В. СЕРИИ некий
В. СЕРПИНСКИЙ
ПИФАГОРОВЫ
ТРЕУГОЛЬНИКИ
перевод с польского
Под редакцией и с примечаниями
с. и. зетеля
ПОСОБИЕ ДЛЯ УЧИТЕЛЕЙ
.J..'" J’	- ............."	...... '-Ч,
ГОСУДАРСТВЕННОЕ УЧЕБНО-ПЕДАГОГИЧЕСКОЕ ИЗДАТЕЛЬСТВО
МИНИСТЕРСТВА ПРОСВЕЩЕНИЯ РСФСР
МОСКВА 1959
Пифагоровы треугольники
в, СЕРПИНСКИЙ
Редактор Сидорова Л. А.
Художественный редактор Максаев А. В.
Технический редактор Головко Б. Н. Корректор Г. С. Попкова.
* * *
Сдано в набор 11/XI 1958 г. Подписано к печати 14/1 1959 г.
84 х Юв1/^ 7 (5,74) п. л. Уч.-изд. л. 5,21. Тираж 10 тыс. экз. А-00920.
* * *
Учпедгиз. Москва, 3-й проезд Марьиной рощи, 41.
Заказ № 2446. Цена без переплета 1 руб. 40 коп.
Переплет 50 коп.
Первая Образцовая типография имени А. А. Жданова
Московского городского Совнархоза.
Москва, Ж-54, Валовая, 28.
ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
Книга известного польского математика Вацлава Сер-
пинского „Пифагоровы треугольники", безусловно,
заслуживает внимания советского читателя. В ней в попу-
лярной форме даны интересные сведения о пифаго-
ровых треугольниках. Этот раздел элементарной теории
чисел интересен для преподавателей средней школы, для
студентов педвузов и учеников старших классов средней
школы.
Скажем несколько слов об авторе книги. Вацлав
Серпинский (род. в 1882 г.) с 1919 г. —профессор Варшав-
ского университета. С 1951 г. В. Серпинский — вице-пре-
зидент Польской Академии наук. Многочисленные иссле-
дования В. Серпинского относятся к теории множеств и
ее приложениям к топологии, к теории функций действи-
тельного переменного, к теории чисел и к другим областям
математики. Вацлав Серпинский — глава Польской мате-
матической школы. В последние годы Серпинским написано
много интересных популярных книг по математике.
К числу их принадлежит книга „Пифагоровы треуголь-
ники".
Для того чтобы сделать книгу более доступной, мы
дали примечания, которые, как нам кажется, помогут
читателю и возбудят у него интерес к пифагоровым тре-
угольникам.
1*	3
В книге 15 параграфов, из которых все, за исключением
двенадцатого, вполне доступны студенту педвуза, ученику
старших классов средней школы и дают хороший мате-
риал для кружковой работы. Двенадцатый параграф очень
интересен, но доступен только хорошо подготовленному
читателю. В этом параграфе дано сложное, хотя элементар-
ное, доказательство одной из теорем Ферма, относящейся
к пифагоровым треугольникам. При первом чтении этот
параграф можно опустить.
Редактор перевода считает своим долгом выразить
благодарность заслуженному учителю школы РСФСР
И. А. Павленко, И. Б. Вейцману и особенно доценту
И. М. Яглому, просмотревшим рукопись перевода и дав-
шим ряд ценных указаний.
§ 1.	ПИФАГОРОВЫ ТРЕУГОЛЬНИКИ.
ОСНОВНЫЕ ПИФАГОРОВЫ ТРЕУГОЛЬНИКИ
1.1.	Пифагоровым треугольником называется прямо-
угольный треугольник, стороны которого выражаются
натуральными числами. С пифагоровыми треугольниками
связано много вопросов, разрешаемых элементарной мате-
матикой. Степень трудности решаемых задач различна.
Прежде всего возникает вопрос о существовании пи-
фагоровых треугольников; если они существуют, то,
конечно, или бесконечно множество пифагоровых треуголь-
ников.
Еще свыше четырех тысяч лет назад египтянам был
известен пифагоров треугольник со сторонами 3, 4, 5.
1.2.	В пифагоровом треугольнике, как известно, боль-
шая сторона называется гипотенузой, меньшие — катетами.
Если обозначим соответственно длины катетов через х
и у, а длину гипотенузы через г, то по теореме Пифа-
гора имеем равенство:
х2 -\-у2 = z2.	(1)
Треугольник Пифагора со сторонами л, у, z условимся
обозначать символом (%, у, z), считая, что на последнем
месте внутри скобки стоит число, выражающее длину
гипотенузы. Стороны треугольника (л, у, z) удовлетво-
ряют уравнению (1), и обратно, если натуральные числа
удовлетворяют уравнению (1), то, как известно из гео-
метрии, треугольник со сторонами х, у, z является пря-
моугольным. Таким образом, исследование пифагоровых
треугольников сводится к исследованию решений в нату-
ральных числах уравнения (1), так называемого уравнения
Пифагора.
5
L3. Если каждую из сторон данного пифагорова тре-
угольника увеличим в одно и то же число раз, то полу-
чим новый прямоугольный треугольник, подобный данному,
со сторонами, выражаемыми натуральными числами, т. е.
получим снова пифагоров треугольник.
Таким образом, из данного пифагорова треугольника
(л, у, z) можно получить бесчисленное множество пифа-
горовых треугольников (kx, ky, kz), где A = l, 2, 3,... .
Например, из треугольника (3, 4, 5) получим треуголь-
ники (6, 8, 10), (9, 12, 15), (12, 16, 20), (15, 20, 25),	,
Итак, для каждого пифагорова треугольника сущест-
вует бесконечное множество ему подобных пифагоровых
треугольников.
1.4.	Среди всех подобных треугольников существует
наименьший; легко догадаться, что это будет треуголь-
ник, стороны которого х и у выражаются взаимно про-
стыми числами (т. е, числа х и у не имеют общего де-
лителя, отличного от единицы).
Действительно, если бы х и у не были взаимно про-
стыми, то существовал бы их общий наибольший делитель
d^>l. В этом случае можно было бы выразить х и у
следующим образом: x = dxr и y — dy^ где хх и ух —
взаимно простые числа. На основании равенства (1) имеем:
z2 х2 + у2 = (dxrf + (dyy d2 (Л* +Х)«
Из полученного равенства следует, что z2 имеет d2
своим делителем, а следовательно, d является делителем г;
z = dz±, где zr— натуральное число.
x = dxiy
y = dylt
z = dzv
Из равенства (1) после сокращения на d2 получаем
равенство:
Из этого равенства следует, что треугольник (л\, у^ zj—
треугольник Пифагора со сторонами, меньшими соответ-
ственных сторон треугольника (%, у, z) и ему подобный.
Итак, числа, выражающие длины катетов наименьшего
из подобных пифагоровых треугольников,— числа взаимно
простые.
Справедливо и обратное заключение: если в пифаго-
ровом треугольнике (л, у, z) хи у — взаимно простые
числа, то не существует меньшего ему подобного пифа-
горова треугольника.
Приведем доказательство от противного. Предположим,
что треугольник (я, Ь, с) подобен треугольнику (х, у, z)
и что а<^х, Ь<^у. Из подобия (а, Ь, с) и (х, у, z) имеем:
х___а
*
Так как дробь у несократима (х и у— взаимно про-
стые числа по условию), то а^х и Ь^у, что противо-
речит предположению.
Итак, среди всех подобных пифагоровых треугольни-
ков наименьший (х, yf z) тот, у которого катеты х, у
выражаются взаимно простыми числами.
Из наименьшего пифагорова треугольника можно по-
лучить все ему подобные, увеличивая его стороны в 2,
3, 4... раз.
1.5.	Пифагоров треугольник (х, у9 z), стороны кото-
рого х и у выражаются взаимно простыми числами,
назовем основным. Для отыскания всех пифагоровых тре-
угольников достаточно найти все основные пифагоровы
треугольники, а остальные пифагоровы треугольники по-
лучим, увеличивая каждую из сторон в 2, 3, 4 ... раз.
Так как среди всех подобных пифагоровых треуголь-
ников основным является наименьший, то два основных
пифагоровых треугольника не могут быть подобными.
Пифагоров треугольник (3, 4, 5) — основной, так как
3 и 4 — взаимно простые числа.
§ 2.	ОТЫСКАНИЕ ОСНОВНЫХ ПИФАГОРОВЫХ
ТРЕУГОЛЬНИКОВ
2.1.	Пусть треугольник (х,у,&) — основной пифагоров
треугольник. Числа х и у — взаимно простые и потому
не могут быть оба четными. Докажем, что они не могут
быть нечетными. Для этого заметим, что квадрат нечет-
ного числа при делении на 8 дает в остатке 1.
Действительно, нечетное число, как известно, можно
представить в виде 2&4~1> где является натуральным
числом.
Отсюда:
(2А + I)2 = 4F 4-4£ + 1 = 4k (k + 1) + 1.
7
Так как из двух последовательных натуральных чисел k
и одно четно, то 4k(k-{~l) делится на 8 и число
(2&Д-1)2 ПРИ Делении на 8 дает в остатке единицу.
2.2.	Сумма квадратов двух нечетных чисел дает при
делении на 8 в остатке два, следовательно, сумма квад-
ратов двух нечетных чисел есть число четное, не кратное
четырем, а потому это число не может быть квадратом
целого числа.
Равенство (1) не может иметь места, если х и у оба
нечетны.
Итак, если пифагоров треугольник (%, у, z) основной,
то среди чисел х и у orw должно быть четным, а дру-
гое нечетным.
2.3.	Пусть число у является четным (необязательно,
чтобы было х<^у). Числа х и z нечетны (нечетность z
следует из равенства (1).
Равенство (1) можно написать в виде
y2 = (z + x)(z — x).	(2)
Числа z-}-x и z — х как сумма и разность двух нечет-
ных чисел — числа четные, а потому
z-]-x = 2a; z — x = 2b,	(3)
где а и b — целые числа.
z = a-}-b, x = a — b.	(4)
Из этих равенств следует, что а и b — взаимно про-
стые числа.
Действительно, если бы у них был общий делитель
d^>l9 то на основании (4) d был бы общим делителем
чисел z и х9 а следовательно, и чисел z Д- х9 z — л и на
основании равенства (2) d2 было бы делителем числа у2.
В таком случае d был бы общим делителем чисел у и л,
тогда как эти числа должны быть взаимно простыми.
Число у, как известно, четно, а потому у = 2с, где с —
натуральное число. Равенство (2) на основании равен-
ства (3) принимает следующий вид:
4с2 — 2a-2b, или c2 — ab.	(5)
Из арифметики известно, что если произведение двух
взаимно простых чисел является квадратом натурального
числа, то каждое из этих чисел также является квадра-
том натурального числа.	[1]1
1 См. примечание стр. 74.
8
Из равенства (5) следует: а = т\ Ь = п\ где т и п —
взаимно простые числа, так как они являются делителями
взаимно простых чисел а и Ь. На основании равенства (4)
имеем:
z = m2-]-n2, х = т2— п2.
Принимая во внимание равенство (5), а также учитывая,
что а = т\ b — п2, находим с = тп и у—2с, следовательно,
у — 2гпп.
Мы доказали, что длины сторон основного пифагорова
треугольника (%, у, z) могут быть выражены через взаимно
простые числа тип:
х = т2— п2*, у = 2тп, z=m2 -\гп2.	(6)
Числа т и п не могут быть оба четными или оба не-
четными, так как в этих случаях х = т2 — п2 были бы
четными, что невозможно. Итак, одно из чисел т или
п четно, а другое нечетно (у = 2тп делится на 4).
Следовательно, в каждом основном, а тем более и не
основном пифагоровом треугольнике хотя бы один из ка-
тетов делится на 4. Отсюда следует, что нет пифагорова
треугольника, все стороны которого были бы простыми
числами. Существуют, однако, пифагоровы треугольники,
у которых гипотенуза и один из катетов — простые числа,
например: (3, 4, 5), (11, 60,61), (19, 180, 181), (61, 1860,
1861), (71, 2520, 2521), (79, 3120, 3121).	[2]
Неизвестно, конечно или бесконечно множество всех
таких треугольников.
2.4.	Предположим, что т и az, где т^>п являются
целыми и взаимно простыми числами, из которых одно
(безразлично, какое) четно, а другое нечетно. Этими
числами по формулам (6) определяются стороны х, у, z
основного пифагорова треугольника. Из тождества
(т2 — /г2)2 4- (2/тш)2 = (т2 Ц- /г2)2,
которое очень легко проверить, а также из равенств (6)
следует, что треугольник со сторонами л, у, z — пифа-
горов треугольник. Остается доказать, что числа х и у
взаимно простые. Пусть у чисел х и у есть общий дели-
тель d 1; принимая во внимание нечетность числа х,
мы должны считать d нечетным числом. На основании
равенства (1) d было бы делителем числа z. Основываясь
на равенстве (6), заключаем, что т2 п2 и от2 — п* имели
бы общим делителем число d, а следовательно, 2m2 и 2л2
также должны делиться без остатка на d. Так как d не-
четно, то т2 и и2 должны делиться на число d, что про-
тиворечит условию, так как т2 и га8 являются взаимно
простыми (т и и — взаимно простые). Следовательно,
числа хну взаимно простые.
2.5.	Заметим, что разным парам чисел тип соответ-
ствуют различные пифагоровы треугольники (х, у, z).
Из равенств (6) следует, что
Можно, кроме того, заметить, что ——несократимая
дробь, равная —— (так как x-\-z=2m2‘, а у = 2тп).
Полученные результаты можно выразить в виде сле-
дующей теоремы.
Теорема 1. Все основные пифагоровы треугольники,
у которых у является четным числом, получаются
из формул:
х = т2— п2, у — 2тп, z=m2 -]-п2, (т^>п),
где тип все пары взаимно простых чисел, из кото-
рых одно (безразлично, какое) является четным, а дру-
гое нечетным.
Каждая основная тройка (л, у, z), где у является
четным числом, определяется этим способом одно-
значно.
2.6.	Вместо того чтобы равенство (1) преобразовать
в равенство (2), как было сделано выше, можно преобра-
зовать его в следующее:
x2 = (z-[-y){z—y),
(7)
где у — четное число, а х и z — нечетные; числа
п = и •v — z—у — нечетные и взаимно простые
(так как пара х и у и пара у и z взаимно простые).
На основании (7) имеем x2 = uv.
Следовательно, существует такая пара взаимно про-
стых чисел k и I, что u — k2 и v=l2.
x = kl', z =
2 ’ У 2	2
10
Рассуждая аналогично, как и при выводе первой тео-
ремы, легко докажем следующую теорему.
Теорема 2. Стороны, всех основных пифагоровых
треугольников (л, у, z), у которых у — четно, вычи-
сляются по формулам:
х = Ы,у = Ч^-. г = Щ, гдеЛ>/ (8)
и где k и I все пары нечетных взаимно простых чисел.
Каждая основная тройка (%, у, z), где у — четно, опре-
деляется этим способом однозначно.	[3]
2.7.	Для определения бесконечной последовательности
основных пифагоровых треугольников (л, у, z), где у —*
четно, следует за число k взять последовательность не-
четных чисел 3, 5, 7, 9, ... , а за I — последователь-
ность нечетных чисел, меньших k и взаимно простых с k,
а затем вычислить х, у, z по формулам (8).
Приведем таблицу двадцати одного основного
k	1	X	У	Z	Площадь
3	1	3	4	5	6
5	1	5	12	13	30
5	3	15	8	17	60
7	1	7	24	25	84
7	3	21	20	29	210
7	5	35	12	37	210
9	1	9	40	41	180
9	5	45	28	53	630
9	7	63	16	65	504
11	1	11	60	61	330
И	3	33	56	65	924
11	5	55	48	73	1320
11	7	77	36	85	1386
11	9	99	20	101	990
13	1	13	84	85	546
13	3	39	80	89	1560
13	5	65	72	97	2340
13	7	91	60	109	2730
13	9	117	44	125	2574
13	И	143	24	145	1716
15	1	15	112	113	840
пифагорова треугольника, составленную по формулам (8).
Для получения всех пифагоровых треугольников следует
каждую основную тройку последовательно умножить на
числа натурального ряда. Таким образом мы получим пи-
фагоровы треугольники, у которых у четно. Добавив к
полученным тройкам тройки, у которых х и у переставлены,
мы получим все пифагоровы треугольники. Так как в пи-
фагоровом треугольнике (а, Ь, с) числа а, Ь, с либо все
четны, либо два из них нечетны, то легко показать, что
радиус круга, вписанного в пифагоров треугольник, всегда
выражается натуральным числом.
Легко доказать, что если г — радиус круга, вписанного
в пифагоров треугольник (а, Ь, с), то
2г = а-{-Ь — с.
Например, радиус круга, вписанного в треугольник (3, 4,5),
равен 1. Отсюда следует, что около круга произвольного
целочисленного радиуса всегда можно описать пифагоров
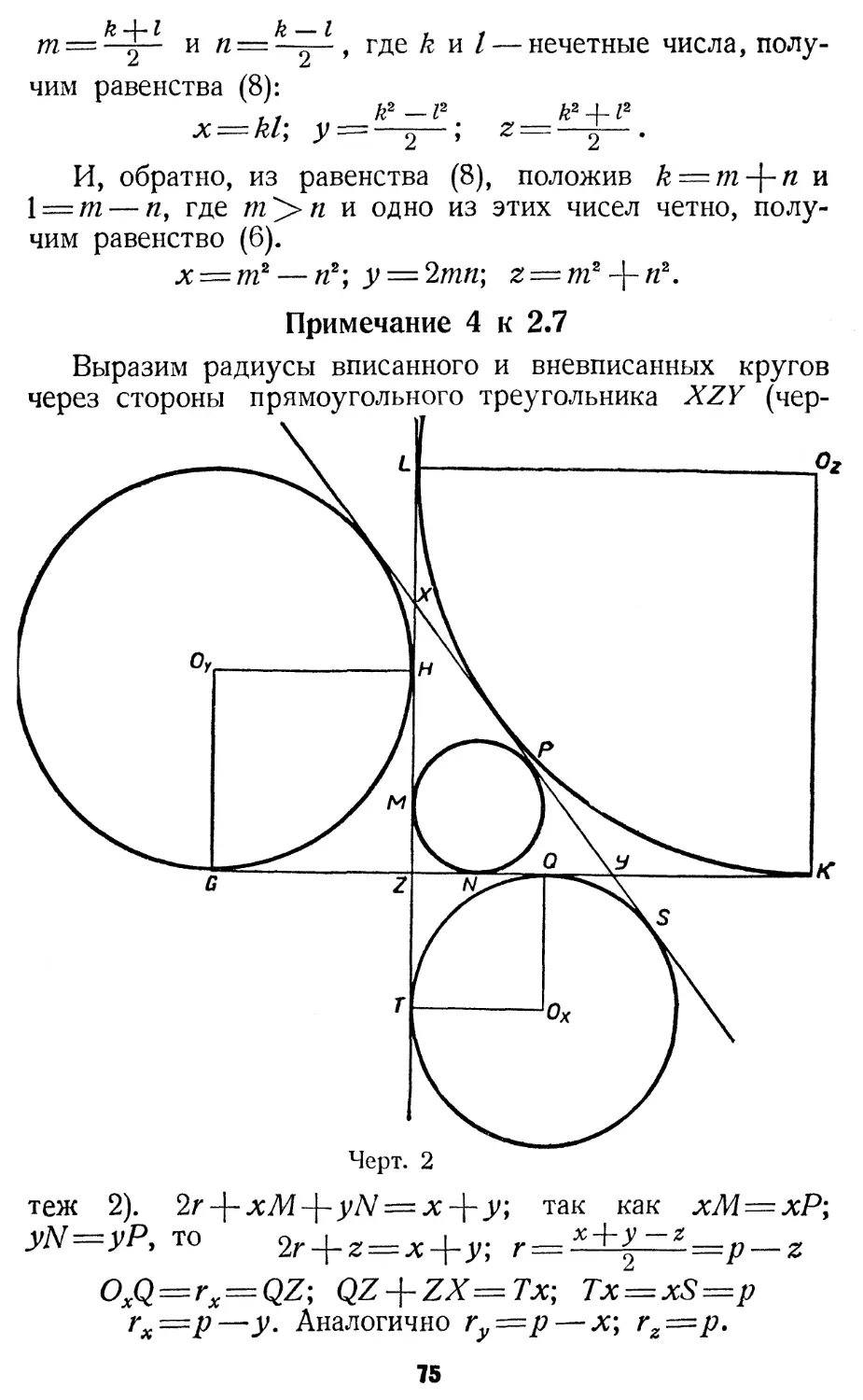
треугольник, подобный треугольнику (3, 4, 5).	[4]
Очевидно, что диаметр круга, описанного около пифа-
горова треугольника, равен его гипотенузе.
§ 3.	ПИФАГОРОВЫ ТРЕУГОЛЬНИКИ СО СТОРОНАМИ,
МЕНЬШИМИ 100
Найдем все пифагоровы треугольники, все стороны
которых меньше ста. Для этого необходимо и достаточно
найти треугольники, у которых гипотенуза менее ста.
Из вышеприведенной таблицы следует, что существует
только 16 таких основных пифагоровых треугольников
(л, у, z), у которых сторона у выражается четным числом.
Действительно, вне нашей таблицы нет основных пи-
фагоровых треугольников с гипотенузой, меньшей 100, и
со стороной у, выражаемой четным числом, так как для
k ^15 имеем:
Написав эти 16 основных треугольников в порядке воз-
растания их гипотенуз (в случае равенства гипотенуз в
порядке возрастания площадей), получим: (3, 4, 5),
(5, 12, 13), (15, 8, 17), (7, 24, 25), (21, 20, 29), (35, 12, 37),
(9, 40, 41), (45, 28, 53), (11, 60, 61), (63, 16, 65), (33, 56, 65),
12
(55, 48, 73), (13, 84, 85), (77, 36, 85), (39, 80, 89) и (65, 72,
97). Стороны первых семи треугольников можно удвоить
(и их гипотенузы все еще останутся меньше 100): (6 8 10)
(10, 24, 26), (30, 16, 34), (14, 48, 50), (42, 40, 58), (70, 24’
74). (18, 80, 82). Стороны первых пяти из наших 16 ос-
новных пифагоровых треугольников можно утроить и по-
лучить пять новых пифагоровых треугольников: (9 12 15)
(15, 36, 39), (45, 24, 51), (21, 72, 75), (63, 60, 87). Стороны
первых трех из наших 16 треугольников можно увеличить в
четыре-пять раз, что даст шесть новых пифагоровых тре-
угольников: (12,16,20), (20,48,52), (60,32,68), (15, 20,
25), (25, 60, 65), (75, 40, 85). Увеличив стороны первых
двух из 16 треугольников в шесть и семь раз, получим
четыре новых треугольника: (18, 24, 30), (30, 72, 78), (21,
28, 35) и (35, 84, 91). Стороны первого из 16 треугольни-
ков можно увеличить в 8,9,10,11, 12, 13, 14, 15, 16,17, 18
и 19 раз, что даст еще 12 новых треугольников: (24 32
40), (27, 36, 45), (30, 40, 50), (33, 44, 55), (36, 48, 60),’ (39*
52,65), (42,56,70), (45,60,75), (48,64,80), (51, 68, 85),
(54, 72, 90) и (57, 76, 95).
Таким образом, всего получаем 50 разных пифагоровых
треугольников со сторонами, меньшими ста.
Меняя местами катеты, мы получим еще 50 пифагоро-
вых треугольников. Итак, из 16 основных пифагоровых
треугольников получим 100 различных пифагоровых тре-
угольников со сторонами, меньшими ста.
§ 4.	ПИФАГОРОВЫ ТРЕУГОЛЬНИКИ, У КОТОРЫХ ДВЕ СТОРОНЫ
ВЫРАЖАЮТСЯ ПОСЛЕДОВАТЕЛЬНЫМИ ЦЕЛЫМИ ЧИСЛАМИ
4.	1. Вернемся к таблице основных пифагоровых тре-
угольников (§ 2.7). Первый из этих треугольников (3, 4, 5)
обладает тем свойством, что стороны его выражаются
последовательными натуральными числами. Легко доказать,
что это единственный пифагоров треугольник, обладающий
этим свойством. Действительно, если стороны пифагоровою
треугольника равны п — 1, п и п -j-1, где п — целое число,
большее 1, то
(п— 1)2 + п2 = (п+1)а.
После упрощения получаем:
az2 = 4zz, откуда п = 4,
искомый треугольник (3, 4, 5).
13
4.2«	Легко найти все пифагоровы треугольники, длины
сторон которых составляют арифметическую прогрессию.
Обозначив соответственно стороны через п — k, п и
n-\-k (где k— целое число и ri^>k), получим:
(п — k)2 Ц- п2 = (п + k)2,
после упрощений получаем:
п2 = 4nk, или n = 4k.
Искомые треугольники (ЗА, 4k, 5k), где k— 1, 2, 3,..., по-
добны основному пифагорову треугольнику (3, 4, 5).
4.3.	Займемся пифагоровыми треугольниками, две сто-
роны которых выражаются последовательными натураль-
ными числами.
Легко видеть, что эти треугольники — основные, так
как два последовательных натуральных числа взаимно
простые.
Равенство z— л=1 невозможно, так как zn х— не-
четные числа.
Предположим, что z—у—\.
На основании теоремы 2 получаем, что /2=1, откуда
7=1. Итак,
^—1	k2 + 1
X — k, у 2 j — 2 >	(9)
где k — нечетно и больше единицы.
По этим формулам можно найти все пифагоровы тре-
угольники (x,y,z), у которых z—у=\.
Приведем десять первых таких треугольников, (3, 4,5),
(5,12,13), (7, 24, 25), (9, 40, 41), (11, 60,61), (13,84,85),
(15, 112, 113), (17, 144, 145), (19, 180, 181), (21, 220, 221).
4.4.	Такие треугольники (конечно не все) можно найти
из тождества Месснера (Moessnera)-.
(10/z — 5)2 + [50п (п — 1) +12]2 = [50/г (п — 1) +13]2.	[5]
Например, для п— 1,2,3,... ,10 получаем треугольники:
(5, 12, 13), (15, 112, 113), (25, 312, 313), (35, 612, 613), (45,
1012, 1013), (55, 1512, 1513), (65, 2112, 2113,), (75, 2812,
2813), (85, 3612, 3613), (95, 4512, 4513).	[6]
4.5.	Существует способ почти механически выписы-
вать сколько угодно пифагоровых треугольников, у ко-
торых z=y-f-l. Если в формулах (9), где k — нечетное
14
число, большее единицы, положить k — 2n-\-l4 то полу-
чим формулы:
л = 2и-|-1, у = 2«(я-|-1), z — 2n(n-\-1)-f-1. (10) [7]
Полагая п = 10s, где s является целым числом, полу-
чаем:
л = 2-10*-]-1 = 20. .. 01,
£— 1 нулей s нулей
y = 2-102S + 2-10s = 20 ... 020...0,
л — 1 нулей J—1нулей
Z = 2- 10SJ + 2.10'r+1=20 ... 020Т?.01
Таким образом, для s=l, 2,... получим треуголь-
ники
21	220	221
201	20200	20201
2001	2002000	2002001
20001	200020000	200020001
и т. д. Каждую следующую тройку сторон получаем из
предыдущей, вписывая в числа предыдущей в соответ-
ствующие места нули. Аналогично, если в формуле (10)
считать равным я = 2- 10s, получим:
s — 1 нулей
х = 4- 10s-|-1 =40... 01,
s — 1 нулей $ нулей
у = 8- 102S-f-4- 10s = 80... 040... 0,
S’ 1 нулей s — 1 нулей
z = 8-102S + 4-10s+1=80.. . 040 ..761.
Таким образом, имеем:
41	840	841
401	80400	80401
4001	8004000	8004001
40001	800040000	800040001	[8]
ИТ. д.1
4.6.	Займемся теперь пифагоровыми треугольниками,
катеты которых выражаются последовательными нату-
ральными числами. Из таблицы основных пифагоровых
1 Рог. „The American Mathematical Monthly", 41 (1943), str. 330
(американский математический журнал).
IS
треугольников (§ 2.7) видно, что такими треугольниками
будут (3, 4, 5), (21, 20, 29). Легко доказать, что имеется
бесчисленное множество таких треугольников. Отсюда
следует, что если для некоторых натуральных чисел х
и z получим пифагоров треугольник вида (л, %4"h z),
то существует тоже пифагоров треугольник (3% 2г 1,
Зх -j— 2% —|— 2, 4% —Зг —2).
Действительно,
(Зх + 2г + 1 )2 + (3% + 2г + 2)2 = 18л2 + 24лг + 8г2 4
4- 18% 4- 12г 4-5,
а так как
%2 4-(% 4- I)2 == г2, или 2х2 4~2%4~ 1 = z2,
то
(3% 4- 2г 4-1)2 4- (3% 4- 2г 4- 2)2 = 16%2 + 24%г 4~ 9г2 4»
4~ 16% 4-12г 4- •= (4% 4- Зг 4~ 2)2.
Таким образом, из каждого пифагорового треуголь-
ника вида (%, %4~h г), катеты которого являются по-
следовательными натуральными числами, можно полу-
чить пифагоров треугольник вида
/(%, %4-1, г) = (3%4-2г4-1, 3%4-2г4-2, 4%4~Зг4-2)
с большими сторонами, катеты которого также выража-
ются натуральными числами.
Из треугольника (3, 4, 5,), пользуясь указанным спо-
собом, получим треугольник со сторонами:
3-34~2-54-1=20, 21 и 4-34-3.54-2 = 29;
из этого треугольника получим следующий со сторонами
3.204-2-294-1 = 119, 120 и 4-24-3.294-2 = 169 и т. д.
Приведем первых шесть треугольников, полученных
таким способом:
3	4	5
20	21	29
119	120	169
696	697	985
4059	4060	5741
23660	23661	33461.
Легко доказать, что в двух последовательно получае-
мых таким образом треугольниках больший катет будет
16
выражаться в одном треугольнике четным, а в другом —
нечетным числом.	[9].
4.7.	Докажем теперь, что вышеприведенным методом
получаем пифагоровы треугольники, у которых катеты
выражаются последовательными натуральными числами.
Теорема. Каждый из пифагоровых треугольников,
катеты которого выражаются последовательными на-
туральными числами, является одним из треугольни-
ков бесконечного ряда.
(3, 4, 5),/(3, 4, 5), //(3, 4, 5), ///(3, 4, 5),... (11)
Для доказательства теоремы предварительно докажем
лемму.
Лемма. Если (%, л-ф-Ь z) является пифагоровым
треугольником, где л>>3, то также
(хх, л,4-1, zj=g(x, л 4-1, z) =
= (3л —2x4-1, Зл — 2г-|-2, Зх —4л —2)	(12)
является пифагоровым треугольником, где х, z.
Докажем, что
л, = Зл — 2х 4~ 1 О и 0 < х, — 3z — 4х — 2 < z,
2х<3л4~1, Зг>4л4~2 и z<2л-(- !•	(13)
Так как л4>3, то имеем:
л2 4> Зл = 2л 4~ х >• 2л 4" 3.
Но так как
л2 4-(л 4- 1)2=х2,
потому что (л, л 4-1, z) — пифагоров треугольник, то
4х2 = 8л2 + 8л -4 4	9л2 4~ 8л 4~ 4 — л2 <<
< 9л2 4-8л 4-4 — (2л 4-3) = 9л2 4-6л +1 = (Зл 4-1)2,
откуда
2х<Зл4-1.
Учитывая, что л>0, усилим неравенство 2z<^4x-\-2,
откуда
z <2л 4~ 1 •
Далее, так как
л2 4-(л 4- 1)2 = х2 и х>0,
то 9z2—18л24" 18л-|-9> 16л24~ 16л4 = (4л4~2)2 и
Зх > 4л 2.
Итак, неравенства (13) доказаны.
17
Остается доказать, что (%1? Xj-f-b — пифагоров
треугольник. Имеем
^44a + 1)2 = 2*i + 2a + i =
= 1 8л2 + 8г2 — 24хг Ц- 18х — 12г + 5,
= 16х2 Ц- 9г2 — 24лг -ф- 16х — 12г Ц- 4,
а так как
г2 = 2л2 + 2х+1,
то имеем:
16л2	9г2 — 24лг 16% — 12г 4 =
= 18л2 4~ 8г2 — 24лг 18% — 12г -ф- 5,
следовательно, z\ — x*-\-(xx -ф- I)2 и +	^) —пи-
фагоров треугольник и лемма доказана.
4.8.	На основании доказанной леммы из пифагорового
треугольника (л, л-|-1, г), катеты которого являются
последовательными натуральными числами ил>3, можно
получить новый пифагоров треугольник:
(л„ Xi + l, £,)=£(*, х+1, х),
катеты которого тоже являются последовательными на-
туральными числами, причем г^ г. Если притом хг >* 3,
то на основании леммы из полученного треугольника
(%i,	-ф- 1, Zi) получим новый пифагоров треугольник:
(л2, %2 + 1, z2) = g(x„ л, + 1, zj^gg^x, л4-1, х),
где г2<г1 и т. д.
Таким способом невозможно получить бесконечный
ряд пифагоровых треугольников с уменьшающимися ги-
потенузами. При некотором целом п мы обязательно
придем к треугольнику
(л„, х„ + 1, z„) = gn(x, х-\-1, z), где хп — 3.
Из равенства х* 4- (х„ 4-1)2 = z2n следует, что zn = 5. Сле-
довательно, при некотором целом п выполняется равенство:
gn(x, х 4-1, х) = (3, 4, 5).	(14)
Как легко проверить, для каждого пифагорового
треугольника (л, л-)-!, z), где л>3, имеем:
fg(x, л-)-1» г)=/(3х — 2г4-1, Зх— 2x4-2,
Зх — 4х — 2) = (л, л 4~ 1, х),	[10]
18
что дает
ffgg(x, л+1, г) = (л, л+1, г)
и в общем случае
fkgk(x, л+1,г) = (л, л+1, z) для k= 1,2,3,... .
Отсюда на основании равенства (14)
(л, л+1, z)=fn& 4, 5),
что и требовалось доказать.
§ 5.	ДЕЛИМОСТЬ ОДНОЙ ИЗ СТОРОН ПИФАГОРОВОГО
ТРЕУГОЛЬНИКА НА 3 ИЛИ НА 5
5.1.	Как нам известно из (§ 2.3), во всяком пифаго-
ровом треугольнике хотя бы один из катетов делится
на 4.
Докажем, что во всяком пифагоровом треугольнике
хотя бы один из катетов делится на 3.
Для доказательства предположим, что в пифагоровом
треугольнике (л, у, z) ни одно из чисел х и у не де-
лится на 3. Тогда имеем:
л = 3£±1, у = 3/±1,
где k и I являются целыми числами и
х2 2 = 3 (3F + З/2 ± 2А ± 2/) + 2.
Полученное выражение не может быть квадратом целого
числа. Действительно, так как это число не делится на 3,
то оно не может быть квадратом числа, кратного трем,
оно не может быть и квадратом числа, некратного трем,
так как квадрат числа 3£ +1 равен
± I)2 = 3 (3£2 ± 2t) +1
и при делении на три дает в остатке единицу, тогда как
z2 = х2 Уa при делении на три дает в остатке два.
Итак, предположение, что ни один из катетов не де-
лится на три, приводит к противоречию. Следовательно,
одно из чисел х или у кратно трем.
5.2.	Легко показать на примерах, что катетом, деля-
щимся на три, может быть катет, делящийся на четыре,
например (5, 12, 13), либо катет, неделящийся на 4, на-
пример (3, 4, 5).
19
Оказывается, что числа 1, 2, 3, 4 являются единст-
венными натуральными числами п, для которых верна
теорема, что в каждом пифагоровом треугольнике хотя
бы один из катетов делится на п. В самом деле, в пи-
фагоровом треугольнике (3, 4, 5) ни один из катетов не
делится на натуральное число, более 4.
5.3.	Докажем, что в каждом пифагоровом треуголь-
нике хотя бы одна из сторон делится на 5.
Для доказательства предположим, что число п не де-
лится на 5. Тогда оно имеет вид:
я = 5^4-1 либо я = 5&-4-2,
где k—целое число.
В первом случае имеем:
п2 5 (5k2 ± 2k) + 1,
во втором случае:
п2 = 5(5/?2+4/?)4-4.
Отсюда следует, что квадрат целого числа, не деляще-
гося на 5, дает при делении на 5 в остатке либо 1,
либо 4.
Если бы в пифагоровом треугольнике (х, у, z) ни
одно из чисел х и у не делилось на 5, то каждое из
чисел х2 и у2 давало бы при делении на 5 остаток 1
либо 4, отсюда число х2-$-у2 давало бы при делении
на 5 остаток 2, 3 или 0. Число z2 — х2 -}-у2 при деле-
нии на 5 не может, как мы видели, давать остаток 2 или 3.
Итак, из трех возможностей остается только принять
последнюю, т. е. предположить, что z2, а следовательно,
и z делится на 5. Если в пифагоровом треугольнике ни
один из катетов не делится на 5, то гипотенуза должна
делиться на 5. Очевидно, что в основном пифагоровом
треугольнике только одна из сторон делится на 5. Легко
заметить, в треугольниках (5, 12, 13), (21, 20, 29) и
(3, 4, 5) делится на 5 только одно из чисел, выражаю-
щих длину либо четного катета, либо нечетного, либо
длину гипотенузы.	[11]
Из примера пифагорового треугольника (3, 4, 5) сле-
дует, что числа 1, 2, 3, 4 и 5 — единственные натураль-
ные числа п, для которых справедлива теорема, что во
всяком пифагоровом треугольнике хотя бы одна из сто-
рон делится на п.
20
§ 6.	ЗНАЧЕНИЕ СТОРОН ПИФАГОРОВЫХ ТРЕУГОЛЬНИКОВ
6.1.	Возникает вопрос, для каких натуральных чи-
сел п существуют пифагоровы треугольники, у которых
один из катетов равен п.
Докажем, что для существования пифагорова тре-
угольника с катетом, равным п, необходимо и доста-
точно, чтобы п было целым числом, большим 2.
Для доказательства необходимости нашего условия
заметим, что в пифагоровом треугольнике (л, Ь, с) имеем:
а2 = с2— Ь2 = (с — b)(c-\-b), причем с и b являются це-
лыми числами и с^>Ь, затем с ^2, с — а
также с-\~Ь~^ 2	1 — 3, откуда а2 3, поэтому а не
может быть равным единице. Не может быть а также
равным двум, так как тогда бы существовало равенство:
4(с — Ь) (с + Ь). Это равенство невозможно, действи-
тельно, если с — Ь^1 и c-j~b^3, то с — Ь=1 и
с b — 4. Следовательно, 2с = 5 и с не может быть на-
туральным числом. Итак, каждый из катетов всякого
пифагорового треугольника больше двух.
Если п является нечетным натуральным числом и
больше 2, то
и2 — 1 п2 1
причем —£— и —~— являются натуральными числами.
Следовательно, имеем пифагоров треугольник
п,
п2 — 1 п2 -|- 1 \
’	2 )•
При четном п (и >2)
где — 1 и -j- + 1 — числа натуральные, получаем пи-
/	^2	^2	х
фагоров треугольник (и,	—1, -j-j-l) с катетом п.
Итак, наше условие достаточно.
Примеры пифагоровых треугольников с катетами
3, 4, ... , 10: (3, 4, 5), (4, 3, 5), (5, 12, 13), (6, 8, 10),
(7, 24, 25), (8, 6, 10), (9, 40, 41), (10, 24, 26).
Покажем, что не для всех целых чисел п S>2 сущест-
вует основной пифагоров треугольник с катетом п.
21
Не существует, например, основного треугольника
с катетом, равным 6. В самом деле, на основании тео-
ремы 1 имеем 6 = 2/шг, так как одно из чисел т или п
должно быть четным, то 3 = тп, что невозможно. [12]
6.2.	Несколько сложнее решается вопрос о существо-
вании таких натуральных чисел, для которых п было бы
гипотенузой пифагорового треугольника. Примем без до-
казательства, что для существования пифагорова тре-
угольника с гипотенузой п необходимо и достаточно,
чтобы число п имело хотя бы один прос той делитель
вида
Итак, для п^ 100 существуют пифагоровы треуголь-
ники с гипотенузой п = 5, 10, 13, 15, 17, 20, 25, 29, 30, 34,
35, 37, 39, 40, 41, 45, 50, 51, 52, 53, 55, 58, 60, 61, 65, 68,
70, 73, 74, 75, 78, 80, 82, 85, 87, 90, 91, 95, 97, 100.
6.3.	Можно доказать, что существует бесконечное
число пар пифагоровых треугольников, гипотенузы кото-
рых определяются двумя последовательными натураль-
ными числами: п и п-1. Это непосредственно следует
из тождества:
(25 + 65Л)2 = (154- 3W + (20 + 5 W,
(26 4- 65Л)2 = (Ю4- 2W + (24 + 6W
для /г = 0, 1, 2, ... .	[13]
6.4.	Можно доказать (несколько сложнее), что для
любого натурального числа п существует т пифагоро-
вых треугольников, у которых гипотенузы определя-
ются т последовательными натуральными числами
п, /г4~1> ^4“2> ••• > п-\-т—1. Например, для т = 3
можно взять « = 39 и получить следующие пифагоровы
треугольники: (15, 36, 39), (24, 32, 40), (9, 40, 41). Для
т — 4 можно взять п, равным 50, и получить следующие
четыре пифагоровых треугольника: (30, 40, 50), (24, 45, 51),
(20, 48, 52), (28, 45, 53).	[14]
§ 7.	ПИФАГОРОВЫ ТРЕУГОЛЬНИКИ С ОБЩИМ КАТЕТОМ
ИЛИ С ОБЩЕЙ ГИПОТЕНУЗОЙ
7.1.	Существует конечное число пифагоровых тре-
угольников с данным катетом а. В каждом треугольнике
(а, Ь, с) на основании разложения а2 = (с— b)(c-}-b),
Ь-{-с должно быть делителем числа а2, следовательно,
22
Ь<^аг и с<й2, количество пар чисел таких, как b и с,
конечно.
7.2.	Легко доказать, что для каждого натурального
числа существует хотя бы п различных пифагоровых
треугольников с общим катетом.
С этой целью примем:
bk = 2k^n~tk— 1);
сй = 2*(22"-2*4-1)
для k = 0,1, 2, ..., п— 1. Числа с0,	..., с„+1 являются,
очевидно, различными, так как при делении на 2" они
дают разные остатки, причем
4-ь2=(2п+1)2.
Полагая а=2"+1, получаем п пифагоровых треугольни-
ков {a, bh, ck), k = 0, 1, 2, ... , п—1 с общим катетом
и с различными гипотенузами. Следовательно, среди всех
пар треугольников нет совпадающих.
Например, для и = 2 получаем этим способом два
различных пифагоровых треугольника (8, 15, 17) и
(8, 6, 10) с общим катетом, равным 8, для я = 3 полу-
чаем три различных пифагоровых треугольника: (16,63, 65),
(16, 30, 34) и (16, 12, 20), с общим катетом 16.	[15]
7.3.	Сложнее доказать, что для каждого натураль-
ного числа п существует по крайней мере п основных
различных пифагоровых треугольников с общим ка-
тетом.
Например, для п = 2 получаем треугольники (5, 12,13)
и (35, 12, 27), а для п = 4 треугольники: (105, 88, 137),
(105, 208, 233), (105, 608, 617) и (105, 5512, 5513). [16]
7.4.	Существует конечное число пифагоровых тре-
угольников с общей гипотенузой с, так как в треуголь-
нике («, Ь, с) должно быть а<^с и Ь<^с, а число таких
пар, как а и Ь, при данном с, конечно. Вместе с тем для
каждого натурального числа п существует хотя бы
п различных пифагоровых треугольников с общей гипо-
тенузой.
Действительно, примем для данного натурального п
с = (32 -]- 1)(42 + 1)(52 +1).. .[(«4-2)2 4-1].
23
Число тг-г-т натуральное для k — 3, 4, ... , п -|- 2, а
потому будут натуральными и следующие числа:
k2- 1
На основании тождества
(15)
получаем с2 = a2k -j- b2k для k = 3, 4, ...
угольники (ak, bk, с) кля k — 3, 4, ...
горовы.
На основании (15) находим
п 2 и тре-
п 2 — пифа-
. ______k2 — 2k - 1 ____________(k —
£>2 11	A2
для k = 3, 4, ... ,
_ 2с
С h2 I
ДЛЯ
также
следовательно, <73<.^4<. ... ял+2.
Итак, в пифагоровых треугольниках (akf bky с), где
k = 3, 4, ... , /гЦ-2, катеты растут с возрастанием k,
а гипотенуза остается постоянной. Мы получаем п раз-
личных треугольников с общей гипотенузой.
7.5.	Сложнее было бы доказать, что существует
произвольное число основных пифагоровых треугольников
с общей гипотенузой.
Шедд (Ch. L. Schedd1) привел 64 основных пифагоро-
вых треугольника с общей гипотенузой
2576450045 = 5-13 17-29 37-41-53.	[17]
§ 8.	ПИФАГОРОВЫ ТРЕУГОЛЬНИКИ С ОБЩИМ ПЕРИМЕТРОМ
8.1.	Можно легко доказать, что для каждого нату-
рального числа п существует хотя бы п различных
не совпадающих пифагоровых треугольников с общим
периметром.
1 „Scripta Mathematical
математический журнал).
15 (1949), str. 132 (научно-популярный
24
В самом деле, среди бесконечного множества основ-
ных пифагоровых треугольников нет ни одной пары по-
добных (§ 1.5). (Случай тождественных треугольников
исключается.)
Возьмем п различных основных пифагоровых треуголь-
ников: (aki bki ск), где k — 1, 2, ... , /г, и обозначим
ak + bk-]-ck = sk для £=1, 2, ... , п,
а также
k ,C. » k o, ’
и2 * * *
? _ CfeS
ck^~ Для
п.
для А =	2, ... , п, при-
чем никакая пара пифагоровых треугольников (a’k, b'k, c'k),
где k = l, 2, ... , /z, не являются подобными, а тем бо-
лее совпадающими.	[18]
8.2.	В предыдущем доказательстве вместо произведе-
ния чисел	s2, ...fsn можно было бы взять их общее
наименьшее кратное. Тогда из треугольников (3, 4, 5) и
(5, 12, 13) получим два треугольника (15, 20, 25) и (10,
24, 26), периметр каждого из которых равен 60. Из тре-
угольников (3, 4, 5), (5, 12, 13) и (15,8, 17) получим три
треугольника (30, 40, 50), (20, 48, 52) и (45, 24, 51), пе-
риметр каждого из которых равен 120.
8.3.	Найдем также три основных пифагоровых тре-
угольника с равными периметрами: (3255, 5032, 5993),
(7055, 168, 7057) и (119, 7080, 7081)х. Существуют ос-
новные пифагоровы треугольники, периметр которых яв-
ляется квадратом натурального числа. Наименьшим таким
треугольником является треугольник (16, 63, 65) с пери-
метром 122. Неосновной пифагоров треугольник того же
периметра (36, 48, 60). Основной треугольник (252, 275,
373) имеет периметр 302, тот же периметр имеют и не-
основные треугольники (150, 360, 390) и (90, 400, 410).
[19], [20]
§ 9.	ПИФАГОРОВЫ ТРЕУГОЛЬНИКИ С ОБЩЕЙ ПЛОЩАДЬЮ
9.1.	Из таблицы (§ 2.7) основных пифагоровых тре-
угольников и их площадей следует, что треугольники (21»
20, 29) и (35, 12, 37) имеют общую площадь, равную 210*
1 „Scripta Mathematica“ 15 (1949), str. 89.
25
Нет меньших основных треугольников с различными ги-
потенузами и равными площадями.
Учтем и неосновные пифагоровы треугольники с гипо-
тенузами, меньшими 37:
X	У	Z	Площадь
6	8	10	24
9	12	15	54
12	16	20	96
15	20	25	150
18	24	30	216
21	28	35	294
10	24	26	120
30	16	34	240
Принимая во внимание и эти треугольники, видим, что
нет двух треугольников с равными площадями, с различ-
ными гипотенузами, меньшими 37 (ни треугольников с
площадями, меньшими 210).
Наименьшая пара основных пифагоровых треуголь-
ников с разными гипотенузами и общей площадью есть
пара (21, 20, 29) и (35, 12, 37).
Заметим, что треугольники с общей площадью и об-
щей гипотенузой совпадают (тождественны).
В самом деле, если Д, bx, cj и (а2, &2, с2) являются
такими треугольниками и а1^Ь1 и а2^Ь2) то из равен-
ства их площадей следует:
аД = аД и ct = c2,
откуда
(«1—V=(«*—и («,+V=(«a+V-
Следовательно,
«1 — Ъ^=аг — bt и a1-{-bl=^a2-\-bt.
Значит а1 = Ьг и #2 = fc2, что и требовалось доказать.
9.2.	Из таблицы (§ 2.7) следует, что пифагоров тре-
угольник (15, 112, 113) имеет площадь, равную 840 =
26
— 4-210, которая в 4 раза больше площадей каждого из
треугольников (21, 20, 29) и (35, 12, 37). Площадь тре-
угольника (15, 112, 113) равна площади каждого из тре-
угольников (42, 40, 58) и (70, 24, 74), полученных из тре-
угольников (21, 20, 29) и (35, 12, 37).
Мы получили три пифагоровых треугольника с раз-
ными гипотенузами и с общей площадью
(15, 112, ИЗ), (42, 40, 58), (70, 24, 74).
Не все они являются основными. Доказано, что наимень-
шая общая площадь для трех основных пифагоровых
треугольников равна 13123110, а треугольники эти сле-
дующие:
(4485, 5852, 7373), (19019,1380,19069),
(3059,8580,9109).	[21]
9.3.	Возникает вопрос, можно ли найти произвольное
число пифагоровых треугольников с разными гипотенузами
и равными площадями. Ответ на этот вопрос дает сле-
дующая теорема Ферма (Fermat.).
Теорема 3. Для каждого натурального числа п
существует п пифагоровых треугольников с разными
гипотенузами и с общей площадью.
Эта теорема может быть доказана по индукции на
основании следующей леммы:
Лемма. Если имеем п^\ пифагоровых треуголь-
ников с различными гипотенузами и с общей площадью
и один из этих треугольников имеет нечетную гипо-
тенузу, то можно найти п -|-1 пифагоровых треуголь-
ников с различными гипотенузами и общей площадью,
из которых один имеет нечетную гипотенузу.
Доказательство. Пусть п1 есть данное нату-
ральное число и пусть дано п пифагоровых треугольни-
ков (ah, bk, ck), где ak<bk<ck, k= 1, 2, 3,. .., n, с раз-
ными гипотенузами и равными площадями, причем число
сг нечетно. Положим
a!k = 2 (Pi — а‘) ciak> b'k = 2 (bi — a-l) ct bk,
c'k = 2(bi-ai)clCft	(16)
для k— 1, 2, ..., /г, а также
=	—«»)2>	и c'n+t = 4albiсЛГ (17)
27
Треугольники (a'k9 b'k9 c*)9 где k= 1, 2, ... , п9 являются
пифагоровыми, потому что стороны их выражаются на-
туральными числами, и они подобны пифагоровым тре-
угольникам (ak9 bk9 ck).
Треугольник (a'n+l9 b’n+l, c'n+1) пифагоров, что видно из
формул (17) и из равенства а2-{-Ь2 — с^.
Действительно,
(&J — ^)4 + Wi + ^i)2 =	+ (а\ 4- Ь\)2]2.
Покажем, что треугольник (afk9 b'k9 c'k)9 где k =
1, 2, ...	отвечает требуемым условиям.
В самом деле, пусть Д (площадь) каждого из треуголь-
ников (ak9 bk9 ck)9 где Л=1, 2,Тогда имеем
akbk = 2& для А=1, 2, ..., п, а площадь треугольника
(a’k9 b'k9 c'k) на основании равенства (16) для Л= 1, 2, .. .,п
выражается следующим образом:
A- a’kb'k = 2(Ьг,- atf c\akbk = 4(b*- atf с^.
Площадь треугольника (а'п+1, b'n+i, с'п+1) на основании ра-
венства (17) равна
~ а'„+1 Ь'п+1 = 2 (Ы - atf = ЦЬ\- atf с^,
£
и треугольники (a'k9 b'k9 c'k)9 где k—l9 2,..., /г-f" h имеют
равные площади. Гипотенузы треугольников (a'kf b'k9 c'k)9
где k = 1, 2,..., п9 различны, так как различны гипоте-
нузы треугольников (ak, bk9 ck) и каждая из гипотенуз вы-
ражается, как видно из равенств (16), четным числом.
Гипотенуза с'п+1 выражается на основании равенств (17)
числом нечетным.
Числа c'kf где & = 1, 2,...,я-|~Ь все различны.
Итак, лемма доказана.
9.4.	Рассмотрим простейший случай леммы, когда
п—1. Наименьший пифагоров треугольник, к которому
применима лемма, — пифагоров треугольник со сторо-
нами
^ = 3, Ьг—49 с1 = Ь.
Получим, исходя из этого треугольника, два пифагоровых
треугольника (a', b'19 с{) и (а'29 Ь29 с2) с равными площа-
дями, где из формул (16) имеем:
2(^ — а2)с1 = 2-7-5 = 70,
а'= 70-3 = 210, Ь[ = 70-4 = 280,	= 70-5 = 350.
28
Из формулы (17) получаем:
а' = (42 —32)2 = 49, fe'=4-3-4-52 = 1200,
^ = 4.32-42-j-54= 1201.
У этих двух треугольников разные гипотенузы (из кото-
рых одна нечетна) и общая площадь, равная 29400.
Если бы мы к полученным треугольникам применили
доказанную лемму, мы нашли бы три пифагоровых тре-
угольника с разными гипотенузами и общей площадью.
Длина каждой стороны выражалась бы больше чем деся-
тизначным числом.
Раньше мы нашли другим способом три таких треуголь-
ника, причем длина сторон каждого выражалась не более
чем трехзначными числами. Найдены также четыре пифа-
горовых треугольника с разными гипотенузами и с рав-
ными площадями, причем стороны этих треугольников
выражаются не более чем четырехзначными числами. Это
следующие треугольники: (518, 1320, 1418), (280, 2442,
2458), (231, 2960, 2969), (111, 6160, 6161), с площадью,
равной 341880.
Найдено также пять таких же треугольников со сто-
ронами, выражаемыми не более чем пятизначными числами:
(2805, 52416, 52491), (3168, 46410, 46518), (5236, 14040,
28564), (6006, 24480, 25206), (8580, 17136, 19164), с пло-
щадью, равной 73513440.	[22]
9.5.	Существует, очевидно, конечное число пифагоро-
вых треугольников с площадью, равной Д, так как катеты
этих треугольников должны быть делителями числа 2Д.
Вместе с тем из доказанной леммы следует, что, напри-
мер, существует бесконечное множество различных пря-
моугольных треугольников с рациональными сторонами
и площадью, равной 6.
В самом деле, из доказанной леммы следует, что если
имеем п 1 пифагоровых треугольников с разными гипо-
тенузами, из которых одна нечетна, и с площадью Д, то
существует п 4~ 1 пифагоровых треугольников с разными
гипотенузами, из которых одна нечетна, и с общей пло-
щадью, равной Дб/2, где d — целое число.
Исходя из треугольника (3, 4, 5) и применяя доказан-
ную лемму п—1 раз, найдем п пифагоровых треуголь-
ников с разными гипотенузами и с площадью, равной
6m2, где т — целое число, зависящее от п. Уменьшая
стороны каждого из треугольников в т раз, получим п
29
различных прямоугольных треугольников с рациональными
сторонами и с площадью, равной 6.
Так как п — произвольное число, то отсюда следует,
что число различных прямоугольных треугольников с ра-
циональными сторонами и площадью, равной 6, не может
быть конечным и, следовательно, таких треугольников бес-
конечное множество, и теорема доказана.
§ 10.	ПИФАГОРОВЫ ТРЕУГОЛЬНИКИ, У КОТОРЫХ ПО КРАЙНЕЙ
МЕРЕ ОДНА СТОРОНА ЯВЛЯЕТСЯ КВАДРАТОМ
10.1.	Можно доказать, что существует бесконечное
множество пифагоровых треугольников, у которых гипо-
тенуза — точный квадрат.
Действительно, пусть (п, т,р), n<Zm<ZP,— про-
извольный основной пифагоров треугольник (как нам из-
вестно, существует бесчисленное множество таких тре-
угольников). Известно (§ 2.5), что одно из чисел т и п
четно, а другое нечетно (безразлично т или п), причем
числа тип взаимно простые. Затем на основании тео-
ремы 1 составим новый основной пифагоров треугольник
(л, у, z\ где л, у и z находятся по формуле (6). Имеем:
г — т*-\-п*=р\
следовательно, гипотенуза — квадрат натурального числа.
Например, из основного треугольника (3, 4, 5) получаем
основной треугольник (7, 24, 25), гипотенуза которого —
квадрат натурального числа, из основного треугольника
(5, 12, 13) получаем основной треугольник (119, 120, 169),
где 169 =132. Существуют пифагоровы треугольники, ги-
потенузы которых являются кубами натуральных чисел,
например треугольник (117, 44, 125), где 125 = 5s. [23]
10.2.	Легко доказать существование бесконечного мно-
жества основных пифагоровых треугольников, у кото-
рых один из катетов является квадратом натураль-
ного числа.
В самом деле, пусть (#, /г, т)— основной пифагоров
треугольник, где п четно, a q н т нечетны, причем
(т, л)=Р.	[24]
1 (т, п) = 1 означает, что тип — взаимно простые числа.
30
Составим новый основной пифагоров треугольник
(%, у, г), выразив х, у, z, пользуясь на основании тео-
ремы 1 формулами (6):
л = 7712 — n2 — q\
следовательно, х (нечетный катет треугольника (л, у, z))—
квадрат натурального числа.
Таким образом, из основного треугольника (3, 4, 5)
получаем основной треугольник (9, 40,41), где 9 = 32, а
из основного треугольника (5, 12, 13) получаем основной
треугольник (25, 312, 313), где 25 —52.
10.3.	Легко доказать существование бесконечного мно-
жества основных пифагоровых треугольников, четный
катет каждого из которых является квадратом.
Это непосредственно следует из тождества:
(А4 — 4)2 + (2£)4 = (А4 + 4)2,
где за k следует взять нечетное число, так как только
в этом случае А4 — 4 и 4Л2 будут взаимно простыми. Для
k — \ получаем треугольник (3, 22, 5), для k — 3 — тре-
угольник (77, 62, 85), для k = 5— треугольник (621, 102,
629).
10.4.	Возникает вопрос, существуют ли пифагоровы
треугольники, две стороны которых являются квадратами.
Ответ на этот вопрос дает теорема Ферма.
Теорема 4. Нет пифагоровых треугольников, у
которых хотя бы две стороны были квадратами.
Доказательство, а) Положим, что существуют
пифагоровы треугольники, у которых оба катета являются
квадратами. Среди таких пифагоровых треугольников есть
один (%, у, z), гипотенуза которого не больше гипотенузы
всякого другого пифагорова треугольника, у которого оба
катета — квадраты. Пусть
х = а2, У — Ь\
где а и b — натуральные числа. Покажем, что а и b —
взаимно простые числа.
31
В самом деле, если бы числа а и b делились на це-
a = dax и b = db
где av и bt — целые числа
Из этого равенства замечаем, что z2 делится на d4, а сле-
довательно, z делится на d2 и z=^d2zlf где zt— целое
число. Равенство d4 й4) — г2 после сокращения наг/4
принимает вид:

19
где zY<Zdzx — z.
Пифагоров треугольник (а2, Ь2, г,) имеет гипотенузу г, < z
и оба катета этого треугольника — квадраты, что проти-
воречит сделанному нами предположению относительно
треугольника (л, у, z).
Итак, числа а и b и, следовательно, а2 и Ь2 — числа
взаимно простые и пифагоров треугольник (л, у, z) =
—(a2, b2, z) — основной. Применяя к этому треугольнику
теорему I, заключаем, что одно из чисел а2 или Ь2 должно
быть четным (пусть Ь2 четно) и что
а2 = т2 — п2,
b2 = 2тп,
z = m2 -\-п2,
(18)
где т и п — взаимно простые числа, из которых одно
четно и т^>п.
Если бы т было четно, а п нечетно, то из первого
равенства (18) а2-\-п2 = т2 следовала бы нечетность чи-
сла а. Одновременно числа а и п не могут быть нечет-
ными, так как треугольник (а, и, т) пифагоров, а в пи-
фагоровом треугольнике (§ 2.5) хотя бы один из катетов
должен быть четным.
Итак, число т нечетно, а п — четно и равняется 2k,
где k— целое число. Числа т и k взаимно простые, так
как т и п взаимно простые. На основании второго ра-
венства (18) имеем:
Ь2 = 2т • 2k = 22 • mk.
Пусть й = 2/, где I — натуральное число и l2 — mk. Учи-
тывая, что т и k взаимно простые, заключаем (см. при-
мечание 1), что т и k являются квадратами, т~г2 и
k — s2, где г и$ — целые числа. Далее имеем: n=2k = 2s2.
Так как т и п— числа взаимно простые, то из пер-
вого равенства (18) заключаем, что а и п — числа взаимно
32
простые и что пифагоров треугольник (я, п, т)— основ-
ной.
На основании теоремы 1, учитывая четность числа пу
заключаем, что существуют такие взаимно простые числа
т1 и из которых одно четно, что
п = 2т1п1, т = т\-{-п\.	(19)
Так как n — 2s* 2y то s2 = m1nl.
Следовательно, т1 и пх каждое в отдельности является
квадратом = и пх = Ь\у где ах и Ьх— натуральные
числа. Подставляя во второе равенство (19) значения т,
и //,, получаем:
«:+^=г2>
причем
г г2 = т т2 + и2 = z-
У пифагорова треугольника (а2, Ь2, г) с гипотенузой г,
меньшей гипотенузы z, оба катета — квадраты, что про-
тиворечит нашему предположению о треугольнике (х,у, z).
Итак, предположение о существовании пифагорова
треугольника, катеты которого квадраты, приводит к про-
тиворечию и, следовательно, таких треугольников нет.
б) Предположим теперь, что существуют пифагоровы
треугольники, у которых один из катетов и гипотенуза —
квадраты.
Пусть треугольник (%, у, z) является таким из этих
треугольников, что его гипотенуза не больше гипотенузы
всякого другого треугольника, у которого гипотенуза и
один из катетов — квадраты.
Пусть х = а2 nz=c\ где а и с — натуральные числа.
Покажем, что пифагоров треугольник (л, у, z) — основ-
ной. Достаточно доказать, что х и z — взаимно простые
числа. Предположим противное, т. е. что х и z имеют
общего делителя, тогда а и с также имеют общего де-
лителя d >* 1.
a — daiy c = dcx.
Числа и сх — натуральные числа:
х — а2 = d2a\, z = с2 = d2c2,
y2=z2-x2 = d\c\-a\\
откуда d^\y2 J), что дает d21у uy = d2yiy где ух является
натуральным числом.
п Символ g | h обозначает, что g является делителем /г.
2 Заказ № 2446
33
Подставляя значения x1,y19z1 в равенство
4
1>
и сокращая на rf4, получаем:
с

причем, так как z = d2c2l и d> 1, имеем c\<Zz. В пифа-
горовом треугольнике (а2, уг, с2^ гипотенуза и один из
катетов — квадраты и гипотенуза меньше г, что противо-
речит нашему предположению относительно треугольника
(л, у, z).
Покажем, что у не может быть четным. Если бы у
был четным, то на основании теоремы 1 существовали бы
взаимно простые числа т и п, где т >* п, такие, что
а2==х — т2— и2,
у = 2тп,
с2 = z — т2 4- /г2,
откуда с2>т2 и (ас)2 — т4— п\
и
п4 4- (ас)2 = т\
В пифагоровом треугольнике (п2, ас, т2) один из ка-
тетов — квадрат и гипотенуза т2 <Z z, что противоречит
нашему предположению.
Итак, у должно быть нечетным, а х = а2 должно быть
четным числом.
Так как а4-^-у2 = с4, где а четно, а у нечетно, то
с — нечетное число, имеем:
Покажем, что нечетные числа с2 а2 к с2 — а2 взаимно
простые. Действительно, их общий делитель является
делителем чисел 2с2 и 2а2, и так как он должен быть
нечетным, то он является делителем взаимно простых
чисел с2 и а2. Итак, числа (c2-j-a2) и (с2 — а2) взаимно
простые.
Так как у2 разлагается на два взаимно простых мно-
жителя, то (см. примечание [1])
с2—а2=г2 и c2-\-a2 = s2,
откуда
и
2с2 = г2 4" s2
34
причем числа S~^r и целые, так как s и г оба нечетны.
Эти числа взаимно простые, так как их сумма и разность —
взаимно простые числа.
На основании теоремы 1 существуют взаимно простые
числа т и п, из которых одно четно, такие, что
либо
= т2 — п2,
= 2тп,
с = т2 Ц- п2
= 2тп;
с = т2 -\-п2.
Откуда в обоих случаях получаем:
2а2 = s2 — г2 = 8тп (т2 — п2).
Так как а четно, то а = 2ал и имеем:
а\ = тп (гп2 — п2) = тп (т — п) (т п).	(20)
Числа т и п — взаимно простые и одно из них четно.
Числа (т— п) и	также взаимно простые, а сле-
довательно, взаимно простыми являются пары т, т— п
и т, т 4~ п. Итак, каждая пара чисел в правой части ра-
венства (20) есть пара взаимно простых чисел. Из этого
следует, что каждый множитель произведения в правой
части равенства (20) есть квадрат:	[25]
m = k2, п = 12, т— п=р2, m-\-n = q2.	(21)
Откуда &4—/4=(да)2, причем А4 — т2 < т2 -j-/z2 = с <Z c2=z
и тем более k2 < z.
В пифагоровом треугольнике (Z2, pq, k2) гипотенуза и
один из катетов — квадраты, причем гипотенуза k2 < z,
что противоречит нашему допущению.
Итак, предположение о существовании пифагоровых тре-
угольников, у которых гипотенуза и катеты — квадраты,
приводит к противоречию. Следовательно, не существует
таких треугольников.
Теорема 4 доказана. Из этой теоремы следует, что
нет пифагоровых треугольников, у которых все стороны
были бы квадратами,
Проф. К. Царанкевич поставил задачу: определит^
существует ли пифагоров треугольник, у которого каж-
дая из сторон была бы треугольным числом (/г-м тре-
2*
35
угольным числом называют число =	, где п—
целое число).
Оказывается, как это легко проверить, примером та-
кого треугольника является пифагоров треугольник
(*13а, М = (8778, 10296, 13530).
10.5	. В алгебре теорема, что нет пифагоровых тре-
угольников, у которых все стороны были бы квадратами,
формулируется следующим образом: уравнение.
л4 4" У1—
не может быть решено в натуральных числах.
Эта теорема—частный случай великой теоремы Ферма:
Теорема. Для целого п^>2 уравнение
xn+yn = zn
не может быть решено в натуральных числах. [26]
Эта теорема доказана для таких степеней /г, что
2 <«<2000, а также для множества других чисел, но
доказательство для всех «<2 неизвестно.
Для наименьшего п = 3 доказательство теоремы сложно.
Сложно также доказательство теоремы Ферма для« = 6,
т. е. доказательства, что нет пифагоровых треугольни-
ков, все стороны которых были бы кубами натураль-
ных чисел.
Для случая п — 3 из великой теоремы Ферма А. Ва-
кулич элементарным путем доказал, что нет пифагоровых
треугольников, у которых катеты — кубы целых чисел.
10.6	. Из теоремы 4 следует, что не существует пи-
фагоровых треугольников, у которых гипотенуза и один
из катетов были бы катетами другого пифагорова
треугольника.
В самом деле, если бы в пифагоровом треугольнике
гипотенуза z и катет х были бы катетами другого пифа-
горова треугольника, то при некоторых натуральных у
и и существовали бы равенства
x2-\~y2 = z2 и х2 -}-z2 =.и2,
откуда
х* + (иу)2 = z4
36
и пифагоров треугольник (%2, иу, z2) имел бы две сто-
роны, которые были бы квадратами, что противоречит
теореме 4.
Из теоремы 4, как легко видеть, следует, что нет
двух натуральных чисел, сумма квадратов которых и раз-
ность квадратов были бы квадратами натуральных чисел.
10.7	. Из теоремы 4 непосредственно получается сле-
дующая теорема Ферма:
Теорема. Не существует пифагоровых треуголь-
ников, площади которых равны квадрату натурального
числа.
Действительно, положим, что существует такой пифа-
горов треугольник (а, Ь, с).
Тогда имеем
а* + Ь2 = с2
и
ab = 2s.
Пусть s равно п2, где п — целое число:
2аЬ = (2п)2
и
с2 + (2п)2 = а2 + Ь2 + 2аЬ = {а + Ь)2,
с2 —(2я)2 = (я —^)2,
что противоречит следствию из теоремы 4.
§ 11.	ТРЕУГОЛЬНИКИ, СТОРОНЫ И ПЛОЩАДИ КОТОРЫХ
ВЫРАЖАЮТСЯ НАТУРАЛЬНЫМИ ЧИСЛАМИ.
ТРЕУГОЛЬНИКИ, ПЛОЩАДИ КОТОРЫХ ВЫРАЖАЮТСЯ
НАТУРАЛЬНЫМИ ЧИСЛАМИ И СТОРОНЫ ВЫРАЖАЮТСЯ
НАТУРАЛЬНЫМИ ПОСЛЕДОВАТЕЛЬНЫМИ ЧИСЛАМИ.
РАЦИОНАЛЬНЫЕ ТРЕУГОЛЬНИКИ
ПЛ. Всякий пифагоров треугольник имеет площадь,
выражаемую натуральным числом, кратным 6. Это сле-
дует из того, что хотя бы один из катетов делится на
3 и хотя бы один делится на 4 (§ 2.3 и 5.1). Площадь
треугольника, определяемая полупроизведением катетов,
должна выражаться числом, кратным 6.
11.2.	Существуют непрямоугольные треугольники, сто-
роны и площади которых выражаются натуральными
37
числами. Такие треугольники можно получить из двух
пифагоровых треугольников с общим катетом.
Например, из пифагоровых треугольников (5, 12, 13)
и (9, 12, 15) можно получить (прилагая один треугольник
к другому так, чтобы совпали их равные катеты) новый
непрямоугольный треугольник со сторонами 13, 14, 15 и
с площадью
(5 4-9). 12
2
Из пифагоровых треугольников (5, 12, 13) и (35, 12, 37)
получаем косоугольный треугольник со сторонами 13, 40
и 37 и площадью, равной 240. Из двух тождественных
пифагоровых треугольников со сторонами (3, 4, 5) можно
составить равнобедренный треугольник со сторонами 5,6,
бис площадью, равной 12, либо равнобедренный тре-
угольник со сторонами 5, 8, 5 и с той же площадью. [27]
В общем случае, имея два пифагоровых треугольника
(an blf сг) и (а2, й2, с2), можно каждый из них увеличить
в соответственное число раз так, чтобы катет одного
треугольника стал равен катету другого. Для этого до-
статочно получить катет, равный наименьшему кратному
двух данных катетов Ьг и Ь2. Из полученных треугольни-
ков с общим катетом легко составить треугольник, сто-
роны и площадь которого выражаются натуральными чис-
лами.
11.3.	Не всякий треугольник, стороны которого и пло-
щадь выражаются натуральными числами, может быть
получен из двух пифагоровых треугольников с общим
катетом. Например, треугольник со сторонами 65, 119, 180
имеет площадь, равную 1638. Число 1638-2 = 3276 =
~22-32-7-13 не делится ни на одно из чисел 65 = 5-13,
119 = 7-17, 180 = 22-32-5. Отсюда следует, что ни одна
из высот этого треугольника не выражается натуральным
числом и рассматриваемый треугольник не может быть
получен из двух пифагоровых треугольников с общим
катетом (катет должен стать высотой рассматриваемого
треугольника).
Если стороны данного треугольника увеличить в пять
раз, т. е. построить подобный треугольник со сторонами
325, 595, 900, то этот треугольник можно составить из
следующих двух пифагоровых треугольников (91,588,595)
и (91, 312, 325) с общим катетом, равным 91.
38
11.4.	Покажем, что если стороны треугольника выра-
жаются последовательными натуральными числами и пло-
щадь выражается натуральным числом, то он может быть
составлен из двух пифагоровых треугольников с общим
катетом.
Сначала покажем, что если треугольник имеет площадь,
выражаемую натуральным числом, и если его стороны вы-
ражаются последовательными натуральными числами, то
наименьшая из сторон определяется нечетным числом.
Действительно, если бы наименьшая сторона была чет-
ным числом 2А, то стороны треугольника определялись
бы числами 2А, 2А-|-1, 2А —2 и по известной из геомет-
рии формуле площадь s определялась бы следующим
образом:
(4s)2 = (6А + 3) (2й + 3) (2й +1) (2k — 1) = 4 (3F + 8k 4~
4-2) .(4Л2 —1)4-4F —1,	[28]
полученное равенство невозможно, так как левая часть
делится на 4, тогда как правая при делении на четыре
дает в остатке 3.
В рассматриваемом треугольнике наименьшая сторона
должна быть нечетным числом 2k — 1 (где k — натураль-
ное число). Стороны треугольника определяются следую-
щими числами: 2k — 1, 2k, 2&4~1 и квадрат площади
s2^= 3k2 (k2 — 1).
Из выражения для площади видно, что s2 кратно k2
и, следовательно, число s делится на число k, s = kh,
где h — целое число. Обозначая через hr высоту треуголь-
ника, перпендикулярную к стороне длиной в 2k, получим
для площади s~kh^
Из сравнения двух выражений для площади заключаем,
что h = hr и, следовательно, высота, перпендикулярная
к стороне 2k, определяется натуральным числом.
Сравнивая формулы s2 — 3k2 (k2— 1) и s2 = k2h2, заклю-
чаем: h2 — 3(k2—1).
Легко проверить, что
3(k2 — 1) = (2k — I)2 — (k — 2)2 = (2k 4- I)2 — (k 4- 2)2.
Следовательно, (k — 2, h, 2k — 1) и (k 4~ 2, h, 2&4~ 1) —
пифагоровы треугольники, из которых можно составить
треугольник со сторонами 2k — 1, 2k, 2,%4“1-
39
Так как 3k2 —h2 -ф-З, то легко проверить, что тре-
угольники (2Л-ф-Л + 2, 3£-[~2^ 4&4“ 2Й ± 1)—пифагоровы
с общим катетом 3k -ф- 2/z.
Из этих двух пифагоровых треугольников легко соста-
вить треугольник со сторонами 4k -ф- 2h — 1, 4k -ф- 2Л,
4k -ф- 2h -ф-1 и с площадью, равной
(2k -ф- h) (3k + 2Л).
Итак, из каждого треугольника, площадь которого
выражается натуральным числом, а стороны натуральными
последовательными числами, можно получить больший
треугольник, отличающийся теми же свойствами.
Применяя найденный нами способ к треугольнику (3,4,5),
где k = 2; h = 3 и s = 6, получаем новый треугольник
(уже не пифагоров) со сторонами 13, 14, 15, где k = 7,
12, s = 84.
Производя аналогичные преобразования со сторонами
найденного треугольника, получим новый треугольник со
сторонами 51, 52, 53, где k — 26, А=45,	1170. Анало-
гично получим треугольник со сторонами 193, 194, 195, где
Л = 97, h —168, s=16296 и т. д.
Очевидно, существует бесконечное множество тре-
угольников, площади которых выражаются натуральными
числами, а стороны — натуральными последовательными
числами. Можно доказать, что таким способом можно
определить все такие треугольники.
11.5.	Возникает вопрос, как можно найти треугольники,
стороны и площади которых выражаются натуральными
числами. Этот вопрос равносилен вопросу, как найти
треугольники, стороны и площади которых выражаются
рациональными числами.
Треугольники, стороны которых и площадь рацио-
нальны, назовем рациональными треугольниками. Уве-
личивая стороны рационального треугольника в целое
число раз, мы снова получим рациональный треугольник.
Покажем, что всякий рациональный треугольник
можно составить из двух прямоугольных треугольни-
ков с рациональными сторонами. Заметим, что во всяком
треугольнике с рациональными сторонами высота, прохо-
дящая внутри треугольника, делит перпендикулярную к
ней сторону на два рациональных отрезка.
В самом деле, пусть а, Ь, с — стороны треугольника,
h — высота, лежащая внутри треугольника и перпендику-
40
лярная стороне с. Обозначим соответственно ал и Ь,
отрезки, которые являются проекциями сторон а и b на
сторону с.
Числа at и Ьг положительны, очевидно, что
а^Ь^с.
Высота h делит наш треугольник на два прямоугольных
треугольника (а19 А, а) и (&,, h, b) (неизвестно, являются
ли стороны треугольников рациональными). На основании
теоремы Пифагора для этих треугольников имеем:
то
откуда
Так как
получаем:
а так как
Из равенства (24) следует рациональность отрезков ал и Ьг
Если данный треугольник с рациональными сторонами
имеет рациональную площадь $, то каждая из высот яв-
ляется также рациональной.
Если h — высота треугольника, перпендикулярная сто-
роне с, то площадь
he t 2s
s = — и h = —.
A-i	c
Рациональность чисел s и с приводит к рационально-
сти числа А.	[29]
Обозначая соответственную сторону с, предполагаем,
что перпендикулярная к ней высота лежит внутри тре-
угольника.
Из доказанного следует, что рассматриваемый тре-
угольник может быть составлен из двух прямоугольных
рациональных треугольников.	[30], [31]
11.6.	Рассмотрим треугольники с натуральными сторо-
нами и рациональными медианами.
41
Длина медианы sa (проходящей через середину сторо-
ны а) выражается по формуле:
(2sJ2 = 2(b24-c2) — а\
Пользуясь этой формулой, можно проверить, что ука-
занный Э й л ером треугольник со сторонами 68, 85, 87
131	127
имеет рациональные медианы sa = 79, sh = -x-, s =-л-.
Доказано, что этот треугольник — наименьший из всех
треугольников, стороны которого выражаются натураль-
ными числами и медианы которого рациональны. Укажем
еще два треугольника с рациональными медианами, это
треугольники со сторонами 127, 131, 158 и 204, 255,261.
11.7.	Интересна следующая теорема Куммера, данная
в 1848 г. и рассматривающая четырехугольники с рацио-
нальными сторонами и рациональными диагоналями.
Теорема. В четырехугольнике с рациональными
диагоналями и сторонами диагонали делятся в точке
пересечения на рациональные отрезки.
При доказательстве Куммер пользуется тригонометри-
ческими функциями и их свойствами.
Дадим элементарное геометрическое доказательство.
Пусть ABCD — четырехугольник, стороны которого и
диагонали— рациональ-
ны, и пусть О — точка
пересечения диагоналей
(чертеж 1).
Пусть BE — высота
треугольника АВС, пер-
пендикулярная к сторо-
не АС. На продолжении
BE отложим отрезок
EG^FD, weFD \EG.
Рассмотрим прямоуголь-
ный треугольник BGD.
Так как у треугольника
АВС рациональные стороны, то, как известно, проекция
АЕ стороны АВ на сторону АС рациональна.
Проекция FC стороны DC рационального треугольника
ADC на сторону АС рациональна
EF=AC — (AE^FC).
42
Из прямоугольного треугольника BGD, у которого ра-
циональны гипотенуза BD и катет GD — EF, заключаем,
что квадрат стороны BG, т. е. ВО2, является рациональ-
ным числом, (BE-{-EG}2 тоже рациональное число. Из
прямоугольного треугольника АВЕ, стороны которого
АВ и АЕ рациональны, следует, что BE2 — рациональное
число.
Аналогично, из прямоугольного треугольника FDC за-
ключаем, что FD2 и EG2 рационально, так как EG = FD.
Из рациональности (BE—ЕG)2=BE2-{-EG2 -|- 2 • BE• ЕG
следует, что произведение BE-EG рационально.
BE EG EG
Выражение —является рациональным.
Из подобия прямоугольных треугольников ВЕО и DFO
имеем
OD___FD___EG
ВО~~~ ВЕ~~~ BE'
Отношение OD к ВО является рациональным, а так как
сумма отрезков BO-\-OD = BD рациональна, то и от-
резки ВО и OD рациональны. Аналогично доказывается
рациональность отрезков АО и ОС. Из теоремы Куммера
следует, что выпуклый четырехугольник с рациональными
сторонами и рациональными диагоналями делится диаго-
налями на четыре рациональных треугольника.
§ 12.	ПИФАГОРОВЫ ТРЕУГОЛЬНИКИ, У КОТОРЫХ
ГИПОТЕНУЗА И СУММА КАТЕТОВ — КВАДРАТЫ
12.1.	В 1643 г. Ферма предложил следующую задачу:
Найти пифагоровы треугольники, у которых гипо-
тенуза и сумма катетов — квадраты.
В письме к Мерсенну Ферма утверждал, что наимень-
шим таким треугольником является треугольник со сто-
ронами:
(4565486027761, 1061652293520, 4687298610289). (25)
Задача Ферма и ее решение имеют более глубокий
смысл, чем кажется на первый взгляд.
Ответом на такую, казалось, простую задачу явля-
ются очень большие числа, которые невозможно найти
случайно или методом подбора. Возникает несколько во-
просов:
1° Как найти решение задачи?
43
2° Показать, что числа, данные Ферма и выражающие
длины сторон, действительно являются наименьшими?
3° Как найти все решения задачи?
Попробуем ответить на поставленные вопросы.
12.2.	Приведем кратчайшее решение задачи Ферма.
Задача, поставленная Ферма, сводится к решению си-
стемы уравнений:
л2-|-^2 = п4, x-\-y = v2	(26)
в натуральных числах. Достаточно найти решение си-
стемы уравнений (26) в рациональных положительных
числах %, у, д, V.
Приведя полученные решения к общему знамена-
телю т и умножая первое из равенств (26) на т4, а вто-
рое равенство — на т2, получим решение системы урав-
нений (26) в натуральных числах т2х, т2у, mu, mv.
Примем за х рациональное число t-.
л = (^ + 5)2 —122, у = 24(^5).	(27)
Получаем тождество:
[(t 4- 5)2 — 122]2 + [24 (t + 5)]2 = [{t + 5)2 + 122]2.
Чтобы числа (27) удовлетворяли системе (26), необхо-
димо и достаточно, чтобы
(^4-5)2+122 = д2, (Z + 5)2— 122 + 24 (^ + 5) = г/2,
или
Z24- 10Z + 169 = п2,	(28)
и
^4-34/4-1= г/2.	(29)
Равенство (29) преобразуем:
169 (^ + 34/4-1) = (13г/)2,
на основании (28) получаем:
(13г/)2 — и2 = 168^ 4-5736£= 1М (12^ + ^). (30)
Равенство (30) будет выполняться, если
13г/ — п= 14£,
13г/4~^= 12£
2868

т. е.
, . 1434
П t J у ,
1434
7-13 *
(31)
44
Первое из этих равенств дает:
14342
72 •
Для того чтобы число и2 удовлетворяло уравнению (28),
необходимо и достаточно, чтобы число t удовлетворяло
уравнению
10/+169=-S + ™\
*	7	1	74 ’
или
14342  (13.7)2  1343-1525
, 2868\	7-2938
(33)
(34)
С другой стороны, если возьмем значение t из ра-
венства (34), а значение и и v из равенства (31), то получим
равенства (32) и (33), из которых получается равенство (28);
на основании второго равенства (31) получается равен-
ство (30), из которого на основании (28) следует равен-
ство (29). Как известно, из равенств (27), (28) и (29) сле-
дует равенство (26).
Если определить t из равенства (34), а числа л, у, и и v
из равенств (27) и (31), то получим решение системы
уравнений (26) в рациональных положительных числах,
причем знаменатель каждой из дробей у, п, v будет, как
легко убедиться, т = 7-2938, а знаменатель дроби х бу-
дет т2. Числа т2х, т2у и т2и2 выражают стороны тре-
угольника (25), найденного Ферма. Существует, следова-
тельно, пифагоров треугольник, гипотенуза которого и
сумма катетов — квадраты целых чисел.
Если (л, у, z)— такой треугольник, а п — произволь-
ное целое число, то, очевидно, треугольник (п2х, п2у, n2z)
будет также удовлетворять условиям задачи.
12.3.	С другой стороны, если (%, у, z)— пифагоров
треугольник, гипотенуза которого и сумма катетов — квад-
раты, и если п — наибольшее натуральное число, квадрат
которого является общим делителем чисел х и у, то,
полагая
х — п2х1У у = п2у1,
получим натуральные числа хг и ух, не имеющие общего
делителя, квадрат которого больше единицы.
45
Из равенства (26), учитывая наше предположение от-
носительно треугольника (х, у, г), имеем:
—и п* (Л1 +л) — ^2-
Из этих равенств видно, что «4]м4, n2\v2, следовательно,
п | и и п |г/ и существуют такие натуральные числа и v19
что
и — пи. и v = nv.9
1	X 9
откуда

Из полученных равенств следует, что в пифагоровом
треугольнике (лп у19 zj гипотенуза и сумма катетов яв-
ляются квадратами, причем xt и уг не имеют общего
делителя, который был бы квадратом и был бы больше 1.
(х,у,г) = (пгхи n2ylt п2и%.
Исследование пифагоровых треугольников, у которых
гипотенуза и сумма катетов — квадраты, сводится к ис-
следованию тех из них, у которых катеты не имеют об-
щего делителя, который был бы квадратом и был больше
единицы.
12.4.	Покажем, что катеты в таких треугольниках
выражаются взаимно простыми числами.
Пусть (х, y,z)— пифагоров треугольник, у которого
гипотенуза и сумма катетов — квадраты и у которых ка-
теты л и у не имеют общего квадратного делителя, боль-
шего 1. Из гипотезы относительно (х,у,г) следует су-
ществование чисел и и V, удовлетворяющих уравне-
ниям (26). Из первого из этих равенств следует, что
одно из чисел х или у, например у, делится на 4 (§2.3).
Если бы число х было четным, то из (26) следовала бы
четность числа v и 4|г/2 или 4|х—}~У, атак как 4|у, то
4|х, что противоречит предположению, что х и у не
имеют общего квадратного делителя, большего единицы.
Итак, число х должно быть нечетным. Пусть d — об-
щий наибольший делитель чисел х и у. Тогда имеем d\x
и d\y и на основании (26) d2\u* и d\v29 т. е. d — об-
щий делитель чисел и2 и v\ Если d^> 1, то числа и и <v
не могут быть взаимно простыми (так как тогда оба
числа и2 и V2 были бы взаимно простыми и не могли бы
иметь общего делителя d^> 1).
46
Пусть 8 — наибольший общий делитель чисел а и v,
тогда 8;>1, Ъ\и, 8 |г/, 84 [ ц4 и 821 г'2, принимая во вни-
мание (26), получим: 841 х2 -{- у2 и 821 х -|-у, откуда
841 (хЦ-у)2, т. е. 84|(хЦ-у)2— (-x2~j-y2), или 84[2ху, а
отсюда 84 (х2 -J-у2 — 2ху, или 84 (х—у)2, что дает
821 х —у, а так как 821 х-|-у, то получаем 821 2х и 821 2у.
Число х нечетно, а число у четно, а потому x-j-y яв-
ляется нечетным числом. Так как 82 |х-у, то 8 — не-
четное число. Из того, что 8212х и 8212у, следует, что
821 х и 821у, что противоречит предположению, что х и у
не имеют общего квадратного делителя, большего 1.
Следовательно, d не может быть больше единицы, а
должно быть равно единице и числа х и у — взаимно
простые, что и требовалось доказать. Доказано также,
что 8 не может быть больше единицы (так как 821 х и
82 |у), т. е. 8=1 и числа и и v также взаимно простые.
Итак, при исследовании пифагоровых треугольников,
гипотенуза и сумма катетов которых квадраты, доста-
точно ограничиться исследованием основных треугольни-
ков. Другими словами, достаточно решить систему урав-
нений (26) в натуральных числах, где х и у являются
взаимно простыми (а также и и v взаимно простые).
12.5.	Предположим, что целые числа х, у, и и *и
удовлетворяют системе (26) и что х и у являются чис-
лами взаимно простыми. Так как число иррациональ-
ное, то х не может быть равным у. Имеем х=^=у, затем
*w — \x—у| является натуральным, причем на основа-
нии (26) имеем:
2ц4 —
z/4 = 2 (х2 +у2) — (х +у)2 = (х — у)2 = w
и, имея в виду (26), получаем:
г>4 — ц4 = (х +у )2 — (х2 +у2) = 2ху > О
и, следовательно <и у> и.
Итак, если натуральные числа х, у, ц, v удовлетво-
ряют системе уравнений (26) и числа х и у взаимно
простые, то целые числа и и v удовлетворяют уравне-
нию (35), где w — натуральное число, а и v и и —
взаимно простые.
Обратно, предположим, что натуральные числа и, v и w
удовлетворяют уравнению (35), причем и и w взаимно
простые и v>u. Из (35), учитывая, что v>u, имеем:
w2 = 2п4 — v4 <С 2г>4 — v4 = v4,
затем ^2<^z/4 и u<Zv2.
Числа
V2 + W	V2 — W
х ——и у = '
(36)
целые, положительные, так как из равенства V4 Ц-^2 = 2zz4
следует, что v и w оба четны или оба нечетны. Итак, х
и у— целые числа. Пусть d — их общий наибольший де-
литель. Тогда d л и d\y и, принимая во внимание (36),
имеем d\ v2 и d w, а из (35) заключаем, что d2\2u4. Но
числа и и v по предположению взаимно простые и, сле-
довательно, и2 и v2 взаимно простые, а так как d\v2,
числа d и и2 взаимно простые, то такими же являются
числа d2 и п4. Из того, что d212&4, следует, что d212
и б/ = 1, так как число 2 не делится ни на один квадрат,
больший единицы. Числа х и у взаимно простые.
Мы доказали, что если натуральные числа и, v и w
удовлетворяют уравнению (35), причем v>uu числа
и и v взаимно простые, то х и у, определенные ра-
венствами (36), взаимно простые и х, у, и, удовле-
творяют системе (26).
Сравнивая полученный результат с ранее найденным,
заключаем, что решение системы (26) в натуральных
числах х, у, и и v, где числа х и у взаимно простые,
сводится к решению уравнения (35) в натуральных чис-
лах и, v, w, где v и и числа и и v взаимно простые.
Итак, вместо системы двух уравнений с четырьмя
неизвестными имеем одно уравнение с тремя неизвестными.
12.6.	Найдем теперь все решения уравнения (35)
в натуральных числах и, v и w, где числа и и v яв-
ляются взаимно простыми (где необязательно v>u).
Одно из решений, очевидно, n = w = ^=l. Каждой си-
стеме решений уравнения (35) в натуральных числах и, v и w,
где числа и и <и взаимно простые и	поставим
в соответствие некоторую систему решений:
(и,, v„	V, W),
где иг и взаимно простые < и.
48
Предположим, что натуральные числа и, v и w удов-
летворяют уравнению (35) и и 1 и числа и и v взаимно
простые. Покажем, что uv^=w. В самом деле, предполо-
жим, что	тогда u2v2 = <w2 и, принимая во вни-
мание (35), получаем: 2п4 — v4 = u2v2 или и2 (2и2 — v2) = v4,
что дает u2\v4 и u\v\ Ввиду того, что (и, с/) = 1,
(п, г/2)—1; учитывая, что u\v\ заключаем, что
что противоречит сделанному выше предположению. Мы
доказали, что
В случае четности числа v на основании (35) число w
было бы также четно и число 2и4 = v4 -\-^2 делилось бы
на 4 и число и было бы четным, что противоречило бы
предположению о том, что числа и и v взаимно простые.
Таким образом, число <и нечетно, а на основании (35)
заключаем, что число также нечетно.
тт V2 4-W V2 — W	г-г
Числа —— и —---------натуральные. Покажем, что
второе число не равно нулю. Действительно, в случае
v2= w имели бы = и, учитывая (35), получили бы
2u4=2v4 и u = v, что противоречит предположению,
что числа uuv взаимно простые и и =^= 1. Число
V2 — W
натуральное число.
n	v2 4- w v2 — w
Легко также показать, что числа —А—• и —~— вза-
имно простые, так как их общий наибольший делитель d
является делителем чисел v2 и w. Принимая во внима-
ние равенство (35), получаем d21 2rz4, что вследствие не-
четности числа d (как делителя нечетного числа w) дает
d2\u4 и d\u2, так как d\v\ а числа и2 и V2 взаимно
простые (так как числа и и v взаимно простые), то d= 1,
что и требовалось доказать.
Заметим еще, что и число и является нечетным.
Вследствие нечетности с/ и w число v4 w2 при делении
на 4 дает в остатке 2, а 2и4 = v4 .
Равенство (35) можно преобразовать в следующее:
2
(37)
Натуральные числа
V2 — W
и и2, из которых пер-
вые два взаимно простые, определяют стороны основного
пифагорова треугольника (37). На основании теоремы 1
49
заключаем, что существуют целые взаимно простые
числа т и п, одно из ко торых четно и что
f	v2 A-w
I в зависимости от четности или нечетности числа —±—
Если V2 > w, находим в обоих случаях
v2 — т2 — п2 -]- 2/ия,
а если	получаем в первом случае
v2 = т2 — п2 — 2тп,
а во втором
— V2 = щ2 — п2 — 2тп.
В каждом из них имеем:
+ г2 = т2 — п2^2тп,
где при v2 и 2тп следует выбрать знак если v2
и знаки 4- и —. если v2 zv и число

нечетно, и
2	V2 4-W
знаки — и —, если	и число —— четно.
Равенство—v2 = m2— 2z/ztz, или v2 — n2 — т2^
^2тп, отличается от равенств z)2 — т2 — п2^-2тп
только тем, что и т и п поменялись местами (при этой
замене сохраняются свойства т и п\ они взаимно простые
и одно из них четно). Во всяком случае заключаем, что
существуют такие натуральные числа т и п взаимно
простые, из которых одно четно, что при знаке плюс
или минус при числе 2тп, получаем:
и2 = т2 -}- п\ v2 = m2 — п2 ± 2тп, (39)
причем, как показано, числа т и п и знак при 2тп
определяются числами и, v и w, удовлетворяющими
равенству (35).
Среди чисел тип, как известно, одно четно, другое
нечетно. Если бы число п было нечетным, то его квад-
рат п2 при делении на 4 давал бы в остатке 1, а так
как числа т2 и 2тп были бы тогда четными, то правая
50
часть второго равенства (39) давала бы при делении
на 4 остаток 3, что невозможно, так как правая часть
равна v2. Число п должно быть четным и, следовательно,
т является нечетным.
Учитывая, что числа т и п взаимно простые и
число п — четно, заключаем из первого равенства (39)
на основании теоремы 1 о существовании взаимно про-
стых чисел г и s таких, что
т = г2— s2, fl = 2rs, u = r2-|-s2.	(40)
(Одно из чисел г и s четно.)
Вторую формулу (39) можно
переписать в виде
2т72 = (ш 4- п)2 — т/2,
что дает
(т ± п — v) (т ± п -J-	— 2/z2,	(41)
где одновременно следует взять либо верхние, либо ниж-
ние знаки.
Так как числа т-А^п и v являются нечетными, то
тЛ-п— v = 2k. m-\-n-4-v = 2l,
		Л	... I	ж
где k и I — целые числа. Отсюда <v = l — k и l^>k.
Покажем, что числа k и I — взаимно простые.
Пусть k и / имеют общий делитель d > 1, тогда
d\m±^n и d\v, откуда на основании (41) d2 было дели-
телем 2я2, т. е. d212п2, что в связи с нечетностью d
(как делителя числа v) дает d2\n2 и d\n. Так как
d\m±n и d\m, что противоречит предположению, что
числа тип взаимно простые. Следовательно, k и I—
взаимно простые.
Из определения чисел k и I и из равенства (41) сле-
дует, что 2kl — n\ затем, учитывая равенство (40), полу-
чаем kl — 2r2 s2, что говорит о четности одного и нечет-
ности другого числа из чисел k и / (числа k и / — вза-
имно простые).
Если k четно, то числа 2k и / взаимно простые, а
так как их произведение — квадрат (числа п), то, следо-
вательно, каждое из них — квадрат. Итак, существуют
натуральные числа а и Ь, такие, что (2k) = (2a)2 и 1 = Ь\
откуда v = l — k = b2 — 2а2. Если число Z четно, то, как
было показано, существуют натуральные числа а и bf
51
такие, что 2Z = (2zz)2 и k = b2, откуда v = l — k = 2az— bz.
Во всяком случае получаем
v = | ‘2а2 — b2\t т± п = k-[-l = 2а2 Ц- Ь2
и п2 = 2AZ = (2аЬ)2, откуда n = 2ab, и, учитывая (40),
получаем:
ab = rs.	(42)
Обозначим через g общий наибольший делитель чисел
г и Ь. Существуют взаимно простые числа и ф19 та-
кие, что r = gut и b = gvi, откуда, учитывая (42), полу-
чаем:
av1 = sux,
а так как числа и взаимно простые, то Фг | s.
Итак, существует такое натуральное число А, что 5 = //^,
но так как avr= su11 находим a — hux. Так как числа г
и s взаимно простые и r = gux, 8 = 1^, то числа g
и h — взаимно простые.
На основании равенства (40), и т —	и полу-
ченных ранее m±n = 2az -\-b2, n = 2ab находим
г2 — sz = 2а2 + А2 + 2аЬ.	(43)
Подставляя в равенство (43) следующие значения:
r =	s = A^, a = hul9 b = gvv, (44)
получаем:
g2zz2 — hzvl = 2h2uz1-\-g2tvl +
что дает
(2zz2 + vi) h2 =F	(v2 — u^g2 = 0.
(45)
Умножая обе части равенства на 2zz24~^t получаем:
= [(«Л)2 — (2«2 + ^2) W — «М g* =	g\
(46)
Отсюда следует, что натуральное число 2^ — отлич-
ное от нуля (так как число является иррациональ-
ным), является квадратом целого рационального числа
1, которое также является квадратом
целого числа Имеем:
2^ —^ = w2,	(47)
52
где au 1?! и Wj — натуральные числа, причем иц—
взаимно простые. Учитывая равенства (40) и (41), полу-
чаем:
и == г2 4- s2 = g2u2 Л2^2 > а2 и а2 а.
Мы получили из определенной системы решений (u, zi, w)
уравнения (35) новую систему решений (uif v19 wt) =
=f(u,v,zv) того же уравнения в натуральных числах
ul9 vx и wr, где и2<^и.
Заметим, что из равенств (46) и (47) следует равенство
Откуда
(2zz24" ^i) ±	= dz
h_____z±z
2zz* + 4 ’
(48)
(49)
принимая во внимание, что числа Ли g взаимно простые,
мы видим из равенства (49), что несократимая дробь —
£
равна рациональному числу
I ± I
2zz2 + 4
при определенном знаке в числителе дроби.
Каждой системе решений уравнения (35) в целых чис-
лах и, v, zv, где и и v — взаимно простые и и 4= 1, мы
приводим в однозначное соответствие некоторую новую
систему решений
уравнения (36) в натуральных числах ul9 v19 zvi9 где
и vr взаимно простые и и\<^и. Если	то системе
решений (zz1? v19 zvx) соответствует новая система решений
(и2, v2, W2)=f(ult wt) =ff(u, V, w),
где числа zz2 и v2 взаимно простые и и2 Если и2 1,
то получаем новую систему решений:
(«„ V,,	И т. д.
Так как ряд уменьшающихся целых чисел и >	> и2...
не может быть бесконечным, то при некотором целом п
мы придем к системе решений (ип, vn9 zvn\ где ип=1,
а следовательно, и vn — zs)n = 1. Для каждой системы
решений уравнения (35) в натуральных числах «, w,
53
где и и я) — числа взаимно простые и и 1, существует
определенное натуральное число п, зависящее от и, v, w,
такое, что
/n(u,v,w) = (l, 1, 1).
12.7.	Обозначим для данного натурального числа п
через Zn совокупность всех решений уравнения (35) в
натуральных числах и, v и w, где числа и и я) взаимно
простые и и=^\, для которых /"(и, я), w) = (l, 1, 1).
Каждое решение уравнения (35) в натуральных числах
и, v, w, где числа и и я> взаимно простые и 1, при-
надлежит к некоторой и только одной из групп Zn, где
п является натуральным числом.
Пусть (zz0, ^0,^0)— решение уравнения (35) в натураль-
ных числах, где числа uQ, wQ взаимно простые и uQ =^= 1, и пред-
положим, что для некоторого натурального числа k решение
это не принадлежит ни одной группе решений Zt, Z2,..., Zk.
Следовательно, оно должно принадлежать группе решений
Z„, где п — натуральное число, большее k.
Примем (и', v', ew')—fn~k(uQ, vQi ^0). Так как реше-
ние (п0, ^0, те>0) принадлежит группе решений Z„, то
/"(«о, ^<»®o) = (l, 1. 1) или/Уп-*(н0,®0,^0) = (1, 1, 1),
что дает f\ur, v’, ям') = (h 1, 1) и доказывает, что ре-
шение (и', v', w') принадлежит группе Zk. Из того, что
(и', v'y w')=fn-k(u0, v0,w0), следует, что («')2<п0.
Если (п0, г>0, w0) является решением (35) в натураль-
ных числах, где числа vQ взаимно простые и
и не принадлежит ни одной из групп Z1? Z2,..Zk, то
число uQ больше квадрата наименьшего среди чисел и,
для которого существует решение (и, v, w) уравнения
(35), принадлежащего группе Zk.
12.8.	Предположим, что нам известно решение урав-
нения (35) в натуральных числах и19 я\ и такое, что
числа и я\ взаимно простые. Поставим следующий
вопрос: существует ли решение уравнения (35) в нату-
ральных числах м, я) и w, где числа и и v взаимно про-
стые и и=^= 1, f(u9 v, w) = (n1, vl9 wj и как его найти?
Предположим, что (п, v9 w) такое решение.
Из приведенных выше рассуждений на основании опре-
деления преобразования/следует, что, определяя для u9v9 я&)
последовательно числа т, п9 r9 s, af b, h ng, придем к ра-
венству (49) для несократимой дроби ~.
54
Так как в формуле (49) имеем знаки ЧН, то, вообще
говоря, имеем две возможности для определения чисел
h и g, за исключением того случая, когда w1 = uxvli что
будет только при их — wx = 1. В этом случае равен-
ство (49) имеет вид:
h uxvx 4"
(так как должно быть положительным числом).
Во всяком случае целые числа Ли g будут определены
одним или двумя способами.
Из равенства (49) получаем равенство (48) и, учитывая
(47), получаем:
[(2м. + h ±	= w2g2 = (2uJ — v*) g\
т. е. равенство (46), из которого легко получаем (45).
Затем определяем числа г, s, а и b из равенства (44) и
получаем равенства (45) и (43).
Так как из равенства (44) следует, что ab = rs, то
равенство (43) дает
г2 — s2 ± 2rs = 2а2 + Ь2.	(50)
Принимаем v = | 2а2 — Ь21.
v — целое число (вследствие иррациональности У~2;
2а2 ^Ь2) и v2 — (2a2— b2}2, откуда на основании (50) и
равенства ab — rs получаем:
(г2 — s2 + 2rs)2 — v2 = 8a2b2 = 8r2s2,
или
v2 = (г2 — s2 + 2rs)2 — 8r2s2,	(51)
где следует брать верхний знак, если в равенстве (49)
выбран верхний знак, и нижний, если в равенстве (49)
выбран нижний знак.
Легко проверить тождество
2 (г2 4“ s2)4 = [(г2 — s2 + 2rs)2 — 8r2s2]2 +
+ [(f2 — s2 — 2rs)2 — 8r2s2]2.
Полагая u = r2-\-s2, w = |(r2 — s2 + 2rs)2 — 8r2s2|
(где знак при 2rs берется верхний, если в (51) взят верх-
ний знак, и нижний знак, если в (51) взят нижний), полу-
чаем, учитывая (51), уравнение (35), причем на основании
(44) имеем:
и = г2 -f- s2 = g2u2	h2v2 >» zz2.
55
Покажем, что найденные нами числа и и v — взаимно
простые.
Для доказательства заметим, что числа и — вза-
имно простые и удовлетворяют уравнению (47), отсюда
следует, что и — взаимно простые.
Если у них есть общий делитель S, то S|wn
откуда, на основании того что = — w2, следует
8|
Так как и учитывая, что 8 | и19 а числа и* и
взаимно простые (числа и vr взаимно простые), то
S=1 и числа иг и взаимно простые.
Пусть d — наибольший делитель чисел их и h. На ос-
новании (49) получаем h(2u\-\~v2) = g	I и так
как d\ur и d| Л, найдем отсюда d|g<wx и, принимая во
внимание, что d\h и g и h—взаимно простые числа, за-
ключаем, что числа d и g взаимно простые. Из того, что
й| gw 1, следует, что d\ew^ так как d\u19 а числа и Wj
взаимно простые, то d= 1 и числа и h взаимно про-
стые.
Пусть dx •— наибольший общий делитель чисел и g.
Также докажем, что dx 2hu2v Так как dx\g и числа g
и h взаимно простые, то и h взаимно простые. Так
как dx как делитель нечетного числа — число нечетное
и dx I 21ш\, заключаем, что dx | и2. Учитывая, что <72|^2 и
что числа v2 — взаимно простые, имеем dx = 1 и чис-
ла и g взаимно простые.
На основании (44) имеем: r — gux и s — hvr9 причем
доказано, что каждый из двух множителей числа г и
каждый из двух множителей числа s взаимно простые.
Отсюда следует, что числа г и s взаимно простые.
Из (47) и из того, что ил и взаимно простые, сле-
дует, что дг, v1 и wt — числа нечетные. Число w1-±=u1v1
0 2 12	л	/г	I w, rt	I
четно, а число 2и2 4- v2 нечетно. А так как — == ।,
1,1	S +	’
где h и g взаимно простые, заключаем, что h четно, а
g нечетно.
Так как s = hv19 то s четно, а число г (взаимно про-
стое с $) нечетно.
Обозначим через общий наибольший делитель чисел
г2-|-$2 и г. Получим | г2 —s2 и | г и тем более Sjr2,
а потому Sj | (г2 + s2) — г2 или Sjs2.
Учитывая, что числа г2 и s2 взаимно простые (г и s
взаимно простые), заключаем, что 81 = 1, т. е. числа
56
г2 Ц- s2 и г взаимно простые. Аналогично доказывается,
что числа г2 —s2 и s взаимно простые.
Принимая во внимание, что число г2 s2 нечетно
(г — нечетно, a s— четно) и по доказанному г и s— вза-
имно простые числа, то r2-\-sz и 2rs тоже взаимно про-
стые.
Из формулы (r2-]-s2) — (г ± s)2 = -F 2rs заключаем,
что числа г2 + s2 и г 4z s взаимно простые. Взаимно про-
стыми являются числа r2-[-sz и 2s(r4:s). Так как
г2 + 2rs — s2 = г2 -ф- s2 4z2s (г 4- s),
то число г2 s2 (иначе и) и число г2 4т 2rs — s2 являют-
ся взаимно простыми, такими же будут числа r2-|-s2 и
4rs и числа г2Ц-52 и 4rs(r24z2rs— s2). Из равенства (51)
г/2 — и2 = 4:4rs (г2 412rs — s2)
заключаем, что и и V2 — и2 взаимно простые, а отсюда
следует, что и и v взаимно простые, что и требовалось
доказать.
12.9.	Легко проверить, что если натуральные числа
ul9 и удовлетворяют уравнению (47) и если nv1
взаимно простые, то можно определить вышеуказанным
методом числа и, v и w, такие, что
/(«, V, w) = (ult ч>„ wt).
Этот метод позволяет найти все решения уравнения
(35) в натуральных числах и, v и w, где числа и и v
взаимно простые и
/(и, V, w)=(ut, v„ wt).
Это дает возможность найти все решения, принадлежа-
щие группе Zn+l, если известны решения, принадлежащие
группе Z„.
12.10.	Из вышеприведенного доказательства заклю-
чаем, что для каждого решения (и19 vl9 wj уравнения (47)
в натуральных числах, где и — взаимно простые
числа, существует не менее одного и не более двух ре-
шений в натуральных числах и9 v и w9 где числа и и
<и взаимно простые и f(u9 v9 w) = (ttn vlf wj. Отсюда
следует, что существуют решения уравнения (35) в чис-
лах и, v и w, где и и v взаимно простые и где и явля-
ется произвольно большим числом.
57
12.11.	Предположим, что —	= В равенст-
ве (49) выбираем только верхний знак и получаем — =-|-,
а так как ~ — несократимая дробь, то h = 2, g=3 и на
g
основании равенств (44) имеем: г — 3, s = 2, а =2, Ь = 3,
затем
w = З2 4- 22 = 13.
В (51) выбираем верхний знак, так как такой знак
выбран в (49), и получаем:
2 — 22 —
Имеем, следовательно, единственное решение уравне-
ния (35), принадлежащее к группе решений Z19 т. е.
2*134— 14 = 2392. Мы получили u=\3^>\—v.
12.12.	Примем ^ = 13, v1—l9 '^1 = 239, так как
u1v1<^w19 то и (49) принимает вид:
h _ 239+ 13
g 339	’
либо при нижнем знаке, либо —=
у, то, учитывая, что h и g взаимно про-
h  226  2
где g	339	3 ’
252	84
=—=— при верхнем знаке.
h
Если —
g
стые, получаем h — 2 и^=3и на основании (44) полу-
чаем г = 39, $ = 2, я = 26, й = 3, затем
а так как в (51) следует выбрать нижний знак, то
г/2 = 13612 — 48672 =1803649 = 13432 и т/= 1343,
w = 16732 — 48672 = 2750257.
Опять получаем u>v.
Если = то /г = 84, §*=113, r=1469, $ = 84,
<7=1092, b= 113, и= 14692 + 842 = 2165017, атак как
в данном случае в (51) следует взять верхний знак, то
^ = 23976972 — 2-2467922 = 23721592 и ^ = 2372159,
w = 19041132 — 2 • 2467Э22 = 3503833734241.
58
В данном случае v^>u.
2 |	2
X =	= 4565486027761, у = v-^- =1061652293520,
z = и2 = 4687298610289 являются сторонами пифагорова
треугольника, сумма катетов которого и гипотенуза —
квадраты. Этот треугольник и был найден Ферма.
Мы нашли два решения уравнения (35), принадлежа-
щие к группе решений Z2, и убеждаемся, что все реше-
ния принадлежат этой группе. Отсюда следует, что в
каждом решении (35) в натуральных числах и, v, w, где
и и *и взаимно простые числа и и 1, не принадлежа-
щие группе и Z2, числа и^> 15252>>225-104, т. е.
больше, чем найденное число и ==2165017, полученное
Ферма. Следовательно, треугольник, найденный Ферма,
имеет наименьшую гипотенузу из всех пифагоровых тре-
угольников, у которых гипотенуза и сумма катетов —
квадраты.
§ 13.	ОПРЕДЕЛЕНИЕ ПИФАГОРОВЫХ ТРЕУГОЛЬНИКОВ
ПРИ ПОМОЩИ ТОЧЕК ПЛОСКОСТИ
13.1.	Пусть (а, Ь, с) — основной пифагоров треуголь-
ник. Установим соответствие между этим треугольником
и точкой плоскости с абсциссой х = — и ординатой — .
с	с
так как а2-{-Ь2 = с2. Точки с координатами (х, у) лежат
на окружности единичного радиуса. Каждому основному
пифагорову треугольнику соответствует точка окружно-
сти х2 ~}~у2 = 1 с рациональными положительными коор-
динатами или так называемая рациональная точка этой
окружности. Обратно, если (х, у) — точка окружности
х2 ±у2 == 1 с рациональными положительными координа-
тами, т. е. если х и у являются положительными раци-
ональными числами, удовлетворяющими уравнению х2 -р
-у2 = 1, то после приведениях и у к общему наимень-
а	Ь
шему знаменателю получим х=— и у== — и установим
соответствие между выбранной точкой и пифагоровым
треугольником (а,	с).
59
Итак, можно установить однозначное соответствие
между пифагоровыми треугольниками и рациональными
точками окружности, находящимися над осью абсцисс и
справа от оси ординат.
Возьмем два произвольных натуральных числа хг и х2,
таких, что 0 < хг <tx2 < 1.
Покажем, что существует основной пифагоров тре-
угольник (а, Ь, с), которому на окружности соответству-
ет точка (x, j?), где х1<^х<^х2.
Действительно, так как	1, то
откуда
Существует такое рациональное число ™ , которое за-
ключено между рассматриваемыми корнями, можно пред-
положить, что тип являются взаимно простыми, причем
т нечетно, а п четно и получим:
Так как
то получим:
И, принимая а = т2— п\ b = 2mn, с — т2-|-«2, получа-
ем (на основании теоремы 1) основной пифагоров треуголь-
ник, причем

х2.
Этому треугольнику соответствует на окружности на-
шего круга точка (л, j), где х =	причем л, <
<^х<л2, что и требовалось доказать.
Отсюда следует, что если на дуге окружности х2 -ф-у2—
— 1, лежащей между точками пересечения окружности
60
с положительными осями координат (на дуге, лежащей в
первой четверти), возьмем две различные точки, то меж-
ду ними имеется точка, которой соответствует некоторый
основной пифагоров треугольник.
Приходим еще к следующему заключению: для про-
извольного угла а, где 0°^а^90°, существует прямо-
угольный треугольник с рациональными сторонами и с
острым углом, сколь угодно близким к углу а. Увеличи-
вая стороны этого треугольника в соответствующее чис-
ло раз, получим пифагоров треугольник. Итак, для каж-
дого прямоугольного треугольника существует пифагоров
треугольник, углы которого сколь угодно мало отличают-
ся от углов треугольника Т.
В частном случае существуют пифагоровы треуголь-
ники, у которых острые углы сколь угодно мало отли-
чаются от угла в 45°. Понятно, что нет пифагоровых
треугольников с острыми углами, равными 45°, так как
в этом случае треугольник был бы равнобедренным и
гипотенуза была бы несоизмерима с катетом. К углу в
45° стремятся острые углы пифагоровых треугольников,
катеты которых выражаются последовательными натураль-
ными числами, и если катеты этих треугольников беско-
нечно возрастают (такие треугольники мы рассматривали
в § 4).
13.2.	Существует и другой способ определения (всех)
пифагоровых треугольников при помощи точек плоскости
с целыми координатами (так называемых решетчатых то-
чек). Пифагорову треугольнику (а, Ь, с) поставим в соот-
ветствие точку плоскости с абсциссой а и ординатой Ь,
Каждому пифагорову треугольнику соответствует опре-
деленная точка плоскости с натуральными координатами
и разным треугольникам соответствуют разные точки.
Обратное заключение неправильно, не каждой точке пло-
скости с натуральными координатами соответствует пи-
фагоров треугольник. Например, точкам (1, 1), (1, 2),
(2, 3) не соответствует пифагоров треугольник. Только
таким точкам (а, Ь) соответствует пифагоров треугольник,
для которых а2 Ь2 является квадратом целого числа.
Легко доказать, подобным пифагоровым треугольни-
кам соответствуют точки плоскости, лежащие на прямой,
проходящей через начало координат и через точку, соот-
ветствующую одному из треугольников.
61
§ 14.	ПРЯМОУГОЛЬНЫЕ ТРЕУГОЛЬНИКИ, СТОРОНЫ КОТОРЫХ
ВЫРАЖАЮТСЯ ЧИСЛАМИ, ОБРАТНЫМИ НАТУРАЛЬНЫМ
ЧИСЛАМ
натуральные числа %, j/, z, такие, что Т=
14.1.	Поставим следующий вопрос: существуют ли
прямоугольные треугольники, стороны которых выража-
ются числами, обратными натуральным числам, и если
они существуют, то как найти все такие треугольники.
Предположим, что Т — такой треугольник. Существуют
J_
X
а так как треугольник Т прямоугольный, то
(52)
Наша задача сводится к решению уравнения (52) в на-
туральных числах. Предположим, что натуральные числа
х, У, z удовлетворяют уравнению (52). Тогда имеем
z“2>x“2 и z2<x2, x">z.
Из уравнения (52) имеем:
(53)
Пусть d—общий наибольший делитель чисел х и z,
тогда существуют взаимно простые числа а и с, такие,
что x = da, z = dc.
Учитывая уравнение (53), имеем:
у2 (а2 — с2) = (dac)2.
(54).
Из (54) заключаем у21 (dac)2 или у | dac и, соответ-
ственно, существует такое целое число Ь, что dac—yb.
Подставляя значение dac в правую часть (54), получаем:
а2 — с2 = Ь2.
Так как числа а и с взаимно простые, то из (55) заклю-
чаем, что числа b и с также взаимно простые. Из (55)
имеем:
№ -Д-с* — а2,
(56)
получаем, что треугольник (fe, с, а} — основной пифагоров
треугольник.
62
На основании теоремы 1 заключаем, что существуют
целые взаимно простые числа т и п, из которых одно
четно, такие, что т^>п и
Ь = т2— п2; с = 2тп; а — т2-\~п2
либо	> (57)
Ь = 2тп; с = т2— п2\ а — т2-\~п2 J
Нам известно, что числа b и с взаимно простые.
Из (56) следует, что b и а взаимно простые, число
будучи взаимно простым с числом а и взаимно простым
с числом с, должно быть взаимно простым с числом ас.
Ранее найденное равенство dac =yb говорит о делимости
числа d на число Ь. Следовательно, существует такое
натуральное число 8, что d = bh.
Получаем x = da — ёаЬ; у = оас (так как yb = dac),
z = dc — ёЬс.
Затем на основании (57) получаем:
х (т2 4- я2) (пг2 — п2) 8,
у = 2тп (т2 -f- п2) 8,
z — 2тп (т2 — п2) S
либо
х — 2тп (т2 4~ п2)
у = (тг 4- п2) (т2 — п2) 8,
z = 2тп (т2 — п2) ё.
С другой стороны, легко проверить, что если мы
определим х, у, z из написанных равенств при произволь-
ных натуральных т, п,ё и п<т и определим Ь, г, а из
равенств (57), то х — ёаЬ, у = ёас, z — ёЬс. Полученные
значения х, у, z удовлетворяют уравнениям (56) и (53),
а следовательно, и (52).
Мы пришли к выводу, что все решения уравнения (52)
в натуральных числах (и только такие решения) по-
лучаем из равенств:
х = (т4 — я4) 8, у = 2тп (т24~ я2) 8,
z = 2тп (т2 — п2) 8	(58)
либо
х — 2тп (т2 4“ ^2) S, У = (т* — п^) 8,
z = 2тп (т2 — п2)ё.
[32]
63
Причем 8 — произвольное натуральное число, а т и п
взаимно простые числа, из которых одно четно и т > п. [32]
14.2.	Легко заметить, что, таким образом, каждое ре-
шение уравнения (52) в натуральных числах получается
только один раз, так как дробь — несократима и равна
С
дроби — , таким образом, числа а и с определены, если из-
вестны х и z. Из равенства (55) определяется число b и числа
т, п и число 5 = Д .
Для т = 2, п=1, 5=1 получаем х — 15, у = 20,
z= 12, что дает решение уравнения (52) в наименьших
целых числах:
Для т = 3, я= 1,5=1 получаем х = 80, у/ = 60, г = 48
(числа в четыре раза больше предыдущих).
Для т = 3, и = 2, 5=1 получаем л = 65, у = 156,
г = 60, откуда
14.3.	Из приведенных равенств (58) следует, что из
решения уравнения (52) каждая пара из тройки чисел
х, у, z не является взаимно простым числом.
14.4.	Заметим, что нет прямоугольного треугольника,
стороны которого были бы обратны квадратам натураль-
ных чисел.
(1 1 1 \
^2 , Ji , ^2 J бЫЛ
таким треугольником, то
£ । _1— 1
х4 ' у4 z*’
откуда (yz)4 4"	— (ЛУ)4> что противоречит теореме 4
(§ 10.4).
§ 15.	ПАРАЛЛЕЛЕПИПЕДЫ, РЕБРА И ДИАГОНАЛИ КОТОРЫХ
ВЫРАЖАЮТСЯ НАТУРАЛЬНЫМИ ЧИСЛАМИ
15.1.	Из каждого пифагорового треугольника можно
получить прямоугольник, стороны и диагонали которого
выражаются натуральными числами, и обратно.
64
При переходе в трехмерное пространство следует от-
ветить на такой вопрос: как найти прямоугольные парал-
лелепипеды, стороны и диагонали которых — натуральные
числа.
Если л, у и z— ребра параллелепипеда, t — его диа-
гональ, то, как известно из элементарной геометрии,
л2-[-у2 -j-z2 = t\	(59)
Обратно, если х, у, z и t удовлетворяют уравнению (59),
то числа x,y,z являются ребрами, a t диагональю пря-
моугольного параллелепипеда.
Отыскание всех прямоугольных параллелепипедов, ребра
и диагонали которых выражаются целыми числами, сво-
дится к решению в целых числах уравнения (59).
15.2.	Предположим, что натуральные числа л, у, z и t
являются решениями уравнения (59). Покажем, что хотя бы
два из чисел л, у, z должны быть четными. Если бы все
три рассматриваемых числа были нечетны, то квадрат
каждого из них при делении на 4 давал бы в остатке
единицу и левая часть уравнения (59) давала бы в ос-
татке три, что невозможно, так как правая часть равен-
ства (59) — квадрат. Если бы только одно из рассматри-
ваемых чисел было четным, то левая часть уравнения (59)
при делении на четыре давала в остатке два, что невоз-
можно, так как правая часть равенства (59) — квадрат.
15.3.	Легко показать, что хотя бы одно из чисел х, у, z
и t делится на три.
Предположим, что ни одно из чисел х, у, z не кратно
трем, докажем, что в этом случае t делится на 3. В самом
деле, квадрат натурального числа, не кратного трем, при
делении на 3 дает остаток, равный единице (§ 5.1). Если
бы ни одно из чисел л, yf z не делилось на 3, то сумма
их квадратов, т. е. число делилось бы на 3 и, следо-
вательно, t было бы кратно трем.
15.4.	Можно доказать, что для каждого натурального
числа х существует бесконечное число троек чисел у, z, t,
удовлетворяющих уравнению (59). Легко проверить (59),
что при всяком натуральном п нечетное число х и у — 2я,
z = х 2/z2 и t = х ~1 2лг2 —[— 1 удовлетворяют урав-
нению (59) и что %, у, z, t — натуральные числа.
3 Заказ № 2446
65
При всяком натуральном п четное число х и у = 2/г -f-1,
z == у 4- 2№ 2л и t = ~ 2я2 4~ 2/z 4~ 1
удовлетворяют уравнению (59) и л, у, z,t — натуральные
числа.
15.5.	Легко доказать, что для всякой пары четных чи-
сел х и у существуют целые z и t, удовлетворяющие
уравнению (59). Если каждое из чисел х и у четно, то
число %24~J2 делится на 4, поэтому числа z — —— 1
и t — —4~ 1 натуральные, удовлетворяющие уравне-
нию (59).
15.6.	Легко доказать, что если одно из чисел х или у
четно, а другое нечетно, то существуют натуральные
числа z и t9 удовлетворяющие уравнению (59). Действи-
2 12 11	х2 4- у2 — I
тельно, число х 4“-У ±1 четно и числа х, у, z——-----
удовлетворяют уравнению (59).
15.7.	Итак, если принять за число, выражающее ребра,
х и у два произвольных числа, с тем условием, чтобы оба
не были нечетными, то можно найти два таких натураль-
ных числа z и t, выражающих соответственно третье ребро
и диагональ прямоугольного параллелепипеда.
15.8.	Покажем, что не существует параллелепипеда
с диагональю, выражаемой натуральным числом и ребра
которого выражались бы тремя последовательными чис-
лами.
Предположим, что ребра параллелепипеда выража-
ются тремя последовательными натуральными числами
у — 1, у, j4~1> а диагональ — целым числом t.
Тогда имеем:
(у _1)* +У4-0 4-1)2 = , или 3/4~2 = ^2.
При нечетном у, у2 при делении на 8 дало бы в остатке
единицу, а сумма Зу24~2 дала бы в остатке 5. Число,
дающее при делении на 8 остаток 5, не может быть точ-
ным квадратом.
При четном у сумма Зу/2 4~ 2 при делении на 4 дала бы
в остатке двойку. Такое число также не может быть
квадратом.
66
15.9.	Можно показать, что диагональ параллелепи-
педа, ребра которого выражаются натуральными числами,
не может быть ни одним из чисел 2\ ни 2^-5, где k равно
О, 1, 2,...
В самом деле, предположим, что существуют такие
целые неотрицательные А, что при t — 2k уравнение (59)
имеет решение в натуральных числах. Среди чисел k су-
ществует наименьшее число т, причем т>>0. Сумма
л2 +у2 + ?2 в уравнении (59) для целых %, у, z должна
быть не меньше трех.
Учитывая, что х2-\-у2-[-z2— 22т и что по крайней
мере два из чисел л, у, z четны, заключаем о четности
третьего числа. Итак, существуют целые числа yl9 zr
такие, что х — 2хх ,у — 2y1,z = 2z1. Откуда
^+Х + ^ = (2т"1)%
что противоречит сделанному нами предположению.
Следовательно, t не может быть равно ни одному из
чисел 1, 2, 22, 23,...
Предположим, что существует такое целое неотрица-
тельное k и что £ = 2*-5. Пусть уравнение (59) решается
в натуральных числах. Обозначим снова через т наимень-
шее среди чисел А. Если бы т — 0, то при некоторых
целых х, у, z мы имели бы
х2 ^у2 ~{-z2==52.
Покажем, что это равенство невозможно при це-
лых х, у, z, t.
Действительно, как нам известно, одно из чисел х,у,
z, t делится на 3. В данном случае t = 5 не делится на 3,
следовательно, одно из чисел х, у, z делится на 3. Пусть
х — кратно 3. Ввиду того, что л2<52, следует, что
х = 3 и у2-[~г2=:52 — 32 = 42. Последнее равенство не-
возможно, так как не существует пифагорова треугольника
с гипотенузой, равной 4,
Итак,
Из уравнения (59)
У2
следует, что если из чисел х, у, z хотя бы два четны, то
вследствие четности правой части уравнения четно и тре-
тье число. При четности чисел х, у, z имеем
x = 2xt, y = 2ylt z — 2zlt
где xl9 у19 zt являются натуральными числами.
3*
67
Числа xlfylf zr удовлетворяют уравнению л2 4”Х + z\—
— (2m-1 -5)2, что противоречит предположению, что т —
наименьшее число, при котором удовлетворяется уравне-
ние л2+>2 + г2 = (2ш.5)2.
Итак, число t не может быть ни одним из чисел
5, 2-5, 22-5,...
15.10.	А. Гурвиц доказал, что числа 2^ и 2^-5, где
А = 0, 1, 2, 3,... —единственные натуральные числа, ко-
торые не могут выражать длину диагонали параллелепи-
педа, у которого ребра выражаются целыми числами.
Среди чисел, меньших 100, следующие числа не могут
выражать длину диагонали параллелепипеда 1, 2, 4, 5, 8,
10, 16, 20, 32, 40, 64, 80.
15.11.	Попытаемся теперь отыскать все параллелепи-
педы, ребра которых и диагональ выражаются натураль-
ными числами. Для этого следует найти все решения
уравнения (59) в натуральных числах. Предположим, что
натуральные числа л, у, z, t удовлетворяют уравнению (59).
Как известно, из чисел л, у, z хотя бы два четны, пусть
у и z четны, т. е.
у — 21, z—2m (60),
где I и т— натуральные числа.
Из уравнения (59) заключаем х2 <Ч2 и t^>x. Число
u = t — х	(61)
натуральное. На основании (59), (60), (61) получаем:
(х + и)2 = х2 Д- 4/2	4т2,
после упрощения имеем 2хи-\~и2 = 412-\-4т2,
и2 = 412	4т2 — 2хи.	(62)
Из уравнения (62), где правая часть есть алгебраическая
сумма четных чисел, следует, что и — четное число.
и = 2/г.	(63).
Подставляя значение и в правую часть уравнения (62)
и сокращая на 4, получаем:
п2 = I2 т2 — хп, откуда I2 т2 = п (п л). (64)
Из последнего равенства следует, что п есть делитель
суммы 12-\~т2’, п 112 —//г2.
Из уравнения (64) имеем
68
Принимая во внимание уравнение (61) и (63), получаем:
п
Так как х — целое число, то из равенства (65) заклю-
чаем, что
zz2 <; Z2 —zzz2.
Итак, мы доказали, что если л, у, z, t—решения урав-
нения (59) в натуральных числах, то существуют це-
лые числа т, п и I, такие, что п является делителем
12-\-т2 и n<zVl2-\-m2, тогда
15.12.	Справедлива и обратная теорема, если нату-
ральные числа I, т.п таковы, что п— делитель числа
I2 -\-т2 и п <Zl- , то х.у. z. t, определяемые из ра-
венств (66), являются решениями уравнения (59) в на-
туральных числах.
Из равенств (66) и из требования, наложенного на
число п. следует, что х, у, z. t — числа натуральные.
Из тождества

следует, что натуральные числа х. у, z, t — решения урав-
нения (59).
15.13.	Кроме того, легко доказать, что каждое из ре-
шений уравнения (59) в натуральных числах, где у и z —
четны, получается из равенств (66) только один раз. Числа
/, т. п однозначно определяются числами х, у, z, t, так
как имеем:
1 у	Z t— X
т =	п=—к- .
Итак, доказана следующая теорема:
Теорема 5. Все решения х.у. z.t уравнения
х2 -\-у2 -\-z2 — t2
в натуральных числах, где у и z четны, получаются
из формул (66), причем за I и т следует взять все
пары чисел, а за п все делители суммы 12-\-т\ при-
чем n^Vl2-\-т2.
69
Каждое решение таким способом получится только
один раз.
Эта теорема дает метод последовательного получения
решений уравнения (59) в целых числах.
15.14.	Легко заметить, что если мы не различаем ре-
шения, отличающиеся одно от другого тем, что у и z
меняются местами, то всегда можно считать m ^ /, а п
выбирать так, чтобы х было нечетным. Таким образом,
мы не получим четных решений для всех неизвестных.
Четные решения уравнения (59) получим из решений, где
х нечетно, умножая их на последовательные степени
числа 2.	[34]
Приведем в виде примера десять первых решений
уравнения (59), найденных этим методом
1	т	I2 -[-т2	п	%	У	Z	t
1	1	2	1	1	2	2	3
2	2	8	1	7	4	4	9
3	1	10	j 1	9	6	2	11
			1 2	3	6	2	7
3	3	18	( 1	17	6	6	19
			J 2	7	6	6	11
			1з	3	6	6	9
4	2	20	Г 1	19	8	4	21
			14	1	8	4	9
4	4	32	1	31	8	8	33
15.15.	Существуют параллелепипеды, все ребра кото-
рых — точный квадрат, а диагональ выражается натураль-
ным числом, например параллелепипед с ребром 122, 152,
202 и с диагональю, равной 481.
Вообще легко показать, что если (а, Ь, с) является
пифагоровым треугольником, то параллелепипед с реб-
рами (ab)2, (ас)2, (be)2 имеет диагональ, равную с4— а2Ь2.
Из треугольника (3, 4, 5) получим, таким образом, при-
веденный параллелепипед.	[35], [36]
15.16.	Эйлер высказал предположение, что не сущест-
вует параллелепипедов, у которых одновременно каждое
ребро и диагональ были бы квадратами целых чисел.
70
М. Вард доказал (1945), что нет таких параллелепипе-
дов среди тех, у которых диагонали 108.	[37]
15.17.	Из пифагоровых треугольников возможно полу-
чить параллелепипеды, у которых все ребра и диагонали
боковых граней выражаются целыми числами.
В самом деле, пусть (а, Ь, с)— пифагоров треугольник
и пусть
л = я(4Ь2 — с2), у = Ь(4а2— с2), z
4abc.
Отсюда, так как а2-[-Ь2 = с2, имеем:
х2-\-у2 = с\ х2 + z2 = а2 (4Ь2	с2)2,
(67)
[38]
Из этих равенств видно, что каждая из диагоналей боко-
вых граней выражается целым числом.
Исходя из пифагорова треугольника (3, 4, 5), получим,
таким образом, параллелепипед с ребрами 117,44 и 240,
найденный Р. Галькего (1719).
Приведем еще некоторые параллелепипеды такого
вида:
X	У	Z
252	240	275
85	132	720
693	140	480
195	748	6336
429	880	2340
15.18.	Легко доказать, что если в параллелепипеде
все ребра и диагонали боковых граней выражаются
натуральными числами, то хотя бы два из этих чи-
сел, определяющих ребра, делятся на 3.
Если х, у, z выражаются такими натуральными чис-
лами, что
х2-\~у2 = t2, x2-[-z2 — u2 и у2 -|-z2 = v2,
где t, и, <v — натуральные числа, и, предположив, что ни
одно из чисел х и у не делится на три, мы бы имели
пифагоров треугольник (х, у, f), у которого ни одно из
71
чисел, выражающих катеты, не делились бы на три, что
противоречит известному свойству пифагоровых треуголь-
ников (§ 5.1). Аналогично доказывается делимость на 4.
15.19.	Можно показать, что если в параллелепипеде
ребра и диагонали боковых граней выражаются нату-
ральными числами, то по крайней мере число, выра-
жающее одно из ребер, делится на 11.
15.20.	Легко доказать, что если в параллелепипеде
ребра выражаются натуральными числами х, у, z
и если диагонали боковых граней выражаются нату-
ральными числами, то и в параллелепипеде, ребра
которого определяются числами ху, xz и yz, диагонали
боковых граней определяются целыми числами.
15.21.	Неизвестно, существует ли параллелепипед,
у которого все ребра, диагонали боковых граней, выра-
жаются натуральными числами.
Итак, существует простая, неразрешенная до сих пор
задача, относящаяся к параллелепипеду, ребра которого
выражаются натуральными числами.
15.22.	Если Р — параллелепипед, у которого ребра и
диагонали боковых граней выражаются натуральными
числами, то каждое из трех ребер, выходящих из одной
вершины, и каждая из трех диагоналей, соединяющих
концы ребер, выражаются натуральными числами и дают
тетраэдр (называемый некоторыми авторами кубоидом),
У
которого все ребра и объем, равный
выражаются
натуральными числами. Исходя из того, что каждое из
двух чисел х, у, z по крайней мере кратно 3 и каждое
из двух делится на 4, заключаем, что 144|лу^. Примерами
такого тетраэдра являются следующие тетраэдры с реб-
рами 117, 44, 240, 125, 267, 244 и объемом 205920.
15.23.	Заметим еще, как указал Литцманн1, объем тет-
раэдра (не кубоида), ребра которого выражаются числами
6, 7, 8, 9, 10 и 11, равен 48.
К. Шверинг приводит, в частности, следующие тет-
раэдры ABCD, ребра которых и объем выражаются ра-
циональными числами.
1 W. Lietzmann, Der Pythagoreische Lehrsatz, Leipzig, 1951, str. 79.
72
ВС	СА	АВ	DA	DB	DC	Объем
						8
4	3	3	4	3	4	3
6	6	8	9	9	9	48
7	7	4	7	7	12	12
12	12	8	9	9	9	96
19	19	12	19	19	20	300
15.24. Существуют			тетраэдры (не		кубоиды), ребра	
которых, площади боковых граней и объем выражаются
натуральными числами. Е. Штарке приводит такой тет-
раэдр, у которого одно из ребер равно 896, противопо-
ложное 990, а каждое из остальных равно 1073. Площадь
каждой из двух боковых граней равна 436800, а каждой
из двух остальных равна по 471240, а объем равен
62092800.
Примечания
Примечание 1 к 2.3
Теорема. Если произведение двух взаимно простых
чисел является квадратом, то каждое из этих чисел
есть также квадрат.
Доказательство. Число, являющееся квадратом,
разлагается на простые множители в степени с четными
показателями, например число
с2 = т2п2р\
где т, п, р — простые числа.
Пусть c2 = ab, где а и b — взаимно простые числа. До-
пустим, что число а — не квадрат, тогда оно должно
содержать в нечетной степени хотя бы один делитель
числа с2, например, а = т-п2р2.
В этом случае, Ь = тр2.
Числа а и b имеют общего делителя т, а потому не
могут быть взаимно простыми, что противоречит условию.
Примечание 2 к 2.3
Не следует думать, что автором последовательно при-
ведены все такие треугольники от (3, 4, 5) до (79, 3120,
3121). Среди приведенных треугольников отсутствуют
(29, 420, 421) и (59, 1740, 1741).
Необходимо отметить, что один из катетов каждого
приведенного треугольника, за исключением (3, 4, 5), де-
лится на 60.
Доказательство этого утверждения дано в примечании
11 к 5.3.
Примечание 3 к 2.6
Равенство (8) можно получить непосредственно из
равенства (6). Действительно, положив в равенствах
х = т2— п\ у = 2тп, z = m2-[-n2,	(6)
74
k — l
т —_х_ и AZ==_____ , где & и i — нечетные числа, полу-
чим равенства (8):
у 2 , - 2 .
И, обратно, из равенства (8), положив k = m-\-n и
1 = т — тг, где т^>п и одно из этих чисел четно, полу-
чим равенство (6).
х = т2 — п2] у = 2тщ z — m2 -f- п2-
Примечание 4 к 2.7
Выразим радиусы вписанного и вневписанных кругов
через стороны прямоугольного треугольника XZY (чер-
о
Черт. 2
теж 2). 2r-\-xM-\-yN = x-\-y\ так как хМ = хР\
rx—p—у. Аналогично ry=p — х\ rz=p
75
Итак,
Преобразуем полученные выражения:
г__„	„___(р —z)p___(* + у —£)(* + >+ 2) __(х + У)2 — Z2
* У	р	2-2/j	2-2/7
; (2)
х р —X	' 7
Из равенств (1), (2), (3), (4) получим Т = Т(5)
'	гX 'у 'Z
Найдем выражение радиусов через k и /:
2
2rz=y-Y-x^z = k(k-^iy,	
Итак, во всяком пифагоровом треугольнике радиусы
вписанного и вневписанного кругов — натуральные числа.
Покажем, что около всякого круга целочисленного
радиуса можно описать хотя бы один основной пифагоров
76
треугольник: один, если г = 2*, и не менее двух, если
г ^=- 2^.
Доказательство. Уравнению 2r = l(k — I) при
нечетных k и /, при 2г = 2* + 1 удовлетворяют только
I = 1 и k — 2r 1.
Итак, получим треугольник со сторонами х = 2г-\-\\
(2г 4-1)2-1
у=	—=2г (г+ 0;
= 2г (г —|— 1) —1.
Катет и гипотенуза выражены двумя последователь-
ными натуральными числами.
Если г — 2t — 1 — нечетному числу, то, кроме тре-
угольника, у которого катет и гипотенуза выражены двумя
последовательными целыми числами, можно найти еще
треугольник:
/ = 2^—1; k —1 = 2\ k = 2t-^ 1;
х= (2t —1)(2<+!) = «—1; у = (а+1)’~<2'~1)‘ = 4<;
г='а+1), + <г,-|)'==«.+ 1; и.™ (х, у, л + 2).
Треугольник, у которого катет и гипотенуза — два
последовательных нечетных числа.
Примеры.
1) г
2) г
8, k = 17, 1=\, (17, 144, 145).
7 / 2г = 14= 14-1;/ = 1; k= 15, (15, 112, 113).
1 \2г=14 = 2-7; / = 7; £ = 9, (63, 16, 65).
Итак, треугольники (15, 112, 113) и (63, 16, 65) имеют
общий радиус вписанного круга и этот радиус равен 7.
2г = 30-1, £ = 31, /=1 (31, 480, 481),
2г=15-2, £ = 17, 7=15 (255, 32, 257),
2г = 5-6, £=11, / = 5 (55, 48, 73),
2г = 3-10, £ = 13, / = 3 (39, 80, 89).
Итак, треугольники (31, 480, 481), (255, 32, 257), (55,
48, 73), (39, 80, 89) имеют общий радиус вписанного
круга и этот радиус равен 15.
77
Примечание 5 к 4.4
Вывод тождества Месснера:
, 1П к ,	1	k2-l2	(10zz —5)г—1
x = k=\0n— 5, Z=l, у =—— = ------т>~-,
Имеем
(10и
(10я — 5)2 + (50я2 — 50n + 12)2 = (50/г2 — 50/г -f-13)*.
Примечание 6 к 4.4
Приведем тождество, аналогичное тождеству Месснера,
дающее все рассматриваемые треугольники:
х= 10п-^-а, где о=+1, ±3,
±5 и Л2г3;
при а= — 5 получаем формулу Месснера:
___(10п 4- а)2 — 1____Юл (10я 4- 2а) 4- а2 — 1
о	о	>
~10я (Юя -f- 2а) 4- о.2 — 1]2
____ '10п(10л4-2а)4-а’4-11«.
о	»
при п = 0, <2=3; 5, (3, 4, 5), (5, 12, 13);
„ я=1, а— — 3, (7, 24, 25);
„ и=1, о = ±1, (9, 40, 41), (11, 60, 61);
„ «=1, а = 3, (13, 84, 85);
„ я=1, а = 5, (15, 112, 113);
„ и = 2, й = —3;±1, (17, 144, 145), (19, 180, 181),
(21, 220, 221).
Примечание 7 к 4.5
Найдем геометрический смысл числа п в равенствах (10)
х=2п-]-1, у = 2п(п-[-1), z = 2ra(ra-]--1)+1;
__ х -|- у '— z %п —1 ~|- 2т22 -|- 2/z — 2/z2 — 2п — 1
Г----------------- —-----------------------------—---- - — *7
78
Итак, n = r — радиусу круга, вписанного в основной пи-
фагоров треугольник [2лг1; 2az (лг —1)]; [2«(n-J“ О П*
Определим для этих треугольников гх, гу, гг;
= П (2я -ф- 1) = г (2г -4- 1);
гх — п —1 — г —1;
rz = 2я2 -|- Зя 4~ 1 — 2г2 -j- Зг	1 = г -ф- гх -ф- Гу.
Применив формулу (см. примечание 4)
к треугольникам:
21,	220,	221,
201,	20200,	20201,
2001,	2002000,	2002001,
20001,	200020000,	200020001,
и пользуясь следующей таблицей:
Г	ГХ	ГУ	
10	11	210	231
100	101	20100	20301
1000	1001	2001000	2003001
10000	10001	200010000	200030001
получим ряд тождеств:
1_1 .Ji _L.
10	11 ^210^ 231 ’
1 _ 1 । 1 . 1
100	101 "Г 20100	20301 ’
1   1 . 1 . 1
1000	1001 “Г 2001000 "Г 2003001 ’
1   1 . 1	, 1
10000	10001 “г 200010000 I 200030001 
Примечание 8 к 4.5
Рассмотрим пифагоровы треугольники, у которых
z—л = 2, т. е. треугольники, у которых катет и гипо-
тенуза выражаются двумя последовательными нечетными
числами.
Так как z = ^-~- и x = kl, то z— х = ^—~\
4 = (& —Z)2 и Aj = Z + 2 (£>Z).
Итак, если z— л = 2, то k—1 = 2.
Обратно, если k—1 = 2, то z — х = 2.
Действительно, ^l-2bl-Z- — Z 2) = Z2 2Z —2 — Z2 —
— 21 = 2.
Следовательно, для получения рассматриваемых тре-
угольников необходимо и достаточно взять за k и Z два
произвольных последовательных нечетных числа.
Например, 1 = 1, k = 9, х = 63, у = 16, z = 65.
Стороны этих треугольников могут быть определены
еще и следующим образом:
у = 4 т = 2-2 т-1
х = (2 т)2— 1
z = (2 m)2-)- 1-
Например: при т= 1(У имеем (10(У—1; 2-1(У, 1О(У-р1)
99,	20,	101,
9999,	200,	10001,
999999,	2000,	1000001,
99999999,	20000,	100000001.
Радиус круга, вписанного в рассматриваемый треуголь-
ник, вычисляется по формуле:
Имеем тождество:
Применяя его к вышезаписанным треугольникам, полу-
чаем:
1-1 ill _L.
9 — 11 ‘ 90 ‘ ПО ’
1-1_ ।	1 I____1_.
99— 101 । 9900 । 10100 ’
I___!____1________.
9999	10001 । 99990000 ' 100010000 ’
1 _ 1 । ___________!____। ______!_____
999999	1000001	999999000000 ь 1000001000000	И Т. Д.
80
Кроме рассмотренных нами треугольников с катетами 99,
999, 9999,..и т. д., можно с теми же катетами полу-
чить еще следующие треугольники:
99,	4900,	4901,
9999, 49990000, 499990001
и т. д.
Примечание 9 к 4.6
Докажем, что в двух последовательно получаемых
таким образом треугольниках больший катет выражается
в одном треугольнике четным, а в следующем треуголь-
нике— нечетным числом.
/(%;%+1; z) == (3% + 2z + 1; 3% + 2г + 2; 4х + 3z + 2);
//(%; х-[- 1; г)=/2(%; % +1; г)=/(3% + 2г +1; 3%-]~
+2г + 2; 4% + Зг + 2) = (9% + 6г + 3 + 8% + 6г + 4 +1;
17%+ 12г —9;	12% + 8г + 4+12% + 9г + 8) = (17% +
+ 12г + 8; 1 7% + 12г + 9; 24%+17г+12).
Больший катет в первом треугольнике 3% + 2г + 2 —
число нечетное (% = 3). Больший катет во втором тре-
угольнике 17%+12г+ 9 — число четное.
Примечание 10 к 4.8
Проверить, что /g(%; %+1; г) = (%; % + 1; г);
/g(%; х+1; г)==/(3% — 2г +1; 3% — 2г + 2; Зг — 4% —
— 2) = (%,у , г );
~х = 9% — 6г + 3 + 6г — 8% — 4 + 1 == %;
у = %+ 1;
г = 12% — 8г+ 4 +9г — 6 + 2 = г.
Примечание И к 5. 3
В примечании 2 к 2.3 отмечено, что в треугольнике,
у которого катет и гипотенуза — простые числа, второй
катет делится на 60, за исключением треугольника (3, 4, 5).
Действительно, так как катет и гипотенуза простые
числа, то второй катет должен делиться на 3, 4 и 5, т. е.
должен делиться на 60.
81
Примечание 12 к 6.1
Покажем, что всякое нечетное число п 3 может
быть катетом основного пифагорова треугольника
x — n^kly полагая /=1, получаем у ——х—=—;
Четное число, кратное четырем, может быть катетом
основного пифагорова треугольника.
Примеры. (3; 4; 5), (5; 12; 13), (7; 24; 25), (9; 40; 41),
(4; 3; б), (8; 15; 17).
Примечание 13 к 6.3
Дадим вывод приведенных формул.
Возьмем два основных треугольника (3; 4; 5) и (5; 12; 13)
и умножим стороны первого на 5, а стороны второго
на 2, тогда получим два треугольника, у которых гипо-
тенузы выражаются двумя последовательными числами
(15; 20; 25), (10; 24; 26).
Для отыскания ряда таких треугольников, умножим
соответственно стороны первого на 5-[-13&, а стороны
второго на 2-[-5£, тогда из тождеств:
52 = 32 Ц-42;
132 = 52 -}-122
получим соответственно:
52 (5 + 13£)2 = З2 (5 + 13&)2 + 42 (5 + 13&)2;
132 (2 + bk)2 = 52 (2 + bk)2 + 122 (2 + 5Л)2,
или
(25 + 65£)2 = (15 + 39Л)2 + (20 + 52&)2;
(26 + 65&)2 = (Ю + 25Л)2 + (24 + 60£)2,
Таких формул можно привести сколько угодно, на-
пример, из тех же основных треугольников получаем:
52 (8 + 13&)2 = З2 (8 + 13£)2 + 42 (8 + 13£)2;
132 (3 + bk)2 = 52 (3 + bk)2 + 122 (3 4- bk)2,
82
или
(40 4- 65&)2 = (24 + 39&)2 + (32 + 52/e)s;
(39 -j- 65&)2 = (15 + 25&)2 + (36 + 60&)2.
Если взять треугольники (3; 4; 5) и (8, 15, 17), то
получим:
(34 + 85£)2 = (30 + 75&)2 + (16 + 40&)2;
(35 + 85£)2 = (28 + 68А)2 + (21 + 5U)2.
Стороны бесконечного множества полученных тре-
угольников (%, у, z) и (%, у, г+ 1) дают системы решений
в целых положительных числах системы двух квадратных
уравнений с пятью неизвестными:
л2 ++ = z2,
tt2_|_^2 = (^+ I)2,
л, положим, равным 30+75 k, у — 16-(-40 Л, г=34+85 k,
« = 28 + б8&, г/ —21+51 k, где k—произвольное целое
положительное число.
Поставим следующую задачу: найти пары пифагоровых
треугольников, у которых гипотенузы —последовательные
нечетные числа.
Исходим из следующей пары треугольников (возможно
взять и другие пары) (5; 12; 13), (9; 12; 15):
52 (1 + 15 k)2 + 122 (1 + 15 k)2 = 132 (1 + 15 А)2,
92 (1 + 13 k)2 + 122 (1 + 13 k)2 = 152 (1 + 13 k)2,
или
(5 + 75 k)2 + (12+ 180 k)2 = (13+ 195 £)2,
(9 + 117 k)2 + (12 + 156 k)2 = (15 + 195 k)2.
Стороны бесконечного множества полученных нами
треугольников (%, у, z) и (л, у, г+ 2) дают системы ре-
шений в целых положительных числах системы двух
квадратных уравнений с пятью неизвестными:
л2++ —г2,
и2 + ^2 = (г + 2)2.
Примечание 14 к 6.4
Приведем формулы для получения троек пифагоровых
треугольников, у которых гипотенузы выражаются тремя
последовательными числами.
83
Исходим из следующей тройки треугольников: (15; 36;
39), (24; 32; 40), (9; 40; 41):
2.
(40-J-5-13-41 ft)2 = (24+ 3-13-41 ft)2+(32 + 4-13-41 Z
5-13-41 ft)2 = (9 + 9-13-5 ft)2 + (40 + 40-13-5 ft)2,
(41
или
2
(39 + 2665 ft)2 = (15 + 1025 ft)2 + (36 + 2460 ft)2;
(24 +1599 ft)2+ (32 + 2132 ft)2;
(41 + 2665 ft)2 = (9 + 585 ft)2 + (40 + 2600 ft)2.
Исходя из следующей тройки треугольников (60; 80; 100),
(20; 99; 101), (48; 90; 102), получаем:
(100 + 5-17-101 ft)2 = (60 + 3-17-101 ft)2+ )
+ (80 + 4-17-101 ft)2;
(101+5-17-101 ft)2 = (20 + 5-17-20ft)2+ I
+ (99 + 5-17-99 ft)2;	f	1
(102 + 5-17-101 ft)2 = (48+ 5-8-101 ft)2 +
+ (90-|-5-15-101 ft)2	J
или
(100 -I	1—8585 ft)2 = (60 + 5151 ft)2-]		-(80-|	-6868 ft)2; )
(101-	- 8585 ft)2 = (20 -	-1700 ft)2-	-(99-	-3989 ft)2; I II
(102-J	- 8585 ft)2 = (48 -]	- 4040 ft)2 -	[-(90-	H 7575 ft)2. J
Равенства I и II являются одними из систем решений
системы трех следующих уравнений с семью неизвестными:
л2+_р2 = г2,
M2 + ^ = (z+l)2,
-у2 + w2 = (г + 2)2 *)•
Приведем формулы для получения четверок пифаго-
ровых треугольников, у которых гипотенузы выражаются
четырьмя последовательными числами:
(50 + 5-13-17-53 ft)2 = (30 + 3-13-17-53 ft)2 +
+ (40 + 4-13-17-53 ft)2;
(51 + 5-13-17-53 ft)2 = (24 + 5-8-13-53 ft)2 +
+ (45 + 5-13-17-53 ft)2;
(52 + 5-13-17-53 ft)2 = (20 + 5-8-17-53 ft)2 +
+ (48 + 5-13-17-53 ft)2;
(53 + 5-13-17-53 ft)2 = (28 +5-13-17-28 ft)2 +
+ (45 + 5-13-17-45 ft)2.
1 Waclaw Sierpinski о Rozwiazy warii rowiieu w lizbach calcowitych
Warszawa, 1956.
84
Нами получена одна из систем решений следующей
системы четырех уравнений второй степени с девятью
неизвестными:
л2-|-_у2 = .г2,
н2 + ^ = (г-|-1)2,
v2	w2 — (z -f- 2)2,
г24-.$2 = (.г4-3)2.
Примечание 15 к 7.2
Дадим вывод и обобщение формул, приведенных в 7.2.
Выберем катет а следующим образом:
« = а0 = 2-2,‘-1=2'1+1.
На основании формул 6 (2.3) имеем:
£0 = 22”—1; с0 = 22И4-1.
Покажем, что
ck — b2k = a2, для сА = 2* (22"-2ft—f—1),
bk = 2k (22"-2*—1).
Действительно,
^2zn"| 2^)2____^2п~к____2^)2 = 4• 22П__(2п+2)2__•а2
Это равенство справедливо при всяком А, но не при
всяком k существует треугольник.
Так как ^>0, то 22Л“2*>> 1 и /г>£, при А = 0,1,2,...
(/г—1) треугольники существуют.
Приведенные в 7.2 формулы могут быть обобщены.
Пусть катет a = aQ = 2 (2р)п-1 (при р = 1 имеем рас-
смотренный выше частный случай), т. е. за общий катет
принимается удвоенная степень произвольного четного
числа.
&о=(2д)2"-1; с0=(2дГ+1.
Для отыскания пифагоровых треугольников с общим ка-
тетом а можно воспользоваться различными формулами:
1)	=	[(2р)2П~^-1],
ch^(2p)k [2^]2”-2Н 1],
2« — 2АД>0, k<Zn\ £ = 0,1,2,... (п — 1):
2)	b'k = 2k [(2р)2П .2~2k — 1],
с'=2а [(2/?)2"2~2* —1J.
85
Так как то если
,2~2^
то (2р)2”2"2\
безусловно, более единицы.
Из равенства 24И-2“2*=1, имеем:
4/z— 2& = 0; 2я — k — 0; k — 2п.
При k= 1,2,..., 2/z
з)	bk=Pk \Ш~2к-Ц
ck=pk [(2р)2>-2*4-1], р2“-2*=1; k = n.
(При некоторых k>nbk может также оказаться положи-
тельным.) Итак, существует не менее 4я пифагоровых
треугольников с общим катетом, равным 2 (2р)п.
Покажем, что общий катет может быть выражен и
нечетным числом вида (2р-1- 1)п.
Выбрав а = а0 = (2р	1)” • 1, найдем bk,ck.
h _(2/? + 1Л[(2р+1Г-2^1]
Ok—-	2	’
_ (2рЧ- 1)Л[(^ + 1)2"~2Л?Ч-1]
Lk	9	,
£=0,1,2,...,(«—!).
Примеры. 2/7 —1 = 5, п = 4, а=54 = 625,
Ьо= 195312,
(625, 195312, 195313),
(625, 7800, 7825),
с0= 195313,
(625, 39060, 39065),
(625, 1500, 1625).
Примеры. р = 3, п=2,
а = 2-62 = 72, ЬО = 1295, с0 = 1297.
1) (72, 1295, 1297),
Ь.=~ 1296 — 6 = 210, с, = 222;
2) (72, 210, 222);
Ь{ = у’ 1296 — 2 = 646; 3) (72, 646, 650);
/?' = у • 1296 — 4 = 320; 4) (72, 320, 328);
Ь'=у-1296 — 8=154; 5) (72, 154, 170);
b’t=• 1296 — 16 = 65; 6) (72, 65,97);
86
6" = у • 1296 — 3 = 429; 7) (72, 429, 435);
5''= у-1296 —9= 135; 8) (72, 135, 153);
b" = ^-1296 — 27 = 21; 9) (72, 21, 75).
Всего 9 пифагоровых треугольников с катетом 72.
Примеры. /2 = 3, л/ = 3, а — 2-63 = 432,
1) (432, 46655, 46657);
2) bt	= У 46656— 6 = 7770,	(432, 7770, 7782).
3) *>2	= — 46656 — 36= 1260, 36	’	(432, 1260, 1332).
4) ь;	= 4- -46656 — 2 = 23326,	(432, 23326, 23340).
5) Ь'2	= y-46656— 4=11660,	(432, 1160, 11668).
6) ь;	= 4--46656— 8= 5824, О	(432, 5824, 5840).
7)	= ^•46656—16 = 2900, 16	’	(432, 2900, 2932).
8) Ь'5	=4г 46656 — 32= 1426,	(432, 1426, 1490).
9) К	= 4г 46656 — 64 = 665, 64	’	(432, 665, 793).
10) Ь"	= 4--46656— 3=15549,	(432, 15549, 15555).
11) Ь”2	= у-46656 — 9 = 5175,	(432, 5175, 5193).
12) Ъ"г	=4?-46656 — 27= 1701,	(432, 1701, 1755).
13) ь\	= 4,-46656 — 81 = 495, О1	(432, 495, 657).
Читатель легко получит 13 треугольников с общим
катетом, равным 2 (2/?)“, при /2 = 5 и п = 3, т. е. я = 2000.
Примечание 16 к 7.3
Покажем, как найти два или более основных пифа-
горовых треугольника с общим катетом, равным нечет-
ному числу.
87
Пусть 2k — 1 и 2k + 1 — два последовательных не-
четных числа.
Примем x = {2k— 1) • {2k	1) = 4А2 — 1, у = 4k,
z = 4&2 + l.
(4&2— 1; 4k; 4&2-|-1) — основной пифагоров треугольник
вида (х; у; % + 2).
Для получения второго основного пифагорова тре-
угольника примем
Л = (4/?2— 1). 1 = 4^2 — 1;
(4£2_ 1)2-1
у = -----~----= 4/г (2k2— 1);
_(4^	—4^2(2^2 -- 1) J;	у, д,_|_ ]).
Пример: л = 5-7 = 35 (35, 12, 37) и (35, 612, 613).
Если один или оба делителя х составные, то можно
найти более двух основных пифагоровых треугольников
с общим катетом.
Примеры.
%—15-17 = 255,
л = 255-1 = 255,
л = 3-85=255,
% = 5-51 = 255,
(255, 32, 257);
(255, 32512, 32513);
(255, 3608, 3617);
(255, 1288, 1313).
Интересно отметить, если вместо простых множите-
лей взять их любые степени с натуральными показателя-
ми, то число основных пифагоровых треугольников с
общим катетом от этого не изменится.
Например.
1) /? —52-73 = 8575; /=1; л = 8575;
2) k = 73; / = 52;	л = 8575;
1) 8575, 36765312, 36765313);
2) (8575, 58812, 58813).
Задача. Найти основные пифагоровы треугольники,
общий катет которых выражается числом, имеющим „т“
простых делителей.
1. Пусть катет пифагорова треугольника равен про-
стому числу. Покажем, что не существует второго пифа-
горова треугольника с тем же катетом.
х=аг, так как аг не разлагается на множители, то/=1,
k = a„
х = ал.
88
Итак, при одном простом делителе пх — 1 = 2° (пг —
число треугольников с общим катетом).
2. Пусть катет пифагорова треугольника выражается
произведением двух простых чисел:
х = а.а9.
Л «*.
Возможны два основных треугольника
1 \	GW — 1	(Я^)1 2 + 1 О\
1) a,az,	; 2) а,а2,
Итак, в этом случае возможны два основных треугольника:
п. — 2 = 2*.
А
3. Пусть х ==ага2аь.
Возможны четыре треугольника:
4. х — ам9аяа.,
1 Л и '
l=z\- k~a.a9axi.,
l = a* k — a9a.a.,
l—a,; k—a.a.a.,
и'	± о z
1 = а • k = a,a9a.,
О '	л. А ’
/ = а,, k — a.ata.,
l = aa k = a.a.,
l = a,a„ k = a9a.9
1 = а9а^ k = a.a.,
A v я	'
Пусть л = гх10!2 ...
Примеры. 1. х = 5; у = 12; z=13.
Не существует других пифагоровых треугольников
с катетом, равным 5, кроме (л, у,
89
2. х = 85 = 5-17. Существует два основных пифаго-
ровых треугольника с общим катетом, равным 85.
1.	/г = 85, 1=1 (85, 3612, 3613),
2.	Л = 17, 1 = 5 (85, 132, 157)
Возможно построить шестьдесят четыре основных пи-
фагоровых треугольника с общим катетом равным х.
х = 2576450045 = 5•13•17•29•37•41•53.
От замены одного или нескольких делителей их сте-
пенями с произвольными натуральными показателями чис-
ло основных пифагоровых треугольников не изменится
х = 2576450045 = 52 • 132 • 172 • 292 • 372 • 412 • 532.
3.	л=П55 = 3-5-7-11 (1155, 68, 1157), (1155, 2852,
3077), (1155, 1292, 1733), (1155, 667012, 667013), (1155,
74108, 74117), (1155, 13588, 13637), (1155, 26668, 26693),
(1155, 5452, 5573).
Примечание 17 к 7.5
В заметке Шедда дана таблица 64 основных пифаго-
ровых треугольников. Таблица дана без вывода. Дадим
обоснование приведенной таблицы.
Пусть даны два основных пифагоровых треугольника
(л,, у1г г,) и (л2, у2, z2), где г, и z2— простые числа
вида 4р —|— 1.
Покажем, что гипотенуза основного пифагорова тре-
угольника выражается числом вида 4р -ф-1.
Действительно, m = 2t, п~2
z=т‘ -ф- п2 — 4t2 -ф- 4s2 -ф- 4s -ф-1 = 4р -ф-1.
Отсюда следует, что если гипотенуза — простое число,
то это число вида 4р -ф-1.
2
1
2
Итак, получены два треугольника с общей гипотенузой
zvz2. Покажем, что полученные треугольники — основные.
Во-первых, л, + и xtx2—yty2 оба четны,
х^—х^ и +	°^а нечетны.
90
Во-вторых, предположим, что катеты xtx2 -j-y^ и
хгу2 — х2ух имеют общий делитель d. Этот делитель либо
либо г2, так как левая часть равенства делится только
на z. или на z*
Л	Л *
Отсюда имеем:
Правая часть равенства делится на zlt тогда как левая
не делится:	a z2— простое число.
Покажем, что и z2 не может быть общим делителем
катетов:
Правая часть делится на za, тогда как левая на z2
не делится.
Итак, у катетов нет общего делителя и полученные
треугольники — основные пифагоровы треугольники.
Примеры. 52 = 324~42
132 = 524-122
652 = (3-5 + 4-12)2 + (3-12 - 4-5)2
652 = (4-12 — 3-5)24-(3-124-4.5)2
(63, 16, 65)
(33, 56, 65).
Получены два треугольника с общей гипотенузой z. Пусть
2 = 5.13.17=1105.
11052 = (632 4-162) (82-f-152);
172 = 82 4-152;
11052 = (562 4- ЗЗ2) (82 4-152).
Получены четыре треугольника: (817, 744, 1105), (264,
1073, 1105), (576, 943, 1105), (45, 1104, 1105) с общей
гипотенузой.
91
Так как 5 • 13 • 17 • 29 = 32045, то
320452 = (8172	7442) (202 4~212)
и мы имеем два треугольника с общей гипотенузой
(2277, 31964, 32045), (32037, 710, 32045).
Аналогично можно найти еще 6 треугольников с той же
гипотенузой.
Если число, выражающее длину гипотенузы, простое —
вида 4/7 4” 1, то существует единственный треугольник с
этой гипотенузой, т. е. nY=%°=\ (пл—число треугольников).
Если число, выражающее длину гипотенузы, равно
произведению двух простых чисел (4/?4~1) и (4#4“Ь» то
существует два основных пифагоровых треугольника с этой
гипотенузой
п = 21 = 2.
Легко видеть, что если число, выражающее длину
гипотенузы, равно произведению t простых множителей
вида 4р Ц-1, то /z/ = 2/"1.
В случае, рассмотренном Шеддом, t = 7, я7 = 26=:64.
Примечание 18 к 8.1
автора, указанным в § 8.1, можно получить
bk« . r' —
k 4 ’
Способом
неосновные пифагоровы треугольники (a'k, b'k, c'k).
Действительно, a'k =.а-^-;	b'k = bj~ •	— CkS- •
ak-b'k'-c'k = ak-.bk:ck.
Так как $>>$£, то a'k>ak; b'k>bk; ck> ck и треуголь-
ник (ак, b'k, ck)— неосновной.
Примечание 19 к 8.3
Для отыскания основных пифагоровых треугольников
с общим периметром найдем выражение периметра пифа-
горова треугольника,
На основании формул (8) имеем:
x = kl; у =
2p = kl-{-kz =	k — число нечетное,
k I — число четное; k 4-1 <Z 2k, так как / << k
92
Рассмотрим несколько примеров на отыскание треуголь-
ников с общим периметром.
Начнем с примера, приведенного в тексте, где даны три
треугольника, периметр каждого из которых равен 14280.
Покажем, как по периметру можно найти треугольник:
14280 = 2.2-2.3.5-7.17,
1)	/4 = 7.17 = 119; kx + 4 = 2-2-2-3-5= 120
4 = 1 (119,7080,7081).
2)	/4 = 5.17 = 85, Л2-|-Z2 = 2-2-2-3-7 = 168;
4 = 83 (7055,168,7057).
3)	/гз = 3-5-7 = 105, /4 + 4=136; Zs = 31.
5032, 5993).
(3255,
Можно построить еще примеры троек (да не только
троек) пифагоровых треугольников с общим периметром.
Найдем треугольники с периметром 2р = 2.3-5.7.11Х
Х13-53= 1591590:
1)	^г = 7.11 -13= 1001; ^ + 4 = 2-3.5.53=1590;
Z, = 589 (589589, 327540 674461);
2)	^ = 3.7-53=1113; k2 4-4 = 2.5-11.13=1340;
4 = 317 (352821, 569140, 669629);
3)	/г8 = 3.5.7.11 = 1155; /4 + 4 = 2.13.53=1378;
4 = 223 (257265, 642148, 691877).
К полученным основным пифагоровым треугольникам
можно добавить несколько неосновных, например, из тре-
угольника (5,12, 13) с периметром 30 = 2-3-5, можно полу-
чить новый с периметром 1591590, умножив стороны перво-
го на 7.11-13.53 = 53053.
Из треугольника (21, 20, 29) с периметром 70 = 2-5.7
можно получить новые с периметром 1591590, умножив сто-
роны основных на 3 -11 -13 - 53 = 22737, (477477, 454740,
659373).
Из треугольника (33, 56, 65) можно получить новый,
умножив стороны основного на 3-5 -13-53= 10335.
Из треугольника (117,44, 125) получим новый, умно-
жив стороны основного на 3-5.7.53 = 5565 и т. д.
Примечание 20 к 8.3
I. Найдем основные пифагоровы треугольники, у кото-
рых периметр является квадратом. Так как 2/7 = k
числа k и I взаимно простые и 2р — квадрат, то k и k +1
93
каждое в отдельности должны быть квадратами (см. при-
мечание 1). Число k — квадрат нечетного числа, число k-{-
4~/ — квадрат четного числа и £Ц-/<2£, так как £>/,
Можно легко найти треугольник с периметром, равным
квадрату.
Для этого достаточно (но не необходимо) выбрать k =
=	I)2; £-j-Z=(2Z)2; / = (2^)2 — (22е—1)2 = 4^—1.
Покажем, что k^>l.
(2£—I)2 — (4£ — 1) = 4£2 — 8^ + 2= 4(Z— I)2 — 2> О
при t 2,
2/7 —[(2/ — 1) 2£]2.
Итак, квадрат произведения двух последовательных
натуральных чисел, из которых меньшее нечетно и не
равно единице, является периметром основного пифагорова
треугольника.
Наименьший пифагоров треугольник, у которого пери-
метр равен квадрату, получается из равенства (1) при t =
= 2.
2/? = (3-4)2= 144 (63, 16, 65).
Следующий основной пифагоров треугольник получает-
ся при г = 3:
2/7 = (5-6)2 = 900, (275, 252, 373).
при £ = 4 получаем:
2/? = (7.8)2 = 562 = 3 1 36, £ = 49, /=15 (735, 1088, 1313).
Таким образом, имеется бесконечное множество основ-
ных пифагоровых треугольников, периметр которых равен
квадрату. Приведем еще несколько пифагоровых треуголь-
ников, периметр которых равен квадрату и которые не
могут быть получены из равенства (1).
Например: 1) 2р = (11.14)2 = 1542 = 237 1 6,
£=121, 7 = 75 (9075, 4508, 10133).
2) 2/7 = (13-16)2 = 2082 = 43264,
£=169, / = 87 (14702, 10496, 18061).
94
II. Аналогично найдем основные пифагоровы треуголь-
ники, у которых периметр является кубом.
Достаточно (но не необходимо) выбрать k = (2.t—I)3,
k-\-l = (2t)3 /=12/2 —6/4-1,
^_/==(2/—l)s—12/2 + 6/ — l = 8/’ — 24/24-12/ —
— 2 = 8/2 (/— 3) —|—12/— 2; при /^3, Л>/.
Полагая / == 3, получим:
2р = (5-6)’ = 27000, /г = 125,/ = 91 (11375, 3672, 11953).
Полагая / = 4, получим:
2р = (7-8)’ = 56’ = 175616; £ = 343, /=169, (57967,
44544, 73105).
Приведем еще примеры (они не получаются из равен-
ства (2))
1) 2р = (17- 20)’ = 340’ = 39304000, £=17’ = 4913,
/ = 3087.
2) 2р = (23 • 28)’ = 644’ = 267089984, Л =12167, / =
= 9785.
III. Найдем основные пифагоровы треугольники, у ко-
торых периметр равен «-ой степени натурального числа.
Достаточно (но необходимо) выбрать Л = (2/— 1)",
k +1=(2/)и; I = (2/)п — (2/ — 1)",
k — / = 2 (2/ — 1 )п — (2/)" = (2/)" — 2п	~1
Х(2/)"-2
2л (п— 1) (л	f/\n-s I 2л (л 1) (п	। I
ПГЗ	1	1-2-3 W
+ (-1Г-2.
Для того, чтобы разность k — I была положительной,
достаточно выбрать t^n.
Пример. Найти наименьший пифагоров треугольник,
у которого периметр равен 5-й степени натурального
числа.
k = (2 - 5 — 1 )5 = 95 = 59049;
Z=105 —— 95 = 40951;
2р = (9 • 10)5 = 905 = 5904900000.
Искомый треугольник (2418115599, 904900000, 2581884401).
95
Покажем, что полученный треугольник — наименьший
из основных пифагоровых треугольников, у которых пе-
риметр равен 5-й степени натурального числа,
Действительно, положив 2/? — (7-8)5 (t положено рав-
ным 4), получим k = 75 = 16807; / = 85 — 75 — 16961,1 > k,
что невозможно.
Примечание 21 к 9.2
Для отыскания пифагоровых треугольников с общей
площадью найдем выражение площади треугольника с
катетами х = т2 — п\ у = 2тп.
Площадь S = тп (гп — п) где каждая пара мно-
жителей— взаимно простые числа, причем один множи-
тель четный, а три другие — нечетные (так как т или п
нечетно). Итак, для отыскания пифагорова треугольника
данной площади следует разложить число, выражающее
площадь, на четыре таких попарно взаимных простых
множителей, чтобы один был равен сумме, другой — раз-
ности двух других.
Это положение можно сформулировать иначе; если
число можно разложить на четыре множителя, из кото-
рых один равен разности арифметической прогрессии, а
три других — трем последовательным членам этой про-
грессии, множители попарно взаимно простые, а один из
них четный, то это число равно площади основного пи-
фагорова треугольника.
Если такое разложение невозможно, то не существует
основного пифагорова треугольника данной площади.
Найдем два наименьших основных пифагоровых тре-
угольника с общей площадью. Естественно положить, что
разность прогрессии для чисел, выражающих площадь од-
ного треугольника, равна единице, а для другого — двум.
Тогда имеем:
(2а— 1)2а (2а+1) = 2(2&— 1) (2^+1) (2^ + 3);
а (2а — 1) (2а + 1— 1) (2^ + 1) (2£ + 3);
а — нечетно.
Положим: а = 2Ь — 1; 2а — 1 = 2b 1.
При а = 3 и Ь~2;
2а —{— 1'== 2Ь —1~ 3,
7 = 7.
Искомая площадь равна 1-5-6-7 = 210 или 2-3-5*7 = 210.
S3
Треугольники с площадью 210 следующие:
т = 6, д=1, (12,35,37);
т = 5, п = 2, (20, 21, 29).
Пример. Найти треугольники, площадь каждого из ко-
торых равна:
13123110 = 2-3-5 7-11 -13-19-23,
13123110 = 38-39-77-115 (щ = 77, и = 38);
13123110 = 55-23-78-133 (т = 78, и = 55);
13123110 = 5-133-138-143 (лп= 138, /г = 5);
(4485, 5852, 7373), (3059, 8580, 9109), (19019, 1380, 19069).
Примечание 22 к 9.4
Найдем треугольники с площадью 341880.
341880 = 55-1-56-111, от = 56, н = 55,
(111, 6160, 6161).
341880 = 37-3-40-77, щ = 40, я = 37,
(231, 2960, 2969).
Кроме полученных основных треугольников, найдем еще
два треугольника.
Так как 341880 = 4-85470, 85470= 15-22-37-7, то,
принимая ///, = 22, п1 — 15, найдем треугольник (259,660,
709) с площадью 85470.
Искомый треугольник подобен треугольнику (259,660,
709) и его стороны в два раза больше сторон последнего
(518, 1320, 1418).
Кроме полученного треугольника, найдем еще один.
Так как 85470 = 2-33-35-37, то ш2 = 35, лг = 2 и тре-
угольник (140, 1221, 1229) подобен искомому.
Примечание 23 к 10.1
Теорема. Из всякого основного пифагорова тре-
угольника можно составить новый, у которого гипоте-
нуза— куб натурального числа.
Действительно, из данного пифагорова треугольника
(xltylf г,) составим следующим образом новый (х2,уг,гг):
4 Заказ № 2446
97
Легко видеть, что полученный треугольник — основ-
ной.
Примеры. 1. (Xjjp 2\) = (3, 4, 5);
г=125
2. (*1, Л, ^i) = (5, 12, 13); х2 = 5 (4-144—169) = 2035;
уа = 12 (169 — 100) = 828; z = 138 = 2197 (2035, 828, 2197).
Из треугольников с равными гипотенузами можно по-
лучить новые, у которых гипотенуза равна кубу исходной
гипотенузы. Например, из треугольников (63,16,65) и
(33, 56, 65) можно получить (201663, 186416, 274625) и
(7336, 274527, 274625). Приняв (х1? zt) за первый тре-
угольник, мы образуем новый (х2, у , г2), который назо-
вем вторым и у которого z* — z^. Из треугольника
(х2,	^г) аналогично составим новый (х8,у8, г8), назовем
его третьим и у которого za = zl = zf. Таким образом,
получим п-й треугольник (хп, уп9 zn), у которого zn =
Пример. Из (3, 4, 5) составляем второй треугольник
(117, 44, 125), а далее третий (922077, 1721764, 1953125).
Из 64 треугольников Шедда (7, 5) можно составить 64
новых основных пифагоровых треугольника с общей ги-
потенузой, равной 25764500458, далее, новых 64 треуголь-
ника с гипотенузой 2576450145® и т. д.
Примечание 24 к 10. 2
Основной пифагоров треугольник, у которого число,
выражающее длину нечетного катета, является квадратом,
получить легко, приняв за k — квадрат нечетного числа,
а за I — квадрат меньшего нечетного числа (проще всего
положить I равным единице).
Например, k — 25; I = 1,
Ы = 25,	= 312, 44 = 313.
Аналогично можно получить треугольник, у которого
катет равен л-й степени нечетного числа, например З4 = 81,
/=1 (81, 3280, 3281).
jfe = 5’ = 3125, /=1; (3125, 48827812, 48827813).
in__1	/"4-1
В общем виде k = in, x = tn-\, у — ——,z ——.
98
Примечание 25 к 10.4
Если произведение нескольких (в данном случае четы-
рех) попарно взаимно простых чисел являются квадратом,
то каждое из этих чисел — квадрат.
Пусть Л2 = abed и h2=-где т, n,p,q — про-
стые числа.
Предположим, что а — не квадрат. Тогда можно пред-
положить, что а = тп2, Ь = тр2, с = pzqz, d = qz.
При этом предположении а и Ъ имеют т общим множи-
телем, что противоречит условию.
Примечание 26 к 10.5
О теореме Ферма см. книгу А. Я. Хинчина „Великая
теория Ферма" и А. О. Гельфонда „Решение уравнений
в целых числах".
Примечание 27 к 11.2
Из двух прямоугольных треугольников с общим кате-
том можно получить два (а не один) треугольника, стороны
которых и площадь выражаются натуральными числами
(такие треугольники будем называть героновыми).
Первый треугольник получается, если два прямоуголь-
ных треугольника с общим катетом приложены друг к другу
так, что один треугольник находится вне другого, вто-
рой — когда один находится внутри другого (черт. 3 и 4).
Например, из пифагоровых треугольников (5, 12, 13)
и (35, 12, 37) получаем треугольник (13, 40, 37) с пло-
щадью 240 и треугольник (13, 30, 37) с площадью 180.
4*
99
В этом случае оба треугольника — тупоугольные.
Из пифагоровых треугольников (5, 12, 13) и (9, 17, 15)
можно получить два: 1) остроугольный со сторонами
(13, 14, 15) и площадью 84 и 2) тупоугольный со сторо-
нами (13, 4, 15) и площадью 24.
Из двух основных пифагоровых можно составить геро-
нов треугольник следующим образом. Возьмем два тре-
угольника (примечание 16): (4&2 — 1, 4&, 4Л2 +1) и[4&2 — 1,
4&2 (2k2 — 1), 4&2 (2k2 —1) +1] с общим катетом 4&2 — 1.
Треугольники 4&2 + 1, 4/г2 (2k2— 1) ±4 A, 4k2 (2k2— 1) +
+ 1 — героновы при любом целом и положительном k.
Площадь их равна [2А2 (2k2 — 1)4- 2k] {4k2 — 1).
Примечание 28 к 11.4
(4s)2 = 2р (2р — 2d) (2р — 2Ь) (2р — 2с) —
= {6k^3)(2k + 3){2k+l)(2k— 1) =
= (12k2 + 24/г + 9) (4 k2 — 1) =
= 4 (3/г26£ + 2) (4Л2— 1) + 4/г2 — 1 =
= 4 (ЗА2 + 6& + 2)(4й2 — 1) + 4&2 — 4+ 3 =
= 4 (3/г2 + 6k + 2) (4А2 — 1) + 4 (/г2 — 1) + 3.
Героновы треугольники, у которых стороны выража-
ются тремя последовательными числами.
Стороны, как мы видели, могут быть обозначены сле-
дующим образом: 2k—1,2А, 2&+1.
Приведем некоторые свойства этих треугольников.
1)	Рассматриваемые треугольники не могут быть тупо-
угольными. В самом деле:
(2k + I)2 = (2k)2 + (2k — I)2 + x.
Покажем, что х ^0 :
4/г2 + 4/г + 1 = 4/г2 4- 4/г2 — 4/г + 1 + л,
8А — 4/г2 = л, 4k (2 — k) = х.
При А=1 не существует треугольника.
При А = 2, л = 0 и геронов треугольник обращается в
основной пифагоров треугольник (3, 4, 5).
При всяком k > 2, х < 0 и геронов треугольник остро-
угольный.
2)	Высота, опущенная на среднюю сторону, делит ее на
два отрезка, разность которых постоянна и равна 4.
100
Назовем отрезки основания, определяемые высотой х
и у и пусть х^>у.
x-}-y = 2k; (1)
(2k + I)2 — х2 = (2k — I)2 —у2;
8/г = л2—-у2; (2)
х—у = 4.
3)	h2 = (2k + 1 )2 — (k + 2)2 = (2k — 1 )2 — (k — 2)2 =
= 3(Л2 — 1) = 3(k + 1) (k — 1).
Так как h2 делится на три, то и h делится на три, а
поэтому h2 делится на девять и один из множителей (k-]~ 1)
или (k — 1) делится на три. Предположим, что k -|-1 =
= 3£, тогда k — l—3t — 2,2k —Qt — 2.
Итак, 2k на 3 не делится.
Так как из трех последовательных чисел одно всегда
делится на три, a 2k на три не делится,то либо
либо 2k — 1 делится на три.
4)	Высота, опущенная на среднюю сторону, делит тре-
угольник на два пифагоровых, из которых только один
основной.
Так как h кратно трем и в одном из треугольников
гипотенуза кратна трем, то этот треугольник не может
быть основным. Если, допустим, что треугольник с гипо-
тенузой 2k — 1 и катетом k — 2 не основной, то треуголь-
ник с гипотенузой 2k -ф-1 и катетом k Ц- 2 — основной.
Действительно, k 2, k — 1 — взаимно простые числа
(тройка не может быть их делителем). Следовательно,
k -f- 2 и 2k 1 взаимно простые.
5)	Найти cosa, если а угол, противоположный стороне
2k — 1.
(2k —
l)2 = (2k + I)2 + (2k)2 — 4k (2k + 1) cosa;
6)	Нельзя ли заменить 2k другим отрезком так, чтобы
две стороны остались без изменения, а треугольник остался
бы героновым, т. е. имел бы площадь, выраженную нату-
ральным числом?
Обозначив искомую сторону через х, получим:
(2k — I)2 = (2k + I)2 + х2 — 2х (2k + 1) cosa,
x2 — 2 (k 4- 2) x Ц- 3k — 0,
x, = 2k, x=4k.
X	J
101
Итак, если в треугольнике со сторонами 2fe—1, 2k
заменить среднюю сторону постоянной, равной 4, то но-
вый полученный треугольник — геронов.
Найдем cos р, где р— наибольший угол.
(2А 4- I)2 = (2k — I)2 + (2k)2 — 4А (2k — 1) cos p;
b _ 9
u	2A2 +1
Наконец, cos у =	.
7)	Так как г — радиус вписанного круга, тогда имеем:
9г2 = 3&2 —3,	3r2 = k2— I, kz — 3r2 = l. (3)
Решая в целых числах последнее уравнение (см. А. И.
Гельфонд, Решение уравнений в целых числах, стр. 31),
получаем:
A = i[(2 + /3)” + (2-/3)"],
JU
h=3r = -£=[(2 + /3)" - (2 - /5)"] =
jy о
[(2 4-/3)”-
-(2-/3)"],
S=^-[(7 + 4/3)" — (7 — 4/3)”].
Пусть kn и hn — решения уравнения (3), покажем, что
kn+l = akn-\-bh„ и hn+1 — ckn-{-dhn также решения и
найдем a, b, с, d.	_
•J( 2 + /3)”+~ (2 — /3)” 4- ^-(2 + /3)" —
— ^р(2—/3)"=(2+/3)”(д	ьУз) 4- (2.~/3)Пх
Х(а-^/3) = £±^
! Al/Т о 1Лп I (2-/3)”
(2—У3)”+1 __(2 + УЗ)”
(a — Z>/3 — 2+/3) =
= 0
|(2 + /3)" +1(2 - / 3)” + ф(2 + /3)" - d-^
X(2 — /3)” = ^(2 + /3)"+I — /?(2 — /3)"+1.
(2 4-/3)"(c4-6f/3 —2/3 —3)4-(2 —/3)”(с —^/3 +
4-2/3 —3) = 0 с —3; (Z=2.
102
Итак, kn+i^=2kn-\-hn и /г„+1 = 3/гп-|-2/гп.
Можно непосредственно проверкой показать, что если
k и h — решения уравнения (3), то 2А —А и ЗА —2/z
также решения уравнения (3).
Действительно, предположив, что
(3k 4- 2Л)2 = 3 (2k + hy — 3,
9 k2 +12hk + 4 A2 = 12A2 4- 12kh + 3h2 — 3.
Получим: h2 = 3k2 — 3.
Доказанное свойство позволяет последовательно на-
ходить решения уравнения (3).
Легко видеть, что так как k — 2 и h — З удовлетво-
ряет уравнению (3), то k2 = 2 • 2	3 = 7 и Л2=12.
^ = 2-7 + 12 = 26, й8 = 21 + 24 = 45.
Приведем таблицу, заключающую первые восемь ге-
роновых треугольников, стороны которых выражаются
тремя последовательными числами.
Г’"					  2k -1	2k	2k +1	h	5
3	4	5	3	6
13	14	15	12	84
51	52	53	45	1170
193	194	195	168	16296
723	724	725	627	226974
2701	2702	2703	2340	3161340
10083	10084	10085	8733	44031786
37633	37634	37635	32592	613283664
И таблицу, получающуюся из первой, заменой сред-
ней стороны на постоянную величину, равную 4.
2k — 1	c	26-H	h	$
3	4	5	3	6
13	4 A	15	12	24
51	4 4	53	45	90
193	4	195	168	336
723	4	725	627	1254
2701	4	2703	2340	4680
10083	4 4	10085	8733	17466
37633	4	j 37635	32592	65184
103
8)	Некоторые из треугольников, приведенных в таб-
лице, могут быть получены очень просто из следующих
соображений.
Пусть 2k — 1, 2k, 2 Л 4~ 1 — стороны геронова треу-
гольника и h = V 3 (k — 1) (k 1) — натуральное число.
Покажем, что треугольник со сторонами 2k' — 1,
2A', 2k' 4“ 1, где К — 2&2 — 1 — геронов. Действительно,
Л'=]ЛЗ(Л' — 1)(А'4-1)= ]/3(2&2 — 2)2Л2 =
= 2k ДЛЗ (/г— 1) (А-(- 1),
h! — натуральное число.
Итак, если треугольник со сторонами 2k — 1, 2k,
2k 4~ 1 — геронов, то треугольник со сторонами 4Л2 — 3,
4А2 — 2, 4Л2 — 1 — геронов.
Например, из треугольника со средней стороной 4 по-
лучаем треугольник со средней стороной 42— 2=14,
треугольник со сторонами 13, 14, 15. Из полученного
треугольника имеем 142 — 2 = 194. Новый треугольник
193, 194, 195.
Следующий треугольник (1942 — 2 = 37634) 37633,
37634, 37635 и т. д. Таким образом, можно получить
сколько угодно новых треугольников, но не все героновы
треугольники, у которых стороны выражаются тремя по-
следовательными числами.
Примечание 29 к 11.5
При разбиении рационального треугольника на два
рациональных прямоугольных, требование, чтобы высота
рационального треугольника проходила внутри треуголь-
ника, излишне.
Действительно, пусть дан тупоугольный рациональ-
ный треугольник АВС, Опустим из вершины С на сто-
рону высоту CD,
Пусть а, Ь, с —стороны треугольника, h — высота.
Обозначив через ах и Ьг соответственно проекции сто-
рон а и b на сторону с, имеем:
а\ — Ь1 = с.
104
(1)
Мы получим два прямоугольных треугольника (at, h, а)
и (bt, h, b). Покажем, что их стороны рациональны.
Для этого надо показать рациональность и bt.
Действительно,
Из равенств (3) следует рациональность отрезков at
и ЪОтсюда следует, что высота, проведенная из вер-
шины рационального треугольника, делит его на два пря-
моугольных рациональных треугольника.
Примечание 30 к 11.5
Пусть дан катет, выражающийся числом, имеющим
своими делителями простые числа.
Покажем, что из основных пифагоровых треугольни-
ников с этим общим катетом можно составить 2"_ 1 (2”-1—1)
рациональных треугольников, где п — число простых де-
лителей числа, выражающего общий катет (см. примеча-
ние 16). Из этих треугольников можно составить
9	2ZZ~1 (2ZZ"1 — 1)
-------------------- пар пифагоровых треугольников,
а так как каждой паре соответствует пара рациональных
треугольников, то общее число треугольников равно
(2"-1 —1).
2л-1
Например, при п=1, получаем нуль треугольников.
При « = 2 получаем два рациональных треугольника.
При и = 3 получаем двенадцать треугольников.
Примеры. Пусть л = 85 (85, 3612, 3613) и (85,
132, 157).
Из этих двух пифагоровых треугольников получаем
два рациональных: (157, 3744, 3613) и (157, 3480, 3613).
105
Площадь первого 159120, площадь второго 147900, а
высота каждого, опущенная на среднюю сторону, равна 85.
При х =195 имеем четыре пифагоровых треугольника
с общим катетом 195 (см. примечание 16): (195,19012,19013),
(195, 2108, 2117), (195, 748, 773), (195, 28, 197).
Из этих треугольников можно составить 12 рацио-
нальных треугольников. Предварительно составим 6 пар
прямоугольных треугольников:
(195,	19012,	19013)	и	(195,	2108,	2117);
(195,	19012,	19013)	и	(195,	748,	773);
(195,	19012,	19013)	и	(195,	28,	197);
(195,	2108,	2117)	и	(195,	748,	773);
(195,	2108,	2117)	и	(195,	28,	197);
(195,	748,	773)	и	(195,	28,	197).
Из каждой пары составим пару рациональных тре-
угольников:
2117, 21120,	19013	и	2117,	16904,	19013,
773, 19760,	19013	и	773,	18264,	19013,
197, 19040,	19013	и	197,	18984,	19013,
773, 2856,	2117	и	773,	1360,	2117,
197, 2136,	2117	и	197,	2080,	2117,
197,	756,	773	и	197,	720,	773.
У каждого из этих треугольников одна из высот
равна 195.
Примечание 31 к 11.5
Героновы треугольники, у которых разность острых
углов равна 90°.
Из основного пифагорова треугольника (х, у, z), у ко-
^2   [2	4- I2
торого X = kl', у = —2 ;	Z~—гДе и *— не“
четные числа и k>lf построим треугольник со сторо-
I %2 - 4)2 1
нами х, у, *---. Этот треугольник легко получается
из (л, у, г). Из вершины С прямого угла радиусом,
равным катету СВ, засекаем гипотенузу в точке В'
(черт. 5). Треугольник ABfС со сторонами х, у,
Z
тупоугольный с разностью двух углов, равной 90°.
Одна из сторон полученного треугольника не выражается
натуральным числом. Треугольник со сторонами xz, yz,
106
|х2— -y2| основной целочисленный треугольник, который
мы будем обозначать {xz, yz, \х2—>2|}. Подставив в
выражения сторон треугольника, вместо х, у и z их зна-
чения, получим треугольник со сторонами:
kt (k2 +12) . k*-i\ (2ki + k2 - z2) (2kl — k2 + z2)
’	4	’	4
треугольника можно
где k и I — произвольные нечетные числа и^>/. Итак,
из каждого основного пифагорова
следующим образом получить ин-
тересующий нас треугольник: про-
изведение числа, выражающего
длину одного катета и числа, вы-
ражающего длину гипотенузы, рав-
но длине одной стороны, аналогич-
но получается длина второй сто-
роны, третья сторона выражается
числом, равным абсолютной вели-
чине разности квадратов чисел,
выражающих длины катетов. Высо-
та полученного треугольника чис-
ленно равна удвоенной площади
пифагорова треугольника; диаметр
окружности описанной около треугольника, численно равен
квадрату гипотенузы, а площадь	~~ F_1=£' | х*—
—у21, где S' — площадь пифагорова треугольника, а л и
у — его катеты.
Действительно, Н—высота полученного треугольника
равна высоте пифагорова треугольника, умноженной на z.
И ~^~ = xy = 2S; sina=^; sin (90° -ф- a) = cos a=^.
Отсюда следует: 1) Из основных пифагоровых тре-
угольников с общей площадью получаются треугольники
с общей высотой, численно равной удвоенной площади,
например из (21, 20, 29) и (35, 12, 37), имеющих общую
площадь, равную 210, получаются {609, 580, 41} и
{ 1295, 424, 1081 } с высотой, равной 420.
2) Из основных пифагоровых треугольников с общей
гипотенузой получаются треугольники с общим радиусом
описанной окружности, например из (63, 16, 65) и (33,
56, 65) получаются {4095, 1040, 3713} и {2145, 3645,
2047} у каждого треугольника 2R = 4225.
107
Из 64 треугольников, указанных Шеддом (см. 7.5 и
примечание 17), можно получить 64 основных целочис-
ленных треугольника, у которых разность углов равна 90°,
и диаметр описанной окружности равен 2 576450 0452.
Из основных пифагоровых треугольников (л, х -f-1, г),
т. е. таких, у которых разность катетов равна единице
(см. 4.6 и примечание 9), легко получаются рассматри-
ваемые героновы треугольники {xz, yz,	Напри-
мер, из треугольника (3, 4, 5) получается {15, 20, 7},
из (20, 21, 29) —(580, 609, 41), из (803760, 803761,
1113689)—{91362515064, 91363651763, 1607521}.
Примечание 32 к 14.1
тт	'Г	111
Для треугольника Т со сторонами —, —, — введем
X у Z
Г1 1	11
1ВОЛ Т’ Т’ Т •
Л/ у &
Из основного пифагорова треугольника (л, у, г) легко
получить треугольник, стороны которого выражаются
числами, обратными натуральным.
Из уравнения z2=x2-^y2 получаем — = ~ +
+^г- Итак, Т=	~ .
Легко видеть, что из пифагоровых треугольников с
общей площадью, получим треугольники с общей гипо-
тенузой.
Например, из треугольников (л, у, z) и (xt, ylf zj, у
которых xy=xtylf получим:
yz ’ XZ
1 1
— и 1\ = —
ху_ 1 _yrzY
1 1 1
Например, из треугольников (21, 20, 29), (35, 12, 37)
получим
ГХ 1 1 Т м Г 1	1 1 1
580’ 609’ 420J	[1295 ’ 424 ’ 420] *
Примечание 33 к 14.2
Найдем выражение высоты, опущенной на гипотенузу
треугольника
’ ZX
108
Так как Т подобен (л, у, z), причем —: Z- — ,
X/ у	Ху Z
hf 1 z, h hz 1
ТО	---- ИЛИ /I =-------=-------
h xyz	xyz xyz2, z2.
Итак, если от пифагоровых треугольников с общей
гипотенузой мы перейдем к треугольникам, у которых
стороны выражаются числами, обратными натуральным,
то у таких треугольников общая высота равна ™ , где
z — общая гипотенуза пифагоровых треугольников.
Например, из треугольников (576, 933, 1105), (744,
817, 1105), (264, 1073, 1105), (47, 1104, 1105) можно по-
лучить четыре треугольника с общей высотой, равной
1 _____ 1
11052	1221025 ’
Из 64 треугольников, указанных Шеддом (см. 7.5 и
примечание 17) можно получить 64 треугольника с об-
щей высотой, равной
1
25764500452’
Примечание 34 к 15.14
Покажем, что существует бесконечное множество
параллелепипедов, у которых ребра, диагональ и диаго-
наль грани — натуральные числа.
Действительно, возьмем основной пифагоров тре-
угольник (л, у, г) и катеты (%, у) этого треугольника
примем за ребра параллелепипеда. Выбор третьего ребра
и диагонали параллелепипеда произведем после доказа-
тельства существования основного пифагорова треуголь-
ника, катет которого равен z— гипотенузе выбранного
нами треугольника. Так как z — нечетное число, то (6.1
и примечание 12), основной пифагоров треугольник с та-
ким катетом существует. Действительно, z—zA. Обо-
значив второй катет треугольника через г, а его гипоте-
нузу— через t, получим:
Р-1 ,	?4-1 ™	,
z —— — , t——jф 1ак как z нечетно, то z и t —
натуральные числа.
109
Примем z за третье ребро параллелепипеда, a t за
его диагональ, & z— за диагональ грани
Итак, существует бесконечное множество параллеле-
пипедов, у которых ребра, диагональ и диагональ боко-
вой грани выражаются натуральными числами; одно из
ребер этого параллелепипеда и диагональ выражаются
двумя последовательными числами. Следует отметить,
что ребра и диагонали являются сторонами основных
пифагоровых треугольников.
Примеры. Исходя из треугольника (5, 12, 13), по-
лучим параллелепипед с ребрами 5, 12, 84, с диаго-
налью 85 и диагональю грани, равной 13. Если за ис-
ходный треугольник взять треугольник (л, л-f-l, г) (см.
4.6), то в параллелепипеде два ребра выразятся последо-
вательными числами, третье ребро (большее ребро) и
диагональ также выразятся последовательными числами.
Например, исходя из треугольника (3, 4, 5), получим
параллелепипед с ребрами 3, 4, 12, диагональю, равной
13; диагональ грани равна 5.
Исходя из треугольника (20, 21, 29), получим парал-
лелепипед со сторонами 20, 21, 420, диагональю, равной
421, и диагональю грани, равной 29.
Треугольник (119, 120, 169) приводит к параллелепи-
педу с ребрами 119, 120 и 14280 и диагональю 14281;
диагональ грани 169 и т. д.
Из основных пифагоровых треугольников
гипотенузой можно получить параллелепипеды с общим
ребром и общей диагональю грани.
Исходя из 64 треугольников Шедда (7.5 примеча-
ние 17), получим 64 параллелепипеда с общим ребром
и
общей
2 576 450 0452 - 1	L	2 576 450 0
-----—гр------ и с общей диагональю ----------2"
с общей диагональю грани, равной 2 576 450045.
Примечание 35 к 15.15
Если (а, Ь, с) пифагоров треугольник, то паралле-
лепипед с ребрами (ab), (яс), (be)2 имеет диагональ
t = c* — а2Ь\
110
Действительно,
аЧ? + а4с4 + 6V = аЧ>* + с4(й4 4- Ь1) =
= а464 4- с4 Г(<2а + by — 2агЬ2] = а464 4- с2 — 2а2/>2с4 =
= (с4 — а2Ь*)\
Примечание 36 к 15.15
Уравнение х4-|~_у4z4 = f2 имеет решения в нату-
ральных числах.
Например: 1) х= 12, у = 15, z = 20, / = 481,
2) х = 420, у = 580, г = 609, / = 530881.
Примечание 37 к 15.16
Предположение Эйлера может быть сформулировано так:
Уравнение х4 -|-у* -ф- = /4 не имеет решений в
натуральных числах.
Примечание 38 к 15.17
Следует писать х = а | (4 Ьг — с2) |, у = b | (4а2 — с2) |.
СОДЕРЖАНИЕ
Предисловие редактора перевода..............................  3
§ 1.	Пифагоровы треугольники...............................
Основные пифагоровы треугольники ........................ 5
§ 2.	Отыскание основных пифагоровых треугольников ...	7
§ 3.	Пифагоровы треугольники со сторонами, меньшими 100 12
§ 4.	Пифагоровы треугольники, у которых две стороны выра-
жаются последовательными целыми числами......................13
§ 5.	Делимость одной из сторон пифагорова треугольника на
3 или на 5...................................................19
§ 6.	Значение сторон пифагоровых треугольников .... . 21
§ 7.	Пифагоровы треугольники с общим катетом или с об-
щей гипотенузой..............................................22
§ 8.	Пифагоровы треугольники с общим периметром .... 24
§ 9.	Пифагоровы треугольники с общей площадью .... 25
§ 10.	Пифагоровы треугольники, у которых по крайней мере
одна сторона является квадратом............................  30
§ 11.	Треугольники, стороны и площади которых выража-
ются натуральными числами. Треугольники, площади которых
выражаются натуральными числами и стороны выражаются нату-
ральными последовательными числами. Рациональные треуголь-
ники 	37
§ 12.	Пифагоровы треугольники, у которых гипотенуза и
сумма катетов — квадраты..............................  ....	43
§ 13.	Определение пифагоровых треугольников при помощи
точек плоскости..............................................59
§ 14.	Прямоугольные треугольники, стороны которых выра-
жаются числами, обратными натуральным числам.................62
§ 15.	Параллелепипеды, ребра и диагонали которых выража-
ются натуральными числами ...................................64
Примечания...............................................74
Цена 1 р. 90 к.