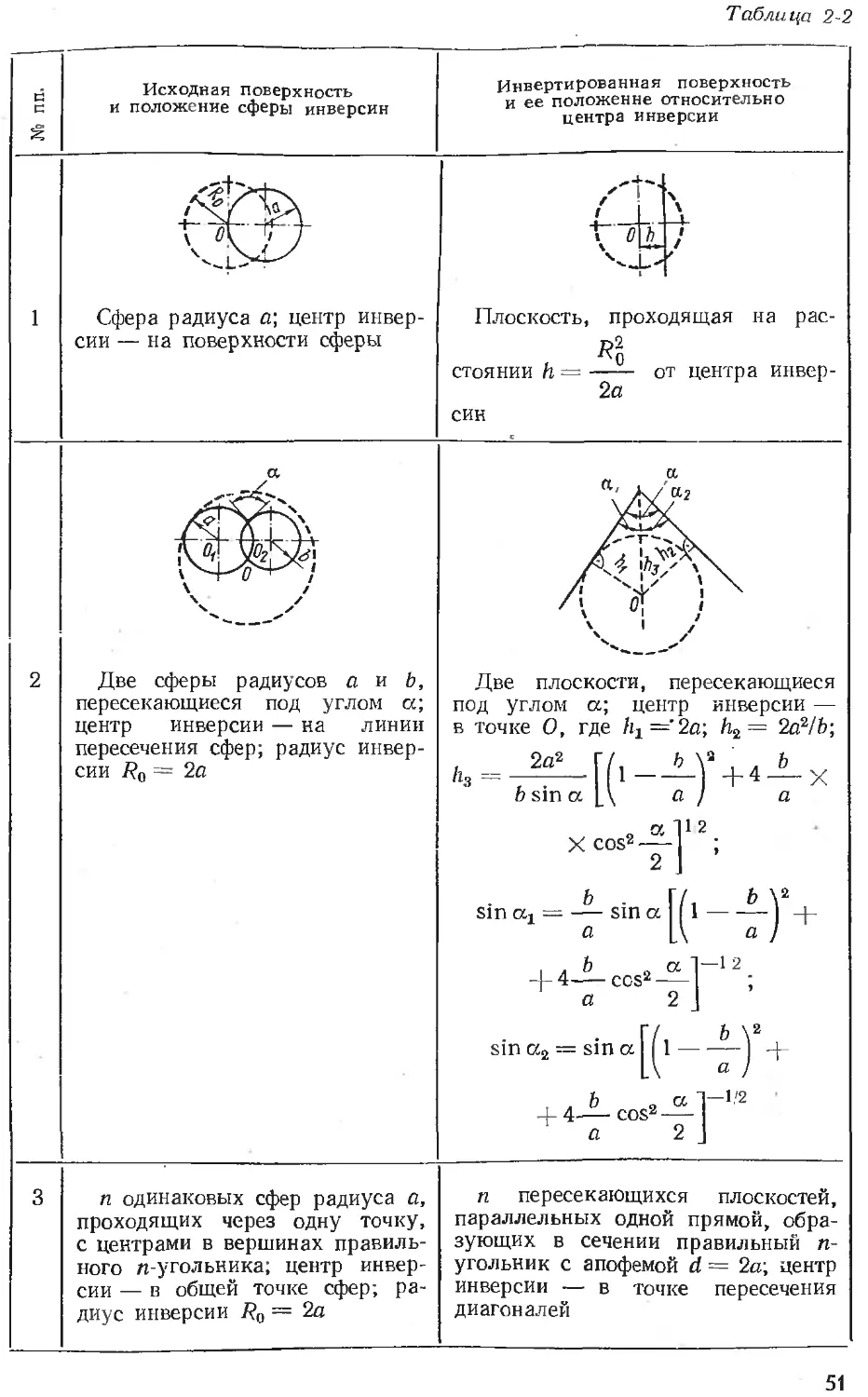
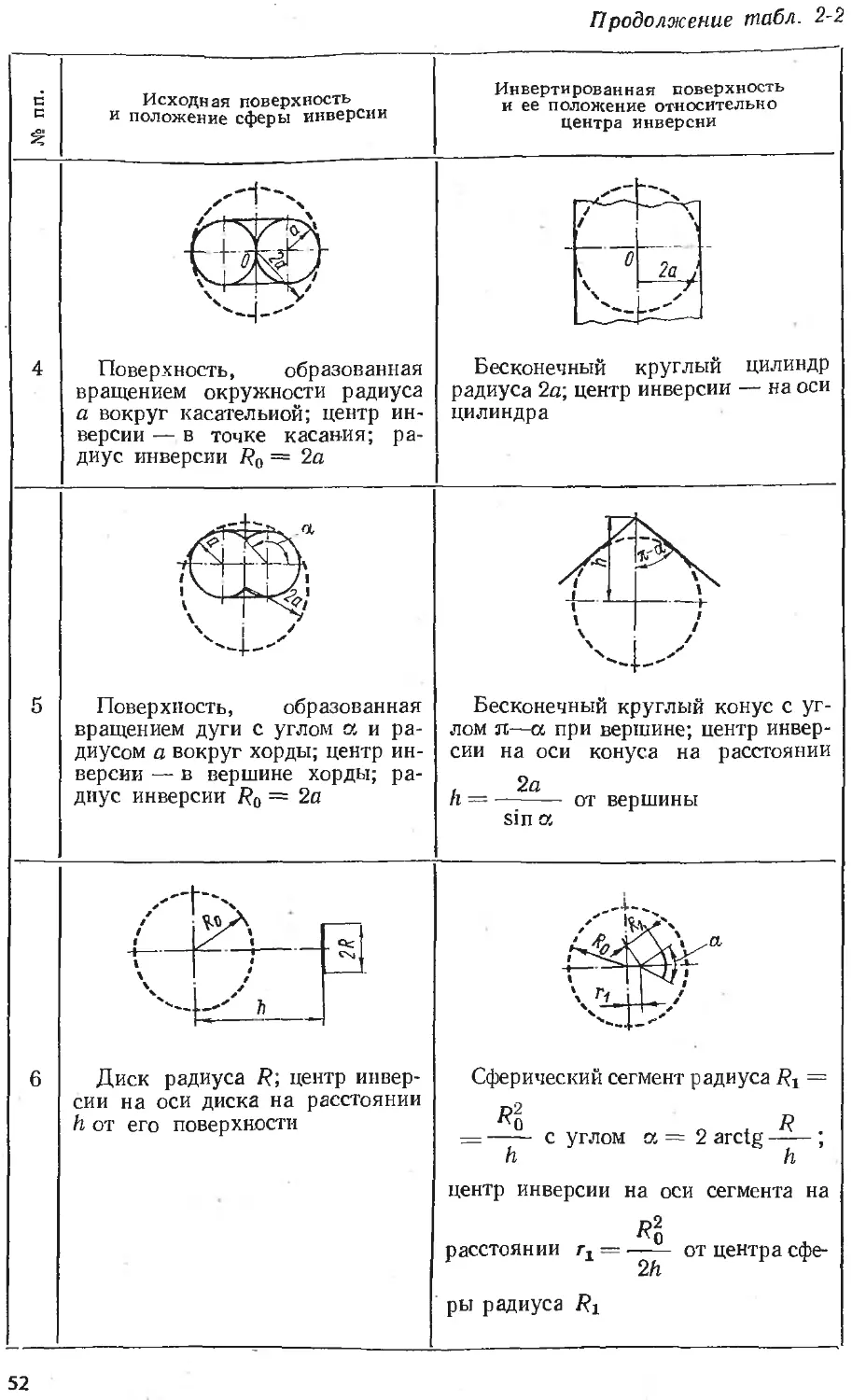
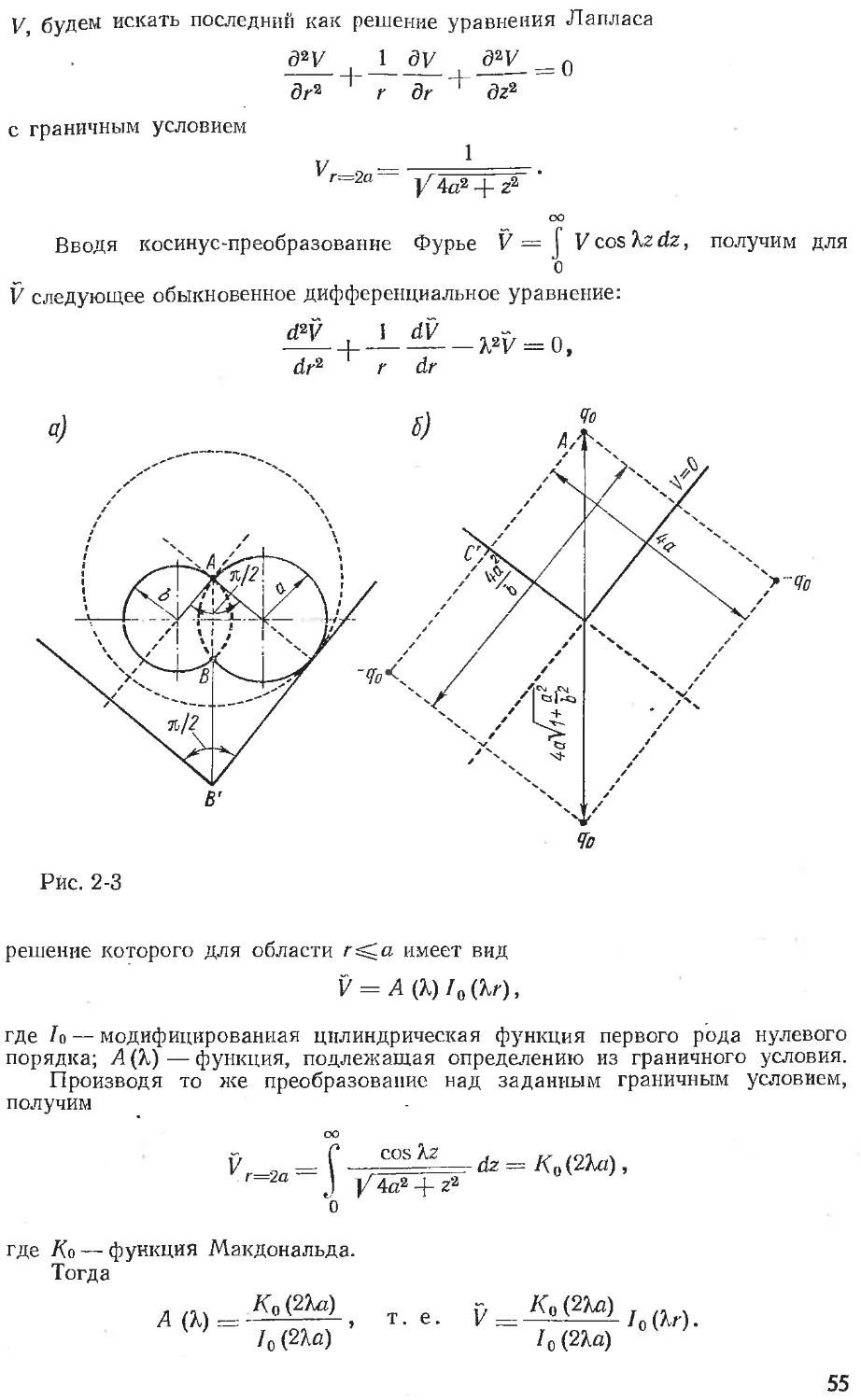
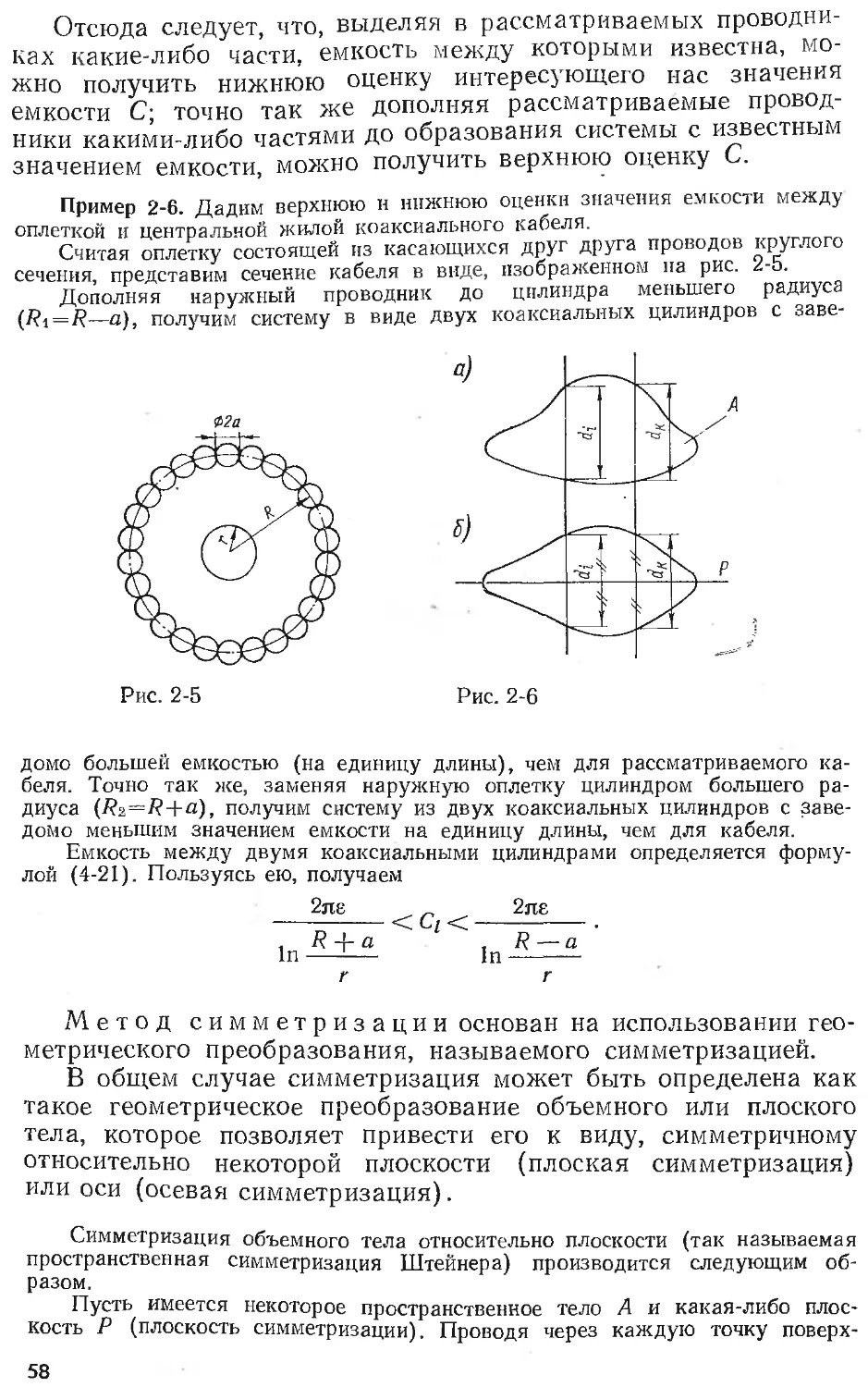
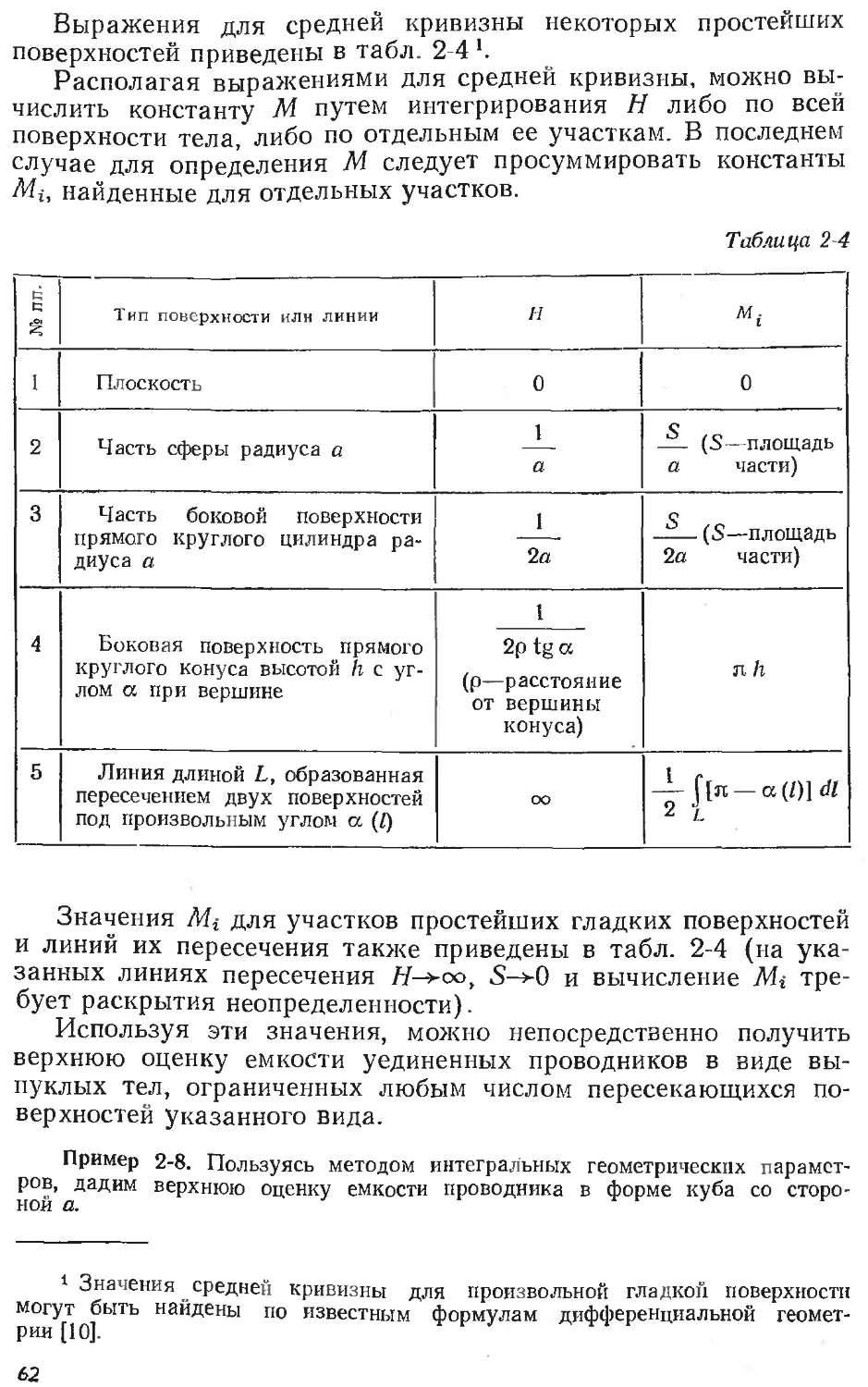
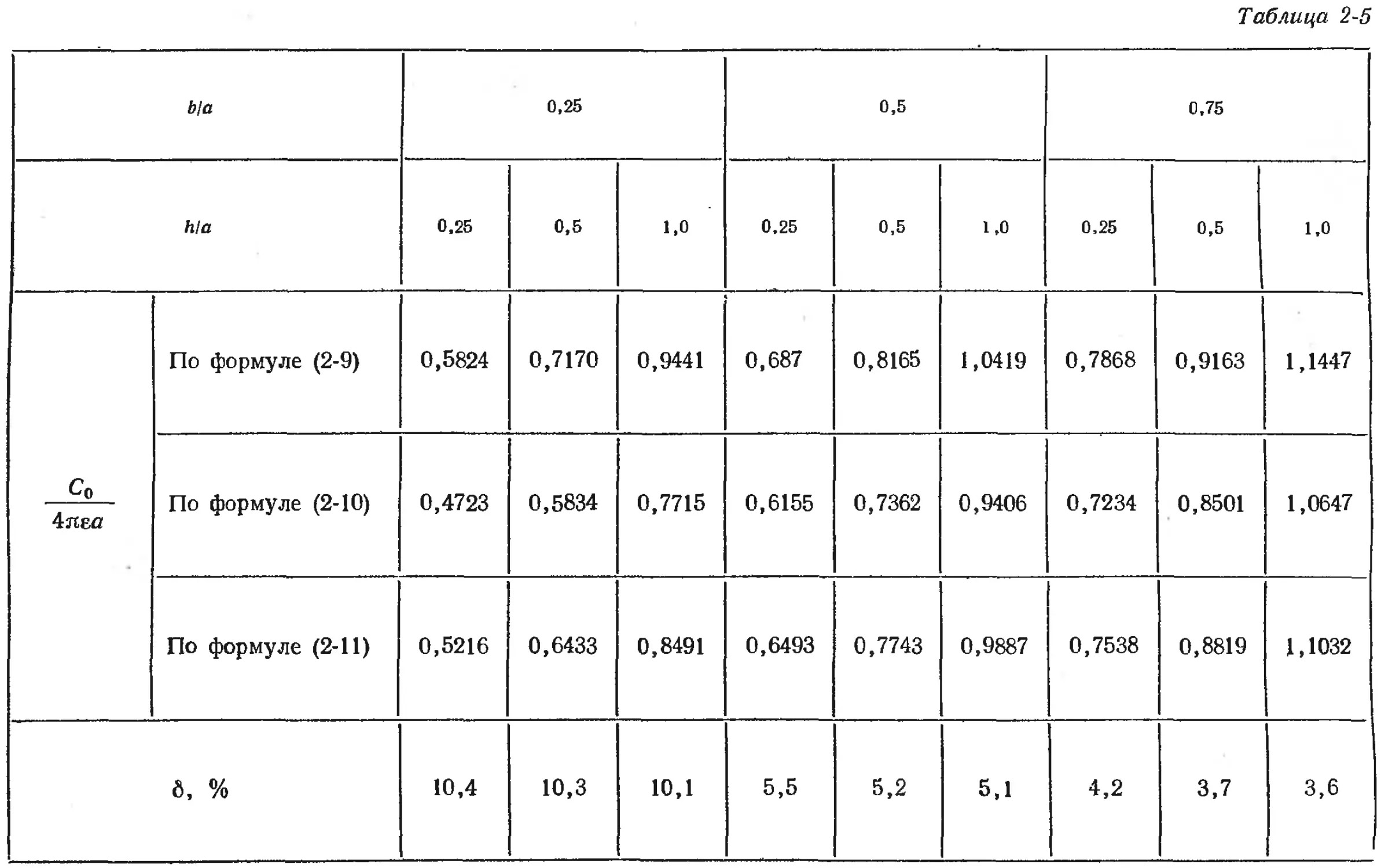
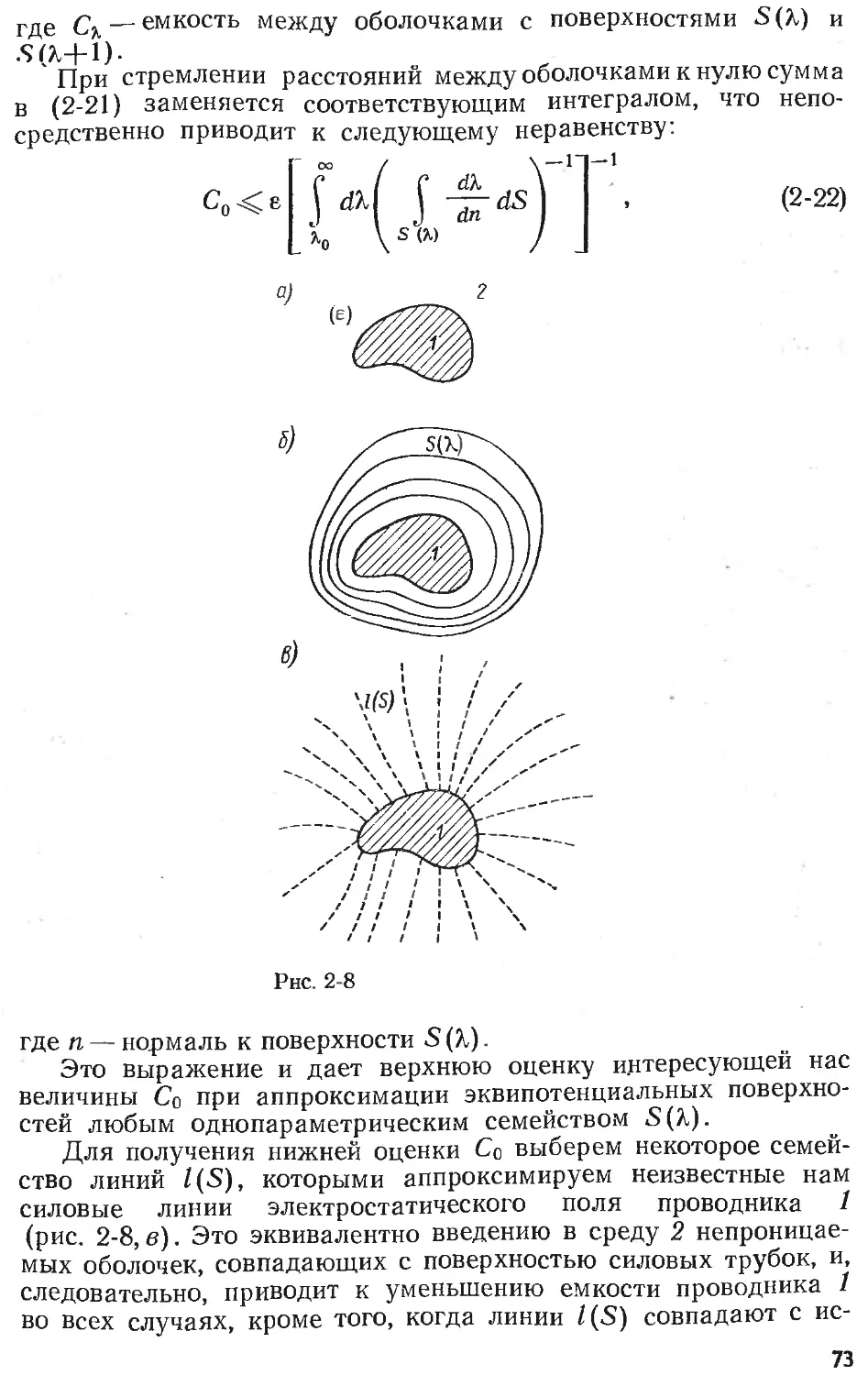
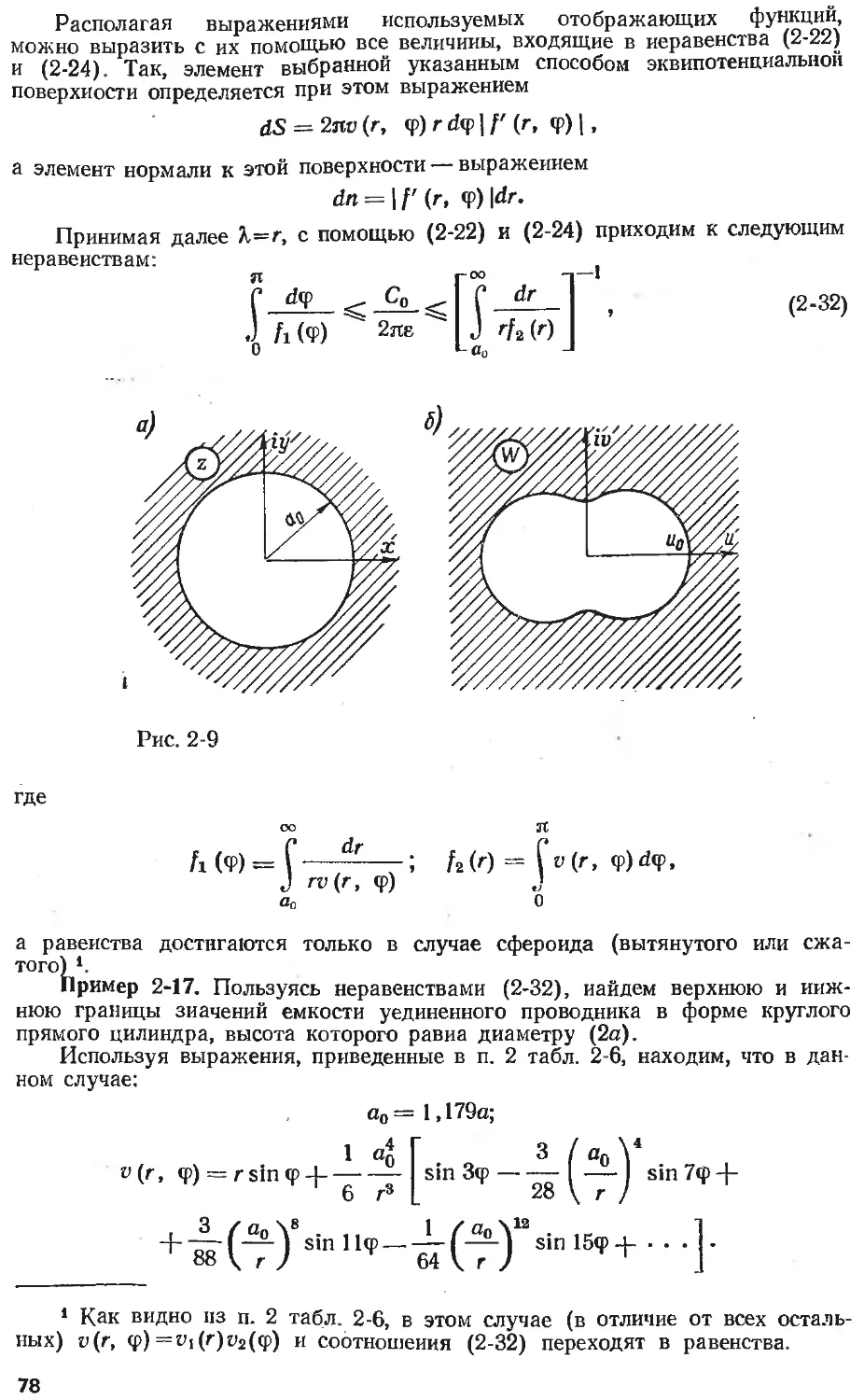
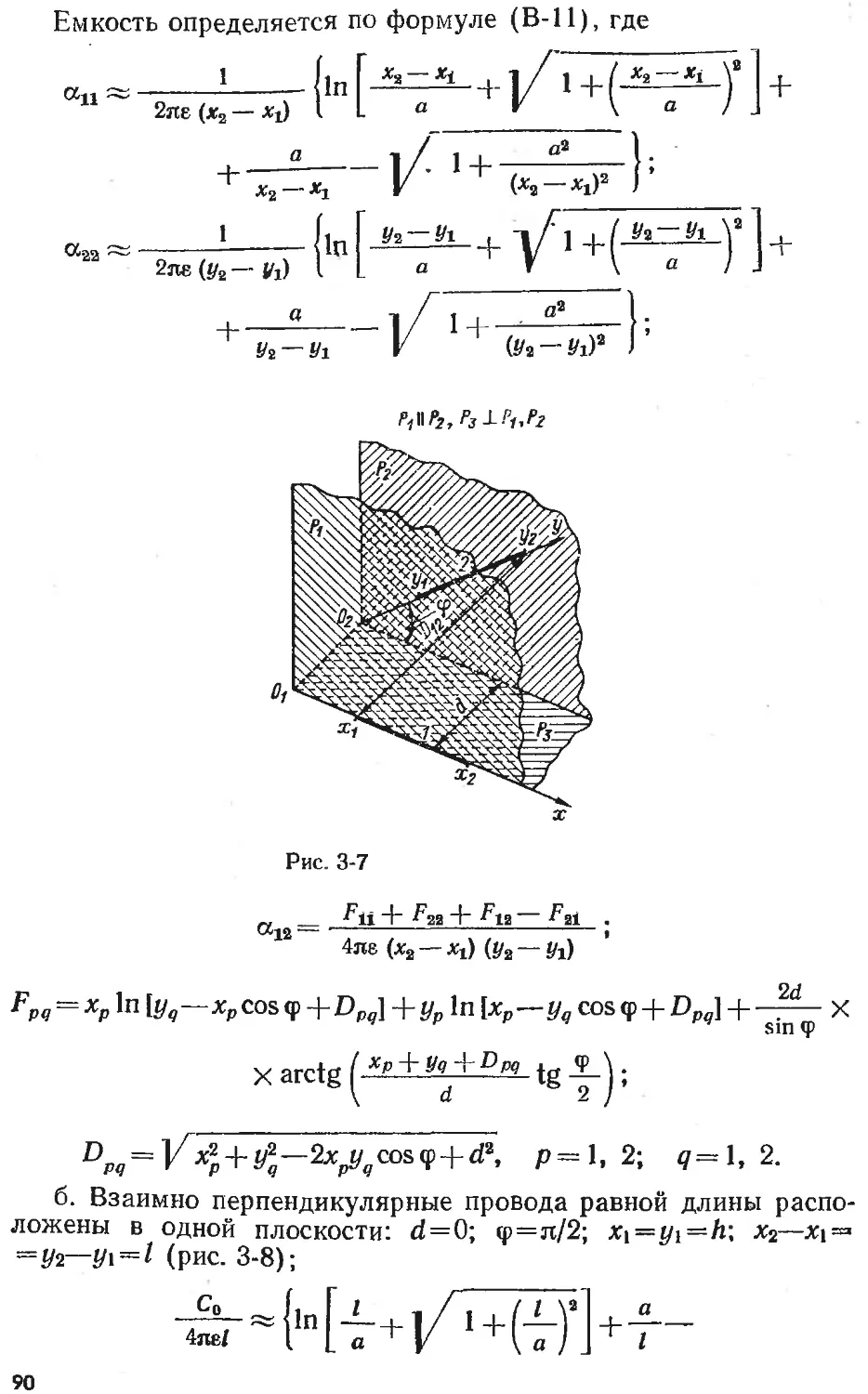
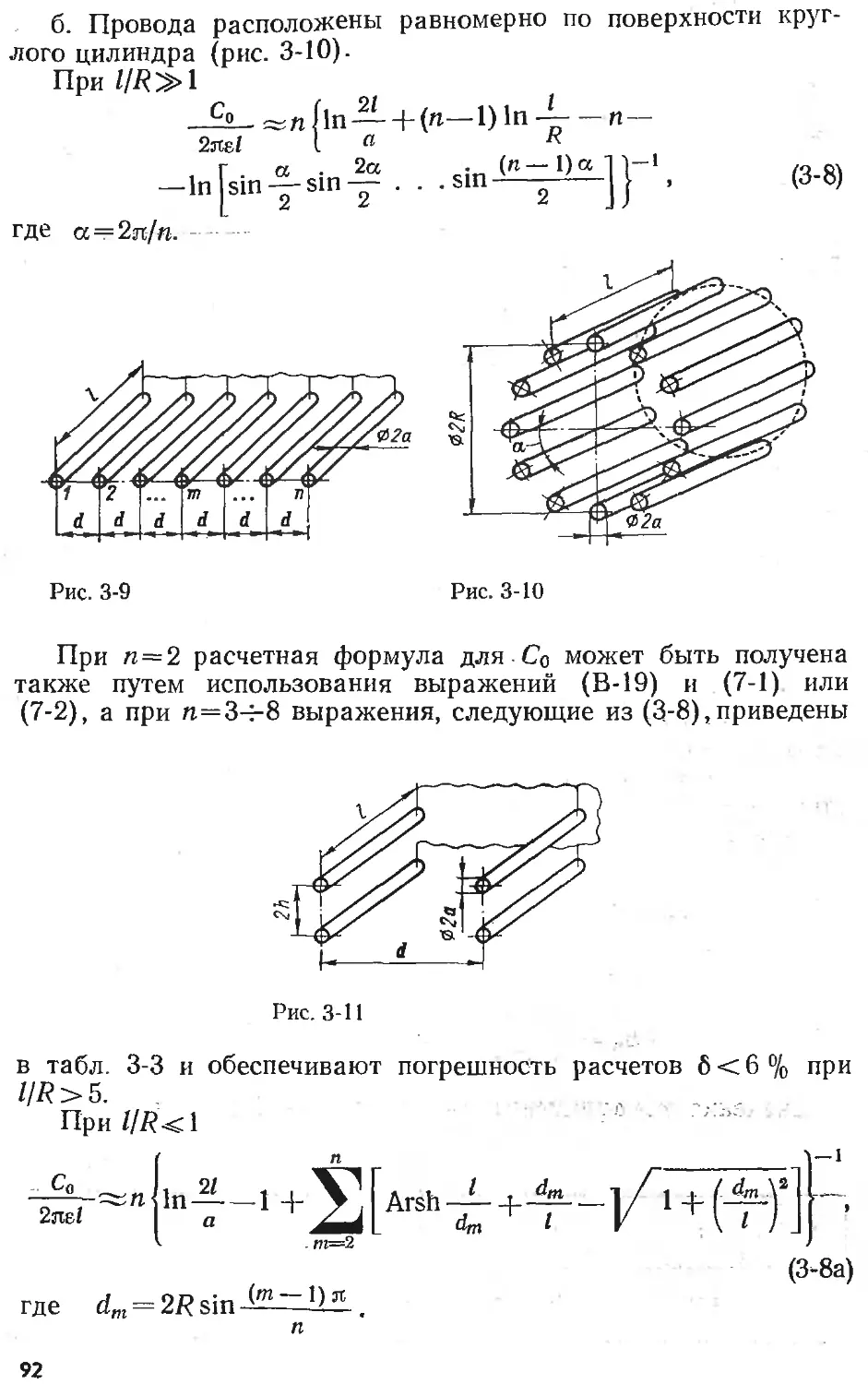
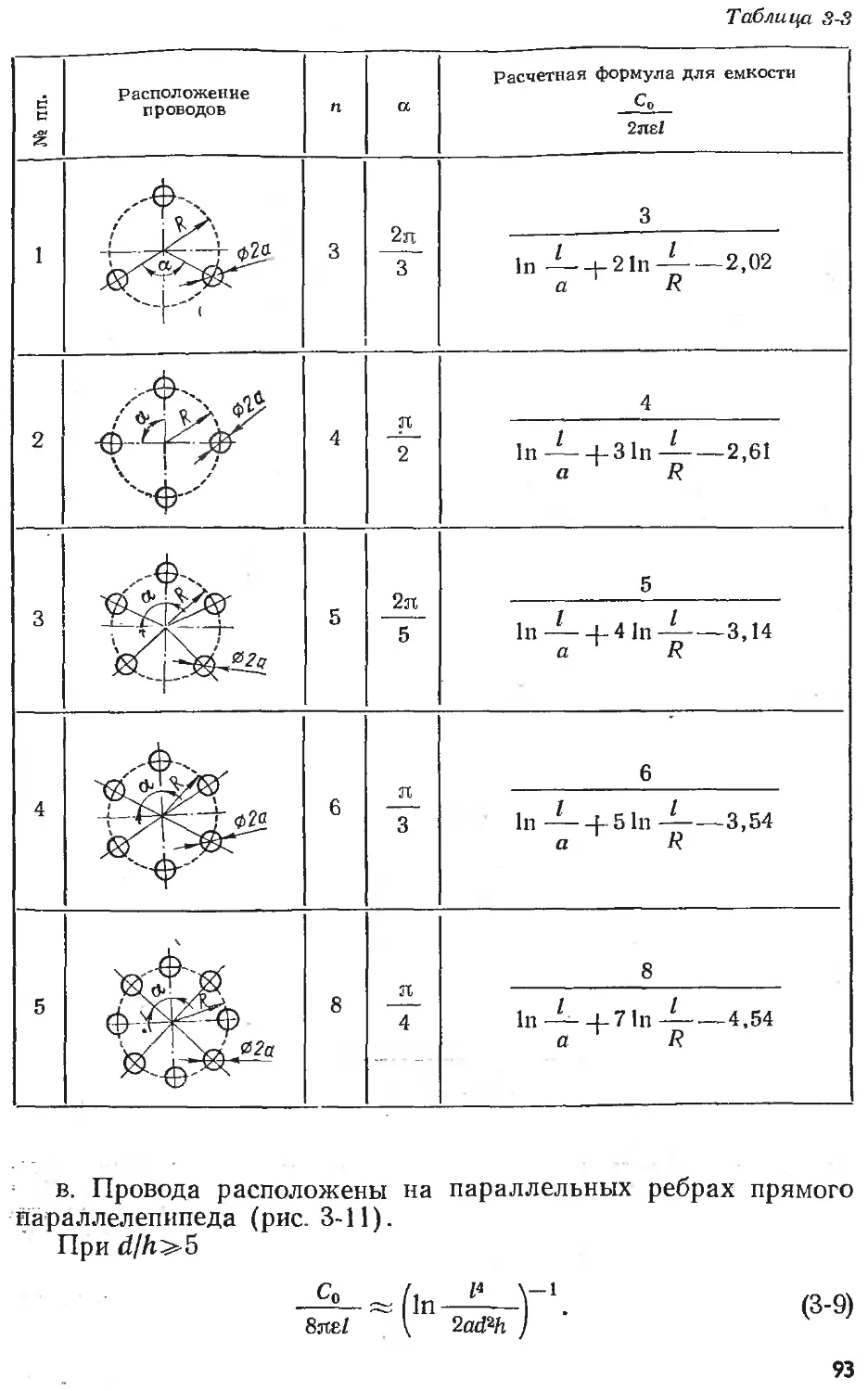
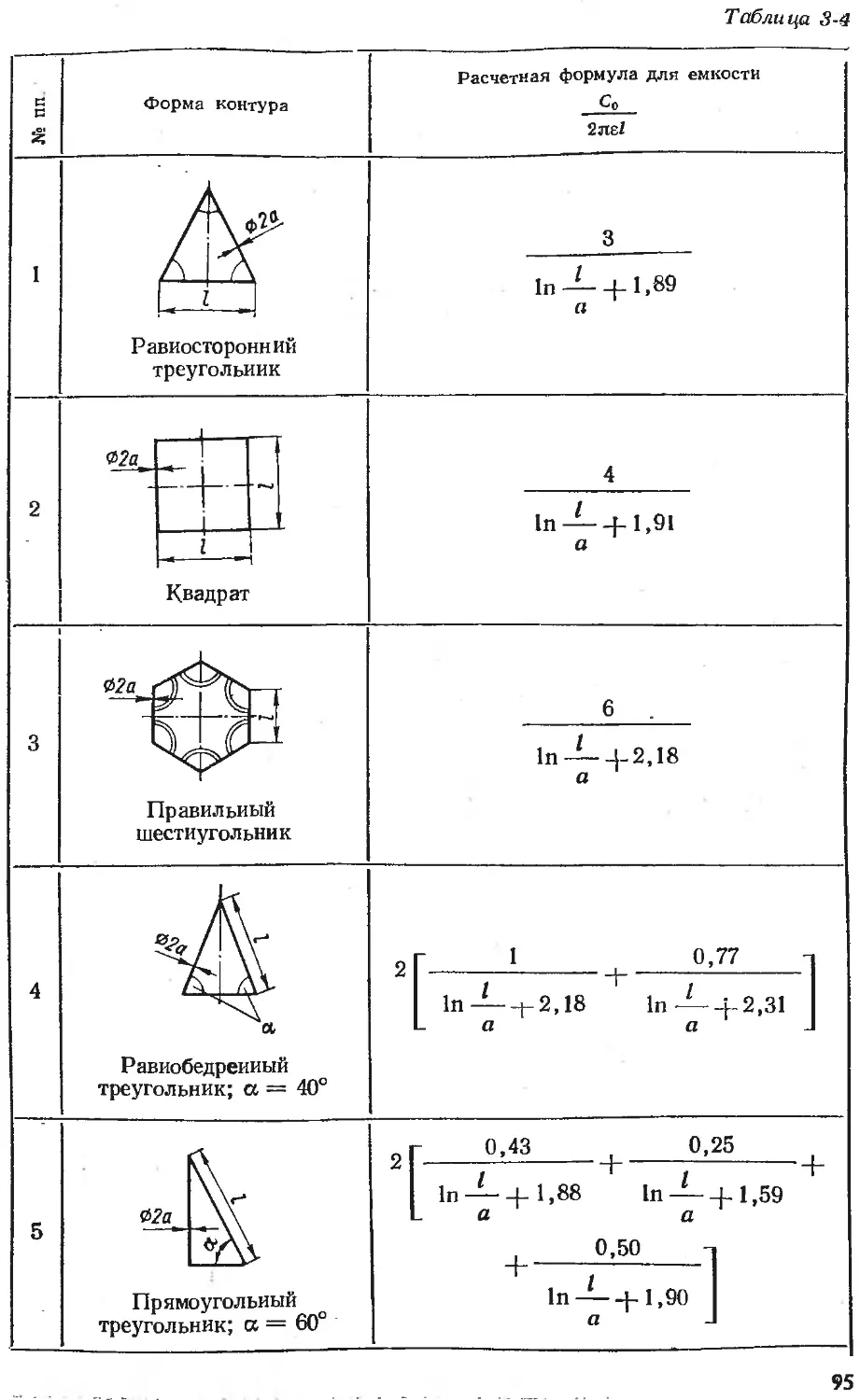
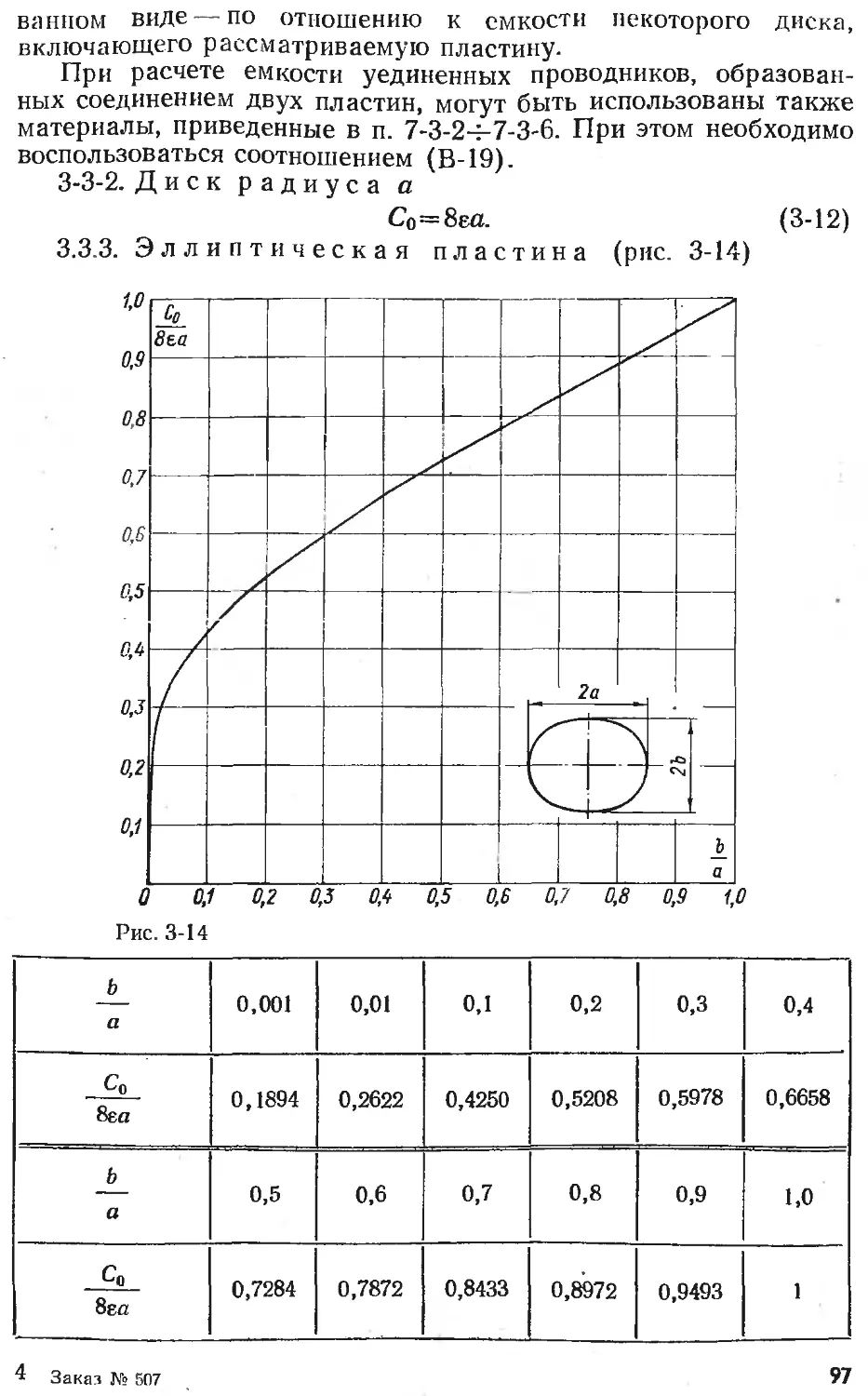
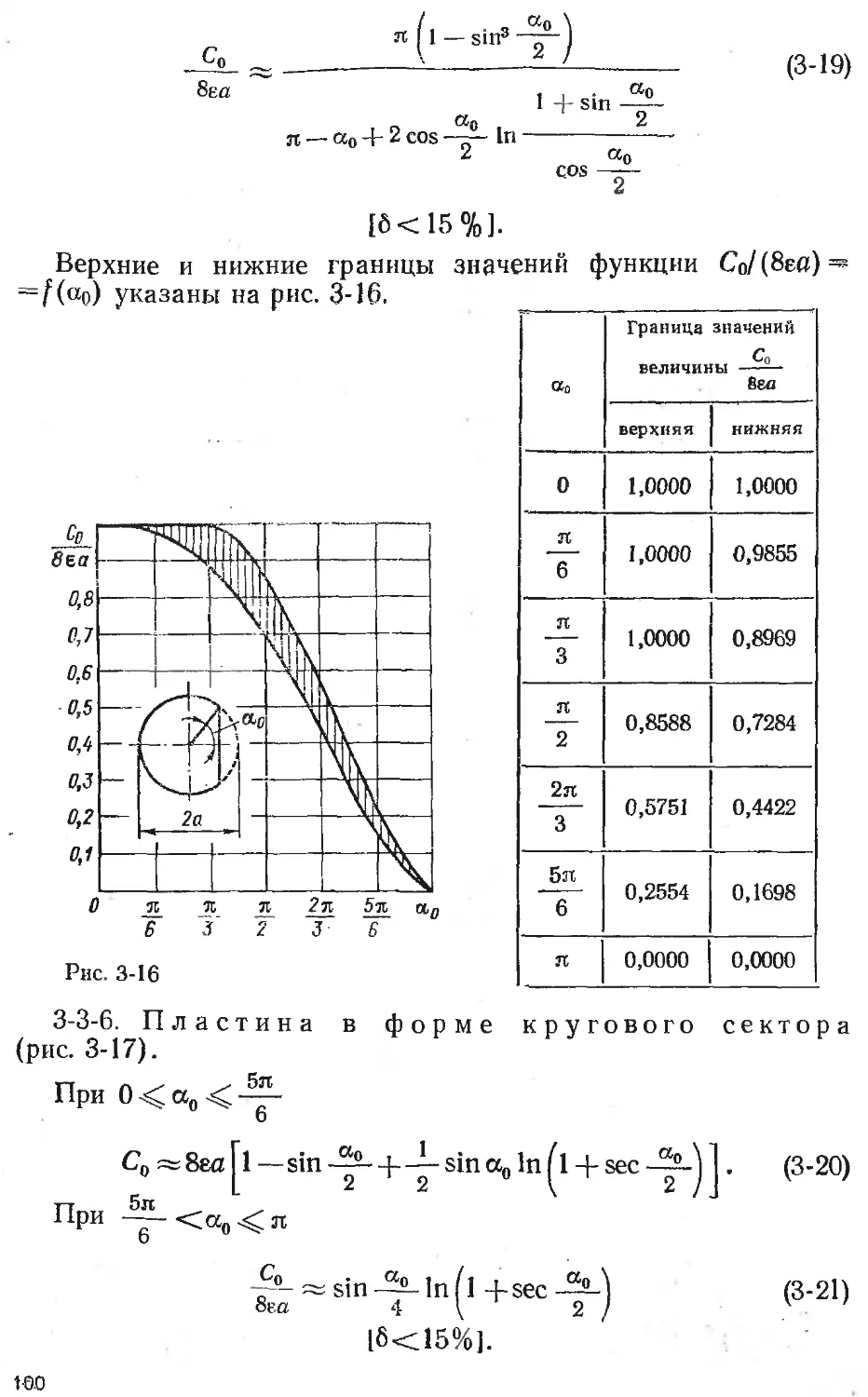
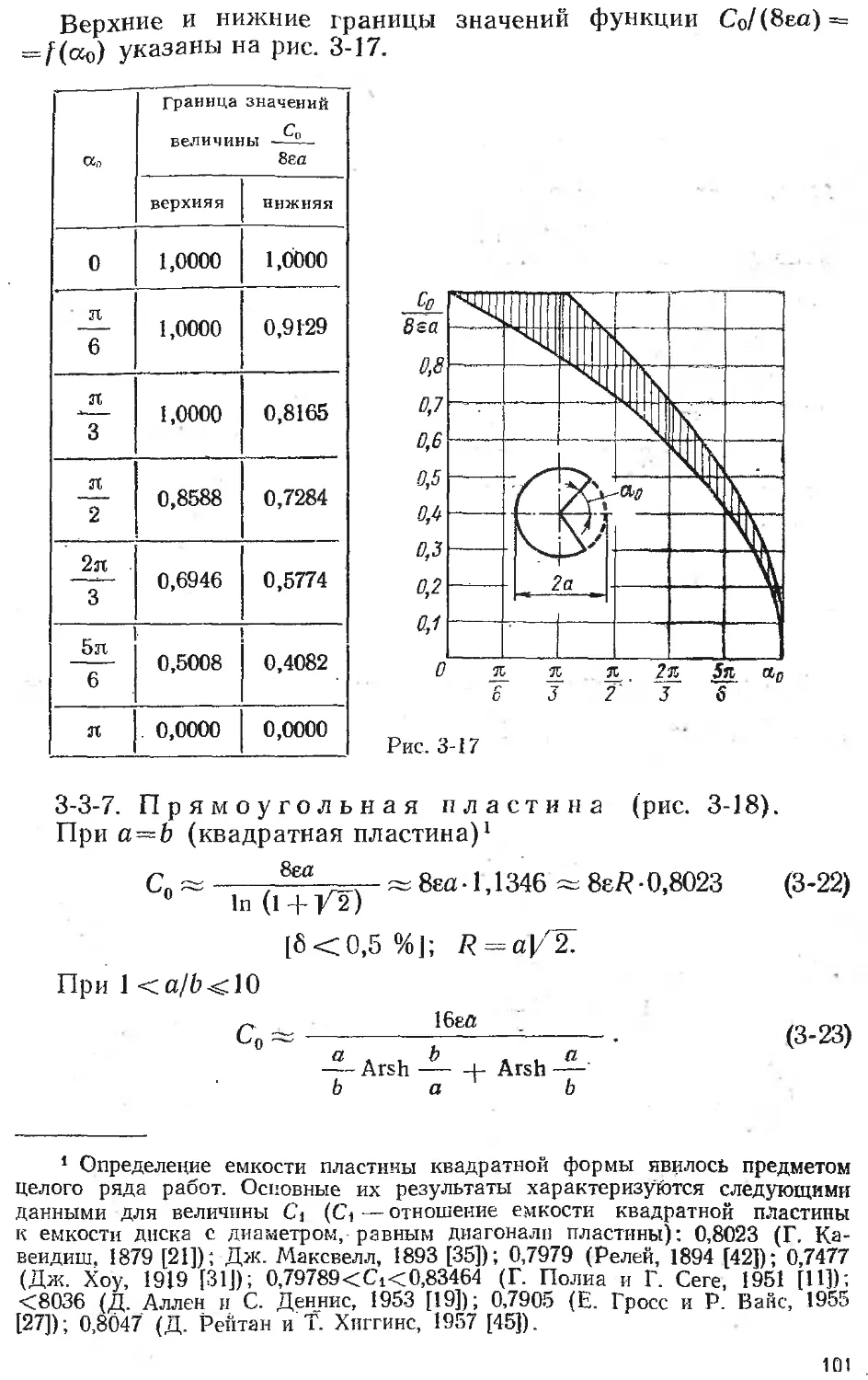
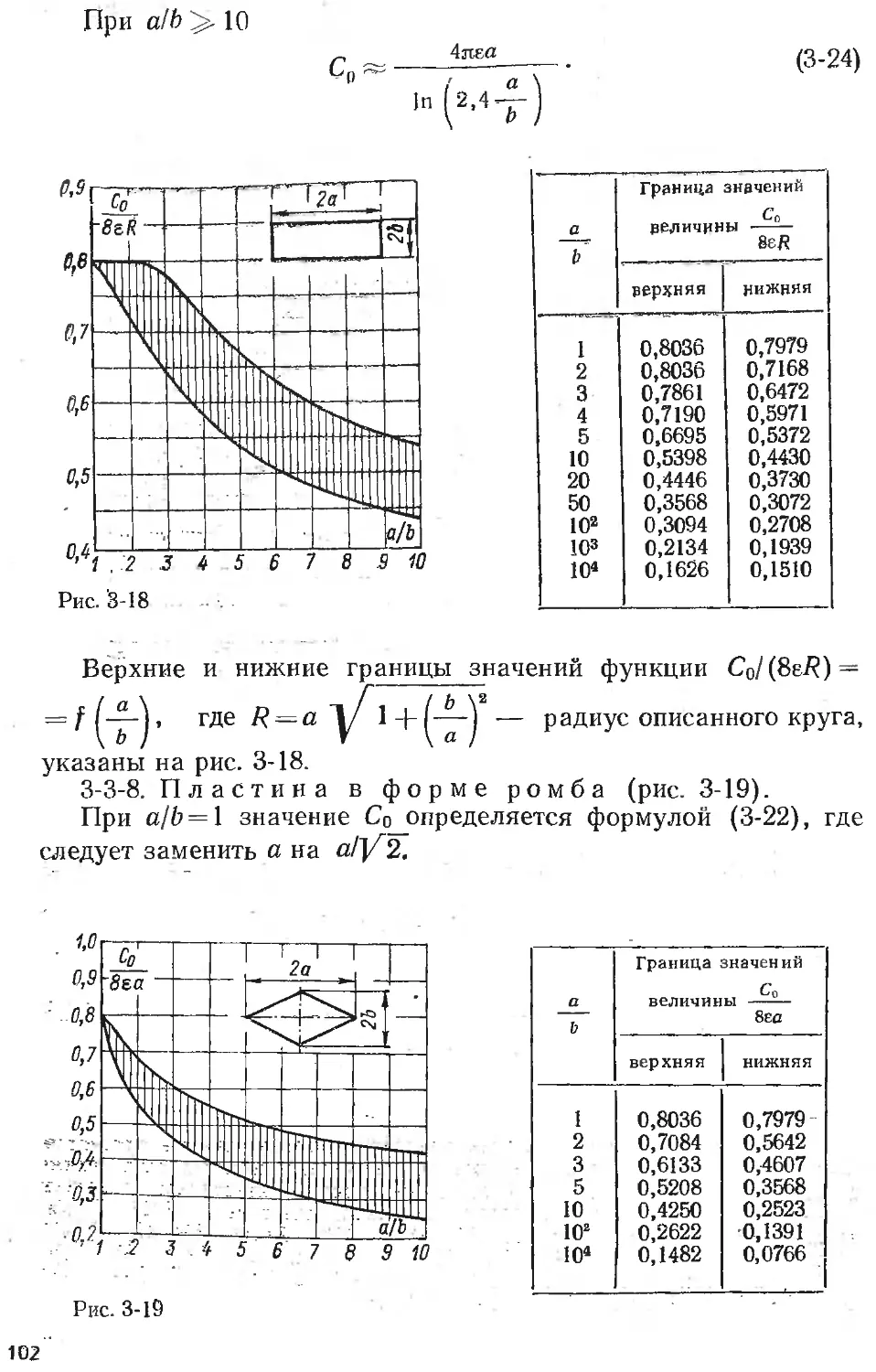
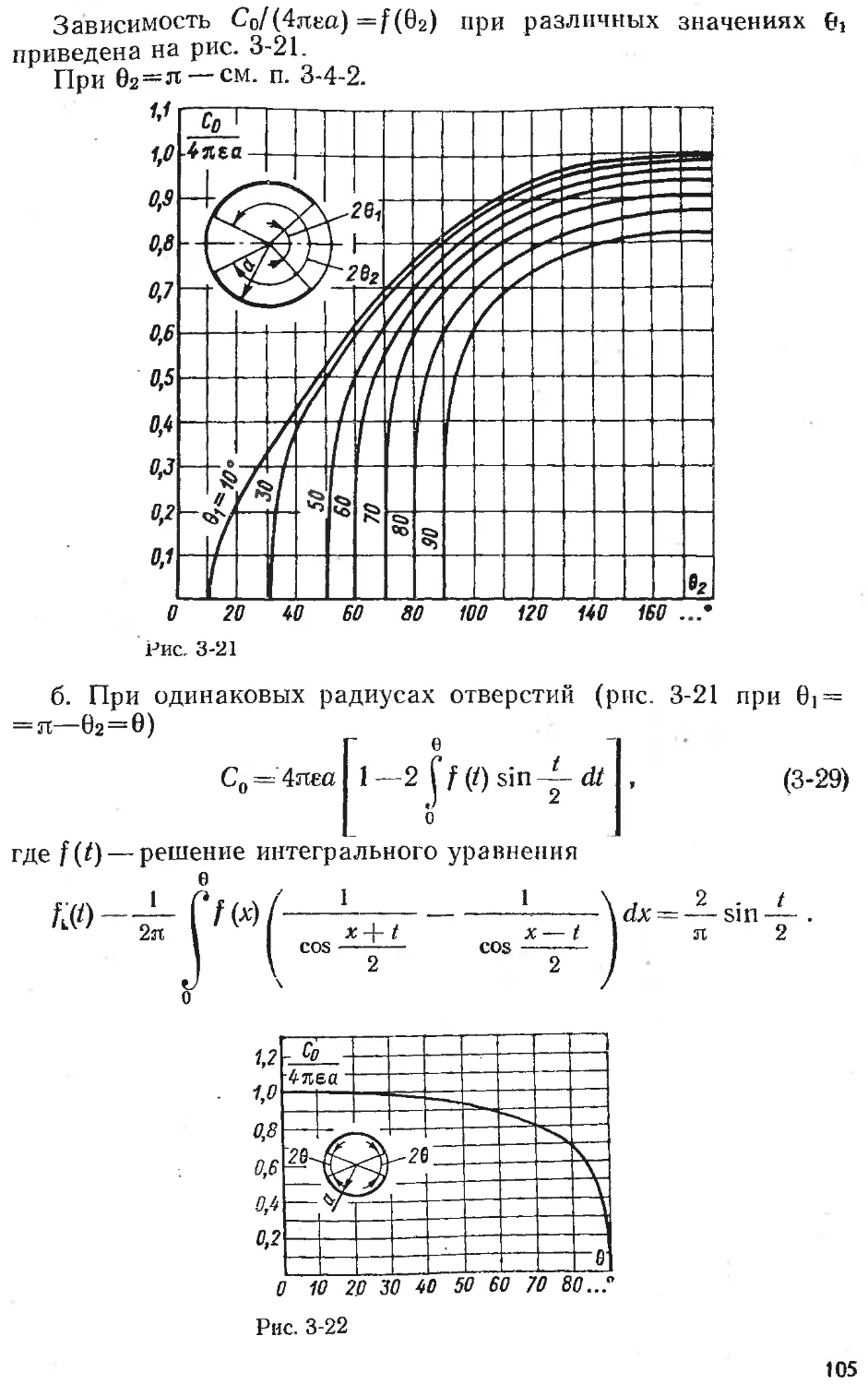
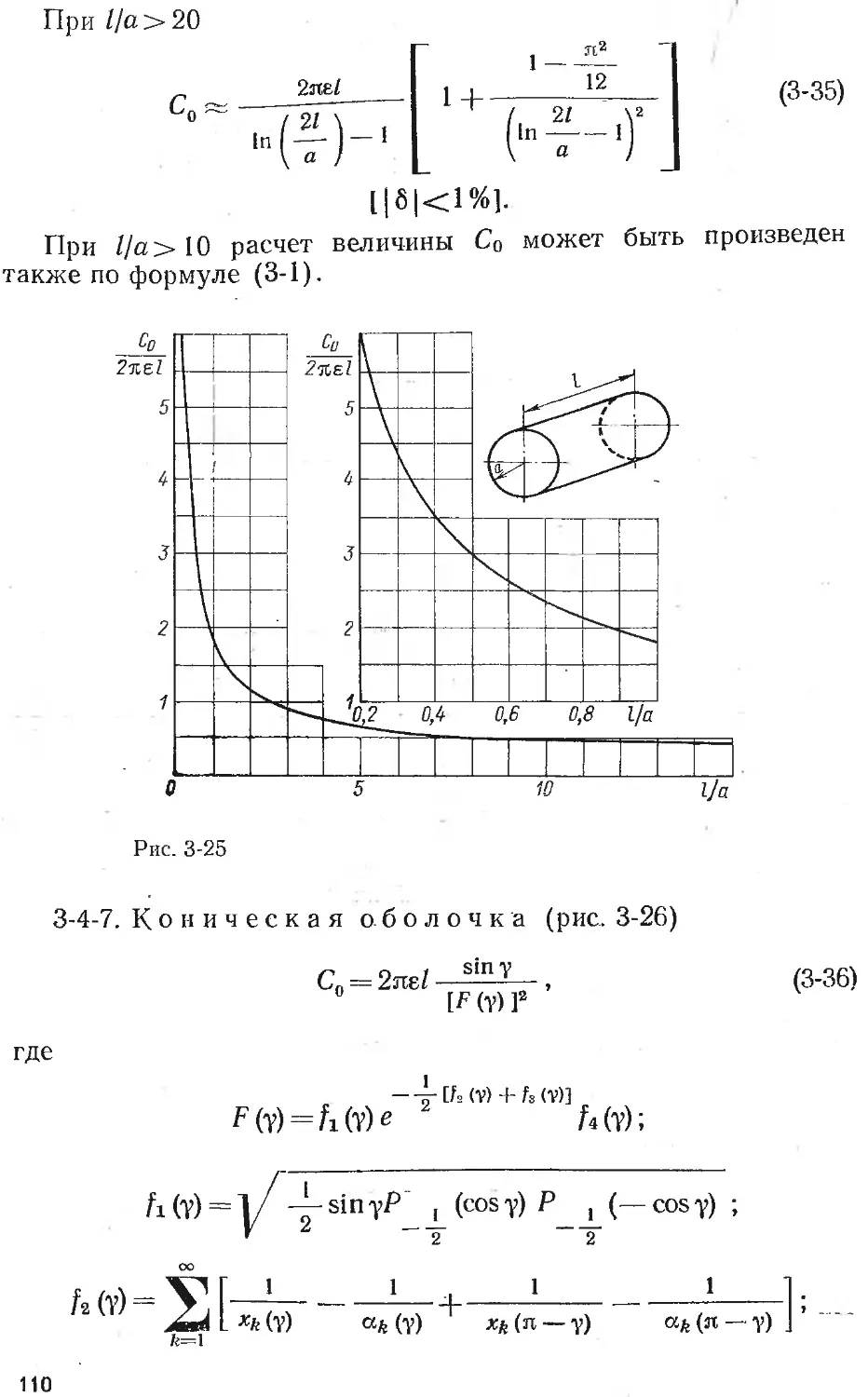
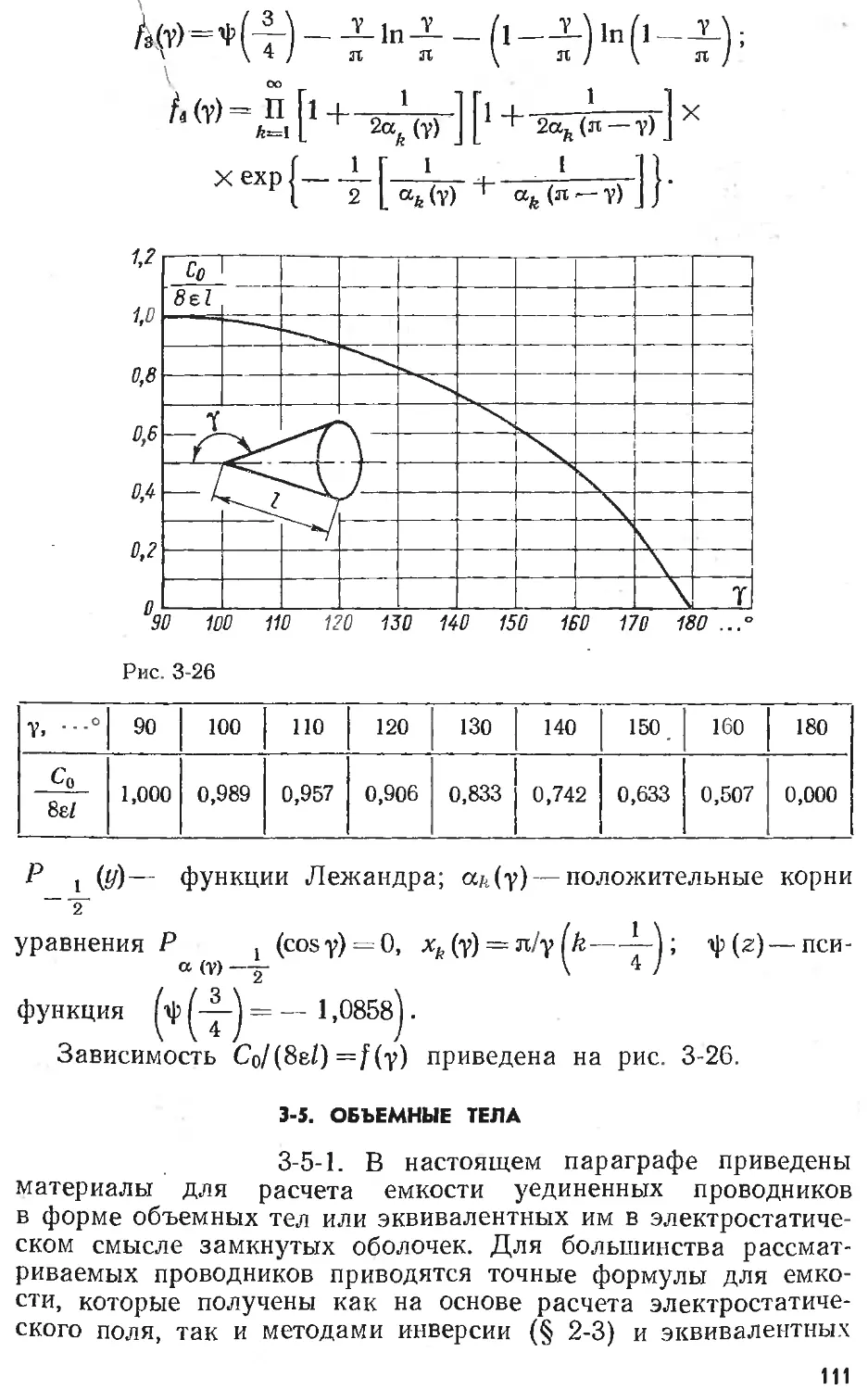
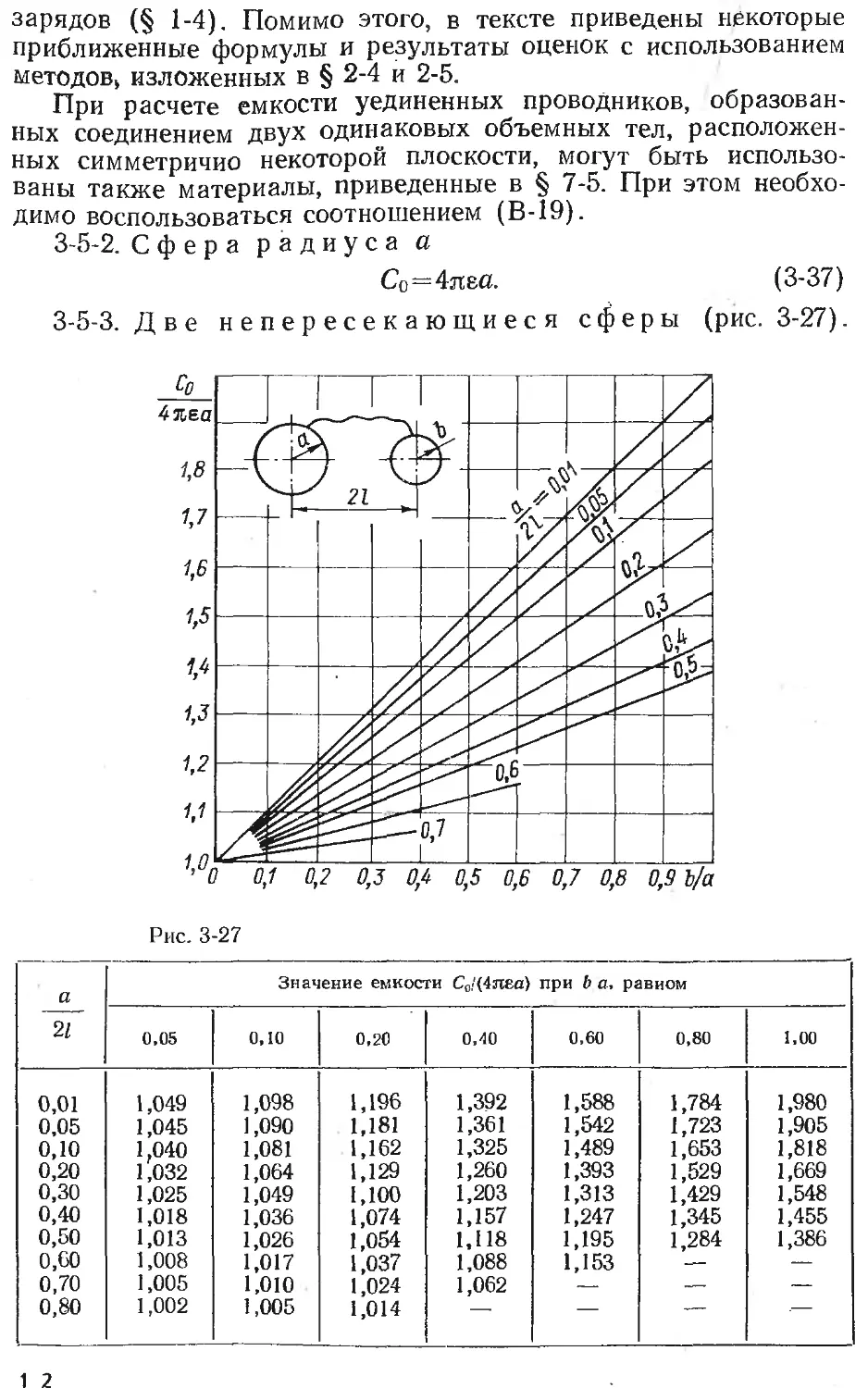
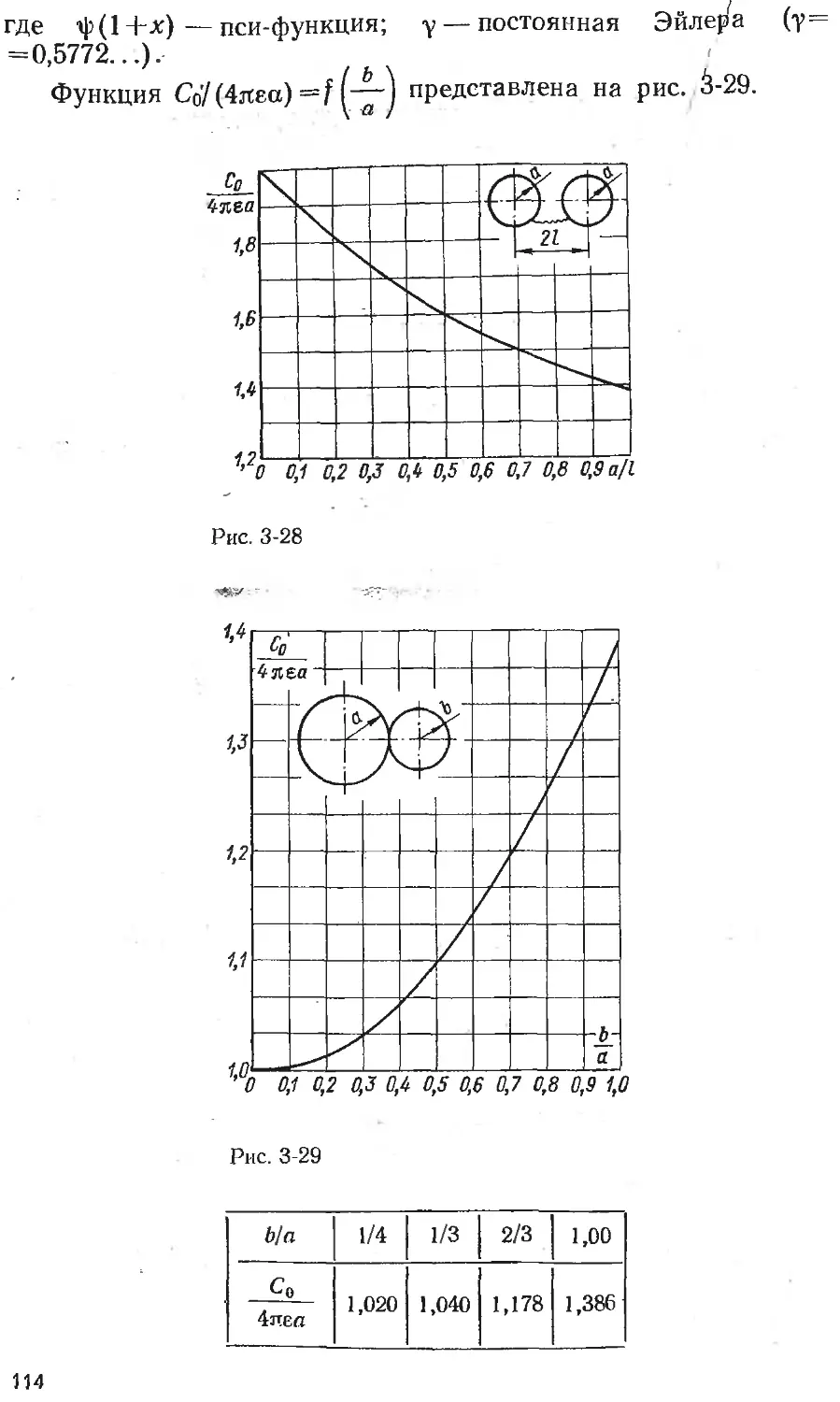
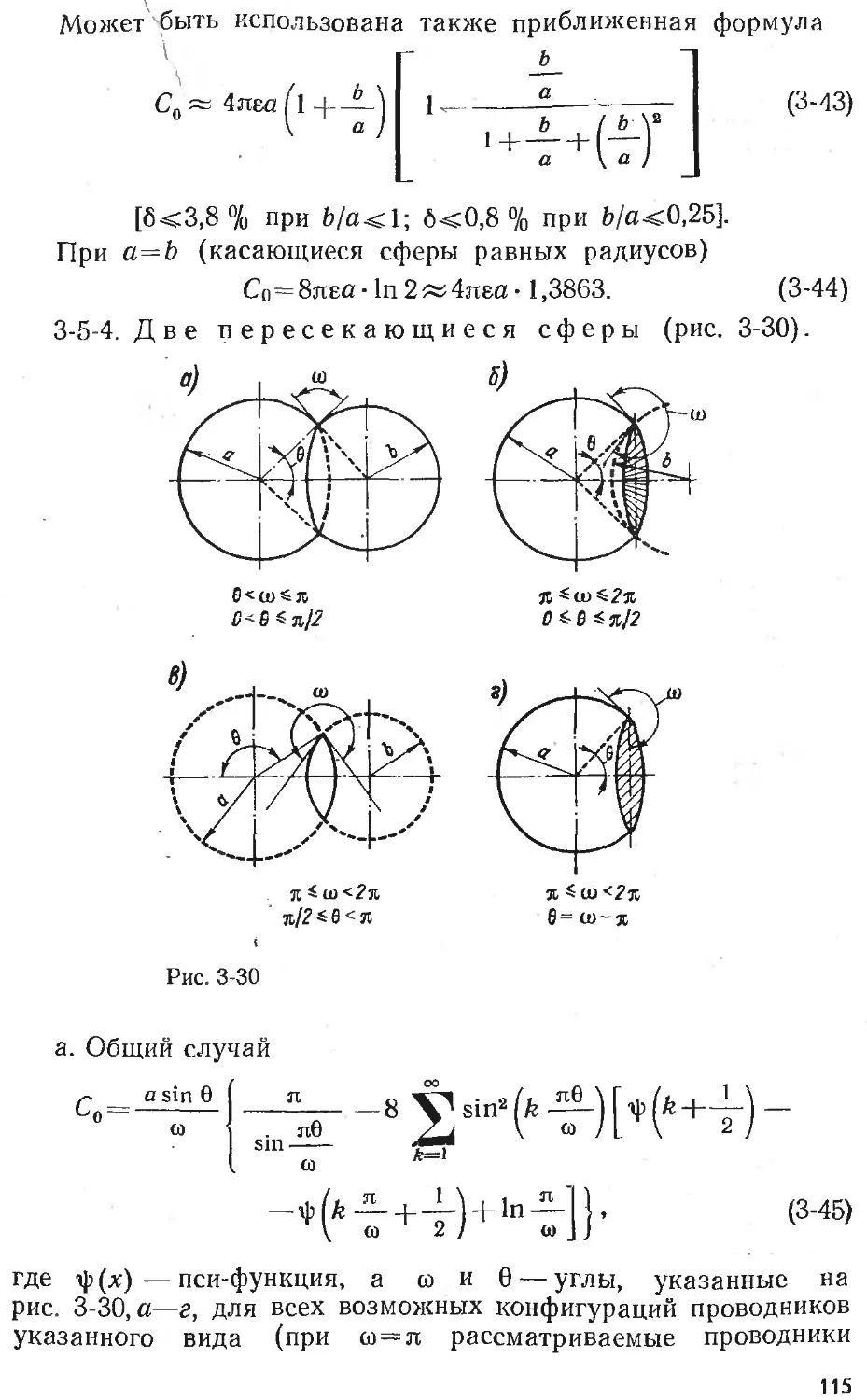
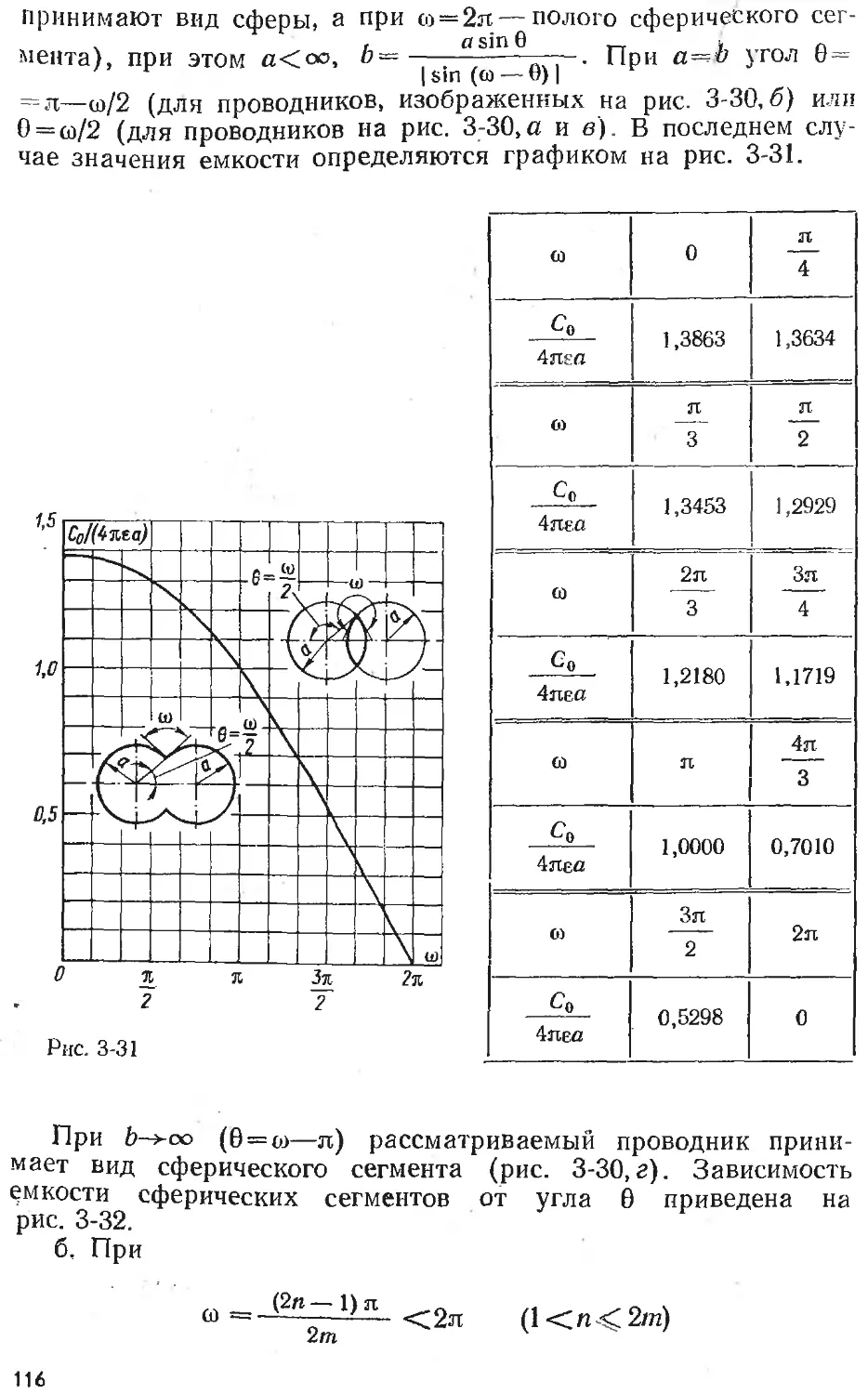
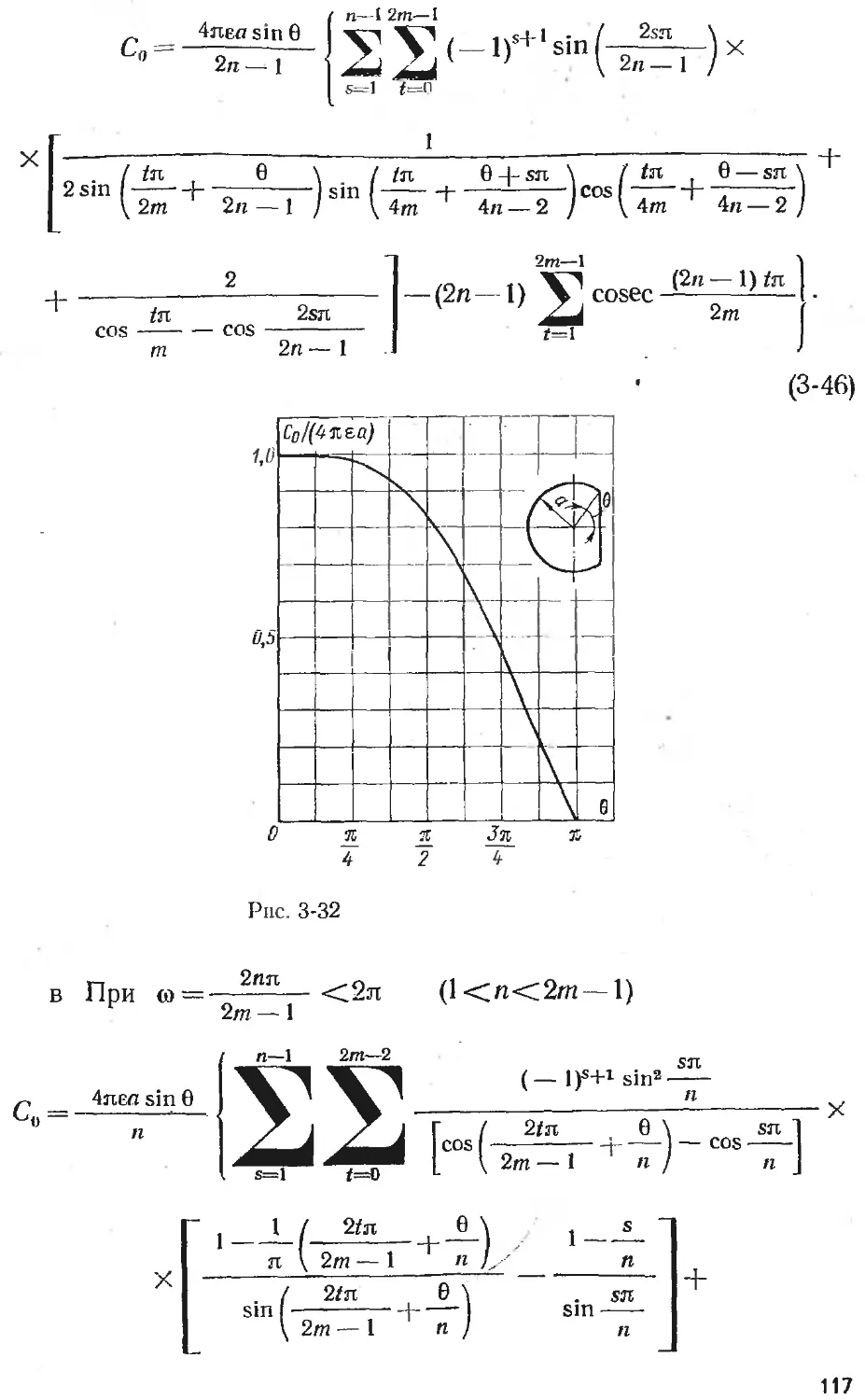
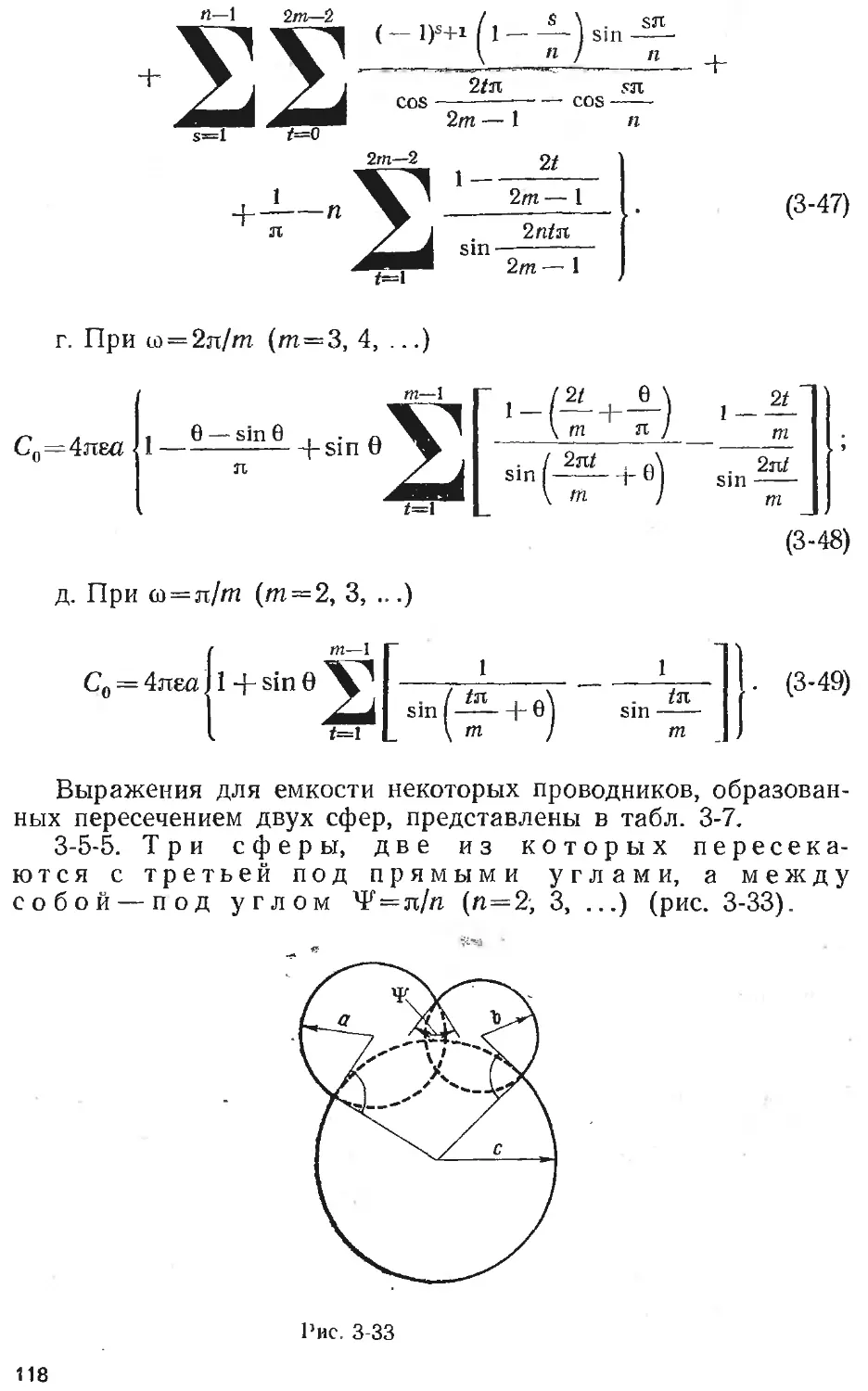
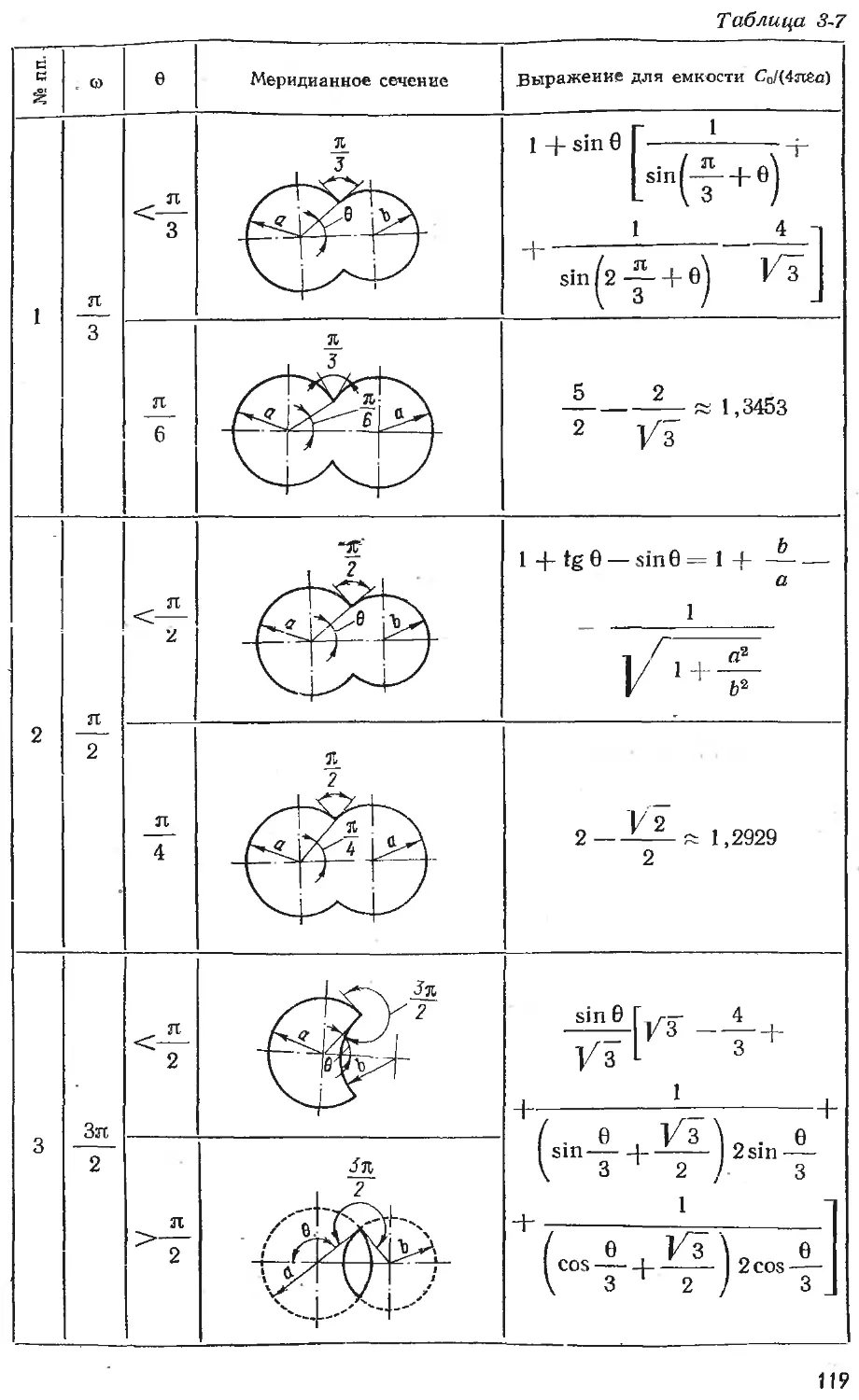
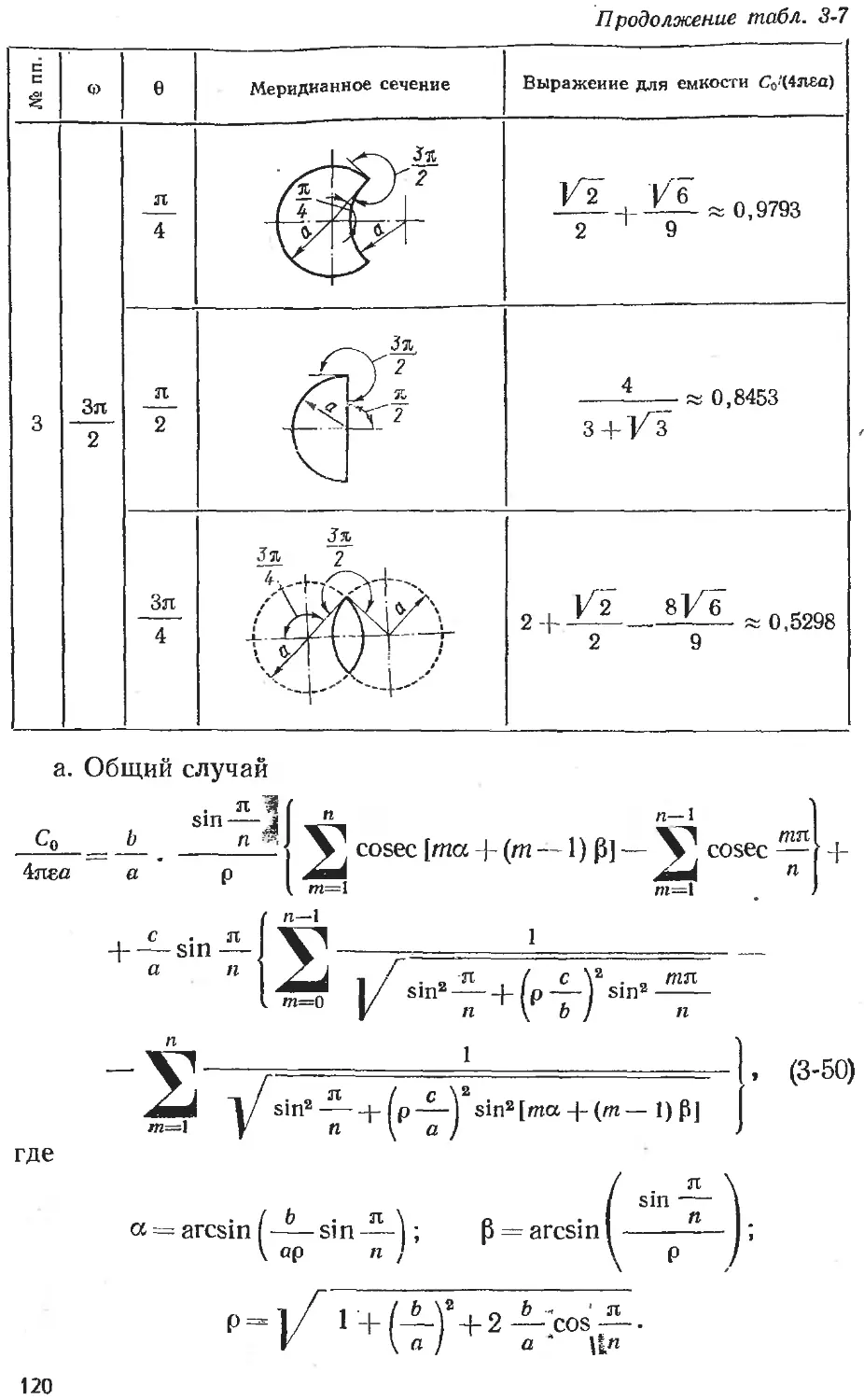
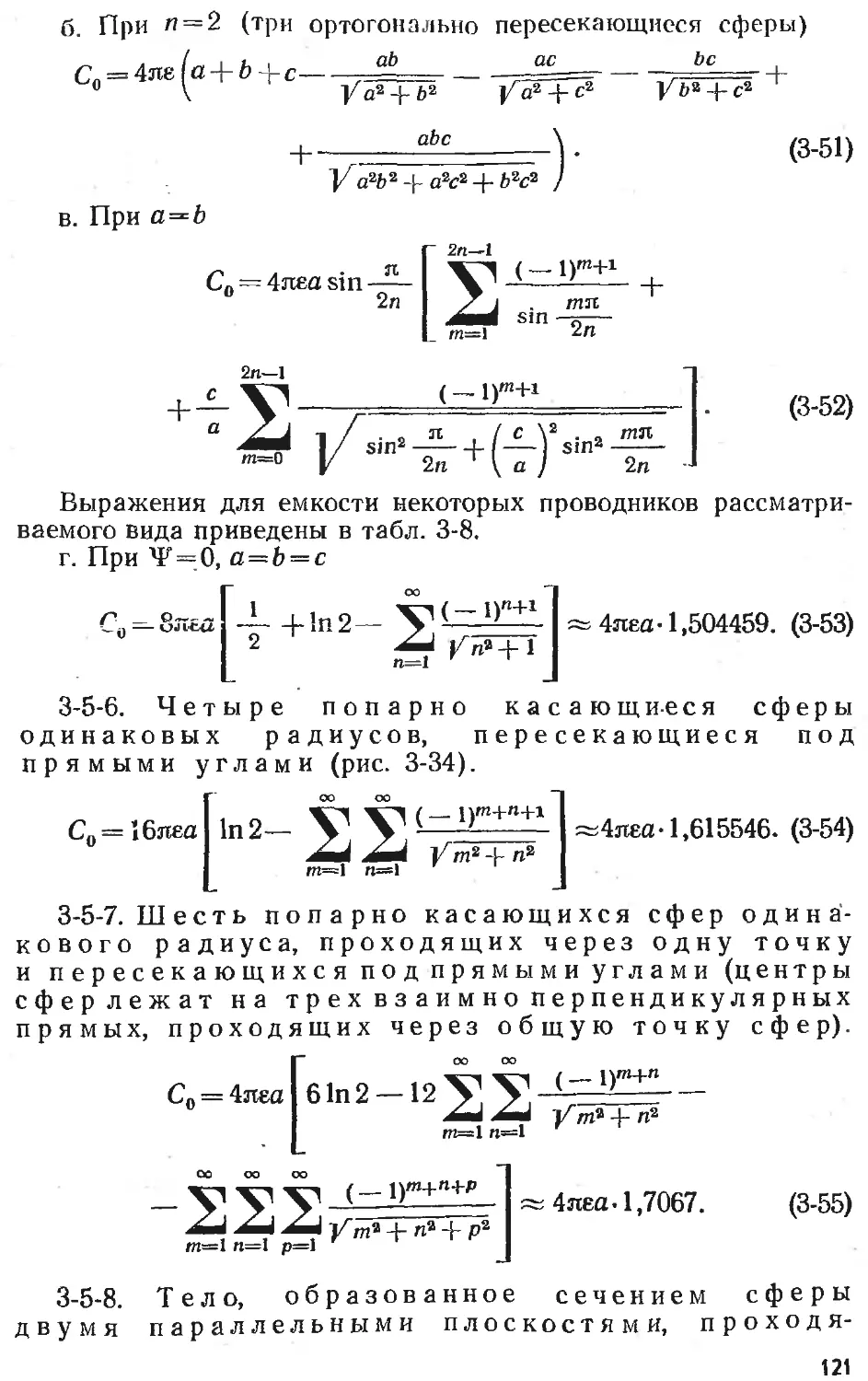
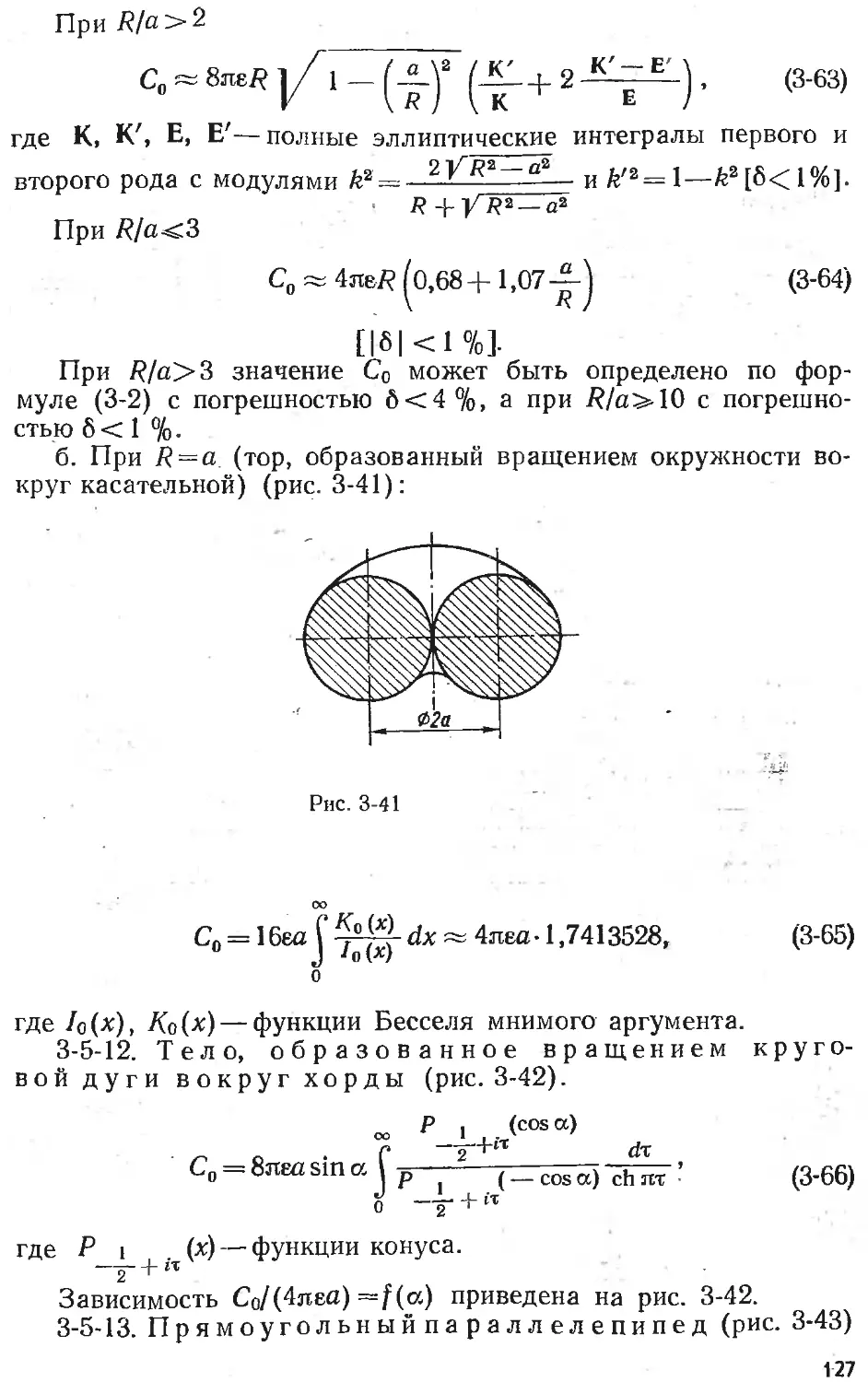
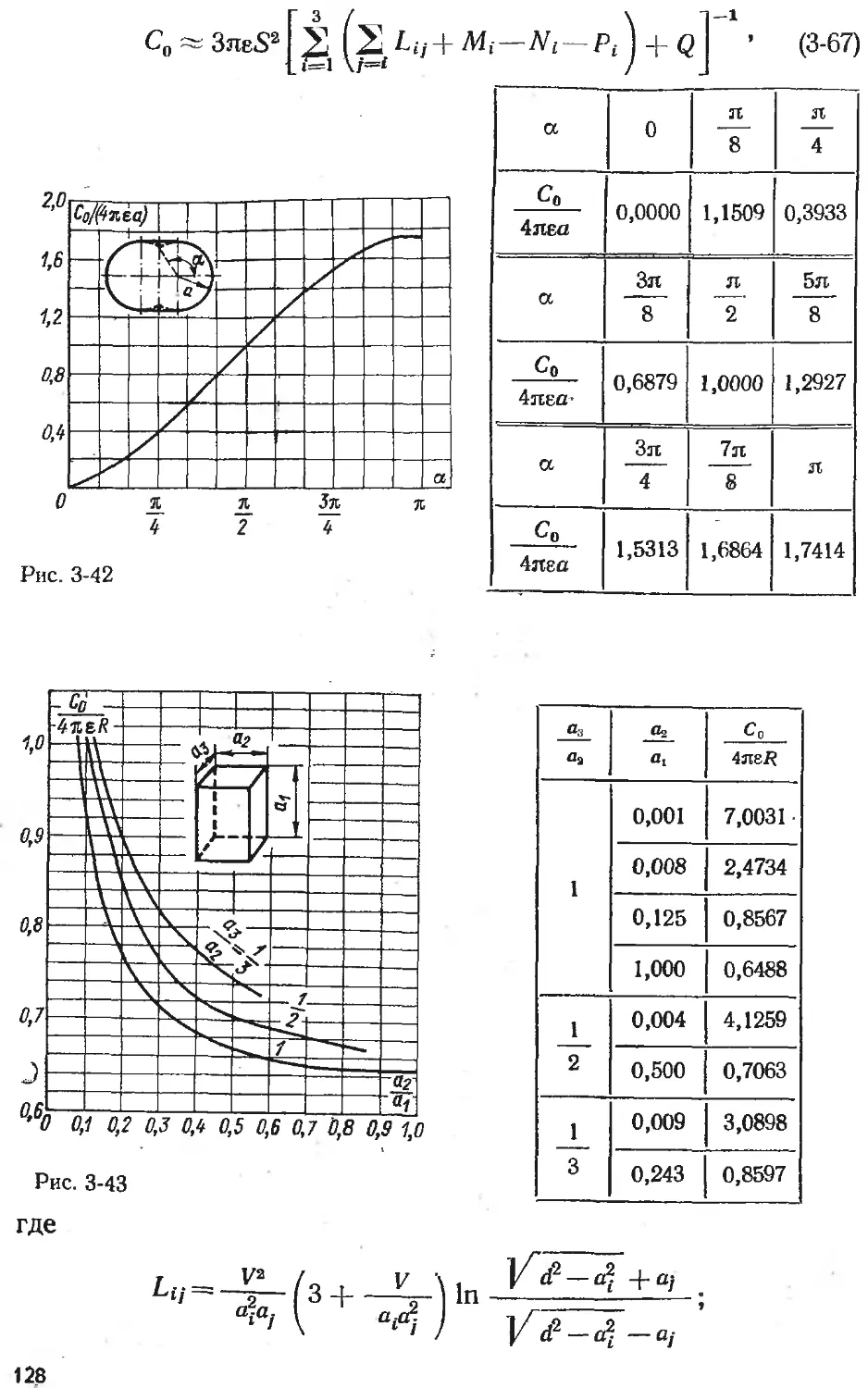
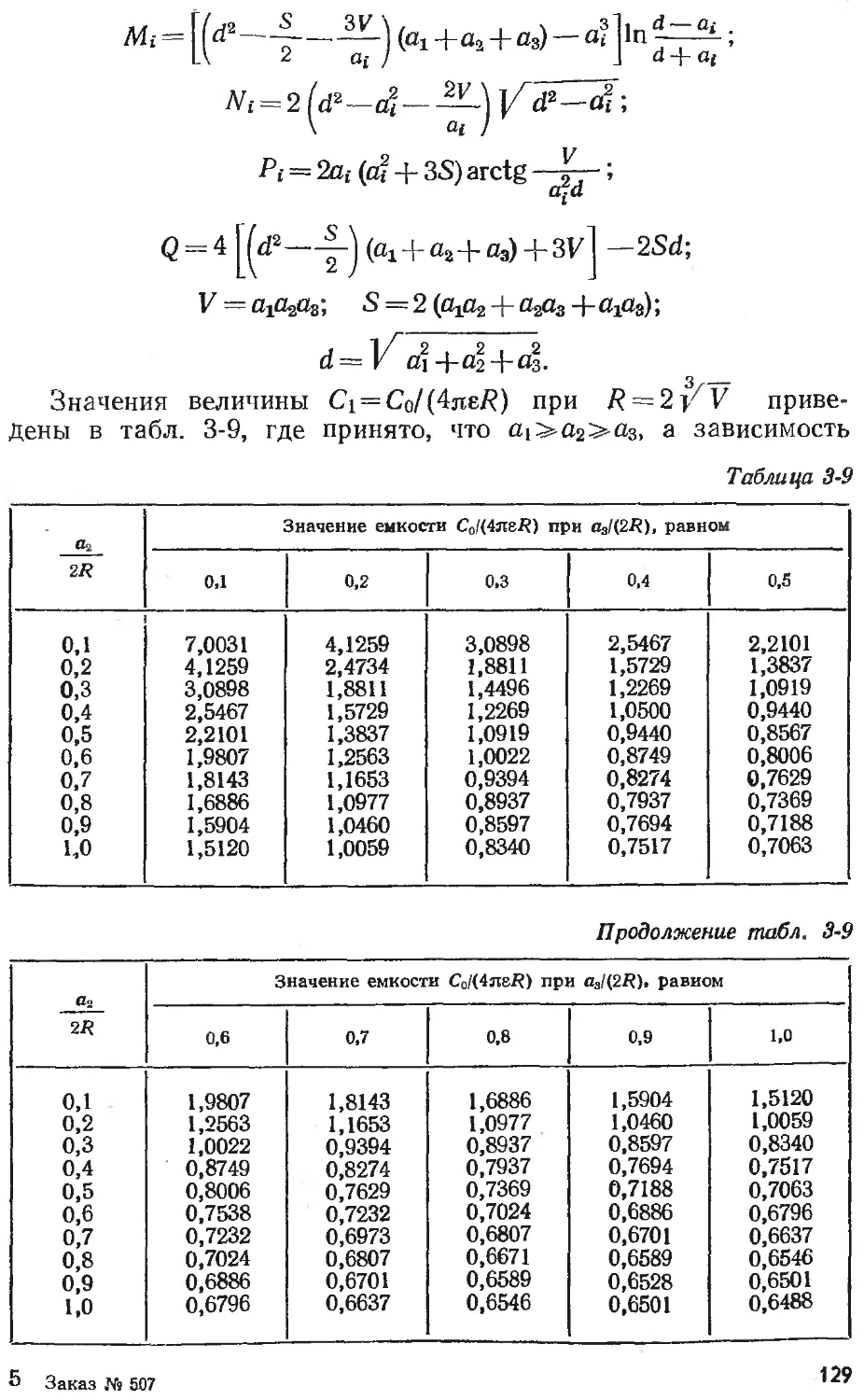
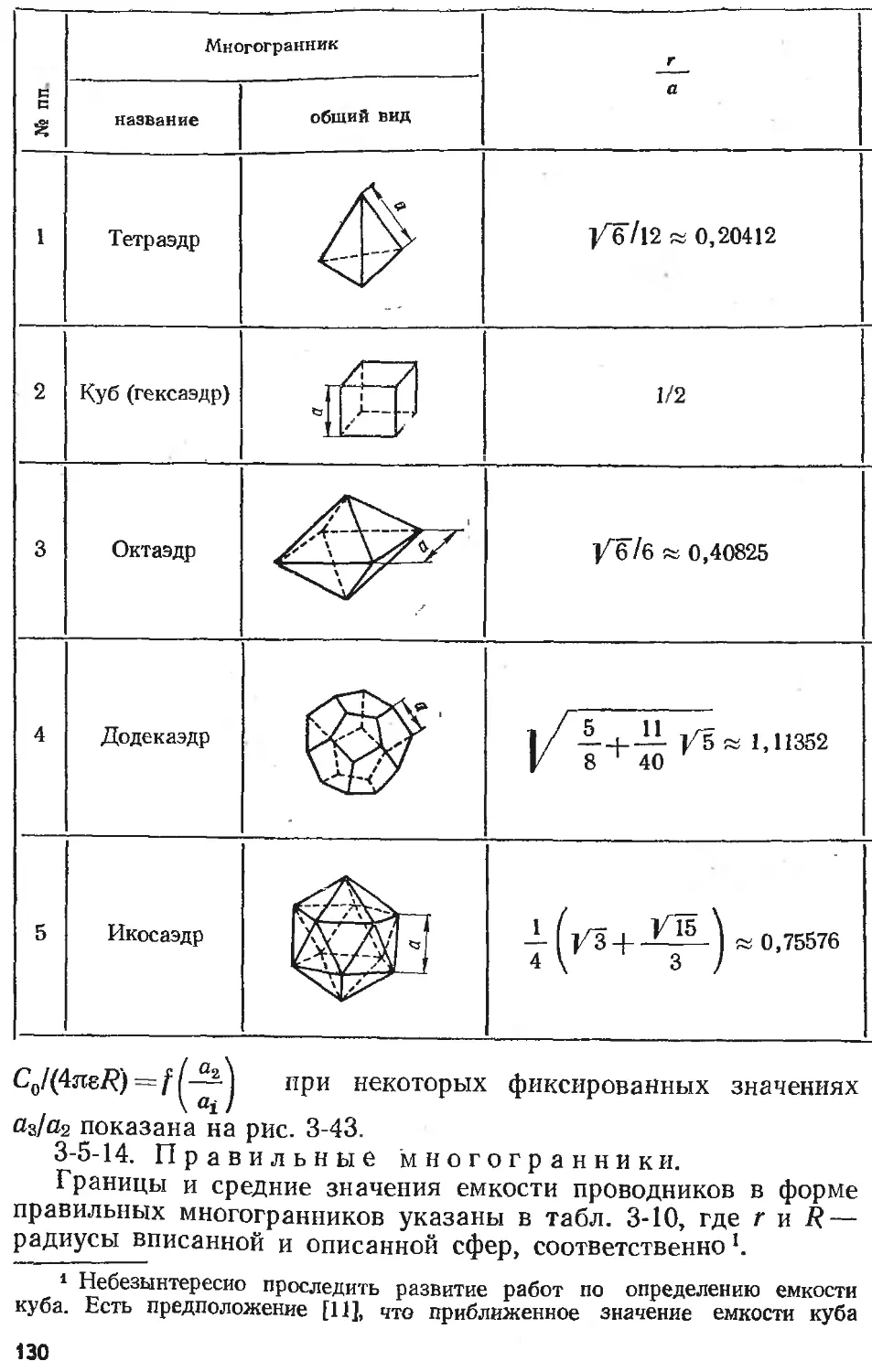
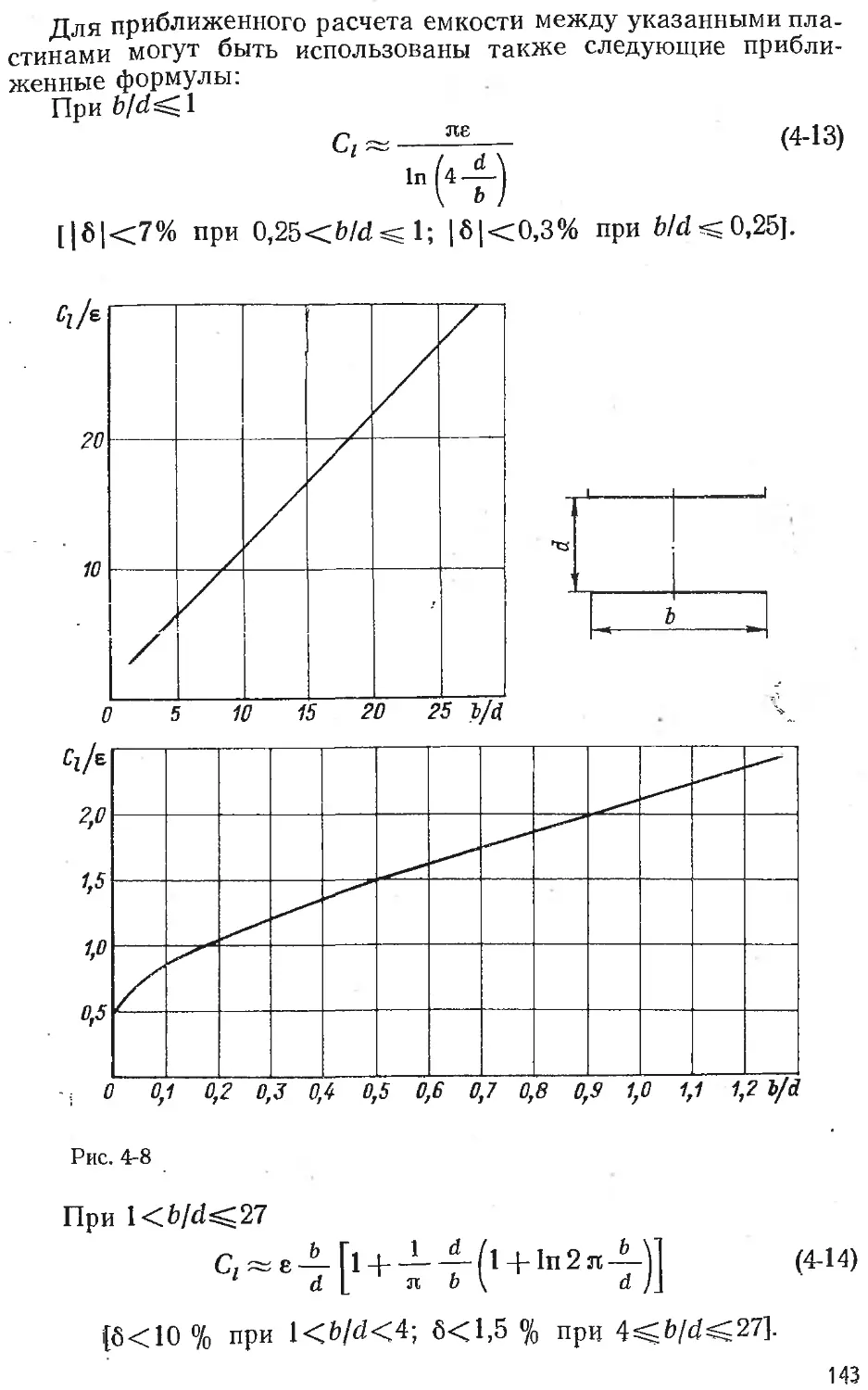
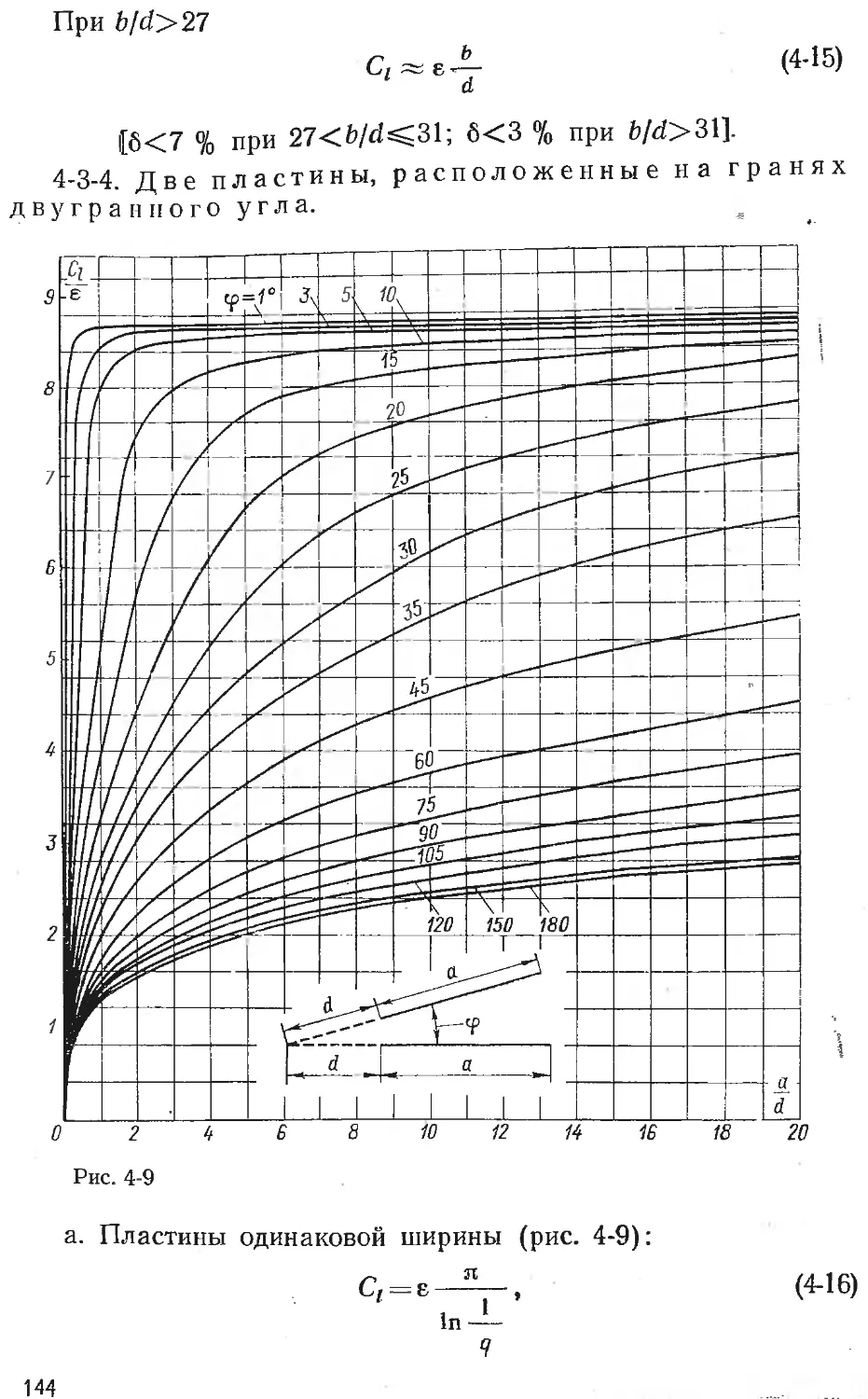
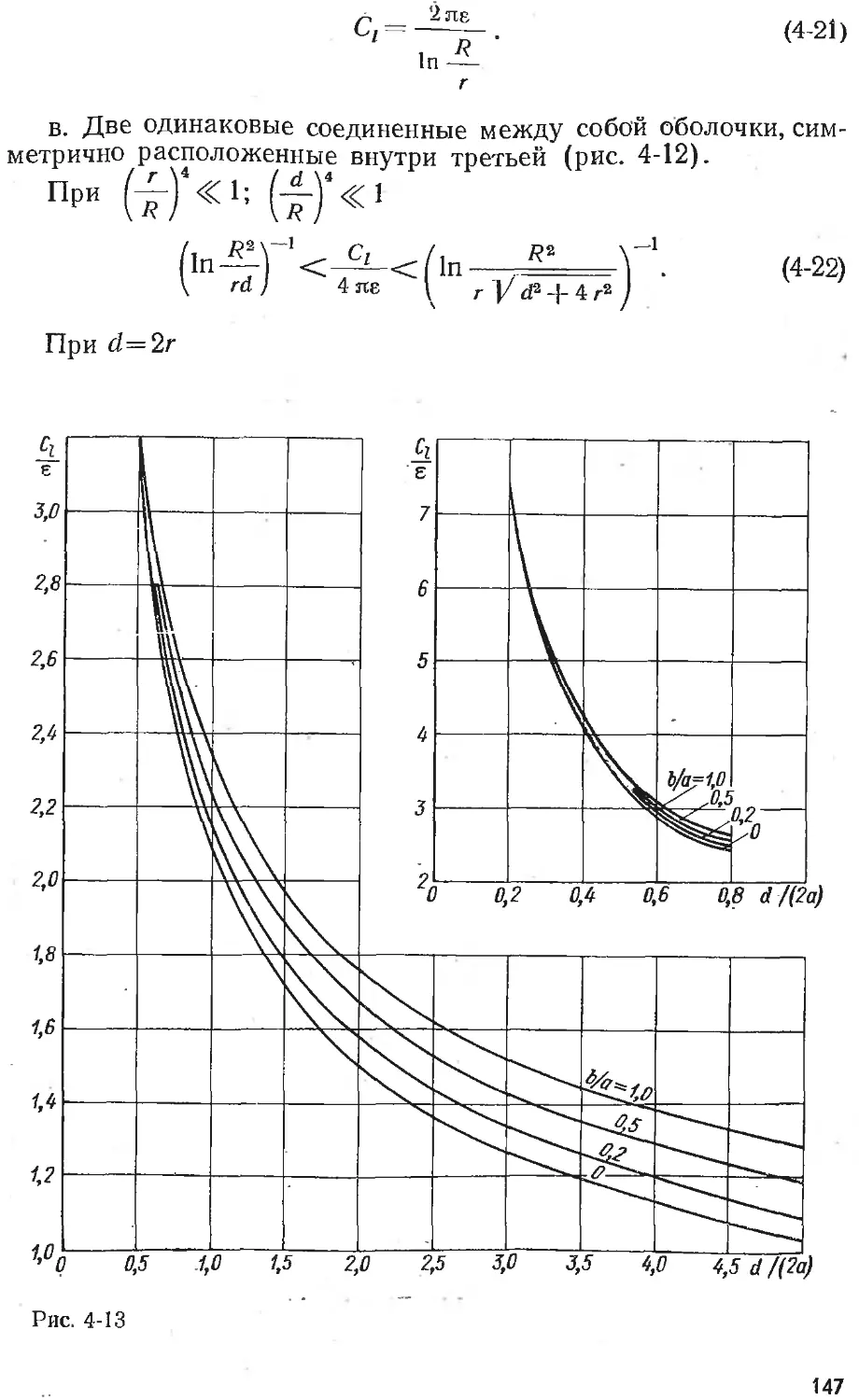
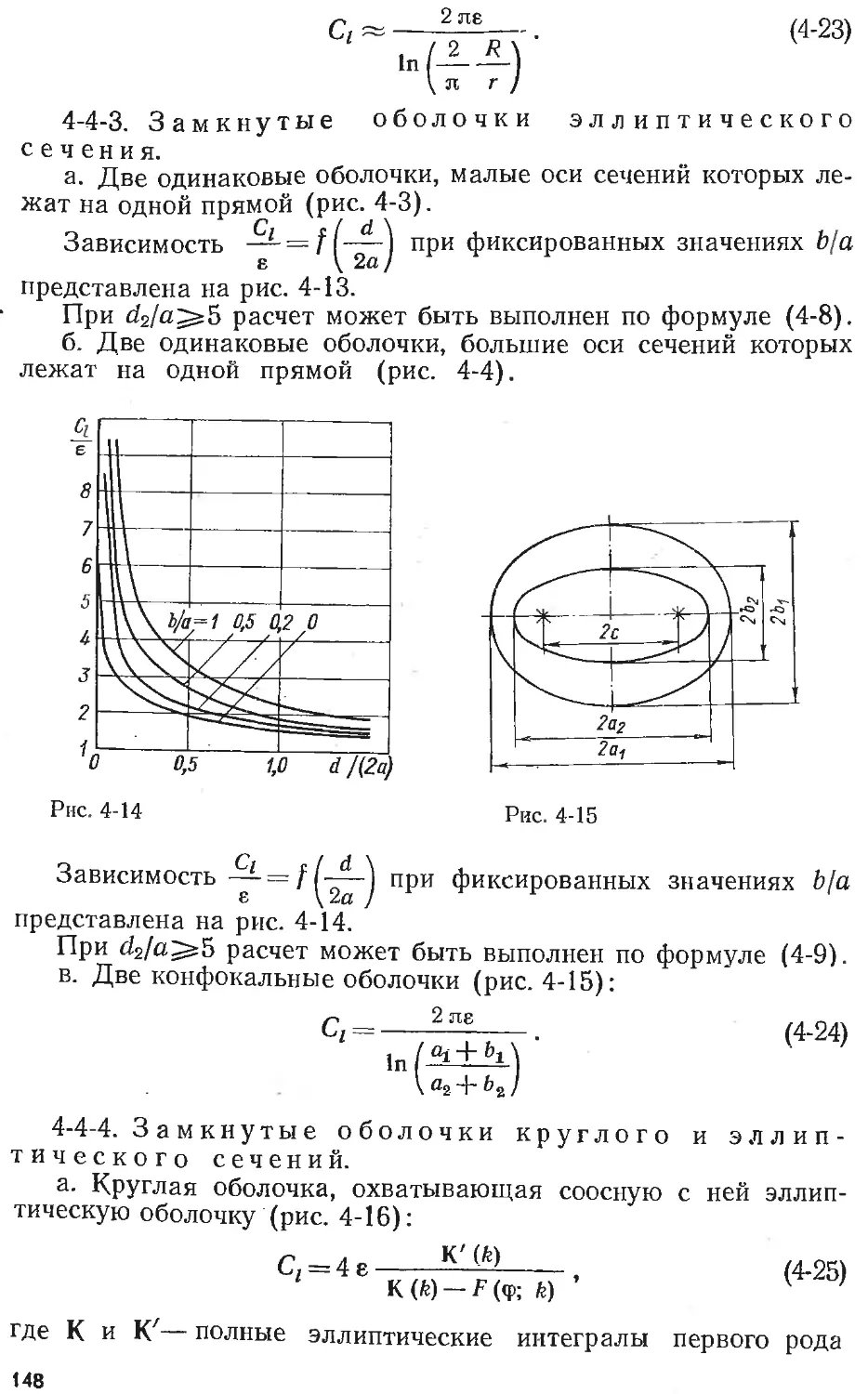
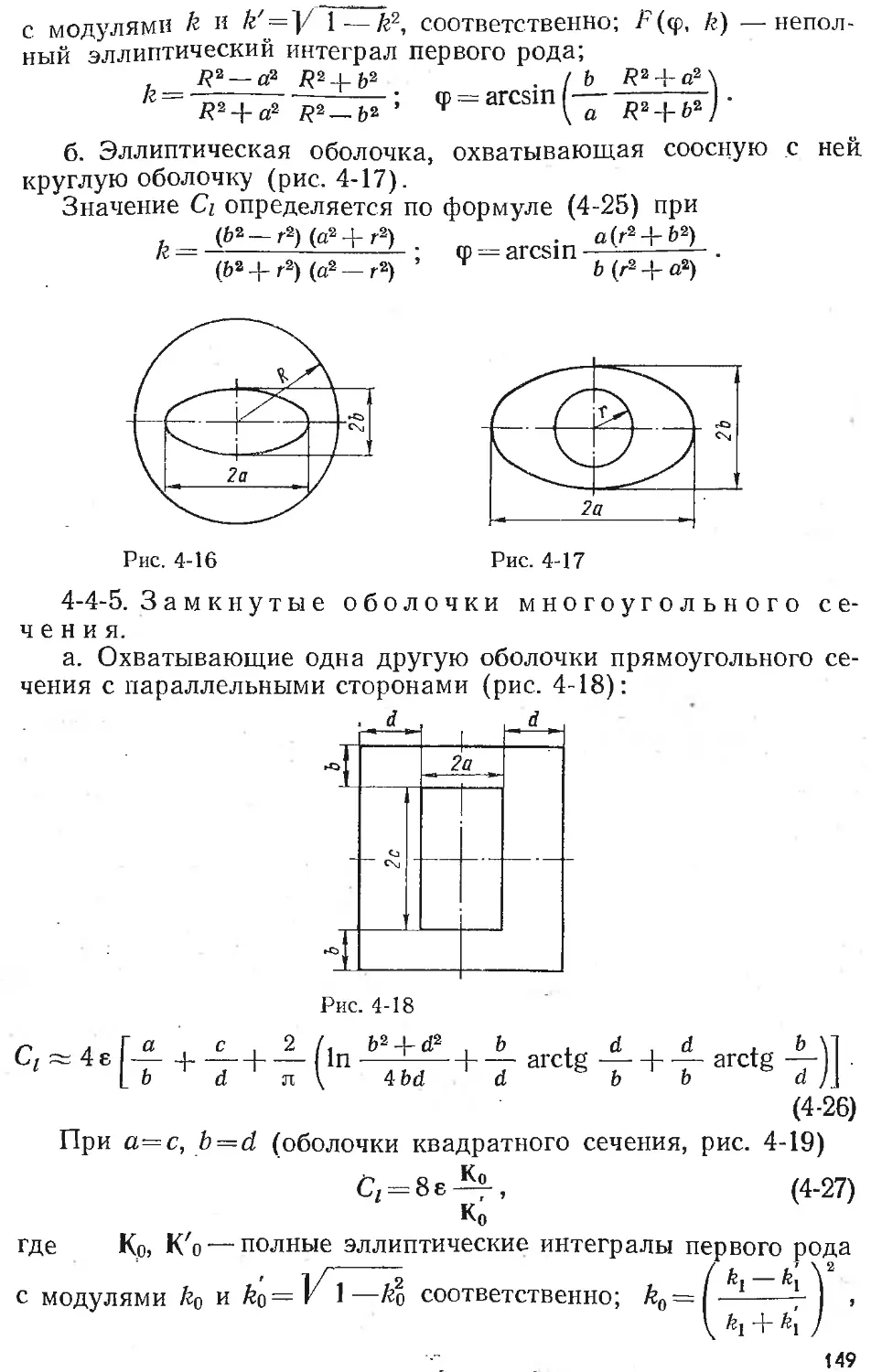
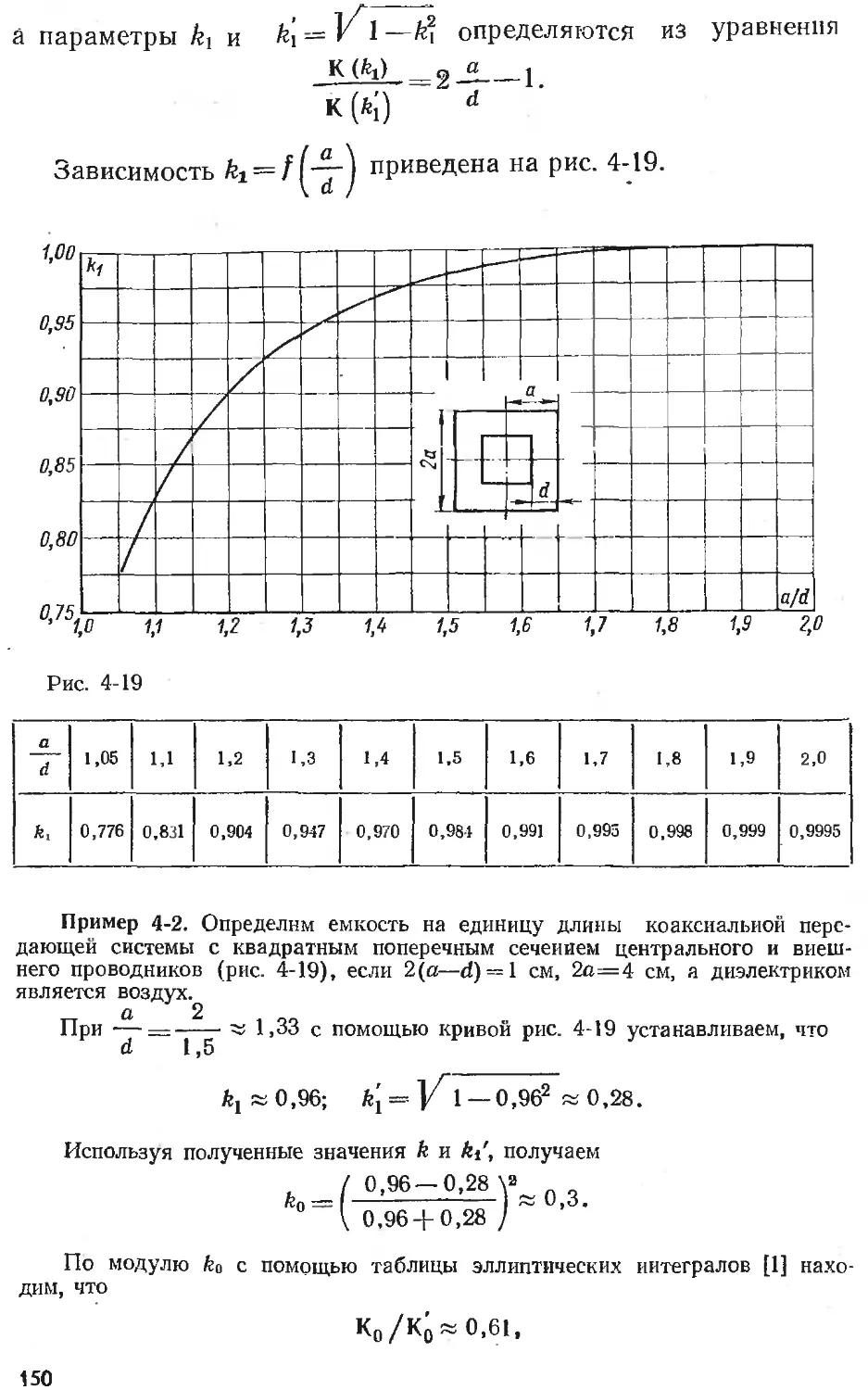
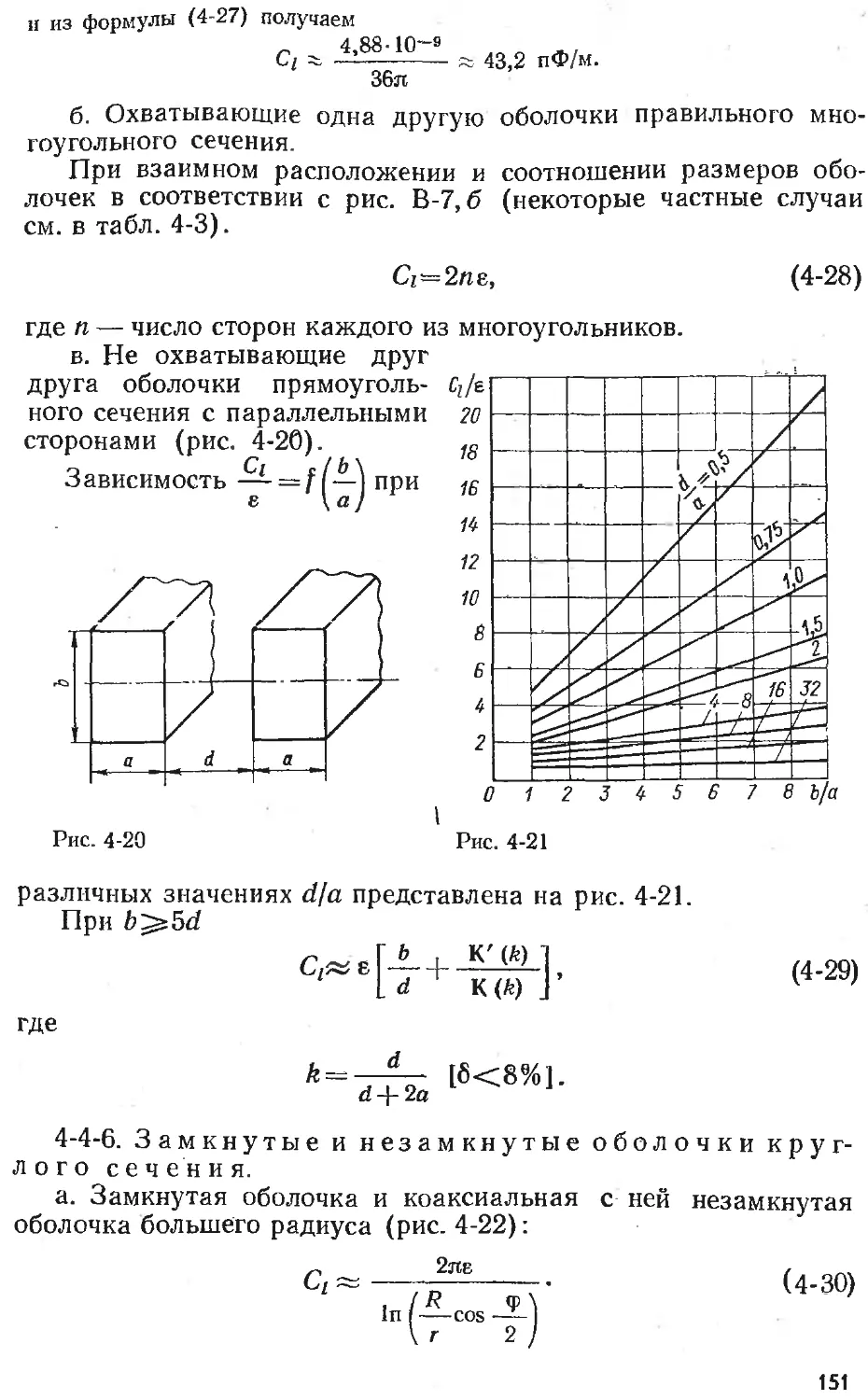
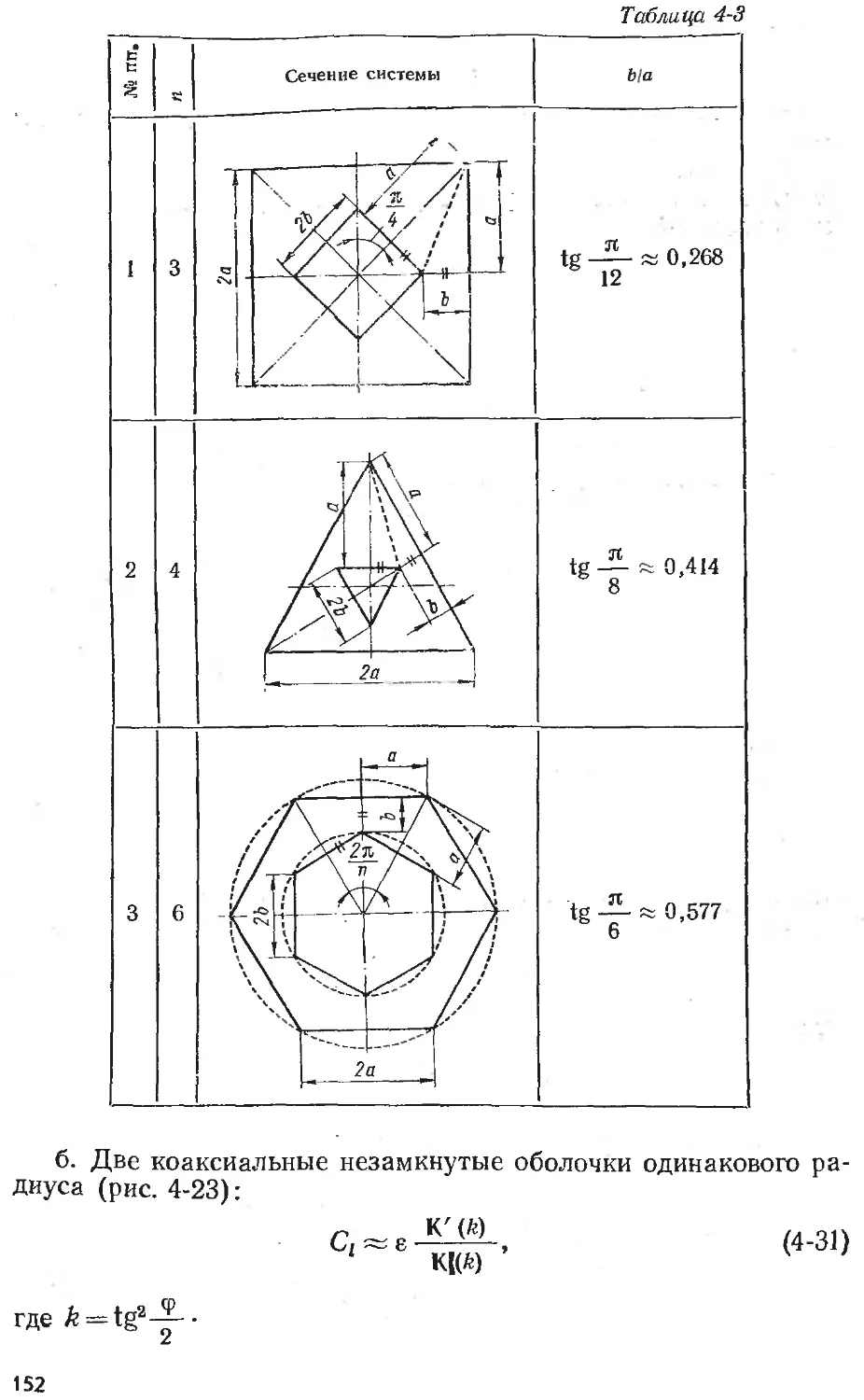
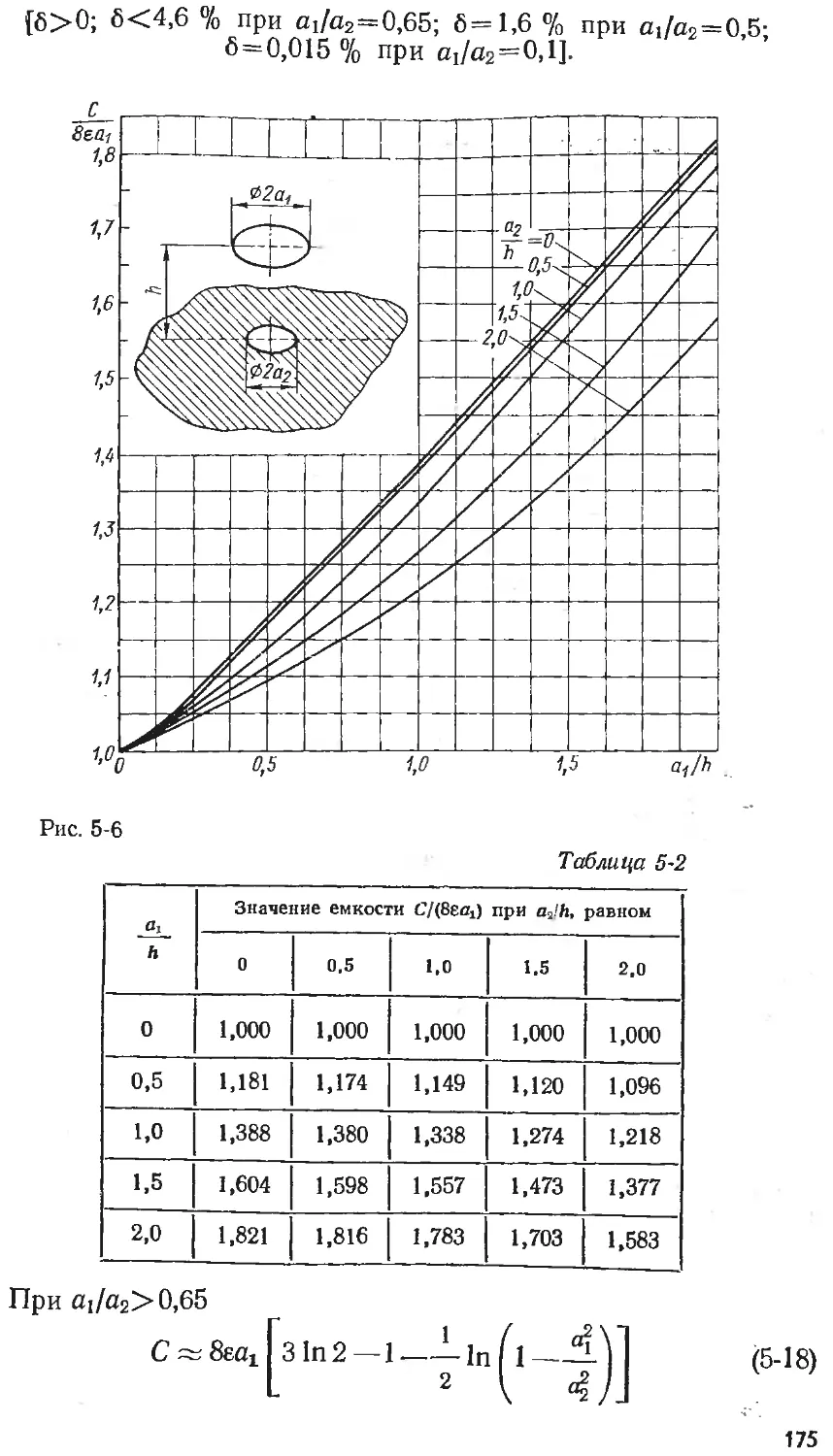
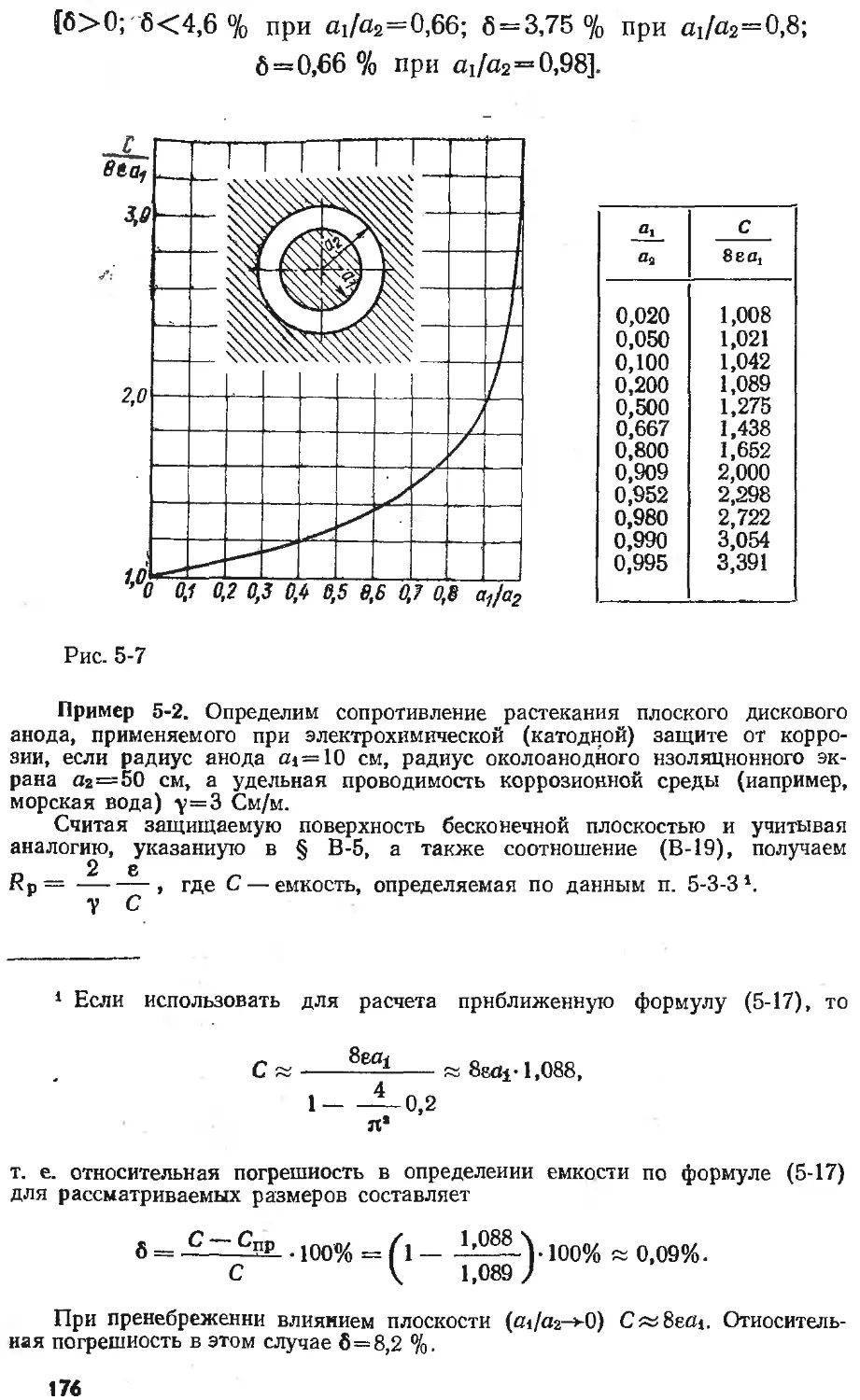
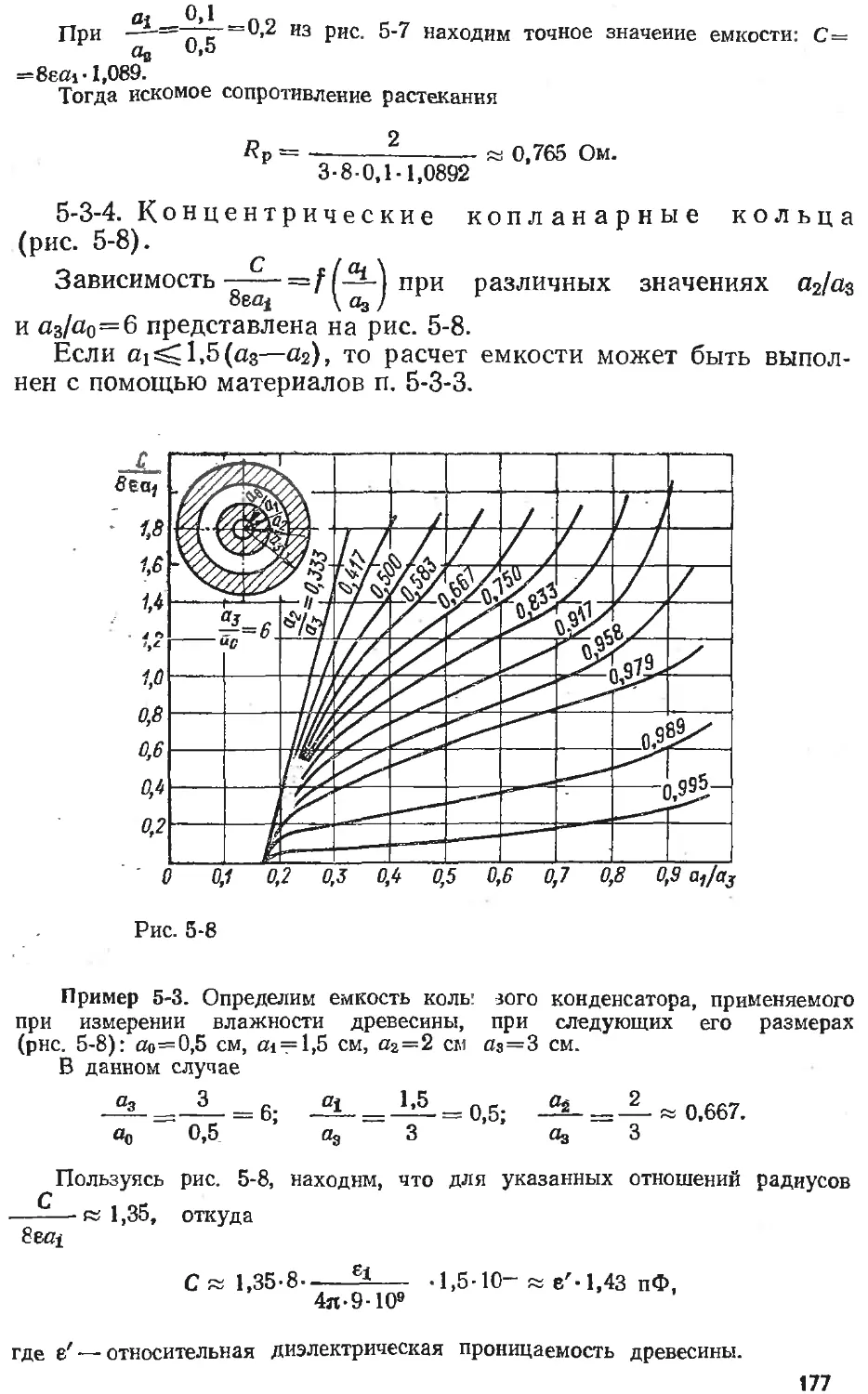
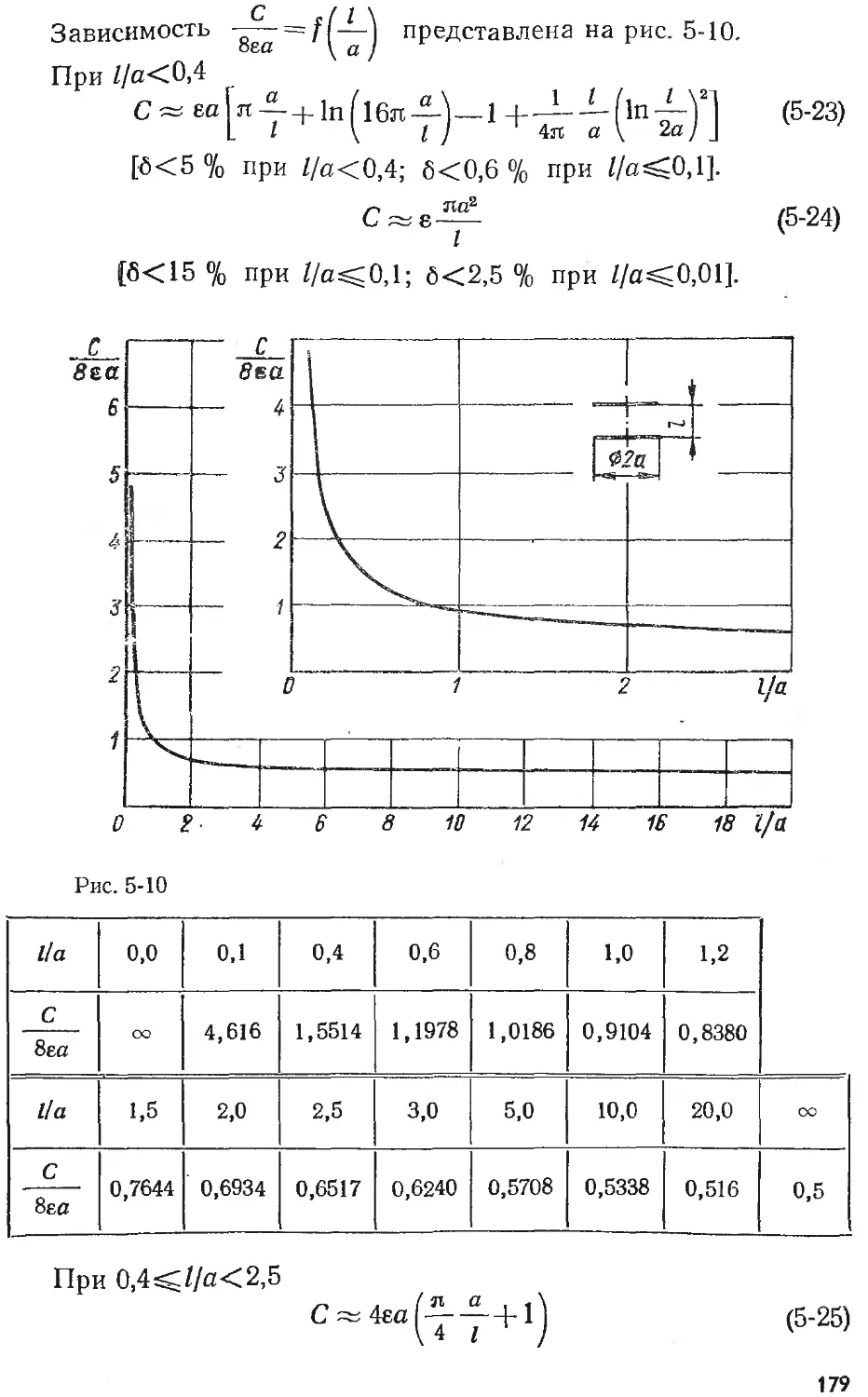
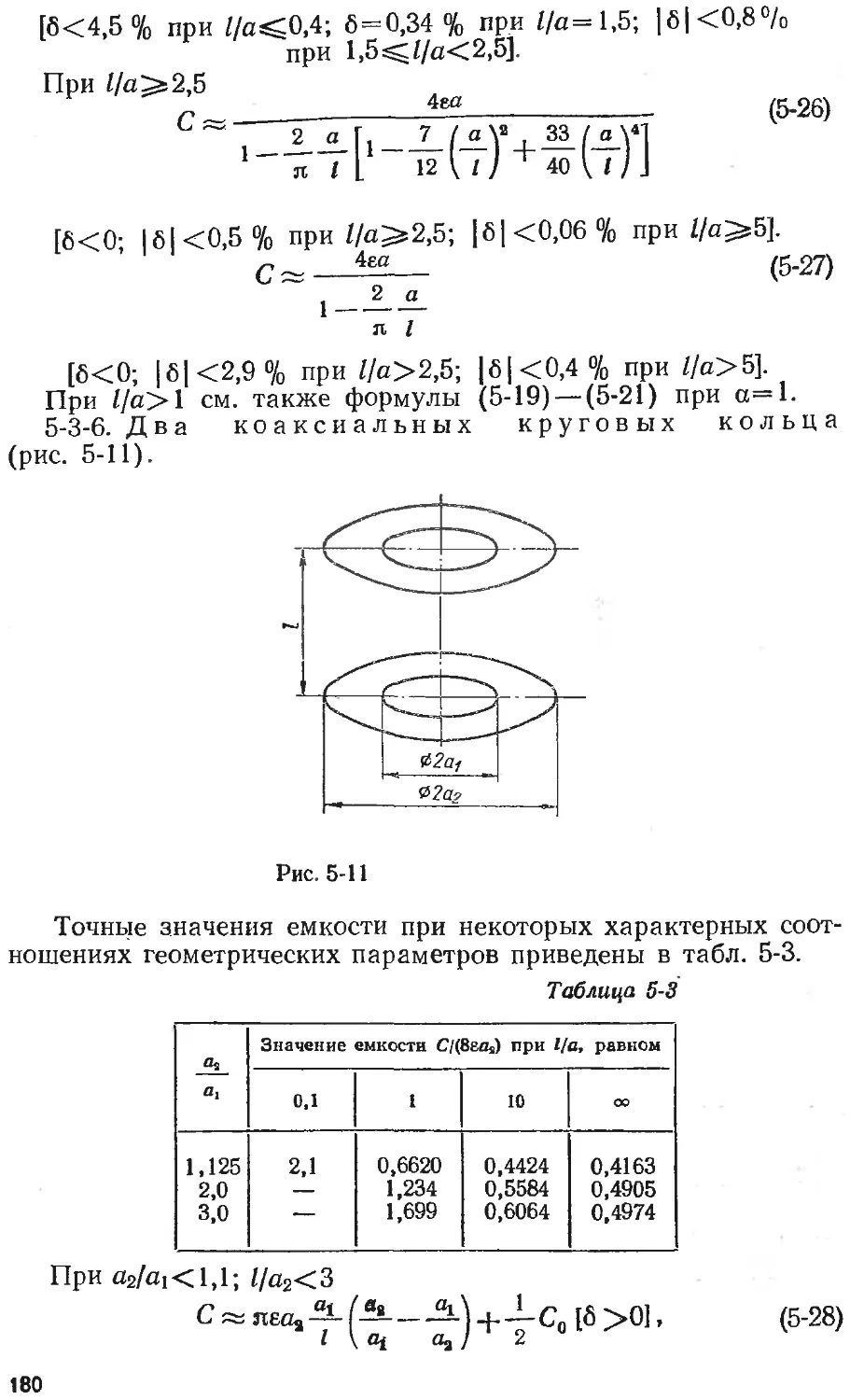
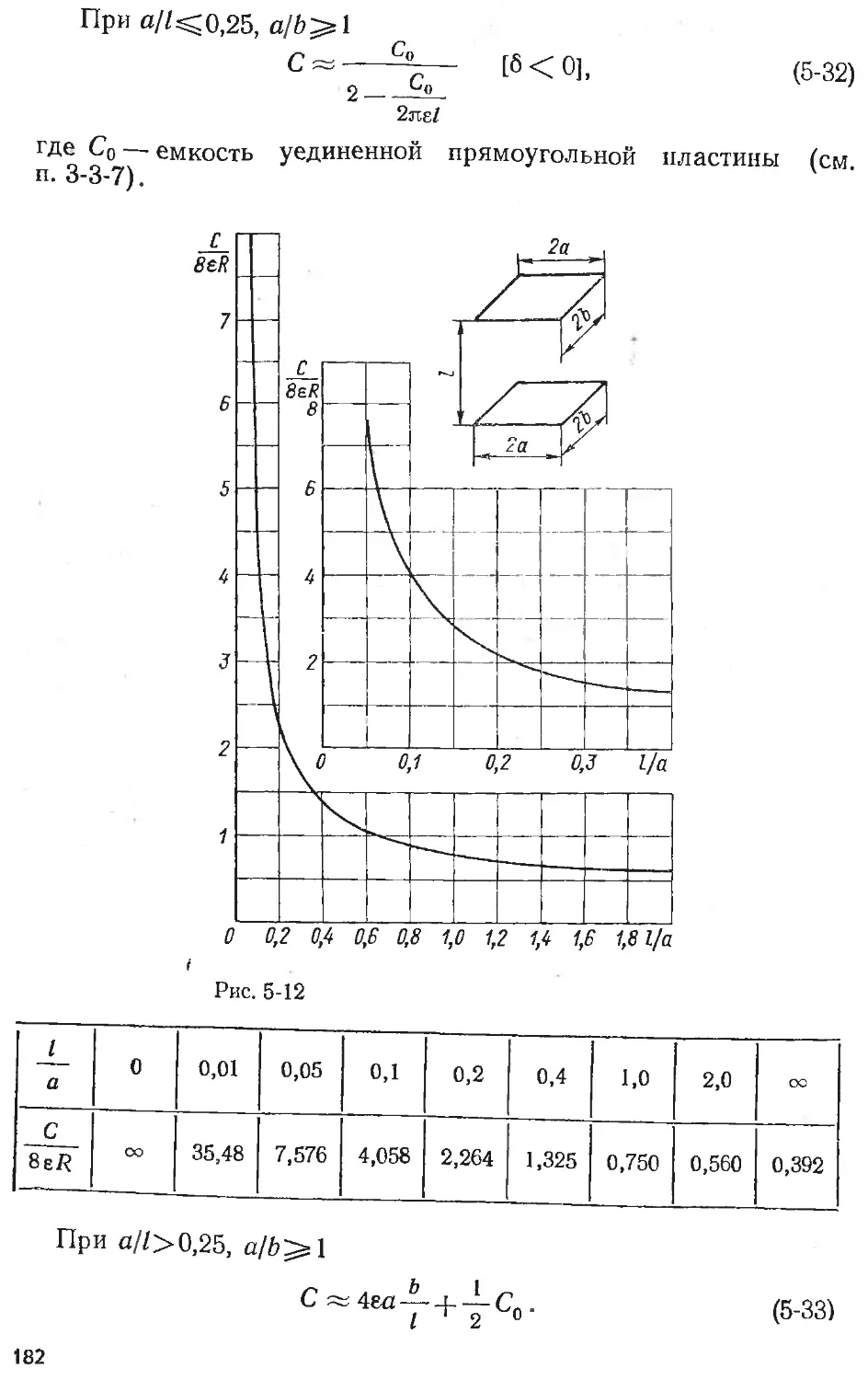
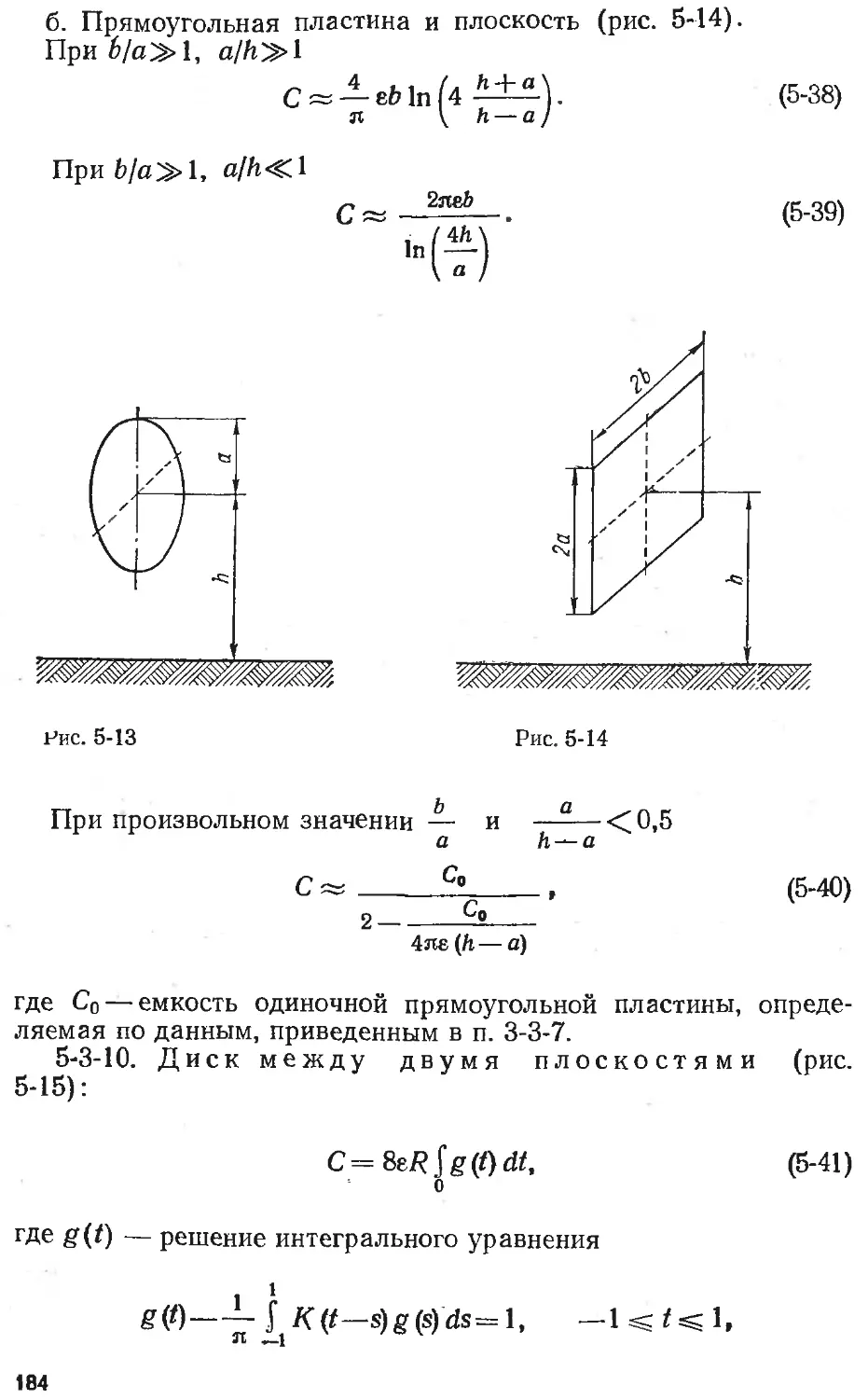
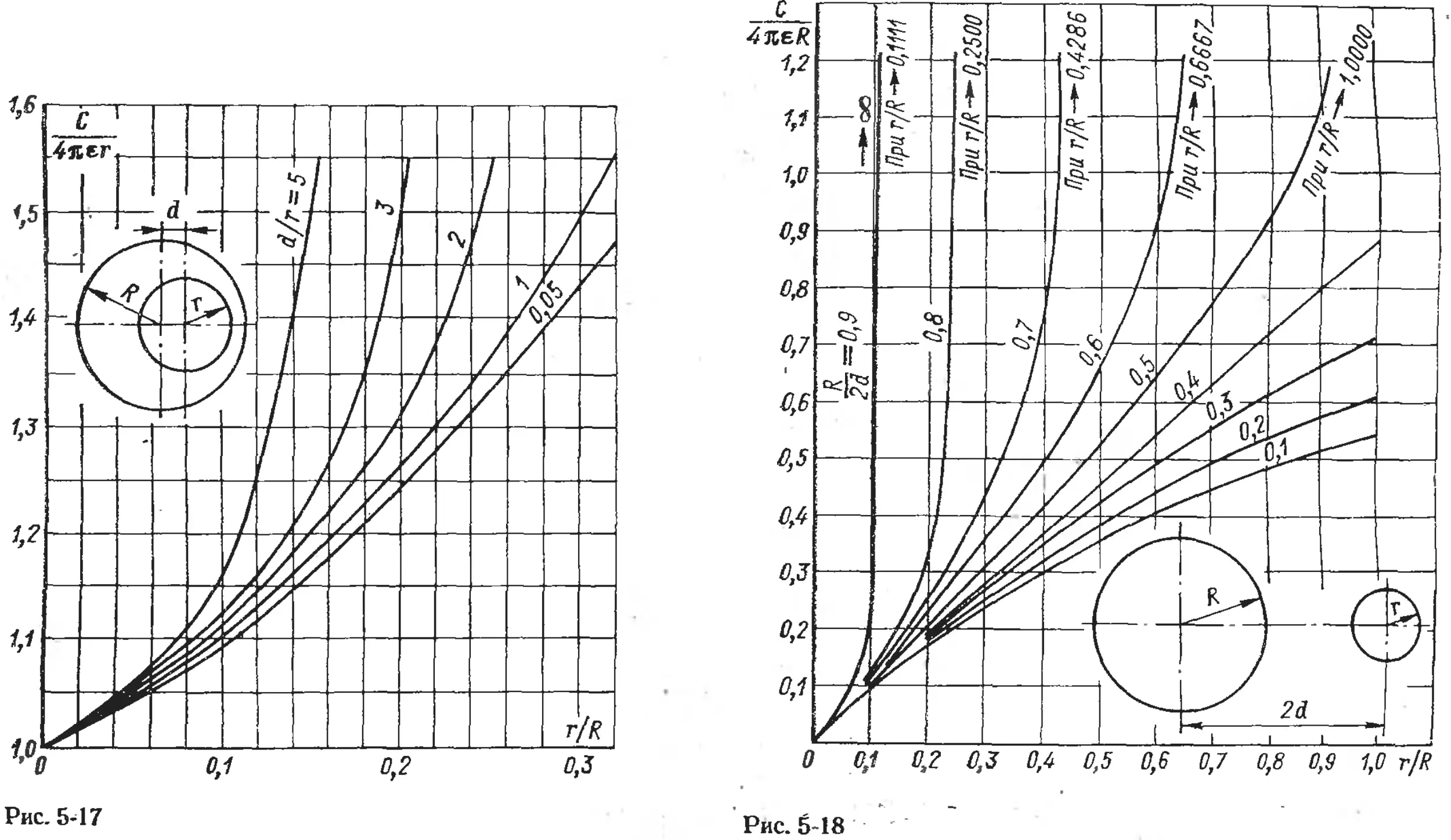
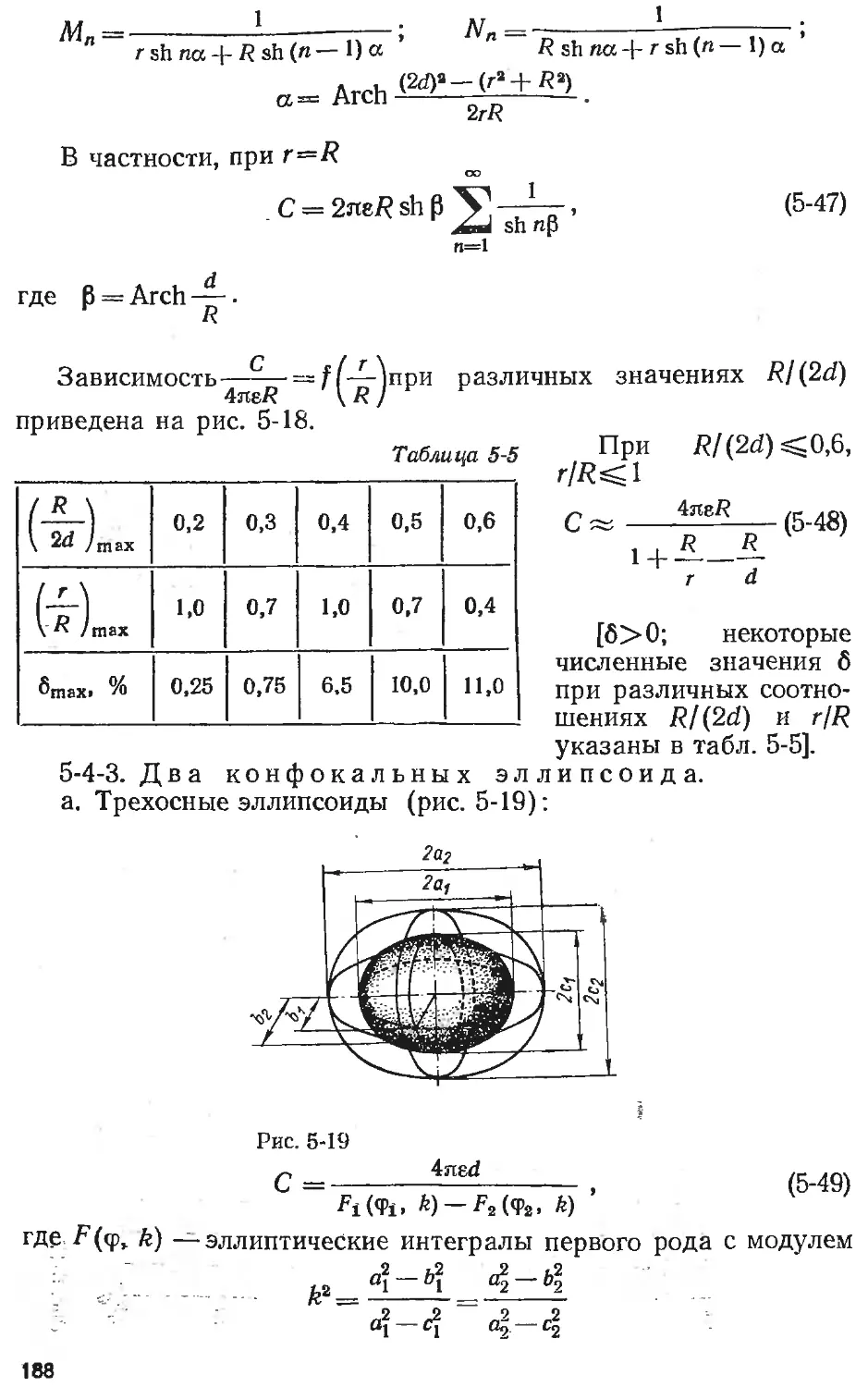
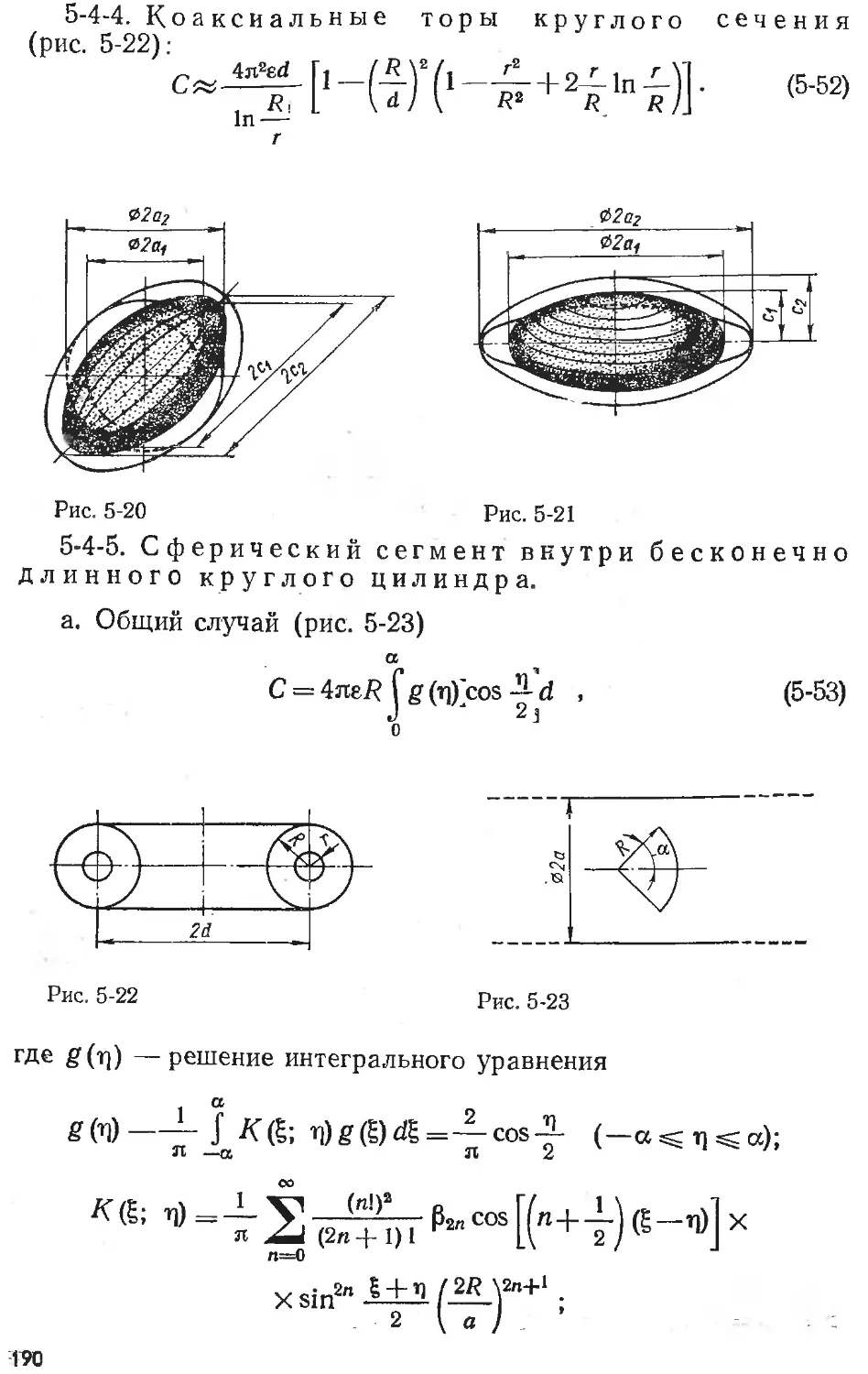
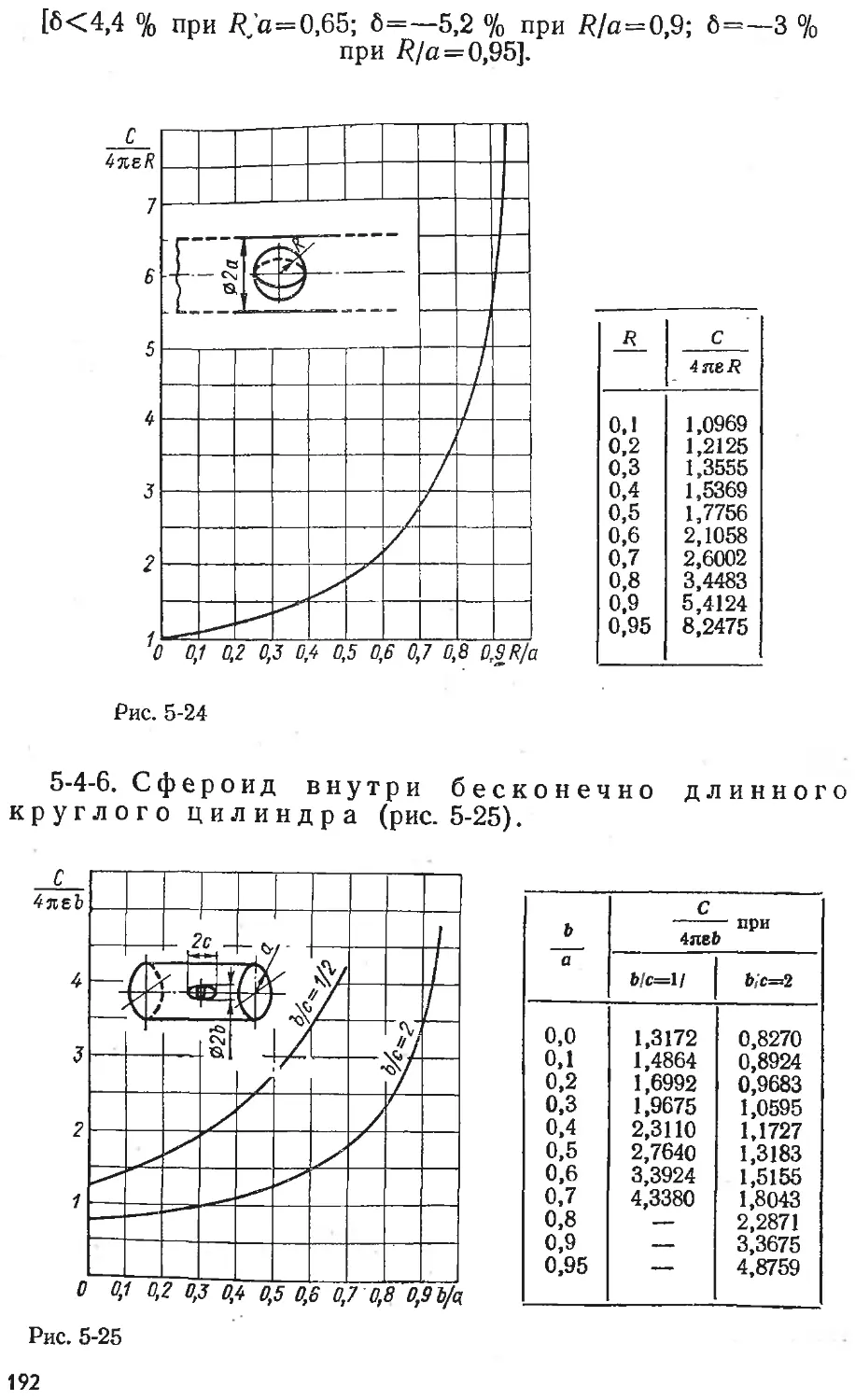
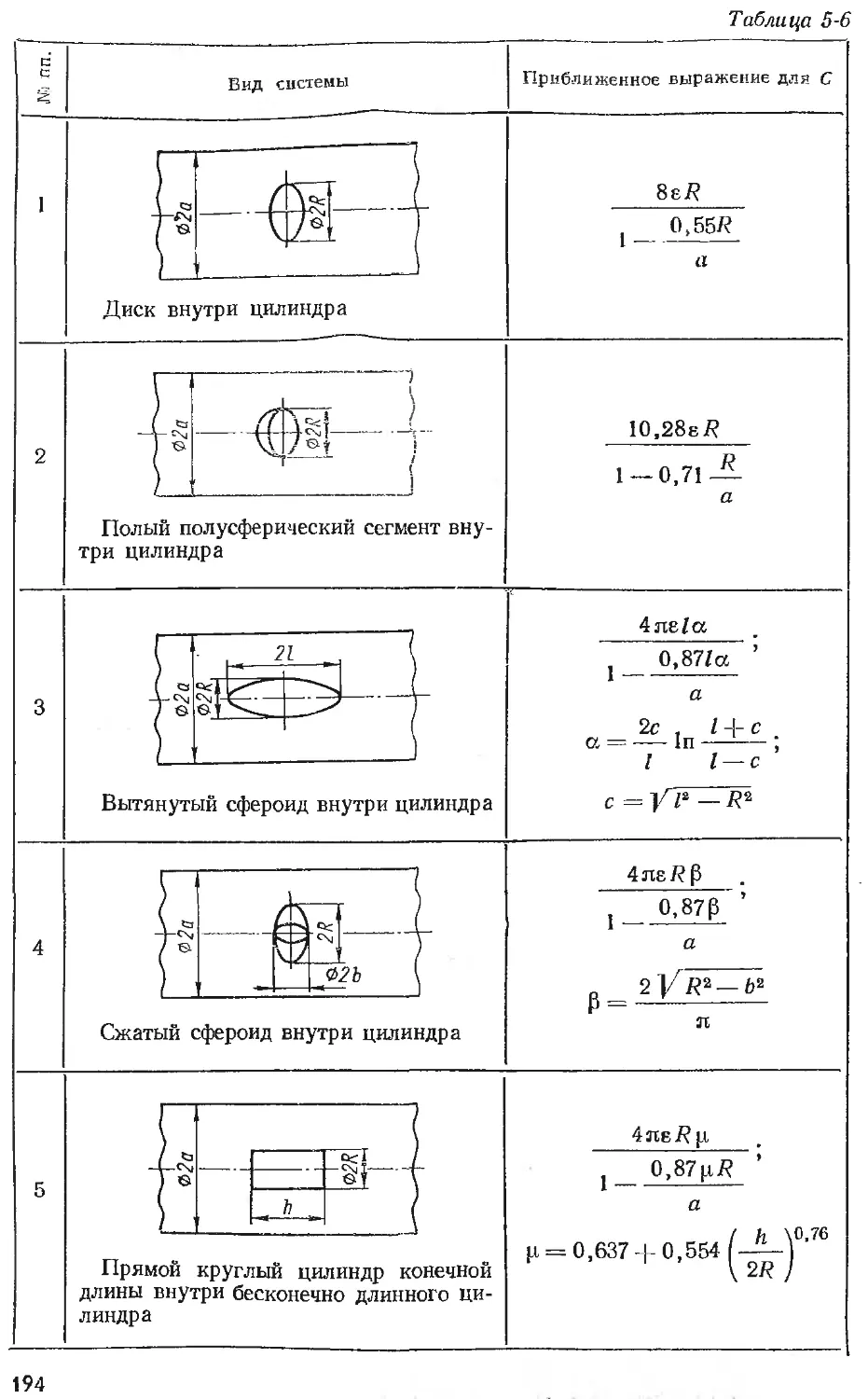
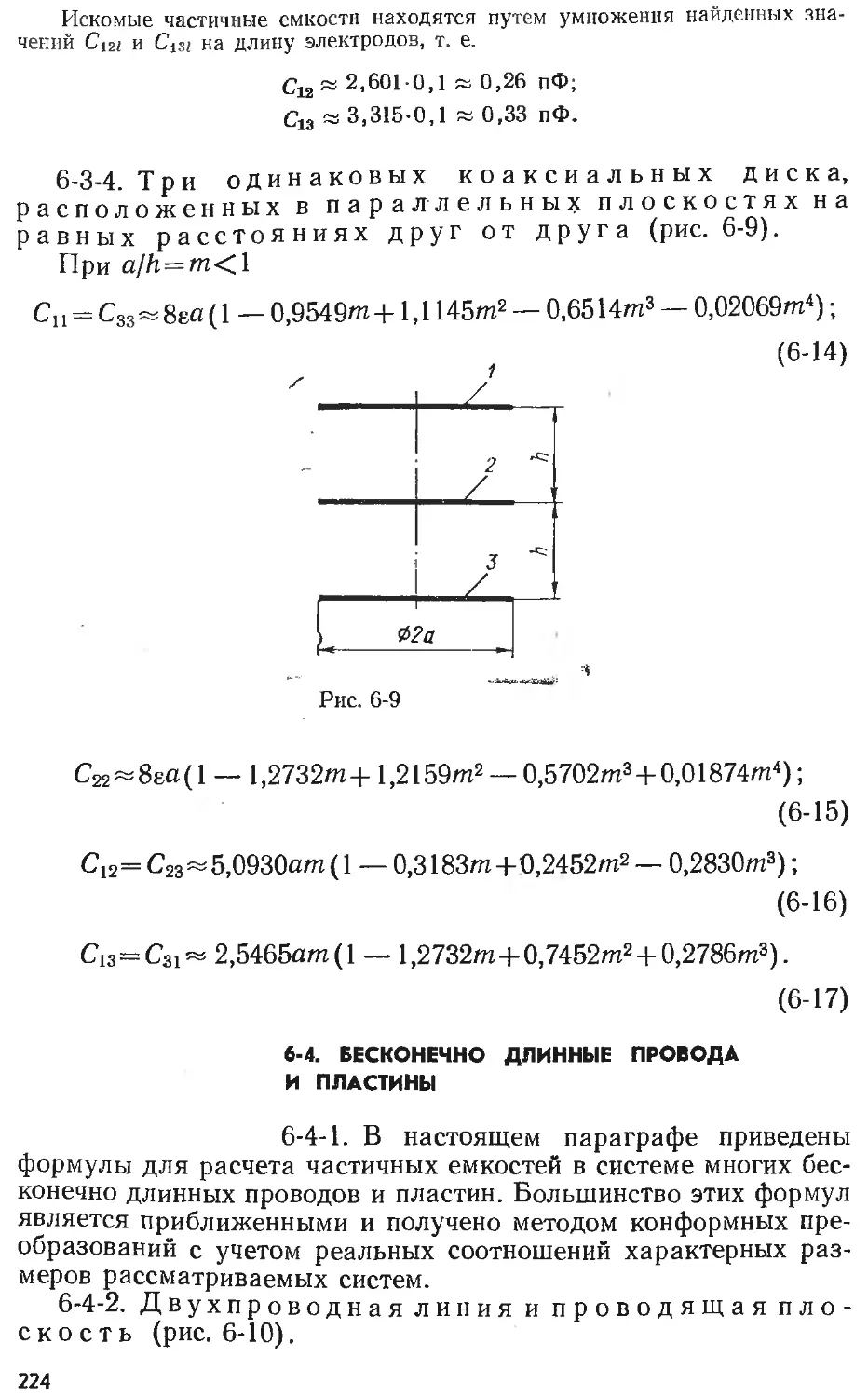
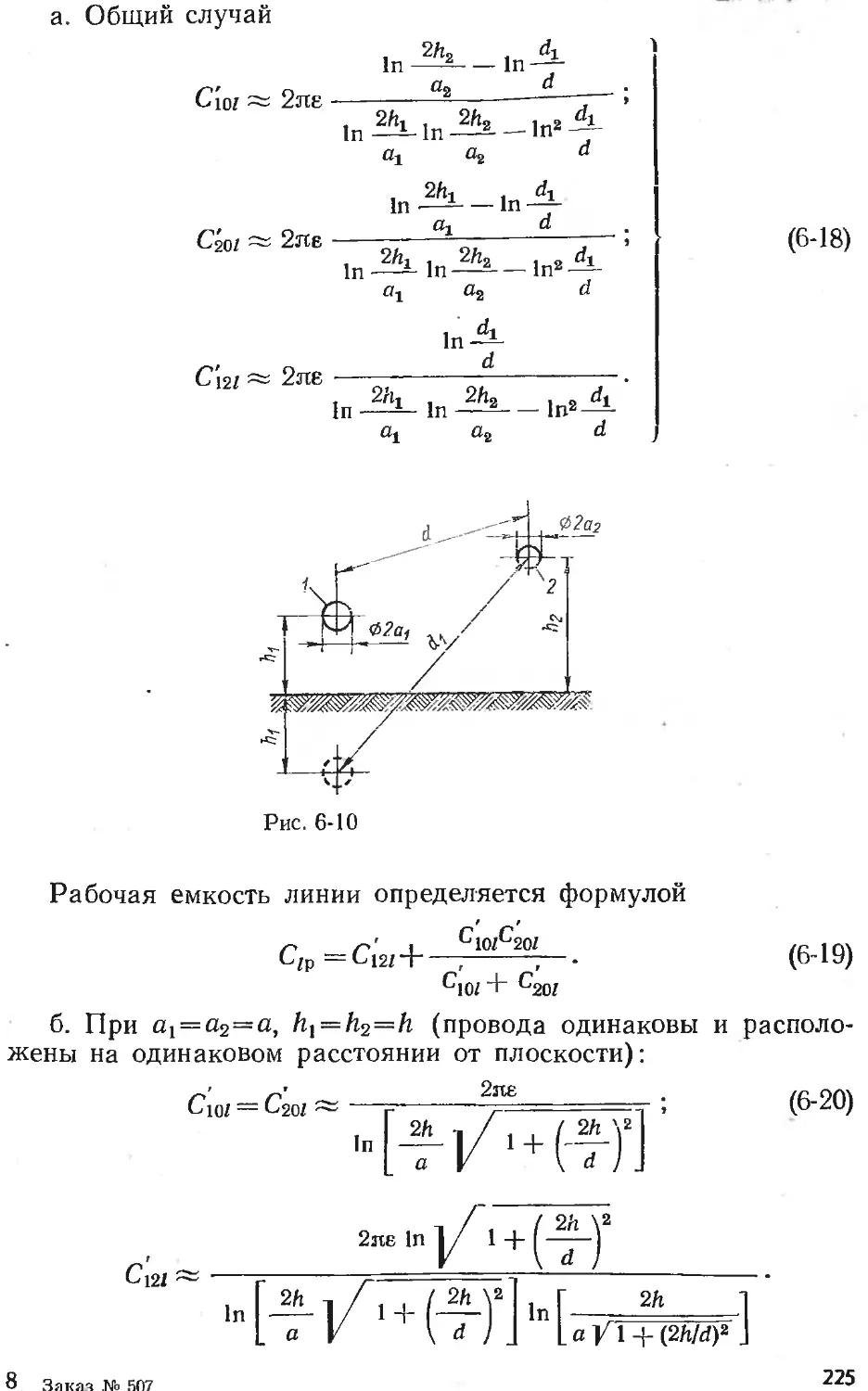
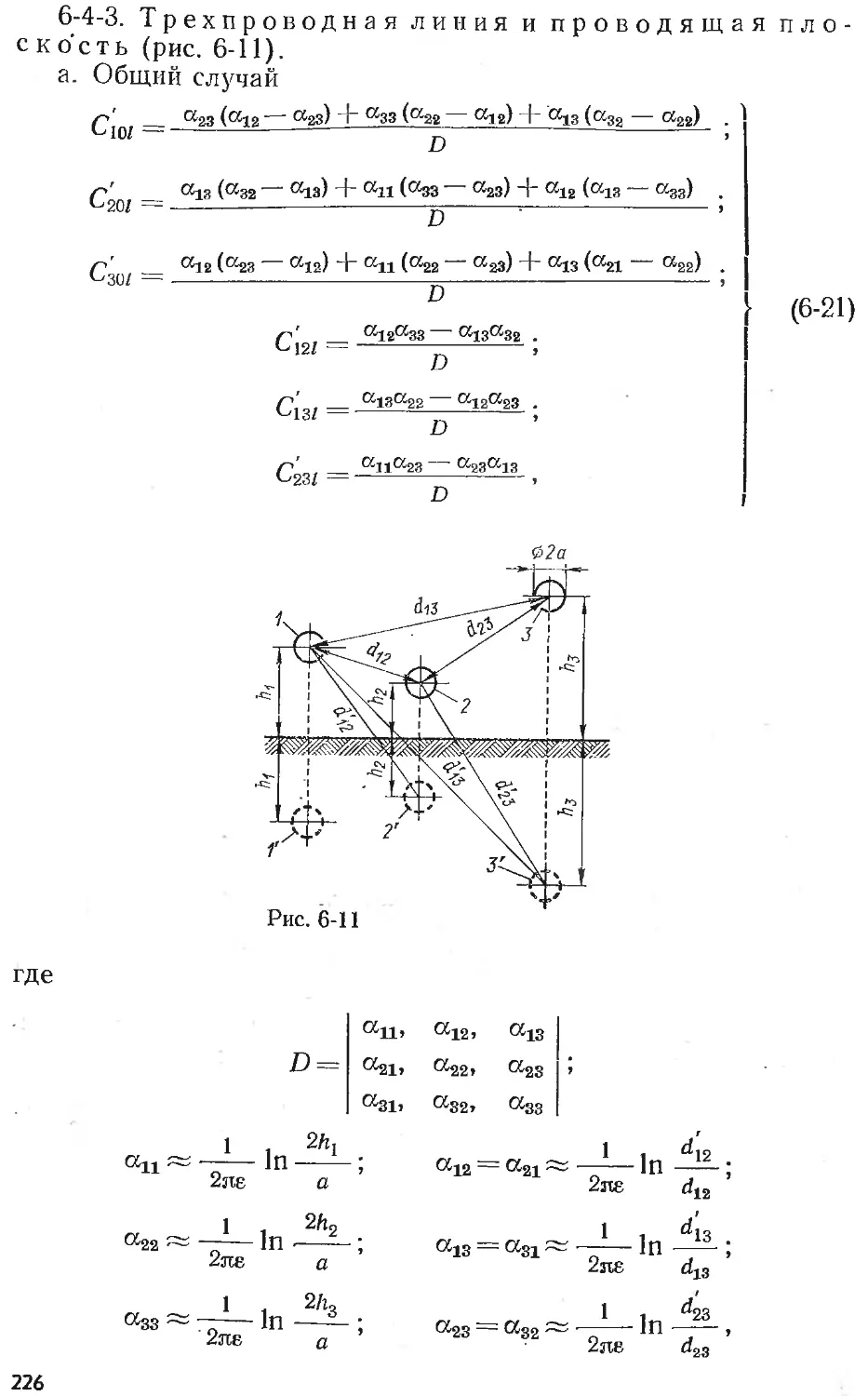
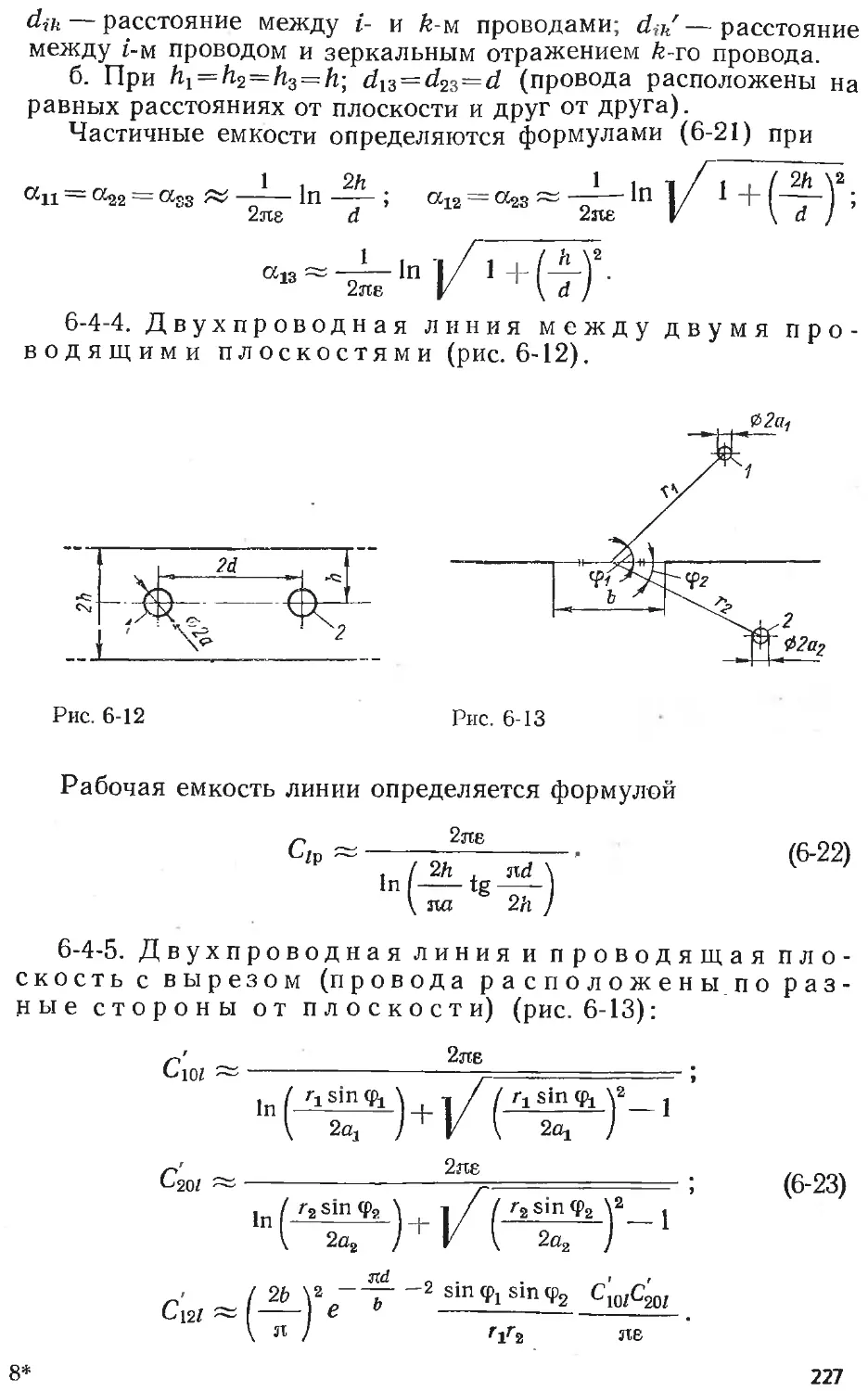
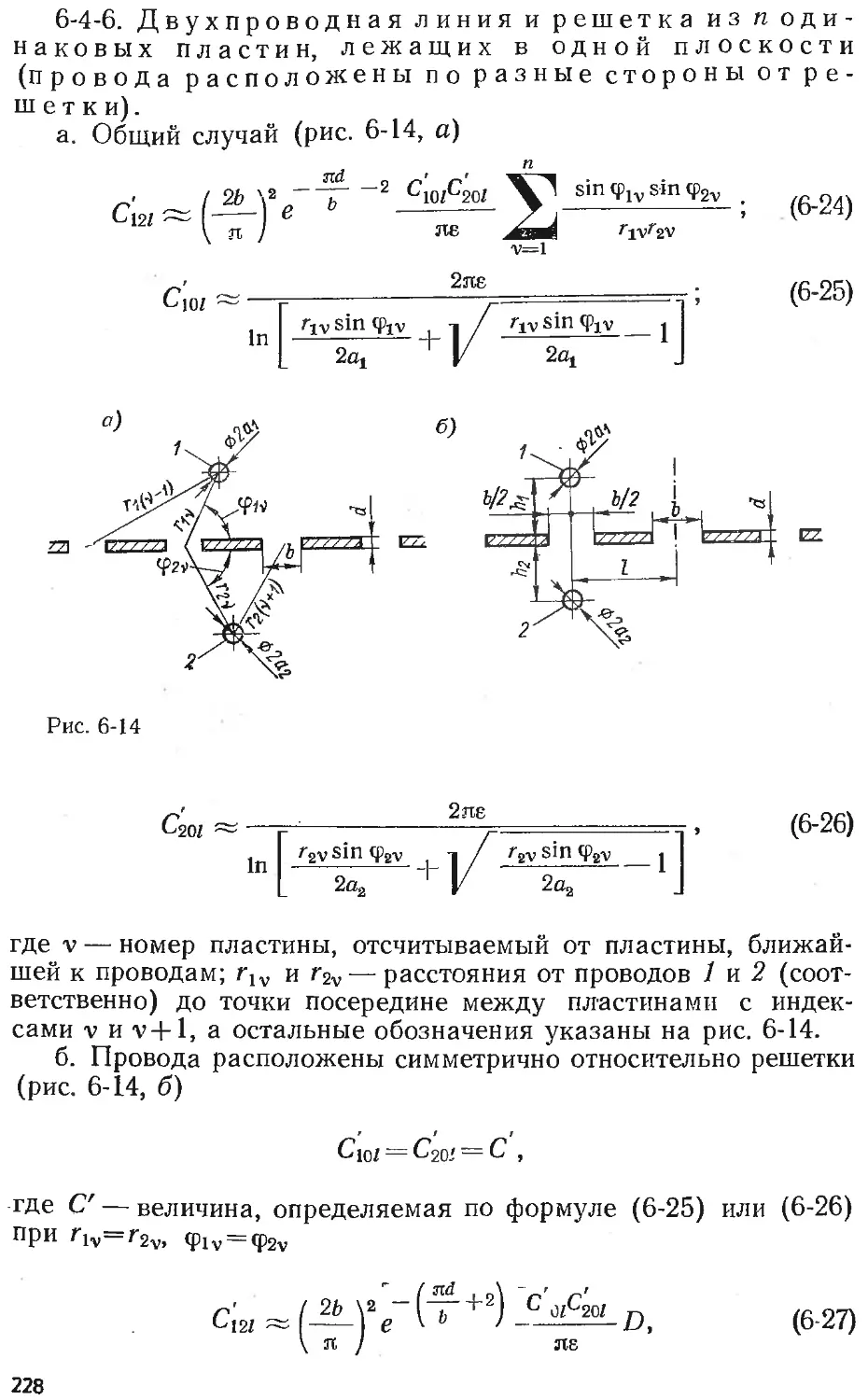
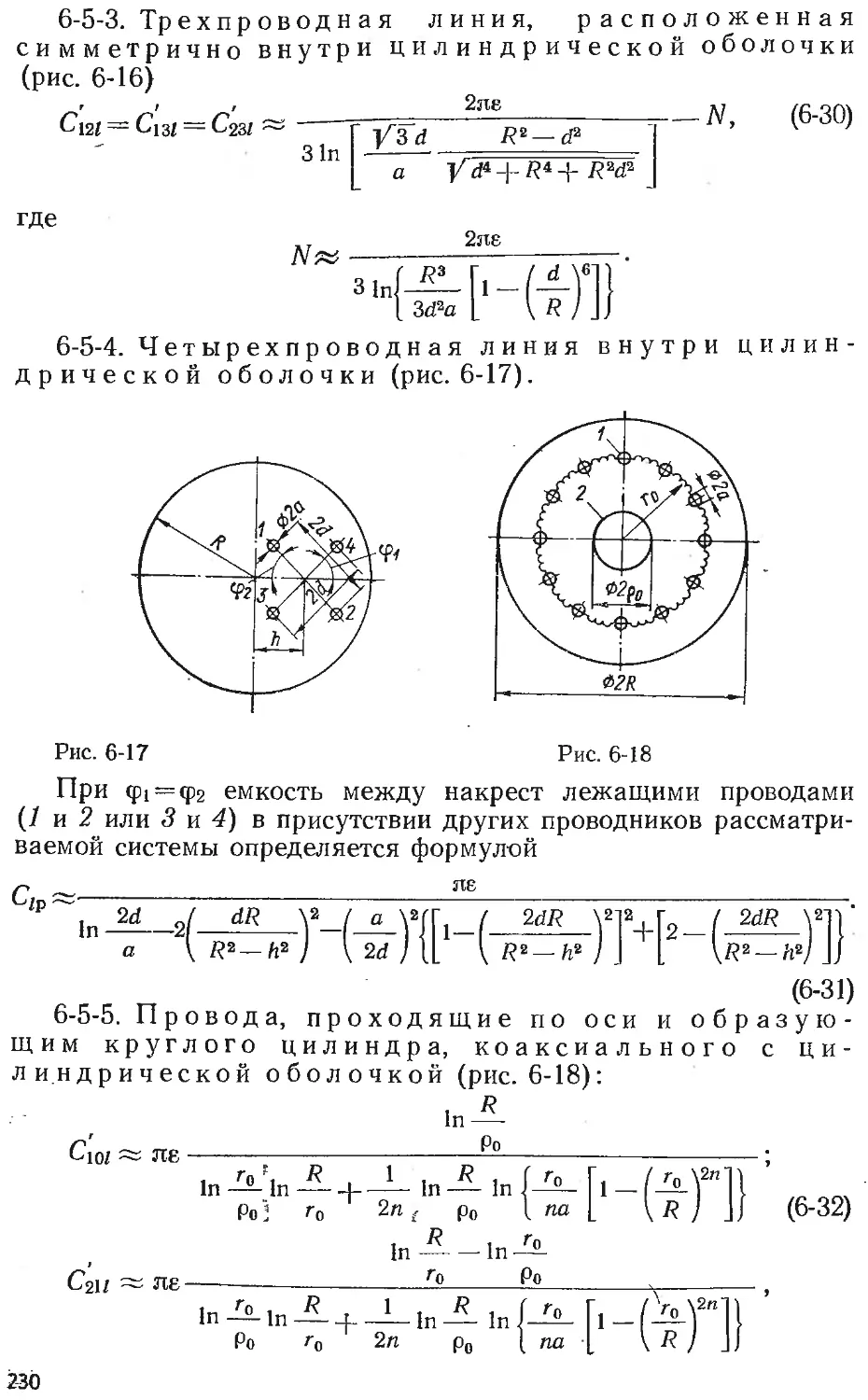
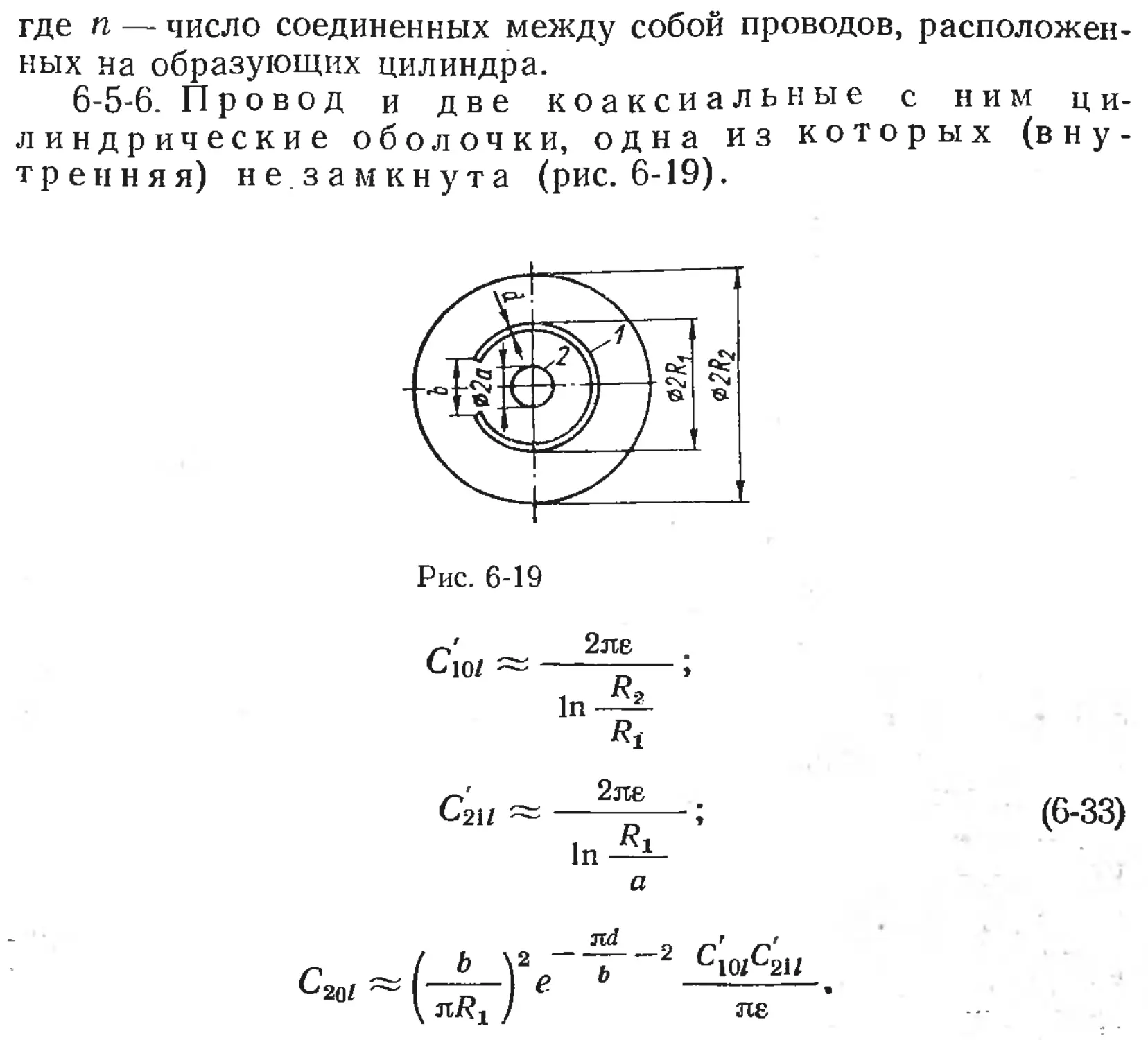
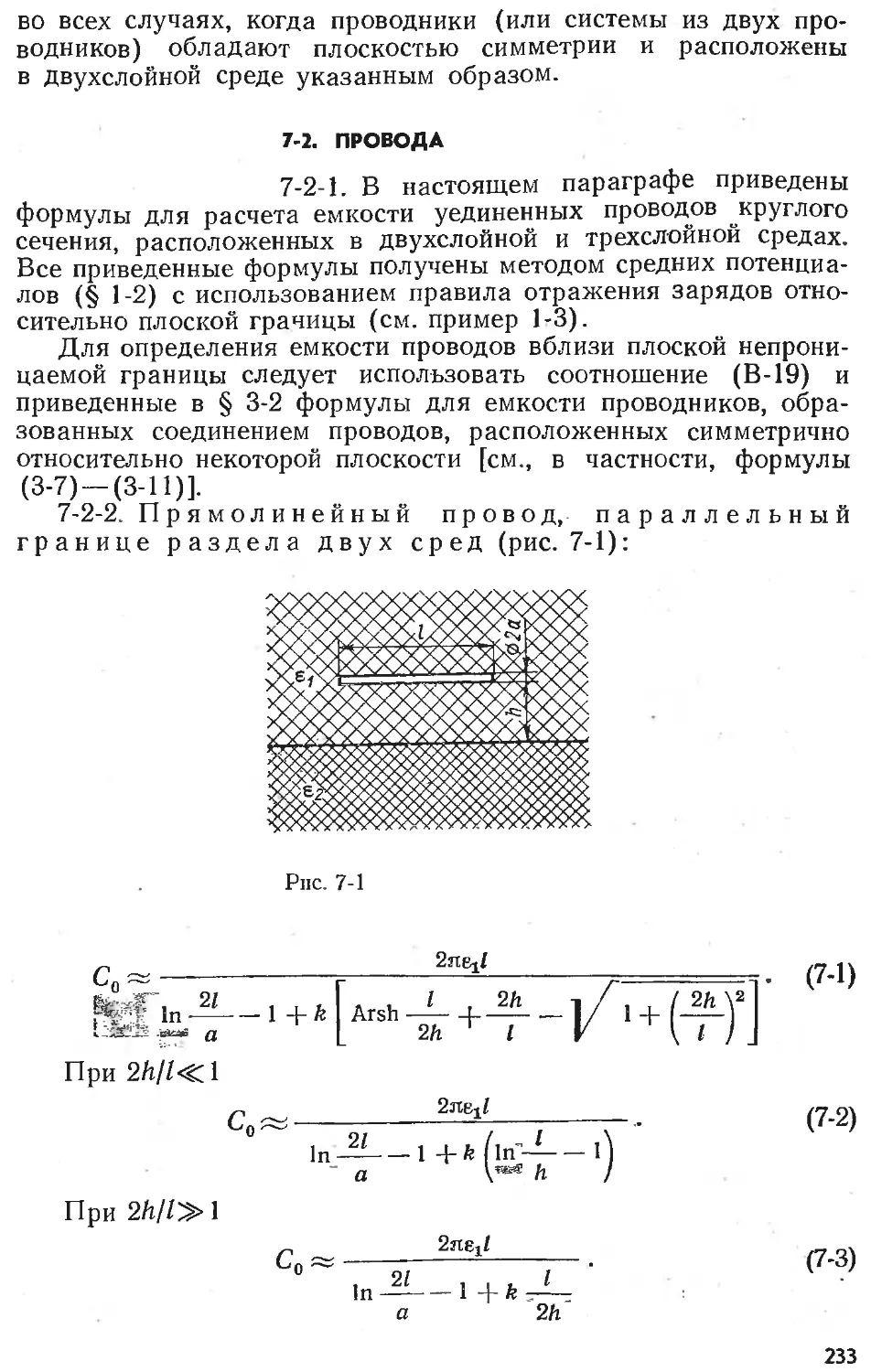
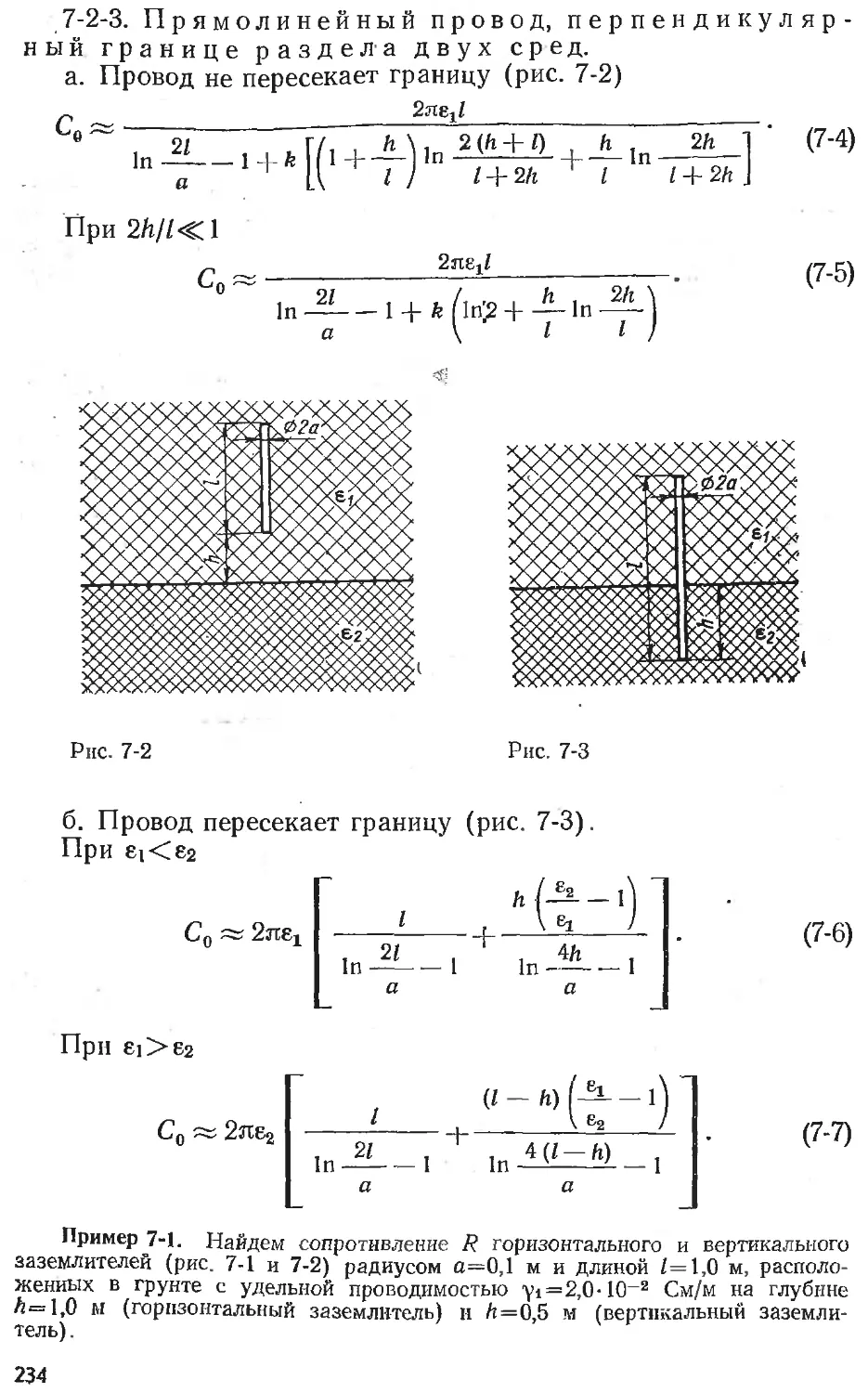
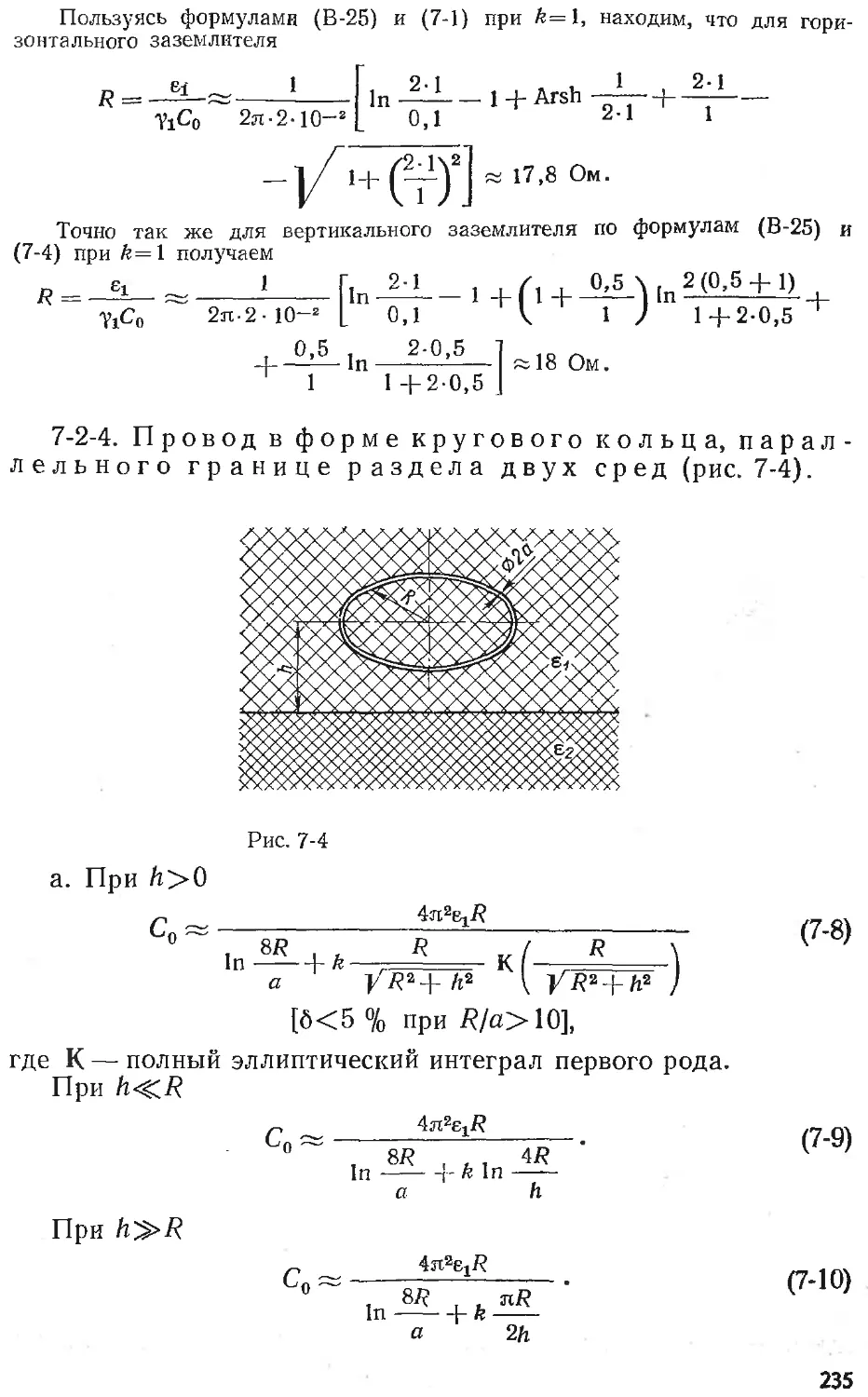
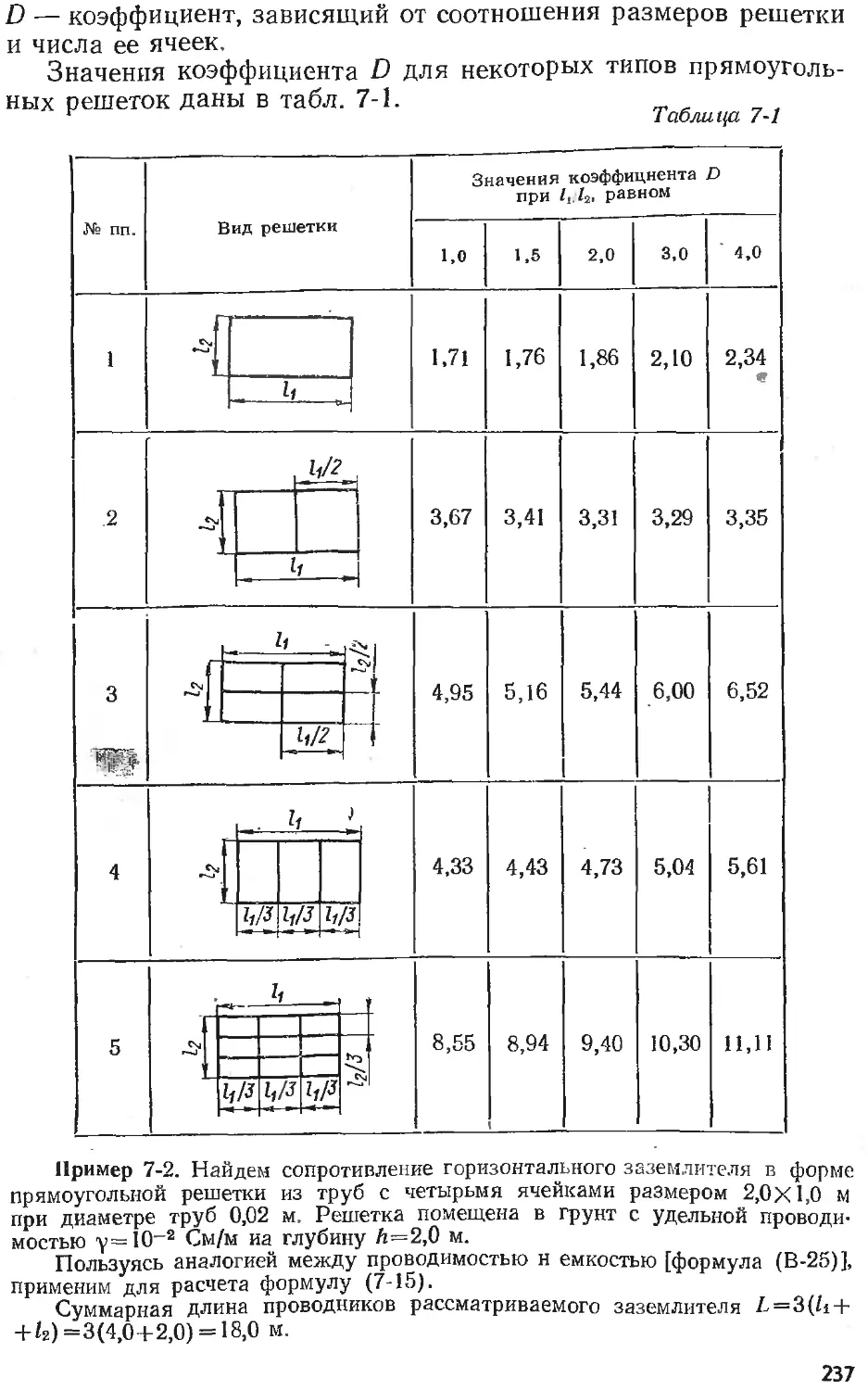
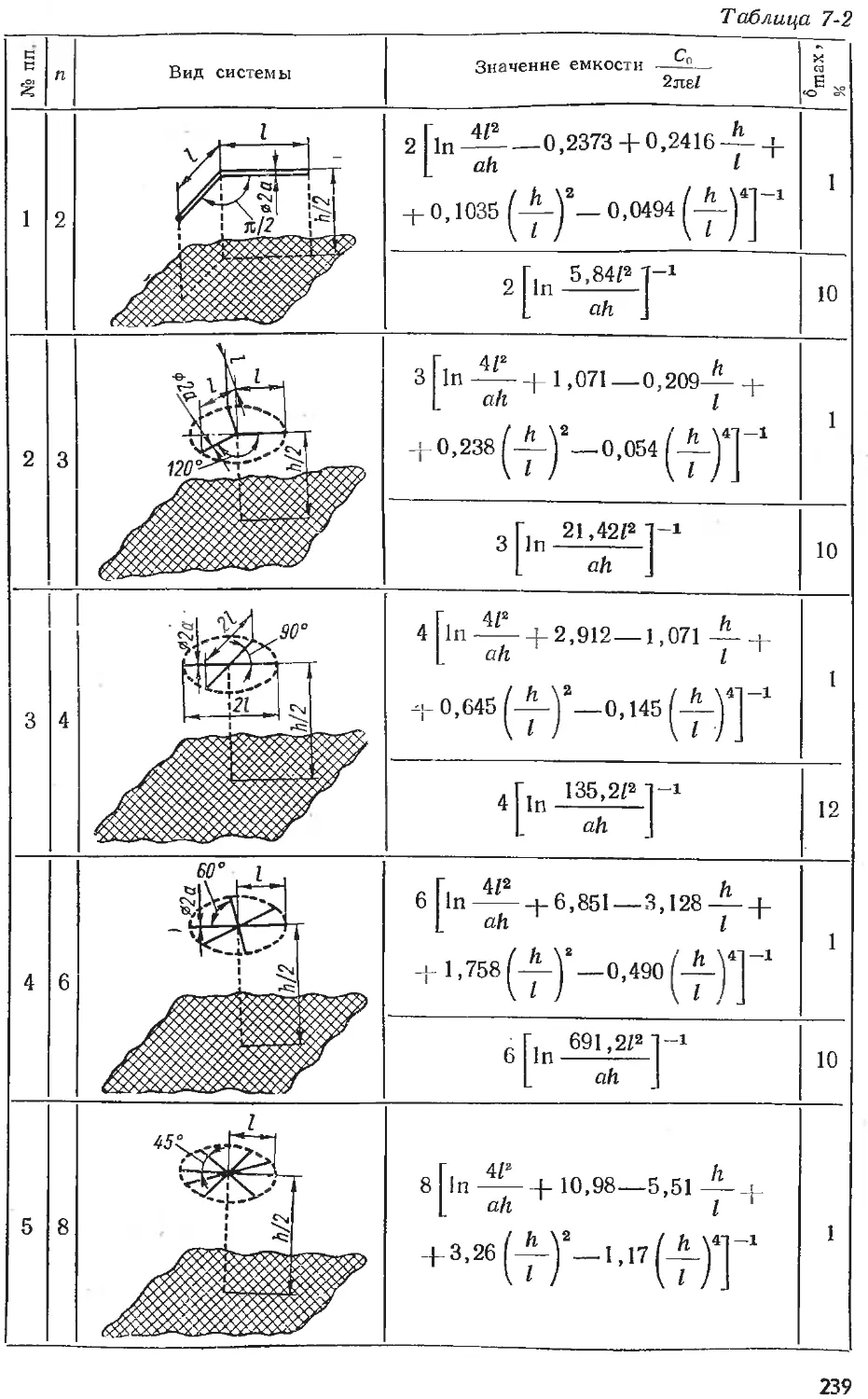
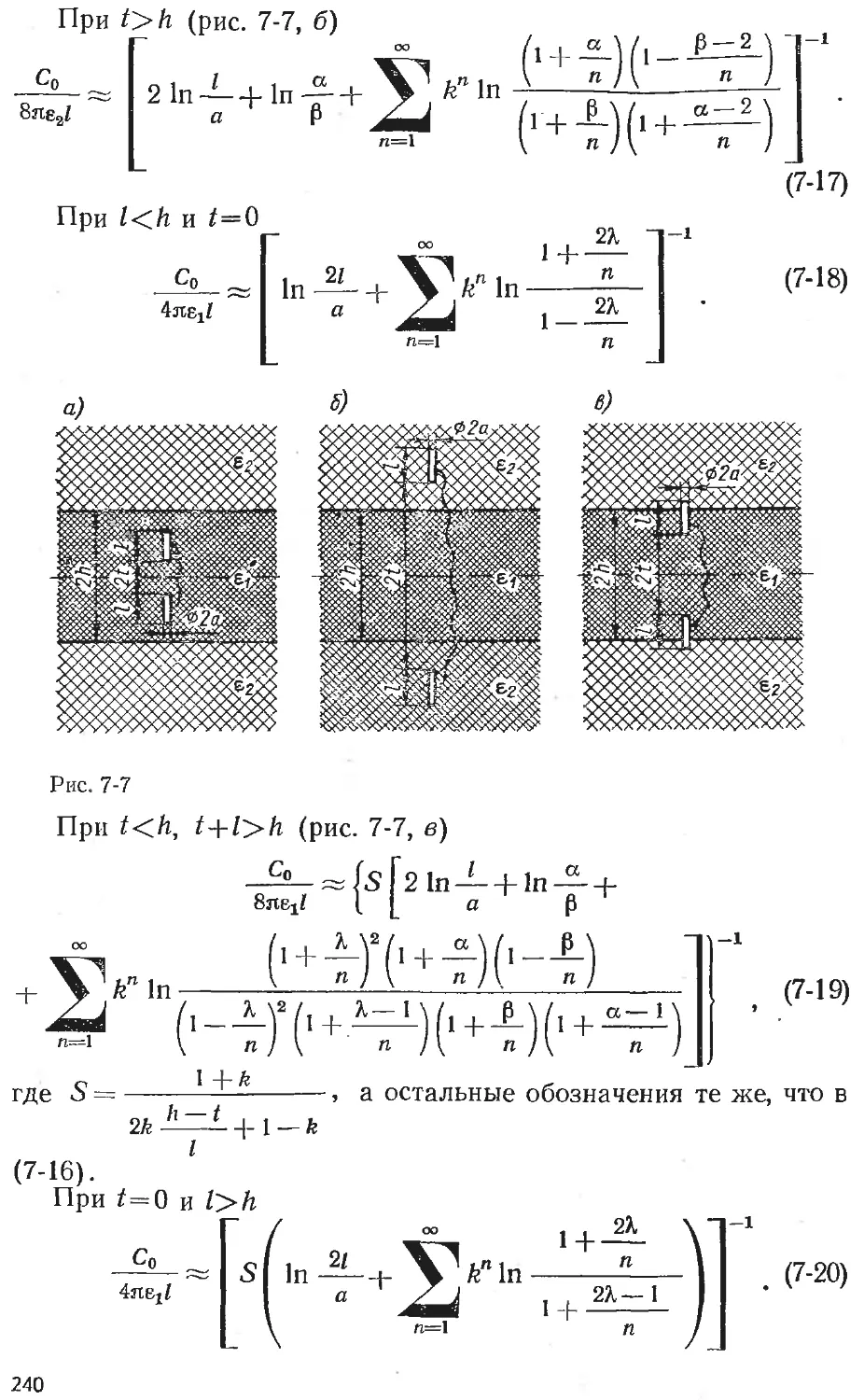
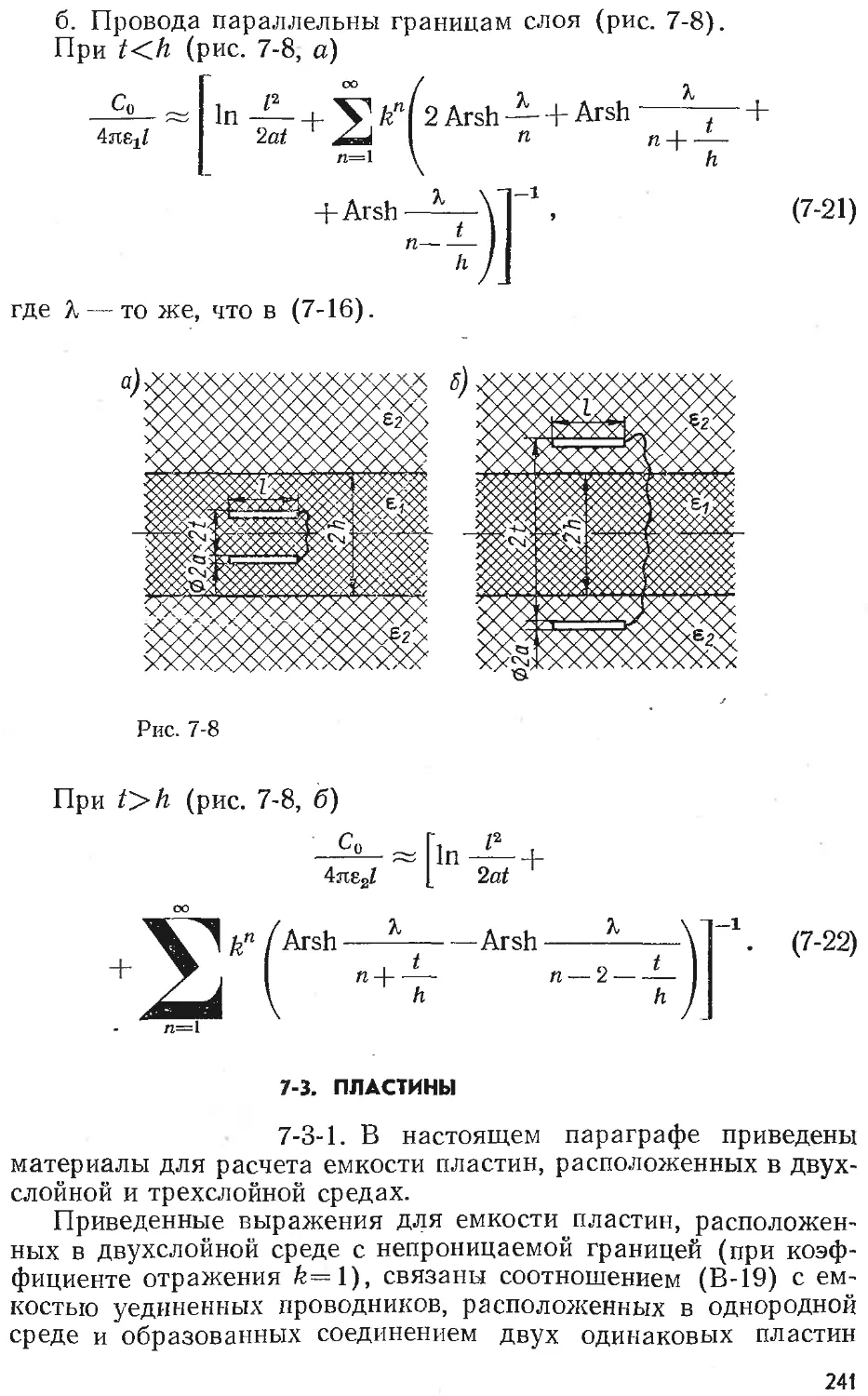
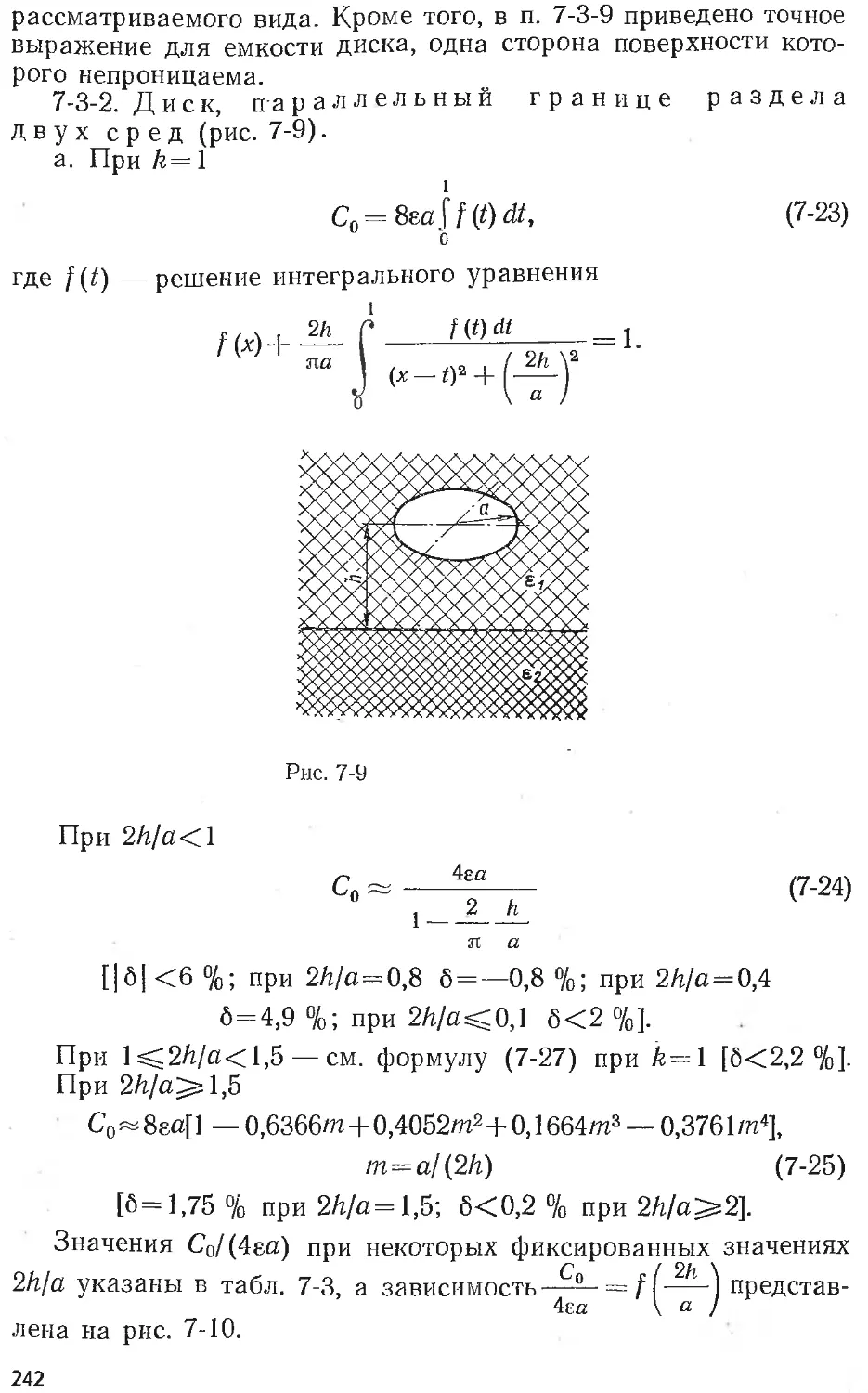
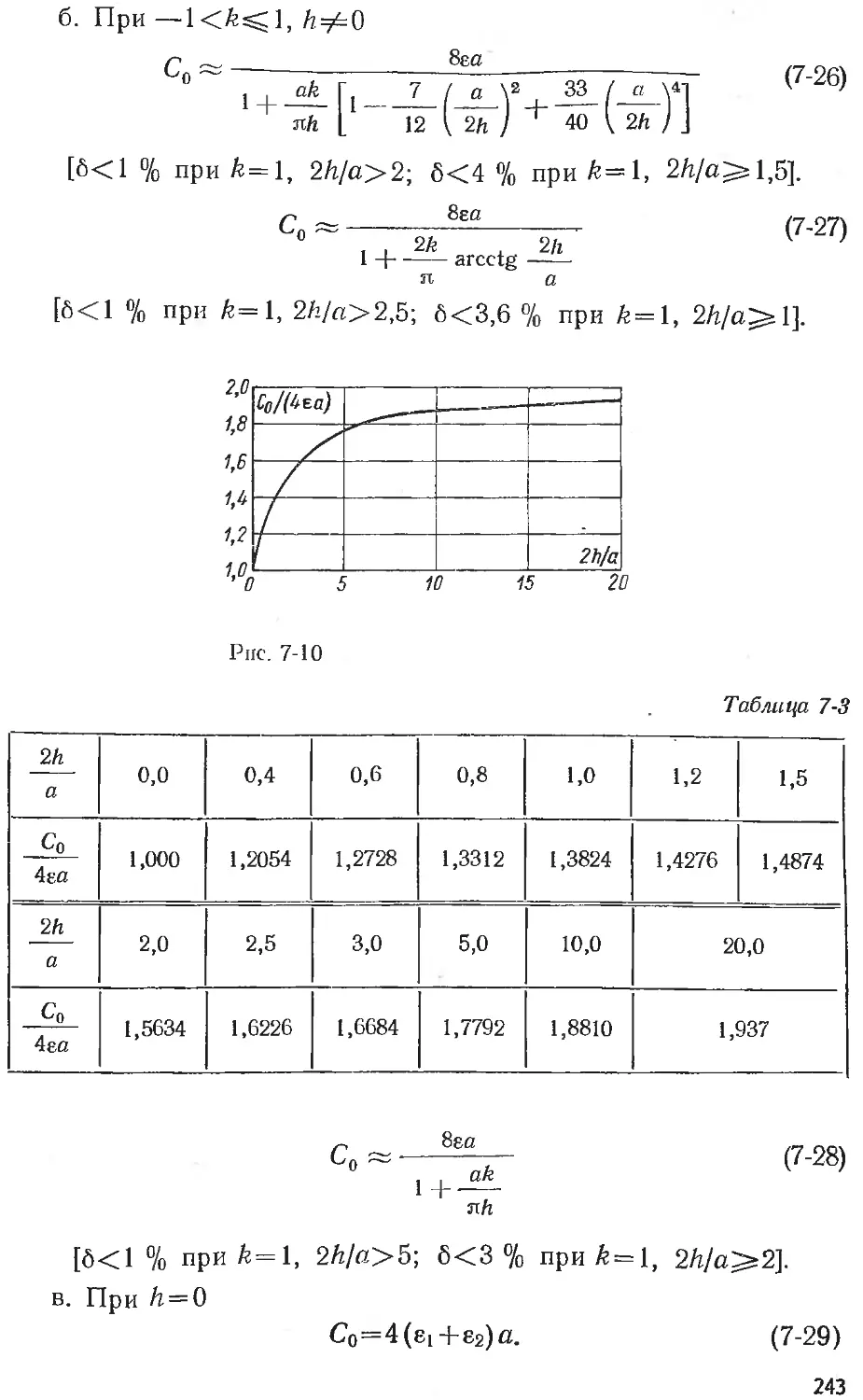
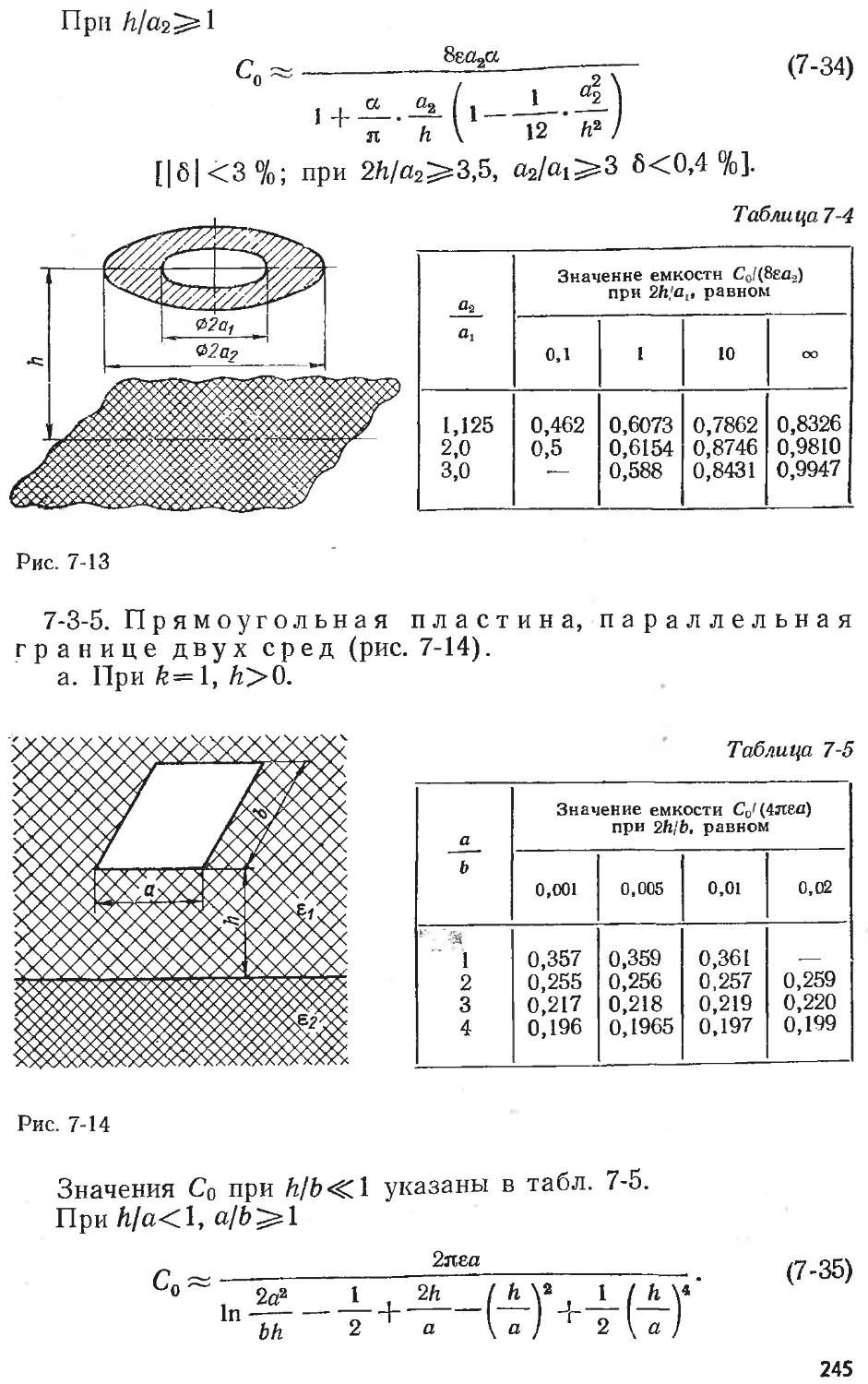
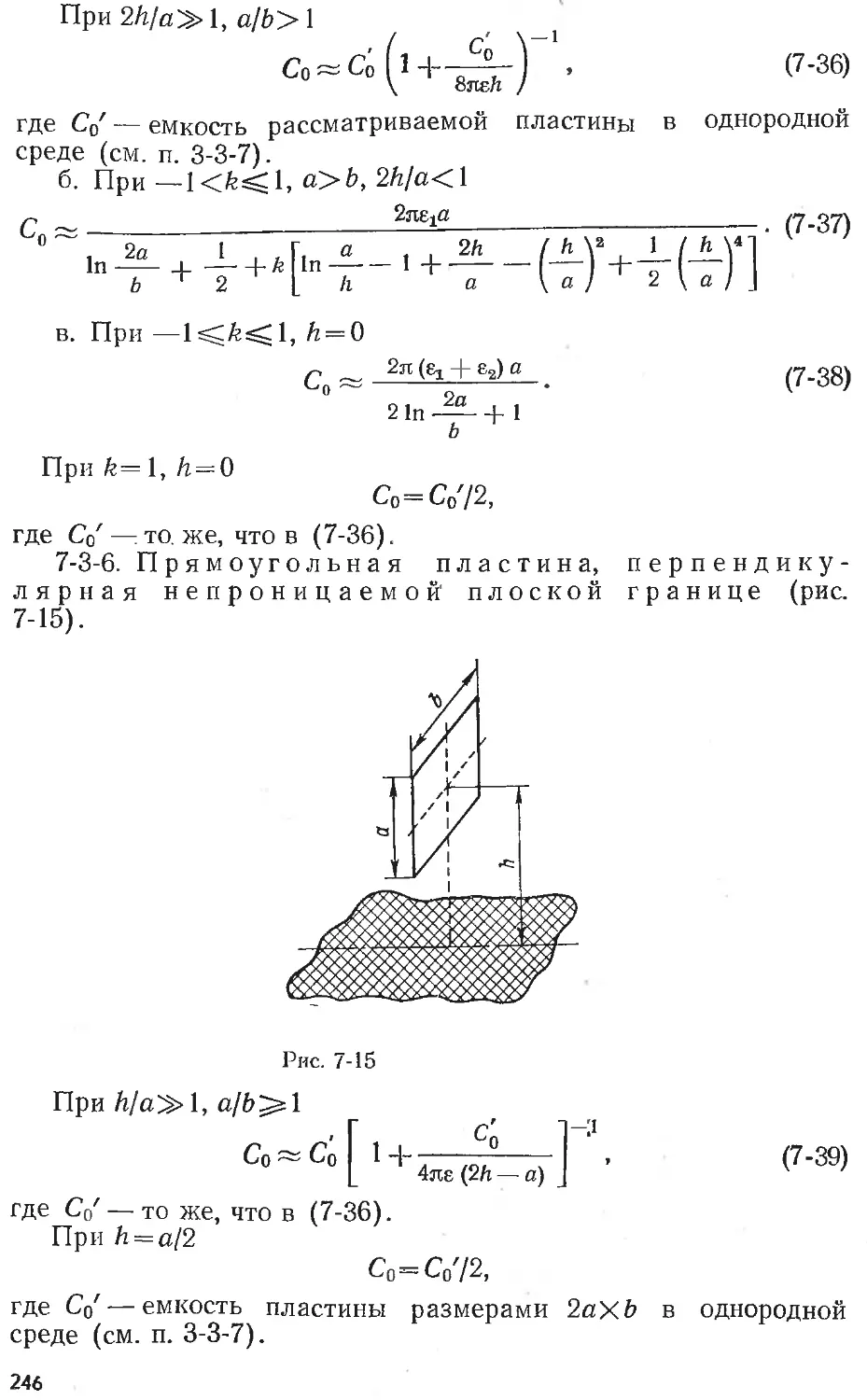
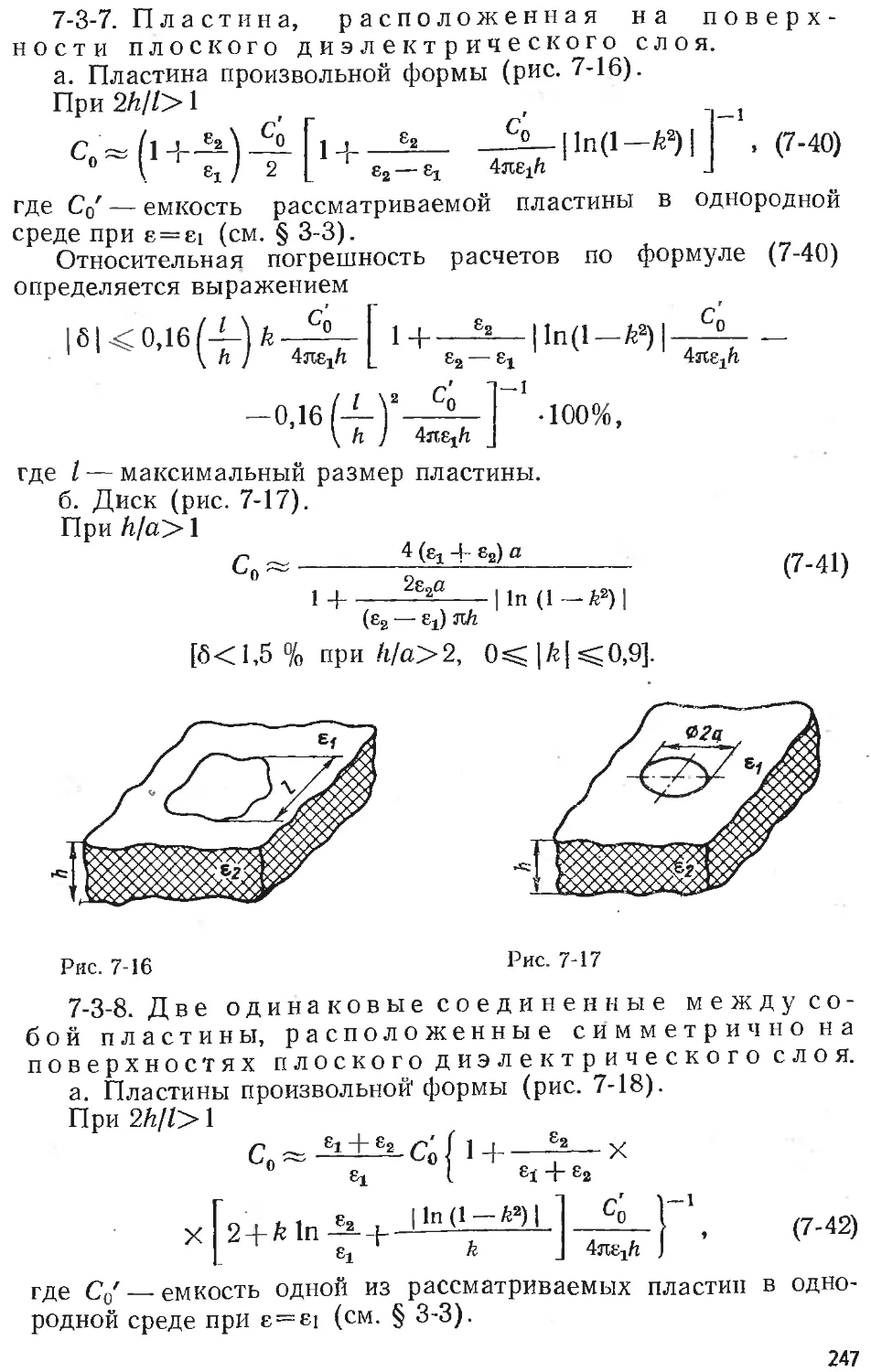
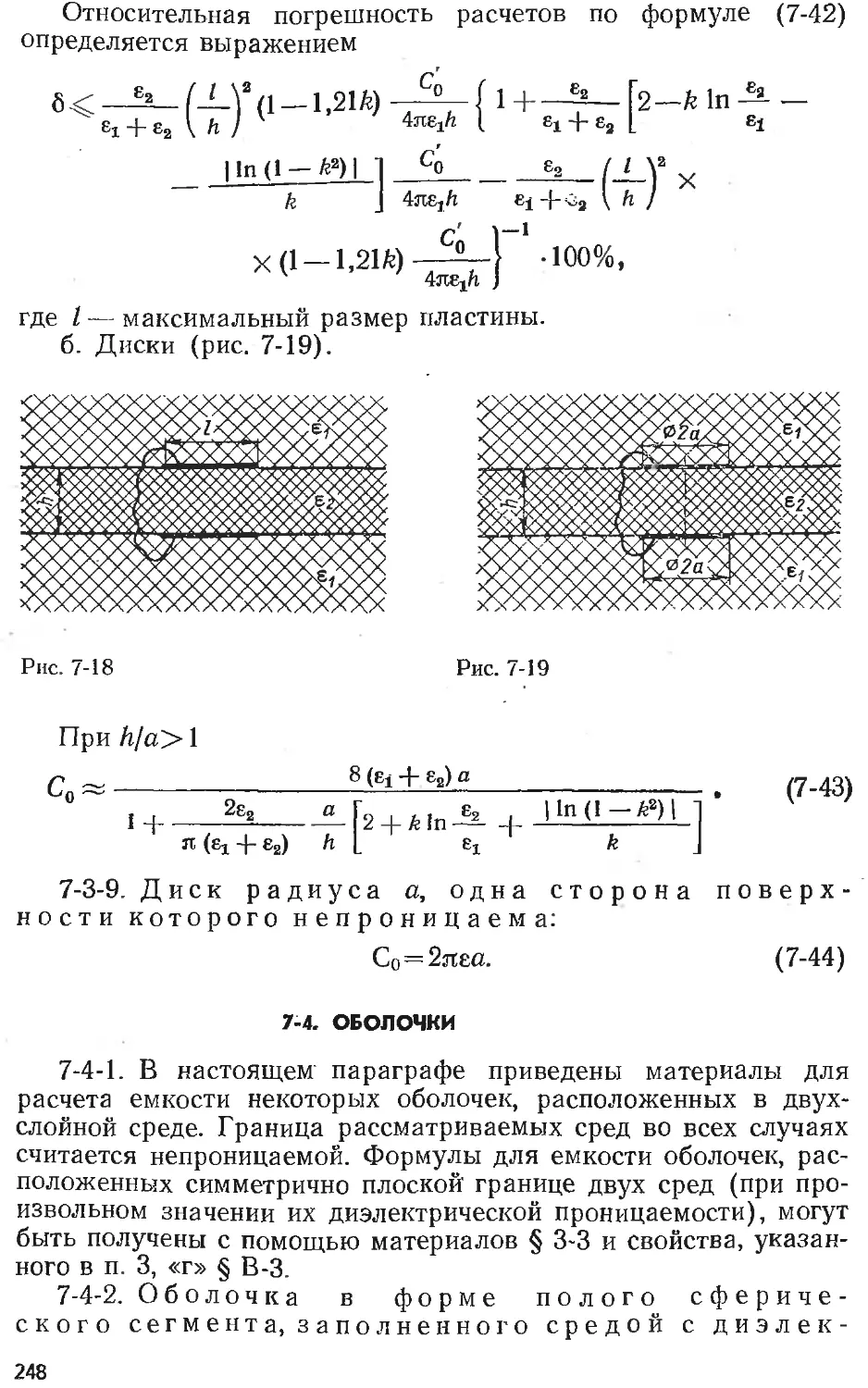
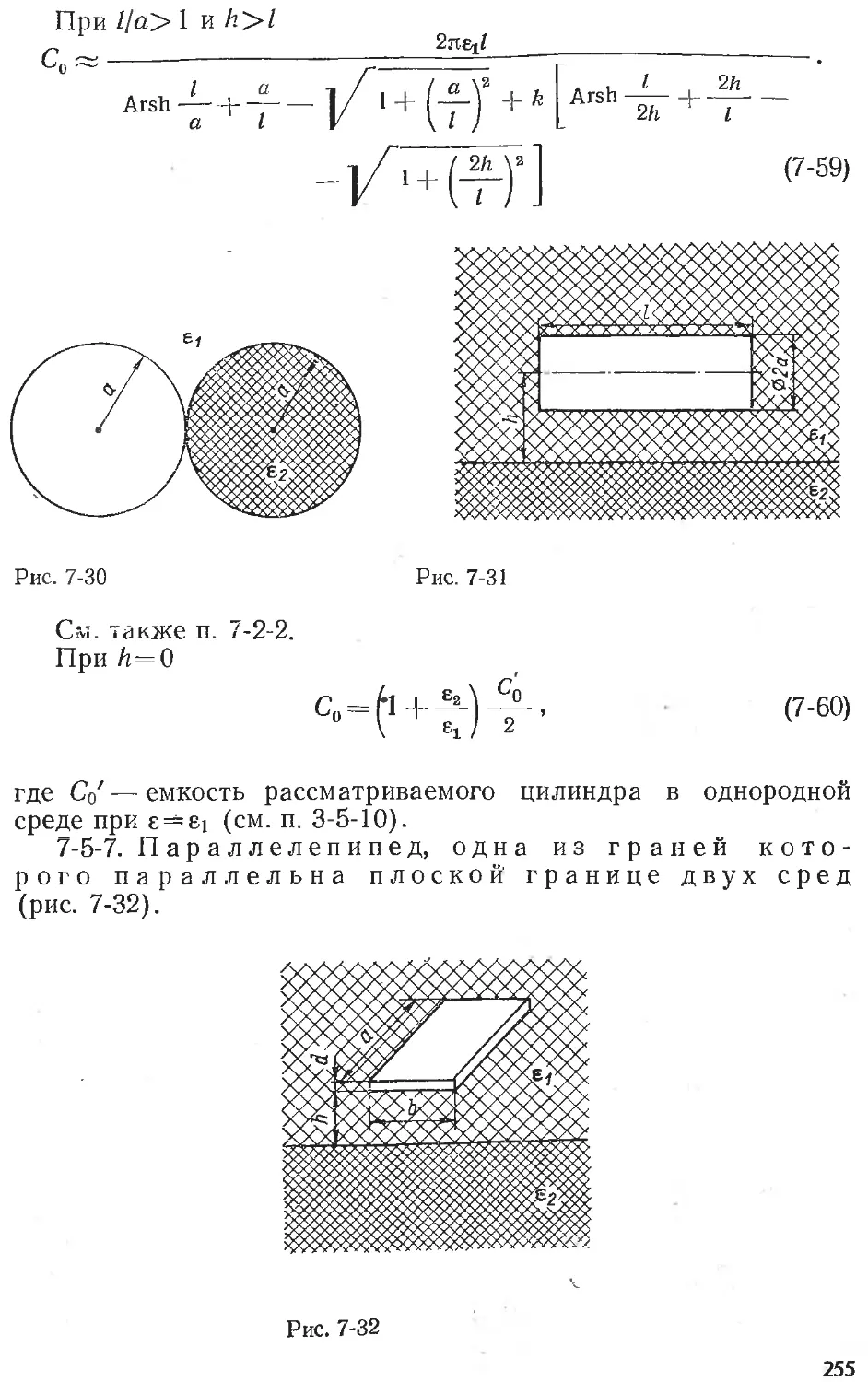
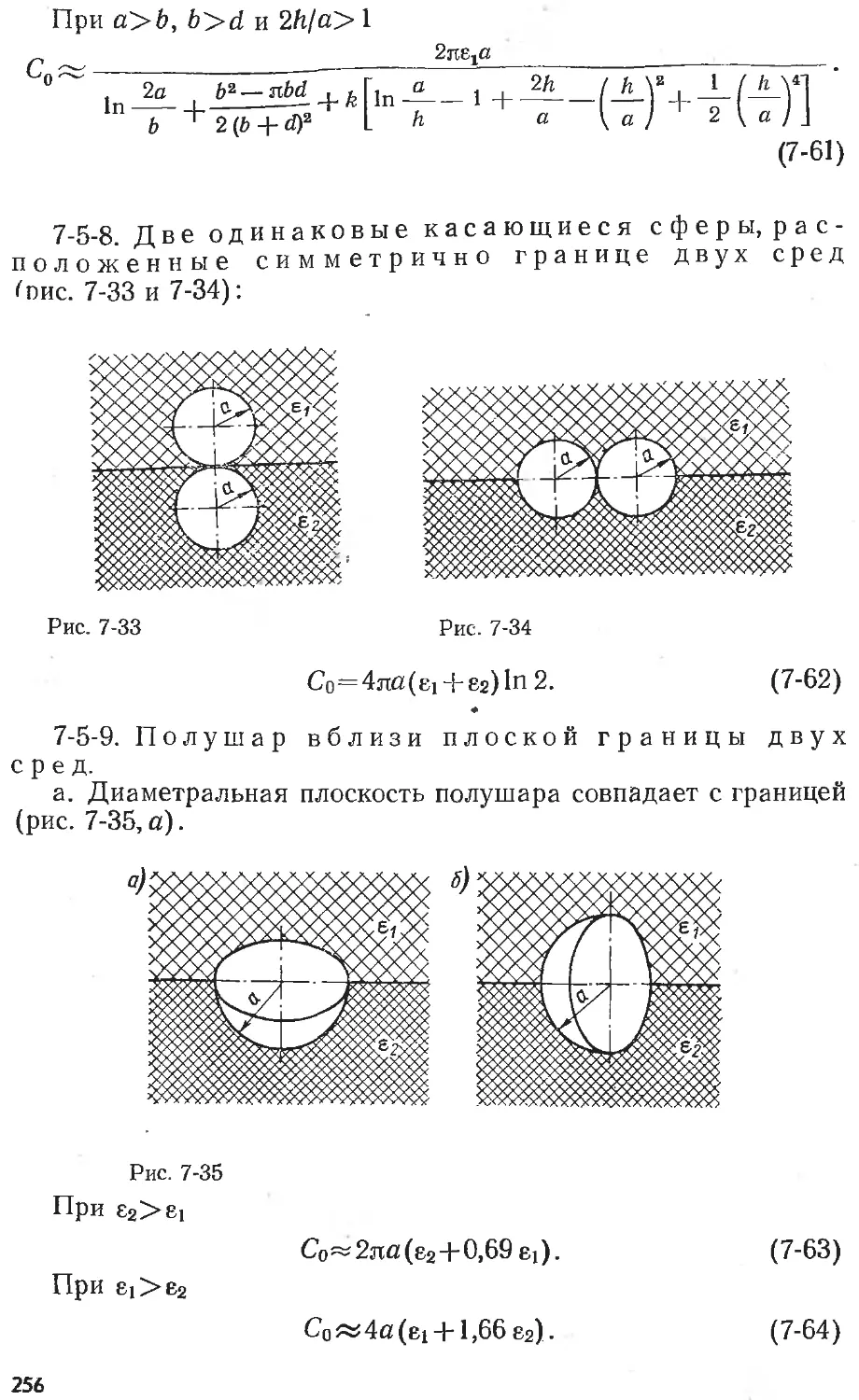
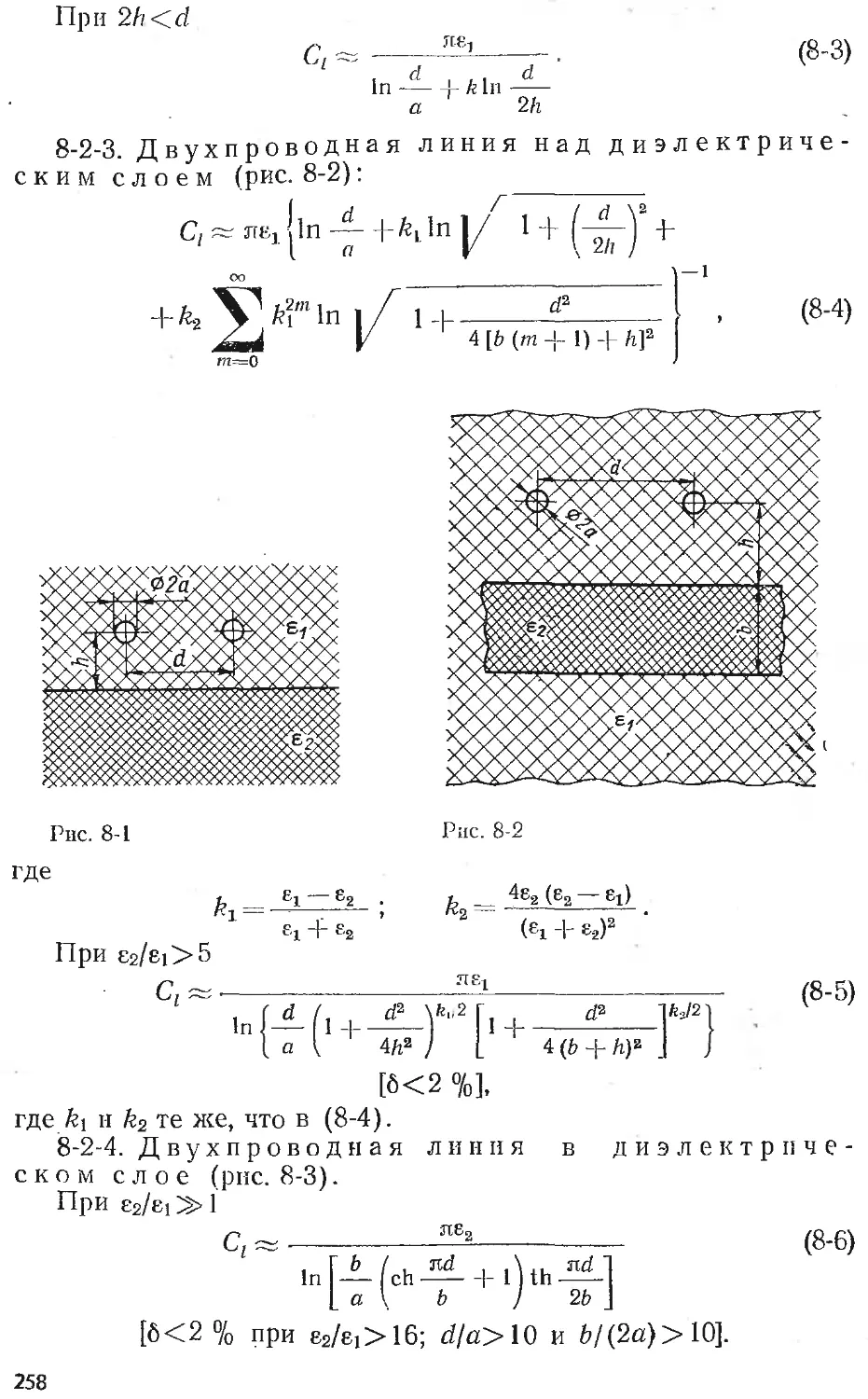
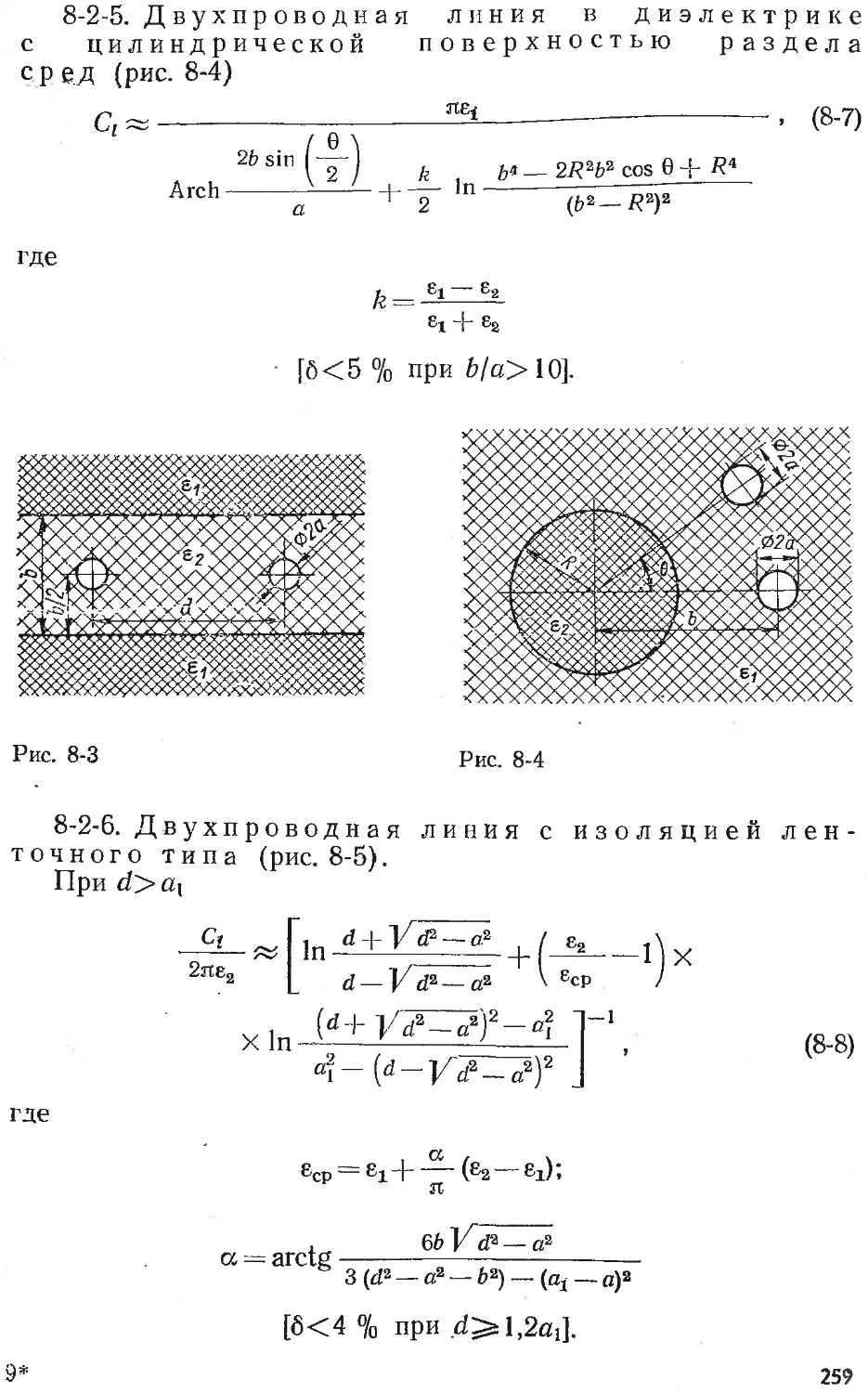
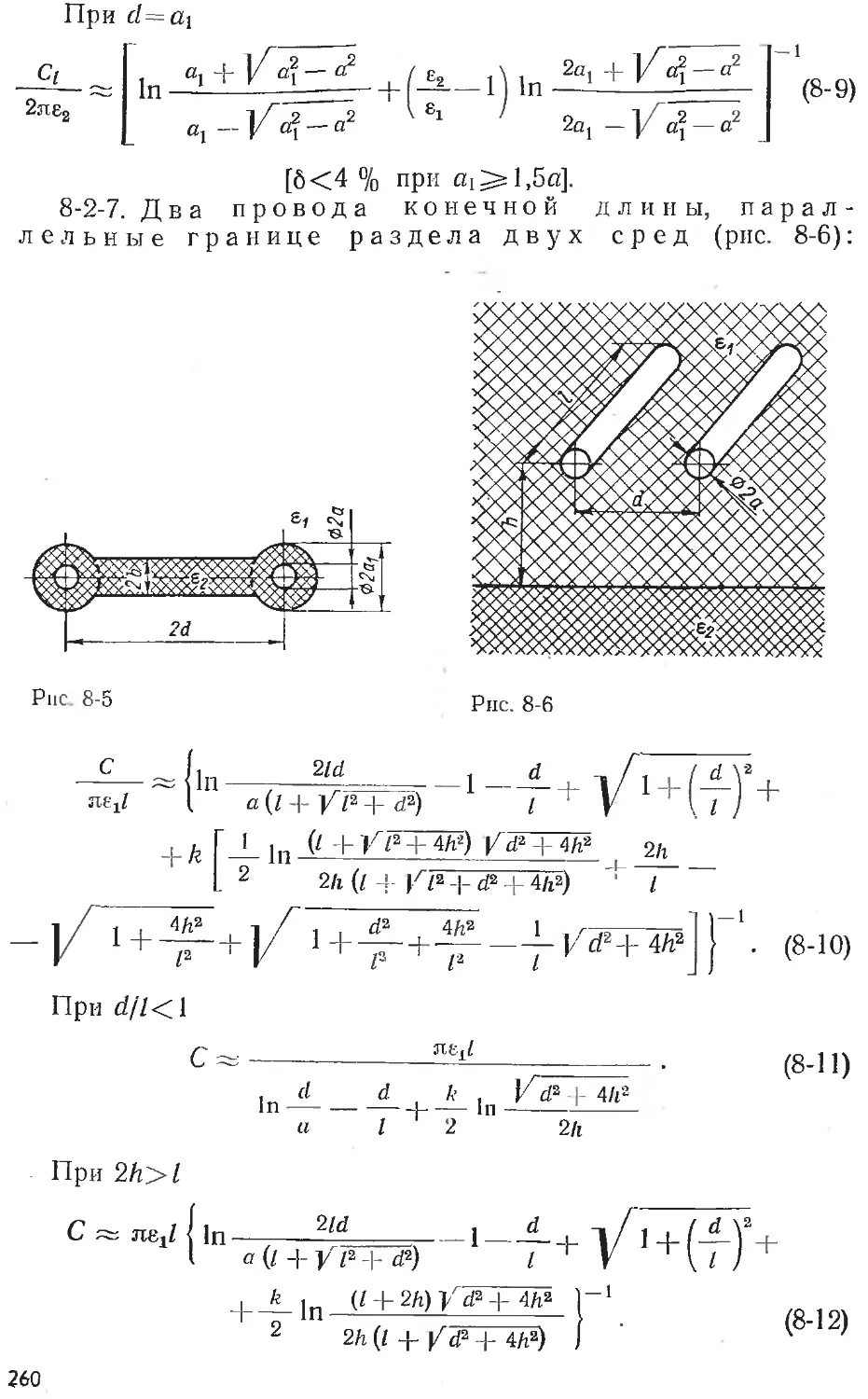
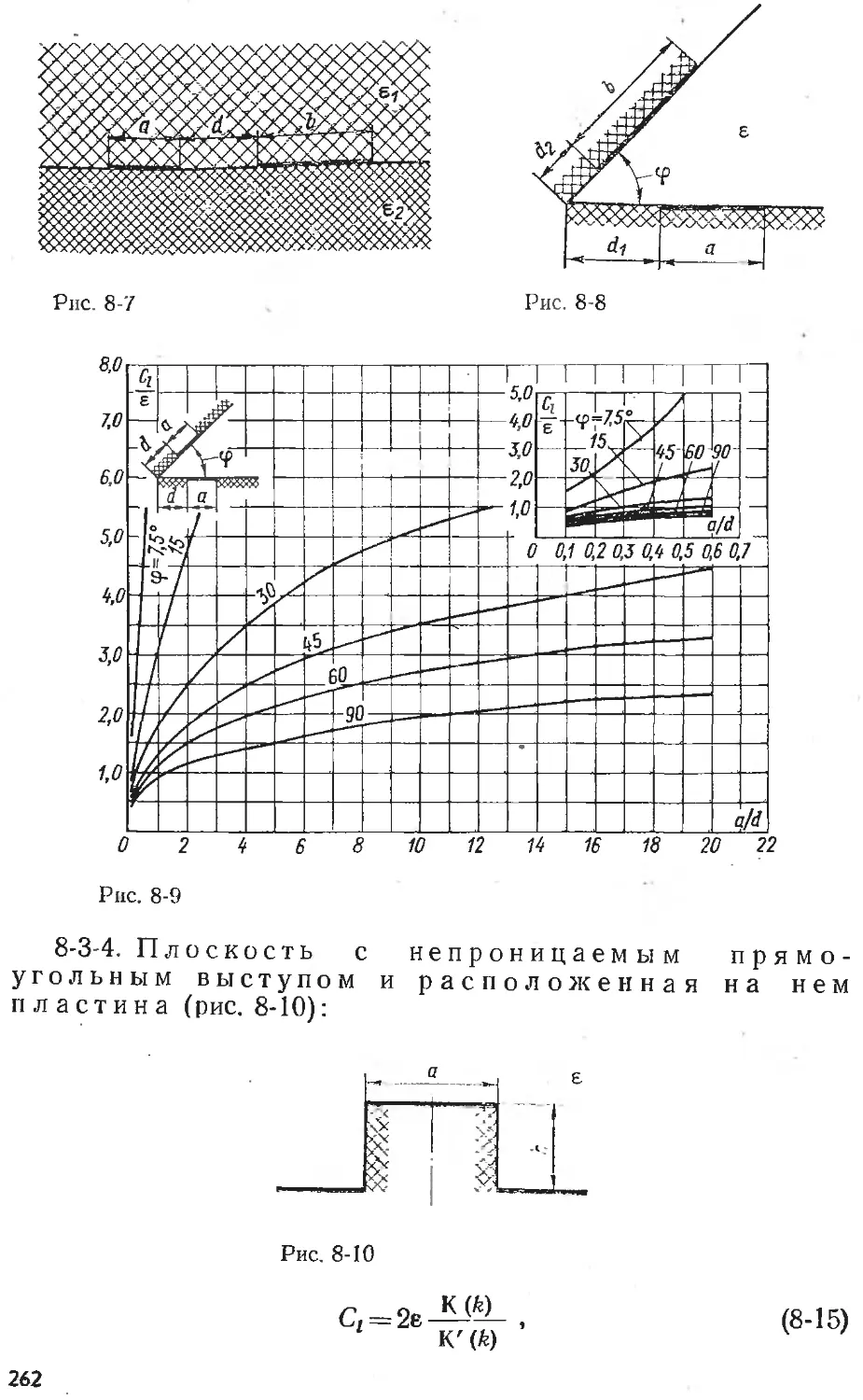
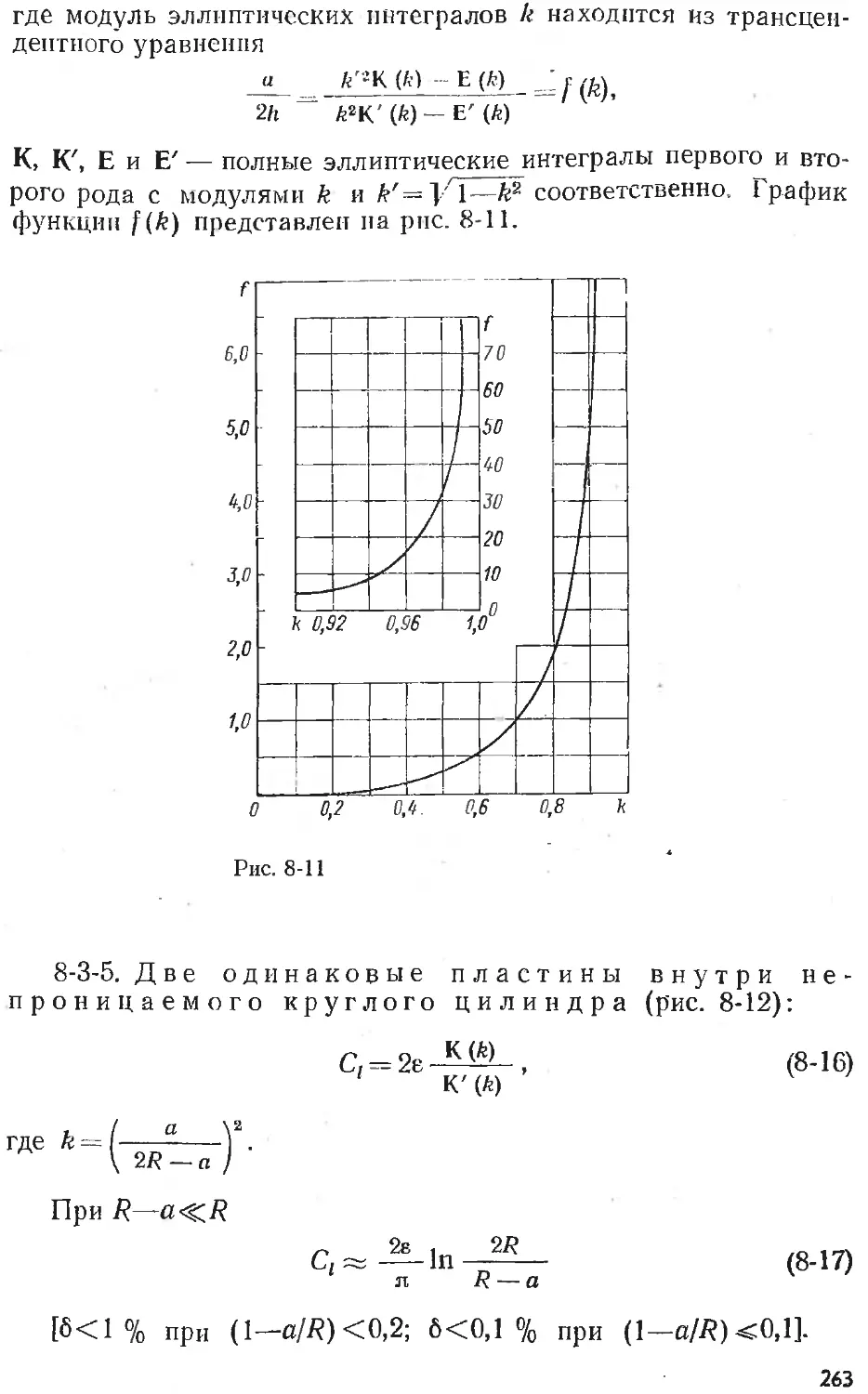
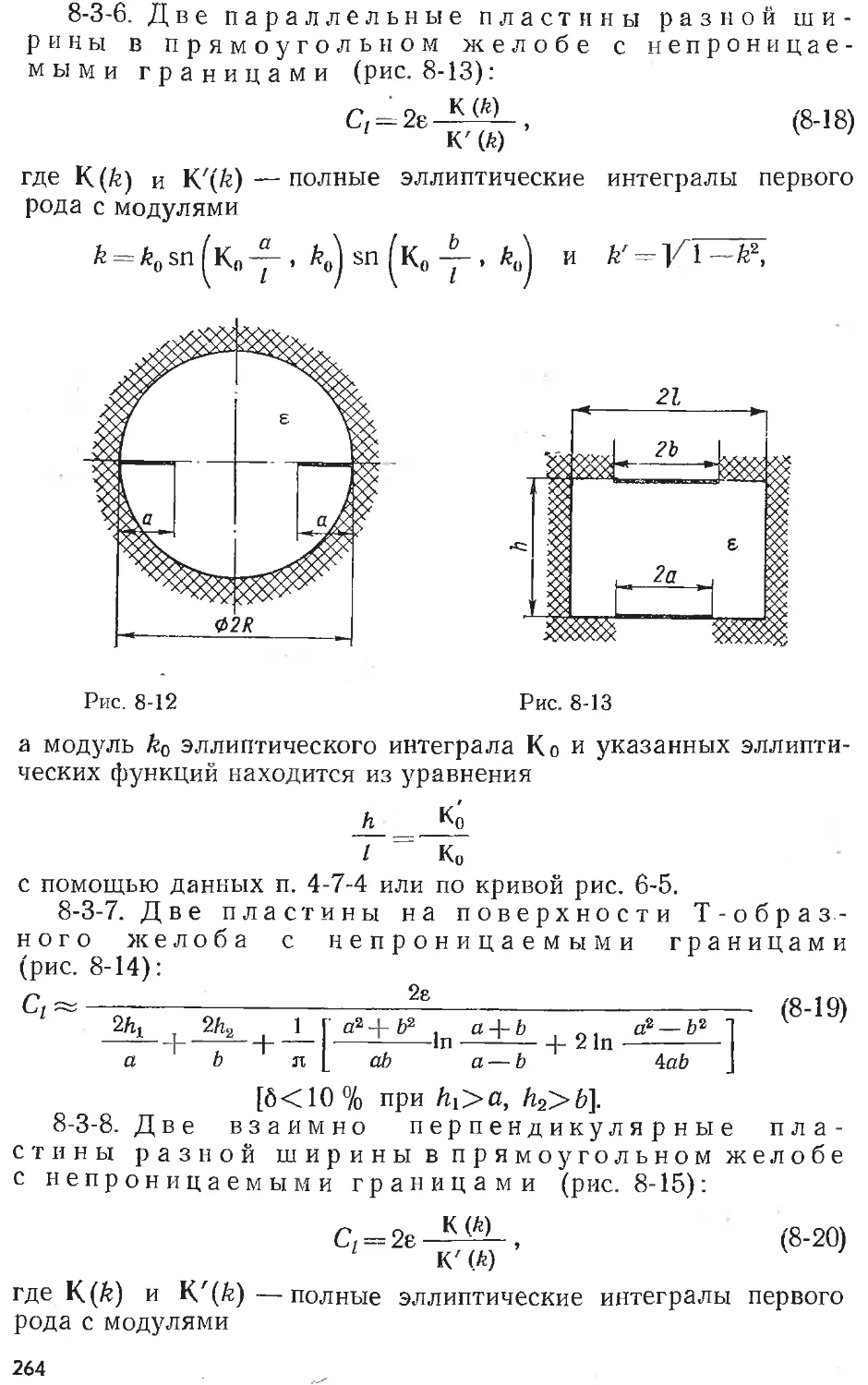
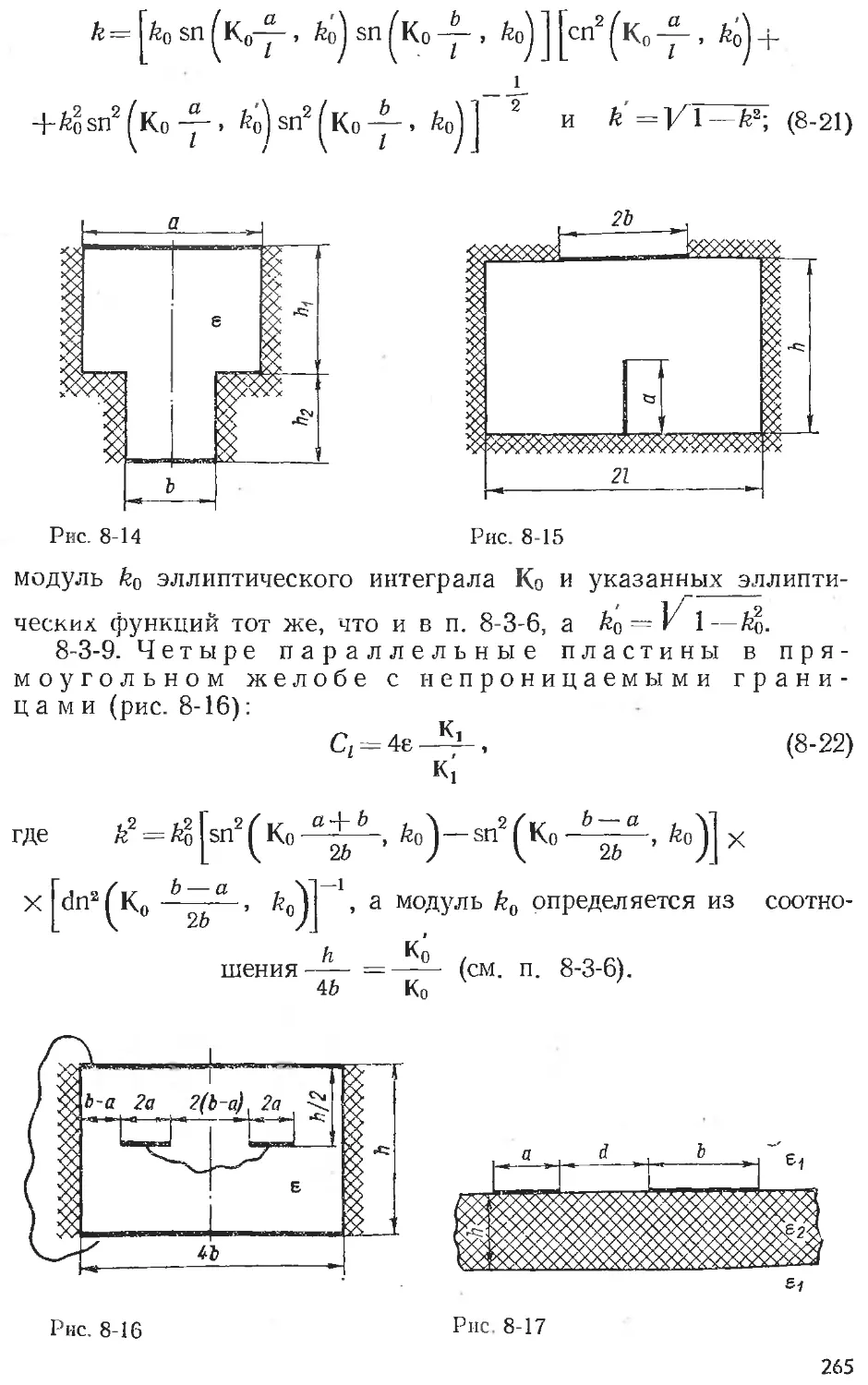
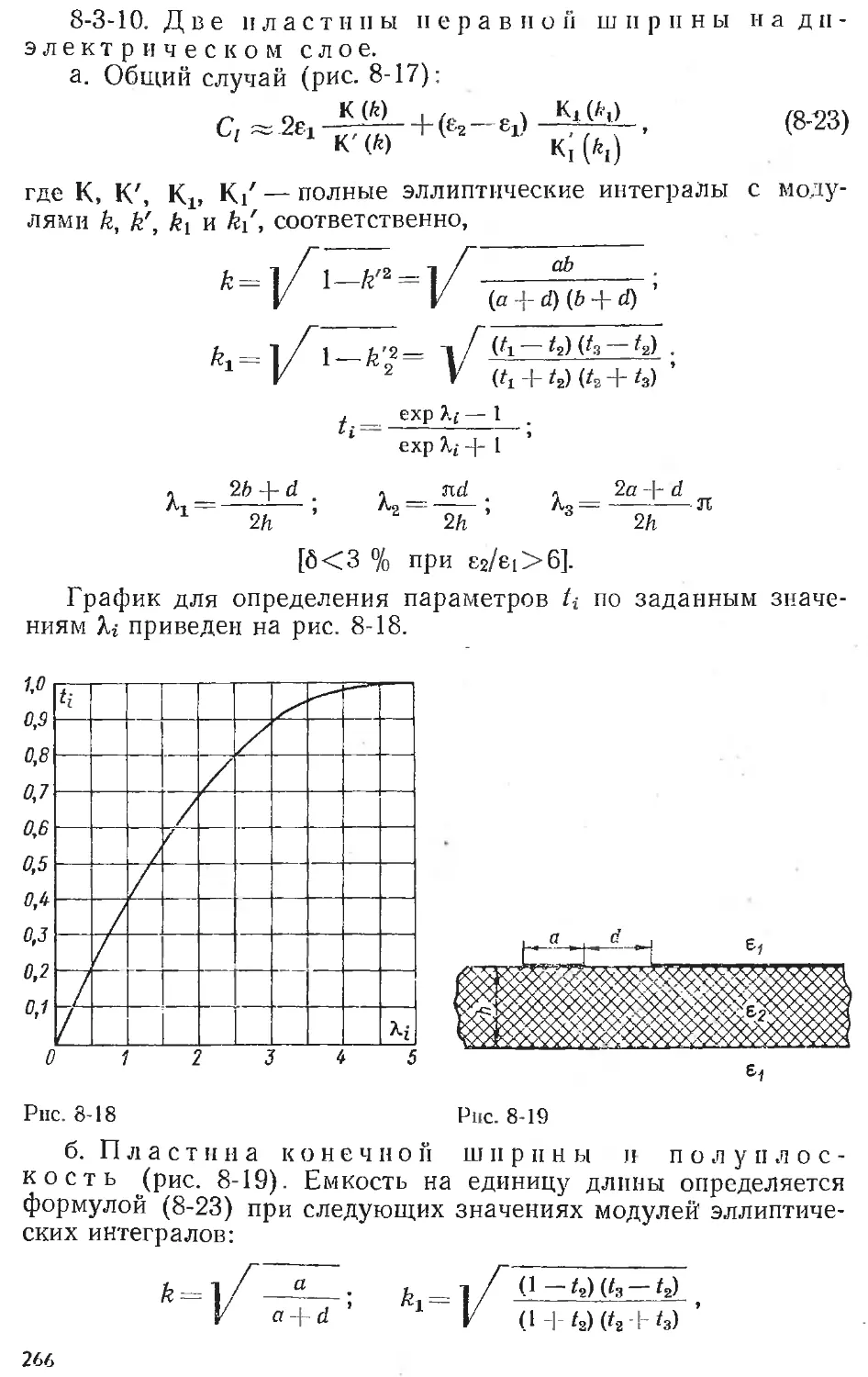
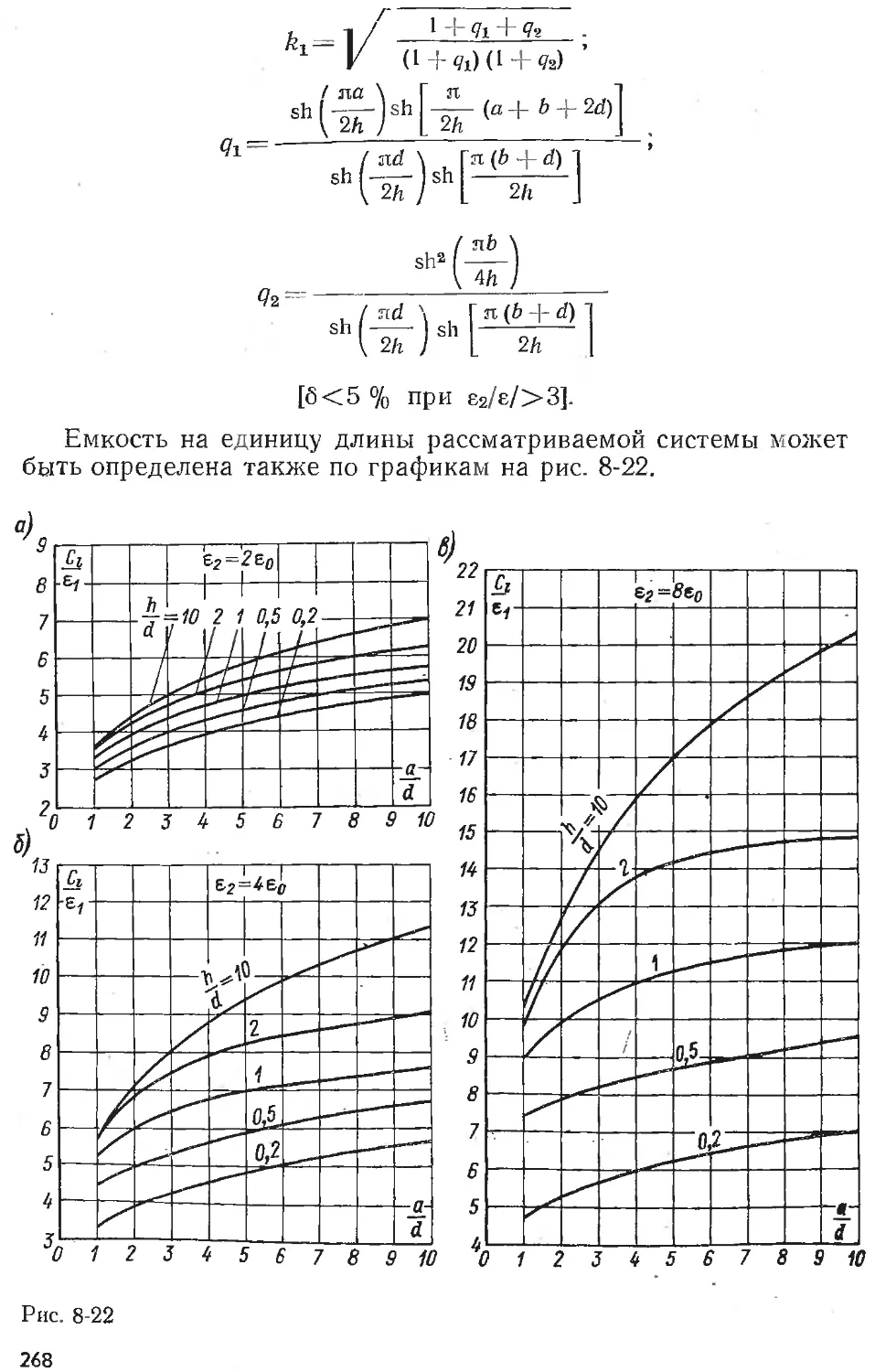
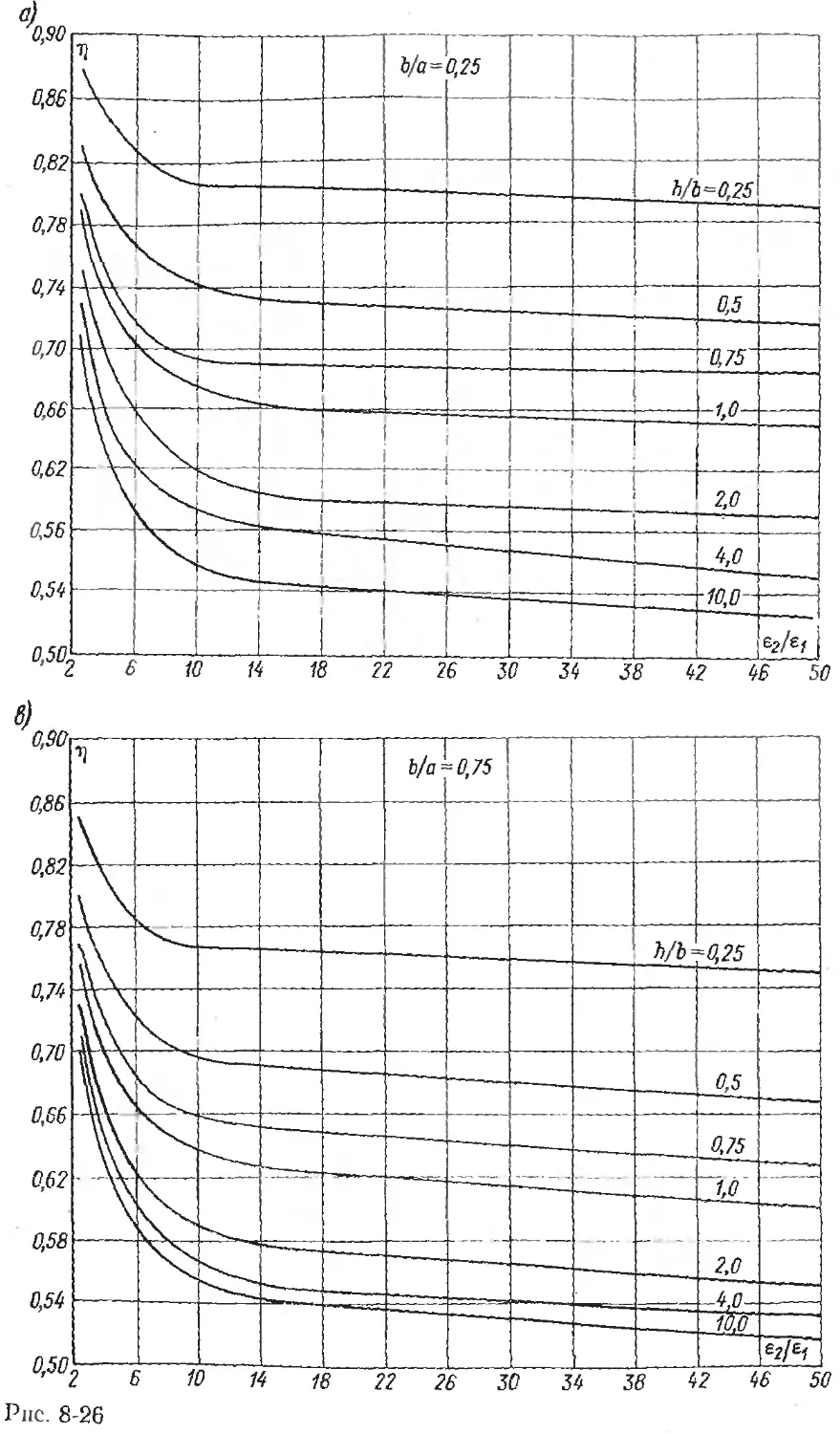
Text
Ю. Я. ИОССЕЛЬ
Э. С. НОЧАМ О В
М. Г. СТРУНСКИЙ
РАСЧЕТ
ЭЛЕКТРИЧЕСКОЙ
ЕМКОСТИ
Издание второе,
переработанное
и дополненное
Ленинград
ЭНЕРГОИЗДАТ
Ленинградское отделение
1981
ББК 31.211
И 75
УДК 621.3.011.4.001.24
Рецензент В. А. Миронов
Юрий Яковлевич Иоссель
Эдуард Степанович Кочанов
Михаил Григорьевич Струнекий
Расчет электрической емкости
Редактор В. Н. Миханкова
Художественный редактор Д. Р. Стеванович
Технический редактор А. Г. Ряб кина
Корректор В. В. Румянцев
Переплет художника Г. В. Смирнова
ИБ № 745 («Энергия»)
Сдано в набор 26.02.81. Подписано в печать 22.07.81. М-21554. Формат бОХЭО’Лб.
Бумага типографская № 1. Гарнитура литературная. Высокая печать. Усл. печ.
л. 18. Уч.-изд. л. 16,4. Тираж 10 000 экз. Заказ 507. Цена 1 р. 10 к.
Ленинградское отделение Энергоиздата. 191041, Ленинград, Марсово поле, 1.
Ленинградская типография № 4 ордена Трудового Красного Знамени Ленинград-
ского объединения «Техническая книга» им. Евгении Соколовой Союзполиграф-
прома при Государственном комитете СССР по делам издательств, полиграфии
и книжной торговли. 191126, Ленинград, Социалистическая ул., 14.
Иоссель Ю. Я. и др.
И 75 Расчет электрической емкости/Ю. Я- Иоссель, Э. С. Ко-
чанов, М. Г. Струнский.— 2-е изд., перераб. и доп,—Л.:
Энергоиздат. Ленингр. отд-ние, 1981.— 288 с., ил.
В пер.: 1 р. 10 к.
Книга посвящена изложению методов расчета электрической емкости н со-
держит сводки расчетных формул, таблиц и графиков, необходимых для опре-
деления емкости проводников различной формы..
Второе издание (первое вышло в 1969 г.) дополняется расчетами электриче-
ской емкости проводников в однородных и неоднородных средах (с приложением
этих расчетов к конкретным инженерным задачам электротехники).
Книга предназначена для инженеров и научных работников, занимающихся
электромагнитными расчетами; она может быть полезна также студентам и ас-
пирантам электротехнических специальностей.
,, 30306—119
И 1)51(01)—81' П2—81 (Э). 2302000000
ББК 31.211
6П2.1.081
© Энергоиздат, 1981
ПРЕДИСЛОВИЕ
КО ВТОРОМУ ИЗДАНИЮ
Первое издание настоящей книги, выпущен-
ное издательством в 1969 г., быстро разошлось и вызвало мно-
гочисленные отзывы читателей. В большинстве отзывов выра-
жались пожелания о том или ином дополнении материала
книги. Идя навстречу этим пожеланиям, издательство приняло
решение о переиздании книги, однако рекомендовало авторам
сохранить неизменным ее объем. Это потребовало от авторов
существенной переработки всего материала книги. Наиболь-
шим изменениям подверглась при этом вторая, справочная,
часть, в которую дополнительно включен раздел о емкости
проводников в неоднородных средах, а также полностью изме-
нена компоновка материала. Помимо этого, в новом издании
освещается более широкий круг методов расчета емкости,
а также значительно изменен весь остальной материал.
ИЗ ПРЕДИСЛОВИЯ
К ПЕРВОМУ ИЗДАНИЮ
Необходимость расчета емкости (или ана-
логичных ей параметров — электрической, магнитной и тепло-
вой проводимости) возникает при проектировании различных
электроавтоматических и радиотехнических устройств, расчете
телефонных, телеграфных и телевизионных кабелей, линий пе-
редачи и линий связи, отдельных элементов телевизионной,
телеметрической и электронно-измерительной аппаратуры, рас-
чете заземлителей, различных магнитных систем и при реше-
нии целого ряда других задач, с которыми приходится встре-
чаться инженерам и научным работникам самых различных
специальностей.
1* 3
По этой причине вопросы расчета емкости и аналогичных
ей параметров уже несколько десятилетий, регулярно рассмат-
риваются в физической, радиотехнической и электротехниче-
ской литературе, и библиография опубликованных к настоя-
щему времени работ, посвященных этой проблеме, весьма об-
ширна.
К сожалению, подавляющее большинство этих работ посвя-
щено изложению лишь отдельных частных вопросов расчета
электрической емкости. Что же касается весьма немногочис-
ленных работ, в которых предпринимались попытки система-
тического изложения вопросов расчета емкости, то они либо
слишком устарели1, либо касаются (подобно книге Р. Бру-
дерлинка2) лишь проводников какого-либо определенного
вида.
В связи с этим уже давно назрела необходимость в изда-
нии справочной книги по расчету емкости, отражающей со-
временное состояние этого вопроса и содержащей как основ-
ные методы расчета емкости, так и готовые формулы, таблицы
и кривые, относящиеся к важнейшим частным случаям. Эту
задачу и призвана решить предлагаемая вниманию читателей
книга.
При разработке плана книги авторы во многом уподобили
его плану известной справочной книги П. Л. Калантарова и
Л. А. Цейтлина по расчету индуктивностей, изданной Гос-
энергоиздатом в 1955 г. Авторам представляется, что это не
только будет удобным для читателей той и другой книг, но
и создаст предпосылки для единообразного изложения во мно-
гом связанных вопросов расчета емкости и индуктивности
в будущем.
Следуя такому плану, авторы разбили основной материал
книги на две части, в первой из которых излагаются методы
расчета емкости, а во второй — даны формулы, таблицы и
графики, необходимые для расчета емкости в различных слу-
чаях.
Одна из особенностей задач по расчету электрической ем-
кости заключается в том, что строгие методы их решения по
существу неотделимы от методов расчета электростатического
поля рассматриваемой системы заряженных тел. Наряду
с этим при расчете емкости используются и приближенные ме-
тоды, не требующие знания электростатического поля в окру-
жающем проводники пространстве, а также вспомогательные
методы, позволяющие привести рассматриваемую систему про-
водников к более удобному для расчета виду.
Учитывая, что методы расчета электростатических полей
в большинстве своем хорошо освещены в электротехнической
1 Orlich Е. Kapazitat und Induktivitat. 1909.
2 Briiderlink R. Induktivitat und Kapazitat der Starkstromfreileitungen.
4
и физико-математической литературе1, в первой части книги
излагаются лишь менее известные приближенные и вспомога-
тельные методы, применяемые при расчете емкости.
Изложение каждого из методов расчета емкости сопровож-
дается примерами, которые должны помочь читателю усвоить
не только идею метода, но и особенности его применения к ре-
шению конкретных практических задач.
Во второй, справочной, части книги авторы стремились
возможно более полно изложить данные, необходимые для
расчета емкости проводников наиболее типичной формы, не
ставя перед собой задачу суммировать все опубликованные
к настоящему времени результаты (в рамках одной книги это
оказалось бы, по-видимому, вообще невозможным). Примене-
ние справочных данных иллюстрируется примерами расчета,
доведенными до численных результатов.
В заключение .авторы выражают искреннюю признатель-
ность рецензенту доктору технических наук Л. А. Цейтлину и
научному редактору кандидату технических наук Р. А. Пав-
ловскому, участие которых в обсуждении и подготовке настоя-
щей книги вышло далеко за рамки их формальных обязан-
ностей.
Авторы надеются, что эта книга будет полезна широкому
кругу инженеров и научных работников, занимающихся элек-
тромагнитными расчетами.
Отзывы и замечания по содержанию книги следует направ-
лять по адресу: 191041, Ленинград, Д-41, Марсово поле, д. 1,
Ленинградское отделение Энергоиздата.
Авторы
1 См., например, Смайт В. Электростатика и электродинамика.— М.:
Йзд-во иностр, лит., 1954; Методы расчета электростатических полей/Н. Н. Ми-
ролюбов, М. В. Костенко, М. Л. Левинштейн, Н. Н. Тиходеев. — Л.: Высшая
школа, 1963.
5
ВВЕДЕНИЕ
В-1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
Между зарядами и потенциалами любых
проводников существует взаимно-однозначная линейная связь,
для выражения которой вводится понятие об электрической
емкости, или просто емкости1.
В зависимости от вида рассматриваемой электростатиче-
ской системы (см. § В-2) различают емкость уединенного про-
водника, емкость между двумя проводниками и емкости в си-
стеме многих проводников.
Емкостью уединенного проводника называют
скалярную величину, характеризующую способность провод-
ника накапливать электрический заряд и равную отношению
заряда проводника к его потенциалу при условии, что все дру-
гие заряженные проводники бесконечно удалены.
Если обозначить заряд уединенного проводника через Q,
а его потенциал через U, то в соответствии с приведенным оп-
ределением емкость этого проводника выразится формулой
C0=Q/t7. (В-1)
Емкостью между двумя проводниками назы-
вают скалярную величину, равную абсолютному значению от-
ношения электрического заряда одного из проводников к раз-
ности их потенциалов при условии, что эти проводники имеют
одинаковые по значению, но противоположные по знаку заряды
и что все другие заряженные проводники бесконечно удалены.
Если заряды проводников равны ±Q, а их потенциалы
имеют значения иг и (72, то в соответствии с приведенным оп-
1 Здесь и в дальнейшем, если не оговорено противное, предполагается,
что диэлектрическая проницаемость среды, окружающей проводники, не за-
висит от напряженности электростатического поля, а потенциал в бесконечно
удаленной точке равен нулю.
6
ределенйем емкость между этими проводниками может быть
выражена формулой
Q
и± — и %
(В-2)
Устройство из двух разделенных диэлектриком проводни-
ков (обкладок), предназначенное для использования емкости
между ними, называют конденсатором, поэтому емкость между
двумя проводниками иногда называют также конденсаторной
емкостью.
Обобщением введенных понятий на случай системы с про-
извольным конечным числом проводников является понятие
о собственных и взаимных частичных емкостях1.
Собственной частичной емкостью проводника,
входящего в систему многих тел, называют скалярную вели-
чину, равную отношению заряда этого проводника к его по-
тенциалу при условии, что все проводники системы (включая
и рассматриваемый) имеют одинаковый потенциал.
Взаимной частичной емкостью между двумя
проводниками, входящими в систему многих тел, называют
скалярную величину, равную отношению заряда одного из
рассматриваемых проводников к потенциалу другого, при ус-
ловии, что все проводники, кроме последнего, имеют потен-
циал, равный нулю.
В соответствии с введенными определениями связь между
зарядами и потенциалами в системе п проводников выража-
ется следующими уравнениями:
Qi = C11t71 + C12(t71—t7a)+ . . . +CV!(t71-t7„);
(?2=^21(^2 ^7])-J-C22t/2 • • • +^2я((^2 л); (В-3)
Qn — Cnl(Un Uj) 4- Сп2 (Un ^2)+ - • • A-CnnUn,
где Qi и Ui — заряд и потенциал i-ro проводника (1=1, 2, ...,
«); Сц — собственная частичная емкость i-го проводника (i=
= 1, 2, ..., /г); Cih — взаимная частичная емкость между i- и
k-м проводниками (1, k=l, 2, ..., п; i=/=k), при этом Cih=Chi-
1 Разделение понятий собственной и взаимной частичных емкостей но-
сит в значительной степени условный характер. Действительно, любую си-
стему из п проводников, занимающую конечный объем, можно условно рас-
сматривать как систему из n-J-1 проводника, где (п+1)-м проводником яв-
ляется сфера бесконечно большого радиуса, имеющая нулевой потенциал.
В новой системе собственную частичную емкость любого проводника, кроме
(п+1)-го, можно интерпретировать как взаимную частичную емкость между
этим проводником и указанной сферой.
7
В частном случае, когда алгебраическая сумма зарядов всех проводни-
ков системы равна нулю (такая система называется электронейтральной),
система уравнений (В-3) может быть преобразована к виду:
= С12 (Ur - 1/2) + . . . +С;п(17т-1/п);
q2=c'1(i/2-i/1)+ . . . + c2'n(t/2-i/„);
(В-4)
Qn = C'ni(Un-U1)+ . . . + с„_(t/„- Un-i),
где C'ik — взаимная частичная емкость между i- и /г-м электродами в элек-
тронейтральной системе (С'1-л=С/л,-).
Значения C'ik могут быть определены так же, как С th, в предположе-
нии, что все проводники, кроме одного, имеют одинаковый (по не обяза-
тельно равный нулю) потенциал. В общем случае значения величины C'ik не
равны значениям С<ь, но могут быть выражены через них.
Уравнения (В-3) или (В-4) можно преобразовать, группируя в правых
их частях члены, имеющие множителем значение 17;. При этом система урав-
нений, связывающих заряды и потенциалы проводников, примет вид:
Q1 — PnCj + Р12172 + • - + Рщ17п;
Q2 = Р21С1 + Р22172 + • • • 4~ Psn^n!
(В-5)
Qn — Pm+ Р«2С72 + . . . +P«n^n
Входящие в эти уравнения величины рг* называются коэффициентами
электростатической индукции (собственными — при i=k и взаимными — при
г =/=£), причем
РгА — Pfei < 0.
Другой формой записи соотношений (В-5) является:
U1 — “nQi + «i2Q2+ • • • + ainQn<
£72 = a21Qi 4~ а2гР2 + • • • + a2nQn>
(В-6)
— tZniQi “Ь 4" • - "В
Входящие в (В-6) величины а;л называются потенциальными коэффици-
ентами (собственными — при i=k и взаимными — при i¥=k), причем аь*>0;
агк>0; aik = aki<Kkk.
Системы уравнений (В-3)—(В-6) являются различными формами выра-
жения одной и той же взаимосвязи между зарядами и потенциалами провод-
ников в системе многих тел. Поэтому коэффициенты, входящие в указанные
уравнения, также оказываются взаимосвязанными. Так,
Qik — PiA!
С** = Pi* + p2fe + • • + P** + • • • + Pnfe;
Pft* = Cik + C2k + • • • + Ckk + • • • + Cnk-
(B-7)
(B-8)
(B-9)
В частном случае, когда система состоит из одного проводника (п=1),
понятие собственной частичной емкости совпадает с понятием емкости уеди-
ненного проводника: Со=Си.
Если при этом уединенный проводник образован соединением нескольких
(т) проводников (см. § В-2), то
Со — Сц + С22 + . . . + Стт,
(В-10)
8
а при /и—2
Со = K11 + K'2g 2al 2 . (В -11)
alla22 a12
В другом частном случае, когда система состоит из двух проводников
(п=2) и электронейтральна, понятие взаимной частичной емкости совпадает
с понятием емкости между двумя проводниками: C=C'iz. При этом справед-
ливы также следующие соотношения:
q __ СцСгв 4- С12С2а -|~ С1гС№ . (В -12)
Сц + С22
с =_____рцр22 ~ р‘2____• (В-13)
Р11 + Рг2 + ^Р12
С =----------1--------- (В-14)
^11 “Ь ^22 2сс13
Как следует из данных выше определений, значения емкости уединен-
ных проводников, емкости между двумя проводниками и частичных емкостей
в системе многих проводников существенно положительны; при этом вели-
чины Со, С, Сгь, C'ik, Ckk, и Psk имеют одинаковую размерность (в от-
личие от потенциальных коэффициентов, имеюших обратную размерность).
В-2. КЛАССИФИКАЦИЯ
ЭЛЕКТРОСТАТИЧЕСКИХ СИСТЕМ
Под электростатической системой ниже
понимается любая совокупность заряженных проводников и
окружающих их диэлектрических сред. Электростатические
системы могут быть классифицированы по числу и форме про-
водников и структуре диэлектрических сред.
Число (п) проводников, образующих электростатическую
систему, определяется с учетом их возможных соединений.
При этом система, образованная соединением нескольких
проводников, рассматривается как один проводник, а влияние
соединительных проводников на значение емкости во всех слу-
чаях считается пренебрежимо малым. Как указано в § В-1,
в зависимости от значения п различают уединенные провод-
ники, системы из двух проводников (в том числе конденса-
торы) и системы многих заряженных тел (п^З).
Типизация геометрических форм проводников приводит
к их разделению на провода, плоские пластины, а также не-
замкнутые и замкнутые оболочки. Последние эквивалентны
в электростатических системах сплошным проводникам той же
формы (за исключением, разумеется, тех случаев, когда внутри
оболочек расположены другие заряженные проводники).
При рассмотрении проводов принимается, что их сечения
неизменны по всей длине, причем линейные размеры сечения
значительно меньше длины провода и расстояний до других
проводников. Кроме того, во всех случаях, когда не оговорено
ч
противное, принимается, что сечение провода является
круглым.
При рассмотрении пластин и оболочек предполагается, что
их толщина постоянна по поверхности и во всех случаях,
когда не оговорено противное, пренебрежимо мала.
Одним из распространенных типов электростатических си-
стем являются так называемые плоскопараллельные системы.
Они могут быть применены при расчете емкости в тех случаях,
когда форма проводников и структура окружающих их ди-
электрических сред таковы, что электростатические поля
в этих средах можно считать плоскопараллельными, а алге-
браическая сумма зарядов всех проводников равна нулю. По-
этому в дальнейшем принято, что число проводников, обра-
зующих любую плоскопараллельную систему, /г^2 а все ве-
личины, характеризующие емкость в таких системах, отнесены
к единице длины проводников.
Структура рассматриваемых диэлектрических сред опреде-
ляется пространственным распределением диэлектрической
проницаемости. С этой точки зрения все рассматриваемые ди-
электрические среды разделяются на однородные (e=const) и
неоднородные. Последние могут быть, в свою очередь, разде-
лены на неоднородные среды с непрерывно изменяющейся ди-
электрической проницаемостью и кусочно-однородные среды,
состоящие из однородных подобластей. Кусочно-однородные
среды классифицируются затем по типу границ, разделяющих
однородные подобласти; простейшими из них являются слои-
стые среды, в которых границами однородных подобластей яв-
ляются параллельные плоскости1 2.
При рассмотрении электростатических систем, содержащих
кусочно-однородные среды, обычно выделяют такие системы,
в которых все проводники целиком расположены в одной из
однородных подобластей. Пусть диэлектрическая проницае-
мость среды в этой подобласти равна еь а в какой-либо гра-
ничащей с ней подобласти — вг- Тогда в зависимости от отно-
шения В1/е2 могут быть выделены следующие характерные
случаи.
Если ei/e2^>l, то границу упомянутых подобластей можно
приближенно считать непроницаемой для силовых линий элек-
тростатического поля и потому рассматривать ее как поверх-
ность некоторой условной среды с нулевой диэлектрической
проницаемостью. Такая граница в дальнейшем называется не-
проницаемой.
1 Для уединенных проводников суммарный заряд всегда отличен от нуля
и потому задача расчета их емкости с помощью плоскопараллельных систем
лишена физического смысла.
2 Помимо этого, могут быть выделены кусочно-однородные среды с сек-
ториальным разделением^ однородных подобластей, а также с цилиндриче-
ской, сферической и другой, более сложной, формой границ.
10
Если Е1/е2<С1, то границу указанных подобластей можно
приближенно считать эквипотенциальной, т. е. рассматривать
ее как поверхность некоторой условной среды с бесконечно
большой диэлектрической проницаемостью. Такая граница
в дальнейшем называется проводящей.
Замена реальных границ однородных подобластей проводя-
щими или непроницаемыми позволяет в ряде случаев получить
двусторонние оценки значения емкости и установить некоторые
общие ее свойства, рассмотренные в § В-3.
В-3. ОБЩИЕ СВОЙСТВА ЕМКОСТИ
Основное свойство электрической емкости
заключается в том, что она зависит только от геометрических
параметров проводников и диэлектрической проницаемости ок-
ружающей среды. В связи с этим ниже сформулированы не-
которые общие положения, выражающие зависимость емкости
от каких-либо из этих параметров при фиксированных значе-
ниях других.
I. При фиксированном значении диэлектри-
ческой проницаемости однородной среды1:
а. Отношения емкостей в двух геометрически подобных си-
стемах проводников равны отношению сходственных размеров
этих систем:
Ci а1 С1 а1 CL а!
— = —; — = —; — =—, (В-15)
С” а11 С" а11 С11 а11
где а1 и а11 — сходственные размеры систем I и II.
б. Емкости (на единицу длины) в геометрически подобных
плоскопараллельных системах двух или более проводников
равны между собой:
Cj = Czn, Cjft./ = C^Z, (В-16)
/и Ст
где С?1 =---; C^k, i = —— ; m = I, II; lm — длина проводников
Im lm
в. Емкость любого уединенного проводника (I) больше ем-
кости любой его части (II), рассматриваемой как другой уеди-
ненный проводник (см. рис. В-1).
г. Емкость любого уединенного проводника меньше суммы
емкостей всех его частей, рассматриваемых как отдельные
уединенные проводники.
д. Емкость между любыми двумя проводниками (С1)
больше емкости между двумя любыми их частями (С11), рас-
сматриваемыми как отдельные проводники, расположенные
1 Свойства, указанные в п. «в» н «д», справедливы и для любой неодно-
родной диэлектрической среды.
11
относительно друг друга так же, как указанные части (см-
рис. В-2).
2. При фиксированных геометрических па-
раметрах проводников:
а. Отношения емкостей двух систем проводников равно от-
ношению диэлектрических проницаемостей окружающих их
однородных сред Ч
z->I „I Щ „I Н gl
- Lo 8 . L 8 . _____, (В-17)
С” ~ е11 ’ С11 ~ ’ С" ~ 8й ’
где е, и Е2 — диэлектрические проницаемости сред I и II.
б. Увеличение диэлектрической проницаемости в любой
части рассматриваемой среды приводит к увеличению емкости
(такое увеличение происходит, в частности, при внесении лю-
бого незаряженного проводника в любую часть рассматривае-
мой среды, тогда как внесение любых тел с непроницаемой
границей приводит к уменьшению емкости).
3. При заданных параметрах электростати-
ческих' систем, содержащих плоские гра-
ницы сред:
а. Емкость между любым проводником и проводящей плос-
костью (С1 на рис. В-3, а) равна удвоенному значению емко-
сти между этим проводником и его зеркальным отражением 2
относительно этой плоскости (С11 на рис. В-3, б):
С1=2СП. (В-18)
1 Равенства (В-17) справедливы и для случая неоднородных сред, если
пространственные распределения их диэлектрических проницаемостей по-
добны; они распространяются и на остальные емкостные коэффициенты,
тогда как для потенциальных коэффициентов справедливы обратные соот-
ношения.
12
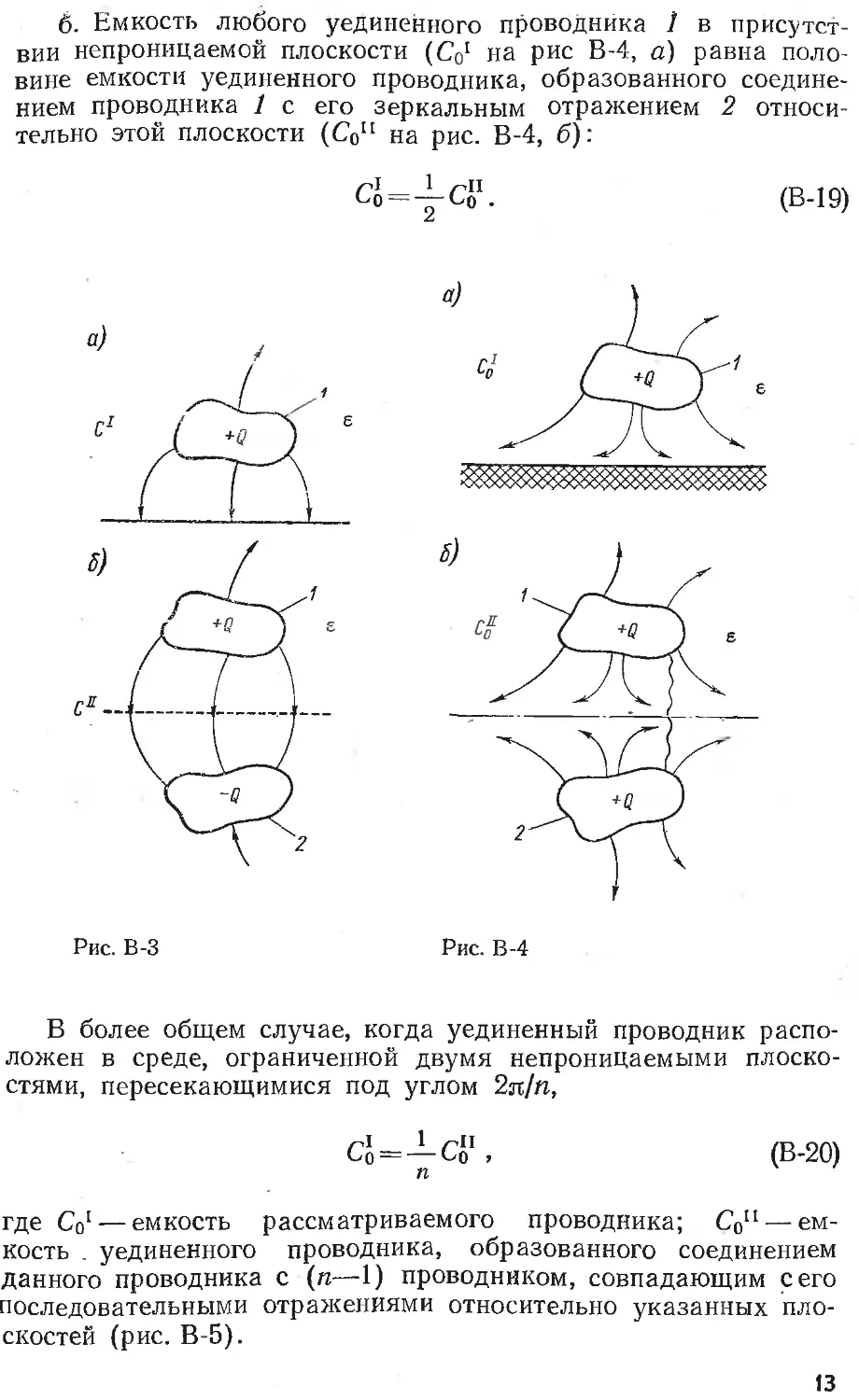
б. Емкость любого уединенного проводника 1 в присутст-
вии непроницаемой плоскости (Со1 на рис В-4, а) равна поло-
вине емкости уединенного проводника, образованного соедине-
нием проводника 1 с его зеркальным отражением 2 относи-
тельно этой плоскости (Соп на рис. В-4, б):
Рис. В-3
Рис. В-4
В более общем случае, когда уединенный проводник распо-
ложен в среде, ограниченной двумя непроницаемыми плоско-
стями, пересекающимися под углом 2л/п,
1 <41
Со==---Со ,
п
(В-20)
где Со1 — емкость рассматриваемого проводника; Сои — ем-
кость . уединенного проводника, образованного соединением
данного проводника с (п—1) проводником, совпадающим сего
последовательными отражениями относительно указанных пло-
скостей (рис. В-5).
13
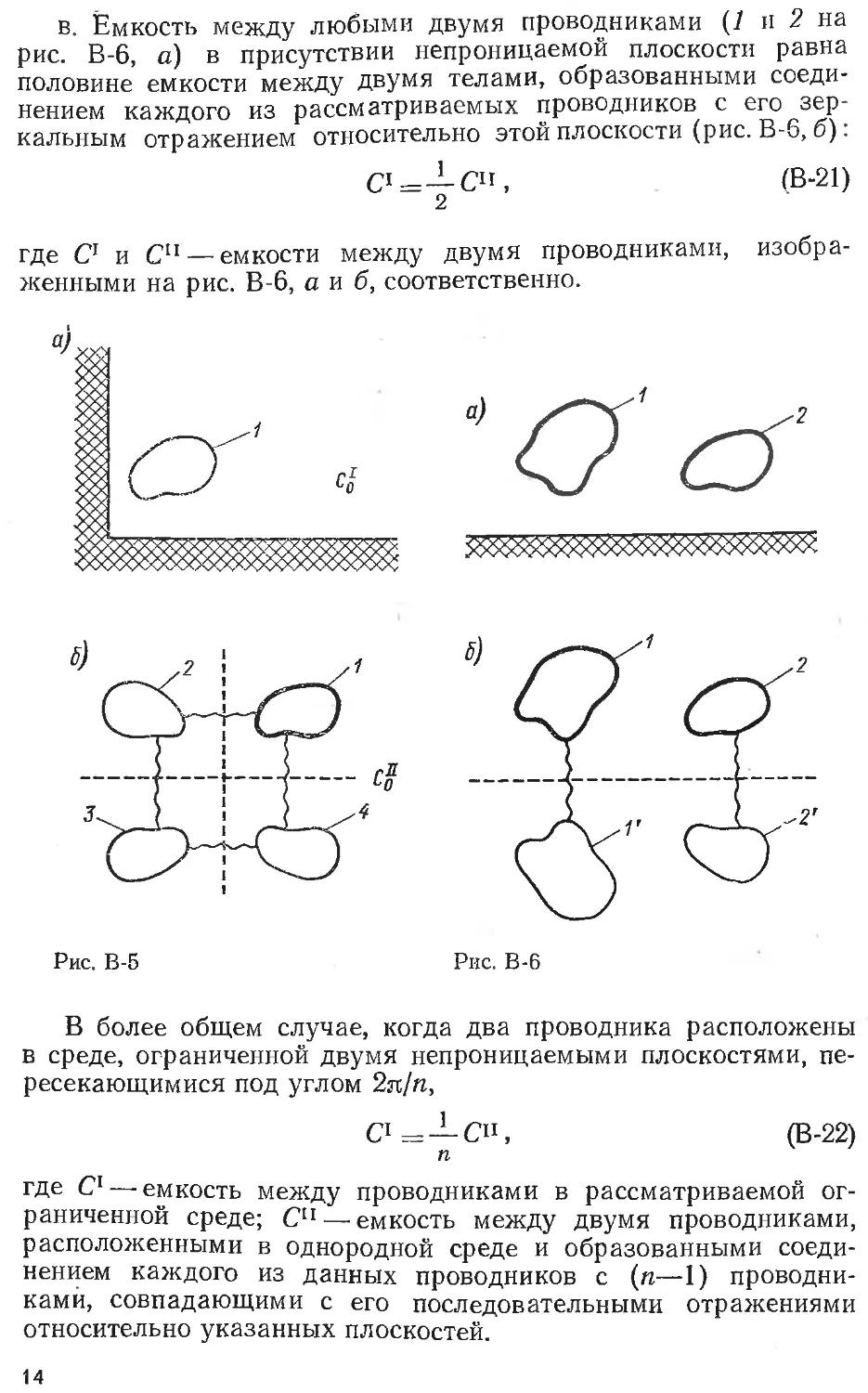
в. Ёмкость между любыми двумя проводниками (1 и 2 на
рис. В-6, а) в присутствии непроницаемой плоскости равна
половине емкости между двумя телами, образованными соеди-
нением каждого из рассматриваемых проводников с его зер-
кальным отражением относительно этой плоскости (рис. В-6, б):
С!= —СП, (В-21)
2
где С1 и С"— емкости между двумя проводниками, изобра-
женными на рис. В-6, а и б, соответственно.
Рис. В-6
В более общем случае, когда два проводника расположены
в среде, ограниченной двумя непроницаемыми плоскостями, пе-
ресекающимися под углом 2л/п,
С1^ —Си, (В-22)
п
где С1 —емкость между проводниками в рассматриваемой ог-
раниченной среде; С"—-емкость между двумя проводниками,
расположенными в однородной среде и образованными соеди-
нением каждого из данных проводников с (п—1) проводни-
ками совпадающими с его последовательными отражениями
относительно указанных плоскостей.
14
. Так, емкость (на единицу длины) между двумя бесконечно
длинными пластинами, сечения которых изображены на
рис. В-7, а, в 2п раз меньше емкости между двумя оболочками
правильного п-угольного сечения, представленными на
рис. В-7, б.
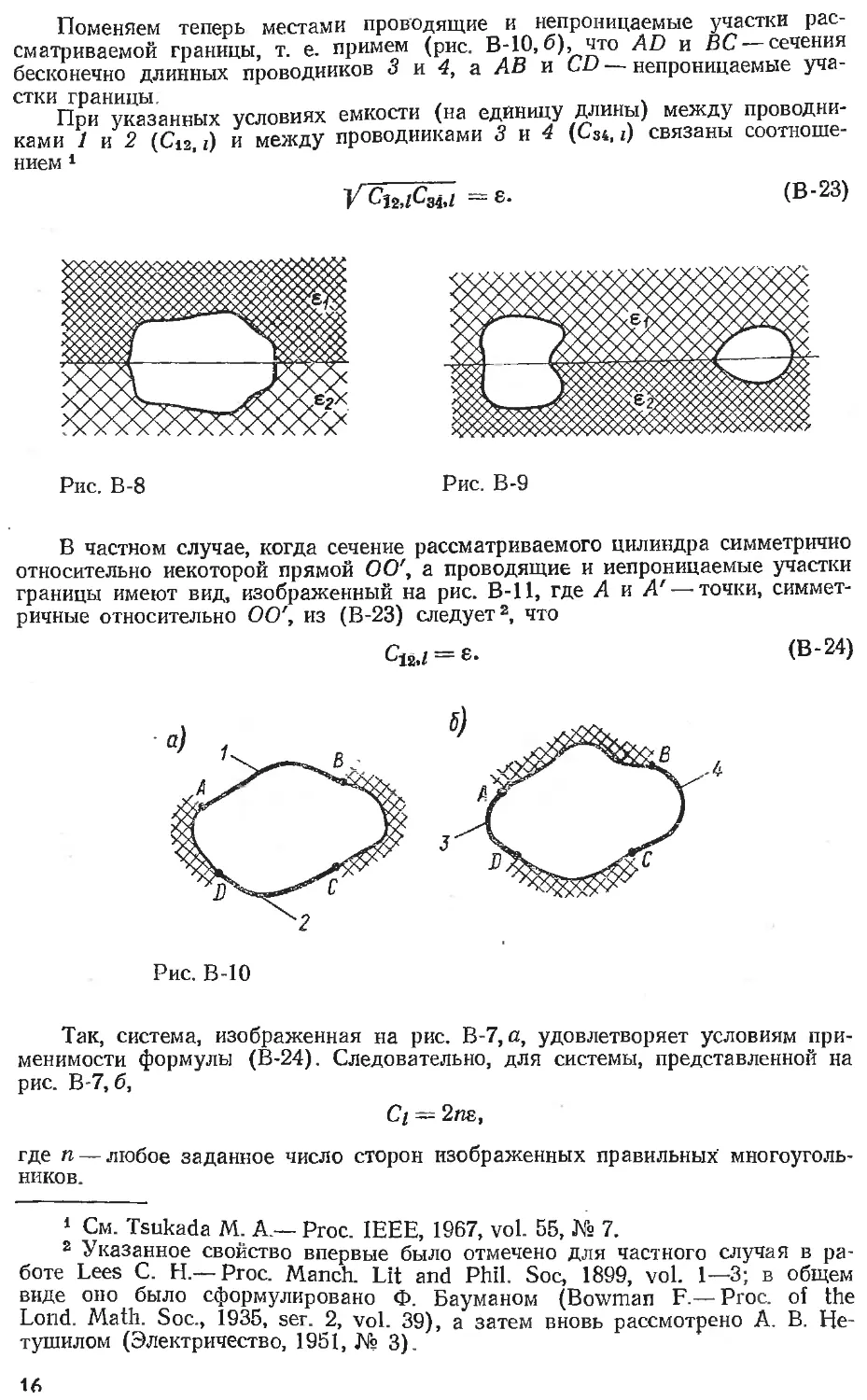
г. Емкость уединенного проводника, расположенного сим-
метрично плоской границе двух сред с диэлектрическими про-
ницаемостями ei и е2 (рис. В-8), равна полусумме значений
емкости того же проводника в однородных средах с диэлек-
трической проницаемостью 81 и е2, соответственно.
д. Емкость между двумя проводниками, каждый из которых
расположен симметрично плоской границе двух сред с диэлек-
трическими проницаемостями ei и е2 (рис. В-9), равна полу-
сумме значений емкости между теми же проводниками в од-
нородных средах с диэлектрической проницаемостью Ei и б2,
соответственно.
Наряду с рассмотренными общими свойствами емкости мо-
жет быть указан ряд таких ее свойств, которые справедливы
лишь для отдельных типов электростатических систем !, на-
пример плоскопараллельных.
Некоторыми характерными свойствами обладает, в частности, емкость на
единицу длины плоскопараллельных систем проводников, сечения которых
изображены на рис. В-10—В-12 сплошными линиями (при этом штриховкой
обозначены, как и раньше, участки непроницаемых поверхностей).
Пусть произвольная кривая ABCD (рис. В-10) представляет собой сече-
ние некоторого бесконечного цилиндра. Рассматривая его поверхность как
внешнюю или внутреннюю границу однородной среды с диэлектрической про-
ницаемостью е, примем сначала (рис. В-10, а), что АВ и CD —сечения беско-
нечно длинных проводников 1 и 2, a AD и ВС — непроницаемые участки
границы'.
1 Некоторые экстремальные свойства емкости уединенных проводников
различной формы указаны в § 2-4.
15
Поменяем теперь местами проводящие и непроницаемые участки рас-
сматриваемой границы, т. е. примем (рис. В-10, б), что AD и ВС — сечения
бесконечно длинных проводников 3 и 4, а АВ и CD — непроницаемые уча-
стки границы. .
При указанных условиях емкости (на единицу длины) между проводни-
ками 1 и 2 (С12, г) и между проводниками 3 и 4 (Cs4, г) связаны соотноше-
нием 1
V Cj2,/C34,/ — е.
(В-23)
Рис. В-8
Рис. В-9
В частном случае, когда сечение рассматриваемого цилиндра симметрично
относительно некоторой прямой 00', а проводящие и непроницаемые участки
границы имеют вид, изображенный на рис. В-11, где А и А'—-точки, симмет-
ричные относительно 00', из (В-23) следует2, что
Cj2j — s.
(В-24)
Так, система, изображенная на рис. В-7, а, удовлетворяет условиям при-
менимости формулы (В-24). Следовательно, для системы, представленной на
рис. В-7, б,
Ci — 2ns,
где п — любое заданное число сторон изображенных правильных многоуголь-
ников.
1 См. Tsukada М. A.— Proc. IEEE, 1967, vol. 55, № 7.
2 Указанное свойство впервые было отмечено для частного случая в ра-
боте Lees С. Н,—Proc. Manch. Lit and Phil Soc, 1899, vol. 1—3; в общем
виде оно было сформулировано Ф. Бауманом (Bowman F.— Proc, of the
Lond. Math. Soc., 1935, ser. 2, vol. 39), а затем вновь рассмотрено А. В. He-
тушилом (Электричество, 1951, № 3).
16
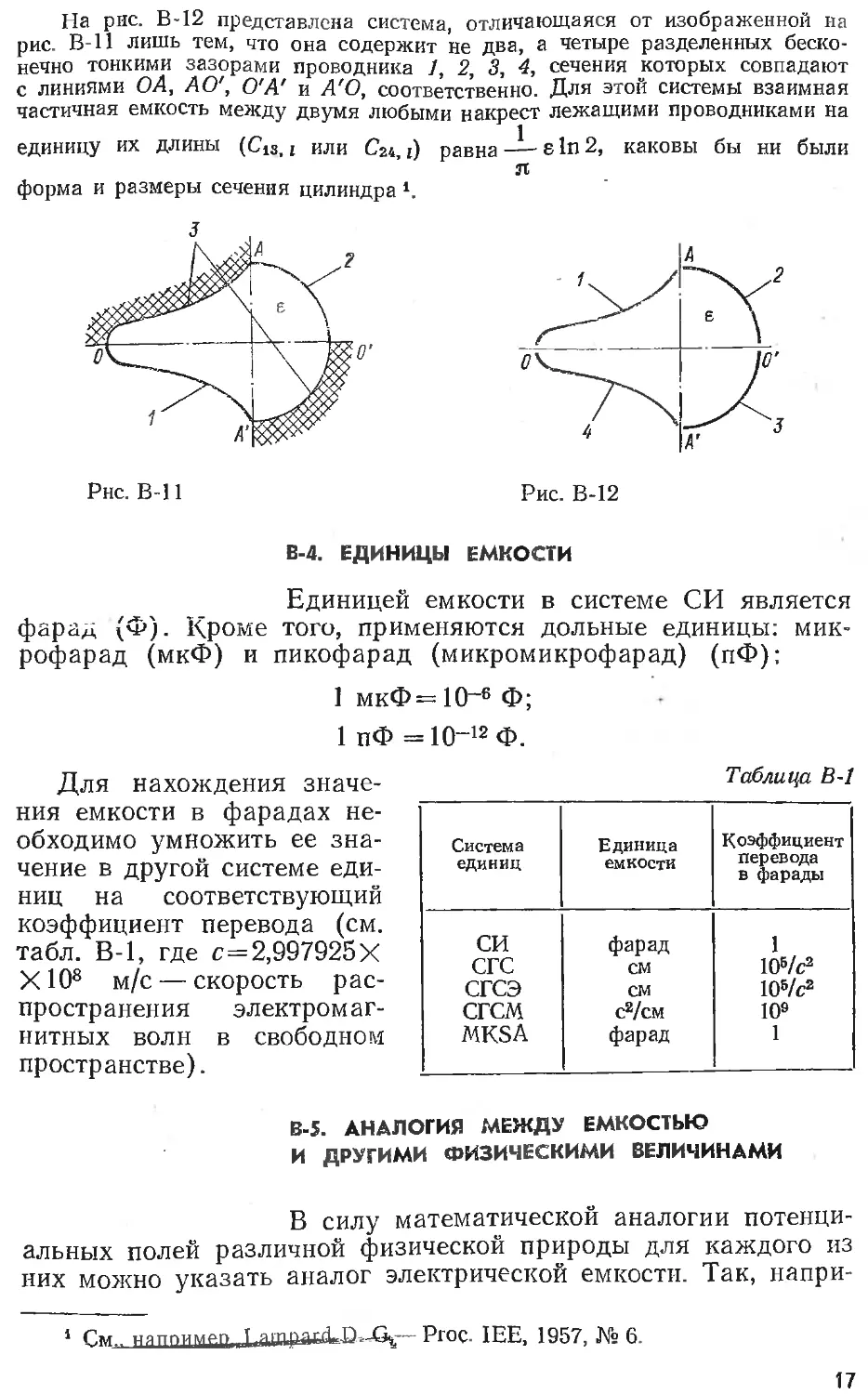
На рис. В-12 представлена система, отличающаяся от изображенной иа
рис. В-11 лишь тем, что она содержит не два, а четыре разделенных беско-
нечно тонкими зазорами проводника 1, 2, 3, 4, сечения которых совпадают
с линиями ОА, АО', О'А' и А'О, соответственно. Для этой системы взаимная
частичная емкость между двумя любыми накрест лежащими проводниками на
единицу их длины (C1S, г или Си, i) равна — е In 2, каковы бы ни были
л
форма и размеры сечения цилиндра *.
В-4. ЕДИНИЦЫ ЕМКОСТИ
Единицей емкости в системе СИ является
фарад (Ф). Кроме того, применяются дольные единицы; мик-
рофарад (мкФ) и пикофарад (микромикрофарад) (пФ):
1 мкФ= 10~6 Ф;
1 пФ = 10~12 Ф.
Для нахождения значе-
ния емкости в фарадах не-
обходимо умножить ее зна-
чение в другой системе еди-
ниц на соответствующий
коэффициент перевода (см.
табл. В-1, где с=2,997925 X
ХЮ8 м/с — скорость рас-
пространения электромаг-
нитных волн в свободном
пространстве).
Таблица В-1
Система единиц Единица емкости Коэффициент перевода в фарады
си фарад 1
сгс СМ 106/с2
сгсэ см 106/с2
сгсм с2/см 10е
MKSA фарад 1
В-5. АНАЛОГИЯ МЕЖДУ ЕМКОСТЬЮ
И ДРУГИМИ ФИЗИЧЕСКИМИ ВЕЛИЧИНАМИ
В силу математической аналогии потенци-
альных полей различной физической природы для каждого из
них можно указать аналог электрической емкости. Так, напри-
1 См., няппимеп 1.ящиаикР.-Х*,-- Ргос. IEE, 1957, 6.
17
мер, для стационарных электрического, магнитного и теплового
полей такими аналогами являются соответственно электриче-
ская, магнитная и тепловая проводимости. При заданных гео-
метрических параметрах системы тел значения величин-анало-
гов и электрической емкости пропорциональны, причем коэф-
фициентами пропорциональности служат отношения соответст-
вующих физических параметров среды к диэлектрической про-
ницаемости. В частности, для двух тел
G=—=—С; (В-25)
R е
GM = J-=^C; (В-26)
GT = — =—С, (В-27)
/?т е
где G — электрическая проводимость между рассматривае-
мыми телами в однородной среде с удельной электрической
проводимостью у; GM — магнитная проводимость между телами
в однородной среде с магнитной проницаемостью р; GT — теп-
ловая проводимость между телами в однородной среде с ко-
эффициентом теплопроводности X; R, RM и RT — электрическое,
магнитное и тепловое сопротивления, соответственно; С—ем-
кость между телами в однородной среде с диэлектрической
проницаемостью е.
Такие же соотношения связывают частичные проводимости
и частичные емкости в системе многих тел.
Помимо указанной, существует также приближенная аналогия между
электрической емкостью и некоторыми параметрами высокочастотных элек-
тромагнитных систем *. При заданной геометрической конфигурации системы
проводников на высокой частоте справедливы, в частности, следующие при-
ближенные соотношения:
Ги/ёр/С, (В-28)
где W — волновое сопротивление между проводниками в однородной среде
с диэлектрической проницаемостью е и магнитной проницаемостью р; С —
емкость между проводниками;
L/wep/Q, (В-29)
где Li — индуктивность (на единицу длины) проводников, расположенных
в однородной среде с магнитной проницаемостью р; Ci — емкость между
этими же проводниками (на единицу их длины) в однородной среде с ди-
электрической проницаемостью е.
1 При этом частота предполагается настолько высокой, что линии маг-
нитного поля можно считать расположенными вне сечений проводников.
Для прямолинейных проводов могут быть указаны также следующие со-
отношения:
Lkk ~ (В-30)
где Lkk — индуктивность провода длиною 1к, расположенного в однородной
среде с магнитной проницаемостью р; akk — собственный потенциальный ко-
эффициент провода, расположенного в однородной среде с диэлектрической
проницаемостью е, вычисленный методом средних потенциалов (см. § 1-2);
Mik ~ eiiltlkcos (plkaik, (В-31)
где Mfk — взаимная индуктивность двух проводов длиной h и Ik, располо-
женных под углом друг к другу в однородной среде с магнитной прони-
цаемостью [X; шь — взаимный потенциальный коэффициент тех же проводов
в однородной среде с диэлектрической проницаемостью е, вычисленный по
методу средних потенциалов (см. § 1-2).
Рассмотренная аналогия делает расчет емкости эквива-
лентным расчету ряда других физических параметров, в част-
ности:
магнитной проводимости различных магнитопроводов;
сопротивления растекания электродов, соединяющих элек-
трические цепи с проводящей средой (например, заземлите-
лей) ;
волнового сопротивления волноводов, полосковых линий,
антенн и других передающих и излучающих систем;
тепловой проводимости между различными нагретыми те-
лами.
В-6. СПОСОБЫ РАСЧЕТА ЕМКОСТИ
Формулы (В-1) — (В-6) не могут быть не-
посредственно использованы для расчета емкости (или свя-
занных с ней величин), так как обычно известны лишь геомет-
рические параметры системы проводников и диэлектрическая
проницаемость окружающей среды. Поэтому для определения
емкости необходимо либо рассчитать заряды проводников, за-
давшись их потенциалами, либо, наоборот, найти потенциалы
проводников, задавшись значением зарядов.
Обе эти задачи могут быть строго решены на основе рас-
чета электростатического поля рассматриваемой системы про-
водников. Действительно, зная распределение потенциала элек-
тростатического поля (С7) в пространстве, окружающем про-
водники, можно найти заряды каждого из них с помощью
соотношения
^=-[e4^dS’ <в-з2>
где Qi — заряд i-ro проводника; Si — поверхность i-ro провод-
ника; W— внешняя нормаль к поверхности проводника.
19
Заряд уединенного проводника может быть определен также по формуле
Q - 4з1б
дЦ \
дд )б-»0
(В-33)
где 6=1/7?; 7?— расстояние от поверхности проводника.
Эта формула более удобна для расчетов, чем (В-32), так как позволяет
исключить интегрирование по поверхности и ограничиться исходными дан-
ными о зависимости потенциала лишь от одной координаты, тогда как при
использовании (В-32) необходимо знать пространственное распределение по-
тенциала.
Пример В-1. Найдем емкость уединенного кругового диска радиуса а,
считая известным распределение потенциала создаваемого им электростати-
ческого поля.
Приняв потенциал рассматриваемого проводника равным некоторому зна-
чению Uo, найдем его заряд, учитывая, что потенциал электростатического
поля кругового диска в произвольной точке с координатами г, z выражается
формулой [16]
.. 27/0 Р 1 '“а / у г \ • 1 «л
U =-------— I — е a70l X------------- sin kdk,
л J к \ a J
о
(В-34)
где За — цилиндрическая функция первого рода нулевого порядка.
Для отыскания значения заряда воспользуемся формулой (В-33). С этой
целью найдем предварительно зависимость потенциала рассматриваемого
электростатического поля от расстояния 7? до поверхности диска. Если при-
нять, в частности, в выражении (В-34) г,=0, то 7?=z, т. е.
СО ___
77Г=О = -2^° С —------------sinX — - arctg — = — °- arctg (аб).
л J к зт г п
о
Тогда в соответствии с выражением (В-33)
<? = 4318 Г----—1 = 8и Efl.
зт Ll+Wh-o
Подставив найденное-значение Q и принятое значение Uo в (В-1), непо-
средственно^ приходим к интересующему нас выражению для емкости диска
Тот же результат может быть получен и при другом представлении
в (В-33) расстояния от диска (например, при г—0, r=R), а также при оп-
ределении значения заряда по формуле (В-34). Однако в последнем случае
вычисления оказываются значительно более громоздкими.
В тех случаях когда расчет электростатического поля вы-
полнен быть не может, используются специальные методы рас-
чета емкости, основанные либо на установлении точной или
приближенной связи заряда проводника непосредственно с по-
тенциалом его поверхности (методы непосредственного опреде-
ления емкости), либо на преобразовании электростатических
систем и приближенной оценке истинных значений емкости
(вспомогательные методы).
Постановка задач по расчету емкости зависит от выбора
исходных величин (зарядов или потенциалов), который, в свою
20
очередь, определяется видом рассматриваемой системы про-
водников.
При расчете емкости уединенного проводника можно задать
произвольно его потенциал или заряд. Если положить, в част-
ности, потенциал равным единице, то заряд уединенного про-
водника будет численно равен его емкости. При расчете ем-
кости между двумя проводниками, как правило, можно за-
даваться лишь их зарядами, причем должно соблюдаться,
условие Q2=—Qj.
Потенциалы обоих проводников в общем случае не могут быть выбраны
произвольно, так как они связаны-соотношением
__ __С22
Си’
(В-35)
следующим из выражения (В-3) прн n=2, Qi=—Q2.
Задание потенциалов в качестве исходных величин возможно лишь в не-
которых частных случаях, например следующих:
1. Система двух проводников симметрична относительно некоторой плос-
кости. В этом случае Сц=С22 и при Qt=—Q2 Ui=—Uz=A, где A— произ-
вольная величина.
2. Размеры одного из проводников (например, первого) велики по срав-
нению с размерами другого. При этом Си^Сгг, Сгг/Сц^О, т. е. J7i~0,
U2=A, где А — произвольная величина.
При расчете частичных емкостей и коэффициентов электро-
статической индукции в системе многих проводников исход-
ными величинами могут являться в общем случае лишь их
потенциалы.
Так, при расчете собственной частичной емкости потен-
циалы всех проводников системы должны быть приняты рав-
ными одному и тому же произвольному постоянному значению,
а при расчете взаимной частичной емкости между I- и /г-м про-
водником потенциал одного из них может быть выбран произ-
вольно, а потенциалы всех остальных проводников должны
быть приняты равными нулю.
При расчете потенциальных коэффициентов в системе мно-
гих проводников исходными данными являются их заряды.
При этом собственный потенциальный коэффициент какого-
либо проводника численно равен его потенциалу при единич-
ном заряде этого проводника и отсутствии свободных зарядов
на других проводниках, а взаимный потенциальный коэффи-
циент между какими-либо двумя проводниками численно ра-
вен потенциалу одного (любого) из них при единичном заряде
другого и отсутствии свободных зарядов на всех остальных
проводниках системы.
В общем случае потенциал указанных проводников (а соответственно и
значение потенциальных коэффициентов) определяется как свободными, так
и индуцированными зарядами. Однако при достаточно большом расстоянии
между проводниками (по сравнению с их размерами) потенциалом индуци-
рованных зарядов можно пренебречь. Это приводит к следующим прибли-
21
Женным выражениям для потенциальных коэффициентов:
(В-36)
^ik
1
4neRik
где Со« — емкость i-ro проводника как уединенного тела; Rik — расстояние
между i- и А-м проводниками.
При тех же соотношениях геометрических размеров емкость между двумя
не охватывающими один другого проводниками определяется в соответствии
с (В-14) следующим приближенным выражением:
^(1)^(2)
С ~ 2лв/?13--------г ... 0 °-------Г|—75г• (В-37)
2Ле/?1г [С'» + С®]
Как уже отмечено в предисловии, методы расчета электро-
статических полей достаточно подробно освещены в литера-
туре; поэтому в последующих двух главах настоящей книги
рассматриваются лишь специальные методы расчета емкости.
Часть первая
Специальные методы
расчета емкости
ГЛАВА ПЕРВАЯ
МЕТОДЫ НЕПОСРЕДСТВЕННОГО
ОПРЕДЕЛЕНИЯ ЕМКОСТИ
1-1. ОБЩИЕ ЗАМЕЧАНИЯ
Методы непосредственного определения
емкости применимы в тех случаях, когда проводники располо-
жены в однородной или кусочно-однородной среде.
Эти методы основаны на замене каждого из рассматривае-
мых проводников диэлектрическим телом, имеющим ту же
форму, что и проводник, и ту же диэлектрическую проницае-
мость, что и окружающая среда. При этом вместо неизвестного
истинного (равновесного) распределения заряда'по поверхно-
сти проводника задается некоторое фиктивное распределение
заряда по поверхности тела o(S) или в его объеме р(У). Спо-
собы задания функций o(S) или p(V) зависят от особенностей
конкретных методов непосредственного определения емкости,
однако при любом выбранном виде этих функций значение
суммарного заряда тела находится из формул:
Qi = f о (S) dS S, (1-1)
или
Q£=fp(17)dl7, vi (1-2)
а потенциал из формул: в произвольной точке Pk поверхности тела —
U(Pb) 1 Vf °(sl ..dS (1-3)
( - 4л8 2^ J R (Pk; Pi) i=l s.
или
tj/рл 1 f P^ dV (1-4)
- 4Яе 2j J R (Pk-, Pi} ’ i=l v(
23
где Pi — точка, расположенная либо на поверхности i-ro тела
(1-3), либо в его объеме (1-4); R(Ph- Pi) — расстояние между
точками Pk и Pi, п — число проводников в системе.
Для плоскопараллельной системы проводников вместо (1-3) и (1-4) еле-
дует применять формулы:
п
U(Pk) = —— Ст(Ь)1п------—-----dL (ЬЗ')
{ k) R(Pk, Pi)
i=l L.
или
п
и (Pfe) = —L V? С о (3) 1п------------dS, (1-4')
2«е 2а J R (Pk, Pi)
i=l S£
где Li — контур сечеиия i-ro тела; т(А) —линейная плотность заряда на кон-
туре сечения i-ro тела; o(S)—плотность распределения заряда по сечению
i-ro тела; Pk — точка контура сечения k-ro тела; Р, — точка, расположенная
либо на контуре сечения i-ro тела (1-3'), либо внутри его сечения (1-4');
R(Pk, Pi)—расстояние между точками Pk и Р,, лежашими в сечении; /о—
линейный масштаб.
При любом распределении заряда, отличном от равновес-
ного, поверхность рассматриваемого тела оказывается неэкви-
потенциальной, тогда как поверхность всякого проводника
эквипотенциальна. Для устранения этого несоответствия всей
поверхности тела приписывается некоторый постоянный потен-
циал Ui, значение которого тем или иным способом определя-
ется по распределению потенциала, найденному при принятом
распределении заряда из (1-3) или (1-4).
Располагая значениями величин Qi и Ui для каждого из
проводников системы (i=l, 2, ..., п), можно приближенно
найти значения емкости в этой системе с помощью формул
(В-1)—(В-4).
1-2. МЕТОД СРЕДНИХ ПОТЕНЦИАЛОВ
Метод средних потенциалов основан на
задании фиктивного распределения заряда по поверхности или
в объеме тел, заменяющих проводники. При этом поверхности
каждого из тел приписывается постоянный потенциал, равный
среднему арифметическому значений потенциала во всех точ-
ках поверхности тела (i7=i7Cp)- Эту величину (Пср) называют
средним потенциалом поверхности или средним потенциалом
проводника.
При указанном способе определения значения U закон фик-
тивного распределения заряда сравнительно мало влияет на
точность определения емкости (поскольку емкость является
интегральной характеристикой электростатического поля) и
обычно выбирается лишь из условий простоты расчета. Наи-
24
более распространенным является допущение о том, что заряд
распределен по поверхности тела равномерно. Основанный на
этом допущении метод расчета емкости был предложен Г. Хоу
[31] и носит его имя *.
При равномерном поверхностном распределении заряда
средний потенциал уединенного проводника может быть опре-
делен по формуле
= f-f-. (1-5)
о J 4лв62 J J К
s s s
где S — поверхность рассматриваемого проводника (а также
площадь этой поверхности); U(Р)—потенциал в произволь-
ной точке Р поверхности S, определяемый формулой (1-3);
Q — заряд; R — расстояние между точками поверхности про-
водника.
Для осесимметричных проводников формула (1-5) может быть упрощена
путем замены внешнего поверхностного интеграла интегралом по контуру
осевого сечения проводника. В этом случае
<1-б>
3 L S
где L — контур осевого сечения проводника; п — расстояние от оси;
R — расстояние между произвольными точками контура L и поверхности S,
а остальные обозначения те же, что ив (1-5).
Из формул (1-5) и (В-1) следует, что емкость уединенного
проводника, вычисленная методом Хоу, определяется выраже-
нием
(1-7)
В частном случае, для осесимметричных проводников,
(Ь8)
При расчете емкости между двумя проводниками средний
потенциал- каждого из них находится из формул:
1 Помимо этого, предлагались и другие способы поверхностного распре-
деления заряда при использовании метода средних потенциалов (см., напри-
мер, [14]). Однако получаемые при этом расчетные формулы для емкости
оказываются обычно более сложными.
25
где Sj и S2 — поверхности каждого из рассматриваемых про-
водников (а также площади этих поверхностей); и R22—
расстояния между двумя точками поверхности одного и того
же проводника (первого и второго соответственно); 7?i2=^2i
расстояние между двумя точками, одна из которых лежит на
поверхности первого проводника, а другая —на поверхности
второго; Q — заряд одного проводника.
При вычислении разности средних потенциалов может быть
использован принцип взаимности, согласно которому средний
потенциал проводника 1, создаваемый зарядом, равномерно
распределенным на проводнике 2, равен среднему потенциалу
проводника 2, создаваемому тем же зарядом, равномерно рас-
пределенным на проводнике 1.
Применение формул (1-9) с учетом указанного принципа
взаимности приводит к выражению
Из формул (1-Ю) и (В-2) следует, что емкость между
двумя проводниками, вычисленная методом Хоу, определяется
выражением
В частном случае, когда система из двух проводников является плоско-
параллельной, вместо (1-11) должна быть использована следующая анало-
гичная ей формула для емкости на единицу длины проводников:
где L± и L2 — контуры сечений рассматриваемых проводников (а также пе-
риметры этих сечений); Ra, Rn и Ra — расстояния между соответствую-
щими точками на контурах сечений (см. обозначения к формуле (1-9)); 10—
линеиныи масштаб.
При расчете частичных емкостей в системе многих тел не-
посредственное использование метода средних потенциалов
затруднительно, так как приводит обычно к громоздким вы-
26
числениям. Поэтому в данных случаях метод средних потен-
циалов применяется, как правило, для расчета потенциальных
коэффициентов с последующим переходом к частичным емко-
стям на основе соотношений, приведенных в § В-1.
Расчет средних потенциалов в системе п проводников базируется на ис-
пользовании формулы
(1-13)
где t/ср; — средний потенциал i-ro проводника; Sl{ — поверхность k-ro про-
водника (k=l, 2, ..., п), а также площадь этой поверхности; Qft— заряд ft-го
проводника; Rik — расстояние между двумя точками, расположенными на по-
верхности разных проводников (ft#=i) или одного проводника (ft=i). При
этом между значениями средних потенциалов любых двух проводников (/
и 2) выполняется соотношение 1 *
Uicp______
U 2СР 01
(1-14)
где (71ср — средний потенциал проводника 1, создаваемый зарядом Qa, рав-
номерно распределенным на проводнике 2; Uzcv — средний потенциал провод-
ника 2, создаваемый зарядом Qit равномерно распределенным на провод-
нике 1.
При определении частичных емкостей заряды всех проводников системы
должны быть приняты отличными от нуля, и расчеты по формуле (1-13),
даже с учетом соотношения (1-14), становятся весьма громоздкими. При
отыскании же потенциальных коэффициентов (когда заряженным следует
считать лишь один из проводников) формула (1-13) сильно упрощается и со-
впадает по виду с (1-5). Это приводит к следующим выражениям для соб-
ственных и взаимных потенциальных коэффициентов, вычисленных по ме-
тоду Хоу:
1
aik
Для плоскопараллельной
мулы принимают вид:
aii,l
4леЗ?
ineStSk
системы
2лв£?
f ЯЧ' f dS
I aS I -----
J J Rii
Si Si
(Ы5)
(Мб)
sk si
из n проводников аналогичные фор-
In -^-dL;
Rii
(1-17)
1
1
«№,z « ———-
C \nJ±_dL,
J Rik
Lk
(1-18)
где Oii, i и ack, i — собственный и взаимный потенциальные коэффициенты,
отнесенные к единице длины проводников; Lt, Lk — контуры сечений i- и
1 В частном случае, когда Qi = <22, эта формула выражает сформулиро-
ванный ранее принцип взаимности средних потенциалов.
27
k-ro проводников, а также периметры этих контуров, Rt, и Rik — расстоя-
ние от какой-либо фиксированной точки на контуре сечения i-ro проводника
до произвольной точки этого же контура (Ra) или контура сечения k-ro про-
водника (Rih), а /о —ТОТ же, что и в (1-12).
Из существа рассмотренного метода следует, что он приво-
дит к точным выражениям для емкости лишь в том частном
случае, когда заряд распределен по поверхности проводника
с постоянной плотностью (такое равновесное распределение
заряда достигается, как известно, лишь для уединенной сферы
или двух концентрических сфер, а также для плоскопарал-
лельных систем, содержащих два коаксиальных цилиндра или
две параллельные плоскости). Во всех остальных случаях ме-
тод Хоу приводит к заниженным значениям емкости ’, причем
относительная погрешность в ее определении для проводников
данной конфигурации зависит от отношения их характерных
размеров и оказывается тем меньше, чем ближе равновесное
распределение заряда к равномерному (так, для прямоуголь-
ных пластин заданной площади относительная погрешность
расчета емкости методом Хоу тем меньше, чем больше отноше-
ние размеров пластины).
Поэтому, определив (путем сопоставления точных и при-
ближенных значений емкости) погрешность метода Хоу для
проводников какой-либо характерной формы (см., в частности,
пример 1-2), можно приближенно оценить эту погрешность и
для проводников другой, близкой формы.
Пример 1-1. Определим емкость проводника в форме прямоугольной пла-
стины размером аХЬ.
Пользуясь формулой
(1-7), вычисляем
f dS
предварительно I -—
J
s
. Для этого
введем прямоугольную систему координат, начало которой совместим с од-
ной из вершин прямоугольного контура пластины, а оси — со сторонами
этого контура. Тогда в некоторой точке с координатами xt, гд
dy
— х±)2 (у —
— | а — *! | f Arsh --— д- Arsh ———Д-
\ а — %! а — xj
+ I'6 — У11 (Arsh --— + Arsh —1 ф- | | (Arsh a~xi । дГ5и i
' ь - У1 b — ylt \ t/j У1 )
+1 *i I f Arsh 6 ~ _p Arsh = f (xt, У1). (1-19)
\ Xi Xi J
1 Доказательство этого утверждения дано в примере 2-12, а также в ра-
ботах [12 и 18]. г г г
2S
Выполняя повторное интегрирование 1, после преобразований получим
У1) с1У1 =
г 6 1—1
= 2 a2b Arsh — b2a Arsh — _]-(a3 ф- 63)-(а2 ф- Ь2)2 •
L а Ь 3 3 J
Подставляя полученное выражение в (1-7), получаем приближенную
формулу для емкости рассматриваемой пластины. В частности, при aJb — \
(квадратная пластина)
-^2- ~ 4,2263.
ей
Пример 1-2. Определим погрешность при расчете методом Хоу емкости
пластины в форме диска радиусом а.
Точное значение емкости рассматриваемого проводника (см. пример В-1)
Со=88«. Найдем теперь то же значение методом Хоу.
Поскольку рассматриваемый проводник является осесимметричным, вос-
пользуемся для расчета формулой (1-8). Для этого введем полярную си-
стему координат (г, 6) н вычислим I—— в произвольной точке п какого-
s
либо радиуса, принятого за линию 6=0.
Тогда
где Е —полный эллиптический интеграл 2-го рода с модулем k^rja.
\ а )
Производя повторное интегрирование, получаем
а 1
Г . Г dS Р ( г\ \ , 8а3
I t\dL I ------ = 4а I rjE / 1 di\ = 4а3 I /гЕ (k) dk -----
L s о о
Подставляя найденное выражение в (1-8), получаем следующее прибли-
женное выражение для емкости диска:
Со ~ 7,4022ва.
Таким образом, в данном случае относительная погрешность расчета по
методу Хоу <5~8 %.
При использовании метода средних потенциалов для рас-
чета емкости проводников в форме замкнутых оболочек фик-
1 Используя симметрию выражения f(xj, у,) относительно входящих
« а
в него величии, а также очевидное соотношение J <р(а—z)dz= J <p(z)dz,
о о
где <р — произвольная функция, достаточно произвести интегрирование лишь
одного из слагаемых, входящих в f(xir гд).
29
тивный заряд можно считать распределенным не только по
поверхности, но и в объеме тел, заменяющих эти проводники.
Это позволяет в отдельных случаях упростить расчетные фор-
мулы.
Так, для вытянутых проводников целесообразно использовать распреде-
ление фиктивного заряда вдоль некоторых линий в объеме тел, что позволяет
заменить объемный интеграл в формуле (1-4) линейным. Если, кроме того,
проводник осесимметричен, то для расчета среднего потенциала может быть
применена формула (1-6). При этом емкость уединенной осесимметричиои
оболочки выразится формулой
Со ~ 2e/S
dl I-1
(1-20)
L L
где I и L — ось и образующая оболочки; 3 — ее поверхность; R — расстоя-
ние между произвольными точками линий / и L; ri — расстояние от оси.
Б другом частном случае, для уединенных (в том числе и криволиней-
ных) проводов,
(1-21)
где R — расстояние между произвольными точками оси (Z) и поверхности
провода.
Метод средних потенциалов может быть использован для
расчета емкости проводников, расположенных не только в од-
нородной, но и в слоистой среде. В этом случае фиктивный за-
ряд, распределенный по поверхности или в объеме тел, заме-
няющих проводники, отражается от плоских поверхностей раз-
дела сред и вычисление среднего потенциала рассматриваемых
тел производится с учетом отраженных зарядов *.
Отражение точечного заряда q относительно плоской границы сред с раз-
личными диэлектрическими проницаемостями производится следующим об-
разом.
Пусть диэлектрическая проницаемость среды, в которой расположен за-
ряд q, равна ei, а диэлектрическая проницаемость граничащей с ней среды —
В2. Тогда отраженный заряд
?о = ^о?> (1-22)
, 81 —- 8о , ,
где kQ == —------коэффициент отражения, и расположен симметрично за-
е1 + е2
ряду q относительно рассматриваемой плоской границы.
Так, средний потенциал уединенного проводника в присут-
ствии плоской границы разнородных сред вычисляется по фор-
муле
Т dS
J
s
(1-23)
5»
и =_____2___С
s
где .Sq — поверхность, полученная путем зеркального отраже-
1 Указанный способ может быть использован и при другой форме границ
раздела сред (например, цилиндрической и сферической), для которой из-
вестно правило отражения точечного заряда.
30
ния S относительно рассматриваемой плоской границы; 7?! —
расстояние между произвольными точками поверхностей S и
So, а остальные обозначения те же, что и выше.
Таким образом, емкость уединенного проводника при нали-
чии плоской границы разнородных тел определяется формулой
(1-24)
Аналогичным образом могут быть получены расчетные фор-
мулы для емкости рассмотренных выше проводников частного
вида, а также для емкостей в системе двух и более провод-
ников.
Пример 1-3. Найдем емкость прямого провода длиной I и радиуса а
расположенного в среде с диэлектрической проницаемостью е.! па-
раллельно ее плоской границе со средой с диэлектрической проницаемостью
82, если расстояние от провода до границы равно h.
Если, как указано выше, считать фиктивный заряд распределенным по оси
провода и затем отразить его относительно рассматриваемой плоской гра-
ницы, то искомая емкость определится формулой
Со «4ji8iZ2
с dx' Г с dx —+ko с , dx —
J J У (x —x')2+a2 J У (x — x')2 + 4ft2
0 *-0 0
После вычисления интегралов, входящих в это выражение, и отбрасыва-
ния величин порядка а/l получаем приближенную формулу (7-1).
1-3. МЕТОД ПЛОЩАДОК
Метод площадок (в отличие от метода
средних потенциалов) основан на непосредственном определе-
нии заряда проводника по его потенциалу.
Он сводится к приближенному решению интегрального
уравнения первого рода, связывающего поверхностную плот-
ность заряда проводника с его потенциалом. Для уединенного
проводника это уравнение может быть записано в соответст-
вии с (1-3) в виде
_1_ б cdS = А (1-25)
4ле J R
s
где А — произвольная постоянная, а остальные обозначения
те же, что в (1-3).
При приближенном решении этого уравнения поверхность
S разбивается на ряд площадок, форма которых выбирается
возможно более простой, а размеры настолько малыми, чтобы
плотность заряда в пределах каждой площадки могла счи-
таться постоянной.
31
Поверхности каждой площадки приписывается постоянный
потенциал Uh, равный потенциалу в какой-либо одной (харак-
терной) точке этой площадки.
При достаточно малых размерах площадок способ распо-
ложения характерных точек на их поверхности сравнительно
мало влияет на результаты расчета. Поэтому его выбирают
обычно лишь из условий простоты расчетов^1.
Потенциал в характерной точке каждой площадки может
быть определен с помощью формулы (1-3) и при принятом за-
коне фиктивного распределения заряда
,, 1 «
Uk= — У >
4ле ^-1
(1-26)
где Uk — потенциал в характерной точке fe-й площадки; п —
число площадок; ст; — плотность заряда на поверхности i-й
площадки; — поверхность i-й площадки; Rm— расстояние
от характерной точки fe-й площадки до произвольной точки на
поверхности i-й площадки;
Значения коэффициентов ам определяются только геомет-
рическими параметрами площадок и их взаимным расположе-
нием. В тех случаях когда расстояние между характерными
точками каких-либо из двух площадок значительно превышает
размеры хотя бы одной из них (например, i-й), значение ам
может быть с достаточной точностью определено как отноше-
ние площади i-й площадки к расстоянию между характерными
точками i- и fe-й площадок.
Найденные из (1-26) значения потенциалов площадок
(Uk=Uh) приравниваются значению величины А, входящей
в (1-25).
Это приводит к следующей системе линейных алгебраиче-
ских уравнений относительно неизвестных значений плотности
заряда на поверхности каждой площадки2:
Пц0'1 +«120'2-1- . . • +а1п<т„ = 4леЛ; 1
a2ia1+a22a2 + • • • +^пОп = 4пеА; }
. ..................................... (1-27)
1 Расположение характерных точек на поверхности одинаковых площадок
обычно выбирают одинаковым, а на поверхности геометрически подобных пло-
щадок — подобным.
2 В ряде случаев из условий симметрии можно заведомо указать неко-
торые площадки с одинаковой плотностью заряда. При этом число неизвест-
ных в (1-27) сокращается.
32
Отсюда плотность
заряда на поверхности Лг-й площадки
Оь = 4 ж А —, (1 -28)
А Д
где
а11а12
^21^22
аи
• &2п
G'lriP'I'l*, ’
• &пп
а Ад— определитель, образуемый из Д заменой всех элемен-
тов fe-ro столбца единицами.
При найденных значениях од суммарный заряд проводника
в общем случае (при произвольном разбиении поверхности
проводника на площадки) определяется формулой
С = ShAh, (1-29)
Д k=i
где Sb — площадь k-й площадки.
Если же все площадки одинаковы, то
С = 4жЛ-42Дь, (1-29а)
пД к=1
где S — суммарная площадь поверхности проводника.
Полученные выражения для суммарного заряда непосред-
ственно приводят к следующим приближенным выражениям
для емкости уединенного проводника:
а) в общем случае
Со ~ 4ле-^-2 (1-30)
Д fc=i
б) для одинаковых площадок
п
С0~4лб-^-2 (1-30а)
пД ft=l
При расчете емкостей в системе двух и более проводников
непосредственное использование метода площадок затрудни-
тельно, так как приводит обычно к громоздким вычислениям.
Поэтому в этих случаях метод площадок применяется, как
правило, для расчета коэффициентов электростатической ин-
дукции с последующим переходом к значениям емкости на ос-
нове соотношений, приведенных в § В-1.
Пусть число проводников в системе равно N, а число площадок, на ко-
торые разбита поверхность р-го проводника, пр (р=1, 2,...., N). Тогда
2 Заказ № 507 ' 33
потенциал в характерной точке каждой площадки может быть найден по фор-
N
муле (1-26) при п= У, Пр. Далее потенциалы всех площадок па поверхности
р =1 „
каждого проводника должны быть приравнены одной и той же постоянной
величине Ар (р=1, 2, .... AQ, однако значения констант Ар уже не могут
быть заданы произвольно (как в случае уединенного проводника), а должны
быть выбраны с учетом условий, указанных в § В-1 и В-6. Эти условия ока-
зываются наиболее простыми при расчете коэффициентов электростатической
индукции, так как при этом потенциалы всех проводников, кроме одного,
должны быть приняты равными нулю.
Пусть, например, нужно определить собственный коэффициент электро-
статической индукции для р-го проводника и взаимный коэффициент элек-
тростатической индукции для р- и 9-го проводников (р, <7=1, 2, ..., N,
P=Aq). Не нарушая общности, можно принять, что площадки с номерами 1,
2, .... пр принадлежат поверхности р-го проводника, а площадки с номе-
рами Пу + 1; пр+2, ..., ПрА-Пд — поверхности р-го проводника. Кроме того,
примем, что потенциал р-го проводника равен некоторой постоянной вели-
чине А.
Тогда система уравнений для определения неизвестных значений плотно-
сти заряда на поверхности площадок принимает вид:
п
У akiGi= 4т,А при k= 1, 2, ...,пр;
1=1
п
У, = 0 при k = пр 1, ..., Пр + nq.
1=0
(1-31)
Решение этой системы вновь приводит к формуле (1-28), где на этот раз
Ль образуется из Л заменой первых пр элементов й-го столбца единицами,
а всех остальных элементов этого столбца — нулями.
Найденные значения плотности заряда позволяют непосредственно опре-
делить значение суммарного заряда р- и с-го проводников, а тем самым и
искомые значения собственного и взаимного коэффициентов электростатиче-
ской индукции. Формулы для определения этих коэффициентов имеют вид:
1 Пр
Ррр~4ле—— 2 Sk^k',
A fe=i
(1-32)
1 np+nq
Ррс ~ 4ле . 2 S/jA/j. (1-33)
Л А=пр+1
Из существа рассмотренного метода следует, что при лю-
бом конечном числе площадок он приводит к точным выраже-
ниям для емкости только при постоянной плотности равно-
весного распределения заряда (т. е. в том же частном случае,
что и метод Хоу). Во всех остальных случаях метод площадок
приводит к приближенным значениям емкости \ причем по-
грешность зависит от выбора характерных точек и числа пло-
щадок (п). При малых значениях п точность метода площадок,
как правило, ниже, чем метода Хоу (см., в частности, пример
1-4), но с увеличением п может быть доведена до любых тре-
1 Доказательство этого утверждения см., например, в [20].
34
буемых пределов L Поэтому существует такое число площадок
«о (различное для проводников различной формы), при кото-
ром точность расчета емкости методом площадок та же, что
и при использовании метода Хоу.
Пример 1-4. Пользуясь методом площадок, рассчитаем емкость уединен-
ного проводника в форме квадратной пластины со стороной а и сопоставим
погрешность расчета методом площадок и методом Хоу.
Для оценки наибольшей погрешности расчета методом площадок рас-
смотрим сначала предельный случай, приняв п=1 (т. е. считая поверхность
пластины одной площадкой).
В этом случае плотность заряда на всей пластине примем постоянной
(oi), а характерную точку совместим с точкой пересечения диагоналей пла-
стины.
При этом согласно (1-27)
а11°1 = 4леЛ,
где значение величины а14 может быть определено по формуле (1-19).
Полагая в (1-19) Ь=а, х1—у1 = а/2, получим а.ц = 4aArsh 1—4-0,8814а~
«3,5256а.
Тогда о, к; ----—----еА « 3,5643-^- и заряд Q«oia1 2«3,5643eaA.
3,5256а а
Отсюда (—} -3,5643.
\ еа /п=1
Сопоставляя зто значение с результатом расчета емкости той же пла-
стины методом Хоу (пример 1-1), устанавливаем, что
Но оба рассматриваемых метода дают заниженные значения емкости;
следовательно, при п=1 метод площадок дает большую погрешность, чем
метод Хоу2.
Примем теперь п—4, разбив поверхность пластины на 4 одинаковые
квадратные площадки со стороной а/2 (рис. 1-1, а). В силу симметрии рас-
положения площадок плотность заряда на каждой из них одинакова (<ч)
и согласно (1-27) удовлетворяет равенству
°i (fiii + й12 ~Ь й1з Ч- а1<) = 4леА .
Входящие сюда значения величин aik вновь определим по формуле
(1-19), где заменим а и b на а/2. Тогда при х1=а/4, получим ац =
=2а Arsh 1« 1,7628а, при xl=a/4, (/i = 3a/4
_ ___ а
fii2 — й1з —
Arsh 3 -|- 3 Arsh - 2Arsh 1
я 0,519a,
1 Расчет емкости методом площадок при больших значениях п требует
использования вычислительной техники (см., например, [9, 44]). При этом сле-
дует учитывать, что в силу некорректности задачи о решении интегрального
уравнения (1-25) решение системы (1-27) неустойчиво и потому должно про-
изводиться с использованием методов регуляризации [15].
2 Это можно установить и непосредственно, так как в данном предель-
ном случае распределение заряда при расчете по методу площадок принято
таким же, как в методе Хоу, а потенциал в выбранной характерной точке
заведомо больше среднего потенциала.
2*
35
а при Xj = !/i=3a/4
а Г
014 ~ L
я: 3,973 Отсюда
а \ еа /п=4
Arsh 1 — 3 Arsh -i-Arsh 3^ a 0,362a.
4л eA
При этих значениях сцО1~- - — — —
3,165 a
— 3,973, t. e. получаем значение емкости, большее, чем при a 1, но все еще
меньшее (и следовательно, менее точное), чем по методу Хоу. Поэтому вновь
увеличим число квадратных площадок, приняв его равным 16 (рис. 1-1,6).
В силу симметрии их расположения al = ©4=©i3=0i6; 02=03=05=08=09=
=012=014=015; Об=о?=oio=оц, т. е. достаточно определить плотность за-
ряда лишь на трех площадках: О(, Ог и ©е. Тогда из (1-27) получим:
Рис. 1-1
(ai,i 4“ 04,1 4" 013,1 4“ fii6,i) 4“ 2о2 (a2il -|- a3-1 -р + 012.1) 4~
-р 06 (°6.i 4" 2 a,, । -р Сцд) — 4леЛ;
al (ИЬ2 4- fi4,2 4- 013,2 4~ й16,г) 4- °2 (°2,2 4" 03.2 4“ С5,2 4" 2Й9,2 4"
4" 012,2 4" 014.2 4" 015,г) 4- °6 (06,2 4" 07,2 4" 010,2 4“ 0Ц,2) = 4ЛвА
ai (01,6 4" 04,6 4- 013,6 4- 01в,е) 4" 2о2 (Оз.б 4_ й2,б 4- 08.6 4- 0i2.e) 4-
4- 06 (06,6 4- 207,5 + 0ц,б) = 4леА .
Значения входящих сюда величин а-;ь определяются по формуле (1-19)
при замене а и b на а/4 и значениях Xj и yi, соответствующих координатам
точки пересечения диагоналей каждой площадки.
В результате приходим к следующей системе уравнений относительно
Ol, О’2 И Об*
1, lOSoj -р 1 ,068о2 0,496©6 = 4яеА,
0,534a! + 1 ,799о2 + 0,679©в = 4леА,
0,496©! + 1,359о2 4- 1,581©6 = 4 ле А .
Отсюда ©! ~ 0,492-^— ; о2л 0,339; ©6-0,186—- . Тогда
f Г \ а а а
I I
I —4,262, т. е. в данном случае погрешность расчета по методу
площадок оказывается уже меньшей, чем при использовании метода Хоу.
Метод площадок, как и метод средних потенциалов, приме-
нйм при расчете емкости проводников, расположенных не
36
только в однородной, но и в слоистой среде. При этом фиктив-
ный заряд отражается от плоских границ раздела сред с ис-
пользованием формулы (1-22) и вычисление потенциала в ха-
рактерной точке каждой площадки производится с учетом от-
раженных зарядов. В простейшем случае — для двухслойной
среды — потенциал в характерной точке любой площадки мо-
жет быть вновь представлен формулой (1-26), где на этот раз
^44^+4^’ (Ь34)
где ko — коэффициент отражения, входящий в (1-22); S't — по-
верхность площадки, расположенной симметрично i-й пло-
щадке относительно рассматриваемой плоской границы; R'ih —
расстояние от произвольной точки поверхности до характер-
ной точки fe-й площадки, а остальные обозначения те же, что
в (1-26).
Это позволяет найти приближенные выражения для емкости
проводников в двухслойной среде путем указанной замены вы-
ражений для ah{ в формулах (1-27) — (1-30).
Пример 1-5. Пользуясь методом площадок, найдем емкость той же пла-
стины, что м в предыдущем примере, считая, что она расположена в плоско-
сти, перпендикулярной плоской границе двух разнородных сред, на расстоя-
нии а/4 от этой границы (рис. 1-2, а); при этом диэлектрическая проницае-
мость среды, в которой расположена пластина, равна Ei, а граничащей с ней
среды 62.
Разделив, как и в предыдущем примере, поверхность пластины на 4 квад-
ратные площадки, показанные на рис. 1-2, а, и учитывая симметрию их рас-
положения (с учетом влияния границы), устанавливаем, что <Ц=Оз; 02=04.
Поэтому достаточно найти плотность заряда лишь на площадках 1 и 2.
Производя отражение фиктивного заряда относительно плоской границы
(рис. 1-2,6), с помощью (1-27) получаем:
(°ii + °si) 4“ °2 (a2i + йгг) = 4лб1 А;
°г (а12 + йзг) + °2 (й22 + й4г) = 4ле1Л ,
йи —
где значения величин определяются формулами (1-34) и (1-19).
Так,
= -|- [4 Arsh 1 +/?0(Arsh 9 —
— Arsh 7—7 Arsh — + 9 Arsh —
7 9 ,
(1,7626-|- 0,1252/?{,)а.
37
Производя аналогичные вычисления для других коэффициентов a th, получаем:
аи + ~ (2.2843 + 0,2468й0) а- с21 + д41 ж (0,7868 + 0,3262^) а;
ай + «32 ~ (1,0434 + 0,3262й{|) а- + «42 « (2,2843 + 0,4781йо) а.
Это позволяет найти значения Ci и а, при любых заданных значениях йо-
Приняв, в частности, б1=2бг (Ао=1/3), получим
Сопоставляя это значение с данными аналогичного расчета в однородной
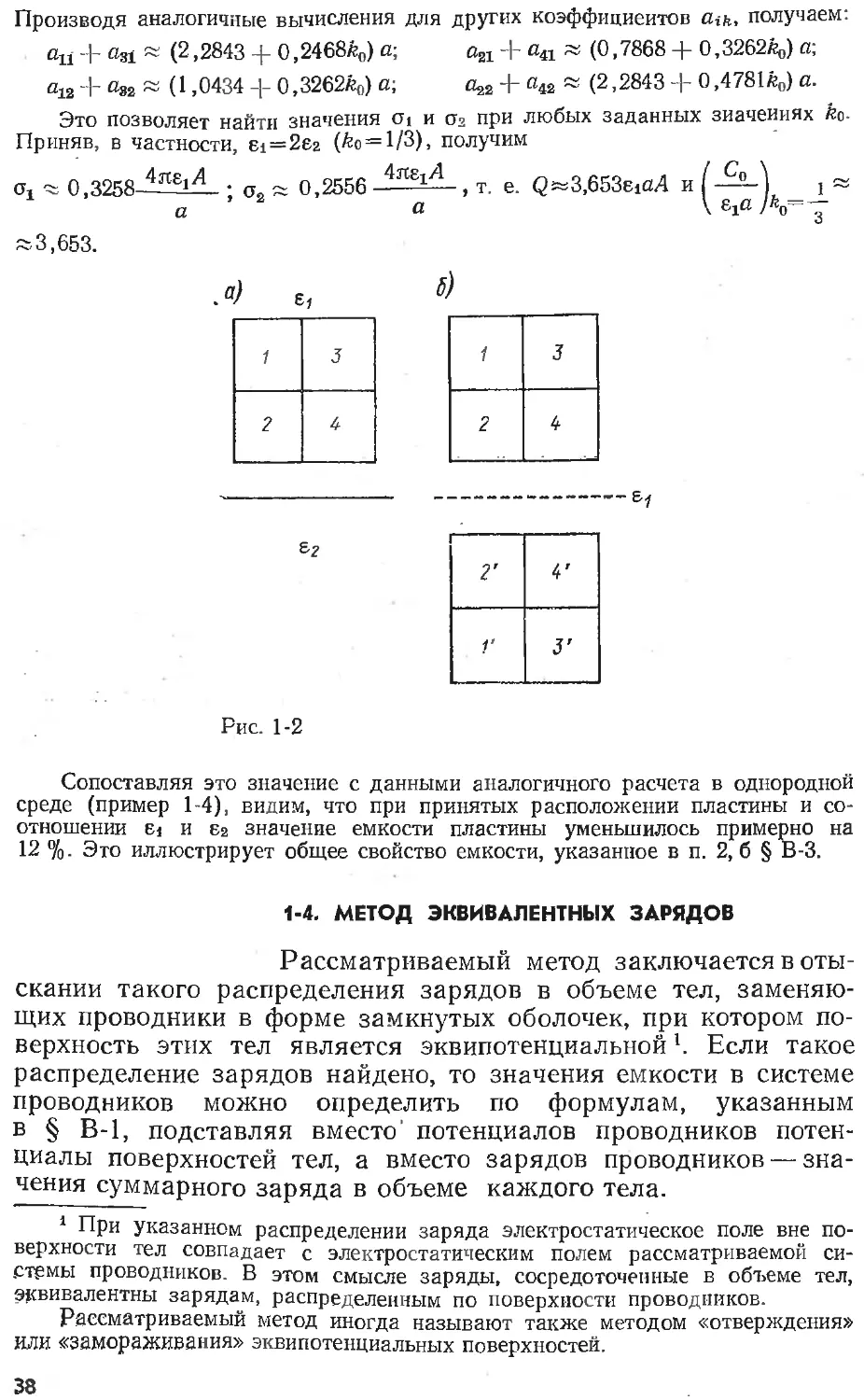
среде (пример 1-4), видим, что при принятых расположении пластины и со-
отношении 61 и бг значение емкости пластины уменьшилось примерно на
12 %. Это иллюстрирует общее свойство емкости, указанное в п. 2, б § В-3.
1-4. МЕТОД ЭКВИВАЛЕНТНЫХ ЗАРЯДОВ
Рассматриваемый метод заключается в оты-
скании такого распределения зарядов в объеме тел, заменяю-
щих проводники в форме замкнутых оболочек, при котором по-
верхность этих тел является эквипотенциальной ’. Если такое
распределение зарядов найдено, то значения емкости в системе
проводников можно определить по формулам, указанным
в § В-1, подставляя вместо' потенциалов проводников потен-
циалы поверхностей тел, а вместо зарядов проводников — зна-
чения суммарного заряда в объеме каждого тела.
1 При указанном распределении заряда электростатическое поле вне по-
верхности тел совпадает с электростатическим полем рассматриваемой си-
стемы проводников. В этом смысле заряды, сосредоточенные в объеме тел,
эквивалентны зарядам, распределенным по поверхности проводников.
Рассматриваемый метод иногда называют также методом «отверждения»
или «замораживания» эквипотенциальных поверхностей.
38
Общего способа отыскания распределения зарядов, создаю-
щих электростатические поля с заданной конфигурацией экви-
потенциальных поверхностей, в настоящее время не существует.
Поэтому при определении емкостей по методу эквивалентных за-
рядов пользуются обычно обратным способом: задаваясь тем
или иным конкретным распределением зарядов, находят для
каждого из них форму эквипотенциальных поверхностей элект-
ростатического поля и получают тем самым некоторый «набор»
распределений зарядов, создающих известные поля. Пользуясь
им, можно в ряде случаев найти такое распределение зарядов,
для которого форма эквипотенциальных поверхностей совпа-
дает (или достаточно близка) с формой поверхностей рассмат-
риваемых проводников.
В отдельных случаях требуемое распределение зарядов мо-
жет быть найдено и непосредственно по заданной форме по-
верхности проводников.
Так, при расчете емкостей в системе проводников, ограни-
ченных поверхностями сферической формы, требуемое распре-
деление заряда может быть найдено непосредственно путем ис-
пользования следующих известных свойств электростатического
поля точечных зарядов.
1. В поле точечного заряда q любая сферическая поверх-
ность с центром в точке расположения заряда является эквипо-
тенциальной. Если потенциал этой поверхности равен А, а ра-
диус R, то заряд, расположенный в центре сферы,
9 = 4ле/?Д.
(1-35)
2. В поле двух разноименных точечных зарядов qi и q% раз-
несенных на расстояние d, существует поверхность нулевого по-
тенциала в форме сферы с центром на линии, проходящей через
точки расположения зарядов, причем радиус этой сферы R и
положение ее центра определяются из соотношений:
Я2=М2;
Л1 = R-
(1-36)
I hi—h% | —d,
где hi и й2— расстояния от центра сферы до зарядов qi и q%,
соответственно.
Формулы (1-36) выражают правило отражения точечного
заряда относительно эквипотенциальной сферы, т. е. позволяют
при заданных радиусе сферы R, а также величине и расположе-
нии одного из зарядов (например, qi) найти величину и распо-
ложение второго заряда (q2). Последний называют при этом
отражением заряда qi относительно сферы или просто отражен-
ным зарядом.
39
Приведенные свойства позволяют указать способ построения
эквивалентного заряда в объеме некоторых тел, ограниченных
сферическими поверхностями.
Так, для тел, ограниченных двумя сферами произвольных радиусов а
и Ь, пересекающимися под углом л/и (п=1, 2, —), этот способ заключается
в следующем.
Располагая в центре одной из сфер (/) точечный заряд, определяемый
выражением (1-35) (при R^=a), многократно отражают его затем [с по-
мощью формул (1-36)] относительно сферы 2 и сферы 1 (последовательно)
При каждом из указанных отражений, до (п—1)-го включительно, экви-
потенциальной оказывается поочередно лишь одна из рассматриваемых
сфер, но после п-го отражения обе они принимают одинаковый потенциал,
так как n-й отраженный заряд всегда попадает в центр сферы 2 и имеет
значение, определяемое выражением (1-35) при R=b.
Таким образом, эквивалентный заряд определяется как сумма заряда,
расположенного в центре сферы /, и п отраженных зарядов
Пример 1-6. Определим емкость уединенного проводника, ограниченного
двумя сферами радиусов а и Ь, пересекающимися под углом л/2 (рис. 1-3).
Принимая потенциал сферы 1 равным произвольной постоянной А, в со-
ответствии с (1-35) расположим в центре этой сферы точечный заряд дю —
=4ле.аА. Отражая заряд дю относительно сферы 2, с помощью (1-36) нахо-
дим, что отраженный заряд
b
у'а2 Ь2
ab
У а2 -|- Ь2
9п =
910 = — 4ле
и расположен на расстоянии
/,11=—
У а2 + Ь2
от центра сферы 2, т. е. на расстоянии
1/V—9 62 fi2
h, , = у сг /г — —, — - — —-
11 ' Уа2А-Ь2 Уа2+Ь2
от центра сферы 1
В поле зарядов д10 и ди потенциал сферы 2 равен нулю, ио сфера 1
не является эквипотенциальной. Для восстановления постоянства потенциала
сферы 1 отражаем относительно нее заряд ди- Отраженный заряд
9И = - 7 • 9ц =
. а2
Т/' ^2 J_ _______
и расположен на расстоянии h12 =-------------= у а2 -ф 62 от центра сферы
а2
1, т е. в центре сферы 2.
Из способа выбора значения и расположения зарядов дю, 9ы. и дю ясно,
что в создаваемом ими электростатическом поле потенциал каждой из рас-
сматриваемых сфер постоянен и равен А.
Суммируя найденные значения величин дю, ди, д12, находим, что эквива-
лентный заряд
Q = 9ю + 911 + 912 = 4леЛ f а Ь-------- Л .
к у а2 + b2 J
Следовательно, емкость рассматриваемого проводника
Со = 4леа (1 -у —-------7 b 7 .
\ а у а2 Ь2 )
Аналогичным способом может быть найден эквивалентный заряд и при
большем числе определенным образом пересекающихся сфер. Так, для тела,
40
Таблица 1-1
L Приведенное значение заряда 4~=д/(4лЕА) Координаты точки расположения заряда
У
1 а 0 0
2 ь а2_ ]/а2+с2 ]/~fl2f,2 -|. агсг + t,2e2 ]/'а2+ с2
3 с V а2 + с2 0
4 ab Vа2+ Ь2 а* (а2 + Ь2) V а2 с2 а2 V а2с2 a2fe2 + Ь2с2 (а2 + Ь2) Vа2 + с2
5 ас У а2 4 с2 а2 V а2 + с2 0
6 Ьс Р Ь2 + с2 а2Ь2 + а2с2 + Ь2с2 (Ь2 -] с2) V а2 4 с2 с2 Vа2Ь2 + а2с2 + Ь2с* (Ь2 + с2) Vа2 + Ь2
7 abc 1 а2Ъ2 + а^с2 + Ь2с2 а2 V а2 + с2 а2с2 Ка2 с2 V а2с2 + Ь2с2 -|- а2Ь2
образованного пересечением трех ортогонально пересекающихся сфер произ-
вольных радиусов (рис. 1-4), значение и расположение точечных зарядов, со-
здающих электростатическое поле с эквипотенциальной поверхностью рас-
сматриваемого вида, приведены в табл. 1-1. Использование этих значений
приводит к формуле (3-51).
Подобным же образом может быть произведен расчет емко-
сти проводников, ограниченных сферическими поверхностями и
расположенных в слоистой среде. В этом случае для нахожде-
ния эквивалентного заряда, помимо (1-35) и (1-36), использу-
ется также формула (1-22), дающая правило отражения точеч-
ного заряда относительно плоской границы разнородных сред.
Это позволяет указать общий способ отыскания эквивалентного
заряда для проводников рассматриваемого вида в присутствии
плоской границы сред. В простейшем случае — для уединенного
проводника в форме сферы, расположенной в двухслойной
среде — этот способ заключается в следующем.
Располагая в центре сферы заряд, определяемый формулой
(1-35), последовательно отражают его затем относительно пло-
скости [по формуле (1-22)] и относительно сферы [по форму-
лам (1-36)]. Тогда изменяющиеся при каждом новом отражении
относительно сферы значения заключенного внутри нее заряда
позволяют определить поочередно верхние и нижние границы
значения емкости. При этом с увеличением числа отражений
эти границы монотонно сужаются и в пределе дают истинное
значение емкости проводника.
Пример 1-7. Найдем емкость проводника в форме сферы радиуса а,
касающейся плоской границы сред с диэлектрическими проницаемостями ei
и е2 (рис. 1-5).
Принимая потенциал рассматриваемой сферы равным некоторой по-
стоянной А, в соответствии с (1-35), поместим в ее центре точечный заряд
qi=4neiaA.
Пользуясь затем формулой (1-22), найдем, что отраженный заряд
и расположен на расстоянии 2я от центра сферы.
При этом выполняются требуемые условия па плоской границе, но потен-
циал сферы оказывается переменным по ее поверхности. Для восстановления
эквипотенциальное™ сферы • отразим относительно нее заряд qT. При этом
получаем отраженный заряд q2, значение и расстояние которого от центра
сферы (OD-) указаны в табл. 1-2, где приведены те же параметры и для
последующих отраженных зарядов, расположенных внутри сферы.
Из рассмотрения этих данных следует, что требуемые значения потен-
циала на сфере и требуемые условия на плоской границе рассматриваемых
сред могут быть достигнуты лишь при бесконечном числе отражений, причем
п й отраженный заряд внутри сферы
= — •
п
Поэтому эквивалентный заряд рассматриваемой сферы
Таблица 1-2 °°
Q = 2 = 4зте1йЛ X
П=1
— In (1 -ф k).
Таким образом, емкость рассматриваемого проводника выражается фор-
мулой
_ . е, + е2 , 2е,
Со = 4ле1а —!—- In-----±,
Ei — е2 ei -ф- е2
совпадающей с (7-49).
В частном случае, при непроницаемой плоской границе (ег/ei-cO),
C0 = 4neic In 2.
Если теперь использовать свойство емкости проводника, расположенного
вблизи бесконечно протяженной плоской непроницаемой границы [см. фор-
мулу (В-19)], то можно непосредственно найти емкость уединенного провод-
ника, образованного двумя соприкасающимися сферами равных радиусов
[см. формулу (3-44)].
В тех случаях когда ни одна из эквипотенциальных поверх-
ностей при выбранном распределении заряда в объеме тела,
заменяющего проводник, не совпадает с поверхностью этого
проводника, расчет его емкости рассматриваемым методом вы-
полнен быть не может. Однако при любом распределении этого
43
заряда можно получить двусторонние оценки емкости провод-
ника.
Если принять суммарный заряд в указанном объеме равным
Q, то
-3-<со<—(1-37)
17 max Pmiti
где [7max и Z7min —наибольшее и наименьшее значения потен-
циала, создаваемого зарядом, распределенным в объеме тела,
на его поверхности.
Пример 1-7. Пользуясь формулой (1-37), дадим двустороннюю оценку
емкости куба со стороной а.
Для простейшей оценки поместим точечный заряд Q в точке пересече-
ния диагоналей куба.
Тогда
О
Umax — ’ >
2яеа
О
б'т'ш — — г~ »
2леа у 3
и в соответствии с (1-37) получаем
0,5 < —^—< 0,866.
4я,еа
Это совпадает с оценками, получаемыми при сопоставлении емкости
куба с емкостями вписанной и описанной сфер (см. § 2-4).
ГЛАВА ВТОРАЯ
ВСПОМОГАТЕЛЬНЫЕ МЕТОДЫ
И ОЦЕНКИ
2-1. ОБЩИЕ ЗАМЕЧАНИЯ
Методы, рассматриваемые в настоящей
главе, делятся на две группы. Методы первой группы (§ 2-2 и
2-3) преследуют цель приведения задач определения емкости
к виду, доступному для расчетов или упрощающему их. Подоб-
ные методы в дальнейшем названы вспомогательными. '
Рассматриваемые вспомогательные методы заключаются
в геометрических преобразованиях проводников и основаны на
том^, что при -некоторых из этих преобразований значения емко-
стей остаются неизменными или меняются известным образом.
При этом задача сводится к расчету емкостей в преобразован-
ной системе, который может быть выполнен либо методами не-
44
посредственного определения емкости, либо путем предвари-
тельного расчета электростатического поля.
Методы второй группы (§ 2-4 и 2-5) имеют целью определе-
ние пределов, ограничивающих истинное значение емкости, т. е.
получение ее верхней и нижней оценок. Методы оценок осно-
ваны на сопоставлении энергии равновесного и фиктивного рас-
пределений зарядов и базируются на использовании неравенств
между величинами, либо непосредственно характеризующими
энергию (§ 2-5), либо известным образом связанными с ней
(§ 2-4).
2-2. МЕТОД КОНФОРМНЫХ ПРЕОБРАЗОВАНИЙ
Метод конформных преобразований приме-
ним при расчете емкостей в плоскопараллельных системах, со-
стоящих из двух или более проводников. В основе метода лежит
свойство емкости сохранять неизменным свое значение при кон-
формных преобразованиях указанных систем (инвариантность
емкости относительно конформного преобразования).
Конформным называют такое геометрическое преобразование на плоско-
сти, при котором углы между любыми двумя пересекающимися линиями ос-
таются неизменными, а длина всех бесконечно малых отрезков, проходящих
через данную точку плоскости, изменяется в одно и то же число раз. Кон-
формное преобразование описывается аналитической функцией комплексного
переменного при условии, что эта функция однозначна, а ее производная
в отображаемой области нигде не обращается в нуль. Аналитичность функ-
ции комплексного переменного’ W(z) =<р(х, у) +гф(х, у) проверяется с по-
мощью условий Коши — Римана1:
5<р <Эф . д<р <Эф
дх ду ду дх
Инвариантность емкости относительно конформного преоб-
разования позволяет заменить задачу определения емкости
в любой плоскопаралеллельной системе проводников расчетом
емкости в другой системе, полученной из исходной путем одного
или нескольких повторных конформных преобразований. Если,
в частности, удается свести исходную систему к какой-либо си-
стеме с известной емкостью, то тем самым необходимость соб-
ственно расчета емкости отпадает.
При практическом использовании рассматриваемого метода
сечение плоскопараллельной системы проводников принимают
за плоскость комплексного переменного z и подбирают такое
конформное преобразование f(z), в результате которого ука-
занная система принимает более простой, доступный для рас-
четов вид.
1 Более подробные сведения о конформных преобразованиях читатель
найдет в многочисленных работах по теории функций комплексного пере-
менного, например в работе [7].
45
Таблица 2-1
№ пп. Форма исходной области в ПЛОСКОСТИ 2 Функция, реализующая конформное отображение области в плоскости z на верхнюю полуплоскость плоскости £ (а0 — размерный коэффициент длины, численно равный единице)
1 iy ш £=—г2 Со
2 iy g = ft th i S' | M
1
3 р / У ? = а0 sh2 / л г 2 h
ш ул /ZZ ///X
4 Лу р X t, = a sin I ю | a O | N
2а
5 а iy
? = Уг2 + г>2
6 iy ? = R (-i±_LV \ z-R J
, 2R ; | '
46
77родолжение табл. 2~]
Форма исходной
области
в плоскости 2
Функция, реализующая конформное отображение
области в плоскости z на верхнюю полуплоскость
плоскости С
(с0 — размерный коэффициент длины,
численно равный единице)
£ =-----------[az - b Kz2- (я2 - ft2) ]
а2 — fe2
— при e=/=fe;
£=--------------при а = Ь
2z
f Z A al . h
t = аг sn Ko —, k0 ; kr. = — ; — ----
A I J a2 I Ko
(nx и a2 — точки вещественной оси в плоскости
t, соответствующие точкам 1 и 2; sn (u, k0) —
эллиптический синус)
Так,, при конформном отображении на верхнюю полупло-
скость (табл. 2-1) любая система электродов, сечения которых
расположены на контуре отображаемой области, преобразуется
в систему бесконечно длинных пластин, лежащих в одной пло-
скости. Это позволяет найти значения емкостей, пользуясь,
в частности, методом непосредственного определения напряжен-
ности поля.
Метод непосредственного определения напряженности поля основан на
рассмотрении вспомогательной величины — угла у, образуемого вектором на-
пряженности электростатического поля с одной из осей декартовой системы
координат. Функция у(х, у) удовлетворяет двумерному уравнению Лапласа
в декартовой системе координат и граничным условиям первого рода, кото-
рые могут быть непосредственно установлены (с учетом ортогональности си-
ловых и эквипотенциальных линий) на тех участках, где задано одно из сле-
дующих условий:
Us = const или
В связи с этим задача определения функции у(х, у) оказывается более
простой, чем расчет потенциала при смешанных граничных условиях ука-
занного вида. Найдя эту вспомогательную функцию, можно затем непосред-
ственно (минуя стадию определения потенциала) найти модуль безразмерной
напряженности электростатического поля Е из соотношений
ду д (In Е) .
дх ~~ ду
ду д(1п£)
ду дх
47
Отсюда может быть найден модуль напряженности плоскопараллельного
электростатического поля, создаваемого системой любого числа (л) пластин,
лежащих в одной плоскости. В точках этой плоскости (</ = 0)
В f(m)
(2-1)
Ее=о =
х— ak I
где
f(m) =
1 — при т = 0.
m, Xoi, yoi — число и координаты точек, в которых £=0; В — постоянная, оп-
ределяемая (наряду со значениями хм и r/ог) по заданным зарядам или по-
тенциалам пластин; а.к — координаты краев пластин.
Располагая выражением для Е, можно непосредственно найти как раз-
ность потенциалов между проводниками, так и их заряд (на единицу длины),
т. е. обе величины, необходимые для определения емкости в преобразованной
(а значит, и в исходной) системе проводников.
Пример 2-1. Определим емкость (на единицу длины) между бесконечно
длинным эллиптическим цилиндром и бесконечной полосой, сечения которых
изображены на рис. 2-1, а.
В соответствии с формулой (В-21) искомое значение емкости равно уд-
военному значению емкости между проводниками, представленными на
рис. 2-1,6. Для расчета емкости этой"вспомогательной системы воспользуемся
методом конформных преобразований. Приняв рассматриваемую область за
часть плоскости комплексного церемонного z, отобразим эту область на верх-
нюю полуплоскость нового комплексного переменного С (рис. 2-1, в). •
Выражение для функции, осуществляющей такое конформное преобразо-
вание, указано в п. 7 табл. 2-1 и позволяет найти все геометрические пара-
метры преобразованной системы. Считая эти параметры известными, рассмот-
рим задачу определения емкости в преобразованной системе проводников,
пользуясь приведенными выше общими методами (представление плоскости
сечения этой системы как плоскости комплексного переменного являлось
лишь вспомогательным приемом, необходимым для перехода к преобразован-
ной системе).
Воспользуемся, в частности, методом непосредственного определения на-
пряженности поля н следующей из него формулой (2-1). Полагая в этой фор-
муле /71=0 (поскольку для электронейтральной системы двух пластин в лю-
бой точке £=/=0), найдем, что разность потенциалов между пластинами
а3 а3
U. - 17, = f Ey=odx = В [ .. dx=.= -„ ,
" J у J V(x — aj)(x — аг)(а3 — х) (а4 — х)
а-2 а 2
а заряд на единицу длины каждой пластины
а, п.
i* dx
т = 2е £ dx 2иВ , .
J J У (X — ctj) (а2 — х) (а3 — х) (а4 — х)
а1
Вычисляя интегралы, входящие в два последних выражения, получаем,
что емкость (на единицу длины) между рассматриваемыми пластинами
Си
т
К\~17г|
о К' (/г)
= 2е--------—
К(£)
(2-2)
48
где K(k)—полный эллиптический интеграл 1 рода с модулем
л = 1 / (Й8 —
V («4 —а2)(а3 —01)
К'(*) = К(ГТ к2), а координаты краев пластин, определяемые из фор-
мулы для отображающей функции, имеют вид:
—ai = a2=a;
а3 = [а (« + d) - t K(a + d)2-(a2-fe2)] 5
а2 — fe2
at =-----— la (a + d + c) — b У (a+ d-\- c)2 — (a2 — b2) ].
a2—b2
Рис. 2-1
Это позволяет найти выражение для k (а соответственно, и для емко-
сти) при любых заданных параметрах а, Ь, с и d.
В. частности, при а=Ь (круговой цилиндр) выражение для модуля эл-
липтических интегралов принимает вид:
-.Л (d-a)(3a + c + d)
|/ (За + d) (с ф- d — а)
Поскольку емкость инвариантна относительно конформного преобразова-
ния, то формула (2-2) определяет емкость системы, изображенной на
рис. 2-1,6. Таким образом, искомая емкость исходной системы (рис. 2-1, а)
определяется выражением
С/= 4е
К' (k)
К (А)
Пример 2-2. Определим емкость (на единицу длины) между двумя про-
водниками, каждый из которых образован соединением двух бесконечно
длинных полос, изображенных на рнс. 2-2, а.
49
Как следует из (В-21), искомая емкость О в 4 раза больше емкости Си
вспомогательной системы, изображенной на рис. 2-2, б. Для отыскания же
значения Си воспользуемся методом конформных преобразований. Принимая
плоскость сечения вспомогательной системы за плоскость комплексного пере-
менного z, выберем отображающую функцию в виде, указанном в п. 1
табл. 2-1, которая переводит рассматриваемую вспомогательную систему
в систему двух пластин, лежащих в одной плоскости (рис. 2-2, в). Емкость
(на единицу длины) между этими пластинами определяется приведенной
выше формулой (2-2), если принять в ней
. = . f (a2 + c2)(fe2 + d2)
|/ (а2 + d2) (62 + с2)
Таким образом, искомое значение емкости
К ГУ
2-3. МЕТОД ПРОСТРАНСТВЕННОЙ ИНВЕРСИИ
Метод пространственной инверсии1 приме-
ним при расчете емкости уединенных проводников, расположен-
ных в однородной среде, и основан на использовании геометри-
ческого преобразования поверхности этих проводников путем
ее отражения относительно сферы.
Отражением (или инверсией) относительно некоторой сферы
радиуса (радиус инверсии) называют такое геометрическое
преобразование, при котором любая точка со сферическими
координатами г; 0; ф переходит в другую (инвертированную)
точку с координатами й?20/г; 6; ф. Геометрическое место инвер-
тированных точек некоторой поверхности образует инвертиро-
ванную поверхность, которая в ряде случаев имеет более про-
стую форму, чем исходная. Отыскание инвертированных поверх-
1 Не путать с плоской инверсией (отражение относительно круга), явля-
ющейся одним из конформных преобразовании.
50
Таблица 2~2
№ пп. Исходная поверхность и положение сферы инверсии Инвертированная поверхность и ее положение относительно центра инверсии
1 ентр инвер- и сферы / 1 Плоскость, стоянии h — - СИН \ \ f / дящая на рас- т центра инвер-
Сфера радиуса а; и сии — на поверхност 0 пре 2с LL )XC о
2 а _ / \v++"4-'j \ / Две сферы радиусов а и Ь, пересекающиеся под углом а; центр инверсии — на линии пересечения сфер; радиус инвер- сии 7?0 = 2с /1 / 1 \ ч Две плоскс под углом а. в точке О, гд , 2а2 Г а, j 0 )СТИ е /13 0 OS2 sin CCS П CL - co a ч/а? к 1 / ne teHTp = 2 h \ \ 1 х 1 / эесекающиеся инверсии — a; h2 = 2а2/Ь; У+4 — X / а 2 1-—У+ а 1 1—1 2 1 » ь \2 + a / 1'2
b sin а [ X с b Sin = а + 4-1 а sin ct2 = si + 4-1 а a T CL *- [( s2- а у CL 2 - CL 2
3 п одинаковых сфер радиуса а, проходящих через одну точку, с центрами в вершинах правиль- ного п-угольника; центр инвер- сии — в общей точке сфер; ра- диус инверсии 7?0 = 2а п пересекающихся плоскостей, параллельных одной прямой, обра- зующих в сечении правильный п- угольник с апофемой d = 2а; центр инверсии — в точке пересечения диагоналей
51
Продолжение табл. 2-2
5
Исходная поверхность
И положение сферы инверсии
Инвертированная поверхность
и ее положение относительно
центра инверсии
Поверхность, образованная
вращением окружности радиуса
а вокруг касательной; центр ин-
версии — в точке касания; ра-
диус инверсии 7?0 = 2а
Бесконечный круглый цилиндр
радиуса 2а; центр инверсии — на оси
цилиндра
Поверхность, образованная
вращением дуги с углом а и ра-
диусом а вокруг хорды; центр ин-
версии — в вершине хорды; ра-
диус инверсии 7?0 = 2а
Бесконечный круглый конус с уг-
лом л—а при вершине; центр инвер-
сии на оси конуса на расстоянии
, 2а
h =------- от вершины
sin а
Диск радиуса R; центр инвер-
сии на оси диска на расстоянии
h от его поверхности
Сферический сегмент радиуса Rr =
RV о t *
=----- с углом а = 2 arctg----,
h h
центр инверсии на оси сегмента на
Rl
расстоянии гх = —— от центра сфе-
ры радиуса
52
ностёй производится либо по заданному уравнению исходных
поверхностей (заменой в нем координаты г координатой п =
= R2o/r)> либо путем непосредственного построения. Последнее
существенно облегчается тем, что пространственная инверсия
сохраняет неизменными углы между любыми двумя пересекаю-
щимися линиями и переводит любую сферическую поверхность
в сферу или плоскость. Кроме того, преобразование инверсии
обратимо, т. е. любая из двух связанных этим преобразованием
поверхностей может рассматриваться и как исходная, и как
инвертированная.
Ряд простейших примеров пространственной инверсии при-
веден в табл. 2-2.
Пространственная инверсия поверхности любого уединен-
ного проводника позволяет определить его емкость по формуле
С0=4шТ?20К0, (2-3)
где Ко — так называемый нормированный потенциал.
Для определения значения Ко необходимо:
1. Расположить в центре инверсии фиктивный точечный за-
ряд д0, численно равный —4ле.
2. Приняв потенциал инвертированной поверхности равным
нулю, найти потенциал искажения К, создаваемого этой по-
верхностью в поле точечного заряда до-
s. Найти нормированный потенциал Ко как значение потен-
циала искажения в центре инверсии.
При достаточно простой форме инвертированной поверхно-
сти расчет потенциала искажения оказывается проще, чем ис-
ходная задача по расчету емкости. Он может быть выполнен
одним из следующих способов:
а. Представить потенциал электростатического поля заряда
до внутри заземленной инвертированной поверхности S в виде
U = ------)-К =---- + к,
4ле7? R
где R— расстояние от центра инверсии до. произвольной точки
внутри S.
Тогда К определяется как решение уравнения Лапласа
(ДК=0) с граничным условием
где Rs — расстояние от центра инверсии до произвольной точки
инвертированной поверхности.
б. Рассчитав электростатическое поле заряда д0 внутри за-
земленной инвертированной поверхности ’, можно найти плот-
1 Эта задача совпадает с определением функции Грина для инвертиро-
ванной поверхности.
53
пость зарядов, индуцированных на этой поверхности, из соотно-
шения
O = S
дЦ
dN
где N — внутренняя нормаль к инвертированной поверхности.
После этого потенциал искажения V определяется с помо-
щью формулы (1-3) как потенциал индуцированных зарядов.
в. Произведя отражение точечного заряда q0 относительно
заземленной инвертированной поверхности, можно найти потен-
циал искажения V как потенциал всех отраженных зарядов.
Пример 2-3. Пользуясь методом пространственной инверсии, определим
емкость того же проводника, что и в примере 1-6 (две сферы, пересекаю-
щиеся под прямым углом).
Рассматривая меридианное сечение этого проводника (рис. 2-3,а), рас-
положим центр инверсии в одной из точек пересечения окружностей, напри-
мер в точке А, а радиус инверсии примем равным диаметру одной из этих
окружностей, например
Ro = 2 а.
Как видно из табл. 2-2 или из непосредственного построения, инвертиро-
ванная поверхность в данном случае образована двумя плоскостями, пересе-
кающимися под углом я/2 в точке В', являющейся инвертированной для точки
В исходной поверхности.
Помещая далее в центре инверсии отрицательный точечный заряд
<Jo=— 4ле, принимаем потенциал инвертированной поверхности равным нулю.
Строя затем систему зеркальных отражений этого заряда относительно ука-
занных полуплоскостей (рис. 2-3, б), находим, что
1 b Ъ
4а 4а2 4а /а2 + Ь2 ’
Подставляя значение Ко в формулу (2-3), имеем
Со = 4ле4а2 — (1 -}- —---- = 4леа (1 -ф —------------------
4а \ а )Ла2 + Ь2 ) \ а J/ а2 + Ь2 ,
что совпадает с формулой, полученной в примере 1-6 методом эквивалент-
ных зарядов.
Пример 2-4. Найдем емкость уединенного проводника в форме тела, об-
разованного вращением окружности радиуса а вокруг касательной (тор без
отверстия).
Вид поверхности рассматриваемого проводника изображен в п. 4
табл. 2-2. Производя инверсию этой поверхности относительно сферы, пара-
метры которой также указаны в табл. 2-2, придем к инвертированной по-
верхности в виде бесконечного круглого цилиндра радиуса 2а. Принимая за-
тем потенциал этой ^поверхности равным нулю п располагая на оси цилиндра
фиктивный точечный заряд ?о=—4ле, найдем значение .величины Ко, входя-
щей в (2-3), первым из указанных выше способов.
Представляя потенциал электростатического поля заряда qo в виде
суммы его потенциала в свободном пространстве н потенциала «искажения»
54
у будем искать последний как решение уравнения Лапласа
d2V 1 dV d2V л
dr2 г dr dz2
с граничным условием
1
Vr=-2a ~-
Вводя косинус-преобразование Фурье V — J V cos Xz dz, получим для
О
V следующее обыкновенное дифференциальное уравнение:
^L+_L<_w = o,
dr
dr2
решение которого для области rsga имеет вид
V = А (X) Io (V),
где /о — модифицированная цилиндрическая функция первого рода нулевого
порядка; А(Х)—функция, подлежащая определению из граничного условия.
Производя то же преобразование над заданным граничным условием,
получим
Vr=-2a= |
€ь
COS Xz , .. /о*; \
— — dz = Ko (zha),
V 4a2 + z2
где Ко — функция Макдональда.
Тогда
/0(2Хс)
т. e.
Р=Ао <2Хд) у (V).
/0(2Xa)
55
Подставив найденное выражение V в формулу обращения, получим
оо 03
у = А С v cos Хг dK = — f 7°(V) cos Лг •
л I я J /0 (2Ля)
*Ь °
Значение величины Vo, входящей в формулу (2-3), определяется как зна
чение V в центре инверсии (при г=0, г=0), т. е.
ОО 00
„ __У = «гИ-Л.
л J /0(2Ха) па J /0(х)
о о
Подставляя найденное значение Vo в (2-3), получаем выражение для
емкости рассматриваемого проводника, приведенное в п. 3-5-11 [формула
(3-65)].
2-4. МЕТОДЫ ОЦЕНКИ ЕМКОСТИ
УЕДИНЕННЫХ ПРОВОДНИКОВ
ПО ИХ ГЕОМЕТРИЧЕСКИМ ПАРАМЕТРАМ
Оценка емкости проводников непосред-
ственно по их геометрическим параметрам является наиболее
простым путем определения пределов, в которых заключено ее
истинное значение. Основными методами решения этой задачи
являются:
метод частей;
метод симметризации;
метод интегральных геометрических параметров.
Все эти методы применяются при оценке емкости уединен-
ных проводников, расположенных в однородной среде.
Ниже рассматривается каждый из указанных методов.
Метод частей позволяет дать двустороннюю оценку
емкости проводников произвольной формы.
В применении к уединенным проводникам он основан на ис-
пользовании указанного выше (§ В-2) положения, согласно
которому емкость уединенного проводника произвольной формы
больше емкости любой его части, рассматриваемой как отдель-
ный проводник. Из этого утверждения следует, что, рассмат-
ривая проводник с искомой емкостью Со как часть другого про-
водника с известным значением емкости, можно получить верх-
нюю оценку для Со. Точно так же, выделяя в проводнике
с искомой емкостью какую-либо часть в виде проводника с из-
вестной емкостью, можно получить нижнюю оценку Со. Точность
этих оценок оказывается тем более высокой, чем ближе поверх-
ность рассматриваемой части к поверхности всего проводника.
Поэтому для проводников различных типовых форм применяют
разные способы выделения (или, наоборот, добавления) каких-
либо частей.
56
Пример 2-5. Пользуясь изложенным методом, оцепим емкость пластины,
изображенной на рис. 2-4.
Выбирая в качестве части рассматриваемой пластины диск радиуса а,
а в качестве включающей ее поверхности — диск радиуса b и пользуясь из-
вестным значением емкости диска [формула (3-12)], непосредственно полу-
чаем следующие оценки:
я Со
b 8еЬ
Рис. 2-4
В приведенном примере, как и для других пластин с отно-
шением характерных размеров, близким к единице, в качестве
части рассматриваемого проводника целесообразно выбирать
диск, ограниченный вписанной окружностью, а в качестве охва-
тывающей поверхности-—диск, ограниченный описанной окруж-
ностью. Если обозначить радиусы этих дисков через а и b
(Ь>а), то для любых пластин указанного вида справедливы
те же неравенства, что и в примере 2-5.
Точно так же для тел и оболочек с близкими по значению
характерными размерами целесообразно использовать при
оценках рассматриваемым методом вписанную и описанную
сферы. В этом случае для емкости проводников такого вида
могут быть указаны следующие неравенства:
Г вп
6*0 /max
4ле 2 ’
(2-4)
где /max — максимальный размер проводника; гвп — радиус впи-
санной в его поверхность сферы.
Если, например, применить эти неравенства для емкости
куба, то придем к тем же результатам, что и в примере 1-7.
Использование метода частей для оценки конденсаторной
емкости базируется на указанном выше (§ В-2) положении,
согласно которому емкость между любыми двумя проводниками
больше емкости между любыми их частями, рассматриваемыми
как отдельные проводники, расположенные относительно друг
друга так же, как указанные части.
57
Отсюда следует, что, выделяя в рассматриваемых проводни-
ках какие-либо части, емкость между которыми известна, мо-
жно получить нижнюю оценку интересующего нас значения
емкости С\ точно так же дополняя рассматриваемые провод
ники какими-либо частями до образования системы с известным
значением емкости, можно получить верхнюю оценку С.
Пример 2-6. Дадим верхнюю и нижнюю оценки значения емкости между
оплеткой и центральной жилой коаксиального кабеля.
Считая оплетку состоящей из касающихся друг друга проводов круглого
сечения, представим сечение кабеля в виде, изображенном па рис. 2-5.
Дополняя наружный проводник до цилиндра меньшего радиуса
(Ri=R—а), получим систему в виде двух коаксиальных цилиндров с заве-
домо большей емкостью (на единицу длины), чем для рассматриваемого ка-
беля. Точно так же, заменяя наружную оплетку цилиндром большего ра-
диуса (Rz—R+a), получим систему из двух коаксиальных цилиндров с заве-
домо меньшим значением емкости на единицу длины, чем для кабеля.
Емкость между двумя коаксиальными цилиндрами определяется форму-
лой (4-21). Пользуясь ею, получаем
2ле _ „ 2ле
< С / < .
1пА±£
г--------------------г
Метод симметризации основан на использовании гео-
метрического преобразования, называемого симметризацией.
В общем случае симметризация может быть определена как
такое геометрическое преобразование объемного или плоского
тела, которое позволяет привести его к виду, симметричному
относительно некоторой плоскости (плоская симметризация)
или оси (осевая симметризация).
Симметризация объемного тела относительно плоскости (так называемая
пространственная симметризация Штейнера) производится следующим об-
разом.
Пусть имеется некоторое пространственное тело Д и какая-либо плос-
кость Р (плоскость симметризации). Проводя через каждую точку поверх-
58
ности тела-А прямые, перпендикулярные Р, откладывают на этих прямых
симметрично относительно Р отрезки, равные суммарным длинам хорд, высе-
каемых на рассматриваемой прямой телом А. Геометрическое место концов
таких отрезков образует поверхность нового тела, симметричного относи-
тельно плоскости Р. Так, например, полушар радиуса а при симметризации
относительно любой плоскости, параллельной его основанию, переходит
в сжатый сфероид с осями 2а и а.
Совершенно аналогичным образом производится и симметризация плос-
кого тела относительно любой лежащей в его плоскости прямой. Один из
примеров такой симметризации приведен на рис. 2-6.
Симметризация пространственного тела относительно оси (симметриза-
ция Шварца) заключается в следующем.
Пусть имеется некоторое пространственное тело А и какая-либо пря-
мая L (ось симметризации). Проводя через точки поверхности А плоскости,
перпендикулярные L, строят в каждой из них круг с центром на L, равнове-
ликий по площади сечению тела А рассматриваемой плоскостью. Геометри-
ческое место таких окружностей образует поверхность нового, осесиммет-
ричного тела. Так, например, куб со стороной а при этом способе симме-
тризации относительно оси, параллельной одному из его ребер, переходит в
прямой круговой цилиндр с высотой а и радиусом аул .
Помимо этого, существуют и другие способы симметризации,
однако во всех случаях симметризация объемных тел сохраняет
неизменным их объем, а симметризация пластин не меняет пло-
щади их поверхности.
Использование симметризации при оценке емкости основано
па том, что емкость любым образом симметризованных уеди-
ненных проводников не превосходит емкости этих проводников
в их исходной форме [11]:
С о СИМ CQ ИСХ • (2-5)
Соотношение (2-5) позволяет:
а) рассматривая какой-либо класс проводников, выделить
среди них проводник с наименьшим значением емкости (см,
например, табл. 2-3);
Таблица 2-3
№ пп. Класс уединенных проводников Проводник i с наименьшей емкостью
1 Прямые провода заданных длины и площади сечения Провод круглого сечения
2 Треугольные пластины заданной площади Пластина в форме равносторон- него треугольника
3 Четырехугольные пластины задан- ной площади Пластина квадратной формы
4 Эллипсоиды заданного объема Сфероид
5 Цилиндры с заданными, объемом и формой поперечного сечения Прямой круглый цилиндр
59
б) найдя тем или иным способом емкость симметризован-
ного проводника, установить тем самым нижнюю границу емко-
сти проводника исходной формы;
в) располагая значением емкости какого-либо уединенного
проводника (отличного от шара или диска), дать верхние
оценки емкости любых проводников, полученных из данного пу-
тем симметризации.
Пример 2-7. Найдем нижнюю границу емкости проводника в форме по-
луэллиптической пластины с полуосями а и Ь (а>Ь).
Точный расчет емкости проводника рассматриваемой формы существую-
щими методами выполнен быть не может. Поэтому для получения нижней
оценки емкости деформируем его путем плоской симметризации относительно
основания. Форма симметризованного проводника может быть определена
следующим образом.
Введем прямоугольные координаты (х, у) с началом в середине основа-
ния, совместив ось х с большой, а ось у — с малой полуосью. Тогда связь
между координатами точек на контуре исходной (х, у) и симметризованной
(Xi, yi) пластин определится равенствами:
Отсюда
т. е. снмметризованный проводник имеет форму эллиптической пластины
с осями 2а и Ь. Выражение для емкости такой пластины известно [см. фор-
мулу (3-13)]. Пользуясь им, находим, что емкость рассматриваемого провод-
ника удовлетворяет неравенству
4леа
4с2
где К — полный эллиптический интеграл первого рода.
В частном случае, при а=Ь (полукруговая пластина)
При установлении нижних границ емкости проводников
в ряде случаев возникает необходимость в их многократной
симметризации.
Если после первой симметризации емкость симметризован-
ного проводника найдена быть не может, то симметризация
производится повторно, до тех пор, пока форма симметризован-
ного проводника не окажется достаточно простой. Однако при
этом точность нижней оценки емкости после каждой симметри-
зации понижается.
60
При бесконечном числе симметризаций любое тело объе-
мом V преобразуется в шар того же объема, а любая пла-
стина — в равновеликий диск.
Это позволяет указать следующие общие неравенства:
а) для емкости произвольного уединенного проводника объе-
мом V
-^->2 6л2У ~ 7,7954 V ;
(2-6)
б) для емкости произвольной пластины с односторонней пло-
щадью S
— >81/ — -4,5134 VS.
е Г л
(2-7)
Метод интегральных геометрических пара-
метров позволяет дать оценку емкости уединенных провод-
ников в форме выпуклых тел 1 и основан на использовании не-
равенств, содержащих интегралы от функций, определяемых
значениями кривизны поверхностей этих проводников.
Так, верхняя граница емкости проводников указанного вида
может быть установлена из соотношения
Со 2Му
\ 1 — У J
(2-8)
где M=[H(S)dS— интегральный геометрический параметр,
s
называемый константой Минковского; H(S) —средняя кривизна
в произвольной точке поверхности тела S; У = ^/~ 1 — 4-^-,
а равенство достигается только в случае сферы.
Константа М имеет размерность длины и может быть най-
дена при любой заданной форме поверхности проводника. Для
ее определения необходимо знать выражение средней кривизны
поверхности Н, определяемой в общем виде равенством
2 \ Rz /
где Ri и /?2 — главные радиусы кривизны в данной точке по-
верхности, т. е. наибольшее и наименьшее значения этих радиу-
сов.
1 Выпуклым называют, как известно, тело, обладающее тем свойством,
что отрезок прямой, соединяющий две любые его точки, целиком содер-
жится в этом теле.
61
Выражения для средней кривизны некоторых простейших
поверхностей приведены в табл. 2-4 *.
Располагая выражениями для средней кривизны, можно вы-
числить константу М путем интегрирования Н либо по всей
поверхности тела, либо по отдельным ее участкам. В последнем
случае для определения М следует просуммировать константы
Mit найденные для отдельных участков.
Таблица 2-4
№ пп. 1 Тип поверхности или линии И
1 Плоскость 0 0
2 Часть сферы радиуса а 1 а с — (S—площадь а части)
3 Часть боковой поверхности прямого круглого цилиндра ра- диуса а 1 2а с (S—площадь 2a части)
4 Боковая поверхность прямого круглого конуса высотой h с уг- лом а при вершине 1 2р tga (р—расстояние от вершины конуса) л h
5 Линия длиной L, образованная пересечением двух поверхностей под произвольным углом а (/) оо — —a(/)] dl 2 L
Значения Mi для участков простейших гладких поверхностей
и линий их пересечения также приведены в табл. 2-4 (на ука-
занных линиях пересечения /У->оо, S->0 и вычисление Mt тре-
бует раскрытия неопределенности).
Используя эти значения, можно непосредственно получить
верхнюю оценку емкости уединенных проводников в виде вы-
пуклых тел, ограниченных любым числом пересекающихся по-
верхностей указанного вида.
Пример 2-8. Пользуясь методом интегральных геометрических парамет-
ров, дадим верхнюю оценку емкости проводника в форме куба со сторо-
1 Значения„средней кривизны для произвольной гладкой поверхности
Найдены по —ным формулам дифференциальной геомет-
62
В соответствии с формулами, приведенными в табл. 2-4, на всех гранях
куба М( = 0> а иа каждом ребре
4
Тогда значение константы (И для .всей рассматриваемой поверхности
М = 1244; = Зла.
Подставляя найденное значение М в выражение для у, найдем, что
4л-6а2
9л2а2
0,3888.
Тогда согласно (2-8) получаем
—^2—<0,7106,
4леа
что дает более точную верхнюю оценку, чем в примере 1-7.
Пример 2-9. Дадим верхнюю оценку емкости проводника в форме полу-
цилиндра, изображенного на рис. 2-7.
Значение константы М для рассматриваемого тела может быть найдено
в виде
М = Mi 4- 2 (М2 + М3 + МД,
где 1 — участок цилиндрической поверхности (r=a), a 2, 3 к 4 — линии, по-
казанные на рисунке.
Пользуясь затем выражениями, приведенными в табл. 2-4, находим, что
.. па „ яа ,, л?а
Mi — М3 =-----; М„ ----------; М. =---------.
2 4 4
Тогда
M = ла
11,2180а.
Определяя далее величину у, входящую в (2-8), при найденном значении
М получаем
у= Г1— 4^'2а2(я+1) и 0 7658.
1 / I Л \2
I л2а212 + у)
Тогда в соответствии с (2-8)
-^2-< 8,5027а.
е
Пример 2-10. Дадим оценку емкости проводника, имеющего форму пря-
мого эллиптического цилиндра с высотой h и полуосями основания а и Ь
(а>Ь).
Точный расчет емкости проводника указанного вида существующими ме-
тодами выполнен быть не может. Поэтому применим для ее приближенного
определения рассмотренные выше методы оценок.
Для получения верхней оценки Со воспользуемся вновь неравенством
(2-8), для чего вычислим входящие в него величины М и у.
63
Вводя параметрические уравнения направляющей цилиндра х—a cos/,
i/ = bsint, можно получить следующее выражение для кривизны в произволь-
ной точке направляющей:
ab
K(t} = (a2 sin2 f J-6а cos2/)3'2 ’
Тогда средняя кривизна в произвольной точке боковой поверхности ци-
линдра
1 ab
Н 2 (д2 sin21 + Ь- cos2 О3 2
и константа М1 па этой поверхности определится выражением
Л2
M1 = 4abh. С ----------—---------= 2лй.
J a2 sin21 + b2 cos21
0
Рис. 2-7
Вычисляя константу Минковского на линии пересечения боковой поверхности
цилиндра с его основанием, воспользуемся формулой, приведенной в п. 5
табл. 2-4. Тогда
где Е — полный эллиптический интеграл второго рода с модулем
Поскольку на основаниях цилиндра кривизна равна нулю, то
( h Г / / ь \2
М — Мл + 2М2 = 2ла <-----|-Е 1/ 1—1-------1
[° у \ о /
Площадь поверхности рассматриваемого проводника определяется вы-
ражением
Подставляя найденные величины в неравенство (2-8), получаем
4лея 1 у
In ——L
1-V
64
где
Численные результаты верхних оценок величины Со с использованием
неравенства (2-9) приведены в табл. 2-5.
Для получения нижней оценки той же величины воспользуемся изложен-
ным выше методом симметризации.
Производя круговую симметризацию рассматриваемого цилиндра относи-
тельно оси, параллельной его образующей, получим симметризованное тело
в форме прямого круглого цилиндра с радиусом R=~\ab.
.Пользуясь далее приближенным выражением для емкости прямого круг-
лого цилиндра [формула (3-61)] и неравенством (2-5), непосредственно по-
лучаем 1 * 3
Численные результаты нижней оценки величины Со с использованием не-
равенства (2-10) также приведены в табл. 2-5.
Находя приближенное значение искомой емкости как среднее гармониче-
ское ее верхней и нижней границ, определяемых неравенствами (2-9) и
(2-10), получаем
где у определяется тем же выражением, что и в (2-9).
Результаты численных расчетов по приведенной формуле и их макси-
мально возможная относительная погрешность 6 также приведены в табл. 2-5.
Как видно, при выбранном диапазоне параметров b/а и h/а значение ве-
личины 6 не превышает 11 % и быстро убывает с увеличением отношений Ь/а
и h/a.
Формулы, приведенные в п. 5 табл. 2-4, позволяют в частном
случае (при а —0) получить следующее неравенство для емко-
сти пластин, ограниченных произвольным выпуклым контуром,
_Со_ -----------------------лДу--, (2_ j 2
е , 1+т
In-----
1—T
1 Коэффициенты в правой части неравенства (2-10) определены с уче-
том максимальной относительной погрешности формулы (3-61).
3 Зякя.ч Ко Г.Г17
65
Таблица 2-5
Ыа 0,25 0,5 0,75
hl а 0,25 0,5 1,0 0.25 0,5 1,0 0,25 0,5 1.0
По формуле (2-9) 0,5824 0,7170 0,9441 0,687 0,8165 1,0419 0,7868 0,9163 1,1447
Ср 4леа По формуле (2-10) 0,4723 0,5834 0,7715 0,6155 0,7362 0,9406 0,7234 0,8501 1,0647
По формуле (2-11) 0,5216 0,6433 0,8491 0,6493 0,7743 0,9887 0,7538 0,8819 1,1032
6, % 10,4 10,3 10,1 5,5 5,2 5,1 4,2 3,7 3,6
32S
; L и S — периметр и односторонняя пло-
где у
щадь поверхности рассматриваемой пластины, соответственно.
Пример 2-11. Дадим верхнюю оценку емкости полукруговой пластины
радиуса а.
В данном случае Д=(л+2)«;
ла2
т =
л24-4я—12
—---------- as 0,6283,
л 2
н из формулы (2-12) непосредственно получаем
< ал (л + 2) —-----------к 6,8702а,
е , 1.6283
In-------
0,3717
5 =
2
т. е. <0,8588.
8еа
Это значение и указано на рис. 3-17.
2-5. ЭНЕРГЕТИЧЕСКИЕ МЕТОДЫ
Методы, рассматриваемые в настоящем па-
раграфе, базируются на теореме Томсона, согласно которой
энергия электростатического поля при равновесном распределе-
нии какого-либо заряда минимальна по сравнению с энергиями
полей при любом другом (фиктивном) распределении того же
заряда.
Это утверждение непосредственно приводит к неравенствам,
позволяющим дать двустороннюю оценку истинного значения
емкости проводников.
Верхняя оценка емкости уединенных проводников может
быть получена из соотношения
f s.(\f)2dV
> (2-13)
fs
где V — область, занятая диэлектриком; f — произвольная ска-
лярная функция координат, принимающая постоянное значение
(fs) на поверхности проводника S, а равенство достигается
только в том случае, когда f — гармоническая функция (Af=O).
В частном случае, при e=const, формула (2-13) выражает
известный принцип Дирихле, согласно которому
(2-14)
е f2s
где D (f) = f (v’f)2 dV = — f f dS—J fAf dV — интеграл Ди-
v sv
3*
67
рихле; N — внешняя нормаль к S, а остальные обозначения те
же, что в (2-13).
Формулы (2-13) и (2-14) могут быть использованы для
верхней оценки емкости и между двумя проводниками, если
под f понимать произвольную скалярную функцию координат,
принимающую постоянные значения fs, и fs.2 на поверхности
каждого из этих проводников (Л?! и 52), а также принять /s=
= fs,—fs2> 5=51+52-
Нижняя оценка емкости уединенных проводников может
быть получена из соотношения
°"' Je|F|«dV
(2-15)
где F— произвольная векторная функция координат, удовлетво-
ряющая в области V условию divF=0; остальные обозначения
те же, что и выше, а равенство достигается только в том случае,
когда F может быть представлена как градиент гармонической
функции, принимающей на S постоянное значение.
В частном случае, при e=const, (2-15) переходит в следую-
щую формулу, выражающую принцип Томсона:
(2-16)
Если заменить проводник телом той же формы с той же
диэлектрической проницаемостью, что и для окружающей
среды (см. § 1-1), то функция F в формуле (2-16) может быть
представлена как градиент потенциала при том или ином рас-
пределении заряда по поверхности или в объеме указанного
тела.
При поверхностном распределении заряда
[ b(S)dSj2
$ U(S)o(S)dS — e j(Vt/)2dV
s v,
(2-17)
где o(S)—принятая поверхностная плотность распределения
заряда; U (S) — потенциал, возбуждаемый при этом распределе-
нии заряда; V! — область, занятая телом, заменяющим провод-
ник, а равенство достигается только при равновесном распре-
делении заряда.
Отсюда может быть получено следующее соотношение, вы-
68
ражающее так называемый принцип Гаусса:
Г f о (S) dS ]2
Г'» \ I S 1
J и (S) о (S) dS
s
(2-18)
где равенство также достигается только при равновесном рас-
пределении заряда, а при любом o(S), отличном от равновес-
ного, неравенство является более слабым, чем в предыдущей
формуле.
При распределении заряда в объеме тела, заменяющего про-
водник, формула (2-16) приводит к соотношению
с.>----
'Н>
S
(2-19)
№(S)
— do
где Q — суммарный заряд внутри S; — внутренняя нормаль
к S, а равенство достигается только при таком распределении
заряда внутри S, когда эта поверхность эквипотенциальна (см.
§ 1-4).
Если теперь представить потенциал U в виде разложения
по сферическим гармоникам и ограничиться конечным числом
членов в этом разложении, то
U ~ 2 а{т}Чт>
гдефт = —2т—\ ’И™ — гармонический полином (Д/7т = 0); R —
R
расстояние от выбранного начала координат; а^>—коэффици-
енты разложения.
Подстановка этого выражения в (2-19) приводит к следую-
щему неравенству для емкости любого проводника, ограничен-
ного аналитической или звездной 1 поверхностью:
где
С0>4леа<п),
ц(«) = 4л ,
1
(2-20)
1 Поверхность называют аналитической, если она в достаточно малой ок-
рестности каждой своей точки допускает параметрическое представление х=
=ft(u, v), y=f2(u, v), z=]'3(u, v), где ft, f2, f3 — аналитические функции (т. e.
функции, представимые степенными рядами). Поверхность называют звезд-
ной относительно некоторой точки, если любой луч, проведенный из этой
точки, пересекает указанную поверхность не более чем в одной точке.
69
дфп
dN(
dS;
^2-dS; .
61 — минор определителя 6n, полученный вычеркиванием первой
строки и первого столбца (при п=\ 6i = l); Ni — внутренняя
нормаль к S.
Пример 2-12. Пользуясь принципом Гаусса, определим знак погрешности
при расчете емкости методом Хоу.
Как указано в § 1-2, при приближенном расчете емкости методом Хоу
принимается, что плотность заряда на поверхности тела, заменяющего про-
водник, постоянна, o(S)=Q/S. Тогда значение величины U(S), входящей
в формулу (2-18), определится выражением
U(S)
Q (* dS
4jieS J R
s
где R — расстояние между двумя произвольными точками поверхности 5.
Подставляя указанные выражения 0(5) и U(S) в формулу (2-18), по-
лучаем
но значение величины в правой части этого выражения в соответствии с (1-5)
определяет емкость, рассчитанную методом Хоу. Таким образом
Со 2а С0хоу>
т. е. расчет методом Хоу приводит, как указано в § 1-2, к заниженным значе-
ниям емкости.
Пример 2-13. Пользуясь формулой (2-20) при и=1, дадим
оценку емкости проводника в форме куба со стороной а.
При п=1 гармонический полином /72=1, и для величины ai(1),
в (2-20), получаем
нижнюю
входящей
Располагая начало прямоугольной системы координат в точке пересече-
ния диагоналей куба и направляя оси координат параллельно его ребрам,
имеем
70
Вычисление интеграла, входящего в это выражение, дает
Тогда
а*1* =--------------------------—----------я 0,6015а.
УТ
За - 2 У 2 arctg —%—
Таким образом, для емкости куба получаем следующее неравенство:
—> 0,6015,
4леа
которое дает значительно лучшую нижнюю оценку, чем в примере 1-7.
При п>1 расчет может быть выполнен аналогичным образом и приводит
к более точным оценкам (см. табл. 3-10).
2-6. МЕТОД АНАЛИТИЧЕСКОЙ АППРОКСИМАЦИИ
ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Рассматриваемый метод (иногда называе-
мый также методом предписанных поверхностей или аналити-
ческим методом ожидаемых путей потоков) позволяет дать дву-
стороннюю оценку значения емкости проводников произвольной
формы и основан на приближенном представлении эквипотен-
циальных поверхностей и силовых линий электростатического
поля этих проводников какими-либо поверхностями и линиями,
выбираемыми из физических соображений. Аналитическое за-
дание таких поверхностей и линий позволяет получить неравен-
ства для определения границ интервала, в котором содержится
искомое значение емкости.
Возможность получения указанных оценок непосредственно
следует из очевидных представлений об изменении емкости лю-
бых проводников при внесении в окружающую их среду каких-
либо незаряженных проводников или диэлектриков.
Действительно, выбирая то или иное семейство эквипотен-
циальных поверхностей, мы фактически приходим к новой
электростатической системе, образующейся при внесении
в среду, окружающую рассматриваемые проводники, тонких не-
_ .... 71
заряженных металлических оболочек, совпадающих по форме
с выбранными поверхностями. Но согласно известной теореме
электростатики внесение таких оболочек (как и любых других
незаряженных проводников) приводит к возрастанию емкости
во всех случаях, кроме того, когда оболочки совпадают по
форме с истинными эквипотенциальными поверхностями элект-
ростатического поля (в последнем случае емкость, очевидно, не
меняется).
Следовательно, при любом выборе эквипотенциальных по-
верхностей может быть получена верхняя оценка искомой ем-
кости.
Подобным же образом можно показать, что при любом вы-
боре силовых линий может быть получена нижняя оценка емко-
сти проводников.
Практические пути получения таких оценок и их точность
зависят, естественно, от принятых способов аналитической ап-
проксимации эквипотенциальных поверхностей и силовых линий
электростатического поля рассматриваемых проводников.
Пусть, в частности, необходимо оценить емкость Со некото-
рого уединенного проводника 1, расположенного в однородном
диэлектрике 2 (рис. 2-8, а).
Для получения верхней оценки величины Со представим се-
мейство эквипотенциальных поверхностей электростатического
поля проводника /, например, в виде однопараметрического се-
мейства охватывающих друг друга замкнутых поверхностей
S(X), одна из которых (при Х=Х0) совпадает с поверхностью
рассматриваемого проводника, а другая (при 7.^-оо) — с поверх-
ностью сферы бесконечного радиуса (рис. 2-8,6).
Выбор такого семейства эквивалентен, как уже указано,
введению в среду 2 тонких проводящих оболочек, совпадающих
по форме с S(X). Обозначив емкость проводника 1 в присут-
ствии этих оболочек через С'о, по указанным выше соображе-
ниям получим
Со-сС'о,
причем равенство достигается здесь только в том частном слу-
чае, когда выбранные поверхности S(X) совпадают с неизвест-
ными нам истинными эквипотенциальными поверхностями
электростатического поля проводника 1 в однородной среде.
Таким образом, для получения верхней оценки Со необхо-
димо найти значение емкости С'о. Но она может быть пред-
ставлена в виде последовательного соединения емкостей между
охватывающими одна другую оболочками S (X).
Если считать расстояния между этими оболочками конеч-
ными (т. е. значения параметра X дискретными, например, Це-
лыми), то
ОО 1—1
со= 2(С>.Г1| . (2-21)
72
где С\ — емкость между оболочками с поверхностями S(X) и
.S(H-i).
При стремлении расстояний между оболочками к нулю сумма
в (2-21) заменяется соответствующим интегралом, что непо-
средственно приводит к следующему неравенству:
(2-22)
Рнс. 2-8
где п — нормаль к поверхности S (X)
Это выражение и дает верхнюю оценку интересующей нас
величины Со при аппроксимации эквипотенциальных поверхно-
стей любым однопараметрическим семейством <S(X).
Для получения нижней оценки Со выберем некоторое семей-
ство линий l(S), которыми аппроксимируем неизвестные нам
силовые линии электростатического поля проводника 1
(рис. 2-8, в). Это эквивалентно введению в среду 2 непроницае-
мых оболочек, совпадающих с поверхностью силовых трубок, и,
следовательно, приводит к уменьшению емкости проводника 1
во всех случаях, кроме того, когда линии l(S) совпадают с ис-
73
тинными силовыми линиями электростатического поля провод-
ника 1 в однородной среде. Поэтому, обозначив емкость про-
водника 1 в присутствии указанных непроницаемых оболочек
через С"о, непосредственно получим
Co^-Cq.
Таким образом, для получения нижней оценки Со необхо-
димо определить значение емкости С"о. Но она может быть
представлена в виде параллельного соединения собственных
частичных емкостей участков поверхности проводника, ограни-
ченных контурами сечений указанных оболочек.
Если считать размеры сечений силовых трубок конеч-
ными, то
Со=2Сй-, (2-23)
£=1
где Си — собственная частичная емкость i-ro участка; N —
число участков.
При стремлении размеров сечений силовых трубок к нулю
сумма в (2-23) заменяется интегралом, что приводит к сле-
дующему соотношению:
ОО “ 1
J hdq , (2-24)
S L <7o(S) J
где q—координата, отсчитываемая вдоль линии Z(<S) [при этом
на поверхности проводника q=qo(S)]-, dS — элемент поверхно-
сти, нормальной к Z(S); hq — коэффициент Ламе.
Приведенное неравенство и дает нижнюю оценку интересую-
щей нас величины Со- Точность такой оценки для конкретных
проводников зависит, естественно, от принятой формы линий
Z(S).
Пример 2-14. Представляя силовые линии лучами, исходящими из неко-
торой точки О, получим общее неравенство для нижней оценки емкости осе-
симметричных проводников с поверхностью, звездной относительно указан-
ной точки.
Рассмотрим сначала какой-либо уединенный проводник указанного вида.
Расположив в точке О центр сферической системы координат (р, 0, <р), со-
вместим ось 0=0 с осью проводника и представим контур осевого сечения
проводника уравнением р=/(0). Тогда в (2-24) необходимо положить ?=р,
Л9 = 1, dS=2np2 sin 0 <10, после чего непосредственно получаем
= 2ле
sin 0 <10.
(2-25)
74
Это соотношение приводит к равенству только для проводника в форме
сферы [Z(0) = о], т. е. в том простейшем частном случае, когда выбранная
форма силовых лнинй совпадает с их истинной формой. Для любых других
проводников неравенство (2-25) является строгим.
Так, для емкости прямого круглого цилиндра высотой 2h и радиуса а
из (2-25) получаем
. а
arctg
Со> 4ле Г/l J
1 О
л
~2
tg 0 dO + a J <Z0
. а
arctg—
. ( i h , h 1 S а VI)
— 4nea J arctg — -f------In 1 -|- I — I }.
I a 2a L \ Л / JJ
В частности, при h—a
ln2^ » 4леа-1,1319.
Подобным же образом можно получить и неравенство для нижней оценки
емкости между двумя охватывающими один другого проводниками с общей
осью симметрии, если поверхности этих проводников звездны относительно
одной и той же точки.
Используя ту же систему сферических координат, представим контуры
осевых сечений рассматриваемых проводников уравнениями p=/1(G) и
p=Z2(0). где при любом фиксированном 0 h>l\. Тогда аналогично предыду-
щему получим неравенство
л
С^2ле
о
к (6) к (0)
Z2(0)-/i(0)
sin 0 dQ,‘
(2-26)
которое является строгим для любых конденсаторов рассматриваемого типа,
кроме сферического (в последнем случае соотношение (2-26) приводит к ра-
венству) .
Пример 2-15. Дадим верхнюю оценку емкости уединенных проводников
того же вида, что и в примере 2-14.
Сохраняя обозначения, принятые в предыдущем примере, аппроксими-
руем семейство эквипотенциальных поверхностей электростатического поля
какого-либо из рассматриваемых проводников однопараметрическим семей-
ством осесимметричных замкнутых поверхностей, контур осевого сечения ко-
торых описывается уравнением
Р = I (9) + X,
где X — размерный параметр, изменяющийся в интервале Ю, оо].
При этом значение Х=0 соответствует поверхности проводника, а с уве-
личением X выбранные поверхности приближаются к сферическим.
Элемент поверхности такого вида определяется выражением
dS == У[I (0) + Х]®+ (/о)2 2л [Z (0) + X] sin 0 ДО,
а элемент нормали к ней —- выражением
K[z(0)+xp + (z;)2
75
Подставляя эти выражения в формулу (2-22), приходим к следующему об-
щему неравенству:
—1
’ (2-27)
Г dX
J # (X)
о
где
<7 (X) = J {IZ (6) + Х]а + (Ze)2} sin Od0.
о
Неравенство (2-27) является строгим для любых проводников указан-
ного типа, кроме сферического [в последнем случае (2-27) приводит к ра-
венству].
Так, для прямого круглого цилиндра, высота которого (2/i) равна диа-
метру (2а),
1(6) =
О- С\ о
-------- при 0 <6^ — ,
sin 6---4
ЗТ 1-l ЗТ
при-------< 6 ,
4 2
и с помощью (2-27) получаем, что
Со •< 4леа-1,2604.
Пример 2-16. Дадим нижнюю оценку емкости проводников в форме пла-
стин, ограниченных контуром, звездным и симметричным относительно неко-
торой точки.
В данном случае для аналитической аппроксимации силовых линий элек-
тростатического поля целесообразно ввести специальную систему координат
(а, р, ср), связанных с декартовыми координатами соотношениями:
х = Z (ср) ch a cos р cos <р;
у = I (ср) ch a cos Р sin <р; (2-28)
z = I (ср) sh a sin р,
где Z(<p)=p— полярное уравнение контура рассматриваемой пластины,
— л<ср<л; 0^а<оо:----------------— ^Р — •
2 2
При этом поверхность а=0 совпадает с поверхностью пластины, а линии
Р=const, ср=const являются дугами гипербол с линейным эксцентриситетом
Z(<p), нормальными к поверхности а=0.
Этими дугами и аппроксимируем силовые линии электростатического
поля рассматриваемых пластин.
Тогда в формуле (2-24) следует положить q=a; ?о—0;
ha = | < | : dS = ^.^“rfpdrp,
I Га I
где r = {Z (<p) ch a cos P cos <p; Z (<p) ch a cos p sin <p; Z (<p) sh a sin P).
Вычисляя входящие сюда выражения, после преобразований получаем
ЗТ
ЗТ 2 Гоо "1—1
76
Таким образом, приходим к следующему неравенству:
Ср
CoSi ----(' I (<р) dtp = 8е/ср, (2-29)
л й
1 л
где ZCp — — f ^(ф)^ф— средний радиус рассматриваемой пластины,
л
Полученное неравенство является строгим для всех пластин указанного
типа, кроме диска; в последнем случае оно переходит в равенство *.
Один из эффективных способов аналитической аппроксимации эквипотен-
циальных поверхностей и силовых линий электростатического поля осесиммет-
ричных проводников основан на использовании аппарата конформных преоб-
разований.
Если, например, произвести конформное преобразование внешности неко-
торого круга в плоскости комплексного переменного z=rel<₽ (рис. 2-9, а)
иа внешность контура меридианного сечения некоторого уединенного осесим-
метричного проводника, представив это сечение как часть плоскости ком-
плексного переменного W=u+iv (рис. 2-9,6), то окружности г=щ>йо пре-
образуются при этом в некоторые замкнутые кривые на плоскости W,
которые и могут быть приближенно приняты за контуры осевых сечений экви-
потенциальных поверхностей электростатического поля заданного проводника.
При этом лучи <р=const в плоскости z перейдут, очевидно, в линии, ортого-
нальные упомянутым замкнутым кривым, и могут быть использованы для
аппроксимации силовых линий того же поля.
Функция W—f(z), реализующая указанное конформное преобразование,
должна удовлетворять очевидным условиям:
lim W (z) = оо; lim = 1,
2->0о 2->оо dz
отражающим особенности эквипотенциальных поверхностей при удалении от
проводника, и в общем виде определяется формулой
я"+*
W^f(z) = z+ (2-30)
zn ’
n=l
где bn—коэффициенты, определяемые видом контура (в данном случае ви-
дом меридианного сечения проводника) 1 2.
Входящая в это выражение величина йо называется внешним (или кон-
формным) радиусом контура и определяется равенством
и0 = —, (2-31)
ОО
1+ 2 ьп
П=1
где t<o=f(fio); А— константа, определяемая выбором начала координат.
Следующие из (2-30) выражения отображающих функций W=f{z) для
некоторых областей приведены в табл. 2-6, где указаны также значения йо
для соответствующих контуров.
1 Как можно показать с использованием неравенства Коши—Буняков-
ского, неравенство (2-29) является более слабым, чем (2-7).
2 Если, в частности, контур симметричен относительно обеих координат-
ных осей, то &2и=0.
77
Располагая выражениями используемых отображающих функции,
можно выразить с их помощью все величины, входящие в неравенства (2-22)
и (2-24). Так, элемент выбранной указанным способом эквипотенциальной
поверхности определяется при этом выражением
dS = 2av(r, <p)rd<p|f (г, <р) |,
а элемент нормали к этой поверхности — выражением
dn = | f' (rt <р) \dr.
Принимая далее с помощью (2-22) и (2-24) приходим к следующим
Рис. 2-9
где
dr
rv (г, ф)
я
/а (И = ( О. <РИ<Р.
о
а равенства достигаются только в случае сфероида (вытянутого или сжа-
того) *.
Пример 2-17. Пользуясь неравенствами (2-32), найдем верхнюю и ниж-
нюю границы значений емкости уединенного проводника в форме круглого
прямого цилиндра, высота которого равна диаметру (2а).
Используя выражения, приведенные в и. 2 табл. 2-6, находим, что в дан-
ном случае:
ав = 1,179а;
1 4 Г 3 /а0\4
<Р) = г sin ф -----sin Зф-------—I sin 7ф
fir3 28 \ г /
JLf^Y
88 k г J
. ,, 1 /а0\1а •
81П11ф —---I----j sin 15ф
* Как видно из п. 2 табл. 2-6, в этом случае (в отличие от всех осталь-
ных) о (г, ф) =Ц1(г)ц2(ф) и соотношения (2-32) переходят в равенства.
78
Тогда
Подставляя это выражение в (2-32) и учитывая, что г^ао, получим
где ai=0,049a4; аг=0,156а4.
При указанных значениях во, «1 н аг находим, что
С < 0,420—.
J rfz (г) а
Тогда в соответствии с (2-32)
< 2,384а.
2 ле
Переходя к нижней оценке, получаем
dr
rv(r, <р)
f.---------------<_1_
J г2 sin <р [1 + р (г, (р)] sin (р
«о
С 1—р(г, <Р) + Р2(г. <Р) dr
J г2
а0
где
Р(г.
sin 3<р
sin <р
3 / а0 у sin7<p
28 \ г J sin <р
причем |р(г, <р)|< 1.
Форма контура в плоскости W'
функция, реализующая конформное
отображение внешности круга
| z I > а, на внешность контура
в плоскости W
Эллипс
а-\- Ь а — Ь а0
2а0 2 г
Квадрат
4 8
6 z’ ' 56 г7 176
z11 384 z«
117 = 2
2 ао
п(п— 1) г”-1
Правильные многоугольники
3
п-2 арп
* n2(2n — l) г2"-1 '
(п —2) (2п —2) «о"
3n3(3n—1) z3"-1 ~'~
। (п~2) (2п —2)(3я —2)
3-4п4(4« — 1)
21п-1 ।
[п — число сторон (на рис. п=4);
7? — радиус описанной окружности]
Таблица 2-6
Мнимая часть отображающей функции I т W = v (г, ф) Внешний радиус меридианного сечения а0
/ a2 —fe2 1 \ . 1 г 1 sin W \ 4 г / 1 а + b 2
Г 4 / 1 ао I sin 3w г sin <р 1 Н 1 L 6 г4 \ sin <р 3aQsin7<p з a® sin 11 ср 28 г’ sin ф ' 88 г8 sin ф 12 \ 1 1 «о sin 15 ф ] 64 г12 sin ф / а
1 1 . 1 1 1 6 1 56 176 1 384 г 1,179 а
( 2 «р г sm ф < 1 X I п(п— 1) гп rsin(n— 1)ф (п—1)(п —2)ч/ [1+—— ч——-—-+ L п(п — 1) 1 п2(2п —1) 1 (п —2)(2п —2)
sin ф 2п(2п—1) ао sin (2п — 1) ф I rn sin ф (п—1) (п —2) (2п —2)
2-3-n2(3n—1) °р sin (Зп—1)ф х r2/1 . sin ф (п-1)(п-2)(2п-2)(3п-2)ч, 3n8(3n—1) (« — 2) (2п — 2) (Зп — 2) 1-1
' 3'4n4-(4n —1)
1 2-3-4-n8 (4п—1) до" sin (4 я — 1) ф 1 х ~ । rsn sin ф J J
Форма контура в плоскости W
Г нпоциклоиды
Функция, реализующая конформное
отображение внешности круга
| z | > а0 иа виешиость контура
в плоскости W
ат
“О
W = Z-{
(m—l)zm—1
[т — модуль (отношение радиусов
неподвижного R и производящего
кругов); на рис. т = 3]
В свою очередь, для последнего интеграла справедливо неравенство
1 С 1— Р(г, ф)~|р1 2(г, <р) . . 1 ,, ...
------ I — V- ~ v -Щ. dr < 11 — q (ф)],
sin Ф J--------------------------------г2-а0 sin ф
«о
где
1 sin Зф 1 sin 7ф 1 sin2 Зф
30 sin ф 18-28 sin ф 9-36 5ш2ф
причем | q (ф) | < 1.
Тогда в соответствии с (2-32)
Л _ ГС
> с0 f - S'n > ав С sin ф [1 + о (ф)1 йф ss2n0-1,006 » 2,372а.
2ле J 1 —?(ф) J
о о
Таким образом, емкость рассматриваемого проводника лежит в следую-
щих пределах:
2,372 <—^5—<2,384,
т. е.
Ср
2леа
~ 2,378 с погрешностью 0,23 % *.
1 Здесь н далее приближенное значение получено как среднее гармониче-
ское верхнего и нижнего предела (см. стр. 85).
82
Часть вторая
Расчетные формулы,
таблицы и графики
1. Настоящая часть состоит из двух разде-
лов. В первом из них (гл. 3—6) приведены материалы для рас-
чета емкости проводников, расположенных в однородной среде,
а во втором (гл. 7 и 8) — проводников, расположенных в неод-
нородных средах.
2. Материал каждого раздела разделен на главы, исходя из
числа проводников, образующих рассматриваемые электроста-
тические системы. При этом система, образованная соединением
нескольких проводников, рассматривается как один проводник
(см. § В-2).
3. Материал каждой главы разделен на параграфы на ос-
нове типизации геометрических форм рассматриваемых провод-
ников (§ В-2) и расположен в порядке усложнения этих форм.
4. При рассмотрении проводов во всех случаях, если не ого-
ворено противное, принимается, что их сечение является круг-
лым, размеры сечения не менее чем в 10 раз меньше длины
провода и его расстояний до других проводников, а под рас-
стоянием между проводами понимается расстояние между их
осями.
5. При рассмотрении пластин и незамкнутых оболочек во
всех случаях, если не оговорено противное, принимается, что
их толщина меньше как характерных размеров самой пла-
стины или оболочки, так и расстояний от них до других провод-
ников.
6. В начале каждого параграфа приводится краткая харак-
теристика особенностей геометрических форм рассматриваемых
проводников и приводимых данных по их емкости, а справоч-
ный материал во всех параграфах расположен, как правило,
в порядке возрастания погрешности приводимых расчетных
формул. Последняя характеризуется величиной
84
g Сточн Спрнбл 10Q %
Сточн
(Сточн и Сприбл — точное и приближенное значения емкости,
соответственно) и во всех случаях, когда нет дополнительных
указаний, не превосходит 10 %.
В тех случаях когда точное значение емкости неизвестно,
а определены лишь пределы, в которых находится это значение
(Cmin И Стах), вместо него в предыдущей формуле используется
среднее гармоническое указанных предельных значений:
__ 2Cmin^max
СР- г —
L,min г ч>тах
а вместо Сприбл значение Cmin*
7. Ссылки на работы, использованные при получении от-
дельных формул, как правило, не даются. Однако для некото-
рых наиболее типичных систем приводится краткое сопоставле-
ние основных результатов, полученных различными авторами.
раздел первый
ЕМКОСТЬ ПРОВОДНИКОВ
В ОДНОРОДНОЙ СРЕДЕ
ГЛАВА ТРЕТЬЯ
ЕМКОСТЬ УЕДИНЕННЫХ ПРОВОДНИКОВ
3-1. ОБЩИЕ ЗАМЕЧАНИЯ
1. Материалы настоящей главы позволяют
найти значения емкости уединенных проводников, определяемой
формулой (В-1).
2. Все характерные размеры рассматриваемых проводников
принимаются конечными, а их отношение к расстояниям от
данного проводника до всех других проводников, входящих
в реальные электростатические системы, пренебрежимо малым.
3-2. ПРОВОДА
3-2-1. В настоящем параграфе приведены
приближенные расчетные формулы для емкости уединенных
проводов, полученные методом средних потенциалов (§ 1-2).
Они следуют из общей формулы (1-7) и приводят к занижен-
ным значениям емкости (погрешность расчета б >0)1
При расчете емкости уединенных проводников, образован-
ных соединением нескольких проводов, могут быть использованы
также материалы, приведенные в § 7-2; для этого необходимо
произвести зеркальное отражение проводов относительно пло-
ской непроницаемой границы и воспользоваться формулой
(В-19).
3-2-2. Прямолинейный провод конечной длины
(рис. 3-1).
_Со_«Г1пЖ_ 11-*
2ле/ \ а / J
(3-1)
, [б <2 %].
При //«<10— см. материалы п. 3-5-10, а при //«>20 —
также формулу (3-35).
86
3-2-3. Провод в форме кругового кольца
(рис. 3-2).
.. С° ... — fin 1 (3-2)
4л9е7? \ а /
[6< 1 % при 2?/а>10].
См. также материалы п. 3-5-11.
3-2-4. Проводник, изогнутый по дуге окруж-
ности (рис. 3-3).
~ / 1п zV‘ (3-3)
2ле/ \ а 0 /
[б <2,0 % при R/a> 10],
Рис. 3-3
где 0 — центральный угол дуги; /=07?— длина провода; / —
параметр, численные значения которого приведены в табл. 3-1,
1— при 0 в радианах;
57,2958— при 0 в градусах.
Пример 3-1. Определим емкость расположенных в воздухе (е=ео=
=-----10—9 Ф/м] проводов в форме круговых кольца и полукольца радну-
36л /
сом 7?=0,1 м с диаметром сечения 2с=0,01 м.
Используя формулу (3-2), для емкости кольца получаем
с х 4ла-0,Ы0 9 ~ 6>88.10_и ф = 6 88 пф
у 0,005 )
87
Для определения емкости полукольца предварительно находим из
табл. 3-1 значение параметра I. При 0=л параметр /=0,916. Таким образом,
для емкости рассматриваемого полукольца имеем
С к 2п' 10~9_________-П (^-1-------~ 4-46'10-12 Ф == 4’46 пф-
збл ——0,916
V 0,005/ л
Отношение найденных значений емкости полукольца и кольца составляет
0,649. С уменьшением R/a это отношение увеличивается.
Таблица 3-1
е, •••° I е, •••° е, •••° / 6, •••°
0 0,0000 360 90 0,7529 270
5 0,1052 355 95 0,7715 265
10 0,1803 350 100 0,7887 260
15 0,2439 345 105 0,8047 255
20 0,3000 340 ПО 0,8195 250
25 0,3506 335 115 0,8332 245
30 0,3968 330 120 0,8548 240
35 0,4393 325 125 0,8572 235
40 0,4786 320 130 0,8676 230
45 0,5151 315 135 0,8774 225
50 0,5492 310 140 0,8852 220
55 0,5809 305 145 0,8925 215
60 0,6107 300 150 0,8988 210
65 0,6385 295 155 0,9041 205
70 0,6645 290 160 0,9083 200
75 0,6889 285 165 0,9117 195
80 0,7117 280 170 0,9141 190
85 0,7330 275 175 0,9155 185
90 0,7529 270 180 0,9160 180
3-2-5. Два соединенных между собой прямоли-
нейных провода конечной длины (рис. 3-4).
а. &=0 (рис. 3-5).
Емкость определяется по формуле (В-11), где
Рис. 3-4
Рис. 3-5
88
+ li In { [2/i4*I2 + li'+ У d2+(2/l-|-/1 -f-/2)2 ]X
X [2h + l1 + Vd^(2h+liy] -1} +
+ /2 in {[2/1 J- 4 + li + У^2 + (27г -f- lz + W2 ] x
X [2ft + /a + Kd*+(2h + l2)2]~l\ +Kd* + (2h+l1)2 +
+ У^2 + (2/г + /2)2- V d2+ (2A+ /г+ /2)2—K^2+ 4А2.
3-2-6. Два соединенных между собой пересе-
кающихся или скрещивающихся прямолиней-
ных провода конечной длины. ;
а. Общий случай (рис. 3-7).
89
Емкость определяется по формуле (В-11), где
М Р2,Ъ1
х
Рис. 3-7
«12 =
+ ^22 + ^12-- Fjj
4ле (х2 —Xi) —
Fpq = Хр In [у9 — хр cos <р + Dp ] + у 1п [хр — Уд cos <р + Dpg] н—X
sin Ф
X arctg
Хр + Уд + Дрд JP_\ .
d ё 2 /’
°рд = Ухр + Уд—2xpt/9cos(p + da, р=1, 2; <7=1, 2.
б. Взаимно перпендикулярные провода равной длины распо-
ложены в одной плоскости: d=0; ф=л/2; Xi=yi=h\ х2—xi =
=У2—У1 = 1 (рис. 3-8);
90
(3-5)
Рис. 3-8
3-2-7. Несколько (и) соединенных между со-
бой одинаковых параллельных прямолинейных
проводов.
а. Провода расположены в одной плоскости на равном рас-
стоянии друг от друга (рис. 3-9).
При
<3’7)
где
Вп =— 2 1)! (и—/п)1].
П т=1.
Значения коэффициента Вп для п = 2-ь12 даны в табл. 3-2.
Таблица 3-2
п 2 3 4 5 6 7 8 9 10 И 12
Вп 0 0,46 1,24 2,26 3,48 4,85 6,40 8,06 9,8 11,65 13,58
91
б. Провода расположены равномерно по поверхности круг-
лого цилиндра (рис. 3-10).
При
«n (in — + (и—1) In- и—
2ле/ Iй к
г а . 2а . (л-1)а1}-1 /о Оч
—In Г sin — sin— . . .sin - | . (3-8)
I 2 A & J /
где а=‘2тх!п. -
Рис. 3-9
Рис. 3-10
При п = 2 расчетная формула для -Со может быть получена
также путем использования выражений (В-19) и (7-1) или
(7-2), а при и=3-?8 выражения, следующие из (3-8), приведены
Рис. з-Н
в табл. 3-3 и обеспечивают погрешность расчетов б<6 % при
//«>5.
При l/R<c\
(3-8а)
где dm = 2R sin Z?2-"1) л _
п
92
Таблица 3-3
в. Провода расположены на параллельных ребрах прямого
параллелепипеда (рис. 3-11).
При d//i>5
Со Л I* \->
—2— 1П-------
8ле/ \ 2ad2h )
(3-9)
93
Пример 3-2. Найдем значением емкости проводника, изображенного на
рис. 3-10, при 1=2,0 м; 2а=0,04 м; /?=0,5 м и различных значениях п, счи-
тая, что .е=ео=1О~д/ (36л) Ф/м.
Пользуясь формулой, приведенной в п. I табл. 3-3, находим, что при
и=3
12ле0_______
1п22®2+21п^1 —2,02
0,'02 0,5
62,3 пФ.
Аналогичные вычисления при п=44-8 приводят к следующим значе-
ниям Со:
п................. 3 4 5 6 8
Со, пФ ........... 62,3 72,1 79,1 83,2 90,8
3-2-8. Прямолинейные провода, соединенные
в форме многоугольного контура.
Расчетные формулы для емкости проводников в форме мно-
гоугольных контуров различного вида приведены в табл. 3-4.
Пример. 3-3. Определим емкость рамочных антенн с контурами в форме
равностороннего треугольника, квадрата н шестиугольника, вписанных в ок-
ружность радиуса /?=5,0 м, считая, что радиус провода а=3-10~3 м, а ан-
тенны расположены настолько высоко над землей, что ее влиянием на ем-
кость можно пренебречь.
Пользуясь формулами, указанными в п. 1, 2 и_3 табл. 3-4, при е=ео=
= 10~9/(36л) Ф/м и параметре /, равном 1^3 R, ]^2R и R (соответственно),
находим, что для рассматриваемой треугольной антенны
У~3 -5,0-10-8
Г уГ-5,0 1
6[ 0,003 + 1’89]
для квадратной антенны
со к-------/2 40-»------ф ~ 162 пф.
9 _1п 0/003 + 1>91]
а для шестиугольной антенны
Г ~ 5'10-9 Л 17Л ич
Со «-------------------- ф и 174 пФ.
„Г. 5,0 „ ,„1
Сопоставляя полученные значения с емкостью проводника в форме круго-
вого кольца того же радиуса (последняя определяется формулой (3-2) и
составляет при принятых значениях е, R и а 184 пФ), находим, что отличие
емкостей рассмотренных и круговой антенн составляет 20,6; 11,9 и 5,4%, со-
ответственно.
3-2-9. Провода, соединенные в форме прост-
ранственных контуров.
94
Таблица 3-4
Форма контура
Расчетная формула для емкости
Ср
2 ле/
1
3
In J_ + l,89
а
Равносторонний
треугольник
4
In —-f-1,91
a
Правильный
шестиугольник
2
Равнобедренный
треугольник; а = 40°
Пр ямоу гольиый
треугольник; а = 60°
In — 4-1,88 In — 4-1,59
а а
! 0,50
In —4-1,90
95
а. Провода расположены на ребрах куба (рис. 3-12).
„ 24ле/
--------
In —+ 6,36
а
(3-1U)
б. Провода расположены по направляющим прямого круг-
лого цилиндра и по четырем его образующим, лежащим в двух
взаимно перпендикулярных плоскостях (рис. 3-13).
При/7/(4/?) < 1
; с ___________________4л2е (hr + И)_________ (3 11)
° 2LlnJK + _^^K+^ln-^ + Л ’
2 а 1 УН2 + 4/?2 Я \ Н J
где К — полный эллиптический интеграл первого рода с мо-
дулем
V 4Д2 + //2
3-3. ПЛАСТИНЫ
З-3-l. Материалы настоящего параграфа
;дают возможность рассчитать значение емкости пластин наибо-
лее типичной формы; вместе с тем при использовании метода
частей и метода симметризации (§ :2-4) они позволяют .оценить
емкость пластин и более сложного вида.
В тексте приведены все известные точные и некоторые при-
ближенные формулы для расчета емкости уединенных пластин.
Последние получены с помощью методов, изложенных в § 2-4
и 2-5, и путем использования некоторых фиктивных распределе-
ний заряда, близких к равновесным.
В параграф включены также данные некоторых численных
расчетов емкости пластин, представленные в виде графиков и
таблиц. При этом все численные результаты даны в нормиро-
96
ванном виде — по отношению к емкости некоторого диска,
включающего рассматриваемую пластину.
При расчете емкости уединенных проводников, образован-
ных соединением двух пластин, могут быть использованы также
материалы, приведенные в п. 7-3-2-=-7-3-6. При этом необходимо
воспользоваться соотношением (В-19).
3-3-2. Диск радиуса а
С0=8га. (3-12)
3.3.3. Эллиптическая пластина (рис. 3-14)
ь а 0,001 0,01 0,1 0,2 0,3 0,4
Со 8еа 0,1894 0,2622 0,4250 0,5208 0,5978 0,6658
ь а 0,5 0,6 0,7 0,8 0,9 1.0
Са 8еа 0,7284 0,7872 0,8433 0,8972 0,9493 1
4 Заказ № 507
97
4леа
к7*Г’
(3-13)
где К (А) — полный эллиптический интеграл первого рода с мо-
, Г. / ь \2
дулем я= \/ 1— — -
г \ a, j
Если отношение а/b монотонно возрастает, то при неизмен-
ной площади пластины ее ёмкость также возрастает.
С / ь \
Зависимость —— = ft — | приведена на рис. 3-14.
8еа \ а }
При а/Ьг> 1,25
4 лес
1 4а
1П~
(3-14)
[6<0; |61<9% приЪ/6 > 1,25; |6|<3,8% при aJb 2;| 61<0,7%
при а/6^5].
3-3-4. Пластина в форме кругового кольца
(рис. 3-15)
arcsec (Ь/а)
C0=8eZ? J Н (6) dB, (3-15)
о
где Н(е) — решение интегрального уравнения
И (0) sin 0 cos2 0 +
„ 2 arcsec (fe/a)
(—) f Я(фИ(0, <рНф=1
\ Л / О
с ядром
К (6, ф) =
ср Е0
sin2 ср sec ср In tg —-------sin2 6 sec 6 In tg —
sec2 0 — sec2 (p
C f b \
Зависимость -~- = f(—(приведена на рис. 3-15.
обо \ а )
Кроме того, могут быть использованы следующие прибли-
женные формулы
1 Точные выражения для емкости плоского кругового кольца получены
сравнительно давно [3, 37], однако они настолько сложны, что представляют
лишь теоретический интерес. Результаты Никольсона [37] были получены не-
достаточно корректно и относились к некоторым частным соотношениям
между радиусами кольца. Хиггинс и Рейтаи [30] и Смайт [47] получили до-
статочно точные численные результаты, причем Смайтом были даны также
и приближенные формулы. Наиболее полные результаты для емкости плоского
кругового кольца получены Куком [24], который дал точное выражение для
расчета емкости и провел некоторые численные расчеты.
98
а. При bjac 1,5
[6<1 %; 6<0,l % при 6/a< 1,1],
(3-16)
Ыа 1,021 1,091 1,125
Cjlteb) 0,6667 0,8011 0,8326
Ь/а 1,20 1,25 1,50
Cj&b) 0,8776 0,8976 0,9494
Ыа 2,0 3,0 4,0
C0/(8efe) 0,9810 0,9947 0,999
Ср 8ъЬ
5\
2 а
1,0 1,2 1,4 1,6 1,8 2,0
Рис. 3-15
б. При 6/а>1,5
03f)[l-0,08(f)*] (3-17)
[|6|<1%],
3-3-5. Пластина в форме кругового сегмента
(рис. 3-16).
При 0<а0<-^-
1 + sin—-
-f2- « 1 — sin + cos2-—In------—. (3-18)
8еа 2 2 а0
cos ~~
2
6<1% при0<ао<^-; 6<10% при — <а
6 6 0 3
3
4*
99
л (1- sin3
_£о_ ~___________5-------------------- (3-19)
8“ l+sin^~
„ аа 2
л — а0 + 2 cos -н~ In---------
2 а0
C0S —
[6<15 %].
Верхние и нижние границы значений функции Со/ (8еа) =®
= f(ao) указаны на рис. 3-16.
а0 Граница значений Со величины 8еа
верхняя НИЖНЯЯ
0 1,0000 1,0000
К | <о 1,0000 0,9855
Л 3 1,0000 0,8969
л т 0,8588 0,7284
2л ”Т” 0,5751 0,4422
5л ~ёГ 0,2554 0,1698
Л 0,0000 0,0000
3-3-6. Пластина в форме кругового сектора
(рис. 3-17).
При 0<а0<-^-
Со 8еа [1 — sin 4—— sin а0 In f 14- sec 1. (3-20)
При <а0 < л
~ sin-^Mnh 4-sec-^2-') (3-21)
8еа 4(2/ V
1б<15%].
изо
Верхние и нижние границы значений функции С0/(8еа) =
= Нао) указаны на рис. 3-17.
Граница значений Со величины -—— Зеа
верхняя нижняя
0 1,0000 1,0000
1 й 1 о 1,0000 0,9129
ы [а 1,0000 0,8165
V 0,8588 0,7284
2эт Т 0,6946 0,5774
5л 0,5008 0,4082
. 0,0000 0,0000
а (рис.
3-18).
3-3-7. Прямоугольная пластин
При а — Ь (квадратная пластина)1
Сп ~---/-8еа-7_, - 8еа • 1,1346 ~ 8е7? • 0,8023 (3-22)
0 In (1 + V2) '
При 1 <а/й<10
п _ 16ей
Со ~ -
а b .. а
— Arsh — + Arsh —
b a b
(3-23)
1 Определение емкости пластины квадратной формы явилось предметом
целого ряда работ. Основные их результаты характеризуются следующими
данными для величины Ci (С)—отношение емкости квадратной пластины
к емкости диска с диаметром, равным диагонали пластины): 0,8023 (Г. Ка-
вендиш, 1879 [21]); Дж. Максвелл, 1893 [35]); 0,7979 (Релей, 1894 [42]); 0,7477
(Дж. Хоу, 1919 [31]); 0,79789«Д<0,83464 (Г. Полна и Г. Сеге, 1951 [11]);
<8036 (Д. Аллен и С. Деннис, 1953 [19]); 0,7905 (Е. Гросс и Р. Вайс, 1955
[27]); 0,8047 (Д. Рейтан и Т. Хиггинс, 1957 [45]).
101
(3-24)
При a/b 10
а b Граница значений Со величины •—— 8еЯ
верхняя НИЖНЯЯ
1 0,8036 0,7979
2 0,8036 0,7168
3 0,7861 0,6472
4 0,7190 0,5971
5 0,6695 0,5372
10 0,5398 0,4430
20 0,4446 0,3730
50 0,3568 0,3072
10® 0,3094 0,2708
103 0,2134 0,1939
104 0,1626 0,1510
Верхние и нижние границы значений функции С0/(8е/?) =
г / а \ г, 1 / л , I Ь \2
= f —). где R=-a 1/ 1—- — радиус описанного круга,
\ b j F \ a j
указаны на рис. 3-18.
3-3-8. Пластина в форме ромба (рис. 3-19).
При а[Ь = \ значение С0_определяется формулой (3-22), где
следует заменить а на а/]^2.
Рис. 3-19
а b Граница значений Со величины 8ес
верхняя НИЖНЯЯ
1 0,8036 0,7979-
2 0,7084 0,5642
3 0,6133 0,4607
5 0,5208 0,3568
10 0,4250 0,2523
102 0,2622 •0,1391
ю4 0,1482 0,0766
102
Верхние и нижние границы
значений функции Со/ (8еа) =
указаны на рис. 3-19.
3-4. ОБОЛОЧКИ
3-4-1. В настоящем параграфе приведены
материалы для расчета емкости уединенных проводников
в форме тонких незамкнутых оболочек (изогнутых пластин), j
Приведенные материалы дают возможность непосредственна
рассчитать емкость оболочек простейшего вида *; вместе с тем
при использовании метода частей и метода симметризация
(§ 2-4) они позволяют оценить емкость оболочек и более слож,-
ной формы.
' Основные формулы настоящего параграфа явдяются точ-
ными и получены путем расчета электростатического поля и ме-
тодом инверсии (§ 2-3).
3-4.2. Полый сферический сегмент (рис. 3-20).
С. /. 0 sin 0
0 = 4пеа 1 ----------—
(3-27)
Функция ,С0/(4леа) =f(6) представлена на рис. 3-20.
При 0 = л/2 (полусферическая оболочка)
Со = 4леа (—4- —) ~ 4леа • 0,8183.
0 { 2 п J
3-4-3. Полая сферическая оболочка с двумя
круглыми коаксиальными отверстиями.
1 Опубликованные результаты по расчету электростатического поля сфе-
рических оболочек с двумя вырезами [2], а также оболочки в форме полого
гиперболоидального сегмента [8] не дают возможности непосредственно рас-
считать емкость этих проводников и потому не приводятся.
103
Рис. 3-20
е 1 — л 8 3 л 16 1 — л 4 5 я 16 3 —- л 8 7 л 16 1 — л 2
Ср 4леа 0,99681 0,98934 0,97508 0,95216 0,91908 0,87469 0,81831
0 9 л 16 5 — л 8 11 л 16 3 — л 4 13 л 16 7 — л 8 15 л 16
Ср 4леа 0,74969 0,66908 0,57716 0,47508 0,36434 0,24681 0,12460
а. Общий случай (рис. 3-21) 61 л С0~4леа 1—J fi(0 sin ~ dt — f f2(/) cos di о G (3-28)
где функции f\(t) и /г(0~Решения системы интегральных урав-
нений:
104
Зависимость С0/(4лео) =f(02) при различных значениях G,
приведена на рис. 3-21.
При 02=л —см. п. 3-4-2.
б. При одинаковых радиусах отверстий (рис. 3-21
= л—02=6)
С0 = 4яеа
t
sin— at
2
где f(t)— решение интегрального уравнения
при 01 =
(3-29)
105
Зависимость Со/(4лея) =f(0) приведена на рис. 3-22.
3-4-4. Полый параболоидальный сегмент
(рис. 3-23). с =8м^(-0Л, (3-30)
о
где 1|)(Т)— решение интегрального уравнения Фредгольма
h а 0,1 0,2 0,3 0,4
Со 8еа 1,0033 1,0128 1,0276 1,0467
h а 0,5 0,6 0,8 1,0
Со . 8еа 1,0697 1,085 1,111 1,134
h а : 1,2 1,5 2,0
Ср Sea 1,153 1,173 1,189
106'
К, е — полные эллиптические интегралы первого и второго рода
с модулями
ц = _ • v = _ Р<т + Е) .
И /1+р2 (т —|)2 ’ /1 + Р2 (т + g)2
При 0</г/а<0,5 может быть использована также следую-
щая приближенная формула
Сп« 8еа Г1 + 0,08333 ( 2—Г — 0,02083 (2 — У +
L \ а ) \ а )
+ 0,00923 (2 —У — 0,00504 (2 —V + 0,00310 (2 — Г1 (3-31)
\ а / \ а / \ а / J
[6<0,1 %],
а при h/a <0,3— формула (3-12) [6 <2,7 %].
Зависимость Сп/(8еа) = Я— | представлена на рис. 3-23
\ а )
(при й/а<0,5 расчеты производились по формуле (3-31), а при
Л/а>0,5 значения Со определены по формуле (3-30) с погреш-
ностью б < 1 %).
3-4-5. Полый тороидальный сегмент (рис. 3-24)
С0=16е/?|/ 1Sh ОС, X
X0Q ( (cha0) + jgnXnQ j (cha0)
~~2 n=l ” 2
(3-32)
где коэффициенты Xn определяются из бесконечной системы
линейных алгебраических уравнений .. . ...
Х„= 5 Ап,тМтХт + Вп (п = 0, 1, 2, . . .),
т-0
107
в которой
До, ,п - IP,П-1 (cos Ро) + Р,п (cos Ро) 1 [2 (1 - In ';
. . P„-! (COS Po) + Pn (COS Po) _ -L I.
An, tn — ^o»m ti 2
n=^0
In. m = f° [Pn-1 (COS 0)- Pn(cos 0) ] ~ [Pm-1 (COS 0) + Pm (cos 0) ] d0;
0 uu
Mm 1 _ 6m sh a0P , (cha0)Q j (cha0),
т~т
( 2 при m = 0,
~ I 2m при m=l, 2, 3,. .
Bn = Дп,о<2_±(с11я«)+1 2 5 Л«,т<2 _l_(chao)'
2 m—I 2
ch a0 = —;
a
COS p0
R cos To + a .
a cos 'Ir(l -|- R
P [(cha0), Q j (ch cQ—-функции Лежандра первою и вто-
" —Т ” г
рого рода; Pn(cost) — полиномы Лежандра.
Значения емкости при некоторых характерных значениях
геометрических параметров приведены в табл. 3-5.
Таблица 3-5
Ra Значение емкости С0'(4леЯ) при 4% •• °
5 90 I7S 180
Ы 2 11 0,746 0,4452 1,6366 1,1988 0,6758 1,647378 1,215831 0,705580 1,647378 1,215836 0,705649
При'Ко = л — см. п. 3-5-11.
3-4-6. Цилиндрическая трубка конечной длины
(рис. 3-25).
Значения емкости цилиндрической трубки конечной длины
приведены в табл. 3-6 и на рис. 3-25 ’.
1 Указанные значения получены на основании результатов работ [4, 26],
а также по данным численных расчетов, любезно предоставленным авторам
проф. Л. А. Вайнштейном.
108
Таблица 3-6
1 а 0,2 0,6 1,0 1,4 1,8 2,2 2,6 3,0
Со 6,192 2,6407 1,8244 1,4487 1,2296 1,0845 0,9806 0,9023
2neZ
1 а 3,4 3,8 4,2 4,6 5,0 5,4 5,8 6,2
Со 0,8406 0,7908 0,7495 0,7146 0,6847 0,6587 0,6359 0,6157
2sieZ
J- а 7,0 7,8 9,0 9,8 11,8 13,8 15,8 17,8
Со 0,5813 0,5531 0,5190 0,5003 0,4629 0,4350 0,4129 0,3950
2iteZ
/ а 19,8 21,0 23,0 25,4 40 50 120 200 2000
С„ 0,3802 0,3724 0,3608 0,3489 0,3026 0,2837 0,2272 0,2033 0,0689
2пе1
Для вычисления емкости могут быть использованы следую-
щие приближенные формулы:
при //а <7
4эт2еа
(а \
32 — I — М
где
При 7<//а<20
.. 1 /. 32а о\ / I V
Л4 = -— 1п----------2 —
64 \ Z } \ a J
[|6|<0,3% при //ПС2]1.
2эте/эт2
(3-33)
(3-34)
1|6|<2%].
Если положить Л'1=0, то |6|<2 %.
109
При Z/cz > 20
2ле/
(3-35)
При 1/а> 10 расчет величины Со может быть произведен
также по формуле (3-1).
3-4-7. Коническая оболочка (рис. 3-26)
где
Со = 2ле/
sin у
И(Т) I2
(3-36)
— 4- [/□ (т) + fs (v)]
Р (Т) = fi(T)e
Мт);
К (т) = 1/ 4"sin ± (cos Р- ± cos
* 2 2
fc—1
—!—-------!----------!---
«Л (т) Х/г (л — У) «Л (л — У)
110
/.ft)=Ч>(4-) - i In - fl -In (1 - JL.V
\ \4/ JX я \ JI / \ JX /
1
>• <T) -£, [’ [' +T4ft=rt] x
X exp { — _y- j j.
у, ° 90 100 ПО 120 130 140 150. 160 180
с0 8е/ 1,000 0,989 0,957 0,906 0,833 0,742 0,633 0,507 0,000
P i (У)— функции Лежандра; а&(у)— положительные корни
— 1Г
уравнения Р . (cos у) = 0, xk(y) = n/y(k----—V ф(г)— пси-
а (V) ~ \ 4 J
функция (ф (—'j = — 1,0858^ .
\ \ 4 у j
Зависимость Со/(8е/) =f(у) приведена на рис. 3-26.
3-5. ОБЪЕМНЫЕ ТЕЛА
3-5-1. В настоящем параграфе приведены
материалы для расчета емкости уединенных проводников
в форме объемных тел или эквивалентных им в электростатиче-
ском смысле замкнутых оболочек. Для большинства рассмат-
риваемых проводников приводятся точные формулы для емко-
сти, которые получены как на основе расчета электростатиче-
ского поля, так и методами инверсии (§ 2-3) и эквивалентных
111
зарядов (§ 1-4). Помимо этого, в тексте приведены некоторые
приближенные формулы и результаты оценок с использованием
методов, изложенных в § 2-4 и 2-5.
При расчете емкости уединенных проводников, образован-
ных соединением двух одинаковых объемных тел, расположен-
ных симметрично некоторой плоскости, могут быть использо-
ваны также материалы, приведенные в § 7-5. При этом необхо-
димо воспользоваться соотношением (В-19).
3-5-2. Сфера радиуса а
С0=4леа. (3-37)
3-5-3. Две непересекающиеся сферы (рис. 3-27).
Рис. 3-27
а ~2Г Значение емкости С0/(4л£а) при b а, равном
0,05 0,10 0,20 0,40 0,60 0,80 1,00
0,01 1,049 1,098 1,196 1,392 1,588 1,784 1,980
0,05 1,045 1,090 1,181 1,361 1,542 1,723 1,905
0,10 1,040 1,081 1,162 1,325 1,489 1,653 1,818
0,20 1,032 1,064 1,129 1,260 1,393 1,529 1,669
0,30 1,025 1,049 1,100 1,203 1,313 1,429 1,548
0,40 1,018 1,036 1,074 1,157 1,247 1,345 1,455
0,50 1,013 1,026 1,054 1,118 1,195 1,284 1,386
0,60 1,008 1,017 1,037 1,088 1,153 — —
0,70 1,005 1,010 1,024 1,062 .—_ -—. —
0,80 1,002 1,005 1,014 — — — —
112
а Обилий случай
\
Co = 4леоЬ sh a V’'----------5---------— +
b sh na -J- a sh (n — 1) a
n=i
4--------------1---------------!---1, (3-38)
a sh na -|- b sh (n—l)a Ishna J
где
a = Arch
(2/)2 —a2—fc2
2ab
(b \
—) представлена на рис. 3-27.
a /
При a/(2/)<l, b/a<l может быть использована также при-
ближенная формула
С,. ~ 4леа-—'-----
’--(-Г
а \21/
(3-39)
[6< 3,8 % при а/(21) <0,5; 6/й<1,0; б<0,6 % при «/(2/) <0,8;
b/a<0,2; a/(2/)<0,5; b/a<0,4; а/(2/)<0,3; Ь/а<1].
б. При а=Ь
Со = 8леа sh р V ~+* » (3-40)
sh пр
п=1
где p = Arch(//a).
Функция С0/(4леа) = представлена на рис. 3-28.
При а! (21) <0,5
С0^8леа--------— (3-41)
[6<4% при а/(2Г) <0,5; 6<1% при а/(2/)<0,35].
в. При 21 = а-\-Ь (касающиеся сферы)
„ ah
С0 = 4лв——
(1 и
——2у—-------—
Ь ' а \ а+Ь
. /, , b \
(3-42)
113
где ф(1+х) — пси-функция; у —постоянная Эйлера (у
=0,5772...).
z / Ь \ А
функция Со'/(4леа)=Ц— представлена на рис. 3-29.
\ /
Рис. 3-28
Рис. 3-29
Ь/а 1/4 1/3 2/3 1,00
Со 4лед 1,020 1,040 1,178 1,386
114
Может быть использована также приближенная формула
’0 ~ 4леа
Ь
1.-----£
1+—
а
(3-43)
2
[б<3,8 % при й/а<1; б<0,8 % при Ь/а<0,25].
При а=Ь (касающиеся сферы равных радиусов)
Со=8л со • In 2 » 4л еа • 1,3863. (3-44)
3-5-4. Две пересекающиеся сферы (рис. 3-30).
0<со«л
Рис. 3-30
а. Общий случай
Со
a sin б
(0
где ф (х) — пси-функция, а со и 0 — углы, указанные на
рис. 3-30, а—г, для всех возможных конфигураций проводников
указанного вида (при со=л рассматриваемые проводники
115
принимают вид сферы, а при со = 2л— полою сферического сег-
, a sin 6 i о
мента), при этом а<о°, о——-—----------——-. При а==6 угол 0—
' г I sin (О) — в) |
=л—<х>/2 (для проводников, изображенных на рис. 3-30,6) или
0 = ы/2 (для проводников на рис. 3-30,а и в). В последнем слу-
чае значения емкости определяются графиком на рис. 3-31.
СО 0 Л V
Со 4 ЛЕА 1,3863 1,3634
0) л 3 Л 2
Cd 4ле.а 1,3453 1,2929
(0 2л 3 Зя 4
Со 4 леи 1,2180 1,1719
€0 Л 4л 3
Ср 4 лес 1,0000 0,7010
0) Зл 2 2л
Ср 4леа 0,5298 0
При Ь->со (0=о>—л) рассматриваемый проводник прини-
мает вид сферического сегмента (рис. 3-30,а). Зависимость
емкости сферических сегментов от угла 0 приведена на
рис. 3-32.
б. При
1>я <2я
2т
(1 2m)
116
_ 4nensin 6
L" "" 2n — 1
„ . / tn , e \ //Л e + sn \ [ tn Q — sn \
2 sin + — —- sin----------1----1---- cos — —
\ 2m 2n — 1 ) \ 4m 4n — 2 / \ 4m 4n — 2 )
2
+
tn 2sn
cos-------cos
m
2m—1
(2n — 1) tn
cosec —------—
2m
2n~ 1
(3-46)
Pnc. 3-32
в При <o=-———<2л (l<n<2m — 1)
2m — 1
n \ 2m — 1_____
/ 2/n 0
sin ----------1--
\ 2m — 1 n
117
(3-47)
г. При со = 2л/т (т=3, 4, ...)
д. При ы = п!т (т = 2, 3, ...)
Со = 4леа
1
/л
sin-----
т
(3-49)
Выражения для емкости некоторых проводников, образован-
ных пересечением двух сфер, представлены в табл. 3-7.
3-5-5. Три сферы, две из которых пересека-
ются с третьей под прямыми углами, а между
собой — под углом Чг = л/п (п=2-, 3, ...) (рис. 3-33).
Рис. 3-33
118
Таблица 3-7
119
Продолжение табл. 3-7
б. При п = 2 (три ортогонально пересекающиеся сферы)
об ас Ьс
У а2 4- 62 У а2 -рс2 Уь2-[-с2
abc
(3-51)
в. При a=b
Г 2n—1
(_ 1)т+1
Сп = 4 лед sin ——
0 2п
тл
sin -д—
т—1 2/1
л
sin2-----
2п
г. / Г. \2 . /пл
sin2-----------------
2n
(3-52)
Выражения для емкости некоторых проводников рассматри-
ваемого вида приведены в табл. 3-8.
г. При г1г=0, а=Ь = с
У — илей
4леа-1,504459. (3-53)
3-5-6. Четыре попарно касающиеся сферы
одинаковых радиусов, пересекающиеся под
прямыми углами (рис. 3-34).
С0 = 16лед In 2— S3
( __ iyn+n+1
/т2 4- п2
4леа-1,615546. (3-54)
(~1)п+1
3-5-7. Шесть попарно касающихся сфер одина-
кового радиуса, проходящих через одну точку
и пересекающихся под прямыми углами (центры
сферлежат на т р е х в з а и м н о п е р пен д и ку л я р н ых
прямых, проходящих через общую точку сфер).
С0 = 4лед 61п2 -12 V V
0 ут2 4- «2
(1)т+«+Р
U- И2 п2
4 лед. 1,7067.
(3-55)
т—1 п=1 р=1
3-5-8. Тело, образованное сечением сферы
двумя параллельными плоскостями, проходя-
121
Таблица 3-8
Значение емкости С0.'(4л£а)
общее выражение
ПРИ
122
щи ми на равном расстоянии от центра сферы
(рис. 3 35) [0,6366 + (0,6996 + 0,7923 63) 6 —
— (0,1359 ф- 0,7807 6 ф- 0,2294 63) 6а].
(3-56)
Зависимость Со/(4лга) = f(0) представлена на рис. 3-35.
3-5-9. Эллипсоиды.
а. Трехосный эллипсоид (а>6>с) (рис. 3-36)
(3-57)
Рис. 3-36
где F(cp, k)—неполный эллиптический интеграл первого рода,
123
При db>Q,l, Ь/а<0,5 может быть использована также при-
ближенная формула
J____I Г/ 6 у / с \21
г « 4ЛЕП--------4 IW... ' d 1. (3-58)
In ( 2 —
\ с 1
Пример 3-4. Определим емкость проводника в форме трехосного эллип-
соида, находящегося в дистиллированной воде (е«83ео). если полуоси его
соответственно а=10 см, Ь=3 см, с=2 см.
Пользуясь формулой (3-57), определяем предварительно модуль и аргу-
мент эллиптического интеграла F(<p, k). Прн заданных размерах
<р = arcsin
78°30'.
По таблице эллиптических интегралов (см., например, [1]) находим
F (<р, k) = F (78°30'( /0^48) « 2,093.
Подставляя это значение в формулу (3-57), получаем
83
С0=4п———-----0,1
4Л-9-10»
4,32-10-м Ф = 432 пФ.
2,093
Если воспользоваться приближенной формулой (3-58), то
« 3,88 10-ю Ф =388 пФ.
Таким образом, относительная погрешность
(3-58) в данном случае составляет
приближенной формулы
432 — 388
432
100 % ж 10 %.
б. Сжатый сфероид (a=fe>c) (рис. 3-37):
С
arccos —
а
(3-59)
124
в. Вытянутый сфероид (а>Ь = с) (рис. 3-38)
(3-60)
Рис. 3-37
Рис. 3-38
92а
2а
3-5-10. Цилиндр конечной длины (рис. 3-39).
При 0<//а<15
С„ « 2ле1 [1,274— +0,654 (—У’241
L I \ I / 1
[6<0,2%]. (3-61)
Зависимость C0/(2ml)=f[—) приведена на рис. 3-39.
\ а /
При //а>10 значение Со может быть определено по фор-
муле (3-1), а при 1/а>2£) — по формуле (3-35).
3-5-11. Тор.
а. Общий случай (рис. 3-40)
С.-Ы ]/1 - (f )2
Q ! (cha0)
Р 1 (ch юр)
Т
Q 1 (cha0)
Р 1 (chan)
П—2-
(3-62)
где Р 1 (ch «□), Q 1 (cha0) — функции Лежандра первого и
второго рода; chtxo=^/a-
Значения функции С0/(4ле/?) даны на рис. 3-40.
___ \Р /
125
Рис. 3-39
I а 2 ле/
0,250 6,008
0,500 3,320
0,750 2,399
1 1,928
2 1,191
3 0,927
5 0,699
10 0,504
15 0,426
R 0,05 0,10 0,15 0,20
сР 4 ле/? 0,616 0,722 0,800 0,868
а R 0,25 0,30 0,35 0,40
Ср 4 ле/? 0,932- 0,992 1,050 1,106
а ~R~ 0,45 0,50 0,60 0,70
Ср 4ле/? 1,161 1,216 1,323 1,429
а R 0,80 0,90 1,00
Ср 4лб/? 1,534 1,638 1,741
126
При 7?/а > 2
Со - 8mR |/1 _ (JL)2 0LL+ 2 , (3-63)
где К, К', Е, Е'— полные эллиптические интегралы первого и
второго рода с модулями fe2 = 2~~fl2 — и £'2=1—&2[6<1%].
₽ + ]<Я2 — а2
При Rla<3
Со ~ 4ле7? ^0,68+ 1,07-^-)
(3-64)
[|6| < 1 %]•
При R/a>?> значение Со может быть определено по фор-
муле (3-2) с погрешностью б<4 %, а при 7?/а>10 с погрешно-
стью б< 1 %•
б. При R = a (тор, образованный вращением окружности во-
круг касательной) (рис. 3-41):
Рис. 3-41
со
Со = 1 бел С ^44-dx ~ 4леа •1.7413528,
J * О W
о
(3-65)
где 10(х), Ко(х) — функции Бесселя мнимого аргумента.
3-5-12. Тело, образованное вращением круго-
вой дуги вокруг хорды (рис. 3-42).
со Р i (cos а)
г с Г ~Г+гг_______dT
Со 8леа sin а I р (_ cos nT (3-66)
о -r + iT
где Р 1 (х)-—функции конуса.
—2~ + гт
Зависимость С0/(4леа) =f(а) приведена на рис. 3-42.
3-5-13. Прямоугольныйпараллелепипед (рис. 3-43)
127
3
3neS2 У 2 M-Nr-Pt + Q
(3-67)
Рис. 3-42
a 0 Л ~8 Л 4
Ce 4nea 0,0000 1,1509 0,3933
a 3л 1 Л 2 5л 8
Co 0,6879 1,0000 1,2927
4леа-
a 3л ~4 7л 8 Л
Co 1,5313 1,6864 1,7414
4iwa
где
да С» с„
4лёД
1 0,001 7,0031
0,008 2,4734
0,125 0,8567
1,000 0,6488
1 2 0,004 4,1259
0,500 0,7063
1 3 0,009 3,0898
0,243 0,8597
128
Mi = i(d2~V~“)(O1 +fl’- + йз) - aHln 7T^:
L\ 2 a,-; J d + at
Nt = 2 (d2 —cfi— —) j/d2—nF;
Pi = 2cii (щ + 3S)arctg ;
Q = 4 |^d2 (fli 4* ^з) 4~ 3Vj 2Sd;
V — d^d<^z\ S = 2 Ч- ^2^3 4~ ^i^s)»
d = Ka|4-al4-at g
Значения величины Ci = C0/(4ne/?) при P~2i/V приве-
дены в табл. 3-9, где принято, что ai>a2>a3, а зависимость
Таблица 3-9
С2 2R Значение емкости С0/(4леЛ) при а3/(2Л), равном
0,1 0,2 0,3 0,4 0,5
0,1 7,0031 4,1259 3,0898 2,5467 2,2101
0,2 4,1259 2,4734 1,8811 1,5729 1,3837
0,3 3,0898 1,8811 1,4496 1,2269 1,0919
0,4 2,5467 1,5729 1,2269 1,0500 0,9440
0,5 2,2101 1,3837 1,0919 0,9440 0,8567
0,6 1,9807 1,2563 1,0022 0,8749 0,8006
0,7 1,8143 1,1653 0,9394 0,8274 0,7629
0,8 1,6886 1,0977 0,8937 0,7937 0,7369
0,9 1,5904 1,0460 0,8597 0,7694 0,7188
1,0 1,5120 1,0059 0,8340 0,7517 0,7063
Продолжение табл. 3-9
а3 2R Значение емкости С0/(4леЛ) при а3/(2Л), равном
0,6 0,7 0,8 0,9 1,0
0,1 1,9807 1,8143 1,6886 1,5904 1,5120
0,2 1,2563 1,1653 1,0977 1,0460 1,0059
0,3 1,0022 0,9394 0,8937 0,8597 0,8340
0,4 0,8749 0,8274 0,7937 0,7694 0,7517
0,5 0,8006 0,7629 0,7369 0,7188 0,7063
0,6 0,7538 0,7232 0,7024 0,6886 0,6796
0,7 0,7232 0,6973 0,6807 0,6701 0,6637
0,8 0,7024 0,6807 0,6671 0,6589 0,6546
0,9 0,6886 0,6701 0,6589 0,6528 0,6501
1,0 0,6796 0,6637 0,6546 0,6501 0,6488
5 Заказ № S07
129
С с •Л Многогранник г а
название обший вид
1 Тетраэдр У§1\2 и 0,20412
2 Куб (гексаэдр) 4® 1/2
3 Октаэдр /б/б « 0,40825
4 Додекаэдр \ * 1 <7 1/ — + — 1/5 ~ 1,11352 V 8 ~ 40
5 Икосаэдр / V? ' \/ К\1 _L (/3 Y15 ~ 0,75576 4 \ 3 /
C0l(4neR)~f ( — | при некоторых фиксированных значениях
\ ai I
а3/а2 показана на рис. 3-43.
3-5-14. Правильные многогранники.
Границы и средние значения емкости проводников в форме
правильных многогранников указаны в табл. 3-10, где г и R—
радиусы вписанной и описанной сфер, соответственно *.
1 Небезынтересно проследить развитие работ по определению емкости
куба. Есть предположение [11], что приближенное значение емкости куба
130
Таблица 3-10
й:| с Границы значений величины С.=С0/(4лел) 9С С г _ 4 1 мин 1 макс
нижняя с 1 мин верхняя С1макс icp.r с ,г 1 мин'1 макс
/6/4 л 0,61237 1,4900 1,8063 1,6330
/з/2 rj 0,86602 1,2976 1,3351 1,3161
/2/2 к 0,70711 1,1826 1,2654 1,2226
-^-(1+ /5) « 1,40126 4 1,0984 1,1254 1,1117
~ V 2 (5 + У5) ~ 0,95106 4 1,0646 1,0839 1,0742
было известно еще Дирихле, однако основные результаты по определению
емкости куба получены сравнительно недавно и характеризуются следующими
г
данными для величины Cj=-------—: 1,24422<С1<1,4210 (Г. Полна, 1947—48
4лег
[40, 41]); 1,264<С1<1,42110 (Г. Полна и Г. Сеге, 1951 [И]); ^«1,3110
(Т. Хиггинс и Д. Рейтан, 1951 [43]); 1,2928; | С j—1,29281 0,064
(В. Гросс, 1952 [28]); ^>1,278546 (Р. Мак-Магон, 1953 [36]); Ci<l,352
(Л. Дабони, 1953 [25]); Ct <1,336 (Л. Пейн и X. Вейнбергер, 1954 [39]);
£,<1,3351 (В. Парр, 1961 [38]); С,«1.31130 (И. Бледл и К. Мэй, 1962 [20]);
С,>1,2976-(А. Г. Рамм и др., 1972 [13]). . . . ..
5* 131
3-5-15. Прямой круглый конус (рис. 3-44).
При 1=а
0710<’_А_< 0,732, (3-68)
4ле/?
где R — радиус описанной сферы.
Рис. 3-44
3-5-16. Тело, ограниченное концентрическими
полусферами с совпадающими основаниями
(рис. 3-45):
ъ а 0 0,1 0,2 0,3 0,4 0,5
Со 4леа 0,8453 0,8459 0,8470 0,8499 0,8556 0,8649
ъ а 0,6 0,7 0,8 0,9 1,0
Ср 4леа 0,8786 0,8979 0,9237 0,9570 1,000
132
(3-69)
Lgm Lftn |<=о
где
________(— l)^+<+i (2m + 1)1 (2Z)!____1
22("Ж)+1 (2z _ 2m - 1) (/ + m + 1) (m!)* (fl)* J,=o ’
а коэффициенты D2m+X находятся из бесконечной системы ли-
нейных алгебраических уравнений
k = 0, 1, 2... ; Nk
i ос оо
^2m+l+ — Mi Dzm+1 2 (4t+l)(2t + l)LtmLtk=NkL0h,
2 m=0 i=0
Г / b \4fe+31
(4Й + 3) 1— —
L \a / J
/ b \4^+3
3fe + 2-J-(fe + 1) I —)
\ a )
Зависимость С0/(4леа) [—приведена на рис. 3-45.
\ a )
ГЛАВА ЧЕТВЕРТАЯ
ЕМКОСТЬ МЕЖДУ .
ДВУМЯ ПРОВОДНИКАМИ
В ПЛОСКОПАРАЛЛЕЛЬНЫХ СИСТЕМАХ
4-1. ОБЩИЕ ЗАМЕЧАНИЯ
1. В настоящей главе приведены материалы
для расчета емкости между двумя проводниками (конденсатор-
ной емкости) в плоскопараллельных электростатических систе-
мах (см. § В-2). Эти материалы позволяют определить значе-
ния емкости Ci, отнесенные к единице длины проводников.
2. Рассматриваемые проводники разделены по форме на бес-
конечно длинные провода, пластины и оболочки (замкнутые и
незамкнутые). Бесконечно длинные пластины в зависимости от
соотношений характерных размеров рассматриваемых систем
разделяются в свою очередь на пластины конечной ширины,
а также проводящие полуплоскости и плоскости.
4-2. ПРОВОДА
4-2-1. В настоящем параграфе приведены
материалы для расчета конденсаторной емкости на единицу
длины параллельных бесконечно длинных проводов.
133
Все формулы настоящего параграфа являются приближен-
ными. Большинство из них получено путем упрощения точных
формул, выведенных методом конформных преобразований
(§ 2-2), с учетом реальных соотношений размеров рассматри-
ваемых систем. Погрешность приближенных формул во всех
случаях, когда отсутствуют дополнительные указания, не пре-
вышает 5 %.
Для расчета емкости проводов, расположенных симметрично
относительно некоторой плоскости, могут быть использованы
также материалы, приведенные в п. 4-5-4 (см. формулу (В-18)).
4-2-2. Д в а провода круглого сечения (рис. 4-1):
~ (inpq-1.
2ле \ CjC2 /
См. также формулу (4-19).
4-2-3. Два провода прямоугольного
(рис. 4-2).
а. Общий случай.
При v>7
(4-1)
сечения
( v = —____________-_____________v = —1.
О1 (—0,171 + 0,447!+0,25) ’ П а, ’
/ 2зТ8
1 1п(^) ’
ь_ «1 0.471- 1,767,- 1
°а 0,47|— 1,7б72— 1 ‘
При V> 10
ж______________________________2ле_____________
In f kvz — v Г——_j-____!___ 1
I [fev—1 k(v—1) J
[6 < 2%],
(4-2)
(4-3)
где v и k — те же, что в (4-2).
б. При ai = a2=&i = &2=a (провода одинакового квадратного
сечения) и произвольном расположении граней.
При dla~>b
ле
0,38 + In (d/o)
При d/n>7
. ' 2ле
—й—dv—
1П (1,47 —)-— 2
L\ а, /
’ f|6| <2 %].
(4-4)
(4-5)
T34
в.
<р = О
Если й1=я2 = />1 = /)2 = а (провода квадратного сечения) и
(попарно параллельные грани), то при
________________________2ле
In fv2__________________
\ V — 1
Cz
(4-6)
me
* = 1,695 —
а
ле
а при d/a>6
Cl
(4-7)
4-2-4. Два одинаковых провода эллиптического
сечения.
а. Малые оси сечений проводов расположены на одной пря-
мой (рис. 4-3) :
ле
. , d , , b
Arsh-------Arsh —
с с
(4-8)
где с= Vа2—Ь2.
См. также рис. 4-13.
б. Большие оси сечений
прямой (рис. 4-4):
проводов расположены на одной
Ct
_______ле__________
. . d . . а
Arch-------Arch —
с с
(4-9)
где с= j/a2—b2.
135
См. также рис. 4-14.
2Ъ
Рис. 4-3
ЦРис. 4-4
4-2-5. Три провода, лежащих в одной плоско-
сти (два крайних провода одинаковы и соеди-
нены) (рис. 4-5):
Ct ------ . (4-10)
, did \ о
In — I— 2
аг \ а2 /
4-2-6. 2п одинаковых проводов чередующейся
полярности, расположенных по образующим
круглого цилиндра (рис. 4-6):
о - 2mR
где 2<п<---.
5а
136
4-3. ПЛАСТИНЫ
4-3-1. В настоящем параграфе приведены
материалы для расчета конденсаторной емкости на единицу
длины проводников в форме параллельных бесконечно длинных
плоских пластин.
Основные формулы настоящего параграфа являются точ-
ными и получены методом конформных преобразований с ис-
пользованием метода непосредственного определения напря-
женности поля (§ 2-2). Большинство этих формул содержит
полные эллиптические интегралы первого рода К(&) =
’ JL
2
Г d6 „ „
= I г , подробные таблицы которых приведены,
J V1 — k2 sin2 е
о
например, в [1]; при этом в тексте используется также обще-
принятое обозначение Kz (k) = К (k'), где k' = ]/1 — k2.
4-3-2. Различные комбинации пластин (в том
числе и соединенных между собой), для которых величина Q
может быть представлена точными замкнутыми выражениями.
Выражения Ci приведены в табл. 4-1.
Пример 4-1. Найдем емкость на единицу длины между двумя копланар-
ными пластинами шириной а=9 см при расстоянии между пластинами
d=2 см.
Расчет производим по формуле п. 2 табл. 4-1. Найдя модули эллиптиче-
ских интегралов
*2 =-----!-----=0,01; k'2= 1— £2 = 0,99,
с помощью таблиц эллиптических интегралов (например, [1]) устанавливаем,
что
К (ft) = 1,5748; К' (k) =3,6956.
Используя эти значения, получаем
3,6956
1,5748
яь 2,3467е.
Приближенное значение емкости может быть определено и без исполь-
зования таблиц эллиптических интегралов. Для этого следует воспользо-
ваться разложениями эллиптических интегралов в ряды [17], сохранив только
; первые члены. Тогда при найденном значении k
к (fe)~—; K'(*)~in4-
2 k
и искомая емкость
с, Л 1 4-2—Al = —In Uf 1 4-2—VI к 2,3484е.
л L V А1 Я L \
137
Таблица 4-1
Выражения для емкости на единицу длины между плоскими бесконечно длинными пластинами
№ пи. Сечение системы ci e
1 а b ND i- 4-A, A
d ' d
_dt (i i-a Vi+ b\
\ d A d)
2 a 1 и K' к 1 \ _i_ 2 a Y
+ d I
3 , _ fl _ L 1 , -i~ 2 к
4 — <k a y di\~ CM 1+ di_ + A a a (i + AV i + A'i \ a )\ a J
5 — d ! g I a I 4jl K' 1 fl+2 Ay V a J
Продолжение табл 4-1
10
d I
2 —
2 —
К
с
№ пп. Сечение системы £
4? ез di - —
2 —
Продолжение табл. 4-1
г<" + м> , W = [I+(A)T\
< (1 + «>(1 + м) 1 U/J
Продолжение табл. 4-1
К2
, л& , л (Ь 4- d) h h Л- + 2h
th2(——] \ 2 h )
. in b ' sin к 2 h , . in 2d + b > sin к 2 h )
.In d+ b\ sin2 \ 2 h ) 2 COS'4 2h
. , / л b \ sin2 — к 2 h )
nb . n(b + d) sin sin h h . nd cos 2h
Относительная погрешность полученной приближенной формулЬ! для рас-
сматриваемого случая
б - (1 -1^1). 100 % » - 0,072 % .
V 2,3467)
С увеличением отношения a/d эта погрешность по абсолютному значе-
нию уменьшается.
4-3-3. Две пластины с общей плоскостью сим-
метрии.
а. Общий случай (рис. 4-7).
Рис. 4-7
О С/ г /
Зависимость —=/ —
е \ d
при некоторых фиксированных зна-
чениях &1/&2 представлена на рис. 4-7.
б. При'&1 = 62=& (пластины одинаковой ширины, рис. 4-8)
С =eLKW_ (4-12)
К' (fe)
где k — корень уравнения
4= — [К (*)£(₽; ^)-E(fe)F(₽, эд,
d л;
о • I 1 I / 1 Е 1
6 = arcsin — I/ 1 — — ,
\ k V К /
F(p, k), K(k), £(р, k), Е(&) — неполные и полные эллипти-
ческие интегралы первого (F, К) и второго (Е, Е) рода.
Зависимость -ф- = представлена на рис. 4-8.
142
Для приближенного расчета емкости между указанными пла-
стинами могут быть использованы также следующие прибли-
женные формулы:
При b/d^ 1
ле
. /л d '
In 4--
\ b ,
[|6|<7% при 0,25<Ш==: 1; |6|<0,3% при bid 0,25].
(4-13)
С/
Рис. 4-8
При 1< 6/а^27
CZ^L
d
е — fl + -L—(1 + 1п2 «А'
d I я b \ d
(4-14)
(6< 10 % при l<b/d<4- б< 1,5 % при 4^b/d^27].
143
При 6/d>27
(4-15)
г ь
Ci X 6-—
1 d
(б<7 % при 27<&/Н^31; б<3 % при &/d>31].
4-3-4. Две пластины, расположенные на гранях
Д в у гр а н по го у г л а.
а. Пластины одинаковой ширины (рис. 4-9):
С, Г--------
1 1
1П -
я
(4-16)
144
где ^(0<^<1)—параметр, определяемый из системы уравне-
ний относительно q и т* 1 * *:
_ 1—2^cos(2jit—<p)-f-2g«cos2(2jiT —<р)~ 2^Bcos3(2nT —<р)+ . . . .
1 — 2<? cos 2 лт -р 2 </* cos 4 лт — 2 «у9 cos 6 лт + ...
д sin (2 лт — <р) — 2 sin 2 (2 лт — <р) + 3 </9 sin 3 (2 лт — <р) — . . . .
q sin 2 лт — 2 gi sin 4 лт -j- 3 д* sin 6 лт — ...
0<т<-£- '
Зависимость-^- = f представлена на рис. 4-9. При <р^90°,
Ai>0,5
G^En[ln21Z1-+X2~2Xcos(p] \ (4-17)
1 — X
Рис. 4-10
Некоторые численные значения 6 при различных углах <р и
параметрах Z. указаны в табл. 4-2.
Таблица 4-2
<р, •••° 5 30 60 90 150
0,95 0,95 0,80 0,66 0,53 0,34 0,16
в >0, % 1,9 0,02 0,4 3,9 1,7 2,8 4,4
б. Пластина и полуплоскость (рис. 4-10):
CZ==E;-^-, (4-18)
In"—
' 4
•О'о ("Г-—
\ 2л/
1 Правая часть первого из этих уравнений равна-А----{_ f а вто.
®о’.(т)
рого уравнения----------------• гДе ^<>W тэта-функция (см., например,
[17])-
145
где q (0<<7<1) определяется по приведенным формулам при
4-4. ОБОЛОЧКИ
4-4-1. В настоящем параграфе приведены
материалы для расчета конденсаторной емкости на единицу
длины проводников в форме бесконечно длинных замкнутых
и незамкнутых оболочек.
Основные формулы настоящего параграфа являются точ-
ными и получены методом конформных преобразований (§ 2-2).
Для приближенного расчета конденсаторной емкости замкнутых
оболочек (при определенном соотношении их размеров) могут
быть использованы также материалы § 4-2.
Большая часть приведенных материалов относится к кон-
денсаторной емкости замкнутых оболочек; расчет емкости не-
которых систем, содержащих незамкнутые оболочки, рассматри-
вается в п. 4-4-6.
4-4-2. Замкнутые оболочки круглого сечения.
а. Две не охватывающих друг друга оболочки (рис. 4-1):
(4-19)
При d/ai^5 и d/a2^5 см. также формулу (4-1).
б. Две оболочки, одна из которых охватывает другую
(рис. 4-11):
Рис. 4-12
Рис. 4-11
2 ле
724-r2-d2 ’
С/=-----
Arch 2 Rr
(4-20)
При d = 0 (цилиндрический конденсатор)
146
'i ле
(4-21)
In
R
r
в. Две одинаковые соединенные между собой оболочки, сим-
метрично расположенные внутри третьей (рис. 4-12).
ПР" (Я<<1; (т)‘«‘
(4-22)
При d=2r
147
Cz
2 ле
(4-23)
4-4-3. Замкнутые оболочки эллиптического
сечения.
а. Две одинаковые оболочки, малые оси сечений которых ле-
жат на одной прямой (рис. 4-3).
Зависимость — = f( — | при фиксированных значениях Ь/а
е \ 2а/
представлена на рис. 4-13.
При d2/zz^5 расчет может быть выполнен по формуле (4-8).
б. Две одинаковые оболочки, большие оси сечений которых
лежат на одной прямой (рис. 4-4).
Зависимость ~ = f j при фиксированных значениях Ь/а
представлена на рис. 4-14.
При </2/а^5 расчет может быть выполнен по формуле (4-9).
в. Две конфокальные оболочки (рис. 4-15):
Cz- Л" (4-24)
In / fr + M
\а2 + 62/
4-4-4. 3 а м кнуты е оболочки круглого и эллип-
тического сечений.
а. Круглая оболочка, охватывающая соосную с ней эллип-
тическую оболочку (рис. 4-16):
Cz = 4e----,
К (fe) —F(<p; k)
где К и К' — полные эллиптические интегралы первого рода
(4-25)
148
с модулями k и k' = }/ 1 — /г2, соответственно; F(<p, k) —непол-
ный эллиптический интеграл первого рода;
^2 —а2 /?2_|_Ь2 . [b R2 + a-\
k~ R2 + a2 R2-b*’ <P-arcsin(a /?2 + 62)-
б. Эллиптическая оболочка, охватывающая соосную с ней
круглую оболочку (рис. 4-17).
Значение Ci определяется по формуле (4-25) при
. а(г2 + &2)
(p = arcsin —
k (fe2-r2j(a2+r2) .
(b®+r2) (a2 —r2) ’
Рис. 4-17
Рис. 4-16
4-4-5. Замкнутые оболочки многоугольного се-
чения.
а. Охватывающие одна другую оболочки прямоугольного се-
чения с параллельными сторонами (рис. 4-18):
Ct
л Г а . с 1 2 Л b2 + d2 , b । d . d , b
4е — + —4---------In —у-------1- — arctg — + — arctg — .
|_6 d л \ 4bd d b b d /J
(4-26)
При a=c, b = d (оболочки квадратного сечения, рис. 4-19)
Cz = 8e-^-, (4-27)
Ко
где Кр, К'о —полные эллиптические интегралы первого рода
с модулями k0 и 1—ko соответственно; k0 =
ky --- ky
2
149
а параметры kx и k\ --= V 1 — k] определяются из уравнения
К (fe^) га а 1
К W) d
Зависимость приведена на рис. 4-19.
Рис. 4-19
а d 1,05 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0
k, 0,776 0,831 0,904 0,947 0,970 0,984 0,991 0,995 0,998 0,999 0,9995
Пример 4-2. Определим емкость на единицу длины коаксиальной пере-
дающей системы с квадратным поперечным сечением центрального и внеш-
него проводников (рис. 4-19), если 2 (а—d) = l см, 2о=4 см, а диэлектриком
является воздух.
При — =-------« 1,33 с помощью кривой рис. 4-19 устанавливаем, что
d 1,5
kx « 0,96; *’ = ]/ 1 — 0,962 «0,28.
Используя полученные значения k и А/, получаем
/ 0,96-0,28 у»
\ 0,96+0,28 )
По модулю feo с помощью таблицы эллиптических интегралов [1] нахо-
дим, что
К0/Ко«0,61,
150
н из формулы (4-27) получаем
„ 4,88-10—э
С/ -------------
Збзт
л 43,2 пФ/м.
б. Охватывающие одна другую оболочки правильного мно-
гоугольного сечения.
При взаимном расположении и соотношении размеров обо-
лочек в соответствии с рис. В-7, б (некоторые частные случаи
см. в табл. 4-3).
Cz=2ne,
(4-28)
где п — число сторон каждого из многоугольников.
в. Не охватывающие друг
друга оболочки прямоуголь-
ного сечения с параллельными
сторонами (рис. 4-20).
Зависимость — — f (—при
е \а)
Рис. 4-20
различных значениях dja представлена на рис. 4-21.
При b^5d
(4-29)
где
k
d
d + 2a
4-4-6. Замкнутые и незамкнутые оболочки круг-
лого сечения.
а. Замкнутая оболочка и коаксиальная с ней незамкнутая
оболочка большего радиуса (рис. 4-22):
2зте
. / R ф \
In I —cos ——
\r 2 )
(4-30)
151
Таблица 4-3
б. Две коаксиальные незамкнутые оболочки одинакового ра-
диуса (рис. 4-23):
Ci ~ е
К' (fe)
К[(й) ’
(4-31)
где £ = tg2-|--
1S2
(4-32)
При <р<л/10
С/ SK------ In-----
л <р
в. Замкнутая оболочка и две коаксиальные с ней, соединен-
ные между собой одинаковые незамкнутые оболочки большего
радиуса (рис. 4-24):
4-5. ПРОВОДА И ПЛАСТИНЫ
4-5-1. В настоящем параграфе приведены
материалы для расчета конденсаторной емкости на единицу
длины проводников в форме бесконечно длинных проводов
и пластин. Последние разделены на пластины конечной ширины,
полуплоскости и плоскости.
Все формулы настоящего параграфа являются приближен-
ными.
Часть из них получена путем упрощения точных формул, сле-
дующих из метода конформных преобразований (§ 2-2), с уче-
том реальных соотношений характерных размеров рассмат-
риваемых систем. Погрешность приведенных формул во всех
случаях, когда отсутствуют дополнительные указания, не превы-
шает 5 %.
Материалы п. 4-5-4 могут быть использованы также для оп-
ределения конденсаторной емкости в системах бесконечно длин-
ных проводов, расположенных симметрично относительно плос-
кости [см. формулу (В-18)].
4-5-2. Провода и пластины конечной ширины.
Значение величины Сг определяется приближенными форму-
лами, приведенными в табл. 4-4, где даны также максимальные
значения относительной погрешности при указанных соотноше-
ниях геометрических параметров рассматриваемых систем.
4-5-3. Провода и полуплоскости.
Значение величины Сг определяется приближенными форму-
лами, приведенными в табл. 4-5.
153
Таблица 4-4
№ пп. с ечение системы Соотношения между геометр ическими параметрами Значение емкости С^/(2зге) ^max> %
1 V/ \ А <10; А<10 а а /. 2Л! W 11” 1 5
_ 2 d ~
2 о л 43 ] Q 6$ Л «I’’3 1. . h* — d? — ah \~1 (Arch \ ad ) 3
,., » ^1 A.V в.|э* II ю в | а. \v о Г / d \1~» Arch 13 — — 2j 3
П Ф/
1 л 2d _
a. |s* II ьэ в [ а. V (in AT1 \ a ) 5
3 /Л 2J. О л ч | в CN Л .е | ч 2 [1 Al12+(1_ AV'2l , L (h+аУ J 1 \ /г* 1 —1 3
z ‘\& , 2d [1 _ d' ]12 Л _ _d‘\1/2 L (h + a)2 J Л* J
ч \ А>3; А> Ю d а (lnr4^ + fc)a -11|~X I L d* 1J 5
Продолжение табл. 4-4
f№ пп. 1 : Сечение системы Соотношения между геометрическими параметрами Значение емкости С^/(2пе) ^maxi %
! 4 ) ф x2d г 1 — >5- — > 1 a d 2 fin ~ ft2 + d2 + ft ]/ (ft - a)2 + d2 | 1 (ft — a) ]/ h2 + d2 — h V (h — ay + d2J —1 3
| 5 □ — > 1; ю d2 а 5
4 —1 -2d1 1 2d? L;h Гц+НК+О—)’!- ]/ df — d| [ ] dg + ft2 — ]/ d| + (d2-df (ft-a) 1Г 4
1 1 6 <9 _ 2d, 2d? О л в | в м I СЧ — м СЧ —' <3 I Q 4- i p-« «1=^ «1=^ c ' Z I CM 1.2-, -1 1,2 3
Таблица 4-5
С с Сечение системы Соотношение между геометриче- скими параметрами Значение емкости С^/(2ле) * E
1 . / Ф2а_ — «1 R [in N [w + Vn2 — 1) т sin —L- 2 ] *, где 3
-1 /"'4
2/?sin — ->1 а 5
- —1
In | 4R sin— \ 2_ a /
— \ I
. 2 J i \2 — 1со о л f 1 '3 ° pn \ ah (i+4 у 1 J 3
3 d — >1 а d 3
[4j — ]/ d2—a2 In » | a. + ft |fx 1
— >1 а [in р —Yl”1 a /J 5
4 ^2 — > 1 а п 1 V In [- 2r0 Y n 2 5
*х a L
156
Пример 4-3. Определим емкость на единицу длины системы, сечение ко-
торой изображено в п. 3 табл. 4-5, при а— 1 мм, <1=5 мм, е=е0.
Пользуясь для расчета первой из формул, указанных в п. 3 табл. 4-5, по-
лучаем
Ci
___________2зт-5-10—»
36л /25 —Г In (5 + /25 — 1)
24,7- 10~и Ф/м = 24,7 пФ/м.
По второй формуле
2m-10—я
Ct » ---i---^24,1-10—12 Ф/м = 24,1 пФ/м.
36m In 10
Как видно, при a/d=0,2 разница в определении емкости по приведенным
формулам не превышает 2,5 %.
4-5-4. Провода и плоскости.
Значение величины Ci определяется приближенными форму-
лами, приведенными в табл. 4-6.
Таблица 4-6
157
Продолжение табл. 4.6
4-6. ПРОВОДА И ОБОЛОЧКИ
4-6-1. В настоящем параграфе приведены
материалы для расчета конденсаторной емкости на единицу
длины некоторых систем, образованных бесконечно длинными
проводами и оболочками.
Рис. 4-25
Все приведенные в тексте формулы являются приближен-
ными; их погрешность не превосходит 5 %
4-6-2. Провод и оболочка круглого сечения.
а. Провод расположен вне оболочки (рис. 4-1)
2пе ( L 2ага2 ' \ 2ага2 J
(4-34)
См. также (4-1) и (4-19).
б. Провод расположен внутри оболочки (рис. 4-11)
. ~ l|„ Г + 1Г‘. (4-35)
2ле ( L 2rR~ V \ 2rR j JJ 1
—См. также-(4-20),.. ..... ... ........................ . ..___ ..
158
4-6-3. Провод в точке пересечения диагоналей
оболочки квадратного сечения (рис. 4-25):
С, ----- (4-36)
In (1,08 — 'j
\ а )
Пример 4-4. В центре тяжести медной трубы квадратного сечення со сто-
роной 2с=40 мм находится линейный провод радиусом 2 мм. Определить
взаимную индуктивность провода и трубы на высокой частоте (на единицу
длины).
Пользуясь формулой (В-29) находим, что
Ь/ = еоро/Сг.
Емкость рассматриваемой системы определяется формулой (4-36), сле-
довательно,
Lt = In (1,08—")=-4л1°~7 Inf 1,08—) к 4,76-10-! Гн/м.
2ft \ a J 2зт \ 2 )
4-6-4. Провод и незамкнутая оболочка, образо-
ванная двумя полуплоскостями (рис. 4-26).
Рис. 4-26
(4-37)
(4-38)
При р=л/2, <р=л/4
2зте
~----". т~т
In (1,41—1
\ ° /
(4-39)
159
4-7. ПЛАСТИНЫ И ОБОЛОЧКИ
4-7-1. В настоящем параграфе приведены
материалы для расчета конденсаторной емкости на единицу
длины систем, образованных бесконечно длинными пластинами
и замкнутыми оболочками. Все приведенные в тексте формулы
являются точными и получены методом конформных преобразо-
ваний (§ 2-2).
4-7-2. Пластины и оболочки круглого сечения,
а. Общий случай.
Значение величины Ci определяется формулой (4-18), где
параметр Л находится в зависимости от размеров и взаимного
расположения рассматриваемых пластин и оболочек из табл.
4-7 при а = 27? sin
Зависимость—= f (7.) при фиксированных значениях ср при-
е
ведена на рис. 4-27.
Рис. 4-27
б. Пластина расположена в плоскости, проходящей через ось
оболочки:
С2 = 2е-^^-, (4-40)
К (k)
где К и Kz полные эллиптические интегралы с модулями k
и к' — у 1 ^г> соответственно; выражения для k в зависимости
160
Таблица 4-7
от соотношений размеров рассматриваемых систем приведены
в табл. 4-8.
Пример 4-5. Определим емкость на единицу длины системы, сечение ко-
торой изображено в п. 1 табл. 4-8, при /?=10 мм, Ь>=5 мм, d=4 мм, При
указанных значениях параметров величина
4(20 — 5 — 4)
(5 + 4) (20-4)
6 Заказ № 507
« 0,306.
161
Таблица 4-9
с £ Сечение системы k
4 Г ' >+^r d
5 <?2 х-" К Ь |Лл1_ 1
(i + 2*W1 + ^ \ Ъ )\ dj
/^ГХ" I
6 (^r
При этом значении k с помощью таблиц эллиптических интегралов (на-
пример, [1]) находим, что ~ 1,62.
К (k)
Тогда в соответствии с (4 40) при е=е0
9-10—»
Q = -±-^—.1,62 - 28,6 пФ/м.
36л
в. Оболочка и плоскость (рис. 4-28):
Cf — е(4-41)
Arch —
а
При А/а^1,5 см. также п. 1 табл. 4-6.
г. Пластина расположена между двумя соединенными между
собой концентрическими круглыми оболочками (рис. 4-29).
При Ra=rR/Ri
с (4.42)
К'И
где К и К' — полные эллиптические интегралы первого рода
с модулями х = k sn Ip К (&), k'\ и v! — 1 —v? (sn х — эллиптиче-
ский синус),
a k — решение уравнения
K'(k} - 1 \п R
К (k) г
4-7-3. Пл астины и оболочка эллиптического
сечения.
6* 163
а. Пластина расположена внутри оболочки.
Если края пластины совпадают с фокусами эллипса (рис.
4-30), то
с -----(4-43)
. , а
Arch —
с
где c=jZa2—Ьг.
Рис. 4-30
б. Пластины расположены вне оболочки в плоскости ее сим-
метрии. Значение величины Ci определяется формулами, приве-
денными в табл. 4-9.
4-7-4. Пл астин а внутри.оболочки прямоуголь-
ного сечения (рис. 4-31):
Рис. 4-31
г О К
Ct —- ,
I к,
Рис. 4-32
(4-44)
где модуль полного эллиптического интеграла первого рода
^2 _ 2 [sn (Ml.fep) — sn (ua, fep)]
[1 + sn (Mt, ftp)] [1 — sn (u2, ftp)] ’
Zi 4 \ iz 26 4- 4 \ «-
“1 = (1—-} Ke; = ---------/ )K°-
Модуль ko эллиптического интеграла Ko и функций sn(w, ko)
находится из уравнения
A=A=_L|„_L
I Ко л q
ГМ
№ пп. Сечение системы Значения емкости Cz/(2e)
1 , °- i _Лч К' (fe) K(fe)
.!
2 I С гЧ К' (fe) К (Ze)
Т
3 -4 S 1^- K(fe) К' (k)
_J_
4 а о K(fe) К'(^)
J dl ~ d ,
Значение k
a2 — b2
(1 —mi)(l + ff?2). = _______________
(1 + mx) (1 — m2) ’ * 1 a(a -\-d)~b У (a 4- d)2 — (a2 — b2) ’
a2 — b2
k =
т.л =--------------------------- ------------------------------
a (a 4- d 4- c) — b V (a 4- d 4- c)2 — (a2 — b2)
a2 — b2
1 — tn
-----; m — ,_____ —
1 4- m a (a 4~ d)—b У (a 4- d)2 — (a2 — b2)
2 (m-L 4- m2)
(1 4- m-j) (1 4- m2)
a2 — b2
о —‘ - -
a (a 4- db 2) — b У\а-}- dlt 2)2 — (a2 — b2)
a2 — b2
a (a+ d) — b -У (a 4- d)2 — (a2 — b2)
№ пп. Сечение системы Значения емкости Cz/(2e)
5 h К' (ft) К (ft)
6 । А tf с . К (ft) К' (ft)
Ц
7 -4 4? К (ft) K'(ft)
8 5 г_^_ о К (ft) К'(ft)
Продолжение табл. 4-9
Значение k
т2 *Ь г 1 + т2 а* — Ь2
----------- ; т-г =-------
m, 4-]/1 4-a(&4-d) — bV (b + dy + (аг — Ь*)
а1 — Ь2
т„ =-----------^7. .
а (Ь 4- с 4- d) — b |Л(& + d 4- с)1 4- (а2 — Ьг)
2 _ g (b + d) — fe К(Ь 4- ^)а + (аг — Ь2)
1 4- jA14-m* ’ т ~ а2 — Ь2
а2 — Ь2
а (Ь 4- d± 2) — b |/ (& 4" dlr 2)* 4~ (°2 Ь2)
1 а (Ь 4- d) — b У(Ь 4- dy + (а2— Ь2)
г — ' т =--------------------------------------------
|1 4- т2 а2 — fe2
или по формуле
, лГ~ ( 1 + <?2п V -л—
k0= V Я П ------~, q = e i .
n=i \ 1 +(?2«-i )
(Значение /г0 может быть найдено по заданному отношению
h/l с помощью кривой, приведенной на рис. 6-5, или по таблицам
эллиптических интегралов [1].)
При симметричном расположении пластины (рис. 4-32)
Cz-4e (4-45)
к j
где k — sn (-у- Ко, k0 , а модуль определяется так же, как и
выше.
В частном случае, когда сечение оболочки имеет квадратную
форму, выражения для емкости между рассматриваемыми про-
водниками принимают вид, указанный в табл. 4-10, где
Таблица 4-10
Ns пп. с ечеш 1е сн стемы Значение емкости Cz/(2s) Значение fea
1 1 K(fe) К' (k) 2 [sn (ui, КбТб) — sn (ы2; р^оТб)] x X {[1 + sn («!; /0^)] [1 — sn (n2; P^5)]}-1; ^=(1 — -y-^K (/0^) « 1,85407(1 —A);
i 2Ь -
« 1,85407(1 —+
2 ’1 О К (fe) K'(fe) sn!^K(/0,5)-y-; ^0,5 sn2fl,85407—; 0,707 \ I ')
3 К' (fe) K(fe) и uz- cn (uj; 1^0,5) [2 — cn (u2; 1^0,5)] )’.
cn (ы2; У 0,5) [2 — cn (u^ p^O,5)] ) l=-^K(/0^)A~ 1,31102— ; 2 I I !.ЗИ02“±^ 2 i I
167
sn (u, j/o,5) и cn —эллиптические синус и косинус,
соответствен но,
Пример 4-6. Определим емкость на единицу длины системы, изображен-
ной на рис. 4-31, если h//=0,78; d//=0,38; (2б+Д)//=0,80, а диэлектриком
является воздух. ,
По заданному отношению—=—-—=0,78 по таблицам [1] находим, что
/ Ко
^о2=0,75; Ко ”2,16.
Значения эллиптических синусов, входящих в формулу (4-42), могут
быть вычислены непосредственно по их таблицам или по таблицам эллипти-
ческих интегралов. Воспользуемся в данном случае последним способом
Вычисляя аргументы эллиптических синусов, имеем:
И1 = (1—0,38)-2,16« 1,34;
и2 = (1 —0,80)-2,16 ^0,43.
Обращаясь далее к таблице, содержащейся в [1], находим, что при
«1 = 1,34 и feo2=0,75 амплитуда <pi«65°. Аналогично <р2«24°.
На основании формулы snu=sin<p имеем-
sn «1 = sin 65° а: 0,906;
sn «2 = sin 24° ss 0,407.
Находим затем модуль k эллиптических интегралов:
2(0.306-0.407)
(1 + 0,906) (1 — 0,407)
Тогда ,К«2,504, К'» 1,620, и по формуле (4-42) получаем
Ci = 2-8,842-10-12- А521 ~ 27,3 пФ/м.
1,620
ГЛАВА ПЯТАЯ
ЕМКОСТЬ МЕЖДУ ДВУМЯ
ПРОВОДНИКАМИ
КОНЕЧНЫХ РАЗМЕРОВ
5-1. ОБЩИЕ ЗАМЕЧАНИЯ
1. В настоящей главе приведены материалы
для расчета конденсаторной емкости между двумя проводни-
ками, хотя бы один из которых имеет конечные размеры. При
этом расположение материала сохранено в основном таким же,
как в гл. 4.
2. Большинство приведенных формул является приближен-
ным. Погрешность их во всех случаях, когда не оговорено про-
тивное, не превышает 10 %.
168
5-2. ПРОВОДА
5-2-1. В настоящем параграфе приведены
формулы для расчета емкости между двумя конечными прово-
дами круглого сечения.
Все приведенные формулы получены методом средних по-
тенциалов и дают заниженные значения емкости между рас-
сматриваемыми проводами (см. § 1-2).
5-2-2. Два параллельных провода конечной
длины (рис. 3-4).
а. При Ь=0 значение С определяется по формуле (В-14) при
следующих выражениях для потенциальных коэффициентов:
Если, кроме того, li = l2=l, ai=a2=a, то значение вели-
чины С может быть найдено также по формуле (В-18), где С1
определяется выражениями, приведенными в п. 5-5-2.
б. При b — li+lm, ах=а2=а (рис. 5-1) значение С опреде-
ляется по формуле (В-14) при следующих выражениях для по-
тенциальных коэффициентов:
(5-4)
_____________ (5-5)
„ ___ 1 ь i„ -f- h2 + P^d2 + (hj -f- /г2)2 ,
а12----~~ niln z- т
+ m + V d2 + (hi + m)2
+h2 in +
h2 + m + Vd^+(h2 + my
169
+ mln{(2m+j/ da+4ma)2x
X {[h1+m + 1/rd2+(h1 + m)2 [ft2+^+]/r^2 + (ft2 + m)2 ]} '} +
+ jAP + fa + m)2' + ]/^ + (Л2 + т)2 -
—]/'d!!+ (^i+ft2)2—~\fd2 + 4m2 }. (5-6)
Если, кроме того, d=0, /i = /z=^ (рис. 5-2), то величина С
может быть найдена также по формуле (В-18), где С1 опреде-
ляется выражениями, приведенными в п. 5-5-2.
Рис. 5-1 Рис. 5-2
5-2-3. Два пересекающихся или скрещиваю-
щихся провода конечной длины.
а. Общий случай (рис. 3-7).
Величина С определяется по формуле (В-14) при следующих
выражениях для потенциальных коэффициентов:
_ Fli 4~ Р22 Р12 ~~ ^21 .
4ле (х2 — Xj) (г/2 — yd
р^ = хр In {yq—хр cos ф+Dpq] + yq In [xp—yq cos ф + Dpq\ +
4—— arctg ( Хв+-уч±£рч. tg _Ф_\ .
sirup \ d 2 )
Dpq = К x2 + у2—2xpyq cos ф + d2;
170
р=1, 2; 9=1, 2.
б. При <р = зт/2; d=0; xx = yx = h-, х2—Х\=У'~У\ = 1 (рис. 3-8)
может быть использована следующая приближенная формула:
5-2-4. Два провода в форме одинаковых круго-
вых колец, расположенных в параллельных
плоскостях (рис. 5-3)
Рис. 5-3
С
4л2е7?
" Й R
In —
а
(5-12)
______К
VR* + h*
где К — полный эллиптический
,2 &
лем я2 — —-------
интеграл первого рода с моду-
Пример 5-1. Определим емкость между проводами, изображенными на
рис. 5-3, считая, что они расположены в воздухе; радиус каждого кольца
равен 5 см, расстояние между ними 10 см, а диаметр провода 0,1 см.
171
Вычисляя модуль эллиптического интеграла, получим
k =
——-------к 0,707.
25 + 25
Тогда из таблиц эллиптических интегралов находим, что К= 1,854.
Подставляя это значение в формулу (5-12), находим, что при е=Во
4л3-10~9-5-Ю~*— ~з(24. Ю-12 ф=з,24 пФ.
36л fin—-0,707-1,854")
V 0,05 J
5-2-5. Бесконечно длинный прямолинейный про-
вод и провод в форме коаксиального кругового
кольца (рис. 5-4)
С
АяРеа!
, 2R
In----
02
(5-13)
5-3. ПЛАСТИНЫ
5-3-1. В настоящем параграфе приведены
материалы для расчета емкости между двумя пластинами, хотя
бы одна из которых имеет конечные размеры.
Большинство приведенных формул и численных результатов
получено приближенными методами (метод площадок, прибли-
женное решение интегральных уравнений и др.) и дает погреш-
ность в определении емкости, не превосходящую, как пра-
вило, 10.%.
При использовании приведенных материалов следует учиты-
вать также соотношение (В-18). Его применение позволяет рас-
пространить материалы п. 5-3-5—5-3-7 на расчет емкости
между соответствующей пластиной и плоскостью, а материалы
п. 5-3-8— на расчет емкости между двумя одинаковыми пласти-
нами, расположенными симметрично относительно плоскости.
172
(5-14)
5-3-2. Диск и соосное ему заземленное плоское
круговое кольцо (рис. 5-5):
а,
С = 8е J <р (0 dt,
О
где ср (0 —решение уравнения
q>(0— $ т)ф(т)йт + 4/^а(Л т)ф(т)4т=1;
о о
Рис. 5-5
т к» <' ’> - «.+(1,+т)-. (ттг » «+W+“«+“<'>)+
+ w+('_t).{7b » и+“»+“ «);
<'’>=£ «->+«] +
+ ft.+(‘,+t). [v W+T P«+“ <”]};
a (r) = arctg -f- arctg Дз~' ;
₽(0 = ln
fta+(«» + /•)» .
№ + (as — r)a ’
T(r)_|„^±£.
a3 — r
173
Зависимость C/(8eai) =f(a3/h) при a2/h = 0,5 и различных зна-
чениях ajh представлена в табл. 5-1 и на рис. 5-5.
Таблица 5-1
а, h Значение емкости С/(8га,) при a:Jh, равном
0,6 0,8 1,0 2,0 3,0 6,0 ОС
0,5 1,077 1,104 1,122 1,154 1,161 1,163 1,174
. 1,0 1,128 1,185 1,228 1,327 1,346 1,353 1,380
1,5 1,144 1,216 1,280 1,483 1,532 1,548 1,598
2,0 1,140 1,214 1,286 1,590 1,704 1,738 1,816
5-3-3. Диск и плоскость с соосным диску круг-
лым отверстием.
а. Общий случай (рис. 5-6)
1
С — 8eaj J to p^dp,
о
(5-15)
где <о — решение уравнения
atlh
“ -----® dy= 1 ’
О
1 1 1
К1х' й=7+<^+4+(^-^ I <Ы6>
а 1х, у, г) = Г—Ш— + —‘-х Г г+и + ‘-ч 1.
|Д + (г + х)а 1 + (г — х)2 |д +(г + {/)2 1 +(г— г/)2]
Зависимость ПРИ различных значениях
представлена в табл. 5-2 и на рис. 5-6.
б. При й=0 ах<а2 (рис. 5-7).
Зависимость—представлена на рис. 5-7.
8еа^ \ /
При О1/а2г^0,65
8eaf
л2 а2
гг2/й
(5-17)
174
[б>0; б<4,6 % при ai/a2=0,65; 6=1,6 % при ai/a2=0 5-
6 = 0,015 % при а1/а2=0,1].
Рис. 5-6 Таблица 5-2
_А1 ft Значение емкости C/(8eai) при a2'h, равном
0 0,5 1.0 1.5 2,0
0 1,000 1,000 1,000 1,000 1,000
0,5 1,181 1,174 1,149 1,120 1,096
1,0 1,388 1,380 1,338 1,274 1,218
1,5 1,604 1,598 1,557 1,473 1,377
2,0 1,821 1,816 1,783 1,703 1,583
При «i/a2>0,65 С~&аг 31п2 —1—-Infl —- 2 \ * 2 \ "I - 1 1 1 (5-18)
175
[б>0; 6<4,6 % при ai/a2=0,66; 6 = 3,75 % при О1/ог=0,8;
6 = 0,66 % при О1/о2=0,98].
Рис. 5-7
Пример 5-2. Определим сопротивление растекания плоского дискового
анода, применяемого при электрохимической (катодной) защите от корро-
зии, если радиус анода «1=10 см, радиус околоанодного изоляционного эк-
рана а2=50 см, а удельная проводимость коррозионной среды (например,
морская вода) у=3 См/м.
Считая защищаемую поверхность бесконечной плоскостью и учитывая
аналогию, указанную в § В-5, а также соотношение (В-19), получаем
2 6
Rp=----------, где С — емкость, определяемая по данным п. 5-3-3 *.
Т С
1 Если использовать для расчета приближенную формулу (5-17), то
С »-----~ 8еаг 1,088,
1-----—0,2
л*
т. е. относительная погрешность в определении емкости по формуле (5-17)
для рассматриваемых размеров составляет
в = . 100% = (1 — -Ь588_\ 100% и 0,09%.
С V 1,089 )
При пренебрежении влиянием плоскости (С1/аг->-0) C«8e«i. Относитель-
ная погрешность в этом случае в=8,2 %.
176
При —0’2 из Рис- находим точное значение емкости: С=
Ов и>°
=8eavl,089.
Тогда искомое сопротивление растекания
Rp =---------£--------0,765 Ом.
3-8-0.1-1,0892
5-3-4. Концентрические копланарные кольца
(рис. 5-8).
Зависимость---=/( —| при различных значениях а2/а3
Дд у
и а3/а0=6 представлена на рис. 5-8.
Если И1 1,5 (а3—а2), то расчет емкости может быть выпол-
нен с помощью материалов п. 5-3-3.
Пример 5-3. Определим емкость колы зого конденсатора, применяемого
при измерении влажности древесины, при следующих его размерах
(рнс. 5-8): ао=0,5 см, ai=l,5 см, а2=2 см йз=3 см.
В данном случае
= -£L. = _LL=o,5; -^-= —» 0,667.
Од 0,5 Яд 3 4Zg 3
Пользуясь рис. 5-8, находим, что для указанных отношений радиусов
--------« 1,35, откуда
8eai
С к 1,35-8-----3--- -1,5-10- и в'-1,43 пФ,
4Л-9-109
где в' — относительная диэлектрическая проницаемость древесины.
177
5-3-5. Два коаксиальных диска (рис. 5-9).
а. При произвольных радиусах дисков.
При значение величины С определяется по
формуле (В-12), где
ж 8ея! (1----— ат+ м]; (5-19)
\ Л /
С22 8еа2(1 —- + /И); (5-20)
\ л /
16сш2те 2 [л2 (1 + а2) — 12а] w2~| (5-21)
^~1 Г
$2аг.
Рис. 5-9
где
а = ^-, М=^т*+2а [n2 (1 + а2) ~ 12aJ m3
йх л2 Зл3
8а [л2 (1 + а2) — 6а] т4>
Зл4
б. При ai = a2=a (конденсатор с одинаковыми круглыми об-
кладками1) (рис. 5-10).
1
C = 4ea^f(f)dt, (5-22)
где f(t) — решение интегрального уравнения
1 Определению емкости конденсатора с круглыми обкладками посвящено
большое число работ (см., например, [5, 6, 11, 22, 23, 29, 32, 33, 34, 37]).
178
c f I \
Зависимость -— = fl— ] представлена на рис. 5-10.
o&a \ a J
При lla<S№
C«eafn4+lnfl6n—V1+—— fln-^-Yl (5-23)
I/ \ l J 4л a \ 2a J J
[6<5 % при //a<0,4; 6<0,6 % ПРИ l/а^СД].
(5-24)
[6<15 % при Z/a^O,l; 0<2,5 % при Z/a^0,01].
Рис. 5-10
l!a 0,0 0,1 0,4 0,6 0,8 1.0 1,2
C 8га oo 4,616 1,5514 1,1978 1,0186 0,9104 0,8380
l!a 1.5 2,0 2,5 3,0 5,0 10,0 20,0 OO
C 8га 0,7644 0,6934 0,6517 0,6240 0,5708 0,5338 0,516 0,5
При 0,4^Z/fl<2,5
C^4ea(^-y+l) (5-25)
179
[6<4,5 % при Z/a^0,4; 6 = 0,34 % при Z/g=1,5; |б| <0,8%
при 1,5^/а<2,5].
При %z^2,5
4еа
с~ _J__[1_______
1 л I L 12 w / + 40 U Л
(5-26)
[б<0- |б| <0,5 % при //п^2,5; [б|<0,06 % при 2/п^5].
4еа (5-27)
i-Ад
л I
[б<0; |б|<2,9 % при //а>2,5; |б|<0,4 % при 1/а>5].
При 1)а>\ см. также формулы (5-19) —(5-21) при а=1.
5-3-6. Два коаксиальных круговых кольца
(рис. 5-11).
Рис. 5-11
Точные значения емкости при некоторых характерных соот-
ношениях геометрических параметров приведены в табл. 5-3.
Таблица 5-3
Значение емкости C/(8eos) при l/а, равном
0,1 1 10 ОС
1,125 2,1 0,6620 0,4424 0,4163
2,0 — 1,234 0,5584 0,4905
3,0 — 1,699 0,6064 0,4974
При а2/П1<1,1; 1/а2<3
С яеа, —f—
j)+TColfi>01’
(5-28)
180
где Со — емкость уединенного кругового кольца (см. и. 3-3-4).
При 1,1 1,5, //а2<3
С « 4еаа Г— -“L +11 (5-29)
L 4 Z \ аа ) J
[6<15 %; 6<10 % при 1/а2> 1].
При a2/«i> 1,5
(5-30)
[|6|<5 % при //оа^О.З]
При Ца2^3
С~---—--
2 — —^'°
2 ле/
(5-31)
[6<0; |6|<3 % при //а2^3; |6|<0,5 % при 1/а2^5].
5-3-7. Две одинаковые параллельные прямо-
угольные пластины (конденсатор с прямо-
угольными обкладками) (рис. 5-12).
Приолиженные численные значения емкости при некоторых
значениях а/l и Ь/l приведены в табл. 5-4, где R = a
— радиус описанной окружности,_а для квадратных пластин
(а=Ь) — на рис. 5-12, где /? = а]/2 .
Таблица 5-4
а 1 0,25 0,33 0,42 0,42 0,50 0,75 1,0
ь 1 0,14 0,25 0,25 0,14 0,25 0,25 0,50
с 8eR 0,372 0,462 0,458 0,370 0,447 0,426 0,570
а 1,33 1,50 1,66 2,0 2,50 2,55 3,0
ь 1 1,0 0,5 1,0 1,0 1,50 0,85 1,50
с 8BR 0,783 0,560 0,811 0,812 1,048 0,748 1,331
181
— [6
с
и<)
0],
(5-32)
При а//<0,25, a/b^\
С~-
2
2зте/
где Со — емкость уединенной прямоугольной пластины (см.
п. 3-3-7).
Рис. 5-12
1 а 0 0,01 0,05 0,1 0,2 0,4 1,0 2,0
с 8еЯ оо 35,48 7,576 4,058 2,264 1,325 0,750 0,560 0,392
При а//>0,25, afb^X
С~4еаА + ±С0. (5-33)
182
5-3-8. Две одинаковые параллельные пластины,
ограниченные выпуклыми кривыми (конденса-
тор с обкладками произвольной формы).
При a/d<0,2
С «----, (5-34)
2 лей
а при a/d>0,2
C~e-T + vC<” (5-35)
а л
где а — половина максимального размера пластины; d — рас-
стояние между пластинами; Со и S— емкость и односторонняя
площадь одиночной пластины, соответственно.
Пример 5-4. Найдем емкость воздушного конденсатора, образованного
двумя одинаковыми пластинами в форме эллипсов, расположенными в парал-
лельных плоскостях, если полуоси эллипсов а=10 см, 6=2 см, а расстояние
между пластинами й=50 см.
Пользуясь данными п. 3-3-3, устанавливаем, что при bla—Q,Q, Со»
«8еа-0,521.
Тогда согласно формуле (5-34)
„ 8-8,842-10—12-0,1-0,521 , .
Л
По формуле (5-35) при площади пластины S=nab—л-0,1-0,02»
»6,283-10-3 м2 находим
С я J,842'10"13'6’283'10^ ..г-— -8-8,842-10~12-0,1-0,521 « 1,954 пФ.
0,5 4 2
Как видно, разница в определении емкости по формулам (5-34) и (5-35)
для рассматриваемого случая (а/й=0,2) не превышает 1 %.
5-3-9. Пластина, перпендикулярная проводя-
щей плоскости.
а. Диск и плоскость (рис. 5-13).
При h/a>2
8еа
а \ К 7 / а \2 99
26/ [ + 24 \26/ + 320
8е^-. (5-37)
1-^-
лб
—VI
26/ J
л \
При значения емкости, вычисленные по формуле
(5-37), отличаются от значений, определенных по формуле
(5-36), не более чем на 0,1 %.
183
б. Прямоугольная пластина и плоскость (рис. 5-14).
При6/а^>1, а//г^>1
С = - efeln/4 (5-38)
а \ h — a j
ПриЬ/а2>1, а//г<^1
При произвольном значении — и —-—<0,5
a h^a
р ____ Со
2 Со
4ns (h—а)
(5-40)
где Со — емкость одиночной прямоугольной пластины, опреде-
ляемая по данным, приведенным в п. 3-3-7.
5-3-10. Диск между двумя плоскостями (рис.
5-15):
C=8eR$g(t)dt,
о
(5-41)
где g(t) — решение интегрального уравнения
. 1
ё (f) —— f К. (t—s) g (s)ds = 1,
— 1 1,
184
с ядром
<30
n=0
А = С 2ы8П du = I 1”2 при П = О;
®" Je^+l I 2-4"(22n —l)(2nl)£(2n-+-l)
оо
£(2n-|-1) = --~+г — дзета-функция Римана.
k—i
при п > 0;
При /</7г<0,6
(5-42)
5-4. ОБОЛОЧКИ
5-4-1. В настоящем параграфе приведены
материалы для расчета конденсаторной емкости между замкну-
тыми или незамкнутыми оболочками, хотя бы одна из которых
имеет конечные размеры.
Приведенные формулы получены, в основном, путем расчета
электростатического поля и являются точными. Помимо этого,
в тексте приводятся некоторые приближенные формулы, полу-
ченные с учетом реальных соотношений геометрических разме-
ров рассматриваемых систем.
При рассмотрении незамкнутых оболочек предполагается,
как и ранее, что их толщина пренебрежимо мала по сравнению
с любыми другими характерными размерами системы.
5-4-2. Две сферы.
185
а. Концентрические сферы (сферический конденсатор)
(рис. 5-16):
С = 4ле —— • (5-43)
R—r
Рис. 5-16
б. Неконцентрические сферы, одна из которых расположена
внутри другой (рис. 5-17):
со
С — 4ле • 2r sh —е (2п+п~ .— , (5-44)
!_в-<?»+*) а»
п=0
где
. , ^2—г2 —А , ^24-Г2—
со = Arch----------; ct2 = Arch-------------
1 2rd 2rR
Зависимость —= f (—'j при
4ner \R J
ведена на рис 5-17.
При d/r^.1, r/R^.0,5
различных значениях d/R при-
z-, . rR
С ~ 4ле---------
R —
1 R di
г (R.—r)(R? — fi}
(5-45)
[<5<10 % при cf/r^l, г//?гС0,3; 6<1 % при d/r^X,
r/R^0,15\.
в. Неконцентрические сферы, одна из которых расположена
вне другой (рис. 5-18):
C=4nzrR shaf (г, R, d), (5-46)
где
f(r,
186
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 r/R
rsh na + R sh (n — 0 « " R sh na+ r sh (« — 1) a
«_ Arch <М),-(С,+ ДД>.
2rR
В частности, при r=R
oo
C = 2mR sh p V —i—,
sh np
(5-47)
n=l
где 6 = Arch — •
R
C / f \
Зависимость-—— ==п —)при различных значениях Rl(2d)
приведена на рис. 5-18. Таблица 5-5 К/(2d) ^0,6,
/ R \ \ 2^ /max 0,2 0,3 0,4 0,5 0,6 С « (5-48) 1 + А_А
{ г \ \ Я /max 1,0 0,7 1,0 0,7 0,4 г d [6>0; некоторые
^гпах» % 0,25 0,75 6,5 10,0 11,0 численные значения б при различных соотно- шениях R! (2d) и r/R указаны в табл. 5-5]. ллипсоида.
5-4-3. Два конфокальных э
а. Трехосные эллипсоиды (рис. 5-19):
Рис. 5-19
С =-----------—------------ , (5-49)
*) — -F2(<P2. k)
где R((fy k) — эллиптические интегралы первого рода с модулем
k2__ al-bi 4~l>2
4ned
188
Ф1
и аргументами
Hf)’; ,ti=ar "’И1
d — Val~cl=]^al—cl [ >6>cJ.
Пример 5-5. Найдем емкость воздушного конденсатора, образованного
конфокальными трехосными_эллипсоидами, полуоси которых Oi=5 см, 61=3 см,
Ci=2 см, 02=7 см, Ь2 = ]/33 см, с2 = 1^28 см.
Для определения емкости необходимо предварительно иайти значения
эллиптических интегралов F(cp, k). Вычисляем сначала их модуль k и аргу-
менты ф1 и <Р2 =
Пользуясь далее таблицей (1], получаем
Л(Ф1. k) к 1,395; Га(<ра, k)x 0,763.
Подставляя в формулу (5-49) численные значения входящих в нее пара-
метров, находим искомую емкость
„ , d . 1
—— 4ттр____ ~ — 4зт• —— — — У
Fi(<Pi. k)-F2(<f2, k) 4Л-9-10»
/5г —2» -10-* ~ 0 806.10_п ф ~ 8 пФ.
1,395 — 0,763
б. Вытянутые сфероиды (рис. 5-20):
£___ 8ned
1П [ ai ~Ь а2 —
\ а1 — Pg “В /
где
d = Val—cl=Vc^—cl [а=Ь<с].
в. Сжатые сфероиды (рис. 5-21):
С__________4ned_______
Сп
arccos —--arccos —
ai а»
(5-50)
(5-51)
где d — V al—ci = aj—cl [a — b> c].
-189
5-4-4. Коаксиальные торы круглого сечения
(рис. 5-22):
c«^[‘-(4)’(1^+2i'ni)]- (5-62)
1п —
г
Рис. 5-20
Рис. 5-21
5-4-5. Сферический
длинного круглого
сегмент внутри бесконечно
цилиндра.
а. Общий случай (рис. 5-23)
С = 4ле7? J g (t])’cos у d ,
о
(5-53)
Рис. 5-22
Рис. 5-23
где g(t\) —решение интегрального уравнения
а
£(11)--- J К(£; ri)g(tyd£,= — cos-—- (—a^rj^a);
л —а л 2
К(Е: ’|>=т2^^)Г^с05[("+1)<5-’Л]х
п=0
vsjn2n 1 + 4/27? \2n4-i .
2 \ а )
190
оо
,2П
-—du.-, /0(и)—модифицированная цилиндриче-
1
Pan = 2 I
(«')2 J
О
ская функция первого рода нулевого порядка Ч
При R/a<.0,7
й С- ~ — (а 4- sin а) 4- (а 4- sin а)3 —
4леЯ л л3 v а
4₽1
л^
( R\2 1
(а 4-sin а)3 —
\ а
₽2 ЗР3
у-р(а) 4-уу (а 4-sin а)4
л3
2₽0₽2 п , . 16Р« .
~^—Р (a)4-~zr~(a + sina)4
О
1
л?
1
4- — (а 4- sin а)
л6-
₽4 2₽о₽9 „ 32fiS
-^- <7 (а) (а 4- sin а)2 р (а) 4—(а 4- sin а)6
л4
л1
R V
а )
(5-54)
/ R
\ а
3
R
а
где
2
р (а) — (2 sin а + sin 2а)2-----(а 4- sin а) (3 sin 2а 4- 2 sin За);
3
<7 (а) = -^- (а 4- sin а) (5 sin 4а 4- 4 sin 5а) —.
-—— (2 sin а + sin 2а) (4 sin За 4- 3 sin 4а) -f — (3 sin 2а + 2 sin За)2;
3 6
ро= 1,3677; ₽2= 1,9407; р4=2,5873.
б. При а=л (сфера внутри цилиндра, рис. 5-24) значение С
определяется зависимостью, представленной на рис. 5-24.
При R/a^.0,65
С
4л87? .[1 4-0,8707.-4-0,7581 .
L а
/ р \4
4-0,5748.1 — ) 4-0,5004-
\ а ]
[6>0; 6<3,2 % при 7?/а^0,65; 6<0,2 % при R/a^0,3\.
При R/a> 0,65
C^8neR---
1-А
а
(5-56)
1 Коэффициенты p2n (0sgnsg41) табулированы в [46].
191
[6<4,4 % при /?,’а=0,65; 6=—5,2 % при /?/а=0,9; 6=—3 %
при /?/а = 0,95].
Рис. 5-24
К с
4 леЯ
0,1 1,0969
0,2 1,2125
0,3 1,3555
0,4 1,5369
0,5 1,7756
0,6 2,1058
0,7 2,6002
0,8 3,4483
0,9 5,4124
0,95 8,2475
5-4-6. Сфероид внутри бесконечно длинного
круглого цилиндра (рис. 5-25).
о 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 Ъ/а
Рис. 5-25
ъ а С
4ле1
Ыс=Ц Ь,'с=2
0,0 1,3172 0,8270
0,1 1,4864 0,8924
0,2 1,6992 0,9683
0,3 1,9675 1,0595
0,4 2,3110 1,1727
0,5 2,7640 1,3183
0,6 3,3924 1,5155
0,7 4,3380 1,8043
0,8 —— 2,2871
0,9 —• 3,3675
0,95 — 4,8759
192
Зависимость-—— = п— при двух характерных значениях Ь/с
4пе.Ь \ (2 I
приведена на рис. 5-25.
См. также п. 3 и 4 табл. 5-6.
5-4-7. Произвольное осесимметричное тело
внутри коаксиального с ним бесконечно длин-
ного круглого цилиндра.
При
С«С0 (1
уС0
4яеа /
(5-57)
где R — наибольший радиус сечения тела; а — радиус цилиндра;
у~0,8707; Со — емкость рассматриваемого тела как уединенного
проводника, определяемая по материалам гл. 3.
Следующие из (5-57) приближенные формулы для емкости
между некоторыми осесимметричными проводниками и беско-
нечно длинным круглым цилиндром приведены в табл. 5-5. При
7?/а<0,4 погрешность этих формул не превышает 10%
5-4-8. Сфера внутри куба (рис. 5-26):
q__ 4ле7?
~~ 16,468
9
(5-58)
£
а
1— 1,7476-р
При а//?>2,5 емкость рассматриваемой систёмы можно рас-
считывать как емкость сферического конденсатора (см. (5-43)),
радиус внешней обкладки которого равен 0,5722а.
Рис. 5-26
5-4-9. Два концентрических полых сфериче-
ских сегмента (рис. 5-27) ’.
1 Материалы п. 5-4-9 основаны на данных, предоставленных авторам
С. Н. Кадниковым.
7 Заказ Ns 507
193
Таблица 5-6
Диск внутри цилиндра
Приближенное выражение для С
8е7?
0,55#
а
2
10,28еЯ
1 — 0,71 —
а
5
Полый полусферический сегмент вну-
три цилиндра
4пе1а
t 0,87/а ’
Вытянутый сфероид внутри цилиндра
а
2с , I + с
о. — — 1п —!:
I 1 — с
с =У 1‘ — #2
Сжатый сфероид внутри цилиндра
4лв#Р
0,87Р ’
а
2]/#2 — Ь2
л
4ле#р
0,87 р./? ’
а
Прямой круглый цилиндр конечной
длины внутри бесконечно длинного ци-
линдра
I h \0.76
и = 0,637-4-0,554 I —-1
\ 2R /
194
Значение С определяется по формуле (В-12) при
е,
Си = 4тг С Д (0 cos 4- dt; (5-59)
2
с22 = 4ле7? J f.2 (t) sin dt-, (5-60)
е2
Л
С12 = 4ле7? Д (0 sin ~ dt, (5-61)
е2
Рис. 5-28
где Д(/), Д(0, h(t) —решения систем интегральных уравнений
fl (0 + 1 Д,3 (X) [К+ (t, х) + (t, х)1 dx = -1 cos -Ц
я е* л 2
?2,з (0 + J Д (х) [/С+ х)—/<_ (t х)] dx = q— sin —,
л о л 2
в которых f2,3=f2 При <7=1; з=/з при <7=0; p = r/R^l (при
r/R=l должно соблюдаться условие 62>6i);
1 — 2р cos (х ± f) + р2
Зависимости ———=/(62) при различных значениях 61 для
4зге7?
Р = 0,4 и р = 0,8 приведены на рис. 5-28.
При 61 = л и 62 = 0 —см. формулу (5-43).
5-5. ПРОВОДА И ПЛАСТИНЫ
5-5-1. В настоящем параграфе приведены
материалы для расчета конденсаторной емкости между прово-
дами и пластинами. Все приведенные формулы (за исключением
формул п. 5-5-12) определяют значение емкости между прово-
дами и плоскостью; они получены с использованием соотноше-
ния (В-18) методом средних потенциалов (§ 1-2) и дают зани-
женные значения емкости.
Применение приведенных материалов иллюстрируется при-
мерами расчета емкости между землей и антеннами различных
типов.
Использование соотношения (В-18) позволяет применить
приведенные материалы и для расчета конденсаторной емкости
между проводами (см. § 5-2).
5-5-2. Прямолинейный провод конечной длины,
параллельный проводящей плоскости (рис. 5-29):
Рис. 5-29
С «.----, (5-62)
In ——
а
где
Oi^lnfl+l/ 1+-T-V——1/1 _|__|_0,307, сс=—.
\ V а2 ) 1 а ]/ a2 2h
Значения Dx даны в табл. 5-7.
196
_________________________________________________Таблица 5-7
а а а D,
20 0,000 0,90 0,838 0,45 1,327
10 0,097 0,85 0,873 0,40 1,421
5 0,189 0,80 0,912 0,35 1,529
2,5 0,362 0,75 0,953 0,30 1,660
2,0 0,440 0,70 1,002 0,25 1,819
1,25 0,652 0,65 1,052 0,20 2,013
1.И 0,714 0,60 1,110 0,15 2,280
1,00 0,774 0,55 1,175 0,10 2,660
0,95 0,806 0,50 1,246 0,05 3,328
Пример 5-6. Определим емкость между землей и прямолинейным прово-
дом длиной 30 м и диаметром 6 мм, расположенным параллельно поверхно-
сти земли на высоте Л=15 м.
I 30
В данном случае а = ---=------- =1 ив соответствии с табл. 5-7
2h 2-15
£>1 = 0,774. Тогда согласно (5-62)
с«---------^3O±°-S_______г зпф.
36л (In ------0,774 А ~
\ 0,003 /
5-5-3. п соединенных между собой одинаковых
прямолинейных проводов, параллельных про-
водящей плоскости.
а. Провода расположены в одной плоскости (рис. 5-30).
При («—\)b^.l, 2h/b^l
г, 2леп/ ,r
In--p (n — 1) In ——-n (D± -|- Bn)
a b
vug Dt находится из табл. 5-7, a
Bn = — X k In (n—k).
n2 fe=l
Значения Bn даны в табл. 5-8.
Таблица 5-8
п Вп п вп п вп п вп
2 0,000 8 0.799 14 1,267 20 1,584
3 0,154 9 0,894 15 1,327 30 1,951
4 0,311 10 0,979 16 1,384 40 2,234
5 0,454 11 1,059 17 1,439 50 2.448
6 7 0,580 0,696 12 13 1,133 1,202 18 19 1,490 1,538 100 3,125
197
При (и— V)bs^l, fe/(2/i)>l
2леп/
In ^L + (п - 1) In А — n (Dt + Вп)
а 2/1
(5-64)
Рис. 5-30
Пример 5-7. Определим емкость между землей и горизонтальной антен-
ной, расположенной на высоте Л=15 м и состоящей из шести параллельных
проводов длиной /=30 м и диаметром 6 мм, если расстояние между прово-
дами b=0,6 м.
В рассматриваемом случае а=//(2й) = 1. При этом значении а, согласно
табл. 5-7, £>1=0,774, а Вп=0,580 (см. табл. 5-8 при /1=6). Поэтому поль-
зуясь формулой (5-63), находим, что
С а-------
36л.
2Л-10-9-30-6
[2-16 2-15
In----— (6 — 1) In------6 (0,774 + 0,580)
0,003 0,6
Ф ~ 484 пФ.
б. Провода расположены в разных плоскостях (рис. 5-31).
Если dr (г=1, 2, ..., п—1)—расстояние от какого-либо
Рис. 5-31
Рис. 5-32
одного провода до остальных проводов, h — наименьшее рас-
стояние проводов ОТ ПЛОСКОСТИ, ТО при d'zmaxCft
2tie.nl
F1 ’
(5-65)
198
где
Fi -= In
a определяется из табл. 5-7 по значению <х=
в. Провода расположены с постоянным шагом по образую-
щим кругового цилиндра (рис. 5-32).
При dr<g.h значение емкости определяется формулой (5-65),
где следует принять dr= 27? sin — (r= 1, 2, ..., п— 1).
Пример 5-8. Определим емкость между землей и горизонтальной антен-
ной, состоящей из шести проводов длиной 30 м и диаметром 6 мм, располо-
женных по поверхности кругового цилиндра диаметром 27?= 1,5 м, ось кото-
рого отстоит от поверхности земли иа расстояние 7i=15 м.
Расстояния между проводами, входящими в систему, di=d5=/?=0,75 м,
da = di = yr3 7?= 1,29 м, d3=2R—1,5 м. Таким образом, даже наибольшее из
этих расстояний удовлетворяет неравенству dr<^h, что позволяет применить
I 30
для расчета формулу (5-65). Пользуясь табл. 5-7, при а =--—---=
2/? 2-15
= 1 находим, что £>!=(),774. При найденных значениях dr и заданных значениях
геометрических параметров коэффициент Fi, входящий в (5-65), оказыва-
ется равным:
г- , 2-15
А = In —---
0,003
2-15 0,75
, 2-15 1,29
In-------• -1-----
1,29 30
In .
0,75 30
9.15 15
+ In ---- 4,644 Й 21,871.
1,5 30
Подставляя найденные значения в (5-65), получаем, что
_ 2л-10-9-30-6 . _
С л-------------Ф ~ 457 пФ.
36я.-21,871
5-5-4. Прямолинейный провод конечной длины,
перпендикулярный
(рис. 5-33):
проводящей плоскости
С
2ле/
In---D2
a
где коэффициент D2 определяется формулами:
при
D2 = i+~ In — + H+-1) In fl——fl +
I I \ I } \ I 1 \
при h!l>\
(5-66)
Dz =
199
Значения D2 даны в табл. 5-9.
Таблица 5-9
h,l D2 НИ d.2 hll D,
0,02 0,928 0,30 0,645 1,0 0,477
0^04 0^884 0,40 0,604 1,11 0,465
0^06 0,850 0,50 0,569 1,25 0,451
0Д)8 0,820 0,60 0,554 2,0 0,408
0,10 О',795 0,70 0,523 2,5 0,392
0,15 0,744 0,80 0,504 5,0 0,352
0,20 0,25 0,702 0,670 0,90 0,489 10,0 ОО 0,332 0
Рис. 5-33
Пример 5-9. Определим емкость между землей н вертикальной антеииой
длиной 12 м и диаметром 6 мм, нижний конец которой находится на рас-
стоянии 3 м от поверхности земли.
В данном случае, при /г//=0,25, из табл. 5-9 находим, что Da=0,670.
Тогда из (5-66) получаем, что
2л-10—9 12
С ~
(12
In ——--------0,670
0,003
Ф ж 87,4 пФ.
5-5-5. п одинаковых проводов, перпендикуляр-
ных проводящей плоскости.
а. Провода расположены в одной плоскости (рис. 5-34).
При (n — l/d^l
С____ 2neln
In — -f- (n - 1) In — — n (D2 + Bn)
a d
(5-67)
где значения D2 определяются из табл. 5-9 при заданном отно-
шении h/l, а значение Вп — из табл. 5-8.
200
При (п— О d^h и l[d<\
fj ____________________________2ле/п______________
In — -I- (п — 1) In — п (D2 + Вп)
а I
(5-68)
Рис. 5-34
Пример 5-10. Определим емкость между землей и вертикальной антен-
ной, образованной шестью прямолинейными проводами длиной Z=12 м и диа-
метром 6 мм, если расстояние между соседними проводами d = 0,6 м, а рас-
стояние нижнего конца каждого провода до земли А=3,0 м.
Пользуясь данными табл. 5-8 и 5-9, находим, что при заданных разме-
рах и числе проводников системы Вп = 0,580, £>2=0,670. Подставляя эти зна-
чения в (5-67), находим, что
С ~
2л-10-М2-6
Г 19 12
36Л In—-----------1-5 In-----6(0,670 + 0,580)
0,003 0,6
Ф к 254
пФ.
б. Провода расположены по образующим круглого цилиндра
(рис. 5-35):
(569)
02R
02а
Рис. 5-35
201
где
F, = ln —
a
In——|——'j—nD2;
d»- I /
dr = 2R sin —
‘ I M
(r=l, 2, . . . , n—1),
а значения D2 находятся из табл. 5-9.
5-5-6. Г-образный провод, расположенный в
Рпс. 5-36
плоскости, перпендикулярной проводящей пло-
скости (рис. 5-36):
С
2ле (Zt -j-12)
1-2 |п 2 (ft + lt)
h. “Ь . а
—|— 2 ,ЗОЗ£>3
(5-70)
где Di определяется из табл. 5-7 при а=------------, a D2 и D3
2 (ft -|- Zt)
находятся соответственно из табл. 5-9 и 5-10.
Пример 5-11. Определим емкость между землей п Г-образной антенной
(рис. 5-36) при Z2=30 м, а=3 мм, /,= 12 м, ft=3 м.
I 30
При заданных параметрах системы а =-----------=—— = 1, и нз табл.
2 (ft + Zj) 2-15
5-7 находим, что £>1 = 0,774; точно так же при Zi/Zi = 3/12=0,25 пз табл. 5-9 полу-
чаем, что £)2 = 0,670, а пз табл. 5-10 (при Zf/Z2= 12/30=0,4 и ft/Zt=0,25) нахо-
дим £>з=0,194. Тогда в соответствии с (5-70)
с ~ ________________________2л.-10-я (30+12) _________
36л —-2... ..(9.210—0,774)4---(8,294—0,670)+2,303-0,194
130+12 30+12 7
к 270 пФ.
Если воспользоваться при приближенном определении емкости рас-
сматриваемой антенны простым суммированием емкостен горизонтального
202
Таблица 5-10
l„ . /, Л ’ l, Значение коэффициента £)3 при
h llr равном li'h, равном
0 0,2 0,4 0,6 0,8 1,0 0,8 0,6 0,4 0,2 0
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 о,9 1,0 0 0,1 0,2 0,3 0,4 0,5 0.6 0,7 0,8 0,9 1,0 0 0,130 0,189 0,222 0,241 0,250 0,254 0,254 0,252 0,248 0,243 0 0.055 0,099 0,135 0,164 0,186 0,204 0,218 0,229 0,237 0,243 0 0,137 0,200 0,237 0,259 0,271 0,277 0,279 0,278 0,275 0,271 0 0,064 0,116 0,157 0,189 0,214 0,233 0,247 0,258 0,265 0,271 0 0,141 0,207 0,247 0,271 0,285 0,292 0,295 0,295 0,293 0,290 0 0,072 0,129 0,173 0,207 0,233 0,253 0,267 0,278 0,285 0,290 0 0,144 0,213 0,254 0,279 0,295 0,303 0,306 0,307 0,306 0,303 0 0,078 0,137 0,184 0,222 0,248 0,267 0,282 0,292 0,298 0,303 При Ijly 0 0,146 0,216 0,260 0,285 0,302 0,310 0,314 0,316 0,315 0,313 При Ijli 0 0,083 0,146 0,-195 0,233 0,260 0,278 0,293 0,302 ' 0,308 0,313 1 0 0,147 0,218 0,265 0,290 0,307 0,317 0,322 0,324 0,323 0,321 > 1 1 0,088 0,155 0,206 0,243 0,269 0,286 0,302 0,311 0,317 0,321 0 0,147 0,221 0,269 0,295 0,312 0,323 0,329 0,331 0,330 0,329 0 0,093 0,165 0,214 0,252 0,278 0,297 0,311 0,320 0,326 0,329 0 0,150 0,224 0,272 0,300 0,318 0,330 0,336 0,340 0,339 0,338 0 0,097 0,174 0,226 0,263 0,290 0,309 0,322 0,330 0,336 0,338 0 0,153 0,228 0,275 0,306 0,325 0,338 0,346 0,350 0,350 0,350 0 0,106 0,187 0,241 0,276 0,305 0,323 0,335 0,342 0,347 0,350 0 0,155 0,232 0,282 0,314 0,335 0,349 0,357 0,362 0,364 0,365 0 0,125 0,207 0,262 0,296 0,323 0,340 0,352 0,358 0,362 , 0,365 0 0,159 0,239 0,291 0,325 0,348 0,360 0,373 0,379 0,382 0,383 0 0,158 0,239 0,291 0,325 0,348 0,363 0,373 0,379 0,382 0,383
и вертикального проводов (см. примеры 5-6 и 5-9), то значение С оказыва-
ется равным 285 пФ, т. е. на 5% больше вычисленного по формуле (5-70),
учитывающей взаимное влияние горизонтального и вертикального проводов
антенны.
5-5-7. п соединенных между собой Г-образных
проводов, лежащих в параллельных плоско-
стях, перпендикулярных проводящей плоскости
(рис. 5-37):
’ r_2ne(/j.+ Z2)
L
(5-71)
где
L = — /—------------------Г1п 2(/|±А). — Djl + -—1±--------
п ( ly + Z2 L a J £ + £
+ (n - 1) f-----------fIn 2 (/-- Z1) - Dj U-------------l-----
L 11 + Z2 \ d / li + Z2
+ 2,303D3 — Bn,
Рис. 5-37
a £>b Bn, £)2 и D3 — коэффициенты, определяемые соответственно
из табл. 5-7 /при а =---------), 5-8—5-10.
( н 2(ft + ZJ )
Пример 5-12. Определим емкость между землей и антенной, образованной
соединением горизонтальных и вертикальных проводов, рассмотренных в при-
мерах 5-7 и 5-10.
В данном случае Zi/Z2= 12/30=0,4; Zi/Zi = 3/12=0,25 и из табл. 5-10 нахо-
дим, что Оз~0,194. Тогда, пользуясь данными, полученными в примерах 5-7
и 5-10, находим
L & _L[----—--- (9,210 — 0,774)-|-—----(8,294 — 0,670) +
6 ( 30+ 12 30+ 12
+ 5 М*—(in -2<3+12->- - 0,774) + —LL- f In Л _ 0,670)1 j +
L 30+12 V 0,6 / 30+12 \ 0,6
+ 2,303-0,194 — 0,580 к 3,656.
Подставляя полученные значения в (5-71), имеем
Са2д.10-..(30+12)фаЮ8пф
36л-3,656
204
Если же просто суммировать емкости, полученные в примерах 5-7 и 5-10,
то С= (484+254) пФ = 738 пФ, что на 15,7 % больше значения, подсчитанного
по формуле (5-71) с учетом взаимного влияния горизонтальных и вертикаль-
ных проводов.
5-5-8. Т-образный провод в плоскости, перпен-
дикулярной проводящей плоскости (рис. 5-38):
с _ 2ле (1У + 2/2)
Л
где
(5-72)
Л
2/г
й + 2/2
+
\ а /
а
й + 2й
2 (Z1 + -2,3Q3DS,
й + 2/2
Рис. 5-38
a Du D2 и D3 — коэффициенты, определяемые соответственно
из табл. 5-7 (при а =--------—), 5-9 и 5-10.
I Л + й /
Пример 5-13. Определим емкость между землей и Т-образной антенной,
если ее горизонтальный и вертикальный провода имеют те же размеры, что и
в примерах 5-6 и 5-9 (й=15 м, /1=12 м, й = 3 м, а = 0,003 м).
При указанных значениях параметров антенны
---------=-----—----~ 0,714; ---l-i-=---------а; 0,286-
2Z2+Zi 30+ 12 2Z2 + Z* 30+12
2(й+ й) = 30 + 24 ~ [ 285; — =0,25; =0,8
2/2+й 30+12 lt /2
и из табл. 5-7, 5-9 и 5-10 находим, что £>1 = 0,774; £>2 = 0,670; £>з~0,263. Тогда
значение Ti в формуле (5-72) оказывается равным:
7\ яв 0,714 Г1п + I2)----0 774 1 _|_ 0,286 (1п ------0,670+
L 0,003 J \ 0,003
+ 1,285-2,303-0,263 и 8,98.
Подставляя найденные значения в формулу (5-72), получаем
2п-10-412+ 30) фк26р
36л-8,98
205
5-5-9. п Т-образных проводов, лежащих в па-
раллельных плоскостях, перпендикулярных
проводящей плоскости (рис. 5-39):
г 2ле (?х + 2/2)
Т
1 2
(5-73)
где
Л
L -dJ + -4--
n [ -[- 2/2 I a I li • I 2/а
О + 2/г
2/8
G + 2/г
—В„ + 2,303- 2(/1 + /г)В3,
Zi + 2/2
Рис 5-39
a Db Вп, В2 и £>3 — коэффициенты, определяемые из табл. 5-7
(при а — —2-----1 , 5-8—5-10, соответственно.
' к к ~Wi /
5-5-10. V-образный провод, параллельный проводящей пло-
скости (рис. 5-40):
2ле (QT /2)
N
(5-74)
где
(’н^-^й+т—7(1П^—оХуз.зоз^-у,);
11Т »2 \ / *1 ”Г *2 \ Й2 /
и О/ — коэффициенты, определяемые из табл. 5-7 при а=
= ^1/(2Л) и а=/г/(2/г) соответственно, а и У2 — коэффициенты,
определяемые из табл. 5-11 и 5-12, соответственно.
206
Таблица 5-11
е. ° Значения коэффициента при 12 равном
1,0 0,9 0,8 0,7 0,6 0,5 0,4 0.3 0,2 о,1
180 0,3010 0,3004 0,2983 0,2942 0,2873 0,2764 0,2598 0,2346 0,1957 0,1323
165 3029 3023 3002 2960 2891 2781 2613 2359 1967 1329
150 3086 3080 3056 3016 2944 2832 2660 2400 1999 1348
135 3185 3179 3156 3112 3037 2920 2741 2469 2053 1380
120 3334 3326 3303 3255 3176 3051 2860 2573 2134 1427
105 3542 3534 3508 3457 3370 3234 2028 2714 2244 1492
90 3828 3820 3780 3732 3635 3483 3254 2911 2393 1578
85 3945 3936 3905 3844 3743 3584 3346 2989 2453 1612
80 4075 4066 4033 3970 3863 3697 3448 3076 2518 1650
75 4220 4211 4176 4109 3997 3823 3560 3172 2591 1691
70 4383 4372 4336 4265 4146 3962 3686 3277 2670 1736
65 4565 4554 4515 4440 4313 4118 3825 3395 2759 1786
60 4771 4759 4718 4636 4501 4292 3981 3526 3857 1842
55 5004 4992 4946 4859 4713 4489 4156 3678 2966 1903
50 5271 5257 5208 5112 4954 4712 4354 3838 3089 1971
45 5579 5563 5509 5404 5230 4966 4580 4025 3227 2048
40 5937 5920 5859 5742 5550 5260 4839 4239 3354 2136
35 6360 6340 6272 6140 5925 5603 5139 4486 3566 2236
30 6870 6846 6767 6616 6371 6009 5494 4778 3780 2354
25 7948 7470 7376 7198 6915 6502 5923 5128 4035 2494
20 8229 8264 8148 7933 7598 7118 6457 5563 4351 2668
15 9376 9330 9180 8909 8499 7926 7155 6129 4762 2892
10 1,0960 1,0892 1,0681 1,0318 9793 9082 8149 6934 5345 3210
5 1,3789 1,3663 1,3314 1,2771 1,2034 1,1079 9863 8320 6346 3757
Таблица 5-12
е, •• Значения коэффициента У2 при 2h/llt равном м,
0,2 0,5 1,0 2,0 5,0
0 0,648 0,359 0,203 0,106 0,043
15 '584 349 202 106 043
30 497 328 197 106 043
45 432 304 191 1045 043
60 384 282 185 103 043
75 348 264 178 102 043
90 321 249 172 101 043 1
105 300 237 167 099 043
120 285 228 163 098 0425
135 274 221 160 097 0425
150 267 216 158 097 0425
165 262 213 156 096 0425
180 261 212 156 096 0425
0 0,571 0,312 0,175 0,091 0,037
15 528 306 174 091 037
30 461 292 171 091 037
45 406 274 167 091 037
60 364 257 163 090 037
75 331 242 158 089 037
90 307 230 154 088 037 0,75
105 288 220 150 087 037
120 274 212 147 086 037
135 264 206 144 086 037
150 257 202 142 085 037
165 253 199 141 085 037
180 251 198 141 085 037
0 0,432 0,239 0,135 0,071 0,029
15 414 236 135 071 029
30 379 229 133 071 029
45 343 221 131 0705 029
60 313 210 129 070 029
75 289 200 126 0695 029
90 270 192 124 069 029 0,5
105 255 186 121 069 029
120 244 180 1195 068 029
135 235 175 118 068 0285
150 230 172 117 0675 0285
165 225 171 116 067 0285
180 223 170 116 067 0285
0 0,238 0,136 0,079 0,042 0,017
15 235 136 079 042 017
30 226 134 079 042 017
45 215 131 078 042 017
60 204 128 0775 042 017 0,25
75 194 126 077 042 017
90 185 122 076 042 017
105 178 120 075 042 017
120 172 117 074 042 017
208
Продолжение табл. 5-12
0. •° Значения коэффициента У2 при равном hl,
0,2 0.5 1.0 2.0 5,0
135 0,167 0,116 0,074 0,041 0,017
150 164 114 073 041 017 0 94
165 162 113 073 041 017
180 161 113 073 041 017
0 0,099 0,059 0,035 0,019 0,008
15 099 059 035 019 008
30 097 059 035 019 008
45 096 058 035 019 008
60 092 058 035 019 008
75 092 057 035 019 008
90 090 057 035 019 008 0,1
105 088 056 035 019 008
120 086 056 034 019 008
135 085 055 034 019 008
150 084 055 034 019 008
165 084 055 034 019 008
180 0835 055 034 019 008
Пример 5-14. Определим емкость между землей и горизонтальной .V-об-
разной антенной, расположенной на высоте /г=15 м и образованной прово-
дами диаметром 2а=6 мм и длиной Z1 = 30 м и lz= 15 м, .пересекающимися
под углом 0=45°.
В данном случае 2й/а= 10 000; 2/i/Zi=l; 2ft/Z2=2 и из табл. 5-7 находим,
что £4=0,774, Р/= 1,246.
Далее из табл. 5-11 при 0 = 45° и Z2/Zi=1/2 получаем, что У1 = 0,497, а из
табл. 5-12 находим, что Уг=0,131. Тогда
= ----—----(in 104 — 0,774) 4-------(In 10—* — 1,246) 4- 0,843 « 9,123.
30— 15 30 4- 15
Подставляя найденные значения в формулу (5-74), находим
_ 2n-10~s-(30+15) . _
С ~1------------!-- Ф яг 2/4 пФ.
36 л-9,123
5-5-11. п одинаковых проводов, расположенных
по образующим круглого конуса с осью, перпен-
дикулярной проводящей плоскости (рис. 5-41):
„ 2ne.nl /с- -уг,
где
U = In ----0,307----— (П2—0,307) + 2,303 V* Ylk,
а cos *₽ и
D2 — коэффициент, определяемый из табл. 5-9 по отношению
hjlcos(f (<р — половина угла при вершине конуса); Yih — коэф-
209
фициент, определяемый из табл. 5-11 для +го провода по зна-
чению угла между каким-либо одним проводом и остальными
при hjl\ = 1.
Рис. 5-41
Пример 5-15. Определим емкость между землей и антенной, состоящей
из шести одинаковых проводов диаметром 2д=6 мм, расположенных по об-
разующим конуса с углом при вершине 2ф=б0°. Длина провода /=30 м, вы-
сота вершины конуса над землей h= 15 м.
В данном случае Z/a=104; /cos<p«26 м; углы между проводами 012=
=61,6=28,9°; 94,3=03,5=51,3° и 01,4=60°.
По табл. 5-9 при----------==-----а; 0,583находим, что £>2=0,548, а из
/ cos <р 26
табл. 5-11 при Z2/Zi=l и указанных значениях 0!, i получаем
У1,2 = 0,705; у113 = 0,520; Г1>1 = 0,477,
Тогда
п—1
у, Ylh = 2 (0,705 + 0,520) + 0,477 = 2,927;
k=i
£7 == in 10* — 0,307----------(548 — 0,307)+ 2,303-2,927 а: 14,023.
cos 30°
Подставляя найденные значения в (5-75), имеем
С а
2л-10~а-30-6
14,023
Ф а 713 пФ .
5-5-12. Прямолинейный
р е з круговой вырез в
(рис. 5-42).
При 27? ~1
провод, проходящий не-
проводящей плоскости
С
2ле1
, Г 21R -
1п -----------
|a(27? + Z)
(5-76)
210
при
2/?</
(5-77)
Рис. 5-42
Пример 5-16. Определим емкость между проводом диаметром 2 мм и
длиной 40 мм и металлической панелью вольтметра, если указанный провод
проходит через отверстие в панели диаметром 10 мм (влиянием изоляции
пренебрегаем).
Пользуясь формулой (5-76), при е=е» находим
2л-10-МО- Ю-s
36л-1п
2-40-5
40+10
= 1,05-10—12 Ф = 1,05 пФ.
По менее точной формуле (5-77)
С
2л-10-9-40- Ю-з
36л-1п-^-
1
Ф = 0,97 пФ.
Сопоставление этих результатов показывает, что при 1/(27?) = 4 формула
(5-77) дает значительную погрешность (примерно 10 %).
При 1/(27?) ^10 разница в значениях, вычисленных по формулам (5-76)
и (5-77), не превышает 6,5 %, а при 1/(27?) ^20 — 0,7 %.
5-6. ПЛАСТИНЫ И ОБОЛОЧКИ
5-6-1. В настоящем параграфе приведены
материалы для расчета конденсаторной емкости некоторых си-
стем, образованных пластинами и оболочками конечных разме-
ров. Все приведенные формулы получены путем расчета элек-
тростатического поля и являются в большинстве своем точными.
Помимо этого, приведены некоторые приближенные формулы,
полученные из точных с учетом реальных соотношений разме-
ров рассматриваемых систем.
5-6-2. Диск внутри прямого круглого цилиндра,
а. Диск, соосный с бесконечно длинным цилиндром
211
C ( R
(рис. 5-43). Зависимость-— = П—
8eR \ а
также табл. 5-6, п. 1).
приведена на рис. 5-43 (см.
R а с 8еД
о,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 0,95 1,0603 1,1272 1,2047 1,2967 1,4093 1,5531 1,7483 2,0420 2,5896 3,1831
Рис. 5-44
21?
1 а R а с 8еД Ртах], *
0,25 0,25 0,50 0,75 1,6105 2,3883 3,3203 0,01 0,07 1,21
0,50 0,25 0,50 0,75 1,2729 1,6371 2,1796 0,14 1,1 3,3
1,0 0,25 0,50 0,75 1,1717 1,4256 1,8944 1,0 10,0 20,0
б. Диск, соосный с цилиндром конечной длины (рис. 5-44).
Зависимость—=/7—^ при различных значениях l/а приве-
о8/< \ а )
дена на рис. 5-44.
5-6-3. Сферический сегмент между двумя пло-
скостями.
а. Общий случай (рис. 5-45):
С = 4леД J g (rj) cos — dr\, (5-78)
о 2
где g(r]) — решение интегрального уравнения
£(П)-- Г К& П)£©= — cos
Л —сс я
(—л «);
X cos (I—т]) j £ (2н-|- 1) |\— l)nsin2n
— (22n+i — 1) cos2n + j ,
g(2n + l) — дзета-функция Римана.
При R!h<G,l
С l/i - \ Fi , In 2 i । ч Я
-------— (a sin a) 1 -| (a + sin a) — -p
4ле/? л [л-h
, ( In 2 \2 . / Д \2-|
+ ----- (a + sin a)2 — 4-
\ л / \ h J J
Рис. 5-45
— LLd! (3a sin 2a + 2a sin 3a + 5 +-^- cos a—3 cos 2a—
л2 L 16 2
_— cos 3a—2 cos 4a) + -ln (a + sin a)4] [ —У+
2 па J \ h /
213
_L | ln 1 2 [2a2 (3 sin 2a+2 sin 3a) + 2a (5 + 7 cos a—
л3 I 16 i
—2 cos 2a—7 cos 3a —3 cos 4a) 4-13 sin a4-11 sin 2a—sin 3a—
__LLsin4a-2sin5al+-^(a4-sina)sl(4yi6>0].(5-79)
б. При а=л (сфера между двумя плоскостями, рис 5-46)
приближенная зависимость-^^-=/ ^приведена на рис 5 46
Рис. 5-46
При R/h^.0,7
/ 4
С ss= 4ле7? I 1 4~ р"
\ n—i
где р = — In 2 [6>0].
h
При 1>/?/й>0,7
1 - Rih
5-6-4. Сфера внутри плоского кольца
При 1,5<Ь/а ^00
к да
(5-80)
(5-81)
(рис. 5-47).
С
_____________sngdg
1
arccos ....т
+ Ь
% — k спа (arcctg Уk ) Е
(5-82)
214
где sn(w, k), cn (и, k). dn(tz, k)—эллиптические функции;
K(k)—полный эллиптический интеграл первого рода, k=
Рис. 5-47
ГЛАВА ШЕСТАЯ
ЕМКОСТИ В СИСТЕМЕ
МНОГИХ ПРОВОДНИКОВ
6-1. ОБЩИЕ ЗАМЕЧАНИЯ
1. В настоящей главе приведены материалы
для расчета емкостей в системе многих (трех и более) провод-
ников. Большая часть этих материалов относится к системам
бесконечно длинных проводников и позволяет найти частичные
(собственные и взаимные) емкости на единицу их длины.
2. Рассматриваемые частичные емкости определяются соот-
ношениями (В-3), (В-4) и связаны формулами (В-7) — (В-10),
(В-12) со всеми остальными величинами, характеризующими
емкость в Системе многих проводников. Помимо этого, в тексте
приводятся некоторые выражения для емкости между какими-
либо двумя проводниками рассматриваемых систем в присут-
ствии остальных (незаряженных) проводников той же системы.
Такие величины в ряде случаев используются в практике элек-
тротехнических расчетов под названием рабочей или полной
емкости (например, рабочая емкость двухпроводных линий
в присутствии земли, полная емкость между двумя проводами
в многофазных линиях и т. п.).
215
6-2. ПРОВОДА
6-2-1. В настоящем параграфе даны при-
ближенные формулы для определения частичных емкостей
в трех- и четырехпроводной линиях с равным расстоянием
между соседними проводами. Приведенные формулы получены
методом средних потенциалов (§ 1-2) и дают заниженные зна-
чения частичных емкостей; их погрешность не превышает 10 %.
6-2-2. Трехпроводная линия с равным расстоя-
нием между проводами (рис. 6-1):
Сш = С231 = Ci'3Z « --. (6-1)
о, d/3
31п—----
а
Рис. 6-1
Емкость между двумя любыми проводами в присутствии
третьего определяется формулой
---ЕЕ__. (6-2)
а
6-2-3. Четырехпроводная линия с равным рас-
стоянием между соседними проводами (два сим-
метрично расположенных провода соединены
между собой) (рис. 6-2).
При dla>^ емкость между проводами / и 2 в присутствии
соединенных проводов 3 и 4 определяется формулой
216
6-3. ПЛАСТИНЫ
6-3-1. В настоящем параграфе приведены
формулы для расчета частичных емкостей и потенциальных
коэффициентов в системе многих пластин. Большая часть этих
материалов относится к бесконечно длинным пластинам, для
которых приводятся точные формулы, полученные методом кон-
формных преобразований (§ 2-2).
6-3-2. Бесконечно длинные пластины, образую-
щие (при соединении) систему трех провод-
ников.
При взаимном расположении пластин (табл. 6-1)
С12г = С2зг = 2е-Л-; (6-4)
где К, К', Ki и К/ — полные эллиптические интегралы первого
рода с модулями k и k', и /г/, указанными в табл. 6-1. При
том же расположении пластин емкость между двумя симмет-
рично расположенными пластинами конечной ширины в при-
сутствии других пластин определяется формулой
Спг = е-£-, (6-6)
К
а полная емкость между соседними пластинами в системе п. 1
табл. 6-1 (1 и 2 или 2 и 3)
Спг = 4е , К'К----, (6-7)
К К! +KKj
где модули эллиптических интегралов определяются формулами,
приведенными в табл. 6-1.
Пример 6-1. Определим частичные емкости (на единицу длины) между
полосками в экранированной связанной полосковой линии с нечетным типом
волн (рис. 6-3), если 2h= 1 см, fe=0,5 см, 2d=0,5 см, а диэлектриком явля-
ется воздух.
Находим сначала частичную емкость между полосками Сш, используя
формулу (6-5).
Вычисляя модули эллиптических интегралов, в соответствии с п. 5
табл. 6-1 имеем
/л 0,25 X
V 2 0,5 J
л 0,25 + 0,5
Т 0,5
sh2
ft2 =------------
я: 0,0276;
*1 =
/ л 0,5 + 0,5 X gh / л 0,5 X
\2 0,5 7 V 2 0,5 /
л 0,25 + 0,5 х
.2 0,5 )
~ 0,9381 ;
217
Продолжение табл. 6-[
(k'f = 1 _ k2 = 1 — 0,0276 = 0,9724;
(fej)2 = I — k\= 1 —0,9381 « 0,0619.
Далее с помощью таблиц для эллиптических интегралов [1] находим, что
К= 1,582; К'=3,196; К,=2,806; К/= 1,596.
Подставляя численные значения в формулу (6-5), получаем
С. . - е ______=8,854 10-« (-------------------2Л)6\ ~ пФ/м.
v к' V 1,582 1,596 )
у К /
Аналогично определяются и частичные емкости каждой из полосок отно-
сительно заземленных плоскостей
C,,z = С23, = 2е = 2-8,854- К)-*2- —80£- «31,1 пФ/м.
±в ' 1 ПОП
Рис. 6-3 Рис. 6-4
Емкость между полосками в присутствии верхней и нижней плоскостей
(полная емкость между полосками) в соответствии с (6-6) оказывается
Спг = е —= 8,854-10--« -3’196- «17,9 пФ/м.
К 1,582
6-3-3. Пять бесконечно длинных пластин
(рис. 6-4):
С12г = — -,-1~ fe° 1 f i-mk0 Г(1 —m)п(ф, п, k) —
л V 14-m&0 L
- + -p) (! - F (Ф, k)\; (6-8)
Cisz
4e
л
И1 —m2^o
1 + fep
fyAo (I + rn.)
К(/г)-
fe0
где ffi = sn(Koy;^oj, a
sn(w, k0) определяется no
шения
7-----ПМ , (6-9)
1 — mk0 J '
модуль k0 эллиптического синуса
заданным размерам h и I из соотно-
h
I
Ко
Ко
=w.
220
в котором Ко и Ко' — полные эллиптические интегралы первого
рода с модулями Ло и k0', соответственно (зависимость k0 от h]L
Дана на рис. 6-5);
1 _ m2fe2
N =________ а___________,
x + mko Г1_2П(^^1
L к (ю J
f((p, k), П(<Р, п, k), К(й), П(пь k), K(k'), П(п2, k') — непол-
ные и полные эллиптические интегралы первого и третьего рода,
модули, аргумент и параметры которых приведены в табл. 6-2.
Таблица 6-2
Модуль Аргумент
k k'=V 1—к- <Р
2 т 1 — т arcsin 1/
1 + т 1 4~ т У 2(1 — mk0)
Продолжение табл. 6-2
Параметры
п П1 n.j
2 (1 4- mk0) 2m (1 — k0) (1 — m) (1 — mfe0)
(1 + т) (1 + ^о) (l + m) (1 + m) (1 + mfe0)
221
Зависимости и ~~~ ~ f (д~)при различных зна-
чениях h/l представлены на рис. 6-6 и 6-7.
При М>0,75, 6//<0,1
с - —
G1SZ~ я
In —
&0
(6 10)
arcsin2 k'o
[б<8 %; 6<1 % при h/l^2, b/l^,\\.
Рис. 6-6
ь 1 ^12^® ПРИ Равном
1,0 1.5 2,0
10—5 0,1887 0,5666 1,0221
ю-4 0,1813 0,5499 0,9994
IO-3 0,1695 0,5234 0,9633
10-2 0,1476 0,4746 0,8973
10-1 0,0969 0,3616 0,7437
0,5 0,0334 0,2015 0,5147
0,9 0,0195 0,1562 0,4440
1,0 0,0190 0,1545. 0,4413
Рис. 6-7
1> 1 С|з;/е при h/l, равном
1.0 1.5 2,0
10-6 0,1279 0,1927 0,2248
10~4 0,1574 0,2366 0,2759
IO-3 0,2046 0,3064 0,3570
IO-2 0,2923 0,4346 0,5055
10-1 0,5142 0,7490 0,8671
0,5 1,231,1 1,6208 1,8201
0,9 3,2321 3,6794 3,9094
0,99 6,1616 6,6112 6,8425
При 0,75, b//s^0,25
^iBz ~2е
arcsin k0
тг±г
\ Ко ь )
[6^1 %; 6<0,1 % при h/l^2, Ь/1^0,1].
(6-П)
222
В частном случае, при /; = /,
(6-12)
(6-13)
Пример 6-2. Определим частичные емкости в трехэлектродыом емкостном
преобразователе, применяемом для измерения малых поперечных размеров
плоских ленточных проводников (рис. 6-8), если 2/= 120 мм, 2/1=150 мм,
Рис. 6-8
длина электродов (в направлении, перпендикулярном плоскости чертежа)
6=100 мм, контролируемая проводящая пластина имеет ширину 2ft =1,2 мм,
а толщина пластины значительно меньше ее ширины.
Наибольший практический интерес представляют частичные емкости Сц
и С{з. Поэтому найдем значения именно этих величин.
ft 75
По заданному отношению-у ——=1,25 с помощью кривой па рис. 6-5
устанавливаем, что £о=О,52; £</=0,854. Тогда, используя таблицы эллиптиче-
ских интегралов (например, [1]), находим, что Ко= 1,697, и из формул (6-10)
и (6-11) получаем:
_ IO”’
^12? ~ ------
18л*
1п ——
0,52
г 10-8
18л
arcsin* 0,854
~ ( 4 60~
In I-------------
\ 1,697 0,6
arcsin 0,854
г 4 60 \ ~
< 1,697 0,6 7
пФ
2,601
м
3,315 -Н*
м
Расчеты по точным формулам (6-8) и (6-9) дают соответственно
6121=2,6040 пФ/м и С1з1=3,3166 пФ/м, т. е. в рассматриваемом случае по-
грешность расчетов по формуле (6-10) не превышает 0,12 %, а по формуле
(6-11) —0,05%.
223
Искомые частичные емкости находятся путем умножения найденных зна-
чений Ci2i и Cis; на длину электродов, т. е.
С12» 2,601-0,1 и 0,26 пФ;
С13 я 3,315-0,1 к 0,33 пФ.
6-3-4. Три одинаковых коаксиальных диска,
расположенных в параллельных плоскостях на
равных расстояниях друг от друга (рис. 6-9).
При a/ft=m<l
Cj j = С33 8еа (1 — 0,9549m + 1,1145m2 — 0,6514m3 — 0,02069m4);
(6-14)
C22 ~ 8ea (1 — 1,2732m + 1,2159m2 — 0,5702m3 + 0,01874m4);
(6-15)
C12 = C23 ~ 5,0930am (1 — 0,3183m+0,2452m2 — 0,2830m3);
(6-16)
C13=C31« 2,5465am(l — 1,2732m+0,7452m2 + 0,2786m3).
(6-17)
6-4. БЕСКОНЕЧНО ДЛИННЫЕ ПРОВОДА
И ПЛАСТИНЫ
6-4-1. В настоящем параграфе приведены
формулы для расчета частичных емкостей в системе многих бес-
конечно длинных проводов и пластин. Большинство этих формул
является приближенными и получено методом конформных пре-
образований с учетом реальных соотношений характерных раз-
меров рассматриваемых систем.
6-4-2. Двухпроводная линия и проводящая пло-
скость (рис. 6-10).
224
а. Общий случай
Сioi ~ 2ле
щА.щА
а2____d
lnAinA-ln’4
аг а2 а
С20/ 2ле
ln_^L 1п^-1п2
«1 а2
(6-18)
C\2i ~ 2ле ——————~ •
1п_А_1п2А_1п2А
at аг d
Рис. 6-10
Рабочая емкость линии определяется формулой
С ip =С{21
C10ZC20Z
С10Z + C20Z
(6-19)
б. При a1 = zz2=a, hi = h2=h (провода одинаковы и располо-
жены на одинаковом расстоянии от плоскости):
Cioi — C2oi
(6-20)
8 Зякяч Ко .407
225
6-4-3. Трехпроводная линия и проводящая пло-
скость (рис. 6-11).
а. Общий случай
Cioi
Qoz
«23 («12-- «2з) 4 «33 («22 «1г) 4~ «13 («32 - «2г) .
D
cc13 (a32 — С<1з) + а11 («33 «2з) + «12 («13 — «33) .
D
СзО/
__ «12 («23 «1г) H- «11 («22 «аз) "Ь «13 («21 «ss) .
D
C«12«33 «13«32 .
12Z = --------
D
__ «13«22 «12«23 .
Czsi
D
«11«23 «аз«1з
02а
Рис. 6-11
D
где
«и,
«21,
«31,
«12,
«22,
«32,
«13
«23 ’
«33
1
2 ле
1 , 2"2
«22 —-----In .----i- ;
2ле а
1 , 2/гз
«33 ~ -— In —2- ;
2эте а,
1 1 ^12
«12 = «21 ~--------In ;
2эте d12
п _ п ~ 1 in di3 .
«13 — «31 — ---- 1П - ,
2ле dis
1 , ^23
«23 = «32 ~ ,n -V- ’
Z3T8 ^*23
226
djk — расстояние между i- и k-ы проводами; —расстояние
между i-м проводом и зеркальным отражением А-го провода.
б. При hl = h2=h3=h; di3=d2s=d (провода расположены на
равных расстояниях от плоскости и друг от друга).
Частичные емкости определяются формулами (6-21) при
1 , 2h 1 ir, т Г1 । ( \2
аи-«22-Озз« — In — ; “i2-“23~ —In |/ 1+(^—j ;
«13--^—1П ]/" 1 +М-)2-
2ле у \ d )
6-4-4. Двухпроводная линия между двумя про-
водящими плоскостями (рис. 6-12).
Рабочая емкость линии определяется формулой
(6-22)
6-4-5. Двухпроводная линия и проводящая пло-
скость с вырезом (провода расположены по раз-
ные стороны от плоскости) (рис. 6-13):
/ 2пе
•WI
Г ( 2Ь \2 Г "2 Sin 4,1 Sin CWlCWl
1>12Z ~ ----) e ---------------------
\ л / ггг2 ле
(6-23)
8*
227
6-4-6. Двухпроводная линия и решетка из п оди-
наковых пластин, лежащих в одной плоскости
(провода расположены по разные стороны от ре-
шетки).
а. Общий случай (рис. 6-14, а)
Рис. 6-14
С201
2 ле
In
r2Vsin qyv
2a2
r2V sin <р8у ___।
2a2
(6-26)
где v — номер пластины, отсчитываемый от пластины, ближай-
шей к проводам; rlv и r2v — расстояния от проводов 1 и 2 (соот-
ветственно) до точки посередине между пластинами с индек-
сами v и v+1, а остальные обозначения указаны на рис. 6-14.
б. Провода расположены симметрично относительно решетки
(рис. 6-14, б)
Сю/ = С2о' = С ,
где С' — величина, определяемая по формуле (6-25) или (6-26)
при rlv=r2v, <plv = <p2v
С121
2b \2^ ( 6 С
л I ле
(6-27)
228
где
D =
—— при h^l,
П1П2
... * . при йх»/, h^l\
I (th + h2)
1 / ,, л/г л/г 1 \ /, к— h
----/ cth-----------------\ при — “2 — “ •
2//г I I sh2_^l I
\ I '
6-5. БЕСКОНЕЧНО ДЛИННЫЕ ПРОВОДА
И ОБОЛОЧКИ
6-5-1. В настоящем параграфе приведены
формулы для расчета частичных и полных (рабочих) емкостей
(Gp) в системе многих бесконечно длинных проводов и обо-
лочек.
Большинство из этих формул получено методом конформных
преобразований (§ 2-2) с учетом реальных соотношений харак-
терных размеров рассматриваемых систем.
6-5-2. Двухпроводная линия внутри цилиндри-
ческой оболочки (рис. 6-15).
Рис. 6-15
Рис. 6-16
а. Общий случай (рис. 6-15, а).
Рабочая емкость линии определяется формулой
3X6
/Р~ ~ 2d 2гРР2 / д \2 г 4d2P2 1
a (R2 — c2)2 \ 2d ) L (Я2 —с2)2]
(6-28)
б. При с = 0 (рис. 6-15,6)
Gp ~
In
ле
R2 — d2 2d
R2 + d2 а
(6-29)
229
6-5-3. Тр ехпр овод н а я линия, расположенная
симметрично внутри цилиндрической оболочки
(рис. 6-16)
C12Z = С131 — С231
2яе
(6-30)
где
Уза —
а + R2d2
6-5-4. Ч ет ы р ех п р о в о д н а я линия внутри цилин-
дрической оболочки (рис. 6-17).
Рис. 6-18
Рис. 6-17
При ф1 = ф2 емкость между накрест лежащими проводами
(/ и 2 или 3 и 4) в присутствии других проводников рассматри-
ваемой системы определяется формулой
(6-31)
6-5-5. Провода, проходящие по оси и образую-
щим круглого цилиндра, коаксиального с ци-
линдрической оболочкой (рис. 6-18):
Сю/ яг ле......................—— -----------------;
гв \ R 1 R , f г0 Г I г0 \2и])
In —— In — -|---In — In J —2- 1 — -Л. I I
Po’ r0 2n ( p0 I na [ \R ) JJ
In — — In
C2U ~ ле------—------------------P®_______>________,
m A in A + _L A ,n fА Г, _ I Afl j
Po r0 2n p0 ( na [ \ R J J J
(6-32)
2-30
где п — число соединенных между собой проводов, расположен-
ных на образующих цилиндра.
6-5-6. Провод и две коаксиальные с ним ци-
линдрические оболочки, одна из которых (вну-
тренняя) не.замкнута (рис. 6-19).
Рис. 6-19
См
2ле
' яГ
1п ——
Ri
2ле
]Г
а
(6-33)
nd
b
зге
С10/С2П
РАЗДЕЛ второй
ЕМКОСТЬ ПРОВОДНИКОВ
В НЕОДНОРОДНЫХ СРЕДАХ
ГЛАВА СЕДЬМАЯ
ЕМКОСТЬ УЕДИНЕННЫХ ПРОВОДНИКОВ
7-1. ОБЩИЕ ЗАМЕЧАНИЯ
1. В настоящей главе приведены материалы
для расчета емкости уединенных проводников в неоднородном
диэлектрике. Расположение материала сохранено, в основном,
таким же, как в гл. 3; при этом для каждой группы проводников
(проводов, пластин, оболочек и объемных тел) последовательно
рассматриваются диэлектрические среды все более сложного
вида.
2. Большая часть приведенных материалов относится к слу-
чаю, когда проводник расположен вблизи плоской границы двух
сред (двухслойная среда) и не пересекает этой границы. При
этом влияние границы учитывается, как правило, с помощью
коэффициента отражения
£____ Е1 ~
е1 + ег
где ei и 62 — значения диэлектрической проницаемости в среде,
содержащей и не содержащей проводник, соответственно, —
В частном случае, при & = 0(ei = e2), приведенные формулы
определяют емкость уединенных проводников в однородной
среде (гл. 3). В другом частном случае, при непроницаемой
границе сред (ег^Сбь kivl), значение емкости проводников мо-
жет быть определено с помощью формулы (В-19) и материалов
гл. 3.
3. Приведенные в тексте формулы для емкости проводников,
расположенных симметрично относительно плоской границы
двух разнородных сред, получены с использованием свойства,
сформулированного в п. 3, д § В-3. Использование материалов
гл- 3—5 позволяет также получить выражения для емкости
232
во всех случаях, когда проводники (или системы из двух про-
водников) обладают плоскостью симметрии и расположены
в двухслойной среде указанным образом.
7-2. ПРОВОДА
7-2-1. В настоящем параграфе приведены
формулы для расчета емкости уединенных проводов круглого
сечения, расположенных в двухслойной и трехслойной средах.
Все приведенные формулы получены методом средних потенциа-
лов (§ 1-2) с использованием правила отражения зарядов отно-
сительно плоской границы (см. пример 1-3).
Для определения емкости проводов вблизи плоской непрони-
цаемой границы следует использовать соотношение (В-19) и
приведенные в § 3-2 формулы для емкости проводников, обра-
зованных соединением проводов, расположенных симметрично
относительно некоторой плоскости [см., в частности, формулы
(3-7)-(3-11)].
7-2-2. П р я м о л и н е й н ы й провод, параллельный
границе раздела двух сред (рис. 7-1):
Рис. 7-1
При
С 2ле11
1 21 1 I ь 1 1
In----------1 "т" к I In--------I
а \гв? h
При 2/г//> 1
2лех1
21 I
In —------1 + k ~
а 2/г
(7-1)
(7-2)
(7-3)
233
7-2-3. Прямолинейный провод, перпендикуляр-
ный границе раздела двух сред.
а. Провод не пересекает границу (рис. 7-2)
2яе}!____________________
и_\ in 2<fe + Q + A in 2/1 1 ' (7-4)
I ) l+2!i I l + 2h J
При 2/i//<Cl
h • (7’5)
In — _ 1 + k (In? + — In — |
a \ ll)
Рис. 7-3
Рис. 7-2
б. Провод пересекает границу (рис. 7-3).
При ei<62
(7-6)
При ei>e2
(7-7)
Пример 7-1. Найдем сопротивление R горизонтального и вертикального
заземлителей (рис. 7-1 и 7-2) радиусом а=0,1 м и длиной 7=1,0 м, располо-
женных в грунте с удельной проводимостью yi=2,0-10-2 См/м на глубине
А=1,0 м (горизонтальный заземлитель) и /г=0,5 м (вертикальный заземли-
234
Пользуясь формулами (В-25) и (7-1) при k=\, находим, что для гори-
зонтального заземлителя
1
Я = —
TiCo 2л-2-10-2
. 2-1
In-----
0,1
1 +Arsh
17,8 Ом.
Точно так же для вертикального заземлителя по формулам (В-25)
(7-4) при /?= 1 получаем
Я = —51— г»-------'----
ухС0 2л-2-10-2
2-1
0,1
2 (0,5 + 1)
1 +2-0,5
i + Ai
и
0,5 , 2-0,5
4------In---------
1 1+2-0,5
18 Ом.
7-2-4. Провод в форме кругового кольца, парал-
лельного границе раздела двух сред (рис. 7-4).
Рис. 7-4
Я
а. При /i>0
__________________________4л2е1Я
In — + k rJl' К
а /Я2+/г2 (
[6<5 % при R/a>\Q],
где К — полный эллиптический интеграл первого рода.
При h^R
р_____________4л2е1Я________
°~ , 8/? - ы 4/?
In-------(' k In----
a h
При h^>R
C — 4л2е1Я
0 ~ . 8Я . . лЯ
In-------1- k---
a 2h
(7-8)
(7-9)
(7-10)
235
б. При h = Q
r _ 2я2 (et -I- e2) R
C°~ ,87?
a
[6<2 % при /?/п>10].
в. При k= \ и h<^.R
f ~ 4л2е17?
0 ~ 7 327? 2
In-----------
ah
(7-11)
(7-12)
7-2-5. Провод в форме прямоугольного контура,
параллельного границе раздела двух сред
(рис. 7-5).
Рис. 7-6
Рис. 7-5
При/г=1 (непроницаемая граница)
__________________________ 2mL
0 ~ ~ aL2 ’
In---------
2ah
где L=2(/i+Z2), а значения коэффициента
отношения /]//2 приведены ниже:
/А..................1,5
а...................3,81
При /] = /2=/
(7-13)
а в
зависимости от
2,0
6,42
3,0
8,17
4,0
10,4
у—. 8жз/
-- ——-
° , 44,24/2
In------
ah
7-2-6. Прямоугольная решетка из проводов, па-
раллельная границе раздела двух сред (рис. 7-6).
При /г=1 (непроницаемая граница)
С __ 2mL
(7-И)
(7-15)
In
2ah
где L — суммарная длина всех проводов, образующих решетку;
236
D — коэффициент, зависящий от соотношения размеров решетки
и числа ее ячеек.
Значения коэффициента D для некоторых типов прямоуголь-
ных решеток даны в табл. 7-1. „
Таблица 7-1
№ пп.
Вид решетки
Значения коэффициента D при li.lz, равном
1,0 L5 2,0 3,0 4,0
1,71 1,76 1,86 2,10 2,34 е
3,67 3,41 3,31 3,29 3,35
4,95 5,16 5,44 6,00 6,52
4,33 4,43 4,73 5,04 5,61
8,55 8,94 9,40 10,30 11,11
1,7?
Пример 7-2. Найдем сопротивление горизонтального заземлителя в форме
прямоугольной решетки из труб с четырьмя ячейками размером 2,0X1,0 м
при диаметре труб 0,02 м. Решетка помещена в грунт с удельной проводи-
мостью у=10 2 См/м иа глубину й=2,0 м.
Пользуясь аналогией между проводимостью н емкостью [формула (В-25)],
применим для расчета формулу (7-15).
Суммарная длина проводников рассматриваемого заземлителя £=3(/i+
+ /2) =3(4,0+2,0) = 18,0 м.
237
Коэффициент D, входящий в формулу (7-15), определяем по заданному
отношению /1//г=2,0 из табл. 7-1, с помощью которой находим, что £>=5,44.
Таким образом,
К =
J_______е_
G — уС0
182
2-0,01-2,0
Ь 5,44
2л-18,0-10-2
а; 13 Ом.
7-2-7. Плоские «-лучевые звезды1, параллель-
ные плоской непроницаемой границе двух сред.
Приближенные выражения для емкости проводников в форме
n-лучевой звезды, параллельной непроницаемой границе (/г=1),
при hll<.0,8 приведены в табл. 7-2.
Пример 7-3. Найдем сопротивление R двухлучевого заземлителя, располо-
женного в грунте с удельной проводимостью у=2-10-2 См/м на глубине
fi/2 = 0,3 м, если длина каждого луча (трубы) £=1,0 м, а его радиус о=0,02 м.
Пользуясь формулой (В-25) и первой из формул, приведенных в п. 1
табл. 7-2, для двухлучевого заземлителя найдем
R
р 1 Г 4-1
as--------------- In----—--------0,2373 + 0,2416-0,6 +
уС0 2-2Л-2-10-2 [ 0,02-0,6
+ 0,1035(0,6)2 —0,0494(0,6)4] а 22,9 Ом.
По второй формуле, приведенной в п. 1 табл. 7-2, для той же величины
получим
1 , 5,84-12
----— In
2-2Я-2-10-2------0,02-0,6
24,6 Ом.
7-2-8. Два соединенных между собой прямоли-
нейных провода, расположенные симметрично
относительно границ плоского диэлектриче-
ского слоя.
а. Провода перпендикулярны границам слоя (рис. 7-7).
При t+l<Ji (рис. 7-7, а)
1 Под n-лучевоп звездой понимается проводник,
линейными проводами, пересекающимися в одной точке.
образованный прямо-
238
Таблица 7-2
239
При t>h (рис. 7-7, б)
оо
При l<h и /=0
(7-17)
2Л
Со
оо
п
(7-18)
In-*
а
п
Рис. 7-7
240
Рис. 7-8
При t>h (рис. 7-8, б)
(7-22)
7-3. ПЛАСТИНЫ
7-3-1. В настоящем параграфе приведены
материалы для расчета емкости пластин, расположенных в двух-
слойной и трехслойной средах.
Приведенные выражения для емкости пластин, расположен-
ных в двухслойной среде с непроницаемой границей (при коэф-
фициенте отражения fe=l), связаны соотношением (В-19) с ем-
костью уединенных проводников, расположенных в однородной
среде и образованных соединением двух одинаковых пластин
241
рассматриваемого вида. Кроме того, в п. 7-3-9 приведено точное
выражение для емкости диска, одна сторона поверхности кото-
рого непроницаема.
7-3-2. Диск, параллельный границе раздела
Двух сред (рис. 7-9).
а. При k= 1
1
Со= 8еа\ f (t) dt, (7-23)
b
где f(t) —решение интегрального уравнения
2/г р f (/) dt _
I I Л 2 I \ 2Л \2
(X — /)2 + -------
V \ a J
Рис. 7-9
При 2Л/с<1
л а
[|б| <6 %; при 2/i/a=0,8 6 = —0,8 %; при 2/z/tz=0,4
6=4,9 %; при 2/г/с^0,1 6<2 %].
При 1^2/г/п<1,5— см. формулу (7-27) при k=l [6<2,2 %].
При 2Л/а^1,5
С о « 8е«[ 1 — 0,6366m+0,4052m2+0,1664m3 — 0,3761 m4],
m = «/(2/z) (7-25)
[6=1,75 % при 2Л/а=1,5; 6<0,2 % при 2/i/«>2).
Значения C0/(4ea) при некоторых фиксированных значениях
‘Zhfa указаны в табл. 7-3, а зависимость—= f(——\ представ-
4еа \ а /
лена на рис. 7-10.
242
б. При—1<Й^1,Й=^0
(7-26)
[б< 1 % при /г=1, 2/г/п>2; 6<4 % при k=A, 2h/a^tl,5],
8sa
. . 2/г 2/г
1 -|------arcctg ------
зг а
(7-27)
[б<1 % при k=l, 2h/a>2,5-, 6<3,6 % при k=l, 2/i/tz>l],
Рис. 7-10
Таблица 7-3
2/г а 0,0 0,4 0,6 0,8 1,0 1,2 1,5
Ср 4еа 1,000 1,2054 1,2728 1,3312 1,3824 1,4276 1,4874
2/г а 2,0 2,5 3,0 5,0 10,0 20,0
Ср 4еа 1,5634 1,6226 1,6684 1,7792 1,8810 1,937
Со 8е~аГ- (7-28)
1 + —
зт/г
[б<1 % при/г=1, 2/г/п>5; 6<3 % приЛ = 1, 2/z/tz^2],
в. При /г = 0
С0=4(е1+е2)а. (7-29)
243
7-3-3. Диск, перпендикулярный границе двух
сред (рис. 7-11).
а. При h^>a
(7-30)
[б<9 % при h/a>\- б<5 % при h/a>3].
с 8еа
l + 2t
ЛЙ
(7-31)
[6<6 % при /г/а>31.
Рис. 7-11 Рис. 7-12
б. При Л = 0 (рис. 7-12)
Со = 4 (ех + е2) а.
(7-32)
7-3-4. Круговое кольцо, параллельное непро-
ницаемой плоской границе (рис. 7-13).
Точные значения емкости при некоторых характерных соот-
ношениях геометрических параметров приведены в табл. 7-4.
При 2/i/«2<1
Р ____ 4еа2а
° ~ [ 2 h
ла а2
(7-33)
где а
Cqi
8еа2
; Со1~ емкость уединенного кольца (см. п. 3-3-4)
[|б| <8 %; при 2/г/«2=0,5, ц2/щ = 2 6 = 4,9 %].
244
При /z/(l2^1
Со -----------------------------—- (7-34)
1 I а fl___________1 —I
л ’ ft \ 12 ft2 )
[|б|<3 %; при 2/i/a2>3,5, а2М>3 б<0,4 %].
Ма, |
Рис. 7-13
Таблица 7-4
Да Д1 Значение емкости С0/(8еа,) при 2h/a„ равном
0,1 1 10 оо
1,125 0,462 0,6073 0,7862 0,8326
2,0 0,5 0,6154 0,8746 0,9810
3,0 — 0,588 0,8431 0,9947
7-3-5. Прямоугольная пластина, параллельная
границе двух сред (рис. 7-14).
а. При k= 1, /г>0.
Рис. 7-14
Таблица 7-5
а b Значение емкости С0/(4леа) при 2hlb, равном
0,001 0,005 0,01 0,02
‘ ’я 1 0,357 0,359 0,361 —
2 0,255 0,256 0,257 0,259
3 0,217 0,218 0,219 0,220
4 0,196 0,1965 0,197 0,199
Значения Со при h/b<^l указаны в табл. 7-5.
При hja<\,
2яеа_______
С°~ 2аг __ ! 2ft 7 h У 1 / ft У'
ftft 2 а (а/г2\а/
(7-35)
245
При 2/z/a>l, alb>\
( С' V1
Со~Со 1+—А- , (7-36)
\ 8neh )
где Со' — емкость рассматриваемой пластины в однородной
среде (см. п. 3-3-7).
б. При — l<fe<l, a>b, 2h/a<l
в. При —Л = 0
2л (ёл + е2) а
2 In — + 1
b
(7-38)
При k= 1, h = 0
Со= Со'/2,
где Со'— то. же, что в (7-36).
7-3-6. Прямоугольная пластина, перпендику-
лярная непроницаемой плоской границе (рис.
7-15).
Рис. 7-15
При hla^> 1, alb^\
Со«Со[ 1+------------
L 4ле(2й — а)
где Со' —то же, что в (7-36).
При h=a[2
Со=Со72,
(7-39)
где Со' — емкость пластины размерами 2яХ& в однородной
среде (см. п. 3-3-7).
246
7-3-7. Пластина, расположенная на поверх-
ности плоского диэлектрического слоя,
а. Пластина произвольной формы (рис. 7-16).
При 2h!l> 1
Со ~ fl Г1 j---_Её_ |1п(1—/г2)[
° \ ех / 2 [ е2 — 4sre1ft
(7-40)
где Со' — емкость рассматриваемой пластины в однородной
среде при e = ei (см. § 3-3).
Относительная погрешность расчетов по формуле (7-40)
определяется выражением
|6|<0,1б/-ЦЛ —Е°- 1+- -£г- |ln(l—fe2)|—Её------------
\ h ) 4ле1/г е2 —е1 4ng1/i
/ / \2 Сп
—0,16/—) ------
\ h J ‘In&jh
•100%,
где I — максимальный размер пластины.
б. Диск (рис. 7-17).
При h!a> 1
4 (®1 4 ч
1+- -2-Ё2- |ln(l-fe2)|
(е2 — Ei) лЛ
(7-41)
[<5<1,5 % при/t/a>2, 0|k | 0,9].
Рис. 7-17
Рис. 7-16
7-3-8. Две одинаковые соединенные между со-
бой пластины, расположенные симметрично на
поверхностях плоского диэлектрического слоя.
а. Пластины произвольной'формы (рис. 7-18).
При Zhll^ 1
С^-Ч+^-Со
ei
X 2 + fe In — 'ln (— - ----Её_1 , (7.42)
£j k J 4nejft J
где Co'— емкость одной из рассматриваемых пластин в одно-
родной среде при e = ei (см. § 3-3).
1+—X
е1 + е2
247
Относительная погрешность расчетов по формуле (7-42)
определяется выражением
g?. —1,21/г) С° ( Н--------Г2—k In ——
ei + е2 \ h ) ineih I ei + еа L Е1
|!п(1 — fe2)| Со________Ё2 / I У х
k 4mrh Bj + <;2 \ h /
С'
х(1 — 1,21/г)----— -100%,
' 4nej/i J
где I — максимальный размер пластины.
б. Диски (рис. 7-19).
Рис. 7-18
Рис. 7-19
При h)a> 1
Со --------------8 (И + Ё*\.а---------(7-43)
1 +---**---Г2 + k 1П-&- + -IM1—1
л (ел -р е2) h L 81 k J
7-3-9. Диск радиуса а, одна сторона поверх-
ности которого непроницаема:
С0=2леп. (7-44)
7-4. ОБОЛОЧКИ
7-4-1. В настоящем параграфе приведены материалы для
расчета емкости некоторых оболочек, расположенных в двух-
слойной среде. Граница рассматриваемых сред во всех случаях
считается непроницаемой. Формулы для емкости оболочек, рас-
положенных симметрично плоской границе двух сред (при про-
извольном значении их диэлектрической проницаемости), могут
быть получены с помощью материалов § 3-3 и свойства, указан-
ного в п. 3, «г» § В-3.
7-4-2. Оболочка в форме полого сфериче-
ского сегмента, заполненного средой с диэле к-
248
три ческой проницаемостью, отличной от ди-
электрической проницаемости окружающей
среды (рис. 7-20).
При e2<Cei
4 пеш------------------— • (1 ’4Ь)
Л ясс
(2л — a) cos — --—
2 (2л — а)
Зависимость —— =
4ле1а
И— ] представлена на рис. 7-21.
Рис. 7-20
7-4-3. Коническая оболочка с осью, перпенди-
кулярной' плоской непроницаемой границе
двух сред.
а. Основание оболочки совпадает с границей (рис. 7-22).
При / = 7?]/2
0,412<—СО,415. (7-46)
4л«/?
б. Вершина оболочки расположена на границе (рис. 7-23)
С0 = 2ле1—-^ , (7-47)
0 [Ф(т)12
где
— 4- Гфз (?)+ Фз (V)]
ф (?) = <Р1 (х)е <Мт);
<Р1 (?) = Г V^sin уР-1/2 (COS у) [Р_ 1-2 (—cos у) + Р_ 1/2 (cos у)];
, , чгл Г 1_______1 , 1_______1 ] .
*Р« W \ (V) « (Т) + а (у) ; (?) ] ’
fe=l 6 К
249
а п 0,1 0,2 0,3 0,4 0,5
Со 0,16320 0,33158 0,49478 0,64339 0,76980
4jtSja
а л 0,6 0,7 0,8 0,9 1,0
Со 0,86889 0,93847 0,97964 0,99714 1,0
4ле1а
Р-чЛу)—функции Лежандра; ф(-г)—пси-функция; аь(у),
а/<(у)—положительные корни уравнений
(—cosy) 4- (cos у) = 0;
ak (Т) — 1/2 ' 17 ' aft (V) — 1/2 ' Г/
250
Хй('у), xfe(y)—асимптотические значения аь. (у) и а&(у), соот-
ветственно *. с
Приближенная [б<7 %] зависимость gg° = f (?) приведена
на рис. 7-23.
Рис. 7-22
7-5. ОБЪЕМНЫЕ ТЕЛА
7-5-1. В настоящем параграфе приведены
материалы для расчета емкости уединенных объемных тел про-
стейшей формы, расположенных в неоднородной среде.
Наиболее полные данные приведены для проводника сфе-
рической формы, емкость которого в неоднородных средах мо-
жет быть представлена рядом точных формул. Помимо этого,
приведены приближенные формулы для емкости проводников
в форме цилиндра, параллелепипеда и полушара, расположен-
ных в двухслойной среде.
7-5-2. Сфера в двухслойной среде.
а. При h>a (рис. 7-24)
Со = 43X6!^ sh р 2 (—k)n 1 cosechnp, (7-48)
ft=l
где р=Arch [hl а).
Зависимость-^2- =f(—) при k=l представлена на рис. 7-25.
2ле1а . \ h )
1 ak (?) = xk (у) + О f-Ц; xk(y) = (k Ц —
\ k ) \ 4 / у
%(?)=м?)+о(4''1: v?)=(^-i)—
к к \ к / Л —
251
При h>2a, k=\
4лва
ч~ —
2h
(7-49)
[6<0,5%].
б. При h=a
Со = 4ле1а -J- In (1 + k). (7-50)
k
При e2/ei->0 (&->1)
Со = 4лв1а • In 2 « 4леха • 0,6931. (7-51)
в. При 0<й<а (рис. 7-26)
Рис. 7-26
252
со « 4ле2а [1 + -1 -а- ₽(—)],
L 62 \ a j J
(7-52)
ГАе Р ("а”) ~ ФУнкЦИя, определяемая графиком на рис. 7-27
[6<2 % при О^р^З].
г. При Л=0
С0 = 2л(е14-е2)а. (7-53)
7-5-3. Сфера в среде с радиально меняю-
щейся диэлектрической проницаемостью.
а. Общий случай:
4л
Со = —--------> (7-54)
f dr
J 8 (г) С2
а
где е(г) — заданная ограниченная функция.
б. е=const в пределах шаровых слоев, концентричных со
сферой (рис. 7-28):
(7-55)
Рис. 7-27
где п — число слоев; т — номер слоя, отсчитываемый от по-
верхности сферы; Ет — значение диэлектрической проницае-
мости в m-м слое; am-i и о™ —границы т-го слоя
причем а0=а, ап — °°-
253
7-5-4. Сфера в неоднородной среде с диэлек-
трической проницаемостью, постоянной в ра-
диальном направлении.
а. Общий случай:
С0 = а\ d<pje(q>, 0)sin0d0, (7-56)
о о
где е(<р, 0)—заданная функция; <р, 0 — сферические коорди-
наты.
Рис. 7-28
б. е=const в пределах
(рис. 7-29):
коаксиальных конических
Со = 2па
п
(COS 9m COS 9m—1)
слоев
(7-57)
где n — число слоев; m — номер слоя, отсчитываемый от оси
конусов; Ет — значение диэлектрической проницаемости в т-м
слое; 0т и 0т_! — углы при вершинах конусов, ограничивающих
772-Й СЛОЙ (0т_ 1<0т), причем 0о = О, 0т = л.
7-5-5. Сфера, соприкасающаяся с диэлектри-
ческой сферой того же радиуса (рис. 7-30).
При е2<е1
0,951 <
Ср
4netft
<0,960.
(7-58)
7-5-6. Цилиндр конечной длины с осью, парал-
лельной плоской границе раздела двух сред
(рис. 7-31).
254
При lla> 1 и h>l
Рис. 7-30
См. также п. /-2-2.
При /г=О
Рис. 7-31
(7-60)
где Со' — емкость рассматриваемого цилиндра в однородной
среде при e = ei (см. п. 3-5-10).
7-5-7. Параллелепипед, одна из граней кото-
рого параллельна плоской границе двух сред
(рис. 7-32).
Рис. 7-32
255
При a>b, b>d и 2h/a> 1
_______2пега_________________
“n 2a_ 1 +2L_/Ay+-LM yi
b + 2(Ь + <У L h a \ a / 2 \ a ) \
(7-61)
7-5-8. Две одинаковые касающиеся сферы, рас-
положенные симметрично границе двух сред
^пис. 7-33 и 7-34):
Рис. 7-33
Рис. 7-34
С0=4лп(е1 + е2)1п 2.
(7-62)
7-5-9. Полушар вблизи плоской границы двух
сред.
а. Диаметральная плоскость полушара совпадает с границей
(рис. 7-35,а).
Рис. 7-35
При e2>ei
При ei>e2
Со~2лп(е2+0,69 ei).
(7-63)
Со ~ 4а (ei +1,66 е2).
(7-64)
256
б. Полушар расположен симметрично относительно границы
(рис. 7-35, б):
Со = 4па (б! + е2) (1
уг)-
(7-65)
ГЛАВА ВОСЬМАЯ
ЕМКОСТЬ МЕЖДУ ДВУМЯ
ПРОВОДНИКАМИ
8-1. ОБЩИЕ ЗАМЕЧАНИЯ
1. В настоящей главе приведены мате-
риалы для расчета емкости между двумя проводниками, распо-
ложенными в неоднородном диэлектрике. Расположение мате-
риала в данной главе сохранено, в основном, таким же, как
в гл. 4 и 5; при этом для каждой системы проводников последо-
вательно рассматриваются неоднородные диэлектрические среды
все более сложного вида.
2. Большая часть приведенных в настоящей главе материа-
лов относится к слоистым средам с плоскими границами раз-
дела. При этом влияние двухслойной среды учитывается с по-
мощью коэффициента отражения k, определяемого так же, как
в § 7-1.
8-2. ПРОВОДА
8-2-1. В настоящем параграфе приведены
формулы для расчета конденсаторной емкости между прово-
дами круглого сечения, радиус которых а считается значительно
меньшим всех остальных характерных размеров рассматривае-
мых систем. Большая часть приведенных материалов относится
к плоскопараллельным системам. Для таких систем в тексте
приведены формулы, характеризующие емкость на единицу
длины проводов.
8-2-2. Д в у х п р о в о д н а я линия в присутствии
плоской границы двух разнородных сред
(рис. 8-1)
При (KZh
а ! 8Д2
9 Заказ № 507
257
При 2h<d
ле,
1 d I , 1 d
In------P k In ----
a 2h
(8-3)
8-2-3. Двухпроводная линия над диэлектриче-
ским слоем (рис. 8-2):
Рис. 8-1 Рис. 8-2
где
fa — Е1 • £ -- (В2 Е1)
1 Е1 + е2 ’ 2 (8i -I- е2)2
При E2/ei>5
Q ____________________________-4S1______________________
1 1 ( d (, , d2 \fc"2 Г, . d? Vhl2
l я ( 4ft2 ) [ 4 (b + /1)2 J
(8-5)
[6<2 %],
где k\ H kz те же, что в (8-4).
8-2-4. Двухпроводная линия в диэлектриче-
ском слое (рис. 8-3).
При е2/в1»1
С; ---------- (8-6)
Г Ь / , nd . ,\ nd 1
In — ch-----pith----
L a \ b ) 2b ]
[6<2 % при e2/ei>16; d/a>!Q и &/(2а)>10].
258
8-2-5. Д в у х п р о в о д н а я линия в диэлектрике
с цилиндрической поверхностью раздела
сред (рис. 8-4)
Q ~------------------------------—------------ > (8-7)
/ 6 )
2Ь ®1П ( 2 / k , М — 2«2fe2 cos 6 + Д4
где
6i + е2
[б<5 % при 6/а>10].
Рис. 8-3 Рис. 8-4
8-2-6. Дв у хп р о в од н а я линия с изоляцией лен-
точного типа (рис. 8-5).
При d>ax
_а_~ [in +i_h__п х
2ле2 L d —]/d2—а2 \ еср )
X 1п
«?-(4-Kd2~fi2)2
(4+ Vd2-^')2-^
(8-8)
где
еср — ei Н— (е2—ei);
Л
а = arctg
6fe]/~da__a2
3 (da — а2 — bz) — (Я1 — а)2
[б<4 % при 4>l,2ai].
9*
259
При с1=а[
Ci
2 ле2
In
и1 +1^4—
at — ] «1 — “2
1г 2°1 1 1/^1—°2
1 ' 201 -
-1
(8-9)
[6<4 % при ai^sl,5a].
8-2-7. Два провода конечной длины, парал-
лельные границе раздела двух сред (рнс. 8-6):
Рис 8-5
Рис. 8-6
2/t
/
+ k Г I 1п (I -I- УУ+w) П^2 + 4Л2
2 2/1 (/ 4- j/Д _|_ ср _|_ 4Л2)
лсД
— -у- |/ds+ 4/г2
(8-10)
При d/K[
При 2h>l
, d d к ,
In----4-- In
a 12
(8-11)
C nej/ I In--------------- 2zd -----------
I a (l -I- VP -I- d2)
Krfs p 4/t2
2/t
J_ ±_ in (l + 2h)Vd^+W 1 -1
2 2/i (/ 4- j/Д + 4Я2) I
(8-12)
260
8-3. БЕСКОНЕЧНО ДЛИННЫЕ ПЛАСТИНЫ
8-3-1. В настоящем параграфе приведены
материалы для расчета конденсаторной емкости на единицу
длины плоскопараллельных систем, образованных бесконечно
длинными пластинами, расположенными в двухслойной или
трехслойной среде. Большинство приведенных формул получено
методом конформных преобразований с использованием зер-
кальных отражений пластин относительно границ разнородных
сред.
Емкость между пластинами, расположенными вблизи плос-
ких непроницаемых границ, может быть определена по фор-
муле (В-21).
8-3-2. Две пластины неравной ширины на гра-
нице раздела двух сред (рис. 8-7):
G = (ei + е2) , (8-13)
К
где К и К' — полные эллиптические интегралы первого рода
с модулями
k-_~\f («+z> + d)d и k,
V (a + d) (b 4- d)
8-3-3. Две пластины неравной ширины, распо-
ложенные на пересекающихся непроницаемых
плоскостях (рис. 8-8).
Общий случай:
G = 8-^, (8-14)
где модуль эллиптических интегралов определяется выраже-
нием
При а=Ь и dt = d2 = d
2<р
k= 2
ч>
-э ci
Зависимость —
в
лена на рис. 8-9.
при различных значениях <р представ-
261
8-3-4. Плоскость с непроницаемым прямо-
угольным выступом и расположенная на нем
пластина (рис. 8-10):
Рис. 8-10
Cz = 2e—(8-15)
K'(k) v ’
262
где модуль эллиптических интегралов k находится из трансцен-
дентного уравнения
a //-К (fe) --Е (fe)
2ft = A2K' (k) — E' (A)
К, К', E и Ez — полные эллиптические интегралы первого и вто-
рого рода с модулями k и k'= ft2 соответственно. I рафик
функции f(k) представлен па рис. 8-И.
Рис. 8-11
8-3-5. Две одинаковые пластины внутри не-
проницаемого круглого цилиндра (рис. 8-12):
С, = 2е -K(fe)-, (8-16)
' К' (k)
При R—a^R
— In ~R - (8-17)
л R — a
[6<1 % при (1—g/7?)<0,2; 6<0,l % при (1—с/7?)<0,1].
263
8-3-6. Две параллельные пластины разной ши-
рины в прямоугольном желобе с непроницае-
мыми границами (рис. 8-13):
С, = 2е К(Л) , (8-18)
К' (А)
где К (k) и K'(fe) — полные эллиптические интегралы первого
рода с модулями
A=^^osn ^Кп-^ . sn (ко-у-. и k' — k2,
Рис. 8-12
Рис. 8-13
а модуль k0 эллиптического интеграла Ко и указанных эллипти-
ческих функций находится из уравнения
h Kp
~Г=-кГ
с помощью данных п. 4-7-4 или по кривой рис. 6-5.
8-3-7. Две пластины на поверхности Т-образ-
ного желоба с непроницаемыми границами
(рис. 8-14):
. 2_ ?!+* 1пл+г. + ,|л .
а Ь л [ а/> а — b 4ab
[б <10 % при hi>a, h2>b],
8-3-8. Две взаимно перпендикулярные пла-
стины разной ширинывпрямоугольном желобе
с непроницаемыми границами (рис. 8-15):
Cz = 2e-^-, (8-20)
К' (*)
где ВД и K'(k)—полные эллиптические интегралы первого
рода с модулями
264
модуль k0 эллиптического интеграла Ко и указанных эллипти-
ческих функций тот же, что и в п. 8-3-6, a k0 = V 1 —ko.
8-3-9. Четыре параллельные пластины в пря-
моугольном желобе с непроницаемыми грани-
цами (рис. 8-16):
Q = 4е -Ь_, (8-22)
к;
Рис 8-17
Рис. 8-16
265
8-3-10. Две пластины неравной ширины на ди-
электрическом слое.
а. Общий случай (рис. 8-17):
(8-23)
где К, К', Кх, К/ — полные эллиптические интегралы с моду-
лями k, k', k\ и ki', соответственно,
^=1/” 1-^ = 1/”----------~
I V (a-]-d)(b + d)
1 — fe'2=
V 1 2 V (G + УОз + 'з)
expXf—1 .
1 exp Kt -J- 1
« 26 -р d л nd . 2ad
Лч — “ ~ • Zvo — ~ ж /vo —- ~ JI
1 2h 2h 2h
[6<3 % при E2/ei>6].
График для определения параметров ti по заданным значе-
ниям Кг приведен на рис. 8-18.
Рис. 8-18 Рис. 8-19
б. Пластина конечно и ш и р и н ы и полуплос-
кость JpHC. 8-19). Емкость на единицу длины определяется
формулой (8-23) при следующих значениях модулей эллиптиче-
ских интегралов:
1 /~ (1 • ^г) Оз ^г)
И (1-н2)ог -Нз) ’
266
a Z2, 13 и ti — те же, что в (8-23).
Параметры i2 и t3 могут быть определены также с помощью
графика на рис. 8-18 по значениям Х2 и Лз-
8-3-11. Три пластины на поверхности раздела
двух сред (рис. 8-20).
При соединении симметрично расположенных пластин между
собой
с,=2(е,+в,)Л_а, (8-24)
где К и К' — полные эллиптические интегралы первого рода
с модулями
d(b-] d)
(а + d) (а -|- b + d)
И k' -= | 1 — k2.
2a~\-b-\~2d
b -1- 2d
Рис. 8-20
Рис. 8-21
8-3-12. Т р и пластины н
трическог о слоя (кра
одинаковую ширину и
бой), e2>ei (рис. 8-21).
а. а<со
а поверхности диэлек-
йние пластины имеют
соединены между с о-
С, ~ 4er К + 2 (е2 — r.J
‘ 1 К (fe)
к; (^1)
(8-25)
где К, К' и Кь К/ — полные эллиптические интегралы первого
рода с модулями k, k' =1^1—k2, ki п Л] = фл1 — k2 соответ-
ственно, ______
267
1 ~Р <71 <7г .
(I + <7i) (1 + <7а)
(a + b + 2d)
sh
<71 =------
п (b + d)
2h
% =------------
sh
л (b -|- d)
2h
[б<5 % при е2/е/>3].
Емкость на единицу длины рассматриваемой системы может
быть определена также по графикам на рис. 8-22.
Рис. 8-22
268
б. а—>оо.
Значение G определяется по формуле (8-25) при
й =-----------------1-----; = 1 / —
j ! 2d V 1+<72
Ь
[б <5 % при e2/ei>3].
8-3-13. Две пластины, расположенные симмет-
рично на границах диэлектрического слоя
(рис. 8-23).
а. Пластины неравной ширины («<(>)
С.»С;(Ч) + 2(%~Ч)-™-. (8-26)
Рис. 8-23
Рис. 8-24
где G(ei) —емкость между теми же пластинами в однородной
среде при e = ei (см. п. 4-3-3); К (k) и К7 (/г) —полные эллипти-
ческие интегралы первого рода с модулями.
[6<5 % при b2/ei >3].
Kl (&1)
б. Пластины одинаковой ширины (а=Ь)
&tCL /1 । h h i 2jT£Z \ t г» / \
Cz« 4- H------------+------In—— +2 (ea—er)
h \ яа яп h )
(8-27)
где Кi7 и Ki — полные эллиптические интегралы первого рода
с модулями
ХЛ , /---------
------------- и =
ch2-----
4/г
[б <5 % при e2/ei > 3].
269
8-3-14. Плоский конденса.тор с бесконечно
длинными пластинами (рис. 8-24).
При е2>81
+ (8-28)
где Cz'(ei)—емкость между рассматриваемыми пластинами
в однородной среде (при e = ei) (см. п. 4-3-3)
[6 <4 % при 82/ei> 2].
При 6z//i<;l
С, I - Je2-_ei)A_ (8-29)
. 4ft h
In---
а
[6<1 % при a/h<0,25 и 82/81 >3].
8-4. ПЛАСТИНЫ КОНЕЧНЫХ РАЗМЕРОВ
8-4-1. В настоящем параграфе приведены
формулы для расчета емкости между двумя пластинами ко-
нечных размеров, расположенными на поверхностях диэлектри-
ческого слоя конечной или бесконечной ширины. Все приве-
денные формулы являются приближенными. Их погрешность
определяется соотношениями геометрических размеров и ди-
электрических проницаемостей и во всех случаях, когда не ого-
ворено противное, не превышает 10 %.
8-4-2. Две одинаковые прямоугольные пла-
стины, расположенные симметрично на гра-
ницах диэлектрического слоя (рис. 8-25).
h
~
Рис. 8-25
При 82/8! >1
JL, _L\
\ ei ь а /
(8-30)
270
где С' — емкость между теми же пластинами в однородной'
среде при е=Е| (см. п. 5-3-7); ц— коэффициент, определяемый
с помощью графиков на рис. 8-26, а—г по заданным значениям
ег/ёь h/b и b/а [б<3 %].
8-4-3. Плоский конденсатор с однородным ди-
электриком (рис. 8-27).
а. Общий случай.
При е2>Б1
(8-31)
h
где h — расстояние между пластинами; К— односторонняя пло-
щадь одной пластины; I—наибольший размер пластины.
При e2>6i
С « С' -ф (s-2~E1),S- , (8-32)
лЛ
где С' — емкость между теми же пластинами в однородной
среде при e=ei
[6<3 % при E2/ei>3],
б. Конденсатор с квадратными пластинами.
При а=/г
С ( 1,008 + 82 81 , (8-33)
\ /
где а — сторона квадрата
[6<3 % при е2/Е1>2].
в. Конденсатор с круглыми пластинами.
При h>a (а — радиус диска)
С » ега (------------------р
, 2 , h Г Е1 h
I 1------srcctg — 1
\ л а
е2 — е£ яа
(8-34)
8-4-4. Плоский конденсатор с неоднородным
по толщине диэлектриком.
а. Общий случай
С------—
h
Г dy
.) е(</)
с
(8-35)
где у — координата, отсчитываемая от одной из пластин по
нормали к ней; е(#) — заданная функция, характеризующая
271
%
UtiJU 0,86 0,82 0,78 0,74 0,70 0,66 0,62 0,58 0,54 ПЧП b/a- --0,75
b/b- ^0,25
— —
— 0,5 f) 74 —
— — — — 1,0' 2,0 —
— 1 : ~ . 10,0 ez/ef
D,5D2 6 10 14 18 22 26 30 34 38 42 46 50
Puc. 8-26
Рис. 8-26
изменение диэлектрической проницаемости ио толщине диэлек-
трика (e(#)min>£i); А — расстояние между пластинами; S —
односторонняя площадь одной пластины.
б. При слоистом диэлектрике (рис. 8-28)
----------— . (8-36)
(Ат ^т—1)
е>п
т^1
где п — число слоев; hm-i и hm — расстояния границ т-го слоя
Рис. 8-27
Рис. 8-28
от одной из
в m-м слое.
.в При
пластин;
с™ — диэлектрическая проницаемость
e = et4----~ у
h
Л In —-
S1
(8-37)
где ei и 62 — значения диэлектрической проницаемости у по-
верхности пластин.
8-4 5. Коаксиальные диск и кольцо, располо-
женные па торцах непроницаемого круглого
Ц и л и и д р а (рис. 8-29):
С^—- , (8-38)
——+ «
ЛР
где а — параметр, определяемый графиком на рис. 8-29.
274
а b Значение а(хЮ’) при kb, равном Макси- мальная абсолют- ная по- грешность
0,10 0,20 0,30 0,40 0,50 0,60 0,80 1,00 СО
0,25 0,144 0,193 0,207 0,212 0,213 0,213 0,214 0,214 0,214 0,003
0,50 0,83 1,33 1,57 1,70 1,75 1,78 1,79 1,79 1,79 0,02
0,75 3,21 5,07 0,08 6,59 6,88 6,97 7,04 7,07 7,07 0,13
8-5. ОБОЛОЧКИ
8-5-1. В настоящем параграфе приведены
формулы для расчета емкости конденсаторов с обкладками
в форме замкнутых или незамкнутых оболочек типичной формы
при учете неоднородности диэлектрика. Для конденсаторов
с обкладками в форме незамкнутых оболочек (цилиндрического
и конического) рассматриваются случаи, когда диэлектрик
однороден в пространстве между обкладками, но отличается по
проницаемости от окружающей среды. Помимо этого, для всех
рассматриваемых систем (кроме конического конденсатора)
учитывается неоднородность диэлектрика и в пространстве
между обкладками.
8-5-2. Цилиндрический конденсатор с одно-
родным диэлектриком (рис. 8-30).
275
При />а2—«ь 6i»e2
с = 2яЕ1£_ (8.38)
In —
ai
8-5-3 Цилиндрический конденсатор с ди-
электриком, неоднородным в радиальном на-
правлении.
а. Общий случай:
С =---, (8-40)
а,
J ге (г)
где й] и а2 — радиусы внутренней и внешней обкладок, соответ-
Рис. 8-30
Рис. 8-31
I
ственно; I — длина обкладок в направлении их оси; е(г) —за-
данная функция, характеризующая изменение диэлектрической
проницаемости в радиальном направлении.
б. При слоистом диэлектрике (рис. 8-31)
С~ —-----—-------(8-41)
2J_ln-^±L
ат
т=1
где п — число слоев; ат и ат+1 — внутренний и внешний ра-
диусы т-го слоя; ет — значение диэлектрической проницае-
мости в т-м слое.
8-5-4. Цилиндрический конденсатор с ди-
электриком, неоднородным в осевом направ-
лен и и.
а. Общий случай:
i
С = л - f е (z) dz, (8-42)
ln-^ 0
«I
где e(z) —заданная функция, характеризующая изменение ди-
электрической проницаемости в осевом направлении, а осталь-
ные обозначения те же, что в (8-40).
б. При слоистом диэлектрике (рис. 8-32)
С=— (8-43)
ln-^ m=I
где п—число слоев; 1т — толщина m-го слоя; ет — значение
диэлектрической проницаемости в m-м слое.
8-5-5. Ц и л и н др и чес к и й конденсатор с ди-
электриком, проницаемость которого зависит
от ф (угла, отсчитываемого от какой-либо полуплоскости, про-
ходящей через ось цилиндрических обкладок конденсатора).
а. Общий случай:
2л
С =-------f е (ф) dtp, (8-44)
, а» о
In ——
аг
где е(ф) —заданная функция, характеризующая изменение ди-
электрической проницаемости, а остальные обозначения те же,
что в (8-40).
б. При секториальном расположении слоев диэлектрика
(рис. 8-33)
п
С = —----- 2 (фт+1 - %,)> (8-45)
ln-^ m=1
где п — число слоев; фт+1 и фт — координаты полуплоскостей,
ограничивающих m-й слой (фт+1>ф»п), причем ф1 = 0, фп+1 = 2я.
При одинаковых слоях
С = 2nl— 2 е,п- (8’46)
^2 "1=1
п In--
01
277
8-5-6. Сферический конденсатор с диэлектри-
ком, неоднородным в радиальном направлении.
а. Общий случай:
С = -~ 4л-----, (8-47)
i‘~ dp
Р2е (р)
at
где at и а2 — радиусы внутренней и внешней обкладок конден-
сатора, соответственно; е(р)—заданная функция, характери-
зующая изменение диэлектрической проницаемости в радиаль-
ном направлении.
Рис. 8-33
Рис. 8-34
б. При слоистом диэлектрике (рис. 8-34)
z-> 4л
(8-48)
где Ет — значение диэлектрической проницаемости в пределах
т-го слоя; ат и am+i — радиусы сфер, ограничивающих /д-й
слой (am+i>am).
8-5-7. Сферический конденсатор с диэлектри-
ком, проницаемость которого зависит от ши-
роты (0).
а. Общий случай:
С = 2этаА - [ 6 (0)sin 0rf0, (8-49)
«2 — Oj 0
где Ci и а2 — радиусы внутренней и наружной обкладок, соот-
ветственно; в(0) — функция, характеризующая изменение ди-
электрической проницаемости с широтой.
278
б. При слоистом диэлектрике (рис. 8-35)
С em (cos 0,„ - cos 0^+1), (gjK
^2 — Oj /71=1
где'em—значение диэлектрической проницаемости в пределах
/tt-го слоя; п — число слоев; 6,п и 6m+i — значения углов при
вершинах конусов, ограничивающих m-й слой (0m+i>0m), при-
чем 01 = 0, 6n+I=jr.
8-5-8. С ф е р и ч е с к и й конденсатор с диэлектри-
ком, проницаемость которого зависит от дол-
готы (ср).
е,=о
Рис. 8-35
а. Общий случай:
9 2я
с== ^2_у e(q))d(p> (8-51)
а2 — а1 о
где е(ф) —функция, характеризующая зависимость диэлектри-
ческой проницаемости от долготы, а остальные обозначения те
же, что в (8-49).
б. При слоистом диэлектрике (рис. 8-33)
С = 2^- 2 ет (фт+1 - фт). (8-52)
(Z2 — @1
где — значение диэлектрической проницаемости в пределах
га-го слоя; срт+) и срт — координаты полуплоскостей, ограничи-
вающих т-н слой (ф/„н><Р)п), причем <pt = 0, ф„+1=2я, а осталь-
ные обозначения те же, что в (8-47).
8-5-9. Конический конденсатор (рис. 8-36).
При ei»B2
С = 2jtei (ь ~а) (8-53)
lnlctgTtg т)
279
С
Зависимость
= /(Р) при различных фиксирован-
ие (Ь — а)
ных значениях а представлена на рис. 8-36.
Для конденсаторов, изображенных на рис. 8-37 и 8-38, фор-
мула (8-53) дает приближенное значение емкости; наибольшая
погрешность ее определе-
ния не превышает значе-
ний, определяемых в зави-
симости от ,|3—а кривыми 1
(для конденсатора на рис.
8-37) и 2 (для конденсатора
на рис. 8-38) рис. 8-39.
8-5-10. Бесконечно
длинные оболочки,
расположенные на
поверхности непро-
Рис. 8 37
Рис 8 39
ницаемого круглого цилиндра1
(рис. 8-40):
1 Приводимая ниже формула справедлива для случаев, когда поверхность
цилиндра является как внешней, так и внутренней границей рассматриваемой
среды.
280
где
Ct = e
KW
K'(*) ’
ПрИ ф!=2л--ф4, (p2 = 2n—фз
(8-54)
длинные оболочки, р а с п о -
8-5-11. Бесконечно
Рис. 8 40
ложенные на поверхности эллиптического ци-
линдра (рис. 8-41)
С _₽
U / — с-----,
к (k)
(8-55)
где k = c{a.
8-6. ПРОВОДА И ПЛАСТИНЫ
8-6-1. В настоящем параграфе даны неко-
торые формулы для конденсаторной емкости между бесконечно
длинными проводами и пластинами, расположенными в неодно-
родной среде специального вида. Она состоит из двух областей,
одна из которых (содержащая рассматриваемые электроды)
имеет вид прямоугольного желоба с непроницаемыми грани-
цами. Путем отражения относительно непроницаемых границ
рассматриваемые системы приводятся к системам, содержащим
бесконечное число одинаковых проводов, параллельных друг
281
другу и одной (для системы на рис. 8-42) или двум (для си-,
стемы на рис. 8-43) плоскостям.
8-6-2. Провод и пластина в желобе (рис. 8-42).
При e2<ei
Ci
2лех
(8-56)
|6<2 % при /г/«>10, t//«> 10].
Рис. 8-42 Рис. 8-43
При 2h]d> 1
2л£^
1 2nh d
Р In
d---------2ла
8-6-3. Провод и две пластины в
(рис. 8-43).
При e2<ei
где О'! — тэта-функция.
При h~b!2
£-> _
, d . „ ла лЬ
b-------sin2 — th------
2л. d d
(8-57)
желобе
(8-58)
(8-59)
282
8-7. ПЛАСТИНЫ И ОБОЛОЧКИ
8-7-1. В настоящем параграфе приведены
некоторые формулы для расчета конденсаторной емкости между
бесконечно длинными пластинами и незамкнутыми оболочками,
расположенными в неоднородной среде. Граница однородных
подобластей во всех рассматриваемых случаях считается непро-
ницаемой.
8-7-2. Бесконечно длинные пластина и обо-
лочка, расположенная на поверхности непро-
ницаемого круглого цилиндра.
а. Пластина расположена вне цилиндра (рис. 8-44):
C. = 2e-^L, (8-60)
К (k)
(R + RJ* .sin2-^-
где № =----------------— ---
.R2+ Rzl — 2RlR cos<p
б. Пластина расположена внутри цилиндра (рис. 8-45). Зна-
чение Ci определяется формулой (8-60) при
<р
(2R — a)acos2^-
/?- ---------
а2 ф- 4.R2 cos -5-8Ra cos2 -~
8-7-3. Пластина и оболочка внутри полукруг-
лого непроницаемого цилиндра (рис. 8-46)
С,= е-К (А) , (8-61)
1 К (й) 4 '
283
Рис. 8-47
где К и К'~ полные эллиптические интегралы с модулями
k ~ tg cf g и k' = ]/l—k2.
2 2
Зависимость Q/e от <pi и <ps представлена на рис. 8-47.
8-7-4. Пластина и оболочка, расположенные на
поверхности прямоугольного желоба с непро-
ницаемыми границами (рис. 8-48):
'—= X' <М2>
где К(k) и К'(&)—полные эллиптические интегралы первого
рода с модулями
/.. а , \
sn Ко— , fe0
k = —J—------и k’ := /гщ
sn ^KG— ,
а модуль k0 эллиптического интеграла Ko и указанных эллипти-
ческих функций sn(w, k0) тот же, что и в п. 8-3-6.
СПИСОК ЛИТЕРАТУРЫ
1. Беляков В. И., Кравцова Р. И., Рапопорт М. Г. Таблицы эллиптиче-
ских интегралов.— М.: Изд-во АН СССР. Т. 1, 1962. Т. 2, 1963.
2. Бреус К. А. Потенциальное поле наэлектризованной сферы с двумя от-
верстиями.— Украинский математический журнал, 1950, т. 2, № 1.
3. Булгаков Н. А. Вычисление электроемкости кольца.— ЖРФХО, 1898,
т. XXX, № 3.
4. Вайнштейн Л. А. Статические граничные задачи для полого цилиндра
конечной длины.— ЖТФ, 1962, т. 32, № 10.
5. Игнатовский В. С. Круговой дисковый конденсатор.— Труды Матема-
тического института им. Стеклова, 1932, т. II, № 3.
6. Клиот-Дашинский М. И., Минков И. М. Задача о поле конденсатора
с круглыми пластинами.— Труды 17-й научной конференции профессорско-
преподавательского состава ЛИСИ, 1959, т. IV.
7. Лаврентьев М. А., Шабат Б. В. Методы теории функций комплексного
переменного.— М.: Фнзматгнз, 1958.
8. Лебедев Н. Н., Скальская И. П. Распределение электричества на тон-
ком гиперболоидальном сегменте.— Журнал вычислительной математики и
математической физики, 1967, т. 7, № 2.
9. Мушенко С. В. Некоторые результаты к обоснованию метода Хоу.—
Известия вузов. Электротехника, 1968, т. 8.
10. Погорелов А. В. Дифференциальная геометрия.— М.: Наука, 1974.
11. Полна Г., Сеге Г. Изопериметрические неравенства в математической
физике. Пер. с англ.— М.: Физматгиз, 1962.
12. Рамм А. Г. Итерационный метод решения интегрального уравнения
теории потенциала.— ДАН СССР, 1969, т. 186, № 1.
13. Рамм А, Г., Голубкова М. Н., Усоскин В. В. Расчет емкости парал-
лелепипеда произвольных размеров.— Электричество, 1972, № 5.
285
14. Русин Ю. С. Метод приближенного расчета электрической емкости.—
Электричество, 1960, № 11.
15. Тихонов А. Н. О некорректно поставленных задачах,—В кн.: Вычис-
лительные методы и программирование,—М.; Изд-во МГУ, 1967, № 8,
16, Трантер Дж. Интегральные преобразования в математической физике.
Пер. С англ.—м.: Гое, изд-во техн.-теор. лит-ры, 1956.
17. Уиттекер Э. Т., Ватсон Дж. Н. Курс современного анализа.—М.: Физ-
матгиз, т. II, 1963.
18. Фихманас Р. Ф-, Фридберг П. Ш. Метод Хоу расчета емкости тел н его
связь с вариационными принципами.— ЖТФ, 1970, т. 40.
19. Allen D., Dennis S. The application of relaxation methods to the so-
lution of differential equations in three dimensions.—Quart. Journ. of Meeh,
and Appl. Math.—London: 1953, vol. VI, pt. 1.
20. Bladel J. Van, Mei K. On the capacitance of a cube.—Appl. Sci. Res.,
1962, vol. 9, № 4—5.
21. Cavendish H. Electrical Researches. Edited by J. C. Maxwell.— Cam
bridge: 1879.
22. Cooke J. C. A solution of Tranter’s dual integral equations problem.—
Quart. Journ. Meeh, and Appl. Math., 1956, № 9.
23. Cooke J. C. The coaxial circular disc problem.— Zeitschrift fiir ang.
Math, und Meeh., 1958, vol. 38, № 9110.
24. Cooke J. C. Triple integral equations.— Quart. Journ. of Meeh, and
Appl. Math., 1963, vol. 16, pt. 2.
25. Daboni L. Applicazione al caso del cubo un metodo per il calculo
per eccesso e per difetto della capacita elettrostatica din conduttore.—
Atti. Accad. Naz. Lincei Rend. Cl. Sci, Mat. Nat., 1953, vol. 14, № 4.
26. Ferguson T., Dunkan R. H. Charged cylindrical tube.— Journ. Appl.
Phys., 1961, vol. 32, № 7.
27. Gross E. T. B., Weiss R. B. Groundig grids for high-voltage stations.
II. Resistance of large rectangular plates.—AIEE Trans., 1955, vol. 74, pt. 3.
28. Gross W. Sul calcolo della cappacita elettrostatica di un condut-
tore.— Atti. Accad. Naz. Lincei Rend. Cl. Sci., Fis. Mat Nat., 1952, vol. 8,
№ 12.
29. Heins A. E. Axially-simmetric boundary-value problems.— Bull.
Amer. Math. Soc., 1965, vol. 71.
30. Higgins T. J., Reitan D. K. Calculation of the capacitance of a cir-
cular annulus by the method of subareas.— AIEE Trans., 1951, vol. 70, pt 1
31. Howe G. W. O. The capacity of rectangular plates and a suggested
formula for the capacity of aerials.— The Radio Review.— Dublin: Oct.
1919—June 1920, vol. 1.
32. Hutson V. The circular plate condenser at small separations.— Proc.
Cambridge Phil. Soc., GB, 1963, vol. 59, pt. 1.
33. Hutson V. The coaxial disc vicosimeter.— Zeitschrift fiir ang. Math,
und Meeh., 1964, № 48.
34. Love E. R. The electrostatic field of two equal circular conducting
disks.—Quart. Journ of Meeh, and Appl. Math., 1949, vol. 2, pt. 4.
35. Maxwell J. C. A treatise of electricity and magnetism.— Oxford Univ.
Press.—London: 1893.
36. McMaxon R. J. Lower bounds for the electrostatic capacity of
a cube.— Proc. Roy. Irish Acad., 1Э53, vol. 55, № 9.
37. Nicholson J. W. Problems relating to a thin plane annulus — Proc.
Royal. Soc.—London: 1922, vol. 101, № 70.
38. Parr W'. E. Upper and lower bounds for the capacitance of the regu-
lar solids.—Journ. Soc. Industr. and Appl. Math., 1961, vol 9, № 3.
39. Payne L. E., Weinberger H. F. New bounds in harmonic and bihar-
monic problems.—Journ. Math. Phys., 1954, vol. 33, № 4.
40. Polya G. Estimating electrostatic capacity.— The Amer. Math.
Monthly, 1947, vol. 54, № 4.
41. Polya G. Torsional rigidity, principal frequency, electrostatic capacity
and symmetrisation.—Quart. Journ. of Meeh, and Appl. Math., 1948, Ns 6.
286
42. Rayleigh (J. W. Strait). The Theory of Sound. 2nd cd —London-
1894—1896. vol. 2.
43. Reitan D. K., Higgins T. I. Calculation of the electrical capacity of
a cube.— Journ. of Appl. Phys., 1951, vol. 22, № 2.
44. Reitan D. K- Accurate determination of the capacitance of rectangular
parallel-plate capacitors.—Journ. of Appl. Phys., 1959, vol. 30, № 2.
45. Reitan D. K-> Higgins T. I. Accurate determination of the capacitance
of a thin rectangular plate.—Trans. Amer. IEE, 1957, vol. 75.
46. Smythe W. R. Charged sphere in cylinder.— Journ. Appl. Phys., 1960,
vol. 31, № 3.
47. Smythe W. R. The capacitance of a circular Annulus.— Amer. Journ.
Appl. Phys., 1951, vol. 22, № 12.
ОГЛАВЛЕНИЕ
Предисловие ко второму изданию................................... 3
Из предисловия к первому изданию................'.................—
Введение . . :.................................................: 6
В-1. Основные определения . . . . : . .......................—
В-2. Классификация электростатических систем................ 9
В-3. Общие свойства емкости . •.............................11
В-4. Единицы емкости................................. ..... 17
В-5. Аналогия между емкостью и другими физическими величинами —
В-6. Способы расчета емкости .............................. 19
Часть первая. Специальные методы расчета емкости . . . 23
ГЛАВА ПЕРВАЯ. МЕТОДЫ НЕПОСРЕДСТВЕННОГО ОПРЕДЕЛЕНИЯ ЕМКОСТИ —
1-1. Общие замечания.........................................—
1-2 . Метод средних потенциалов ................ . ... 24
1-3. Метод площадок.........................................31
1-4. Метод эквивалентных зарядов ........ ... 38
ГЛАВА ВТОРАЯ. ВСПОМОГАТЕЛЬНЫЕ МЕТОДЫ И ОЦЕНКИ ...............44
2-1. Общие замечания.........................................—
2-2. Метод конформных преобразований........................45
-2-3. Метод пространственной инверсии.......................50
2-4. Методы оценки емкости уединенных проводников по их геомет-
рическим параметрам....................................56
2-5. Энергетические методы..................................67
2-6. Метод аналитической аппроксимации электростатического поля 71
Часть вторая. Расчетные формулы, таблицы и графики . . 84
Раздел первый. ЕМКОСТЬ ПРОВОДНИКОВ В ОДНОРОДНОЙ СРЕДЕ 86
ГЛАВА ТРЕТЬЯ. ЕМКОСТЬ УЕДИНЕННЫХ ПРОВОДНИКОВ......................—
3-1. Общие замечания ..............
3-2. Провода . 96
3-3. Пластины.............................................' щч
3-4. Оболочки . . ...... 111
3-5. Объемные тела...................................... - •
287
ГЛАВА ЧЕТВЕРТАЯ ЕМКОСТЬ МЕЖДУ ДВУМЯ ПРОВОДНИКАМИ В ПЛОСКО-
ПАРАЛЛЕЛЬНЫХ СИСТЕМАХ ......................................133
4-1. Общие замечания
4-2. Провода . . . . —
4-3. Пластины 137
4-4. Оболочки ................. . . . 146
4-5. Провода и пластины ... . 153
4-6. Провода и оболочки .............................. 158
4-7. Пластины и оболочки . . . . . 160
ГЛАВА ПЯТАЯ. ЕМКОСТЬ МЕЖДУ ДВУМЯ ПРОВОДНИКАМИ КОНЕЧНЫХ
РАЗМЕРОВ ...................................................168
5-1. Общие замечания . —
5-2. Провода 169
5-3. Пластины . 172
5-4. Оболочки .... .185
5-5. Провода и пластины . : 196
5-6. Пластины н оболочки . 211
ГЛАВА ШЕСТАЯ. ЕМКОСТИ В СИСТЕМЕ МНОГИХ ПРОВОДНИКОВ 215
6-1. Общие замечания ....... . . ................—
6-2. Провода..................... ...................... 216
6-3. Пластины.................... ......................217
6-4. Бесконечно длинные провода и пластины . 224
6-5. Бесконечно длинные провода и оболочки ........229
Раздел второй. ЕМКОСТЬ ПРОВОДНИКОВ В НЕОДНОРОДНЫХ СРЕ-
ДАХ ......................... ........... 232
ГЛАВА СЕДЬМАЯ. ЕМКОСТЬ УЕДИНЕННЫХ ПРОВОДНИКОВ —
7-1. Общие замечания.....................................—
7-2. Провода . 233
7-3. Пластины 241
7-4. Оболочки ... 248
7-5. Объемные тела 251
ГЛАВА ВОСЬМАЯ. ЕМКОСТЬ МЕЖДУ ДВУМЯ ПРОВОДНИКАМИ 257
8-1. Общие замечания . . :...............................—
8-2. Провода......................................... —
8-3. Бесконечно длинные пластины 261
8-4. Пластины конечных размеров . . . 270
8-5. Оболочки .................. . . ...........275
8-6. Провода и пластины ......... 281
8-7. Пластины и оболочки ... ..................... 283
Список литературы...........................................285
ЗАМЕЧЕННАЯ ОПЕЧАТКА
На странице 250 вместо строки третьей и четвертой сверху следует
читать:
<рДт) = П Г1
fe=i L
I г 1 . I
, 1 1 Г1 , 11 2 Ь™
---------1 -]— --------е
2«fe (Т) J 2а/г fy) ]