Text
А.Я.ХАЛАМАЙЗЕР
К0МБИИАТВР1ЛКА
И БИНОМ НЬЮТОНА
А. Я. ХАЛАМАЙЗЕР
КОМБИНАТОРИКА
И БИНОМ НЬЮТОНА
ПОСОБИЕ ДЛЯ УЧАЩИХСЯ 9—10 КЛАССОВ
МОСКВА «ПРОСВЕЩЕНИЕ» 1980
22.141
Х17
СОДЕРЖАНИЕ
Введение 3
1. Волейболисты меняются ме-
стами 4
2. Проверка гипотез 7
3. Четырехбуквенные «слова» 8
4. Упорядоченные и неупорядо-
ченные подмножества 10
5 Два состава из общего спи-
ска 12
6. Выбор делегации 14
7. Три вида соединений —
8. Баскетболисты тренируются в
зале 16
9. Треугольник Паскаля 18
10. Коэффициенты многочлена 18
11. Биномиальная формула 19
12. Решение задач 20
13. Некоторые приближенные
формулы 21
14. Наташа нанизывает бусы 22
15. Сережа штампует номера 23
16. В государственном совете
Швамбрании 24
17. Азбука Морзе 26
18. Из истории комбинаторики 28
Ответы и указания 31
Литература для дополнительного
чтения 32
Халамайзер А. Я.
Х17
и бином Ньютона: Пособие для
, 1980-
X
Комбинаторика 1
учащихся 9—10 кл.— М.: Просвещение,
32 с., ил.
В брошюре посредством задач раскрывается содержание основ-
ных понятии комбинаторики. Предназначена для учащихся старших
классов.
60601—183 ББК 22.141
———— 263-80 4306020400
103(03)—80 , 512
© Издательство «Просвещение», 1980 г,
ВВЕДЕНИЕ
В Большой советской энциклопедии говорится, что комби-
наторика— это раздел математики, в котором изучаются неко-
торые операции над конечными множествами, т. е. над опреде-
ленным числом предметов (или точнее, объектов). Сами эти
объекты называются элементами множества. Основными и ти-
пичными операциями и связанными с ними задачами комбина-
торики являются следующие:
1) Образование упорядоченных множеств, состоящее в уста-
новлении определенного порядка следования элементов множе-
ства друг за другом,— составление перестановок.
2) Образование подмножеств, состоящее в выделении из
данного множества некоторой части его элементов,— составле-
ние сочетаний.
3) Образование упорядоченных подмножеств — составление
размещений.
В учебной и научной литературе элементы комбинаторики
включаются обычно в виде отдельной главы в курс алгебры. По-
нимание проблем комбинаторики, умение подсчитывать число
различных возможностей, связанных с упорядочением множеств
и выделением из них подмножеств (как упорядоченных, так и
неупорядоченных), является весьма важным для правильного
восприятия статистических закономерностей, проявляющихся
в природе и технике, для восприятия законов природы, носящих
вероятностный характер, и в конечном итоге Для формирования
личности сознательного строителя коммунистического общества.
Поэтому настоящее пособие представляется полезным как
для самостоятельного чтения любознательными старшеклассни-
ками, так и для использования на факультативных и кружковых
занятиях. Упражнения, приводимые для самостоятельного ре-
шения в конце каждого раздела, помогут учителю уяснить дета-
ли. Выполнение их поможет сознательному усвоению темы.
Автор не считает целесообразным при первоначальном зна-
комстве с предметом излагать строгие доказательства вводимых
правил и формул. Предполагается, что «правдоподобные рас-
суждения» и аналогии, приводящие как бы к самостоятельному
выводу нужных предложений, являются достаточно убедитель-
ными и будут легче восприняты читателем. Вполне строгие дока-
зательства (если они вообще окажутся необходимыми) лучше
отложить на следующий этап изучения.
Автор
1. ВОЛЕЙБОЛИСТЫ МЕНЯЮТСЯ МЕСТАМИ
Тренер волейбольной команды решил изменить расположение
игроков.
— Следующую встречу будем начинать по-другому,— объя-
вил он после очередного проигрыша.— Ты, Сергей, встанешь на
подачу; Володя — на четвертый номер, в нападение, а ты, Ни-
колай...
— А если опять проиграем? — спросил капитан.
— Тогда опять переставлю,— хладнокровно ответил тре-
нер.— Пока не перепробуем всех возможных расположений.
— Долговато пробовать будем,— усмехнулся Сергей, кото-
рый был не только перворазрядником, но и инженером-расчет-
чиком в конструкторском бюро.— Ты даже не представляешь
себе, сколько игр пройдет, пока все способы перепробуем...
Как же подсчитать, сколькими способами можно расставить
6 волейболистов на 6 различных мест? И сколько потребуется
времени, если, например, каждый месяц пробовать 10 различных
способов?
Представьте себе две геометрические фигуры: квадрат и тре-
угольник. Если говорить о порядке их расположения, то можно
найти два способа: сначала квадрат, потом треугольник (рис. 1, а)
или сначала треугольник, а потом квадрат (рис. 1,6).
Точно так же из двух букв А и Б можно составить два двух-
буквенных «слова» АБ и БА. Вообще, множество из двух эле-
ментов можно расположить (упорядочить) ровно двумя спосо-
бами.
Третий элемент (букву) В можно поместить впереди пары —
получим «слово» из трех букв ВАБ; можно поместить посреди
пары — получим АВБ; можно поместить позади пары — полу-
чим АБВ. Точно так же из пары БА можно получить ВБА, БВА
и БаВ. Значит, для трех элементов существует 2-3=6 способов
расположения по порядку; из
трех элементов можно соста-
вить 6 «перестановок» — ком-
бинаций, отличающихся друг "l Л А
от друга порядком расположе- / \ \
ния элементов. Или иначе: мно- L—J Z_____A Z______А ------
жество, содержащее 3 элемен- а) б)
та, можно упорядочить шестью
различными способами. Рис. 1
4
Установленный в конечном множестве порядок расположения
его влементов называется перестановкой.
Число перестановок обозначается латинской буквой Р. Зна-
чит,
Р2=2; Р3=2-З=6.
Символ Р3 читается так: «Число перестановок из трех эле-
ментов».
Пусть теперь у нас имеется k предметов (элементов), из ко-
торых составлены всевозможные Рь перестановок. Возьмем одну
из них:
Ob аз1 • • »
Добавим еще один (Л-Н)-й элемент. Его можно поместить!
1) впереди первого элемента ас,
2) впереди второго элемента «г;
3) впереди третьего элемента аз;
k) впереди Л-го элемента а*;
Л-Н) позади всех имеющихся k элементов, т. е. всего
fe-H способом. Значит, количество перестановок из /г 4-1 элемен-
тов в (£-Н) раз больше, чем число перестановок из k элемен-
тов, т. е.
Рл+1=Рл.(Л+1).
Заметим, что Р2 и Р3 вычислены нами непосредственно; про-
должим наши рассуждения, добавляя для симметрии множи-
тель 1:
Р2= 1-2=2;
Р3=1- 2-3=6;
Р<= 1-2-3-4=24;
Р5=1-2-3-4-5=120;
Ра=1-2-3- ... -Л;
Pft+I=l-2-3- ... .*.(*+1).
Замечание. Произведение натуральных чисел от 1 до
данного натурального числа m называется факториалом числа m
и обозначается ш\
Например: Р2= 1-2=2!
Р5=1-2-3-4-5=5!
РА = 1-2-3- . . . -k=k\ (1)
Итак, из k элементов можно составить Рл=1-2- ... -k=kl
различных перестановок, или, иначе, k\ различных упорядочен-
ных множеств.
Подсчитаем теперь число перестановок из 6 элементов (столь-
кими способами можно расставить на площадке 6 волейболи-
стов) :
Р6= 1 -2-3-4-5-6=720.
б
Согласно условию тренер может
пробовать 10 различных способов
расс+ановки волейболистов в месяц.
Значит, на проверку всех способов
уйдет 72 месяца, или 6 лет.
Если считать различными толь-
ко те расстановки, при которых ме-
няется порядок следования волейбо-
листов, то разных порядков следо-
вания окажется только (6—1)! =
= 120; в этом случае на проверку
всех способов расстановки тренеру
достаточно будет одного года. Вооб-
ще, когда важен только порядок
следования элементов (начальный элемент безразличен), то для
упорядочения множества из k элементов существует (Л—1)1 спо-
собов.
Изменение расположения элементов, не меняющее порядка
их следования (первый элемент «следует» за последним), иног-
да называют циклической перестановкой. Так, например, слово
«осел» циклической перестановкой может быть преобразовано
в «село». Другой пример циклических перестановок изображен
на рисунке 2.
Факториал иногда рассматривают как функцию, определен-
ную на множестве натуральных чисел. В таблице 1 приведены
значения факториала для небольших значений п. Для больших п
вычисление факториала оказывается затруднительным; однако
приближенное значение можно вычислить с хорошей точностью
по формуле Стирлинга:
(е«2,718...)‘.
Таблица 1
1
2
3
4
5
6
7
8
9
10
1
2
6
24
120
720
5 040
40 320
362 880
3 628 800
11
12
13
14
15
16
17
18
19
20
39 916 800
479 001 600
. 6 227 020 800
87 178 291 200
1 307 674 368 000
20 922 789 888 000
355 687 428 096 000
6 402 373 705 728 000
121 645 100 408 832 000
2 432 902 008 176 640 000
6
2. ПРОВЕРКА ГИПОТЕЗ
При нахождении количества различных перестановок (или
числа перестановок) мы воспользовались принципом математи-
ческой индукции. Для этого пришлось:
а) непосредственно подсчитать число перестановок из двух
(или трех) элементов;
б) подметить закономерность изменения числа перестановок
при добавлении еще одного элемента (при увеличении числа
элементов на единицу); сформулировать гипотезу*;
в) доказать эту гипотезу.
Рассмотрим еще один пример применения математической
индукции. Пусть требуется найти сумму дробей следующего
вида:
= -L_ + —+ __L_ +...+ _L_.
1-2 2-3 3-4 Л(Ж)
Выпишем гаемых: суммы Si = для 1 1.2 ОДНОГО, - = —. ‘ — 2 ’ двух, трех, четырех ела- •
1 1 1 = _2_
02 — 12 2-3 3 ’
1 । > 1 1 - = Л.
03 — 1*2 1 2*3 + 3-4 4 ’
S4= 1 L2 +-Л" Z • о . 4 5 *
Нетрудно подметить закономерность: каждая из этих сумм —
дробь, числитель которой равен числу слагаемых, а знамена-
тель— на одну единицу больше; значит, суммы имеют вид:
k
£+1 ’
Предположим, что для k слагаемых выполняется равенство
Sh= ——|—!—h..-Н---------------------— = —-—,
1-2 2-3 Л(Ж) Ж
и докажем, что в этом случае равенство выполняется и для
(&+1) слагаемых, т. е.
о = 1 , 1 , . __1 I 1 = &+1
ft+1 1-2 2.3 (^+0(^+2) k+2 ' 1
1 Гипотезой называется предположение, объясняющее какую-либо зако-
номерность; проверка или доказательство гипотезы — рассуждение, в резуль-
тате которого гипотеза • становится законом (правилом, формулой) или от-
вергается как ошибочная. Одной из форм доказательства гипотез является
применение математической индукции.
7
Для доказательства достаточно заменить первые k дробей
их суммой (исходя из подмеченной закономерности) и сделать
упрощения. Рекомендуем читателю самостоятельно проделать
необходимые действия.
Иногда закономерность (гипотеза) предполагается заранее
и дается в готовом виде; это несколько облегчает задачу.
Проверьте следующие гипотезы:
1. 14-34-54-7+ ... +(2£-l)=fe2 * *.
2.
3.
4.
12+22+32+ ... +*2= -
1-3 3-5 5-7
Вычислите: а) б)
ft-(ft-H)-(2ft+l)
6
_________1 _ k
(2ft—l)-(2ft-|-l) ft+1 ’
Azfi. B) -IL + JL
Pe ’ ' 61 + 71 ’
5. Найдите сумму цифр во всех пятизначных числах, состав-
ленных из цифр 1, 4, 6, 7, 8 (без повторений).
6. Сколько различных пятизначных чисел можно составить
из цифр 2, 4, 6, 8, 0 (без повторений)?
7. Найдите сумму всех пятизначных чисел из упражнения 5.
3. ЧЕТЫРЕХБУКВЕННЫЕ «СЛОВА»
Тридцать букв русского алфавита изображены на карточках
(рис. 3) без повторений. Сколько различных четырехбуквенных
«слов» можно из них составить? 1
Для решения задачи подготовим «наборную доску» для че-
тырехбуквенного «слова» (рис. 4). Очевидно, первую букву
можно выбрать 30 способами: каждая из 30 имеющихся карто-
чек может быть уложена в первую клетку. Вторая буква выби-
рается из оставшихся 29 букв: буква, которая заняла первое
место, не может быть использована вторично. Таким образом,
с буквы А начинается 29 двухбуквенных «слов», с буквы Б —
тоже 29..., с буквы Я — тоже 29, от Я А до ЯЮ. Всего получится
30-29 двухбуквенных «слов».
4
Б
Рис. 3
ЬукЬы-. 1-я 2-я 3-я 4-я
Рис. 4
1 Разумеется, многие «слова», например «ФРЦХ», не будут иметь смыс-
лового значения. Но мы хотим подсчитать все «слова». Отметим еще, что
слово «МИША» мы из этих букв составить можем, а слово «МАША»—не
можем, так как по условию буквы не должны повторяться.
8
Продолжая рассуждение, заметим, что третью букву можно
выбрать 28 способами (так как две буквы уже заняли первое и
второе места); значит, получим 30-29-28 трехбуквенных и
30-29-28-27=657 720 четырехбуквенных «слов». Вот некоторые
из них:
КРАН БРАК
КРАБ ФРАК
Первые два из этих «слов» отличаются выбором одной бук-
вы; второе и третье состоят из одних и тех же букв, но отлича-
ются порядком их расположения; третье и четвертое отличают-
ся выбором одной буквы. Вообще, различные слова могут от-
личаться друг от друга либо выбором букв, либо порядком их
расположения.
Наши четырехбуквенные «слова» представляют собой четы-
рехэлементные упорядоченные подмножества, входящие в мно-
жество из 30 элементов — букв русского алфавита. Упорядочен-
ные подмножества данного конечного множества называются
размещениями.
Как видно, различные размещения (в нашей задаче — по
4 элемента из 30) отличаются друг от друга либо выбором эле-
ментов, либо порядком их расположения. Количество размеще-
ний (или число размещений) обозначается буквой А с соответ-
ствующими индексами. Следовательно, число размещений из
30 элементов по 4: Азо4=ЗО-29-28-27.
8. Сформулируйте правило: как найти число размещений из m
элементов по п (естественно, что n^tri)—и напишите со-
ответствующую формулу.
9. Вычислите: а) AJ0; б) A ; в) А^.
10. Сколько различных четырехзначных чисел можно составить
из цифр: а) 2, 3, 4, 5; б) 2, 3, 4, 5, 6; в) 2, 3, 4, 5, 6, 7; г) 2,
3, 4, 5, 6, 7, 0?
Для записи числа размещений иногда удобно использовать
факториалы, например
A' -3Q.29-28-27- .3°,29,28'27'<26'25‘ -3 2-1) =3°!
30 1-2-3- ... -25-26 261
или в общем виде
A" =m(m—1) • (т—2) • (т—3) • ... - (тп-п+1)= ~^п)1- (2)
11. Вычислите: а) —1Ц-——; б) 10 _------, где п<10.
лЗ Но
Л13 9 12
12. Решите уравнения: а) Д2х=90; б) А2 =42; в) =56х<
9
4. УПОРЯДОЧЕННЫЕ И НЕУПОРЯДОЧЕННЫЕ
ПОДМНОЖЕСТВА
Сколько различных трехзначных чисел можно составить
из цифр 1, 2, 3, 4, 5, 7 (без повторений)?
Решение. Сгруппируем (столбцами) числа, записанные
одними и теми же цифрами:
123 124 ... 579
231 241 795
312 412
132
213
321
В каждом столбце ровно 6 различных трехзначных чисел,
составленных из одних и тех же цифр, но в различном порядке
(объясните, почему именно 6). Эти трехзначные числа отлича-
ются друг от друга либо выбором цифр в различных столбцах,
либо порядком их расположения в одном и том же столбце. Как
уже известно, такие соединения называются размещениями; зна-
чит, для ответа на вопрос задачи нужно найти число размеще-
ний из 7 элементов по 3:
А3 =7-6-5=210.
7
Сколько различных произведений по 3 сомножителя можно
составить, используя те же -цифры в качестве множителей?
Решение. Воспользуемся написанными выше столбцами.
Одно'из возможных произведений будет 1-2-3; все другие про-
изведения, записанные по образцу этого же столбца (2-3-1
и т. д.) отличаются только порядком множителей и, следова-
тельно, не являются различными произведениями *. Различных
же произведений будет лишь столько, сколько выше было
столбцов, т. е. во столько раз меньше, чем различных трехзнач-
ных чисел, сколькими способами можно переставлять эти три
цифры. Значит, ответ на вопрос получается делением:
.3 7-6-5
Л наР„ т. е._1=—=
Различные произведения, о которых шла речь в этой задаче,
представляют собой различные трехэлементные неупорядоченные
подмножества, входящие в множество из семи элементов: 1, 2,
3, 4, 5, 7, 9.
1 Если бы в этом примере в качестве сомножителей были и числа 6 и 8,
то разные сомножители могли бы дать одно и то же произведение (напри-
мер, 1-8=2-4; 2-6=3-4 и т. д.), так что подсчет числа различных произве-
дений был бы сложнее.
10
Произвольные неупорядоченные подмножества данного мно*
жества называются сочетаниями. Различные сочетания отлича-
ются друг от друга только составом (выбором) элементов.
Количество сочетаний (или число сочетаний) обозначается
латинской буквой С с соответствующими индексами. Возвра-
щаясь к предыдущему примеру, получим, что число сочетаний
из 7 элементов по 3:
С7 — — 7-6-5
— Р3 ~ 1-2-3
=35г.
В классе 10 юношей-допризывников. Сколькими способами
они могут избрать четверых для участия в слете ДОСААФ?
Решение. Порядок, в котором будут избраны 4 делегата
на слет, безразличен. Значит, речь идет о сочетаниях из 10 эле-
ментов по 4:
10-9-8:7 _2ю
1-2-3-
13. Сформулируйте правило: как найти число сочетаний из m
элементов по п (n^m)—и напишите соответствующую
формулу.
14. Вычислите: а) С^; б) С3; в) С|.
15. Решите уравнения: а) Сх=21; б) 5С3х=С*х+2;
в) С3х+С2 = 15 (*-0; г) = 15(у—2).
16. В некотором коллективе 20 комсомольцев. Сколькими спо-
собами можно выбрать из них трех членов комитета?
17. Агрохимик проверяет 6 типов минеральных удобрений; ему
нужно провести несколько опытов по изучению совмест-
ного влияния любой тройки удобрений. Для каждого опы-
та берется участок 0,25 га. На какой площади проводится
все исследование?
18. На окружности отмечено 8 различных точек, а) Сколько
хорд можно провести, соединяя любые 2 из этих точек?
б) Сколько различных треугольников с вершинами в дан-
ных точках можно построить? в) Сколько выпуклых четы-
рехугольников с вершинами в этих точках можно постро-
ить? г) Сколько невыпуклых четырехугольников?
19. Очевидно, что С^ = С|. Проверьте также равенстваС]2 = С32;
С.^=С ^.Сформулируйте аналогичное свойство в общем
виде.
* Иногда встречается обозначение числа сочетаний из 7 элементов по 3
в форме (J) ;этот символ имеет то же значение, что и С.
11
5. ДВА СОСТАВА ИЗ ОБЩЕГО СПИСКА
Таблица 2
Команды
по 2 че- ловека по 3 чело- века
АБ вгд
АВ БГД
АГ БВД
АД БВГ
БВ АГД
БГ АВД
БД АВГ
ВГ АБД
вд АБГ
ГД АБВ
Шестеро ребят во дворе большого до-
ма часто играли в лапту строе на трое».
Однажды один из мальчиков уехал, и
наши друзья остались впятером. Стали
играть вдвоем против троих. А чтобы
никому не было обидно, стали составлять
команды всеми возможными способами.
Сколько различных команд по три участ-
ника и сколько — по два участника мож-
но составить из пяти человек?
Решение. Назовем наших ребят
Андреем, Борисом, Виктором, Григори-
ем и Дмитрием и попробуем составить
всевозможные команды (в таблице 2
оставлены лишь начальные буквы имен).
Легко понять, что команд по 2 человека существует ровно С|,
а команд по 3 человека — ровно С|. Но каждой команде
из двух человек соответствует одна и только одна (часто го-
ворят: ровно одна) команда из трех человек. И обратно: каж-
дой команде из трех человек соответствует ровно одна команда
из двух человек. А это и означает, что количество тех и других
команд совпадает, т. е.
Если бы т спортсменов нужно было разбить на 2 команды,
в одной из которых п человек, а в другой — остальные т—п че-
ловек, то, дословно повторив наше рассуждение, мы пришли бы
к выводу, что число сочетаний из т элементов по п равно числу
, сочетаний из т элементов по т—п, т. е. получили бы ту же фор-
мулу в общем виде:
гт—п ,-,п
Рассмотрим еще один пример. 20 выпускников одной школы
подали заявления на механико-математической факультет Мос-
ковского университета. После сдачи вступительных экзаменов
в алфавитном списке принятых оказались семеро из них. Сколь-
ко разных списков по 7 человек в каждом можно составить из
20 выпускников нашей школы?
Очевидно, два разных (алфавитных) списка счастливцев
должны отличаться друг от друга хотя бы одной фамилией. Зна-
чит, разных списков существует столько, сколько есть сочетаний
из 20 элементов по 7, или С^о.
В алфавитном списке непринятых, конечно, остальные ^вы-
пускников нашей школы. Им предстоит выполнить неприятную
12
обязанность: забрать обратно аттестаты в другие документы.
Разумеется, разных списков таких неудачников столько, сколько
есть сочетаний из 20 элементов по 13, или
Но каждому списку принятых соответствует один и только
один список непринятых. И обратно: каждому списку неприня-
тых соответствует ровно один список будущих студентов.
Множество X (различные списки принятых) и множество У
(различные списки непринятых) находятся во взаимно-однознач-
ном соответствии. Каждому элементу первого множества соот-
ветствует ровно один элемент второго множества, и обратно.
Очевидно, оба эти (конечные) множества содержат одинаковое
число элементов. Отсюда сразу же вытекает, что —С7^.
Если бы в университет поступали т абитуриентов, п из кото-
рых приняты, а остальные т—п не приняты, то, дословно повто-
рив наше рассуждение, мы сделали бы вывод, что
с т^п = спт. о):
Заметим, что эти выводы получены без вычислений, на осно-
ве одних только логических рассуждений. Впрочем, этот же ре-
зультат можно получить непосредственно из формулы для числа
сочетаний, если записать ее с помощью факториалов:
Сп - = т1
т Рп (m-n)t nt ‘
о <чз 201 т 20
В нашем случае С12 = ———; CL ----------------------, oi
3 20 (20—13)113! 20 (20—7)17!
куда непосредственно следует, что С^ — С72О.
20. Решите системы уравнений: а) С*+* : С? i С>-> =5 : 5 : 3;
-ФлГ'-Ю,
С’-1 : С’ .=«Л
2L На кафедре математики 9 преподавателей. Сколькими спо-
собами можно составить расписание консультаций на 9 дней,
если каждый преподаватель дает консультацию ровно один
раз?
22. В комитете комсомола 9 членов. Сколькими способами мож-
но составить из них делегацию в составе трех человек для
поездки к шефам?
13
23. 9 членов профсоюзного комитета должны избрать из своего
состава председателя, секретаря и казначея. Сколькими
способами это можно сделать?
24. Проверьте равенства: а) С|4-С2 = С’; б) С*;/4-С* ! =
6. ВЫБОР ДЕЛЕГАЦИИ
В комитете комсомола 7 членов (включая секретаря). Из них
решено выбрать тройку — делегацию к шефам. Сколькими спо-
собами это можно сделать?
Решение. Различные тройки должны отличаться хотя бы
одним делегатом. Значит, ответом на вопрос будет число соче-
таний из семи элементов по 3:
Сколько различных троек (делегаций) включают секретаря
комитета и сколько — не включают?
Решение. Если секретарь — один из делегатов, то еще дво-
их можно выбрать из остальных шести членов комитета; для
этого существует
2 6*5 1 я
Св = — = 15 способов-
Если же секретарь не входит в делегацию, то всех троих де-
легатов придется выбирать из шести членов комитета (кроме са-
мого секретаря). Для этого существует
Ct— 6'5'4. =20 способов.
1-2-3
Итак, делегаций, включающих секретаря, существует С| = 15,
не включающих секретаря — С|=20. Таким образом, общее чи-
сло делегаций, равное С3, разбилось на 2 группы, а именно
и С|. Значит, С26+С3 = С3.
Если бы в составе комитета было п комсомольцев, а в деле-
гацию избрали k членов, то, дословно повторив наше рассужде-
ние, мы получили бы общую формулу, которую иногда назы-
вают правилом Паскаля:
c‘z!+c;ul = c‘. (si 7
7. ТРИ ВИДА СОЕДИНЕНИЙ
Итак, мы рассмотрели 3 вида соединений: перестановки, раз-
мещения и сочетания (без повторений). Напомним, что:
перестановки отличаются друг от друга только порядком рас-
положения элементов;
14
размещения отличаются либо выбором элементов, либо по-
рядком их расположения;
сочетания отличаются только выбором элементов.
В следующих упражнениях сначала определите вид соедине-
ния, а потом произведите вычисления.
25. 25 учителей, встретившись перед педсоветом, обменялись
рукопожатиями. Сколько было сделано всего рукопожатий?
26. 25 выпускников школы решили обменяться фотокарточка-
ми. Сколько было всего заказано фотокарточек?
27. Ученики изучают 9 различных предметов. 1 сентября в
классе должно быть 5 уроков. Сколькими способами мож-
но составить расписание уроков для этого класса на 1 сен-
тября, чтобы в этот день было 5 различных предметов?
28. Для передачи сигналов вывешиваются одно под другим три
разноцветных полотнища. Сколько разных сигналов мож-
но передать при наличии белого, желтого, красного, зеле-
ного, синего и черного полотнищ?
29. Решите уравнение = 120.
30. Сколько существует различных четырехзначных чисел с не-
повторяюшимися цифрами?
31. На железной дороге 25 станций. На каждом билете печата-
ются станция отправления и станция назначения. Сколько
всего различных билетов нужно печатать: а) Если каждый
билет действителен только в указанном направлении?
б) Если каждый билет годен либо на поездку «туда», либо
на поездку «обратно»? в) Если, кроме билета на одну по-
ездку «туда», нужно печатать билет на поездку «туда и об-
ратно»?
32. а) Сколькими способами можно назначить в патруль трех
солдат и одного офицера, если имеется 15 солдат и 4 офи-
цера?
б) В спортобществе 10 сильных лыжников и 8 сильных
лыжниц. Сколькими способами можно сформировать ко-
манду из четырех лыжников и трех лыжниц?
в) Футбольная команда составляется из вратаря, трех
защитников, двух полузащитников, пятерых нападающих.
Сколько разных команд может составить тренер, если
в клубе 3 хороших вратаря, 6 защитников, 5 полузащитни-
ков, 8 нападающих (команды считаются разными, если
они отличаются хотя бы одним участником, причем пред-
полагается, что нападающий не может играть в полузащи-
те, но может играть на любом месте в линии нападения)?
33. Автомобильные номера состоят из трех букв, за которыми
идут 4 цифры, например МКМ 07-37. Сколько машин можно
снабдить различными номерами, если используется 25 букв
(буквы Ь,Ъ, Е, й и Ы не используются)?
15
84. Аня, Вера, Галя, Дина, Жанна, Зоя, Ира и Катя отправи-
лись в путешествие на двух лодках, в меньшей из которых
могли поместиться не более четверых, а в большей — не бо-
лее шестерых. Сколькими различными способами они мо-
гут распределиться в разные лодки? (Распределения счи-
таются различными, если хотя бы одна из девушек окажет-
ся в другой лодке.)
8. БАСКЕТБОЛИСТЫ ТРЕНИРУЮТСЯ В ЗАЛЕ
Зимой баскетболисты приходили на тренировки неаккурат-
но. Иногда собирались все 9 членов секции, а порой только двое-
трое. Однажды тренер решил подсчитать, сколько же всего ва-
риантов появления в зале разных составов.
— Вот сегодня пока никто не явился. Один вариант. А мо-
жет, кто-то один еще придет, хоть мяч в сетку покидает. 9 чело-
век— 9 вариантов.— И тренер записал: 1+9=10.
— Могут прийти двое,— продолжал он размышлять.— Вчера
были Алексей и Борис, позавчера — Борис и Виктор.'Опять раз-
ные составы.
Считал, считал тренер и сбился.
Сколько разных составов баскетболистов может собраться в
зале? Составы считаются разными, если они различаются числом
участников или самими участниками.
Решение I. Чтобы подсчитать число разных составов, ра-
зобьем их на группы по числу явившихся участников:
1) не явился никто—1 вариант;
2) явился один участник — 9 вариантов (т. е. Сэ=9);
3) явились двое из девяти — число вариантов равно С ;
10) явились все 9 участников — число вариантов равно Сэ = 1.
Общее число вариантов получается сложением:
с^+с’ + сЧс’ + сЧсЧ’ + с’ + с’+с;
Это же выражение можно записать короче, если воспользовать-
ся знаком суммы:
Здесь суммирование ведется при изменении k от k=0 до 9.
Решение II. Первый из баскетболистов (например, по ал-
фавиту) может либо явиться, либо не явиться; имеем два вари-
анта. Второй спортсмен также может либо присутствовать, ли-
бо отсутствовать. Для двоих участников имеем 4 варианта (см.
табл. 3).
Третий участник может при этом либо отсутствовать (оста-
ются имеющиеся 4 варианта), либо присутствовать (еще 4 ва-
16
Таблица 3
№ варианта Первый участник Второй участник
1 нет нет
2 да нет
3 нет да
4 да да
Обобщая это рассуждение
важную формулу:
рианта). Таким образом, при-
сутствие или отсутствие каж-
дого следующего баскетболи-
ста увеличивает число воз-
можных вариантов вдвое; для
девяти членов секции будет
29=512 различных составов,
в том числе юдин вариант,
когда явятся все 9 участни-
ков, и один вариант — пустой
зал.
п спортсменов, можно получить
^ + <+<+•+^=2". (6)
или
пк п
2 с = 2 . (6а)
№0 П
35. Каждого из семи студентов можно направить для прохож-
дения практики на один из двух заводов. Сколькими раз-
личными способами можно это сделать?
36. В классе 29 учеников. Сколько существует различных ва-
риантов присутствия (отсутствия) этих учеников в классе?
37. Сколькими различными способами можно разложить 8 мо-
нет различного достоинства в два кармана?
38. Сколько различных четных делителей имеет число 2310?
39. Имеются катушки с омическим сопротивлением 1, 3, 5, 10
и 20 ом. Сколько цепей с различным сопротивлением мож-
но получить, соединяя некоторые из этих катушек после-
довательно?
40. Выполните упр. 35, ес^ли для практики можно выбрать лю-
бой из трех заводов.
41. После окончания всех экзаменов бывшие десятиклассники
устроили вечер, на котором к чаю предлагали торты «Чаро-
дейка», фруктовый, шоколадный, ореховый и вафельный.
Оказалось, что каждый отобрал себе разный набор кусоч-
ков тортов, а Сережа, которому врач запретил сладкое, пил
чай без торта. Сколько выпускников было в X классе?
На сколько кусочков пришлось разрезать каждый торт?
В городе N автобусы ходят без кондукторов.
Пассажиры заранее приобретают талоны,
пробиваемые компостером, причем вид про-
бивки меняется два раза в день. Сколько
различных пробивок можно установить на
компостере, если он пробивает отверстия не
менее чем на трех из девяти возможных мест,
но не на всех девяти (рис. 5) ?
42.
Рис. 5
£ Заказ № 3266
17
9. ТРЕУГОЛЬНИК ПАСКАЛЯ
Выше доказана справедливость важной формулы Паска-
ля (5), которую можно записать в виде С*+1 = C*+I +С*.
Замечая, что С£ = С£=1 и C\—k, получим последовательно:
Са = С1 + С3=2+1=3;
3 2 2
с3= с1 4- с2 =3+3=6 и т. д.
4 3 3
Объединим найденные числа в таблицу 4 (чисел сочетаний):
Таблица 4
Из сколь-
ких эле-
ментов
По сколько элементов
3 4 5 6 7
1
2
3
4
5
6
7
8
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8
Полученная нами таблица обычно называется арифметиче-
ским треугольником или треугольником Паскаля. В качестве
упражнения продолжите эту таблицу до 12-й строки включитель-
но (для контроля: среднее число в 12-й строке должно быть рав-
но 924).
10. КОЭФФИЦИЕНТЫ МНОГОЧЛЕНА
Легко найти произведение двучленов:
(х—а) (х—Ь) =х2— (a-\-b)x+ab.
Можно найти произведение трех двучленов:
(х—а) (х—Ь) (х—с) =x3-(a+b+c)x2+(ab+ac+bc)x-~abc.
Пусть теперь требуется найти произведение п таких дву-
членов:
Pn(x) = (x—a)(x—b)(x—c)(x—d) ... (х—р). (7)
Раскрывая скобки и группируя члены с одинаковыми степе-
нями х, получим многочлен, расположенный по убывающим сте-
пеням х: Рп(х)—хп—хп~'(а-1-Ь-}-с+ ... +р)-^-хп~2(аЬ-}-ас-{-
+ &с+ ...)— xn~3(abc-{-abd+ ...) + ... +(— l)n(abcd ...р),
или, короче, Рп(Х)=$о*п+51*п_|+$2*п_2+ ••• +3п. (7а)
18
Нетрудно заметить, что:
старший коэффициент $о многочлена Рп(х) равен 1;
члены имеют знакочередующиеся коэффициенты;
каждый коэффициент Sk равен сумме всевозможных произве-
дений вторых членов, стоящих в скобках,— по. k сомножителей
в каждом произведении.
43. Раскройте скобки и расположите получившиеся многочлены
по убывающим степеням х:
а) (х-2)(х-4)(х-3);
б) (х+1)(х+2)(х+3)(х+4);
в) (х-1)(х+2)(х-5)(х-Н);
г) (х— 1) (х—2) (х—3) (х+1) (х+2).
Замечание. Если Рп(х)=0, то, раскрывая скобки, полу-
чим уравнение степени п относительно х. Ойо, очевидно, имеет
ровно п корней: Xi—a, x2—b и т. д., так как эти корни обращают
в нуль одну из скобок в выражении (7). Решение таких уравне-
ний здесь не рассматривается.
11. БИНОМИАЛЬНАЯ ФОРМУЛА
Предположим, что в выражении (7) все вторые члены равны
между собой, т. е. Р(х) — (х—а)п. Тогда s0=l; $i =—(а+а4-
+ ... па; s2=(a2-|-a2+ ... 4-а2) = С2а2, ибо слагае-
мых в скобках будет столько, сколько существует всевозможных
парных произведений из п сомножителей, а именно С2п‘, следую-
щие коэффициенты будут s3=—С3а3; s4=C4a4 и т. д. «Общий»
коэффициент, стоящий на (Л4-1)-м месте, будет (— l)hC*-aft; на-
конец, последний коэффициент будет (—l)nan.
Окончательно получим:
(х-а)п=хп—пахп~,-}-С1па2хп-2—С3па3хп-3 + ...+
+ (-1)*С?а*х"-*+ ... +(-l)nan. (8)
Формула (8) называется формулой разложения бинома Нью-
тона 1 и применяется для возвышения в натуральную степень
бинома (х—а). В этой формуле (&+1)-й член имеет вид:
7л+1 = (-1)*с" aftxn_ft. (9) 1
1 Впрочем, формула (8) была известна в Европе уже М. Штифелю
(середина XVI в.), а на Востоке, вероятно, еще раньше. В 1678 г. Ньютон
обобщил эту формулу, показав возможность разложения в «биномиальный
ряд» степени (l-f-x)a при любом действительном значении а. Подобные ря-
ды изучаются в вузовских курсах математического анализа. Формулу (8)
часто называют просто биномиальной формулой или биномиальной теоремой.
2* 19
В некоторых задачах все члены разложения, кроме одного,
обращаются в нуль. По формуле (9) можно находить требуе-
мый член, не выписывая всего разложенияцеликом.
Замечания. 1) Если в натуральную степень возвышается
сумма (х-)-а), то все члены разложения становятся положитель-
ными, например:
(х-|-а)6=х6-|-6ах5-|-15а2х4-|-20а3х3-]-15а4х24-6а5х-|-ав;
2) под х и под а можно понимать любое число или любое
алгебраическое выражение, например:
(Зх—2а)5= (Зх)5-5-2а(Зх)4+10(2а)2(Зх)3-10 (2а)3- (Зх)2-};
+5 (2а) 43х-(2а)5=243x5-810ах4+1080а2х3—
—720а3х2-}-240а4х—32а5.
Отметим некоторые свойства формулы (8):
1) число членов разложения на единицу больше показате-
ля п;
2) показатели степени первого числа (х) убывают, а пока-
затели степени второго числа (а) возрастают от члена к члену
на одну единицу; сумма показателей в каждом члене равна п;
3) коэффициенты членов разложения, равноудаленных от
концов, равны между собой (они совпадают с числами соответ-
ствующей строки треугольника Паскаля);
4) сумма всех биномиальных коэффициентов равна 2П (сравни-
те с формулой (6));
5) сумма биномиальных коэффициентов, стоящих на четных
местах, равна сумме биномиальных коэффициентов, стоящих
на нечетных местах; каждая из этих сумм, равна 2П-1.
44. Докажите сформулированные выше свойства (1), (3), (4),
(5).
Указание. Для доказательства свойств - (4) и (5) приме-
ните формулу бинома к двучленам (1-|-1)п и (1—1)п.
45. Найдите разложения: а) (2у2—Зу)5; б) (1— V2)6; в) (2|Лх—
—4Ух)4. - _
46. Найдите: а) девятый член разложения (a-j-fx)12; б) шестой
член разложения (а2—х3)13.
12. РЕШЕНИЕ ЗАДАЧ
Найдите член разложения (Vy— |/У)20> содержащий у7.
Решение: Сначала запишем общий вид разложения
k /4 г— \ k / 1—\20—й * — — *
rfc+1=c«>(/У ) -(Ку) =СЖу4 у 2 = с20у 4 .
р-г 40—k __ 7 40—k __7
По условию У~~^~ =У* т- е. —= '
20
Отсюда находим 6=12 и искомый член T12+i = C%y>=C&f~
= 216970 у1.
В разложении коэффициент пятого члена от-
носится к коэффициенту третьего члена, как 7:2. Найдите член
разложения, содержащий х в первой степени.
Решение (получается в три этапа).
1) Из условия следует, что
СР = 7 р(р—1) (р—2) (р—3) 12 = 7_
са 2 ’ или 1-2-3-4 " />(/>-!) 2 •
р
откуда находим р=9;
2) записываем общий член разложения
*/ 1 \* _ *
Г*+,^С9|Г^) •(Vx)9_ft=c,х 3x2 •
\ г /
Так как ищется член, содержащий х в первой степени, то
_ 2fe . 9—k
3 + 2
откуда находим k=3;
3) искомый член Т3+1 = Сз9х1 = 84 х.
47. В разложении f——(-г/Укоэффициент четвертого члена от-
\ У /
носится к коэффициенту шестого члена, как 5:18. Найдите
в этом разложении член, не содержащий у.
— 1 \р
а/а-р . который после
упрощений содержит а5, если сумма биномиальных коэффи-
циентов этого разложения составляет 128.
49. Имеется многочлен х(1—х)|04-х2(1—2х)204-х3(1—Зх)30. Оп-
ределите коэффициент при члене, содержащем х4, если вы-
полнить все указанные действия.
50. Второй, третий и четвертый члены разложения (х+у)р
равны соответственно 240, 720 и 1080. Найдите х, у, и р.
51. Выведите формулу для (х-\-а)п методом математической
индукции по п. 13 * * * * *
13. НЕКОТОРЫЕ ПРИБЛИЖЕННЫЕ ФОРМУЛЫ
Вычислим 1,0025 с точностью до 0,000001.
Решение. Воспользуемся формулой бинома:
(14-0,002) 5= 154-5 • 14 • 0,0024-10 • 13 • 0,0022.4-10 • 12 • 0,00234-
4-5-1 •0,00244-0,0025= 14-0,014-0,000044-0,000000084-
4-0,000000000000032 «1,010040.
21
Когда второе число бинома значительно меньше единицы, то
члены разложения (1 4-х)п, содержащие высокие степени х,
становятся очень малыми. При вычислениях, не требующих вы-
сокой точности, можно отбросить эти малые члены, если они
меньше допустимой погрешности вычислений. В частности, пре-
небрегая второй и более высокими степенями х, получаем при-
ближенные формулы:
\±kx. (10)'
52. Вычислите: а) 1,04е (с точностью до 0,0001); б) 0.9974
(с точностью до 0,000001).
Вычислим приближенно 10,02®.
Решение. 10,025= 10-(1,002)5= 105- 1,0025=105Х
XI,010040 ... «101004,0 (с точностью до 0,1).
53. Вычислите: а) 6,ОЗ4 (с точностью до 0,1); б) 4,975 (с точ-
ностью до 1). _____
Вычислим приближенно у 1,012.
Р е ш е н и е. Приближенная формула (10) применяется для
любых, значений k (а не только для натуральных)1. Поэтому
1,012=(1+0,012)°-5=1+0,5-0,012=_12006. _____ _________
54. Вычислите приближенно; а) ^Х1,02; б) |Х'8,024; в) >/"999.
14. НАТАША НАНИЗЫВАЕТ БУСЫ
В самом начале книги было сказано, что из трех букв можно
составить 31=6 различных трехбуквенных «слов». Вот, напри-
мер, слова, составленные из букв К, О, Т:
КОТ, КТО, ОКТ, ОТК, тко, ток.
Составим теперь трехбуквенные слова из букв К, К, О. Ес-
ли бы одинаковые буквы можно было различить (например, Кг
и Ki), то мы тоже получили бы 6 «слов»:
1) KiK2O; 2) К2К1О; 3) К^Кг; 4) К2ОКг, 5) О^Кг;
6) ОКгКь
Легко заметить, что «слова» (1) и (2), а также (3) и (4),
(5) и (6) отличаются только индексами; без индексов эти пары
слов неразличимы. Поэтому из букв К, К, О можно составить не
6, а только 3 различных «слова»: ККО, КОК, ОКК-
Можно рассуждать так: перестановка одинаковых букв не
меняет «слова»; поэтому общее число перестановок с повторе-
ниями во столько раз меньше числа перестановок без повторе-
ний, сколькими способами можно переставлять повторяющиеся
буквы (элементы). В нашем простейшем примере было всего
3 элемента, из которых 2 повторяющихся; поэтому число пере-
становок оказалось равным
Рз _ 31 _о
__________ Р, 21
1 Сравните с замечанием о биномиальном ряде.
22
Наташа получила в подарок 10 просверленных шариков из
оргстекла: 5 белых, 2 красных и 3 голубых. Она продела в них
нитку и надела как ожерелье на шею. Потом стала менять по-
рядок расположения шариков, и каждый день ожерелье при-
нимало другой вид. Сколько разных видов ожерелья может
получить Наташа?
Решение. Если бы шарики одного и того же цвета были
различимы (индексированы), то общее число разных располо-
жений составило бы 101=3 628 800 способов. Однако при любой
перемене мест пяти белых шариков ожерелье не меняет своего
вида, поэтому разных видов ожерелья будет меньше в 5! =120 раз.
Те же соображения относятся и к двум красным и к трем го-
лубым шарикам.
Ответ. ------—----- =2520 видов.
5! 21 3!
Если еще учесть, что ожерелье замкнуто, т. е. последний ша-
рик примыкает к первому, и циклическая перестановка шариков
не меняет вида ожерелья, то окажется, что в действительности
возможны только 252 различных вида.
Рассуждая точно так же в общем случае, можно получить
формулу для числа перестановок из п элементов, среди которых
п( — первого вида, п2 — второго вида, ... п-ь — k-ro вида. Это
л!
здесь п=П14-п2+ ....
число оказывается равным
4-Пл, а некоторые элементы могут и не повторяться, так что мо-
жет быть, например, nt = l. Общепринятого символа для этого
выражения нет; количество видов Наташиного ожерелья мож-
но было, например, обозначить
Р(10; 5, 2, 3) =
101
51213! '
55. Подсчитайте число перестановок из букв слова МИССИ-
СИПИ.
56. Женщина, оставшаяся в захваченной врагом деревне, по-
стоянно передавала информацию о вражеских войсках. Для
этого она развешивала в условленном порядке выстиранное
белье: 4 синих полотенца, 2 белые рубашки и 3 черных тру-
сов. Сколько различных сигналов она могла передавать?
57. Решите задачу 56, если развешиваются 4 белых полотенца
и одна, или две, или три голубые рубашки.
15. СЕРЕЖА ШТАМПУЕТ НОМЕРА
У Сережи остались от набора для настольной игры штампы
с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести
на все книги пятизначные номера — оставить каталог. Первая
книга получила номер 11 111, следующая 11 113, потом 11 117,
23
11 131 и т. д. Сколько различных пяти-
значных номеров может составить Се-
режа?
Решение. Составим сначала все-
возможные двузначные номера из цифр
1, 3, 7 (см. табл. 5).
Таких чисел оказывается 3-3=9.
Третья цифра может быть добавлена к
Таблица 5
Первое число Второе число
1 1 3 1 7
1 11 13 17
3 31 33 37
7 71 73 П
каждому из этих девяти двузначных чи-
сел ровно тремя способами, получится 9-3 = 27 трехзначных чи-
сел. Точно так же можно’ тремя способами добавить четвер-
тую и пятую цифры, получится 27-3=81 четырехзначное и
81-3=243 пятизначных числа.
Эти пятизначные числа отличаются друг от друга либо са-
мими цифрами (например, 11 113 и 11 117), либо порядком их
расположения (например, 11 113 и 31 111). Таким образом мы
составили размещения с повторениями; их число оказалось
равным
Л* =3-3-3-3-3=35.
Если различных штампов будет не 3, а п и если Сережа со-
ставит ими не 5, a k знаков, то общее число различных обозна-
чений окажется п*. Это и есть формула для числа размещений
с повторениями из п элементов по k.
58. В двоичной системе счисления, применяемой в ЭВМ, суще-
ствует только 2 знака: 0 и 1 (иначе: включено — выключе-
но, соединено — разъединено, есть ток — нет тока). В од-
ной из ЭВМ каждое «машинное слово» записывается в
ячейке «памяти», содержащей 37 пронумерованных двоич-
ных разрядов. Сколько различных «слов» можно записать
в такой ячейке?
16. В ГОСУДАРСТВЕННОМ СОВЕТЕ ШВАМБРАНИИ
В домино играют двойными фишками, на каждой половинке
которых изображены точки в количестве от нуля (пустая) до
шести. Сколько всего разных фишек в полном наборе домино?
Решение. Обозначим фишки, изображенные на рисунке 6,
2 4 Л -
через — и —. Фишки с одинаковым числом очков на обеих
5 4
——I половинках назовем дублями, а с разным чис-
• • • лом очков — простыми. Все простые фишки
• • можно обозначить правильными дробями, т. е.
---— ” в случае, изображенном на рисунке, обозначим
2 5
е е именно —, а не —. Значит, нужно найти
число правильных дробей со знаменателями не
Рис. 6 более шести и добавить к ним 7 дублей. Но чис-
24
ло правильных дробей со знаменателями не более шести равно
числу сочетаний из семи элементов (0, 1, 2, 3, 4, 5, 6) по 2, т. е.
Ответ. Разных костей домино всего 214-7=28.
Каждая кость домино соответствует паре чисел, одинаковых
или разных, выбираемых из множества {0, 1, 2, 3, 4, 5, 6}. Лю-
бую фишку можно обозначить последовательностью нулей и еди-
ниц, причем ‘единицы будут стоять на тех местах, которые соот-
ветствуют числам, изображаемым на фишке: для нуля — на
первом месте, для единицы — на втором, для двойки — на треть-
ем... Если фишка — дубль, то две единицы окажутся записанны-
ми подряд, в противном случае после единицы пишем дополни-
тельный нуль, которым отделяются символы разных элементов.
Например, фишке— соответствует запись (0, 0, 0, 0, 1, 1, 0, 0),
4
4 2
фишке —-----запись (0, 0, 0, 0, 1, 0, 1, 0), фишке------запись
5 5
(0, 0, 1, 0, 0, 0, 1, 0); выделенный здесь дополнительный нуль
является разделительным.
Нетрудно убедиться, что каждому способу записи двух еди-
ниц и шести нулей соответствует ровно одна фишка домино.
Значит, количество разных фишек равно числу перестановок из
двух единиц и шести нулей, или
^(8;2,6)= 7~ =28.
' ' 2161 8
Государственный совет Швамбрании подал в отставку. Пред-
стоит формирование нового совета из семи человек, причем в
него могут быть избраны представители четырех политических
партий: 1) Желтой, 2) Оранжевой, 3) Синей и 4) Фиолетовой
(сокращенно: Ж. О, С, Ф). Сколько различных советов можно
составить, если иметь в виду только численное представитель-
ство партий?
Решение. Обозначим совет из трех членов Желтой партии,
двух — Оранжевой и двух — Фиолетовой последовательностью
(1, 1, 1, 0, 1, 1, 0, 0, 1, 1); три первые единицы указывают трех
членов первой партии, следующие после нуля две единицы —
двух членов второй партии, затем после нуля нуль членов треть-
ей партии и две единицы — двух членов четвертой партии. В ито-
ге у нас получилось 7 единиц и 3 нуля. Аналогично запись (1,0,
1, 1, 1,0, 1, 0, 1, 1) обозначает одного члена Ж, трех членов О,
одного члена С и двух членов Ф. Для перестановок из семи еди-
ниц и трех нулей существует
Л10;7,3)= — =с’ способов.
25
Вообще, а единиц и b нулей можно расположить числом спо-
собов, равным
5 _ (а+ь)! а
р(а+Ь;а,Ь) — а/Ь! ~Са+в-
При составлении последовательностей нулей и единиц, со-
ответствующих фишкам домино, нам пришлось добавить один
нуль, чтобы отделить единицы, соответствующие различному
числу очков на половинках фишек домино. При составлении
последовательностей, соответствующих числам членов четырех
политических партий в совете, пришлось добавить 3 нуля; вооб-
ще, составляя обозначения из единиц и нулей для сочетаний с
повторениями по п элементов, среди которых есть т различных,
придется добавить /п—1 разделительных нулей. Полученное по-
сле этого количество различных перестановок с повторениями
из п единиц и m— 1 нулей в точности совпадает с количеством
сочетаний с повторениями из т элементов по п. Значит, число
сочетаний с повторениями выражается формулой
Гп —р — (т+л—1)! _г п
Ст P(m+n-i:n,m-l)- (m_1)!n! -Cn+'-t.
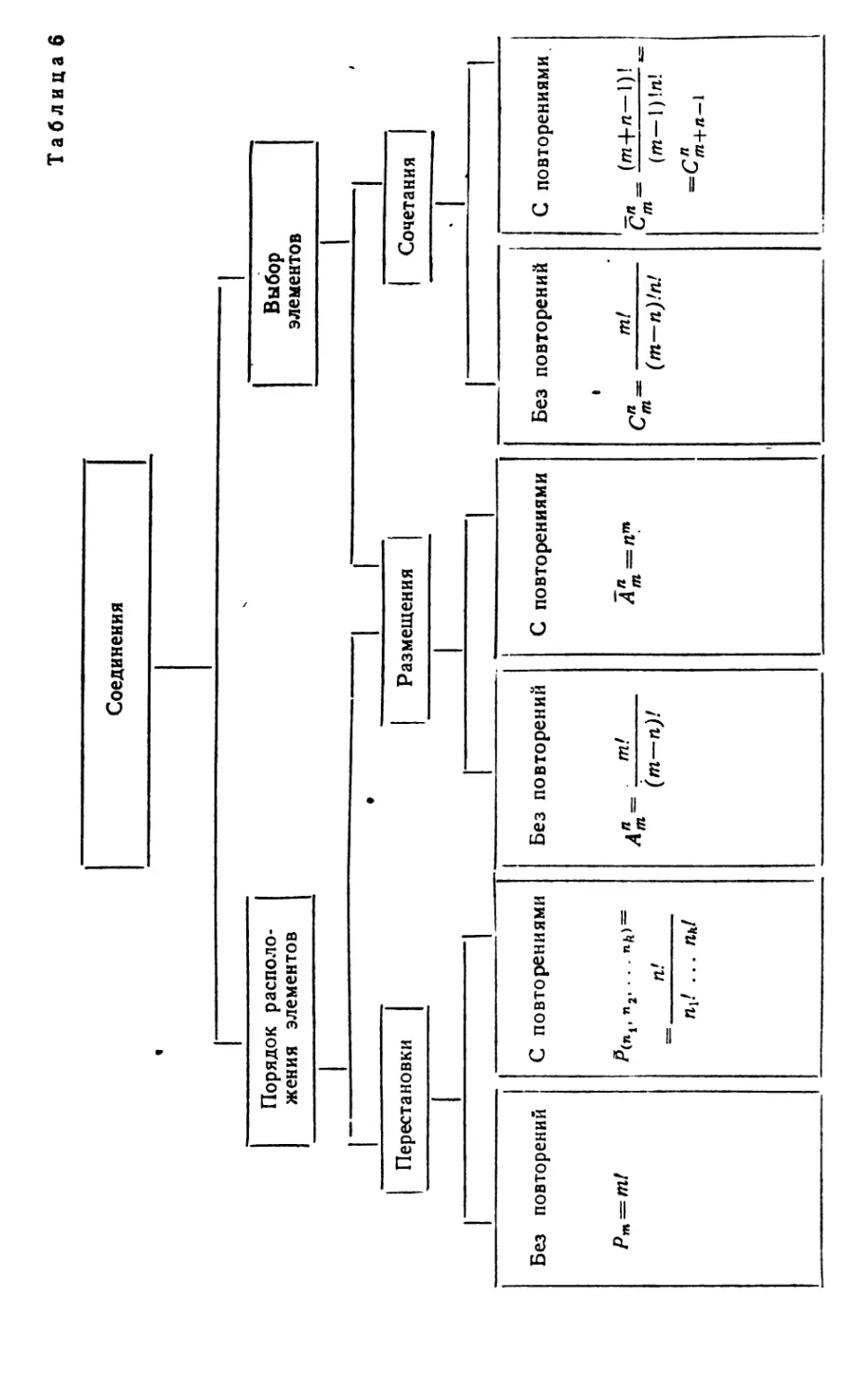
Примечание. Сводка формул всех видов соединений при-
ведена в таблице 6.
59. В школьный комитет комсомола избирают 9 членов, кото-
рые могут быть учениками VIII А, или VIII Б, или IX, или
X класса, причем из одних десятиклассников комитет со-
ставить нельзя. Сколько различных комитетов, отличаю-
щихся представительством классов, можно избрать?
60. Сколько существует различных целых чисел, меньших
10 000, в написании которых содержатся цифры 1, 2, 3
(каждая цифра не менее одного раза)?
17. АЗБУКА МОРЗЕ
В азбуке Морзе, которая используется для телеграфных со-
общений, содержится только два знака: точка и тире. Каждая
буква или цифра кодируется определенной последовательностью
точек и тире. Например:
А — 1
Б -------- 2
В -------- 3
Г -------- 4
д + •
Е - -
Э -------- и т. д.
26
Таблица 6
Некоторые символы передаются одним знаком, как буква Е,
другие — двумя, тремя и даже пятью знаками. Попробуем под-
считать, сколько различных символов можно передать.
Одним знаком можно, очевидно, передать ровно два различ-
ных символа: «•» (буква Е) или «—» (буква Т). Двумя знака-
ми можно передать «• • », или «—», или «—», или «-», т. е.
четыре различных символа. Присоединяя к каждому из этих
четырех символов точку или тире, получим еще восемь символов.
Далее, присоединение каждого нового знака дает возможность
увеличить число различных символов вдвое; с помощью k зна-
ков можно передать 2* различных символов. Таким образом,
используя код, содержащий от одного до пяти знаков, можно пе-
редать 21+22+23+24+25=62 различных символа, которых и
оказалось достаточно для телеграфной азбуки Морзе. Позднее
для некоторых знаков были присоединены шестизначные сим-
волы (например, минус, кавычки, двоеточие, восклицательный
знак, запятая, дробная черта и т. п.).
61. В азбуке Брайля (для слепых) каждый символ обознача-
ется шестью точками; на некоторых из них имеются вы-
пуклости, которые легко определяются осязанием (на на-
шей схеме выпуклости обозначены плюсом):
+ О + О • ++ + +
ОО + О +О + +
ОО ОО + О + О
А Б П Ч
Ощупывая пальцами эти знаки, слепые могут «читать» любой
текст. Сколько различных символов может быть в азбуке Брай-
ля?
62. В телефонной сети города Безпятска запрещен набор циф-
ры 5. Сколько различных «безпятских» абонентов можно
вызвать набором четырехзначного номера, если ни один но-
мер не должен начинаться с нуля?
18. ИЗ ИСТОРИИ КОМБИНАТОРИКИ
Уже в школе пифагорейцев (VI—IV вв. до н. э.) изучались
«треугольные числа», которые представляют собой сочетания
по 2 элемента.
В документах, относящихся к началу нашей эры, упомина-
ются «четырехгранные» или «пирамидальные» числа, представ-
ляющие собой С£. «Треугольными» называются числа вида
л(лЧ-1) . П П А
—-—придавая п значения 1, 2, 3, 4 ..., получим треуголь-
ные числа 1, 3, 6, 10, ... .
Если одинаковые шары выложить на плоскости в виде тре-
угольника, в верхнем ряду которого один шар, в следующем —
28
два, затем — три, четыре и т. д.,
то общее количество шаров в
первых рядах выразится тре-
угольными числами. Можно
представить себе также несколь-
ко одинаковых кругов (например,
монет), выложенных на стол
вплотную друг к другу (рис. 7)-
Точно так же «пирамидаль-
ные» или «четырехгранные»
числа связаны с числом шаров,
сложенных в виде пирамиды, в
Рис. 7 - верхнем ряду которой один шар,
лежащий в углублении между
тремя касающимися друг дру-
га шарами следующего ряда (слоя); каждый следующий слой
содержит следующее «треугольное» число шаров (1, 3, 6, 10,
15, ...), так что первыми пирамидальными числами служат 1,
4, 10, 20, 35, ..., представляющие собой числа сочетаний из
трех, четырех, пяти и т. д. элементов по три.
Во всех странах мира люди с давних времен играли в кости.
Особенно широкое распространение получили азартные игры
с развитием денежного обращения. Сиятельные графы и морские
пираты, византийские купцы и золотоискатели Невады, блиста-
тельный д’Артаньян и его товарищи-мушкетеры — все были за-
ражены азартом этой древней игры. Атос оценил своего слугу
Гримо в десять ставок; выигрыш и проигрыш состояний,
дворцов, поместий хорошо известны в истории. Игра рас-
пространилась настолько, что христианской церкви пришлось
издавать указы и постановления, запрещавшие или огра-
ничивающие игру. Участникам третьего крестового похода
не разрешалось проигрывать более 20 шиллингов в сутки. Лю-
довик IX (XIII в.) запретил не только игру, но даже изго-
товление костей. Издавались законы о запрещении игры и
на Руси (царь Алексей Михайлович — в 1649 г., Екатерина II —
в 1782 г.).
В XVII в. в Европе стали распространяться таблицы, в кото-
рых перечислялись возможности получения разного числа очков
на двух и трех костях. Математики стали анализировать ком-
бинации, получающиеся при бросании костей. Наиболее полно
сделали это Галилей, Паскаль и Ферма.
Паскаль и Ферма излагали свои результаты в письмах.,
В 1653 г. Паскаль писал друзьям о подготовленной им рукопи-
си; однако его «Трактат об арифметическом треугольнике» был
опубликован посмертно лишь в 1665 г. Рукописи Галилея увиде-
ли свет только в 1718 г.
Вероятно, систематическое изложение формул и законов ком-
бинаторики было впервые опубликовано в 1666 г. Г. Лейбницем
29
в книге «Рассуждения р комбинаторном искусстве»; в 1713 г.
появилась книга Я. Бернулли «Искусство предположения», со-
державшая также формулы комбинаторики; наконец, великий
Л. Эйлер рассмотрел ряд комбинаторных задач, из которых впо-
следствии развились самостоятельные отрасли науки, находя-
щие в наши дни Самое широкое применение.
Уже много сотен лет люди пользуются различными формами
тайнописи — криптографии. Чтобы текст не могли прочитать
непосвященные, слова иногда записывали в обратном порядке,
т. е. от конца к началу; иной раз пользовались заменой одних
букв алфавита другими; чтобы прочитать такую запись, нужно
было знать «ключ»— способ замены букв.
Развитие комбинаторных методов позволило расшифровы-
вать такие записи. Победа Кромвеля в гражданской войне (Анг-
лия, середина XVII в.) была в значительной мере облегчена
раскрытием намерений монархистов. Заговорщики думали, что
их планы выданы тайным агентом Кромвеля. А после реставра-
ции Стюартов стало известно, что один из лучших английских
математиков того времени сумел очень быстро разгадать не-
сложные шифры заговорщиков.
Несколько сотен лет назад ученый, сделавший какое-либо
открытие, публиковал об этом сообщение или даже книгу. Ес-
ли же открытие было еще недостаточно проверено, то публика-
ция могла оказаться преждевременной, а задержка публикации
грозила потерей приоритета. Поэтому многие ученые публико-
вали (или посылали другим ученым в письмах) краткое сооб-
щение в форме анаграммы.
Анаграмма — слово (или фраза), составленное из тех же
букв, но в другом порядке. «Нева» и «Вена» — анаграммы.
Получивший сообщение «Вена» может довольно быстро со-
ставить остальные 23 четырехбуквенных слова из тех же букв
и догадаться, что зашифровано «Нева». А если в анаграмме, ска-
жем, 30 букв (причем некоторые повторяются от двух до шести
раз), то существует---------—----------- , или около 7-Ю22,
' J J 2! 2! 31 314! 5! 5f 6!
способов их перестановки.
Галилей, наблюдая в 1610 г. Сатурн с помощью построенно-
го им телескопа, заметил у него два спутника. Однако, не будучи
уверен в своем открытии, он возвестил об этом анаграммой,
зашифровав по-латыни сообщение, которое можно перевести так:
«Высочайшую планету тройною наблюдал».
Полвека спустя голландский ученый Христиан Гюйгенс с по-
мощью более мощного телескопа обнаружил кольцо Сатурна
и поместил в очередной брошюре анаграмму своего открытия.
А английский математик Уоллис (тот самый, который помогал
Кромвелю дешифровать переписку монархистов) сумел рас-
шифровать ее и, шутки ради, послал в свою очередь Гюйгенсу
сообщение, также в форме анаграммы, о своем аналогичном от-
30
крытии. Говорят, что Гюйгенс, сам большой любитель и знаток
комбинаторики, не захотел принять шутки и рассердился.
Современный вид формулы комбинаторики приняли к началу
XIX в.; в это время уже почти полностью сформировалась и со-
временная алгебраическая символика.
В наши дни комбинаторные задачи приходится решать физи-
кам, химикам, биологам, экономистам, специалистам самых раз-
нообразных профессий.
ОТВЕТЫ И УКАЗАНИЯ
1. 1) Проверяем гипотезу, например, для Л=2: 1+3 = 4. 2) Пусть гипо-
теза верна для некоторого числа k слагаемых, т. . е. верно, что 1+3+5+ ...
+ (2Л—1)=Л2; докажем, что в этом случае гипотеза (формула) верна и для
(Л+1) слагаемых, т. е. что 1+3+5+ ... + (2Лг—1) + (2£-+1) = (&+1)2. В са-
мом деле, сумма первых k слагаемых по предположению равна k2\ остается
доказать, что Л2+(2&+1) = (&+1)2, а это проверяется непосредственно.
120 1
4. а) 90; б) 49; в) — = —. 5. 3120. 6. 5! — 41=96. 7. Выпишем некоторые
из рассматриваемых пятизначных чисел, например,
1 4 6 7 8 и подсчитаем сумму только единиц во всех 120 слагае-
4 6 7 8 1 мых; эта сумма будет состоять из 24 единиц, 24 четве-
6 7 8 1 4 рок, 24 шестерок, 24 семерок и 24 восьмерок,, что со-
7 8 1 4 6 ставит 24(1+4+6+7+8) =624 единицы-, точно так же
получим 624 десятка, 624 сотни и т. д., а всего 624+6420+62 400+624 000-|-
+6 240 000=6 933 264. 8. См. формулу (2) в пункте 3. 9. а) 720; б) 132;
в) 3024. 10. а) Л^ = Р4 = 24; б) /4^=120; в) Л^=360; г) обшее количество
«четырехзначных» чисел составило бы Л? = 840; однако, например, число
0123, начинающееся с нуля, не является «четырехзначным»; с нуля начи-
нается ровно — общего .количества «четырехзначных» чисел; значит, собст-
венно четырехзначных остается 840— — -840 = 720 чисел. Возможен и дру-
гой способ рассуждения: на первом месте в собственно четырехзначном* числе
может стоять любая из шести цифр, кроме нуля; на следующем месте — лю-
бая из оставшихся шести цифр (включая и нуль), далее —любая из остав-
шихся пяти, а на последнем месте — любая из оставшихся четырех цифр.
Ответ. 6-6-5-4 = 720. 11. а) 100; б) 10. 12. а) 10; б) 7; в) 9. 14. а) 126;
б) 56; в) 56. 15. а) 7; б) 14; в) 9; г) 10. 16. с^0 = =1140. 17. Чи-
сло опытов С|=20; площадь 5 га. 18. а) С|=28; б) С| = 56; в) 70. Ука-
з а н и е. Любые четыре точки, выбранные на окружности, могут служить вер-
шинами трех различных четырехугольников, лишь один из которых — выпук-
лый. 19. См. формулу (3) в пункте 5. 20. а) х=7, г/=3; б) х=12, у=5;
в) л=15, 0=6. 21. Л®=Р9=362 880. 22. С|=84. 23. Яд = 504. 25. С'|5=300.
26. Л 25 = 600. 27. Яд = 15 120. 28. Л|=120. 29. х=5. 30. 4536. См. указание
к задаче 10 (г). 31. а) Л 2s =600; б) С ^=300; в) 1200. 32. а) С?5-С} = 1820.
33. 253-104= 156 250 000. 34. В меньшей лодке могут находиться либо двое
(число вариантов С|), либо трое (число вариантов С|), либо четверо (число
вариантов С«). Ответ. С|+С’+С£= 154. 35. у. С*=2’=128. 36. 2”.
л=о 7
37. 28 = 256. 38. Заметим, что 2310 = 2-3-5-7-11; различные четные делители
31
получаются, если единственный четный простой делитель 2 умножить на неко-
торые из остальных четырех простых делителей, в том числе на все четыре
простых делителя (это будет число 2310, которое, конечно, является дели-
телем самого себя) и ни на один из остальных делителей (это будет число 2,
4 k
которое тоже является делителем числа 2310). Ответ. V С = 24 = 16.
Л=0 4
39. 25—1=31 (32-я цепь не содержала бы ни одной катушки). 40. З7; каж-
дого студента можно направить 4ча практику не двумя, а тремя способами.
41. 2»=32; на 16. 42. С^+С9+С^+С^+С^+С|=84+126+126+84+36+
+9=465. 45. а) 32у'°-240^+720/-1080^+810^-243г/5; б) 99-70V2.
46. a) Te+1=Cf2(x)8a<=495a4x4; б) T6+l=Cj3 (х’)5(а»)’= 1237а'*х'\ 47. Задача
С3Х 5
решается в три этапа: 1) —— =, откуда х=12; 2) 711+1 =
С® 18
(1 \ х
— ji2-fc==c*2^(),5fc^-,2; так как искомый член не должен содер-
жать у, то 0,5^+Л—12 = 0, откуда Л=8; 3) Т6+1 = С^2 =495. 48. 35а5. Задача
решается в три этапа аналогично предыдущей. 49. Следует найти четвертый
член в разложении первого бинома, третий член в разложении второго би-
нома, второй член в разложении третьего бинома; затем умножить их со-
ответственно на х, на х2, на х3 и сложить с учетом знаков. Ответ. 550.
50. Выписав названные члены, получим систему: рг/хр”1 = 240,
——у2хР~2=720, ——е/3хР-3=1080,
1-2 1-2-3
которая решается почленным делением. Ответ. х=2, {/=3, р=5.
52. а) 1,2653; б) 0,908054. 53. а) 1322,115; б) 3032,368. 54. а) 1 005; б) 2,002;
9! * 91
В) 9,997. 55. Р(9;4.э,!!)= =2520. 56. Лэл.з.з) = , =1260.
*1 01 4 I 11 *1 01 лЛ
51 6!
57. При одной рубашке: Р(5;4.о = тгт =5; при двух рубашках: Р<в;4,2)=——=
*1 II 4Н х!
7!
= 10; при трех рубашках: Р(7;4>Э)а=; =35. Ответ. Всего 5+10+35 =
= 50 различных сигналов. 58. 237 «слов»; в каждом разряде может быть
записан либо 0, либо 1. 59. Пусть в комитете а\ учеников VIII А класса, аг —
из VIII Б, а3 —из IX и а4 —из X класса, причем а!+а2+аз+а4=9; тогда
состав комитета может быть охарактеризован последовательностью, состоя-
щей из 9 единиц и 3 нулей, а число таких различных последовательностей
12!
составляет Р(12;9,з)= =220. Однако комитет, характеризующийся по-
9! □!
следовательностью (0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1), состоит из одних десяти-
классников, что запрещено условием. Ответ. 219. 60. 204. 61. 2в=64; каж-
дый символ состоит из шести знаков в двух вариантах. 62. 5832 абонента.
Литература для дополнительного чтения
1. Петер Р. Игра с бесконечностью. М., Просвещение, 1968.
2. Мостеллер Ф., Рурке Р. и Томас Дж. Вероятность. М., Мир,
1969.
3. Виленкин Н. Я. Комбинаторика. М., Наука, 1969.
4. В и л е н к и н Н. Я. Популярная комбинаторика. М., Наука, 1975.
5. Ежов И. И., Скороход А. В., Я Д р е н к о М. И, Элементы ком-
бинаторики. М., Наука, 1977,
А. Я. Халамайэер
КОМБИНАТОРИКА И БИНОМ НЬЮТОНА
Редактор В. И. Ефимов
Художник В. Л. Николаев
Художественный редактор Е. Н. Карасик
Технический редактор Л. Е. Пухова
Корректор В. И. Громова
ИБ № 4962
Сдано в набор 12.03.79. Подписано к печати 04.07.79. Формат 60X90’/ie.
Бум. газетная. Гарнит. литерат. Печать высокая. Усл. печ. л. 2. Уч.-изд. л.
1,84. Тираж 100 тыс. экз. Заказ № 3266. Цена 05 коп.
Ордена Трудового Красного Знамени издательство «Просвещение» Государ-
ственного комитета РСФСР по делам издательств, полиграфии и книжной
торговли.
Москва, 3-й проезд Марьиной рощи, 41.
Типография им. Смирнова Смоленского облуправления издательств, поли-
графии и книжной торговли, г. Смоленск, пр. им. Ю. Гагарина, 2.