Author: Бабич Н.П. Жуков И. А
Tags: блоки обработки данных процессоры вычислительная техника компьютерные технологии
ISBN: 966-96415-2-7
Year: 2004
Text
МКПрссс МММВЦНМс
Н. П. Бабич, И. А. Жуков
МЕТОДЫ ПОСТРОЕНИЯ И ПРОЕКТИРОВАНИЯ
“МК-Пресс” Киев, 2004
Рецензенты: член-корреспондент НАН Украины, профессор В.Ф. Евдокимов — директор Института проблем моделирования в энергетике НАН Украины; доктор технических наук, профессор Г.М. Луцкий — заведующий кафедрой "Вычислительная техника" НТУУ “КПИ''.
Бабич Н. П., Жуков И. А.
Б125 Компьютерная схемотехника. Методы построения и проектирования: Учебное пособие. — К,: “МК-Пресс”, 2004. — 576 с., ил.
ISBN 966-96415-2-7
В этом учебном пособии систематизировано изложены информационные, арифметические и логические основы микроэлектронных схем современных компьютеров. Рассмотрены принципы построения и функционирования логических и запоминающих элементов, типовых функциональных узлов, аналого-цифровых и цифро-аналоговых преобразователей, электронной памяти, арифметико-логических и управляющих устройств, микропроцессоров, интерфейсных контроллеров, а также представлены технологии производства печатных плат. Особое внимание уделено правилам составления конструкторской и программной документации, а также требованиям оформления схем и иллюстративных документов.
Рассчитано на студентов инженерно-технических специальностей высших учебных заведений.
ББК з973.2-04я73-5
BN 966-96415-2-7
© Бабич Н.П., Жуков И.А., текст, иллюстрации, 2004 © "МК-Пресс ’, оформление, дизайн обложки, 2004
Содержание 3
Содержание
Введение
Перечень используемых сокращений
Глава 1. Основы теории компьютерной схемотехники
1 1 Информационные основы компьютерной схемотехники
1 2 Арифметические основы компьютерной схемотехники
1 3 Логические основы компьютерной схемотехники
1 4 Основные хаоактеристики цифровых микросхем
Глава 2. Элементы компьютерной схемотехники
2 1 Логические элементы — диодные, транзисторные, ИИЛ и ДТЛ
2 2 Транзисторно-транзисторные логические элементы
2 3 Логические элементы эмиттерно-связной логики
2 4 Логические элементы на МОП-транзисторах
2 5 Импульсная и потенциально-импульсная системы элементов
2 6 Магнитная схемотехника
2 7 Асинхронные и синхронные RS-триггеры
2 8 Триггеры типов JK, Т D и DV
Глава 3. Последовательностные (накапливающие) узлы компьютерной схемотехники
3 1 Регистры
3 2 Счетчики
Глава 4. Комбинационные функциональные узлы компьютерной схемотехники
4 1 Дешифраторы
4 2 Шифраторы
4 3 Мультиплексоры и демультиплексоры
4 4 Схемы сравнения и контроля
4 5 Преобразователи кодов
4 6 Двоичные сумматоры
4 7 Двоично-десятичные сумматоры
Глава 5. Цифро-аналоговые и аналого-цифровые преобразователи
5 1 Цифро-аналоговые преобразователи
5 2 Аналого-цифровые преобразователи
Глава 6. Основы компьютерной техники
6 1 Общая характеристика компьютерной техники и короткая история ее развития
6 2 Архитектура и структура компьютеров
6 3 Принцип программного управления
6 4 Основные характеристики компьютеров
6 5 Поколения компьютеров
6
7 10
10
18 40
51 65
65 73
83
86
S3 97 103 110
119 119 128
141
141 147
151 157
166 173 186
190
190 196
202
202 203
207 208 209
4 Введение
Глава 7. Память компьютеров 213
7 1 Общая характеристика памяти 213
7 2 Основные структуры полупроводниковой памяти 219
7 3 Кэш-память 223
7 4 Постоянная память 227
7 5 Флэш-память 235
7 6 Статические запоминающие устройства 240
7 7 Динамическая память 243
Глава 8. Арифметико-логические устройства и устройства управления 254
8 1 Классификация арифметико-логических устройств 254
8 2 Языки описания операционных устройств 256
8 3 Устройства управления 258
8 4 Управляющие автоматы со схемной логикой 261
8 5 Структурный синтез управляющего автомата со схемной логикой 264
8 6 Синтез микропрограммного автомата с программируемой логикой 267
8 7 Центральное устройство управления 273
Глава 9. Проектирование специализированных арифметико-логических устройств 277
9 1 Реализация операции сложения 277
9 2 Реализация операции вычитания 285
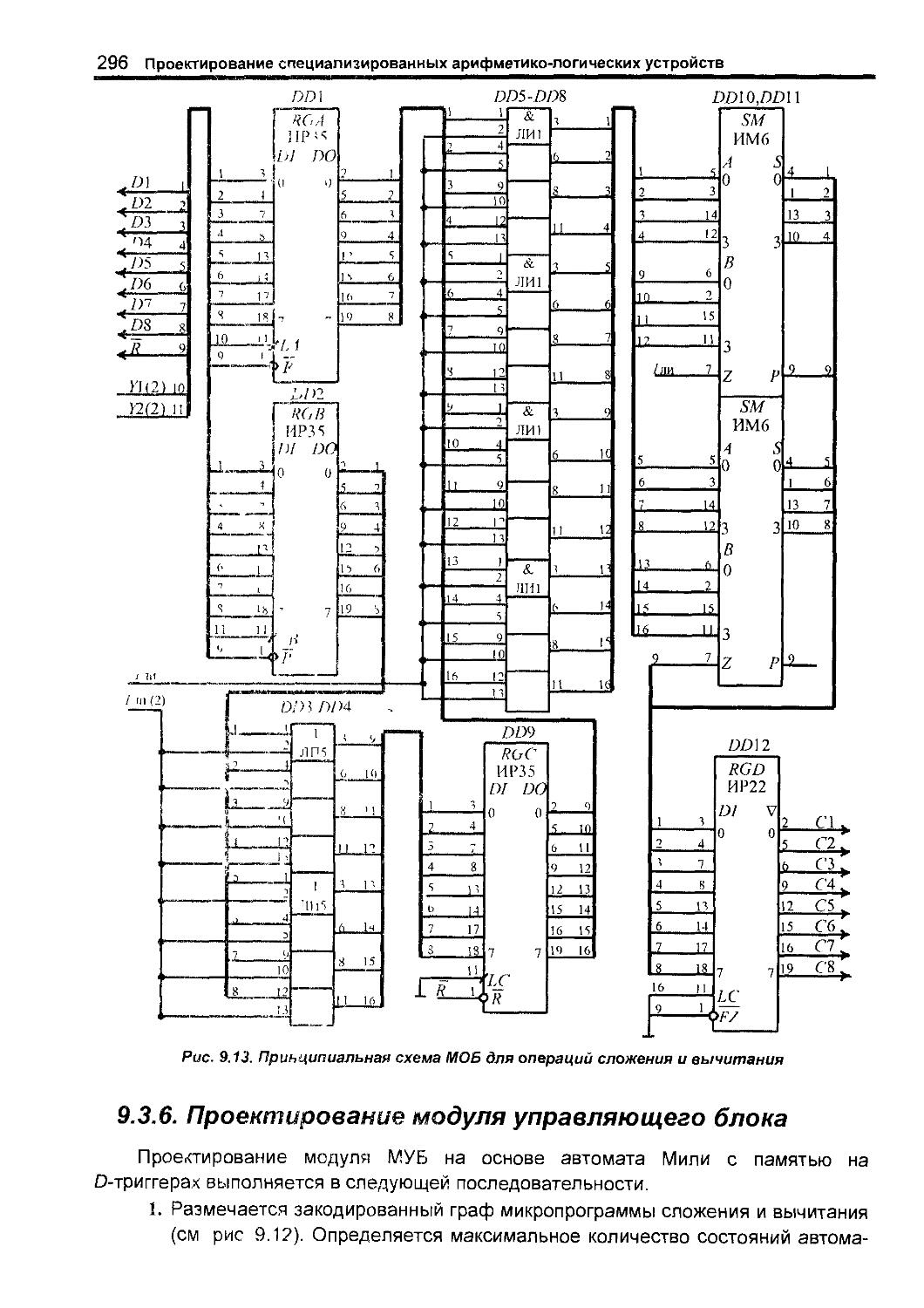
9 3 Реализация операций сложения и вычитания 291
9 4 Реализация операции умножения 299
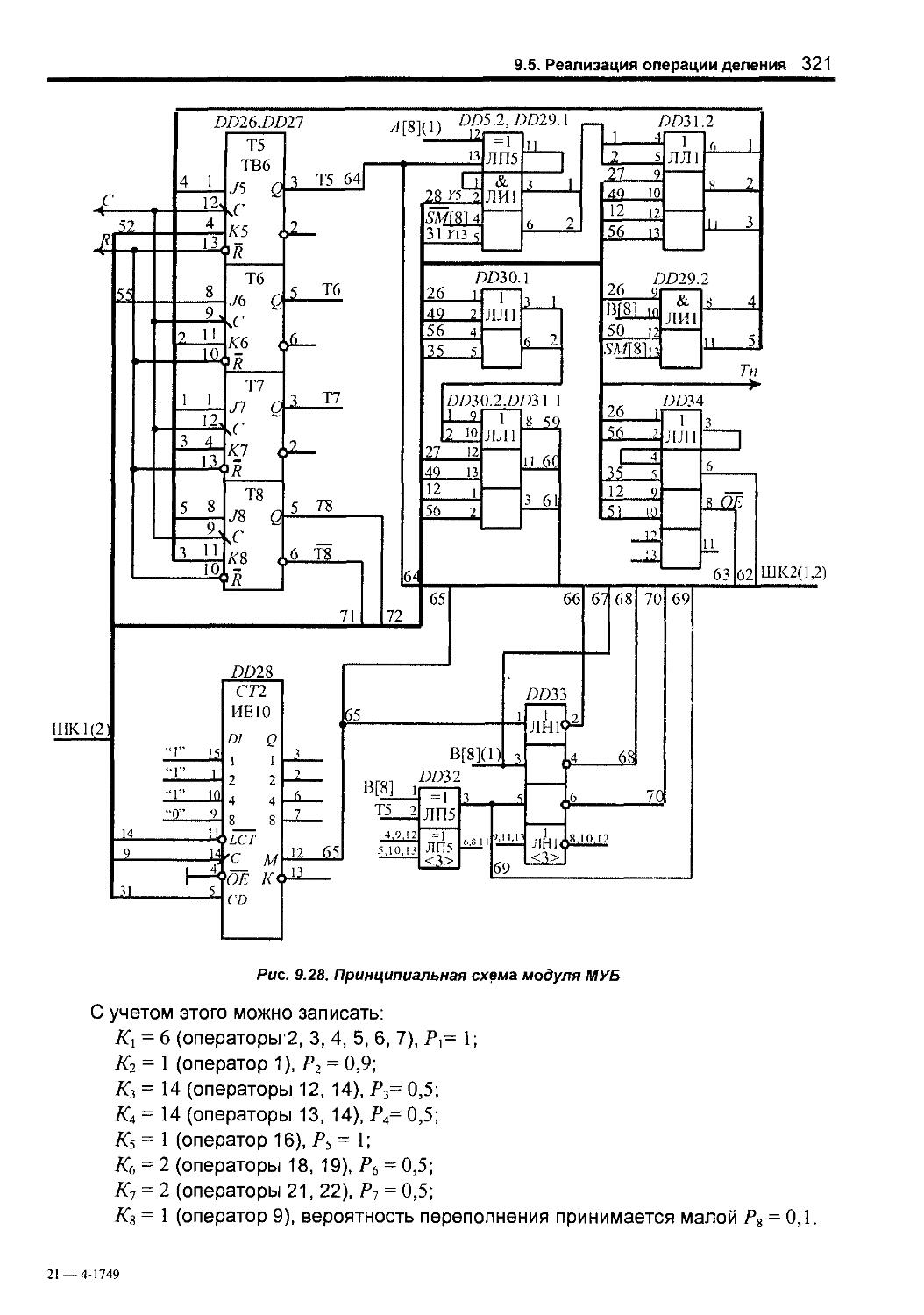
9 5 Реализация операции деления 308
Глава 10. Микропроцессоры 323
10 1 Общая характеристика процессоров и микропроцессоров 323
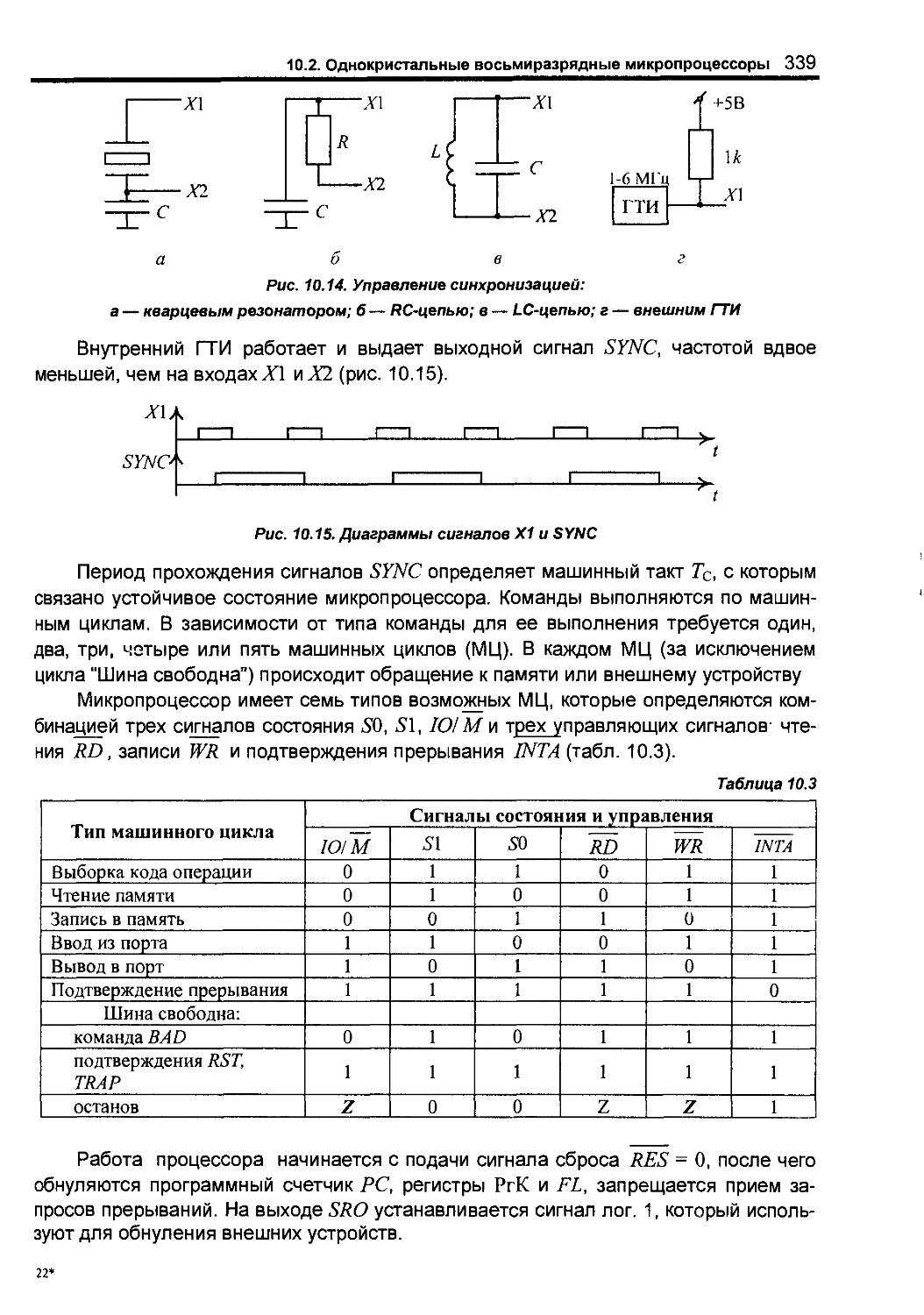
10 2 Однокристальные восьмиразрядные микропроцессоры 335
10 3 Однокристальные шестнадцатиразрядные микропроцессоры 368
10 4 Арифметические сопроцессоры 376
10 5 Суперскалярные 32-разрядные микропроцессоры с C/SC-архитектурой 378
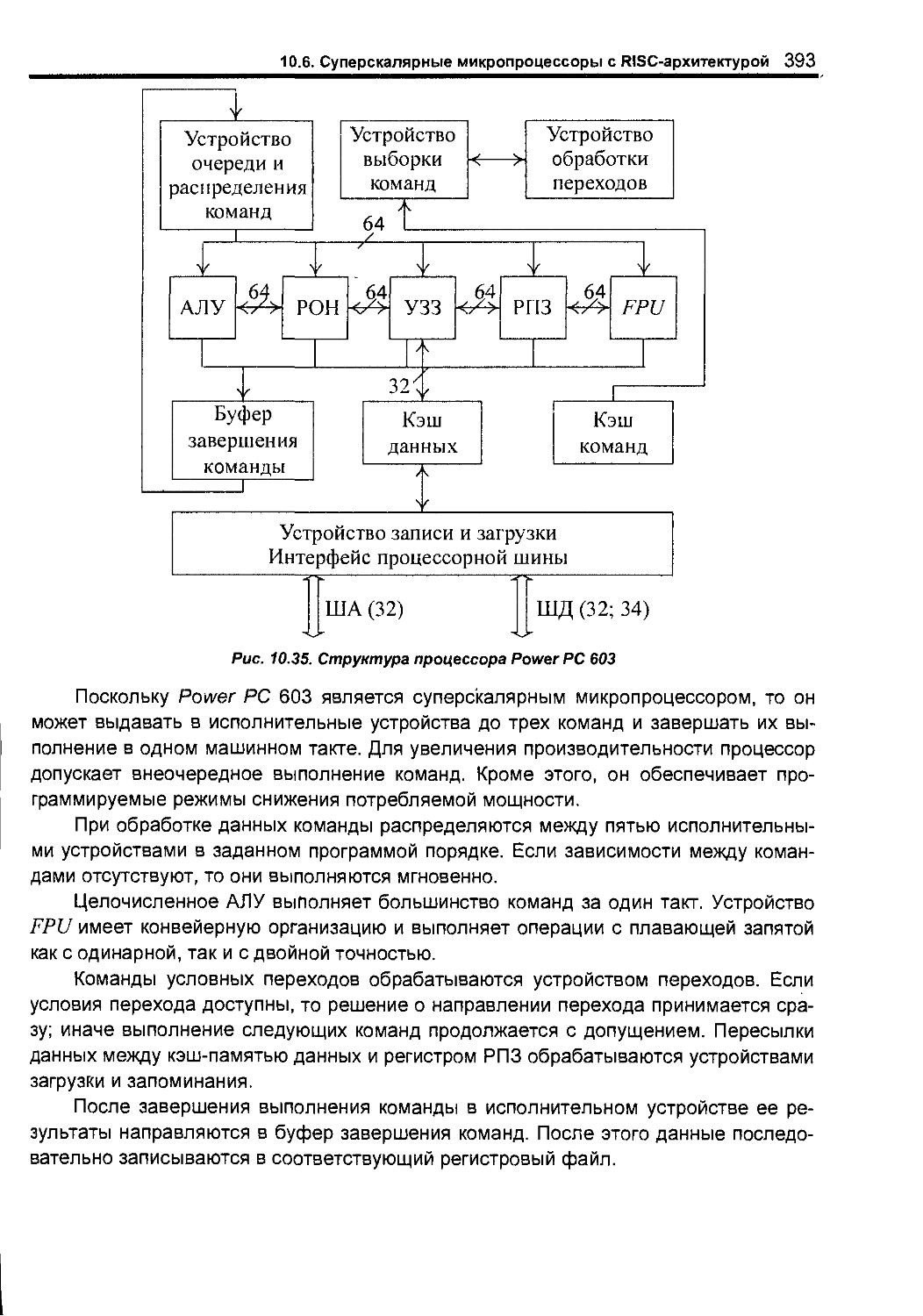
10 6 Суперскалярные микропроцессоры с R/SC-архитектурой 390
Глава 11. Интерфейсы микропроцессорных систем 395
111 Общая характеристика микропроцессорных систем 395
112 Общая характеристика интерфейсов 401
113 Интерфейсные микросхемы 406
114 Программируемые интерфейсные контроллеры 417
Глава 12. Проектирование печатных плат 434
12 1 Основные определения 434
12 2 Виды печатных плат и кабелей 434
12 3 Материалы для печатных плат 436
12 4 Входной контроль и механическая обработка печатных плат 437
12 5 Чертеж печатной платы 439
12 6 Изготовление оригиналов и фотошаблонов 446
Содержание 5
12.7. Типовые процессы изготовления печатных плат.............452
12.8. Последовательность технологических процессов изготовления печатных плат................................454
Глава 13. Конструкторская документация............................457
13.1. Виды конструкторской документации....................... 457
13.2. Общие требования к оформлению проектов..................458
13.3. Обозначение стандартов ЕСКД.............................458
13.4. Обозначение конструкторских документов..................459
13.5. Форматы.................................................460
13.6. Основные надписи и порядок их заполнения................461
13.7. Конструкторские изделия.................................464
13.8. Стадии разработки конструкторской документации..........467
13.9. Правила оформления пояснительной записки................468
Глава 14. Требования к выполнению схем и иллюстративных документов.........................................480
14.1. Понятие схем и общие требования к их выполнению.........480
14.2. Правила выполнения схем цифровой вычислительной техники.488
14.3. Условные графические обозначения элементов цифровой техники в схемах...........................496
14.4. Требования к выполнению иллюстративных документов.......510
Глава 15. Программная документация 518
15.1. Программное обеспечение систем обработки информации.....518
15.2. Единая система программной документации..................521
15.3. Обозначение программных документов.......................523
15.4. Виды программ и программной документации................524
15.5. Стадии разработки программ и программной документации...524
15.6. Требования к содержанию и оформлению....................525
15.7. Символы в схемах алгоритмов, программ, данных и систем...530
Список литературы..................................................542
Приложения.........................................................546
А. Образцы форм документов проекта.............................545
Б. Соотношения размеров условных графических обозначений на модульной сетке...........................................552
В. Обозначения функций элементов, меток выводов...............553
Г. Примеры чертежей печатной платы............................559
Д. Условные графические обозначения элементов цифровой техники.562
Е. Перечень стандартов........................................567
Ж. Словарь общих терминов.....................................569
6 Введение
Введение
Компьютерная схемотехника — это научно-техническая дисциплина, которая изучает теоретические методы анализа и синтеза схем компьютеров (электронных вычислительных машин) и способы их технической реализации. Развитие компьютерной схемотехники является основой усовершенствования архитектуры компьютеров, качественного повышения их производительности и надежности, существенного уменьшения весогабаритных показателей. Компьютеры широко используются в различных отраслях народного хозяйства.
Цель применения компьютеров заключается в информатизации общества — обеспечении повсеместного использования автоматизированных методов сбора, передачи, обработки и хранения информации. Решение проблемы информатизации обеспечивает выход страны на новый уровень цивилизации.
Данное учебное пособие предназначено для студентов, которые обучаются по специальностям “Компьютерные системы и сети", “Информационные управляющие системы и технологии”, "Программное обеспечение автоматизированных систем”. Здесь нашли отражение результаты методологических исследований по оптимизации учебного процесса, полученные на кафедре вычислительной техники Института компьютерных технологий Национального авиационного университета Украины.
В пособии изложены информационные, арифметические, логические и схемотехнические основы компьютерной схемотехники. Рассмотрены элементы и типовые функциональные узлы, а также основные устройства компьютеров: электронная память, арифметико-логические, управления и системы ввода/вывода информации. В сжатой форме представлены характеристики процессоров, микропроцессоров и компьютеров, даны определения, классификация, основные области их применения. Рассмотрен также процесс проектирования печатных плат. Особое внимание уделено правилам разработки конструкторской и программной документации, а также требованиям к выполнению схем и иллюстративных документов.
Авторы благодарны рецензентам — директору Института проблем моделирования в энергетике НАН Украины, члену-корреспонденту НАН Украины, профессору В. Ф. Евдокимову и заведующему кафедры “Вычислительная техника” НТУУ “КПИ”, доктору технических наук, профессору Г. М. Луцкому за ценные замечания.
Авторы выражают благодарность кандидату технических наук А. А. Бабич за помощь в подготовке книги к изданию, а также ответственному редактору издательства “МК-Пресс” Юрию Шпаку, выполнившему всю работу по обработке авторского материала.
Перечень используемых сокращений 7
Перечень используемых сокращений
А аккумулятор
АК арифметический канал
АЛБ арифметико-логический блок
АЛУ арифметико-логическое устройство
АЦП аналого-цифровой преобразователь
АШ арбитр шины
БАД буфер адреса данных
БМУ блок местного управления
БИС большая интегральная схема
БИФ блок интерфейса
ВЗУ внешнее ЗУ
ГПК гибкий печатный кабель
ГПП гибкая печатная плата
ГТИ генератор тактовых импульсов
ДПП двусторонняя печатная плата
ЕСКД единая система конструкторской документации
ЕСПД единая система программной документации
ЗГ задающий генератор
ЗУ запоминающее устройство
И2Л интегральная инжекционная логика
ИМС интегральная микросхема
КВВ канал ввода-вывода
КМОП комплементарная МОП-структура
КОП код операции
КПДП контроллер ПДП
КПР контроллер прерываний
КПТО комплекс программ технического обслуживания
KLLI контроллер шины
МЕП структура “металл-полупроводник"
МИС малая интегральная схема
МК микрокоманда
МНОП структура "металл-нитрид-оксид-полупроводник”
МОП структура “металл-оксид-полупроводник”
МП микропроцессор
МПА микропрограммный автомат
МПК микропроцессорный комплект
8 Введение
мпп многослойная печатная плата
МПС микропроцессорная система
мц мэт машинный цикл многоэмиттерный транзистор
СБИС сверхбольшая интегральная схема
НГМД НЖМД НМЛ накопитель на гибких магнитных дисках накопитель на жестких магнитных дисках накопитель на магнитных лентах
НОД ОА накопитель на оптических дисках операционный автомат
ОЗУ оперативное ЗУ
ок открытый коллектор
оп ОПП оперативная память односторонняя печатная плата
ОС операционная система
ОУ операционный усилитель
ПД пдп ПЗУ переключатель Джозефсона прямой доступ к памяти постоянное ЗУ
пмк память микрокоманд
ПУ периферийное (внешнее) устройство
ППА ППЗУ программируемый параллельный адаптер программируемое ПЗУ
ппи ппп программируемый последовательный интерфейс пакеты прикладных программ
пт программируемый таймер
ПЭВМ персональная ЭВМ
РОН РПЗУ-ЭС РПЗУ-УФ регистр общего назначения репрограммируемое ПЗУ с электрическим стиранием репрограммируемое ПЗУ со стиранием данных ультрафиолетовым лучом
рт распределитель тактов
СДНФ СКНФ совершенная дизъюнктивная нормальная форма совершенная конъюнктивная нормальная форма
сис средняя интегральная схема
сои СУП сш система обработки информации схема ускоренного переноса системная шина
Перечень используемых сокращений 9
тз техническое задание
тл транзисторная логика
ТТЛ транзисторно-транзисторная логика
ттлш транзисторно-транзисторная логика с диодами Шотки
УА управляющий автомат
УВВ устройство ввода-вывода информации
УВв устройство ввода информации
УВыв УГО УУ устройство вывода информации условное графическое обозначение устройство управления
ФАМК формирователь адреса МК
ЦАП ЦП ЦУУ ША цифро-аналоговый преобразователь центральный процессор центральное устройство управления шина адреса
ШВВ шина ввода-вывода
ШД ШУ ЭВМ шина данных шина управления электронная вычислительная машина
эп эсл элемент памяти; эмиттерный повторитель эмиттерно-связная логика
10 Основы теории компьютерной схемотехники
Глава 1
Основы теории компьютерной схемотехники
1.1. Информационные основы компьютерной схемотехники
1.1.1. Информатика, информация, сигналы и их представление
Широкое применение компьютеров способствует научно-техническому развитию страны. Сфера использования компьютеров охватывает практически все виды человеческой деятельности.
Компьютер — это программно управляемая физическая система, предназначенная для алгоритмической обработки информации, представленной сигналами.
В широком смысле слова информация является отражением реального мира. Информация — это единственный неубывающий ресурс жизнеобеспечения. Более того: ее объем в настоящее время удваивается ежегодно. Информация, подготовленная для обработки на компьютерах, называется данными.
Информационный процесс включает в себя такие этапы:
I . сбор информации от различных источников и представление ее в форме, необходимой для ввода в компьютер;
2 . передачу (пересылку) информации от источника к приемнику;
3 . хранение — процесс передачи информации во времени;
4 . обработку — систематическое выполнение операций над данными;
5 . выдачу результата обработки пользователю.
На всех этих этапах используют средства компьютерной схемотехники. К информации предъявляют следующие требования:
• корректность (однозначность восприятия);
• ценность (полезность) и оперативность (актуальность);
• точность, достоверность и устойчивость (способность реагировать на изменения исходных данных);
• достаточность (полнота) — наличие минимально необходимого объема информации для принятия правильного решения.
Структуру и общие свойства информационных процессов изучают в информатике, которая включает:
• теорию информации;
• алгоритмические, программные и компьютерные средства обработки информации;
1.1. Информационные основы компьютерной схемотехники 11
• архитектуру компьютеров, системы искусственного интеллекта, вычислительные сети и т.д.
В теории информации изучают процессы передачи, преобразования и хранения информации, в том числе:
• методы определения количества информации в сообщении;
• рациональные способы представления информации с помощью различных символов (букв, цифр и т.д.);
• способы формирования, обнаружения и оценки параметров информационных процессов.
Упорядоченную последовательность символов (букв, цифр, математических знаков, предназначенных для передачи информации), закодированную в материальной форме, называют сообщением.
Информационное сообщение всегда связано с источником и приемником информации, соединенных каналом передачи (рис. 1.1).
Рис. 1.1. Информационная модель канала передачи
Источником и приемником информации могут быть как люди, так и технические устройства (компьютеры, датчики, индикаторы и др.). Каналом передачи (связи) называется совокупность устройств, имеющих один вход и один выход, предназначенных для передачи информации на расстояния. Сообщения'могут иметь различные формы: звука, текста, изображения, электрического напряжения от датчиков (например, от термопар).
Информационные сообщения размещают на машинных носителях информации. Носитель информации — это любая запоминающая предметная среда, предназначенная для записи и хранения информации с целью ее непосредственного ввода в компьютер. Носитель информации является промежуточным звеном между компьютером и первичным документом, содержащим числовые данные, текстовые материалы, схемы, графики, различные измерения.
Хранение сообщений — это, как правило, три вида операций: запись, собственно хранение и считывание. Информация записывается в носитель посредством изменения физических или механических свойств запоминающей среды. Данные считываются посредством преобразования их в электрические сигналы. Считают, что в носителе информации сигнал хранится в закодированной форме.
Носители информации различаются по следующим признакам:
• средой накопления: непрерывные (магнитные ленты и диски) и дискретные, где каждой хранимой единице данных отводится свой дискретный участок или элемент (ферритовые сердечники, перфокарты, перфоленты, триггеры, криотроны и т.д );
• типом материала: бумага с текстом или рисунком; бумажные перфоленты, перфокарты; магнитные ппенки, магнитные ленты и диски; полупроводниковые схемы памяти;
12 Основы теории компьютерной схемотехники
• способом считывания данных: механические, оптические, магнитные, электрические;
• конструктивным исполнением: ленточные, дисковые, электронные и др.
Для передачи информации от источника к приемнику сообщение преобразовывают в сигналы. Согласно ДСТУ 2938-94 “сигнал — это изменение физической величины, используемой для передачи данных”. Таким образом, сигнал образуется на основе некоторой физической величины (электромагнитные или акустические колебания, электрическое напряжение и др.), традиционно называемой энергетическим носителем, и изменения одного или нескольких ее параметров (амплитуды, частоты, фазы, длительности и др.) по закону передаваемой информации. Считают, что сигнал — это материально-энергетическое воплощение сообщения. Посредством совокупности сигналов можно представить любое сложное сообщение. Сигнал может преобразовываться без изменения смысла информации из одной физической величины в другую, более удобную для передачи по каналу связи и обработки в схемах компьютера. Изменение параметров физической величины по закону передаваемого сообщения называют модуляцией, а изменяемые параметры — информативными
Сигналы классифицируют по таким признакам:
• степени определенности ожидаемых значений — случайные и детерминированные;
• структуре временного изменения — непрерывные и дискретные;
• роли переданной информации в компьютеры — адреса, данные и управления;
• особенностям спектрального представления — низкочастотные и высокочастотные, узкополосные и широкополосные;
• способу преобразования — кодированные, декодированные, усиленные, дискретизированные и т.д.;
• принадлежности к виду связи — телеграфные, телефонные, радиолокационные, междумашинные и внутримашинные;
• характеру изменения кодированных сигналов в синхронизированные моменты времени-— потенциальные и импульсные.
В процессе передачи сигналов от источника к приемнику физические величины и способы их модуляции могут многократно изменяться, но содержание сообщения остается неизменным, поскольку оно определяется только законом модуляции.
Для информационного обмена используют знаки различного ранга:
• первый ранг — символы. Символ — это элементарная единица сообщения. Если число различных символов ограничено, то их совокупность называют алфавитом (например, буквы латинского алфавита, двоичные символы 0 и 1 — в технических устройствах);
• второй ранг — слова (группы символов), из которых строятся фразы и выражения.
В общем случае способ формализованного описания различных сигналов (и соответственно сообщений) называется представлением информации. В теории информации рассматривают не физическое, а математическое представление сиг
1.1. Информационные основы компьютерной схемотехники 13
налов, то есть их описание с помощью различных функций, формул, графиков, законов распределения вероятностей.
Наиболее распространенными способами представления сигналов являются временной, спектральный, статистический. Во многих случаях информация о протекании некоторого физического процесса поступает от соответствующих датчиков в виде электрических сигналов, которые непрерывно изменяются во времени. Различают следующие разновидности сигналов, описываемых временной функцией y(f).
1. Непрерывная функция непрерывного аргумента в интервале времени О <t <tk (рис. 1.2, а).
2. Дискретная функция непрерывного аргумента (рис. 1.2, б). Значения, принимаемые функцией y(t), образуют дискретный ряд чисел i = 1, 2, .... к. Значение аргумента может быть любым в заданном интервале времени О <t <tk. Преобразование непрерывной функции y(t) в дискретное множество значений)/, называется квантованием по уровню.
3. Непрерывная функция дискретного аргумента (рис. 1.2, в). Значения функции y(t) определяются только на дискретном множестве th i = 1,2, ..., к. Функция y(tt) может принимать любые значения в заданном диапазоне. Преобразование функции y(t) непрерывного аргумента t в функциюy(t,) дискретного аргумента t, называется дискретизацией (квантованием) во времени.
4. Дискретная функция дискретного аргумента (рис. 1.2, г). Значения, принимаемые функцией и аргументом, образуют дискретные ряды чисел у0, уь , у к и to, t\, ..., tk.
Рис. 1.2. Математическое представление сигналов
Первая из рассмотренных разновидностей описывает непрерывные (аналоговые) сигналы, вторая и третья — дискретно-непрерывные, а четвертая — чисто дискретные. Совместное применение дискретизации и квантования позволяет преобразовывать непрерывную функцию в чисто дискретную.
Согласно теореме Котельникова сигнал, описываемый функцией с ограниченным спектром, определяется своими дискретными значениями, которые отсчитываются через интервалы времени t = \/2Fc, где Fc — ширина спектра. Таким образом, сигнал y(t) можно передавать отдельными мгновенными значениями, которые отсчитываются через конечный интервал времени. По этим значениям компьютер полностью восстанавливает первичный непрерывный сигнал.
К дискретно-непрерывным функциям относят также время-импульсное представление первичного сигнала y(t) прямоугольными импульсами с непрерывным
14 Основы теории компьютерной схемотехники
информативным параметром (,/Т. где /, — длительность импульсов, пропорциональная значению сигнала; Т — период повторения импульсов (рис. 1.3, а).
Рис. 1.3. Представление сигналов:
а — время-импульсное; 6 — число-импульсное; в — импульсно-кодовое
При число-импульсном представлении (рис. 1.3, б) информативным параметром является количество импульсов за период. В телеграфной связи используют импульсно-кодовое представление символов. Например, в коде Бодо передачу символов реализуют последовательной посылкой во времени пяти импульсов разной полярности, как показано на рис. 1.3, е для букв А и Б.
В компьютерной схемотехнике используют разрядно-цифровое (или просто цифровое) кодирование, в котором первичный сигнал представляется группой символов, отображайэщих значения цифр 0 и 1 двоичной системы счисления электрическими сигналами, например, импульсами. Наличие импульса соответствует цифре 1, отсутствие— 0. Разряды двоичного числа характеризуются весом, кратным степени двойки — 1, 2, 4, 8, ... (в направлении от младших к старшим разрядам), например. для четырехразрядного двоичного числа имеем:
.х - ,т3 л:2 • Л', • т0 = То • 21 -г х2 • Т + л', 21 т ,у() 2° =
= л'з -8 <- х2 • 4 т л', 2 + л'о • I
Если двоичное число х2 -- 1 101, то получим следующий десятичный эквивалент:
Хю == 1-8+ 1-4+ 0-2+ 1-1 = 13
Цифровой код передают последовательно во времени (последовательный код) с помощью одного канала передачи (рис. 1.4. а) или одновременно (параллельный код) с помощью многоканальной передачи (рис.1.4, б).
На практике последовательный код используют при передаче информации на большие расстояния (например, между компьютерами), а параллельный код — при передаче информации на малые расстояния (например, внутримашинные).
Рис. 1.4. Передача информации: а — последовательным кодом; б — параллельным кодом
1.1. Информационные основы компьютерной схемотехники 15
1.1.2. Информационные меры
В теории передачи и преобразования информации установлены информационные меры количества и качества информации — семантические, структурные, статистические.
Семантический подход позволят выделить полезность или ценность информационного сообщения. В структурном аспекте рассматривают строение массивов информации и их измерение простым подсчетом информационных элементов или комбинаторным методом. Структурный подход используют для оценки возможностей информационных систем вне зависимости от условий их применения. При использовании структурных мер информации учитывают только дискретное строение сообщения, количество содержащихся в нем информационных элементов, связей между ними. При структурном подходе различают геометрическую, комбинаторную и аддитивную меры информации.
Геометрическая мера определяет параметры геометрической модели информационного сообщения (длина, площадь, объем) в дискретных единицах. Эту меру применяют как для оценки информационной емкости всей модели, так и для оценки количества информации в одном сообщении.
В комбинаторной мере количество информации 1 определяют количеством комбинаций элементов (символов), которые совпадают с числом:
• сочетаний из q элементов по п:
1 = -^--, п\(q - п)!
например, для множества цифр 1, 2, 3, 4 можно составить шесть сочетаний по две цифры: 12, 13, 14, 23, 24, 34;
• перестановок I = q!, например, для множества букв а, в, с можно получить шесть перестановок: аве, асе, вас, вса, сав, сва\
• размещений с повторениями из q элементов по it.
I = q".
Например, для q = 0, 1 и а = 3 имеем: ООО, 001, 010, 01 1, 100, 101, 110, 111.
Широкое распространение получила аддитивная мера. Пусть N — число равновероятных сообщений, а — их длина, q — число букв алфавита, используемого для передачи информации. Количество возможных сообщений длины п равняется числу размещений с повторениями
N-~-q. (1.1)
Эту меру наделяют свойством аддитивности, чтобы она была пропорциональна длине сообщения и позволяла складывать количество информации ряда источников. Для этого Хартли предложил логарифмическую функцию как меру количества информации:
I = log N = п log q. (1.2)
Количество информации, которое приходится на один элемент сообщения, называется энтропией:
H = - = log(/. (1.3)
п
16 Основы теории компьютерной схемотехники
Основание логарифма зависит от выбора единицы количества информации. Если для алфавита используют двоичные цифры 0 и 1, то за основание логарифма принимают q = 2, в результате чего I = п log2 2 = п. При длине п = 1 получают Z = 1 и это количество информации называют битом.
Передача сообщения длиной п = 1 эквивалентна выбору одного из двух возможных равновероятных сообщений — одно из них равно единице, другое — нулю. Двоичное сообщение длины п содержит п битов информации. Если основание логарифма равно 10, то количество информации измеряется в десятичных единицах — дитах, причем 1 дит = 3,32 бита. Например, текст составлен из 32 букв алфавита и передается последовательно по телетайпу в двоичном коде. При этом количество информации I = log2jV = log232 = 5 битов. Далее используются логарифмы с основанием два.
В общем случае сообщения появляются с разной вероятностью. Статистическая мера использует вероятностный подход к оценке количества информации. Согласно Шеннону каждое сообщение характеризуется вероятностью появления, и чем она меньше, тем больше в сообщении информации. Вероятность конкретных типов сообщений устанавливают на основе статистического анализа.
Пусть сообщения образуются последовательной передачей букв некоторого алфавита xj... х„ xq с вероятностью появления каждой буквы р(х\) = р},
р(х) = р„ р(х:1) = рч, при этом выполняется условие:р< + ... +р, + ... + рч = 1.
Множество с известным распределением элементов называют ансамблем. Согласно Шеннону количество информации, которое содержится в сообщении х„ рассчитывают по формуле
/(*,) = log—• (1.4)
Р,
Для абсолютно достоверных сообщений р, = 1, количество информации 1(х) = 0; при уменьшении значенияр, количество информации увеличивается.
Пусть в ансамбле все букры алфавита хь ..., х„ ... , хч — равновероятны, то есть р\ = р2 = ... = pq = \/q, и статистически независимы. Тогда количество информации в сообщении длиной п букв с учетом выражения (1.4)
” ”11 1
/ = УЛх,) = У log—= log—+ ...+ log— = n\ogq, Zf P, P-. A
что совпадает с мерой Хартли в соответствии с выражениями (1.1) и (1.2).
Согласно Шеннону информация — это снятие неопределенности, что понимают следующим образом. До опыта событие (например, появление буквы х,) характеризуют малой начальной вероятностью рн, которой соответствует большая неопределенность. После опыта неопределенность уменьшается, поскольку конечная вероятность рк > рн. Уменьшение неопределенности рассчитывают как разность между начальным 7Н и конечным 1К значениями количества информации. Например, для рн = 0,1 и рк = 1 получим:
А/ = IH -1к = log —— log — = log 10 - log 1 - 3,32 бит.
Рн Рк
1.1. Информационные основы компьютерной схемотехники 17
Пусть сложное сообщение характеризуется алфавитом из букв хь х2, ..., xq, их вероятностями р\, р2, ..., рч и частотой появления каждой буквы т,, т2, .... mq. Все сообщения статистически независимы, при этом + т2 + ... + mq = т. Общее количество информации для всех q типов сообщений с учетом выражения (1.4)
я 1
h = У-Jog- м Р,
Среднее значение количества информации на одно сообщение (энтропия) согласно формуле Шеннона
гг Л: V"1 mi 1 1 V"1 1 1
^= —= у—log—= XAlog—, (1.5)
- ,=i - А ,=1 А
где при большом значении т отношение mjm характеризует вероятность р, каждой буквы. Выражение logl//>, рассматривают как частную энтропию, которая характеризует информативность буквы х,, а энтропию Н— как среднее значение частных энтропий. При малых значениях р, частная энтропия велика, а с приближением р. к единице она приближается к нулю (рис. 1.5, а).
Функция г| = (pj = р, logl/p, отражает вклад буквы х, в энтропию Н. Как видим, при р, = I эта функция равна нулю, затем возрастает до своего максимума и при уменьшении р, приближается к нулю. Функция q(p) при значении р, = 0,37 имеет максимум 0,531.
Интерес представляют сообщения с использованием двухбуквенного алфавита Х| и х2 (например, цифры 0 и 1). Поскольку при q = 2 вероятность букв алфавита Р\ + Pi = 1, то можно положить, чтор\ = р и р2 = 1 -р. Тогда энтропию определяют соотношением
Н = ?7() + 7(Рг) = Р log - + (1 - р) log 1 , р О-/’)
график которой показан на рис. 1.5, б. Он образуется суммированием двух графиков, определяющих энтропию каждой из двух букв. Из графиков видно, что при р = 0 или р = 1 энтропия равна нулю и неопределенность полностью снимается. Это означает, что с вероятностью, равной единице, можно знать, каким будет следующее сообщение.
Рис. 1.5. Гоафики функции Н: а — для частной энтропии; б — для двоичных сообщений
2 — 4-1749
0,2 0,4 0,6 0,8 1,0 Р
18 Основы теории компьютерной схемотехники
Энтропия двухбуквенных сообщений достигает максимального значения, равного 1 биту, при р = 0,5, и ее график симметричен относительно этого значения. Это тот случай, когда наиболее трудно предугадать, какое сообщение будет следующим, — то есть ситуация наиболее неопределенная.
В общем случае энтропия обладает следующими свойствами.
1. Энтропия — величина вещественная, непрерывная, ограниченная и неотрицательная.
2. Энтропия равна нулю, если сообщение заранее известно. В этом случае некоторое сообщение задано с вероятностью р, = 1, а вероятность остальных равна нулю.
3. Энтропия максимальна, если все сообщения равновероятны: рх = р2 = ... = = рч = \lq... В этом случае на основании выражения (1.5) получим:
ч 1 4 1
•Og—= X-1Qg9 = log^
Pi 7^ Я
что совпадает с выражением (1.3). В этом случае оценки количества информации по Хартли и Шеннону совпадают.
4. При неравных вероятностях количество информации по Шеннону меньше меры Хартли.
5. При объединении энтропий двух независимых источников сообщений их энтропии складываются.
В компьютере наименьшей возможной единицей объемной (геометрической) меры информации является бит. Объем (или емкость) информации вычисляется по количеству двоичных символов 0 и 1, записанных в памяти компьютера. При этом возможно только целое число битов в отличие от вероятностного подхода, где может быть и нецелое число.
Для удобства использования введены также единицы количества информации, превышающие бит. Так, двоичное слово из восьми символов содержит 1 байт информации, 1024 байт составляют килобайт (Кбайт), 1024 Кбайт — мегабайт (Мбайт) и 1024 Мбайт — гигабайт (Гбайт); при этом 1024 = 210.
Между объемным и вероятностным количествами информации соотношение неоднозначное. Если сообщение допускает измерение количества информации и объемно и вероятностно, то они не обязательно совпадают. При этом вероятностное количество не может быть больше объемного. В дальнейшем тексте количество информации понимается в объемном значении.
1.2. Арифметические основы компьютерной схемотехники
1.2.1. Принципы построения системы счисления
Числовая информация в компьютерах характеризуется:
• системой счисления (двоичная, десятичная и др.);
• видом числа (числа вещественные, комплексные, массивы);
• типом числа (смешанное, целое, дробное);
1.2. Арифметические основы компьютерной схемотехники 19
• формой представления числа (место запятой) — с природной (переменной), фиксированной, плавающей запятой;
• разрядной сеткой и форматом числа;
• диапазоном и точностью представления чисел;
• способом кодирования отрицательных чисел — прямым, обратным и дополнительным кодами;
• алгоритмами выполнения арифметических операций.
Системой счисления называется совокупность цифр и правил для записи чисел. Запись числа в некоторой системе счисления называется его кодом. Все системы счисления делятся на позиционные и непозиционные. Для записи чисел в позиционной системе счисления используют определенное количество графических знаков (цифр и букв), которые отличаются один от другого. Число таких знаков q называют основанием позиционной системы счисления. В компьютерах используют позиционные системы с разным основанием.
Система счисления с основанием два (цифры 0 и 1) называется двоичной, система счисления с основанием три (цифры 0, 1,2) — троичной и т.д. В системах счисления с основанием меньше десяти используют десятичные цифры, а для основания больше десяти добавляют буквы латинского алфавита — А, В, С, D, Е, F. Далее в обозначениях в случае необходимости пишут десятичный индекс, равный применяемому основанию системы счисления (табл. 1.1).
Таблица 1.1
Основание q Система счисления Знаки
2 Двоичная 0, 1
3 Троичная 0, 1,2
5 Пятеричная 0, 1,2, 3,4
8 Восьмеричная 0, 1,2, 3,4,5, 6,7
10 Десятичная 0, 1,2, 3,4, 5, 6, 7, 8,9
16 Шестнадцатеричная 0, 1,2, 3,4, 5, 6, 7, 8, 9, А, В, С, D, Е, F
В позиционных системах счисления значение каждой цифры определяется ее изображением и позицией в числе. Отдельные позиции в записи числа называют разрядами, а номер позиции — номером разряда. Число разрядов в записи числа называется его разрядностью и совпадает с длиной числа.
В непозиционных системах счисления значение каждой цифры не зависит от ее позиции. Самой известной непозиционной системой является римская, в которой используются семь знаков — I, V, X, L, С, D, М, соответствующих таким значениям:
I
1
V X L С D М
5 10 50 100 500 1000
Например: III — 3; LIX — 59; DLV — 555.
Недостатком непозиционной системы является отсутствие нуля и формальных правил записи чисел и соответственно арифметических действий с ними (хотя по традиции римскими числами часто пользуются при нумерации глав в книгах, веков в истории и др.). Система счисления должна обеспечивать:
• возможность представления любого числа в заданном диапазоне;
2*
20 Основы теории компьютерной схемотехники
• однозначность, сжатость записи числа и простоту выполнения арифметических операций;
• достижение высокого быстродействия машины в процессе обработки информации.
Число в позиционной системе можно представить полиномом:
к
Aq = ak-qk + а^_, -qk 1 +...+а0 -q' +а_, -q 1 + -q т = -q , (1.6)
i=-m
где q — основание системы счисления; q‘ — вес позиции; а, е {0, 1, - 1)} —
цифры в позициях числа; 0, 1, ..., к — номера разрядов целой части числа; -1, -2, ..., -т — номера разрядов дробной части числа.
Позиционные системы с одинаковым основанием в каждом разряде называют однородными. Поскольку на значение q нет никаких ограничений, то теоретически возможно бесконечное множество позиционных систем счисления.
На практике применяют сокращенную запись полинома (1.6) в виде последовательности цифр со знаком в зависимости от типа числа:
• для смешанного числа
Aq - +ак ак-] ... а\ а0, а_\ ... С1-т, (1.6, а)
• для целого числа Aq = +ак Я*-| Щ а0; (1.6,6)
• для правильной дроби Aq = ± 0, ... (2 _т . (1.6, в)
\ Пример 1.1
Иллюстрация записи чисел в виде последовательности цифр (1.6) и соответствующего полинома (1.5):
• двоичная система: q = 2; cq е {0, 1}:
А2 = 111,01 = 1-22 + 1-2' + 1-2°+ 0-2*' + 1 -2 2 = 7,2510;
• восьмеричная система: q = 8; а,- е {0, 1, 2, ..., 7}:
Л8 = 45,21 =4-8' + 5-8° + 2-81 + 1-8“2 = 37,26510;
• десятичная система: q = 10; а, е {0, 1, 2, ..., 9}:
А10 = 135,64 = 1 -102 + 3-101 + 5-10° + 6 10“' + 4-10“2
• шестнадцатеричная система: q = 16; cq= {0, 1, ..., F}\
Al6 = DEAB = D-161 -ь^-160 + 1-16"' + 5-16“2 = = 13-16' + 14-16° + 1-16"' + 11-16 2 = 222,10510.
Рассмотренные записи чисел показывают один из способов перевода недесятичных чисел в десятичные. При одинаковой разрядности в системах счисления с большим основанием можно записать больше разных чисел.
1.2. Арифметические основы компьютерной схемотехники 21
Достоинством двоичной системы является: простота выполнения арифметических операций; наличие надежных микроэлектронных схем с двумя устойчивыми состояниями (триггеров), предназначенных для хранения значений двоичного разряда— цифр 0 или 1. Двоичные цифры называют также битами. В двоичнодесятичной системе счисления каждая десятичная цифра записывается четырьмя двоичными разрядами (тетрадами).
Пример 1.2
Запись десятичного числа в двоично-десятичной системе:
8 7 3 2 5
Aw = 873,25 = 1000 01110011,0010 0101.
1.2.2. Перевод чисел из одной системы в другую
Для перевода целого числа из одной системы счисления в другую необходимо разделить переводимое число на новое основание по правилам исходной системы. Полученный первый остаток является значением младшего разряда в новой системе, а первое частное необходимо снова разделить. Этот процесс продолжается вплоть до получения неделимого частного. Результат записывают в порядке, обратном их получению в виде формулы (1.6, б).
Для перевода правильной дроби из одной системы счисления в другую необходимо, действуя по правилам исходной системы, умножить переводимое число на основание новой системы; от результата отделить целую часть, а оставшуюся дробную часть снова умножить на это основание. Процесс такого умножения повторяется до получения заданного числа цифр. Результат записывают как целые части произведения в порядке их получения, располагаемых в виде формулы (1.6, в).
22 Основы теории компьютерной схемотехники
Пример 1.4
Перевод правильной десяти стью до четвертого знака: 0, 1 0 1 0 Результат: А = 0,62510 = 0,10 чной дроби А = 0,625 в двоичное число с точно- 625 2_ 0; 250 2_ a-i = 1; 500 2 а_2=0; 000 2_ а-з=1; 000 <7-4 = 0. 102.
Для перевода смешанных чисел в двоичную систему требуется отдельно переводить их целую и дробную части. В записи результата целая часть перевода отделяется от дробной в соответствии с формулой (1.6, а).
Г Пример 1.5
Перевод смешанного десятичного числа А = 118,62510 в двоичное. Используя результаты перевода целого числа 118 в примере 1.3 и дробного числа в примере 1.4, запишем результат:
________________________А= 118,62510 = 1110110,10102._______________________
В восьмеричных и шестнадцатеричных числах основание системы счисления кратно степени двойки: 23 = 8; 24 = 16. По этой причине перевод этих чисел в двоичные реализуется очень просто: каждую цифру записывают тремя двоичными цифрами (триадами) для восьмеричных чисел и четырьмя двоичными цифрами (тетрадами) для шестнадцатеричного числа в направлении влево и вправо от запятой. При этом крайние незначащие нули опускаются.
Пример 1.6
Иллюстрация перевода восьмеричных и шестнадцатеричных чисел в двоичные:
Г-°-, Г-'-, Г-Л-,
А = 305,428 = 011000101,100 0102’
л—। ,_Х_, ,-5—, ^-3-^ ,-3—,
А = 1AB,EFX6 = 011110101011,111011112-
Для перевода двоичного числа в восьмеричное исходное число разбивают на триады влево от запятой; отсутствующие крайние цифры дополняют нулями. Затем каждую триаду записывают восьмеричной цифрой. Аналогично осуществляется перевод двоичного числа в шестнадцатеричное, при этом выделяют тетрады, заменяемые шестнадцатеричными цифрами.
1.2. Арифметические основы компьютерной схемотехники 23
Пример 1.7
Иллюстрация перевода двоичных чисел в восьмеричные и шестнадцатеричные:
Д-, Д_,
А = 110011,1000102 = 110011,1000102 = 63,428;
А = 110011,1000102 = 00110011,100010002 = 33,88]6
Рассмотрим правила, облегчающие расчеты с двоичными числами.
1. Необходимо знать представление десятичных чисел от нуля до 15 в системах счисления с основанием q = 2, 8, 16 и 2-10 (табл. 1.2).
Таблица 1.2
q = 10 гч II О" QO II О" q = 16 q = 2-10
0 0 0 0 0000
1 1 1 1 0001
2 10 2 2 0010
3 и 3 3 ООП
4 100 4 4 0100
5 101 5 5 0101
6 по 6 6 оно
7 111 7 7 0111
8 1000 10 8 1000
9 1001 11 9 1001
10 1010 12 А 0001 0000
11 1011 13 В 0001 0001
12 1100 14 С 0001 0010
13 1101 15 D 0001 ООП
14 1110 16 Е 0001 0101
15 1111 17 F 0001 0101
2. Необходимо знать десятичные значения чисел 2к от к = 0 до к = Ю
(табл. 1.3).
Таблица 1.3
к 0 1 2 3 4 5 6 7 8 9 10
2к 1 2 4 8 16 32 64 128 256 512 1024
3. Полезно знать следующие соотношения для двоичных целых и дробных чисел:
А = Ю0...00 = 2к, например , А = 1000 2 = 23 = 8|0; к
А = 11... 11 = 2к -1, например , А = 111112 = 25 -1 = 31|0; к
А = 0,11...И = 1-2”*, например, Л = 0,1111 = 1-2”4=| — |
'—Г' 2 Ы10
24 Основы теории компьютерной схемотехники
А ~ 0,00...01 = 2“‘, например, А = 0,00001 2 = 2-5 = — •
Двоичные дробные числа в десятичном виде записываются так: к разрядов справа от запятой определяют целое положительное число в числителе, а в знаменателе — число 2а. Например, А = 0,10112 = (11/24)10 = (11/16)10, что читается как “одиннадцать шестнадцатых”.
1.2.3. Специальные системы счисления
Рассмотренные позиционные системы счисления относят к классическим. Кроме них, в компьютерах используют ряд специальных позиционных двоичных систем, в том числе:
• систему с использованием символов 0, -1, или_1, -Г, для удобства символ -1 обозначают как 1 ; систему с символами 1 и 1 называют системой счисления (1, 1);
• системы с отрицательным основанием q < -1 и символами 0, 1, ...,(<?- 1); систему с основанием q = -2 и символами 0, 1 называют минус-двоичной;
• избыточную систему с основанием q и количеством символов больше q, например, при q = 2 используют символы (1,0, 1), такую систему называют также симметричной знакоразрядной.
Преимуществом специальных систем счисления является упрощение и ускорение выполнения ряда арифметических операций (сложение, вычитание, умножение, деление) и представление единым кодом положительных и отрицательных чисел без дополнительного знакового разряда. Недостатком специальных систем является сложность правил перевода их в классические системы счисления и наоборот, а также неоднозначное представление ряда чисел.
Если в формуле (1.6) учесть, что символы а, принимают значение 1 или 1, то для основания q = 2 число А = 99|0 будет иметь вид 1111111. В системе чисел (1,1) отсутствует символ “нуль”, поэтому некоторые целые и дробные числа в ней не могут быть представлены конечным множеством символов. Например, десятичное чис-ло_ А =_20|0 в системе чисел (1,1) записывается как^ бесконечное число 11111,111 ..., что обуславливает погрешность в системе (1, 1). В то же время есть числа, которые не имеют единого изображения.
В минус-двоичной системе может быть представлено любое положительное или отрицательное число. Например, для q = -2, п = 4 с учетом формулы (1.6): А = 5ю = 0101 (_2); А = -5ю =1111(_2). Некоторые числа представлены неоднозначно и только бесконечными дробями: А = 1/3 = 0,010101... или А = 1,101010...
Избыточная двоичная система связана с обычной соотношением:
2= £ 2' = 2* -1 = 100...01. к '=0 к
На основании выражения (1.6) осуществляется переход от обычной двоичной системы к избыточной с символами 1,0, 1 и наоборот. Избыточная система имеет следующие свойства:
1.2. Арифметические основы компьютерной схемотехники 25
• одно и то же число не имеет единой записи: А = 12ю = 011002 — 10 1 00, = = 11100;
• положительные и отрицательные числа изображаются без_использования дополнительного знакового разряда: А = 13|0 = 011012 = 10101; А = -1310 = = -011012= 10101 (при смене знака достаточно заменить в записи числа 1 на 1 и наоборот);
• возможно уменьшение количества единиц в записи числа, что позволяет упростить и ускорить выполнение арифметических операций, особенно сложение и вычитание.
Преобразование двоичных чисел в избыточную систему с минимальным числом единиц в разрядах осуществляют так. На первом этапе все комбинации в записи числа вида 01. ..11 заменяют равнозначной комбинацией вида_10...01 с тем же числом разрядов; затем выполняют замену сочетаний 11 на 01 и 11 на 0 1, например:
А = 10 0111 0 01Н0И012 = 10100101 ООП 011 =10100101000101. 1 1 з
Количество единиц в записи числа уменьшилось с десяти до четырех.
1.2.4. Выбор системы счисления
В компьютерах в основном используют однородные позиционные системы счисления. При выборе основы q этих систем учитывают такие показатели.
1. Наличие физических элементов для изображения цифр системы в виде одного из q состояний, например, разницы напряжений. Уменьшение числа состояний упрощает физический элемент, поэтому наиболее приемлемой является двоичная система.
2. Экономичность системы счисления. Система с большим основанием q обеспечивает представление определенного числа меньшим количеством разрядов. Однако при этом усложняется построение физического элемента с большим числом состояний.
Эффективность системы счисления с основанием оценивается количеством цифровых разрядов D„ необходимых для изображения определенного числа с длиной то есть D, = qrn,. При этом учитывается, что уменьшение значения D, приводит к уменьшению электронных схем для представления чисел в компьютерах.
Для представления любого десятичного числа длиной, например, «ю = 6 используют Di0 = (fio’Hio = Ю-6 = 60 цифроразрядов. В двоичной системе для представления того же числа (с учетом соотношения п2 = З-ию) требуется иметь D2 - q2-3-n]0 = 2-3-6 = 36 цифровых разрядов.
Наиболее экономичной является система с основанием q = 2,73 ... « 3. Двоичная система по экономичности уступает троичной на 5,8%, однако имеет более надежные физические элементы. Кроме того, для запоминания цифр троичной системы 0, 1, 2 используют два двоичных физических элемента. Из этого следует, что самой эффективной является двоичная система счисления.
26 Основы теории компьютерной схемотехники
3. Трудоемкость и быстродействие выполнения арифметических операций. Чем меньше основание q, тем меньше цифр принимают участие в вычислении данных и тем выше быстродействие компьютера. Например, быстродействие машины в двоичной системе превышает быстродействие в троичной на 26,2%, а в десятичной — в 2,7 раза.
4. Наличие формального математического аппарата для анализа и синтеза цифровых схем. Таким аппаратом для двоичных элементов является булева алгебра.
Таким образом, из перечисленных показателей видно, что самой приемлемой для применения в компьютерах является однородная позиционная двоичная система счисления. Двоичные системы счисления используют в больших и средних компьютерах, предназначенных для решения научно-технических задач с большим объемом вычислений и сравнительно малым количеством исходных данных.
Двоично-десятичную систему применяют для решения экономических задач, которые характеризуются большим объемом входных и выходных данных в сравнении с малым объемом вычислений.
Двоично-десятичная система имеет следующие достоинства:
• не требуется перевод исходных данных из одной системы в другую;
• удобство контроля результатов изображением их на экране дисплея;
• удобство автоматического контроля через наличие избыточных кодов в изображении цифр: 1010, 1011, .... 1111.
1.2.5. Формы, диапазон и точность представления чисел
Двоичные числа в компьютерах размещаются в ячейках памяти или в регистрах, которые состоят из запоминающих элементов — триггеров. В ячейке или триггере хранится значение одного двоичного разряда — бит информации. Разрядной сеткой компьютера называется совокупность запоминающих элементов для размещения одного двоичного числа. Для разных классов компьютеров длина разрядной сетки составляет 8, 16, 32, 64 и больше разрядов. Форматом называется способ размещения компонентов числа в разрядной сетке, то есть последовательность и позиции знака, мантиссы, порядка и др.
В компьютерах используются две формы представления числа:
• с фиксированной запятой перед старшим разрядом числа (для правильной дроби) или после младшего (для целого числа);
• с плавающей запятой, место положения которой задается порядком числа.
Место запятой в обоих форматах понимается неявно, без использования дополнительных разрядов. По традиции нумерация разрядов в больших машинах осуществляется слева направо, а в мини- и микрокомпьютерах и микропроцессорах — справа налево.
В числах со знаком выделяют дополнительный знаковый разряд (обычно, крайний слева). В нем для знака плюс записывают цифру 0, а для знака минус — цифру 1. В числах без знака все разряды числа определяют модуль. Форматы двоичных дробных и целых чисел со знаком, с нумерацией разрядов справа налево и значением их веса показаны на рис. 1.6.
1.2. Арифметические основы компьютерной схемотехники 27
6 5 4 3 2 1 0
2’1 2'2 2‘3 2’4 2'5 2-б 2'7
Рис. 1.6. Формат байта: а — для правильной дроби; б — для целого числа
Числа в разрядную сетку записывают в соответствии с весом позиций. Не занятые разряды заполняют нулями, как это показано на рис. 1.7 для чисел +0,725ю = = .+0,101112 и-4710 =-1011112.
7 6 5 4 3 2 1 0
0.
1 0 1 1 1 0 0
А
7 6 5 4 3 2 1 0
1 0 1 0 1 1 1 1
Рис. 1.7. Запись чисел: а — дроби +0,101112; б — целого числа -1011112
Интервал числовой оси, заключенный симметрично между максимальным и минимальным значением числа, называется диапазоном представления. Абсолютное значение целого числа Л изменяется в пределах:
Amin IА | < Лтах; Лт|П = 1; Атах = 2 — 1, (1.7)
где к— количество разрядов цифровой части числа.
Из выражения (1.7) следует, что числа, по абсолютному значению меньше единицы, воспринимаются как “машинный нуль”; числа, больше Л,пах, вызывают переполнение разрядной сетки. Диапазон представления целых чисел с учетом симметрии относительно нуля числовой оси
Д>я=2Лтах = 2(2*-1)«2* ’. (1.8)
Пример 1.8
Рассчитать максимальное значение и диапазон представления целого числа со знаком в 16-разрядной сетке. На основе выражений (1.7) и (1.8) для к = 15 получаем:
Лтах = 215 - 1 = 32767; D = 2Лтах = 65534.
Абсолютное значение правильной дроби В изменяется в пределах:
. Д„,п < IВ | < Bmax; Bmin = Тк; Втт = 1-2* (1.9)
Правильная дробь, по модулю меньше 2”*, воспринимается как “машинный нуль”; числа, больше единицы, вызывают переполнение разрядной сетки. Диапазон представления правильной дроби
DB = 2Дпах = 2(1- 2 *) « 2, так как 1 » 2"*.
Точность представления чисел в компьютере определяется абсолютной и относительной погрешностью. Абсолютная погрешность представления чисел в компьютере составляет:
для целых чисел
АЛ = 1/2 = 2"';
(1.10)
28 Основы теории компьютерной схемотехники
для правильной дроби
АВ = 2 к/2 =2"(А+,). (1.11)
Из выражения (1.10) следует, что абсолютная погрешность представления целых чисел в форме с фиксированной запятой равна половине младшего разряда и не зависит от длины разрядной сетки. Из выражения (1.11) видно, что абсолютная погрешность представления правильной дроби в форме с фиксированной запятой уменьшается при увеличении длины разрядной сетки.
Относительная погрешность 8 представления числа задается отношением абсолютной погрешности к текущему значению числа и находится в пределах
8min — 8 Зщах.
Для целых чисел в форме с фиксированной запятой минимальное и максимальное значения относительной погрешности
Зл,™ = ЛА/Лтах = 2~7(2*- 1) « 2-(И|);
8Лтах = Жш = 2’71 = 0,5.
Такими же формулами определяются минимальное и максимальное значения относительной погрешности для правильной дроби с фиксированной запятой. Относительная погрешность представления чисел в форме с фиксированной запятой существенно зависит от значения числа и значительно возрастает для малых чисел.
В форме с плавающей запятой числа представляются в виде произведений:
С = qn -М = ХМ, (1.12)
где q — основание системы счисления (обычно целая степень числа 2); П — порядок числа длиной £+1 (целое число со знаком); М— мантисса числа длиной г+1 (правильная дробь со знаком); X — характеристика числа. Знак всего числа определяется знаком мантиссы. Для мини-компьютеров основания порядка и мантиссы совпадают (далее предполагается этот случай), а для больших машин — они различны. Представление числа формулой (1.12) называют также полулогарифмическим, потому что только часть числа — характеристика — представляется в логарифмической форме.
Мантисса называется нормализованной, если ее значение определяется неравенством вида
\/q<\M\<1, (1.13)
то есть в старшем разряде модуля мантиссы должна быть записана единица. Так, для основания q = 2 имеем: 2'1 < М< 1.
Пример 1.9
Иллюстрация записи числа в форме с плавающей запятой:
Л2 = 2'110,111 = 22-1 1,01 11 - 24-0,1 1011 1.
Значение порядка указывает на количество позиций, на которые “плавает" запятая.
Формат числа с плавающей запятой в 16-разрядной сетке показан на рис. 1.8. Тут для модулей порядка и мантиссы отведено соответственно пять и девять разря
1.2. Арифметические основы компьютерной схемотехники 29
дов. Запятая в порядке размещена (условно) после младшего разряда, а в мантиссе— перед старшим. Знаки порядка и мантиссы размещены перед их старшими разрядами.
15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 О
± Порядок ± Мантисса
Рис. 1.8. Формат чисел в форме с плавающей запятой
Абсолютное значение числа С в форме с плавающей запятой с учетом формул (1.7), (1.9) и (1.13) изменяется в пределах
Ainin Akinin “ Cmjn < | С* | < C*max — -Aqnax Л/1Пах, (1.14)
где Xmnl = 2 n- ; Af,nill = 2~’; Xmax = 2+n- ; Mmax = 1 -2~‘; Птах = T - 1;
г л к— разрядность модулей порядка и мантиссы.
Диапазон представления чисел в форме с плавающей запятой
Dc =2Cmax = 2-2+n"M>(l-2~*)«2+n”"'+1. (1.15)
Пример 1.10 I
Рассчитать значение диапазона Dc для числа С при г = 5, к = 9. С учетом \ выражения (1.15) получаем:
П,„ах = 2/<- 1 = 25 - 1 - 31; Dc = 23|+|= 232,
что приблизительно соответствует десятичному числу 1О320’3 ~ 109. Диапазон представления чисел с плавающей запятой приблизительно больше в Птах раз диапазона представления чисел в форме с фиксированной запятой.
—-----—-----------------------------------------------__----,-----,----.-
Абсолютная погрешность представления чисел в форме с плавающей запятой зависит от погрешности мантиссы и порядка числа:
АС = АЛ/-2±П; АЛ/ = 2(Ж), (1.16)
где АЛ/— погрешность представления мантиссы.
Минимальная и максимальная относительные погрешности представления чисел в форме с плавающей запятой не зависят от характеристики (она записывается в числителе и знаменателе выражения и потому сокращается). С учетом формул (1.14) и (1.16) относительные погрешности рассчитывают из соотношений:
=
Ш 2~(t+l)
“ ~ 2“’
(1.17)
Из выражений (1.17) следует, что относительные погрешности представления чисел в форме с плавающей запятой практически постоянны во всем диапазоне чисел.
30 Основы теории компьютерной схемотехники
1.2.6. Представление информации в микропроцессорах класса Pentium
Рассмотрим представления операндов в 32-разрядных микропроцессорах класса Pentium. В них используются такие типы данных: целые числа, вещественные числа, двоично-десятичные числа и строки битов, байтов и слов. Целые числа представляются со знаком и без знака в форматах байта, слова, двойного и учетверенного слова длиной соответственно 8, 16, 32 и 64 бит (рис. 1.9).
7 0 7 0 15 8 7 0 15 8 7 0
l± I Байт | | Байт | Слово | | Слово I
a б в г
31 16 15 0 31 16 15 0
|± | Двойное слово | I Двойное слово
д е
61 0
l± I Учетверенное слово I
Рис. 1.9. Форматы целых чисел: а, в, д, ж— со знаком; б, г, е— без знака
Над числами в этих форматах выполняются операции сложения, вычитания, умножения, деления и др. Диапазоны представления знаковых и беззнаковых значений в данных форматах представлены в табл. 1.4.
Таблица 1.4
Формат числа Диапазон представления чисел
без знака со знаком
Байт 0...255 “128... + 127
Слово 0...65535 -32768...+32767
Двойное слово 0...4-Ю9 -2-1О9...+2-1О9
Учетверенное слово 0...5-1019 -2,51019. ..+2,5Ю19
Вещественные числа представлены в формате с плавающей запятой в коротком (32 бит), длинном (64 бит) и расширенном (80 бит) форматах (рис. 1.10). Числа с плавающей запятой длиной 32 и 64 бит, которые используются во многих компьютерах, например, в ЕС ЭВМ, СМ ЭВМ, обычно называют числами с одинарной и двойной точностью. Расширенный формат характерен только для процессоров класса Pentium.
31 30 27 26 0
| Порядок 1 Мантисса |
63 62 a 52 51 0
1 ± 1 Порядок 1 Мантисса 1
79 78 б 64 63 0
Ь L Порядок 1 Мантисса
в
Рис. 1.10. Форматы чисел с плавающей запятой: а — короткий; б — длинный; в — расширенный
1.2. Арифметические основы компьютерной схемотехники 31
В данных форматах чисел с плавающей запятой используются смещенные по-
рядки Псм ’
П + 127 для г = 8;
Псм = П + АП = П +2г-'~
1 = •! П + 1023 для г = 11;
П + 16383 для г = 15,
где П — значение истинного порядка; АП = 2'1 - 1 — смещение; г — длина порядка, которая равна 8, 11 или 15 бит соответственно для короткого, длинного и расширенного формата. Значение ПСм всегда положительное, поэтому знаковый разряд не нужен. Представление порядка со смещением упрощает операции сравнения чисел с плавающей запятой, что особенно важно для алгоритмов сортировки.
Значение числа с плавающей запятой и смещенным порядком определяется по формуле
где 5— знак числа; п — число, которое для разных форматов равно 23, 52 или 63.
В машине мантисса представлена в нормализованной форме, которая состоит из целой части Fo = 1 и дроби в таком виде:
М — 1, F, F2, .... Fi, ...,Fn.
В коротком и длинном форматах бит Fo при передаче чисел и хранении их в памяти не фигурирует. Это — скрытый (неявный) бит, который в нормализованном числе всегда равен единице.
Пример 1.11
Представить десятичное число -247,375 в коротком формате. Двоичный код этого числа равен -11110111,011; истинный порядок будет +7 (запятая сдвигается влево на семь разрядов), а смещение достигнет значения Псм = 127 + 7 = 134. С учетом скрытого бита Fo = 1 имеем:
Знак Порядок Мантисса
1 1000 0110 ,1110 1110 1100 0000 0000 0000.
Параметры форматов вещественных чисел представлены в табл. 1.5.
Таблица 1.5
Параметры Формат
короткий ДЛИННЫЙ расширенный
Длина формата, бит 32 64 80
Длина мантиссы, бит 24 53 64
Длина порядка, бит 8 П 15
Смещение порядка + 127 + 1023 +16383
Диапазон Ю±з8 1О±308 10±4932
Числа в коротком и длинном форматах существуют только в памяти. При загрузке чисел в одном из этих форматов в микропроцессор они автоматически преобразуются в 80-битный формат, который используется только для внутренних one-
32 Основы теории компьютерной схемотехники
раций. Аналогично данные из процессора преобразуются в короткий или длинный формат для хранения в памяти.
Точность вычислений чисел с плавающей запятой возрастает с увеличением длины мантиссы. Диапазон представления чисел с плавающей запятой зависит от длины порядка и основания счисления q. В машинах ЕС ЭВМ значение q = 16. В процессорах Pentium диапазон представления чисел в коротком формате для q = 2 находится в пределах 10±38. Если же для этого формата взять основание q = 16, то получим значение диапазона в пределах 10±152.
В микропроцессорах Pentium используются двоично-десятичные цифры в таких форматах:
• восьмиразрядные упакованные, которые содержат в одном байте две десятичные цифры в коде 8421, например, 3910 = 0011 Ю012_10;
• восьмиразрядные неупакованные, которые содержат одну десятичную цифру в байте (младшая тетрада) вместе с признаком (зоной) 00112 в международном коде ASCII, например, 3910 = 0011 0011 0011 Ю012_10.
Представление десятичного числа 136492 в неупакованном и упакованном форматах показано на рис. 1.11;
7______0 7_______0 7______0 7______0 7_______0 7______0
|00П 0001 |0011 ООП |0011 0П0|00П 0100|00П 100110011 оою|
а
7______0 7_______0 7______0
[0001 ООП |0П0 0100 |1001 0010 I
б
Рис. 1.11. Представление десятичных цифр в форматах: а — неупакованном; б — упакованном
• 80-разрядные упакованные, в которые записываются 19 десятичных цифр, и в старшую тетраду записывается знак числа.
1.2.7. Кодирование отрицательных чисел
Для записи знака числа, замены операции вычитания чисел сложением их кодов, а также для определения переполнения разрядной сетки используют прямой, обратный и дополнительный коды, где для представления знака числа отводится знаковый разряд, который располагается слева от числа и отделяется запятой. В знаковый разряд записывают нуль (для положительного числа) или единицу (для отрицательного). Запятая в машине в явном виде не изображается, а только подразумевается.
Числа, представленные в прямом, обратном и дополнительном кодах, называют машинными изображениями. Они состоят из знакового разряда и цифровой части (модуля числа). Положительные числа во всех кодах записываются одинаково. Если обозначить машинные изображения числа А в прямом коде [Л]Пр, в обратном коде [Л]0Б, в дополнительном коде [Л]д, то для положительных чисел имеем:
[Л]пр = [Л]об = И]д.
1.2. Арифметические основы компьютерной схемотехники 33
Для отрицательных чисел с длинной мантиссы к битов коды определяют по таким правилам:
прямой код:
Г1 + |Л| -для дроби;
МпР = ] А. I I
2 + -для целого числа;
обратный код:
[2-|л|-2“а' -для дроби;
И]оБ=1 л+| | |
2 -Л -для целого числа;
дополнительный код:
[2-|л| -для дроби;
Ид Н А.+| I , 12 - |Л| - для целого числа;
Пример 1.12 ]
Запись двоичных чисел А = 10102 и В = —10102 в прямых кодах:
[Л]Пр = 0,1010; [5]пр= 1,1010. |
Обратный код отрицательного числа образуется из его прямого кода после инвертирования значений разрядов цифровой части, то есть заменой нуля на единицу и единицы — на нуль; значение знакового разряда не изменяется. Дополнительный код отрицательного двоичного числа образуется из его обратного кода путем добавления единицы к младшему разряду.
Пример 1.13
Представление в обратном и дополнительном кодах двоичных чисел: целого А =-10012 и дробного В = —10012:
И]0Б= 1,0110; №=1,0111;
[5]об= 1,0110; [5]д= 1,0111.
Из этих примеров видно, что обратный и дополнительный коды целых и дробных чисел по виду записи совпадают; расхождения между ними отражены в алгоритмах обработки информации.
В модифицированных кодах знак числа дублируется в двух знаковых разрядах.
Пример 1.14
Представление в модифицированных кодах чисел А = 11012 и В = -11012: №р=№б=№ = 00,1101;
[5]пр= 11,1101; Моб = 11,0010; [5]д = 11,0011.
Для перехода от обратного кода отрицательного числа к прямому коду требуется инвертировать значения разрядов цифровой части, не изменяя значения знакового разряда. Для перехода от дополнительного кода отрицательного числа к прямому сначала получают его обратный код, а затем добавляют единицу к младшему разряду. 3-4-1749
34 Основы теории компьютерной схемотехники
1.2.8. Арифметические операции сложения и вычитания
Все операции в компьютере выполняются в арифметико-логическом устройстве (АЛУ). Числа, которые участвуют в операциях, называются операндами. Основной операцией в АЛУ является сложение. Операция вычитания заменяется сложением операндов в обратном или дополнительном кодах. Операции умножения и деления сводятся к многократным сложениям и сдвигам.
Правила выполнения операций сложения, вычитания, умножения и сложения по модулю 2 в двоичной арифметике представлены в табл. 1.6. При сложении двух единиц возникает перенос в старший разряд; при вычитании из нуля единицы требуется заем из старшего разряда.
Таблица 1.6
Сложение Вычитание Умножение Модуль 2
0+0 = 0 0-0 = 0 00 = 0 0+0 = 0
0+1 = 1 1-0=1 01 =0 0+1 = 1
1+0 = 1 1-1=0 1-0 = 0 1+0=1
1 + 1 = 10 т Перенос 0-1 = 11 t Заем 11 = 1 1 + 1=0
Операция сложения в АЛУ выполняется типовым функциональным узлом — сумматором. Он состоит из отдельных логических схем, называемых одноразрядными сумматорами. Связь между отдельными одноразрядными сумматорами реализуется с помощью цепей переноса в направлении от младших разрядов к старшим.
Операнды А и В поступают с выходов регистров операндов. Комбинационный сумматор строится на логических элементах и не обладает свойством запоминания информации, поэтому результат сложения записывается в регистр результата.
Во всех компьютерах имеются команды сложения и вычитания чисел. Однако в сумматорах реализуются только операции сложения условно положительных машинных изображений. Машинные изображения положительных операндов во всех кодах совпадают. Машинные изображения отрицательных операндов получают по правилам представления чисел в обратном и дополнительном кодах. В операциях вычитания знак второго операнда (вычитаемого) автоматически изменяется на противоположный и после этого получают его машинное изображение. Поэтому в последующих примерах рассматриваются только операции сложения.
В машинных изображениях (для обратного и дополнительного кодов) знаковый разряд и цифровая часть числа рассматриваются как одно целое. Они одинаково участвуют в операции сложения. При сложении в обратных кодах перенос из старшего знакового разряда результата поступает на вход переноса младшего разряда (циклический перенос). При сложении в дополнительных кодах перенос из старшего знакового разряда результата не учитывается, поэтому в сумматоре цепь циклического переноса разрывается. Знак результата при сложении машинных изображений образуется автоматически.
При сложении двоичных л-разрядных чисел А = а,„ ..., а, и В = Ь„, ..., Z>„ ...,
Ьх результат в каждом разряде определяют по формулам:
1.2. Арифметические основы компьютерной схемотехники 35
а, + bj +Zi — Si + 2P,+l,
f 0 при а, + Ь, < 1;
/+l [1 при at + bi > 2;
где а„ bj — значения z-x разрядов; Z, — перенос из младшего разряда; S, — результат; Р1+, — перенос в старший разряд.
Пример 1.15
Сложить двоичные числа А = 1010 и В = 0011 в обратном коде:
[Л]Об = 0,1010
+ [^]ОБ = 0,0011
[С]об = 0,1101; С= 11012 = 1310.
Пример 1.16
Сложить двоичные числа А = -1010 и В = ном кодах: [Л]Об = 1,0101 + [^]об = 1,1100 -0011 в обратном и дополнитель- [Л]д= 1,0110 + [5]д= 1,1101
1,0001 | +1 [С]Об = 1,0010; С = -11012 =-1310. [С]д= 1,0011; С =-11012 =-1310.
При сложении чисел одного знака возможно переполнение разрядной сетки, признаком чего является несовпадение знака результата со знаками операндов. В АЛУ имеются специальные логические схемы, которые автоматически формируют признак переполнения.
Пример 1.17
Сложить двоичные числа А = 1011 и В = 0111 в обратном и дополнительном
кодах:
[Л]об = 0,1011 [Л]д = 0,1011
+ [5]об = 0,0111 + [5]д = 0,0111
[Qoe# 1,0010; [С]д# 1,0010.
В этом примере сложение положительных чисел привело к положительному переполнению: операнды — положительные, результат — отрицательный.
Пример 1.18
Сложить двоичные числа А = -1011 и В = -0111 в обратном и дополнительном кодах:
|/4]об — 1,0100 + [5]об= 1,1000 [Л]д= 1,0101 + [Я]д= 1,1001
[С]об # 0,1101; [С]д # 0,1110.
з*
36 Основы теории компьютерной схемотехники
В этом примере сложение отрицательных чисел привело к отрицательному переполнению; операнды — отрицательные, результат — положительный.
Для упрощения обнаружения переполнения разрядной сетки используются модифицированные коды, для которых знаковый разряд в сумматоре дублируется. Положительному переполнению в знаковых разрядах соответствуют цифры 01, а отрицательному — 10. Значение знаковых разрядов 00 соответствует правильному положительному результату, а цифры 11 — отрицательному.
Пример 1.19
\ Сложить двоичные числа А = -1010 и В = 1100 в обратном и дополнительном
\ модифицированных кодах:
I [Л]МОБ= 11,0101 [Л]мд= 11,0110
I +[^]МОБ = 00,1100 + [£]мд = 00,1100
I ’ 100,0001” [С]мд = 00,0010;
I I* +1
I 1-----►
[С]Моб = 00,0010; С = 00102 = 2|О. С = 00102 = 2|О.
Пример 1.20
Сложение чисел А = -1101 и В = фицированных кодах: -1010 в обратном и дополнительном моди-
[Л]МОБ = 11,0010 [Л]мд= 11,0011
+ [£]МОБ= 11,0101 + [£]мд= 11,0110
[С]МОБ^ 10,1000; [С]мд^ 10,1001.
В этих примерах произошло отрицательное переполнение в результате.
1.2.9. Арифметические операции умножения и деления
Операция умножения чисел состоит из к циклов, где к — число цифровых разрядов множителя. Результат умножения z-го разряда множителя на множимое называется частичным произведением, а их последовательное сложение — суммой частичных произведений (СЧП). В каждом цикле анализируется следующая цифра множителя: если это 1, то к СЧП прибавляется множимое, если 0, то сложение не выполняется. Цикл завершается сдвигом на один разряд множимого относительно СЧП или сдвигом СЧП относительно неподвижного множителя. Множимое и множитель размещаются в разрядной сетке на основе специальных схем-регистров, а СЧП — в сумматоре-регистре.
Умножение можно выполнять одним из четырех способов:
• с младших разрядов множителя со сдвигом его и СЧП вправо при неподвижном множимом (рис. 1.12, а). Старшие разряды произведения находятся в сумматоре, а младшие — в регистре множителя;
• с младших разрядов множителя при сдвиге множимого и неподвижной СЧП;
• со старших разрядов множителя при сдвиге СЧП влево и неподвижном множимом;
1.2. Арифметические основы компьютерной схемотехники 37
• со старших разрядов множителя при сдвиге его и СЧП влево (рис. 1.12, б).
Если хотя бы один из сомножителей равен нулю, то произведению сразу присваивается нулевое значение.
п 1
а б
Рис. 1.12. Способы умножения: a — первый; б — четвертый
Алгоритм умножения целых чисел, представленных в прямом коде, на основе первого способа реализуется в такой последовательности:
1. взять модули сомножителей и обнулить исходное значение СЧП;
2. если младшая цифра множителя равна 1, то к СЧП прибавляется множимое; если это 0, то сложение не происходит;
3. сдвиг вправо на один разряд СЧП и множителя;
4. пп. 2 и 3 последовательно выполняются к раз, после чего произведению присваивается знак, определяемый сложением по модулю 2 знаков сомножителей.
Пример 1.21
Перемножить первым способом числа А = 13 )0 = 11012 и В = 1110 = 10112,
представленные прямыми кодами.
1101 — модуль множимого
1011 — модуль множителя
0000 — исходная СЧП
+1101 — первое частичное произведение (ЧП)
1101 — первая СЧП
01101 — сдвиг вправо СЧП на 1 разряд
+ 1101 — второе ЧП
100111 — вторая СЧП
0100111 — сдвиг вправо СЧП на 1 разряд
+0000 — третье ЧП
100111 — третья СЧП
0100111 — сдвиг вправо СЧП на 1 разряд
+1101 — четвертое ЧП
10001111 • — четвертая СЧП
10001111 — сдвиг вправо СЧП на 1 разряд.
Произведение С = А В = 100011112= 143,0-
38 Основы теории компьютерной схемотехники
Разработаны также методы ускоренного умножения и умножения в дополнительных кодах.
Операция деления числа С = А / В обычно сводится к последовательности вычитаний делителя В сначала из делимого А, а затем из создаваемых в процессе деления остатков Числа А и В поступают в прямом коде. В зависимости от способа вычитания делителя различают два алгоритма деления: без восстановления остатка и с восстановлением.
Для обоих алгоритмов общим является следующее:
• деление осуществляется над модулями чисел А и В (при делении целых чисел в машинах длина делимого А вдвое больше длины делителя В)-,
• знак частного определяется сложением по модулю 2 знаков Л и В;
• перед делением анализируются числа А и В на равенство нулю: если А = О, то частному присваивается значение 0 и операция завершается; при В = О выполнение программы прерывается;
• умножение частного на два осуществляется сдвигом его влево на один разряд, а операция вычитания делителя В заменяется его сложением в дополнительном коде;
• первый остаток R} определяет по формуле
R} =2-\А\-В = 2-\А\+[-В]а,
причем, если 7?| < 0, то деление возможно, если R} > 0, то возникает переполнение разрядной сетки;
• цифры частного определяются, начиная со старших разрядов:
при R, < 0;
при R, > 0,
i - 1,2, ..., к, где к — заданное количество цифр частного. Обычно первый разряд С,- отводится для записи знака.
Алгоритм деления без восстановления остатка определяют по следующему ре-курентному соотношению:
' 2Rt +15
2R, + [б 1ц
при R,< 0; при R, >0.
Алгоритм деления с восстановлением остатка определяют по следующему ре-курентному соотношению:
47?,-, + [- 5]д при Ri < 0; 2Rj + В]д при Rj > 0.
при R, > 0.
[ Пример 1.22
Разделить числа А = 49|0 и В - -7]0 на основе алгоритма без восстановления остатка. Прямой код операндов: [Л]Пр = 0,0110001, [В]Пр = 1,111; [-5]д = = 1,001:
1.2. Арифметические основы компьютерной схемотехники 39
Пример 1.22. Продолжение
[Л]Пр = 0,0110001 + [5]ПР= 1,111
2 |Л = 0,1100010 + [-В]д= 1,001
7?, = 1,1110010 < 27?, = 1,1100100 + \В\ =0,111 0 С, =0
Т?2 = 0,1010100 > 27?2= 1,0101000 + [-7?]д= 1,001 0 С2 = 1;
7?з = 0,0111000 > 27?3 = 0,1110000 + Н?]д= 1,001 0 С3 = 1; частное [С]пр = 1,111; С = -111 = -7)0; остаток равен нулю.
Т?4 = 0,0000000 > 0 С4 = 1; Знак частного А[7] Ф В[7] = 0 Ф 1 = 1.
Пример 1.23
Разделить числа А остатков: [Л]пр = 0,0110001 + [5]ПР= 1,111 = 49ю и В = -710 на основе алгоритма с восстановлением
2|Л| = 0,1100010 + [-7?]п= 1,001
7?! = 1,1110010 < 47?0= 1,1000100 + [-7?]д= 1,001 0 С, = 0
Т?2 = 0,1010100 > 27?2 = 1,0101000 + [-7?]д= 1,001 0 С2 = 1;
7?з = 0,0111000 > 27?3 = 0,1110000 + [-Д]д= 1,001 0 С3 = 1; частное [Л]ПР = 1,111; С = -111 = -710.
Т?4 = 0,0000000 > 0 С4 = 1;
40 Основы теории компьютерной схемотехники
Описанные способы выполнения арифметических операций над числами с фиксированной запятой применяют также для выполнения их над мантиссами чисел с плавающей запятой. Сложение и вычитание чисел А и В с плавающей запятой может осуществляться только при равенстве их порядков Пл и Пя. Для этого они предварительно выравниваются сдвигом одного из них. При умножении или делении чисел А и В с плавающей запятой порядок результата ПР равен соответственно сумме или разности порядков этих чисел, то есть ПР = ПА± Пй.
1.3. Логические основы компьютерной схемотехники
1.3.1. Булева алгебра
Теоретической основой компьютерной схемотехники является алгебра логики — наука, которая использует математические методы для решения логических задач. Алгебру логики называют булевой в честь английского математика Дж. Буля, внесшего наибольший вклад в развитие этой науки.
Основным предметом булевой алгебры является высказывание — простое предложение, о котором можно утверждать: истинно оно (обозначают символом 1) или ложно (обозначают символом 0). Обычно простые высказывания обозначают буквами, например, Хъ которые в компьютерной схемотехнике называют переменными (аргументами). С помощью логических связок НЕ, ИЛИ, И, ЕСЛИ... ТО... строят сложные высказывания, которые называют булевыми (логическими) функциями и обозначают буквами F, L, К, М, Р и др.
В настоящее время главная задача алгебры логики — анализ, синтез и структурное моделирование любых дискретных конечных систем. Аппарат булевой алгебры распространяется на объекты самой различной природы безотносительно их сути, лишь бы они характеризовались двумя значениями или состояниями: контакт включен или выключен, наличие высокого или низкого уровня электрического напряжения, выполнение или невыполнение некоторого условия работы и т.д.
Использование аппарата алгебры логики в компьютерной схемотехнике основано на том, что цифровые элементы характеризуются двумя состояниями и благодаря этому могут быть описаны булевыми функциями. Стандарт ДСТУ 2533-94 “Арифметические и логические операции. Термины и определения” конкретизировал основные понятия булевой алгебры в системах обработки информации.
Переменную с конечным числом значений (состояний) называют переключательной, а с двумя состояниями — булевой. Функция, которая имеет как и каждая ее переменная конечное число значений, называется переключательной (логической). Логическая функция, число возможных значений которой и каждой ее независимой переменой равно двум, является булевой. Таким образом, булева функция — это частный случай переключательной.
Операция — это четко определенное действие над одним или несколькими операндами, которое создает новый объект (результат). В булевой операции операнды и результат принимают “булево значение 1” (далее просто значение 1) и “булево значение 0” (далее просто значение 0). Булеву операцию над одним операндом называют одноместной, над двумя — двуместной и т.д.
1.3. Логические основы компьютерной схемотехники 41
Булевы функции могут зависеть от одной, двух и в целом от п переменных. Запись F(AS,, AS, ... , XJ означает, что некоторая булева функция F зависит от переменных AS,, AS, ..., AS„. Основными булевыми операциями являются отрицание (операция НЕ, инверсия), дизъюнкция (операция ИЛИ, логическое сложение, объединение) и конъюнкция (операция И, логическое умножение). _
Отрицание — это одноместная булева операция F = X (читается “не X’), результатом которой является значение, противоположное значению операнда.
Дизъюнкция — это булева операция F = Х} vX2 (читается “Х} или AS”), результатом которой является значение нуль тогда и только тогда, когда оба операнда имеют значение нуль.
Конъюнкция — это булева операция F = ХгХ2 (читается “AS, и Х2"), результатом которой является значение единица тогда и только тогда, когда значение каждого операнда равно единице. В выражении AS,AS2 точку можно опускать; часто используют запись AS, л Х2 или Х} & Х2.
Операции отрицания, дизъюнкции и конъюнкции можно задать с помощью таблиц истинности (табл. 1.7 и 1.8), в которых слева представлены значения операндов, а справа — значения булевой функции.
Таблица 1.7
X F ~X
0 1
1 0
Таблица 1.8
Xi x2 F = X, vX, F = X, X2
0 0 0 0
0 1 1 0
1 0 1 0
1 1 1 1
В табл. 1.8. булевы функции ИЛИ, И заданы для двух переменных Хь Х2.
Для булевых операций отрицания, дизъюнкции и конъюнкции справедливы следующие законы, свойства и тождества:
• коммутативность (переместительный закон):
Х^ vAS = AS vAS; Хх X2 = AS X;
• ассоциативность (сочетательный закон):
X vX2 vX3 = (X vX2) vX3; X X2 X3=(XX2)X3;
• дистрибутивность (распределительный закон):
AS, (AS v AS) = AS AS v AS AS; XvX2X3 = (X^X2)(XvX3);
• идемпотентность (исключение повторения):
XvXvX = X; XXX = X;
• закон поглощения:
Xi v AS AS = AS; Хх {Хх v AS) = X;
• закон склеивания:
X X ^X X = Жv(*i v T2) = AS,;
• закон де Моргана:
,Y,v J, =XX; XxX2 =^v^;
• свойства отрицания и констант:_
ASvX=l; ASX=0; X = .Y; 1 = 0; 0=1;
ASvO=AS; Avl = l; XI =X; ^-0=0;
42 Основы теории компьютерной схемотехники
• тождества:
Х} vIX = Х} чХ2; Х}(х^ Х2)=Х}Х2.
Справедливость приведенных законов булевой алгебры проверяется путем подстановки в логическое выражение нуля и единицы, как показано в табл. 1.9 для формулы Х\Х"2 =X'2vX'2.
Таблица 1.9
Xi х2 Xi -х2 *1 х2 vX2
0 0 0 1 1 1 1
0 1 0 1 1 0 1
1 0 0 1 0 1 1
1 1 1 0 0 0 0
Областью определения булевой функции F(JVb Х2, ... , Х„) является конечное множество различных двоичных наборов длиной п, на каждом из которых указывается значение функции нуль или единица. Количество разнообразных двоичных наборов равно множеству «-разрядных двоичных чисел т = 2". Например, для функции двух переменных Х} и Х2 имеется четыре двоичных набора: < 0,0 >; < 0,1 >; < 1,0 >; < 1,1 >.
Часто наборы нумеруются десятичными эквивалентами двоичных чисел от нуля до 2п-1. Например, для п = 4, наборы < 0, 1, 0, 1 > и < 1, 0, 0, 1 > имеют соответственно номера 5 и 9. Две функции отличаются одна от другой, если их значения будут разными хотя бы в одном наборе. Число различных булевых функций от п переменных равно 2т, где т = 2".
Произвольную булеву функцию можно задать разными способами: словесным описанием, временными диаграммами, геометрическими фигурами, графами, таблицами истинности и аналитическими выражениями.
Словесное описание некоторой булевой функции F(JVb Х2) можно представить так: F = 1 при Х} Х2 = 1 и F = 0, если Х} Х2 = 0. Такую функцию можно изобразить временной диаграммой (рис.1.13, а) или геометрически с помощью двухмерного куба (рис.1.13, б), в котором точками выделены единичные вершины (данная функция принимает значение единицы на наборе < 1, 1 >), а также графом, где вершины отображают значение нуля и единицы, а на ориентированных дугах переменные указывают условия переходов (рис. 1.13, в).
Рис. 1.13. Способы задания булевых функций
1.3. Логические основы компьютерной схемотехники 43
С помощью таблиц истинности показывают все возможные функции одной переменной (всего четыре функции) и двух переменных (всего 16 функций). Для и = 3 число возможных булевых функций равно 256, для п = 4 их количество - 21е = 65536.
Булевы функции одной переменной представлены в табл. 1.10. Как видим, из четырех булевых функций практический интерес вызывает только операция отрицания L2 = X.
Таблица 1.10
Lt Xi Выражение Название операции
0 1
Lty 0 0 Fo = O Константа 0
F, 0 1 F, =X Повторение X
Fj 1 0 f2 =x Отрицание X
F3 1 1 F3 = 7 Константа 1
Все 16 булевых функций Fn-Fi5 двух переменных Хг, Х2 представлены в табл. 1.11.
Таблица 1.11
х, 00 11 Выражение Название операции
х2 0 10 1
Fo 0000 F0=0 Константа 0
F} 000 1 F=X}X2 Конъюнкция
f2 00 10 f2= XxX2 Запрет по Х2
F3 00 11 F3=Xx ПовторениеF,
F< 0 100 F4=X,A'2 Запрет по Xt
f5 0 10 1 f5=x2 Повторение Х2
F6 0 110 F6 = X{®X2 Сумма по модулю 2
f7 0 111 Fj = Xi v X2 Дизъюнкция
f8 1000 Fs = X}lX2 Отрицание дизъюнкции
f9 100 1 F9=Xi~X2 Эквивалентность
F,o 10 10 f}0 = x~2 Отрицание Х2
F,. 10 11 Fu=X<-X2 Импликация от Х2 к А)
Fn 1100 Fn = X{ Отрицание X)
F13 110 1 Fl3=X^X2 Импликация от X] к Х2
FM 1110 f»=xfx2 Отрицание конъюнкции
f15 1111 F,5=l Константа 1
Как следует из табл.1.11, функции Fo и F]5 — константы, F3 и Fs— повторяют, а Fio и F)2 — отрицают одну из переменных, Fi и F7 — конъюнкция и дизъюнкция, которые рассмотрены ранее. К новым булевым функциям (операциям) относятся следующие.
Исключение (запрет) — двухместная булева операция, результатом которой является значение единицы тогда и только тогда, когда значение одного операнда равно единице, а другого — нулю. Записывается в виде:
44 Основы теории компьютерной схемотехники
F2 = Х}Х2 илиР4=Х1Х2.
Сумма по модулю два (исключающее ИЛИ, отрицание эквивалентности) — двухместная булева операция, результатом которой является значение единицы тогда и только тогда, когда операнды имеют разные значения. Обозначается в виде:
F6 = X, ® Х2 =Y^X2 v X, Y .
Отрицание дизъюнкции (операция НЕ ИЛИ, стрелка Пирса) — булева операция, результатом которой является значение единицы тогда и только тогда, когда оба операнда равны нулю. Обозначается в виде:
F8 =.¥, 1х2 = X, V,¥2 .
Обобщая для п переменных, имеем:
.¥, 1х21х3 ... lX„=Y}Y2...Y„ = X, vX2 vX3v...vX„.
Эквивалентность (равнозначность) — двухместная булева операция, результатом которой является единица тогда и только тогда, когда операнды принимают одинаковые значения. Обозначается в виде:
F9 =Х, ~Х2 =Х, Х2 V Х\ Y2 .
Импликация (включение) — двухместная булева операция, результатом которой является значение нуль тогда и только тогда, когда значение одного из операндов равно нулю, а другого — единице. Обозначается в виде:
Fn =Х^Х2=Х 'Y_; Fl3 =Х->Х2 = X~jvX2.
Отрицание конъюнкции (операция НЕ И, штрих Шеффера, отрицание пересечения) — булева операция, результат которой равен нулю тогда и только тогда, когда оба операнда равны единице. Обозначается в виде:
Fu /Х2 = Х,Х2 .
Обобщая для п переменных, имеем:
х}/х2/... xn=Y^Y2^..7Yn=xxx2... хп.
Булевы функции одного и двух аргументов называют элементарными. Схему, которая осуществляет элементарную логическую операцию, называют логическим элементом (вентилем). Совокупность взаимозависимых логических элементов с формальными методами описания называется логической схемой.
Названия и условные графические обозначения основных логических элементов, применяемых в компьютерной схемотехнике, представлены в табл. 1.12. Значения переменных (операндов) отображаются электрическими сигналами с двумя четко выраженными уровнями значений.
Таблица 1.12
Название операции Название элемента Условное графическое обозначение
Отрицание НЕ X 1 С —
1.3. Логические основы компьютерной схемотехники 45
Таблица 1.12. Продолжение
Название операции Название элемента Условное графическое Обозначение
Дизъюнкция ИЛИ х2 1
Конъюнкция и У] х2 & Х\Х2
Отрицание дизъюнкции НЕ ИЛИ х2 1 А', уУ
Отрицание конъюнкции НЕИ у. х2 & С ) Х'Х2
Отрицание эквивалентности Исключающее ИЛИ х2 х{®х2
Эквивалентность Эквивалентность Х{ х2 -1 С х}®х2 ь - -
Импликация ЕСЛИ, ТО Х2 bi Х; v X-}
Запрет НЕТ Х2 )& xXi
С помощью суперпозиций, то есть подстановки в логические формулы вместо переменных некоторых других булевых выражений, можно получить более сложные функции любого числа переменных, например,
Y = v Х2, Л] = Zi Z2; Х2 = Z3v Z4, тогда У = Z, Z2 v Z3 v Z4.
Одной из интерпретаций булевых операций являются схемы, состоящие из ключей, источника напряжения Е и лампочки Л. Для реализации операции дизъюнкции двух переменных Хх и Х2 используют два параллельно соединенных нормально разомкнутых ключа (рис. 1.14, а).
При нажатии любого ключа = 1 или Х2 = 1) или обоих вместе лампочка горит (значение 1). Для реализации операции конъюнкции двух переменных Х} и Х2 применяют два последовательно соединенных нормально разомкнутых ключа (рис. 1.14, б). При нажатии одновременно обоих ключей (.Y| = Х2 - 1) лампочка горит (значение 1).
46 Основы теории компьютерной схемотехники
Для реализации операции отрицания применяют нормально замкнутый ключ (рис. 1.14, в). При Х= 0 ключ замкнут и лампочка горит; при X = 1 ключ размыкается и лампочка не горит.
Рос. 1.14. Интерпретация булевых операций: а — дизъюнкция; б — конъюнкция; в — отрицание
1.3.2. Аналитическое представление булевых функций
Разработаны универсальные (канонические) формы представления булевых функций, дающие возможность получить аналитическую форму произвольной функции непосредственно из таблицы истинности. Эта форма в дальнейшем может быть минимизирована или упрощена. Поскольку между множеством аналитических представлений и множеством схем, реализующих эту функцию, имеется взаимнооднозначное соответствие, то отыскание канонической формы записи является начальным этапом синтеза логических схем. Наиболее широкое распространение получили совершенная дизъюнктивная нормальная форма (СДНФ) и совершенная конъюнктивная нормальна форма (СКНФ). Для получения этих форм вводятся понятия мин-термов (конституента 1) и макстермов (конституента 0).
Минтерм — это функция п переменных, равная единице только на одном наборе. Минтерм получают как конъюнкцию п переменных, которые входят в него в прямом виде, если значение данной переменной в наборе Л) = 1, и — с отрицанием, если Х; = 0. При п переменных имеется 2П минтермов т0, ть ..., mR, где R = 2" - 1. Все минтермы двух переменных приведены в табл. 1.13.
Таблица 1.13
Xi Хг F, / Минтермы Макстермы
0 0 1 /о=1 т0 = Х} Х2 М0=Л1
0 1 0 />=о т\= X, Х2 Mi =Xi v *2
1 0 0 /2=0 т2 = Х} Х2 М2= Х^ j Х2
1 1 1 /=1 т2 = Х\ Х2 M2 = Xt v
Значения функции Fg, соответствующие, согласно таблице истинности, каждому z-му набору, обозначены как/о,/,/,/. Представление функции F9 в СДНФ является дизъюнктивной суммой минтермов, соответствующих наборам переменных, для которых/ = 1:
1.3. Логические основы компьютерной схемотехники 47
Fg = f0 • та v f • т, v /2 т2 v f3 • т} = 1 • т0 v 0 m, v 0 т2 v 1 m3 = = т0 v m3 — Х2 v Х\ Х2.
Макстерм — это функция п переменных, равная нулю только на одном наборе. Макстерм получают как дизъюнкцию всех переменных, которые входят в него в прямом виде, если^значение X, = 0, или в инверсном виде, если значение JV, = 1. Число макстермов равно 2п, для функции двух переменных они приведены в табл. 1.13. Представление функции Fg в СКИФ записывается в виде:
Fg = (/0 vM0 ) (/ vM,) (A VM2) (/3 V _ = (lvMo)(OvM,)(0vM,)(lvM3) = M2 ={X} V X2 )(X> vl2).
Поясним на примере табл. 1.14 аналитическую запись функции трех переменных в СДНФ и СКИФ. Для записи функции Р в СДНФ требуется дизъюнктивно сложить те минтермы, для которых функция равна единице:
Р = Х^Х3 v Х^Х2 Х2 v X Х^ Х^ v X Х2Х^ v X Х2Х2.
Таблица 1.14
х, х2 Х1 р
0 0 0 0
0 0 1 1
0 1 0 0
0 1 1 1
1 0 0 1
1 0 1 0
1 1 0 1
1 1 1 1
Для записи функции Р в СКИФ необходимо записать конъюнкцию макстермов, для которых функция равна нулю:
Р = (X,vX2v^3) (X-vX2v Х3) ( X{-v ,Y,v Х3).
По этому способу производится запись в СДНФ и СКНФ функций с произвольным числом переменных.
Система функций, суперпозицией которых может быть представлена любая булева функция, называется функционально полной; она образует базис в логическом пространстве.
Систему функций называют минимально полным базисом, если удаление из нее любой функции превращает эту систему в неполную. В теории алгебры логики доказано, что функционально полные системы образуют следующие наборы функций:
1. Х_, JV, v Х2, Xt Х2 (булев базис, избыточный);
2. X , v ;
3. X, ХхХ2,
4. х~х;
5. X, v Х2 и др.
48 Основы теории компьютерной схемотехники
Другая алгебра логики строится на основе функции суммы по модулю два и конъюнкции (алгебра Жегалкина). Через операции алгебры Жегалкина можно выразить все другие булевы функции:
Хх -> Х2 - ~Х\ V Х2 = 1 © Xt © Х2;
.¥,-%,= (Л\ vJ¥2)G¥, vX)-1® .V,© .¥2;
Х} <г- Х2 = X, -» Х2 = Х{ ®Х}Х2.
В булевой алгебре широко используется разложение Шеннона — формула, позволяющая перейти к представлению функции п переменных через функции от (и-1) переменных:
F(X},X2,...,Xn)~X]f(l,X2,...,Xi:)'v'x\f(Q,X2,...,Xn).
Выражение легко обобщается для любого числа переменных, если обе функции его правой части подвергнуть такому же разложению по другим переменным. Отметим, что в результате разложения по всем переменным получится СДНФ.
1.3.3. Минимизация булевых функций
Важным этапом проектирования компьютерных схем является минимизация булевых функций, то есть нахождение их выражений с минимальным числом букв. Минимизация обеспечивает построение экономичных схем компьютеров. Для минимизации функций с числом букв п < 6 используют карты Карно. Их строят в виде таблиц из 2П клеток с разметкой строк и столбцов переменными. Карты Карно для функции трех переменных F(X\, Х2, Х3) показаны на рис. 1.15. Строки карты отмечены значениями переменной J¥,, а столбцы — значениями переменных Х2, Х2. Каждая клетка карты Карно однозначно соответствует одному набору таблицы истинности для функции трех переменных (рис. 1.15, а) или минтермам этой функции (рис. 1.15, б). Клетки карты Карно часто нумеруют десятичными цифрами — номерами наборов (рис. 1.15, в).
При минимизации для каждого минтерма, входящего в СДНФ функции, ставится единица, а другие клетки не заполняются. Например, заполнение карты Карно для функции, заданной табл. 1.14, показано на рис. 1.15, г.
Минтермы в соседних клетках карты Карно в строке (включая верхние и нижние) или в столбце (включая крайние) отличаются значением одной переменной, что позволяет выполнить операцию склеивания по этой переменной.
Например, на рис. 1.15, г минтермы Х}Х2Х2 и X,Х2Х3 (клетки с номерами 1 и 3) отличаются значением переменной Х2, поэтому они склеиваются по ней и представляются конъюнкцией двух переменных Х,Х2. Аналогично для минтермов А", Х2Х2 и Х}Х2Х2 (номера клеток 4 и 6) склеивание происходит по переменной Х2 и получают конъюнкцию Х\ Х3. В результате минимизации функции Р(Х}, Х2, Х3) получают ее минимальное выражение Р = Х,Х2 vХ2Х2 v Xt X3.
1.3. Логические основы компьютерной схемотехники 49
Рис. 1.15. Карты Карно для функции трех переменных
Перечислим общие правила минимизации.
1. Изображают карту Карно для п переменных и производят разметку ее строк и столбцов. В клетки таблицы, соответствующие минтермам (единичным наборам) минимизируемой функции, записывают единицу.
2. Склеиванию подлежат прямоугольные конфигурации, заполненные единицами и содержащие 2, 4 или 8 клеток. Верхние и нижние строки, крайние левые и правые столбцы карты как бы склеиваются, образуя поверхность цилиндра.
3. Множество прямоугольников, покрывающих все единицы, называется покрытием. Чем меньше прямоугольников и чем больше клеток в прямоугольниках, тем лучше покрытие. Из нескольких вариантов выбирают тот, у которого меньше коэффициент покрытия z = г / s, где г — общее число прямоугольников, 5 — их суммарная площадь в клетках. Например, для изображенного покрытия (рис. 1.15,г) имеем z = 3/5.
4. Формулы, полученные в результате минимизации, содержат г элементарных конъюнкций (по числу прямоугольников в покрытии). Каждая конъюнкция содержит только те переменные, которые не меняют своего значения в склеиваемых наборах в соответствующем прямоугольнике. Число переменных в конъюнкции называется ее рангом. При склеивании двух соседних клеток получают ранг конъюнкции п-1, четырех клеток — п-2 , восьми клеток — п-3 и т.д.
Разметка карт Карно для функций четырех переменных показана на рис. 1.16.
00 01 II________10 х 00 01 11 10
0000 0001 ООН 00! 0
оюо 010! ОН! 0! Ю
иоо НО! ИИ пю
1000 100! юи юю
0 I 3 2
4 5 7 6
12 13 15 14
8 9 И Ю
a б
Рис. 1.16. Карты Карно для функции четырех переменных: а — двоичное значение минтермов; 6— десятичное значение минтермов
4 — 4-1749
50 Основы теории компьютерной схемотехники
В клетки карт записаны значения минтермов соответственно в двоичном и десятичном эквивалентах.
Пример 1.25
! Минимизировать булевы функции Lt, L2 и четырех переменных. Функция ! задана двумя способами — в СДНФ и с десятичными эквивалентами минтер-: мов:
• L. = Х}Х2X3 J4 v Х}Х2 v Х\Х2Х.Х4 v Х}Х2Х3Х4 v
i v XtX2X2X4 v X,X,Х3Х4 v Х,Х2ХХ. v Х}Х2Х3Х4 =
: = 0 v 1 v 2 v 3 v 4 v 8 v 12 v 15.
Функции L2 и Ц для упрощения заданы десятичными эквивалентами мин-. термов:
: L2 = 2v3v6v7v8v9v12v13; L2 =1v3v5v7v9v11v13v15.
Минимизация функций Lx, L2 и L3 производится на основе карт Карно, пока-
! занных на рис. 1.17. Результаты минимизации:
Рис. 1.17. Карты Карно для минимизации булевых функций четырех переменных: а — L ,; б — L2; в — Из
Л = 77T7V Х,Х2Х2Х4-, z, =3/8;
L2 = V A”, J7; z2 = 2/8;
L, = X 4; z3 = I /8.
Для минимизации булевых функций используют также диаграммы Вейча, кото-
рые аналогичны картам Карно и отличаются от них способом разметкиизместо символов 0 и 1 используют булевы обозначения аргументов — Х}, Х: , Х2 и др.
(рис. 1.18). X X Л А, X,
V, и 10 ио 111 101 юо
у 01 00 ОН . 001 000
X ою
х - X х, X
х- 1100 1101 1001 юоо X
1110 11 и 1011 юю X;
X, 01 10 01 11 0011 оою
0100 0101 0001 0000 X
X . в X, X Рис. 1.18. Диаграммы Вейча:
а — для двух переменных; б — для трех переменных; в — для четырех переменных
1.4. Основные характеристики цифровых микросхем 51
I Пример 1.26
\ Минимизировать с помощью диаграмм Вейча функцию £2 из примера 1.25. ! Запись значения минтермов функции £2 в клетки Вейча показан на рис. 1.19. Ре-\ зультат минимизации:
[ L2=V3v/X z2=1/4
j совпадает сданными примера 1.25.
Рис. 1.19. Диаграмма Вейча для минимизации функции L2
1.4. Основные характеристики цифровых микросхем
1.4.1. Понятие элементов, узлов и устройств компьютерной схемотехники
Технические средства компьютерной схемотехники в зависимости от выполняемых функций, делят на элементы, функциональные узлы и устройства, а также микропроцессоры и компьютеры (рис. 1.20). Они предназначены для обработки дискретной информации и потому называются цифровыми.
Технические средства компьютерной схемотехники в настоящее время основаны на интегральных микросхемах (ИМС) разной степени сложности.
Элементы ) Узлы ? Устройства Компьютеры
Рис. 1.20. Состав технических средств компьютерной схемотехники
Элементами в компьютерной схемотехнике называются наименьшие неделимые микроэлектронные схемы (изделия), предназначенные для выполнения логических операций или хранения бита информации. К элементам условно относятся и вспомогательные схемы — усилители, повторители, формирователи и др. Элементы строятся на основе двухпозиционных ключей, что технически реализуется наиболее просто. Элементы с двумя состояниями называются двоичными.
На входах и выходах двоичного элемента действуют напряжения, которые принимают в установившемся режиме два значения — высокого U/., и низкого UL уровней (индексы от английских слов High и Low). Эти напряжения отображают электрические сигналы. Сигнал с двумя состояниями называется двоичным. Переход эле
4*
52 Основы теории компьютерной схемотехники
мента из одного состояния в другое называется его переключением. На основе элементов строят типовые функциональные узлы.
Элементарные действия, выполняемые в компьютерах за один машинный такт, называются микрооперациями. Например, инкремент или декремент слова, сдвиг, инверсия, сложение и др. В компьютерах команды выполняют последовательностью микроопераций над двоичными словами (числами). Типовыми функциональными узлами компьютеров называются микроэлектронные схемы, предназначенные для выполнения одной или нескольких микроопераций. По логике работы функциональные узлы разделяют на комбинационные и последовательностные схемы.
В комбинационных схемах логическое состояние выходов элементов зависит только от комбинации входных сигналов в данный момент времени. К функциональным узлам комбинационного типа относятся сумматоры, дешифраторы, шифраторы, мультиплексоры и демультиплексоры, схемы сравнения (компараторы) и контроля по четности, кодопреобразователи.
В последовательностных схемах логическое значение выходов определяют как комбинацией выходных сигналов, так и состоянием памяти схемы в данный момент времени. К функциональным узлам последовательностного типа относятся регистры, счетчики, генераторы чисел и управляющие автоматы. На основе типовых функциональных узлов строят различные устройства компьютеров.
Универсальность компьютеров обеспечивает возможность приема и выдачи информации, ее хранения и арифметико-логической обработки, а также управления всем вычислительным процессом. Эти функции реализуют соответствующими устройствами ввода, вывода, запоминающими, арифметико-логическими и управления.
Во всех компьютерах используют генератор тактовых импульсов (ГТИ), который вырабатывает периодическую последовательность прямоугольных импульсов, называемых тактовыми (С). Начало каждого импульса С называется тактовым моментом. Временной интервал между двумя соседними импульсами С называется машинным тактом Тс. Вначале каждого импульса С происходит смена информации на входах элементов и узлов машины (рис. 1.21).
Частота ГТИ измеряется десятками, сотнями мегагерц и гигагерцами. В литературе ГТИ часто называют генераторами синхронизирующих импульсов, а сами импульсы называют синхронизирующими или синхроимпульсами. Амплитуда и полярность импульса С зависит от физических принципов построения машины. Принцип подачи информации на входы элементов и узлов в тактовые моменты называется дискретизацией сигналов во времени.
В компьютерной схемотехнике используются два основные вида двоичных сигналов: потенциальные и импульсные (рис. 1.22).
1.4. Основные характеристики цифровых микросхем 53
Рис. 1.22. Диаграммы потенциальных (ПС) и импульсных (ИС) сигналов
Сигнал, который изменяется только в тактовые моменты времени, называется потенциальным. Сигнал, который нарастает в тактовый момент, а спадает в пределах данного такта, называется импульсным. Длительность потенциального сигнала равна или кратна длительности машинного такта.
В логике значения двоичного сигнала и соответствующей переменной X кодируются символами 0 (лог. 0) и 1 (лог. 1). Напряжение, отображающее символ 1, обозначим через U', а символ 0 — через U0. Различают два способа кодирования логических сигналов Xi потенциальными сигналами — положительный и отрицательный. При положительном кодировании (положительная логика или соглашение) больший уровень напряжения UH с учетом знака отображает лог. 1, а меньший UL — лог. 0, то есть X = 1, если I/1 = UH, и X = 0 при if = UL (рис. 1.23, а). При отрицательном кодировании (отрицательная логика или соглашение) больший уровень напряжения UH с учетом знака отображает лог. 0, а меньший UL — лог. 1, то есть Х= 1, если U' = UL, и X = 0 при if = UH (рис. 1.23, б).
Рис. 1.23. Логические соглашения: а — положительное X ; б — отрицательное X
Для импульсных сигналов различают два рода кодирования (рис. 1.24): первый — наличие импульса отображает лог. 1, отсутствие — лог. 0; второй — наличие импульса одной полярности отображает лог. 1, а другой полярности — лог. 0.
Рис. 1.24. Импульсное кодирование: а — первого рода; б — второго рода
54 Основы теории компьютерной схемотехники
Элементы компьютеров классифицируют по следующим признакам:
• используемым физическим приборам;
• виду информационных сигналов;
• функциональному назначению;
• конструктивно-технологическому изготовлению;
• уровню и степени сложности.
По типу физических приборов различают следующие элементы: построенные на электронных лампах — первое поколение; на транзисторах — второе поколение; на ИМС малой и средней степени интеграции — третье поколение; на больших и сверхбольших ИМС — четвертое поколение.
По виду информационных сигналов выделяют:
• потенциальные элементы — используются только потенциальные сигналы;
• импульсные элементы — используются только импульсные сигна. ,ы;
• потенциально-импульсные элементы — используются потенциальные и импульсные сигналы.
По функциональному назначению элементы компьютерной схемотехники делятся на следующие классы:
• логические элементы, предназначенные для выполнения логических операций — НЕ, И, ИЛИ, НЕ И, НЕ ИЛИ, НЕ И ИЛИ и др.;
• запоминающие элементы — триггеры, предназначенные для хранения значения одной двоичной переменной — нуля или единицы, то есть одного бита информации;
• вспомогательные элементы (усилители, формирователи, преобразователи сигналов, схемы временного согласования, генераторы импульсов и др.), предназначенные для обеспечения работы элементов первых двух классов.
По конструктивно-технологическому изготовлению элементную базу современной компьютерной схемотехники составляют интегральные микросхемы. Это — микроэлектронные изделия с высокой плотностью упаковки электрорадиоэлементов (резисторов, диодов, транзисторов) и соединений между ними. С точки зрения спецификации, испытаний, поставки и эксплуатации ИМС рассматриваются как единое целое.
В ИМС электрорадиоэлементы называются элементами, если они неотделимы от схемы, и компонентами, если их можно использовать самостоятельно. Далее, во избежание путаницы с элементами компьютеров, электрорадиоэлементы называют просто компонентами.
Микросхемы классифицируют по следующим основным признакам:
• технологии изготовления — полупроводниковые, гибридные, пленочные;
• конструктивному оформлению — корпусные и бескорпусные;
• форме обработки информации —• аналоговые, цифровые и аналого-цифровые;
• степени интеграции (сложности) — малые, средние, большие, сверхбольшие и ультрабольшие;
• типу активных элементов — построенные на биполярных и МОП-транзисторах;
1.4. Основные характеристики цифровых микросхем 55
• области применения — широкого применения, специализированные, в том числе заказные и полузаказные;
• используемым материалам — кремниевые, арсенид-галлиезые;
• перспективным направлениям — криомикроэлектронные, акустоэлектрон-ные, оптоэлектронные, молекулярной электроники и др.
Набор цифровых микросхем с общими конструктивно-технологическими и схемотехническими признаками образует серию ИМС. В компьютерной схемотехнике широко применяются цифровые полупроводниковые корпусные ИМС на основе кремния и арсенида галлия. В полупроводниковых ИМС все компоненты и соединения между ними выполнены в объеме и на поверхности кристалла площадью от 4 до 100 мм2. В гибридных ИМС навесные компоненты крепятся на поверхности диэлектрической подложки. В пленочных ИМС все компоненты и соединения между ними выполнены в виде тонких пленок на диэлектрической подложке.
Сложность микросхем характеризуется уровнем интеграции N, степенью интеграции К = lg/V и степенью функциональной сложности F = IgA, где N— число компонентов, комп.; L — число двухвходовых логических элементов (вентилей); значение десятичного логарифма округляется до большего целого числа. Промышленность изготовляет ИМС от первой (менее 10 комп.) до шестой (менее 1 млн комп.) и выше степени интеграции.
Возможности интегральной технологии определяет плотность упаковки: соотношение числа компонентов к объему (иногда к площади) кристалла. Плотность упаковки в полупроводниковых ИМС составляет 107 комп, /см3, а для гибридных — 100-200 комп. /см3.
Малая интегральная схема (МИС) содержит до 100 комп, включительно, средняя микросхема (СИС) — 100-1000 комп., большая интегральная схема (БИС) — до 100000 комп., сверхбольшая интегральная микросхема (СБИС) — до 1 млн комп., а ультрабольшая (ультра-БИС) — до 10 млн комп, и больше. На МИС строят элементы, на СИС реализуют типовые узлы, на БИС, СБИС и ультра-БИС обеспечивается построение микропроцессоров и микрокомпьютеров.
Каждая элементарная логическая функция реализуется соответствующим логическим элементом: ИЛИ (дизъюнктор), И (конъюнктор), НЕ (инвертор). Для реализации сложных функций логические элементы объединяются в логическую схему. Функционально полная система логических элементов позволяет построить любую сложную логическую схему. Такие системы образуются следующими наборами логических элементов: 1) ИЛИ, НЕ; 2) И, НЕ; 3) НЕ ИЛИ; 4) НЕ И и другими. В технически полной системе элементов обеспечивается значение электрических параметров двоичных сигналов, для этого используются вспомогательные элементы — усилители, повторители, формирователи и др.
С учетом вышеизложенного можно сказать, что система элементов представляет собой функционально и технически полный набор элементов, который использует одинаковые способы представления информации, а также имеет общие конструктивно-технологические характеристики.
56 Основы теории компьютерной схемотехники
1.4.2. Характеристики логических элементов
Логические, схемотехнические и эксплуатационные свойства логических элементов определяются совокупностью характеристик и параметров, к которым относят:
• функции логических элементов;
• логические соглашения;
• коэффициенты объединения по входу и выходу;
• коэффициент разветвления;
• быстродействие;
• мощность потребления;
• работа переключения;
• входные и выходные напряжения и токи;
• статическая и динамическая помехоустойчивость;
• надежность элементов;
• допустимые величины механических воздействий, диапазоны давления и температуры окружающей среды, устойчивость к радиационным воздействиям;
• масса, стоимость и конструктивное оформление.
В большинстве случаев указанные характеристики и параметры относятся и к ИМС, на которых реализованы логические элементы.
Коэффициент объединения по входу Ni характеризует число логических входов логического элемента — обычно 1,2, 3, 4 или 8 (рис. 1.25).
N=3 N=8 N{ = 2И-2И-ЗИ-ЗИЛИ-НЕ
Рис. 1.25. Примеры значений коэффициента Nt
Коэффициент объединения по выходу No характеризует допустимое количество соединенных между собою выходов логических элементов с целью создания новых функций.
Коэффициент разветвления по выходу Np характеризует нагрузочную способность логического элемента, то есть максимальное число входов идентичных схем, которое может быть одновременно подключено к выходу данного элемента без нарушения его работоспособнрсти (рис. 1.26). В состав серий ИМС обычно входят элементы с малой нагрузочной способностью (Np = 3...15) и с большой (Np = 30...50).
1.4. Основные характеристики цифровых микросхем 57
а б
Рис. 1.26. Подключение нагрузки: а — N„ = 3; б— Nv = 4
Приняты следующие определения и буквенные обозначения электрических параметров цифровых микросхем (ДСТУ 2883-94):
• входные Ut и выходные Uo уровни напряжений (индексы — от английских слов Input и Output)',
• входные напряжения низкого UIL и высокого UIH уровней; для них устанавливаются максимальное значение низкого уровня U1L П1ах и минимальное значение высокого уровня UlHniin (рис. 1.27, а);
• выходные напряжения низкого U0L и высокого UOh уровней; для них установлены максимальное значение низкого уровня U()L пмх и минимальное значение высокого уровня J7(Wniin (рис. 1.27, б);
• входной I/ и выходной 10 токи;
• входной ток I!L — при низком уровне напряжения на входе, 1т — при высоком;
• выходной ток Iql — при низкому уровне напряжения на входе, а 10н — при высоком;
• UCc — значение напряжения источника питания;
• 1( (—ток, потребляемый ИМС от источника питания;
• Ра— мощность, потребляемая ИМС от источника питания;
• входные пороговые напряжения, при которых происходит переключение элемента: UTih — наименьшее значение для высокого уровня и UTIL — наибольшее значение для низкого уровня. _
а б
Рис. 1.27. Обозначение уровней напряжения: а — входных; б— выходных
Основные параметры логических элементов определяют с помощью входной, выходной и передаточной характеристик. Типовые графики этих характеристик для
58 Основы теории компьютерной схемотехники
инвертирующих элементов транзисторно-транзисторной логики представлены на рис. 1.28.
Входная характеристика логического элемента I, = flUi) — это зависимость входного тока от изменения входного напряжения. Токи, втекающие в схему элемента, считаются положительными, а вытекающие — отрицательными (рис. 1.28, а). Из этой характеристики определяют входные токи I!L для напряжения U/Lnax и то 1!Н для напряжения U!Hт[п.
Выходная характеристика логического элемента Uo = fll()) определяет зависимость выходного напряжения от тока нагрузки для состояний высокого и низкого уровней (рис. 1.28, б). Из этой характеристики определяют допустимые значения токов: +IOL — при низком уровне выходного напряжения UOL п1ах и -10н — при высоком уровне напряжения (7oWmi„ (рис. 1.28, б).
в
Рис. 1.28. Характеристики логического транзисторно-транзисторного элемента: а — входная; б — выходная; в — передаточная
Передаточная характеристика Uo = fill,) — это зависимость выходного напряжения от входного (рис. 1.28, в). Из этой характеристики определяют значение помехоустойчивости для низкого уровня на входе ML (отпирающая помеха) и для высокого уровня на входе Мн (запирающая помеха):
= Util ~ UlLmux, Мн = Uiffmn - UTIH-
Средняя мощность Р сс, потребляемая элементом от источника питания вычисляется по формуле
Р сс = Р'сс (Iccl + Icch) / 2 = UCc I сс.
где ICCl, Icch — токи потребления при низком и высоком уровнях напряжения на выходе соответственно; /*сс — средний ток потребления. Современные элементы потребляют мощность от микроватт до десятков милливатт.
Потенциальные сигналы характеризуются значением логического перепада (амплитудой) UM = UH - UL и длительностью положительного tWH и отрицательного
1.4. Основные характеристики цифровых микросхем 59
twL перепадов (рис. 1.29). Перепады напряжений часто называют положительными и
Для измерения временных параметров сигнала устанавливают условные уровни в долях амплитуды — 0,1; 0,5 и 0,9.
Быстродействие микросхем определяют по значениям следующих длительностей:
• фронта tLH и спада tHL (рис. 1.30, а);
• собственно включения tTHL и выключения tTLH (рис. 1.30, б); и их задержки соответственно tDHL и tDL/f,
• задержек распространения сигнала при включении tPHL и выключении tPLH (рис. 1.30, в).
Рис. 1.30. Измерение временных параметров сигналов:
а — фронта tw и спада tm.; б — времени включения Ithl и выключения tnn:
в — времени задержек распространения сигнала при включении tPHL и выключении tTLH
Для практических расчетов используют среднее время задержки распространения сигнала
tp ~ (tpHL + tPLH) I "P
Для оценки качества элемента широко используют обобщенный параметр — работу переключения
Л-п — Р сс ’ tp-
60 Основы теории компьютерной схемотехники
Если мощность Р*сс измеряется в милливаттах, а время задержки — в наносекундах, то работа переключения Лп выражается в пикоджоулях (пДж). Значение обобщенного параметра Лп находится в пределах 0,1-200 пДж. Чем меньше значение Ап, тем лучшими характеристиками обладает логический элемент.
Надежность ИМС характеризуется тремя взаимозависимыми показателями:
• интенсивностью отказов А = n / (mt), где п — число отказов за время испытания, час; т — общее количество испытуемых микросхем;
• наработкой на отказ Т = 1/2;
• возможностью безотказной работы на протяжении заданного интервала времени Р = ехр(-Лг).
Для современных ИМС интенсивность отказов А = (10“7 ... 10'8). Приняв, что А = 10~8, t = 15000, получим значение вероятности безотказной работы P(t) = 0,998 или 99,8%.
По конструктивно-технологическому исполнению микросхемы подразделяются на пять групп, которым присвоены следующие обозначения (ДСТУ 3212-95):
• полупроводниковым на биполярных транзисторах— 1, 6;
• полупроводниковым на полевых транзисторах — 5, 7;
• гибридным — 2, 4;
• другим (пленочным, вакуумным, керамическим и т.д.) — 3;
• резервным — 0, 8, 9.
Указанные группы микросхем по конструктивно-технологическому исполнению подразделяются на подгруппы, которым присваиваются следующие обозначения:
• для первой группы: комбинированные структуры с биполярными и полевыми транзисторами — 0; структура на биполярных транзисторах с изоляцией р-n переходами или диэлектриком — соответственно 1, 2; на транзисторах с инжекционной интегрированной логикой — 3; резерв — 4-9;
• для второй группы: структура на полевых транзисторах п- или р- типа — соответственно 5, 6; с симметричной комплементарной структурой — 7; структуры с зарядовой связью — 8; резерв — 1-4, 9;
• для третьей группы (гибридные микросхемы): толстопленочные — 1; тонкопленочные — 2; комбинированные — 3; резерв — 4-9;
• для четвертой группы: толстопленочные — 4; тонкопленочные — 2; комбинированные — 3; резерв — 4-9.
По функциональному назначению микросхемы подразделяются на группы, которым присваиваются следующие обозначения:
• генераторы — Г;
• коммутаторы и ключи — К;
• логические элементы — Л;
• многофункциональные схемы — X;
• наборы элементов — Н;
• преобразователи сигналов — П;
• схемы источников вторичного электропитания — Е;
• схемы задержки — Б;
• схемы сравнения — С;
• триггеры — Т;
1.4. Основные характеристики цифровых микросхем 61
• усилители — У;
• формирователи —А;
• схемы запоминающих устройств — Р;
• схемы цифровых устройств — И;
• схемы вычислительных средств — В.
В каждой функциональной группе различают виды, например:
• логических елементов: ЛИ — элемент И; ЛН — элемент НЕ; ЛЛ — элемент ИЛИ; ЛА — элемент НЕ И; ЛЕ — элемент НЕ ИЛИ; ЛР — элемент НЕ И' ИЛИ; ЛД — расширители; ЛП — прочие;
• триггеров: ТВ — универсальные (тип JK); ТР — с раздельной записью (тип RS); ТМ — с задержкой (тип О); ТК — комбинированные; ТП — прочие;
• схем вычислительных средств: BE — микро-ЭВМ; ВМ — микропроцессоры; ВС— микропроцессорные секции; ВУ — схемы микропрограммного управления; ВБ — схемы синхронизации; ВВ — схемы интерфейса; ВН — время-задающие схемы; ВП — прочие.
Для характеристики материала и типа корпуса по ГОСТ 174-67 перед цифровым обозначением серии добавляются следующие буквы;
• Р — для пластмассового корпуса типа 2;
• М — для керамического, металлокерамического корпуса типа 2;
• Е — для металлополимерного корпуса типа 2;
• С —для стеклокерамического корпуса типа 2 и др.
Для некоторых микросхем буквенные обозначения типа корпуса не применяют.
Присвоение обозначений микросхемам осуществляет в централизованном порядке главная организация по стандартизации изделий электронной техники.
Обозначение микросхемы должно состоять из следующих элементов:
• первый и второй элементы — две цифры, характеризующие соответственно группу и подгруппу микросхемы по конструктивно-технологическому исполнению;
• третий элемент — две цифры, обозначающие порядковый номер разработки серии микросхем;
• четвертый элемент — две буквы, характеризующие соответственно группу и вид микросхемы;
• пятый элемент — две цифры, обозначающие порядковый номер разработки микросхемы.
Три первых элемента определяют серию микросхем. В случае необходимости после обозначения порядкового номера разработки микросхемы по функциональному назначению дополнительно проставляются буквы от А до Я, характеризующие отличие микросхем одного типа по электрическим параметрам. Такая буква во время маркировки может быть заменена цветной точкой. Буква или цвет маркировочной точки указываются в технических условиях микросхем конкретных типов.
Примеры условного обозначения микросхем:
• 5704ВГ03 — полупроводниковый программируемый контроллер управления динамической памятью с симметричной комплементарной структурой серии 5704; номер разработки серии — 04, номер разработки микросхемы в данной серии по функциональному назначению — 03 (рис. 1.31);
62 Основы теории компьютерной схемотехники
• 1101УД06 — полупроводниковая микросхема серии 1101, порядковый номер разработки серии — 01, структура на биполярных транзисторах с изоляцией р-п переходом, операционный усилитель постоянного тока, порядковый номер разработки микросхемы в данной серии по функциональному назначению — 06.
Серия
( /X
5 7 04 ВГ 03
Третий в данной серии
Контроллер
Порядковый номер разработки серии
Симметричная комплементарная структура
Вторая полупроводниковая группа на полевых транзисторах
Рис. 1.31. Структура условного обозначения программируемого контроллера памяти с симметричной комплементарной структурой 5704ВГ03
Перед условным обозначением микросхем указывается сокращенное название государства-разработчика — У (Украина). Для микросхем с шагом 1,27 или 2,54 мм между выводами корпуса, которые поставляются на экспорт, вначале условного обозначения после буквы У проставляется буква Е, например:
• УЕ1217УД06 — микросхемы серии 1217, выпущенные в Украине в экспортном исполнении (шаг выводов 1,27 или 2,54 мм) в пластмассовом корпусе типа 2.
В ранее принятых обозначениях ИМС широкого применения вначале ставили букву К.
^Примечание j
| Условные обозначения ИМС, которые выпускались до 1991 года в СССР, ус- ] | танавливались по ОСТ 11073.915-80. В соответствии с отраслевым стандартом, | условное обозначение микросхем состояло из четырех цифро-буквенных злемен-; тов.
| Первый элемент — цифра, которая обозначает конструктивно-
| технологическую группу: полупроводниковых — 1, 5, 6, 7; гибридных — 2, 4 8;
J прочих (пленочных, керамических) — 3.
| Второй элемент, состоящий из двух или трех цифр, обозначает порядковый
| номер серии.
j Третий двухбуквенный элемент определяет функциональное назначение
! ИМС: первая буква — подгруппу; вторая — вид в подгруппе, что совпадает с
) ДСТУ 3212-95.
j Четвертый элемент — это порядковый номер разработки ИМС данного типа j в серии. Первый и второй элементы вместе обозначают серию ИМС, перед кото-j рой могут проставляться буквы, характеризующие тип корпуса.
1.4. Основные характеристики цифровых микросхем 63
\ В дальнейшем условные обозначения ИМС выбираются по отраслевому ; стандарту. Для ИМС коммерческого назначения условное обозначение начинает-’ ся с буквы К, а в экспортном варианте — с букв ЭК. Пример условного обозначения D-триггера ТТЛШ серии КР1333ТМ2 представлен на рис. 1.32.
К Р 1 333 Т М 2
— ————"————————— 5
i Порядковый номер разработки |
| по функциональному признаку |
| Вид: D-триггер \
I L........-------------------- !
I Подгруппа: триггер I
. Порядковый номер серии |
„ . .. i
। Конструктивно-технологическое исполнение ।
| Пластиковый корпус типа 2 |
I Коммерческое назначение [
i I
I Рис. 1.32. Пример условного обозначения ИМС по ОСТ 11073.915-80 j
I.......... ; ; ... . ...................................... , j
Корпусы микросхем состоят из трех основных частей: кристалла, корпуса для защиты кристалла от климатических воздействий и для удобства монтажа, а также проводников для электрической связи кристалла и выводов корпуса. Имеется четыре основных конструктивно-технологических варианта корпусов (рис. 1.33): пластмассовый, металлокерамический, металлостеклянный и керамический.
Рис. 1.33. Конструкции корпусов ИМС:
1 — кристалл ИМС; 2 — проволочные проводники; 3 — кристаллодержатель; 4 — выводы; 5— низкотемпературный припой; 6 — крышка корпуса;
7 — стекло (стеклоприпой); 8 — монтажная площадка; 9 — основание корпуса
64 Основы теории компьютерной схемотехники
Контрольные вопросы
1. Какие методы и технические средства изучает дисциплина “Компьютерная схемотехника”?
2. Что такое информатика?
3. Что такое сигнал?
4. Охарактеризуйте основные системы счисления, используемые в компьютерах.
5. Дайте определение логических функций инверсии, дизъюнкции и конъюнкции.
6. Назовите основные технические характеристики цифровых микросхем.
7. Назовите буквенно-цифровые элементы, определяющие условные обозначения микросхемы.
8. Поясните количественные меры информации — бит, байт, килобайт.
9. Запишите число А = -0101 в прямом, обратном и дополнительном кодах и их модификациях.
10. Поясните, зачем используют минимизацию булевых выражений.
11. Назовите отличия между картами Карно и диаграммами Вейча.
12. Дайте определение потенциального информационного сигнала.
13. Поясните отличие между положительным и отрицательным кодированием логических переменных потенциальными сигналами.
14. Что такое импульсный информационный сигнал?
15. Поясните способы кодирования логических переменных импульсными сигналами.
16. Назовите функционально полные системы логических элементов.
17. Охарактеризуйте классификационные признаки элементов компьютерной схемотехники.
18. Что такое серия ИМС?
2.1. Логические элементы — диодные, транзисторные, ИИЛ и ДТЛ 65
Глава 2
Элементы компьютерной схемотехники
2.1. Логические элементы — диодные, транзисторные, ИИЛ и ДТЛ
В компьютерной схемотехнике в основном используют потенциальную систему элементов. Она обладает следующими особенностями:
• на входах и выходах логических элементов действуют только потенциальные сигналы;
• с выхода одного элемента на вход другого передаются как переходные, так и установившиеся значения сигналов;
• на пути потенциального сигнала не допускается включать конденсаторы и обмотки трансформаторов, поскольку длительность потенциального сигнала в общем не ограничена (такой вид электрической связи называется гальваническим или непосредственным);
• отсутствие конденсаторов и трансформаторов в цепях связи способствует упрощению технологии изготовления микросхем;
• реализуется ограниченный набор булевых функций: НЕ, ИЛИ, И, НЕ ИЛИ, НЕ И, НЕ И-ИЛИ, “Исключающее ИЛИ”, что облегчает применение автоматизированных методов проектирования.
Потенциальные элементы различают по схемотехническому признаку — способом соединения транзисторов, диодов и резисторов между собой в пределах одной схемы типового базового элемента. Принято считать, что совокупность элементов с общим признаком построения образует вид схемной логики или просто логику.
Различают следующие виды логики потенциальных элементов:
• диодную (ДЛ) и диодно-транзисторную логику (ДТЛ);
• транзисторную логику (ТЛ), в которой выделяют схемы с непосредственными связями (ТЛНС), с резисторными связями (ТЛРС) и резисторноконденсаторными связями (ТЛРКС);
• интегральную инжекционную логику (ИИЛ или И2Л);
• транзисторно-транзисторную логику (ТТЛ) и ее модификации с диодами Шотки (ТТЛШ);
• эмиттерно-связанную логику (ЭСЛ);
• МОП-транзисторную логику (p-МОП, n-МОП, КМОП);
• логику на основе арсенида галлия (AsGa).
5-4-1749
66 Элементы компьютерной схемотехники •
2.1.1. Диодные логические элементы
Диодные логические элементы являются исторически первыми и самыми простыми схемами, которые реализуют булевы функции ИЛИ, И, И-ИЛИ, ИЛИ-И. Диодные элементы не усиливают входных сигналов и не могут выполнять операцию НЕ.
При рассмотрении работы логических элементов принимают (если не оговорено особо) положительное кодирование: высокий уровень напряжения Ун отображает лог. 1, а низкий уровень UL — лог. 0.
Элемент ИЛИ
Логика работы логического элемента ИЛИ на два входа и Х> представлена в табл. 2.1, на основе которой получают выражение для выходной булевой функции элемента F = Х-Х X-,.
Таблица 2.1
Xt х2 F
0 0 0
0 1 1
1 0 1
1 1 1
Используя принцип суперпозиции, функцию F можно записать для произвольного числа входных переменных
F=X} v%2v ,.ухп.
Схема двухвходового элемента ИЛИ, его условное графическое изображение и временные диаграммы работы показаны на рис. 2.1.
Рис. 2.1. Диодный элемент ИЛИ: а — схема; б — условное графическое изображение; в — временные диаграммы работы
Высокий уровень напряжения У()н на выходе диодного элемента ИЛИ устанавливается при подаче на один или оба входа высоких уровней напряжения У1Н, при которых открываются соответствующие кремниевые диоды FD1 или VD2, либо оба вместе. В резистор нагрузки RH втекает выходной ток 10н, определяемый по формуле
1он ~ Uон/ Rh.
Значение выходного высокого уровня УОн зависит от входных напряжений:
Уон — Уш — У !
где U = 0,8 В — прямое падение напряжения на кремниевом диоде.
Для Um = 5 В, RH =1 кОм получим:
Уон = Уш-У' = 5 - 0,8 = 4,2 В;
Ion ~ Уон / Rh ~ 4,2/10 = 4,2 мА.
2.1. Логические элементы — диодные, транзисторные, ИИЛ и ДТЛ 67
При подаче одновременно на оба входа низких уровней напряжения UIL < 0,4 В, диоды закрыты, ток в цепи нагрузки не протекает и выходное напряжение U0L почти равно нулю.
На выходе элемента обычно имеется паразитная емкость Сп = 25...100 пФ, вследствие чего длительность фронта tLH очень мала (емкость быстро заряжается от источника входных сигналов через малое прямое сопротивление открытого диода), а длительность спада tHL велика (диоды закрыты и емкость разряжается через резистор 7?н). Поэтому для диодных схем ИЛИ выполняется неравенство tLH « tHL (рис. 2.1, в).
Элемент И
Логика работы логического элемента И на два входа Хх и Х2 представлена в
табл. 2.2, на основе которой получают выражение для выходной булевой функции
элемента F = X, Х2.
Используя принцип суперпозиции, функцию F можно записать
для произвольного числа входных переменных: xt Х2 F
F = Xt X ... Хп. 0 0 0
Схема двухвходового элемента И, его условное графическое 0 1 0
изображение и временные диаграммы работы, показаны на 1 0 0
рис. 2.2. 1 1 1
9 +(7
I <->сс
а б в
Рис. 2.2. Диодный элемент И: a — схема; б — условное графическое изображение; в — временные диаграммы работы
Высокий уровень напряжения U0H на выходе диодного элемента И устанавливается только при одновременной подаче на оба входа высоких уровней напряжения U1H, при которых закрываются кремниевые диоды FD1 и VD2. При этом от источника питания Ucc через резисторы R и RH протекает ток нагрузки
1он = Ucc RR + R\i)>
который определяет значение высокого уровня выходного напряжения
Uqh =IohRh ~ Ucc R» t(R + Ru)-
Как правило, используют значения R = 1... 2 кОм и RH > R. Длительность фронта выходного сигнала tLH определяется временем заряда паразитной емкости Сп через большое сопротивление резистора R. Если на один из входов, например Хь подан низкий уровень напряжения UIL, то диод VD1 открывается. При этом от ис-5*
68 Элементы компьютерной схемотехники
точника питания Ucc по цепи: резистор R, открытый диод VDi и источник входного сигнала Xt — протекает ток, значение которого определяют из выражения
IIL= [t/cc - (t/’ + UIL) ]/R, и на выходе устанавливается низкий уровень напряжения Uol = Ucc —IjlR ~ Uл + U , где U* = 0,8 В — прямое падение напряжения на открытом диоде VD1. Источники входных сигналов строят так, чтобы они пропускали втекающий в них ток IIL.
Длительность спада выходного сигнала определяется временем разряда паразитной емкости Сп через малое прямое сопротивление открытого диода. Поэтому в диодных схемах И длительность фронта выходного сигнала значительно больше длительности спада: tLH » tHL.
2.1.2. Элемент НЕ
Логика работы логического элемента НЕ (инвертора) представлена в табл. 2.3, на основе которой получают выражение для выходной булевой функции F = X .
Таблица 2.3
X F
0 1
1 0
Схема элемента НЕ, его условное графическое изображение и временные диаграммы работы показаны на рис. 2.3. Схема элемента НЕ включает: VT1 — кремниевый транзистор п-р-п типа; резисторы в цепи коллекторной нагрузки 7?к и базы 7?б; UCc — источник питания. Такую схему часто называют транзисторным ключом.
а — схема; б— условное графическое обозначение; в — временные диаграммы работы
Рис. 2.3. Элемент НЕ:
Транзистор VT1 может находиться в трех основных режимах: отсечки коллекторного тока (закрытое состояние), насыщения (открытое состояние) и активной работы (усиление). В режиме отсечки коллекторный и базовый переходы закрыты (на вход подан низкий уровень напряжения UfL), в цепи коллектора протекает очень малый обратный ток коллекторного перехода Тк0 < 1 мкА и на коллекторе транзистора устанавливается высокий уровень напряжения, определяемый из выражения
Uoh = UCc - Лео ~ UcC'
В режиме насыщения (на вход подан высокий уровень напряжения иОн) на кремниевом переходе база-эмиттер прямое падение напряжения равно С/Бн = U* = = 0,8 В, через коллектор протекает максимально возможный ток, который называет- ся током насыщения коллектора Ан- Значение этого тока находят из соотношения
2.1. Логические элементы — диодные, транзисторные, ИИЛ и ДТЛ 69
7rh = (Рсс ” ^KhW
где (7КН = UOL <0,4 В — напряжение на коллекторе насыщенного транзистора. Например, для типовых значений Ucc = 5 В, йк= 1 кОм получим для тока /Кн ~ 5 мА. Для получения этого тока требуется минимальный базовый ток насыщения /БН, значение которого вычисляют из соотношения
= Лсн/р, где р — коэффициент передачи базового тока в транзисторе, включенном по схеме с общим эмиттером. Для обеспечения надежного насыщения транзистора значение базового тока насыщения рассчитывают из выражения
Л| ~ S Тбн,
где 5 = 3...10 — степень насыщения. Например, если р = 50, то /БН = ОД мА и прямой ток базы, включающий транзистор, 1ы = 0,5 мА для 5=5.
Значение сопротивления резистора Т?Б получают из условия обеспечения необходимого значения включающего тока
Re ~ (Um- )/ 7Б1.
Для UIH = 5 В, и" = 0,8 В получим: Т?Б = 8,4 кОм.
В режиме насыщения в базе транзистора накапливается избыточный заряд, значение которого пропорционально степени насыщения. При подаче низкого уровня входного сигнала транзистор закрывается. Однако коллекторный ток остается постоянным в интервале времени - h, называемом временем рассасывания /рас избыточного заряда в базе (рис. 2.3, в). После окончания рассасывания коллекторный ток спадает и формируется фронт выходного сигнала tLH. Таким образом, наличие насыщения вызывает задержку выключения инвертора, что является недостатком данной схемы.
Уменьшение длительности переходных процессов обеспечивается схемой элемента НЕ (рис. 2.4, а), в которой вместо резистора Т?Б включены два последовательно включенных диода VD1 и VD2.
Рис. 2.4. Элемент НЕ с диодами в цепи базы: а — схема; б — временные диаграммы базовых токов
Диоды VDI и VD2 называются смещающими, поскольку они смещают пороговый уровень входного открывающего напряжения в большую сторону на значение 2(7*. Емкость СБ называется ускоряющей (форсирующей), поскольку она при включении быстро заряжается, увеличивая при этом прямой ток базы ГБ1 > /Бн, а при выключении быстро разряжается, создавая обратный, выключающий ток с амплитудой /Б2. Этот ток ускоряет рассасывание избыточного заряда в базе транзистора.
70 Элементы компьютерной схемотехники
2.1.3. Элементы ДТЛ
В этих элементах операции дизъюнкции и конъюнкции реализуются с помощью диодных схем, а операцию отрицания выполняет инвертор на основе транзисторного ключа. Логика работы двухвходового элемента НЕ ИЛИ представлена в табл. 2.4, на основе которой получают выражение для булевой функции
т л F = X vX2.
Таблица 2.4 12
Используя принцип суперпозиции, функцию F можно за-
X, хг F писать для произвольного числа переменных:
0 0 1 F = X, v Х2 v... v Хп . Схема ДТЛ-элемента, которая реализует булеву операцию HE-ИЛИ для двух переменных, и его условное графическое изо-бражение показаны на рис. 2.5.
0 1 0
1 0 0
1 1 0
Рис. 2.5. Элемент НЕ ИЛИ: а — схема; б — условное графическое обозначение
Схему ДТЛ-элемента НЕ ИЛИ строят путем подключения выхода диодного элемента ИЛИ ко входу инвертора. Смещающие диоды FD3 и FD4 играют ту же роль, что и в схеме, изображенной на рис. 2.4, а. Через резистор смещения 7?см протекает ток ZK0. Транзистор УТ\ открывается и формирует низкий уровень выходного напряжения UC,L только в том случае, когда на одном или обоих входах имеется высокий уровень напряжения Um. При этом включающий ток /Б1 проходит от источников входных сигналов.
Временные диаграммы работы (идеализированные) элемента НЕ ИЛИ показаны на рис. 2.6. Длительность переходных процессов практически определяется быстродействием транзистора.
Рис. 2.6. Временные диаграммы работы элемента НЕ ИЛИ
2.1. Логические элементы — диодные, транзисторные, ИИЛ и ДТЛ 71
Логика работы двухвходового элемента НЕ И представлена в табл. 2.5, на основе которой получают выражение для булевой функции F = XxX2. Используя принцип суперпозиции, функцию F можно записать для произвольного числа переменных:
Р = Х,Х2...Х„.
Схема ДТЛ-элемента, реализующего булеву операцию НЕ-И для двух переменных X, иХ2, и его условное графическое изображение показаны на рис. 2.7.
Таблица 2.5
X, Х2 F
0 0 1
0 1 1
1 0 1
1 1 0
Схему ДТЛ-элемента НЕ И строят путем подключения выхода диодного элемента И ко входу инвертора. Смещающие диоды VD3 и VD4 играют ту же роль, что и в схеме, изображенной на рис. 2.4.
Транзистор ИЛ открывается и формирует низкий уровень выходного напряжения Uql только при совпадении высоких уровней входных сигналов UtH на обоих
входах одновременно. При этом включающий ток протекает от источника тока Усс по цепи: резистор R, диоды VD3, VD4 и база транзистора УЛ. При подаче хотя бы на один из входов (или на оба) сигнала низкого уровня весь ток от источника пита-
Рис. 2.8. Временные диаграммы работы элемента НЕ И
ния Ucc замыкается по цепи: резистор R, диод ИО1 или VD2 (или оба) на соответствующий источник входных сигналов. В результате этого транзистор ИЛ закрывается и на выходе устанавливается высокий уровень напряжения UOH. Длительность переключения элемента практически определяется быстродействием транзистора. Временные диаграммы работы элемента НЕ И показаны на рис. 2.8.
2.1.4. Транзисторная логика
Элементы ТЛ строят путем параллельной подключения коллекторов транзисторов к общему резистору коллекторной нагрузки 7?к. Выходное напряжение снимается с объединенных коллекторов. Если на один из входов поступает высокий уровень напряжения UIH, то соответствующий транзистор открывается и на выходе устанавливается низкий уровень сигнала U0L. Высокий уровень напряжения формируется на выходе только в случае подачи на все входы низких уровней UIL.
72 Элементы компьютерной схемотехники
Логика работы элементов ТЛ представлена в табл. 2.4. В элементах ТЛНС входные сигналы подают непосредственно на базы транзисторов VT\ и VT2 (рис. 2.9, а). В схеме ТЛРС в цепи баз транзисторов включены резисторы Т?Б (рис. 2.9, б).
Рис. 2.9. Элементы ТЛ: а — ТЛНС; б — ТЛРС; в — ТЛРКС
В схеме ТЛРКС для ускорения переходных процессов резисторы Т?Б шунтированы конденсаторами СБ. Их роль описана при рассмотрении схемы инвертора (см. рис. 2.4). Временные диаграммы работы элементов ТЛ совпадают с процессами, изображенными на рис. 2.6.
Интегральная инжекционная логика
Разновидностью транзисторных схем являются элементы интегральной инжекционной логики (ИИЛ или И2Л). Схемотехнику И2Л используют для построения микропроцессорных и запоминающих БИС (серии К582, К583, К584 и др.).
Схема логического элемента И2Л показана на рис. 2.10.
Схема включает инжекционные р-п-р транзисторы VT1, VT2, включенные по схеме с общей базой, и входные многоколлекторные п-р-п транзисторы VTi, VTA, включенные по схеме с общим эмиттером. Эмиттеры транзисторов Г7Т, VT1 называются инжекторами, а протекающий через них дырочный ток — инжекционным. Каждый из транзисторов VT\, VT2 образует вместе с источником питания и внешним резистором R источник тока, который питает индивидуальным током ZT входы транзисторов F73, VTA.
2.2. Транзисторно-транзисторные логические элементы 73
Особенностями элементов И2Л являются:
• “безрезисторность”, характерная для МОП-структур, которая впервые была реализована в схемотехнике И2Л;
• соединение областей базы и коллектора инжекционных р-п-р транзисторов соответственно с областями эмиттера и коллектора входных п-р-п транзисторов, а также малое число схемных компонентов и соединений между ними (количество операций маскирования и диффузии в два раза меньше сравнительно с элементами ТТЛ);
• низкий уровень напряжения UL = 0,01 В снимается с коллектора насыщенного транзистора, а высокий уровень напряжения £/#= 0,8 В — с коллектора закрытого транзистора, причем этот уровень ограничивается напряжением базы насыщенного транзистора нагрузки; используется режим микротоков, в котором токи коллектора изменяются от десятков до сотен микроампер; работоспособность элементов сохраняется при изменении значения тока в них на несколько порядков;
• на коллекторах входного транзистора реализуется инверсия переменной, а на соединенных коллекторах транзисторов И73, VT4 выполняются операции НЕ-ИЛИ.
Входные транзисторы управляются переключением тока на их входах. Если ко входу X] подключен коллектор левого насыщенного транзистора, то ток /т замыкается на него и не поступает в базу транзистора VI3, который закрывается и создает на своих коллекторах режим разомкнутых контактов. Если ко входу X, подключен коллектор левого закрытого транзистора, то ток /т втекает в базу И73, насыщает его и обеспечивает на коллекторах режим замкнутых контактов.
Задержка распространения сигнала в элементе И2Л при токе 100 мкА составляет примерно 5-10 нс, мощность потребления — до 20 мкВт, работа переключения равна 0,1 пДж (например, в ТТЛШ серии КР1533 работа переключения составляет 6 пДж). Отмеченные свойства элементов И2Л и БИС на их основе придают им технологичность и компактность, они имеют невысокую стоимость при большом быстродействии.
2.2. Транзисторно-транзисторные логические элементы
2.2.1. Общая характеристика транзисторнотранзисторных логических элементов
Элементы ТТЛ появились в результате развития схем ДТЛ в направлении сокращения числа компонентов, уменьшения емкости переходов и учета специфики интегральной технологии. Первоначально главной особенностью элементов ТТЛ было использование на входе многоэмиттерного транзистора (МЭТ) для реализации операции И. Каждый эмиттер МЭТ используют как логический вход. Число эмиттеров определяет коэффициент на входе N, = 1.. .8 и более.
74 Элементы компьютерной схемотехники
Промышленность выпускает следующие серии ТТЛ и ТТЛШ:
• стандартного среднего быстродействия (ТТЛ) — К133, К155, быстродействующие — К130, К131, К599 и маломощные — К134, К158 (1963 г.);
• стандартные быстродействующие (ТТЛШ) — К530, К531 и маломощные — К533, К555 (1970 г.);
• сверхбыстродействующие (ТТЛШ) — КР1530 (тип AS), высокого быстродействия — КР1531 (тип FAST) и маломощные — КР1533 (тип ALS) (1980 г.). В этих сериях применена изопланарная технология на основе ионной имплантации, прецизионной фотолитографии, обеспечивающих малые площади и емкости переходов.
В микросхемах серий К533, К555, КР1531 и КР1533 вместо МЭТ на входы снова поставили диодные схемы совпадения, однако название схемотехники ТТЛШ сохранилось.
2.2.2. Транзисторно-транзисторный логический элемент с простым инвертором
Схема простейшего ТТЛ-элемента содержит МЭТ, коллектор которого подключен к базе инвертирующего транзистора VT2 (рис. 2.11, а).
Рис. 2.11. Элемент ТТЛ с простым инвертором: а — схема; б — топология
Многоэмиттерный транзистор выполняет операцию И, транзистор VT2. — операцию НЕ. Поэтому элемент в целом реализует функцию/7 = ХхХ2. В первом приближении МЭТ с топологией, показанной на рис. 2.11, б, рассматривают как совокупность из п (по числу эмиттеров) отдельных транзисторов с общими базой и коллектором. Для исключения взаимного влияния эмиттерные переходы располагают друг от друга на расстоянии 10...15 мкм, что превышает диффузионную длину пробега носителей в базовом слое.
В схеме ТТЛ-элемента МЭТ работает в двух основных режимах: инверсном и насыщения. Процессы, происходящие в инверсном режиме, отображают эквивалентной схемой (рис. 2.12, а).
Инверсный режим возникает после подачи на все входы высоких уровней напряжений U!H. В результате эмиттеры Э1 и Э2 закрываются, коллекторный переход находится под прямым напряжением U* = 0,8 В и инжектирует электроны в общую базу.
2.2. Транзисторно-транзисторные логические элементы 75
Рис. 2.12. Эквивалентные схемы элемента ТТЛ: а — е инверсном режиме; б — в режиме насыщения
С целью уменьшения втекающих в эмиттер обратных токов 1/н, технологическими методами специально уменьшают значение инверсного коэффициента передачи тока /?/0т базы к эмиттеру до 0,01-0,02. В этом случае значение тока 11Н находят из соотношения
1/н = Pi 4м >
где 7gM — ток базы МЭТ.
На основе схемы рис. 2.12, а для тока 1^м, вытекающего из коллектора МЭТ, справедливо выражение
4м ~ 4м + 2-4 = 4м + 2р,- /БМ = /БМ (1+2 pj).
Ток /БМ находят из равенства
4м =(Ucc-2UyR, где 2U* = 1,6 В — суммарное падение напряжения на двух последовательно включенных кремниевых переходах — коллектора МЭТ и базы VT2. Для типовых значений Ucc = 5 В, R = 3 кОм, получим:
4М=(5- 1,6)/3-103= 1,12 мА;
1,н = 0,02-1,12-10“3 = 25 мкА;
4м = 4м(1+2-0,02)- 7’м=1,12мА.
Таким образом, значение коллекторного тока 4м достаточно для надежного насыщения транзистора VT2, при этом на выходе устанавливается низкий уровень напряжения t/oz.<0,l В.
Режим насыщения возникает при подаче на один из входов (или на оба), например низкого уровня входного напряжения UIL (рис. 2.12, б). При этом эмиттер Э1 открывается, поскольку на нем падение напряжения if = 0,8 В, и инжектирует электроны в базу МЭТ.
Коллекторный переход МЭТ также находится под прямым смещением. Однако он не может собирать (“коллекционировать”) электроны; это равнозначно появлению втекающего в коллектор тока, что не допускает база транзистора VT2. Считают, что в цепи коллектора МЭТ включено бесконечно большое сопротивление нагрузки, поэтому в области коллектора МЭТ накапливается объемный заряд электронов, что
76 Элементы компьютерной схемотехники
характерно для режима насыщения. Транзистор VT2 — закрытый и на его коллекторе устанавливается высокий уровень напряжения U0H~ UCc-
Значение вытекающего (отрицательного) из открытого эмиттера Э1 тока IIL находят из равенства
IfL~[Ucc-(U,L+U*)]/R.
Допустив, что UIL = 0,4 В, получим IIL= 1,23 мА.
Таким образом, в рассмотренной схеме элемента ТТЛ практически постоянный ток базы 7бМ коммутируется или в базу транзистора VT2 (инверсный режим), или в открытый эмиттер МЭТ (режим насыщения).
2.2.3. Транзисторно-транзисторный логический элемент со сложным инвертором
В микросхемах ТТЛ используют сложные инверторы, которые повышают быстродействие и нагрузочную способность элементов. Схема базового (типового) элемента ТТЛ со сложным инвертором содержит три основных каскада (рис. 2.13, а):
1. Входной каскад, реализующий операцию И (транзистор И7Т, резистор RA). Ко всем входам МЭТ подключены демпфирующие (антизвонные) диоды, ограничивающие влияние импульсов помех отрицательной полярности.
2. Фазоинверсный каскад (транзистор VT2, резисторы 7?к и 7?э), управляющий выходными транзисторами с помощью противофазных изменений напряжений на коллекторе и эмиттере VT2.
3. Выходной двухканальный усилитель (транзисторы V73, VT4, смещающий диод VD3, резистор Яо). Сложный инвертор образуется совместной работой фазоинверсного и выходного каскадов.
При совпадении на входах элементов высоких уровней напряжений МЭТ переключается в инверсный режим и своим коллекторным током открывает транзистор VT2. Часть эмиттерного тока транзистора VT2 втекает в базу транзистора ИТ4 и открывает его. После быстрого разряда паразитной емкости Сп через коллектор насыщенного транзистора VT4 на выходе устанавливается низкий уровень напряжения. При этом транзистор VT3 — закрытый, поскольку напряжение, прикладываемое к последовательно включенным переходам базы и диода VD3, недостаточно для его открывания.
2.2. Транзисторно-транзисторные логические элементы 77
При подаче на один из входов напряжения низкого уровня МЭТ переключается в режим насыщения, ток его коллектора равен нулю, вследствие чего закрываются транзисторы VT2 и VT4. При этом открытый транзистор VT3 работает в режиме эмиттерного повторителя: на его вход поступает высокий уровень напряжения с коллектора закрытого транзистора VT2, а нагрузкой служит сопротивление закрытого транзистора VT4. Эмиттерный повторитель передает на выход высокое напряжение
UOH=UCC-2U\
где 2U"— прямое падение напряжения на двух последовательно включенных переходах — базы транзистора VI3 и диода VD3. Повторитель создает в нагрузке ток, в 50-100 раз превышающий его входное значение. Это также обеспечивает быстрый заряд паразитной емкости Сп. Временные диаграммы работы ТТЛ элемента совпадают с рис. 2.8.
В процессе переключения имеется кратковременный интервал, когда транзистор VT4 уже открыт, a VT3 — еще не успел закрыться. При этом возникает значительный импульс тока от источника питания на землю (сквозной ток). Для уменьшения амплитуды сквозного тока в коллекторе транзистора VT3 поставлен ограничительный резистор Ro = 100...200 Ом.
Рассмотренная схема элемента ТТЛ со сложным инвертором является типовой для ТТЛ серий К131, К133, К155 и др.
Принцип работы транзисторов Шотки
Элементы ТТЛШ в сравнении с ТТЛ имеют более высокое быстродействие и меньшую потребляемую мощность, что достигается применением диодов Шотки. Принцип работы диода Шотки основан на использовании потенциального барьера, который образуется в приконтактной области между металлом и полупроводником. В диодах Шотки нет накопления избыточных зарядов, поскольку ток определяется переходом основных носителей из полупроводника в металл. Время переключения диодов Шотки очень мало (до 0,1 нс) и не зависит от температуры. В сравнении с кремниевыми диодами прямое падение напряжения в диодах Шотки вдвое меньше (около 0,3-0,4 В).
В режиме насыщения на коллекторе кремниевого транзистора действует прямое напряжение (7КБ = 0,7 В, вследствие чего коллектор открывается и инжектирует электроны в базу. Это вызывает задержку выключения, обусловленную временем рассасывания грас(рис. 2.14, а).
Рис. 2.14. Распределение напряжений в открытом транзисторе: а — обычном; б — с диодом Шотки; в — условное обозначение транзистора Шотки
78 Элементы компьютерной схемотехники
При наличии между базой и коллектором диода Шотки (рис. 2.14, б) коллектор при открывании транзистора не переходит в режим насыщения, поскольку прямое напряжение Ukb = 0,4 В. Транзистор с диодом Шотки между базой и коллектором называют транзистором Шотки (рис. 2.14, в).
Таким образом, транзистор Шотки не переходит в режим насыщения и тем самым исключается задержка выключения. При этом быстродействие увеличивается приблизительно в 3-5 раз.
Элементы ТТЛШ серий К530, К531
Схема типового элемента ТТЛШ серии К530 и К531 показана на рис. 2.15. Элемент реализует операцию НЕ-И для двух переменных Х1 иХ2.
Рис. 2.15. Схема элемента ТТЛШ серий К530, К531
В сравнении с элементом ТТЛ со сложным инвертором (см. рис. 2.13) в схеме ТТЛШ серии К530 и К531 внесены следующие изменения:
• используются только диоды и транзисторы Шотки (за исключением транзистора VT4, который не переходит в режим насыщения);
• в фазоинверсный каскад добавлена корректирующая цепочка (транзистор VT6, резисторы R3 и /?4), которая смещает порог включения элемента в сторону больших входных напряжений, благодаря чему повышается помехоустойчивость схемы;
• в выходной каскад встроена схема Дарлингтона на транзисторах VT3 и VT4, которая удваивает значение коэффициента усиления базового тока, что обеспечивает большие токи в нагрузке и повышает быстродействие элемента;
• в коллекторе транзистора VT4 включен резистор R6, который ограничивает амплитуду “сквозного" тока от источника питания на общий провод в моменты переключения выходных транзисторов; резистор 7?5 обеспечивает прохождение обратного тока /к0 транзистора VT4.
Схема работает аналогично элементу ТТЛ со сложным инвертором. При описании работы элементов ТТЛШ других серий сохранены буквенно-цифровые обозна
2.2. Транзисторно-транзисторные логические элементы 79
чения резисторов, диодов и транзисторов, назначение которых описано применительно к схеме, изображенной на рис. 2.15. Условное графическое обозначение рассмотренного элемента представлено на рис. 2.13, б.
Элементы ТТЛШ серий К533, К535
Схема типового элемента ТТЛШ серий К533 и К535 показана на рис. 2.16. Элемент реализует операцию НЕ-И для двух переменных Хх и Х2.
ЯЗ Я4
Рис. 2.16. Схема элемента ТТЛШ серий К533, К535
В схеме рассматриваемого элемента не применяют МЭТ. Входной каскад образуется схемой совпадения на диодах VD3, VD4 и резисторе 7?1. Коллектор транзистора VT2 дополнительно соединен с базой транзистора VT4- через диод VD5 и резистор 7?5; это способствует уменьшению времени перезарядки паразитных емкостей нагрузки. При совпадении высоких уровней входных напряжений диоды VD3 и FD4 закрываются и ток от источника питания через резистор R1 открывает транзистор 1-72; при этом включается также транзистор /7’5 и на выходе устанавливается низкий уровень напряжения.
Если на один из входов подать низкий уровень напряжения, то данный диод открывается и через него протекает ток, создаваемый источником питания через резистор 7?1. В этом случае транзисторы VT2 и VT5 закрыты и схема Дарлингтона устанавливает высокий уровень выходного напряжения.
Элементы ТТЛШ серий КР1531 и КР1533
Элементы ТТЛШ новых серий КР1531 (условное название FAST) и КР1533 (условное название ALS) изготовляют по новейшей технологии “Изопланар II”, которая использует ионную имплантацию (точное дозированное внедрение атомов примеси в области полупроводника), прецизионную фотолитографию, что позволяет в восемь раз уменьшить площадь, которую элементы занимают на кристалле. Существенно уменьшены потребляемая мощность и работа переключения, входные токи при низких уровнях входных напряжений (I!L < 0,1 мА). Схема типового элемента
80 Элементы компьютерной схемотехники
ТТЛШ серии КР1531 показана на рис. 2.17. Элемент реализует операцию НЕ-И для двух переменных и Х2.
Рис. 2.17. Схема элемента ТТЛШ серии КР1531
Рис. 2.18. Схема элемента ТТЛШ серии КР1533
В рассматриваемом элементе на выходе диодной схемы совпадения включен дополнительный усилитель на транзисторе УТ1. При совпадении высоких входных уровней напряжения диоды VD3 и TD4 закрываются, а транзистор УТ1 открывается. Ток его эмиттера создает на резисторе 7?8 падение напряжения, которое управляет фазоинверсным каскадом. Дополнительные диоды VD6, VD1 емкостными токами своих переходов ускоряют процесс переключения транзистора УТ\.
В элементах серии КР1533 (рис. 2.18) в качестве диодов схемы совпадения используют эмиттерные переходы р-п-р транзисторов УП и УТЬ. Переходы закрыты при совпадении высоких уровней на входах; открываются транзисторы УТ1, УТ2, VT5 и УТ6. Если хотя бы на один из входов подан низкий уровень, то ток, протекающий через резистор R\, замыкается на общий провод по цепи эмиттер-коллектор открытого р-п-р транзистора. Вследствие этого транзисторы VTl, VT2, VT5 и VT6 закрываются, a УТЗ, УТА — открываются. Применение схемы совпадения на переходах р-п-р транзисторов позволило в сравнении с ТТЛШ серии КР1531 в 20 раз уменьшить входные токи IIL.
2.2.4. Элементы ТТЛ и ТТЛШ с открытым коллекторным выходом и тремя состояниями
Для работы на нестандартную нагрузку (например, лампу накаливания (ЛН) или обмотку реле) выпускают схемы элементов ТТЛ и ТТЛШ с открытым коллектором (рис. 2.19, а). При совпадении высоких уровней на входах транзистор УТЗ открывается и ЛН светится. Если хотя бы на одном из входов будет низкий уровень напряжения, то транзистор УТЗ размыкается и ЛН гаснет.
Если выходы нескольких элементов с открытым коллектором подключаются к источнику питания через общий коллекторный резистор, то такая схема реализует функцию НЕ-И-ИЛИ (рис. 2.19, в).
2.2. Транзисторно-транзисторные логические элементы 81
Рис. 2.19. Элемент ТТЛШ с открытым коллектором: а — схема; б — условное обозначение; в — подключение к общей нагрузке
В схемах элементов ТТЛ и ТТЛШ соединение выходов нескольких элементов во избежание протекания большого тока от выхода с высоким уровнем иОнна выход с низким уровнем U0L недопустимо, поскольку может привести к выходу из строя микросхемы. При необходимости такого прямого соединения выходов (способ “монтажное ИЛИ”) используют элементы с тремя состояниями.
Два состояния выходов — это обычная выдача значений лог. О и лог. 1. Третье состояние характеризуется бесконечно большим выходным сопротивлением, когда элемент практически полностью отключается от нагрузки, то есть не потребляет и не выдает тока. Это достигается рядом схемных решений, в том числе и простейшим, показанным на рис. 2.20, а. В том случае, когда диод РТЛ подключен к эмиттеру и коллектору транзисторов VT\ и VT2, а на катод диода подается управляющий сигнал Z с высоким уровнем напряжения (лог. 1), схема работает как элемент НЕ И.
Рис. 2.20. Элемент ТТЛ с тремя состояниями: а — схема; б — условное обозначение; в — подключение к общей нагрузке
Если управляющий сигнал Z представлен низким уровнем напряжения (лог. 0), то МЭТ и коллектор транзистора 7Т2 (а соответственно и база транзистора Р73) подключаются через открытый диод VDI к шине земли. В этом случае все транзисторы закрыты и элемент переходит в третье состояние (Z-состояние). В сериях микросхем часто управляющий сигнал является инверсным. При объединении выходов^элементов ТТЛ с тремя состояниями (рис. 2.20, в) управляющие сигналы Zi, Z-i и Zj должны подаваться только поочередно.
6-4-1749
82 Элементы компьютерной схемотехники
Для элементов с тремя состояниями введены следующие временные параметры для задания задержек распространения:
• tuz. и ?hz — длительность задержки при переходе из низкого и высокого уровней выходного напряжения в состояние “выключено” соответственно;
• (ть и <zh — длительность задержки при переходе из состояния “выключено” в состояние низкого и высокого уровней выходного напряжения соответственно.
2.2.5. Сравнительный анализ параметров элементов ТТЛ и ТТЛШ
Серии микросхем ТТЛ и ТТЛШ включают широкий функциональный набор логических элементов, триггеров, узлов (регистры, счетчики, сумматоры и др.). Наличие готовых узлов в сериях позволяет уменьшить число корпусов микросхем и получить значительный выигрыш в объеме аппаратуры.
Серии элементов ТТЛ и ТТЛШ обладают функциональной и технической полнотой, работают от источника напряжения плюс 5 В, совместимы по уровням логических сигналов, а часть — и по разводке выводов корпуса микросхемы. Уровни напряжения лог. О и лог. 1 при положительном кодировании составляют: для элементов ТТЛ — UL< 0,4 В; UH > 2,4 В; для элементов ТТЛШ — UL < 0,5 В; UH > 2,7 В.
В элементах ТТЛ и ТТЛШ удачно сочетаются схемотехнические, технологические и конструктивные достоинства:
• высокий уровень схемно-технологической отработанности, обеспечивающий высокий процент выхода годных микросхем и низкую стоимость изготовления;
• сравнительно высокое быстродействие и помехоустойчивость;
• высокая нагрузочная способность No = 10...30 и умеренная потребляемая мощность;
• широкий функциональный набор элементов и удобство применения (монтаж, компоновка, охлаждение).
Значение задержек и потребляемой мощности элементов ТТЛ и ТТЛШ различных серий приведены в табл. 2.6.
Таблица 2.6
Группы микросхем Номер серии /р, нс /'со мВт Лп, пДж
Стандартные ТТЛ К133, К135 9 10 90
Быстродействующие ТТЛ К130, К131 6 22 132
Маломощные ТТЛ К134, К136 33 5 165
Стандартные ТТЛШ К530, К531 3 19 57
Маломощные ТТЛШ К533,К531 9,5 2 19
FAST КР1531 3 4 12
ALS КР1533 4 1,2 4,8
К недостаткам элементов ТТЛШ относятся: меньшее быстродействие в сравнении с элементами ЭСЛ, трудности согласования с низкоомной нагрузкой, высокий уровень создаваемых помех и рост потребляемой мощности с повышением частоты
2.3. Логические элементы эмиттерно-связной логики 83
переключения, значительное импульсное потребление тока во время переключения, особенно при емкостной нагрузке. Усилия разработчиков направлены на расширение функционального состава серий элементов ТТЛШ, функций элементов и узлов, а также на повышение быстродействия, уменьшение потребляемой мощности и снижение стоимости.
Элементы ТТЛ и ТТЛШ в настоящее время составляют основу элементного базиса компьютерной схемотехники. Выбор конкретной серии микросхем для построения цифровых устройств производится на основе следующих рекомендаций:
• если к устройствам не предъявляются особые требования, то используют стандартные серии;
• если по условиям работы следует обеспечить малое энергопотребление и допустимо понижение быстродействия, то используют маломощные (экономичные) серии;
• устройства повышенной продуктивности проектируют на быстродействующих сериях элементов.
2.3. Логические элементы эмиттерно-связной логики
Схемотехника элементов ЭСЛ основана на использовании дифференциального усилителя в режиме переключения тока. Элементы ЭСЛ появились в 1967 г. и в настоящее время являются самыми быстродействующими среди полупроводниковых элемен ,0В на основе кремния. Задержки распространения сигналов в элементах ЭСЛ уменьшились до субнаносекундного диапазона (приблизительно 1 нс).
Сверхбыстродействие элементов ЭСЛ достигается за счет использования ненасыщенного режима работы транзисторов, выходных эмиттерных повторителей, малых амплитуд логических сигналов (около 0,8 В). В логических элементах ЭСЛ имеется парафазный выход, что позволяет одновременно получать прямое и инверсное значение реализуемой функции. Это дает заметное снижение общего количества микросхем в аппаратуре.
Особенностями схемотехники ЭСЛ и ее характеристик являются:
• возможность объединения выходов нескольких элементов для образования новых функций;
• возможность работы на низкоомную нагрузку благодаря наличию эмиттерных повторителей;
• небольшое значение работы переключения и независимость потребляемой мощности от частоты переключения;
• высокая стабильность динамических параметров при изменении температуры и напряжения питания;
• использование отрицательного источника питания и заземления коллекторных цепей, что уменьшает зависимость выходных сигналов от помех в шинах питания.
К недостаткам элементов ЭСЛ относят сложность схем, значительное потребление мощности и трудности согласования с микросхемами ТТЛ и ТТЛШ.
Промышленность выпускает ряд серий ЭСЛ: 100, 137, 138, 187, 223, 229, 700, 500 и К1500. Высокие технико-экономические характеристики микросхем серий 500
6*
84 Элементы компьютерной схемотехники
и К1500 обусловили их широкое применение в быстродействующих цифровых устройствах. Типовые значения параметров элементов ЭСЛ представлены в табл. 2.7.
Таблица 2.7
Номер серии элементов ЭСЛ tp, нс Рсс, мВт Ап, пДж
500 2 25 50
К1500 0,75 40 30
Микросхемы ЭСЛ серии 500 изготовляют по полупроводниковой диффузионной планарно-эпитаксиальной технологии. Все компоненты микросхемы размещают в одном кристалле кремния и изолируют обратно смещенными р-п переходами. Компоненты формируются диффузией примесей в тонком эпитаксиальном слое монокристаллического кремния.
Схема типового логического элемента ЭСЛ серии 500 показана на рис. 2.21.
Рис. 2.21. Элемент ЭСЛ серии 500: а — схема; б — условное обозначение
Схема ЭСЛ включает:
• переключатель тока (логические транзисторы РТ1, VT2, опорный транзистор KZ3, резисторы R1, R2, R2);
• источник опорного смещения (транзистор VT4, диоды VD1, VD2, резисторы R5,R6)\
• выходные эмиттерные повторители (транзисторы Р75, К7’6).
Напряжение на открытом переходе база-эмиттер кремниевого транзистора является постоянным параметром U = 0,8 В. При описании работы элемента берут соглашение отрицательной логики: значение лог. 0 отображается высоким (с учетам знака) уровнем напряжения UH = -0,9 В; значение лог. 1 отображается низким уровнем напряжения UL= -1,7 В. Амплитуда (перепад) логического сигнала Um = = UH- UL = 0,8 В. Опорное напряжение переключателя тока располагается симметрично относительно уровней двоичных сигналов и определяется как их среднее: UOn = ~(UH + UL)I2 =-1,3 В.
2.3. Логические элементы эмиттерно-связной логики 85
Если хотя бы на один из входов подано напряжение UH = -0,9 В, то данный транзистор открывается, на него переключается ток Лэ, что создает на резисторе 7?, падение напряжения минус 0,9 В. При этом опорный транзистор закрытый и на резисторе R2 падение напряжения равно минус 0,1 В.
Если на всех входах поданы уровни UL = -1,7 В, то транзисторы VT\ и VT2 закрываются, а транзистор К73 открывается и на него переключается ток 1Э. В этом случае падение напряжения на резисторе 7?1 равно минус 0,1 В, а на резисторе R2 минус 0,9 В. При этом на коллекторах левого и правого плеча уровни напряжения не соответствуют принятому значению двоичного сигнала. Эмиттерные повторители на транзисторах VT5 и VT6 смещают уровни сигналов, поступающих на их базы с левого и правого плеча переключателя, на U* = 0,8 В в сторону отрицательных сигналов:
UOH = - (J7* + 0,1) В = - 0,9 В; Uql = -(£/’ + 0,9) В = -1,7 В.
Вследствие этого уровни входных и выходных сигналов соответствуют принятому стандарту. Временные диаграммы работы элемента ЭСЛ показаны на рис. 2.22.
Рис. 2.22. Временные диаграммы работы элемента ЭСЛ
Как следует из временных диаграмм, входные и выходные логические сигналы изменяются на ±0,4 В относительно опорного напряжения.
В отрицательной логике элемент ЭСЛ реализует на прямом выходе F функцию И, а на инверсном выходе Y — функцию НЕ-И, что записывается как НЕ-И/И. В положительной логике элемент ЭСЛ реализует функцию НЕ-ИЛИ/ИЛИ.
Резисторы 7?7 и 7?8 сопротивлением 50 кОм подключены к источнику отрицательного питания и обеспечивают протекание обратного базового тока, а также надежное запирание неиспользуемых входных транзисторов (незадействованные входы не требуется подключать к лог. 1). Кроме того, эти резисторы служат нагрузкой для источников входных сигналов.
В элементах ЭСЛ серии 500 нагрузочные резисторы эмиттерного повторителя (ЭП) вынесены за пределы микросхемы, что снижает рассеиваемую мощность на кристалле и обеспечивает возможность организации монтажной логики. Внешние нагрузочные резисторы сопротивлением 0,3-3,0 кОм подключаются между выходом ЭП и основным источником отрицательного питания минус 5,2 В. При работе на низкоомную нагрузку 50-200 Ом резисторы могут подключаться к дополнительному пониженному источнику питания минус 2,0 В.
86 Элементы компьютерной схемотехники
Подключение отрицательного напряжения питания к эмиттерной цепи и заземление коллекторов обеспечивает лучшую помехоустойчивость и меньшую зависимость выходных сигналов от наводок в цепях эмиттера. Сопротивление резистора R3 в несколько раз больше сопротивлений 7?1 и R2, чем достигается постоянство тока 1Э в плечах переключателя тока. Кроме того, соотношение сопротивлений резисторов 7?1, R2 и R3 подобрано таким образом, чтобы на выходе закрытого плеча устанавливалось напряжение минус 0,1 В за счет протекания тока базы ЭП, а на выходе открытого плеча напряжение составляло минус 0,9 В за счет протекания тока 1Э.
Коллекторы ЭП подключены к отдельной шине земли. Это связано с тем, что токи повторителей носят импульсный характер и создают помехи в, проводниках, подводящих напряжение.
В элементах ЭСЛ допускается объединение выходов, как показано на рис. 2.23. Объединение прямых выходов увеличивает коэффициент объединения по И; объединение инверсных выходов позволяет реализовать функцию НЕ-И-ИЛИ.
Рис. 2.23. Объединение выходов элемента ЭСЛ
Элементы ЭСЛ серии 500 обладают функциональной и технической полнотой. Серия 500 включает широкий набор микросхем: логические элементы, триггеры, регистры, счетчики, дешифраторы, мультиплексоры, АЛУ.
2.4. Логические элементы на МОП-транзисторах
Развитие компьютерной схемотехники на основе МОП-транзисторов началось с появлением в 1962 г. полевого транзистора с индуцированным каналом. Схемы на МОП-транзисторах характеризуются относительной простотой изготовления, компактностью, малой потребляемой мощностью, высокой помехоустойчивостью к изменению напряжения питания.
МОП-транзисторы имеют структуру: металл-диэлектрик-полупроводник и в общем случае называются МДП-транзисторами (рис. 2.24). Поскольку диэлектрик реализуется на основе оксида SiO2, то применяют название МОП-транзисторы (униполярные, канальные).
Металлический электрод, на который поступает управляющее напряжение, называется затвором (3) а два других электрода — истоком (И) и стоком (С). От истока к стоку протекает рабочий ток. Для p-канала полярность стока отрицательная, а для п-канала — положительная. Основная пластина полупроводника называется подкладкой (П). Канал — это приповерхностный проводящий слой между истоком и стоком, в котором величина тока определяется с помощью электрического поля.
2.4. Логические элементы на МОП-транзисторах 87
Процессы инжекции и диффузии в канале отсутствуют. Рабочий ток в канале обусловлен дрейфом в электрическом поле электронов в n-каналах и дырок в р-каналах.
р-МОП
-OCCQ
А/
п-МОП
Рис. 2.24. Топология и условные обозначения МОП-транзисторов: а, б — p-МОП; в, г — п-МОП
При нулевом значении управляющего напряжения канал отсутствует и ток не протекает. Канал, который образуется под действием внешнего управляющего напряжения, называется индуцированным. Напряжение, при котором образуется канал, называется пороговым J7TIH. Канал с начальной дополнительной концентрацией зарядов называется встроенным.
Быстродействие n-МОП транзисторов в 5-8 раз выше быстродействия р-МОП транзисторов, поскольку подвижность электронов существенно больше дырок. В МОП-схемах полностью исключены резисторы, их роль выполняют МОП-транзисторы.
Схемы логических элементов НЕ на МОП-транзисторах показаны на рис. 2.25.
Рис. 2.25. Схемы элементов НЕ на МОП-транзисторах: а — с p-каналами; б — с п-каналами
В схеме элемента НЕ на p-МОП транзисторах применяют нагрузочный транзистор VT\, сток которого подключается к отрицательному источнику питания минус Ucc (рис. 2.25, а). Напряжение отрицательной полярности входной переменной X поступает на затвор входного транзистора VT2. В этой схеме применяют транзисторы с индуцированными каналами.
В схеме элемента НЕ на n-МОП транзисторах используют нагрузочный транзистор VT\ со встроенным каналом, который подключается к положительному источнику питания плюс UCc- Положительное напряжение входной переменной X посту
88 Элементы компьютерной схемотехники
пает на затвор входного транзистора VT2 с индуцированным каналом (рис. 2.25, б). Нагрузочные транзисторы включены по схеме двухполюсника.
Если входное напряжение U < Utih, то транзистор VT2 закрытый, a VT1 — открытый и на выходе устанавливается уровень напряжения, близкий к значению UCc-
Если входное напряжение U > Utih, то оба транзистора открыты и выходное напряжение снимается с делителя, образованного сопротивлением каналов
Uq = (Lcc-^b) / (*в + 7?н), где RB и 7?н — сопротивления каналов входного и нагрузочного транзисторов. Пороговые напряжения для p-МОП UTih = - (5...7) В, а для n-МОП UnH = +(1,5...2) В.
Для того чтобы напряжение UOl было меньше 0,1 В, требуется выполнение условия RB « RH, которое достигается изготовлением транзисторов с разными сопротивлениями каналов. В схемах на р-МОН транзисторах сопротивление каналов транзистора УТ\ в 25 раз больше сопротивления канала транзистора VT2. Специфика n-МОП транзисторов такова, что достаточно соотношения сопротивлений около четырех.
Схемы элементов НЕ ИЛИ и НЕ И на n-МОП транзисторах показаны на рис. 2.26.
Рис. 2.26. Логические элементы на n-МОП транзисторах: а — НЕ ИЛИ; б — НЕ И
Элемент НЕ ИЛИ образуется параллельным соединением входных транзисторов (рис. 2.26, а), а элемент НЕ И последовательным соединением (рис. 2.26, б). Значение лог. 0 отображается напряжением UL = 0,1 В, а лог. 1 — напряжением Uh = Ucc- На выходе элемента НЕ ИЛИ устанавливается инверсное значение логической суммы входных переменных, а на выходе элемента НЕ И устанавливается инверсное значение логического произведения входных переменных. Например, на выходе элемента НЕ ИЛИ уровень лог. 0 устанавливается при наличии хотя бы на одном входе единичного сигнала. На выходе элемента НЕ И уровень лог. 0 устанавливается при совпадении высоких уровней напряжений на двух входах, когда одновременно открываются транзисторы VT2 и УТЬ.
В комплементарной МОП-структуре (логика КМОП) используются одновременно р- и n-канальные транзисторы. Элемент НЕ в схемотехнике КМОП построен на двух транзисторах с индуцированными каналами: нагрузочном VT2 с каналом р-типа и входном УТ1 с каналом n-типа (рис. 2.27, а). Исток транзистора VT2 подключен к
2.4. Логические элементы на МОП-транзисторах 89
источнику положительного питания Ucc, напряжение входной переменной X поступает на затворы обоих транзисторов; выходное напряжение снимается с объединенных стоков.
Рис. 2.27. Схемы элементов КМОП: а — НЕ; 6 — НЕ ИЛИ; в — НЕ И
При входном уровне UJH транзистор VT1 открыт, a VT2 — закрыт, поскольку между его затвором и истоком есть нулевое напряжение. На выходе устанавливается уровень UOL и ток в цепи не протекает. При входном уровне U1L транзистор VT1 закрыт, a VT2 — открыт, потому что между его затвором и истоком есть напряжение Ucc. На выходе — уровень UOh и ток в цепи не протекает.
На рис. 2.27, б показана схема КМОП элемента НЕ ИЛИ, в которой входные транзисторы VT\, VT2 включены параллельно, а нагрузочные F73, КГ4 — последовательно. Если хотя бы на одном из входов имеется уровень напряжения Um, то данный транзистор открывается, на выходе устанавливается уровень U0L, нагрузочные транзисторы закрыты, ток в цепи не протекает. Если на обоих входах имеется уровень напряжения U1L, то транзисторы VT1 и К72 закрыты, а К73 и РТ4 — открыты, на выходе устанавливается напряжение UOh и ток в цепи не протекает.
На рис. 2.27, в показана схема КМОП-элемента НЕ И, в которой входные транзисторы КП и VT2 включены последовательно, а нагрузочные VT3 и КГ4 — параллельно. Если на затворы входных транзисторов одновременно поступают сигналы U/H, то транзисторы КП и VT2 открываются, выходной уровень равен UOl, нагрузочные транзисторы закрыты, ток в цепи не протекает. Если хотя бы на одном из входов имеется уровень напряжения UIL, то транзисторы КП и КГ2 закрыты и открывается один из нагрузочных транзисторов К73 или VT4. На выходе устанавливается уровень ион и ток в цепи не протекает.
Таким образом, в схемах КМОП в статическом состоянии протекает очень малый рабочий ток, поскольку при открытых входных транзисторах закрыты нагрузочные и наоборот. Суммарная мощность потребления в основном определяется энергией, расходуемой на перезаряд паразитных емкостей.
Промышленность выпускает следующие серии КМОП: 176, 564, 561, КР1561 й КР1554. Микросхемы быстродействующей серии КР1554 имеют функциональную и техническую полноту и включают логические элементы, триггеры, регистры, счетчики, дешифраторы, мультиплексоры и др.
90 Элементы компьютерной схемотехники
Элементы серии КР1554 характеризуются следующими параметрами: диапазон напряжения питания составляет 3-6 В; уровни логических сигналов: U0L = 0,1 В, UOh = исс, U/L < 1,35 В, U,H > 3,15 В; ток потребления в статическом режиме на логический элемент — 0,25 мкА (в тысячу раз меньше в сравнении с серией КР1533); мощность потребления на элемент — 2,5 мкВт; задержка распространения сигналов — 4 нс; работа переключения Лп = 0,01 пДж; частота переключения D-триггера — 150 МГц; диапазон температур: минус 40 ... плюс 85°С. Как следует из этих данных, микросхемы КМОП серии КР1554 являются серьезным конкурентом схемам ТТЛШ.
2.4.1. Логические элементы на МЕП-транзисторах
Полевые транзисторы МЕП-типа имеют структуру “металл-полупроводник”; их строят на основе арсенида галлия (AsGa — соединение галлия с мышьяком). В сравнении с германием AsGa имеет следующие преимущества:
• более высокую подвижность электронов в слабых электрических полях (приблизительно в пять раз);
• почти в полтора раза шире запрещенную зону, которая обеспечивает высокое удельное сопротивление подкладки (как следствие, подкладки из AsGa служат полуизолирующим материалом);
• очень малые паразитные емкости между электродами МЕП-транзистора.
На основе арсенида галлия достигается десятикратное повышение быстродействия схем при снижении мощности потребления вдвое. Однако арсенид галлия Не позволяет строить МОП-транзисторы с изолированным затвором, поскольку он не образует стойких оксидов. В полевых МЕП-транзисторах используют барьер Шотки на границе контакта металла с полупроводником. Поэтому МЕП-транзисторы также называют “полевыми транзисторами с барьером Шотки” (ПТШ).
Структура арсенид-галлиевого МЕП-транзистора (поперечный разрез) показана на рис. 2.28, а. Транзистор создается на подкладке из нелегированного AsGa. На поверхности подкладки ионным методом формируют сильно легированные п+-области истока и стока, а потом тонкий слой канала /7-типа толщиной d0 = 0,2 мкм. На поверхность подкладки в канале наносят металлический электрод затвора (например, сплав титан-вольфрам)
Рис. 2.28. МЕП-транзистор: а — поперечный разрез; б — сток-затворные характеристики
Для обеспечения омических контактов с истоком и стоком применяют металлические электроды на основе композиции германий-золото. На поверхность подклад-
2.4. Логические элементы на МОП-транзисторах 91
ки между контактами наносят слой диэлектрика, например, диоксида кремния. Металлический электрод затвора создает в канале обедненный электронами слой — барьер Шотки высотой 0,8 В. Пространственные размеры барьера изменяются под действием напряжения затвора. Собственно проводящий канал толщиной dK ограничен областью барьера и подкладкой. Между затвором и истоком подается управляющее напряжение (7ЗИ, а на сток — напряжение питания плюс Ucc. При изменении управляющего напряжения изменяется толщина обедненного слоя <УБ и проводящего канала dK = d0- d^, его проводимость и ток стока.
Пороговое напряжение Un определяется из уравнения UT}=C}-C2Ndd^l, где С], С2 — константы, Nd — концентрация доноров в канале. Если напряжение (7ЗИ (затвор-исток) достигает порогового значения, то граница обедненного слоя смыкается с подкладкой <7К = d0- d5 = 0; при этом толщина проводящего слоя и ток стока 7С равны нулю.
Если при напряжении 7/зи = 0 есть проводящий канал и протекает рабочий ток, то МЕП-транзистор называется нормально открытым, он работает в режиме обеднения. Если при 7/зи = 0 барьер Шотки перекрывает весь канал и рабочий ток не протекает, то МЕП-транзистор называется нормально закрытым; он работает в режиме обогащения.
На рис. 2.28, б представлены сток-затворные характеристики нормально открытого (кривая 1) и нормально закрытого (кривая 2) МЕП-транзистора, а также их входная характеристика (кривая 3). Для нормально открытых МЕП-транзисторов управляющее напряжение на затворе, при котором протекает ток стока /с, может изменяться от отрицательных значений до небольших положительных (не больше 0,6 В). При напряжениях, больших (7ЗИ > 0,6 В, в его канале возникает ток затвора 73, поскольку открывается переход металл-полупроводник. Поэтому ток стока ограничен значением /СМ1. Для нормально закрытых транзисторов напряжение затвора, при котором протекает ток стока, положительное и может изменяться только в узких пределах (0...0,6 В). Максимальный ток стока ограничен значением 1СМ2. Для транзисторов с одинаковыми размерами канала (длиной и шириной) /Cmi » /смз- В схемотехнике применяют нормально закрытые и нормально открытые МЕП-транзисторы.
Варианты схем логических элементов НЕ, НЕ ИЛИ на МЕП-транзистбрах показаны на рис. 2.29.
Рис. 2.29. Логические элементы на МЕП-транзисторах: а — НЕ; б, е — НЕ ИЛИ
Схема НЕ (рис. 2.29, а) содержит пассивный транзистор VT\ (нормально открыт) и входной активный транзистор VT2 (нормально закрыт). Пассивный транзистор Р71 включен по схеме двухполюсника и выполняет роль источника стокового тока, зна
92 Элементы компьютерной схемотехники
чение которого практически не изменяется в широком диапазоне изменения напряжения между стоком и истоком.
К выходу элемента НЕ подключается аналогичный инвертор. Он в статическом режиме представлен эквивалентной схемой из последовательно включенных диода Шотки (барьера металл-полупроводник) и сопротивления между затвором и истоком Ази. Напряжение источника питания в схеме Ucc = 1,5 В; усредненные значения пороговых напряжений для транзисторов УТ\ и VT2 соответственно равны (7П1 = = -0,3 В и [/гл = 0,15 В.
При £/Вх = UlL < Um транзистор VT2 закрыт, ток стока 7С2 = 0 и на выходе устанавливается уровень напряжения U0H. Ток 1С] открытого транзистора УТ\ переключается в затвор инвертора нагрузки. Поскольку ток 1С2 составляет единицы миллиампер, а сопротивление 7?зи измеряется десятками ом, то выходной уровень практически определяется прямым напряжением на диоде VD'.
U()n ~и^щ + 7С1 7?3и = t/дш ~ 0,6 В.
Уровень напряжения UOH мало зависит от значений источника питания Ucc, тока /С| и понижается с увеличением коэффициента объединения и температуры.
При U^x = UIH > Um транзистор VT2 открывается и через него протекают токи стоков транзистора УТ\ и предыдущего транзистора (источник входного сигнала). На выходе устанавливается низкий уровень U0L = 0,05 В.
Уровень U0L понижается с уменьшением токов стоков и сопротивления 7?си между стоком и истоком. Если допустить, что U'=UH, U°=Ul, то амплитуда логического сигнала Um = U} - U° = 0,55 В. Помехоустойчивость элемента НЕ Л/л= 0,16 В, Мн = = 0,26 В, что значительно меньше, чем для схем на л-МОП транзисторах.
Схема двухвходового элемента НЕ ИЛИ содержит нормально открытый пассивный транзистор УТ1, входные нормально закрытые транзисторы VT2 и УТЗ, включенные параллельно (рис. 2.29, б).
При UX\ = Цу2 = UIL транзисторы VT2 и УТЗ закрыты, на выходе У устанавливается высокий уровень напряжения иПн- Если на одном из входов или на обоих действует напряжение Um, то соответствующий транзистор (или оба) открываются и на выходе устанавливается уровень U()L. Параметры элемента НЕ ИЛИ аналогичны схемам, изображенным на рис. 2.29, а.
Схема двухвходового элемента НЕ ИЛИ с повышенной помехоустойчивостью показана на рис. 2.29, в. Входные диоды Шотки VD\ и VD2 реализуют операцию ИЛИ, транзисторы УТ\ и VT2 создают инвертор, а транзистор УТЗ вместе с диодами — это цепь смещения уровня порога транзистора VT2.
В данном элементе в сравнении со схемами, изображенными на рис. 2.29, а и б, обеспечивается большая помехоустойчивость и меньшая ее зависимость от технологического разброса пороговых напряжений транзисторов. Это достигается усложнением схемы, увеличением ее площади на кристалле и использованием другого источника питания минус UCC2- В схеме применяют только нормально открытые транзисторы с напряжениями питания t/Cci = 1,5 В; UCC1 = -1 В. Для транзисторов УТ\ и УТЗ (7П1 = t/пз = - 0,7 В, а для транзистора VT2 Um = - 0,45 В.
Прямое напряжение на диодах Шотки при протекании через них тока 7СЗ равно приблизительно 0,7 В (минус на катоде). Напряжение на затворе транзистора VT2 определяется из зависимости изи= UBX - t/дш, которая является практически линейной, поскольку (7ДШ = const.
2.5. Импульсная и потенциально-импульсная системы элементов 93
При (7Вх = UIL = 0 напряжение (7ЗИ = - 0,7 В, что меньше t/nz, и транзистор VT2 закрыт, на его выходе устанавливается высокий уровень напряжения U0H ~ 1 В. При [/вх = Um = 1 В напряжение (73и = +0,3 В, что больше Um, и транзистор VT2 открыт, на его выходе устанавливается низкий уровень напряжения = 0,01 В. Таким образом, использование цепи смещения позволяет уменьшить значение U0, увеличить [/' и логический перепад U„, = I/1 - U° = 1 В.
Промышленность выпускает схемы на МЕП-транзисторах серии К6500, которые характеризуются следующими параметрами: UCC] = 4 В, UCC2 = -2,4 В; UH= 0,9 В; UL = 0,1 В; средняя задержка распространения /п = 0,15 нс, мощность, потребляемая одним логическим элементом, Рсс = 5 мВт.
2.5. Импульсная и потенциально-импульсная системы элементов
2.5.1. Импульсная система элементов
В импульсной системе элементов используются только импульсные информационные сигналы. В этой системе обычно применяются логические элементы ИЛИ, И, НЕ и импульсные (динамические) триггеры. Информационные сигналы с выходов одних импульсных элементов поступают на входы других через конденсаторы, обмотки трансформаторов, которые исключают взаимосвязь элементов по постоянному току.
Импульсные элементы характеризуются относительно простой схемою и малой потребляемой мощностью. Недостатком импульсных элементов являются трудности реализации конденсаторов большой емкости и трансформаторов методами интегральной технологии.
Схема импульсного диодного элемента ИЛИ показана на рис. 2.30, а. Она отличается от аналогического потенциального элемента наличием на входе разделительной RC-цепи, причем постоянная времени т = RC » t,, где Г, — длительность входных информационных импульсов. Сигнал на выходе элемента ИЛИ возникает в случае наличия импульса хотя бы на одном входе (рис. 2.30, б).
Рис. 2.30. Импульсный диодный элемент ИЛИ: а — схема; б — временные диаграммы работы
94 Элементы компьютерной схемотехники
Схема импульсного диодного элемента И показана на рис. 2.31, а, она отличается от аналогичного потенциального элемента наличием на входе разделительной RC-цепи, причем постоянная времени т = RC » t,, и должно выполняться условие R1 » R. Сигнал на выходе элемента И возникает при совпадении импульсов на всех входах (рис. 2.31, б).
а
б
Рис. 2.31. Импульсный диодный элемент И: a — схема; б — временные диаграммы работы
Схема импульсного элемента НЕТ, которая реализует логическую функцию Y = Х\Х2 , показана на рис. 2.32, а. Если АЛ? = 0, то на выходе элемента повторяется значение переменной Х}. При наличии импульса на входе Х2 на вторичной обмотке W2 трансформатора Тр наводится напряжение, которое компенсирует запирающее смещение плюс Сем- По этой причине диод VD2 открывается и выход элемента практически подключается к потенциалу земли, то есть обеспечивается значение лог. О (рис. 2.32, б).
Рис. 2.32. Импульсный диодный элемент НЕТ: а — схема; б — временные диаграммы работы
В импульсных схемах часто используются искусственные линии задержки, состоящие из £.С-звеньев_Т-образного типа. Длительность задержки определяется из соотношения Г3 = n^LC, где п — количество звеньев, L — индуктивность, мкГн; С — емкость, Пф (рис. 2.33, а).
Для исключения помех на входе и выходе линии задержки включают резисторы с волновым сопротивлением р = -]ЫС .
2.5. Импульсная и потенциально-импульсная системы элементов 95
Рис. 2.33. Искусственная линия задержки: а — схема; б — условное обозначение
DEL
2.5.2. Потенциально-импульсная система элементов
В потенциально-импульсной системе элементов используют потенциальные и импульсные информационные сигналы. В этой системе применяют как чисто импульсные и потенциальные элементы, так и специальные потенциальноимпульсные схемы на основе диодов, транзисторов и трансформаторов. Потенциально-импульсные элементы широко применялись в компьютерах первого и второго поколений; сейчас их используют в специализированных цифровых устройствах. Потенциально-импульсные элементы по энергопотреблению занимают промежуточное положение в сравнении с импульсными и потенциальными схемами.. Схема потенциально-импульсного диодно-трансформаторного логического элемента И ИЛИ, который реализует функцию Y = 7177lv72772, где L, Z2 — импульсные сигналы; 77,, П2— потенциальные сигналы, показана на рис. 2.34, а. Наличие импульса положительной полярности заданной амплитуды отображает лог. 1, а его отсутствие — лог. 0. Низкий уровень потенциального сигнала кодирует лог. 1, высокий уровень — лог. 0.
6- б
Рис. 2.34. Потенциально-импульсный элемент И ИЛИ: а — схема; б — временные диаграммы работы
В диодно-трансформаторной схеме И ИЛИ диоды VD1 и VD2 выполняют роль ключей: они открываются в том случае, если на аноде действует отпирающий положительный импульс, а на катоде — потенциал земли. При этом к первичной обмотке или W\2 прикладывается импульс напряжения, который трансформируется на выходной обмотке W2 трансформатора Тр (рис. 2.34, б). Резистор 7?ш и диод Дш образуют шунтирующую (демпфирующую) цепь, которая уменьшает выходные после-импульсные колебания. При наличии на потенциальных входах П< и П2 высокого уровня напряжения, диоды VD\ и VD2 закрываются, и первичные обмотки отключаются от импульсов напряжения: на выходе импульсный сигнал отсутствует.
96 Элементы компьютерной схемотехники
Схема потенциально-импульсного элемента И ИЛИ с усилителем-формирователем на выходе показана на рис. 2.35. Усилитель-формирователь построен на транзисторе VT1 с импульсным трансформатором Тр2 в электрической цепи коллектора.
Рис. 2.35. Элемент И ИЛИ с усилителем-формироеателем
Основное назначение усилителя-формирователя состоит в том, чтобы обеспечить выходной сигнал необходимой формы (обычно прямоугольный), амплитуды и длительности. В исходном состоянии транзистор п-р-п типа Р71 закрыт отрицательным напряжением смещения Есм = -1 В, которое подается через обмотку W2 трансформатора Тр1 на базу, ток в электрической цепи коллектора не протекает, и выходной импульс отсутствует.
При совпадении импульсного и потенциального сигналов на входах обмоток Wu или Г7|2 (или обеих одновременно) на выходной обмотке трансформатора Тр1 индуцируется напряжение, которое компенсирует запирающее напряжение и открывает транзистор VT\. Потенциал между коллектором и эмиттером насыщенного транзистора близок к нулю, поэтому напряжение источника питания Ucc практически полностью прикладывается к обмотке WK трансформатора Тр2. На выходной обмотке W4 формируется импульс напряжения с постоянной амплитудой Um = = {Ucc Длительность выходного импульса определяется временем заряда
эмиттерным током конденсатора Сэдо уровня напряжения, которое закрывает транзистор VT\. Цепь из резистора и диода Дш уменьшает послеимпульсные выбросы во вторичных обмотках трансформаторов.
Для повышения надежности и помехоустойчивости цифровых систем используют мажоритарные логические элементы. Мажоритарные элементы, инвертор, константы “0” и “1” создают функционально полную систему логических элементов.
Мажоритарный логический элемент имеет непарное количество входов п = 3, 5, 7, ... и один выход, состояние которого определяется по большинству входов. В минимизированной дизъюнктивной нормальной форме мажоритарной функции в каждом произведении имеется т = (и+1)/2 переменных без инверсии. Например, мажоритарная функция для п = 3 имеет вид:
М{Х}, Х2, Х3) = Х} Х2 V X Х3 v X, Х3.
В 1960 г. была введена операция мажоритарности с символическим изображением #. В этом случае мажоритарная функция на п входов имеет вид:
М{Х,, Х2,..., Х„) = X,#х2#х3#...#х„.
2.6. Магнитная схемотехника 97
Наибольшее практическое применение нашли мажоритарные элементы с количеством входов п = 3 (рис. 2.36) реже — с п = 5.
Рис. 2.36. Мажоритарные элементы: а — схема на элементах НЕ И;
б— условное обозначение; в — строенный мажоритарный элемент типа КР1533ЛПЗ
Микросхема КР1533ЛПЗ (рис. 2.36, в) представляет собой три мажоритарных элемента с общим входом стробирования Е. При Е = 0 логическое состояние каждого выхода определяется совпадением единиц на любых двух входах из трех. Если £ = 1, то выходы элементов повторяют состояние третьего входа.
2.6. Магнитная схемотехника
2.6.1. Общая характеристика магнитных схем
Магнитные схемы (МС) строят на основе электромагнитной цепи, частью которой является магнитный материал. Их применяют для преобразования, обработки и хранения информации. Для построения МС используют ряд физических явлений: ферромагнитных, магнитно-полупроводниковых, магнитооптических, сверхпроводимости и др.
Явление ферромагнетизма характеризуется:
• нелинейным характером процесса намагничивания и высокой магнитной проницаемостью;
• эффектом магнитного гистерезиса, который используется для хранения информации.
К достоинствам МС относят: высокую надежность работы и радиационную стойкость; хранение информации без потребления энергии; высокую температурную стабильность и помехозащищенность.
Применяют несколько методов интеграции и миниатюризации МС:
• конструктивный (технологический) — переход к интегральной схемотехнике;
• функциональный — МС выполняет несколько функций;
• физический — в одном и том же ферромагнетике используются различные физические явления, например, магнитные и магнитоакустические.
7-4-I749
98 Элементы компьютерной схемотехники
По виду обрабатываемой информации МС подразделяются на аналоговые и цифровые. В магнитной схемотехнике выделяют следующие основные направления:
• на кольцевых сердечниках;
• на конструкциях со сложным магнитопроводом;
• на магнитных доменах и эффекте Джозефсона.
Магнитные схемы на кольцевых сердечниках
В компьютерной схемотехнике применяют магнитные элементы на ферритовых кольцевых сердечниках. Предельная кривая намагничивания В = /(Я) представляет собой почти прямоугольную петлю гистерезиса (рис. 2.37, а). На этой характеристике используются следующие обозначения: Н — напряжение магнитного поля; В — магнитная индукция; ±В, — остаточная магнитная индукция; Вт — индукция насыщения (максимальное значение), достигаемое в сердечнике под действием импульса напряжения Нт.
Простейшим магнитным элементом является кольцевой ферритовый сердечник с информационной, управляющей и выходной обмотками (рис. 2.37, б).
Рис. 2.37. Магнитные схемы: а — кривая намагничивания; б, в — магнитные элементы
Информационная ИзП и управляющая Исч обмотки служат для записи и считывания информации. Выходная обмотка WB предназначена для получения электрического сигнала, который отображает значение функции элемента. В общем случае количество обмоток, их использование и наименование определяются назначением данного магнитного элемента.
Обычно допускается, что положительная остаточная индукция плюс В,, отображает состояние “1”, а отрицательная минус Вг — состояние “0”. Начала обмоток сердечника обозначены точками. Условно считают, что ток считывания 7СЧ, втекающий в начало обмотки 1УСЧ, намагничивает сердечник в состояние “0", а ток записи /зп, вытекающий из начала обмотки РГЗП, перемагничивает сердечник в состояние “1". Намагничивающая сила, действующая в сердечнике, определяется алгебраической суммой ампервитков во всех одновременно действующих обмотках. Поэтому, в зависимости от направления тока и включения обмоток, отдельные составляющие магнитной индукции могут складываться или вычитаться, что расширяет возможно
2.6. Магнитная схемотехника 99
сти использования магнитных элементов. Ток записи и ток считывания должны иметь амплитуду, которая обеспечивает расчетное значение напряжения поля Н,„ и длительность, не меньше времени переключения т сердечника.
В процессе перемагничивания сердечника из одного состояния в другое на выходной обмотке WB индуцируется знакопеременный импульс напряжения U,n = = ± Ив5АВ/т, где JFB — количество витков выходной обмотки; А — площадь поперечного сечения сердечника; АВ = 2ВГ + А, где А = В„, - В,.; т — время переключения (рис. 2.37, б). Переключение сердечника в состояние “1” сопровождается индуцированием на выходной обмотке отрицательного импульса напряжения; для его отсечки от нагрузки в выходной цепи включается ограничивающий диод VD1 (рис. 2.37, в).
При повторной подаче импульсов записи или считывания магнитная индукция изменяется на А, и на выходе возникают импульсы помехи небольшой амплитуды. К особенностям кодирования информации относится то, что входной электрический сигнал записи преобразуется в магнитную остаточную индукцию и только при считывании вновь преобразуется в электрический сигнал. Наличие положительного импульса на выходной обмотке в момент считывания считается лог. 1, а его отсутствие— лог. 0.
Для изображения магнитного элемента используют “зеркальный" метод, при котором сердечник обозначают утолщенной вертикальной линией, обмотки — в виде горизонтальных тонких линий. Ток по входных обмотках протекает слева направо. Способ включения обмоток изображен тонкими наклонными линиями под углом 45°. Входной ток, отражаясь по наклонной линии вверх, переключает сердечник в состояние “1”, а отражаясь вниз — в состояние “0”. На выходной обмотке появление положительного импульса напряжения возникает в момент переключения из состояния “1” в состояние “0” (рис. 2.38).
Рис. 2.38. Ферродиодные (а, б) и ферротранзисторные (в) логические элементы
В магнитных схемах используют ферродиодные и ферротранзисторные элементы.
Функционально полным набором логических элементов на ферродиодных схемах являются дизъюнктор, НЕТ и генератор “1”. Схема дизъюнктора, который реализует функцию F -Xt v X, показана на рис. 2.38, а. Сердечник переключается в состояние “1” в первом такте сигналами Xt или Х2 или одновременно обоими. Выходной сигнал F возникает в выходной обмотке во втором такте при считывании. Схема НЕТ, которая реализует функцию F =Х}Х2 показана на рис. 2.38, б. Информационные входные обмотки включены встречно, поэтому переключение сердечника возможно только при условии Х1 = 1, Х2 = 0.
7*
100 Элементы компьютерной схемотехники
Упрощенная схема ферротранзисторного дизъюнктора, в которой с помощью транзистора VTI и коллекторной обмотки И7К образована положительная обратная связь, ускоряющая перемагничивание сердечника из состояния “1” в состояние “0”, показана на рис. 2.38, в. В исходном состоянии транзистор VT1 закрыт, при считывании лог. 1 на базовой обмотке возникает положительный импульс напряжения, который открывает транзистор ИЛ. Ток коллектора создает дополнительный перемагничивающий поток, действующий согласно с потоком обмотки считывания. В результате время переключения сердечника значительно уменьшается.
Универсальная магнитная схема для реализации восьми минтермов для трех переменных А7], Х2, X (рис. 2.39) имеет вид:
М() = Хх Х2 Х3; Мх = Хх Х2 Х3; М2= Хх Х2 Х3 ;
Рис. 2.39. Универсальная магнитна схема
Если прошить общим проводом несколько сердечников, то реализуется дизъюнкция минтермов. Для примера в схеме (рис. 2.39) с помощью прошивки реализуются следующие функции:
Fx = м0 = Yx ~Х2 Y3;
f2 = м2 v л/4 v м2 v мх = х, х2 х3 v хх x^ Y3 v Yx x2 Y3 v Yx Y, X3.
Для усиления сигналов в соединениях между магнитными схемами используются интегральные усилители и формирователи тока (серии 146, 169, 170), а также диодные и транзисторные микросборки.
2.6. Магнитная схемотехника 101
2.6.2. Магнитные элементы со сложным магнитопроводом
К магнитным элементам со сложным магнитопроводом относятся многоотвер-стные пластины, трансфлюксоры и ряд других.
Многоотверстные пластины — это конструкции из феррита, имеющие до ста отверстий диаметром 0,65 мм. На такой пластине может размещаться более 25 RS-триггеров или несколько десятков логических элементов И ИЛИ, НЕ ИЛИ.
Трансфлюксор — это ферритовый диск с двумя неодинаковыми отверстиями (рис. 2.40, а), который может находиться в двух состояниях, характеризующихся разным распределением магнитного поля вокруг большого отверстия и отображают лог. 1 (рис. 2.40, б) и лог. 0 (рис. 2.40, в). Характерной особенностью RS-триггера на трансфлюксоре является считывание информации без ее разрушения.
Рис. 2.40. Трансфлюксор: а — конструкция; б, е - состояния “1" и “0".
Криоэлектронные магнитные элементы
Криоэлектронные магнитные элементы строятся на основе сверхпроводимости, при которой электрическое сопротивление ряда металлов и сплавов при их охлаждении скачком падает до нуля — ниже определенной критической температуры Тк. Под действием управляющего магнитного поля с напряженностью выше критической Нк, сверхпроводимость исчезает. Чем больше охлажден материал, тем больше магнитное поле требуется для разрушения сверхпроводимости.
Простейший криоэлектронный логический элемент с двумя входами и одними выходом называется криотроном. Конструктивно криотрон выполнен в виде двух тонкопленочных металлических полосок, разделенных диэлектриком и помещенных на сверхпроводящий металлический экран. Полоску для рабочего тока называют вентилем “В”, а для управляющего тока — затвором ”3”. Если затвор помещен поперек вентиля, криотрон называют поперечным (рис. 2.41, а), а если параллельно — продольным (рис. 2.41, б).
Рис. 2.41. Криотроны: а — поперечный; б — продольный, в, г — условное обозначение
102 Элементы компьютерной схемотехники
При подаче в затвор тока управления, который создает критическое магнитное поле 7/к, вентиль переключается из состояния сверхпроводимости в нормальное омическое состояние, при этом его сопротивление увеличивается в 1012- 1017 раз Сверхпроводящее состояние затвора не меняется, поскольку он выполнен из материала с более высоким значением магнитного поля Нк, чем вентиль. Если рабочий ток вентиля отображает переменную А, а управляющий ток затвора — переменную В, то криотрон выполняет функцию запрета АВ. Включение криотронов для реализации элементарных логических функций переменных показано на рис. 2.42.
а б
Рис. 2.42. Логические элементы на криотронах: а — И, НЕ И; б — ИЛИ, НЕ ИЛИ
В 1962 г. английский физик Б. Джозефсон показал, что сверхпроводимость может возникать в пластинках, разделенных диэлектриком толщиной в несколько нанометров (рис. 2.43, а). При этом происходит туннелирование электронов. Конструкции, называемые туннельными переходами или переключателями Джозефсона (ПД), имеют вольтамперную характеристику, показанную на рис. 2.43, б.
a б в
Рис. 2.43. Переключатель Джозефсона:
а — конструкция перехода; б — вольт-амперная характеристика;
в — зависимость /к = f(H, Но)
При токе Io < I < /к (участок 7) переключатель находится в состоянии сверхпроводимости. При достижении значения тока 1> 1К (участок 2) сверхпроводимость исчезает и на ПД скачком возникает напряжение А// ~ 3 мВ. Дальнейшее увеличение тока I (участок 3) сопровождается почти линейным ростом напряжения на ПД. Уменьшение тока возможно до минимального значения 70 (участок 4), после чего происходит скачкообразный возврат в состояние сверхпроводимости (участок 1). Такая характеристика с петлей гистерезиса позволяет строить на ПД логические элементы. Например, состоянию сверхпроводимости приписывается значение лог. 0, а его отсутствию, при котором на ПД имеется напряжение, — значение лог. 1.
Магнитное поле “сплющивает” петлю гистерезиса в вертикальном направлении (рис. 2.43, в), в результате чего ПД переключается в нормальное состояние (так называемое “включение”) при меньшем токе 7К. Обратное переключение происходит
2.7. Асинхронные и синхронные RS-триггеры 103
или после снятия входных сигналов, или специальным понижением тока ПД ниже уровня 70.
Упрощенные схемы логических элементов на ПД показаны на рис. 2.44.
а б в
Рис. 2.44. Логические элементы на ПД: а — ИЛИ; б — И; в — НЕТ
Питание схем — импульсное; ток питания равен 0,32 мА; критический ток — 0,4 мА; управляющий ток — 0,2 мА. Схема ИЛИ включается на входах А или В, а схема И — при совпадении сигналов на входах А и В. Сигнал лог. 1 на выходе элемента НЕТ формируется при условии, что в момент поступления тактового импульса Л = 1 и В = 0.
Время переключения ПД составляет пикосекунды, работа переключения равна 10‘6 пДж. Плотность компоновки и степень интеграции криоэлектронных элементов достаточно высокие.
К недостаткам криоэлектронных элементов относится сложность обеспечения компактного, экономичного и надежного охлаждения.
2.7. Асинхронные и синхронные RS-триггеры
2.7.1. Определение и назначение триггеров
Триггер — это запоминающий элемент с двумя устойчивыми состояниями, изменение которых происходит под действием входных сигналов. Как элемент компьютера, триггер предназначен для хранения одного бита информации, то есть лог. 0 или лог. 1. Схема триггера обеспечивает запись, считывание, стирание и индикацию хранимой двоичной информации. На основе триггеров строят типовые функциональные узлы компьютеров — регистры, счетчики, накапливающие сумматоры, а также микропрограммные автоматы.
Все разновидности триггеров представляют собой элементарный автомат, включающий собственно элемент памяти (ЭП) и схему управления (СхУ), которая образует входную логику (рис. 2.45).
Состояние триггера определяется сигналами на прямом Q и инверсном Q выходах. При положительном кодировании информации высокий уровень напряжения на прямом выходе отображает значение лог. 1 (состояние Q = 1), а низкий уровень — значение лог. 0 (состояние Q = 0).
104 Элементы компьютерной схемотехники
Рис. 2.45. Структура триггера в виде ЭП и СхУ
Изменение состояния триггера (его переключение) обеспечивается внешними сигналами и сигналами обратной связи на выходе триггера, поступающие на входы СхУ. Обычно внешние сигналы, как и входы триггера, обозначают латинскими буквами R, S, Т, С, Ии др.. В простейших схемах триггеров отдельная СхУ может отсутствовать. Поскольку функциональные свойства триггеров определяются их СхУ, то названия основных входов переносятся на всю схему триггера.
2.7.2. Классификация триггеров
Триггеры классифицируют по следующим признакам:
• логике функционирования (RS, JK, D, Т и др.);
• способу записи информации (асинхронные и синхронные);
• моменту реакции на тактовый сигнал (статические, динамические);
• количеству тактов синхронизации (одно-, двух- и трехтактные);
• количеству ступеней (одно- или двухступенчатые триггеры); '
• составу логических элементов (триггеры на элементах НЕ И, НЕ ИЛИ, НЕ И ИЛИ и др.).
В соответствии с логикой функционирования различают следующие триггеры:
• с раздельной установкой состояний “0” и “1” (MS-триггеры);
• с одним информационным входом (D-триггеры);
• со счетным входом (Т-триггеры);
• универсальные с раздельной установкой состояний “0” и “1” (JK-триггеры);
• комбинированные (RST-, RSJK-триггеры);
• со сложной входной логикой.
Входы триггеров разделяются на информационные (R, S, Т и др.) и управляющие (С, V). Информационные (логические) входы предназначены для приема сигналов запоминаемой информации. Названия входных сигналов отождествляют с названиями входов триггера. Управляющие входы служат для управления записью информации. В триггерах может быть два вида управляющих сигналов: синхронизм-рующий (тактовый) сигнал С, поступающий на С-вход (тактовый вход) и разрешаю-щий сигнал V, поступающий на К-вход.
По способу записи (приема) информации различают асинхронные и синхрон-ные (тактируемые) триггеры. Триггеры, не имеющие С-входа, называются асинхронными (рис. 2.46, а и б). В асинхронных триггерах запись информации производится в любой момент времени при поступлении сигналов на информационные входы.
2.7. Асинхронные и синхронные RS-триггеры 105
Триггеры, имеющие С-вход, называются синхронными. В синхронном триггере запись информации возможна при совпадении сигналов на информационном и синхронном входах. Этим объясняется более высокая помехоустойчивость синхронных триггеров в сравнении с асинхронными.
а бег
Рис. 2.46. Условные обозначения триггеров: а, б — асинхронных; е, г — синхронных
На К-входы триггера поступают сигналы, которые разрешают (V = 1) или запрещают (Г = 0) запись информации. В синхронных триггерах с К-входом запись информации возможна при совпадении сигналов на информационном, С- и V- входах (рис. 2.46, г).
В зависимости от количества тактовых сигналов, необходимых для формирования нового состояния, различают однотактные, двухтактные и многотактные триггеры.
По способу управления записью (моменту реакции на тактовый сигнал) выделяют синхронные триггеры со статическим (по уровню), динамическим (по фронтам) и двухступенчатым управлением. В асинхронных триггерах запись нуля и единицы возможна в любой момент времени, при этом входной информационный сигнал одновременно является и управляющим. В синхронных триггерах с управлением по уровню запись информации возможна только в течение длительности тактового сигнала. При этом тактовые сигналы могут быть прямыми (изменяться от нуля к единице) или инверсными (изменяться от единицы к нулю) (рис. 2.47, а и б).
Рис. 2.47. Управляющие входы триггера: а — прямой статический;
б — инверсный статический; в - прямой динамический; г — инверсный динамический
При управлении фронтами разрешение на запись информации дается только в момент перепада тактового сигнала от нуля к единице (прямой динамический вход) или от единицы к нулю (инверсный динамический вход). В другие моменты времени триггер не реагирует на входные информационные сигналы независимо от уровня тактового импульса (рис. 2.47, в и г).
106 Элементы компьютерной схемотехники
2.7.3. Динамические параметры триггеров
Для триггеров установлены следующие динамические параметры, измеряемые на уровне половины амплитуды сигналов (рис. 2.48):
• минимальная длительность импульса t( на тактовом входе;
• минимальное время предварительной установки сигнала на информационном входе /уС1;
• время восстановления (фиксации) /вос — минимальное время между нарастанием синхросигнала С и спадом информационного сигнала D; для асинхронных триггеров /впс — просто длительность входного сигнала;
• время переключения триггера /пт— временной интервал между фронтом входного переключающего сигнала и фронтом сигнала на выходе Q или Q (который
Рис. 2.48. Измерение временных параметров триггеров D-muna
позже принимает новое состояние). Минимальная длительность синхросигнала на входе триггера определяется максимальным временем переключения триггера k > /птmax- В двухступенчатом триггере с однотактной синхронизацией время переключения второй ступени определяется по отношению к спаду синхроимпульса.
2.7.4. Таблица переходов и логические уравнения RS-триггера
RS-триггером называют запоминающий элемент с раздельными информационными входами для установки его в состояние “0” (Л-вход) и в состояние “1" (5-вход). Название “RS-триггер” образовано от первых букв слов RESET (сброс) и SET (установка).
В таблице переходов RS-триггера (табл. 2.8) приняты обозначения: R,, Sb Qt — значения логических переменных в момент времени t на входах R, S и выходе Q, Ql+i — состояние триггера после переключения; К6, К7 — неопределенные коэффициенты на тех наборах, где входные сигналы R, и S, одновременно принимают значение единицы (запрещенная комбинация сигналов).
Таблица 2.8
R, 5 0/+I
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 1
1 0 0 0
1 0 1 0
1 1 0 кь
1 1 1
0 I
0 1 0
1 1 К7 0
0
1
00 01 11 10
0 /Г 0
С1__ \D 0
б
0 а 0 0
C£Z 0 0
Рис. 2.49. Карта Карно для RS-триггеров
о
2.7. Асинхронные и синхронные RS-триггеры 107
Таблице переходов соответствует карта Карно (рис. 2.49, а), где значения функции Q,+ l для минтермов Rh S„ Qt и Rh St, Qt заменены неопределенными коэффициентами Кь и К-,. Предположив, что комбинации входных сигналов R, S, = 1 не существует, получим карты Карно для К6 = Ку = 1 (рис. 2.49, б) и К6 = Ку = 0 (рис 2.49, в).
Из карт Карно получаем логические уравнения асинхронного RS-триггера: А-6=А-7=1, Ql+l =5^^, (2.1)
K6 = K7 = 0, Q^R'tS'VQ,). (2.2)
Логические выражения (2..1) и (2.2) определяют новое состояние триггера Ql+i в зависимости от старого состояния Q, и входных сигналов R, и S,. В дальнейшем для простоты индекс t в правой части логического выражения опускается.
Асинхронный RS-триггер на элементах НЕ И
Преобразуем логическое выражение (2.1) к виду, удобному для реализации на элементах НЕ И:
QM=SvRQ = SR-Q. (2.3)
Схема асинхронного RS-триггера на двух элементах НЕ И с логическими связями на основе выражения (2.3) показана на рис. 2.50, а. Особенностью этого триггера является инверсное управление по информационным входам, что отражается в условном графическом обозначении. Из анализа диаграмм работы RS-триггера следует, что элементы НЕ И в схеме переключаются последовательно. Имеется интервал времени, когда на обоих выходах устанавливаются одинаковые сигналы Q = 1 и Q = 1 (рис. 2.50, в, заштрихованные области) — явление “риск”.
Рис. 2.50. Асинхронный RS-триггер на элементах НЕ И: а — схема; б — условное обозначение; е — временные диаграммы
Длительность переключения триггера определяется суммой задержек: /пт = 2ГР. Длительность входного сигнала определяется из условия Г, > /Пт На практике для надежности переключения триггера длительность входного импульса увеличивают на одну задержку, то есть г, = 3/р. Максимальная и рабочая частоты переключения триггера соответственно равны_/тах = 1/(2Гр) и fp = 1/(3/р).
108 Элементы компьютерной схемотехники
Асинхронный RS-триггер на элементах НЕ ИЛИ
Преобразуем логическое выражение (2.2) к виду, удобному для реализации на элементах НЕ ИЛИ:
&+1=/?(5v0 = /?v(Sv0. (2.4)
Схема асинхронного RS-триггера на двух элементах НЕ ИЛИ с логическими связями на основе выражения (2.4) показана на рис. 2.51, а.
Из анализа диаграмм работы RS-триггера следует, что элементы НЕ ИЛИ в схеме переключаются последовательно. Имеется интервал_времени, когда на обоих выходах устанавливаются одинаковые сигналы Q = 0 и Q = 0, — явление “риск” (рис. 2.51, в). Временные параметры данного триггера аналогичны параметрам триггера, изображенного на схеме рис. 2.50, а.
Рис. 2.51. Асинхронный RS-триггер на элементах НЕ ИЛИ: а — схема; б — условное обозначение; в — временные диаграммы
Синхронный RS-триггер на элементах НЕ И
Для построения синхронного RS-триггера на элементах НЕ И следует заменить в логическом выражении (2.3) переменные S и R на сочетания CS и CR, где С — синхросигнал:
й+1 = CS CRQ . (2.5)
Схема синхронного RS-триггера на четырех элементах НЕ И с логическими связями на основе выражения (2.5) показана на рис. 2.52, а. Элементы D\ и D2 образуют схему управления с прямыми входами, а элементы D3 и D4 образуют фиксатор (асинхронный RS-триггер).
При значении сигналов CS = 1 на выходе элемента D1 устанавливается лог. О, и триггер переключается в состояние “1”. При значении сигналов CR = 1 на выходе элемента D2 устанавливается лог. 0. и триггер переключается в состояние “0”. Комбинация входных сигналов CSR = 1 запрещена, поскольку приводит к неопределенному состоянию триггера.
Из временной диаграммы (рис. 2.52, б) следует, что время переключения триггера /пт = 3tp, а длительность синхросигнала (с учетом запаса на одну задержку)
2.7. Асинхронные и синхронные RS-триггеры 109
определяется из условия t( = 4гр. Максимальная и рабочая частоты переключения триггера соответственно равны: = 1/Згр и/р = l/4zp.
Рис. 2.52. Синхронный RS-триггер на элементах НЕ И: а — схема; б — временные диаграммы
Синхронный RS-триггер на элементах НЕ ИЛИ
Для построения синхронного RS-триггера на элементах НЕ ИЛИ следует заменить в логическом выражении (2.4) переменные S и R на сочетания CS и CR :
0,+1 =Cflv(CSv0 = Cv2?v(CvSv0. (2.6)
Схема синхронного RS-триггера на четырех элементах НЕ ИЛИ с логическими связями на основе выражения (2.6) показана на рис. 2 53. Элементы D\ и D2 составляют схему управления с инверсными входами, а элементы D3 и D4 образуют фиксатор (асинхронный RS-триггер).
Рис. 2.53. Синхронный RS-триггер на элементах НЕ ИЛИ: а — схема; б — условное обозначение; в — временные диаграммы
При значении сигналов С = 0 и S = 0 на выходе элемента D2 устанавливается лог. £(то есть_С$ = 1), и триггер переключается в состояние “1”. При значении сигналов С = 0 и R = 0 на выходе элемента D1 устанавливается лог. 1 (то есть CR = 1), и
110 Элементы компьютерной схемотехники
триггер переключается в состояние “0”. Комбинация сигналов С = S =R = 0 запрещена, так как приводит к неопределенному состоянию триггера. Временные параметры такого триггера аналогичны параметрам триггера, изображенного на схеме рис. 2.52.
Двухступенчатые RS-триггеры
Двухступенчатые триггеры строятся по способу “М-S” и обеспечивают совмещение двух процессов — одновременной записи новой информации и считывания старой. Во время действия синхроимпульса С первая ступень “М" (Master— основная) принимает новую входную информацию, а вторая ступень “S” (Slave — вспомогательная) в это же время передает во внешние схемы старую информацию. После окончания синхроимпульса С информация из первой ступени переписывается во вторую ступень.
При однофазном (однотактном) обмене информацией связь между ступенями реализуется с помощью инвертора (рис. 2.54, а), запрещающих связей (рис. 2.54, б) или разнополярного управления (рис. 2.54, в). При двухтактном обмене связь между ступенями обеспечивается двумя сериями синхросигналов — СТ и С2 (рис. 2.54, г).
Рис. 2.54. Организация связи между ступенями триггера: а — с инвертором; б — с запрещающими связями; в — с разнополярным управлением; г — с двухфазным обменом
2.8. Триггеры типов JK, Т, D и DV
2.8.1. Триггеры типа JK
Триггером типа JK называется запоминающий элемент с двумя устойчивыми состояниями и информационными входами J (аналог S) и К (аналог R), которые обеспечивают соответственно раздельную установку состояний “1” и “0”. Он функционирует подобно RS-триггеру, однако при совпадении сигналов JK = 1 переключается в противоположное состояние, то есть реализует сложение сигналов по модулю два. Таким образом, JK-триггер не имеет запрещенных комбинаций входных
2.8. Триггеры типов JK, Т, D и DV 111
сигналов. Триггер типа JK является универсальным, поскольку может выполнять функции RS-триггера (при раздельном поступлении сигналов/и К), Т-триггера (при одновременной подаче сигналов J и К), D-триггера (при подаче сигнала от входа J через инвертор на вход К). Изменение состояний JK-триггера приведено в табл. 2.9; с помощью карты Карно (рис. 2.55) получаем следующее уравнение для триггера:
0,+l=^Gv7,-a- (2-7)
Таблица 2.9
К, J, Qt+\
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 1
1 0 0 0
1 0 1 0
1 1 0 1
1 1 1 0
KJ
\ 00 01 И 10
0 Cl_ __D 0
CL_ _D 0 0
Рис. 2.55. Карта Карно для JK-триггера
Для построения одноступенчатого синхронного JK-триггера на элементах НЕ И требуется заменить в уравнении (2.7) переменные К и J на сочетания СК и JK, после чего выполнить преобразования на основе правил двойной инверсии и правил де Моргана:
Qt+} = C K QvC J Q = C K Q C J Q. (2.8)
Схема одноступенчатого JK-триггера с логическими связями на основе уравнения (2.8).показана на рис. 2.56.
Рис. 2.56. Одноступенчатый JK-триггер: а — схема; б — условное обозначение
В схемотехнике потенциальных триггеров в основном применяют двухступенчатые синхронные JK-триггеры на элементах НЕ И (рис. 2.57). Новая информация снимается с выходов Q* основной /W-стулени, а старая — с выходов Q вспомогательной S-ступени.
Из временных диаграмм (рис. 2.57, б) следует: при использовании JK-триггера для хранения информации сигналы на входы J и К подаются поочередно; при совпадении сигналов на входах J и К реализуется счетный триггер (на практике эти входы часто монтажно объединяются). Время переключения JK-триггера определяется суммой задержек первой и второй ступеней и составляет /птт = 7/р. На выходе S-ступени новая информация возникает после спада сигнала С.
112 Элементы компьютерной схемотехники
Рис. 2.57. Двухступенчатый JK-триггер на элементах НЕ И: а — схема; б— временные диаграммы; в — условное графическое обозначение
2.8.2. Таблица переходов и логические уравнения Т-триггера
Триггером типа Т называется запоминающий элемент с двумя устойчивыми состояниями и одним информационным Т-входом. Состояние Т-триггера изменяется на противоположное после каждого поступления счетного сигнала на Т-вход. Логика функционирования асинхронного счетного триггера представлена таблицей переходов (табл. 2.10) и описывается логическим уравнением
Q^TQ^t-q,.
(2.9)
Таблица 2.10
Т, Qt бг+1
0 0 0
0 1 1
1 0 1
1 1 0
Для построения асинхронного RS-триггера на элементах НЕ И уравнение (2.9) преобразуется к виду, удобному для реализации в заданном элементном базисе:
Qt+л =TQvTQ = TQQ-TQ. (2.10)
_В уравнении (2.10) для исключения инверсии сигнала Т используется тождество Т • Q = (Т Q) • Q. Переключение триггера определяется совместным действием счетных сигналов “Т” и обратной связи выходов Q и Q. Для исключения “гонок” в
триггере сигналы обратной связи не должны изменяться во время действия счетно-
го сигнала “7"”. Задержка выходного сигнала может осуществляться линией задерж-
ки (в импульсно-потенциальной системе элементов) или дополнительным триггером (в потенциальной системе элементов). Схема одноступенчатого асинхронного Т-триггера на элементах НЕ И с логическими связями согласно уравнению (2.10) показана на рис. 2.58. Сигналы с выходов элементов DI и D2 задерживаются на время Az, что равно длительности счетного сигнала на
Рис. 2.58. Схема одноступенчатого Т-триггера
Г-входе.
2.В. Триггеры типов JK, T, D и DV 113
Надежные структуры счетных триггеров строят с использованием двухступенчатых триггеров или триггеров с динамическим управлением по фронту сигнала С.
2.8.3. Двухступенчатые Т-триггеры
Схема двухступенчатого асинхронного Т-триггера на элементах НЕ И с логическими связями согласно уравнению (2.10) показана на рис. 2.59, а.
Рис. 2.59. Асинхронный двухступенчатый Т-триггер: а — схема; б — временные диаграммы работы
Асинхронный Т-триггер включает в себя два синхронных RS-триггера, при этом на Т-вход основной ступени додается считаемый сигнал, а входы S и R соединены соответственно с выходами Q и Q вспомогательной ступени.
Пусть в начальном состоянии Q* = Q = 0. При поступлении первого счетного импульса происходит совпадение лог. 1 на входе элемента DI (Т = 1, Q = 1), а основной триггер переключается в состояние “1". После окончания входного импульса инвертор в цепи связи между ступенями разрешает перезапись информации во вспомогательный триггер (рис. 2.59, б). После поступления второго импульса триггер переключается в состояние “0”, то есть осуществляется сложение входных сигналов по модулю два. В общем случае, в Т-триггерах с однофазным обменом информацией связь между ступенями реализуется на основе трех основных способов (см. рис. 2.54). В схеме двухступенчатого синхронного Т-триггера переключение “ЛТ-ступени происходит при совпадении считаемого импульса с синхросигналом (рис. 2.60, а). В схеме двухступенчатого синхронного Т\/-триггера переключение происходит при совпадении считаемого импульса с синхросигналом при условии V = 1 (рис. 2.60, б).
Рис. 2.60. Синхронные двухступенчатые счетные триггеры: а — типа Т; б — типа TV
8 — 4-1749
114 Элементы компьютерной схемотехники
2.8.4. Таблица переходов и логическое уравнения
• D-триггера
Триггером типа D называется синхронный запоминающий элемент с двумя устойчивыми состояниями и одним информационным D-входом. Закон функционирования D-триггера описывается логическим уравнением:
C2r+i = CtDt.
Это уравнение показывает, что после переключения состояние D-триггера повторяет значение сигнала на D-входе в тактовые моменты времени. Поэтому в литературе D-триггеры часто называют триггерами задержки (от Delay — задержка).
Схему D-триггера можно построить на основе синхронного RS-триггера, если сигнал по входу S одновременно подавать через инвертор на вход R (рис. 2.61, а). Схемы D-триггера строят также на основе самостоятельного логического уравнения. Преобразуем уравнение (2.5) путем замены сигнала S на D и сигнала R на D:
е,+1 ^C^S-'C^RQ = 'C^DC-DQ. (2.11)
Схема D-триггера на элементах НЕ И с логическими связями согласно уравнению (2.11) показана на рис. 2.61, б.
Рис. 2.61. D-триггер: а — на основе RS-триггера;
б — на элементах НЕ И; в — временные диаграммы работы
D-триггер “следит” за изменением сигнала на D-входе во время действия синхросигнала С и сохраняет ту информацию, которая имелась в момент его окончания. RS-триггеры таким свойством не обладают и потому они менее помехозащищенные в сравнении с D-триггерами.
Для задержки информации в D-триггере на произвольное число тактов используется разрешающий /-вход, как показано штриховой линией на рис. 2.61, б. Если V = 1, то DV-триггер функционирует как обычный триггер задержки; если V = 0, то работа схемы по входам блокируется и DV-триггер сохраняет предыдущую информацию.
Схема двухступенчатого однотактного О\/-триггера на элементах НЕ И с запрещающими связями между ступенями показана на рис. 2.62.
2.8.5. D-триггер с динамическим управлением
Во всех синхронных триггерах со статическим управлением (по уровню) возможно ложное переключение в случае изменения сигналов на информационных входах во время действия синхросигнала С. Например, если в D-триггере информа-
2.8. Триггеры типов JK, T, D и DV 115
ционный сигнал изменяет свое значение от единицы к нулю до окончания сигнала “С", то триггер может вновь переключиться из единичного в нулевое состояние. Поэтому для надежной работы D-триггера требуется определенный интервал времени между фронтом синхроимпульса С и спадом сигнала на D-входе (параметр /вос).
Рис. 2.62. Двухступенчатый DV-триггер: а — схема; б — временные диаграммы
В триггерах с динамическим управлением записью информации синхроимпульс С активен лишь на коротком интервале времени в окрестности фронта или спада. Поэтому D-триггеры с динамическим управлением обладают высокой помехоустойчивостью. На практике широкое распространение получили D-триггеры с прямым динамическим управлением по схеме “трех триггеров”. Схема такого D-триггера с прямым динамическим управлением показана на рис. 2.63, а, а его условное графическое изображение — на рис. 2.63, б.
Рис. 2.63. D-триггер с динамическим управлением: а - схема; б - условное обозначение; в — временные диаграммы
Здесь хранение информации осуществляет основной выходной синхронный RS-триггер (элементы D5 и D6) с инверсным управлением, а прием тактового и информационного сигналов и задание динамического режима работы обеспечивают 8*
116 Элементы компьютерной схемотехники
два выходных коммутирующих триггера (элементы Di, D2, D3, D4). Элемент 04 подает инверсное значение входного сигнала О на входы элементов О1 и 03 (рис. 2.63, в). Элемент О1 повторяет значение сигнала О.
При С - D - 1 включается элемент D2 и устанавливает основной триггер по входу Si в состояние “1”; одновременно блокируется работа элемента 03, в связи с чем схема уже не реагирует на изменение входного сигнала. При С = 1,0 = 0 включается элемент 03 и устанавливает основной триггер в состояние “0”; одновременно происходит прием новой информации элементом 04. При С = 0 обеспечивается режим хранения записанной информации.
Время переключения триггера по С-входу Згр. После окончания сигналов на О- и С-входах начинается этап восстановления, который характеризуется переходом коммутирующих триггеров в исходное состояние за время 3/р. Максимальная частота переключения D-триггера с динамическим управлением определяется суммарным временем задержек/тах = 1/(6/р).
На рис. 2.64 показаны схемы ряда триггеров серии КР1533: ТР2 — четыре RS-триггера; ТВ9 — два JK-триггера; ТВ11 — два JK-триггера с общим входом сброса и синхронизации по спаду С; ТМ2 — два D-триггера с динамическим управлением по фронту С.
ТВ9 ТВ1Л
а б в г
Рис. 2.64. Триггеры серии КР-1533: a — ТР2; б — ТВ9; в — ТВ11; г — ТМ2
Микросхемы указанных триггеров характеризуются следующими параметрами: UCc = 5 В; 7сс = 4...5 мА; РСс = 20...25 мВт; время переключения — 15...20 нс. Схема импульсного (динамического) RS-триггера на элементах ИЛИ И с линией задержки (ЛЗ), реализованная на основе уравнения Ql+l =Rl(Sl v Qt)Ct, показана на рис. 2.65, а.
Рис. 2.65. Импульсный RS-триггер: a — схема; б— временные диаграммы работы
2.8. Триггеры типов JK, T, D и DV 117
Импульсный триггер устанавливается в состояние лог. 1 сигналами St = 1 и R, =0. После этого в замкнутой цепи схемы триггера циркулируют импульсы с периодом синхронизации Т (рис. 2.65, б). Для сброса триггера подается сигнал R, = 1, после чего схема НЕТ прерывает циркуляцию импульсов.
Схема RST’-триггера в потенциально-импульсной системе элементов показана
На потенциальные входи вентилей 1 и 4 подаются сигналы обратной связи с инверсного Q и прямого Q выходов статического триггера, а импульсные входы объединяются и образуют 7-вход. Импульсные входы вентилей 2 и 3 образуют S- и R- входы.
Схема магнитного RS-триггера, в котором ток Is переключает сердечник в состояние "1”, а ток IR — в состояние “0”, показана на рис. 2.67, а. При считывании состояния “1" на выходе возникает положительный импульс (рис. 2.67, б). Одновременная подача токов Is и IR запрещена.
Рис. 2.67. RS-триггер: а — условное обозначение; б— временные диаграммы работы
Функция переходов RS-триггера описывается уравнением
QM=Stv~RtQt,
где индексы t и /+1 определяют состояния входов до и после переключения. Магнитный RS-триггер может реализовать функцию конъюнкции вида:
Yl+i=S,R,+it
где переменные S, и R, подаются соответственно в первом и втором такте.
Увеличением числа обмоток по входам S и R логическая функция схемы расширяется. Согласное включение нескольких обмоток по входам S и R дает функцию
п т
i=i /=1
118 Элементы компьютерной схемотехники
Например, для п = 2, т = 2 получим:
Если принять, что в первом такте S, = 1, а во втором такте по нескольким обмоткам Rt+], включенных согласно, поступает т аргументов Х„ а сигнал на выходе схемы снимать в третьем дополнительном такте Rl+2, то реализуется функция НЕ ИЛИ (рис. 2.68, а).
Рис. 2.68. Магнитный элемент НЕ ИЛИ: а — схема; б — временные диаграммы работы
Например, для т = 3 получим:
т
= v Xt ;
1 = 1
У,+2 = X, v X, v Х3 = X, X, Х3 .
Контрольные вопросы
1. Поясните работу диодных логических элементов ИЛИ, И.
2. Охарактеризуйте свойства логических элементов ТТЛШ.
3. За счет каких факторов достигается сверхвысокое быстродействие логических элементов ЭСЛ?
4. Что такое криотрон?
5. Укажите на отличия между триггерами типов RS, JK, D 1лТ.
6. В каких случаях используют двухступенчатые триггеры?
7. Опишите достоинства элементов на КМОП-структурах.
8. В чем заключаются преимущества синхронных триггеров в сравнении с асинхронными.
9. Поясните, почему JK-триггер называют универсальным.
10. Поясните назначение логических элементов с открытым коллектором.
11. Охарактеризуйте работу логических элементов с тремя состояниями.
12. Какие преимущества имеют логические элементы на основе арсенида галлия в сравнении с кремниевыми схемами?
13. Поясните работу элемента ИЛИ на магнитных схемах.
14. Охарактеризуйте особенности построения потенциальной, импульсной и потенциально-импульсной систем элементов.
3.1. Регистры 119
Глава 3
Последовательностные (накапливающие) узлы компьютерной схемотехники
3.1. Регистры
3.1.1. Общая характеристика регистров
Регистром называется типовой функциональный узел компьютера, предназначенный для приема, временного хранения, преобразования и выдачи «-разрядного двоичного слова. Регистр содержит регулярный набор однотипных триггеров, в каждом из которых хранится значение одного двоичного разряда машинного слова. Наиболее часто используют триггеры типов RS, JK\a D (рис. 3.1).
Регистры, предназначенные только для приема (записи), хранения и передачи информации, называются элементарными или фиксаторами. Регистры, в которых хранение данных совмещается с микрооперациями сдвига, называются сдвиговыми. Элементарные регистры строят на одноступенчатых триггерах, а сдвиговые — на двухступенчатых или D-триггерах с динамическим управлением. Логическая функция регистра обозначается буквами RG (register). Регистры обеспечивают хранение команд, адресов памяти, результатов операций, индексов и т.д.
Регистры классифицируют по следующим признакам:
• способу управления записью — асинхронные и синхронные;
• способу записи и выдачи двоичных слов — параллельные, последовательные и универсальные; в параллельных регистрах запись и выдача слов производится одновременно всеми разрядами, а в последовательных — разряд за разрядом в направлении от младших разрядов к старшим или наоборот; универсальные регистры обеспечивают как параллельный, так и последовательный обмен информацией;
• числу линий для представления значения одного разряда слова (бита информации) — однофазные и парафазные; при однофазном представлении значение каждого разряда слова передается по одной линии связи, а при
120 Последовательностные (накапливающие) узлы компьютерной схемотехники
парафазном — по двум линиям (одновременно отображается прямое и инверсное значение разряда);
• числу тактов для записи слова — одно-, двух- и многотактные;
• составу выполняемых микроопераций — установочные, записи, считывания, поразрядные логические и сдвига, а также преобразования последовательного кода в параллельный и наоборот;
• направлению сдвига — односторонние (левый или правый сдвиг) и двухсторонние (реверсивные);
• типу используемых триггеров;
• элементной структуре — потенциальные, импульсные и потенциальноимпульсные.
3.1.2. Установочные микрооперации. Однофазный и парафазный способ записи информации
Установочные микрооперации служат для переключения регистров в определенное состояние. Например, установка регистра в состояние “0” или “1”; установка парных разрядов в состояние “0”, а непарных — в состояние “1”; запись в регистр некоторой константы или обнуление некоторых байтов и т.д. Установочные микрооперации преимущественно используют асинхронные входы регистра, например, вход сброса Л для схемы, изображенной на рис. 3.1.
В регистрах на RS- или JK- триггерах возможен однофазный или парафазный способ записи информации. При однофазной записи значение каждого разряда слова А = А„ А,А, ...А} поступает по одной линии связи на вход S (или J) соответствующих триггеров. После считывания записанной информации регистр должен обнулиться по общему Л-входу (рис. 3.2). Таким образом, при однофазной записи частота обмена информацией уменьшается, поскольку процессы ввода и сброса чередуются.
При парафазной записи информации значение каждого разряда слова А передается по двум линиям связи. При этом прямое значение А, поступает на вход 5 (или J) соответствующих триггеров, а инверсное значение Д — на вход R (или К). В этом случае не требуется предварительного сброса регистра в состояние “0”, потому что такую функцию выполняет сигнал Д (рис. 3.3).
В регистрах на D-триггерах, имеющих один информационный вход, возможен только однофазный способ записи информации. С приходом очередного синхроимпульса записывается новая информация или, при отсутствии данных на входной шине, состояние регистра автоматически обнуляется (см. рис. 3.1).
3.1. Регистры 121
Рис. 3.3. Схема регистра с парафазией записью данных
При необходимости сохранения информации на несколько тактов в регистрах на D-триггерах следует использовать разрешающий К-вход, или блокировать прохождение синхроимпульса на С-вход.
3.1.3. Запись информации от двух источников
Для записи информации от нескольких источников (направлений) на входе каждого триггера ставят дополнительные комбинационные схемы, образующие входную логику регистра. Каждое направление имеет свою совокупность электрических линий (шину), по которым передаются сигналы, отображающие значения разрядов слова. Если «-разрядное слово передается однофазным кодом, то шина имеет п линий связи, а если парафазным кодом — то 2п линий. Запись каждого слова инициируется соответствующим управляющим сигналом У,, У2 и т.д.
Для записи в регистр на RS-триггерах однофазным кодом слов А и В требуется реализовать следующие поразрядные функции возбуждения входа
Si=Y}Al\fY2B„ (3.1)
где А, и В, — двоичные разряды слов А и В\ У, и У2 — сигналы управления приема слов А и В соответственно. Схема входной логики z-ro разряда регистра на основе уравнения (3.1) показана на рис. 3.4, а.
Для записи в регистр на JK-триггерах парафазным кодом слов А и В требуется реализовать следующие поразрядные функции возбуждения входов / i АГ,:
J, = YtA,v Y2B,; К/ = YtA,v Y2B,. (3.2)
Схема входной логики z-ro разряда регистра на основе уравнений (3.2) показана на рис. 3.4, б.
Рис. 3.4. Схемы разряда регистра с записью слов от двух источников: а — однофазным кодом; б — парафазным кодом
122 Последовательностные (накапливающие) узлы компьютерной схемотехники
3.1.4. Считывание информации
Информация, хранимая в регистрах, может передаваться во внешние схемы однофазным или парафазным способом в прямом или обратном коде. Для реализации микроопераций считывания к выходам каждого триггера подключаются комбинационные схемы, образующие выходную логику регистра.
Схемы выходной логики строятся на основе следующих поразрядных логических уравнений:
• для считывания однофазным прямым или обратным кодом
ОД= Knp0vyo6a; (3.3)
• для считывания парафазным прямым или обратным кодом
Ш' = YnpQt v УПР2,; Ш- = Уоб Ql v Уоб2,; (3.4)
где Упр и Уоб — управляющие сигналы выдачи соответственно прямого или обратного кода; Q, и Qi — прямое и инверсное значение выхода z-ro разряда регистра; Ш,— разряд однофазной шины данных; Ш,‘ и Ш’ — разряды парафазией шины данных.
Очевидно, что управляющие сигналы Упр и Уоб не должны совпадать во времени. Например, при считывании информации парафазным обратным кодом получим:
Упр = 0; Уоб = Ш* = Q,.
Схемы выходной логики для z-ro разряда на основе уравнений (3.3) и (3.4) показаны на рис. 3.5.
Рис. 3.5. Схемы выходной логики i-го разряда регистра для считывания информации: а — однофазным кодом; б — парафазным кодом
3.1.5. Логические микрооперации в регистрах
В регистрах могут выполняться следующие поразрядные (без переносов) логические микрооперации над словами А и В: логическое сложение и умножение:' RG1 := AvB; RG1 := АлВ; сложение по модулю два и его отрицание: RG1 := А®В; RG1 ;= А®В; инверсия слова: RG1 : = А .
Логические микрооперации предполагают наличие первого слова А в регистре. С учетом этого логическое сложение слов А и В в регистре на RS- или JK-триггерах с однофазной записью выполняется вводом слов В без предварительного сброса. Логическое умножение реализуется подачей инверсных значений разрядов слова В на входы R (или К) триггеров регистра. Действительно, если значение В, = 0, то
3.1. Регистры 123
Bl = 1 и соответственно триггеры обнуляются, что и требуется для поразрядного логического умножения.
Микрооперации сложения по модулю два и его отрицания реализуются в регистрах на Т-триггерах. Вначале записывается слово Л а затем без предварительного сброса по счетному входу вводится слово В. После этого на прямых выходах триггеров фиксируется результат операции Q = А ® В, а на инверсных выходах — Q = А ® В. Микрооперация инвертирования состоит в подаче импульса на все Т-входы триггеров регистра, в которых хранится слово Л. В итоге на прямых выходах триггеров устанавливается результат согласно соотношению Q, = А,® 1 = А,.
3.1.6. Микрооперации сдвига
Сдвиг — это одновременное пространственное перемещение двоичного слова в разрядной сетке с сохранением порядка следования нулей и единиц. Регистры, предназначенные для выполнения микроопераций сдвига, называются регистрами сдвига или сдвиговыми.
Микрооперации сдвига используют в процессе выполнения команд умножения, деления и нормализации. Кроме того, с помощью сдвига осуществляется преобразование параллельного кода в последовательный или наоборот (например, при обмене информацией с магнитными лентами и дисками).
Сдвиг слова может выполняться вправо (в сторону младших разрядов) или влево (в сторону старших разрядов). Обозначим одноразрядные микрооперации сдвига вправо и влево символами R и L соответственно. Различают правый и левый арифметический (/?а, Та), логический (/?.,, Ьл) и циклический (7?ц, Ц,) сдвиги слова.
Пусть в регистре А записано слово А„ А„_} ...А2 Ah где А} — младший разряд; А,,— старший разряд. Символически микрооперации сдвига записываются следующим образом:
• арифметические сдвиги (знаковый разряд не сдвигается):
RGA := Ra(A)=A„0A„4 ...А2; RGA :-La(A) = Л„ Ац_2 ...А, 0;
• логические сдвиги (одновременно сдвигаются все разряды):
RGA := R„(A) = 0 А„А„^ ...А2; RGA := ВЛ(А) = А„ч А„_2 ...А, 0;
• циклические сдвиги (между старшим и младшим разрядами имеется кольцевая связь):
RGA := RU(A) = А} А„ А„ f ...А2; RGA := LU(A) = А„ t А„_2 ...At А„.
Арифметические и циклические сдвиги преимущественно используют при выполнении команд в процессорах, а логические сдвиги обеспечивают преобразование последовательного кода в параллельный и наоборот в устройствах связи с магнитными лентами и дисками.
Сдвиговые регистры проектируют на двухступенчатых RS- (или JK-) или D-триггерах с динамическим управлением по фронту. Такие триггеры обеспечивают разделение во время процессов приема новой информации в каждом разряде и выдачи (сдвига) старой.
Примем, что в реверсивном регистре должны выполняться параллельная запись слова А по сигналу управления Узп и сдвиги информации влево и вправо под
124 Последовательностные (накапливающие) узлы компьютерной схемотехники воздействием управляющих сигналов Ьл и R,. Функции возбуждения S, и R, для каждого разряда регистра сдвига на двухступенчатых RS-триггерах имеют вид:
S; = Y3nAjV R„Qi+]v L„Qi4; R, = Y3n A, v Rn Ql+I v 1Л Q,_,. (3.5)
Схема одного разряда регистра сдвига на RS-триггерах согласно уравнениям (3.5) показана на рис. 3.6, а.
Экономичная схема разряда регистра, в которой функция на Л-входе триггера образуется инвертированием сигнала S,, показана на рис. 3.6, б. Однако в этом случае время записи данных увеличивается за счет задержки инвертора.
Для регистра сдвига на D-триггерах функции возбуждения имеют вид:
Д = ГзпЛ^лС,+1^лб,ч. (3.6)
Схема разряда регистра сдвига на D-триггерах согласно уравнению (3.6) показана на рис. 3.6, в.
Рис. 3.6. Схема разряда регистра сдвига: а — на RS-триггере; б — с инвертором на входе R; в — на D-триггере
Пример построения реверсивного трехразрядного регистра сдвига на D-триггерах с динамическим управлением представлен на рис. 3.7.
Рис. 3.7. Схема реверсивного регистра сдвига на D-триггерах
Реверсивный регистр сдвига работает следующим образом. При значении сигнала Узп = 1 в регистр записывается информация параллельным однофазным кодом. При значении сигнала 7?л = 1 хранимая информация одновременно сдвигается
3.1. Регистры 125
в сторону младших разрядов, при этом разряд Q3 обнуляется. При значении сигнала La = 1 информация в регистре одновременно сдвигается в сторону старших разрядов, при этом разряд обнуляется. Запись и сдвиг информации происходят по фронту синхроимпульса.
3.1.7. Преобразование последовательного кода в параллельный и наоборот
Схема четырехразрядного регистра сдвига вправо на JK-триггерах, которая обеспечивает преобразование кодов, показана на рис. 3.8, а. Старший разряд регистра с помощью инвертора на /<-входе работает в режиме D-триггера.
Рис. 3.8. Регистр сдвига :
а — схема ; 6, в — преобразование последовательного кода в параллельный и наоборот
Пусть от накопителей на магнитных дисках или лентах на вход регистра по линии D поступает последовательный код слова А = 1101 в направлении от младших разрядов к старшим. Значение разрядов слова поступает одновременно с синхроимпульсами, которые обеспечивают как прием кода в старший разряд, так и одновременный сдвиг содержимого регистра вправо (рис. 3.8, б). После прихода четырех синхроимпульсов на выходах регистра Qi - 2i устанавливается код 1101. Таким образом осуществляется преобразование последовательного кода в параллельный, часто называемое последовательным вводом слова в регистр.
Преобразование параллельного кода в последовательный также выполняется сдвигом хранимого слова. Процесс преобразования параллельного кода слова Л = 1101 в последовательный в направлении от младших разрядов к старшим с помощью сдвига вправо показан на рис. 3.8, в.
3.1.8. Распределители тактов
В системах синхронизации и устройствах управления используют распределители тактов (РТ), которые вырабатывают серии импульсов. Простейший способ построения распределителя тактов состоит в делении счетными триггерами частоты прямоугольных импульсов f от задающего генератора (ЗГ).
126 Последовательностные (накапливающие) узлы компьютерной схемотехники
На прямом и инверсном выходах триггера с помощью схем совпадения образуются две последовательности импульсов фаз С, = f Q и С2 =/Q (рис. 3.9, а). Длительность такта синхронизации Т( в два раза больше периода следования импульсов ЗГ (рис. 3.9, б).
Рис. 3.9. Распределитель тактов: а - схема; б - временные диаграммы
Распределители тактов строятся также на кольцевых регистрах, в которых выход младшего разряда соединен с информационным входом старшего, если реализован сдвиг вправо (рис. 3.10, а), или имеется связь от старшего разряда к младшего при сдвиге влево.
Кольцевой регистр в качестве распределителя тактов функционирует следующим образом. Вначале через схему ИЛИ в старший разряд Q4 записывается единица. Затем по фронту каждого синхроимпульса единица сдвигается вправо и поочередно появляется на выходах Q3, Q2 и Q}. С приходом четвертого синхроимпульса единица из младшего разряда Q, по кольцевой связи и через схему ИЛИ снова записывается в старший разряд. Число выходов распределителя тактов определяется количеством триггеров кольцевого регистра. В распределителе тактов на основе четырехразрядного кольцевого регистра формируются импульсы фаз С,, С2, С3 и С4, которые образуют машинный такт Т длительностью в четыре периода синхроимпульсов, то есть Т ~ 4 Тс (рис. 3.10, б).
3.1. Регистры 127
Недостатком схемы, изображенной на рис. 3.10, а, является возможность сбоя — появления лишних единиц в разрядах, например, 1100, 1001.
В кольцевом регистре с самовосстановлением после сбоя используется схема контроля, которая при неправильной работе автоматически возвращает регистр в исходное состояние.
3.1.9. Регистры в микросхемах серии КР1533
Серия микросхем КР1533 содержит широкий набор регистров. Большинство регистров — восьмиразрядные с третьим состоянием выхода и одно- или двухсторонним сдвигом (рис. 3.11). Микросхема КР1533ИР13 (рис. 3.11, а) — это восьмиразрядный реверсивный сдвиговой регистр. Он имеет входы для параллельной записи данных D0-D7, синхронизации С, последовательного приема DR и DL, задания режимов работы 51, S0 и вход сброса R. Информация считывается с параллельных выходов 00-07. Разряды нумеруются слева направо: QQ — старший разряд, Q7 — младший.
a б в
Рис. 3.11. Регистры серии КР1533: а — ИР13; 6 — ИР24; в — ИР34
Регистр обеспечивает четыре режима работы: 51-50 = 00 — хранение данных (блокировка); 01 — последовательный прием со сдвигом вправо по входу DR; 10 — последовательный прием со сдвигом влево по входу DL; 11 — параллельная запись по входу D0-D7. Запись и последовательный прием данных осуществляются по фронту синхроимпульса С. Во время записи последовательный ввод данных блокируется. При R = 0 все входы регистра устанавливаются в состояние “0".
Микросхема КР1533ИР24 (рис. 3.11, б) — это восьмиразрядный реверсивный сдвиговой регистр с двунаправленными выводами DQ D7 для приема и выдачи информации. Выводы D0-D7 имеют Z-состояния, в которые они переключаются при подаче сигнала лог. 1 хотя бы на один из входов Z1 или Z2. Регистр содержит так-
128 Последовательностные (накапливающие) узлы компьютерной схемотехники
же дополнительные выводы DO и D7, которые связаны соответственно со старшим и младшим разрядами, но не имеют Z-состояний.
Регистр обеспечивает четыре синхронных режима работы в зависимости от сигналов на входах 51 -SO: 00 — хранение (блокировка); 01 — последовательная запись по входу DR со сдвигом вправо; 10 — последовательная запись по входу DL со сдвигом влево; 11 — параллельный прием данных. Первые три режима реализуются при Z1 =Z2 - 0; при этом информация передается на выводы D0-D7, а четвер-тый режим осуществляется независимо от значений сигналов на выходах Z1 и Z2. Все операции выполняются по фронту сигнала синхронизации С.
Регистры ИР13, ИР24 серии КР1533 используют для временного хранения информации, преобразования данных из параллельной формы в последовательную и наоборот.
Микросхема КР1533ИР34 (рис. 3.11, в) — это два независимых четырехразрядных регистра с тремя состояниями на выходах О()- Q3. Параллельная запись данных по входам D0-D3 выполняется при сигнале лог. 1 на входе разрешения L; если L_= 0, то регистр переходит в режим хранения. Высокий уровень сигнала на входе Z переключает выходы регистра в третье состояние. Однако при этом в регистр могут записываться новые данные или сохраняться предыдущие. Микросхема обладает большой нагрузочной способностью, что в сочетании с тремя состояниями позволяет использовать регистр в магистральных структурах без дополнительных интерфейсных схем.
Мощность потребления регистров ИР13, ИР24 и ИР34 серии КР1533 составляет примерно 200 мВт, а время записи информации — 15-20 нс.
3.2. Счетчики
3.2.1. Общая характеристика счетчиков
Счетчиком называется типовой функциональный узел компьютера, предназначенный для счета входных импульсов. Счетчик представляет собой связанную цепочку Т-триггеров, образующих память с заданным числом устойчивых состояний (рис. 3.12).
Рис. 3.12. Логическая структура счетчика
Разрядность счетчика п равна числу Т-триггеров. Каждый входной импульс изменяет состояние счетчика, которое сохраняется до поступления следующего сигнала. Значения выходов триггеров счетчика Q„, Q„_}, ..., Q} отображают результат счета в принятой системе счисления. Логическая функция счетчика обозначается буквами СТ (counter). Список микроопераций счетчика включает предварительную
3.2. Счетчики 129
установку в начальное состояние, инкремент или декремент хранимого слова, выдачу слов параллельным кодом и др.
Входные импульсы могут поступать на счетчик как периодически, так и произвольно распределенными во времени. Амплитуда и длительность счетных импульсов должны удовлетворять техническим требованиям для используемых серий микросхем.
Счетчик является одним из основных функциональных узлов компьютера, а также различных цифровых управляющих и информационно-измерительных систем. Основное применение счетчиков:
• образование последовательности адресов команд программы (счетчик команд или программный счетчик);
• подсчет числа циклов при выполнении операций деления, умножения, сдвига (счетчик циклов);
• получение сигналов микроопераций и синхронизации; аналого-цифровые преобразования и построение электронных таймеров (часов реального времени).
Счетчик характеризуется модулем и емкостью счета. Модуль счета Ксч определяет число состояний счетчика. Модуль двоичного «-разрядного счетчика выражается целой степенью двойки М = 2"; в счетчиках других типов справедливо неравенство /<сч М. После счета числа импульсов /VI!X = Ксч счетчик возвращается в начальное состояние. Таким образом, модуль счета, который часто называют коэффициентом пересчета, определяет цикл работы счетчика, после которого его состояние повторяется. Поэтому число входных импульсов и состояние счетчика однозначно определены только для первого цикла.
Емкость счета 7Vmax определяет максимальное количество входных импульсов, которое может зафиксировать счетчик при одном цикле работы. Емкость счета Nnm = Ксч - 1 при условии, что работа счетчика начинается с нулевого начального состояния.
В счетчиках используются три режима работы: управления, накопления и деления. В режиме управления считывание информации производится после каждого входного счетного импульса, например, в счетчике адреса команд. В режиме накопления главным является подсчет заданного числа импульсов либо счет в течение определенного времени. В режиме деления (пересчета) основным является уменьшение частоты поступления импульсов в КСч раз. Большинство счетчиков может работать во всех режимах, однако в специальных счетчиках-делителях состояния в процессе счета могут изменяться в произвольном порядке, что позволяет упростить схему узла.
Счетчики классифицируют по следующим признакам:
• способу кодирования — позиционные и непозиционные;
• модулю счета — двоичные, десятичные, с произвольным постоянным или переменным (программируемым) модулем;
• направлению счета — простые (суммирующие, вычитающие) и реверсивные;
• способу организации межразрядных связей — с последовательным, сквозным, параллельным и комбинированным переносами (заемом);
• типу используемых триггеров — Т, JK, D в счетном режиме;
9 — 4-1749
130 Последовательностные (накапливающие) узлы компьютерной схемотехники
• элементному базису — потенциальные, импульсные и потенциальноимпульсные.
В счетчиках с позиционным кодированием числовое выражение текущего состояния счетчика определяется формулой:
}) v
N = ^riQi = r„Ql, + r„^Q„_]+...+ r}Q}, /=1
где г,- — вес z-ro разряда; Q, — значение выхода z-го разряда; п — число разрядов. Нулевое значение всех разрядов обычно принимается за начальное состояние счетчика. Остальные состояния нумеруют по числу поступивших входных импульсов.
В счетчиках с непозиционным кодированием (например, в кодах Грея) разряды не имеют постоянных весов и каждом набору состояний Q„, Q,,^, .... Q, приписывается определенное количество входных импульсов. В компьютерах преимущественно используют счетчики с позиционным кодированием.
По виду переходов простые счетчики (Сч) подразделяются на суммирующие (прямого счета) и вычитающие (обратного счета). В суммирующих счетчиках каждый прибавляемый импульс if увеличивает состояние на единицу, то есть реализуется микрооперация инкремента Сч := Сч + 1. Граф переходов суммирующего счетчика показан на рис. 3.13, а, где вершины обозначают устойчивые состояния. Из Л/-1-го состояния очередной сигнал if возвращает счетчик в начальное состояние и выдает сигнал переполнения Р.
В вычитающих счетчиках каждый вычитаемый импульс 1Г уменьшает состояние на единицу, то есть реализуется микрооперация декремента Сч := Сч - 1. Граф переходов вычитающего счетчика (рис. 3.13, б) характеризуется наличием переходов только в обратном направлении от некоторого (например, Л/-1-го) предварительно установленного состояния. После вычитания М импульсов счетчик выдает сигнал заема Z и возвращается в исходное М-\-е состояние.
в
Рис. 3.13. Гоафы счетчиков: а — суммирующего; б — вычитающего; в — реверсивного
Реверсивные счетчики имеют переходы в прямом и обратном направлениях, что позволяет считать прибавляемые и вычитаемые импульсы (рис. 3.13, в). В процессе счета должно выполняться условие Ylf + Nn > YlT, где 7Vn — предварительно записанное число. По текущему состоянию выходов счетчика определяется результат реверсивного счета:
\N = Xlf +Nn ZU-
К временным характеристикам счетчиков относятся разрешающая способность, быстродействие и время установления (переключения) кода.
3.2. Счетчики 131
iMii)>i>i..itiii»i.HiiiiwiiiiJii(i»Hi(((oiii(ioiiii«i)UHiiJTO:H):wM)WH'ir;iiiiTiiiMii)i«iiiiiiiiHiii(i>iit»oiitiiiirriiiiiiiiiii>:iict:,iniiiiiini(ii-i ^^Lll»и^.:l^мlrlffiiffilrntll^^',^,*,.•tmi'Hi4iiiri'iiiiiiiiTiiii!"'i‘,,,i......
Разрешающая способность /рс определяется минимальным интервалом времени между двумя входными импульсами, при котором еще сохраняется работоспособность счетчика. Параметр tpL задают временем переключения // первого (младшего) триггера счетчика, то есть /рс = /Л поскольку он переключается под воздействием каждого входного импульса.
Быстродействие счетчика определяется максимальной частотою F„, поступления входных импульсов в режиме деления и вычисляется по формуле F„, = l//z Время установления кода /уст отсчитывается от начала входного импульса до момента получения нового состояния. Данный параметр позволяет рассчитать быстродействие счетчика в режиме управления из соотношения FnK = 1/(г,сг + /еч), где t„ — время считывания информации.
Межразрядные связи обеспечивают выработку сигналов переноса в старшие разряды при суммировании импульсов и сигналов заема — при вычитании От вида реализации межразрядных связей существенно зависят параметры /уст и F,„K.
В счетчиках с последовательными переносами триггеры переключаются поочередно после каждого входного импульса в направлении от младших разрядов к старшим. Такие счетчики называются последовательными или асинхронными. В счетчиках с параллельными переносами триггеры переключаются одновременно после каждого входного импульса, такие счетчики называются параллельными или синхронными.
3.2.2. Двоичные суммирующие и вычитающие счетчики
Двоичные счетчики реализуют счет входных импульсов в двоичной системе счисления. Число разрядов п двоичного суммирующего счетчика для заданного модуля М находят из выражения п - log2M Значение текущего числа N* входных импульсов «-разрядного суммирующего счетчика при отсчете с нулевого начального состояния определяют по формуле
л^= X2'-1 Q' =2"~' Q"+ 2"2 + -+2°
1=\
где 2'“' — вес z-ro разряда; Q, е {0,1} — логическое значение прямого выхода триггера /-го разряда. Разряды двоичного счетчика строятся на двухступенчатых Г-триггерах или D-триггерах с динамическим управлением по фронту синхросигнала (в счетном режиме).
В двоичном суммирующем счетчике перенос Р, в соседний старший разряд Ql+[ возникает в том случае, если в момент поступления очередного счетного импульса !/ все младшие разряды находятся в единичном состоянии, то есть Р, = U* QiQi-i Qi = 1- После выработки переноса старший разряд переключается в состояние “1”, а все младшие разряды — в состояние “0”.
Асинхронные суммирующие счетчики на двухступенчатых Т-триггерах строятся так, чтобы входные импульсы if поступали на счетный вход только первого (младшего) разряда. Сигналы переноса передаются асинхронно (последовательно во времени) с прямых выходов младших разрядов на Т-входы соседних старших, как показано на рис. 3.14 для трехразрядного счетчика.
Изменение состояний триггеров происходит по спаду счетного импульса для первого разряда, а для остальных — по спаду сигнала переноса (рис. 3.14, б). 9’
132 Последовательностные (накапливающие) узлы компьютерной схемотехники
Рис. 3.14. Асинхронный суммирующий счетчик на двухступенчатых Т-триггерах: а — схема; б — временные диаграммы работы
После подсчета семи импульсов на выходе трехразрядного счетчика устанавливается двоичный код gjgzQi = И1 (то есть максимальное значение или емкость счета), После прихода восьмого входного импульса if трехразрядный суммирующий счетчик переключается в исходное нулевое состояние последовательно (асинхронно) во времени: вначале спадает напряжение на выходе Qi, затем — на выходе Q2 и т.д.
С помощью импульса по входу сброса R счетчик возвращается в нулевое состояние в любой момент времени.
Временные параметры «-разрядного асинхронного счетчика на двухступенчатых триггерах определяются из соотношений:
• разрешающая способность /рс = гГ1+ = 2tr, где tTi и tn — время переключения первой и второй ступени триггера, причем = tn = tf,
• время установки гус1 = + ntn ~ ntT\
• максимальная частота счета в режиме деления и управления соответственно: Fm = l/2tT;FmK* \/ntT.
В режиме управления быстродействие асинхронного счетчика примерно в п раз меньше, чем в режиме деления.
Схема трехразрядного асинхронного двоичного суммирующего счетчика на Т-триггерах с динамическим управлением по фронту показана на рис. 3.15. Счетные импульсы If поступают на 7-вход только первого (младшего) разряда; последующие триггеры переключаются асинхронно от сигналов переноса с инверсных выходов соседних младших разрядов.
Рис. 3.15. Асинхронный суммирующий счетчик на триггерах с динамическим управлением по фронту: а — схема; б — временные диаграммы работы
Временные параметры асинхронного «-разрядного двоичного счетчика на триггерах с динамическим управлением: /рс = tT, /уст = ntT, F„, = l/tT, Fm к ® \/ntT.
Достоинством асинхронных счетчиков является простота схемы: увеличение разрядности производится подключением необходимого числа триггеров. К недостаткам асинхронных счетчиков относятся сравнительно низкое быстродействие в
3.2. Счетчики 133
режиме управления и ее зависимость от числа разрядов, а также появление промежуточных выходных двоичных кодов в процессе последовательного переключения триггеров в новое состояние.
Для получения минимального времени переключения счетчика используют параллельные переносы (рис. 3.16). Для этого в каждом разряде синхронного счетчика имеется схема совпадения, с помощью которой анализируются состояния всех предыдущих младших триггеров и вырабатываются функции переноса согласно следующим логическим соотношениям:
л = trg,; л = стае,; л = л =
При поступлении очередного счетного импульса if переключаются только те триггеры, для которых все предыдущие (младшие) разряды находятся в этот момент в единичном состоянии.
Время установления синхронного счетчика не зависит от числа разрядов и равна /уст = tri + tP, где Г/7-— время переключения двухступенчатого триггера; t,— время задержки распространения сигнала вентилем в цепи переноса. Максимальная частота счета в режиме управления F,„ ® l/trr. Таким образом, синхронные счетчики обеспечивают наибольшее быстродействие в режиме управления.
При построении многоразрядных синхронных счетчиков появляются трудности — рост числа входов вентилей в цепи переноса и увеличение нагрузки на выходы триггеров.
В двоичном вычитающем счетчике каждый вычитаемый импульс W уменьшает состояние на единицу. Текущее значение количества входных импульсов «-разрядного двоичного вычитающего счетчика определяется по формуле
где К — значение кода на прямых выходах триггеров счетчика; N„ — предварительно записанное начальное число; при этом должно выполняться условие 11Г < Nn.
В вычитающих счетчиках сигналы межразрядной связи называются заемами. По правилу двоичного вычитания в момент поступления счетного импульса LT заем из старшего разряда с единичным значением возникает при условии, что все младшие триггеры находятся в нулевом состоянии. После этого все они переключаются в состояние “1”, а старшие — в состояние “0”. Сигналы заема образуются на инверсных выходах двухступенчатых триггеров или на прямых выходах триггеров с динамическим управлением по фронту.
Параметры вычитающего счетчика (модуль и емкость счета, быстродействие) совпадают с аналогичными характеристиками суммирующих счетчиков.
Схема трехразрядного двоичного асинхронного вычитающего счетчика на двухступенчатых триггерах показана на рис. 3.17, а.
134 Последовательностные (накапливающие) узлы компьютерной схемотехники
а б
Рис. 3.17. Асинхронный вычитающий счетчик на двухступенчатых триггерах: а — схема; 6 — временные диаграммы работы
Перед началом работы с помощью сигнала на общем входе 5 все триггеры счетчика устанавливаются в состояние “1”, образуя выходной код 111. Вычитаемый импульс 1Г поступает на счетный вход только первого младшего разряда, межразрядные сигналы заема снимаются асинхронно с инверсных выходов триггера.
После поступления семи вычитаемых импульсов все триггеры счетчика устанавливаются в состояние “0”, образуя выходной код ООО. Восьмой вычитаемый импульс переключает счетчик в состояние 111 (при условии, что рассматривается трехразрядная схема).
В вычитающем счетчике на триггерах с динамическим управлением по фронту сигналы заема снимаются с прямых выходов триггеров.
3.2.3. Двоичные реверсивные счетчики
Двоичные реверсивные счетчики имеют переходы в двух направлениях: в прямом (при счете суммируемых сигналов if) и в обратном (при счете вычитаемых сигналов 1Г). Текущее значение разности подсчитанных импульсов определяется из соотношения
Xlf -1.1Г = N-Nn , где N— значение кода на прямых выходах триггеров счетчика; N„ — предварительно записанное в счетчик начальное число.
В процессе счета должно выполняться условие fU Nn+£.lf < 2"-1.
Различают одноканальные и двухканальные реверсивные счетчики. В одноканальных реверсивных счетчиках суммируемые if и вычитаемые LT сигналы поочередно поступают на общий счетный вход, а направление счета задается направлением цепей межразрядных переносов или заемов. Для переключения межразрядных связей в одноканальном реверсивном счетчике требуются дополнительные управляющие сигналы.
Двухканальные реверсивные счетчики имеют два счетных входы: один для суммируемых импульсов if, другой — для вычитаемых 1Г. Переключение цепей межразрядных связей осуществляется автоматически счетными сигналами: для переносов — импульсами 1Г, для заема — импульсами 1Г. Схема одноканального трехразрядного двоичного реверсивного счетчика показана на рис. 3.18. Межразрядные связи коммутируются с помощью логических элементов И ИЛИ.
Для задания направления счета используют дополнительный RS-триггер: с его прямого выхода снимается сигнал управления сложением Усл (включает цепи переноса), а с инверсного выхода — сигнал управления вычитанием Увч (включает
135
цепи заема). На выходах элементов И ИЛИ (которые называются “схемы реверса”) вырабатывается сигнал Т) для счетных входов старших разрядов:
Г.-ГдЙУГвё, / = 1,2,3,...,».
Рис. 3.18. Схема одноканального реверсивного счетчика
Таким образом, если управляющий RS-триггер находится в состоянии “1”, то счетчик реализует режим прямого счета входных импульсов (то есть суммирование), в противном случае — обеспечивает режим обратного счета (вычитание). В обоих режимах работы триггеры переключаются асинхронно.
Схема двухканального четырехразрядного двоичного реверсивного счетчика показана на рис. 3.19.
Рис. 3.19. Схема двухканального реверсивного счетчика
Счетные Г-входы в триггерах внутренне связаны схемой ИЛИ. Суммирующие импульсы if поступают на счетный вход первого (младшего) разряда счетчика и одновременно — на входы всех вентилей в цепи параллельного переноса. При этом формируются импульсы межразрядных переносов на основе логических выражений:
f = U+QX; Р2 ~U+QXQ2; Р2 =U+QtQ2Q2; P,=U+QXQ2Q&.
Вычитаемые импульсы LT поступают на счетный вход первого разряда счетчика и одновременно на входы всех вентилей в цепи параллельных заемов. При этом
136 Последовательностные (накапливающие) узлы компьютерной схемотехники
формируются импульсы межразрядных заемов на основе следующих логических выражений:
Z, -L7-Q; Z2 =U-Q&, Z2=IJ-Q£2Q2- Z4 =U~QQ2Q2Q4.
Таким образом, в двухканальных реверсивных счетчиках направление счета непосредственно задается суммируемыми if или вычитаемыми IP импульсами. Запрещается одновременное поступления на входы двухканального реверсивного счетчика суммируемых и вычитаемых импульсов.
На практике с учетом схемотехнических возможностей микросхем средней степени интеграции многоразрядные реверсивные счетчики строятся в виде групповой структуры. При этом каждая группа представляется, например, микросхемой четырехразрядного реверсивного счетчика с параллельными переносами и заемами. Между группами могут бути образованы последовательные или параллельные связи.
Схема 12-разрядного двухканального реверсивного счетчика групповой структуры с последовательными переносами между группами (микросхемы КР1533ИЕ7) показана на рис. 3.20; СТ2 — функция двоичного счетчика.
Рис. 3.20. Схема 12-разрядного двухканального реверсивного счетчика с групповой структурой
Микросхема КР1533ИЕ7 — это двоичный четырехразрядный реверсивный синхронный счетчик, имеющий следующие режимы работы:
• параллельная загрузка начальных данных D3-D0 при L = 0 ;
• суммирование импульсов If по входу “+Г;
• вычитание импульсов IP по входу “-1”;
• сброс в начальное состояние сигналом лог. 1 на Л-входе.
Информация считывается с выходов gll-QO счетчика. Суммируемые импульсы if в счетчике с групповой структурой поступают на вход прямого счета “+1” первой младшей группы. Для другой группы сигналы переноса формируются при условии Р = If QiQiQiQo- Вычитаемые импульсы IP поступают на вход обратного счета “-1”. Для второй группы сигналы заема вырабатываются при условии Z = IP Q2Q2QiQ0. Аналогично строятся связи и между старшими группами.
Длительность импульсов на счетных входах должна быть не меньше 20 нс, а максимальная частота счета не должна превышать 30 МГц.
137
3.2.4. Двоично-десятичные счетчики
Двоично-десятичные счетчики реализуют счет импульсов в десятичной системе счисления, причем каждая десятичная цифра от нуля до девяти кодируется четырехразрядным двоичным кодом (тетрадой), Эти счетчики часто называют десятичными или декадными, поскольку они работают с модулем счета, кратным десяти.
Многоразрядный двоично-десятичный счетчик строится на основе регулярной цепочки декад, при этом первая (младшая) декада имеет вес 10°, вторая — 101, третья — 102 и т.д.
Декада строится на основе четырехразрядного двоичного счетчика, в котором исключается избыточное число состояний. Исключение лишних шести состояний в декаде достигается многими способами:
• предварительной записью числа 6 (двоичный код ОНО); после счета девятого импульса выходной код равен 1111 и десятичный сигнал возвращает счетчик в исходное состояние ОНО. Таким образом, здесь результат счета фиксируется двоичным кодом с избытком 6;
• блокировкой переносов: счет импульсов до девяти осуществляется в двоичном коде, после чего включаются логические связи блокировки переносов; с поступлением десятого импульса счетчик заканчивает цикл работы и возвращается в начальное нулевое состояние;
• введением обратных связей, которые обеспечивают счет в двоичном коде и принудительное переключение счетчика в нулевое начальное состояние после поступления десятого импульса.
Схема синхронного десятичного счетчика с блокировкой переносов показана на
Рис. 3.21. Схема десятичного счетчика на JK-триггерах
В этой схеме С-входы используются как счетные. С приходом десятого импульса на С-вход младшего разряда JK-триггера обнуляются первый и четвертый разряды и сигналом с выхода блокируют переключения второго и третьего разряда. Схема суммирующего счетчика с обратными связями (один разряд) показана на рис. 3.22.
138 Последовательностные (накапливающие) узлы компьютерной схемотехники
Рис. 3.22. Схема десятичного суммирующего счетчика с обратными связями
После сброса в нулевое начальное состояние на счетный вход первого триггера поступают суммируемые импульсы if. Сигналы переноса в старшие разряды формируются обычным асинхронным способом. Счет до девяти ведется в двоичном коде. После прихода десятого входного импульса обратная связь на основе схемы совпадения вырабатывает сигнал P = U+Q^Q^Q2QXt который является переносом для старшей декады и одновременно переключает счетчик в нулевое состояние. Далее цикл работы счетчика повторяется.
Схема пятиразрядного суммирующего двоично-десятичного счетчика показана на рис. 3.23.
10°=1 10=10 10=100 ioJ=iooo io4=ioooo
Рис. 3.23. Схема пятиразрядного суммирующего двоично-десятичного счетчика
Модуль данного счетчика составляет Ксч = 105 = 100000, емкость счета N„,ax = Ксч - 1= 99999.
Выходы триггеров каждой декады подключаются ко входам дешифраторов, которые обеспечивают визуальную индикацию состояния счетчика с помощью разного рода световых табло.
3.2.5. Счетчики с единичным кодированием
При единичном (унитарном) кодировании состояния «-разрядного счетчика различаются только местоположением одной единицы, называемой маркирующим кодом; в других разрядах записаны нули. В отдельных случаях маркирующий код состоит из двух единиц и называется парно-единичным.
Счетчик с единичным кодированием — это цепочка триггеров, в которой обеспечивается сдвиг предварительно записанного маркирующего кода по “кольцу” в направлении старших разрядов (прямой счет) или младших (обратный счет). Такие счетчики часто называют кольцевыми (по аналоги с кольцевыми регистрами сдвига).
Счетчик с единичным кодированием характеризуется модулем Ксч = п и емкостью счета Nmax = п - 1. Таким образом, число состояний кольцевого счетчика равно его разрядности и существенно меньше в сравнении с другими типами счетчиков.
139
В кольцевых счетчиках каждый разряд имеет вес, равный номеру состояния О, 1, 2,(п - 1). Из состояния (п - 1) после поступления очередного импульса счетчик образует на выходе сигнал окончания цикла (переполнения) и возвращается в начальное состояние с помощью цепи обратной связи с выхода старшего разряда Q„ на вход младшего разряда Qt. Схема четырехразрядного кольцевого счетчика пока-
Рис. 3.24. Кольцевой счетчик: а— схема; б— временные диаграммы
Перед началом работы по входу D схемы ИЛИ в младший разряд счетчика записывается единица и устанавливается начальный код Q4Q3Q2Q1 = 0001. С поступлением каждого счетного импульса по входу синхронизации единичный код последовательно сдвигается в сторону старших разрядов; при этом младшие разряды, выполненные на D-триггерах с динамическим управлением, обнуляются. После прихода четвертого импульса счетчик возвращается в начальное состояние с помощью сигнала с выхода Q4 на вход схемы ИЛИ.
Практическое использование кольцевых счетчиков объясняется следующими его достоинствами:
• не требует выходного дешифратора, поскольку все состояния отличаются наличием единицы только в одном каком-либо триггере;
• в процессе счета всегда переключается в единичное состояние только один триггер, что обеспечивает минимальное значение />ст;
• упрощается построение схемы контроля счетчика.
Схема счетчика Джонсона (рис. 3.25) строится на основе кольцевого, в котором обратная связь реализуется подключением инверсного выхода старшего разряда ко входу младшего.
Рис. 3.25. Счетчик Джонсона: а— схема; б— временные диаграммы
Счетчик Джонсона характеризуется модулем счета Ксч = 2п и емкостью счета Nmm = In - 1. Таким образом, число состояний счетчика Джонсона в два раза больше аналогичного параметра кольцевого счетчика Однако информация на выходах
140 Последовательностные (накапливающие) узлы компьютерной схемотехники
счетчика Джонсона представляется не в двоичной позиционной системе счисления, которая требует дополнительного преобразования. Как видно из временных диаграмм (рис. 3.25, б), в процессе счета вначале двигается “волна” единиц, а затем — “волна” нулей. Дешифрация состояний счетчика Джонсона осуществляется проще в сравнении с двоичными позиционными счетчиками.
Контрольные вопросы
1. Что такое регистр?
2. Каковы области применения регистров?
3. Сформулируйте признаки классификации регистров.
4. Охарактеризуйте микрооперации, которые может выполнять регистр.
5. Что такое сдвиги? Перечислите основные виды сдвигов.
6. Какие логические операции реализуются в регистрах?
7. Что такое счетчик?
8. Перечислите области применения счетчиков.
9. Сформулируйте признаки классификации счетчиков.
10. Охарактеризуйте два режима работы счетчика: управления и деления.
11. Как можно повысить быстродействие счетчика в режиме управления?
12. Чем отличается двоичный счетчик от десятичного?
13. Какие ограничения накладываются на работу реверсивного счетчика?
14. По каким правилам организуются связи между триггерами суммирующего и вычитающего счетчиков?
15. Каковы особенности работы счетчика на двухступенчатых триггерах в сравнении с D-триггерами с динамическим управлением?
16. Перечислите способы построения счетчиков с произвольным модулем счета.
17. Охарактеризуйте счетчик Джонсона.
4.1. Дешифраторы 141
Глава 4
Комбинационные функциональные узлы компьютерной схемотехники
4.1. Дешифраторы
4.1.1. Общая характеристика дешифраторов
Дешифратором называется функциональный узел компьютера, предназначенный для преобразования каждой комбинации входного двоичного кода в управляющий сигнал только на одном из своих выходов. В общем случае дешифратор имеет п однофазных входов (иногда 2п парафазных) и т = 2" выходов, где п — разрядность (длина) дешифрируемого кода. Дешифратор с максимально возможным числом выходов т = 2" называется полным. Функционирование полного дешифратора описывается системой логических выражений вида:
Fo = ...ВД,-
F, = ХпХ„^...Х2Хх;
F„,_\ ...Х2Хх,
где Х}, ..., Х„ — входные двоичные переменные; Fo, Fit ..., F,„_| — выходные логические функции, представляющие собой минтермы (конституенты 1) п переменных.
Индекс функции F, определяет номер выбранного выхода и соответствует десятичному эквиваленту входного кода. Выход, на котором появляется управляющий сигнал, называется активным. Если значение сигнала на активном выходе отображается лог. 1, то на остальных пассивных выходах устанавливается лог. 0. Двоичный код, включающий всегда только одну единицу, а остальные — нули, называется унитарным. Поэтому дешифратор является преобразователем входного позиционного кода в унитарный выходной код.
В дешифраторах в интегральном исполнении состояние активного выхода часто отображается значением лог. 0, а на остальных пассивных выходах устанавливается лог. 1. Функционирование полного дешифратора с инверсными выходами представляется системой вида:
Lo = X п v X v ... v 2Г2 v Х};
Lx = X ,,v Х„_, v ... v Х2 v Х};
L т-1 = X „ V X п_} V ... V Х2 V У,, где Lo, L\, ... , Lm_x — выходные логические функции, которые являются макстермами (конституенты 0) п переменных.
142 Комбинационные функциональные узлы компьютерной схемотехники
Индекс функции L, определяет номер выбранного выхода и соответствует десятичному эквиваленту входного кода. Между двумя видами выходных функций существует простая связь: Ft = Д.
Дешифраторы классифицируют по следующим признакам:
• способу структурной организации — одноступенчатые (линейные) и многоступенчатые, в том числе пирамидальные и прямоугольные (матричные);
• формату входного кода — двоичные, двоично-десятичные;
• разрядности дешифрируемого кода — 2, 3, ..., и;
• форме подачи входного кода — с однофазными и парафазными входами;
• количеству выходов — полные и неполные дешифраторы;
• виду входных стробирующих сигналов — в прямом или инверсном значениях;
• типу используемых логических элементов — И, НЕ, ИЛИ, НЕ И, НЕ ИЛИ и т. д.
К основным характеристикам дешифратора относят: число ступеней (каскадов) дешифрации, количество используемых логических элементов или микросхем, общее число входов логических элементов, время дешифрации и потребляемую мощность. Условные графические обозначения дешифраторов на электрических схемах показаны на рис. 4.1.
а — на функциональных схемах; б, в — на принципиальных схемах
Логическая функция дешифратора обозначается буквами DC (decoder). Метки левого дополнительного поля в условном обозначении отображают десятичные веса входных переменных, а метки правого дополнительного поля соответствуют десятичным эквивалентам входных комбинаций двоичных переменных. В схему дешифраторов встраиваются один или два стробирующих (разрешающих) входа, например, W (рис. 4.1, б). С помощью сигнала на входе W определяется момент срабатывания дешифратора; кроме того, вход IV используется для наращивания разрядности входного кода. На практике полный дешифратор на п входов и т выходов для краткости называют дешифратором “из п в т" или “п -> т". Например, дешифратор “из 3 в 8” — активизируется одна из восьми выходных линий.
В компьютерах дешифраторы используют для выполнения следующих операций:
• дешифрации кода операции, записанного в регистр команд процессора, что обеспечивает выбор требуемой микропрограммы;
• преобразования кода адреса операнда в команде в управляющие сигналы выбора заданной ячейки памяти в процессе записи или чтения информации;
• обеспечения визуализации на внешних устройствах;
4.1. Дешифраторы 143
• реализации логических операций и построения мультиплексоров и демультиплексоров.
Использование дешифраторов для дешифрации кода операции и адреса операнда, размещенных в регистре команд процессора, показано на рис. 4.2. Дешифрация кода операции в устройстве управления (УУ) определяет тип машинной команды. Дешифрация адреса операнда в оперативной памяти (ОП) обеспечивает доступ к указанной ячейке памяти для записи или считывания данных.
Рис. 4.2. Иллюстрация использования дешифраторов
4.1.2. Линейные дешифраторы на два входа и четыре выхода
В линейном дешифраторе “из п в т" каждая выходная функция F, реализуется полностью отдельным и-входным логическим элементом при использовании пара-фазного входного кода. Логика работы полных дешифраторов на два входа X,, Х2 и четыре прямых выхода Fo, F}, F2, F3 и четыре инверсных выхода Lo, L}, L2, X представлена в табл. 4.1 и 4.2 соответственно.
Таблица 4.1
Х2 х. Fo F, f2 F3
0 0 1 0 0 0
0 1 0 1 0 0
1 0 0 0 1 0
1 1 0 0 0 1
Таблица 4.2
x2 Xt L0 Lt L2 L3
0 0 0 1 1 1
0 1 1 0 1 1
1 0 1 1 0 1
1 1 1 1 1 0
По данным табл. 4.1 получают систему логических функций в СДНФ:
Fo = Х~2 F, = Х~2Х}-, F2=X2Y}; F3=X2X}. (4.1)
Для линейного дешифратора со стробирующим входом IV система уравнений (4.1) принимает вид:
Fo = JF F,-F2 - Fo -As A', JF (4.2)
Схемы линейных дешифраторов на основе уравнений (4.1) и (4.2) показаны на рис. 4.3.
В схеме, изображенной на рис. 4.3, б используется однофазный входной код, поскольку инверсии переменных образуются элементами НЕ. Если сигнал на стробирующем входе W = 0, то работа дешифратора блокируется — на всех выходах
144 Комбинационные функциональные узлы компьютерной схемотехники
устанавливаются логические нули независимо от значений входных переменных. При W = 1 дешифратор функционирует согласно табл. 4 1.
Рис. 4.3. Схемы линейных дешифраторов на элементах И: а — с парафазными входами; б — с однофазными входами и стробированием
По данным табл. 4.2 записывается система логических функций в СКНФ:
£0 — A?vХ\', L] = Аг v Х1 Ьг = А\ v Ац X. — Х2 v Х}. (4.3)
Схема линейного дешифратора с парафазным входным кодом и инверсными выходами, построенная в соответствии с уравнением (4.3) на элементах ИЛИ, показана на рис. 4.4, а.
Для линейного дешифратора со стробирующим И/-входом система уравнений (4.3) принимает вид:
L-^2v.Yr< L^X^T^W-, (44)
L, = Y2 v Хх v W; L3=X}vX\vJ7.
Схема линейного дешифратора на основе уравнений (4.4) показана на рис. 4.4, б.
Рис. 4.4. Схема линейных дешифраторов на элементах ИЛИ: а — с парафазными входами; б — с однофазными входами и стробированием
Здесь используется однофазный входной код, поскольку инверсии переменных образуются элементами НЕ. Если сигнал на стробирующем входе W = 1, то работа дешифратора блокируется — на все/ выходах устанавливаются лог. 1 независимо от значений входных переменных. При W = 0 дешифратор функционирует согласно с табл. 4.2.
4.1. Дешифраторы 145
4.1.3. Пирамидальные дешифраторы
В пирамидальном дешифраторе число ступеней на единицу меньше разрядности входного кода, то есть К = п - 1. Во всех ступенях используются только двухвходовые логические элементы. На первой ступени используются линейные дешифраторы на два входа и четыре выхода. Число логических элементов в каждой ступени равно М, = 2'+|, где i = 1,2, ..., к. Это означает, что каждая последующая ступень имеет в два раза больше элементов, чем предыдущая. Выход элемента z-й ступени подключается ко входам только двух элементов (?+1 )-й ступени.
Пирамидальная структура для реализации полного дешифратора “из 3 в 8” описывается системой минтермов вида:
F, = ...F7=X,X2Xi.
Схема пирамидального дешифратора с парафазным входным кодом на три входа и восемь выходов показана на рис.4.5.
Рис. 4.5. Схема пирамидального дешифратора на три входа и восемь выходов
На первой ступени дешифрируются переменные и Х}, на второй ступени добавляется разряд Хз. При большем числе разрядов дешифрируемого кода, например, п > 10, пирамидальный дешифратор в п/4 раз экономичнее линейного.
Основным недостатком пирамидального дешифратора является большое число ступеней, что существенно увеличивает время дешифрации кода.
4.1.4. Прямоугольные дешифраторы
Прямоугольный дешифратор строится по двухступенчатой схеме. При этом входной код разбивается на две группы по и/2 разрядов при четном и; при нечетной разрядности группы содержат неравное число переменных. Две группы переменных декодируются на первой ступени двумя полными линейными (возможно и пирамидальными) дешифраторами, а на второй ступени формируются выходные функции
10 — 4-1749
146 Комбинационные функциональные узлы компьютерной схемотехники
Усповно считают, что один из дешифраторов первой ступени формирует адреса строк матрицы, а второй — адреса столбцов матрицы. На пересечении линий строк и столбцов подключается т = 2" двухвходовых схем совпадения, которые образуют вторую, выходную ступень дешифратора. При четном п матрица вентилей квадратная, при нечетном п — прямоугольная. Поэтому такие дешифраторы назы-ваются матричными или прямоугольными.
Запишем систему выходных функций полного дешифратора “из 4 в 16" в виде следующих сокращенных обозначений:
Л.)=Д0^0’ ^8~fl2^0’ ^12=fl3^O’
F5-axb}\ F^a2bx' Fx3 = a3bx-
(4.0)
F3~rt0F; F6-t2]Z)2; F\o~a2b2, F\A-a3b2\
F3^aob3, Fj - axb3; Ftl=a2b3; FX5=a3b3.
где введены двухразрядные функции а, и Ь,, которые реализуются дешифраторами строк и столбцов соответственно:
t\=X2Xx, Ьг~Х2Хх, Ь.-Х2Х,', (4 6)
«0-ВД; ах-Х4Х3, а2 = Х4Х3, а3=Х4Х3.
Схема прямоугольного дешифратора на основе уравнений (4.5) и (4.6) показана на рис 4 6.
Рис. 4.6. Схема прямоугольного дешифратора
При большом числе разрядов прямоугольный дешифратор почти в и/2 раза экономичнее линейного и в два раза — пирамидального.
4.1.5. Многоступенчатые дешифраторы. Каскадирование дешифраторов
Принцип построения многоступенчатых дешифраторов состоит в последовательном разбиении входного многоразрядного кода до получения в каждой группе двух-трех разрядов. В качестве примера на рис. 4.7 показано разбиение дешифри-
4.2. Шифраторы 147
руемого кода для п = 10 и п = 13. После этого многоступенчатая схема дешифратора изображается в виде соединения ряда линейных схем.
Рис. 4.7. Разбиение входного дешифрируемого кода на группы: а — при п = 10; б — при п = 13
Под каскадированием (наращиванием) понимают способ соединения дешифраторов в виде микросхем средней степени интеграции для получения большей
разрядности входного кода. Соединение двух трехразрядных дешифраторов для
декодирования четырехразрядного кода показано на рис. 4.8.
Рис. 4.8. Каскадирование дешифраторов
Входные переменные Хъ Х2 и Х3 подаются параллельно на входы обоих дешифраторов: переменная Х4 подается непосредственно на вход стробирования W первого дешифратора, через инвертор — на вход стробирования второго дешифратора.
Такая каскадная схема работает следующим образом. Если значение старшего разряда входного кода Х4 = 0, то в работу включается первый дешифратор с инверсными восемью выходами Lo, ..., L2, при этом второй дешифратор блокирован (выключен) и на его выходах £8, ..., £,5 устанавливаются высокие уровни. При Х4 = 1 блокируется первый дешифратор и включается в работу вторая микросхема.
Таким образом, благодаря наличию стробирующего входа два трехразрядных дешифратора образуют схему дешифрации четырехразрядного кода.
4.2. Шифраторы
4.2.1. Общая характеристика шифратора
Шифратором называется функциональный узел компьютера, предназначенный для преобразования входного m-разрядного унитарного кода в выходной n-разрядный двоичный позиционный код. Двоичные шифраторы выполняют функцию, обратную функции дешифратора. При активизации одной из входных линий дешифратора на его выходах формируется код, отображающий номер активного входа. Полный двоичный шифратор имеет т = 2'1 входов и п выходов. Условные графические обозначения шифраторов на схемах показаны на рис. 4.9.
10*
148 Комбинационные функциональные узлы компьютерной схемотехники
Рис. 4.9. Условные графические обозначения иифратора: а — на функциональных схемах;
б — на принципиальных схемах
Функция шифратора обозначается буквами CD (coder). Входы шифратора нумеруются последовательными десятичными цифрами 0, 1, т-1, а метки
выходов отображают веса выходных двоичных переменных 1, 2"
В цифровых устройствах шифраторы используются для следующих операций: преобразования унитарного входного кода в выходной двоичный позиционный код; ввода десятичных дан
ных с клавиатуры; указания старшей единицы в слове; передачи информации между
различными устройствами при ограниченном числе линий связи.
4.2.2. Приоритетный шифратор клавиатуры
Одно из основных применений шифратора — ввод данных с клавиатуры, например, десятичных цифр. Нажатия клавиши с десятичной цифрой 0, 1, ..., 9 должны приводить к передаче в цифровое устройство двоично-десятичного кода этой цифры. Для этого используется неполный шифратор “из 10 в 4”.
Шифраторы, которые при одновременном нажатии нескольких клавиш вырабатывают код только старшей цифры, называются приоритетными. Приоритетные шифраторы, предназначенные для поиска старшей (левой) единицы в слове и формирования на выходе двоичного номера искомого разряда, называются указателями старшей единицы. Их применяют в устройствах нормализации чисел с плавающей запятой, в системах с приоритетным обслуживанием запросов на прерывание работы компьютера.
Логика работы приоритетного шифратора на восемь входов представлена в табл. 4.3, где приняты следующие обозначения: Fo, F[,...,F1 — входные инверсные сигналы, записанные в порядке возрастания приоритета: Fo — самый низкий, /ч — самый высокий; _¥3, Х2, ¥, — выходной инверсный позиционный код; W— сигнал стробирования; Р — функция, указывающая на поступление входного сигнала; V — функция, указывающая на отсутствие входных сигналов.
Таблица 4.3
W F. F, F, F. F. F2 Fo X. 2G *1 р V
1 X X X X X X X X 1 1 1 1 1
0 1 1 1 1 1 1 1 1 1 1 1 1 0
0 1 1 1 1 1 1 1 0 1 1 1 0 1
0 1 1 1 1 1 1 0 X 1 1 0 0 1
0 1 1 1 1 1 0 X X 1 0 1 0 1
0 1 1 1 1 0 X X X 1 0 0 0 1
0 1 1 1 0 X X X X 0 1 1 0 1
0 1 1 0 X X X X X 0 1 0 0 1
0 1 0 X X X X X X 0 0 1 0 1
0 0 X X X X X X X 0 0 0 0 1
4.2. Шифраторы 149
В табл. 4.3 значения входных переменных справа от диагонали, образованной цифрами 1, не должны определять выходной код (они обозначены крестиком). Это объясняется тем, что сигнал с большим приоритетом блокирует запросы с меньшими приоритетами.
Из табл. 4.3 получаем выражения для выходного кода шифратора Х3, Х2, X, и функций V и Р, которые соответственно определяют отсутствие информационных сигналов на всех выходах и наличие сигнала хотя бы на одном входе. Для упрощения выражений используем тождество F, v FlFk = F( v Fk и законы де Моргана:
Х2 = W v WY}F3F2 v 17F7F6F5 v HT7F6F4;
X} = WvWY}F3F2 v WY,F3Ft v WF2Fb v WF2F3F^
P = WvWY{Y2; V =W vY^Y2WvY{vY2-, Y^F^F^- Y2=F3F2FXFQ.
На основе этих выражений построена схема приоритетного шифратора “8 —> 3” (рис. 4.10).
Рис. 4.10. Схема приоритетного шифратора “8 —> 3”
При W = 1 работа схемы блокируется и независимо от сигналов на входах на инверсных выходах получаем: Х3Х2Х, = 111, Р=1, V -1. Если, например, F6=0 и F2 = 0 , то схема формирует на выходах код номера входа со старшим приоритетом: Х3Х2Хх = 001 или в прямом коде Х3Х2Хх = 1102 = 6|0. Активное состояние выхода
150 Комбинационные функциональные узлы компьютерной схемотехники
отображается значениями функций Р =0 и V =1, которые передаются в процессор, а также используются при каскадировании шифраторов. Схема, изображенная на рис. 4.10, является аналогом шифратора К555ИВ1.
4.2.3. Каскадирование шифраторов
Каскадирование шифраторов используется для увеличения разрядности входного слова. Схема каскадирования двух восьмивходовых шифраторов К555ИВ1 для приоритетного обслуживания 16-разрядного слова Ft5 -Fo показана на рис. 4.11.
Рис. 4.11. Каскадирование двух восьмивходовых приоритетных шифраторов
Разряды Fl5 -Fg старшего байта входного слова поступают на первый шифратор CD1, а разряды F7 - Fo младшего байта подаются на второй шифратор CD2. Вход 7^5 имеет наивысший приоритет, a Fo — наинизший. Информационные выходы обоих шифраторов объединяются с помощью логических элементов ИЛИ, образуя трехразрядный инверсный код Z3Z2Zj. Значение старшего разряда Z4 обеспечивается непосредственно сигналом Рг
Информация с выходов первого шифратора подается на входы элементов ИЛИ с помощью схем совпадения ЛИ1 при /1= 1 (микросхема CD1 воспринимает входные данные, a CD2 — заблокирована). Информация с выходов второго шифратора подается на входы элементов ИЛИ с помощью схем совпадения ЛИ2 при V2 = 1 (микросхема CD2 воспринимает входные данные, CD\ — блокируется).
Схема работает следующим образом: когда на входе имеется активный сигнал из старшего байта входного слова, например, F14 =0 (Р1 = 0 И1 = 1), то работает шифратор CF1 и на выходах элементов ИЛИ формируется инверсный код Z4Z3Z2Zj =0001, что соответствует прямому значению Z4Z3Z2Z, = 1110 = 1410. Если активный входной сигнал относится ко младшему байту слова, например, F6 = 0, то
4.3. Мультиплексоры и демультиплексоры 151
работает шифратор CD2 (Р1 = 1, /1 = 0, V2 = 1) и на инверсных выходах формируется код =1001, что соответствует прямому числу Z4Z3Z,Z, = 01 10 = 6|(|.
4.3. Мультиплексоры и демультиплексоры
4.3.1. Общая характеристика мультиплексоров
Мультиплексором называется функциональный узел компьютера, предназначенный для поочередной коммутации (переключения) информации от одного из п входов на общий выход. Номер конкретной входной линии, подключаемой к выходу в каждый такт машинного времени, определяется адресным кодом Ло, Ait А„ ,.
Связь между числом информационных и и адресных т входов определяется соотношением п = 2'". Таким образом, мультиплексор реализует управляемую передачу
данных от нескольких входных линий в одну выходную.
Условное графическое обозначение мультиплексоров показано на рис. 4.12. Функция мультиплексоров записывается буквами MUX (multiplexor).
Рис. 4.12. Условное обозначение мультиплексора: а - на функциональных схемах; б - на принципиальных схемах
Мультиплексоры применяют для следующих операций: коммутации как отдельных линий, так и групп линий (шин); преобразования параллельного кода в последовательный; реализации логических функций; построения схем сравнения, генераторов кодов.
Мультиплексор символически часто обозначают: “л-1”.
Логика работы четырехвходового мультиплексора представлена в
табл. 4.4, где Ао, А\ — адресный код; Fo, F}, F2, F3 — выходы внутреннего дешифратора; Хо, Xt, Х2, Х2 — входная информация; D — общий информационный выход.
Таблица 4.4
Ад Fo f2 F3 D
0 0 1 0 0 0 FoX)
0 1 0 1 0 0 FX
1 0 0 0 1 0 f2x2
1 1 0 0 0 1 FX
На основе табл. 4.4. выражение для выходной функции D можно представить с использованием выходов F0~F3 внутреннего дешифратора в виде:
D = F(Xo v FjjYj v F2X2 \/ F-..X 3, (4.7)
или с минтермами адресного кода:
О = А\ Ао v Zj А0Х) v А\ А,.: Х2 \у А, А о Х3. (4 8)
Схемы мультиплексоров, соответствующие уравнениям (4.7) и (4.8), показаны на рис. 4.13.
152 Комбинационные функциональные узлы компьютерной схемотехники
Рис. 4.13. Схемы мультиплексоров: а — с внутренним дешифратором; б — с адресными минтермами
При построения схемы мультиплексоров с внутренним линейным дешифратором требуются логические элементы с меньшим числом входов, однако при этом увеличивается время установления выходного сигнала. При исключении дешифратора быстродействие повышается, однако требуются схемы совпадения с большим числом входов
4.3.2. Каскадирование мультиплексоров
В интегральном исполнении мультиплексоры выпускают на четыре, восемь или шестнадцать входов. Каскадирование позволяет реализовать коммутацию произвольного числа входных линий на базе серийных микросхем мультиплексоров меньшей разрядности.
Пример построения схемы мультиплексора на 16 входов на основе типовых четырехвходовых мультиплексоров показан на рис. 4.14.
Младшие разряды адреса At, Ао подключаются к адресным входам всех мультиплексоров первого уровня, на выходах которых вырабатываются следующие функции:
А = № v F\X\ v F2X2 х/ FyXy,
D{ —FХа v F\XS v ^2^6 v FyXi',
D'2 — FXs v FX> v F-X\ 0 v FyX\ 1 '>
D'3 ~ FXn v v ^12^14 v FX\s,
4.3. Мультиплексоры и демультиплексоры 153
где Fo-F3 — выходы внутренних дешифраторов: Fo= А,. ; Ft=A,A0; F2= AtAn; /'.= At А»; .AGs-JVo — входные переменные.
Старшие разряды адреса А3, А2 подаются на адресные входы мультиплексора второго уровня, на выходе которого формируется окончательная функция
D = Ft; D'o v F; D\ v F,' £>' v F’ D\ , где внутренние выходы дешифратора определяются следующими минтермами: Fo' = А2 А2', F{ = А2 А2; F2 = А3А2; F2 = А3 А2 .
Пусть, например, значение адреса А3 А2 А} Ао = 10112 = Ню- При этом функция младшей части адреса принимает значение F3 = At Ао = 1 и на выходах мультиплексоров первого уровня одновременно формируются сигналы D'o = F3 Xlt D' = F,F7, D'2 = F3 A'n, D’3 = F2X\5. Функция старшей части адреса F2 = А3А2 = 1 обеспечивает передачу на выход значение сигнала 1У2, то есть
F - F,' D'2 = F'2F2Xw =АъТ2А{АйХи.
4.3.3 Реализация логических функций мультиплексорами
С помощью мультиплексоров реализуются логические функции с числом переменных т, равным разрядности адресного кода. Выполняемая функция должна быть представлена в СДНФ. При этом переменные поступают на адресные входы, а информационные входы используются как настроечные — на них подаются константы нуля и единицы в зависимости от реализуемой функции.
Выходная функция трехадресного мультиплексора на восемь входов описывается уравнением:
F(A) = А., ф А(,Х$ А2 A., Aq Xt v А2 А । AqХ2 \/ А2 A i Aq Х2 v
v А2 Д, AqXj v А2 AjAtj Х$ v А2 А । А,, Х<, v А2 А \ Aq Х2.
Если требуется получить логическую функцию с десятичными эквивалентами минтермов 1, 3, 5 и 7, то на четные входы Хо, Х2, Х4 и Х6 необходимо подать кон
станту “0”, а на нечетные Х\, Хъ, Xs и (рис. 4.15):
/1) A, А,АП\/ A7AtAov
v А2 A] Aq v А2 А1 Aq.
С помощью дополнительных логических преобразований можно реализовать логические функции с числом переменных т+l, то есть на единицу больше разрядности адресного кода мультиплексора.
Возможны и другие схемотехнические применения мультиплексоров. Мультиплексор может выполнять функции преобразователя //-разрядного двоичного параллельного кода в последовательный.
— константу “1”. В результате получаем
Рис. 4.15. Схема мультиплексора для реализации логической функции трех переменных с десятичными эквивалентами минтермов 1,3,5 и 7
154 Комбинационные функциональные узлы компьютерной схемотехники
Для этого требуется подать параллельный код на информационные входы мультиплексора и затем изменять код на адреса в необходимой последовательности.
4.3.4 Мультиплексирование шин
Мультиплексирование шин — это поочередное переключение шин (групп линий) от нескольких источников информации к одному приемнику. Такие микрооперации реализуются схемами на основе мультиплексоров одиночных линий. При выборе количества и типа мультиплексоров учитывают следующее:
• число коммутируемых шин равно 2т, где т — длина адресного кода;
• г-й номер входа всех мультиплексоров служит для подключения разрядов определенной одной шины.
Схема мультиплексора четырех Ди), К(и), Z(w) и 5(и) шин показана на рис. 4.16. Для ее построения требуется и двухадресных четырехвходовых мультиплексоров, где и — произвольная разрядность коммутируемых шин.
Л
S2Z2Y2X.
.1.1 J,
1 J? *11
Ж
Ж
-L 1? ,L «L
A MUX /
W1
Рис. 4.16. Мультиплексор шин
4.3.5. Общая характеристика демультиплексоров
Демультиплексором называется функциональный узел компьютера, предназначенный для коммутации (переключения) сигнала с одного информационного входа D на один из и информационных выходов. Номер выхода, на который в каждый такт машинного времени передается значение входного сигнала, определяется адресным кодом Д0,Д|,Д2,...,Л,„_1. Адресные входы т и информационные выходы и связаны соотношением и = 2'" или т = log2n.
Демультиплексор выполняет функцию, обратную функции мультиплексора. Применительно к мультиплексорам и демультиплексорам пользуются также термином “селекторы” данных. В условных графических обозначениях (рис. 4.17) функция демультиплексора обозначается буквами DMX.
Рис. 4.17. Условные графические обозначения демультиплексоров: а — на функциональных схемах; б — на принципиальных ^хемах; в — типовое соединение с мультиплексором
4.3. Мультиплексоры и демультиплексоры 155
Демультиплексоры используют для следующих операций:
• коммутации как отдельных линий, так и многоразрядных шин;
• преобразования последовательного кода в параллельный;
• реализации логических функций и др.
Демультиплексоры часто обозначают: “1 —>п ”.
Логика работы двухадресного демультиплексора на языке микроопераций представлена в табл. 4.5, где D — информационный вход; Fo, Ft,F2viF} — выходы внутреннего дешифратора адреса.
Таблица 4.5
А, Ад Fo F, Fi F3 х» х, Xi X2
0 0 1 0 0 0 F0D — — —
0 1 0 1 0 0 — FD — —
1 0 0 0 1 0 - - f2d —
1 1 0 0 0 1 - - - F3D
По данным табл. 4.5 записываем систему уравнений для информационных выходов:
Хо = FaD = Д ДD- X, = F,D = ДАо£);
X2=F2D=Ai1<)D;X3=F3D=AiA0D;
На основе уравнений (4.9) построены схемы демультиплексоров с внутренним дешифратором (рис. 4.18, а) и с совмещением адресных и входных переменных на трехвходовых элементах И (рис. 4.18, б).
Рис. 4.18. Схема демультиплексоров:
а — с внутренним дешифратором; б — с совмещением адресных и входных переменных
Схема демультиплексора с совмещением адресных и входных переменных обеспечивает высокое быстродействие, однако требует применения логических элементов с большим числом входов.
1 56 Комбинационные функциональные узлы компьютерной схемотехники
4.3.6. Каскадирование демультиплексоров
Каскадирование позволяет реализовать коммутацию одного входного сигнала на произвольное число выходных линий на базе серийных микросхем меньшей разрядности. Пусть требуется реализовать демультиплексирование входного сигнала на и выходных линий, определяемых m-разрядным адресным кодом, на базе типовых микросхем меньшей размерности вида “1 -^п”.
Для этого следует использовать L = п/п, типовых демультиплексоров с числом адресных входов т\ = log2 щ каждый. Число старших адресных разрядов, равное разности т - mlt используется дополнительным “ведущим” демультиплексором, который располагается в первом уровне схемы каскадирование. Ведущий демультиплексор определяет поочередное включение одного из L микросхем демультиплексоров второго уровня. Каскадирование демультиплексоров вида “1 ->4” для реализации коммутатора “1 —> 16” показано на рис. 4.19.
Рис. 4.19. Каскадирование демультиплексоров
Пусть для схемы (рис. 4.19) адресный кодЛ^/Мо = ЮЮ и значение входного сигнала 0=1. Тогда на выходе ведущего демультиплексора D2 = A3A2D = 1, а на остальных выходах устанавливаются нулевые значения. Единичное значение сигнала D', передается на выходку ведомого демультиплексора согласно соотношению
Х10 = А। А() D2 ~ А3 А2А\ AqD.
Демультиплексоры не выпускаются как самостоятельные изделия на интегральных микросхемах. Функцию демультиплексора обычно реализуют на дешифраторах, имеющих входы стробирования (дешифраторы-демультиплексоры).
4.3.7. Демультиплексирование шин
Под демультиплексированием шин понимается поочередное переключение групп линий от одного источника информации ко многим приемникам. Такие микрооперации реализуются обычно на основе демультиплексоров одиночных линий. При выборе количества и типа демультиплексоров учитывают:
• число коммутируемых шин равно 2т, где т — длина адресного кода;
• количество используемых демультиплексоров определяется разрядностью и демультиплексируемых шин;
• адресные входы всех мультиплексоров параллельно объединяются.
4.4. Схемы сравнения и контроля 157
Схема демультиплексора входной шины £>(//) на четыре выходные шины Х(п), Y(n), Z(n) и S(„) показана на рис. 4.20
Рис. 4.20. Демультиплексор шин
Типовое включение мультиплексоров и демультиплексоров для коммутации входных и выходных шин //-разрядных регистров Л, В, С и D показано на рис. 4 21
Рис. 4.21. Типовая коммутация входных и выходных шин регистров АЛУ
В АЛУ такая коммутация обеспечивает использование в качестве первого операнда сумматора содержимого любого регистра и запись результата операции в любой регистр, указанный микропрограммой выполняемой команды.
4.4. Схемы сравнения и контроля
4.4.1. Общая характеристика схем сравнения
Схемой сравнения (компаратором) называется функциональный узел компьютера, предназначенный для выработки признаков отношений между двоичными словами (числами). Признаки отношений записываются в виде:
F, := А*К или F, rA или F/(*A;
F,:=A*B или F, или F(*w,
где А и В — двоичные или двоично-десятичные числа; К — двоичная константа; i — номер отношения (часто пропускается); * - операция отношения вида =, #, <, >, <, > и т. д.; F, — функция, задающая результат отношения: лог. 1 — если отношение выполняется, то есть истинно, и лог. 0 — если отношение не выполняется, то есть ложно. Функция компаратора обозначается буквами COMP (comparator) или знаками = =.
158 Комбинационные функциональные узлы компьютерной схемотехники
Основными отношениями считаются: “равно” FA.K, “больше” FA>t} и “меньше” FA<I1. Часто схемы, реализующие отношения FA>I} или FA<ji, называют схемами сравнения “на больше” или “на меньше". Располагая основными признаками отношений, можно на их основе получить ряд дополнительных признаков, например:
Fa в ~ ^а=в S Fa<b=Fa>h\ FAsB = FA/j v F,tB-
Признаки отношения используются как логические условия (осведомительные сигналы) в микропрограммах, командах передачи управления, а также в устройствах контроля и диагностики. После выполнения каждой команды в машине автоматически формируются признаки результатов операции. Эти признаки, называемые флагами (флажками), помещаются в специальный регистр флагов. К флагам обычно относят признаки нулевого результата, переполнения разрядной сетки, знак результата, наличие переносов из старшего разряда сумматора, четное или нечетное число единиц в результате и др.
Отметим, что формирование и использование признаков (флажков) — это основное отличие компьютера от калькулятора. Только с помощью флагов машина принимает решение про ход вычислительного процесса, то есть обладает интеллектуальными свойствами.
4.4.2. Схемы сравнения слов с константой
Примем, что требуется получить признаки отношений двоичного слова А=А2АtA0 со следующими заданными константами:
Ft:=(A=000); F2:=(A=lll) и F3 := (Л<011).
На основе табл. 4.6 значения признаков отношения слова А с константами запишутся в виде:
F\ ~ Л4Л; f2=a2A\Aq, f2 = a2 (4.10)
Схема сравнения слова с константой согласно выражениям (4.10) показана на рис. 4.22.
Таблица 4.6
Аг Л1 Ао F, F2 F
0 0 0 1 0 1
0 0 1 0 0 1
0 1 0 0 0 1
0 1 1 0 0 1
1 0 0 0 0 0
1 0 1 0 0 0
1 1 0 0 0 0
1 1 1 0 ' 1 0
4.4.3. Схемы сравнения двоичных слов А и В
Многоразрядные двоичные слова равны, когда одновременно попарно равны все их разряды, то есть Л(и) = 5(и), если А, = Bt, i = 1, 2, ..., п.
4.4. Схемы сравнения и контроля 159
На основе табл. 4.7, задающей условие равенства г, двух z-x разрядов А и В, получим:
г, = 2,13,4 А1В1 = А,® В, = М, , (4.11)
где М, — функция сложения по модулю два (“Исключающее ИЛИ").
Схемная реализация функции (4.11) показана на рис. 4.23.
Таблица 4.7
А, В, г,
0 0 1
0 1 0
1 0 0
1 1 1
Рис. 4.23. Элемент “Исключающее ИЛИ": а — схема; б — условное обозначение
Признак равенства двух zz-разрядных слов Р4.в определяется логическим произведением поразрядных условий г,:
Ъ=в = r„r^t ... = Мп -М^...МХ. (4.12)
Схема сравнения двух четырехразрядных слов А и В согласно выражению (4.12) показана на рис. 4.24. Схема включает четыре логических элемента “Исключающее ИЛИ” и один конъюнктор.
При большой разрядности сравниваемых слов можно на первом уровне получить при
Рис. 4.24. Схема сравнения двух четырехразрядных слов А и В
знаки для четырехразрядных групп и на втором уровне реализовать общий флаг логическим умножением групповых признаков. На
пример, при разрядности сравниваемых слов и = 16 получим четыре групповых при
знака сравнения.
’ 1 4 , г4 5 8 , г, 9 12 . г413 16
’ ГА = В > Г А=В ’ ГА=В ’
где верхние индексы обозначают номера разрядов в группах. Тогда признак сравнения двух 16-разрядных слов запишется в виде:
Z7 - Z714 .//58 .^912 ^13,16
1 Л-Ц ГА=В гА=В ГА=В гА-И
Схема сравнения двух 16-разрядных слов показана на рис. 4.25, а.
Сравнение может быть реализовано и на других схемотехнических принципах. Схема сравнения двух четырехразрядных чисел А и В на основе дешифратора и мультиплексора показана на рис 4.25, б. Дешифратор вырабатывает единичное значение сигнала на том выходе, номер которого также определяется десятичным эквивалентом входного кода. Например, при А4А3 А2А\ = 0111 логическая единица появится на выходе с номером семь Мультиплексор подключает к выходу тот вход, номер которого также определяется десятичным эквивалентом входной комбина-
160 Комбинационные функциональные узлы компьютерной схемотехники
ции. Если В4 В3 В2В, =0111, то разрешается прохождение на выход сигнала с седьмого входа. Таким образом, если слова А и В равны, то формируется флаг FA-K = 1
Л .4, л2 Я,
б
Рис. 4.25. Схема сравнения двух слов на равенство: а — групповая структура; б — на основе дешифратора и мультиплексора
4.4.4. Схемы сравнения двух слов “на больше”
Схема сравнения двух слов А и В “на больше” по абсолютному значению вырабатывает признак FA,B и строится по следующему алгоритму:
• анализ неравенства слов Л и В выполняется последовательно в направлении от старших разрядов к младшим;
• младшие разряды включаются в анализ в том случае, если старшие разряды равны (эквивалентны),
• для получения признака строится дизъюнктивная сумма поразрядных
условий.
Логика сравнения
Таблица 4.8
Я, в, С, Г,
0 0 0 1
0 1 0 0
1 0 1 0
1 1 0 1
разрядов А и В представлена в табл. 4.8, где С, — признак А, >В,; г, — условие подключения к анализу соседних младших разрядов обоих слов.
На основе табл. 4.8 получаем такие выражения:
С, = Л В,,/; =Л,В, v4B, =Л, ©В, =М, (4.13)
С учетом выражения (4 13) и алгоритма анализа функцию признака FA,B представляем в виде'
Fa>B ~ G; v rn^n-\ v v rnrn-\ (4.14)
Для сравнения двух четырехразрядных слов “на больше” признак неравенства согласно выражению (4.14) представляем следующим образом.
4.4. Схемы сравнения и контроля 161
fa>b = с4 v г4С3 V г4г2С2 V г4г2г2С, = _ _ _--------------------------- (4.15)
= А4Ва vМлА3Вз vМлМзА2В2 vМаМзМ2А{В\.
Схема сравнения “на больше” двух четырехразрядных слов А и В согласно соотношению (4.15) показана на рис. 4.26.
Рис. 4.26. Схема сравнения двух слов “на больше"
4.4.5. Многоразрядные схемы сравнения “на больше”
При реализации схем сравнения многоразрядных слов “на больше” возникают технические трудности, связанные с необходимостью использования вентилей с большим количеством входов. Поэтому сравниваемые слова разбиваются на группы, состоящие, например, из четырех разрядов. Каждая группа вырабатывает свой признак неравенства и условие подключения к анализу М\-р младшей группы согласно выражению (4.15) и схеме (рис. 4.26). Например, для п = 16 имеем четыре группы, которые объединяются согласно соотношению
fa>b(4.16) где — флаг сравнения “на больше” в самой старшей группе с разрядами А|6-А13, В]6--й,3 и Л/гр = М16М15М}4М[3 — условие для подключения к анализу соседней младшей группы; Р*А>В — флаг сравнения “на больше” в группе с разрядами Л12-Л|9, ВГВР и Л/гр = М{2МпМ[0Мч — условие анализа младшей группы; F2A.B— флаг сравнения “на больше” в группе с разрядами Л8-Л5, Й8-/Л и Л/2гр = = — условие подключения младшей группы; F'a>b — флаг сравнения “на
больше” в группе с разрядами Аа-А\, В4-В,.
Схема сравнения “на больше” двух 16-разрядных слов А и В на основе уравнения (4.16) показана на рис. 4.27.
II .4-1749
*
162 Комбинационные функциональные узлы компьютерной схемотехники
Рис. 4.27. Схема сравнения “на больше" двух 16-разрядных слов
4.4.6. Применение компараторов
Контроль (обнаружение) и коррекция (исправление) результатов операций является важным условием грамотной эксплуатации машин. Контроль может быть программным или аппаратным. К аппаратным методам относятся дублирование операций и восстановление входных сигналов.
Контроль операций сложения методом дублирования реализуется двумя одинаковыми сумматорами (SM), на входы которых одновременно поступают слагаемые Л(п) и В(п). Оба результата ^(/z) и S2(n) поступают на входы схемы сравнения (рис. 4.28, а).
a б
Рис. 4.28. Применение схемы сравнения для контроля операций
4.4. Схемы сравнения и контроля 163
Если оба результата равны, то на выходе схемы сравнения значение признака /-\1-v2 = 1 и ошибок нет При нулевом значении признака операцию следует повторить или остановить работу ЭВМ.
Схема контроля методом восстановления входных сигналов показана на рис. 4.28, б. Двухразрядное слово А2А} декодируется и значение унитарного кода с выходов дешифратора поступает на входы шифратора. При правильной работе дешифратора и шифратора входной код A2At должен совпадать с выходным кодом шифратора В?В> При этом на выходе схемы сравнения установится единичное значение признака
При передаче информации из одного регистра в другой контроль правильности пересылки может осуществляться поразрядным сравнением содержимого этих двух регистров. На рис. 4 28, в показан один из вариантов контроля пересылок слов между регистрами После передачи информации из регистра А в регистр В (или наоборот) проводится сравнение их содержимого. Если значения двух слов совпадают, то признак равенства принимает единичное значение, в противном случае — вырабатывается сигнал ошибки.
4.4.7. Общая характеристика схем контроля четности
В компьютерах широко используется контроль четности (синоним — по паритету или соответствию). Этот способ основан на допущении, что в двоичном числе чаще всего возникают одиночные ошибки — потеря или появление лишней единицы. В обоиЛ случаях число единиц изменится на одну. Если двоичное число имело нечетное количество единиц, то после одиночной ошибки оно окажется четным и наоборот.
На практике контроль четности осуществляется следующим образом Для повышения эффективности контроля двоичное слово разбивается на части, как правило, байты. К каждому байту добавляется дополнительный контрольный разряд Содержимое контрольного разряда зависит от выбранного способа контролю (по четности или нечетности). При контроле по четности значение контрольного разряда выбирается таким, чтобы общее число единиц в байте и контрольном бите было четным. В этом случае значение контрольного (паритетного) бита определяется сложением по модулю два значений разрядов байта (рис. 4 29, а):
FK4 = А,® А2® А.® А4® As® Ап® А, ® А,,,. (4.17)
Яч 8 7 6 5 4 3 2 1
0 1 0 1 0 1 1 ] 1
1 1 1 1 0 1 1 0 J 0
a
ГМ-8 I 7 ! о
М
О
1
1
1
О
О
б
t—
Рис. 4.29. Контроль байта: а — по четности; б — по нечетности
В результате операции сложения по модулю два значений разрядов байта с четным числом единиц получаем значение контрольного байта ?’кч - 0. При сложении по модулю два значений разрядов байта с нечетным числом единиц значение контрольного байта FK ч = 1.
и*
164 Комбинационные функциональные узлы компьютерной схемотехники
При контроле по нечетности значение контрольного бита выбирается из условия, чтобы количество единиц в байте с учетом содержимого контрольного разряда было нечетным. В этом случае значение контрольного бита определяется следующим выражением:
fkh=4®4®4®^®4®A®4®4^k4- (4.18)
На практике контроль нечетности используется чаще, поскольку он фиксирует полное пропадание информации. Контроль четности (нечетности) предполагает формирование значений контрольных разрядов до выполнения операции и проверку байта после выполнения операции с учетом контрольных разрядов. Например, при записи байта в память компьютера одновременно автоматически формируется (генерируется) значение его контрольного разряда. При считывании хранимого байта осуществляется сложение по модулю два значений его разрядов совместно с контрольным битом согласно принятому способу контролю четности или нечетности. Таким образом, контроль по паритету требует использования дополнительных разрядов.
Схемы, которые обеспечивают получение значения контрольного разряда и проверку двоичного числа по признаку четности или нечетности, называются схемами контроля четности. Их часто называют схемами свертки, схемами контроля по модулю два, схемами контроля по паритету. Для получения условия четности (4.17) требуется сложение по модулю два восьмиразрядного слова, что реализуется с помощью ступенчатого включения двухвходовых элементов “Исключающее ИЛИ”:
• на первом уровне получают функции F\ - F4:
^|=Л|Фу42; F2=43©t44; F3 = А5®А6; F4 = А7®А$; (4.19)
• на втором и третьем уровнях реализуются функции:
F5 = Fi®F2; F6 = F3®F4; М = Fs®Fb. (4.20)
Функция М согласно выражениям (4.19) и (4.20) принимает значение лог. 1 при нечетном числе единиц во входном байте и значение лог. 0 — при четном числе единиц во входном байте.
Для задания признака контроля вводится управляющий сигнал F, который вместе с сигналом Мпоступает на входы схемы “Исключающее ИЛИ” в четвертом уровне. На прямом и инверсном выходах этого уровня формируются прямое и инверсное значения контрольного разряда:
F = M®V; F = M®F.
Логика работы схемы контроля, показанной на рис. 4.30, а, представлена в табл. 4.9.
Таблица 4.9
Входы А8- А। V F F
На входах: Четное число единиц 0 0 1
Нечетное число единиц 0 1 0
На входах: Четное число единиц 1 1 0
Нечетное число единиц 1 0 1
4.4. Схемы сравнения и контроля 165
а б
Рис. 4.30. Схемы контроля по четности: a — ступенчатое включение элемента "Исключающее ИЛИ"; б — условное обозначение
Из табл. 4.9 видно, что при V = 0 на выходе F генерируется значение контрольного разряда для контроля четности, при V = 1 на выходе F генерируется значение контрольного разряда для контроля нечетности.
Пример схемы контроля нечетности пересылок байта от источника информации (ИИ) к приемнику информации (ПИ) показан на рис. 4.31.
Рис. 4.31. Контроль пересылок байта
Схема контроля на стороне источника информации выступает как генератор значения контрольного разряда нечетности Fm. Схема контроля на стороне приемника информации обеспечивает сложение по модулю два значений разрядов принятого байта совместно с принятым контрольным битом нечетности. Прием информации возможен только при выполнении условия нечетности Гпи = 1 на стороне приемника.
166 Комбинационные функциональные узлы компьютерной схемотехники
4.5. Преобразователи кодов
4.5.1. Общая характеристика преобразователей кодов
Преобразователем кода называется функциональный узел компьютера, предназначенный для преобразования двоичного кода из одной формы в другую.
Для представления информации используют разнообразные двоичные и двоично-десятичные коды, прямой, обратный, дополнительный и их модификации, циклический с избытком три и др. Существует множество кодов, которые обеспечивают.
• простоту выполнения арифметико-логических операций;
• удобство перевода чисел из десятичной системы в двоичный код,
• надежность выполнения заданных алгоритмов функционирования и эффективный контроль результатов вычислений,
® уменьшение аппаратных затрат при построении цифровых устройств.
Наиболее распространенными являются прямой, обратный и дополнительный коды, которые обеспечивают представление знака числа и замену операции вычитания сложением (табл. 4.10). К преобразователям кода относятся шифраторы и дешифраторы, однако по традиции эти функциональные узлы выделены в отдельные самостоятельные классы
Таблица 4.10
Коды тля положительных чисел Коды для отрицательных чисел
десятичный -'0 прямой обратный дополнительный десятичный прямой обратный дополнительный
0.000 0,000 0,000 0 1,000 1,111 0,000
• 1 0,001 0,001 0,001 -1 1,001 1,110 1,111
4-2 ___ 0,010 0,010 0,010 -2 1,010 1,101 1,110
0,011 0,011 0.011 -3 1,011 1,100 1,101
+4 и, 100 0,100 0,100 —4 1,100 1,011 1,100
0,101 0,101 0,101 -5 1,101 1,010 1,011
4 6 >,110 0,110 0,110 -6 1,110 1,001 1,010
7 7 0,111 0,111 0,111 -7 1,111 1,000 1,001
Прямой, обратный и дополнительный коды используются для записи знака числа, замены операции вычитания чисел сложением их кодов, а также для определения переполнения разрядной сетки. Для представления знака числа в них отводится знаковый разряд, который располагается слева от числа и отделяется запятой В знаковый разряд записывается нуль — для положительного числа и единица — для отрицательного.
4.5.2. Преобразователь прямого кода в обратный
В прямом двоичном коде А’ПР - АЛЗН А7,,^, ..., Х{ один разряд, обычно старший, отображает знак числа, остальные — значение цифровых разрядов; при этом для положительного числа Адн = 0, а для отрицательного Хзн - 1. Обратный код положи
4.5. Преобразователи кодов 167
тельного двоичного числа совпадает с прямым кодом, а для отрицательного числа
цифровые разряды прямого кода инвертируются.
В процессе преобразования прямого кода в обратный значение знакового разряда Jf3H используется в качестве управляющего сигнала, который обеспечивает получение следующего выражения:
Yi = X3UXt v Хзн - Хзн © Xt , (4.21)
где Yt — значение z-ro разряда обратного кода; Х,— значение z-ro разряда положительного входного числа (Хзн = 0); X,— значение z-ro разряда отрицательного входного числа (Хзн = 1).
Схема пятиразрядного преобразователя прямого кода в обратный, построенная на элементах “Исключающее ИЛИ” соответственно выражению (4.21), показана на рис. 4.32.
Рис. 4.32. Схема преобразователя прямого кода в обратный
4.5.3. Преобразователь прямого кода в дополнительный
Дополнительный код положительного двоичного числа совпадает с его прямым и обратным кодами. Дополнительный код отрицательного двоичного числа образуется из его обратного кода добавлением к младшему разряду единицы. Таким образом, операция преобразования прямого кода в дополнительный не является поразрядной и выполняется значительно сложнее, чем получение обратного кода.
Соответствие между прямым и дополнительным кодами на примере четырех цифровых разрядов (беззнаковых) представлено в табл. 4.11.
Таблица 4.11
Прямой код Дополнительный код Прямой код Дополнительный код
х4 X Х2 Xt y4 Уз Уг У, х4 Хз Хг X, У< Уз Уг у.
0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0
0 0 0 1 1 1 1 1 1 0 0 1 0 1 1 1
0 0 1 0 1 1 1 0 1 0 1 0 0 1 1 0
0 0 1 1 1 1 0 1 1 0 1 1 0 1 0 1
0 1 0 0 1 1 0 0 1 1 0 0 0 1 0 0
0 1 0 1 1 0 1 1 1 1 0 1 0 0 1 1
0 1 1 0 1 0 1 0 1 1 1 0 0 0 1 0
0 1 1 1 1 0 0 1 1 1 1 1 0 0 0 1
Знаковый разряд прямого кода используется в качестве управляющего сигнала: если Хзн = 0, то выходной код повторяет значение входного; при Jf3H = 1 реализуется преобразование согласно табл. 4.11.
Карта Карно, соответствующая табл. 4.11, для получения минимальных форм функций преобразования прямого кода в дополнительный показана на рис. 4.33.
168 Комбинационные функциональные узлы компьютерной схемотехники
Рис. 4.33. Карта Карно для функций преобразователя прямого кода в дополнительный: a— Y1;6— Y3; в— Y3;e — Y4
На основе карт Карно с учетом знакового разряда прямого кода для функций У,, Yi, У3, У4, представляющих выходы преобразователя, получаем:
^зн ~ ^зн; = -^i; У2 = ^2 ® Хзн;
У3-ЛЛз©(Х2 V Y4=X4®(X3v Х2 vX{)X3li.
В общем виде для У, справедливо уравнение:
Y, = Xt Ф v Xt2 v... v X.) Хзн. (4.23)
Схема преобразователя прямого кода в дополнительный на основе выражений (4.22) и (4.23) показана на рис. 4.34, а. Данный преобразователь характеризуется высоким быстродействием. Время установления выходного кода определяется тремя задержками распространения сигнала, однако по мере возрастания номера разряда линейно возрастает и требуемое число входов используемых элементов ИЛИ.
a б
Рис. 4.34. Схемы преобразователей прямого кода е дополнительный
Второй вариант схемы преобразователя (рис. 4.34, б) использует только двухвходовые элементы ИЛИ, при этом дизъюнктивная сумма переменных образуется последовательным способом. В такой реализации схема преобразователя упрощается, однако время установления выходного кода существенно увеличивается.
Практическое правило получения дополнительного кода состоит в том, что справа от первой единицы (учитывая и саму единицу) в прямом коде числа значения разрядов — неизменны, а слева от единицы (кроме знакового) — инвертируются. Например, для прямого кода 10100100 дополнительным будет код 11011100.
Для преобразования в дополнительный код многоразрядных двоичных чисел часто используют перевод числа в обратный код с последующим прибавлением единицы к его младшему разряду с помощью сумматора.
4.5. Преобразователи кодов 169
4.5.4. Преобразователь двоичных чисел в код Грея
Код Грея образован последовательностью двоичных чисел, в которых два любых соседних числа отличаются только одним разрядом (табл. 4.12). Первое и последнее число считаются соседними. Код Грея, называемый также цикличным, относится к невзвешенным двоичным кодам.
К достоинствам кода Грея относят: удобство кодирования угловых перемещений; простота кодирующей логики; сокращение времени преобразования в связи с изменением значения только одного разряда; высокая эффективность защиты от сбоев. Недостатками кода Грея являются затруднения при выполнении арифметических операций и цифро-аналоговых преобразований. Поэтому при необходимости код Г рея преобразуют в двоичный код.
Таблица 4.12
х4 х. Хг X, Л !з h /| Х4 Х3 Х1 х, Л h h
0 0 0 0 0 0 0 0 1 0 0 0 1 1 0 0
0 0 0 1 0 0 0 1 1 0 0 1 1 1 0 1
0 0 1 0 0 0 1 1 1 0 1 0 1 1 1 1
0 0 1 1 0 0 1 0 0 0 1 1 1 1 1 0
0 1 0 0 0 1 1 0 1 1 0 0 1 0 1 0
0 1 0 1 0 1 1 1 1 1 0 1 1 0 1 1
0 1 1 0 0 1 0 1 1 1 1 0 1 0 0 1
0 1 1 1 0 1 0 0 1 1 1 1 1 0 0 0
По данным табл. 4.12 в клетки карт Карно (рис. 4.35) внесены значения разрядов Ц кода Г рея.
Рис. 4.35. Карта Карно для кода Грея: а — Л, б — 12, в —13, г —14
С помощью карт Карно получаем следующие выражения для разрядов кода Грея:
1Х = Х2ХЛ v Х2Хх = Хх ®Х2; I2=X3X2vX3X2 = Х2 © Х3.
(4.24)
13 = ^Х4Х3 = Х3 ®Х4; 14 =Х4.
Схема преобразователя прямого кода в код Грея на основе соотношений (4.24) показана на рис. 4.36.
По аналогичной методике, используя табл. 4.12 и новые заполнения карт Карно, получаем обратное преобразование кода Грея в прямой код:
Хх =1Х ®12®13®14, Х2=12®13®14, Х3=13®14, Х4—14. (4.25)
170 Комбинационные функциональные узлы компьютерной схемотехники
Схема преобразования кода Грея в прямой код на основе соотношений (4.25) показана на рис. 4.37.
Рис. 4.36. Преобразователь прямого кода в код Грея
Рис. 4.37. Преобразователь кода Грея в прямой код
4.5.5. Преобразователь двоично-десятичных чисел в код семисегментного индикатора
Визуальное отображение двоично-десятичных чисел часто выполняется с помощью семисегментных индикаторов на основе электролюминисцентных приборов, жидких кристаллов или светодиодных матриц. Количество семисегментных индикаторов определяется разрядностью чисел, отображаемых на световом табло — обычно шесть и белее десятичных цифр.
Выводимый из компьютера десятичный код отображаемой цифры поступает на вход двоично-десятичного преобразователя, выходы которого а, Ь, с, ..., g подключаются к соответствующим сегментам индикатора (рис. 4.38, а).
Рис. 4.38. Подключение преобразователя к индикатору (а) и отображение цифр (б)
Единичное значение выходного сигнала преобразователя вызывает свечение сегмента, подключенного к этому выходу. Комбинации единичных сигналов на выходах преобразователя образуют изображение десятичной цифры в своем разряде (рис. 4.38, б).
4.5. Преобразователи кодов 171
Соответствие между двоично-десятичным числом и необходимыми для отображения десятичной цифры наборами сегментов представлено в табл. 4 13.
Таблица 4.13 '
х4 Ху Хг х, a ь с d е / к Х4 Ху хг X. a h с d е / А'
0 0 0 0 1 1 1 1 1 1 0 0 1 0 1 1 0 1 1 0 1 1
0 0 0 1 0 1 1 0 0 0 0 0 1 1 0 1 0 1 1 1 1 1
0 0 1 0 1 1 0 1 1 0 1 0 1 1 1 1 1 0 0 0 0 0
0 0 1 1 1 1 1 1 0 0 1 1 0 0 0 1 1 1 1 1 1 1
0 1 0 0 0 1 1 0 0 1 1 1 0 0 1 1 1 1 1 0 1 1
На основе данных табл. 4.13 и после их минимизации с помощью карт Карно получаем систему логических уравнений для сегментов преобразователей кодов:
a ~ Х2 v X, v X, Х3 v X, Х3;
b = X}X2v Х'Х2 v Х3 V X.;
с - Х{ v Х2 v Х3 v Х4;
d = Х{Х2 v Х2Х3 v X,Х3 v Х,Х2Х3 v Х4;
e = XtX2 vX,J3;
f = Х{Х2 v XtX3 v Х2Х3 v Az4;
g = X,X2v X,X3 v X2X, v X4
Схема преобразователя двоично-десятичного кода в управляющие сигналы семисегментного индикатора локазана на рис 4 39.
Рис. 4.39. Схема преобразователя кода “8421" в код семисегментного индикатора (для выходов а, Ь, с)
4.5.6. Двоично-десятичные преобразователи
В компьютерах широко используется двоично-десятичное кодирование, в котором каждая десятичная цифра изображается четырехразрядным двоичным кодом, то есть тетрадой двоичных символов. Количество различных двоично-десятичных кодов определяется числом возможных комбинаций по десять из 16 комбинаций, которые допускаются тетрадой Десятичные числа могут представляться в коде “с избытком 3”, в коде с весом “5421" или “2421” (код Айкена) и др.
Наиболее распространенным является код прямого замещения “8421”, в котором каждая десятичная цифра 0, 1, ..,9 заменяется ее двоичным эквивалентом 0000, 0001, ..., 1001. Такой код называют также взвешенным Д-кодом. Например,
172 Комбинационные функциональные узлы компьютерной схемотехники
число 72910 в двоично-десятичном коде записывается в виде трех тетрад: 0111001010012-ю
Для Д-кодов разработаны машинные алгоритмы операций сложения, вычитания, умножения, деления и других. Операции над десятичными числами (десятичная арифметика) входят в состав команд компьютеров различных классов.
Особенностью Д-кодов является наличие десяти разрешенных и шести запрещенных комбинаций двоичных символов в тетраде. Появление запрещенной комбинации при выполнении операций над числами свидетельствует о возникновении ошибки или же о необходимости коррекции результата.
В разрядной сетке машины двоично-десятичные коды представляются в форме с плавающей или фиксированной запятой. При этом отрицательные числа отображаются в прямом, обратном или дополнительном кодах. Для Д-кодов не выполняется условие получения обратного кода инвертированием разрядов тетрады.
Применение Д-кодов в компьютерах не требует выполнения разного рода преобразований: двоично-десятичных чисел в двоичные и наоборот. Например, с помощью шифратора обеспечивается сравнительно простой способ ввода в машину десятичных цифр двоично-десятичным кодом.
Значение одной тетрады Д-кода, дополнение тетрады до девяти “9-Д” (обратный код) и до десяти “10-Д” (дополнительный код), а также коды с “избытком 3” и с весом “5421" представлены в табл. 4.14
Таблица 4.14 '
Код Д Код “9-Д” Код “10-Д” Код “Д+3” Код “5421”
Х4 Ху хг х. г4 Уз У1 У| /з F3 F2 F, 2$ 2^ 2i 2\ Е4 Еу Ег Е{
0 0 0 0 0 0 0 1 0 0 10 0 0 11 0 10 0 0 10 1. 0 110 0 111 10 0 0 10 0 1 10 0 1 10 0 0 0 111 0 110 0 10 1 0 10 0 0 0 11 0 0 10 0 0 0 1 0 0 0 0 10 10 10 0 1 10 0 0 0 111 0 110 0 10 1 0 10 0 0 0 11 0 0 10 0 0 0 1 0 0 11 0 10 0 0 10 1 0 110 0 111 10 0 0 10 0 1 10 10 10 11 110 0 0 0 0 0 0 0 0 1 0 0 10 0 0 11 0 10 0 0 10 1 0 110 0 111 10 0 0 110 0
Систему минимальных логических выражений обратного двоично-десятичного кода получаем с помощью карт Карно (рис. 4.40), в которые вносятся значения разрядов У|-У4 по данным табл. 4.14.
Рис. 4.40. Карты Карно для получения обратного Д-кода;
знаком “х” помечены неопределенные наборы: а — Y,, б — Y2, в — Y3, г — Y»
4.6. Двоичные сумматоры 173
На основе карт Карно получаем систему уравнений для разрядов У! - У4 обратного Д-кода:
Y^X}; Y2=X2; Y3=X2®X3; Y4=X4X3X2=X^X^Jx'2. (4.26)
Из выражений (4.26) следует, что значение второго разряда тетрады прямого и обратного Д-кодов совпадают. Схема преобразователя прямого Д-кода в обратный на основе соотношений (4.26) показана на рис. 4.41, а.
Рис. 4.41. Схемы преобразователей Д-кода в обратный:
а — на основе логических уравнений; б — с использованием элемента "Исключающее ИЛИ"
а
Возможен и другой способ построения преобразователя Д-кода в обратный: вначале инвертируются цифры всех тетрад (получается код с избытком шесть) и затем производится вычитание из каждой тетрады числа минус ОНО, что эквивалентно добавлению в дополнительном коде плюс 1010 (без учета переносов между тетрадами). Например, А = —148, прямой Д-код £Л]Пр = 1 0001 0100 1000; после инвертирования имеем: [Л]*ПР = 1 1110 1011 0111; после прибавления плюс 1010 к каждой тетраде получаем значение обратного Д-кода: [Л]Об = 1 Ю00 0101 0001.
Схема преобразователя на основе инвертирования и коррекции тетрад показана на рис. 4.41, б. В данной схеме инвертирование значений разрядов тетрад осуществляется логическими элементами “Исключающее ИЛИ", а коррекция реализуется типовой микросхемой четырехразрядного комбинационного сумматора. Дополнительный Д-код тетрады получается из обратного прибавлением единицы к младшему разряду.
4.6. Двоичные сумматоры
4.6.1. Общая характеристика сумматоров
Сумматором называется функциональный узел компьютера, предназначенный для сложения двух n-разрядных слов (чисел). Операция вычитания заменяется сложением слов в обратном или дополнительном коде. Операции умножения и деления сводятся к реализации многократных сложений и сдвигов. Поэтому сумматор является важной частью арифметико-логического устройства. Функция сумматора обозначается буквами SM или L.
174 Комбинационные функциональные узлы компьютерной схемотехники
Сумматор состоит из отдельных схем, которые называются одноразрядными сумматорами; они выполняют все действия по сложению значений одноименных разрядов двух чисел (операндов). Сумматоры классифицируются по следующим признакам:
• способу сложения — параллельные, последовательные и параллельнопоследовательные;
• числу входов — полусумматоры, одноразрядные и многоразрядные сумматоры;
• организации хранения результата сложения — комбинационные, накапливающие, комбинированные;
• организации переноса между разрядами — с последовательным, сквозным, параллельным или комбинированным переносом (с групповой структурой);
• системе счисления — позиционные (двоичные, двоично-десятичные, троичные) и непозиционные, например, в системе остаточных классов;
• разрядности (длине) операндов — 8-, 16-, 32-, 64-разрядные;
• способу представления отрицательных чисел — в обратном или дополнительном кодах, а также в их модификациях;
• времени сложения — синхронные, асинхронные
В параллельных //-разрядных сумматорах значения всех разрядов операндов поступают одновременно на соответствующие входы одноразрядных суммирующих схем. В последовательных сумматорах значения разрядов операндов и перенос, который запомнился в предыдущем такте, поступают последовательно в направлении от младших разрядов к старшим на входы одного одноразрядного сумматора. В параллельно-последовательных сумматорах числа разбиваются на части, например, байты, разряды байтов поступают на входы восьмиразрядного сумматора параллельно (одновременно), а сами байты — последовательно, в направлении от младших к старшим байтам с учетом запомненного переноса
В комбинационных сумматорах результат операции сложения запоминается в регистре результата. В накапливающих сумматорах процесс сложения объединяется с хранением результата. Это объясняется использованием 7-триггеров как одноразрядных схем сложения.
Организация переноса практически определяет время выполнения операции сложения. Последовательные переносы схемно образуются просто, однако являются медленнодействующими. Параллельные переносы схемно организуются значительно сложнее, однако дают высокое быстродействие.
Разрядность сумматоров находится в широких пределах: 4-16 — для микро- и мини-компьютеров и 32-64 и более — для универсальных машин.
Сумматоры с постоянным интервалом времени для сложения называются синхронными. Сумматоры, в которых интервал времени для сложения определяется моментом фактического окончания операции, называются асинхронными. В асинхронных сумматорах имеются специальные схемы, которые определяют фактический момент окончания сложения и сообщают об этом в устройство управления. На практике преимущественно используют синхронные сумматоры
Сумматоры характеризуются следующими параметрами:
• быстродействием — временем выполнения операции сложения /v, которое отсчитывается от начала подачи операндов до получения результата, часто
4.6. Двоичные сумматоры 175
быстродействие характеризуется количеством сложений в секунду имея в виду операции типа регистр-регистр (то есть числа хранятся в регистрах АЛУ);
• аппаратными затратами: стоимость одноразрядной схемы сложения определяется общим числом логических входов используемых элементов; стоимость многоразрядного сумматора определяется общим количеством используемых микросхем;
• потребляемой мощностью сумматора.
4.6.2. Одноразрядные сумматоры
Одноразрядным сумматором называется логическая схема, которая выполняет сложение значений i-x разрядов X, и Y, двоичных чисел с учетом переноса Z, из младшего соседнего разряда и вырабатывает на выходах функции результат S, и
перенос Р, в старший соседний разряд. На основе одноразрядных схем сложения на
три входа и два выхода строятся многоразрядные сумматоры любого типа Алгоритм работы одноразрядного сумматора отображается таблицей истинности [табл. 4.15). На основе табл. 4.15 записывается система логиче- Таблица4.15
ских функций для результата 5, и переноса Р, в СДНФ. s, = vj,y;z, vx,^z, vx,y,z,,- (4.27) Д =X,YlZ, vX,Y,Z, vX^Z, VX^Z,. (4.28) Минимизация функций (4.27) и (4.28) с помощью карт Карно показана на рис. 4.42. Л[ Y, X, Y, 00 01 11 10 /Z, 00 01 11 10 i 0 1 0 1 | 0 0 0 j fT] j J 1 0 1 _L_ 0 . L JL 1Л J 1 0 Щ 1 Ш 1 О , 1 a б х, Y, Z, S, р,
0 0 0 0 0
0 0 1 1 0
0 1 1 0 1 0
0 1 0 1
1 0 0 1 0
1 0 1 0 1
1 1 0 0 1
1 1 1 1 1
Рис. 4.42. Карты Карно для минимизации функций: а — S,; 6 — Р,
Как видно из карт Карно, функция результата S, не минимизируется, а функция Р, минимизируется с понижением ранга конъюнкции и использует только прямые значения переменных:
/)=^vI,Z,V};Z,=^vkv^. (4 29)
При проектировании комбинационных одноразрядных сумматоров учитывают следующие факторы:
• схема должна характеризоваться регулярностью (одинаковостью) структуры и минимальной стоимостью, то есть иметь по возможности наименьшее число логических входов всех элементов,
• с целью повышения быстродействия многоразрядного сумматора требуется минимальное время получения функции переноса /п =• k tP, где к — число последовательно включенных элементов от входов к выходам Р, или Pt, гР — средняя задержка распространения сигнала одним логическим элементом в выбранной серии интегральных микросхем; параметр к часто на
176 Комбинационные функциональные узлы компьютерной схемотехники
зывают каскадностью (этажностью) схем. Таким образом, для минимизации времени получения переноса необходимо уменьшить каскадность схемы и использовать интегральные микросхемы с малым временем задержки распространения сигнала;
• для схем одноразрядных сумматоров на основе уравнений (4.27) и (4.28) необходимо вырабатывать как прямые Р„ так и инверсные Pt значения функции переноса. Такая организация переносов называется парафазной.
Для построения схемы одноразрядного сумматора на универсальных логических элементах НЕ И уравнения (4.27) и (4.28) преобразуются на основе правил двойной инверсии и де Моргана к следующему виду:
S, = XXZ-XX.Z.-XXZ,-X^Z,; Р, = ~ХХ • ~X^Zi • \Zt. (4.30)
Схема одноразрядного сумматора, построенная на элементах НЕИ соответственно уравнениям (4.30), показана на рис. 4.43, а; ее стоимость, измеряемая числом логических входов всех элементов, составляет 27, каскадность к = 3.
Уравнения (4 27) и (4.28) могут быть выражены через функцию “Исключающее ИЛИ”:
S, = (X, © YI)ZI v (^, © jjz, = X, ©, Y®ZI; (4.31)
Р, = XX, v (X,Y, v X,Y,)Zl = X,Y, v (x, © Y,)z,. (4.32)
Схема одноразрядного сумматора на элементах “Исключающее ИЛИ” согласно уравнениям (4.31) и (4.32) показана на рис. 4.43, б; ее стоимость составляет восемь входов и каскадность к = 2
Функции одноразрядного сумматора — самодвойственны, то есть их инверсии образуются инвертированием значений аргументов без изменения местонахождения знаков дизъюнкции и конъюнкции, например, для переноса из уравнения (4.28):
р,=ххх vXXX, ^ХХХ^ХХХ- (4.зз)
Умножая левые и правые части соотношения (4.33) на макстерм (X,vy,vZ,), получают:
Р,Х, vPXvP'Z, = XX,Z, \zX,Y,Z, vXXZr (4.34)
После подстановки левой части соотношения (4.34) в правую часть выражения (4 27) получают уравнения для функции S, с использованием собственного переноса.
S, = PtX, ^РХ^ P.Z, vХУЛ (4.35)
Схема одноразрядного сумматора соответственно уравнениям (4.35) и (4.29) показана на рис. 4.43, в; ее стоимость равна 17 входов, каскадность к = 2. Важным свойством этой схемы является использование только прямых значений входных переменных и однофазной цепи формирования переноса Р, в старший разряд.
Полусумматором называется логическая схема, которая выполняет сложения значений z'-x разрядов X, и Y, двоичных чисел X и Y и реализует на выходе значение результата М, и перенос в старший соседний разряд R,:
М^ХХ^ХХ^Х,®^- Rt=XX. (4.36)
Таким образом, полусумматор выполняет лишь часть задачи суммирования в z-м разряде, поскольку не учитывает перенос из соседнего младшего разряда. Схема полусумматора, построенная на основе уравнений (4.36), показана на рис. 4.44. Из уравнений (4.31) и (4.32) следует, что схема одноразрядного сумматора может
4.6. Двоичные сумматоры 177
быть построена на основе двух полусумматоров и дополнительного логического элемента ИЛИ, как показано на рис. 4.44, в.
Рис. 4.43. Схемы одноразрядных сумматоров: а — на элементах НЕ И;
б — на элементах “Исключающее ИЛИ”; в — с использованием собственного переноса
Рис. 4.44. Схемы суммирования: а, б — полусумматор и его условное обозначение; в, г — одноразрядный сумматор и его условное обозначение
12-4-1749
178 Комбинационные функциональные узлы компьютерной схемотехники
4.6.3. Последовательный многоразрядный сумматор
Последовательный двоичный многоразрядный сумматор включает в себя, «-разрядные сдвиговые регистры операндов А' и У, регистр результата S, одноразрядный сумматор SM и двухступенчатый D-триггер для запоминания переноса. Все регистры обеспечивают одновременный сдвиг вправо, в сторону младших разрядов (рис. 4.45).
Рис. 4.45. Схема последовательного многоразрядного сумматора
В последовательном сумматоре попарная подача значений разрядов X, и У, начинается с младших разрядов. Образуются значения суммы S, и переноса РИ которые записываются соответственно в регистр результата и в триггер запоминания переноса на один такт Тс.
Последовательное сложение выполняется за столько тактов, сколько разрядов в числе. Поэтому время сложения определяется соотношением: ~ пТс, где rc — длительность машинного такта.
Отрицательные числа рекомендуется представлять в дополнительном коде.
Последовательный сумматор требует минимальных аппаратных затрат, однако длительность операции сложения пропорциональна разрядности операндов Поэтому последовательный сумматор можно использовать в относительно медленнодействующих цифровых устройствах.
4.6.4. Параллельные многоразрядные сумматоры
Параллельный многоразрядный сумматор содержит « одноразрядных схем
4.6. Двоичные сумматоры 1 79
Значения всех разрядов двух чисел X и Y поступают на входы соответствующих одноразрядных сумматоров параллельно (одновременно). В параллельных сумматорах с последовательным переносом значение сигнала переноса Р, передается от разряда к разряду последовательно во времени (асинхронно). При использовании обратного кода перенос из самого старшего разряда подается на вход переноса младшего разряда по цепи циклического переноса (рис. 4.46, а). При использовании дополнительного кода цепь циклического переноса разрывается, а на вход переноса младшего разряда подается логический нуль.
В параллельных сумматорах с последовательным переносом время сложения определяется соотношением:
= (п-1) Гп + ts , где /и — время формирования переноса в каждом разряде, ts — время сложения в самом старшем разряде. В худшем случае возможен вариант, когда сигнал переноса последовательно распространяется от первого до /г-го разряда.
4.6.5. Параллельные сумматоры с параллельными переносами
Для повышения быстродействия сумматоров используют //-разрядные сумматоры с параллельными переносами. При этом сумматор разбивается на две части: собственно схему сложения и схему выработки ускоренных переносов (СУП). Схема сложения содержит п упрощенных одноразрядных сумматоров SM на три входа и только на один выход суммы S,; они могут строиться по выражениям типа (4.27), (4.30) и т.д.
Схема ускоренных переносов вырабатывает сигналы переноса Р, одновременно во всех разрядах на основе уравнений, которые учитывают значение переменных X, и Y, как в данном разряде, так и в предыдущем младшем. Например, перенос Р, в первом (младшем) разряде является функцией переменных X, и У, и внешнего переноса Z]:
Pi=f](Xi,Yl,Zl) = Z2.
Для второго разряда функция переноса Р2 записывается в виде:
р2 =/2(x2,y2,z2) = /2(x2,y2,xi,y,zl) = z3.
Аналогично для z-го разряда
P^f{Xl,Yl,X,_},Yl-},-.X},Y}X^ = Zl^
а в последнем (старшем) разряде имеем:
Для уменьшения аппаратных затрат при построении схемы и сокращении записи функций переноса Р, вводят две вспомогательные функции: генерации (порождения) переноса в z-м разряде R, = X,Y< и распространения (транзита или передачи) переноса через z-й разряд. Функция транзита имеет две эквивалентные по результатам применения формулы: М, = X,®Y, — из неминимизированного уравнения переноса (4.30) и F, = Х1\Х1 — из минимизированного уравнения переноса (4.29). Перенос из z-го разряда в старший генерируется при условии, что /?, = X,-Y, = 1, то есть Р, = 1 при Xt = У, = 1. Сигнал переноса из младшего разряда передается транзитом в старший при условии, что Z, = 1 и М, = Xt®Y, = 1 или F, - X,vy, = 1. С учетом
12’
180 Комбинационные функциональные узлы компьютерной схемотехники
функций переноса и транзита уравнения (4.29) и (4.30) запишутся соответственно в виде:
р = X.Y. v (Xi v K)Z, = 7?,. v FZ,;
' ' ' v ' '7 ' ' ' ' (4.37)
= Xft v (Xi Ф Yi)Zi = 7?,. v 7H,.Z,..
Для образования в сумматоре параллельных (одновременных) переносов необходимо, чтобы уравнения (4.37) строились с учетом значений переменных всех младших разрядов. Это достигается последовательной подстановкой в каждую функцию переноса Р, вместо переменной Z, ее значение Р,_! в направлении от младших к старшим разрядам:
Д = 7?! v FiZ] = Z2;
Р2 = Т?2 v F2Z2 =R2vF2P} =R2vF2R} v F2F}Z} = Z3;
P3 = P, v F3Z3 = R3 v F3P2 = R3v F3R2 v F3F2R} v F^F^ - Z4;
P4 = P4 v F4Z4 = T?4 v F4F3 =
= P4 v F4F3 v F4F37?2 v F4F3F2P, v F4F3F2F,Z, = Z5. (4.38)
Для i -го разряда:
P, = R< vFJ^R,-, у...уХХ}...Р^.
Схема четырехразрядного сумматора с параллельными переносами между разрядами на основе системы уравнений (4.38) показана на рис. 4.47.
Рис. 4.47. Схема четырехразрядного сумматора с параллельными переносами
Для выработки функций генерации R}-R4 и транзита F]-F4 использовано по четыре логических элемента соответственно И и ИЛИ, которые показаны на схеме пакетным изображением.
Время сложения в схеме (рис. 4.47) вычисляется по формуле = tr + /п, где учтены задержки при выработке сигналов генерации tr = tp, переноса t„ = tp и сложения ts = 2/р. С учетом этого /i=4zp. Например, для гр = 5 нс имеем: F = 20 нс. Таким образом, длительность операции сложения в данном сумматоре не зависит от числа
4.6. Двоичные сумматоры 181
разрядов п, если не учитывать ухудшение временных характеристик логических элементов при увеличении числа входов и нагрузки на выходе.
В четырехразрядном сумматоре элементы И ИЛИ в схеме переносов вместе имеют 30 входов совпадения. В 32-разрядном сумматоре общее число входов совпадения в элементе И ИЛИ составит 6550. Поэтому строить многоразрядные сумматоры с параллельными переносами сложно по конструктивно-технологическим причинам В схемотехнике часто используют частично параллельные переносы: «-разрядный сумматор разбивается на к групп по т разрядов в группе (обычно т = 4). Перенос между группами может быть последовательным, параллельным или сквозным.
Для построения w-разрядных сумматоров с параллельными переносами в группе для т = 4 (первый уровень) и универсальными способами переносов между группами в уравнении (4.38) выделяют вспомогательные функции генерации переноса из группы
G, = R3 vF4R3 vF4F3R2 vF4F3F2R} (4.39)
и транзита через группу
H}=F4F3F2F}. (4.40)
С учетом формул (4.39) и (4.40) уравнение для параллельного переноса и первой группы имеет вид:
= Р3 = vHXZ{.
По аналогии записывают уравнения для Gt, Я, и Д, где / = 1,2, ..., к.
Для организации универсальных способов переносов в схему (см. рис. 4.47) включают дополнительные схемы выработки функций G„ Н, и L, (рис. 4.48).
Рис. 4.48. Сумматор с универсальными выходами переносов: а — схема для G,; 6 — условное обозначение первой группы сумматора
С помощью функций G,, II,, L, реализуют следующие способы переносов между группами:
• последовательный, если используется выход/,, (рис. 4.49);
• параллельный, если используются выходы G, и Я,;
• сквозной с использованием выхода Я,.
Во всех этих случаях в группах используют параллельный перенос.
182 Комбинационные функциональные узлы компьютерной схемотехники
Рис. 4.49. Сумматор с параллельными переносами в группах и последовательными — между группами
Время сложения в сумматоре (рис. 4.49) определяется задержками сигналов последовательного переноса 2(к- 1)/р и выполнения действия в последнем разряде группы ts = 2tp, то есть = 2(к- 1)гр + 2гр. Например, для к = 8, Гр = 5 нс имеем: - 14/р + 2гр = 16гр = 80 нс.
Параллельные переносы между группами сумматора (второй уровень параллелизма) реализуют на основе системы уравнений, описывающих функцию переноса С, в каждую старшую группу с учетом уравнений (4.39) и (4.40) (по аналогии с параллельными переносами первого уровня — между разрядами в группе):
G = GjvH.C,; С, =Z,;
С3 = G2 vН2С2 = G2 vHfi, nH2HxC}-,
С4 = G3 v Н3С3 = G3 vH3G2 vH3H2G} у Н3Н2Н}Сй
С4 = G4 у Н4С4 = G4 у H4G3 у HJ13G2 у у Н4 Н3Н2Н}С,.
(4.41)
В уравнениях (4.41) выделяют функции генерации переноса D и транзита Vдля обеспечения третьего уравнения параллелизма:
D = G4 у H4G3 у H,H3G2 у HJIilhGi, V = H,H3H2H}. (4.42)
Реализация функций С2-С4, а также D и Н на логических элементах И ИЛИ, И показана на рис. 4.50, а. На их основе проектируется СУП (рис. 4.50, б)
Рис. 4.50. Реализация функций С2, С3, Ct, D и V: а — схемы; б — условное обозначение микросхемы СУП
4.6. Двоичные сумматоры 183
Микросхема CRU (символ функции СУП) в сериях ТТЛШ обозначается как ИПЧ, например, КР1533ИПЧ. Она имеет входы и Я„ i = 1, 2, 3, 4, на которые поступают сигналы генерации и транзита от четырехразрядных сумматоров с параллельными переносами между разрядами в группах (см. рис. 4.49). С выходов микросхемы CRU сигналы ускоренного переноса С2, С3 и С4 подаются соответственно на входы переноса С второй, третьей и четвертой (старшей) групп сумматоров.
Таким образом, с помощью микросхемы CRUстроится 16-разрядный сумматор с параллельными переносами в четырехразрядных группах и между группами (рис. 4.51).
Рис. 4.57. Схема блока 16-разрядного сумматора SM16 с параллельными переносами в четырех группах и между группами
Время сложения в этом сумматоре определяется задержками сигналов: генерации (или транзита) tG = 2/р в группе; переноса из CRU tc = 2tp и времени выполнения действия в последнем разряде четвертой группы ts = 2/р. Таким образом, h = tG + tc + ts = 67Р. Для /р = 5 нс имеем время сложения t = 30 нс.
Схема 64-разрядного сумматора с третьим уровнем параллелизма строится на основе системы уравнений, полученных по аналогии с соотношениями (4.41) и (4.42):
К2 = A v ИСТ,; С, = Z,;
)?3=P2vK2C2=D2vK251vW1; (4-43)
Я4 = Dy v RyCy = Dy v VyD2 v Vy V2D} v Vy V2 Г, C,
Схема 64-разрядного сумматора с третьим уровнем параллелизма показана на рис. 4.52. Она содержит четыре блока сумматоров 57И16 и дополнительно одну микросхему CRU.
Время сложения в этом сумматоре определяется задержками формирования сигналов генерации (или транзита) в группах tG = 2/р, задержкой в двух схемах CRU tc = 4/р и задержкой времени выполнения действия в последнем разряде старшей группы: = tG + tc + ts = 7tp. Для tp = 5 нс имеем = 35 нс.
184 Комбинационные функциональные узлы компьютерной схемотехники
Рис. 4.52. Схема 64-разрядного сумматора с третьим уровнем параллелизма
4.6.6. Схемы для выполнения логических микроопераций
Все компьютеры могут выполнять определенный список поразрядных логических операций. Для их реализации используют отдельный блок логических операций (рис. 4.53).
Рис. 4.53. Структура блока логических операций
В простых компьютерах этот блок совмещается со схемой параллельного сумматора. Каждую логическую операцию в блоке задают кодом £3-£0, который подается на входы дешифратора. Сигналы Fl5-F0 с выходов дешифратора непосредственно управляют выбором определенной логической операции. Составим список буле-
вых выражений для шести поразрядных логических микроопераций: L0(. := £0(^, v логическое ИЛИ >;
Li; := F^JV,. v У)]
4, )
< логическое НЕ ИЛИ >;
< логическое И >;
< логическое НЕ И >;
L4l := F4(X, ® < исключающее ИЛИ >;
L5l := F5 (х, ® Y,) < равнозначность >.
Каждая поразрядная логическая операция выполняется одним из определенных логических элементов ИЛИ, НЕ ИЛИ, И, НЕ И и другими. Функции L5i-LOi в каждом разряде объединяются элементом ИЛИ по формуле:
4.6. Двоичные сумматоры 185
(4.44)
Схема для реализации поразрядных логических микроопераций над z'-ми разрядами операций Х(п) и Y(ri) согласно выражению (4.44) показана на рис. 4.54.
Рис. 4.54. Схема реализации поразрядных логических микроопераций над i-ми разрядами операндов
Блок логических поразрядных операций над двумя «-разрядными операндами должен иметь п схем, аналогичных изображенным на рис. 4.54.
4.6.7. Микросхемы ALU
Промышленность выпускает микросхемы с символом функции ALU для выполнения 16 арифметических и 16 поразрядных логических микроопераций в зависимости от входных сигналов настройки. В сериях ТТЛШ 530, 531, 533, 555 и 1533 они имеют обозначения ИПЗ; в сериях ЭСЛ 100, 500 и 700 используются обозначения ИП179.
Микросхема ALU в сериях ТТЛШ имеет (рис. 4.55):
• информационные входы для представления двух четырехразрядных операндов Хи Y;
• входы настройки Е3-Ео для задания номера одной из микроопераций;
• вход М для задания типа микрооперации: М = 0 — арифметические, М = 1 — логические; _
• вход переноса С1, необходимый только при исполнении арифметических микроопераций;
• выходы: результата микрооперации F4-F,, последовательного переноса L, генерации G, транзита Н, а также выход с открытым коллектором от внутреннего компаратора для выработки признака равенства операндов Fa=B-
Рис. 4.55. Условные обозначения микросхемы ALU 1533ИПЗ
186 Комбинационные функциональные узлы компьютерной схемотехники
Перечень арифметических и логических операций, выполняемых ALU, представлен в табл. 4.16. При исполнении логических операций перенос между разрядами не используется. Арифметические операции реализуются с учетом переносов и заемов. В арифметические операции включены фрагменты логических действий. Например, запись (X vK) + XY означает, что сначала выполняется операция инверсии (Y ), затем — логического сложения (XvK) и логического умножения (X Y ), а затем полученные таким образом два числа складываются арифметически с учетом переносов.
Таблица 4.16
Дз Ег Е\ Еп Логика М=1 Арифметика M=Q
0 0 0 0 х x
0 0 0 1 XvY X + Y
0 0 1 0 XY X vF
0 0 1 1 0 -1
0 1 0 0 XY X + XY
0 1 0 1 Y (X v Y) + XY
0 1 1 0 X®Y X-Y-l
0 1 1 1 XY XY-1
1 0 0 0 XvY X + XY
1 0 0 1 X®Y X + Y
1 0 1 0 Y (X + Y) + XY
1 0 1 1 XY XY-1
1 1 0 0 1 X + Y
1 1 0 1 X vf (X v У) + X
1 1 1 0 XvY (X v Y ) + X
1 1 1 1 x X-l
Микросхема ALU выполняет операцию арифметического сложения двух четырехразрядных операндов X и Y, если на входы настройки поданы сигналы Е3Е2Е1Ео = Ю01 и М = 0. В этом случае микросхема ALU выполняет функцию сумматора. Наращивание разрядности ALU осуществляется с помощью микросхемы CRUсогласно рис. 4.51 и рис. 4.52.
4.7. Двоично-десятичные сумматоры
Двоично-десятичные сумматоры используются для обработки массивов десятичной информации по сравнительно простым алгоритмам, поскольку при этом исключаются затраты времени на перевод чисел из десятичной системы счисления в двоичную и наоборот.
4.7. Двоично-десятичные сумматоры 187
Каждая десятичная цифра X, кодирует двоичным кодом прямого замещения “8421” (двоичной тетрадой), то есть Xt = Xl4Xl3Xl2Xl} и Y, = Y,4Yl3Yl2Y,,. Например, X, = 7,о = 011 12-ю. Y, = 9io = 10012-ю; Для двухразрядных десятичных чисел:
ХХ-1 = 16,о = 0001011О2.|О; Y,Y, 1 = 28,о = 001010002.,о
Один разряд двоично-десятичного сумматора (декада) содержит четырехразрядный сумматор SM1 для получения предварительной суммы в тетраде, четырехразрядный сумматор SM2 для коррекции результата и логический элемент И ИЛИ для выработки признаков коррекции, как показано на рис. 4.56.
Рис. 4.56. Одноразрядный двоично-десятичный сумматор: а — схема; б — условное обозначение
Декада работает следующим образом. Двоичные тетрады десятичных цифр X, = Х14Х,зХ,2Х,} и Y, = Y^Y^Y^Y,! вместе с переносом поступают на входы сумматора SM1, и на его выходах образуется предварительная сумма S’,T = где
S’,Т—десятичный эквивалент тетрады (табл. 4.17).
Таблица 4.17
До коррекции После коррекции Примечание
Р' S3 s'2 s', P s4 s3 S2 s,
0 0 0 0 0 0 0 0 0 0 0<Si7-<9 Коррекция не требуется
0 0 0 0 I 0 0 0 0 1
0 0 0 1 0 0 0 0 I 0
0 1 0 0 I 0 I 0 0 I
1 0 0 0 0 0 I 0 I 0 10<Si7-< 15 Коррекция требуется: минус 10 и перенос в старшую декаду г
1 0 0 0 I 0 I 0 I I
1 0 0 0 0 0 I I I 0
1 0 1 0 I 0 I 1 1 I
1 0 1 1 0 I 0 0 0 0 16<S,T< 19 Коррекция требуется: плюс 6
1 0 1 1 1 1 0 0 0 1
1 1 0 0 0 1 0 0 1 0
1 1 0 0 I 1 0 0 1 I
188 Комбинационные функциональные узлы компьютерной схемотехники
При этом возможны три случая:
1. для значения 0 < S'lT <9 коррекция не требуется;
2. для значений 10 < S'lT < 15 требуется вычесть из предварительной суммы число 10 и выполнить перенос в старшую соседнюю декаду; вычитание числа 10 в дополнительном коде соответствует добавлению с помощью сумматора SM2 к предварительному результату числа шесть, то есть плюс 01102; признаком такой коррекции является единичное значение функции коррекции суммы и переноса
F'r=S',4S',2vS'i4S'2, (4.45)
которое реализуется элементом И ИЛИ;
3. для значений 16 < S'T < 19 на выходе сумматора SM1 возникает перенос P'lT с весом 1610. Однако в старшей декаде его значение воспринимается как 10, поэтому требуется прибавить к предварительному результату с помощью сумматора число шесть, то есть 01102.
С учетом уравнения (4.45) функцию коррекции результата и переноса можно записать в виде:
Pa = P'TvF'T = P'TvS'4S'3vS'i4S'i2.
Таким образом, во всех случаях, когда Р'1Г = 1, к предварительной сумме добавляется число плюс 01102 и формируется перенос в старший разряд.
Схема четырехразрядного двоично-десятичного сумматора с последовательным переносом в тетрадах и между декадами показана на рис. 4.57. Быстродействие таких сумматоров рассчитывают по аналогии с двоичными последовательными переносами. Для двоично-десятичных сумматоров можно использовать групповые структуры ускоренных переносов.
X,— SM} 0 1.0 0 21. X.— 5ЛЛ 0 1.0 0 5. Л’Л/10 1.0 0 1 । 8Ш 0 1.0 0
I — 2 0 У2 — 2 0 У31 — 2.0 ^41 2.0
^2 — 1.1 1 X,— 1.1 1 22 X,— 1.1 1 32 х2— 1.1 1 42
2.1 1.2 2.2 1.3 2 3 313 5.4 24 2.1 1 2 2.2 1.3 2 3 ^23 । Г'J г' L 2.1 1.2 2.2 1.3 2 3 2 1 1.2 2.2 1.3 2 3 3.43 1)4
^14 2.3 Г24 2.3 У34 — 2.3 Г44~ 2.3
z р 7 р 7 р 7 Р
Рис. 4.57. Схема четырехразрядного двоично-десятичного сумматора.
Операция вычитания в двоично-десятичном сумматоре заменяется сложением операндов в обратном или дополнительном кодах. Обратный код отрицательных десятичных чисел получают заменой каждой цифры ее дополнением до девяти. Схема одного десятичного сумматора с преобразователями прямого кода операндов и результата в обратный код показана на рис. 4.58.
Значение отрицательных чисел при Хзи = 1, Узн = 1, Хн = 1 инвертируется схемой “Исключающее ИЛИ”; при этом образуется двоичный код тетрад с избытком шесть. Коррекцию результата выполняют сумматорами SMI, SM2 и SM3, в которых
Контрольные вопросы 189
вычитание заменяется сложением двоичной тетрады с обратным кодом числа шесть, то есть плюс 10102.
Рис. 4.58. Схема одного разряда десятичного сумматора с преобразователями прямого кода в обратный
Контрольные вопросы
1. Назовите области применения дешифраторов и шифраторов.
2. Как строятся мультиплексоры и демультиплексоры шин?
3. Поясните назначение компараторов.
4. Что такое контроль по модулю два?
5. Назовите основные типы кодопреобразователей.
6. По каким признакам классифицируют сумматоры?
7. Поясните отличия в построении двоичного и двоично-десятичного сумматоров.
8. Назовите способы увеличения быстродействия сумматоров.
9. Поясните функции микросхем ALU.
10. Поясните назначение микросхемы CRU.
11. Поясните способ преобразования прямого двоично-десятичного кода в обратный.
12. Как строится последовательный многоразрядный сумматор?
13. Что такое функция генерации переноса?
14. Что такое функция транзита переноса?
15. В чем отличие синхронного сумматора от асинхронного?
16. Поясните построение матричного дешифратора.
17. Поясните принцип работы приоритетного шифратора.
18. Дайте определение типового функционального узла компьютера.
190 Цифро-аналоговые и аналого-цифровые преобразователи
Глава 5
Цифро-аналоговые и аналого-цифровые преобразователи
5.1. Цифро-аналоговые преобразователи
5.1.1. Общая характеристика цифро-аналоговых преобразователей
Цифро-аналоговые преобразователи (ЦАП) предназначены для преобразования цифровой информации в аналоговую форму в виде напряжения (иногда тока). Их используют в системах управления технологическими процессами, в аналоговых микропроцессорах, в дисплеях, графопостроителях, робототехнике.
Цифро-аналоговое преобразование состоит в том, что для входного параллельного n-разрядного кода
X = Х,2~' + Х22~2 + ... + Х,2~‘ + ... + Х„2~", где X, — цифры 0 или 1, а 2“'— вес г-го разряда, сначала получают ток 1,:, пропорциональный значению числа X, а затем преобразуют его в выходное напряжение. Значение тока Д определяется суммой эталонных токов /„ создаваемых для каждого разряда числа
/г = XJ{ + Х212 + ... + Х^ + .. + ХП1П, причем суммируются токи только тех разрядов, для которых Л) = 1. Значения эталонов тока I, пропорциональны весу позиции двоичного числа и уменьшаются в два раза при переходе от старшего г-го разряда к соседнему младшему с номером г+1.
5.1.2. Схемы цифро-аналоговых преобразователей
Структура ЦАП включает- резистивную или транзисторную матрицу для формирования эталонных токов; ключи для коммутации эталонных токов согласно входному коду к общей точке суммирования; операционный усилитель (ОУ) для преобразования тока Д в выходное напряжение; вспомогательные схемы для согласования с входными уровнями сигналов; стабилизированный источник опорного напряжения Доп-
Резистивные матрицы строят или из набора двоично-взвешенных по номиналам резисторов, или в виде лестничной (многозвенной) цепочки резисторов лишь двух номиналов R-2R. Схема ЦАП с резистивной матрицей на основе двоичновзвешенных сопротивлений вида R-2R- ...~2"~lR показана на рис. 5.1. В этой схеме сопротивление резисторов матрицы удваивается при переходе от старшего разряда к младшему, а эталонные токи уменьшаются в два раза. Например, если для первого, самого старшего разряда принять значение тока Ц = 1 мА, то для второго разряда Д = 0,5 мА, для третьего Д = 0,25 мА и т. д.
5.1. Цифро-аналоговые преобразователи 191
Рис. 5.1. Схема ЦАП со взвешенными резисторами
Ключи А") - К„ управляются уровнями напряжений, отображающих цифры “нуль” и “один” соответствующих разрядов входного кода. Источник опорного напряжения С/оп чаще всего бывает внешним, однако в некоторых случаях его встраивают в микросхему ЦАП. На входе ОУ всегда имеется практически нулевой потенциал, поэтому суммирование разрядных токов определяется соотношением
= — (Xi +2~'Х2 +2“2Jf3 + ... + 2-('",)^„) = -^^^, •2“('~,). (5.1)
A R
Напряжение на выходе ЦАП рассчитывают по формуле
t/BbIX=-ZXc=-^onE^-2"', (5.2)
i=i
где Аос = R/2 — сопротивление в цепи обратной связи усилителя.
Пример 5.1
Рассчитать напряжение на выходе ЦАП при преобразовании входного шестиразрядного цифрового кода2С = 101011. Опорное напряжение Uon = 10 В.
На основе выражения (5.2) имеем:
С/ВЬ1Х = -1о(1 • 2’’ + 0-2’2 + 1-2'1 + 0-2’4 + 1-2~5 + 1-2"6) = = -10 (2’1 + 2’3 + 2'5 + 2'6) = -6,72 В.
Основной недостаток рассмотренной структуры ЦАП — это огромный диапазон сопротивлений матрицы, особенно при большой разрядности входного кода. Схема ЦАП на основе лестничной матрицы R-2R показана на рис. 5.2. Здесь используются резисторы только двух номиналов, с помощью которых реализуются соотношения (5.1) и (5.2), то есть при переходе от старшего разряда к младшему эталонный ток уменьшается в два раза.
Для быстродействующих ЦАП токовые ключи строят на диодах и биполярных транзисторах; для преобразователей среднего и низкого быстродействия используют ключи на КМОП-структурах. Схема диодного ключа, который можно использовать в рассмотренных схемах ЦАП, показана на рис. 5.3, а.
192 Цифро-аналоговые и аналого-цифровые преобразователи
Ux, i
Рис. 5.3. Диодный ключ: а — схема; б — входной сигнал i-го разряда
Входной сигнал С7г „ отображающий цифру в разряде входного кода, является двухполярным: положительный уровень (лог. 1) закрывает диод VD1 и эталонный ток /, через диод VD2 поступает на вход ОУ; отрицательный уровень (лог. 0) закрывает диод VD2 и ток I, замыкается на источник входного сигнала J7,,.
В схемы ЦАП часто встраивают генераторы токов (ГТ), предназначенные для термостабилизации токов. Один из вариантов ГТ с обратной связью показан на рис. 5.4.
Рис. 5.4. Схема ГТ с узлом управления
5.1. Цифро-аналоговые преобразователи 193
В этой схеме транзисторы VT1-VT4 стабилизируют токи резистивной матрицы R-2R-4R-8R. Вспомогательный транзистор КЛ) вместе с усилителем образуют схему управления, которая стабилизирует токи транзисторов VT1-VT4. Изменение эталонных токов от расчетных величин контролируется по току коллектора транзистора VT0, идентичного транзисторам VT1-VT4 и находящегося с ними в одинаковых температурных условиях. Если через коллектор транзистора VTQ протекает заданный ток ZK, то сигнал коррекции с выхода ОУ не будет поступать на базы транзисторов Р7О-Р74 (баланс ОУ) и режим работы транзисторов не изменится. При отклонении /к от заданного значения на базы транзисторов VT1-VT4 будет подаваться сигнал коррекции.
5.1.3. Двоичные коды, используемые в цифро-аналоговых преобразователях
Ввод информации в ЦАП осуществляется, в основном, в параллельном коде. В ЦАП используют три основных двоичных кода: прямой, смещенный и дополнительный (рис. 5.5). Прямой код удобен при преобразовании сигналов следящих систем, так как при переходе через нуль не меняются старшие разряды кода, что позволяет реализовать линейный переход от малых положительных к малым отрицательным выходным напряжениям. Для преобразования положительных и отрицательных кодов используют знаковый разряд, который управляет переключением выходного напряжения ЦАП (рис. 5.5, а).
Для исключения из схемы ЦАП коммутирующих элементов используют смещенный код, который является наиболее простым (рис. 5.5, 6). В дополнительном коде (рис. 5.5, в) положительные числа преобразуются так же, как и в прямом коде, а отрицательные — двоичным дополнением соответствующего положительного числа (инверсия всех разрядов с последующим добавлением единицы в младший разряд).
13 — 4-1749
194 Цифро-аналоговые и аналого-цифровые преобразователи
5.1.4. Умножающие цифро-аналоговые преобразователи
Цифро-аналоговые преобразователи могут работать с постоянным или переменным опорным напряжением. Преобразователи, работающие с переменным напряжением Uon, называются умножающими. Операция умножения выполняется схемой ЦАП непосредственно в виде:
^-Аых Авх! ^вх2> (5-3)
где Хвх] = Uon, Хвх2 = -¥(АЛь Х2, Х„). На основе выражения (5.3) воспроизводится
операция умножения аналогового сигнала ХвхЛ на цифровой кодХх?-
Производительность вычислительных систем повышается, если на входах используются ЦАП, которые реализуют умножение аналоговых и цифровых сигналов Цифро-аналоговые преобразователи могут быть одно- и многоканальными, что достигается объединением в одной БИС нескольких идентичных преобразователей, работающих независимо друг от друга, либо использованием на входах и выходах ЦАП коммутаторов аналоговых и цифровых сигналов.
Структура многоканального умножающего ЦАП показана на рис. 5.6.
Рис. 5.6. Структура многоканального умножающего ЦАП
Коммутаторы аналоговых каналов АК1 и AJC2 и мультиплексор цифровых каналов MUXуправляются трехразрядными адресными кодами: АуА2А.,, В2В2В\ и С3С2С, соответственно. Если А2А2А[ = 011 и С2С2С} = 110, то получим для выхода с адресом В3В2В{ = 100 значение операции умножения С/вых4 = С/вх3 JVBx6.
Изменяя кодовые комбинации на адресных входах, можно получить любое произведение вида:
^-Аых/ ^-Аху ^-АхЛ, С j> k 1 5 ..., 8.
В умножающих ЦАП в основном используются токовые ключи на МОП-транзисторах в режимах малых напряжений и токов, что дает им возможность работать с опорным напряжением произвольного знака и формы. Выходной сигнал такого ЦАП может располагаться в любом из четырех квадрантов в зависимости от знаков, принимаемых сомножителями.
5.1. Цифро-аналоговые преобразователи 195
5.1.5. Основные параметры и характеристики цифро-аналоговых преобразователей
Основными параметрами ЦАП являются число разрядов входного цифрового кода, разрешающая способность, погрешности преобразования, диапазон выходных сигналов, динамические параметры (табл. 5.1).
Таблица 5.1
Тип микросхемы Разрядность, п Максимальное отклонение <5ЛД, % Время установления Густ, мкс Технология
К427ПА4 16 0,0015 20 КМОП
К572ПА2 12 0,025 15 Биполярная
КМ1118ПА1 8 0,75 0,02 Биполярная
К1108ПАЗ 8 0,5 0,05 Биполярная
КМ1148ПА1 10 0,75 1 Биполярная
Число разрядов п входного кода для различных типов ЦАП составляет от восьми до восемнадцати. Число разрядов определяет максимальное количество кодовых комбинаций на входе ЦАП, равное 2П.
Диапазон изменения выходного напряжения (без учета знака) определяется из соотношения (5.2) при Л) = 1, i = 1, 2, ..., п:
UBbn тах= С/Оп(2~1+2“2+...+2^')= С7оп(1-2 л), если п = 10, Uon = 10 В, то С/вь,хтах = 10 В.
Разрешающая способность h характеризуется минимальным квантом выходного напряжения, который соответствует изменению входного кода на единицу младшего разряда: h = Uon/T ~ 10 мВ для предыдущего примера.
Абсолютная погрешность преобразования <5А — отклонение выходного напряжения от расчетного в конечной точке характеристики преобразования. Типичная погрешность ЦАП не превышает ± 1/2 младшего разряда.
Нелинейность <5л— максимальное отклонение реальной характеристики преобразования от теоретической (прямой линии, соединяющей точку нуля и минимального выходного сигнала).
Дифференциальная нелинейность <5ЛД — максимальное отклонение разницы двух аналоговых сигналов соседних кодов от значения младшего разряда.
Параметры <5А, <5Л и <5ЛД выражаются в долях младшего разряда или в процентах от полной шкалы выходного напряжения.
Время установления /уст — интервал времени от подачи входного кода до момента достижения выходным сигналом установившегося значения с заданной погрешностью (обычно ±1/2 младшего разряда). Это время определяет общее быстродействие ЦАП.
В зависимости от значений параметров выделяют прецизионные (8Л <0,1%) и быстродействующие (густ < 100 нс) ЦАП.
Цифро-аналоговые преобразователи различаются структурой резистивной матрицы (взвешенные резисторы или R-2R), элементной базой, функциональной полнотой, согласующими устройствами, числом источников питания и т.п.
13*
'196 Цифро-аналоговые и аналого-цифровые преобразователи
Реализуются ЦАП в виде гибридных и полупроводниковых микросхем. Большинство микросхем ЦАП — полупроводниковые, функционально законченные. Ряд ЦАП используют внешние источники опорного напряжения и выходные операционные усилители.
Питание ЦАП может осуществляться от одного или от нескольких источников, что определяется элементной базой. Перспективами развития ЦАП являются повышение быстродействия и точности, удобство согласования с микропроцессорами, снижение потребляемой мощности.
5.2. Аналого-цифровые преобразователи
5.2.1. Общая характеристика аналого-цифровых преобразователей
Аналого-цифровые преобразователи (АЦП) предназначены для преобразования аналоговой информации (обычно в виде напряжения) в цифровой код. Используют АЦП в микропроцессорных системах, в цифровых измерительных приборах Во многом области их применения аналогичны ЦАП, поскольку они часто используются совместно, например, в автоматизированных системах управления (АСУ) (рис. 5.7).
Рис. 5.7. Аналого-цифровой и цифро-аналоговый преобразователи в контуре управления
Основными параметрами и характеристиками АЦП являются:
• число разрядов и выходного кода;
• разрешающая способность h — минимальный квант входного напряжения, за который выходной код изменяется на единицу младшего разряда;
• нелинейность <5Л— максимальное отклонение выходного кода от расчетного значения во всем диапазоне шкалы;
• абсолютная погрешность <5А — наибольшее отклонение выходного кода от расчетного в конечной точке шкалы;
• время преобразования гпр — интервал от момента начала преобразования до появления на выходе установившегося кода; часто вместо /пр быстродействие АЦП характеризуется частотой преобразования;
• диапазон и полярность входного напряжения, число источников питания, ток потребления, возможность общей работы с микропроцессорами.
В АЦП используются следующие методы преобразования:
• последовательного счета (с использованием ЦАП или с двухтактным интегрированием);
• поразрядного кодирования (последовательного двоичного приближения);
• параллельного действия (считывания);
• параллельно-последовательные (комбинированные).
5.2. Аналого-цифровые преобразователи 197
Аналого-цифровые преобразователи последовательного счета
Метод последовательного счета с применением АЦП основан на уравновешивании входного напряжения суммой эталонов, подсчитываемых счетчиком. Момент уравновешивания определяется аналоговым компаратором.
Схема АЦП последовательного счета показана на рис. 5.8, а. В ней по сигналу “Пуск” RS-триггер переключается в состояние “1” и разрешает прохождение импульсов от генератора G через элемент И на вход суммирования двоичного счетчика СП.
а б
Рис. 5.8. Аналого-цифровой преобразователь последовательного счета с ЦАП: а — схема; б — временные диаграммы работы
Нарастающий цифровой код с выхода счетчиков СТ2 преобразуется с помощью ЦАП в напряжение, которое подается на вход компаратора КОМП. На второй вход КОМП поступает измеряемое напряжение С7ВХ.
В момент равенства напряжений С7ВХ = С/ЦАП компаратор вырабатывает сигнал сброса триггера. После этого счет импульсов прекращается и на выходе счетчика СТ2 фиксируется цифровой эквивалент входного напряжения. Время преобразования /Г1р зависит от значения напряжения С7ВХ (рис. 5.8, б).
В АЦП с двухтактным интегрированием (рис. 5.9, а) преобразование реализуется за два такта.
В первом такте сигнал “Пуск” переключает RS-триггер Т\ в состояние “1”. Входное напряжение минус С7ВХ через ключ 771, управляемый выходом Q}, поступает на интегратор ИНТ. Импульсы от генератора G через схему И ИЛИ подаются на вход суммирования счетчика СТ2. После подсчета 2П импульсов (и — разрядность счетчика) сигнал с выхода Q„ старшего разряда счетчика СТ2 сбрасывает триггер Т1 и устанавливает в состояние “1” RS-триггер 72. На этом первый этап интегрирования заканчивается.
Во втором такте на интегратор поступает опорное напряжение плюс С70П через ключ 772, управляемый выходом Q2. Одновременно высокий уровень напряжения с выхода Q2 разрешает прохождение импульсов от генератора G на суммирующий вход счетчика С72 (начинается новый счет).
198 Цифро-аналоговые и аналого-цифровые преобразователи
Рис. 5.9. Аналого-цифровой преобразователь с двухтактным интегрированием: а — схема; б — временная диаграмма работы
В момент, когда напряжение на выходе ИНТ равно нулю, компаратор обнуляет триггер Л, прохождение импульсов на вход счетчика блокируется, и на его выходах фиксируется цифровой код Nx, пропорциональный входному напряжению. Для интегратора приросты напряжений в первом и втором тактах равны (рис. 5.9, б):
£4х(^2~ ~ Uon(t2 — t2).
Поскольку t2 - /| = T02", t3- t2 = Nx То, где To— период следования импульсов генератора G, то получим:
t/Bx = (t/on№)/2". (5.4)
Пример 5.2
При измерении десятиразрядный АЦП с опорным напряжением Uon = 10 В, зафиксировал в счетчике число импульсов Nx = 455. Найти значение входного напряжения UBX.
На основе выражения (5.4) имеем:
U вх=1^ . 4,48 В.
2° 1024
Аналого-цифровые преобразователи с поразрядным кодированием
В схеме АЦП с поразрядным кодированием (уравновешиванием) входное напряжение С/вх сравнивается скачкообразно с выходным напряжением С/ЦАП по определенной программе (рис. 5.10, а).
Сигнал “Пуск” включает генератор периодических импульсов G и одновременно записывает единицу в старший разряд сдвигового регистра поразрядного приближения РгПП, а остальные разряды обнуляет. В первом такте с помощью компаратора КОМП сравниваются входное напряжение С/Вх и напряжение с выхода ЦАП, соответствующее значению старшего разряда РгПП. Алгоритм сравнения следующий: если [7цап > С7ВХ, то в следующем такте эта единица исключается, а вместо нее в РгПП добавляется следующая из соседнего разряда. Если же С/ЦАП < С/вх, то единица в старшем разряде сохраняется и к ней прибавляется единица из соседнего разряда и т. д.
5.2. Аналого-цифровые преобразователи 199
Л'
X
а
б
Рис. 5.10. Аналого-цифровой преобразователь поразрядного кодирования:
а — схема; б — временные диаграммы работы
Преобразование заканчивается за время гпр = n0T0 + 1, где п0— разрядность РгПП; То — период следования тактирующих импульсов. Временные диаграммы поразрядного уравновешивания для С/вх = 4,5 В и п = 4 показаны на рис. 5.10, б.
Аналого-цифровой преобразователь параллельного и параллельно-последовательного действия
Принцип работы АЦП параллельного действия основан на одновременном сравнении входного сигнала с 2П-1 эталонами напряжений, где п — разрядность выходного кода. Сравнение осуществляется с помощью компараторов, результат сравнения запоминается в регистре и в дальнейшем шифруется в л-разрядный двоичный выходной код (рис. 5.11).
Рис. 5.11. Схема АЦП параллельного действия
В АЦП опорные напряжения формируются с помощью резистивного делителя. Каждое опорное напряжение Uoni подается вместе с входным напряжением С/Вх на входы соответствующих компараторов КОМП. Срабатывают только те компараторы, в которых С7ВХ > Uo„, Результат сравнения через фиксирующие триггеры Т подается на шифратор CD, который преобразовывает его в выходной «-разрядный двоичный код. Аналого-цифровые преобразователи параллельного действия являются наиболее быстродействующими, поскольку преобразование осуществляется за одну операцию сравнения. К недостаткам этого АЦП относится большое число источников опорного напряжения и соответствующих им компараторов.
Параллельно-последовательные АЦП имеют повышенную разрядность, высокое быстродействие и приемлемую сложность (рис. 5.12).
200 Цифро-аналоговые и аналого-цифровые преобразователи
Рис. 5.12. Схема АЦП параллельно-псследоеательного действия
В таких комбинированных преобразователях несколько малоразрядных АЦП параллельного действия соединяются последовательно между собой.
Входной аналоговый сигнал подается на первый АЦП (АЦП1), на выходе которого формируются старшие разряды N„ выходного кода. Эти разряды подключаются также на вход ЦАП. Выходной сигнал с ЦАП сравнивается в усилителе разности (УР) с входным сигналом. Усиленная разность этих сигналов подается на вход другого АЦП (АЦП2), который преобразует ее в выходной код Умл младших разрядов.
5.2.2. Основные параметры и характеристики аналого-цифровых преобразователей
В АЦП используют методы поразрядного кодирования, последовательного счета с двоичным интегрированием и параллельного преобразования. Микросхемы АЦП выполняют по гибридной и полупроводниковой технологии. В последние годы выпускают, в основном, полупроводниковые АЦП. Основные параметры и характеристики некоторых полупроводниковых АЦП представлены в табл. 5.2.
Таблица 5.2
Тип микросхемы Разрядность, п Максимальное отклонение, <5Лд, % Время преобразования Тп, мкс Технология Примечание
КР572ПВЗ 8 ±0,75 7,5 КМОП МК, СМ
К1107ПВ1 6 ±0,5 0,1 Биполярная —
М1107ПВ6 10 ± 1,5 0,06 Биполярная ФЗ, СМ
К1108ПВ2 12 ± 1 0,9 Биполярная ФЗ
Примечание. В табл. 5.2: СМ — совместимость с микропроцессорами; ФЗ — функциональная законченность; МК — многоканальность.
Некоторые АЦП являются функционально законченными, однако большинство требуют дополнительных внешних элементов: операционных усилителей, источников опорного напряжения, генераторов тактовых импульсов, резисторов и конденсаторов.
Микросхемы АЦП обычно имеют диапазон изменения входного напряжения 0-10 В, а некоторые АЦП допускают использование двухполярного входного сигнала. Разрядность АЦП составляет 6-12, причем ряд АЦП допускают наращивание разрядности.
Контрольные вопросы 201
Быстродействие АЦП определяется, в основном, методом преобразования и элементной базой (ТТЛШ, ЭСЛ, КМОП). Наибольшее быстродействие имеют АЦП ' параллельного действия на базе ЭСЛ-елементов (гпр < 20 нс). Преобразователи по уровням выходных сигналов согласуются с ТТЛШ-, ЭСЛ- и КМОП-микросхемами. Большинство современных АЦП совместимы с микропроцессорными устройствами. Выходные цепи в таких АЦП имеют три устойчивых состояния (лог. 0, лог. 1 и Z).
Выходным кодом АЦП чаще всего является двоичный. В АЦП с двоичным интегрированием применяется двоично-десятичный код для сопряжения с индикаторами и измерительными приборами. Здесь для представления каждого десятичного знака используются четыре двоичных разряда. Используются также обратный и дополнительный коды.
Некоторые АЦП — это БИС аналого-цифровой системы сбора данных, включающей в свой состав, кроме преобразователя, многоканальный мультиплексор, оперативное запоминающее устройство, схемы буферов и управления.
Основными направлениями совершенствования АЦП являются:
• повышение быстродействия основных узлов, особенно компараторов;
• использование АЦП комбинированного действия;
• повышение точности преобразования, в частности, увеличение разрядности до 16 и более;
• снижение потребляемой мощности;
• достижение удобства и гибкости применения, особенно согласования с микропроцессорными устройствами.
Контрольные вопросы
1. Назовите области применения ЦАП.
2. Расскажите о принципе преобразования цифрового кода в напряжение.
3. Назовите отличия в структуре резисторных матриц со ступенчатыми резисторами типа R-2R.
4. Каково назначение токовых ключей?
5. Какую функцию в схеме ЦАП выполняет ОУ?
6. Охарактеризуйте основные параметры ЦАП.
7. Назовите серии микросхем отечественных ЦАП.
8. Каковы основные параметры и характеристики АЦП?
9. Поясните структуру АЦП последовательного счета.
10. Нарисуйте временные диаграммы АЦП последовательного счета.
11. Поясните принцип построения АЦП с двухтактным интегрированием.
12. Нарисуйте структурную схему АЦП поразрядного кодирования.
13. Поясните временные диаграммы работы АЦП поразрядного кодирования.
14. Охарактеризуйте работу АЦП параллельного действия.
15. Поясните работу АЦП параллельно-последовательного действия.
16. Как строится умножающий ЦАП?
202 Основы компьютерной техники
Глава 6
Основы компьютерной техники
6.1. Общая характеристика компьютерной техники и короткая история ее развития
Компьютерная техника — это совокупность средств для автоматизации процессов обработки информации, а также отрасль техники, которая занимается разработкой, изготовлением и эксплуатацией компьютеров.
Комплекс электронного оборудования, которое предназначено для автоматизации процессов обработки дискретной информации и имеет общее управление, называют цифровой электронной вычислительной машиной (ЭВМ). В наше время диапазон использования ЭВМ существенно расширился: называют более 20 тыс. областей их применения — от научно-инженерных задач до искусственного интеллекта, математического моделирования, робототехники. Поэтому вместо термина ЭВМ используют его более современный синоним — компьютер.
Первые сведения о вычислительных устройства относятся к 1500 г., когда Леонардо да Винчи разработал эскиз 13-разрядного суммирующего устройства с десятизубцовыми колесами. В 1642 г. Б. Паскаль во Франции создал первую действующую модель восьмиразрядного цифрового устройства “Паскалина”. Каждая цифра в нем определялась положением десятисекторного колеса. Сложение осуществлялось поворотом колеса на соответствующее число секторов. Немецкий ученый Г. Лейбниц в 1670 г. описал механическую счетную машину, которая выполняла операции сложения, вычитания, умножения и деления.
В 1833 г. английский математик Ч. Беббидж спроектировал и почти 30 лет совершенствовал “аналитическую машину", в которую были заложены фундаментальные для компьютерной техники принципы:
• автоматическое (без остановки) выполнение операций;
• необходимость памяти (“склада") для хранения чисел, набранных зубчатыми колесами;
• работа по программе, вводимой “на ходу” с перфокарты в исполнительное устройство (“фабрику”) со скоростью выполнения операций в машине.
Ограниченные технические возможности того времени не позволили реализовать эти прогрессивные идеи.
Автоматические цифровые машины на механических и релейных элементах создавали одновременно и независимо во многих странах. Так, в 1936 г. А. Тьюринг в Англии и Э. Пост в США разработали концепцию абстрактной автоматической цифровой машины, которая могла решать любую алгоритмическую задачу. В 1941 г. немецкий инженер К. Зюс разработал две электромеханические машины с программным управлением “Зюс-1” и “Зюс-2”.
6.2. Архитектура и структура компьютеров 203
В 1944 г. в США под управлением Г. Айкена была разработана электромеханическая машина “Марк-1", где впервые были использованы идеи Ч. Беббиджа. В том же году в США под управлением Д. Эккерта, Д. Моучли и Дж. фон Неймана был создан первый в мире компьютер ENIAC с применением электронных ламп и электромеханических реле. В машине было задействовано 18 тыс. ламп и 1,5 тыс. реле; она выполняла за одну секунду 5 тыс. операций сложения, 300 — умножения, потребляла мощность 150 кВт.
У этих первых машин были следующие недостатки:
• программы не хранились в памяти, а набирались с помощью внешних сложных и продолжительных коммутаций;
• данные представлялись и обрабатывались в десятичной системе счисления последовательно (разряд за разрядом).
6.2. Архитектура и структура компьютеров
Архитектура — это наиболее общие принципы построения компьютеров. Она охватывает круг вопросов, существенных в первую очередь для пользователя: функциональный состав технических и программных средств и их взаимодействие в процессе обработки информации; систему команд, их форматы и способы кодирования; методы адресации команд и данных.
Основные принципы построения компьютеров изложили в 1946 г. американские математики Дж. фон Нейман, К. Голдстайн и А. Беркс. Совокупность этих принципов породила классическую неймановскую архитектуру, которая остается актуальной и сегодня.
В общем неймановская архитектура обладает следующими основными признаками:
• наличие одного вычислителя, имеющего процессор, память, средства ввода-вывода информации, а также средства управления;
• применение двоичной системы счисления как для представления информации, так и для выполнения арифметико-логических операций;
• размещение в единой общей памяти команд и чисел фиксированной длины;
• линейную структуру адресации ячеек памяти, что требует наличия в процессоре счетчика команд;
• централизованное автоматическое последовательное считывание команд из памяти и интерпретацию их процессором; данные обрабатываются параллельно — одновременно над всеми разрядами машинного слова;
• низкий уровень машинного языка.
Первый компьютер EDSAC с хранимой программой в памяти на 512 ртутных линиях задержки был построен М. Уилксом (Англия) в 1949 г. Машина выполняла 15 тыс. сложений и 120 умножений за одну секунду. В 1950 г. под управлением Дж. фон Неймана был создан первый полностью электронный компьютер классической архитектуры EDVAC, который положил начало машинам первого поколения.
В 1948-1950 гг. в Институте электротехники в Киеве была создана малая электронная счетная машина “МЭСМ". Ее разработкой руководил выдающийся ученый и конструктор многих компьютеров академик С. А. Лебедев. В машине “МЭСМ” были
204 Основы компьютерной техники
использованы (независимо от Неймана) основные принципы классической архитектуры. Компьютер содержал 3500 ламп, 2500 диодов, занимал площадь 60 м2, потреблял мощность 25 кВт и выполнял 50 операций за одну секунду.
Компьютер классической архитектуры включает в себя (рис. 6.1):
• арифметико-логическое устройство (АЛУ);
• оперативную память (ОП);
• средства хранения и ввода-вывода информации: внешние запоминающие устройства (ВЗУ); устройства ввода информации (УВв); устройства вывода информации (УВыв); все эти устройства называют внешними или периферийными (ПУ);
• устройство управление (УУ). Вместе с АЛУ оно образует процессор. При наличии в машине нескольких процессоров выделяют центральный (ЦП).
Рис. 6.1. Структура компьютера
Арифметико-логическое устройство предназначено для выполнения арифметических и логических операций, предусмотренных системой команд данного компьютера. В состав АЛУ входят регистры и комбинационные схемы. Данные для обработки в АЛУ поступают из ОП и называются операндами. Результаты операций пересылаются в ОП или временно сохраняются в регистрах АЛУ.
Устройство управления (УУ) считывает и дешифрирует в соответствующей последовательности команды, формирует и подает управляющие сигналы для других устройств компьютера.
Оперативная память предназначена для временного хранения программ и данных, в ней выполняются операции записи и считывания информации. Кроме ОП, используют также постоянную память, в которой выполняются только операции считывания. Оперативную (ОЗУ) и постоянную память (ПЗУ), а также регистры АЛУ называют внутренней памятью (рис. 6.2). Процессор и ОП вместе образуют ядро
компьютера.
Рис. 6.2. Внутренняя память компьютера
Операции ввода-вывода — это обмен информацией между ядром машины и ПУ. Операция ввода передает информацию из ПУ в ядро компьютера, а операция вывода — наоборот.
6.2. Архитектура и структура компьютеров 205
Внешняя память предназначена для длительного и энергонезависимого хранения больших объемов информации. Физически ее реализуют в виде накопителей (рис. 6.3):
• на гибких магнитных дисках (НГМД);
• на жестких магнитных дисках (НЖМД); они называются винчестерами;
• на оптических (лазерных) дисках (НОД);
• на магнитных лентах (НМЛ).
Накопители на дисках имеют электромеханический привод (дисковод), который обеспечивает вращение диска, блок магнитных головок для считывания или записи, систему установки (позиционирования) магнитной головки в требуемое положение и электронный блок управления.
Рис. 6.3. Внешняя память компьютера
Все виды внешней памяти обеспечивают обмен информацией с ядром компьютера, однако ВЗУ выделяют в отдельный вид ПУ по следующим признакам:
• внешняя память обеспечивает хранение больших массивов информации и быстродействующий обмен с ядром компьютера (более 30 тыс. байт/с);
• информация в ВЗУ хранится в виде, недоступном для непосредственного восприятия человеком.
Устройства ввода и вывода информации (УВВ) рассматривают как единую функциональную часть компьютера. Различные по своим функциями, принципам построения и характеристикам УВВ и ВЗУ вместе образуют группу очень разнообразных внешних или периферийных устройств.
К УВв информации относятся (рис. 6.4):
• клавиатура, предназначенная для ввода программ и данных и управления работой машины;
• сканеры, предназначенные для ввода графической информации;
• ручные манипуляторы — мышь, шариковый манипулятор и джойстик — предназначенные для быстрого перемещения курсора в заданную точку экрана дисплея и выполнения других действий;
• устройства речевого ввода, предназначенные для управления машиной с помощью речевых команд;
• устройства ввода с перфолент, перфокарт и др.
К УВыв информации относят (рис. 6.5):
• принтеры (матричные, струйные, лазерные);
• дисплеи (на электронно-лучевых трубках (ЭЛТ), на жидких кристаллах, плазменные, люминесцентные), предназначенные для отображения информации, которая вводится с клавиатуры (для контроля правильности набора данных) или из памяти машины;
206 Основы компьютерной техники
• плоттеры (графопостроители), предназначенные для печати чертежей высокого качества;
• синтезаторы звука и языка, предназначенные для преобразования аналоговых сигналов в цифровой код и наоборот;
• устройства вывода информации на перфоленты и перфокарты.
Рис. 6.4. Устройства ввода информации
Рис. 6.5. Устройства вывода информации
Связь между функциональными частями машины осуществляют с помощью интерфейса — совокупности шин, сигналов, вспомогательных микросхем и алгоритмов, предназначенных для обмена информацией между устройствами компью-
тера
Выделяют три шины (рис. 6 6):
• адреса (ША), предназначенная для передачи адреса ячеек ОП и регистров ПУ;
• данных (ШД), предназначенная для передачи данных;
• управления (ШУ), предназначенная для передачи управляющих сигналов от процессора к устройствам и наоборот
Рис. 6.6. Структура процессора
6.3. Принцип программного управления 207
6.3. Принцип программного управления
В компьютере реализуют принцип программного управления, суть которого следующая. Для решения каждой задачи разрабатывают алгоритм на основе числовых методов вычислений. Алгоритм переводится на язык, свойственный данной машине, в виде программы— языковой конструкции, которая является упорядоченной последовательностью описаний и команд, предназначенных для обработки информации. Каждая команда определяет действия компьютера в отношении выполнения любой операции, реализующей аппаратные (технические) и программные средства. Программа записывается в ОП в виде машинных слов, которые кодируются цифрами 0 и 1 и различаются только способом применения. Код операции поступает в регистр команд IR (instruction register) и затем дешифрируется, а данные — в регистры АЛУ (см. рис. 6.6).
Команды программы размещены в ОП линейно (одна за другой) и выполняются последовательно. Номер команды в ОП определяется программным счетчиком PC (program counter). Управляющий автомат (УА) вырабатывает множество управляющих сигналов, которые подаются на все устройства машины. Регистр команд, программный счетчик и управляющий автомат входят в состав УУ. Последовательное управление обусловлено наличием одного процессора. Команды условного и безусловного ветвления изменяют линейный порядок считывания и выполнения команд.
Множество всех операций, реализуемых в компьютере, составляет его операционные ресурсы. Компьютеры, операционные ресурсы которых обеспечивают выполнение любого алгоритма обработки информации, называют универсальными. Для этого теоретически достаточно иметь в операционных ресурсах только четыре операции: пересылку слова между любыми ячейками ОП, прибавление единицы к слову (вычитание единицы из слова), условный переход по совпадению слов и безусловную остановку компьютера. Однако в компьютерах операционные ресурсы состоят из десятков и сотен команд, что упрощает программирование.
В общем в компьютерах используют список команд, который обеспечивает выполнение следующих групп операций:
• пересылки данных между регистрами АЛУ, регистрами и ОП;
• арифметических операций над двоичными числами с фиксированной и плавающей запятой: сложение, вычитание, знаковое и беззнаковое умножение и деление;
• логических операций отрицания, дизъюнкции, конъюнкции, сложения по модулю два;
• установления соотношений — больше, меньше, неравно, больше-равно и др.;
• сдвига влево или вправо — арифметического, логического, циклического;
• управления программой: условными и безусловными переходами и вызовами процедур, безусловными и условными возвратами из процедур, прерыванием программ; некоторые компьютеры имеют специальные команды для организации циклов;
• ввода-вывода данных между ядром машины и ПУ;
• специальных операций для машин с сопроцессорами (математическими расширителями): вычислений квадратного корня, синуса, косинуса, логарифмические и др.;
208 Основы компьютерной техники
• преобразования из одного формата в другой (например, из восьмибитного в 16-битный);
• системных операций — загрузки служебных регистров, защиты памяти;
• мультимедийных операций для выполнение действий со звуком, графикой, изображением.
С ростом производительности процессора увеличивается и количество команд.
Компьютеры, в зависимости от их сложности и назначения, работают в следующих режимах (рис. 6.7):
Рис. 6.7. Режимы работы компьютеров
• однопрограммном — каждая программа отдельно загружается в ОП и выполняется до получения результата;
• многопрограммном — в память загружается несколько программ; когда выполнение одной из программ останавливается из-за необходимости обратиться к ПУ, то машина переключается на выполнение другой программы;
• пакетном — в ВЗУ формируется пакет задач, которые затем считываются в ОП группами и выполняются в многопрограммном режиме;
• распределения времени (коллективного пользования) — доступ к компьютеру пользователей с помощью собственного терминала;
• реального времени — обеспечивается взаимодействие компьютера с внешними объектами в темпе, который требует быстродействие объекта.
6.4. Основные характеристики компьютеров
Важной характеристикой компьютера является производительность — объективная количественная мера работы машины. Используют следующие меры производительности: пиковую, номинальную, системную и эксплуатационную (рис. 6.8).
Пиковая производительность — среднее число коротких операций типа “регистр-регистр” в секунду (оп./с) без операций обмена с ОП. За границей пиковую производительность оценивают для команд типа “Нет операции” в миллионах операций в секунду (млн. оп./с) или в MIPS (Million Instruction per Second). Пиковую мощность часто называют быстродействием компьютера.
Номинальная производительность — среднее число смеси команд Vc с учетом их статистического веса (частоты повторения), которые выполняет ядро компьютера в выбранном классе задач (зависит от скорости ОП):
К^1/(Р1/1+Р2Г2+... + ^,+... + ^„), где Р, и /, — соответственно весовой коэффициент каждой z-й команды и время ее выполнения; п — число команд.
6.5. Поколения компьютеров 209
Рис. 6.8. Основные характеристики компьютеров
Номинальную производительность часто называют “быстродействием компьютера на смеси команд”. Производительность мощных машин часто измеряют в мегафлопсах (MFLOPS) — в миллионах операций в секунду над операндами с плавающей запятой.
Системную производительность измеряют с помощью типовых оценочных программ (бенчмарков), реализованных на языках высокого уровня. Результаты оценки сис1вмной производительности компьютера конкретной архитектуры представлены в числовых таблицах.
Эксплуатационную производительность оценивают данными о реальной рабочей нагрузке в основных областях применения; при этом учитывают необходимую площадь размещения машины, механические и климатические условия эксплуатации, потребляемую мощность и т. д.
К характеристикам компьютеров также относят:
• разрядность машинного слова, которое хранится, пересылается и обрабатывается как единое целое; измеряется в битах, байтах;
• объем оперативной памяти в битах, байтах, килобайтах, мегабайтах, гигабайтах;
• надежность, которая характеризует среднюю наработку на отказ — не менее 15 тыс. час; время восстановления работоспособности, срок службы (не менее 10 лет).
6.5. Поколения компьютеров
Поколение — это категория в исторической классификации компьютеров, основанная преимущественно на технологии производства их элементной базы. Различают пять поколений компьютеров (рис. 6.9).
С каждым новым поколением компьютеров увеличиваются их операционные ресурсы, производительность и надежность; уменьшается потребляемая мощность, масса и габариты; совершенствуются языки программирования; упрощается взаи
14-4-1749
210 Основы компьютерной техники
модействие пользователя с машиной. Приведем приблизительный даты образования поколений и основные их характеристики.
Рис. 6.9. Поколения компьютеров
Первое поколение (с 1945 г.): элементная база — электронные лампы; объем ОП — 100 байт; быстродействие — 10 тыс. оп./с; язык программирования — машинный код. В нашей стране использовались машины первого поколения “МЭСМ”, “Киев”, “Урал-1”, “Урал-4”, “Минск-1, “Минск-14” и др.
Второе поколения (с 1954 г.): элементная база — транзисторы и полупроводниковые диоды; объем ОП — 1000 байт; быстродействие — 1 млн оп./с; язык программирования — ассемблер. Модели компьютеров второго поколения — “Мир”, “Днепр" (руководители разработки академики В. М. Глушков и Б. М. Малиновский), “Урал-11”, “Урал-14”, “Минск-22”, “Минск-32” и др.
Третье поколение (с 1965 г.): элементная база — малые и средние интегральные схемы; объем ОП — 10 тыс. байт; быстродействие — 10 млн оп./с; язык программирования — процедурные языки высокого уровня. В нашей стране были созданы крупные унифицированные и программно совместимые большие и средние универсальные машины единой системы от ЕС-1010 до ЕС-1066 (прототип — машина IBM 360)j мини- и микрокомпьютеры — от СМ-1 до СМ-4, “Электроника-60” и другие (прототип — машина PDP-11 фирмы DEC); в компьютерах третьего поколения в сравнении с первым быстродействие и надежность возросли примерно в ЮОО раз и настолько же уменьшилась потребляемая мощность.
Четвертое поколение (с 1976 г.): элементная база — большие и сверхбольшие интегральные схемы; объем ОП — 0,1-1 Мбайт; быстродействие — 100-1000 млн оп./с; язык программирования — непроцедурные языки высокого уровня; к четвертому поколению относят персональные компьютеры на базе микропроцессоров типа Pentium фирмы Intel.
Пятое поколение — контуры его архитектуры только разрабатываются и возможны следующие характеристики: элементная база — оптоэлектроника, криозлек-троника, СБИС; объем ОП — 1-10 Гбайт; быстродействие — 1000 млрд оп./с; средства обмена с пользователем — устройства голосовой связи; язык программирования — новые непроцедурные языки высокого уровня.
В зависимости от производительности, размеров, функционального назначения и стоимости выделяют суперкомпьютеры, большие компьютеры, мини- и микрокомпьютеры (рис. 6.10).
Суперкомпьютер определяется только относительно — это самая мощная вычислительная система, действующая в соответствующий исторический период. В наше время наиболее известны суперкомпьютеры “Cray” и “IBM SP2” (США). Модель “Cray”, которая выпускается с начала 90-х годов 20 столетия, содержит 16 процессоров и обладает быстродействием свыше 10 MFLOPS; в модели CS 6400 число
6.5. Поколения компьютеров 211
процессоров доведено до 64. В наше время создаются супермашины на основе сотен и тысяч процессоров. Суперкомпьютеры требуют стабильного температурного режима. Стоимость такого компьютера достигает десятков миллионов долларов. Суперкомпьютеры используют для решения крупных научных и технических задач.
Рис. 6.10. Классификация компьютеров
Большие компьютеры (мейнфреймы) — это машины общего назначения с производительностью до 400 тыс. оп./с, объемом памяти — несколько мегабайт, разрядностью — 32 или 64 бит. Их используют в узлах региональных систем обработки данных, на крупных производствах. Стоимость мейнфреймов — около одного миллиона долларов. К большим машинам относятся модели ЕС-1065 (Россия) и IBM-370 (США).
Миникомпьютеры появились в начале 70-х годов 20 столетия; их традиционное применение — управление технологическими процессами. Классической минимашиной является модель “PDP-11” фирмы DEC. Стоимость миникомпьютеров составляет примерно 100 тыс. долларов.
Микрокомпьютеры строят на микропроцессорах, выполняющих функции процессора. Составные части микропроцессора размещены в одной или нескольких интегральных микросхемах. Первый микропроцессор был разработан фирмой Intel в 1971 г. С этого времени развитие компьютерной техники носит новый количественный и качественный характер. Стоимость микрокомпьютеров составляет несколько тысяч долларов. На основе микрокомпьютеров построены управляющие системы, автоматизированные рабочие места и персональные компьютеры.
Выделяют два направления построения компьютеров:
• с полным набором сложных и многоформатных команд CISC (Complex Instruction Set Computer);
• с ограниченным набором команд RISC (Reduced Instruction Set Computer); все команды работают с операндами, расположенными в регистрах АЛУ, при этом команды имеют одинаковый формат.
Компьютеры RISC работают в 2-4 раза быстрее CISC-компьютеров при одинаковой тактовой частоте.
I4*
212 Основы компьютерной техники
Контрольные вопросы
1. Дайте общую характеристику компьютерной техники.
2. Опишите коротко историю развития компьютерной техники.
3. Что понимают под архитектурой компьютеров?
4. Нарисуйте классическую структуру компьютера.
5. Назовите составные части внутренней памяти компьютера.
6. Что относится к устройствам ввода-вывода информации компьютеров?
7, Охарактеризуйте принципы программного управления.
8. Поясните основные характеристики и режимы работы компьютеров.
9. Что понимают под поколениями компьютеров?
7.1. Общая характеристика памяти 213
Глава 7
Память компьютеров
7.1. Общая характеристика памяти
7.1.1. Функция памяти
Памятью компьютера называется совокупность различных устройств, предназначенных для приема, хранения и выдачи двоичной информации. Отдельное устройство называется запоминающим (ЗУ) или просто памятью. Термин “запоминающее устройство” употребляют тогда, когда требуется подчеркнуть принцип его построения: на магнитных сердечниках, полупроводниках и т.д. Термин “память” применяют, когда указывают на выполняемую функцию: основная, постоянная и т.п.
Память компьютера функционирует под управлением операционной системы, которая размещает массивы информации в памяти, обеспечивает их защиту от несанкционированного доступа и выполняет другие функции. Производительность и вычислительные возможности компьютера в значительной мере определяются составом и характеристиками используемых ЗУ.
Память современных компьютеров классифицируют по функциональному назначению, виду носителя информации, способу организации доступа к информации. По функциональному назначению память компьютеров подразделяется на две основные группы: внешнюю и внутреннюю.
Внешние ЗУ предназначены для длительного хранения больших массивов информации с емкостью до гигабайта и более и малым быстродействием. Внешняя память включает в себя накопители на магнитных лентах, дисках, барабанах и оптических дисках.
Внутренние ЗУ предназначены для хранения программ и данных, обрабатываемых в текущий момент времени. К внутренней памяти относятся:
• сверхоперативные (регистровые) ЗУ, которые используют регистры общего назначения процессора; они обладают небольшой информационной емкостью и быстродействием работы процессора;
• кэш-память, которая служит для хранения копий информации, используемой в текущих операциях обмена. Высокое быстродействие кэш-памяти повышает производительность компьютера;
• оперативные, которые характеризуются высоким быстродействием и информационной емкостью до сотен мегабайт; оперативная память компьютеров первых поколений строилась на магнитных сердечниках. В настоящее время ОП реализуется на полупроводниковых БИС ЗУ. В процессе работы информация из внешней памяти при необходимости переписывается в оперативное ЗУ (ОЗУ);
214 Память компьютеров
• постоянные, которые строятся на полупроводниковых БИС. В постоянную память информация записывается заранее и ее можно только считывать. Оперативные и постоянные ЗУ образуют основную память компьютера;
• специализированные виды памяти — многопортовые, ассоциативные, видеопамять и др.
По физическому принципу построения память компьютера бывает:
• магнитная (на сердечниках и пленках, на цилиндрических и плоских магнитных доменах);
• ультразвуковая(магнитострикционная, электрострикционная);
• сегнетоэлектрическая и голографическая (лазерная), на основе сверхпроводимости;
• полупроводниковая на БИС и СБИС, ультра-БИС.
Полупроводниковые БИС ЗУ в свою очередь характеризуются:
• технологией изготовления: на биполярных транзисторах (ТТЛШ, ЭСЛ, И2Л), на МОП-структурах (p-МОП, п-МОП, КМОП); среди новейших разработок следует отметить ЗУ, в которых используются ПТШ на основе арсенида галлия;
• способом хранения информации — статические и динамические (в статических ЗУ элементом памяти является триггер, а в динамических элемент памяти строят на конденсаторе и МОП-транзисторах);
• энергозависимостью: различают энергозависимые БИС ЗУ, в которых при отключении источника питания хранимая информация разрушается (что справедливо в настоящее время для большинства полупроводниковых микросхем памяти), и энергонезависимые (обычно на сегнетоэлектриках), в которых информация сохраняется;
• структурной организацией БИС ЗУ, символически представляемой в виде N х 1V. где N — количество хранимых адресуемых единиц информации; т — разрядность (организацию в виде Nx 1 называют одноразрядной, а Nx т — словарной, при этом т > 1).
Элементный базис памяти современных компьютеров составляют микросхемы различной степени интеграции. Основой любого ЗУ является элемент памяти (ЭП) статического или динамического типа, предназначенный для записи, хранения и считывания одного бита информации — цифры 0 или 1. Совокупность ЭП, которые образуют /^-разрядное слово, называют ячейкой памяти (ЯП). Множество ЯП образует запоминающий массив, называемый матрицей М элементов памяти.
7.1.2. Основные параметры памяти
Основными операциями в памяти являются запись и считывание определенной единицы информации, например, байта. Эти операции называются также обращением к памяти. Память характеризуется информационной емкостью, физическим объемом, удельной емкостью и стоимостью, шириной выборки, потребляемой мощностью и быстродействием.
Информационная емкость Е представляет собой максимальный объем данных, который может одновременно храниться в памяти. Емкость выражается в битах, байтах (8 бит = 1 байт), килобайтах (210 байт = 1 Кбайт), мегабайтах (210 Кбайт =
7.1. Общая характеристика памяти 215
= 1 Мбайт) и гигабайтах (210 Мбайт = 1 Гбайт) (при этом следует учитывать, что 210 = = 1024).
Удельная емкость определяется отношением информационной емкости ЗУ к его физическому объему. Удельная стоимость — это отношение стоимости ЗУ к его информационной емкости. Ширина выборки представляется числом разрядов, которые записываются в ЗУ или считываются из него за одно обращение.
Потребляемую мощность задают либо для всего ЗУ, либо на хранение одного бита информации. Основными требованиями к памяти являются максимально большая информационная емкость, высокое быстродействие (малое время обращения- 70бр < 10 нс), минимальная потребляемая мощность (менее-1 мкВт на 1 бит хранимой информации).
В настоящее время ни один вид ЗУ не удовлетворяет этим требованиям в полной мере. Поэтому в памяти используются различные виды ЗУ, которые отличаются принципами построения и своими характеристиками.
Быстродействие ЗУ измеряется временем записи и считывания, а также продолжительностью соответствующих им циклов. Время записи tWK — это интервал между моментами появления управляющего сигнала записи и установкой ЯП в состояние, задаваемое входными сигналами. Время считывания — это интервал между моментами появления управляющего сигнала чтения tRD и данных на выходе памяти. Минимально допустимый интервал между последовательными чтениями t(YR и записями tCYw образует соответствующий цикл. Длительность циклов может превышать время чтения или записи, поскольку после этих операций необходима дополнительная задержка для установки исходного состояния памяти. В качестве длительности цикла обращения к памяти берут величину /Сг = тпах (lrw, tent)-
7.1.3. Входные и выходные сигналы микросхемы памяти
Микросхемы ОП имеют типовые выводы, на которых действуют определенные адресные, информационные и управляющие сигналы (рис. 7.1, а).
Назначение выводов и сигналов:
• A (Address) — входы адреса, разрядность которого к определяется соотношением к = log2M где N = 2'“ — максимально возможное число данных (бит, байт, слов), которые хранятся в памяти и адресуются как единое целое;
• DI (Data Input) — шина входных данных;
• DO (Data Out) — шина выходных данных;
• W / R (Write/Read) — сигнал записи данных при W / R = 0 или считывания при W / R = 1; __
• CS (Chip Select) или СЕ (Chip Enable) — сигнал разрешения при CS (СЕ) = 0 или запрета, если CS (СЕ) = 1, работы данной микросхемы.
Особенностью работы динамических ЗУ является мультиплексирование ША (рис. 7.1, б). Адрес, например, Л=Л|5, Аы, Ао делится на старший полуадрес Аг=А15, А14,..., А8 и младший А1=А1,А6, Ао. Полуадреса подаются на одни и те же входы адреса микросхемы памяти. Подача полуадреса А. сопровождается сигналом RAS (Row Address Strobe), а полуадреса А} — сигналом CAS (Column Address Strobe). Такой способ адресации уменьшает число выводов корпуса ИМС. Часто выводы D/и DO объединяются в общий вывод DIO.
216 Память компьютеров
Рис. 7.1. Микросхемы ОП: а, 6— условные графические обозначения; в — временные диаграммы сигналов
7.1.4. Временные характеристики микросхем памяти
Требования ко взаимному временному положению двух сигналов (A-В) задают следующими параметрами:
• временем предварительной установки tsu (А~В) сигнала А относительно сигнала В, то есть интервалом между начальными моментами обоих сигналов;
• временем удержания (щл-ву — интервалом времени между началом сигнала А и окончанием сигнала Б;
• временем хранения — интервалом между окончанием сигналов А и В.
Длительность сигналов обозначается как tlv (Width — ширина).
Для ЗУ характерна следующая последовательность сигналов во времени (рис. 7.1, в): вначале адрес, затем выбор микросхемы CS, затем строб записи-чтения W / R. Индексом A (Access) обозначают интервалы времени от появления управляющего сигнала до появления данных на выходе (рис. 7.1, в).
7.1.5. Способы доступа к данным е полупроводниковой памяти
В полупроводниковых ЗУ выделяют адресные, последовательные и ассоциативные способы доступа к данным (рис. 7.2).
При адресном доступе адресный код указывает номер ячейки памяти, с которой должен производиться обмен. Все ячейки в момент обращения равнодоступны. К адресным ЗУ относят:
7.1. Общая характеристика памяти 217
• RAM (Random Access Memory), русские синонимы: ОЗУ (оперативное ЗУ) или ЗУПВ (ЗУ с произвольной выборкой);
• ROM (Read Only Memory), русский термин — ПЗУ (постоянные ЗУ).
Полупроводниковые ЗУ
Адресные
RAM | ROM |
ROM(M)
PROM
EPROM
EEPROM
FLASH
Последо вател ьн ы е
~-| FIFO
— Стековые
— Файловые
L- Циклические
Ассоциативные
_ Полностью ассоциативные
_ С прямым размещением
_ Наборно-
ассоциагивные
| Статические
- Асинхронные - Тактируемые
| Динамические
Синхронные (конвейерные)
| Стандартные |
Г Квазистатические|
Повышенного быстродействия ~— FPM — EDORAM — BEDORAM — MDRAM — SDRAM — RDRAM — DRDRAM — CDRAM
Рис. 7.2. Классификация полупроводниковых ЗУ
Оперативные ЗУ хранят данные, необходимые при выполнении текущей программы; они могут быть изменены в любой момент времени. Оперативные ЗУ по большей части энергозависимые. В постоянных ЗУ содержимое ячеек или вообще не изменяется, или изменяется редко в специальных режимах.
Запоминающие устройства RAM подразделяются на статические SRAM (Static RAM) и динамические DRAM (Dynamic RAM). В статических RAM элементами памяти являются триггеры. Они хранят свое состояние, пока схема имеет напряжение питания и новые данные не записываются. В динамических RAM данные хранятся в виде зарядов конденсаторов, создаваемых компонентами МОП-транзисторов. Саморазряд конденсаторов приводит к разрушению данных, поэтому они периодически (каждые 2-30 мс) должны регенерироваться. Однако плотность упаковки динамических ЭП превышает в 4-5 раз этот же показатель для статических RAM. Регенерация данных осуществляется с помощью специальных контроллеров. Разработаны также DRAM с внутренними схемами регенерации; такие ЗУ называются квазистати-ческими.
Статические ОЗУ разделяют на следующие типы:
• асинхронные — управляющие сигналы можно задавать как импульсами, так и уровнями;
• тактируемые — в них некоторые сигналы должны быть обязательно импульсами, например, сигнал разрешения работы CS;
218 Память компьютеров
• синхронные, в которых организован конвейерный канал передачи данных, синхронизируемый от тактовой системы процессора.
Динамические ЗУ характеризуются самой большой информационной емкостью и невысокой стоимостью, поэтому они используются как основная память компьютеров. Разработаны варианты схем DRAM высокого быстродействия, которые представлены в классификации и детально рассмотрены в п.7.7. Статические ЗУ в 4-5 раз дороже динамических и приблизительно в столько же раз меньше их информационная емкость. Их достоинством является высокое быстродействие, а типовой областью применения — схемы кэш-памяти.
Постоянная память типа ROM(M) программируется при изготовлении с помощью масок, поэтому ее называют ПЗУ масочным. В последующих разновидностях ROM в обозначениях имеется буква Р (от Programmable). Это — память, которая одноразово программируется пользователем — PROM (в русской терминологии ППЗУ — программируемые ПЗУ) и многократно программируется — EPROM, EEPROM (подробности см. в п. 7.3).
Память типа Flash по ЭП подобна EEPROM (иначе E2PROM), однако имеет структурные и технологические особенности, которые позволяют выделить ее в отдельный тип.
В ЗУ с последовательным доступом записываемые данные, образуют очередь. Считывание выполняется слово за словом в порядке записей или наоборот. Прямой порядок считывания используется в буферах FIFO с дисциплиной “первый пришел — первый вышел (First In — First Out)", а также в файловых и циклических ЗУ.
Разница между памятью FIFO и файловым ЗУ состоит в том, что в FIFO запись в пустой буфер сразу доступна для чтения (то есть, поступает в конец цепочки модели ЗУ). В файловых ЗУ данные поступают в начало цепочки и появляются на выходе после некоторого числа обращений, равного числу элементов в цепочке.
В циклических ЗУ слова доступны одно за другим с постоянным периодом, определяемым емкостью памяти. К ним относится видеопамять (VRAM).
Считывание в обратном порядке свойственно стековым ЗУ с дисциплиной “последний пришел — первым вышел”. Такие ЗУ называются буферами LIFO (Last In — First Out).
Время доступа к конкретной единице информации, хранимой в последовательных ЗУ, является случайной величиной. В наихудшем случае для такого доступа требуется просмотреть весь объем информации, хранимой в этой памяти.
Ассоциативный доступ реализует поиск информации по некоторому признаку, а не по адресу. В наиболее полной версии все слова, хранимые в памяти, могут одновременно проверяться на соответствие признаку, например, на совпадение определенных полей слов — тегов (от tag) по признаку, который задает входное слово (теговый адрес). На выход передаются слова, которые удовлетворяют признаку. Дисциплина выдачи слов, если тегу удовлетворяет несколько слов, и дисциплина записи новых данных могут быть различными. Основная область применения ассоциативной памяти в компьютерах — кэширование данных.
7.2. Основные структуры полупроводниковой памяти 219
7.2. Основные структуры полупроводниковой памяти
7.2.1. Понятие структуры памяти
Каждая матрица М в устройстве памяти имеет систему адресных и разрядных линий (проводников). Адресные (словарные) линии служат для выделения по адресу любой ЯП Совокупность различных адресных кодов образует адресное пространство памяти. Разрядные линии записи (ЛЗП) служат для ввода в каждый разряд выбранной ЯП цифры 0 или 1 в соответствии с входной информацией Разрядные линии считывания (ЛСЧ) служат для съема хранимой информации с разряда выбранной ЯП. Часто используют общую линию записи-считывания (ЛЗС). Адресные и разрядные линии вместе называются линиями выборки. Если длина адресного кода равна к, то количество слов N, которые хранятся в памяти как отдельные единицы данных, определяется из соотношения N = 2k.
Структуру памяти определяет способ распределения ЯП между адресными и разрядными линиями. По этому признаку выделяют следующие структуры памяти. 2D, 3D, 2,5D и модифицированную — 2.DM (D от Dimention — размерность)
В системе 2D каждый ЭП имеет одну адресную линию Аи (одну D), линии записи ЛЗП, и считывания ЛСЧ,, которые совместно образуют второе D (рис. 7.3, а) В структуре 3D адрес разделяют на две части: старшая Лг определяет адреса строк, а младшая А} — адреса столбцов; вместе они образуют 2D. Линии записи и считывания образуют третье D (рис 7.3, б). В структуре 2,5D одна из ЛЗП или ЛСЧ совмещена с полуадресом А1и или AVJ (рис. 7 3, в) В модифицированной системе 2DM используется общая линия ЛЗС/, которая объединена с адресной линией А,и
Рис. 7.3. Обобщенное понятие структуры памяти: а — 2D; б — 3D; в — 2,5D; г — 2DM
Рассмотренные структуры характерны для статических ОЗУ и памяти типа ROM. Структуры динамических ОЗУ имеют свою специфику.
7.2.2. Память со структурой 2D
Организация микросхемы ОЗУ со структурой 2D показана на рис. 7.4.
В состав микросхемы памяти входят:
• матрица элементов памяти М, которая содержит N строк и т столбцов (по числу разрядов слова);
• буфер ВА и дешифратор DCA адреса с числом выходов N = 2к;
220 Память компьютеров
• буферные формирователи входных DI и выходных DO информационных сигналов в режимах записи и считывания и BD\
• блок местного управления (БМУ).
Рис. 7.4. Память со структурой 2D
При обращении к памяти выбираются ЭП, расположенные на возбужденном выходе дешифратора адреса DCA. Запись данных осуществляется при значении сигнала W / R = 0, а считывание при W / R = 1. Емкость памяти 2D равна Е = = Ххт бит. Организация матрицы М памяти со структурой 2D (три строки и три столбца) показана на рис. 7.5.
Рис. 7.5. Организация матрицы М памяти со структурой 2D
Недостатком структуры 2D является сложность построения дешифратора адреса с числом выходов N, равным числу хранимых в памяти слов. Поэтому структура типа 2D используется в ЗУ малой информационной емкости.
7.2.3. Память со структурой 3D
В памяти со структурой 3D адресный код разделяется на две равные части Ах и А, (для четного к), каждая из которых декодируется отдельными дешифраторами соответственно DCX и DCY (рис. 7 6).
Матрица М состоит из т подматриц по числу разрядов слова. Каждая матрица хранит значение своего /-го разряда всех N слов. Каждая подматрица является квадратной: г строк и г столбцов, что записывается как г х г, при этом r = 4N =2ш(рис. 7.7).
При обращении к памяти выбирают т запоминающих элементов (по одному из каждой подматрицы), которые лежат на пересечении строки и столбца возбужденных выходов дешифраторов DCX и DCY. Такая структура часто используется и с одноразрядной организацией Ух 1 бит. Для этой памяти емкостью 1 К слов требуется
7.2. Основные структуры полупроводниковой памяти 221
иметь два дешифратора с числом выходов в каждом N = 25 = 32. Для памяти со структурой 2D такой же емкости дешифратор имеет 1024 выхода.
Недостатком структуры 3D является применение сложных ЭП, допускающих двухкоординатную выборку и более сложную структуру матрицы М. В памяти по модифицированной структуре 2DM объединяются достоинства структур 2D и 3D.
7.2.4. Память со структурой 2DM
В ЗУ типа SRAM, ROM со структурой 2DM адресный код длиной к разбивается на две части: Ах = Ак Акч... Аг^, поступающую на дешифратор строк DCX, и Ау = А, АгЧ ... At, поступающую на входы мультиплексоров MUX с организацией “2^1” (рис. 7.8).
Дешифратор DCX обслуживает 2к~г строк, каждая из которых хранит 2к ш-разрядных слов. В каждой группе хранятся значения одноименных разрядов и обслуживается она своим буфером BD и мультиплексором MUX с организацией “2к—И” (рис. 7.9).
Таким образом, активизированный выход дешифратора DCX выбирает строку, а младшие разряды адреса с помощью мультиплексоров обеспечивают формирование выходного слова DO (по одному разряду из каждой группы).
Структура 2DM для ЗУ типа RAM в общем виде показана на рис. 7.10. Из матрицы М считывается “длинная” строка. Данные в соответствующие группы строки записываются или считываются буферами данных BD, которые управляются
222 Память компьютеров
сигналами с выходов дешифратора DCY. Буфер BD также определяет направление обмена данными с помощью сигнала W / R
Рис. 7.8. Память SRAM и ROM со структурой 2DM
do, do. do2 do}
Рис. 7.9. Матрицы М с организацией 4 х 4 2
Рис. 7.10 Память типа RAM со структурой 2DM
Организация памяти со структурой 2DM является наиболее распространенной, особенно для микросхем большой емкости
7.3. Кэш-память 223
7.2.5. Память с последовательным доступом
Представителями памяти с последовательным доступом являются буфер FIFO и стек. Буфер FIFO — это память для хранения очередей данных (списков). Слова из очереди выбираются в порядке их поступления. Моменты записи слов в буфер и считывания из него задаются внешними управляющими сигналами независимо друг от друга. Данные поступают в темпе источника информации, а считываются с частотой, необходимой для приемника. Новое слово ставится в конец очереди, а считывание осуществляется с начала очереди. В схеме (рис. 7.11) перед началом работы оба счетчика адресов записи CTW и чтения CTR сбрасываются.
Рис. 7.11. Структура буфера FIFO
При записи данных адреса увеличиваются на единицу при каждом обращении. То же происходит и при чтении данных. Адреса сравниваются при чтении компаратором. С помощью схемы совпадения определяется момент полной загрузки буфера. Эти проверки автоматически выполняются при подаче сигналов RD или WR. Если буфер полный, то требуется прекратить прием данных, а если пустой — то прекратить чтение.
7.3. Кэш-память
7.3.1. Общая характеристика кэш-памяти
Кэш-память (от Cache — тайник) — это способ копирования и хранения блоков данных основной памяти типа DRAM в процессе выполнения программы. Кэшпамять построена на быстродействующих триггерных ЭП, однако имеет небольшую емкость в сравнении с основной динамической памятью. Кэш хранит ограниченное число данных и тегов. Тег содержит информацию о физическом адресе и состояние данных.
При каждом обращении к основной памяти специальный контроллер проверяет по тегу наличие этой копии в кэше. Если она имеется, то вырабатывается сигнал Ни (кэш-попадание) и происходит обращение к кэш-памяти (рис. 7.12). Если копии нет (кэш-промах), то сигнал Hit не вырабатывается и выполняется чтение из ОП и одновременное размещение считанных данных в кэше.
224 Память компьютеров
Рис. 7.12. Структура кэш-памяти
Обмен с ОП может осуществляться двумя способами:
• первый: обращение к ОП сочетается с одновременным поиском информации в теге. Обращение при попадании в ОП аннулируется;
• второй: обращение к ОП осуществляется только после выявления кзш-промаха.
В современных компьютерах кэш строят по двухуровневой схеме:
• первичный кэш (Z.1 Cache) имеет объем десятки Кбайт и встраивается в процессор. Для повышения производительности часто используются раздельные кэши для команд и данных (Гарвардская архитектура);
• вторичный кэш (/.2 Cache), обычно устанавливают на системной плате, он имеет объем несколько Мбайт.
Большинство прикладных программ имеет циклический характер и многократно использует одни и те же данные, поэтому наличие кэша уменьшает количество обращений к относительно медленной ОП.
7.3.2. Полностью ассоциативный кэш
В зависимости от способа установки соответствия между данными в кэше и ОП используют следующие структуры кэш-памяти:
• полностью ассоциативный кэш;
• кэш с прямым размещением;
• наборно-ассоциативный кэш.
В полностью ассоциативной кэш-памяти каждая ячейка хранит данные, а в поле Тег находится полный физический адрес единицы информации, копия которой записана (рис. 7.13).
Рис. 7.13. Структура полностью ассоциативного кэша
7.3. Кэш-память 225
Во время обменов записываемый физический адрес данных сравнивается с полем Тег всех ячеек. Если выявляется совпадение с адресом любой ячейки, то она выставляет сигнал Hit. При чтении, когда значение сигнала Hit = 1, данные выдаются на ШД. Если совпадения нет (Hit = 0), то при чтении из ОП данные вместе с адресом размещаются в свободной или давно не используемой ячейке кэш-памяти.
Строки кэша загружаются адресами и данными при операциях чтения из ОП. Данные без копии в кэше записываются только в ОП. Данные, имеющие копии в кэше, записываются в ОП сквозным или обратным способом.
Во время сквозной записи данные одновременно загружаются в копию кэша и в ОП. Затрачивается время на относительно большую длительность записи в DRAM, что снижает быстродействие всей памяти.
Во время обратной записи данные вначале записываются в свою копию и помечаются признаком модификации. После освобождения системной шины кэш-контроллер переписывает модифицированную строку в ОП. Обратный способ записи сложнее сквозного, однако более эффективный. В обоих случаях кэш-контроллер обеспечивает когерентность, то есть согласование данных в кэше и ОП.
Полностью ассоциативная кэш-память обеспечивает наибольшую функциональную гибкость, однако является очень сложным устройством.
7.3.3. Кэш-память с прямым размещением
В кэш-памяти с прямым размещением ОП условно разбивается на страницы, например, 512. Размер каждой страницы совпадает с размером кэш-памяти. Данные в кзше хранятся в строках, которые являются наборами байтов (часто 32 байта). Если кэш-память имеет, например, 256 строк, то ее объем равен 256 х 32 = 8 Кбайт. При этом объем ОП должен составлять 512 х 8 К = 4 Мбайт. В строках кэша могут храниться данные любой страницы ОП.
Адрес от процессора делится на три части (рис. 7.14).
Рис. 7.14. Организация кэш-памяти с прямым размещением
Младшие разряды (смещение) определяют положение младшего байта 32-разрядного слова. Средние разряды адреса задают номер строки. Вместе номера строки и байта в ней называются индексом. Информация о номере страницы ОП, данные из которой занимают соответствующую строку в кэше, называется тегом.
I5 —4-1749
226 Память компьютеров
Каждый тег занимает ячейку памяти, которая связана со своей строкой. Совокупность этих ячеек образует память тегов. Разрядность ячеек тега должна быть достаточной для записи номера страницы ОП. Например, для 256 страниц длина ячейки тега должна составлять 8 бит.
При обращении к ОП вначале считывается строка кэша с заданным индексом, а затем сравниваются значения тегов данной строки и заданного в адресе от процессора. При кэш-попадании сигнал Hit = 1 и слово данных мультиплексируются из выбранной строки и пересылаются в процессор. При кэш-промахе сигнал Hit = 0 и данные выбираются из ОП; при этом по указанному адресу загружается вся строка кэша (пакетный обмен).
Кэш с прямым размещением имеет простую схему, малую разрядность тега, однако и существенный недостаток — не допускается размещение в кэше строк с одинаковыми индексами, но разными тегами. Это приводит к беспрерывной очереди кэш-промахов. Этот недостаток устраняется в наборно-ассоциативном кэше.
7.3.4. Наборно-ассоциативный кэш
В наборно-ассоциативной структуре кэш-память делится на наборы с небольшим числом строк, кратным двойке, то есть 2, 4, 8 и т.д. Средние разряды адреса от процессора определяют не одну строку, а весь набор.
Каждая строка в наборе обслуживается собственным блоком кэш-памяти, тегом, компаратором и буфером данных. Это подобно параллельной и согласованной работе нескольких каналов прямого замещения. Контроллер кэш-памяти принимает решение о том, в какой из строк наборов размещается очередной пакет данных.
В простом случае каждый пакет данных из ОП может загружаться в одну из двух строк в наборе. Такой кэш содержит два блока кэш-памяти: А — для четных строк и В — для нечетных (рис. 7.15). Такие кэши называются двухвходовыми.
Адрес от процессора
| Тег Набор | Смещение
Индекс * Индекс-------------я
Рис. 7.15. Двухвходовой наборно-ассоциативный кэш
Страницу данных из ОП можно поместить только в тот набор, номер которого равен адресу страницы по модулю, например, 64 или 128 и т.д. Место страницы в наборе произвольное.
Одновременно считываются и сравниваются четные и нечетные строки (слова из них). Считывание данных идет от того блока, где имеется совпадение тега и тего
7.4. Постоянная память 227
вого адреса от процессора. При отсутствии совпадений выполняется обращение к ОП и замещение строки в одном из блоков кэша.
7.4. Постоянная память
7.4.1. Общая характеристика постоянной памяти
Постоянная память предназначена для хранения программ, констант, табличных функций и другой информации, которая записывается заранее и не изменяется в процессе текущей работы компьютера. Она применяется также в преобразователях кодов, знакогенераторах, в микропрограммных устройствах управления. Общим для всех микросхем постоянной памяти является энергонезависимость, словарная организация и применение режима считывания как основного.
Микросхемы постоянной памяти разделяются на следующие группы:
• ПЗУ или ROM (Read Only Memory) — программируются одноразово заводом-изготовителем, часто называются масочными;
• ППЗУ или PROM (Programmable ROM) — программируются одноразово электрическим способом пользователем;
• РПЗУ-УФ или EPROM (Erasable PROM) — программируются многократно (репрограммируются) с ультрафиолетовым стиранием и электрической записью;
• РПЗУ-ЭС или EEPROM (Electrical EPROM) — программируются и стираются многократно электрическим способом.
7.4.2. Микросхемы постоянных запоминающих устройств
В микросхемах ПЗУ и ППЗУ элементами памяти являются диоды, биполярные и МОП-транзисторы, а также КМОП-структуры. Элементы памяти размещаются в узлах матрицы, образованных адресными линиями строки X, и столбца У,- Состояние “1” соответствует соединению ЭП с разрядной линией, а состояние “0” означает отсутствие связи (для прямых выходов микросхемы памяти). В масочных ПЗУ разрыв соединений ЭП с разрядными линиями при записи информации выполняет завод-изготовитель (рис. 7.16).
а б в
Рис. 7.16. Элемент памяти масочных ПЗУ:
а — на диодах; б — на многоэмиттерных транзисторах; в — на МОП-транзисторах
Характеристики ряда серий БИС ПЗУ представлены в табл. 7.1, а их условные обозначения показаны на рис. 7.17. 15*
228 Память компьютеров
Таблица 7.1
Тип микросхемы Емкость, бит Технология Время выборки — tA, нс P,.L, мВт
КР1656РЕ4 8Кх8 ТТЛШ 40 90
КР568РЕЗ 16Кх8 п-МОП 300 300
КМ568РЕ5 128Кх8 п-МОП 200 300
К536РЕ2 32Кх8 КМОП 500 20
КР1656РЕ4
КР568РЕЗ
Рис. 7.17. Условное обозначение БИС ПЗУ
К563РЕ2
Микросхема К563РЕ2 имеет вмонтированную схему самоконтроля и исправления одиночных ошибок с помощью кода Хеминга с установлением признака-ошибки на выходе ЛТ. Корректор можно выключить сигналом /<2 = 0, при этом данные считывают без исправления ошибок.
7.4.3. Микросхемы программируемых постоянных запоминающих устройств
В микросхемах ППЗУ, которые поставляются заводом изготовителем, все ЭП, расположенные в узлах матрицы, соединены со столбцами плавкими перемычками (рис. 7.18).
Рис. 7.18. Элемент памяти микросхем ППЗУ;
а — на диодах; б — на многоэмиттерных транзисторах; в — на диодах Шотки
Запись информации в ППЗУ осуществляется пользователем пережиганием перемычек (рис. 7.18, а, б) или электрическим пробоем диодов Шотки (рис. 7.18, в). Для плавких перемычек используют тонкие пленки из нихрома или поликристалли-
7.4. Постоянная память 229
ческого кремния; ток пережигания равен 50-100 мА, в результате чего перемычка необратимо разрушается.
Структура ППЗУ с ЭП на многоэмиттерных транзисторах показана на рис. 7.19. Память построена по системе 2,50 с организацией 4x2 бит. Каждый многоэмиттер-ный транзистор в матрице представляет собой два ЭП (по числу эмиттеров) и программируется на запоминание двухразр'ядного слова.
Рис. 7.19. Структура ПЗУ с организацией 4x2 бит
В ЭП на транзисторах ГЛ-КГД запрограммированы для хранения соответственно слова 01,10,11 и 00.
Пусть значение адреса строки Хо = 1 (At = 0) и столбца У, = 1 (Л2 = 1); при этом открываются транзисторы VT2 и VT1 и через них протекает в буфер ток, отображающий лог. 1. Транзистор VT& — закрытый, поскольку его коллектор не имеет связи с эмиттером VT2, который отображает лог. 0.
В результате считывания на выходе буфера BD формируется слово DJX = 01. Число транзисторов, подключаемых к каждому выходу адреса столбца, определяется разрядностью хранимого слова.
Микросхема ППЗУ по структуре аналогична масочным, однако допускает однократное программирование пользователем. Наиболее распространены микросхемы ППЗУ серии К556, изготовленные по ТТЛШ-технологии. Функциональный состав этой серии включает микросхемы емкостью от 1 К до 64 Кбит со словарной (четырех и восьмиразрядной) организацией с временем выборки 45-85 нс и потребляемой мощностью 0,6-1 Вт (рис. 7.20).
Разновидностью ППЗУ являются программируемые логические матрицы (ПЛМ или PLM), к которым относятся микросхемы КР556 (РТ1, РТ2). Они имеют идентичные характеристики и конструктивные параметры, однако отличаются по типу выхода: РТ1 имеют выход с открытым коллектором, РТ2 — с тремя состояниями (рис. 7.20, в). Обе микросхемы предназначены для реализации устройств, выполняющих логические операции над двоичными переменными.
Анализируемые ПЛМ рассчитаны на 16 входных переменных, инверсии от которых получают внутри микросхемы. Функциональные возможности данных ПЛМ:
230 Память компьютеров
восемь логических сумм, каждая из которых может включать до 48 логических произведений из 16 переменных и их инверсий.
КР556(Р 15.РТ17)
КР556И 16
Рис. 7.20. Условное обозначение БИС ППЗУ
КР556(РГ1,РГ2)
Программирование ПЛМ заключается в пережигании плавких перемычек в требуемых узлах. Это выполняют вмонтированные в ПЛМ специальные схемы, которые управляются сигналом PR. Вначале программируют матрицу I, затем матрицу 4М и выходные усилители. Для управления доступом к микросхеме используют сигнал CS, наличие которого позволяет также наращивать число входных переменных и выходных функций способом объединения нескольких ПЛМ.
Широко применяются микросхемы ПЛМ, которые программируются способом заказного фотошаблона. Такие микросхемы включены в комплект некоторых микропроцессорных серий БИС как ПЗУ микрокоманд.
Характеристики наиболее распространенных микросхем РПЗУ-ЭС на МНОП-транзисторах представлены в табл. 7.2., а условные графические обозначения некоторых из них показаны на рис. 7.21.
Способность к многократному программированию обеспечивается применением ЭП с качествами управляемых перемычек. Эту функцию выполняют транзисторы типа ЛИЗМОП или МНОП. Они представляют собой специальные МОП-транзисторы, в которых область под затвором и подкладкой может накапливать и сохранять заряд, создаваемый электрическим способом.
Таблица 7.2
Тип микросхемы Тип транзистора Емкость, бит t, мкс Рсс, мВт £/„, В
КР558РР1 р-МНОП 256x8 5.0 300 5-12
КР1601РР1 р-МНОП 1Кх4 1,8 625 5-12
КР1601РРЗ р-МНОП 2Кх8 1,6 825 5-12
КР558РР2 п-МНОП 2Кх8 0,35 480 5
КР558РРЗ п-МНОП 8Кх0,4 0,4 400 5
КР1611РР1 п-МНОП 8Кх8 0,3 850 5
7.4. Постоянная память 231
КР558РР2
К573РР2 КМ1609РР1
БЕРНОМ.
КМ558РРЗ
КР1601РР1
Рис. 7.21. Условные обозначения микросхем РПЗУ-ЭС на МНОП-транзисторах
Для программирования ППЗУ и репрограммируемых ПЗУ используют специальные устройства — программаторы. Для ряда микросхем памяти программирование выполняют с помощью компьютера.
7.4.4. Микросхемы РПЗУ-ЭС на МНОП-транзисторах
Для построения памяти типа РПЗУ-ЭС широко используют транзисторы МНОП (от слов металл-нитрид-оксид-полупроводник) с двухслойным подзатворным диэлектриком. На поверхности кристалла находится тонкий слой диоксид кремния S/O2, дальше — более толстый слой нитрида кремния S/'3A/4, а затем уже металлический затвор (рис. 7,22, а).
Рис. 7.22. Элементы памяти на МНОП-транзисторе: а — топология; б — характеристика lc=f(UC4); в — схема ЭП.
Элемент памяти на МНОП-транзисторе работает в следующих режимах: программирования, хранения, считывания и стирания информации.
Программированием называется процесс занесения заряда под затвор транзистора. При этом к затвору и-канального МНОП-транзистора, в котором создается заряд, прикладывают положительный импульс напряжения амплитудой около 20 В. Под действием сильного электрического поля электроны обретают достаточную энергию и туннелируют из подкладки через тонкий слой оксида толщиной около 5 нм
232 Память компьютеров
в слой нитрида, где они захватываются “ловушками”. В нитриде появляется неподвижный отрицательный заряд, выполняющий функцию носителя информации. Считают, что наличие заряда отображает лог. О, а его отсутствие — лог. 1. Транзистор, в котором заряд отсутствует, открывается рабочим сигналом. В «-канальных МНОП-транзисторах заряд экранирует действие положительного напряжения на затворе и соответственно повышает пороговое напряжение настолько, что рабочий сигнал не может открыть транзистор (рис. 7.22, б).
В схеме ЭП на МНОП-транзисторе выходной ток И„ых, отображающий лог. 1, появляется при следующих условиях: А', = Y, = 1, заряд под затвором транзистора VTX отсутствует. После программирования новое состояние МНОП-транзистора сохраняется месяцами или годами. Перед новой записью старая информация стирается записью нуля в ЭП. Число перезаписей информации находится в пределах 104-106 раз.
В режиме считывания на затворы МНОП-транзисторов подают напряжение С7Сч. значение которого лежит между двумя предельными уровнями. Если в ЭП записана лог. 1, то транзистор открывается; если лог. О — транзистор буде закрытым.
Итак, в зависимости от состояния транзистора при подаче на его затвор напряжения считывания 1/Сч (по координате А\) в разрядной шине Y, ток протекает или нет (рис. 7.22, в). Усилитель считывания трансформирует состояние разрядной шины в выходное напряжение высокого (ток протекает) или низкого (ток отсутствует) уровней.
Если транзистор имеет заряд в диэлектрике, то есть находится в состоянии лог. О, то для его перехода в состояние “1” накопленный заряд вытесняют из-под затвора отрицательным импульсом напряжения 30-40 В, который подается на затвор относительно подкладки. Такой процесс называют режимом стирания.
Структура микросхемы КР1601РРЗ емкостью 2 К х 8 бит на р-канальных МНОП-
Микросхема КР1601 РРЗ содержит:
• матрицу ЭП из 128 строк и 128 столбцов, на пересечении которых расположены 16384 транзисторов;
7.4. Постоянная память 233
• дешифратор адреса строк DCX, на входы которого поступают семь старших разрядов адреса A4-Aw; он имеет 128 выходов, каждый из которых управляет выборкой одной из строк матрицы;
• дешифратор адреса столбцов DCY, на входы которого поступают четыре . младших разряда адресного кода Ло-Л3. Выходы DCY управляют селектором. На входы селектора поступают сигналы, считанные из ЭП выбранной строки. Селектор выбирает из 128-разрядного слова (16 байт) одно восьмиразрядное (байт) и передает его через буфер ввода-вывода BIO на внешнюю шину;
• узел управления, на входы которого поступают инверсные управляющие сигналы: CS — выбор микросхемы; PR — разрешение на программирование (запись); ER — сигнал разрешения стирания информации. На узел подается также напряжение программирования UPR. Узел управления обеспечивает режимы хранения, считывания, стирания и записи. Состояния управляющих сигналов, обеспечивающих перечисленные режимы работы, представлены в табл. 7.3.
Таблица 7.3
Режимы работы Сигналы состояния uPR, в tA, мкс
CS RD PR ER
Стирание 0 1 1 0 -36 200
Запись 0 1 0 1 -36 20
Считывание 0 0 1 1 -12 0,4
Хранение I X X X X
Стирание начинается с момента подачи импульса ER длительностью 100-200 мс. По окончанию стирания все ЭП матрицы переходят в состояние лог. 0; допускается также построчное стирание.
В режиме записи на выводы микросхемы подают значения разрядов записываемого байта данных, адресный код, управляющие сигналы и затем импульсный сигнал программирования PR - 0 на время 20 мс. Для программирования в автоматическом режиме всей микросхемы с числом адресов, равным 2048, требуется 41 с. В режиме считывания на вывод UPR коммутируют напряжение питания минус 12 В для понижения используемой мощности, затем подают код адреса и сигнала управление соответственно табл. 7.3. Через 0,4 мкс на информационных выходах появляется считываемое слово. __
Режим хранения определяется сигналом CS, который запрещает обращение к микросхеме независимо от состояния сигналов на других входах. В режиме хранения при отключении источника питания заряд под затвором может храниться несколько лет. Достоинством микросхем РПЗУ-ЭС является возможность их перепрограммирования без изъятия из устройства, а также значительное число циклов перепрограммирования, достигающее 10 тыс.
Эта особенность наряду с энергонезависимостью позволяет широко применять их в компьютерах в качестве встроенных ПЗУ со стиранием информации.
234 Память компьютеров
7.4.5. Микросхемы РПЗУ на ЛИЗМОП-транзисторах
Запоминающий элемент типа ЛИЗМОП — это МОП-транзистор с индуцированным р- или n-каналом. Металлический затвор этого транзистора размещен в толще диэлектрика (обычно диоксида кремния) и не имеет металлического вывода. Этот затвор называется плавающим (ПЗ). От кристалла ПЗ отделен диэлектриком толщиной 0,1 мкм (рис. 7.24, а).
и с и з с
a б в
Рис. 7.24. Элемент памяти на ЛИЗМОП-транзисторв:
а, б — топология транзистора с одним и двумя затворами; в — схема с одним затвором; г — схема с двумя затворами.
При наличии заряда на ПЗ образуется проводящий канал и транзистор открыт— это соответствует записи лог. 1; при отсутствии заряда транзистор закрыт (записан лог. 0).
Структурная схема ЛИЗМОП-транзистора с дополнительным затвором выборки (двухзатворный транзистор) показана на рис. 7.24, б. В режиме программирования на исток и сток транзистора относительно подкладки подается положительный импульс напряжения амплитудой 25 В. На обратно смещенных n-р-переходах исток-подкладка и сток-подкладка возникает процесс лавинной инжекции заряда (отсюда происходит обозначение транзистора ЛИЗМОП). Часть электронов попадает на ПЗ; в результате наложения на ПЗ отрицательного заряда пороговое напряжение на передаточной характеристике смещается в область более высокого уровня (сдвиг вправо), что соответствует записи лог. 0. Отсутствие зарядов электронов на ПЗ соответствует записи лог. 1.
Стирание записанной информации состоит в вытеснении заряда из ПЗ. Эту операцию в транзисторах ЛИЗМОП осуществляют двумя методами: в группе РПЗУ-ЭС — импульсом напряжения, который подается на затвор; в группе РПЗУ-УФ — с помощью ультрафиолетового (УФ) облучения сквозь прозрачное стекло в крышке корпуса. В первом случае накопленные на ПЗ электроны вытесняются в подкладку электрическим полем и восстанавливается состояние “1”. Во втором случае электроны рассасываются с ПЗ в подложку в результате усиления теплового движения за счет полученной от источника УФ-излучения энергии.
Режим считывания осуществляется так же, как и в микросхеме РПЗУ на МНОП-транзисторах. В режиме хранения обеспечивается отсутствие напряжения на электродах ЭП с тем, чтобы исключить рассасывание заряда на ПЗ в диэлектрической среде. Например, в микросхеме К573РФ6 гарантированный срок хранения информации без питания составляет пять лет, а в КМ1609РР2 — до 10 лет.
Схема включения в ЭП транзистора VT1 с одним затвором показана на рис. 7.24, в, а с двумя затворами — на рис. 7.24, г.
7.5. Флэш-память 235
В современных компьютерах используют:
• память типа РПЗУ-УФ с емкостью до 8 Мбит и временем доступа 45 нс (фирма Atmel);
• память типа РПЗУ-УФ с емкостью до 256 Кбит, временем доступа 90 нс, допустимым числом циклов перезаписи 105 и продолжительностью хранения данных более 10 лет; эти ЗУ используют один источник напряжения 5 В и потребляют ток 5 мА в активном режиме и 0,1 мА при отсутствии обращений (фирма SGS-Thomson).
В энергонезависимой постоянной памяти широко используют режим импульсного питания: напряжение подается только на ту микросхему памяти, к которой имеется обращение. Это во много раз уменьшает энергопотребление, улучшает тепловой режим ИМС и повышает их надежность.
7.5. Флэш-память
7.5.1. Общая характеристика флэш-памяти
Флэш-память (Flash Memory) использует ЭП на транзисторах ЛИЗМОП с электрическим стиранием и записью информации. Она относится к постоянной памяти типа EEPROM, однако ряд архитектурных и функциональных особенностей позволили выделить флэш-память в отдельный класс. Флэш-память использует наряду с традиционными адресными и управляющими сигналами специальные команды. Информация в микросхемах флэш-памяти записывается и сохраняется в блоках определенного размера, иногда — назначения. При этом стирание информации осуществляется или для всей памяти сразу, или для больших блоков; это упрощает схемы ЭП. Флэш-память превосходит EEPROM в том, что не требует специальной аппаратуры для записи или стирания данных.
Различают следующие виды флэш-памяти:
• файловая флэш-память (Flash File) — массив ЭП разделен на блоки одинакового размера (симметричная архитектура);
• флэш-память с несимметричной архитектурой (Boot Block) — массив ЭП разделен на блоки разного размера; один из блоков имеет аппаратные средства для защиты информации в нем;
• флэш-память с возможностью стирания только всего массива ЭП (Bulk Erase);
• флэш-память с возможностью записи информации при различных напряжениях программирования (Start Voltage);
• память с использованием новых ЭП с четырьмя состояниями, которые хранят по два бита (Strata Flash).
Файловая флэш-память ориентирована на замену жестких магнитных дисков. Такие ЗУ в сотни раз уменьшают потребляемую мощность, увеличивают механическую прочность и надежность, уменьшают их размеры и массу и на несколько порядков повышают быстродействие при чтении данных. Микросхемы, заменяющие магнитные диски, имеют идентичные блоки и развитые средства обмена информа
236 Память компьютеров
цией. Микросхемы файловой флэш-памяти фирмы Intel имеют информационную емкость 4-32 Мбит, время доступа — 70-150 нс.
Микросхемы Boot Block используют однобайтовую или переключательную одно- или двухбайтовую организацию и состоят из нескольких блоков разного размера. Один из блоков имеет дополнительные аппаратные средства защиты от изменения данных; он предназначен для хранения очень важной информации, которая не изменяется при модификации данных в других блоках. Микросхемы Boot Block предназначены для хранения компонентов системного программного обеспечения. Привилегированный блок содержит программу-загрузчик, которая записывает с диска необходимые данные для инициализации устройств компьютера.
Микросхема Boot Block типа 2QF00BXIN, которая часто применяется для хранения программ базовой системы ввода-вывода (BIOS) в ПЭВМ, имеет время доступа 75-150 нс, гарантируется 105 циклов стирания-программирования.
Микросхема 28F00BX содержит:
• основной блок объемом 112 Кбайт;
• два блока параметров емкостью по 4 Кбайт каждый;
• блок-загрузчик объемом 4 Кбайт, стирание и программирование которого возможно только при особых условиях.
Основной блок и блоки параметров защиты — равноправные. Выделение небольших блоков параметров позволяет хранить в них часто изменяемую информацию.
Микросхемы Bulk Erase имеют однобайтовую организацию емкостью 32-256 Кбайт, время доступа 65-200 нс и представляют собой единый массив, который стирается сразу.
7.5.2. Микросхема файловой флэш-памяти 28F008SA
Микросхема файловой флэш-памяти 28FQQ8SA разработана фирмой Intel в 1989 г. на основе новой технологии ETOX III (EPROM Tunnel Oxide). К особенностям технологии ETOX III относятся:
• разрешающая способность — 0,8 мкм;
• применение однотранзисторных ЭП на ЛИЗМОП-структурах с размерами 2,5 х 2,9 мкм и плавающим поликремневым затвором.
В основе программирования флэш-памяти лежит механизм канальной инжекции горячих электронов. Во время программирования управляющий затвор ЭП подключается к внешнему напряжению UPR = 12 В. При стирании электроны одновременно вытесняются из всех выбранных ЭП обратным туннелированием. Структура микросхемы 28F008SA показана на рис. 7.25. Она является типовой для флэш-памяти.
Опишем основные компоненты микросхемы и их функциональное назначение. Микросхема 28F008SA содержит:
• матрицу ЭП емкостью 8 Мбит с организацией 1 М х 8 бит, которая разбита на 16 блоков по 64 Кбайт в каждом. Блок состоит из 1024 строк и 512 столбцов;
• буфер адреса ВА, регистр RGA и счетчик СТА адреса. Буфер ВА соединен с адресными входами А19-ЛО. При обращении к памяти адрес фиксируется
7.5. Флэш-память 237
в регистре, с которого он подается на дешифраторы строк DCX и столбцов
DCY;
Рис. 7.25. Структура СБИС 28F008SA
• буферы входных BID и выходных BOD данных. Обмен данными осуществляется по двунаправленным входам-выходам DJ-DQ. Входная информация записывается во внутренний регистр данных RGD. Выходные данные из матрицы ЭП через мультиплексор MUX подаются на выход через буфер BOD. Оба буфера имеют по три состояния;
• регистр-идентификатор RID; предназначен для выдачи кода фирмы-разработчика и кода микросхемы;
• командный интерфейс (блок команд) пользователя CUI (Command User Interface), в составе которого имеется регистр команд RGK. Блок CUI выполняет роль интерфейса между микропроцессором и внутренними операциями в микросхеме;
• автомат записи байта и стирания блока WSM (Write State Machine). Он воспринимает команды от блока SUI и автоматически выполняет алгоритм записи байта или стирания блока с последующей верификацией (проверкой) результата. Запись данных в память выполняется побайтно с типовым временем 9 мкс. При этом типовой ток потребления от источника программирования IPR < 30 мА. Напряжение записи байта и стирания блока UPR = 12 В;
• регистр состояния RGS (Status Register); хранит информацию о состоянии автомата WSM и служит для контроля коррекции операций записи или стирания;
• компаратор СОМР; используется при контроле правильности записи байта данных;
• коммутатор напряжений KUPR.
238 Память компьютеров
Для управления работой микросхемы служат входы, сигналы на которых активны в состоянии низкого уровня (рис. 7.26).
ША
28F008SA
^19-ЛО
Выбор микросхемы! — Разрешение записи 1 7777, Разрешение выдачи!^
Режим -----
энергопотребления
ШД
7)7-DO :---
„ — Готово/Занято
R1/BY *
Напряжение питания
5 В-----------------и
исс
т г Напряжение программирования
С//’Я ---------------
Корпус >
Рис. 7.26. Условное графическое обозначение микросхемы 28F008SA
Ко входным сигналам относят:
• СЕ — выбор микросхемы; WE — разрешение записи, ОЕ — разрешение выдачи данных;
• PWD — управление энергопотреблением: PWD = 1 — нормальная работа; PWD =0 — режим микропотребления (типовое значение тока I = 0,2 мкА, мощность потребления — 1 мВт) и блокировка операций записи и стирания;
• — вход для подачи напряжения стирания блока или записи байта. Если
Urr < UPr, то изменить данные невозможно;
• UC(— напряжение питания плюс 5 В;
• GND — корпус микросхемы.
Выход RY / BY (Ready/Busy) показывает состояние автомата WSM. Если RY/BY = 1, то автомат занят, а если RY/BY = 0, то готов к приему новой команды.
Операции в памяти выполняются после записи соответствующей команды:
• “Чтение массива” (код FFH)\
• “Идентификатор" (код 90/7). Вначале считывается код фирмы-производителя 897/, затем код микросхемы А2Н. Эти коды позволяют автоматически определять алгоритм работы с памятью;
• “Чтение регистра состояния” (код 7077);
• “Сброс регистра состояния “RGS” (код 50/7);
• “Установка стирания” (код 20/7); “Подтверждение стирания” (код Z>0/7). Команды следуют одна за одной;
• “Приостановить стирание” (код ВОН)-, “Возобновить стирание” (код 7)0/7);
• “Установить запись байта” (код 40/7); “Запись”.
Значения разрядов регистра состояний:
• 57 = 1 — автомат WSM готов;
• 56 = 1 — стирание приостановлено;
• 55 = 1 — ошибка при стирании блока;
• 54 = 1 — ошибка при записи байта;
7.5. Флэш-память 239
• S3 = 1 — низкий уровень напряжения питания;
• 52 - 50 — резерв.
7.5.3. Основные направления развития флэш-памяти
Для улучшения технико-экономических характеристик флэш-памяти используют различные средства и способы.
1. Прерывание длительного процесса записи при необходимости чтения памяти.
2. Создание внутренней очереди команд, которая позволяет организовать конвейерный процесс работы.
3. Программирование длины слов.
4. Ввод пониженного энергопотребления в режиме покоя, когда ток уменьшается до 2 мкА.
5. Приспособление для работы с различными напряжениями питания: 5; 3,3 и даже 2,6 В.
6. Ввод в структуру памяти буферов, которые обеспечивают одновременно запись и вывод данных.
7. Совершенствование средств защиты от случайного стирания или несанкционированного доступа.
В качестве примера представим параметры файловой микросхемы флэш-памяти 28F0Q2SA (изделие фирмы Intel, 1997 г.);
• организация 2 М х 16 или 4 М х 8 бит (емкость 32 Мбит) по выбору пользователя;
• напряжение питания — 3,3 или 5 В, напряжение программирования — 12 В, до 106 циклов стирания на блок;
• число независимых блоков: 64 х 64 Кбайт или 64 х 32 Келов;
• корпус — типа TSOP размерами 1,2 х 14 х 20 мм с 56 выводами;
• технология — с разрешающей способностью 0,6 мкм;
• время доступа при чтении — 70 или 150 нс при напряжениях 5 и 3 В соответственно;
• время записи слова или байта — не более 9 мкс;
• время записи блоку — не более 2,1 с для байтового режима и не более 1с — для словарного режима;
• время стирания блока — не более 10 с и стирания кристалла — не более 25,6 с.
7.5.4. Память типа Strata Flash
Флэш-память типа Strata Flash разработана фирмой Intel в 1997 г. В ней впервые в одном ЭП хранятся два бита. Это обеспечивается созданием в плавающем затворе транзистора ЛИЗМОП четырех значений зарядов. Запись двух битов осуществляется практически на тех же размерах ЭП, которые использовались для хранения одного бита. Таким образом, это позволило от емкости 32 Мбит, например, сразу перейти к емкости 64 Мбит.
240 Память компьютеров
Запоминающие ЭП программируются путем ввода в плавающий затвор одного из четырех количеств зарядов, каждое из которых соответствует паре двоичных цифр: 11, 10, 01 и 00. В зависимости от заряда ЭП имеет одно из четырех пороговых напряжений. При считывании информации ток элемента памяти имеет четыре значения, на. их основе выходные схемы формируют двухразрядный код.
7.6. Статические запоминающие устройства
7.6.1. Общая характеристика статических запоминающих устройств
В статических ЗУ функцию запоминания бита информации выполняют триггеры. Они реализуются по любой схемотехнике — ТТЛШ, И2Л, ЭСЛ, л-МОП, КМОП и др. Наиболее интенсивно развираются ОЗУ на КМОП-структурах, которые при уменьшении разрешающей способности до 0,2 мкм достигают высокого быстродействия. При этом они сохраняют свои традиционные достоинства — большую информационную емкость и очень малое энергопотребление — до долей микровольта на один ЭП.
Статические ОЗУ (SRAM) обычно имеют структуру 2DM, а при небольшой информационной емкости строятся по структуре 2D. Они широко используются в кэшпамяти, которая должна иметь максимально возможное быстродействие.
Для построения ЭП статических ЗУ широко используют RS-триггеры по схемотехнике КМОП. Типовая схема такого RS-триггера содержит:
• собственно триггер на транзисторах VT3 и VT5 (л-тип) и на нагрузочных транзисторах VT2. и VTA (р-тип);
• ключи выборки на транзисторах РТ1 и VT6 (рис. 7.27).
Рис. 7.27. Схема RS-триггера на КМОП-структурах
7.6. Статические запоминающие устройства 241
С прямым Q и инверсным Q выходами триггера через ключи выборки связаны разрядные линии записи-считывания РЛ07 и РЛ17. В режиме хранения транзисторы VTI и VT6 закрыты (лог. 1). При выборе данного триггера (линия выбора ЛВ, = 1) для записи единицы устанавливают РЛО, = О, РЛ1, = 1, а при записи нуля — наоборот.
Во время считывания данных сигнал ЛВ, = 1, и двунаправленные ключи VT\ и VT6 открываются. При этом напряжение паразитной емкости Сщ или СП2 увеличивается на значение AZ7 в плече закрытого транзистора VT5 или К73. Например, если триггер находится в состоянии лог. 1, то заряжается паразитная емкость Спг- Если триггер находится в состоянии лог. О, то заряжается паразитная емкость Ст. При этом состояние триггера не изменяется. Значения напряжений с паразитных емкостей подаются на дифференциальный усилитель, подключение которого показано на рис. 7.27 штриховой линией. Усилитель формирует на выходе соответствующее значение лог. 1 или лог. 0.
Схема выходного каскада с тремя состояниями, который широко используется в статической памяти на КМОП-структурах, показана на рис. 7 28, а.
Рис. 7.28. Выходной каскад с тремя состояниями на КМОП-структурах: а — схема; б — эквивалентная схема для открытого состояния
Транзисторы VTI и VT2 построены по p-МОП технологии, a VT3, VT4 — по л-МОП технологии. Сигнал передается на выход инверсным кодом только при условии CS = 0, W IR = \. В этом случае транзисторы VT1 и VT3 образуют инвертор, а транзисторы VTI и VT4 открыты и насыщены. Для других комбинаций управляющих сигналов CS, W /R схема находится в третьем состоянии.
16-4-1749
242 Память компьютеров
7.6.2. Модуль статической памяти
Условное графическое изображение микросхем SRAM серий К132РУ9 и К541РУ2 показано на рис. 7.29, а.
К132РУ9
К541РУ2
а
а — полное; б — упрощенное
Построение модуля памяти с организацией 1 К х 16 бит на основе четырех микросхем К132РУ9 показано на рис. 7.30.
ША(Ю)
ШД(16)
Рис. 7.30. Построение модуля памяти 1Кх 16 бит
Для построения данного модуля памяти необходимо:
• подключить десятиразрядную ША (10) к адресным входам всех микросхем;
• на входы всех микросхем подать совместные управляющие сигналы CS, W/R;
• к двунаправленным входам-выходам подключить соответствующие разряды ШД(16).
Рассмотренный способ построения блока памяти с большей разрядностью называют расширением по горизонтали.
Основные параметры ряда отечественных серий микросхем SRAM представлены в табл. 7.4 (значения параметров усреднены).
7.7. Динамическая память 243
Таблица 7.4
Серия Емкость, бит tcv, нс Ucc, В Рсс, Вт Схемотехнология
К500 64 х 4 4 Кх 1 30 -5,2 0,8 ЭСЛ
К1500 16 К х 1 1 Кх4 20 -4,5 0,8 ЭСЛ
К132 4Кх4 70 5 0,6 И2Л-ТТЛ
К541 1 Кх4 130 5 0,4 И2Л-ТТЛ
К537 64 К х 1 200 5 0,02 КМОП
К1809 1 Кх 16 800 5 0,6 п-МОП
К6500 1 Кх41 4 4; -2,4 1,6 GaAs
Американская электронная промышленность выпускает микросхемы типа SRAM с организацией 8Кх8, 16Кх8, 32Кх8, 64Кх8и128Кх8 бит и временем доступа 8-20 нс.
7.7. Динамическая память
7.7.1. Принцип построения динамического запоминающего элемента
В динамической памяти типа DRAM информация сохраняется в виде зарядов на очень малой емкости С3=0,01...0,05 пФ, образованной между стоком и подкладкой МОП-транзистора (рис. 7.31).
ЛЗСу
ЛВ ч (_!_
и
Рис. 7.31. Динамической однотранзисторный ЭП: а — схема; б— топология
Стык транзистора не имеет внешнего вывода. Для записи информации на линию выборки ЛВ,- подается высокий уровень напряжения, которое открывает транзистор Ту. Создается проводящий канал, и уровень напряжения на разрядной линии записи-считывания ЛЗС; определяет состояние конденсатора С3: заряжен при высоком уровне (состояние “1”) и разряжен при низком (состояние “0”)
Фрагмент ЗУ (рис. 7.32) показывает два динамических ЭП в одном столбце, усилитель считывания УСЧ, а также ключи и Ко соответственно для записи единицы и нуля.
16*
244 Память компьютеров
Рис. 7.32. Фрагмент динамического ЗУ: а — схема; б — временные диаграммы считывания
Линия ЛЗС,- длинная, к ней подключено много транзисторов (определяются количеством строк), поэтому она имеет большую емкость Сл, которая многократно превышает С3 запоминающего элемента. Перед считыванием линия ЛЗС, (собственная емкость Сл) предварительно заряжается до уровня С7с-с/2 (возможны и другие значения в ряде микросхем памяти). При считывании нуля (сигнал ЛВ, = 1) линия ЛЗС, подключается к емкости С3 с нулевым потенциалом, поэтому часть заряда емкости Сл перетекает в емкость С3 и напряжение на них выравнивается. Потенциал линии ЛЗС, понижается на значение АС/. Это — сигнал лог. О, поступающий на УСЧ. При считывании единицы, наоборот, напряжение на емкости С3 вначале равно значению Ucc- При подключении емкости С3 к линии ЛЗС, часть ее заряда передается на емкость Сл и напряжение на линии ЛЗС, увеличивается на АС/. Это — сигнал лог. 1, поступающий на УСЧ.
До выборки ЭП емкость Сл имела заряд Q = CnUcc /2 , а после — этот же заряд имеет общая емкость С3 + Сл, поэтому справедливо равенство: 2 = (СЛ + С3)(С/сс/2-АС/). Сравнивая выражения для одного и того же заряда Q, запишем:
СлС/(Г/2 = (Сл+С3)(С/сс/2-АС/), откуда для АС/ получаем
АС/ = U(XC3/2Cn.
Вследствие того, что Сл » С3, сигнал АС/ оказывается слабым. Кроме того, считывание является разрушительным — емкость С3 существенно изменяет свой потенциал.
Эти недостатки можно устранить увеличением емкости С3 (без изменения площади ЭП) или уменьшением емкости Сл.
Уменьшение емкости Сл достигается при разрезании ЛЗС на половины и включении между ними дифференциального усилителя-регенератора УРЕГ. Такой способ вдвое уменьшает емкость Сл и соответственно сигнал АС/ увеличивается в два раза (рис. 7.33).
7.7. Динамическая память 245
Рис. 7.33. Способ уменьшить емкость С„:
а — разрезание разрядной линии на половины; б — схема УРЕГ
О ПДГ
Схема УРЕГ строится на основе триггеров с использованием дополнительного сигнала подготовки ПДГ для управления нагрузочными транзисторами Тн{ и Тн2 (рис. 7.33, б). Вначале сигнал ПДГ = 0 и транзисторы THi и Тн2 закрыты. Входы-выходы УРЕГ подключены соответственно к ЛЗСл и ЛЗСД. При считывании сигнал ПДГ = 1 и транзисторы и Тн2 открываются. Потенциал ЛЗС с выбранным ЭП увеличивается или уменьшается на АСУ, а вторая линия хранит постоянное напряжение [/«72. Состояние триггера определяется тем входом-выходом, на котором изменяется напряжение.
При увеличении напряжения на А[/ данный вход-выход принимает значение лог. 1 (противоположный — лог. 0). При уменьшении напряжения на А[/ данный вход-выход принимает значение лог. 0 (противоположный — лог. 1).
После переключения триггер хранит на выводах А и В значения записанных данных, с помощью которых он восстанавливает на емкости С3 полное значение считанного сигнала. Тем самым автоматически осуществляется регенерация данных в ЭП. Состояние триггера определяет также выходные сигналы считанной информации.
7.7.2. Схема динамического запоминающего устройства
Типовая схема динамического ЗУ с однобитной организацией Nx 1 содержит (рис. 7.34):
• матрицу ЭП (раскрыт частично один столбец);
• буферы адресов строк и столбцов;
• дешифраторы адресов строк DCX и столбцов DCY;
• формирователи ФС1 и ФС2, вырабатывающие тактовые сигналы Ф1 - Ф4;
• усилитель-регенератор УРЕГ;
• инверторы и ключевые схемы KI - К4 и К8.
С помощью схемы УРЕГ линии записи-считывания разрезаны на две равные части ЛЗСл и ЛЗСД, при этом емкость разрядных линий уменьшается до значений Сл/2. ____
В исходном состоянии высокий уровень сигнала RAS = 1 замыкает ключи А"1, которые подают напряжение Uccl^ Для заряда ЛЗС^ и ЛЗСЙ. При обращении к памя-
246 Память компьютеров
ти одновременно с сигналом RAS = 0 подается старшая половина адресного кода
Ключи А"1 размыкаются и ЛЗС изолируются от напряжения Ucc/2-. При этом во всех ЭП выбранной строки происходят процессы зарядки или разрядки запоминающего конденсатора С3 и создается дисбаланс напряжений на входах схемы УРЕГ.
Второй тактирующий импульс Ф2 снимает сигнал ПДГ с усилителей-регенераторов, и они переключаются. При этом на их входах-выходах формируются полные уровни сигналов, которые восстанавливают состояние ЭП выбранной строки.
На исполнительном этапе операции записи или считывания необходимо наличие сигнала CAS = 0 — прием младшей части адресного кода Ау (адреса столбцов).
7.7. Динамическая память 247
Формирователь ФС2 вырабатывает вторую пару тактирующих импульсов ФЗ и Ф4. Сигнал ФЗ позволяет загрузку в буфер BAY адреса столбцов; сигнал Ф4 активизирует работу дешифратора DCY, в результате чего открываются ключи К2 выбранных столбцов.
Если W / R = 1, то выполняется операция считывания бита информации с правого плеча схемы УРЕГ и передача его значения через ключи К2 и КА на выходную линию данных DO. При этом данные, считанные с ЛЗСл, передаются инверсным кодом.
При W / R = Q выполняется операция записи бита информации с входной линии DIчерез ключи КЗ. При этом данные, которые записываются на ЛЗСА, инвертируются.
Операция регенерации осуществляется внутри ЗУ и для него достаточно только подать сигнал RAS (вместе с адресами регенерируемых строк) и выработать тактирующие сигналы Ф1 и Ф2.
7.7.3. Динамические запоминающие устройства повышенного быстродействия
Динамические ЗУ повышенного быстродействия функционируют на основе предположения, что адреса текущего и следующего обращения к памяти с большой вероятностью расположены рядом (совокупность адресов). Это позволяет уменьшить длительность исполнительного и подготовительного этапов обмена данными или выключить один из них.
Рассмотрим кратко основные структуры в развитии DRAM. Считается, что память условно разбивается на страницы, адреса которых подаются старшей частью Ах адресного кода (записывается по стробу RAS). Слова в странице адресуются младшей частью Ау адресного кода (записывается по стробу CAS). Например, для адреса длиной к = 20 имеем 1024 страницы и 1024 слова в странице.
FPM
Структура FPM (Fast Page Mode) обеспечивает быстрый пакетный доступ к строке (страницы) и слова в нем. В данной памяти адрес строки А< подается только один раз по стробу RAS . В дальнейшем изменяется только адрес столбца по стробу GAS'(рис. 7.35)
Рис. 7.35. Временные диаграммы работы памяти типа FPM
248 Память компьютеров
Таким образом, пакетный обмен осуществляется при одном подготовительном этапе и многократном исполнительном. Для FPM характерную пропорцию интервалов времени первого и последующих обращений записывают как 5-3-3...
EDORAM
Структура с расширенным выводом данных EDORAM (Extended Data Out RAM) отличается от FPM модификацией процесса считывания данных. В этой памяти по окончанию строба CAS схемы УРЕГ не обнуляются. Они образуют как бы статический регистр, обеспечивающий дальнейшее быстрое считывание в пределах данной строки. Как и раньше, используется только один сигнал CAS, однако его длительность сокращается. Это повышает быстродействие ЗУ. Для памяти EDORAM характерную пропорцию интервалов времени между первым и последующими обращениями представляют как 5-2-2... Разработанные EDORAM обеспечивают работу до 50 МГц.
BEDORAM
В структуре с пакетным расширенным доступом BEDORAM (Burs EDORAM) имеется дополнительный счетчик адресов столбцов. При обращении к пакету (группе слов) адрес столбца формируется только в начале пакетного цикла. В дальнейшем адреса столбцов образуются инкрементом содержания счетчика (рис. 7.36).
Рис. 7.36. Временные диаграммы считывания памяти BEDORAM
Для BEDORAM характерную пропорцию интервалов времени между первым и последующими обращениями представляют как 5-1-1-1, однако и сами интервалы существенно сокращаются.
MDRAM
В многобанковых структурах MDRAM (Multibank DRAM) память разбита на банки (части). Обращение к банкам осуществляется по очереди. Пока идет обмен с одним банком, в остальных заканчиваются переходные процессы. Эффект ускорения работы такой памяти достигается уже при ее делении на два банка — с четными и нечетными адресами. Банки типа MDRAM могут строиться на обычных микросхемах динамической памяти без каких-либо изменений.
7.7. Динамическая память 249
SDRAM
Синхронная память типа SDRAM (Sinchronous DRAM) — это быстродействующая динамическая память, которая работает на частоте системной шины без тактов ожидания в середине пакетного цикла. От обычной асинхронной динамической памяти, в которой все внутренние процессы инициируются только сигналами RAS, CAS, W / R, память SDRAM отличается использованием сигналов тактовой частоты системной шины. Это позволяет создать внутри микросхемы высокопроизводительный конвейер с использованием обычных динамических ЭП с временем доступа 50-70 нс. Синхронный интерфейс обеспечивает трехкратный выигрыш в продуктивности в сравнении с обычными микросхемами DRAM с таким же быстродействием.
Синхронная память типа SDRAM была предложена в 1994 г. как двухбанковая система с трехступенчатым конвейером. Она обеспечивала пропускную способность 250 Мбайт/с и работала на частоте 125 МГц.
В целом микросхема SDRAM — это устройство с программируемыми параметрами, внутренней организацией чередования банков и собственным набором команд, в том числе:
• MRS — программирование параметров пакетного цикла;
• ACIT — активизация верхнего Т или нижнего В банка и ввод адреса строки;
• DEAC — предварительный заряд шин;
• WRT, RED — запись или чтение и ввод адреса столбца;
• REFR — автоматическая регенерация (рефреш) с периодом 15,6 мкс. Возможно задать рефреш с большим периодом;
• SLER — самогенерация без внешних сигналов, при этом чтение и запись запрещены;
• PDE — режим хранения с пониженным энергопотреблением (питание внешних буферов отключается).
Рис. 7.37. Временные диаграммы работы памяти SDRAM
Длина пакетного цикла может программироваться на 1-, 2-, 4-, 8- или 256 байт. Трехступенчатая конвейеризация позволяет инициировать следующий цикл обращения до завершения предыдущего.
Временные диаграммы работы синхронной памяти SDRAM показаны на рис. 7.37. Первое слово после формирования адреса появляется с запозданием на несколько тактов. Адреса последующих слов формируются внутренним счетчиком и слова появляются в каждом такте.
250 Память компьютеров
RDRAM
Микросхемы RDRAM (Rambus DRAM) — это байт-последовательная память, в которой синхронизация осуществляется двумя фронтами тактовых импульсов и применяется новый интерфейс Rambus Channel (имя фирмы-разработчика). В первой разработке при частоте тактирования 250 МГц темп передачи байта составляет 500 МГц, затем частота стала больше еще в 1,5-3 раза. Интерфейс Rambus Channel имеет всего 13 сигнальных линий без специализированных линий адреса. Вместо обычной адресации по интерфейсу посылаются вначале пакеты команд, затем следует пакет подтверждения, а далее — пакет данных. Первый доступ к данным сильно запаздывает: в первых разработках — до 128 нс.
Память типа RDRAM эффективна при пакетном обмене: например, для 256 байт в пакете частота обмена равна 400 МГц, а для 64 байт — 250 МГц и т.д. Такая память идеально подходит для графических и мультимедийных применений с типовым для них процессом — быстрой выдачей последовательности слов при формировании изображения на экране или для других подобных задач.
DRDRAM
Память типа DRDRAM (Direct RDRAM) в сравнении с RDRAM имеет меньшее запаздывание при первом доступе к данным. В DRDRAM пропускная способность в середине пакета составляет 1,6 Гбайт/с. Это превышает частотные возможности современных системных шин.
CDRAM
В кэшированных структурах CDRAM (Cached DRAM) на одном кристалле с DRAM размещена также статическая кэш-память уровня L1. При этом кэш обеспечивает быстрый обмен с процессором при наличии информации в кэше, а также быстрое обновление своего содержимого. Это объясняется тем, что связи между обоими выводами на кристалле являются внутренними. При этом разрядность шин может быть большой и обмен может осуществляться большими блоками данных. Например, в CDRAM фирмы Ramtron применяется 2048-разрядная шина для обновления содержимого кэша.
7.7.4. Регенерация динамической памяти
Поскольку в процессе работы памяти обращение к ее строкам происходит через различные интервалы времени, то требуется принудительная регенерация. Она состоит из регулярных циклических обращений к q строкам матрицы ЭП по адресам, которые формируются внешним или внутренним счетчиком адреса. Такие циклы называются холостыми, поскольку в них не происходит обмен информацией.
Максимальный период обращения к каждой строке TRF (refresh time) для гарантированного хранения информации в современных микросхемах памяти находится в пределах 8-64 мс. В зависимости от объема и организации матрицы памяти для однократной регенерации требуется 512, 1024, 2048 или 4096 циклов обращений (то есть, по числу строк q).
7.7. Динамическая память 251
При распределенной регенерации одиночные циклы регенерации выполняются равномерно с периодом tRF = TRF/q, который для стандартной памяти составляет 15,6 мкс (рис. 7.38, а).
Рис. 7.38. Регенерация динамической памяти: а — распределенная; б — пакетная; е — комбинированная
пппппяп
12 3 4 5 q
П П П П П у г П )
12 3 4 5 a t
Для памяти с расширенной регенерацией допустимый период циклов — до 125 мкс. Возможен также вариант пакетной регенерации, когда все циклы регенерации собираются в пакет (рис. 7.38, б), во время которого обращение к памяти для записи и считывания блокируется. При количестве циклов 1024 эти пакеты будут периодически занимать шину памяти приблизительно на 130 мкс, что в ряде применений недопустимо. По этой причине практически всегда используют распределенную регенерацию, хотя возможный и промежуточный вариант — пакетами по несколько циклов (рис. 7.38, в)
Циклы регенерации могут организовываться различными способами. Классическим является цикл без импульса CAS, который сокращенно именуется ROR (RAS Only Refresh — регенерация только импульсом RAS). В этом случае адрес очередной регенерированной строки на магистрали адреса (МА) вырабатывается контроллером памяти до спада импульса RAS очередного цикла регенерации (рис. 7.39, а).
RAS
МЛ
t
t
t
‘ a
Рис. 7.39. Цикли регенерации динамической памяти: а — ROR; б — CBR
Другой вариант — цикл CBR (CAS Before RAS), который поддерживается прак-тически всеми современными микросхемами памяти (рис, 7.39, б). Здесь спад импульса RAS осуществляется при низком уровне сигнала CAS (в обычном цикле об
252 Память компьютеров
ращения такая ситуация невозможна). В этом случае микросхема выполняет регенерацию строки, адрес которой находится во внутреннем счетчике БИС ОЗУ, и в задачу контроллера входит только периодическое формирование таких циклов. Дополнительным преимуществом данного цикла является экономия потребляемой мощности за счет неактивности внутренних адресных буферов.
Разновидностью цикла CBR является цикл скрытой регенерации: в конце полезного цикла считывания или записи сигнал CAS удерживается на низком уровне, а сигнал RAS поднимается и вновь опускается, что является указанием микросхеме памяти выполнить цикл регенерации по внутреннему счетчику. При этом после цикла считывания выходные буферы хранят только что считанные данные (в обычном цикле CBR выходные буферы находятся в третьем состоянии).
В современных компьютерах регенерацию памяти берет на себя контроллер и его задача — по возможности использовать для регенерации циклы шины, не занятые ее абонентами (процессорами и активными контроллерами).
“Самые ловкие” контроллеры регенерации ставят запросы на регенерацию в очередь, которую обслуживают в свободное для шины время, и только когда запросов нагромождается больше предельного количества, откладывается текущий цикл обмена по шине, и цикл регенерации выполняется незамедлительно.
Динамическая память, которая используется в видеобуферах графических адаптеров, специальных циклов регенерации не требует, поскольку частота считывания для отображения информации вполне достаточная для сохранения информации.
7.7.5. Модуль динамической памяти
Динамические ЗУ отечественного производства (1990 г.) в основном представлены микросхемами К565РУ1-К565РУ9, которые характеризуются следующими параметрами:
• емкостью — от 4 Кбит до 4 Мбит;
• организацией — 4Кх1, 16 К х 1, .... 256 К х 1;
• временем доступа — 150-500 нс;
• потребляемой мощностью: при хранении информации 20-40 мВт, при обмене 150-400 мВт.
Поколения микросхем динамической памяти сменяются через пять лет. Недавно группа фирм IBM, Siemens и др. представили свои ультра-БИС памяти с параметрами:
• технологические нормы — 0,25 мкм;
• количество транзисторов на кристалле площадью 286 мм2 — 280 млн.;
• время доступа в пакетном режиме — 26 нс.
Модуль динамической памяти емкостью 64 Мбит, построенный на четырех микросхемах типа 2100 фирмы Motorola с организацией 4 М х 4 бит, показан на рис. 7.40.
Длина адресного кода к = 22. Код разделен на две равные части, которые подаются мультиплексным способом одновременно на адресные входы микросхем. По стробу RAS подается старшая часть адреса, по стробу CAS— младшая.
Контрольные вопросы 253
Рис. 7.40. Схема модуля динамической памяти с организацией 4М х 16 бит
Сигнал WE позволяет записывать информацию, а ОЕ позволяет запись выходного буфера при чтении. Информационные входы Div выходи DO объединены в общую шину DIO. Микросхему выпускают в корпусе с 26 выводами.
Контрольные вопросы
1. Охарактеризуйте понятие “память компьютера”.
2. Назовите основные параметры памяти.
3. Почему информация в ЗУ хранится в двоичном коде?
4. Для чего предназначена внутренняя память?
5. Для чего предназначена внешняя память?
6. Что такое адресный доступ к данным?
7. Охарактеризуйте принципы построения постоянной памяти.
8. Какими достоинствами обладает динамическая память в сравнении со статической?
9. Что такое кэш-память?
10. Охарактеризуйте флэш-память.
11. Дайте анализ структур быстродействующих динамических микросхем па-
мяти.
254 Арифметико-логические устройства и устройства управления
Глава 8
Арифметико-логические устройства и устройства управления
Рис. 8.1. Структура математической модели АЛУ
8.1. Классификация арифметико-логических устройств
Арифметико-логическое устройство функционирует на основе микропрограммного управления. Каждая машинная операция разделяется на последовательность элементарных действий (передача слов, инверсия слов и др.), реализуемых в тактах. Элементарное функциональное вычисление, выполняемое в одном машинном такте, называется микрооперацией. Каждая микрооперация инициируется соответствующим управляющим сигналом. Совокупность микроопераций, выполняемых в одном такте, называется микрокомандой. В частности, микрокоманда может содержать одну микрооперацию или ни одной.
Для выбора порядка прохождения микроопераций анализируются логические условия, которые принимают значение единицы (да) или нуля (нет) в зависимости от значений операндов и результатов вычислений. Микроалгоритм операции, записанный в терминах микроопераций и логических условий, называется микропрограммой. Каждая машинная операция имеет свою микропрограмму.
Любой цифровой вычислитель, в том числе и АЛУ, может быть представлен композицией операционного и управляющего устройств. В операционном устройстве выполняются арифметико-логические операции. Управляющее устройство обеспечивает выполнение операций с помощью последовательности управляющих сигналов, которую он вырабатывает в зависимости от микропрограммы. В математических моделях АЛУ первое устройство представлено операционным автоматом, а второе — управляющим автоматом (рис. 8.1).
Операционный автомат (ОА) принимает по входу А операнды, по входу Y — управляющие сигналы {у,}, передает на выход Z результаты операции и формирует множество значений логических условий {л,}.
Управляющий автомат (УА) принимает по входу X логические условия {л:,} и в зависимости от их значений и кода операции по входу F формирует последовательность управляющих сигналов {у,}.
Арифметико-логические устройства классифицируют по следующим признакам:
• способу обработки данных — параллельные, последовательные, параллельно-последовательные;
8.1. Классификация арифметико-логических устройств 255
• системе счисления — двоичные, восьмеричные, десятичные, шестнадцатеричные, а также устройства на основе специальных систем (остаточных классов, с искусственным порядком веса, чисел Фибоначчи) и др.;
• форме представления чисел — с плавающей запятой, с фиксированной запятой, целые двоичные и десятичные числа;
• времени выполнения операций — синхронные и асинхронные;
• способу выполнения микроопераций — с закрепленными микрооперациями, с общими операциями;
• типу управляющего автомата — со схемной или программируемой логикой;
• методу построения — многофункциональные и блочные.
В синхронных АЛУ на выполнение различных операций отводится один и тот же интервал времени, а в асинхронных время выполнения зависит от типа операции.
В АЛУ с закрепленными микрооперациями каждый из регистров с помощью дополнительных комбинационных схем выполняет определенный набор микроопераций. При этом комбинационные схемы часто повторяются, что требует значительных аппаратных затрат.
В АЛУ с общими микрооперациями выделяют запоминающую часть — блок регистров, в которых выполняются однородные микрооперации (прием операндов, их хранение и выдачу), и комбинационную часть, в которой сосредоточены все схемы для выполнения микроопераций (формирование кодов, сдвиги, сложение и др.). Обе части соединяются между собой с помощью мультиплексоров и демультиплексоров. Арифметико-логические устройства с общими микрооперациями часто называют магистральными (к числовым магистралям по очереди подключаются регистры).
Многофункциональные (универсальные) АЛУ используются для выполнения всего списка операций, что достигается соответствующей настройкой и коммутацией узлов. Блочные АЛУ состоят из отдельных блоков, ориентированных на выполнение отдельных типов операций (например, блок умножения чисел с плавающей запятой). Такие структуры используются в высокопроизводительных компьютерах.
В АЛУ возможны два типа УА:
• со схемной (“жесткой”) логикой, которая состоит из элементов памяти (триггеров) и комбинационных схем. Они генерируют соответствующие управляющие сигналы {у,} в машинные такты в зависимости от кода операции;
• с программируемой (хранимой в памяти) логикой: для каждой операции в специальной памяти (чаще всего — различные виды ПЗУ) записывается микропрограмма в виде последовательностей управляющих слов — микрокоманд. Они содержат информацию о микрооперациях, которые должны выполняться в данном такте, и адрес следующей микрокоманды.
Обобщенная и наиболее распространенная структура АЛУ показана на рис. 8.2.
В состав ОА универсальных компьютеров входят:
• арифметико-логический блок (АЛБ);
• набор регистров общего назначения (РОН);
• блок контроля.
В АЛБ выделяют комбинационный сумматор SM, входные регистры А и В для приема операндов и выходной регистр С для записи результата. В АЛБ.имеются ло-
256 Арифметико-логические устройства и устройства управления
гические схемы, вырабатывающие множества {л:,} сигналов логических условий (признаков результата), например, нулевой или отрицательный результат и др.
Рис. 8.2. Обобщенная структура АЛУ
Регистры общего назначения используют для приема и хранения операндов, промежуточных и конечных результатов. Блок контроля обеспечивает проверку правильности выполнения арифметико-логических операций одновременной реализацией той же команды дублирующей аппаратурой и сравнением результатов или путем выполнения действий над специальными кодами, полученными от операндов при сложении по модулю два, три и др. При обнаружении ошибок и сбоев в работе ОА блок контроля посылает в УА код ошибок {£,}.
В АЛУ поступает код операции от центрального устройства управления. Применение в АЛУ устройств управления со схемной логикой ускоряет выполнение операций. Применение УА с программируемой логикой обеспечивает гибкость микропрограммирования, позволяет изменять состав микропрограмм при вводе новых команд. В современных АЛУ могут объединяться оба типа УА.
8.2. Языки описания операционных устройств
Для описания операционных устройств на различных уровнях используются соответствующие языки, а именно:
• язык электрических уравнений для токов и напряжений в цепях схем, состоящих из резисторов, диодов, транзисторов и т.д.;
• язык булевых функций для описания логических и запоминающих элементов;
• язык микроопераций для описания типовых функциональных комбинационных и последовательностных узлов;
• язык микропрограмм для описания работы операционных устройств на уровне микроалгоритмов машинных операций;
• алгоритмические языки для описания вычислительного процесса в компьютере на уровне программ (Ассемблер, Паскаль, Си и др.)
8.2. Языки описания операционных устройств 257
В языке микроопераций описание слова содержит идентификатор А, В, RGA, СТ\л разрядный показатель количества разрядов Л(32), 5(16), или номера старшего (слева) и младшего (справа) разрядов: Л(32:1), 5(16:1). Разрядный показатель может быть опущен, если слово было описано ранее. Регистр и слово в нем часто обозначают одним и тем же идентификатором: RGA, А(32). Слово может быть представлено своими частями: Л(32:16), ^4(15:12), Л(11:1). Значение конкретного z-ro разряда слова записывают какЛ[/], например, Л[1], 5[л].
Микрооперация описывается оператором и идентификатором управляющего сигнала в виде:
yi: А(п):= В(п)*С(п), где у/ — управляющий сигнал, отделяемый от оператора двоеточием; А(п) — результат; := — знак присваивания; * — вид преобразования в двухместной микрооперации (в одноместной пропускается); 5(/z) и С(и) — //-разрядные операнды. Выражение справа от знака присваивания называется формулой оператора. Двоичное значение, полученное на основе вычисления по формуле оператора, в конце такта присваивается слову А(п).
Наиболее распространены следующие микрооперации:
• установка константы: Л(3:1):=111;
• инвертирование слова: В(п):- В(п) ;
• складывание (конкатенация) слова из отдельных слов или их полей: Л(16:1):=5(16:8).С(7:1);
• передача слов: А(п):~ В(п}, RGC := RGD\
• сложение двух слов: А:- В + С;
• инкремент и декремент слова на единицу: А : = А+ 1,А := А - 1;
• поразрядные логические операции: дизъюнкция A:=BvC, конъюнкция А\=В лС, сложение по модулю два А В © С;
• левый и правый логические сдвиги L, R; арифметические сдвиги LA, RA и циклические сдвиги Вц, Вц. Например, логический сдвиг слова А(п) влево на один разряд: А(и):~ L(a)= А(п -1:1).О; циклический сдвиг вправо на один разряд: А := 5Z/ (л) = Л[1] А(п: 2).
Язык, предназначенный для описания микропрограмм в терминах операторов, называется языком микропрограммирования. Операторы в микропрограмме выполняются последовательно от начала до конца; для изменения такого порядка используют операторы перехода и метки.
Оператор
Перейти
переносит действие к оператору с меткой
Оператор
Перейти, если х, то М-, переносит действие к метке М,, если х = 1,,иначе при х - 0 операторы выполняются последовательно.
Оператор
Перейти, если х, то иначе Mj
переносит действие к МА при х = 1, иначе выполняется оператор с меткой Mj.
17 — 4-1749
258 Арифметико-логические устройства и устройства управления
Микропрограммы представляют также направленным графом (рис. 8.3), который состоит из вершин: “Начало”, “Конец”, операторных (соответствуют одной микрокоманде каждая) и условных (эквивалентных условным переходам к двум меткам).
J ( Конец ) | А;=А+В |
I
а б в
Рис. 8.3. Вершины графа микропрограммы: а — "Начало"; б — “Конец"; в — операторная; г — условная
Все вершины, кроме начальной, имеют произвольное (не менее одного) число входов. При всех возможных значениях логических выражений в условных и переключающих вершинах должен существовать путь из начальной в конечную вершину (рис. 8.4).
Если операторные и условные вершины графа содержат полное описание микроопераций и булевых выражений (логических условий), то его называют содержательным (рис. 8.4, а). Если микрооперации представлены идентификаторами управляющих сигналов, а логические условия — булевыми аргументами, то такой граф называется закодированным (рис. 8.4,6).
Примечание. Проектирование специализированных арифметико-логических устройств рассматривается в следующей главе.
a б
Рис. 8.4. Граф микропрограммы: а — содержательный; б — закодированный
8.3. Устройства управления
Устройством управления (УУ) называется функциональна часть компьютера, предназначенная для автоматического управления вычислительным процессом с помощью последовательности управляющих и синхронизирующих сигналов. Уст
8.3. Устройства управления 259
ройство управления обеспечивает координацию работы всех функциональных узлов компьютера в процессе выполнение программы.
Время, за которое выполняется одна машинная команда, называется машинным циклом. На протяжении машинного цикла УУ обеспечивает выполнение следующих действий:
• считывание очередной команды из ОП, ее дешифрацию и хранение на протяжении цикла;
• формирование адресов операндов из информации, содержащейся в коде команды;
• выборку операндов из ОП или РОН и пересылку их в АЛБ;
• выработку необходимой для выполнения данной команды последовательности управляющих сигналов;
• пересылку результата операции в РОН или ОП;
• формирование адреса следующей команды;
• переадресацию по безусловным и условным признакам;
• реализацию пультовых операций управления (запуска, остановки машины, автоматического или покомандного выполнения программы), контроль и обеспечение различных режимов работы, связанных с устройствами ввода-вывода и др.
В УУ выделяют две основные функциональные части — программную и микропрограммную. Программная часть реализуется центральным устройством управления (ЦУУ). Оно определяет последовательность выполнения команд программы, выполняет расшифровку команд, вырабатывает исполнительные адреса, пересылает операнды в операционное устройство и подготавливает его к выполнению заданной операции.
Микропрограммная часть УУ предназначена для выполнения микропрограмм в операционных устройствах, которые имеются в АЛУ, в каналах ввода-вывода информации, в накопителях на магнитных дисках и лентах и т.д.
Например, в микропроцессорах может быть два АЛУ целочисленной арифметики и арифметический сопроцессор для выполнения операций с плавающей запятой. Конструктивно микропрограммная часть реализуется в виде блоков местного управления (БМУ). Таким образом, в общем случае УУ компьютера — это иерархическая структура, состоящая из ЦУУ и ряда БМУ.
Решение любой задачи в машине сводится к последовательной выборке и выполнению команд соответствующей программы, организованной в ЦУУ. В связи с этим ЦУУ может быть представлен как преобразователь первичной командной информации во вторичную, которая подает исполнительные адреса и управляющие сигналы. Кроме команд, к первичной командной информации относятся коды и сигналы, характеризующие состояние отдельных узлов, блоков и устройств.
Устройства управления классифицируют по следующим признакам:
• программной ориентации — универсальные и специализированные;
• принципу выработки сигналов во времени — синхронные и асинхронные;
• способу построения УА — со схемной или программируемой логикой;
• способу реализации машинных команд — централизованные или смешанные;
• методу хранения программ — с использованием ОП или с вводом извне;
260 Арифметико-логические устройства и устройства управления
• порядку прохождения команд — с естественным или произвольным порядком;
• числу уровней управления — одно- и многоуровневые.
Универсальные УУ позволяют выполнять любые программы, записанные в виде последовательности команд с учетом ограничений, связанных с емкостью памяти машины, длины разрядной сетки и быстродействия.
Специализированные УУ работают по фиксированным программам, которые изменяются соответствующими переключениями в них. Специализированные УУ используют в компьютерах, выполняющих один или определенный класс задач.
В зависимости от длительности микроопераций УУ подразделяют на синхронные и асинхронные. В синхронных УУ частота работы генератора синхросигналов выбирается двумя способами:
• с учетом времени, необходимого для самой продолжительной микрооперации;
* ? учетом времени, необходимого для наиболее распространенной микрооперации. При этом для реализации самых продолжительных (“долгих”) микроопераций отводят несколько тактов, например, два.
В асинхронных УУ длительность такта переменная и зависит от времени выполнения текущей микрооперации. Сигнал окончания данной микрооперации является сигналом начала следующей. Устройства управления современных компьютеров используют комбинированный способ тактирования, в котором выгодно сочетаются преимущества обоих принципов.
По способу построения различают УА со схемной и программируемой логикой. Последний содержит специальный блок памяти для хранения микропрограмм.
Управляющий автомат, функционирование которого задают с помощью микропрограмм,/называется микропрограммным автоматом (МПА).
Исторически сложилось так, что во многих пособиях термин “микропрограммный автомат” используют только относительно УА с программируемой логикой, что методически не обосновано.
По способу реализации машинных команд УУ подразделяют на централизованные и смешанные. При централизованном способе управления единое УУ вырабатывает все управляющие сигналы, необходимые для выполнения любой операции из системы команд машины. Такие УУ часто используют асинхронный принцип тактирования и применяются преимущественно в одноадресных машинах со сравнительно небольшим числом микроопераций.
При смешанном способе управления ЦУУ вырабатывает основные управляющие сигналы — приема команды, ее дешифрации, модификации и др. Управление выполнением арифметико-логических операций обеспечивается БМУ.
По числу уровней управления УУ относят к одно- или многоуровневым. Это в одинаковой мере относится как к УУ в целом, так и к его части — программной и микропрограммной.
На первом, самом низком уровне, базовыми операторами служат микрооперации, а логическими условиями — извещающие сигналы из операционного устройства. На втором уровне базовые операторы и логические условия имеют такой же порядок сложности, что и команды традиционных машин. На третьем уровне базовые
8.4. Управляющие автоматы со схемной логикой 261
операторы аналогичны микрокомандам одноуровневых машин, однако реализуются техническими средствами и являются неотъемлемой частью У'У.
По порядку прохождения команд программы различают УУ с естественной и с произвольной последовательностью. В большинстве компьютеров команды размещаются в памяти в ячейках с последовательными номерами и адрес следующей команды определяется автоматически — прибавлением константы к счетчику команд. В УУ с произвольным порядком адрес следующей команды указывают в текущей команде.
По методу хранения программ выделяют машины с внутренним прогоаммиро-ванием (команды хранятся в ОП) и с внешним (программа вводится с помощью перфокарт, магнитных карточек, специальных панелей и др.).
8.4. Управляющие автоматы со схемной логикой
Термин “автомат” используют двояко. В технике с понятием “автомат” связывают некоторое устройство, способное выполнять определенные функции без вмешательства человека или с его ограниченным участием. В другом, широком аспекте, автомат — это математическая модель, отображающая физические или абстрактные явления самой разнообразной природы (вычислительные машины, системы управления и связи, лингвистика и др.). Универсальность теории автоматов позволяет рассматривать с единой точки зрения различные объекты, устанавливать связи и аналогии между ними, переносить результаты исследований из одной области в другую. Обобщенным примером цифрового автомата является компьютер, выполняющий прием, хранение и преобразование дискретной информации по заданным алгоритмам.
Общая теория автоматов подразделяется на абстрактную и структурную. Абстрактная теория изучает поведение автомата относительно внешней среды и не рассматривает способы его построения. Структурная теория автоматов изучает способы построения логических схем автоматов на основе алгоритма, заданного на абстрактном уровне.
Абстрактный автомат как систему задают упорядоченной совокупностью шести объектов {X Y, Z, S, Л, zj], где;
Х= {хь х2, ..., хт} — множество входных сигналов;
У= {у,,_у2, •••,%} —множество выходных сигналов;
Z= {zi,z2, ...,zr} — множество внутренних состояний, определяемых памятью автомата;
S— функция переходов, задающая отображение множеств X*Z-XZ;
Z — функция выходов, задающая отображение множеств X*Z->Y или Z-XY\ z, — начальное состояние автомата.
Множества X, Y, Z называются алфавитами, а их элементы — буквами. Последовательности входных и выходных букв образуют соответственно входные и выходные слова.
Понятие “память” (внутренние устойчивые состояния) автомата введено для описания систем, сигналы на выходах которых зависят как от входных сигналов в данный момент времени, так и от предыдущей истории развития процесса. В общем
262 Арифметико-логические устройства и устройства управления
множество устойчивых состояний автомата — это совокупность текущих значений физических параметров элементов памяти (например, напряжение на выходах триггеров), которая сохраняется до поступления соответствующего входного сигнала. Внутреннее состояние автомата соответствует некоторой памяти о прошлом и позволяет устранить время как явную переменную и выражать выходные сигналы в виде функции входов и памяти.
Автомат работает в дискретном времени и переход из состояния в состояние происходит мгновенно. По способу ввода дискретного времени автоматы подразделяются на синхронные и асинхронные. В синхронных автоматах дискретное время задают генератором синхросигналов: t = 0, 1,2, ..., где t — номер машинного такта. В асинхронных автоматах моменты перехода из одного состояния в другое предварительно не определены и зависят от некоторых событий. В таких автоматах интервал дискретности переменный.
В теории наиболее полно описаны и на практике широко применяются синхронные автоматы. Автомат, имеющий начальное состояние, называется инициальным. В начальный момент времени t = 0 инициальный автомат всегда находится в начальном состоянии zj g Z.
По способу формирования выходных сигналов различают автоматы Мили, Мура и С-автоматы. Функция переходов всех автоматов одинакова и записывается в виде:
Z(r) = <5[X(f), Z(t-\)].
Функции выходов задают выражения:
Y(t) = Л [Х(/), Z(t-l)] —для автоматов Мили;
У(0 = X [Z(t)] — для автоматов Мура;
С-автомат объединяет свойства автоматов Мили и Мура.
Абстрактные автоматы Мили и Мура характеризуются одноканальными входами и выходами (рис. 8.5).
Х= {х } --------------- Y= {у }
------------► Z={z} ------>
Рис. 8.5. Структура абстрактных автоматов Мили и Мура
Функция переходов ^показывает все возможные переходы из одного состояния памяти Zj в другое z, под действием входных сигналов. Функция выходов X задает все возможные выходные сигналы, вырабатываемые автоматом в дискретные мо-? менты времени в зависимости от х,(г) и z,(z).
В автоматах Мили выходные сигналы являются функцией входных сигналов и состояния памяти. В автоматах Мура выходные сигналы определяются только состоянием памяти.
Автомат называется конечным, если его множества X, Y и Z конечны; иначе автомат является бесконечным. В конечном автомате переход из одного состояния в любое другое заканчивается за конечное число тактов.
Ряд процессов, которыми управляют автоматы, не требуют для своей работы предыдущей истории, в них выходной сигнал y^t) определяется только входными сигналами х,(г). Такие автоматы имеют только одно состояние, их задают тройкой X, X, Y, где функция выходов X — зто отображение вида y(f) = X [х(/)]. Автоматы с од
8.4. Управляющие автоматы со схемной логикой 263
ним внутренним состоянием называются автоматами без памяти или комбинационными схемами.
На уровне абстрактной теории функционирование автомата рассматривается как преобразование входных букв (слов) в выходные буквы (слова).
Абстрактный автомат можно задавать с помощью таблиц переходов и выходов, графов, матриц соединений или аналитическим способом. Абстрактный автомат называется полным, если его функции переходов определены для всех пар (х/; z7) и частичным — в противном случае.
В таблице переходов и выходов полного автомата Мили строки и столбцы обозначены буквами входных сигналов и состояния памяти. В клетках таблицы переходов на пересечении строки х, и столбца zj записывается новое состояние — результат перехода zk = 8(х,-, zz), а в таблице выходов — выходной сигнал ут = Я (х,-, гД Для полного автомата Мили с произвольными множествами X = {хь х2, х3}, Y = {yi,y2, Уз} и Z = {zb z2, z3, z4} функция переходов представлена в табл. 8.1, а функция выходов — в табл. 8.2. Часто при представлении автомата Мили используют одну совмещенную таблицу переходов и выходов (табл. 8.3), которую называют отмеченной.
Таблица 8.1
X Z
Z1 Z2 Z3 Z4
X, Z| z3 Z3 Z3
х2 Z2 z4 Z1 Z1
х3 Z3 Z2 z4 Z2
Таблица 8.2
X z
Zi Z2 Z3 Z4
X, Vi Уз ,У2 ,У2
x2 ,Vi .Уз Zi /3
X3 У2 Уз Уз Уз
Таблица 8.3
X Z!Y
Zi Zi Z3 Z,
X, Z\ty\ z-i/Уз г3/Уг zy>2
x2 z2/Vi г^Уз z\/y\ zfyi
x3 Zifyl г21уз zy>3 ггУз
Вид таблицы переходов не зависит от типа автомата (Мили, Мура или С-автомата). В частичном автомате Мили с произвольными множествами X, Y и Z для неопределенного перехода ставится'прочерк, и любая входная буква, приводящая к этому, запрещена. В клетках таблицы выходов частичного автомата Мили
может стоять прочерк, что означает отсутствие выходного сигнала. При этом прочерк обязательно ставится в тех клетках таблицы выходов, которые соответствуют таким же клеткам с прочерком в таблице переходов. Отмеченная таблица переходов частичного автомата Мили све
Таблица 8.4
X Z/Y
Zi Zi Z3 Z4
Xi z2/y\ — Zi/уз —
x2 — z4/y2 Z\!~ Z2/>3
дена в табл. 8.4.
В таблице выходов полного автомата Мура с множествами Х= {хьх2}, У = {ji,у2,уз} и Z = {zb z2, z3, z4) каждому состоянию памяти приписывают свой выходной сигнал, не зависящий от букв входного алфавита. Прочерки в некоторых
клетках таблицы выходов частичного автомата не связаны с прочерком в его таблице переходов. Отмеченная таблица произвольного частичного автомата Мура сведена в табл. 8.5.
При графическом способе описания абстрактный автомат Мили представляют ориентированным графом, в котором состояния изобра-
Таблица 8.5
X Z/Y
Z1 Zi Z3 Z4
,Fi У1 Уз
X| z2 Z3
x2 — z4 Z\ Z2
264 Арифметико-логические устройства и устройства управления
жаются вершинами графа, а переходы между состояниями — дугами с обозначением входного и выходного сигналов. Пример графа автомата Мили с отмеченной табл. 8.3 показан на рис. 8.6, а. При представлении графом абстрактного автомата Мура выходные сигналы записываются рядом с вершинами состояний. Пример автомата Мура, заданного табл. 8.5, показан на рис. 8.6, б.
Рис. 8.6. Гоафы автоматов: а — Мили; б — Мура
8.5. Структурный синтез управляющего автомата со схемной логикой
Академик В.М. Глушков разработал канонический метод структурного синтеза цифровых устройств, в котором закон функционирования абстрактного автомата реализуется комбинационной схемой и набором триггеров. Процесс построения такой схемы называют структурным синтезом.
Набор триггеров и логических элементов является структурно полным, если на их основе можно построить любой автомат. Для этого набор должен содержать функционально полную систему логических элементов и хотя бы один триггер с полной системой переходов и выходов.
При структурном синтезе автоматов используют RS-, JK-, D-, и Т-триггеры, которые являются элементарными автоматами Мура с полными системами переходов и выходов. Они имеют два внутренних состояния, которым соответствуют два различных сигнала. Это дает возможность обозначать состояния, входные и выходные сигналы триггеров двухзначным структурным алфавитом (символами 0 и 1), как показано в табл. 8.6 для основных типов триггеров.
Таблица 8.6
ЛУ-триггер JK-триггер О-триггер Т-триггер
R 5 Q J К Q D Q Т Q
0 1 0 1 0 1 0 1
0 0 0 1 0 0 0 1 0 0 0 0 0 1
0 1 1 1 0 1 0 0 1 1 1 1 1 0
1 0 0 0 1 0 1 1
1 1 - - 1 1 1 0
8.5. Структурный синтез управляющего автомата со схемной логикой 265
Конечные автоматы Мили и Мура являются основой для построения управляющих автоматов со схемной логикой.
Для построения структурного автомата необходимо иметь память и две комбинационные схемы: КС1 —для выработки функций возбуждения и КС2 —для формирования выходных управляющих сигналов (рис. 8.7).
Рис. 8.7. Схема структурного автомата
Структурный синтез МПА со схемной логикой содержит следующие этапы:
1. Разработка микропрограммы операции и запись ее на языке микроопераций.
2. Построение содержательного графа микропрограммы.
3. Построение закодированного графа микропрограммы (рис. 8.8, а).
Рис. 8.8. Графы операции сложения:
а — закодированный; б — размеченный; в — переходов и выходов автомата Мили
4. Для получения числа состояний памяти N автомата выполняют разметку закодированного графа. Разметку графа микропрограммы для автомата Мили выполняют по следующим правилам (рис. 8.8, б):
• символом состояния z\ обозначают выход вершины “Начало” и вход вершины" Конец”;
266 Арифметико-логические устройства и устройства управления
• выходы операторных вершин обозначают символами z2, Z3, zN, где индекс N определяет максимальное число состояний памяти автомата Мили (рис. 8.8, б).
5. Строят граф автомата Мили (рис. 8.8, в):
• изображают Nвершин zb z2, ..., zN\
• путь между двумя вершинами включает одну операторную и произвольное число условных вершин и изображается ориентированной дугой. Между двумя вершинами может быть несколько путей и соответственно — ориентированных дуг;
• возле дуги записывают конъюнкцию произвольного числа сигналов х„ записанных в условных вершинах на данном пути размеченного графа;
• для выходы из условной вершины, обозначенной единицей, записывают х„ а обозначенной нулем —х,;
• возле сигналов условий на дуге записывают перечень управляющих сигналов^,;
• при отсутствии на пути условных вершин вместо них записывают единицу;
• в случае отсутствии управляющих сигналов записывают прочерк.
6. Размечая граф микропрограммы для автомата Мура, символом z, обозначают вершины “Начало" и “Конец”. Все остальные операторные вершины обозначают символами z2, z3, ..., zL, где L — максимальное число состояний памяти. Каждому состоянию z, приписывают свой набор выходных сигналов (рис. 8.9, а). На дугах графа переходов автомата Мура записывают только сигналы логических условий, а сигналы управления проставляют возле вершин графа (рис. 8.9, б).
Рис. 8.9. Графы операций вычитания: а — закодированный и размеченный; б — переходов и выходов автомата Мура
8.6. Синтез микропрограммного автомата с программируемой логикой 267
7. Кодирование состояний памяти автомата выполняют двоичными наборами сигналов Q„, Qn-\, Q\ с выходов триггеров. При кодировании состояний позиционным кодом количество триггеров п = ]log2M (для автомата Мили) и п = ]log2Z[ (для автомата Мура). Обычно число состояний автомата Мура больше числа состояний автомата Мили.
8. При построении комбинационных частей автомата для формирования выходных сигналов и функций возбуждения входов триггеров памяти используют прямую структурную таблицу МПА, которая содержит в своих столбцах:
• последовательность предыдущих состояний z„ и их код
• последовательность последующих состояний z7, и их код K[zj];
• наборы входных сигналов {%,}, вызывающих переход (z,,z;), и выходных сигналов уа,ур...у а, которые формируются на данном переходе;
• наборы информационных входов триггеров, что должны переключаться на переходе (z,,£,). Если используют RS- и JK- триггеры, то они имеют по два информационных входа, а если D- и Т- триггеры, то они имеют по одному входу. Переключение триггеров на переходах осуществляется согласно с данными табд. 8.6.
8.6. Синтез микропрограммного автомата с программируемой логикой
Микропрограммный автомат с программируемой логикой строят на основе опе
рационно-адресной структуры с использованием общих принципов программного
управления. При этом алгоритм управления представляют упорядоченными набо
рами управляющих слов-микрокоманд. Они определяют порядок функционирования
дискретного устройства на протяжении машинного цикла. Совокупность из Р ^-разрядных микрокоманд образует их массив, который хранится в памяти микрокоманд ПМК[Р:1] автомата.
Структура МПА с программируемой логикой содержит (рис. 8.10):
• формирователь адреса микрокоманды (ФАМК);
• регистр адреса микрокоманды (7?(7АМК);
• дешифратор адреса микрокоманд (DCA);
• память ^-разрядных микрокоманд ПМК[Р:1] (Л);
• регистр микрокоманд RGMK, разделенный на поля микроопераций Y (операционная часть), логических условий Xи адреса А;
• дешифратор микроопераций Z5CMO, на выходе которого формируются управляющие сигналы для ОА; в некоторых типах МПА он отсутствует.
Рис. 8.10. Структура МПА с программируемой логикой
268 Арифметико-логические устройства и устройства управления
В общем случае микрокоманда содержит информацию о микрооперациях, которые должны выполняться в данном такте, адрес следующей микрокоманды и анализируемые логические условия.
Выполнение каждой микропрограммы сводиться к последовательности следующих действий:
• считывание микрокоманд из ПМК по адресу, формируемому узлом ФАМК. Адрес первой микрокоманды задают кодом операции КОП в регистре команд RGK машины;
• запись считанной микрокоманды в регистр 7?GMK, дешифрация содержимого полей Y и А'и выдача набора управляющих сигналов в ОА;
• формирование адреса следующей микрокоманды с учетом полей Хи Y;
• выработка сигнала “Конец” микропрограммы.
Микропрограммные автоматы с программируемой логикой классифицируют по следующим признакам:
• типу памяти микрокоманд — статические (динамические) и постоянные (масочные, программируемые и др.);
• способу кодирования микроопераций — горизонтальные, вертикальные, горизонтально-вертикальные, вертикально-горизонтальные;
• времени выполнения микрокоманд — синхронные и асинхронные и наличию фаз в такте — одно- и многофазные;
• способу адресации — естественные, произвольные (принудительные) и способу организации условных и безусловных адресных переходов;
• направлению совершенствования структуры и алгоритмов функционирования.
В качестве ПМК используют различные типы постоянной памяти, а также ОП, загружаемую микропрограммами с гибких магнитных дисков при каждом включении машины.
Различают одно- и многофазные микрокоманды. В первом случае все микрооперации, указанные в микрокоманде, выполняются одновременно за один такт. В другом — такт разбивается на интервалы, называемые фазами или микротактами; при этом указанные в микрокоманде микрооперации выполняются в различных фазах.
При горизонтальном кодировании поле Y содержит М разрядов, где М— общее число микроопераций (рис. 8.11, а). Если в разряде стоит единица, то соответствующая микрооперация выполняется независимо от значений остальных разрядов. Достоинством горизонтального кодирования является возможность одновременного выполнения в одном такте микрокоманды с любым набором из М микроопераций и простота формирования управляющих сигналов — они представляются на выходах разрядов поля Y. Недостатком горизонтального кодирования является большая длина микрокоманды, поскольку число М может достигать более 100 значений.
При вертикальном кодировании все множество из Ммикроопераций кодируется «-разрядным двоичным позиционным кодом (рис. 8.11, б). Например, для М = 60 имеем длину кода п = ]Iog2A/[ = 6. При данном кодировании в каждом такте выполняется микрокоманда с одной микрооперацией. Достоинством вертикального коди-
8.6. Синтез микропрограммного автомата с программируемой логикой 269
рования является короткая микрокоманда, а недостатком — необходимость исполь-
а б
Ум У, Ум >’i
\ в г
Рис. 8.11. Кодирование микроопераций: а — горизонтальное; б — вертикальное; в — горизонтально-вертикальное; г — вертикально-горизонтальное
При горизонтально-вертикальном кодировании операционная часть Y микрокоманды разбивается на Я полей У,, У2.. Ун (рис. 8.11, в). В каждом поле горизон-
тально размещаются множества из М микроопераций у}, у2, ..., ум, которым присвоены номера 1,2,..., М. Эти номера кодируются вертикальным способом — //-разрядным двоичным кодом. Если поле У, пустое (содержит только нули), то оно не инициирует никакой микрооперации. Таким образом, в зависимости от кода в полях У,- микрокоманда может одновременно инициировать от нуля до Я микроопераций. Каждое поле У,-дешифрируется дешифратором на п входов и М выходов.
При вертикально-горизонтальном кодировании (рис. 8.11, а) все множество из М микроопераций распределяется на к подмножеств. В каждом из них объединяются микрооперации, которые чаще всего выполняются вместе в одном такте. Подмножества по возможности создают равномощными — с одинаковым числом микроопераций.
Операционная часть У микрокоманды состоит из двух полей. В первом поле Уи используется горизонтальный способ кодирования, а второе поле YI2 показывает, к какому подмножеству принадлежит микрооперация в первом поле.
Способ адресации задает правила определения адреса следующей микрокоманды. Существуют следующие способы адресации:
• естественная с последовательным размещением микрокоманд;
• с произвольным порядком прохождения микрокоманд;
• относительная — произвольная в диапазоне адресов, определенных базовым адресом;
• по фиксаторам — адрес следующей микрокоманды определяется содержимым специальных ячеек ПМК.
В каждом из способов адресации можно использовать горизонтальные, вертикальные и смешанные способы кодирования.
Естественная адресация микрокоманд реализуется следующим образом,
270 Арифметико-логические устройства и устройства управления
1. Используют два формата микрокоманд (рис. 8.12): операционный и адресный. Форматы отличаются наличием нуля в старшем k-м разряде операционной микрокоманды и единицы — в адресной.
К КА 6 5 4 3 2 1
0 ут • • • • |у6 3’5 •V4 Ь 3'1
к КА 6 5 4 3 2 1
1 БП х А . ... А. п т 6 А Л ^3 А? Л
Рис. 8.12. Форматы микрокоманды: а— операционной; б— адресной
2. В операционной микрокоманде записываются микрооперации {у,}, которые должны быть выполнены в данном такте. Естественная адресация обеспечивается счетчиком адреса микрокоманд СТАМИ, содержимое которого автоматически увеличивается на единицу после выполнения текущей микрокоманды.
В адресной микрокоманде записывают три параметра: одноразрядные значения логического условия х,- (берется из графа автомата) и безусловного перехода БП, а также адреса перехода Ат, А„,^, ..., Аг. Адрес следующей микрокоманды задают выражением
R = МВДх,x'i v МК[Л] БП, где МК[А] —значение старшего разряда микрокоманды, х',-— логическое условие с выхода ОА.
Таким образом, если R = 0, то происходит естественная адресация; при R = I адрес следующей микрокоманды определяется ее адресным полем А„„ Ат_\, ..., А{. Описанный метод позволяет использовать ряд логических условий, однако единичное значение должно воспринимать только одно х,.
Схема МПА, использующего естественную адресацию и горизонтальное кодирование, показана на рис. 8.13.
Рис. 8.13. Схема МПА с естественной адресацией и горизонтальным кодированием
8.6. Синтез микропрограммного автомата с программируемой логикой 271
В данной схеме при МК[А] = 1 блокируется выдача управляющих сигналов уг, .... yt и происходит условный переход. При МК[А] = 0 выдача управляющих сигналов разрешена. Информация из памяти микрокоманд считывается по сигналу “СЧТ”.
Схема МПА с естественной адресацией и вертикальным кодированием имеет выходной дешифратор микроопераций. Поле микроопераций, как и поле адреса, кодируется двоичным позиционным кодом, что значительно сокращает длину микрокоманды (рис. 8.14). Адресация в схеме автомата на рис. 8.14 реализована аналогично схеме рис. 8.13.
Рис. 8.14. Схема МПА с естественной адресацией и вертикальным кодированием для выполнение микропрограммы сложения
Принудительная адресация предусматривает наличие в едином формате микрокоманды одного или двух адресных полей, в которых указывают адрес следующей микрокоманды. Если имеется одно поле адреса, то для выполнения условных и безусловных переходов используют дополнительную комбинационную схему для инкремента на единицу содержимого адресного поля.
Схема МПА с горизонтально-вертикальным кодированием микроопераций и принудительной адресацией с помощью двух адресных полей АО и А\ показана на рис. 8.15. При такой структуре микрокоманды в каждом такте может выполняться не более двух микроопераций.
Рис. 8.15. Схема МПА с горизонтально-вертикальным кодированием и принудительной адресацией
272 Арифметико-логические устройства и устройства управления
На основе закодированного графа микропрограммы для операции деления в табл. 8.7 разработано кодирование микрокоманд для реализации МПА с горизонтальным кодированием и принудительной адресацией.
Таблица 8.7
Адрес ПМК У, У2 X АО А1
А 28 Ую Уп 0 А 29
А 29 У12 0 Азо
Азо У20 У21 х4 Аз1 А 32
Ал у22 0 Конец
Аз2 Т16 0 Азз
А зз х4 А34 Азз
А 39 У18 0 Азь
Лз5 У19 0 А зб
А зб у2о у21 0 Аз7
Л 37 У14 0 Азз Аз8
Аз8 У2з х4 A4i А 39
А 39 У19 0 А4о
А 40 У2о 0 A4i
А41 у24 0 а42
Л47 Уз1 &
В пятиразрядных операционных полях К, и У2 можно закодировать вертикальным способом до 32 микроопераций. В трехразрядном поле X кодируют до восьми логических условий. Шестиразрядные адресные поля А\ и АО обеспечивают обращение к ПМК [63:0](25). Параметры МПА (см. рис. 8.15) предусматривают выполнение микроопераций сложения, вычитания, умножения и деления.
Микрооперации логические условия л;, адреса в полях АО и А\ кодируются двоичным позиционным кодом. Его десятичный эквивалент используется в качестве индекса соответствующего сигнала микрооперации и адреса.
Значение ^32 = 1 означает конец операции. Адреса АО или А\ передаются через мультиплексор MUX на вход ПМК в зависимости от выполнения условия F = Ux,x' v БП. В поле логических условий при необходимости указывают на единичное значение только одного из условий х2, ..., х8, которое сравнивают с соответствующими физическими условиями от ОА. Таким образом, если
F = 0, то адрес выбирается из поля А1, иначе — из поля АО. При безусловном переходе БП = 1 адрес определяется полем АО.
Микропрограммные автоматы с программируемой логикой характеризуются временем, затрачиваемым на формирование одной микрокоманды. Это время состоит из трех компонентов:
• времени формирования адреса следующей микрокоманды;
• времени обращения к ПМК;
• времени дешифрации операционной части микрокоманды.
8.7. Центральное устройство управления 273
Основная доля времени приходится на считывание микрокоманды из ПМК, поэтому повышение быстродействия может достигаться или за счет уменьшения времени обращения к памяти, или за счет уменьшения числа таких обращений.
Увеличение быстродействия МПА с программируемой логикой достигается при следующих условиях:
• применение быстродействующей ПМК;
• параллельной выборке нескольких микрокоманд;
• опережающей выборке микрокоманд (то есть до окончания выполнения предыдущей).
Использование МПА с программируемой логикой сравнительно со схемной имеет следующие преимущества:
• обеспечивается большая гибкость и наглядность, повышается регулярность структуры МПА и процессора в целом;
• повышается эффективность математического обеспечения и производительность работы процессора;
• облегчается модернизация микропрограмм МПА как в процессе автоматизированного проектирования, так и при работе компьютера, что увеличивает срок морального устаревания машины;
• облегчается построение эффективной микродиагностики.
Микропрограммный автомат с программируемой логикой имеет самое широкое применение в процессорах с малой и средней производительностью. Оба способа построения автоматов управления получили дальнейшее развитие на основе программируемых БИС, однородных сред и т.д.
8.7. Центральное устройство управления
Устройство, выполняющее основные функции управления компьютером, называется центральным устройством управления. Под ЦУУ подразумевают совокупность узлов и блоков процессора, которые обеспечивают координацию функционирования всех устройств машины и управление ими для всех принятых режимов работы.
Центральное устройство управления реализует системные и рабочие программы, организовывает все необходимые действия по оценке и преобразованию начальной информации для получения результата вычислений.
Решение любой задачи сводится к последовательности выборки и выполнения команд программы под управлением ЦУУ. Таким образом, ЦУУ — это преобразователь первичной командной информации, представленной командами программы, во вторичную командную информацию — исполнительные адреса и управляющие сигналы. К первичной командной информации относятся также коды и сигналы, характеризующие состояние процессора и отдельных блоков. Часто в мини- и микрокомпьютерах, основным требованием которых является минимум стоимости, оборудование совмещают по функциональному назначению, например, ЦУУ и МПА процессора.
В УУ условно выделяют две основные части — микропрограммную и программную. Микропрограммная часть — это МПА, вырабатывающий сигналы управления микрооперациями в АЛУ. Программная часть определяет последователь
274 Арифметико-логические устройства и устройства управления
ность выполнения команд программы, их дешифрацию, вырабатывает исполнительные адреса, по которым считываются из памяти операнды в АЛУ и записывается результат операции. Функции программной части реализует ЦУУ.
Для выполнения своих функций ЦУУ содержит (рис. 9.15):
• регистр команд RGK с полем кода операции КОП и полем адреса АДР;
• счетчик адреса команд СТАК;
• управляющий автомат МПА;
• дешифратор кода операций РСКОП;
• операционный блок (ОБ), в который входят сумматор адреса, схемы анализа режимов работы: готовности памяти и периферии к обмену информацией, запросов прерываний и прямого доступа к памяти; интерфейсные схемы и др.;
• пульт управления “Пульт”.
Рис. 8.16. Структура взаимодействия УУ, АЛУ и памяти
Регистр команд RGK предназначен для приема команды из ОП и хранения ее на протяжении рабочего цикла. В зависимости от типа машины и сложности операции команда может иметь длину от одного до 10 и более байтов. В зависимости от длины шины выборки данных за одно обращения к ОП может считываться вся команда, ее часть или несколько команд.
Счетчик адреса команд СТАК предназначен для определения адреса команды. После считывания текущей команды содержимое СТАК автоматически увеличивается на константу, равную длине команды в байтах.
Микропрограммный автомат МПА1 расшифровывает команды и обеспечивает управляющими сигналами выполнение программной части, а МПА2 —выполнение собственно микропрограмм операций в АЛУ. Каждый из автоматов может строиться на основе схемной или программируемой логики. При централизованном управлении оба автомата объединяются в единый МПА.
Сумматор адреса служит для формирования исполнительных адресов операндов и результата операции по информации, содержащейся в коде команды. В общем случае исполнительные адреса получают сложением трех компонентов: базового адреса и индекса, расположенных в блоке РОН, и кода смещения в команде.
8.7. Центральное устройство управления 275
Пульт управления “Пульт” предназначен для управления работой компьютера пользователем. Он содержит клавиатуру, переключающие кнопки и средства индикации для визуального контроля состояния отдельных устройств и проведения профилактики. На клавиатуре “Пульта” набирается команда ввода и адрес первой команды программы, которая должна выполняться после нажатия на кнопку ЗАПУСК (или любой клавиши). Эта информация поступает в ЦУУ, которое управляет вводом с магнитных дисков программы и исходных данных в ОП. После окончания ввода программы ЦУУ пересылает в счетчик СТАК адрес первой предназначенной для выполнения команды.
Функционирование компьютера состоит из рабочих циклов, каждый из которых соответствует выполнению одной команды программы.
В каждом рабочем цикле в общем случае выполняются следующие типовые действия:
• выборка из ячейки ОП команды, которая должна выполняться, и формирование адреса следующей команды. При этом содержимое счетчика адреса СТАК пересылается в регистр адреса памяти 7?СА0П. Считанный по данному адресу код поступает в регистр данных памяти, а оттуда пересылается в регистра команд RGK, после чего содержимое счетчика адреса СТАК увеличивается на константу — длину команды в байтах;
• формирование исполнительных адресов и считывание по ним операндов из ОП. Содержимое адресной части команды пересылается в ОБ, где вырабатываются исполнительные адреса. Считанные операнды поступают в ОА и хранятся в блоке РОН;
• расшифровка кода операции в МПА2: выполняется последовательность микроопераций, яки определены микропрограммой данной операции и запись результата операции в память или в РОН;
• выработка в МПА2 сигнала конца операции. Переход к п. 1.
При каждом обращении к памяти проверяется сигнал готовности “Гт” памяти к обмену информацией. Обмен (считывание или запись) возможен при “Гт” = 1, иначе процессор переходит в режим ожидания. После каждого обращения к ОП проверяется наличие сигнала запроса прямого доступа к памяти. Если такой сигнал имеется, то процессор переключает свои шины в третье состояние и обеспечивает периферийным устройствам режим прямого доступа к памяти. После окончания каждой команды проверяется наличие сигнала запроса на прерывание программы от периферии.
При запросе на управление выполняется процедура реализации подпрограммы обслуживания того внешнего устройства, которое установило запрос на прерывание. После обслуживания внешнего устройства компьютер возвращается к выполнению прерванной программы.
276 Арифметико-логические устройства и устройства управления
Контрольные вопросы
1. Охарактеризуйте назначение АЛУ.
2. Поясните структуру АЛУ в виде композиции ОА и УА.
3. Перечислите классификационные признаки АЛУ.
4. Охарактеризуйте язык микроопераций.
5. Охарактеризуйте функции УУ.
6. Что такое программная и микропрограммная части УУ?
7. Поясните функцию МПА.
8. Укажите на отличия построения УА со схемной и программируемой логикой.
9. Дайте сравнительную характеристику горизонтального и вертикального кодирования в микрокомандах.
10. Поясните структуру ЦУУ.
И. Что такое структурный синтез автомата?
12. Запишите функцию переходов автомата Мили.
13. Запишите функцию переходов автомата Мура.
14. Поясните функцию выходов автомата Мили.
15. Поясните функцию выходов автомата Мура.
16. Нарисуйте схему структурного автомата.
17. Что такое инициальный автомат?
18. Как проводится разметка микропрограммы для графа Мили?
19. Как проводится разметка микропрограммы для графа Мура?
20. Поясните структурную таблицу автомата Мили.
21. Поясните структурную таблицу автомата Мура.
9.1. Реализация операции сложения 277
Глава 9
Проектирование специализированных арифметико-логических устройств
9.1. Реализация операции сложения
9.1.1. Исходные данные
• Тип арифметической операции — сложение двоичных чисел;
• исходный код представления операндов — дополнительный;
• разрядность операндов — 8 бит;
• код выполнения операции в сумматоре — дополнительный модифицированный;
• структура операционного блока — с закрепленными микрооперациями;
• тип управляющего блока — автомат Мура с памятью на JK-триггерах;
• схема логического признака переполнения разрядной сетки;
• схема логического поразрядного сложения кодов входных операндов Л и В.
9.1.2. Элементная база — интегральные схемы ТТЛШ серий К1531, КР1533
Перечень обязательного графического материала:
• граф-схемы микропрограммы сложения;
• схема электрическая функциональная;
• схема электрическая принципиальная;
• перечень элементов (спецификация).
Требуется выполнить расчеты:
• количества микросхем в устройстве АЛУ;
• потребляемой мощности;
• быстродействия АЛУ на примере операции сложения типа “регистр-регистр”.
9.1.3. Алгоритм сложения двоичных чисел
Сложение и вычитание двоичных чисел можно выполнять в обратных или дополнительных кодах и их модификациях. В современных компьютерах часто операнды хранятся в памяти в дополнительных кодах. Использование дополнительных кодов в операциях сложения и вычитания, а также для хранения операндов в памяти обладает следующими преимуществами:
278 Проектирование специализированных арифметико-логических устройств
• однозначное представление знака результата как положительного, так и отрицательного;
• во время записи в память отрицательного результата не затрачивается время для его преобразования в прямой код;
• меньше действий для анализа знака результата, в частности переполнения разрядной сетки.
Алгоритм сложения двоичных чисел:
• в первом и втором машинных тактах с входной шины параллельным кодом записываются операнды А и В в соответствующие регистры RGA и RGB. Считывание операндов осуществляется ЦУУ;
• на протяжении одного машинного такта выполняется микрооперация сложения;
• при отсутствии переполнения разрядной сетки результат записывается в регистр RGC\
• при наличии переполнения результат не фиксируется и в ЦУУ подается сигнал переполнения ПП.
9.1.4. Функциональная схема АЛУ для выполнения операции сложения
Функциональная схему восьмиразрядного АЛУ для выполнения операции сложения показана на рис. 9.1.
Схема АЛУ содержит:
• регистры RGA и RGB для приема и последующего хранения с входной шины Ш1 первого и второго операндов;
• параллельный комбинационный сумматор с дополнительным старшим разрядом знака П для создания модифицированного дополнительного кода;
• регистр результата RGC, данные из которого пересыпаются по выходной шине 1112 в оперативную память;
• схемы электронных ключей SJFl и SW2;
• схему выработки признаков переполнения ПР;
• схему дизъюнкторов OR для выполнения операций поразрядного логического сложения кодов операндов Л и В.
Признаки результата вычисляются с помощью булевых выражений:
Pi = Т7-5А/[«] — положительный результат (знаки 00);
< Рг - II • — отрицательный результат (знаки 11);
(рз = II • 5A/[z?]v П • >Ш[и] — переполнение разрядной сетки ПП (знаки равны 01 или 10);
н-*1__
(Pi - —нулевой результат.
После окончания операции УА анализирует признаки результата и устанавливает значения соответствующих триггеров признаков. Признак переполнения проверяется до окончания операции и при ее наличии выполнение программы прерывается.
9.1. Реализация операции сложения 279
Признак OR реализуется с помощью восьми логических двухвходовых элементов ИЛИ по соотношению
^=(4v5,), i = 1,2,...,8,
где Ft — z-й выход узла логического сложения. Эта операция выполняется автоматически независимо от кода команды.
280 Проектирование специализированных арифметико-логических устройств
9.1.5. Микропрограмма сложения
Микропрограмма сложения двоичных чисел в дополнительных кодах имеет следующий вид.
Начало. Если А'[ 1 ], то М\, иначе — ожидать
М\ у. : RGA := А <приема первого операнда>
у2 : RGB := В <приема второго операнда>
у3 : 5Л/ := А + В <сложения>
Если <рг, то Мг, иначе
:RGC '.= SM <присвоения результата>
у5 : Ш2 -RGC <пересылка в память>
Перейти к А£3
М2 уь: Гп :=ПП <триггеру переполнения Тп присваивается признак ПП> Конец.
Примечание. /€[ 1 ] — одноразрядный код команды сложения.
Содержательный и закодированный графы микропрограммы сложения показаны на рис. 9.2.
9.1.6. Принципиальная схема модуля операционного блока
Модуль операционного блока (МОБ) строится на микросхемах ТТЛШ серии КР1533 за исключением сумматора, взятого из серии К1531.
Для построения принципиальной схемы МОБ использованы следующие микросхемы (рис. 9.3):
• два входных восьмиразрядных регистра RGA и RGB типа ИР35, позиционное обозначение DD\, DD2\
• две микросхемы типа ЛЛ1, каждая из которых содержит по четыре двухвходовых логических элемента ИЛИ, позиционное обозначение DD2, DD4. Их используют для реализации поразрядной дизъюнкции над кодами операндов Л и В. Изображение представлено пакетным способом;
• четыре микросхемы типа ЛИ1, каждая из которых содержит по четыре двухвходовых конъюнктора, позиционное обозначение DD5-DD&. Используют, для подключения выходов регистров RGA и RGB ко входам сумматора SM-,
• микросхему типа ЛП5, которая содержит четыре логических элемента “Исключающее ИЛИ", позиционное обозначение DD9. Используют для создания старшего знакового разряда сумматора и логического признака = х, и %!;
• выходной восьмиразрядный регистр RGC типа ИР22 с тремя состояниями, позиционное обозначение £>£>10. Используют для приема результата сложения и его передачи на выходную шину;
• два четырехразрядных комбинационных сумматора SM типа ИМ6, позиционное обозначение £>£>11, £>£>12.
9.1. Реализация операции сложения 281
Содержательный граф сложения
Закодированный и размеченный граф сложения
Рис. 9.2. Гоафы микропрограммы сложения
282 Проектирование специализированных арифметико-логических устройств
Рис. 9.3. Принципиальная схема МОБ для операции сложения
9.1.7. Проектирование модуля управляющего блока
Проектирование модуля управляющего блока (МУБ) на основе автомата Мура с памятью на JK-триггерах выполняется в следующей последовательности.
1. Размечается закодированный граф микропрограммы сложения (см. рис. 9 2). Определяется максимальное количество состояний автомата
9.1. Реализация операции сложения 283
Мура, что равно L = 7. Для реализации такого числа состояний необходимо использовать п = ]log27[ = 3 триггера.
2. На основе размеченного графа микропрограммы строится граф автомата Мура (рис. 9.4), интерпретирующий микропрограмму сложения.
Рис. 9.4. Граф автомата Мура для микропрограммы сложения
3. Состояния автомата Мура кодируются значениями выходов JK-триггеров: z\ = 636261 > z2 = 636261 • 2з = 636261 • zt ~ Q2Q2Q\ •
4. На основе графа автомата Мура записывается его структурная таблица переходов (табл. 9.1).
Таблица 9.1
Z, A (z,) Z/ A (z>) {*/} {y,} JK
к J
Z1 ООО Zi Zl 000 001 A У1 Ji
Z2 001 Z3 010 1 У2 Ki Ji
Z3 010 Z4 Oil 1 Уз - J\
z4 Oil Z5 z6 100 101 %, Xi У4 У6 K2, Ki к2 J3 J3
Z3 100 Z7 110 1 Уз - J2
Z6 101 zi 000 1 - Кз, К} -
27 110 z\ 000 1 - Кз,К2 -
5. На основании данных табл. 9.1 записываются системы логических уравнений для функций возбуждения входов JK-триггеров и выходов:
• для функций возбуждения входов:
^1 ~ Z\P\ Z3’ J2 ~~ Z2 Z5' ^3 ~ Z4’
K}-z2v z4x}v z6; K2=z4\/z2; K2^z6\/z2.
• для выходных управляющих сигналов:
Ji =г2; Уз =z3; Уз =z4’ У4 =z5’ Уз =z7; у6 =z6-
6. Строится принципиальная схема модуля управления МУБ (рис. 9.5).
Соответствие между входами управления микросхем МОБ и сигналами микроопераций представлено в табл. 9.2.
Таблица 9.2
Входы LA LB ЛИ1 LC EZ
Сигналы микроопераций Ух У2 Уз У4 Уб Уз
284 Проектирование специализированных арифметико-логических устройств
Рис. 9.5. Принципиальна схема МУБ для операции сложения
Для построения принципиальной схемы модуля МУБ (рис. 9.5) использованы следующие микросхемы:
• £>£>13, £>£>14 — две микросхемы типа ТВ6, каждая из которых содержит по два JK-триггера (память автомата Мура);
• £>£>15 — дешифратор типа ИД7. Используется для выделения состояний автомата;
• £>£>16, DD17.1 — две микросхемы типа ЛН1, каждая из которых содержит шесть инверторов;
• DD18 — микросхема типа ЛИ1, которая содержит четыре конъюнктора;
• DD\9, £>£>20 — две микросхемы типа ЛЛ1.
Перечень микросхем, использованных для построения АЛУ, реализующего операцию сложения, представлен в табл. 9.3.
Таблица 9.3
Позиции Наименование микросхемы Количество
£>£>1,£>£>2 КР1533ИР35 2
£>£>3, £>£>4, £>£>19, £>£>20 КР1533ЛЛ1 4
£>£>5-£>£>8,£>£>18 КР1533ЛИ1 5
£>£>19 КР1533ЛП5 1
£>£>10 КР1533ИР22 1
£>£>11, £>£>12 КР1533ИМ6 2
£>£>13, £>£>14 КР1533ТВ6 2
£>£>15 КР1533ИД7 1
£>£>16, £>£>17 КР1533ЛН1 2
9.2. Реализация операции вычитания 285
9.1.8. Характеристики АЛУ
Риме (тип F, серия КР1531) = 180 мВт;
Рлп5 ~ зо мВт;
Рлш = 16 мВт.
j°TB6 = 22,5 мВт;
Рлш = 22,5 мВт;
Микросхемы ТТЛШ серии КР1533, которые используются для построения АЛУ, реализующего операцию сложения, потребляют следующую мощность:
Рир?5 = 122 мВт; Pnpi2 = 100 мВт;
Рид? = 50 мВт;
Рлш = 13 мВт;
Мощность, потребляемая данным АЛУ, рассчитывается путем сложения мощностей всех микросхем:
Р АЛУ = 2РиР35 + РиР12 + 2Рцмб + Рр1Д7 + 2Р|'В6 + РпП5 + 2РлН1 + 4РдЛ1 + 5РдИ1 =
= (2-122 + 100 + 2-180 + 50 + *2-22,5 + 30 + 2-13 + 4-22,5 + 5-16)10”3 = 1,125 Вт.
Микросхема КР1531ИМ6 реализует сложение двух четырехразрядных операндов за tSM! =15 нс. При сложении восьмиразрядных операндов длительность микроопераций удваивается, то есть tSM2 -2-tSMi =30 нс. Учитывая задержки сигналов, поступающих на входы сумматора, рекомендуется выбирать длительность машинного такта Тс =2-tSM2 =60 нс. При этом быстродействие АЛУ, выраженное количеством операций сложения типа “регистр-регистр” в секунду, составит F -\/Т( = 16 млн оп/с.
9.2. Реализация операции вычитания
9.2.1. Исходные данные
• Тип арифметической операции — вычитание двоичных чисел;
• исходный код представления операндов — дополнительный;
• разрядность операндов — 8 бит;
• код выполнения операции в сумматоре — дополнительный модифицированный;
• структура операционного блока — с закрепленными микрооперациями;
• тип управляющего блока — автомат Мили с памятью на О-триггерах;
• схема логического признака переполнения разрядной сетки;
• схема логического поразрядного умножения кодов входных операндов А и В.
Элементная база, перечень обязательного графического материала и необходимые расчеты — согласно пункту 9.1.2.
9.2.2. Алгоритмы вычитания двоичных чисел
Алгоритм вычитания двоичных чисел реализуется в следующей последовательности:
• в регистры RGA и RGB с входной шины один за одним параллельным кодом записываются соответствующие им операнды А и В;
• операнд В безусловно инвертируется;
• микрооперация вычитания выполняется в дополнительных модифицированных кодах на протяжении одного машинного такта;
286 Проектирование специализированных арифметико-логических устройств
• анализируется результат вычитания. При отсутствии переполнения разрядной сетки результат записывается в регистр RGC и затем пересылается в оперативную память, при наличии переполнения результат не фиксируется и в ЦУУ передается сигнал переполнения Тп.
9.2.3. Функциональная схема АЛУ для выполнения операции вычитания
Функциональная схема восьмиразрядного АЛУ для выполнения микропрограммы вычитания показана на рис 9.6:
Рис. 9.6. Функциональная схема АЛУ для вычитания чисел
9.2. Реализация операции вычитания 287
Схема АЛУ содержит:
• регистры RGA и RGB для приема из входной шины Ш1 операндов А и В и их хранения на протяжении времени выполнения микропрограммы;
• схему инвертирования BIN содержимого регистра RGB\
• электронные ключи SW1 и SW2 для коммутации операндов;
• схему поразрядного логического умножения AND\
• комбинационный сумматор SM с дополнительным знаковым разрядом П для создания модифицированного кода. На вход переноса первого разряда сумматора подается “лог. 1”;
• регистр результата 7?G'C;
• схему признака переполнения ПР;
• модуль управляющего блока (МУБ) на основе автомата Мили с памятью на О-триггерах.
9.2.4. Микропрограмма вычитания
Микропрограмма вычитания двоичных чисел в модифицированных дополнительных кодах имеет следующий вид:
Начало. Если А?[2], то Мь иначе — ожидать
М\ у, : RGA := А <приема первого операнда>
у2 : RGB := В <приема второго операнда>
у2: SM :-А + 5 + 1 микрооперация вычитания в дополнительных кодах>
Если <р2, то М2, иначе
у4 : RGC :=SM <присвоение результата:*
ys : Ш2 .- RGC <пересылка в память*
Перейти к М2
М2 уь: Гп :=ПП <триггеру переполнения Тп присваивается признак ПП>
М2 Конец.
Примечание. А?[2] — одноразрядный код команды вычитания.
Содержательный и закодированный графы микропрограммы вычитания показано на рис. 9.7.
9.2.5. Принципиальная схема модуля операционного блока
Модуль операционного блока (МОБ) строится на микросхемах ТТЛШ серии КР1533 за исключением сумматора, взятого из серии КР1531.
Принципиальная схема МОБ содержит (рис. 9.8):
• два входных восьмиразрядных регистра RGA и RGB типа ИР35, позиционное обозначение DD1, DD2-,
• две микросхемы типа ЛН1, позиционное обозначение DD3, DD4A. Предназначены для инвертирования кода операнда В;
• четыре микросхемы типа ЛИ1, позиционное обозначение DDS-DDR. Предназначены для построения двух схем электронных ключей SW1, SW2;
288 Проектирование специализированных арифметико-логических устройств
• микросхему типа ЛП5, позиционное обозначение DD9. Используется для создания старшего знакового разряда сумматора и выработки логического признака переполнения ;
• две микросхемы сумматоров ИМ6, позиционное обозначение £>£>10, £>£>11;
• выходной 8-разрядный регистр RGC типа ИР22 с тремя состояниями, позиционное обозначение £>£>12. Используется для приема результата вычитания и его передачи на выходную шину Ш2.
Содержательный граф Закодированный граф
микропрограммы вычитания микропрограммы вычитания
Рис. 9.7. Гоафы микропрограммы вычитания
9.2. Реализация операции вычитания 289
9.2.6. Проектирование модуля управляющего блока
Проектирование МУБ на основе автомата Мили с памятью на О-триггеоах выполняется в следующей последовательности:
19-4-1749
290 Проектирование специализированных арифметико-логических устройств
1. Размечается закодированный граф микропрограммы вычитания (см. рис. 9.7). Определяется максимальное количество состояний автомата Мили, которое равно L = 5. Для реализации такого количества состояний необходимо использовать п = ]log25[ = 3 триггера.
2. На основе размеченного графа микропрограммы строится граф автомата Мили (рис. 9.9), интерпретирующий микропрограмму вычитания.
Рис. 9.9. Граф автомата Мили для микропрограммы вычитания
3. Состояния автомата Мили кодируются значениями выходов D-триггеров: z\ = 636261’ 22 = 636261 ’ ••• ’ ZS ~ 636261 •
4. На основе графа автомата Мили записывается его структурная таблица переходов (табл. 9.4).
Таблица 9.4
Zi A (z,) Z/ {*<•} D-триггеры D3, Dz,
Z1 000 000 Zi Z2 000 001 A A У1 Dr
Z-) 001 ?3 010 1 У2 d2
z3 010 Z4 Oil 1 Уз D2,Di
z4 Oil z5 z\ 100 000 *1 ‘ Xi У4 Уб D,
Zs 100 Zi 000 *1 Уз -
5. На основании данных табл. 9.4 записываются системы логических уравнений:
• для функций возбуждения входов:
£>i = z$vz3 - j, vz3;
О, = z, v ;
Z?3 = y4;
• для выходных сигналов:
У1 = z,/?,, у2 = z2; у2 = z3; у4 = z4xy, у5 = z5; у6 = z4xv
6. Строится принципиальная схема модуля управления МУБ (рис. 9.10).
Соответствие между входами управления микросхем модуля МОБ и сигналами микроопераций представлено в табл. 9.5.
Таблица 9.5
Входы LA LB Тли LC EZ Тп
Сигналы микроопераций У1 У1 Уз У4 Уб Уь
9.3. Реализация операций сложения и вычитания 291
£>Z>13 £>£>16 DDY1
£>£>14. £>£>1 5
АШ1
1 4.9 12 & ЛИ1
.....4.9,12 ~Т~
2.ч.10.13 ЛИ 1
1.£4»
WJ8 &
ЛИ1
1111) 22Ц) 14(1)
2К1)
Рис. 9.10. Принципиальная схема МУБ для операции вычитания
Принцмпиальна схема на рис. 9.10 содержит:
• £>£>13 — микросхему типа ТМ9, которая содержит шесть D-триггеров. Три триггера образуют память автомата Мили, триггер на выходе £п фиксирует сигнал переполнения. На выходе £п пятого триггера формируется сигнал управления длительностью в машинный такт для управления микросхемами DD5 £>£)8;
• £>£>14, £>£>15 — две микросхемы типа ЛИ1, реализующие поразрядную конъюнкцию кодов операндов А и В на основе соотношения Ft = (А, а5,), где z= 1,2, ..., 8;
• £>£>16 — микросхема дешифратора типа ИД7;
• DD17-DD19 — микросхемы логических элементов типа ЛН1, ЛИ1, ПЛ1, реализующих функции комбинационных схем автомата Мили.
Расчеты схемы АЛУ выполняют аналогично разделу 9.1.
9.3. Реализация операций сложения и вычитания
9.3.1. Исходные данные
• Типы арифметических операций — сложение и вычитание двоичных чисел;
• исходный код представления операндов — дополнительный;
• разрядность операндов — 8 бит;
• код выполнения операций в сумматоре — дополнительный модифицированный;
19'
292 Проектирование специализированных арифметико-логических устройств
• структура операционного блока — с закрепленными микрооперациями;
• тип управляющего блока — автомат Мили с памятью на D-триггерах;
» схема логического признака переполнения разрядной сетки;
• схема логической поразрядной операции “Исключающее ИЛИ” кодов исходных операндов Л и В.
Элементная база, перечень обязательного графического материала и необходимые расчеты — согласно пункту 9.1.2.
9.3.2. Алгоритмы сложения и вычитания двоичных чисел
Алгоритм сложения и вычитания двоичных чисел можно выполнять в обратных или дополнительных кодах. В современных компьютерах часто операнды хранятся в памяти и обрабатываются в дополнительных кодах, преимущества которых описаны в разделе 9.1.
Алгоритм сложения (код команды A’fl]) или вычитания (код команды #[2]) выполняется в следующей последовательности:
• в регистры RGA и RGB со входной шины один за другим параллельным кодом записываются соответствующие им операнды А и В;
• во время операции вычитания (код команды #[2] = 1) операнд В безусловно инвертируется;
• микрооперации сложения или вычитания выполняются в дополнительных кодах на протяжении одного машинного такта;
• анализируется результат операции. При отсутствии переполнения разрядной сетки (знаки операндов А и В и результата совпадают) результат записывается в регистр RGD и затем пересылается в оперативную память, при наличии переполнения (знаки операндов А и В и результата на выходе сумматора не совпадают) результат не фиксируется и в ЦУУ подается сигнал переполнения ПП.
9.3.3. Функциональная схема АЛУ для выполнения операций сложения и вычитания
Функциональная схема восьмиразрядного АЛУ для выполнения микропрограммы сложения и вычитания представлена композицией модуля операционного блока МОБ и модуля управляющего блока МУБ (рис. 9.11).
Схема содержит:
• регистры RGA и RGB для приема со входной шины И11 операндов А и В и их хранения на протяжении времени выполнения микропрограммы;
• схему инвертирования BIN содержимого регистра RGB\
• схему XOR для поразрядного логического “Исключающее ИЛИ" кодов операндов А и В;
• схемы электронных ключей SJFI и SW2 для коммутации операндов;
• комбинационный сумматор SM. На вход переноса сумматора подается лог. 1 при операции вычитания;
• регистр результата RGD\
• схему признака переполнения ПР;
9.3. Реализация операций сложения и вычитания 293
модуль управляющего блока МУБ на основе автомата Мили с памятью на D-триггерах.
Ш1
Рис. 9.11. Функциональная схема АЛУ для сложения и вычитания чисел
294 Проектирование специализированных арифметико-логических устройств
9.3.4. Микропрограмма сложения и вычитания двоичных чисел
Совмещенная микропрограмма сложения и вычитания двоичных чисел имеет вид:
Начало Если К[ 1 ] или /С[2], то Мь иначе — ожидать
у, : RGA := А <приема первого операнда^
у2 : RGB := В <приема второго операнда>
Если A’fl], то
у3: RGC :=В, иначе
у4 : RGC :=В <пересылка с инвертированием второго операнда>
Если 7Ц11, то
у5 : SMВ + С , иначе у6: SM := В + С +1
Если qy, то перейти к М2, иначе
у2 : RGD \=SM <присвоение результата>
у8 : П12: - D <пересылка результата в оперативную память>
Перейти к Л/3
Мг у9 :7п:=ПП <фиксация переполнения>
ЛЛ Конец.
Содержа: ел ьный и закодированный графы микропрограммы сложения и вычитания показаны на рис. 9.12.
9.3.5. Принципиальная схема модуля операционного блока
Модуль операционного блока (МОБ) строится на микросхемах ТТЛШ серии КР1533 за исключением сумматора, взятого из серии К1531.
Принципиальная схема МОБ содержит (рис. 9.13):
• ОО1, DD2 — два входных восьмиразрядных регистра RGA и RGB типа ИР35;
• DD?>, DD4 — две микросхемы типа ЛП5. Предназначены для инвертирования содержимого регистра RGB\
• 005-008 — четыре микросхемы типа ЛИ1. Реализуют схемы электронных ключей;
• 009 — микросхему вспомогательного регистра RGC типа ИР35, позиционное обозначение;
9.3. Реализация операций сложения и вычитания 295
• DDK), DD\ 1 — две микросхемы четырехразрядных сумматоров типа И Мб; • DD12 — микросхему регистра результата с тремя состояниями типа ИР22.
Содержательный граф
Закодированный граф
Рис. 9.12. Графы микропрограммы сложения и вычитания
296 Проектирование специализированных арифметико-логических устройств
DD\
DD5-DD&
Рис. 9.13. Принципиальная схема МОБ для операций сложения и вычитания
9.3.6. Проектирование модуля управляющего блока
Проектирование модуля МУБ на основе автомата Мили с памятью на D-триггерах выполняется в следующей последовательности.
1. Размечается закодированный граф микропрограммы сложения и вычитания (см рис 9.12). Определяется максимальное количество состояний автома
9.3. Реализация операций сложения и вычитания 297
та Мили, равное L = 6. Для реализации такого количества состояний необходимо использовать п = ]log26[ = 3 триггера.
2. На основе размеченного графа микропрограммы строится граф автомата Мили (рис. 9.14), интерпретирующий микропрограмму сложения и вычитания.
Рис. 9.14. Гоаф автомата Мили для интерпретации микропрограммы сложения и вычитания
3. Состояния автомата Мили кодируются значениями выходов трех О-триггеров:
Zl = 636261 > Z2 = 636261 > ••• • Z6 = 636261 •
4. На основе графа автомата Мили записывается его структурная таблица переходов (табл. 9.6)
Таблица 9.6
Zl k (z,) k (zj) {Xj D-триггеры
Di, Dt
Zl 000 Р1Р1 - -
Z\ 000 Zl 001
Zl 001 PxPl У1
Zl 001 z3 010 1 Di
Z3 010. z4 z4 Oil Oil Al A У1 У4 Di, D\ Di, D\
z4 Oil z5 zs 100 100 A Al У5 Уб
z5 100 z6 Zl 101 000 A *1 У7 У9 Di, Dt
Zb 101 zl 000 1 У8 -
5. На основании данных табл. 9.6 записываются системы логических уравнений:
• для выходных сигналов:
У! = zxpx = zJ3x '^zxpi (используется тождество
A v P\Pi — P\v Pi)’
^2=z2; >’3=2зА; >’4=2зД;
У5=2аР\'-> У<:>~2\Р\' -У7=25Х1’
У % = Z6’ У9 ~ Z5XI>
298 Проектирование специализированных арифметико-логических устройств
• для функций возбуждения входов D-триггеров
D, - z,Д v Zj Д Д, v z3 v zsx, = zji, v v z3 v z5x, = j, v z3 v y7 (учитываются выражения для выходных сигналов микроопераций);
= Z2 V Z3’
D3 =z4 vzjXj =z4 v J'7;
• признак переполнения (p3 - x( определяется по формуле:
= Х| = I[8]C[8]W[8] v Л[8]С[8]ЯИ[8].
6. Строится принципиальная схема МУБ (рис 9 15)
0013
7
1 \19
4
.ш.
Tim In 7’ш
ЯН
DD\ 6
№18
0021, DD22
12
0019, 0020
О
ЛЛ1
2 2
Л111Т
я Г\ 1 -----* Л [8]
и 04, -g_[8]
SM [81
ЛИ1
и
ЛИ1
6
&
8____I9
i____Q
4_____I
Jj_____u
ос
ИД7
Au.
/3014,7)015 _ 0017
< ду 4МГ& Г 1 ’ Д|8.1
ЯЯ...Д
Л115
ф] н, _Щ1_С яь JliLu ЯМи JJ.6L-4
Ц71 9 Д|7] ,0 Ф) !2 Я|8] в
ЛП5
II Я)
л- 7
Л' «
9
К)
М— 11
j_____4
6_____s
Ц_____2
15...1.(1
ЛЛ1
23
24
И 3,(1)
2 I/D
Ы Я(0
15 14Л)
U —ML»
LZ
12 J/D
6 М»
12 Зо(1)
24 _Ш1)
J Д-.
Q
сД—i
д
Рис. 9.15. Принципиальная схема МУБ для операций сложения и вычитания
Соответствие между входами управления микросхем и сигналами микроопераций представлено в табл 9 7
Таблица 9.7
Входы LA LB LC Tim LD EZ D4 = 7},H Т’п
Сигналы микроопераций У1 У2 V, V у4 У4 3’7 У8 Тли ".Л v Уь 3'9
9.4. Реализация операции умножения 299
Пояснения к табл. 9.7:
• LA = уу LB = у2— запись операндов в регистры RGA, RGB\
• LC = у3 v у4 — запись в регистр RGC, при этом одновременно формируется сигнал LC = у3 v у4 для управления микросхемами “Исключающее ИЛИ”;
• Гип — сигнал на выходе четвертого триггера микросхемы ТМ9 для управления электронными ключами и входом переноса Z сумматора;
• LD = у7 — запись результата в регистр RGD\
• EZ - у8 — пересылка результата в память;
• Т1т = y5vy6= 7)4 — выход четвертого триггера микросхемы ТМ9 для управления электронными ключами;
• Гп ~ уч — выход пятого триггера микросхемы ТМ9 для фиксации переполнения.
9.4. Реализация операции умножения
9.4.1. Исходные данные
• Тип арифметической операции — умножение двоичных чисел;
• исходный код представления операндов — прямой;
• разрядность — 8 бит;
• код выполнения микрооперации в сумматоре — дополнительный;
• структура операционного блока — с закрепленными микрооперациями,
• тип управляющего блока — автомат Мили с памятью на /?Э-триггерах.
Элементная база, перечень обязательного графического материала и необходимые расчеты — согласно пункту 9.1.2.
9.4.2. Алгоритм умножения двоичных чисел со сдвигом суммы частичных произведений вправо
Умножение двоичных чисел А и В сводится к вычислению произведения их модулей и присвоения ему знака. Произведение двух «-разрядных операндов содержит 2л-1 цифровых разрядов и один знаковый. Если перемножаются целые числа, запятая размещается после младшего разряда, а если дроби — перед старшим разрядом.
1. Множимое и множитель в прямых кодах последовательно записываются соответственно в регистры А и В. Регистры С и D обнуляются. В счетчик СТ записывается количество циклов.
2. Для разрядов множителя 1, 2, ..., /7-1 выполняются следующие действия:
• если младшая цифра множителя 7?[1J=1, то к сумме частичных произведений прибавляется модуль множимого, иначе — не прибавляется;
• далее для обоих случаев содержимое регистров С и В сдвигается вправо на один разряд, причем младший разряд регистра С передается в старший разряд регистра В. После каждого сдвига в младший разряд регистра В по-
300 Проектирование специализированных арифметико-логических устройств
ступает следующий разряд множимого, по которому определяется очередное частичное произведение (нуль или множимое);
• после л-1 циклов выполняется дополнительный сдвиг вправо для передачи в триггер Т знака множителя и определяется знак произведения сложением по модулю два знаков множимого и множителя.
3. Результат представляется конкатенацией чисел С и В; при этом в регистре С размещаются старшие разряды произведения, а в регистре В — младшие разряды.
9.4.3. Функциональная схема АЛУ для операции умножения
Функциональная схема АЛУ для умножения целых двоичных чисел со сдвигом вправо частичных произведений содержит (рис. 9.16):
• регистры А и В для приема с входной шины Ш1 соответственно множимого и множителя;
• параллельный комбинационный сумматор <571/;
• регистр С для приема частичной суммы из SM при единичном значении синхросигнала;
• регистр D для приема и временного хранения частичной суммы из регистра С при спаде синхросигнала;
• счетчик циклов СТ;
• триггер Л для управления ключами 5W1, SW2;
• триггер Т2 для записи знака множителя.
Ш1
Рис. 9.16. Функциональная схема АЛУ для умножения
9.4. Реализация операции умножения 301
Регистры С ]л В обеспечивают сдвиг вправо чисел, при этом значение младшего разряда регистра С[ 1 ] пересылается в старший разряд регистра Дп].
9.4.4. Микропрограмма умножения целых чисел
Начало. Если /<[3], то М}, иначе — ожидать
Мх :RGA:= Л; Т2.Т1;=0.0 <приема множимого и обнуления триггеров
Л, Т2>
у2: RGB := В; Т2 := В[«] <приема множителя и дублирования его знака в триггере Т2>
у3 -.RGC.RGD -.-Q.G «обнуления регистров>
уь :СТ := л -1 «запись количества циклов>
Mi Если В[1], то М
ys: SM := |Л| + D <сложение>
у6: RGC := SM «пересылка частичной суммы>
Мз у7 : RGC.RGB ;= R(C.B) «одноразрядный сдвиг вправо>
у8: СТСТ -1 «декремент счетчика>
Если СТ # 0, то М2, иначе
у7 : RGC.RGB := R(C.B)
y9: RGC = L(C) «одноразрядный сдвиг влево>
7IO : RGCT2.R(c) «запись знака результата в регистр RGC>
Конец.
Содержательный и закодированный графы микропрограммы умножения показаны на рис. 9.17.
302 Проектирование специализированных арифметико-логических устройств
Рис. 9.17. Содержательный и закодированный графы микропрограммы умножения
9.4. Реализация операции умножения 303
9.4.5. Модуль операционного блока для умножения целых чисел
Модуль МОБ для умножения целых чисел содержит (рис. 9.18, 9.19):
ХШ1[1] .<1II.11.2L «ШЧЗ. .<mi„H,L ХШ1Г51 ЛШ1Г6] ..«.ШАШ.
—
и п
>3
Y4
Л_
)7 №
УЧ
ПО
Ш1(2)
1
3
4
5
6
7
8
9
10
1L
13
14
I 5
16
17
1£
19
20
Рис. 9.18. Принципиальная схема МОБ для операции умножения (начало)
• DD1 — регистр множимого RGA типа ИР35;
• DD11 — вспомогательный регистр RGD типа ИР35;
• -DD12 — регистр частичной суммы ЯСС типа ИР13;
• DD9, DD1Q — комбинационный параллельный сумматор 5Л/типа ИМ6;
• DD\3 — счетчик циклов СТ2 типа ИЕК);
• DDA-DD7 — микросхемы электронных ключей типа ЛИ 1;
304 Проектирование специализированных арифметико-логических устройств
вспомогательные микросхемы DD3, DD%, DD1A, DD15, DD16 для управления входами функциональных узлов согласно логическим уравнениям на основе таблицы соответствия.
Рис. 9.19. Принципиальная схема МОБ для операции умножения (продолжение)
9.4. Реализация операции умножения 305
9.4.6. Модуль управляющего блока
Проектирование модуля МУБ на основе автомата Мили с памятью на RS-триггерах выполняется в следующей последовательности.
1. Размечается закодированный граф микропрограммы умножения (см. рис. 9.17) и определяется максимальное количество состояний памяти и требуемое количество триггеров: L = 8,n = log28 = 3.
2. Строится граф автомата Мили, интерпретирующий микропрограмму умножения (рис. 9.20). Состояния памяти кодируются следующим образом: Z1 ~ 030201 ' Z2 = 030201 ' Z3 ~ Q-iQzQx ••• > Z6 = 030201 •
УУю
Рис. 9.20. Граф автомата Мили для микропрограммы умножения
3. Записывается структурная таблица переходов и выходов автомата Мили с памятью на RS-триггерах (табл. 9. 8). Логические условия закодированы так: /73 = 2С[3]; Х] =/?[!]; х2-(СТ = 0).
Таблица 9.8
z, Zj Ш) x(Zi,Zj) j(Zi,Z2) R
Zi 000 Zi 000 Pl - - -
Z2 001 Pl У1 S1 -
Z2 001 Z3 010 1 У2, Уз, У4 S2
z3 010 z4 Oil Уб -
z6 101 X| У7,У8 St, 5, r2
Z4 Oil z5 100 1 Уб 53 r2,
z5 100 z6 101 1 5) -
z6 101 z6 101 1 M*1 1 24 УъУ« - -
z4 on *2*1 Уб □ 2 Ri
Z7 110 Xl У7 s2
z7 110 z8 111 1 У9 5, -
Z« 111 Zi 000 1 Ую - R2, Rt, Ry
4. На основании данных структурной таблицы записываются системы уравнений:
• для выходных сигналов:
у, у2 =у3 =y4=z2> ys =z3^ivWi* Уб =z4;
y2 = z3X] v z5 v z6x2X] v z6x2 = z3Xj v z5 v z6x2 v z6x, (используется тождество x2x, v x, - x2 v x,);
yg - z3X] v z5 v z6x2Xj;
Уд = z2', Ую = zs •
20-4-1749
306 Проектирование специализированных арифметико-логических устройств
• для функций возбуждения входов RS-триггеров:
S’, = z,/?3 vz3vz,vz7; /?, = z2 v z4 vz6x2 vz8;
S2 = z2 v z6x2x, v z6x2 = z2v z6x, v z6x2 (используется тождество x2x} v x2 = x2 v x,);
R2 = z3xt v z4 vz8;
S’3 = zixi v z4; 7?3 = z6x2x, v zg.
В записанных системах уравнений имеются общие двухбуквенные логические выражения, для которых вводят обозначение:
а\ ~ = Z6X2 > «3 = Z6^1 > ~ Z3X1’
а5 ~ Z6X2X1 ’ a6 ~ Z2X\ i а7 = Z5XI '
С учетом вспомогательных функций ах - а2 и дополнительных преобразований по правилу двойной инверсии и закону де Моргана системы уравнений представляются в следующем виде:
• для функций возбуждения входов RS-триггеров:
S, = tz, v z3 v z5 v z7 = tz, • z3 • z5 • z7;
Rx = z, v z4 v tz2 v z8 = z2 • z4 • Zz2 • z8;
S’2 = z2 v a2 v tz3 = z2 • a2 • oy;
T?2 £Z4 V z4 V z8 6Z4 • z4 * z8,
S\ = tz4 vz4 =a4-z4;
7?3 = a2 v zs = • z8;
• для выходных сигналов микроопераций:
У\^а\\ л ~у3 =л = ?2; л =абv«5 уб = г4;
у2 = tz4 v tz5 v tz2 = а4 • а5 • а2;
у8 = tz4 V z5 V tz5 = Zz4 • z5 • a5;
Уд = Z7’ Л’ю = Z8-
9.4.7. Принципиальная схема модуля управляющего блока
Принципиальная схема модуля МУБ содержит (рис. 9.21):
• DDZ1 — микросхему четырех асинхронных RS-триггеров типа ТР2 с инверсными входами (память автомата);
• DD\8, DD19.1 — микросхемы НЕ И типа ЛАЗ, которые обеспечивают синхронное прямое управление RS-триггерами;
• DD20 — дешифратор типа ИД7, предназначенный для расшифровки двоичного позиционного кода состояний памяти;
• DD23, DD24 — две микросхемы инверторов типа ЛН1, предназначенные для инвертирования инверсных сигналов с выходов дешифратора;
• Z)Z>19.2, DD21 — микросхемы элементов НЕ И типа ЛАЗ, предназначенные для формирования вспомогательных функций -а7;
9.4. Реализация операции умножения 307
• DD25, DD26 - микросхемы элементов НЕ И типа ЛА1 и ЛА4, формирующие сигналы для входов RS-триггеров и выходные сигналы микроопераций.
£>£>22
£>/3>25,£)£>26-£>£>28
АД 9
Х2 10
/33__П
2
4
2 5
,3 9
10
12
4 13
5 1
, 2
4
6 5
£>£>18,£>£)19.1
& ЛАЗ
& ( ЛАЗ
&S
53
<65
51
Я1
52
R2
R3
52 £2
Т
ТР2
ТР2
2
2 2
£>£>20 DC | ИД7
о Ан. .114 АЙ л п ю
£1 £2
£3
Z7£>23,£>£>24
14
Ji
1______11
1
ЛН11
А
7Q-Z_____1
1_Л
1Щ.
J2
13 9
12 10
18 12
10 13
18 1
?1 2.
15 4
9 5
15 9
?|
17 12
21 13
& । ЛАЗ
£>£>19.2,£>£>21
&А-
ЛАЗ
3
12
13
6 13
ЛН1Т
2 19
20
£____т
14
8
1211
Ат
22
6 о—
12
з ?
S 4
7 £
2 9
4 И)
U 12
8 13
э 1
13 2
14 13
15 з
4 4
8 5
15 9
4 10
11
17 1
8 2
13
16 3
25 4
5
15 9
24 10
13 11
15 1
5 2
24 13
18 3
2i 4
9 5
JIA1
&
&
А-^
А-^
ЛА4
&
12
24
14
J1A4
з—У7(1)
2
ЛА4
&
У5(1)
16
19
20
Г 2(1)
У3(1) Г4(1) Г6(1)
У9(1) И 0(1)
Рис. 9.21. Принципиальная схема модуля МУБ для операции умножения
20*
308 Проектирование специализированных арифметико-логических устройств
Соотношения между множеством выходных сигналов микроопераций и управляющими входами микросхем операционного блока заданы табл. 9.9.
Таблица 9.9
У. LA SOB S1B S0C SJ с LD LCT CD Л к. Л к. RC RB RGC[8] RGB[8]
У| У1 У1 У1
)’2 у-' У1 F,
у-» >’з Уз
,У4 Ул
V5 УУ
Уъ Уь Уб уХ
Уч У? У-! Уч Fz
У» ,Уз
Уч Уч
Ую Ую Ую'Т2
Примечание. 1. F; =_у2С4[8] © В[8]).
2. F2 = y7FGC[l],
На основании данных табл. 9.9 записываем систему уравнений, которая является основой для построения второго уровня управления операционным блоком:
LA = y}; S0B = y2vyy-, SIB - у2;
>S'OC'= у6 v _у7 v _у|0; SlC = y6 vy9;
LD = ^C-, ~LCT = y4; CD = y^; J2 =_у2(Л[8]©В[8]);
К?=УА -Ц=У^ RC = y3- RD = y3\ -
FGF[8] - y7 FGC[1]; FGC[8] = yl0 • T2.
Для построения второго уровня управления операционным блоком на основе полученных уравнений используются микросхемы DD3, DDR, DD14-DD17 (см. рис. 9.19, 9.20).
9.5. Реализация операции деления
9.5.1. Исходные данные
• Тип арифметической операции — деление двоичных чисел;
• исходный код представления операндов — прямой;
• разрядность — делимое X— 16 бит, делитель Y — 8 бит;
• код выполнения микрооперации в сумматоре — дополнительный;
• структура операционного блока — с закрепленными микрооперациями;
• тип управляющего блока — автомат с памятью на JK-триггерах.
Элементная база, перечень обязательного графического материала и необходимые расчеты — согласно пункту 9.1.2.
9.5. Реализация операции деления 309
9.5.2. Алгоритм деления целых чисел
Операция деления целых чисел Z=X/Y сводится к последовательности вычитаний делителя Y вначале от делимого X, а затем — от образующихся в процессе деления остатков 7?,.
В зависимости от способа вычитания делителя Y различают два основные алгоритма деления: без восстановления остатка R, и с восстановлением остатка. Оба способа реализуются приблизительно одинаковыми аппаратными затратами, однако для деления без восстановления остатка требуется больше микроопераций сложения и вычитания. В универсальных компьютерах обычно используют деление без восстановления остатка.
В случае деления целых чисел делимое X зачастую представляют в 2«-разрядном формате, а делитель Y — в «-разрядном.
Алгоритм деления целых чисел в прямом коде без восстановления остатка реализуется в следующей последовательности.
1. В регистры А, В и С последовательно записываются с входной шины «-разрядный делитель Y и 2«-разрядное делимое X. В счетчик циклов СТ заносится число циклов л-1.
2. Делимое X и делитель Y анализируются на равенство нулю. Если делимое Х= 0, то частному Z присваивается нулевое значение и деление заканчивается. Если делитель Y = 0, то деление прерывается.
3. Устанавливается возможность деления без переполнения разрядной сетки. Для этого значение делимого удваивается сдвигом влево на один разряд. Из сдвинутого делимого вычитается делитель. Операция вычитания делителя заменяется его сложением в дополнительном коде, и определяется первый остаток Ro по формуле
S0=2|jr|-r = 2|X| + |-r|;/.
Если 7?0 < 0, то деление возможно; если Ro>0, возникает переполнение разрядной сетки и деление прекращается.
4. Если деление возможно, выполняются следующие основные действия:
• частичный остаток в регистре В и содержимое регистра С сдвигаются влево на один разряд (то есть удваиваются);
• из сдвинутого остатка вычитается делитель, если предыдущий остаток 7?,_j >0, или прибавляется, если7?,_, <0. Это определяется рекурентным соотношением
*,=
27?,+|к|, если 7?,_, <0;
27?,+|- У| если 7?,_, > 0,
где i = l,2..«-1.
• если происходит сдвиг влево, в младший разряд регистра С записывается цифра частного г,- согласно соотношению
0, если 7?,_, < 0;
1, если 7?,_] > 0.
Это означает, что текущая цифра частного является инверсией знака остатка;
310 Проектирование специализированных арифметико-логических устройств
• содержимое счетчика циклов СТ уменьшается на единицу;
• п. 4 повторяется до обнуления счетчика циклов СТ.
Значение первого (старшего) разряда частного отводится для записи знака результата на основании выражения г0 = Л[и]® В[п].
5. Остаток деления размещается в регистре В на месте старших разрядов делимого, а частное — в регистре С. Делитель, остаток и частное имеют формат «-разрядного числа со знаком. Остаток должен иметь тот же знак, что и делимое, нулевые остатки и частное всегда положительные. Если знак последнего остатка отрицательный, то он корректируется прибавлением к нему модуля делителя, после чего остатку присваивается знак делимого.
9.5.3. Функциональная схема АЛУ для микропрограммы деления
Функциональная схема АЛУ для выполнения микропрограммы деления показана на рис. 9.22.
Рис. 9.22. Функциональная схема АЛУ для операции деления
9.5. Реализация операции деления 311
Представленная схема АЛУ содержит:
• регистр RGA для приема восьмиразрядного делителя У;
• регистры RGB и RGC для приема 16-разрядного делимого X;
• комбинационный восьмиразрядный сумматор SM;
• мультиплексор MUX, который обеспечивает запись информации в регистр RGB со входной шины Ш1 или с выходов сумматора SM;
• схему BIN для представления прямого или обратного кода делителя на входе сумматора SM;
• счетчик количества циклов СТ;
• схему выработки признаков результата ПР;
• триггеры 71-74 для создания второго уровня управления модулем операционного блока МОБ;
• местный управляющий блок МУБ на основе автомата Мили с памятью на JK-триггерах.
9.5.4. Микропрограмма деления целых чисел без восстановления остатка
Начало. Если Х[4], то М{, иначе — ожидать
М{ у, :RGA:=Y; 71.72.73.74 :=0.0.0.0 <загрузка делителя и обнуление триггеров>
у2 : RGB := XI; Т1 := B[ri\ <загрузка старшей части делимого; присвоения триггеру 71 знака делимого>
у3: RGC := Х2 <загрузка младшей части делимого>
у4 : RGB.RGC := ЦВ.С).Т2 <сдвиг влево на один разряд содержимого регистров RGB и RGC. Передача значения старшего разряда регистра RGC в младший разряд регистра RGB, а в младший разряд регистра RGC — содержимого триггера 73>
у5:73:=ЗНАК= Дл]® 71 «запись в триггер 73 знака результата де-ления>
yb: СТ := п -1 «загрузка в счетчик СТ количества циклов>
у2: SM := В + [-Л]д «вычитание делителя в дополнительном коде от значения данных в регистре RGB>
у8: ADR.RGB :=i.SM «загрузка результата вычитания в регистр RGB. Входу адресации ADR мультиплексора MUX присваивается значение единицы>
уч: 74 := SAY[и] «присвоение знака остатка триггеру 74>
312 Проектирование специализированных арифметико-логических устройств
Если ГД, то М2, иначе
у10 : ?\л'•= ПП «присвоение признака переполнения триггеру Тп в ЦУУ>. Перейти к М2 (конец)
М2 у, : RGB.RGC := ь(В.С)ТЗ .
М2 Еслй Т4, то М4, иначе
y7-.SM -.= В + [-А]а
yl2: ТЗ.Т4 := 0.0 «обнуление триггеров 73, Т4> Перейти к М5
М4 у,, : SM := В+ \А | «прибавление делителя к остатку>
у12 : ГЗ.7’4 := 0.0
М5 ys : ADR.RGB := I .SM
у9-Т4
у|3: ТЗ :- 5А/[п] «присвоение триггеру 73 инверсного значения знака сумматора — формирование цифры частного>
у|4: СТ := СТ -1 «декремент содержимого счетчика>
Если СТ / 0, то М2, иначе М5
М5 у15 := RGC := £(С).ТЗ «сдвиг влево содержимого регистра RGC и запись последней младшей цифры частного>
Если 5[я], то М6, иначе
ун : SM := Д+|Л|
v8 : ADR.RGB :=] ,SM
Мь Если 5[и] = Т\, то М2. Иначе
у|5 := RGB := L(B.O) «сдвиг влево остатка>
у16: RGB :=T1.R(B) «сдвиг вправо частного и присвоение ему знака делимого
М2 Конец.
Содержательный и закодированный графы микропрограммы деления показаны на рис. 9.23 и 9.24.
9.5.5. Принципиальна схема модуля операционного блока для микропрограммы деления
Принципиальная схема модуля МОБ для микропрограммы деления (рис. 9.25, 9.26) содержит:
• 7)7)1 — восьмиразрядный регистр делителя RGA типа ИР35;
• 7)7)2, 7)7)3 — двухканальный восьмиразрядный мультиплексор MUX на двух микросхемах типа КП16;
9.5. Реализация операции деления 313
• 7)7)4, 7)7)5, 7)7)32 — микросхемы логических элементов “Исключающее ИЛИ” типа ЛП5;
• 7)7)6, 7)7)9 — восьмиразрядные регистры делимого RGB и 7?ССтипа ИР13;
• DD1, DD8 — восьмиразрядный сумматор SM на двух микросхемах типа ИМ6;
• 7)7)10, 7)7)11, 7)7)26, 7)7)27 — восемь JK-триггеров типа ТВ6;
• 7)7)12-7)7)15 — четыре микросхемы логических элементов НЕ И типа ЛАЗ;
• 7)7)16 — дешифратор типа ИДЗ;
• 7)7)17, 7)7)18, 7)7)33 — микросхемы инверторов типа ЛН1;
• 7)7)19, 7)7)29 — микросхемы логических элементов И типа ЛИ1;
• 7)7)20-7)7)22 — микросхемы логических элементов НЕ И типа ЛА2;
• 7)7)23, 7)7)25 — микросхемы логических элементов НЕ И типа ЛА4;
• 7)7)24 — микросхема логических элементов НЕ И типа ЛА1;
• 7)7)28 — двоичный четырехразрядный счетчик циклов типа ИЕ10;
• 7)7)30, 7)7)31, 7)7)34 — микросхемы логических элементов ИЛИ типа ЛЛ1.
Рис. 9.23. Содержательный граф микропрограммы деления
314 Проектирование специализированных арифметико-логических устройств
Рис. 9.24. Закодированный и размеченный граф микропрограммы деления
9.5. Реализация операции деления 315
Рис. 9.25. Принципиальная схема МОБ для микропрограммы деления (начало)
316 Проектирование специализированных арифметико-логических устройств
DD)0,DDH DD\6
9 9(2)* т ТВ6 3 1 1 23 DC I ,идзоL и
10 10(2), 2 22 7 k-2 12
Н Г1 3 21 4 АЗ 13
1 1 л ./1 KI 1 4 20 8 14
15 15
2 4 5 ? L и
4 X Ь 12
Т2 J2 К2 । 1$ ц
7lj> и
3 11 ? 3 IlO 20
5 1 Хи ц
113 22
73 Л КЗ '
1!4 23
7 4 , pi 115 24
'bl Q " ' 1F7 А1£_
X
in
7'4 J4
Рис. 9.26. Принципиальная схема МОБ для микропрограммы деления (продолжение)
9.5. Реализация операции деления 317
9.5.6. Схема второго уровня управления операционным блоком
Традиционно при проектировании произвольного цифрового вычислительного устройства управляющий автомат Мили или Мура рассматривается как первый уровень управления. Это справедливо и для управляющих автоматов на основе программируемой логики.
Сигналы с выходов управляющего автомата инициируют в операционном блоке выполнение некоторого множества микроопераций. Обычно каждый сигнал микрооперации поступает на вход соответствующего управляющего входа функционального узла.
В случае использования современных микросхем среднего уровня интеграции (регистров, счетчиков, мультиплексоров и т. д.) для реализации сложных микропрограмм типа умножения, деления и др. проектирование усложняется. Это обусловлено следующими факторами:
• один управляющий сигнал может одновременно поступать на несколько входов одной микросхемы;
• один и тот же сигнал микрооперации может одновременно поступать на входы нескольких различных микросхем;
• регистры в серии КР1533 построены на D-триггерах, что почти исключает возможность записи в них информации по отдельным разрядам, например, знака произведения или знака деления в старший разряд.
В таком случае возможно использовать схему второго уровня управления, которая строится в следующей последовательности:
• записывается таблица соответствия между входами управления микросхем операционного блока и сигналами микроопераций <р:;
• на основе таблицы соответствия записываются дизъюнкции сигналов микроопераций для каждого управляющего входа микросхем операционного блока;
• на основании полученных логических уравнений определяется необходимый состав микросхем и строится схема второго уровня управления.
Соответствие между управляющими входами микросхем операционного блока МОБ представлено в табл. 9.10.
В табл. 9.10 показаны управляющие входы микросхем, на которые подаются сигналы микроопераций:
• J5J8 — установка триггеров 75-ТВ;
• АЗ-АВ - обнуление триггеров Т5-ТВ;
• S\B, SOB — задание режимов универсального регистра RGB (00 — хранение данных, 11 — запись данных, 01 и 10 соответственно — сдвиг вправо и влево);
• 51 С, S0C — задание режимов работы регистра RGC;
• ОЕ — разрешение передачи данных мультиплексору;
• ADR — адресует канал мультиплексирования: ADR = 0, ОЕ = 0 — передаются данные с входной шины; ADR = 1, ОЕ =0 — коммутируются данные с выходов сумматора;
318 Проектирование специализированных арифметико-логических устройств
• LCT — загрузка счетчика числом циклов —константой 0111 (2)=7(10);
• LA — загрузка регистра RGA\
• КА — восприятие сигнала переполнения;
• CD — вход вычитания счетчика.
Таблица 9.10
У, Т5 Тб 77 Т8 RGA RGB RGC MUX СТ2 SM тп
К5 J5 Кб J6 КП Л К8 J8 LA SIB SOB SIC SOC ADR ОЕ LCT CD •7п
У1 У| У> У>
У? У/5[8] Уг Уг Уг Уг
Уз /з /з
У4 /4 /4
У5 У5-зн
Уб Уь
,У7 У1 72
Уя /8 /8 /8 /8
У9 Л5М[8]
/к> Ую
Ун /и 72
,У|2 У>2 /|2
/в
/14 /14
Ув /15
Z16.
На основании данных табл. 9.10 записывается система логических уравнений, которые являются основой для схемной реализации второй ступени управления ОБ:
J5 = y25[8]; ^5 = y,; ADR = y2 v y8
J6 = y7; K6 = yt v/ц; OE^y2 vy8;
Л = у5 • ЗН v у,3 SM[8]; ^7 = y, vy12; Zl = 72;
J8 = у9 5М[8]; /С8 = У1 vy12; LA = y{;
5/5 = у2 vy4 vy8 vyl6; 5OC = y3; LCT = y6-,
505 = у2 vy8 vy16; KA = y10.
5/С = у3 vy4;
9.5.7. Принципиальная схема автомата Мили для операции деления
На рис. 9.24 выполнена разметка графа микропрограммы деления для автомата Мили. На основе закодированной и размеченной микропрограммы строится граф автомата Мили для реализации операции деления (рис. 9.27).
Максимальное количество состояний автомата L = 14.
9.5. Реализация операции деления 319
Состояния кодируются логическими выражениями следующим образом:
zi =64636261! ^5 = 64636261 ’ ^9 = 64636261 ’ z13 = 6463626U z2 =64636261; z6 =64636261; z10 =64636261; z14 =64636261;
z3 =64636261; z7 =64636261; Z11 =6463626,; z15 =64636261;
z4 =64636261; ZS =64636261; z12 =64636261; z16 =64636261-
Puc. 9.27. Граф автомата Мили для операции деления
На осноре графа автомата Мили для операции деления строится прямая структурная таблица переходов и выходов (табл. 9.11).
Таблица 9.11
Zi к&) Zj K(zj) KfcZy) JK
J к
Z| 0000 21 0000 А - - -
0000 22 0001 А . «1 JI -
z2 0001 23 0010 1 a2 J2 KI
z3 0010 24 ООН 1 a2 J\ -
24 ООП 25 0100 1 aA,as,a6 J3 K2, KI
25 0100 26 0101 1 «7 J\ -
2б 0101 z7 оно 1 a8,6z9 J2 KI
z7 оно 28 0111 *1 «4 JI -
оно 21 0000 *1 «10 - КЗ, KI
z8 0111 29 1000 *1 «11 ’«12 J4 КЗ, KI, K\
0111 29 1000 *1 «7>«12 J4 КЗ, KI, KI
z9 1000 ' 210 1001 1 «8’«9 JI -
«13’«14
2 IO 1001 Z|| 1010 Х2 «15 J2 KI
1001 29 1000 Xj -х2 «11 ’«12 - KI
320 Проектирование специализированных арифметико-логических устройств
Таблица 9.11. Продолжение
Z, K(z,) Zj K(zj) K(z„zy) JK
J к
1001 z9 1000 Xj a7, a]2 - KI
41 1010 Z]2 1011 x3 «И JI -
Z13 1100 *3 - J3 K2
Z12 1011 Z|3 1100 1 «8 J3 K2, KI
Z13 1100 -14 1101 X4 «15 J\ -
1100 Z1 0000 X4 - - K4,K3
-14 1101 Zi 0000 1 «16 - K4, КЗ, KI
По данным структурной табл. 9.11 записываем системы логических уравнений: • для функций возбуждения:
JI = z,/74 vZhX3 vzI3x4 vz3vz5vz7 V29; KI = z2v z4 v z6 v zs vz10;
J2 = Z-. v z. v z,nx,; K2 = z.v z7x, v z„ v z,,x, v zl7;
J3 = z. v z„ v z..x3; КЗ = z7x, vz. v z.,x4 v z,4;
J4 = zs; К 4 = z13x4 v z14.
• для выходных сигналов:
a^zxp4, a2~z2\ ay=zy\ «4=z4vz7x,; «5=z4; «6 = z4; cr7 = z5 v z8x, v z10X|, a8-z6vz9vz,2, «9—z6vz9, «10—z7Xj, «и — z8Xj vz10x2X] vzHx3; a]2 = zsxi v zi<A vzio4
«13 “4 «[4=z9; al5=z|3x4.
На основе полученных систем уравнений строится логическая схема автомата Мили для операции деления (рис. 9.28). В данном случае устройство АЛУ реализуется на основе синхронного принципа управления, при котором:
• длительность машинного такта Тс для всех микрокоманд, представленных операторными вершинами микропрограммы деления, постоянна;
• все микрооперации подразделяются на две группы: короткие (приема и пересылки операндов, сдвиги, мультиплексирование и др.) и длинные (сложения или вычитания делителя от делимого);
• длительность машинного такта Тс выбирается из условия выполнения за один такт длинной микрооперации;
• длительность синхросигнала tcc выбирается из условия выполнения коротких микроопераций;
• длительность машинного такта связана с длительностью синхросигнала соотношением Тс =(2...3)tcc.
Все множество операторных вершин микропрограммы деления (см. рис. 9. 23) последовательно разбивается на группы Л), К2, ..., К7 с определенным количеством операторов с одинаковыми вероятностями обращения Ръ Р2, .... Р7. Группы 7<4 и К5 выполняются в цикле «-1=7 раз.
9.5. Реализация операции деления 321
Рис. 9.28. Принципиальная схема модуля МУБ
С учетом этого можно записать:
К = 6 (операторы'2, 3, 4, 5, 6, 7), Р,= 1;
К2 = 1 (оператор 1), Р2 = 0,9;
К = 14 (операторы 12, 14), Р3= 0,5;
КЛ = 14 (операторы 13, 14), Р4- 0,5;
К5 = 1 (оператор 16), Р5 = Г,
Кь = 2 (операторы 18, 19), Рь = 0,5;
К-, = 2 (операторы 21,22), Р2 = 0,5;
К^, = 1 (оператор 9), вероятность переполнения принимается малой Р8 = 0,1.
21-4-1749
322 Проектирование специализированных арифметико-логических устройств
Длительность tcc синхросигнала определяется двумя составляющими:
^СС “ ty Амо»
где ty < 5t,> — максимальное время формирования управляющих сигналов, tP~ 10 нс — средняя задержка распространения сигнала в логических элементах, /м0 < 30 нс — максимальное время выполнения короткой микрооперации в операционном блоке. С учетом этих данных запишем:
tcc - 5tP + 30 = 50 + 30 = 80 нс;
Тс = 2tCc = 2 • 80 = 160 нс.
Длительность выполнения микропрограммы деления Тс = 24Т( = 24 160 нс « = 3,86 мкс.
Контрольные вопросы
1. Напишите микропрограмму сложения целых чисел.
2. Поясните фрагмент схемы АЛУ для сложения целых чисел.
3. Напишите микропрограмму вычитания целых чисел.
4. Поясните фрагмент схемы АЛУ для вычитания целых чисел.
5. Напишите микропрограмму умножения целых чисел.
6. Поясните фрагмент схемы АЛУ для умножения целых чисел.
7. Напишите микропрограмму деления целых чисел.
8. Поясните фрагмент схемы АЛУ для деления целых чисел.
10.1. Общая характеристика процессоров и микропроцессоров 323
Глава 10
Микропроцессоры
10.1. Общая характеристика процессоров и микропроцессоров
10.1.1. Процессоры
Универсальные компьютеры делятся на три функционально связанные аппаратные части: процессор, память и периферийные устройства.
Процессор — это основная функциональная часть компьютера, которая ин
терпретирует и выполняет команды, то есть непосредственно реализует программно-управляемый процесс обработки данных. Процессор, выполняющий в вычислительной системе основные функции, называют центральным (ЦП). Специализированный процессор, предназначенный для управления внешними устройствами (накопителями, дисплеями, принтерами и т.д.) называют контроллером.
Процессор характеризуется архитектурой, к которой относят:
• список арифметико-логических операций (система команд);
• типы и форматы команд и данных;
• организацию адресного пространства памяти и периферийных устройств;
• способы адресации команд и данных;
• функции составных частей и структуру связей с другими устройствами машин, а также режимы работы.
Процессор состоит из устройства управления, арифметико-логического устройства и блока интерфейса (БИФ) для соединения с внешней средой — памятью, пе
риферийными устройствами (рис. 10.1).
Обработка данных осуществляется в АЛУ, которое содержит арифметико-логический блок АЛБ, блок РОН, блок контроля БК и местный блок управления при децентрализованном управлении.
Арифметико-логический блок содержит универсальный двоичный комбинационный сумматор, двоичнодесятичный сумматор или схему десятичной коррекции, регистры для временного хранения двух операндов и ре
зультата операций, а также регистр флажков. Для повышения производительности в АЛУ могут включать специализированные узлы сдвига и умножения, схемы ускоренного переноса и другие устройства.
Ряд процессоров имеет по два и более АЛУ. Разрядность АЛУ определяет раз
рядность всего процессора. 21*
324 Микропроцессоры
В РОН хранятся исходные данные, промежуточные и конечные результаты, адреса данных, константы, необходимые в процессе выполнения команды. Все операции в АЛУ реализуются как пространственно-временные последовательности микроопераций над двоичными словами, каждая из которых является совокупностью булевых операций над битами слов. В АЛУ реализуются следующие типовые микрооперации:
• передачи слов между регистрами и регистрами и памятью;
• сложение двух слов, декремент (минус 1) или инкремент (плюс 1) слова;
• арифметические, логические и циклические сдвиги вправо или влево;
• поразрядные логические операции ИЛИ, И, исключающее ИЛИ и сравнение операндов;
• преобразование кодов слов — инверсия, дополнение, расширение и др.
Устройство управления УУ руководит процессом обработки данных, обеспечивает основные режимы работы (начальных установок, ожидания, прерывания, прямого доступа к памяти, диагностики и контроля) и взаимодействие всех устройств компьютера. Для выполнения этих функций УУ имеет в своем составе регистр и дешифратор команд, программный счетчик для задания адреса следующей команды, блок управления и схемы синхронизации, диагностики и контроля.
В состав процессора могут входить специальные системные средства (служба времени, средства межпроцессорной связи, пульт управления и др.).
Устройство управления последовательно считывает код команды из памяти и размещает его в регистр команд (инструкций). Блок управления дешифрирует команду и формирует последовательности управляющих сигналов. Для выполнения одной микрооперации в АЛУ необходим один управляющий сигнал. В одном машинном такте реализуется совокупность микроопераций — микрокоманда. Множество микрокоманд образует микропрограмму команды. Каждая команда имеет свою микропрограмму, время выполнения которой называется командным циклом.
Различают аппаратные, микропрограммные и комбинированные блоки управления. Аппаратные блоки управления построены на основе схемной логики, а микропрограммные — программируемой логики (имеют память микропрограмм). Комбинированные блоки управления используют оба способа их реализации.
При централизованном управлении одно УУ руководит процессом обработки команд и данных во всей машине. При децентрализованном управлении УУ формирует основные управляющие сигналы, а обработкой данных управляет местный блок управления, расположенный в АЛУ.
Отметим, что все команды в компьютере реализуются на основе принципа микропрограммного управления, то есть выполнения микропрограмм. В то же время УУ с программируемой логикой также называют микропрограммными. Методологически эти понятия следует различать.
10.1.2. Микропроцессоры
Микропроцессор представляет собой процессор, составные части которого миниатюризированы и размещены в одной или нескольких микросхемах. История микропроцессоров началась в 1971 г., когда фирма Intel разработала первый в мире четырехразрядный процессор 4004, а через год — восьмиразрядный 8008. На осно
10.1. Общая характеристика процессоров и микропроцессоров 325
ве микропроцессоров создана новая элементная база — микропроцессорные средства, на которых строят современные компьютеры. В наше время термины “процессор" и “микропроцессор” воспринимают как синонимы.
Микросхема, выполняющая функции микропроцессора или его части, называется микропроцессорной. Совокупность микропроцессорных и других микросхем, совместимых по конструктивно-технологическому исполнению и предназначенных для совместного использования, называется микропроцессорным комплектом (МПК).
К характеристикам микропроцессорных ИМС относятся: размеры кристалла и количество транзисторов в нем, тип корпуса и количество выводов.
Наиболее важными статическими и динамическими электрическими параметрами микропроцессоров как микроэлектронных изделий являются:
• количество источников питания и их напряжение;
• ток и мощность потребления;
• количество серий синхроимпульсов, их частота и амплитуда; уровни логических сигналов;
• входная и выходная емкости, нагрузочная способность;
• время задержки распространения сигналов, число операций в секунду над операндами, хранимыми в регистрах-аккумуляторах.
В зависимости от условий эксплуатации к микропроцессорным ИМС могут предъявляться специальные требования относительно:
• температурного диапазона работы и режима хранения;
• устойчивости к радиационным и электромагнитным влияниям, вибрациям и ударам;
• массы и габаритов;
• интенсивности отказов, наработки на отказ, надежности функционирования.
Микропроцессор, предназначенный для использования функционально полного набора операций, является универсальным, иначе — специализированным. По конструкции различают следующие микропроцессоры:
• однокристальные — выполнены в виде единой микросхемы (рис. 10.2, а); ,
• многокристальные (модульные) — построены из микросхем, каждая из которых выполняет функции устройства компьютера (рис. 10.2, б);
• разрядно-наращиваемые (секционные); их разрядность может увеличиваться за счет нескольких микропроцессорных секций, объединенных общими шинами (рис. 10.2, в).
АЛУ
АЛУ
Секция АЛУ
УУ
УУ
УУ
ИФ
ИФ
Секция ИФ
Рис. 10.2. Конструкции микропроцессоров: а — однокристальные; б — многокристальные; в — секционные
326 Микропроцессоры
Все микропроцессоры имеют средства сопряжения с внешними устройствами — интерфейсы (ИФ).
Для производства микропроцессоров используют все виды схемотехники (технологии): ТТЛШ, ЭСЛ, И2Л, л-МОП, p-МОП, КМОП и др.
В зависимости от режима работы различают следующие процессоры:
• однопрограммные (выполняют одну программу) и многопрограммные (имеют средства для одновременного выполнения нескольких программ);
• мультипроцессоры (системы, в которых одновременно могут быть активны несколько процессоров);
• конвейерные (команды выполняются последовательно рядом устройств, причем различные устройства могут одновременно обрабатывать соответствующие части нескольких команд);
• матричные (имеют специальную архитектуру, рассчитанную на обработку числовых массивов);
• сопроцессоры (арифметические расширители) — предназначены для расширения списка команд ЦП; самостоятельно не используются;
• периферийные — выполняют функции ввода-вывода информации
• ассоциативные процессоры, в которых характер обработки данных определяется содержимым самих данных.
По виду обрабатываемой информации различают цифровые (обычные) и аналоговые микропроцессоры. В аналоговых микропроцессорах на входе используют АЦП для преобразования аналоговых величин в цифровой код, а на выходе — схемы ЦАП, преобразующих цифровые данные в аналоговые.
10.1.3. Микропроцессорные комплекты
Для построения современных компьютеров используют микропроцессорные средства — комплексы аппаратно и программно совместимых ИМС различной степени сложности (СИС, БИС, СБИС и ультра-БИС). Основой микропроцессорных средств являются микропроцессорные комплекты МПК и базовые кристаллы, БИС памяти (рис. 10.3).
Рис. 10.3. Состав микропроцессорных средств
10.1. Общая характеристика процессоров и микропроцессоров 327
В нашей стране разработан и выпускается микроэлектронной промышленностью широкий набор серий МПК. Основные параметры большинства МПК (серия, подгруппа и вид базового микропроцессора, технология, быстродействие F в MIPS для операций типа регистр-регистр, разрядность пв битах, потребляемая мощность Рсс в ватах и число микросхем в серии) представлены в табл. 10.1.
Таблица 10.1
Серия МПК Тип ИМС Технология F, MIPS п, бит Рcci Вт Число БИС, шт.
К58О ВМ80 п-МОП 0,5 8 1,5 21
К581 ВЕ1 И2Л 0,4 0,9 6
К582 ВМ1 И2Л 1,5 0,3
К583 ВС1 И2Л 0,1 8 0,6 И
К584 ВМ1А И2Л 0,5 4 0,25 4
К586 ВМ1 п-МОП 0,5 0,9
К587 ВМ2 КМОП 0,5 0,005 4
К588 ВС2А КМОП 0,5 16 0,05 21
К589 ВС02 ТТЛШ 1,0 2 1,0 8
К1800 ВС01 ЭСЛ 3,0 4 1,7 10
К1801 ВМ1 п-МОП 0,5 16 1,4 9
К1802 ВС1 ТТЛШ 0,8 8 1,4 15
К1804 ВС1 ТТЛШ 0,8 4 1,5 29
К18О8 ВМ1 И2Л 0,3 8 0,05 4
К1810 ВМ86 п-МОП 0,7 16 0,9 22
К1811 ВМ1 л-МОП 0,5 16 1,1 5
К1813 ВЕ1 п-МОП 1,2 28 1
К1815 ВФ1 И2Л 0,5 16 0,3 9
К1816 ВЕ51 л-МОП 1,0 8 0,7
К1820 ВЕ1 и-МОП 0,5 8 0,6 2
К1821 ВМ85 и-МОП 0,5 8 1,0 12
К1827 ВЕ1 и-МОП 0,5 16 11
К1838 ВМ1 ЭСЛ 5,0 16 1 11
В зависимости от вида и типа базовой программируемой БИС выделяют следующие МПК:
• с одним или несколькими однокристальными микропроцессорами: серии КР580, КР581, К1810, К1518, К1821, КР1828, КМ1831, К1838;
• с многокристальными (модульными) микропроцессорами: К581, К588;
• с секционными (разрядно-модульными) микропроцессорами: К583, К1800, К1802, К1804, К1822;
• с однокристальными микро-ЭВМ: К1813, К1816, К1820, К1827.
Однокристальные микропроцессоры имеют фиксированную структуру и систему команд; предназначены для построения микро- и мини-компьютеров широкого применения. Однокристальные микро-ЭВМ встраиваются в технические системы, в которых они выполняют функции контроля, управления и диагностики.
328 Микропроцессоры
Модульные микропроцессоры ориентируют на реализацию конкретного класса алгоритмов (обработка цифровых сигналов, графические преобразования и т.д.). Секционные микропроцессоры обеспечивают построение высокопроизводительных универсальных компьютеров методом наращивания необходимого числа секций.
В состав МПК входит широкий спектр специализированных микропроцессорных ИМС, в том числе:
• процессорные элементы (секции АЛУ); блоки регистров общего и специального назначения; многорежимные буферные регистры (порты, фиксаторы); схемы ускоренных переносов и расширители вычислительных функций;
• схемы синхронизации и генераторы тактовых импульсов; блоки управления обменом с памятью и формирования адресов микрокоманд;
• контроллеры: клавиатуры, видеотерминалов, накопителей на магнитных дисках и лентах, ввода-вывода данных, прямого доступа к памяти и прерываний;
• контроллеры шин и протоколов, шинные формирователи;
• программируемые таймеры и схемы арбитража.
По характеру работы во времени микропроцессоры подразделяются на синхронные (время выполнения команд в них постоянно) и асинхронные, где каждая команда реализуется за время ее фактического выполнения. Микропроцессоры имеют различные устройства управления со схемной или программной логикой и комбинированные.
Появление микропроцессоров — это эволюционный процесс в технологии производства микросхем, а для вычислительной техники — переход в новое качественное состояние.
К технико-экономическим преимуществам микропроцессоров относят:
• высокое быстродействие и надежность, малую мощность потребления, малые размеры и массу, низкую стоимость;
• простоту технического обслуживания, составление и расширение микропроцессорных систем;
• возможность построения мощных микропроцессорных комплексов с параллельной обработкой информации;
• реализацию распределенных систем контроля, диагностики и управления.
Достоинства микропроцессоров обеспечили массовое применение их в науке, технике и нетрадиционных областях народного хозяйства.
Развитие микропроцессоров во времени иллюстрирует табл. 10.2 для изделий фирмы Intel.
Таблица 10.2
Название МП Год выпуска Технология W, бит Адресное пространство F, MIPS Мт
4004 1971 р-МОП 4 640 байт 0,1 , 2800
4040 1972 р-МОП 4 0,15 3500
8008 1973 р-МОП 8 16 Кбайт 1,0 4500
8080 1974 п-МОП 8 64 Кбайт 5,0 5000
8085 1975 п-МОП 8 64 Кбайт 5-10 6500
8086 1978 и-МОП 16 1 Мбайт 5-10 29000
10.1. Общая характеристика процессоров и микропроцессоров 329
Таблица 10.2. Продолжение
Название МП Год выпуска Технология W, бит Адресное пространство F, MIPS •'Утр
80186 1980 . КМОП 16
80286 1982 КМОП 16 16 Мбайт 134000
80386 1985 КМОП 32 4 Гбайт 275000
80486 1991 КМОП 32 4 Гбайт 1,2 млн
Pentium 1993 КМОП 32 4 Гбайт 75-200 3,1 млн
Pentium Pro 1995 КМОП 32 4 Гбайт 180-200 5,5 млн
Pentium MMX 1997 КМОП 32 4 Гбайт 166-200 4,5 млн
Pentium II 1997 КМОП 32 4 Гбайт 233-450 —
Pentium III 1998 БиКМОП 32 4 Гбайт 450-933 —
Itanium (Merced) 2000 БиКМОП 64
Примечание: МП — микропроцессор, УТР — число транзисторов в МП.
Конструктивно-технологическое развитие микропроцессоров происходит в следующих направлениях.
1. Используют новые технологии, например, БиКМОП, в которых комбинируют биполярные транзисторы (для увеличения скорости) и КМОП-структуры (для уменьшения потребляемой мощности и повышения плотности компоновки). Если в первых микропроцессорах расстояние между соседними линиями составляло 10 мкм, то в последних изделиях она равна 0,18 мкм.
2. Увеличивается уровень интеграции: от 2800 транзисторов в чипах первых микропроцессоров до 10-12 млн и более в последних изделиях типа Itanium. По закону Мура характеристики микросхем должны улучшаться в два раза каждые 18 месяцев при сохранении стоимости. По прогнозу экспертов в 2012 г. на чипе будет размещаться 1,4 млрд транзисторов, которые должны работать на частоте 2700 МГц.
3. Увеличивается разрядность обрабатываемых данных: от четырех — в первых микропроцессорах до 64 — в Itanium (возросла в 16 раз).
4. Ускоряется смена поколений микропроцессоров. Если до 1994 г. новые поколения появлялись каждые три года, то теперь этот цикл уменьшился до двух лет. Стоимость современного завода, выпускающего чипы с размерами транзисторов 0,25 мкм, составляет $ 2 млрд, а через 5-10 лет такой комплекс будет стоить $ 4 млрд.
10.1.4. Архитектура микропроцессоров
Архитектуру микропроцессора характеризуют: список команд и их форматы; способы адресации; разрядность и емкость адресуемой памяти; структура регистров и их функции и т.д.
Исторически первыми сложились следующие основные архитектуры микропроцессоров: с аккумулятором, с РОН, со стековой организацией и комбинированные (рис. 10.4).
330 Микропроцессоры
Рис. 10.4. Структура микропроцессоров: а — с аккумулятором и стеком; б — с РОН
Структура всех микропроцессоров содержит следующие одинаковые устройства, узлы и блоки, объединенные общей внутренней шиной данных: АЛБ; УУ; IR — регистр команд (инструкций); FL — регистр признаков (флажков); EAR — регистр исполнительного адреса; БИФ — блок интерфейса с выходными шинами адреса, данных и управления.
В архитектуре микропроцессора с аккумуляторами (рис. 10.4, а) дополнительно используют индексный регистр X и указатель стека SP\ регистр R выполняет функции аккумулятора А. При выполнении арифметико-логических операций первый операнд предварительно размещается в аккумуляторе, а второй — из ОП непосредственно поступает на вход АЛБ. Результат операции размещается в аккумуляторе, а в регистр FL автоматически записываются признаки операции.
В архитектуре микропроцессора с РОН (рис. 10.4, б) обычно используют от восьми до 16 регистров, каждый из которых может выполнять функции аккумулятора. Увеличение числа РОН значительно уменьшает количество обращений к ОП, что повышает производительность компьютера. Однако увеличение числа регистров приводит к потерям машинного времени в случаях прерывания программ: при этом необходимо сохранить содержимое РОН в памяти (обычно в стеке), а затем вЬсстановить его после обработки прерывания. Поэтому при выборе количества РОН учитывают этот фактор.
В микропроцессоре со стековой архитектурой (рис. 10.4, а) отсутствуют аккумулятор и РОН, a R выполняет функции регистра временного хранения данных ОП на время выполнения операции. Чтение данных и их запись в стековую память осуществляют с помощью указателя стека SP. Все операции с данными выполняют соответственно польской записи: операнды размещают в стеке в последовательности выполнения над ними действий. В стек последовательно загружают числа a, b и с (рис. 10.5).
10.1. Общая характеристика процессоров и микропроцессоров 331
Рис. 10.5. Иллюстрация работы стека
По команде умножения MUL получаем произведение a-b, которое записывается по адресу Ь. По команде сложения ADD имеем a-b + c, что записывается по адресу с. После команды инвертирования NEG в ячейке по адресу с записывается обратный код результата a b + с .
В микропроцессорах с комбинированной архитектурой объединяют в значительной мере свойства архитектур с аккумулятором, РОН и стеком. К ним относят однокристальный микропроцессор 8080 (1974 г., фирма Intel, аналог в нашей стране— КР580ВМ80А), более совершенную его модель 8085А (аналог — КР1821ВМ85А), а также модель Z80 фирмы Zilog (рис. 10.6).
Рис. 10.6. Структура микропроцессора з комбинированной архитектурой (близкой к модели 8085А)
Комбинированная структура содержит:
• сложный комбинированный сумматор SM (в нем выполняется большинство арифметических и логических операций), регистры А и ТР; вместе они образуют АЛБ;
• блок РОН (регистры В, С, D, Е, Н, L), программный счетчик PC, указатель стека SP, регистр исполнительного адреса EAR-,
• блок ИФ с ША, ШД и ШУ;
• устройство управления УУ с регистром команд IR.
Совокупность вычислительных средств, в которые входят один или несколько микропроцессоров и полупроводниковая память, а также средства интерфейса, называется микропроцессорной системой (МПС).
332 Микропроцессоры
10.1.5. Программно управляемый обмен информацией
Между ядром машины и периферией реализуются следующие виды программно управляемого обмена информацией:
• синхронный и асинхронный обмены в последовательных и параллельных двоичных кодах, выполняемые по схеме, изображенной на рис. 10.7, а;
• с прерыванием программы по запросу ПУ.
он
ЦП
ПУ
Рис. 10.7. Синхронный обмен: а — схема, б — алгоритм; в, г — последовательный обмен без стробирования; д, е — параллельный обмен со стробированием
a
При синхронной передаче источник информации ИИ всегда готов к обмену в соответствии с алгоритмом (рис. 10.7, б). Источник информации выставляет и удерживает значение данных на линии последовательного обмена ЛОб на протяжении времени т, которое состоит из длительности задержки распространения сигнала на линии, его распознавания и фиксации в регистре приемника ПИ (рис. 10.7, в, г).
При синхронном параллельном обмене часто используют сигнал квитирования, который передается и принимается по отдельной линии Лк и определяет интервал времени надежного приема данных приемником (рис. 10.7, д, е).
Асинхронный обмен выполняется при готовности (Ready) внешнего устройства к обмену данными в соответствии с алгоритмом (рис. 10.8, а). При асинхронной передаче параллельного кода по ШД используют метод квитирования, в котором объединяются совместное действие сигнала квитирования Лк от источника ИИ и сигнала подтверждения приема Лп от приемника ПИ (рис. 10.8, б, в).
Основным недостатком синхронного и асинхронного обмена является значительная загрузка процессора операциями ввода-вывода, что приводит к существенному уменьшению производительности компьютера. Поэтому синхронный и асинхронный обмены используют при передаче одиночных байтов или слов. Обмен в режиме прерывания осуществляют аппаратно по инициативе внешнего устройства или программно — командой прерывания INT. Процессор, получив аппаратный запрос на прерывание, заканчивает текущую команду, пересылает в ОП содержимое своих регистров и переходит на подпрограмму обслуживания прерывания. После ее завершения процессор восстанавливает содержимое своих регистров и продолжает выполнение прерванной программы (рис. 10.9, а).
10.1. Общая характеристика процессоров и микропроцессоров 333
в
Рис. 10.8. Асинхронный обмен: а — алгоритм; б — схема; в — временные диаграммы работы с квитированием
Аппаратно режим прерывания обеспечивается контроллером прерываний (КПР), к которому подключаются ПУ. Выход INT контроллера подается на соответствующий вход ЦП, а на ШД пересылается начальный адрес подпрограммы обслуживания (рис. 10.9, б). При программном прерывании адрес подпрограммы передается в самой команде прерывания INT.
Рис. 10.9. Обмен по прерыванию: а — алгоритм; б — схема подключения контроллера КПР
Прямой доступ к памяти (ПДП) используют для быстрого обмена массивами информации между основной памятью и периферией. При этом процессор (микропроцессор) освобождается от непосредственного управления операциями ввода-вывода.
ПДП реализуется в соответствии с алгоритмом (рис. 10.10, а). В мини- и микрокомпьютерах прямым доступом управляет контроллер прямого доступа к памяти
334 Микропроцессоры
(КПДП). Перед началом обмена процессор пересылает в КПДП следующую информацию (программирование контроллера):
• начальный адрес области памяти, которая принимает участие в обмене;
• направление операции обмена — ввода или вывода;
• количество байтов, подлежащих передаче.
Рис. 10.10. Режим ПДП: а — алгоритм; б, в — схемы подключения контроллеров КПДП
Особенность режима ПДП — обмен данными может происходить между машинными циклами в команде (“Захват цикла”), а также после завершения команды.
Контроллер ПДП управляет обменом данными между ОП и ПУ без участия процессора (рис. 10.10, б). При необходимости в компьютере используют программно-управляемый обмен отдельными байтами (он не требует программирования КПДП) и обмен массивами в режиме ПДП (рис. 10.10, в).
В универсальных компьютерах обмен информацией между ОП и ПУ обеспечивают специальные устройства — каналы ввода-вывода (КВВ) или просто каналы (рис. 10.11).
В каналах используют два режима обмена информацией: монопольный и распределения во времени. Монопольный режим реализуют селекторным каналом, а
10.2. Однокристальные восьмиразрядные микропроцессоры 335
распределение во времени — мультиплексным каналом. Средства канала, предназначенные для обслуживания одного ПУ, называются подканалом.
Селекторные каналы обслуживают быстродействующие устройства, в первую очередь ВЗУ (накопители на дисках и магнитных лентах). Селекторный канал имеет один подканал. После установки связи он монопольно обслуживает только одно ПУ: остальные устройства ожидают завершения данной программы обмена. В малых компьютерах используют один селекторный канал, в больших — до шести.
Мультиплексный канал (один в машине) параллельно обслуживает сотни медленнодействующих ПУ в режиме распределения времени (клавиатура, принтеры, перфораторы и т.д.).
10.2. Однокристальные восьмиразрядные микропроцессоры
Однокристальные восьмиразрядные микропроцессоры имеют фиксированную систему команд. Они рассчитаны на разнообразное применение в составе МПС.
Известны следующие основные типы восьмиразрядных однокристальных микропроцессоров: КР580ВМ80А (i8080), КР1821ВМ85 (i8085), 6800 (фирмы Motorola), Z-80 (фирмы Zilog) и др. Рассмотрим детально микропроцессор КР1821ВМ85А.
10.2.1. Общая характеристика микропроцессора К1821ВМ85А
Микропроцессор К1(821ВМ85А (далее сокращенно ВМ85) — это однокристальный восьмиразрядный процессор с фиксированной системой команд. Он имеет классическую архитектуру с одним аккумулятором и отдельными шинами адреса и данных. Основная область применения микропроцессора ВМ85 — контроллеры, работающие по фиксированной программе. Микросхема ВМ85 выполнена по п-МОП технологии и выпускается в 48-контактном керамическом корпусе с двухсторонним вертикальным размещением выводов (тип DIP).
Микропроцессор ВМ85 имеет следующие характеристики:
• напряжение питания — плюс 5 В; потребляемая мощность — 0,2 Вт;
• тактовая частота — 5 МГц. Длительность выполнения операции сложения типа “регистр-регистр” равна 0,8 мкс;
• нагрузочная способность — один вход ТТЛ-схемы;
• может обслуживать 256 устройств ввода и 256 устройств вывода;
• выходы напряжений: U0L < 0,4 В; Uo/;> В;
• число команд — 80; адресное пространство памяти — 64 Кбайт;
• число транзисторов в кристалле — около 5000.
Процессор ВМ85 (аналог i8085) программно и конструктивно совместим с популярным микропроцессором К580ВМ80А (аналог i8080).
10.2.2. Структура микропроцессора ВМ85
Микропроцессор ВМ85 содержит АЛУ, УУ и схемы интерфейса (рис. 10.12).
336 Микропроцессоры
RST5S
IN7\
-VI,
RDY, REN SR0
TRAP,
RST7.5
RST6.5
SID, SQD
HOLD HLDA SYNC IO/М SO SI EA WR RD
Puc. 10.12. Структура микропроцессора BM85
Арифметико-логическое устройство содержит:
• арифметико-логический блок, в который входят: параллельный комбинационный сумматор SM; регистр-аккумулятор А\ регистр временного хранения данных ТР (от femp); регистр флажков (признаков) FL (от flag); схема десятичной коррекции ДК;
• блок регистров общего назначения В, С, D,E,Hv\ L.
Все регистры и сумматоры в АЛУ — восьмиразрядные.
В УУ входят:
• восьмиразрядный регистр команд РГК и дешифратор команд ДШК;
• шестнадцатиразрядный программный счетчик PC (от program counter) и указатель стека SP (от stack pointer) и регистр адреса со схемой инкремента-декремента РАИД;
• буфер старшего байта адреса (БА) и совместимый буфер младшего байта адреса и байта данных (БАД), который работает в мультиплексном режиме,
• блок выработки управляющих сигналов и синхронизации (БУС).
Схема интерфейса содержит блоки последовательного обмена данными (ПОД) и обработки прерываний (БПР). Все функциональные компоненты микропроцессора объединены внутренней восьмиразрядной шиной.
В АЛБ выполняются арифметико-логические операции над двоичными и двоично-десятичными операндами. Аккумулятор А построен на двухступенчатых триггерах. При выполнении большинства арифметико-логических операций используют сложный комбинационный сумматор SM. При этом в аккумуляторе хранится первый операнд, а в регистре ТР — второй; результат операции записывается в аккумулятор.
Регистр ТР принимает участие в операциях межрегистровых передач, а аккумулятор используется также при параллельном и последовательном вводе-выводе
10.2. Однокристальные восьмиразрядные микропроцессоры 337
данных. В регистр флажков FL после выполнения большинства операций автоматически записываются следующие признаки:
• CY — флажок переноса, устанавливается при наличии переноса из старшего бита результата (в операциях вычитания он становится флажком заема);
• S — флажок знака, совпадает со значением старшего бита результата;
• Z— флажок нуля, устанавливается при нулевом результате;
• Р — флажок паритета, устанавливается при наличии в результате парного числа единиц;
• АС— вспомогательный флаг, устанавливается при наличии переноса между тетрадами результата.
В сумматоре SM выполняются все арифметико-логические операции и сдвиги. Схема ДК предназначена для коррекции результатов сложения двоично-десятичных чисел в двоичном сумматоре SM.
Регистры В, С, D, Е, Н и L предназначены для хранения данных (как операндов, так и результатов) в процессе выполнения программы. В ряде операций они объединяются в регистровые пары ВС, DE и HL, хранящие двухбайтовые данные или указатели адресов операндов в памяти.
Программный счетчик PC предназначен для хранения адреса следующей выполняемой команды. Содержимое PC автоматически увеличивается на константу, равную числу байтов в команде.
Указатель стека SP хранит адрес ячейки стека, по которому было последнее обращение При записи в память содержимое SP уменьшается, а при чтении — увеличивается.
Регистр РАИД позволяет увеличивать или уменьшать на единицу содержимое программного счетчика PC, указатель стека SP и регистровых пар.
Регистр команд РГК используется для приема и хранения на время выполнения операции первого байта команды, который содержит код операции. Содержимое РГК расшифровывается дешифратором команд ДШК и передается в блок БУС. Последний вырабатывает сигналы синхронизации и управления вычислительным процессом в компьютере.
Блок управления прерываниями (БПР) переключает микропроцессор с выполнения одной программы на другую с помощью внешних сигналов прерывания. Введены следующие входы и соответствующие им уровни прерываний:
• TRAP— имеет наивысший приоритет и не может отключаться или маскироваться; предназначен на случай появления ошибки, которую нельзя устранить (например, при повреждении источника питания или появления неисправности в шинах);
• RST7.5, RST 6.5, RST 5.5, INT — сигналы прерывания на этих входах могут маскироваться (программно запрещается их восприятие). Вход /NT предназначен для обслуживания векторных прерываний по командам RSTn и CALL п с использованием контроллера КР580ВН59.
В начале каждого машинного цикла буфер БА выставляет и удерживает на линиях шины Я15 - А8 старший байт адреса памяти, а буфер БАД передает на короткое время младший байт адреса на линии АД1 - ДДО, который по сигналу AEN должен записаться во внешний регистр-фиксатор. После этого двунаправленный буфер
22 — 4-1749
338 Микропроцессоры
БАД переключается на запись или считывание данных. Периферийные устройства адресуются восьмиразрядным кодом, который одновременно поступает на две части шины адреса. При необходимости буферы БА и БАД переключаются в Z-состояние.
Блок ПОД по команде RIM выполняет последовательный ввод данных, а по команде SIM — последовательный вывод.
Условное графическое обозначение микропроцессора ВМ85 показано на рис. 10.13. Обозначения выводов микропроцессора совпадают с именами сигналов на них.
CPU
ВМ85
Входы_________
синхронизации >
XI
Х2
Шина адреса
Готовность
RDY
Прерывание тддр
Маскированные прерывания
___$ RST7.5
—) RST6.5
—) RST5.5
---Э 1NT
-..3а'^-с..ПДГ1 ) HOLD
Последовательный
-------2223------) SID
СбРос_____J) RES
А15-А8
АД7-А ДО 1Шинаадреса/дан^1х
Синхронизация ч
SO Состояния к
С1 микропроцессора ( 1>
Ю/М Порты/память
AEN Строб адреса
X Запись________
~RD А Чте^ --------»
Подтверждение
1NTAИв------------->
Подтверждение
HLDA -----23П------->
S0D Последовательный^выход
SRO Выход сброса ч
Рис. 10.13. Условное графическое обозначение микропроцессора ВМ85 и функций выводов
В сравнении с программно совместимым микропроцессором КР580ВМ80А микросхема ВМ86 имеет следующие отличия: двухфазная синхронизация заменена однофазной; увеличена в два раза частота синхронизации; вместо трех источников питания используется один; добавлены две команды последовательного ввода-вывода.
10.2.3. Функционирование микропроцессора ВМ85 во времени
Функционирование микропроцессора ВМ85 во времени определяется внутренним генератором тактовых (синхронизирующих) импульсов (ГТИ). Его возбуждение может задаваться внешним кварцевым резонатором, RC- или LC-цепями или внешним генератором, которые подключаются ко входам XI, Х2 микропроцессора (рис. 10.14).
10.2. Однокристальные восьмиразрядные микропроцессоры 339
Г-------1
Рис. 10.14. Управление синхронизацией: а — кварцевым резонатором; б — RC-цепью; в — LC-цепью; г — внешним ГТИ
Внутренний ГТИ работает и выдает выходной сигнал SYNC, частотой вдвое меньшей, чем на входах XI и Х2 (рис. 10.15).
Рис. 10.15. Диаграммы сигналов Х1 и SYNC
Период прохождения сигналов SYNC определяет машинный такт Тс, с которым связано устойчивое состояние микропроцессора. Команды выполняются по машинным циклам. В зависимости от типа команды для ее выполнения требуется один, два, три, четыре или пять машинных циклов (МЦ). В каждом МЦ (за исключением цикла “Шина свободна”) происходит обращение к памяти или внешнему устройству
Микропроцессор имеет семь типов возможных МЦ, которые определяются комбинацией трех сигналов состояния SO, S1, Ю/ М и трех управляющих сигналов- чтения RD, записи WR и подтверждения прерывания INTA (табл. 10.3).
Таблица 10.3
Тип машинного цикла Сигналы состояния и управления
IO/M S1 so RD WR INTA
Выборка кода операции 0 1 1 0 1 1
Чтение памяти 0 1 0 0 1 1
Запись в память 0 0 1 1 0 1
Ввод из порта 1 1 0 0 1 1
Вывод в порт 1 0 1 1 0 1
Подтверждение прерывания 1 1 1 1 1 0
Шина свободна:
команда BAD 0 1 0 1 1 1
подтверждения RST, TRAP 1 1 1 1 1 1
останов Z 0 0 z z 1
Работа процессора начинается с подачи сигнала сброса RES = 0, после чего обнуляются программный счетчик PC, регистры РгК и FL, запрещается прием запросов прерываний. На выходе SRO устанавливается сигнал лог. 1, который используют для обнуления внешних устройств.
22*
340 Микропроцессоры
При работе микропроцессора ВМ85 возможны три режима: ожидания, захвата цикла и останова. Режим ожидания предназначен для согласования обмена информацией между быстродействующим процессором и медленными внешними устройствами. Если они не готовы к обмену, то на входе RDY устанавливается сигнал лог. 0 длительностью Tw = пТс, где п — произвольное число тактов. Обмен продолжается при условии, что RDY = 1.
Режим захвата цикла обеспечивает прямой доступ внешних устройств к ОП. Для этого ПУ выставляет на входе HOLD сигнал лог. 1. После завершения текущего цикла микропроцессор переключает свои шины в Z-состояние и выставляет на входе HLDA сигнал лог. 1 разрешения на захват цикла. При условии, что HOLD = О, микропроцессор продолжает свой работу.
. В режим останова процессор переходит после выполнения команды HLT. В этом режиме обслуживаются также запросы прерывания и захвата цикла. Выход из режима останова осуществляется после сброса (начальной установки).
Блок управления и синхронизации (БУС) обеспечивает выполнение в тактах типовых машинных действий, представленных в табл. 10.4.
Таблица 10.4
Номер такта Типовые действия в такте
7Т Выдача адреса на ША
Т2 Анализ сигналов RDY, HOLD
Tw Переход в режимы ожидания при RDY= 0
73 Обмен данными. Выполнение операций
74, 7’5 Выполнение внутренних действий для ряда операций
Типовые машинные циклы чтения и записи показаны на рис. 10.16.
73 J.71
SYNC
А8
Адрес
AD'" f дАдресД Данные
ЛДУ'Ч---
WR'*
t
1
Рис. 10.16. Диаграммы машинных циклов: а — чтение; б — запись
При тактовой частоте Fc = 5 МГц длительность такта Тс = 0,2 мкс.
10.2. Однокристальные восьмиразрядные микропроцессоры 341
10.2.4. Форматы команд и данных. Способы адресации
Формат команд микропроцессора зависит от типа операции и может быть одно-, двух- или трехбайтовым (рис. 10.17). Первый байт содержит КОП, остальные — данные или адрес операнда. Двух- и трехбайтовые команды хранятся в последовательных ячейках ОП. Для чтения команды из памяти указывают адрес ее первого байта.
7 Н 6 4JL..+2-..о
ADR । । КОД ОПЕРАЦИИ , ’ a
ADR
ADR+\
7 4- 6 4—5 3 ,2,1,0
, , КОД ОПЕРАЦИИ ,
Восьмибитовые данные или адрес oh
7-+ 6-Н-5..Л-4-3-...............I-,
ADR , , КОД ОПЕРАЦИИ , ,
ADR+1 _щестнадцатибитовь1е данные или адрес ОП—
Рис. 10.17. Формат команд: а — однобайтовый; б — двухбайтовый; в — трвхбайтовый
Символически содержимое второго байта команды записывают как <В2>, третьего — <ВЗ>, а в формате конкатенации — как <ВЗ><В2>.
В микропроцессоре данные представляются в формате восьмибитового двоичного слова (числа). Имеются команды, оперирующие 16-битовими данными, которые запоминаются в двух последовательных ячейках памяти. В арифметических операциях микропроцессор интерпретирует байт данных как число со знаком в дополнительном коде. Старший бит D7 такого числа является знаковым (0 — для положительного числа, 1 — для отрицательного). Остальные семь битов образуют значение числа.
Числа в формате байта в дополнительном коде изменяются в диапазоне: для положительных чисел — от 0 до плюс 127; для отрицательных чисел — от минус 1 до минус 128. Отрицательные числа хранятся в ОП в дополнительном коде. Если знаковая интерпретация чисел не обусловлена, то число считается положительным в диапазоне 0-255.
В микропроцессоре ВМ85 используют следующие способы адресации операндов:
• неявный, который не требует операндов (например, HLT — останов, EI — разрешение прерывания);
• прямой — адрес операнда определяется значениями второго и третьего байтов команды;
• непосредственный — операнд задается непосредственно в команде;
• регистровый — в качестве операнда используют содержимое регистра, указанного в первом байте команды;
• непрямой — адрес операнда определяется содержимым регистровой пары ВС, DE и HL.
342 Микропроцессоры
Адресация с указателем стека SP называется непрямой с автоиндексацией.
При выполнении некоторых команд применяются комбинированные адресации, например, регистровая для аккумулятора и непрямая для ячейки памяти по адресу М = (ВД.
10.2.5. Язык ассемблера
Систему команд микропроцессора описывают на языке ассемблера.
Язык ассемблера — это машинно-ориентированное средство программирования. Программа на языке ассемблера называется исходной. Ассемблер транслирует исходную программу в символах в двоичные машинные коды. Такая программа называется объектной, ее можно загружать в память для выполнения.
Программа готовится в виде последовательности предложений, называемых операторами языка ассемблера. Каждый оператор записывается в одной отдельной строке и после трансляции порождает одну машинную команду. Строка оператора имеет четыре поля, в которых записывают метку, мнемокод (код операции), операнд^) и комментарии. На практике поля оператора выравниваются программистом.
Все операторы записываются с помощью символов кода ASCII.
Метки отделяются от поля мнемоники двоеточием:
МЕТКА: MOV А, В; Команда пересылки
Метки начинаются с буквы и отличаются первыми пятью символами. Нельзя записывать одинаковую метку в нескольких операторах, однако в одном операторе можно записать зразу несколько разных меток. Метками помечают только те операторы, на которые есть ссылка из других операторов программы. При трансляции каждой метке присваивается 16-разрядный адрес первого байта помеченной команды:
JMP МЕТКА; Команда перехода
MOV В, с-
МЕТКА: INR Л; Помеченный оператор
В поле операции записывают мнемонику команды. Мнемоника отделяется от поля операндов как минимум одним пробелом.
В поле операндов размещают один или два операнда. В командах без операндов это поле свободное. В качестве операндов используют имена регистров и регистровых пар, метки или непосредственные данные. Двоичные данные заканчиваются символом В, восьмеричные — Q, десятичные — D (может опускаться), шестнадцатеричные — Н; если в шестнадцатеричном числе первый знак — буква, то перед ней пишут цифру 0. Пример загрузки данных:
МЕТКА: MVIA, ОЕН; шестнадцатеричных
MVIВ, 15; десятичных
MVI С, 15 g; восьмеричных
MVI L, 11115; двоичных
В операнд можно записывать один или два символа кода ASCII, которые берутся в кавычки. После трансляции записи символов подставляются их двоичные коды.
10.2. Однокристальные восьмиразрядные микропроцессоры 343
Значения операндов можно задавать выражениями, которые вычисляются во время трансляции:
МЕТКА: MVI В, (30+40)/2
MOV 7/2+4, 0477
В поле комментариев, которое отделяют от предыдущего поля точкой с запятой, размещают описание назначения оператора. В языке ассемблера используют директивы, которые предназначены для передачи информации, используемой при трансляции.
К основным директивам относятся:
• управления трансляцией ORG, END',
• определения данных и резервирования в памяти области данных DB, DW, DS.
Директива ORG (начало) используется для установки начального адреса программы:
МЕТКА: ORG 080077
При трансляции ассемблер присваивает своему счетчику адреса значение 080077; по этому адресу в программе буде расположен первый байт команды или данных. Если в начале программы директива ORG отсутствует, то счетчику адреса присваивается нулевое значение. Если у директивы ORG имеется метка, то ей присваивается адрес ячейки памяти, следующей за последним байтом объектного кода предыдущего оператора.
Директива END (конец) записывается в последней строке исходной программы и сообщает ассемблеру о ее завершении:
МЕТКА: END z
Если в директиве END записана метка, то ей присваивается адрес байта, следующего за последним байтом объектного кода предыдущего оператора.
Директиву DB (определение байтов) используют для записи в память массива однобайтовых данных:
МЕТКА: DB СПИСОК
Операнд СПИСОК может быть последовательностью байтов данных, отделенных друг от друга запятыми, или символов, взятых в кавычки. Если в директиве DB используется метка, то ей присваивается адрес первого байта массива данных. Использование меток в директиве DB позволяет организовать символическую адресацию данных:
МЕТКА1: DB 15, 1, 24, 50; Запомнить четыре байта данных
МЕТКА2: DB “Строка”; Запомнить пять символов
В первой директиве число 15 запоминается по адресу МЕТКА1, число 1 — по адресу МЕТКА 1+1 и т. д.
Директиву DW (определение слова) используют для записи в память массива двухбайтовых данных:
МЕТКА: DWСПИСОК
Операнд СПИСОК задает последовательность 16-разрядных данных. При выполнении директивы DW младший байт первого данного запоминается по текущему
344 Микропроцессоры
адресу (адрес метки), а старший байт — по адресу на единицу больше. Затем эти действия выполняются для следующих данных:
DATA: DW 11007/, 02227/
В этом примере число 110027 запоминается по адресу DATA, DATA+1, а число 02227/ — по адресу DAГЛ+2, DATA+2>. Начальный адрес может задавать директива ORG.
Директиву DS (определение памяти) используют для резервирования области памяти для данных:
МЕТКА: DS ЧИСЛО
Значение операнда ЧИСЛО определяет количество ячеек (байтов) памяти, резервируемых для запоминания данных. Содержимое этой области не определяется. Если в директиве DS используют метку, то ей присваивают адрес первого байта резервируемой области памяти:
TABLE: DS 64; Резервируют 64 байта данных
10.2.6. Система команд микропроцессора ВМ85
Общая характеристика
Система команд ВМ85 содержит 80 команд, разбитых на пять функциональных групп:
• пересылки;
• арифметические операции;
• логические операции;
• передачи управления;
• управления стеком, вводом-выводом и состоянием микропроцессора.
Команды описываются символическими названиями. Каждая команда записывается в одной строке, которая в общем случае имеет три поля: мнемоники, операндов и комментариев. В поле мнемоники записывают символическое название команды, заменяющее машинный двоичный код операции. Большинство мнемоник— это аббревиатуры английских слов, характеризующие основные функции команды, например:
• MOV (MOVe) — передать, переслать;
• ADD (ADD) — прибавить;
• SUB (SUBtract) — отнять;
• LDA (LoaD Accumulator) — загрузить аккумулятор;
• STA (Story Accumulator) — запомнить аккумулятор;
• ACI (Add with Carry Immediate) — сложение с переносом, непосредственное;
• JNZ (Jump if Non Zero) — перейти, если не нуль.
Обычно длина мнемоники не превышает четырех позиций, а соседнее поле справа отделяется минимум одним пробелом. В поле операнда записывают данные — один или два операнда. Это могут быть имена регистров, регистровых пар, непосредственные данные или адреса.'В ряде команд операнды отсутствуют, на
10.2. Однокристальные восьмиразрядные микропроцессоры 345
пример, HLT— останов машины. Поле комментариев отделяется точкой с запятой, в нем указывают пояснительный текст.
Далее система команд ВМ85 описывается по функциональным группам. Командам в группах даны названия команд, их запись в формате языка'ассемблера и машинного кода, а также комментарии. Для описания команд используется символика:
• R, Rl, R2 — один из регистров Л, В, С, D,E,H и L;
• М — ячейка памяти, адрес которой задает содержимое регистровой Ж-пары, то есть М = (Н, Z);
• RP — одна из регистровых пар: ВС, DE, HL или SP\
• (R) или (RP) — содержимое регистра или регистровой пары;
• [<53><52>], [<ЯР>] — содержимое ячейки памяти, адресуемой двумя байтами памяти или содержимым регистровой пары;
• <->,<--операторы обмена и пересылки соответственно;
• D8, D16 — непосредственные восьми- или 16-битовые данные;
• ADR — название 16-битового адреса, указанного во втором и третьем байтах команды;
• SSS i DDD — коды регистра-источника и регистра-приемника.
Команды пересылок
Команды пересылок микропроцессора ВМ85 представлены в табл. 10.5, в которой число тактов выполнения операции обозначено ^ып.
Таблица 10.5
Команда Комментарий Машинный код V 1 ’вып
Пе эесылка
MOVR1, R2 MOVR,M MOV М, R (Л1)НЯ2) (А0«-(Я) 0 1 DDDSSS 4 7 7
0 1 DDD1 1 0
0 111 0SSS
Непосредственная загрузка
MVIR, D8 MVIM, D8 LXIRP, D\6 (/?)<—Z>8 (jW)<-Z)8 (PP)<-D16 0 1 DDD1 1 0 7 10 10
<В2>
00110110
<D8>
00PP0001
<В2>
<ВЗ>
Загрузка аккумулятора
LDA ADR LDAXRP (A)<-(ADR) (Л)<-[(ЛР)] 00111010 13 7
<В2>
<ВЗ>
00ЯР1010
346 Микропроцессоры
Таблица 10.5. Продолжение
Команда Комментарий Машинный код /V /твып
Запоминание аккумулятора
STA ADR (ADR)<r-(A) 00110010 13
<В2>
<ВЗ>
STAXRP [(ЛР)]<-(Л) 00ЯР0010 7
Прямая загрузка /77-пары
LHLDADR (7>[(Л7)Я)] 00101010 16
(Л)<-[(ЛДЛ+1)] <В2>
<вз>
Запоминание /77-пары
SHLD ADR [<ВЗхВ2>]<—(7) 00100010 16
[<ВЗхВ2>+1 ]<—(//) <В2>
<вз>
Обмен содержимым HL и DE пар
XCHG aS t т a s 11101011 4
Команды пересылок выполняют следующие действия:
• обмен данными между регистрами MOVR1, R2, регистрами и памятью MOV М, R, или MOVR, М;
• непосредственную загрузку регистров MVIR, 7)8, ячейки памяти MVIМ, 7)8, регистровой пары LXIRP, 7)16;
• прямую загрузку LDA ADR и запоминание STA ADR аккумулятора;
• непрямую загрузку LDA RP и запоминание STAXRP аккумулятора;
• прямую загрузку LHLD ADR и запоминание SHLD ADR регистровой-' 777-пары;
• обмен данными HCHG регистровых HL и DE пар.
Команды пересылок не изменяют значений флажков в регистре признаков.
Примеры команд пересылок;
MOV А, В; Переслать содержимое регистра В в аккумулятор А;
MVIA, 15Н; Записать в аккумулятор число 1577;
MVIH, 10/2+2; Записать в регистр Н число 7;
LXIH, 100077; Загрузить в регистровую /77-пару адрес 100077;
MOVМ, А; Запомнить по адресу 100077содержимое аккумулятора, если (77, 7) = 100077;
STA 200077; Запомнить по адресу 2000/7 содержи мое аккумулятора.
Команды арифметических операций микропроцессора ВМ85
Команды арифметических операций микропроцессора ВМ85 представлены в табл. 10.6.
10.2. Однокристальные восьмиразрядные микропроцессоры 347
Таблица 10.6
Команда Комментарий Машинный код №вып
Сложение с аккумулятором
ADD R (A)^(A)+(R) 1 OOOOSSS 4
ADD М (А)<—(А)+(М) 1 0000 1 1 0 7
ADID8 (Я)<-(Л)+ £>8 11000110 7
<В2>
Сложение с аккумулятором с переносом
ADCR (Л)Н^)+(Л)+(СУ) 10001SSS 4
ADCM (А)<-(А)+(М)+(С¥) 10001110 7
ACID8 (A)<-(A)+D8+(CY) 11001110 7
<В2>
Вычитание из аккумулятора
SUB R (A)<-(A)-(R) 100 1 0SSS 4
SUB М (А)^(А)-(М) 10010110 7
SUID8 (A)t-(A)-D8 11010110 7
<В2>
SB В R (A)<-(A)-(R)-(CY) 100115S5 4
SBBM (A)<-(A)-(M)-(CY) 10011110 7
SBID8 (A)<-(A)-D8-(CY) 11011110 7
<В2> 7
Инкремент
INRR (*)<-(*)+1 GGDDD 1 00 5
INRM (Af)<—(ЛУ)+1 00110100 10
INXRP (PP)<-(PP)+1 00ЯР0011 5
Декремент
DCRR (WH 00DDD 1 0 1 5
DCRM (Л/)<-0И)-1 00110101 10
DCXRP (ЯР)<-(ЯР)-1 00 ЯР 101 1 5
Двойное сложение регистровой пары
DADRP (Ж)<-(Ж)+(ЯР) 00ЯР1001 10
Десятичная коррекция аккумулятора
DAA 00100111 4
Арифметические команды выполняют операции сложения, вычитания, инкремента, декремента и т.д.
Операции сложения и вычитания выполняются в дополнительном коде над содержимым аккумулятора и операнда. Результат операции хранится в аккумуляторе, и в зависимости от него устанавливаются все флажки. Операнды представляются в формате целого числа со знаком в дополнительном коде в диапазоне минус 128 -плюс 127. При этом старший бит является знаковым.
По командам сложения ADD R, ADD М, ADI D8 содержимое указанного регистра R, ячейки памяти по адресу М или непосредственные данные прибавляются к содержимому аккумулятора, и результат записывается в аккумулятор. Команды ADCR, ADCM, ACID8 выполняют сложение с учетом значения бита переноса (СУ).
348 Микропроцессоры
Пример выполнения команды сложения ADD С:
Аккумулятор (Л) 1111 0001 = -15ш
Регистр (С) = 0101 1100 = +9210
Результат (А) = 0100 1101 = 7710
Флажки: СУ = 1; ЛС = 0; S = 0; В = 1; Z = 0._________________________
По командам вычитания SUB R, SUB М, SUID8 содержимое указанного регистра R или ячейки памяти по адресу или непосредственные данные отнимаются от содержимого аккумулятора, и результат записывают в аккумулятор. По командам вычитания SBB R, SBB М, SBID8 эти же действия выполняются с учетом значения бита заема (СУ). Если при вычитании есть заем (то есть, уменьшаемое меньше вычитаемого), то из старшего разряда сумматора переноса не будет, и бит СУ устанавливается в состояние “1”. Если же этот перенос был (заем не требуется), то СУ бит сбрасывается в состояние “0".
Пример выполнения команды вычитания SUB Н:
Аккумулятор (Л) = 1.111 0001 =-1510
Регистр (7/) =”1.111 И10 =-210
Результат (Л) = 1.111 ООН = -13ю
Флажки: СУ = 0; ЛС = 0; 5 = 1; Р = 1.________________________________
Команды сложения и вычитания с учетом переносов (заема) позволяют организовать обработку многобайтовых чисел последовательно по байтам, которые хранятся в смежных ячейках памяти и адресуются, начиная с младшего байта.
Для увеличения или уменьшения содержимого регистров или ячейки памяти на единицу используются соответственно команды инкремента INR R, INR М и декремента DCRR, DCR М. Эти операции в отношении к результатам операции устанавливают флажки S, Z, Р, АС, бит переноса (заема) не изменяется.
Команды инкремента INX RP или декремента DCX RP соответственно увеличивают или уменьшают на единицу содержимое регистровых пар RP.
Команда двойного сложения DAD RP суммирует содержимое двух регистровых пар: фиксированной HL и RP, которая указывается в команде. Результат записывается в Ж-паре; устанавливается только флажок СУ, остальные признаки не изменяются.
Пример выполнения команды DAD ВС:
Регистровая пара (Ж) = 0000 1100 0000 0000 = ЗО721О
Регистровая пара (ВС)+= 1111 1111 1111 1111 =-110
Результат_______(Ж) = 0000 1011 1111 1111 = ЗО711О.__________________
В формате байта можно записать две двоично-кодированные десятичные цифры (BCD-числа). При сложении BCD-чисел операнды суммируются как двоичные числа. Затем промежуточный результат корректируется командой DAA по правилам:
• если младшая тетрада больше девяти или установлен флажок АС = 1, то содержимое аккумулятора увеличивается на шесть и к старшей тетраде прибавляется единица;
10.2. Однокристальные восьмиразрядные микропроцессоры 349
• если после этого старшая тетрада аккумулятора больше девяти, CY = 1, то к ней прибавляют цифру 6.
Отметим, что в командах сложения и вычитания результат в аккумулятор записывается в такте 72 цикла М\ новой команды, что повышает производительность микропроцессора.
Команды логических операций микропроцессора ВМ85
Команды логических операций микропроцессора ВМ85 представлены в табл. 10.7.
Таблица 10.7
Команда Комментарий Машинный код дг 1 ’ вып
Логическое И с аккумулятором
“ ANA R (Л)<-(Л)л(Я) 1 0 1 00555 4
ANA М (Л)<—(Л)а(Л/) 10100110 7
ANI 7)8 (Л)<-(Л)а 7)8 11100110 7
<В2>
Логическое ИЛИ с аккумулятором
OR A R (A)<-(A)v(R) 10110SSS 4
ORAM (A)<-(A)v(M) 10110110 7
ORID8 (A)<-(A)vD8 11110110 7
- <В2>
“Исключающее ИЛИ” с аккумулятором
XRAR (Л)<-(Л)Ф(Л) 10101555 4
XRA М (A)<r-(A)®(M) 10101110 7
XRID8 (Л)<-(Л)Ф£>8 11101110 7
<В2>
Сравнение с аккумулятором
CM PR 10111555 4
CMPM (Л)-(Л7) 10111110 7
CPI D8 (A)-D8 11111110 7
<В2>
Сдвиг аккумулятора
RLC >4i 00000111 4
RRC Ат ^т-1 00001111 4
Сдвиг аккумулятора с переносом
RAL 00010111 4
RAR 00011111 4
Инверсия
СМ А 00101111 4
СМС (СУ) <-(СУ) 4
Установка переноса в положение “1”
STC (СУ)<-1 00110111 4
350 Микропроцессоры
Логические команды выполняют поразрядные операции И, ИЛИ, “Исключающее ИЛИ", а также операции сравнения, сдвига, инвертирования аккумулятора и бита переноса, установки бита переноса.
По командам логического И (ЛЛС4 R, ANA М, ANID8) или логического ИЛИ (ORA R, ORA М, ORID8) и исключающего ИЛИ (XRA R, XRA М, XRID8) выполняются соответствующие поразрядные логические операции над содержимым:
• аккумулятора и указанного регистра /?;
• аккумулятора и ячейки памяти по адресу М;
• аккумулятора и непосредственных данных D8.
Результат записывается в аккумулятор.
Примеры логических поразрядных операций И, ИЛИ, “Исключающее ИЛИ”
Содержимое аккумулятора и регистра В до операции: (А) = 10011011, (5) = = 11001101. Результаты операции:
ANA В; (А) = 10001001, 5=l,Z = 0,P = 0
ORA В; (А) = 11011111,5= l,Z = 0,P = 0
XRA В; (А) = 01010110, S = 0,Z = 0,P = 1____________________________
По командам сравнения CMP R, CMP М, CPI D8 из содержимого аккумулятора вычитается операнд, однако результат операции не хранится; при этом значения сравниваемых данных не изменяются, и по правилам вычитания устанавливаются все флажки.
В командах сравнения данные интерпретируются как числа в дополнительном коде в диапазоне минус 128 - плюс J27. Результат сравнения однобайтовых чисел со знаком трактуется следующим образом:
'(J) = (R? CY = 0,Z = l
Если- (А) * (/?) (J) > (/?) >, имеем • Z = 0 CY-0
,(Л) < (/?) CY = 1
Когда сравниваемые данные рассматриваются как положительные числа без
знака от нуля до 255 и их старшие биты разные, то программист должен трактовать
результат сравнения следующим образом:
Если-
[(А) > (У?)]
.(Л) <(/?)?
имеем <
CY = 0]
СУ = 1
Команды сдвига предназначены для циклического сдвига содержимого аккумулятора на один разряд влево (команды RLC, RAL) или вправо (команды RRC, RAR). Команды RAL и RAR включают в поле сдвига флажок переноса (рис. 10.18).
К логическим командам относят команды СМА — инвертирования содержимого аккумулятора, STC — установки в положение “1” флажка переноса CY и его инвертирования СМС.
10.2. Однокристальные восьмиразрядные микропроцессоры 351
RLC RRC
RAL
RAR
Рис. 10.18. Выполнение операций сдеига
Команды передачи управления микропроцессора ВМ85
Команды передачи управления микропроцессора ВМ85 представлены в табл. 10.8.
Таблица 10.8
Команда Комментарий Машинный код N 1 ’ выл
Безусловный переход
JMP ADR (PQ<- ADR 11000011 10
<В2>
<ВЗ>
Условный переход
JMP COND ADR Если ССС, то (РС)<-<ВЗ><В2>, (РС)<-(РС)+3 11ССС100 10
<В2>
<ВЗ>
Безусловный вызов подпрограммы
CALL ADR (PC)^ADR 11001101 17
<В2>
<ВЗ>
Условный вызов подпрограммы
С COND ADR RET Если ССС, то (РС)<-<ВЗ><В2>, (РС)<-(РС)+3 (РС)<—(STACK) 1 1ССС10 1 17 11
<В2>
<ВЗ>
1 1 00 1 00 1
Возврат по условию
R COND Если ССС, то (PC)<-(STACK) (РС)<-(РС) + 1 1 1 сссооо 17/11
Непрямой переход
PCHL 11101001 5
Повторный запуск (рестарт)
RST п 1 1 А А А 1 1 1
Команды передачи управления изменяют естественную последовательность выполнения команд программы (табл. 10.8), однако не изменяют значений флажков. Различают безусловные и условные команды передачи управления.
352 Микропроцессоры
По команде JMP ADR выполняется безусловная передача управления по адресу <ВЗ><82>, загружаемому в программный счетчик PC; старое содержимое счетчика теряется. Например:
JMP 4040#; Переход по адресу 4040#
При выполнении условия осуществляется переход по новому адресу, в противном случае выполняется следующая команда. Для удобства программирования предусмотрены проверки условий по единичным и нулевым значениям флажков СУ, Z, 5, Р. Мнемоника команд условного перехода образуется добавлением буквы J к названию условия: JC — переход, если СУ = 1; JNC — переход, если NC = 1 и т.д. Например:
JNC 4040#; Переход, если NC = 1
В условных командах передачи управления проверяется текущее значение условия, которое указывается в трехбитовом поле ССС кода операции (табл. 10.9).
Таблица 10.9
Условие Название условия Код ССС Мнемоника
переход вызов возврат
СУ=1 Перенос 011 JC СС RC
NC=\ Нет переноса 010 JNC CNC RNC
Z=1 Нулевой результат 001 JZ CZ RZ
wz Ненулевой результат 000 JNZ CNZ RNZ
м Отрицательный результат 111 JM СМ RM
р Положительный результат по -JP СР RP
РЕ Четный результат 101 JPE с ре' RPE
РО Нечетный результат 100 JPO СРО RPO
По команде CALL ADR выполняется безусловный вызов подпрограммы по адресу <ВЗ><В2>, загружаемом в программный счетчик. Содержимое PC временно запоминается в стеке как адрес возврата. Например:
CALL 4040#; Вызов подпрограммы по адресу 4040#
Команды условного вызова подпрограмм передают управление по адресу <ВЗ><В2> только при выполнении условия, записанного в поле ССС кода операции. При этом адрес возврата запоминается в стеке. Если заданное условие не выполняется, то выполняется следующая по последовательности команда. Мнемоника команды условного вызова подпрограммы строится добавлением буквы С к названию условия (табл. 10.9); СС— вызов, если СУ = 1; CNC— вызов, если NC = 0 и т.д.
Команда безусловного возврата из программы передает управление по адресу возврата, хранимому в двух верхних ячейках стека. Команды условного возврата из подпрограмм выполняются при выполнении условия в поле ССС (табл. 10.9).
Команда повторного запуска (рестарт) RSTn предназначена для обработки прерывания и ввода контрольных точек (разрывов) при отладке программ. В коде операции рестарт 11ААА111 три бита п = ААА называются вектором; их задает программист или схема прерывания. По команде RSTn текущее содержимое программного счетчика PC засылается в стек, а в счетчик загружается код PC <- 0000 0000 МАА Л000 = 8-п.
10.2. Однокристальные восьмиразрядные микропроцессоры 353
Таким образом, в зависимости от значений вектора реализуются передачи управления по адресу: RST 0 -> 0000//; RST 1 -> 0008//; RST 7-> 0038//. Обычно в восьми байтах, отведенных для каждой команды, записывают начальный адрес подпрограммы обслуживания прерываний. Выход из подпрограммы обслуживания прерываний выполняется по команде возврат RET.
Команды CALL и С COND (при выполнении условия) выполняются за пять циклов и 17 тактов; если условие вызова не удовлетворено, то эти команды реализуются за три цикла и 11 тактов. Команды JMP и J COND выполняются за три цикла и 11 тактов. Команды RET и R COND (при выполнении условия) реализуются за три цикла и пять тактов. Команда RST выполняется за три цикла и 11 тактов.
Команды управления вводом-выводом, стеком и состояниями микропроцессора ВМ85
Команды управления вводом-выводом, стеком и состояниями микропроцессора ВМ85 представлены в табл. 10.10.
Таблица 10.10
Команда Комментарий Машинный код N 1 ’ ВЫП
Ввод данных из порта
IN PORT (Л)<- (PORT) 11011011 10
<B2>
Вывод данных в порт
OUT PORT (PORT)<-(A) 11010011 10
<B2>
Запись в стек
PUSH RP (STACK)<—(RP) 1 1RP0101 11
Чтение стека
POP RP (RP)<—(STACK) 1 1RP000 1 10
Обмен со стеком
XTHL (L)<r>(SP) (H)<r>((SP)+l) 11100011 17
Загрузка SP
SPHL (SP)<-(HL) 11111001 5
Разрешение прерывания
EI INTE+-A 11111011 4
Запрет прерывания
DI INTE<- 0 | 11110 0 11 4
Отсутствие операций
NOP 00000000 4
Останов
HLT 01110110 7
Чтение маски
RIM (A)t-(IM) 00100000 4
Установка маски
SIM (IM)^(A) 00110000 4
23 — 4-1749
354 Микропро цессоры
Для обмена данными с процессором внешние устройства имеют на своих входах и выходах регистры, называемые портами ввода-вывода.
По команде IN PORT байт данных из порта внешнего устройства пересылается в аккумулятор. По команде OUT PORT пересылается байт данных из аккумулятора во внешний порт; PORT — это символическое обозначение адреса порта, находящегося в диапазоне 0-255.
По команде PUSH RP содержимое одной из регистровых пар ВС, DE, HL или PSW, адресуемой кодом RP в поле команды, записывается в стек. В ячейку памяти по адресу (SP)-1 пересылается содержимое старшего регистра пары, а по адресу (SP)-2 — содержимое младшего регистра пары. Содержимое этого значения стека SP уменьшается на два.
По команде POP RP два соседних байта с вершины стека пересылаются в одну из регистровых пар ВС, DE, HL или PSW, адресуемых кодом в поле RP. В младший регистр пары загружается содержимое ячейки с адресом [5Р], а в старший — с ад-оесом [(5Р)+1 ]. После этого значение указателя стека SP увеличивается на два.
По команде SPHL содержимое Ш-пары переписывается в указатель стека SP.
По команде XTHL выполняется обмен содержимым между //L-парой и двумя верхними ячейками стека, адресуемых SP (рис. 10.19).
5Р|Ю 00| F0 1000 ЗС 5Р|10 00|
0D 1001 0F
Н L 1002 Н L
Н \QF ЗС| H\0D Л)|
a б
Рис. 10.19. Выполнение команды XTHL: а — до выполнения команды; б — после выполнения команды
Программное управление запросами прерываний от внешних устройств осуществляется командами EI (разрешение прерывания) и DI (запрет прерывания). По команде NOP операция не выполняется, поскольку она используется для формирования временных задержек или для резервирования места в программе. По этой команде содержимое счетчика PC увеличивается на единицу и, таким образом, указывает на адрес следующей команды. По команде останова HLT значение PC увеличивается на единицу и микропроцессор переходит в режим останова до появления запроса на прерывание от внешнего устройства. Запрос на прерывание обслуживается, если командой EI до этого был установлен внутренний триггер прерывания, после этого микропроцессор снова переходит в режим останова. Для продолжения обычной работы необходимо выполнить сброс микропроцессора. Все команды управления не изменяют значений флажков.
По команде SIM содержимое аккумулятора пересылается в регистр маски прерывания и одновременно значение старшего разряда аккумулятора передается в однобитный порт вывода SOD. По команде RIM в аккумулятор пересылается содержимое маски прерывания и одновременно в старший разряд аккумулятора передается значение последовательного порта ввода.
10.2. Однокристальные восьмиразрядные микропроцессоры 355
10.2.7. Примеры программ на языке ассемблера для микропроцессора ВМ85
Пример 1. Выделение шестнадцатеричной цифры
Шестнадцатеричные цифры 0, 1, ... 9, А, ... F кодируются тетрадой (четырьма двоичными разрядами). Требуется выделить в байте по адресу 0840Н младшую тетраду, обнулить старшую и результат записать по адресу 0841Н. В программе используется косвенная адресация ячейки памяти М с помощью содержимого регистровой пары Н, L.
Адрес Объектный код Программа ORG 0800Н Комментарий
0800 21 40 08 LXI Н, 0840Н ;Установка указателя
0803 7Е MOV А, М ;3агрузка А
0804 Е6 0F ANI 0FH ;Маска
0806 23 INXH ;Инкремент Н-пары
0807 77 MOV М, А Запоминание А
0808 76 HLT ;Останов
ORG 0840Н ;Начало массива
0840 9С DB 9С
Пример 2. Разделение байта на две части
Требуется выделить из исходного байта по адресу 0840Н младшую и старшую тетрады и запомнить их по адресам 0841Н и 0842Н соответственно.
Адрес Объектный код Программа ORG 0800H Комментарий
0800 21 40 08 LXI H, 0840H ;Установка указателя
0803 7Е MOV A, M ;3агрузка А
0804 47 MOV B, A ;Пересылка в В
0805 Е6 0F ANI 0FH ;Маска
0807 23 INXH ;Инкремент Н-пары
0808 77 MOV M, A ;Пересылка в память
0809 78 MOV A, В ;Пересылка в В
080А OF RRC Четырехкратный
080В OF RRC циклический
080С OF RRC ;сдвиг
080D OF RRC ;вправо
080Е E6 OF ANI 0FH ;Маска
0810 23 INXH ;Инкремент Н-пары
0811 77 MOV M, A ;Пересылка в память
0812 76 HLT ;Останов
ORG 0840H ;Начало массива
0840 AB DB AB
23*
356 Микропроцессоры
Пример 3. Суммирование массивов байтов
Начальный адрес массива данных равен 0842Н; длина массива указана в ячейке с адресом 0841Н. В программе используется счетчик циклов. Результат последовательного сложения байтов запоминается по адресу 0840Н.
Адрес Объектный код Программа ORG 0800Н Комментарий
0800 97 SUB А ;Обнуление А
0801 21 41 08 LXI Н, 0841Н ;Установка указателя
0804 46 MOV В, М ;Счетчик цикла
0805 23 MET: INXH ;Инкремент Н-пары
0806 86 ADDM ;Сложить с памятью
0807 05 DCRB ;Декремент В
0808 С2 05 08 YNZ МЕТ ;Переход к метке, если не ноль
080В 32 40 08 STA 0840Н Запоминание
080Е 76 HLT ;Останов
ORG0841H ;Начало массива данных
0841 03 DB 03 35 72 0А
Пример 4. Пересылка массива байтов
Длина массива байтов записана по адресу 0840Н; начало пересылаемого массива — 0841Н; начало области пересылки — 0851Н. В программе используется косвенная адресация с помощью регистровых пар Н, L и D, Е. В качестве счетчика циклов используется регистр В.
Адрес Объектный код Программа ORG 0800Н Комментарий
0800 21 40 08 LXI Н, 0840Н ;Установка указателя
0803 46 MOV В, М ;Длина массива в В
0804 11 50 08 LXI D, О85ОН ;У станов ка указателя
0807 13 МЕТ: INXD ;Инкрементирование
0808 23 INXH указателей
0809 7Е MOV А, М ;3агрузка А
080А 12 STAXD Запоминание А
080В 05 DCRB Декремент счетчика
080С С2 07 08 YNZ МЕТ ;Переход к метке, если не ноль
080F 76 HLT ;Останов
ORG 0840Н ;Начало массива
0840 02 DB 02 7F 55
Пример 5. Нахождение максимума
Длина массива задана в ячейке по адресу 0841Н. Элементы массива — это восьмиразрядные числа без знака. Максимальное значение в массиве данных помещается в ячейку по адресу 0840Н. Вначале за максимальное значение принимается первый байт. Затем идет последовательное сравнение со следующим байтом.
10.2. Однокристальные восьмиразрядные микропроцессоры 357
Значение нового байта принимается за максимальное, если оно больше предыдущего.
Адрес Объектный код Программа ORG 0800Н Комментарий
0800 21 40 08 LXIН, 0840Н ;Установка указателя
0803 46 MOV В, М ;Длина массива в В
0804 05 DCRB Декремент В
0805 23 INXH ;Инкремент Н-пары
0806 7Е MOV А, М ;3агрузка А
0807 23 МАХ: INXH ;Инкремент Н-пары
0808 BE СМРМ Сравнение с памятью
0809 D2 0D 08 YNC NOC ;Переход к метке NOC, если С=0
080С 7Е MOV А, М ;3агрузка А
080D 05 NOC: DCRB Декремент В
080Е С2 07 08 YNZ МАХ ;Переход к метке МАХ, если не ноль
0811 32 40 08 STA 0840Н Запоминание А
0814 76 HLT ;Останов
ORG0841H ;Начало массива данных
0841 03 DB 03 37 F2 С6
Пример 6. Сложение многобайтовых чисел
Длина массива задается в ячейке по адресу 0840Н. Многобайтовые числа находятся в памяти, начиная с адресов 0841Н и 0851Н соответственно, причем сначала хранятся младшие байты. Результат сложения записывается по адресу первого числа.
Адрес Объектный код Программа ORG 0800Н Комментарий
0800 97 SUB А ;Обнуление A
0801 21 40 08 LXI Н, 0840Н ;Установка указателя
0804 46 MOV В, М ;Длина массива в В
0805 И 50 08 LXI D, 0850Н ;У станов ка указателя
0808 13 MADD INXD ;Инкремент
0809 23 INXH указателей
080А 1А LDAXD ;3агрузка А
080В 8Е ADCM ;Сложение с переносом
080С 77 MOV М, А Запоминание А
080D 05 DCRB Декремент В
080Е С2 08 08 YNZ MADD ;Переход к метке MADD, если не ноль
0811 76 HLT ;Останов
ORG 0840H ;Начало первого массива
0840 03 DB 03 29 A4 50
ORG 0850H ;Начало второго массива
0850 FB DB FB 37 28
358 Микропроцессоры
Пример 7. Сложение десятичных чисел
Двоично-десятичные числа заданной длины, указанной в ячейке по адресу 0840Н, находятся в массивах с начальными адресами 0841Н и 0851Н соответственно. Сложение начинается с младших цифр. После каждого сложения используется команда десятичной коррекции DAA. Результат сложения запоминается по адресу
первого массива.
Адрес Объектный код Программа Комментарий
ORG 0800Н
0800 97 SUB А ;Обнуление A
0801 21 40 08 LXI Н, 0840Н ;Установка указателя
0804 46 MOV В, М ;Длина массива в В
0805 11 50 08 LXI D, О85ОН ;Установка указателя
0808 13 ADD: INXD ;Инкремент
0809 23 INXH указателей
080А 1А LDAXD ;3агрузка А
080В 8Е ADCM ;Сложение с переносом
080С 27 DAA ;Коррекция
080D 77 MOV М, А Запоминание А
080Е 05 DCRB •Декремент счетчика
080F С2 08 08 YNZ ADD ;Переход к метке ADD, если не ноль
0812 76 HLT ; Останов
ORG 0840H ;Начало первого массива
0840 03 DB 03 29 65 37
ORG 0851H ;Начало второго массива
0851 08 DB 88 43 22
Пример 8. Таблица квадратов
Использование таблиц результатов, хранимых в памяти, повышает производительность ЭВМ. Для трехразрядного двоичного числа в диапазоне от ООО до 111 таблица квадратов образует следующим образом: О2 = 0(0Н), 12= 1 (1Н), 22 = 4(4Н), 32= 9(9Н), 42= 16(1 ОН), 52 = 25(19Н), 62 = 36(23Н) и 72= 49(31 Н). Таблица квадратов в шестнадцатеричном коде размещается в памяти с базового адреса 0850Н. Число, которое возводится в квадрат, записано в ячейке 0841Н. Адрес искомого результата определяется сложением исходного числа и базового адреса размещения таблицы квадратов.
Адрес Объектный код Программа ORG 0800Н Комментарий
0800 11 50 08 LXI D, О85ОН ;Установка указателя
0803 ЗА 40 08 LDA 0840Н ;3агрузка А
0806 6F MOV L, А ;Пересылка
0807 26 00 MVIН, ООН ;Обнуление Н
0809 19 DADD Двоичное сложение
080А 7Е MOV А, М результат в А
080В 32 41 08 STA 0841Н Запоминание А
10.2. Однокристальные восьмиразрядные микропроцессоры 359
080Е 76 HLT ORG 0840Н ;Останов ; Число
0840 04 DB 04 ORG О85ОН ;Таблица квадратов
0850 00 DB 0, 1,4, 9, 10, 19, 23,31
Пример 9. Определение длины строки символов
Массив символов в коде ASCII размещается в памяти, начиная с адреса 0841Н. Конец строки отмечается символом “точка” (код 2ЕН). Результат запоминается по адресу 0840Н.
Адрес Объектный код Программа ORG 0800Н Комментарий
0800 06 00 MVI В, ООН ;Обнуление В
0802 ЗЕ2Е MVI А, 2ЕН ;Код “точка” в А
0804 21 41 08 LXI Н, 0841Н ;Установка указателя
0807 BE СИМВ: СМРМ Сравнение
0808 СА 10 08 JZEND ;Переход к метке END, если ноль
080В 04 INR В ;Инкремент В
080С 23 INXH ;Инкремент Н-пара
080D F2 07 08 JMP СИМВ безусловный переход к метке СИМВ
0810 78 END MOV А, В результат в А
0811 32 40 08 STA 0840Н Запоминание А
0814 76 HLT ; Останов
ORG 0840H ;Начало массива
0840 03 DB 03 43 41 54 2E
Пример 10. Преобразование цифры из кода ASCII в десятичную систему
Для преобразования цифры из кода ASCII в десятичную систему достаточно’ вычесть из этого кода значение ЗОН (ноль в коде ASCII). Преобразуемая цифра находится в ячейке 0840Н; результат записывается по адресу 0841Н. Если преобразуемый символ не является цифрой, то в ячейку результата записывается код FFH.
Адрес Объектный код Программа ORG 0800Н Комментарий
0800 ЗА 40 08 LDA 0840Н ;3агрузка А
0803 D6 30 SUI ЗОН ;Вычитание нуля
0805 FE 0А CPI 0AH ; Цифра
0807 DA ОС 08 JC МЕТ ;Переход к метке МЕТ, если перенос
080А ЗЕ FF MVI A, 0FFH ;Код ошибки
080С 32 41 08 МЕТ: STA 0841Н Запоминание А
080F 76 HLT ; Останов
ORG 0840Н ;Начало массива
0840 36 DB 36
360 Микропроцессоры
Пример 11. Сравнение строк символов
Сравнение состоит в проверке совпадения некоторой симврльной строки с заданной. Пусть две строки символов расположены в памяти, начиная с адресов 0842Н и 0852Н соответственно. В ячейке 0841Н указана длина строк. Программа посылает в ячейку с адресом 0840Н ноль, если строки совпадают, и FFH, если не совпадают.
Адрес Объектный код Программа ORG 0800Н Комментарий
0800 21 41 08 LXIH, 0841Н ;Установка указателя
0803 46 MOV В, М ;Длина строки в В
0804 11 51 08 LXID, 085 Ш ;Установка указателя
0807 23 МЕТТ. INXH ;Инкремент Н-пары
0808 13 INXD ;и D-пары
0809 1А LDAXD ;3агрузка А
080А BE CMPM Сравнение с памятью
080В С2 18 08 JNZ МЕТ2 ;Переход к метке МЕТ2, если не ноль
080Е 05 DCRB ;Декремент счетчика
080F С2 07 08 JNZ MET1 ;Переход к метке МЕТ1, если не ноль
0812 3F 00 MVI A, 00H ;3агрузка нуля в С
0814 32 40 08 STA 0840H Запоминание А
0817 76 HLT
0818 ЗЕ FF МЕТ2 MVI A, FFH ;3агрузка FFH в С
081А 32 40 08 STA 0840H Запоминание А
081D 76 HLT ;Останов
ORG 0841H ;Начало первого массива
0841 04 DB 04 43 41 54 53
ORG 0852H ;Начало второго массива
0852 43 DB 43 41 50 45
Пример 12. Преобразование десятичного числа в десятичный символ в коде ASCII
Преобразуемая десятичная цифра хранится в ячейке 0841Н. Проверяется соответствие этого кода десятичной цифре, а затем добавляется значение ЗОН (ноль в шестнадцатеричном коде). Результат записывается в ячейку 0841Н.
Адрес Объектный код Программа ORG 0800Н Комментарий
0800 ЗА 40 08 LDA 0840Н Загрузка А
0803 FE 0А CPI0AH Сравнение
0805 DA 0D 08 JCM1 ;Переход к метке Ml, если ноль
0808 3EFF MVI A, 0FFH ;Код ошибки
080А СЗ 0F 08 JMP М2 безусловный переход к метке М2
080D С6 30 Ml: ADI ЗОН ;Сложение с ЗОН
080F 32 41 08 М2: STA0841H Запоминание А
0812 76 HLT ;Останов
10.2. Однокристальные восьмиразрядные микропроцессоры 361
0840 05
ORG 0840Н
DB 05
;Число
Пример 13. Умножение двух байт
Множитель и множимое хранятся в ячейках 0840Н и 0841Н соответственно. Множимое загружается в регистр С, множитель — в регистр А. Производится суммирование командой двоичного сложения DAD В с накоплением в регистровой паре Н, L. Суммирование производится m раз, где m — значение множителя. В итоге в регистровой паре Н, L формируется 16-разрядное произведение.
Адрес Объектный код Программа ORG 0800Н Комментарий
0800 21 00 00 LXI Н, 0000Н ;Обнуление Н, L и
0803 01 00 00 LXI В, 0000Н В, С пар
0806 ЗА 40 08 LDA 0840Н ;Множимое в
0809 4F MOV С, А регистре С
080А ЗА 41 08 LDA 0841Н ;3агрузка А
080D 09 МЕТ2: DAD В ;Двойное сложение
080Е 3D DCRA Декремент А
080F СА 15 08 JZ МЕТ1 ;Переход к метке МЕТ1, если ноль
0812 СЗ 0D 08 JMP МЕТ2 безусловный переход к метке МЕТ2
0815 11 50 08 МЕТ1: LXID, 0850Н ;Установка указателя
0818 7D MOV A, L Запоминание
0819 12 STAXD ;младшего байта
081А 7С MOV А, Н Запоминание
081В 13 INXD ;старшего
081С 12 STAXD ;байта
081D 76 HLT ;Останов
0840 06 ORG 0840Н DB 06, 03 Два байта
Пример 14. Получение временной задержки
В задачах управления часто требуется выдавать управляющие сигналы с определенными временными задержками. Это обеспечивается как аппаратно с помощью линий и схем задержки, так и программными средствами. Сущность программного способа получения задержки — выполнение некоторого количества команд, время выполнения которых известно.
Рассмотрим универсальную подпрограмму получения требуемой задержки tw на основе трех циклов над содержимым регистров В, С и D.
t3a = 0,7 [(15JC+ 22)М + 22]Усек,
где N, М и К — содержимое регистров В, С И D соответственно. Если К = М = FFH, то получаем следующую расчетную формулу.
Гзд = 0,7 N сек.
Для получения требуемой задержки вызывающая программа загружает в регистр В значение У = /зд и передает управление подпрограмме DELS-.
362 Микропроцессоры
Адрес Объектный код Программа DELS: ORG0900H Комментарий
0900 0EFF Ml: MVI С, FFH ;3агрузка С
0902 16 FF М2: MVI D, FFH ;3агрузка D
0904 15 М3: DCRD ;Декремент D
0905 С2 04 09 INZM3 ;Переход к метке М3, если не ноль
0908 0D DCRC ;Декремент С
0909 С2 02 09 JNZ М2 ;Переход к метке М2, если не ноль
090С 05 DCRB ;Декремент В
090D С2 00 09 JNZ Ml ;Переход к метке Ml, если не ноль
0910 С9 RET безусловный возврат
Программа включения-выключения светового индикатора с полупериодом
772 = Гзд, выглядит следующим образом:
Адрес Объектный код Программа Комментарий
ORG 0800Н
0800 ЗЕ 82 MVI А, 82Н ;Настройка программируемого
0802 D3 83 OUT 83Н периферийного адаптера
0804 ЗЕ 00 MVI А, ООН ;Обнуление А
0806 ЕЕ 55 Ml: XRI 55Н Исключающее ИЛИ с А
0808 06 0А MVI В, 0AH ;3агрузка числа N
080А CD 00 09 CALL DELS ;Вызов подпрограммы DELS
080D D3 80 OUT 80Н ;Вывод в порт А
080F СЗ 06 08 JMP Ml безусловный переход к метке Ml
Пример 15. Контроль состояния внешнего пульта
В микропроцессорных системах управления технологическими процессами и объектами важное место занимает контроль за состоянием пультов операторов и выдачи осведомительной информации на световые индикаторы.
Контроль состояния внешнего пульта оператора осуществляется с помощью' платы, на которой размещена микросхема программируемого периферийного адаптера (ППА). Эта микросхема программируется на работу в режиме, при котором порт А (адрес 80Н) настраивается на вывод, а порт В (адрес 81Н) — на ввод информации в микропроцессор. Такая работа ППА обеспечивается кодом 82Н, который засылается в регистр управляющего слова по адресу 83Н.
Программа контроля пульта для варианта 21Н/32Н или 42Н/15Н выглядит следующим образом:
Адрес Объектный код Программа ORG 0800Н Комментарий
0800 ЗЕ 82 MVI А, 82Н ;Настройка
0802 D3 83 OUT 83Н ;ППА
0804 DB81 М3 IN81H ;Ввод с тумблера
0806 ЕЕ 21 XRI21H ;Маска
0808 СА 19 08 JZM1 ;Переход к метке Ml, если ноль
10.2. Однокристальные восьмиразрядные микропроцессоры 363
080В DB 81 IN81H ;Ввод с тумблера
080D ЕЕ 42 XRI42H ;Маска
080F СА 20 08 JZ М2 ;Переход к метке М2, если ноль
0812 ЗЕ 00 MVI А, ООН ;3агрузка кода вывода
0814 D3 80 OUT 80Н ;Вывод
0816 СЗ 04 08 JMP М3 ^Безусловный переход к метке М3
0819 ЗЕ 32 МТ MVI А, 32H ;3агрузка кода вывода
081В D3 80 OUT 80H ; Вывод
081D СЗ 04 08 JMP М3 безусловный переход к метке М3
0820 ЗЕ 15 М2- MVI A, 15H ;Загрузка кода вывода
0822 D3 80 OUT 80H ; Вывод
0824 СЗ 04 08 JMP М3 безусловный переход к метке М3
В программе состояние внешнего пульта непрерывно записывается в аккумулятор командой ввода IN81H. Команда XRI2XH суммирует содержимое аккумулятора с маской по модулю два. При равенстве кодов аккумулятора и маски устанавливается флажок нулевого результата. В этом случае на световой индикатор выдает заданный код. Аналогично проверяется и второе состояние пульта.
Пример 16. Считывание числа из памяти, его инвертирование и запись в память
Представленная ниже программа извлекает .число из ячейки с адресом 0B00H, инвертирует его и записывает результат в ячейку с адресом 0В01Н.
Адрес Объектный код Программа ORG 0800Н Комментарий
0800 21 00 0В LXI Н, 0B00H ;3апись в регистры Н, L числа 0B00H
0803 7Е MOV А, М ;Получение числа из адреса, указанного ;в регистрах Н, L
0804 2F СМА Инвертирование числа в аккумуляторе
0805 23 INXM ;Увеличение на 1 числа в регистрах Н, L
0806 77 MOV М, А ;3апись числа из аккумулятора по ;адресу, указанному в регистрах Н, L
0807 CF RST 1 ;Прервать выполнение программы
Пример 17. Обмен числом между устройствами
Представленная ниже программа перезаписывает число из входного устройства (по адресу 20) во входное (по адресу 30).
Адрес Объектный код Программа ORG 0800Н Комментарий
0800 DB 20 CNT: IN 20 ;3апись числа из входного устройства
0802 D3 30 OUT 30 ;с адресом 20 в аккумулятор ;3апись числа из аккумулятора в
0804 СЗ 00 08 JMP CNT ;выходное устройство с адресом 30 безусловный переход к метке CNT
364 Микропроцессоры
Пример 18. Маскирование отдельных разрядов числа
Ниже представлена программа маскирования отдельных разрядов числа, записанного во входном устройстве. Результат маскирования помещается в выходное устройство.
Адрес Объектный код Программа ORG 0800Н Комментарий
0800 DB 20 CNT: IN 20 ;3апись числа из входного устройства ;с адресом 20 в аккумулятор
0802 Е6 20 ANI20 выполнение логической операции
0804 D3 30 OUT 30 ;3апись числа из аккумулятора в ;выходное устройство с адресом 30
0807 СЗ 00 08 JMP CNT безусловный переход к метке CNT
Пример 19. Определение единицы в разряде числа
Ниже представлена программа определения единицы в пятом разряде числа, записанного во входном устройстве. Используется маскирование числа и условный переход.
Адрес Объектный код Программа ORG 0800Н Комментарий
0800 DB 20 WAIT: IN 20 ;3апись числа из входного устройства
;с адресом 20 в аккумулятор
0802 Е6 20 ANI 20 ;Проверка состояния 5-го разряда числа
0804 СА 00 08 JZ WAIT ;Переход к метке WAIT, если в пятом
;разряде был нуль (Z=0)
0807 CF RST 1 Завершение выполнения программы
Пример 20. Ожидание появления единицы в разряде
Ниже представлена программа ожидания появления единицы в пятом разряде числа, записанного во входном устройстве. Эта программа содержит два цикла.
Адрес Объектный код Программа ORG 0800Н Комментарий
0800 DB20 WAIT1: IN 20 Запись числа из входного устройства
;с адресом 20 в аккумулятор
0802 Е6 20 ANI 00000100 ;Выключен ли второй переключатель?
0804 СА 00 08 JZ WAIT1 ;Если нет, то переходим к метке WAIT1
0807 3EFF MVI A, FF ;Если да, зажечь светодиоды
0809 D3 30 OUT 30 ;выходного регистра
080В DB 20 WAIT2 IN 20 ;Получаем число из входного устройства
080D Е6 20 ANI 00100000 ;Выключен ли пятый переключатель?
080F СА 0В 08 JZ WAIT2 ;Если нет, перейти к метке WAIT2
0812 ЗЕ 00 MVI A, 00 ;Если да, погасить светодиоды
0814 D3 30 OUT 30 ;выходного регистра
0816 СЗ 00 08 JMP WAIT1 ;Повторить программу
10.2. Однокристальные восьмиразрядные микропроцессоры 365
Пример 21. Генерация звуковых сигналов с заданной частотой
В подпрограмме DLY реализована временная задержка.
Адрес Объектный код Программа ORG 0900Н Комментарий
0900 41 DLY MOV В, С ;3апись числа из регистра С в регистр В
0901 00 NOP ;Нет операции
0902 05 DCRB ;Уменьшить число в регистре В на 1
0903 С2 00 09 JNZ DLY ;Если число в регистре В не равно нулю,
;то переходим к метке DLY
0906 С9 RET ;Возврат из подпрограммы
Рассмотрим пример использования подпрограммы DLY при организации звуковых сигналов. Будем считать, что устройство формирования звуковых сигналов имеет адрес 80.
Адрес Объектный код Программа ORG 0A00H Комментарий
0А00 AF ВРР XRA А ;Очистка аккумулятора
0А01 D3 80 OUT 80 ;3апись кода 00 в выходное устройство
0А03 CD 00 09 CALL DLY ;Вызов подпрограммы задержки
0А06 2F СМА ;3апись кода FF в аккумулятор
0А07 D3 80 OUT 80 ;3апись кода FF в выходное устройство
0А09 CD 00 09 CALL DLY ;Вызов подпрограммы задержки
0A0C С9 RET ;Выход из подпрограммы
Программа MAIN генерирует сигналы с частотой, заданной числом из входного регистра.
Адрес Объектный код Программа ORG 0800Н Комментарий
0800 DB 20 MAIN IN 20 ;3апись числа из входного регистра
;в аккумулятор
0802 4F MOV С, А ;3апись числа в регистр С
0803 CD 00 0А CALL ВРР ;Вызов подпрограммы ВРР
0804 СЗ 00 08 JMP MAIN безусловный переход к метке MAIN
Пример 22. Сложение массива однобайтных чисел с получением двухбайтного результата
Ниже представлена программа сложения массива однобайтных чисел с получением двухбайтного результата. Слагаемые располагаются в ячейках памяти с последовательными адресами. Входные параметры: регистры Н, L — адрес первого слагаемого; регистр В — число слагаемых. Выходной параметр программы — сумма, старший байт которой записан в регистре С, а младший — в аккумуляторе А. После прибавления каждого элемента массива определяется переполнение аккуму
366 Микропроцессоры
лятора (разряд С= 1). Если такое переполнение присутствует, то содержимое регистра С увеличивается на 1. Таким образом, за счет суммирования единиц переноса получается старший байт суммы.
Адрес Объектный код Программа ORG 0800Н Комментарий
0800 21 00 0В MAIN LXIH, 0B00H ;3апись в регистры Н, L адреса первого
0803 06 05 MVI В, 05 слагаемого ;3агрузка в регистр В количества слагаемых
0805 CD 09 0В CALL ADDB ;Вызов подпрограммы сложения
0808 CF RST 1 Прерывание выполнения программы
0809 AF ADDB: XRAA ;Очистка аккумулятора
080А 4F MOV C, A ;Очистка счетчика переносов
080В 86 CNT: ADD M Прибавление к содержимому аккумулятора
080С D2 JNCTRM ;числа из массива слагаемых ;Если переноса нет, то переход к метке TRM
080D ОС INRC Увеличиваем содержимое регистра С на 1
080Е 23 TRM: INXH Указываем на следующий адрес слагаемого
080F 05 DCRB Уменьшаем содержимое счетчика
0810 С2 0В 08 JNCCNT Слагаемых ;Если не все слагаемые, то переходим к
0813 С9 RET ;метке CNT
Пример 23. Нахождение разности чисел
Ниже представлена программа нахождения разности чисел одинаковой длины. Входные параметры: С — длина чисел (в байтах); регистры Н, L — адрес младшего байта вычитаемого; регистры D, Е — адрес младшего байта уменьшаемого. Каждое из чисел записывается в последовательных адресах памяти начиная с младших байтов. Результат заносится в область памяти, отведенной под вычитаемое. В случае если уменьшаемое меньше вычитаемого, выдается звуковой сигнал.
Адрес Объектный код Программа ORG 0800Н Комментарий
0800 AF SBN: XRA А ;Очистка аккумулятора и флага С
0801 1А CNT: LDAXD ;3апись в аккумулятор уменьшаемого
0802 9Е SBBM ;Из содержимого аккумулятора
;вычитается вычитаемое
0803 77 MOV М, А ;Разность записывается на место вычитаемого
0804 23 INXH Указывается следующий байт вычитаемого
0805 13 INXD Указывается следующий байт уменьшаемого
0806 0D DCRC Уменьшается содержимое счетчика длины
0807 С2 01 08 JNZ CNT ;Если не последний (старший) байт числа,
;то переходим к метке CNT
080А D0 RNC ;Если байт старший и результат без заема
;(С=0), то выполняется возврат
10.2. Однокристальные восьмиразрядные микропроцессоры 367
080В CD 1200 CALL ВЕЕР ;Если был заем (С=1), то подать сигнал
080Е CF RST 1 Прерывание выполнения программы
Пример 24. Деление чисел
Деление чисел представляет собой последовательное вычитание делителя из делимого и остатков от деления. Однако двоичное деление реализуется проще, поскольку нет необходимости в каждом цикле деления определять количество делителей, содержащихся в текущем значении делимого или остатка (достаточно только сравнить их). Входные параметры программы: регистр Е — делимое; регистр D — делитель. Выходные параметры: регистр Н—частное, регистр С — остаток.
Адрес Объектный код Программа ORG 0800Н Комментарий
0800 21 0В 00 DIVB: LXI Н, 000BH ;3агрузка счетчика битов (регистр L) и ;очистка регистра частного Н
0803 0Е 00 MVI С, ООН ;Очистка регистра промежуточного ;делимого
0805 7В МХТВ MOV А, Е ;3агрузка делимого в аккумулятор
0806 17 RAL ;Сдвиг старшего бита в разряд С
0807 5F MOV Е, А ;Возврат делимого в регистр Е
0808 79 MOV А, С ;3агрузка в аккумулятор промежуточного ;делимого из регистра С
0809 17 RAL ;Сдвиг старшего бита в разряд С
080А 92 SUB D ;Вычитание делителя из содержимого ;аккумулятора
080В 080Е D2 0F09 JNC NOADD В2 ADD D ;Если С=1, то восстановить содержимое ;аккумулятора
080F 4F NOADD: MOV С, А Промежуточное данное возвращается ;в регистр С
0810 3F СМС Инвертирование разряда С
0811 0812 0813 7С MOV А, Н 17 RAL 67 MOV Н, А ;Сдвиг разряда С в младший бит регистра ;частного Н
0814 2D DCR L Проверены ли все восемь разрядов?
0815 С2 05 08 JNZ МХТВ ;Если нет, то продолжить
0818 CF RST 1 ;Если да, прервать выполнение программы
Пример 25. Определение номера нажатой клавиши
Алгоритм программы основан на последовательной записи нуля в каждый из разрядов матрицы клавиатуры. Если какая-либо клавиша нажата, то определяется ее номер по номеру разряда, в котором записан нуль. Другими словами, номер нажатой клавиши определяется по номеру ряда клавиатуры, в котором обнаружена нажатая клавиша, и номеру разряда входного устройства, в котором записан нуль.
368 Микропроцессоры
Адрес Объектный код Программа ORG 0800Н Комментарий
0800 06 00 MVI В, ООН ;Обнуление счетчика клавиш
0802 0Е FE MVI С, 11111110 ;Начальная установка маски сканирования рядов
0804 16 03 MVI D, ОЗН ;Установка счетчика рядов
0806 79 FROW: MOV А, С ;3апись маски сканирования в ;аккумулятор
0807 D3 KBDOT OUT KBDOT Запись маски сканирования в ;выходное устройство (адрес KBDOT)
0809 07 RLC ;Изменение маски сканирования
080А 4F MOV С, A Сохранение маски в регистре С
080В DB KBDIN IN KBDIN ;Получение числа с входного устройства ;(адрес KBDIN)
080D Е6 07 ANI 00000111 ;Маскирование пяти старших разрядов
080F FE 07 CPI 00000111 ;Есть ли в трех младших разрядах 0?
0811 С2 1F08 JNZ FCOL ;Если да, то переход к метке FCOL
0814 78 MOV A, В ;Изменить содержимое
0815 С6 03 ADI3 ;счетчика номера
0817 47 MOV B, A ;клавиш
0818 15 DCRD Уменьшение счетчика рядов
0819 С2 06 08 JNZ FROW ;Если не последний ряд, то повторить ;для следующего ряда
081С СЗ 27 08 JMP DONE ;Переход к метке DONE
081F IF FCOL: RAR Определение номера разряда,
0820 D2 27 08 JNC DONE ;в котором записан 0,
0823 04 INRB ;и определение номера
0824 СЗ 1F 08 JMP FCOL ;нажатой клавиши
0827 СЗ 27 08 DONE: JMP DONE ;Конец
10.3. Однокристальные шестнадцатиразрядные микропроцессоры
Однокристальные 16-разрядные микропроцессоры имеют: расширенную систему команд (в том числе умножения, деления одно- и двухбайтных чисел); увеличенное адресное пространство до.1-16 Мбайт; дополнительные способы адресаций.
Известны следующие микропроцессоры данного класса: К1810ВМ86 (/8086), К1810ВМ88 (/8088), Z-800 (фирмы Zilog), 680X0 (фирмы Motorola) и др. Рассмотрим детально микропроцессор К1810ВМ86А.
10.3.1. Общая характеристика микропроцессора К1810ВМ86А
Микропроцессор К1810ВМ86А (далее ВМ86) используют как центральный микропроцессор в управляющих, информационных и контрольно-измерительных МПС. Микропроцессор ВМ86 (аналог/8086) имеет следующие характеристики:
10.3. Однокристальные шестнадцатиразрядные микропроцессоры 369
• схемотехнология — л-МОП, размер кристалла — 5,5 х 5,5 мм, содержит около 29000 транзисторов;
• однофазная синхронизация импульсами частотой 5 МГц от внешнего генератора;
• выпускается в корпусе типа DIP с 40 выводами;
• источник питания — плюс 5 В, потребляемая мощность — 1,7 Вт;
• число базовых команд — 111;
• количество операций сложения типа “регистр” — около 1,6 млн/с.
Структурная схема микропроцессора ВМ86 (рис. 10.20) имеет арифметико-логическое устройство, шинный интерфейс и устройство управления и синхронизации.
Рис. 10.20. Структурная схема микропроцессора ВМ86
Арифметико-логическое устройство содержит:
• арифметико-логический блок с двумя регистрами RA и RB на входах;
• блок регистров общего назначения АХ, ВХ, СХ, DX,
24 - 4-1749
370 Микропроцессоры
• регистры-указатели стека SP, базы ВР, индексные регистры SI, DS-,
• регистр флажков FL-,
• блок микропрограммного управления (БМПУ).
В состав шинного интерфейса (ШИФ) входят:
• буфер адреса/данных (БАД);
• сумматор адреса операндов SMA-,
• блок сегментных регистров CS, DS, SS, ES',
• регистры очереди команд R 1-7?6;
• указатель команд IP (instruction pointer)-,
• регистр обмена R7 с АЛУ.
Устройство управления и синхронизации (УУС) имеет в своем составе следующие схемы:
• буфера адреса/состояния (БАС);
• обработки запросов на прерывание;
• управления прямым доступом к памяти;
• выработки сигналов записи и чтения памяти или внешних портов ввода-вывода;
• обеспечения внутренней синхронизации.
Регистры очереди команд R1-R6 являются восьмиразрядными, а все остальные — шестнадцатиразрядные.
Функции арифметико-логического устройства
Арифметико-логический устройство предназначено для хранения данных и выполнения операций над ними. Блок АЛБ реализует арифметико-логические операции, в том числе сдвиги над восьми- и шестнадцатиразрядными операндами.
Регистры общего назначения (или регистры данных) АХ, ВХ, СХ, DX используются для хранения операндов и результатов операций. Они программно доступны и используются во всех арифметико-логических операциях. Во многих командах регистры данных имеют свое специфическое назначение: АХ — аккумулятор; ВХ— регистр базы; СХ— счетчик циклов; DX— регистр данных. Каждый регистр данных состоит из двух частей, к которым можно обращаться по именам АН, ВН, CH, DH (старший байт — High) и AL, BL, CL, DL (младший байт — Low). Это обеспечивает обработку байтов данных, а также программную совместимость с микропроцессорами ВМ80, ВМ85.
Регистры-указатели SP, ВР и индексные регистры используют в арифметико-логических операциях и при определении адресов операндов. Указатели стека SP и базы ВР содержат относительные адреса в границах сегмента стековой памяти. Индексные регистры SI и DI обеспечивают автоинкрементную адресацию в операциях со строками данных.
В регистре признаков FL используют только девять битов, причем пять признаков эквивалентны признакам микропроцессоров ВМ80, ВМ85: SF — знак результата; ZF — нулевой результат; AF — перенос между тетрадами младшего байта; PF— четный результат; CF — перенос из старшего разряда результата (рис. 10.21).
10.3. Однокристальные шестнадцатиразрядные микропроцессоры 371
15_____________________________________________________________0
OF DF IF TF SF ZF AF PF CF
Рис. 10.21. Регистр признаков
К новым признакам относятся: TF — разрешение пошагового режима (трассировка); IF — разрешение или запрет маскированных прерываний; DF — управление направлением автоадресации: DF = 1 — индексные регистры автоматически декрементируются, DF = 0 — инкрементируются; OF— переполнение разрядной сетки.
Функции блока интерфейса с шиной
Данный блок осуществляет связи с модулями МПС, виборку команд и данных из памяти, формирует очередь команд. Шесть восьмиразрядных регистров очереди команд 7?1-7?6 обеспечивают временное хранение шести байтов кодов команд. Блок интерфейса следит за состоянием очереди и при необходимости пополняет ее, когда другие модули системы не занимают памяти. При выполнении команд передачи управления очередь сбрасывается и после завершения перехода заполняется опять.
Микропроцессор ВМ86 может адресовать память емкостью до 1 Мбайт. Адресное пространство логически разбивается на сегменты по 64 Кбайт каждый. Начальный адрес сегмента размещается в сегментных регистрах: CS — регистр программного сегмента памяти; его содержимое вместе с содержимым указателя задает адрес следующей команды; DS — регистр сегмента данных; SS — регистр сегмента стека; ES — дополнительный сегментный регистр данных. Таким образом, содержимое сегментного регистра — это базовый адрес сегмента.
Физический адрес (ФА) памяти, поступающий на 20-разрядную ША, получают добавлением двух частей: адреса необходимого сегмента (Seg), который увеличивается на четыре влево (умножается на 16), и исполнительного (эффективного) адреса (ЭА):
ФА = 16&?£ + ЭА.
Формирование ФА в блоке ШИФ показано на рис. 10.22.
15 0
Рис. 10.22. Формирование ФА
Исполнительный адрес ЭА может быть константой (смещением в команде), содержимым регистра или ячейки памяти или суммой нескольких значений (например, двух регистров и константы), однако эта сумма является 16-разрядной (перенос игнорируется). Таким образом, значение ФА никогда не переходит границы 64 Кбайт.
24*
372 Микропроцессоры
Сегментация памяти по 64 Кбайт повышает защиту программных файлов друг от друга, однако неудобна при написании больших программ. В 32-разрядных микропроцессорах ограничения на объем сегментов памяти сняты.
Микропроцессор может обращаться как к одному байту памяти, так и к слову из двух байтов или к двойному слову — из четырех байтов.
Устройство управления и синхронизации
При описании микросхемы ВМ86 название вывода (контакта, линии) совпадает с названием передаваемого по нему сигнала.
Для увеличения коммуникационных возможностей микропроцессора используют:
• мультиплексирование во времени, при котором сигналы на одном и том же выводе имеют различное функциональное назначение;
• изменение конфигурации;
• двунаправленные выводы обмена данными;
• третье состояние (Z-состояние), в который переводится часть выводов в режиме захвата локальной шины и обработки прерываний.
Микросхема имеет вывод MN/MX для выбора конфигурации: минимальной -вывод подключается к источнику питания Ua- и максимальной — вывод соединяют с шиной земли. Минимальная конфигурация используется в простых системах, при этом микропроцессор ВМ86 сам вырабатывает все необходимые управляющие сигналы. Максимальную конфигурацию выбирают при построении сложных МПС, а управляющие сигналы получают с помощью внешних контроллеров.
Совокупность линий, связывающих микропроцессор с буферными регистрами адреса, формирователями данных и контроллерами, образуют локальную шину. Сигналы с выходов указанных модулей образуют системную шину (магистраль).
Цикл обмена информацией с магистралью состоит из четырех машинных тактов 71-74 (в некоторых командах вводится такт 75). В такте 71 на локальную шину АД15- АДО, А19-А16 выдается адрес памяти или порта, затем шина переключается на обмен данными в цикле записи (такты 72, 73, 74), или в цикле чтения (такты 73, 74). Для согласования с медленно действующей памятью или с портами между тактами 73 и 74 могут вводиться дополнительные такты ожидания Т№, на протяжении которых данные в магистрали не изменяются.
Часть сигналов микропроцессора ВМ86 аналогична сигналам микропроцессоров ВМ80 и ВМ85: CLK — синхронизация; RES — сброс; RDY — готовность к обмену; RD — чтение; WR — запись; ALE — строб адреса; DEN, DTIR, HOLD и HOLDA, INTvi INTA, М НО.
В микросхеме микропроцессора ВМ86 введены новые выводы и сигналы:
• ВНЕ — разрешение на передачу старшего байта адреса;
• MNI— вход сигнала немаскированного прерывания; _____
• TEST — состояние сигнала прерывания WAIT (при TEST-0 микропроцессор переходит в состояние ожидания до появления логического нуля, используется для согласования работы с сопроцессором);
• LOCK — блокирование системной шины (при выполнении микропроцессором команды с префиксом LOCK на выводе WR формируется логический
10.3. Однокристальные шестнадцатиразрядные микропроцессоры 373
нуль, который запрещает доступ к магистрали других модулей МПС до завершения команды).
На двухфункциональных выводах после завершения основных сигналов формируется информация про тип цикла S2, Si, So: ООО — подтверждение прерывания; 001/010 — запись / чтение ПУ; 011 — останов; 101/110 — запись / чтение памяти. Сигналы S3, S4 указывают на сегментный регистр, который используется в данном цикле: 00 — ES, 01 — SS, 10 — CS, 11 — DS.
Система команд микропроцессора ВМ86
Микропроцессор имеет 133 команды, составляющих пять функциональных групп:
• пересылки данных типа регистр-регистр, регистр-память, память-память, циклические передачи, ввод-вывод;
• арифметические: сложения, вычитания, сравнения и коррекции;
• логические: поразрядные дизъюнкции, конъюнкции, по модулем два, инверсии, арифметические и логические сдвиги вправо или влево;
• передачи управления и безусловного и условного перехода, вызова подпрограмм и возврат из них, многократного выполнения, программные и внешние прерывания;
• управления микропроцессором: останов, установка и сброс флажков, поддержка функционирования схемы в мультипроцессорных системах.
Мнемоника большинства команд микропроцессора ВМ86 совпадает с символикой команд микропроцессоров ВМ80 и ВМ85. Команды имеют длину 1-6 байт. Код операции содержится в одном или в двух первых байтах. Разряд W в первом байте команды указывает на тип операнда: 17-0 — 1 байт; W = 1 — 2 байта (слово). В двухместных командах источник данных (правый операнд) может быть константой, в этом случае приемник данных (левый операнд) является регистром или памятью. Во всех остальных случаях один из двух операндов содержится в регистре, а второй — в регистре или памяти.
Вид адресации задают во втором байте (постбайте), который имеет три поля: метода адресации MOD, регистра REG и регистра или памяти RJM. Следующие один или два байта в команде могут содержать смещение (DISP) в команде или непосредственные данные. Смещение представляется восьмиразрядным (DISP8) или 16-разрядным (DISP16) числом со знаком в дополнительном коде (рис. 10.23, а, б). Данные также записываются в виде байта DATA8 или слова 7Х47И16 (рис. 10.23, в, г). В командах из шести байтов могут быть последовательно записаны смещение и данные.
Двухбитное поле MOD показывает условия вычисления исполнительного адреса ЭА: 00 — без смещения; 01, 10 — соответственно со смещением 7)8 или 7)16; 11 — операнд находится в регистре. Трехбитное поле R/М указывает вместе с MOD способ формирования адреса ЭА, размещенного в памяти или регистре (табл. 10.11).
374 Микропроцессоры
7654 3 210765432107 0
Рис. 10.23. Формат команд: а, б— со смещением; в, г — с непосредственными данными; д — со смещением и данными
Таблица 10.11
R/M MOD
00 01 10 11
w=o W= 1
ООО (ВХ) + (Si) (ВХ) + (SI) + D8 (BX) + (ST) + D16 AL AX
001 (BX)+(DI) (ВХ) + (DI) + D8 (BX) + (DI) + D\6 CL CX
010 (ВР) + (SI) (BP) + (SI) + D8 (BP) + (S/) + D16 DL DX
011 (BX) + (DI) (BX) + (DI) + D8 (BX) + (DI) + D\6 BL BX
100 (si) (SI) + D8 (Sl) + D\6 AH SP
101 (DI) (DI) + D8 ' (Dl) + D16 CH BP
110 Прямой (BP) + D8 (BP) + D\6 DH SI
111 (ZLY) (BX) + D8 (BX) + D16 BH DI
Трехбитное поле указывает имя регистра, который содержит операнд (табл. 10.12). Отметим, что при двух операндах в команде каждый из них может адресоваться своим способом.
Таким образом, постбайт определяет два адреса: регистров в поле REG и ис-
полнительный ЭА в поле R/М с помощью MOD. В командах пересылки один из них является адресом источника данных, другой — адресом приемника. При d = 0 поле определяет источник данных, а адрес ЭА — приемник данных; при d = 1 — наоборот. В двухместных операциях при d = 1 адрес ЭА задает полный операнд и приемник данных, а поле REG — правый операнд; при d = 0 — наоборот. В ряде операций (с одним операндом или с непосредственными данными) поле КОП используют для размещения КОП.
Таблица 10.12
REG W = 1 w = o
000 AX AL
001 CX CL
010 DX DL
Oil BX BL
100 SP AH
101 x BP CH
110 SI DH
111 DI BH
10.3. Однокристальные шестнадцатиразрядные микропроцессоры 375
Способы адресации
В микропроцессоре используют следующие способы адресации.
• Неявный:
NOP — нет операций;
НЕТ — останов;
LOCK — на выходе устанавливается сигнал блокировки шины на время выполнения следующей команды.
• Прямой регистровый (операнд в регистре):
ADD AL, BL; (AL) <- (AL) + (BL) — оба операнда имеют прямую регистровую адресацию
AND АХ, ВХ; (АХ) <- (АХ) л (ВХ)
JMP СХ — безусловный переход по адресу (СХ)
• Непосредственный (второй операнд в команде):
ADD АХ, DATA16; (АХ) <- (АХ) + DATA16
SUB BL, DATA8; (BL) <- (BL) + ШГЛ8
• Прямая адресация (исполнительный адрес ЭА находится в команде):
OR 1213, DATA16; (1213) <- (1213) v DATA16
• Относительная адресация (адрес определяется в отношении регистра IP): JMP 2530; безусловный переход по адресу (IP) <- (IP) + 2530
• Индексная адресация (с регистрами SI, DI):
MOV[SI], 2СА077; (ST) <- 2СА077
MOV [DI], 5555H; (DI) <- 555577
• Индексная адресация co смещением:
MOV5[DI], 5 50177; ((DI) +5) <- 550177
• Базово-индексная адресация:
MOV AX, [5A][S7]; (AX) <- ((BX) + (SI))
• Базово-индексная адресация co смещением:
MOV BX, 100[5A][S7]; (BX) <- ((BX)(SI) + 100)
• Адресация с многоразовым повторением:
REP MOVS STR1, STR — содержимое ячейки памяти сегмента DS, к которому обращаются по адресу в регистре SI, пересылается в ячейку памяти вспомогательного сегмента ES по адресу 7)7. Содержимое индексных регистров SI и DI автоматически декрементируется или инкрементируется в зависимости от значений D.
Префикс REP перед командой MOVS вызывает декрементирование содержимого СХ и многократное повторение команды до того времени, пока СХ = 0. Затем осуществляется переход к следующей команде.
Для передачи сопроцессору кода операции или операнда предназначена команда ESC: после этой команды микропроцессор не выполняет операций, а только считывает операнды из памяти и выдает их на шину.
При выполнении команд по умолчанию используют сегменты кода CS, данных DS, стека S.S' и вспомогательного ES. При необходимости сменить сегмент в команде записывают префикс (имя нового сегмента): вместо сегмента данных используют вспомогательный сегмент.
376 Микропроцессоры
Микропроцессор К1810ВМ88 является практически полным программным и аппаратным аналогом процессора ВМ86, однако обмен данными выполняется байтами по восьмиразрядной ШД. Такая модификация обеспечивает совместимость с широким набором интерфейсных схем.
10.4. Арифметические сопроцессоры
10.4.1. Сопроцессор К1810ВМ87
Арифметические сопроцессоры предназначены для повышения производительности ЦП в 100 и более раз при выполнении операций с многоразрядными целыми и действительными числами. Сопроцессор работает только в паре с определенным микропроцессором. Сопряжение микропроцессора и сопроцессора обычно выполняют простым объединением их выводов без дополнительных микросхем. Взаимодействие двух микросхем поддерживается с помощью контроллера прерываний. Рассмотрим принцип построения и функционирования сопроцессора на основе сопроцессора К1810ВМ87.
Микросхема К1810ВМ87 (далее ВМ87) — зто однокристальный 80-разрядный арифметический сопроцессор (АСП), выполненный по n-МОП схемотехнологии. Он расположен на кристалле размером 5,5 х 5,5 мм, содержит 65000 транзисторов, потребляет мощность не более 3 Вт от источника питания плюс 5 В. Схема АСП выпускается в 40-выводном корпусе, имеет однофазную синхронизацию частотой 5 МГц от внешнего генератора.
Структура АСП содержит операционное устройство и устройство ШИФ.
Операционное устройство имеет в своем составе:
• группу из восьми 80-разрядных регистров, организованных в стек, которые служат для хранения операндов в расширенном формате;
• модуль обработка мантиссы, который имеет 68-разрядный сумматор, регистр сдвига и регистр результата и выполняет заданные операции над мантиссами операндов и формирует признаки;
• модуль обработки порядка, который выполняет действия над значениями полей порядка начальных операндов;
• постоянное запоминающее устройство констант, хранящее в расширенном формате семь часто используемых числовых констант;
• блок управления, связанный с выходом очереди байтов команд и построенный по микропрограммному принципу. Он дешифрирует очередную команду, а также формирует управляющие сигналы, определяющие режим работы АСП.
Устройство шинного интерфейса содержит группу вспомогательных регистров, буферный регистр, а также регистры очереди команд и операндов.
Сопроцессор работает только в паре с ЦП ВМ86, установленным в максимальный режим (MN/MX = 0 ), как показано на рис. 10.24.
Команды из памяти выбирает только ЦП. Сопроцессор находится в активном режиме, следит за работой ЦП и также записывает в свою очередь команды. Арифметический сопроцессор анализирует код состояния очереди команд по линиях QS1,
10.4. Арифметические сопроцессоры 377
QSQ. Как только на этих линиях появится код первого байта команды ESC = 11011, сопроцессор переходит в активный режим.
Если команда ESC указывает, что операнд является источником и расположен в памяти, то АСП перехватывает адрес и записывает операнд в свой регистр, а байты данных размещает по очереди команд. Если в команде ESC адрес определяет приемник операнда, то сопроцессор после выполнения команды записывает результат по перехваченному адресу.
Система команд АСП ВМ87 содержит 69 мнемоник и построена на основе команды ESC, которая имеет машинный код 11011, расположенный в начале каждой команды сопроцессора. Мнемоника каждой команды начинается с буквы F [float — плавающий), что позволяет различать в программе на языке ассемблера команды микропроцессора и сопроцессора.
Система команд АСП ВМ87 по функциональным признакам разбивается на четыре группы:
• передачи данных — загрузки, запоминания, обмена;
• арифметические — сравнения, анализа, сложения, вычитания, умножения и деления;
• специальные — вычисления квадратного корня, тангенса, котангенса, логарифма и др.;
• управления — инициализации сопроцессора, разрешения / запрета прерывания, обработки особых ситуаций.
Арифметический сопроцессор ВМ87 оперирует данными семи форматов: целыми двоичными числами (два байта, четыре и восемь байтов); целыми двоично
378 Микропроцессоры
десятичными числами (10 байтов); действительными числами в коротком, длинном и расширенном форматах.
10.5. Суперскалярные 32-разрядные микропроцессоры с С/SС-архитектурой
10.5.1. Скалярные и суперскалярные микропроцессоры
Процессоры с одним конвейером называются скалярными. Процессоры, имеющие два и более конвейеров, называются суперскалярными; они могут выполнять несколько команд за один машинный такт.
Современные 32-разрядные микропроцессоры имеют архитектуру CISC, RISC, Alpha, Power и др. Типовыми изделиями с CISC-архитектурой (сложные команды, много способов адресации, мало регистров общего назначения) являются микропроцессоры фирмы Intel, в том числе скалярные:
• 80386, выпущенный в 1985 году, содержит 275000 транзисторов, технология — 1,2 мкм, адресное пространство — 4 Гбайт, внутренняя очередь команд — 16 байт. Это первый 32-разрядный процессор фирмы Intel’,
• 486, появился в 1989 г., число транзисторов — 1,2 млн, технология — 1 мкм, имеет встроенный сопроцессор.
К суперскалярным микропроцессорам фирмы Intel относятся:
• Pentium, разработан в 1993 г., содержит 3,1 млн транзисторов, технология — 0,8 мкм, имеет два конвейера;
• Pentium Pro, разрабатывался одновременно с процессором Pentium. В одном корпусе размещено 5,5 млн транзисторов ядра и 15,5 млн транзисторов для вторичного кэша объемом 256 Кбайт;
• Pentium MMX, разработан в 1997 г. Имеет 4,5 млн транзисторов, технология — 0,35 мкм. Обеспечивает параллельную обработку группы операндов одной командой, что ускоряет выполнение мультимедийных задач;
• Pentium II, появился в 1997 г. Это — сокращенный вариант ядра Pentium Pro, в который ввели поддержку ММХ. Кристаллы ядра и статической памяти вторичного кэша размещены на печатной плате-картридже и закрыты общей крышкой.
В 2000 г. фирма Intel выпустила 64-разрядный процессор Itanium (кодовое название разработки Merced).
Перечисленные модели микропроцессоров имеют модификации, которые отличаются частотой работы (от 66 до 500 МГц и более), энергопотреблением, стоимостью, областью использования (стационарные, мобильные, портативные и др.).
Ряд фирм (AMD, Cyrix, IBM) выпускают процессоры, совместимые с перечисленными моделями Intel и имеют свои характерные особенности. У фирм DEC, Motorola, Texas Instruments, IBM имеются разработки более мощных процессоров с RISC-a рхите кту ро й.
10.5. Суперскалярные 32-разрядные микропроцессоры с CISC-архитектурой 379
10.5.2. Структура микропроцессора Pentium
Микропроцессор Pentium изготовлен по 0,8-микронной БиКМОП-технологии с комбинированным использованием биполярных транзисторов (для повышения быстродействия) и КМОП-структур — для уменьшения потребляемой мощности и увеличения плотности компоновки. Первый процессор Pentium был рассчитан на частоты работы 60 и 66 МГц, выпускался в корпусе типу PGA-273 (матрица 21*21), имел напряжение питания плюс 5 В и потреблял мощность 16 Вт.
Структура микропроцессора Pentium включает (рис. 10.25):
• исполнительные U- и Г-конвейеры с АЛУ каждый;
• устройство вычислений с плавающей запятой FPU\
• регистровый файл;
• раздельные кэш команд и кэш данных;
• дешифратор команд и устройство управления;
• буферы предвыборки с опережением;
• буферы прогнозирования адреса переходов;
• шинный интерфейс с 64-разрядной ШД.
Рис. 10.25. Структура микропроцессора Pentium
Целочисленные U- и Г-конвейеры имеют следующую пятиступенчатую структуру (рис. 10.26):
• PF (Pre Fetch) — предварительная выборка (предвыборка);
• Z>1 (Decode Stage!) — декодирование команд и определение возможности запуска на выполнение сразу двух команд;
• D2 (Decode Stage2) — генерация адресов операндов;
• EX (Execute) — буфер обратной записи завершения выполнения команды и возможное изменение состояния процессора;
• XI, Х2, WF — используются FPU.
Каждый конвейер имеет свое АЛУ, совокупность устройств генерации адресов на ступени D2 с использованием многоканального сумматора и интерфейса с кэшами.
380 Микропроцессоры
Рис. 10.26. Конвейеры микропроцессора Pentium
Процесс выдачи на выполнение одновременно двух команд называется четным запуском; он никак не ограничивает программирование задач. Оба конвейера функционально подобны, однако главный (7-конвейер выполняет все целочисленные операции, а К-конвейер — только простые и некоторые команды с плавающей запятой. Конвейеры работают одновременно и при четном запуске сначала в (7-конвейер подается более сложная команда, а затем в К-конвейер поступает более простая команда. Если две команды запустить нельзя, то работает (7-конвейер, а F’-конвейер простаивает. Если выполнение команды останавливается на любой ступени, то команда во втором конвейере останавливается на той же ступени (за отдельными исключениями).
Четные запуски возможны при отсутствии зависимости между двумя командами, например, при обращении к одному и тому же регистру. Команды FPU не запускаются в паре с целочисленными командами.
Каждый конвейер имеет 64-разрядный буфер записи WB, из которого информация передается в память в порядке ее генерации процессорным ядром.
Математический сопроцессор FPU реализован на трехступенчатом конвейере с плавающей запятой, который пристроен к целочисленному конвейеру. Команды FPU проходят по общему конвейеру к ступени ЕХ, после этого они проходят по ступеням XI, Х2, WE конвейера FPU. Устройство FPU поддерживает операции с операндами 32-, 64- и 80-разрядного формата.
Для хранения текущих операндов селекторов сегментов памяти и информации про состояние процессора предусмотрен регистровый файл, который содержит восемь общих регистров, шесть сегментных регистров и два регистра состояний и управления. Отдельные кэши команд и данных объемом 8 Кбайт каждый исключают конфликты при одновременном обращении к командам и данным на стадии предварительной выборки. Каждый кэш — это два двухканальных ассоциативных модуля с длиной строки 32 байта и шириной внешней шины 8 байт. Память каждого кэша разбита на восемь банков с чередованием по границам в 4 байт. Кэш данных имеет два интерфейса, по одному для каждого конвейера.
Если конвейерам необходимы данные из различных банков, то они обслуживаются одновременно в одном такте. С каждым кэшем связан свой ассоциативный буфер трансляций, который преобразовывает логические адреса в физические.
Информация в строках кэша данных имеет следующие признаки: модифицированная; принадлежащая только данному кэшу; распределенная с другими кэшами; недействительная. Это обеспечивается протоколом MESI (Modified - Exclusive -Shared - Invalid— протокол поддержки когерентности памяти при наличии кэша, названный в соответствии с состояниями строк). Кэш данных может настраиваться на алгоритм сквозной или обратной записи.
10.5. Суперскалярные 32-разрядные микропроцессоры с CISC-архитектурой 381
Кэш команд защищен от случайных записей и его строки помечаются как общие с другими кэшами команд или как недействительные.
Блок предвыборки команд имеет четыре 32-байтовых буфера, работающих вместе с буфером адресов переходов ВТВ (Branch Target Buffer). Выборка проводится последовательно до появления команды переходов, после чего блок 577? прогнозирует — будет переход или нет. Например, после выполнения каждого программного цикла (а это может быть сотни раз) вычисляется условие — вернуться в начало цикла или выйти из него. Эти два решения (пути) называются прогнозированием адресов переходов.
Блок ВТВ запоминает адрес и команду первого вхождения в цикл и предвидит, что с появлением команды перехода цикл будет продолжаться. Если прогноз правильный, то переход выполняется без задержки. В противном случае используются дополнительные три-четыре такта для вычисления условий действительного перехода и считывания следующей команды.
Внешняя шина имеет 32 линии адреса или 64 линии данных, однако внутри обрабатываются 32-разрядные данные. Эта шина обеспечивает возможность пакетных пересылок (скорость до 528 Мбайт/с) и циклов пакетного согласования информации между кэшами и ОЗУ при использовании алгоритма обратной записи.
10.5.3. Функциональные регистры
Архитектура 32-разрядных C/SC-микропроцессоров 386, 486, Pentium, Pentium Pro, Pentium II и Celeron характеризуется общей базовой программной моделью, которая охватывает набор регистров процессоров, формат команд и способы адресации, типы данных, организацию памяти, ввод-вывод, прерывания и т.д.
Набор основных функциональных регистров указанных C/SC-микропроцессоров показан на рис. 10.27.
Восемь 32-разрядных регистров общего назначения EAX, ЕВХ, ЕСХ, EDX, ESP, EBP, BSI, EDI используют для хранения данных и адресов; их младшие 16 разрядов доступны отдельно с именами АХ, ВХ, СХ, DX, &Р, ВР, SI, DI. При операциях с байтами регистры АХ, ВХ, СХ, DX разделяются на младшие байты (AL, BL, CL, DL) и старшие байты (АН, ВН, CH, DH). Доступ к отдельным байтам обеспечивает дополнительную гибкость при операциях с данными.
31 15 0 15 0
АН АХ AL ЕАХ CS
ВН ВХ BL ЕВХ SS
СН СХ CL ЕСХ DS
DH DX DL EDX ES
SP ESP FS
ВР ЕВР GS
S1 ESI Регистры
DI EDI сегментов
Регистры общего назначения 31 0 31 0
EIP IP ЕFLAGS
Рис. 10.27. Основные функциональные регистры CISC-микропроцессоров
382 Микропроцессоры
Шесть 16-разрядных регистров сегментов CS, SS, DS, ES, FS и GS содержат значения селекторов, адресующих текущие сегменты памяти. Селектор в CS обеспечивает обращение к текущему сегменту команд, селектор в SS — к текущему сегменту стека, селектор в DS, ES, FSvt GS — к текущим сегментам данных.
В указатель команд EIP входит смещение следующей выполняемой команды относительно базы сегмента кода. При 16-разрядной адресации используются IP (младшие 16 бит). Регистр флажков EFLAGS содержит признаки результата выполнения команды, управляет обработкой исключений и маскированных прерываний.
Разряды, определенные для процессоров ВМ80, ВМ85 и ВМ86, имеют одинаковые обозначения и функции.
Процессоры могут работать в одном из двух режимов:
• реальной адресации (или просто — реальный режим — Real Mode), который полностью совместим с 8086 и может адресовать до 1 Мбайт физической памяти;
• защищенный режим виртуальной адресации (или просто — защищенный режим — Protected Mode). В этом режиме адресуется до 4 Гбайт памяти, через которые при использовании механизма страничной адресации может отображаться до 4 Тбайт виртуальной памяти для каждой задачи.
Существенным дополнением способов адресации является режим виртуальной адресации процессора 8086 VM (Virtual 8086 Mode). Он устанавливается битом VMb регистре флажков и является особенным состоянием защищенного режима, в котором процессор функционирует как 8086, однако может адресовать до 4 Мбайт физической памяти.
10.5.4. Типы данных
Процессоры непосредственно поддерживают (используют как операнды) знаковые и беззнаковые целые числа, строки битов, байтов, цифр и символов, указатели и числа з плавающей запятой. Рассмотрим эти типы данных подробнее:
• бит (Bit) — единица информации; задается адресом слова и своим номером в слове;
• битовое поле (Bit Field) — группа до 32 смежных битов, расположенных не более, чем в четырех байтах;
• битовая строка (Bit String) — набор смежных битов длиной до 4 Гбит;
• числа без знака и со знаком:
• байт (Byte) — 8 бит; слово (Word) — 16 бит; двойное слово (Double Word) — 32 бит; учетверенное слово (Quadre Word) — 64 бит.
Отрицательные числа хранятся в памяти в дополнительном коде; единичное значение старшего бита определяет отрицательное число.
Действительные числа в формате с плавающей запятой обрабатываются сопроцессором FPU. К ним относятся следующие данные:
• одинарная точность — 32 бит (23 бит отведено для мантиссы, 8 бит — для порядка);
• двойная точность —64 бит (52 бит — мантисса, 11 бит — порядок);
• повышенная точность — 80 бит (64 бит — мантисса, 15 бит — порядок).
10.5. Суперскалярные 32-разрядные микропроцессоры с CISC-архитектурой 383
Двоично-десятичные BCD-числа:
• 8-битные упакованные, содержат две десятичные цифры в одном байте;
• 8-битные неупакованные, содержат одну десятичную цифру в байте;
• 80-битные упакованные.
Процессоры используют указатели для обращений, например, к подпрограммам. Близкий (внутрисегментный) указатель NEAR — это 32-битное смещение от базы текущего сегмента. Далекий (межсегментный) 48-битный указатель FAR (16-битный селектор и 32-битное смещение) применяется при передачах управления в другой сегмент.
В процессорах х86, как правило, слова записываются в двух смежных ячейках памяти, начиная с младшего. Адресом слова является адрес его младшего байта. Двойное слово записывается в четырех смежных байтах; его адрес определяется адресом младшего байта. Такой порядок адресации называется Little-Endian Memory Format.
В других семействах процессоров применяют обратный порядок Big-Endian Memory Format, в котором адресом слова или двойного слова является адрес его старшего байта, а младшие байты размещаются в последующих адресах. Для взаимного преобразования форматов слова имеется инструкция XCHG, а для двойного слова — BSWAP.
10.5.5. Форматы команды
Обобщенный формат команд показан на рис. 10.28.
КОП MODR/M SIB Смещение Операнд
1 или 2 байт 0 или 1 байт 0 или 1 байт 0, 1, 2 или 4 байт 0, 1, 2 или 4 байт
Рис. 10.28. Обобщенный формат команд
Команды содержат от одного до 11 байт. В среднем длина команды составляет 4-5 байт. Рассмотрим назначение основных полей формата команд.
Код операции КОП занимает 1 или 2 байта. Перед КОП в отдельных случаях записывается один или несколько префиксных байтов, модифицирующих выполняемую операцию. Во многих командах арифметико-логических операций и пересылок значение бита W в первом байте КОП определяет разрядность операндов: W = 0 — операции с байтами; W = 1 — операции с 16- или 32-разрядними операндами.
Разрядность слов (16 или 32 бит) определяется режимом работы микропроцессора и устанавливается битом D в дескрипторе сегмента кода. При выполнении отдельных команд разрядность операндов изменяется соответствующим префиксом.
В ряде команд первый байт содержит поле REG (три бита) или поле SREG (два или три бита), которые определяют соответственно регистр операндов (табл. 10.13) или сегментный регистр (табл. 10.14).
Байт адресации MOD RIM содержит три поля (рис. 10.29, а). Поля MOD и R/M задают адрес одного из операндов, который хранится в регистре или в ячейке памяти.
384 Микропроцессоры
Таблица 10.13 Таблица 10.14
Поле REG Разрядность операндов SREG 2 бита SREG 3 бита Регистр сегмента
8 16 32
ООО 001 010 011 100 101 111 AL CL DL BL АН СН ВН АХ СХ DX ВХ SP ВР DI ЕАХ ЕСХ EDX ЕВХ ESP ЕВР EDI 00 01 10 11 000 001 010 011 ES CS SS DS
100 101 FS GS
7 654321 0 7 6543210
MOD REGAUQM R М \ SS INDEX BASE
a б Рис. 10.29. Форматы байтов: а — MOD R/М; б — SIB
Байт SIB содержит поля INDEX, BASE и SS. Они определяют соответственно регистры, используемые в качестве базовых и индексных, а также масштабный коэффициент для модификации значения индекса (рис. 10.29, б).
В поле смещения задают значение смещения длиной 8, 16, или 32 бит. При выполнении операций с непосредственными данными один из операндов записывают в последних байтах команды.
10.5.6. Защищенный режим. Дескрипторы
Защищенный режим обеспечивает защиту аппаратных и программных ресурсов одной задачи от возможного влияния другой. Основным защищаемым ресурсом является память, в которой хранятся команды, данные и системные таблицы.
Защита памяти основана на сегментации. Это — механизм, с помощью кото-' рого память разделяется на отдельные области адресного пространства определенного назначения. Такая область с множеством ячеек памяти со смежными адресами называется сегментом.
Сегменты памяти задают слова-селекторы, которые операционная система загружает в сегментные регистры. В режиме реальной адресации прикладная программа может ошибочно записать в сегментный регистр селектор чужого сегмента. В защищенном режиме такая ситуация исключена — доступ к своему сегменту обеспечивается как селектором, так и предварительно сформованными таблицами дескрипторов сегментов (их значения прикладная программа не может изменить).
Дескриптор — это восьмибайтовая структура данных, используемых для определения свойств сегментов: базовый адрес сегмента BASE и его размер LIMIT, его назначение TYPE (тип), характеристики защиты и дополнительная информация. Обобщенный формат дескриптора сегмента показан на рис. 10.30.
Рассмотрим назначение отдельных полей дескриптора сегмента.
Поле базового адреса BASE длиной 32 бит занимает байты 3, 4, 5 и 8 формата и определяет начальный адрес сегмента в линейном адресном пространстве 4 Гбайт.
10.5. Суперскалярныв 32-разрядные микропроцессоры с CISC-архитектурой 385
Байт 4 Байт 3 Байт 2 Байт 1
31 24 23 16 15 8 7 0
BASE LIMIT
15 -0 15 -0
Байт 8 63 56 Байт 7 55 52 51 48 Байт 6 - AR 47 44 40 Байт 5
BASE 31-24 G D X и LIMIT 19-16 Р DPL S TYPE А BASE 23-16
Рис. 10.30. Формат дескриптора
Поле границы LIMIT длиной 20 бит занимает байты 1, 2 и младшую тетраду байта 7. Граница сегмента задает размер сегмента. Если в байте 7 бит гранулярности (дробности) G = 0, то максимальный размер сегмента составляет 1 Мбайт; при G = 1 максимальный размер сегмента равен 4 Мбайт.
В байте управления доступом AR {Access Rights) поля имеют следующие назначения:
• А — бит обращения; при А = 0 — к сегменту не было обращения; если А = 1, то селектор данного сегмента загружен в регистр сегмента;
• TYPE — трехбитное поле типа, которое определяет целевое использование сегмента и операций, которые в нем могут выполняться (например, сегменты коду, стека, данных);
• DPL — двухбитное поле атрибутов привилегий сегмента;
• S — системный бит;
• Р — бит присутствия в памяти; при Р = 1 сегмент отображен в физической памяти; при Р = 0 сегмента в памяти нет, поэтому поле базового адреса и лимита не используется.
В старшей тетраде байта 7 биты имеют следующее назначение:
• U — бит пользователя (системного программиста);
• X— резерв, содержит лог. 0;
• D — определяет разрядность адресов и операндов: по умолчанию: D = 0 — 16 бит; D = 1 — 32 бит.
Процессоры имеют специальные средства, которые в защищенном режиме не допускают несанкционированного доступа к памяти. Двухбитное поле DPL устанавливает четыре уровня привилегий с номерами от нуля (максимальная привилегия) до трех (минимальная привилегия). Наиболее защищенным является ядро операционной системы (инициализация работы, управление доступом к памяти и т.д.), а наименее защищены прикладные программы.
Определенное в адресном пространстве памяти множество дескрипторов называется таблицей дескрипторов. Каждый дескриптор занимает в памяти 8 байт. Количество дескрипторов в таблице — произвольное, однако не может превышать максимальных значений 8192; при этом необходимый объем памяти для размещения таблицы равен 8192 8 = 64 Кбайт. Порядок размещения дескрипторов в таблице роли не играет.
25 - 4-I749
386 Микропроцессоры
Дескрипторы размещают в общесистемных таблицах дескрипторов трех типов:
• GDT — глобальная таблица дескрипторов;
• LDT — локальная таблица дескрипторов;
• IDT—таблица дескрипторов прерываний.
Глобальная таблица дескрипторов используется совместно всеми задачами, выполняемыми в данном компьютере.
Локальна таблица LDT определяет сегменты, доступные только конкретной задаче. Таблицы LDT создаются при необходимости по одной для каждой задачи. Для однозадачных систем таблица LDT может отсутствовать (вся информация содержится в глобальной таблице).
Таблица прерываний IDT содержит дескрипторы специальных объектов, которые определяют точки входа процедур обработки прерываний и особых случаев.
Доступ к таблице дескрипторов обеспечивают специальные регистры (рис. 10.31):
• GDTR — регистр глобальной таблицы дескрипторов;
• LDTR — регистр локальной таблицы дескрипторов;
• IDTR — регистр таблицы дескрипторов прерываний.
47 0
Г раница Базовый адрес GDTR
Граница Базовый адрес IDTR
15- 0
63 16 SELECTOR LDTR
LIMIT BASE ATRIBUTE
Рис. 10.31. Форматы регистров дескрипторов
Регистры GDTR и IDTR имеют одинаковый формат и функциональное содержимое полей. Регистр LDTR имеет специфическую структуру, содержащую:
• 16-битное поле SELECTOR, содержимое которого выполняет функцию селектора сегментного регистра;
• 64-битное поле собственно локального дескриптора с полями базы BASE, границы LIMIT и атрибутов ATRIBUTE (то есть, формат обычного дескриптора).
Для доступа к глобальной таблице GDI процессор загружает селектор в один из сегментных регистров CS, SS, DS и др. Формат селектора показан на рис. 10.32.
15 3210
Индекс n RPL
Рис. 10.32. Формат селектора
В двухбитном поле RPL записывается номер привилегии, который требует задача. Однобитное поле Л задает тип таблицы дескрипторов: при Л = 0 — глобальная, при Л = 1 — локальная. Поле индекса длиной 13 бит задает смещение в адресе таблицы дескриптора. Процессор автоматически умножает значение индекса на 8 (три нуля справа), складывает с базовым адресом, содержащимся в регистре GDTR, и считывает необходимую таблицу. Одновременно выполняется проверка,
10.5. Суперскалярные 32-разрядные микропроцессоры с CISC-архитектурой 387
чтобы значение умноженного индекса не превышало границы, заданной в регистре GDTR. Если это условие не выполняется, то программа прерывается.
Дескриптор локальной таблицы LDT расположен в глобальной таблице GDT. Для доступа к локальному дескриптору процессор предварительно загружает поле SELECTOR регистра LDTR. Поле SELECTOR определяет смещение адреса локального дескриптора в таблице GDT. Значение этого поля складывается с базовым адресом глобального регистра и образует адрес локального дескриптора. После проверки допустимых границ 8 байт локального дескриптора считывается и записывается в основной части регистра LDTR (он размещен в процессоре). Таким образом, доступ к локальному дескриптору выполняется быстрее, чем к глобальному.
Считанный дескриптор автоматически засылается в соответствующий “теневой" регистр быстродействующей кэш-памяти (рис. 10.33). Каждый сегментный регистр (CS, SS и др.) имеет функционально связанные теневые регистры дескрипторов, что ускоряет доступ к данным.
Регистры дескрипторов
Рис. 10.33. Теневые регистры дескрипторов сегментов
Команды загрузки селекторов используют прикладные программы. Команды загрузки глобальных и локальных регистров доступны только сегментным программам.
Защита памяти с помощью сегментации не позволяет:
• использовать сегменты не по назначению;
• нарушать права доступа (например, запись в сегмент, предназначенный только для чтения);
• адресовать сегменты, выходящие за пределы сегмента;
• изменять содержимое таблицы дескрипторов без достаточных привилегий.
10.5.7. Способы адресации в процессорах с CISC-архитектурой
При сегментной организации памяти 32-разрядный физический адрес ячейки памяти формируется сложением базового адреса сегмента и относительного адреса ячейки внутри сегмента.
Эффективный адрес операнда ЭА формируется в зависимости от полей MOD, RIM и SAB.
Значение ЭА образуется арифметическим сложением трех компонентов:
• содержимого базового регистра ЕВР или ЕВХ\
• содержимого индексного регистра ESI или EDT,
• 8-, 16- или 32-разрядного смещения <78, 716 или 732, заданного в команде.
25*
388 Микропроцессоры
В 32-разрядных процессорах способы адресации являются развитием и модификацией методов адресации процессора 8086. Перечислим основные способы адресации.
• Непосредственная — операнды задаются в байтах команды.
• Регистровая — операнд выбирается из регистра, который определяется полем R/M.
• Непрямая регистровая — адрес операнда находится в регистрах общего назначения.
• Прямая — относительный адрес задается байтами команды.
• Базовая — относительный адрес формируется сложением содержимого базового регистра ВХ или ВР и смещения в команде.
• Базово-индексная — относительный адрес образуется сложением содержимого базового и сегментного регистров.
• Базово-индексная со смещением — это вариант базово-индексной адресации с добавлением смещения.
• Индексная с масштабированием — относительный адрес образуется добавлением масштабированного индекса (умножение на 1, 2, 4 и 8) и 32-разрядного смещения.
• Базово-индексная с масштабированием — относительный адрес образуется добавлением масштабированного индекса и базы.
• Базово-индексная со смещением и масштабированием — это вариант предыдущего способа с дополнительным добавлением смещения.
• Относительная — адрес формируется как сумма содержимого регистра IR, которая соответствует текущему моменту и смещению.
Структура формирования 32-разрядного физического адреса в памяти показана на рис. 10.34.
Рис. 10.34. Формирование адреса памяти 32-разрядного процессора в защищенном режиме
10.5.8. Команды суперскалярных CISC-микропроцессоров
Система суперскалярных C/SC-микропроцессоров в сравнении с Intel 80486 существенно расширена и модифицирована. Увеличена разрядность адреса и one-
10.5. Суперскалярные 32-разрядные микропроцессоры с CISC-архитектурой 389
рандов, создана более гибкая система адресации, используются новые типы команд и данных. Систему команд разделяют на функциональные группы.
• Команды пересылки данных (всего около 40) позволяют передавать константы или переменные между регистрами и памятью, а также портами ввода-вывода.
• Команды двоичной арифметики (около 15) выполняют все арифметические действия с байтами, словами и двойными словами.
• Команды десятичной арифметики (около 10) позволяют оперировать с неупакованными и упакованными двоично-десятичными данными. Операции с этими числами требуют применения команд коррекции форматов.
• Команды логических операций (4) реализуют все функции булевой алгебры с байтами, словами и двойными словами.
• Логические и циклические сдвиги (всего 10) выполняют над содержимым регистров или операндов в памяти. Число позиций, на которое осуществляется сдвиг, можно задавать операндом и другими способами.
• Команды обработки битов и байтов (26) позволяют проверять и устанавливать значение указанного операнда или бита.
• Команды передачи управления (около 30) осуществляются с помощью команд безусловных и условных переходов. Команда вызова процедур CALL передает управление в точку перехода, при этом адрес следующей за ней команды хранится в стеке.
• Строковые операции (24) выполняются с операндами в памяти.
• Операции с флажками (всего 13) позволяют изменять значения отдельных флажков, а также сохранять их значения в стеке и восстанавливать эти значения.
• Команды загрузки указателей (5) обеспечивают загрузку указателей из памяти в регистр общего назначения и соответствующий сегментный регистр.
• Команды математического сопроцессора FPU (92) выполняют операции с действительными, целыми и двоично-десятичными числами, представленными в формате с плавающей запятой.
• Системные команды (32) — это операции управления защитой, загрузкой и хранением регистров дескрипторов, проверки привилегий, тестирования, управления кэшированием памяти, останова процессора и др.
Количество команд в каждой группе указано только для базовых мнемоник.
10.5.9. Обобщенная характеристика суперскалярных CISC-микропроцессоров
Поколение суперскалярных C/SC-микропроцессоров началось с процессора Pentium и характеризуется:
• большим количеством сложных машинных команд различной разрядности и преимущественно двухоперандного формата (у команд R/SC — трехопе-рандный формат);
• наличием предвыборки, конвейера команд и динамического прогнозирования условных переходов;
• большим числом способов адресации;
390 Микропроцессоры
• использованием всего восьми регистров общего назначения (в RISC — как минимум 32);
• широким использованием микрокоманд;
• раздельными кэшами команд и данных и их заполнением в пакетном режиме;
• встроенным сопроцессором FPU.
Архитектура Pentium является оптимизированной, поскольку имеет свойства современных RISC-микропроцессоров:
• аппаратную реализацию простых команд, выполняемых за один машинный такт;
• суперскалярность и 64-разрядную внешнюю шину данных;
• приблизительно одинаковую производительность конвейерного FPU для операций с одинарной, двойной и расширенной точностью;
• прогнозирование переходов, наличие 64- и 256-разрядных шин на кристалле;
• эффективные средства обеспечения многопроцессорности и др.
Таким образом, Pentium относится к C/SC-архитектуре, однако имеет много свойств RISC-микропроцессоров.
Следующее поколение CISC-микропроцессоров отсчитывается от выпуска Pentium Pro, Pentium II, Pentium III и Celeron. Они имеют следующие основные архитектурные усовершенствования:
• возможность выполнения команд не в порядке их размещения в программе;
• встроенный вторичный кэш объемом до 2 Мбайт;
• появление двух независимых внутренних шин: одну — для связи с памятью, вторую — для обмена с вторичным кэшем;
• управление энергопотреблением;
• наличие встроенных средств контроля операций по модулю два;
• расширение возможностей построения многопроцессорных МПС с симметричной архитектурой.
Развитие современных микропроцессоров определяется конкуренцией между фирмами, развивающими направления CISC- и R/SC-архитектур.
10.6. Суперскалярные микропроцессоры с RISC-архитектурой
10.6.1. Основные положения
R/SC-архитектура является основой современных рабочих станций и серверов. Элементы архитектуры с упрощенной системой команд применяли в суперкомпьютерах Cray. В 1980 г. были разработаны машины R/SC-I и R/SC-II. Их главными идеями было отделение медленной памяти от быстродействующих регистров и использование регистровых окон. Годом позднее было опубликовано описание машины MIPS, основным аспектом которой была эффективная реализация конвейерной обработки с помощью детального планирования компилятором его загрузки.
10.6. Суперскалярные микропроцессоры с RISC-архитектурой 391
Окончательно понятие архитектуры RISC в современном виде сформировалось на базе проектов трех компьютеров — RISC, 801 фирмы IBM и MIPS.
Е? общем R/SC-архитектура имеет следующие черты:
• Сравнительно небольшой (сокращенный) набор команд, которые больше всего применяются в прикладных программах;
• трехоперандный формат команд с длиной операндов 32 или 64 разряда,
• мало способов адресации;
• большой регистровый файл (16, 32, 64 и более регистров);
• аппаратная реализация простых команд за один машинный такт;
• обращение к памяти с помощью специальных команд загрузки-запоминания, обрабатывающих группу регистров;
• широкое использование регистровых окон при переключениях задач;
• суперскалярность — за один машинный такт выполняются две и более команд;
• предвидение переходов;
• наличие средств поддержки многопроцессорности.
В целом структура R/SC-процессоров содержит;
• два и более исполнительных устройств, в том числе с плавающей запятой;
• раздельные кэши команд и данных;
• блок прогнозирования переходов;
• интерфейс с 64-разрядной внешней шиной данных.
Разработкой и промышленным выпуском R/SC-процессоров занимается ряд известных фирм. Они присваивают своим изделиям собственные названия архитектур, например:
• POWER — фирма IBM, PowerPC — фирмы Motorola, Apple и IBM;
• Alpha — фирма DEC;
• MIPS — фирма MIPS Technology и др.
Рассмотрим особенности построения и функционирования процессоров с архитектурой POWER.
10.6.2. Архитектура POWER
Архитектура POWER — это развитие идей, которые были заложены в основу процессора IBM 801 в направлении реализации суперскалярной обработки, сокращения длины конвейера и времени выполнения команд и приоритетной ориентации на эффективное выполнение операций с плавающей запятой.
Архитектура POWER во многих отношениях является традиционной R/SC-архитектурой, которая имеет фиксированную длину команд, простые способы адресации, операции регистр-регистр и трехоперандный формат команд. Однако архитектура POWER имеет дополнительные свойства, отличающие ее от других архитектур:
• Набор команд основан на идее суперскалярной обработки. В процессоре команды распределяются между тремя независимыми исполнительными устройствами: переходов, с фиксированной и плавающей запятой. Команды одновременно поступают и заканчиваются в этих трех устройствах.
392 Микропроцессоры
• Архитектура POWER расширена несколькими “смешанными” командами: групповой загрузки и запоминания регистров, автоинкрементной адресации, операций с полями битов и др.
• Архитектура переходов в POWER организована по принципу “предварительного просмотра условных переходов”.
• Архитектура POWER определяет расширенные свойства регистра условий (флажков). Для этого вводится специальный бит в коде операции в каждой команде для модификации регистра условий, а также используются восемь регистров флажков. Это расширяет количество битов условий.
После первой реализации архитектуры POWER (1990 г.) появились процессоры POWER2 и P0WER2+.
Многокристальный набор POWER2 состоит из восьми полузаказных микросхем:
• блок кэш-памяти команд — 32 Кбайт;
• устройство целочисленной арифметики АЛУ — содержит два конвейера и два блока регистров. В каждом блоке имеется 32 регистра длиной 32 бит. Выполняет целочисленные и логические операции и все обращения к памяти;
• устройство операций с плавающей запятой FPU — содержит два конвейера для выполнения операций с двойной точностью, а также 54 регистра длиной 64 бит;
• четыре блока кэш-памяти данных — всего 256 Кбайт;
• блок управления памятью.
Этот набор кристаллов содержит 23 млн транзисторов на площади 12,17 см2, выполнен по КМОП-схемотехнике с проектными нормами 0,45 мкм, на частоте 66,5 МГц потребляет мощность 65 Вт.
Система PowerPC использует однокристальную реализацию архитектуры POWER для построения малых машин. На основе архитектуры Power PC последовательно были разработаны кристаллы 601 (для настольных рабочих станций), 603 (для портативных машин), 604 (для высокопроизводительных настольных систем), 620 (для серверных конфигураций с 64-битовой организацией). В этих процессорах были внесены несколько изменений в направлениях:
• упрощения архитектуры с целью реализации на однокристальных процессорах;
• исключения команд, препятствующих повышению тактовой частоты;
• ввода выполнения команд без очереди;
• расширения средств поддержки симметричной многопроцессорной обработки.
Процессор Power PC 603 содержит (рис. 10.35):
• устройство обработки переходов и выборки команд;
• целочисленное устройство АЛУ;
• устройство для операций с плавающей запятой FPU\
• кэш-память для данных и команд емкостью по 8 Кбайт каждый;
• набор из 32 целочисленных регистров РОН;
• набор из 32 регистров РПЗ для чисел с плавающей запятой;
• устройство очереди и распределения команд;
• буфер завершения команд;
• буферы записей и загрузки, а также интерфейс с внешними ША и ШД.
10.6. Суперскалярные микропроцессоры с RISC-архитектурой 393
Рис. 10.35. Структура процессора Power PC 603
Поскольку Power PC 603 является суперскалярным микропроцессором, то он может выдавать в исполнительные устройства до трех команд и завершать их выполнение в одном машинном такте. Для увеличения производительности процессор допускает внеочередное выполнение команд. Кроме этого, он обеспечивает программируемые режимы снижения потребляемой мощности.
При обработке данных команды распределяются между пятью исполнительными устройствами в заданном программой порядке. Если зависимости между командами отсутствуют, то они выполняются мгновенно.
Целочисленное АЛУ выполняет большинство команд за один такт. Устройство FPU имеет конвейерную организацию и выполняет операции с плавающей запятой как с одинарной, так и с двойной точностью.
Команды условных переходов обрабатываются устройством переходов. Если условия перехода доступны, то решение о направлении перехода принимается сразу; иначе выполнение следующих команд продолжается с допущением. Пересылки данных между кэш-памятью данных и регистром РПЗ обрабатываются устройствами загрузки и запоминания.
После завершения выполнения команды в исполнительном устройстве ее результаты направляются в буфер завершения команд. После этого данные последовательно записываются в соответствующий регистровый файл.
394 Микропроцессоры
Контрольные вопросы
1. Что такое процессор?
2. Охарактеризуйте архитектуру процессора.
3. Нарисуйте и поясните структуру процессора.
4. Что такое микропроцессор?
5. Назовите характеристики микропроцессора.
6. Что относится к статическим и динамическим параметрам микропроцессора?
7. Как подразделяют микропроцессоры по конструкции?
8. Что входит в микропроцессорные комплекты?
9. Назовите типы микропроцессоров.
10. Перечислите технико-экономические преимущества микропроцессоров.
11. Назовите виды архитектур микропроцессора.
12. Охарактеризуйте программно управляемый обмен информацией.
13. Нарисуйте и поясните структуру однокристального восьмиразрядного микропроцессора.
14. Охарактеризуйте список команд восьмиразрядного микропроцессора.
15. Нарисуйте и поясните структуру 16-разрядного микропроцессора.
16. Поясните особенности суперскалярных микропроцессоров.
17. Охарактеризуйте R/SC-архитектуру.
18. Охарактеризуйте C/SC-архитектуру.
19. Нарисуйте и поясните структуру микропроцессора Pentium.
20. Нарисуйте и поясните структуру процессора Power PC 603.
11.1. Общая характеристика микропроцессорных систем 395
Глава 11
Интерфейсы микропроцессорных систем
11.1. Общая характеристика микропроцессорных систем
Микропроцессорной системой называют совокупность информационновычислительных средств, куда входит один или несколько микропроцессоров.
Для построения МПС требуется ограниченный набор микроэлектронных ресурсов, поскольку реализация большинства функций возлагается на программное обеспечение. Таким образом, МПС — это цифровые системы обработки информации и управления, функциональные возможности которых определяются программным обеспечением, а взаимосвязь с внешней средой осуществляется ПУ. На основе МПС реализуют микрокомпьютеры, персональные компьютеры, информационные сети, системы искусственного интеллекта и т.д.
Как и компьютер, МПС содержит следующие устройства:
• процессор, выполняющий основные функции управления и обработки информации;
• запоминающие устройства на полупроводниковых микросхемах, предназначенные для хранения программ и данных;
• устройства ввода-вывода, которые обеспечивают взаимосвязь с внешними устройствами.
Устройства МПС объединены между собой внутрисистемным интерфейсом и взаимодействуют по адресному принципу (рис. 11.1).
1Г.. II -'П""...."Т
। ША
i ШУ
J ПУ
--- I ШД
Рис. 11.1. Структура магистральной МПС
Конкретный состав и структура МПС определяется ее назначением. В однопроцессорных системах все функции обработки информации и управления выполняет один процессор. В многопроцессорных системах имеется ряд равноправных процессоров или один центральный и несколько подчиненных для решения специализированных задач (арифметики с плавающей запятой, операций ввода-вывода). В многопроцессорных МПС может быть общая системная память и локальная (резидентная) память отдельных процессоров.
396 Интерфейсы микропроцессорных систем
Микропроцессор в МПС обрабатывает информацию трех типов: данные, адреса и команды программы. Для выполнения этих функций микропроцессор содержит: средства обработки данных и адресов и их хранения в регистрах; схемы микропрограммного управления, синхронизации и обеспечения режимов работы.
Внутрисистемный интерфейс чаще всего реализуют на основе общей системной шины, по которой передаются адреса, данные и команды. Системная шина может иметь отдельные шины для адресов и данных или совмещенные шины адре-сов/данных, передаваемых мультиплексным способом.
В однопроцессорных МПС системная шина управляется одним процессором (шина одного пользователя). В многопроцессорных МПС системная шина используется в режиме распределения времени. В них может применяться многошинная структура: общая системная шина и несколько резидентных для отдельных процессоров.
Микропроцессорные системы делятся на универсальные, специализированные и многопроцессорные (рис. 11.2).
Рис. 11.2. Состав микропроцессорных систем
Универсальные МПС ориентированы на решение широкого класса задач. Наиболее распространены микро-ЭВМ — компьютер малых размеров на основе микропроцессора, полупроводниковой памяти и средств связи с внешней средой. При настольном исполнении микро-ЭВМ имеет единую несущую конструкцию, пульт управления и источники питания. Ряд одно- или двухплатных микро-ЭВМ встраивают в технические системы, в которых они выполняют функции управления, контроля и диагностики. На основе модификаций микро-ЭВМ созданы следующие компьютеры:
• персональные (ПЭВМ), рассчитанные на массового пользователя;
• рабочие станции — автоматизированные рабочие места для конструкторов;
• серверы — выполняют часть функций обслуживания группы пользователей (распределение ресурсов памяти, принтеров, баз данных);
11.1. Общая характеристика микропроцессорных систем 397
• мейнфреймы (мейнфрейм — синоним понятия “большой универсальный компьютер”);
• Х-терминалы — комбинации бездисковых рабочих станций и стандартных терминалов;
• кластерные системы — объединения машин с единым механизмом управления и программного обеспечения. Кластерные МПС очень надежные в работе — при отказе одного процессора его функции перераспределяются между остальными процессорами. В общем кластерные системы обеспечивают распределение ресурсов, высокую готовность, удобство расширения конфигурации.
Многопроцессорные МПС предназначены для распараллеливания вычислительного процесса, что обеспечивает высокую производительность системы.
Специализированные МПС ориентированы на решение специализированных задач управления или обработки информации в составе технических систем (микрокомпьютеры), цифровой обработки сигналов (процессоры сигналов), обработки графики (графические процессоры). Их аппаратные средства реализуют в виде одноплатных конструкций или наборов плат, объединенных внутрисистемным интерфейсом.
Универсальные МПС ориентированы на решение широкого круга вычислительных задач. Работают они в автономном режиме и содержат широкий набор ПУ.
Многопроцессорные системы обеспечивают функционирование многих процессоров под совместным управлением.
Основными техническими характеристиками МПС являются: разрядность, емкость памяти, производительность, число внешних устройств и их пропускная способность, функции системы и состав программного обеспечения.
11.1.1. Программное обеспечение микропроцессорных систем
Программное обеспечение МПС содействует эффективному функционированию и использованию системы в разных областях науки и техники. Основными составляющими программного обеспечение являются операционные системы (ОС), пакеты прикладных программ (ППП) и комплексы программ техничного обслуживания (КПТО).
Основными компонентами ОС являются (рис. 11.3):
• управляющая программа, которая планирует ресурсы МПС, обеспечивает взаимодействие с внешней средой, выявляет неисправности технических средств;
• программа обслуживания, которая выполняет вспомогательные функции (копирование данных, подготовка носителей данных и др.);
• средства генераций, которые настраивают МПС на конкретный состав и .конфигурацию технических средств, и программы обеспечения необходимых режимов работы.
При описании работы управляющей программы важным является понятие процесса обработки данных (задач) — совокупность действий одной или нескольких программ над распределенными ресурсами процессоров, памяти, периферии.
398 Интерфейсы микропроцессорных систем
Рис. 11.3. Состав программного обеспечение МПС
Основными режимами обработки данных являются режимы распределения времени, реального времени (в темпе сравнительно со скоростью процесса), интерактивный, диалоговый и пакетной обработки. Основными понятиями системы программирования являются язык программирования, транслятор и компилятор программ, программный модуль.
Язык программирования — это формализованный язык представления программ. Важными языками программирования являются машинный, ассемблер, проблемно ориентированный. Машинный язык представляет программы в форме, готовой к выполнению. Язык ассемблера (автокод или мнемокод) машинноориентированный: его операторы аналогичны командам конкретной машины. Проблемно-ориентированные языки предназначены для решения определенного класса задач (языки Паскаль, Турбо-Паскаль, Си, Пролог и др.).
Трансляция программ — это преобразование программы из одного языка программирования в равноценную на другом языке. Компиляцией программы называют трансляцию ее на язык, близкий к машинному. Частичным видом компиляции является ассемблирование — компиляция программ из языка ассемблера. Форма представления программы после компиляции называется объектным кодом.
Средства, преимущественно программные, которые выполняют трансляцию или компиляцию, называются соответственно трансляторами или компиляторами. Основными видами компиляторов являются кросс-компилятор (транслирует из авто
11.1. Общая характеристика микропроцессорных систем 399
кода одной МПС в объектный код другой), препроцессор (преобразовывает исходную программу перед последующей компиляцией), отладочный компилятор (средства спецификации различных процедур отладки).
Пакеты прикладных программ — это функционально завершенный комплекс программных средств, ориентированный на решение определенного логично целостного класса задач. Они развивают ОС в прикладном направлении.
Пакет прикладных программ классифицируют по следующим признакам:
• области использования и классу решаемых задач. Это — ППП, расширяющие возможности ОС (обеспечивают нестандартные режимы эксплуатации МПС), общего назначения (программы для решения прикладных научно-технических и экономических задач);
• ориентации на определенный метод или процедуру обработки (методоориентированные, технологически или проблемно ориентированные);
• способу реализации и принципам функционирования (библиотеки подпрограмм, специальные языки, программные системы).
Методо-ориентированные пакеты программ предназначены для решения задач числового анализа, статистических задач. К проблемно ориентированным относятся пакеты для решения задач планирования, оперативного управления, материально-технического снабжения и т.д.
Библиотека прикладных программ — это набор отдельных программ, предназначенных для решения некоторого класса задач; каждая программа из библиотеки имеет самостоятельное значение и применяется для решения несложных задач.
Программная система предназначена для решения сравнительно большой по объему типовой задачи.
Комплекс программ технического обслуживания обеспечивает процедуру контроля работы и диагностики МПС.
11.1.2. Понятие архитектуры микропроцессорной системы
Архитектура МПС в широком понимании включает понятие многоуровневой организации системы, в том числе процессора, памяти, системной магистрали и средств ввода-вывода данных. Относительно МПС многоуровневая архитектура определяется как распределение функций системы, точнее — очерчивание границ между уровнями.
Архитектура первого уровня характеризует функции, выполняемые МПС, и средства ее взаимодействия с внешней средой: язык оператора, графический интерфейс, управление заданиями и программным обеспечением.
В программном обеспечении выделяют уровни логического управления ресурсами (базой данных, файлами, виртуальной памятью, сетевой телеобработкой) и физического (внешней и оперативной памятью и процессами, осуществляемыми в МПС). Второй уровень отображает границу между программным обеспечением и аппаратурой, а затем — распределение функций между отдельными частями физической системы, например:
• центральным процессором и каналами ввода-вывода;
• каналами и контроллерами внешних устройств;
400 Интерфейсы микропроцессорных систем
• контроллерами и внешними устройствами (терминалами, модемами, НГМД и др.).
Архитектура таких уровней часто называется архитектурой физического ввода-вывода. В узком понимании архитектура МПС — это архитектура набора команд. Она служит границей между аппаратурой и программным обеспечением и представляет собой часть системы, которую видит программист или разработчик компиляторов.
На современном этапе развития МПС используют две основные архитектуры наборов команд:
• с полным набором команд CISC (Complete Instruction Set Computer);
• с сокращенным набором команд RISC (Reduced Instruction Set Computer).
Архитектура CISC является стандартом для мирового рынка микрокомпьютеров, изготовленных фирмой Intel.
Для C/SC-микропроцессоров характерны:
• большое количество машинных команд, некоторые из которых загружены семантически аналогично операторам высокоуровневых языков программирования. Команды выполняются за много тактов;
• большое количество методов адресации и форматов,команд и данных разной разрядности. Преимущественно используются двухадресные форматы команд;
• сравнительно малое количество регистров общего назначения (от восьми до 16);
• широкое использование микрокоманд, конвейеризация команд и прогнозирование переходов. Наличие команд обработки данных типа регистр-память;
• отсутствие жесткого ограничения на доступ операндов к памяти;
• раздельное использование кэша команд и данных и заполнение кэш-памяти в пакетном режиме.
Архитектура RISC является основой современных рабочих станций и процессоров. Она применена также при создании серии суперкомпьютеров фирмы Cray Research.
Для архитектур RISC, RISC\, RISCW характерны:
• небольшое число простых команд, которые аппаратно реализуются за один машинный такт;
• команды имеют фиксированную длину и формат, что упрощает логику их декодирования;
• достаточно большой регистровый файл (32 и более регистров). Это обеспечивает хранение значительного объема данных в регистрах, что упрощает роботу компилятора по распределению регистров под данные;
• как правило, используется трехадресный формат.
В последних разработках фирмы Intel (Pentium, Pentium II) используют идеи R/SC-микропроцессоров, поэтому отличия между RISC- и C/SC-архитектурами постепенно стираются.
11.2. Общая характеристика интерфейсов 401
11.2. Общая характеристика интерфейсов
Современные МПС имеют магистрально-модульную организацию, основанную на принципах агрегирования и унификации. Модульность (агрегирование) — это разделение МПС на простые функционально и конструктивно законченные блоки, называемые модулями, например: модуль микропроцессора, модуль памяти и т.д.
Унификация состоит в оптимизации состава модулей, связей между ними и в их конструктивных оформлениях.
Связь устройств МПС одного с другим осуществляют с помощью сопряжений, называемых интерфейсами. Интерфейс — это совокупность информационнологических и конструктивных средств и требований (правил), которые обеспечивают оптимальный алгоритм взаимодействия всех модулей МПС.
Информационно-логические требования определяют структуру и состав линий и сигналов, способы кодирования и форматы данных, адресов и команд, протоколов обмена для разных режимов и фаз работы. Они непосредственно влияют на пропускную способность, надежность обмена и аппаратурные расходы.
Электрические требования задают необходимые статические и динамические параметры сигналов на сигнальных линиях интерфейса: уровни напряжений, длительность фронтов, нагрузочная способность, помехоустойчивость и др.
Конструктивные требования указывают на тип соединительных элементов и распределение линий по их контактам, геометрические размеры плат, каркаса и другие признаки.
Сигнальная линия — это проводник (электрическая цепь), который физически соединяет источник и приемник информации. Совокупность сигнальных линий, по которым передают сигналы одинакового функционального назначения, называют шиной. Различают шины данных, адреса и управления.
Интерфейс должен обеспечивать:
• построение машин с переменным составом оборудования (переменной конфигурацией, открытостью архитектуры);
• параллельное во времени выполнение программ и процедур ввода-вывода;
• увеличение скорости обмена информацией;
• упрощение и стандартизацию программирования операций ввода-вывода и их независимость от особенностей периферийных устройств,
• автоматическое распознавание и реакцию ЦП на разнообразные ситуации в ПУ (готовность устройства, отсутствие носителя данных, нарушение нормальной работы).
Особенно актуальным является решение этих задач для машин большой производительности, которые содержат сотни различных внешних устройств.
Периферийные устройства соединяются с интерфейсом МПС при помощи контроллеров КПУ, которые обеспечивают выполнение каждым ПУ своих специфических функций.
Термин “интерфейс” применяют как к аппаратуре МПС, так и к ее программному обеспечению.
26 - 4-1749
402 Интерфейсы микропроцессорных систем
• 11.2.1. Классификация интерфейсов
Интерфейсы классифицируют по следующим основным признакам.
По функциональному назначению интерфейсы подразделяются на такие типы:
• внутренние — внутриплатные, межплатные и системные;
• внешние — для периферийных устройств, для локальных сетей, для распределенных систем управления (рис. 11.4).
Рис. 11.4. Классификация интерфейсов по функциональному назначению
По направлению обмена информацией различают следующие интерфейсы:
• симплексные — обмен в одном направлении (рис. 11.5, а);
• полудуплексные — поочередный обмен в двух направлениях (рис. 11.5, б);
• дуплексные — одновременный обмен в двух направлениях (рис. 11.5, в);
• мультиплексные — обмен реализуется с помощью общей магистрали (шины), в которой в каждый момент времени взаимодействуют источник и приемник информации (рис. 11.5, г).
a б в
Рис. 11.5. Направления обмена информацией:
а — симплексное; б — полудуплексное; в — дуплексное; г — мультиплексное
Все устройства (модули), подключаемые к каналу передачи данных, называются абонентами (АБ).
По структуре связей между абонентами МПС различают интерфейсы с радиальным, кольцевым, каскадным и магистральным подключениями (рис. 11.6). В радиальных интерфейсах (рис. 11.6, а) к ЦП с помощью двунаправленных шин и заданного приоритета подключаются абоненты (рабочие станции, удаленные периферийные устройства, схемы промышленной автоматики). Сообщения между абонентами передаются через ЦП, который выполняет функции концентратора и обеспе
11.2. Общая характеристика интерфейсов 403
чивает независимость и параллельность работы абонентов. Радиальный интерфейс — логически простой, однако требует больших аппаратных затрат. Кроме этого, его живучесть зависит от надежности ЦП.
а б
г
Рис. 11.6. Структура соединений абонентов: а — радиальная; б — кольцевая; в — каскадная; г — магистральная
В кольцевом интерфейсе (рис. 11.6, б) каждый абонент связан с двумя соседними. В кольце могут одновременно циркулировать несколько сообщений от источников к приемникам на основе заданных способов адресации и управления. При расширении МПС дополнительные модули включаются в кольцо системы. Недостатком кольцевых интерфейсов является сложность взаимодействия абонентов.
В каскадных интерфейсах (рис. 11.6, в) абоненты соединены по цепочке и обслуживаются в порядке их подключения к линиям интерфейса. Каскадные интерфейсы характеризуются малым числом линий и ограничением по скорости.
В магистральных интерфейсах (рис. 11.6, г) используется коллективная шина, которую также называют магистралью. Информация, передаваемая по магистрали, доступна всем абонентам, которые к ней подключены. Обычно в каждый момент времени только один абонент может быть источником информации. Приоритет абонентов определяется арбитром шины (АШ). Магистральный интерфейс является гибким, экономичным и используется в большинстве системных интерфейсов МПС.
По способу передачи информации во времени различают следующие интерфейсы:
• синхронные — с фиксированной длительностью операций обмена;
• асинхронные — с переменной длительностью операций обмена;
• синхронно-асинхронные — с комбинированным соединением двух способов.
По разрядности передаваемых данных различают интерфейсы с параллельным (словами), последовательным (битами) и параллельно-последовательным обменами.
26*
404 Интерфейсы микропроцессорных систем
К классификационным признакам интерфейсов МПС также относят:
• организацию прерываний (векторный или последовательный опрос) и прямого доступа к памяти;
• способ арбитража доступа модулей к шинам (параллельный, последовательный, циклический);
• число линий адресации данных, управления, синхронизации;
• длину и тип линий связи (проводники, радиоканал, волоконно-оптический тип);
• максимальное число абонентов, которые могут одновременно подключаться к шине;
• способ адресации устройств периферии — с собственным адресным пространством (характерно для изделий фирмы Intel) или с отображением на адресное пространство памяти (используется в изделиях фирмы DEC).
11.2.2. Системные интерфейсы
В МПС широко используются параллельные системные стандартные интерфейсы, в которых унифицируются: форматы команд и данных и процедуры обмена; алгоритм функционирования; состав и типы линий связи; быстродействие передачи; конструктивные требования; допустимые расстояния между модулями системы; возможность расширения и совместимость с предыдущими интерфейсами.
Для обеспечения высоких скоростей обмена информацией используют асинхронные мультиплексные интерфейсы с параллельным способом передачи информации. К ним относятся: восьмиразрядные — Microbus; 16-разрядные — Unibus; Q-bus; Multibus I; 32-разрядные — Vercabus. Основные технические характеристики этих интерфейсов представлены в табл. 11.1.
Таблица 11.1
Технические характеристики Microbus Z-bus Unibus Q-bus Multibus I Vercabus
Число линий: общее 37 56 43 86 260
данных 8 8 16 16 16 32
адресных 16 — 18 — 20 35
управления 13 20 — 11 —
Скорость передачи, Кбит/с 103 — 2103 800 104 105
Длина линий, м — — 15 15 — —
Число абонентов - — 20 15 —
Интерфейс Multibus I (стандарт российский — И41, зарубежный — IEEE-796) предназначен для построения микро-ЭВМ, ПЭВМ и сосредоточенных многопроцессорных МПС. Он обеспечивает:
• четыре операции обмена — запись в память или порт, чтение памяти или порта;
• прямой доступ к памяти и обработки прерываний программы;
11.2. Общая характеристика интерфейсов 405
• использование двух независимых адресных пространств для адресации ячеек памяти и внешних устройств (их портов);
• функционирование на основе принципа — ведущий (задатчик) и ведомый (исполнитель).
Сигналы на линиях интерфейса активны при низких уровнях напряжений, назначения линий и сигналов на них совпадают.
Магистраль содержит следующие основные функциональные группы линий и сигналов на них (цифры даны в шестнадцатеричной системе счисления):
• передачи адреса: ADRE-ADRI) с возможностью расширения до ADRV1 - ADR1A на дополнительном разъединителе. Сигнал BHEN позволяет считывание старшего байта данных, а сигнал ALE разрешает запись адреса во внешний регистр-фиксатор;
• передачи данных: DATE-DAT® обеспечивает двунаправленную передачу слов или байтов данных. Информация на ШД может выдаваться только задатчиком. Линии PAR1 и PAR2 предназначены для передачи сигналов четности младшего и старшего байтов данных. На линии INX1, INX2 подают сигналы запрета обращения к ОЗУ или ПЗУ соответственно;
• управление передачей данных: MWTC, IOWC — запись в память или порт; MRDC, IORC — чтение памяти или порта, ХАСК — подтверждение передачи;
• синхронизации и арбитража приоритетов: BCLK, CCLK — синхронизация шины и системных модулей; BUSY— шина занята; BREQ, CBRQ — запрос и совместный запрос шины; BPRN, BCR0 — вход и выход разрешения приоритета;
• управления состояниями системы; INIT — начальная установка; HALT— останов; AUX RESET — дополнительный сброс; WAIT — ожидание;
• управление электропитанием и его контроль: ACLO — снижение напряжения в сети или ее неисправность; PFIN — прерывание при неисправности электропитания; MPRQ — защита памяти.
Электропитание: плюс 5 В — девять линий питания; плюс 12 В —три линии дополнительного питания; плюс 12 В, минус 12 В — по две линии дополнительного питания; GND — 23 линии заземления.
К интерфейсам Multibus I относят системную магистраль персонального компьютера IBM PC/AT-bus.
Интерфейс Multibus II используют в многопроцессорных 16- и 32-разрядных МПС. Он содержит три основные и три дополнительные магистрали.
Основная магистраль системы — параллельная система iPSB (Parallel System Bus), предназначенная для организации обмена данными с производительностью до 40 Мбайт/с. Магистраль имеет пять групп линий, возможен обмен восьми-, 16-, 24- и 32-разрядными данными. Адреса передаются по 32-разрядной мультиплексной ШАД.
406 Интерфейсы микропроцессорных систем
Магистраль iLBX обеспечивает быстродействующий локальный обмен данными с памятью. Асинхронная немультиплексная шина iLBX предназначена для расширения ШВВ. Асинхронная мультиплексная магистраль MDMA обеспечивает прямой доступ к отдаленной памяти.
Магистраль iSSB предназначена для создания последовательной системной шины. Локальная шина связи с модулями промышленной телеуправляемой системы использует магистраль BitBus.
В наше время большинство стандартных системных интерфейсов МПС оптимизированы для конкретных типов микропроцессоров.
11.3. Интерфейсные микросхемы
В МПС широко используют интерфейсные микросхемы, реализующие типовые функции, а именно: генерацию тактовых импульсов, запоминание адресов, обеспечение двунаправленного обмена данными между модулями системы, выработку сигналов управления записью-считыванием памяти или в портах, арбитража, приоритетного доступа к системной шине многих микропроцессоров и т.д.
В составе МПК КР580 и К1810 имеется большой набор интерфейсных микросхем (аналогов изделий фирмы Intel). Рассмотрим некоторые из них.
11.3.1. Генератор тактовых импульсов
Генератор тактовых импульсов обеспечивает синхронизацию работы МПС. В составе МПК К1810 имеется микросхема К1810ГФ84 (далее ГФ84), предназначенная для формирования серий синхроимпульсов, сигналов сброса и готовности системы на основе микропроцессора ВМ86.
Генератор ГФ84 характеризуется: схемотехнологией — ТТЛШ; частотой синхронизации — до 80 МГц; напряжением питания — плюс 6 В и потребляемой мощностью — 0,7 Вт; амплитудой импульсов — 4,5 В (рис. 11.7).
Рис. 11.7. Структура ГТИ К18ЮГФ84
11.3. Интерфейсные микросхемы 407
Микросхема ГФ84 содержит схемы задающего генератора G, делители частоты на три DIV3 и два DIV2, которые вместе с логическими элементами вырабатывают прямоугольные импульсы CLK, PCLK и синусоидальный сигнал OSC. Они предназначены соответственно для тактирования работы микропроцессора ВМ86, портов
периферии или внешних устройств системы. Сигналы синхронизации могут форми-
роваться из колебаний основной входам Л иА2 (рис. 11.8).
частоты кварцевого резонатора, подключенного к
ГФ84
XI
XI
TANK OSC ----
F/C
EFI CLK -----
CSYN
RDY\
RDY2
AEN2
+5 В
Рис. 11.8. Генератор тактовых импульсов ГФ84: а — условное графическое обозначение; б — схема подключения кварцевого резонатора
С помощью ZC-фильтра, соединенного с входом TANK, можно изменить частоту колебаний резонатора.
Генератор может синхронизироваться и от внешнего источника сигналов, который подключается ко входу EF1. Режим синхронизации задают уровнем сигнала на входе F!С\ при высоком — от внешнего генератора, при низком — от кварцевого генератора. В обоих режимах синхронизации частота сигналов CLK вдвое больше частоты PCLK, однако в три раза меньше частоты OSC или внешнего генератора (рис. 11.9, а).
a
Рис. 11.9. Временные диаграммы сигналов: а — синхронизации; б — готовности
CLK
RDY1 ‘ AEN1 ' RDY'
>
б
408 Интерфейсы микропроцессорных систем
Вход CSYN служит для синхронизации нескольких ГТИ системы: если CSYN = 1, то на выходах CLK и PCLK устанавливаются высокие уровни; при CSYN = 0 на выходы CLK и PCLK поступают синхросерии.
Схема формирования сигнала сброса RESET имеет на входе триггер Шмидта, а на выходе — D-триггер, который формирует фронт сигнала RESET по спаду CLK. Обычно ко входу RES подключается 7?С-цепь, которая обеспечивает автоматическое формирование сигнала сброс при включении источника напряжения.
Схема формирования сигнала готовности к обмену данными RDY построена с учетом шины Multibus. Она имеет две пары одинаковых сигналов RDY1, AEN1 и RDY2, AEN'l, объединенных схемой И ИЛИ:
REDY = REDYX AEN\ v RE DY 2 AEN2.
D-триггер формирует фронт сигнала RDY по спаду CLK и подает его на вход готовности микропроцессора.
11.3.2. Буферные регистры и двунаправленные шинные формирователи
Буферные регистры и двунаправленные шинные формирователи обеспечивают в МПС соответственно временное хранение (фиксацию) адреса с выходов ЦП и двунаправленный обмен данными между локальной и системной шинами. В составе МПК КР580 для выполнения этих функций имеется регистр КР580ИР82 (далее ИР82) и шинный формирователь КР580ВА86 (далее ВА86).
Восьмиразрядный буферный регистр ИР82
Восьмиразрядный буферный регистр ИР82 с тремя состояниями характеризуют следующие параметры: схемотехнология — ТТЛШ; число транзисторов на кристалле — 524; напояжение питания — плюс 5В и потребляемая мощность 1 Вт.
Регистр ИР82 имеет восемь триггеров, стробированная запись данных в которые выполняется по сходам D77-DZ0 при значении сигнала STB = 1 (рис. 11.10). Прямые выхо ды D07-D00 регистра подключены к буферным схемам SW тремя состояниями.
При значении сигнала ОЕ-Q буферы открываются и данные передаются на выход. Если ОЕ = 1, то буферы устанавливаются в Z-состояние. Сигнал ОЕ не влияет на состояние триггеров и функцию записи информации.
Шинный формирователь ВА86 обеспечивает двунаправленный обмен данными между локальной и системной шинами, усиление сигналов и отключение от шины в определенные моменты времени. Микросхема ВА86 характеризуется следующими параметрами; ТТЛШ схемотехнологией, числом транзисторов на кристалле — 567; напряжением питания — плюс 5 В и потребляемой мощностью — 1 Вт.
Шинный формирователь (ШФ) имеет двунаправленные входы-выходы А7-А0 и B7-BQ, вход Т для управления направлением обмена и вход ОЕ для снятия Z-состояния определенного направления переходу (рис. 11.11).
Каждый разряд формирователя содержит две схемы SW с тремя состояниями каждая. При ОЕ = 1 все SW-схемы находятся в Z-состоянии, при ОЕ = 0 и Т = 0 об-
11.3. Интерфейсные микросхемы 409
мен данными выполняется в направлении от А кВ. При ОЕ - 0 и Т = 1 обмен дан-
ными выполняется от В к А.
Рис. 11.10. Буферный регистр ИР82: а — условное обозначение; б — функциональная схема
Рис. 11.11. Шинный формирователь ВА86: а — условное обозначение; б — функциональная схема
410 Интерфейсы микропроцессорных систем
Формирователь потребляет от ЦП ток около одного миллиампера, а может отдавать в системную шину десятки миллиампер.
11.3.3. Контроллер системной шины
Для управления обменом данными в МПС используется системный контроллер. В составе МПК К1810 имеется микросхема К1810ВГ88 (далее ВГ88), которая реализует функции системного контроллера шины (КШ). Микросхема ВГ88 имеет следующие технические характеристики: схемотехнология — ТТЛШ; частота синхронизации — 8 МГц; напряжение питания — плюс 5 В; потребляемая мощность — 0,85 Вт.
Контроллер шины реализует в МПС следующие функции: дешифрацию состояний микропроцессора, формирование управляющих и командных сигналов для локальных и системных шин; выработку сигналов управления ШФ, буферными регистрами и контроллером прерываний. В состав КШ входят (рис. 11.12): дешифратор состояний ДшС, схема управления СхУ, формирователь командных Ф1 и управляющих Ф2 сигналов.
Командные сигналы интерфейса
CEN юв
MCE/PDEN
Сигналы управления
Рис. 11.12. Структура контроллера шины ВГ88
Функциональное назначение входных сигналов КШ: S2, 51, S0 — состояния микропроцессора; CLK — синхронизация от ГТИ; AEN— разрешение выдачи сигналов по командным выводам; CEN — разрешение выдачи командных сигналов и сигналов управления DEN, PDEN; ЮВ — управление режимом работы.
Выходные сигналы КШ по функциональным признакам распределены на командные сигналы интерфейса и сигналы управления.
К командным сигналам интерфейса относятся: MRDC — чтение памяти; MWTC — запись в память; IORC — ввод из порта; IOWC — вывод в порт; AMWC , AIOWC — предупреждающие подготовительные сигналы записи в память или вывода в порт; INTA — подтверждение прерывания.
К выходным управляющим сигналам АШ относятся: DT/R — выбор направления передачи данных через ШФ; DEN — разрешение выдачи данных; ALE —
11.3. Интерфейсные микросхемы 411
строб записи адреса в буферный регистр; MCE/PDEN — в режиме работы с системной шиной используется как строб чтения номера ведомого контроллера прерываний. При работе с ШВВ используется для управления состоянием “включен” ШФ.
Основной информацией для работы КШ является код состояния S2, 51, 50, который декодируется дешифратором (табл. 11.2).
Таблица 11.2
Код состояния Состояние Управляющие сигналы
50 54 52
0 0 0 Подтверждение прерывания INTA
0 0 1 Чтение УВВ IORC
0 1 0 Запись УВВ IOWC, ALOWC
0 1 1 Останов
1 0 0 Выборка команды MRDC
1 0 1 Чтение памяти MRDC
1 1 0 Запись в память MWTC, AMWC
1 1 1 Холостое состояние -
Входные сигналы ЮВ, CEN, AEN определяют два режима работы контроллера — с СШ и ШВВ. Режим работы с СШ устанавливается при ЮВ = 0, при этом КШ формирует командные сигналы и сигналы управления ALE, DEN, DT / R фиксаторами адреса и ШФ.
Типовая схема включения КШ в однопроцессорных системах на основе ЦП ВМ86 в максимальном режиме показана на рис. 11.13.
На входах формируются постоянные значения AEN = 0 и CEN = 1, которые разрешают выдачу командных сигналов и сигналов управления. На выходе MCE/PDEN при таком включении формируется сигнал MCE. Он используется в МПС с каскадированием контроллеров прерываний для определения момента передачи номера ведомого контроллера, который запрашивает прерывание. Сигнал ALE определяет момент фиксации адреса в буферных регистрах ИР82. Выходные сигналы DT/ R и DEN используются для управления работой ШФ. Сигнал DEN имеет высокий уровень, поэтому он должен инвертироваться перед подачей на вход ОЕ микросхемы ВА86.
Системна шина в этом случае работает только с памятью и ЦП получает доступ к ней по сигналу AEN от арбитра шин, а командные сигналы для портов не используются.
412 Интерфейсы микропроцессорных систем
Рис. 11.13. Типовая схема подключения ВГ88 к ЦП ВМ86
11.3.4. Арбитр шин
В многопроцессорной МПС приоритетный доступ к СШ обеспечивает АШ. В составе МПК К1810 имеется микросхема К1810ВБ89 (далее ВБ89), которая реализует функции арбитра.
В структуру АШ входят (рис. 11.14):
• схема арбитра АРБ и дешифратор состояний ДшС;
• схема управления арбитражем СхУ и блок шинного интерфейса БИФ.
В АШ входы и сигналы на них имеют следующее функциональное назначение:
• S2, 51, 50—сигналы состояний микропроцессора;
• CLK—вход синхронизации;
• BCLK — вход системной синхронизации;
• INIT — начальная установка (сброс) АШ;
• LOCK — блокирование СШ;
• RESB — выбор резидентной шины;
• ЮВ — выбор режима работы с ШВВ;
• CRCK — сигнал совместного блокирования СШ;
• AQST — любой запрос;
• SB!RB — выбор системной или локальной шины.
11.3. Интерфейсные микросхемы 413
<k— IOB_ _|ч— SB/RB
АШ
S1
S2 BPRO i—
-- CLK ___
—qBCLK BUSY О—
—QINTT
—0LOCKCBRQ о—
--RESB
-- ЮВ
—QCRCK
--AQST ___
--SB/RB ANE 6—
a
Puc. 11.14. Арбитр шин ВБ89: а — структура; б — условное графическое обозначение
Функциональное назначение выходов и сигналов на них:
• BREQ,BPRO,BUSY,CBRQ — используются для организации схемы определения приоритетов;
• AEN — разрешение СШ.
В многопроцессорной МПС с помощью АШ организовывают следующие схемы обработки приоритетов: последовательные; параллельные с фиксированным приоритетом; параллельны с циклично изменяемыми приоритетами. В многопроцессорной МПС каждый ЦП имеет свой АШ.
В схеме последовательного арбитража приоритетный выход BPQ0 арбитра с высшим приоритетом подключается ко входу BPRN арбитра с низшим приоритетом (рис. 11.15)
BPRQ BPRN BPRQ BPRN BPRQ
.....................
। ЛШ21
BPRN
+5В
| AHLV |
—BCLK jtjt
— J' CBRQ
BUSZ
Puc. 11.15. Схема последовательного арбитра
Вход BPRN арбитра с наивысшим приоритетом подключается к земле. Если нескольким АШ необходим доступ к СШ, то сигнал BPR0 = 0 у арбитра с наивысшим приоритетом поступает на вход BPRN соседнего арбитра и запрещает ему захват шины.
Схема последовательного определения приоритета наиболее проста и не требует дополнительных микросхем. Однако при таком соединении приоритет к последнему АШ приходит с задержкой. Поскольку доступ к СШ должен осуществлять
414 Интерфейсы микропроцессорных систем
ся за один период сигнала BCLK, то при частоте 10 МГц можно последовательно соединить не более трех АШ.
Схема параллельного определения приоритетов позволяет подключиться к 16 арбитрам, для их организации дополнительно используются приоритетный шифратор и дешифратор (рис. 11.16).
Рис. 11.16. Схема параллельного арбитража
Сигнал с выхода запроса шины BPRQ каждого АШ подается на вход приоритетного шифратора, который формирует двоичный код номера запроса с наивысшим приоритетом. Этот код декодируется дешифратором и поступает на вход BPRN выбранного АШ, разрешая ему захват шины.
Схема циклического определения приоритетов аналогична схеме параллельного арбитража, однако она имеет более сложные дополнительные микросхемы, с помощью которых приоритеты обрабатываются по очереди.
Во всех схемах арбитража имеется линия BUSY, на которую выставляется низкий уровень арбитром, запрашивающим СШ. Если СШ свободна, то арбитр, который получил доступ к шине, формирует сигнал AEN = 0. После этого для выбранного КШ разрешается выдавать на СШ командные сигналы с КШ, а также адрес и данные соответственно с фиксаторов и формирователей.
В зависимости от конфигурации МПС и сигналов на входах ЮВ, RESB можно задавать четыре режима работы с АШ. Сигнал на входе SYSB! RESB выполняет вспомогательную роль — определения условий доступа к СШ. ___
Режим работы с СШ задают сигналы ЮВ = 1, RESB = 0, вход SB! RB игнорируется. При этой комбинации сигналов ЦП может подключиться только к одной СШ (рис. 11.17).
При исполнении цикла обращений к СШ арбитр вначале получает приоритетный доступ, затем формирует сигнал AEN = 0 и подает его на схему шинного интерфейса СШ1 (она содержит КШ, фиксатор адреса и формирователь данных). Арбитр удерживает СШ и использует адресное пространство памяти (то есть, управляется сигналами MRDC и MWTC).
Режим работы с СШ памяти и резидентной ШВВ задают сигналы ЮВ = RESB = = 0 и SB!RB = 0. При этой комбинации сигналов ЦП подключается к СШ, которая
11.3. Интерфейсные микросхемы 415
обслуживает только память, и к резидентной ШВВ, которая выполняет обмен данными с периферией (рис. 11.18)
Рис. 11.18. Схема подключения АШ
АШ к системной шине
к СШ и резидентной ШВВ
Рис. 11.17. Схема подключения
В этом режиме сигнал AEN = 0 вырабатывается арбитром только при необходимости ЦП обратиться к памяти и наличии приоритетного разрешения. Доступ к резидентной ШВВ предоставляется процессору всегда при исполнении команд ввода IN и вывода OUT сигналом PDEN = 0. Схема СШ2, которая связывает локальную шину с резидентной ШВВ, не содержит системного контроллера ВГ88. Его функции выполняет КШ в блоке СШ1, установленный в режим ЮВ = 1. При этом командные сигналы управления памятью (MRDC, MWTC) поступают на СШ, а управления вводом-выводом (IORC, IOWC), а также INTA — на резидентную ШВВ.
Детальная схема расширенного ЦП в режиме обслуживания СШ и резидентной ШВВ показана на рис. 11.19.
____Режим работы с системной и резидентной шинами задают сигналами ЮВ = RESB = 1. Он используется в МПС с системной и резидентной шинами и в каждой из них обеспечивается доступ к памяти и УВВ (рис. 11.20).
Сигнал AEN, который обеспечивает доступ к СШ, вырабатывается при SB!RB = 1 (при условии, что АШ получил разрешение на доступ). Для формирования сигналов доступа к системной SB / RB = 1 или к резидентной SB/ RB = 0 шине используют дешифратор адреса ДША, подключенный к СШ.
Режим работы с СШ памяти, резидентной шиной и резидентной ШВВ задают сигналы ЮВ = 0 и RESB = 1. Эту комбинацию сигналов используют в МПС, где наряду с СШ, которая обеспечивает доступ только к памяти, имеется две резидентные шины. Одна из них выполняет доступ как к памяти, так и к УВВ, вторая — только к УВВ.
416 Интерфейсы микропроцессорных систем
ГФ84
ВМ86
ВМ89
TANK
XI RESB
RDY
CLK
F!C PCLK
,1019-ЛОО
RES RDY СЕК
LOCK*
~S2- so :
|— RESB
7ob*
LOCK
V S2-S0
AEN
—9----
4-5В
, LORC c HJWC
.. ВГ88
—о------
AEN
S2- SO
- CLK IORC /UWC
МИ-7С
A-'--.--;
MRDC
PDEN dtCr DEN
IIJBB
Адрес
Данные
с=з
ИР82
ИР87
Рис. 11.19. Схема ЦП в режиме обслуживания СШ и резидентной ШВВ
ВА87>
<2>
ВА86
<2>
Адрес
=>
Данные
СШ
ОЗУ
УВВ
СШ1 ft
ЛШ
ВМ86 £
СШ1 £
5'2
AEN
SB/RB е-
____ЮВ RESB +5B-1
} ДША
Резидентная ШВВ
CEN
ОЗУ
ОЗУ
Puc. 11.20. Схема использования АШ с системной и резидентной шинами
11.4. Программируемые интерфейсные контроллеры 417
11.4. Программируемые интерфейсные контроллеры
11.4.1. Общая характеристика программируемых интерфейсных контроллеров
Периферийные устройства подключаются к компьютеру с помощью специализированных адаптеров или контроллеров. Адаптер — это средство сопряжения некоторого внешнего устройства с определенной шиной МПС. Контроллер также выполняет подобные функции, однако он способен на самостоятельные действия после получения команд от машины. Сложный контроллер может иметь и собственный процессор. Сегодня часто термины “адаптер” и “контроллер” считают почти синонимами. Все внешние интерфейсы имеют в своем составе адаптер или контроллер.
Микропроцессорные комплекты КР580 и К1810 имеют следующие программируемые интерфейсные контроллеры (адаптеры):
• контроллер прерываний — К1810ВН59 (ВН59);
• контроллер ПДП — КР580ВТ57 (ВТ57);
• программируемый таймер — КР580ВИ53 (ВИ53);
• параллельный интерфейс — КР580ВВ55 (ВВ55);
• последовательный интерфейс — КР580ВВ51 (ВВ51).
11.4.2. Программируемый контроллер прерываний
Во время выполнения текущей (фоновой) программы в компьютере возникают заранее неизвестные события, которые требуют мгновенной реакции на них (авария в системе, готовность ПУ к передаче данных, деление на нуль и др.). Реакция состоит в прерывании фоновой программы, переходе к подпрограмме обслуживания данного события и возврате программы в предыдущее состояние. Каждое событие, требующее прерывания, сопровождается сигналом — запросом прерывания. Прерывания — важная архитектурная особенность машины, позволяющая эффективно организовать работу процессора при наличии нескольких параллельных процессов.
Для технической реализации прерываний используют программируемые контроллеры прерываний (ПКП). К ПКП относится микросхема ВН59 (аналог модуля 8259) со следующими характеристиками: схемотехнология — л-МОП, напряжение питания — плюс 5 В, потребляемая мощность — 1 Вт? Структура ПКП ВН59 показана на рис.11.21.
В состав ПКП ВН59 входят :
• двунаправленный восьмиразрядный буфер данных БД;
• блок управления (входы CS, WR, RD, AD, INTA, INI},
• регистры запросов прерываний IRR (входы IR7-IR0), управляющих слов РУС, состояния ISR, маскирования IMR',
• блок каскадирования (вход SP, двунаправленные выходы CAS3-CAS0)',
• блок обработки приоритетов (БОП).
Программируемый контроллер прерываний воспринимает запросы на прерывания от восьми ПУ; за счет каскадирования с помощью выходов CAS3-CAS0 число входов для запросов может увеличиваться до 64.
27-4-1749
418 Интерфейсы микропроцессорных систем
IR7 — IR0
Puc. 11.21. Структура ПКП BH59
CS
WR
RD AO
INTA INT
CASO
CAS1
CAS2
SP
Запросы, поступающие на входы IR7-IR0, фиксируются в регистре запросов прерывания IRR. Блок обработки приоритетов определяет наиболее приоритетный запрос Блок управления формирует сигнал запроса прерывания INT, который поступает на такой же вход микропроцессора. Если в микропроцессоре прерывание разрешено, то он отвечает контроллеру сигналом INTA, поступающим на такой же вход ПКП. В результате на ШД от КПК видается сначала первый байт — код команды CALL (переход на подпрограмму обработки прерывания), а затем второй и третий байты, определяющие адрес подпрограммы. После этого разряд регистра запросов IRR, на который поступил запрос с высшим приоритетом, обнуляется и устанавливается единица в соответствующем разряде регистра состояний ISR.
С помощью загрузки управляющих слов инициализации ICW в режиме настройки и операционных слов OCW при обслуживании запросов ПКП может программироваться на такие режимы обслуживания прерываний:
• приоритеты внешних устройств фиксированы;
• циклический сдвиг приоритетов;
• специального маскирования;
• последовательного опроса ПКП.
В режиме с фиксированными (неизменными) приоритетами вход IRO имеет наивысший приоритет, а вход IR7 — самый низкий. Программируемый контроллер прерываний всегда обслуживает запросы с высшим приоритетом. Если во время обслуживания одного из запросов приходит запрос высшего приоритета, то ПКП переключается на его обслуживание.
При циклическом сдвиге приоритеты могут динамически изменяться: входу после обслуживания присваивается низший приоритет (рис. 11.22).
В данном режиме после каждого сдвига необходимо загружать управляющее слово Режим циклического сдвига приоритетов позволяет устранять недостатки, когда при частых обращениях ко входам с высшими приоритетами игнорируются запросы с низшими приоритетами. Применение этого способа целесообразно при обслуживании внешних устройств с одинаковыми приоритетами.
11.4. Программируемые интерфейсные контроллеры 419
Запись единиц в разряды регистра маски IMR1-IMRQ запрещает прием запросов на известных входах IRR7-IRR0.
В режиме специального маскирования разрешаются прерывания на входах с меньшими приоритетами, чем запрос, обслуживаемый в данное время.
В режиме последовательного опроса микропроцессор с помощью ПКП последовательно опрашивает источники запросов. Контроллер выставляет на ШД информа-
б
Рис. 11.22. Иллюстрация циклического сдвига приоритета: а — запросы на входах IR2 и IR5; б — после обслуживания
цию, в которой в младших разрядах байта указывается номер ПУ с высшим приори-
тетом, а единица в старшем разряде байта указывает на наличие запроса. В микропроцессоре эта информация обрабатывается программой.
11.4.3. Контроллер прямого доступа к памяти
Режим прямого доступа к памяти обеспечивает непосредственный обмен информацией между ОП МПС и внешними быстродействующими устройствами, например, НГМД. Реализация такого обмена достигается с помощью БИС программируемых КПДП.
Функции КПДП выполняет микросхема ВТ57 (аналог модуля 8257), упрощенная структура которой показана на рис. 11.23. Технические характеристики микросхемы: схемотехнология — л-МОП; напряжение питания — плюс 5 В и потребляемая мощность — 0,7 Вт.
Рис. 11.23. Структура микросхемы контроллера ВТ57
Микросхема контроллера ВТ57 содержит:
• двунаправленный БД;
• четыре независимых канала (channel) CH3-CHQ-,
• блок задания приоритетов БПР;
• блок управления процессом программирования контроллера и обменом между системной памятью и внешними устройствами.
27*
420 Интерфейсы микропроцессорных систем
Двунаправленный восьмиразрядный БД обеспечивает обмен информацией между микропроцессором и КПДП в режимах программирования и проверки.
Каналы осуществляют непосредственный обмен данными между системной памятью и внешними устройствами. Каждый из каналов содержит:
• 16-разрядний регистр адреса РАК, с помощью которого задают адресное пространство до 64 Кбайт;
• 16-разрядний регистр числа циклов (РЧЦ), причем старшие два разряда определяют тип обмена: 00 — проверка; 01 — запись в ОП данных от ПУ; 10— чтение данных из ОП и пересылка их в ПУ; И — запрещенная комбинация; регистры числа циклов (без двух старших разрядов) обеспечивают обмен данными блоками объемом до 16 Кбайт;
• схему запросов подтверждения, на входы которой поступают сигналы запроса захвата цикла DRQ, а на выходе DACK формируется сигнал подтверждения захвата.
БПР обслуживает каналы с фиксированным приоритетом (канал СЯ0 имеет наивысший приоритет, СНЗ — самый низкий приоритет) или с циклическим — после обслуживания канала ему присваивается самый низкий приоритет.
Блок управления контроллера содержит: __
• схему приема сигналов выбора микросхемы CS, синхронизации CLK, сброса RES, готовности от периферии RDY и подтверждения захвата цикла IILDA от микропроцессора;
• буферы адреса Л7-Л4 иЛЗ-ЛО (двунаправленные);
• регистр управляющего слова (РУС) и регистр состояния;
• схему выработки выходного сигнала захвата цикла HRQ для микропроцессора, сигналов записи-чтения памяти MEMW, MEMR и портов TioR, ITow-
• формирователь адресных стробов AEN, STB, ADS',
• генератор сигнала конца обмена “ТС" и сигнала MARK — “до окончания передаваемого блока осталось число циклов, кратное 128”.
В режиме программирования информацию в каналы записывают в следующей последовательности: младший, а затем старший байт адреса; младший, а затем старший байт числа циклов (уменьшено на единицу) и типа обмена. Адрес реестров задают кодом АЗ-АО, как это показано в табл. 11.3. Запись двух байтов в регистрах выполняется командой OUT по одному адресу с помощью специального триггера, который определяет вначале младший байт, а затем старший.
Таблица 11.3
АЗ А1 А1 АО Регистр АЗ А1 А1 АО Регистр
0 0 Q 0 РАО
0 0 0 1 РЦО 0 1 0 1 РЦ2
РА1 0 1 1 0 РАЗ
0 0 1 0
0 0 1 1 РЦО 0 1 1 0 РЦЗ
РА2 1 0 0 0 РСС
0 1 0 0
Формат управляющего слова, показанный на рис. 11.24, записывается в РУС.
11.4. Программируемые интерфейсные контроллеры 421
D2 D6 D5 D4 D3 D2 01 ОО
AL TCS EW RP EN3 EN2 ENl EN0
Автозагрузка Расширенная запись ? т т т СН3 СН2 СН\СНО Разрешение обмена каналов Циклический приоритет
Отключение
Рис. 11.24. Формат управляющего слова
Сигналы EN3-EN0 при единичных значениях разрешают обмен с соответствующим каналом, а при нулевых — запрещают. Сигнал устанавливает последовательность обслуживания каналов: RP = 0 — фиксированный приоритет; RP = 1 — циклический приоритет. Сигнал EW = 1 увеличивает длительность сигналов MEMW и IIOW, которые генерирует КПДП; это согласовывает роботу системной памяти и периферии, имеющих различные цикли обращений.
Когда значение сигнала TSC = 1, появление сообщения ТС в одном из каналов СЕЕЗ-СЕГЗ сбрасывает его сигнал разрешения ENQ-EN3 на обмен и этот канал отключается.
В режиме автозагрузки может работать только канал СН2. После появления сигнала конца обмена “ТС" в канале СН2 он автоматически загружает в свои регистры адреса и числа из регистров канала СЕГЗ. Это позволяет организовывать пересылки БД с одинаковыми параметрами или соединять несколько блоков с разными параметрами.
Схема подключения в МПС контроллера ПДП, памяти и внешнего устройства показана на рис. 11.25.
Рис. 11.25. Структурная схема МПС с контроллером ПДП
Контроллер ПДП по запросу берет на себя управление системной шиной и выполняет циклы чтения-записи до получения нулевого содержания его счетчика циклов.
11.4.4. Г1рограммируемый таймер
Программируемый таймер (ПТ) предназначен для организации работы МПС в режиме реального времени и позволяет формировать сигналы с разными временными интервалами и частотными характеристиками.
422 Интерфейсы микропроцессорных систем
В МПС широко используют ПТ ВИ53 (аналог модуля 8253). Технические параметры микросхемы: схемотехнология — n-МОП, число транзисторов — 1500; тактовая частота — 2 МГц; напряжение питания — плюс 5 В и потребляемая мощность — 1 Вт.
Структура ПТ ВИ53 показана на рис. 11 26.
GATE 0
OUT 0
В состав ПТ ВИ53 входят: буфер БД для связи с микропроцессором; блок сопряжения, который обеспечивает выполнение операций ввода-вывода информации; регистр управляющего слова РУС; счетчики С70-С73. __
___ Назначение сигналов на входах и выходах ПТ: CS— выбор микросхемы, RD ,WR — чтение и запись; АЛ, АО — адресные входы для выбора канала ПТ или РУС; CLK0-CLKA — входы синхроимпульсов, каждый из которых уменьшает содержимое соответствующего счетчика на единицу; GATE0-GATE2 — входы управления счетчиками; OUTO-OUT2 — выходные сигналы счетчиков.
Операции обмена информацией между микропроцессором и ПТ, задающие сигналы адреса и управления, представлены в табл. 11.4
Таблица 11.4
Операция Сигналы управления
CS RD WR А\ АО
ШД-»РУС 0 1 0 1 1
ШД-»СЛ) 0 1 0 0 0
ШД-»С7Т 0 1 0 0 1
ШД->С72 0 1 0 1 0
СТО—>ШД 0 0 1 0 0
СП—>111Д 0 0 1 0 1
С72—>ШД 0 0 1 1 0
Z-состояние 1 X X X Z
Режим работы каждого канала программируется записью управляющего слова в РУС и исходного значения содержания счетчиков. Формат управляющего слова и назначения его отдельных разрядов показаны на рис. 11.27.
11.4. Программируемые интерфейсные контроллеры 423
СТО СТ\ СТ2 0 0 0 1 1 0 " 2-10 " КОД Двоичный код 1 0
Ф Ф _А_
DI D6 D5 D4 D2 D2 DI DO
Фиксация Младший байт Старший байт Два байта 0 0 0 1 1 0 1 1 С 5 Э 010101 001100 0 0ХХ11
1 Режим 0 1 2 345
Рис. 11.27. Формат управляющего слова
Во время работы ПТ на входы GATE поступают сигналы разрешения или запрета счета. Уровень выходного сигнала OUT изменяется в зависимости от записанных в счетчик данных, заданного режима и сигнала на входе GATE. Каждый канал ПТ можно программировать на работу в одном из шести режимов:
“О” — программируемая задержка (рис. 11.28, а);
“1” — программируемый ждущий мультивибратор (рис. 11.28, б);
“2” — программируемый генератор тактовых импульсов (рис. 11.28, в)
“3” — генератор прямоугольных сигналов (рис. 11.28, г);
“4” — программно-управляемый строб;
“5” — аппаратно-управляемый строб.
Рис. 11.28. Временные диаграммы работы ПТ:
а — режим “0"; б — режим “1”; в — режим “2"; г — режим “3"
Схема подключения ПТ к магистрали МПС показана на рис. 11.29.
424 Интерфейсы микропроцессорных систем
Рис. 11.29. Схема подключения ПТ к магистрали МПС
Длительность управляющих сигналов на входах GATE должна быть не меньше 150 нс.
11.4.5. Программируемый параллельный интерфейс.
Программируемый параллельный адаптер (ППА) типа ВВ55 предназначен для организации параллельного обмену информацией между ядром МПС и периферией (клавиатурой, индикаторами и др.). Технические характеристики: схемотехноло-гия— n-МОП, число транзисторов — 1600; напряжение питания — плюс 5 В и потребляемая мощность — 0,3 Вт. В состав ППА входят (рис. 11.30):
• двунаправленный буфер данных БД, который подключается к системной шине МПС;
• блок сопряжения и управления;
• три регистра РА, РВ и PC, которые вместе с серийными двунаправленными буферами образуют порты ввода-вывода А, В и С. Порты связаны с периферией каналами КА, КВ и КС;
• регистр управляющего слова РУС.
Рис. 11.30. Программируемый параллельный адаптер ВВ55: а — условное обозначение; б — функциональная схема
11.4. Программируемые интерфейсные контроллеры 425
Все регистры, буферы и каналы — восьмиразрядные. При этом порт С разбивается на две независимые части. Порт Л и старшие разряды порта С образуют группу А; порт В и младшие разряды порта С образуют группу В. _
На блок сопряжения и управления поступают сигналы выбора микросхемы CS, чтения RD, записи WR . Эти сигналы определяют направление передачи: ввод (команда IN ADR) и вывод (команды OUT ADR). Значения разрядов адресов А1, АО адресуют конкретный порт в ППА: А1*А0 = 00 — А, 01 — В, 10 — С, И — РУС. Старшие разряды адреса Л15-ДЗ поступают на адресный селектор, который формирует сигнал выбора всей микросхемы CS (табл. 11.5)
Таблица 11.5
Операция CS RD WR Al АО Направление обмена
IN (ввода) 0 0 1 0 0 ШД<—А
0 0 1 0 1 ШД<-В
0 0 1 1 0 ШД<-С
OUT (вывода) 0 1 0 0 0 ШД—>А
0 1 0 0 1 ШД->В
0 1 0 1 0 ШД->С
0 1 0 1 1 ШД->РУС
Z-состояние 1 X X X X
Группа А может настраиваться на один из трех режимов обмена: 0 — полудуплексный синхронный; 1 — полудуплексный асинхронный; 2 — дуплексный асинхронный. Группа В может настраиваться только на режим 0 или 1.
Управляющие слова (рис. 11.31) задают режимы работы портов (при Д7 = 1) или побитно (при Д7 = 0) устанавливают разряды порта С; при этом значение бита записывают в разряд D0 слова управления.
ппа,
D6 D5
D4 D3 D2
D\
DO
ппа
Режимы 00-0 01-1 10-2
РА
0 - OUT-, 1- IN
РС\]: 4]; 0 - OUT-, 1-IN ь
0-OUT
1- IN РВ 0-QUTA-IN Режимы В L~0 - режим 0; 1 - режим 1
DI D6 D5 D4 DI D2 DI DO
0 о.-- •••' 1 О.--' Z1 0/ /1 о.--' /1
Значение бита
Номер разряда
б
Рис. 11.31. Структура управляющего слова ППА: а — для задания режимов; б — для побитной установки
426 Интерфейсы микропроцессорных систем
Раздельную установку используют для последовательного обмена данными и организации обмена по прерываниям. В портах Л и В имеются триггеры разрешения прерывания соответственно ТА и Тв. Установка в режим 1 этих триггеров разрешает обмен по прерываниям.
В режиме 0 порты А и В и две равные части порта С независимо настраиваются на ввод или вывод информации без сопровождающих сигналов управления. Данные, которые выводятся из микропроцессора, всегда предварительно загружаются в аккумулятор. По команде OUT содержимое аккумулятора пересылается в адресуемый порт, где оно запоминается. Данные, которые вводятся в микропроцессор по команде IN, поступают в аккумулятор; после чего прочитанный порт обнуляется.
Пример 11.1
Настроить порт Л на вывод, лорты В и С— на ввод данных в режиме 0. Адрес РУС ППА равен 1103Я. Команды программирования:
MVIA, 100010115;
оятпозя.
В режиме 1 порты А и В используют для асинхронной передачи данных, а линии порта С — для выработки и восприятия управляющих сигналов. Функциональное назначение управляющих сигналов порта С при выводе данных:
• STB — входной сигнал стробирования записи данных в порт;
• IBF— выходной сигнал сообщения для периферии, что входной буфер заполнен;
• INT — выходной сигнал запроса на прерывание.
Управляющее слово для ввода в режим, конфигурация порта С и временные диаграммы работы показаны на рис. 11.32.
D7 D6 D5 D4 D3 D2 D\ DO
Рис. 11.32. Работа ППА при вводе в режиме 1:
а — управляющее слово; 6 — конфигурация порта С; в — временные диаграммы
Триггеры разрешения прерывания в этом режиме предварительно устанавливаются в режим 1 по разрядам РС4 — для порта А и РС2 — для порта В. Свободные линии PCS и 5С4 используют для последовательного обмена данными.
11.4. Программируемые интерфейсные контроллеры 427
Функциональное назначение управляющих сигналов порта С при выводе данных в режиме 1:
• OBF— сигнал для периферии сообщает, что выходной буфер полон;
• АСК — входной сигнал от периферии, подтверждающий прием данных;
• INT— выходной сигнал запроса прерывания микропроцессора.
Управляющее слово при выводе в режиме 1, конфигурация порта С и временные диаграммы работы показаны на рис. 11.33.
Рис. 11.33. Работа ППА при выводе в режиме 1: а — управляющее слово; б— конфигурация порта С; в — временные диаграммы
Триггеры разрешения прерывания при выводе в режиме 1 предварительно устанавливаются в положение 1 по разрядам РС6 — для порта А и РС2 — для порта В.
Режим 2 обеспечивает дуплексный обмен между портом А и периферией и сопровождается пятью управляющими сигналами PC1-PCS. Последние 11 интерфейсных линий могут настраиваться на режимы 0 или 1. Управляющее слово для режима 2, конфигурация порта С и временные диаграммы работы ППА показаны на рис. 11.34. Функции управляющих сигналов аналогичны режиму 1. Установка в положение 1 триггеров разрешения прерывания при вводе осуществляется по разрядам РСА, а при выводе — РС6.
Схема подключения ППА к СШ МПС, к восьмиразрядным индикаторам и клавиатуре показана на рис. 11.35.
Пример 11.2
Запрограммировать ППА для обслуживания клавиатуры (ввода данных) и индикаторов (вывода данных) в режиме 1. Программирование выполняют следующими командами:
MVIA, 10110100В;
оитиозн.
428 Интерфейсы микропроцессорных систем
7 6 5 4 3 2 1 0
1 1 0 0 0 1 0 0
а
Рис. 11.34. Работа ППА в режиме 2: а — управляющее слово; б — конфигурация порта С; в — временные диаграммы
Рис. 11.35. Подключение ППА к системным шинам, клавиатуре и индикатору: АС — адресный селектор
11.4.6. Программируемый последовательный интерфейс
В МПС для последовательного обмена информацией между микропроцессором и терминалом (телетайпом, дисплеем и др.) используют БИС, которую называют программируемым последовательным интерфейсом (ППИ). Обобщенная структура МПС с ППИ показана на рис. 11.36.
Программируемый последовательный интерфейс содержит передатчик (transmitter) и приемник (receiver). Передатчик получает от микропроцессора по ШД данные (data) в параллельном коде и передает их последовательно по линии TXD в терминал. Приемник получает от терминала по линии RXD данные в последователь-
11.4. Программируемые интерфейсные контроллеры 429
ном коде, преобразовывает их в параллельные слова и пересылает по ШД в микропроцессор. Система обмена может быть асинхронной или синхронной, симплексной, полудуплексной или дуплексной.
Рис. 11.36. Структура МПС с ППИ
Асинхронный режим используют для последовательного обмена данными в виде единичных символов (букв, цифр, знаков), которые программируют на длину 5-10 бит (рис. 11.37).
12 11 10 98765432 1 0
СТБ D0 D\ D2 D3 D4 D5 D6 D7 К СБ
СТБ D0 D\ D2 D3 D4 D5 D6 К СБ
СТБ DO D\ D2 D3 D4 D5 К СБ
СТБ D0 D1 D2 D3 D4 D5 К СБ
СТБ D0 D\ D2 D3 D4 К СБ
Рис. 11.37. Формат символов в асинхронном режиме:
СТБ — старт-бит; D7 (6,5,4),—, D0— информационные биты;
К — бит контроля; СБ — стоп-бит
Передатчик автоматически обрамляет каждый символ в асинхронном режиме дополнительными служебными битами: нулевым старт-битом (начало передачи); информационными битами, начиная с младшего разряда 7)0; битом контроля на четность или нечетность; единичным стоп-битом (конец передачи) длительностью 1; 1,5 или 2 бит. В таком же формате в асинхронном режиме данные поступают от терминала, а приемник ППИ автоматически исключает служебные биты. Временной интервал между символами при асинхронном обмене - фиксированный.
При синхронном обмене стартовые и стоповые биты исключаются, а синхронизация осуществляется за помощью одного или двух синхросигналов, которые предварительно записываются в ППИ (рис. 11.38.)
$0 S> ... s„ Sfl Si ... S„ D D D D D D К
Синхросимвол 1 Синхросимвол 2 Данные
Рис. 11.38. Формат данных при синхронном обмене
При синхронном приеме приемник выполняет побитное сравнение входного потока данных с записанными синхросимволами, пока не обнаружит их прохождения.
430 Интерфейсы микропроцессорных систем
После этого он интерпретирует каждую группу длиной от 5 до 8 бит (в зависимости, от программирования) как символ. Символы идут один за другим непрерывно. При неготовности данных передатчик продолжает работу, посылая для поддержки синхронизации специальные коды.
Синхронный режим обмена используют для пересылок массивов данных; он повышает быстродействие обмена, которое измеряется числом битов, пересылаемых за секунду. Единицу бит за секунду (бит/с) называют бодом.
В МПС широко применяют микросхему ВВ51 (аналог модуля 8251), которая является универсальным асинхронно-синхронным ППИ. Технические характеристики микросхемы: схемотехнология — n-МОП, число транзисторов — 3000; тактовая частота — 2 МГц; напряжение питания — плюс 5 В и потребляемая мощность — 0,4 Вт; быстродействие обмена в асинхронном режиме — 0...64-103 бод, в асинхронном —• 0...19.2-103 бод.
Микросхема ВВ51 содержит буфер БД, блок сопряжения с управляющими сигналами, магистрали, передатчик, приемник и блок связи с терминалом (рис. 11.39).
CTS RTS DSR DTR
Рис. 11.39. Функциональная схема БИС ВВ51
Буфер БД обеспечивает двунаправленный обмен параллельными восьмиразрядными данными между микропроцессором и ППИ. На входы блока сопряжений поступают сигналы, инициирующие направление обмена между микропроцессором и ППИ, и виды слов: данные, программирования и состояния ППИ (табл. 11.6).
Таблица 11.6
Операция CS C/D RD IVR
ППИ ->ШД; чтение данных 0 0 0 1
ШД -> ППИ; запись данных 0 0 1 0
ШД -> ППИ; запись управляющих слов 0 1 1 0
ППИ —>ШД; чтение слова состояния 0 1 0 1
Z-состояние 1 X X X
Назначение входных сигналов блока сопряжения: CLK— синхронизация; CS — выбор микросхемы; RD — разрешение чтения информации из ППИ на ШД; WR—
11.4. Программируемые интерфейсные контроллеры 431
разрешение на запись информации из ШД в_ППИ; С!D (control data) — тип слов: С/D= 1 — запись управляющего слова; С/D = 0 — передача данных.
На входах и выходах передатчика действуют следующие сигналы:
• TXD — последовательная передача данных;
• ТХС — синхронизация передачи данных;
• TXRDY— готовность передатчика к приему данных из ШД;
• ТХЕ — регистр данных передатчика пустой;
На входах и выходах приемника действуют следующие сигналы:
• RXD — последовательные данные из терминала;
• RXC— синхронизация приема данных;
• RXRDY —данные готовы к записи в микропроцессор;
• SYND— вход/выход; его назначение задают программно в синхронном режиме;
На входах и выходах блока связи с терминалом сигналы имеют следующее назначение:
• CTS — готовность приемника терминала;
• RTS — готовность ППИ передавать данные;
• DSR — готовность передатчика терминала;
• DTR —готовность ППИ принять данные.
В асинхронном режиме скорость обмену кратна частоте сигналов синхронизации по входу ТХС для передачи и RXC — для приема. Коэффициент кратности устанавливается программно и равен 1,16 и 64. Например, для скорости обмена 100 бод частота сигналов синхронизации на входах ТХС или RXC должна быть 100 Гц при кратности 1; 1,6 КГц — при кратности 16 и 6,4 КГц — при кратности 64.
В режиме синхронного обмена с внутренней синхронизацией скорость обмена равна частоте сигналов на входе ТХС для передатчика и RXC —для приемника.
Режим работы и функции ВИС ВВ51 задает программа с помощью слов инициализации и слов команд. Слово инициализации определяет асинхронный или синхронный режим работы, кратность коэффициента деления частоты, длину данных в битах, наличие контроля на четность или нечетность, длительность стоп-бита, количество синхросимволов и вид синхронизации — внешняя или внутренняя. Формат слова инициализации ППИ для асинхронного режима и назначение разрядов показаны на рис. 11.40.
D1 D6 D5 D4 D3 D2 D] D0
XСтоп-биты \ / КонтрошГ^\/Длина, бит Кратность \
01- 1 01 - по четности 00- 5 . 01- 1
10- 1.5 01- 6 10- 16
И- 2 11 - по нечет- 10- 7 И- 64
ности 11- 8
Рис. 11.40. Формат слова инициализации для асинхронного режима
432 Интерфейсы микропроцессорных систем
В формате слова инициализации для синхронного режима (DI-D0 = 00) разряд D6 определяет способ синхронизации: нуль — внешняя, единица — внутренняя; D7 — задает количество синхросимволов: нуль — 1, единица — 2.
С помощью слова команды (рис. 11.41) работа ППИ программируется на выполнение следующих функций (при “1” в разрядах): D0 — передача; DI — запрос на передачу; D2 — прием; D3 — конец передачи; Z)4 — сброс флажков ошибок; D5 — запрос на прием; D6 — программный сброс ППИ ; D7 — поиск синхросимволов в синхронном режиме.
D7 D6 D5 D4 D3 D2 D1 D0
Поиск синхросимволов Сброс Запрос приема Сброс они Конец Разрешение передачи на прием шажков 1бок Разрешение на передачу Запрос передачи
Рис. 11.41. Формат слова команды
.Управляющие слова должны формироваться после сигнала “RES" в такой последовательности: слово инициализации (режима); синхросимвол “1”; синхросимвол “2" в синхронных режимах; слова команды; данные; слова команды; данные и т.д.
Для контроля состояния ППИ в процессе обмена данными микропроцессор командой ввода считывает слово состояния из специального регистра состояния. Формат слова состояния и назначение разрядов показаны на рис. 11.42.
D1 D6 D5 D4 D3 D2 D\ DO
PCR SYND FE OE PE TXE RXRD] TXRDY
Рис. 11.42. Формат слова состояния ППИ
В разрядах слова состояния формируется информация (при “1” в разрядах): D0— разрешение для передатчика; DI — разрешение для приемника; D2 — регистр передатчика пуст; D3 — ошибка четности РЕ; D4 — ошибка переполнения (микропроцессор не прочитал символ); D5 — не выявлен стоп-бит (в асинхронном режиме); D6 — отсутствие синхронизации; D7 — готовность терминала к выдаче данных.
При синхронной передаче данные поступают на выход сигнала TXD. Если следующие данные не поступили в ППИ от микропроцессора, то выходной сигнал ТХЕ = 1. После завершения передачи символа выходной сигнал TXRDY = 1. Запись в ППИ следующего символа от микропроцессора может осуществляться двумя способами: первый — чтение слова состояния; второй — использование сигнала TXRDY в качестве запроса на прерывание.
Асинхронный прием данных начинается с поиска стоп-бита, который устанавливается на выходе сигнала RXD низким уровнем напряжения (лог. 0). Наличие этого уровня повторно проверяется стробированием его середины внутренним импуль
Контрольные вопросы 433
сом. Если старт-бит найден, то запускается внутренний счетчик, который определяет начало и конец битов данных, бит контроля и стоп-бит.
После этого на выходе готовности приема RXRDY устанавливается лог. 1. Передача принятого символа в микропроцессор может осуществляться двумя способами: первый — чтение слова состояния; второй — использование сигнала RXRDY в качестве запроса на прерывание.
Во время синхронной передачи на выходе TXD с частотой синхронизации на входе ТХС формируется последовательность битов, которая начинается с синхросимволов. Затем передаются данные, которые предварительно поступают в ППИ из микропроцессора. Если очередной символ не загружен к моменту передачи, то ППИ вставляет в последовательность синхросимволы. Конец передачи определяется записью в слове команды D3 = 1.
Во время синхронного приема с внутренней синхронизацией ППИ начинает роботу с поиска во входной последовательности синхросимволов и сравнивает принимаемые символы с записанными синхросимволами во время программирования. После выявления синхросимволов устанавливается значение SYND = 1 и начинается прием данных; этот сигнал автоматически сбрасывается при чтении слова состояния.
При синхронном приеме с внешней синхронизацией на вход SYND поступает сигнал (строб) от внешнего устройства, который разрешает прием данных на входе RXD со скоростью синхроимпульсов на входе RXC. В этом режиме поиск синхросимволов не выполняется, поэтому нет необходимости подавать их в начале кодовой последовательности.
Контрольные вопросы
1. Что такое микропроцессорная система?
2. Назовите основные составные части микропроцессорной системы.
3. Поясните структуру магистральной МПС.
4. Назовите основные составные части программного обеспечение МПС.
5. Охарактеризуйте понятие архитектуры МПС.
6. Что такое интерфейс?
7. Какие функции в МПС должен обеспечивать интерфейс?
8. Поясните классификацию интерфейсов.
9. Какие технические характеристики унифицируются в параллельных системных стандартных интерфейсах?
10. Охарактеризуйте интерфейсные микросхемы: генератор тактовых импульсов, буферные регистры, двунаправленные шинные формирователи.
11. Поясните назначение контроллера системной шины.
12. Поясните функции арбитра шин ВБ89.
13. Что такое системная и резидентная шины?
14. Дайте характеристику программных интерфейсных контроллеров.
15. Назовите режимы работы контроллера прерываний ВН59.
16. Поясните функции КПДП ВТ57.
28-4-1749
434 Проектирование печатных плат
Глава 12
Проектирование печатных плат
12.1. Основные определения
Печатные платы — это составные части конструкции компьютеров и радиоэлектронной аппаратуры. Платы состоят из плоских проводников в виде участков металлизированного покрытия, размещенных на диэлектрической основе. Проводники на плате соединяют печатные или навесные электрорадиоэлементы (резисторы, конденсаторы, индуктивность) и транзисторы, реле, микросхемы и др.
Печатные платы обеспечивают:
• увеличение плотности монтажных соединений и возможность микроминиатюризации изделий;
• получение печатных проводников, элементов и экранирующих поверхностей в одном технологическом цикле;
• гарантированную стабильность и повторение электрических характеристик;
• повышенную устойчивость к механическим и климатическим воздействиям;
• унификацию и стандартизацию конструктивных и технологических решений;
• увеличение надежности изделий;
• возможность комплексной автоматизации проектирования и монтажносборочных и контрольно-регулирующих работ;
• снижение трудоемкости, материалоемкости и себестоимости.
К недостаткам печатных плат относят сложность внесения изменений в схему и ограниченную ремонтопригодность.
12.2. Виды печатных плат и кабелей
Основными видами печатных плат и кабелей являются:
• односторонние печатные платы (ОПП) — с одной основой, на одной стороне которой выполняют проводящий рисунок (рис. 12.1, а);
• двухсторонние печатные платы (ДПП) — с одной основой, на обеих сторонах которой выполняют проводящие рисунки (рис. 12.1, б);
• многослойные печатные платы (МПП) — состоят из чередующихся слоев изоляционного материала с проводящими рисунками на двух и более слоях (до 20) с необходимыми соединениями (рис. 12.1, в);
• гибкие печатные платы (ГПП) — имеют гибкую основу, аналогичную ОПП и ДПП;
• гибкий печатный кабель (ГПК) — состоит из тонких от 5 до 50 и более полосок проводящего материала (обычного меди); они размещены параллельно и заклеены между двумя изоляционными пленками (рис. 12.1, г).
12.2. Виды печатных плат и кабелей 435
Рис. 12.1. Печатные платы и кабели:
а — односторонние; б — двухсторонние; в — многослойные; г — ГПК
Конструирование печатных плат и гибких кабелей выполняют ручным, полуав-томатизированным и автоматизированным методами.
При ручном методе размещение элементов на плате и трассировку печатных проводников выполняет непосредственно конструктор. Этот метод обеспечивает оптимальное распределение проводящего рисунка.
Полуавтоматический метод предусматривает размещение навесных элементов с помощью ЭВМ в случае ручной трассировки печатных проводников. Этот метод значительно повышает производительность в сравнении с ручным.
Автоматизированный метод проектирования предусматривает размещение навесных элементов и трассировку печатных проводников с помощью ЭВМ; допускается доработка отдельных соединений вручную. Метод обеспечивает высокую производительность работы конструктора.
Основными этапами проектирования печатных плат являются:
• выбор материалов и их входной контроль;
• обоснование способов механической обработки платы;
• выполнение чертежа платы;
• создание оригиналов, фотошаблонов или сеточных трафаретов;
• реализация химических и электрохимических технологических операций;
• сборка печатной платы;
• контроль, консервация и сдача готовых плат.
Перед выполнением чертежа платы требуется определить:
• форму и размеры печатной платы;
• положение, форму и размеры монтажных, контактных, крепежных и фиксирующих отверстий платы;
• шаг координатной сетки и рисунок печатной платы;
28:
436 Проектирование печатных плат
• параметры элементов печатной платы: ширину проводников, расстояние между ними, размеры контактных площадок, расстояние между контактными площадками или проводником и контактной площадкой, размеры незанятых зон, экранов и печатных контактов;
• сторону монтажа и положение базовых элементов устанавливаемых компонентов;
• допустимые отклонения размеров, формы и размещения, а также шероховатости поверхности элементов платы;
• содержимое, положение, размеры маркировки и клеймения;
• материал основы печатной платы и вид ее поставки;
» метод и способ получения рисунка платы;
• способ нанесения покрытия, способ и содержание контроля.
Чертежи ОПП и ДПП имеют наименование “Плата". На чертеже изображают основные проекции платы (две — для ОПП и три — для ДПП) с рисунками проводников и отверстиями.
Допускается выполнять дополнительный вид платы без проводящего рисунка и координатной сетки, на котором проставляют размеры для механической обработки отверстий, сведения о маркировке и клеймении, а также о покрытии. Над этим видом делают надпись: “Вид без проводников”.
12.3. Материалы для печатных плат
Для изготовления основы печатной платы используют фольгированные и не-фольгированные диэлектрики — гетинакс, стеклоткань, фторопласт, полистирол, керамические и металлические (с поверхностным изоляционным слоем) материалы.
Фольгированные материалы — это многослойные прессованные пластики из электроизоляционной бумаги или стеклоткани, пропитанные искусственной смолой. Они покрыты с одной или двух сторон электролитической фольгой толщиной 18; 35 и 50 мкм.
Фольгированный стеклотекстолит марок СФ выпускают листами размерами 400x600 мм и толщиной листа до 1 мм и 600x700 мм с большей толщиной листа. Он рекомендуется для плат, которые эксплуатируются при температуре до 120° С.
Более высокие физико-механические свойства и теплостойкость имеют стеклотекстолиты марок СФПН .
Диэлектрик слофодит имеет медную фольгу толщиной 5 мкм, которую получают испарением меди в вакууме.
Для многослойных и гибких плат используют теплостойкие стеклотекстолиты марок СТФ и ФТС; они эксплуатируются в диапазоне температур от минус 60 до плюс 150° С.
Нефольгированный диэлектрик СТЭФ металлизируется слоем меди в процессе изготовления печатной платы.
Фольгу изготовляют из меди высокой чистоты (содержание примесей не превышает 0,05%). Медь имеет высокую электропроводность, она относительно устойчива к коррозии, хотя и требует защитного покрытия.
12.4. Входной контроль и механическая обработка печатных плат 437
Для печатного монтажа допустимое значение тока выбирают: для фольги 100...250 А/мм2, для гальванической меди 60. ..100 А/мм2.
Для производства печатных кабелей используют армированные фольгированные пленки из фторопласта.
Керамические платы могут работать в диапазоне температур 20...700°С. Их изготовляют из минерального сырья (например, кварцевого песка) прессовкой, литьем под давлением или отливанием пленок.
Металлические платы используют в изделиях с большой токовой нагрузкой. В качестве основы используют алюминий или сплавы железа с никелем. Изоляционный слой на поверхности алюминия получают анодным оксидированием с толщиной от десятков до сотен микрон и сопротивлением изоляции 109... 1010 Ом.
Толщину проводника берут 18; 35 и 50 мкм. По плотности проводящего рисунка печатные платы подразделяют на пять классов:
• первый класс характеризуется наименьшей плотностью проводящего рисунка и шириной проводника и пробелов более 0,75 мм;
• пятый класс имеет наибольшую плотность рисунка и ширину проводника и пробелов в пределах 0,1 мм.
Поскольку печатный проводник имеет малую массу, то сила его сцепления с основой достаточна, чтобы выдержать действующие на проводнике знакопеременные механические перегрузки до 40<? в диапазоне частот 4...200 Гц.
12.4. Входной контроль и механическая обработка печатных плат
Во время входного контроля фольгированного диэлектрика проверяют:
• размеры листа и состояние его поверхности;
• прочность сцепления фольги перед и после действия гальванических растворов, расплавленного припоя;
• коробление листов и их способность к механической обработке: штамповке, сверлению отверстий, прессовке и др.;
• поверхностное сопротивление, электропроводность и др. (ГОСТ 10326-78).
Выполняя визуальный осмотр листов, устанавливают наличие царапин, проколов, пузырей и других повреждений.
Прочность сцепления фольги с диэлектриком характеризуется усилием, необходимым для отрыва полоски фольги от ее основы.
Коробление и изгиб диэлектрика проверяют погружением материала в расплавленный припой. При этом выявляются трещины на поверхности листа и дефекты сцепления между слоями.
Штампуемость материала определяют его способностью поддаваться механической обработке без образования сколов на гранях отверстий.
Способность материала к сверлению определяют пробным сверлением нескольких отверстий различного диаметра. Это позволяет установить наличие прожига во время сверления и оплавление поверхности или шероховатость из волокон в отверстиях, затрудняющие проведение металлизации отверстий.
438 Проектирование печатных плат
Механическая обработка включает:
• раскрой листового материала на полоски и получение из них заготовок;
• выполнение технологических, фиксирующих, переходных и монтажных отверстий;
• получение чистого контура платы после всех химических и электрохимических операций.
12.4.1. Получение заготовки
Заготовка печатной платы — это материал основы определенного размера, обрабатываемый во всех производственных операциях.
Заготовки вырезают на одцу или несколько плат (соответственно одиночный и групповой способы) с технологическим полем припуска по периметру листа шириной 10 мм для ОПП и ДПП и 30 мм для МПП (рис. 12.2).
<ьЧН11 ФЛН12 <г>ЧН11 &SH12
a б
Рис. 12.2. Заготовки плат: а — на одну деталь; б — групповая
На плате, в том числе и технологическом поле, формируется ряд отверстий с определенным функциональным назначением:
• технологические — используются для выполнения отдельных технологических операций;
• крепежные — служат для закрепления платы в блоке или для механического соединения элементов на плате;
• монтажные — предназначены для соединения выводов навесных элементов с печатной платой, а также для любого электрического подсоединения к проводящему рисунку;
• фиксирующие — служат для точного размещения платы и совмещения с фотошаблонами и отдельными слоями платы;
• контактный переход — токопроводящий участок, который обеспечивает электрический контакт между проводниками в разных слоях МПП;
• контактное отверстие — используют в ДПП для электрического соединения проводников, размещенных с двух сторон платы;
• металлизированные — с наличием на своих стенках слоя осажденного проводящего материала.
Размеры заготовок определяются требованиями чертежа. Малогабаритные платы размером до 100 мм размещают на групповой заготовке с расстоянием между ними 10 мм. Они обеспечивают лучшее использование материала и повышают производительность выполнения ряда операций; платы с размерами одной из сторон больше 100 мм размещают одиночным способом.
12.5. Чертеж печатной платы 439
Выбор метода получения заготовок определяется серийностью производства В крупносерийном выполнении раскрой листового материала выполняется штамповкой на прессах с одновременной пробивкой фиксирующих отверстий на технологическом поле. Заготовки плат в одиночном и мелкосерийном производстве получают разрезанием на роликовых или гильотинных ножницах. Лист из фольгированного материала можно резать дисковой фрезой.
Все отверстия, которые требуется металлизировать, получают сверлением, поскольку пробитые отверстия имеют низкое качество и не годятся для металлизации. Стенки отверстий должны бути гладкими, без заусениц, расслоения и т.п. Диаметр просверленного отверстия выполняется больше конечного на 100 мкм, что позволяет нанести слой меди толщиной 25 мкм и припой толщиной 10 мкм. Сверление монтажных отверстий выполняют в кондукторе со специальными сверлами без охлаждающей жидкости. Заготовки собирают в пакеты толщиной до 15 мм.
Монтажные и контактные отверстия получают штамповкой в случаях, когда они не металлизируются и их диаметр не больше 1 мм.
Фиксирующие и технологические отверстия изготовляют пробиванием или сверлением. Пробивку обычно выполняют при толщине материала до 0,5 мм. Фиксирующие отверстия диаметром 4...6 мм выполняют штамповкой или сверлением с высокой точностью — до 10...50 мкм.
12.4.2. Обработка по контуру
Остаточный (чистовой) контур платы, показанный на рис. 12.2 штрихами, получают вырубкой штампом, отрезанием гильотинными ножницами или фрезерованием после изготовления печатных проводников. Это объясняется тем, что травитель, используемый в химических процессах изготовления плат, может глубоко проникать в диэлектрик и вызывать короткие замыкания и снижение сопротивления изоляции. Вырубка по контуру может совмещаться с пробивкой отверстий, пазов и других элементов, которые не требуют металлизации.
Для чистовой обработки плат все чаще используют контурно-фрезерные многошпиндельные станки с числовым программным управлением, которые обеспечивают высокое качество краев платы и точность размеров в пределах ±25 мкм, позволяют обрабатывать внешние и внутренние контуры за одно закрепление, характеризуются надежностью и высокой производительностью — до 2000 плат/час. Они оснащены устройствами для автоматической замены фрез, защитными скафандрами для ограждения оператора от шума, пыли, стружки во время обработки, бесступенчатой регулировкой частоты вращения инструмента в диапазоне 15...60 тыс/мин.
12.5. Чертеж печатной платы
12.5.1. Координатная сетка
Габаритные размеры печатной платы, координаты и диаметры отверстий на чертеже платы указывают одним из следующих способов:
440 Проектирование печатных плат
• соответственно требованиям ГОСТ 2.307-68 с помощью размерных и выносных линий;
• нанесением координатной сетки в прямоугольной или полярной системе координат;
• комбинированным способом с помощью размерных и выносных линий и координатной сетки в прямоугольной или полярной системе координат.
За нуль (начало координат) в прямоугольной системе координат на главном виде печатной платы принимают:
• центр крайнего нижнего левого отверстия на поверхности платы, в том числе и технологического (рис. 12.3, а);
• левый нижний угол печатной платы (рис. 12 3, б);
• левую нижнюю точку, образуемую линиями построения (рис. 12.3, в);
• центр круглой платы в прямоугольной системе координат (рис. 12.3, г).
Рис. 12.3. Варианты задания нуля печатной платы в прямоугольной системе координат: а — центр крайнего левого нижнего отверстия; б — левый нижний угол;
в — левая нижняя точка, образованная линиями построения;
г — центр круглой печатной платы
Координатную сетку наносят тонкими сплошными линиями. Основной шаг координатной сетки должен составлять 2,50 мм. Используя шаг координатной сетки меньше основного, необходимо использовать шаг 1,25; 0,625 мм.
Линии координатной сетки требуется нумеровать арабскими цифрами с определенным шагом, например 0, 1, 2, 3,... (рис. 12.4, а), или 0, 2, 4,... (рис. 12.4, б), или 0, 5, 10, 15,... (рис. 12.4, в).
Рис. 12.4. Варианты нанесения линий координатной сетки:
а—с нанесением каждой линии с выделением пятой; б—с выделением через один; в — без нанесения на поле чертежа сетки
12.5. Чертеж печатной платы 441
Для уменьшения частоты сетки допускается наносить линии сетки через одну (см. рис. 12.4, б). При этом в технических требованиях пишут: “Линии сетки нанесены через одну”. Если частота линий сетки большая, то можно выделить каждую пятую или десятую линии, увеличивая их толщину до половины толщины контурных линий (см. рис. 12.4, а).
Координатную сетку наносят или на все поле чертежа платы, или на часть его поверхности. Линии координатной сетки можно не наносить на изображение, а их нумерацию указывают черточками по контуру платы или ниже его (см. рис. 12.4, в).
Чертежи печатных плат выполняют в натуральную величину, или с увеличенным масштабом 2:1,4:1, 5:1, 10:1; преимущество отдается четной кратности.
12.5.2. Монтажные и переходные (контактные) отверстия
Печатные платы в общем случае содержат значительное количество монтажных и переходных (контактных) металлизированных и не металлизированных отверстий. Монтажные отверстия предназначены для соединения выводов навесных элементов (резисторов, транзисторов, микросхем и др.) с печатной платой, а также для любого подсоединения к проводящему рисунку. В каждое монтажное отверстие платы устанавливают только один вывод навесного элемента.
Переходные (контактные) отверстия предназначены для соединения проводников, расположенных с двух сторон (или двух слоев) печатной платы. На сторонах металлизированных отверстий платы осаждается проводящий материал.
Диаметры монтажных, переходных металлизированных и не металлизированных отверстий требуется выбирать из ряда от 0,4 до 3,0 мм с шагом 0,1 мм за исключением диаметра 1,9 мм. При этом учитывают диаметры выводов навесных эле
ментов.
Центры всех отверстий должны быть расположены в узлах координатной сетки. Используя навесные элементы с шагом выводов, не четным шагу координатной сетки, требуется в узле сетки разместить одно из отверстий как основное. Остальные отверстия размещают соответственно рабочим чертежам элемента.
Необходимость зенковки отверстий определяется конструктивным заданием и методом изготовления. Круглые отверстия, которые имеют зенковки и круглые контактные площадки с круглыми отверстиями (в том числе с зенковкой), следует изображать одним кругом (рис. 12.5). Их формы и размеры определяют на поле чертежа.
Рис. 12.5. Изображение отверстий: а — кругом; б — со штриховкой; в — с зачернением; г — с зачернением и меткой в середине
442 Проектирование печатных плат
Для упрощения графики чертежа платы все отверстия показывают с одинаковым диаметром, однако с разным рисунком в середине (табл. 12.1).
Таблица 12.1
Диаметр, мм 0,6 0.8 1,0 1,3 1,5 1,8 2,0 5,0
Условное обозначение
Сведения об отверстиях (условное обозначение, диаметры отверстия и зенковки, наличие металлизации и количество отверстий) рекомендуется объединять в таблицу, заполняя ее в меру увеличения размеров отверстий (табл. 12.2).
Таблица 12.2
Обозначение Диаметр, мм Диаметр зенковки, мм Наличие металлизации Количество отверстий
0,6+| 1,1+0’2 х100 Есть 28
ф 0,8+1 1,Г0'2 хЮО Есть 35
1,5+0’12 2,040’2 хЮО Есть 18
-V 2,7+0,1 - Нет 4
З,6+о'3 - Есть 2
Положения центров монтажных отверстий задают одним из следующих способов:
• нанесением выносных и размерных линий (рис. 12.6, а);
• нумерацией отверстий и указанием их координат по оси Хи Y(рис. 12.6, б);
• по координатной сетке.
12.5.3. Проводники и контактные площадки
Печатные проводники — это участки токопроводящего покрытия, нанесенного на изоляционную основу, эквивалентные обычному монтажному проводу. Форма, длина, ширина и размещение печатных проводников могут быть произвольными в зависимости от схемы и конструкции платы.
Печатные проводники изображают отрезками линий, совпадающими с линиями координатной сетки, или расположенными под углом, кратным 15°.
Проводники шириной меньше 2,5 мм изображают одной сплошной линией, а больше 2,5 мм —двумя линиями со штриховкой под углом 45° или зачернением.
Печатные проводники требуется выполнять одинаковой ширины на всем протяжении; в узких местах проводники сужают до минимально допустимого значения на возможно меньшей длине. Проводники шириной больше 5 мм выполняют в виде экранов.
12.5. Чертеж печатной платы 443
а
Рис. 12.6. Задание положения центров отверстий: а — выносными и размерными линиями, мм; б — нумерацией отверстий с занесением номеров в таблицу координат
Номер отверстия 1 2 3 4 5 6 7 8
Координаты X 0 0 0 0 2 4 7 4
Y 9 6 4 0 9 7 4 2
б
С целью упрощения чертежа платы допускается изображать проводники любой ширины одной утолщенной линией. При этом в технических требованиях указывают действительную ширину проводников (рис. 12.7, а).
Рис. 12.7. Варианты чертежа проводников: а — утолщенными линиями;
б — двойными линиями с радиусом закругления не меньше 1 мм; в — комбинированное изображение проводников и указание участка, который должен быть свободным
Не допускается резких перегибов, острых углов и переходов. Плавный переход компенсирует разницу в тепловых деформациях фольги и диэлектрика. Радиус закругления в местах сгиба должен быть не меньше 1 мм (рис. 12.7, б). Резкое изменение ширины и острые углы уменьшают прочность сцепления проводника с диэлектриком.
Границы участков платы, которые не допускается занимать печатными проводниками, на чертеже показывают штриховыми линиями (рис. 12.7, в).
444 Проектирование печатных плат
В широких частях проводника (больше 2,5 мм) необходимо делать точечные, кольцевые или щелеподобные разрывы, которые предотвращают вспучивание фольги во
Рис. 12.8. Изображение проводников время пайки погружением, поскольку эти от-шириной больше 5 мм верстия обеспечивают выход газов
(рис. 12.8).
Печатные проводники не должны иметь бесконтактных разветвлений (рис. 12.9).
Рис. 12.9. Изображение печатных проводников: а— правильное; б— неправильное
Концы печатных проводников (ламели), предназначенные для подключения платы, размещают с учетом удобства использования разъемов (рис. 12.10).
Рис. 12.10. Размещение концевых контактов: а — правильное; б — неправильное
Навесные элементы на печатной плате размещают симметрично (рис. 12.11).
Рис. 12.11. Размещение навесных элементов: а — рекомендуется; б-не рекомендуется
12.5. Чертеж печатной платы 445
Шероховатость поверхности монтажных неметаллизированных отверстий должна составлять Rz < 80. Шероховатость поверхности монтажных и переходных металлизированных отверстий Rz < 40.
Все монтажные отверстия для соединения с навесными элементами должны иметь контактные площадки. Это металлизированный участок вокруг монтажного отверстия, который обеспечивает электрическую связь навесных элементов с печатными проводниками. Их форма может быть произвольной — круглой, прямоугольной или близкой к ней. Для создания контактных площадок проводники в местах пайки расширяются на 2,5 ...3 мм больше диаметра отверстия (рис. 12.12).
Рис. 12.12. Формы монтажных площадок
Круглые контактные площадки с зенковкой можно изображать одним кругом, диаметр которого должен соответствовать минимальному размеру контактной площадки. Диаметр контактных площадок указывают в технических требованиях на чертеже.
Для точного представления размеров групповых контактных площадок их изображение в увеличенном масштабе отдельно выносят на чертеже платы. Если расстояние между соседними контактными площадками невелико, то можно сделать срез (см. рис. 12.12). Центр контактной площадки симметричной формы должен совпадать с центром монтажных отверстий.
Рекомендуется делать плавный переход контактной площадки в проводниках. При этом ось симметрии печатного проводника должна быть касательной контура площадки. Расстояние между краями проводника, контактной площадки, неметалли-зированного отверстия и краем платы должно быть не меньше толщины площадки платы.
12.5.4. Запись технических требований на чертеже платы
На чертеже печатной платы указывают ее габаритные размеры, ширину проводников, диаметры и координаты крепежных, технологических и других отверстий, не связанных с печатным монтажом.
На поле чертежа указывают:
• метод изготовления платы;
• технические условия, если не все данные содержатся на чертеже;
• шаг координатной сетки, ширину проводников и расстояние между ними;
• расстояние между контактными площадками; между контактными площадками и проводниками;
• допуски на выполнение проводников, отверстий, особенности конструкции и другие параметры печатной платы.
446 Проектирование печатных плат
Технические требования размещают над основной надписью и формулируют и излагают в такой последовательности:
1. Плату изготовить......методом.
2. Плата должна соответствовать ГОСТ.......
3. Шаг координатной сетки.......мм.
4. Конфигурацию проводников выдерживать по координатной сетке с отклонением от чертежа.........мм.
5. Допускается округление контактных площадок проводников.
6. Места, обведенные штриховыми линиями, проводниками не занимать.
7. Требования к параметрам элементов платы — согласно конструктивным данным.
8. Ширина проводников в свободных местах...мм, в узких.....мм.
9. Расстояние между двумя проводниками, между двумя контактными площадками или проводником и контактной площадкой в свободных местах ......мм, в узких.....мм.
10. Форма контактных площадок произвольная.
11. Предельные отклонения расстояний между центрами отверстий в узких местах ±.......мм, в свободных местах ±..мм.
12. Предельные отклонения расстояний между центрами контактных площадок в группе ±.....мм.
13. Маркировка эмалью по ГОСТ....шрифт......
12.6. Изготовление оригиналов и фотошаблонов
12.6.1. Изготовление оригиналов
Оригинал рисунка печатной платы — это реальное изображение на основе чертежа технологического слоя платы, выполненное в увеличенном масштабе, обычно в позитивном изображении. При этом рисунок оригинала соответствует рисунку чертежа по степени почернения (проводники и контактные площадки черные, а пробелы белые).
Если на плате имеются экраны, занимающие большую площадь, то оригинал рисунка платы выполняют в негативном изображении (рисунок оригинала противоположен рисунку печатной платы по степени почернения).
Основными методами получения оригиналов являются черчение, наклеивание липкой ленты, резание по эмали и др.
Черчение оригинала печатной платы выполняют на специальной бумаге или малоусадочной пленке с предварительно нанесенной координатной сеткой с помощью сдвоенных рейсфедеров, плакатных перьев, лекал и др. Из-за высокой трудоемкости процесса, низкой точности изготовления оригинала (в пределах ±0,2 ...0,5 мм) этот способ используют редко.
Наклеивание липкой ленты (метод аппликации) значительно сокращает трудоемкость оригинала. При этом на прозрачную основу наносят центры отверстий и контактных площадок из калиброванных темных заготовок, а проводники получают приклеиванием непрозрачной липкой ленты. Метод обеспечивает совмещение ори
12.6. Изготовление оригиналов и фотошаблонов 447
гинала и чертежа с точностью ± 0,2 мм; он рекомендуется для изготовления ОПП и ДПП простых по конструкции и с пониженной плотностью монтажа.
Наибольшую точность изготовления оригиналов (±0,05мм) обеспечивает метод вырезания по эмали. Для этого на прозрачную основу распылителем краски наносят равномерный слой черной эмали толщиной 30 ...50 мкм. После сушки заготовку устанавливают на универсально-растачивающих станках или на координатографах с ручным или программным управлением. Для резки эмали используют различные инструменты — пунктирные иглы, граверные резцы, рейсфедеры с алмазными наконечниками. Путем оптимального давления на инструментах добиваются удаления эмали на всю толщину слоя из светлых мест (для позитивного изображения). Для достижения более высокой точности оригинал выполняют в увеличенном (в 2-10 раз) масштабе.
12.6.2. Изготовление фотошаблонов
Фотошаблоны обеспечивают нанесение рисунка оригинала (или непосредственно чертежа) на поверхность заготовки печатной платы (метод фотопечати).
Фотошаблон — это графическое позитивное или негативное изображение рисунка платы в натуральную величину (масштаб 1:1) на светопроницаемой фотопластинке или пленочном материале, полученное путем фотографирования оригинала.
По назначению фотошаблоны подразделяют на контрольные, которые хранятся как эталоны, и рабочие, которые изготовляются с контрольных. Рабочие фотошаблоны служат для переноса имеющегося на них рисунка на плату.
Изображение элементов на фотошаблоне должно соответствовать требованиям чертежа и быть черно-белым, контрастным, с четкими и ровными краями. Размеры печатных проводников и контактных площадок устанавливают с учетом степени подтравливания.
На рабочем поле фотошаблона не допускаются ореолы, пятна, точки, разрывы, полоски и другие видимые дефекты. Фотошаблон должен быть износостойким, малоусадочным, иметь минимальную деформацию при изменении температуры и влажности окружающей среды, а также в процессе производства. В большой мере этим требованиям соответствуют сверхконтрастные пластинки типа “Микрат - НК” и пластинки из полированного силикатного стекла с металлизированными поверхностями.
Из готового оригинала контрольные фотошаблоны получают масштабным фотографированием на фоторепродуктивных полиграфических камерах с объективами, имеющими высокую разрешающую способность.
Рабочие фотошаблоны изготовляют из контрольных способом контактной печати. Если технологический процесс предусматривает обработку групповой заготовки, то на специальном оборудовании (фотоштампах) методом мультипликаций получают групповой фотошаблон с точным размещением элементов рисунков, специальными отверстиями совмещения и общим машинным нулем отсчета координат программного сверления отверстий.
Более прогрессивным является метод получения фотошаблонов сканирующим световым лучом непосредственно на фотопластинке (без изготовления оригинала).
448 Проектирование печатных плат
Он реализуется с помощью высокопроизводительных координатографов под управлением ЭВМ.
Рис. 12.13. Схема работы координатографа для получения фотошаблонов печатной платы без оригинала ляют определенный элемент рисунка г
Координатограф (рис. 12.13) состоит из вакуумного стола 6, на котором закрепляется фотопластинка и блок управления 1. Стол перемещается с высокой точностью в двух взаимно перпендикулярных направлениях с помощью прецизионных ходовых винтов 4 и 5, которые приводят во вращение шаговыми двигателями 2 и 3. Фотоголовка включает осветитель 7, фокусирующую систему 8, круглую диафрагму 9 и фотозатвор 10. Диафрагма имеет набор отверстий (от'25 до 70), которые оформ-аты и закрепляются на валу шагового дви
гателя.
В случае ввода программы в блок управления сигналы подаются на шаговые двигатели привода стола и диафрагмы, а также на осветитель. В результате их программируемой работы на фотопластинке последовательно засвечиваются все элементы платы. Современные координатографы оснащаются системами автоматической поддержки постоянного светового режима и обеспечивают: размер рабочего поля от 500x500 до 1200x1200 мм; точность позиционирования ± (0,01...0,03 мм); максимальную скорость перемещения 3...10 м/мин; ширину экспонируемой линии 0,1 ...5 мм; дискретность перемещения по координатах 0,025 мм.
Если для изготовления фотошаблона используют обычный чертеж платы, то он с помощью координатографа кодируется на перфоленту.
12.6.3. Фоторезисты
Фоторезисты — это специальные светочувствительные материалы в виде органических растворов или сухих пленок, которые наносят слоем на подготовленную поверхность платы. Фоторезисты вместе с фотошаблонами обеспечивают создание на поверхности платы соответствующего рисунка схемы методом фотопечати.
Фоторезисты подразделяют на негативные и позитивные. Они отличаются способом образования защитной маски после экспонирования — непродолжительного действия ультрафиолетового излучения. В качестве источника света используют дуговые ртутные и люминесцентные лампы.
Участки негативного фоторезиста, которые находятся под прозрачными местами фотошаблона, под действием света получают свойства не растворяться во время проявления. Участки фоторезиста, которые расположены под непрозрачными местами фотошаблона, легко удаляются во время проявления в растворителе. Таким образом, образуется рельеф, который представляет собой изображение светлых элементов фотошаблона (рис. 12.14, а).
Позитивный фоторезист под действием излучения изменяет свои свойства так, что в процессе обработки в проявителе растворяются его облученные участки, а не-
12.6. Изготовление оригиналов и фотошаблонов 449
Излучение
а б
Рис. 12.14. Создание защитного слоя фоторезиста: -а — негативного; б — позитивного
облученные (те, которые находятся под непрозрачными участками фотошаблона) остаются на поверхности платы (рис. 12.14, б).
Фоторезисты должны иметь:
• высокую разрешающую способность, что определяется количеством проводящих линий, которые можно нанести на одном миллиметре поверхности платы;
• светочувствительность и устойчивость к воздействиям различных химических растворов;
• хорошую адгезию с поверхностью платы.
Негативные фоторезисты изготовляют на основе поливинилового спирта. Их широкое применение обусловлено нетоксичностью, високой разрешающей способностью (до 50 линий/мм), простотой проявления и низкой стоимостью.
Недостатком негативных фоторезистов является невозможность хранения больше 3-4 лет заготовки платы с нанесенным на ней слоем, поскольку фоторезист задубляется не только под действием света, но и в темноте. Кроме того, с понижением влажности и температуры окружающей среды уменьшается механическая прочность светочувствительного слоя и его адгезия с фольгой.
Для позитивных фоторезистов применяют материалы на основе диазосоединений, которые состоят из светочувствительной полимерной основы, растворителя и других материалов.
Позитивные фоторезисты превосходят негативные1 по адгезии, разрешающей способности (до 350 линий/мм), химической стойкости, отсутствием дубления в темноте во время хранения заготовки с нанесенным светочувствительным слоем. Однако они содержат токсические вещества и имеют высокую стоимость. Позитивные фоторезисты широко используют в сеточных трафаретах.
В технологическом процессе производства печатных плат используют жидкие и сухие (пленочные) фоторезисты.
Жидкие фоторезисты значительно дешевле пленочных, и для работы с ними требуется несложное оборудование.
Использование пленочных фоторезистов значительно упрощает технологический процесс (исключает операции сушки, дубления, ретуширования). Он легко поддается автоматизации, обеспечивает равномерное нанесение защитных слоев при наличии монтажных отверстий.
Среди жидких фоторезистов наиболее распространен светочувствительный материал на основе поливинилового спирта, который проявляется в нагретой до 40 °C воде. Он нетоксичен, пожароустойчив. Ограниченный срок хранения увеличивают, используя различные примеси.
Негативные фоторезисты наносят на поверхность платы различными способами: погружением, поливом с центрифугированием, накатом ребровым валом, разбрызгиванием.
Для нанесения фоторезиста погружением заготовку платы опускают в кювету с фоторезистом и вытягивают с постоянной скоростью до 50 см/мин. Погружение яв-29 — 4-1749
450 Проектирование печатных плат
ляется самым простым способом покрытия слоем фоторезиста с обеих сторон платы. Толщина полученного слоя зависит от скорости вытягивания, вязкости раствора и колеблется от 4 до 8 мкм. Для получения толстых слоев используют многократное погружение с дальнейшей сушкой каждого слоя. Способ не требует дорогого оборудования; недостатком является неравномерное нанесение слоя фоторезиста.
Поливом с центрифугированием можно получить покрытие почти без пор. Толщина полученного слоя зависит от вязкости фоторезиста и частоты вращения центрифуги. Для получения тонких пленок используют высокую частоту вращения, при этом необходимы фоторезисты с достаточно низкой вязкостью. Толщина слоя обычно составляет 2 ...4 мкм, а неравномерность толщины — 0,5 ...1,0 мкм.
Накат фоторезиста ребристым валиком обеспечивает большую равномерность слоя покрытия.
Недостатками всех жидких фоторезистов является малая толщина и неравномерность слоя покрытия, большая трудоемкость процесса нанесения и невозможность его использования для нанесения на платы с отверстиями.
Сухие фоторезисты теперь широко используются и заменяют жидкие как более технологические и простые в применении. Сухой пленочный фоторезист — это тонкая пленка, которая полимеризируется под действием ультрафиолетового облучения. Он состоит из трех слоев: оптически прозрачной пленки, светочувствительного полимера и защитной лавсановой пленки, которая защищает фоторезист от механических повреждений и возможного загрязнения.
Наносят сухой пленочный фоторезист с помощью валкового механизма — ламинатора (рис. 12.15).
а б в г
Рис. 12.15. Последовательность фотопечати с использованием сухого фоторезиста: а — нанесение фоторезиста; б — экспонирование;
в — удаление несущей пленки; г — удаление неэкспонированных участков
Накатный валик 4 оснащен устройством для обеспечения заданного давления на заготовку 1. Процесс осуществляется при повышенной температуре. При этом защитная пленка 3 удаляется, а открытая поверхность полимера 5 приклеивается к медной фольге 6, поскольку адгезия светочувствительного материала к фольге больше, чем к несущей пленке 2. В результате экспонирования инициируется фотохимическая реакция и на плате образуется изображение светлых мест фотошаблона. Оптически прозрачная пленка 8 отделяется от несущей поверхности и изображение проявляется в теплой воде. При этом неэкспонированные участки удаляются.
Промышленность выпускает сухие фоторезисты толщиной 20, 40 и 60 мкм и защитой 90, 110, 130 мкм. Тонкие слои сухого фоторезиста используют как маски для вытравливания меди из пробелов, средние — для создания рисунка для нанесения слоя металлизации, а толстые — для защиты отверстий с металлизацией во время вытравливания.
12.6. Изготовление оригиналов и фотошаблонов 451
Метод фотопечати обеспечивает высокую разрешающую способность — ширина проводников составляет 0,1 мм.
12.6.4. Офсетная печать
Метод офсетной печати заключается в изготовлении печатной формы, на по-
верхности которой формируется рисунок слоя трафаретной краской, а затем офсетный цилиндр переносит краску с формы на подготовленную поверхность платы (рис. 12.16).
Метод используют в условиях массового и крупносерийного производства с минимальной шириной проводников и пробелов между ними 0,3 ...0,5 мм (платы 1-го и 2-го классов плотности монтажа) и с точностью воспроизведения изображения ±0,2 мм. Его недостатком является высокая стоимость оборудования и сложность изменения рисунка платы.
платы. Форма закатывается валиком
Рис. 12.16. Схема установки офсетной печати: 1 — диэлектрик; 2 — медная фольга; 3 — основа; 4 — печатная форма; 5 — офсетный цилиндр; 6 — валик для нанесения краски; 7 — краска;
8 — прижимной валик
По конструкции формы для офсетной печати подразделяются на три вида: высокой печати, глубокой печати и с размещением печатных участков в одной плоскости. Изготовляют их из алюминия, цинка, сплавов на их основе с помощью вытравливания, гравировки, прессовки, сборки из отдельных элементов и др.
Наиболее технологичной, точной и надежной является печатная форма для сухого офсета. Это пластина из алюминия толщиной 0.5...1 мм, на которую наносится тонкая пленка силиконового лака, не смачиваемого трафаретной краской. На пленке с помощью лазерного гравировального автомата выжигается рисунок платы. При этом обеспечивается производительность 300 отпечатков в час.
Рис. 12.17. Принцип трафаретной печати:
1 — рама; 2 — фиксатор подкладки;
3 — диэлектрик; 4 — основа;
5 — трафаретная краска; 6 — трафарет;
7 — напечатанный рисунок; 8 — ракель
12.6.5. Сеткография
Сеткографический метод (трафаретная печать) заключается в нанесении рисунка схемы на поверхность фольги продавливанием защитной краски резиновой лопаткой (ракелем) через сеточный трафарет (рис. 12.17).
Сеточные трафареты — это рама из алюминиевого сплава, на которую натянута эластичная сетка из шелковых, капроновых или лавсановых ниток. Наиболее точными и долговечными являются металлические сетки из нержавеющей стали или фосфористой бронзы с размерами ячеек 40...50 мкм. Металлическая сетка выдерживает большое количество отпечатков и используется в серийном производстве. Ее недостатком в сравнении с неметаллическими сетками является малая эластичность и склонность к окислению,-29*
452 Проектирование печатных плат
Для изготовления сеточного трафарета на поверхность рамы наносят клей и на него накладывают нарезанную сетку. В пневматических устройствах сетка равномерно натягивается, приклеивается к раме и обезжиривается. На сетку накладывают временную подкладку из полиэтиленовой пленки, на которую методом полива наносят фоторезист. После экспонирования через фотошаблон и проявления на поверхности сетки получают проводящий рисунок.
Краска для защитного слоя должна быть кислотостойкой, иметь хорошую адгезию с платой, минимальное время сушки и сметаноподобную консистенцию. Краску на плату можно наносить вручную в случае малосерийного производства. Разработаны и автоматизированы устройства нанесения краски на поверхность платы с помощью сеточных трафаретов. Получение рисунка схемы методом офсетной печати на 60% дешевле, чем фотопечатью.
12.7. Типовые процессы изготовления печатных плат
12.7.1. Субтрактивные, аддитивные и полуаддитивные процессы
В зависимости от способа обработки проводящего покрытия платы (удаления или нанесения фольги) все процессы изготовления печатных плат подразделяют на субтрактивные, адитивные или полуадитивные.
Субтрактивный процесс (subtractio — отнимать) — получение проводящего рисунка заключается в выборочном удалении участков проводящей фольги.
Аддитивный процесс (additio — добавлять) — это выборочное осаждение проводящего материала на нефольгированную основу.
Полуаддитивный процесс предусматривает предварительное нанесение тонко-' го вспомогательного проводящего покрытия, которое затем удаляется из пробелов.
12.7.2. Методы изготовления печатных плат
Соответственно ГОСТ 23751-86 конструирование печатных плат осуществляют с учетом следующих методов изготовления:
• химического для ОПП, ГПК;
• комбинированного позитивного для ДПП, ГПП;
• электрохимического (аддитивного) для МПП.
Все рекомендованные методы (кроме полуаддитивного) являются субтрактивными.
Основное назначение химических и гальванических процессов заключается в металлизации контактных отверстий и защите рисунка печатной платы во время вытравливания. Типовой технологический процесс химической и гальванической металлизации печатных плат состоит из следующих этапов:
• подготовка поверхности, сенсибилизация и активация;
• химическое и гальваническое меднение;
• гальваническое осаждение сплава SnPb.
12.7. Типовые процессы изготовления печатных плат 453
12.7.3. Подготовка поверхности. Сенсибилизация и активация
Подготовка поверхности монтажных отверстий печатных плат заключается в гидроабразивной обработке, подтравливании диэлектрика в отверстиях серной кислотой и фтористым водородом, промывке в проточной воде.
Сенсибилизация (повышение чувствительности к меди) осуществляется в растворе двухлористого олова, соляной кислоты и металлического олова на протяжении 5...7 мин с последующей промывкой в дистиллированной воде. В результате сенсибилизации на поверхности стенок отверстий адсорбируется пленка ионов двухлористого олова, которые служат восстановителем для палладия.
Активацию проводят в водном растворе двухлористого палладия и аммиака на протяжении 5...7 мин. Металлический палладий служит центром кристаллизации в процессе химического меднения. Для сокращения технологического цикла и улучшения качества металлизации используют активирующий раствор, в состав которого входят соли палладия и олова.
12.7.4. Химическое и гальваническое омеднение
Химическое меднение заключается в восстановлении меди на активированных поверхностях из раствора, в состав которого входят соли меди, никеля и др. Процесс осуществляется с плавным покачиванием плат или с наложением ультразвукового поля. Осадок меди при этом имеет более плотную структуру, что объясняется лучшими условиями удаления пузырьков водорода, закрывающих поверхность диэлектрика. Длительность осаждения слоя меди толщиной 0,25...0,5 мкм составляет 15...20 мин.
Гальваническую металлизацию используют для увеличения ранее полученного тонкого слоя меди до толщины 5...8 мкм и для последующего создания проводящего рисунка схемы с толщиной меди возле отверстия 25 мкм. Гальваническое меднение требует замкнутого проводящего покрытия, которое осуществляется технологическими проводниками, прошивкой отверстий медным проводом. Медь наращивают в сернокислых и других электролитах в специальных гальванических ваннах. Электроды из электролитической меди и плата подключаются соответственно к “плюс” и “минус” источника тока. На плате, которая является катодом, оседает медь.
Гальваническое осаждение сплава олово-свинец толщиной 8...20 мкм проводится с целью защиты проводящего рисунка во время травления плат и обеспечения качественной пайки.
Возможное применение специальных покрытий (палладий, золото и др^) толщиной 2 ... 5 мкм.
12.7.5. Химическое травление
Травление — это химический процесс, во время которого участки медной фольги, не защищенные резистом, удаляются с диэлектрической основы, а участки, покрытые резистом, сохраняются и формируют рисунок печатной платы. В качестве резиста используют фоторезисты, трафаретную краску или стойкий к действию травителей гальванически нанесенный слой оловянно-свинцового сплава или драго
454 Проектирование печатных плат
ценного металла. Процесс травления включает предварительную очистку, собственно вытравливание металла, промывку и удаление фоторезиста из пробелов.
Травление печатных плат с рисунками, защищенными сплавом олово-свинец или драгоценными металлами, проводят в растворах на основе хлорной меди. Такие растворы дешевые, простые в изготовлении и легко удаляются с платы после травления. В случае, когда рисунок защищен печатными красками, травление проводят в железомедном хлоридном растворе.
Травлеание набрызгиванием проводят в ваннах, где травильный раствор подается на плату лопастями вращающегося ротора. Такое травление обеспечивает равномерное удаление фольги и незначительное ее подтравливание. Однако этим методом обрабатывается одновременно мало плат при невысокой скорости травления.
Струйное травление обеспечивает высокую производительность. Травитель под высоким давлением через систему сопел распыляется на поверхность платы. Постоянное попадание на плату свежего раствора обеспечивает высокие скорости травления с высокой разрешающей способностью.
Защитный слой трафаретной краски или фоторезиста снимаются в щелочных растворах. Для снятия некоторых красок используются дополнительно механические вращающиеся щитки.
После травления плату необходимо тщательно промыть в горячей проточной воде для удаления остатков травильного раствора.
12.8. Последовательность технологических процессов изготовления печатных плат
12.8.1. Сеткографический метод
По сеткографическому методу изготовление печатных плат с помощью, например, капроновой сетки, реализуется в такой последовательности.
1. Подготовка поверхности. Она заключается в очистке поверхности платы латунными или капроновыми щетками с последующей очисткой в кислотах.
2. Нанесение рисунка схемы на поверхность платы с помощью кислотостойких красок, сушка и ретуширование.
3. Травление медной фольги с последующим смыванием краски и зачисткой проводников.
4. Нанесение на поверхность платы защитного слоя бакелитового лака, сверление, обезжиривание.
5. Сенсибилизация платы и лужение.
6. Смывание краски с ламелей ацетоном, покрытие ламелей серебром и палладием.
7. Вырубка контура платы, контроль и сдача.
12.8. Последовательность технологических процессов изготовления печатных плат 455
12.8.2. Фотохимический метод
Схема типового технологического процесса изготовления печатных плат включает следующие этапы.
1. Подготовка поверхности фольги латунными или капроновыми вращающимися щетками с последующей очисткой в кислотах (рис. 12.18, а).
Рис. 12.18. Основные этапы получения проводников фотохимическим методом:
1 — фольга; 2 — фоторезист; 3 — фотошаблон и экспонирование; 4 — проявление;
5 - травление фольги; 6 - снятие фоторезиста.
2. Нанесение слоя фоторезиста (рис. 12.18, 6) и его сушка на протяжении 20 мин при температуре 65°С.
3. Экспонирование позитивного фотошаблона с помощью ультрафиолетового излучения (рис. 12.18, в).
4. Проявление схемы и вымывание тех участков фоторезиста, которые находятся под светлыми местами (рис. 12.18, г). Дефекты фоторезиста устраняются химическим дублением.
5. Последующие этапы являются общими для фотохимического и сеткографического методов. Они содержат (рис. 12.18, б, е):
• предварительную очистку;
• собственно травление металла;
• очистку после травления и удаление слоя фоторезиста или краски.
6. Проводится механическая обработка платы — штампование или фрезерование по контуру и получение отверстий.
Химические методы простые, обеспечивают крепкое сцепление проводников с основой, равномерную толщину проводников и их высокую электропроводность. Недостатком химических методов является низкая прочность в местах установки выводов, поскольку они не металлизируются.
Пример выполнения чертежа печатной платы и ее сборочный чертеж для фрагмента блока индикации фазометра представлен в прил. Г. Принципиальная электрическая схема (см. прил. Г, рис. Г.1) выполняет функцию подсчета и индика
456 Проектирование печатных плат
ции количества импульсов, которые подаются на ее вход. Блок выполнен в виде схемы со статической индикацией и запоминанием. На микросхемах DDY-DD3 собран трехразрядный десятичный счетчик. Перед началом каждого измерения выполняется установка счетчиков в нулевое состояние короткими импульсами (подаются на вход “/?”)• После подсчета импульсов результат с выходов счетчика записывается в регистры дешифраторов DD^-DD6. Запись осуществляется коротким импульсом (подается на вход “С”). На выходах дешифратора появляется код для управления семисегментными индикаторами HG1-HG3. Для отображения результата используются вакуумно-люминесцентные индикаторы. В схеме блока применены интегральные микросхемы серии 176 — десятичные счетчики К176ИЕ2, дешифраторы К176ИД2 и индикаторы ОВ6. Для подсоединения к другим частям схемы фазометра используется разъем для печатного монтажа (вилка ГРППМ5-18Ш1).
Конструктивно блок выполнен на двухсторонней печатной плате, которая изготовляется комбинированным позитивным методом по третьему классу точности (см. прил. Г, рис. Г.2). По этому методу проводниковый рисунок получают субтрактивным процессом (химическим травлением медной фольги), а металлизацию монтажных отверстий — аддитивным процессом (химическим меднением с последующим гальваническим наращиванием полученного слоя). Для платы использован двусторонний фольгированный стеклотекстолит марки СФ-2-35-1,5 (2 — двусторонний, 35 обозначает толщину фольги в микрометрах, 1,5 — толщина диэлектрика (мм)).
Сборочный чертеж печатной платы блока индикации показан на рис. Г.З (см. прил. Г).
Контрольные вопросы
1. Дайте определение печатной платы?
2. Что обеспечивает применение печатных плат?
3. Перечислите виды печатных плат и кабелей.
4. Перечислите основные этапы проектирования печатных плат.
5. Какие материалы используются в качестве основы печатных плат?
6. Дайте определение заготовки печатной платы?
7. Какие существуют виды заготовок печатной платы?
8. Перечислите виды отверстий печатной платы по их функциональному назначению.
9. Опишите методы создания чертежа печатной платы.
10. Перечислите способы, которыми задают положение центров монтажных отверстий.
11. Опишите особенности черчения печатных проводников.
12. Опишите особенности черчения монтажных площадок.
13. Перечислите основные методы получения оригиналов.
14. Что такое фотошаблон и как его изготовляют?
15. Что такое фоторезист и для чего он применяется?
16. Опишите особенности офсетной печати.
17. Опишите особенности сеткографии.
18. Опишите типовые процессы изготовления печатных плат.
13.1. Виды конструкторской документации 457
Глава 13
Конструкторская документация
13.1. Виды конструкторской документации
Проектирование — это процесс разработки нового продукта: технических и программных средств, структурных, функциональных, принципиальных схем устройств, компьютерных систем и сетей, концептуальной и физической модели баз данных и т.д. Проект содержит входные данные, необходимые для дальнейшего изготовления нового продукта.
Обычно проект состоит из комплекта документации, содержащего информацию об объекте проектирования. Совокупность взаимосвязанных документов, имеющих отношение к объекту проектирования, составляет конструкторскую документацию.
Существует несколько систем государственных стандартов, определяющих правила оформления технической документации. Основной среди них является Единая система конструкторской документации (ЕСКД), которая содержит комплекс государственных стандартов, определяющих правила и положения разработки, оформления, оборота конструкторских документов.
В технике конструкция — это схема, устройство и принцип работы технического предмета (машины, аппарата, строения и т.д.), а также сам предмет и его составные части. Конструкция предусматривает взаимное размещение частей и элементов технического предмета, способ их соединения и взаимодействия, а также материалы, из которых должны быть изготовлены составные части.
Конструкторская документация состоит из текстовых и графических документов, которые определяют конструкцию технического изделия и содержат данные, необходимые для разработки, изготовления, контроля, приема, эксплуатации и ремонта.
Текстовые конструкторские документы содержат информацию, записанную естественным или формальным языком. Их подразделяют на два вида:
1. документы, содержащие сплошной текст (пояснительные записки, технические условия, расчеты, паспорта, инструкции и т.д.);
2. документы, содержащие текст, разделенный на графы (таблицы, спецификации, ведомости и т.д.).
Графическое изображение — это воспроизведение комплекса геометрических особенностей изделия в образной форме с помощью средств графики: линий, штрихов, точек. Под геометрическими особенностями подразумевают форму, размеры и взаимное размещение составных частей изделия. К графическим конструкторским документам относятся чертежи и схемы.
Чертеж — это документ, содержащий изображение технического изделия или его составных частей и другие данные, которые поясняют функциональное назначение предмета и позволяют его изготовить.
458 Конструкторская документация
Схема — это документ, содержащий условные графические изображения составных частей технического изделия и связи между ними. В зависимости от физического строения элементов изделия схемы подразделяют на виды: электрические, гидравлические, пневматические, газовые, кинематические, вакуумные, энергетические, деления и комбинированные. Назначение схемы определяет ее тип: структурная, функциональная, принципиальная (полная), соединений (монтажная), подключения, общая, размещения и объединенная.
Чаще всего используют следующие документы: чертеж общего вида, чертеж детали, сборочный чертеж, схемы, спецификации, пояснительные записки.
13.2. Общие требования к оформлению проектов
Результатом выполнения проектов являются технические описания, расчеты, таблицы, графики, чертежи, схемы, плакаты и пояснения к ним. Эти материалы оформляются в виде пояснительной записки и соответствующего графического материала. Виды, комплектность и оформление всех документов проекта должны соответствовать стандартам ЕСКД, ЕСПД и другим действующим стандартам. Каждое положение должно быть обосновано расчетами, фактическим материалом и ссылками на литературные источники, научно-технические отчеты и т.д. Не допускаются ссылки на устные указания руководителей, консультантов, преподавателей и других лиц. За принятые в проекте решения и правильность всех данных отвечает автор проекта.
13.3. Обозначения стандартов ЕСКД
Стандарты ЕСКД распределены по группам, представленным в табл. 13.1.
Таблица 13.1
Шифр группы Содержание стандарта в группе
0 Общие положения
1 Основные положения
2 Классификация и обозначение изделий в конструкторских документах
3 Общие правила выполнения чертежей
4 Правила выполнения чертежей изделий
5 Правила оборота
6 Правила выполнения эксплуатационной и ремонтной документации
7 Правила выполнения схем
8 Правила выполнения документов строительства и кораблестроения
9 Другие стандарты
Обозначение стандарта ЕСКД выполняется по классификационному признаку и состоит из указания категорий стандарта, системы, группы, порядкового номера стандарта в группе и года утверждения. Пример обозначения стандарта ЕСКД “Правила выполнения электрических схем” показан на рис. 13.1.
13.4. Обозначения конструкторских документов 459
ГОСТ 2. 7 02 -75*
Категория - государственный стандарт Класс стандартов - ЕСКД----------
Классификационная группа---------
Порядковый номер в группе--------
Год регистрации стандарта
Примечание: символ обозначает изменения в стандартах
Рис. 13.1. Пример обозначения стандарта ЕСКД "Правила выполнения электрических схем"
13.4. Обозначения конструкторских документов
Проекты — это комплекты текстовых и графических документов (конструкторских, программных, технологических, автоматизированных систем управления), которые обязательно выполняются на основе задания. В учебных заведениях необходимое количество документов и их виды устанавливает выпускающая кафедра.
Вся техническая документация проектов, за исключением иллюстративной, должна иметь обозначения. Для основных конструкторских документов установлена следующая структура обозначения согласно ГОСТ 2.201-80 “Обозначение изделий и конструкторских документов" (рис. 13.2).
хххх хххххх ххх
Код организации-разработчика_____
Код классификационной характеристики________
Порядковый регистрационный номер
Рис. 13.2. Структура обозначения основных конструкторских документов
Четырехразрядный буквенный код организации-разработчика определяют по кодификатору организаций-разработчиков. Для конструкторских документов, которые выполняют студенты, этот код определяется сокращенным названием учебного заведения с точкой в конце (например: “НАУ.”).
Шестизначный цифровой код классификационной характеристики присваивают изделию и конструкторскому документу по классификатору ЕСКД. Структура кода классификационной характеристики показана на рис. 13.3.
хх х х х х
Класс____________________
Подкласс______________________
Группа______________________________
Подгруппа________________________________
Вид
Рис. 13.3. Структура кода классификационной характеристики
460 Конструкторская документация
К примеру, для проектов в Киевском национальном авиационном университете принято условную классификацию, в которой записывают следующие данные, разделенные пробелами:
• первые две цифры (класс) — последние две цифры года защиты проекта;
• следующие две цифры (подкласс и группа) — порядковый номер темы проекта;
• последние две цифры (подгруппа и вид) — последние две цифры номера зачетной книжки студента-выпускника.
Порядковый регистрационный номер присваивают по квалификационной характеристике от ООО до 999 в пределах кода организации-разработчика. Регистрационный номер присваивают в пределах одного проекта.
Обозначение основного конструкторского документа совпадает с обозначением изделия. Обозначение других конструкторских документов (пояснительная записка, сборочный, габаритный, монтажный или электромонтажный чертеж, схемы, ведомости, эксплуатационные документы и т.д.) должны состоять из обозначения основного документа (спецификации или детали) и кода документа, установленных соответствующими стандартами ЕСКД (рис. 13.3).
хххх хххххх хххх
Обозначение основного документа Код неосновного документа
Рис. 13.4. Обозначение неосновных конструкторских документов
Код неосновного документа должен иметь не более четырех знаков. Например:
• обозначение основного конструкторского документа (спецификации)
НАУ 04 12 20 001;
• обозначение сборочного чертежа изделия
НАУ 04 12 20 002 СЧ;
• обозначение схемы электрической структурной
НАУ 04 12 20 001 Э1.
Общее обозначение основного конструкторского документа имеют документы одного уровня вхождения.
13.5. Форматы
Графические конструкторские документы выполняют на листах определенного размера, называемого форматом. Форматы листов определяют по размерам внешней рамки. Согласно требованиям ГОСТ 2.301-68 “Форматы” выделяют основные и дополнительные форматы листов. Обозначения и размеры основных форматов представлены в табл. 13.2.
Таблица 13.2.
Обозначения форматов АО А1 А2 АЗ А4
Размеры сторон, мм 1189x841 594x841 , 594x420 297x420 297x210
В случае необходимости, используют формат А5 с размерами сторон 148x210 мм. Допускается применение дополнительных форматов, которые образу-
13.6. Основные надписи и порядок их заполнения 461
ют увеличением коротких сторон основных форматов на величину, кратную его размерам, например:
А0х2 А1хЗ А2х4 А4х4
1189x1648 841x1783 594x1685 297x841
Выбирая форматы, учитывают:
• объем и сложность проектируемого изделия;
• необходимую степень детализации данных, обусловленный назначением схемы;
• условия хранения и обращения схем;
• особенности и возможности техники выполнения, репродуцирования и (или) микрофильмования схем;
• возможности обработки схем средствами вычислительной техники.
Выбранный формат должен обеспечивать компактное выполнение схемы без нарушения ее наглядности и удобства использования. Формат схемы, выполненной на нескольких листах, должен быть одинаковым. При этом следует стремиться к уменьшению формата за счет увеличения общего количества листов.
Каждый лист, на котором выполняется схема, должен иметь порядковый номер. Первый лист схемы выполняют по форме 1, а следующий — по форме 2а согласно ГОСТ 2.104-68 “Основные надписи”. Основные и пояснительные надписи на схеме выполняют вручную шрифтом согласно ГОСТ 2.304-81 “Шрифты чертежные" или машинным способом.
Если схему выполняют на нескольких листах, то линии, переходящие с одного листа на другой, прерывают за пределами изображения схемы. Рядом с прерванной линией указывают обозначение или наименовании этой линии. Например, номер провода, наименование сигнала или его сокращенное обозначение и в круглых скобках — номер листа, на котором продолжается линия. Допускается к номеру листа добавлять после символа обозначение зоны, в которой находится продолжение линии.
13.6. Основные надписи и порядок их заполнения
Вся конструкторская документация сопровождается основной надписью и дополнительными графами к ней. Основные надписи располагают в правом нижнем углу документа, а на листах формата А4 — только по короткой стороне листа, то есть формат А4 всегда имеет вертикальное положение.
Размещение основных надписей и дополнительных граф к ним на листах различных форматов показано на рис. 13.5. Графы, показанные штриховыми линиями, вводятся в случае необходимости.
Требования к форме, размерам и порядку заполнения конструкторской документации устанавливает ГОСТ 2.104-68. Предусмотрены три типа основных надписей шириной 185 мм:
• для первых листов чертежей и схем высотой 55 мм (рис. 13.6);
• для первых (или заполненных) листов текстовых документов высотой 40 мм (рис. 13.7);
462 Конструкторская документация
для последующих 15 мм (рис. 13.8).
листов любых конструкторских документов высотой
Рис. 13.5. Размещение основных надписей: а — формат А4; б, е — формат больше А4 с основной надписью соотеетстеенно по короткой и длинной стороне; I — основная надпись; II, III — дополнительные графы
185 70 > ' 50
(2) у
( 14) (15) (16) (17) (18) Литера Масса Масштаб А ! л
Изм Лит \<> ()ОК\ И lltxtnucb J(ama 5 5 5 s 17 , 18
Выпи пни (1) (4) (5) (6)
Руковооит
Копсу }ът Лист (7) | Листов (8)
(Ю) (И) (12) (В) (3) (»)
Н контр
Зан каф
Рис. 13.6. Основная надпись для чертежей и схем
185
- 7> -10> < 23 > < 15 ^<|0> z 70 .1, " г 50 >
(14) (И) (16) (17) (18) (2) К 15 , 15 , 20
Him 1ип> А® ()оку м Подпись Лота 4
Выпоипи Литера Лист Листов о
Ру га водит (4) (7) (8)
(10) (I I) (12) (13) (1) У
// контр (9) U1
iae каф
Рис. 13.7. Основная надпись для текстовых документов
7Ч к 23 ^-.15 > Z Юч L ио . И Юч
Лист. ~~4.
(14) (В) (16) (17) (18) (2)
Нзм Лит А®докуй НодПНСЬ Дата (7)
Рис. 13.8. Основная надпись для следующих листов чертежей, схем и текстовых документов
13.6. Основные надписи и порядок их заполнения 463
В основной надписи для текстовых документов нет граф “Масса”, “Масштаб”, “Обозначение материала”. Основные надписи и рамки выполняют сплошными основными и тонкими линиями.
В графах основной надписи (номера граф на рис. 13.6-13.8 показаны в скобках) указывают следующую информацию.
Графа 1. Наименование изделия (тема проекта), а также наименование документа, если ему присвоен шифр. Наименование изделия записывают в именительном падеже единственного числа.
В наименовании, состоящем из нескольких слов, на первом месте записывают существительное, например: “ПРОЦЕССОР ЦЕНТРАЛЬНЫЙ”. Наименование документа располагают в отдельной строке после наименования изделия и записывают шрифтом меньшего размера малыми буквами (первая буква большая). Например:
ПРОЦЕССОР ЦЕНТРАЛЬНЫЙ
Схема электрическая структурная.
Графа 2. Большими буквами записывают обозначение документа согласно указаниям п. 13.4.
Графа 3. Материал детали (графа заполняется только для чертежей деталей).
Графа 4. Литера, присвоенная документу согласно ГОСТ 2.103-68 в зависимости от стадии разработки конструкторской документации. Графу заполняют последовательно, начиная с крайней левой клетки. В учебных документах проставляют: Д — дипломный проект; К — курсовой проект; КР — курсовая работа; РР — расчет-1 ная работа.
Графа 5. Масса изделия в килограммах без единицы физической величины. Допускается указывать массу в других единицах с их обозначением, например 0,5 т, 10 г. ,
Графа 6. Масштаб согласно ГОСТ 2.302-68.
Графа 7. Порядковый номер листа. На документах, состоящих из одного листа, эту графу не заполняют.
Графа 8. Общее количество листов документа, имеющих одинаковое обозначение. Эту графу заполняют только на первом листе.
Графа 9. Сокращенное наименование учебного заведения и факультета, номер группы и специальности.
Графа 10. Характер работы лица, подписывающей документ. Свободная строка заполняется на усмотрение разработчика.
Графы 11 и 12. Фамилии лиц, подписавших документ, и их подписи. Подписи лиц, разработавших данный документ, и ответственных за нормоконтроль обязательны.
Графа 13. Дата подписи документа.
Графы 14-18. Возможные изменения согласно ГОСТ 2.503-74.
В надписях на последующих листах чертежей и схем заполняют графы 2, 7 и в случае необходимости — графы 14, 15, 16, 17 и 18.
464 Конструкторская документация
13.7. Конструкторские изделия
13.7.1. Виды изделий
Изделие — это любой предмет или их набор, которые требуется изготовить на предприятии. ГОСТ 2.101-68 устанавливает следующие виды изделий:
• деталь — изделие, изготовленное из однородного по наименованию и марке материала без применения сборочных операций;
• сборочная единица — изделие, составные части которого подлежат соединению на предприятии-изготовителе сборочными операциями;
• комплекс — несколько изделий, не соединенных сборочными операциями, однако предназначенных для выполнения взаимосвязанных сложных операций;
• комплект — набор деталей или сборочных единиц, имеющих общее эксплуатационное назначение вспомогательного характера.
13.7.2. Виды и комплектность конструкторских документов
Виды и комплектность конструкторских документов устанавливает ГОСТ 2.102-68. К конструкторским документам (дЬлее просто “документ’) относятся графические и текстовые документы, которые отдельно или в совокупности определяют состав и строение изделия и содержат необходимые данные для его разработки или изготовления, контроля, приема, эксплуатации и ремонта.
Документы подразделяют на виды. Основные виды перечислены в табл. 13.3.
Таблица 13.3
Вид Шифр Содержание"
Чертеж детали Изображение детали
Сборочный чертеж СЧ Изображение сборочной единицы
Чертеж общего вйда ов Определение конструкции изделия и взаимодействия его основных составных частей
Теоретический чертеж тч Определение геометрической формы изделия
Габаритный чертеж гч Контурное изображение изделия
Монтажный чертеж эч Контурное изображение изделия и данные, необходимые для его монтажа на месте применения
Схема* Изображение составных частей изделия с помощью условных обозначений (ГОСТ 2.708-81)
Спецификация Определяет состав сборочной единицы, комплекса или комплекта
Ведомость спецификации ВС Перечень всех спецификаций составных частей изделия
Пояснительная записка* ПЗ Описание устройства и обоснование принятия решения
Техническое задание* тз Содержит основные требования к изделию и процессу проектирования
13.7. Конструшорские изделия 465
Таблица 13.3. Продолжение
Вид Шифр Содержание
Программа и методика испытаний МИ Определяет технические данные, проверяемые во время испытаний
Таблица* ТБ Указывает данные, сведенные в таблицу
Расчет* РЧ Содержит выполненные расчеты
Эксплу атац ион ны й доку- мент Перечень документов, использованных в процессе эксплуатации
Патентный формуляр ПФ Содержит данные о патентной чистоте изделия
Карта технического уровня и качества изделия КУ Содержит данные о соответствии уровня разработки современным достижениям науки и техники
Инструкция и Содержит правила составления, регулирования и контроля и т.п.
Описание альбома* ОА Перечень всех документов проекта
Примечание. В табл. 13.3. значком обозначены Документы, разработка которых обязательна в дипломном проектировании.
Документы.в зависимости от стадии разработки подразделяют на проектные (техническое предложение, эскизный проект, технический проект) и рабочие (рабочая документация).
В зависимости от способа изготовления конструкторских документов и характера их использования различают:
• образцы — выполняются на любом материале и предназначены для изготовления оригиналов;
• оригиналы — документы, заверенные официальными подписями, позволяющие многократно снимать с них копии;
• дубликаты — копии идентичного воспроизведения оригиналов;
• копии — идентичны оригиналу (дубликату) и предназначены для непосредственного использования в работе.
Определяя комплектность конструкторских документов на изделия, различают:
1. Основной конструкторский документ. Он однозначно определяет изделие и его состав. В качестве основных конструкторских документов приняты:
• для деталей — чертеж детали;
• для сборочных единиц, комплексов и комплектов — спецификация.
2. Основной комплект конструкторских документов изделия объединяет конструкторские документы на все изделие, а не только на составные части. Например, сборочный чертеж, схема электрическая принципиальная, технические условия, эксплуатационные документы.
3. Полный комплект конструкторских документов изделия состоит из основного комплекта конструкторских документов и основных комплектов конструкторских документов на все составные части изделия.
30 — 4-1749
466 Конструкторская документация_________________________________________
13.7.3. Техническое задание на конструкторские изделия
Техническое задание на конструкторские изделия разрабатывают согласно ГОСТ 15.001-73. Техническое задание является обязательным исходным документом для проектирования новых изделий и модернизации серийных.
Техническое задания разрабатывают на основе требований заказчика, изложенных в заявке. При этом учитывают результаты выполнения научно-исследовательских и экспериментальных работ, научного прогнозирования, анализа передовых достижений науки и техники, изучение патентной документации.
Техническое задание состоит из следующих разделов:
• наименование и область использования;
• основание для разработки;
• цель, назначение и источники разработки;
• технические требования и экономические показатели;
• стадии и этапы разработки;
• порядок контроля и приема.
Техническое задание оформляют согласно общим требованиям к текстовым конструкторским документам на листах формата А4 с основным надписями (см. прил. А).
Требования к продукции в техническом задании требуется задавать с учетом действующих государственных стандартов, а также рекомендаций международных организаций.
13.7.4. Спецификация изделий
Стандарт ГОСТ 2.108-71 устанавливает форму и порядок спецификации изделий всех отраслей промышленности. Спецификацию составляют на отдельных листах на каждую сборочную единицу, комплекс и комплект по форме 1 и 1а. Спецификация определяет состав сборочной единицы, комплекса и комплекта. Она необходима для изготовления, комплектации конструкторских документов и планирования запуска производства указанных изделий.
В спецификацию вносят составные части, входящие в состав специфицируемого изделия, а также конструкторские документы, имеющие отношение к изделию и к тем его частям, которые не специфицируются.
Спецификация в общем случае состоит из разделов, расположенной в следующей последовательности:
• документация, комплексы, сборочные единицы, детали;
• стандартные и другие изделия, материалы и комплекты.
Наличие тех или иных разделов определяется составом определенного изделия. Наименование каждого раздела указывают в виде заголовка в графе “Наименование’’ и подчеркивают.
В раздел “Документация” заносят документы основного комплекта конструкторских документов изделия. В разделы “Комплексы”, “Сборочные единицы” и “Детали” заносят комплексы, сборочные единицы и детали, непосредственно входящие в состав изделия. Указанные изделия записывают по алфавиту.
Раздел “Стандартные изделия” содержит изделия, используемые согласно го
13.8. Стадии разработки конструкторской документации 467
сударственным, республиканским и отраслевым стандартам, а также стандартам предприятий.
В раздел “Другие изделия” записывают изделия, используемые не по основным конструкторским документам (по техническим условиям). В раздел “Материалы” заносят все материалы, непосредственно входящие в изделие. В разделе “Комплекты” указывают ведомости эксплуатационных документов, документов для ремонта и т.д.
Графы спецификации заполняют следующим образом.
В графе “Формат” указывают форматы документов, обозначения которых записывают в графе “Обозначения”. Если документ выполнен на нескольких листах различных форматов, то в графе проставляют “звездочку”, а в графе "Примечания” перечисляют все форматы по мере их увеличения.
Для документов, указанных в разделах “Стандартные изделия”, “Другие изделия”, “Материалы”, графу “Формат” не заполняют. Для деталей, на которые не выпущен чертеж, в этой графе указывают “БЧ”.
В графе “Зона” указывают обозначение зоны, в которой находится номер позиции сборочной единицы. В графе “Поз.” указывают порядковые номера составных частей.
После каждого раздела спецификации требуется оставлять несколько свободных строк для дополнительных записей.
13.8. Стадии разработки конструкторской документации
Стандарт ГОСТ 2.0103-71 устанавливает следующие стадии разработки конструкторской документации:
• техническое предложение;
• эскизный проект;
• технический проект;
• рабочая документация: опытного образца, серийного производства.
Техническое предложение (ГОСТ 2.118-74) содержит:
• проверку изделия на предмет патентной чистоты;
• оформление заявок на изобретения;
• оценку качества рассматриваемых вариантов и выбор оптимального для обеспечения наилучшего технического и экономического эффекта (иногда по изготовленному макету).
Наиболее целесообразно выполнять оптимизацию с помощью компьютерной графики в диалоговом режиме. При этом используют математические модели и количественные методы минимизации.
Эскизный проект (ГОСТ 2.119-73) разрабатывают для установки принципиальных (конструктивных, схемных и др.) решений. По эскизной документации изготовляют и испытывают макет. На этом этапе для компоновки вариантов конструкций из стандартных и типовых модулей полезны графические средства автоматизации. Они позволяют создавать новые конструкции с учетом эргономики, эстетики и оптимизации.
30*
468 Конструкторская документация
На этапе технического проекта (ГОСТ 2.120-73) принимают окончательное решение с подробной разработкой общих видов, чертежей и схем изделия. Они позволяют оценить его соответствие требованиям ТЗ, технологичность, удобство эксплуатации и т.д.
Технический проект не повторяет работы, проведенные на предыдущих этапах, если они не содержат дополнительных сведений. Для его разработки можно использовать документы с предыдущих стадий с соответствующей корректировкой замечании к эскизному проекту. Технический проект служит основанием для разработки рабочей конструкторской документации. Для детального конструирования особенно важно использовать ЭВМ-с накопленной информационной базой, содержащей изображения стандартных и типовых элементов, узлов, а также выполнять на ней проверочные расчеты.
На стадии рабочего конструкторского проекта (ГОСТ 2.109-73) выполняют:
• разработку документов для изготовления и испытания опытного образца;
• изготовление и испытание опытного образца;
• корректировку конструкторских документов по результатам испытаний опытного образца;
• приемочные испытания опытного образца и дальнейшую коррекцию документации;
• изготовление и испытание установочной серии;
• корректировка документации по результатам испытаний установочной серии;
• изготовление и испытание главной (контрольной) серии (в случае необходимости).
13.9. Правила оформления пояснительной записки
13.9.1. Общие требования
Пояснительную записку оформляют в соответствии с требованиями следующих стандартов-
• ГОСТ 2.105-95 “Общие требования к текстовым документам”;
• ДСТУ 3008-95 “Документация. Отчеты в сфере науки и техники. Структура и правила оформления”;
• ГОСТ 19.105-78 “Общие требования к программным документам”;
• ГОСТ 19.404-79 “Пояснительная записка. Требования к содержанию и оформлению”;
Согласно ГОСТ 2.105-95 пояснительную записку выполняют одним из следующих способов:
• машинописным. Шрифт печатной машинки должен быть четким, высота — не менее 2,5 мм, лента — только черного цвета (полужирная);
• рукописным. Чертежный шрифт с высотой букв и цифр не менее 2,5 мм, написанных черными чернилами или черной пастой;
• с использованием печатных и графических устройств вывода компьютеров;
• на магнитных носителях данных.
13.9. Правила оформления пояснительной записки 469
В отдельных случаях после согласования с руководителем допускаются другие способы выполнения пояснительной записки.
Для дипломных проектов объем пояснительной записки составляет 100-120 ' страниц печатного текста с учетом таблиц, схем, графиков, диаграмм, приложений, выполненных в одном экземпляре. Готовая пояснительная записка брошюруется так, чтобы листы были плотно стиснуты. Не допускается их соединение скрепками или скоросшивателем.
Выполняя записку, требуется выдерживать равномерную густоту, контрастность и четкость изображения по всему тексту. Все линии, буквы, цифры и знаки должны быть одинаково черными по всей записке.
Отдельные слова, формулы и знаки, которые вписывают в напечатанный текст, должны быть черного цвета, а густота вписанного текста — максимально приближаться к густоте основного цвета.
Ошибки, описки и.графические неточности, обнаруженные в процессе выполнения, допускается исправлять подчисткой или забеливать корректором с дальнейшим нанесением на этом месте исправленного текста (графики). Повреждения листов текстовых документов, помарки и следы не полностью удаленного старого текста (графики) не допускаются.
На всех листах текстового документа наносится сплошной основной линией рамка с полями: слева — 20 мм, сверху, справа и снизу — 5 мм.
Расстояние от рамки до края текста в начале и в конце строки должно быть не меньше 3 мм. Расстояние от верхней или нижней строки текста до верхней рамки формы — не меньше 10 мм. Абзацы в тексте начинают с отступом 15-17 мм (пять знаков).
Сокращения слов и словосочетаний в записке выполняют в соответствии с действующими стандартами библиотечного и издательского дела. Перечень допустимых сокращений слов устанавливает ГОСТ 2.316-68.
13.9.2. Построение пояснительной записки
В общем пояснительная записка состоит из структурных элементов. Структурные элементы “СОДЕРЖАНИЕ”, “ВСТУПЛЕНИЕ”, “ОСНОВНАЯ ЧАСТЬ” (3-4 раздела), “ВЫВОДЫ И РЕКОМЕНДАЦИИ”, “ПЕРЕЧЕНЬ УСЛОВНЫХ ОБОЗНАЧЕНИЙ”, “ПЕРЕЧЕНЬ ТЕРМИНОВ”, “СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ”, “ПРИЛОЖЕНИЯ” не нумеруются, а их названия являются заголовками структурных элементов. Разделы основной части также являются структурными элементами; их нумеруют, а их количество и названия зависят от темы проекта.
Все названия структурных элементов рекомендуется начинать с новой страницы и писать большими буквами. После названия структурного элемента непосредственно размещают (в случае необходимости) заголовки подразделов или пунктов, а далее — соответствующий текст.
На первом листе бумаги структурного элемента “СОДЕРЖАНИЕ” выполняют основную надпись по форме 2, а на всех последующих листах записки — уменьшенную надпись по форме 2а.
470 Конструкторская документация
В записке подразделы обязательно должны иметь заголовки, а для пунктов и подпунктов их использовать не обязательно. Все заголовки в тексте не подчеркивают и в конце них точку не ставят.
Заголовки подразделов, пунктов и подпунктов начинают с абзаца и печатают малыми буквами, кроме первой большой. Абзацы должны быть одинаковыми по всему тексту записки.
Если заголовок состоит из двух и более предложений, то их разделяют точкой. Переносы слов в заголовках не допускаются. Расстояние между заголовком и следующим или предыдущим текстом в случае компьютерного способа выполнения не должно быть меньше двух строк. Не допускается располагать наименование раздела, подраздела, а также пункта и подпункта в нижней строке страницы, если ниже расположена только одна строка текста.
Расстояние между названиями структурного элемента и подраздела — 10-15 мм, а между названием подраздела и пункта (или текста) — 5-10 мм.
13.9.3. Нумерация составных частей
Разделы, подразделы, пункты и подпункты записки нумеруют арабскими цифрами. Порядковые номера записывают с абзаца и в конце их точку не ставят. Если порядковый номер состоит из нескольких цифр, то их разделяют точкой.
Разделы записки последовательно нумеруют в пределах документа, например, 1, 2, 3 и т. д. Подразделы последовательно нумеруют в пределах каждого раздела, например, 2.1 (первый подраздел второго раздела).
Разделы, как и подразделы, могут состоять из нескольких пунктов. Если раздел не имеет подразделов, то пункты нумеруют в пределах раздела; при этом пункты не имеют наименования и их записывают с абзаца, например, 2.4 (четвертый пункт второго раздела). Если записка имеет подразделы, то номер пунктов в них состоит из номера раздела, подраздела и порядкового номера пункта, например, 1.2.1, 1.2.2 и т. д. Пункты, в случае необходимости, разбивают на подпункты с порядковой нумерацией в пределах каждого пункта, например, 1.3.4.1, 1.3.4.2 и т. д.
К страницам записки применяют сквозную нумерацию арабскими цифрами. Номер страницы на титульном листе не ставят. Иллюстрации, схемы, таблицы, расположенные на отдельных страницах записки, включают в общую нумерацию записки.
В середине пункта или подпункта можно указывать перечень требований, указаний и положений. Перед каждой позицией перечня требуется ставить дефис или, в случае необходимости ссылки в тексте записки на одну из позиций перечня — малую букву, после которой ставят скобку. Для.дальнейшей детализации перечня в пределах позиции используют арабские цифры со скобкой, а запись выполняют с абзаца, например:
а)
б)
1)
2)
а)
Каждую строку перечня начинают с абзаца.
13.9. Правила оформления пояснительной записки 471
13.9.4. Изложение текста записки
Полное наименование проекта на титульном листе, основной надписи и при первом упоминании в тексте записки должно быть одинаковым с его названием в основном конструкторском документе. В последующем тексте порядок слов в названии должен быть следующим: на первом месте определение (прилагательное), а затем название изделия (существительное). При этом допускается использовать сокращенное название изделия. Названия, которые указывают в тексте записки и на иллюстрациях, должны быть одинаковыми.
Текст записки должен быть четким и не допускать различных толкований. Излагая обязательные требования в записке необходимо использовать слова “должен быть”, “требуется”, “не требуется”, “разрешается только”, “не допускается”, “запрещено". Используя другие положения, требуется применять слова “может быть”, “как правило”, “в случае необходимости” и т.д.
В тексте пояснительной записки не рекомендуется употреблять обороты с местоимениями первого лица, например, “Я считаю...”, “Мы считаем...” и т.п. Рекомендуется вести изложение, не употребляя местоимений, например, “Считаем...”, “...находим...” и т.п. Допускается использовать повествовательную форму изложения текста записки, например, “указывают”, “применяют” и т.д.
В документе требуется применять научно-технические термины, обозначения и определения, установленные существующими стандартами, а при их отсутствии — общепринятые в научно-технической литературе.
Если в документе используется специфическая терминология, то в его конце перед списком литературы приводят перечень используемых терминов с соответствующими пояснениями.
В тексте записки не допускается:
• применять для одного и того же понятия различные научно-технические термины, близкие по смыслу (синонимы), а также иностранные слова и термины, если такие используются в русском языке;
• сокращать обозначения единиц физических величин, если их применяют без цифр, за исключением физических величин в заголовках таблиц и в расшифровках буквенных обозначений, входящих в формулы;
• записывать сокращения слов, кроме установленных правилами русской орфографии и соответствующими государственными стандартами;
• располагать в тексте математический знак минус (-) перед отрицательными значениями величин. Вместо знака (-) следует писать слово “минус”. Например, минус 5 В, а не “-5 В”;
• использовать без числовых значений математические знаки, например, < (меньше или равно), > (больше или равно), * (не равно), а также № (номер), % (процент);
• использовать знак “0” для обозначения диаметра (следует писать слово “диаметр”);
• применять индексы стандартов, технических условий и других документов (ГОСТ, ДСТУ, ТУ и т.п.) без регистрационного номера.
Если в записке указаны пояснительные надписи, нанесенные непосредственно на проектируемое изделие (планки, панели, таблички с элементами управления), то
472 Конструкторская документация
их выделяют шрифтом (без кавычек), например, ВКЛ., ВЫКЛ., или кавычками, если надпись состоит из цифр и знаков.
В тексте записки перед обозначением параметра указывают его пояснение, например, “Длительность фронта сигнала tHL". Числовые обозначения величин в тексте указывают с необходимой степенью точности, при этом в ряду величин выравнивание числа знаков после каждой запятой не обязательно.
13.9.5. Правила написания обозначений и наименований физических величин
Применение и написание единиц физических величин должны соответствовать требованиям ГОСТ 8.417-81 "Основные метрологические термины”.
4.5.1. Для написания значений величин требуется использовать обозначения их единиц буквами или специальными знаками (...°, ...', ..."). При этом устанавливают два вида буквенных обозначений: международные (с использованием букв латинского или греческого алфавита) и кириллица. Использование обоих видов обозначений в одном документе не допускается.
4.5.2. Буквенные обозначения единиц выполняют шрифтом без наклона. В обозначениях единиц точку как знак сокращения не ставят, обозначения единиц следует применять после числовых значений и располагать в строке с ними (без переноса на следующую строку).
4.5.3. Последнюю цифру и обозначение единицы записывают через пробел:
• правильно 150 kW; неправильно 150/cUV.
Исключением являются обозначения в виде знака, поднятого над строкой, перед которым пробел не оставляют:
• правильно 20°; неправильно 20 °.
4.5.4. При наличии десятичной дроби в числовом значении величины обозначения единимы измерения ставят после всех цифр:
• правильно 423,06 т; неправильно 423 т, 06.
4.5.5. Указывая значения величин с предельными отклонениями, числа берут в скобки, после которых пишут обозначения единицы:
• правильно (100,0±0,1) mA; неправильно 100,0±0,1 mA.
4.5.6. Буквенные обозначения единиц, входящие в произведение, отделяют точками на середине линии как знаками умножения, или пробелами, если не возникает недоразумений:
• правильно N-m; неправильно Nm.
4.5.7. В буквенных обозначениях отношений единиц для знака деления используют только одну черту: косую или горизонтальную.
Допускается исгГользовать обозначения единиц, возведенных в степень (положительные или отрицательные)
W W
• правильно —2 х ; неправильно —
• правильно W пГ2 - К ; неправильно W /т2 / К .
4.5.8. Обозначения единиц в числителе и знаменателе с помощью косой черты размещают в одной строке:
13.9. Правила оформления пояснительной записки 473
• правильно m/s; неправильно т/ .
4.5.9. Для сложных единиц, которые состоят из двух и более простых, не допускается комбинировать буквенные обозначения и названия единиц (то есть для одних — обозначения, для других — названия):
• правильно 50 т/s', неправильно 50 rn/sec.
4.5.10. Единица физической величины одного и того же параметра в пределах пояснительной записки должна быть одинаковой. Записывая группу числовых значений, выраженных одинаковой единицей физической величины, ее указывают после последней цифры в ряду, например, 5, 9; 8,5; 12,0 тт.
4.5.11. Числовые значения величин с обозначением единицы пишут с цифрами, а без обозначения физических величин — словами, например: “струм не больше 2 mA”, “сопротивление увеличить в три раза”.
4.5.12. Если в тексте документа указывают диапазон числовых значений однородной физической величины, то ее обозначения указывают после последнего числового значения, например: от 1 до 5 тпг, от плюс 10 до минус 40°С.
Недопустимо отделять единицу физической величины от числового значения (переносить их на разные строки или страницы).
4.5.13. Числовые значения величин в тексте указывают со степенью точности, необходимой для обеспечения требуемых свойств изделия. При этом в ряду величин выравнивают количество знаков после запятой, одинаковое для изделия одного наименования. Например, если градация толщины стальной ленты 0,25 тт, то весь ряд толщин ленты требуется указывать с таким же количеством десятичных знаков—1,50; 1,75; 2,00.
4.5.14. Дробные числа указывают в виде десятичных дробей, за исключением Г Г размеров в дюймах, которые требуется записывать 1/4", 1/2" (но не —, —).
4 2
13.9.6. Представление формул и уравнений
В тексте пояснительной записки обычно используют формулы и уравнения. Формула — это совокупность величин, выраженных символами и соединенных с помощью математических знаков =, *, >, < и т.д. Уравнения — это аналитическая запись задачи о нахождении неизвестных значений аргументов.
Формулы и уравнения размещают непосредственно после текста, в котором они упоминаются впервые, посредине страницы. Выше и ниже каждой формулы или уравнений оставляют по одной свободной строке.
Формулы и уравнения последовательно нумеруют в пределах раздела. Номер формулы или уравнения состоит из номера раздела и порядкового номера формулы или уравнения, разделенных точкой. Номер указывается в круглых скобках на уровне формулы в крайней правой позиции строки, например, (4.5) — пятая формула четвертого раздела.
Пояснения обозначений символов и числовых коэффициентов, входящих в формулу или уравнение, указывают непосредственно под выражениями в той последовательности, в которой они представлены в формуле или уравнении. Первая строка пояснения начинается с абзаца словом “где” без двоеточия после нее.
474 Конструкторская документация
Например:
I = U/R, (4.5)
где I— сила тока, A; U — напряжение, В; R — сопротивление электрическому току, Ом.
Расчеты по представленным формулам размещают непосредственно за ними. В случае расчетов и печати результатов с помощью компьютера указывают тип машины и названия используемых алгоритмов и программ. Переносить формулы или уравнения на следующую строку допускается только на знаках выполнения операций, при этом знак операции в начале следующей строки повторяют. В случае переноса формулы или уравнения на знаке операции умножения применяют знак“х”.
Если в записке имеется только одна формула или уравнение, то их также нумеруют по указанным правилам.
Формулы, следующие одна за другой и не разделенные текстом, отделяют запятой. Например:
fl(x,y) = Sl и 51 <51 max, (4.1)
/2(х, у) = S2 и S2 < S2 max, (4.2)
Числовой результат расчетов получают только после подстановки в формулу вместо символов их числовых значений:
т и 100 _
• правильно I- — =----= 2А;
R 50 т U ,
• неправильно 1 = — -2 А.
Ссылку в тексте на номер формулы указывают в скобках, например,"... в формуле (2.4)”.
13.9.7. Оформление иллюстраций
Все иллюстрации в пояснительной записке (чертежи, схемы, фотографии, диаграммы, графики) называют рисунками.
Количество иллюстраций должно быть достаточным для пояснения излагаемого текста. Иллюстрации необходимо располагать как по тексту записки (как можно ближе к соответствующим частям текста), так и в конце его или указывать в приложениях. Иллюстрации следует выполнять в соответствии с требованиями стандартов ЕСКД и ЕСПД.
Все иллюстрации последовательно нумеруют в пределах раздела арабскими цифрами. Номер иллюстрации состоит из номера раздела и порядкового номера иллюстрации, разделенных точкой, например, “Рисунок 2.5”. Ссылки на иллюстрации добавляются по типу "... на рис. 2.5 Повторная ссылка на иллюстрацию указывают с сокращением слова “смотри”, например, "... см. рис. 2.5 ...”. Допускается нумерация иллюстраций в пределах всей записки.
Если иллюстрация одна, то ее обозначают "... Рисунок 1 ...” Номер иллюстрации в приложениях определяют отдельной нумерацией с добавлением перед арабской цифрой обозначения приложения, например, “... Рисунок А.1 ...”.
Иллюстрации могут иметь название, которое размещают под иллюстрацией в одной строке с ее номером, например, “Рисунок 3.2. Схема электрическая структур
13.9. Правила оформления пояснительной записки 475
ная”. В случае необходимости под названием иллюстрации записывают поясняющие данные (рис. 13.9).
Графические обозначения элементов цифровой техники
а б
Рис. 13.9. Условные графические обозначения логических элементов: а — логический элемент НЕ И; б — логический элемент «Исключающее ИЛИ»
Допускается, в случае необходимости, записывать над иллюстрацией обобщенный смысловой заголовок, например, для рис. 13.9: “Графические обозначения элементов цифровой техники”. Размер шрифта всех без исключения надписей в рисунках такой, как и в тексте пояснительной записки.
Иллюстрации размещают таким образом, чтобы их можно было рассматривать без поворота или поворачивая по часовой стрелке.
Если в тексте записки имеется иллюстрация, на которой изображены составные части изделия, то на ней указывают номера позиций этих составных частей, по мере их возрастания.
На электрических схемах, представленных в записке, возле каждого элемента указывают его позиционное обозначение и, в случае необходимости, номинальные значения величин.
Допускается сквозная нумерация иллюстраций в пределах всей записки.
13.9.8. Построение таблиц
Таблицы используют для большей наглядности и удобства сравнения показателей. Название таблицы при ее наличии должно отображать ее содержанине, быть точным и кратким. Название следует располагать над таблицей. В случае переноса части таблицы на ту же самую или другую страницу название размещают только над первой частью таблицы.
Цифровой материал обычно оформляют в виде таблиц (рис. 13.10). Горизонтальные линии, разделяющие строки таблицы, а также линии, ограничивающие таблицу слева, справа и снизу, можно не проводить, если их отсутствие не затрудняет пользование таблицей.
Таблицу размещают непосредственно после текста, в котором она упоминается впервые, или на следующей странице. На все таблицы должны быть ссылки в тексте записки.
Таблицы последовательно нумеруют арабскими цифрами в пределах раздела, за исключением таблиц в приложениях. Номер таблицы состоит из номера раздела и порядкового номера таблицы, разделенных точкой, например, “Таблица 2.1” — первая таблица второго раздела. Допускается сквозная нумерация таблиц в пределах всей записки.
476 Конструкторская документация
Таблица_____________-_____________________
номер название таблицы
Шапка
Заголовки граф
Подзаголовки граф
Строки (горизонтальные ряды)
Боковик Графы (колонки)
(заголовки строк)
Рис. 13.10. Формат таблиц
Если в записке только одна таблица, то ее также нумеруют по перечисленным правилам.
Заголовки граф и строк таблицы пишут с большой буквы, а подзаголовки — с малой буквы, если они составляют одно предложение с заголовком, или с большой буквы, если они имеют самостоятельное значение. Заголовки и подзаголовки указывают в единственном числе, и в конце их точку не ставят.
Разделять заголовки и подзаголовки боковика и граф диагональными линиями не допускается. Заголовки граф записывают параллельно строкам таблицы, однако, в случае необходимости, допускается их вертикальное размещение. Шапка отделяется линией от остальной таблицы. Высота строк должна быть не менее 8 мм. Допускается располагать таблицу вдоль длинной стороны листа.
Если строки или графы таблицы выходят за формат страницы, то ее делят на части, которые размещают одну под другой или рядом; при этом в каждой части таблицы повторяют ее шапку и боковик.
В случае деления таблицы на части допускается ее шапку или боковик заменять в соответствии с номерами граф или строк. При этом нумеруют арабскими цифрами графы и (или) строки первой части таблицы.
Слово “Таблица” указывают один раз слева над первой частью таблицы, над остальными частями пишут: “Продолжение таблицы” с указанием номера таблицы.
13.9.9. Оформление примечаний и ссылок
Примечания в записке указывают, если требуются пояснения или справочные данные к содержанию текста, таблиц или графического материала. Примечания не содержат требований; их размещают непосредственно после материала, которого они касаются.
13.9. Правила оформления пояснительной записки 477
Одно примечание не нумеруют. Слово “Примечание” печатают с большой буквы с абзаца, не подчеркивая. После слова “Примечание” ставят тире и с большой буквы в этой ж строке указывают текст примечания.
Примечание —_______________________________
Несколько примечаний нумеруют последовательно арабскими цифрами с точкой. После слова “Примечания" ставят двоеточие и с новой строки с абзаца после номера примечания с большой буквы указывают текст.
ПРИМЕЧАНИЯ:
1._____________________________
2.______:______________________
Ссылку в тексте записки на источники следует указывать порядковым номером по перечню ссылок, выделенных двумя квадратными скобками, например, "... в работах [1-7] показано...”.
В случае ссылок на разделы, подразделы, пункты и подпункты, рисунки, формулы, таблицы и приложения указывают их номера; следует писать "... в разделе 4...’’, "... см. 3.4.1...”,"... в приложении Б”.
Примечание к таблице размещают внизу в пределах ее рамки.
13.9.10. Оформление приложений
Иллюстративный материал, таблицы или текст вспомогательного характера допускается указывать в приложениях. Их оформляют как продолжение записки на последующих листах или как самостоятельный документ по общим правилам.
Приложения бывают обязательными или информационными. Информационные приложения могут быть рекомендуемого или справочного характера. Приложения выполняют на листах формата А4; допускается использование других форматов.
Каждое приложение начинают с новой страницы. Приложение имеет заголовок, напечатанный сверху малыми буквами с первой большой симметрично относительно текста страницы. Посередине строки над заголовком малыми буквами с первой большой печатают слово “Приложение
Приложения обозначают последовательно большими буквами русского алфавита, например, приложение А, приложение Б и т. д. Одно приложение обозначают как приложение А. Приложения имеют общую с остальной частью записки сквозную нумерацию страниц.
Если необходимо, текст приложения делят на разделы, подразделы, пункты и подпункты, которые нумеруют в пределах каждого приложения по общим правилам Например, Г.3.1 — подраздел 3.1 приложения Г.
Если в тексте приложения имеются рисунки, таблицы, формулы и уравнения, то их нумеруют в пределах каждого приложения, например, рис. Г.З — третий рисунок приложения Г; табл. А.2 — вторая таблица приложения А; формула (Д.З) — третья формула приложения Д.
Если приложение содержит по одной иллюстрации, таблице, формуле или уравнению, то их нумеруют, например, Рис. А.1, Таблица А.1, Формула (В.1).
478 Конструкторская документация
13.9.11. Оформление списка литературы
Список литературы содержит перечень источников, использованных в пояснительной записке. Источники размещают в списку в порядке появления ссылки на них в тексте записки и последовательно нумеруют арабскими цифрами. Допускается располагать литературные источники по алфавиту.
Литературными источниками могут быть книги, многотомные издания, периодические издания (газеты, журналы), специальные виды нормативно-технических документов (стандарты, патенты, каталоги) и др. Названия литературных источников указывают языком, на котором они написаны — русским, английским и т.д.
Сведения о литературных источниках указывают в соответствии с требованиями ГОСТ 71-84 “Библиографическое описание произведений печати”.
Обязательные элементы библиографического описания литературных источников следующие:
• фамилии и инициалы автора или коллектива авторов в именительном падеже;
• название издания;
• характеристика издания и сведения о повторном издании;
• место издания, издательство;
• год издания, количество страниц.
Фамилия и инициалы одного, двух или трех авторов записывают, как правило, перед названием книги, а четырех и больше — после названия. Допускается запись книги трех авторов под фамилией и инициалами одного автора, указанного первым, с дополнением “и др.”.
Название книги указывают в описание в той форме, в которой она указана на титульном листе. Для повторного издания указывают его порядковый номер, например, 2-е изд., 3-е изд., и т. д. В характеристике издания пишут: исправленное, дополненное, стереотипное, например, 5-е изд., испр. и доп.
Названия места издания указывают полностью в именительном падеже, за исключением названий городов: Москва — М., Киев — К., Санкт-Петербург — С.Пб.
Название издательства записывают в сокращенной форме, например, К.: “МК-Пресс". Год издания обозначают арабскими цифрами. В конце описания книги указывают фактическое количество страниц, например, 125 с. Использование разделительных знаков (точек, запятых, двоеточий, дефисов) показано в представленных ниже примерах.
Библиографическое описание книг индивидуальных авторов:
1. Глушков В. М. Синтез цифровых автоматов. - М.: Физматгиз, 1996. - 467 с.
2. Бабич М. П., Жуков И. А. Компьютерная схемотехника. Методы построения и проектирования: Уч. пособ. - К.: “МК-Пресс”, 2004. - 576 с.
3. Самофалов К. Г., Корнейчук В. И., Тарасенко В. П. Цифровые вычислительные машины. - К.: Вища шк., 1983. - 455 с.
Описание многотомных изданий:
4. Хоровиц П., Хилл У. Искусство схемотехники: В 3-х т.: -Пер. с англ. - 4-е изд., перераб. и доп. - М.: Мир, 1993. -Т. 3, - 367 с.
Контрольные вопросы 479
Описание периодических изданий:
5. Уэнспи Д. X. Высоконадежная система с тройным резервированием для управления технологическими процессами. - Электроника, 1983 - №2. - С. 32-39.
Библиографическое описание стандарта содержит его индекс, цифровое обозначение, название, дату ввода в действие, например:
6. ГОСТ 2.105-95.ЕСКД. Общие требования к текстовым документам. - Введ. 01.07. 96.
Описывая патентный документ, указывают:
• сокращенное название документа (“А. с." — авторское свидетельство, ”Пат.” — патент);
• название государства, видавшего документ;
• название изобретения;
• фамилию или название заявителя, а также фамилии авторов;
• номер заявки, даты заказа и публикации;
• номер бюллетеня и количество страниц.
Например:
7. А. с. 1449986 СССР. Устройство для формирования остатков по модулю/Н.
В. Черкасский. - №4122318/24 - 24. Заявл. 19.09.86; опубл. 07.06.88. Бюл. № 19. -2 с.
Все цитаты, а также взятые из литературы данные должны иметь ссылку на первоисточники. Ссылку указывают в тексте в квадратных скобках, в которых ставят порядковый номер источника, указанного в списке используемой литературы, номер тома (при наличии) и страницу, например: [3], [8, Т. 3, с. 42], [15, с. 55]; ссылаясь на стандарт, указывают его номер, например, ГОСТ 16263-70.
Контрольные вопросы
1. Дайте определения проектирования.
2. Дайте определение конструкторской документации.
3. Перечислите виды конструкторской документации.
4. Что такое графическое изображение?
5. Что такое чертеж?
6. Что такое схема?
7. В чем заключаются общие требования к оформлению проектов?
8. Как обозначаются стандарты ЕСКД?
9. Опишите форматы конструкторских документов.
10. Перечислите виды основных надписей.
11. Перечислите виды конструкторских изделий.
12. Из каких разделов состоит техническое задание?
13. Что входит в состав спецификации изделия?
14. Опишите стадии разработки конструкторской документации.
480 Требования к выполнению схем и иллюстративных документов
Глава 14
Требования к выполнению схем и иллюстративных документов
14.1. Понятие схем и общие требования к их выполнению
1 4.1.1. Термины и определения
Стандарт ГОСТ 2.701-84 “Схемы. Виды и типы. Общие требования к выполнению” распространяются на схемы, которые выполняются ручным или автоматизированным способом, для изделий всех отраслей промышленности. Стандарт использует следующие термины и определения.
Схема — это графический конструкторский документ, на котором показаны в виде условных графических изображений или обозначений составные части изделия и связи между ними.
Элемент схемы — составная часть схемы, которая выполняет определенную функцию в изделии и не может быть разделена на части с самостоятельным функциональным назначением (резистор, трансформатор, муфта и др.).
Устройство — совокупность элементов, представляющих собой единую конструкцию (блок, плата и др.). Устройство может не иметь в изделии определенного функционального назначения.
Функциональная группа — совокупность элементов, которые выполняют в изделии определенную функцию и не объединены в единую конструкцию.
Функциональная часть — элемент, устройство, функциональная группа.
Функциональная цепь — линия, канал, тракт определенного назначения (канал звука, видеоканал и др.).
Линия взаимосвязи — линия на схеме, указывающая на наличие связи между функциональными частями изделия.
1 4.1.2. Виды и типы схем
В зависимости от физической реализации элементы подразделяют на виды, которые обозначаются большими буквами: электрические — Э; гидравлические — Г; пневматические — П; газовые -X; вакуумные —В; оптические — Л; энергетические — Р; автоматизации — А; деления — Д; комбинированные — С.
В зависимости от основного назначения все схемы делят на типы, которые обозначают цифрами:
• структурные — 1;
• функциональные — 2;
• принципиальные (полные) — 3;
14.1. Понятие схем и общие требования к их выполнению 481
• соединений (монтажные) — 4;
• подключения — 5;
• общие — 6;
• размещения — 7;
• объединенные — 0;
Структурная схема определяет основные функциональные части изделия, их назначение и взаимосвязь.
Функциональная схема поясняет определенные процессы, происходящие в отдельных функциональных цепях изделия или в изделии в целом.
Принципиальная (полная) схема определяет полный состав элементов и связей между ними и обычно дает подробное представление о принципах работы изделия.
Схема соединений (монтажная) показывает соединения составных частей изделия и определяет проводы, жгуты, кабели, с помощью которых они соединены, а также места их соединений.
Схема подключения показывает внешние подключения изделия.
Общая схема определяет составные части комплекса и соединение их между собой на месте эксплуатации.
Схема размещения определяет относительное размещение составных частей изделия, а в случае необходимости, также проводов, жгутов, кабелей и т.д.
Схема объединенная — схема, когда на одном конструктивном документе выполняют схемы двух или нескольких типов на одно изделие.
1 4.1.3. Наименование и код схемы
Наименование и код схемы определяют по их виду и типу. Код схемы должен состоять из буквенной части, определяющей вид схемы, и цифровой части, определяющей тип схемы. Например:
• схема электрическая принципиальная — ЭЗ;
• схема гидравлическая соединений — Г4;
• схема электрическая структурная — Э1;
• схема электрическая соединений и подключений — Э0;
• схема электрогидропневмокинематическая принципиальная — СЗ.
В основной надписи (графа 1) указывают наименование изделия и наименование схемы (см. рис. 13.6).
На изделие допускается выполнять схему определенного вида и типа на нескольких листах.
1 4.1.4. Общие требования к выполнению схем
Организация рисунка схемы
Схемы выполняют без выдерживания масштаба, действительное пространственное размещения составных частей изделия не учитывают или учитывают приблизительно. Графические обозначения элементов, устройств и функциональных групп и соединительные линии следует размещать на схеме так, чтобы обеспечить 31 -4-1749
482 Требования к выполнению схем и иллюстративных документов наилучшее представление о структуре изделия и взаимодействии его составных частей. Допускается размещать условное графическое обозначение (УГО) элементов на схеме в таком же порядке, в каком они размещены в изделии, если не нарушается удобство чтения схемы.
Линии должны состоять из горизонтальных и вертикальных отрезков и иметь, по возможности, наименьшее количество изломов и взаимных пересечений. В отдельных случаях, если это упрощает графику схемы, допускается применять наклонные участки линии, длину которых по возможности следует ограничивать. Промежуток между любыми двумя параллельными линиями должен быть не менее 3 мм независимо от принятой толщины линий.
Направления линий связи сверху вниз и слева направо берут за основные; допускается их стрелками не обозначать. В других случаях направление линий связи обозначают по ГОСТ 2.721-74 “Обозначения условные графические в схемах. Обозначения общего применения”.
Слияние линий связи следует обозначать точкой в отличие от их пересечения.
Допускается:
• выполнять схемы в пределах условного контура, который тонкими сплошными линиями упрощенно изображает конструкцию изделия;
• изображать на схемах УГО элементов и функциональных частей разнесенным способом. В этом случае на поле схемы можно указывать полные УГО и (или) таблицы, указывающие размещение их отдельных частей.
Элементы, которые составляют устройство, имеющее самостоятельную принципиальную схему, выделяют на схемах сплошной линией, которая вдвое толще линий связи. Элементы, которые составляют функциональную группу или устройство, но не имеют принципиальной схемы, допускается на схемах выделять штрих-пунктирными линиями, одинаковыми по толщине с линиями связи.
На схеме одного вида можно изображать элементы схем другого вида, которые непосредственно влияют на работу схемы этого вида, а также элементы и устройства, которые не входят в изделие, однако необходимы для пояснения принципов его работы. Графические обозначения таких элементов и устройств выделяют на схеме штрихпунктирными линиями, равными по толщине линиям связи.
Графические обозначения
Для выполнения схем применяют следующие графические обозначения:
• УГО, установленные в стандартах ЕСКД, а также построенные на их основе;
• прямоугольники и упрощенные внешние изображения, в том числе аксонометрические.
В случае необходимости применяют нестандартные УГО с соответствующими разъяснениями на схеме.
На схемах, которые выполняют средствами печатающих устройств, должны применяться только те графические изображения, для которых соответствующими государственными стандартами предусмотрена возможность их выполнения методом алфавитно-цифровой печати.
Условные графические обозначения, для которых установлено несколько допустимых (альтернативных) вариантов выполнения, которые отличаются геометри-
14.1. Понятие схем и общие требования к их выполнению 483
ческой фигурой или степенью детализации, следует применять с учетом вида и типа разрабатываемой схемы и информации, которую необходимо показать на схеме графическими средствами. При этом на всех схемах одного типа, входящих в комплект документации, применяется один выбранный вариант обозначения. Применение на схемах тех или иных УГО определяют по правилам выполнения схем определенного вида и типа. Условные графические обозначения элементов изображают в размерах, близких к стандартным условным обозначениям. Если размеры УГО в стандартах не установлены, то их изображают на схемах в размерах, в которых они выполнены в соответствующих стандартах на УГО. Размеры УГО, а также толщина их линий должны быть одинаковыми на всех схемах для определенного изделия.
Допускается все обозначения пропорционально изменять. Графические обозначения следует выполнять линиями той же толщины, что и линии связи. Если в УГО элементов имеются утолщенные линии, то их следует выполнять толще линий связи в два раза.
Условные графические обозначения элементов изображают на схеме в положении, в котором они представлены в соответствующих стандартах, или повернутыми на угол, кратный 45°, или изображают повернутыми зеркально. Если при повороте или зеркальном изображении УГО может нарушаться содержание или удобство чтения, то такие обозначения следует изображать в положении, в котором они представлены в соответствующих стандартах.
Условные графические обозначения, содержащие цифровые или буквенноцифровые обозначения, допускается поворачивать против часовой стрелки на угол 90 или 45°.
Линии связи
В зависимости от вида и типа схем линиями изображают электрические (функциональные, логические и т.д.) и механические взаимосвязи, материальные проводники (провода, кабели, шины), экранирующие оболочки, корпуса приборов, условные границы устройств и функциональных групп и др.
Линии на схемах всех типов выполняют в соответствии со стандартом ГОСТ 2.751-73 “Электрические связи, провода, кабели и шины”.
Толщину линий выбирают в зависимости от формата схемы и размеров УГО. На одной схеме рекомендуется использовать не более трех типоразмеров с толщиной: тонкую s, утолщенную 2s и толстую 35...4\, где 5 — толщина линии, которую выбирают в зависимости от размеров схемы. Выбранные значения толщины линий должны быть постоянными во всем комплекте схем на изделие. Электрические связи в основном изображают тонкими линиями.
Если необходимо выделить наиболее важные цепи (например, электропитания), используют утолщенные и толстые линии. УГО и линии связи выполняют линиями одной и той же толщины. Оптимальная толщина линии s = 0,3...0,4 мм, что соответствует по ГОСТ 2.303-68 “Линии” сплошной тонкой линии.
Наименование и изображение, толщина линий и основное назначение представлено в табл. 14.1. Длину штрихов в штриховых и штрихпунктирных линиях выбирают в указанных пределах в зависимости от размеров схемы. Штрихи в линии, а также промежутки между штрихами должны быть приблизительно одинаковой длины.
31*
484 Требования к выполнению схем и иллюстративных документов
Таблица 14.1
Наименование Изображение Толщина Основное назначение
Сплошная линия — S Линия электрической связи, провод, кабель, шина, линия групповой связи, линии УГО
Сплошная толстая линия — 2s, 3s..As Допускается для линий групповой связи применять утолщенные 2s и толстые 35...45 линии
Штриховая — s Линия экранирования, механичной связи
Штрих-пунктирная — s Линия для выделения на схеме групп элементов, составляющих устройство или функциональную группу
Штрих-пунктирная с двумя точками — s Линии разъединительные (для графического разделения частей схемы)
Для уменьшения количества линий, изображенных на схеме, рекомендуется использовать условное графическое слияние отдельных линий в групповые линии по таким правилам:
• линии групповой связи изображают утолщенными и толстыми;
• каждую линию в месте слияния обозначают условным порядковым номером (рис. 14.1, а); допускается обозначать линии буквами или комбинацией букв и цифр;
• каждый условный номер следует наносить на линии групповой связи два раза. При наличии разветвлений их количество указывают после порядкового номера через черту дроби (рис. 14.1, б);
• условные порядковые номера не присваивают, если сливающиеся линии уже имеют обозначения, например, номера проводов (рис. 14.1, в).
Рис. 14.1. Построение линий групповой связи: а — обозначение линий номерами; б - обозначение количества разветвлений; в — обозначение линий номерами проводов
Линии, которые сливаются на всех схемах комплекта, изображают под прямым углом (рис. 14.2, а) или с изломом под углом 45° к групповой линии (рис. 14.2, б).
Текстовая информация
На схемах допускается размещать различные технические данные, характер которых определяется назначением схемы. Такие сведения указывают или возле графических обозначений (по возможности справа или сверху), или на свободном
14.1. Понятие схем и общие требования к их выполнению 485
месте схемы. Около графических обозначений элементов и устройств размещают, например, номинальные значения их параметров, а на свободном поле схемы — диаграммы, таблицы, текстовые указания (диаграммы последовательности временных процессов, циклограммы и т.д.).
Рис. 14.2. Способы слияния линий в групповую линию: а — под прямым углом; б — с изломом под углом 45°
Содержание текста должно быть сжатым и точным. В надписях на схемах не следует применять сокращения слов, за исключением общепринятых или установленных в стандартах.
Текстовые данные в зависимости от их содержания и назначения можно размещать:
• рядом с графическими обозначениями;
• в середине графического обозначения;
• над линиями связи или в разрыве линий связи или рядом с концами линий связи;
• на свободном поле схемы.
Текстовые данные, имеющие отношение к линиям, ориентируют параллельно горизонтальным участкам соответствующих линий. В случае большой плотности схемы допускается вертикальная ориентация данных.
На поле над основной надписью допускается размещать необходимые технические указания. Если схему выполняют на нескольких листах, технические указания, общие для всей схемы, следует размещать на свободном поле первого листа схемы.
Буквенно-цифровые обозначения выполняют с применением больших букв латинского алфавита, арабских цифр и знаков (квалификационных символов) согласно ГОСТ 2.710-81 “Обозначения буквенно-цифровые в электрических схемах”.
Условное буквенно-цифровое обозначение записывают в виде последовательности букв, цифр и знаков в одну строку без пробелов, и их количество в обозначении не устанавливают.
Например, DA2 — вторая схема интегральная аналоговая; DD4 — четвертая схема интегральная цифровая; DS— устройство хранения информации.
Буквенно-цифровой код элемента на схеме присваивают в направлении сверху вниз и слева направо. Он является обязательной частью. Дополнительную информацию обозначают квалификационными символами, обозначения которых перечислены в табл. 14.2.
486 Требования к выполнению схем и иллюстративных документов
Таблица 14.2
Тип условного обозначения Квалификационный символ
Устройство высшего уровня =
Функциональная группа высшего уровня или #
Конструктивное обозначение +
Обозначение элемента —
Обозначение контакта
Адресное обозначение 0
Порядок записи составного обозначения определяют порядком вхождения, например: ^Л=Л2-Л5 означает, что резистор R5 входит в устройство А2, входящее в функциональную группу Л.
Перечень элементов
Перечень элементов размещают на первом листе схемы или выполняют в виде самостоятельного документа. Перечень элементов оформляют в виде таблиц, которые заполняются сверху вниз (рис. 14.3).
- Обозначение Наименование Кол-во Примечания
СС
20 НО < 10 >
185
Рис. 14.3. Форма таблицы перечня элементов
В графах таблицы указывают следующие данные:
• графа “Обозначение” — позиционное обозначение элементов, устройств и функциональных групп;
• графа “Наименование" — для элемента (устройства) — наименование соответственно документу, на основе которого этот элемент (устройство) применяют, и обозначение этого документа (основной конструкторский документ, государственный стандарт, отраслевой стандарт, технические условия);
• графа “Примечания” — рекомендуется указывать технические данные элемента (устройства), которые не содержатся в его наименовании.
Перечень элементов на первом листе схемы размещают, как правило, над основной надписью. Расстояние между перечнем элементов и основной надписью — не менее 12 мм. Продолжение перечня элементов размещают слева от основной надписи, повторяя шапку таблицы.
В случае выпуска перечня элементов в виде самостоятельного документа его код должен состоять из буквы “П” и кода схемы, для которой выпускают перечень, например ПЭЗ — код перечня элементов к электрической принципиальной схеме.
14.1. Понятие схем и общие требования к их выполнению 487
При этом в основной надписи (графа 1) указывают наименование изделия, а также наименование документа “Перечень элементов”.
Перечень элементов записывают в спецификации после схемы, к которой он выпущен. Перечень элементов в виде самостоятельного документа выполняют форматом А4. Основная надпись и дополнительные графы к ней указывают по ГОСТ 2.104-68 (форма 2 и 2а), как показано на рис. 14.4.
Обозначение Наименование Кол-во Примечания
НАУ 03 15 41 005 ПЭ
Ч н т доку v Надпись [ата
Кыпо min Сумматор. Перечень элементов . Читера v Чист Листов
/’1 КОвООнт । 1
А' о нс v 1ын
И КОНГИ/)
Зов каф
Рис. 14.4. Сумматор. Перечень элементов
Разбивая поля схемы на зоны, перечень элементов дополняют графой “Зона” (рис. 14.5); в ней указывают обозначения зоны, в которой размещен элемент (устройство).
Зона Обоя тачание Наименование Кол-во Примечания
СС
< 8 > 20 но < 10 В
185
Рис. 14.5. Форма таблицы перечня элементов с разбивкой поля схемы на зоны
Элементы в перечень записывают группами по алфавиту буквенных обозначений. В пределах каждой группы, имеющие одинаковые буквенные обозначения, элементы размещают по возрастанию их порядковых номеров.
Для облегчения внесения изменений допускается оставлять несколько незаполненных строк между отдельными группами элементов, а в случае большого количества элементов — ив середине групп.
488 Требования к выполнению схем и иллюстративных документов
Элементы одного типа с одинаковыми параметрами, имеющие на схеме последовательные номера, допускается записывать в перечень в одну строку. В этом случае в графу “Обозначение” вписывают только позиционные обозначения с наименьшим и наибольшим порядковыми номерами, например, 7?3, 7?4, С8...С12, а в графу “Кол-во”.— общее количество таких элементов.
14.2. Правила выполнения схем цифровой вычислительной техники
14.2.1. Общие положения
Электрические схемы для изделий цифровой техники требуется йыполнять согласно ГОСТ 2.708-81 и с учетом требований согласно ГОСТ 2.702-75, ГОСТ 2.751-73, ГОСТ 2.710-81.
При чрезмерной насыщенности листов схем условными графическими обозначениями и линиями связи допускается делить поле листа на колонки, ряды, зоны, применять метод координат и т.д.
Колонки обозначают по верхнему краю листа (по горизонтали) слева направо последовательными порядковыми номерами с постоянным количеством знаков в номере, например, 01, 02, ...10...20 и т. д. Допускается дополнительно обозначать колонки по нижнему краю листа.
Ряды обозначают по вертикали (по левому краю листа) сверху вниз большими буквами латинского алфавита. Допускается дополнительно проставлять обозначения рядов по правому краю листа. Высота ряда должна равняться минимальной высоте УГО элемента. В технически обоснованных случаях допускается изменять ширину и высоту колонки ряда.
Обозначение зоны состоит из обозначения ряда (буквы) и обозначения цифры, например, ДОЗ, А'12 и т.д. (рис. 14.6, а).
Рис. 14.6. Разделение поля листа: а — на зоны; б — координатным методом
Разделяя поле листа методом координат (рис. 14.6, б), вертикальные и горизонтальные координаты обозначают большими буквами латинского алфавита.
14.2. Правила выполнения схем цифровой вычислительной техники 489
Нельзя обозначать ряды и координаты буквами I и О в случае, когда они не отличаются от единицы и нуля. Разделение листа разрешается выполнять без изображения на поле листа сетки, ограничившись только нанесением обозначений рядов, колонок, шкал.
Входными линиями листа схемы показывают электрические связи с входными выводами изделия, изображенного на этом листе, а также связи, изображения которых начинаются на других листах схемы. Выходными линиями показывают электрические связи с выходными линиями изделия, изображенного на этом листе, а также связи, изображения которых начинаются на этом листе и продолжаются на других листах и других схемах. Понятие входных и выходных линий распространяется на линии электропитания.
Начало входных линий изображают, начиная с левой стороны и (или) сверху листа. Выходные линии заканчиваются на правой стороне и (или) внизу листа.
При чрезмерной насыщенности листа УГО и линиями связи допускается:
• входные и выходные линии связи начинать и обрывать в середине листа;
• прерывать отдельные линии связи между отдаленными друг от друга УГО, изображенными на одному листе;
• пояснять размещения мест обрывов на поле схемы.
Всем входным, выходным и прерванным на этом листе в месте обрыва линиям присваивают обозначения (цифровые, буквенные или буквенно-цифровые), которые должны отличаться друг от друга. Обозначения можно указывать над линией, на уровне линии или в разрыве линии.
Для обозначений линии связи используют:
• наименование (обозначение сигнала, порядковые номера и т.д.);
• адресное обозначение.
Адресным обозначением линии связи могут быть или координаты места выхода линии связи из элемента (источника) или координаты места обрыва линии. На прерванной в пределах листа линии допускается после обозначения указывать в круглых скобках адрес места продолжения прерванной линии или через черту дроби количество ее разветвлений (рис. 14.7).
Начало разрыва
4 А£Х#08)
,4D(XO3)
Конец разрыва
Начало разрыва
Конец разрыва
Рис. 14.7. Адресные обозначения: а — координатный метод; б— обозначения количества разветвлений
490 Требования к выполнению схем и иллюстративных документов
На выходных лийиях, продолжение которых изображается на других листах схемы, после обозначения в круглых скобках указывают адреса мест продолжения прерванной линии. Если она продолжается на нескольких листах, то в круглых скобках указывают все номера листов, на которых продолжается эта линия. Номера листов разделяют запятой и пишут в порядке возрастания (рис. 14.8). Когда выходная линия продолжается на большом количестве схем, допускается:
• в случае перехода выходной линии на листы с последовательными номерами записывать первые и последние номера листов, разделяя их знаком “дефис”, например, запись (2, 4-8, 10) равносильна записи (2, 4, 5, 6, 7, 8, Ю);
• адрес продолжения прерванной линии не указывать, а записывать их в таблице, размещенной на поле схемы. Вместо адреса на прерванной линии указывают в круглых скобках знак букву Т и номер таблицы, например (*Т6). Знак можно не проставлять в случае однозначного понимания адреса, указанного в скобках. Таблица может содержать и другие графы, например, обозначения сигналов, источников, приемников и т.д.
Лист 2
Лист 3
Лист I
18(2,3)
18(1)
18(1)
Рис. 14.8. Обозначения адресов продолжения линии
Электропитание на схеме допускается показывать в виде таблиц, текста или на прерванной линии, изображающей связь по питанию. При этом в УГО элементов и устройств обозначения выводов электропитание допускается не указывать.
На схемах допускается выделять функциональные части штрихпунктирной линией (рис. 14.9).
Рис. 14.9. Выделение функциональных частей
На структурных и функциональных схемах допускается в УГО функциональной части выделять ее составные части (рис. 14.10). Каждая выделенная составная часть должна иметь наименование или условное обозначение с пояснениями на поле схемы или в документации на выбор.
14.2. Правила выполнения схем цифровой вычислительной-техники 491
Процессор .Y.YXXXY
YYY ZZZ
Рис. 14.10. Выделение составной части в УГО на структурных и функциональных схемах
В случае необходимости направление потоков информации на структурных и функциональных схемах допускается показывать стрелками на линиях взаимосвязи (рис. 14.11).
В случае выполнения на одно изделие не- ,.
скольких схем одного типа, эти схемы должны ------------
иметь однозначное обозначение. Допускается ин- ,, ------
формационная взаимосвязь схем, например, типов ------►!____—J 1...... .
2 и 3, выполнять самостоятельным документом в ]
виде таблицы с присвоением ему соответствующе-----------------------------
го шифра, например, Т2,3 или ТЕ2ТЕЗ. Если схемы
_ Рис. 14.11. Показ направлении
выполняют машинным способом, допускается
_ потоков информации
применять другие способы организации взаимо-
связи между элементами схем, не установленные стандартом. При этом выбранный способ следует описать на поле схемы или в документации на изделие. В случае автоматического выполнения схем с помощью алфавитно-цифровых печатающих устройств допускается контуры УГО выполнять с применением знаков “звездочка” или “точка”, “минус”, “подчеркивание”, “вертикальна черта”, “латинская буква I”, “знак равенства”и др.
14.2.2. Правила выполнения структурной схемы цифровой вычислительной техники
Выполняя структурные схемы, функциональные части изображают в виде прямоугольников или УГО, представленных в табл. 14.3.
Таблица 14.3
Наименование
Устройства с носителями данных на перфокартах
Устройства с носителями на перфолентах
Печатающие устройства
Накопитель на магнитных картах
Накопитель на магнитной ленте
Визуальное устройство ввода-вывода (дисплей)
Наименование
Обозначение
492 Требования к выполнению схем и иллюстративных документов
Таблица 14.3. Продолжение
Наименование
Накопитель на магнитных дисках
Наименование Обозначение
Запоминающее устройст- I [ J
во (RAM, ROM и т. д.) И
Примечание. Размер Н рекомендуется выбирать из ряда 10;15 мм и далее через 5 мм, а
размер L = 1,57/.
В схеме УГО указывают наименование каждой функциональной части и (или) ее тип или условное обозначение. Допускается над УГО делать пояснительные надписи. Всем функциональным частям на схеме допускается присваивать порядковые номера сверху вниз в направлении слева направо. Допускается указывать сведения о конструктивном размещении устройств, места их присоединения и другую информацию в таблицах, которые размещаются на схемах, или выпускаются самостоятельно с присвоением шифра Т1.
Пример электрической структурной схемы с магистральной структурой показан на рис. 14.12.
Рис. 14.12. Компьютер. Схема электрическая структурная (Э1): Р — процессор; RAM — оперативная память; ROM — постоянная память; HDD — накопитель на магнитных дисках; DISP — дисплей
14.2.3. Правила выполнения функциональной схемы цифровой вычислительной техники
Функциональные схемы выполняют на изделия и их функциональные части. Функциональные части на схеме изображают в виде прямоугольников, а двоичные логические элементы — по ГОСТ 2.743-91. Допускается функциональные части изображать в виде УГО, представленных в табл. 14.4.
Таблица 14.4
Наименование Обозначение Наименование Обозначение
| Чисто
Комбинационная схе- ю/\ /
l\ н Элемент памяти Н
ма, общее обозначение
O25W—♦[— —► — 5мм ь
Сумматор на два числа 60° Приоритетные схемы 1 Н п , ,
0 25 It—» М у 1
14.2. Правила выполнения схем цифровой вычислительной техники 493
Таблица 14.4. Продолжение
На схеме для каждой функциональной части в середине ее УГО должно быть указано ее наименование и (или) условное обозначение. Допускается указывать символ функции.
Всем функциональным частям и функциональным группам допускается присваивать порядковые номера в последовательности сверху вниз в направлении слева направо.
В случаях, когда листы схемы разделены на адресуемые части, порядковые номера могут быть заменены адресными обозначениями. Порядковые номера или адресные обозначения проставляют под наименованием или обозначением функциональной части.
В случае необходимости на функциональных схемах записывают дополнительную информацию, например, обозначения конструктивного размещения, состояние функциональных частей и др.
Условное обозначение функциональных частей допускается поворачивать на 90°. Допускается в УГО указывать цифрами разрядность функциональных частей (рис. 14.13).
Допускается объединять УГО функциональных частей по большей стороне условного обозначения, если выходы одной части полностью совпадают с входами другой (рис. 14.14).
Рис. 14.14. Объединение условных обозначений
/8
RGA
Рис. 14.13. Условное графическое обозначение регистра с обозначением разрядности
Линии связи подразделяют на информационные и управляющие. Информационные линии связи подводят к большей стороне УГО, а отводят от противоположной стороны. Управляющие линии подводят к меньшей стороне УГО. Если необходимо уточнить, что входы и выходы относятся к соответствующим составным частям функциональной части, то эти составные части показывают горизонтальными линиями, расположенными параллельно над (под) ее УГО. Горизонтальные линии, обозначающие определенные составные части, должны быть с ограничителями (рис. 14.15). На горизонтальных линиях допускается показывать разрядность функциональной части и ее составных частей.
494 Требования к выполнению схем и иллюстративных документов
Рис. 14.15. Обозначения составных частей УГО: а — с выделением функциональных составляющих; б — с единой горизонтальной линией для всего УГО
Если к УГО подведено много управляющих сигналов, то допускается продолжение условных обозначений или ограничителей линий, к которым их подводят (рис. 14.16).
Рис. 14.16. Способы подвода управляющих сигналов: а — к единой вертикальной линии слева или справа; б — с выделением отдельных линий для подачи управляющих сигналов
Пример функциональной схемы — фрагмента арифметико-логического устройства — показан на рис. 14.17.
Рис. 14.17. Фрагмент арифметико-логического устройства. Схема электрическая функциональная (Э2): RGA, RGB, RGC, RGD — регистры-фиксаторы; SRGE — регистр сдвига; MUX1, MUX2 — мультиплексоры; DMX — демультиплексор; SM — сумматор; DC — дешифратор;
СТ2— двоичный счетчик
14.2. Правила выполнения схем цифровой вычислительной техники 495
14.2.4. Правила выполнения принципиальных схем цифровой вычислительной техники
Двоичные логические элементы изображают в виде УГО по ГОСТ 2.743-91. Логические элементы с п состояниями (например, с тремя состояниями), а также элементы и устройства, которые не выполняют логические функции, однако применяются в изделии (например, аналоговые и аналого-цифровые элементы, диодные, резисторные сборки и т.д.) допускается изображать на схеме прямоугольниками. Для указанных элементов действуют все положения ГОСТ 2.743-91.
Если непосредственное электрическое соединение выходов нескольких логических элементов в одну цепь приводит к образованию логической связи между этими выходами (по И или ИЛИ), то такое соединение на схеме допускается изображать в виде псевдоэлемента монтажной логики.
В основном поле УГО элементов и устройств размещают следующую информацию:
• в строке 1 — символ функции по ГОСТ 2.743-91;
• в строке 2 — полное или сокращенное наименование типа или кода устройства (элемента);
• в следующих строках — буквенно-цифровое обозначение или порядковый номер; обозначение конструктивного размещения; адресное обозначение УГО элемента на листе и другую информацию. При этом указание буквенно-цифрового обозначения обязательно. Характер и размещения информации в следующих строках требуется пояснять на поле схемы или в нормативно-технической документации.
Адресное обозначение показывает размещение УГО элемента на схеме и выражается координатами левого верхнего угла этого УГО в зонном формате. Буквенно-цифровое обозначение допускается размещать над УГО. Для устройств, однозначно выраженных в изделии своими конструктивными обозначениями, его можно не указывать, в этом случае конструктивное обозначение используют вместо буквенно-цифровых обозначений.
При совместном способе изображения конструктивно объединенных логических элементов, выполняющих одинаковую логическую функцию, допускается проставлять информацию строки в одном верхнем элементе.
Обозначение выводов устройств (номера контактов) указывают над соответствующими линиями связи или в их разрыве рядом с УГО элементов. Если логический элемент имеет группу равноценных входов (выходов), то обозначения номеров контактов таких выводов допускается указывать в произвольном порядке.
14.2.5. Таблицы сигналов
На поле структурных, функциональных и принципиальных схем допускается указывать таблицы сигналов. В них указывают информацию, необходимую для прослеживания сигналов в изделии. Форму таблицы выбирают в зависимости от сведений, требуемых для удобства исследования сигналов в процессе наладки и эксплуатации изделия.
496 Требования к выполнению схем и иллюстративных документов
В таблицах указывают следующую обязательную информацию:
• наименование или обозначение сигналов и (или) порядковый номер сигнала;
• конструктивное обозначение контактов, через которые проходит сигнал.
В таблицу допускается вводить дополнительные графы. Информация в таблицах сигналов упорядочена по алфавитному размещению сигналов, и (или) по упорядоченным конструктивным адресам и (или) по схемным адресам.
Таблицы сигналов допускается выполнять в виде самостоятельных документов с шифром, например, ТСЗ (или ТСЭЗ). Если таблицы сигналов имеют отношение к двум и более типам схем, то в шифре таблицы перечисляют все шифры схем, на которые распространяется таблица, начиная с меньшего порядкового номера типа схемы, например, ТС2,3 (или ТСЭ2ЭЗ).
14.3. Условные графические обозначения элементов цифровой техники в схемах
14.3.1. Общие положения
Элемент цифровой техники (далее элемент) — цифровая или микропроцессорная микросхема, ее элемент или компонент. К элементам цифровой техники условно относят элементы, которые не используются для обработки дискретных сигналов, однако применяются в логических цепях, например, конденсатор, генератор и т.д.
Для построения УГО используют символы “0” и “1” для идентификации двух логических состояний “логического нуля” и “логической единицы” (ГОСТ 2.743-91 “Обозначения условные графические в схемах. Элементы цифровой техники”).
14.3.2. Правила построения условных графических обозначений элементов
Условное графическое обозначение элемента имеет форму прямоугольника, к которому подводят линии выводов. Он может содержать три поля: основное и два дополнительных, которые размещают слева и справа от основного (рис. 14.18).
Рис. 14.18. Полная форма УГО элемента
14.3. Условные графические обозначения элементов цифровой техники в схемах 497
Кроме основного и дополнительного полей, УГО элемента может содержать также контур общего блока управления и контур общего выходного элемента.
В первой строке основного поля УГО обозначают функцию элемента. В следующих строках основного поля размещают информацию по ГОСТ 2.708. Допускается размещать информацию в основном поле с первой позиции строки, если это не приводит к неоднозначности понимания. В дополнительных полях размещают информацию о назначении выводов (метки выводов, указатели). Допускается проставлять указатели на линиях выводов, на контуре УГО, а также между линией вывода и контуром УГО.
Условное графическое обозначение может состоять только из основного поля (табл. 14.5, п.1), или из основного поля и одного дополнительного, которое размещают справа или слева от основного (табл. 14.5, пп. 2, 3), а также из основного поля и двух дополнительных (табл. 14.5, п.4). Допускается дополнительные поля разделять на зоны, отделяемые горизонтальной чертой (табл. 14.5, п.4).
Таблица 14.5
Рис. 14.19. Графическое разделение совмещенных УГО линиями связи
Основные и дополнительные поля можно не отделять линиями. При этом расстояние между буквенными, цифровыми или буквенно-цифровыми обозначениями, размещенными на полях, определяют однозначностью понимания каждого обозначения. Для обозначений, размещенных в одной строке, расстояние должно быть не меньше двух букв (цифр, знаков), которыми выполнены эти обозначения.
Допускается элементы, изображенные совмещенным способом, разделять графически линиями связи, при этом расстояние между концами контурных линий должно быть не меньше 1 мм (рис. 14.19).
Выводы элементов подразделяют на входы, выходы, двунаправленные выводы и выводы, не несущие логической информации.
Входы элемента изображают с левой стороны УГО, а выходы — с правой. В случае подвода линий выводов к контуру УГО не допускается:
• проводить их на уровне стороны прямоугольника;
32 —4-1749
498 Требования к выполнению схем и иллюстративных документов
• проставлять на них возле контура УГО стрелки, указывающие направление информации.
Допускается другая ориентация УГО, при которой входы размещают сверху, а выходы — снизу (рис. 14.20, а). При ориентации УГО, когда входы находятся справа или снизу, а выходы — слева или сверху, необходимо на линиях выводов (связи) проставлять стрелки, указывающие направление распространения информации. При этом обозначения функции элемента должно соответствовать рис. 14.20, б.
_L_
ГД
Рис. 14.20. Допустимые ориентации УГО: а — входы сверху, выходы снизу; б — входы справа (снизу), выходы слева (сверху)
Размеры УГО определяют:
• по высоте — количеством линий выводов, интервалов и строк в основном и дополнительных полях, размером шрифта;
• по ширине — наличием дополнительных полей, количеством знаков в одной строке в середине УГО (с учетом пропусков), размером шрифта.
Соотношение размеров обозначения функций, меток и указателей выводов в УГО, а также расстояние между линиями выводов должны соответствовать представленным в прил. Б. Надписи в середине УГО выполняют основным шрифтом по ГОСТ 2.304-81. Выполняя УГО с помощью устройств вывода ЭВМ, применяют шрифты, наличные в них.
14.3.3. Обозначение функций элементов
Обозначение функций элементов или их совокупности (далее — функций), которые выполняет элемент, образуют из больших букв латинского алфавита, арабских цифр и специальных знаков, записанных без пробелов. Количество знаков в обозначении функции не ограничено, однако следует достигать их минимального количества с сохранением однозначности понимания каждого значения.
Обозначения функций элементов представлены в прил. В, табл. В.1. Знак проставляют перед функцией элемента, если все его выводы являются нелогическими. Допускается справа к обозначению функций добавлять технические характеристики элемента, например: резистор сопротивления 47 Ом — *7?47.
Задержку элемента указывают способом, показанным на рис. 14.21. Если эти две задержки одинаковые, то указывают только одно значение:
। 5 нс . . 10 нс ,
14.3. Условные графические обозначения элементов цифровой техники в схемах 499
10 нс 5 нс
если
*— 5 нс
10 нс
Рис. 14.21. Графическое изображения задержки
Задержку, заданную в секундах или в единицах, основанных на количестве слов или битов, можно указывать как в середине контура УГО элемента задержки, так и вне его.
Допускается указывать значения задержки десятичным числом |------13 или
DEL3, при этом значение единицы задержки записывают на поле схемы или в технических требованиях.
В УГО элемента допускается опускать пробел между числовым значением и единицей измерения, например: RAM16K, 10нс, +5В.
В случае необходимости указать сложную функцию элемента допускается составное (комбинированное) обозначение функции. Например, если элемент выполняет несколько функций, то обозначение его сложной функции образуется из нескольких более простых обозначений функций. При этом их последовательность определяется последовательностью функций, выполняемых элементом:
• четырехразрядный счетчик с дешифратором на выходе — CTR4DC’,
• преобразователь двоично-десятичного кода в семисегментный код —
BCD\7SEG.
Обозначение сложной функции элемента может также состоять из обозначения функции и метки вывода. При этом метка вывода стоит перед обозначением функции, например:
• генератор ускоренного переноса — CPG',
• регистр данных—DRG\
• селектор (устройство селекции) — SELDEV.
В случае использования обозначений функций элементов, не установленных стандартом, их поясняют на поле схемы.
14.3.4. Обозначение выводов элементов
Выводы элементов подразделяют на несущие или не несущие логическую информацию. Выводы, несущие логическую информацию, подразделяют на статические и динамические, а также на прямые и инверсные.
На прямом статическом выводе двоичная переменная имеет значение “1”, если сигнал на этом выводе в активном состоянии находится в состоянии “логическая единица” (далее LOG1) в принятом логическом соглашении. На инверсном статическом выводе двоичная переменная имеет значение “1”, если сигнал на этом выводе в активном состоянии находится в состоянии “логический нуль” (далее LOGQ)
На прямом динамическом выводе' двоичная переменная имеет значение “1”, ' если сигнал на этом выводе изменяется из состояния LOGQ в состояние LOG1 в принятом логическом соглашении. На инверсном динамическом выводе двоичная 32*
500 Требования к выполнению схем и иллюстративных документов
переменная имеет значение “1”, если сигнал на этом выводе изменяется из состояния LOG1 в состояние LOGO в принятом логическом соглашении.
Рассмотренные свойства выводов обозначают указателями (табл. 14.6).
Таблица 14.6
Наименование
1. Прямой статический вход
2. Прямой статический выход
3. Инверсный статический вход
4. Инверсный статический выход
5. Прямой динамический вход
6. Инверсный динамический вход
7. Статический вход с указателем полярности
8. Статический выход с указателем полярности
9. Динамический вход с указателем полярности
10. Вывод, не несущий логической информации: изображение слева
Изображение справа
Примечания. 1. Указатели в пп. 7-9 применяют в случае, когда состоянию LOG1 соот-
ветствует менее положительный уровень. 2. Преимущество отдается форме 1.
Метку вывода образуют из больших букв латинского алфавита, арабских цифр и (или) специальных знаков, записанных в одной строке без пропусков. Количество знаков в метке не ограничивается, однако, по возможности, должно быть минимальным с сохранением однозначности понимания каждого обозначения.
Обозначения основных меток выводов элементов представлены в прил. В, табл. В.2.
В случае необходимости указать сложную функцию выводов допускается построение составной метки, которую образуют из основных меток. При этом рекомендуется выдерживать обратный порядок присоединения меток, например:
14.3. Условные графические обозначения элементов цифровой техники в схемах 501
• адреса считывания — RDA\
• байт данных — DBY\
• выбор байта — BYSEL.
Для обозначения метки выводов, имеющих по очереди две функции, эти функции указывают через косую черту, например:
• ввод-вывод — I/O',
• запись-считывание — WR/RD-,
• управление-данные — C/D.
Порядок прохождения меток определяет логический уровень разрешительного сигнала: первая функция осуществляется при LOG\, вторая — при LOGQ. Порядок прохождения меток выводов, не несущих логической информации, произвольный.
Если выполняется УГО элемента, имеющего два порта приема и передачи информации А и В, метка вывода A/В означает разрешение приема информации портом А и передачи информации портом В по логическому уровню сигнала на этом выводе, который равен LOGY
В роли меток допускается применять обозначения функций, например:
• сравнение — СОМР\
• результат операции вычитания — P-Q.
Допускается также создавать сложную метку вывода с обозначением функции и метки вывода, при этом рекомендуется прямой порядок их присоединения, например:
• чтение из памяти — RDM.
Изображая составную функцию или метки вывода, допускается выполнять ее в двух строках, например:
RAM DOUT
256x1 о
Если в УГО требуется изобразить свободный вывод (не имеющий соединений в середине элемента), то он должен иметь указатель вывода, не несущего логической информации, и иметь метку вывода “NC”.
Выводы питания элементов показывают или на свободном поле схемы, или одним из способов, показанных на рис. 14.22.
Рис. 14.22. Изображения выводов питания: а — в общем блоке управления;
б — в одном из элементов DD2, изображенных разнесенным способом; в — е отдельном элементе микросхемы DD3
502 Требования к выполнению схем и иллюстративных документов
Нумерацию выводов элементов указывают над линией слева для входов или справа для выходов от контура УГО или указателя вывода (при его наличии). Допускается нумеровать выводы элементов в разрыве линий вывода.
Обозначения основных меток, не несущих логической информации, представлены в прил. В, табл. В.З.
14.3.5. Обозначения групп выводов
Выводы элементов подразделяют на логически равнозначные, то есть взаимозаменяемые без изменения функции элемента, и логически неравнозначные. Условное графическое обозначение элемента выполняют без дополнительных полей или без правого или левого дополнительного поля в следующих случаях:
• все выводы логически равнозначные;
• функции выводов однозначно определяются функцией элемента.
При этом расстояния между выводами должны быть одинаковыми, а метки выводов не указываются.
При наличии логически равнозначных входов или выходов элемента они могут быть графически объединены в группу выводов, которой присваивают метку, обозначающую их функцию. Такую метку проставляют на уровне первого вывода группы (рис. 14.23).
&R
Рис. 14.23. Объединение групп равнозначных выводов: а — по И; б — по ИЛИ (каждый вход устанавливает элемент в нуль); в — по И с обнулением элемента
Нумерацию выводов таких групп логически равнозначных выводов допускается указывать произвольно.
Если несколько последовательных выводов имеют части, отображающие одинаковые функции, то такие выводы можно объединять в группу выводов, и эту часть метки вынести в групповую метку. Ее размещают над группой меток, записанных без интервала между строками (рис. 14.24, а).
Рис. 14.24. Обозначение меток групп выводов: а — вынос общей метки группы; б — вынос общих меток двух групп
14.3. Условные графические обозначения элементов цифровой техники в схемах 503
Группы выводов разделяют интервалом в одну строку или размещают в отдельную для каждой группы зону. Из нескольких групповых меток можно выделить групповую метку более высокого порядка. Эту метку проставляют над группами выводов, которых они касаются, отделяя от них интервалом. Группы, имеющие отношение к метки более высокого порядка, размещают в отдельной зоне (рис М 24, б).
Допускается не делать пропуск между группами выводов, имеющими метку более высокого порядка.
Номера разрядов в группах выводов обозначают числами натурального ряда, начиная с нуля. При этом метки выводам присваивают одним из способов, показанных на рис. 14.25.
р 0 ____ р 0
Р0
I I или Р1 1Г1И
2 Р2
з f — — _2__J
Рис. 14.25. Обозначения номеров разрядов: а — для входов; б — для выходов
Для выходов допускаются метки выводов, состоящие только из номеров разрядов. Обязательным являются только метки открытого выхода и выхода с тремя состояниями.
Если в группе разрядов однозначно определены весовые коэффициенты, то вместо номера разряда можно проставлять его весовой коэффициент. Например, для двоичного счисления ряд весов имеет вид 2°, 21, 22, 23,... = 1, 2, 4, 8,... Тогда информационный вход нулевого разряда будет иметь метку D1 или 1, третьего разряда — D8 или 8.
Если требуется пронумеровать группы и разряды в середине группы, метку каждого вывода составляют из номера группы (первая цифра) и номера разряда в группе, отделенных друг от друга точкой, например: метка информационного входа первого разряда нулевой группы — D0.1.
При наличии в элементе двух информационных каналов (портов) допускается их обозначения А и В, которые выносят как групповую метку для информационных входив и (или) выходов, если это не приведет к неоднозначности понимания меток выводов.
Двунаправленный вывод обозначают меткой “<>" или которую проставляют или в УГО элемента — над или рядом с меткой функции (групповой меткой функции) вывода (выводов), как показано на рис. 14.26, а, б, или на выводах элемента (рис. 14.26, в). При этом метки выводов, обозначающие входную и выходную функции, проставляют через косую черту.
504 Требования к выполнению схем и иллюстративных документов
Допускается метки входных и выходных функций вывода проставлять над и под меткой двунаправленного вывода непосредственно (рис. 14.26, г).
Рис. 14.26. Обозначения метки двунаправленного вывода; а— над меткой функции, б — рядом с меткой функции; в — на выводах элемента; г — между метками функций
14.3.6. Взаимосвязь выводов
Выводы элементов подразделяют на влияющие и зависимые. Влияющий вывод действует на один или несколько зависимых от него выводов. Чтобы показать взаимосвязь выводов элемента, используют обозначения зависимости. Зависимости выводов обозначают присвоением им меток выводов:
• для влияющего вывода — буквенным обозначением зависимости и порядковым номером, проставленным после буквенного обозначения без пропусков;
• для каждого зависимого от влияющего вывода — таким же порядковым номером, проставленным без пропусков перед буквенным обозначением метки вывода.
Если влияющий вывод действует на зависимый своим дополнительным логическим состоянием, то над порядковым номером, проставленным перед меткой зависимого вывода, ставят черту (рис. 14.27, а). В случае, когда вывод зависит от нескольких влияющих выводов, порядковый номер каждого из них указывают через запятую (рис. 14.27, б).
a б
Рис. 14.27. Обозначения выводов: а — влияющего дополнительным логическим состоянием на зависимый вывод; б — зависимость нескольких выводов от одного влияющего
Допускается дополнять обозначения зависимости меткой, которая поясняет функциональное назначение вывода и проставляется в круглых скобках.
Если вывод выполняет несколько функций и (или) имеет несколько влияющих действий, то обозначения каждой из этих функций и (или) зависимостей соответствующей меткой можно показывать в следующих строках. При этом каждой метке может быть поставлен в соответствие указатель (рис. 14.28, а), или одной строкой
14.3. Условные графические обозначения элементов цифровой техники в схемах 505
через косую черту (рис. 14.28, б). Порядок меток, обозначающих несколько функций или зависимостей, произвольный.
Рис. 14.28. Обозначения выводов с несколькими функциями: а — с помощью мЬпки и указателей; б — одной строкой через косую черту
Если трёбуется указать несколько меток одного вывода в следующих строках, допускается линии выводов к ним не подводить.
14.3.7. Обозначения монтажной логики
Непосредственное соединение логических выходов нескольких элементов на общую нагрузку (монтажная логика) следует обозначать, как показано на рис. 14.29, а. Монтажную логику можно рассматривать как элемент, который изображают в виде УГО элемента монтажной логики (рис. 14.29, б).
1. Термину “элемент монтажной логики" соответствует термин “элемент DOT”.
2. В зависимости от вида выполняемой логической функции знак следует заменить знаком (монтажное “И”) или знаком “1” (монтажное “ИЛИ").
3. Допускается изображать монтажную логику, как показано на рис. 14.29, в, если это не приведет к неоднозначности понимания.
4. Если выходам элементов присвоены метки открытых выходов, то допускается изображать монтажную логику соответственно рис. 14.29, г.
Рис. 14.29. Изображение монтажной логики: а — общее; б — в виде УГО элемента монтажной логики; в — упрощенное изображение; г — для элементов с открытым коллекторным выходом
14.3.8. Сокращенное обозначения групп УГО
Для уменьшения объема документации допускается сокращенное обозначение групп УГО. Условные обозначения элементов можно изображать совместно; в этом случае они прилегают друг к другу одной или двумя сторонами, параллельными
506 Требования к выполнению схем и иллюстративных документов
распространению информации (рис. 14.30, а). При этом логического соединения между этими элементами нет.
Допускается изображать УГО элементов с общей стороной (рис. 14.30, б). В этом случае имеется как минимум одно логическое соединение между этими элементами. При наличии таких элементов считается, что имеется только одно логическое соединение между ними (рис. 14.30, в).
Рис. 14.30. Изображения групп УГО элементов: а — совмещены двумя сторонами; б — с общей стороной; в — нет соединений
Условные графические обозначения группы однотипных элементов, которые изображены совместно и имеют одинаковую информацию и общие выводы, могут содержать общий графический блок управления (рис. 14.31).
0 1 с RG XXX
0 1 с RG XXX
С R(J XXX
0 1
0 1
1_______Г
0 1 0 1
0 1 0 1
Рис. 14.31. Способы изображения групп однотипных элементов
В группе совместно изображенных элементов одинаковую информацию в основном поле размещают в верхнем УГО (рис. 14.32, а).
Допускается отделять такие элементы друг от друга штриховой линией (рис. 14.32, б). Две последовательные группы элементов следует изображать так, как показано на рис. 14.32, в. Сокращенное обозначения группы из пар элементов показано на рис. 14.32, г.
14.3. Условные графические обозначения элементов цифровой техники в схемах 507
Группу элементов с идентичными выводами (входами и выходами), которые
Рис. 14.33. Изображения групп элементов с одинаковыми выводами: а — с общим блоком управления; б — без блока управления
В схемах, имеющих элементы с большим количеством выводов одного функционального назначения, допускается сокращенное обозначения таких элементов (рис. 14.34). В схемах, в которых элементы повторяются, допускается также применять пакетный метод сжатия информации, то есть пакетное изображение УГО элементов и линий связи.
Пакет элементов — это группа однотипных элементов, изображенных в виде одного УГО. Пакет сигналов — это группа сигналов (логических связей элементов), изображенных одной линией. Пакеты элементов и сигналов поясняют на схеме с помощью пакетов информации.
Номер вывода 8 7 6 5 4 3 2 I 23 22
Метка вывода .10 .11 /2 ЛЗ .44 Л 5 Л6 Л7 .48 /19
Номер вывода 9 10 И 13 14 15 !6 17
Метка вывода D0 D1 D2 D3 04 D5 Об 07
Рис. 14.34. Сокращенное обозначение элементов с большим количеством выводов
508 Требования к выполнению схем и иллюстративных документов
Пакет информации — это сжатый перечень следующих данных:
• идентификаторов сигналов (логических связей элементов);
• конструктивных адресов элементов и сигналов;
• координат элементов на схеме;
• количества элементов или сигналов в пакете и т.д.
Таблицу (первый способ сокращенного обозначения элементов) следует размещать на поле схемы.
Короткую запись пакета можно представить следующими способами:
• 0,1; 0,1; 0,1; 0,1 = (0,1)4 — последовательность 0,1 повторяется четыре раза;
• 0,0,0,1,1,1 = 3(0,1) — каждый элемент указанной последовательности повторяется три раза подряд;
Пакетное изображение информации применяют в случае одновременного выполнения следующих условий:
• однотипность элементов в группе;
• однотипность входных и выходных сигналов элементов группы;
• регулярность сигналов в каждом пакете, которая допускает их удобный перечень.
В середине основного поля УГО пакета элементов размещают:
• в первых трех строках информацию по ГОСТ 2.708;
• в следующих строках информацию о пакете.
В случае недостачи мест в основном поле информацию о пакете элементов допускается размещать на поле схемы. Пример УГО пакета элементов показан на рис. 14.35.
Рис. 14.35. Пример изображения УГО пакета элементов
14.3.9. Логические соглашения
Двоичная логика оперирует с переменными, которые могут принимать два логических состояния — состояние “логическая единица” (далее — LOG\) и состояние “логический нуль” (далее — LOGO). Символы логических функций, определенных стандартами, представляют собой связь между входами и выходами элементов в терминах логических состояний, не связанных с физической реализацией.
14.3. Условные графические обозначения элементов цифровой техники в схемах 509
При конкретной физической реализации элементов логические состояния представляют физическими величинами (электрический потенциал, давление, световой поток и т.д.). В логике не требуется знание абсолютного значения величины, поэтому физическая величина идентифицируется просто как более положительная — Я и менее положительная —L (рис. 14.36). Эти два значения называются логическими уровнями.
L , Н УН
। i L —।—
Рис. 14.36. Два логических уровня
Соответствие между определенными понятиями устанавливается следующими соглашениями:
Соглашение положительной логики:
• более положительное значение физической величины (логический уровень Н) соответствует LOG1. Менее положительное значение физической величины (логический уровень/,) соответствует LOGO',
Соглашение отрицательной логики:
• менее положительное значение физической величины (логический уровень L) соответствует LOG\. Более положительное значение физической величины (логический уровень Н) соответствует LOGO.
Для указания соответствий между логическими состояниями и значениями (логическими уровнями) физических величин, используемых для представления этих состояний, применяют два метода:
• метод единого соглашения для всей схемы (соглашение положительной логики или соглашение отрицательной логики);
• использование указателя полярности.
Для того чтобы установить на схеме однозначное соответствие между логическим состоянием и логическим уровнем, на выводе элемента используют указатель инверсии (о) или указатель полярности (с или с).
Указатель инверсии используют тогда, когда для всей схемы принято единое, соглашение. Если в схеме применяют соглашение положительной и отрицательной логики, то следует применять указатель выводов, для которых справедливо соглашение отрицательной логики. В схеме с указателями полярности указатель инверсии не используют.
На поле схемы или в технических условиях требуется указывать, в какой логике выполнена схема.
Логические элементы могут иметь логические эквивалентные формы. Например, элемент, имеющий таблицу истинности, выраженную в уровнях сигнала (рис. 14.37, а), имеет эквивалентные формы в положительной и отрицательной логике (рис. 14.37, б, в).
510 Требования к выполнению схем и иллюстративных документов
XI XI Y
L L II
L Н И
Н L Н
Н Н L
2И-НЕ
'-ПУЛ2-Л1А2
XI XI у-
I 1 0 1 1 0 1 0 0 0 0 1
&
в
Рис. 14.37. Эквивалентные формы логических элементов в положительной и отрицательной логике
С учетом положений, изложенных в этом разделе, построены принципиальные электрические схемы арифметико-логических устройств, разработанных в главе 9 (см. рис. 9.3, 9.5, 9.8, 9.10 и т.п.).
14.4. Требования к выполнению иллюстративных документов
14.4.1. Общие положения
К иллюстративным документам относятся фотографии, рисунки, диаграммы, графики, в тому числе сетевая, экспериментальная документация и др. Иллюстративную документацию часто называют плакатами. Они предназначены для наглядного отображения темы проекта и носят вспомогательный или справочный характер.
Иллюстративные материалы, не содержащие элементов самостоятельной работы проектанта, в перечень обязательных листов графической части не включаются. Плакаты в уменьшенных размерах подаются в приложениях к записке.
Главными требованиями к плакатам являются наглядность, полнота отображения и сжатость представления материала. Плакаты изготовляют на листах формата А1 в черно-белом варианте. В случае необходимости допускается многоцветное оформление плакатов (не более шести цветов на одном листе).
Основная надпись на плакатах не выполняется. Для определения принадлежности плаката к проекту в правом нижнем углу листа выполняют рамку размеров 185x40 мм. Вдоль длиной стороны листа записывают:
Дипломный проект (аттестационная работа) на тему:
Выполнил студент(ка)__________________
Факультет_________________
Г руппа
Руководитель_________________
14.4. Требования к выполнению иллюстративных документов 511
Каждый плакат должен иметь заголовок, написанный большими буквами (не менее 10 мм) посередине верхней части листа, и изобразительную часть с пояснительным текстом, которая содержит данные, необходимые для показа и пояснений во время защиты проекта.
14.4.2. Правила выполнения диаграмм
Традиционно в технической литературе понятие диаграммы и графика представляют следующими определениями:
• диаграмма — это графическое изображение, которое наглядно показывает линейными отрезками или геометрическими фигурами соотношения между различными величинами;
• график — это геометрическое наглядное изображение функциональной зависимости между величинами с помощью линий на плоскости. В выбранной системе координат график функций/(х) — это множество тех точек плоскости, координаты которых удовлетворяют уравнению у =flx).
В рекомендациях ЕСКД Р 50-77-88 “Правила выполнения диаграмм” используют обобщенный единый термин — “диаграмма”. Рекомендации устанавливают основные правила выполнения диаграмм, изображающих функциональную зависимость двух и более переменных величин в системе координат.
14.4.3. Оси координат
Значения величин, связанных изображаемой функциональной зависимостью, следует откладывать на осях координат в виде шкал. Допускается выполнять диаграммы без шкал значений величин. В прямоугольной системе координат независимую переменную следует откладывать на горизонтальной оси (оси абсцисс), а положительные значения величины — на осях вправо и вверх от точки начала отсчета (рис. 14.38).
В полярной системе координат начало отсчета углов (угол 0°) должен находиться на горизонтальной или вертикальной оси; при этом положительное направление угловых координат должно соответствовать вращению против часовой стрелки (рис. 14.39).
Рис. 14.38. Диаграмма в прямоугольной системе координат без шкал
Рис. 14.39. Диаграмма в полярной системе координат
/
512 Требования к выполнению схем и иллюстративных документов
Оси координат в диаграммах без шкал и со шкалами следует заканчивать стрелками, указывающими направление возрастания значений величин (см. рис. 14.38). В диаграммах со шкалами оси координат заканчивают стрелками за пределами шкал или обозначают самостоятельными стрелками после обозначения величины параллельно осям координат (рис. 14.40, 14.41)
Скорость вытяжки, м/мпп
1 - без смазывания; 2 - маловязкое масло;
3 - олеат кальция; 4 - графит с жиром; 5 - ланолин
Рис. 14.40. Диаграмма со шкалами
Рис. 14.41. Диаграмма в системе трех координат
Выполняя диаграммы в прямоугольной (пространственной) системе трех координат, функциональные зависимости следует изображать в аксонометрической проекции.
14.4.4. Масштабы, шкалы и координатная сетка
Значения переменных величин следует откладывать на осях координат в линейном (см. рис. 14.38) или нелинейном (например, логарифмическом, как показано на рис. 14.42) масштабах изображения.
Рис. 14.42. Диаграмма со шкалами на координатной оси и линии координатой сетки
14.4. Требования к выполнению иллюстративных документов 513
Масштаб, который может быть различным для каждого направления координат, должен выражать шкалой откладываемых значений величины. В качестве шкалы используют координатную ось или линию координатной сетки, ограничивающей поле диаграммы. Диаграммы без шкал выполняют по всем направлениям координат в линейном масштабе изображения.
В диаграммах, изображающих несколько функций различных переменных и
диаграммах, в которых одна и та же переменная одновременно выражается в раз
личных единицах, допускается использовать как шкалы координатной оси, так и линии координатной сетки, ограничивающие поле диаграмм (см. рис. 14.42) и (или) прямые, расположенные параллельно координатным осям (рис. 14.43).
с
Рис. 14.43. Диаграммы с дополнительными шпалами на прямых параллельно координатной оси
Координатные оси как шкалы изображаемых величин разделяют на графические интервалы одним из трех способов:
1. координатной сеткой (см. рис. 14.39, 14.41);
2. штрихами делений (см. рис. 14.40);
3. сочетанием координатной сетки и штрихов делений (см. рис. 14.43).
Шкалы, расположенные параллельно координатной оси, разделяют только штрихами делений (см. рис. 14.43).
Размер графического интервала (расстояние между штрихами делений и (или) линиями координатной сетки) выбирают с учетом назначения диаграммы, удобства отсчета с интерполяцией и репрографии.
Рядом с делениями, соответствующими началу и концу шкалы, требуется указывать соответствующие числа (значения величин). Если началом отсчета шкал является нуль, то его указывают один раз в точке пересечения шкал.
33 —4-1749
514 Требования к выполнению схем и иллюстративных документов
Частоту нанесения числовых значений и промежуточных делений шкал выбирают с учетом удобства пользования диаграммой. Штрихи делений, соответственно кратные графическим интервалам, допускается продлевать (см. рис. 14.40). Числа на шкалах следует размещать горизонтально вне поля диаграммы (см. рис. 14.39 и 14.40). Допускается наносить числа на шкалах внутри поля диаграммы (см. рис. 14.39).
Многозначные числа желательно выражать как кратные 10", где п — целое
Рис. 14.44. Диаграммы с обозначением многозначных чисел, кратных 1(Г
14.4.5. Линии и точки
Для выполнения диаграмм линии выбирают с учетом размера, сложности и назначения диаграммы, а также требований репрографии. Оси координат и шкал, ограничивающих поле диаграммы, выполняют сплошной основной линией. Допускается выполнять линии сетки, кратные графическим интервалам, сплошной линией, толщина которой 2S (см. рис. 14.44).
На диаграмме одной функциональной зависимости ее изображение следует выполнять сплошной линией толщиной 2S. Допускается изображать функциональную зависимость сплошной линией меньшей толщины (толстой или тонкой), если требуется обеспечить необходимую точность отсчета (см. рис. 14.44).
14.4. Требования к выполнению иллюстративных документов 515
Если в одной общей диаграмме изображают две и более функциональные зависимости, то допускается выполнять их различными типами линий (например, сплошной и штриховой — см. рис. 14.41 и 14.42).
При наличии на диаграмме пучков или серий линий допускается использовать линии разной толщины и разных типов (см. рис. 14.44). Пучок линий, которые выходят из одной точки или пересекаются в одной точке под небольшими углами, не доводят до точки пересечения, за исключением крайних линий (рис. 14.45).
Рис. 14.45. Изображение пучков линий
Если в некоторой области совпадают две и более линий, чертят одну из них. В случае совпадения линии, изображающей функциональную зависимость, с осью координат или с линией сетки, наносят линию функциональной зависимости.
Характерные точки линий функциональной зависимости (то есть обозначенные числами, буквами, символами и т.п.) допускается изображать кружком (рис. 14.46).
На шкалах допускается наносить числовые значения величин для характер
Рис. 14.46. Изображения характерных точек
ных точек (см. рис. 14.46). точки диаграммы. Полученные измерением или расчетами, можно обозначать графически, например, кружком, крестиком и т.п.
33*
516 Требования к выполнению схем и иллюстративных документов
(см. рис. 14.40). Обозначения точек разъясняется в записке. Допускается выделять зону между линиями функциональных зависимостей штрихами.
14.4.6. Обозначения величин
Переменные величины необходимо указывать одним из следующих способов:
• символом (см. рис. 14.38 и 14.46);
• названием (см. рис. 14.40);
• названием и символом (см. рис. 14.42);
• математическим выражением функциональной зависимости (см. рис. 14.45).
В диаграммах со шкалами обозначения величин следует размещать в середине шкалы с ее внешней стороны, а в случае объединения символом с обозначением величины измерения в виде дроби — в конце шкалы последнего числа.
Обозначения в виде символов и математических выражений следует размещать горизонтально (см. рис. 14.38 и 14.41), обозначения в виде названия или названий и символов—параллельно соответствующим осям (см. рис. 14.40).
Если в диаграмме системой линий изображают функциональную зависимость трех переменных, соответствующие числовые значения (параметры) переменной величины указывают возле отдельных линий системы на поле диаграммы (см. рис. 14.44) или вне поля диаграммы (см. рис. 14.45).
14.4.7. Нанесение единиц измерения
Единицы измерения наносят одним из следующих способов:
• в конце шкалы между последним и предпоследним числами шкалы (см. рис. 14.41, 14.42, 14.46); если не хватает места, допускается не наносить предпоследнее число (см. рис. 14.39);
• вместе с названием переменной величины после запятой (см. рис. 14.39);
• в конце шкалы после последнего числа вместе с обозначением переменной величины в виде дроби, в числителе которой — обозначение переменной величины, а в знаменателе — обозначение единицы измерения (см. рис. 14.43). Единицы измерения углов (градусы, минуты, секунды) следует наносить один раз возле последнего числа шкалы (см. рис. 14.39). Допускается единицы измерения углов наносить возле каждого числа шкалы.
Диаграмма также может содержать:
• названия, поясняющие изображенную функциональную зависимость;
• пояснительную часть (текстовую, графическую), которая разъясняет обозначения. Ее следует размещать после наименования диаграммы или на свободном месте (см. рис. 14.40).
Не допускается пересечение надписей и линий. Если не хватает места, линию прерывают. Это правило не распространяется на диаграммы, выполненные на листах с напечатанной координатной сеткой.
Контрольные вопросы 517
Контрольные вопросы
1. Дайте определение схемы.
2. Перечислите виды и типы схем.
3. Как определяются наименования и коды схем? Приведите примеры.
4. Какие типы линий допускаются в схемах?
5. Как выполняется перечень элементов схемы?
6. Нарисуйте условные графические обозначения устройств цифровой вычислительной техники.
7. Нарисуйте условные обозначения функциональных элементов вычислительной техники.
8. Из каких частей может состоять условное графическое изображение элемента цифровой техники в схемах?
9. Нарисуйте обозначения различных комбинаций статических и динамических, прямых и инверсных выводов элементов.
10. Как на схемах изображается монтажная логика?
11. Объясните суть логических соглашений.
12. Чем отличается диаграмма от графика?
13. Какие системы координат могут применяться в диаграммах?
14. Перечислите способы разбиения шкалы на графические интервалы.
15. Как на графиках могут обозначаться переменные величины?
16. Перечислите способы нанесения единиц измерения.
518 Программная документация
Глава 15
Программная документация
15.1. Программное обеспечение систем обработки информации
Система обработки информации (СОИ) — это комплекс технических и программных средств и обслуживающего персонала, предназначенный для механизации и автоматизации обработки информации.
Стандарт ГОСТ 19781-90 устанавливает термины и определения понятий, имеющих отношение к программному обеспечению СОИ.
15.1.1. Основные понятия
Для программного обеспечения СОИ установлены следующие основные понятия.
Программирование. Научная и практическая деятельность по созданию программ.
Программа. Данные, предназначенные для управления конкретными компонентами СОИ с целью реализации определенного алгоритма.
Программное обеспечение. Совокупность программ СОИ и программных документов, необходимых для эксплуатации этих программ.
Система программирования. Система, предназначенная для подготовки программ в форме, пригодной для выполнения.
Кросс-система программирования. Система, программные компоненты которой порождают программы на машинном языке, отличном от того, на котором работают компоненты.
15.1.2. Виды программ
В процессе программирование обычно используют следующие виды программ.
Системная программа. Предназначена для поддержки работоспособности СОИ в процессе выполнения прикладных программ.
Управляющая программа. Системная программа, реализующая набор функций управления: ресурсами и взаимодействием с внешней средой СОИ, восстановлением работы системы после неполадок.
Супервизор. Часть управляющей программы, координирующая распределение ресурсов СОИ.
Прикладная программа. Программа, предназначенная для решения задачи или класса задач в определенной сфере использования СОИ.
Программа обслуживания. Программа, предназначенная для предоставления услуг общего характера пользователям и обслуживающему персоналу СОИ.
Абсолютная программа. Программа на машинном языке, выполнение которой зависит от ее местонахождения в оперативной памяти.
15.1. Программное обеспечение систем обработки информации 519
Перемещаемая программа. Программа на машинном языке, выполнение которой не зависит от ее местонахождения в оперативной памяти.
Реентерабельная программа. Программа, которая размещена в оперативной памяти и может выполняться многократно.
Мобильная программа. Программа, написанная для ЭВМ одной архитектуры, однако может выполняться в машинах другой архитектуры.
Драйвер. Программа, предназначенная для управления работой периферийных устройств.
Подпрограмма. Программа, которая является частью другой программы и удовлетворяет требованиям языка программирования к структуре программы.
Программный модуль. Программа или ее завершенный фрагмент, предназначенный для хранения, трансляции, объединения с другими программными модулями и загрузки в оперативную память.
Исходный модуль. Программный модуль на исходным языке, который обрабатывается транслятором.
Объектный модуль. Программный модуль, получаемые в результате компиляции исходного модуля.
Загрузочный модуль. Программный модуль, представленный в форме, пригодной для загрузки в основную память для выполнения.
Рекурсивная подпрограмма. Подпрограмма, которая может обращаться сама к себе.
15.1.3. Языки и технология программирования
Стандарт устанавливает следующие основные понятия языков и технологий программирования.
Язык программирования. Формализованный язык, предназначенный для описания алгоритмов решения задач на ЭВМ.
Алгоритмический язык. Искусственный язык, предназначенный для выражения алгоритмов.
Проблемно-ориентированный язык. Язык программирования, соответствующий понятиям определенного класса прикладных задач. Обычно он имеет набор специфических изобразительных средств.
Исходный язык. Язык программирования, который используется для первичного представления программы.
Машинный язык. Предназначен для представления программ в форме, позволяющей выполнять их непосредственно в СОИ без использования трансляторов, компиляторов и интерпретаторов.
Автокод. Символьный язык программирования, предложения которого по своей структуре подобны командам и обрабатываемым данным конкретного машинного языка.
Язык ассемблера. Представляет собой символьную форму машинного языка с рядом возможностей, характерных для языков высокого уровня. Язык ассемблера обычно включает в себя макрокоманды.
Ассемблер. Программа или техническое средство, выполняющее ассемблирование.
Ассемблирование. Компиляция программ с языка ассемблера.
520 Программная документация
Язык высокого уровня. Язык программирования, понятия и структура которого удобны для восприятия человеком.
Декларативный язык. Язык программирования для выражения определений, например, язык описания данных.
Объектно-ориентированный язык. Соответствует концепциям объектно-ориентированного программирования.
Процедурный язык. Язык программирования, в котором действия над данными выражаются в терминах последовательностей команд.
Функциональный язык. Язык программирования, в котором действия над данными выражаются в виде обращений к функциональным процедурам.
Транслятор. Программа или техническое средство, выполняющее трансляцию программы. Кроме этого, он диагностирует ошибки, формирует словари идентификаторов, выдает на печать тексты программы.
Трансляция программы. Преобразование программы, представленной одним языком, в программу на другом языке, равнозначную первой.
Компилятор. Программа или техническое средство, выполняющее компиляцию.
Компиляция. Трансляция программы из языка высокого уровня в форму, близкую к программе машинным языком.
Интерпретация. Последовательное считывание команд исходной программы из оперативной памяти, компиляция их машинным языком и выполнение.
Интерпретатор. Программа или техническое средство, выполняющие интерпретацию.
Редактор связей. Программа, предназначенная для создания загрузочных модулей на основе объектных модулей.
Библиотека программ. Организованная совокупность программ или их частей. Библиотеку программ часто называют в соответствии с природой содержащихся в ней элементе з.
Спецификация программы. Формализованное представление требований к разрабатываемой программе.
Верификация программы. Доказательство того, что поведение программы соответствует ее спецификации.
15.1.4. Виды программирования
Для создания программ широко используют следующие виды программирования.
Структурное программирование. Метод построения программ, использующий только иерархически вложенные конструкции, каждая из которых имеет единую точку входа и единую точку выхода. Тут используют три вида структур, связанных передачей управления: последовательную, условного перехода и циклическую.
Объектно-ориентированное программирование. Метод построения программ как совокупностей объектов и их классов, которые могут вызывать друг друга для выбора и выполнения операций. Объекты состоят из данных и операций над данными.
15.2. Единая система программной документации 521
15.2. Единая система программной документации
Единая система программной документации — это комплекс государственных стандартов, которые устанавливают взаимосвязанные правила разработки, оформления и обращения программ и программной документации (ГОСТ 19.001-77).
В стандартах ЕСПД устанавливают требования, регламентирующие разработку, сопровождение, изготовление и эксплуатацию программ, что обеспечивает возможность:
• унификации программных изделий для взаимного обмена программами и использования ранее разработанных программ в новых разработках;
• снижения трудоемкости и повышения эффективности разработки, сопровождения, изготовления и эксплуатации программных изделий;
• автоматизации изготовления и хранения программной документации.
Сопровождение программы содержит анализ функционирования, развития и совершенствования программы, а также внесения изменений в нее с целью устранения ошибок.
15.2.1. Сфера использования и состав ЕСПД
Правила и положения, установленные стандартами ЕСПД, распространяются на программы и программную документацию для вычислительных машин, комплексов и систем независимо от их назначения и сферы использования.
В состав ЕСПД входят:
• основополагающие и организационно-методические стандарты;
• стандарты, которые определяют формы и содержание программных документов, использованных для обработки данных;
• стандарты, которые определяют автоматизацию разработки программных документов.
Разработка организационно-методической документации, которая определяет и регламентирует деятельность организации по разработке, сопровождению и эксплуатации программ, должна производиться на основе стандартов ЕСПД.
15.2.2. Классификация и обозначения стандартов ЕСПД
Стандарты ЕСПД подразделяют на группы, представленные в табл. 15.1.
Таблица 15.1
Код группы Наименование группы
0 Общие положения
1 Основополагающие стандарты
2 Правила выполнения документации разработки
3 Правила выполнения документации изготовления
4 Правила выполнения документации сопровождения
5 Правила выполнения эксплуатационной документации
6 Правила обращения программной документации
7, 8 Резервные группы
9 Другие стандарты
522 Программная документация
Стандарты ЕСПД обозначают по классификационному признаку. Обозначение стандарта ЕСПД содержит:
• цифра 19, присвоена классу стандартов ЕСПД;
• одна цифра (после точки), обозначающая код классификационной группы стандартов согласно табл. 15.1;
• двузначное число, определяющее порядковый номер стандарта в группе;
• двузначное число (после тире), указывающее год регистрации стандарта.
Пример обозначения стандарта “ЕСПД. Общие положения” представлен на рис. 15.1.
ГОСТ 19. 0 01-77
Категория стандарта - государственный
Класс (стандарт ЕСПД)
Классификационная группа стандартов Порядковый номер стандарта в группе Год регистрации стандарта
Рис. 15.1. Пример обозначения стандарта ЕСПД
15.2.3. Термины и определения в ЕСПД
ГОСТ 19.004-80 устанавливает термины и определения основных понятий ЕСПД, используемых в науке, технике и производстве.
К ним относятся следующие документы:
1. Алгоритм — согласно ГОСТ 19781-74.
2. Программа вычислительной машины (программа) — согласно ГОСТ 19781-74.
3. Программирование — согласно ГОСТ 19781-74.
4. Документ — согласно ГОСТ 6.102-75.
5. Программное изделие: программа на носителе данных — продукт программного производства.
6. Программный документ: содержит сведения, необходимые для разработки, изготовления, эксплуатации и сопровождения программного изделия.
7. Эксплуатационный программный документ: содержит сведения, необходимые для обеспечения функционирования и эксплуатации программного изделия.
8. Проверка программы: проверка правильности реализации заданного алгоритма выполнением программ на ЭВМ.
9. Отладка программы: выявление, локализация и устранение ошибок в программе ЭВМ.
10. Испытание программы: установка соответствия программы ЭВМ заданным требованиям и программным документам.
11. Отладка программы: формирование конкретного варианта программы ЭВМ со свойствами многовариантности с учетом состава и структуры технических средств, возможных режимов работы и классов решаемых задач.
15.3. Обозначение программных документов 523
12. Сопровождение программы: процесс модификации существующей программы ЭВМ, обусловленный необходимостью устранения выявленных в ней ошибок и (или) изменения ее функциональных возможностей.
15.3. Обозначение программных документов
Обозначение программ и программных документов следует выполнять в соответствии с ГОСТ 19.103-77. Структура обозначения программы и ее программного документа — спецификации показана на рис. 15.2.
_ А. В. ХХХХХ - XX
Обшая часть ооозначения программы и -р- -т- —-------
программных документов
Код страны
. Код организации-разработчика
Регистрационный номер
Номер издания (для документа) или редакции (для программы)
Рис. 15.2. Структура обозначения программы и ее спецификации
Код страны и код организации-разработчика разделяют точками, после регистрационного номера ставят дефис. Правила обозначения кода страны, кода организации-разработчика и регистрационного номера аналогичны правилам обозначения конструкторских документов (см. главу 13, п.13.4).
Структура обозначения других программных документов показана на рис. 15.3.
А. В. ХХХХХ-XX XX XX-XX
Общая часть обозначения
программы и ее программных документов
Номер редакции документа
Код вида документа
Номер документа данного вида
Номер части документа
Рис. 15.3. Структура обозначения других программных документов
Номер издания программы или номер редакции документа присваивают по мере возрастания от 01 до 99 в пределах каждого проекта.
Код вида документа присваивают в соответствии с требованиями ГОСТ 19.101-77 “Виды программ и программных документов”, например, для текста программы — 12. Номер документа этого вида присваивают по мере возрастания от 01 до 99, а номер части документа — от 1 до 9 в пределах проекта.
Если документ состоит из одной части, то дефис и порядковый номер части не указывают. Номер редакции спецификации и ведомости эксплуатационных документов должен совпадать с номером издания той же программы.
524 Программная документация
15.4. Виды программ и программной документации
ГОСТ 19.101-77 устанавливает виды программ и программных документов для ЭВМ, комплексов и систем.
Программу допускается идентифицировать и использовать самостоятельно и (или) в составе других программ.
Программы подразделяют на следующие виды:
• компонент: рассматривается как единое целое, которое выполняет законченную функцию и используется самостоятельно или в составе комплекса;
• комплекс: программа состоит из двух и более компонентов и (или) комплексов, выполняющие взаимосвязанные функции;
К программным относятся документы, содержащие сведения, необходимые для разработки, изготовления, сопровождения и эксплуатации программ.
Виды программных документов и их содержание представлены в табл. 15.2.
Таблица 15.2
Код вида документа Виды программного документа Содержание программного документа
— Спецификация Состав программе и документации на нее
05 Ведомость держателей оригиналов Перечень организаций, в которых хранятся оригиналы программных документов
12 Текст программы Запись программы с необходимыми комментариями
13 Описание программы Сведения о логической структуре и функционировании программы
51 Программа и методика испытаний Требования, которые проверяются во время испытания программы, а также порядок и методы их контроля
31 Техническое задание Назначение и сфера использования программы
81 Пояснительная записка Схема алгоритма, его общее описание и (или) функционирования программы, а также обоснование принятых технических и технико-эКономических решений
20 Эксплуатационные документы Сведения об обеспечении функционирования и эксплуатации программ
15.5. Стадии разработки программ и программной документации
ГОСТ 19.102-77 устанавливает пять стадий разработки программ и программной документации для ЭВМ, комплексов и систем- техническое задание; эскизный проект, технический проект; рабочий проект; внедрение.
1. На стадии техничного задания выполняют:
• постановку задачи;
• обоснование потребности в разработке программы;
15.6. Требования к содержанию и оформлению 525
• научно-исследовательские работы (в случае необходимости);
• выбор и обоснование критериев эффективности и качества разрабатываемой программы;
• разработка и утверждение технического задания.
2. На стадии эскизного проекта разрабатывают:
• структуру входных и выходных данных;
• методы решения задачи;
• общее описание алгоритма решения задачи;
• технико-экономическое обоснование;
• эскизный проект, который подают на утверждение.
3. На стадии технического проекта:
• уточняют структуру входных и выходных данных;
• определяют форму представления входных и выходных данных семантики и синтаксиса языка;
• остаточно определяют конфигурацию технических средств;
• утверждают технический проект.
4. На стадии рабочего проекта выполняют:
• программирование и отладку программы;
• разработку программных документов в соответствии с ГОСТ 19.107-77;
• разработку, согласование и утверждение методики исследований;
• проведение предварительных государственных приемо-сдаточных испытаний;
• корректировку программы и программной документации по результатам испытаний.
5. На заключительной стадии внедрения:
• готовят и передают программу и программную документацию для сопровождения и (или) изготовления;
• оформляют и утверждают акт о передаче программы;
• передают программу в фонд алгоритмов и программ.
15.6. Требования к содержанию и оформлению
15.6.1. Общие требования к программным документам
Общие требования к оформлению программных документов устанавливает ГОСТ 19.105-78.
Программный документ может подаваться на различных типах носителей данных и состоять из следующих условных частей:
• титульной,
• информационной,
• основной,
• регистрации изменений.
Титульная часть состоит из листа утверждения и титульного листа согласно ГОСТ 19.104-78.
526 Программная документация
Информационная часть состоит из аннотации и содержания. В аннотации указывают сведения о назначении документа и сжатое изложение его основной части. Содержание содержит перечень записей о структурных элементах основной части документа, в каждую из которых входят:
• обозначения структурного элемента (номер разделу, подраздела);
• наименование структурного элемента;
• адрес структурного элемента на носителе данных (например, номер страницы, номер файла и т.д.).
Правила обозначения структурных элементов основной части документа и их адресации устанавливают стандарты ЕСПД для каждого типа носителя. Состав и структуру основной части программного документа устанавливают правила ЕСПД на соответствующие документы. О каждом изменении программного документа делают запись согласно ГОСТ 19.603-78.
15.6.2. Описание языка
Требования к содержанию и оформлению программного документа по описанию языка (программирование, управление заданием, организация вычислительного процесса) устанавливает ГОСТ 19.506-79. При этом учитываются положения ГОСТ 19.105-78 “Общие требования к программным документам”. Составление информационной части (аннотации и содержания) является обязательным.
Описание языка должно содержать следующие разделы.
1. Общие сведения. Указывают назначение и дают описание общих характеристик языка, его возможностей, основных сфер использования и т.д.
2. Элементы языка. Дают описание синтаксиса и семантики базовых и составляющих элементов языка.
3. Способы структурирования программы. Указывают способы вызова процедуры, передачи управления и другие элементы структурирования программы.
4. Средства обмена данными. Указывают описание языковых средств обмена данными (например, средства ввода-вывода, внутреннего обмена данными и т.д.).
5. Встроенные элементы. Дают описание встроенных в язык элементов (например, функции, классы и т.д.) и правила их использования.
6. Средства отладки программ. Указывают описание наличных средств отладки программ, семантику этих средств, рекомендаций относительно их использования.
В случае необходимости содержание разделов можно пояснять примерами. В приложениях к описанию языка можно указывать вспомогательные материалы (формализованные описания языковых средств, иллюстрации, таблицы, графики, формы бланков и т.д.).
15.6. Требования к содержанию и оформлению 527
15.6.3. Текст и описание программы
Структуру и оформление текста программы устанавливают в соответствии с ГОСТ 19.105-78 “Общие требования к программным документам”. Составление информационной части (аннотации и содержания) является обязательным.
Основная часть документа должна состоять из текстов одного или нескольких разделов, которым дают наименование. Каждый из этих разделов реализуется одним из типов символической записи, например:
• символические записи исходным или промежуточными языками;
• символическое представление машинных кодов и т.д.
В символическую запись разделов рекомендуется включать комментарии, которые могут отображать, например, функциональное назначение, структуру (ГОСТ 19.401-78).
Описание программы должно содержать следующие разделы (ГОСТ 19.402-78):
1. Общие сведения. Указывают обозначение и наименование программы; программное обеспечение, необходимое для функционирования программы; язык программирования, которым написана программа.
2. Функциональное назначение. Указывают классы решаемых задач и (или) назначение программы и сведения о функциональных ограничениях программы.
3. Описание логической структуры. Указывают алгоритм программы, использованные методы, структуру программы с описанием функций составляющих частей и связи между ними. Описание логической структуры программы выполняют с учетом текста программы на исходном языке.
4. Использованные технические средства. Перечисляют типы ЭВМ и устройства, используемые для работы программы.
5. Вызов и загрузка. Указывают способ вызова программы с соответствующего носителя данных, входные точки программы. Допускается указывать адреса загрузки, сведения об использовании оперативной памяти, объем программы.
6. Входные данные. Указывают характер, организацию и предварительную подготовку входных данных, а также формат и способ кодирования входных данных.
7. Выходные данные. Указывают характер и организацию выходных данных, а также формат и способ кодирования выходных данных.
Допускается содержание разделов иллюстрировать пояснительными примерами, таблицами, схемами, графиками. В приложениях к описанию программы допускается указывать различные материалы, которые не целесообразно указывать в описании программы.
15.6.4. Пособие системного программиста
Требования к содержанию и оформлению программного документа "Пособие системного программиста” устанавливает ГОСТ 19.563-79. При этом учитываются положения ГОСТ 19.105-78 “Общие требования к программным документам”. Составление информационной части (аннотации и содержания) является обязательным.
528 Программная документация
Пособие системного программиста должно содержать следующие разделы.
1. Общие сведения о программе. Указывают назначение и функции программы и сведения о технических и программных средствах, которые обеспечивают выполнение этой программы.
2. Структура программы. Указывают сведения о структуре программы, ее составные части и связи между ними и другими программами.
3. Настройка программы. Указывают описание действий по настройке программы на условия конкретного использования (настройка на состав технических средств, выбор функций и др.).
4. Проверка программы. Указывают описание способов проверки, позволяющие оценить работоспособность программы (контрольные примеры, методы прогона, результаты).
5. Сообщения системному программисту. Указывают тексты сообщений, выдаваемых в ходе выполнения настройки и т.п.
В приложениях к пособию можно указывать вспомогательные материалы (примеры, иллюстрации, таблицы, графики и т.д.).
15.6.6. Пособие программиста
Требования к содержанию и оформлению “Пособия программиста” устанавливает ГОСТ 19.504-79. При этом учитываются положения ГОСТ 19.105-78 “Общие требования к программным документам”. Составление информационной части (аннотация и содержание) является обязательным.
Пособие программиста должно содержать следующие разделы.
1. Назначение и условия использования программы. Указывают назначение и функции, которые должна выполнять программа, и условия, необходимые для выполнения программы (объем оперативной памяти, требования к составу и параметрам периферийных устройств, программного обеспечения и т.д.).
2. Характеристика программы. Описывают основные характеристики и особенности программы (временные характеристики, режим работы, средства контроля и т.д.).
3. Обращение к программе. Указывают описание процедур вызова программы (способы передачи управления и параметров данных и т.д.).
4. Входные и выходные данные. Представляют описание организации используемой входной и выходной информации.
5. Сообщения. Указывают пакеты сообщений, выдаваемые программисту или оператору в ходе выполнения программы, описание их содержания и действия, которые необходимо выполнять по этим сообщениям.
В приложениях можно указывать вспомогательные материалы (примеры, иллюстрации, таблицы, графики и т.д.).
15.6. Требования к содержанию и оформлению 529
15.6.7. Техническое задание. Требования к содержанию и оформлению
Порядок построения и оформления ТЗ на разработку программы или программного изделия устанавливает ГОСТ 19.201-78.
Техническое задание содержит следующие разделы.
1. Вступление. Указывают наименование, сжато характеризуют сферу использования программы (изделия) и объекта.
2. Основания для разработки.
В этом разделе указывают:
• документ, на основании которого выполняется разработка;
• организации, утвердившие этот документ;
• наименование и (или) условное обозначение цели разработки.
3. Назначение разработки. Указывают функциональное и эксплуатационное назначение программы (изделия).
4. Требования к программе или программному изделию.
Этот раздел состоит из следующих подразделов:
• требования к функциональным характеристикам и надежности;
• требования к составу и параметрам технических средств, их информационной и программной совместимости;
• условия эксплуатации, специальные требования.
5. Требования к программной документации. Указывают предварительный состав программной документации и, в случае необходимости, специальные требования к ней.
6. Технико-экономические показатели.
В этом разделе указывают:
• ориентировочную экономическую эффективность;
• предусмотренную потребность на год;
• экономические преимущества в сравнении с лучшими образцами (аналогами).
7. Стадии и этапы разработки. Устанавливают необходимые стадии разработки, этапы и содержание работ (перечень программных документов, которые должны быть разработаны, согласованы и утверждены), а также термины разработки, определяют исполнителей.
8. Порядок контроля и приемки. Указывают виды испытаний и общие требования к приемке работ.
В приложениях к ТЗ в случае необходимости указывают:
• перечень научно-исследовательских и других источников и работ, обосновывающих разработку;
• схемы алгоритмов, таблицы, описания, обоснования, расчеты и другие документы, которые могут быть использованы в разработке.
34 — 4-1749
530 Программная документация
15.7. Символы в схемах алгоритмов, программ, данных и систем
ГОСТ 19.701-90 (международный стандарт ICO 5807-85) все символы разделяет на четыре группы: данных, процессов, линий и специальных символов.
15.7.1. Символы данных
К первой группе относятся основные и специфические символы данных. К основным символам относятся:
1. Данные. Символ изображает данные с неопределенным носителем данных (рис. 15.4, а).
2. Запоминаемые данные. Символ изображает эти данные в виде, пригодном для обработки; носитель данных
a б
Рис. 15.4. Основные символы данных: а — данные; б — запоминаемые данные
не определен (рис. 15.4, б).
К специфическим символам данных относятся:
1. Оперативное запоминающее устройство. Символ изображает данные, хранимые в оперативному запоминающем устройстве (рис. 15.5, а).
2. Запоминающее устройство с последовательным доступом. Символ изображает данные, хранимые в запоминающем устройстве с последовательным доступом — магнитная лента, кассета с магнитной лентой, магнитофонная кассета (рис. 15.5, б).
3. Запоминающее устройство с прямым доступом. Символ изображает данные, хранимые в запоминающем устройстве с прямым доступом — магнитный диск, магнитный барабан, гибкий магнитный диск (рис. 15.5, в).
4. Документ. Символ изображает данные, представленные на носителе в удобной для чтения форме — машинограмма, документ для оптического или магнитного считывания, микрофильм, рулон ленты с результирующими данными, бланки ввода данных (рис. 15.5, г).
5. Ручной ввод. Символ изображает данные, вводимые вручную во время обработки с устройства любого типа — клавиатура, переключатели, кнопки, световое перо, полоски с штриховым кодом (рис. 15.5, д).
6. Карта. Символ изображает данные, представленные на носителе в виде карты — перфокарты, магнитные карты, помеченные карты для считывания, карты с отрывным ярлыком, помеченные карты для сканирования (рис. 15.5, е).
7. Бумажная лента. Символ изображает данные, представленные на носителе в виде бумажной ленты (рис. 15.5, ж).
8. Дисплей. Символ изображает данные в виде экрана для визуального наблюдения, индикатора ввода информации (рис. 15.5, к).
15.7. Символы в схемах алгоритмов, программ, данных и систем 531
Рис. 15.5. Специфические символы данных: а — оперативное запоминающее устройство; б — запоминающее устройство с последовательным доступом; в — запоминающее устройство с прямым доступом; а — документ; д — ручной ввод; е — карта; ж — бумажная лента; к— дисплей
15.7.2. Символы процесса
Ко второй группе относятся основные и специфические символы процесса.
Основной символ процесса
Символ отображает функцию обработки данных любого -----------
вида — выполнение определенной операции или группы операций, присед я щих к изменению значения, формы или раз- мещения информации, или определение, в каком из несколь- Рис. 15.6. Основной ких направлений потока следует двигаться (рис. 15.6). символ процесса
Специфические символы процесса
1. Обусловленный процесс. Символ отображает обусловленный процесс, который состоит из одной или нескольких операций или шагов программы, определенный в другом месте — в подпрограмме, модуле (рис. 15.7, а).
2. Ручная операция. Символ отображает любой процесс, выполняемый человеком (рир. 15.7, б).
3. Подготовка. Символ отображает модификацию команды или группы команд с целью воздействия на некоторую следующую функцию — установка переключателя, модификация индексного регистра или инициализация программы (рис. 15.7, в).
4. Решение. Символ отображает решение или функцию переключательного типа с одним входом и рядом альтернативных выходов, из которых только один может быть активизирован после вычисления условий, определенных внутри этого символа. Соответствующие результаты вычислений могут быть записаны рядом с линиями, отображающими эти пути (рис. 15.7, а).
5. Параллельные действия. Символ отображает синхронизацию двух или более параллельных операций (рис. 15.7, д).
6. Граница цикла. Символ состоит из двух частей и отображает начало и конец цикла. Обе части символа имеют один и тот же идентификатор. Условия для инициализации, прироста, завершения и т.д. помещаются внутри
34*
532 Программная документация
символа в начале или в конце в зависимости от размещения операции,
проверяющей условие.
6
Рис. 15.7. Специфические символы процесса: а — обусловленный процесс; б — ручная операция; в — подготовка; г — решение; д — параллельные действия
Пример синхронизации нескольких параллельных операций показан на рис. 15.8.
Рис. 15.8. Принцип синхронизации параллельных операций
Процессы С, D, Е не могут начаться до тех пор, пока не завершится процесс Л; аналогично процесс F должен ожидать окончания процессов В, С и D, однако процесс С может начаться и (или) завершиться раньше, чем соответственно начнется и (или) завершится процесс D. <
Пример использования границ цикла показан на рис. 15.9.
a б в
Рис. 15.9. Символ границы цикла: а — общее обозначение; б — условие окончания в начале цикла; в — условие окончания в конце цикла
15.7.3. Символы линий
Третья группа содержит основные и специфические символы линий.
15.7. Символы в схемах алгоритмов, программ, данных и систем 533
Основной символ линии
Символ отображает поток данных или управ-
ления (рис. 15.10). В случае необходимости ИЛИ Рис. 15.10. Основной символ линии для удобства чтения и понимания можно использовать стрелки-указатели.
Специфические символы линий
1. Передача управления. Символ отображает непосредственную передачу управления от одного процесса к другому. Тип передачи управления должен быть назван внутри символа — например, запрос, вызов, событие (рис. 15.11, а).
2. Канал связи. Символ отображает передачу по каналу связи (рис. 15.11, б).
3. Пунктирная линия. Символ отображает альтернативную связь между двумя или более символами. Символ используют также для обвода аннотированных участков (рис. 15.11, в).
а б в
Рис. 15.11. Специфические символы линий: а — передача управления; б — канал связи; в — пунктирна линия
15.7.4. Другие специфические символы
К четвертой группе относятся следующие специфические символы.
1. Соединитель. Символ отображает выход в часть схемы и вход из другой части этой схемы и используется для обрыва линии и продолжения ее в другом месте. Соответственно символы-соединители должны иметь одно и то же уникальное обозначение (рис. 15.12, а).
2. Терминатор. Символ отображает выход во внешнюю среду и вход из внешней среды — начало или конец схемы программы, внешнее использование и источник или пункт назначения данных (рис. 15.12, б).
3. Комментарий. Символ используют для добавления описательных комментариев или пояснительных записей для пояснения или примечаний. Пунктирные линии в символе комментария связаны с соответствующим символом или могут обводить группу символов. Текст комментариев или примечаний может быть расположен возле ограничительной фигуры (рис. 15.12, в).
4. Пропуск. Символ (три точки) используют в схемах для изображения пропуска символа или группы символов, у которых не определены ни тип, ни количество символов. Символ используют только в символах линий или между ними. Его используют главным образом в схемах, изображающих общие развязки с неизвестным числом повторений (рис. 15.12, г, д).
534 Программная документация
Рис. 15.12. Специальные символы: а — соединитель; б — терминатор; в — комментарий; г — пропуск в символе линий; д — пропуск между символами линий
Пример использования комментария показан на рис. 15.13, а, а использования символа пропуска — на рис. 15.13, б
Данные А
---' Комментарий I
Процесс I
Данные В / ~
- -j Комментарий 2
П роцесс 2
6
a
Рис. 15.13. Использование специальных символов: а — комментария; б — пропуска
15.7.5. Правила использования символов и схем
Символ предназначен для графической идентификации функции, которую он отображает, независимо от текста внутри этого символа. Символы в схеме следует размещать равномерно, придерживаясь разумной длины соединений и минимального количества долгих линий.
Большинство символов задуманы так, чтобы можно было поместить текст внутрь символа. Формы символов, установленные стандартом, должны служить пособием для фактически используемых символов. Не должны изменяться углы и другие параметры, влияющие на соответствующую форму символов. Символы должны быть по возможности одного размера. Символы могут быть начерчены в любой ориентации, однако лучше использовать горизонтальную ориентацию. Зеркальное изо-
Рис. 15.14. Запись текста для пояснения функции символа
бражение формы символа означает одну и ту же функцию, однако ему не следует отдавать преимущество.
Минимальный объем текста, необходимый для понимания функции данного символа, требуется размещать внутри этого символа. Текст для чтения следует записывать слева направо и сверху вниз независимо от направления потока (рис. 15.14).
Если объем текста, который необходимо поместить внутри символа, превыша
ет его размеры, то следует использовать символ комментария. Если использование
15.7. Символы в схемах алгоритмов, программ, данных и систем 535
символов комментария может запутать или разрушить ход схемы, текст необходимо размещать на отдельном листе и давать перекрестную ссылку на символ.
В схемах можно использовать идентификатор символов. Это связанный с определенным символом идентификатор, определяющий этот символ для использования в справочных целях в других элементах документации (например, в листинге программы). Идентификатор символа следует размещать (рис. 15.15).
слева над символом
Рис. 15.15. Запись идентификатора
^ZZZ...Z ZZZ...
Рис. 15.16. Описание символов
В схемах можно использовать описание символов — любая другая информация, например, для отображения специального применения символа с перекрестной ссылкой или для лучшего понимания функции как части схемы. Описание символа должно быть размещено справа над символом (рис. 15.16).
В схемах работы системы символы, отображающие носители данных, во многих случаях показывают способы ввода-вывода. Для использования в качестве ссылки на документацию текст для символов, отображающих способы ввода, следует размещать справа над символом, а текст для символов, отображающих вывод — справа под символом (рис. 15.17).
В схемах можно использовать подробное
XXX.
г j ZZZ...Z
Рис. 15.17. Способы обозначения
ввода и вывода
ZZZ...Z
изображение, которое обозначают символом с полосой для процесса или данных. Символ с полосой указывает, что в этом же комплекте документации в другом месте имеется более подробное изображение.
Символ с полосой представляет собой любой символ, внутри которого в верхней части проведена горизонтальная линия. Между этой линией и верхней линией символа расположен идентификатор, указывающий на подробное изображение этого символа. В качестве первого и последнего символа подробного изображения необходимо использовать символ указателя конца. Первый символ указателя конца должен содержать ссылку, которая также находится в символе с полосой (рис. 15.18).
Потоки данных или потоки управления в схемах представляют линиями. Направление потока слева направо и сверху вниз считается стандартным. В случаях, когда требуется внести больше ясности в схему, на линиях используются стрелки. Если поток имеет направление, которое отличается от стандартного, то стрелки должны указывать это направление.
| АВ4
h--------
a
Рис. 15.18. Подробное изображение процесса или данных: а — символ с полосой;
б — полное представление
< ХМ >
< НАЧАЛО J
( Х№. >
< КОНЕЦ J
б
536 Программная документация
В схемах требуется избегать пересечения линий. Линии, которые пересекаются, не имеют логической связи между собой, поэтому изменение направления в точках пересечения не допускается (рис. 15.19, а).
Две или более входных линии могут объединяться в одну выходную линию. Если две или более линий объединяются в одну линию, то место объединения должно быть уменьшено
а б
Рис. 15.19. Изображение линий: а — пересечение; б — объединение
(рис. 15.19, б).
Линии в схемах должны входить в символ слева или сверху, а выходить справа
или снизу и быть направленными к центру символа.
В случае необходимости линии в схемах требуется разрывать во избежание чрезмерных пересечений или слишком длинных линий, а также, если схема состоит из нескольких листов. Соединитель в начале разрыва называют внешним, а соеди-
нитель в конце разрыва — внутренним.
Ссылку на страницы можно указывать вместе с символом комментария для их соединителей (рис. 15.20).
Qb,')---] К с. 3 Из с. 1 I----
a б
Рис. 15.20. Соединители: а — внешние; б—внутренние
Несколько выходов из символа следует показывать:
• несколькими линиями от этого символа к другим символам (рис. 15.21, а);
• одной линией от этого символа, которая затем разветвляется на соответствующее количество линий (рис. 15.21, б).
Рис. 15.21. Изображение нескольких выходов: а — несколькими линиями от одного символа; б — одной линией с последующим разветвлением
Рис. 15.22. Запись значений логических условий: а — для нескольких выходов из одного символа, б — для одного выхода с разветвлением
Каждый выход из символа должен сопровождаться соответствующим количеством условий. Таким образом показывается логический путь для того, чтобы эти условия и соответствующие ссылки были идентифицированы (рис. 15.22).
Вместо одного символа с соответствующим текстом можно использовать несколько символов с перекрытием изображения, каждый из которых содержит текст
15.7. Символы в схемах алгоритмов, программ, данных и систем 537
описания (использование или формирование нескольких носителей данных или файлов, выработка множества копий печатных отчетов или форматов перфокарт).
Если несколько символов представляют собой упорядоченное множество, то это упорядочивание должно располагаться от переднего (первого) к заднему (последнему).
Приоритет или последовательный порядок нескольких символов не изменяется с помощью точки, в которую линия входить или из которой выходит.
15.7.6. Схемы алгоритмов, программ, данных и систем
ГОСТ 19.701-90 (международный стандарт ICO 5807-85) определяет следующие схемы: алгоритмов, данных, программ, работы систем, взаимодействие программ и ресурсы системы.
Схемы алгоритмов, программ, данных и систем (далее — схемы) состоят из символов, имеющих заданное значение, короткого пояснительного текста и соединительных линий.
Схемы можно использовать на различных уровнях детализации, причем количество уровней зависит от объема и сложности задания обработки данных. Уровень детализации должен быть таким, чтобы различные части и взаимосвязь между ними были понятны в целом.
Используют следующие понятия:
• основной символ — символ, который используют в тех случаях, когда точный тип (вид) процесса или носителя данных неизвестен или нет потребности описывать фактический носитель данных;
• специфический символ — символ, который используют в тех случаях, когда известен точный тип (вид) процесса или носителя данных или когда требуется описать фактический носитель данных;
• схема — графическое изображение определения, анализа или метода решения задачи, в котором используются символы для отображения операций, данных, потока, оборудования и т.д.
Схемы данных отображают путь данных во время решения задач и определяют этапы обработки, а также различные носители используемых данных.
Схема данных состоит из следующих символов:
• данных (символы данных могут также указывать вид носителей данных);
• процесса, который следует выполнить над данными (символы процесса могут также указывать функции, выполняемые вычислительной машиной);
• линий (указывают потоки данных между процессами и (или) носителями данных);
• специальных (используют для облегчения написания и чтения схемы).
Схема данных начинается и заканчивается символами данных за исключением специальных символов (рис. 15.23).
538 Программная документация
1 .Банковский чек.
Виды денежных j , I поступлений от . , продажи билетов |
— : Полученные по почте
Банковский чек
\ Проверить
\ детали
\ и исправить
\ ошибки /
_____г т!
Виды денежных пошупиений 01 продажи билетов
11рочесть документ
Ввести номер клиента в сумму
Регистрация । видов денеж-| ных поступ-। пений
Банковский чек
Список чсков.под- | лежащих возврату, и сумма для I заполнения,..----_ ,
Письма “билетов !
пет” 1
Билеты для отправки
Пересортировка / \ банковских /— \ чеков '
Банковский чек
“Пустые” |
банковские чеки I
1 Чеки, подлежащие возврату
Составить итоговые су ммы и список
\ Внеси, сумму в /
\ пустой /
\ чековый /
\ список /
Список чеков и су ммы для заполнения
Итоговые суммы^
| Заполненные чеки
Файл
Составить итоговые^ суммы и список ,
Банковский чек
Итоговые суммы П
Рис. 15.23. Схема данных
Схемы программ отображают последовательность операций в
Схема программы состоит из следующих символов (рис. 15.24):
• процесса (указывают фактические операции обработки данных);
• линейных (указывают поток управления);
• специальных (используют для облегчения написания и чтения схемы).
программе.
15.7. Символы в схемах алгоритмов, программ, данных и систем 539
/ Начало программы /
; Арифметическая ^обработка в ЭВМ' ------------I___________,_____—!
Перезапуск 1----------
Передача результата в запоминающее устройство
/' П ередач а'.^Н ет успешная X
_Х
4Да----------
I Передача резуль-'
I тата в запоминаю*
| шее устройство
Ошибка !
Остановка программы.
По ручному перезапуску - -- вернуться к месту появления ошибки и попробовать еще раз
Х^Персда1laX^HeTj
Контрольная) \ успешная/ । , передача ,
Да
Останов
Рис. 15.24. Схема программы
Схемы работы системы отображают управление операциями и поток данных в системе.
Схема работы системы состоит из следующих символов (рис. 15.25):
• данных (указывают на наличие данных);
• процесса (указывают операции, которые требуется выполнить над данными, и определяют логический путь, которого следует придерживаться);
• линейных (указывают потоки данных между процессами и (или) носителями данных, а также поток управления между процессами;
• специальных (используют для облегчения написания и чтения блок-схемы).
Схемы взаимодействия системы отображают путь активации программ и взаимодействий с соответствующими данными. Каждая программа в схеме взаимодействия программ показывается только один раз.
Схема взаимодействия программ состоит из следующих символов (рис. 15.26):
• данных (указывают на наличие данных);
• процесса (указывают операции, которые следует выполнить над данными);
• линейных (указывают поток между процессами и данными, а также инициацию процессов);
• символов (используют для облегчения написания и чтения схемы).
540 Программная документация
{ Начало заказа на товары
___ ____—1 ' I Г—---------
___ — ( ' Начальная обработка L 1 Данные j Вызов отображения _J данных Г отображения !
/ Начальное
( отображение
для запроса описи
I Запрос входных данных ।
'' |П1ифр
[покупателя, I Шифр к— товара,
количество
Файл покупателя
Файл товаров, внесенных ] — в опись___‘
Ошибка ввода, ответ на запрос
Контроль данных, ! запрос описи, распределение товаров1
^рсменный\ файл /
Запрос Заказ илн запрос9
Проверить заказ
Заказ
Обработка заказа 1
(? пет [филировать заказ
(Файл товаров,! Ji внесенных j в опись
Счета
Обработка накладных
Конец работы
Рис. 15.26. Схема взаимодействия программы
Контрольные вопросы 541
Схема ресурсов системы отображает конфигурацию блоков данных и обрабатывающих блоков, необходимую для решения задачи или набора задач.
Схема ресурсов системы состоит из следующих символов (рис. 15.27):
• данных (отображают входные, выходные и запоминающие устройства вычислительной машины);
• процесса (отображают процессоры);
• линейных (отображают передачу данных между устройствами ввода-вывода и процессорами, а также передачу управления между процессорами);
• специальных (используют для облегчения написания и чтения схемы).
f Файл \ (транзакций!
Рабочий файл
Корректировка Ч Главный файл
Отчет >
Список ошибок
Рис. 15.27. Схема ресурсов системы
Контрольные вопросы
1. Дайте определение системы обработки информации
2. Что такое программирование?
3. Какие два вида программирования существуют?
4. Что входит в состав ЕСПД?
5. Что содержит обозначение стандарта ЕСПД?
6. Опишите структуру обозначения программного документа.
7. Перечислите виды программных документов.
8. Перечислите стадии разработки программ и программной документации.
9. Из каких условных частей может состоять программный документ?
10. Какие разделы входят в описание языка программирования?
11. Какие разделы входят в описание программы?
12. Какие разделы входят в пособие системного программиста?
13. Какие разделы входят в пособие программиста?
14. Какие разделы входят в техническое задание?
15. На какие четыре группы разбиваются символы схем программной документации?
16. Перечислите символы, входящие в каждую из четырех групп.
17. Перечислите виды схем программной документации.
542 Список литературы
Список литературы
1. Алексенко А.Г., Шагурин И.И. Микросхемотехника. - М.: Радио и связь, 1990. - 496с.
2. Бабак В.П., Хандецкий В.С., Шрюфер Е. Обработка сигналов: Учебник. 2-е изд., пе-рераб. и доп. - К.: Лыбидь, 1999. - 496 с.
3. Бабич Н.П., Нагорный Л.Я. Элементы и узлы цифровых вычислительных машин: Курс лекций. - К.: КИИГА, 1971. - 209 с.
4. Бабич Н.П., Кубицкий В.И., Ефимец В.Н. Импульсные и цифровые устройства: Учеб, пособ. - К.: КИИГА, 1975. - 95 с.
5. Бабич Н.П., Ефимец В.Н. Элементы и узлы ЭЦВМ: Учеб, пособ. - К.: КИИГА, 1983. -48 с.
6. Бабич Н.П., Жуков И.А. Компьютерная схемотехника: Метод, указания. - К.: КМУГА, 2000. - 72 с.
7. Балашов Е.П., Григорьев В.Л., Петров Г.А. Микро- и мини-ЭВМ: Учеб, пособ. для вузов. - Л.: Энергоатомиздат, 1984. - 376 с.
8. Башков Е.П. Аппаратное и программное обеспечение зарубежных микро-ЭВМ: Учеб пособ.. - К.: Вища шк., 1990. -207 с.
9. Белоус А.И., Блинков О.Е., Силин А.В. Биполярные микросхемы для интерфейсов систем автоматического управления. - Л.: Машиностроение, 1990. - 272 с.
10. Бойко В.А., Клименко Ю.В., Корнейчук В.И. Курсовые и дипломные проекты — требования к оформлению документации. - К.: “Корн1йчук”, 2003. - 176 с., ил.
11. Бродин В.Б., Шагурин ИИ. Микропроцессор i486. Архитектура, программирование, интерфейс. - М.: ДИАЛОГ-МИФИ, 1993. - 240 с.
12. Букреев И.Н., Мансуров Б.М. Микроэлектронные схемы цифровых устройств. 3-е изд. - М.: Радио и связь, 1990. -415 с.
13. Вишенчук И.М., Черкасский Н.В. Алгоритмические операционные устройства и суперЭВМ. - К.: Техника, 1990. - 197 с.
14. Гальперин М.В. Практическая схемотехника в промышленной автоматике. - М.: Энергоатомиздат, 1987. - 320 с.
15. Горбунов В.Л., Панфилов Д.И. Микропроцессоры. Лабораторный практикум: Учеб, пособие для втузов/Под ред. Л.Н.Преснухина. - М.: Высш, шк., 1984 - 104 с., ил.
16. Гоигорьев В.Л. Программное обеспечение микропроцессорных систем. - М.: Энергоатомиздат, 1983. - 208 с.
17. Гоигорьев В.Л. Архитектура и программирование арифметического сопроцессора. - М.: Энергоатомиздат, 1991. - 208 с.
18. Григорьев В.Л. Микропроцессор i486. Архитектура и программирование (в 4-х книгах). - М.: Гранал, 1993. - Кн. 1 - 346 с., кн. 2, 3, 4 - 382 с.
19. Гук М. Аппаратные средства IBM PC. Энциклопедия. - СПб.: Питер Ком, 1999. -816 с.
20. Гук М. Процессоры Pentium II, Pentium Pro и просто Pentium. - СПб.: Питер Ком, 1999.-288 с.
21. Гусев В Г, Гусев Ю.М. Электроника: Учеб, пособ. для приборостроит. спец, вузов. - 2-е изд., перераб. и доп. - М.: Высш, шк., 1991. - 622 с.
22. Евдокимов В.Ф., Стасюк А.И. Параллельные вычислительные структуры на основе разрядных методов вычислений. - К.: Наук, думка, 1987. - 312 с.
23. Жабин В.И., Ткаченко В.В. Однокристальные и микропрограммируемые ЭВМ / Под ред. В.И. Корнейчука. - К.: Диалектика, 1995. - 115 с.
24. Жабин В.И., Ткаченко В.В., Зайцев А.А., Антонов Р.Л. Логические основы и схемотехника цифровых ЭВМ: Практикум. - К.: ВЕК+, 1999. - 128 с.
25. Жуков И.А., Плющ Ю.А. Математические модели вычислительных структур функционально-ориентированных оперативных блоков. Препринт-95 - 461. - К.: ИМПЭ, НАН Украины, 1995. - 76 с.
543
26. Изделия электронной техники. Цифровые микросхемы. Микросхемы памяти. Микросхемы ЦАП и АЦП: Справ. / О.Н. Лебедев и др.; Под ред. А.И. Ладика и А.И. Сташкевича. - М.: Радио и связь, 1994. - 248 с.
27. Интегральные микросхемы энергонезависимой памяти 28F008SA 28F008SA-L: INTEL CORPORATION: Пер. с англ. - М.: БИНОМ, 1992.-78 с.
28. Информатика: Учеб, пособие для студ. пед. вузов / А.В. Могилев, Н.И. Пак, Е.К. Хеннер; Под ред. Е.К. Хеннера. - М.: Академия, 1999. - 816 с.
29. Каган Б.М. Электронные вычислительные машины и системы: Учеб, пособ. для вузов. - 2-е изд., перераб. и доп. - М.: Энергоатомиздат, 1985. - 552 с.
30. Калабеков Б.А. Цифровые устройства и микропроцессорные системы: Учеб, для техникумов связи. - М.: Горячая линия - Телеком, 2000. - 336 с.
31. Компьютерная схемотехника: Лаб. практикум / Н.П. Бабич, Л.Я. Нагорный, И.А. Жуков. - К.: КМУГА, 1998. - 82 с.
32. Кончаловский В.Ю. Цифровые измерительные устройства: Учеб, пособ. для вузов. - М.: Энергоатомиздат, 1985. - 304 с.
33. Корячко В.П. Микропроцессоры и микро-ЭВМ в радиоэлектронных средствах: Учеб, для вузов. - М.: Высш, шк., 1990. - 407 с.
34. Кравец В.А., Шпильберг А.Я. Зарубежные ЭВМ. Оборудование и программное обеспечение: Учеб, пособ. для иностр, студентов. - Харьков: Основа, 1991. - 216 с.
35. Лихтциндер Б.Я., Кузнецов В.Н. Микропроцессоры и вычислительные устройства в радиотехнике: Учеб, пособ.. - К.: Вища шк., 1988. - 272 с.
36. Логические ИС КР1533, КР1554: Справ.: В 2-х частях /И.И. Петровский, А.В. При-быльский, А.А. Троян, В.С. Чувелев. - М.: БИНОМ, 1993. - 496 с.
37. Луцкий Г.М., Корочкин А.В. Алгоритмы деления в полуавтономном режиме вычислений И Электронное моделирование. - 1982. - №5. - С. 9-15.
38. Майоров С.А., Новиков Г.И. Принципы организации цифровых машин - Л.: Машиностроение, 1974. - 432 с.
39. Микропроцессоры: В 3-х кн.: Учеб, для втузов / В.Д. Вернер, Н.В. Воробьев, А.В. Горячев и др.; Под ред. Л.Н. Преснухина. - М.: Высш, шк., 1986. - Кн.2 - 383 с.
40. Микропроцессоры и микро-ЭВМ в системах автоматического управления: Справ. / С.Т. Хвощ, Н.Н. Варлинский, Е.А. Попов; Под ред. С.Т. Хвоща. - Л.: Машиностроение, 1987. - 640 с.
41. Микропроцессорный комплект К1810: Структура, программирование, применение: Справ, книга / Ю.М. Казаринов и др.; Под ред. Ю.М. Казаринова. - М.: Высш, шк., 1990.-269 с.
42. Микропроцессорный комплект БИС серии К1810 для цифровой обработки сигналов: Справ. / А.И. Белоус, О.В. Подрубный, В.М. Журба; Под ред. А.И. Сухопаро-ва. - М.: Радио и связь, 1992. - 256 с.
43. Мячев А.А. Мини- и микро-ЭВМ систем обработки информации: Справ. - М.: Энергоатомиздат, 1991. - 304 с.
44. Мячев А.А., Степанов В.Н. Персональные ЭВМ и микро-ЭВМ. Основы организации: Справ. /Под ред. А.А. Мячева. - М.: Радио и связь, 1991. - 320 с.
45. Нефедов А.В. Интегральные микросхемы и их зарубежные аналоги: Справ. Т.З. -М.: КУбК-а, 1997.-544 с.
46. Прикладная теория цифровых автоматов / К.Г. Самофалов, А.М. Романкевич, В.Н. Валуйский и др. - К.: Вища шк., 1987. -375 с.
47. Применение интегральных микросхем памяти: Справ. / А.А. Дерюгин, В.В. Цыркин, В.Е. Красовский и др.; Под ред. А.Ю. Гордонова, А.А. Дерюгина. - М.: Радио и связь, 1994. - 232 с.
48. Проектирование микропроцессорной электронно-вычислительной аппаратуры: Справ. / В.Г. Артюхов, А.А. Будняк, В.Ю. Лапий и др. - К.: Техника, 1988. - 263 с.
49. Рабинович З.Л., Раманаускас В.А. Типовые операции в вычислительных машинах. - К.: Техника, 1980. - 264 с.
50. Савельев А.Я. Прикладная теория цифровых автоматов: Учеб, для вузов. - М.: Высш, шк., 1987. - 272 с.
544 Список литературы
51. Самофалов К.Г., Виктороа О.В. Микропроцессоры. - Б-ка инженера. - 2-е изд., лерераб. и доп. - К.: Техника, 1989. - 312 с.
52. Самофалов К.Г., Корнейчук В.И., Тарасенко В.П. Цифровые ЭВМ: Теория и проектирование / Под общ. ред. К.Г. Самофалова. - 3-е изд., перераб. и доп. - К.: Вища шк., 1989. -424 с.
53. Сигорский В.П. Математический аппарат инженера. - К.: Техника, 1975. - 768 с.
54. Соломатин Н.М. Логические элементы ЭВМ: Практ. пособ. для вузов. 2-е изд., перераб. и доп. - М.: Высш, шк., 1990. - 160 с.
55. Схемотехника ЭВМ: Учеб. /Под ред. Г.Н. Соловьева. - М.: Высш, шк., 1985. - 391с.
56. Схемотехника БИС постоянных запоминающих устройств / О.А. Петросян, И.Я. Козырь, Л.А. Колядов, Ю.И. Щетинин. - М.: Радио и связь, 1987. - 304 с.
57. Схемотехника ЭВМ: Лаб. практикум /Н.П. Бабич, В.И. Андреев, И.А. Жуков. - К.: КМУГА, 1997.-245 с.
58. Угрюмое Е.П. Проектирование элементов и узлов ЭВМ: Учеб, пособ. - М.: Высш, шк., 1987. - 318 с.
59. Угрюмое Е.П. Цифровая схемотехника. - СПб.: БХВ - Петербург, 2001. - 528 с.
60. Хоровиц П., Хилл В. Искусство схемотехники: В 3-х томах: Т.З. Пер. с англ. - 4-е изд., перераб. и доп. - М.: Мир, 1993. - 367 с.
61. Цапенко М.П. Измерительные информационные системы: Учеб, пособ. для вузов. - 2-е изд., перераб. и доп. - М.: Энергоатомиздат, 1985. - 439 с.
62. Цифровые устройства и микропроцессорные системы. Задачи и упражнения: Учеб, пособ. для вузов. / Л.М. Гольденберг, В.А. Малев, Г.Б. Малько. - М.: Радио и связь, 1992.-256 с.
63. Шагурин И.И., Бродин В.Б., Мозгоаой Т.П. 80386: описание и система команд. - М.: Малип, 1992. - 160 с.
64. Шевкопляс Б.В. Микропроцессорные структуры. Инженерные решения. - М.: Радио и связь, 1986. - 264 с.
65. Шило В.Л. Популярные микросхемы КМОП: Справ.. - М.: Ягуар, 1993. - 64 с.
66. Электроника СБИС. Проектирование микроструктур: Пер. с англ. / Под ред. Н. Айнслрука. - М.: Мир, 1989. - 256 с.
67. Юшин А.М. Цифровые микросхемы для электронных устройств: Справ, для ПТУ. -М.: Высш, шк., 1993. - 176 с.
68. Microprocessors. Intel Corporation. - New-York, 1990. - 1424 с.
А. Образцы форм документов проекта 545
Приложения
А. Образцы форм документов проекта
А.1. Титульный лист пояснительной записки
НАЗВАНИЕ МИНИСТЕРСТВА Название учебного заведения
Кафедра______________________________________________
ДОПУСТИТЬ К ЗАЩИТЕ Заведующий кафедрой
“__”200_г.
ДИПЛОМНЫЙ ПРОЕКТ
(ПОЯСНИТЕЛЬНАЯ ЗАПИСКА)
Тема:________________________________________________
Выполнил_____________________________________________
Руководитель_________________________________________
Консультанты по раздела^:
Нормоконтролер по ЕСКД (ЕСПД)________________________
35 — 4-1749
546 Приложения
А. 2. Задание на выполнение проекта и составление календарного плана
НАЗВАНИЕ УЧЕБНОГО ЗАВЕДЕНИЯ
Факультет Кафедра_________________________________________________________
Образовательно-квалификационный уровень___________________________________
Специальность_____________________________________________________________
УТВЕРЖДАЮ
Заведующий кафедрой
“____”200_г.
ЗАДАНИЕ на выполнение дипломного проекта студента
(фамилия, имя, отчество)
1. Тема проекта:__________________________________________________________
утверждена приказом ректора от “_”200__________________г. №
2. Срок выполнения проекта: с по
3. Выходные данные к проекту: ,___________________________________________
4. Содержание пояснительной записки (перечень вопросов, подлежащих разработке):
5. Перечень обязательного графического материала:
А.. Образцы форм документов проекта 547
КАЛЕНДАРНЫЙ ПЛАН
№ п/п Этапы выполнения дипломного проекта Срок выполнения этапов Примечание
Студент_________________________________________________________________
Руководитель дипломного проекта_________________________________________
6. Консультанты по отдельным разделам проекта:
Раздел Консультант (должность, Ф.И.О.) Дата, подпись
здание выдал задание принял
7. Дата выдачи задания_________________________
Руководитель_________________________________________________________
(подпись)
Задание принял к выполнению________________________________________________
(подпись студента)
Дата_________________________
35*
548 Приложения
Д.З. Образец оформления реферата
РЕФЕРАТ
Пояснительная записка к дипломному проекту “Цифровая математическая модель динамики полета самолета в режиме автоматической стабилизации", 105 с., 26 рисунков, 15 таблиц, 5 приложений, 15 литературных источников.
Объект исследования — динамика полета самолета Ил-96-300 в режиме автоматической стабилизации заданной приборной скорости через микропроцессорную систему управления тягой и исследование его динамических и статических характеристик.
Метод исследования — цифровое математическое моделирование в детерминированной постановке.
Установлено, что разработанная цифровая математическая модель динамики полета самолета Ил-96-300 на заданном режиме подобна реальному объекту; исследованы динамические и статические характеристики автоматически управляемого движения самолета; даны предложения относительно использования разработанной цифровой математической модели.
Результаты дипломного проектирования рекомендуется использовать для научных исследований и в практической деятельности специалистов авиационных конструкторских бюро.
Прогнозные допущения относительно развития объекта исследования — Синтез оптимальной структуры законов функционирования микропроцессорных систем управления полетом и тягой.
Ключевые слова:
САМОЛЕТ
ДИНАМИКА ПОЛЕТА
АВТОМАТИЧЕСКОЕ УПРАВЛЕНИЕ
МОДЕЛИРОВАНИЕ
МИКРОПРОЦЕССОРНАЯ СИСТЕМА
АЛГОРИТМ
А. Образцы форм документов проекта 549
А.4. Примеры оформления альбома и технического задания
,О1 I Формат Обозначение Наименование Документация общая Количество листов № экз Примечания
2 : 3 ‘ Разработана по-новому _ .
4 5 6 А4 НАУ 03 15 4I 000Д АЛУ1 Реферат 1
7 8 А4 НАУ 03 I5 4I 002 ГЗ АЛУ 1. Техническое задание 2
9 Ю А4 НАУ 03 I5 41 003 НЗ АЛУ1. Пояснительная записка 17
II 12 Л4 НАУ 03 15 4I 004 Э2 АЛУ 1. Схема электрическая функциональная 1
13
I4 I5 А4 НАУ 03 I5 4I 005 I'M АЛУ 1. Графы микропрограммы 1
I6 17 А4 НАУ 03 I5 41 006 ЭЗ АЛУ1 Схема электрическая принципиальная 2
18 I9 А4 НАУ 03 15 41 007 ПЭ АЛУ1, Перечень элементов 1
20
2I 22
23 24
25
НАУ 03 15 41 001 ОН
Лит докум Подпись Дата
Выпоиш! Петренко И П АЛУ У Описание альбома Литера Лист Листов
Руководит Пеанов И И к|п| 1
Проверил НАУ ФКСИКТ 301 091501
Н контр
Зав каф СнОоренко С С
Рис. А.1. Описание альбома
550 Приложения
1. НАЗВАНИЕ ТЕМЫ ПРОЕКТА. СФЕРА ИСПОЛЬЗОВАНИЯ
Название темы курсового проекта: Специализированное арифметико-логическое устройство (АЛУ) для выполнения операции сложения.
Сфера использования АЛУ — в составе бортового вычислителя с упрощенной системой команд для решения пилотажно-навигационных задач и автоматического контроля работы авиационных агрегатов.
2. ОСНОВАНИЕ ДЛЯ РАЗРАБОТКИ
2.1. Основанием для разработки АЛУ служит техническое задание на курсовой проект по дисциплине “Компьютерная схемотехника” согласно учебному плану.
2.2. Вариант технического задания задается таблицей, в которой номер строки (варианта) совпадает с номером студента в списке академической группы.
3. ЦЕЛЬ ПРОЕКТА
3.1. Цель проекта — получение новых теоретических знаний и обретение практических навыков в сфере цифровой схемотехники и закрепление методологии проектирования специализированных АЛУ.
3.2. Проект должен выполняться на основе современных интегральных микросхем с соблюдением требований действующих государственных стандартов.
4. ВЫХОДНЫЕ ДАННЫЕ
4.1. Арифметическая операция — сложение чисел в дополнительных кодах.
4.2. Разрядность входных операндов — 16 бит.
4.3. Код входных операндов — дополнительный.
4.4. Тип сумматора — параллельный комбинационный.
5. ТЕХНИЧЕСКИЕ ТРЕБОВАНИЯ
5.1. Структура АЛУ — с закрепленными микрооперациями.
5.2. Состав АЛУ — композиция операционного и управляющего блоков.
5.3. Тип управляющего блока — автомат Мура с памятью на /?5-триггерах.
5.4. Элементная база — микросхемы ТТЛШ серий КР1533, КР1531.
5.5. Время выполнения операции (быстродействие) — не более 100 нс.
5.6. Потребляемая мощность — не более 5 Вт.
5.7. Средняя наработка на отказ — не менее 25000 часов.
НАУ 03 15 41 002 ТЗ
Из.и Лит Л» докум Подпись Лата
Мынонни Петренко П.П АЛУ\ Техническое задание Питера Лист Листов
Ну-оворит. Иванов И И. кТп 1 2
Привсри / НА У ФКС ИКГ 301 091501
II.контр.
Зав каф. (.'.иаоренко С (
Рис. А.2. Техническое задание (начало)
А. Образцы форм документов проекта 551
6. УСЛОВИЯ ЭКСПЛУАТАЦИИ
6.1. Устойчивость к климатическим воздействиям.
Климатические воздействия по ГОСТ 18725-88, в том числе:
• максимальная допустимая влажность при 25°С — 80 %;
• изменения температурной среды — от минус 60 до плюс 85°С;
• атмосферное давление — от 84 до 106 кПа.
6.2. Устойчивость к механическим воздействиям.
Механические воздействия по ГОСТ 18725-88, в том числе линейное ускорение 500 м/с2 (500 g).
6.3. Характеристики надежности микросхем серии КР1533.
Наработка микросхем на отказ — 5000 часов, в облегченном режиме — 60000 часов. Интенсивность отказов — не более 0,9-10-4 час-1.
Во время изготовления схемы АЛУ должны быть обеспечены правила безопасности, охраны труда и окружающей среды согласно действующим стандартам.
7. ЭТАПЫ ПРОЕКТИРОВАНИЯ
7.1. Согласование технического задания с руководителем проекта.
7.2. Изучение научно-технической литературы по теме курсового проекта.
7.3. Разработка алгоритма заданной операции и функциональной схемы АЛУ.
7.4. Написание микропрограммы операции и разработка принципиальной схемы операционного блока.
7.5. Структурный синтез управляющего автомата и построение его принципиальной схемы.
7.6. Выполнение расчетов технических характеристик АЛУ (стоимости, быстродействия, потребляемой мощности, средней наработки на отказ).
7.7. Оформление текстовых и графических материалов проекта.
7.8. Защита курсового проекта.
8. ПЕРЕЧЕНЬ ТЕКСТОВОЙ И ГРАФИЧЕСКОЙ ДОКУМЕНТАЦИИ
8.1. Реферат.
8.2. Описание альбома.
8.3. Техническое задание.
8.4. Пояснительная записка.
8.5. АЛУ. Схема электрическая функциональная.
8.6. АЛУ. Графы микропрограмм.
8.7. Операционный блок. Схема электрическая принципиальная.
8.8. Управляющий блок. Схема электрическая принципиальная.
8.9. АЛУ. Перечень элементов.
НЛУОЗ 15 41 002 73 Лист
2
Пзм Лит Хв (Юкум. Подпись Дита
Рис. А.З. Техническое задание (окончание)
552 Приложения
Б. Соотношения размеров условных графических обозначений на модульной сетке
1. Минимальное расстояние между линиями выводов
2. Указатель полярности 1111111 Н
3. Указатель инверсного вывода ПТ?- J IB III и!
4. Указатель нелогического вывода
5. Указатель динамического вывода 4т р
6. Метка двунаправленного вывода на входе г-Н
То же с указателем полярности ДМ 111И11 п
7. Метка вывода с изменением состояния после возврата сигнала на исходный уровень
8. Метка вывода “сдвиг” вправо
9. Метка открытого выхода
10. Метка открытого выхода 1-го типа 1 и 1
11. Метка двухпорогового входа
12. Группирование битов многобитового входа 4 к- - !,1 г! Н
13. Обозначение функции “усилитель” — ST ---
14. Обозначение функции “элемент задержки”
15. Обозначение функции “моностабильный элемент” ---
16. Обозначение функции “множитель” —
17. Обозначение функции “сумматор”
18. Обозначение функции “Исключающее ИЛИ” --Ч--
19. Обозначение аналогового сигнала
20. Обозначение цифрового сигнала
21. Метка выхода с тремя состояниями
22. Общий блок управления и единый выходной элемент “Г Г-- --
В. Обозначения функций элементов, меток выводов 553
В. Обозначения функций элементов, меток выводов
Наименование Обозначение
Буфер BUF
Вычислитель СР
Секция вычислителя CPS
Вычислительное устройство CPU
Вычитатель Р-Q или SUB
Делитель DIV
Демодулятор DM
Демультиплексор DX
Дешифратор DC
Дискриминатор DIC
Дисплей DPY
Интерфейс периферийный программируемый PPI
Инвертор, повторитель I
Компаратор COMP
Микропроцессор MPN
Модулятор, модификатор MD
Память M
Главная память MM
Основная память GM
Быстродействующая память FM
Таблица В.1. Обозначения функций элементов
Наименование Обозначение
Память типа “first in, first out” FIFO
ПЗУ ROM
ППЗУ PROM
ППЗУ с многократным стиранием RPROM
Репрограммируемое ПЗУ с ультрафиолетовым стиранием UVPROM
ОЗУ RAM
ОЗУ статическое SRAM
ОЗУ динамическое DRAM
Энергонезависимая память ' NVRAM
Ассоциативная память CAM
Программируемая логическая матрица PLM
Преобразователь X/Y
Преобразователь аналоговый о или A
Преобразователь цифровой # или D
Преобразователь двоичный BIN
Преобразователь десятичный DEC
Преобразователь восьмеричный OCT
Преобразователь двоичнодесятичный BCD
Преобразователь 16-ричный HEX
Преобразователь в код Грея GRAY
554 Приложения
Наименование Обозначение
Преобразователь семисегментный 7 SEG
Преобразователь уровня ТТЛ TTL
Преобразователь уровня МОП MOS
Преобразователь уровня ЭСЛ ESL
Преобразователь аналого-цифровой ADC
Преобразователь цифро-аналоговый DAC
Приемо-передатчик RTX
Процессор Р
Секция процессора PS
Регистр RG
Регистр сдвига ^разрядный SRGN
Сумматор S или SM
Счетчик CTR
Счетчик TV-разрядный CTRN
Счетчик по модулю два CRTDIVN
Триггер Т
Триггер двухступенчатый ТТ
Множитель П или МР2
Усилитель > или >
Устройство DEV
Арифметико-логическое устройство ALU
Таблица В. 1. Продолжение
Наименование Обозначение
Устройство приоритета HPR1
Электронный ключ SW
Шина BUS или В
Шифратор CD
Элемент задержки DEL или Н
Элемент логический “Больше” >п или >=п
Элемент логический “Исключающее ИЛИ” EXOR или =1
Элемент логический “И” &
Элемент логический “ИЛИ” >1 или 1
Элемент логический “п и только п" =п
Элемент логический “Нечетность” 2Н1
Элемент логический “Четность” 2к
Элемент “Монтажное ИЛИ” 1 0 или 1
Элемент “Монтажное И” & 0 или &#
Элемент моностабильный, одновибратор с перезапуском 1 1
Элемент моностабильный, одновибратор без перезапуска J_TL
Элемент нелогический *
Стабилизатор, общее обозначение *ST
Стабилизатор напряжения *STY
Стабилизатор тока *ST1
Наборы резисторов *R
В. Обозначения функций элементов, меток выводов 555
Наименование Обозначение
Наборы конденсаторов *С
Наборы индуктивностей *L
Наборы диодов с указанием полярности *D-> или *D<-
Наборы транзисторов
Наборы трансформаторов *TR
Наборы индукторов ЗОГОСГ2,764
Наборы предохранителей *FY
Наборы предохранителей диоднорезистивных *DR
Элемент нестабильный — генератор, общее обозначение JML
Таблица В.1. Продолжение
Наименование Обозначение
Генератор с синхронизацией пуска
Генератор с синхронизацией останова |—|G'|—|
Генератор с синхронизацией пуска и останова П'СП
Генератор серии прямоугольных импульсов Gn
Генератор с непрерывной последовательностью импульсов GN
Генератор линейноизменяемого напряжения G/
Генератор синусоидального сигнала GSIN
Элемент пороговый, гистерезисный —' или TM
Наименование Обозначение
Адрес ADR или А
Байт BY
Бит младший LSB
Бит старший MSB
Блокировка: запрет INH
Блокировка: захват Н
Блокировка: сигнал неисправности ALI
Ввод (информации) I
Вектор VEC
Таблица В.2. Обозначения меток выводов элементов
Наименование Обозначение
Ветвление BR
Восстановление REC
Вход гистерезисный или ТМ
Вход запроса САМ ?
Вход обратного счета (вход уменьшения) -п или DOWN
Вход операнда, над которым выполняется одна или несколько операций Рп
Вход прямого счета (вход увеличения) +п или UP
Вход, который переключается каждый раз с подачей LOG1 Т
Вход цифрового компаратора: больше >
556 Приложения
Наименование Обозначение
Вход цифрового компаратора: меньше <
Вход цифрового компаратора: равно =
Выбор (селекция) SEL или SE
Выбор адреса столбца CAS
Выбор адрес строки RAS
Выбор кристалла CS
Вывод информации О
Вывод двунаправленный <> или о
Свободный вывод (без внутренних соединений) NC
Вывод фиксированного режима (состояния) “1”
Выход, изменение состояния которого задерживается до возврата сигнала в исходное состояние п
Выход открытый 0
Открытый коллекторный выход и-типа
Выход с открытым «-коллектором
Выход с тремя состояниями V
Выход САМ 1
Данные D
Данные входные DIN
Данные выходные DOUT
Данные последовательные D-> или D<-
Таблица В. 2. Продолжение
Наименование Обозначение
Входная информация запоминающих устройств D
Выходная информация запоминающих устройств Q
Загрузка (разрешение параллельной записи) LD
Задержка DEL
Задержка двойная DD
Заем BI
Вход приема заема ВО
Вход выдачи заема BG
Занято BUSY
Запись WR
Запрос на обслуживание SRQ
Знак SI
Запрос REQ или RQ
Имитация SIM
Инвертирование N
Инструкция, команда INS
Квитирование AK
Код CODE
Коммутация (электронная) SW
Конец END
В. Обозначения функций элементов, меток выводов 557
Наименование Обозначение
Коррекция CORR
“Логический 0” LOGO
“Логическая 1” LOG\
Маска, маскирование МК
Маркер MR
Мультиплексирование МРХ
Нечетность ODD
Ожидание WAIT или WT
Операция OP
Останов STOP
Ответ AN
Отказ REJ
Очистка CLR
Ошибка ERR или ER
Слово ошибки EW
Передача TX
Перенос CI
Вход приема переноса CO
Образование переноса CG
Распространение переноса CP
Переполнение DF
Таблица В. 2. Продолжение
Наименование Обозначение
Подтверждение приема АСК
Позиция РО
Прерывание INT
Подтверждение прерывания INTA
Программное прерывание PCI
Прием RX
Приоритет PRI или PR
Продолжение GOON
Пуск, начало START или ST
Работа RUN
Разрешение EN
Разрешение прохождения импульсов, работа цепи CE
Разрешение третьего состояния EN
Режим M
Результат нулевой RZ
Сброс общий SR
Обнуление RES или R
Сдвиг вправо -+n или SHRn
Сдвиг влево (если л=1, то он опускается) П±~ или SHLn
Синхронизация SYNC или SYN
Состояние SA
558 Приложения
Наименование Обозначение
Средний ML
Строб (сигнал выборки) STR или ST
Счет СТ
Считывание RD
Такт CL или CLK
Кодирование С
Таблица В.2. Продолжение
Наименование Обозначение
Условие СС
Установка в“1” SET или S
Установка ТЛГ-триггера в LOGI J
Установка -///-триггера в LOGO) К
Функция F
Четность ЕУЕХ
Наименование Обозначение
Напряжение питания Усс или U
Способы записи номинала напряжения Vcc + 5V -*-+54
Пояснительная информация: порядковый номер 2 Усс
Пояснительная информация: питание цифровой части # Усс
Пояснительная информация: питание аналоговой части П Усс
Земля, корпус GND или О
Ток /или 4..20 мА
Выводы для подключения конденсатора СХ
Выводы для подключения резистора RX
Выводы для подключения индуктивности LX
Таблица В.З. Обозначения меток нелогических выводов
Наименование Обозначение
Выводы для подключения кварцевого резонатора BQ
Выводы полевого транзистора: исток S
Выводы полевого транзистора: сток D
Выводы полевого транзистора: затвор G
Выводы транзистора: коллектор К
Выводы транзистора: база В
Выводы транзистора: эмиттер Е
Выводы транзистора: эмиттер и-р-л-транзистора Е-*
Выводы транзистора: эмиттер р-л-р-транзистора Е<—
Г. Примеры чертежей печатной платы (разработаны Ю.И. Миронченко) 559
Г. Примеры чертежей печатной платы (разработаны Ю-И. Миронченко)
НАУ 03 07 67 000 ЭЗ
БЛОК ИНДИКАЦИИ Схема электрическая принципиальная Литера Масса Macumat.
Him Лит j\s докум Подпись Дата Н
Выполнил Миронченко
Руководит Шевченко
Консульт Лист I | Листов
Проверив ФКСИКТ гр. 503 091501
Н.контр.
Зав каф. Белецкий
Рис. Г.1. Блок индикации. Схема электрическая принципиальная
72л
Рис. Г.2. Плата. Чертеж блока индикации
12 -
0
Сторона установки навесных элементов
68-
56
52-
48-
44-
4Q.
36
32 -
28 :
8 -
4 -
64-
63-
24 Z
20 -
16 -
01' а
Блок индикации
04 8 12 16 20 24 28 32 36 40 44 48 52 56
2
3
4
60 64
- 60
- 48
35
32
28
8
4
: 44
- 40
: 20 г W Е 12
64 60 56 52 48 44 40 36 32 28 24 20 16 12 8 4 0
г 72
- 68
- 64
: 56 1 52
24
0
Rz V
560 Приложения
‘Размеры для справок
Плата должна соответствовать ГОСТ 23752-79 Группа жесткости 3
Шаг координатной сетки 1,25 мм
Плату изготовить позитивным комбинированным методом
Класс точности 3 согласно ГОСТ 23751-86
Конфигурацию проводников выполнить согласно координатной сетке
Ширина проводников 0,27 мм в узких местах согласно группе жесткости 3
Форма контактных площадок произвольная
Первые выводы микросхем обозначены площадками в виде прямоугольников 6 Место для нанесения маркировки ‘
7 Обозначение платы выполнить в процессе вытравливания Покрытие - сплав Розе чистый ТУ 6-09-4065-88 8 Маркировку выполнить краской трафаретной ТНПФ-01 черной ТУ 29-02-889-88 У2 Шрифт 2,5 Допускается отклонение в размещении маркировки
9 Ставить штамп ОТК на свободном от проводников месте
10 Параметры элементов проводящего рисунка представлены в табл 1
Условное обозначение отверстий Диаметр отверстий Наличие металлизации в отверстиях Диаметр контактной площадки Количество отверстий
О 9 ±0,01 металл 1 43±0,05 142
П 9 ±0.01 металл 1,43г0 05 10
О 3.0 без металл 4
/7±и Лит Л? догам Подпись Дата
Выполни! Миронченко
Р) ководит Шевченко
Консу.1Ь)п
Проверил
Н контр
Зав каф Бслсцкни
НАУ03 07 67 001 П
БЛОК ИНДИКАЦИИ Плата печатная
Литера Масса Масштаб
н 1:1
Лист 1 | Листов
ФКС И КТ
<'Р 503 091501
I
*
72 5
I»
Рис. Г.З. Плата. Сборочный чертеж
10 max
80* к — ►
1 ‘Размеры для справок
2 Установку элементов выполнять согласно ОСТ 4ГО 010 030 80
Шаг координатной сетки 1 25 мм
Элементы DD1 DD6 HG1 HG3 установить согласно варианту Villa
3 Паять припои ПОС 61 ГОСТ 21930 76
4 Маркировка показана условно
5 Печатные проводники условно не показаны
6 Плату после сборки покрыть лаком УР 231 ТУ-6 10 863-84 У2
НАУ 03 07 67 001 СЧ
БЛОК ИНДИКАЦИИ Плата печатная Сборочный чертеж . htmepa Масса Macwmat
Лит )окум Пооти. i Цата н 1 1
Выпо шил Миронченко
Руководит Шевченко
Копсу ibm Лист 1 | Листов
Проверил ФКС ИК1 ер 501 091501
Н контр
iae каф Бетеикии
Г. Примеры чертежей печатной платы (разработаны Ю.И. Миронченко) 56
562 Приложения
Д. Условные графические обозначения элементов цифровой техники
л
Рис. Д. 1. Логические элементы: а — элемент НЕ; б — элемент НЕ ЗИ; е — элемент НЕ 2И с открытым коллекторным выходом и повышенной нагрузочной способностью; г — элемент НЕ И с открытым коллекторным выходом; д — элемент НЕ ЗИЛИ; е — комбинированный элемент 2И ИЛИ с инвертированным выходом; ж— элемент 2И ИЛИ с инвертированным выходом и расширяющим входом; к — расширитель; л — элемент проверки четности или нечетности
Рис. Д.2. Приемо-передатчики и гистерезисные элементы: а — четыре шинных усилителя с двухпороговым входом и выходом на три состояния с общим входом разрешения третьего состояния; б— двунаправленный шинный приемо-передатчик еосьмиканальный; в — шестиканальный буферный элемент с тремя состояниями на выходе с сигналом разрешения по выходу; г — инвертирующий усилитель с порогом Шмидта; д — триггер Шмидта с логическим элементом ИЛИ на входе
Д. Условные графические обозначения элементов цифровой техники 563
Рис. Д.З. Бистабильные (триггеры), моностабильные и нестабильные элементы: а — два триггера с раздельными входами, один с дополнительным входом; б — два триггера задержки D-типа; в — шесть D-триггеров с общими входами управления и сброса; г — триггер D-типа с пуском по фронту; д — триггер JK-muna с пуском по фронту; е — два JK-триггера с общими входами управления и сброса; ж— мультивибратор с перезапуском; к— два генератора, управляемые напряжением, с указанием выводов питания
CTRD/V'.O
СТ=0
ГО
С7]2
1з
Рис. Д.4. Счетчики: а — двоичный 14-разрядный счетчик со сквозным переносом; б — асинхронный десятичный счетчик из делителей на 2 и 5 с параллельной записью; в — четырехразрядный асинхронный десятичный счетчик из делителей на 2 и 5с предварительной установкой и синхронным сбросом; г — синхронный десятичный счетчик с параллельной загрузкой; д — десятичный синхронный реверсивный счетчик
36*
564 Приложения
SRG4 :W1 >('‘2/1 -► R Н г
1,20 3V 1,2К I.2D ИЛИ
1.20
SRG4
— (PlS)
— >с
— (Т/1.)
R
J0
КО
D
0 0
3 3
SRGZ
>С
С LR
EN(.4/.D)
-►/<-
D -►
D-4-
D V
е*
0 0
7 7
б
в
Рис. Д.5. Регистры: а — четырехразрядный регистр с параллельными входами; б — четырехразрядный последовательно-параллельный регистр с прямым и дополнительным кодами на выходе; в — регистр сдвига двунаправленный универсальный; г — универсальный восьмиразрядный регистр; д — восьмиразрядный регистр сдвига с последовательным и параллельными входами и выходами; е — восьмиразрядный регистр сдвига с параллельной загрузкой
Д. Условные графические обозначения элементов цифровой техники 565
Рис. Д.6. Арифметические элементы: а — полный одноразрядный сумматор; б — четырвхраз-рядный сумматор-вычитатель; в — четырехразрядный сумматор; а — четырехрвзрядное АЛУ; д — генератор ускоренного переноса для АПУ; е — четырехразрядный цифровой компаратор
Рис. Д.7. Преобразователи (дешифраторы) и кодирующие устройства (шифраторы): а — преобразователь двоично-десятичного кода в десятичный; б — преобразователь из трех линий на восемь; в — преобразователь двоичного кода в двоично-десятичный; г — преобразователь-усилитель двоичного кода в семисегментный; д — приоритетный шифратор из восьми линий на три; е — два дешифратора, принимающие двухразрядный код; ж — преобразователь уровней ТТЛ в уровни МОП; к— преобразователь уровней ЭСЛ в уровни ТТЛ
566 Приложения
гпттттгш
Рис. Д.8. Мультиплексоры, демультиплексоры и коммутаторы: а — мультиплексор на восемь входов со стробированием; б — демультиплексор на три линии; в — мультиплексор четырехканальный, каждый по два входа; а — мультиплексор двухканальный, каждый по четыре входа; д — электронный коммутатор
Ж4Л/25&1 RAS О
3 CAS
О
3
D Q —
WRIRD -
Рис. Д. 9. Запоминающие устройствам— ПЗУ на 32 слова по восемь битов; б— ОЗУ с произвольной выборкой на 16 слов по четыре бита; в — ОЗУ с произвольной выборкой на четыре слова по четыре бита с отдельной адресацией при записи и считывании; г — статическое ОЗУ на четыре слова по четыре бита; д — статическое ОЗУ на 256 слое по одному биту
Е. Перечень стандартов 567
J
б
! ! ;
в
Рис. Д.10. Шины: а — обозначение шин; б— пересечение шин; в — ответвление от шины отдельных линий
Е. Перечень стандартов
Е.1. Стандарты ЕСКД
• ГОСТ 2.101-68 ЕСКД. Виды изделий.
• ГОСТ 2.102-68 ЕСКД. Виды и комплектность конструкторских документов.
• ГОСТ 2.103-68 ЕСКД. Стадии разработки.
• ГОСТ 2.104-68 ЕСКД. Основные надписи.
• ГОСТ 2.105-95 ЕСКД. Общие требования к текстовым документам.
• ГОСТ 2.106-68 ЕСКД. Текстовые документы.
• ГОСТ 2.108-68 ЕСКД. Спецификация.
• ГОСТ 2.109-73 ЕСКД. Основные требования к чертежам.
• ГОСТ 2.112-70 ЕСКД. Ведомость держателей оригиналов.
• ГОСТ 2.114-70 ЕСКД. Технические условия. Правила построения, изложения и оформления.
• ГОСТ 2.118-73 ЕСКД. Техническое предложение.
• ГОСТ 2.119-73 ЕСКД. Эскизный проект.
• ГОСТ 2.120-73 ЕСКД. Технический проект.
• ГОСТ 2.201-80 ЕСКД. Обозначение изделий и конструкторских документов.
• ГОСТ 2.301-68 ЕСКД. Форматы.
• ГОСТ 2.302-68 ЕСКД. Масштабы.
• ГОСТ 2.303-68 ЕСКД. Линии.
• ГОСТ 2.304-81 ЕСКД. Шрифты чертежные.
• ГОСТ 2.307-68 ЕСКД. Написание размеров и предельных отклонений.
• ГОСТ 2.309-73 ЕСКД. Обозначение шероховатости поверхностей.
• ГОСТ 2.316-86 ЕСКД. Правила написания на чертежах надписей, технических требований и таблиц.
• ГОСТ 2 321-84 ЕСКД. Обозначения буквенные.
• ГОСТ 2.414-75 ЕСКД. Правила выполнения чертежей жгутов, кабелей и проводов.
• ГОСТ 20406-75 ЕСКД. Платы печатные. Термины и определения.
• ГОСТ 2.417-78 ЕСКД. Правила выполнения чертежей печатных плат.
• ГОСТ 10317-79 ЕСКД. Платы печатные. Основные размеры.
• ГОСТ 23770-79 ЕСКД. Платы печатные. Типовые технологические процессы химической и гальванической металлизации.
568 Приложения
• ГОСТ 23751-86 ЕСКД. Платы печатные. Основные параметры конструкции.
• ГОСТ 2.601-68 ЕСКД. Эксплуатационные документы.
• ГОСТ 2.605-68 ЕСКД. Плакаты учебно-технические. Общие технические требования.
• ГОСТ 2.701-84 ЕСКД. Схемы. Виды и типы. Общие требования к выполнению.
• ГОСТ 2.702-75 ЕСКД. Правила выполнения электрических схем.
« ГОСТ 2.708-81 ЕСКД. Правила выполнения электрических схем цифровой вычислительной техники.
• ГОСТ 2.709-72 ЕСКД. Система обозначения цепей в электрических схемах.
• ГОСТ 2.710-81 ЕСКД. Обозначения буквенно-цифровые в электрических схемах.
• ГОСТ 2.721-74 ЕСКД. Обозначения условные графические в схемах. Обозначения общего использования.
• ГОСТ 2.770-73 ЕСКД. Обозначения условные графические. Приборы полупроводниковые.
• ГОСТ 2.743-91 ЕСКД. Обозначения условные графические в схемах. Элементы цифровой техники.
• ГОСТ 2.747-68 ЕСКД. Обозначения условные графические в схемах, размеры условных графических обозначений.
• ГОСТ 2.759-82 ЕСКД. Обозначения условные графические в схемах. Элементы аналоговой техники.
• ГОСТ 2.761-84 ЕСКД. Обозначения условные графические в схемах. Компоненты волоконно-оптических систем передачи.
• ГОСТ 2.764-86 ЕСКД. Обозначения условные графические в электрических схемах. Интегральные электронные элементы индикации.
• ГОСТ 2.765-87 ЕСКД. Обозначения условные графические в электрических схемах'запоми-нающих устройств.
Е.2. Стандарты ЕСПД
• ГОСТ 19.001-77 ЕСПД. Общие положения.
• ГОСТ 19.101-71 ЕСПД. Виды программ и программных документов.
• ГОСТ 19.102-77 ЕСПД. Стадии разработки.
• ГОСТ 19.103-77 ЕСПД. Обозначения программ и программных документов.
• ГОСТ 19.104-78 ЕСПД. Основные надписи.
• ГОСТ 19.105-78 ЕСПД. Общие требования к программным документам.
• ГОСТ 19.106-78 ЕСПД. Описание к программным документам, выполненных печатным способом.
• ГОСТ 19.202-78 ЕСПД. Спецификация. Требования к содержанию и оформлению.
• ГОСТ 19.401-78 ЕСПД. Текст программы. Требования к содержанию и оформлению.
• ГОСТ 19.402-78 ЕСПД. Описание программы.
• ГОСТ 19.404-79 ЕСПД. Пояснительная записка. Требования к содержанию и оформлению.
• ГОСТ 19.701-90 ЕСПД. Схема алгоритмов, программ, данных и систем. Условные обозначения и правила выполнения.
• ГОСТ 19.781-90 ЕСПД. Обеспечение систем обработки информации программное. Термины и определения.
Е.З. Другие стандарты
• СТД 24.101-80. Виды и комплектность документов.
• СТД 24.102-80. Обозначения документов.
• СТД 24.203-80. Требования к содержанию общесистемных документов.
• СТД 24.301-80. Общие требования к текстовым документам.
• СТД 24.302-80. Общие требования к выполнению схем.
• СТД 24.303-80. Обозначения условные графические технических средств.
• СТД 24.304-80. Требования к оформлению чертежей.
• ГОСТ 34.602-89. Информационная технология, комплекс стандартов на автоматизированные системы. Техническое задание на создание автоматизированной системы.
• ГОСТ 34.003-90. Информационные технологи. Комплекс стандартов на автоматизированных системах. Автоматизированные системы.
• ГОСТ 28907-91. Системы обработки информации. Локальные вычислительные сети. Протокол и услуги уровня управления логическим звеном данных.
• ГОСТ 29099-91. Сети вычислительно-локальные. Термины и определения.
Ж. Словарь общих терминов 569
Ж. Словарь общих терминов
Автомат Математическая модель, отображающая физические или абстрактные явления
Автомат без памяти Автомат с одним внутренним состоянием
Автомат Мили Автомат, в котором выходные сигналы являются функцией входных сигналов и состояния памяти
Автомат Мура Автомат, в котором выходные сигналы определяются только состоянием памяти
Агрегирование Разделение микропроцессорной системы на простые функционально и конструктивно законченные блоки — модули
Адаптер Средство сопряжения некоторого внешнего устройства с определенной шиной микропроцессорной системы
Активный выход (дешифратора) Выход, на котором появляется управляющий сигнал
Аналого-цифровой преобразователь Устройство, предназначенное для преобразования аналоговой информации (обычно в виде напряжения) в цифровой код
Ансамбль Множество с известным распределением элементов
Арифметико-логическое устройство Устройство, предназначенное для выполнения арифметических и логических операций, предусмотренных системой команд данного компьютера
Архитектура компьютера Наиболее общие принципы построения компьютеров, которые охватывают круг вопросов, существенных в первую очередь для пользователя: функциональный состав технических и программных средств и их взаимодействие в процессе обработки информации; систему команд, их форматы и способы кодирования; методы адресации команд и данных
Асинхронный сумматор Сумматор, в котором интервал времени для сложения определяется моментом фактического окончания операции ч
Асинхронный триггер Триггер без тактового входа
Ассемблер Машинно-ориентированный язык программирования
Байт 8 бит
Бит Наименьшее количество информации, двоичная цифра
Бод Единица бит за секунду (бит/с)
Большой компьютер Машина общего назначения с производительностью до 400 тыс. оп./с, объемом памяти — несколько мегабайт, разрядностью — 32 или 64 бит
Булева алгебра Наука, которая использует математические методы для решения логических задач
Булева переменная Переменная с двумя значениями (состояниями)
Булева функция Сложное высказывание, построенное с помощью логических связок НЕ, ИЛИ, И, ЕСЛИ... ТО...
Ваод-вывод Обмен информацией между ядром компьютера и периферийными устройствами
Вентиль Схема, которая осуществляет элементарную логическую операцию
Вмонтированный канал (МОП-транзистора) Канал с начальной дополнительной концентрацией зарядов
Внешняя память компьютера Предназначена для продолжительного и энергонезависимого хранения больших объемов информации
Внутренняя пам'ять Оперативная и постоянная память, а также регистры арифметико-логического устройства
Время записи Интервал между моментами появления управляющего сигнала записи и установкой ячейки памяти в состояние, задаваемое входными сигналами
Время считывания Интервал между моментами появления управляющего сигнала чтения и данных на выходе памяти
Входная характеристика логического элемента Зависимость входного тока от изменения аходного напряжения
Выходная характеристика логического элемента Зависимость выходного напряжения от тока нагрузки для состояний высокого и низкого уровней
Г игабайт 1024 мегабайт
Глобальная таблица дескрипторов Таблица дескрипторов, которая используется совместно всеми задачами, выполняемыми в компьютере
График Геометрическое наглядное изображение функциональной зависимости между величинами с помощью линий на плоскости
Графическое изображение Воспроизведение комплекса геометрических особенностей изделия в образной форме с помощью средств графики: линий, штрихов, точек
Данные Информация, подготовленная для обработки на компьютерах
Двоичная система счисления Система счисления с основанием два 1
Двоичный элемент Элемент с двумя состояниями |
570 Приложения
Двухместная булева операция Булева операцию над двумя операндами
Демультиплексирование шин Поочередное переключение групп линий от одного источника информации ко многим приемникам
Демультиплексор Функциональный узел компьютера, предназначенный для коммутации (переключения) сигнала с одного информационного входу на один из информационных выходов
Дескриптор Восьмибайтовая структура данных, которые используются для определения свойств сегментов базовый адрес сегмента и его размер, его назначение (тип), характеристики защиты и дополнительная информация
Дешифратор Функциональный узел компьютера, предназначенный для преобразования каждой комбинации входного двоичного кода в управляющий сигнал только на одном из своих выходов
Диаграмма Графическое изображение, которое наглядно показывает линейными отрезками или геометрическими фигурами соотношения между различными величинами
Диапазон представления Интервал числовой оси, заключенный симметрично между максимальным и минимальным значением числа
Дизъюнкция Булева операция, результатом которой является значение нуль тогда и только тогда, когда оба операнда имеют значение нуль
Динамическая память Память, в которой информация хранится в виде зарядов на очень малой емкости, созданной между стоком и подкладкой МОП-транзистора
Диод Шотки Диод, в котором нет накопления избыточных зарядов, поскольку ток определяется переходом основных носителей из полупроводника в металл Время переключения диодов Шотки очень мало и не зависит от температуры
Дисковод Электромеханический привод, который обеспечивает вращение диска накопителя
Дискретизация во времени Преобразование функции непрерывного аргумента в функцию дискретного аргумента
Дискретизация сигналов во времени Принцип подачи информации на входы элементов и узлов в тактовые моменты
Дит 3,32 бита
Заготовка печатной платы Материал основы определенного размера, обрабатываемый во всех производственных операциях
Закодированный граф Граф микропрограммы, в котором микрооперации представлены идентификаторами управляющих сигналов, а логические условия — булевыми аргументами
Запрет Двухместная булева операция, результатом которой является значение единицы тогда и только тогда, когда значение одного операнда равно единице, а другого — нулю
Затвор Металлический электрод МОП-транзистора, на который поступает управляющее напряжение
Защищенный режим Обеспечивает защиту аппаратных и программных ресурсов одной задачи от возможного влияния другой
Импликация Двухместная булева операция, результатом которой является значение нуль тогда и только тогда, когда значение одного из операндов равно нулю, а другого — единице
Импульсный сигнал Сигнал, который нарастает в тактовый момент, а спадает в пределах данного такта
Инверсия См “Отрицание”
Индуцированный канал (МОП-транзистора) Канал МОП-транзистора, который образуется под действием внешнего управляющего напряжения
Инициальный автомат Автомат, имеющий начальное состояние
Интегральная микросхема Микроэлектронное изделие с высокой плотностью упаковки электрорадиозле-ментов (резисторов, диодов, транзисторов) и соединений между ними
Интерфейс Совокупность шин, сигналов, вспомогательных микросхем и алгоритмов, предназначенных для обмена информацией между устройствами компьютера
Информативные параметры Изменяемые параметры физической величины по закону передаваемого сообщения
Информатика Фундаментальна дисциплина, которая изучает процессы передачи, обработки, хранения и использования научной информации
Информационная емкость Максимальный объем данных, который может одновременно храниться в памяти
Исходная программа Программа на языке ассемблера
Канал (МОП-транзистора) Приповерхностный проводящий слой между истоком и стоком МОП-транзистора, в котором величина тока определяется с помощью электрического поля
Канал ввода-вывода Специальное устройство универсального компьютера, которое обеспечивает обмен информацией между оперативной памятью и периферийным устройством
Ж. Словарь общих терминов 571
Канал передачи (связи) Совокупность устройств, имеющих один вход и один выход, предназначенных для передачи информации на расстояния
Квантование по уровню Преобразование непрерывной функции в дискретное множество значений
Килобайт 1024 байт
Кластерная система Объединение машин с единым механизмом управления и программного обеспечения
Код Г рея Код, образованный последовательностью двоичных чисел, в которых два любых соседних числа отличаются только одним разрядом
Код числа Запись числа в некоторой системе счисления
Командный цикл Время выполнения микропрограммы команды
Комбинационная схема Схема, в которой логическое состояние выходов элементов зависит только от комбинации входных сигналов в данный момент времени
Компаратор Функциональный узел компьютера, предназначенный для выработки признаков отношений между двоичными словами (числами)
Компиляция программы Трансляция программы на язык, близкий к машинному
Компонент Электрорадиоэлемент интегральной микросхемы
Компьютер Программно управляемая физическая система, предназначенная для алгоритмической обработки информации, представленной сигналами
Компьютерная техника Совокупность средств для автоматизации процессов обработки информации, а также отрасль техники, которая занимается разработкой, изготовлением и эксплуатацией компьютеров
Конечный автомат Автомат, в котором переход из одного состояния в любое другое заканчивается за конечное число тактов
Конструкторская документация Совокупность взаимосвязанных документов, имеющих отношение к объекту проектирования
Контроллер Специализированный процессор, предназначенный для управления внешними устройствами компьютера
Контроль четности Способ контроля, основанный на допущении, что в двоичном числе наиболее часто возникают одиночные ошибки — потеря или появление лишней единицы
Конъюнкция Булева операция, результатом которой является значение единицы тогда и только тогда, когда значение каодогооперанда равно единице
Криотрон Простейший криоэлектронный логический элемент с двумя входами и одним выходом
Кэш-память Служит для хранения копий информации, используемых в текущих операциях обмена
Линия взаимосвязи Линия на схеме, указывающая на наличие связи между функциональными частями изделия
Логическая схема Совокупность взаимозависимых логических элементов с формальными методами описания
Логическая функция См “Булева функция”
Логический элемент См “Вентиль”
Локальная таблица дескрипторов Таблица дескрипторов, определяющая сегменты, доступные только конкретной задаче
Локальная шина Совокупность линий, связывающих микропроцессор с буферными регистрами адреса, формирователями данных и контроллерами
Магистраль Совокупность сигналов с выходов буферных регистров адреса, формирователей данных и контроллеров
Макстерм Функция п переменных, равная нулю только на одном наборе
Маркирующий код Единица, по размещению которой можно различить состояние счетчика при единичном кодировании
Машинные изображения Числа, представленные в прямом, обратном и дополнительном кодах
Машинный такт Временной интервал между двумя соседними тактовыми импульсами
Машинный цикл Время, за которое выполняется одна машинная команда
Мегабайт 1024 килобайт
Мегафлопс Миллион операций в секунду над операндами с плавающей запятой
Мейнфрейм См. "Большой компьютер"
Микрокоманда Совокупность микроопераций, выполняемых в одном такте
Микрокомпьютер Компьютер, построенный на микропроцессорах, составные части которых размещены в одной или нескольких интегральных схемах
Микрооперация Элементарное действие, выполняемое в компьютерах за один машинный такт
Микропрограмма Микроалгоритм операции, записанный в терминах микроопераций и логических условий
Микропрограммный автомат Управляющий автомат, функционирование которого задают с помощью микропрограмм
Микропроцессор Процессор, составные части которого миниатюризированы и размещены в одной или нескольких микросхемах
572 Приложения
Микропроцессорная система Совокупность вычислительных средств, в которые входят один или несколько микропроцессоров и полупроводниковая память, а также средства интерфейса
Микропроцессорный комплект Совокупность микропроцессорных и других микросхем, совместимых по конструктивно-технологическому исполнению и предназначенных для совместного использования
Минимально полный базис Система функций, которая превращается в неполную в случае удаления из нее любой функции
Минтерм Функция и переменных, равная единице только на одном наборе
Минус-двоичная система счисления Позиционная двоичная система счисления с основанием -2 и символами 0,1
Модульность См. “Агрегирование"
Модуляция Изменение параметров физической величины по закону передаваемого сообщения
Мультиплексирование шин Поочередное переключение шин (групп линий) от нескольких источников информации к одному приемнику
Мультиплексор Функциональный узел компьютера, предназначенный для поочередной коммутации (переключения) информации от одного из л входов на общий выход
Непозиционная система счисления Система счисления, в которой значение каждой цифры не зависит от ее позиции
Номинальная производительность компьютера Среднее число смеси команд с учетом их частоты повторения, которые выполняет ядро компьютера в выбранном классе задач
Носитель информации Любая запоминающая предметная среда, предназначенная для записи и хранения информации с целью ее непосредственного ввода в компьютер
Объектная программа Программа в двоичных машинных кодах
Объектный код Форма представления программы после компиляции
Одноместная булева операция Булева операция над одним операндом
Одноразрядный сумматор Логическая схема, выполняющая сложение значений соответствующих разрядов двоичных чисел с учетом переноса из младшего соседнего разряда и вырабатывает на выходах функции результат и перенос в старший соседний разряд
Однородная позиционная система счисления Позиционная система счисления с одинаковым основанием в каждом разряде
Операнд Число, которое участвует в операциях
Оперативная память Предназначена для временного хранения программ и данных, в ней выполняются операции записи и считывания информации
Операционные ресурсы Множество всех операций, реализуемых в компьютере
Операция Четко определенное действие над одним или несколькими операндами, которое создает новый объект (результат)
Оригинал рисунка печатной платы Реальное изображение на основе чертежа технологического слоя платы, выполненное в увеличенном масштабе, обычно в позитивном изображении
Основание позиционной системы счисления Количество графических знаков, которые используются для записи чисел
Отрицание Одноместная булева операция, результатом которой является значение, противоположное значению операнда
Пакет прикладных программ Функционально завершений комплекс программных средств, ориентированный на решение определенного логически целостного класса задач
Память компьютера Совокупность различных устройств, предназначенных для приема, хранения и выдачи двоичной информации
Параллельная передача кода Одновременная передача в такте значения всего слова с помощью многоканальной передачи
Передаточная характеристика логического элемента Зависимость выходного напряжения от входного
Переключательная переменная Переменная с конечным числом значений (состояний)
Переключение элемента Переход элемента из одного состояния в другое
Печатная плата Составная часть конструкции компьютеров и радиоэлектронной аппаратуры, состоящая из плоских проводников в виде участков металлизированного покрытия, размещенных на диэлектрической основе
Печатный проводник Участок токопроводящего покрытия, нанесенного на изоляционную основу, эквивалентный обычному монтажному проводу
Пиковая производительность компьютера Среднее число коротких операций типа “регистр-регистр" в секунду без операций обмена с оперативной памятью
Подканал Средства канала ввода-вывода, предназначенные для обслуживания одного периферийного устройства
> Подкладка Основная пластина полупроводника в МОП-транзисторе
Ж. Словарь общих терминов 573
Позиционная система счисления Система счисления, в которой для записи чисел используют определенное количество графических знаков (цифр и букв), отличающихся друг от друга
Поколение компьютеров Категория в исторической классификации компьютеров, основанная преимущественно на технологии производства их элементной базы
Полный дешифратор Дешифратор с максимально возможным числом выходов
Полусумматор Логическая схема, которая выполняет сложения значений разрядов двоичных чисел и реализует на выходе значение результата и перенос в старший соседний разряд
Пороговое напряжение Напряжение, при котором образуется канал МОП-транзистора
Порт ввода-вывода Регистр на входе или выходе внешнего устройства для обмена данными с про-- цессором
Последовательная передача кода Передача в такте значения одного разряда слова с помощью одного канала передачи
Последовательностная схема Схема, в которой логическое значение выходов определяют как комбинацией выходных сигналов, так и состоянием памяти схемы в данный момент времени
Постоянная память Предназначена для хранения программ, констант, табличных функций и другой информации, которая записывается заранее и не изменяется в процессе текущей работы компьютера
Потенциальный сигнал Сигнал, который изменяется только в тактовые моменты времени
Представление информации Способ формализованного описания различных сигналов и сообщений
Преобразователь кода Функциональный узел компьютера, предназначенный для преобразования двоичного кода из одной формы в другую
Прерывание Особенная операция, которая приостанавливает работу программы для выполнения специальных системных действий
Приоритетный шифратор Шифратор, который при одновременном нажатии нескольких клавиш вырабатывает код только старшей цифры
Программа Языковая конструкция, которая является упорядоченной последовательностью описаний и команд, предназначенных для обработки информации
Процессор Основная функциональная часть компьютера, которая интерпретирует и выполняет команды, то есть непосредственно реализует программноуправляемый процесс обработки данных
Разложение Шеннона Формула, которая позволяет переходить к представлению функции п переменных через функции от (л -1) переменных
Разряд Отдельная позиция в записи числа
Разрядная сетка компьютера Совокупность запоминающих элементов для размещения одного двоичного числа >
Разрядность Число разрядов в записи числа
Регистр Типовой функциональный узел компьютера, предназначенный для приема, временного хранения, преобразования и выдачи «-разрядного двоичного слова
Сдвиг Одновременное пространственное перемещение двоичного слова в разрядной сетке с сохранением порядка следования нулей и единиц
Сдвиговой регистр Регистр, в котором хранение данных совмещается с микрооперациями сдвига
Сегмент Область памяти с множеством ячеек со смежными адресами
Сегментация памяти Механизм, с помощью которого память разделяется на отдельные области адресного пространства определенного назначения
Сервер Компьютер, который выполняет функций обслуживания группы пользователей (распределение ресурсов памяти, принтеров, баз данных)
Серия интегральных микросхем Набор цифровых микросхем с общими конструктивно-технологическими и схемотехническими признаками
Сигнал Изменение физической величины, используемой для передачи данных
Сигнальная линия Проводник, который физически соединяет источник и приемник информации
Символ Элементарная единица сообщения
Симметричная знакоразрядная система счисления Избыточная система счисления с основанием q и количеством символов больше q
Синхронный сумматор Сумматор с постоянным интервалом времени для сложения
Синхронный триггер Триггер с тактовым входом
Система счисления Совокупность цифр и правил для записи чисел
Системная шина См “Магистраль"
Системная производительность компьютера Измеряется с помощью типовых оценочных программ (бенчмарков), реализованных на языках высокого уровня
Скалярный процессор Процессор с одним конвейером — может выполнять только одну команду за один машинный такт
Слово Группа символов
Содержательный граф Граф микропрограммы, в котором операторные и условные вершины содержат полное описание микроопераций и логических условий
574 Приложения
Сообщение Упорядоченная последовательность символов (букв, цифр, математических знаков, предназначенных для передачи информации), закодированная в материальной форме
Статическое запоминающее устройство Устройство, в котором функцию запоминания бита информации выполняют триггеры
Стрелка Пирса Булева операция, результатом которой является значение единицы тогда и только тогда, когда оба операнда равны нулю
Структурный синтез Синтез цифровых устройств, в котором закон функционирования абстрактного автомата реализуется комбинационной схемой и набором триггеров
Сумма по модулю два Двухместная булева операция, результатом которой является значение единицы тогда и только тогда, когда операнды имеют разные значения
Сумматор Функциональный узел компьютера, предназначенный для сложения двух п-разрядных слов (чисел)
Суперкомпьютер Самая мощная вычислительная система, действующая в соответствующий исторический период
Суперпозиция Подстановка в логические формулы вместо переменных некоторых других булевых выражений
Суперскалярный процессор Процессор, имеющий два и более конвейеров —может выполнять несколько команд за один машинный такт
Схема Документ, содержащий условные графические изображения составных частей технического изделия и связи между ними
Схема сравнения См. "Компаратор"
Счетчик Типовой функциональный узел компьютера, предназначенный для счета входных импульсов
Таблица дескрипторов Определенное в адресном пространстве памяти множество дескрипторов
Таблица прерываний Содержит дескрипторы специальных объектов, которые определяют точки входа процедур обработки прерываний и особых случаев
Тактовый момент Начало каждого тактового импульса
Тетрада Четыре двоичных разряда
Типовой функциональный узел компьютера Микроэлектронная схема, предназначенная для выполнения одной или нескольких микроопераций
Травление Химический процесс, во время которого участки медной фольги, не защищенные резистом, удаляются с диэлектрической основы, а участки, покрытые резистом, сохраняются и формируют рисунок печатной платы
Транзистор Шотки Транзистор с диодом Шотки между базой и коллектором
Трансляция программы Преобразование программы из одного языка программирования в равноценную на другом языке
Трансфлюксор Ферритовый диск с. двумя неодинаковыми отверстиями, который может находиться в двух состояниях, характеризующихся разным распределением магнитного поля вокруг большого отверстия и отображающих лог. 1 и лог. 0
Триггер Запоминающий элемент с двумя устойчивыми состояниями, изменение которых происходит под действием входных сигналов
Удельная емкость Отношение информационной емкости запоминающего устройства к его физическому объему
Указатель старшей единицы Приоритетный шифратор, предназначенный для поиска старшей (левой) единицы в слове и формирования на выходе двоичного номера искомого разряда
Универсальный компьютер Компьютер, операционные ресурсы которого обеспечивают выполнение любого алгоритма обработки информации
Унитарный код Двоичный код, включающий всегда только одну единицу, а остальные — нули
Устройство Совокупность элементов, представляющих собой единую конструкцию (блок, плата и др.)
Устройство управления Функциональна часть компьютера, предназначенная для автоматического управления вычислительным процессом с помощью последовательности управляющих и синхронизирующих сигналов
Фиксатор См. “Элементарный регистр"
Флаги Признаки результатов операции, которые формируются автоматически после выполнения каждой команды
Флэш-память Использует элементы памяти на транзисторах ЛИЗМОП с электрическим стиранием и записью информации
Формат Способ размещения компонентов числа в разрядной сетке
Фоторезист Специальный светочувствительный материал в виде органического раствора или сухой пленки, который наносят слоем на подготовленную поверхность платы
Фотошаблон Графическое позитивное или негативное изображение рисунка платы в натуральную величину на светопроницаемой фотопластинке или пленочном материале, полученное путем фотографирования оригинала
Ж. Словарь общих терминов 575
Функциональная группа Совокупность элементов, которые выполняют в изделии определенную функцию и не объединены в единую конструкцию
Функциональная цепь Линия, канал, тракт определенного назначения (канал звука, видеоканал и др )
Функциональная часть Элемент, устройство, функциональная группа
Функционально полная система функций Система функций, суперпозицией которых может быть представлена любая булева функция
Центральное устройство управления Совокупность узлов и блоков процессора, которые обеспечивают координацию функционирования всех устройств машины и управление ими для всех принятых режимов работы
Центральный процессор Процессор, выполняющий в вычислительной системе основные функции
Цифро-аналоговый преобразователь Устройство, предназначенное для преобразования цифровой информации в аналоговую форму в виде напряжения или тока
Чертеж Документ, содержащий изображение технического изделия или его составных частей и другие данные, которые поясняют функциональное назначение предмета и позволяют его изготовить
Шина Совокупность сигнальных линий, по которым передают сигналы одинакового функционального назначения
Шифратор Функциональный узел компьютера, предназначенный для преобразования входного m-разрядного унитарного кода в выходной п-разрядный двоичный позиционный код
Штрих Шеффера Булева операция, результат которой равен нулю тогда и только тогда, когда оба операнда равны единице
Эквивалентность Двухместная булева операция, результатом которой является единица тогда и только тогда, когда операнды принимают одинаковые значения
Эксплуатационная производительность компьютера Оценивается данными о реальной рабочей нагрузке в основных областях применения, при этом учитывают необходимую площадь размещения машины, механические и климатические условия эксплуатации, потребляемую мощность и т д
Электронно-вычислительная машина Комплекс электронного оборудования, которое предназначено для автоматизации процессов обработки дискретной информации и имеет общее управление
Элемент Наименьшая неделимая микроэлектронная схема (изделие), предназначенная для выполнения логических операций или хранения бита информации
Элементарная булева функция Булева функция одного или двух аргументов
Элементарный регистр Регистр, предназначенный только для приема (записи), хранения и передачи информации
Элемент схемы Составная часть схемы, которая выполняет определенную функцию в изделии и не может быть разделена на части с самостоятельным функциональным назначением (резистор, трансформатор, муфта и др )
Энтропия Количество информации, которое приходится на один элемент сообщения
Ядро компьютера Процессор и оперативная память
Язык микропрограммирования Язык, предназначенный для описания микропрограмм в терминах операторов
Язык ассемблера См “Ассемблер"
Язык программирования Формализованный язык представления программ
Ячейка памяти Совокупность элементов памяти, которые образуют ^-разрядное слово
D-триггер Синхронный запоминающий элемент с двумя устойчивыми состояниями и одним информационным D-входом
JK-триггер Запоминающий элемент с двумя устойчивыми состояниями и информационными входами J (аналог S) и К (аналог R). которые обеспечивают соответственно раздельную установку состояний "1” и "0"
RS-триггер Запоминающий элемент с раздельными информационными входами для установки его в состояние "0" (Я-вход) и в состояние “1" (S-вход)
Т-триггер Запоминающий элемент с двумя устойчивыми состояниями и одним информационным Т-входом Состояние Т-триггера изменяется на противоположное после каждого поступления счетного сигнала на Т-вход
ББК з973.2-04я73-5
Б125
УДК 004.31 (075.8)
Рецензенти: член-кореспондент НАН УкраТни, профе.сор В Ф. Свдокимов — директор 1нституту проблем моделювання в енергетиф НАН УкраТни; доктор тех-жчних наук, професор Г.М. Луцький — завщувач кафедри “Обчислювальна техФ-ка" НТУУ “КП".
Бабич М. П., Жуков I. А.
Б125 Комп’ютерна схемотехыка. Методи побудови та проекту-вання: Навчальний пособник. — К.: “МК-Прес”, 2004. — 576 с., in.
ISBN 966-964Т5-2-7
В цьому навчальному поабнику систематизовано викладен! ФформафйФ, арифметичж i лопчн! основи м!кроелектронних схем сучасних комп’ютер1в. Роз-глянуто принципи побудови i функфонування лопчних та запам’ятовуючих еле-менлв, типових функфональних вузл!в, аналого-цифрових i цифро-аналогових перетворювач!в, електронноТ пам’ял, арифметико-лопчних та керуючих пристро-Тв, м!кропроцесор|в, Ытерфейсних контролер(в, а також наведено технологи виро-бництва друкованих плат. Особливу увагу прид'тено правилам складання конс-трукторськоТ та програмноТ документафТ, а також вимогам оформления схем та Фюстративних документов.
Розраховано на студентов онженерно-техночних спефальностей вищих навчаль-них закладов.
ББК з973.2-04я73-5
Навчальний пособник
Бабич Микола Павлович Жуков Irop Анатолиевич
Комп’ютерна схемотехшка
МЕТОДИ ПОБУДОВИ ТА ПРОЕКТУВАННЯ
Комп’ютерна верстка: Ю. О. Шпак Дизайн обкладинки: М. В. Шашкова
Пдписано до друку 31.08.2004. Формат 70 х 100 1/16. Папор газетний. Друк офсетний. Ум. друк. л. 23,8. Ум.-вид. л. 36,8.
Тираж 2000 екз. Замовлення № 4-1749
ПП Савченко Л.О., УкраТна, м.КиТв, тел./ф.: (044) 517-73-77; e-mail: info@micronika.com.ua. Свдоцтво про внесения суб’екта видавничоТ справи до Державного реестру видавниюв, вигопвниюв та розповсюджувач!в видавничоТ продукфТ: cepia ДК №51582 вщ 28.11.2003 р.
Надруковано в ЗАТ “ВИТОЛ”. 03151, м. КиТв, вул. Волинська, 60
ISBN 966-96415-2-7
© Бабич М.П., Жуков I.A., текст, Фюстраци, 2004
© “МК-Прес”, оформления, дизайн обкладинки, 2004