Author: Боровков А.А.
Tags: теория вероятностей математическая статистика комбинаторный анализ теория графов математика учебник гипотезы теоремы теории оценок
ISBN: 978-5-8114-1013-2
Year: 2010
КЛАССИЧЕСКАЯ УЧЕБНАЯ ЛИТЕРАТУРА
ПО МАТЕМАТИКЕ
А. А. БОРОВКОВ
МАТЕМАТИЧЕСКАЯ
СТАТИСТИКА
УЧЕБНИК
Издание четвертое,
стереотипное
HAUL®
ЛАНЬ*
САНКТ-ПЕТЕРБУРГ · МОСКВА · КРАСНОДАР
2010
ББК22.172я73
Б 83
Боровков А. А.
Б 83 Математическая статистика: Учебник. 4-е изд., стер. —
СПб.: Издательство «Лань», 2010. — 704 с. — (Учебники для
вузов. Специальная литература).
ISBN 978-5-8114-1013-2
В учебнике излагаются основания современной математической
статистики, предельные теоремы для эмпирических распределений и
основных типов статистик, основы теории оценок и теории проверки гипотез.
Рассматриваются методы отыскания оптимальных и асимптотически
оптимальных процедур. Значительное внимание уделено статистике разно-
распределенных наблюдений и, в частности, задачам однородности,
задачам регрессии и дискретного анализа, распознаванию образов и задаче
о разладке. Излагается единый теоретико-игровой подход к задачам
математической статистики. Изучаются статистические игры и основные
принципы отыскания оптимальных и асимптотически оптимальных
решающих правил. Многие результаты теории оценивания и теории
проверки гипотез обобщаются на случай произвольной функции потерь.
Учебник рассчитан на студентов и аспирантов математических и
физических специальностей вузов.
ББК22.172я73
Обложка
А Ю. ЛАПШИН
Охраняется законом РФ об авторском праве.
Воспроизведение всей книги или любой ее части
запрещается без письменного разрешения издателя.
Любые попытки нарушения закона
будут преследоваться в судебном порядке.
© Издательство «Лань», 2010
© А. А. Боровков, 2010
© Издательство «Лань»,
художественное оформление, 2010
ОГЛАВЛЕНИЕ
Предисловие ко второму изданию 11
Введение 18
Глава 1. Выборка. Эмпирическое распределение. Асимптотические
свойства статистик 21
§ 1. Понятие выборки 21
§ 2. Эмпирическое распределение (одномерный случай) 24
§ 3. Выборочные характеристики. Основные типы статистик 28
1. Примеры выборочных характеристик (28). 2. Два типа статистик (29).
3. L-статистики (31). 4. М-статистики (32). 5. О других статистиках (33).
§ 4. Многомерные выборки 33
1. Эмпирические распределения (33). 2*. Более общие варианты теоремы
Гливенко-Кантелли. Закон повторного логарифма (34). 3. Выборочные
характеристики (35).
§ 5. Теоремы непрерывности 35
§6*. Эмпирическая функция распределения как случайный процесс.
Сходимость к броуновскому мосту 40
1. Распределение процесса ni^(i) (40). 2. Предельное поведение процесса
wn(t) (43).
§ 7. Предельное распределение для статистик первого типа 46
§8*. Предельное распределение для статистик второго типа 51
§9*. Замечания о непараметрических статистиках 62
§ 10*. Сглаженные эмпирические распределения. Эмпирические
плотности 63
4
Оглавление
Глава 2. Теория оценивания неизвестных параметров 69
§11. Предварительные замечания 69
§ 12. Некоторые параметрические семейства распределений и их свойства 71
I. Нормальное распределение на прямой (71). 2. Многомерное нормальное
распределение (71). 3. Гамма-распределение (72). 4. Распределение «хи-
квадрат» Н* с к степенями свободы (73). 5. Экспоненциальное
распределение (74). 6. Распределение Фишера с числом степеней свободы к\у
&2 (74). 7. Распределение Стьюдента Т* с к степенями свободы (75).
8. Бэта-распределение (В-распределение) (77). 9. Равномерное
распределение (78). 10. Распределение Коши Κα,σ с параметрами (α, σ) (80).
II. Логнормальное распределение La<72 (80). 12. Вырожденное
распределение (81). 13. Распределение Бернулли В£ (81). 14. Распределение Пуассона
Па (81). 15. Полиномиальное распределение (81).
§ 13. Точечное оценивание. Основной метод получения оценок.
Состоятельность, асимптотическая нормальность 82
1. Метод подстановки. Состоятельность (82). 2. Асимптотическая
нормальность. Одномерный случай (85). 3. Асимптотическая нормальность. Случай
многомерного параметра (86).
§ 14. Реализация метода подстановки в параметрическом случае. Метод
моментов. М-оценки 87
1. Метод моментов. Одномерный случай (87). 2. Метод моментов.
Многомерный случай (89). 3. М-оценивание как обобщенный метод моментов
(90). 4. Состоятельность М-оценок (92). 5. Состоятельность М-оценок (95).
6. Асимптотическая нормальность М-оценок (96). 7. Замечания о
многомерном случае (98).
§15*. Метод минимального расстояния 99
§ 16. Метод максимального правдоподобия. Оптимальность оценок
максимального правдоподобия в классе М-оценок 101
1. Определения. Общие свойства (101). 2. Асимптотические свойства о. м. п.
Состоятельность (109). 3. Асимптотическая нормальность о. м.п.
Оптимальность в классе М-оценок (ИЗ).
§ 17. О сравнении оценок 115
1. Среднеквадратический подход. Одномерный случай (116). 2.
Асимптотический подход. Одномерный случай (119). 3. Нижняя граница рассеивания
для L-оценок (121). 4. Среднеквадратический и асимптотический подходы в
многомерном случае (124). 5. Некоторые эвристические подходы к
определению дисперсий оценок. Методы складного ножа и будстрэп (127).
§ 18. Сравнение оценок в параметрическом случае. Эффективные оценки 128
1. Одномерный случай. Среднеквадратический подход (129). 2.
Асимптотический подход. Асимптотическая эффективность в классах М- и L-оценок
(131). 3. Многомерный случай (138).
§ 19. Условные математические ожидания 140
1. Определение у.м. о. (140). 2. Свойства у.м.о. (143).
§ 20. Условные распределения 146
§21. Байесовский и минимаксный подходы к оцениванию параметров . . 150
§ 22. Достаточные статистики 157
Оглавление
5
§23*. Минимальные достаточные статистики 164
§ 24. Построение эффективных оценок с помощью достаточных
статистик. Полные статистики 171
1. Одномерный случай (171). 2. Многомерный случай (173). 3. Полные
статистики и эффективные оценки (173).
§ 25. Экспоненциальное семейство 178
§26. Неравенство Рао-Крамера и Д-эффективные оценки 185
1. Неравенство Рао-Крамера и его следствия (185). 2. Я-эффективные и
асимптотически Я-эффективные оценки (191). 3. Неравенство Рао-Крамера
в многомерном случае (194). 4. Некоторые выводы (200).
§27*. Свойства информации Фишера 200
1. Одномерный случай (200). 2. Многомерный случай (203). 3. Матрица
Фишера и замена параметра (206).
§ 28*. Оценки параметра сдвига и масштаба. Эффективные эквивариант-
ные оценки 207
1. Оценки параметра сдвига и масштаба (207). 2. Эффективная оценка
параметра сдвига в классе эквивариантных оценок (208). 3. Минимаксность
оценки Питмена (211). 4. Об оптимальных оценках параметра масштаба
(212).
§29*. Общая задача об эквивариантном оценивании 215
§30. Интегральное неравенство типа Рао-Крамера. Критерии
асимптотической байесовости и минимаксности оценок 218
1. Эффективные и сверхэффективные оценки (218). 2. Основные неравенства
(220). 3. Неравенства в случае, когда функция q(6)/I(6) не дифференцируема
(224). 4. Некоторые следствия. Критерии асимптотической байесовости и
минимаксности (225). 5. Многомерный случай (228).
§31. Расстояния Куль бака-Лейблера, Хеллингера и χ2. Их свойства . . . 228
1. Определения и основные свойства расстояний (228). 2. Связь расстояний
Хеллингера и других с информацией Фишера (232). 3. Существование
равномерных границ для γ(Δ)/Δ2 (233). 4. Многомерный случай (234). 5*. Связь
рассматриваемых расстояний с оценками (236).
§ 32*. Свойства информации Фишера.Разностное неравенство типа Рао-Крамера 238
§ 33. Вспомогательные неравенства для отношения правдоподобия.
Асимптотические свойства оценок максимального правдоподобия 243
1. Основные неравенства (244). 2. Оценки для распределения и моментов
о. м.п. Состоятельность о. м. п. (246). 3. Асимптотическая нормальность
(247). 4. Асимптотическая эффективность (249). 5. Асимптотическая байе-
совость о. м. п. (250).
§ 34. Асимптотические свойства отношения правдоподобия. Дальнейшие
свойства оптимальности о. м. π 251
§35*. Приближенное вычисление оценок максимального правдоподобия . 260
§ 36. Результаты § 33, 34 для случая многомерного параметра 269
6
Оглавление
1. Неравенства для отношения правдоподобия и свойства о. м. п.
(результаты §33) (269). 2. Асимптотические свойства отношения правдоподобия
(результаты §33, 34) (271). 3. Свойства о.м.п. (результаты §33, 34) (275).
4. Приближенное вычисление о.м.п. (278). 5. Свойства о.м.п. при
отсутствии условий регулярности (результаты § 14, 16) (278).
§ 37. Равномерность по θ асимптотических свойств отношения
правдоподобия и оценок максимального правдоподобия 278
1. Равномерные закон больших чисел и центральная предельная теорема
(278). 2. Равномерные варианты теорем об асимптотических свойствах
отношения правдоподобия и оценок максимального правдоподобия (280).
3. Некоторые следствия (283).
§ 38*. О статистических задачах, связанных с выборками случайного
объема. Последовательное оценивание 284
§ 39. Интервальное оценивание 285
1. Определения (285). 2. Построение доверительных интервалов в
байесовском случае (286). 3. Построение доверительных интервалов в общем случае.
Асимптотические доверительные интервалы (287). 4. Построение точного
доверительного интервала с помощью заданной статистики (290). 5. Другие
методы построения доверительных интервалов (293). 6. Многомерный случай
(295).
§ 40. Точные выборочные распределения и доверительные интервалы для
нормальных совокупностей 296
1. Точные распределения статистик х, S* (296). 2. Построение точных
доверительных интервалов для параметров нормального распределения (298).
Глава 3. Теория проверки гипотез 301
§41. Проверка конечного числа простых гипотез 301
1. Постановка задачи. Понятие статистического критерия. Наиболее
мощный критерий (301). 2. Байесовский подход (303). 3. Минимаксный подход
(308). 4. Наиболее мощные критерии (309).
§42. Проверка двух простых гипотез 311
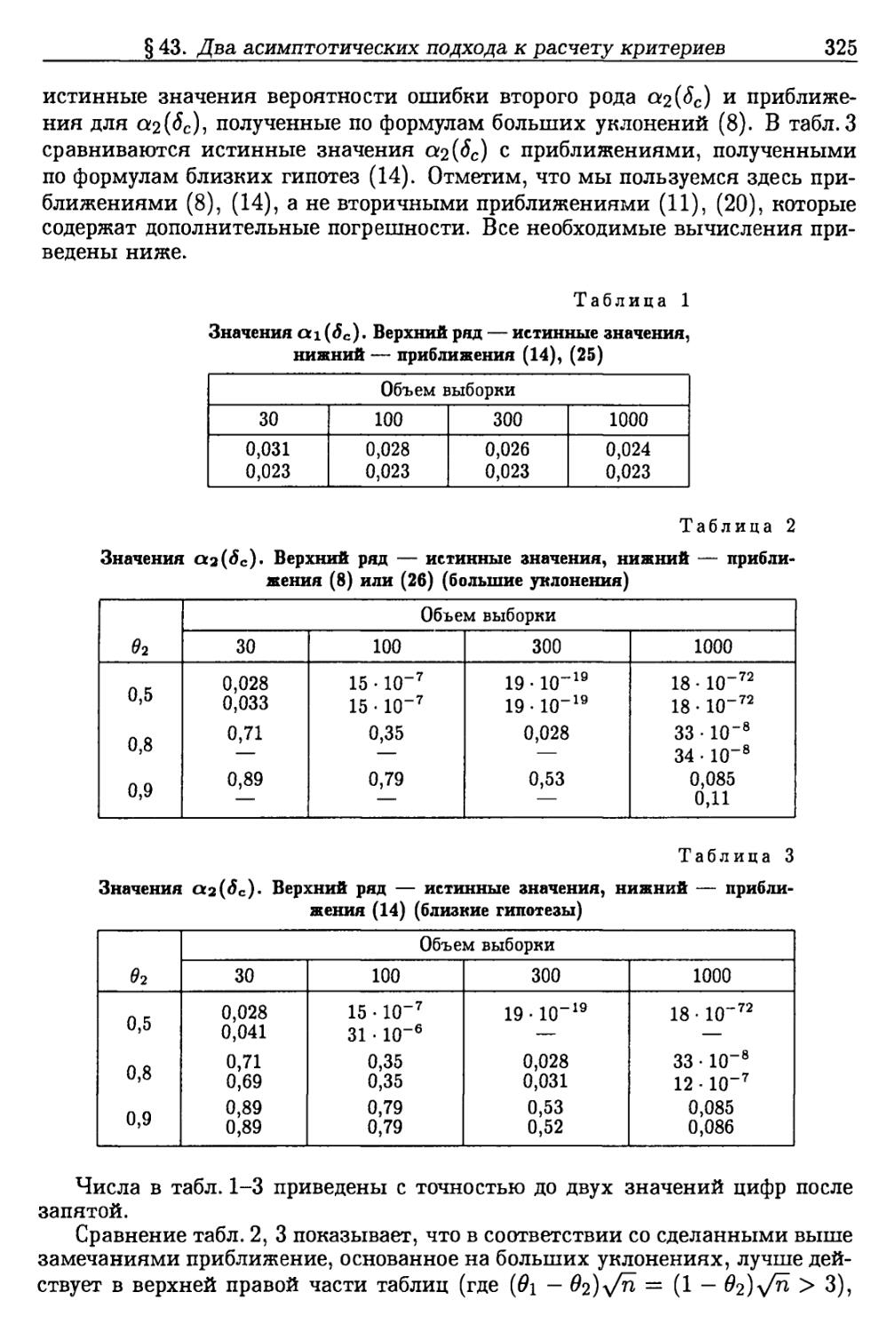
§43*. Два асимптотических подхода к расчету критериев. Численное
сравнение 315
1. Предварительные замечания (315). 2. Фиксированные гипотезы (316).
3. Близкие гипотезы (320). 4. Сравнение асимптотических подходов.
Числовой пример (323). 5. Связь н.м. к. с асимптотической эффективностью
о.м.п. (328).
§ 44. Проверка сложных гипотез. Классы оптимальных критериев 329
1. Постановка задачи и основные понятия (329). 2. Равномерно наиболее
мощные критерии (331). 3. Байесовские критерии (332). 4. Минимаксные
критерии (333).
§ 45. Равномерно наиболее мощные критерии 333
1. Односторонние альтернативы. Монотонное отношение правдоподобия
(333). 2. Двусторонняя основная гипотеза. Экспоненциальное семейство
(336). 3. Другой подход к рассматриваемым задачам (341). 4. Байесовский
подход и наименее благоприятные априорные распределения при построении
н.м.к. и р.н.м.к. (342).
Оглавление
7
§46*. Несмещенные критерии 344
1. Определения. Несмещенные р. н.м. к. (344). 2. Двусторонние
альтернативы. Экспоненциальное семейство (347).
§47*. Инвариантные критерии 349
§48*. Связь с доверительными множествами 353
1. Связь статистических критериев и доверительных множеств. Связь
свойств оптимальности (353). 2. Наиболее точные доверительные интервалы
(356). 3. Несмещенные доверительные множества (359). 4. Инвариантные
доверительные множества (360).
§ 49. Байесовский и минимаксный подходы к проверке сложных гипотез 363
1. Байесовские и минимаксные критерии (363). 2. Минимаксные критерии
для параметра α нормальных распределений (366). 3. Вырожденные
наименее благоприятные распределения для односторонних гипотез (373).
§ 50. Критерий отношения правдоподобия 375
§51*. Последовательный анализ 378
1. Вводные замечания (378). 2. Байесовский последовательный критерий
(379). 3. Последовательный критерий, минимизирующий среднее число
испытаний (383). 4. Вычисление параметров наилучшего последовательного
критерия (385).
§ 52. Проверка сложных гипотез в общем случае 388
§53. Асимптотически оптимальные критерии. Критерий отношения
правдоподобия как асимптотически байесовский критерий для проверки
простой гипотезы против сложной 397
1. Асимптотические свойства к. о. п. и байесовского критерия (397).
2. Асимптотическая байесовость к. о. п. (399). 3. Асимптотическая
несмещенность к.о. п. (403)
§ 54. Асимптотически оптимальные критерии для проверки близких
сложных гипотез 404
1. Постановка задачи и определения (404). 2. Основные утверждения (407).
§ 55. Свойства асимптотической оптимальности критерия отношения
правдоподобия, вытекающие из предельного признака оптимальности . . 412
1. А. р. н. м. к. для близких гипотез с односторонними альтернативами (412).
2. А.р.н.м.к. для двусторонних альтернатив (413). 3. Асимптотически
минимаксный критерий для близких гипотез, касающихся многомерного
параметра (415). 4. Асимптотически минимаксный критерий о принадлежности
выборки параметрическому подсемейству (417).
§56. Критерий χ2. Проверка гипотез по сгруппированным данным .... 423
1. Критерий χ2. Свойства асимптотической оптимальности (423). 2.
Применения критерия χ2. Проверка гипотез по сгруппированным данным (427).
§57. Проверка гипотез о принадлежности выборки параметрическому
семейству 430
1. Проверка гипотезы X € В^(а). Группировка данных (430). 2. Общий
случай (434).
§ 58. Устойчивость статистических решений (робастность) 438
8
Оглавление
1. Постановка задачи. Качественная и количественная характеризации ро-
бастности (438). 2. Оценка параметра сдвига (445). 3. Статистики Стьюдента
и So (448). 4. Критерий отношения правдоподобия (449).
Глава 4. Статистические задачи с двумя и более выборками 450
§ 59. Проверка гипотез об однородности (полной или частичной) в
параметрическом случае 450
1. Рассматриваемый класс задач (450). 2. Асимптотически минимаксный
критерий для проверки близких гипотез об обычной однородности (452).
3. Асимптотически минимаксные критерии для задачи об однородности при
наличии мешающего параметра (458). 4. Асимптотически минимаксный
критерий для задачи о частичной однородности (463). 5. Некоторые другие
задачи (466).
§ 60. Задачи об однородности в общем случае 466
1. Постановка задачи (466). 2. Критерий Колмогорова-Смирнова (467).
3. Критерий знаков (469). 4. Критерий Вилкоксона (470). 5. Критерий χ2
как асимптотически оптимальный критерий проверки однородности по
сгруппированным данным (475).
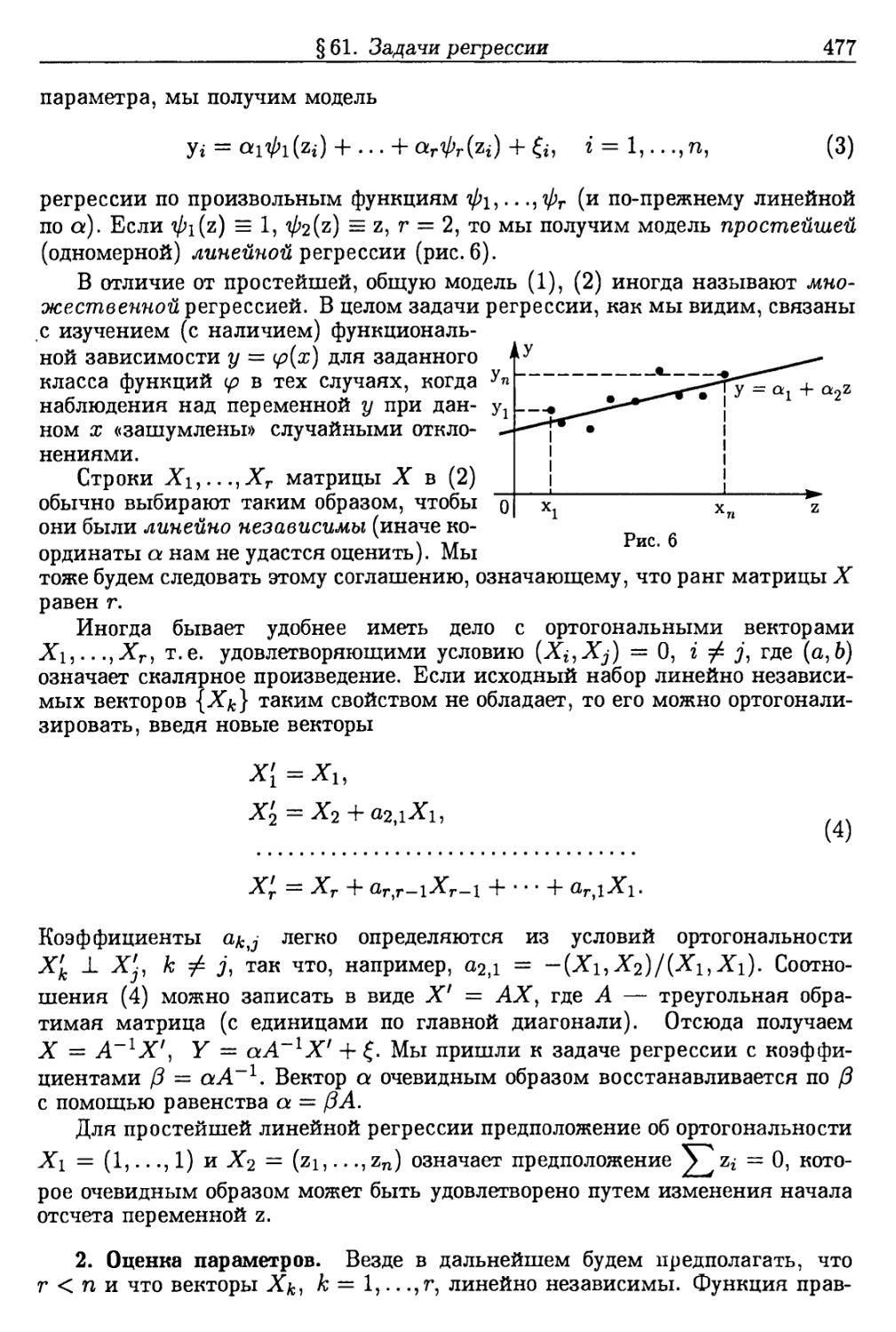
§61. Задачи регрессии 476
1. Постановка задачи (476). 2. Оценка параметров (477). 3. Проверка гипотез
относительно линейной регрессии (484). 4. Оценивание и проверка гипотез
при наличии линейных связей (488).
§62. Дисперсионный анализ 491
1. Задачи дисперсионного анализа как задачи регрессии. Случай одного
фактора (491). 2. Влияние двух факторов. Элементарный подход (494).
§ 63. Распознавание образов 496
1. Параметрический случай (497). 2. Общий случай (497).
Глава 5. Статистика ρазнораспредеденных наблюдений 500
§ 64. Предварительные замечания. Примеры 500
§ 65. Основные методы построения оценок. М-оценки. Состоятельность
и асимптотическая нормальность 507
1. Предварительные замечания и определения (507). 2. М-оценки (508).
3*. Состоятельность М-оценок (514). 4. Состоятельность М-оценок (519).
5. Асимптотическая нормальность М-оценок (521).
§66. Оценки максимального правдоподобия. Основные принципы
сравнения оценок. Оптимальность о. м. п. в классе М-оценок 524
1. Оценки максимального правдоподобия (524). 2. Асимптотические свойства
о. м.п. (526). 3. Основные принципы сравнения оценок. Асимптотическая
эффективность о.м.п. в классе М-оценок (531).
§ 67. Достаточные статистики. Эффективные оценки. Экспоненциальные
семейства 533
§ 68. Эффективные оценки в задаче оценивания «хвостов» распределений
(пример 64.7). Асимптотические свойства оценок 535
Оглавление
9
1. Оценки максимального правдоподобия (535). 2. Асимптотическая
нормальность Θ* в задаче В (537). 3*. Асимптотические нормальность и
оптимальность в задаче А (540).
§ 69. Неравенство Рао-Крамера 545
§ 70. Неравенства для отношения правдоподобия и асимптотические
свойства о. м. π 547
1. Неравенства для отношения правдоподобия и состоятельность о. м. п.
(547). 2. Асимптотическая нормальность о.м.п. (550). 3. Асимптотическая
эффективность (552). 4. Замечания об о.м.п. для многомерного параметра
(552).
§ 71. Замечания о проверке гипотез по неоднородным наблюдениям .... 553
§ 72. Задача о разладке (пример 64.6) 556
1. Задача о разладке как задача проверки гипотез (556). 2. Задача о разладке
как задача оценки параметра (563). 3. Последовательные процедуры (566).
Глава 6. Теоретико-игровой подход к задачам математической статистики 575
§ 73. Предварительные замечания 575
§ 74. Основные понятия и теоремы, связанные с игрой двух лиц 576
1. Игра двух лиц (576). 2. Равномерно оптимальные стратегии в подклассах
(577). 3. Байесовские стратегии (577). 4. Минимаксные стратегии (579).
5. Полный класс стратегий (587).
§ 75. Статистические игры 587
1. Описание статистических игр (587). 2. Классификация статистических
игр (590). 3. Две фундаментальные теоремы теории статистических игр
(591).
§ 76. Байесовский принцип. Полный класс решающих функций 593
§ 77. Достаточность, несмещенность, инвариантность 599
1. Достаточность (599). 2. Несмещенность (600). 3. Инвариантность (602).
§78. Асимптотически оптимальные оценки при произвольной функции
потерь 605
§ 79. Оптимальные статистические критерии при произвольной функции
потерь. Критерий отношения правдоподобия как асимптотически
байесовское решение 616
1. Свойства оптимальности статистических критериев при произвольной
функции потерь (616). 2. К. о. п. как асимптотически байесовский критерий
(616).
§ 80. Асимптотически оптимальные решения при произвольной функции
потерь в случае близких сложных гипотез 620
Таблицы 625
Приложение I 634
Приложение II 637
Приложение III 644
Приложение IV 647
10 Оглавление
Приложение V 658
Приложение VI 664
Приложение VII 669
Приложение VIII 679
Библиографические замечания 685
Список литературы 692
Список основных обозначений 698
Предметный указатель 701
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
Предлагаемая книга является существенно переработанной и
дополненной версией книги «Математическая статистика», вышедшей в 1984 г. в двух
частях: первая часть имела подзаголовок «Оценка параметров, проверка
гипотез», вторая — «Дополнительные главы». Позже эти две книги были
опубликованы в виде монографии на французском (1987) и испанском (1988)
языках. В 1997 г. дополненная и переработанная версия книги издана на
английском языке.
Одним из главных нововведений в предлагаемой книге по сравнению с
изданиями 1984 г. является появление новой главы, посвященной
статистике разнораспределенных наблюдений.
В целом в основу предлагаемой книги положены лекции по
математической статистике, которые автор в течение многих лет читал на
математическом факультете Новосибирского университета. Со временем курс лекций
неоднократно менялся в поисках варианта, который был бы по возможности
более стройным, доступным и в то же время соответствовал современному
состоянию этой науки. Были испробованы варианты, начиная с курса
преимущественно рецептурного характера с изложением основных типов задач
(построение оценок, критериев и изучение их свойств) и кончая курсом
общего теоретико-игрового характера, в котором теория оценок и проверка
гипотез представлялись как частные случаи единого подхода. Ограничения
во времени не позволяли объединить эти дополняющие друг друга
варианты, каждый из которых в отдельности обладал очевидными недостатками.
В первом случае набор конкретных фактов мешал развитию общего взгляда
на предмет. Второй вариант испытывал недостаток в простых конкретных
результатах и оказывался загруженным многими новыми непростыми
понятиями, трудными для усвоения. По-видимому, наиболее приемлемым
является вариант, в котором изложение элементов теории оценок и
теории проверки гипотез сочетается с последовательным проведением линии
на отыскание оптимальных процедур.
Основу книги составляет объединение материала, читавшегося в
разное время в лекциях, расширенное за счет разделов, присутствие которых
диктуется самой логикой изложения. Главной целью являлось изложение
современного состояния предмета в сочетании с максимально возможной
доступностью и математической цельностью и стройностью.
Содержание книги распадается на 6 глав и приложения.
В главе 1 изучаются свойства (в основном асимптотические)
эмпирических распределений, лежащие в основе математической статистики.
В главах 2, 3 излагаются соответственно теория оценок и теория
проверки статистических гипотез. Первые части каждой главы посвящены
описанию возможных подходов к решению поставленных задач и отысканию
оптимальных процедур. Вторые части посвящены построению
асимптотически оптимальных процедур.
Такую же структуру имеет глава 6, где излагается общий теоретико-
игровой подход к задачам математической статистики.
12
Предисловие
Глава 4 посвящена задачам, связанным с двумя и более выборками.
Статистические выводы для разнораспределенных наблюдений в более общей,
чем в главе 4, постановке задачи рассматриваются в новой главе 5, которая
уже упоминалась выше.
Книга содержит также 8 приложений. Они связаны с теми
утверждениями в основном тексте, доказательство которых выходит за рамки основного
изложения либо по своему характеру, либо по трудности.
Имеются еще библиографические замечания, не претендующие на
полноту, но позволяющие проследить возникновение и развитие основных
направлений математической статистики. При этом везде, где это возможно,
оказывалось предпочтение ссылкам на монографии (как на более доступный
вид литературы), а не на оригинальные статьи.
В настоящее время существует довольно много книг по математической
статистике. Выделим из них следующие, в которых представлено большое
количество материала, отражающее современное состояние предмета — это
книги Г.Крамера [58], Э.Лемана [66, 67], Ш. Закса [48], И.А.Ибрагимова
и Р.З.Хасьминского [49], L.Le Cam [63], G.R.Shorak, J.A.Wellner [139].
Из них наибольшее влияние на изложение настоящей книги оказали
монографии [49] (некоторые идеи этой книги использовались в §33, 34, 36, 37
главы 2) и [67] (изложение §45-48 главы 3 близко по содержанию к
соответствующим разделам [67]). Остальное изложение мало связано по строю с
имеющимися книгами.
Существует много других книг, занимающих заметное место в
статистической литературе (такие, как книги Блекуэлла и Гиршика [9], Кендалла и
Стьюарта [50], Кокса и Хинкли [54], Фергюссона [112], Рао [96] и ряд
других — все перечислить невозможно), но они по духу и по подбору материала
существенно отличаются от предлагаемой монографии.
Наряду с известными результатами и подходами в настоящую книгу
включены некоторые новые разделы, упрощающие изложение, ряд
методологических улучшений, а также некоторые новые результаты и результаты,
впервые публикуемые в монографической литературе.
Ниже приводится краткое описание методологической структуры книги
(см. также оглавление и краткие предисловия к каждой из глав).
Глава 1 излагает основные результаты, связанные с понятиями выборки,
эмпирического распределения и статистик.
В § 1, 2 вводятся понятия выборки, эмпирического распределения и
устанавливается теорема Гливенко-Кантелли, которую можно рассматривать как
фундаментальный факт, составляющий основу статистических выводов.
В §3 вводится два типа статистик (статистики I и II типов),
включающие в себя подавляющее большинство практически интересных статистик.
Эти статистики определяются как значения G(P*) функционалов G
(удовлетворяющих некоторым условиям) от эмпирического распределения Р*.
Класс рассматриваемых статистик расширен включением в него также так
называемых L-, М- и [/-статистик. Позже, в § 7, 8, устанавливаются
предельные теоремы о распределении этих статистик. Это разгружает
последующее изложение и освобождает от необходимости для каждой конкретной
статистики проводить очень схожие рассуждения, не относящиеся притом к
самому предмету статистики.
Предисловие
13
В § 5 собраны вспомогательные теоремы (названные в книге теоремами
непрерывности) о сходимости распределений статистик и о сходимости их
моментов. Это также разгружает последующее изложение.
В § 6 (он не обязателен при первом чтении) устанавливается, что
эмпирическая функция распределения F£{t) есть условный пуассоновский процесс,
и приводится формулировка теоремы (доказанной в приложении I) о
сходимости процесса у/п (F*(t) — F{t)) к броуновскому мосту.
В § 10 вводятся сглаженные эмпирические распределения, позволяющие
приближать не только само распределение, но и его плотность.
Глава 2 посвящена оценкам неизвестных параметров.
В § 13 вводится единый подход к построению оценок, названный
методом подстановки. Он состоит в том, что оценку Θ* для параметра 0,
представимого в виде функционала θ = G(P) от распределения Ρ выборки,
следует искать в виде Θ* = G(P*), где Р* -— эмпирическое распределение.
Все «разумные» оценки, используемые на практике, являются оценками
подстановки. Оптимальность оценки достигается путем выбора подходящего
функционала G. Если статистика Θ* = G(P*) является статистической I
или II типов, то теоремы главы 1 позволяют немедленно установить
состоятельность этих оценок и их асимптотическую нормальность.
В § 14, 15 этот подход иллюстрируется на оценках, полученных с
помощью метода моментов и метода минимального расстояния. Там же доказаны
состоятельность и асимптотическая нормальность М-оценок.
С тех же позиций в § 16 рассматриваются и оценки максимального
правдоподобия. Кроме того, установлена нижняя граница рассеивания М-оценок
и доказана асимптотическая оптимальность оценок максимального
правдоподобия в классе М-оценок. Более полное изучение асимптотических свойств
оценок максимального правдоподобия проводится позже, в § 34, 34.
В § 17 установлена нижняя граница рассеивания для L-оценок. Это дает
возможность для параметра сдвига строить в явном виде асимптотически
оптимальные L-оценки, асимптотически эквивалентные оценкам
максимального правдоподобия.
Сравнение оценок в главе 2 происходит на основе двух подходов: сред-
неквадратического (сравниваются Е#(0* — Θ)2) и асимптотического
(сравниваются дисперсии предельного распределения у/п (θ* — Θ) в классе
асимптотически нормальных оценок). В качестве иллюстрации с помощью
таких подходов строятся асимптотически оптимальные оценки в классе
L-оценок. В параметрическом случае такие подходы позволяют выделить
три типа оптимальных оценок: эффективные оценки в классах Кь с
фиксированным смещением Ь, байесовские и минимаксные оценки. На основе тех
же принципов выделяются классы асимптотически оптимальных оценок при
асимптотическом подходе. Для построения эффективных оценок
используются следующие традиционные методы: первый носит качественный
характер и связан с принципом достаточности (§ 22-24); второй метод основан на
количественных соотношениях, вытекающих из неравенства Рао-Крамера
(§ 26); третий связан с соображениями инвариантности (§ 28, 29),
позволяющими сузить класс рассматриваемых оценок. Отысканию асимптотически
оптимальных оценок, а также изучению асимптотических свойств функции
правдоподобия посвящены § 30-38. Параграф 30 содержит интегральное не-
14
Предисловие
равенство типа Рао-Крамера, которое позволяет, в частности, получить
простые критерии асимптотической байесовости и минимаксности оценок, а
также обосновать выделение некоторого подкласса оценок Ко, которым
следует ограничиться в поисках асимптотически эффективных оценок. Это
позволяет путем изучения асимптотических свойств оценок максимального
правдоподобия в § 34 сразу установить асимптотическую байесовость и
минимаксность названных оценок и их асимптотическую эффективность в Ко.
Параграфы 31-33 носят вспомогательный характер.
Интервальное оценивание параметров рассматривается в §39, 40, 49
главы 3.
Глава 3 посвящена проверке гипотез.
В § 41, 42 рассматривается случай конечного числа простых гипотез.
Выделяются (аналогично теории оценивания) три типа оптимальных
критериев — наиболее мощные в подклассах, байесовские и минимаксные.
Устанавливаются связи между этими критериями и находится их явный вид.
При этом в основу рассмотрений положен байесовский принцип (а не лемма
Неймана-Пирсона), что, на наш взгляд, упрощает изложение и делает его
более прозрачным.
В § 43 излагаются два асимптотических подхода к расчету критериев для
проверки двух простых гипотез и производится их сравнение.
В § 44 рассматривается общая постановка задачи о проверке двух
сложных гипотез и определяются классы оптимальных критериев (равномерно
наиболее мощные, байесовские, минимаксные).
Параграф 45 посвящен отысканию равномерно наиболее мощных
критериев в тех случаях, когда это возможно.
В §46, 47 решается та же задача, но в классах критериев, суженных
на основании соображений несмещенности и инвариантности. При этом в
основу рассмотрений, как и в §41, 42, положен байесовский подход.
В § 48 с помощью полученных результатов строятся наиболее точные
доверительные множества.
В § 49 рассматриваются байесовские и минимаксные критерии.
Параграфы 50, 53 посвящены критерию отношения правдоподобия. Он
оказывается равномерно наиболее мощным во многих частных случаях и
обладает свойством асимптотической байесовости при весьма широких
предположениях.
Изучение свойств асимптотической оптимальности критерия отношения
правдоподобия продолжено в § 55-57.
В §51 установлена оптимальность этого критерия в задачах
последовательного анализа.
Параграфы 54, 55 посвящены отысканию асимптотически оптимальных
критериев для проверки близких гипотез и найден их простой явный вид
для основных статистических задач.
Существенной особенностью первых трех глав является тот факт, что в
них рассмотрены лишь статистические задачи, связанные с использованием
одной выборки.
Глава 4 книги, как уже отмечалось, посвящена задачам с двумя и более
выборками. К ним относятся прежде всего задачи об однородности (полной
или частичной, §59, 60), задачи регрессии (§61) и дисперсионного анализа
Предисловие
15
(§62). На основании результатов главы 3 для задач однородности в
параметрическом случае построены асимптотически оптимальные критерии в
предположении, что альтернативные гипотезы являются близкими к
основной гипотезе об однородности. Для задач регрессии (как для линейной
регрессии, так и для регрессии по произвольным функциям) с помощью
результатов глав 2, 3 найдены эффективные оценки неизвестных параметров
и построены критерии для проверки основных гипотез. Рассмотрены также
так называемые задачи распознавания образов (§ 63), которые появляются в
учебной литературе, по-видимому, впервые.
Новая глава 5 «Статистика разнораспределенных наблюдений» по своей
структуре во многом повторяет главу 2. Ее появление в настоящем издании
вызвано тем, что в приложениях стало появляться все больше задач,
связанных с неоднородными наблюдениями, типичным примером которых могут
служить задачи нелинейной регрессии (но не только они). В то же время
общие методы исследования таких задач были разработаны лишь
фрагментарно, отсутствовало их систематическое изложение. Не претендуя ни в
какой мере на то, чтобы полностью заполнить этот пробел, автор имел своей
целью перенести на неоднородный случай основные результаты и подходы,
изложенные в исходной книге для статистики однородных наблюдений.
В § 64 приведен ряд типичных задач (некоторые из них представляют
самостоятельный интерес), относящихся к статистике разнораспределенных
наблюдений. Эти примеры в дальнейшем используются для иллюстраций и
для более детального изучения.
В § 65 излагаются основные методы построения оценок. В основном это
метод М- и М-оценивания. На эти оценки переносятся основные результаты
главы 2 о состоятельности и асимптотической нормальности этих оценок.
В §66 с помощью результатов §65 устанавливаются асимптотические
свойства оценок максимального правдоподобия (состоятельность,
асимптотическая нормальность, асимптотическая оптимальность в классе М-оценок).
В § 67 содержатся комментарии об использовании результатов,
связанных с достаточными статистиками и экспоненциальными семействами в
случае разнораспределенных наблюдений.
В § 68 в качестве иллюстрации детально изучаются асимптотические
свойства оценок параметров хвостов распределений.
В § 69 рассмотрено обобщение на случай разнородных наблюдений
неравенства Рао-Крамера и близких задач; § 70 посвящен обобщению (на тот же
случай) результатов главы 2 об асимптотических свойствах оценок
максимального правдоподобия (§33, 34).
Перенос большинства результатов главы 3 на случай
разнораспределенных наблюдений либо не требует подробных рассмотрений, либо основан на
обобщениях результатов главы 2, упомянутых выше (комментарии по этому
поводу см. в § 71).
В § 72 изучается задача о разладке. Для нее найдены асимптотически
оптимальные процедуры.
Глава 6 посвящена общему теоретико-игровому подходу к задачам
статистики. Он способствует выработке общего взгляда на предмет
математической статистики и позволяет обобщить многие результаты глав 2, 3.
В § 74 излагаются основные понятия и результаты «обычной» теории игр
(рассматриваются лишь игры двух лиц). В частности, устанавливаются
16
Предисловие
связи между основными типами оптимальных стратегий — байесовскими,
минимаксными, равномерно наилучшими в подклассах.
В § 75 изучаются статистические игры.
В § 76 формулируется и доказывается так называемый байесовский
принцип, который позволяет свести задачу отыскания байесовского
статистического решения к значительно более простой задаче построения байесовской
стратегии для обычной игры двух лиц.
В § 77 обсуждаются принципы достаточности, несмещенности и
инвариантности для построения решений, равномерно наилучших в
соответствующих подклассах.
Параграфы § 78-80 посвящены отысканию асимптотически оптимальных
решающих правил. В § 78 изучаются асимптотически оптимальные оценки
параметров при произвольной (не только квадратической) функции потерь.
В этом случае удается установить результаты, близкие к результатам главы 2
об асимптотической оптимальности оценок максимального правдоподобия.
В § 79, 80 изучаются асимптотически оптимальные критерии при
произвольной функции потерь. В § 79 доказана асимптотическая байесовость критерия
отношения правдоподобия; в § 80 установлен предельный признак
оптимальности критериев для проверки близких гипотез (обобщение результатов § 54,
55 главы 3 на случай произвольной функции потерь).
Из приложений выделим приложение VII, в котором найдены
асимптотически оптимальные процедуры в задаче о разладке, и приложение VIII,
в котором доказаны две фундаментальные теоремы теории статистических
игр. Чтение приложений требует более высокой математической подготовки.
Книга имеет многоцелевое назначение. В ее полном объеме она, конечно,
ближе к программе кандидатского минимума по специальности
«математическая статистика», чем к учебному пособию для студентов. Однако в книге
предусмотрена система мер, упрощающих первое чтение, которая делает
книгу доступной и для студентов. Параграфы повышенной трудности или
«более продвинутые» по своему содержанию отмечены звездочкой, их
следует при первом чтении опускать, как и текст, набранный петитом. Кроме
того, изложение технически более сложного случая, относящегося к
многомерному параметру, почти везде выделено в отдельные разделы и параграфы,
которые также можно пропускать.
Преподаватели вузов, уже знакомые хотя бы частично с предметом, могут
выбирать из книги совокупность параграфов (вариантов может быть много),
используя которые (не обязательно полностью) можно составить
семестровый курс математической статистики. Вот один из вариантов: § 1, 3, 5
главы 1; § 12-14, 16-22, 24, 26 (31, 33, 34), 40, 49 главы 2; §41, 42, 44, 45, 52
(53, 56) главы 3. Параграфы, взятые в скобки, посвящены асимптотически
оптимальным процедурам. Их следует в зависимости от подготовленности
студентов либо максимально облегчить, либо опустить вовсе.
Чтение книги предполагает знакомство с курсом теории вероятностей,
например, в объеме учебника А.А. Боровкова [17]. (Возможно, конечно,
использование и других источников.) Ссылки на эту книгу, в отличие от
других ссылок, появляются в тех местах, которые предполагаются читателю
известными, и служат, главным образом, для напоминаний. При этом мы
будем использовать сокращенную запись этих ссылок. Например, вместо § 3
главы 13 в [17] мы будем писать [17, § 13.3].
Предисловие
17
Нумерация параграфов в книге сквозная; нумерация теорем, лемм,
примеров и т. д. в каждом параграфе самостоятельная. Для удобства чтения
используются разные системы для ссылок на теоремы, леммы, примеры,
формулы и т. д. в зависимости от того, в каком параграфе они находятся.
Если делается ссылка на теорему 1 или формулу (12) читаемого параграфа,
то ссылки на них будут выглядеть так: теорема 1, формула (12). Если
делается ссылка на теорему 1 и формулу (12) одного из предыдущих
параграфов (например, §13), то ссылки будут иметь такой вид: теорема 13.1,
формула (13.12).
Значок < означает окончание доказательства.
Разделы, помеченные звездочкой, при первом чтении можно опустить.
Для удобства читателя в конце книги помещены список основных
обозначений и предметный указатель.
Написание этой книги было весьма трудным многоэтапным делом.
Значительную помощь при подготовке первоначальных записок лекций к
печати и по устранению недостатков в них мне оказал И.С.Борисов. Второй
вариант рукописи прочел по моей просьбе К.А. Боровков, который
представил мне длинный список полезных советов и замеченных им погрешностей.
Он же существенно помог мне при «чистке» окончательного варианта
рукописи. В поисках новой критики я обратился с просьбой ознакомиться
с рукописью к А.И. Саханенко. Он также представил мне длинный список
замечаний и предложений по улучшению изложения, многими из которых
я воспользовался. Наиболее существенные изменения при этом коснулись
доказательств в §26, 31, 33, 37 главы 2, §53-55 главы 3, приложениях II,
IV, VIII (см. также библиографические замечания).
Много ценных замечании, направленных на улучшение книги, было
сделано Д.М. Чибисовым. Рукопись просматривали В.В. Юринский и А.А.
Новиков и также сделали ряд полезных замечаний. Всем названным коллегам
и всем тем, кто так или иначе помогал мне при работе над книгой, я хотел
бы выразить здесь свою глубокую и искреннюю признательность и
благодарность за их труд и содействие в написании книги.
А. А. Боровков
Памяти моего учителя
Андрея Николаевича Колмогорова
посвящается
ВВЕДЕНИЕ
Настоящая книга посвящена изложению основ раздела математики,
который называется математическая статистика. Последнюю для
краткости называют иногда просто статистикой. Однако следует иметь в виду,
что такое сокращение возможно лишь при достаточно хорошем
взаимопонимании, поскольку сам по себе термин «статистика» соответствует часто
несколько иному понятию.
Что представляет собой предмет математической статистики? Можно
приводить разные описательные «определения», которые в большей или
меньшей степени отражают содержание этого раздела математики. Одно из
самых простых и грубых основано на сравнении, связанном с понятием
выборки из конечной генеральной совокупности и с задачей о
гипергеометрическом распределении, которая обычно рассматривается в начале курса
теории вероятностей. Зная состав генеральной совокупности, там изучают
распределения для состава случайной выборки. Это типичная прямая
задача теории вероятностей. Однако часто приходится решать и обратные
задачи, когда известен состав выборки и по нему требуется определить,
какой была генеральная совокупность (это делается, например, при
социологических опросах общественного мнения). Такого рода обратные задачи и
составляют, образно говоря, предмет математической статистики.
Несколько уточняя это сравнение, можно сказать так: в теории
вероятностей мы, зная природу некоторого явления, выясняем, как будут вести себя
(как распределены) те или иные изучаемые нами характеристики, которые
можно наблюдать в экспериментах. В математической статистике
наоборот — исходными являются экспериментальные данные (как правило, это
наблюдения над случайными величинами), а требуется вынести то или иное
суждение или решение о природе рассматриваемого явления. Таким
образом, мы соприкасаемся здесь с одной из важнейших сторон человеческой
деятельности — процессом познания. Тезис о том, что «критерий истины
есть практика» имеет самое непосредственное отношение к математической
статистике, поскольку именно эта наука изучает методы (в рамках точных
математических моделей), которые позволяют отвечать на вопрос,
соответствует ли практика, представленная в виде результатов эксперимента,
данному гипотетическому представлению о природе явления или нет.
При этом необходимо подчеркнуть, что, как и в теории вероятностей,
нас будут интересовать не те эксперименты, которые позволяют делать
однозначные, детерминированные выводы о рассматриваемых в природе
явлениях, а эксперименты, результатами которых являются случайные события.
С развитием науки роль такого рода задач постоянно возрастает, поскольку с
увеличением точности экспериментов становится все труднее избежать
«случайного фактора», связанного с разного рода помехами и ограниченностью
наших измерительных и вычислительных возможностей.
Введение
19
Математическая статистика является частью теории вероятностей в том
смысле, что каждая задача математической статистики есть по существу
задача (иногда весьма своеобразная) теории вероятностей. Однако сама по
себе математическая статистика занимает и самостоятельное положение в
табеле о науках. Математическая статистика может рассматриваться как
наука о так называемом индуктивном поведении человека (и не только
человека) в условиях, когда он должен на основании своего
недетерминированного опыта принимать решения с наименьшими для него потерями*).
Математическую статистику называют также теорией статистических
решений, поскольку ее можно характеризовать как науку об оптимальных
решениях (последние два слова требуют пояснения), основанных на
статистических (экспериментальных) данных. Точные постановки задач будут
даны позже, в основном тексте книги. Здесь же мы ограничимся тем, что
приведем три примера наиболее простых и типичных статистических задач.
Пример 1. Для многих изделий одним из основных параметров,
которым характеризуется качество, является срок службы. Однако срок службы
изделия (скажем, электролампы), как правило, случаен, и заранее
определить его невозможно. Опыт показывает, что если процесс производства в
известном смысле однороден, то сроки службы ξι, ξ2,· ■ · соответственно 1-го,
2-го и т. д. изделий можно рассматривать как независимые одинаково
распределенные величины. Интересующий нас параметр, определяющий срок
службы, естественно отождествить с математическим ожиданием θ = Εξ;.
Одна из стандартных задач состоит в выяснении, чему равно Θ. Для того
чтобы определить это значение, берут η готовых изделий и проверяют их.
Пусть χι,Χ2,.. .,хп — сроки службы этих проверенных изделий. Мы знаем,
что
ι п
П ^—' п.н.
г=1
1 п
при η -* оо. Поэтому естественно ожидать, что число χ = ~~/\]х* ПРИ
г=1
достаточно большом η окажется близким к θ и позволит в какой-то мере
ответить на поставленные вопросы. При этом очевидно, что мы
заинтересованы в том, чтобы требуемое число наблюдений η было по возможности
наименьшим, а наша оценка числа θ по возможности более точной
(завышение параметра 0, как и его занижение, приведут к материальным потерям).
Пример 2. Радиолокационное устройство в моменты времени t\, t^ ...
.. .,£п зондирует заданную часть воздушного пространства с целью
обнаружения там некоторого объекта. Обозначим через χι,...,χη значения
отраженных сигналов, принятых устройством. Если в заданной части
пространства интересующий нас объект отсутствует, то значения Х{ можно
рассматривать как независимые случайные величины, распределенные так же, как
некоторая случайная величина ξ, природа которой обусловлена характером
различных помех. Если же в течение всего периода наблюдений объект
находился в поле зрения, то х; будут наряду с помехами содержать «полезный»
сигнал о, и значения х; будут распределены как ξ + α. Таким образом, если
*) Подробнее об этом см. в [72].
20
Введение
в первом случае наблюдения х^ имели функцию распределения F(x), то во
втором случае их функция распределения будет иметь вид F(x — а). По
выборке χι,.. .,хп требуется решить, какой из этих двух случаев имеет место,
т. е. существует в заданном месте интересующий нас объект или нет.
В этой задаче окажется возможным указать в известном смысле
«оптимальное решающее правило», которое будет решать поставленную задачу с
минимальными ошибками. Сформулированная задача может быть
усложнена следующим образом. Сначала объект отсутствует, а затем, начиная с
наблюдения с неизвестным номером 0, появляется. Требуется по
возможности более точно определить момент θ появления объекта. Это так
называемая задача о разладке, имеющая и целый ряд других интерпретаций,
важных для приложений.
Пример 3. Некоторый эксперимент производится сначала щ раз в
условиях А и затемп^ раз в условиях В. Обозначим через χι,...,хП1 иу1г..,уП2
результаты этих экспериментов соответственно в условиях А и В.
Спрашивается, сказывается ли изменение условий эксперимента на его результатах?
Иными словами, если обозначить через Ρ а распределение х^, 1 ^ г ^ ηχ, и
через Рв — распределение yi? 1 ^ г ^ П2, то вопрос состоит в том,
выполнено соотношение Рд = Рв или нет.
Например, если нужно установить, влияет ли некоторый препарат на
развитие, скажем, растении или животных, то параллельно ставятся две
серии экспериментов (с препаратом и без), результаты которых необходимо
уметь сравнивать.
Часто возникают и более сложные задачи, когда аналогичный вопрос
ставится для многих серий наблюдений, проведенных в различных условиях.
Если результаты наблюдений зависят от условий, то бывает необходимым
проверить тот или иной характер этой зависимости (так называемая задача
о регрессии).
Список примеров типичных статистических задач, разных по сложности
и по своему существу, можно было бы продолжить. Однако общими для всех
них будут следующие два обстоятельства.
1. Перед нами не было бы никаких проблем, если бы распределения
результатов наблюдений, которые фигурируют в задачах, были нам известны.
2. В каждой из этих задач мы должны по результатам экспериментов
принимать какое-то решение относительно распределения имеющихся
наблюдений (отсюда и название «Теория статистических решений»,
упоминавшееся выше).
В связи с этими двумя замечаниями принципиальное значение для всего
дальнейшего и, в частности, для решения приведенных в качестве примеров
задач, приобретает следующий факт. Оказывается, по результатам
наблюдений χι,.. .,хп над некоторой случайной величиной ξ можно при больших η
сколь угодно точно восстановить неизвестное распределение Ρ этой
случайной величины. Аналогичное утверждение справедливо и для любого
функционала θ = Θ(Ρ) от этого неизвестного распределения.
Этот факт лежит в основе математической статистики. Ему и более
точным постановкам задач будет посвящена глава 1.
Глава 1
ВЫБОРКА, ЭМПИРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ·
АСИМПТОТИЧЕСКИЕ СВОЙСТВА СТАТИСТИК
В § 1-4 вводятся понятия выборки и эмпирического распределения и
рассматриваются их простейшие свойства, главным образом, асимптотические, лежащие
в основе математической статистики.
В §5 излагаются так называемые теоремы непрерывности (о сходимости
распределений функций от последовательностей случайных величин), используемые
на протяжении всей книги.
Параграфы 6-10 посвящены более тонким асимптотическим свойствам
эмпирических распределений и изучению предельных распределений для основных типов
статистик.
§ 1· Понятие выборки
Исходным материалом любого статистического исследования является
совокупность результатов наблюдений. В простейших случаях они
представляют собой экспериментальные (полученные в результате опытов)
значения некоторой случайной величины ξ. Мы уже отмечали, что в задачах
статистики распределение Ρ этой случайной величины хотя бы частично
неизвестно.
Точнее, пусть G — эксперимент, связанный со случайной величиной ξ.
Формально для этого эксперимента со случайной величиной ξ мы должны
построить математическую модель, в которую входит вероятностное
пространство (Χ, ©,ν,Ρ), и задать на нем подходящим образом измеримую
функцию, которая и называется случайной величиной ξ (см. [17]).
Пространство (X, ЯЗ;г,Р), не ограничивая общности, можно считать
«выборочным» (см. [17]), т.е. считать, что X есть пространство значений ξ(χ) = χ.
В этом случае Ρ можно называть распределением ξ. Если ξ — числовая
случайная величина, то X есть числовая прямая К; если ξ — вектор, то
X = Km5 m > 1. В дальнейшем мы, как правило, и будем иметь в виду
только эти два случая, т. е. под X понимать R (одномерный случай) или
Мт, т > 1 (многомерный случай). В качестве 93χ чаще всего выбирают
σ-алгебру борелевских множеств.
В то же время следует отметить, что многие результаты книги, особенно
в главах 2-6, вообще никак не связаны с природой выборочного
пространства X, поскольку там рассматриваются не сами наблюдения, а функции от
них со значениями в R или IRm, m > 1.
Если заранее известно, что Ρ сосредоточено на части В Ε ΐ&χ
пространства X, то может оказаться удобным под X понимать В, а под *Βχ — сужение
σ-алгебры 93 д* на В.
22
Гл. 1. Выборка. Эмпирическое распределение
Рассмотрим η независимых повторений эксперимента G (см. [17, § 1.3])
и обозначим через χχ,.. .,хп совокупность полученных наблюдений. Вектор
Хп — (ХЬ · · ·)χη)
называется выборкой объема η из совокупности с распределением Р.
Иногда используются укороченные или более полные варианты этого термина:
выборка из распределения Ρ или простая выборка объема η из
генеральной совокупности с распределением Р.
Символически соотношение «Хп есть выборка из распределения Р» будет
записываться с помощью знака €= следующим образом:
Хп €= Р. (1)
Такого рода запись будет использоваться нами и для других случайных
величин. Например, соотношение
ξί= Ρ (2)
будет означать, что ξ имеет распределение Р. Такое использование
символа €= находится в соответствии с (1), поскольку последнее определено для
любого п, в частности для η = 1.
Если ξ и η есть две случайные величины (вообще говоря, заданные на
разных пространствах) с одинаковыми распределениями, то этот факт будем
обозначать ξ = τ/, так что если Хп и Yn есть две выборки одинакового объема
d
из распределения Р, то можем писать Хп = Yn.
d
В правых частях (1), (2) вместо распределения Ρ иногда может
стоять функция распределения, соответствующая Р. Так что если F(x) =
= Р((—оо,х)), то запись
Xn^F
будет тождественна с (1).
Само понятие «выборки из генеральной совокупности» встречается также
при рассмотрении простейших вероятностных моделей, связанных с
извлечением шаров из урны в классическом определении вероятности (см. [17,
§1.2]). Следует отметить, что введенное выше определение выборки
находится в полном согласии с этим понятием, введенным ранее, и по существу
совпадает с ним. Если х^ (или случайная величина ξ) могут принимать
лишь s значений αχ,.. .,α5 и вероятности этих значений рациональны, т.е.
ρ(ξ = «,·) = $, Σ>, = ;ν,
то выборку Хп можно представить как результат «выборки с возвращением»
(в смысле [17, § 3.2]) из урны с N шарами, из них на N\ шарах написано αχ,
на Л^2 шарах написано аг и т. д.
Как математический объект выборка X = Хп (индекс п мы часто будем
опускать) есть не что иное, как случайная величина (χχ,.. ·,χη) со
значениями в «n-мерном» пространстве Xй — Χ χ Χ χ •••хЛ'и распределением,
§ 1. Понятие выборки
23
определяемым для В = В\ χ Въ χ · - · χ Βη, Bj Ε *Βχ равенствами
η
ρ(Χ ε В) = Р(Х1 е Si,.. ,χη е вп) = JJ р(х* е я*), (з)
Другими словами, распределение Ρ на Хп есть η-кратное прямое
произведение заданных «одномерных» распределений.
Относительно обозначений для распределения Ρ и других будем
придерживаться следующих соглашений, которые мы отчасти уже использовали
в (3) и которые нигде не приведут нас к недоразумениям.
1. Мы будем использовать один и тот же символ (в частности, Р) для
распределений в (Χ,ΐβχ) и для прямого произведения этих распределений
в (Л"\933>) (см. (3)), где 05^ — σ-алгебра борелевских множеств в Χν.
Различие будет определяться лишь аргументом функции Р.
2. Вероятность попадания величины X в множество Л, скажем, из 93^,
нам иногда будет удобно обозначать через Ρ (В), а иногда через Р(Х Ε В).
Это одно и то же в силу того, что Хп есть выборочное пространство для X.
3. Наконец, символ Ρ будем использовать для обозначения общего
понятия вероятности (т.е. для вероятности, относящейся к каким-то другим
случайным величинам без конкретизации вероятностного пространства).
В силу (3) можем рассматривать выборку X как элементарное событие в
выборочном вероятностном пространстве (#,93^, Р) (см. [17, §3.5]).
Отметим, что относительно выборки X будем допускать двойственное толкование
этого обозначения и объекта: как случайной величины и как вектора
реальных числовых данных, полученных в фактически осуществленных
экспериментах. Как показывает опыт, такое двойное толкование вполне приемлемо
и не приводит к недоразумениям, хотя и допускает одновременное
существование записей вида Ρ(χχ < ί) = F(t) и вида χχ = 0,74, х2 = 0,83 и т.д.
Отметим также, что координаты х; выборки X мы обозначаем
«прямыми» буквами х, оставляя «наклонные» буквы χ для обозначения
переменных величин. Вектор (χχ,. ..,xn) Ε Хп, хг Ε Χ, мы будем обозначать
полужирными буквами χ = (χχ,.. .,χη)·
Выборка является основным исходным объектом в задачах
математической статистики. Однако на практике ее элементы χχ, хг,..- далеко не
всегда являются независимыми. В своих рассмотрениях мы также не будем
исключать такой возможности. Чтобы при этом не делать дополнительных
оговорок, мы в случае зависимых наблюдений будем считать, что имеем
дело с выборкой объема η = 1, а наблюдения представляют собой
координаты вектора χχ (ведь природа пространства X произвольна).
В следующих рассмотрениях нам часто придется иметь дело с
выборками Хп неограниченно возрастающего объема п. В таких случаях удобно
предполагать, что задана выборка Хоо = (χχ,Χ2, · · ·) бесконечного объема, а
X = Хп есть совокупность ее первых η координат. Под выборкой
бесконечного объема Хоо мы будем понимать элемент выборочного вероятностного
пространства (A'oo,03;j?,P), где Х°° — пространство последовательностей
(#ъ^2,.. .); сг-алгебра 05^ порождена множествами f] {χι Ε 5г}, В{ Ε 93χ,
Ν = 1,2,...; распределение Р обладает свойством (3). По теореме
Колмогорова [17] такое распределение всегда существует. Стало быть, предположение
24
Гл.1. Выборка. Эмпирическое распределение
о существовании выборки Х^ бесконечного объема никак не ограничивает
общность.
Саму бесконечную последовательность (бесконечную выборку) Xqq в
рассмотрениях, носящих теоретико-вероятностный характер, можно
трактовать как элементарное событие (ср. с [17]).
В тех случаях, когда нам нужно будет понимать Хп как подвектор -Хоо,
мы будем писать
где [·]η — оператор проектирования из Х°° в Хп, определенный очевидным
образом. В соответствии с предыдущим запись
*оо€= Ρ
будет означать, что Xqq есть выборка бесконечного объема из
распределения Р.
Если возникает необходимость особо отметить тот факт, что речь идет
о распределении в (Л^°°,23^) (или (Х71,^7^) при п<оо), а не в (Л\ Ъх),
то будем использовать также обозначение Р°° (Рп). Сохранение верхних
индексов ос и η во всем тексте привело бы к громоздким обозначениям.
§ 2. Эмпирическое распределение (одномерный случай)
Пусть дана выборка X = (xi,...,xn) Ε Ρ, χ* Ε Χ = Ш. Рассмотрим
вещественную прямую М с сг-алгеброй борелевских множеств 03 и дискретное
распределение Р* на (К, 93), сосредоточенное в точках χχ,.. ,,хп, для
которого вероятность значения х* полагается равной 1/п. Другими словами, для
любого В £ 23 по определению
К(В) = *&, (1)
Π
где и {В) — число элементов выборки X, попавших во множество В.
Распределение Р* называется эмпирическим распределением, построенным по
выборке X (или соответствующим выборке X). Его можно представить также в
следующем виде. Пусть 1Х(В) — распределение, сосредоточенное в точке х:
«*>={£ %%
η
тогда, очевидно, и {В) = У^1Х.(2?),
= 1
*η{Β)=1~ΣΚ{Β). (2)
<=1
η
г=1
Ясно, что Ρ* (β) для любого борелевского В как функция от выборки есть
случайная величина. Таким образом, мы имеем здесь дело со случайной
функцией множеств, или со случайным распределением.
Предположим теперь, что Хоо €=Р, Хп = [Хоо]п и га —>· оо. Мы получим
тогда последовательность эмпирических распределений Р*. Замечательный
§ 2. Эмпирическое распределение (одномерный случаи) 25
факт состоит в том, что эта последовательность неограниченно сближается с
исходным распределением Ρ наблюдаемой случайной величины. Этот факт
имеет принципиальное значение для всего последующего изложения,
поскольку он показывает, что неизвестное распределение Ρ может быть сколь
угодно точно восстановлено по выборке достаточно большого объема.
Теорема 1. Пусть В Ε 23 и Хп — [Χοο]η €=Ρ· Тогда при η —» оо
К(в) ^ р(в).
Сходимость с вероятностью 1 здесь имеется в виду относительно
распределения Ρ = Р°° в (М00,©00,?). Предположение Хп = [Хоо] нужно нам для
того, чтобы случайные величины Р^(-В) были заданы на одном
вероятностном пространстве.
Доказательство. Обратимся к определению (2) и заметим, что
IXi{B) есть независимые одинаково распределенные случайные величины,
Е1Х.(В) = P(IXi(B) = 1) = Ρ(χϊ е В) = Ρ {В). Так как Έ>*η{Β) есть
среднее арифметическое этих величин, то остается воспользоваться усиленным
законом больших чисел. <
Теорема 1 устанавливает сходимость Р£(-5) и Р(-В) в каждой «точке» В.
Однако имеет место и более сильное утверждение о том, что такая
сходимость в известном смысле равномерна по В.
Обозначим через 3 совокупность множеств 5, являющихся
полуинтервалами вида [а, Ь) с конечными или бесконечными концами, и предположим
опять, что Хп = [Хоо]п-
Теорема 2 (Гливенко-Кантелли).
sup|P;(B)-P(B)|—>0.
Собственно, с именами Гливенко и Кантелли связано несколько иное
утверждение, относящееся к важному понятию эмпирической функции
распределения. По определению это есть функция распределения,
соответствующая Р*. Другими словами, эмпирической функцией распределения F£{x)
называется функция
F:(x) = P*n((-oo,x)).
Величина nF*(x) равна числу элементов выборки, которые меньше, чем х.
В реальных условиях для построения F£{x) часто используют следующую
процедуру. Элементы выборки (χι,...,χη) упорядочивают по возрастанию,
т. е. образуют из нее последовательность
х(1) < х(2) ^ · < х(п)>
которая называется вариационным рядом. Тогда можем положить
к
Fn(x) = ~ при χ Ε (x(*),X(*+i)],
где к пробегает значения от 0 до п, Х(0) = —оо, Χ(η+ΐ) = °°· Очевидно, F£{x)
представляет из себя ступенчатую функцию, имеющую скачки величиной
1/го в точках Хг, если все х; различны.
26
Гл.1. Выборка. Эмпирическое распределение
Пусть F(x) = Р((—оо, ж)) есть функция распределения ξ (или, что то
же, χι) и Χη = [-Χ"οο]η· Теорема Гливенко-Кантелли состоит в следующем.
Теорема 2А. При η —> оо
8υΡ^η*(χ)-^(χ)|-4θ.
χ Π·Η·
Ниже индекс η у обозначений F* мы будем опускать и писать просто F*.
Доказательство теоремы 2А. Предположим сначала для
простоты, что функция F непрерывна. Пусть ε > 0 — произвольно малое заданное
число такое, что число N = l/ε целое. Так как F непрерывна, то можно
указать числа zq = — оо, z\,.. .,гдг_1, ζχ = оо такие, что
F(*0) = 0, F(*i) = е = ^, · · ·, ^Ы = ке = -, ..., F(zn) = 1.
При 2 G [zjt,zjt+i) справедливы соотношения
F*(z) - F(z) < F*(zfc+1) - F(zk) = F*(zk+1) - F(zk+1) + ε,
F*{z) - F{z) > F*(zk) - F(zk+1) = F*(zk) - F{zk) -ε. U
Обозначим через А^ множество элементарных событий ω = Xqq, на которых
F*(zk) -> F(zic). По теореме 1 Р{А^) = 1. Стало быть, для каждого ω G А =
лг
= IJ -Ajt найдется n(cj) такое, что при всех η ^ η(ω) будет выполняться
А;=0
|F*(zfc)-F(zfc)|<e, k = 0,l,...,N. (4)
Но вместе с (3) эти неравенства влекут за собой
sup \F*(z) - F(z)\ <2ε. (5)
Ζ
Итак, это соотношение имеет место для произвольного ε > О, всех ω Ε А
и всех достаточно больших η ^ η(ω). Так как 'Р(А) = 1, то теорема для
непрерывной функции F доказана.
Для произвольной функции F(x) доказательство происходит совершенно
аналогично. Надо лишь воспользоваться следующим обстоятельством: для
любой F(x) существует конечное число точек — оо = zq < z\ < ■ · · < ζ^-ι <
< ζм — оо таких, что
F(zk+l)-F(zk+0)^e, k = 0,l,...,N-l (6)
(для определенности можно считать, что множество {zj} содержит все точки
скачков F, по величине больших, чем, например, ε/2). Совершенно
аналогично (3) получаем, что при ζ Ε (ζ^,ζ^+ι]
F*{z) - F{z) < F*(zk+1) - F{zk+l) + ε,
F*(z) - F(z) > F*(zk + 0) - F(zk + 0) - ε. U
§ 2. Эмпирическое распределение (одномерный случай) 27
К множествам А^, которые определяются как прежде, добавим множества
AjJ", k = 0,1,..., iV, на которых F*(z^ + 0) -> F(zfc + 0). Тогда по теореме 1
N
Р{Ак) = Р(А^) = 1, и на множестве А = f) А*л4£, Р(А) = 1, при ДОСта-
А^О
точно больших η ^ η(ω) будет справедливо (4), а также неравенства
\F*(zk + 0) - F(zA + 0)| < ε, А; = 0,1,.. , Ν.
Вместе с (7) эти неравенства влекут за собой (5). <
Теорема 2А является частным случаем теоремы 2, так как множества
(—οο,χ) принадлежат 3; с другой стороны, теорему 2 нетрудно получить в
качестве следствия теоремы 2А, поскольку для В = [а, 6)
\К(В) - Р(В)\ < \К(Ь) - F(b)\ + \F*(a) - F(a)\,
и, стало быть,
sup\K(B) ~ Р(В)| < sup[|Fn*(b) - F(b)\ + \F*(a) - F(a)\] —► 0.
Bed ajb Π·Η·
Замечание 1. Нетрудно видеть, что такого же рода рассуждения
позволяют нам в качестве совокупности множеств 3 в теореме 2 брать
совокупности интервалов (а, 6), отрезков [а, 6] и их конечных (в числе не более
некоторого Ν) объединений.
С другой стороны, если в качестве 3 в теореме 2 взять достаточно богатый
класс множеств, то утверждение теоремы перестает быть верным.
Например, если 3 содержит объединения любого конечного числа интервалов, то
множество
Bn = U (Х* ~ ~2^ Хк + ~2 ) Ε α' Ρη(Βη) = 1,
А;=1 ^ П П '
а для равномерного на [0,1] распределения P(i?n) < 2/п, так что
suP|p;(b) - р(в)| ^ р;(в„) - р(вп) -> ι.
вез
В заключение этого параграфа отметим, что представление (2) позволяет
получить для Р* и более точные теоремы об асимптотическом поведении,
чем теоремы типа Гливенко-Кантелли (эти результаты будут представлены
в §4, 6). Чтобы проиллюстрировать возможности, которые здесь есть, на-
71
помним, что yjlxi(i?) в (2) есть сумма независимых одинаково распреде-
ленных случайных величин в схеме Бернулли,
EIXi(B)=P(IXi(B) = l)=P(B),
тЦв) = р(в), mXi(B) = p(b)(i - р(в)).
Поэтому из центральной предельной теоремы немедленно вытекает
следующее утверждение.
28
Гл.1. Выборка. Эмпирическое распределение
Теорема 3. P£(i?) представило в виде
Р*п(В) = Р(В) + ζ-^ψ-, (8)
1 n
где распределение ζη(Β) = —^=)(1Х.(В)-Р(В)) сходится к нормальному
распределению с параметрами (0,P(i?)(l — Р(1?))).
Дальнейшее изучение Р£(5) в этом направлении содержится в § 6. Более
точные теоремы о сходимости с вероятностью 1 см. в § 4.
§ 3. Выборочные характеристики. Основные типы статистик
1. Примеры выборочных характеристик. Выборочными
характеристиками называют обычно различные измеримые функционалы от
эмпирического распределения или, другими словами, функции от выборки, которые
предполагаются измеримыми. Наиболее простые среди них — выборочные
(или эмпирические) моменты. Выборочным моментом порядка к
называется значение
J ηί=ι
Выборочный центральный момент порядка к равен
а? = а*к°(Х) =/"(*- <)kdK(x) = Ι Σ> " <)к.
J n i=i
Для выборочных моментов а* и а™ в литературе распространены
специальные обозначения χ и S2:
В статистических задачах используются самые различные выборочные
характеристики. Например, выборочная медиана ζ* — это среднее значение
вариационного ряда, т.е. значение ζ* = X(m), если η = 2га — 1 (нечетно),
и ζ* = (x(m) + X(m+1))/2, если η = 2га (четно). Напомним, что медианой ζ
непрерывного распределения Ρ называется решение уравнения Ρ(ζ) = 1/2.
Более общим понятием является понятие квантили ζρ порядка р. Это
число, для которого F((p) = р. Так что медиана есть квантиль порядка 1/2.
Если F имеет точки разрыва (дискретную компоненту), то это
определение теряет смысл. Поэтому в общем случае будем пользоваться следующим
определением.
Квантилью ζρ порядка ρ распределения Ρ называется число
ζρ = sup {x : F(x) <p}.
Как функция от р квантиль ζρ есть не что иное, как функция F~1(p),
обратная к F(x).
§ 3. Выборочные характеристики
29
Такое определение ζρ (или F~l(p)), в отличие от предыдущего, очевидно,
имеет смысл для любых F{x).
Ясно, что наряду с выборочными медианами можем рассматривать
выборочные квантили ζ* порядка р, равные по определению значению Х(/), где
/ = [пр] + 1, Х(д.) — члены вариационного ряда для выборки Х) к = 1,.. .,п.
Для ρ = 1/2 мы сохраним определение ζ* = ζ*/2, данное выше (оно
совпадает с приведенным лишь при нечетных п).
2. Два типа статистик. Пусть дана измеримая функция S от η
аргументов. Выборочная характеристика S(X) = S(xi,.. .,хп) часто называется
также статистикой. Из сказанного выше ясно, что любая статистика есть
случайная величина. Ее распределение полностью определяется
распределением Ρ {В) = Ρ(χι Ε В) (напомним, что S(X) можно рассматривать как
случайную величину, заданную на (#n,Q3^,P), где Ρ — η-кратное прямое
произведение одномерных распределений χι).
Мы выделим здесь два класса статистик, которые часто будут
встречаться в дальнейшем. Они будут построены с помощью следующих двух
видов функционалов G(F) от функций распределения F.
I. Функционалы вида
G(F)=hl I g(x)dF(x)
где g — заданная борелевская функция, h — функция, непрерывная в точке
а = / g(x) dFo(x), где Fq такова, что X €= F0.
II. Функционалы G(F), непрерывные в «точке» Fq в равномерной
метрике: G(F^) -> G{F0), если sup \fW(x) - ад| -> о, носители*) рас-
х
пределений принадлежат носителю Fo. Здесь Fo опять есть функция,
для которой X €= Fo·
Соответствующие классы статистик мы определим с помощью равенства
s(x) = g{f:),
где F* — эмпирическая функция распределения. Мы получим тогда:
I. Класс статистик I типа, представимых в виде
S(X) = h (/ д(х) dFn*(s)) = h (^ J2g(xi) J .
Очевидно, все выборочные моменты имеют вид аддитивных статистик
1 п
— 2_.9{хг) и относятся к статистикам I типа.
г=1
') Носитель Nf распределения Ρ с функцией распределения F есть множество, для
которого Ρ(Νρ) = 1.
30
Гл. 1. Выборка. Эмпирическое распределение
II. Класс статистик, которые будем называть статистиками II типа
или статистиками, непрерывными в точке Fq.
Ясно, что, например, выборочная медиана будет непрерывной
статистикой в точке F, если существует медиана ζ, F(() = 1/2, и F непрерывна и
строго возрастает в точке ζ.
Принадлежность функционалов одному из названных классов, конечно,
не является альтернативной. Функционал G(F) может не принадлежать ни
одному из этих классов или принадлежать обоим сразу. Например, если G
есть функционал I типа, носитель F сосредоточен на отрезке [a, b] {F(a) = 0,
F(b) = 1), а функция g имеет ограниченную вариацию на [а, 6], то G будет
одновременно функционалом II типа, так как в этом случае функционал
о
j g(x) dF(x) = g(b) - j F{x) dg(x)
непрерывен относительно F в равномерной метрике. Сказанное означает,
что статистики I типа χ и 52 будут также статистиками II типа, если X €= Ρ
и Ρ сосредоточено на конечном интервале.
Статистики вида G(F*) иногда называют также статистическими
функциями. Их систематическое исследование было начато фон Мизесом
(см. [75, 76, 115]).
Теоремы 2.1 и 2.2 можем дополнить здесь следующим утверждением о
п. н. сходимости выборочных характеристик.
Теорема 1. Пусть, как и прежде, Хп = [Xoo]n^F. Тогда если
S(X) = G(F*) есть статистика I или II типа, то при η —> оо
G(F;) -► G(F).
Здесь предполагается, конечно, что значение G(F) существует.
Таким образом, выборки большого объема позволяют оценивать не
только само распределение Р, но и функционалы от этого распределения —
по крайней мере те, которые принадлежат одному из названных в теореме
классов.
Доказательство утверждения для обоих классов статистик почти
очевидно. Пусть, например, G(F) = h Ι / g(x)dF(x) J . Тогда
S = S(X)= i9(x)dF*{x) = ^g(xi)
J n i=i
есть сумма независимых случайных величин с математическим ожиданием
Eg(xi)= fg{x)dF(x).
Поэтому по усиленному закону больших чисел S —> Ε<?(χι). Пусть теперь
А = {Хоо : S(X) -> ΕίΚχι)}. Тогда Р(А) = 1, и если Хоо € А, то S(X) ->
—> E<?(xi)) h(S(X)) —> /ι(Ε<?(χι)). Другими словами, на множестве А
G(F*) -> G(F).
§ 3. Выборочные характеристики
31
Утверждение теоремы для функционалов второго типа есть прямое
следствие теоремы Гливенко-Кантелли. <
Из теоремы вытекает, что абсолютные и центральные выборочные
моменты п. н. сходятся при η -> оо к соответствующим моментам
распределения Р:
4 = 4(x) = ^i^.E^
1=1
ι п
a? = a*k°(X) = - 2>i - х)* гт> Ε(χι - EXl)\
П ^ ' π.η.
В частности,
г=1
Таким образом, мы установили важный факт, имеющий для нас
принципиальное значение: эмпирическое распределение и широкий класс
функционалов от него с ростом объема выборки неограниченно сближаются с
соответствующими «теоретическими» значениями.
3. L-статистики. Так называются статистики, являющиеся линейными
комбинациями членов вариационного ряда или функций от них:
Здесь функция д и коэффициенты φη^ заданы. Очевидно, что все
выборочные квантили являются L-статистиками.
Если положить φη{ί) = φη % при t Ε ( , — ) , то статистику Sn(X)
\ η η J
можно представить в виде
1
Sn(X) = JtpnMF-Htfidt, (1)
о
где F~l — обратная функция к эмпирической функции распределения F*.
Если φη(ΐ) сближается при η —> сю в подходящем смысле с функцией
(p(t), то естественно ожидать, что Sn(X) будет близко к статистике G(F^),
где
ι
G(F) = J<p(t)g(F-l(t))dt = J<p(F(u))g(u)dF(u). (2)
о
Очевидно, что G(F*) есть L-статистика при φη^ = φ ( ] . Считая на
время, что F*(u) непрерывна справа (это предположение ничего не меняет
32
Гл. 1. Выборка. Эмпирическое распределение
в последующих доказательствах), получим несколько более удобную запись
ψη г — φ ( ~~ ) · Представление (2) доставляет весьма широкий «регулярный»
выбор для коэффициентов φη^ в определении Sn(X). Поэтому, чтобы
избежать технических осложнений, ограничимся в дальнейшем рассмотрением
L-статистик вида G(F*), построенных на основании функционала G,
определенного в (2).
Отметим, что выборочная квантиль порядка ρ и крайние значения
вариационного ряда Х(х) и Х(п) являются L-статистиками вида (1), для которых
φη{ί) сходятся при η —> ос к (S-функциям Дирака. В дальнейшем будем
предполагать, как правило, что φ(ί) в (2) является «обычной» (не обобщенной)
функцией.
Так как функции φ и g в представлении (2) определены неоднозначно
(с точностью до постоянных множителей, произведение которых равно еди-
1
нице), то можно фиксировать значение φ$ = I ip(t) dt.
О
Запись (2) показывает, что статистики I типа при h(x) = χ являются
L-статистиками, а L-статистики при φ = 1 являются статистиками I типа.
4. М-статистики. Пусть ψ{χ,θ) — некоторая функция Χ χ Шк —> R.
Рассмотрим функционал G(F), который определяется как точка максимума
по
θ функции ,φ(χ.θ)1Ρ(άχ).
Μ-статистикой (или Μ-оценкой) называется значение Θ* = G(F£)
или, что то же, точка #*, в которой достигается
шахУ^^(хг,^) — шахη / ψ{χ,θ) dF^(x). (3)
Если точек максимумов несколько, то любая из них является М-оценкой.
Часто используется и несколько иное (более регулярное в известном
смысле) определение. Μ-статистикой (М-оценкой) называется решение
уравнений
5>(χ,,0) = ο, (4)
где #, как и ψ, есть некоторая заданная функция на X х Шк. Кроме того,
термин М-статистика будем использовать иногда и как собирательный,
включающий в себя оба вида упомянутых выше М- и М-статистик.
Если функция ψ в (3) дифференцируема по 0, то очевидно, что
М-статистика (в смысле определения (3)) будет М-статистикой (в смысле
определения (4) при замене в (4) g производной ф1 по Θ). При этом определение (4)
может добавлять «ненужные» значения #*, в которых достигаются
локальные экстремумы.
Более подробно М-статистики будут изучены в главе 2. Они играют
важную роль в теории асимптотически оптимальных оценок.
§ 4. Многомерные выборки
33
5· О других статистиках. Имеют распространение и некоторые другие
«собирательные» классы статистик такие, например, как ίΖ-статистики,
построенные на основе функционалов
G{F) = h(xi,...,xm)P(dxi)...P(dxm), 1 ^ т < га,
где h — симметрическая функция, называемая иногда ядром функционала.
U-статистикой называется статистика
G{F;)=n-mJ2h(x4,...,xim),
где суммирование ведется по всем ii,..., im между 1 и гг.
Очевидно, что выборочные моменты являются [/-статистиками.
Почти все встречающиеся в приложениях статистики принадлежат
одному из названных выше классов. С другой стороны, асимптотическое
поведение распределений статистик для каждого из этих классов может быть
изучено весьма полно. Результаты в этом направлении будут изложены в § 7, 8
и в главе 2.
§ 4. Многомерные выборки
1. Эмпирические распределения. Совершенно аналогичным образом
выглядят построения эмпирического распределения и выборочных
характеристик в многомерном случае, когда наблюдаемая случайная величина ξ, а
вместе с ней и выборочные значения χι,...,χη есть векторы размерности
т > 1: χ*; = (xfc,i·. .,Xfc,m)· Здесь Έ*(Β) = Ρ(ξ £ В) есть распределение
в X = Rm, а выборочным пространством здесь будет (Α^,Ώ^,Ρ), где Ρ
есть η-кратное прямое произведение распределений Ρ в (Km,53^ = 23д)·
Обозначение X €= Ρ полностью сохраняет свой смысл.
Эмпирическое распределение Р* по выборке X строится, как и раньше,
как дискретное распределение с массами величины \/п в точках χι,..., хп,
так что
вд-^—Ем*),
η η .
где ν(Β) — число точек, попавших в множество J3, IXi — распределение,
сосредоточенное в точке хг.
Утверждение теоремы 1 о сходимости Р£(£?) —> Р(£?) здесь, очевидно,
сохранится.
Обобщение теоремы Гливенко-Кантелли на многомерный случай связано
с появлением качественно новых вопросов. Один из них — обобщения
понятия интервалов на многомерный случай. Таких обобщений может быть
несколько — это могут быть, например, прямоугольники, выпуклые
множества и др.
Простейший вариант обобщения теоремы Гливенко-Кантелли таков.
Пусть у = (yi,.. .,уш) есть точка Rm и Bt есть угол с вершиной в точке
Bt = {y£mm:yk<tk, *=1,...,го}.
34
Гл. 1. Выборка. Эмпирическое распределение
Функция
iS(t) = p;(Bt)
называется эмпирической функцией распределения.
Теорема 1. Пусть Хп = [Хоо]П5 Xoo^F. Тогда
sup|Fn*(i)-F(i)|^0
при η —> оо.
2*. Более общие варианты теоремы Гливенко-Кантелли. Закон
повторного логарифма. Одно из возможных обобщений теоремы типа Гливенко-
Кантелли состоит в следующем. Пусть С — класс всех выпуклых множеств
вЕт.
Теорема 2. Пусть Хп = [Хоо]т Аоо^Р? распределение Ρ
абсолютно непрерывно относительно меры Лебега в Мт. Тогда
suP|p;(B)-p(B)|—>о. (1)
вес Π·Η·
Другие возможные обобщения теоремы 1 можно получить с помощью
утверждений приложения I.
Замечание 1. Требование абсолютной непрерывности
распределения Ρ относительно меры Лебега в теореме 2 существенно. На это указывает
следующий пример. Пусть Ρ есть равномерное распределение на единичной
окружности (т.е. на границе круга) в R2. Построим замкнутый
многоугольник Βχ с вершинами в точках χι,...,χη, лежащих на окружности. Это
выпуклое множество. Однако Ρ (Β χ) = О, Ρ^(Βχ) = 1, и, следовательно,
соотношение (1), где £ — класс выпуклых множеств, не верно.
Утверждения теорем типа Гливенко-Кантелли можно существенно
уточнить — по крайней мере для простейших классов множеств. Например, для
эмпирических функций распределений F*(t) (см. теорему 1) можно указать
такую детерминированную последовательность Ьп —> 0 при η -> оо, для
которой с вероятностью 1 (для почти всех «точек» Хоо)
\imswpb-lsnp\F*(t)-F(t)\ = l.
n-teo t
/In In η
Оказывается, что порядок малости Ъп такой же, как \ — .
γ η
Теорема 3 (закон повторного логарифма). Если F(t) непрерывна, то
,*%?\/Ж'Г\г"м-™\-1)
= 1.
Теорема 3 тесно связана с нормальным приближением для F*(t) вида
(2.8), которое в многомерном случае, очевидно, также имеет место.
Доказательство теорем 1, 2 отнесено нами в приложение I.
Доказательство теоремы 3 см. в [52].
§ 5- Теоремы непрерывности
35
3. Выборочные характеристики. В многомерном случае, как и в
одномерном, они представляют различные измеримые функции от выборки.
Простейшие из них — выборочные моменты. Например, выборочные моменты
первого порядка равны
1 п
моменты второго порядка (обычные и центральные) —
1 п
ahj = a2,ijW = - X^xMxA:j, г, j = 1,.. .,m,
1 n
<*ад = Sij = - 5Z(xfc,i - αϊ,<) (xfcj - αί j)
Jc=l
и т.д. Как и в одномерном случае, легко убедиться с помощью
усиленного закона больших чисел, что эти характеристики с вероятностью 1
сходятся к соответствующим «теоретическим» моментам. В частности, Sn —>
J П.Н.
—> E(xi,i — Exi)i)(xi>j — Exij). Нетрудно убедиться (подробнее об этом см.
в следующем параграфе), что этим же свойством обладают и выборочные
коэффициенты корреляции
r _ Sjj Е(хм-Ехм)(хи-Ехц)
y/SiiSjj Π·Η- ^/Dxi}iDxij
Отметим, что все типы статистик, введенные в §3, за исключением
L-статистик, допускают естественное обобщение на многомерный случай и
случай произвольного выборочного пространства X.
Для получения более точных теорем о распределении выборочных
характеристик нам будут полезны так называемые теоремы непрерывности.
§ 5· Теоремы непрерывности
В дальнейшем нам понадобятся некоторые вспомогательные
утверждения, которые мы будем часто использовать и которые можно было бы назвать
теоремами непрерывности. Для удобства выделяем их в отдельный
параграф. Одну теорему такого типа мы уже использовали — это теорема 3.1.
Первая теорема непрерывности будет очень близка к этой теореме.
Теорема 1 (первая теорема непрерывности). Пусть X = [Х00]П^Р.
Тогда если Sn = Sn(X) есть последовательность скалярных или
векторных статистик таких, что Sn —> SO, и H(s) — функция, непрерывная
п.н.
почти всюду относительно распределения случайной величины SO (га. e.
H(s) непрерывна в каждой точке множества В, Ρ (So Ε: В) — 1), то
H(Sn(X)) —* H(S0).
п.н.
Если Sn сходится к So no вероятности (Sn —> So), то при тех -же
ρ
прочих условиях H(Sn) —> Η (So).
36
Гл.1. Выборка. Эмпирическое распределение
Доказательство теоремы почти очевидно. Так как вероятности
событий А = {Хоо : Sn(Хоо) -> 50(Хоо)} и С - {Хоо : 50(Хоо) G В} равны 1,
то в силу равенства Р(АПС) = Р(Л)+Р(С)-Р(АиС) вероятность события
А П С (на котором Я(5,п(Х0о)) -> Я"(5о(-Х"оо)) также равна 1.
Чтобы упростить доказательство о сходимости по вероятности,
предположим дополнительно, что Sq — const (нам только этот случай и
понадобится). Для заданного ε > 0 найдется δ > 0 такое, что событие Ап =
= {Хоо : |5П — 5о| < ί} влечет за собой \H(Sn) — Я(5о)| < ε и, кроме того,
Р(АП) > 1 — ε при всех достаточно больших п. Следовательно, для таких η
имеем 1 - ε < Р(ЛП) ^ Р(|Я(5П) - Я(50)| < ε). <
Прежде чем формулировать последующие теоремы, введем некоторые
обозначения, которые будут удобны в дальнейшем.
Пусть дана последовательность случайных векторов ηη = (% ,.. .,r/n )
(не обязательно на одном вероятностном пространстве). Если
распределения ηη слабо сходятся при η —> оо к распределению некоторой случайной
величины 77, то этот факт будем обозначать символом
Vn => τ/· (1)
Здесь мы используем для случайных величин знак => слабой сходимости
распределений. Этот знак будет употребляться по-прежнему и для самих
распределений, так что соотношение (1) эквивалентно тому, что
где Qn и Q суть соответственно распределения ηη и η. Такое соглашение
удобно и не приводит к недоразумениям.
Ясно, что из ηη —* η или ηη —► η следует ηη => '/7 (ср. с [17, § 6.2]).
р п.н.
Таким образом, если речь идет о соотношении (соответствующем слабой
сходимости) между объектами одной природы (между случайными
величинами или между распределениями), будем использовать символ =>. Наряду
с этим нам было бы удобно иметь также символ для выражения
«распределения ηη слабо сходятся при п —> оо к Q». Это соотношение будем
записывать в виде
Vn & Q, (2)
так что символ €> выражает тот же факт, что и =>, но соединяет объекты
разной природы так же, как это делает символ €= в соотношении η €= Q
(слева в (2) стоят случайные величины, а справа — распределение).
Пусть ηη и η есть случайные векторы из W.
Теорема 2 (вторая теорема непрерывности). Если ηη => η и H(t),
t Ε Μ5, есть непрерывная функция из Rs θ Rk, mo Η(ηη) => Η(η).
Отметим, что эта теорема на самом деле верна и в более общей форме*):
Если ηη =ϊ η и H(t) непрерывна в точках множества Α Ε 235, Ρ (г/ Ε Α) =
= 1, то Η{ηη) => Η{η).
*) Подробнее об этом см. в [7].
§ 5. Теоремы непрерывности
37
Доказательство теоремы 2. Пусть Qn и Q есть соответственно
распределения ηη и η. Слабая сходимость Qn => Q означает по
определению, что для любой непрерывной и ограниченной функции /: Rs —)► К
выполняется
/ f(y)Qn(dy) -> J f(y)Q(dy),
или, что то же самое,
Е/Ы -> E/fo). (3)
Аналогичное соотношение мы должны получить и для распределений
Η(ηη) и Η(η). То есть мы должны установить, что для любой непрерывной
ограниченной функции д: Rk —> К справедливо Ед(Н(щ)) —> Eg(Hfa)). Но
это очевидным образом следует из (3), так как суперпозиция 'д = доН :RS —>
—> К непрерывна и ограничена. <
Теорема 3 (третья теорема непрерывности). Пусть ηη => η £ Κ, .#(£),
t Ε 1, есть функция, дифференцируемая β точке а. Тогда если Ьп —> О
есть числовая последовательность, то
H(a + bnV)-H(a) ^
On
Доказательство. Рассмотрим функцию
Н{а + х)-Н(а)
х^О,
h(x) = { χ
.Η'(α), χ = 0,
которая будет непрерывной в точке χ = 0. Так как Ьпг\п => 0, то в силу
первой теоремы непрерывности h{bnr\n) =Ф- h(0) = Η1 [а). Пользуясь второй
теоремой непрерывности, получим
Н(а + 6П?7П) - Н{а) ,
Г = HbnVnWn =* Η (α)η. <
On
Мы приведем теперь два последовательных обобщения теоремы 3 на
многомерный случай, которые будут нам полезны.
Теорема ЗА. Пусть ηη = (ηηι\ .. .,Vns)) =>η = (t/W, .. .,τ/β>), H{t) -
скалярная функция вектора t = (£ι,...,£5) такая, что существует про-
изводная Hit) = { ——,..., -ζ— Ι β точке а. Тогда при Ъп —> 0
Н(а + Ьпч)-Н(а) ^ η{Η,{α))Τ = А вЯМ^Ю (5)
Здесь индекс Τ соответствует транспонированию.
38
Гл.1. Выборка. Эмпирическое распределение
Если т/(Я'(а))т = О с вероятностью 1 (например, Н'(а) = 0), а ма-
трица Η [t) производных — существует в точке а, то
atiOtj
Н{а + Μη) - Н{а) 1 „ т 1 А
ш =ϊ-ηΗ(α)η = -^
52Я(а)
ь1 2' к J' 2.4^ aiiS*
7/«т/Л· (6)
<J = 1 '^J
Пусть теперь H(t) — векторная функция. Тогда, очевидно, предельное
распределение для каждой компоненты Hj будет описываться теоремой ЗА,
а относительно совместного распределения будет справедлива
Теорема ЗВ. Пусть ηη => η Ε IK5, Я(£) Ε R* — векторная
функция такая, что производные Я'·, j = !,...,&, удовлетворяют условиям
теоремы ЗА. Тогда
Ща + ЬпПп)-Ща) ^ η(Η,{α))τ
On
Если 77(Я'(а))т = 0 с вероятностью 1, α матрицы Я'7, j = 1,...,/с,
существуют в точке а, то
Доказательства этих утверждений по существу ничем не
отличаются от доказательства теоремы 3, и поэтому предоставляем их читателю
в качестве упражнений. Кроме того, предлагаем убедиться, что символ =>
в (4)-(6) можно заменить на —► или —>, если соответственно выполняется
4 ' п.н. ρ
ηη —> η или ηη —> η.
п.н. ρ
Содержание теорем 1-3 можно резюмировать следующим образом. Пусть
~* означает один из символов —», —►, =ϊ . Тогда если Я непрерывна, то из
П.Н. ρ
ηη ~» η следует Η(ηη) ~> Η (η).
Если Я дифференцируема в точке а, т^ ~* ?7, то для Ьп —> О
Я(а + 6п;?п)-Я(а) ^ ^
£>п
Замечание 1. Нетрудно видеть, что если α = ап зависит от п так,
что ап = ао + ^(1), и производные в теоремах 3, ЗА, ЗВ непрерывны, то
соотношение (7) сохранится в форме
#К + Μη) - #К) ^ я,(ао) (
On
Для доказательства достаточно заметить, что левая часть (8) предста-
вима в виде Η'(αη)ηη, где ап = 9ап + (1 - 0)(αη 4- bn^n) ~* «о» 0 ^ 0 < 1, и
воспользоваться второй теоремой непрерывности.
§ 5. Теоремы непрерывности
39
То же самое замечание справедливо для многомерных аналогов этого
утверждения в теоремах ЗА, ЗВ.
Сформулированные теоремы касались сходимости почти наверное и
сходимости распределений. Четвертая теорема непрерывности относится к
сходимости интегралов.
Теорема 4 (теорема непрерывности для моментов). Пусть {ηη} —
последовательность числовых случайных величин и ηη=> η при п —> оо.
Тогда если выполнено хотя бы одно из следующих условий:
1) limsup / Р(|??п| > #) dx —> 0 при N —> оо,
п—юо J
N
оо
2) Р(|тм| > ζ) < φ(χ), \ φ{χ)άχ < оо,
о
|1+α
3) Е|т7п| < с < оо для некоторого а > О,
то lim Έηη = Е77.
η—юо
ОС
/
Отметим, что условие 1) означает равномерную по п сходимость к нулю
Р(|*7п| > х) dx при N -> оо.
N
Доказательство. Из обобщенного неравенства Чебышева
Р(Ы>я?)
х1+а
следует, что условие 3) влечет за собой условие 2). В свою очередь, условие 2)
влечет за собой условие 1).
Пусть выполнено условие 1). Для простоты рассуждений предположим
сначала, что ηη ^ 0. Тогда, интегрируя по частям, получим
оо оо
Ет?п = - / χάΡ(ηη ^ х) = / P(?7n ^ x) dx.
о о
Из этого представления, из сходимости Ρ (77η ^ χ) —> Ρ (г/ ^ χ) для почти
00
всех а: и из равномерной по η сходимости интеграла / P(?7n ^ я) dx следует
о
законность предельного перехода под знаком интеграла, в силу которого
оо оо
lim Έηη = lim / Ρ(ηη ^ x)dx = / Ρ(η ^ x)dx — Ε77.
η-»οο π-»οο у у
О О
В общем случае следует воспользоваться представлением г\п = η£ — η~,
где 7/+ = max (т/п,0), η~ = max (-τ?η,0). <
40
Гл. 1. Выборка. Эмпирическое распределение
Отметим, что условие 1) можно рассматривать так же, как условие
равномерной интегрируемости ηη, из которой немедленно следует сходимость
Εηη -> Εη (см., например, [17, гл. 6; 72, §6.2)].
§ 6·* Эмпирическая функция распределения
как случайный процесс· Сходимость к броуновскому мосту
В этом параграфе будем предполагать известным понятие случайного
процесса (скажем, в объеме [17]) и, в частности, определения и простейшие
свойства винеровского и пуассоновского процессов.
1. Распределение процесса nF£(t). Ограничимся рассмотрением случая
X = Ж. Пусть, как и прежде, F*(t) = Р*((—оо,£)) есть эмпирическая
функция распределения, соответствующая выборке X = Хп €=Р.
Функция F*(t) есть функция двух переменных: t и X, или, что то же,
случайная функция от t или случайный процесс.
Найдем конечномерные распределения этого процесса. Пусть t\ <
< Ϊ2 < ... < tm — произвольные т точек числовой оси. Положим ίο = — оо,
im+i = оо и обозначим через
Aj0 = 0(*j+i)-0(*i)
приращения функции g(t) на полуинтервалах Δ^· = [ij, ij+i)> J = 0,1,..., m.
Рассмотрим приращение Δ^πη процесса
πη(ί)=η^(ί).
Очевидно, это есть число элементов выборки, попавших в Δ^. Вероятность
попадания одного элемента выборки (скажем, χχ) в Δ^ равна pj = Ρ(Δ^).
Так как попадания в Δ^, j = 0, 1,...,га, представляют собой т + 1
несовместных событий, то, очевидно, имеем здесь полиномиальное
распределение (см. [17, § 5.2]) для вектора (Δοπη,..., Аткп) с вероятностями ро> · · *,Рт,
ТП
y~]pj = 1· Как известно,
i=o
Ρ(Δ0πη = fc0l.. ·, Δ™πη = fcm) = П> fp£°.. .ρ*Γ, (1)
ko\...km\
m
где V^ kj = n.
j=o
Пусть теперь η(ν), и Ε [0,1], есть непрерывный слева пуассоновский
процесс (см. [17, § 16.4]) с параметром λ, 77(0) = 0. Приращения этого процесса
независимы,
P(iW=*)=e-to1^.
Если функция распределения F(t) = Р((—οο,ί)) непрерывна, то можем
сделать непрерывную замену времени, положив и = F(t), — 00 < t < 00,
§ 6. Эмпирическая функция распределения как случайный процесс 41
и определить тем самым процесс n(t) = η(Ρ(ί)) на всей оси. Рассмотрим
приращения этого процесса
Δ,π = n(tj+1) - π(ί,) = v(F(tj+i)) - v(F(tj))
на интервалах Δ^. Тогда
Ρ(Δ0π = fc0,..,A^ = U = Де-^ШИ = e-^"J] Г7-
m
а условная вероятность того же события при условии π(οο) = \^Δ^π = η
j=o
будет равна
Ρ Δ0π = feo,.. ·, Δ™π = fc,
^Δ,π = η ι =
i=o
Ρ(Δ0π = fcp,..., Δ7ηπ = fcm)
Ρ(π(οο) = η)
λ ! rn r) J
= Ρ(Δ0π = fc0>. · -, Am* = km)^- = η! JJ -i-. (2)
Мы получили при любом λ > 0 то же самое выражение, что и в правой
части (1). Таким образом, мы доказали следующее утверждение.
Теорема 1. EcAuF(t) непрерывна, то распределение процесса nF*(t)
совпадает с условным распределением процесса π(ί) = (η(Ρ(ί)) при
условии π(οο) = η (77(1) = η).
Теорема показывает, что отклонения n[F^{t) — F(t)) распределены так
же, как 7/(F(i)) — nF(t) при условии η(1) — η, и задача с точностью до
замены времени и = F(i) сводится к изучению отклонений т/(и) — тш для
условного (?7(1) = п) пуассоновского процесса на отрезке [0,1] или, что то же,
к изучению отклонений n{F^(t) — t), где F£{t) соответствует равномерному
на [0,1] распределению.
Полезным бывает и другое представление для процесса nF*(t). Пусть
Сь Сг> ■ · · — точки скачков пуассоновского процесса т;(£), так что ^(Ofc+O) ~ ^-
Как известно [17], разности ^ — Cfc — Сл—ι (Со = 0), А = 1,2,..., независимы
и показательно распределены,
Ρ (ξ* > х) = е~Хх,
ζΐς имеет Г-распределение с плотностью (см. также § 12)
42
Гл. 1. Выборка. Эмпирическое распределение
Чтобы упростить формулировки, предположим, что F(t) — ί, t G [0,1], to =
= 0, im+i = 1, так что η(ί) — π(ί).
Теорема 2. Распределение процесса nF*(t) совпадает при любом
ν > 0 с условным распределением процесса 7г(£г>), 0 < ί < 1, npw условии
Cn+l = U>
Другими словами, утверждение теоремы 1 сохранится, если условие
π(1) = η заменить значительно более узким условием π(1) = η, π(1 + 0) =
= η + 1 (мы считаем, что траектории π(ί) непрерывны слева).
Поскольку вероятность этого нового условия равна 0, то, возможно,
следует добавить (см. [17, §4.8 об условных математических ожиданиях, а
также §19]), что под условным распределением мы понимаем здесь
вероятности
τ>(Δ//- ·λ Р(Л;Сп+1 edv)
где А = {Δοπ(ίυ) = fco, · ·>, Δ771π(^) = fcm}, Δ^π(ίυ) = π(^>ι^) - n(tjv).
Доказательство. Событие {ζη+ι € dv} представим в виде
произведения двух событий
В = {π{υ) = η}, С = {π(υ 4- cfo) - π(υ) = 1}.
События 5 и АВ не зависят от С, так как события В и АВ, с одной
стороны, и событие С — с другой относятся к приращениям процесса π на
непересекающихся интервалах времени. Поэтому
Р(Л/С„+1 = ν) = Щ^ = ^ = Ρ(Λ/π(«) = η). (3)
Точно так же, как в (2), убеждаемся, что это выражение от ν (как и от λ) не
зависит и совпадает с (1). <
Следствие 1. Распределение процесса nF*(t) совпадает с
распределением π(£ζη+ι), 0 ^ t ^ 1.
Это вытекает из того, что для
В = {Δ0π(*(η+ι) = fc0,. - ■> Am^(<Cn+i) = fcm}
имеем в силу (3)
Р(5) = У Р(Л/С„+1 = г;)Р(Сп+1 € rf«) = η! Ц -^-.
Из следствия 1 вытекает
Следствие 2. Совместное распределение элементов вариационного
ряда Х(!),.. .,Х(П) выборки X из равномерного распределения совпадает с
§ 6. Эмпирическая функция распределения как случайный процесс 43
совместным распределением
Cl Сп
Сп+1 Сп+1
или, что то же, совместное распределение разностей х^), Х(2) — X(i),...
■ · ·5χ(η) — χ(η-ΐ)> 1 — х(п) совпадает с совместным распределением
£ΐ ξη+1
Cn+1 Cn+1
В заключение этого пункта найдем моменты второго порядка для
приращений процесса n(F*(t) — F(t))> Нам будет удобнее иметь дело с процессом
wn(t) = yfr{FZ(t)-F(t)).
Очевидно, что EAjWn = О, E{AjWn)2 = AjF(l - AjF). Для вычисления
смешанных моментов заметим, что (г φ j)
E(AiWn ■ AjWn) = i £ Ε(ΙΧ4(Δ<) - Ρ(Δ;))(ΙΧ,(Δ,·) - Ρ (Δ,·)) =
= τ Σ {ΕΙχ,(Δί)Ιχ,(Δ,·) - Ρ(Δ<)Ρ(Δ,·)}.
η
k,l=
"*,!=
Так как
ew*.)ma,)={r-)P(^ ^ίϊί:
το Ε(Δ<ιι;η · Ajwn) = -Ρ(Δ,)Ρ(Δ;) = -A,F · AjF.
Таким образом, приращения процесса wn отрицательно коррелированы.
2. Предельное поведение процесса wn(t). Мы будем считать, что F(t)
непрерывна. В предыдущем пункте мы видели, что задача отыскания
распределения nF^(t) для произвольной непрерывной функции распределения F
может быть редуцирована в известном смысле к той же задаче для функции
распределения U(t) = £, 0 < t ^ 1, соответствующей равномерному на [0,1]
распределению. Такой редукцией будем пользоваться и в дальнейшем.
Сделаем в связи с этим несколько предварительных замечаний.
Пусть x(F) = ini{t: F(t) > 0} — левая граница носителя
распределения F. Положим F~~l(0) = χ(ρ\ Ρ~λ(η) =sup{ir. F(v) < и} при и > 0.
Функция F_1(u) называется обратной к F, она так же, как и F, непрерывна
слева. Если F непрерывна, то F~l(u) есть минимальное решение
уравнения F(v) = и (решение единственно, если F(v) строго монотонна).
Нетрудно видеть также, что если F непрерывна, то F(F~l(t)) = ί, t Ε [0,1].
В этом случае функции от наблюдений у^ = -^(ха;) представляют собой
выборку У из равномерного на [0,1] распределения, так как по определению
обратной функции
P(yfc < t) = P(F(xfc) < ί) = P(xfc < ^_1(ί)) = F(F~4t)) = t.
44
Гл. 1. Выборка. Эмпирическое распределение
Так как, кроме того,
PiF-Hyk) <t) = P(y* < F(t)) = F(t),
ТО
Y = (yi,...,Vk)eU, (F-Hy^.-.F-HykV^F.
Если U£ — эмпирическая функция распределения, соответствующая
выборке Υ из равномерного на [0,1] распределения, то из сказанного следует,
что
Fn*(t) = K(F(t)). (4)
Действительно, левая и правая части этого соотношения равны k/n при
t € (х(*),Х(А;+1)] или, что то же, при
F{t) е {F{x{k),F{x{k+l})] = (у(*),У(*+1)], Л = 1,...,п.
Итак, если найдем способы приближать тем или иным образом
распределение процесса U*(t) при больших п, то тем самым в силу (4) мы найдем
подходы и к приближенному описанию распределения процесса F*(t) для
произвольной непрерывной F.
В дальнейшем в этом пункте будем считать, что F(t) = U(t) есть
равномерное на [0,1] распределение.
Обозначим через w(t) стандартный винеровский процесс, т.е. процесс
с независимыми приращениями, для которого w(t) распределено нормально
с параметрами (Ο,ί). Процесс
w°{t) = w(t)-tw(l)
называют броуновским мостом (по той причине, что у него закреплены
оба конца: w°(0) = w°(l) = 0). Распределение этого процесса совпадает с
условным распределением процесса w(t) при условии w(l) — 0 (более точно,
надо взять условие |ги(1)| < ε и перейти к пределу при ε ~> 0).
Оказывается, что конечномерные распределения процессов
wn(t) = ^(F*(t)-F(t)), i G [0,1],
сходятся при η —> оо к соответствующим распределениям броуновского
моста w°(t).
Этот факт позволяет приближать процессы wn(t), которые называют
иногда эмпирическими процессами, с помощью процесса w°(t). Именно, мы
можем представлять себе, что при больших η имеет место приближенное
равенство
V^{F:(t)-F(t))*w°(t), (5)
описывающее распределение уклонений F£{t) от F(t) (напомним, что мы
считаем здесь F(t) = t, t Ε [0,1]).
Однако утверждение типа (5) нам понадобится в более сильной форме.
Рассмотрим, например, статистику S~\/nsup[F^(t) — (t)). Высказанное
t
утверждение делает естественным предположение о том, что при больших η
§ 6. Эмпирическая функция распределения как случайный процесс 45
случайная величина S приближенно распределена так же, как sup w°(t).
Однако из нашего утверждения это никак не следует, поскольку 5 нельзя
представить как функцию от значений wn(t) = y/n (F^(t) — f{t)) в каком-
либо конечном числе точек. Поэтому существенно более сильным является
следующее утверждение.
Обозначим через D(a,b) пространство функций на отрезке [а,6],
непрерывных слева (в точке α справа) и имеющих лишь конечное число
скачков, и через C(a, b) пространство всех непрерывных на [а, 6] функций.
Через i^o(a, 6), Со(а, Ь) будем обозначать подпространства функций из D(a,b),
С(а, Ь) соответственно, обращающихся в нуль в точках а и Ь. Очевидно,
что траектории wn(t) принадлежат А)(0,1). Кроме того, известно (см. [17,
§16.2]), что траектории w°(t) принадлежат Со(0,1) с вероятностью 1. Для
простоты можем считать, что все траектории w(t) и, следовательно, w°(t)
лежат в С0(0,1) (см. [17]). Поскольку С0(0,1) С D0(0,1), то (£>о(0, l),crD),
где σο есть σ-алгебра подмножеств из ί>ο(0,1), порожденная
цилиндрическими множествами*), мы можем считать выборочным пространством**)
процессов wn и w°.
Теорема 3 (функциональная предельная теорема для эмпирических
процессов). Пусть f — функционал, определенный на пространстве
Do(0,1) и обладающий следующими свойствами:
1) f(wn) uf(w°) являются случайными величинами (m.e.f(y)
осуществляет измеримое отображение (Dq(0,1),<7£>) в (R, 93));
2) /(у) есть функционал, непрерывный в «точках» пространства
Со(0,1) относительно равномерной метрики, т.е. f(yn) —> /(у) при η —>
-> оо, если у е Со(0,1) и р{уп,у) = sup \yn{t) - y(t)\ -> 0.
Если эти условия выполнены, то
f(wn) => f(w°).
Если функционал f непрерывен в равномерной мелп,рике в любой точке
у Ε Do(0,1), то условие 1) выполняется автоматически.
Очевидно, что функционал S, рассмотренный выше, удовлетворяет
условиям теоремы, так что при η —> оо
S=> sup w°{t).
Поскольку распределение правой части в этом соотношении можно найти в
явном виде (см., например, [7, 104])
Р{ sup w°{t) > ζ} = e~2z\
*) To есть множествами вида {y(t\) 6 £ι,.. .,y(im) € Вт}> где В\,.. .,Bm — борелев-
ские множества.
**) (-D, σ) есть выборочное пространство процесса ξ(ί), если на нем задано распределение
процесса £, так что траектории £(£) лежат в D.
46
Гл. 1. Выборка. Эмпирическое распределение
то мы получаем таким образом приближенное выражение для
распределения 5.
Использование теоремы 3 для вычисления предельного распределения
других статистик рассмотрено в последующих параграфах.
Доказательство теоремы 3 отнесено нами в приложение II.
Возвращаясь к произвольным непрерывным функциям распределения F
и пользуясь (4), можем записать
Kit) = U*(F(t)) = F(t) + -±=wn(F(t)), (6)
где поведение процесса wn(t) описано в теореме 3.
Отметим, что левая и правая части (6) равны и без предположения о
непрерывности F.
§ 7. Предельное распределение для статистик первого типа
Напомним, что статистиками первого типа мы называем статистики
Sn(X) = G(F*)i где функционал G имеет вид G(F) = Μ / g(x)dF(x)) .
Другими словами,
Sn(X) = /J±f>(Xi)J.
Мы уже видели (теорема 3.1), что если Χ ξ= Fq и h непрерывна в точке
a = / g(x) dFo(x), то Sn —> h(a).
Теорема 1.
Если X €= Fo, h дифференцируема в точке a, g (x)dFo(x) < оо, то
yfr{Sn{X)-h{a))=>ti{a)t,
где £ ξ= Φ л „г, σ2 = J(9(x)-a)2dFo(x), Φο,σ2 — нормальное
распределение с параметрами (Ο,σ2).
Доказательство. Статистику Sn(X) представим в виде
где по центральной предельной теореме (см. [17], гл. 8 или приложение IV)
1 "
Лп = -7= 53(з(хг) - а) ©■ *ο,σ2,
σ2 = Ε(0(χι) - ο)2 = j{g{x) - a)2 dF0(x).
§ 7. Предельное распределение для статистик первого типа 47
Отстается воспользоваться третьей теоремой непрерывности при bn =
= 1/у/п. <
Иногда функционалы первого типа удобнее рассматривать в виде G(F) =
g{x) d(F — Fq) 1 . Очевидно, все сказанное сохраняется и для них с
-AI
той лишь разницей, что α следует положить равным нулю.
Приведем аналог теоремы 1 для случая, когда функция g = (<7ь.. ·, <7S)
есть
вектор (т.е. G{F) = h(jgi{x)dF{x),...,ig8{x)dF(x)j\
Теорема 1А. Пусть Sn(X) = G(F*), h(t) дифференцируема β точке
= [ 9{x)dF0{x), а матрица вторых моментов σ = ||о"^*|| = Е(д(х\) —
а
a)T(g(xi) —α) конечна. Тогда
dh{a)
(Sn(X) - h[a))Ji => ξ(Λ'(α))τ = £ ^fr W
с вероятностью 1, α матрица вторых производных
существует в точке а, то
Л"«)
dijdi
■ли
№№-Μ«))η*1ί»·(.)£τ.ΐΣ|^
*- Я2',.,,.,,
ί=α
Для доказательства теоремы ΙΑ следует воспользоваться теоремой
непрерывности 5.ЗА и многомерной центральной предельной теоремой, в силу
1 п
которой —1= У^(<7(хг) — а) => ζ (см. приложение IV).
Совершенно аналогично выглядит теорема о предельном распределении
5П(Х), когда функция /г, а вместе с ней и статистика 5П(Х) являются
векторами. Читатель без труда воспроизведет ее формулировку и доказательство
с помощью теоремы 5.3В.
Пример 1. Пусть X ^ Ро и Ро таково, что Εχι = а > 0, Dxi =
= d2 < оо. Что из себя представляет в этих условиях предельное
распределение статистики
1 / 1 п \
S = - Ι χ = — > Хг I ? Условия теоремы 1 здесь, очевидно,
х V nU )
выполнены при h(t) = 1/ί, g(x) = χ, при этом α = α, σ2 = d2, /ι(α) = 1/α,
fr'(a) = —1/α2. В силу теоремы 1
a/ or
48
Гл.1. Выборка. Эмпирическое распределение
так что
IS- -) \/η&Φ042/α*.
Пример 2. Найдем предельное распределение статистики
524ς(*<-*)2>
t=l
если Εχι = α, Dxi = d2 и Ex4 < oo. (Мы уже знаем, что в силу первой
теоремы непрерывности S2 —> (Р.) Найти требуемое предельное распреде-
п.н.
ление нетрудно непосредственно, воспользовавшись представлениями
η
s2 = -X>-«)2-(*-«)2.
ni=i
1 n
(S2 - d2)yfr = 4= Y[(*i ~ a)2 - d2} - y/H(x - a)2.
Однако мы воспользуемся теоремой ΙΑ. В условиях этой теоремы мы
должны положить
G{F)= f{x-a)2dF{x)- (fxdF{x)-a\ ,
так что gi(x) = {χ — α)2, дъ(х) — х, h(t) = t\ — fa — a)2. Поскольку в точке
a = (d2,a)
dh(a) _ dh(a) _
то
(S2 - d2)V^ =* ξ, ξ ^ Φ0,^5 ^2 = E(xi - a)4 - d\
Пример 3. Статистика χ2. В заключение этого параграфа
рассмотрим пример статистики, которую можно относить к статистикам как I, так
и II типов.
Рассмотрим статистики, построенные с помощью функционалов вида
G(F) = h\^J gdFj, (2)
где д есть функция ограниченной вариации на отрезке [a, b] таком, что
F(a) = 0, F(b) = 1 (α и Ъ могут быть бесконечными). Так как / gdF =
= g(b) — / Fdg, то функционал G(F) будет непрерывным в равномерной
§ 7. Предельное распределение для статистик первого типа 49
метрике, если только непрерывна функция Л. Нетрудно понять, что
выделенный класс статистик представляет собой пересечение классов статистик
I и II типов.
То же самое справедливо в случае, когда g есть векторнозначная функция
с компонентами #, имеющими ограниченную вариацию.
Рассмотрим теперь разбиение вещественной оси (пространства X) на
непересекающиеся интервалы Δι,...,ΔΓ и положим щ = ηΡ*(Δζ), pi =
= Ρο(Δζ·) (Ро есть распределение, соответствующее Fq, так что X €= Ро)·
Статистикой «хи-квадрат» ξ2 = χ2{Χ) называют статистику
t=l ПРг
Очевидно, что это есть статистика II типа, так как она с точностью до
множителя η соответствует функционалу
Чтобы представить χ2{Χ) как статистику I типа, рассмотрим
функционал вида (2)
-(/
G(F) = h[ gd(F-Fo)
с функцией h(u) = У^^ и векторной функцией g с координатами
J —— при χ Ε Aj9
[О при χ φ Aj.
Так как функция h дифференцируема, dh(0)/duj = О, д2!г(0)/дщ duj = 2δψ
(5ij — символ Кронекера), то, положив Sn{X) = G(F£), мы получим
„4№ _„£ [(a _W)_L]'_,»(*,.
При X ^ Pq ъ силу второй части теоремы 1А
x2{x)^J2il (з)
3 = 1
где ξ = (ξι,.. .,£г) есть нормально распределенный вектор (предельный для
*Ί ~ "Pi ντ--ηρΛ\ 2
— , - -.,—# ] ι с нулевым средним и с матрицей σΔ = σ^·
y/ηρι y/npr J J
вторых моментов,
<*ij = Щ£з = E(5i(xi) - y/Pi)(9j(xi) ~ V^J)
50
Гл. 1. Выборка. Эмпирическое распределение
(из определения gj следует, что E#j(xi) = у/р])> Так как gi{x)gj{x) = 0 при
г φ J и P(^?(xi) = l/Pj) = ρ,, PfaJ(xi) = 0) = 1 - Pj, то
Выясним теперь, что из себя представляет распределение правой части
в (3) (т.е. предельное распределение χ2{Χ)).
Рассмотрим ортогональное преобразование в W с матрицей С и
рассмотрим вектор
η = ξϋ.
Вектор η так же, как и ξ, будет нормально распределен. Действительно,
нормальность величины ξ означает, что ее характеристическая функция (х. ф.)
равна (см. [17, § 7.6])
Ее^Т=е-^2'т,
где σ2 = ||σ^|| есть матрица вторых моментов. Но х.ф. для η
ΕβίίηΤ = EeiicT^T = е-№т°2с*т
имеет тот же вид и, следовательно, η есть нормальный вектор, но с матрицей
вторых моментов d2 = С a2C — ||dyl|j так чт0
di3 = E^r/j = 22,cuaikCkj = 2^сц(81к - y/ptPkVkj =
ΣСнС1з ~ (ΣciiVPi) (ΣСк'зV^fc) · (4)
Выберем теперь матрицу С так, чтобы ее первый столбец имел координаты
Qi = y/pi (это соответствует фиксированию первого вектора преобразован-
г
ной системы координат и возможно, так как Υ^ c?i = Σ^ = 1)· Тогда, оче-
видно, второе слагаемое в (4) в силу ортогональности С равно единице лишь
при г — j = 1 и нулю в противном случае. Это означает, что с/ц = Е771 = 0,
dij — Er/i^j = Sij при г ^ 2, и, следовательно, 771 = 0 с вероятностью 1, а
величины щ,.. .,т}т независимы и нормально распределены с параметрами
(0,1). На основании ортогональности С получаем
j=i i=i j=2 i=2
Распределение правой части в этом равенстве называется распределением χ2
(«хи-квадрат») с г — 1 степенями свободы (см. [17, §7.7], а также § 12). Мы
будем встречать это распределение в последующем изложении неоднократно.
Еще одно доказательство (5) будет получено в следующем параграфе.
Кроме того, (5) будет доказано в § 56 с помощью более общих соображений.
Некоторые другие примеры использования теорем 1, 1А будут
содержаться в последующих главах.
§ 8. Предельное распределение для статистик второго типа 51
§ 8.* Предельное распределение для статистик второго типа
В этом параграфе будем изучать предельное распределение G(F*) в
случае X — R, где G{F) есть функционал второго типа, осуществляющий
измеримое отображение (Ζ)(-οο,οο),σ£)) в (К, 55) (или измеримое отображение
(V(—οο,οο),σν) в (К, 05), где V(—οο,οο) — пространство функций
ограниченной вариации на (—οο,οο), σγ — σ-алгебра, порожденная
цилиндрическими множествами).
Применительно к рассматриваемым задачам в дальнейшем под С(—оо, оо)
(D(—οο,οο)) можно понимать пространство функций / на (—οο,οο),
полученных из элементов / Ε С(0,1) (/ Ε 12(0,1)) путем непрерывной замены
«времени»: f(t) = f(F(t)), где F — непрерывная функция распределения.
Отметим прежде всего, что для статистик II типа справедлива
Теорема 1. Если Хп = [Х^]п <^ F0, mo G(F*) —► G(F0).
Это утверждение немедленно следует из теоремы 2.2А.
Для того чтобы можно было найти предельное распределение для
функционала второго типа G(i^), необходимо, как и в предыдущем параграфе,
наложить на функционалы G(F) некоторые условия гладкости.
Положим для краткости \\х\\ — sup |#(£)|.
—оо<£<оо
Определение 1. Функционал G{F) называется непрерывно
дифференцируемым порядка к в точке Fo, если существует функционал G'(-Fo,^),
который для любой функции ν Ε С(—οο,οο) и любой последовательности
Vh € D(—оо, оо) такой, что Цг^ — г>|| -> 0 при h -> 0, удовлетворяет
соотношениям
G{F° + hV^-GiFo)->G'(F0,v), G'{F^vh)->G\Fo,v). (1)
Последнее соотношение означает, очевидно, непрерывность в
равномерной метрике в точках из С(—οο,οο) функционала G'(Fq,v), который можно
называть производной порядка к от G по направлению v.
Замечание 1. Введенное понятие производной шире понятий
производных по Гато и Фреше, так как здесь не предполагается линейность
функционала С по г) и равенство к = 1. Названные производные применительно
к задачам робастности (см. § 58) называются также функционалами влияния
(подробнее см., например, [124-126] и §58). Значение G'(Fo,v) совпадает,
очевидно, с обычной производной функции G(Fq + hv) по h в точке h = 0.
Рассмотрим несколько примеров.
В дальнейшем будем обозначать через F~l функцию, обратную F*
(см. §6):
F"1(0)=x(i), F-l{u) = sup {v :Fn»< и} при и > 0.
52
Гл. 1. Выборка. Эмпирическое распределение
Пример 1. Пусть G(F) есть квантиль порядка ρ функции
распределения F, т.е. G{F) = F~l(p). Это значит, что G(F*) = F~l(p) = ζ* есть
выборочная квантиль порядка р. Покажем, что в этом примере G(F)
дифференцируем первого порядка в точке i*o, если Fo(t) дифференцируема в точке
CP = JF0-1(p)1F%)>0.
Действительно, по определению
G(F0 + hvh) = max{t: F0{t) + hvh(t) < ρ}.
Так как этот функционал является непрерывным в равномерной метрике в
точке Fo, то мы можем положить G(Fq + hvh) = ζρ + £, где 6 = 6(h) -> 0 при
h —► 0. Далее, из соотношения \\vh - v\\ -+ 0, υ Ε С(—оо, оо), следует
|«л(р + *)-ил(р)| ξγ(Λ) ->0
при /ι —> 0. Так как
FoiCP + S)=p + SF^p) + o{S),
то для £ = G(Fo + hvh) = ζρ + # получаем
*b(i) + /юл(<) = Ρ + Мо(Ср) + о(*) + ΛνΛ(ζρ + «) =
= Ρ + ^о(Ср) + ο{δ) + Η{υΗ{ζρ) + rr{h)) < ρ,
где |г| ^ 1. Аналогичное обратное неравенство можно написать, пользуясь
тем, что Fo(t + 0) + hvh{t 4-0) ^ р. Отсюда следует, что
ό + о(6) = -τ-— , |п| < 1,
так что
G(Fo + ^)-G(Jb) = £ ν(ζΡ)
h h F^PY
Таким образом, производная G'(Fq,v) в этом примере равна
Пример 2. Рассмотрим функционал
G[F) = sjip\F(t)-F0(t)\.
t
Очевидно, что он дифференцируем первого порядка по любому
направлению ν Ε С(—οο,οο), так как G(Fq) = 0,
, G(F0 + hv)
G{F0,v) = ^—r = sup v(t) ,
Л t
при этом G^Fqjv) от Fq не зависит.
§ 8. Предельное распределение для статистик второго типн 53
оо
Пример 3. Функционал G{F) = / \F{t) - F0(t)\k dR(t) для любой
функции ограниченной вариации R(t) является непрерывно
дифференцируемым порядка к по любому направлению ν Ε С(—οο,οο), так как
оо
0'(Ρ0,ν) = 0{Ρο+Ηυ) = f\v(t)\4R(t).
-оо
Пример 4. Рассмотрим функционал
G{F) ~ ^ A~F0 '
где AjF суть приращения функции F на интервалах Δ^· = [ij,<j-+-i)>
образующих разбиение вещественной прямой. Очевидно, что nG(F*) есть не
что иное, как статистика χ2, рассмотренная в примере 7.3 в качестве
статистики I типа. Рассматриваемый функционал будет непрерывно
дифференцируемым второго порядка, так как для него
G'(F0,v) =
G(F0 + hv) ,Α (Δ^)2
h?
Обобщением функционалов в примерах 2-4 являются функционалы вида
G(F) = Gi(F — Fo), где функционал Gi является однородным в том смысле,
что Gi(hv) = hkGi(v). Очевидно, все такие функционалы будут
дифференцируемыми.
Пример 5. Статистики I типа, введенные в § 3, соответствуют
функционалам G{F) =h( J g{x)dF{x)) .
Эти функционалы будут одновременно функционалами II типа, если
функция h непрерывна в точке / g(x) dFo(x), a д имеет ограниченную вариацию.
В этом случае, считая, не ограничивая общности, д{—оо) = 0, получим, что
интеграл / g(x)dF(x) = / (1 — F(x))dg(x) непрерывен относительно F в
равномерной метрике. Если вариация д не ограничена, то такая
непрерывность, вообще говоря, будет отсутствовать. Если, например, h(x) = χ,
д{х) =х, FM = (l--jF04--Fi, где a = xdF0{x) < оо, ί xdFx{x) =
= оо, то ||F(n) - Foil -+ 05 G(F0) = a, G{F^) = оо при всех п.
Если функция h дифференцируема в точке a = / g(x)dFo(x), g имеет
ограниченную вариацию, то функционал G дифференцируем первого по-
54
Гл.1. Выборка. Эмпирическое распределение
рядка в точке Fo, при этом (\\νε — υ\\ -> 0 при ε -> 0)
G;(Fo,t;) = lime""1 (h (α- ε / ^(ж)^(х) J -Λ(α)) =
= -Λ#(α)^Φ)*(^)
Пример 6. L-статистики были введены в §3. Мы будем рассматривать
L-статистики, соответствующие функционалу
1
G(F) = JV(t)g(F-1(t))dt, (3)
о
где F"1 — функция, обратная к F\ ψ и g — заданные функции. Пусть
ι
f<p(FQ(t))gf(t)dt <оо, (4)
о
функции Fq и g непрерывно дифференцируемы.
Опуская ввиду громоздкости обоснование предельного перехода под
знаком интеграла, в силу примера 1 будем иметь (F^(t) = f(t))
ОД + hvh) = J <p(t)g hoHt) ~ уШШ + °(Л)) dt =
1 1 / _! ч
= J' v(t)<p(F0-\t)) dt -hJ^y(F-\t))V-^^+ o(h);
0
1
lim /^[ОД + hvh) - G(F0)} = - Кш^Ч*))^}^·
Это значит, что функционал G, определенный в (3), дифференцируем
первого порядка,
1 _, оо
G'(F0,v) = - J φ(ι)9'{F0-\t))V-^^ = - J V(Fo(t))^(t)t;(t)dt.
О —оо
(5)
Сформулируем теперь основную теорему о предельном распределении
функционалов второго типа. Через fg мы будем обозначать функцию fg{x) —
§ 8. Предельное распределение для статистик второго типа 55
Теорема 2. Пусть Fq непрерывна, X ^ Fq u функционал G(F)
дифференцируем (порядка к в смысле определения 1). Тогда
nk'2{G{F*n) - G(F0)) => G'(Fo,w°F0), (6)
где w° есть броуновский мост.
Доказательство. Воспользуемся теоремой 6.3. В ней доказана
сходимость распределений функционалов от процесса wn(t) = y/n(F*(t) — F(t)),
где X ^ Fq = U, U есть равномерное на [0,1] распределение. В
соответствии с этим функционалы в теореме 6.3 определены на пространстве
(ί}(0,1),σ£>), а не на (D(—οο,οο)σ#), как в общем случае. Поэтому
предварительно мы должны произвести редукцию рассматриваемой задачи к
условиям теоремы 6.3. Для этого воспользуемся соотношением F£ = U^Fq
(см. (6.4)), где U£ — эмпирическая функция равномерного на [0,1]
распределения, Fq — распределение, соответствующее выборке X. Это
соотношение позволяет сводить изучение распределения G(F£) (G определен на
D(—оо, оо)) к изучению распределения Gq(U*), где функционал Go
определен на элементах Η из D(0,1) равенством Gq(H) = G(HFq), так что
Go(·) есть значение исходного функционала G, но от функции, у которой
произведена замена «времени» t на Fo(t). При таком определении Go имеем
G(F) = GiFF-'Fo) = GoCFFo"1).
Так как F^Fq1 = U* соответствует согласно (6.4) выборке из
равномерного на [0,1] распределения, то
g{f;)=g0(u:).
Покажем теперь, что если функционал G дифференцируем, то Go также
дифференцируем, G'Q(U,v) = G'(Fq,vFq).
Действительно, при Цг^ — υ\\ —> 0 имеем
G'Q(U,v) = limh-k[GQ{U + hvh)-GQ{U)] =
= lim h-k[G(F0 + hvhF0) - G(F0)} = G'(F0>vF0).
Итак, нам достаточно доказать теорему 2 в предположении Fq = U.
Рассмотрим величину
[G{F$ - G(U)]nk/2 = G'(U,wn) + Hn(wn),
где Нп{х) = [G{U+x/y/n)-G{U)]nk/2-G'{U,x). Так как в силу теоремы 6.3
и определения 1 G'{U,wn) => G'(i7,ги°), нам достаточно убедиться, что
Я„Ю -^ 0. (7)
56
Гл.1. Выборка. Эмпирическое распределение
Заметим, что для любого компакта К С С(0,1) и любой
последовательности hn —> 0 при η —> оо
sup |Яп(ж)| -> О, (8)
xGD(0,l)
xe(K)hn
где (if)e есть ε-окрестность множества К. Допустив противное, придем к
существованию последовательности xn G jD(0, 1) такой, что \\хп — х\\ -> 0,
χ Ε С(0,1). limsup\Hn(xn)\ > О, что противоречит дифференцируемое™ G.
п—юо
Напомним теперь (см., например, [7]), что компакты в метрическом
пространстве непрерывных функций С(0,1) с равномерной метрикой
описываются следующим образом. Каждой функции <£>(Δ) > О, </?(Δ) -* 0 при Δ —> О,
и числу N > 0 соответствует компакт
К = Κ(φ, N) = {ye С(0,1) : шА(у) ^ φ(Α), |у(0)| ^ Ν},
где о>д(у) есть модуль непрерывности у:
^д(у) = sup |y(i)-y(tz)|.
Обозначим через К^ множество
Kh = {ye £>(0,1) : соА{у) < φ{Α) для всех Δ ^ Л; |у(0)| ^ Ν}.
Множества Kh можно было бы назвать «предкомпактами» (этот термин
используется в функциональном анализе в ином смысле), порожденными ком-
оо
пактом К. Ясно, что К^ С К^2 при h\ < /12, Π К ι/η = К и что К^ С
71=1
с {K)^hl
Покажем теперь, что для заданного δ > 0 существуют компакт К (и,
стало быть, соответствующее ему семейство предкомпактов К^) и
последовательность hn —¥ 0 при η —> оо такие, что
limsupP(wn £#,>„) О- (9)
71—VOO
Действительно, по теореме 6.3 для любого функционала /,
непрерывного в равномерной метрике, выполняется f{wn) =>· /(w°), где wn(t) =
= y/n(F*(t) — ί), 0 < t < 1. Так как о>д(у) является таким
функционалом, то а>д (ги71) =>> о>д(м°). Но о>д(м°) —^ 0 при Δ -» 0, так как траектории
п.н.
ги° почти наверное непрерывны. Следовательно, для заданных ε и δ при
достаточно малом Δ
Ρ{ωΑ{υι°)>ε)^δ.
Считая, не ограничивая общности, число ε точкой непрерывности
распределения и;д(^°), мы получим
HmsupP^ACu/1) > ε) ^ δ.
η—>·οο
§ 8. Предельное распределение для статистик второго типа 57
Пусть теперь ε^ I 0 — некоторая последовательность, а числа Δ& | О
таковы, что
г
limsupP(o;Afc(ujn) > ek) < -j-^.
η—>·οο -ώ ^
Образуем функцию <£>(Δ) = ε& при Δ G [Δ^+ι, Δ^). Ясно, что <^(Δ) -> 0
при Δ —> 0, и мы можем рассмотреть предкомпакты К^ построенные по
функции ψ. Тогда для любого к < оо
HmsupP(ti;n £ К^к) ^ HmsupУ^(^ (wn) > Sj) <
η—юо п->оо . -
fc+1 ,
^ VlimsupP^^71) > е,-) ^ -
1 п—»оо ^
.7=1
(при к — оо это неравенство может быть неверным). Полученное
соотношение означает, что при каждом δ существует последовательность hn —> 0 при
η —¥ оо такая, что выполнено (9).
На основании (8), (9) получаем
P(\Hn(wn)\ >е)^ Р(|ЯПК)| >*,«;»€ #Лп) + P(wn i Khn),
HmsupP(|tfn(wn)| > ε) ζ δ.
η-»οο
Так как £ произвольно, το соотношение (7), а вместе с ним и утверждение
теоремы доказаны. <
Вернемся к рассмотрению примеров. В примере 1 для выборочной
квантили ζ* = F~l(p) порядка ρ имеем согласно (2) и теоремы 2.
Следствие 1. Если Xn €= Fo, Fq непрерывно дифференцируема в
точке Ср, ^о(Ср) > О? wo
Для доказательства надо заметить лишь, что условия следствия 1
означают непрерывную дифференцируемость F^~ в точке р:
{F°~1{p))' щроЧр)) тРг
Так как Ew°(p) = О, Ow°{p) = E(w{p) - pw(l))2 = Е(ги(р)(1 - ρ) +
+ p(w(l) — w(p)))2 = p(l -p)2 +p2{l —p) =p(l ~ p)» то утверждение след-
58
Гл.1. Выборка. Эмпирическое распределение
ствия 1 можно записать также в виде
(c;-Cp)^e>*o^ *2 = й^· <
О распределении выборочных квантилей см. также п. 12.9.
В примере 2 функционал G(F) — sup \F(t) - Fo(i)| дифференцируем и,
стало быть, по теореме 2
G(F*)^^sjip\w°{FQ(t)\ = sup |u;0(i)|.
Это соответствует тому, что для произвольной непрерывной функции
распределения Fq распределение статистики
D(X)=snp\F*{t)-F0(t)\
t
остается тем же, что и для случая Fo(t) = t, t Ε [0,1].
Распределение η = sup |tu°(<)| найдено в явном виде [104]:
оо
Ρ(η < ζ) = К (ζ) Ξΐ+2 ]£(-1)*е-2*2*2.
Jc=l
Функция К (ζ) называется функцией Колмогорова.
Мы получили, таким образом,
Следствие 2 (теорема Колмогорова). Если X €= Fo, Fo непрерывна,
то
y/^D{X) & К.
Это означает, что максимальное уклонение -D(A") функции F*(t) от Fo(£)
имеет порядок \j\fn и может быть приближенно представлено в виде D(X) «
В примере 3 в силу теоремы 2 получаем
nk'2 j\F*{t) - F0(t)\k dR{t) => f\w°(F0(t))\kdR(t).
В частности, при к = 2 и R(t) = Fo(t) мы получим статистику,
обозначаемую о;2, распределение которой инвариантно относительно Fo и для которой
справедливо
Следствие 3. Если X ^ Fo, Fq непрерывна, то
ι
,2
о
f[w°{t)]2dt.
1
12
/[»°(*)]
Распределение / [ги (t)] dt также найдено в явном виде и наряду с рас-
о
пределением К [ζ) табулировано.
§ 8. Предельное распределение для статистик второго типа 59
Применительно к примеру 4 теорема 2 дает
X^l· W
Если обозначить через SjF приращение F на интервалах Sj = [tj, τ^+ι), ту =
= Fo(tj) и обозначить той же буквой 5j длину интервала <5у, то мы получим
Следствие 4. ЕЪш А" ^ Fq, Fq непрерывна, mo
г 'Γ „0Л2
Σ
.2 . \^ W
(ίΧ)2
■ 1 *J
Если положить ξ = (ξι,...,ξΓ)ϊ fj — $jw°/y/fij) T05 пользуясь тем, что
(^•гу° = SjW — w(l)Sj, где w — стандартный винеровский процесс, получим
г
Здесь матрица σ2 = \\σ^\\ та же, что и в примере 7.3, так как
5jW° = SjW - ί Χ) **™ ) *7 = Σ akjhw>
^ k ' k=l
akj = ifej - *j, E(^tu)(J^) = £fc/4
(£jw — символ Кронекера),
Ε(<^)(<^°) 1 ^
σΐ3 = /ΊΓΊΤ = /ΤΤ~ / > akiakjOk =
'#t<5j
(£y Ji — ί,-ij) = % - y/S{Sj.
Повторяя рассуждения примера 7.3, получим, что 2_] £у имеет распределение
χ2 с г — 1 степенями свободы.
Для примера 5 справедливо
Следствие 5. Если X^Fq, Fq непрерывна, функция g имеет
ограниченную вариацию, h непрерывно дифференцируема в точке а —
= / g{x)dFo{x), то
yfc{G(FZ-h{a)) => -ti(a)Jw0(FQ(x))dg(x). (10)
60
Гл.1. Выборка, Эмпирическое распределение
Правая часть здесь имеет нормальное распределение с параметрами
(o,(h'(a))2J(g(x)-a)2dF0(x)y (11)
Чтобы вычислить распределение правой части в (10), можно
воспользоваться простейшими свойствами стохастических интегралов, в силу
которых (интегрирование по частям)
- J w°(F0(x))dg(x) = J g(x)dw°(F0(x)) =
= Jg(x)dw(F0(x))-w(l)J(g(x)dF0(x)) = J'(g(x) - a)dw(F0(x)).
Этот интеграл имеет нормальное распределение с параметрами
(o,J(g(x)-a)2dF0(x)y
Если названные свойства стохастического интеграла (правило интегри-
1
Ib{t)dw{t)
рования по частям и нормальность / b{t) dw[t) читателю не известны,
о
можно воспользоваться аналогичными свойствами сумм случайных
величин,
η
, поскольку / b(t) dw(t) для непрерывных &(-) можно рассматривать как
η
предел /~^£а:,п&(&/п)> гДе £fe,n = w{k/n) — w((k — Ι)/η) суть независимые,
A;=l
одинаково (нормально) распределенные случайные величины с параметрами
(0,1/п). Аналогичную трактовку следует использовать для исходного
интеграла вида
fw\t)dg(t) W£)=5>.»·
-Ί;)-^)-^1»
Тогда, меняя порядок суммирования (аналог интегрирования по частям), мы
придем к асимптотическому равенству допредельных сумм, а следовательно,
и к равенству пределов.
Замечание 2. Второе утверждение следствия 5 (см. (11)), как
показывает теорема 7.1, справедливо и при более общих предположениях, когда
вместо ограниченности вариации функции g требуется лишь существование
g2(x)dF0(x).
I
Для L-статистик G(F*) в примере 6 (функционал G определен в (3))
в силу теоремы 2 справедливо
§ 8. Предельное распределение для статистик второго типа 61
Следствие 6. Если X €= i<o, g и Fo непрерывно дифференцируемы и
выполнено (4), то
ι
v^(G(Fn*) - ОД)) =► Ja(t)w°(t)dt, (12)
о
a(t)=<p(t)g'{F0-l(t))/f{F0-1(t)).
Правая часть в (12) нормальна с параметрами
О,
о
1
,j A*(t)dt-A2Y (13)
zdeA{t) = I a{t)dt, A= I A(t)dt.
t о
Чтобы убедиться в последнем утверждении, надо, как и в предыдущем
следствии, воспользоваться интегрированием по частям:
1 1
J a(t)w{t) dt = ( A(t)dw{t),
о о
11 11
ί a{t)w°(t)dt = ( A(t)dw(t)-w{l) fta{t)dt = /{A(t) - A)dw(t),
0 0 0
где правая часть нормальна с параметрами
), Г {A{t) - A)2 dt) = (θ, ΓA2{t)dt-A2
Замечание 3. Можно показать (см., например, [102]), что второе
утверждение следствия 6 (о нормальном предельном распределении
y/n(G(F*) — G(Fq)) с параметрами (13)), как и в следствии 5 (см.
замечание 2), остается справедливым и при более широких условиях, когда
ι
требуется лишь / A (t) dt < со
JA\t),
о
Существует много других примеров, показывающих, что теорема 2
остается справедливой и при условиях более широких, чем те, что сфор-
62
Гл.1. Выборка. Эмпирическое распределение
мулированы в теореме 2. Если воспользоваться представлением F£{t) —
= Fo(t) -i—y=wn(Fo{t)) (см. (6.6)), где поведение wn описано в теореме 6.3,
то можно записать
Vii{G{F*) - G(F0)) =^(g (f0 + -^™nF0) - G(F0)\ « G'(F0,wnF0),
(14)
где производная
G'(F0,v) = lim h-^GiFo + hv) - G{F0))
может быть определена на элементах ν из какого-нибудь другого
пространства (не обязательно С( —οο,οο)), а функционал G'(F$,v) не обязан
быть непрерывным относительно ν в непрерывной метрике. Тем не
менее в этих условиях мы по-прежнему можем иметь требуемую сходимость
Gf(Fo,wnFo) =*► G'(Fo,w°Fo) (как это имело место в примерах 5, 6), если,
конечно, правая часть этого соотношения имеет смысл (см. также
результаты § 14 о распределении М-оценок).
По своему существу теоремы 1 и 2 близки соответственно теоремам
непрерывности 5.1 и 5.3, но они действуют в функциональных пространствах.
В заключение этого параграфа отметим, что далеко не все
статистики, представляющие интерес, могут быть отнесены к статистикам I и
II типа. Достаточно рассмотреть, например, [/-статистики (скажем, U(X) =
η
= 2_\ h{xi,Xj); см. §3) или статистики 5, связанные с функционалами
Gn(F), где функционалы Gn «существенно» зависят от η (не только
через выборку), такие, как, скажем, максимальный член вариационного ряда
S{X) =x(n) = СГ_1/Пидр.
§ 9.* Замечания о непараметрических статистиках
Есть одно свойство, в отношении которого статистика ζ* в примере 8.1
существенно отличается от статистик в примерах 8.2-8.4. Это свойство
состоит в том, что предельное распределение статистик в примерах 8.2-8.4
(см. следствия 8.2-8.4) никак с функцией распределения Fo не связано.
Этого нельзя сказать о статистике ζ* и о статистиках в примерах 8.5, 8.6
(ср. со следствиями 8.1, 8.4, 8.5).
Определение 1. Статистика S(X) называется асимптотически
непараметрической, если S(X) ©► Q, когда η -> оо, и Q не зависит от
распределения X, т.е. не зависит от Fq, если X ^ Fq.
Отметим, что сама функция S при этом может зависеть от Fq. Сам
термин «непараметрическая» является не совсем удачным; однако он весьма
распространен (он оправдан в случае, когда Fq принадлежит некоторому
параметрическому семейству — тогда распределение Q не зависит от
параметра и в этом смысле является непараметрическим). Иногда используется
другой термин — «свободный от распределения».
§10. Сглаженные эмпирические распределения
63
Мы видели в §6-8, что статистики y/nD(X), ηω2(Χ), χ2{Χ) являются
асимптотически непараметрическими.
Заметим теперь, что теорема 6.1 делает возможным введение и более
узкого понятия. В теореме 6.1 установлено, что nF^(t) распределено так же,
как 77(^0(^)5 где v{u) — условный пуассоновский процесс с произвольным
параметром λ > 0 при условии 77(1) = η (см. § 6), т. е. процесс, от Fq не
зависящий. Таким образом, если статистика S построена как функционал G(F£)
(или G(F£ — Fq)), который инвариантен относительно замены «времени» t
у аргумента, то распределение S от Fq зависеть не будет. Например,
D = snp\FZ{t)-Fo{t)\ = -suvfo{FQ(t))-nFo(t)\ = - sup \η(η)-ηη\.
t d Π t пиф,1]
(1)
Сказанное делает уместным
Определение 2. Статистика S(X) называется непараметрической,
если ее распределение не зависит от Fq (X ^ Fq).
Соотношения (1) означают, что статистика D является
непараметрической.
Мы отмечали также (см. следствие 8.3), что статистика ω2 наряду с D
не зависит от Fq и, стало быть, тоже является непараметрической.
Статистика χ2, являясь асимптотически непараметрической, не будет
обладать свойством непараметричности. В этом легко убедиться
непосредственно на примере, положив г = 2, η = 1.
Другие примеры непараметрических статистик мы получим, если
рассмотрим значения F*((p), где ζρ — квантиль порядка р, так что nF*((p) =
d
= η(ρ) (см. §6). Число rj элементов выборки X, меньших, чем х^, — так
d
называемая ранговая статистика — также будет непараметрической
статистикой.
Понятия непараметрической и асимптотически непараметрической
статистик весьма полезны в теории проверки статистических гипотез (см.
главу 3), так как распределение этих статистик, знать которое необходимо при
построении критериев, достаточно вычислить лишь один раз (например, для
равномерного распределения Fq) и оно будет годиться для любых других
распределений выборки.
§ 10.* Сглаженные эмпирические распределения.
Эмпирические плотности
В § 2 мы каждой выборке X поставили в соответствие распределение
P*j, которое назвали эмпирическим и которое представляет собой сумму η
атомарных распределений, сосредоточенных в точках χχ,.. .,хп. Это
распределение обладает рядом замечательных свойств, описанных в предыдущих
параграфах. Однако использованное нами определение Р* далеко не
единственно возможное, а в ряде случаев и не самое естественное. Существуют и
другие подходы к определению Р£, при которых изученные выше полезные
свойства эмпирических распределений не только полностью сохраняются,
но и дополняются рядом новых.
64
Гл. 1. Выборка. Эмпирическое распределение
Мы ограничимся здесь обсуждением вопроса о природе распределений,
которые мы помещаем в точки х^. В использованном нами определении Р*
это были вырожденные распределения IXi(i?), так что
ρη(β) = ^Σ^(β)· w
В этом случае эмпирическое распределение оказывается сингулярным
относительно меры Лебега и, стало быть, не имеет плотности. Это может
оказаться неудобным в тех случаях, когда нам заранее известно, что исходное
распределение Ρ имеет плотность. При этом условии было бы желательно
иметь такое гладкое эмпирическое распределение Р*, для которого вместе
со сходимостью Р£ -4 Ρ во всех установленных выше смыслах имела бы
место также сходимость плотностей /* —> /, где /* и / есть плотности,
соответствующие Р* и Р.
Этого нетрудно добиться следующим образом. Пусть Q — какое-нибудь
распределение, имеющее плотность. Положим
•WJ-sEQ^)· (2)
В -χ
где —;— есть множество точек у € •£, для которых χ 4- yh € В] hn —» О
h
при η —> оо.
Очевидно, что Р**(В) есть не что иное, как «средняя сумма»
распределений Q, сжатых до размеров hn и «посаженных» в точки х^. Определение (2)
обобщает (1). Формула (1) получается из (2), если положить Q = Ιο, так
как IXi(B) = Iq(B — xt·) = Ιο Ι —г—- ] при любой последовательности {hn}.
Отметим следующие свойства распределения Р**, которое будем
называть сглаженным эмпирическим распределением.
1. Распределение Р** есть свертка распределений Р£ и Q(B/hn), a
РП(В) = ЕКЧВ) = J Q {^) РШ
есть свертка распределений Ρ и Q(B/hn). Другими словами, Рп(В) есть
распределение случайной величины ξ + /ιη77, где ξ ^ Ρ, η €= Q. Из теорем
непрерывности следует, что при hn —> О
Рп => Р. (3)
Напомним, что для распределения Р£ мы имели точное равенство
ер; = р.
§ 10. Сглаженные эмпирические распределения
65
2. Распределение Р** будет удовлетворять теоремам типа теоремы Гли-
венко-Кантелли. Действительно, в этом случае сходимость (3) будет
означать равномерную сходимость распределений по всем интервалам.
Ограничиваясь для простоты одномерным случаем, будем иметь (F**(x), Fn(x)
и Q(x) обозначают функции распределения, соответствующие Р**, Рп и Q)
F? - F(x) = |Q (^) dF*n{y) - F(x) =
= -JF*n{y)dyQ{^>j-F{x) =
= Fn(x) - F(x) - f{F*{y) - F(y)) dyQ (^) .
Здесь, как уже отмечалось, разность Fn(x) — F(x) -* 0 равномерно по я, а
интеграл, присутствующий в правой части, не превосходит
syxV\F*n{y)-F{y)\—Ю.
у П.Н.
3. Преимущество Р** перед Р£, ради которого это распределение и
вводилось, состоит в том, что это распределение имеет плотность
я»-±р{Ч?)-Ы'{Ч?)'х
(У) (4)
(q(x) есть плотность распределения Q), которая при каждом χ при η —> оо,
hn -> 0 сближается с плотностью f(x) распределения Р.
Прежде чем доказывать соответствующее утверждение, заметим, что для
получения хороших результатов о сближении f^\x) с f(x) следует
пользоваться гладкими ограниченными плотностями q. При выборе, скажем,
неограниченных q оценка f^{x) гладкой плотности f(x) будет нарочито
портиться. Так как выбор q находится в наших руках, то мы можем считать,
что по крайней мере выполнено условие
d2= ί q2{t)dt <ос. (5)
Теорема 1. Если q удовлетворяет условию (5), f(x) непрерывна и
ограничена, hn -> 0 при η —> оо так, что nhn —> оо, то
км = /„(*) + ^Ы=, (6)
y/nhn
где /п(ж) есть неслучайная функция
fn(X)=Bf*(x)=m-1q(^^-
= ^Jq(^1^)f(t)dt = Jq(z)f(x-zhn)dz^f(x) (7)
66
Гл.1. Выборка. Эмпирическое распределение
при hn —> 0. Случайные величины ζη(χ) асимптотически нормальны,
ζη{χ) & Φ0,σ2(*), <72(ζ) = f{x)d2.
Доказательство. Сумма в (4) есть сумма независимых одинаково
распределенных случайных величин в схеме серий, при этом /η(#) = Έ/*(χ)
представлено в (7). Положим
hnfn{x)\
s/c,n —
y/nhn
hn
Тогда
1 n
Vnhn^
hn \ hn J hn J \ hn J
= fq2{z)f{x-zhn)dz->f{x)fq2{z)dz = f{x)d2. (8)
Таким образом, Εξ^η ~ f(x)d2/n, если f(x) > 0. Условие Линдеберга в
нашем случае имеет форму
ηΕ(£?,η;|£ι,η|>ε)-»0
при η —>· оо и любом ε > 0. Так как
hnfl{x) -> О,
<«<2(^(^)+*"/«<*))'
то для выполнения (9) достаточно, чтобы
'№№> .(^)>.^)-а
Это соотношение имеет место, так как левая часть его равна (ср. с (8))
/ q2{z)f{x- zhn)dz ^c / q2(z) dz -> 0.
(9)
ς(^)>εν/η/ιη
q(z)>ey/nhn
Таким образом, к случайной величине ζη(χ) = /_~]£а;,п применима цен-
k=l
тральная предельная теорема. Это доказывает теорему 1. <
§10. Сглаженные эмпирические распределения
67
В рассматриваемой задаче естественно возникает вопрос об
оптимальном выборе hn и функции q(t). Однако ответ на него зависит от свойств
гладкости f(x). В самом деле, пусть, например, f(x) положительна лишь на
конечном интервале и дважды непрерывно дифференцируема с
фиксированным значением φ = / (f"{x))2 dx. Предположим также, что / zq(z) dz = 0
(это всегда так для симметричных q(z)) и что D2 = / z2q(z) dz < оо. Тогда
fn(x) = / q{z)f(x - zhn) dz =
= Jq(z) [/(χ) - zhnf'(x) + ^f"(x) + o{z2h2n)] dz =
= f{x)^l^^jz2q{z)dz + o{hl).
Мы видим, что
Я(.)-/(.)-^И + ^ + .(«).
E[№)-/(x)]2=(^^)2 + ^ + oW).
Минимизация этого выражения по hn и q даст, в силу асимптотической
нормальности ζη(χ)·> наименьший возможный «разброс» f^[x) около
значения fix). Однако минимизирующие значения hnnq при этом будут зависеть
от χ через неизвестные значения f(x) и f"(x). Чтобы избавиться от этого
эффекта и получить оптимальность «в среднем», естественно рассмотреть
интеграл
"E[/*(x)-/(x)]2dx, (И)
/'
главная часть которого будет равна (Ζ)2/ι2/2)2<£> + d2/nhn (это получится,
если в (10) убрать ο(Λ„))·
Минимум этого выражения достигается при hn — (d2/nD4<p)1/5. При
таком выборе hn интеграл (11) будет равен
!»>,/5(1И2)4/5„-4/5 + (>(„-4/5)>
дм - т - (gf (Ш + /(х)^?„) + «.-«·). (12)
ξη & Φθ,1·
68
ГлЛ. Выборка. Эмпирическое распределение
Таким образом, скорость сходимости здесь составляет лишь η 2'5 в
отличие от скорости η""1'2, которая имеет место для сходимости функций
распределения. Это естественный факт, так как в оценке значения f(x)
принимает участие, грубо говоря, не вся выборка, а лишь те наблюдения, которые
сосредоточились в некоторой убывающей окрестности точки х.
Выражение (12) позволяет оптимальным образом выбрать и функцию
q{z), т.е. функцию, для которой минимизируется Dd2. Считая, не
ограничивая общности, что D = 1, получим задачу минимизации d2 = / q2(z)dz
при условиях
/ q(z) dz = / z2q(z) dz = 1, / zq{z) dz = 0.
Отметим, что если / имеет непрерывные производные более высокого
порядка 2га > 2, то можно получать и более высокие скорости сходимости
к нулю разности f^{x) — }{x)· При этом, однако, надо использовать
обобщенные распределения Q, «плотность» которых q может принимать
значения обоих знаков и позволяет удовлетворять условиям / z2mq(z)dz = 1,
/
z3q(ζ) dz = 0 при всех 1 ^ j < 2га — 1. В этом случае путем прежних
рассуждений мы сможем получить скорость сходимости порядка η 2m/(4m+1) =
= n-i/2+i/2(4m+i) ? к0т0рая будет тем лучше, чем больше т. Этот факт
объясняется тем, что для более гладких f(x) к оценке значения f(x) привлекаются
элементы выборки, лежащие во все более широких окрестностях точки х.
С другой стороны, выбирая гладкие функции q(z), мы можем обеспечить
возможность оценивать не только плотности /(ж), но и их производные.
В этом также можно убедиться с помощью приведенных выше рассуждений.
Функции fn(x) вида (4) называют часто оценками Розенблата-Парзена
плотности f(x) или ядерными оценками /(ж). Функции q(z) называют при
этом ядрами. На практике часто используют «прямоугольные» ядра, т.е.
полагают
«(*) = {
1 при ζ Ε
0 при ζ £
1 1
2'2
1 1.
2'2
Иногда поступают еще проще — разбивают вещественную прямую на
маленькие интервалы Δ^ (длиной hn) и полагают f^{x) = Vjjnhn при
χ Ε Aj, где Vj — число элементов выборки, попавших в Δ^. Такая
функция fn{x) называется гистограммой выборки. Нетрудно проверить, что
если f(x) непрерывна, то гистограмма fnix) наряду с функцией,
определенной в (4), также обладает свойством сходимости f^{x) —> /(#), если
только hn —> 0, nhn —> оо.
Глава 2
ТЕОРИЯ ОЦЕНИВАНИЯ НЕИЗВЕСТНЫХ ПАРАМЕТРОВ
Параграф 12 содержит описание наиболее распространенных параметрических
семейств распределений и их основных свойств.
В § 13-16 излагаются основные методы получения точечных оценок.
В § 17, 18 обсуждаются подходы к сравнению оценок.
Параграфы 19-30 посвящены методам построения оптимальных (в том или
ином смысле) оценок. Выделены следующие 4 направления:
1) (§ 19-21, 30) Байесовский и минимаксный подходы к построению
оптимальных оценок. Параграфы 19, 20 носят вспомогательный характер и содержат
определения и изложение основных свойств условных математических ожиданий и
условных распределений.
2) (§ 22-25) Построение оптимальных (эффективных) оценок с помощью
принципов достаточности и несмещенности.
3) (§ 26, 27, 30-32) Построение оптимальных (эффективных) оценок на основе
неравенства Рао-Крамера.
4) (§ 28, 29) Использование соображений инвариантности.
В §31, 33-37 изучаются асимптотические свойства отношения правдоподобия.
На этой основе устанавливается асимптотическая оптимальность оценок
максимального правдоподобия. Результаты этих параграфов составляют также основу
теории асимптотически оптимальных критериев, развитой в главе 3.
Параграфы 39, 40 посвящены интервальному оцениванию.
§ 11. Предварительные замечания
Как мы уже отмечали в предыдущей главе, исходным объектом
статистических исследований является выборка
Хп — (хь · · ·>χη)> χ^ Ε А',
из распределения Р, которое полностью или частично неизвестно. В
математической статистике традиционно выделяют в качестве основных два
следующих класса задач.
1. Оценка неизвестных параметров.
2. Проверка статистических гипотез.
Задачи первого класса возникают, когда по выборке X = Хп нужно
оценить какую-нибудь неизвестную числовую характеристику θ
распределения Ρ (оно ведь неизвестно). То есть для заданного функционала
θ = 0(Р)
от распределения Ρ мы должны указать функцию от выборки (или, что то
же, статистику)
Θ* = 0*(ХП),
70
Гл. 2. Теория оценивания неизвестных параметров
предназначенную для использования вместо параметра θ в качестве его
приближения. Мы видели в предыдущей главе, что предпосылки для этого
существуют. Статистику Θ* называют оценкой параметра Θ. Разумеется,
оценок для параметра θ может быть очень много. Теорема 3.1 показывает, что,
например, для оценки функционала θ = 0(Р) вида
θ = Jg(x)dF(x)
естественно использовать статистику
«* = ££>(*)■
Но можно, конечно, рассматривать и другие оценки, скажем L-статистики
- п-и2
^i/i + l
(см. пример 8.5), где xyj, j — l,...,n, — элементы вариационного ряда
и т. д. В качестве Θ* можно брать и значения, не зависящие от выборки.
Можно положить, например, Θ* = 0, хотя это не всегда разумно и совсем
плохо, если множество возможных значений θ не содержит 0.
В связи с последним замечанием отметим, что часто в постановке
задачи об оценивании содержится указание на то, каким является множество
Θ возможных значений параметра Θ. Например, если оценивается доля θ
какого-нибудь минерала в руде, то ясно, что θ Ε [0,1].
Во многих случаях бывает заранее известно также, что распределение Ρ
выборки X не может быть произвольным, а принадлежит какому-то
определенному семейству распределений V»
К задачам оценки параметров относится пример 1 из введения.
Задачи второго класса имеют дело с проверкой того или иного
предположения (гипотезы) о неизвестном распределении Р. Например, мы можем
проверять гипотезу о том, что Ρ имеет тот или иной заданный вид. К этому
типу задач относится пример 2 из введения.
Позже мы увидим, что качественной разницы между задачами первого
класса (теории оценок) и второго класса (проверка статистических гипотез)
не существует.
В этой главе мы приведем постановки задач и подходы, которые тесно
связаны с результатами предыдущей главы и которые можно назвать «чисто
статистическими» в отличие от более общих теоретико-игровых подходов,
изложенных в главе 6.
В известной мере чисто статистические подходы выражают существо
методов математической статистики. Исторически они были осознаны
значительно раньше, чем более общие методы. Что же касается их применения,
то, по-видимому, человек пользовался ими, явно или неявно, на протяжении
всего пути процесса познания.
Все это оправдывает отдельное изложение чисто статистических
подходов несмотря на то, что некоторые моменты этого изложения в рамках более
общих концепций можно рассматривать как частные случаи. Одновременно
§ 12. Некоторые параметрические семейства распределений 71
мы обнаружим некоторую недостаточность чисто статистического подхода
для более точных постановок задач. Это поможет нам понять
целесообразность других точек зрения.
§ 12. Некоторые параметрические семейства распределений
и их свойства
Рассмотрим некоторые семейства распределений, зависящих от
параметров (или параметрические семейства распределений), которые часто
возникают в приложениях и будут появляться в дальнейшем изложении как по
существу его, так и в качестве иллюстраций.
1. Нормальное распределение на прямой. Символом Φα>σ2 мы будем
обозначать нормальное распределение с параметрами (α,σ2), т.е.
распределение с плотностью
-(х-а)2/2<72
так что
σ\/2π
в
Если ξ €= Φο,ι и к ^ 0 — целое число, то, очевидно,
щ2к+1 = 0
Для моментов четного порядка, пользуясь заменой χ = \/2и, находим
00 00
ъ+2к 2 f 2k -x*/2 J 2 + Г к -и du 2к _ / 1
щ2к = _^ / х2ке χ /2 άχ = _^ ι ике и—^ = ρ А: + -
х/2^ J yfa J V2u A V 2
где
оо
Γ(λ)= f x^e^dx (l)
о
есть Г-функция, Γ(λ) = (λ - 1)Γ(λ - 1), Г(1/2) = χ/тг, так что
Е£2/с = (2* - 1)!! = (2к - l)(2fc - 3)... 1.
Такой же результат мы получили бы, дифференцируя 2к раз
характеристическую функцию е~ь /2 в точке t = 0.
2. Многомерное нормальное распределение. В многомерном случае # =
= Мт символ Φα?σ2 означает нормальное распределение в Шт с вектором
математических ожиданий а — (ai,...,am) и матрицей центральных
вторых моментов а2 — ||σ^||, i,j = l,...,m. Если А есть матрица, обратная
72
Гл. 2. Теория оценивания неизвестных параметров
к σ2 (в тех случаях, когда она существует), то плотность φα,σ2(χ) Β
распределения Фа^2 будет иметь вид (см. [17, §7.6])
Ψν,σΦ) = ,2^)m/2 ехр ί --(χ ~ a)Aix ~ α)Τ) >
где χΎ есть транспонированный вектор. Напомним также (мы этим фактом
уже пользовались в §7), что х.ф. величины ξ €= &α,σ2 равна
где t = (*ι,..., tm) есть вектор в Rm.
3. Гамма-распределение. Символ Га>д будет означать так называемое
гамма-распределение (или Г-распределение) с параметрами (а, А). Плотность
7α,λ(χ) эт01,0 распределения зависит от двух параметров а>0иА>0и
равна (см. [17, §7.7])
( ^λ
7α,λ(χ) = <
α -а*-^-**, я>0,
Γ(λΓ , ~^, (2)
10, ζ<0,
где Γ(λ) есть Г-функция, определенная в (1). Характеристическая функция
Г-распределения имеет вид [17]
Jeitx7aiX(x)dx=^^ . (3)
о
Если ξ ^ rQjA, то
оо _ оо
О О
Такой же результат при целых t > 0 можно было бы получить,
дифференцируя характеристическую функцию. Полагая t = 1,2, находим
Εξ = -, ϋξ = Α (5)
Из формул (3), (4) видно, что параметр α играет роль масштаба, так что
- ^ Γα>λ, если η ξ= Γι)λ.
α
В силу этого обстоятельства многие свойства Г-распределения достаточно
изучать при каком-нибудь одном значении а, например при α = 1 или
a = 1/2. Второе значение часто будет для нас более удобным, так как
распределение Γ!/2,λ играет важную самостоятельную роль в математической
§12. Некоторые параметрические семейства распределений 73
статистике и называется распределением «хи-квадрат» (или %2-распределе-
нием).
4. Распределение «хи-квадрат» Щ с к степенями свободы. Так
называется распределение Н* = Г1/2,А;/2 пРи целых к > 0. Мы сохраним это
название за распределением Щ и при произвольных к > 0.
Характеристическая функция распределения Щ равна в силу (3)
(1-2ί*Γ*/2.
Отметим следующие три свойства распределения Н*.
1) Если щ независимы, щ €= Hfct, г = 1,..., s, то
S S
<=1 t=l
Это свойство сразу вытекает из вида характеристической функции
распределения Η&.
2) Если ξ €= Φα>σ2, где Φα>σ2 есть к-мерное нормальное распределение
с невырожденной матрицей вторых моментов σ2, то
ρ(ξ) = (ξ-α)σ-2(ξ-α)τ^Η*.
Действительно, характеристическая функция случайной величины Q(£)
равна
Ββ*κ° = (^Р / βΧΡ (4Q(*)(1 " Ш)) dxi··-dxk-
Произведя замену переменных Xj\/1 — 2it = у^, мы получим выражение
(l-2i*)-*^Iy'e-i«Wc^...^fc=:(l-2it)-t>
что и требовалось доказать. Независимость интеграла в левой части от
изменения области интегрирования вытекает из аналитичности
подынтегральной функции и ее быстрого убывания при \у\ —> оо.
Из сказанного вытекает, что распределение Η*, имеет случайная
величина
где £j независимы, £j ^ Φο,ι· Термин «число степеней свободы» связан
именно с этим представлением.
3) Так как Εξ2 = 1, Щ* = 3, Όξ% = 2 для ξι ^ Φ0,ι, то в силу
центральной предельной теоремы при к —> оо
v2 -jfe
-ж^*°->- (6)
74
Гл. 2. Теория оценивания неизвестных параметров
Отсюда и из теорем непрерывности § 5 следует, что наряду с (6)
2χ2 - VU^l @> Фод.
Эта сходимость служит основой для приближенного (при больших к и х)
равенства Hfc((0,:r)) « Ф(л/2я - \/2fc - 1), Ф(х) = Φο,ι((-οο,ζ)),
которое, как правило, оказывается более точным, чем приближение Н^((0,ж)) «
« Φ [ — J , вытекающее из (6).
Отметим еще один частный случай Г-распределения, часто
встречающийся в приложениях.
5. Экспоненциальное распределение. Это есть распределение Гад с
плотностью
ae~ax, х > 0.
Из формул (5) получаем для ξ ^ Гад
щ = -, Ώξ = \
α az
Рассмотрим теперь некоторые распределения, связанные с нормальным и
Г-распределениями и играющие важную роль в математической статистике.
В отличие от предыдущих эти распределения нам прежде не встречались.
6. Распределение Фишера с числом степеней свободы &ι, &2· Так
называется распределение случайной величины
Μι
κ= ι—>
«1*72
где щ независимы, r/j Ш Η*., j = 1,2. Нам будет удобнее изучать
распределение Ffcb*2 случайной величины
которая, очевидно, связана с ус соотношением ус = --—. Причина введения в
определении ус нормирующего множителя — состоит в том, что при к\ -> оо,
«1
/с2 —> со в силу закона больших чисел будет выполняться ус —> 1.
Р
Из свойств Г-распределений следует, что распределение ζ останется тем
же при щ €= Та,к/2 и любом о: > 0 и что ζ при целых kj допускает
представление
, *? + ··· + &
где случайные величины £j, ζ& независимы, ^· ^ Фод, Cfc €= Φο,ι-
§ 12. Некоторые параметрические семейства распределений 75
Найдем плотность распределения Ffcb£2. Имеем
Р(С < х) = Л T1M(du)T1M(dv) =11 ^'^'^e-^dudv;
u/v<x ^=0 u=0
00
. , , <iP(C<i) /,(»ι)Λι-1»Λ>-1 _^„ ^
0
00
Γ(λι)Γ(λ2)
/,υλ1+λ2-1 -„(!+«) rf _ ?_! Γ(Λ1 + Λ2) /7Ν
Требуемая плотность получится, очевидно, если подставить сюда Xj = kj/2.
Нетрудно найти моменты случайной величины ζ (если они существуют):
w Γ(λ!+λ2) Г х>*+1-1 , _ Г(Л! + рГ(А2 -1)
оо
/Χλ
(1+ж)А1+А2^= ' Γ(λ!)Γ(λ2) '- (8)
О
В частности, при / = 1,2 находим
λι _2 λι(λι + 1)
Е< = ^, ЕС-
λ2-1' (λ2-1)(λ2-2)'
Распределение Фишера называют иногда также распределением Снеде-
кора. Это связано с тем, что Фишер предложил использовать и
табулировал, собственно, не распределение х, а распределение случайной величины
-1η χ. Распределение же к было несколько позже подробно табулировано
Снедекором.
В дальнейшем в формулировках результатов, связанных с
распределением Фишера (см., например, §61, 62), нам будет удобнее использовать
распределение Ffcb£2. При этом следует иметь в виду, что при отыскании
квантилей распределения FkiM c помощью таблиц распределения Фишера
надо вводить поправочный множитель: если /ε, >сЕ — квантили порядка 1-е
распределений Fkifa и Фишера, соответственно, то f£ = —-—.
7. Распределение Стьюдента*) Т& с к степенями свободы. По
определению это есть распределение случайной величины
\/м«?+-+ш'
*) Стьюдент — псевдоним В. С. Госсета.
76
Гл. 2. Теория оценивания неизвестных параметров
где £j независимы, £j ^ Фо,ь 3 = О,...,Л. Очевидно, что —ί имеет то же
самое распределение и, стало быть, распределение Стьюдента симметрично
относительно начала координат. Далее,
ίΔ =
2 оо~ '
где щ независимы, 771 ^ Hi, 772 €= Щ. Это значит, что t2 /к имеет
распределение Фишера. Рассмотрим случайную величину τ — >/С, С = Vi/V2j
щ €= Н^. Так как Ρ (г < χ) = Ρ (ζ < я2), то плотность /(т)(я) случайной
величины г будет равна
/(т) W ^;(ς)1χ ) ^Γ(λι)Γ(λζ) (1 + 3.2)λ1+λ2
_Γ(ΛΧ + Λ2) 2s2*'-1 _^
ΓίλΟΓ^α+χψι+λ»' j 2' 1>υ·
Отсюда при λι = 1/2, λ2 = λ/2 очевидным образом можно получить
плотность \t\/vk. Так как распределение t симметрично, то для плотности f(t)(x)
случайной величины t окончательно получаем
, , . Г((*+1)/2) {, i2V(l+1)/2
Ясно, что все моменты t нечетного порядка (если они существуют) равны
нулю. Для моментов четного порядка 2/ имеем в силу (8)
m -кЕС-к Γ(λι)Γ(λ2) ,
где следует положить λι — 1/2, Аг = fc/2, 2/ < /с. При / = 1 получаем
ЕГ
/с-2"
По своей форме функция f(t){x) напоминает плотность нормального
закона. Более того, с ростом к
f(t)(x)
-х2/2
что означает сходимость t ©► Фод при к —> со. Однако fm{x) имеет более
«толстые хвосты», поскольку функция (9) убывает с ростом |д;| значительно
медленнее, чем е~х /2, так что при всех Ъ > О
Тк((-Ь,Ь))<Ф0А((-Ь,Ь)). (10)
При этом разница между правой и левой частью в (10) при небольших к
может быть существенной.
§12. Некоторые параметрические семейства распределений 77
Сходимость t = у/Що/у/П2 к нормальному закону читатель может
доказать и другим путем с помощью теорем непрерывности. Например,
достаточно заметить, что — = —(ξ? + · · · + ξϊ) —> 1; и, стало быть, t —> £о>
к к п.н. п.н.
8. Бэта-распределение (В-распределение). Так называется распределение
ВдьА2 с ПЛОТНОСТЬЮ
[о, χ £ [ο,ι].
Своим названием оно обязано бета-функции
ι
В(АЬ А2) = jx^~\l - χ)**'1 Лх = Щ^
Γ(λχ)Γ(λ2)
λ2)'
Бета-распределение связано с гамма-распределением и с распределением
Фишера путем следующего утверждения.
Если щ независимы, η^ ^ Га>д; {или щ ^ Н^д,), mo
m + m ζ +1
где ζ = 771/772 ^F2Ab2A2.
Доказательство этого утверждения весьма просто, так как в силу (7)
Для моментов случайной величины β имеем
1
ЪР ~ r(A0r(A2) J [1 X) dX~ Γ(λΟΓ(λι + λ2
О
При 1 — 1,2 находим
±R
2+0'
λΐ πα2_ Αι(Λι + 1)
Έβ = -—L—, Εβ
λι + λ2' и (λι + λ2)(λι+λ2 + 1)'
78
Гл. 2. Теория оценивания неизвестных параметров
9. Равномерное распределение. Частным случаем В-распределения
является равномерное на [0,1] распределение, которое получится, если положить
λ! = λ2 = 1.
Символом \Jafb мы будем обозначать равномерное распределение на
отрезке [а, 6], так что Вхд = Uo,i.
С помощью В-распределения можно описать распределение членов
вариационного ряда X(fe) выборки X.
Теорема 1. Если X €= Ρ есть выборка из распределения Ρ с
непрерывной функцией распределения F, то
У (к) = ^(Х(А;)) ^ Вк,п-к+1-
Доказательство. Так как yk^Ffa) €=Uo,i, то y^j =F(x^) можно
рассматривать как член вариационного ряда выборки У^Иод. Найдем
P(y(fc) ε (u,u + du)). Событие {у(^) G (u,u + du)} можно представить как
объединение непересекающихся событий
Аз = {у* ^ (гх,и + Ах), у,- = y(jb)},
которые происходят, когда yj попадает в (и, и + du) (вероятность этого
равна du), к—1 иг оставшихся п — 1 наблюдений попадает в область (0, и), п — &
наблюдений — в область (и, 1). Следовательно,
P{Aj) = C^V-^l - u)n-*du,
Р(У(*) е (и, и + du)) = пС^и*-1 (1 - u)n"*du.
Это и значит, что плотность у^) существует и равна
ϋ! ^(l - u^-* = Г(п + 1) uk-i(1 _ )П-к
На основании теоремы 1 можно без большого труда получить и
предельное распределение членов вариационного ряда, когда объем выборки X
неограниченно возрастает. Мы остановимся здесь лишь на одном результате,
вытекающем из теорем непрерывности.
Теорема 2. Если а = —> ац Ε (0,1) при η —> оо, πιο
η + 1
. \Λο(1 ~αο) t t ^ -
У(А;) = « + " -д ξη, ξπ ©> *0,1-
Доказательство. В силу теоремы 1 у^ ^ Β^η_£+ι и? стало быть,
в силу свойств В-распределения справедливо представление
77т
У(к) = —Τ—» %^Hfc., ki = 2k, k2 = 2(n-k + l).
κ ' d ηι + η2 J
§ 12. Некоторые параметрические семейства распределений 79
Положим для удобства αϊ = а, а2 = 1 - а и предположим, что а = ао
фиксировано. Тогда, очевидно, kj/(n + 1) = 2aj, j = 1,2, ив силу свойств
распределения χ2
У(*) =
. / Ql t(l) , / Q2 >(2)
Остается воспользоваться теоремой непрерывности 5.ЗА при
Так как щ (а стало быть, и ξη ) независимы и
ая *2 зя ίι
ati (*i+*2)2' dt2 (*ι+ί2)2'
то мы получаем
(У(*) - οι)λ/π + 1 =► α2λ/αΓ^(1) - ^л/^ £(2) = χ/αΐ^ f, ξ ^ Φ0|ι·
Если α зависит от η, то следует воспользоваться замечанием 5.1. <
Следствие 1. Если a = k/(n+ 1) —> αο Ε (0,1) w непрерывная
функция F непрерывно дифференцируема в точке ζ$ = F~l(aa) (квантиль
порядка ао), тпо
X(fc) = C+ /(Co)v^ ' &е>*°.ь (11)
г<?е ζ = F"1(a) — квантиль порядка α, f(x) = F'(x).
Это утверждение получается сразу из теоремы непрерывности 5.3 (с
учетом замечания 5.1), если воспользоваться представлением
dF~llx) 1
и тем фактом, что —
dx HF^ix))'
тверждение (11) неск
обобщить и в другом
\F(x)-F(C)\~c\x-C\\ 7>0.
Замечание 1. Утверждение (11) несколько обобщает утверждение
следствия 8.1. Его можно обобщить и в другом направлении. Пусть при χ —> ζ
80
Гл. 2. Теория оценивания неизвестных параметров
Тогда нетрудно видеть, что при у -> a
|1/7
\F-l(y)-F-1(a)\r.
и что, стало быть,
(xW-On^^iaoil-oo))1^
3/-α
ξΙ1^
sign£, ξ^Φο,ι. (12)
При 7 = 13 с — /(С) отсюда следует (11).
10· Распределение Коши Καί<τ с параметрами (α, σ). Так называется
распределение с плотностью
σ 1 1
π[σ2 + (χ - α)2] πσ (χ-α.
Κα,σχΖ') —
Как и в случае нормального закона, параметры α и σ здесь являются
соответственно параметрами сдвига и масштаба. Форма распределения Код очень
похожа на форму Фод, однако Atyi, как и плотность распределения Стью-
дента, имеет значительно более «толстые хвосты» (т.е. более медленное
убывание при |д;| —> со), так что распределение Код не имеет даже
конечного математического ожидания. В [17, гл.8] отмечалось, что распределения
Κα>σ, как и нормальные распределения, обладают свойством устойчивости.
Характеристическая функция ход(0 распределения Код равна
поэтому
*r0,iW = exp(-|i|),
^α,σ(ί) = exp{iat - σ|ί|},
(ί) = ехр{г(с*1 + a2)t - (σι + σ2)|ί|},
так что свертка Και>σι и KQ2)(T2 равна Και+α2>σι+σ2.
Нетрудно видеть, что Код = Τι-
В приложениях часто приходится иметь дело с разного рода функциями
от нормально распределенных случайных величин. Одна из них —
экспоненциальная функция, с которой связано так называемое логнормальное
распределение.
11. Логнормальное распределение La<T2. Мы будем говорить, что η ^
^ Ι»ασ2, если 1ητ/ €= Φα,σ2. Другими словами, η = е^, где ξ €= Φα,σ2. Отсюда
видно, что распределение La<72 сосредоточено на положительной полуоси.
Плотность η €= LaiT2 в силу формул для плотности функции от случайной
величины (см. [17, §3.2]) равна
φα%σ2{]ιιχ)χ
§ 12. Некоторые параметрические семейства распределений 81
Кроме того, находим
Ет/ = / ехру—7=ехр
J σγ2π
(v-<*)
2σ2
(α + σ2)2_α2
dy = exp — χ
(у - α-σ2)2λ , ία + σ2
ay = exp
exp (2y)-^ exp1 КУ }
dy - exp (2a 4- 2σζ).
12. Вырожденное распределение. Символ Ια (это обозначение нами уже
использовалось в § 2) будет означать вырожденное распределение,
сосредоточенное в точке а.
В общем случае, когда рассматривается произвольное семейство рас-
пределенищ зависящих от параметра θ (скалярного или векторного), мы
будем использовать обозначение Р#. Само семейство будет обозначаться
символом
{Рв}вев,
где Θ — множество возможных значений параметра Θ. Такие же обозначения
будут применяться к семействам распределений 1-12. Например, {Φα,ι}α^κ
будет означать семейство всех нормальных распределений с единичной
дисперсией.
Распределения 1-11 абсолютно непрерывны относительно меры Лебега.
Введем теперь обозначения для трех хорошо известных дискретных
распределений (абсолютно непрерывных относительно считающей меры μ{Β):
μ(Β) = А;, если В содержит к целочисленных точек).
13. Распределение Бернулли В™. По определению ξ €= В£ (п целое, ρ Ε
G [0,1]), если
P(£ = *) = C*p*(l-p)n-*, 0O<n.
14. Распределение Пуассона Ид. Это распределение определяется
равенством
Пл(В)=Е^в"А' λ>°·
кев,
15. Полиномиальное распределение. Мы будем обозначать его В£, где
г
η > 0 — целое число, р= (pi,.. ·,ρΓ)> Pj ^ 0, /^Pj = 1· Для целочисленного
i=i
случайного вектора ν — {у\,..., vr) мы будем писать ν €= В™, если для к =
г
= (fci,..., fcr), kj ^ 0, 2_] kj ==: n справедливо
82
Гл. 2. Теория оценивания неизвестных параметров
Распределение В£ соответствует последовательности η независимых
испытаний, в каждом из которых наступает один из г несовместных
возможных исходов Αι,.. .,АГ; при этом вероятность появления исхода А3 в одном
испытании равна р3. Координаты v3 вектора ν означают частоты появления
событий А3 после η испытаний (см., например, [17, §3.3]). Очевидно, что
при каждом j = 1,..., г
Исход j-το испытания в описанном эксперименте можно описать г-коорди-
натным вектором xj5 у которого г — 1 координат равны нулю и одна
координата равна единице. Номер этой координаты есть номер события, которое
η
произошло при j-м испытании. Очевидно, что ν — /^Xj. Относительно
j = l
выборки X, составленной из χι,.. .,хп, нам будет удобнее писать
X €= Вр,
где Вр = Вр. Пространство X для такой выборки, очевидно, конечно и
состоит из г точек. Если ρ = (рьрг), Pi + Р2 = 1» то мы получим схему
Бернулли, для которой мы будем использовать те же обозначения,
отождествляя В(рьр2) с ВР1 = Βρχ (см. п.13). В общем случае распределение Вр
зависит на самом деле лишь от (г — 1)-мерного параметра (ρχ,.. .,pr_i), так
что вместо индекса ρ можно было бы писать (рь .. .,pr_i).
Многие из рассмотренных выше распределений, например
распределения Фо,ь Нь ^kuk2i Tjt, 1Г\, табулированы в руководствах по
математической статистике и в специальных таблицах (см., например, [10]).
§ 13. Точечное оценивание. Основной метод получения оценок.
Состоятельность, асимптотическая нормальность
1. Метод подстановки. Состоятельность. Понятие оценки было введено
нами в § 11. Формально оценка — это то же самое, что и статистика, т.е.
любая измеримая функция Θ* от выборки. Неформально смысл,
вкладываемый в этот новый термин, состоит в том, что оценками Θ* мы называем
лишь статистики, предназначенные для использования вместо неизвестного
параметра Θ. Другими словами, Θ* есть некоторое приближение для 0,
основанное на выборке. Величину Θ* называют также точечной оценкой для θ
в отличие от интервальных оценок, которые будут рассмотрены позже.
Задание оценки обычно предполагает задание функций (от выборок Хп),
определенных при всех возможных значениях п. Поэтому в дальнейшем
термин «оценка», будет означать семейство статистик Θ* = 0*(Хп),
определенных при всех η = 1,2,..., где Θ* есть функция на Xй, или, что то же,
одну функцию Θ* = 0*(гг,Хоо), определенную на произведении множества
целых чисел и Х°°.
В соответствии с § 11 мы будем считать, что в постановке задачи об
оценивании определено множество Θ возможных значений параметра θ и
семейство V возможных распределений Ρ выборки X (это могут быть, скажем,
лишь нормальные распределения Фад или распределения Пуассона Щ, для
которых требуется оценить неизвестные параметры α, λ). Если какие-либо
§13. Точечное оценивание. Основной метод получения оценок 83
ограничения на θ (на Р) отсутствуют, то можно считать, что Θ (V) совпадает
с евклидовым пространством соответствующей размерности (с множеством
всех распределений).
Если для обозначения параметра вместо θ используется какая-нибудь
другая буква, например λ, то оценки этого параметра будут обозначаться
тем же способом: добавлением к λ верхнего индекса «звездочка». Например,
для параметра α нормального закона естественно рассматривать оценку
1 п
а* = -У^Хг·
г=1
Выборочные моменты, используемые для оценки
Εχι = / χ = P(dff), Dxi = / (χ - Exi)2P(cb),
имеют свои специальные традиционные обозначения
η г--' τι г—'
г=1 г=1
Мы уже отмечали, что для данного параметра можно указать сколь угодно
много разных оценок, и прежде чем обсуждать, каким образом в каждой
конкретной ситуации следует сравнивать их достоинства, мы остановимся
на некоторых общих «регулярных» методах их построения.
Эти методы объединяют в себе наиболее разумные подходы к проблеме
оценивания и позволят нам получать в дальнейшем наилучшие в том или
ином смысле оценки.
В основе почти всех приемов оценивания лежит следующий основной
метод, который можно было бы назвать методом подстановки эмпирического
распределения (или, для краткости, методом подстановки.)
Пусть Хп §Ри неизвестный параметр θ представим в виде некоторого
функционала G от распределения Р:
θ = G(P).
Пусть, далее, Ρ*, как и прежде, означает эмпирическое распределение. Тогда
метод подстановки предписывает в качестве оценки Θ* взять функцию
θ* = 0(Ρ*η).
Такие оценки мы будем называть оценками по методу подстановки
или просто оценками подстановки.
Функционал G иногда бывает задан в неявном виде как решение
некоторого уравнения #(#, Р) = 0, разрешимого относительно Θ. В этом случае
оценками подстановки в соответствии с основным определением мы будем
называть любое решение уравнения #(0,Р*) = 0.
Если известно, что множество возможных значений параметра θ Ε Шк
ограничено областью θ из Rfc, не совпадающей с Kfc, то эту информацию
можно учесть при построении оценок подстановки. Допустим, что область Θ
замкнута, и пусть V есть множество возможных распределений выборки X,
84
Гл. 2. Теория оценивания неизвестных параметров
Θ = {<7(Р)}рер. Определим функционал Gi(P) для произвольного Ρ как
значение t Ε Θ, для которого достигается
min|i-G(P)| = |G1(P)-G(P)|, (1)
так что (?ι(Ρ) есть точка из Θ, ближайшая к G(P). Так как Gi(P) = G(P) =
= 0, если Ρ Ε V, то оценка
e* = Gi(P;) (2)
вместе с G(P^) будет оценкой подстановки, при этом множество возможных
значений Θ* будет принадлежать Θ.
Про оценки (1), (2) мы будем говорить, что они получены сужением
метода подстановки.
Пусть, например, оценивается параметр а нормального распределения
Фад, и нам заранее известно, что а Ε [0,1]. Тогда может оказаться, что
оценка а* = χ ^ [0,1] (очевидно, что χ = J t dF*(t) есть оценка подстановки).
Сужение метода подстановки рекомендует в качестве оценки взять точку из
[0,1], ближайшую к х.
Отметим теперь, что в сформулированном виде метод подстановки не
всегда имеет смысл. Дело в том, что исходный функционал G может
оказаться не определенным на множестве эмпирических распределений. Пусть,
например, заранее известно, что распределение Ρ принадлежит классу V
абсолютно непрерывных относительно меры Лебега распределений, так что
каждое Ρ Ε V имеет плотность /. Нас интересует значение
θ = G(P) - J/2(x) dx=[ №\ dx.
Ясно, что в этом случае (?(Р*) не имеет смысла, так как Р* есть
дискретное распределение. В таких случаях метод подстановки всегда можно
естественным образом модифицировать так, чтобы он сохранил свое существо.
В приведенном примере, где б(Р) есть функционал от плотности /, следует
в качестве Θ* в соответствии с методом подстановки рассмотреть значение
G(P**), где Р** — сглаженное эмпирическое распределение (см. § 10),
обеспечивающее сходимость эмпирической плотности к /(х).
Может оказаться также, что в некоторых случаях С?(Р*) будет иметь
смысл не для всех Хп, а лишь для Хп Ε Ап, где "Р{Хп Ε Ап) —> 1 при η —> оо.
Это обстоятельство для существа дальнейшего изложения роли играть не
будет, и для определенности можно положить G(P*) = 0 для Хп ^ Ап.
В этом параграфе мы для простоты будем предполагать, что (7(Р£) имеет
смысл при всех Хп Ε Хп и что Θ* есть случайный вектор, т.е. функция
G(P*) осуществляет измеримое отображение Хп в R*, где к есть
размерность Θ.
Принцип подстановки представляет собой весьма естественный подход
к задаче, поскольку, как мы уже знаем, распределение Р* неограниченно
сближается с Ρ с ростом п.
ПуСТЬ Хп = [Хоо]п-
§13. Точечное оценивание. Основной метод получения оценок 85
Определение 1. Оценка Θ* = 0*(ХП) (или последовательность Θ^(Χ))
называется состоятельной, если
Θ* —>θ
р
при η —> оо.
Оценка θ* называется сильно состоятельной, если при η —> оо
0*—> б.
п.н.
Пусть F, как обычно, есть функция распределения, соответствующая Р.
Теорема 1. Пусть θ = G(P) w функционал G принадлежит одному
из двух классов: либо он представим в виде
G(P) = h^jg(x)dF(x)y (I)
где h — функция, непрерывная в точке а = g(x)dFo(x) (функционал
I типа), либо в виде
G(P) = d(n (И)
где функционал G\ непрерывен в точке Fo в равномерной метрике
(функционал II типа). Тогда если X ^ Fo, то Θ* — G(P*) есть сильно
состоятельная оценка:
Θ* —> Θ.
п.н.
Утверждение этой теоремы немедленно следует из теоремы 4.1.
2. Асимптотическая нормальность. Одномерный случай
Определение 2. Оценка Θ* параметра θ называется асимптотически
нормальной (а.н.) с коэффициентом σ1 > 0, если (Θ* — в)у/п ©► Φο,σ2·
Последнее соотношение может читаться также следующим образом:
оценка Θ* а.н. с параметрами (θ,σ2/η). Коэффициент σ2 мы будем иногда
называть также коэффициентом рассеивания (или разброса).
Пусть Θ* есть оценка подстановки параметра θ = G(P) и выполнено (I),
т.е.
θ* = h[lΣ,^(χгη (3)
есть статистика I типа. Тогда из результатов § 7 вытекает следующее
утверждение. Предположим, что θ — скалярный параметр, a g — скалярная
функция.
Теорема 2. Пусть X€=Fo, h дифференцируема в точке а =
= / g(x)dF0(x), 0 < \ti(a)\ < оо, / g2(x)dF0(x) < оо. Тогда Θ* — а.н.
оценка с коэффициентом
a2 = [ti(a)]2 J(g(x)-a)2dF0(x).
86
Гл. 2. Теория оценивания неизвестных параметров
Примеры, рассмотренные в § 7, можно взять в качестве иллюстраций и
к этой теореме, так как статистики, рассмотренные в них, используются в
качестве оценок.
Аналогичным образом мы могли бы, пользуясь результатами § 8,
получить условия асимптотической нормальности оценок, являющихся
статистиками II типа. Читатель может получить нужные утверждения, если
воспользуется теоремой 8.1 без каких-либо ее изменений, потребовав, однако,
чтобы в ее формулировке выполнялось к = 1, а производная д была такой,
что g{F0,w°) ^Φ0,σ2·
3. Асимптотическая нормальность. Случай многомерного параметра
Определение 2А. Оценка Θ* — (0f,...,0£) называется а. н. оценкой
θ = (01,..., 6k) с матрицей σ2, если
(θ*-θ)^^Φ0<σ2, (4)
где Φο,σ2 есть ^-мерное нормальное распределение с нулевым вектором
математических ожиданий и матрицей вторых моментов σ2 = ||о\;||. Плотность
этого распределения равна (см. §12)
где А — матрица, обратная к σ2, χ — (д;χ,.. .,£*). Матрицу σ2 мы будем
называть также матрицей рассеивания (или разброса).
Если Θ* есть оценка подстановки и она является статистикой I типа (т. е.
представима в виде (3), где д, вообще говоря, вместе с Θ* и h есть векторная
функция), то для выяснения условий асимптотической нормальности можно
воспользоваться теоремой 7.1 А и замечанием к ней. Мы получим тогда
следующее утверждение.
Теорема 2А. Пусть θ* Ε Rk определяется равенством (I), где
g = (gi,...,ffs) E Ms, а вектор-функция h(t) — (Λχ(ί),..., Λ*(ί)), t ==
= (ίι,.. .,is), имеет в точке а = (αϊ,.. .,αβ), α? = / <7j0&) di*o(s)j
ΟΙ
производные ——(α), / = 1,..., /с, j = 1,..., 5. Тогда если X ^ Fo, mo
{θ* -0)\Λ^ξ#τ,
где ξ = (£ι,···,£δ) €= ^od2 ^cmb нормально распределенный вектор с
нулевым средним и матрицей вторых моментов d = ||<%||, d*j —
= E(<7i(xi) — ai)(<7j(xi) ~ aj)> Μ = 15···55; -Η" — ||Лу|| есть матрица
размера к χ s с элементами hij = тг^(а)? г = 1,..., fc; j = 1,.. .,5.
Otj
Это означает, в свою очередь, что 0* при выполнении условий теоремы 2А
является а. н. оценкой с матрицей σ1 = Hd2HT = ΈΗξτξΗτ. Отметим, что
матрицы σ2 и d2 здесь имеют, вообще говоря, разные размерности (к и s).
частные
§14. Метод подстановки в параметрическом случае
87
§ 14. Реализация метода подстановки
в параметрическом случае. Метод моментов. iVi-оценки
Пусть Χ ^ Р#, где {Ρθ}θεΘ есть известное нам семейство
распределений Pfl, зависящих от параметра Θ. Неизвестный параметр θ из множества
Θ может быть в наших рассмотрениях как скалярным, так и векторным.
Например, если X €= Φα)σ2, то θ = (α,σ2) двумерно, а множество Θ может
быть как полуплоскостью {—оо < α < οο, σ ^ 0}, так и какой-нибудь ее
частью.
Математическое ожидание и дисперсию статистики S — S(X) по
распределению Р# будем обозначать соответственно E^S, OqS.
Мы рассмотрим ниже несколько методов оценивания, каждый из
которых можно трактовать как реализацию принципа подстановки эмпирике
ского распределения.
1. Метод моментов. Одномерный случай. Выберем д(х) так, чтобы
функция
πι(θ) = Εθ9(χ1) = Jg(x)Pe(dx) (l)
была монотонной и непрерывной. Область т(0) значений га(0), θ Ε Θ,
имеет ту же «природу», что и Θ. Если, например, Θ есть отрезок
вещественной оси, то ττι(Θ) также будет отрезком.
Очевидно, что уравнение τη(θ) = t однозначно и непрерывно разрешимо в
области ττι(Θ) относительно θ: θ = m-1(£), и что (1) эквивалентным образом
можно записать в виде
e = m-4J g(x)Pe(dx)\. (2)
Предположим для простоты, что
Г 1 "
д= 9(χ)άΡ·η(χ) = -Σ9(χί)£τη(θ)
J nU
при всех X е Хп.
Определение 1. Оценкой по методу моментов называется оценка
в* = т-\д). (3)
Если д ψ m(0), то можно положить согласно (13.1), (13.2)
в* = т-1(д0),
где (?о ^ τη(θ) есть ближайшая к ~д точка из т(0).
Нетрудно видеть, что это есть оценка по принципу подстановки. Выбор
функции т{в) позволил нам выразить θ в виде функционала (2). Ясно также,
что оценка (3) является статистикой I типа, так что в силу теоремы 13.1
оценки по методу моментов будут сильно состоятельны. Если к тому же
88
Гл. 2. Теория оценивания неизвестных параметров
функция m дифференцируема в точке 0, / д2(х)Р$(ах) < оо, то по
теореме 13.2 оценка по методу моментов будет а. н. с коэффициентом рассеивания
(m'(0))-2D,5(Xl).
Метод моментов был предложен К.Пирсоном (в несколько более
частном виде) и исторически является первым регулярным методом построения
оценок.
Свое название «метод моментов» получил потому, что его существо
состоит в приравнивании друг другу «теоретических» и эмпирических
моментов (математических ожиданий) величины д(х\): ведь оценка (3) есть не
что иное, как решение уравнения
** · 1
Можно добавить также, что в качестве д(х) часто выбирают функцию
д(х) = χ или д(х) = хк, к > 1, так что наше уравнение превращается в
уравнение для обычных моментов.
Равенство (4) можно рассматривать так же, как результат
приравнивания среднего значения величины g{xi) «по пространству» ее среднему
значению «по времени».
Неоднозначность метода моментов, как и всего принципа подстановки,
здесь видна особенно хорошо: ведь выбор функции д(х) почти ничем не
ограничен.
Пример 1. Пусть X €= Гад и α не известно. Построим оценки по методу
моментов с двумя простейшими функциями д(х): д\{х) = х и ^(^) = я2·
Справедливы следующие равенства (см. п. 12.2):
00
mi (a) = EQffi(xi) = / xTQti(dx) = -,
J Οί
о
оо
m2{a) = EQ#2(xi) = / x2Tail{dx) = —^.
о
1 n
Решая уравнения m\{a) = χ, 7712(a) = — Ух?, мы получим оценки по
методу моментов
/ η 4-1/2
Обе эти оценки являются статистиками I типа, и мы можем описать их
асимптотические свойства. На основании равенств (12.4) получаем
1 20
Daffi(xi) = Daxi = —, Da^2(xi) = Daxj = —т.
ΟίΔ ОТ
§14. Метод подстановки в параметрическом случае 89
Так как для первой оценки m[(a) = —Ι/α2, а для второй га'2(а) = — 4/а2,
то на основании теорем 13.1, 13.2 мы получаем, что обе оценки а* и а**
являются сильно состоятельными и а.н. с коэффициентами рассеивания
соответственно
1 4 2 20 а6 5 2
—а =а , — · — = -а .
а1 а4 16 4
Видимо, оценку а* следует предпочесть, так как ее «разброс» при
больших η вокруг истинного значения а, измеряемый дисперсией предельного
распределения, меньше, чем «разброс» для а**.
2· Метод моментов. Многомерный случай. Совершенно аналогичным
образом рассматривается случай, когда θ — многомерный параметр.
Пусть, как и прежде, к есть размерность Θ. Выберем вектор-функцию
g{x) = {gi{x),...,9k{x)) так, чтобы уравнение
т(0) = ί,
где
t =(tb...,**), т(0) = (т!(0),...,т*(0)),
mj{9) = Ε^-(χι) = / gj{x]PB(dx),
было однозначно и непрерывно разрешимо относительно θ — m 1(t) в
области τη(Θ) значений т(0), 0 Ε Θ. Допустим для простоты, что вектор
= (-Σ^(χ«)'···'^Σ^(χί)
\ г=1 г=1 /
принадлежит области га(Э) при всех Χ Ε Л"\
Определение ΙΑ. Оценка θ* = m~l(jj) называется оценкой по методу
моментов.
Как и прежде, из теоремы 13.1 следует, что такие оценки Θ* будут сильно
состоятельными.
Для того чтобы имела место а.н. #*, нужно потребовать дополнительно,
чтобы функция т была дифференцируемой, / д^(х)Р$(ах) < оо.
Утверждение о предельном распределении Θ* нетрудно получить с помощью
теоремы 13.2А.
Пример 2. Рассмотрим в качестве {Р#} семейство нормальных
распределений Φα>σ2. Полагая д\{х) — х, д2{%) = χ2, получим следующие
уравнения для метода моментов:
1 п
— 2 2 ■*· Ч Л 2
а = х, σ + α = - > χ»,
п. * *
П · 1
г—1
решение которых есть
=* (^2г = ^Ехг2-(х)2 = 52.
α
г=1
90
Гл. 2. Теория оценивания неизвестных параметров
Мы предлагаем читателю в качестве упражнения найти оценки по методу
моментов для всех параметрических семейств, приведенных в § 12.
3. М-оценивание как обобщенный метод моментов. Возможно
следующее обобщение метода моментов, которое существенно расширяет
рассмотренный выше класс оценок.
Пусть 0о — истинное значение параметра: X €= Р#0. Оценка по методу
моментов была основана на том, что уравнение относительно θ
τη(θ) = j9(x)Pe(dx) = Jg(x)P(dx) (6)
имело единственное решение θ = G(P) = πι λ ί / g(x)P(dx) I , совпадаю-
■ (/*>
щее при Ρ = Р#0 с #о> так что оценка по методу моментов Θ* — G(P*), как
мы уже отмечали, оказывается оценкой подстановки.
Первое соотношение в (6) можно записать в виде
/<
(0(х)-т(0))Рв(<*г)=О, (7)
а уравнение (6) в виде
' (д(х)-т(в))Р((1х) = 0.
/<
Основываясь на этих двух соотношениях, мы можем рассмотреть теперь
более общее уравнение. Пусть функция д{х,в) ^ 0 такова, что
/
9{χ,θ)Έ>θ{άχ)=0 (8)
(д(х,9) = д(х) — πι(θ) в (7)). Функцию д{х,9), удовлетворяющую (8),
можно получить из любой интегрируемой функции д\{х,в), положив д{х,в) =
= 9ι(χ,θ) — / 9iix^)Pe{dx)· Если уравнение
/
g{x,0)P{dx) =0 (9)
имеет единственное решение θ — G(P), то в силу (8) выполняется G(P^0) =
= 0q. Стало быть, метод моментов допускает следующее естественное
обобщение.
Определение 2. Значение 0*, являющееся решением уравнения
£>(xi,0) = O (Ю)
(ср. с (9) при Ρ = Ρ*), называется оценкой решения θ уравнения (9) по
обобщенному методу моментов или М-оценкой.
Очевидно, что М-оценка является М-статистикой (см. п. 3.4).
§ 14. Метод подстановки в параметрическом случае
91
Здесь, как и прежде, 0* = G(P*), где G(P) есть решение (9)
относительно 0. Нетрудно видеть, что определение 2 М-оценки допускает выход
за рамки параметрического случая и сохраняется в более общем случае,
когда речь идет об оценке по выборке X ^ Ρ фукционала θ = G(P),
который определяется как решения уравнения (9) при некоторой функции
д(х,9)\ при этом Ρ может быть произвольным распределением, не
обязательно принадлежащим параметрическому семейству. Равенство (8) в
параметрическом случае нужно лишь для справедливости равенства G(Pfl0) = во*
Если 0 Ε Шк — многомерный параметр, то в качестве g в (9), (10)
следует брать вектор-функцию той же размерности, что и 0, так, чтобы
уравнения (9), (10) представляли собой систему из к независимых уравнений.
Иногда М-оценки определяют иначе. Пусть ψ(χ,θ) — заданная
скалярная измеримая функция.
Определение 2А. М-оценкой 0* называется значение 0, при котором
достигается
η
тахУ^(хп0). (И)
θ
t=l
Если φ для п.в. χ дифференцируема по 0, то, полагая д(х,в) = ^(х,0),
мы получим, что М-оценка будет М-оценкой в смысле определения 2.
Обратное, вообще говоря, не верно, так как М-оценки в смысле определения 2
могут быть точками локальных экстремумов У^?/>(х;,0). Если решение 0*
уравнения (10) единственно и в точке 0* достигается максимум, то, очевидно,
0* будет М- и М-оценкой.
Использование М-оценок естественно в тех случаях, когда
существует функция ^(я,0) такая, что неизвестный параметр 0о максимизирует
ψ{χ,θ)Ρ{άχ).
I
Пример 3. Среднее 0 распределения Ρ минимизирует / (х — 0) P(dx)>
Поэтому М-оценкой параметра 0 будет значение 0*, минимизирующее
/J(xj — 0)2, или, что то же, решение 0* = χ уравнения /J(xi — 0) =0,
являющееся М-оценкой. Здесь ip{x,t) = —(χ — 0)2, g(x,t) = 2(х — θ).
Так как 0 = / xP(dx), то сказанное согласуется, очевидно, с тем, что 0*
является также «непосредственной» оценкой подстановки 0*= xP^(dx) =x.
Аналогичное замечание справедливо и относительно медианы
выборки X. Предварительно заметим, что квантиль ζρ порядка ρ распределения Ρ
с функцией распределения F может быть определена как решение уравнения
/
д(х - Θ) dF(x) = 0,
-1
0
Ρ
1 ~
при χ < 0,
при χ = 0,
при ж > 0.
92 Гл. 2. Теория оценивания неизвестных параметров
где
I 1 — ρ
Поэтому выборочная квантиль ζ* является М-оценкой в смысле
определения 2. Она определяется как решение уравнения
- ^/(х,- < е)+^- χ;/(χί > б) = о.
Медиану ^/2 распределения Ρ с непрерывной в точке Ci/2 функцией
распределения F можно рассматривать также как значение, минимизирующее
/ \χ—θ\ dF(x), т. е. М-оценку. Действительно, производная этого интеграла
п. в. существует и равна Р((0, оо)) — Р((—оо,0)). Она монотонно убывает с
ростом 0 и обращается в нуль при 0 = ζ\/2· Мы получили, что ζ^2 является
одновременно М- и М-оценкой. Она является решением уравнения
£j(xi>0)-£;/(xj<0)=o.
(Если η нечетно, то ζ*/2 = χ((η+ΐ)/2)· Если η четно, то левая часть этого
уравнения обращается в нуль при любом 0 Ε (x(n/2)>x(n/2+i)); Для
Определи х(п/2+1) + х(п/2) _ \
ленности можно положить θ — —^ — K—L-L = ζ*,2·)
Более содержательные примеры М-оценок рассмотрены в § 16,33,34. Там
же можно найти примеры М-оценок, не являющихся М-оценками (см.
пример 16.5).
Легко построить также примеры М-оценок, не являющихся
М-оценками. Таким образом, классы М- и М-оценок близки, но не совпадают.
В известном смысле М-оценки имеют более широкую область определения:
М-оценки определены и в тех случаях, когда функция φ не
дифференцируема, и уравнение (10) для д = ф'е не определено. Если же φ'θ существует, то
М-оценки являются М-оценками.
М-оценки были введены П. Хьюбером в [127] как обобщение оценок
максимального правдоподобия (см. § 16; об М-оценках см. также [129, 67, 102]).
Основное внимание в настоящей книге уделяется регулярному случаю, когда
функция φ является гладкой. Изучение асимптотических свойств М-оценок
(а стало быть, и М-оценок) посвящены п. 4-6. Для полноты картины мы
приводим также условия состоятельности М-оценок в «нерегулярном»
случае, когда не предполагается гладкость ф.
4. Состоятельность М-оценок. Мы приведем здесь условия сильной
состоятельности М-оценок при весьма слабых ограничениях на функцию
φ(χ,θ) в (11). Введем в рассмотрение следующие условия.
§14. Метод подстановки в параметрическом случае 93
/·
(Ас) Множество Θ компактно.
Это условие вводится для упрощения. С точки зрения приложений
всегда можно указать достаточно большой компакт К = [ίο,ίι] такой, что
искомое 0о наверняка принадлежит внутренности К и, следовательно, можно
ограничиться поисками точки Θ* максимума (11) лишь в компакте К. При
этом под Θ* можно понимать любую точку максимума (11),
принадлежащую К, Если же максимум достигается вне К, скажем в точке θ > t\, то
можно положить Θ* равной t\ или равной точке максимума на К, Содержание
последующих утверждений от этого не зависит.
[Ао] Функция φ[χ,ί) такова, что
φ(χ,ί)Ρ(άχ)
достигает своего максимума в единственной точке t = 0, так что
Φ(ί, 0,Ρ) = ί{φ{χ, t) - φ{χ, θ))Ρ{άχ) < 0
при всех t φ 0, t £ Θ.
Эти два условия мы будем предполагать выполненными на протяжении
всего этого параграфа.
Далее, по выборке Χ ^ Ρ строится М-оценка 0*, являющаяся точкой
максимума Υ^?/>(χ;,ί), или, что то же, Φ(ί,0, Ρ*).
Нам понадобится также следующий равномерный вариант условия [Ао].
(Ао) Для любого δ > О
inf Φ(ί,0,Ρ) < -ε
t:\t-e\^S
при некотором ε = ε(δ) > 0.
Очевидно, что условие (Ао) будет следствием (Ас), [Ао] и непрерывности
Ф(£,0,Р) по t. Обозначим
φ (ζ,ί) = sup φ(χ,ί + ύ)
|ι*|$Δ
и наряду с [Ао], (Ао) рассмотрим также условие
(А^) Для любого δ > 0 существует Δ = Α(δ) такое, что при всех £,
\ί-θ\>δ
\φΑ{χ,ί) -φ{χ,θ))Έ>{άχ) < -ε (12)
/<
при некотором ε > 0.
Теорема 1. Если выполнено (А^), то М-оценка 0* сильно
состоятельна.
94
Гл. 2. Теория оценивания неизвестных параметров
Как будет показано в § 16, одного условия (Ао) для состоятельности Θ*
недостаточно.
Доказательство. Так как
*{θ;β,ρ·η) >φ(θ,θ,Κ) = о,
то для доказательства теоремы нам достаточно убедиться, что с
вероятностью 1
limsup sup Φ(ί,0,Ρ*) < -ε
п-юо \ί-θ\^δ
при некотором ε > 0. (Это и будет означать, что для п. в. Х^ €? Р, начиная
с некоторого η = n(Xoo) < ε, выполняется \θ* — θ\ < δ.)
Пусть δ фиксировано, Δ удовлетворяет (12), (θ)δ есть ^-окрестность
точки 0. Покроем множество Θ \ (θ)δ окрестностями Δ^ = {t : \t — tk\ ^ Δ},
к = 1,.. .,iV < oo, где ijt € Θ, ijt ^ {θ)δ. Тогда по усиленному закону
больших чисел в силу (12)
\t-9\>6 * "" * ί€Δ,
sup Φ (ί, θ, Ρ;) < max sup Φ (ί, 0, Ρ*η) ζ
k teAk
1 η
< max - У^ SUP [^(ХЬ *) ^ ФЫ, θ)} —>
к П *—" л . п.н.
к Π .
—► ma.xE[ipA{xutk) -ф(хиЬк)] < -ε. <
п.н. к
Условие (Aq ) можно эквивалентным образом представить в несколько
иной форме. Обозначим φ°(χ,ί) = limsup^(x, u).
u-*t
Теорема 2. Условие (А^) эквивалентно одновременному
выполнению следующих двух условий:
(Aq) для всех t φ θ
[φΌ{χ,ί)-φ{χ,θ)]Ρ{(Ιχ) <0;
/
(J) при всех t и некотором Δ > 0
[φΑ(χ,ή - φ{χ,θ)]Έ>(άχ) < oo.
/
Условие (J), как, впрочем, и (А§), (А^), означает интегрируемость
положительных частей подынтегральных функций. Такие функции естественно
называть интегрируемыми сверху.
Условие (J) в силу (Ас) по существу эквивалентно ограниченности сверху
интеграла
/
[ф{х, Θ) - ф{х, θ)]Ρ{άχ) < oo,
где φ(χ,θ) = δ\ιρφ(χ, t).
§ 14, Метод подстановки в параметрическом случае
95
Доказательство теоремы 2. Тот факт, что из (А^) следует (Aq)
и (J), очевиден. Пусть теперь выполнены (Ад) и (J). Если допустить, что
(А^) не имеет места, то найдутся последовательности tk —> t Ε Θ, Δ^ —> 0,
Sk —> 0 такие, что
J[rl>*b(x,tk) -φ(χ,θ)]Έ>(άχ) > -ek.
Здесь подынтегральная функция мажорируется в силу условия (J)
интегрируемой сверху функцией, поэтому в силу леммы Фату
limsup [[tpAk{x,tk) -φ{χ,θ)]Ρ{άχ) ^ f[tl>°{x,t) - φ{χ,θ)]Ρ{άχ) < 0.
/c-»oo J J
Мы получили противоречие, доказывающее теорему. <
Более простые достаточные условия, обеспечивающие выполнение (А§)
и (J) для конкретных функций ψ(χ,ί), приведены в § 16.
Асимптотическая нормальность М-оценок требует выполнения
условий гладкости по t функции ψ(χ, t). Поэтому ее естественно изучать в рамках
п. 6, посвященного асимптотической нормальности М-оценок.
5. Состоятельность М-оценок. Сначала мы ограничимся рассмотрением
одномерного случая Θ С Μ и вновь для простоты будем предполагать везде,
что выполнено условие (Ас) о том, что Θ С [£ο>*ι] — компакт. Положим
з(0)=Ед(хив) = Jg(x,9)P(dx). (13)
Нам понадобятся следующие условия.
(Μι) Пусть
sup|0(a;,0)| ^j{x), / nf{x)P{dx) < °о.
0€Θ J
(М2) Функция g(x,9) для п. β. χ непрерывна по Θ.
(Мз) Уравнение s{9) = 0 имеет внутри Θ единственное решение во.
Теорема 3. При выполнении условий (Mi)-(Ma) М-оценка Θ* сильно
состоятельна.
Для доказательства теоремы нам понадобится следующее утверждение.
Положим
п *—'
Лемма 1. При выполнении (Μι), (Μ2) wn-4oo
функция s(t) непрерывна.
sup|<(i)-s(i)|—>0,
tee Π·Η·
96
Гл. 2. Теория оценивания неизвестных параметров
Доказательство. Чтобы упростить рассуждения, везде в
дальнейшем мы будем считать g(x,t) непрерывной по t при всех χ (этого можно
добиться, выбросив из X множество нулевой Р-вероятности). Обозначим
через
шА{х)= sup \g{x,t + u) - g{x,t)\
модуль непрерывности функции s{i) на θ. Тогда
ω δ = Εο;δ(χι) = / u)&(x)P(dx) -> О
при Δ —> оо. Это следует из теоремы о мажорируемой сходимости, так как в
силу (Μι), (М2) имеем с^д(я) -> 0 при Δ -> О, ω^(χ) < 2j(x). Из этих же
соображений вытекает непрерывность s(t).
По усиленному закону больших чисел
1 п
ω*±{Χ) = sup \s*n{t + u) - s*n{t)\ < -ΣωΑ№ ΤΪ ωΔ'
i€0,i+ue©,|u|^A ηχτ{ Π·Η·
Далее, пусть η^ = ίο + ΑΔ, к = Ο, l,...,m (τ0 = to, rm = ίι), — точки
разбиения отрезка [ίο,ίι] D Θ. Тогда s£(tj) —> s(r,·) при всех г. Остается
заметить, что п,н"
5n = sup|5*(i) -a(i)| ^тах|5*(гг)-5(гг)| + ω*Α{Χ) +ωΛ —► 2ωΔ,
te& г Π,Η·
где левая часть от Δ не зависит, а правая выбором Δ может быть сделана
сколь угодно малой. Это доказывает утверждение леммы.
Доказательство теоремы 3. Пусть δ таково, что (#о — S,#о + δ) С Θ
и для определенности s(t) > О при t > θο и s(t) < 0 при t < 9q. Ясно, что
для любого δ > 0 найдется δι = δ\(δ) такое, что
inf s{t) > 2ib sup s{t) < —2*i. (14)
t>9o+S t<e0-6
В силу леммы 1 для п. в. Χ ^ Ρ найдется n(Jf) такое, что при всех
η ^ п(Х) будет выполняться inf s*(£) > δ\, sup 5*(ί) < —ίχ. Так как
функция 5* (ί) непрерывна, то при η ^ п(Х) существует б* G (#о — #, #о + Я)
такое, что s^(0*) = 0. Итак, мы получили, что для заданного δ > 0
существует п(Х) такое, что при всех η ^ п(Х) выполняется |0* — θο\ < δ. <
6. Асимптотическая нормальность М-оценок. Здесь в дополнение к (Μι),
(М2) нам понадобятся следующие условия.
(Mj) Функция д(Х)О) для η. β. χ непрерывно дифференцируема по 0,
s\ip\g'(x,t)\ < 71 (ζ), / 7i(s)P(<*x) <
l€© У
оо.
§ 14. Метод подстановки в параметрическом случае 97
Из этого условия следует, что в (13) законно дифференцирование по Θ:
5'(0) = Е</(хь0).
(М4) a2 = Eff2(xi,0o) <oo.
В этих условиях #о — решение уравнения (9).
Теорема 4. При выполнении условий (М^), (М^), (Мз), (М4) М-оцен-
ка 0* асимптотически нормальна с коэффициентом σ2[5'(0ο)]-2·
Доказательство. Так как (М'х), (М^) влекут за собой (Μι), (Мг), то
условия теоремы 3 выполнены и Θ* —> 0q.
Так как s^(t) непрерывно дифференцируема, то (полагаем для краткости
βη(θη = 0 = sn(90) + (θ* - θοΚ(θ), θ£ [0О,П (15)
где θ—> θο.
Π.Η.
Заметим теперь, что в силу (M'J, (М'2) функция s'n(t) удовлетворяет
условиям леммы 1 и, следовательно, sf(t) непрерывна,
supl^O-*'(*)| —>0.
tee Π·Η·
Это значит, что з'п(в) - з'(в) —> 0, и так как s'(0) —> s'(9o), то з'п(в) —>
=·«■
Итак, в силу (15)
^(Г - 0О) =-ч/^п(0о)К(0))
-1
где згп(в) —> sf(9o) φ 0 и по центральной предельной теореме — \fnsn{Oo) &
& Φο,σ2· Нам остается воспользоваться второй теоремой непрерывности. <
Из сказанного в доказательствах теорем 1, 2 легко извлечь также, что
для любой последовательности δη —> 0 случайный процесс у (и) = y/nsnx
χ (00 + и/у/п) допускает в области \и\ < 6пу/п представление
где ξη <Ξ> Ν0>σ2, \εη(θο,Χ,ύ)\ ^ εη(θ0,Χ) -^> 0 при η -> оо.
Замечание 1. Предельное распределение для М-оценок можно
получать и пользуясь подходами §8, где изучалось асимптотическое поведение
статистик второго типа (см. замечание в конце §8). Так как М-оценка
параметра θ есть значение G(i^), где функционал G(F) является решением
98
Гл. 2. Теория оценивания неизвестных параметров
относительно
θ уравнения / д(х,9) dF(x) = О, то мы имеем тождество
/
g(x,G(F))dF(x) = 0, (16)
пользуясь которым можно найти значение производной G'(Fq,v) (cm. §8).
Пусть ν = F\ — Fo, где Fi, как и Fo, есть функция распределения. Тогда
Fo + hv — снова функция распределения, и, подставляя в (16) Fq + hv
вместо F, получим
/
[д(х, G{F0 + hv))] d{F0(x) + hv{x)) = 0.
Предположим, что функция д(х,6) для всех χ непрерывно дифференцируема
по Θ. Так как G'(Fq,v) является обычной производной функции G(Fo + hv)
по h в точке h = 0 (см. замечание 8.1), то, пользуясь процедурой отыскания
производной от неявной функции, получим
Jg'(x,G(F0))G'(Fo,v)dFo(x) + jg(x,G(F0))dv(x) = 0,
G'(F0,v) = -Jg(x,G(F0))dv(x) (Jg'(x,G(Fo))dFo) .
Стало быть, в силу (8.10), (16)
^(G(Fn*)-G(F0))»
*-Jg(x,G(F0))dwn(F0(x)) (Jg'(x,G(F0))dFo(xf) =>
=Ф -(s'tfo))-1 J g(x,0Q)dwo(Fo(x)) = -(s'tfo))-1 J g(x,eQ)dw(F0(x)).
Это значит, что v^ (^(F^) — G(Fo)) асимптотически нормально с
параметрами, указанными в теореме 2.
7. Замечания о многомерном случае. Если неизвестный параметр θ =
= (01,...,0*) E R* многомерен (к > 1), то исходным при построении
М-оценок является предположение о том, что 0 является решением системы
уравнений з(в) = 0, где s(0) = (si(0),.. .,s*(0)),
Si(6) = Jgi(x,e)P(dx).
В соответствии с этим М-оценка определяется как решение системы урав-
нений s*n(t) = 0, где <(ί) = «д(<),.. .,<,*(*)),
1 п
' 77 *■" ·*
П ι
§15. Метод минимального расстояния
99
Утверждения, относящиеся к состоятельности и асимптотической
нормальности М-оценок, сохранятся при естественной модификации условий.
Основным для доказательства асимптотической нормальности является
следующий аналог уравнения (15):
<i(O = O = <j((9) + ((6*-(9,grad<i<(6))+o(|(9*-0|), г = 1,...,к. (17)
1К<(*)
_ dsj{9)
dtj
сходится п. н. к матрице з'{9) = ||s^||, s^ —
t=e
Здесь матрица
, i,j = l,...,fc. Поэтому уравнение (17) в векторной форме можно
Эвг
записать в виде
3*η(θ) + (θ*-θ)3'(θ)+ο(\θ*-θ\) = 0,
которое в предположении \s'(0)\ Φ 0 дает соотношение
(θ*-θ)*-3*η(θ)(3'(θ)Γ\
означающее асимптотическую нормальность в*:
Μ = [(3'(θ))-ψϋ(3'(θ))-\ D = \\дЩ, д&) = E5i(xi,%(xb^).
§ 15·* Метод минимального расстояния
Метод, указанный в заголовке, как и методы § 14, является реализацией
принципа подстановки и состоит в следующем. Рассмотрим какой-нибудь
функционал от двух распределений d(P,Q), который обладает тем
свойством, что как функция от Q он достигает своего минимума при Q = Ρ и
d(P, Q) > d(P,P) при Q φ Р. Мы будем рассматривать величину d(P, Q)
(или d(P,Q) — d(P,P) как «расстояние» между Q и Р, так что Ρ можно
определить как значение Q, при котором d(P, Q) достигает своего
наименьшего значения.
Пусть теперь X €= Ρ, Ρ неизвестно и принадлежит семейству V.
Обозначим через {Q)v распределение из Р, ближайшее к распределению Q в
смысле расстояния d, и допустим, что оно существует:
d((Q)p,Q) = mjnd(II,Q),
так что {Q)v = Q> если Q Ε V.
Определение 1. Оценкой распределения Ρ по минимуму
расстояния d называется распределение Р* = (Р^)^ Ξ Φι гДе Р£> как и прежде,
эмпирическое распределение.
Таким образом, при Π = Ρ*! = (Р£)^ минимизируется с/(П, Ρ*). Если
V совпадает с множеством всех функций распределения, то, очевидно, Р* =
= Р*
100
Гл. 2. Теория оценивания неизвестных параметров
Пусть теперь V = {Ρθ}θξΘ еСть параметрическое семейство,
удовлетворяющее следующему условию.
(Ао) Пусть
ΡΘι φ Ρθ2 при θλ φ 02.
В этом случае отображение 0 -» Ρ# взаимно однозначно, так что
распределение Ρ € V позволяет единственным образом восстановить параметр 0, для
которого Ρ = Р#. Этот факт можно выразить и иначе: существует
функционал G, определенный на V, такой, что 0 = G(P^).
Введем в рассмотрение функционал G\(Q) = G((Q)p). Это есть,
очевидно, значение 0 Ε Θ, при котором Р# будет ближайшим к Q
распределением в смысле расстояния d, так что
G1(Pe) = G(Pg)=e. (1)
Определение 2. Оценка 0* = Gi(P*) называется оценкой
параметра θ по минимуму расстояния d.
Другими словами, 0* есть значение из Θ, для которого
ά(Έ>θ.,Ρ*η) = Μά(Ρθ,Ρ*η).
Очевидно, что здесь мы снова имеем дело с принципом подстановки. Это
вытекает из определений и (1). Разумеется, расстояние d и семейство V = {Р#}
должны обладать свойствами, обеспечивающими измеримость отображения
Xй в R*, осуществляемого функционалом (?ι(Ρ*) так, чтобы 0* была
случайной величиной.
Отметим теперь, что β параметрическом случае при выполнении
условия (Ао) сужение метода подстановки (см. (13.1), (13.2)) и метод
минимального расстояния дают один и тот же класс оценок.
Действительно, мы уже знаем, что оценки минимального расстояния 0*
являются оценками по методу подстановки, при этом 0* £ Θ. Пусть теперь 0*
есть оценка по методу подстановки: 0* = G(P£), где G{Pq) = 0, 0* G Θ.
Определим расстояние rf(P, Q) = |G(P) —G(Q)|. Тогда, очевидно, при 0 = 0*
достигается
mf d(p,,p;) = mf |σ(ρ,) - g(p;)| = ы \θ- о{р*п)\ = о.
Ясно, что можно указать много «разумных» расстояний с/, которые можно
использовать для построения оценок. Мы могли бы в качестве d взять
расстояние
d(P,Q)=sup\FP(x)-FQ(x)\
X
ИЛИ
d(P, Q) = J(FP(x) - FQ(x))2 dFQ{x),
где Fp(x) — функция распределения, соответствующая распределению Р.
Оценками 0* по минимальному расстоянию здесь будут значения 0, для
§ 16. Метод максимального правдоподобия
101
которых достигается соответственно
mfsup\FPe(x)-FZ(x)\,
ν χ
/ι η / k — 1 \2 (^)
(*■*(*) - FZ(x))2dK(*) - У" Σ (*Ь(*<*>) " —J ·
В некоторых задачах (ср. с [58]) используются так называемые оценки
по минимуму χ2 (хи-квадрат). Это есть оценки по минимуму расстояния
^■«»-§(Р(^У.
где Δί,..., ΔΓ — разбиение R (или Мт, если х^ га-мерны) на г < оо интер-
г
валов, так что |J Δ, = R. Таким образом, оценка Θ* по минимуму χ2 есть
t=l
значение 0, при котором минимизируется
η
(Pfl(Ai) - ι/j/n)2 ^ (nPg(Aj) - vjf
Здесь ι/, = ηΡ*(Δϊ) есть число наблюдений х^, попавших в интервал Δ*.
Статистика в правой части (3) есть уже известная нам статистика χ2, отсюда
и происходит название оценки.
Ниже мы увидим, что существует такой функционал G, θ = G(P$),
для которого оценки по принципу подстановки, называемые оценками
максимального правдоподобия, будут в известном смысле наилучшими. Эти
оценки будут являться также М-оценками, М-оценками (при некоторых
условиях регулярности) и оценками минимального расстояния.
Расстояние, минимизируемое этими оценками, будет близко к расстоянию Кульба-
ка-Лейблера между распределениями, которое будет введено в §31.
§ 16. Метод максимального правдоподобия.
Оптимальность оценок максимального правдоподобия
в классе М-оценок
1. Определения. Общие свойства. Пусть снова V есть
параметрическое семейство {Ρθ}θ€θ· Относительно этого семейства будем предполагать
в дальнейшем везде, где это потребуется, выполненным условие
(Ао) Пусть
Ρ*ι/Ρ*2 при θχ+θϊ,
а также условие
(Αμ) Существует σ-конечная мера μ в фазовом пространстве
(Х,Ъх) такая, что все распределения Р# £ V имеют относительно
102
Гл. 2. Теория оценивания неизвестных параметров
этой меры плотность f$(x) = —:—(я), так что
αμ
Έ>Θ(Β) = f !9{χ)μ{άχ).
в
В этом случае говорят, что мера μ доминирует распределения Р#.
Все семейства распределений, рассмотренные в § 12, очевидно,
удовлетворяют условиям (Ао), (А^). В качестве μ для одних распределений надо взять
меру Лебега (абсолютно непрерывные распределения), для других —
считающую меру (дискретные распределения). Считающая мера μ определяется
так: μ {В) = &, где к есть число точек с целочисленными координатами,
принадлежащих В.
К первым относятся нормальное Φα>σ2, логнормальное LQ σι
распределения, Г- и В-распределения, равномерное распределение, распределение
Коши, распределения Стьюдента и Фишера. Ко вторым — распределения
Бернулли, Пуассона, вырожденное в нуле и полиномиальные распределения.
Вид плотностей fe{x) этих распределений приведен в § 12. В дискретном
случае (когда μ есть считающая мера) плотность fe{x) совпадает с
вероятностью Р$({х}) события {χχ = χ}; здесь {χ} означает множество,
состоящее из одной точки х. Можно отметить также, что, например, нормальное
распределение Φα>σ2 и распределение Пуассона взаимно сингулярны.
Вместо меры Лебега и считающей меры мы могли бы брать и другие меры —
например, нормальное распределение Фод и распределения Пуассона Πι
соответственно. Однако в этом случаи плотности fe(x) будут, очевидно,
другими. Мы предлагаем читателю найти их. Приведенные выше примеры
относились к случаю X = R или X — Rm, m > 1. В произвольном фазовом
пространстве (X, 55^) природа меры μ может быть более сложной.
Введение условия (Αμ) удобно прежде всего тем, что оно позволит нам
в дальнейшем с единой точки зрения рассматривать два наиболее важных
в приложениях типа распределений — абсолютно непрерывные и
дискретные. С точки зрения условия (Αμ) качественная разница между ними
отсутствует. Кроме того, становится несущественной размерность фазового
пространства X.
Условимся писать
f{x)=g{x) п. в. [μ],
если существует множество Α, μ{Α) = 0 такое, что f(x) = g(x) для всех
χ £ А. Очевидно, f(x) = g(x) п. в. [μ] тогда и только тогда, когда
1(/(χ)-9(χ))2μ(άχ) = 0.
Лемма 1. Пусть fug — две плотности вероятности
относительно меры μ. Тогда
Ι' /{χ)1η/{χ)μ{άχ) > f /{χ)\η9{χ)μ{άχ), (1)
если оба эти интеграла конечны. Знак равенства возможен лишь в
случае f = gn.e. [μ].
§ 16. Метод максимального правдоподобия
103
Здесь принято соглашение, что интегралы в (1) по множеству А, на
котором f(x) = 0, равны нулю при любой д{х).
Доказательство. Нам надо доказать, что
/
Так как 1п(1 + х) ^ χ при всех χ ^ — 1 и знак равенства возможен лишь при
χ = 0, то
и знак равенства здесь возможен лишь при f(x) = д(х). Поэтому
Jf(x)\n^(dx) < Jf(x) (№ - l) „(ώ) =
= J 9{χ)μ{άχ)- J f{xM<b)=Q. (2)
Если соотношение f = д п.в. [μ] не имеет места, то, очевидно, знак
неравенства в (2) будет строгим. <
Рассмотрим теперь семейство V = {Ρθ}θβΘι удовлетворяющее условиям
(Ао), (Αμ), и «расстояние» d(Pe, Q) между произвольным распределением Q
и распределением P^GP
d(Pe,Q) = -J\nfe(x)Q(dx). (3)
Определим функционал G(Q) как значение Θ, при котором достигается
mmd(Pe,Q) = d(PG(Q),Q).
Из леммы 1 и условия (Ао) следует, что
- / Ль 1η/β/ί(ώ;) > - / /в„ \η/θομ(άχ),
ά(Ρθ,Ρθο)>ά(Ρθο,Ρθο)
при # т^ $ο· Это означает, что
<?(Ρθ0) = б0. (4)
Определение 1. Оценкой максимального правдоподобия (о.м.п.)
называется значение Θ* = <7(Р*), т.е. значение б, при котором достигается
Г 1 п
max / In/0(0;) Ρ* (da;) — max — У^ ln/g(xj). (5)
104 Гл. 2. Теория оценивания неизвестных параметров
Символ «~» над обозначением оценки везде в дальнейшем будет
соответствовать о. м. п.
Из определения и (4) следует, что о. м. п. является оценкой
подстановки. Ее можно рассматривать также как М~оценку и оценку по
минимуму расстояния (3). Это расстояние, как уже отмечалось, тесно связано с
расстоянием Кульбака-Лейблера между распределениями, которое играет в
математической статистике особую роль и будет нами рассмотрено позже.
В определении 1 семейство {Р#} предполагается таким, чтобы Θ* была
случайной величиной *).
Поскольку максимум некоторой функции может достигаться в
нескольких точках, то о.м.п., вообще говоря, не единственна. Соответствующий
пример мы приведем несколько позже.
Название этой оценки связано со следующей важной интерпретацией
выражения
η η
£>/,(*) =1пП/*(х<),
2=1 2=1
присутствующего в (5). Для простоты рассмотрим сначала дискретный слу-
п
чай, когда μ — считающая мера. Тогда ТТ/^(хг) есть вероятность появле-
г=1
ния исхода X = (χι,.. .,хп). Стало быть, мы выбираем в качестве Θ*
значение параметра, которое максимизирует эту вероятность (ведь функции
φ(θ) > 0 и \ηψ(θ) достигают экстремумов в одних и тех же точках).
Аналогичное толкование имеет место и в общем случае. В силу
независимости хг· имеем для множеств В = В\ χ - · · χ Бп, В{ £ Я$х
Р9(Х е В) = J MzMdxi)- · · f ίθ(Χη)μ(άχη)' (6)
Βι Βη
Напомним, что Х{ в отличие от элементов выборки хг обозначают переменные
величины, вектор (а;ι,.. >,хп) обозначается через х. Пусть μη есть гг-кратное
прямое произведение мер μ, так что μη(άχ) = Υ^μ(άχ{). Тогда (6) означает,
2=1
ЧТО
Т?9{Х € В) = J (f[h(xi) J μη(άχ)
В
η
и, стало быть, функция /я (ж) = ТТЛ(^г) есть плотность распределения
г=1
случайного вектора X в Хп относительно меры μη,
ff0(x№(dx) = l.
хп
*) То есть Θ* осуществляет измеримое отображение (^п,53дг) в (Rk,*Sk).
§16. Метод максимального правдоподобия
105
Таким образом, Τ\/θ{χί)μη{άχ) можно интерпретировать (аналогично дис-
г=1
кретному случаю) как вероятность попадания выборки в параллелепипед,
образованный пересечением «полос» (xi,x% + dxi), и оценка максимального
правдоподобия максимизирует по θ эту вероятность.
Функция
η
как функция от θ называется функцией правдоподобия, а функция
η
где 1(χ,θ) = lnfe(x), — логарифмической функцией правдоподобия.
Такое же название за функциями / и L мы будем сохранять и в том
случае, когда в качестве аргумента вместо X стоит переменный вектор ж.
Таким образом, функция правдоподобия fe{x) есть функция на Хп χ Θ,
являющаяся при каждом θ Ε θ плотностью вероятности относительно меры μη,
так что плотность feixi) в X также есть функция правдоподобия для случая
п = 1.
С другой стороны, /#(^0, например, в случае X = Ш можно
рассматривать как функцию правдоподобия выборки объема 1 в многомерном случае,
когда X = Rm = Rn.
Важно отметить, что о. м. п. от выбора меры μ никак не зависит, так как
при замене μ на какую-нибудь эквивалентную меру μι функция правдоподо-
άμη
бия fe{x) изменится лишь на множитель —~{х), от θ не зависящий.
αμι ^
В соответствии с определением 14.2А о. м. п. является М-оценкой для
функции φ(χ)θ) = 1(χ,θ). Это соответствует тому, что значение t = θ
максимизирует
Jl(x,t)Pe(dx) = j 1η/,(*)/β(α0μ(ώ0. (7)
Если 1(χ,θ) имеет непрерывные производные 1'{χ,θ) по 0, то точка 0*, в
которой достигается максимум (5), будет с необходимостью удовлетворять
уравнению
η
L'(X,e) = J2H^0) = 0. (8)
i=l
В соответствии с определением 14.2 и замечаниями к нему это означает,
что в этом случае о. м. п. Θ* является М-оценкой (надо положить в
определении 14.2 g(x,9) = l'(x,t)). Это соответствует тому, что значение t = θ
в предположении законности дифференцирования интеграла (7)
удовлетворяет уравнению
' l'{x,t)Pe(dx) = 0. (9)
/-
106
Гл. 2. Теория оценивания неизвестных параметров
Тот факт, что о.м.п. является М-оценкой, можно получить и из других
соображений, не связанных с максимизацией (как и тот факт, что t — 0
является решением уравнения (9)). Для этого в рамках параметрического
случая надо предполагать, что законно дифференцирование по 0 равенства
/·
/θ{χ)μ{άχ) = 1,
что дает нам равенство вида (14.8) при д = V
ίΐ'(χ,θ)Ρθ(άχ) = [ϊ{χ,θ)Μχ)μ(άχ) = [ ffaMdx) = 0. (10)
В этом случае согласно определению 14.2 решение уравнения (8) (или
уравнения (14.10)) является М-оценкой параметра 0.
Обратное утверждение о том, что М-оценка, соответствующая функции
д(х, 0) = /'(ж, 0), является о. м. п., вообще говоря, не верно. Функция L(X, 0)
может иметь несколько изолированных точек локальных максимумов, в
которых будет удовлетворяться (8), однако maxL(X, 0) достигаться не будет.
Это будет иметь место в тех случаях, когда J(t) = f 1(χ,ί)Ρβ(άχ) имеет
несколько точек максимума по t и, следовательно, решение уравнения (9)
не единственно. Соответствующие примеры легко построить, если взять
в качестве 0 параметр сдвига: /^(ж) = /(ж — 0) (# = R, θ = R), а в
качестве f(x) симметричную «двухгорбную» функцию (например, f(x) =
= -(φ(χ + 1) + φ{χ — 1)), где φ — плотность нормального распределения
с параметрами (0,1)). Тогда интеграл J(0) будет иметь три точки 0 = 0,
0 = ±0ι, 01 > 0, в которых J(0) достигает локальных максимумов, J'(0) =
= J'(±0i) = 0, при этом J(0) > J(±0i). Примерно такая же картина при
больших η будет иметь место и для функции L(X,9).
Найдем функции правдоподобия и о.м.п. для некоторых распределений
из § 12. Для гладких функций правдоподобия максимум проще всего искать
путем приравнивания нулю первых производных.
Пример 1. Нормальное распределение Φα>σ2 и X = R имеет плотность
(χ - α)2Ί
Ψ"·ΑΧ) = ^^[ Ίο*
Полагая в этом случае θ = (α,σ2), получим
-оо < α < оо, σ > 0.
Мх) = (2π)-"/2σ-"βχρ { -^ £> - «)2| ,
ЦХ,в) = -| 1η2π - ηίησ - ~ ]Г(х* - а)2.
г=1
§16. Метод максимального правдоподобия
107
Так как In есть монотонная функция, то, как уже отмечалось, / и L
достигают максимума при одних и тех же Θ. Имеем
dL 1 ^, ч dL η Ι χ^, ч2
г=1 г=1
Решая для точки максимума систему уравнений
9α 'da
получаем
α* = χ, (σ2)* = 52 = ±][>-ϊ)2.
Нетрудно проверить, что в этой точке действительно достигается
максимум L.
Пример 2. Рассмотрим Υ-распределение с плотностью
1а{х) = ^ду^"16"^' * ^ °> α > °>
в случае, когда параметр λ известен. Имеем
η η
L(X,a) = ληΐηα - η1ηΓ(λ) + (λ — 1) ^1ηχζ - α^χ^,
i=l i=l
dL Xn _ λ
•χ- = χη, α = -.
σα α χ
Пример 3. Биномиальное распределение Вр. Здесь для X ^ Вр имеем
Р(х, = 1)=р, Р(х,=0) = 1-р,
/р(Х)=р1/(1-р)яЛ
где ν — число появлений 1 среди элементов χι,.. .,хп. Стало быть,
L(X,p) = *Лпр + {п — ^)1п(1 — р),
dL ν η — ν ^+ ν
op ρ I — ρ η
Мы предлагаем читателю в виде упражнения попытаться найти о.м.п.
для всех параметрических семейств, приведенных в § 12, и сравнить их с
оценками по методу моментов.
Приведем теперь два примера несколько иного типа, когда функция fe
не является гладкой по θ и методы отыскания о.м.п., связанные с
дифференцированием, не действуют.
108 Гл. 2. Теория оценивания неизвестных параметров
Пример 4. Пусть X ё U^i+fl (равномерное распределение на [Θ, 1+0]).
Здесь
/·(*)
хе[в,1 + θ],
χϊ[θ,ι + θ],
fe(X) = lh 0<χ(ΐ)^χ(η)<1+0,
\θ в противном случае,
где Х(!) ^ ... ^ Χ(η) — вариационный ряд. Оценка м.п. в этом примере
не единственна. Действительно, f$(X) = 1 (т.е. максимальному значению)
при любых 0, удовлетворяющих соотношениям Х(п) -1^0^ х^. Так как
х(п) ~~ х(1) ^ 1» т0 такие 0 всегда существуют. Мы можем взять, в частности,
0* = х(1) или 02 = х(п) - 1· Та« как θ\ > 0, 02 < 0, то лучше, по-видимому,
взять
^ = |Й + ^) = ^(х(1)+Х(п)-1).
Пример 5. Пусть Χ £ Uq,0. Здесь
Λ(χ) = \о,
х£[О,0],
, /л_ч Г0~п> если χ, G [0,0] при всех г = 1,2, ...,п,
1^0 в противном случае.
Чтобы получить более простую запись функции fe(X) как функции от 0,
перепишем условие х^ Ε [0,0], i = Ι,.,.,η, в эквивалентной форме 0 ^
> таххг = Х(„). Таким образом, fe(X) = 0 при 0 Ε [0,Х(П)) и /^(Х) = 0"п
при 0 £ [х(п),оо). График этой функции представлен на рис.1. Здесь, как
* ив предыдущем примере, функция /# раз-
| AW рывна. Максимум fg достигается в точке
^=Х(п)·
Аналогичным образом читатель может
найти о. м. п. для двумерного неизвестного
параметра (α.β), когда Χ ^ υα,β·
χ Q Если fe[x) не ограничена и точки xq, в
которых fe(xe) = оо, зависят от 0, то ме-
Рис· 1 тод максимального правдоподобия в
значительной мере теряет свой смысл (мы приняли здесь соглашение fei^e) = оо,
если fe(x) -> оо при χ I xq или χ ^ xq). Проще всего это понять на
примере параметра сдвига, когда fe(x) = f{x - 0), f(x) > 0, /(0) = оо. Тогда
fe{X) = оо при 0 = χι,..., 0 = хп и, стало быть, 0* принимает по
крайней мере η значений, совпадающих с элементами выборки. Существо этого
эффекта в том, что в этом случае «всплески» fe(X) не дают возможности
судить о положении точки «истинного» максимума fe{X), обусловленного
влиянием всей выборки (ср. с §34). Чтобы получить таковой, следовало бы
каким-то образом «сгладить» выбросы fe{X)-
§ 16. Метод максимального правдоподобия
109
Оценки м. п. обладают следующим важным свойством инвариантности
относительно замены параметра.
Теорема 1. Пусть β(θ) есть функция, осуществляющая взаимно од-
позначное отображение множества θ на множество В. Тогда если Θ*
есть о.м.п. по выборке X параметра 0, то β* = β(θ*) будет о.м.п.
по выборке X параметра β = β(θ) для параметрического семейства
{Qp = *Ρ0(β)}β€Β, где θ(β) есть функция, обратная κ β(θ).
Доказательство теоремы мы опускаем ввиду его очевидности.
Отметим, что неявно мы уже пользовались теоремой 1 в примере 1, где в
поисках о. м. п. для σ2 искали максимум L по σ и затем взяли (σ2)* = (Э*)2.
Другой пример использования теоремы 1 — отыскание о. м. п. в случае
X €= La<72, т.е. в случае, когда распределение хг- логнормально: 1пхг- ^
€= Φασ2. Для таких х^ среднее а и дисперсия d2 равны соответственно
(см. § 12)
а — ехр < а + — >, d2 = a2(exp (σ2) — 1).
Если обозначить α* и (d )* о.м.п. для а и d2, то в силу свойства
инвариантности получим для функции (a,d2) = /3(α,σ2) (см. пример 1)
{-#}·
а* = ехр (У + "f j ι (*)* = (S*)2(«P(#) - 1),
1 п 1 п
где У = (у1,...,уп), Уг = lnxi, у = - УЧЙ, S£ = -У)(уг-у)2·
г—I г=1
Приближенному вычислению о. м. п. в более сложных ситуациях
посвящен § 35.
2. Асимптотические свойства о.м.п. Состоятельность. Как уже
отмечалось, о. м. п. являются М-оценками и при выполнении некоторых условий
регулярности — М-оценками. Если сравнивать условия состоятельности,
которые можно получить для о. м. п., используя соответствующие результаты
для М- и М-оценок, то окажется, что М-оценки являются более общими уже
потому, что не требуют дифференцируемости /(я, Θ) по Θ. Поэтому для
получения условий состоятельности о. м. п. мы воспользуемся результатами § 14
о состоятельности М-оценок.
Следуя п. 14.1, мы будем предполагать везде, что выполнено условие (Ас)
о компактности Θ (замечания по этому поводу см. в п. 14.1). Условие [Ао]
и его аналоги в § 14 мы будем использовать в новой редакции
применительно к функциям ψ(Χ)θ) = 1(χ,θ) и Р{А) = Pq(A). Эта новая редакция
[Aq] следует из леммы 1 и приведена в начале параграфа в виде условия (Ао).
по
Гл. 2. Теория оценивания неизвестных параметров
Она означает, что расстояние Кульбака-Лейблера (см. §31)
p(9,t)= ί\η^.Μχ)μ(άχ)>0
J ft[x)
при t φ θ. Условия (Ао), (А(^) будут иметь соответственно вид:
(Ао) Для любого δ > 0 inf ρ(θ,ί) > ε при некотором ε = ε(<5) > 0.
(ΑΑ) Для любого δ > 0 существует Δ = Δ(<5) > 0 такое, что при
всех ί, \t — θ\ > <5,
Jlnj^yfe(xMdx)>e (11)
при некотором ε > О, где
ftA{x) = sup ft+u{x)·
Из теоремы 14.1 вытекает
Следствие 1. Если выполнено (А^), то о.м.п. Θ* сильно
состоятельна.
Пусть Л°(я) = limsup/u(a;). Из теоремы 14.2 вытекает
u-*t
Следствие 2. Условие (Aq ) эквивалентно одновременному
выполнению следующих двух условий.
(Aq) Для всех t φ θ
I
\ηψ&·Μχ)μ(άχ)<0.
(J) При всех t и некотором Δ > О
/
fAlx)
\ηψ^-'/θ{χ)μ{άχ) <оо.
Условие (J), означающее интегрируемость положительных частей
подынтегральных функций, эквивалентно по существу ограниченности
/
fQ(x)
In —7— - /θ(χ)μ(άχ) < оо,
где
/θ(x) = sup ft(x).
tee
Приведем теперь более простые достаточные условия, обеспечивающие
выполнение (А§) и (J) и, стало быть, сильную состоятельность о.м.п.
Определение 2. Будем говорить, что ft(x) принадлежит классу Д),
если для каждого t € Θ существует множество Ct € 93,*, Pe(Ct) — 1, на
котором ft{x) непрерывна по t ftk(x) —> ft(x) при t^ —> t, x Ε Ct.
§16. Метод максимального правдоподобия
111
Классу -Do помимо непрерывных (по t) ft{x) на не зависящем от t
множестве С, Р#(С) = 1> принадлежат, конечно, и многие другие функции такие,
например, для которых ft{x) в плоскости (£,я) имеет изолированные линии
разрыва, не имеющие участков, параллельных оси х. Так будет, в
частности, если ft{x) как функция от χ имеет изолированные разрывы в точках
(1) (2)
х\ ' ,х\ ,..., которые непрерывно зависят от t.
Теорема 2. Если ft{x) £ -Do и выполнено (J), то выполнено условие
(Aq), Щ следовательно о.м.п. Θ* сильно состоятельна.
Доказательство. Если ft(x) G Д>, то ft{x) = ft(x) при χ Ε Ct и,
стало быть,
/
In £М · MxMdx) = -р(0, <) < 0. <
Следствие 3. Ясли /*(ж) € Do ограничена, а интеграл
/θ{χ)1η/θ{χ)μ{άχ) (12)
/·
конечен, то о. м. п. сильно состоятельна.
Утверждение следствия 3 немедленно вытекает из теоремы 2, так как
ограниченность ft(x) и конечность интеграла (12) влекут за собой
условие (J).
Следствие 4. Если
φ(Α) = / sup \ft+u(x) - Μχ)\μ{άχ) -> 0 (13)
J \u\^A
при Δ —> 0, то о. м. п. сильно состоятельна.
Доказательство. Воспользуемся теоремой 2. Принадлежность
ft{x) £ Dq очевидна, так как (13) может выполняться лишь в случае, когда
ft+u{x) -* ftix) при гл —> 0 для п. в. [μ] значений х. Далее,
J £[χ)μ{άχ) < φ(Α) + jίι{χ)μ{άχ) = φ(Α) + 1,
fA(X)
и условие (13) означает также интегрируемость f^(x). Так как In f ^
few
fA(x)
^ ь v — 1, то отсюда получаем, что интеграл в условии (J) не превосходит
ЛИ
Ι/ίΑ(χ)μ(άχ)-1^φ(Α). <
Вместо (13) мы могли бы требовать сходимости к нулю величины
<Ρι(Δ)= / sup {y/ft+u{x) - y/ft{x) )2μ{άχ),
J Ы\<А
112
Гл. 2. Теория оценивания неизвестных параметров
так как φ(Δ) можно оценить с помощью φι{Δ) неравенством
φ(Δ) ^ / sup \y/ft+u(x)- \βάχ)\ sup \y/ft+u(x) + \ίΰ(χ)\μ{άχ) <
< φ\Ι2{Δ)
/ sup (Vft+u(x) - у(Щ+ 2\/7t(^) )V(<*r) <
<[2¥>1(Δ)(^1(Δ)+4)]1/2.
Следствие 5. Если ft(x) дифференцируема no t для η. β. [μ]
значений χ и
(14)
\ίΆχ)\μ(άχ) <с<оо,
то о. м. п. Θ* сильно состоятельна.
Доказательство. Принадлежность ft(x) G Do очевидна. Для
выполнения условия (J) достаточно, как мы видели в доказательстве следствия 4,
интегрируемости /гЛ(я). Но
f &(χ)μ(άχ) ^ J Шх) + f\ft+u{x)\ du
μ(άχ) =
= 1 +
Δ
- f [f\fl+u{x)№dx)
-Δ
du < 1 + 2Δα
Остается воспользоваться теоремой 2.
Следствие 6. Пусть θ есть параметр сдвига семейства fe(x) =
= f(x — 9), J f(x) lnf(x) dx > — оо. ^слг/ функция f(x) ограничена (иначе
метод максимального правдоподобия теряет свой смысл; см. замечание
перед теоремой 1) и имеет множество В точек разрыва, лебегова мера
замыкания которого μ(Β°) равна нулю, то о. м. п. Θ* сильно
состоятельна.
Доказательство. Проверим выполнение условий теоремы 2.
Условие (J) выполнено очевидным образом. Принадлежность ft{x) G Do
вытекает из определения Do, в котором надо положить Ct — Bc — t (это есть сдвиг
множества Вс на t, Bc есть дополнение к замыканию множества В). Так как
множество Вс открыто, то χ — t G Bc — t влечет за собой χ — ί* G Bc — t при
достаточно малых |ί* — ί|. Это означает, что f{x — tk) —> f(x — t). Следствие
доказано. <
Отметим, что в условиях следствия б предполагать выполненным
условие (Ао) излишне — оно выполняется автоматически. Если допустить, что
§16. Метод максимального правдоподобия
113
(Ао) не имеет места, то мы придем к периодичности функции /(ж), что
невозможно.
Относительно условий следствия 6 заметим, что условие на
«непрерывность» /(я), сформулированное в нем, является весьма слабым. Но и оно,
по-видимому, не существенно. На это указывает в какой-то мере следующий
пример.
Пример 6. Пусть f(x) — произвольная функция, имеющая
ограниченный носитель (а, Ь) = {х : f(x) > 0}. Тогда
Р*# - 0| > *U (1 - F0(a + δ))η + F£(b - ί), (15)
χ
где Fo(x) = / f(y)dy. Неравенство (15) означает сильную состоятель-
-00
ность Θ*. Оно следует из соотношений вида
(71 ") П
Ц/,+,(*,) > О I С р|{хг ^ α + θ + δ},
i~l J i=l
Ρθ{θ* -0>S)<^[l-Fo{a + 9 + δ)]η = [1 - F0(a + i)]n.
Условие на конечность интеграла / f(x)lnf(x)dx в следствии 6 в
известном смысле тоже не существенно: легко построить пример, когда этот
интеграл обращается в —оо, а условие (J) будет выполнено. Все сказанное
в следствии 6 и после него полностью сохраняет свою силу для параметра
масштаба.
Если бы для отыскания условий состоятельности о. м. п. мы стали
применять теорему 14.3 о состоятельности М-оценок, то мы столкнулись бы
среди других с требованием дифференцируемости ft(x) по £, которое само
по себе есть намного более сильное условие (при выполнении (Ао)), чем,
скажем, (11).
Замечание 1. В целом применительно к о.м.п. имеет место в
известном смысле парадоксальная ситуация (мы будем убеждаться в этом на
примерах): для доказательства состоятельности (и особенно асимптотической
нормальности; см. ниже) мы предполагаем выполнение некоторых свойств
гладкости ft{x)· На самом же деле, чем менее регулярна /^(а:), тем, как
правило, лучше оказываются свойства о. м. п. Иллюстрации этого факта можно
найти в § 30, 32.
3. Асимптотическая нормальность о.м. п. Оптимальность в классе
JVf-оценок. Обратимся теперь к свойству асимптотической нормальности
о. м. п. Она будет вытекать из следующего утверждения, являющегося
следствием теоремы 14.4. Это утверждение устанавливает также нижнюю
границу для разброса М-оценок и оптимальность о. м. п. в классе М.
Теорема 3. Предположим, что функцияд(х,0) удовлетворяет
условиям теоремы 14.4 и законно дифференцирование под знаком интеграла
114
Гл. 2. Теория оценивания неизвестных параметров
β равенстве
9{χ,θ)/θ{χ)μ{άχ) = 0.
/■
Пусть, кроме того, выполнены следующие условия:
a) Ι(χ,θ) дважды непрерывно дифференцируема по 0;
sup|Z"(x,0)| </(z), [1{χ)/θ{χ)μ(άχ) < οο; (16)
0€θ J
b) пусть
0 < Ι(θ) = Εβ(ΐ'(χι, θ))2 = J(l'(x, θ))2Μχ)μ(άχ) < οο; (17)
c) законно дифференцирование под знаком интеграла в равенствах
j ίθ{χ)μ{άχ) = 1, [ ϊ(χ,θ)Μχ)μ(άχ) = 0;
d) уравнение относительно t
1'(χ,ί)Μχ)μ(άχ)=0
l·
имеет единственное решение t = Θ.
(В с) второе равенство получается дифференцированием первого; из с)
вытекает, что Ε^/7(χι,θ) = —7(0).)
При выполнении этих условий М-оценка 0*, соответствующая
функции д, и о. м. п. Θ* асимптотически нормальны. Коэффициент разброса Θ*
(см. теорему 14.4) удовлетворяет неравенству
Έθ92(χ1,θ)(Εθ9'(χ1,θ))-2 > Г1 (θ) (18)
и достигает своего наименьшего значения, равного Ι~ι(θ) при д(х,в) =
= Ι'(χ,θ) (т. е. коэффициент разброса 0* всегда больше или равен
коэффициенту разброса 0*).
Доказательство. Заметим прежде всего, что условия a)-d)
достаточны для того, чтобы функция V(x,6) наряду с д(х,9) удовлетворяла
условиям теоремы 14.4. Поэтому нам надо доказать лишь последнюю часть
теоремы, связанную с неравенством (18). Имеем (аргументы для краткости
опускаем)
УV/ + jV = o = уV/ + Уgi'f,
Евд'(хив) = Jg'f = -jgl'f = -Ввд(хив)1'(хив).
§ 17. О сравнении оценок
115
По неравенству Коши-Буняковского отсюда находим
(Евд'(хив))2 = (Евд(хив)1'(хив))2 < Εβ92(χ1,θ)Εθ(ϊ(χ1,θ))2. (19)
Это доказывает неравенство (18).
В силу a)~d) все сказанное применимо и к функции д = /', для которой
в (19) достигается равенство. Теорема доказана. <
Замечание 2. Условие с) о законности дифференцирования будет
выполнено, если эти интегралы после дифференцирования сходятся
равномерно по θ (в окрестности точки Θ). Это условие, в свою очередь, будет
выполнено, если в (16) и в условии {М[) из § 14 потребовать, чтобы оценочные
интегралы вида / 1(χ)/β(χ)μ(άχ) сходились равномерно по θ (в окрестности
точки Θ); см. об этом также в §34 и в приложении V.
Значение Ι(θ) = Ε0(/'(χι,0))2, присутствующее в (17), (18), играет
значительную роль в теории оценивания параметров. Оно будет
характеризовать наименьший возможный разброс оценки около истинного значения
параметра θ не только в классе М-оценок, но и в классе вообще всех оценок.
Асимптотические свойства о.м.п. будут более подробно изучены в § 33-37.
В примерах 1-5 мы имели дело с распределениями, для которых о. м. п.
без труда могла быть найдена в явном виде. В общем случае поиски о. м. п.
сопряжены обычно со значительными вычислительными трудностями.
Например, для параметра сдвига θ распределения Коши с плотностью
[π(1 + (χ — 0)2)]"1 о.м.п. θ* является решением уравнения
степени 2п — 1, так что при больших η отыскание Θ* становится весьма
сложным. Все условия теорем 2, 3 при этом выполнены, так что Θ* будет
в этом случае 1'{χ,θ) = ; —,
1 + (ж — θγ
Ε»«'<^»2 = !/(ΤΤ^ = {)-
Процедура приближенного вычисления Θ* в этом примере приведена в § 35
(см. также §18 об асимптотической эквивалентности Θ* L-оценке). Там
же содержатся другие примеры, удовлетворяющие условиям теорем 2, 3 и
иллюстрирующие процедуру вычисления о. м. п.
§ 17· О сравнении оценок
Мы видели, что существует много весьма естественных подходов к
получению оценок. Возникает вопрос — как сравнивать между собой разные
оценки и какие оценки следует предпочитать другим? В этой главе мы
выделим два подхода к сравнению оценок — среднеквадратический и
асимптотический. Более общий подход, основанный на использовании элементов
116
Гл. 2. Теория оценивания неизвестных параметров
теории игр и произвольных (не только квадратических) функций потерь,
изложен в главе 6.
Первый из двух названных подходов основан на сравнении
среднеквадратичных уклонений. Второй подход применим лишь к выборкам большого
объема, так как он основан на сравнении «рассеиваний» распределений для
(0* — 0)у/п при больших п. Основанием для такого сравнения служит обычно
вид предельных распределений для (0* — в)у/п при η —> со (если таковые
существуют). Соответствующие предельные теоремы дают нам условия, при
которых распределение (0* — 9)у/п при больших η можно приближать с
помощью упомянутых предельных распределений.
В этом параграфе предполагается, что оценки сравниваются при каком-то
одном неизвестном, но фиксированном распределении выборки Р.
1. Среднеквадрэтический подход. Одномерный случай. Этот подход
используется при рассмотрении оценок по выборке X любого фиксированного
(не обязательно большого) объема. Он состоит в сравнении
среднеквадратичных уклонений Е(0* — 0)2.
Правило 1. Оценку 0*, в соответствии со среднеквадратическим
подходом, будем считать лучшей, чем 0£, если
Έ,{ΘΙ-Θ)2<Έ,{Θ*2-Θ)\ (1)
Широко распространено представление о том, что среднеквадратичная
погрешность является наиболее подходящей числовой характеристикой
точности оценки, хотя это обстоятельство со многих точек зрения является
спорным — ведь можно сравнивать, скажем, величины Е|0* — 0|, также
описывающие средние значения уклонений 0* от 0.
Несомненное преимущество характеристик Е(0* — Θ)2 составляет тот
факт, что (0* — 0)2 есть аналитическая функция разности 0* — Θ. Это
делает многие рассмотрения более удобными, а также позволяет приближать,
как мы увидим позже, значения Е/(0* — 0) для гладких функций /.
Наряду со среднеквадратичным уклонением для описания свойств оценок
часто используется также величина смещения.
Определение 1. Смещением оценки 0* называется величина
b = Е0* - 0.
Оценка 0*, для которой 6 = 0, называется несмещенной.
Среднеквадратичное уклонение связано со смещением и дисперсией
оценки равенством
Е(0* - 0)2 = D0* + б2,
так что для несмещенных оценок среднеквадратичное уклонение совпадает
с дисперсией.
Само по себе свойство несмещенности представляется, очевидно,
желательным свойством оценок, поскольку оно означает, что в данной
последовательности оцениваний среднее значение оценок будет совпадать с истинным
значением параметра. Если этого свойства нет, то оценка называется
смещенной.
§17. О сравнении оценок
117
Пример 1. Рассмотрим следующие три оценки для среднего значения
θ = Εχι распределения Ρ
6>Г = х, (?| = Г, ^з = Х(1)2Х(П)' (2)
где ζ* — выборочная медиана, Х(м, к = 1,..., п, — значения вариационного
ряда, так что С* = Χ((η+ΐ)/2)ι если п нечетно, и (* = ^(п/2) + Χ(η/2+ΐ))ι
если η четно (при η = 1,2 все три оценки совпадают). Все оценки являются
несмещенными, если распределение Р, из которого извлечена выборка,
симметрично относительно θ (Р((—оо, θ — t)) = Р((0 + t, оо)) при любом t ^ 0).
Это следует из того, что распределение всех трех оценок также будет
симметричным относительно 0. Для χ утверждение о несмещенности Ех = 0
очевидно и без предположения о симметрии.
Вычислим среднеквадратичные уклонения оценок (2). Для простоты мы
ограничимся случаем Ρ = Uo,i, n = 3, для которого оценки (2) перейдут в
д* _ = д* _ ν й* _ χ(ΐ) + Х(3)
Имеем
2
36
^-/(.-i)'*-!, ЕИ-^ = И-^-^
Далее, в силу определения медианы (п нечетно) {С* < х} — {F^{x) > 1/2}
и, стало быть,
^ ' к=(п+1)/2
(3)
Для η = 3
p{f;(x) = ι) = ρ т{* < *}) = **(*).
P(3F3*(z) = 2) =3i?2(s)(l-*"(*))■
Вероятность Р(С* € (гх,г* + с/и)) складывается из вероятностей событий вида
{xi Ε (г*, г* + du)}{x2 < ^}{хз > ^}· Так как всего возможно шесть таких
комбинаций, то Р(С* £ {щи + du)) = 6f{u)F{u){l — F{u))du, и,
следовательно, С* имеет плотность, равную (это вытекает и из (3))
6f(u)F(u)(l-F(u)),
118
Гл. 2. Теория оценивания неизвестных параметров
где F(u) = / f{t)dt = Ρ(χι < и). В случае Р = Uo,i эта плотность будет
— 00
равна 6х{\ — х) при χ Ε [0,1], так что
ι
Е(С*)2 = |б*3(1 - x)dx = 6 Q - \} - iQl
о
DC* = Е(С*)2 - (ЕС*)2 = — - - = —.
s ^ ; ^ ^ 10 4 20
Нам осталось найти дисперсию оценки
0* _ x(i) + х(з)
3 2
Рассуждая аналогично предыдущему, нетрудно убедиться, что
вероятность Ρ(χ(ΐ) £ {u,u + du), Х(з) € (υ,υ + ώ)) при u < ν равна 6f(u)f(v) x
χ (F(i;) — i^(w)) dudv. Поэтому для Р = Uo,i
ι ν 2
Значение этого интеграла равно 11/40 (вычисления читатель может
провести самостоятельно), так что
ва; = ЕИ)'-(Е*з)2 = 1Н = |;.
Итак, оценка θ% оказалась наилучшей. Для других значений η и других
распределений Ρ положение может оказаться другим. Мы увидим,
например, что для Ρ = Φα?σ2 наилучшей оценкой для α будет 0* = х.
При мер 2. Несмещенные оценки дисперсии. Рассмотрим оценку для
дисперсии
а также оценку
S! = -T(xi- Ex;)2 = - У; х2 + (ЕхО2 - 2хЕХ1
(обе по принципу подстановки) в том случае, когда Εχι известно. Оценка S\,
очевидно, является несмещенной. В то же время
52 = - ]Г(х; - χ)2 = i J> - χ ± ΕΧ1)2 =
= - Σ(χ< - ЕхО2 - (χ - ЕхО2 = Sf - (χ - EX1)2 < Si
§ 17. О сравнении оценок
119
Таким образом, оценка S2 является смещенной,
ES2 = Dxi - Dx = (1 - - J Dxi.
Это соотношение показывает, что мы можем рассматривать и в случае
неизвестного Εχι несмещенную оценку дисперсии, равную
So2 = -V2 = -Ц- Σ(χ< - χ)2' Е5о = Dxi·
П — 1 П — 1 ^—-'
Перейдем теперь к асимптотическому подходу к проблеме сравнивания
оценок. В этом случае правило для предпочтения оценок выбирается
однозначно.
2. Асимптотический подход. Одномерный случай. Пусть даны две оценки
0* и 0£ такие, что
-U UL- ^ q5 L* L ^ q5 (4)
σι σ2
где Q — некоторый предельный закон распределения, один и тот же для 0*
и #2? ^ σ2 > 01- Тогда при больших η распределения (0* — 0) χ/η/σ^, г = 1,2,
будут близки к Q, и несомненно, что «рассеивание» 0£ вокруг 0 будет больше
«рассеивания» 0*, и нам следует предпочесть θ\. Числа <т; естественно
называть коэффициентами рассеивания.
Таким образом, существо асимптотического подхода состоит в сравнении
предельных распределений оценок.
Мы уже видели и будем убеждаться в этом и в дальнейшем, что многие
возникающие естественным образом оценки, в том числе и оптимальные (об
этом ниже), являются асимптотически нормальными, т.е. для них
справедливо (4) при Q = Фол· Это позволяет нам сформулировать следующее
естественное правило сравнения а. н. оценок.
Пусть даны две а. н. оценки 0* и 0£ с коэффициентами рассеивания σ\
и σ? соответственно
2
Правило 2. Оценку 0* следует признать лучшей, чем 0£, если σ\ < σ\.
Мы использовали это правило для выделения оптимальных оценок
в п. 16.3.
В дальнейшем, при использовании этих и других правил, будем наряду
с термином «лучше» использовать, где это требуется, также слова «не хуже»,
«хуже», «не лучше». Они будут соответствовать знакам неравенства ^, >, ^
между σ\ и σ\ (или между Е(0* — 0) и Ε(02 - θ) в (1)). Если σ\ = σ\, то
оценки мы будем называть асимптотически эквивалентными. Предлагаемое
соглашение естественно, и в дальнейших определениях мы оговаривать его
каждый раз не будем, а будем ограничиваться лишь определением
отношения «лучше» или аналогичных ему.
Отметим, что в классе а. н. оценок минимальность рассеивания 0*
означает, что величина
lim Р(|0*-0|/<г^)
π—юо
120
Гл. 2. Теория оценивания неизвестных параметров
будет максимальной при каждом и. Это обстоятельство делает указанное
правило для сравнения а. н. оценок бесспорным.
Асимптотический подход при всей своей естественности обладает
существенным недостатком: он применим лишь к выборкам большого объема
и лишь в классе a. w. оценок.
Отмеченные два подхода в известном смысле близки друг к другу —
в обоих случаях дело сводится к сравнению дисперсий или величин, близких
к ним. Конечно, величина σ2/η в (4) при Q = Ф0д может, вообще говоря,
существенно отличаться от Е(#* — Θ)2. Однако примеры, иллюстрирующие
этот факт (мы предлагаем читателю построить их), носят, как правило,
искусственный характер.
Дальнейшее изложение этой главы во многом связано с построением
оценок, оптимальных для каждого из двух введенных подходов.
Пример 3. Пусть X €= Γαιι· В примере 14.1 было показано, что обе
оценки
-1/2
«ί-m-. «4-(sE^)'
являются оценками по методу моментов. Кроме того, а* является также
о. м. п. Было установлено, далее, что обе оценки а.н. с коэффициентами
соответственно а2 и ~а2, так что оценка а* лучше, чем а^, с точки
зрения асимптотического подхода. Тот же результат при η ^ 2 получим для
среднеквадратического подхода.
Приведем теперь пример, показывающий, что в зависимости от свойств
распределения одна и та же оценка может быть лучше или хуже, чем
некоторая другая фиксированная оценка.
Пример 4. Рассмотрим задачу об оценке θ = Εχχ, если известно, что
I § Ρ иР — симметричное относительно точки θ распределение (ср. с
примером 1). В этом случае медиана распределения ζ совпадает с Θ. Мы
рассмотрим две оценки для θ (обе по принципу подстановки): среднее 0* = χ
и выборочную медиану Q\ = ζ*. Пусть, для определенности, η нечетно. Из
следствия 12.1 при к = (п + 1)/2 следует, что если функция распределения F
непрерывно дифференцируема в точке θ = £, то
(С*-СЬ/^=*2Лё), ^фо,ь f(x) = F'(x).
Иными словами, в этом случае ζ* является а.н. оценкой с коэффициен-
том а\ = 1/(4/2(0).
С другой стороны, а.н. оценка χ имеет коэффициент σ\ = Dxi. Таким
образом, если
/
Ϊ2 — ν . 1
(x-CYdF{x) <
4/2(С)'
то мы должны предпочесть оценку х. Если знак неравенства будет обратным,
то С*. Следует отметить, что числа / (х — ζ)2 dF(x) и /(ζ) представляют
очень мало связанные между собой характеристики распределения.
§17. О сравнении оценок
121
Рассмотрим важный частный случай, когда мы оцениваем параметр α по
выборке X €= Φα,σ2. В этом случае /(α) = /(ζ) = 1/<7\/27г, так что
2 π 2 ^ 2 2
^2 = 2σ >σ =σι·
Это значит, что статистика х, являющаяся в данной ситуации о. м. п. для а,
лучше, чем ζ*. Это обстоятельство тесно связано с общим фактом, который
будет установлен нами несколько позже, что в широких классах а. н.
оценок Θ* о. м. п. Θ* является асимптотически наилучшей: ее коэффициент
рассеивания является наименьшим в этих классах.
Возвращаясь к примеру 4 о сравнении выборочных медианы и среднего,
еще раз отметим, что, как было показано, существуют распределения, для
которых выборочная медиана будет предпочтительнее х.
Пример с медианой весьма поучителен и в другом отношении. Он
показывает, что скорость убывания степени рассеивания ζ* — ζ с ростом η
может быть любой. Чтобы убедиться в этом, достаточно обратиться к
замечанию 12.1. В условиях этого замечания нормирующим множителем,
который обеспечивает сходимость распределения ζ* — ζ к предельному
распределению, является величина nl^2l\ где 7 может быть любым
неотрицательным числом (см. (12.12)). Множитель у/п соответствует лишь гладким
распределениям.
Приведем теперь один численный эксперимент с выборкой X объема η =
= 101 из нормальной совокупности Фдд и посмотрим*), как значения χ
и ζ* приближают 0 при η = 11, 21, 51, 101. Полученные данные приведены
в следующей таблице:
η
X
г
11
-0,283
-0,291
21
-0,254
-0,292
51
-0,148
-0,078
101
-0,072
-0,044
В этом примере оценка ζ* при η = 51, 101 ведет себя лучше, что есть
результат случайного отклонения. Чтобы почувствовать преимущества х,
надо было бы провести много таких экспериментов.
Приведем теперь некоторые общие результаты, связанные с
рассмотренными примерами.
3. Нижняя граница рассеивания для Ь-оценок. В связи со
сформулированным выше правилом сравнения а. н. оценок возникает естественный
вопрос, насколько малым может быть сделан коэффициент рассеивания этих
оценок. Для некоторых классов оценок нижняя граница возможных
значений рассеиваний может быть найдена в явном виде. Для М-оценок такие
границы были найдены в теореме 16.3. Здесь мы остановимся на этой задаче
для L-оценок, т.е. для оценок, являющихся L-статистиками,
рассмотренными нами в §3, 8. Это есть класс оценок (или статистик), представимых
в виде линейной комбинации членов вариационного ряда (мы предполагаем,
*' Выборка X построена с помощью случайных чисел, взятых из таблиц в [10] (взяты
первые 101 чисел на с. 434).
122
Гл. 2. Теория оценивания неизвестных параметров
что Xi ЕМ), или функций от них. Как и в главе 1, ограничимся L-оценками
не самого общего вида:
η . °°
θ* = 1^φ(^9^{ΐ))= j ψ(Ρ*{η))9{η)άΡ*{η) = 0{Ρ*η), (5)
1=1 -оо
или в несколько иной, близкой, записи:
1
o* = fv>(t)g{F;1{t))dt, (6)
о
где ψ, д — заданные функции, F~l — функция, обратная к F£- В §8 было
установлено (см. следствие 8.6, замечание 8.3), что если X €= F, φ и F
непрерывно дифференцируемы, то L-оценки являются а.н. оценками:
yfr{G{FZ)-G{F))&*w,
1
σ2- /A2{t)dt-A\
о
1
A{t) = J α(ί)Λ, ο(ί)
t
Так как σ2 инвариантно относительно замены A(t) на ±A(t) + с, то можно
сказать также, что в (7) A(t) — любая функция с производной Л'(£),
равной —α(ί), и считать ее выбранной так, что А = 0. Простоты ради положим
^(х) ξ я. Это не очень ограничивает общность, так как для монотонной д
значения #(x(i)) вместе с х^ образуют вариационный ряд (см. (5)). В этом
случае все разнообразие L-оценок доставляется функцией φ. Фиксируем
значение
ι
/ ψ{ί) dt = const = φο, (8)
о
где φο может выбираться, например, так, чтобы оценка Θ* была
несмещенной.
Итак, если X €= F) F имеет плотность /, то в сделанных
предположениях мы можем записать
ι
a2 = jA\t)dt, А'(*) = -"М = -п%-щу О)
О
где φ удовлетворяет (8). Через /, /, /, I будем обозначать производные f(x)
и 1{х) — In/(а;) по х, сохраняя обозначения /#. /^', /', I" для производных
fe{x) и Ι(χ,θ) = Infe(x) по параметру Θ,
ι
А= J A{t)dt,
о
4>W(F-l(t))
F'(F-Ht)) ■
(7)
§17. О сравнении оценок
123
Теорема 1. Если f имеет производную /, то при всех φ,
удовлетворяющих (8),
σ2 > σΐ = ψΐΓ\ (10)
iij^du^J{i{u))2f(u)du. (11)
7 =
Если I < oo, / имеет вторую производную f и существует / f(u)du,
то I — — If {и) du и равенство в (10) достигается при
<p{t)=<p0r4(F-1{t)),
(12)
где φο из условия (8).
Здесь мы опять сталкиваемся с тем, что интеграл 7, аналогичный (16.17),
определяет нижнюю границу возможных значений коэффициентов разброса.
Доказательство. Так как f(u) —> 0 при и —> ±оо, то, интегрируя по
частям, получим в силу (9)
i 1 1
φ0= I\p{t)dt = fa{t)f(F-l(t))dt = ί A(t)
о о
По неравенству Коши-Буняковского
1 1г.
f(F-4t))
dt.
Ψο ^
ίA2{t)dt ί
ο ο L
f(F-4t))
dt,
(13)
где второй интеграл после замены t = F(u) превращается в 7. Отсюда
следует (10). Равенство (11) следует из соотношений
/ = *"/, f = 'if + (i)2f, y/(«)d« = o,
последнее из которых получается, если два раза продифференцировать по θ
в точке θ = 0 равенство
/
f{u + 0)du = 1.
Знак равенства в (13) достигается при
^i)=c/Pi=c,'(F"1(i))·
Отрицательная производная этой функции равна
'i(F-Ht))
(14)
a(t) = —с
f(F-4t)Y
124
Гл. 2. Теория оценивания неизвестных параметров
Сравнивая это с (9), получаем
<p(t) = -d(F-1(t)).
Для этой функции A(t) = cl(F~l(t)) +с\. Условие А = 0 и соотношение (14)
будут выполнены при с\ = 0. Условие (8) будет выполнено при с = —φοί"1.
Теорема доказана. <
Заметим, что свойство l(u) = const реализуется лишь для нормального
закона. С другой стороны, из (6) видно, что оценка Θ* будет статистикой
I типа (см. § 3) лишь при φ(η) = const. Это означает, что нижняя граница
возможных значений σ2 может достигаться на статистиках I типа (в классе
L-статистик) лишь для выборок из нормальных совокупностей.
Посмотрим теперь, как выглядят два подхода к сравнению оценок,
сформулированные в п. 1,2 в многомерном случае, когда θ есть вектор (0ι,..., θ^)·
4. Среднеквадрэтический и асимптотический подходы в многомерном
случае. Асимптотический подход, как и прежде, мы будем использовать
лишь в классе а. н. оценок. В этом случае все дело сводится к сравнению
многомерных нормальных распределений (предельных для (Θ* — 0)\/п),
которые полностью описываются матрицей вторых моментов σ2 (см.,
например, теорему 13.2А).
Если рассматривать среднеквадратический подход к сравнению точных
распределений 0*, то дело также сведется к возможности сравнивать два
распределения в Шк на основании знания моментов (θ* — Θ) второго порядка.
Таким образом, в обоих случаях мы должны уметь сравнивать по «степени
рассеивания» матрицы моментов второго порядка.
Рассмотрим наиболее естественные способы сравнения. Пусть Qi и Q2 —
произвольные распределения в Шк. Обозначим через ξι и £2 какие-нибудь
случайные векторы, обладающие этими распределениями: ^ €= Q^.
Определение 2. Мы будем говорить, что среднеквадратичное
рассеивание распределения Qi около точки α Ε Шк не больше, чем рассеивание Q2,
если для любого вектора α = (αϊ,..., α&)
Ε(ξι-α,α)2<Ε(ξ2-α,α)2, (15)
к
где (х, a) = 2_.xiai есть скалярное произведение.
i=l
Будем говорить, что рассеивание для Qi меньше, чем для Q2, если в (15)
имеет место знак строгого неравенства хотя бы для одного а.
Если а = Εξι = Е^2? то неравенство (15) означает, что по любому
направлению а дисперсия распределения Qi (т.е. дисперсия проекции ξι на а)
не превосходит такой же величины для Q2.
Если df = \\dJ\\ — матрица вторых моментов Qj, I = 1,2, то, раскрывая
скобки в (5) при α = 0, получим для любых αϊ,..., α&
к к
Σ 4))а^ < Σ diij)aiaj' (16)
ij=l i,j=l
§17. О сравнении оценок
125
Это соотношение на языке матриц мы будем обозначать
4 ^ 4 (17)
Оно означает неотрицательную определенность матрицы d| — ^ϊ·
Таким образом, среднеквадратичное рассеивание Qi около нуля не
превосходит такового для Q2 тогда и только тогда, когда для матриц моментов
второго порядка имеют место неравенства (16), (17).
Правила предпочтения оценок в многомерном случае можно
сформулировать следующим образом.
Среднеквадратический подход: оценка 0* лучше, чем 0£, если
среднеквадратичное рассеивание 0* около точки 0 меньше, чем такая же
величина для #2- Если df есть матрица вторых моментов 0г* — 0, то утверждение
«оценка 0* лучше, чем 0£» означает, что d\ < d\.
Асимптотический подход: оценка 0* лучше, чем 0г[, если
среднеквадратичное рассеивание около нуля предельного распределения для (0* — 0) у/п
меньше, чем такая же величина для (02 — в)у/п.
Другими словами, если (0* — 0) у/п ©► Φα σ2, то утверждение «оценка θ\
лучше, чем 0£» означает, что σ\ <σ\.
Можно показать, что если 0* и 02 — две а. н. оценки и 0* лучше, чем 02,
то
lim ((0? - 0)7^ £ В) > lim Р((0£ - 0)^ Ξ В) (18)
для любого центрального эллипсоида*) В.
Мы видим, что в обоих случаях сравнение оценок сводится к
установлению неравенств для матриц моментов второго порядка. Некоторое отличие
состоит в том, что в первом случае моменты не обязательно центральные.
Установим теперь некоторые соотношения, эквивалентные (16), (17).
Положим
<;(0*) = E(0*-0)F(0*-0)T
и обозначим через 93+ множество всех неотрицательно определенных
матриц V = \\vij\\. Если \\dij\\ есть матрица вторых моментов 0* — 0, то,
очевидно, ν{θ*) = Y^Vijdij.
Лемма 1. d\ ^ d\ тогда и только тогда, когда г>(0*) ^ ^(0^) для
любых V G 55+.
Доказательство. В одну сторону утверждение очевидно, так как
матрица Va = ||α;α^'|| Ε 55+, и для такой матрицы
να{θΙ) = Ε (β? - Θ)να{θΐ - θ)Τ = Σ*αί4'}
(см. (16)).
А:
*' Ради краткости условимся область Σ dijXiXj ^ с называть эллипсоидом в R*, а
к
поверхность Σ dijXiXj = с — эллипсом.
126
Гл. 2. Теория оценивания неизвестных параметров
Чтобы доказать утверждение в обратную сторону, заметим, что
частичный порядок, основанный на неравенствах (15), инвариантен относительно
вращения осей координат. Именно, если С — матрица ортогонального
преобразования и Θ* лучше #2 Для параметра 0, то 9\С лучше Q\C для
параметра 0С. Это следует из равенств
(θΐΟ - ΘΟ, а) = ((в; - в)С, а) = (θ\ - 0, аСт)
и определения 2.
Пусть теперь d\ < ά%, т.е.
Σφααι, К^ЛУащ. (19)
Это означает, что ν(βΐ) < ν {θ2) для матриц V вида Va = ||ai%"||> a стало
быть, и для диагональных матриц Vdiag Ε 23+, поскольку последние пред-
ставимы в виде суммы к матриц вида Va. Пусть теперь V — произвольная
матрица из 55+, С есть ортогональное преобразование такое, что CTVC —
= Vdiag- ТогД3
υ{θΙ) = Έ(θί - θ)ν(θ{ - Θ)Ύ = E(0J - θ)θνάΪΆ&Οτ{θΙ - Θ)Τ.
Из сделанных выше двух замечаний и из (19) следует, что правая часть
этого равенства меньше, чем
Е(02* - e)CVdiaeCT(ΘΪ - Θ)Τ = Ε{θ*2 - θ)ν(θ*2 - θ)Τ = υ(θ*2). <
Существует и другой способ сравнения рассеивания (см. [58]), который
предполагает, однако, что оба распределения Qi и Q2 не вырождены в Rfc
и имеют нулевое среднее. В этом случае матрицы центральных вторых
моментов df будут положительно определены, и для них существуют обратные
4 = КГ1.
Пусть d2 есть матрица вторых моментов распределения Q и А = (d2) l.
Определение 3. Эллипсоидом рассеивания распределения Q
называется эллипсоид
tAtT ^ к + 2,
который однозначно выделяется среди всех эллипсоидов следующим своим
свойством: если рассмотреть равномерное распределение U на этом
эллипсоиде (т. е. распределение вКАс постоянной плотностью внутри эллипсоида
и нулевой плотностью вне его), то первые и вторые моменты Q и U
совпадают (см. [58, с. 333]).
Лемма 2. Пусть матрицы d2, I = 1,2, невырождены.
Среднеквадратичное рассеивание Qi около нуля не больше рассеивания Q2 тогда и
только тогда, когда эллипсоид рассеивания для Qi лежит в эллипсоиде
для Q2-
Доказательство. Пусть эллипс tA\tT — 1 лежит внутри tA2tT —
— 1. Как известно, существует невырожденное линейное преобразование
§17. О сравнении оценок
127
t = uL, которое переводит эллипс tA\tT = 1 в единичную сферу 5ι, а
эллипс tA2tT = 1 — в эллипс #2 с главными осями по направлениям осей
координат. Это означает, что А\ = LA\LT — Ε (единичная матрица),
A2 = LA2LT = diag (λ?,...,λ|), 0 < Aj < 1, j = 1,...,Л. Так как If1 = β,
Α^1 = diag (λ^2,..., λ^2), то эллипс tA^t1 = 1 будет инверсией
относительно единичной сферы S\ эллипса 5г, и, следовательно, он будет
располагаться в S\. Так как А^ = {L )~lA2L~l, то, делая «обратное»
преобразование и — tLT, получим, что эллипс tA^ltT = td\tT = 1 лежит снаружи от
tA^t1' = td\tT = 1. Очевидно, что такое же соотношение справедливо для
эллипсов td\tT = с и td\tT = с. Но это означает, что равенство tdftr -=- с
влечет за собой td\t^ = с ^ td2tT. Утверждение в обратную сторону
доказывается точно так же. <]
Важно заметить теперь, что в отличие от одномерного случая сравнение
рассеиваний распределений с помощью матриц вторых моментов
устанавливает лишь частичный порядок на множестве всех распределений. Например,
матрицы d\ = ( 9 J и d2 = ( п ) не лучше и не хуже одна другой, так как
для вектора a = (1,0) неравенство (16) справедливо, а для вектора a = (0,1)
оно будет обратным. Это существенное неудобство введенного порядка, хотя
сам по себе он сомнений не вызывает.
Мы можем сделать множество оценок (или множество распределений)
вполне упорядоченным, если будем сравнивать, скажем, Έ\θ* — 0|2, где | · |
есть евклидова норма в R*, так что
к
Е\в*-в\2 = Е^2(в*г-9г)\ (20)
Такой способ упорядочивания является уже спорным, так как в разных
обстоятельствах точность по различным направлениям может цениться по-
разному. Чтобы как-то учесть это обстоятельство, можно в качестве
обобщения рассматривать меру точности
ν{θ*) = Ε{θ*-θ)ν{θ*-θ)τ,
где V — неотрицательно определенная матрица (случай (20) соответствует
V = E).
Из леммы 1 следует, что если рассеивание 0* около θ меньше, чем
рассеивание #2> т0 ν{θι) < v(02i)· Обратное, вообще говоря, неверно — выполнение
неравенства ν (β*) < ν[θ2) для какой-нибудь одной матрицы V
(предложенный выше полный порядок основан на фиксированной матрице) не означает
еще, что рассеивание Θ* около θ меньше, чем рассеивание 6%.
5. Некоторые эвристические подходы к определению дисперсий оценок.
Методы складного ножа и будстрэп. Мы видели, что важнейшую роль при
сравнении оценок играют величины дисперсий этих оценок. Однако
вычисление этих величин может представлять значительные трудности. В связи
128
Гл. 2. Теория оценивания неизвестных параметров
с этим был предложен ряд эвристических процедур (иногда они могут быть
теоретически обоснованными) для определения дисперсий оценок по самой
выборке. Мы ограничимся рассмотрением лишь одномерного случая θ Ε R.
L Метод складного ножа (jacknife; см. [78, 107]). Для определения
дисперсии заданной оценки Θ* = 0£(Х), построенной по выборке X объема η
(т.е. заданной функции от X и п) предлагается рассмотреть η «подвыборок»
Χ^,.,.,χΜ объема η - 1, где X® получается из X выбрасыванием г-го
наблюдения xj. По каждой из этих подвыборок строятся оценки 9^_г(Х^)
1 п
и Θ*(Χ) = — ^ 0*_Χ(Χ^) (последняя оценка, как правило, имеет меньшее
г—1
смещение по сравнению с Θ*(Χ)). В качестве оценки дисперсии σ2 = ΌΘ*
предлагается использовать значение
(σ2)* = ^ΣΚ-ι(*(ί)) -Θ*{Χ))\
г=1
2. Вудстрэп (bootstrap; см. [47]). Здесь для оценки σ2 = ΌΘ* = a2(F),
Χ €= F предлагается использовать значение σ2 (F*), а для оценки σ2 (i^) —
следующую процедуру типа Монте-Карло. По выборке X = (χι,.. .,хп)
строятся новые выборки Х^\ ..., χ(Ν\ каждая из которых получается
независимым образом как выборка из распределения F£* Иначе говоря, элементами
χΜ — (xj',. .., Xn ) являются χι,..., хп, при этом х^ есть результат
случайного равновероятного выбора с возвращением из совокупности (χι,.. .,хп).
Точно также независимо от х^ определяется х^ и т. д. Оценкой будстрэпа
для 0, построенной по Х^г\ называется значение 0* (Х^). В качестве оценки
значения a2(F*) принимается величина
г=1 г=1
которая выбором N может быть сделана сколь угодно точной.
Вернемся к общей задаче оценивания и перейдем к рассмотрению
важного параметрического случая, когда оцениваются неизвестные параметры
распределений из параметрических семейств.
§ 18· Сравнение оценок в параметрическом случае.
Эффективные оценки
В предыдущем параграфе мы выделили два подхода (среднеквадрати-
ческий и асимптотический) к сравнению качества оценок. Введем теперь
некоторые понятия, связанные с этими подходами в параметрическом
случае, когда распределение выборки X принадлежит некоторому семейству
V = {Р#}. Символами Е# и Ό о обозначаем, как и прежде, математическое
ожидание и дисперсию по распределению Р#.
§18. Сравнение оценок в параметрическом случае
129
1. Одномерный случай. Среднеквадратический подход. Напомним, что
в соответствии со среднеквадратическим подходом мы должны говорить,
что θI лучше, чем 0£, если
d\{9) = Έ6{θ\ - θ)2 < Εθ(θ*2 - θ)2 = 4(θ). (1)
Но в параметрическом случае g^(0), / = L2, суть функции от θ, и мы
должны говорить «0J1 лучше 0£ β точке 0», если d\{9) < d<2.(6).
Аналогичным образом дело обстоит при использовании
асимптотического подхода, когда сравниваются а.н. оценки при больших объемах
выборки η путем сравнения их предельных распределений. Оценка 0*
считается лучше, чем 0£, в точке 0, если в соотношениях
{Θ! - Θ) = yfc & Ф0^{в), 1 = 1,2, (2)
справедливо σ\(θ) < σ2{θ)*).
Таким образом, в обоих случаях задача сравнения оценок приводит к
вопросу о сравнении функций, скажем, άι(θ), 0 Ε Θ. Это множество
неупорядоченное, и в классе всех оценок можно ввести частичный порядок
следующим образом.
Правило 1. Оценка 0* лучше, чем 0£, если d\{9) ^ с^(0) (или
соответственно σ\(θ) ^ σ2(0)) при всех 0 Ε Θ и хотя бы для одного 0 выполняется
строгое неравенство ά\(θ) < cfeW·
Если оценка 0* такова, что для нее существует оценка 0|, которая лучше,
чем 0*, то в таких случаях говорят, что 0* — недопустимая оценка.
Остановимся сначала на среднеквадратическом подходе в одномерном
случае и рассмотрим существующие тут возможности сравнивать оценки.
Прежде всего следует отметить, что наилучшей оценки в смысле
приведенного определения, вообще говоря, не существует. То есть не существует
оценки 0* такой, что для любой другой оценки 0* справедливо неравенство
d(9) < di(0), где d\{9) определено в (1), d{9) соответствует 0*.
Действительно, если взять оценку 0* = θ\ = const Ε Θ, το ά\(θ) =
= Ε^(0ι — 0) =0 при 0 = 0ι, и для наилучшей оценки 0* (если бы такая
существовала) будет выполняться d2(0i) = Έθι{θ* — #ι)2 = 0. Поскольку 0χ
произвольно, то d2(0) = 0. Но это возможно лишь в «вырожденном» случае,
когда наблюдения однозначно определяют значение параметра 0. Например,
когда X €= 1θ или X ^ U^+i и Θ = {1,2,...}.
Таким образом, нижняя огибающая всех функций d2{9) равна нулю, но
в «невырожденных» случаях ни для какой оценки 0* эта функция не
реализуется.
Задачу можно сделать более содержательной, если искать наилучшие
оценки 0* в тех или иных подклассах оценок, которые выбираются
достаточно разумным образом. Одним из возможных способов выделения таких
подклассов является фиксирование смещения 6(0).
*) Мы уже отмечали, что в широком классе случаев d](6) = η~ισ?(θ) + о{п~1). Однако
из определений чисел df (θ) и af(9) это не следует.
130
Гл. 2. Теория оценивания неизвестных параметров
Определение 1. Оценка θ$ Ε К называется эффективной в классе
К, если для любой другой оценки Θ* Ε К Έο(θ^ -θ) ^ Εο{θ* - θ)2 при
всех θ е Θ.
Особую роль играет класс Kq несмещенных оценок — это класс оценок,
для которых Ь(в) = 0.
Эффективные оценки в классе Ко = {Θ* : Едв* = 9} несмещенных
оценок называются просто эффективными. Так что эффективные оценки —
это несмещенные оценки с минимальной дисперсией.
Само по себе свойство несмещенности, как уже отмечалось, является
несомненно желательным, так как оно означает отсутствие систематической
погрешности при использовании оценки.
Вопрос о существовании оценок с данным смещением Ъ{в) (в частности,
несмещенных оценок) сводится к разрешимости интегрального уравнения
относительно д(х)
[д{х)Ре{Хеах)=в + Ъ(в)) (3)
где д{Х) = Θ*; левая часть этого уравнения представляет собой Eq6*.
η
Если выполнено условие (Αμ) и fe{x) = ТТ/0(#г) есть функция правдо-
подобия, то уравнение принимает вид
J 9(χ)/θ(χ)μη(άχ) = в + Ь{в). (4)
Следует отметить, что решение (4) для заданной Ъ{9) существует далеко не
всегда, и, в частности, не для всех семейств {Ре} существуют
несмещенные оценки параметра Θ. Рассмотрим, например, схему Бернулли с
неизвестным параметром ρ (вероятностью исхода {х\ = 1}) и допустим, что
нам дано оценить параметр θ = <р(р), где φ — заданная функция. Тогда
уравнение (4) для несмещенной оценки будет иметь вид
2>(а)Л(а) = 0
X
или, что то же,
f^G(k)pk(l-p)n-k = <p(p), (5)
А;=0
где G(k) = \2 9{χ)·> Ak есть множество точек я, у которых к коорди-
нат равны единице. Но левая часть (5) есть полином от ρ степени п. Это
означает, что уравнение (5) может быть разрешимо, если только φ(ρ) есть
полином степени не выше п.
Рассмотрим теперь класс Кь оценок с фиксированным смещением Ь(в) и
допустим, что существует эффективная в Кь оценка.
§18. Сравнение оценок в параметрическом случае
131
Теорема 1. Эффективная в Кь оценка единственна с точностью
до значений на множестве А С Xй, для которого Р#(А) = 0 при всех
Доказательство. Пусть 0J, θ* — две эффективные в Кь оценки.
Обозначим
Ό = Όθθΐ At = e;-e, в* = ?Ц?±, ι = ο,ι.
Так как
(6)
то
/Δρ + ΔΛ2 + /Δο-ΔΛ2 = Δ^ + Δ2
Εθ(θ* - θ)2 + -АЩ{в1 - θ*,)2 = D + Ь2{0). (7)
Но θ* е Kb, и, стало быть, Έθ{θ* - θ)2 ^ D + Ь2(в). Из (7) вытекает тогда,
что
0* = 0о*п.в.*) <
Проведенное обсуждение проблемы сравнения оценок относилось к сред-
неквадратическому подходу. К нему же относится по существу и следующее
Определение 2. Оценка θ{ Ε К называется асимптотически
эффективной (а. э.) в классе К, если при η —> оо для любой другой оценки Θ*
из К и каждого θ Ε Θ
Εθ(θ*}-Θ)2
"iSPs&bsH1· (8)
2. Асимптотический подход. Асимптотическая эффективность в классах
Λί- и L-оценок. Мы перейдем теперь к асимптотическому подходу, с
которым определение 2 тесно связано. Задача здесь, как и прежде, состоит в
сравнении функций σ(#), характеризующих предельное нормальное
распределение, но проблема в целом несколько упрощается. Дело прежде всего в
том, что сравнение происходит лишь в классе а. н. оценок, который мы в
дальнейшем будем обозначать через Кф.
*) Справедливо следующее утверждение, обобщающее в известном смысле теорему 1.
Если во — эффективная в Кь, о, Θ* — произвольная в Кь оценки, так что h =
= Όβθο/Όβθ* ζ 1, то коэффициент корреляции ρ{θ{,θ*) между оценками 6q и Θ* равен
Доказательство читатель может провести самостоятельно, убедившись, что при
р(#о>0*) Φ \/h и соответствующем выборе а оценка θ\ — (1 — α)θο + <*θ* 6 Кь будет
удовлетворять неравенству Oq9{ < Όβθ^ противоречащему эффективности 0J.
132 Гл. 2. Теория оценивания неизвестных параметров
Пусть К — некоторый класс оценок из Кф. Временно вместо (8) мы
будем использовать несколько иное определение асимптотически эффективной
оценки.
Определение 3. Оценка 0* Ε К называется асимптотически
эффективной в К, если для любой другой оценки θ* Ε К
σ\{θ) ^ σ2{θ)
при всех θ £ Θ, где σ2(0) и σ\(θ) — коэффициенты рассеивания 0* и 0J
соответственно.
Позже мы покажем, что при широких предположениях определения 2 и 3
эквивалентны.
Если в качестве К взять класс М-оценок Км, построенных по
функциям д, удовлетворяющим условия теоремы 14.4 (об асимптотической
нормальности), то из теоремы 16.3 немедленно вытекает следующее
утверждение.
Следствие 1. При выполнении условий регулярности, приведенных
в теореме 16.3, о. м. η. Θ* является а. э. оценкой в Км с коэффициентом
рассеивания
σ*(θ) = Γι{θ); Ι(θ) = Ι{ΐ'(χ1,θ))2Μχ)μ(άχ), (9)
где fe(%) — плотность наблюдений х^.
Класс Км является весьма широким (в него входят, например, все
оценки, являющиеся статистиками I типа; достаточно положить д{х,в) =
= д(х) — h~l(9), где jh/i — функции из определения статистик I типа
в §3). Однако остается неясным, содержит ли Км все а.н. оценки, т.е. все
оценки из класса Кф, в котором нам хотелось бы построить а.э. оценки.
Чтобы двигаться в этом направлении, мы произведем несколько позже иное
сужение класса Кф, по-видимому, менее существенное.
Обратимся теперь к L-оценкам применительно к задачам оценивания
параметров (изначально определение L-статистик с параметрическими
семействами не связаны).
Использование результатов теоремы 17.1 в параметрическом случае будет
эффективно, если функция l(FQl{t),e) (см. (17.12)) от Θ не зависит. По-
видимому, это возможно лишь для параметров сдвига и масштаба.
Рассмотрим сначала задачу об оценке параметра сдвига θ = а для
параметрического семейства Ра(А) = Ρ (А — а) (А — а = {х : х + а Ε Α}, Χ = К,
Θ = R). В этом случае Fa(x) = F(x - α), /α(χ) = f{x — α), где функции F
и / = F' известны, F~l{t) = а + F^t); fQ{F-l(t)) = f{F~l(t)) от α не
зависит.
Заметим, что
ι ι
G(Fa) = /\>{t)F-l{t)dt ^ftpWia + F-1®) dt = ау>о + ОД) = a + G{F)
о о
§ 18. Сравнение оценок в параметрическом случае
133
при любой функции </?, удовлетворяющей условию
Ψο= f<p{t)dt = l. (10)
Поэтому оценка подстановки a* = G(F*) — G(F) является с точностью до
постоянной G(F) (зависящей от φ\) L-статистикой, зависящей от φ, и
естественно поставить вопрос об оптимальном выборе </?. Оценки, являющиеся с
точностью до постоянных слагаемых L-статистиками, также будем называть
L-оценками. Пусть / имеет вторую производную / и φ удовлетворяет (10).
Обозначим через Kl класс L-оценок вида
а* = G{FZ) - G(F), a* = J<p(FZ(u))udK(u) ~ G(F).
Тогда согласно следствию 8.6 и замечанию 8.3 Kl С Кф.
Несомненное преимущество L-оценок перед М-оценками состоит в том,
что первые выписываются в явном виде. Из теоремы 17.1 вытекает
Следствие 2. Пусть 1(х) = 1η/(α:),
0 < I = f(i{x))2f{x) dx < ос. (11)
Тогда L-оценка a* G Kl при φ(χ) = I"4(F~1(x)) является а.э. в классе
Kl и имеет коэффициент рассеивания 7-1.
Очевидно, что для параметра сдвига θ = а значение /(а) в (9) от а не
зависит и совпадает с I. Это означает, что оценка
а* = J"1 yV"1^)))"^») - <W =
= (n/)"1X;r(li-1(i))x(0-G(i·) (12)
(мы считаем здесь в соответствии с договоренностью в § 3, что F*(и)
непрерывна справа, так что F*(x^) = г/п) асимптотически эквивалентна о.м.п.
(имеет то же предельное распределение) и в этом смысле оценку (12) можно
рассматривать также как М-оценку, соответствующую решению уравнения
2_]ЧХ1 "~ а) — 0-* она будет обладать всеми свойствами асимптотической
оптимальности, каким обладает о.м.п. δ*.
Замечание 1. Так как 1{и) = const лишь для нормального
распределения, то представление (12) дает следующую характеризацию этого
распределения: а.э. оценка параметра сдвига (или о. м. п.) реализуется как
статистика вида — YJ φ Ι — J x, (статистика I типа) лишь для нормального
закона F = Ф.
134
Гл. 2. Теория оценивания неизвестных параметров
Аналогично обстоит дело с оценкой параметра масштаба θ — σ для
параметрического семейства Ί?σ{Α) = Ρ Ι —-
В этом случае
*·,(*) = *■(!), 1М = У(1), (13)
где функции F и / = F' известны, F~] (t) = aF~l(t). Имеем
1 1
G(Fa) = J<p(t)F^(t)dt = aj<p(t)Fr1(t)dt = aG(F), (14)
о о
так что при любой φ такой, что G(F) = G(F, φ) -ψ 0
* ~ "ОД"· (15)
Это делает естественным рассматривать в качестве оценки σ* параметра σ
значение
» G(Fn)
" G(F) '
являющееся L-оценкой. Для этой оценки функция φ в «исходном»
представлении L-оценок (как / ip(t)F~l (t) dt) удовлетворяет условию
f<p(t)F-4t)
dt = 1. (16)
(Это равенство дает возможность аналогично (17.10) получать с помощью
неравенства Коши-Буняковского другие нижние границы для разброса
L-оценок.)
Следствие 3. Если выполнено (11) и
то L-оценка
h = [l{u)uf{u)du/0, (17)
соответствующая функции φ(ί) = l(F l{t))1 является а.э. в классе
L-оценок, удовлетворяющих (16), и имеет коэффициент рассеивания
σ2ΐΓ2Ι.
Доказательство. Воспользуемся теоремой 17.1, в которой роль F,
7, f(F~l(t)), /'(F"1^)) бУлУт играть соответственно Fa, σ~2Ι, -/(F"1^)),
σ
§18. Сравнение оценок в параметрическом случае
135
—l(F 1{t)), где F и / из (13) от σ не зависят. Согласно этой теореме в каче-
&
стве оптимальной ψ надо взять φ(ί) = φοΙ~ 1/(F~1(i)), где </?о определяется
из (16):
φ0Γ1 fl(F-l(t))F-1(t)dt=h φο^ΐΓ1!·
Следствие доказано. <]
Для весьма распространенного класса симметричных распределений F
(/(—х) — /(#), /(—х) = /(х)) условие (17) не выполнено. В этом случае
можно перейти к наблюдениям у* = |х;| (в §22 увидим, что {|χϊ|} образуют
здесь достаточную статистику и потери информации при переходе от хг к |х^|
не происходит). После этого можно перейти к наблюдениям ζ; = In у*, для
которых
P(z, < t) - Р(|хг| < ег) = 2Fa{el) - 1 = 2Р{ег~1псг) - 1 = F{t- α),
где α = Ιησ, F(u) = 2F(ew) - 1. Мы свели задачу об оценке параметра
масштаба σ к оценке параметра сдвига для параметрического семейства с
плотностью f(u — α), f(u) = 2f(eu)eu, и > 0. Остается воспользоваться
следствием 2. При этом в новой задаче при очевидном соглашении
относительно обозначений
Т(и) = 1{еи) + In 2 + щ Т{и) = 1{еи)еи + 1, Г= /"(eu)e2u + /(eu)eu,
так что
оо
7 = -2 f f{t)dt[i{t)t2 + l{t)t]. (18)
о
Итак, из следствия 2 вытекает
Следствие 4. Если распределение F симметрично, то оценка
a- = (nf)-1X;f(ii-1(i))zw-G(ii),
G(F) = 7"1 il(F-l{u))F-\u)du = Г1 [T(u)uf(u)du,
(19)
будет а. э. β классе оценок L и будет иметь коэффициент разброса I 1.
Оценка σ* = еа* будет а. к. с коэффициентом разброса σ2/-1.
Для стандартного нормального распределения 1(и) = — и, /(гх) = —1,
7 = 2 (см. (18), а также §26,27) и оценка σ* = ea* будет иметь разброс
σ2/2. Такой же разброс будет иметь о.м. п.
σ*~
ϊΣ*
Τ 1/2
(20)
136
Гл. 2. Теория оценивания неизвестных параметров
Это вытекает из следствия 1 или непосредственно из соотношений
„„-2/^2 ^ тт с ... ησ-2{σ*)2-η
ησ (σ) § Ηη, ξη — ί== ©> Φο,ι
(см. 12.4), так что
""-'('WI) =σ(1+^;ίη+ε")'
где εη —> 0. Таким образом, для нормальных распределений оценка σ* =
= еа* оказалась асимптотически эквивалентной а. э. оценке σ* в классе Км-
Отметим еще раз, что несомненным преимуществом оценки σ* — еа*
является наличие ее явного вида.
Сравним оценки (19), (20) с естественной несмещенной L-оценкой
параметра σ вида
σ* = — V>,|, (21)
па ^—'
00
где а = 2 / xdF(x), так что Е|х;| = ασ (X ^ Fa, распределение F симме-
о
оо
трично). Если обозначить d = χ dF(x) < ос, то мы получим, что σ*
— 00
является а. н. оценкой с коэффициентом разброса
(σ* - σ)ν^ = ^ Σ ("t" " σ) ^ φο,^2σ2·
Для нормального закона а2 = —, d2 = 1, D2 = σ2 Ι— — 1) . Так как — —
π V 2 / 2
— 1 > -, то коэффициент разброса для оценки (21) больше, чем для
оценок (19), (20).
Вернемся теперь к общим определениям 2, 3 асимптотической
эффективности и введем в рассмотрение несколько иное сужение Кф, упоминавшееся
выше, которое, по существу, обеднять Кф не будет. Именно, будем
рассматривать класс Кф}2 С Кф а.н. оценок 0*, обладающих тем свойством, что
для них сходимость
происходит вместе с двумя первыми моментами:
Εθ(θ* - 0)Vn -» Ο, Εθ{θ* - θ)2η -> σ2(0). (22)
§ 18. Сравнение оценок в параметрическом случае
137
Отметим, что первое из этих двух соотношений нетрудно получить из второго
с помощью теоремы непрерывности для моментов (см. §5).
Сужение Кф до класса Кф% мало обедняет первый из этих классов по
двум причинам. Во-первых, а.н. оценки, в которых (22) нарушено,
практически не встречаются (мы отмечали, что для этого обычно нужны
искусственные построения). Во-вторых, для θ* Ε Кф по лемме Фату
\ιπιΜΕθη{θ* - θ)2 > σ2(θ)
n-юо
(мы имеем дело с интегралами от неотрицательных функций), так что
Ε#η(0* — θ)2 при больших η может отличаться от σ2(θ) лишь в сторону
больших значений. Но оценки с таким свойством вряд ли могут
конкурировать с оценками, для которых (22) выполнено.
Таким образом, при асимптотическом подходе мы можем в качестве
класса а.н. оценок, в котором производится сравнение, рассматривать класс
Кфу2- Он будет для нас удобнее.
Если К — класс оценок такой, что К С Кф^, то определение 3
асимптотической эффективности эквивалентно определению 2.
Эквивалентность определений вытекает из того, что для θ* Ε Кф^
Εθ{θ*-Θ)2= 2-^1(1+ rn(0)), rn(0)->O при η "Чоо.
η
В этом случае соотношение (8), означающее, что
Εθ{θί - θ)2 < Εθ(θ* - Θ)2{1 + r'n(9)), τ'η{θ) -». О,
для любой θ* Ε К, очевидно, эквивалентно неравенству в определении 3. <
Упомянутое ранее некоторое упрощение проблемы сравнения при
асимптотическом подходе состоит в том, что здесь мы сравниваем лишь
дисперсии предельных законов. Роль смещения Ь{в) оценок здесь исчезает,
поскольку в классе Кф$ в силу (22) выполняется соотношение 6(0) = о(1/>/п),
означающее «почти несмещенность» оценок или «асимптотическую прене-
брегаемость» смещения с точки зрения соотношений (2).
Аналогично теореме 1 может быть получена
Теорема 2. Пусть К С Кф^· Тогда если θ\ и θ% — две а.э. оценки
в К такие, что —{θ* + #£) ^ ^ то они асимптотически совпадают,
га. е.
νϊι{θΐ-θ*2)^ο, Εθ[νϊϊ{θΐ-θ*2)}2->ο.
Доказательство. Нам достаточно установить второе соотношение,
так как первое из него следует. Пусть
Μι>η = Εθη{θϊ-θ)2, Αι = θ!-Θ, θ* = %^1, 1 = 1,2.
138
Гл. 2. Теория оценивания неизвестных параметров
Тогда на основании (6) получаем
в,п(в. _ θγ + ι-Έθη(θι - θΐγ = Μ^ + Μ2,η (23)
Но θ* Ε К и, стало быть, после перехода к пределу в последнем равенстве
получим в силу асимптотической эффективности 0*
lim Εθη(θ{ - ΘΧ)2 < 0. <
Приведенные выше рассмотрения содержали лишь один из возможных
путей выделения оценок (в нашем случае — эффективных оценок), которые
по ряду естественных соображений следует предпочесть другим. Однако
возможны, конечно, и иные подходы (напомним, что нам приходится
сравнивать неупорядоченные элементы — функции ά(θ) или σ(θ)). Поскольку
оценок с наименьшим при каждом θ возможным значением с/(0), вообще говоря,
не существует, можно сравнивать, скажем, средние значения / d(t)q(t)dt,
где q(t) ^ 0, / q(t)dt = 1, или максимальные значения maxd(0). Это есть
J 0€θ
способы упорядочивания множества всех оценок.
Первый из этих двух способов мы назовем позже байесовским, второй —
минимаксным. Байесовские и мимимаксные оптимальные оценки будут
рассмотрены нами в § 21, эффективные оценки — в более поздних параграфах.
Более подробно проблема выбора оценок будет рассматриваться в главе 6.
3. Многомерный случай. Рассмотрим теперь случай, когда θ и Θ* есть
векторы из R*. Здесь задача сравнения оценок становится труднее. Дело в
том, что в многомерном случае нам пришлось ввести частичный порядок
уже для сравнения оценок при фиксированном Θ. Для сравнения оценок на
всем множестве Θ, как и в одномерном случае, также приходится вводить
частичный порядок, но уже в «другом направлении» (ведь в основе сравнения
лежит среднеквадратичное уклонение, которое есть функция двух
переменных: θ и вектора о, на который проектируется уклонение θ* — Θ).
Наилучшие оценки в «обоих направлениях» и составляют предмет
следующих определений.
Определение 4. Оценка θ$ является эффективной в классе К, если
для любой оценки Θ* из К среднеквадратичное рассеивание Θ* около θ при
всех θ Ε Θ не меньше, чем рассеивание 0q.
Это определение эквивалентно следующему.
Векторная оценка θ$ параметра θ эффективна в К, если для любого
вектора а оценка aj = (#ο>α) является эффективной оценкой скалярного
параметра а = (0,а) в классе оценок а* = (#*,а), Θ* £ ЯГ, т.е. если при всех
θ е Θ, а е Rk, 0* е к
Εθ(ΘΖ-θ,α)2^Εθ{θ*-θ,α)2.
(24)
§ 18. Сравнение оценок в параметрическом случае 139
Как мы уже видели, это неравенство эквивалентным образом
записывается в виде άΙ(θ) ^ бР(0) или
id id
при всех 0 е Θ, a£Rk, где ά2{θ) = ||dy (0)|| и d§(0) = ||^O)(0)|| — матрицы
вторых моментов 0* — 0 и 0q — 0 соответственно.
Эффективные оценки в классе Kq несмещенных оценок называются
просто эффективными.
Поскольку определение (24) эффективности строится на использовании
одномерного случая, из теоремы 1 нетрудно установить, что эффективная
оценка в классе Къ оценок с фиксированным смещением Ь(в) = Е0* — θ
единственна.
Определение а. э. оценок в многомерном случае аналогично
определениям 2, 3.
Определение 5. Векторная оценка θ\ параметра 0 асимптотически
эффективна в К, если для любого вектора а оценка (0*,а) является а. э.
оценкой скалярного параметра а = (0,а) в классе оценок а* = (0*,а) € К.
Другими словами (см. §17), среднеквадратичное рассеивание
предельного распределения (0* — в)у/п для а. э. оценки является наименьшим. Это,
в свою очередь, означает что для любых 0* Ε К, a Ε R*, 0 G Θ выполняется
σ?(0Κσ2(0), или
^σ^\θ)αια^ ^ ]Γσ^·(0)α^·,
id id
гдеа2(0) = ||o"ij(0)||, σΊ(θ) = \\σ\„; (0)|| суть соответственно матрицы вторых
моментов предельных распределений (0* — 9)у/п и (0* — 9)у/п.
Из рассмотрений предыдущего параграфа можно заключить, что
множество оценок в многомерном случае при фиксированном 0 можно сделать
упорядоченным, если качество оценки измерять количеством (при средне-
квадратическом подходе)
υ{θ*) = Εθ(θ* - θ)ν{θ* - 0)τ = ν{θ\ 0), (25)
где V — неотрицательно определенная матрица. Аналогичное количество,
связанное с матрицей вторых моментов предельного нормального
распределения, можно рассматривать и при асимптотическом подходе в классе Яф,2·
Двигаясь дальше по этому пути, можно сделать вполне упорядоченным
множество всех оценок и на всем множестве Θ. Именно, можно проводить
сравнение средних
( ν{θ*,t)q(t) dt, q{t) > 0, Jq{t)dt = 1,
аксималы
в (25).
или максимальных тахг;(0*,£) значений количеств г>(0*,0), определенных
140 Гл. 2. Теория оценивания неизвестных параметров
Если окажется, что оценка, наилучшая при таком подходе, будет
оставаться наилучшей при любой неотрицательно определенной матрице V, это
будет означать в силу леммы 17.1, что эта оценка будет наилучшей и в
смысле частичного порядка, установленного в § 17 (т.е. усредненное
среднеквадратичное уклонение будет наименьшим в любом направлении).
Чтобы строить оценки, оптимальные в смысле определений,
рассмотренных в этом параграфе, нам понадобятся понятия и свойства условных
математических ожиданий и достаточных статистик.
§ 19. Условные математические ожидания
В этом параграфе напомним определение и основные свойства условных
математических ожиданий (у.м. о). Более полное изложение см. в
приложении III, а также в [17, 35, 46, 72, 137].
1. Определение у. м. о· Пусть ξ и η есть две случайные величины,
заданные на вероятностном пространстве (Ω,#, Ρ).
Условное математическое ожидание Έ(ξ/Β) случайной величины ξ
относительно события i?, Ρ (В) > 0, определяется равенством
т/в) = Щ^, (1)
где Έ(ξ]Β) = / ξάΡ = Ε(ξΙ#), 1в = Ib{u) есть случайная величина,
в
равная индикатору множества В.
Допустим, что ξ и η независимы, В = {η = χ} и Ρ (Β) > 0. Тогда для
любой измеримой функции φ(χ,ν) согласно (1)
«г (t w ί Е<^(^у/)/{т?=х} Ey^aQi^s}
4<P&v)h = *]= Р(,Л) = P{f,Jx) '=ίΜ&*)- (2)
Последнее равенство справедливо, так как случайные величины φ(ξ)χ) и
Ιίη-Χ\ как функции соответственно от £ и η независимы и, стало быть,
Εφ{ξ,χ)Ι{η=χ} = Εφ{ξ,χ)ΕΙ{η=χ} = Εφ{ξ,χ)Ρ(η = χ).
Соотношения (2) показывают, что понятие у.м.о. может сохранять свой
смысл и в случае, когда вероятность условия равна нулю — ведь само по
себе равенство
Ε[φ{ξ,η)/η = χ]=Εφ{ξ,χ)
для независимых ξ и η представляется естественным и с предположением
Ρ (η = χ) > 0 никак не связано.
Пусть 21 есть σ-подалгебра #. Определим теперь понятие у.м.о.
случайной величины ξ относительно 21, которое будем обозначать через Ε(ξ/21).
Определение дадим сначала для «дискретного» случая, но так, чтобы оно
легко обобщалось.
§ 19» Условные математические ожидания
141
«Дискретным» мы называем случай, когда σ-алгебра 21 образована
(порождена) не более чем счетной последовательностью непересекающихся
событий Αι, ^2,...; UAi = Ω, P{Ai) > 0. Этот факт мы записываем в виде
21 = σ(Αι, Α<ι,...); это означает, что элементами 21 являются всевозможные
объединения множеств Αι, Α<ι,...
С помощью случайной величины ξ и системы событий (Αι, Α<ι,...) по-
строим новую случайную величину ξ = ξ (ω) следующим образом:
£=Ук = Щ/Ак) = Щ^ при ые4Ь1,2,...
Другими словами,
ζ~^ Ρ(Λ) Л*'
А;
где Ια есть индикатор множества А,
^+*
Определение 1. Случайная величина ξ называется у. м. о. ξ
относительно о-алгебры 21 и обозначается Е(£/21).
Таким образом, в отличие от обычных математических ожиданий у. м. о
Е(£/21) есть случайная величина. В нашем случае она постоянна на
множествах Ак и равна на этих множествах усреднению ξ по А^. Если ξ и 21
независимы (т.е. Ρ(ξ Ε В;Ак) = Ρ(ξ G B)P(Ak)), то, очевидно, Е(£; Afc) =
Если же 21 = #, то 5 тоже «дискретна», ξ постоянна на множествах А^
и, стало быть, ξ = ξ.
Отметим следующие два основных свойства у. м. о.:
1) ξ измерима относительно 21;
2) для любого события А £ 21
Е(£Л)=Е(е;Л).
Первое свойство очевидно. Второе следует из того, что любое событие
А Е 21 представимо в виде Л = (J А^ и, стало быть,
к
Β(ξ;Λ) = ΣΒ(6^Λ) = Σ»*Ρ^Α) = Σ>(^Λ) = Ε^ ^
Это свойство довольно ясно: усреднение по множеству А величины ξ дает
тот же результат, что усреднение уже усредненной по Ajk величины ξ.
Лемма 1. Свойства 1), 2) однозначно определяют у. м. о. и
эквивалентны определению 1.
Доказательство. В одну сторону утверждение леммы уже доказано.
Пусть теперь выполнены условия 1), 2). Измеримость ξ относительно 21
означает, что ξ постоянна на множествах Аь- Обозначим значение ξ на А^
через у к- Так как А^ £ 21, то из свойства 2) следует, что
Щ&Ак)=укР(Ак) = ЩЬАк)
142
Гл. 2. Теория оценивания неизвестных параметров
и, стало быть, при wE4
Теперь мы может дать общее определение у.м. о.
Определение 2. Пусть ξ есть случайная величина на вероятностном
пространстве (Ω,#, Ρ) и 21 С # есть σ-подалгебра $. Условным
математическим, ожиданием ξ относительно 21 называется случайная величина ξ,
обозначаемая Ε (ξ/21), которая обладает следующими свойствами:
1) ξ измерима относительно 21;
2) для всякого А Е 21 справедливо Ε(ξ; Α) = Ε(ξ; А).
В этом определении случайная величина ξ может быть как скалярной,
так и векторной.
^+*
Сразу возникают вопросы: существует ли такая величина ξ и
единственна ли она? В «дискретном» случае мы видели, что ответ на эти вопросы
положителен. В общем случае справедлива
^+*
Теорема 1. Если Έ\ξ\ конечно, то функция ξ = Е(£/21) в
определении 2 всегда существует и единственна с точностью до значений на
множестве вероятности нуль.
Доказательство. Предположим сначала, что ξ скалярна, ξ ^ 0. Тогда
функция множества
Q(A) = f£dP=E(bA), Ae%
А
будет мерой на (Ω,21), которая абсолютно непрерывна относительно Р,
поскольку Ρ {А) = 0 влечет за собой Q{A) = 0. Следовательно, по теореме
Радона-Никодима (см. [17, приложение 3]). существует 21-измеримая функ-
ция ξ = Е(£/21), единственная с точностью до значений на множестве меры
нуль такая, что
' ξάΡ.
Q(A) = fl
А
В общем случае положим ξ = ξ+ — ξ~, ξ+ = max(0,£) ^0, ξ~ =
= max(0, -ξ) > 0,
ξ = ξ+-ξ-,
где ξ* — у.м.о. для ξ*. Этим доказано существование у.м.о., так как
ξ будет удовлетворять условиям 1), 2) определения 2. Отсюда же следует
и единственность, так как предположение о неединственности ξ будет
означать неединственность ξ+ или ξ~. Доказательство для векторных ξ сводится
к одномерному случаю, так как свойствами 1), 2) будут обладать коорди-
наты ξ, существование и единственность которых нами доказана. <
§19. Условные математические ожидания
143
Существо проведенного доказательства достаточно прозрачно: ведь по
условию 2) для всякого А Ε 21 задано Ε(ξ;Α) = / £dP, т.е. заданы зна-
А
чения интегралов от ξ по всем множествам А Ε 21. Ясно, что это должно
определять 21-измеримую функцию ξ однозначно с точностью до значений
на множестве меры нуль.
Смысл Ε(ξ/21) остается прежним — грубо говоря, это есть усреднение ξ
по «неделимым» элементам 21.
Если 21 = #, то, очевидно, ξ = ξ удовлетворяет свойствам 1), 2) и, стало
быть, Е(е/$) = ξ.
Определение 3. Если ξ = 1с есть индикатор множества С G 5, то
E(/c/2t) будет называться условной вероятностью Ρ (С/21) события С
относительно 21. Функция множеств Ρ (ξ Ε С/21) называется условным
распределением ξ относительно 21.
Рассмотрим теперь важный специальный случай, когда σ-алгебра 21
порождена некоторой случайной величиной η.
Определение 4. Пусть ξ и 77 — случайные величины на (Ω,^,Ρ),
21 = σ(η) есть σ-алгебра, порожденная случайной величиной η. Тогда Ε(ξ/21)
называется также условным математическим ожиданием величины ξ
относительно η.
Иногда ради упрощения записи будем вместо Έ(ξ/σ(η)) писать Έ(ξ/η).
Это не приводит к недоразумениям.
Так как Ε(ξ/η) по определению есть а(т7)-измеримая случайная
величина, это означает (см. [17, §3.4]), что существует измеримая функция д(х),
для которой
4tft) = Sfo)· (3)
По аналогии с дискретным случаем мы можем истолковывать здесь величину
д(х) как результат усреднения ξ по множеству {77 = я}. (Напомним, что в
дискретном случае д(х) = Έ(ξ/η = х).)
Аналогично определению 3 в случае 21 = σ(η) будем называть функцию
множеств Ρ (ξ Ε С/η) условным распределением ξ относительно η (см.
также §20).
2. Свойства у. м. о.
1. У. м. о. обладает свойствами обычных математических ожиданий
(см. [17, §4.9]) с той лишь разницей, что они выполняются почти наверное
(с вероятностью 1):
1а) Е(с£/21) = сЕ(£/21), если с = const,
lb) Ε(ξ! + ξ2/21) = Ε^/21) + Ε(ξ2/21),
1с) если ξι ζ ξ2 п. к., то Ε(ξι/21) < Ε(ξ2/21).
2. Справедливо неравенство типа Чебышева: если ξ вещественна, ξ ^
> 0, то для любого χ > 0
Р(?г1/я)<5Ш).
144
Гл. 2. Теория оценивания неизвестных параметров
Это соотношение между у.м. о., как и равенства п. 1, выполняется п.н.
Такое же соглашение будет справедливо в дальнейшем для всех соотношений
между у.м.о.
3. Если σ-алгебры 21 и σ(ξ) независимы, πιο Ε(ξ/21) = Εξ.
Отсюда следует, в частности, что если ξ и η независимы, то Ε(ξ/η) = Εξ.
Если σ-алгебра 21 тривиальна, очевидно, также получим Ε(ξ/21) = Εξ.
4. Для у. м. о. верны теоремы сходимости, справедливые для обычных
математических ожиданий, например теорема о монотонной сходимости:
если ξη f ξ, ξη > 0, το Ε(ξη/2ί) t Ε(ξ/21) п. н.
5. Если η скалярна и измерима относительно 21, Ε|ξ| < оо, Ε|ξη| < оо,
то
Ε(ηξ/Κ) = ηΕ(ξ/Χ).
Другими словами, 21-измеримые случайные величины ведут себя
относительно операции у.м.о. как постоянные (ср. со свойством 1а)).
6. Для у. м> о. остаются справедливыми все основные неравенства
для обычных математических ожиданий, в частности неравенство Коши-
Буняковского
E(|fcfc|/a) ^ [Ε(ξ?/2ΐ)Ε(ξ22/2ΐ)]1/2
и неравенство Иенсена: если Ε|ξ| < оо, то для любой выпуклой вниз
функции д(х)
9(Ε(ξ/Ζ)) < Е((/(0/Я).
7. Формула полной вероятности (свойство 2 определения 2 при А — Ω)
Εξ = ΕΕ(ξ/21).
8. Последовательное усреднение (обобщение свойства 7): если 21 С
С Qli С 3, то
Ε(ξ/21)=Ε(Ε(ξ/211)/21).
Доказательство этих свойств можно найти в приложении III.
Очевидно, что свойства 1, 3-5, 7, 8 справедливы как для скалярных, так
и для векторных случайных величин ξ.
Отметим, что если рассматривать у. м. о. ξ = Ε(ξ/η) относительно
случайной величины η, то их, пользуясь свойствами 5, 7, иногда удобно
определять эквивалентным (по отношению к определению 2) образом так:
Определение 2А. Случайная величина ξ является у.м.о.
относительно 77, если она измерима относительно σ(77), и для любой измеримой
функции т
Ε(ξπι(η)) = Ε(ξτη(η)). (4)
Действительно, если ξ = Ε(ξ/η), то согласно свойствам 5, 7
Ε(ξτη(η)) = ΕΕ(ξπι{η)/η) = Επι(η)Ε{ξ/η) = Ε(ξτη(η)).
§19. Условные математические ожидания
145
Обратно, если выполнено (4), то, полагая гп(у) = /с, получим
Е(£ η 6 С) = Etfmfa)) = Е(£; ту 6 С),
что означает выполнение условий определения 2.
Вернемся к свойствам у.м. о. в общем случае. Следующее свойство
проясняет «геометрическую» сущность у.м.о.
9. Известно, что функция φ(α) = Ε(ξ — α)2 достигает своего минимума
при α == Εξ (см., например, [17, §4.5]). Аналогичное свойство справедливо и
для у.м.о.: при α(ω) = Ε(ξ/21) достигается минимум Έ(ξ — α(ω))2 среди
всех ^измеримых функций α(ω).
Действительно, Ε(ξ - α(ω))2 = ΕΕ((ξ — (ω))2/21), но α(ω) ведет себя как
постоянная относительно операции Ε(·/21) (см. свойство 5), так что
Ε((ί - а(и,))2/Ъ) = Ε((ξ - E(£/2l))2/2l) + Ε((Ε(ξ/21) - а(и))2/Щ,
и минимум этого выражения достигается при α(ω) = Ε(ξ/21). Это свойство
можно рассматривать как определение у. м. о., эквивалентное определению 2.
Согласно нему Ε (ξ/21) можно трактовать как «проекцию» ξ на 21.
Свойство 9 допускает обобщение на многомерный случай, когда ξ =
= (£ъ · · ->6?) есть случайный вектор в Ms.
9А. Пусть V = \\vij\\ — произвольная неотрицательно определенная
матрица размера s x s, a EW,
ζ(α) = (ξ-α)ν(ξ-α)τ
(в частности, при V = Ε получим ζ(α) — |ξ —α|2). Тогда на функции α(ω) =
= Ε(ξ/21) достигается минимум ιηΐηΕζ(α) по классу А всехШ-измеримых
авЛ
функций.
Доказательство этого факта протекает так же, как и в одномерном
случае. Положим α = Ε(ξ/21). Тогда Εζ{α) = EE(C(a)/2l),
В(С(а)/Я) = Ε((ξ - α)ν(ξ - α)τ/21) =
= Ε((ξ - α)ν(ξ - α)τ/21) + Ε((α - α)V(ξ - α)1» +
+ Ε((ξ - a)V(a - α)Τ/21) + Ε((α - a)V{a - a)T/2t). (5)
Так как а — а есть 21-измеримый вектор, то по свойству 5
Е((а - а)У (ξ - а)т/21) = (а - а)УЕ((£ - а)т/21) = О,
Ε((ξ - а)У(а - а)т/21) = [Е((£ - а)/21)]У(а - а)т = 0.
Поскольку последнее слагаемое в (4) неотрицательно и равно нулю при о =
= а, утверждение доказано. <
146
Гл. 2. Теория оценивания неизвестных параметров
§ 20. Условные распределения
Наряду с у.м. о. можно рассматривать условные распределения
относительно σ-подалгебр и относительно случайных величин. В этом параграфе
остановимся лишь на последних.
Пусть ξ и η — две случайные величины на (Ω,#, Ρ) со значениями
соответственно в Rs и Шк и 05s — σ-алгебра борелевских множеств из R5.
Определение 1. Функция Р(В/у) двух переменных у Ε Rfc, В Ε 535
называется условным распределением ξ при условии η = у, если:
1) при каждом В Ε 55s Ρ(Β/η) есть условная вероятность (условное
распределение) Ρ(ξ Ε Β /η) события {ξ Ε В} относительно η, т.е. Р(В/у)
есть борелевская функция от у такая, что для любого А Е 93fe
Ε(Ρ(Β/η);η Ε Л) = J P(B/y)P(V E dy) - Ρ(ξ Ε 5, r/ Ε Α);
Л
2) при каждом у Р(В/у) есть распределение вероятностей по В.
Функцию Ρ (В/у) мы будем иногда записывать в более «расшифрованной
форме» в виде
р(в/у)=Р((ев/п = у).
Мы знаем, что для каждого В Ε 535 существует борелевская функция
5в(у) такая, что <7в(?7) = Ρ(ξ Ε #/77). Таким образом, положив Р(В/у) =
= 9в{у), мы удовлетворим условию 1) определения 1. Однако условие 2)
при этом из свойств у.м.о. никак не следует и выполняться совсем не
обязано — ведь условная вероятность Ρ (ξ Ε Β /η) определена при каждом В
с точностью до значений на множестве Νβ меры нуль (так что существует
много вариантов у. м. о.), и это множество может быть своим для каждого В.
Поэтому если объединение N — (J Νβ имеет не нулевую вероятность, то
Be*ss
может оказаться, что, например, равенства
Ρ(ξ Ε Вг U Β2/η) = Ρ(ξ е Βι/η) + Ρ(ξ Ε Β2/η)
(аддитивность вероятности) сразу для всех непересекающихся В\, В2 из 555
не выполняются ни для одного ω из iV, т. е. на ω-множестве N
положительной вероятности функция дв{у) не будет распределением как функция В.
Однако в нашем случае, когда ξ есть случайная величина со
значениями в W с σ-алгеброй борелевских множеств *В5, дв{я) = Р(£ € Β/η)
всегда можно выбрать таким образом, что дв{у) будет условным
распределением (см. [35, 46]).
Как и следовало ожидать, условные распределения обладают тем
естественным свойством, что у. м. о. выражаются в виде интегралов по условным
распределениям.
§ 20. Условные распределения
147
Теорема 1. Для любой измеримой функции д(х), отображающей Ks
β IK, такой, что Ε|^(ξ)| < со, справедливо равенство
Ε(9(ξ)/η)=Ι9(χ)Ρ(άχ/η). (1)
Доказательство. Достаточно рассмотреть случай, когда g(x) ^ 0.
Если д(х) = /л(х) есть индикатор множества А, то формула (1), очевидно,
верна. Стало быть, она верна для любой простой функции дп(х) (т.е. для
функции, принимающей конечное число значений). Остается взять
последовательность дп | д и воспользоваться монотонностью обеих частей в (1)
и свойством 4 в § 19. <
В реальных задачах для подсчета условных распределений часто можно
пользоваться следующим простым правилом, которое для наглядности мы
запишем в форме
Очевидно, что формально оба условия определения 1 будут удовлетворены.
Если ξ и 77 имеют плотности распределения, этому равенству будет
придан точный смысл.
Определение 2. Пусть условное распределение Р(В/у) при каждом у
абсолютно непрерывно относительно некоторой меры μ в W
>(ξ£Β/η = ν)= J f{x/yMdx).
В
Тогда плотность f{x/y) называется условной плотностью ξ
(относительно меры μ) при условии η = у.
Другими словами, измеримая по паре переменных гг, у функция f(x/y)
есть условная плотность ξ при условии η = у, если
1) для любых борелевских множеств А С К*, В С Rs
f J f(x/yMdx)P(V e dy) = Ρ(ξΕΒ,ηΕ Α); (3)
уел хев
2) при каждом у функция f{x/y) есть плотность распределения
вероятностей.
Из теоремы 1 вытекает, что если существует условная плотность, то
ЕШМ = Jg(x)f(x/vMdx).
Если предположить дополнительно, что распределение η имеет
плотность q(y) относительно некоторой меры λ в Rfc, то (3) можно записать
в виде
J f f{xlv)q{vMte)\(dy) = Ρ(ξ е в, η е А). (4)
уеАхеВ
148
Гл. 2. Теория оценивания неизвестных параметров
Рассмотрим теперь прямое произведение пространств Rs и Шк и на нем
прямое произведение мер μ χ λ (если С = В χ А, В С Is, А С КА, то
μ χ λ (С) = μ(Β)λ(Α)). В этом пространстве соотношение (4) означает,
очевидно, что совместное распределение ξ и η в W χ Шк имеет плотность
относительно μ χ λ, равную
ffav) = /(я/уМу)·
Справедливо и обратное утверждение.
Теорема 2. ^слг/ совместное распределение ξ и η β Κ5 χ Шк имеет
плотность /(#,у) относительно μ χ λ, mo функция
f(x/y) = ^^-, где q{y) = j f{x,yMdx\
есть условная плотность ξ при условии η = у, а функция q(y) есть
плотность η относительно меры λ.
Доказательство. Утверждение теоремы относительно q(y)
очевидно, так как / q{y)^{dy) = Έ*(η £ А). Остается заметить, что f{x/y) =
А
= 1{хтУ)/я{у) удовлетворяет всем условиям в определении 2 условной
плотности (равенство (4), эквивалентное (3), выполнено очевидным образом). <
Замечание 1. Случайные величины ξ и η в теореме 2 можно
поменять местами. Тогда получим, что наряду с f(x/y) существует условная
плотность
q(y/x) = ^0-, f(x) = J f(x,y)X(dy),
случайной величины η при условии ξ — х. Это простое следствие теоремы 2
будет играть существенную роль в последующем изложении.
Применительно к задачам статистики оно позволит нам в следующем параграфе
получить формулу Байеса, которая будет затем часто использоваться на
протяжении всего курса.
Пример 1. Пусть Φα,σ2 есть двумерное нормальное распределение
величин ξι и ξ2, где α = (аьа2), а* = Е&, а2 = ||ау||, σ# = Е(& -а*)^· -ау),
i,j = 1,2. Определитель матрицы вторых моментов равен
\σ | = аца22 - σ12 = <гц<Г22(1 - Ρ ),
где ρ есть коэффициент корреляции между ξι и £г- Таким образом, если
\р\ φ 1, то матрица вторых моментов не вырождена и для нее существует
обратная матрица
1 Ρ
§ 20. Условные распределения
149
Стало быть, совместная плотность ξι и £2 (относительно меры Лебега)
равна (см. § 12)
/(я, у) =
2πΛ/σιισ22(1 - Ρ2)
ν *™ / 1 |>-αι)2 2p(s-a1)(y-a2) , (y~Q2)211
X exp < ; тг 7= 1 > .
L 2(1-/^)L ση \Μισ22 ^22 J J
Одномерные плотности ξι и £г соответственно равны
V/πσιι νζπσ22
Поэтому условная плотность ξι при условии £г = У равна
Ηχ,ν) ι
ЯФ)
q(y) y/2nan{l-p2)
хехр -r-7—~2T (a;-0!i-pA/?ii(y-a2)
2σιι(1-^) V V σ22
)'l·
это есть плотность нормального распределения со средним αχ + р\/&п/&22 х
х {у — #2) и дисперсией ац(1 — р2). Отсюда следует, в частности, что у. м. о.
ξι относительно ξ2 равно
Β(ξι/ξ2)=αι + Ρ*/^(ξ2-α2).
V σ22
Прямую χ = αχ 4- P\JonJG<i2 {у — #2) называют линией регрессии ξι на £г-
Она дает наилучшие среднеквадратичные приближения величины ξι при
данной ξ2 = у.
Пример 2. Рассмотрим задачу о вычислении плотности случайной
величины ξ = φ{ζ,η), где С и 77 независимы. Из формулы (3) при А = К*
вытекает, что плотность f(x) распределения ξ выражается через условную
плотность f{x/y) равенством
f(x) = Jf(x/y)P(Vedy). (5)
Применительно к рассматриваемой задаче под f{x/y) надо понимать
плотность случайной величины <^(С,у), поскольку Ρ(ξ Ε Β/η = у) =
= РМС,у)ев).
Формула (5) бывает очень полезной при вычислении распределений
различных статистик. Например, в п. 12.6 мы могли бы формулу (12.7) для
для плотности распределения Фишера выписывать сразу, а не выводить ее
из вида функции распределения.
150
Гл. 2. Теория оценивания неизвестных параметров
§ 21. Байесовский и минимаксный подходы
к оцениванию параметров
Суть байесовского подхода состоит в том, что неизвестный параметр θ
рассматривается как случайная величина с некоторой (известной или
неизвестной) плотностью распределения q(t), ί Ε θ, относительно меры А,
которая, как и мера μ в условии (Αμ), чаще всего будет представлять из себя
либо меру Лебега, либо считающую меру. Плотность q(t) называется
априорной, т. е. данной до эксперимента. Байесовский подход предполагает,
что неизвестный параметр θ выбран случайным образом из распределения
с плотностью q{t)>
Пусть, далее, ft{x), t Ε Θ, χ Ε Χη, есть функция правдоподобия,
введенная нами в §16. Как мы отмечали, ft{x) при каждом t есть плотность
распределения в Xй. Поэтому функция
f(x,t)=ft(x)q(t)
есть плотность некоторого распределения в Хп χ Θ относительно меры μη χ λ,
которую можно интерпретировать как плотность совместного
распределения X и Θ. При таком подходе в силу теоремы 20.2 функция /г(ж), χ Ε Χη,
есть условная плотность X при условии θ = t
ft(x) = f(x/t), Έθ9(Χ) = Β(9(Χ)/Θ).
В этих рассмотрениях формальная сторона дела требует, чтобы ft{x)
была измеримой по t и χ функцией. В дальнейшем везде, где это потребуется,
будем предполагать, что это свойство имеет место.
В последующем параметр, как случайную величину, везде будем
обозначать через 0, в то время как для фиксированных значений параметра часто
будем использовать обозначения £, и и др., так что
Etg(X) = Ε(9(Χ)/Θ = t).
Наряду с f{x/t) мы можем выписать условную плотность q{t/x)
величины θ при условии X = х:
q{t/x) = М*$*\ /И = /Mx)q(t)\(dt). (1)
Эта плотность определяет так называемое апостериорное (т.е. после
эксперимента) распределение #, которое мы будем обозначать через Qx.
Равенство (1) называется формулой Байесаяля плотности апостериорного
распределения. В дальнейшем эта формула будет играть существенную роль.
Свойство 9 у.м. о. применительно к байесовскому случаю означает
следующее: среди всех функций θ* = φ{Χ) наилучшей оценкой для θ (в смысле
минимизации Έ(θ — φ(Χ))2) является функция
e*Q = Щв/Х) = Jtq(t/X)X(dt) = JtQx{dt). (2)
Определение 1. Оценка 0q, определенная формулами (2), (1),
называется байесовской, соответствующей априорному распределению Q с
плотностью q(t).
§21. Байесовский и мимимаксный подходы
151
Отметим еще раз, что для байесовской оценки безусловное
среднеквадратичное уклонение
Ε{Θ*-Θ)2 = ΕΕ{{Θ*-Θ)2/Θ)=ΕΕΘ{Θ*-Θ)2 = (Et{e* -t)2q{t)\{dt) (3)
принимает наименьшее возможное значение. Соотношение (3) показывает,
что байесовская оценка минимизирует среднее значение (с данной весовой
функцией q(t)X(dt)) величины Et(6* — t)2.
Другими словами, если θ выбирается случайно, с плотностью q(t): то
байесовская оценка является наилучшей в смысле среднеквадратичес-
кого подхода. Среднеквадратичное уклонение (3) байесовской оценки можно
представить в виде (см. (1))
E{e*Q - θ)2 = JEt{e*Q - t)2q(t)X(dt) =
= J/(t - 9*Q)2ft(x)q(t)X(dt№(dx) = ΙσΙα/(χ)μη(άχ) = Ba2Qx,
где Oq есть дисперсия апостериорного распределения Qx:
σ1χ = /(* - e*Qfq{tlX)\{dt) = |(ί - E(0/X))2Qx(dt). (4)
Это был байесовский подход к отысканию наилучших оценок.
Другой подход к сравнению оценок, который отмечался нами в § 18,
основан на сравнении supE^(0* — £)2, где Г С Θ — заданное подмножество Θ
teT
(Г либо совпадает с Θ, либо равно той его части, относительно которой
удалось установить, что θ Ε Γ).
—*
Определение 2. Оценка θ называется минимаксной, если для любой
другой оценки Θ*
supEt(0* - t)2 ^ supEi(0* - t)2.
ter ter
Другими словами, для минимаксной оценки достигается
inf supEt{9* - t)2 = supEttfP - *)2. (5)
θ* ter ter
Установим некоторые полезные связи между байесовскими и
минимаксными оценками.
Теорема 1. Обозначим через 0q байесовскую оценку для априорного
распределения Q с плотностью q. Если существуют оценка Θ* и
распределение Q такие, что при всех t
Μθ*ι-*Ϋ< 1ВЛвЪ-и)2я(и)Ч<1и), (6)
то оценка Θ* минимаксна.
152
Гл. 2. Теория оценивания неизвестных параметров
Доказательство. Пусть Θ* — любая другая оценка. Тогда
supEt(0* - t)2 > [ει{Θ* - t)2q(t)\{dt) >
> JEt(9*Q - t)2q(t)X(dt) > Et(ei - t)\ <
Заметим, что почти для всех /, принадлежащих носителю Nq =
= {t : q(t) > 0} распределения Q, в неравенстве (6) с необходимостью
должно выполняться равенство, так как в противном случае мы получили бы
J Et(0i - t)2q(t)X(dt) < JEt{e*Q - t)2q(t)X(dt),
что противоречит определению байесовской оценки.
Это замечание позволяет нам сформулировать следующий критерий
минимаксной оценки, эквивалентный теореме 1.
Теорема 2. Если оценка Θ*
1) является байесовской для некоторого распределения Q,
2) Еь{в* -t)2 = с = const при t e Nq,
3) Et(6* — t)2^c для остальных ί,
то θ* является минимаксной оценкой.
Если Θ* = 9q = θ удовлетворяет этому критерию, то, очевидно,
supE*(0* - tf = /*Е*(Г - t)2q{t)X(dt). (7)
Таким образом, минимаксная оценка — это есть байесовская оценка,
которая «выравнивает» погрешности Ει(θ — t)2 при различных t. Это
значит, что априорное распределение Q, соответствующее этой оценке,
заставляет быть одинаково внимательным ко всем возможным значениям 0, а не
ориентироваться, как это делают байесовские оценки 0q, соответствующие
другим априорным распределениям Q φ Q, на какие-то выделенные
(более вероятные) значения Θ. Поскольку в последнем случае мы используем
дополнительную информацию о #, то естественно, что при Q φ Q оценки
0q будут обладать меньшими значениями безусловных среднеквадратичных
уклонений
У Et(0£ - t)2Q(dt) < У Et(^ - t)2Q(dt).
В связи с этим распределение Q в теореме 2, соответствующее минимаксной
оценке θ , часто называют наихудшим,
Так как такое наихудшее распределение Q не всегда существует (это
бывает обычно в случаях, когда Θ — неограниченное множество), то можно
предложить следующий модифицированный критерий для отыскания
минимаксной оценки.
§21. Байесовский и мимимаксный подходы
153
Теорема 3. Если существует оценка Θ* и последовательность рас-
пределений Q^) с плотностями q(k' такие, что при всех t
Et(0i - tf < limsup (Μθ*α<*> ~ t)2qW(t)X(dt),
k-юс J
то оценка θ\ минимаксная.
Доказательство этой теоремы столь же просто. Для любой оценки Θ*
справедливо
8upEt(0· - tf > JВД* - t)2qW(t)\(dt) > JEt(FQW - t)2qW(t)X(dt).
Отсюда следует, что
supEt(0*-i)2^ Hmsup f E<(0* (k) - t)2q^{t)X(dt) > Et(ej - if. <
ί jfe-юо У v
Пример 1. Пусть X ^ Φα,ι· Выясним, что из себя представляет
байесовская оценка ct*(k) параметра а с априорным нормальным распределением
Q(*0 = Ф0)А;. В этом случае мы должны положить X(dt) = dt.
Апостериорное распределение Q^' будет иметь плотность q(k'(t/X),
пропорциональную (как функция от t) q^(t)ft{X) или, что то же,
пропорциональную
«ρ{-δ-ϊΣί*-«>2}·
Из равенства
следует, что
п(*) л
Чх — φχη£/(1+ηΑ;),Α;/(1+ηΑ;)·
Так как байесовская оценка ot*^ параметра а равна математическому
ожиданию апостериорного распределения, то отсюда получаем
^ хпк __ χ
пк
154
Гл. 2. Теория оценивания неизвестных параметров
к
Дисперсия апостериорного распределения σ2 {к) = от X не зави-
Qх 1 -г τικ
сит. Стало быть, в силу (4) среднеквадратичная ошибка байесовской оценки
равна
к 1
1 + пк η
при к —> оо. Поэтому для оценки α* = χ имеем
Εί(χ-ί)2 = - = lim /Et(a* w -<)Vfc)(<)*.
и, стало быть, по теореме 3 оценка α* = χ минимаксна. «Наихудшим»
распределением здесь было бы равномерное распределение на всей прямой
(«предельное» для Φο,λ), если бы таковое существовало*).
В следующем примере множество θ компактно и «наихудшее»
распределение существует.
Пример 2. Пусть X €? Вр, т. е. xj, j = 1,..., η, принимают значения 1
и 0 соответственно с вероятностями ρ и 1 — ρ, ρΕ θ = [0,1]. Как мы знаем,
в этом случае для оценки ρ* = χ справедливо
так что критерий теоремы 2 не выполнен. Рассмотрим оценку
_ х + 1/2у^
р - тттмг· (8)
Для нее погрешность
η fp{l-p) + (1 ~ 2р)2
(l + v^)2V n 4n j 4(1+ ^η)2
не зависит от р. Если мы убедимся теперь, что оценка (8) является
байесовской, мы установим тем самым ее минимаксность. Рассмотрим априорное
распределение Q = Вдг+1,лг+ъ где Вдьа2 есть бэта-распределение с
плотностью (см. п. 12.8)
Γ(Λι + Λ2) Λι_1η _ -чАа-l
Тогда, поскольку
MX) = Р41 - *)n(1-*\ g(t) = p^^W -<)N'
*) Интересно отметить, что оценка α* = χ перестает обладать отмеченным свойством,
если X есть выборка из многомерного нормального распределения размерности, большей
двух (xj е Шк, a € Rfc, к ^ 3). Подробнее об этом см. в [49].
§21. Байесовский и мимимаксный подходы 155
то апостериорное распределение будет иметь плотность q(t/X), которая как
функция от t будет пропорциональна ft{X)q(t) или, что то же,
пропорциональна
Это означает, что апостериорное распределение совпадает с
B;v+xn+i,iv+n(i-x)+i· Так как среднее значение распределения Вдьд2 равно
λχ/(λι 4- Аг) (см. п. 12.8), то байесовская оценка рд, соответствующая Q,
будет равна
„ _ Ν + ήχ + 1 _ х+ (Ν + 1)/п
Pq~ 2Ν + Π + 2 ~ 1 + 2{Ν + 1)/η
При N 4- 1 = у/п/2 эта оценка будет совпадать с оценкой р*,
определенной в (8), ив силу теоремы 2 будет минимаксной. Распределение Q
будет наихудшим. Оно концентрируется с ростом η около «наихудшего»
значения параметра ρ = 1/2, при котором дисперсия оценки х, равная
р(1 —р)/п = 1/(4п), будет максимальна. Сама оценка χ не является
минимаксной, так как
р(1-р) . ι ^ ι
SpP n 4η 4(1 +V"")2'
В то же время ясно, что для всех значений р, лежащих вне узкой
окрестности точки ρ = 1/2, оценка χ все же будет лучше, чем р%, — это будет иметь
место для всех р, для которых
ρ(ΐ-ρ)<
4(1 + 1Д/п)2'
В общем случае отыскание точных выражений (явных функций от X)
для байесовских и минимаксных оценок не всегда возможно. Поэтому
естественно использовать также асимптотический подход.
Прежде чем вводить соответствующие определения, напомним, что
байесовские и минимаксные оценки 0д и 0 определялись неравенствами
Е(0£-0)2-Е(0*-0)2 <0,
supE<(0* - t)2 - supEt(0* - t)2 < 0 (9)
для любой оценки 0*. Было бы неразумно определять асимптотическую байе-
совость и минимаксность оценок, просто добавляя к левым частям знак
предельного перехода lim , так как обычно для а.н. оценок Е#(0* — θ)2 ~
п-»оо
~ σ2(θ)/η и левые части в (9) будут сходиться к нулю. Поэтому естественно
рассматривать, скажем, отношение слагаемых в (9). Учитывая, что в
дальнейшем мы будем иметь дело главным образом с оценками, для которых
Е#(0* — 0)2 имеет порядок малости 1/го, можно эквивалентным образом
использовать следующее определение.
156
Гл. 2. Теория оценивания неизвестных параметров
Определение 3. Оценка 0* называется асимптотически байесовской
или асимптотически минимаксной, если для любой другой оценки 0*
выполняется соответственно
limsup[En(0J - θ)2 - Εη(θ* - θ)2] < О,
η—юо
limsup[supEtn(0i - t)2 - supEtn(0* - t)2} ^ 0.
n-юо ter гег
Отыскание асимптотически байесовских и асимптотически
минимаксных оценок возможно, как мы увидим, при весьма широких
предположениях.
В многомерном случае (когда θ Ε Rk есть вектор) свойство 9 у.м.о., как
мы видели, сохраняется, и оценка
e*Q = щв/х)
будет минимизировать
υ(θ*) = Ε{θ* - 9)V{9* - θ)τ = ЕЕ„(0* - θ)ν(θ* - θ)τ =
= [ε№* - t)V(0* - t)Tq(t)\(dt)
для любой неотрицательно определенной матрицы V или, что то же (см. § 18),
минимизировать усредненное (с весом q(t)) среднеквадратичное уклонение
0* — θ по любому направлению а € R*.
Определение 4. Оценка 0д называется байесовской, если для любой
другой оценки 0* и для любой неотрицательно определенной матрицы V
Оценка θ\ называется асимптотически байесовской, если
lim sup[m>(0f) -ηυ(θ%)] < 0.
η—>оо
Определение 5. Оценка 0 называется минимаксной, если для любой
другой оценки 0* и для любой неотрицательной определенной матрицы V
supE*(0* - t)V{T - t)T - supEt(0* - t)V{9* - t)T < 0.
ter ter
Оценка 0* называется асимптотически минимаксной, если
Hmsup[supEtn(01* - £)ν(θ\ - t)T - supEtn(0* - t)V{0* - t)T] < 0.
n->oo ter ter
В заключение этого параграфа еще раз отметим, что обозначения Е^5,
Рв(А), fe(x) в байесовском случае можем рассматривать, если потребуется,
с новой точки зрения — как условные относительно 0 математические
ожидания, вероятности и плотности Е(5/0), Έ*(Α/Θ), /(χ/θ).
§ 22. Достаточные статистики 157
§ 22. Достаточные статистики
В предыдущем параграфе мы рассматривали вопрос о построении двух
типов оптимальных оценок — байесовских и минимаксных. В этом
параграфе введем понятие достаточной статистики, которое позволит нам
строить эффективные оценки — другой тип оптимальных оценок, выделенный
нами в § 18.
Понятие достаточной статистики играет важную роль в математической
статистике вообще и в теории оценок в частности. Условимся обозначать
статистики, т. е. произвольные измеримые (скалярные и векторные)
функции от X символом 5 = S(X).
Пусть X €= Р#, Р# G V = {Р#}. Рассмотрим условное относительно
случайной величины S распределение Р#(Х Ε B/S), В Ε 93^, порожденное
распределением Р# в Хп.
Определение 1. Статистика 5 = S{X) называется достаточной
для параметра Θ, если существует вариант условного распределения
Ί?β(Χ £ B/S), не зависящий от Θ.
Очевидно, что это определение эквивалентно следующему (ср. с
определением 19.2А и теоремой 20.1): статистика S является достаточной,
если для любой статистики Τ = Т(Х) существует вариант у. м. о. Е^(Т/5),
не зависящий от Θ.
Мы знаем, что Vq{X £ B/S) при каждом В есть у. м. о. и, следовательно,
существует функция P[B/s), борелевская по s при каждом В такая, что
Pe(XeB/S) = P(B/S).
Мы можем считать (см. §20), что P(B/s) как функция от В есть условное
при условии 5 = 5 распределение вероятностей. Это распределение можно
интерпретировать как распределение X на поверхности S(x) = s.
Но если S -— достаточная статистика, то это распределение не зависит
от ΘΙ Это означает, что знание того, где находиться выборочная точка X на
поверхности S{x) = s, не сообщает нам никакой дополнительной
информации о параметре Θ. (Ведь ясно, что никто не станет определять неизвестный
параметр в примере 1 введения с помощью подбрасывания монеты по той
причине, что распределение числа «гербов» или «решек» при таком
подбрасывании от θ никак не зависит.)
Это важное обстоятельство означает, в свою очередь, что вся информация
о параметре θ содержится в значении статистики 5. Отсюда и происходит
ее название — достаточная статистика; грубо говоря, знания S(X)
достаточно для построения оценки параметра 0; остальные данные,
содержащиеся в выборке X, бесполезны.
η
Пример 1. Пусть X ^ ГГ\. Покажем, что статистика S = ήχ = У^х»
является достаточной для параметра закона Пуассона λ. Нам надо убедиться,
η
что распределение положения точки X на поверхности yj Х{ = s (s целое)
·=ι
158
Гл. 2. Теория оценивания неизвестных параметров
то
от А не зависит. Так как Ρ ( Χ = χ, Υ^ хг· = s) = Р(Х = χ) при \^ ^ = s,
г=1
η
г=1
η
О, если 2_] хг Φ 5.
г=1
η
Поскольку Х{ независимы, У^хг' €= Ппд, то правая часть (1) равна
Р(Х = ж/пх = 5) = <
J ХГ\Х\ — Х\, . » -?Χη — #п)
Р(ггх = 5)
η
если
г=1
η
Ε
г=1
(1)
г=1
-1 η
И^1) π
е Л — = —
г=1 Ж<· ns Π *i!
t=l
Таким образом, условное при условии S = s распределение X совпадает с
полиномиальным распределением В£ (см. § 12) с η равновероятными
исходами (т. е. с вектором вероятностей ρ = (1/п,..., 1/п)) и с 5 независимыми
испытаниями. Очевидно, это распределение от λ не зависит, так что S = пх
является достаточной статистикой для λ.
Понятие достаточной статистики было введено Фишером в 1922 г.
Следующая теорема Неймана-Фишера носит название факторизационной
теоремы, она устанавливает простой критерий существования достаточной
статистики.
Предположим, что выполнено условие (Αμ) о существовании плотности
Л(.) - f М-
Теорема 1. Для того чтобы S была достаточной статистикой
для Θ, необходимо и достаточно, чтобы функция правдоподобия /#(ж) =
TT/fl^i) была представима в виде
i=l
Mx)=t(S(x),e)h{x) п. в. [μη], (2)
где каждая из функций φ ^ 0 и h ^ 0 зависит только от своих
аргументов, φ{δ,θ) измерима по s, h(x) измерима по х.
Понятно, что представление (2) неоднозначно. Компоненты его
определены с точностью до произвольной положительной функции от S(x).
В рассмотренном нами выше примере с распределением Пуассона
/л(*) = Пе_А^т = е'пААП5ЕПЛ' ™ = f>>
i\ Xil tiXil έί
§ 22. Достаточные статистики
159
так что мы можем положить при S = пх
V>(S,A)=e"nAA5, h(x) = f[—.
Отсюда в силу теоремы 1 будет следовать, что S = пх есть достаточная
статистика.
Из методических соображений мы приведем два варианта
доказательства теоремы 1. Первый — для наиболее простого специального случая,
когда наблюдения хг· дискретны. В этом случае доказательство оказывается
весьма простым. Второй, несколько более сложный вариант доказательства
теоремы Неймана-Фишера, будет относиться к некоторому обобщению
теоремы 1, в котором условие (Αμ) не предполагается.
Доказательство теоремы 1 в дискретном случае.
В дискретном случае μ есть считающая мера на счетном множестве X
возможных значений χι, и, стало быть, fe{x) — Ρ#(χι — я), я Ε Χ. Пусть
сначала выполнено (2). Тогда для фиксированной точки χ Ε Xй
τ>θ(χ = x/s(x) = s[x)) = Ρθ{8{χ) = s{x)) . (3)
Так как {Χ — ж, S(X) — S(x)} = {Χ = ж}, то правая часть (3) равна
Ре(Х = х) __ Мх)
Pe(S(X) = S(x)) Σ Л(У)
y:S(y)=S(x)
iP{S{x),0)h{x) h{x)
Σ *(S(x),e)h(y) Σ НуУ
y:S(y)=S(x) y:S(y)=S(x)
Таким образом, Vq{X = x/S(X) = S(x)) от в не зависит.
Наоборот, если левая часть в (3) от θ не зависит, то, обозначая ее через
Л(ж), из (3) находим
Рв(Х = х)= Мх) = Έ>Θ(Χ = ж; S(X) = S(x)) = h(x)Pe(S(X) = S(x)),
где "Pq(S(X) = S{x)) = ip(S(x),9) зависит только от S(x) и θ. <
Лишь немногим сложнее доказывается теорема 1 и в другом важном
частном случае — «гладком», когда μ есть мера Лебега в К, а статистика
S(X) предполагается гладкой функцией от X.
Чтобы доказать теорему 1 в общем случае, сначала несколько изменим
ее формулировку. Заметим прежде всего, что для простоты мы можем, не
ограничивая общности, считать η = 1, так как выборку X мы можем
рассматривать как выборку объема 1 из совокупности с плотностью распределения
η
/β(χ) = ТТ /^(^i). Тогда теорема 1 будет эквивалентна следующему утверж-
i=l
дению.
160
Гл. 2. Теория оценивания неизвестных параметров
Теорема 1А. Для того чтобы S была достаточной статистикой,
необходимо и достаточно, чтобы при каждых 0, Θ' отношение
Л'(я)
было функцией от S(x), га. е. чтобы существовала измеримая по s
функция rQ}or(s) такая, что
Ш-ге^Б{х)\ (4)
Л'(я)
Действительно, если верно (2), то (4) очевидно. Если верно (4), то,
фиксируя θ1, получим равенство
Л (я) = refi>(S(x))f9'(x),
которое влечет за собой (2) при h(x) = /#'(#), ^{6,s) = rofit(s) [θ'
фиксировано). <
Характеризация достаточности с помощью теоремы 1А обладает двумя
пр еиму ще ства ми.
1. В ней отсутствует проблема неоднозначности представления (2),
связанного с неопределенным множителем, зависящим от S. (Поэтому в ряде
случаев для отыскания достаточной статистики S удобнее пользоваться
теоремой 1А, а не теоремой 1.)
2. Она позволяет получать критерии достаточности, не связанные с
условием (Αμ).
Чтобы убедиться в последнем, заметим, что теорему 1А можно
переформулировать следующим образом.
Статистика S является достаточной тогда и только тогда, когда
при каждых θ, Θ1 отношение
М*)'+М*) ΞΚθ"'{Х) = 1 ТгеХ) (5)
является функцией от S(x).
Рассмотрим теперь усредненное распределение
P = iV = 2(p* + ]EV)·
Очевидно, что распределение Р# абсолютно непрерывно относительно Ρθ,Θ'
и, стало быть, существует плотность
/v(*) = ^-(«) (6)
(она всегда ограничена, так как fe,e'{x) + ίθ',θ(χ) = 2). Если выполнено
условие (Αμ), то
ίθ,θ'{χ) = 2Β>θ}θ'{χ)-
Таким образом, функция R, присутствующая в (5), допускает определение,
никак не связанное с условием (Αμ) (этого нельзя сказать о функции г в
§ 22. Достаточные статистики
161
теореме 1А, так как Р# не всегда абсолютно непрерывно относительно Ρ#>,
как, например, в случае, когда θ есть параметр сдвига: Έ*θ{Β) = Р(В — 0),
Р0О([0,1]) = 1 при некотором 9q).
Теперь мы можем сформулировать характеризационную теорему в виде,
не связанном с условием (Αμ).
Теорема 1В. Статистика S является достаточной тогда и
только тогда, когда при каждых θ, Θ' плотность /θ,θ'{χ) есть функция от S,
т. е. существует измеримая по s функция g9fl(s) такая, что /$β'(χ) =
Из сделанных выше замечаний ясно, что при выполнении (Αμ) это
утверждение эквивалентно теореме 1А и, следовательно, теореме 1. Доказав
теорему 1В, тем самым докажем теорему 1.
Доказательство теоремы 1В. Необходимость. Пусть
статистика S является достаточной. Тогда для любой статистики Τ = Г(Х)
Ев(Г/5) = Ey(T/S) ξ H(S(x)) (7)
от θ и θ' не зависит. Наряду с у^м. о. Е#, построенным по распределению Р#,
можем строить также у.м.о. Ε по усредненному распределению Ρ = Т?е,е'-
Покажем, что Е(Т/5) = Е^(Т/5) и, следовательно, также не зависит от 0, Θ'.
Действительно, для любой измеримой функции т в силу (7) и свойств у. м. о.
B(Tm(5)) = |pB,(Tm(S)) +E,(Tm(S))] =
= i[E*(tf (S)m(S)) + Eef(H(S)m(S))} = ЁЯ (S)m(S).
Отсюда следует, что (см. определение 19.2А)
ЩТ/S) = H(S) (8)
от θ и θ1 не зависит (т. е. S является достаточной статистикой и для
семейства Ρ = Р(9,0')·
Нам надо доказать, что / = /θ,Θ'(χ) является функцией от S(x). Для
этого покажем, что
Л,ИХ)=Ё(Л,ИХ)/5) п. в.
или, что то же,
d = Ё[/ - Ё(//5)]2 = Ё/2 - 2Ё/Ё(//5) + Ё(Ё(//5))2 = 0.
Но в этом соотношении в силу свойств у. м. о.
Ё/Ё(//5) = Ё(Ё(//5)Ё(//5)) = Ё(Ё(//5))2
и, стало быть,
d = E/2-E/E(//5),
162
Гл. 2. Теория оценивания неизвестных параметров
где в силу равенства (6)
Ё/2 = J f ■ fPefi,{dx) = JfPeidx) = E9f,
(9)
Ё/Ё(//5) = JvUIS)rP0fi.(dx) = JE(f/S)Pe(dx) = E9E(f/S).
Но согласно (7), (8) Е(//5) = Ee(f/S). Следовательно, правая часть (9)
будет равна E$E0{f/S) = Ε*/, d = 0.
Достаточность. Пусть теперь Jqji(x) = gej'{S(x)) является
функцией от 5(ж). Покажем, что тогда для произвольной статистики Τ и
произвольных б, Θ'
E9(T/S) = E9,(T/S), (10)
что означает независимость E9(T/S) от 0 и достаточность S. Положим
H(S) = E(T/S). Тогда для любой измеримой функции m
Евт(5)Я(5) = f m{S{x))H(S(x))Pe(dx) =
= [m(S(x))H(S(x))fe,9.(x)P(dx) = ί m(s)H(s)g9,9l(S)P(S(X) G ds) =
= Em(S)H(S)g9,9.(S) = Em(S)Tg9i9.(S).
Те же рассуждения в обратном направлении позволяют продолжить эти
равенства следующим образом:
= fm{S{x))T{x)gBtei{S{x))P{dx)= Im{S{x))T(x)Pe{dx) = Eem{S)T.
Отсюда следует
H(S)=E9(T/S).
Поменяем теперь местами θ и Θ1. Функция /^/^(ж) также будет функцией
от S(x). Поэтому совершенно аналогично получим
H(S) = E9,(T/S),
что доказывает (10). Теорема доказана. <
Вернемся теперь к теореме 1 и примерам достаточных статистик.
Пример 2. Пусть Χ ξ= Φα>σ2. Здесь параметр θ = (α,σ2) двумерный.
Имеем
§ 22. Достаточные статистики
163
Полагая S = (Si, S2), Si = пх, S2 = /Jx*» получим представление (2), где
t=l
*(5,*) = α-exp {-52"^1+а2} , НХ) = (2π)""/2.
Здесь мы могли бы, конечно, множитель (2π)~η/2 отнести и к функции ψ,
положив h(X) = 1.
Таким образом, мы получили, что статистика (Si, S2) является
достаточной векторной статистикой для (α, σ2). Из всей информации, содержащейся
в выборке, нам достаточно знать χ и 2_] xi -
Предлагаем читателю найти достаточные статистики для всех семейств
распределений, приведенных в § 12.
Остановимся подробнее лишь на одном их этих семейств.
Пример 3. Пусть X €= Uo,0. Здесь условие (Αμ) выполнено
относительно меры Лебега и
-г
, если 0 ^ х2^ θ при всех г = 1,..., п,
ίθ{Χ) = i п
в противном случае.
Пусть Х(!) = minxj, X(nj = таххг. Тогда, как мы видели в примере 16.5,
функцию f$(X) можно записать в виде f${X) = ψ{χ.(η),θ)Ιι(Χ), где
Ηχ) = μ> еслих(1)^0,
в противном случае,
ч (θ~η
/ ( а\ )~ при 5 ^ Θ,
в противном случае.
Это означает, что S(X) = Х(п) есть достаточная статистика для Θ.
Аналогичным образом читатель может убедиться, что для выборки X €=
€= Ueti+o достаточной статистикой для параметра θ является двумерная
статистика S(X) — (x(i),X(n)). Такой же будет достаточная статистика и для
двумерного параметра θ = (α, 6), когда выборка извлечена из
распределения Ufl)6.
Приведем некоторые следствия теоремы 1.
Следствие 1. Если S — достаточная статистика для 0, то оценка
максимального правдоподобия зависит лишь от S.
Точнее, о. м.п. Θ* не зависит от X при фиксированном S(X).
Это следствие очевидно, так как о.м.п. есть значение 0, при котором
достигается максимум fe{X) = Ψ(8(Χ),θ)}ι(Χ) или, что то же, максимум
Следствие 2. Если S — достаточная статистика и функция φ
такова, что отображение и = φ(ν) взаимно однозначно и измеримо в
обе стороны, то Si = ip{S) также будет достаточной статистикой.
164
Гл. 2. Теория оценивания неизвестных параметров
Это следствие также очевидно, поскольку ip(S, Θ) в (2) можно записать в
Bmef/>{<p-l{Si),e)=tl>i{Sue).
Следствие 3. Пусть нам надо оценить параметр η = φ{θ), где φ
осуществляет взаимно однозначное отображение, так что определена
функция θ = φ~ι(Ί)' Пусть, далее, S — достаточная статистика для Θ.
Тогда S будет также достаточной статистикой для у.
Это следствие вытекает из тех же соображений, что и в следствии 2.
Действительно, функция правдоподобия для 7будет иметь вид /φ(8(Χ),ψ~ι(^)) χ
χ h(X), где первый множитель можно записать в виде t/>i(S(X),7)·
Справедлив еще один критерий достаточности статистики 5, который
можно рассматривать как некоторую модификацию теоремы 1В.
Теорема 2. Статистика S является достаточной для θ тогда и
только тогда, когда для любого априорного распределения Q
параметра θ апостериорное распределение Qx зависит от X только через
S(X) (т. е. остается неизменным на поверхности S(X) = s).
Доказательство. Пусть S — достаточная статистика, q(t) —
плотность Q относительно какой-нибудь меры λ. Тогда апостериорная плотность
q{t/X) относительно этой меры будет по формуле Байеса равна
дШХ) = МШ*) = iKS(X)tt)q(t)
ί fu{X)q{u)X{du) ί 1/>{S{X), u)q{u)X{du)
Докажем теперь обратное утверждение теоремы. Выберем априорное
распределение так, чтобы q(t) > 0 всюду на Θ и при всех t
ft{x) = q{t/xq(/){x)> пх) = /шшч<ь).
Если q{t/X) = g{t,S{X)), то, полагая tp{s,t) = g{t,s)/q(t), h{X) = f(X),
получим представление (2). <
Следствие 4. Если S — достаточная статистика, то все
байесовские оценки и минимаксные оценки, определенные с помощью
теоремы 21.2, зависят лишь от S.
В дальнейшем получим много других подтверждений того, что
достаточная статистика S содержит в себе исчерпывающую информацию о 0.
§ 23.* Минимальные достаточные статистики
Рассмотрим теперь вопрос о выборе достаточных статистик. Ясно, что их
может быть очень много. Например, статистика S(X) = X, очевидно, всегда
является достаточной. Эта достаточная статистика называется
тривиальной достаточной статистикой. Однако мы заинтересованы (и в дальнейшем
станет ясно, почему) в более «экономных» статистиках. Оказывается, далеко
не всегда можно построить достаточные статистики, которые были бы
существенно «экономнее» тривиальной достаточной статистики. К этому вопросу
мы вернемся после того, как определим более точно понятия, связанные с
§ 23 Минимальные достаточные статистики
165
«экономностью» достаточных статистик. Для этого введем на множестве
всех достаточных статистик (для некоторого параметра Θ) частичный
порядок.
Определение 1. Будем говорить, что статистика Si подчинена 5г,
если Si есть измеримая функция от S2'. Si = ^(S^)·
Это соотношение и означает, что Si «экономнее» #2-
Определение 2. Если 5χ подчинена S2 и 5г подчинена 5Ί, то
статистики Si и 5г называются эквивалентными.
Очевидно, S\ эквивалентна 5г тогда и только тогда, когда Si = ^(^г) и
φ — взаимно однозначное измеримое в обе стороны отображение.
Определение 3. Достаточная статистика Se называется
минимальной, если она подчинена любой другой достаточной статистике S.
Минимальная достаточная статистика является самой экономной. Если
мы построили минимальную достаточную статистику S, то при сохранении
свойства достаточности дальнейшее сокращение данных по сравнению с S
невозможно. Остальные данные, содержащиеся в выборке, можно
рассматривать как порожденные некоторым случайным механизмом, не зависящим
от 0. Они не несут в себе никакой информации о Θ.
Введенные понятия, как и исходное понятие достаточной статистики,
можно в слегка обобщенной форме излагать на языке σ-алгебр,
который в ряде случаев оказывается более удобным и наглядным. В самом
начале — в определении 22.1 предыдущего параграфа — условное
распределение Ρθ(Χ € B/S) можно заменить на условное распределение Pq(X Ε
G В/21) относительно σ-подалгебры 21 С 25д> и называть 21 достаточной
σ-алгеброй, если существует вариант Рв(Х € В/%), не зависящий от Θ.
Факторизационная теорема при таком подходе сохранится, если
функцию ifj{S{X),9) заменить на 21-измеримую по X функцию ψ(Χ,θ).
Доказательство этой теоремы по существу останется прежним.
Достаточную статистику теперь можно определить как статистику S, для
которой порожденная ею σ-алгебра σ(5) будет достаточной.
Подчиненность достаточных статистик (см. определение 1) на языке
σ-алгебр не требует введения дополнительных понятий и совпадает просто с
вложением σ-алгебр: Si подчинена S2, если σ(ί>ι) С σ^)· Таким образом,
S\ экономнее 5г, если σ-алгебра σ(5ι) беднее (грубее), чем а(5г).
Эквивалентность Si и 52 означает, что σ(5ι) = а(5г).
Минимальная достаточная σ-алгебра 21о определяется как σ-алгебра,
которая вкладывается в любую достаточную σ-алгебру.
Минимальная достаточная σ-алгебра всегда существует. Прежде
чем сформулировать соответствующее утверждение, заметим, что существует
распределение Q на Θ такое, что все Р# абсолютно непрерывны
относительно распределения Pq = / PtQ(dt). Действительно, рассмотрим
байесовскую постановку задачи, когда θ есть случайная величина с априорным
распределением Q. Пусть q(t) > 0 есть плотность распределения
относительно подходящей меры λ на Θ.
166
Гл. 2. Теория оценивания неизвестных параметров
Допустим для простоты, что для п. в. χ функция ft(x) в каждой точке t Ε
Ε Θ непрерывна справа и слева. Тогда все распределения Pt будут абсолютно
непрерывны охношхельно Р, = /р„(()А(<й), «, „ак Рв(Л) = 0 влечет
за собой Р^ (А) = 0 для всех t.
Это означает, что либо /q{X) = / ft{X)Q(dt) > 0 при всех X, либо из
равенства }q{X) — 0 следует fe{X) = 0 при всех Θ. В этом случае говорят,
что Pq доминирует семейство {Р#}, так что мы могли бы Pq взять в
качестве меры μ. Плотность распределения Р# относительно этой меры равна
dPQ[x) /«И ( ' )-
Ясно (ср. с теоремой 22.2), что если S — достаточная статистика, то г(х,6)
зависит от χ лишь через S{x).
Теорема 1. σ-алгебра Slo = σ(τ(Χ,θ)\ θ Ε Θ), порожденная
случайными величинами τ(Χ,θ) = fg(X)//q(X) при различных 0 Ε θ, является
минимальной достаточной σ-алгеброй.
Доказательство теоремы весьма просто. Достаточность 51о следует
из факторизационной теоремы и того, что
fg(X)=r(X,e)fQ(X), (1)
где }q{X) не зависит от 0, а г(Х,Θ) измерима относительно Slo.
Пусть теперь 31 есть любая достаточная σ-алгебра. Тогда fe{X) =
= ф{Х)в)к{Х)^ где функция ψ(Χ,θ) 51-измерима. Рассмотрим σ-алгебру
ЗЦ = σ(ψ(Χ,θ), θ Ε Θ) С SI. Из определения г(Х,в) следует, что
fi,(X,W(dt)'
и, стало быть, Sto С ЗЦ С 31. <
С этой теоремой и теоремой 22.2 тесно связано другое полезное
замечание. Апостериорная плотность, соответствующая q(t), равна
яШХ) = У^=г(ХЛф),
и, стало быть, минимальную достаточную σ-алгебру Slo можно
рассматривать как порожденную апостериорным распределением:
α0 = σ(9(ί/Χ);ί€θ).
Отыскание распределений Q и Pq, фигурирующих в теореме 1, обычно
труда не составляет. Например, если носитель Νρθ распределения Ρ я от θ не
зависит, что имеет место для большинства распределений, перечисленных
в § 12, то можно взять Pq = Р#0 при любом #о € Θ.
§ 23. Минимальные достаточные статистики 167
Таким образом, мы располагаем теоремой существования и
конструктивным способом построения минимальных достаточных сг-алгебр*).
Однако в большинстве случаев нам все же будет удобнее иметь дело со
статистиками. Основная задача этого параграфа — отыскание
минимальных достаточных статистик.
Прежде всего, каким образом можно проверить, что данная достаточная
статистика Sq является минимальной?
Одна из возможностей состоит в использовании теоремы 1. Если σ(5ο)
совпадает с σ-алгеброй, порожденной fe{X)/Jq(X), to Sq есть минимальная
достаточная статистика.
Пример 1. Мы видели, что статистика S = пх является достаточной
для параметра λ распределения Пуассона Пд. Это будет минимальная
достаточная статистика, так как a(S) совпадает, очевидно, с σ-алгеброй,
порожденной fx(X)/f\l(X) = βη(λι_λ)(λ/λι)5 (мы взяли здесь
распределение Q, сосредоточенное в точке λι).
Пример 2. Пусть X €= Uo,0. Тогда статистика 5 = X(n) = тахх*
является минимальной достаточной статистикой. В самом деле, возьмем в
качестве Q какое-нибудь распределение на [0, оо) с плотностью q(t) > 0 при всех
t > 0. Тогда
0, θ < 5,
00 ОО
/qW = J ft(X)q(t)dt = jrnq(t)dt > О
О 5
при всех X. При этом 5 = sup{0: fo{X)/Jq(X) = 0}. Это означает, что 5
измерима относительно минимальной σ-алгебры 21ο, σ(5) С 21о и что, стало
быть, 5 — минимальная достаточная статистика.
Можно указать другой способ отыскания минимальных достаточных статистик,
также связанный с функцией правдоподобия. В самом деле, любая статистика, и
в частности достаточная статистика 5, порождает разбиение выборочного
пространства на классы эквивалентности — т.е. на подмножества точек χ с одинаковым
значением S(х).
Если Si подчинена S%, т.е. S\ = <^(52), то> очевидно, разбиение для Si
будет более крупным, так как классы эквивалентности для S2 содержатся в классах
эквивалентности для S\. Таким образом, минимальной достаточной статистике
соответствует самое «крупное» среди разбиений, порожденных достаточными
статистиками.
Можно рассматривать просто разбиения пространства на классы
эквивалентности, не связывая их непосредственно со статистиками. Класс эквивалентности,
содержащий точку ж, обозначим через D{x). Каждый класс однозначно
определяется какой-нибудь одной своей точкой. Разбиение на классы D будем называть
достаточным, если
Μχ) = φ(χ,θ)Η(χ), (2)
ίθ(Χ)
-
*) Существование минимальной достаточной σ-алгебры 21о можно установить и иным
путем, доказав, что 21о есть пересечение всех пополненных достаточных σ-алгебр.
168
Гл. 2. Теория оценивания неизвестных параметров
где φ(χ,θ) = φ(χο,θ) постоянно при χ G D(xq) (т.е. φ{χ,θ) = const внутри
класса эквивалентности). Если классы D(x) определяются соотношениями S(x) =
= 5, то из теоремы 21.1 сразу вытекает, что статистика S(x) достаточна тогда и
только тогда, когда разбиение на классы D достаточно.
Рассмотрим теперь разбиение, построенное следующим образом: возьмем
точку хо и объявим, что χ принадлежит классу D(xq), если отношение
AM"*"·"·' <3)
не зависят от Θ. Очевидно, что при таком построении D{x\) = D{x2) = D(xq),
если χι Ε D(xo), χ<ι € Ώ(χ§), так что правило (3) порождает разбиение всего
пространства на непересекающиеся классы.
Это разбиение соответствует разбиению, порожденному минимальной
достаточной статистикой S.
В самом деле, пусть S — минимальная достаточная статистика. Возьмем
произвольную точку xq. Тогда на поверхности S(x) = S(xq) отношение fe(x)/fe(xo)
равно h(x)/h(x0) и, стало быть, от θ не зависит. Таким образом, разбиение на
кассы D не менее крупное, чем разбиение для 5.
С другой стороны, это разбиение достаточное. Действительно, каждой
поверхности D мы можем поставить в соответствие одну какую-нибудь ее точку χ в, по
которой эта поверхность будет однозначно определяться. Рассмотрим функцию Хо(х),
которая определяется соотношением хо(х) = xd-> если χ € D. Тогда в силу (3) при
xeD
fe{x) = fe(xD)h(x,xD) = fe(xo(x))h(x,x0(x)), (4)
что означает выполнение (2).
Проведенные рассмотрения были не совсем строгими, так как мы не связывали
их с вопросом об измеримости функций, входящих в (4).
Сказанное можно резюмировать следующим образом. Пусть дана
статистика S(X) такая, что S(x) = S(xo) тогда и только тогда, когда
отношение (3) не зависит от Θ. В этом случае S есть минимальная достаточная
статистика.
В отличие от подходов, связанных с теоремой 1, где рассматривались
отношения fe{x)lIq{x) или fe(x)/fe1(x) при разных θ и θχ (называемые часто
отношениями правдоподобия), правило, сформулированное выше, использует отношение
fe(x)/fe(xo) при одинаковых значениях параметра Θ. В примере 1, например,
отношение
А (ар = ТТ bXi~XioXiol = Λη(*-*ο) ТТ ££:
Д(*о) И Хг\ И Хг\
1 п
не будет зависеть от λ тогда и только тогда, когда χ = х0 = — У^ЯгО, где Хю —
ι=1
координаты вектора xq. Этого достаточно, чтобы заключить, что S(x) = χ есть
минимальная достаточная статистика.
Рассмотрим теперь с помощью предложенного правила пример, когда
«экономных» достаточных статистик не существует. Прежде заметим, что вариационный
ряд Sy = (х(!),Х(2),.. .,Х(П)), построенный по выборке X, очевидно, всегда является
η η
достаточной статистикой, так как fe{X) = ТТ/#(хг) = ТТ fe(*(k))· Эта статистика
г=1 к=1
«чуть-чуть экономнее» самой выборки X. Отсюда, в частности, следует, что
любая минимальная достаточная статистика инвариантна относительно перестановки
координат χι в выборке X.
§ 23. Минимальные достаточные статистики
169
Если плотность fe(x) симметрична, т.е. /#(—х) — fe(%) при всех 0, то,
очевидно, будет существовать еще немного более «экономная» достаточная статистика,
представляющая из себя упорядоченную по возрастанию совокупность (х2,.. .,х^),
которую мы обозначим через Sy2.
Пример 3. Если Χ ^ Κο,σ, га. е. если х* имеют плотность распределения
Коши с параметром θ — σ
£θ,σ0*0
π(χ2 + σ2)1
mo статистика Буг является минимальной достаточной статистикой.
Действительно, в этом случае
/^)=©пгЫ+*2)_1>
г=1
так что
fa(x) _ ТТ 4) + °2
=пз& и
Ισ(Χθ)
есть отношение двух полиномов от σ2. Оно не зависит от σ тогда и только тогда,
когда коэффициенты при соответствующих степенях σ2 в числителе и знаменателе
совпадают. Это, в свою очередь, имеет место тогда и только тогда, когда множества
«нулей» {—xfQ} и { —х2} совпадают. Другими словами, для независимости (5) от σ
необходимо и достаточно, чтобы точка х2 = (я2,..., х2п) имела координаты, которые
отличаются от координат х\ разве лишь перестановкой их мест. Это и означает,
что Sy2 есть минимальная достаточная статистика.
Совершенно аналогично можно показать, что Sy является минимальной
достаточной статистикой для параметра а и, стало быть, для параметра θ = (α,σ)
распределения Κα>σ.
Другой пример, в котором Sy будет минимальной достаточной статистикой,
получим, если рассмотрим семейство
Pajlts2 = &Ρθι + (1 - α)Ρθ2, α G [0,1],
где {Ρ β} — экспоненциальное семейство (см. § 25; в качестве Р# можно взять
нормальное распределение или распределение Пуассона) и где хотя бы один из
параметров а, #1, 02 неизвестен.
Докажем теперь теорему, указывающую простой «конструктивный»
способ отыскания минимальных достаточных статистик.
Для простоты изложения рассмотрим случай одномерного параметра Θ.
Теоре ма 2. Пусть функция правдоподобия fe{x) при всех χ как
функция от θ непрерывна справа (или слева). Тогда если оценка м.п.
Θ* единственна и является достаточной статистикой, то Θ* есть
минимальная достаточная статистика.
Доказательство. Пусть S — произвольная достаточная статистика.
Мы докажем теорему, если покажем, что Θ* измерима относительно a(S) и,
стало быть, Θ* подчинена S.
170
Гл. 2, Теория оценивания неизвестных параметров
В силу факторизационной теоремы
fe(x)=il>(S{x),e)h{x) п. в. [μη], (6)
где h(x) — измеримая функция по ж, ip(s,t) непрерывна (справа или слева)
по t и измерима по s. Так как Р# не изменится, если плотность /я (ж)
изменить на множестве /лп-меры 0, мы можем считать, что (6) справедливо при
всех ж.
В силу (6) точка абсолютного максимума /#(#) является точкой
абсолютного максимума и для ?/>(5(ж),0). Поэтому в силу единственности Θ*
{Θ* < t} = {sup</>(SpO,0) > sup</>(S(X),0)}.
0<t θ^ί
Так как ip{S(X),0) при каждом S(X) непрерывна по θ справа (или слева),
то существует счетное всюду плотное множество Эс = {%}^ι С Θ (одно и
то же для всех S(X)) такое, что
sup</>(S(X),0) = sup ^(S(X),0,)· (7)
9<t »j<t
Такое же соотношение будет справедливо для области θ ^ t. Так как
tJ)(S(X), 6j) измеримы относительно cr(S), то в силу (7) значения sup^(5f,θ)
0<t
и sup ip(S, θ) будут случайными величинами, также измеримыми
относите*
тельно σ(5). Следовательно, {Θ* < t} Ε cr(S'), и теорема доказана. <
Условие достаточности о. м. п. Θ* в условии приведенного утверждения
существенно, поскольку оценка м. п. Θ* сама по себе не обязана быть
достаточной статистикой. Соответствующий пример легко получить, рассмотрев
любое семейство распределений {Р#} со скалярным параметром θ и
векторной (размерности, большей единицы) минимальной достаточной
статистикой 5. В этом случае оценка м. п. Θ* будет также скалярной, так что σ-алгебра
σ(5) будет более богатой, чем σ(θ*), и, стало быть, включение σ(5) С 0-(0*),
вытекающее из минимальности S и достаточности 0*, невозможно.
Пример 4. Пусть X ^ U^i+0, Θ = R. Тогда, как мы видели в
примере 16.4,
f (χ) = <Г при θ ^ Χ(1) ^ Χ(η) ^1 + θ>
\θ в противном случае,
■β
так что fe(X) зависит от X только через Χ(χ) и Х(п\. Это означает, что
S = (χ^,χ^)) есть достаточная статистика. Ни одна из величин х^), Х(п)
в отдельности не является достаточной статистикой, на что указывают
следующие соотношения:
η
Р(х(1) > щ χ(η) < ν) = Π Р(хг е [щ ν)) = (ν - гх)п
г=1
при гх > 0, г> ζ 1 + 0, г; > гх.
§ 24. Достаточные статистики и эффективные оценки 171
Поэтому совместная плотность распределения (х^\,х^п\) будет равна
(п(п - 1)(ν - u)n~2 при u^ θ, ν ^ 1 + 0, υ > u,
l^U в остальных случаях.
Далее, P(x(i) ^ и) = (1 + 0 — u)n при θ < u < 1 + θ, так что плотность x^j
равна
g(u) = n(l 4- (9 - и)71"1 при б < ti < 1 + 0.
Отсюда уже легко получить, что условная плотность g(v/u) величины Х(п)
при условии Х(!) = и (а стало быть, и соответствующее условное
распределение) будет зависеть от 0. Это означает, что х^) (как и Х(п)) в отдельности
не являются достаточными статистиками. Так как в качестве о. м. п. Θ* мы
можем взять Θ* = х^) (см. пример 16.4), то мы доказали, что для семейства
Ήθ,ι+θ о. м. п. 0* не является достаточной статистикой.
Предлагаем читателю с помощью теоремы 1 убедиться, что S=(x^, X(n))
является минимальной достаточной статистикой для ияд+я.
Условие о достаточности Θ* в теореме 2 будет автоматически выполнено,
если предположить, что существуют скалярная (для одномерного 0)
достаточная статистика So, для которой функция φ в равенстве Θ* = ^(SO) будет
взаимно однозначной (т.е. Θ* и So будут эквивалентными).
§ 24. Построение эффективных оценок с помощью
достаточных статистик. Полные статистики
Определение 1. Оценка 0* называется достаточной, если она
является достаточной статистикой.
1. Одномерный случай. Будем предполагать здесь, что 0 — скалярный
параметр. Пусть Кь есть класс всех оценок 0* со смещением Ь(0), так что
0* е Кь если α{θ) = Εθθ* = θ + 6(0). Для 0* Ε Kb имеем
ΕΘ{Θ* - θ)2 = Εθ{θ* - α(0))2 + (α(0) - θ)2 = Ό0Θ* + 62(0).
Индекс θ у символов Е#, D# будем в этом параграфе иногда опускать.
Следующее утверждение было получено независимо Блекуэлом, Рао и
Колмогоровым.
Теорема 1. Пусть S — достаточная статистика, 0* £ К\>. Тогда
функция 9*s = E$(6*/S) является оценкой, обладающей свойствами:
1) e*s e кь,
2) θ $ зависит от выборки лишь через S{X),
3) Εθ(θ*8 - θ)2 < Εθ{θ* - θ)2 при всех 0.
Последнее неравенство превращается в равенство, если только 0* = 9*s
п. е. относительно Р#.
172
Гл. 2. Теория оценивания неизвестных параметров
Другими словами, в классе Кь применение к 0* операции Е^(-/5)
равномерно улучшает оценку 0*.
Доказательство. Тот факт, что 0J является оценкой, означает, что
9*s не зависит от 0 и является измеримой функцией от X. Независимость от 0
вытекает из свойств достаточных статистик, так как распределение X при
фиксированном 5 от 0 не зависит (Eq(9*/S) для произвольной статистики 5,
вообще говоря, от 0 зависит). В то же время в силу свойств у.м. о. θ*3 есть
измеримая функция от 5, а стало быть, и от X. Таким образом, 0J является
оценкой, удовлетворяющей свойству 2 теоремы.
Равенство
Εθθ*3 = EeEe(e*/S) = Εθθ*,
доказывающее, что θ3 € Кь, также следует непосредственно из свойств
у.м.о. Далее,
Εθ{θ* - θ)2 = ΕΘ(Θ*-Θ± θ*5γ =
= Εθ(θ3-θ)2 + Εθ{θ*-θ3)2 + 2Εθ(θ3-θ){θ*-θ*3).
Используя опять свойства у.м.о., получим
εθ{θ3-θ){θ*-θ3)=εθεθ[{θ3-θ){θ*-θ;)/8] =
= Εθ[{θ3-θ)Εβ{θ*-θ3/8)]=0,
и, следовательно,
Έθ(θ* - θ)2 = Εθ{θ*3 - θ)2 + Εβ(θ* - θ*3)2. <
Собственно, неравенство З) теоремы 1 можно получить непосредственно
из свойства у.м.о. (Ε(ξ/5))2 < E(£2/S), так как тогда
(0£ - θ)2 = [Εθ((θ* - 0)/S)]2 ^ Ε9[(θ· - Θγ/Sl
®θ{θ*3-θ)2 <E(0*-0)2.
Факт, изложенный в теореме 1, можно интерпретировать следующим
образом. Пусть S и Τ — две достаточные статистики, 0* = φ(Τ) и S
подчинена Г, тогда Εθ(θ*3 - θ)2 < Efl(0* - 0)2.
Другими словами, чем «экономнее» достаточная статистика S (или чем
беднее соответствующая σ-алгебра), тем оценки 9*s лучше. Таким
образом, для построения оптимальных оценок мы должны искать минимальные
достаточные статистики (или минимальные достаточные σ-алгебры). При
этом в качестве исходных оценок 0* могут фигурировать и «плохие» оценки,
не обладающие, например, даже свойством состоятельности. Поучительным
в этом отношении является следующий
Пример 1. Пусть X ^ Пд. Оценка λ* = χι, очевидно, является
несмещенной Ελ* = Εχι = λ (b(X) = 0), но не состоятельной, так как она от η не
зависит. Минимальной достаточной статистикой для λ является статистика
S = пх = /™]xi- Из примера 22.1 следует, что условное относительно S
§ 24. Достаточные статистики и эффективные оценки 173
распределение χι есть распределение В[/ в схеме Бернулли с вероятностью
успеха 1/п
Pfc-*/*-.)-<*(£)'(l-i)~\
Следовательно,
AJ = E(x,/5) = !>C!(iHl-ir' = f=x·
В одном из последующих примеров покажем, что χ — эффективная
оценка.
2, Многомерный случай. Получим аналоги теоремы 1 для многомерного
случая, когда θ и Θ* есть векторы из Шк.
Как и в одномерном случае, вектор Ь{9) — Е#0* — θ будем называть
смещением оценки Θ* и обозначать через Kf, класс всех оценок со смещением Ь.
Теорема 1А. Пусть S — достаточная статистика и θ* Ε Κ\>.
Тогда оценка θ$ = E#(0*/5) обладает свойствами:
1) θ*5 е Кь;
2) θ*3 зависит лить от S(X)\
3) среднеквадратичное рассеивание θ$ не превосходит
среднеквадратичного рассеивания 0*, или, что то же, для любого вектора оЕМА
Εθ{θ*3-θ,α)2ζΕθ(θ*-θ,α)2. (1)
Равенство (при всех а) здесь возможно лишь в случае θ* = θ*8 η. е.
относительно Pq.
Доказательство. Первые два утверждения очевидны. Неравенства (1)
следуют из теоремы 1, поскольку все сводится к рассмотрению одномерных
оценок (0*,а) и Е^[(б*,а)/5] = (0£,а) параметра (0,а). Если в (1) при всех α
справедливо равенство, то при каждом а будем иметь (θ^,α) = {θ*, а) п. в.
Это и означает, что 9*s = θ* п. в. <
Таким образом, в многомерном случае роль достаточных статистик та
же: квадратичная форма 2_Ισ4α*α3ΐ где σ2 = \\συ\\ есть матрица вторых
моментов для 9*s — 0, будет тем меньше, чем меньше σ-алгебра cr(S'),
порожденная S.
3. Полные статистики и эффективные оценки. Приведем теперь весьма
простой критерий неулучшаемости оценок, основанный на понятии полноты
статистики S. Размерность статистики S будем обозначать через I. Обычно
она больше или равна размерности к параметра 0.
Для двух измеримых функций /i(s) и /2(5): Rz —> Шк будем писать
/ι(5) = /2(5) п.в. [V], где V — семейство распределений в (К*,93*), если
/ι(5) = /2(5) всюду, за исключением множества N такого, что P(iV) = О
для всех Ρ 6 Р.
174
Гл. 2. Теория оценивания неизвестных параметров
Определение 2. Семейство Q = {G#} распределений в (Мг,*8г),
зависящих от fc-мерного параметра θ € Θ С R , называется полным, если
равенство η
y{s)Ge{ds) = 0 при всех Θ е Θ (2)
влечет за собой y(s) =0п.в. [Q]. Уравнение (2) рассматривается в классе
функций у\ R1 —> М.к, для которых интеграл (2) существует.
Определение 3. Статистика S называется полной, если семейство Q
ее распределений G#, индуцированных распределением Р# в (Л^Шд,),
является полным.
Уравнение (2) для статистик может быть написано в виде Е^у(5) = О
при всех θ е Θ С К*.
Теорема 2. Статистика S является полной тогда и только тогда,
когда при каком-нибудь bo(9) a(S)-измеримая*) оценка Θ* единственна
в классе К^ всех a{S)-измеримых оценок из Кь0.
Если σ(5)-измеримая оценка единственна в К^о, то σ(5)-измеримые
оценки будут обладать свойством единственности и в любом другом
классе К^'.
Доказательство этого утверждения почти очевидно, так как наличие
в Кь0 двух а(5)-измеримых оценок в\ = <£>i(S), 0£ = ^2 (5) означает, что
f <Pi{s)Ge(ds) = Ъо{в), г = 1,2,
/ [ψι{3) — WzMJGflids) = О при всех θ G Θ,
так что полнота S влечет за собой <^i(s) = ψ2{^) п>в· [£/]· Наоборот, пусть
для всех θ 6 Θ, θ* — φ\ (s) E Къ- Тогда θ\ = φι (s)+y(s) G Кь,
единственность а(5)-измеримой оценки означает, что y(s) = 0 п. в. [Q]. <
Теорема 3. Если достаточная статистика S является полной и
θ* Ε Кь, то оценка 9*s = Efl(0*/S) является единственной эффективной
оценкой в Кь*
Эта теорема дает нам достаточно простые критерии эффективности
оценок.
Доказательство. В силу теоремы 2 а(5')-измеримая оценка в
классе К^ единственна.
Пусть Θ** — любая другая оценка из Кь. Тогда θ§* = Ee(6**/S) € Κξ и,
стало быть, θ*<? = θ*§ п. в. [£]. Отсюда и из теоремы 1 следует, что
Εθ{θ3 -θ)= Εθ(θ*3* - θ)2 ζ Εθ(θ** - θ)2,
и равенство возможно лишь при θ** = θ*8 п. н. <
*) То есть измеримая относительно σ-алгебры a(S), порожденной 5, и, стало быть, пред-
ставимая в виде w(S). где <р — борелевская функция.
§ 24. Достаточные статистики и эффективные оценки 175
Следствие L Если S — достаточная полная статистика, α Θ* —
несмещенная оценка, то θ$ есть эффективная оценка и она единственна.
Пример 2. В примере 1 с распределениями Пуассона мы получили, что
для λ* = χι
A£ = EA(xi/S)=x,
где S = пх. Покажем, что S — полная статистика и, стало быть, χ —
эффективная оценка. Уравнение (2) для статистики S имеет вид
^у{к)е~пХ^-^ = 0 при всех λ>0
или, что то же,
zk
v(z) ^ 2J^)t7 = о при всех z ^ о. (з)
Это, очевидно, влечет за собой у (к) = 0, так как из сходимости ряда (3),
скажем, при ζ = 1 следует, что υ (ζ) аналитична при \ζ\ < 1 и тождественно
равна нулю. Стало быть, коэффициенты у(к) ее разложения в ряд равны
нулю.
Пример 3. Пусть X €= Uo^. Покажем, что статистика S = Х(п) =
= maxxi является полной. Достаточность (и минимальность) S была уста-
новлена в примере 23.2. Распределение 5 определяется равенством
Р(5 < 5) = (s/0)n, 0 < 5 < б,
так что S имеет плотность, равную nsn~le~n при s € [0,6]. Уравнение (2) в
этом случае имеет вид
θ
ι
nsn~l
y(s) ds = 0 при 0<Е(О,оо).
о
θ
есть единственная
Из равенства / y(s)sn 1 ds = 0 при всех θ следует, очевидно, что y{s)sn l —
о
= 0, y(s) = 0 п. в.
Мы предлагаем читателю проверить, являются ли полными
достаточные статистики, найденные методами § 22, для других параметрических
семейств. В частности, установить, что а* = - [ 1 1
χ V nj
эффективная оценка параметра а семейства Гад (см. § 12).
Замечание 1. Во всех приведенных выше утверждениях и примерах
молчаливо предполагалось, что множество возможных значений оценок Θ*
принадлежит Θ. Если это не так, то в изложение надо внести некоторые
коррективы. Проиллюстрируем сказанное на примере 2, в котором мы
показали, что λ* = χ является эффективной оценкой параметра λ для
распределения Пуассона Пд. Рассмотрим теперь простейшую модификацию этого
176
Гл. 2. Теория оценивания неизвестных параметров
примера. Пусть по-прежнему надо оценить параметр λ распределения
Пуассона, но нам даны в качестве наблюдений не значения ъ\ €= Пд, а «зашум-
ленные» значения х; = Ъ{ + у», где у г Ш Πχ, у^ не зависят от Zj. Это значит,
что мы должны в этом случае оценить λ по выборке X €= Πλ+ι· Как и в
примере 2, здесь полной достаточной статистикой является х. Однако при этом
мы не можем воспользоваться конструкцией примера 2. Действительно, там
в качестве основы для построения эффективной оценки параметра θ = λ + 1
мы использовали несмещенную оценку θ* = χχ. В нашем случае
аналогичная оценка могла бы иметь вид λ* = χχ — 1. Но это невозможно, так как λ* с
вероятностью е~х~~1 принимает «недопустимое» значение —1, которое
естественно заменить на ближайшее допустимое значение, равное нулю, так что
«подправленная» оценка имеет вид λ* = max(0,xx — 1). Эта оценка имеет
положительное смещение, равное е~А_1 и не годится для построения
эффективной оценки. Более естественно подправлять не исходную оценку, а
эффективную оценку в примере 2, взяв в качестве оценки А* = max (0, χ — 1).
Эта оценка также не является несмещенной, но смещение ее при больших η
очень мало*).
К тому же ее качество по сравнению с «недопустимой» оценкой χ — 1
может только улучшиться, так как
Ελ(λ* - λ)2 = Ελ((χ - 1 - λ)2; χ > 1) + Ελ(λ2; χ < 1)<
^Ελ(χ-1-λ)2 = ^±1.
η
Смещение оценки λ* равно
η к
]ζΡλ(χ- 1 = -Λ/η)- <Ρ(ηχ<η) =
= Ρ(-η(χ - λ - 1) > λη) < 6"ηλ(λ + 1)η.
Последнее неравенство получается, если воспользоваться неравенством Че-
бышева для сумм Sn = —п(х — λ — 1) центрированных случайных величин
и тем, что Exe~tn* = en(A+i)(e-*-i) (CMt также [17, §8.8]). Таким образом,
смещение λ* экспоненциально убывает при n-^оои пренебрежимо мало по
сравнению с «разбросом» оценки, имеющим порядок 1/у/п.
*) Несмещенных оценок в этом случае вообще не существует. Пусть для простоты η = 1.
Существование несмещенной оценки для λ означало бы существование функции φ ^ 0 такой,
что
при всех λ > 0. Полагая λ 4- 1 = θ, последнее соотношение запишем в виде
Ё^.л.-.) —+Ё«'(ГгЬ5-н)·
Из этого равенства двух степенных рядов следует с необходимостью φ{0) = — 1, что
противоречит предположению о существовании несмещенной оценки λ* = φ(χι) ^ 0.
§ 24. Достаточные статистики и эффективные оценки 177
Аналогичным образом дело будет обстоять и в других примерах,
поскольку замена значений #*, вышедших за пределы допустимой области Θ,
на подходящие значения, лежащие на границе этой области, будут приводить
лишь к уменьшению разброса исходной «недопустимой» оценки Θ* около
истинного значения. Величины смещений при этом будут экспоненциально
малы.
Отметим теперь, что теорема 3 указывает на существование связей между
понятиями полноты и минимальности. На этот счет справедливо следующее
утверждение, дающее вместе с теоремами § 23 критерий минимальности
достаточных статистик.
Теорема 4. Всякая полная достаточная статистика S является
минимальной достаточной статистикой.
Доказательство. Пусть 21о — минимальная достаточная сг-алгебра
(по теореме 23.1 такая существует). Предположим, что Е#5 существует, и
рассмотрим функцию φ = S — Eo(S/$io)> Так как 21о С сг(5), то φ будет
а(5)-измеримой, так что φ = "0(5). Обозначим через Ge распределение S.
Тогда при всех 0, очевидно, Έβφ(8) = 0 или, что то же,
^(s)Ge{ds)=0 при всех θ G θ.
Отсюда в силу полноты S следует, что φ(β) = О п. в. [£/], Q = {G^}. Это
означает, что S = Еб(5'/21о) п.в. [Q] и, стало быть, S измерима относительно*)
Ио, σ(5) - Яо-
Если EqS не существует, надо вместо 5 рассмотреть статистику arctgS',
которая, очевидно, эквивалентна S относительно свойств достаточности,
полноты и минимальности. <
Отметим, что обратное утверждение не верно: минимальная
достаточная статистика не обязана быть полной. Соответствующие примеры
легко получаются в случаях, когда размерность I статистики больше, чем
размерность к параметра Θ. Например, в § 23 мы видели, что совместная
плотность минимальной достаточной статистики S = (x(i),X(n)) для
семейства и#д+0 равна
(п(п - l)(v - u)n~2 при и ^ θ, ν < 1 + 0, ν > щ
9θ\η,ν) = <
1^0 в остальных случаях.
Если взять функцию у (и, ν) = (p(v — u) и сделать ортогональное
преобразование (ν — и)/у/2 = tj (υ + и)/у/2 = я, то интеграл в (2) (по треугольнику
и ^ 0, υ ^ 1 + 0, ν > и) будет равен
ι
/ y{u,v)go{u,v) dudv = п(п — 1)1 φ(χ)χη~2(1 — χ) dx.
о
Очевидно, что интеграл в правой части от 0 не зависит и легко подобрать
функцию φ(χ) ^ 0, обращающую его в нуль.
*) Под 21о здесь надо понимать σ-алгебру, пополненную множествами Ν, для которых
Έ>Θ(Ν) = 0 при всех θ
178
Гл. 2. Теория оценивания неизвестных параметров
§ 25. Экспоненциальное семейство
Пусть θ = (#ι,.. .,#&) — А;-мерный параметр и плотность fe(x) предста-
вима в виде
Мх) = h(x)exp Ι Х>(0)ВД + ν(θ) Ι , (1)
где все функции, входящие в правую часть, конечны и измеримы.
Определение 1. Семейства распределений {Р#} с плотностью такого
вида будем называть экспоненциальными семействами и обозначать их
символом £.
Чтобы сделать представление (1) по возможности более однозначным,
предположим, что функции αο(θ) = 1, αχ(0),.. .,α^(0) линейно независимы
на Θ.
Как мы увидим, экспоненциальные семейства занимают особое место
среди параметрических семейств распределений, так как для них многие
общие конструкции математической статистики можно реализовать в явном
виде.
Иногда экспоненциальными семействами называют семейства
распределений более частного вида*), когда aj{9) = θ у
К эскпоненциальным семействам относятся, например, семейства
распределений {Φα>σ2}, {Πλ}, {Βρ}, {rQjA} и ряд других.
Пример L Рассмотрим распределение Га>/\. Плотность 7α,λ(^) этого
распределения можно представить в виде
Ία,Λχ) = ρηΛ^"1 ехР (~ах) = Х~Х ехр < Alns - as + In —— \, χ > О,
так что здесь можно положить
(х-\ х>0,
"(1) = {о, *«0,
U\(x) = In2:, U2{x)=x, V(a, λ) = In
Γ(λ)'
αι(α,λ)=λ, α2{α,λ) =-α> <
Функция правдоподобия для X ^Р £ Ε равна
η
f$(X) = ехр {(α(0), S) + nV(6)} Ц /ι(χ,),
ί=1
*) По существу это то же самое: мы придем к частному виду, если сделаем взаимно
однозначное преобразование η — ί(Θ), η = (7ι»···>7*) над параметром 0, положив jj =
= aj(9).
§ 25. Экспоненциальное семейство
179
где
а(0) = Ы0),...,М0)), S=(Su...,Sk),
П
г=1
(α, S) есть скалярное произведение. Отсюда и из теоремы 22.1 следует, что
S есть достаточная статистика для Θ. Мы докажем, что S является
минимальной достаточной статистикой.
Так как функции ау(0), Uj(x), V{6) конечны, экспонента в (1) всегда
положительна. Это означает, что в качестве распределения Q в теореме 23.1
(при котором все Р# абсолютно непрерывны относительно Рд = / PjQ(di))
можно взять распределение, сосредоточенное в любой фиксированной
точке 0°. Поэтому из теоремы 23.1 вытекает, что σ-алгебра 21о> порожденная
функцией
ν(Χ,θ) = j№- = ехр{(а(0) - a(0°),S) +n(V(Θ) - ν(θ°))},
является минимальной достаточной σ-алгеброй.
Теорема L Статистика S является минимальной достаточной
статистикой.
Доказательство. Из линейной независимости функций 1, α\(Θ),...
...,ajt(0) на Θ следует линейная независимость α\{θ) — αι(00),.. .,α*(0) —
— α&(0°). Это значит, что в Θ найдутся к точек 01,..., вк таких, что значения
&ij = аг
(θί) - αί{θ°) образуют матрицу А с определителем, отличным от
нуля. Это означает, в свою очередь, что уравнения
(α(θή - α(θ°), S) = lnr(X,Ρ) - n(V(0>') - ν(θ0)), j = 1,..., к,
однозначно разрешимы относительно S и, стало быть, σ(5) С a(r(X,6j)\
j = l,...,fc) C2l0. <
В примере 1 мы рассмотрели Г-распределение и установили, что для него
справедливо представление (1) при θ — (α, λ) с функциями
U\(x) = In χ, U2{x) = χ,
αι(α,Α) = Α, α2(«, λ) = —α.
Очевидно, что условия теоремы 1 выполнены, и статистика S = iV^lnxj,
/_^х») или? чт0 т0 же5 статистика (ТТхг>У^хг) является минимальной
достаточной статистикой.
Если условия теоремы 1 несколько усилить, то статистика S будет
полной достаточной статистикой (в этом случае минимальность S можно было
бы получить как следствие полноты).
180
Гл. 2. Теория оценивания неизвестных параметров
Теорема 2. Пусть X €= Ρ Ε £. Если функция α и множество Θ
таковы, что α(θ) зачеркивает k-мерный параллелепипед, когда θ
пробегает Θ, то S — полная достаточная статистика.
Условия теоремы относительно параллелепипеда, очевидно, будут
выполнены, если множество Θ «телесно», т.е. содержит внутренние точки (а
вместе с ними и сферы в Rk достаточно малого радиуса), а функции clj(9) в
окрестности какой-нибудь «телесной» точки 0° являются линейно
независимыми и гладкими. Тогда преобразование а = α(θ) переводит окрестность
точки 0° в телесное множество.
Очевидно, что пример 1 с Г-распределением удовлетворяет условиям
теоремы 2, так что статистика (ТТхмУ^хг) является полной.
Столь же просто читатель может проверить, что для нормального
распределения Φα>σ2 статистика (У^хг?У^х?) является также полной
достаточной статистикой.
Доказательство теоремы 2. В нашем случае функции z/>(s,0) и
h(x) в факторизационной теореме Неймана-Фишера равны
ф(з, θ) = ехр {(а(в),з) + ηΚ(0)},
η
Ηχ) = JJMsj).
Рассмотрим на (R*,93*) не зависящую от θ меру
и{В) = ί Η{χ)μη{άχ),
s-цв)
где S"1(B) есть множество всех я, для которых S(x) Ε В.
Выделим в виде лемм следующие два вспомогательных утверждения.
Лемма 1. Распределение Gq(B) = T?e{S{X) Ε В) статистики S
абсолютно непрерывно относительно и и имеет плотность в точке s,
равную tp(s,6).
Доказательство следует из равенства
G$(B)= ί ψ(3(χ),θ)Η(χ)μη(άχ) = ί\l>(s,9)v{ds),
s(x)eB seB
которое является следствием замены переменных. <
Лемма 2. Пусть G\ и G2 — две σ-конечные меры в (Rk,*&k). Тогда
если / e'a,ti'Gi(dzz) = / е^а^G2{du) существуют для всех а из
некоторого параллелепипеда I в Шк, то G\ = G2.
§ 25. Экспоненциальное семейство
181
Доказательство. Чтобы упростить рассуждения, рассмотрим
одномерный случай к = 1 и будем считать, что 7 = {х : \х\ ^ а}. Тогда
hj(a) = j eauGj{du), j = 1,2,
есть аналитические функции при \а\ < а. Кроме того, при всех b Ε Ш
определены функции hj(z) — \ е'а+г 'uGj(du) комплексного переменного ζ =
= a + ib. Ясно, что hj{z) будут аналитическими в полосе \а\ < а, —оо < b <
< оо. Так как h\(z) = h<i(ζ) на отрезке прямой 6 = 0, \а\ < а, то h\(z) =
= h,2{z) при всех ζ из указанной полосы. Стало быть,
fe^Giidu) = feibuG2(du). (2)
Заметим, что так как /ij(0) = / Gj(dw) < оо, то Gj можно считать
вероятностными мерами. Из теоремы о взаимно однозначном соответствии
между характеристическими функциями и распределениями (см. [17, § 7.2])
и из (2) следует, что Gi = G2.
Если параллелепипед I имеет вид {х : \х — αο| ^ с*}, то следует перейти
к мерам G^du) = ea°uGj{du).
В многомерном случае А; > 1 доказательство проходит точно так же. <
Мы можем перейти теперь непосредственно к доказательству теоремы 2.
Нам надо доказать, что если φ — измеримая функция в (Rfe,55fc) и
существует
/■
<p(s)Ge(ds)=0 при всех Θ Ε Θ, (3)
то <p(s) = 0 п. в. [Q], Q = {Ge}eee- Пусть φ = φ+ - φ~, где φ± ^ 0. Тогда
из (3) следует / (p*(s)Gs(ds) = / </?~(s)G0(ds) или в силу леммы 1
j φ+{8)ψ{81θ)ν{ά3) = j4>~{a)${s,e)v{ds),
Если образовать оконечные меры i/^ds) = ^(sji^ds), получим
/"β<*·β>ι/+(ώ)== fe^v-{ds)
при всех α из некоторого параллелепипеда в R*. Остается воспользоваться
леммой 2. <
Следствие 1. £7сли X § Ρ G f, б* G -Кь, w выполнены условия
теоремы 2, то оценка 0J = E(0*/S) является эффективной оценкой в Къ-
182
Гл. 2. Теория оценивания неизвестных параметров
Предположим теперь, что нам надо оценить параметр η = φ(β), где φ
осуществляет взаимно однозначное непрерывное отображение θ в Г,
множество Г телесно в Rk. В этом случае определена непрерывная функция
θ = φ~ι(η), переводящая Г в Θ, и согласно теореме 2 статистика S(X) =
η
= 2_] и(хг) будет полной достаточной статистикой и для параметра 7 (см.
г-1
также следствие 22.3). Следовательно, для η сохраняется и утверждение
следствия 1: если 7* £ Кь1 — оценка 7> т0 7s = ^(7* I S) будет
эффективной оценкой в классе Кь1, 61(7) = Е#7* —η = Έφ-\^η* — η.
Если φ — линейная функция и Θ* — эффективная оценка, то 7* = φ{@*)
будет эффективной оценкой для 7·
Пример 2. Задача восстановления изображения.
Рассмотрим следующую простейшую задачу восстановления «дискретного»
изображения, представляющую существенный интерес в томографии, астрофизике
(см., например, [106]) и в других приложениях. Имеется источник
излучения, которому на плоской фотопластине (будем считать ее квадратной)
соответствует изображение, описываемое функцией (полем) яркости θ(ν) =
= 9(u\ ,1x2), u £ [0,1]2. Дискретизируем это изображение, разбивая пластинку
ί Г*-! Л \з -1 з \\
на маленькие квадраты Ду = < и: щ Ε , — , и^ 6 , — г и
[ [ m mj ι m m J J
введя для описания изображения усредненные яркости θ^ = I 6(u)du,
i, j = 1,..., га. Значения полей 9{и) и, стало быть, {θ^} неизвестны.
Наблюдателю доступно лишь «зашумленное» и «размытое» («рассеянное»)
изображение источника. Более точно, будем предполагать, что имеем
фотографическое изображение суммарного воздействия двух пуассоновских источников
частиц. Первый соответствует изучаемому источнику. Для него «в идеале»
каждая частица попадает в квадрат Ду с вероятностью θ^/θ (θ = / θ (и) du
есть интенсивность источника). Однако из-за присутствия эффекта
рассеивания этого не происходит. Реальная интенсивность 7ij попадания частиц
в Ду определяется не только «идеальной» интенсивностью 0у, но и интен-
сивностями соседних квадратов, так что 7ij есть взвешенное среднее
7ij = EMUJ)> ΣΛ*/) = 1. iJ = l...-,m. (4)
к,I i,j
Здесь суммирование в первой сумме ведется по 1 ^ к ^ га, 1 ^ / ^ т, так
что (4) исключает влияние «квадратов», расположенных вне фотопластины.
Во многих случаях рассеивание можно считать инвариантным относительно
сдвига, т.е. считать, что
г (*+aJ+6) __ , (i,j)
в области, не затрагивающей границу.
§25. Экспоненциальное семейство
183
Второй пуассоновский поток частиц представляет собой «шум»: число
частиц второго потока, попавших в Δ^ за единицу времени имеет
распределение Пуассона с параметром aij. Если поток однороден, то а^ = а не
зависят от г, j.
(i i)
Значения α^·, hKk^ нам известны. В приведенном выше описании мы
имеем дело с «расщеплением» и сложением пуассоновских потоков. Если
пуассоновский поток частиц с параметром θ I вероятность появления к ча-
стиц за единицу времени равна е — I, то под «расщеплением» будем
понимать разделение этого потока на г «подпотоков» следующим образом: каждая
частица независимо от других с вероятностью ρ*;, к = l,...,r, /Jpjt = 1,
направляется в к-ft подпоток. Полученные подпотоки снова будут пуассо-
новскими (с интенсивностями Opk) и независимыми. Действительно,
вероятность иметь набор fci,...,A;r, \&i = &, частиц соответственно в
первом, ..., г-м подпотоке равна
6 A:! *1!...*r!Pl ~'Pr "Пе Л-1 "
При сложении независимых пуассоновских потоков мы, очевидно, также
будем получать в результате пуассоновский поток с интенсивностью, равной
сумме интенсивностей слагаемых.
В силу сказанного рассматриваемое фотографическое отображение можно
описывать как результат воздействия га2 независимых пуассоновских
потоков частиц, соответствующих квадратам Δ^·, г, j = 1,.. .,га. Интенсивности
этих потоков равны соответственно λ^· = 7zj +&ij· Стало быть, количества
Vij частиц, попавших в Δ^· за время п, независимы и будут иметь
распределение Пуассона с параметрами ηλ^,
Набор частот ν = {fij} можно рассматривать как достаточную статистику
для параметра λ = {λ^·} (построенную по выборке X = {^· },.·., {^,·" }?
где ν\· — число частиц, попавших в Δ^· за к-ю единицу времени). Функция
правдоподобия в этом случае имеет вид
Ш) = Π П*"^ = ГК*^ Π -щ-
fc=l ij vij · ij к vij ·
Очевидно, что мы имеем дело с экспоненциальным семейством и ν является
полной достаточной статистикой для λ при этом λ* = u/n будет эффективной
оценкой А.
Если матрица Η = {Щ\ } имеет обратную, отображение (4), которое
можно записать в виде
λ = ΘΗ + α,
184
Гл. 2. Теория оценивания неизвестных параметров
обратимо: θ = (λ — α)Η~ι и, стало быть, ν будет полной достаточной
статистикой и для θ (см. замечания, предшествующие примеру 2). При этом было
бы естественно положить θ* = (λ* — a)if_1. Однако здесь возникают
ограничения, сьязанные с областью возможных значений θ ^ 0. Эти ограничения
были рассмотрены на простом примере в замечании 24.1. В соответствии со
сказанным в этом замечании мы должны положить
θ*^[{Χ*-α)+Η^]+}
где [0]+ для θ = {0ij} означает «вектор» {<й}, #Л = max(0,^j). При этом
качество оценки от введения операции []+ только улучшится (см.
замечание 24.1).
С технической стороны наибольшие трудности во всем этом может
представлять вычисление обратной матрицы Я"**1. Если изображение сосредо-
s τη — s
(#zj = 0 при г φ [s + 1, m — s] или j $
точено в квадрате
m m
t [s + 1, m - s], s > 0) и hffiffi = Л$ = 0 при \i - k\ > s, \j - l\ > s
(ограниченное однородное рассеивание), то построение обратного
преобразования можно осуществить с помощью производящих функций (отметим,
что при этом будем иметь дело с (т — 2s)2 независимыми параметрами 0$j,
i, j = 5 + 1,.. -,77i — 5, и таким же числом независимых 7ij> hj = 1,.. .,m).
Действительно, положим hkl α> ' = /ια^,
S 771 — S ТП
h{y,z)= Σ hajbzazb, 9(y,z)= Σ Wz\ 7(y.*) = ^7i^V·
a,b=-s i,j=s+l i,j
Тогда уравнение (4) можно записать в виде свертки
s
Ί%3 = X, 9i-kj-ihk,h
k^—s
что при переходе к производящим функциям дает
га s
7(У>*) = Σ V%Z% Σ ei-k,j-lhk,l =
s m
= 53 ^yV^y^V-^j.^My.^^z), (5)
%i*) =7(y^)^"1(y,^).
Разлагая /i_1(y,^) в ряд по положительным и отрицательным степеням у
и ζ (в подходящей области изменения у и ζ)
h"l{y,z)^^9^ykzl
§ 26. Неравенство Рао-Крамера и R-эффективные оценки 185
и приравнивая коэффициенты при одинаковых степенях в (5), получим
обратное линейное преобразование
га
θυ = Σ lkji9i-kj-u г, j = s + 1,.. .,m - s.
kJL-l
Если, например, h-Si-s > 0, то h(y,z)y$zs образует полином, отличный
от нуля в точке у = ζ — 0, так что при достаточно малых у, ζ
00
h-1(y,z)=yszs[yszsh(y,z)}-1 = £ 9k,lVkzl.
k,l=s
Если теперь воспользоваться теми же, что и прежде, правилами построения
оценок, получим
Ясно, что во всех этих рассмотрениях для получения достаточно хороших
оценок нужно, чтобы частоты v^l были велики или, что то же, чтобы время
наблюдения η было велико по сравнению с размерностью га2 (или (га — 2s)2)
неизвестного параметра θ — {0Zj} (считаем, что θ сравнимо с единицей).
Точность оценки поля θ = {&ij} можно значительно увеличить, если
уменьшить размерность оцениваемого параметра. Это можно сделать, если
нам заранее известна возможная форма поля θ^ (или θ(η)). Если, например,
9{j есть «одновершинное» поле вида
9ij = сехр{&!(г-а!)2 + b2{j ~α2)2},
то дело сводится к оценке всего лишь пяти (а не га2) неизвестных
параметров с, αϊ, α2, bi, ί>2·
§26· Неравенство Рао-Крамера и Д-эффективные оценки
1. Неравенство Рао-Крамера и его следствия. Результаты предыдущих
параграфов дали нам ряд критериев эффективности оценок. Однако эти
критерии носили в известном смысле качественный характер. В этом параграфе
мы продолжим изучение вопроса об эффективных оценках, но с несколько
иной точки зрения. Выясним прежде всего, какова минимальная величина
среднеквадратической погрешности, которую можно получить.
Рассмотрим сначала одномерный случай, когда θ — скалярный параметр.
Относительно множества Θ будем предполагать для определенности, что это
есть конечный или бесконечный интервал, замкнутый или открытый.
Для того чтобы ответить на поставленный вопрос, нам понадобятся
условия регулярности на fe(x)- Пусть, как и прежде,
η
Ζ (χ, θ) = 1η/,(χ), ЦХ, θ) = Σΐ{χύ θ), α{θ) = Εθθ* = θ + b{0).
1 -τ-
Σ (Xh~awY9i-kj-i
ΠΜ=ι
' η
186
Гл. 2. Теория оценивания неизвестных параметров
Предположим, что выполнено условие
(R) Функции \/fe{x) для η. β. [μ] значений χ непрерывно
дифференцируемы по 6 Ε Θ, интеграл
1{θ)= ί^ψ^μ{άχ)^ΒΘ[ΐ\^θ)γ (1)
существует, положителен и непрерывен по 6. (Здесь и в дальнейшем
штрих означает дифференцирование по 6.)
Относительно интеграла (1) необходимо отметить следующее. Если χ
вместе со своей окрестностью не принадлежит носителю Νρθ = {χ : fe(x) >
> 0} распределения Р^, то подынтегральная функция (/ρ{χ)) /ίθ(χ)
превращается в неопределенность типа 0/0. Условимся считать это отношение
равным нулю. Такого же правила будем придерживаться относительно
производной 1'{χ,θ) = /${х)//в{х) ПРИ ее интегрировании. Этих оговорок можно
не делать, если с самого начала рассматривать интегралы вида Έ$φ(χι,θ)
лишь по области Νρθ.
Функция 7(6) носит название информации Фишера. Мы уже встречали
ее в § 16. Она играет важную роль в математической статистике и будет
неоднократно встречаться в дальнейшем. Некоторые свойства функции 7(6)
обсуждаются в § 27.
Если множество Θ компактно, то непрерывность 7(6) в условиях (R)
эквивалентна условию
supE,(p'(xi,0)]2; |/'(xi,0)| > Ν) -> 0
вее
при N —> со, которое можно назвать равномерной сходимостью интеграла
7(6) (см. приложение VI).
Имеет место следующее неравенство для дисперсии оценок 6* со
смещением Ь.
Теорема 1 (неравенство Рао-Крамера). Еслив* Ε ϋΓ&, выполнено
условие (R) и Ея(0*)2 < с < оо, то
Όθθ > ηΙ(θ) ■ (2)
Если в этом неравенстве достигается равенство на некотором отрезке
6 Ε [61,62] С Θ и Όβθ* > 0 на этом отрезке, то функция правдоподобия
fe{X) при 6 Ε [61,62] представима в виде
MX) = ехр {Θ*Α(Θ) + В{9)ЩХ), (3)
где Л(6), Β(θ) от X не зависят.
Обратно, если 6* = const или если справедливо представление (3), то
в неравенстве (2) достигается равенство.
Условие (3), очевидно, означает принадлежность распределения в Хп с
плотностью f$(x) к экспоненциальному семейству S.
§ 26. Неравенство Рао-Крамера и R-эффективные оценки 187
Следствие 1. При выполнении условий теоремы 1
Для любой несмещенной оценки Θ*
Εθ(θ*-Θ)2> *
Таким образом, в классах К^ наименьшее возможное значение
среднеквадратичных уклонений отлично от нуля и определяется правыми частями
выписанных неравенств.
Замечание 1. По поводу условия Έθ(Θ*)2 < с < оо можно заметить,
что при Έθ(Θ*)2 — оо выполняется Όρθ* = оо и неравенство (2) становится
тривиальным. Условие D#0* > 0 в силу (2) можно заменить на (1+ί/(0))2 > 0.
Замечание 2. Наряду с условием (R) можно указать несколько других
условий, обеспечивающих утверждение теоремы 1, которые будут отличаться
друг от друга очень мало. Мы остановились на том из них, которое нам
будет удобнее в последующих параграфах. Условия несколько иного вида
будут приведены в § 32.
Нам понадобится одно вспомогательное утверждение.
Лемма 1. Пусть выполнено условие (R) и S = S{X) есть любая
статистика, для которой Е#52 < с < оо при θ Ε θ. Тогда функция
α$(θ) = EeS = J 3(χ)Μχ)μη(άχ) (4)
непрерывно дифференцируема по 0, причем
α'3(θ) = f 3(χ)Ι'θ(χ)μη(άχ) = E6SL'(X, θ). (5)
Это утверждение носит технический характер, а его доказательство
существенно отяготило бы рассмотрения. Поэтому доказательство леммы 1
отнесено нами в приложение V.
Доказательство теоремы 1. Полагая в (5) S = 1, получим
as(0) = 1,
EeL' = О, E9a{9)L' = 0. (6)
Используя снова (5) при S = Θ* и (6), получаем
Евв*Ь' = α! (θ), Е9(в*-а{в))Ь' = а'{в). (7)
По неравенству Коши-Буняковского
(α'(θ))2ζΕθ(θ*-α(θ))2Εθ(1')2 (8)
или, что то же,
Όθθ > Ee{Vf ■ (9)
188
Гл. 2. Теория оценивания неизвестных параметров
Так как случайные величины lj = i'(xj,0) независимы, одинаково
распределены и имеют в силу (6) ненулевое математическое ожидание EqIj — О,
то Eeklj = 0 при г φ j, E^L')2 = Εβί Σ1*) = ΣΕ<^ = ηΕ^ι =
з hj
= ηΙ(θ). Вместе с (9) это доказывает неравенство (2).
Докажем второе утверждение теоремы. Для простоты будем считать, что
Θ совпадает с [01,0г] и чт0 X совпадает с объединением носителей X =
= U Ήν
tee
Итак, пусть в (2) (или в (8)) достигается знак равенства. Тогда функция
&θθ* = —тТТгГ вместе с α'{θ) и 1{θ) непрерывна по θ и
ηΐ (Θ)
(Εθ(θ* - α(θ))Σ')2 = Εθ(θ* - α(θ))2Εθ(Σ')2.
Последнее равенство вместе с (7) при с(в) = \/ тл п дает
Εθ(ο(θ)(θ* - α(θ)) - L'f = ηΙ(θ) - 2^~^^Ώθθ*-ηΙ{θ) + ηΙ{θ) = О
или, что то же,
У(с(0)(0· - α(θ)) - L'(x, θ))2Μχ)μη(άχ) = 0, (10)
где функции а(0), с(0) непрерывны.
Пусть M(t) — множество точек χ Ε Xn, для которых
[ф)(0* - α(ί)) - L'(*, *)]λ/Λ(^) = 0. (11)
Из (10) следует, что μη(Μ(ί)) = 0, где Μ(ί) — дополнение к М(£).
Обозначим Μ = Ρ| Μ(ί), где Τ — счетное всюду плотное на Θ множество.
teT
Тогда, очевидно, μη(Μ) = 0. Фиксируем точку χ Ε Μ. Так как ft(x)
непрерывна по t и Я* совпадает с объединением носителей, найдется интервал
(*ь*2) С Θ, <2 > *ь на котором /г (ж) > 0 и, стало быть (см. (11)),
£'(ж, i) = c(i)(0* - α(ί)) для teT f] [ib t2]. (12)
Обе части этого равенства непрерывны на [ίι,^] и> следовательно, это
равенство справедливо всюду на (ίι,^)· Кроме того, правая часть равномерно
ограничена на (ίι, £г)· Но это означает, что L(x, t) также равномерно
ограничена, a ft(x) равномерно положительно всюду на (^ь^)· Эт0 противоречит
допущению о существовании интервала (ίι,^)? на котором /*(ж) > 0, но
mm(f^(x), ft2(x)) = 0. Поэтому ft{x) положительно всюду на Θ = [0ι,#2]?
так что (12) справедливо при всех t. Интегрируя (12) в пределах от θ\ до 0,
§ 26. Неравенство Рао-Крамера и R-эффективные оценки 189
получим
θ θ
L{x,0) = Θ* c{t)dt- c{t)a{t)dt + L(x,ei),
что эквивалентно (3) для [μη] п. в. х. Так как изменение /я (я) на множестве
дп-меры нуль роли не играет, то (3) доказано.
Обратимся к последнему утверждению теоремы. Если Θ* = const, то
Ь'(в) — — 1, и обе части неравенства (2) обращаются в нуль. Пусть теперь
выполнено (3). Тогда, дифференцируя по θ функцию L(J*f, 0), получим
1'{Χ,Θ) = Θ*Α'(Θ) + Β'{Θ).
Из (7) следует, что α(θ)Α(θ) + Β(θ) = 0. Поэтому
£,'{Χ,θ)=Α'(θ){θ*-α{θ))
и, стало быть (см. (12)), в (2) достигается равенство. <
θ
Замечание 3. Так как в представлении (3) Α(θ) = / c(t)dt > 0,
то (3) означает, что носитель Νρθ = {χ: h(x) > 0, θ* > —οο} от θ не
зависит, и можно считать Νρθ = X. Таким образом, если Νρθ зависит от θ
(как, например, в задаче оценки параметра сдвига, когда fe{x) = f(x — θ)
и f(x) > 0 лишь для а; Е [0, а], 0 < a ^ оо), то не существует оценок 0*, для
которых в (2) достигалось бы равенство.
Если доказывать второе утверждение теоремы 2 лишь для случая Νρθ =
— X, то доказательство можно несколько упростить, сделав ненужными
рассмотрения, связанные с (11), (12) и непрерывностью функций с(0), α(θ).
Чтобы получить требуемое представление для L(x,0), достаточно заметить,
что при fe{x) > 0, χ Ε Хп, наряду с (10) справедливо
ί[φ){θ*-α(ί))-1'{χ,ί)]φ(χ)μη{άχ)=0
для любой ограниченной измеримой функции φ. Надо теперь
проинтегрировать это равенство по t в пределах от θι до 0, поменять порядок
интегрирования и воспользоваться произвольностью φ.
В дальнейшем тривиальный случай 0* = const будем исключать из
рассмотрений и предполагать, что Όβθ* > 0 всюду на Θ. Тогда справедливо
Следствие 2. При выполнении условий (R) для достижения нижней
границы в неравенстве Рао-Крамера необходимо и достаточно, чтобы
оценка Θ* была достаточной и функция ^(0*, 0) в факторизационном
равенстве имела вид
ψ{θ\θ) = ехр{в*А{в) + Β{θ)}>
где Α(θ) и Β(θ) — дифференцируемые функции.
190
Гл. 2. Теория оценивания неизвестных параметров
Следствие 3. Если выполнены условия (R), θ* Ε Кь, и в
неравенстве Рао-Крамера достигается равенство, то Θ* — эффективная в Кь
оценка.
Это утверждение следует из представления
Ев{в*-в)2=Ввв* + Ъ2(в).
Заметим, что обратное, вообще говоря, не верно: оценка может быть
(1 + *>'(0))2
эффективной в К&, но нижняя граница -ггт:— для дисперсии может не
достигаться.
Пример 1. Пусть X €? ГаД. Здесь fa(X) = апе~ап*. Условия (R) в
области Θ С {а ^ δ > 0} выполнены. Очевидно, S = пх есть полная
достаточная статистика. Поэтому оценка а* = х-1 = Еа(х_1/5) является
эффективной в классе Кь со смещением Ь(а) = EQx-1 — α.
Заметим теперь, что S €= Га)П, так что при η > 1 (см. § 12) Εαχ_1 =
^ η 1 П
= nEaS-1 = -а.
η — 1
Таким образом, оценка а** = —— = а* ( 1 1 будет при η > 1
пх \ п/
несмещенной.
Аналогично при η > 2 находим (см. § 12, а также пример 14.1)
EQ(02 = (n-l)2EQS-2 = ^a2,
п — I
Όαα** = α
»-!_■
η-2
α2
η-2'
Итак, при η > 2 оценка α** является эффективной. Однако критерий (3) не
выполнен, так как
fa(X) = α-η6-α(η-1)/α·^
Следовательно, в неравенстве Рао-Крамера нижняя граница не достигается.
В этом можно убедиться и непосредственно. В самом деле, здесь /(я, а) =
= In а — ах, 1'(х,а) = 1/а — а: и
/(α)=Εβ[/'(χι,α)]2=Ββ^-χΛ = ^.
Стало быть, при η > 2
1 с? сг
_ — < _ JJ α #
η/(α) η η — 2
Таким образом, достижение нижней границы в (2) есть более жесткое
требование, чем эффективность.
§ 26. Неравенство Рао-Крамера и R-эффективные оценки 191
2· R-эффективные и асимптотически Д-эффективные оценки. Пусть
выполнены условия (R). В этом случае достижение нижней границы (точное
или асимптотическое) для дисперсии в неравенстве Рао-Крамера может
служить важным показателем качества оценок, тесно связанным с понятием
эффективности.
Определение 1. Оценка Θ* £ i£&, для которой
называется R-эффективной (или регулярно эффективной) в классе Кь-
jR-эффективная оценка в классе Kq несмещенных оценок называется
просто R-эффективной.
Оценка Θ* называется асимптотически R-эффективной (а.Д-э.), если
Έθ{θ ~θ) - пЩ '
Мы видим, что в отличие от определений § 18, которые носили более
качественный характер, определения Τϊ-эффективности основаны на
сравнении с известными числовыми значениями, связанными, главным образом,
с информацией Фишера, точнее, с количеством (ηΙ(θ))~ι.
Для ϋ-эффективности оценки Θ* необходимо и достаточно
выполнение (3).
Из сказанного выше следует, что R-эффективные оценки являются
эффективными, но не наоборот; Д-эффективные оценки просто реже
существуют, что является недостатком нижней границы в неравенстве Рао-
Крамера, а не оценок.
В существующей литературе по математической статистике Л-эффек-
тивные оценки называются просто эффективными. Однако нам
представляется более естественным сохранить термин «эффективность» для
наилучших оценок в более широком понимании (см. определение 18.1).
Теорема 2. Если выполнены условия (R) и R-эффективная оценка
существует, то она совпадает с оценкой м. п.
Доказательство. Мы уже видели, что выполнение (3) влечет за собой
равенство (см. (11))
L'{X,0) = (0*-0)c(0).
Кроме того, так как Ь(в) — 0, из (12) следует
для любых θ Ε Θ. Это означает, что Lf(X,0) < 0 при Θ > θ* и Ι'(Χ,Θ) > 0
при θ < θ*. Следовательно, при θ = Θ* достигается максимум L(X,0). <
Приведенный выше пример 1 показывает, что эффективные оценки в
отличие от Д-эффективных могут не совпадать с о.м. п. В этом примере
192
Гл. 2. Теория оценивания неизвестных параметров
о. м.п. есть (х) , в то время как эффективная оценка равна (х) .
η
Обе эти оценки являются, очевидно, а. R-э. оценками.
Рассмотрим класс Kq оценок 0*, для которых
\Ь(в)\^Щ£, |6'(0)|<ε(0,π), Έθ(θ*)2 < с < оо
при некоторой функции ε(0, η) — о(1) при η —> оо и каждом θ Ε Θ.
Каждый такой класс замечателен тем, что для него нижняя граница в
неравенстве Рао-Крамера имеет вид (1 + ο(1))/[ηΙ(θ)]. В § 30 мы увидим, что
в ряде случаев при отыскании асимптотически оптимальных оценок можно
ограничиться изучением оценок Θ* из таких классов.
Теорема 3. Пусть выполнены условия (R). Тогда всякая а. R-э.
оценка из Kq является а. э. в Kq оценкой.
Доказательство теоремы очевидно: если 0* есть а. R-э. оценка, то
Кроме того, как уже отмечалось, по неравенству Рао-Крамера для всех
Θ*£Κ0
limmfE<,n(0* - θ)2 > Γ\θ) = lim E<jn(0f - θ)2. <
η—юо η-»οο
Ясно также, что если а. R-э. оценка существует, любая а. э. оценка в Kq
будет а. R-э. оценкой.
Позже мы увидим (см. §34), что при некоторых дополнительных
предположениях а. R-э. оценки существуют всегда. Ими оказываются о.м.п. 0*.
Этот факт тесно связан с теоремой 16.3, в силу которой у/п(в* — Θ) &
& &oj-i(0)· Чтобы установить, что Θ* является а.Д-э. оценкой, нужны
дополнительные рассмотрения, которые будут проведены в §33. Сказанное
означает, что утверждение теоремы 3 справедливо и в обратную сторону: а. э.
оценка в Kq является а. R-э. оценкой, т.е. для нее Е#(0* — θ)2 ~ [ηΙ(θ)]~ι.
Теорема 4. Пусть выполнены условия (R). Если 0*, 0£
принадлежат Kq и являются а. R-э. оценками, то они асимптотически
эквивалентны в следующем смысле:
sft (θ{ - θ*2) -+ о.
Доказательство этого утверждения проходит точно так же, как в
теореме 18.2. Так как Θ* — (θ* + б^)/2 £ ^о, на основании (18.11) и
неравенства Рао-Крамера получаем
lim sup Εθη(θΙ - θ*2)2 <0. <
§ 26. Неравенство Рао-Крамера и R-эффективные оценки 193
Пример 2. Оценка а* = χ среднего значения α нормальной
совокупности Фа5(Т2 при известном σ2 является Д-эф фективной оценкой. В этом
легко убедиться, проверив, например, условие (3). Другая возможность
состоит в сопоставлении Όαα* = σ2/η с наименьшим возможным значением
(nl(a))~l дисперсий несмещенных оценок. В нашем случае
Ι(χ,α) = -1ην2πσ —ъ—,
l'{x,a) =
2σ2
χ — a
σ*
w ч -г. г,// м9 Εα(χι - α)2 Ι
1(a) = Εαρ#(χι,α)]2 = ^4 = ^,
так что Daa* = (nZ(a))^1 = σ2/η.
1 η
Пример 3. Рассмотрим оценку θ* = S2 = — 7 (χ; — α)2 параметра
η г—'
г=1
θ = σ2 нормальной совокупности с известным а. Нетрудно подсчитать, что
D#0* = Έο(θ* - σ2)2 = 2σ4/η. С другой стороны, здесь
/(хьв)-~20+ 202 '
/(б) = Ε,[ί'(χι, *)]2 = ^Е,[(Х1 - а)2 - 0]2 = ^ = ^1 ·
Таким образом, здесь также D#0* = (ηΖ(θ))"1, и оценка Θ* = 52 является
jR-эф фективной.
тт <-»2 ^ \~""V —\2 ^®
Дисперсия несмещенной оценки Ьп = г > (х* — х) равна г, так
η — 1 ^—' η — 1
что она не является Д-эф фективной или просто эффективной оценкой σ2.
В то же время очевидно, что 52 есть а. Д-э. оценка.
Если мы будем в качестве неизвестного параметра оценивать не σ2, а θ = σ, то
i?-эф фективной оценки мы не получим. Несмещенной оценкой σ будет оценка
V2r/n + l
Ч-
так как
,^2
где
Εσ5ι = -*,Ε,^5>-α)»,
—^- = — 2j(xt - о)2 имеет распределение Ηη = Γι/2,„/2, поэтому (см. § 12)
г. п + 1
aV2 2 ,
vs Γ (ι
194
Гл. 2. Теория оценивания неизвестных параметров
Так как S\ есть минимальная и полная достаточная статистика, то σ* является
эффективной оценкой. С помощью формулы Стирлинга нетрудно убедиться, что
σ*=5ι(1 + 0(1/η)).
Сравним теперь величину Όσσ* с нижней границей (η/(σ))-1. Имеем
Όσσ* = Εσ
rr5f
(13)
С другой стороны, здесь
ι// ч 1 (х-а)2
Ι(σ) - Ε,Ρ'(χι,*)]2 = ΛΕσ[(χι - ос)2 - σ2]2 = 2
2'
так что (η/(σ)) * = σ2/(2η). Но это значение отличается от (13). Их отношение,
например, для η = 3 равно 0,936. Таким образом, Λ-эффективных оценок здесь не
существует. При η —> оо коэффициент при σ2 в (13) ведет себя асимптотически как
i+°(*)·
так что σ* есть а. Д-э. оценка.
3. Неравенство Рао-Крамера в многомерном случае. В этом пункте θ =
= (0i,...,0fc) есть Aj-мерный вектор, как и оценка Θ* = (0*,...,0£). Как и
прежде, положим
а(0) = Е<,0* = θ + 6(0), 6(0) = (6ι(0),..., bk(0))
и рассмотрим классы Кь оценок с фиксированным смещением Ь{9).
Обобщение условий (R) на многомерный случай будет выглядеть
следующим образом. Обозначим
l(x,e) = \ogfe(x), Ι'άχ,θ) = щЦх,в),
Iij(e) = E9l'l(xue)l'j(xue)
и предположим, что выполнено условие
(R) Функции y/feW) непрерывно дифференцируемы no 6j для η. в. [μ]
значений х. Матрица
1(0) = ||';#)||, 1ц{В) = J 1'ί(χ;θ)1^χ;θ)Μχ)μ(άχ)
непрерывна по 0*), ее определитель \1{θ)\ отличен от нуля.
*) Для этого достаточно требовать равномерной сходимости интегралов Uj{9) (см.
приложение V).
§ 26. Неравенство Рао-Крамера и R-эффективные оценки 195
Так как 1(0) есть матрица вторых моментов Eehlj случайных величин
1{ = ί|·(χι, 0), то она будет положительно определенной матрицей, так как для
любого вектора α = (αϊ,..., α&) φ 0 выполняется
]Г aiajEelilj = Ε* (^ αώ) ^ 0,
где равенство нулю исключается условием |/(0)| Φ 0.
Неравенство между матрицами σ\ ^ σ|, как и раньше, будем
понимать как неравенство ασ2α ^ ασ|ατ для любой вектор-строки α =
= (αϊ,.. .,α*;) т^ 0. Это эквивалентно, очевидно, тому, что матрица σ\ — σ\
неотрицательно определена. Строгое неравенство будет соответствовать
положительной определенности, так что, например, Ι(θ) > 0.
Теорема 1А. Если Θ* £ Кь и выполнено условие (R), то для матрицы
вторых моментов σ2 = ||σ^·|| = Е#(0* — α(θ))τ(θ* — α(θ)) любой оценки Θ*
вектор-строки θ справедливо неравенство
σ2>-{Ε + Ό{Θ))Γ\Θ){Ε + D{0))T, (14)
η
где Ε есть единичная матрица, D(0) = \\Ь^(в)\\, °ij(Q) = ~~^bj—·
OVj
Пусть \σ2\ > 0 (или \E + D(6)\ > 0) при всех θ. В этом случае знак
равенства в (14) достигается тогда и только тогда, когда распределение
выборки принадлежит экспоненциальному семейству специального вида,
т. е. когда для некоторых скалярных функций Β(θ) и h(X) выполняется
MX) = ехр {(*·, А(9)) + В(в)ЩХ), (15)
где вектор Α(θ) = (Αι(θ),..., Аь{в)) имеет матрицу производных,
равную
IIAjll —
дАг{в)
d9j
= η[(Ε + ϋ(θ)Γιγΐ(θ)
Для несмещенных оценок Θ*, очевидно,
σ2 > (ηΙ(θ)Γ1,
и равенство возможно лишь при выполнении (15), где \\Aij\\ = ηΙ(θ).
Таким образом, если нам удастся найти несмещенную оценку Θ* с
матрицей вторых моментов [ηΙ(θ)]~ι, то она будет эффективной оценкой.
Отметим, что
Εθ{θ* - θ)τ(θ* - θ) = σ2 + bT{9)b{0).
Доказательство теоремы ΙΑ. Положим
η
Ц = L'jiX, Θ) = Σ l'j(xu θ), L' = L'(X,θ) = {L[,.. .,L'k).
196
Гл. 2. Теория оценивания неизвестных параметров
Тогда совершенно аналогично одномерному случаю устанавливаем, что
справедливы равенства
Egl'j (χι , 0) = О, Е„ОД (Χ, 0) = 1 + bij (θ),
в которых bij (θ) непрерывны, или, что то же, равенства
EeL' = О, (16)
Ee{e*)TL' = E + D{0), (17)
в которых матрица D{6) непрерывна. Отсюда получаем
Εθ{θ* - a(0))TL' = Ε + Ό(Θ). (18)
Докажем теперь следующее неравенство (матричный вариант
неравенства Коши-Буняковского).
Лемма 2. Пусть ξ и η — матрицы одинакового размера (не
обязательно квадратные) со случайными элементами, матрица Εηητ имеет
обратную. Тогда
ΕξξΤ > ΕξηΤ{ΕηηΤ)-1ΕηξΤ. (19)
При этом равенство возможно лишь в случае ξ = ζη> ζ = Έξη^(Έηη^)~ι.
Доказательство. Так как для любой матрицы А справедливо
неравенство ААТ > О (ААТ неотрицательно определена), то
О < Ε(ξ - ζη)(ξ - ζη)Τ = ΕξξΤ - ζΕηξΤ - ΕξηΤζΤ + ζΕηηΤζΤ.
Полагая ζ = Έξη (Έηη )~ι, получим требуемое неравенство.
Утверждение относительно условий равенства в (19) очевидно. <
Вернемся к доказательству теоремы 1А. Положим в (19) ξ = (0* — α(0))Τ,
η = (Ζ/)Τ. Тогда
ΈθξξΤ = Εθ(θ* - α(θ))Τ(θ* - α(θ)) = σ2.
Из (16) и независимости хг· получаем
Εθηητ = Ee{L')TL' = nl(0).
Наконец, из (18) находим
Εθξητ = Εθ{θ* - a(0))TL' = Е + D{9).
Неравенство (14) доказано.
Равенство в (14) возможно в силу леммы 2, если только для точек (аз,0)
таких, что fe(x) > 0, справедливо
(0· - α(θ))τ = (Ε + ϋ(θ))(ηΙ(θ))-1{Ώ')τ
или, что то же,
V = (Θ* - α(θ))η[{Ε + ZW))-1]1"/^). (20)
§ 26. Неравенство Рао-Крамера и R-эффективные оценки 197
Заметим теперь, что из равенства в (14) следует
\Ε + ϋ(θ)\2 = η\σ2\.\Ι(θ)\,
и отделенность от нуля определителя \σ2\ означает то же самое для \Е +
+ D(0)\ и означает существование равномерно ограниченной обратной
матрицы (Е 4- D(0))~l. Поэтому производная V в (20) будет ограниченной,
/#(ж) > 0 всюду на Θ и само равенство (20) будет справедливо всюду на Θ.
Если теперь s есть любой путь, соединяющий точки #о и θ в области Θ, то
ВД0)= f(L\ds)+L(X,e0)t
S
где ds означает векторный элемент пути s, ((Lf,ds) = (Z/, sf(l)) dl есть
приращение L(X, θ) на этом пути, I — «длина» пройденного пути). Стало быть,
в силу (20)
ЦХ, θ) = Θ*Α{Θ) + Β{θ) + # (Χ), (21)
где Β(θ) и Н(Х) — скалярные функции, Α(θ) = (А\ (0),..., Α^{β)) — вектор,
зависящий только от своих аргументов. Это означает справедливость (15).
Если выполнено (21), то
L' = θ*\\Αιό\\ +Β'(Θ),
где в силу равенства EgZ/ = 0 справедливо
ВЧв) = -а(в)\\А15\\.
Умножая обе части равенства V = (Θ* — α(θ))\\Α^\\ слева на (θ* - α(θ))τ,
получим в силу (18), что для выполнения условия (20), означающего равенство
в (14), должно выполняться
WAuW^nHE+Dm-vw). <
В многомерном случае сохраняют свою силу все замечания, сделанные
к одномерному неравенству Рао-Крамера, а также определение Д-эффектив-
ности, в которые следует внести лишь очевидные изменения, связанные с
размерностью Θ.
В частности, а. Д-э. оценками будем называть оценки 0*, для которых
Е*(0* - θ)τ{θ* -θ)=σ2 + Ът{в)Ь{в) = {ηΙ{θ))~ι + ο(1/η).
Аналог теоремы 2 здесь будет выглядеть следующим образом.
Теорема 2А. Пусть выполнены условия (R). Если Θ* есть R-эффек-
тивная оценка, то это есть оценка максимального правдоподобия.
Доказательство. Чтобы доказать, что Д-эффективная оценка
является единственной точкой максимума, достаточно убедиться, что L'(X, 0*) =
= 0и что при 0 = 0* + w, и φ 0
(gradL(X,0),u) = (L'(X,0), θ-Θ*) <0.
198
Гл. 2. Теория оценивания неизвестных параметров
Но в случае существования Я-эффективной оценки выполняется (см. (20))
L'(X,0) = (0*-0)nJ(0),
откуда немедленно вытекают оба требуемые соотношения. Второе следует
из того, что
(L',u) = -unI(0)uT,
где ul(0)u есть положительно определенная квадратичная форма. <
Пример 4. Рассмотрим двупараметрическое семейство нормальных
распределений Φασ2. Оно принадлежит экспоненциальному семейству, так как
(здесь θ = (0Ь02), 01 = а, 02 = σ2)
. , ч 1 / (я-а)2\ 1 [ х2 ха а2 л Л
1 п
Оценка 0* = (0?,05), где 0f = χ, ^ = S^ = —— £(х; - х)2 =
п 1 «=ι
— г f/Jxf ~~ ηχ2) 5 является эффективной, поскольку она принадлежит
Ко и статистика (/Jxi> У^ХП > как мы видели в §25, является полной
достаточной статистикой (см. теорему 24.4).
Оценка м.п. (х, — /(х» — х) ) отличается от 0* лишь множителем
η — 1
при второй координате, что делает ее смещенной. Для выбранной
η
оценки Θ* специальное экспоненциальное представление (15) функции fe(X)
реализовываться не будет, так как
= (2.) п/2ехр|_,Г___^__(,Г) ____η1ησ|.
Это значит, что нижняя граница в многомерном неравенстве Рао-Крамера
достигаться не будет.
Наименьший эллипсоид рассеивания, определяемый по теореме 1А
матрицей 1(0) (или /_1(#)), будет достигаться лишь асимптотически при η —>
—> оо, так что оценка 0*, не являясь Д-эффективной, будет а. /2-э. оценкой.
Убедимся в этом непосредственно.
Вычислим сначала матрицу 1(0). Имеем
;' t„ m (х~а) // {tr й\ (χ -α)2 !
§ 26- Неравенство Раю-Крамера и R-эффективные оценки
199
(напомним, что 1'2 есть производная по σ2, а не по σ; ср. с примером 3).
Поэтому
Ιηψ) - Έ,θ -ι -ζ,
Ι12(Θ)=Ι21(Θ) = ΕΘ
1
(χι — α)3 χι — α
2σ6
2σ4
1
0,
Ы0) = ^Е,[(х1-а)2-а2]2 = ^.
Отсюда находим
(пЩГ1 =
η
0
0
2σΑ
η J
(22)
Вычислим теперь для сравнения матрицу вторых центральных моментов
оценки Θ*.
Имеем
Ее(^-0!)2 = Ее(х-а)2 = ^,
Ε,(^-^2)2 = Ε(?(502-σ2)2= 2σ4
n-V
Εθ{θ*ι-θ1)(θ*2-θ2)=0.
Последние два равенства устанавливаются непосредственным подсчетом
Рассмотрим, например, второе из них. Нам достаточно убедиться, что
Efl(x-a)5g = 0. (23)
Но
5ο = ^[Σ(χ*-")2-(χ--«)2],
<*" °rt = ^Ьт) [Σ<* - °>] [Σ<* - «)2] - ет (χ ~ «)3·
Поскольку
Εβ(χ - a)3 = Εθ{χ{ - a)3 - Εθ{χ{ - α) (χ, - a)2 = 0,
то (23) доказано.
Таким образом, матрица вторых моментов Θ* — θ равна
* о
η
о ^
п-1.
Ясно, что различие между этой матрицей и матрицей (п/(0))-1 может быть
существенным лишь при небольших значениях п.
200
Гл. 2. Теория оценивания неизвестных параметров
4. Некоторые выводы. В заключение этого параграфа подведем
некоторые итоги исследований, проведенных в последних шести параграфах.
Главная их цель состояла в отыскании способов построения оптимальных
(в том или ином смысле) оценок и установлении нижних границ для их
среднеквадратичных уклонений. В результате можно указать следующие
четыре основные направления, по которым можно идти в поисках
наилучших оценок.
1. Построение байесовских (если есть априорная информация о Θ) и
минимаксных оценок.
2. Отыскание полных (или минимальных) достаточных статистик S.
Тогда оценка θ§ = Ε^(θ*/5) будет эффективной в том классе К\>, которому
принадлежат Θ*.
3. Использование о. м. п. в тех случаях, когда выполнен критерий (3)
теоремы 1 (или критерий (15) теоремы 1А). При этом также получим
эффективные (и даже Д-эффективные) оценки в классах с фиксированным
смещением.
4. Количественный подход, основанный на сравнении
среднеквадратичного уклонения Έβ(θ* — θ)2 оценки 0*, которую хотим использовать, с
нижней границей Д, определяемой неравенством Рао-Крамера. Если отношение
Eq(0* — θ)2/R будет близко к единице, то оценка Θ* может быть
рекомендована к использованию. На этом пути мы получим в дальнейшем весьма
общие результаты, связанные с построением асимптотически эффективных,
асимптотически байесовских и асимптотически минимаксных оценок.
Сделаем также следующее замечание. Во всех отмеченных выше
направлениях существенную роль играет форма зависимости распределения
выборки Р# от оцениваемого параметра Θ. На практике, однако, нередко
возникают задачи оценки не самого 0, а некоторой функции от него φ{θ).
При этом нетрудно видеть (см. пример со схемой Бернулли в (18.4), (18.5)),
что оценка φ* = φ{θ*) далеко не всегда будет обладать теми же свойствами,
которыми обладала оценка Θ* (несмещенность, эффективность и т.д.
Сохранятся лишь свойства асимптотической эффективности, если φ —
гладкая функция). С этой точки зрения представляется естественным с самого
начала рассматривать задачу оценивания функций φ(θ) от исходного
параметра Θ. Мы отказались от такого подхода, так как на этом пути
многие основные результаты, полученные нами, существенно усложнились бы.
С другой стороны, если φ осуществляет взаимно однозначное отображение,
то задача об оценке φ(θ) сводится к задаче, рассматриваемой нами путем
«перепараметризации», т.е. введения нового параметра η = φ{θ), которому
будет соответствовать семейство распределений G7 = Ρ^,-ι^.
§ 27.* Свойства информации Фишера
Мы уже видели и будем убеждаться в дальнейшем, что информация
Фишера играет важную роль в математической статистике. В связи с этим
выясним некоторые ее полезные свойства.
1. Одномерный случай. Информация Фишера
Щ = Ι^^-μ(άχ) = Ев(1'(хи0))2
§27 Свойства информации Фишера
201
появилась в рассмотрениях § 16, 26. Величину
Ιχ(θ) = Εθ[Σ'(Χ,θ)}'2
принято рассматривать как меру количества информации, содержащейся
в выборке X относительно параметра Θ. В теореме 26.1 мы доказали
аддитивность информации: Iх(θ) = ηΙ{θ), т.е. что Iх(Θ) равна сумме
информации /Xt(0) = Έθ[1'{χι,Θ)}2 = Ι(θ), содержащихся в независимых
наблюдениях χ χ,..., χη.
Докажем еще одно свойство информации Фишера. Пусть S = S(X) есть
некоторая статистика со значениями в R1 и ge(s) есть плотность ее
распределения, индуцированного распределением Ρ в в (A*n,93^) относительно
некоторой меры λ в (Кг, 05'). В соответствии с предыдущими обозначениями
величину
/s(0) = E*[(log5*(S))']2
будем называть информацией, содержащейся в статистике S
относительно параметра Θ.
Отметим, что значение Is(Θ) не зависит от выбора меры λ.
Действительно, пусть λ — какая-нибудь другая мера и ν = λ + λ. Тогда λ и λ
абсолютно непрерывны относительно и, а плотность g^(s) распределения S
относительно меры ν равна
~ m dX dX
где qq — плотность относительно А. Так как — и — от θ не зависят, то
dv dv
производные от логарифмов всех трех выражений будут совпадать.
Теорема 1. Пусть плотности f${x) и ge{s) удовлетворяют
условиям (R). Тогда
Ι3(θ)ζΙχ(θ). (1)
Равенство здесь достигается тогда и только тогда, когда S есть
достаточная статистика.
Доказательство. Для любого В Ε 93* обозначим через 5-1 (В) Ε 93д>
множество χ (Ξ Xй, для которых S(x) Ε В. Тогда по определению у.м. о.
/
L'(x,9)Pe{dx) = ΕΘ[Σ'(Χ,Θ); Χ Ε S~l(B)] =
S'1(B) = Ee[Ee(L'(X,e)/S); S Ε В]. (2)
С другой стороны,
J Σ'(χ,θ)Έ>θ(άχ) = ^ J Μχ)μη(άχ) = ^ Jge(s)X(ds) =
s-^B) s-цв) в
= I ^ge(s)X(ds) = E,[(logff6(5))'; S € B]. (3)
в
202
Гл. 2. Теория оценивания неизвестных параметров
Сравнивая (2) и (3), видим, что п. в. [Pq]
E<,(L'(X,9)/S) = (\ogge(S))'. (4)
Далее, имеем
0 < E9[L'(X,9) - (\ogge(S))'}2 = Ιχ(θ) + Is(9) - 2EeL'(Χ, 9) (log ge(S))',
где в силу (4)
EeL'(X,9)(logge(S))' =
= Ee[(]ogge(S))'Ee(L'(X,e)/S)] = Ee[(log^(5))']2 = Is(9).
Это доказывает неравенство (1).
Пусть теперь S — достаточная статистика для Θ. Тогда
fe(X)=iP(S,9)h(X). (5)
Возьмем в качестве А меру
А(В) = Ι Η{χ)μη{άχ).
s-нв)
Тогда, как показано в лемме 25.1, распределение S будет абсолютно
непрерывно относительно λ и будет иметь плотность go(s), равную ge(s) = φ(β, 0).
Отсюда в силу (5) получаем
Iх (Θ) = ΕΘ[Σ'(Χ,Θ)}2 = E9[(log^(S,9))'}2 = Is(9).
Покажем теперь, что из равенств Iх (Θ) = Is(Θ) при всех θ следует, что
S — достаточная статистика. Действительно, Iх(Θ) есть дисперсия L'(X, 0),
так что
Iх(9) = E9[L'(X,9) - Ee(L'(X,9)/S)}2 + Ee[Ee(L'(X,9)/S)}2. (6)
Но в силу (4) последнее слагаемое равно
Ee[(\ogge(S)y\2 = Is(9).
TaKnaKlx(9) = Is(9), то в (6) п. в. [Pq] при всех θ
L,(X,e)-Ee{L'(X,e)/S)=0.
То есть L'(X,9) измерима относительно σ(5) и, стало быть, существует
измеримая функция </?(5. Θ) такая, что
L'(X, 9) = tp(S,9), L(X, θ) = Ф(5, θ) + /ц (Χ),
Л(Х) = ехр[Ф(5,е) + /ц(Х)]. <
Мы уже отмечали, что достаточные статистики являются тем
единственным типом статистик, которые сокращают выборочные данные без потери
информации о параметре Θ. Теорема 1 придает этому утверждению точный
смысл применительно к информации Фишера.
§ 27. Свойства информации Фишера
203
Пример 1. Пусть X ^ Вр. Здесь
где χ равно нулю или единице, fp{x) есть плотность относительно
считающей меры. Поэтому
χ 1 — χ
1(х,р) = χ In p + (1 - х) In (1 - ρ), 1'{χ,ρ) = - - ,
ρ 1-ρ
Таким образом, информация одного наблюдения в схеме Бернулли равна
(р(1 — р))-1 и достигает своего наименьшего значения при ρ = 1/2.
Информация всей выборки равна п/(р(1 — р)). Обозначим теперь через ν
число «успехов» в выборке X (число единичных исходов) и найдем
информацию этого наблюдения. Плотности (опять относительно считающей меры)
для ν будут равны
9Р{х) = Схпрх{1-р)п-х, х = 0,1,...,п,
так что \oggp(x) = χ logp + (η - χ) log (1 - ρ) + log Cx,
r{p) = Ep[0oggp{u))f =
г-х(х-пр)2
= Σθχ(ΐ -рГ~х (f - γτ|У = Σ^ρχ(ι -Ρ)η"
χ=0 ^^ Ρ' χ=0
(ρ(ι-ρ))
1 т-ч П
rDi/
(ρ(1-ρ))2 Ρ(1-Ρ)'
Это равенство полностью согласуется с теоремой 1.
Мы предлагаем читателю найти в виде упражнений информации
наблюдений для выборок из распределений, зависящих от одномерного параметра
и приведенных в § 12.
2. Многомерный случай. Пусть теперь θ £ Rfc, к > 1. В этом случае
будем иметь дело с информационной матрицей Фишера наблюдения χχ
Ι(θ) = ||Jy(0)||, 1ц{9) = Еощ^в^Цхив),
где предполагается, конечно, что функция fe{x) дифференцируема.
Если положить
φ{χ,θ) = (φι(χ,θ),...,φ^χ,θ)) =
о( /Γμυ * fdfe{x) dfe{xA
=2(х/Ш)=7Ш1^Г'-'"^г)'
204
Гл. 2. Теория оценивания неизвестных параметров
то матрицу Ι(θ) можно записать также в виде
1(0) = J φΤ{χ,θ)φ{χ,θ)μ{άχ).
Χ
Мы уже установили в §26, что, как и в одномерном случае,
информация Фишера аддитивна, т.е. информационная матрица Фишера выборки X
равна сумме информационных матриц отдельных наблюдений. Если
обозначить
то Iх {θ) =ηΙ{θ).
Теорема 1 также сохраняется полностью. Пусть ge{s) — плотность
некоторой статистики 5 = S(X) со значениями в R1 относительно некоторой
меры λ. Положим
Ι8(θ) = ||jg(0)||, ф) =Ee^.\ogge(S)-^-loggg(S).
Это есть информационная матрица наблюдения 5.
Теорема 1А. Если плотности fe{x) и ge{s) удовлетворяют
условиям (R) §26, то
Ι3(θ)ζΙχ(θ), (7)
т.е. матрица Iх (Θ) — 1(9) является неотрицательно определенной.
Равенство в (7) имеет место тогда и только тогда, когда S —
достаточная статистика.
Доказательство этой теоремы вполне аналогично доказательству
теоремы 1, и для сокращения текста мы его опускаем. Это доказательство можно
найти, например, в [48, 49].
Пример 2. В §26 мы уже вычисляли информационную матрицу для
нормального распределения. Вычислим теперь информационную матрицу
для двупараметрического семейства распределений
И^)·
Μχ) = -/
где θ = (α, σ), / — заданная дифференцируемая функция, для которой
существуют интегралы
U = fxi{-^fdx = Ε(0ι1)χί(ί'(χι))2, i = 0,1,2.
Здесь l(x) = log/(x), штрих означает обычное дифференцирование,
параметры а и σ суть параметры сдвига и масштаба распределения с плотностью
/(х). Таким образом, нам известен вид распределения, но лишь с точностью
до линейного преобразования аргумента. Параметры а и σ нормального
§27. Свойства информации Фишера
205
распределения Фа5(Т2, очевидно, являются параметрами сдвига и масштаба.
Параметр α Г-распределения при фиксированном А является параметром
масштаба, как и параметр θ в распределении Uq,0.
Имеем
/о™ /у
1{χ,θ) = hgfe(x) = -loga + Z
Θ1{χ,θ)
da
\(χ,θ) __ 1 (ж - α) . /д; — сЛ
да σ σ2 \ σ )
Отсюда находим
1
Ιη(θ) = -ζΕ$
■г/х^а\12_ 1 r[f{X σ)\
. V ο )\ σ2 J ^Jx-a\
12
;— dx = —tzIq,
Ι12(θ) = \ΈΘ1> ( Xl °
σ*
1 + ίυΐ^^χι-α
_ 1 г
Τ^1
σΑ
/22 W
σ*
ΓΕ0
l + ^LZ^r^1-"
= £fc " 1],
так как
/χ ~~ ol /χ — cx\ dx Γ
/' ί J — = -2 / f{x) dx = -2. Таким образом,
г/m _ 1 К0 х
σ^ ||ii i2 — J-
Если / — симметричная функция, то, очевидно, 1\ = 0.
Вырождение матрицы Ι(θ) означает, что ее определитель обращается в
нуль или, что то же,
[Eio.Di'ixOCl+xi/'ixO^^E^a'ixO^o.DCl + Xi/'ix!))2.
Это возможно лишь в случае, когда либо l + xV(x) = cl'(x) при каком-нибудь
с, либо 1'{х) = 0. Из первого равенства следует, что
eCl
1{х) = — In (ж — с) + ci, /(χ) = .
χ — с
Ясно, что такая функция f{x) не может быть плотностью
распределения. Аналогично рассматривается возможность 1'{х) = 0. Стало быть, Ι(θ)
положительно определена.
206
Гл. 2. Теория оценивания неизвестных параметров
В частности, для нормального семейства [Φα>σ2] при θ = (α, σ)
w - ?
1 0
0 2
так как в этом случае 1(х) = —х2/2 — 1η\/2π, V{x) = —я, /о = Е^пх? = 1,
h = Ε(ο,ΐ)χι = ^ ^2 = E(0ji)Xi = 3. Тот же самый результат мы могли бы
получить с помощью примера 26.4, используя п. 3 этого параграфа, где
выяснено поведение информационной матрицы при замене параметра (в
примере 26.4 θ = (α, σ2), а не (α, σ)). Предлагаем читателю убедиться теперь,
что в соответствии с теоремой 1А статистика f x, \_\ xi) имеет
информационную матрицу
ЛЧ = £
1 0
0 2
= ηΙ{θ).
3. Матрица Фишера и замена параметра. Рассмотрим вопрос о том, как
ведет себя информационная матрица при замене параметра. Положим θ =
= υ (β), β Ε R*, где υ — дифференцируемая вектор-функция, и рассмотрим
параметрическое семейство Р*' = Ρυ(β)- Чтобы найти информационную
матрицу J (β) для этого семейства, мы должны найти производные
к
Я-1ЫМР)) = Еж*(*ь«(0)п^. (8)
щ
Если обозначить V =
i=l
двг
dPj
dVitf)
δβ<
, г, j = 1,..., fc, то мы получим, что вектор
производных в (8) Ιβ(χι,υ(β)) представим в виде Ι'θ(χι,υ(β))ν, так что
JC9) = E/J(^(x1>t;(/9))V)T(Zi(xi>«G9))V) = FT/(«(/3))K
В частности, если θ = /ЗС, С = ||с^||, г, j = 1,..., А:, то V = Ст и
m = с/(^)ст. (9)
Отметим, что если мы рассмотрим в параметрическом пространстве
эллипсоид
(Θ - ΘΧ)Ι{Θ){Θ - 0:)Τ < с, (10)
то запись (10) этого множества инвариантна относительно линейного
обратимого преобразования С над параметром Θ. Именно, если положим θ = /ЗС,
то в новых переменных множество (10) будет иметь вид
(/3-A)j(/3)(/3-A)T<c
где βι = в\С~1. Это немедленно получится, если подставить θ = βΟ в (10)
и воспользоваться (9).
§ 28. Оценки параметра сдвига и масштаба
207
§ 28·* Оценки параметра сдвига и масштаба.
Эффективные эквивариантные оценки
Мы видели в § 22-26 и будем убеждаться в дальнейшем, насколько
полезным является понятие достаточной статистики вообще и при построении
эффективных оценок в частности. Круг идей, связанный с использованием
достаточных статистик, можно было бы назвать принципом достаточности.
Принцип достаточности мы сочетали при построении эффективных
оценок с другим — принципом несмещенности. Он состоит в выделении
классов оценок с фиксированным и, в частности, с нулевым смещением. Без
фиксации смещения выделение эффективных оценок было бы невозможно.
В этом и следующем параграфах (а также в главе 3) мы рассмотрим еще
один важный принцип математической статистики — принцип
инвариантности.
Смысл введения всех названных принципов один и тот же — они
позволяют естественным образом сужать класс рассматриваемых оценок так,
что в полученных сужениях оказывается возможным отыскание
эффективных оценок.
1. Оценки параметра сдвига и масштаба. Задачей об оценке параметра
сдвига называется задача оценки параметра α в семействе распределений
{Ра}, обладающих свойством
Ρα(Α) = Ρ(Λ-α).
Здесь Ρ — некоторое фиксированное распределение, А—а = {х : х+а Ε А},
и предполагается, что параметрическое множество Θ имеет ту же природу,
что и X. В случае X = Rm можно, конечно, рассматривать сдвиги θ и
«меньшей размерности», например скалярные, но тогда надо фиксировать
направление (вектор е € X) сдвига и рассматривать Ра{А) = Р(А — ае). Будем
рассматривать для определенности лишь первую возможность и считать, что
Θ = X = Шт.
Заметим, что Ра-распределение х; 4- с (с Ε Шт) совпадает с
распределением Ра+с величины χ,, т.е. сдвиг всех наблюдений на с приводит к
выборке из распределения PQ+C. Это делает естественным рассматривать
лишь те оценки а* = а*(Х) параметра а, которые обладают свойством
а*(Х + с)=а*(Х)+с. (1)
Здесь и в дальнейшем X + с означает вектор с координатами (χχ + с,...
.. .,хп + с). Нарушение этого равенства означало бы, что оценка а* зависит
от начала отсчета, т. е. от выбора начала координат в пространстве X = Шт.
Аналогичный подход возникает при оценке параметра масштаба, когда
оценивается параметр σ в семействе {Ρσ} со свойством Ρσ{Α) = Ρ(Α/σ),
σ (Ξ (0, οο). Мы считаем здесь σ скалярным, хотя можно рассматривать и
матричный случай. В этом случае Ρσ-распределение значений Х{С совпадает
с распределением Рас величин х$, т.е. умножение наблюдений на с
приводит к выборке из Р<7С. Стало быть, в этом случае естественно ограничиться
рассмотрением оценок, обладающих свойством
а*{Хс) =са*{Х), (2)
где Хс = (xic,.. .,хпс), поскольку при изменении в с раз масштаба
наблюдений во столько же раз меняется и параметр.
208
Гл. 2. Теория оценивания неизвестных параметров
Следующие утверждения читатель может легко получить самостоятельно.
Если семейство Р# удовлетворяет условию (Αμ), то параметр θ
будет параметром сдвига (масштаба) тогда и только тогда, когда
Л(*) = /(*-*) (/·(*) = J/(f))·
Если X — R = Θ, I § PQ и α есть параметр сдвига, то Υ = ех =
= (еХ1,.. .,eXn) €= Q<7, где для распределений Qa параметр σ — еа есть
параметр масштаба. Это сразу следует из того, что плотность у ι = eXl равна
(см. [17, §3.2])
i/(b»-a)-if2/(l«S)l.
у σ [у \ σ/\
Наоборот, если X = (Ο,οο) = Θ, Χ €= Ρσ и σ есть параметр масштаба,
то Υ = ΙηΧ = (lnxi,.. .,lnxn) ^ Qa, где a = Ιησ есть параметр сдвига
распределений Qa. Таким образом, задачи оценивания параметров сдвига и
масштаба могут быть сведены одна к другой.
Можно рассматривать задачу и об одновременной оценке неизвестных
параметров α и σ в случае, когда Va^(A) = Ρ Ι j . В этих условиях в
качестве оценки σ естественно рассматривать функции, обладающие
свойством
а*(Х + с) = а*рГ), а*(Хс) - са*(Х). (3)
Оценки, удовлетворяющие в рассмотренных примерах условиям (1)-(3),
называются эквивариантными (общее определение см. в §29). Смысл
введения таких оценок состоит в сужении класса всех рассматриваемых оценок,
что упрощает задачу поиска оптимальных оценок. Так, в § 18 нами было
установлено, что найти равномерно (т. е. при всех Θ) наилучшие оценки в
классе всех оценок невозможно. Оказывается, что в классе эквивариантных
оценок такие равномерно наилучшие оценки уже существуют и могут быть в
ряде случаев найдены в явном виде. На примере оценок параметров сдвига
и масштаба мы этот факт и проиллюстрируем.
2. Эффективная оценка параметра сдвига в классе эквивариантных
оценок. Будем предполагать здесь, что выполнено условие (Αμ) и, стало быть,
/а(я) = /(# — <*) и что μ есть мера Лебега.
Обозначим через So статистику
So = So{X) = (X2 -Xi,...,Xn -Xl),
очевидно, инвариантную относительно сдвига: Sq(X + c) = Sq(X). Через К ε
обозначим класс всех эквивариантных оценок а*, т.е. оценок,
удовлетворяющих (1), и через |а|2 — квадрат евклидовой нормы a £ Km.
§ 28. Оценки параметра сдвига и масштаба 209
Теорема 1. Пусть а* = а*(Х) — любая эквивариантная оценка с
конечным значением Е0а*. Тогда оценка
a*0 = a*-E0(a*/S0) (4)
от выбора а* не зависит и является единственной эффективной в Ке
оценкой, т. е. Εα|αί — а| = min EJa* - а\2 при всех а и Еа|а* — а|2 =
1 ' а*екЕ
= Еа|«о — а| , если только Ео(а*/5о) = 0 п. е. Оценка οβ может быть
представлена в форме
, fufu{X)du = JufjX -u)du
а° Jfu(X)du Jf(X-u)du' [0)
Оценка aj называется оценкой Питмена. Из (4) нетрудно видеть, что
она является эквивариантной и несмещенной. Эквивариантность следует
из эквивариантности а* и инвариантности относительно сдвига функции
V(Sq) = Eo(a*/5o), зависящей только от Sq. Несмещенность вытекает из
равенств
Eaa*Q =a + Eaa*{X -a)- EQF(50), (6)
где EaV(So) = E0F(5o), Eaa*(X - a) = Е0а*(Х). Последнее соотношение
вытекает из того, что X — а €= Ро, если X €= PQ. Поэтому сумма двух
последних слагаемых в (6) равна
Е0а* - Ео[Ео(а*/5о)] = 0, EaaJ = а.
Доказательству теоремы предпошлем следующее вспомогательное
утверждение.
Лемма 1. Пусть X ^ Ро- Для любой статистики S = S(X) с
конечным математическим ожиданием Ео|5| < оо у.м.о. S относительно So
равно
■*/ад-»сх)-"ЭДЙ?*··
Доказательство. Все функции под знаками интегралов в (7) есть
функции от X — и. Стало быть, после замены х\ — и = ν они будут функциями
от (г>, Х2 — χι + г>,..., хп — χ ι + г;). Это означает, что правая часть (7) зависит
лишь от SO· В силу свойств у. м. о. нам для доказательства леммы достаточно
убедиться, что для любого А Е <t(5q)
Ео(51;Л)=Е0(5;Л).
(8)
210 Гл. 2. Теория оценивания неизвестных параметров
Пусть Ζ = Z(So) — любая ограниченная а(5о)-измеримая статистика,
тогда
Z{S0)fS(x-u)fu(x)du
EoZSi= / ° . . , f(x)dx =
J I fu(x) du
//
f fu(x)du
xn θ
Z(SQ)S(x-u)f(x~u)f(x) άχ ^
f f(x — v)dv
θ xn θ
После замены χ — u —> χ во внутреннем интеграле получим (So(я) ПРИ этом
перейдет в себя)
Г [ Z^o)S(X)f(x)Hx + u) άχάη = Γ z{So)S{x)f{x) dx = EoZS_
J J J f{x + u-v)dv J
Θ Χη 0 Xn
Это доказывает (8). Изменение порядка интегрирования, которое мы
дважды производили, законно в силу абсолютной интегрируемости S и
ограниченности Z. <
Доказательство теоремы 1. Заметим прежде всего, что для экви-
вариантной оценки Εα|α* — α|2 не зависит от а. Действительно,
Εα\α*(Χ) - а|2 = EQ\a*(X - a)\2 = Ε0|α*(Χ)|2.
Таким образом, для отыскания равномерно оптимальной эквивариантной
оценки надо найти оценку а*, минимизирующую Ео|а*|2.
Пусть а* — любая эквивариантная оценка а. В силу свойств у.м.о.
Е0|а*|2 = Е0|а*-Ео(а75о)|2+Е0|Ео(а75о)|2 >Ео|а*-Е0(а75о)|2. (9)
Остается заметить, что в силу леммы 1 оценка aj = a* — Eo(a*/5o) равна (5)
и от выбора а* не зависит. Равенство в (9), очевидно, возможно тогда и
только тогда, когда Ео(а*/5о) -Оп.в. <
Из доказательства теоремы видно, что особую роль в построении
оптимальной эквивариантной оценки играет статистика SO = (хг — χι,...
. ..,χη — χι), инвариантная относительно преобразования сдвига.
Инвариантность статистики есть качество, в известном смысле противоположное
достаточности, а конструкция оценки 0q = θ* — Eo(0*/So) на основе
произвольной оценки 0* представляет собой подход к улучшению оценки 0*, также
в некотором смысле противоположный подходу, при котором для улучшения
оценки θ* с помощью достаточной статистики S рассматривалась оценка
0£ = Έο(θ*/S). Противоположность состоит в следующем. Достаточная
статистика содержит в себе всю информацию о параметре Θ; инвариантная
статистика — никакой. В поисках наилучших оценок мы искали минимальные
достаточные статистики; Здесь, как мы увидим, нам нужны максимальные
инвариантные статистики (таковой является статистика So). Оценка θ$ есть
§ 28. Оценки параметра сдвига и масштаба
211
П < -\2
2(а-х).
«проекция» Θ* на S, в то время как оценка θ$ получается вычитанием из Θ*
ее «проекции» на 5Ό·
В конечном счете результаты, полученные этими двумя путями, часто
совпадают, как это будет видно из следующих двух примеров.
Пример 1. Пусть X = R, X е Фад. Тогда
Здесь второй множитель как функция α есть функция плотности
нормального закона с параметрами (х, 1/п). Так как первый множитель от α не
зависит, то он сократится в (5), и оценка Питмена будет равна а* = х.
Таким же будет результат в многомерном случае.
Пример 2. Пусть X = Μ, Χ €= \3ο,\+θ- Тогда
f (χ) = J1 при Х(п)~1 ^ θ ^ Х(1)'
\θ в остальных случаях.
Поэтому в силу (5)
Χ(ΐ)
Л* Г udu 1, , ч
|_ У ■w-^ti-i'1"'^-"·
X(n)-i
Мы видим, таким образом, что в классе ЯГ# эквивариантных оценок
можно в явном виде строить эффективные оценки, при этом не требуется
никаких условий на гладкость /#(£)> и сама эффективность носит точный
(не асимптотический) характер.
3. Минимаксность оценки Питмена. Обратим теперь внимание на форму
оценки Питмена. Грубо говоря, это есть байесовская оценка для
«равномерного на всей оси» априорного распределения. Так как указанного
распределения не существует, то мы сформулируем высказанное утверждение более
точно. Пусть X = К и Q(^) есть равномерное распределение на [-ЛГ, ЛГ],
т. е. распределение с плотностью
q [t) ~ \о, |<| > ν.
Байесовская оценка, соответствующая Q^N\ будет равна
N
/*гч Г ufu{X)du
aQ<N) JqW{u)fu{X)du " y.. '
J fu(X)du
-Ν
212
Гл. 2. Теория оценивания неизвестных параметров
Очевидно, что для всех X оценка Питмена aj есть предел aj =
= lim a%(N)- Это обстоятельство наводит на мысль, что одновременно бу-
дут сходиться и моменты второго порядка:
Ea iaQ(N) ~ a)2 -> EQ (aS - a)2 ·
Оказывается, что в области ]a\ ^ N — y/N это так и есть, причем сходимость
будет равномерной по α в указанном интервале значений а. (Доказательство
связано с оценкой Ea(aQ —a* (7V))2, носит в основном технический характер,
и мы его опускаем.)
Но в таком случае мы можем воспользоваться критерием минимаксности
оценок в теореме 21.3: если оценка а* такова, что при всех а
Еа(а* - а)2 < limsup [Et(a*iN) - t)2Q^{dt) (10)
ЛГ-юо J W
для некоторой последовательности априорных распределений Q^ (не
обязательно равномерных) и соответствующих им байесовских оценок
a* (7V), то а* — минимаксная оценка.
В нашем случае т = Ea(ag — α) от α не зависит. Поэтому в силу
отмеченных выше свойств сходимости вторых моментов
limsup [Et(a*Q(N)--t)2QW(dt) >
> limsup—- / Et(a*(N) - t)2 dt ^
\t\<N-y/N
^ limsup—-2(N - y/N)(m - ε) = m - ε
ДГ-К50 2iV
при любом ε > 0. Это означает, что свойство (10) выполнено.
Таким образом, оценка Питмена является минимаксной в классе всех
оценок параметра сдвига (то, что она минимаксна в классе инвариантных
оценок, очевидно, следует из эффективности).
Сказанное можно интерпретировать также следующим образом:
«наихудшим» априорным распределением (см. §21) для параметра сдвига является
«равномерное на всей оси» распределение.
Указанием на минимаксность оценки Питмена могла бы служить также
отмеченная выше независимость Ea(ag — а) от α (ср. с теоремой 21.2).
4. Об оптимальных оценках параметра масштаба. Как мы уже
отмечали, проблема оценки параметра масштаба σ может быть сведена в
известном смысле к проблеме оценки параметра сдвига. Пусть для простоты
Χ = (Ο,οο) = Θ. Тогда если X g= Ρσ, Ρσ{Α) = Ρ(Α/σ), το Υ = Ια Χ =
= (Ιηχι,..., 1ηχη) ёРц , где α = 1ησ, а распределение Р^ имеет плотность
§ 28. Оценки параметра сдвига и масштаба 213
величины у! = 1ηχι в точке у (условие (Αβ) выполнено, —-—- = /(#)),
(JLLL
равную (см. [17, §3.2])
fW(y) = f(ey)ey.
Таким образом, мы можем оценить наилучшим образом параметр α с
помощью оценки Питмена а* = а*(У), а затем положить σ*(Χ) = ea*(Y\
Нетрудно видеть, что σ*(Χ) будет эквивариантной, так как
a*{cX) = ea*(y+lnc> = eQ*(y)+lnc = ca*{X).
Однако здесь важно отметить, что оценка Питмена минимизирует
Εα(α* — α)2. Стало быть, полученная оценка σ* будет минимизировать
К)2·
E^ln-J , (11)
а не величину Εσ(σ* — σ)2, с которой мы обычно имели дело. Но в задаче об
эквивариантной оценке параметра σ и неразумно было рассматривать
среднеквадратичную погрешность, поскольку она, в отличие от (11), зависит
от преобразования сжатия, примененного одновременно к σ* и σ. Аналогом
инвариантной статистики So здесь будет статистика (хг/хь- ..,χη/χι).
Наряду с (11) возможно, конечно, рассмотрение и других погрешностей. Если,
например, мы будем минимизировать величину
наилучшей эквивариантной оценкой будет
fa-^nX/a)d*
fa-»-*f{X/a)da [ }
(см. [112, с. 191]).
Пример 3. Обнаружение источника излучения. Приведем
пример реальной физической задачи, которая связана с оценками
параметров сдвига и масштаба.
Предположим, что в некоторой неизвестной точке ζ трехмерного
пространства находится источник 7~излучения. Задача состоит в том, чтобы,
используя плоский детектор (пусть он совпадает с одной из координатных
плоскостей) и фиксируя на нем следы излучения, т. е. следы взаимодействия
7-квантов, испускаемых точкой ζ, с чувствительной поверхностью детектора,
определить координаты точки ζ.
214
Гл. 2. Теория оценивания неизвестных параметров
Эта задача намного упростилась бы, если бы мы имели источник
излучения заряженных частиц высокой энергии. Тогда можно было бы
поставить один за другим два параллельных плоских детектора и фиксировать
на них точки прохождения, т.е. взаимодействия с поверхностью экрана,
всего лишь двух частиц. Это дало бы нам направления полета этих частиц
и вместе с ними координаты точки ζ как точки пересечения этих
направлений. Однако для слабого 7-излучения, используемого в рентгеноскопии, это
неосуществимо, и возможно введение лишь одного детектора.
Направление, в котором распространяются излучаемые 7-ΚΒ<ίΗΤΜ,
случайно и имеет равномерное распределение на поверхности сферы (если
направление определять точкой на сфере с центром в точке ζ).
Чтобы упростить задачу, рассмотрим ее двумерный вариант. Пусть
источник находится на плоскости переменных (я, у) в неизвестной точке ζ —
= (α, σ), σ > 0. Угол направления излучения, составленный с осью Оу имеет
равномерное распределение на [0,2π]. Чувствительный детектор совпадает с
осью абсцисс. Результатами наблюдений будут точки χι,Χ2,..., в которых
было зафиксировано взаимодействие 7-квантов с детектором (осью абсцисс).
Некоторое своеобразие этой задачи состоит в том, что объем η выборки,
полученной за фиксированное время t будет случайным: число 7~квантов,
испускаемых источником за время £, имеет распределение Пуассона,
число 7-квантов, достигших детектора, также
ζ = (α, σ) распределено по закону Пуассона, так как
ч каждый квант достигает оси абсцисс с ве-
β\ роятностью 1/2. Однако в нашем случае η
\ и наблюдения χι,Χ2,... независимы. По-
\ = этому мы можем рассматривать то число
\ η наблюдений, которое получилось, и счи-
\ тать его фиксированным (для каждого та-
\ кого фиксированного η распределение хг
\ ^ будет одним и тем же).
α χ Итак, пусть даны наблюдения X =
рис 2 — (хь ■ · ·? Хп)· Наша задача состоит в
оценке координат (α, σ). Покажем, что X €?
^ Κα,σ, т.е. хг имеют распределение Коши с параметрами сдвига α и
масштаба σ.
Действительно, условное распределение угла β направления движения
7-кванта с осью (0, —у) при условии, что квант достиг детектора (ось
абсцисс), будет равномерным на отрезке [—π/2,π/2]. Так как (х — α)/σ = tg/?
(см. рис. 2), то
_ , ч 1 1 χ — a
Ρα,σ(Χΐ < Χ) = о + -~ arctS ·
δ π σ
Стало быть, плотность распределения χι будет равна плотности
распределения Коши (см. § 12)
к ли = 1 I = σ
α'σ1 ] πσ (1 + ((χ - α)/σ)2) π(σ2 + (χ - α)2)'
Предположим теперь, что σ известно, пусть, например, σ = 1. Тогда
наилучшей инвариантной оценкой параметра сдвига α будет оценка Питмена,
§ 29. Общая задача об эквивариантном оценивании
215
которая получается как среднее значение а* =? / u<p(u) du распределения с
плотностью
φ{η) = <p(u, Χ) = г " , ku(X) = Yl ku(xi),
ίΚ{Χ)άυ'
1
π(1 + (ιχ~χζ)2)·
Ο. μ. π. α* будет представлять из себя точку, в которой достигается
max<^(w). Позже мы покажем (см. §34), что а* и а* асимптотически
эквивалентны и имеют а. н. распределение с коэффициентом 1/1 = 2 (в
рассматриваемом случае / = / (&q) /kodx = 4π~1 / χ2(1 + я2)-3 da; = 1/2). Из
сказанного следует, что погрешность оценок а* и а* при больших η имеет
порядок малости 1/у/п.
Интересно отметить, что в рассматриваемой задаче можно добиться
путем вмешательства в эксперимент более высокой степени точности. Это
можно сделать, поставив между точкой ζ = (α, 1) и детектором экран,
параллельный оси абсцисс, с отверствием #, через которое лишь и могут
проходить 7-кванты. Положение экрана и отверствия выбираются
экспериментатором и, стало быть, нам известны.
В этом случае распределение наблюдений на экране будет разрывным и
при небольших отверствиях Η будет близко к Uaa?aa+6 при некоторых
известных нам постоянных α и 6. Вид эффективной эквивариантной оценки а*н
для такого распределения был найден в примере 2. Оценка а*н
определяется крайними значениями выборки и имеет точность порядка 1/п#, где
пн ^ τι — число элементов выборки, которые соответствуют квантам,
прошедшим через щель (п#, как и га, на самом деле случайно и распределено
по закону Пуассона). Так как в среднем п# пропорционально га, то при
достаточно больших η получим 1/га# <^ 1/у/п.
§ 29.* Общая задача об эквивариантном оценивании
Рассмотрим группу G измеримых преобразований g пространства Хп в
себя, обладающих следующими свойствами.
1. Каждое g отображает Хп на все пространство Хп, т.е. для любого
Х2 £ Хп найдется х\ Ε Хп такое, что х^ = дх\.
2. Отображения д взаимно однозначны.
Измеримость д нужна для того, чтобы дХ была случайной величиной.
Групповое свойство означает, что д2д\ Ε G, если д\ Ε G, дъ Ε G;
тождественное преобразование е и обратное преобразование д~1 принадлежат G
(так что д~1д = е).
Определение 1. Семейство распределений {Р#} называется
инвариантным относительно группы преобразований G (или, для краткости,
просто инвариантным), если для каждых д Ε G и θ Ε Θ существует
единственное вд Ε Θ такое, что соотношение X €= Р# влечет за собой дХ €= Р^.
216
Гл. 2 Теория оценивания неизвестных параметров
Значение θ9, однозначно определяемое θ и #, обозначим через θ9 = дв.
Тогда определение означает, что
ΡΘ(9Χ ЕА) = Ρ-9θ(Χ € А).
Так как в силу определения 1 условие (Ао) выполнено, то множество G
всех преобразований д пространства Θ в себя образует группу.
Действительно, распределение gig\X дается одновременно распределениями Рд^е
и Pgtgtf- Из условия (Ао) следует, что Щр[ = ~g^gY и что д±l e G
(достаточно положить #2 = 9\1)· Преобразования 'д из G автоматически взаимно
однозначны. Однако изоморфизма между G и G может и не быть. Пусть,
например, Χ ^ Φο,σ2* σ € (0, оо). В этом случае плотность f^a2(X)
(функция правдоподобия) зависит лишь от /Jx»· Стало быть, если в качестве
G рассмотреть группу вращений (ортогональных преобразований Л'71), то
условия определения 1 будут выполнены, но 'д — ё, и группа G состоит из
единственного элемента ё — тождественного преобразования Θ = (0, оо) в
себя.
Мы предоставляем читателю возможность в качестве упражнения
проверить, что если {Р#} инвариантно относительно группы G и G\ есть
подгруппа G, то {Р#} инвариантно относительно G\.
При рассмотрении общей задачи эквивариантного оценивания нам
необходимо иметь несколько более общую постановку задачи относительно
сравнения оценок. До сих пор мы делали это с помощью среднеквадратичных
уклонений, меряя погрешность оценки величиной (Θ* — 0)2. Будем теперь
предполагать, что измерение погрешности Θ* происходит с помощью
функции ιυ(θ*,θ) и что эта функция обладает свойством «однородности»*):
ю(дв,дв*) = ιυ{θ,θ*) при всех Θ. (1)
Именно этим свойством обладают функции w(9, θ*) = (θ—θ*)2 для параметра
сдвига (преобразование сдвига) и ιυ(θ,θ*) = f In— ] или f —- — 1 J для
параметра масштаба (преобразование сжатия).
Мы видели в п. 28.4, что задача отыскания наилучшей эквивариантной
оценки может быть весьма чувствительной к выбору меры погрешности
τν(θ,θ*) оценки Θ*.
Обратимся теперь к проблеме оценивания для инвариантных семейств
{Ря}. Пусть мы имеем выборку X и по ней построили оценку θ* = Θ*{Χ)
параметра 0. Если мы рассмотрим выборку Υ = дХ ^ Р^, то Θ*[Υ)
будет оценкой для ~дв. При этом естественно предполагать, что оценки Θ*(Χ)
и Θ*(Υ) связаны между собой так же, как оцениваемые параметры θ и дв,
т. е. преобразованием д
Θ*(Υ)=$Θ*(Χ). (2)
*) Это свойство не обязательно в теории эквивариантного оценивания. Можно лишь
требовать существования дд* такого, что w(g6,g6*) = ιυ(θ,θ*) при всех θ (см. [112]).
§ 29. Общая задача об эквивариантном оценивании
217
В силу (1) оценка Θ*(Υ) параметра Ί}θ дает ту же самую ошибку, что и оценка
Θ*(Χ) параметра Θ. Таким образом, имеем две «одинаковые» проблемы
оценивания. Произведенные преобразования дХ и 1дв можно интерпретировать
как замены систем координат. Тогда (2) означает, что оценка Θ* не зависит
от выбора системы координат и удовлетворяет соотношению
θ\χ) = д-'еъх)· (3)
Иными словами, если выбрана 0*, удовлетворяющая (2), то безразлично,
какую из двух проблем оценивания, указанных выше, решать, поскольку
выводы о 7}θ во второй проблеме можно превратить в выводы ойв первой с
помощью равенства (3).
Определение 2. Оценка Θ* параметра θ инвариантного семейства Р#,
удовлетворяющая (3), называется эквиваршнтной*).
Рассмотрим какую-нибудь точку θο Ε Θ и множество «эквивалентных»
точек θ = <7#о> д € G. Такое выделение классов «эквивалентных» точек
делит все пространство Θ на подмножества, называемые орбитами.
Теорема 1. Значение Eqw{9,9*) для эквиваршнтной оценки Θ*
постоянно на орбите, га. е.
E9w{e,e*)=Eg9w{g0,0*)
при любых θ Ε Θ и g Ε G.
Доказательство. Имеем
Εβν(θ,θ*(Χ)) = Eew(g9,g9*(X)) = E9w(g9,9*(gX)) = Ε&χυβθ,θ*{Χ)). <
Если орбита {θ : θ = дво, g Ε G} совпадает с Θ (как это имело место для
параметров сдвига и масштаба), то ¥jqw(6,Θ*) = const на Θ. Выполнение
этого равенства есть характерный признак минимаксности Θ* (ср. с
теоремой 21.2), так что наилучшие эквивариантные оценки часто оказываются
минимаксными в классе всех оценок (подробнее см. [112]).
Из теорем §21 вытекает, например,
Теорема 2. Если Θ является орбитой и эквивариантная оценка Θ*
оказалась байесовской (или пределом байесовских оценок Θ*Ν со
сходимостью Е^гу(0,0*) = lim E0w(0,0^)), то 0* — минимаксная оценка.
Ν—>оо
Отметим также следующее важное свойство эквивариантных оценок. Нам
будет удобно через v(gdx)/u(dx) обозначить плотность меры vg, vg{B) =
= v(gB) относительно меры ν в точке χ Ε Χη.
Теорема 3. Пусть выполнено условие (Αμ) и μη(gdx)/μη(dx)
конечно и положительно при каждом g Ε G и п. в. [μη] значений ж. Пусть,
*) Такие оценки называют иногда инвариантными. Однако этот термин менее точен.
Его лучше оставить для оценок, обладающих свойством 9*(дХ) = Θ*(Χ) (т.е. для случая,
когда д = е для любого д).
218
Гл. 2, Теория оценивания неизвестных параметров
кроме того, о. м. η. Θ* единственна при каждом X. Тогда если
семейство Р# инвариантно, то Θ* является эквивариантной оценкой.
Доказательство. Имеем
, ,у. PHx){dx) Pejdx) ш
fs. (Χ) = / , ч— = max —-—г (4)
J° y μη{άχ) θ μη(άχ) κ '
в точке х = X. Полагая Υ = gX, мы можем записать также
f.m (y)=Mii=maxi^i.
J0*(Y)\ > μη{9άχ) θ μη{ράχ)
В силу инвариантности Р# и конечности μη(g dx)/μη (dx) > О это
эквивалентно тому, что
pri?-(y)(da?) Vg-ie(dx) Ρθ(άχ)
—- тт^: = max /, ч = max —гтт·
μη(άχ) θ μη(άχ) θ μη{άχ)
Сравнивая с (4) и пользуясь единственностью Θ*(Χ), получаем g~l9*(gX) =
= Θ*{Χ). <
§ 30. Интегральное неравенство типа Рао-Крамера.
Критерии асимптотической байесовости и минимаксности оценок
Этот параграф можно было бы назвать также «Неравенство для
среднеквадратичного уклонения в байесовском случае». В значительной своей
части он относится к асимптотической теории оценивания.
Вопросы, связанные с асимптотическим подходом к сравнению оценок,
затрагивались нами и раньше. Теперь, и главным образом в §33-37, они
станут основным объектом изучения.
1. Эффективные и сверхэффективные оценки. В §26, посвященном
неравенству Рао-Крамера, остался невыясненным следующий важный вопрос.
Пусть выполнено условие (R). Тогда для несмещенных оценок
Е*(0*-0)2> *
η
Щ'
Правую часть этого неравенства называют иногда границей Рао-Крамера.
Она достигается для R-эффективных оценок. Вопрос состоит в том, можно
ли за счет выбора смещения сколько-нибудь существенно улучшить Д-эф-
фективные или а. Л-э. оценки? Это есть вопрос о существенности границы
Рао-Крамера и о роли смещения.
Тот факт, что в отдельной фиксированной точке во значение Έ$(θ* — θ)2
может быть сделано значительно меньше, чем граница Рао-Крамера, нами
уже отчасти обсуждался. Достаточно взять в* — во. Однако при этом в других
точках эта оценка будет очень плохой.
Можно привести другой, менее тривиальный пример, где улучшение
достигается не за счет других точек. Пусть Χ ^ Фа,ь а ё θ — [0, оо). Тогда
оценка α* = χ является эффективной и даже Л-эффективной. Однако оценка
§ 30. Интегральное неравенство типа Рао-Крамера 219
а** = max(0,x) в нашем случае, когда Θ = [0, оо), будет, очевидно, лучше,
поскольку она уменьшает среднеквадратичные уклонения, заменяя
недопустимые отрицательные значения на нуль. Оценка а**, очевидно, будет уже
смещенной: Еаа** > а, но в точке а = 0 имеем 1(a) = 1, Ео(а*)2 = —,
Е°<а">2 - £ < Ш
В этом примере улучшение связано с тем, что мы сузили область
значений оценки а* до множества θ. Приведем еще один пример (принадлежащий
Ходжесу), в котором улучшение а* происходит не за счет ограничения Θ.
Пусть опять X €= Φα,ι, Οι G Θ = (—οο,οο). Наряду с эффективной
оценкой α* = χ рассмотрим при β < 1 оценку
** /χ, если |х| ^ п"1/4,
Οί —- \
I /йс, если |х| < п-1/4.
Нетрудно видеть, что при α > 0 по центральной предельной теореме
PQ(|x| < η"1/4) ^ Ρα((χ - α)V^ < η1/4 - ay/n) -> 0
при η —> оо. Аналогичное утверждение верно при α < 0. Поэтому а** при
а^О совпадает с χ на множестве вероятности, сходящейся к единице, и,
стало быть, по теореме непрерывности при α φ Ο
(α** - a)y/n & Ф0,ь
При α = 0
Ρο(|χ| < η"1/4) = Po(|xV^| < η1/4) -> 1,
и α** на множестве вероятности, сходящейся к единице, совпадает с /?х, так
что (а** — a)y/n & Фо,/32· Таким образом, при всех α оценка а** является
а. н., (а** - a)y/n & Ф0,<т2(сф ™e
2/ ч Г1 ПРИ а^°>
a(a) = V<l при а = 0.
Таким образом, в точке α = 0 коэффициент рассеивания сг2(0) оказался
меньше нижней границы Рао-Крамера, равной единице.
Асимптотически нормальные оценки в приведенных примерах, когда
коэффициент рассеивания для них σ2(θ) ^ 1~1{β) оказывается при
некоторых 0 строго меньше /-1(0), называют иногда суперэффективными.
Однако оказалось, что эти примеры все же мало меняют правильную в
целом картину о предпочтительности эффективных оценок. Именно, Ле Ка-
мом было установлено, что добиться проиллюстрированного выше
улучшения оценок можно, грубо говоря, лишь в малом числе точек.
Здесь мы покажем, что наряду с соотношением inf Е$(0* — t)2 = 0,
и*
справедливом при каждом £, для интеграла от Е*(0* — t)2 уже существует
положительная нижняя граница, не зависящая от 0* и тесно связанная
220
Гл. 2. Теория оценивания неизвестных параметров
с аналогичным интегралом от функции {nl(t)) x. Именно, мы получим в
одномерном случае θ G R неравенство для
inf [Et(9*-t)2q(t)dt (1)
при любой весовой функции q(t) ^ 0, / q(t)dt = 1, правая часть которого
не зависит от Θ* (в том числе и от смещения b(t), присутствующего в
неравенстве Рао-Крамера) и близка к значению J/n, где
'-/$* »
2. Основные неравенства. Прежде чем сформулировать соответствующие
теоремы, заметим, что интеграл в (1) можно рассматривать как
безусловное математическое ожидание Е(0* — Θ)2 в байесовском случае, когда θ
имеет априорное распределение с плотностью q(t) относительно меры
Лебега. В этом случае J = Ε/-1 (θ).
Обозначим через f(x,t) = ft(x)Q(t) плотность совместного
распределения X и 0; //(ж), как и прежде, будет означать производную ft{x) no t.
Пусть, далее, Nh С Θ есть носитель функции /ι, определенной на Θ;
iV/j = {ί: h(t) φ 0}, и ΛΓ есть носитель /(ж,<) в Afn χ θ.
Теорема 1. Предположим, что ft{x) дифференцируема по ί, α
функция \fl{t) интегрируема на любом конечном интервале. Тогда для любой
финитной {т. е. равной нулю вне конечного интервала)
дифференцируемой функции h(t) такой, что Nh С Nq, справедливо неравенство
щг-v* ттшт
ηΕ(Ι(θ)[ΗΘ)/ς(θψ) + Ε[ν(θ)/ς(θψ
U h{t) A]2
(3)
η f I(t)h2(t)/q(t) dt + J h'(t)2/q(t) dt
Доказательство. В силу финитности h(t) имеем
f(Mx)h(t))'dt = Jd(ft(x)h(t)) = 0,
I t(ft(x)h(t))' dt = - f ft(x)h{t)dt.
Стало быть, для любой θ*
ί [{θ* -t){ft{x)h{t))'άίμη{άχ)= ί ί ft(x)h(t) άίμ11 (dx) = fh{t)dt.
Χη θ Χη Θ θ
(4)
§ 30. Интегральное неравенство типа Рао-Крамера 221
Эти интегралы можно рассматривать в силу условия Nh С Nq как
интегралы по N. Стало быть, мы можем умножить и разделить подынтегральное
выражение в (4) на /(a?,i). Тогда получим
Б
В силу неравенства Коши-Буняковского отсюда следует
же* - β* > тм/яш2 (.
*{" "> 'Е[(МХ)Н(9)У/(МХ)я№Г W
Остается привести это неравенство к виду (3). Заметим предварительно, что
Et\L'(X,t)\ζn^/Щ
и что для почти всех *) t
EtL/(X,i)=0. (6)
Первое из этих утверждений следует из соотношений
Et\L'(X,t)\ < nEt|/'(xbi)| < n{Et[l'(xut)]2}^2 = п^Щ,
вытекающих из неравенства Коши-Буняковского. Чтобы доказать второе
утверждение, возьмем произвольную финитную функцию ρ(ί)> имеющую
всюду непрерывную производную </(ί). Тогда
jg{t)f't{X)dt = -jg,{t)ft{X)dt.
Кроме того,
y"|0(t)|Et|L'(Xfi)l<tt <njШ\уДЩя<оо.
Отсюда следует, что можно менять порядок интегрирования в следующем
выражении:
Jg(t)EtL'(X,t)dt = f J9{ί)ί[{χ)άίμη{άχ) =
χη θ
= - / faf(t)ft(x) άίμη(άχ) = -fgf(t) dt = -Jdg{t) = 0.
Χη Θ Θ Θ
Вьшолнение этого равенства для всех д и означает справедливость (6).
*) В § 26 мы доказали, что это равенство при выполнении условий (R) имеет место при
всех t. Здесь нам будет достаточно его выполнения для почти всех t.
222
Гл. 2. Теория оценивания неизвестных параметров
Теперь можем преобразовать правую часть (5). Опуская для краткости
аргументы функций, получим
Ε
(fe(X)h(e))'
L ΜΧΜθ) J
l2
Ε
vh- + h-
Ε
+ 2E
h
4
/\ 2
я gj
'h/h
Я
Здесь мы воспользовались тем, что в силу (6)
+
E,(L')2
М"(т)'-[(;)
+ Е
/\ 2
E^EeL'^f^EtL'dt = 0
Nq
и что (см. §26) Efl(L')2 = ηΙ{θ). <
В последующих утверждениях везде будем предполагать, что ft{x)
удовлетворяет условиям теоремы 1.
Теорема 2. Если функция h{t) — ho(t) = q{t)/I(t) является
финитной и дифференцируемой, то
(7)
где
щ
dt
Замечание 1. Неравенства в теоремах 1, 2 являются интегральными
в том смысле, что они относятся к интегралам от Ε*{θ* — Θ)2. В этом смысле
неравенства § 26 можно называть локальными.
Доказательство. Это утверждение немедленно вытекает из
теоремы 1, так как правая часть в (3) при h — q/I преобразуется к виду
J2/(nJ + H). <
Мы видим, таким образом, что нижняя граница возможных значений
Ε (θ* — 0)2 при больших η лишь немногим отличается от границы — =
η
= / —ггт-, равной значению E(0q - Θ)2 для R-эффективной оценки 0q.
J Til [t)
Это указывает на целесообразность использования эффективных оценок,
поскольку для них при любой функции q почти достигается экстремальное
значение Е(0* -Θ)2.
Оценка (7) неулучшаема, на что указывает
Пример 1. Пусть X €= Фад. Как мы знаем, в этом случае 1(a) = 1.
Пусть, далее, параметр а выбирается случайно с гладкой плотностью q(t),
t Ε (—со, оо). Тогда правая часть (7) превращается в (п + Н)~1, где
#= i^--dt = E[{\nq(a)y}2.
§ 30. Интегральное неравенство типа Рао-Крамера
223
В нашем случае байесовская оценка an, соответствующая априорному
распределению Q с плотностью q и минимизирующая Ε (α* — а)2, равна
(см. § 20)
, _Jtq(t)ft(X)dt _
&Q Jq(t)ft(X)dt
f tq{t) expjnxt - t2n/2) dt f tq(t) exp(-n(x - t)2/2) dt
~ fq{t)exp{nxt-t2n/2)dt ~ f q[t) exp(-n(x - i)2/2) dt ' ^ '
Нетрудно найти асимптотическое представление этого отношения и
показать, что
olq = х Л тзг +
* nq(x)
°Ш· ■w-"),-M+o(a)·
Однако мы поступим проще, предположив, что q(t) = /—β * /2.
Тогда, очевидно, Я = 1, и правая часть в (7) превращается в 1/(п -f 1).
Но в примере 21.1 было установлено, что
\2 *
Q } п + 1
Ε(α^-α)2 =
Тем самым неулучшаемость неравенств (7) и (3) доказана.
Теорема 3. Если интервал (а - ε,α + ε) содержится в Θ, mo длл
любой оценки Θ*
max Et(0* - *)2 ^ — =—о ■
*€(α-ε,α+ε) η max i (£) + ΈΔΖ~Δ
te(a—ε,α+ε)
Доказательство. Воспользуемся неравенством
α+ε
max
ί€(α-ε,α+ε)
Ef(0*-<)2> f Et{6* - t)2q(t) dt,
справедливым для любой плотности q(t), равной нулю вне (о — ε,α + ε).
Требуемое утверждение следует из теоремы 1, если положить в ней
h(t) = q(t) = -cos2 n{t~a\ \t-a\^e.
S ΔΕ
Тогда
Е(6Г ~ θ)2 > nfl(t)q(t)dt + f(q>(t))2/q(t)dt>
где
/■(•(*))' ?l2^-2COS^Sm27j ^ 1 > 2 . 2π* π2
ι чч ν yy rf< = ι _\ / df = — / тГ SilT — dt = —. <
У <z(*) J C0S2?1 e2J 2
_£ 2e _1
224
Гл. 2. Теория оценивания неизвестных параметров
Можно отметить, что на функции q(t) = cos2(7r£/2) достигается минимум
ι
функционала I (qf(t))2/q(t) dt в классе всех дифференцируемых плотнос-
-1
тей q(t).
Из теоремы 3 вытекает, в частности, что интервал значений 0, при
которых оценка Θ* является сверхэффективной, не может иметь длину, большую
чем 0(1/у/п).
3. Неравенства в случае, когда функция ς(θ)/Ι(θ) не дифференцируема.
Если функция До = я/1 не удовлетворяет условиям теоремы 1,
справедливо следующее полезное утверждение, позволяющее оценивать асимптотику
Е(0* — Θ)2 в общем случае.
Теорема 4. Пусть последовательность функций /ιε(£), зависящих
от параметра ε > О, такова, что каждая функция h£ удовлетворяет
условиям теоремы 1 и
1) h£(t) < Λο(ί),
Тогда для любого ε > О
Е(* "б) > п7 + Я(е) ·
Доказательство немедленно вытекает из теоремы 1, если положить
h = he.
Из теоремы 4 получаем следующее важное следствие.
Теорема 5. Если функция q интегрируема по Риману, J < оо, то
Ε(θ*-θ)2>-(1 + δη),
п
где δη = о(1) при η —> оо.
Доказательство. Положим <fe(£) = ming(t + w),
/j\ _/&(*), еСЛИ 4e{t)^e,
\θ, если <?ε(£) < ε,
Je(i) = max (ε,/(£)),
ί+ε
Очевидно, что функция he финитна и дифференцируема при любом ε > 0.
§ 30. Интегральное неравенство типа Рао-Крамера 225
Из того, что q(t) интегрируема по Риману, следует, что qe(t) f q(t) почти
всюду при ε -> 0. Чтобы доказать это, убедимся, что
/1
6
[q(t)-qe(t)]dti0. (9)
α
Из интегрируемости q(t) по Риману вытекает сходимость
J2 qs(2kS)2S t / q{t) dt, £ q5{(2k + 1)^)25 f ί q(t) dt
k Ί k Ί
при δ -> 0. Поэтому
b
fqe{t)dt>Y^q2e(2ke)2e =
= \ (Σ ?2ε(4*ε)4ε + £ Ы(4A + 2)ε)4ε) ->■ /g(i)
Соотношение (9) и вместе с ним сходимость q£(t) f <?(£) доказаны.
Пользуясь теперь этой сходимостью, получаем утт t ^о(£),
J "■' J 2eJ /,(« + «) 2£j / /,(i| //«(()
-e —e
Кроме того,
Ιλ'οΜ 1 \Qe(t + e) ge(t-e)\ g(f)
di.
Мы можем воспользоваться теперь теоремой 3. Полагая ε = ε(η) =
= η""1/5, η —> οο, получим ε(η) —> 0,
4. Некоторые следствия. Критерии асимптотической байесовости и
минимаксности. Один из основных выводов, которые можно сделать из
результатов этого параграфа, состоит, грубо говоря, в следующем. Если существует
а. Я-э. оценка, то какую бы другую оценку мы не взяли, мы не получим «в
целом» (или «в среднем») асимптотически лучшего результата. Этим фактом
226 Гл. 2. Теория оценивания неизвестных параметров
мы воспользуемся позже в § 33. Здесь же мы приведем критерии
асимптотической байесовости и асимптотической минимаксности оценок, вытекающие
из теорем 2, 5.
Определение L Оценка 0*, обладающая свойством
Εη(θΙ-θ)2 = J + o(l) (10)
при η —> оо, называется асимптотически R-байесовской.
Это есть оценки, для которых асимптотически достигается нижняя
граница для среднеквадратичных уклонений, определенная в теоремах 2, 5. Их
можно было бы назвать также асимптотически R-эффективными «в
целом» (или «в среднем»).
Напомним (см. §21), что оценка 0* называется асимптотически
байесовской (относительно распределения Q), если для всякой другой оценки Θ*
limsup[En(0i - θ)2 - Εη(0* - θ)2] < 0. (11)
η->οο
Следствие 1. Пусть выполнены условия теоремы 1 и функция q(t)
интегрируема по Риману. Тогда асимптотически R-байесовская оценка
является асимптотически байесовской.
Доказательство. Пусть 0* — асимптотически Д-байесовская оценка.
В силу теоремы 5 для любой оценки 0*
liminfEn(0*-0)2^ J.
n->oo
Отсюда и из (10) следует (11). <
Ясно также, что если асимптотически Д-байесовская оценка существует,
то любая асимптотически байесовская оценка будет асимптотически Д-байе-
совской (ср. с замечаниями к теореме 26.3).
Из теоремы 5 вытекает также
Следствие 2. Пусть выполнены условия теоремы 1 и функция q{t)
интегрируема по Риману. Еслив\ ив\ — две асимптотически R-байесов-
ские оценкщ они асимптотически эквивалентны в следующем смысле:
Εη(0ί - ΘΙ)2 -> 0, (0ί - 0£)>/n —> 0,
где сходимость по вероятности понимается относительно совместного
распределения Хиве Хп χ Θ.
Доказательство совершенно аналогично доказательствам теорем 18.2,
26.4. Исходным является равенство (18.23), которое в силу теоремы 5 дает
HmsupEn(0?-0£)2 ^ 0. <
П->00
В § 18, 21 мы отмечали, что для сравнения оценок наряду со средними
значениями / ςτ(£)Εί(0* — t) dt можно рассматривать максимальные
значения
supEt(0*-*)2, Г С Θ.
ter
§ 30. Интегральное неравенство типа Рао-Крамера 227
В качестве Г берется либо все множество Θ, либо та его часть, которая по
предварительным данным содержит неизвестное значение 0. Напомним, что
оценка 0 называется минимаксной, если для любой оценки 0*
supE*(0* - tf <; supE*(0* - t)2.
ter ter
Оценка 0* называется асимптотически минимаксной, если для любой
оценки 0*
limsupsupEjv/n(0i - t)]2 < liminfsupEjx/n(0* - t)]2.
п-юо ter n->°° ter .
Следствие 3. Пусть информация Фишера I(θ) существует и
непрерывна. Тогда если для любого отрезка Г С Θ
\ims\ips\ipEt[Vn{0l-t)}2 ^sup/_1(£), (12)
n-*oo ter ter
то оценка θ* асимптотически минимаксна.
Доказательство. Нам достаточно убедиться, что для любой оценки 0*
liminfsupE*[>/n(0* -t)f ^ sup/_1(*). (13)
n"-»°° ter ter
Для любого распределения Q на Г с гладкой плоскостью q(t) относительно
меры Лебега
supEt[>/n (0* - t)}2 > /Et[Vn (0* - t)fq{t) dt.
ter J
По теореме 2 интеграл в правой части для любой оценки 0* не меньше, чем
J — Н/п. Поэтому левая часть (13) больше или равна
J= [ rl[t)q(t)dt.
= jr\t)q{t)
Но q — произвольная гладкая плотность, и для заданного ε > 0 ее всегда
можно выбрать в силу непрерывности I~l(t) так, чтобы
J^supΓl(t)-ε.
ter
Так как ε произвольно, (13) доказано. <
В заключение этого пункта сделаем одно важное замечание. Оно
состоит в том, что при отыскании асимптотически оптимальных оценок можно
ограничиться классом Kq асимптотически несмещенных оценок, введенным
нами в §26. Это вытекает из следующих соображений.
Мы уже отмечали, что правая часть неравенства теоремы 5, равная
J/n + о(1/п), от смещения 6(0) никак не зависит. В то же время, если
для построения нижней границы для Е(0* — 0)2 мы будем исходить из
неравенства Рао-Крамера в § 26, то мы получим
^2
чг-^ф/тР^+М
dt.
228 Гл. 2. Теория оценивания неизвестных параметров
Можно показать (ср. с [131]), что этот минимум по всем смещениям Ь{9)
имеет (при некоторых предположениях на гладкость q(t) и I(i)) тот же вид
J/n + о(1/п) и, что для нас существенно, достигается на смещении 6(6),
обладающем при η —> оо свойствами
b'(t) = o(l), b(t)=o(^=y
Класс оценок Θ* с такими смещениями и есть Ко (см. §26). Выход Θ*
из класса Ко делает границу J/n + о(1/п) недостижимой. Таким образом,
при асимптотическом подходе, когда а. н. оценки сравниваются с помощью
значений Е(0* — Θ)2 при гладких q(t) и /(ί), можно ограничиться
рассмотрением оценок из класса К = Кф$ Π Ко (класс Кф$ обсуждался нами в § 18),
поскольку оценки вне класса Ко являются «недопустимыми» в указанном
выше смысле.
5· Многомерный случай. В случае θ Ε Шк можно получить аналоги для
всех теорем этого параграфа и сделать те же выводы, которые нами были
получены для одномерного случая.
В частности, утверждение теоремы 5, одной из основных в этом
параграфе, будет иметь вид
d*>J- + o(l-\,
η \nj
где S = \\dijl dkj = E(0? - 9i) {θ] - θ,), J = ΈΙ-^Θ).
Рассуждения, связанные с байесовскими и минимаксными оценками,
также сохранятся, если в качестве погрешности оценки рассматривать
значение
ν{θ*)=Εθ(θ*~ θ)ν{θ* -0)τ,
где V — неотрицательно определенная матрица. Байесовскими и
минимаксными оценками (или асимптотически байесовскими и минимаксными)
следует называть оценки, погрешности которых удовлетворяют
соответствующим неравенствам для любой неотрицательно определенной матрицы V.
§31. Расстояния Кульбака-Лейблера, Хеляингера и χ2.
Их свойства
Результаты этого параграфа будут существенны для получения основных
результатов асимптотической теории оценивания, а также для результатов
главы 3.
1. Определения и основные свойства расстояний. Пусть Ρ и G — два
распределения на (Af, 95д'), абсолютно непрерывных относительно меры μ.
Обозначим
dP dG _
άμ άμ
Νρ — носитель распределения Ρ: Νρ = {χ : ρ(χ) > 0}.
§31. Расстояния Кульбака-Лейблера, Хеллингера и χ2 229
Определение 1. Расстоянием Кульбака-Лейблера между
распределениями Ρ и G называется величина
Pl(P,G) = |ln^P(dz) = |ΐη^|ρ(χ)μ(ώ).
ΝΡ Νρ
На самом деле /?i(P, G) не есть, конечно, расстояние или метрика в
общепринятом смысле, поскольку /9i(P,G) не есть симметричная функция
от Ρ и G. Тем не менее мы увидим, что /?i(P,G) очень по существу (со
статистической точки зрения) характеризует отклонение G от Р.
Из неравенства 1п(1 4- г;) — ν ^ 0 и представления
^•g>=-/K-(H
ρμ(άχ)
следует, что всегда /?i(P, G) ^ 0. В лемме 16.1 было установлено, что
равенство pi(P, G) = 0 возможно, лишь если Ρ = G.
Определение 2. Расстоянием χ2 между распределениями Ρ и G
будем называть величину
Р2{ ' )= У —Ф)—μ{ у
Np\jNG
К этому расстоянию относятся почти все замечания, сделанные к
определению 1. Название χ2 объясняется причинами, которые станут ясны позже.
Определение 3. Расстоянием Хеллингера между распределениями
Ρ и G называется величина
рз(Р.О) = J (y/^-^/^))^(dx).
NpUNG
Расстояние Хеллингера является уже симметричной функцией Ρ и G, а
значение д//?з(Р, G) обладает всеми свойствами метрики (между функциями
у/р(х) и у/д{х) в метрическом пространстве Ь^{Х^ μ)). Нетрудно видеть, что
р3(Р, G) = 2 (l - f ^ξμ{άχ)\ < 2. (1)
Все три введенных нами расстояния играют существенную роль в
различных задачах математической статистики. В какой-то мере мы в этом
убедимся.
Если с помощью этих расстояний характеризовать степень близости
распределений, когда отношение р/д близко к единице, то окажется, что все они
асимптотически ведут себя одинаково с точностью до постоянных
множителей. Действительно, пользуясь разложением
%£ЧЧЧИИ-КН2+о
9--1
Ρ
230
Гл.2. Теория оценивания неизвестных параметров
получаем
pi(P,G) = -|ln^ ·ρμ(άχ) -Ц^-1) РИ№) = |P2(P,G),
р2(Р,С) = |^^-М^) = |(х/р-%/5)2(1 + д/|) /i(<fe)«4p3(P,G).
Из последнего равенства следует также, что p2(P,G) ^ /93(P,G). Кроме
того, /?i(P,G) ^ /9з(Р, G). Действительно, так как 1η(1 + χ) ^ х, то
1п^ = 21п[ 1+ ( л/^-1 ) ) ^2( fi-l ) ,
Ρ V VVP // VVP /
/οι(Ρ,G) = -ίΐη^-ρμ(άχ) > -2 (j>/ρξμ{άχ) - Λ = p3(P,G).
В дальнейшем будем рассматривать параметрический случай и
предполагать, что выполнено условие (Ад). Нас будут интересовать расстояния
Pi, г = 1,2,3, между распределениями Ρ — Р^ и G = Р^2 в (Х,Ъх),
а также между соответствующими выборочными распределениями
(обозначим их здесь через Р£ , Р^2) в (А^ЯЗ^-). (Отметим, что расстояния имеют
смысл для произвольных распределении и с природой пространств никак не
связаны.) Если Νρβ С Νρβ , то мы можем записать
/ea(xi)'
ριίΡ^,Ρ^) = jlJ-^-fe^idx) = Bfll In
«(Ρβχ,Ρ*) = / {/θι~θίθ2)2μ(άχ) = Εβι
Ρ3(Ρ9ι,Ρθ2)= Ι(^-νϋ2)2μ(άχ) = Εθι (J:
/<?2(χι) τ
/*2(χι) 1
/*ι(χΐ)
Если условие iVp^ C iVF^ не выполнено, то P2(P^,P^2)i Рз(Р01,Р02)
будут больше соответствующих математических ожиданий в (2).
Отметим, что наряду с (2) имеет место следующее полезное равенство,
вытекающее из (1):
EolyJfo2(xl)/fo1(xl) = J }//θ2{χ)/θι{χ)μ{άχ) = 1 - ^(Pft.Pft)· (3)
Связь между расстояниями ^(Ρ^,Ρ^) и ^(Ρ^,Ρ^) устанавливается
следующим утверждением.
§31. Расстояния Кульбака-Лейблера, Хеллингера и χζ 231
Теорема 1. Справедливы равенства
Ρι(ΡΙ,Ρΐ)=ηΡι(Ρθι,Έ>θ2),
ι + Ρ2(Ρ?1,Ρ?2) = (ΐ + Ρ2(Ρ*1,Ρί2))η, (4)
1 - ~Ρ3{-ΡΙ,ΡΙ) = (l- \ps(Pei,Pe2)J■
Доказательство почти очевидно, если предположить для простоты,
что Νρθ С Νρθ (в общем случае выкладки по существу сохранятся, но
станут чуть более громоздкими). Действительно, в этом случае мы можем
воспользоваться равенствами (2). Тогда первое из соотношений (4)
немедленно следует из того, что
1n/giP0 ^f]n/gi(xi)
Далее, в силу (2), (3)
Ι+^,Ρ^Ε,,^Μ)2,
и такие же соотношения справедливы для расстояний между Р^ и Р£2 (с
заменой в правых частях χ ι на X). Так как
Е" Кмщ) -Е" Π {-ш) - h {им))
то отсюда при а = 2 и а = 1/2 получаем (4).
Доказательство теоремы в общем случае (т. е. если условие Νρθ С Νρθ
не выполнено) мы предоставляем читателю. <
Из теоремы 1 вытекает
Следствие 1. Справедливо неравенство
ρ3{ΡΙ,ΡΙ)^ηρ3(Ρθι,Ρθ2).
Действительно, 1 — β71 ^ (1 — β)η при любом /3^0. Полагая β =
= 1 - 2^3(P*'Pfc)' полУчим из (4)
p3(P?1,Pgl) = 2(l-/yi)<2(l-./?)n = np3(Pex,Pfa). <
232
Гл. 2. Теория оценивания неизвестных параметров
2. Связь расстояний Хеллингера и других с информацией Фишера. Среди
трех введенных в предыдущем пункте расстояний наибольший интерес для
нас в дальнейшем будет представлять расстояние Хеллингера. В то же время
характер главных утверждений, приводимых ниже (теоремы 2, 3), и
характер доказательств будет один и тот же для всех трех расстояний. Поэтому
для краткости изложения ограничимся в этом пункте изучением расстояния
Хеллингера, которое будем обозначать теперь (опуская индекс у символа рз)
ρ(Ρ9ι)Ρβ2) = J{y/fc- ^/7ϊ2γμ{άχ).
Положим r(0i,02) = />(P0j,P02).
Лемма 1. Если f$(x) при п. β. \μ] значениях χ непрерывна по θ, θ\ φ
Φ 02, mo
Если функция \/fe{x) при п. β. [μ] значениях χ дифференцируема по 0, то
^nfi^r^—· (6)
Кроме тогО)
О
Здесь предполагается, конечно, что значения &\ 0", 0χ, 02, θ
принадлежат Θ.
Доказательство. Чтобы проверить (5), достаточно воспользоваться
леммой Фату и непрерывностью fe{x) в соотношении
θ"-+θ2 θ"->$2
Так как при θ\ = 02 = 0 подынтегральное выражение в последнем интеграле
равно (/^) /(4/0), то мы получаем (6).
Чтобы доказать (7), положим о = 02 — θ\ и представим приращение
\/1н ~ \fhl в виДе
θ2 ι
1 [ ft м _ а [ foi+*v АщЁ
θι О
§31. Расстояния Кульбака-Лейблера, Хеллингера и χ2 233
В силу неравенства Коши-Буняковского
ι
{у/Ы- n/Ю2 = j
/Ж* «т/
yfOi+ay
1,„ ^2
^±^dy.
ίθι+ay
О
Пользуясь неотрицательностью подынтегральной функции, мы можем
менять порядок интегрирования в следующих соотношениях:
1
dy Ι μ(ώ) = J / Α#ΐ + ay) dy·
x \o / о
Неравенство (7) доказано. <
Положим γ(Δ) = г(0,0 + Δ). Из леммы 1 непосредственно вытекает
Теорема 2. lfo/ш функция \ffo(x) при п. в. [μ] значениях χ
дифференцируема по θ и Ι(θ) непрерывна, то существует
Δ->ο Δ2 4 ν '
Замечание 1. Это утверждение остается справедливым и для
расстояний pi, p2, если положить
γ(Δ) = ^2(Ρ*,Ρ*+δ), γ(Δ) = ^ι(Ρ*,Ρ*+δ).
Соотношение (6) доказывается при этом точно так же, как в лемме 1.
Доказательство же (8) может потребовать привлечения дополнительных
условий регулярности (близких к условиям (R)), обеспечивающих законность
предельного перехода под знаком интеграла.
Итак, рг(Р0,Р0+д)5 г = 1,2,3, ведут себя асимптотически одинаково, и
7(0) характеризует скорость их стремления к нулю при Δ —> 0 (ведь ~τΙ(θ)
пропорционально второй производной г (υ) в точке ν = 0).
Если положить Γ^η)(Δ) = p(P$+a>^)> то из теорем 1, 2 будет следовать
,. Γ<η)(Δ) ηΙ{θ)
km ——τ— = —-—.
Δ->ο Δ2 4
Такие же соотношения сохранятся для расстояний ρι, ρ2·
3. Существование равномерных границ для τ·(Δ)/Δ2. Наличие таких
границ позволит нам в дальнейшем получить весьма полезные оценки для
моментов отношения правдоподобия.
Для того чтобы упростить изложение и избежать введения других более
громоздких условий, часто будем предполагать в последующих
рассмотрениях выполненным условие
(Ас) Множество Θ компактно.
234
Гл. 2. Теория оценивания неизвестных параметров
С точки зрения приложений это условие, означающее ограниченность и
замкнутость параметрического множества, как правило, не представляется
ограничительным.
Ниже мы будем использовать также условие (Aq), которое было введено
нами в §14, 16 и которое означает, что fex φ }θ2 при θ\ φ 02- При этом
УСЛОВИИ r(0i,#2) > 0 При #ι φ 02.
Теорема 3. Если выполнены условия (Ао), (Ас) и 0 < 1(0) ^ ih < оо
при всех 0 Ε Θ, то существует постоянная д > 0 такая, что для всех
01, 02 е Θ
„ . Г(0!,02)
Доказательство. Оценка сверху следует непосредственно из (7).
Покажем теперь, что
Допустим, что (10) неверно, тогда найдется последовательность (0χ , 0^ )
такая, что
г(0[пЫп)) / ч
при η -> оо. В силу условия (Ас) можем считать, не ограничивая общности,
что θ[η) -> 01 Ε Θ, 0j° -> 02 G Θ. Если 0ι ^ 02, то (11) противоречит (5),
так как в силу условия (Ао) r(0i,02) > 0. Если же 0г = 02 = 0, то (11)
противоречит (6), так как 1(0) > 0. <
4. Многомерный случай. В этом пункте получим аналоги утверждений
п. 2, 3 для многомерного параметра (содержание п. 1 с размерностью 0 не
связано). Обозначим через φ(χ,θ) вектор-функцию с координатами
ψΛχ'β) vm и. ·
Тогда производная функция yfe(x) п0 направлению единичного вектора
о; = (uju...,uk) равна ((y/fe(x) );,ω) = (grad y/fe{x),u) = -(φ(χ,θ),ω).
Матрица Фишера 7(0) равна в этих обозначениях
Ι(θ)= Ι φΎ(χ,θ)φ(χ,θ)μ((Ιχ).
Пусть |w| означает евклидову норму и = (щ,..., и^).
В многомерном случае имеет место следующее обобщение леммы 1.
Лемма 1А. Первое утверждение леммы 1 (см. (5)) при к > 1
полностью сохраняется.
§31. Расстояния Кульбака-Лейблера, Хеллингера и χ2 235
Если функция yfe{x) при τι. в. [μ] значениях χ дифференцируема по Θ,
Θ' -> 0, θ" = θ' + ω"δ, ω" -»■ ω, \ω"\ = |ω| = 1, δ -> Ο, mo
l™Mw^>rW)*T.
(12)
Кроме того, если ω, \ω\ = 1, есть вектор, коллинеарный 62 — 61, так что
02 = #1 4- αα>, α = |^2 — #i|, mo
r(0b02) ^ 1
\θι-θ2\
< ~ / ω/(#ι + аи>у)и)Т dy.
(13)
Доказательство. Первое утверждение леммы 1 с размерностью не
связано. Второе вытекает из леммы Фату и соотношений
Kminf.y^.l Ξ* / liminf
\θ' -θ"\2
I
:„:„,Ь/Ж-л/7Й2
μ(άχ) =
\θ' - θ"\2
= ±Ι(φ(χ,θ),ω)2μ(άχ) = ±ωΙ(θ)<.
Чтобы доказать (13), заметим, что
а 1
\ff(h- л/fa = 2 (ψ(χ,θι+νω),ω)άν = \ \{φ{*,β\ + ayu),u>)dy,
τ
~{θι,θ2) = ^ Γ \[{φ(χ,θχ+ανω),ω)
dy
χ L0
μ(άχ) =ξ
^ Τ / (φ(χ>θι +ανω)ιω)2άνμ{(1χ) =
χ ο
1 Λ 1
α2 Γ Γ α2 Γ
= — / / (φ{χ,θ\ + ayω),ω)2μ(dx)dy = — / cj/(0i +ayu))u>T dy. <
о # о
Положим, как и прежде, γ(Δ) = г(#,0 4- Δ). Из леммы 1А вытекает
Теорема 2А. J5o/m функция y/fe(x) дифференцируема при η. β. [μ]
значениях χ и матрица Ι(θ) непрерывна, то для любого вектора ω
единичной длины существует
τ{δω) 1 т
lim г9 = -ωΙ(θ)ω .
Я_>о δ2 4 w
236
Гл. 2. Теория оценивания неизвестных параметров
Как и в одномерном случае, из леммы 1А мы можем получить также
следующее следствие. Обозначим через Sp/(0) след матрицы 1{θ).
Теорема ЗА. Если выполнены условия (Ао), (Ас), матрица 1(9)
является положительно определенной в Θ, 4Λ = supSp/(0) < оо, то суще-
θ
ствует постоянная g > О такая, что при всех 0ι, 02 Ε θ
^ϊ*γ=~^°· (14)
Доказательство. Обозначим через Λι(0) и Л*(0) соответственно
минимальное и максимальное собственные числа матрицы 7(0), так что
при |ω| = 1
Λι(0)<α;/(0)α;τ<Λ*(0). (15)
А:
По условию теоремы Λι(0) > О всюду на Θ. Так как (</?,ω)2 < \φ\2 == yZ ¥^> т0
/<
{φ,ω)2μ(άχ) = ωΙ{θ)ωτ < Sp/(0)
A'
и, стало быть, Л&(0) ^ Sp/(0) ^ 4Л. Из неравенства (13) получаем
ι
r(0i - 02) 1
-0J2
|0ι-02|
^ - / Ak{6i+ ayu)dy < Л.
Докажем теперь второе неравенство в (14). Предположим, что оно не
верно. Тогда, как и в теореме 3, найдется последовательность (0| , 02 )>
01 -> 01 £ Θ, 02 -> 02 ^ θ, для которой будет справедливо (11). Если
01 Φ 02 5 то это будет противоречить (5). Если 0ι = 02 = 0, то в силу
компактности сферы |cj| = 1 можно считать, не ограничивая общности, что
фп) = 0(п) + δω{η)^ ω(η) _^ ^ μ(η)| = |^| = L Но в етом случае (И) будет
противоречить (12), (15). <
5*. Связь рассматриваемых расстояний с оценками. Рассмотрим
расстояние Кульбака-Лейблера между распределениями Р# и не зависящим от 0
распределением G
Pi(G,-pe) = fln^G(dx) - j \nfe{x)G{dx).
Здесь от 0 зависит лишь второе слагаемое
d(Pe,G) = - J\nMx)G(dx).
§31. Расстояния Кульбака-Лейблера, Хеллингера и χ2 237
С другой стороны, напомним, что о. м. п. определялась нами в § 16 как
значение 0, при котором минимизируется d(P0,P*). Если распределение χι
дискретно, а μ — считающая мера, то выражение
/JP*
ln-^P^x)
Ρ'
имеет смысл, /?i(P*,Pfl) = d(P^,P*) -d(P*,P*) и, следовательно, мы
можем считать, что о. м. п. минимизирует расстояние Кульбака-Лейблера
ρΐ(Ρ*,Ρ#) между Р# и Р*. В общем случае такое толкование можно
принимать лишь условно.
Основанием для такого толкования может служить приближенное
описание распределения Ρ я с помощью дискретного распределения Р^. Для
этого надо предположить, например, что существуют множества Δχ,..., An
такие, что при больших N (малых Δ;) fe{x) при χ Ε Δ, хорошо
приближается (в подходящем смысле) значениями fe(xi), У% £ Δ^, % = l,...,iV.
Тогда можно считать, что fe{x) постоянна на Δ; и равна fe{yi)> а
наблюдения, попавшие в Δζ·, отождествляются (объединяются в группы). Полученное
новое сгруппированное эмпирическое распределение обозначим через Р^.
Соответствующие вероятности попадания в г-ю группу равны
»?(Δ<) = Jfe(xMdx) ~ fe(ViMbi).
Δ,
В этом случае будем иметь дело с выборкой из распределения Р^ дискретного
типа. При этом о. м.п. Θ* будет близка значению 0^, максимизирующему
^ln/fl(yj)P;(A,·)» flnMx)P*n(dx).
i J
Другими словами, Θ*Ν будут сближаться с ростом N с 0*, где Θ*Ν суть
значения, минимизирующие расстояния Кульбака-Лейблера р1(Р*^,Р^).
Более содержательный «предельный переход» здесь построить трудно, так как
значения Pi(Pn^jP^)» как и ^{^nN5?Л' неограниченно возрастают при
iV->oo (μ(Δ0->0).
Для дискретных распределений χι можно рассматривать также
расстояния /?i(P^,P^) при г = 2,3 и оценки, минимизирующие эти расстояния.
Например, при г = 2 получим
„/р р«\ _ S^ Ып ~ fe(ai))2
где щ — число элементов выборки, попавших в точку а*, для которой fei^i) =
= Рв({аг·}) > 0. Это есть статистика χ2 (см. §7, 8), в связи с чем это
наименование присвоено нами и расстоянию р2·
Так как расстояния pi обладают близкими асимптотическими
свойствами, то оценки, минимизирующие эти расстояния, как это выяснится позже,
будут асимптотически совпадать.
238
Гл. 2. Теория оценивания неизвестных параметров
§32.* Свойства информации Фишера.
Разностное неравенство типа Рао-Крамера
Этот параграф стоит несколько в стороне от основного изложения. В нем
мы попытаемся хотя бы частично ответить на вопрос о том, что происходит
с нижней допустимой границей для Е#(0* — Θ)2 в нерегулярном случае, т.е.
в случае, когда функция fe{x) не дифференцируема по θ или когда 1(9) = оо.
Начнем с примера, который показывает, что при этих условиях
поведение среднеквадратичных уклонений оценок (или их дисперсий) может быть
совсем иным, чем поведение правой части неравенства Рао-Крамера.
Пример 1. Пусть X€=Uo,0. Условие (R) здесь не выполнено, так
как функция fo(χ) разрывна. Как мы знаем, для этого семейства
статистика S = maxxi является полной и достаточной (см. пример 24.3).
Возьмем несмещенную оценку Θ* = 2χχ. Тогда в силу результатов §24 оценка
θ§ = 2Efl(xi/5) будет эффективной. Вычислим значение E^xi/S). Так как
Р#(5 < ζ) = (ζ/θ)η, ζ Ε [0,0], το S имеет плотность, равную ηζη~1/θη на
[0,0] и нулю вне этого интервала. Для отыскания условного распределения
P(B/s) = Ρ#(χι Ε B/S = s) величины χι при условии S = s воспользуемся
правилом (20.2):
ίμα ι \ о / г- j /с \ Pfl(xi edy, S e ds)
P(dy/s) = Р,(Х1 Ε dy/S = s) = re{Seds) ■
Здесь числитель равен
[dy (η — l)sn~2ds
Pfl(xi edy, S e ds) = {
θ θη.χ при y<s,
ds sn~l
ПрИ у = 5
0 при у > 5.
Отсюда следует, что P(dy/s) = при 0 < у < s, Ρ({5}/θ) = —.
Таким образом,
5
0
Имеем
0 2
D^ = E^)2-02 = |s2(l + i) ™^ά8-θ> =
(n + 1)2 iV- <?2 ш
n(n + 2) у n(n + 2)"
§ 32. Разностное неравенство типа Рао-Крамера
239
Так как 0£ эффективна, для любой несмещенной оценки Θ* получаем
ϋθθ* > -j^-ry (2)
η(η + 2)
Таким образом, при больших η среднеквадратичное уклонение Е# (θ*3 — θ)
будет иметь порядок малости 1/п2. С точки зрения нижней границы
неравенства Рао-Крамера, имеющей порядок 1/п, это ненормально высокая
точность*). Можно показать, что это есть точность, с которой по выборке
определяются любые точки скачков fe(x) (запрещаемые условием (R)). Мы
видели в примере 17.4 об оценке медианы, что точки, где плотность fe(x)
бесконечна, можно определить с еще большей точностью, так что, грубо говоря,
чем больше нарушение регулярности в точке, тем точнее эта точка
оценивается по выборке. Скажем, если X €= Р#, где Р# = Τϊ^οβ + ~Ϊ05 Ifl есть
распределение, сосредоточенное в точке 0, то Ря(5 Φ Θ) — 2~n (S — maxxi),
так что дисперсия Θ* — θ при Θ* = S будет убывать с ростом η
экспоненциальным образом.
Можно ли в этих условиях указать нижнюю границу для дисперсии
оценок? Ниже мы получим неравенство, аналогичное неравенству Рао-Крамера,
с помощью которого такие границы можно строить при более слабых
условиях регулярности, чем условие (R).
Будем предполагать лишь, что выполнено условие (Αμ), хотя оно и не
очень существенно (см. замечание в конце параграфа).
Обозначим через Δφ{θ) приращение функции φ(β) на интервале
(θ,θ 4- Δ), через Νρ — носитель в Хп распределения выборки: Νρ =
= {χ : fe{χ) Φ 0} и положим Νη = N£g U ΛΓρ,+Δ·
Теорема 1 (Неравенство Чепмена-Роббинса). Пусть θ Ε Θ, θ + Δ Ε
G Θ, α(θ) = Έθθ*. Тогда при любом Δ ф 0
Όαθ* > (Μ<?))2 = (Δα«?))2 ,
Ue ' ![ΑΜχψ/Μχ)μ»(άχ) ρ2(Ρ£,Ρ?+Δ)' [)
где р2 есть расстояние χ2, рассматривавшееся в §31. Для несмещенных
оценок числитель здесь следует заменить на Δ .
В силу теоремы 31.1 знаменатель в (3) имеет вид ^(Р^Р^+д) =
= (ΐ + Γ2(Δ))η-1, где
г2(А)=Р2(Ре,Ро+А)= [ [Αίθ^]2μ(άχ). (4)
Таким образом, чем больше расстояние P2(Pq,Pq+a) между Ρ#+Δ и Р#
(при фиксированном Δ), тем меньше нижняя граница для ΌΘ*.
*) Для параметра θ существуют также оценки, дисперсия которых имеет порядок 1/п.
Например, для оценки Θ** = 2х имеем Е0** = θ, ΌΘ** = 4Dxi/rc = θ2/3η.
240
Гл. 2. Теория оценивания неизвестных параметров
Если Р#+д абсолютно непрерывно относительно Р#, то Νρ Α С Ν%Λ =
Νη и Ρ2(Ρ^Ρ^+δ) можно записать в виде (см. (31.2))
Р2(Р£,Р£+д)=Е,
т2
L /»W J '
аналогично гг(Д) = Е#
ΔΛ(χι)
l2
Λ(χι) J
Если же распределение Ρ#+Δ не абсолютно непрерывно относительно Р#,
то существует подмножество из Νρθ+Α положительной Ря+д-меры, на
котором fe{x) = 0, так что интеграл в (4) обращается в бесконечность, а само
неравенство (3) становится тривиальным. Следует вновь отметить, что
выражение Е$[А/$(Х)//е(Х)]2, понимаемое как интеграл по Νρθ, может при
этом оставаться конечным.
Доказательство теоремы 1. Из сказанного выше следует, что, не
ограничивая общности, можем считать, что Ρ#+Δ абсолютно непрерывно
относительно Р#, так что Νρ С Νρθ = Νη. Так как f${x) и /$+δ(®) есть
плотности в Хп, то
Кроме того,
Отсюда следует, что
/
[ ΑΜχ)μη{άχ)=0.
θ*ΑΜχ)μη(άχ) = Αα(θ).
I
(0* - α{θ))Α/θ(χ)μη{άχ) = Αα{θ).
(5)
На множестве Νη можем подынтегральную функцию в (5) представить в
виде произведения
yfeyx)
Применяя затем неравенство Коши-Буняковского, получим
(Δα(0))2 < у (61· - α(θ))2Μχ)μη(άχ) J {-^^-μη{άχ). <
Νη
tfn
В дальнейшем, в соответствии со сделанным выше замечанием, как и
в доказательстве теоремы 1, ограничимся случаем, когда Р#+д абсолютно
непрерывно относительно Р# (ведь иначе неравенство (3) становится
тривиальным).
§32. Разностное неравенство типа Рао-Крамера
241
Следствие 1. Если выполнены условия регулярности,
обеспечивающие существование (см. замечание 31.1 к теореме 31.2) lim Γ2(Δ)/Δ2 =
= 7(0), то
ηΙ(θ)
(6)
где αΛΘ) = am sup—-—.
Δ-»ο Δ
Чтобы получить (6) из теоремы 1, надо лишь заметить, что мы можем
выбрать последовательность Δ —> О так, чтобы —- > а+(#)· ^
Неравенство (6) является по форме некоторым обобщением неравенства
Рао-Крамера (обобщением, скорее всего, фиктивным, так как упомянутые
условия регулярности, по-видимому, влекут за собой существование α!{β)).
Неравенство (3) естественно называть разностным в отличие от
неравенства (6), которое можно было бы назвать дифференциальным.
Таким образом, если Γ2(Δ) ~ Ι(Θ)Α2 (это соответствует тому, что fg
дифференцируема), то из разностного неравенства Чепмена-Роббинса
следует дифференциальное неравенство Рао-Крамера.
Однако если функция fg не дифференцируема, поведение Γ2(Δ) при
уменьшении Δ будет иным.
Если, скажем, fg дифференцируема всюду за исключением конечного
числа точек разрыва θ = θ(χ), зависящих от я, то мы будем иметь
г2(А)~с\А\. (7)
Проще всего это прояснить на довольно типичном примере,
рассмотренном в начале параграфа.
Пусть X €= Uo,0. Чтобы было выполнено условие абсолютной
непрерывности Pfl+Δ относительно Р#, будем считать в случае Рд = Uo,0, что Δ < О,
|Δ| < 0. Тогда
1 1 ГЛ Л .,
Δ/*(*) = <
Θ + Α~
1
θ
Ιο
- - при it[u,t;t £Л|,
σ
при χ е[в + Α,θ],
при χ $. [0,0],
γ2(Δ)
Ι
(Д/«(*))а
/θ(χ)
άχ =
Θ+Α
-/[
Δ
τ2
θ(θ + Α)\
θάχ +
υ
ίϊ
Θ+Α
Δ2 |Δ|
242
Гл. 2. Теория оценивания неизвестных параметров
Существенным здесь является наличие интервала длины, сравнимой с |Δ|,
на котором |Δ/^(α:)| > с > О, где с от Δ не зависит. Это и обеспечивает
порядок малости (7) для Γ2(Δ).
Возвращаясь к нашему примеру, видим, что для несмещенных оценок
параметра θ
"^-gv ιδι/Ά' γ ;·
[i+ β +β(β + Α)) '
Каков порядок малости правой части этого неравенства при η —> со? Полагая
|Δ| = ув/п, получим
Θ2 у2
ΌΘ* > — max · у
\ η n{n-y)J
Ясно, что выражение со знаком max асимптотически эквивалентно h =
= m&xy2/(ey — 1) « 0,65, так что
D0*^(/i + o(l)).
Это неравенство имеет ту же по порядку малости правую часть, что и не-
улучшаемое неравенство (2), однако постоянный множитель при θ2 /η2 в (2)
«лучше» и равен единице.
Наряду с (7) могут возникать и другие скорости сходимости Γ2(Δ) к
нулю при Δ —> 0. Мы можем получить, например, и Γ2(Δ) ~ βΔα, α < 1,
если /я(ζ) имеет линии θ — θ(χ) φ const, при приближении к которым
/θ(χ) —> оо; и Γ2(Δ) ~ οΔα, 2 > α > 1, если /# непрерывна по 0, но не
дифференцируема, а удовлетворяет лишь условию Гёльдера в окрестности
некоторой линии θ = θ(χ) φ const. Нетрудно видеть, что порядок малости
Δ2
max ■
Δ (l + cAa)n-l
при a < 2 будет определяться значением Δ = (у/сп)1/", так что
Όθ* > τ—ϊ5μ max i—г*1 + °M)·
{cn)z/a у еУ — 1
В «регулярном» случае α = 2 максимум по у достигается в предельной точке
у = 0 (Δ = 0).
В заключение этого параграфа отметим, что оценки для ΌΘ*
аналогичным образом могут быть получены и для взаимно не абсолютно
непрерывных Р# и Pfl+Δ- Для этого в (5) подынтегральную функцию следует
умножать и делить на y/fe(x) + /я+д(#)> а не на y/fe{x)- Условие (А^) также не
столь существенно, так как меры Р# и Ρ^+Δ всегда абсолютно непрерывны
относительно -(Р# +Ρ#+δ)·
§ 33. Вспомогательные неравенства. Свойства о. м. п. 243
§ 33. Вспомогательные неравенства для отношения правдоподобия.
Асимптотические свойства оценок максимального правдоподобия
В § 22-26 мы изучали вопросы, связанные с существованием и
отысканием в явном виде эффективных и Д-эффективных оценок. Мы видели, что
существуют они далеко не всегда, а найти их удается лишь когда функция
правдоподобия имеет специальный вид или когда мы знаем в явном виде
полную достаточную статистику (первое из этих условий часто влечет за
собой второе (см. §25)).
Перейдем теперь к построению асимптотически оптимальных оценок.
Здесь условия их существования будут значительно более широкими.
Соответствующие результаты будут опираться прежде всего на асимптотические
свойства функции
ОД = %^ =exp{L(X,0 + u) -L(X,0)}, (I)
η
где, как и раньше, Σ(Χ,Θ) = Υ^/(χ;,0). Число Θ в (1), как правило, будет
считаться фиксированным и представлять собой истинное значение
параметра, т.е. такое, что X ^ Р#. В этом случае Z(u) есть функция двух
переменных и и X и, стало быть, вместе с функцией правдоподобия fo+u(X)
будет случайной функцией переменного и. Функцию Z(u) будем называть
отношением правдоподобия, она играет важную роль в математической
статистике. Основная задача этого и следующего параграфов — изучить
свойства Ζ (и).
Будет установлено, что Z(u) близко к нулю вне окрестности точки и = 0.
В окрестности этой точки Z(u) сближается в известном смысле с дельта-
функцией, точнее, Z(v/y/n) сближается асимптотически при η —> оо с
функцией плотности нормального закона.
В § 33, 34 будем рассматривать лишь одномерный случай. Случай
многомерного параметра будет рассмотрен отдельно в § 36.
Важную роль в последующих оценках будет играть расстояние Хеллин-
гера
r{u) = p(P,+u,P,) = J{y/f9+u{x) - у/Ш)^(ах)
между распределениями Ρθ+u и FV Оно рассматривалось нами в §31.
Напомним, что
0 < г(и) = 2 (1 - j ^/θ^(χ)/θ(χ)μ{άχ)\ < 2,
так что
Е //e+u(xi) [ ic ,_w ,_, ..,„_, , г {и)
Λ(χι)
= / ^ίθ+η{χ)ίθ{χ)μ{άχ) = 1 - Τ-ψ, (2)
*Z*(«)=(l-^)". (3)
244 Гл. 2. Теория оценивания неизвестных параметров
Относительно параметрического семейства {Р#} будем предполагать в
этом и последующих параграфах, что наряду с (Αμ) выполнены условия
(Ао) {/θι(χ) Φ ίθ2{χ) nPu 01 Φ 02) w (Ac) (Θ есть компакт).
Несущественность с точки зрения приложений последнего условия мы уже отмечали. Это
связано с тем, что в реальных задачах из априорных соображений обычно
бывает возможно указать границы возможных значений Θ. Для простоты
там, где это потребуется, будем предполагать также, что Θ выпукло (в
одномерном случае это означает, что Θ = [α, 6], —оо < a <b < оо).
Кроме того, в этом параграфе будем предполагать, что функция у/Jq
дифференцируема для п. β. [μ] значений х, а информация Фишера
rim [<J№L ич π (ЯМУ
строго положительна и ограничена в Θ (это есть условие (R) без свойства
непрерывности). При этих условиях в теореме 31.3 было доказано, что при
всех допустимых θ и θ + u (т.е. таких, что θ £ Θ, θ + u Ε θ) для величины
r(u) = p(P0+u,Pfl) справедливо неравенство
inf^^ff>0. (4)
0,u U2·
1. Основные неравенства. Обозначим для краткости р(и) = Z*/*(u) и
будем считать, что все перечисленные выше условия выполнены.
Теорема 1. Справедливы неравенства
ΈθΖιΙ2{η) < е"п^2/2, Еер{и) < е"п^2/4,
о t (5)
Е9\р'(и)\ < -^/п1{в + и)е-^и21\
Из рассмотрений § 31 следует, что для значений и = о(1) вместо g в этих
неравенствах можно брать значения, сколь угодно близкие к 7(0)/4.
Доказательство. Имеем в силу (3), (4)
ΈΘΖι'2{η) = (1 - т{и)/2)п ^ е-пг^12 ^ е"п^2/2.
Далее, в силу неравенства Коши-Буняковского
Евр(и) < [ΈθΖ^2(η) · EeZ(u)}V2 = [ΕβΖ1/2(«)]1/2 ^ «.-«'η*/^
Используя снова неравенство Коши-Буняковского и соотношение
j/(ti) = |Ll(X>e + ti)Z3/4(ti)l
находим
Ев\р'(и)\ = ^Ев\Ь'(Х,9 + и)\г^2(и)г^(и) <
< \ШЬ'{Х,θ + u)]2Z(u) ■ Έ,θΖχ/2{η)γΙ2 <
^ l[Ee+u[L'(X, θ + η)}ψ2β-η4^. <
§ 33, Вспомогательные неравенства. Свойства о. м. я. 245
Теорема 2. При всех ζ, п^ 1
Р9( sup Z (^=) > ez) ζ ce-3*/Vu2*/4,
\\v\2u \Vn/ J
где с = 1 + Зу/lo/g, h = sup Ι(θ) om θ не зависят.
Для доказательства теоремы нам понадобится
Лемма 1. При всех χ ^ О
00
/V^d^v^e-*2/2.
Доказательство*). Характеристическая функция случайной
величины ξ €= Фод равна Ее1^ = е*"' /2 и определена во всей плоскости. Полагая
t = —га;, получим Ее3* = ех /2. Отсюда с помощью неравенства Чебышева
получаем
Ρ{ξ >х) = Р{е*х > е*2) ^ е-^Ее** = е"*2/2. <
Доказательство теоремы 2. Оценим функцию
#(ί) = Efl supp(i;).
Если ΐϋ € [б + ί,6], то
w-θ ъ-θ
ρ(<ιν-θ)=ρ{δ)+ J p'{u)du^p(S)+ I \p'{u)\du.
δ δ
Так как правая часть здесь от w не зависит, то
supp(u) ζρ(δ)+ / \p\u)\du,
η^δ J
4>δ
Η+{δ) = Εθsupp{u) ^ Εθρ{δ) + / Ee\p'{u)\du.
η>.δ J
η>δ
*) При больших χ более точными являются следующие неравенства:
х + 1 J χ
χ
которые читатель без труда может получить, сравнив производные рассматриваемых
функций (значения самих функций при χ = оо совпадают).
246
Гл. 2. Теория оценивания неизвестных параметров
В силу теоремы 1 отсюда получаем
Η+{δ) < e-n9i2/4 + jV" f yJl{e + u)e-n9u2'Adu.
На основании леммы 1
Η+(δ) < e-"^2/4 + |^fQ J e-ngu>/4 du «.
v^6y/ng/2
Ясно, что точно такая же оценка будет справедлива для функции
#_ (δ) — sup p(u).
Поэтому
Я(5) <тах(Я+(*),Я_(*)) < (l + 3*№) &~η^Ι\
Остается воспользоваться неравенством Чебышева
P*(sup Z(t) > ez) = P,(supp(t) > е3г/4) < Я (£)е"3г/4. <
2. Оценки для распределения и моментов о. м. п. Состоятельность о. м. п.
Теорема 3. Существуют значения с < со, д > 0 такие, что
Р*(\/^|0*-0|^Ксе-^2/4 (6)
<λ/υι всея г; « η ^ 1.
Доказательство. Из теоремы 2 вытекает, что
Р,( sup Ζ(ί) > 1) < ce~^l\
Остается воспользоваться соотношением
{\θ* - θ\ > δ} = {sup Z(t) > sup Z(t)} С {sup Z(t) > Z(0) - 1} (7)
Ш* IW l*l£*
при £ = v/y/n. <
Следствие 1. Пусть un —> оо — любая неограниченно
возрастающая последовательность. Тогда
(^-^ίν°· (8)
§ 33. Вспомогательные неравенства. Свойства о. м. л. 247
Если же ип таковы, что при любом а > О
2>~QU"<°°' (9)
то
{θ*-θ)^—>0. (10)
Un п.н.
Эти соотношения являются, очевидно, усилениями соответственно состо-
ятельности (Θ* — θ —> 0) и сильной состоятельности (Θ* — б —> 0) о. м. п.
Ρ п.н.
Доказательство. Соотношение (8) следует непосредственно из (6),
если в последнем положить ν = 6ип. Соотношение (10) также вытекает
из (6), так как сумма правых частей в (6) при выполнении (9) будет
образовывать сходящийся ряд. <]
Например, даже такая медленно растущая последовательность, как ип =
= Inn, удовлетворяет условию (9), так что*)
\ПП п.н.
Следствие 2. Существует значение с\ < оо, не зависящее от п, 0,
такое, что при любом а ^ д/Ъ
Ебехр{а(и*)2}<С1, (11)
где и* = у/п{9*-в).
Доказательство. Интегрируя по частям, получаем
оо оо
Εβαξ2 = - / еау2 άΡ{\ξ\ >ν) = 1 + 2α ί νβαν2Ρ{\ξ\ > ν) dv.
о о
Поэтому в силу теоремы 3
00
еИ°2 < 1 + ψίνβ"^20 dv = Cl<oo. <
о
3. Асимптотическая нормальность. Доказательство асимптотической
нормальности о. м. п., как мы видели в § 14, 16, требует более сильных, чем (R),
условий регулярности. Обозначим эти условия символом (RR), чтобы
отметить таким способом, что это есть условия регулярности и что они усиливают
условия (R).
Условия (RR).
1. Выполнены условия (Aq), (Ac), (R).
*) Из замечания 34.2 будет следовать, что (10) справедливо и для еще более медленно
растущих ип>
248
Гл. 2. Теория оценивания неизвестных параметров
2. Функция 1(χ,θ) для η. β. [μ] значений χ дважды непрерывно
дифференцируема по Θ. Функция \lff(x,t)\ мажорируется функцией ί(#), не
зависящей от t: \lf/(x,t)\ < /(#), для которой
Et>
i(xi) = ί 1{χ)Μχ)μ{άχ) < ос. (12)
3. Законно дифференцирование по θ под знаком интеграла в
равенствах
J /θ(χ)μ(άχ) = 1, Ιϊ(χ,θ)Μχ)μ(άχ)=0.
Свойство 3 вместе с равенствами (аргументы для краткости опускаем)
'-f 4-(ff
означает, что
Е/(хь0) = 0, Е/'(хь0) = -E6(/'(xi,^))2 = -Ι(Θ).
Условие о единственности решения t = θ уравнения (относительно t)
ι
ΐ{χ:ί)/θ{χ)μ{άχ) = 0
здесь не требуется, так как состоятельность в силу следствия 1 уже
установлена (см. условие d) в теореме 16.3).
Как увидим ниже, условие 3 является излишним, если потребовать,
чтобы интеграл (12) сходился равномерно (см. §34 и приложение V).
Условия (RR), по-видимому, завышены для последующих утверждений;
см. об этом ниже замечание 34.3. Напомним основной результат п. 16.3.
Теорема 4. При выполнении условий (RR)
(Θ* - 0)Vn = ξηΓ^ΘΚΐ + εη(Χ,θ)),
где
ξη = ^^ ©► Фо,/(*), εη(Χ, θ) -f 0.
Это утверждение можно дополнить следующим образом.
Теорема 5. Сходимость
г? = (&-в)у/И&Ф0г1-чв) (13)
имеет место вместе с моментами любого порядка, т. е. вместе с (13)
при любом к > 0 выполняется
Efl(u*)*-► Вт;*, ^Φ0ι/-ΐ(ί). (14)
Более того, для любой непрерывной функции w(t) такой, что \w(t)\ <
< е*<2/б (см. 4)),
Eew(u*) -> Его (η), η Φ Φ0,/-ΐ(β)· (15)
§ 33. Вспомогательные неравенства. Свойства о. м. я. 249
Доказательство. Соотношения (14), (15) получаются из (13) и
теоремы непрерывности для моментов (см. §5), так как в силу следствия 2
W/e(«*)<E*«p{^}
< с < оо. <!
Замечание 1. Из (13), (14) вытекает, что Θ* принадлежит классу оце-
нок ЛГф,2? в котором сходимость (Θ* — 9)у/п €= Φο,σ2(0) имеет место вместе
со сходимостью Ε#(0* — б)2 -* σ2(θ) двух первых моментов. Как уже
отмечалось в § 18, в этом классе асимптотический подход к сравнению оценок
совпадает по существу со среднеквадратическим.
Установим теперь один из центральных результатов этой главы,
состоящий в том, что о. м. п. при выполнении условий (RR) обладает всеми
возможными свойствами асимптотической оптимальности, которые мы
рассматривали выше, т.е. является а. э., асимптотически байесовской (для любого
априорного распределения, имеющего плотность) и асимптотически
минимаксной оценкой одновременно.
Асимптотическая эффективность М-оценок в классе Км оценок была
доказана в § 16.
4. Асимптотическая эффективность. В §26 мы ввели в рассмотрение
класс Ко асимптотически несмещенных оценок, т.е. оценок 0*, смещение
которых Ъ{9) = Έβθ* — θ обладает свойствами
b(0) = o(-j=y 1/(0) = о(1).
(16)
В § 30 были приведены соображения, по которым в поисках асимптотически
эффективных «в целом» оценок можно ограничиться классом Kq.
Установим теперь следующий факт.
Следствие 3. Справедливо θ* Ε Ко·
Доказательство. Первое из соотношений (16) вытекает из (14) при
к = 1. Чтобы доказать второе, заметим, что (см. § 26)
1 +Ь\в) = Е0в*Ь'(Х,в) = Εθ(θ* - Θ)Σ,'{Χ,Θ) =
= Е,((0* - θ)^ξη) = Е*щ(! + *η(-Μ)),
εη(Χ,θ)—*0.
п.н.
Если здесь верна теорема непрерывности для моментов, получим отсюда
требуемое соотношение 1 4- Ъ'{9) —у 1 или, что то же, У (Θ) —>> 0. Чтобы
установить справедливость этой теоремы в нашем случае, достаточно убедиться
(см. §5), что
Έθ\{θ*-θ)^ξηγΙ2<ο<οο, (17)
250 Гл. 2. Теория оценивания неизвестных параметров
где с от η не зависит. Воспользуемся неравенством Гёльдера
Ρ Q
при г = 3/2, ρ = 4, q = 4/3. Получим тогда для левой части (17) оценку
(Eq[(9* — 0)у/п]6)1^[Щ^) ' , которая в силу (13) дает нам требуемое
неравенство. <
Следующее следствие ввиду его важности сформулируем в виде теоремы.
Теорема 6. О.м.п. Θ* является a.R-э. оценкой. Кроме того, Θ*
является а.э. в Kq.
^+*
Доказательство. Тот факт, что Θ* есть а.R-в. оценка, следует
непосредственно из определения 26.1 и того, что
т? (в* т2 1+°(1)
Εθ{θ ~θ) =~^W
Асимптотическая эффективность в Kq следует из теоремы 26.3. <
Теорема 2 вместе с замечаниями к теореме 26.3 означает, что при
выполнении условий (RR) любая а. э. оценка в Kq будет а. Д-э. оценкой.
Отметим, что сужение множества рассматриваемых оценок до Kq — да-
^+*
леко не единственное сужение, при котором Θ* становится а. э.
Укажем другое сужение, связанное на этот раз со свойством θ быть
асимптотической медианой распределения а. н. оценок, т. е. со свойством
Р*(0* > В) -> \ (18)
при η —>· сю.
Обозначим через К° класс оценок 0*, для которых (18) выполняется
равномерно по Θ. Класс К0 можно было бы назвать классом асимптотически
центральных оценок.
Теорема 7. О.м.п. θ* Ε К0 и является а.э. оценкой в классе К0.
Доказательство этой теоремы мы отложим до п. 37.3 и 43.5.
5. Асимптотическая байесовость о.м.п. В этом пункте всюду, где будет
предполагаться существование плотности q(t) априорного распределения Q
относительно меры Лебега на Θ, будем предполагать также, не оговаривая
это особо, что плотность интегрируема по Риману, так что будут
удовлетворяться условия теоремы 30.5.
Теорема 8. О.м.п. Θ* является асимптотически R-байесовской
оценкой. Если Q есть произвольное априорное распределение, имеющее
плотность q(t) относительно меры Лебега, то Θ* является также и
асимптотически байесовской оценкой, соответствующей
распределению Q.
§ 34. Дальнейшие свойства оптимальности о. м. п.
251
Доказательство. Асимптотическая Д-байесовость о.м.п. следует из
соотношений
lim Е[у/п(в* - θ)]2 = lim EE0U/nt<r - θ)]2 =
n->oo n->oo
= Ε lim Ee[Vn (^ - Θ)}2 = E/"1^) = J
n—>oo
Предельный переход под знаком математического ожидания здесь законен
по теореме о мажорируемой сходимости, так как в силу следствия 2 значение
Ед[у/п(9* — Θ)]2 равномерно ограничено постоянной, не зависящей от η и Θ.
Асимптотическая байесовость вытекает из следствия 30.1. <
Из замечаний к следствию 30.1 и теоремы 8 следует, что любая
асимптотически байесовская оценка является асимптотически Д-байесовской.
Утверждение теоремы 8 можно усилить. Оказывается, что о. м. п. и
байесовская оценка для любой априорной плотности q «почти» совпадают.
Теорема 9. Справедливы соотношения
Εη(θ* - e*Qf -> 0, (fl£ - 0*)v^ -у 0,
где 6q есть байесовская оценка, соответствующая распределению Q;
сходимость по вероятности понимается относительно совместного
распределения X и θ на Χ χ Θ.
Теорема 9 немедленно вытекает из следствия 30.2. Ее утверждение
эквивалентно тому, что для почти всех t
Etn{e*-e*Q)2->0.
§ 34. Асимптотические свойства отношения правдоподобия.
Дальнейшие свойства оптимальности о.м.п.
В предыдущем параграфе нами были изучены свойства отношения
правдоподобия Z(u) вне окрестности точки и = 0. Теперь рассмотрим поведение
Z(u) в окрестности этой точки. Как и в п. 3 предыдущего параграфа, будем
предполагать, что выполнены условия (RR). Из полученных ниже
результатов будет следовать, в частности, уже доказанная нами асимптотическая
нормальность о. м. п. Θ*. Мы приведем доказательство этого факта в таком
виде, который позволяет без труда переносить его на многомерный случай.
Некоторые из последующих утверждений повторяют отчасти
рассуждения § 14. Нам понадобятся соотношения
Е/(хь0)=О, (1)
Е/'(хь0) = -Εβ(Ζ'(χι,0))2 = -Ι(θ), (2)
вытекающие из условий (RR), и следующая
252
Гл. 2. Теория оценивания неизвестных параметров
Лемма 1. Если выполнены условия (RR), то имеет место
непрерывность 1"(χ,θ) «β среднем» в следующем смысле:
Ε^(χι) = J ω%{χ)}θ{χ)μ{άχ) -> О
при Δ —> О, где и>^{х) — модуль непрерывности функции 1"(χ,θ):
ω^{χ) = sup \1"(χ,θ + η)-1"{ζ,θ)\.
вее,в+иее
(3)
(4)
Доказательство. В силу теоремы о мажорируемой сходимости
соотношение (3) будет следствием обычной непрерывности Ζ", так как в этом
случае ш'^(х) —>· 0 для п.в. [μ] значений χ при Δ —>· 0 и, кроме того,
\ω^(χ)\^21(χ). <
Положим
\L'{X,0 + v)-L'{X,e)
7η(Δ, θ) = sup
|ν|ζΔ
ην
+ Щ
Лемма 2. Пусть выполнены условия (RR), δη > О, η = 1,2,..., есть
любая последовательность, сходящаяся к нулю. Тогда для любого θ Ε Θ
и для Χ €= Ρ#
Ίη(δη,θ)—>0, 7η(<*η,0*)—+ 0.
Π.Η. Π.Η.
Β smwa; соотношениях Ι(θ) можно заменить на I{θ*) и наоборот.
Доказательство. Докажем сначала первое утверждение. Так как
Eel' (χι,θ) = —Ι{θ), L"(X,0)/n —> —I{Θ), то нам достаточно убедиться,
что 7п(<5п) -* 0, где
\1'(Χ,θ + ν)-Ι,'{Χ}θ) L"{X,0)\
7η(Δ) = sup
\vKA
ην
η
Но
7n(*nK sup VW + u)-L"(X,0)|^£^^^
η
г=1
где с^д(х) означает модуль непрерывности ί"(χ,0), определенный в (4).
Очевидно, что для любого фиксированного Δ > 0 при достаточно больших η
й?1(х)<й>ых).
Кроме того, по усиленному закону больших чисел
ωΙ(Χ)τ^Έθω4(χ1)=ωΙ.
В силу леммы 1 о>д —> 0 при Δ -» 0. Отсюда следует, что
=№т?0. (5)
§ 34. Дальнейшие свойства оптимальности о. м. л.
253
Первое утверждение доказано. Из (5) и определения п. н. сходимости
следует, что наряду с (5)
для любой последовательности случайных величин ηη —> 0. Нам остается
п.н.
sup
Μ<δη
L'{X,e* + v)-L'{X,(l·) L"{X,0)
ην η
<
*L+p-*\W- ^
и воспользоваться следствием 33.1. Возможность замены 7(0) на Ι(θ*) также
вытекает из следствия 33.1 (и непрерывности Ι(θ)). <
Мы можем теперь сформулировать основные утверждения об
асимптотическом поведении отношения правдоподобия Z(t). Положим
и условимся обозначать через εη(Χ, θ) (иногда с дополнительными
индексами) различные последовательности случайных величин, п. н. сходящиеся
к нулю относительно распределения Р# выборки Х^.
Теорема 1. Пусть выполнены условия (RR), δη > 0 есть
произвольная последовательность, сходящаяся к нулю. Тогда при \и/у/п\ < δη
У (и) = ηξη - ^Ι(θ)(1 + εη(Χ,θ,η)), (7)
где
|ε„(Χ,Μ)| < εη{Χ,θ) ^ 0, ξη = ^{Χ,θ) @> Φ0,/(*)·
Точка u* = (θ* — 9)у/п, в которой Y(u) достигает максимального
значения, обладает свойствами
"* = щ(1 + *п (*,*)), (8)
2Y(u*) = 21ηΖ(θ* -θ) = ^(1 + εη(Χ,θ)) @> Ηχ. (9)
Наряду с (7) справедливо представление
Y(u)=Y(u*) - {и~и*)21(в)(1 + еп(ХАи)),
\εη(Χ,θ,η)\<εη(Χ,θ).
Во всех приведенных утверждениях Ι(θ) можно заменить на ΐ(θ*).
254
Гл. 2. Теория оценивания неизвестных параметров
В этой теореме, как и в лемме 2, предполагается, что θ + uy/n Ε θ. Это
соотношение будет автоматически выполнено при достаточно больших п5
если θ — внутренняя точка Θ.
Замечание 1. Важно отметить, что в (7) случайные величины ξη
и εη(-Χ", θ) от и не зависят. Поэтому первое утверждение теоремы можно
записать в виде
„2
sup
\η\ζδη\/η
Υ(η)-ηξη + γΙ(θ)
0.
Если δη таково, что
Σ
е-пд&ЦА < 00)
(И)
из теоремы 33.2 следует, что в дополнительной области |и| > δη\/η
sup Y{u)
—00.
|u|>i„Vn
Доказательство теоремы 1. Из леммы 2 при |υ| ^ δη получаем
L'(X,0 + υ) = L'(X,0) - ηυΙ(θ)(1 + εη(Χ,θ,υ)),
\εη(Χ,θ,ν)\ζεη(Χ,θ).
Интегрируя это равенство по υ в пределах от нуля до u/y/n, находим
L[X,
:,θ + -^=) - L(X,θ) = -^=uL'{X,θ) - ^-Ι(θ)(1 + εη(Χ,θ,u)),
\εη(Χ,θ,η)\ζεη(Χ,θ).
(12)
Это есть, очевидно, разложение в ряд Тейлора, в котором Ь"(Х,9)/п
заменено на —/(б), а остаточный член допускает равномерную оценку. Так как
у/71 y/ΐΐ ^—'
есть сумма независимых одинаково распределенных случайных величин с
нулевым средним и дисперсией Ι(θ) (см. (2)), то по центральной предельной
теореме ξη ©► Фо,/(0)· Представление (7) доказано. Чтобы доказать (8),
вернемся к лемме 2. Она означает, что существует множество Л, Έ*#(Α) — 1,
такое, что для Xqq Ei, η —> оо
sup
\ν\<δη
L'{X,e + v)-L'{X,e)
ην
+m
0.
(13)
Кроме того, в силу следствия 33.1 существуют последовательность un —> оо,
ν>η/\/η Ξ 7η —> 0 (un должна удовлетворять (33.9)) и множество 5, Р#(.В) =
= 1, такие, что для Xqq G5, η —> оо
ν* = (θ*-θ) = ο(Ίη).
(14)
§ 34. Дальнейшие свойства оптимальности о. м. п.
255
Так как последовательность δη —> 0 в (13) произвольна, то при -Xqq Ε АПВ,
P#(j4 Π S) = 1, в силу (14) величина под знаком sup в (13) в точке ν = ν*
будет сходиться к нулю. Вспоминая, что L'(X,θ + ν*) = Lf(X,0*) = 0,
получим для -Хоо £ Α Π β
ад-^>
п(0* - Θ)
0.
Это означает, что ξη — 1{θ)η* — ιι*εη(Χ,θ), и доказывает (8).
Пользуясь теми же аргументами, можно подставить
„ = и* = У*уД = (Θ* - в)у/^ = Щ(1 + Ζη(Χ, Θ))
в (12). Это дает
L(X,9*)-L(X,0) = JL(i + En(X,e))
и доказывает первую часть соотношения (9). Сходимость распределений
ξ^/Ι(θ) к распределению χ2 с одной степенью свободы следует из теорем
непрерывности, так как ξη/\//(0) ©► Φο,ι-
Соотношение (10) доказывается совершенно аналогично (7), если
воспользоваться вторым утверждением леммы 2 и найти на его основе предста-
вление для L(X,0 + Uy/n) — L(X,0*). <
Замечание 2. Соотношение (8) позволяет также точно описать
«максимальные уклонения» (Θ* — 6)у/п при η —> оо. Именно, известно, (см. [17,
72, 137]), что нормированные суммы ξη независимых одинаково
распределенных величин с нулевым средним и дисперсией Ι(θ) удовлетворяют закону
повторного логарифма в силу которого
Ρ (limsup-7=JM = 1 j = 1.
\ n^oo y/2I{0)ln\nn J
Так как в (4) limsupen^,θ) = 0 п.н., то получаем, что
П-*00
Ро hmsup , — = 1=1.
γ n-юо V 2 In In П /
Замечание 3. На языке распределений первое утверждение теоремы 1 можно
сформулировать следующим образом:
Υ (и) ©> Ф-.и*Цв)/2,иЧ(в)' (15)
Мы отмечали выше, что второе условие (RR) (о существовании /"(ж,0)) не всегда
существенно для доказываемых утверждений. В несущественности этого условия
для сходимости (15) можно убедиться путем следующих рассуждений. Величина
У» = L (х,в+-^Л-ЦХ,в) = £ \l (хг,0+ -jA -/(*,*)
г=1
256
Гл. 2. Теория оценивания неизвестных параметров
есть сумма независимых одинаково распределенных величин. Поэтому по
центральной предельной теореме для схемы серий (слагаемые зависят от п, проверку условий
Линдеберга опускаем)
Υ (и) ^ Фв(щ)^(«),
где
a(u) = lim ηΈ$
1\хи9 + -т=) -/(хь0)
= цт „в,in W(*> = _u2 lim Pi(P>,P>fA) = _Н!М
"->°° Λ(χι) Δ^° Δ2 2
(см. теорему 31.2 и замечание 31.1). Далее
σ (ή) = lim nEg
71—ΪΟΟ
/(χι,0 + ^)-/(χι,0)1
= ti2 lim
Δ->0
/
Ι(ζ,θ + Δ)-Ι(χ,θ)
/θ(χ)μ(άχ) =
= u2 [(Ι'(χ,θ))2/Θ(χ)μ(άχ)=η21(θ).
Если бы при вычислении α (ti) и σ2(^) мы воспользовались разложением
1{χ,θ + u/y/η) в ряд с двумя производными, то получили бы тот же результат.
Однако мы убедились, что это делать не обязательно.
В заключение этого параграфа получим из теоремы 1 еще одно полезное
следствие, которое потребуется в дальнейшем и которое касается поведения
интегралов от отношения правдоподобия.
Теорема 2. Пусть выполнены условия (RR), функция w(t)
удовлетворяет условию
\w{t)\^ceaM\ с<оо, а = ^
(д > 0 определено в §31), а функция q(t) непрерывна в точке t = θ и
ограничена. Пусть, кроме того, Π — любая мера на (R, 03) такая, что
J е-аН2/4П(А*) <оо. Тогда если θ — внутрення точка Θ и X ^ Р#, то
JS/«<«--«)g(*+^)z(^)n(*0-
= eY^q{9) Г /"ш(и* -^-(V^Mf/Wnj^) + εη(Χ,0)1 . (16)
5 частности, если Π есть л«ера Лебега, U(du) = c?u, то
J =
/ 2π
7(0)
ey(u*)a(0)(E™(r?) + £n(*,0)),
где εη(Χ,0) —► 0, r/ e *ο,/-ΐ(*)·
§ 34. Дальнейшие свойства оптимальности о. м. л.
257
Утверждение (16) весьма естественно, так как множитель q{9 + u/y/n)
«почти постоянен», а функция Ζ(u/y/n) = eY^ сближается с точностью
до постоянного множителя по теореме 1 с плотностью нормального
распределения.
Доказательство. Чтобы упростить запись, ограничимся
рассмотрением случая, когда Π есть мера Лебега. Переход к общему случаю никаких
затруднений не вызывает.
Оценим сначала часть интеграла (16) по области \и\ > г. Обозначим
ее через J(r). Так как fe(X)/f^(X) ^ 1, то, полагая для краткости Ζ —
= Z{u*/y/n) = ey(u*), t = θ + u/y/n, получим
z~lzШ=Щ^(Ш)) *zmШ'
Поэтому в силу неравенства Коши-Буняковского, теоремы 33.1 и
следствия 33.2
EBw{u*-u)Z-lZ (уЛ ζ [Е9т2{у/й{в* - t))E9Z^2 (4=)] ζ «Γ*2*/4.
Так как maxg(£) < оо, то отсюда и из леммы 33.1 находим
EoZ-lJ{r)^ce-9r2l\
Пользуясь неравенством Чебышева, получим оценки того же порядка и для
P$(Z~l J (г) > δ). Поэтому если г = гп —> оо так, что
£е-г^4<оо, (17)
то при у ^ гп
Z~lJ{y) -^ о. (18)
Выберем тп — о(у/п) и рассмотрим оставшуюся часть V(y) =· J — J(y)
интеграла J при у = 2rn. По теореме 1
Z^V{2r) = Z^1 ί q(e+^)w{u*-u)z(-^j du =
\u\<2rn
= Γ (g(0)+en(u)Mtz*-u)^^
\u\<2rn
где |εη(^)| < εη —* 0, \εη(Χ,θ,u)\ ^ εη(Χ,θ) —> 0 при η —* оо. Поэтому в
силу (18) для доказательства теоремы нам достаточно убедиться в близости
258 Гл. 2. Теория оценивания неизвестных параметров
интегралов
J w(u* - и) ехр { -J(u ~ п*)2/(0)(1 + ε^Χι θ>и))} du>
\u\<2rn
Jj^Ewfr) = jw(u* - и) ехр |-±(u - η*)2Ι(θ)\ du.
В силу (17) и следствия 33.1 существует множество А, Р#(А) = 1, такое, что
\и*\ ^ т*п Для ^оо € А при всех достаточно больших η = η(Χοο). Так как
Ι(θ) > g, |u — гх*|2 > гх2/2 при |it| > 2rn, |u*| < rn, то на множестве А (см.
лемму 33.1)
ί w{u* - и) ехр \-\(и ~ и*)2Щ\ du < се"9** ~> 0.
Поэтому нам остается оценить
ί ^*-Ti)|exp|-i(Ti-Ti*)2/(0)(l + 6n(X,0,Ti))|-
\u\<2rn
- ехр j --(и - η*)2Ι{θ) \\du^
fw{v)\βχρί~ν2Ι{θ){1 + εη{Χ,θ,ν + η*))\ - expi-^v2I{9)\\dv.
Но этот интеграл сходится на множестве АВ к нулю, где В = {Хоо :
εη(Χ,θ) -» 0}, P#(i?) = 1. Это следует из сходимости к нулю при
каждом ν подынтегральной функции и того, что она мажорируется
интегрируемой функцией. <
Мы можем усилить теперь утверждение теоремы 33.9.
Теорема 3. Пусть θ — произвольная внутренняя точка Θ, Χ ^ Р#.
Пусть, далее, q(t) — произвольная непрерывная и положительная
внутри Θ плотность априорного распределения. Тогда у/п (θ* — 9q) —> 0.
Доказательство следует из теоремы 2. Действительно,
fl. fr_f(t-e*)q(t)ft(X)dt
« fq(t)ft(X)dt ■
Делая замену переменных t = θ + и/у/п и деля числитель и знаменатель в
этом выражении на f${X), получим
θ* _$* = /(" ~ и*Мв + u/\fo)Z{u/y/H) du
Q y/n$q{e + u/y/n)Z{u/>fn)du
§ 34. Дальнейшие свойства оптимальности о. м. п.
259
Надо воспользоваться теперь теоремой 2 при w(t) = t и w(t) = 1. Так как в
первом случае Έχυ(η) = Ет/ = 0, то мы получаем
г & = Щ&, £п(х,в)->о. <
4 у/п п.н.
Имеет место также асимптотическая минимаксность о. м. п. Чтобы
установить этот факт, нам будет удобнее пользоваться несколько иной формой
условий (RR) (см. §33). В новой версии (RR^) этих условий будет
отсутствовать свойство 3, а интеграл (33.12) будет предполагаться сходящимся
равномерно по Θ. Приведем полностью эту новую версию условий (RR).
Условия (RRu).
1. Выполнены условия (Ао), (Ас), (R).
2. Функция Ι(χ,θ) для η. β. [μ] значений χ дважды непрерывно
дифференцируема по Θ. Функция \lf/(x^t)\ мажорируется функцией /(ж), не
зависящей от t: |//7(χ,ί)| < /(χ), для которой интеграл
Ei
jj(xi) = / 1{χ)/ι{χ)μ{άχ)
сходится равномерно по t Ε Θ*).
Под равномерной сходимостью интеграла мы понимаем сходимость**)
sup / 1(χ)/β(χ)μ(άχ) -¥ О
θ J
x:\l(x)\>N
при Ν —> οο.
В дальнейшем нам понадобятся следующие два свойства, вытекающие
из (RRu).
*) Все последующее изложение полностью сохранится, если условие о существовании
мажоранты ослабить следующим образом: область θ может быть покрыта конечным числом
областей θι,...,θβ так, что при θ 6 θ; функция \1"(χ,θ)\ мажорируется функцией ί(;)(ζ),
не зависящей от Θ: |/"(я,0)| < /(;)(я), для которой интеграл
Ε*Ό)(χΟ = J Ιω(χ)ίβ(χ)μ(άχ)
сходится равномерно по θ £ Bj, j = 1,..., s.
**) Такое понимание равномерной сходимости находится в согласии с равномерной
сходимостью, использовавшейся в теореме 5.4 — там оно относилось к функции 1(х) = х. В то
же время это не есть равномерная сходимость / φ(χ,θ)μ(άχ) при φ(χ,θ) = l(x)fe(x), когда
предполагается, что при N —► со
sup / φ(χ, θ)μ(άχ) -+ 0.
θ J
Χ:\φ{*,9)\>Ν
260
Гл. 2. Теория оценивания неизвестных параметров
1. Законность двойного дифференцирования по параметру под знаком
интеграла в равенстве
Ι /θ(χ)μ{άχ) = 1,
означающая справедливость соотношений
j ί'θ{χ)μ{άχ) = 0, J /2(χ)μ(άχ) = 0.
2. Равномерная сходимость интеграла
Ι(θ) = Ι(1'(χ,θ))2ίθ(χ)μ(άχ).
(Это свойство вытекает из (R) и понадобится в §37.)
Чтобы разгрузить основное изложение, доказательство этих следствий
условий (RRu) отнесено в приложение V.
Для большинства утверждений этого параграфа безразлично, какой
версией условий (RR) пользоваться: они будут справедливы при выполнении
хотя бы одного из этих условий, при этом доказательства останутся
прежними. Поэтому под (RR) мы можем понимать любую версию этих условий.
Однако в утверждениях, связанных со свойством минимаксности, нам нужно
будет условие (RRu).
Теорема 4. При выполнении (RR^) о.м.п. Θ* является
асимптотически минимаксной оценкой.
Эта теорема выводится непосредственно из следствия 30.3 и следующего
утверждения.
Лемма 3. Справедливо равенство
lim supEen(e* - θ)2 = sup/_1(0),
n-foo ееГ ееГ
где Г — любой отрезок, лежащий внутри Θ.
Лемма 3 вытекает из равномерной по θ сходимости (33.14).
Равномерность будет доказана в §37 (см. п. 37.3).
В дальнейшем под (RR) будем понимать любой из двух приведенных
выше вариантов этих условий. (В теореме 4 приложения V будет доказано,
что условия (RRu) влекут за собой (RR).) В утверждениях, связанных с
минимаксностью о.м.п., под (RR) будем понимать (RRu).
§ 35/ Приближенное вычисление оценок
максимального правдоподобия
Мы видели, что в задачах оценивания параметров наибольший интерес
представляют эффективные и а. э. оценки, каковыми часто являются о. м. п.
Возникает вопрос о практическом отыскании таких оценок. Отыскание точ-
^+*
ного значения о.м.п. Θ* в реальных задачах может представлять
значительные трудности. Особенно это относится к распределениям, не имеющим
сравнительно простых достаточных статистик.
§ 35. Приближенное вычисление о. м. л.
261
С другой стороны, отыскание какой-нибудь а. н. оценки Θ* обычно
трудностей не вызывает.
Приведем здесь способ приближенного отыскания М-оценок и, в
частности, о. м. п., используя в качестве исходной какую-нибудь состоятельную
или а. н. оценку Θ*. С помощью Θ* будет построена оценка 0*,
асимптотически эквивалентная о. м. п. и, стало быть, а. з. В основе этого способа
лежит известный метод Ньютона (метод касательных) приближенного
решения уравнения s(t) = 0, где s — некоторая непрерывно дифференцируемая
функция. Напомним предварительно его суть. Пусть θ — решение
уравнения s(t) = 0, и пусть в каждой точке ί мы можем вычислить значения s(t)
и sf(t). Будем предполагать также, что s'(0) ^Ои что «исходное» для
приближений значение ίο близко к θ и, стало быть, s'(io) φ 0. Тогда, обозначив
Δ = ίο — #5 будем иметь
s(0) = 0 = а(«0 - Δ) = s(t0) - As'{to) + ο(Δ),
s{to)
Поэтому если положить
Δ + ο(Δ).
то получим
(1=у"°>^»-!щ· (1)
ί1-β = £ί(ί0)-β = Δ--^=ο(Δ).
Таким образом, применение к ίο преобразования U дает значение ίι, которое
«на порядок» ближе к 0, чем ίο·
Перейдем теперь к статистическим оценкам. Положим
U(t) = t - L'{X,t){L"(X,t))~l, t e Θ,
(2)
£7ι(ί) = ί + L'{X,t){nI{t))-\ ί e Θ,
где L(X, ί), как и прежде, логарифмическая функция правдоподобия.
Теорема 1. Пусть выполнены условия (RR), X Ε Р# и Θ* — любая
а. н. оценка:
(Θ* - в)у/И θ- Ф0,аЦв)·
Тогда оценка Θ* = U(9*) (или Θ* = Ui(0*)) будет асимптотически
эквивалентной 0*, т. е.
Доказательство теоремы будет опираться на следующую лемму.
Лемма 1. Пусть выполнены условия (RR), X €= Р#, δη > 0 есть
произвольная последовательность, сходящаяся к нулю. Тогда, если θη
262
Гл. 2» Теория оценивания неизвестных параметров
таково, что \θη — θ\ ^ <$п, то
υ(θη)-<Τ = (θη-θ*)εη(θηΑΧ),
гдееп= max \εη(θη,θ,Χ)\—> 0.
Θη·.\θη-Θ\<ζδηι Ре
То dice самое утверждение будет справедливо, если вместо U
использовать функцию U\.
Другими словами, если пользоваться методом последовательных
приближений к 0* и положить 0q = θη, θ* = U(9q) (или θ* = ί/ι(0ο))> τ0
β* — θ* — ο[ΘΙ — б*), так что приближение θ{ существенно лучше, чем 0q.
Доказательство. Из рассмотрений §34 и непрерывности L"
вытекает (см, например, лемму 34.1), что
L'(-Mn) = (Θη-<Γ)1"(Χ,Θ), 1"(Χ,Θ) = -η(/(0) + <(*», *,*)),
где б Ε [0η,0*]> max εήί^τυ^-Χ") —> 0 при любой последовательности
θη'\θη— θ\ζδη Ρθ
δη -> 0. Далее,
£"(ΧΑ) = -η(/(0) + <#),
где ε'ή, εη обладают тем же свойством, что и ε'η. Следовательно,
Щ9п) -θ* = θη-θ*- L\X,en){L"{X,0n))-1 =
= θη-θ*- {θη - θ*)(1 + εη) = (θη - θ*)εη.
Доказательство для функции U\ проводится точно так же. <]
Доказательство теоремы 1. Выберем какое-нибудь δη —> 0 такое,
что 5пу/п —> оо, и представим (0J — в*)у/п в виде
(υ(θ*) -θ*)^= \/^(θ* -θ*)εη(θ*,θ,Χ)Ι(1θ._ΘΚδη)+Γη,
где rn φ О лишь на множестве Вп = {X : \θ* — θ\ > <Jn}, и в силу леммы 1
εη = max εη(£, 0, Χ)—)► 0.
|t-*|<*n ft
Так как, кроме того, P#(i?n) -4 0, то отсюда следует, что
\θ{ - 0*|^ < л/^|0* - θ\εη + ν^|0* - θ\εη + τη —+ 0. <
§ 35. Приближенное вычисление о. м. л.
263
Теорема 1 показывает, что метод последовательных приближений,
отправляясь от любой а. н. оценки, за один шаг приводит нас в точку Θ* с
точностью до значений о(1/у/п).
Однако при выполнении некоторых условий последовательные
приближения можно начинать с произвольного значения £, принадлежащего
некоторому множеству. Тогда можно за «небольшое» число итераций
преобразования U(t)} определенного в (2), получить оценку, асимптотически
эквивалентную о. м.п. Обратимся сначала к неслучайной функции s(t).
Справедливо следующее вспомогательное предложение, которое поясняет суть дела.
Пусть U(t) — преобразование, определенное в (1).
Лемма 2. Пусть отрезок К = [ui,^] такое, что решение θ
уравнения s(t) = 0 принадлежит К и при всех t€K выполняется s'(t) φ0 и
г'«(г1Ь)<г2 (з)
при некоторых г\ Ε (0,1), гг Ε (1,2). Тогда
\U{t) - ί| < p\t - 0|, ρ = max (r2 - 1, 1 - η) < 1. (4)
Значение θ неизвестно, и поэтому проверять условие (3), по-видимому,
удобнее с помощью следующего более сильного достаточного условия: при
всех ί, и Ε К
s{t) - s{u)
Γ1 < (t-uMt) < Г2· (5)
Ясно также, что при достаточно малом отрезке К условие (3) всегда
выполнено.
Из леммы 2 следует, что если Uk(t) есть fc-я итерация преобразования U
и все ТО
\uW(t)-e\<pk\t-0\.
Принадлежность U^(t) £ К будет всегда иметь место по крайней мере для
одного из концов ui, ^2 отрезка К (для значения щ, ближайшего к 0; это
проверяется по ходу вычислений).
Доказательство леммы 2. Пусть для определенности t > 0, Δ =
= t - 0. Тогда
J7(i) - θ = Δ _ ΐΆ > Δ _ Γ2Δ = _(Γ2 _ ι)Δ,
U{t)-θ ^Α-ηΑ = (1-η)Δ.
Отсюда следует (4). Случай £ < θ рассматривается аналогично. <
Из леммы 2 вытекает следующая рекомендация. Пусть с помощью
оценки Θ* или априорных сведений нам удалось выделить отрезок К С Θ
такой, что выполнено (5) для s(t) = L'(X,t). Тогда для одного из значений
t = Tii или t = U2 все £/(*)(£) будут принадлежать К и будет иметь место
264
Гл. 2. Теория оценивания неизвестных параметров
экспоненциальная сходимость U^(t) к θ (на самом деле сходимость будет
еще более быстрой, так как при уменьшении К числа г\ и Г2 сближаются с
единицей). Признаком, по которому следует прекратить итерации, является,
очевидно, первое совпадение (в рамках принятой точности) значений £Λ*'(ί)
H[/(fe+1)(i).
Описанную процедуру можно применять и без предварительной проверки
условия (5). Критерием того, что она привела к значению Θ* = U^k°\t)
является совпадение U^k°\t) при всех к, начиная с некоторого ко (Lf(X^ U^(t)) =
= 0; t — нулевое приближение), и неравенство
В многомерном случае θ G R*, к > 1, дело обстоит аналогичным образом.
Как и прежде, рассмотрим сначала соответствующую детерминированную
задачу: найти приближенное решение θ системы уравнений
Si(t) = 0, г = l,...,fc,
для непрерывно дифференцируемой функции s(t) = (si(£)> · · -isk{t))- Здесь,
полагая Δ = (Δι,..., Δ^) — t — 0, будем иметь
8i(9) = 0 = Si{t - Δ) = *(ί) - (A,gracU(i)) + ο(|Δ|).
Предположим, что dets'(0) φ 0, где
*'(*) = \\Sij(t)\\, ey(i) = ^.
Тогда при малых Δ будем иметь также dets'(£) φ 0 и можно записать в
векторной форме
s(t) = Δβ'(ί) + ο(|Δ|), βίίΧβ'Μ)"1 = Δ + ο(Δ).
Полагая аналогично предыдущему
U{t)=t-8(t){s4t))-\
получим
ί/(ί)-0 = Δ-5(ί)(5'(ί))-1=ο(|Δ|).
Это дает возможность перенести на многомерный случай все основные
результаты, полученные выше. В частности, сохраняет свою силу теорема 1,
в которой в определениях (2) под L"(X,t) и I(t) следует понимать
соответствующие матрицы.
Пример 1. Классификация частиц. Рассмотрим источник,
который излучает частицы двух типов: с вероятностью ρ — частицы типа А и
с вероятностью 1 — ρ — частицы типа В. Энергия частиц случайна и имеет
плотность /ι(χ) для частиц типа А и /2(2) для частиц типа В. Функции fi{x)
известны. Зарегистрировано η частиц с энергиями χι,...,χη. Чему равна
вероятность р? Функция правдоподобия здесь равна
/рРО = ПШъ) + (ι -р)/2(х<)),
t=l
§ 35. Приближенное вычисление о. м. п. 265
так что
η
/l(*i) ~ /г(х<)
γ'(υ n\-V m*i)-m*i)
(6)
Мы видим, что отыскание о. м. п. р* приводит к уравнению V = 0 степени
π - 1 относительно р, решать которое при больших η весьма сложно.
Воспользуемся теоремой 1. Для этого нам нужна какая-нибудь а. н. оценка р*.
Предположим, что
/
(Fi - F2)2 dx < оо,
где Fi(x) = / fi(t)dti и рассмотрим следующий естественный подход.
—оо
Определим р* как значение, минимизирующее
J'{F*(x) - F(x))2 dx, F(x)=pF1(x) + (l-p)F2(x). (7)
Приравнивая нулю производную от (7), получим / (F* — F) (F\ — F2) dx = О,
,_f(FZ-F2)(F1-F2)dx
Р f(Fi - F2)2 dx
Оценка ρ* является, очевидно, М-оценкой. Нетрудно видеть, что Ер* = ρ и
что
<* ~ P)V" ~ №-F2ydx · {8)
Из результатов §6-8 следует, что ρ* есть а. н. оценка, а предельное
распределение (8) совпадает с распределением
fw°(F{x)№-F2)dx
${Fx-F2Ydx ■
Следовательно, в силу теоремы 1 оценка
pl=p*-L(X,p*)(L"(X,p*)r\
где V определено в (6),
(/l(xi)-/2(xi))2
L" = -E
(ρ/ι(χί) + (ΐ-ρ)Λ(χί))
,U2'
266
Гл. 2. Теория оценивания неизвестных параметров
будет асимптотически эквивалентной о. м. п. р*. Коэффициент рассеивания
р\ будет определяться информацией
/«-/:
(Л(*)-/2(*))2 dx
p/i(x) + (1-p)/2(x)
и будет меньше, чем коэффициент рассеивания р*.
Пример 2. Предлагаем читателю аналогичным образом найти
приближение для о. м. п. параметра α распределения Коши Кад с плотностью
тг(1 + (а;-а)2)'
В качестве «предварительной» а. н. оценки можно взять выборочную
медиану ζ* (см. § 12 или §3, 8; оценку α* = χ здесь брать нельзя, так как Εαα*
не существует). Оценка
-1
αΙ = ζ*-1'(Χ,ζ·)(Σ,»(Χ,ζ*))
где
будет асимптотически эквивалентной о. м. п. а*. Так как
/(q)-/(l^W)'d.-l/· *' * = 1
1 ' У *»,lW π У (l+x2)5dI 2'
то коэффициенты рассеивания ζ* и α* будут равны соответственно (см. § 12)
(й-Ы'-©'· /"w=2' ©2>2·
Предлагаем читателю с помощью следствия 18.2 построить в явном виде
другую оценку, асимптотически эквивалентную о. м. п. а* и являющуюся
L-оценкой. Здесь в обозначениях следствия 18.2 будем иметь
ПХ) = ^ГЬ)' F(X)=i-+1-vctgX, F-4t) = ig[*(t-\)
'W 1+X2' W (1 + χ2)2 ·
Пример З. Каждый человек имеет кровь, принадлежащую одной из
четырех групп, которые обозначим через 0 (ноль), А, В, АВ. Наследование
групп крови управляется тремя генами: А, В, 0, при этом ген 0 «подавляется»
генами А и В. Поэтому если р, g и г — 1 — ρ — q обозначают вероятности
появления генов А, В и 0 у родителей, то вероятности появления групп
крови у потомка будут равны следующим величинам:
§ 35. Приближенное вычисление о. м. п.
267
Таблица 1
г (номер
группы)
1
2
3
4
Группа
0
А
В
АВ
Комбинации генов,
дающие эту группу
00
АА, АО
ВВ, ВО
АВ
Вероятности
г2
р2 + 2рт
q2 + 2qr ;
2pq j
Пусть ζ/χ, ζ/2, ^з> Щ — частоты появления соответствующих групп крови
в обследуемой популяции обшей численностью η человек. Как найти о. м. п.
для ρ и q? В нашем случае вероятности рг(0), θ = (ρ, g), появления г-й
группы крови и их частные производные по ρ и ς представлены в табл. 2.
Таблица 2
р.(0)
5р
dq
г
1
г2
-2г
-2г
2
р(р + 2г)
2г
-2р
3
g(g + 2r)
-ч
2т
4
2Р5
2<7
2р i
4
Поэтому для логарифмической функции правдоподобия L(X, 0)=У^ Щ \ир%(в)
получим
51/ __ γ-ν Z^i $Рг __ 2ζ/ι 2ΓΖ/2 2z/3 ΖΛ*
dp " pi 5p r p(p + 2r) g + 2r ρ '
(9)
dL _ γ-> z/^ 9p£ _ 2^i 2z/2 2rz/3 z/4
dq ^ pi dq r p + 2r q(q + 2r) g '
Приравнивая к нулю эти производные, мы придем к системе из двух
уравнений для Θ* четвертого порядка. Решение такой системы связано с
техническими трудностями. Поэтому проще воспользоваться теоремой 1. Для
этого заметим, что справедливы равенства
Pi=r2, pi +P2 = (p + r)2, Pi +рз = {q + r)2. (10)
Эффективные оценки для pi равны ρ* = щ/п. Подставляя в (10) эти оценки
и решая полученные уравнения, получим
Р* = Vp*+P2 " у/ΡΪ > 9* = λ/Ρι+Рз - у/Л ·
Так как р? есть а.н. оценка р,- (т.е. (р* -pi)>/n ©► *o,pi(i-pi))j то Р*> 9* в
силу теоремы § 5 также будут а. н. оценками для р, д.
268
Гл. 2. Теория оценивания неизвестных параметров
Чтобы воспользоваться теоремой 1, остается вычислить матрицу
(L"{X,9*))-1 или матрицу (ηΙ{θ*))-\ θ* = (ρ',ςΓ).
Приведем пример реальной выборки X, полученной в результате
обследования η = 353 человека.
Распределение людей по группам крови приведено в табл. 3.
0
121
0,343
А
120
0,340
В
79
0,224
Таб
АВ
33
0,093
л и ц а 3
Всего
353
1
Из этой таблицы находим р* = 0,241, q* = 0,167, г* = 1 — р* — q* = 0,592.
С помощью табл. 2 для элементов матрицы 1(9) при θ = 0* получаем
Σ
1
Ορί(θ)
dp J р№
δΡί(θ)\2 1
= 4 +
4r2
+
4g
2σ
р[р + 2r) q + 2r ρ
^ дрг(в) dPi(0) 1
4p
+
4r2
2p
η ■ / η ч + — = 13>761>
p + 2r q(q + 2r) q
4-
4r
4r
•^ dp c?g pi(^) * p + 2r q + 2r
Отсюда находим |/(0*)| = 130,512,
+ 2 = 2,585.
ГНР)
0,105 -0,020
-0,020 0,076
Из формул для — и — (см. (9)) получаем
L'(e*,X) = (25,443; 34,161),
так что для второго приближения #j имеем
0? = 0· + -L'(0*, А")7_1(0*) = (0,246; 0,173).
η
Это дает нам в дополнение к табл. 3 оценки, приведенные в табл. ЗА.
Таблица ЗА
(И)
(12)
МП
р№)
0
0,351
0,337
А
0,343
0,347
В
0,226
0,231
АВ
0,080
0,085
Применение еще одной итерации вида (12) оценку Θ* уже не меняет (в
рамках используемой нами точности), так как
L'(e\,X) = (-0,076; -0,167)
(ср. с (11)), так что третье приближение для Θ* и все последующие будут
совпадать с Θ*.
§ 36. Результаты §33, 34 для многомерного параметра 269
§ 36. Результаты § 33, 34 для случая многомерного параметра
В этом параграфе мы перенесем на многомерный случай все основные
результаты §33, 34. Излагаться эти результаты будут в той же
последовательности, что и в указанных параграфах, при этом мы будем
останавливаться лишь на тех моментах, где многомерность либо меняет формулировку
результата, либо требует модификации рассуждений.
Итак, пусть θ £ Θ С RA, к > 1. Формулировки условий (Αμ), (Ас), (Ао),
как и определения отношения правдоподобия
и расстояния Хеллингера
г(и) = р(Рв+и,Ре) = J{y/fe+u(x) - ^/Μχ))2μ{άχ),
с размерностью никак не связаны.
1. Неравенства для отношения правдоподобия и свойства о.м.п.
(результаты §33). Для изучения поведения функции Z{u) в окрестности нуля нам
понадобится следующее условие: функция \/fe{x) дифференцируема по 0,
информационная матрица Фишера
т = \ы°)\\ =
E°w^e)w/{xi'e)
(1)
при всех θ Ε Θ ограничена и положительно определена.
При этом условии из теоремы 31.ЗА следует, что при всех θ
Ο<0<ίπτΟ = 7SupSp/(0) < °о. (2)
Μ 4 Θ
4
Здесь и в дальнейшем \и\ означает евклидову норму \и\ = \JU\ + - ·
вектора и = (щ,..., и&).
Первое утверждение теоремы 33.1 и его доказательство переносится на
многомерный случай без каких-либо изменений, так как они с размерностью
по существу не связаны.
Теорема 1. Если выполнено (2), то
ΈθΖιΙ2{η) < e"n^l2/2.
Для обобщения теоремы 33.2 нам понадобится дополнительное условие,
которое состоит в том, что
7 = supE*|i/(xi10)|e<oo (3)
θ
при некотором s > к.
270 Гл. 2. Теория оценивания неизвестных параметров
Теорема 2 (аналог теоремы 33.2). Если выполнены условия (2), (3),
то при любых 2, η ^ 1
Р, ( sup Ζ (-уЛ > ez) ζ Π(β-Ζ + е'ж12)е^\ (4)
где с < оо, β > 0 зависят лишь от к, g и s.
Для доказательства этого утверждения в одномерном случае мы использо-
1
оценивать sup р(и) через значения ρ(0) и / \pf(u)\du>
«€(0,1) J
Такой же подход в многомерном случае наталкивается на трудности,
поскольку максимальное значение р(и) в некоторой области D С К*, к > 1, не
удается оценить, вообще говоря, через значения р{щ), щ £ D и интеграл
от |p'(u)| (p'(u) = gradp(ii)) по какой-нибудь одной фиксированной кривой
из D. Существует по крайней мере три пути преодоления этой трудности.
Первый является полной аналогией одномерному подходу и состоит в
использовании оценки вида (в этой формуле мы для простоты ограничиваемся
двумерным случаем к = 2)
вали возможность
иек0
ι ι
du\du2,
supp(U)<|p(0)|+/|^^|dn2 +
€Xo,i J \ <™2 |
О
J дщ J J \duidu2
о оо
где и = (111,112), -Код — единичный куб: К^\ = {и : 0 ^ щ ζ 1, j =
= l,...,fc}. Однако для использования этого подхода мы должны
предполагать существование производных k-το порядка функции Iq(x) {fe{x)) (см.
определение функции ρ в § 33) и уметь оценивать нужные нам средние
значения производных функции ρ /-го порядка, / ^ к.
Второй путь использует неравенства, восходящие к С. Л. Соболеву, об
оценке sup p{u) через значения р(0) и
u£Kotx
/ \p'{u)\sdu (p'(u) = gradp(u), u = («i,...,ufc))
Κο,ι
при некотором s > к (при s = к оценка невозможна). При этом, разумеется,
мы должны располагать оценками для E^|p'(u)|s при s > к*).
В этой книге мы остановимся на третьем варианте, использующем
некоторые идеи А. Н. Колмогорова об оценке распределения максимума
случайного процесса. Ввиду того, что доказательство теоремы 2 занимает довольно
много места, мы поместили его в приложение VI.
Этот вариант доказательства приведен в испанском издании [19] книги.
§ 36. Результаты § 33, 34 для многомерного параметра 271
Доказательства утверждений о состоятельности о. м.п. и об оценках для
моментов п. 33.2 с размерностью не связаны. Сами утверждения сохранятся
в следующем виде.
Теорема 3 (аналог теоремы 33.3). Если выполнены условия (2), (3),
то при любых ν, η ^ 1 справедливо (33.6) с заменой числа #/4 на β (см.
теорему 2).
Утверждения следствий 33.1, 33.2 сохраняются полностью с той же
заменой д/4 на /?.
2. Асимптотические свойства отношения правдоподобия (результаты
§ 33, 34). Под условиями (RR) в многомерном случае будем понимать
совокупность следующих условий.
1. Условия (Ао), (Ас), (R).
2. Непрерывная дифференцируемость второго порядка по θ внутри Θ
функции l(x,t) для п. в. [μ] значений х. При зтом предполагается, что
производные
9^(М)
№г)- dUdtj
допускают мажоранту /(я), не зависящую от t: \l"j(x,t)\ ^ /(χ), для
которой интеграл
Е;
;/(χι) = / 1(χ)^{χ)μ(άχ)
сходится равномерно*) по t £ Θ.
3. Кроме того, будем предполагать, когда зто потребуется, что
выполнено условие (3).
Как и в одномерном случае, нам понадобятся следующие два свойства,
вытекающие из (RR).
1. Возможность дважды дифференцировать по θ под знаком
интеграла в равенстве
J /θ{χ)μ{άχ) = 1,
означающая справедливость соотношений
/£л<«м*) = о, /грилем*»-а <5)
2. Равномерная сходимость интеграла 1{θ):
supE^xi,*))2; \№ι,θ)\ > iV] -> О (6)
θ
при Ν -> οο, где 1[(χ,θ) = —^—.
Доказательство этих свойств отнесено в приложение V. Для упрощения
изложения они могут быть введены в условия (RR).
** См. сноску о равномерной сходимости в §34.
272
Гл. 2. Теория оценивания неизвестных параметров
В силу равенств
,!,„ дч 1 dfejx)
/β (a;) dfli
ij[,) feMMiMj β(χ) d9i dOj '
из соотношений (5) следует, что
Εθ1'ί(χ1,θ) = 0,
Е,*£(хь0) = -ЕоЩхивЩхив) = -WO).
Как и в одномерном случае, условия (RR) означают, что будут иметь
место утверждения теорем 2, 3 об оценках для sup Z(v/y/n) и для у/п(в* — 0).
\v\^u
При выполнении условий (RR) справедливы также следующие аналоги
лемм 34.1, 34.2.
Лемма 1. Функции 1"Λχ,θ) непрерывны «в среднем»:
Ε*α£(χι)->0
равномерно по θ при Δ -> 0, гдеш'Пх) = max sup \1'1Лх,в+и) — Ι'^(χ,θ)\.
ij θ,\η\<Δ
Доказательство в точности повторяет рассуждения леммы 34.1. <
Положим
χΐ'{Χ,θ + ωΔ),ω)-{Σ,'{Χ,θ),ω)
7π(Μ) = sup
ηΔ
+ ωΙ{θ)ω'
Лемма 2 (аналог леммы 34.2). Пусть выполнены условия (RR),
δη > 0 — любая последовательность, сходящаяся к нулю. Тогда для
Ίηίδη,θ)—>0, Ίη{δη,θ*)—»0.
П.Η. П.Η.
В этих соотношениях значения Ι(θ) и Ι(θ*) можно заменить одно
другим.
Доказательство. Как и в одномерном случае, нам достаточно
убедиться, что 7п(#п) -► 0, где
7п(*) = sup
(Ι,'{Χ,θ + ωΔ),ω) - {1'{Χ,θ),ω) ωΣ"{Χ,θ)ωτ
ηΔ
η
§ 36. Результаты §33, 34 для многомерного параметра 273
Но 7п(^п) ^ — 2_1 y^^ni^)!^^'!' где ωδ(χ) есть максимальный модуль
^ I ·
непрерывности функций Ι^(χ,θ). Так как
Y^\ukUj\ ^ к\и>\2 = к,
то
г
Дальнейшее доказательство основано на лемме 1 и в точности повторяет
рассуждения леммы 34.2. <
Обобщением теоремы 34Л на многомерный случай здесь является
Теорема 4. Пусть выполнены условия (RR), δη > О, η = 1,2,..., —
любая последовательность, сходящаяся κ нулю. Тогда если X €= Р$, то
для и таких, что \и/у/п\ ^ δη,
Y(u) = In Ζ (^=\ = (ξη,η)-^ηΙ(θ)ητ(1 + εη(Χ,θ,η)), (8)
\εη{Χ,θ,υ)\^εη{Χ,θ)—>0,
-j=gra,dL(X,e) = -j^i
ξη = -^gradL(X,e) = -^Ь'{Х,в) θ- Φ0)/(β).
Значение и* = л/п(в* — θ), при котором Υ (и) достигает максимума,
представимо в виде
η·=ξηΓ\θ){Ε + εη(Χ,θ)), ε„(Χ,0)^>Ο, (9)
где Ε есть единичная матрица. Кроме того,
2Υ(η*)=ξηΓ1(θ)ξϊ(1 + εη(Χ,θ)) ^ξΓ1(θ)ξτ ^Hfc, ξ ^ Фот. (10)
Наряду с (8) справедливо представление
Y(u) - Υ(u*) = |(и - ti*)/(0)(ti - tx*)T(l + εη(Χ, θ, и)),
\εη{Χ,θ,η)\^εη(Χ,θ).
Во всех приведенных утверждениях Ι(θ) можно заменить на 7(0*).
В этом параграфе мы, как и в §34, понимаем под εη(Χ,θ) различные
последовательности, обладающие свойством εη(Χ, θ) —> 0 относительно Ра.
п.н.
Отметим также, что главную часть в (8) можно записать в виде
ξηητ - \и!{в)иТ = -1-{и - ξηΓι(θ))Ι(θ)(η - ξηΓ1(θ))τ + \ξηΓ1№η·
274
Гл. 2. Теория оценивания неизвестных параметров
Это соответствует плотности многомерного нормального распределения со
средним ξηΙ~ι(θ) и матрицей вторых моментов Ι~ι(θ).
Доказательство теоремы 4 вполне аналогично доказательству
теоремы 34Л. Из леммы 2 при Δ < δη получаем
{Ь'{Х,в + Аи>),ш) = (Ζ/(-Μ),ω) -ηΔωΙ{θ)ωτ{1+εη{Χ,θ,Αω)),
\εη(ΧΑΔω)\<εη(Χ,θ).
Интегрируя это равенство по Δ от нуля до \u\/y/n и полагая ω = гх/|гх[,
получим
ь(х,0+-у=)-ЦХ,в) = ί {L'{X,0 + Au),u)dA =
о
II I |2
= ЩЬ\Х,9),Ш) - ]-^-ωΙ(θ)ωτ(1 + εη(Χ,θ,η)) =
= (ξη,η)-^ηΙ(θ)ητ(1+εη(Χ,θ,η)), \εη(Χ,θ,η)\^εη(Χ,θ).
Здесь по многомерной центральной предельной теореме (см. приложение IV)
1 п
Представление (8) доказано. Остальные утверждения теоремы доказываются
точно так же, как в теореме 34.1, с учетом продемонстрированных
изменений, связанных с многомерностью. Соотношение
СГ'№Т§Щ
в (10) следует из свойств нормального распределения (см. п. 12.4). <
В связи с соотношением (10) полезно также следующее
Замечание 1. Матрица Ι~^1(θ) вместе с Ι(θ) является положительно
определенной, и существует матрица /_1/2(0), являющаяся корнем квадратным из /^(0),
т.е. удовлетворяющая соотношению
Γ1'2(Θ)Γ1'2(Θ)=Γ1(Θ).
Действительно, если некоторая матрица Μ > 0 (положительно определена), то
существует ортогональная матрица С, для которой СМСТ = diag (λι,..., λ*) есть
диагональная матрица с положительными элементами λ* > 0 на диагонали. Если
положить теперь М1/2 = CTdiag(A/ ,.,.,λ/ )С, то получим, очевидно, корень
квадратный из М.
Пользуясь этим и симметричностью матрицы Ι~ι(θ), мы можем (10) записать
в виде
(ξηΙ-1/2(θ))(ξηΓ1/2(θ))Ύ.
§ 36. Результаты § 33, 34 для многомерного параметра 275
Здесь вектор ηη = ξηΙ~1'2(θ) есть, очевидно, нормированная сумма η независимых
одинаково распределенных случайных векторов с нулевым средним и матрицей
вторых моментов
Εβ(ξηΓ1/2(θ))τ{ξηΓ1/2{θ)) = ^I-l,2{9)CinI-l/2{9) = Ε,
поскольку
Ee£f„ = Е,(*'(х1,*))Т(/'(хь0)) = Ι(θ).
Это означает, что по многомерной центральной предельной теореме ξηΙ"1^2(θ) ©►
& Фо.я-
Теорема 5 (аналог теоремы 34.2). Пусть выполнены условия
теоремы 34.2 для многомерного θ £ Rk и при a = /3/2 (β определено в
теореме 2). Тогда
/Β/«(«·-«),(β + ^)ζ(^)π(Λ)-
= eY^q{9) \iw(u*-u)expi-^(u-u*)I(e)(u-u*)T\ x
χη(άη) + εη{Χ,θ)]. (11)
Если П есть мера Лебега, TL(du) = du, то
J=^^^eY^q(e)(Ew(V)+en(X,e)), (12)
где εη(Χ,θ) —► 0, η €= Фо,/-1^) (последовательность εη(Χ,θ) является
векторной, если w(t) есть вектор-функция).
Доказательство теоремы 5 проходит так же, как доказательство теоремы
34.2, поскольку последнее с размерностью не связано.
3. Свойства о.м.п. (результаты §33, 34). Здесь мы будем предполагать
везде выполненными условия (RR).
Аналог теоремы 33.5 будет иметь следующий вид.
Теорема 6. О.м.п. Θ* является асимптотически нормальной
оценкой, при этом сходимость
η*^{θ*-θ)^ θ>Φ0|/-ΐ(*)
имеет место вместе со сходимостью моментов любого порядка. В
частности,
Εθη{θ* - θ)τ(θ* -θ)-> Г1 (θ). (13)
Более того, для любой непрерывной функции w(t) такой, что \w(t)\ <
< еРЩ /2 (число β определено в теореме 2),
Eew(u*) -> Ειν{η), η €= Φ0|/-ι(β).
276
Гл. 2. Теория оценивания неизвестных параметров
Соотношение (13) означает, что 0* Ε ΛΤφ,2·
Утверждение теоремы 6 следует из теоремы 4 (см. (9)) и многомерного
аналога следствия 33.2, вытекающего из теоремы 3 (ср. с доказательством
теоремы 33.5). <
Определим класс Kq как совокупность оценок 0*, для которых смещение
6(0) = (6ι(0),..., Ьк{в)) = ΈΘΘ* - 0 обладает свойствами
при η -> со.
Аналог теорем 33.6, 33.7 имеет здесь ту же самую форму.
-^ .^ —
Теорема 7. 0* является a.R-э. оценкой. Кроме того, 0* Ε Ко
является асимптотически эффективной в К$.
Асимптотическая R-эффективность 0*, эквивалентная (13), очевидно,
имеет место. Доказательство принадлежности 0* Ε Kq и асимптотической
эффективности в ifo происходит совершенно аналогично одномерному
случаю.
Перейдем теперь к свойству асимптотической байесовости.
Асимптотическая Д-байесовость оценки 0* означает по определению, что (ср. с § 30)
Е(0* - 0)т(0* - 0) = ^ + о QV J = frl{t)Q{dt). (14)
Асимптотическая байесовость 0* означает
limsup[nv(0*) - nv(0g)] ^ 0, (15)
п—юо
0д — байесовская оценка, минимизирующая г;(0*) = Е(0* — θ)ν(θ* — 0)т
для любой неотрицательно определенной матрицы V.
Теорема 8 (аналог теоремы 33.8). 0* является асимптотически
R-байесовской оценкой. Если априорное распределение Q имеет
плотность относительно меры Лебега на Θ, то Θ* — асимптотически
байесовская оценка.
Доказательство вполне аналогично теореме 33.8. Соотношение (14)
для 0* = 0* следует из того, что
lim Еп(0* - 0)т(0* - 0) = Ε lim Εθη{θ* - 0)τ(0* - 0) = ΕΓι(θ) = J.
η~>οο η~>οο
Предельный переход под знаком математического ожидания (т.е.
интеграла) здесь законен, так как величина Ε#η(0* — 0)т(0* — 0) ограничена
постоянной, не зависящей от η и 0 (ср. со следствием 33.2).
Чтобы доказать (15), заметим, что в соответствии с §30 интегральное
неравенство Рао-Крамера в случае, когда Q имеет плотность, имеет вид
Еп(0*-0)т(0*-0) > J + o(l).
§ 36. Результаты § 33, 34 для многомерного параметра 277
Это означает, что
nv{e*Q) ^ Y^VijJij +o(l),
^^
где \\Jij\\ = J, H^ijll = K С другой стороны, в силу (14) при θ* = Θ*
ην(θ*) = ^VijJij + о(1).
Из этих соотношений, очевидно, вытекает (15) при θ* = 0*. <
Аналоги теорем 33.9, 34.3 также будут иметь место. Например, из
теоремы 5 вытекает
Теорема 9 (аналог теоремы 34.3). Пусть X ^ Р# и θ есть
произвольная внутренняя точка Θ. Если q(t) — произвольная непрерывная и
положительная внутри Θ плотность априорного распределения Q, то
где 9q есть байесовская оценка, соответствующая q(t).
Асимптотическая минимаксность Θ* может быть установлена аналогично
теореме 34.3 с помощью многомерного аналога критерия асимптотической
минимаксности в следствии 30.3:
lira supEen(0* - θ)ν(θ* - θ)τ = supV/^1^·,
\\^г(в)\\ = ГЩ,
и равномерного характера сходимости в (13), которая будет вытекать из
результатов следующего параграфа.
Свойства асимптотической оптимальности Θ* в случае многомерного
параметра 0, когда его размерность к велика, следует использовать с
осторожностью. Нужно следить за тем, чтобы отношение п/к было велико (число
наблюдений на один скалярный параметр). В противном случае выводы
могут оказаться ошибочными.
Пример 1. В лаборатории проверяется концентрация η растворов.
Каждая из неизвестных η концентраций μι,.. .,μη проверяется дважды.
Предполагается, что дисперсия σ2 всех η наблюдений (xi,yi),..., (xn,yn) одна и
та же, а сами наблюдения независимы и нормально распределены, так что
/β(Χ) = ^4^βχρ{~έΣκχ«-^)2+(^-^)2]}'
где
θ= (μι,...,μ„,σ ).
О. м. п. для μι здесь равны
278
Гл. 2. Теория оценивания неизвестных параметров
Очевидно, эти оценки являются несмещенными, но не состоятельными.
0. м. п. для σ2 равна
1 2
(σ2)* = — ]Г(Хг-Уг)2"^ У ПРИ П->°°>
Эта оценка с большой надежностью дает ложное значение для параметра σ2
(вдвое меньшее).
4. Приближенное вычисление о.м.п. Как мы видели в §35, содержание
этого параграфа в многомерном случае полностью сохранится.
5. Свойства о.м.п. при отсутствии условий регулярности (результаты
§14, 16). Условия состоятельности 0*, сформулированные в теоремах 14.1,
14.2 и в п. 16.2, с размерностью по существу не связаны. Доказательство
этих теорем полностью сохраняется с точностью до очевидных изменений,
связанных с тем, что множество θ надо покрывать теперь (в силу
условия (Ас)) не конечным числом интервалов, а конечным числом шаров. То
же самое можно сказать и по поводу теоремы 16.2 и следствий 16.1-16.6.
§ 37. Равномерность по θ асимптотических свойств отношения
правдоподобия и оценок максимального правдоподобия
В последующих рассмотрениях, главным образом в §53-55 следующей
главы, будут полезны утверждения § 33, 34 и 36 в их равномерной по θ
форме. Большинство этих утверждений (скажем, утверждения о предельном
Ря-распределении (0* — 0)у/п) были получены в предположении, что θ —
фиксированная точка из Θ. Нас будет интересовать теперь, что будет
происходить, если θ не фиксировано, а меняется вместе с п. Ясно, что при этом
вместе с η будут меняться и распределения Р#, так что каждая выборка Хп
будет иметь «свое» распределение при η = 1,2,...
Мы приходим, таким образом, к схеме серий (см. [17, гл. 8]), для которой
формулировки основных предельных теорем будут уже несколько иными.
В частности, усиленный закон больших чисел, вообще говоря, теряет свой
смысл, так как рассматриваемые случайные величины перестают быть
заданными (при разных п) на одном вероятностном пространстве.
1. Равномерные закон больших чисел и центральная предельная теорема.
Пусть Χ ^ Ρ*, ηη# = ηη(Χ,θ).
Определение 1. Мы будем говорить, что последовательность ηηβ
равномерно сходится по вероятности к постоянной а(0), если для любого
ε > О при η —> оо
supP*(ton|0-a(0)| >e) -> 0.
θβθ
Это соотношение будем записывать в форме «τ/η,Α —► я(0) равномерно
по Θ».
Определение 2. Мы будем говорить, что ηηβ сходится по
распределению к случайной величине щ равномерно по Θ, если для любой
непрерывной и ограниченной функции φ при η —> оо
*νρ\Εθφ{ηη,θ) - Εφ(ηθ)\ -> 0. (1)
θ
§ 37. Равномерность по θ асимптотических свойств о. м. л. 279
Это соотношение будем записывать в виде «ηηβ => щ равномерно по 0».
Такой же смысл будем придавать соотношению «77^0 ©► G$ равномерно по 0»,
где G# означает распределение щ.
Мы предоставляем читателю самостоятельно убедиться, что если
функции распределения ηβ непрерывны равномерно по 0, то соотношение (1)
эквивалентно
suplPfl^ < χ) - Ρ(ηΘ < х)\ -> 0.
Отметим, что равномерная сходимость ηηβ —>· α(β) и равномерная схо-
димость по распределению ηηβ => α(θ) к вырожденной случайной
величине α(Θ) эквивалентны.
Отметим также, что для равномерной сходимости сохранятся все
основные теоремы непрерывности. Например, если Η есть непрерывная функция,
то из равномерной сходимости ηηβ => щ следует равномерная сходимость
Η(ηη,θ) => Η(ηθ). (2)
Эти утверждения вытекают непосредственно из определений.
В приложении IV доказаны следующие «равномерные» предельные
теоремы.
Пусть X g= Р# и α(χ,θ) — заданная измеримая вектор-функция: Χ χ
χ θ —> Rl. Рассмотрим суммы
*n(0) = J>(x.,0)
независимых случайных векторов, зависящих от параметра θ Ε Θ как
непосредственно через функцию α(ζ,0), так и через распределение хг €= Р#.
Напомним, что интеграл / ψ(χ,θ)1?ο((Ιχ) мы называем сходящимся
равномерно по θ в области Θ, если
sup / \ψ(χ,θ)\Ρθ{άχ) ->0
ее® J
ее®
\ψ(χ,θ)\>Ν
при N —> оо.
Теорема 1 (равномерный закон больших чисел). Если интеграл α(θ) =
= / α(χ^θ)Ρθ(άχ) сходится равномерно по θ Ε θ, то при п —> оо
^ -> α(θ)
Π Ρθ
равномерно по Θ.
Следствие 1. Если последовательность {θη} Ε Θ, то в условиях
теоремы 1
9п (
п
- а(вп)
> ε -> 0.
280
Гл. 2. Теория оценивания неизвестных параметров
Этот факт будем обозначать
sn(0n)
- α(θη) —► 0.
При рассмотрении центральной предельной теоремы для сумм sn(6)
нам будет удобнее считать α(θ) равным нулю. (Это не есть ограничение
общности, так как мы можем рассмотреть новые слагаемые α1(χι^θ) =
= α(χχ,θ) — α(#)0 Положим σ2(θ) = Έβ(ατ(χι1θ)α(χι,θ)) и обозначим
через aj(xi,0), j = 1,2,...,/, координаты векторов a(xi,0).
Теорема 2 (равномерная центральная предельная теорема). Пусть ин-
%,0 = —~ =*Ώθ <^ φΟ,σ2(0)
у То
равномерно по Θ.
2. Равномерные варианты теорем об асимптотических свойствах
отношения правдоподобия и оценок максимального правдоподобия. Заметим
предварительно, что при выполнении условий (RR) результаты §33 являются
равномерными по θ по самой своей форме, так как правые части неравенств
в теоремах 33.1-33.3 (и в теоремах 36.1-36.3) от θ не зависят. Перейдем к
результатам §34, 36 об асимптотическом поведении Z(u/y/n).
При этом под условиями (RR) в одномерном случае будем понимать
условия (RRJ (см, §34).
Утверждения лемм 34.1, 36.1, 34.2, 36.2 можно сделать равномерными
по Θ.
Лемма 1. При Δ —> 0
supE^(xi)^0, (3)
θ
где ω^(χι) есть максимальный модуль непрерывности функций 1"Λχ,θ).
Доказательство. Справедливость (3) при фиксированном θ доказана
в лемме 36.1. Если допустить при этом отсутствие равномерности по 0, то
мы придем к существованию ε > 0 и последовательностей θη -+ θ Ε Θ,
Δη —>· 0 таких, что
Ε0ηω£η(χι)>ε· (4)
Полагая для краткости и>д (χι) = и/7, получим
Εθηω" = Efln(a;";/6n(xi) < 2/θ(Χι)) + Εβη(α/';/*„(χι) >
> 2/e(Xl),J(Xl) ^ Ν) +E0>";/0„(xi) > 2/„(χι),/(χι) > Ν).
Здесь первое слагаемое не превосходит 2Έιρω" и сходится к нулю в силу
леммы 36.1, второе — не превосходит 2NJn, где
Jn= Ι /θη(χ)μ{άχ) = 1 - / ίθη{χ)μ(άχ) -» 0
Λη(χ)>2Λ(») Λ„(*)^2/,(χ)
§ 37. Равномерность по θ асимптотических свойств о. м. п. 281
по теореме о мажорируемой сходимости. Наконец, последнее слагаемое не
превосходит Ε^η(2/(χι); 1{χι) > Ν) и в силу (RR) может быть сделано
выбором N сколь угодно малым. Мы получили противоречие с (4), доказывающее
лемму. <
Лемма 2. Утверждение леммы 36.2 сохранится, если в нем п. н.
сходимость заменить сходимостью 7п(^п>0) —> О, 7п(^п>#*) —* 0, равно-
Ρθ Ρθ
мерной по Θ.
Доказательство. Будем следовать доказательству леммы 26.2.
Заметим предварительно, что в силу теоремы 1 и равномерной сходимости
интеграла в (RR)
та _ -т
Π Ρθ
равномерно по θ (сходимость матриц понимается поэлементно). Кроме того,
из теорем 33.3, 36.3 вытекает, что Θ* —> θ равномерно по Θ. Отсюда следует,
Р$
что в соотношении 7п(^п>#) —> О (см· лемму 36.2) можем Ι(Θ) заменить на
Рв
L"{9)/n и на Ι(θ*).
В силу неравенства (36.7) задача оценки Ύη{δη,θ) сводится к оценке
где и;д(#,0) — максимальный модуль непрерывности функций 1"Λχ,θ). Из
неравенства Чебышева получаем
supP^'JX) >ε) < -supE^(xbe).
θ ε θ
Но в силу леммы 1 supE^o;^(xi,0) -» 0 при Δ -* 0. Это доказывает, что
θ
ωΙ(Χ)—>0, Ίη(δη,θ)->0 (5)
равномерно по 0.
Далее, из неравенств (34.6) следует, что задача оценки 7п(^п? #*) сводится
к оценке ω" ,- ЛХ)· Так как Θ* — θ —> 0 равномерно по 0, то из (5)
получаем, что
равномерно по Θ. <
Теорема 3 (аналог теоремы 36.4). При выполнении условий (RR)
утверждения теоремы 36.4 сохранятся при следующих изменениях:
εη(Χ,θ) —> 0 равномерно по 0, ξη ©► Фо>/(0), 2Y(u*) ©► Н^ равномерно
Ρθ
по Θ.
282 Гл. 2. Теория оценивания неизвестных параметров
Доказательство теоремы полностью основано на лемме 2 так же,
как доказательство теоремы 36.4 — на лемме 36.2. Поэтому требуемое
доказательство получается путем внесения очевидных изменений в
доказательство теоремы 36.4, связанных с заменой (вытекающей из леммы 36.2)
сходимости εη(Χ, θ) —ϊ 0 на равномерную сходимость εη(Χ, θ) —> 0. Кроме
П.Н. Рд
того, надо добавить, что
1 п
равномерно по θ в силу теоремы 2 и равномерной сходимости (36.6)
интеграла Ι(θ) (это есть матрица вторых моментов для ί'(χι,0)), которая
вытекает из условий (RRW) (см. приложение V). Отсюда и из замечаний,
касающихся (2), получаем равномерную сходимость
2У(и*)©>НЛ. <
Те же изменения, что и в теореме 3 (по сравнению с теоремой 36.4),
могут быть внесены в теоремы 36.5, 36.6.
Приведем здесь следующие два следствия теоремы 3.
Теорема 4.
ν,* = ν^(θ*-θ)&Φ0;-4θ) (6)
равномерно по Θ. При этом для любой функции w(x), непрерывной п. в.
относительно меры Лебега и такой, что |ги(а;)| < Се^х\ /2 (значение
β > 0 определено в теореме 36.2), выполняется
sup \Egw{u*) - Ευ)(ηθ)\ -> 0, (7)
θ
где щ ^ *o,/-4*)-
Доказательство. Первое утверждение вытекает из соотношений
ν* = ξηΓι{θ)№ + εη{Χ,θ)),
|εη(Χ,0)| —>0, ξη ©► Φ0|/(*)ι
равномерных по θ и содержащихся в теореме 3.
Чтобы доказать второе утверждение, допустим, что (7) не верно. Тогда
найдутся δ > 0 и последовательность θη —> θ Ε Θ такие, что
|Eenti;(tx*)-Eti;(WJ|>i (8)
при всех п.
Но ΦΟ)/-ΐ(0η) => ΦΟ)/-ΐ(0) и, стало быть, в силу (6) Р#П-распределение
и* (w(u*)) слабо сходится к распределению ηο (ΐϋ(η$)). Кроме того, по
следствию 33.2 (см. также §36)
π 3/2/ .ч ^ х, |3(u*)2/3
supE^iud/J(u*) ^supEaexp1 —^^
θ
4
< Ci < 00.
§ 37. Равномерность по θ асимптотических свойств о. м. п. 283
Отсюда и из теорем непрерывности для моментов следует, что
Eenw(u*) -4 Eiu(rfe).
Так как Ewfyen) -> Егу(%), то полученное соотношение противоречит (8). <
Пусть Ап С Л'71.
Теорема 5. Если Ρ#(Αη) -4 0, то при любом фиксированном N
sup Pe+u/VE{An) -+ 0.
Это свойство последовательностей распределений P^^w/v^n ПРИ п ~~> °°
называется контигуалъностъю (см. [100]). Мы будем использовать его в
главе 3.
Доказательство. Имеем
< Ее f Z f-J0 ; Ап η {У(и) < с}) + Pe+u/VE(Y(u) > с) <
<ecPe(An)+P,+u/v^(F(u)>c).
Так как Р#(ЛП) —» 0, то для доказательства теоремы нам надо рассмотреть
лишь sup Рв+и/^(У(и) > с)· Согласно теореме 3 равномерно по и
Y(u) = (£„,*) - \ηΙ{θ)ητ (l + en ^χ,θ+^У) & Φ_ισ2,σ2, (9)
где σ2 = uI(9)uT ^ N2Ak(6) при |u| ^ JV, Λ*(0) — максимальное
собственное число матрицы Д0). Так как Φ_ισ2 σ2((ο,οο)) < Ф0)(Т2((с, 0)), то в силу
равномерности в (9)
lim sup Т?в+и/у/п{у(ц) > с) < SUP фо,^((с,оо)) = Фо,лг2Ль(0)((с,оо)).
Это значение выбором с может быть сделано сколь угодно малым. <
3. Некоторые следствия.
1) В §33 была сформулирована теорема 33.7, в которой утверждалось, в
частности, что θ* Ε if0, где К0 есть класс асимптотически центральных
оценок, определяемый соотношением (рассматривается одномерный случай)
ρθ(β* > θ) _> I
284
Гл. 2. Теория оценивания неизвестных параметров
равномерно по 0. Из теоремы 4 вытекает, что упомянутая часть теоремы
верна, так как
Ρθ(θ* >θ)= Рв(уД(в* - θ)Γι'2{θ) > 0) -»> Φο,ι((0,οο)) = l-
равномерно по 0. <Ι
2) В § 34 была сформулирована теорема 34.4 об асимптотической мини-
максности 0*. Для доказательства этой теоремы нужно установить
справедливость леммы 34.3 о том, что
lim supEen{9* - θ)2 = sup Г1 {θ), (10)
n-ЮО 9еГ деГ
где Г — любой отрезок из Θ. Но это утверждение есть прямое следствие
равномерной по θ Ε Θ сходимости Ε^η(θ* — θ)2 —>- /_1(0), которая делает
законным предельный переход под знаком sup
еег
lim s\xpEen(e* - θ)2 = sup lim Εθη(θ* - θ)2 = sup/_1((9). <
П-ЮО Θ£Γ деГ П-ЮО деГ
Утверждение, аналогичное (10) и обеспечивающее асимптотическую
минимаксность 0*, будет иметь место, очевидно, и в многомерном случае:
lim supE*n(0* - θ)ν(θ* - 0)т = sup Υ VijIf.1 (θ),
n-уоо веГ 9еГ t—' J
\\ΐΓ3\θ)\\=ι-4θ),
для любой матрицы V.
§ 38.* О статистических задачах, связанных с выборками
случайного объема. Последовательное оценивание
Тот факт, что выборки случайного объема возникают на практике и
являются естественными, подтверждают примеры 25.2, 28.3. Еще один пример
связан с так называемым последовательным оцениванием. Оно применяется
в тех случаях, когда мы можем производить наблюдения последовательно —
одно за другим, и когда мы заинтересованы в минимизации числа этих
наблюдений, скажем, в силу их высокой стоимости. При этом наряду с
правилом оценивания (т.е. конструкцией оценки 0*) мы должны задать правило
остановки эксперимента. Эти правила могут быть различными: например,
можем суммировать заданные стоимости с(х^) наблюдений хг- до тех пор,
пока не исчерпаем некоторое допустимое количество t. В этом случае
момент ν остановки (номер последнего наблюдения или объем выборки) будет
определяться как
min < к : Y^ c(xi) ^ W
— это есть «время первого прохождения уровня t» в блуждании со
скачками с(хг) (см. [17, гл. 9]). Можно суммировать «информации» /(х^,0) =
= (Ζ'(χί,0))2 и прекращать наблюдения, когда будет достигнут заданный
уровень, и т.д.
§ 39. Интервальное оценивание 285
В этих примерах ν есть марковский момент, т. е. \у > п} £ σ(χι,..., хп).
Это есть одно из основных предположений, при которых рассматриваются
задачи последовательного оценивания. При этом предположении и
выполнении ряда дополнительных, менее существенных условий сохраняется
неравенство Рао-Крамера в виде
где Θ* = 0*(xi,.. .,х„) — несмещенная оценка 0, 7(0) — информация
Фишера. Доказательство этого неравенства вполне аналогично
доказательствам § 26; надо лишь для вычисления информации Фишера, содержащейся в
выборке (χι,.. .,Χί/), воспользоваться тождеством Вальда (см. [17, §14.2]).
Если ν зависит от некоторого параметра £, как это было в примере 28.3,
так что ν —► оо п. н. при t —> оо, то возможно построение асимптотически
оптимальных оценок со среднеквадратичной погрешностью, асимптотически
эквивалентной (Ι(θ)Έι/)^1.
§ 39. Интервальное оценивание
1. Определения. До сих пор мы изучали свойства и способы отыскания
наилучших точечных оценок неизвестного параметра 0, который определяет
распределение Р# из семейства V = {Р#}, соответствующее выборке X.
Точечные оценки используются в тех случаях, когда мы должны назвать
некоторое число 0*, предназначенное для использования вместо неизвестного 0.
Однако весьма распространен и другой подход к проблеме.
Будем считать 0 скалярным параметром (многомерный случай будет
рассмотрен в п. 6). Как мы знаем, точное определение θ по данной выборке
невозможно. Но мы могли бы попытаться указать такой интервал (0~,0+),
что он с заданной достаточно высокой вероятностью будет накрывать
неизвестное значение 0. При этом несомненно, что чем уже этот интервал, тем
лучше. Во многих задачах заранее требуется, скажем, путем увеличения
объема выборки построить такой интервал (0~,0+), чтобы его ширина не
превосходила заданных размеров.
Определение 1. Пусть для заданного ε > 0 существуют случайные
величины θ± = θ±(ε,Χ) такие, что
Ρθ{θ-(ε,Χ)<θ, 0+(ε,Χ)>0)>1-ε. (Ι)
Тогда интервал (0~,0+) называется доверительным интервалом для θ
уровня 1 — ε.
Очевидно, что (1) можно записать в виде
Р*(0- <θ<θ+)>1-ε.
Событие, стоящее здесь под знаком вероятности, состоит в том, что
случайный интервал (0~,0+) накрыл неизвестное значение 0. Читать это
событие как «попадание 0 в интервал (0~,0+)» было бы несколько менее
аккуратно, так как 0, вообще говоря, не случайно.
286
Гл. 2. Теория оценивания неизвестных параметров
Значения θ± называются границами доверительных интервалов, число
1 — ε — коэффициентом или уровнем доверия.
Итак, отличие интервального оценивания от точечного состоит в
следующем.
1. Доверительный интервал как оценка менее «точен», так как
указывается целое множество возможных значений 0.
2. С другой стороны, утверждение «Θ £ (θ~,θ+) с вероятностью ^ 1 — ε»
является истинным, в то время как событие 9 = 0*, как правило, имеет
вероятность, равную нулю.
В качестве ε выбирается обычно малое число. По нему строятся #*(£, X),
и затем на основании выборки объявляется, что θ Ε (θ"(ε, AT), 0+(ε, X)).
Поступая таким образом, мы будем ошибаться в длинном ряду экспериментов
примерно в 100ε % всех случаев. Например, если ε = 0,001, то ошибка будет
происходить примерно 1 раз на 1000 случаев.
Объявляя верным соотношение θ Ε (0~,#+), мы используем тот факт,
что если некоторое событие имеет вероятность ε и это ε мало, то
практически невозможно, чтобы это событие произошло при единичном испытании.
Авиапассажир, садясь в самолет, интуитивно твердо верит в это. Ему
достаточно знать, что вероятность того, что полет закончится благополучно,
довольно высока (ведь ему известно, что она не равна 1). Именно такой
подход и лежит в основе построения многих статистических процедур.
Мы выделим сначала один случай, когда построение доверительных
интервалов особенно естественно и может быть произведено без существенных
затруднений. Это так называемый байесовский случай, который уже
рассматривался нами в §20, 21, 30.
2· Построение доверительных интервалов в байесовском случае. Мы
предполагаем здесь, что параметр θ выбирается случайно с известной нам
априорной плотностью распределения q(t) относительно некоторой меры λ
на Θ. После этого производится выборка X ^ Р#, и нам надо построить
доверительный интервал для выбранного значения Θ.
Если выполнено условие (Αμ), то, как мы знаем из §20, в этом
случае существует апостериорное распределение θ (условное относительно X) с
плотностью
относительно меры λ. Это означает, что в качестве 0*(ε, Χ) достаточно взять
любые два числа θ±, для которых
Iq{u/X)\{du) = 1-ε
θ-
t
(или ^ 1 — ε, если / q(u/X)\(du) меняется при изменении t дискретно).
-00
Другими словами, в качестве θ~ и Θ+ следует взять квантили апостериорного
§ 39. Интервальное оценивание
287
распределения соответственно порядков 1 — 62 и ε χ при любых ει и 62 таких,
что е\ + 62 = ε.
Здесь в соотношении θ~ ^ θ ^ 0+ в отличие от небайесовского
случая случайными являются все три элемента: границы интервала θ± и сама
величина Θ.
Нетрудно видеть, что в описанной процедуре существует некоторый
произвол, связанный с выбором чисел е\ и €2- Иногда этот произвол устраняется
самой постановкой задачи — например, в случаях, когда нам важно
установить лишь верхнюю или нижнюю доверительную границу. В этом случае
одно из чисел ει, 62 следует положить равным нулю, а соответствующую
границу сделать бесконечной. Если же границы играют симметричную роль,
то естественно следует выбирать е% так, чтобы сделать интервал (0~,0+) по
возможности более коротким. Для распределений g(i/X), близких к
симметричным, это достигается при е\ = S2 = ε/2.
3. Построение доверительных интервалов в общем случае.
Асимптотические доверительные интервалы. Основные методы построения
доверительных интервалов базируются на использовании точечных оценок. Рассмотрим
сначала асимптотический подход к построению доверительных интервалов.
Определение 2. Пусть X = [Хсс]п ^ Р#> и для заданного ε > О
существуют случайные величины θ^ε,Χ) такие, что
liminf P,(0-(ε,Χ) < θ < θ+{ε,Χ)) > 1 - ε. (2)
η—>οο
Тогда интервал (0",0+) называется асимптотическим доверительным
интервалом уровня 1 — ε.
В этом определении необходимо подчеркнуть, что речь идет на самом деле
о последовательности интервалов (θ~,θ+), определенных для каждого п.
Формально понятие асимптотического доверительного интервала
применительно к выборке фиксированного объема является малосодержательным.
Тем не менее соотношением (2) пользуются при больших η — так же, как
пользуются центральной предельной теоремой для приближенного
вычисления распределений сумм конечного числа случайных величин.
Мы видели в предыдущих пунктах, что большинство рассматривавшихся
нами точечных оценок асимптотически нормальны. Ниже мы приводим
конструкцию асимптотических доверительных интервалов, основанных на
таких оценках.
Пусть Θ* — а.н. оценка:
(0*-0h/ne^O|iF2Wl (3)
и σ(θ) есть непрерывная функция. Так как Θ* —> 0, то последнее условие
означает, что σ(θ*) —> σ{θ). Отсюда и из (3) по второй теореме
непрерывности следует, что
(0*-0)v^ ,
~^т *Фод- (4)
Обозначим через \$ квантиль нормального распределения порядка 1 — £,
т.е. такое число, что Φο,ι((—°ο, λ^)) = 1 — J, или Р(|£| < Xs) = 1 — 2J, если
288
Гл. 2. Теория оценивания неизвестных параметров
ξ ^ Ф0д. Для λε/2 при заданном фиксированном ε > 0 введем временно
более короткое обозначение, положив
Тогда из (4) следует
lim Τ?θ
η—>оо
λε/2 = β·
(θ* -9)y/n
<β)=1-ε.
σ{θ*)
Но это соотношение можно переписать в виде
п->оо у у/п у/П )
Таким образом, числа
β± = θ·±Εψ (5)
Vη
удовлетворяют определению 2 и, стало быть, являются границами
асимптотического доверительного интервала уровня 1 — ε.
Если теперь для заданной фиксированной выборки X объема η построим
интервал (5), его истинный уровень будет, вообще говоря, отличаться от ε,
но будет мало отличаться, если η достаточно велико. Поэтому обращаться с
асимптотическими доверительными интервалами надо с известной
осторожностью, выяснив предварительно, начиная с каких η вероятность события
{Θ £ (0~,0+)} достаточно точно приближается к предельным значениям.
Обычно чем меньше ε, тем выше требование к объему выборки п.
Необходимый объем зависит также от распределения Р# и от статистики Θ*.
Пример 1. Пусть X €= Γαχ, и мы пользуемся эффективной оценкой
п- 1
а* = —— > В примерах 14Л, 26Л было установлено, что
пх
Εαα* = α, Όαα* =
a2
n-2'
так что здесь σ2(α) = α2. Соотношение (5) дает нам
ηχ V νη/
Чему на самом деле равен уровень этого интервала?
Нам надо найти Гад — вероятность неравенства
пх
или, что то же, неравенства
п-1 / β \ п-1 Λ β \
пх \ y/nj пх \ у/п/
β ηαχ . β
γ/η П — I у'П
§ 39. Интервальное оценивание 289
где пах €= 1\п. Так как α есть параметр масштаба, то 2ηαχ €= Τι/2,η — Η2η·
Таким образом, точный уровень интервала (6) равен
2(n-l)(l+/Vv^)
7i/2,n(s)<fo, (7)
2(п-1)(1-Р/у/П)
гДе 7ι/2,η определено в § 12*).
При ε = 0,05, η = 30 имеем β = 1,96, (η - 1)(1 - β/^/η)/η « 0,6201,
(η - 1)(1 + fi/y/n)/n « 1,3126.
Таким образом, асимптотический доверительный интервал уровня
1 — ε = 0,95 применительно к случаю η = 30 представляет собой
интервал (0,620/х, 1,313/х).
Если воспользоваться таблицами распределения χ2 с 60 степенями
свободы, то мы в силу (7) обнаружим, что точный уровень значимости этого
доверительного интервала равен (с точностью до трех знаков) 0,937 = 1—0,063.
При этом «вклады» левого и правого конца доверительного интервала далеко
не равнозначны (ср. с нормальным приближением) и составляют
соответственно 0,010 и 0,053.
Для η — 50 асимптотический доверительный интервал уровня 0,95 будет
иметь вид (0,708/х, 1,252/х). Истинный уровень его значимости будет равен
0,942 = 1 — 0,058 (вклады равны соответственно 0,014 и 0,044). Ясно, что
если продолжать увеличивать п, то эти вклады будут сближаться с 0,025.
Вернемся к доверительному интервалу (5), построенному нами с
помощью а. н. оценки 0*. В отличие от байесовского случая здесь имеется
произвол, связанный с выбором оценки 0*. Форма границ интервала показывает,
что достичь заданных размеров интервала можно как за счет увеличения
объема выборки η (что по разным причинам не всегда осуществимо), так
и за счет возможного уменьшения σ(θ*)> Здесь мы приходим к важному
выводу, что при равных объемах выборки лучший доверительный интервал
будет давать оценка с меньшим рассеиванием σ(0). Таким образом,
наилучшие асимптотические доверительные интервалы будут получены при
использовании асимптотически эффективных оценок.
При выполнении условий (RR) и принадлежности Θ* классу Ко Π Κφ$
(см. § 18, 26) наилучший асимптотический доверительный интервал имеет
границы
sftrfW)
где 0* — любая а.э. оценка, например о.м.п.
Некоторые другие методы построения асимптотических доверительных
интервалов будут рассмотрены в п. 6.
*' Замечание о том, что Г^г.п = Нгп, полезно, так как оно позволяет для вычисления
Га,А (если 2λ целое) использовать таблицы распределения χ2, приведенные в приложении,
а также во многих других руководствах по математической статистике.
/
290
Гл. 2. Теория оценивания неизвестных параметров
4. Построение точного доверительного интервала с помощью заданной
статистики. Допустим, что в качестве статистики мы выбрали оценку 0*.
Тогда симметричный доверительный интервал уровня 1 — ε с помощью этой
оценки было бы естественно искать в форме θ* ± Δ(ε,Χ) или в форме
θ*(1 ± Δ(ε, X)), как это было в рассмотренном выше примере. Однако если
мы попытаемся реализовать такой план, то окажется, что дело обстоит не
так просто, так как в общем случае границы ±Δ(ε,Χ) будут зависеть от
неизвестного параметра θ — ведь Δ(ε, -Χ") надо выбрать из условия
Έ>θ{θ* - Δ(ε, Χ) < θ < θ* + Δ(ε, Χ)) > 1 - ε,
в которое θ входит существенным и весьма сложным образом, прежде всего
через само распределение Р#.
Поэтому требуется некоторая специальная конструкция для построения
доверительных интервалов с помощью данной оценки Θ*.
В приводимом ниже построении наряду с оценкой Θ* может участвовать
любая статистика 5. Обозначим символом G# распределение 5 и положим
GG{x) = Ge{{-oo,x)).
Определение 3. Будем говорить, что статистика 5 по распределению
монотонно зависит от 0, если при любых χ, θ\ < 02
G6l((x,oo)) ^ G02((x,oo))
или, что то же,
ββι(χ)>βφ). (8)
Все разумные оценки Θ* обычно этим свойством обладают.
Если дополнительно монотонная зависимость Gq(x) от θ является
непрерывной, то уравнение
<ЗД=7
всегда разрешимо относительно θ при каждом η £ (0,1). Решение этого
уравнения обозначим через 6(х,7)·
Теорема 1. Если ει+εζ = ε, статистика S по распределению
монотонно зависит от θ и функция Gq(x) непрерывна по θ и я, то значения
^ = 6(5,1»ε2), θ+ = 6(5,ει)
образуют доверительный интервал уровня 1 — ε.
Доказательство теоремы почти очевидно. Воспользуемся тем
фактом, что если функция распределения F(x) непрерывна и ξ €= F, то F(£) ^
^ U0,i (P(F(0 < х) = Р(£ < F~l{x)) = F{F-l{x)) = χ). В силу этого
замечания Gq(S) €= Uo,i и, стало быть,
Ρ*(ει<σ*(5)<1-ε2) = 1-ε,
Ρ^(6(5,1-ε2)<0<6(5,ει)) = 1-ε. <
§ 39. Интервальное оценивание
291
Часто «обращение» функции Ge(S), используемое в теореме, удобно
проводить в два этапа. Сначала Gq(x) обращается относительно я, т.е.
определяются квантили G^ij) как решения уравнений Gq(x) = 7? а затем
решаются относительно θ уравнения
Gel(ei) = S, Gjl(l-e2) = S.
Такие решения всегда будут существовать, так как по условию теоремы
Ggl(y) монотонно и непрерывно зависит от Θ.
На рис. 3 представлены кривые у = G^l(ei) и у = G^l — £2),
определяющие при каждом θ область значений у, вероятность попадания в которую
для некоторой оценки 5 = Θ* равна 1 — ε. Как
уже отмечалось, процедура построения
доверительного интервала есть обращение функций
y = Gg\el), y = GJl{l-ei),
т. е. отыскание точек пересечения
соответствующих им кривых с уровнем у =■ S. Полученные
точки пересечения и дают требуемый интервал
Если условие о непрерывности Gq(x) не
выполнено, что будет иметь место для
дискретных случайных величин 5, то в целом изло- Рис· 3
женная процедура и утверждение теоремы 1 сохранятся с той лишь
разницей, что при соответствующем определении квантилей G^ (7) следует
удовлетворить неравенству G^((G^1(ei),G^1(l — £2))) ^ 1 - ε> на месте
которого мы прежде имели точное равенство. В соответствии с этим
утверждение теоремы 1 в этом случае будет иметь вид
Р*(0- <0<0+)>1-ε,
где θ± есть решения уравнений Gjl(e\) = 5, G^1{1 — 62) = S. При этом мы
будем, как и прежде, называть интервал (θ~~ ,θ+) доверительным интервалом
уровня 1 — ε.
Если мы строим доверительный интервал (0~, 0+) с помощью оценки 0*,
то из рис. 3 видно, что этот интервал будет тем уже, чем уже интервал
{Gj1(ei)i G^l(l — ε2)) или, что то же, чем более сконцентрировано
распределение Θ* около Θ. Таким образом, мы приходим здесь к той же проблеме,
что в теории точечных оценок — к отысканию оценок 0*, наиболее точно
оценивающих 0.
Проблема построения наилучших доверительных интервалов более
подробно будет рассмотрена в § 48.
Так как вид функций распределения Go{x) даже для простых семейств
распределений, приведенных в § 12, оказывается обычно достаточно
сложным, то указанная процедура обращения G$(x) становится на практике
довольно трудным делом. Поэтому вычисление доверительных границ во
многом табулировано. В следующем примере, где мы проиллюстрируем по-
292
Гл. 2. Теория оценивания неизвестных параметров
строение доверительных интервалов по схеме, описанной в теореме 1, мы
для упрощений будем пользоваться нормальным приближением.
Пример 2. Пусть X €= Вр. В качестве оценки для ρ возьмем
эффективную оценку ρ* = ν/η, где ν — число успехов в η испытаниях (числом
ν может быть, например, число бракованных изделий, обнаруженных при
контрольной проверке η образцов). Требуется построить доверительный
интервал для доли брака р.
Имеем (q = 1 — ρ)
^ / ч ^ / * ч ^ (ν — ηρ χη — ηρ\
GP{x) = РР(р* < χ = РР —=& < .—F .
V y/ηρξ Jnpq J
В соответствии с теоремой 1 нам надо решить уравнение
GP(p*) = 7 (9)
для значений 7> равных ε/2 и 1 — ε/2. При больших η в силу центральной
предельной теоремы Gp(x) ~ Ф((х — р)гь/ y/npq), где Ф(у) = Фод((-ос,у)),
и, стало быть, уравнение (9) можно заменить его приближением
\ у/пРЯ / II
или, что то же, \{р* -~p)n/y/npq\ = \ε/2 = /?,
η
Это уравнение для границ р± доверительного интервала представляет собой
уравнение эллипса, вытянутого при больших η вдоль биссектрисы ρ*— ρ = 0.
Решая это уравнение относительно р, получим
p±„p.±JSGZ>.
V η
Нетрудно проверить, что такой же результат мы получили бы, пользуясь
асимптотическим подходом, изложенным в п. 3.
Если η невелико, то приходится Gp(x) вычислять по точной формуле
Gp(x)= £СпУ(1-р)"-*,
к<пх
применяя затем процедуру теоремы 1.
Пусть, например, из η = 10 изделий ν = 2 оказались бракованными.
Тогда при ε = 0,05 точные границы доверительного интервала оказываются
равными р~~ = 0,037, р+ = 0,507. Большая ширина интервала объясняется
незначительной информацией, которой мы располагаем.
Если же η = 100, ν = 20, то при ε = 0,05
ρ- = 0,137, р+ = 0,277.
§ 39. Интервальное оценивание
293
Эти цифры заимствованы из специальных таблиц, дающих численное
решение задачи о доверительных интервалах для числа ρ при разных η и и
(см. [10]).
5. Другие методы построения доверительных интервалов. В этом пункте
мы рассмотрим некоторые обобщения предложенной ранее процедуры
построения доверительных интервалов.
Теорема 2. Допустим, что на Θ х Хп существует такал функция
G(9,x), что распределение H(J5) = ¥q(G(6,X) £ В) не зависит от 0.
Предположим также, что G{9,x) при каждом χ непрерывна и
монотонна по Θ.
Пусть, далее, у~, у+ удовлетворяют соотношению Н((у~,у+))=1—е.
Тогда статистики
θ-^Ο-^ν-,Χ), θ+^Ο-^ν+,Χ), если G(0,-)t,
θ- = G~l{y+,X), Θ+ = G~l{y-,X), если G{9,-)i,
являются границами доверительного интервала уровня 1-е. Здесь
G~1(y,X) есть решение уравнения G(0,X) = у.
Доказательство. В силу монотонности G{9,x) (пусть для
определенности G{6,x) возрастает по Θ) событие {G~1(y~,X) < θ < ΰ^ι^,Χ)}
совпадает с событием А = {у~~ < G{9,X) < у4*}.
По определению Н(·) и у± имеем
Ρθ(θ- <θ<θ+)= Pe(G-\y-,X) < θ < G~\y+,X)) =
= Р,(Л)=Н((у-,у+)) = 1-б. <
Замечание 1. В теореме 1 в качестве G{9, X) мы рассматривали
функцию Ge(S). При этом выполнялось Η = Uoj.
Замечание 2. Можно рассмотреть асимптотический аналог теоремы 2,
допустив существование последовательности функций {Gn(6,x)},
непрерывных и монотонных по θ и таких, что при η —> оо
Ρθ(Οη(θ,Χ)£Β)->Η(Β),
где Η(·) не зависит от Θ. Мы получим тогда способ построения
асимптотических доверительных интервалов, обобщающий изложенный в п. 3 метод
построения асимптотических доверительных интервалов с помощью а. н.
оценок.
Предложим теперь еще один способ (наряду с теоремой 1) выбора
функции G(9,x), фигурирующей в теореме 2.
Теорема 3. Пусть Fg{x) = Ρ#(χι < ζ), причем
1) Fe{x) непрерывна по χ для всех θ Ε Θ,
294
Гл. 2. Теория оценивания неизвестных параметров
2) Fq{x) непрерывна и монотонна по θ для любого фиксированного х.
Тогда функция
г=1
удовлетворяет условиям теоремы 2.
Если числа у^ таковы, что
у+
щ1а»-1е-*<Ь = 1-е, (10)
у~
то у± = G~l(y±,X) образуют границы доверительного интервала
уровня 1 — ε.
Доказательство. Проверим выполнение условий теоремы 2.
Поскольку по условию 1 Fe{xi) распределена равномерно на [0,1], то — lni^(xj) E
Ε Γι,ι и G{6,X) е Ι\η. Другими словами, Ί?0(Ο{θ,Χ) G В) = Γ1>η(5)
и Η = Ι\η на зависит от б. Монотонность и непрерывность G(9,x) при
каждом ж следуют из условия 2. Кроме того, в силу (10)
Н((2Г,у+))=Г1)П((у-)У+)) = 1-е. <
Можно указать и некоторые другие конструкции доверительных
интервалов. При этом так же, как в теории точечного оценивания, сразу же возникает
вопрос о том, какой доверительный интервал, если их получено несколько,
считать лучшим. Подходов, которые здесь существуют, мы коснемся в §48.
Однако из предыдущего изложения ясно, что по существу задача поиска
оптимального доверительного интервала во многом очень близка к задаче
оптимального точечного оценивания. Ясно также, что если мы строим
доверительные интервалы с помощью точечных оценок, то предпочтение следует
отдавать доверительным интервалам, построенным с помощью лучших
оценок.
Близость задач оптимизации точечного и интервального оценивания
можно проиллюстрировать на примере следующего утверждения.
Теорема 4. Рассмотрим асимптотический доверительный
интервал (0~,0+) уровня 1 — ε и предположим, что случайная величина Θ* —
= (θ^,θ~)/2 есть асимптотически центральная (см. п. 33.4) а.н.
оценка, а величина Δ = (θ+ — θ~)/2 такова, что δ = liminf у/пА от X не
п-*оо
зависит. Тогда δ^β/у/Щ.
Это значит, что ширина доверительного интервала (0~,0+) не может
быть существенно меньше, чем 2β/у/п1(в), т.е. чем ширина интервала
1-е, построенного с помощью о.м.п. Θ*.
Доказательство. Допустим противное. Тогда найдется
подпоследовательность чисел {п'}, для которых Δ\Ζη' -> с/3/\/ΐ(θ), с < 1. Так как
§ 39- Интервальное оценивание 295
θ± = θ*± Δ, то
1 - ε = lim Ρβ(0- < θ < θ+) = lim Ρθ(\θ* -Θ\<Α) =
η'~>οο η'—юо
-j!»p.(i»--«i^<^)<
<iillmP»(r-^<^). (11)
Последнее неравенство следует из того, что о. м. п. Θ* является а. э. в
классе К0 асимптотически центральных оценок (см. теорему 33.7). Так как
правая часть в (11) строго меньше 1 — ε, мы получили противоречие,
доказывающее теорему. <
6. Многомерный случай. Понятие доверительного интервала обобщается
в случае многомерного параметра θ Ε Шк в понятие доверительной области
или доверительного множества.
Определение 4. Случайное*) подмножество θ* = θ(ε,Χ)
параметрического пространства θ называется доверительным множеством уровня
1 — ε, если
Ρ*(θ*30)^1-ε. (12)
Другими словами, доверительное множество уровня 1 — ε накрывает
неизвестное истинное значение θ с вероятностью, не меньшей 1 — ε.
Определение 5. Если X = [-Xoojn €= Р#, и случайное множество Θ*
удовлетворяет соотношению
liminfP*(e*9 0)^l-e,
п-юо
то Θ* называется асимптотическим доверительным множеством уровня
1-ε.
Изучению «точных» доверительных множеств, в том числе
оптимальных, посвящен §48 следующей главы.
Что касается асимптотических доверительных множеств, то принцип их
построения остается прежним. Учитывая теорему 4, рассмотрим сразу
доверительные множества, построенные с помощью о. м. п. Θ*. Как мы знаем,
при выполнении условий (RR), X €= Ρ θ
Отсюда следует, что
{в*-в)у/п11'2{в)&Фо,Е.
η(θ*-θ)Ι{θ)(θ*-θ)τ ©>Щ,
η{θ*-θ)Ι(θ*)(θ*-θ)τ &Hk.
*) В этом контексте множество θ*(ε,Χ) будем называть случайным, если при каждом t
множество {X : t € θ*(ε,Χ)} измеримо и, стало быть, определена вероятность (12) (ср.
с §48).
296
Гл. 2. Теория оценивания неизвестных параметров
Другими словами, если h£ означает квантиль порядка 1 — ε распределения
χ2 с к степенями свободы, то
lim Έ>θ(η{θ - θ*)ΐ(θ*)(θ - θ*)τ < Лс) = 1 - ε. (13)
η->οο
Мы построили асимптотическое доверительное множество Θ* уровня
1 — ε, которое представляет собой эллипсоид с центром в точке Θ* и с осями,
определяемыми матрицей nl(9*)/h£> Вычислять матрицу Ι(θ) для
построения θ* при этом не обязательно. Как мы знаем, при выполнении
условий (RR), Χ ^ΡΘ
L(X, θ) - L(X, θ*) « -%(θ - Θ*)Ι(Θ*)(Θ - θ*)τ.
Поэтому эллипсоид Θ*, определенный в (13), можно представить как
совокупность значений 0, для которых
L(X,e)-L(X,0*)^-^.
В § 36 было установлено, что предел Р^-вероятности этого неравенства (см.
замечание 36.2) равен 1 — ε.
Отсюда следует, в частности, что в одномерном случае границы θ±
асимптотического доверительного интервала уровня 1 — ε можно определять как
решения уравнения
Κχ,θ)-κχ,θ*) = -^ = -ζ.
§ 40. Точные выборочные распределения и доверительные
интервалы для нормальных совокупностей
Среди всех распределений, перечисленных в § 12, нормальное
распределение наиболее распространено в приложениях. Поэтому в этом параграфе
мы остановимся отдельно на построении точных доверительных интервалов
для параметров α и σ2 распределения Φα,σ2.
1. Точные распределения статистик х, S%. Пусть X ^ Фо,ь и С = ||с^||
(г, j = 1,2,..., η) есть ортогональная матрица.
Изучим распределение n-мерного вектора
η
Υ = ХС, Υ = (у1,...,уп), Yi = Y^XjCji.
i=i
Лемма 1. Если С — ортогональная матрица, то Υ ^ Фо,ь т· е-
координаты yi,...,yn есть независимые случайные величины, γι €= Фо,ь
г = 1,2,.. .,п.
Доказательство. Пусть t есть вектор (£ι,...,ίη)· Нормальность
распределения X означает, что его характеристическая функция равна
§ 40. Выборки из нормальных совокупностей
297
где m = \\mij\\ есть матрица вторых моментов, равная в нашем случае еди-
п
ничной матрице Е% для которой tEtT = 7 vt2,
n
Εβ**Τ=β '&'.
Характеристическая функция совместного распределения yi,.. -,уп (или
распределения вектора У) имеет вид
/(t) = Ее'*уТ = Ее"1
Делая замену переменных t = гхС и замечая, что ССТ = ЕЛ получим
η л
f{t) = Ее-суГ = Ее^Г = е"Г<5 * = е"*^.
Это означает, что Υ имеет ту же характеристическую функцию и, стало
быть, то же распределение, что и X. <
Теперь докажем важное для дальнейшего утверждение, которое носит
название леммы Фишера.
Лемма 2. Пусть по-прежнему X €= Фо,ь С — ортогональная
матрица, Υ = (yi,.. .,уп) = ХС. Тогда квадратичная форма
Т(Х) = 5>г2-у?-...-уг2
<=1
we зависит от случайных величин yi,...,yr w имеет распределение χ2
с η — г степенями свободы: Т(Х) ^ НП_Г.
Доказательство почти очевидно, так как после применения
ортогонального преобразования С получим
T(X)^f^y^y2l yr2 = yr2+i+"-+j£
i=l
Остается лишь воспользоваться леммой 1. <
Перейдем теперь к изучению совместного распределения статистик χ и
г—\
Теорема 1. Пусть X €= Φα,σ2· Тогда
1) {х-а)у/п/а ^ Ф0|1,
2) (n-l)502/a2^Hn_lL
3) случайные величины χ и 52 независимы.
298
Гл. 2. Теория оценивания неизвестных параметров
Доказательство. Утверждение 1 очевидно. Далее, ясно, что, не
ограничивая общности, можем считать α = О, σ = 1. Имеем
(п - 1)S2 = £х2 - пх2.
Заметим, что
г- 1 1
у/П X = -7=х1 + - · - + ~7=χη
Vn у/η
Л/чМ
и что n-мерный вектор-столбец ... (его норма равна единице) всегда
Vi/vV
можно дополнить до какой-нибудь ортогональной матрицы С. Тогда yi =
= у/пх есть первая координата У = ХС, и в силу леммы 2 получаем, что
(п - 1)S02 = f>? - у2 €= Η*-!
г=1
и что случайные величины (п - 1)Sq и у ι = у/пх независимы. <
Следствие 1. Пусть X €= Φα>σ2. Тогда случайная величина t =
= (χ — а) у/п/So ^ Tn_i, m. е. имеет распределение Стьюдента с η — 1
степенями свободы.
Это следует из теоремы 1 и представления
(х — а)у/п 1
ί =
1 (rc-l)Sp2
η — 1 σ2
Утверждения теоремы 1 о независимости 52 и χ можно немного
усилить. Пусть е = (1,..., 1) есть вектор с единичными координатами. Тогда
χ не зависит не только от 52, но и от вектора X — хе (т.е. от слагаемых
суммы, определяющей 52). Действительно, из леммы 1 и рассуждений в
доказательстве теоремы 1 следует, что ортогональные векторы X — хе и хе
независимы, что означает, очевидно, независимость жиХ-хе.
2. Построение точных доверительных интервалов для параметров
нормального распределения. Разберем сначала две простейшие ситуации.
а) Пусть X €= Φα>σ2 и σ2 известно. Требуется построить доверительный
интервал уровня 1 — ε для параметра а. Вид доверительного интервала в
этом случае очевидным образом вытекает из равенств
{х-а)у/п\ А „/ σβ _ σβ\ Λ
к 1У—1 <β\ = Р ί—-ρ <χ-α<-7=)==1-ε,
σ
у/п у/п
где, как и прежде, β = А£/2> *o,i((—οο,λ,?)) = 1 — £, так что
, ГГЙ
α^ε,Χ) = х±
V^'
§ 40. Выборки из нормальных совокупностей 299
Читателю в виде упражнения предлагается воспользоваться несколько
более формальной процедурой, изложенной в теореме 39.2, с использованием
функции G{a,X) = (χ - a)y/n/a ^ Ф0д.
б) Пусть теперь известно а. Требуется построить доверительный
интервал уровня 1 — ε для сг2.
Положим
5ι = ^Σ(χ*-α)5
t=l
Тогда, очевидно, nS\jo1 €= Ηη и, стало быть,
Ρ
/ - nS\ Л тт „ _ +чч _ (nS\ о nS\
Таким образом, границы доверительного интервала уровня 1 — ε будут иметь
вид
2^± _ nSj
yff
при любых у± таких, что Нп((у~,у+)) = 1 - ε.
Если использовать процедуру теоремы 39.2, то следует положить
G(a,X)=nSJ7a2€=Hn.
Перейдем теперь к случаю, когда оба параметра α и σ2 неизвестны.
в) Для построения доверительного интервала для σ2 воспользуемся
статистикой G\(a,X) = (η — 1)52/σ2. На основании теоремы 1 Gi(a,X) €=
^ Ηη_ι- Далее поступаем так же, как и в случае б). Границы доверительного
интервала для σ1 будут иметь вид
(σ2)± = (η-1)5^_ι·
Легко видеть, что статистики G(a,X) и G\(o,X) в случаях б) и в) имеют
одинаковое распределение и, стало быть, дают одинаковые доверительные
интервалы для σ2, если только в случае в) мы имеем на одно наблюдение
больше, чем в б). Образно говоря, в случае в) мы «теряем» одно наблюдение
ввиду наличия дополнительной неопределенности — неизвестного
параметра а. Это наблюдение как бы предназначается для устранения
«мешающего» параметра*) а.
** Интересно отметить, что вопреки первоначальным интуитивным представлениям по
•одному наблюдению χι @ Фа,<72 возможно построить доверительный интервал для σ2 при
неизвестном а. Следующие рассуждения, показывающие это, были сообщены нам Л. Н. Боль-
шевым.
Выберем и так, чтобы Ф(1/и) — Ф(—1/и) = е, где Ф(х) = Φο,ι((—οο, ж)). Тогда
^/ ι #ч -г> / О" σ\ __ ( 1 α (χι — α) 1 α\
Ρ(σ>ΜΧι ) = Ρ( <χι < -) =Ρ [ < ^ L < ) =
\ и и/ \ и σ σ и σ)
"(Η)-(-Η)«·®-·(-ί)-"
300
Гл. 2. Теория оценивания неизвестных параметров
г) Построим теперь доверительный интервал для а. Воспользуемся
статистикой Gi(a,X) = (χ — a)y/n/So. В силу следствия теоремы 1
Так как функция G\(a,X) удовлетворяет условиям теоремы 39.2, то
дальнейшие рассуждения в точности повторяют соответствующие
рассуждения в случаях а)-в). Границы доверительного интервала имеют вид (для
простоты возьмем симметричный интервал)
а* =х±ге50/\Лг,
где τε определяется из равенства
Ρ(|ίη-ι| < те) = Τη-ι{{-τε,τε)) = 1 - ε.
Заметим, что если значение So близко к σ, то полученный доверительный
интервал будет шире, чем интервал в а), так как τε > β (см. замечание
в §12). Это опять же объясняется наличием «мешающего» параметра σ
который в а) известен.
Числа у^, для которых в приведенных рассмотрениях выполнилось
соотношение
Р(0(в,Х)ш(у-,у+)) = 1-е,
на практике обычно определяются с помощью таблиц математической
статистики.
В § 48 мы покажем, что доверительные интервалы, построенные в этом
параграфе, в известном смысле являются наилучшими.
Глава 3
ТЕОРИЯ ПРОВЕРКИ ГИПОТЕЗ
В § 41-43, 51 излагается теория проверки конечного числа (в частности, двух)
простых гипотез.
Параграфы 44-52 посвящены методам построения оптимальных критериев для
проверки двух сложных гипотез. В частности, рассмотрены байесовские и
минимаксные критерии (§ 44, 49) и использованы принципы достаточности,
несмещенности и инвариантности для построения равномерно наиболее мощных критериев.
В § 53-57 изучаются методы построения асимптотически оптимальных
критериев.
Параграф 58 посвящен устойчивости (робастности) статистических решений.
§ 41. Проверка конечного числа простых гипотез
1. Постановка задачи. Понятие статистического критерия. Наиболее
мощный критерий. В этой главе речь будет идти о проверке каких-либо
предположений (гипотез) относительно распределения Р, из которого извлечена
выборка X. Здесь, как и в теории оценок, проблема отсутствовала бы, если
бы распределение Р, из которого извлечена выборка X, было известно.
Решение о том, справедлива данная гипотеза Η или нет, должно
основываться лишь на знании выборки X €= Р, которая нам дана, и, возможно,
также на знании априорной информации относительно Р, если таковой мы
располагаем.
Таким образом, чтобы определить процедуру принятия решения по
выборке X, мы должны задать в той или иной форме отображение выборочного
пространства Хп на множество рассматриваемых гипотез. Такое
отображение называют обычно статистическим критерием. Точные определения для
различных конкретных ситуаций будут даны ниже.
Мы начнем с наиболее простой задачи — проверки конечного числа
простых гипотез.
Определение 1. Простой гипотезой будем называть любое
предположение, однозначно определяющее распределение выборки X.
Пусть даны г распределений Pi,...,Pr и пусть нам известно, что X
есть выборка из одного из этих распределений. Задача состоит в том, чтобы
определить, к какому именно Pj, j = 1,2,.. .,г, относится X. Каждая из г
гипотез
Я, = {Х#Р,} (1)
будет простой, и, стало быть, речь идет о проверке г простых гипотез.
В этой главе, как и в главе 2, мы часто будем рассматривать
параметрический случай, когда выборка X извлечена из распределения Р# Ε V =
= {Рв}вее- В этом случае при выполнении условия (Aq) простые гипотезы
302
Гл. 3. Теория проверки гипотез
будут записываться в виде Hj = {X ^ T?0j}, где 0Ь ..., 0Г — фиксированные
точки из Θ. Случай (1) тоже можно рассматривать как параметрический с
конечным множеством Θ = {1,..., г}.
Эти рассуждения показывают, что принципиальной разницы между
задачами оценки параметров и проверки гипотез нет — и там, и там определяем
неизвестное значение Θ. Некоторое различие все же имеется, и состоит оно в
том, что в рассматриваемой задаче проверки гипотез возможные значения θ
дискретны и подходы, связанные со сравнением, скажем,
среднеквадратичных уклонений, развитые нами в главе 2, тут не всегда применимы. Здесь
нами будут выбраны другие критерии для сравнения правил принятия тех
или иных гипотез по выборке X.
С дискретностью множества возможных значений θ связано и другое
новое качество, которое здесь появляется, — мы можем теперь с ненулевой
вероятностью точно указать неизвестное значение θχ (или распределение Р^),
в то время как в задачах оценки параметров вероятность такого события,
как правило, равна нулю.
Отметим, что существуют задачи, связанные с дискретными
параметрами, в которых естественным образом применимы оба подхода: с позиций
теории оценивания и с позиций теории проверки гипотез. Одной из таких
задач является задача о разладке, упомянутая в примере 2 введения. Эта
задача (она имеет дело с параметром случайного процесса) будет детально
рассмотрена в § 72 главы 5.
Вернемся к общей задаче о проверке конечного числа простых гипотез.
Определение 2. Статистическим критерием для проверки г
гипотез ίίι,...,#Γ называется любое измеримое отображение δ: Χη —>
->{Ни...,Нг}.
Другими словами, δ(Χ) есть случайная «величина», принимающая
значения #ι, #2,...,#г: если δ(Χ) = #*, то принимаем гипотезу #& (т.е.
считаем, что θ = θ^ в параметрическом случае).
Отображение δ(·) иногда называют решающим правилом или
решающей функцией. Понятно, что задание решающего правила эквивалентно
разбиению пространства Хп на г непересекающихся борелевских множеств
Ωι,Ω2,.. ·,ΩΓ, на которых принимаются соответственно гипотезы -ΗΊ,
Качество критерия чаще всего характеризуется набором вероятностей
ошибочных решений
оц = oti(S) = Pi(X i ΩΟ = ΡΜΧ) φ Hi).
Число cti есть вероятность отвергнуть гипотезу Н{, когда она на самом деле
верна. Это число называют вероятностью ошибки i-го рода критерия δ.
Если нам удалось выбрать критерий δ так, что все числа щ малы, то
в соответствии с нашим основным принципом, упомянутым в §39, будем
считать, что в одном испытании ошибка практически невозможна, и будем
объявлять, что верна гипотеза #&, если δ(Χ) = Нь- При этом будем
ошибаться примерно в доле случаев с^ = Ρ{(δ(Χ) Φ Щ), если на самом деле
верна Н{.
Желательно, конечно, провести проверку гипотез таким образом, чтобы
свести к минимуму вероятности всех ошибок. Однако если объем выборки X
§ 41. Проверка конечного числа простых гипотез 303
задан, то мы не можем управлять всеми вероятностями ошибок
одновременно. Можно лишь, фиксируя некоторые из вероятностей ошибок,
пытаться минимизировать остальные.
Мы приходим здесь к вопросу о том, как сравнивать между собой
различные критерии. Введем на множестве всех критериев для проверки гипотез
Н\,..., Нг частичный порядок.
Определение 3. Критерий δ\ лучше критерия #2, если для всех г =
= 1,2,..., г
(*ΐ{δι) < оц{62)
и хотя бы для одного г имеет место строгое неравенство.
Однако далеко не всегда критерии δ\ и #2 могут быть сравнимы в этом
смысле. Точно так же, как могут быть не сравнимы две оценки θ{ и θ%
с точки зрения среднеквадратического подхода, когда в качестве критерия
качества мы берем Έβ{θ* — 0)2. Чтобы иметь возможность сравнивать
критерии, надо сузить множество рассматриваемых решающих правил. Для
этого введем в рассмотрение классы
Kaw..,aT-i ={δ :aji5) =aj! 3 = l,2,...,r-l}.
В классах ΛΤαι,...,αΓ_ι уже можно установить отношение порядка между
критериями по величине ar\ чем меньше аг(£), тем лучше критерий.
Определение 4. Критерий #о Ε i^a1,...,Qr^1 называется наиболее
мощным критерием (н.м.к.) β классе Kaiimmmjar_l^ если для любого δ €
£ -Και,...,αΓ-ι
αΓ(5ο) < αΓ{δ).
Напомним, что нечто подобное мы делали в главе 2, когда занимались
сравнением оценок. Там мы выделяли, например, классы Кь оценок с
фиксированным смещением.
Наряду с только что введенным в теории проверки гипотез так же, как
и в теории оценок, существуют два других подхода, которые позволяют
упорядочить множество всех решающих правил с помощью одной числовой
характеристики, — это байесовский и минимаксный подходы.
Прежде чем изучать методы построения наиболее мощных критериев в
классах ΑΓαι,...,αΓ_ι> мы рассмотрим эти два подхода.
2. Байесовский подход. Этот подход предполагает, что распределение Pj,
из которого извлечена выборка X, было выбрано случайно. В этом случае
гипотезы Hj = {X ^ Р;}, j = 1,.. .,г, становятся случайными событиями,
и мы обозначим вероятности этих событий через
Q(^) = q(j),
так что Q есть априорное распределение на множестве гипотез {ifi,..., #r},
a q(j) есть априорные вероятности этих гипотез (ср. с §21). В этом случае
сравнивать критерии становится проще, поскольку мы можем определить
304
Гл. 3. Теория проверки гипотез
здесь среднюю вероятность oq(6) ошибки критерия δ:
г г
<*q(S) = Σ<ΧΗ№(δ(Χ) φ Hj) = ^i^jW (2)
3=1 j=l
и тем самым полностью упорядочить множество критериев по величине
aQ(S).
Определение 5. Критерий δ = £q, который минимизирует
вероятность ошибки ад(£), называется байесовским критерием,
соответствующим априорному распределению Q.
Пусть выполнено условие (Αμ), т.е. распределения Pj имеют
плотности fj{x) относительно некоторой σ-конечной меры μ. Функцию fj(X) =
η
= TT/j(xj)j как и прежде, будем называть функцией правдоподобия.
г=1
Функция f(x) = ^Z^U)/j(x) есть безусловная плотность
распределения X относительно меры μη, a q(j)fj(x) есть плотность совместного
распределения пары (0, Х), в которой номер θ гипотезы выбирается случайно.
Таким образом, если дана выборка X, то в байесовском случае можно
построить апостериорное распределение Qx гипотез Hj (мера λ,
фигурирующая в §21, здесь — считающая мера), которое определяется по формуле
Байеса
Ях{нк) = ф/х) = д-Ц1^. О)
Это есть условное относительно X распределение Θ.
Через Ε будем обозначать безусловное математическое ожидание,
соответствующее распределению Ρ пары (0,Х).
Теорема 1. 1) Вероятность ошибки &q^) любого критерия δ
удовлетворяет неравенству
aQ{6)>l-Emaxq(j/X). (4)
з
2) Для того чтобы критерий δ = 6q был байесовским для априорного
распределения Q, необходимо и достаточно, чтобы для Р-почти всех
значений X он удовлетворял соотношениям
δ{Χ) = Hk, если q{k/X) = max q(j/X). (5)
i
При δ = 6q в неравенстве (4) достигается равенство.
Отметим, что правая часть в (4) от δ не зависит.
Доказательство. Пусть дан критерий δ. Рассмотрим событие Д$,
состоящее в том, что критерий δ приводит к ошибочному решению:
г
§41. Проверка конечного числа простых гипотез
305
Тогда очевидно, что αρ(ί) = Ρ (ДО и запись (2) есть результат
последовательного усреднения: сначала по X при фиксированном θ = j, потом по Θ.
Но мы можем cxq(S) записать и иначе: сначала провести усреднение по θ
при фиксированном X, а потом по X:
<*q(S) = fP(Ds/X = χ)}{χ)μη{άχ)
= ЕР(£5/Х) = Ε £ Pi* = J. W * fii/X).
Но 5(Х) измеримо относительно X, поэтому
р(й> = з, δ(Χ) Φ Hj/X) = /{W*,}P(0 = i/*) = (i - I{s(x)=hj})q(j/x)-
Отсюда получаем
г
aQ(5) = l^E^2q(j/X)I{S{x)=Hj} > 1-Emaxq(j/X).
3=ι 3
Первое утверждение теоремы доказано.
Достаточность второго утверждения теоремы с очевидностью вытекает
из первого утверждения, так как установленная нижняя граница для cxq(5)
достигается для критерия ig, определенного в (5). Изменение 5q(X) на
множестве нулевой Р-вероятности, очевидно, olq(5q) не меняет.
Необходимость второго утверждения доказывается столь же просто.
Действительно, пусть δ = 6q есть байесовский критерий и пусть δ(Χ) = Я^,
q{k/X) < q{l/X) = maxq(j/X) при Χ € А, Т?(А) > 0. Тогда для критерия
з
#ιΡΟ, который отличается от δ(Χ) лишь на множестве Α: δ{(Χ) = Hi при
iGi, получим
P(DSi;A) = -P{A)-E
\Σς(3/Χ)Ι{δι{χ)=Ηι};Α\ =
'- j
= Έ>(Α) - E[q(l/X); A] <P(A)- E[q(k/X); A] = P(DS; A);
P(DSl)<P(Ds) = P(DsQ).
Мы получили противоречие. <
Отметим теперь, что запись (5) еще не полностью определяет критерий
Sq: из нее не ясно, какую гипотезу следует принимать, если максимальными
оказались два или более значений q(j/x). Речь идет, очевидно, об
определении функции Sq(X) на границах
Tk = {xeXn: q(k)fk(x) = maxflfUJ/ji®)}
Зфк
множеств
Ω? = {х 6 Xn : q(k)fk(x) > maxq{j)fj(*)h (6)
на которых согласно (5) критерием 5q принимается гипотеза Нк.
306
Гл. 3. Теория проверки гипотез
Стало быть, Ω^; есть «внутренность» области
ili = {x£Xn:SQ(x) = Hk}
приема гипотезы Яд., и нам надо в дополнение к (6) определить лишь, какие
точки границы Г^ относятся к щ и какие нет. Но эта задача, как видно из
приведенных рассуждений, может быть решена весьма просто: мы можем
присоединять точки Г* к любой из «прилегающих» областей Ω^; при этом
мы получим то же значение olq{5), поскольку (5) будет выполнено. Точнее,
если А С Г^ Π... Π Г*р то при X £ А согласно байесовскому критерию
безразлично, какую из гипотез Я^,..., Я^ принимать. Мы можем принимать
решение случайно — с вероятностью pki выбирать гипотезу Я^, % = 1,..., ί,
/
/Jpfc, = 1. Значение clq{8) при этом не изменится.
i=l
Мы приходим здесь к более общему понятию рандомизированного
статистического критерия (от английского слова random), которое оказывается
весьма полезным.
Определение 6. Рандомизированным статистическим критерием
для проверки гипотез Н\,...,НГ называется любое измеримое
отображение π: Xй -> R(r\ где Ш^ есть множество векторов (πι,...,πΓ), щ ^ 0,
t=l
Рандомизированный критерий каждому χ £ Xй ставит в
соответствие распределение вероятностей π{χ) — (πι(χ),.. .,7гг(ж)) на множестве
{Н\,.. .,ЯГ}, и окончательное решение о приеме гипотезы «разыгрывается»
случайным образом с этим распределением (уже независимо от X, после того
как π2·(Χ) определены).
Обычный статистический критерий, очевидно, есть частный случай
рандомизированного, когда все π, равны нулю и лишь одно — единице. Такие
критерии будем называть нерандомизированными.
Вероятность ошибки г-го рода α{(π) для рандомизированного критерия
определяется аналогично:
α{{π) = Pi (не принять Я;) = 1 — ^щ(Х).
В байесовском случае задача минимизации
г
3=1
рассматривается совершенно аналогичным образом. Если через 0, как и
раньше, обозначить номер случайно выбранной гипотезы с априорным
распределением Q, так что Q(0 = j) = q(j), и через Ε, как и прежде, символ
§41, Проверка конечного числа простых гипотез
307
безусловного математического ожидания, то
г
α0(π) = 1 - J2q(j)EMX) = 1 - Ещ(Х) = 1 - ΕΕ(πθ(Χ)/Χ) =
Г
= 1 -ЕТЧ{ЦХ)^{Х) > 1-Emax q(j/X).
7=1 J
Итак, мы получили ту же нижнюю границу для ад (π), что и для
нерандомизированных критериев. Это значит, что, расширяя класс критериев,
мы не можем в нашем случае улучшить значение ctQ{S). Более того,
наименьшее значение достигается на нерандомизированном критерии Sq.
Однако при этом число байесовских рандомизированных критериев π^, т.е.
критериев, для которых ад(π^) = olq(Sq), будет значительно больше, чем
нерандомизированных, так как на множестве
1
где Г = Xй \ Г, мы можем взять в качестве π®(χ) любой вектор из
подмножества Rku...,ki С №>г\ состоящего из векторов π, у которых отличны
от нуля лишь координаты с номерами fci,...,fcj. Очевидно, что Rk состоит
из единственного вектора е&, у которого Л;-я координата равна единице, а
остальные — нулю, и мы должны положить
π®(χ) = e\z при χ Ε fijjr.
Поскольку приведенные соотношения с точностью до значения π®(χ) на
множестве Р-меры 0 необходимы и достаточны для того, чтобы
<xq{kQ) = olq{Sq) = 1 - Emaxgu/X),
то мы можем наряду с теоремой 1 сформулировать следующее утверждение.
Теорема 1А. 1) Для любого рандомизированного критерия
ад (π) ^ 1 - Emaxq{j/X).
j
2) Для того чтобы критерий π® был байесовским, необходимо и
достаточно выполнения соотношений
π®{χ) = ek при χ G Ω^τ,
nQ{x) е Д*1 ,...,*, при χ G Г^Ь...Л
<?лл Р-почти всех значений х.
308
Гл. 3. Теория проверки гипотез
г
3) Для любых gj ^ 0, j = 1,.. .,r; }tfj = 1 справедливо неравенство
3=1
г г
ifo/ш minify > 0 w we все /г(ж) совпадают, т. е. если существуют значе-
з
нил fc, j w множество А, Р(А) > 0, на котором Д(аг) 7^ fj{x)i mo знак в
неравенстве (8) будет строгим.
Замечание 1. Из (8) следует, что
(xq{kQ) < 1 - maxg(j). (9)
В правой части здесь стоит вероятность ошибки критерия, который
выбирает Hk, если q(k) = max q(j) (это есть байесовский критерий среди всех
з
критериев, не зависящих от выборки X).
Доказательство теоремы 1А. Первые два утверждения нами уже
доказаны. Чтобы доказать последнее утверждение, достаточно сравнить
байесовский критерий π^ с критерием π°{Χ) = g = (gi,..., <7Г), не зависящим
от X, для которого, очевидно, α^(π°) = 1 — gj,
αβ(π0) = έ9ω(1-»)^«9(^)-
Если в (8) имеет место равенство, то критерий π°{Χ) = g = const будет
байесовским. По второму утверждению теоремы это возможно лишь в
случае, когда q(l/X) = ... = q(r/X) Р-почти всюду. Это, в свою очередь,
возможно, лишь когда fi{X) = -.. = fr{X) Р-почти всюду, q(l) =■ ... — q(r). <
Итак, введение рандомизированных критериев не позволяет уменьшить
вероятность ошибки ад, но увеличивает само разнообразие критериев и,
в частности, число байесовских критериев π^. Это обстоятельство иногда
оказывается полезным.
В дальнейшем под статистическим критерием мы, как правило, будем
понимать рандомизированный критерий π.
3. Минимаксный подход. Если в байесовском случае мы измеряли
качество критерия средней величиной ад (π) = У^<70)оу(7г), то теперь мы
будем сравнивать максимальные значения
α(π) = maxaj(7r) = тахад(7г).
з Q
Очевидно, это тоже позволяет упорядочить множество всех критериев.
Определение 7. Критерий π = π, для которого
α(π) = mina(7r),
π
называется минимаксным.
§ 41. Проверка конечного числа простых гипотез
309
Следующее утверждение является полным аналогом теоремы 21.2.
Теорема 2. Пусть существует байесовский критерий π
(соответствующий некоторому априорному распределению Q), для которого
αι(π) = ... = αΓ(π). (10)
Тогда π — минимаксный критерий.
Доказательство. Обозначим через q(j) априорные вероятности,
соответствующие Q. Тогда для любого критерия π имеем
г г
α(π) > Σϊϋ)αί(π) ^ Σ tfl?)0^) = max α, (π) = α(π). <
ί=ι i=i J
Распределение Q = {^(j)}, соответствующее критерию π, называют wau-
худшим (или наименее благоприятным, ср. с §21). Это связано с тем, что
при Q = Q достигается
max giq^^) = maxminaQ(7r),
так что минимаксный критерий (10) есть байесовский критерий с самой
большой вероятностью ошибиться. Доказательство этого факта можно найти
в § 75. Там же будет показано, что наихудшее распределение и минимаксный
критерий всегда существуют.
Следует, однако, отметить, что в отличие от байесовских критериев
минимаксные нерандомизированные критерии существуют далеко не всегда.
Дело в том, что разделяющие границы Г^ множеств Ω^; (см. (6)) могут иметь
ненулевую вероятность Pfc(X £ Г*) > 0 и, стало быть, значения а&(5д) при
непрерывном изменении Q могут меняться скачками. Это означает, в свою
очередь, что г — 1 уравнения g:i(5q) = ... = ar(5g) для г — 1 неизвестного
#(1),.. .,g(r — 1) ( q{r) = 1 — /JtfO) ) могут не иметь решения. Однако
^ j=i '
в классе рандомизированных байесовских критериев минимаксный
критерий существует всегда. В качестве иллюстрации подробно рассмотрим этот
вопрос для случая г = 2 в следующем параграфе.
Итак, мы нашли явный вид байесовских критериев и установили, что
с их помощью можно строить минимаксные критерии. Оказывается, что
аналогичным образом можно строить и наиболее мощные критерии в
классах ΛΤαι,...,αΓ-ι> введенных в п. 1.
4. Наиболее мощные критерии. Определение нерандомизированного
н. м. к. было дано в п. 1. Нам будет удобно здесь распространить это
определение на класс рандомизированных критериев. Пусть аналогично п. 1
^αι,...,αΓ-ι означает класс рандомизированных критериев с фиксированными
значениями вероятностей ошибок j-ro рода, j = 1,..., г — 1,
Καΐ9...,ατ-ι = {тггаДтг) = ау; j = 1,...,г-1}.
310
Гл. 3. Теория проверки гипотез
Определеннее. Критерий π0 Ε #αι,...,αΓ_ι называется w. ле. к. β
Каи...,аг-1> если Для любого π G /faif...far_i
αΓ(π0) < αΓ(π).
Теорема 3. Предположим, что существует распределение Q =
= {#(1),.. ·,<ζ(Γ)} такое, что
aj(*(*) = l-Ejir9(X) = aj, j = l,...,r-l (И)
(по существу, мы имеем здесь г - 1 уравнение для неизвестных ςτ(1),...
...,g(r — 1)). Тогда байесовский критерий π^, определенный в (6), (7),
будет наиболее мощным в классе KaijtmmtCtr_1.
Доказательство. По определению байесовского критерия
Это значит, что для π Ε i^ai,...,ar_i будем иметь
г г —1
J^g(j)ay(7rQ) < 5^?(j)aj +9(Γ)αΓ(π).
J=l j=l
Ho α^-(π^) = otj при j ^ r - 1 и, стало быть, αΓ(π^) ^ αΓ(π). <
Здесь по той же причине, что и при отыскании минимаксных критериев,
уравнения (11) в классе нерандомизированных критериев δ не всегда
разрешимы. В классе рандомизированных критериев положение существенно
меняется. Это обстоятельство будет проиллюстрировано в следующем
параграфе.
Приведем теперь пример довольно распространенной реальной задачи о
проверке конечного числа простых гипотез.
Пример 1. Пусть гипотеза Η ι означает, что пациент, пришедший на
осмотр к врачу, здоров, а Н^ — болен некоторой определенной болезнью А^,
k ^ 2. Задача врача состоит в том, чтобы на основании наблюдений
(которые можно записать в виде вектора χι = (xn,xi2> · ■ ·>χι«)> представляющего
из себя многомерную выборку X единичного объема) принять одну из
гипотез Hj. Болезни Ak фиксируются нами для того, чтобы гипотезы Η^ были
простыми и тем самым полностью определяли распределение выборки X.
Если врач принимает гипотезу Η к, к ^ 2, в то время как на самом деле
верна Н\, он совершает ошибку одного типа. Если же наоборот — он
больного (i/fc) признает здоровым (Hi), — то совершает ошибку другого рода.
Нетрудно понять, что «эффекты» от ошибок этих двух типов могут быть
существенно различными.
Из результатов, изложенных выше, мы видим, что для построения
наилучшего решающего правила мы должны знать распределение вектора
наблюдаемых величин (хц,.. .,xis) для здоровых людей и людей, больных
болезнью Α^ (для этого нужны обширные статистические данные
медицинских обследований). Разумеется, значительная часть проблемы состоит в
самом выборе s и наблюдений (хц,Х12> · · ->xis)· Во многом именно здесь
проявляется искусство и опыт врачей.
§ 42. Проверка двух простых гипотез
311
Если же вектор (хц,.. .,хь) выбран достаточно обоснованным образом,
то теоремы 1, 2 указывают нам прямой путь для алгоритмизации задач
диагностики заболеваний.
§ 42. Проверка двух простых гипотез
В этом параграфе мы несколько подробнее остановимся на частном
случае, когда проверяются г = 2 простые гипотезы.
В задачах проверки гипотез последние часто играют несимметричную
роль, как это было, скажем, в примере 41.1. Поэтому одну из гипотез,
например //"χ, принято называть основной или нулевой, а остальные —
альтернативами. Вероятность ошибки первого рода αι(δ) критерия δ в этом
случае называют также размером, а число 1 — αι(δ) — уровнем критерия.
Число β(δ) = 1 — α2{δ) называется мощностью критерия.
Область Ω2 С Xй приема гипотезы Нч нерандомизированным
критерием δ в случае г = 2 называют критической областью. Вероятность
Рг(Х Ε Ω2) попадания в эту область, когда верна Яг, будет равна мощности
критерия β{δ). Отсюда происходит название «наиболее мощный критерий»
для критерия £, на котором β(δ) достигает своего максимума при
фиксированном уровне критерия δ.
Отметим теперь, что в случае г = 2 любой критерий, в том числе и
рандомизированный, можно характеризовать одной числовой функцией.
Действительно, произвольный рандомизированный критерий 7г(ж) полностью
определяется значением его г координат (πι(ж),.. .,7гг(ж)). Но так как
У^7Г;(ж) == 1, то в случае г = 2 достаточно задать одну функцию, скажем
π2(χ). Эта функция определяет вероятность принятия альтернативы i?2- Мы
будем обозначать ее через 7г(ж) и называть критической функцией
критерия π, который будем обозначать той же буквой π. Очевидно, что для
нерандомизированных критериев π (ж) принимает лишь значения нуль и единица;
в общем случае 0 ^ π (ж) ^ 1.
Размер αϊ (π) критерия π (или δ) и его мощность /3(π) выражаются через
7г(ж) следующим образом:
αϊ (π) = Ειπ(Χ), β{π) = 1 - α2(π) = Ε2π(Χ).
Обозначим через Ζ отношение правдоподобия
Ζ = Ζ(χ) =
№)'
которое будем рассматривать лишь для значений ж, при которых оно
определено, т.е. для ж, при которых /ι(ж) + /г(ж) > 0.
Теорема 1. 1) Пусть с = g(l)/g(2), где Q = (?(1),д(2)), q{2) = l-g(l)
есть заданное априорное распределение. Тогда критерий 7rCjP с
критической функцией
[1, если Z(x) > с,
кс#(х) = { Ρ(χ)ι если ζ(χ) — с> (*)
^0, если Ζ(χ) < с,
312
Гл. 3. Теория проверки гипотез
при любой измеримой функции р(х), 0 ^ р(х) < 1, является байесовским
для распределения Q: 7rCjP = π^.
Параметры αι(π0|Ρ), α2(π0>ρ) критерия nCiP удовлетворяют
неравенству
2 2
£?(;>,·(тгс,р) ^ 5^g(j)(l -и) (2)
npw любых gj ^ О, 51 +52 = 1·
2) Длл заданного ε > О такого, что Έ*ι(Ζ > 0) > ε, существуют с > О
и р(ж) = ρ = const такие, что nCiP Ε Χε = {π : αχ (π) = ε} u 7rCjP является
н. ж. κ. β ΑΓε. Числа сир определяются как решение уравнения
ai(nc<p) = EmCJ,(X) = Ρι{Ζ(Χ) > с) +ρΡι(Ζ(Χ) = с) = е. (3)
Яри этож мощность критерия β{π0)ρ) = 1 — #2(я"с,р) удовлетворяет
неравенству
/?Кр) > е. (4)
£^сли соотношение /г(ж) = /ι(ж) η. β. [μ] не выполнено (аналог
условия (Ао) главы 2), то неравенства (4) и (2) при 0 < gi < 1 являются
строгими.
Kpumepuu7TCiP минимизирует вероятность ошибки первого родаа,\(к)
в классе К всех критериев π с фиксированной вероятностью ошибки
второго рода: К = {π : α2(π) = α2(π0>ρ)}.
3) Существуют с > 0 и р{х) =р = const такие, что критерий -кСф
будем минимаксным. Числа сир определяются из уравнения α?ι(π0ιΡ) =
— ^2(тгс,р) или, что то же-> из уравнения
Ρι(Ζ(Λ·) > с) +Ρ2(Ζ(Χ) > с) +p\P1(Z(X) = c) + P2(Z(X) = с)] = 1. (5)
Очевидно, что если Pi-распределение Ζ(Χ) непрерывно, т.е. Έ*ι(Ζ(Χ) =
= с) = 0 при всех с ^ 0, то в последних двух утверждениях теоремы можем
положить ρ = 1 или ρ ξ 0.
Заметим также, что
P!(Z(X)=c)= j Μχ)μη(άχ)= f ^μη(άχ) = ^Ρ2(Ζ(Χ) = ο),
Z(x)=c Z(x)=c
так что непрерывность на (Ο,οο) Pi-распределения Ζ влечет за собой
непрерывность ^-распределения Ζ.
Критерий 7гс,р, основанный на отношении правдоподобия Ζ, называют
критерием отношения правдоподобия.
Теорема 1 показывает, что все оптимальные критерии являются
критериями отношения правдоподобия.
Второе утверждение теоремы 1 носит название леммы
Неймана-Пирсона. Если в нем условие Ρι(Ζ > 0) > ε не выполнено, т. е. если Ρι(Ζ = 0) =
— 1 — 7> 7 < ε-> τ0 Η· Μ· κ· 7Г(Ж) — Ι{ζ(χ)>ο] будет иметь мощность 1 и размер
§ 42. Проверка двух простых гипотез
313
7 < ε. Например, если носители распределений Pi и Р2 не пересекаются, то
Ζ = 0 на множестве, где /ι(ж) > 0 и, стало быть, Ρ\{Ζ > 0) = 0. В этом
случае гипотезы Н\ и #2 различаются по одному наблюдению с вероятностями
ошибок, равными нулю, т. е. различаются детерминированным образом.
Доказательство теоремы 1. Первое утверждение теоремы
является прямым следствием теоремы 41.1А.
Для доказательства второго утверждения можно воспользоваться
теоремой 41.3. Покажем сначала, что уравнение (3) всегда разрешимо
относительно сир. Очевидно, что функция φ(ο) = Pi (Z > с) не возрастает
на [0, оо). Случайная величина Ζ относительно распределения Ρ χ является
собственной, т.е.
V?(c)=Pi(Z>c) =
= ί Μχ)μη{άχ)<^ ί Μχ)μη(άχ) = ^Ρ2(Ζ>ή->0
Z(x)>c Z(x)>c
при с —► оо. Так как по условию φ(0) ^ ε, то найдется се Ε (О, оо) такое, что
(φ(ό) непрерывна справа)
<ρ(θε-0)^ε, (р(се)^е. (6)
Если мы положим в (3) с = се и обозначим Δε = φ{οε — 0) — φ(ο€), то получим
aifrcdO = φ{οε)+ρΔε.
8 силу (6) здесь, очевидно, всегда можно выбрать ρ £ [0,1] так, чтобы*)
φ{θε) +ρΑε =ε.
Теперь мы можем поступить так же, как в доказательстве теоремы 41.3.
Положим q(l) = q£ = с£/(с£ + 1) и фиксируем выбранное нами р. Тогда
критерий 7гС€)Р будет байесовским, соответствующим распределению Q€ =
= (<7ε, 1 —9е), и в то же время αι(πβ(ΓϊΡ) = ε. Это означает в силу теоремы 41.3,
что 7rCffjP является н. м. к. в ΛΓε.
Если взять критерий 7г(ж) = ε, получим
π G Κε, α2(π^ιΡ) < α2(π) = 1 - ε, β{π0ε,Ρ) ^ ε.
Это есть не что иное, как неравенство (2) (ср. (41.8)) при #2 = £· Стало быть,
если соотношение /2(2;) = /ι(χ) п. в. [μ] не выполнено, то эти неравенства
будут строгими. Утверждение теоремы о минимизации αϊ (π) на критерии
7гС)Р в классе К = {π : α2(π) = a2(7rCjP)} следует из приведенных выше
рассуждений и симметрии относительно гипотез Н\ и i/2 постановки задачи
в первом утверждении теоремы.
Для доказательства третьего утверждения теоремы 1 следует
воспользоваться теоремой 41.2. Для этого нам надо проверить лишь, что уравнение
*) Ясно, что если φ(ο) непрерывна в точке сс, то проблема решения (3) сводится к
отысканию квантиля распределения Ζ порядка 1 — ε.
314
Гл. 3. Теория проверки гипотез
^ι(ττο,ρ) = «2(тгс,р) разрешимо относительно сир. Это уравнение можно
записать в виде
Е17гС)Р(Х) = 1^Е27гс,р(Х)
или, что то же, в виде (5). Разрешимость его устанавливается точно так
же, как разрешимость уравнения (3). Надо заметить лишь, что всегда
Ρι(Ζ > 0) + P2(Z> 0)^1, так так Ρ2(Ζ>0) = / /2{χ)μη{άχ) = 1. <
/2(χ)>ο
Мы видели еще раз, что цель введения рандомизированных
байесовских критериев состоит в обеспечении «непрерывного» изменения
параметров этих критериев (возможные значения размеров критериев π0}Ρ
заполняют весь интервал (0,1)). Отсутствие такого непрерывного изменения
параметров, связанное с тем, что на множестве положительной Ρ ι-вероятности
возможно равенство fi(x) = 0/2(2;), составляет основное препятствие при
отыскании критериев заданного уровня или минимаксных критериев в
классе нерандомизированных критериев. Эта картина полностью сохраняется и
в случае проверки большего числа гипотез.
Важно отметить, что два вида оптимальных критериев — наиболее
мощные и минимаксные — оказываются байесовскими при тех или иных
априорных распределениях. Нетрудно видеть также, что класс всех наиболее
мощных критериев совпадает в известном смысле с классом всех
байесовских критериев. Такое положение, при котором в качестве основы для
выбора оптимальных критериев можно использовать байесовский подход, во
многом сохранится и в дальнейшем.
Пример 1. Рассмотрим пример 2, приведенный во введении. В этом
примере гипотезы #χ и #2 имеют вид Н\ = {х* ^ F(x)}y Я2 = {xi €=
€= F(x — о)}, где F(x) — заданная функция распределения, а — данное
число. Предположим, что F(x) имеет плотность f(x) и что случайная
величина /(χι — α)//(χι) имеет непрерывное распределение. Тогда по лемме
Неймана-Пирсона (п. 2 теоремы 1) среди всех критериев уровня 1 — ε
критерий
Тт/(* -">;-.
будет наиболее мощным в рассматриваемой задаче о проверке гипотезы Н\
(объект отсутствует) против гипотезы i/2 (объект присутствует). Число се
определяется из условия
Р.(Ёь^>ь.)-..
При больших η для вычисления этой вероятности мы можем пользоваться,
очевидно, центральной предельной теоремой.
§ 43. Два асимптотических подхода к расчету критериев 315
§43.* Два асимптотических подхода
к расчету критериев. Численное сравнение
1. Предварительные замечания. В §41, 42 мы нашли форму
оптимальных критериев для проверки простых гипотез. Термин «расчет критериев»,
который мы употребили в заголовке, будет означать вычисление
параметров, характеризующих критерий. В задаче о н. м. к. в случае г = 2 это
есть отыскание величин с£ и ρ для заданного ε > 0 и определение
вероятности ошибки второго рода Οί2(π0ε#) или, что то же, мощности критерия
β(ποε,ρ) = 1 — <22(тгСе,р)· Можно поставить вопрос и несколько иначе. Мы
видели, что все оптимальные критерии в случае г = 2 имеют вид функций
7tCjP, представленных в (42.1). Пусть дан критерий nCjP. Как определить для
него вероятности ошибок aj(7rCjP)?
Этот же вопрос возникает, конечно, и в общем случае г > 2 для критерия
(41.7), но мы в этом параграфе ограничимся для простоты лишь случаем
двух простых гипотез.
Ниже рассматриваются асимптотические подходы, позволяющие
приближенно (при больших п) решать эти задачи. Такие же подходы можно
использовать и для расчета критериев, которые будут рассматриваться в
дальнейшем.
Итак, пусть дан критерий (42.1) и пусть для простоты распределение
Z(X) непрерывно, так что можем положить ρ = 1. Тогда критерий (42.1)
станет нерандомизированным (обозначим его через £с), и нам требуется найти
значения
ai№) = Pl(fm>c)' аЛ) = Р2(Ш<с)· (1)
П
Так как fj{X) = ТТ/Дх»)» т0 событие, стоящее под знаком вероятности
в (1), можно записать в виде
Σ»
^ In с,
i=1 7ife)
где слагаемые
m = ь χι
/l(xt)
очевидно, есть независимые, одинаково распределенные в каждом из случаев
X ё Pj, j = 1,2, случайные величины.
η
Таким образом, дело сводится к изучению распределений сумм 2~^т?г
i=l
случайных величин щ.
В дальнейшем мы будем предполагать, что объем η выборки X
неограниченно возрастает. При этом под критерием мы будем понимать на самом
деле последовательность критериев, определенных при каждом η (такое
же соглашение мы использовали для оценок в главе 2).
316
Гл. 3. Теория проверки гипотез
2, Фиксированные гипотезы· В этом пункте мы будем предполагать,
что распределения Р; фиксированы, т.е. от объема η —> оо выборки
Хп = [-Хоо]п не зависят. Рассмотрим задачу расчета н. м. к.
фиксированного уровня 1 — ε. Имеем
Eitfc = -α = Г/1(χ)\η^\μ(άχ) = -pi(PbP2) < О,
J л (я)
E27?i = b = /"/а(я:) h^L(<fe) = ρι(Ρ2,Ρι) > 0,
где pi есть расстояние Кульбака-Лейблера (см. §31).
1 п
Это означает в силу закона больших чисел, что Ρ ι-распределение — V^ щ
П · 1
г=1
будет сосредоточено в окрестности точки —а, а Р2-распределение — в
окрестности точки Ь. И это «разделение» распределений будет в смысле леммы
Неймана-Пирсона наилучшим. Положим σ| = Dj77i и предположим, что
a'j < оо. Тогда
αϊ(<У = Pi ( έ*Κ ^ lnc) = Pl ( ~^ Σ^ + α)
>!f±|2 . (2)
Выберем в качестве с = с(п) любую последовательность, для которой
In с + an
G\y/n
λε,
где Αε, как и прежде, квантиль нормального распределения уровня 1 — ε.
Тогда из (2) и центральной предельной теоремы следует
ai(ic) - 1 - Φ 7=^ ~* ε· 3
Определение 1. Критерий π, удовлетворяющий соотношению
lim αϊ (π) = lim Ειπ(Χ) = ε,
η—>οο η—>οο
называется критерием асимптотического уровня 1 — ε (или
асимптотического размера ε).
Стало быть, при
lnc = —an 4- \εσ\\/η + о(\Лг) (4)
критерий 5С будет иметь асимптотический уровень 1 — ε.
Соотношение (4) можно рассматривать как приближенное решение
уравнения для числа се, для которого ai(5Ce) = ε.
§ 43. Два асимптотических подхода к расчету критериев 317
Положим для определенности In с = — αη + \εσ\ \Jn и найдем для
выбранного с асимптотическое поведение вероятности ошибки второго рода
г—1
σ2
(5)
Так как —(α + b)y/n/a2 + \εσ\/σ2 —► —οο при η -» οο, то применение здесь
центральной предельной теоремы дает нам лишь, что &2(8С) —> 0.
Задача вычисления точного асимптотического поведения правой
части в (5) приводит нас к задаче о вероятностях больших уклонений для
сумм случайных величин щ.
Приведем здесь результаты о вероятностях больших уклонений,
изложенные в [17, §8.8]. Пусть нам надо вычислить асимптотическое поведение
Ρ I 2_]ζί > х ] ПРИ п -* °°> х ~* °°> гДе ζι независимы и одинаково
распределены. Предположим, что распределение & имеет абсолютно непрерывную
компоненту и что
< οο
при некоторых А > 0. Пусть, далее,
А+ = sup {λ : ψ(\) < οο},
(6)
A(a)=inf{-aA + ln^(A)}, V '
и λ (α) есть значение А, при котором этот inf{·} достигается.
Тогда справедливо следующее утверждение. (См. [17, § 8.8,
теоремы 12, 13, теоремы 9, 10]. Условия D£2 = 1, Έξ{ = 0, фигурирующие в
этих теоремах, не играют роли.)
Теорема 1. Пусть 1= > οο так, что
у/П
* №+)
limsup - < a+ == .
η_>οο η ν(λ+)
Тогда уравнение
αψ(\)=ψ'(\) (7)
<?лл точки λ(α) имеет при а < а+ единственное решение,
p(yji>x)= \ _ехр{-пЛ(а)}(1 + о(1)), (8)
У σ(ο;)|λ(θ!)|ν2πη
318
Гл. 3. Теория проверки гипотез
где
а = -, σ (а) = - а .
η ψ(λ(α))
Кроме того, справедливы соотношения
A(Bfi)=0, Λ'(α) = λ(α),
А/// Ч _ Х/Г ΐ - ^(Л(а))
W ~~ W <№(<*)) - α2^(λ(α))'
Вернемся теперь к вычислению асимптотического поведения величины
а2(5с)> определенной в (5) и равной
Р2 (-][]% >ап-уу/п) =Р2 I J^Hfc + b) > {a + b)n-yy/n\
при у = λεσχ. Чтобы воспользоваться приведенной теоремой, надо положить
, Л(хЛ /-
ξι = -% = Ь , ,, х = ап- уу/п.
/2№;
Тогда получим при 0 ^ λ ^ 1
V(A) = Е2е"^ = | /2(*) (Щ) μ(άχ) =
= J ti(x)ftx(xMdx) < (/ Μχ)μ(άχή (|/2(*М^)) = ι-
Отсюда следует также, что ψ(\) будет конечным и в некоторой
окрестности точки λ = 1, если
/л(*)М,"<*,<00 (9)
при каком-нибудь 7 > 0. Далее, уравнение для точки λ (α) будет иметь вид
« 4- ^λ) - П
-α + Τ7νΓ U
ν»(λ)
или
^w-/aw(Ш)ЛьШ"^ = а/ЛМ(ш)Л"(*)-(10)
Если а = о = /3ι(Ρι,Ρ2) = / /i(ir)b jgy^(dz), то (10) будет
удовлетворено при А = 1. Это означает, что
λ(ο) = 1, ф(Х(а)) = ф(1) = 1.
§ 43. Два асимптотических подхода к расчету критериев 319
Отсюда следует, что
Л(а) = аА(а) — \ηψ(λ(α)) = а,
</>"(λ(α)) = V"(l) = fh{x) (ln£^\(dx),
σ2{α)=ψ"(1)-α2 = σΙ
Λ'(α) = λ(α) = 1, Λ"(α) = af2.
Условия приведенной теоремы будут выполнены, если:
1) Рг-распределение In ——г имеет абсолютно непрерывную компо-
ненту;
2) / /ι(χ)(/ι(χ)//2{χ))Ίμ(άχ) < оо при каком-нибудь 7 > 0.
Учитывая, что в нашем случае функции σ(α), λ(α), Λ"(α) непрерывны
в окрестности точки α = α и что α = χ/η = α — у/л/n, мы получаем Λ(α) =
= a - y/y/n + y2/2ajn + o(l/n).
Итак, мы можем сформулировать теперь следующее следствие
цитированной теоремы.
Следствие 1. Пусть выполнено условие (9) и ^^-распределение
In -7-7—г имеет абсолютно непрерывную компоненту. Тогда при η —> оо
Λ(χι)
а2(5с) = Рг ( - Х)*К > ап - у\Лг) -== ехр |-па + уу/п - ^-Л =
1
βχρ|-η/9ΐ(Ρι,Ρ2)+λ6σιν^- у}· (И)
σι \/2πη
Таким образом, a2(ic) убывает при гг -> оо экспоненциально*).
*) Мы получили заодно возможность дать еще одно определение (интерпретацию)
расстояния Куль бака-Лейб л ер а:
pi(Pi,P2) = — lim — lna2(5c) = — Ит — inf 1паг(^).
В связи с этим отметим, что тот же порядок малости ехр{—η/9ι(Ρι,Ρ2)} имеет Рг-веро-
ятность того, что эмпирическая функция распределения F„ попадет в окрестность функции
распределения Fi, соответствующей Рь Точнее, если η = η(η) -* 0 достаточно медленно, то
- lim ±lnP2(sup|^*)-iM*)|<7)=Pi(Pi.P2) (12)
п-юо п χ
(теорема Санова). Таким образом, расстояние ρι(Ρι,Ρ2) имеет глубокий вероятностный
смысл. Доказательство соотношения (12) читатель может получить, преодолев
незначительные трудности, из теоремы б в [17, §5.2].
320
Гл. 3. Теория проверки гипотез
Нетрудно видеть, что если мы возьмем фиксированное с в (1), то обе
вероятности α\(δ0) и с*2(<У будут убывать экспоненциально, как и значение
OiQ(SQ) при любом фиксированном Q.
Так как
Е,е^ = JMx) (^^j μ(άχ) = ψ(1-\),
miii7/j(A) = min?/>(l — λ),
то ai(£c), a2(<y будут при этом убывать с одинаковой скоростью
(зависимость от η будет одна и та же). Это означает, что минимаксный критерий
будет соответствовать некоторому фиксированному с, приближенное
значение которого нетрудно найти, решая уравнение α\(δ0) = а2{6с) и пользуясь
асимптотическим анализом правой части (8) при a = c/η, η -+ оо.
Экспоненциальное приближение (11) действует достаточно хорошо при
больших п, если только нормированное уклонение
^i = V-(Pl(PbP2) + PlPbP2 )--£-i (i3)
<72Vn σ2 &2
также велико (см. формулировку теоремы).
В тех прикладных задачах, где число η ограничено значениями
порядка 100, это условие выполняется довольно редко, и значение (13) часто
оказывается сравнимым с единицей. Это делает затруднительным
использование описанного подхода к вычислению аг(5с) и соответствует той
ситуации, когда значение аг(^с) вместе с ai(£c) не очень мало (имеет величину,
сравнимую, скажем, с 0,1). В то же время значения η порядка 100 вполне
достаточны для удовлетворительного применения центральной предельной
теоремы в зоне «нормальных уклонений».
Таким образом, вопрос, интересующий нас, состоит в том, когда мы
можем пользоваться нормальными приближениями
«2(У = Р2(|><.пс)«ф(!2^)
(14)
для вычисления обоих значений а\(6с) и ot2($c)·
Для обоснования формул (14) возникает другой подход, основанный на
предположении, что гипотезы Н\ и Ή.2 являются близкими.
3. Близкие гипотезы. Мы будем здесь рассматривать выборку X в схеме
серий и предполагать, что распределения Pi, P2 зависят от η так, что
Ρι(Ρι,Ρ2)+Ρι(Ρ2,Ρι)->0 (15)
при η —> оо, а последовательность (13) сходится к конечному
положительному пределу.
§ 43. Два асимптотических подхода к расчету критериев 321
Чтобы облегчить рассуждения и сделать их полезными для дальнейшего,
мы ограничимся здесь параметрическим случаем, когда X €= Р#,
а семейство {Р#} удовлетворяет условиям регулярности (RR) (см. §33).
Сделаем сначала несколько неформальных замечаний, поясняющих
существо дела. Мы рассматриваем близкие гипотезы, т. е. предполагаем, что
#2 = #1 + 7> гДе 7 мало. Тогда логарифм отношения правдоподобия, на
котором построен н.м.к., представим в виде*)
ымТ)~"ьЧхл)- (16)
Статистику U = L'(X,9\) — главную часть в (16) — называют иногда
эффективным вкладом. Если верна гипотеза Н\, то
Е^С/ = 0, Όθιυ = ηΙ(θ1).
Так как
L'(-Mi) " Ь'{Х,02) ~ lL"(X,e2), Εθ2Σ"(Χ,θ2) = -ηΙ(θ2),
TO
Εθ2υ ~ ηη1{θ2) ~ τη/(0ι), D*2E7 - η/(02) ~ η/(0ι).
Это означает, что распределения U при гипотезах ffi, Я2 и при больших η
будут различимы, если только величина Е^2С/ — Е^:{7 ~ ^ηΙ{θ\) будет
значительно больше или сравнима с y/D^U ~ \/ηΙ(θι). Другими словами,
должно выполняться равенство уп = ϋι/η, г> ^ О, или, что то же, 7 = v/y/n.
Итак, переходя к более точному изложению, мы будем предполагать, что
02 = 01 + 4=, (17)
уп
где величины в\ и г? будем считать фиксированными.
Положим, следуя обозначениям главы 2,
*<*>-№■ ™-ь*Ш-
Тогда
В силу теоремы 37.3 при X ^ P^j имеем
Υι(ν)=ξην-\ν2(Ι(θ1) + εη), (19)
*) Знак ~, используемый здесь, означает асимптотическую эквивалентность при 7 -* 0.
322
Гл. 3. Теория проверки гипотез
где εη —> О, ξηΙ ιΙ2{β\) & Φ0,ι· Аналогично при X ^ Р02
-Υ2(-ν)=ξην + ±ν2(Ι(θ2)+εη),
тдееп—>0, ξηΙ-ι/2{θ2) & Φ0|ι-
Так как /(62) —► ^(#ι)> получаем, что при гипотезе Hj, j = 1, 2,
Это означает, что из теоремы 37.3 вытекает
Следствие 2. Пусть выполнены у словил (RR), (17). Тогда при
любом фиксированном с справедливы формулы (14) или, более точно,
/V
оч{6с) = Ρ* ( Σ^ > 1пс Ι -» χ ~ φ
α=1
J(0i)+lnc
V
Нл/Що
/
α2
(<У=Р<?2 (]Г><1пс -*Φ
'--/(gQ+lnc*
(20)
4t=l
V
M>/W
J
Определение 2. Критерии πι иπ2 называются асимптотически
эквивалентными, если
limsup|aj(7ri) -а^г)| = 0, j = 1,2.
Критерий π называется асимптотически наиболее мощным критерием
(а. н. м. к.), если он асимптотически эквивалентен н.м. к.
Так как в представлениях (18), (19) ξη = L'(X,θ\)η~ιΙ2, то из этих
представлений следует, что критерий δ с критической областью
vL'{X,ei) J J v2I{0) + 2\nc
> να, a =
yfiW)
ЩуДЩ
(здесь играет роль знак ν) будет иметь те же предельные значения αι(δ),
что и критерий 5С, и, следовательно, является а.н. м.к.
Кроме того, в силу результатов § 37
ξη = ЩЬ2£ = (§* -θι)^ϊΙ(θ1)(1 + εη(Χ,θ1)),
§ 43. Два асимптотических подхода к расчету критериев 323
εη(Χ,θ\) —> 0. Отсюда следует, что критерий с критической областью
ν(β*-0ι)>/η/(0ι) >vd (21)
также будет а. н. м. к.
Чтобы получить н. м. к. 6С асимптотического уровня 1 — ε, достаточно
в (20) положить d — λε. Вероятность ошибки второго рода а2(5с) будет
сходиться к Φ(—ν\/ΐ(θι) + λε).
При с = 1 оба предела в (20) будут иметь одно и то же значение
г /п *( ^\/ША\
lim otj{5c) = Φ ζ— .
п-юо J I 2 I
В этом случае критерий 6С (ср. с теоремой 41.2) естественно называть
асимптотически минимаксным.
4. Сравнение асимптотических подходов. Числовой пример. В п. 2, 3 мы
рассмотрели два асимптотических подхода, каждый из которых оправдан
в определенных условиях и которые позволяют указывать приближенные
значения вероятностей ошибок первого и второго рода н. м. к. *). В случае
фиксированных гипотез эти формулы даны в (3), (5), (11), в случае
близких гипотез — в (14), (20). Формулы (11), (20) являются «вторичным»
приближением по сравнению с (8), (14). Поэтому при возможности следует
отдавать предпочтение последним (т.е. (8), (14)).
Мы уже отмечали, что для малых значений αϊ (<$), &2(δ) (скажем,
порядка 0,01 и менее) целесообразнее использовать подход, связанный с
фиксированными гипотезами. Здесь нам важно иметь достаточно хорошую
относительную точность приближения, которая обеспечивается формулами (8) и
не гарантируется центральной предельной теоремой. Если же αϊ (δ) и ct2{$)
сравнимы с 0,1 (скажем, ^ 0,1), то можно рекомендовать второй подход,
рассматривая данную вторую гипотезу #2 = {& = #2} как элемент
последовательности близких гипотез Н2уП = {0 = #i + v/y/n}, где, очевидно, надо
при данных 01, #2 положить ν = у/п(в2 — θι). Так как ожидаемые значения
αι(ί), α2(#) не являются очень малыми, то абсолютная величина ν/y/ΐψι)
не должна быть большой.
Пример L Приведем теперь числовой пример, который иллюстрирует
в какой-то мере соотношение между двумя предложенными выше способами
аппроксимации.
Пусть X €= Гяд, т.е. х^ имеют плотность
Мх)=ве~вх, х>0,
*) Отметим, что наряду с предложенными двумя подходами можно рассматривать
целый спектр промежуточных случаев, которые на параметрическом языке можно представить
в форме (ср. с (17)) 02 = 0ι + ζη~Ί, 0^7^ 1/2· Такого рода близкие гипотезы
представляют интерес при подборе приближенных формул, наиболее точно отражающих данную
конкретную ситуацию.
324
Гл. 3. Теория проверки гипотез
и пусть основная гипотеза Н\ имеет вид Н\ = {Θ = 1}. В качестве
альтернатив рассмотрим простые гипотезы Щ — {Θ = 0,5}, Щ = {Θ = 0,8},
#<3> = {θ = 0,9}.
По выборке X гипотеза i/χ будет проверяться против одной из гипотез
(i)
#2 , J — 1,2,3. Таким образом, здесь 0\ = 1, а для 62 имеются три
варианта: 02 = 0,5, 02 = 0,8, 02 — 0,9, два последних из которых мы попытаемся
рассматривать как соответствующие гипотезам, «близким» к Н\. Мы
произведем расчет критериев для выборок объемов η = 30,100,300,1000.
В нашем случае
г/< = 1п^Ей = 1п02-(б2-1)х<, (22)
/01 (xi)
/'(Xi,0i) = 1 - xi, (23)
ГЛ.
X
Отсюда следует, что н. м. к. йс, а также оба а.н.м.к., рассмотренные выше
(с критическими областями вида
di = ά^/ηΙ(θι)) будут иметь форму JC(X) = Я^, если
£>-1)>*1. (24)
2 = 1
Если Χ ί= Ι\ι (гипотеза Я1), то
BiX! = 1, DlXl = 1 = 1(1) = Bi[/#(xi, Ι)]2·
Стало быть, если положим di = 2^/п, то (ср. с (14))
αϊ
№) = Ρι (X>i--l)><*i) =
U=l
(-^^(хг-l) >2J -> 1 - Ф(2) « 0,023
(25)
при η —> оо. Так как в нашем случае /J 77г = η 1п#2 + (1 — #г) /J*г, то 1пс
i=l г=1
в (14) (или в (20)) связан с d\ соотношением
In с = п(1п02 + 1 - θ2) + (1 - 02)di.
Ниже мы приводим три таблицы. Во всех трех d\ предполагается
выбранным так, что выполнено (25) (т.е. d\ = 2^/п). В табл.1
сравниваются истинные значения α\(δ0) с приближением (25). В табл.2 приведены
§ 43. Два асимптотических подхода к расчету критериев 325
истинные значения вероятности ошибки второго рода с*2($с) и
приближения для a2(ic)5 полученные по формулам больших уклонений (8). В табл.3
сравниваются истинные значения a2(ic) с приближениями, полученными
по формулам близких гипотез (14). Отметим, что мы пользуемся здесь
приближениями (8), (14), а не вторичными приближениями (11), (20), которые
содержат дополнительные погрешности. Все необходимые вычисления
приведены ниже.
Таблица 1
Значения ai (Sc). Верхний ряд — истинные значения,
нижний — приближения (14), (25)
Объем выборки
30
0,031
0,023
100
0,028
0,023
300
0,026
0,023
1000
0,024
0,023
Таблица 2
Значения аз(£с)· Верхний ряд — истинные значения, нижний —
приближения (8) или (26) (большие уклонения)
02
0,5
0,8
0,9
Объем выборки
30
0,028
0,033
0,71
0,89
100
15 · Ю-7
15 -КГ7
0,35
0,79
300
19-Ю-*19
19-Ю-19
0,028
0,53
1000
18 ■ Ю-72
18 · Ю-72
33-Ю"8
34 · Ю-8
0,085
0,11 1
Таблица 3
Значения ct2(Sc). Верхний ряд — истинные значения, нижний —
приближения (14) (близкие гипотезы)
02
0,5
0,8
0,9
Объем выборки
30
0,028
0,041
0,71
0,69
0,89
0,89
100
15 · Ю-7
31 ■ Ю-6
0,35
0,35
0,79
0,79
300
19-Ю-19
0,028
0,031
0,53
0,52
1000
18 · 10~72
33 · Ю-8
12-Ю-7
0,085
0,086
Числа в табл. 1-3 приведены с точностью до двух значений цифр после
запятой.
Сравнение табл. 2, 3 показывает, что в соответствии со сделанными выше
замечаниями приближение, основанное на больших уклонениях, лучше
действует в верхней правой части таблиц (где {θ\ — #2)4/^ = (1 — 02)л/п > 3),
326 Гл. 3. Теория проверки гипотез
а приближение, основанное на близких гипотезах — в нижней левой
части таблиц (где (1 — 02)у/п < 3). Прочерки в таблицах проставлены там,
где применение рассматриваемого подхода бессмысленно (в табл. 2,
например, приближение (8) не применяется во всех случаях, когда a2(ic) > 0,1).
Вычисление с*2(<У> когда это значение меньше, скажем, 10~6, редко имеет
практический смысл. Очень малые значения <Χ2{δ0) в табл. 2 при 02 = 0,5,
η = 300,1000 подсчитаны нами для сравнения результатов вычислений.
Для завершения комментариев к таблицам нам осталось пояснить, как
вычислялись истинные значения ai(ic), г = 1,2, и во что превращаются
приближения (8), (14) в нашем конкретном случае.
Значение а2(6с) равно
a2(Jc) = P,2 i£(Xi-l)<2v^b
Так как Ея2хг· = 1/02, &θ2χί — 1/^г> т0 нормальное приближение (14) для а2(6с)
будет иметь вид
φ te [i1 ~ j;)n+2v^l)= φ^2 -1)v/"+ 2Θ^·
Рассмотрим теперь формулу (8), в которой в нашем случае надо положить & =
= хг-, χ = —η - 2у/п. Здесь условие теоремы 1
х - пЩг -п-2у/И + п/в2 (1-θ2\
выполнено. Далее,
оо
ψ(λ) = Ee2e~Xxi = θ2 ίβ-χχ-θ2Χ dx =
λ + 02'
λ+ = οο, α+ = lim -—- =0, α = - = -1 γ=.
+ λ-юо ^(λ) П V^
Так как lim a = -1 < 0, то условие lim sup- < a+ также выполнено. Уравне-
П-ЮО П-ίΟΟ ^
ние (7) имеет в нашем случае вид
αθ2 02
λ+ 02 (λ + 02)2'
и его решение есть λ(α) = — 1/α - 02· Отсюда находим
Л(а) = -1п(-а02) - 1 - а02, σ2(α) = -^— = а2.
Таким образом, в силу (8) получаем
а2(6с) = Ρθ2 [Σ& >х)= Р*2 ( f>i " Х) < 2^Ч ~
1
(1 + α02)λ/2πη
exp {η[1η(-α02) + 1 + αθ2]}· (26)
§ 43. Два асимптотических подхода к расчету критериев 327
Полагая здесь α = — 1 - 2/у/п, мы получим формулы, по которым вычислялись
значения а2(<5с) B табл.2 (нижний ряд).
Отметим для сравнения, что правая часть (11) превращается в нашем случае в
выражение
1 ехр {π[1η<92 + 1 - 02] + 2(1 - 02)л/^ - 2}, (27)
{1-92)у/2жп
которое можно получить из (26), подставляя туда α = — 1 — 2у/п и отбрасывая после
разложений в ряд члены порядка 1/у/п и выше.
Первый множитель в знаменателе (26), равный σ(α)|λ(α)| = 1 + αθ2 = 1—02 -
— 202/y/n, заменяется в (27) на σι = 1 — θ2. Если θ2 близко к единице, то
относительная погрешность, связанная с поправочным слагаемым — 2в2/л/п, может
оказаться значительной. Например, для θ2 = 0,8, η = 100 получаем 262/у/п = 0,16,
σχ = 1 - #2 = 0,2, σ(α)|Α(α)| = 0,2 - 0,16 = 0,04, так что первый множитель в (27)
в пять раз (!) больше, чем в (26). Этот пример показывает, что в случае
близких гипотез, когда множитель σ\ в (11) мал, приближения (11) (или (27)) надо
использовать с большой осторожностью.
Для вычисления истинных значений αι(δ€) использовался следующий факт.
Пусть η(ί) есть процесс восстановления (см. [17, гл. 9]) для блуждания со скачками
хьх2,..., т.е.
η{ί) = min < k : ^2 х* ^ * (
Тогда если х, €= Г^д, то, как показано в [17, §16.4], процесс ξ(ί) = η{ί) — 1
представляет собой при t > 0 процесс Пуассона с параметром 0, т. е.
Ρ(„(ί) - 1 = *) = е"" = М.
Заметим теперь, что < 22х* ^ * Г = №№) ^ п}> и> стало быть,
, г=1
-\-et(0t)k
?*{Σχ^ή = Σ*-Η^- (28)
Поэтому при t = η 4- 2y/n
η \ η—1
a2(5c) = Ρθ2 £>i < t = 1 - J2e'
■e2t
(θ2ί)"
k\
Эти равенства и использовались для вычислений точных значений αι(δ€), г = 1,2.
Отметим, что наряду с (28) можно выписать и другие формулы для распределе-
η η
ния /Jxij основанные на том, что У^Хг ^ Γθ,η-
«=1 г=1
328
Гл. 3. Теория проверки гипотез
5. Связь н.м. к. с асимптотической эффективностью о. м.п. Используя
проведенные вычисления и результаты §41, 42, мы можем доказать теперь
теорему 33.7 об асимптотической эффективности о.м.п. Θ* в классе К0
асимптотически центральных оценок (принадлежность Θ* G К0 была
установлена в п. 37.3).
Доказательство теоремы 33.7. Допустим противное, что
существует а. н. оценка Θ* такая, что при каком-нибудь θ\
lim Εθιη{θ* ~ θι)2 = σ2(θι) < Г1{9г) = lim Εθιη{θ* ~ ^ι)2·
η->οο η-)·οο
Рассмотрим задачу проверки гипотезы Н\ = {X ^ Р^} против Щ =
= {X # Р$, θ = θι + υη~ιΙ2} и построим для этого критерий δ следующего
вида:
6(Х) = {Нъ еСЛИ 0*<0ι+υη"1/2>
{Я2, если 0* > θι + υπ"1/2,
где мы приняли для определенности, что ν > 0. Тогда
«!(£)= Ре1(0* > 01+υη-1/2) =
Далее, принадлежность θ* ζ Κ° означает, что
α2(δ) = Ρβ(β* Οι + υη"1/2) = Ρβ(0* < 0) -> i.
Рассмотрим теперь другой критерий io(-X') с критической областью
0*-01>-ПД, 7>0,
который, как мы установили, будет а.н. м. к. (см. (21)). Так как при
достаточно малом 7 > 0
то для этого критерия
lim αι(δο) = 1 - Ф((« + 7)л/Д^У) > 1 - Φ (-^т) ,
lim a2(J0) = Hm Ρβ [0* < 0 + -2= ) > J.
n-юо n-юо у νη J 2
Это означает, что начиная с некоторого η критерий δ будет лучше, чем
н. м. к. Полученное противоречие доказывает теорему. <
§ 44. Проверка сложных гипотез. Классы оптимальных критериев 329
§ 44. Проверка сложных гипотез. Классы оптимальных критериев
1. Постановка задачи и основные понятия. В §41, 42 мы
рассмотрели наименее сложные задачи проверки гипотез, когда эти гипотезы
являются простыми. Однако часто проверяемые гипотезы имеют более сложную
природу. В параметрическом случае, например, гипотеза может иметь вид
{X ^ Р#; θ £ Θι}, где Θι — данное подмножество Θ. Такая гипотеза,
очевидно, уже не определяет однозначно распределение выборки.
Всякую гипотезу i/, не являющуюся простой, мы будем называть
сложной.
Например, гипотезы {X €= Φο,σ25 σ ^ 1}> {X €= Фад; α ^ 0} являются
сложными.
Везде в дальнейшем в этой главе будем рассматривать задачи о
проверке двух гипотез, которые будем обозначать через Н\ и i?2· При этом в
ближайших параграфах ограничимся изучением параметрического случал
X €= Р#, θ Ε Θ. Гипотезы Щ в этом случае можно записать в виде
щ = {X €= Ρ*; θ е θ,}, ©г СЭ, Θι Π Θ2 - 0.
Так как остальные значения 0, не принадлежащие Θιυθ2, вообще не
рассматриваются, то, не ограничивая общности, можем считать, что Θ = Θι U©2 и
что #2 есть гипотеза, дополнительная (или противоположная) к Н\, так что
гипотезу #2 можно записать также в виде Η<χ — {Н\ не верна}. Аналогично
тому, как это делалось в § 42, одну из гипотез — в нашем рассмотрении Н\ —
будем называть основной или нулевой. Простые гипотезы Hq — {X ^ Р^},
θ Ε ©2, будем называть альтернативами.
Выделение среди гипотез основной часто отражает отношение
исследователя к изучаемому объекту. Основная гипотеза обычно соответствует
некоторой концепции, а альтернатива — отклонениям от нее, наличие которых
надо либо доказывать, либо отвергать. Обычно имеется одна или небольшое
количество основных гипотез и огромное количество мыслимых
альтернатив.
Процедура приема гипотез основывается на статистическом критерии.
Так как мы рассматриваем всего две гипотезы, то, как и в § 42, любой
(рандомизированный) критерий π однозначно определяется измеримой функцией
7г(ж), 0 ^ π(χ) ^ 1, которая определяет вероятность принятия π{Χ)
гипотезы Ή.2 для каждой выборки X (реализация случайного выбора с
вероятностью π{Χ) должна производиться с помощью независимого дополнительного
устройства). Функция π(χ) называется, как и в §42, критической. Для
нерандомизированного критерия δ функция π(χ) — δ(χ) принимает лишь два
значения 0 и 1; область Ω2 пространства Хп, в которой δ(χ) = 1 (область
приема #2), называется в этом случае критической, ее часто отождествляют
с критерием δ.
Определение 1. Размером или вероятностью ошибки первого рода
критерия π называется число
αχ (π) = sup Ε^π(Χ).
θ£Θι
330
Гл. 3. Теория проверки гипотез
Для нерандомизированных критериев очевидно
αι(ί) = sup Έ>Θ{Χ е Ω2).
0€θι
Это есть максимальная (по θ Ε Θι) вероятность отвергнуть гипотезу #ι,
когда она на самом деле верна. Обычно, чтобы облегчить поиски оптимальных
критериев, рассматривают критерии π, удовлетворяющие условию
αχ(π)=ε (или αι(π) < ε).
Класс таких критериев обозначим через Κε.
Число 1 — &χ(π) = 1 — ε будем называть уровнем (значимости) *)
критерия π.
Статистически использование критерия δ Ε Κε означает, что в длинном
ряду экспериментов по проверке гипотезы Н\ с помощью критерия δ Ε Κε
будем ошибаться не чаще, чем в доле случаев ε, если на самом деле была
верна гипотеза Н\.
Выбор уровня значимости критерия в значительной степени
произволен. Часто в качестве ε выбирают одно из стандартных значений таких, как
0,005; 0,01; 0,05; 0,1. Эта стандартизация имеет то преимущество, что
позволяет сократить объем таблиц, используемых статистиком в своей работе.
Никакой другой специальной причины для выбора именно этих значений
нет. Выбирая уровень значимости критерия π, нужно обращать внимание
на мощность критерия
βπ(θ)=ΕΘ7τ(Χ), 0Εθ2.
Если она окажется слишком малой, то, возможно, следует заменить уровень
1 — ε на меньшее значение.
Важным обстоятельством, которое может влиять на выбор уровня
значимости, является наше отношение к гипотезе до проведения эксперимента.
Если мы твердо верим в истинность гипотезы (априорная вероятность Q(i?i)
в байесовской постановке задачи велика), то потребуются убедительные
свидетельства против нее для того, чтобы мы отказались от своей
уверенности. В таких условиях нужны критерии высокого уровня, и ε выбирается
очень малым (тогда попадание в Ω2 будет крайне неправдоподобным, если
верна Η χ).
Здесь используется та же концепция, которую мы излагали при
построении доверительных интервалов. Она состоит в следующем: если
вероятность ε некоторого события А мала, то мы считаем практически
невозможным, что это событие произойдет при единичном испытании.
Среди ряда специалистов по математической статистике существует и
другая точка зрения. Она состоит в том, что нет надобности задавать
фиксированный уровень значимости и что для его предварительного выбора
*) Часто уровнем значимости называют число ε, а не 1 — ε. Но это несколько
противоестественно: ведь естественнее считать, что чем выше уровень значимости, тем «значимее»
критерий. Именно из этих соображений мы определяли уровень значимости (или доверия)
для доверительных интервалов. Так как между статистическими критериями и
доверительными интервалами существует прямая связь (см. §48), то было бы неразумно менять
терминологию при переходе к критериям на противоположную.
§ 44. Проверка сложных гипотез. Классы оптимальных критериев 331
нет разумного правила. Они рассматривают проверку гипотез не как
процедуру, ведущую обязательно к приему одной из двух гипотез, а как
некоторый процесс в сознании исследователя, определяющий его отношение к
гипотезам. С этой точки зрения фиксированному уровню значимости можно
предпочесть «фактически достигаемый» уровень, который определяется
следующим образом. Рассмотрим семейство нерандомизированных критериев δ
уровня 1 — ε, когда ε пробегает значения из интервала (0,1), и обозначим
через Ω2,ε критическую область <J, предположив, что Ω2,ε2 С Ω2,ει ПРИ ε2 < εχ.
Определение 2. Фактически достигаемым уровнем семейства
критериев δ на выборке X называется случайная величина 1 — ε(Χ), где
ε{Χ)=Μ{ε:ΧΕΩ2,ε}·
Чем больше 1 — ε(Χ), тем сильнее свидетельствует выборка против
гипотезы Ηχ.
Значение ε(Χ) дает возможность принимать или отвергать гипотезу при
любом заранее данном уровне 1 — ε путем простого сравнения ε{Χ) с ε.
Пример 1. В предыдущем параграфе мы построили н. м. к. для
проверки гипотезы Ηχ = {X ^ ГЧд} против гипотезы #2 = {X ^ Г^д}· Этот
критерий имеет критическую область
Ω2 = J χ е Χη : 5^(xj - 1) >άχ \ .
10
Допустим, что для выборки X объема η = 10 оказалось У^Хг — 18.
г=1
η
Так как при гипотезе Н\ ]Рхг €= 1\п и ΐγη((α,6)) = Η2η((2α,26)), то
г=1
Γι,ιο((18,οο)) = Н2о(36,оо)) = 0,0154 (см. табл. III или [10]) и фактически
достигаемый уровень в этом случае будет равен 1 — ε{Χ) = 1 — 0,0154 =
= 0,9846, так что гипотеза Ηχ будет отвергаться н. м. к. с уровнем 1—ε = 0,98
и не будет отвергаться н. м. к. с уровнем 1 — ε = 0,99.
2. Равномерно наиболее мощные критерии. Вернемся к произвольным
рандомизированным критериям π, которые мы договорились задавать
критической функцией 7г(ж), χ £ Xй. (Функцию π(χ) можно называть также
статистической (рандомизированной) решающей функцией.)
Если существует достаточная статистика S(X), то можно ограничиться
критериями π(Χ), которые зависят от X только через достаточную
статистику 5(Х), т.е. критериями, представимыми в форме π(Χ) = tp{S(X)).
Ведь мы знаем, что вся информация о неизвестном параметре сосредоточена
в 5 и привлечение других статистик (другой информации о выборке X) не
имеет смысла.
Как мы уже отмечали, для отыскания оптимальных критериев обычно
сужают множество рассматриваемых критериев до класса Κε критериев
фиксированного уровня. Среди них можно пытаться отыскать такой критерий,
для которого мощность
βπ(θ)=Εβπ(Χ)
332
Гл. 3. Теория проверки гипотез
в области ©2 максимальна (т.е. вероятность ошибки второго рода 1 — βπ(θ)
минимальна). Другими словами, максимальной должна быть вероятность
принять гипотезу Н2, когда она верна.
Функция βπ{θ) = Έβπ(Χ) часто называется также функцией мощности
критерия π.
Определение 3. Критерий π° Ε Κε называется равномерно наиболее
мощным критерием (р. н. м. к.) в Κε, если для любого π Ε Κε
βΛΘ) > βπ{θ) при всех θ Ε Θ2. (1)
Конечно, р. н. м. к. существуют далеко не всегда. Если такой критерий π°
существует, то для него функция мощности βπο(θ) располагается на графике
выше любой другой функции βπ(θ) в области ©2 при условии, что обе они
не превосходят значения ε в области θ ι (ведь αϊ (π) = sup /?π(0)), так что
0€Θι
βπο{θ) есть огибающая семейства {β<κ(θ)} в области ©2-
Допустим, что θι = {#ι}, Έθ1τγ°{Χ) = ε. Тогда р. н.м.к. π° будет,
очевидно, н. м. к. уровня 1 — ε для проверки гипотезы {θ = θ\} против
альтернативы {θ = Θ2} при любом 02 Ε ©2- Так как форма н. м. к. известна, то
отсюда возникает следующий естественный путь отыскания р. н.м. к.: мы
найдем его, если окажется, что н. м. к. в поставленной выше задаче о
проверке гипотез {Θ = θι} и {Θ = 02} не зависит от 02·
Верно и обратное: если н.м.к. из Ке для проверки гипотезы {0 = θ\}
против {0 = 02}, 02 € ©2, существенно зависит от 02, это будет означать,
что р.н.м. к. для проверки {0 = θ\} против {0 Ε ©г} не существует.
Если гипотеза Н^ простая (©2 состоит из одной точки 02), то
понятие р. н. м. к. частично теряет свой смысл и превращается в понятие
обычного н.м.к., т.е. критерия, для которого в классе Ке максимизируется
Ε*2π(Χ).
Определим теперь байесовские и минимаксные критерии для проверки
сложных гипотез.
3. Байесовские критерии. При проверке сложных гипотез будем
различать два байесовских подхода.
1. Полный байесовский подход. Он состоит в предположении,
что гипотезы Hq = {X €= Р0}, 0 Ε ©, выбираются случайно с априорным
распределением Q. Другими словами, на © = ©χ U ©2 фиксируется
некоторая σ-алгебра подмножеств Θ, ©ι Ε ©, ©2 Ε ©, и 0 рассматривается как
случайная величина на выборочном пространстве (©,©,Q).
Распределение Q индуцирует Qj на ©;, i = 1,2, и вероятности дг =
= Q(0 Ε ©г), так что Q = qiQi + 92Q2· Гипотезу о том, что 0 Ε ©г
выбирается случайным образом с распределением Q2, обозначим через #q..
Определение 4. Критерий πg называется байесовским, если он
является байесовским критерием, соответствующим априорному распределению
(<7ь<72) для проверки двух простых гипотез Hq1 и Hq2 (cm. §41).
2. Частично байесовский подход. Здесь предполагаются
заданными априорные распределения Qj на ©j, но отсутствуют априорные веро-
§ 45. Равномерно наиболее мощные критерии
333
ятности <7ι, (72· В этом случае имеем дело с проверкой двух простых гипотез
HQl И HQ2-
Положим, как и прежде,
Κε = {π : sup Εθπ(Χ) ζ ε}, Κ^ = {π : Ε0ιπ(Χ) ^ ε},
0<Εθι
где Egt. обозначает безусловное математическое ожидание по распределению
на Θ2 χ Хп, порожденному Q; и Р#.
Определение 5. Критерий ттдьд2 называется байесовским в Κε
если это есть н. м. к. уровня 1 — ε для проверки двух простых гипотез Hq1
и tfg2.
Если одна из гипотез Hi вырождается в простую (θι или ©2
одноточечно), то будет вырождаться и соответствующее распределение. В этом
случае индекс у обозначения 7TQbg2 будем укорачивать и писать, например,
πQ1 вместо тгдьд2, если 02 = {#2} одноточечно.
Построение критериев 7гдьд2 трудностей не вызывает. Они будут
использоваться нами как вспомогательное средство для построения р. н. м. к.
и минимаксных критериев.
4. Минимаксные критерии
Определение 6. Критерий π для проверки Н\ = {θ Ε θι} против
#2 = {θ Ε 62} называется минимаксным в К£ (в Κε), если π Ε Κε
(π Ε Κε) и для него максимизируется
inf Εθπ{Χ) = inf /?π(0).
0ее2 0<Ξθ2
Такой критерий правильнее было бы называть максиминным
(максимизируется минимум). Однако будем использовать все же единый термин
«минимаксный», тем более что он сохраняет свой смысл, если иметь дело не
с мощностью, а с вероятностями ошибок второго рода.
Более подробно байесовские и минимаксные критерии будут изучаться
в §49. Ближайшие же параграфы будут посвящены выяснению условий,
при которых возможно построение р. н. м. к.
§ 45. Равномерно наиболее мощные критерии
В этом параграфе мы рассмотрим два важных частных случая,
относящихся к одномерному параметру Θ, когда р. н. м. к. удается построить. Мы
получим также один полезный результат, касающийся построения н. м. к.
1. Односторонние альтернативы. Монотонное отношение правдоподобия.
Пусть основная гипотеза Hi состоит в том, что θ ^ 0ι, а альтернативная
гипотеза Н^ в том, что θ > θ\. Такую гипотезу Н^ будем называть
односторонней в отличие, скажем, от гипотезы Щ = {θ Φ θ\} (дополнительной
к Hi = {θ = 0ι}), которая является двусторонней, так как допускает
отклонения от 01 в обе стороны.
334
Гл. 3. Теория проверки гипотез
Другое наше предположение будет состоять в следующем. Пусть
выполнено условие (Ао) и существует функция Т(х) такая, что при всех 0, #о>
θ > #о> отношение правдоподобия
ΙΜ. (1)
является неубывающей (или невозрастающей) функцией от Т(х). В этом
случае говорят, что семейство {Р#} имеет монотонное отношение
правдоподобия.
Так как Г — достаточная статистика, то fe{x) = ψ{Τ(χ),θ)ίι(χ), и
сформулированное условие будет относиться к отношению ψ(Τ,θ)/'ψ(Τ,θο).
Это условие означает, что при всех θ > θο и любом d > 0 неравенство
fe(x)/fe0{x) > d будет разрешимо в виде Т(х) > Cn(0,0o,d) (или Т(х) <
Например, семейства {Фад} и {Φ0>σ2} имеют монотонное отношение
правдоподобия, так как
^=ехр{(а-„0)п*-2(а>-аЭ},
и соответствующие неравенства будут иметь вид (а > ао, σ > σο)
х> Сп(а,а0,бО = г(а + а0) + "т г {Т{Х) = 5с),
^ тца — aoj
£х? > c^.ob.d) = 2-^^lnd (т(Х) = £хА .
Многие параметрические семейства § 12 также имеют монотонное отношение
правдоподобия. В дальнейшем для определенности будем считать, что (1)
есть неубывающая функция Т(х)>
Теорема 1. Пусть θ — одномерный параметр, а семейство {Р#}
имеет монотонное отношение правдоподобия. Тогда:
1) в Κε существует р. н. м. к. для проверки гипотезы Ηχ = {θ ^ θχ}
против альтернативы Η<ι = {θ > #ι}, который имеет вид
{1, если Т(Х) > с,
р, если Т{Х) = с, (2)
0, если Т{Х) < с,
где сир определяются из условия
Εθιπ0(Χ) = Рв1 (Г(Х) > с) + PPfll(Т(Х) = с) = ε; (3)
§ 45. Равномерно наиболее мощные критерии
335
2) функция мощности βΌ{θ) = Ε^π°(Χ) строго возрастает по θ при
всех 0, для которых β°{θ) < 1;
3) при всех во критерий (2) является р. н. м. к. в классе Κβο/ρ0\ для
проверки гипотезы Н^ = {Θ ^ во} против Щ = {Θ > во}]
4) для любого в < в\ критерий (2) минимизирует β(θ) — Eqk(X) β
классе Κε.
Доказательство. Рассмотрим сначала простые гипотезы {в = в\}
и {в = #2}> #2 > #ι· Η. м. к. для проверки этих гипотез в классе
критериев π, для которых Εθ1π(Χ) = ε, имеет согласно теореме 42.1 вид (2),
так как неравенство Z(X) > d для отношения правдоподобия эквивалентно
неравенству Т(Х) > с (при надлежащем соответствии между сие/), где
постоянные сир определяются из (3) (ср. с (42.3)). Так как числа сир
из уравнения вида (3) определяются единственным образом, то мы
получаем также, что критерий (2) будет н. м. к. в Κβο^ для проверки гипотезы
{в = #о} против {в = 02}> #2 > #о- Отсюда и из теоремы 42.1 (см. (42.4))
следует, что β°{θ2) > β°{θ0).
Так как β°(θ) не убывает, то
ΕθπΌ{Χ)^ε при θ^θχ. (4)
Класс Ке критериев π, удовлетворяющих (4), содержится в классе {π:
Ε^χπ(Χ) = ε}. Так как критерий (2) максимизирует β{02) в этом
последнем классе, он будет максимизировать β(02) и в Κε. Остается заметить, что
критерий (2) никак не зависит от 02 и, стало быть, сделанные выводы
справедливы при любом 02 > θ\. Тем самым первые три утверждения теоремы
доказаны.
Четвертое утверждение теоремы следует из первых трех, если их
применить к задаче о проверке гипотезы Н[ = {θ ^ θ\} против Н^ = {θ < θι}^ для
которой р. н. м. к. в классе {ЩХ) : ЕвЩХ) < 1 — ε, θ ^ θ\} будет иметь вид
П°(Х) = 1 - π°(Χ), а функция 1 - β°{θ) = EeU°(X) станет максимальной
при θ < θ\ функцией мощности. <
Важный класс семейств распределений, допускающих монотонное
отношение правдоподобия, образует однопараметрическое экспоненциальное
семейство (см. §25), когда плотность fe{x) представима в виде
Мх) = h(x) exp {a(0)U(x) + V(0)}. (5)
Действительно, в этом случае
|^ = ехр | (α(θ) - α(θ0)) £ Ufa) + n{V{9) - V{90)) J ,
71
и отношение правдоподобия будет монотонно зависеть от Т(х) = У^ U(xi)>
г=1
если α(θ) — α(#ο) сохраняет знак при всех 0, #о> θ > 9q.
336 Гл. 3. Теория проверки гипотез
Следствие 1. Пусть f$(x) имеет вид (5), где α(θ) есть монотонная
функция. Тогда существует р. н. м. к. π° в классе Κε для проверки
гипотезы Ηι = {θ < 0ι} против #2 = {θ > θι}. Если α(θ) возрастает, этот
критерий имеет вид (2), (3). Если α(θ) убывает, неравенства в (2), (3)
заменяются на противоположные.
Отметим, что если проверяется двусторонняя альтернатива, например
гипотеза Ηχ — {Θ = θ\} против Я2 — {θ φ θι}, то р. н. м. к. для
экспоненциального семейства (5) уже не существует. Действительно, допустим для
η
простоты, что α(θ) возрастает и что Р#-распределение Т(Х) = V^ U(xi) при
г=1
всех 6 абсолютно непрерывно. Тогда согласно теореме 42.1 н. м. к. для
проверки {θ = θ{\ против {0 = 02 } будет нерандомизированным и будет иметь
критическую область Т(Х) ^ с, если 02 > θ\. Если же 02 < #ь то
критическая область будет иметь вид Т(Х) < с. Мы видим, что максимальная
мощность в точке 02 будет достигаться на существенно разных критериях
в зависимости от знака разности 02 — θ\. Из теоремы 1 видно, что если мы
возьмем какой-нибудь из этих двух критериев, например тот, для которого
π(Χ) = 1 при Т{Х) ^ с, то он будет р.н. м.к. для всех 02 > θι и заведомо
не будет таковым для 02 < θι-
Уже отмечалось, что положение двух простых гипотез в теореме 42.1 о
н. м. к. в известном смысле симметрично (н. м. к. минимизирует
вероятность ошибки второго рода с*2(7г), если фиксировано значение &ι(π), и
наоборот — минимизирует αϊ (π), если фиксировано α2(π)). Такой симметрии
в постановке задачи о проверке сложных гипотез нет. С этим
обстоятельством связан следующий интересный факт. Мы только что видели, что для
экспоненциального семейства не существует р. н. м. к. для проверки
гипотезы Hi = {0 = θι} против Н2 = {θ φ θι}. Из приведенных рассмотрений
легко понять, что не существует также р.н.м.к. для проверки гипотезы
{θι < θ < Θ2} против альтернативы {0 £ (0ь#2)}· Однако если рассмотрим
теперь в качестве основной гипотезы Hi гипотезу Hi = {θ φ (0i,02)}? a B
качестве альтернативы гипотезу Н2 = {Θ £ (θι, Θ2)}ι то р.н. м. к. в Κε будет
уже существовать. Итак, мы рассмотрим теперь вторую возможность, когда
удается построить р. н. м. к.
2. Двусторонняя основная гипотеза. Экспоненциальное семейство.
Теорема 2. Пусть /#(#) определяется равенством (5) и
проверяется гипотеза Hi — {θ £ (θι,02)}, θι < 02, против альтернативы Н2 —
= {θ Ε (Θι,θ2)}· Тогда если функция а(0) монотонна, то:
1) В классе Κε = {π : sup Ε^π(Χ) ^ ε} существует р. н. м. к. π°,
ецвив2)
который имеет вид
{1, если ci < Τ (χ) < С2,
Pi, если Τ (χ) = ci, i = 1,2, (6)
О, если Т(х) φ [ci,c2],
§ 45. Равномерно наиболее мощные критерии
337
гдеТ{х) = ^и{хг), α постоянные щ, р^ определяются из условий
i=l
Εβιπ0(Χ)=Εβ2π0ΡΟ = ε.
(7)
2) Этот критерий максимизирует функцию мощности β(θ) =Έΐοπ(Χ)
при условии (7) внутри интервала (0i,02) w минимизирует ее вне этого
интервала (см. рис.4).
3) При О < ε < 1 функция β°(θ) имеет максимум в некоторой точке
θο Ε (#ι,#2) w строго убывает при удалении θ от во вправо или влево.
При этом мы исключаем тот случай, когда распределение Т(Х)
сосредоточено в двух точках, т. е. когда существуют такие t\, £2, что
ΡΘ{Τ{Χ) = h) + Έ>Θ{Τ{Χ) = ί2) = 1 при всех θ. (8)
В приводимых рассмотрениях полезно также следующее утверждение.
Лемма 1. Уравнения (7) при 0 < ε < 1 всегда разрешимы
относительно Cj, ^, г = 1,2.
Доказательство этой леммы мы приведем позже.
Доказательство теоремы 2. Запишем функцию правдоподобия в
виде
Мх) = с(в)еа^Т^Н(х), (9)
где будем считать для определенности, что α(θ) строго возрастает.
Рассмотрим следующую
байесовскую постановку задачи. Пусть
проверяется основная «смешанная»
гипотеза Н, которая состоит в том,
что {Θ = 01} с вероятностью q и
[β = 02} с вероятностью 1 — 9,
против альтернативы Щ = {0 = 0о},
00 6 (0ι>02)· Пусть, далее,
априорные вероятности гипотез Η и Но
равны соответственно г и 1 — г. Так
как гипотезы Η и Но полностью
Рис. 4. Вид функции мощности β°(θ) =
= Ея7г0(Х) и функции /3(0) = Έ,βπ(χ) для
произвольного критерия π £ Κε
определяют распределение выборки, то их можно считать простыми и
воспользоваться результатами §42. Байесовский критерий (обозначим его
через π0) будет иметь в этом случае вид
Λχ) = <
1,
р(х.
о,
если
1, если
если
R(X) =
R(X) =
R{X)<
ίθο(Χ)
qfei(X) + (l-q)fe2(X)
г
>
1-г'
1-г'
г
1-г"
(10)
338
Гл. 3. Теория проверки гипотез
Неравенство R(X) > r/(l - г) в силу (9) эквивалентно неравенству
д£Ше(а(*1)-а(*0))Г + (1 _ д)£^)е(а№)-в№))Т < Lzl (n)
Так как α(θι) - α(0ο) < 0, α(02) - а(#о) > 0, то левая часть здесь есть
выпуклая функция от Т. Это означает, что (11) можно записать в виде
с\ < Τ < с2,
где Ci = Ci(q, г); числа с\ < с2 пробегают при изменении qnr все возможные
значения. Функцию р{Х) в (10) положим равной pi, если Т(Х) == с\, и р2,
если Т(Х) = с2.
Согласно лемме 1 найдутся q, г = 1,2 (или, что то же, q и г), и р^ такие,
что (7) будет выполнено. Покажем теперь, что функция π°(Χ), определенная
в (10) или, что то же, в (6), будет обладать всеми сформулированными в
теореме 2 свойствами. Сказанное означает, что мы стали теперь рассматривать
π0 одновременно как решающую функцию для проверки Н\ против i/2. Так
как критерий π° байесовский (для проверки Η против #о)> то для любого
другого критерия π
г[дЕЛ7г° + (1 - q)Eo27r0} + (1 - г)Е,0(1 - π°) <
< Γ[9Εβιπ + (1 - 9)Ε^2π] + (1 - r)E*0(l - π). (12)
Стало быть, если критерий π наряду с π° будет удовлетворять (7), то
Εθ0π ^ Ε^0π.
Это значит, что в каждой внутренней точке #о € (#ъ#2) критерий π°
максимизирует функцию мощности β(θ) = Ε#π в классе критериев π,
удовлетворяющих (7). Но условия (7) выделяют класс критериев, более широкий,
чем Ке. Следовательно, π° будет максимизировать β(θ) и в Κε. Так как
критерий π0 не зависит от #о> то он будет р. н. м. к. в Κε.
Отметим еще, что в силу теоремы 42.1
β°(θ0) = Εθαπ° > ε
и равенство здесь возможно лишь в случае, когда
qfe1(x) + (l-q)fe2(x) = fe0(x) (13)
/хп-почти всюду.
Совершенно аналогично с помощью (12) можно убедиться, что π°
будет минимизировать Ε^π при фиксированных Ε^0π, Ε#2π (мы используем
здесь те же соображения, что и в доказательстве теорем §41).
Покажем теперь, что π° минимизирует β(θ) вне (#ι,#2). Пусть Θ0 < θ\.
Заменим в предыдущих рассмотрениях тройку точек (0ι,0ο5#2) на тройку
(0о}0ь#2) и заметим, что для новой задачи критерий π° снова будет
байесовским (ведь его форма от выбора точек θ{, г = 0,1,2, не зависит) в классе
критериев π, для которых Ε#οπ = /3°(0°), Ε#2π = ε. Но согласно сделанному
§ 45. Равномерно наиболее мощные критерии
339
выше замечанию π° будет минимизировать Ε#οπ при фиксированных Ε^π
и Е027г. Первые два утверждения теоремы доказаны.
Докажем третье утверждение. Заметим предварительно, что, пользуясь
заменой переменных интегрирования, мы можем записать
Р*(Г е А) = с(0) /" е^^ВД^я) - с(0) /" ea^V(cft),
{ж:Г(ж)бА} «€Л
где мера ν определяется соотношением
у{А) = / Λ(*)μη(ώί).
{s:T(z;)€A}
Это означает, что распределение Τ относительно меры ν имеет плотность
(см. также лемму 25.1) g$(t) = с(9)еа^г и, стало быть, также принадлежит
экспоненциальному семейству. Далее, в силу монотонности а{9) можно
ввести новый параметр η = α(0), совершенно не изменив при этом задачи и ее
условий. Следовательно, мы можем считать, не ограничивая общности, что
1-1
(dt)
и /?°(0) = ΕΘπΌ(Χ)
α(θ) = θ. В этом случае функции с(0) = / ewi/
будут, очевидно, непрерывными. Допустим теперь, что утверждение теоремы
о характере поведения β°(θ) неверно. Тогда найдутся три точки Θ1 < Θ" < θ"',
для которых
/3°(0') = βΡ(θ") = /3°(0'") = α е (0,1). (14)
Мы видели, что π° максимизирует β(θ") при условиях /?(0') = /9(0") = α,
при этом если не выполнено условие вида (13), то β°(θ") > а. Но равенство
(13) в нашем случае означает, что
QL· + а _ α)ίΐΐ = аЕЦ!1е{*-пт + α _ Q\W!lev»-nT = χ
*/*" 9j/*' ~9с(0") +U *jc(0")
г/-почти всюду. В силу выпуклости левой части по Г это равенство
возможно не более чем для двух значений Т. Стало быть, если (8) исключено,
то /?°(0") > /3°(0') = а, и (14) невозможно. <
Доказательство леммы 1. Проведем доказательство при
упрощающем предположении, что распределение Т(Х) непрерывно, т. е. Р#(Т =
= с) = 0 при всех 0 и с. Это освободит нас от несущественных усложнений.
В этом случае в силу замечаний, сделанных в конце доказательства
теоремы 2, мы можем записать
С2 С2
Εθπ°(Χ) - ΡΘ(Τ Ε (сг,с2)) = Jge{t)v{dt) = с{в) f eetu{dt).
Это будет непрерывная функция от 0, ci, c<i.
340
Гл. 3. Теория проверки гипотез
Обозначим через с+ значение с, для которого Рех (Т ^ с+) = 1 — е. Тогда
на (—со, с+) определена функция d(c) такая, что
d(c)
\(Te(c,d(c)))= J gei(t)u(dt) =
Ясно, что d(c) есть непрерывная возрастающая функция.
Докажем требуемое утверждение, если убедимся, что функция
d(c)
ф{с) = Р*2(Т е (c,d(c))) = J ge2{t>{dt)
С
непрерывно возрастает, ф(—оо) < ε, ф{с+) > ε. В этом случае найдется со
такое, что ф{со) = ε, и, стало быть, Р^.(со,с/(со)) = ε, i = 1,2.
Непрерывность ф(с) очевидна. Докажем монотонность. Запишем ф(с) в
виде
d(c)
Ф(с)= J g0l(t)r(tHdt), (15)
с
где r(t) есть плотность Р#2-распределения Τ относительно
Ρ#χ-распределения:
r(t) =
£ίΜρ(<?2-βΐ)ί
c(6»i)
Пусть Δ для определенности таково, что с + Δ < d(c). Тогда так как
c+Δ d(c+A)
J g$1(t)v(dt)= j g9l{t)v{&)> (16)
d(c)
TO
d(c+A) c+Δ
ф(с + Δ) - </>(c) = Ζ" Wl (t)r(t)v(dt) - У №l (i)r(i)i/(di) Ξ*
d(c) с
>[r(d(c))-r(c + A)}\>0,
где λ есть общее значение интеграла (16).
Убедимся теперь, что ф(—оо) < ε. Обозначим через to решение
уравнения r(t) = 1. Есди d(—oo) ^ to, то г(£) < 1 на интервале (—oo,d(—oo)),
и требуемое неравенство в силу (15) очевидно. Если же d(—со) > to, то
аналогично находим
^(-оо) = 1 - Ρθ2(Τ е (d(-oo), oo)) <
< 1-Рв1(Те (d(-oo),oo)) =Ρθι(ΤΕ (-oo,d(-oo))) = ε.
Точно так же устанавливается, что ф{с+) > ε. <
§ 45. Равномерно наиболее мощные критерии
341
Замечание 1. Мы предоставляем читателю самому убедиться в том,
что при θ\ < 02 утверждение теоремы 2 и все проведенные рассмотрения
сохранятся, если мы интервал (#ι,Θ2) заменим на отрезок [0ι, 0г]> τ. е. будем
проверять гипотезу #ι = {θ £ [#ι,#2]} против #2 = {θ G [0ι,#2]}·
Замечание 2. Требование экспоненциальное™ семейства {Р#}, как
это видно из доказательства теоремы, может быть ослаблено до условия
выпуклости отношения
qh0(X)+(L q)fe0(X)
относительно некоторой статистики Τ (ср. с (10), (11)).
Замечание 3. Обратим внимание еще раз на то, что если бы основной
гипотезой была Η<ι = {θ G {61,62)}, а альтернативой Н\ = {θ φ (#ι,02)}>
то р. н. м. к. не существовало бы, так как в этом случае «односторонние»
критерии вида Τ > с или Τ < с соответственно для альтернатив θ > 02
и θ < θ\ оказались бы более мощными, чем критерий вида Τ ^ (ci,C2).
Например, для альтернатив θ > 02 будет существовать р. н. м. к. вида Τ > с,
а условие π G Κε приведет к единственному ограничению Ε#2π ^ ε (см.
замечания в конце п. 4).
Тем не менее окажется, что если класс Κε дополнительно несколько
сузить вполне естественным образом (см. §46, 47), то р.н. м. к. будет
существовать и в этой задаче.
3. Другой подход к рассматриваемым задачам. Математическое существо
главного утверждения теоремы 2, а также теорем §41, 42 весьма просто и
заслуживает того, чтобы его выделить. Например, в теореме 2 оно состоит
в следующей вариационной задаче. В классе функций π, удовлетворяющих
условиям
/
π(χ)/θί(χ)μη(ώϋ)=ε, г = 1,2,
мы ищем элемент π°, для которого максимизируется
/
π{χ)/θο(χ)μη(άχ).
Следующее утверждение называется обычно обобщением
фундаментальной леммы Неймана-Пирсона.
Лемма 2. Пусть /ι,...,/m+i — действительные функции,
определенные на Xй и интегрируемые относительно меры μη. Пусть
критические функции π таковы, что
I
π(χ)/ι(χ)μη(άχ) = а, г = 1,..., т. (17)
342 Гл. 3. Теория проверки гипотез
Тогда элемент π°, на котором / π{χ)/τη+ι{χ)μη(άχ) достигает
максимума, имеет вид
*(*Л -
тги(ж)
1, если fm+i{x) >^2кг/г{х),
i=l
т
О, если /m+i(aj) < ^) *»/<(«),
»=1
где fci,...,A;m определяются из условий (17).
Доказательство. Положим Ή(π)= / π(χ)/{(χ)μη(άχ), t=l,.. .,m+l.
Элемент π, удовлетворяющий условиям Ή (π) = ε«, г = l,...,m,
максимизирует Fto+i(tt) тогда и только тогда, кода он максимизирует Fm+i(n) —
771
— yZ ^iFi{7r) при каких-нибудь &χ,..., Л;т (ведь значение суммы здесь фик-
г=1
сировано). Стало быть, нам достаточно, чтобы π максимизировало
т \
fm+i{x)-Y^kifi{x) j тг(ж)/хп(с/ж).
Но это выражение делается максимальным, если положить π (ж) = 1 там,
m
где /т+1(ж) - У^&г/г(я) > 0, и 7г(ж) = 0 там, где это выражение отри-
i=l
цательно. Постоянные &j, от которых зависит это π, а также «свободные»
ί m 1
значения π на множестве < /т+х(ж) = Х,^г/г(ж)} > следует подобрать так,
чтобы выполнялось (17). <
4. Байесовский подход и наименее благоприятные априорные
распределения при построении н.м.к. и р.н.м.к. Лемма 2 выясняет
математическое существо построений, которые проводились нами в этом параграфе.
В этом пункте речь будет идти также о существе этих рассмотрений, но с
несколько иной точки зрения. Дело в том, что при доказательстве теоремы 2
мы неявно использовали подход, связанный с построением минимаксных
критериев с помощью байесовских (ср. с теоремой 41.2). Этот подход позже
будет рассматриваться более подробно. Здесь же мы получим одно общее
утверждение, полезное при построении р. н. м. к. в общем случае, и поясним
его связь с минимаксным подходом.
Пусть проверяется основная гипотеза #χ = {θ £ θι} против простой
альтернативы Η<ι = {θ = #2}> #2 ^ Θχ. В качестве #2 здесь можно взять
и произвольную альтернативу {X €= G}, где G имеет плотность g
относительно μ и с семейством {Ρ#} никак не связано. Задача состоит в отыскании
§ 45. Равномерно наиболее мощные критерии
343
н. м. к. π уровня 1-е для проверки Н\ против Η<ι. Другими словами, надо
найти функцию π из Κε,
Κε = {π: sup ΈΘπ{Χ) ζ ε}, (18)
θβθι
которая минимизирует β{02) = Έο2π(Χ). В предыдущих рассмотрениях
мы не раз наблюдали известную «дуальность» в постановке задачи:
максимизация мощности при фиксированной вероятности ошибки первого рода
эквивалентна минимизации последней при фиксированной мощности. Но
при таком обращении мы приходим в нашей задаче к проблеме
минимизации (18), а это и есть проблема построения минимаксного критерия (более
подробно эта проблема будет обсуждаться в §50). Это объясняет в какой-то
мере сходство доказываемого ниже утверждения с теоремой 41.2.
Итак, рассмотрим частично байесовскую постановку задачи, в силу
которой параметр θ на множестве Θ ι выбирается случайным образом с
распределением Qi. Сложная гипотеза Hi заменяется при этом простой
гипотезой Hq1 , при которой плотность X определяется как усредненное по мере Qi
значение
/gi(aO = //i(aOQi(<*0).
Для проверки Hq1 против #2 в классе Κε = {π : Eq^(X) < ε}
критериев уровня 1 — ε существует н. м. к. 7Tq1 , имеющий вид (πς^ есть критерий
π<2ι<?2 в обозначениях §44, где Q2 — вырожденное в точке 02 распределение):
(1, если д(х) > cfQl(x),
(0, если g{x)<cfQl{x)
(здесь д(х) = fe2(x) B параметрическом случае).
Теорема 3. Допустим, что существует такое распределение Qi,
сосредоточенное на подмножестве ©J С ©i(Qi(©?) = l), для которого:
1) имеем
πο,ΕΚ?1, (20)
2) справедливы равенства
EokQi(X) = const = sup Έθ-kq^X) (21)
0<Εθι
для всех θ Ε ©J.
Тогда критерий 7Tq1 Ε Κ£ является н. м. к. для проверки Н\
против #2·
Доказательство. Проверим сначала принадлежность πg1 € Κε.Β
силу условий теоремы
sup BenQl(X) = I EgnQl(X)Q1(de) = EQlnQl(X) < ε. (22)
©?
344
Гл. 3. Теория проверки гипотез
Пусть теперь π — любой другой критерий из Κε, т.е. критерий уровня
1 — ε для проверки Н\ против #2· Тогда
Щхж{Х) = Jπ(χ)^ι(χ)μη(άχ) = jEen(X)Q1(d9) < ε,
β!
и, стало быть, π € Kg . Но тогда в силу определения π^1
Ee2KQl(X)>E92n(X),
что и требовалось доказать. <
Распределение Qi, фигурирующее в теореме, называют наименее
благоприятным. Это связано со следующим обстоятельством. Величина βζ^)^ (Θ2) =
= 'Eq2kq1(X) есть наибольшее значение мощности, которое можно достичь
в Κε при «априорном» распределении Qi на ©ι. Если мы возьмем теперь
любое другое распределение Q' на θι, то получим
А?'№) > fiQl (Θ2), Азх№ = inf Pq>(92)
(это и есть смысл термина «наихудшее распределение»). В самом деле, -kq1
в силу (22) принадлежит Κε и, стало быть, Κε - Это означает, что его
мощность Pq1{02) = 'Eo2ttq1(X) не будет превосходить мощности н. м. к. в Κε ,
равной по определению /?q/(02)·
Мы могли бы теперь с помощью теоремы 3 доказывать теоремы 1 и 2.
Множество θ?, на котором сосредоточено наименее благоприятное
распределение в теоремах 1 и 2 , состоит соответственно из одной {θι} и двух {0χ, Θ2}
точек. Условия (20), (21) превращаются соответственно в условия (3) и (7).
Аналогичным образом следует использовать теорему 3 для построения
р. н. м.к. и в других случаях: если построенный критерий kqx не зависит
от 02 Ε 02, то он будет р.н.м.к. для проверки Н\ = {θ Ε ©ι} в классе Κε.
Наименее благоприятное распределение Qi, удовлетворяющее условиям
теоремы 3, существует при весьма широких предположениях, которые в
реальных задачах обычно выполнены. Достаточно требовать компактность
©ι и непрерывность f${x) по θ для п. в. χ (подробнее об этом см. [65] и
главу 6).
Дальнейшее обсуждение связей между байесовским и минимаксным
подходами см. в §49.
§46.* Несмещенные критерии
В этом и следующем параграфах мы будем использовать принципы
несмещенности и инвариантности для естественного сужения класса
рассматриваемых критериев. Цель такого сужения — отыскание оптимальных
критериев в построенных подклассах.
1. Определения. Несмещенные р.н.м.к. Пусть, как и в предыдущем
параграфе, мы рассматриваем проверку сложной гипотезы Н\ = {Θ Ε ©ι}
§ 46. Несмещенные критерии
345
против #2 = {θ € ©2} по выборке X €= Р#, θ Ε θ = θι U Θ2. Рассмотрим
критерии π из класса Κε = {π : sup Ε^π ^ ε}.
0€Θι
Если, например, Θι состоит из одной точки θι, Ε^π = ε, το ε есть
вероятность отклонения Hi, когда Н\ верна. Естественное требование к
критерию π состоит в том, чтобы вероятность отклонения Hi, когда Н\
неверна, должна быть больше ε. Если это не так, то найдутся
альтернативы, при которых принятие Н\ более вероятно, чем в случаях, когда Н\
верна. Такое положение является нежелательным. Мы приходим к
необходимости выделить следующий важный класс критериев.
Определение 1. Критерий π называется несмещенным, если для него
inf ЕятгрО ^ sup Έθπ(Χ). (1)
0£θ2 0€θι
Таким образом, критерий π Ε Κε, для которого sup Ε^π = ε, будет
вевг
несмещенным, если βπ(θ) ^ ε при θ £ ©2- Класс несмещенных критериев
уровня 1 — ε мы обозначим через Κε.
Односторонний критерий π с критической областью Τ > с (или Τ < с)
для экспоненциальных семейств, упоминавшийся в предыдущем параграфе,
не может быть несмещенным для проверки Н\ = {X €= Р^Л против #2 =
= {X ^ p0li θ φ θι}, так как здесь ©2 = {0 : θ φ θι}, Εθπ < ε при θ < θι,
если Ε^π = ε (см. теорему 45.1).
Наоборот, р. н. м. к., если они существуют, с необходимостью являются
несмещенными, так как для них мощность /3(0) при θ Ε ©2 не может быть
меньше мощности тривиального критерия π(Χ) = ε.
Принцип несмещенности*) представляет самостоятельный интерес,
поскольку он дает возможность естественного сужения класса критериев. Это
позволяет нам строить р.н. м. к. в классе Ке в тех случаях, когда р. н. м.к.
в классе Κε не существуют.
Как мы увидим, это относится, в частности, к задаче о проверке
гипотезы Hi = {θ Ε [Θι,θ2]}ι θι ^ 02, против двусторонней альтернативы Ή.2 =
= {0g[0i,02]} (°Ρ· с п. 45.2).
Отыскание р. н. м. несмещенных критериев во многом может быть
сведено к использованию уже применявшихся приемов, существо которых
изложено в лемме 45.2. При этом может быть полезным следующее утверждение.
Допустим, что существует общая непустая граница Г множеств ©ι и ©2
из Шк:
Γ = θθιΠ д&2
(сЮг обозначает границу ©^), т.е. множество точек, предельных
одновременно для ©ι и ©2- Допустим, кроме того, что для всех π Ε Κε
βπ{θ)=Έθπ{Χ)=ε при всех θ е Г. (2)
*) Термин «несмещенность» использовался и применительно к оценкам. Свойство
несмещенности оценки в известном смысле аналогично свойству несмещенности критерия: если
оценка Θ* является смещенной, то Е$о0* φ во и найдутся другие значения параметра θ φ θο,
при которых среднее значение Е$0* будет равно во.
346 Гл.З. Теория проверки гипотез
Это свойство будет, очевидно, всегда выполнено, если βη(θ) непрерывно
зависит от θ для любого критерия π из Κε.
Так как
/Ш = J ττ(χ)Μχ)μη(άχ), (Ктг(а0<1,
то непрерывность βπ(θ) будет иметь место, если непрерывной по θ для
μη-π. в. χ будет функция /#(ж). Это вытекает из следствия 1 приложения V.
Обозначим через Κε класс всех критериев π, удовлетворяющих (2).
Лемма 1. Пусть Ке С КЕ (т. е. выполнено (2)). Тогда если π есть
р. н. м. к. в ΚεΠ Κε) то π — р.н. м. к. в Κε.
Доказательство. Нам достаточно убедиться, что π Ε Κε и что
Κε С_Ке Π Κε. Второе из этих соотношений вытекает из предположения
Κε С Κε. Первое следует из того, что критерий π = ε принадлежит Κε Π Κε
и, стало быть, inf Τ&απίΧ) ^ inf Ε#π = ε. <
θ€θ2 θ€θ2
Таким образом, лемма 1 позволяет свести поиски р. н. м. несмещенных
критериев к поискам обычных р. н. м. к., но при наличии граничных
условий (2). Если число точек границы Г конечно, то мы окажемся в
условиях леммы 45.2, где нам останется проверить независимость полученной
оптимальной критической функции π от значения й G 02, для которого
максимизировался функционал Ε^π(Χ). Это и будет означать равномерную
наибольшую мощность.
Отметим теперь следующее обстоятельство, связанное с вырождением
условий (2), которое проще всего пояснить для одномерного случая. Если
Θι = [Яьбг], а ©2 есть дополнение к Θι, то условия (2) будут
представлять собой два уравнения Ε^π(Χ) = ε, г = 1,2. Однако в предельном
случае θ\ = #2 эти уравнения превратятся в одно. Но в силу
несмещенности критерия π его мощность βπ(θ) должна будет в точке в\ достигать
своего минимума (см. (1)). Стало быть, если βπ{θ) дифференцируема, то
роль уравнений (2) в случае θι = 02 будут играть равенства
/Μ0ι)=ε, &(0ι)=Ο. (3)
Условия дифференцируемости / /ο(χ)μ(άχ), а тем самым и βπ(θ) =
= Ε^π(Χ), выяснены в приложении V. Если эти условия выполнены, то
β'Μ = j π{χ)}'θ{χ)μη{άχ) = J π(χ)ϊ(χ,θ)Μχ)μη(άχ) =Εθπ(Χ)Σ'(Χ,θ).
Это означает, что условия (3) вновь можно записать в терминах интегралов:
Εθιπ(Χ)=ε, E9lir(X)L'(X,e1) = 0. (4)
Например, для экспоненциального семейства (45.9)
ϊ(χ,θ) = ^ + α'(θ)Τ(χ).
§ 46. Несмещенные критерии 347
Так как EeL'(X,9) = 0, то с/(0)/с(0) = -α'{θ)ΕθΤ{Χ),
Eeir(X)L'{X,0) = -α'(θ)ΕθΤ(Χ) ■ Εθπ(Χ) + α'(θ)Εθπ{Χ)Τ(Χ),
и уравнения (4) примут вид
Εθι (π(Χ) - ε) = 0, Εθι (π(Χ) - ε)Τ(Χ) = 0.
В качестве иллюстрации рассмотрим случай, к разбору которого, по
существу, уже все подготовлено.
2. Двусторонние альтернативы. Экспоненциальное семейство.
Теорема 1. Пусть fe{x) определяется равенством 45.9 и
проверяется гипотеза Н\ = {θ Ε [0ι,02]}5 ^ι ^ ^2> против альтернативы
#2 = {θ £ [#ι,#2]}· Тогда если функция α(θ) монотонна, то:
1) в классе Κε несмещенных критериев уровня 1 — ε существует
р. н. м. к, π, который имеет вид
ГО, если с\ < Т(х) < С2,
7г(я) = < pi, если Т(х) = С{, г = 1,2, (5)
[l, если Т(х) £ [сьс2],
η
где Т(х) = У^Ща^), α постоянные с^, р*, г = 1,2, определяются из
условий
Ε6ίπ(Χ) = ε, г = 1,2, (6)
если θ\ < Θ2, и из условий
Εθιπ(Χ)=ε, Εθι(π(Χ) - ε)Τ(Χ) = 0, (7)
если θ γ = 02;
2) критерий π минимизирует функцию βπ(θ) = Egn(X) при условиях
(6) внутри отрезка [#ь#2] ^ максимизирует ее вне [#ι,#2] ^ф^ условиях (6)
или (7) (последнее при θχ = 62);
3) гари 0 < ε < 1, θχ < 02 функция /3(0) = Ε^π(Λ*) имеет минимум в
некоторой точке 0о £ (^ь^г) ^ строго возрастает при удалении θ от во
вправо или влево. При зтом исключаем случай (45.8).
Нетрудно видеть, что формулировка этой теоремы почти повторяет
утверждение теоремы 45.2 с той, однако, разницей, что сами утверждения иногда
носят «противоположный» характер и не исключается равенство θχ = 02.
Доказательство. В случае θχ < 02 оно полностью следует
доказательству теоремы 45.2. В замечании 1 к упомянутой теореме сказано, что при
θχ < 02 все рассуждения теоремы полностью сохранятся в случае, когда
проверяется основная гипотеза {0 £ [0ι,02]} против {0 £ [01,02]}, т.е. в
обозначениях этого параграфа — гипотеза i?2 против Ηχ. Положим π(χ) = 1—π°(χ),
где π° — функция, определенная в (45.6) при условиях Ε^π°(Χ) = 1 — ε,
г — 1,2, вместо (45.7). Тогда, очевидно, утверждения 2), 3) будут прямыми
следствиями соответствующих утверждений теоремы 45.2.
348
Гл. 3. Теория проверки гипотез
Первое утверждение теоремы следует из второго, так как класс критериев
π, удовлетворяющих (6), шире, чем Κε, и, стало быть, π будет
максимизировать Ε^π(Χ) в классе Κε в любой точке θ вне [61,62]· Это означает, что π
есть р. н. м. несмещенный критерий.
Нам осталось рассмотреть случай 9\ — θ2. Здесь, по-видимому, проще
воспользоваться леммой 45.2. Возьмем любое θ φ θ\ и рассмотрим задачу
максимизации Εβπ{Χ) при условиях
Εβιπ(Λ·)=ε, Εβιπ(Χ)Γ(Χ)=εΕβιΓ(Λ·). (8)
Очевидно, мы будем находиться в условиях леммы 45.2, если положим га =
= 2, /ι = fBl, h = Tfe^ /з = Λι ει = ε, ε2 = εΕθΤ{Χ). Согласно этой
лемме максимум Ε#π будет достигаться на функции
-/х\ = J1' если Л(ж) > к^Лх) + k2T{x)f6l{x),
[О, если fe{x)<klfel{x) + k2T{x)fel{x).
Рассмотрим последнее неравенство, которое можно записать в форме
с(0)
е(.(м»1))г(»)<к1 + ]ь2Г(а.).
Ясно, что для любых с\ < с2 можно всегда выбрать fci, k2 так, чтобы это
неравенство было эквивалентно
ci < Τ < с2.
Это доказывает, что критерий вида (5) максимизирует Έβπ(Χ) при условиях
(7), если только сг-, pi, i = 1,2, в (5) можно выбрать так, чтобы
удовлетворялось (7) (или (8)). Этот критерий будет, очевидно, р. н. м. несмещенным
критерием, так как класс критериев π, удовлетворяющих (8), шире, чем Κε,
и, стало быть, π будет максимизировать Εβπ(Χ) и в Κε. Итак, для
доказательства теоремы нам осталось убедиться, что справедлива
Лемма 2. Уравнение (7) при 0 < ε < 1 разрешимо относительно с^
Pi, г = 1,2.
Доказательство этой леммы мы приведем, как и доказательство
леммы 45.1, при упрощающем предположении, что Т?$1 -распределение Т(Х)
непрерывно, т. е. Ρ#χ {Т(Х) = с) = 0 при всех с.
Напомним, что плотность распределения Τ относительно некоторой
меры ν можем считать равной (см. §45) ge(t) = c(9)eet. Тогда уравнения (7),
(8) будут эквивалентны соотношениям
С2
Εθι (1 - тгрО) = c(0i)У e^i/frfi) = 1 - ε,
(9)
С2 С2 ν '
Εβι(1 - π(Χ))Τ(Χ) = c(0i) fteeitv{dt) = (1 - e)c(0i) ί te9ltv(dt).
§ 47. Инвариантные критерии
349
Обозначая r(t) = t, m = ΕθιΤ{Χ) = ο(θχ) I te6ltv{dt), мы можем
уравнения (9) записать в виде
С2 С2
c(0i) Ie9ltv(dt) = 1 -ε, c(0i) Ιr{t)eeitu(dt) = (1 - e)m. (10)
Мы пришли к задаче, совпадающей с задачей, рассматривавшейся в лемме
45.1, с той лишь разницей, что распределение с плотностью r(t)gQl (t) может
быть обобщенным (т.е. принимать и отрицательные значения). В этих
новых условиях сохраняются рассуждения леммы 45.1. <
§ 47.* Инвариантные критерии
В этом параграфе рассмотрим еще один способ сужения класса всех
критериев, основанный на этот раз на соображениях инвариантности.
Предположим, что X €= {Р#} и {Р#} есть инвариантное семейство.
Напомним необходимые обозначения и понятия (см. § 29). Пусть дана группа G
измеримых преобразований д пространства Хп в себя. Семейство {Р#} будет
инвариантным относительно G, если для каждого д Ε G и θ Ε Θ найдется
элемент вд Ε Θ такой, что
Рвд(ХеА) = Рв(дХеА)
для любого А Е 95д».
Преобразования д пространства θ, определяемые равенством дв = 9д,
при выполнении условий (Ао) образуют группу G (см. §29).
Определение 1. Будем говорить, что задача проверки гипотезы Н\ =
= {θ Ε θι} против #2 = {θ Ε 02/, θι U ©2 = θ, является инвариантной,
если выполнены следующие два условия:
1) семейство {Рв} является инвариантным относительно G;
2) множества θ ι и ©2 являются инвариантными относительно д Ε G,
т.е. дЭ{ = ©г, г = 1,2.
Если задача проверки гипотез является инвариантной, то для ее решения
естественно воспользоваться инвариантным критерием.
Определение 2. Критерий π называется инвариантным, если π(Χ)
есть инвариантная относительно д статистика*):
тг(дх) = 7г(ж) для всех χ Ε Хп\ д Ε G.
Если π есть нерандомизированный критерий и Ω^ есть область приема
гипотезы Hj, то инвариантность π означает, что 67Ω7 = f}j, j = 1,2.
Естественность использования инвариантных критериев, по-видимому,
проще всего понять на примерах. Общее обсуждение, связанное с
трактовкой д как замены координат и нечувствительности к этой замене
соответствующих статистик, содержится в § 29.
*) См. сноску в § 29.
350 Гл. 3. Теория проверки гипотез
Пример 1. Наиболее простые примеры относятся к тому случаю, когда
группа G тривиальна, т.е. ~д для любого д есть тождественное
преобразование ё пространства Θ.
Пусть Χ ^ Φο,σ2 и проверяется гипотеза Н\ = {σ\ ^ σ ^ σ2} против
дополнительной альтернативы #2. В этом случае
Очевидно, что семейство Φο,σ2 инвариантно относительно группы G
ортогональных преобразований д (вращений) пространства Хп, при этом 'д =
= е для любого д. Поэтому естественно рассматривать критерии π, зави-
п
сящие от статистики Т(Х) = У^х?. Так как σ~2Τ(Χ) €= ^i/2}n/2 ^ Нп,
то Т(Х) €= Γα,η/2 ПРИ α ^ 1/(2°"2)> и мы приходим к задаче о проверке
гипотезы i?i = {αϊ ^ а ^ а2}, ol\ = 1/(2σ2), «2 = 1/(2сг^), по
наблюдению Т(Х), имеющему распределение Γαη/2 из экспоненциального
семейства. С помощью результатов предыдущих параграфов мы можем построить
р. н. м. несмещенный критерий уровня 1 — ε, принимающий Н\ при
С1 < Т(Х) < с2, (1)
где Ci выбираются так, чтобы Га1)П/2(К\ [ci,c2]) = ra2j7l/2(R\ [ci,c2]) = ε.
Отметим, что критерий вида (1) в этом примере мы могли бы построить
и из других соображений, основываясь на принципе достаточности, так как
статистика Τ является достаточной. Ведь мы знаем, что вся информация о
параметре σ2 сосредоточена в Τ и привлечение других статистик (т. е. другой
информации о выборке) не имеет смысла.
В дальнейшем там, где это возможно, мы будем сразу редуцировать
задачу к задаче о достаточных статистиках.
Пример 2. Пусть X €= Φα,σ2, Н\ — {σ\ ^ σ < σ2}. В этом случае
θ = (α,σ2), и преобразование сдвига дХ — X + с — (χι + с,. ..,хп + с)
индуцирует преобразование Tja — а + с, которое оставляет гипотезу Hi
неизменной. Если ограничиться рассмотрением достаточных статистик
η
Т1=х, Т2-£](хг--х)2,
то преобразование д дает
Т1(дХ)=х + с, Т2(дХ)=Т2(Х).
Таким образом, статистика Т2 является инвариантной относительно G. То
есть инвариантный критерий π, основанный на достаточных статистиках,
должен быть функцией от Т2. (Ниже мы увидим, что любой инвариантный
критерий π должен быть функцией от Т2.) В силу §40 σ~2Τ2 €= Γι/2,(η-ΐ)/2>
и мы приходим к задаче, разобранной в предыдущем примере. Р.н. м.
инвариантный несмещенный критерий будет иметь вид с\ < Г2 ^ с2.
§ 47. Инвариантные критерии
351
Пример 3. Оба рассмотренные выше примера касались нормального
распределения. Применительно к распределению выборки X это было
многомерное нормальное распределение с диагональной матрицей вторых
моментов. Для дальнейшего полезно отметить, что семейство произвольных
многомерных нормальных распределений Φα)(72, α £ Rm, σ2 = ||σ^||, г, j =
= 1,...,га, является инвариантным относительно группы G линейных
невырожденных преобразований
дх = (х — а)С,
где С — обратимая матрица. В самом деле, мы должны убедиться, что
при некотором преобразовании д выполняется Рд$(А) — Т?д(д~1А), где
Р# = Φα,σ2, θ = (α, σ2), g~lA, как обычно, означает множество д~1А =
= {х € Rm : дх е Л}. Имеем (σ = vW)
*a^(g"1^)=(27r)L/2(y / exp|^^(a;^a)a-2(^^a)T|^.
После замены у = дх получим
Учитывая, что <7-1у = уС~1 + а, мы можем показатель у экспоненты в
последнем интеграле записать в виде
(у - (а - а)С)С-1о-2{С-1)т{у - (а - а)С)т.
Стало быть, если положить
дв = д(а, о2) = (да, Ста2С) = ((a - а)С, Ста2С), (2)
то мы получим
фа,А9-1А) = ФЖа,(Т2)(А). (3)
Пример 4. Пусть гипотезы Hj имеют следующий вид: Hj = {X ^
^ Pj,a}, а € X, j = 1,2, где Pjjtt есть распределения с плотностями
fj(x — a), j = 1,2. Другими словами, нас интересует, какому из двух
типов распределений, с точностью до сдвига, принадлежит выборка X. Здесь
следует положить θ = (ι/,α), ν = 1,2, α Ε Λ', и рассмотреть
преобразование gX = I + c, которое в параметрическом пространстве индуцирует
преобразование 'дв = (ζ/, а + с). Ясно, что гипотезы Hj = {ι/ = j}, j = 1,2,
инвариантны относительно <; и, стало быть, задача проверки этих гипотез
является инвариантной. Статистика
У = {Xl - Хп, . . ., Хп-1 - Хп)
352
Гл. 3. Теория проверки гипотез
будет инвариантом относительно д (ср. с §28). Ее распределение в точке
У = (j/b ..., 2/η-ι) ПРИ гипотезе Hj имеет плотность
ffM = / Π /i(w + z)fj(*Mdz). (4)
J t=i
Отсюда видно, что для наблюдения У гипотезы ifj превращаются в
простые гипотезы, в соответствии с которыми плотности jj для Υ имеют
вид (4). В этих условиях мы можем воспользоваться леммой
Неймана-Пирсона и построить н.м.к. π, который принимает Н2, если
£^>с (5)
ΙΪ(Υ) (5)
Так как этот критерий от а не зависит, он будет р. н. м. к. для проверки
Н\ против #2 среди всех инвариантных критериев, основанных на
статистике У.
В связи с рассмотренными примерами желательно иметь уверенность
в том, что остальные инвариантные критерии в этих задачах также
являются функциями выбранных нами инвариантных статистик. Особенно это
относится к последнему примеру, так как в двух предыдущих наш выбор
критериев определялся также соображениями достаточности.
Для того чтобы выяснить взаимоотношения между инвариантами,
введем некоторые понятия. Две точки ж и ж' из Хп будем называть
эквивалентными относительно группы G, если найдется д G G такое, что х' = дх.
Так как G есть группа, все пространство Xй разбивается на
непересекающиеся классы эквивалентности, которые в § 29 мы называли орбитами.
Чтобы получить некоторую орбиту, достаточно взять какую-нибудь одну ее
точку xq и применить к ней все преобразования д из G. Например, для
ортогональных преобразований в примере 1 орбиты образуют сферы с центром
в начале координат.
Инвариантность статистики Τ относительно G равнозначна тому, что Τ
постоянно на каждой орбите.
Определение 3. Статистика Τ называется максимальным
инвариантом, если она инвариантна и из Т(х') = Т(х) следует х1 = дх при
некотором д G G.
Это означает, что максимальный инвариант принимает разные значения
на разных орбитах.
Теорема 1. Пусть Τ — максимальный инвариант. Статистика S
инвариантна тогда и только тогда, когда S зависит от X через Т,
т. е. когда существует функция φ такая, что S(X) = φ(Τ(Χ)).
Для упрощения изложения мы не затрагиваем здесь важный вопрос об
измеримости φ. Отметим лишь, что в рассматриваемых в этом параграфе
примерах такая измеримость будет иметь место*).
*) Подробнее см., например, [48, 65].
§ 48. Связь с доверительными множествами
353
Доказательство. Если S(x) = φ(Τ(χ)), то S(gx) = <p{T{gx)) =
= φ(Τ(χ)) = 5(ж), и, стало быть, S инвариантна. Чтобы доказать обратное
утверждение, нам надо убедиться, что из Т(х) = Т(ж') следует S(x) = 5(ж;).
Но это так в силу того, что Т(ж) = Т(ж') влечет за собой существование g
такого, что х1 — дх. Так как 5 — инвариант, то S(x) = S(xf). <
Рассмотрим в качестве примера группу G сдвигов
д(х) = χ + с = (х\ + с,..., хп + с).
Как мы уже отмечали, статистика Υ (χ) = (ху — яп,..., хп-\ — хп) является
инвариантом. Покажем, что это максимальный инвариант. Действительно,
изУ(ж) = Υ{χ') ξ Ц-<,....я^-а^) следует, что яй - аг„ = a?J - а;^ при
всех г = 1,..., η — 1. Полагая х^ — ζη = с, получим xj = х, + с, г = 1,..., п,
ж' = ж + с = до, что и означает требуемую эквивалентность х1 и ж.
Мы можем вернуться теперь к примеру 3 и утверждать, что критерий (5)
является р. н. м. среди всех инвариантных критериев, поскольку все
инвариантные критерии являются по теореме 1 функциями от У и, стало быть,
предположение о существовании более мощного инвариантного критерия,
чем (5), будет противоречивым.
Аналогично предыдущему читатель может убедиться, что статистика
η
V^Xf в примере 1 также является максимальным инвариантом.
i=l
Если существуют достаточные статистики, то исходную задачу бывает
удобно редуцировать сначала к задаче относительно распределения
достаточных статистик, а затем уже применять соображения инвариантности,
η
как это было в примере 2, где статистика Τι = /~^(χΐ ~ х) является, оче-
г=1
видно, максимальным инвариантом в наблюдении (х, Тг).
В заключение этого параграфа отметим еще раз, что существо подхода,
связанного с инвариантностью, состоит в редукции рассматриваемых задач
о проверке гипотез к более простым задачам, относящимся к распределению
максимальных инвариантов. В этих новых более простых условиях в ряде
случаев оказывается возможным построить н. м. или р. н. м. критерии.
В этом отношении «принцип инвариантности» близок к «принципам»
достаточности и несмещенности, в соответствии с которыми исходная задача
редуцируется к задаче в терминах достаточных или несмещенных
статистик.
§48/ Связь с доверительными множествами
1. Связь статистических критериев и доверительных множеств. Связь
свойств оптимальности. Понятия доверительного множества и
статистического критерия тесно связаны между собой. Определение доверительного
множества было дано в § 39. Напомним его.
Пусть Χ €?Τ?θ, 0 6 Θ.
354
Гл. 3. Теория проверки гипотез
Определение 1. Случайное подмножество Θ* = Θ*(Χ,ε)
параметрического пространства Θ называется доверительным множеством уровня
1 — ε, если
Ρβ(Θ*(Χ,ε)Βθ)>1-ε (1)
для всех θ € Θ.
Очевидно, доверительный интервал есть частный случай доверительного
множества. Последнее сохраняет тот же смысл: с вероятностью ^ 1 — ε оно
накрывает истинное значение параметра.
Положим
Ω(0,ε) = {хеХп:ве θ*(ж, ε)}. (2)
Тогда соотношения
θ Εθ*(ж, ε) и хеП{в,е) (3)
будут эквивалентными.
Определение доверительного множества предполагает, что множество
Ω(0, ε) в (2) является измеримым, так что вероятность в (1) имеет смысл и
равна Έ>Θ{Χ ΕΩ(0,ε)).
Доверительные множества и статистические критерии для проверки
гипотезы Η ι = {θ = θχ} против дополнительной альтернативы Щ = {Θ Ε 02},
θ\ $. 02? связаны между собой следующим образом. Пусть для каждого θ\
определено свое множество 02 = ©2(#ι) ^ #1-
Теорема 1. 1) Рассмотрим для каждого θ\ нерандомизированный
критерий π = δ уровня 1 — ε для проверки гипотезы Н\ против Η<ι и
обозначим через Ω(#ι,ε) его область принятия гипотезы Н\. Тогда
множество
θ*(Χ,ε) = {0Ε0:ΧΕΩ(0,ε)}
будет доверительным множеством уровня 1 — ε.
Наоборот, если Θ*(Χ,ε) — доверительное множество уровня 1 — ε,
то множество Ω(#ι,ε) С А'71, определенное в (2) и взятое в качестве
области приема Н\, будет определять критерий для проверки Н\ —
= {Θ = θ\} против Ή.2 = {θ Ε ©2(#i)} уровня 1 — ε d/иг любого ©2(#i),
0飩2(0ι).
2) £Ъш критерий 7Г с областью приема Ω($ι,ε) гипотезы Н\
является р.н.м.к., то соответствующее множество θ*(Χ,ε)
минимизирует вероятность
Р*(0' € θ*(Χ,ε)) длл всех 0,0', 0 € θ2(0')ι (4)
в классе всех доверительных множеств уровня 1 — ε.
Верно и обратное утверждение: минимальность (4) означает, что
соответствующее множество Ω(0,ε) будет порождать р. W. Mf 7ъ.
Для одномерного параметра наиболее употребительными являются
случаи θ2(0') = {θ:θφ θ') и ©2(0') = {0 : θ > 0'} (или {0 : θ < θ1}). В первом
из них в (4) будет иметь место минимизация при всех 0' φ 0, во втором —
при всех 0' < 0.
§48. Связь с доверительными множествами
355
Итак, теорема утверждает в (4), что для Θ* минимизируется вероятность
Р# того, что в доверительное множество попадет любое другое значение θ' φ
Φ θ такое, что θ £ 02(0')· Это есть один из способов выделения оптимальных
доверительных интервалов.
Определение 2. Доверительные множества, для которых
минимизируется (4) при условии (1), называются наиболее точными
доверительными множествами (уровня 1 —ε) относительно альтернатив Θ1 таких,
что θ е θ2(0')·
Ниже будет приведено некоторое дополнительное обоснование для такого
понимания оптимальности доверительного интервала.
Таким образом, теорема 1 устанавливает, что «обращение» множества
Ω(#ι,ε) для р. н. м. к. дает наиболее точное доверительное множество. При
этом важно отметить, что рассматриваемая процедура построения
доверительных множеств с размерностью θ никак не связана. Можно даже
рассматривать бесконечномерные параметры θ или отождествлять θ с самим
распределением Ρ выборки X. Тогда соотношения эквивалентности (3),
где Ω(0, ε) = Ω(Ρ,ε) есть область приема гипотезы {Х€=Р} при
альтернативе {Χ €=Ρι 5^Р}, позволяют построить доверительное множество
для Р. Например, мы видели в §6, что распределение статистики Dn =
= л/пsup \F£(t) — F(t)\ при условии X €= Ρ, где F есть непрерывная функ-
t
ция распределения, соответствующая Р, от F не зависит и может быть
найдено. Стало быть, можем найти такое d — d(e)y что P(Dn $C d(e)) = 1 — ε.
Таким образом, неравенство
VGsup|F*(t)-F(i)|<d
t
определяет область приема гипотезы {X €= Р} для критерия уровня 1 — ε.
Но это же неравенство определяет и доверительное множество для F —
просто ввиду симметрии этого неравенства относительно F и F£
специальной процедуры «обращения» здесь не требуется.
Доказательство теоремы 1 почти очевидно. В основе его лежит
эквивалентность (3), в силу которой
Ρθ(θ е Θ*(Χ,ε)) = Ре(Х е Ω(0, ε))>1-ε.
Это доказывает первое утверждение. Чтобы доказать второе, рассмотрим
какое-нибудь другое доверительное множество Θ*(Χ,ε), и пусть Ω(0,ε) —
соответствующее ему подмножество в Xй. Тогда
ΡΘ(Χ е ОДе)) = Ρθ(θ € θ*(Χ,ε)) > 1 - ε,
ΡΘ{Χ е ОД,ε)) > ΡΘ{Χ G Ω(0ι,ε))
при θ £ 02 (#ι) и, стало быть,
Ρθ(θιΕβ*(Χ,ε))^Ρθ(θ1£θ*(Χ,ε)). <
Рассмотрим теперь важный частный случай, связанный с одномерным Θ.
356
Гл. 3. Теория проверки гипотез
2. Наиболее точные доверительные интервалы
Теорема 2. Пусть множество Ω(0,ε) ρ. н. м. к., рассмотренного в
теореме 1, имеет вид
ο1{θ,ε)^Τ(χ)ζο2{θ,ε),
где с\(в,е) монотонно и непрерывно*) зависят от Θ. Пусть для
определенности Ci(6,e) возрастают. Тогда наиболее доверительное
множество [уровня 1 —ε) относительно альтернатив Θ' таких, что θ Ε θ2(0')>
будет иметь форму интервала
где Т = Т(Х), cjl{t,e) есть решения относительно θ уравнений
<Η(θ,ε)=ί.
Мы видим, таким образом, что процедура построения доверительного
интервала здесь, по существу, та же, что и в §39, — с той лишь
особенностью, что в качестве статистики S здесь используется статистика Τ р. н. м.
критерия.
Доказательство теоремы вполне очевидно, и оно предоставляется
читателю.
Рассмотрим теперь более подробно односторонние доверительные
интервалы для скалярного Θ. Они используются там, где наибольший
интерес представляет лишь одна граница для оцениваемого параметра. Такие
ситуации возникают, когда оценивается вероятность какого-нибудь
нежелательного события или, скажем, оценивается величина разрывающего усилия
для нового сплава.
Ввиду симметрии можно ограничиться рассмотрением нижней
доверительной границы Θ~(Χ,ε), для которой
Р,(0-(ад<0)>1-е. (5)
Определение 3. Граница θ" = 0~(Х, ε), для которой Ρβ(θ~ ^ Θ')
минимальна при всех Θ' < 0, называется наиболее точной нижней
доверительной границей уровня 1 — ε.
Допустим, что ιυ(θ~,θ) есть какая-нибудь мера потерь, возникающих от
«недооценки» θ: ιυ(θ~,θ) = 0 при θ~ > 0 и w(0~)9) > О при θ~ < 0; при
этом ιν{θ~, θ) непрерывно возрастает при удалении θ~ от 0, Hjqw(0~, θ) < oo.
Следующее утверждение в какой-то мере поясняет смысл определения 3.
Лемма 1. Наиболее точная нижняя граница 9~ минимизирует
значение Εθό)(Θ~,Θ) при условии (5) и при любой функции w, обладающей
сформулированными выше свойствами.
*) Свойства монотонности и непрерывности Ci(9, ε) обычно вытекают из таких же свойств
функции распределения Рв(Т(Х) < с). В обозначениях §39 с\{9,е) = Gg1(ei)1 сг(0,ε) =
= С^Ч1 — £2), где Ge — функция распределения Т(Х), ει + ει = ε.
§ 48. Связь с доверительными множествами
357
Доказательство. Пусть 0 — другая нижняя граница. Тогда, так как
приращения duw{u,9) по и в области и < 0 отрицательны, то
θ θ
Εθ<ω{θ-,θ)= / w{u,e)duPe{e- <u) = - [ Ρθ{θ~ <u)duw{u,9)^
-00 -OO
θ
ζ - / Ρθ(θ- < u)duw{u,e) = ΕΘν)(θ",θ). <
—oo
Мы видим, таким образом, что подход к определению наиболее точных
доверительных множеств в случае односторонних множеств является вполне
естественным. Можно теперь с помощью теорем 1, 2 и результатов §45
построить в явном виде односторонние доверительные интервалы для случая,
когда отношение правдоподобия монотонно.
Теорема 3. Пусть X €= Ρ о, семейство {Рв} имеет монотонное
отношение правдоподобия относительно статистики Т(Х), Рв-распреде-
ление которой Go(t) = Ρρ(Τ(Χ) < t) непрерывно по θ и t> Тогда
статистика Τ по распределению монотонно и непрерывно зависит от 0, т. е.
Ge{t) непрерывно убывает с ростом 0 (см. определение 39.3). Если b(t^)
есть решение относительно θ уравнения Ge{t) = 7> то наиболее точная
нижняя граница θ~~(Χ,ε) уровня 1 — ε равна
0-{Х,е) = Ь(Т(Х),1-е).
Другими словами, в утверждении теоремы 39.1 мы получим наиболее
точную нижнюю доверительную границу, если будем использовать в
качестве S статистику Т.
Доказательство. В нашем случае в условиях теорем 1, 2 надо
положить ©2(0) = {t : t > 0}. В силу теоремы 45.1 существует
нерандомизированный р. н. м. к. для проверки Н\ = {0 = θ{\ против Η<ι = {0 > θ\} с
областью Ω(#ι,ε) = {Χ : Τ(Χ) < с} принятия Яь где с = с(в\) 1-е) = Gj^(l—e)
определяется из условия
Рв1(Т{Х)<с{ви1-е)) = 1-е.
При этом
Рв(Т(Х)>с)>е = -рв1(Т(Х)>с)
при 0 > 01. Последнее означает, что c(0i, 1 — ε) < c(0,1 — ε) при 0ι < 0, т. е.
функция с(0,1 — ε) возрастает по 0. Непрерывность с(0,1 — ε) = G^l(l — ε)
по 0 следует из непрерывности Gg.
Мы видим, что условия теорем 1, 2 полностью выполнены при С2(0, ε) =
= с(0,1 — ε) и, стало быть, наиболее точное доверительное множество имеет
форму полуинтервала (с_1(Т(Х),1 — ε),οο), где, как мы видели в
теореме 39.1, с'1(Т, 1 - ε) = 6(Г, 1 - ε). <
358
Гл. 3. Теория проверки гипотез
Точно так же можно построить наиболее точную верхнюю границу
θ+(Χ,ε).
Пусть теперь 0 (Χ, ει) < θ*(Χ, 62) обозначают верхнюю и нижнюю
доверительные границы уровней 1 — ει и 1 — в2 соответственно. Так как
события {Θ~(Χ,ει) > 0} и {Θ+(Χ,62) < 0} не пересекаются, то
Ρθ{θ-{Χ,ει) <θ< 0+(Χ,ε2)) = 1 - ει - ε2,
и (0~(Х,ει),0+(Χ, 62)) представляет собой доверительный интервал уровня
1 - ει - ε2.
Пусть ΐϋι(θ , 0) и 1^(0 ,0) — функции потерь для границ 0^,
обладающие свойствами, описанными в формулировке леммы 1.
Лемма 2. Пусть ги(0~,0+,0) = wi(0~,0) + ΐϋ2(0+,0)· Тогда
доверительный интервал (0~,0+), образованный наиболее точными верхними и
нижними границами, минимизирует Ε#ΐί;(0~,0+,0) при условиях
Ρ*(0~>0Χει, Ρ*(0+<0Κε2.
Эта лемма является очевидным следствием леммы 1. Она показывает,
что доверительный интервал, построенный с помощью точной нижней и
точной верхней границ, также будет обладать свойством оптимальности.
Теорема 3 дает возможность в явном виде строить такие интервалы для
параметрических семейств с монотонным отношением правдоподобия.
Предлагаем читателю убедиться с помощью сделанных замечаний, что
доверительные интервалы, построенные в §40 для среднего и дисперсии
нормального распределения, будут иметь наиболее точные верхние и нижние
границы.
В теореме 1 и последующих рассмотрениях фигурировало условие, что
р. н. м. к. является нерандомизированным. Однако это ограничение не
является существенным. Любой рандомизированный критерий π можно
представить как нерандомизированный, если ввести в рассмотрение
дополнительное наблюдение У, независимое от X и равномерно распределенное на [0,1].
Действительно, рассмотрим для новой выборки (Χ, У) критическую область
Ω = {(ж,у) :тг(ж) ^у},
т.е. положим δ(Χ,Υ) = 1, если (X,У) G Ω, и δ(Χ,Υ) = 0 в противном
случае. Тогда при любом распределении X
ι
Ρ(δ(Χ,Υ) = 1) = Ρ(π(Χ) £ У) = /р(тг(Х) > y)dy == Επ(Χ)
о
и, стало быть, критерий δ по своим параметрам эквивалентен π.
Как воспользоваться этим обстоятельством для построения
доверительных интервалов в условиях теоремы 3? Допустим для простоты, что
статистика Т(Х) целочисленна (как мы видели, отсутствие нерандомизированных
р. н. м. к. может быть вызвано лишь дискретностью распределения Т). Тогда
наблюдение S(X, Υ) = Т(Х) + У, Υ ^ Uo,i, сохраняет всю информацию,
содержащуюся в Т(Х), так как Т(Х) есть целая часть S(X,Y). Р.н. м.к.
§ 48. Связь с доверительными множествами
359
уровня 1 — ε можно придать выбором нецелого с(9,е) следующую форму:
принимается гипотеза Н\, если
S(X,Y)^c(eul-e).
Тем самым мы построили требуемые множества Ω (0, ε) и остается лишь
«обратить» их тем же способом, что и прежде. Получим нижнюю границу
θ-(Χ,Υ,ε)=ο-1(Τ(Χ) + Υ,1-ε),
где с"1 — функция, обратная к с по первому аргументу. Здесь из самой
формы записи видно, что для определения θ~ нужно произвести
дополнительное наблюдение У.
Пример 1. Пусть X ^ Вр, и нас интересует верхняя доверительная
граница р+ уровня 1 — ε для вероятности ρ = P(xj = 1) = 1 — P(xj = 0).
Семейство распределений {Вр} экспоненциально и удовлетворяет условиям
η
теоремы 3, где следует положить Т(Х) = У^х*. Рассмотрим наблюдение
η
S = Y,Xi + Y, r<=U0ll.
Оно имеет в точке ί, 0 < ί ^ η + 1, плотность Cn pM(l — р)п~И.
Обозначим через Gp(t) функцию распределения с этой плотностью. Тогда р+ будет
решением уравнения Gp(t) = ε.
3. Несмещенные доверительные множества. Вернемся к вопросу о
наиболее точных доверительных множествах. С помощью теоремы 3 можем
строить наиболее точные верхние и нижние границы, основываясь на том,
что для односторонних альтернатив {Θ > #ι}, {θ < θ\} гипотез {θ — θ\} в
ряде случаев существует р. н. м. к. Если же попытаться использовать
теоремы 1, 2 непосредственно при построении наиболее точных доверительных
интервалов, то нам потребуется существование р. н. м. к. для проверки
гипотезы {Θ = θι} против {θ φ #ι}, что бывает весьма редко. Выход из этого
положения состоит в естественном сужении класса рассматриваемых
доверительных интервалов на той же основе, на которой мы сужали классы
рассматриваемых критериев в § 47, 48. Именно, введем понятия несмещенных
и инвариантных доверительных множеств.
Пусть, как и прежде, каждому В соответствует множество ©2(6), θ ^
i β2(0).
Определение 4. Доверительное множество θ*(Χ,ε) для θ уровня
1 —ε называется несмещенным относительно альтернатив в' таких, что
θ<Ξθ2{θ'), если
Р*(0' € θ*(Χ,ε)) ^ 1 - ε при всех 0,0', θ Ε θ2(0')· (6)
Множество θ* (Χ, ε) называется просто несмещенным, если (6)
справедливо для всех θ' φ 0.
360
Гл. 3. Теория проверки гипотез
Несмещенность доверительного множества означает, что вероятность
покрытия им ложного значения Θ' не больше, чем истинного.
Определение 5. Доверительные множества, для которых
минимизируется (4) при условиях (1), (6), называются наиболее точными
несмещенными доверительными множествами (уровня 1 — ε) относительно
альтернатив, для которых θ Ε Θ2(0')·
Теорема 4. 1) Несмещенные нерандомизированные критерии
порождают в силу эквивалентности (3) несмещенные доверительные
множества, и наоборот.
2) Если Ω(θ\,ε) при каждом θ\ Ε Θ есть область принятия
гипотезы {θ = θ\} нерандомизированного р. н. м. несмещенного критерия при
альтернативе {θ Ε θ2(#ι)}, то соответствующее множество Θ*(Χ,ε)
будет наиболее точным несмещенным доверительным множеством, и
наоборот.
Доказательство теоремы полностью повторяет рассуждения
теоремы 1, к которым надо добавить лишь, что свойство несмещенности при
переходе от критериев к доверительным множествам и обратно сохраняется.
Действительно, соотношения (1), (6) эквивалентны
sup Έ>Θ{Χ Ε Ω(0ι,ε)) <1-^Р^е Ω(0ι,ε)).
θ€Θ2(θι)
Если π(Χ) есть критическая функция нерандомизированных критериев,
фигурирующих в теореме {π{Χ) = 0 при Χ Ε Ω(0χ,ε)), то мы получаем
Έθπ{Χ) = 1 -Vo(X е Ω(0ΐ5ε)), inf Έθπ{Χ) > ε > Έθιπ{Χ).
Это и есть, очевидно, свойство несмещенности, эквивалентное (6). <
Если воспользоваться результатами §46 и построить несмещенное
наиболее доверительное множество для параметра θ экспоненциального
семейства, то мы получим тот же доверительный интервал (0~,0+), который мы
строили, используя монотонность отношения правдоподобия, т. е. интервал,
у которого θ~ и 0+ есть соответственно наиболее точные нижняя и верхняя
границы уровней 1 — ε/2.
4. Инвариантные доверительные множества. Следующее определение
использует обозначения и понятия предыдущего параграфа. Пусть {Р#} —
инвариантное семейство относительно G.
Определение 6. Доверительное множество Θ*(Χ,ε) называется
инвариантным*) относительно группы G, если
θ*(9Χ,ε)=9θ*(Χ,ε) (7)
для всех g Ε G.
*) Если следовать замечанию, сделанному в сноске в §29, то доверительное множество
со свойством (7) было бы естественнее называть эквивариантным.
§ 48. Связь с доверительными множествами
361
Смысл этого понятия аналогичен смыслу эквивариантной оценки (§29).
Если преобразования g и g интерпретировать как замену системы
координат, сохраняющую распределение, то (7) означает, что доверительное
множество не зависит от координатной системы, в которой выражены исходные
данные.
Определение 7. Доверительное множество Θ*(Χ,ε) называется
наиболее точным инвариантным доверительным множеством уровня 1 — ε,
если на нем минимизируется Р#(0' Ε Θ*(Χ, ε)) при всех θ' φ θ в классе всех
множеств Θ*, удовлетворяющих (7) и условию Р#(0 Ε Θ*(Χ,ε)) = 1 — ε.
Пусть Ω(#ι,ε) есть область приема гипотезы Н\ = {0 = θ\) при
альтернативе {0 φ θ{\ для инвариантного критерия уровня 1 — ε. Отметим,
что есть существенное различие в определениях инвариантного критерия и
инвариантного доверительного множества (его не было бы, если бы
требовалось выполнение равенства #Ω(0,ε) = Ω(£0,ε), а не #Ω(0,ε) = Ω(0,ε)).
С этим фактом связано то обстоятельство, что соответствие между р. н.м.
инвариантными критериями и наиболее точными инвариантными
доверительными интервалами выглядит несколько сложнее, чем в предыдущих
теоремах.
Рассмотрим группу преобразований G и предположим, что для каждого θ\
в ней есть подгруппа G[0i], оставляющая инвариантной задачу проверки
гипотезы Н\ — {0 = 01}. Другими словами, дв\ = 9\ при д Ε G[6{\.
Теорема 5. Пусть Θ*(-Χ",ε) — инвариантное относительно G
доверительное множество уровня 1 — ε. Тогда:
1) область Ω(0,ε) = {χ : 0 Ε Θ*(χ,ε)} будет инвариантной
относительно G[9] при каждом 0;
2) если область Ω(0ι,ε), соответствующая θ*(Χ,ε), есть область
приема Н\ при альтернативе {0 ^ 0ι} (?лл р.н.м. инвариантного
критерия уровня 1-е, то Θ*(Χ,ε) будет наиболее точным доверительным
инвариантным множеством.
Доказательство. 1) Пусть g Ε G[0]. Тогда #0 = 0,
5Ω(0,ε) = {^:0ΕΘ>,ε)} =
= {ж : 0 Ε θ'^'^,ε)} = {ж : 0 Ε ^©'(χ,ε)} =
= {χ : £0 Ε θ*(χ,ε)} - {ж : 0 Ε θ*(χ,ε)} = Ω(0,ε).
2) Пусть θ* — любое другое инвариантное доверительное множество
уровня 1 — ε. Согласно первому утверждению ему соответствует
инвариантный критерий уровня 1 — ε с областью Ω(0χ,ε) приема Н\.
Так как по предположению
ΡΘ(Χ еП(в1,е))^Рв(Х ζ^θ,,ε)),
то _
Ρβ(0ι е θ*(Χ,ε)) > νβ{βχ Ε θ*(Χ,ε))
при 01 =^ 0, что и требовалось доказать. <
362
Гл. 3. Теория проверки гипотез
Пример 2. Пусть Χ ^ Φα,<72· Требуется построить наиболее точное
доверительное множество для параметра σ2 при неизвестном а. Мы
видели в примере 2 предыдущего параграфа, что семейство Φα>σ2
инвариантно относительно преобразований сдвига дХ = X + с, если положить
1 п
#(α,σ2) = (а + с,сг2). Статистика 5q = -; (χι — χ) является мак-
i=l
симальным инвариантом, построенным по достаточной статистике. Кроме
того, гипотеза Н\ = {σ = σι} инвариантна относительно G. Согласно
примеру 47.2 р. н. м. инвариантный несмещенный критерий для проверки Н\
имеет вид
Λι>βσ?<(η-1)52<Λ2ι6σ?, (8)
где hij£ определяются из условий (см. условие (46.7) теоремы 46.1)
V{hlie<X2n_1<h2ie) = l-e,
Ε(*η-ι;4ε < xLi < h2ie) = (1 - ε)Εχ2_υ
Xn-i ^Η„_ι-
Соответствующее (8) доверительное множество Θ*(Χ, ε) имеет вид
интервала
("-l)So2 . σ2 . (η - 1)Sq2 (9)
Этот интервал, очевидно, инвариантен относительно #, как и критерий (8)
(в этом примере G[a\] = G для любого σι). Следовательно, в силу вторых
утверждений теорем 4, 5 интервал (9) есть наиболее точное инвариантное
несмещенное доверительное множество уровня 1 — ε.
Пример 3. Пусть X €= Φα,σ2· Требуется построить наиболее точное
доверительное множество для параметра α при неизвестном σ. Здесь
/ο^(χ) = (2^^^{-άέ(χ<"ο)8}·
Семейство Фа)(72 будет инвариантно относительно группы G линейных
преобразований дХ = аХ + Ь, если положить #(α,σ) = (аа + 6, ασ). Пара
наблюдений (х, Sq) образует достаточную статистику. Нетрудно видеть, что с
ее помощью нельзя построить статистику, инвариантную относительно G.
Однако для каждого αϊ можно выделить подгруппу G[a{\ преобразований
дХ = а(Х — αϊ) + αϊ, относительно которой статистика (χ — αϊ)/So будет
максимальным инвариантом. Гипотеза Н\ = {а = а\} остается
инвариантной относительно G[ai]. Исследуя плотность (χ — αι)/5ο, можно
показать с помощью методов §47 (ввиду сложности этих рассмотрений мы их
опускаем*)), что при каждом σ р.н.м. несмещенный инвариантный
критерий для проверки гипотезы Hi против {а Ф ol{\ существует и имеет область
*) Подробнее об этом см. [65, с. 312].
§ 49. Байесовский и минимаксный подходы
363
приема Hi вида
V^|x-ai| ^ _
~~So <Τε'
где те определяется из условия Ρ(|ίη_ι| ^ τε) = ε, tn-\ €= Τη-χ.
Соответствующее доверительное множество Θ* имеет вид
(10)
х--^г <а<х + —=-. (11)
Легко видеть, что этот доверительный интервал является
инвариантным (Θ*(ρΧ, е) = дЭ*(Х, ε)). В соответствии с первым утверждением
теоремы 5 критерий (10) будет инвариантным относительно G[ai]. Согласно
второму утверждению доверительный интервал (11) будет наиболее точным
(равномерно по σ) инвариантным несмещенным доверительным интервалом
уровня 1 — ε.
Таким образом, в этом параграфе мы установили, что все
доверительные интервалы, построенные нами в §40, являются в известном смысле
оптимальными.
§ 49. Байесовский и минимаксный подходы
к проверке сложных гипотез
1. Байесовские и минимаксные критерии. Байесовский и минимаксный
подходы были описаны в § 44. Там же были даны соответствующие
определения, которые мы по ходу изложения напомним.
Пусть, как и прежде, проверяется гипотеза Н\ = {Θ G Θι} против Нч =
= {Θ G ©г} по выборке X €= Pfl.
Полный байесовский подход предполагает, что θ выбирается случайно с
априорным распределением Q на Θ = Θιϋθ2. Распределение Q индуцирует
распределения Q* на θ*, г = 1,2, и вероятности q(i) = Q(0 G θ;), так что
Q = q(l)Qi + g(2)Q2. Гипотезу о том, что θ G θ* выбирается случайным
образом с распределением Qj, обозначим через Hq{. В соответствии с этой
гипотезой X имеет плотность
fQi{*) = f 1е{хШЩ-
Подразумевается, конечно (см. §44), что на θ* определены σ-алгебры 6j,
на которых заданы Q;, и что fe{x) измерима относительно Θι χ 55^.
Из результатов §41, 42 следует, что байесовский критерий kq для
проверки Hqx против Hq2 в описанной выше задаче будет иметь вид
Γΐ, если Jq2{X) > cfQl{X),
icQ(X) = Ι ρ, если fQ2(X) = cfQl(X), (1)
[θ, если fQ2{X) < cfQl{X),
где с = q(l)/q(2), ρ G [0,1] произвольно.
364 Гл.З. Теория проверки гипотез
Частично байесовский подход связан с проверкой гипотезы Hq1
против Hq2 в том случае, когда априорное распределение между Hqx и Hq2
(определяемое вероятностями д(1), <?(2)) отсутствует. Положим
К?> = {π : EQl7r(X) < ε}.
Тогда критерий kqxq2 мы называем байесовским в , если это есть
н.м.к. уровня 1 — е для проверки Hqx против Hq2. Критерий /^q1q2 будет
иметь тот же вид (1), где с, ρ выбираются из условия 'Bjq1ttq1q2(X) — ε·
Вместо 7гдхд2 мы будем писать kqx или π<22, если одно из множеств Θι
или ©2 вырождается в одноточечное множество {θχ} или {#2}·
В приложениях не часто встречаются задачи, в которых
распределения Qi полностью известны. Однако, как мы уже не раз видели, польза
байесовского подхода не ограничивается лишь возможностью его
непосредственного применения. Он позволяет строить р. н.м. к., а также
минимаксные критерии (ср. с §41, 45, 46). Позже мы будем использовать
байесовский подход также для построения асимптотически оптимальных критериев.
Пусть, как и раньше,
Ке = {π : sup ΕΘπ(Χ) < ε}. (2)
θβΘι
Тогда критерий π мы называем минимаксным в Ке (в Κε), если π Ε
£ Кε (π Ε Κε1) и для него максимизируется
inf Ε,π(Χ) = inf β(θ). (3)
Следует отметить, что если функции мощности β(θ) = Ε^π(Χ)
непрерывны и множества θι и ©2 соприкасаются, то
β = sup inf /3(0) < ε (4)
и неравенство β > ε выполняться не может. Поэтому если желать, чтобы
гарантированная мощность (3) была достаточно большой (во всяком
случае больше ε), то следует рассматривать «разделенные» множества ©ι и ©2-
Другими словами, зону значений 0, где β(θ) близка к ε, как зону
«безразличия» критериев следует изъять и рассматривать в качестве ©2 множество,
не соприкасающееся с ©ι.
Если все же множества соприкасаются, то любой несмещенный
критерий в Ке будет минимаксным. Действительно, для несмещенных
критериев β(θ) = Ε^π(Χ) > ε, θ е ©2, и, стало быть, β = inf β(θ) ^ ε достигает
в силу (4) своего максимального значения.
Обратное утверждение верно в общем случае: минимаксный критерий,
если он существует, является несмещенным. Это следует из того, что
β = sup inf β(θ) ^ ε
(мы можем взять π (Χ) = ε), и того, что для минимаксного критерия
inf β(θ) = β.
§ 49. Байесовский и минимаксный подходы
365
Р. н. м. несмещенный критерий π β классе Κε всех несмещенных
критериев является минимаксным в Κε. Действительно, пусть β(θ) —
функция мощности критерия π. Тогда для любых π Ε Κε, θ £ Θ2
β(θ)>β(θ), ϊηΐβ(θ)>ίηΐβ(θ),
(5)
inf β(θ) = sup inf β{θ) = sup inf β(θ).
Последнее равенство объясняется тем, что добавление к Κε критериев из Κε,
для которых inf β(θ) < ε, величины sup в (5) не меняет. <]
ве&2 πεκε
В теореме 45.3 мы использовали байесовские критерии для отыскания
р. н. м. к. Следующее утверждение есть некоторое «развитие» теоремы 45.3.
Оно является также аналогом теорем 41.2, 21.2 и устанавливает, что
минимаксные критерии следует искать в классе критериев (1), явный вид которых
нам известен.
Теорема 1. Пусть существуют распределения Qj, сосредоточенные
соответственно на подмножествах Θ^ С Θ;, г = 1,2, и постоянные с up
такие, что критерий ^qxq2^ определенный в (1), обладает свойствами:
1) *QlQieK?lt
2) E<,irQlQ2(X)= sup EeirQlQ2(X) (6)
0601
при всех θ G Θ",
3) EenQlQ2(X) = inf EenQlQi(X) (7)
при всех θ e ©2-
Тогда t^q1q2 € Κε и является минимаксным критерием в Κε для
проверки Η ι против Hi.
Пара распределений Qi, Q2, обладающая свойствами 2), 3),
является наименее благоприятной в том смысле, что для любых двух других
распределений Q[, Qf2
inf Εβπη1η2 < inf Εθπη<ο<,
oee2 0۩2 Vl^2
где kq'q' — критерий вида (1) из Κε.
Последнее утверждение означает, что среди всех байесовских
критериев (1) критерий kqxq2 обладает наименьшей гарантированной
мощностью.
Доказательство. Так как
sup EenQlQ2{X) = / E^QlQ2Qi(ci(9) = Eq^Qiq2 = ε,
θ?
366
Гл. 3. Теория проверки гипотез
то kqxq2 € Ке. Гарантированная мощность tcq1q2 равна (см. (7))
<4П©2 Ε*π<2ι<^Χ) = / Ee*Q1Q2Q2{de) = Eq2ttQiQ2 ξ /3QlQ2. (8)
Пусть теперь π — любой другой критерий из Κε для проверки Ηχ
против #2. Тогда π будет одновременно критерием из Κε для проверки Hqx
против Hq2, так как
EQitt{X) = [Een{X)Q1{de) < sup Ε0π(Χ) < ε. (9)
У 0€©ι
Θ?
Но критерий kqxq2 является н.м.к. в ЯГ^1 для проверки Hqx против Hq2.
Стало быть, в силу (8)
inf EeirQlQ2(X) = PQlQ2 > EQMX) > inf Ебтг(Х). (10)
Первое утверждение теоремы доказано. Пусть теперь Q^, Q2 — два
любых других распределения на θχ, &2 соответственно. Критерий kqxq2) как
Qf
и 7Гдг Qf, будет критерием из Κε ι для проверки Hgt против Hqi , так как
Eq'TQi^PO = [ EenQlQ2(X)Q[(de) < sup E^glQ2(X) < ε.
θι
Но критерий 7Tq/ q/ является н. м. к. для этих гипотез, поэтому в силу (8)
/-
Ee7rQlQ2(X)Q'2(d9) > u^Ee*QlQ2{X) = /3Qiq2. <
Θ2
Основная трудность в применении теоремы 1 к реальным задачам
состоит в отыскании (или угадывании) наименее благоприятных
распределений Qi и Q2. Иногда при этом могут оказаться полезными соображения
инвариантности, как это имеет место в примерах следующего пункта. Эти
примеры представляют самостоятельный интерес и будут использоваться в
дальнейшем.
2. Минимаксные критерии для параметра α нормальных распределений
Пример 1. Пусть X = χ χ €= Фа,я есть выборка объема η = 1 из га-мер-
ного нормального распределения со средним а = (ai,...,am) и единичной
m
матрицей вторых моментов. Положим \а\2 = У^<*? и рассмотрим задачу о
г=1
проверке гипотезы Н\ — {\а\ ^ а} против Н2 = {|а| ^ Ь}, b > а (здесь
имеется «разделяющая» зона a < |a| < Ь).
§ 49. Байесовский и минимаксный подходы
367
Если, например, X определяет в канале связи амплитуды вектор-сигнала,
состоящего из «шума» Хо €= Φο,Ε и полезного сигнала а, |а| ^ 6, то
гипотезы Щ при a = 0 можно рассматривать как гипотезы о наличии полезного
сигнала.
Так как рассматриваемый пример будет неоднократно использоваться
нами в дальнейшем, то утверждение, относящееся к виду минимаксного
критерия, мы сформулируем в виде теоремы.
Теорема 2. Минимаксный критерий π £ Κε для проверки Н\ =
= {\а\ ^ а} против #2 = {|а| ^ Ь}, а < Ь, по наблюдению X ^ Фа,Е
имеет вид
fl, если \Х\>се,
П ' \θ, если \Х\ < с£,
где се выбирается из условия рс{о) = £, гарантированная мощность π
равна рСе{Ъ),
ξι ^ Ф01 и независимы.
Доказательство. Начнем с наводящих соображений. В нашем
случае для χ = (χ(ι\ .. .,z(m)) имеем
fa{x) = щ^ехр \1{х"а)(х"а)Т}'
где хТ — вектор-столбец. Отсюда видно, что рассматриваемое семейство
распределений инвариантно относительно ортогонального преобразования
дх = яС, где С есть матрица ортогонального преобразования в Rm. При
этом надо положить 'да = аС. Гипотезы Hi будут инвариантными
относительно д.
Пусть для простоты а — 0. Если бы распределение Q2 на ©2 = {ос: |α| ^ &}
не обнаруживало инвариантности относительно # (так будет, например, если
оно сосредоточено в окрестности какой-нибудь точки ао), эту несимметрию
можно было бы как-то использовать при решении задачи (при сделанном
только что допущении мы были бы близки к задаче проверки двух простых
гипотез {а = 0} и {а = ао} и получили бы при этом критерий с большой
мощностью). Стало быть, такое распределение не может быть наименее
благоприятным. Им должно быть распределение Q2, инвариантное
относительно д. Кроме того, ясно, что наихудший вариант мы получим, если
все распределение будет сосредоточено на границе ©2 (чем ближе гипотезы,
тем труднее их различать). Аналогичные наводящие рассуждения можно
проводить относительно Qi, если а ф 0.
Итак, представляется естественным, что наименее благоприятные
распределения Qi и Q2 в нашем примере есть равномерные распределения
на сферах ®\ — {а : \а\ = а} и Θ% = {а : \а\ = Ь}. В этом случае
согласно теореме 1 минимаксный критерий π будет иметь вид π(χ) = t^q1q2{^)^
368
Гл. 3. Теория проверки гипотез
где ■kq1q2{x) = 1, если
[ ( 1, w ,т) dV(v) Г ί 1, .. ,т1^(«)
/ e*pi--{x-v)(x-v) *>—γ—>οΙβχρ<--{χ-ν){χ-ν) Ϊ ~у~
&Ϊ ©?
(И)
и πg1Q2(α:) = 0 в противном случае. Здесь dV(v) означает площадь элемента
соответствующей сферы, V{ = mes©^, г = 1,2.
Рассмотрим любой из этих интегралов, например правый, и заметим,
что его можно записать в виде
Г 1 Τ 2\ ί г Τι<ΠΦ)
ехр < —-XX — α > / expjxi; }———.
θ?
Интеграл здесь равен
/ exp{\x\aexvT}———, V = mes©0,
θο
где Θ° — поверхность единичного шара, ех = х/\х\. Стало быть, если
обозначить
ф{1) = ί exp{texvT} dV{v), (12)
θ°
то область (11) приема Η<ι примет форму
ф{\х\Ъ) > сф{\х\а) (13)
(через с обозначаем здесь постоянные, не обязательно совпадающие со
значением в (11)). Но φ(ί), очевидно, от χ не зависит, поскольку значение
интеграла (12) не зависит от направления единичного вектора ех. Поэтому
φ{ί) = fexp{tvi}dV(v),
θ°
где vi есть первая координата вектора г>.
Так как ф'(0) = 0, ф"(Ь) > 0 при t > 0, то ф{Ь) есть выпуклая
возрастающая функция на [0, оо). Отсюда следует, что неравенство (13) (или (11))
эквивалентно
\х\ > с. (14)
Это есть, очевидно, инвариантный критерий. Проверим для него
выполнение условий 1)-3) теоремы 1 и установим тем самым, что это минимаксный
критерий.
Имеем
EanQlQ2{X) = Ра(\Х\ > с) = ΦοΜ{χ ' Iх ~ <*\ > с»>
§ 49. Байесовский и минимаксный подходы
369
Ясно, что перемещение точки α по сфере \a\ = const этой вероятности не
меняет. Стало быть, она зависит лишь от \а\ и, следовательно,
EanQlQ2(X)=P(\(-a\2>c2) =
= ρ(^(ξί-αίγ>Α=Ρ((ξ1-\α\)2 + ξ2 + ...+ξΙι>οη,
где ξι €= Φο,ι есть независимые координаты вектора £.
Лемма 1. Функция pc(t) = Ρ ((ξι — ί)2 + ξ2 + · · - + £m > °2) при каждом
с является возрастающей функцией \t\.
Из этой леммы вытекает, что
Ea7TQiQ2 РО = Рс(\<*\) ^ Рс(а) при |а| < а,
Ea7TQiQ2(^) = Pc{\ot\) ^ Pc{b) при \а\ ^ 6,
Эти соотношения эквивалентны условиям 2), 3) теоремы 1. Чтобы
критерий kq1q2 был критерием уровня 1 — ε, мы должны положить с равным
решению с£ уравнения рс(а) = е. Таким образом, t^q1q2 есть минимаксный
критерий уровня 1 — ε, и его гарантированная мощность равна рСе{Ъ)· <
Доказат ельство леммы 1. Так как pc(t) = рс(—ί), то мы можем
ограничиться рассмотрением значений t ^ 0.
Рассмотрим сначала случай т = L Обозначим функцию рс(£) в этом
случае через ρ(ί). Имеем
p(t) = pflft - *|2 > с2) = Ф(* - с) + 1 - Φ(ί + с).
Стало быть, производная по t равна
ρ'(ί) = 1 [е-(*-с)а/2 _ е-(С+*)2/2| = 1е-(С2+^)2/2[еС« _ e-ct] ^ 0>
ν2π ν2π
и функция ρ(ί) возрастает при t ^ 0.
При m > 1 функция pc(i) есть свертка функции p(t) — p{t,c2) с
распределением χ2 с m — 1 степенями свободы:
00
pc(t) = / p{t,c2 -u)dHm-i{u).
о
Очевидно, это также есть возрастающая функция t при t ^ 0. <
По поводу теоремы 2 можно заметить следующее. Пусть для простоты
а = 0. Тогда гипотеза Hi = {α = 0} станет простой. Если мы построим
н. м. к. для каждой альтернативы а € 02, получим критерий вида
XGL > С.
370
Гл. 3. Теория проверки гипотез
Это значит, что каждое направление а = оо£, ао € Θ2, t ^ 1, будет иметь
свой н. м. к. уровня 1 — ε
xaj > се, (15)
где се зависит только от ε, так как Eo(XaJ) = 0, Όο(Χα^) — |αο|2 = b.
Но критическая область минимаксного (инвариантного) критерия должна
быть одинаково чувствительна по всем альтернативам. В соответствии с
этим она имеет форму объединения полупространств (15), представляющего
собой внешность сферы.
Пример 2. Пусть теперь X = χ χ ^ Φα,σ2, где σ2 = ||σ^|| есть
произвольная положительно определенная матрица вторых моментов. Рассмотрим
задачу о проверке гипотезы Н\ — {ασ~2ατ < о2} = {|ασ_1| ^ а} против
Я2 = {ασ~2ατ ^ Ь2} = {|ασ_1| ^ 6}, а < 6. Из теоремы 2 вытекает
Теорема 2А. Критическое множество минимаксного критерия
уровня 1-е для проверки Hi против Н^ имеет вид
—2 Τ 2
χσ χ > се
и гарантированную мощность рСе{Ь), где с£, как и прежде, есть решение
уравнения рс{а>) = ε.
Доказательство. Положим дх — χσ и заметим, что в силу (47.3)
&аМА) = *5(α,β)(^)ι
где д(а,Е) = (ασ, σ2). Для шара А = {χ : \х\ < с} будем иметь
дА = {у = χσ : χα:τ < с2} = {у : уа~2уТ < с2},
(16)
Φα,Ε(Α) = Φασ^{{χ : xa 2ят < с2}).
Множество {а : |а| ^ о} переходит после преобразования д в множество
{/3 = ασ : αατ ^ α2} = {β : βσ~2βτ < a2}.
Таким образом, все соотношения, установленные нами в примере 1 для
&a,E{A) при \а\ ^ а или |а| ^ 6, будут справедливы для Ф/?)<72 ({χ : χσ~2χτ <
< с2}) при |/?σ-1| ^ а или |/?σ_1| ^ 6 соответственно. Это доказывает
теорему 2А. <
Пример 3. Рассмотрим снова выборку из нормального распределения
Фа,Е с единичной матрицей вторых моментов. Однако в отличие от
примера 1 проверяемые гипотезы Hi будут касаться лишь части координат
вектора а. Представим α в виде набора двух векторов a = (a7, a/y), где
а7 = (αϊ,..., а/), а" = (а/+ь .. .,ат), и рассмотрим задачу о проверке
гипотезы Н\ = {|a77| ^ α} против Η<ι — {\а"\ > b] по выборке X = χχ —
ь*--5х1,т) объема η — 1. Величина а7 при каждой из гипотез одна
и та же и может принимать произвольное значение. Поступим точно так
§ 49. Байесовский и минимаксный подходы
371
же, как в примере 1, но выберем в качестве Qi, Q2 равномерные
распределения на «сферах» Θ? = {а : |а/7| = а, а7 = αό}, θί> = {а : \а"\ =
= 6, а7 = αό}, где αό — какая-нибудь фиксированная точка. Если
обозначить х[ = (х1д,.. .,χι,ι), χ7/ = (χι,ί+ь .. .,xi,m)i то мы получим в результате
минимаксный критерий
К| > Се,
где с£ есть решение уравнения
Ρ((£ι - о)2 + CI + · · · + d-i > с2) = ε (17)
(множители ехр < — - (х[ — а'0) (х[ — а'0) > в неравенстве /q2 {X)/ Jq1 (Χ) > с
сократятся, и оно перейдет в неравенство типа (11)). Этот результат
является вполне естественным, так как координаты x\j в нашем случае
независимы и, стало быть, подвектор х^ не несет в себе никакой информации
относительно а77. Поэтому из всей выборки X = х\ достаточно
рассматривать лишь подвектор х'/, а в этом случае задача сводится к примеру 1.
Проверка гипотез в примере 3 относится к классу задач при наличии так
называемого «мешающего» параметра. В нашем случае мешающим
параметром служил вектор а'. В силу отмеченных выше причин он на самом
деле практически не мешал построению минимаксного критерия, который
автоматически получился не зависящим от а7.
Несколько иначе дело обстоит в следующем более общем примере, когда
координаты xij зависимы.
Пример 4. Пусть X = χ ι €= Φα,σ2 · Рассмотрим задачу о проверке
гипотезы
Ηι = {α<Γ2ατ ^ а2} против Я2 = {ad~2aT ^ б2}, (18)
где d~2 — неотрицательно определенная матрица ранга т — I < m,
полученная из σ~2 заменой элементов каких-нибудь I строк и I столбцов (с теми
же номерами) на нули. Для определенности можно считать, что для
положительно определенной матрицы σ^~ порядка {т — Ι) χ (ттг — Ζ), обратной к
матрице
σ22 = ΕΩ,σ2κ-"'')τΚ-«''),
образованной последними т — I столбцами и строками матрицы а2 = ||cr2j||,
проверяется гипотеза Н\ = {α/7σνΓ2α7/Τ < α2} против H*i = {α77σ^~2α7/Τ ^ 62},
где χ7/, α77 означают те же подвекторы векторов х\ и а, что и в предыдущем
примере. Мешающий параметр а7 может быть в каждой из гипотез Hi
произвольным.
В этом примере распределение x7l5 вообще говоря, зависит от а". Сделаем
следующее преобразование по превращению χι в вектор с «ортонормирован-
ными» координатами. Положим
y = xiA, (19)
372
Гл. 3. Теория проверки гипотез
где Л = \\atJ\\ — треугольная матрица с элементами а13 = О при j > г.
Оставшиеся элементы выбираются из условия у €= Ф/з,я> где β = (А» · · ·? An) =
= αΛ. Это всегда можно сделать, так как из (19) получаем
У τη = xl,m^m,mj
Ут-1 = х1,тат,т-1 + х1,т-1ат-1,т-Ъ
Отсюда и из условий
Εαισ2(γ,-Α)2 = 1,
Еа^(Уг-А)(У^А) = 0' «VJ,
поочередно определяются значения
ат,т »
Gmjm0,mim—1 » &т—1,тат— 1,т— 1 = U,
О л О
^Vn,mflm,m—1 ' ^τη,τη—lam,m—lam— l,m— 1 τ στη—\^πι—Ι0, γη—\^τη—\ == ■*■»
Таким образом, треугольная матрица Л такова, что
EQ)(72(y - /?)т(у - /?) = ΕΩι(72Λτ(Χι - α)τ(Χι - α)Λ = Λτσ2Λ = Ε.
Из треугольности Λ следует, что вектор β" = (Α+ι>···>Αη) зависит лишь
от а" и наоборот. Если обозначить через Λ2 треугольную матрицу
порядка (т — I) х (т — ί), полученную из последних га — / строк и столбцов
матрицы Λ, то мы получим, очевидно, β" = α"Λ2, Aja|A2 = £?. Множество
0Х = |α : α7/σ^"2α//Τ < α2} перейдет в множество
{/? : /3 = αΛ, οί'σ;2α"τ ζ α2} = {β : βηΚ^σ^Κ^τβηΎ < α2} =
= {/? : ΑΆ,Τ < α2} = {/? : |ΑΊ < α}.
«Подпараметр» β' может быть произвольным, если произвольно α'.
Мы пришли к задаче примера 3. Минимаксный критерий уровня 1-е
для проверки Н\ против Ή.2 имеет, следовательно, вид у"у//Т > с£ или
(л2л2т = 0
χ1σ2 χ1 -> се->
где се — решение уравнения (17).
Последний пример является наиболее общим из примеров 1-4. Он
резюмирует содержание этих примеров следующим образом.
Теорема 2В. Если по выборке X = х\ ^ Φασ2 проверяются
гипотезы (18), связанные со значением ad~2aT, то минимаксный критерий
уровня 1 — ε имеет вид
xid~2xj > c£, (20)
где с£ определяется в (17), т — 1 есть ранг d~2.
§ 49. Байесовский и минимаксный подходы
373
Гарантированная мощность критерия (20) равна
Ρ((ίΐ - Ъ)2 +ξ2 + ... +£m-l > Ce2), 6 е Фо,1.
Если выборка X имеет объем п, то χ €= Φα,σ2/η будет достаточной
статистикой, а минимаксный критерий будет иметь вид
х<Г2хт > ^.
η
Следующий пример будет носить несколько иной характер.
Пример 5. Пусть, как и в примере 1, X = χ ι €= Фа,я есть выборка
объема η = 1 из m-мерного нормального распределения со средним α =
= (ai,...,am). Пусть Н\ — {а = 0}, а гипотеза #2 состоит в том, что а
принадлежит некоторому множеству ©2, не содержащему точки a = 0.
Обозначим через ©2 выпуклое замыкание множества ©2 (наименьшее выпуклое
замкнутое множество, содержащее ©г), и пусть β есть точка из ©2,
ближайшая к началу координат. Тогда если β Ε ©2, то распределение Q2,
сосредоточенное в точке β, будет наименее благоприятным, и минимаксный
критерий π будет иметь вид π(Χ) = 1, если
{Χ-β){Χ-β)τ <ΧΧΤ + ci
или, что то же, если
Χβτ
Ж>С2'
где С2 выбирается из условия π £ Κε.
В самом деле, нам достаточно проверить условие (7). Имеем
Εαπ{Χ)=Ρα(η^τ->ο2
где Χβτ/\β\ & Φα/3Τ/|/3|,1> так чт0
αβτ
Εαπ (Χ) = 1 - Φ С2 -
\β\
Эти значит, что минимум Εαπ(Χ), a G ©2, достигается при α,
минимизирующем функцию αβΎ/\β\. Но очевидно, что а/?т ^ /?/?т = |/3|2 при всех
аЕ 02, так что
Ε0π(Χ) = inf Εαπ(Χ). <
aG©2
Мы предлагаем читателю построить минимаксный критерий в той же
задаче, когда X €= Фа?<г2, σ2 есть произвольная матрица вторых моментов.
3. Вырожденные наименее благоприятные распределения для
односторонних гипотез. Пусть X €= Р#, где θ и элементы х^ выборки X
вещественны.
374
Гл. 3. Теория проверки гипотез
Предположим, что мы проверяем одностороннюю гипотезу Н\ = {Θ < θχ]
против #2 = {Θ ^ #2} при наличии непустой «зоны безразличия» θ\ <
< θ < 02- При каких условиях наименее благоприятные распределения будут
сосредоточены в точках θ\ и 02? Ведь в этом случае минимаксный критерий
π уровня 1 — ε выглядел бы весьма просто:
W(X) = {
1, если fo2{X) > cf0l{X),
ρ, если f02(X)=cfel(X)) (21)
О, если fo2{X)<cfei{X),
где рис определяются равенством Έοιπ(Χ) = ε.
Мы уже знаем, что если отношение правдоподобия монотонно, то такой
критерий будет р. н.м., а стало быть, и минимаксным. Следующее
утверждение дает другое достаточное условие для того, чтобы критерий был
минимаксным.
Теорема 3. Пусть плотность fe{x) обладает тем свойством, что
отношение fe'{x)lfe{?) не убывает по χ при любых θ1 > Θ. Тогда
наименее благоприятные распределения Qi и Q2 будут, сосредоточены
соответственно в точках θ\ и 02 Щ стало быть, критерий (21) будет
минимаксным.
Доказательство. Пусть сначала η = 1. По условию теоремы найдутся
такие а < 6, что fe'(x)/fe{x) ^ 1 при χ е (-οο,α], fe'{x)/fe{x) = 1 при
χ Ε (α, 6), fe'(x)l ίθ{χ) ^ 1 при χ Ε [6, οο). Так как π (χ) не убывает, то
W(b) ^ W(a) и
Εθ<π{Χ) - Εθπ{Χ) ^
α οο
^ π(ο) ί {fу {χ) - /θ{χ))μ(άχ) + π(6) f{fo>{x) - /θ(χ))μ{άχ) =
ΟΟ
= (π(6) - π(α)) /(/И*) " ίθ{χ))μ{άχ) > 0.
Если η > 1, то для получения такого же неравенства нужно
воспользоваться последовательным интегрированием (сначала по χι, затем по Х2 и
т.д.) и тем, что π{Χ) не убывает по каждому из своих аргументов.
Таким образом, мы установили, что мощность β(θ) — Ε^π(Χ) является
неубывающей функцией.
Отсюда следует, что уровень π равен 1 — ε и β{0\) — sup β{θ), β(θ2) =
θζθ!
= inf β(θ). Это означает, что выполнены все условия теоремы 1. Теорема 3
доказана. <
Если θ — параметр сдвига: /#{x) = f(x — 9), то можно показать, что
ίθ'(χ)/ίθ{χ) будет монотонно по χ тогда и только тогда, когда функция
— lnf(x) является выпуклой (см. [65]).
§ 50. Критерий отношения правдоподобия
375
§ 50. Критерий отношения правдоподобия
В предыдущих параграфах мы получили ряд результатов, касающихся
построения разного рода оптимальных критериев. Важный вывод, который
можно сделать из приведенных рассмотрений, состоит в том, что эти
оптимальные критерии существуют лишь при весьма ограниченных условиях.
В теории оценивания мы имели примерно ту же ситуацию: эффективные
оценки существуют также лишь при ограничительных условиях. Однако
мы видели в главе 2, что если рассматривать не точное, а
асимптотическое свойство эффективности, то оценки, обладающие этим свойством,
существуют уже довольно часто, при весьма широких условиях, связанных
главным образом с регулярностью семейства {Ря}· Такими оценками
являются о. м. п.
Другое выражение асимптотической оптимальности о. м. п., как мы
видели, состоит в том, что о. м. п. асимптотически эквивалентны байесовским
оценкам для любого фиксированного гладкого априорного распределения.
В теории проверки гипотез некоторым аналогом о. м. п. является так
называемый критерий отношения правдоподобия (к. о. п.). При широких
предположениях он совпадает с оптимальными критериями, если таковые
существуют, и оказывается асимптотически эквивалентным байесовскому
критерию в случае Θι = {#ι} при любом фиксированном гладком
априорном распределении Q2 на 02- Это свойство и ряд других асимптотических
свойств к. о. п. будут установлены в ближайших параграфах.
Дадим определение к. о. п. Пусть в параметрическом случае, когда X €=
€= Р#, проверяется гипотеза Н\ = {θ Ε Θι} против гипотезы #2 = {θ Ε Θ2}.
Определение 1. Критерий π(Χ) с критической областью
sup f0(X)
RW Ξ Tnfm > C (1)
SUp MA)
0€θι
называется критерием отношения правдоподобия (к. о. п.) для проверки
гипотезы Hi против #2·
Постоянная с обычно выбирается из условия
supPe(R(X)>c)=e, (2)
0€θι
при котором к. о. п. будет иметь уровень 1 — е.
Наряду с критерием (1) часто рассматривают, по существу,
эквивалентный ему критерий (который также называется к. о. п.) вида
supfe(X)
Rl{X) = ^—— = fr(*> > с. (3)
u ; supfo{X) sup UW
θεθι 0€θι
376
Гл. 3. Теория проверки гипотез
Близость этих критериев вытекает из того, что при Θ = θ ι U Θ2
/?.PO=max{sup/,(X), sup fe(X)},
0€Θι 0€Θ2
и, стало быть, ^(Х) = max{l,R(X)}.
Если гипотеза #i простая: Θι = {0ι}, #2 = {θ Φ θ\}, так что Θ2 =
= θ \ {θι}, то для fe(χ), непрерывных по θ, будем иметь
R{X) = Ri(X) =
MX)'
По своей форме критерий (1) естественным образом обобщает н. м. к.
для проверки простых гипотез в лемме Неймана-Пирсона. И хотя
точных свойств оптимальности этот критерий в общем случае, по-видимому, не
имеет, асимптотически он часто оказывается наилучшим (см. §53-56).
Многие несмещенные инвариантные и минимаксные критерии,
рассмотренные выше, являются к. о. п. Рассмотрим для иллюстрации
примеры 49.1-49.4, в которых строились минимаксные критерии для параметра а
нормальных совокупностей. Во всех этих примерах минимаксные
критерии являются к. о. п. Докажем это. Задачи примеров 49.2, 49.4 с
точностью до линейных преобразований параметра сводились к задачам
примеров 49.1, 49.3. Так как отношение правдоподобия (1) от таких замен (при
соответствующем изменении областей Θ;) не зависит, нам достаточно
рассмотреть лишь примеры 49.1, 49.3.
В примере 49.1 по выборке X ^ Ф&,е единичного объема из многомерной
нормальной совокупности с единичной матрицей Ε вторых моментов
проверялась гипотеза Н\ = {\а\ ^ а} против Ή.2 = {|а| ^ 6}, а < Ь. Оказалось,
что минимаксный критерий имеет форму
1*1 > с. (4)
В нашем случае sup fe{X) определяется значением
еевг
mf(X-a)(X-a)T= inf|X-а|2,
так что для статистики R(X) в (1) будем иметь
(-\{\Х\-Ъ)2, если |ХКа,
1пЯ(Х) = <
-\{\Х\-Ь)2+1-{\Х\-а)\ если а < \Х\ < Ь,
-h\X\-a)2, если \Х\ > Ь.
Это есть непрерывная возрастающая функция от \Х\. Поэтому области (1)
и (4) при подходящих значениях с совпадают.
Предлагаем читателю убедиться, что критерий (3) в этом примере также
имеет вид (4).
§ 50. Критерий отношения правдоподобия
377
В примере 49.3 по выборке χ ^ Φα,Ε единичного объема проверялась
гипотеза Ηλ = {\α"\ < α} против Н2 = {|α"| ^ Ь}, где α" = (α/+ΐι···>αίη)
есть подвектор вектора а, составленный из его последних m — / координат.
Минимаксный критерий имеет вид
\Х"\ > с, (5)
где X" составлен из га — / последних координат вектора X. Но в этом случае
inf (X - а)(Х - а)Т = inf (X" - а")(Х" - <*")Т
aG0i α":|α"|ζα
Аналогичное неравенство справедливо для ©2. Поэтому все сводится к
рассмотрениям, проведенным для примера 49.1, и к. о. п. (1) и (3) будут
совпадать с (5).
В условиях § 45 построенные там р. н. м. к. для экспоненциальных
семейств
Мх) = с{в)евт^к{х) (6)
также будут совпадать с к. о. п. Читатель может проверить это
самостоятельно, заметив, что функция
φ(θ)
= 1п(0) = - In ( ί βθτ^Η{χ)μη{άχ)
является выпуклой, поскольку φ'(β) = — Ε#Τ, φ"{θ) = —OgT < 0. Из
выпуклости φ вытекает однозначная разрешимость уравнения
φ'(θ)+Τ{Χ)=0
для о.м. п. θ* — ψ{Τ) и монотонность функции ψ. При этом один из
sup }е{Х) будет достигаться в точке #*, а другой — в точках θ\ или 02.
Проверка сделанного утверждения для нормальных семейств Фа)£,
являющихся частным случаем (6), содержится в §55.
Несколько иначе обстоит дело в примере 49.5, в котором по выборке
Χ ξ= Φα?£ проверялась гипотеза Н\ = {а = 0} против ^ = {а G Θ2}.
Предполагается, что множество ©2 и его выпуклое замыкание ©2 не
содержит точки а = 0. Если ближайшая к началу координат точка β
множества ©2 принадлежит ©2, то минимаксный критерий существует и имеет
вид
Χβτ > с. (7)
Этот критерий не является инвариантным относительно какой-либо группы
преобразований. Предлагаем читателю убедиться, что в этом случае к. о. п.
будет отличным от (7) и будет иметь вид
Р2(х,е2)-р2(х,о)<с,
где р(Х,Э2) = inf \Х - а\, р(Х,0) = \Х\.
а€вг
Установим теперь, что при выполнении некоторых предположений
критерий отношения правдоподобия обладает свойствами инвариантности. Пусть
378
Гл. 3. Теория проверки гипотез
G — любая группа преобразований в Хп, относительно которой задача
проверки гипотез Н\ и #2 инвариантна, и пусть G — соответствующая группа
преобразований д на Θ.
Теорема 1. Если Jq{x) обладает свойством
fe{gx) = c{g,x)fge{x), (8)
критерий отношения правдоподобия инвариантен относительно G.
По поводу условия (8) отметим, что оно всегда выполнено, если μ есть
мера Лебега и g — преобразование, сохраняющее меру (сдвиг, поворот).
В этом случае с(#, х) = 1. Для преобразований сжатия c(g,x) = const.
Доказательство теоремы 1. В силу того, что ^Θ; = Θί, г = 1,2,
будем иметь
sup fe{gx) sup c{g,x)fge{x) sup fe{x)
R(gx) = —,—r = 7 ^ , , ^ = гт~т = λ(®)· <
sup fe{gx) sup c{g, χ)fge{x) sup f0(x)
0€θι 0€θι θβρΘι
Другие свойства к. о. п. см. в §51, 53-56.
§51/ Последовательный анализ
1. Вводные замечания. Во всех предыдущих рассмотрениях объем η
выборки X — Хп, которой мы располагаем, был фиксированным. При этом
условии мы искали критерии, обладающие теми или иными свойствами
оптимальности. Например, в самом простом случае, когда проверяются две
простые гипотезы Щ = {X €= Рг}, г = 1, 2, оказалось, что существует н. м. к.
π уровня 1 — ε, который имеет вид (см. теорему 42.1)
fl, если MX) > ch(X),
тг(Х) = Ь, если f2{X) = cfi{X),
[θ, если /2{Х)<сМХ).
Здесь сир определяются из условия Έιπ(Χ) = ε, f%(x) суть плотности
распределений Р^, г = 1,2, относительно некоторой меры μ.
Возможно ли дальнейшее улучшение этой статистической процедуры?
В сформулированных условиях, конечно, нет. Но если отказаться от
фиксации объема выборки, т. е. сделать число наблюдений η случайной
величиной, зависящей от уже проведенных наблюдений, то улучшения возможны.
Имеется в виду сокращение числа наблюдений, необходимых для
построения критерия с заданными параметрами. Это обстоятельство существенно
для тех экспериментов, где проведение опытов сопряжено с затратами.
Принципиальную возможность такого улучшения критериев можно
пояснить на следующем примере. Допустим, что распределения Pi и Рг не
являются взаимно абсолютно непрерывными, и пусть существуют
множества В\ и i?2 из Ъх такие, что j\{x) > 0, /2(х) = 0 при χ Ε Βχ и fi{x) = О,
/г(ж) > 0 при χ £ 2?2· Тогда ясно, что если χ ι Ε В\ (χχ Ε Въ), то мы
безошибочно можем утверждать, что имеет место гипотеза Ηγ (#2)· При этом
нет никакой необходимости делать дальнейшие наблюдения.
§51. Последовательный анализ
379
Таким образом, если проводить эксперименты не сразу в количестве η
штук, а последовательно, рассматривая результат каждой новой серии
полученных наблюдений, то можно объем наблюдений сократить.
Введение последовательной процедуры представляется очень
естественным и с точки зрения байесовского подхода. В самом деле, байесовский
критерий, рассмотренный нами в §42, предписывает принимать гипотезу i?2,
если апостериорная вероятность q(2/X) этой гипотезы не меньше 1/2. При
этом в критическом множестве среди других будут находиться как
выборки X, для которых q(2/X) близка к единице (для таких X прием i?2
представляется целесообразным), так и выборки X, для которых q(2/X) близко
к 1/2. Эти последние было бы естественно рассматривать как
«недостаточные» для приема решения и требующие дополнительных экспериментов.
Кроме того, как и в приведенном выше примере, апостериорная вероятность
q(2/X) может оказаться большой уже после первых опытов, и тогда
решение можно было бы принимать без последующих испытаний (в упомянутом
примере q(2/X) = 1 при X = χι Ε Β<ι для любого априорного распределения
(q(l),q(2)),q(2)>0).
Ниже мы рассмотрим последовательную процедуру для проверки двух
простых гипотез, на которой будет достигаться максимально возможное
сокращение числа наблюдений.
2. Байесовский последовательный критерий· Рассмотрим сначала
байесовскую постановку задачи и обозначим через q(l) = g, q{2) = 1 — q
априорные вероятности гипотез #ι, #2· Тогда апостериорная вероятность
гипотезы Hi после наблюдений X = Хп будет равна
„/■/ν χ Q(i)fi(Xn) m
Я{г/ n)-Q(imXn)+Q(2)f2(XnY W
Будем проводить наблюдения последовательно и при каждом η будем
вычислять значения q(2/Xn), η = 1,2,... (или q(l/Xn)). В плоскости
переменных (п, у) рассмотрим случайную траекторию апостериорных
вероятностей (случайную ломаную), выходящую при η = 0 из точки у = q(2) и
принимающую в точках η = 1,2,... значения у = q(2/Xn). С помощью
этой траектории можно построить следующий критерий для проверки
гипотезы Н\ против #2· рассмотрим в плоскости (п,у) две прямолинейные
границы у = 7г, г = 1,2; 0 < 71 < 72 < 1> для переменной q(2/Xn).
Принимается гипотеза Яг, если траектория q(2/Xn), η = 0,1,..., впервые выйдет
из полосы (7ь7г) через верхнюю границу 72- Если траектория q(2/Xn),
η = 0,1,..., выйдет из этой полосы через нижнюю границу 7ь
принимается Н\. Позже мы увидим, что Pj-вероятность (г = 1,2) того, что q(2/Xn)
никогда не выйдет из полосы (7ъ72)> т.е. вероятность события
{71 < <?(2/Хп) < 72, η = 0,1,...} (2)
равна нулю.
Число испытаний ζ/, которое потребуется для того, чтобы принять одну
из гипотез (т.е. чтобы нарушить неравенства (2)), очевидно, является
марковской случайной величиной (моментом остановки) относительно
последовательности χι,Χ2,... для каждого из распределений Ρχ, ?2· В этом смысле
приведенное правило принятия гипотез является последовательным. Оно
380
Гл. 3. Теория проверки гипотез
довольно хорошо согласуется с правилами, которыми руководствуется
человек в своей практической деятельности, — принимать то или иное решение
только после того, как наблюдения позволят уменьшить в достаточной
степени неопределенность, имеющуюся в отношении изучаемого объекта.
Построенный критерий зависит от q = q(l) и вектора 7 — (7ь72)·
Поэтому обозначим его через ίρ/γ. Установим теперь, что критерий δ4α является
оптимальным. Для этого введем сначала общее понятие последовательного
критерия, существенными характеристиками которого наряду с
вероятностями ошибок первого и второго рода становятся средние значения Ει ν
и Е2^ для числа наблюдений ζ/, необходимых для принятия решения.
Пусть на (λ*00,©^) дана произвольная целочисленная случайная
величина ν ^ 0, являющаяся марковской относительно последовательности
xi, X2,... {{у ^ п} € σ(χι,...,χη) = 55^). Обозначим через Xй
пространство векторов (η,Χη) таких, что iy(Xoo) = Щ Хп — [Хоо[п* На Xй
введем σ-алгебру 93", порожденную событиями {у = η, Χη Ε В71}, Bn G 93^,
η = 0,1,... Ясно, что любое распределение на (X, 55^) (или на (Х°°,93#))
индуцирует соответствующее распределение на (ХУ,^8У).
Определение 1. Последовательным критерием δ для проверки Hi
против Ή.2 называется пара (ι/, Ω), где Ω Ε 55" представляет собой область
приема Ή.2 (критическую область), а случайная величина ν предполагается
собственной относительно обоих распределений Pi, P2 (Р*(^ < 00) = 1,
i = 1,2).
В тех случаях, когда необходимо будет отметить, что ν и Ω относятся к
критерию ί, будем писать v[S) и Ω(£).
Ясно, что эквивалентным образом последовательный критерий можно
задать с помощью двузначной измеримой функции на Ху. Ясно также, что
последовательный критерий δ можно задавать и с помощью построения
критической области (обозначим ее снова через Ω) во всем пространстве Х°°.
Однако при таком отображении области Ω и Ху \ Ω приема гипотез i?2 и Н\
не обязательно покрывают все элементы из Х°°: на тех из них, для
которых z/(Xoo) = 00, не принимается никакая гипотеза. Но в соответствии с
определением, Pj-вероятности множества таких Х^ равны нулю.
Обычный нерандомизированный критерий δ является частным случаем
последовательного, когда ν(δ) = η постоянно (если z/(J) = 0, то решение
принимается без проведения испытаний).
Последовательный критерий ί, как и любой обычный критерий для
проверки простых гипотез, характеризуется вероятностями α{(δ) ошибок г-го
рода (г = 1,2):
αί(ί)=Ρί((ι/,Χι/)^Ω<),
где Ω2 = Ω, Ωχ = Xй \ Ω2. Кроме того, как уже отмечалось, мы будем
характеризовать последовательный критерий средними значениями Ε^ζ/,
i = 1,2. Очевидно, что для обычного критерия £, построенного по выборке
Хп, выполняется Ечи(6) =n.
Чтобы учесть появление этих новых факторов в постановке задачи (т. е.
характеристик, связанных с величиной ζ/), мы будем считать, что
проведение каждого наблюдения требует затрат величиной а. Нам будет удобно
также характеризовать потери, возникающие при неправильном решении,
§51. Последовательный анализ
381
различными значениями w\ и w2. Именно, будем считать, что потери г-го
рода, возникающие при ошибочном решении, когда верна Hi, равны W{,
г = 1,2.
При этих соглашениях математическое ожидание R(q, δ) потерь, которые
возникают при использовании критерия δ, равно
R{Q,S) = q[ai{S)wi+aEiv{5)] + (1 - q)[a2(S)w2 + αΕ2ι/(ί)]. (3)
Это выражение называют байесовским риском в рассматриваемой задаче.
Если положить здесь а = О, w\ = w2 = 1, то получим выражение для
вероятности ошибочного решения критерия £, которое нами уже неоднократно
использовалось в §41, 42.
Определение 2. Последовательный критерий δ) минимизирующий
байесовский риск (3), называется байесовским.
Следующее утверждение устанавливает оптимальность (байесовость)
критерия 59)7, построенного в начале этого пункта.
Теорема 1. Для заданных а, доi, w2 существуют 7ι, 72 такие, что
критерий δ4Π является байесовским.
Доказательство. Обозначим через δι критерий, который принимает
гипотезу Hi без проведения испытаний, так что ν{δι) = 0, Oi(5i) = 0.
Выясним сначала, в каких случаях критерий δ, минимизирующий R(q, δ),
совпадает с δι или #2- Очевидно, что
R{q,Si) = (1 -q)w2, R{q,S2) = qwi.
Пусть К — класс критериев {δ = δ(Χ)}, которые зависят хотя бы от одного
наблюдения, т.е. класс критериев δ, для которых ι/(δ) ^ 1. Очевидно, что
R(q, δ) ^ а для δ Ε К. Положим
R(q)= inf R(q,S).
Так как критерий δ, основанный на одном испытании {и{δ) = 1),
принадлежит К, то R(q) < ос.
Для любого ρ Ε (0,1) имеем в силу линейности R(q, δ) как функции от q:
R(pqi + (1 -р)«) = inf \pR{qu5) + (1 -р)Д(»,*)] ί* pilfai) + (1 - р)Д(й)·
Это означает, что Д(д) —
вогнутая функция. Так как а < R(q) <
< 00, то отсюда следует, что R(q)
является также непрерывной на [0,1]
функцией. Сравним теперь риски
критериев δ{ и δ Ε К в зависимости
от g (см. рис. 5).
Одно из двух: либо R(q) ^
Рис. 5
D ( w2 \ wiw2 \
ветствует тому, что К ^ , либо существуют решения,
\W\+W2J Wi+W2J
^ mini?(g, δι) при всех q I это coot
382
Гл. 3. Теория проверки гипотез
которые обозначим 1 — 7ь 1 ~~ 72 5 1 — 7ι > 1 ~~ 72? соответственно уравнений
Д^,^) = Л(д), i?(g, £2) = Д(?)· Очевидно, что i?(g) < mini2(qr,^) внутри
i
интервала (1 — 72 > 1 — 7ι)· Для пеРвой из перечисленных двух возможностей
положим
1-71 = 1- 72 = : ,
Wi + W2
так что
Д(1-Τι,ίι) = Я(1-7i, fc).
Из приведенных рассуждений и рис. 5 вытекает следующее оптимальное
правило действий. По данным а, до ι, г^2 вычисляем 1 — 7ь 1 ~ 72· Если
q ^ 1—72 или, что то же, 1 — g ^ 72 > то наименьший риск среди всех
критериев дает #2 (т-е- надо немедленно принимать #2)· Если q ^ 1 — η
(1 — # ^ 7ι)5 т0 наименьший риск дает δι (надо принимать Hi). И лишь
в случае 1 - 72 < 1 — 7ь 9 £ (1 - 72> 1 - 7ι) (или 1-?^ (7ь7г)) следует
воспользоваться критерием из К, т. е. необходимо проводить эксперимент.
Воспользуемся теперь индукцией. Пусть проведено π наблюдений и мы
имеем выборку Хп. Перед (п + 1)-м наблюдением мы имеем ту же
альтернативу: либо больше не проводить наблюдений и принять одну из гипотез
Н{ тут же, либо продолжить наблюдения. Тот факт, что мы уже понесли
потери an, роли не играет, так как они ничем уже устранены быть не могут.
Существенные изменения касаются лишь априорного распределения. Теперь
роль вероятностей q(l) = q и q(2) = 1 — q должны играть апостериорные
вероятности q(l/Xn), q(2/Xn). Применительно к этой новой ситуации уже
выработанное нами оптимальное правило дает, что нужно принимать #2,
если q(2/Xn) ^ 72, и #ι, если q(2/Xn) ^ 7ι· Если же q(2/Xn) E (7ъ72), то
следует продолжать наблюдения. Но полученное правило есть не что иное,
как критерий 8qn. Таким образом, мы нашли 7г = 7г(а> ^i, it^), обладающие
тем свойством, что критерий 8ЯП минимизирует риск R(q,S). <
Отметим, что числа 7г(а5^ь^2) остаются неизменными при умножении
a, ti;i, W2 на одно и то же число; это очевидно из их определения, так как
такая операция приводит лишь к умножению на то же число всех рисков
R(q,S). Таким образом, на самом деле 7г есть функция лишь двух
переменных, например а и tui, если считать, что w<i = 1 — w\.
Что собой представляет байесовский критерий Sq^? Он предписывает не
проводить наблюдений в двух случаях: если 71 = 72 (это бывает, когда а
велико по сравнению с wi, W2) либо если q(2) ^ 71 или 9(2) ^ 72· В остальных
случаях следует проводить эксперименты до первого нарушения неравенств
71 < q(2/Xn) < 72
или, что то же (см. (1)), при первом нарушении неравенств
719(1) h{Xn) 729(1) ..
(1 - 7i)9(2) </i(X„)< (1-72)9(2)· W
При этом принимается гипотеза Н^·, если впервые нарушается правое
неравенство, и гипотеза Hi — если левое. В таком виде «переменная» часть
§51. Последовательный анализ
383
критерия 5qn с байесовской постановкой задачи уже не связана, и мы
можем, обозначив через Γι, Γ2 левую и правую границы в (4), рассматривать
последовательный критерий όγ, Γ = (Γχ,^), который называют
последовательным критерием отношения правдоподобия. Он был впервые введен
Вальдом.
3. Последовательный критерий, минимизирующий среднее число
испытаний
Теорема 2. Пусть Г χ < 1 < Г2. Обозначим через αχ, а2
вероятности ошибок первого и второго рода критерия δγ. Тогда среди всех
последовательных критериев J, для которых α\(δ) ^ αϊ, α2(δ) ^ α2,
критерий δγ имеет наименьшие значения Εχΐ/(£) и Ε2ν(δ).
Эта теорема означает, в частности, что если δ есть критерий,
построенный по выборке Хп фиксированного объема, для которого α\(δ) ^ αχ,
&2{δ) < α2, то
ΕΜδΓ) <η, * = 1,2.
Доказательство. Байесовский критерий δ4ιΊ, рассматривавшийся в
теореме 1, определяется набором чисел (</, a, w\, w2). Но, как уже отмечалось,
умножение а, W\, w2 на одно и то же число не меняет границ 7t» тзк что
6яп на самом деле определяется тремя параметрами, например (д, а, ги), если
принять г^х = г^, w2 = 1 — ги.
Если исходить из этого соглашения, то в теореме 1 мы по заданным
(α,ΐϋ) построили числа 7г = 7i(a>™), ПРИ которых критерий J9j7 является
байесовским. Теперь нам потребуется в известном смысле обратное
утверждение о том, что для данных 7ь 72 существуют a, w такие, что л(а,ш) =
= 7г? т-е- такие а, ги, для которых критерий δςη будет байесовским в
задаче, соответствующей набору (д, а,ги). Это утверждение носит технический
характер и доказывается довольно сложно (см. [65]). Поэтому мы примем
его как допущение*).
Итак, рассмотрим критерий δγ и при данном q найдем 7г из уравнений
ИЧ =Г
(1-70(1-9) '"
Для полученных значений 7ΐ = Γ,·(1 — <?)/(Гг(1 — q) + q) найдем α, ги, при
которых критерий <^7 будет байесовским в задаче, соответствующей набору
(q,a,w). Так как Γχ < 1 < Г2, то 7ι < 1 — Я < 72 и ί/(ίς,7) ^ 1. Это означает,
что δ^Ί — δγ.
Пусть теперь δ — любой другой критерий, для которого α{(δ) ^ α^. Так
как критерий δ4Π = δγ минимизирует байесовский риск, то
q[aiw + αΕιν{δγ)] + (1 - q)[a2(l - w) + αΈ,2ν(δγ)] ^
^ q[ax{S)w + αΕιΐ/(ί)] + (1 - q)[a2(S){l - w) + αΕ2ν(δ)].
*) Мы не доказываем здесь и другое полезное утверждение о том, что для непрерывных
Р»-распределений величины f2(X)/fi(X) и любых заданных αϊ, α.ι найдутся Γι, Г 2 такие,
что αι(δν) = αϊ, аг(<5г) = аг. По своему существу это утверждение близко к леммам 46.1 и
47.1, но доказывается труднее.
384
Гл. 3. Теория проверки гипотез
Отсюда следует, что
qEMSr) + (1 - q)E2v{Sr) < дЕц/(Я) + (1 - g)E2i/(i).
Так как число q E (О,1) здесь произвольно, то Ειζ/(ίρ) ^ Ει^(ί), Е2гу(#г) ^
^ Ε2ν{δ). <
Мы использовали здесь для доказательства тот же прием сравнения с
байесовскими критериями, который применяли в §41, 42, 45.
Рассмотрим некоторые свойства критерия ir> Обозначим через Ω"
подмножества из А*00, которые определяются следующим образом (Х^ = [Хоо]^):
П? = {Хоо:Г1<^<Г2>* = 1>...,п-1,^^Г11.
I л№) η\χη) J
Множество Ω" определяется так же, но последнее неравенство надо заменить
00
на f2{Xn)/fi{Xn) ^ Г2. Очевидно, что Ω™ не пересекаются, Ω^ = Μ Ω" есть
71=1
область приема i/г, ζ/(ίρ) — η Β области {ж G Λ*00 : χ е Ω?},
αϊ
оо оо «
(ίΓ) = ΣΡι(Ω2} = Σ у /ι(*)/Λ<^Κ
00 /»
s /
71-1 Λ^ΠΩ?
/2(x)r2-Vn(dx) = L_^M (5)
'2
Аналогично устанавливается, что
α2(ίΓΚΓι(1-αι(£Γ))> (6)
Положим для краткости ai(ip) = &%· Степень точности полученных
неравенств
Г2<^, Г^-^_ (7)
αϊ 1 — αϊ
обсудим позже. А сейчас выясним свойства критерия, который получим,
если воспользуемся соотношениями (7) в качестве основы для
определения Т{ по заданным аг·. Если положить
Γι = , Г2 = , ai = ai(drOi
1 — αϊ αϊ
для полученного критерия δν* будем иметь в силу (7)
* ϊ ^7' ^^— ^ "77—· W
— αϊ 1 — а^ αϊ aj
Отсюда следует, что
αι(ΐ-α'2) αϊ , α2(ΐ-αΊ) a2
1 — a2 1 — a2 1 — αχ 1 — αχ
§51. Последовательный анализ
385
Приводя неравенства (8) к общему знаменателю и складывая их, получим
также
Таким образом, если ol{ малы, то критерий ίρ' будет иметь значения с^,
которые в сумме не превышают αϊ + α2, и каждое из а^ может превышать
щ лишь незначительно и в известных нам пределах.
Пример L Пусть хг- имеет биномиальное распределение с вероятностью
успеха ρ (распределение Бернулли В*). Задача состоит в проверке гипотезы
Н\ = {р = р\} против Η<ι = {р = ρ2}5 Pi < Р2> В этом случае
MX) = рГ(1-Р2)п~т?" = /p2(i-Pi)y- (1-P2V
MX) ρψ{\-Ριγ-ηη \Pl(l-p2)j \l-pj '
где 77n есть число успехов в η испытаниях. Для значений р\ — 0,05, р2 =
= 0,17, αϊ = 0,05, α2 = 0,10 получаем*) Γ'ι = 0,105, Г'2 = 18, α'ι = 0,031,
α'2 = 0,099,
Eii/(irv) = 31,4, Ε2ι/(ίρ) = 30,0.
С другой стороны, процедура с фиксированным объемом выборки и
вероятностями ошибок первого и второго рода 0,05 и 0,10 требует η = 57
наблюдений. Таким образом, последовательная процедура в этом примере почти
вдвое сокращает среднее число наблюдений.
4. Вычисление параметров наилучшего последовательного критерия.
Соотношения (7), (8) дают возможность устанавливать некоторое соответствие между
границей Г и вероятностями ошибок оц{6г). Рассмотрим теперь задачу расчета
критерия 6г более подробно.
а) Точные формулы. Положим
**=1п£{Ц, fc = 1,2 Ai = ]nTu i = l,2.
/i(xfc)
Тогда критерию ίρ можно придать следующую форму: если Α ι < 0 < А2, то
последовательно проводятся эксперименты и суммируются независимые одинаково
η
распределенные значения 2* до тех пор, пока сумма Zn = V^ г^ не коснется впер-
вые одной из границ А{. Если верна гипотеза Я"2, то описанное блуждание будет
направлено в среднем вверх, так как
Ε2*ι = ί\ηψ^-Μχ)μ(άχ) =ρι(Ρ2,Ρι) >0
(см. лемму 16.1). Аналогично устанавливается, что ΕχΖι = -/?ι(Ρι,Ρ2) < 0.
Если границы Αι удаляются от начала координат, то это соответствует (ср. с (5),
(6)) уменьшению вероятностей ошибок первого и второго рода.
*) Числовые данные заимствованы из [65, с. 143].
386
Гл. 3. Теория проверки гипотез
Множества Щ в терминах блуждания {Zk} будут иметь вид
Щ = {АХ <Zk<A2y fc = l,...,n-l, Zn^A2}.
Аналогичную форму будут иметь множества Ω".
Обозначим через η(ί) случайную величину, равную времени первого выхода
случайного блуждания Zq = О,Z\,Z2l... за границу t:
_ /m^n{^ '· %к^ t} при t > О,
^ ' " \min{fc : Zk ^ i] при t < 0.
Это есть процесс восстановления, соответствующий последовательности {Zk} (см.
[17, гл. 9]). Разности χ(Α{) = Ζη(Λ.) - Αι будут представлять собой величины
эксцессов (перескоков) через уровни Αι в блуждании {Zk} (см. [17]).
Для вероятности ошибки первого рода можем записать
α1(ίΓ) = Σρι(Ω2) = Σ / Μ^Μχ)μη№) =
οο
= y£E2(e-z->^)^T^1E2(e-^A^;il2), (9)
n=l
oo
где Ω2 = Μ Щ есть область приема Н2. Аналогично
п=1
α2((5Γ) = ΓιΕ^β^^ίΩι), Πι = (J Ω?. (10)
Далее, для значений Е^, г = 1,2; ν = ^(<5r)} в силу тождества Вальда находим
Ei(Z„) = E^iEii/, г = 1,2.
Так как Zu = А2 + х(А2) на множестве il2 и Zu = Αι + χ(Αι) на множестве Ωι, то
Ειΐ/==Λ-[αιΑ2 + Ει(χ(Λ2);Ω2) + (1-αιμι+Ει(χ(^ι);Ωι)],
ι (11)
Ε2ι/ = - [(1 - а2)А2 + Е2(х(Л2); Ω2) + α2Αλ + Ε^χ^);Ωι)].
rj2z\
В ряде случаев правые части в формулах (9)—(11) могут быть найдены в явном
виде. Эти формулы оказываются весьма полезными и в приближенных
вычислениях.
б) Приближенные формулы (при больших А\, А2) и неравенства.
Мы уже отмечали, что большие значения |Л»|, i = 1,2, соответствуют малым
вероятностям ошибок α{(δγ). Рассмотрим значение
c*i(*r)=Pi( sup Zk> Ла) =
= P1{supZk>A2)-P1{ sup Zk<A2, sup Zk > A2). (12)
§51. Последовательный анализ
387
Последнее слагаемое здесь не превосходит в силу марковости случайной величины
η(ί) значений
Pi( sup (Zk-Zrj{Al))>A2-ZT){Al))^P1(supZkZA2-A1).
Так как почти во всех практически интересных случаях вероятность и(А) =
= Pi (sup Z* ^ А) убывает экспоненциально с ростом А (см., например, [111, т. 2];
это же можно извлечь из главы 11 в [17], где изложены методы вычислений и(А) *)),
то при больших \Αι\ значение и(А2 — Αχ) будет иметь более высокий порядок
малости, чем и(А2). Это означает в силу (12), что
αι(δτ) * Pi(supZfc ^ А2) = и(Л2), (13)
Jk^O
так что второй границей при больших Αι, А2 в (12) можно пренебречь. Точно так
же получается приближение
a2(ir)«P2(inf гк^Аг). (14)
Если \Ai\ велики, cci малы, то главные части в (11) дают
Вц/и^, Е21/«^2_. (15)
В основе этих формул также лежит пренебрежение второй границей (их можно
получить и с помощью приближений Eji/ та Eff(Ai) та Αχ/ΈχΖι. Последнее соотношение
имеет место в силу теоремы восстановления [17]).
Учет следующих по порядку малости членов в (11) дает
Ец/ = =—(Ах + αι(Α2 - Аг) + Еш),
ΆιχΖχ
(16)
Е2*/ = -—(А2 - α2(Α2 - Αχ) + Ε2χ2),
^2*1
где at определяются приближениями (12), (13), значения Е^ = lim Έιχ(Αί)
|>tj|->oo
могут быть найдены методами главы 11 в [17].
Рассмотрим теперь неравенства (8). Так как χ(Α\) ^ 0, χ(Α2) ^ 0, то эти
неравенства следуют из (9), (10), если χ(Α{) заменить на нуль. Стало быть, точность
этих неравенств определяется погрешностью, вызываемой такой заменой.
Если случайные величины Ζχ ограничены, Ь\ ^ Zi ^ 62, то, очевидно, χ(Α2) ζ
^ b2) χ(Α\) ^ bi, и наряду с (5), (6) могут быть написаны обратные неравенства.
Именно,
αι(ίΓ) = Γ2-1Ε2(β-^2>;Ω2) ί> I^V^l - а2),
(17)
α2(ίΓ)£Γι6>ι(1-αι).
*) Подробнее об этом см. [12].
388
Гл. 3. Теория проверки гипотез
Чтобы проиллюстрировать полученные соотношения, обратимся к примеру 1.
Для него
Ζη = ??„ In — + nln ,
Pi(l-P2J 1-pi
где ηη есть число успехов в η испытаниях. Это значит, что Ζ\ для Pj-распределе-
ния принимает значение 62 = b(p2/pi) « 1,224 с вероятностью pi и значение
1 "" Р2
6i = In « -0,135 с вероятностью 1 -pi, г = 1,2. Отсюда находим
1 -Pi
Ειζι = -0,067, Ε2ζι = 0,096, еЬг = 3,400, ebl = 0,874.
Из двух последних значений близко к единице лишь второе, так что
сравнительно точным будет лишь второе из неравенств (17). Используя это неравенство
и (7) для критерия 6г>, получим
0,102= ^^ГК^-^. = 0,117.
Это дает довольно точные границы для значения Г[ = 0,105. В нашем случае
А[ = In Г; « -2,254, А'2 = 1пГ^ » 2,890.
Отсюда, используя приближенные формулы (15), получим для Ejj/, г = 1,2,
значения
_j4i оо «on ^2
= 33,639, —ί- = 30,108.
Ει^ι Ε2Ζ1
Мы видим, что даже довольно грубые приближения такие, как (15), дают
правильное представление о величинах E^i/. Результаты будут значительно более
точными, если воспользоваться формулами (16).
§ 52, Проверка сложных гипотез в общем случае
В этом параграфе мы не будем предполагать, что выборка относится к
какому-либо параметрическому семейству.
Задача проверки двух гипотез в общем случае выглядит следующим
образом. Пусть Р\ и Т>2 — два семейства распределений такие, что
распределение Ρ выборки X принадлежит V\ U 7^· Проверяется гипотеза Н\ = {X €=
§ Ρ, Ρ G Pi} против #2 — {Χ ^ Ρ, Ρ £ Рг}· Общий принцип
построения (нерандомизированного*)) критерия π(Χ) = δ(Χ) здесь остается
прежним — таким же, каким он был описан в § 44 для параметрического случая.
Именно, строится критическое множество Ω С Хп (часто отождествляемое
с понятием критерия) такое, что мы принимаем i?2, если Χ Ε Ω, и
принимаем Н\ в противном случае. Число
1-ε= inf Р{Х ΦΩ)
*) В дальнейшем для единообразия обозначений мы будем статистические критерии
обозначать символом π, хотя в пределах этой главы это будут, как правило,
нерандомизированные критерии.
§ 52. Проверка сложных гипотез в общем случае
389
называется уровнем значимости критерия. Величина
Дг(Р)=р(ХеП), ре?2,
есть значение мощности критерия π в «точке» Ρ Ε TV
Сравнивать мощности /?π(Ρ) критериев π в случае, когда множество Т>2
альтернатив Ρ очень богато, и строить оптимальные критерии в этих
условиях весьма затруднительно или просто невозможно. Минимальные
требования к критериям в этом случае состоят обычно в том, чтобы для каждого
фиксированного Ρ Ε V<i выполнялось
lim /?π(Ρ) = 1.
П~>00
Определение 1. Критерий π, обладающий этим свойством,
называется состоятельным.
Существо рассматриваемых критериев, как и всех статистических
критериев, соответствует основному принципу математической статистики, о
котором уже говорилось в § 4 и в § 39. Если ε мало, то при выполнении
гипотезы Hi и при многократном использовании построенного критерия уровня
1-е мы будем ошибаться (т.е. попадать в критическую область) в среднем
лишь в 100ε % всех испытаний. Поэтому попадание при выполнении
гипотезы Н\ в эту область в единичном испытании мы считаем практически
невозможным. Так что если мы все-таки туда попали, значит, сделанное
предположение неверно, и мы объявляем, что гипотеза Н\ неверна. В этом
случае говорят, что результаты эксперимента не согласуются с
гипотезой Н\ с точки зрения критерия уровня 1-е.
Очень распространенными являются критерии проверки простой
гипотезы Н\ = {X €= Ρχ} против сложной альтернативы #2 — {X §Р/ Pi};
гипотеза #2 означает, что X есть выборка из произвольного распределения
Р^Рь
В основе построения критериев для проверки простой гипотезы Н\ =
= {X ^ Pi} обычно лежит «удаленность» эмпирического распределения Р*
от распределения Pi в смысле некоторого «расстояния» d(P,Q).
Желательным свойством этого расстояния является обращение d(P, Q) в нуль лишь
при Q = Р, а также непрерывность d(P,Q) в «окрестности» точки Q = Р,
например в равномерной метрике (иначе малые отклонения Q от Ρ могут
приводить к большим значениям расстояния d). Напомним, что в
параметрическом случае аналогичные соображения мы использовали при
построении оценок неизвестного параметра по методу минимального расстояния.
Итак, пусть d(P, Q) есть некоторое расстояние (не обязательно метрика)
в пространстве распределений. Предположим, что по заданному ε > 0 можно
найти такое с > 0, для которого
Pi(rf(Pi,p;)>c)=e. (ι)
Тогда критерий строится следующим образом:
ГО, если d(PbP;) <c,
^{Х) = < 1
[1 в противном случае.
Очевидно, что π есть критерий уровня 1 — ε.
390
Гл. 3. Теория проверки гипотез
Так же, как и в § 43, можно ввести понятие критерия асимптотического
уровня 1 — ε, для которого
limPi(d(Pi,P;)>c)=e. (2)
Описанные критерии часто называют критериями согласия (с
предположением {X ^ Pi})· Их конструкцию можно эквивалентным образом
представить и в несколько иной форме. Пусть дан функционал G(P) (или
последовательность функционалов Gn(P)) такой, что G(P) Φ G(Pi) при
Ρ φ Pi. Тогда можем положить π(Χ) = 1, если |G(P*) - G(Pi)| > с, и
-к{Х) — 0 в противном случае, где с выбирается из тех же соображений,
что и в (1), (2). Нетрудно проверить, что этот второй подход
эквивалентен первому, поскольку по функционалу G можно построить расстояние
d(P,Pi) = |G(P) — G(Pi)| (ср. с принципом подстановки в теории
оценивания), и наоборот по расстоянию d(P,Px) можно построить функционал
G(P) = d(P,Pi) (G(Pi) = 0), удовлетворяющий требуемым свойствам.
Если функционал G в описанной конструкции критерия обладает к тому
же свойством G(P*) —> G(P) при X €= Ρ (это всегда так, если G
является функционалом первого или второго типа; см. §3), то построенный
критерий будет состоятельным. Действительно, в этом случае число
с = с(п), обеспечивающее равенство (2), должно сходиться к нулю (так
как Pi(|G(P*) — G(Pi)| > ε) -► 0 при любом ε > 0) и, следовательно,
будем иметь G(P*) —► G(P), P(|G(P;) - G(Pi)| > c{n)) -> 1 при каждом
фиксированном Ρ φ Ρχ.
Рассмотрим теперь некоторые хорошо известные критерии согласия,
которые являются реализацией описанного выше подхода.
1. Критерий Колмогорова. Рассмотрим статистику (расстояние)
D(PbP;)=Sup|Fn*(<)-F(<)|,
где F*(t) и F(t) — функции распределения, соответствующие мерам Р*
и Ρχ. В § 8 нами было установлено, что если F(t) непрерывна, X €= Ρχ, то
dK(PuK)=yfcD{lPuPmn)=> sup |ιι/°(ί)|,
где w°(t) — броуновский мост. Отсюда следует
Теорема 1 (А.Н.Колмогоров). ЕслиР(Ь) непрерывна, то существует
lim PifefPbP;) <x) =K{x)=P( sup |tu°(i)| < χ).
Функцию К (χ) можно найти в явном виде. Она равна
оо
К(х) = Σ (-l)fce"2fc2x2·
fc=-oo
§ 52. Проверка сложных гипотез в общем случае
391
С помощью этой теоремы можно конструировать критерии
асимптотического уровня 1 — ε. Функция К(х) табулирована во многих руководствах по
математической статистике. Поэтому для заданного ε можем с помощью
таблиц найти постоянную с = се, для которой К (с) = 1 — ε. Положив π(Χ) = 1
при d#(Pi,P*) > се, мы получим критерий согласия асимптотического
уровня 1-е. Нетрудно видеть, что полученный критерий состоятелен, так
как функционал G(P) = sup|FP(i) - F{t)\ (здесь FP{t) = Ρ((-οο,ί))),
t
с помощью которого построен критерий Колмогорова, непрерывен
относительно Fp в равномерной метрике и, стало быть, является функционалом
II типа (см. главу 1), для которого G(P^) —> G(P) при X €= Ρ» Остается
воспользоваться сделанными выше замечаниями об условиях
состоятельности критериев согласия.
С помощью результатов главы 1 мы можем найти асимптотическое поведение
мощности критерия Колмогорова относительно близких альтернатив (см. §43).
Допустим, что X €= Р, где распределение Ρ имеет функцию распределения
FP(x)=F(x)+p(x)n-1/2. (3)
Будем предполагать для простоты, что р(х) непрерывна, a F(x) непрерывна и строго
монотонна. Мощность /?(Р) критерия Колмогорова в «точке» Ρ будет равна
/3(Р) = P(d*(РЬР;) > с) = P(sup|F(i) - Fn*(<)|v^ > с) =
= P(sup|FP(i) -pWn-1'2 - F«(t)|>/n > с).
Если сделать замену t = Fpl(u), где Fp1 есть функция, обратная к Fp, то мы
получим выражение
р( sup \u-p{Fp1(u))n^2^F:{Fp1(u))\y/K>c). (4)
Здесь Un(u) = F*{Fpl(u)) есть эмпирическая функция, соответствующая
равномерному на [0,1] распределению С/од, так что (4) равно
Ρ ( sup |u - £/» -p{Fp1(u))n-1/2\V^ > с) .
Кроме того, Fpl(u) ->· F~l(u) в силу строгой монотонности F. Отсюда и из
непрерывности ρ следует, что
lim /?(Р) = Ρ ( sup \w°(t) - a(t)\ > с) , (5)
rj&a(t)=p(F-l(t)).
Можно показать, что это выражение минимально при a(t) = 0 {р = 0). В этом
смысле критерий Колмогорова является асимптотически несмещенным.
392
Гл. 3. Теория проверки гипотез
2. Критерий Мизеса-Смирнова (критерий ω2). Рассмотрим в
качестве расстояния между Pi и Р* статистику
ω2η = ^(РьР;) = nj{F(x) - F*(x))2dF(x),
с помощью которой также можно построить критерий согласия заданного
уровня. В главе 1 доказано, что здесь, как и в предыдущем случае,
справедлива
Теорема 2. Существует предельное распределение
Ιιι^Ρ^ωΙ <х) =Ω(χ)ξΡ | i{w°{t))2dt<x\ .
Функция Ω,(χ) имеет весьма сложный вид (см. [10]), и мы ее приводить
здесь не будем.
Так как функционал
G(P) = J{F(t)-FP(t))2dF(t)
является функционалом II типа (§3), то по тем же соображениям, что и в
случае критерия Колмогорова, критерий ω2 является состоятельным.
Следуя рассуждениям предыдущего пункта, можно найти и асимптотическое
поведение мощности β(Ρ) критерия ω2 для близких альтернатив Ρ вида (3). Получим
совершенно аналогичным образом, что
/?(Р) = РК > с) -> Р (/(»Л«) - а(*))2 dt > с) ,
где a(t) определено в (5). Полученное предельное значение так же, как и (5),
минимально при a(t) = 0, так что критерий ω2 тоже является асимптотически
несмещенным.
Рассмотренные два критерия, как и другие критерии согласия с
гипотезой Hi = {X €= Pi}, построенные с помощью расстояний d(P,Q),
позволяют сразу получать доверительные множества для неизвестной функции
распределения F(x) или для неизвестного распределения Pi выборки X.
Действительно, соотношение (1) (или (2)) можно трактовать и так:
вероятность того, что с-окрестность «точки» Р£ (в смысле расстояния d) накроет
«точку» Pi, равна 1 — е. (Для (2) мы получим асимптотический вариант
этого утверждения.) Это означает (см. §48), что с-окрестность точки Р£
представляет собой доверительное множество уровня 1 — ε для неизвестного
распределения Pi, X €= Pi. Критерий Колмогорова, например, определяет
эту окрестность в терминах функций распределения: это множество всех
F(x), для которых
sup\F(t)-F:(t)\<^=,
где се определяется из (1).
§ 52. Проверка сложных гипотез в общем случае
393
Вернемся к критериям. Мы уже отмечали, что асимптотическим уровням
значимости можно доверять лишь при больших п. Если же объем выборки
невелик, то при построении критерия (точнее, при нахождении с — се)
необходимо использовать точные формулы для распределения d(Pi, P*). Однако
их получение связано, как правило, с большими трудностями. В этой связи
важную роль играют так называемые непараметрические критерии,
основанные на статистиках, распределение которых не зависит от истинного
распределения Pi (или не зависит от параметра 0, если X €= Р#).
В этом случае вероятности Pi (d(Pi, P*) < χ) от Pi не зависят, и, стало
быть, можно один раз произвести вычисления, составить таблицы и затем
использовать их при любых Pi.
Критерий Колмогорова и критерий ω2 являются
непараметрическими критериями. Этот факт установлен в §6.
Непараметрические критерии возникают и при проверке двух сложных
гипотез.
3. Критерий знаков. Пусть F(x) есть функция распределения для
Pi и гипотеза Н\ состоит в том, что F(a) = ρ для заданной точки а.
Очевидно, это есть сложная гипотеза. Гипотеза Ή.2 является дополнительной:
Н2 = {X €= Р, Fp(a) φ ρ}. В этом случае естественно воспользоваться
следующей статистикой: обозначим через ν{Χ) число наблюдений х^, для
которых знак разности х^ — а отрицателен. В качестве критического
множества Ω рассмотрим все выборки X, для которых
р{Х)£{сис2)
При неКОТОрЫХ С\ < С2-
Если верна гипотеза i?i, то
РМХ) = к) = С№(1-р)п-к.
Итак, распределение v(X) при гипотезе Н\ от Pi не зависит, так что
наш критерий является непараметрическим. Числа с% следует выбрать так,
чтобы
Р(1/(Х)е(с1>С2))£1-е
(знак равенства из-за дискретности v(X) здесь может не достигаться).
Неоднозначность в выборе С{ можно устранить требованием несмещенности
относительно изменений р. В целом эта задача эквивалентна проверке
гипотезы о том, что вероятность успеха в схеме Бернулли равна р.
Аналогичным образом можно строить «односторонние» критерии для проверки
гипотез F(a) < р.
Если в качестве обобщения рассмотренной задачи мы будем проверять
гипотезу F(cii) = р^, i — 15 · · ·, г, для заданных значений бц, р^, то придем к
критерию χ2, который подробно рассматривается в §56.
4. КритерийМорана. Так называется следующий критерий для
проверки гипотезы о том, что X ^ Pi. Пусть Χ(ι),.. .,Х(П) — вариационный
ряд, построенный по выборке X. Предположим, что Pi имеет непрерывную
394
Гл. 3. Теория проверки гипотез
функцию распределения F, и составим статистику
η
Mn = J>(x(fc+1))-F(x{fc))]2, (6)
где принято F(x(0)) = 0, ^(х(п+1)) = 1· Критерий Морана отвергает гипотезу
{X g= Pi}, если Мп >с.
Очевидно, этот критерий является непараметрическим, так как F(x}c) ^
€f Uo,i· Стало быть, достаточно рассматривать критерий Мп > с,
основанный на статистике
η
Mn = ^(x(jt+1)-x(jt))2
А;=0
и предназначенный для проверки равномерности распределения X.
Использование статистики Мп в этом случае представляется естественным, так как
η η
величина S~^ yf достигает своего минимума при условии У^Уг = 1 в точке
г=0 г=0
Для вычисления асимптотического уровня критерия Морана может
служить следующая
Теорема 3. Если X €= Pi, mo
Γ(ηΜη \
Vn[— 1J & Фод-
Доказательство. Пусть £j независимы и £j ^ Гад, j = 1,2,...
к
Тогда ζΐς = y^Cj €= Г^А;, и в силу следствия 6.2 совместное распределение
разностей
χ(1)ιχ(2) -χ(1)5···5χ(η) ~х(п-1)Д ~χ(η)
совпадает с совместным распределением
ζι & ζη+l
ζη+Ι Cn+1 Cn+1
так что*)
n+1
Знак = означает совпадение распределений.
§ 52. Проверка сложных гипотез в общем случае
395
Распределение Мп от α не зависит, и можно положить α = 1. Тогда (см. § 12)
Е# = Г(А + 1) = *«, D0 = 1, D£j = 20,
- 2) @> Φθ!
.20·
Имеем
η
ηΜη-ι =
2п+Е(Й-2)
Я=1
тг(2п + г?пЧ/й) 2 + τ&,η-1/2
η+Σ(^-ΐ)Ι
(7)
(ηΜη_ι - 2)>/η ^
??η - 4ρη - 2ρ2 η ^2
(1+ΡηΠ-1/2)2 ■
Здесь
Εξ^ = -2, D^ = Efo4-8£f + 16£2)-4 = 4.
Стало быть, 77η — 4ρη ©► Φο,4> так что в силу теорем непрерывности из (7)
получаем
г(пМп-х Л ЛЛ
Это доказывает утверждение теоремы. <
Приведем теперь соображения, показывающие что критерий Морана является
состоятельным. Рассмотрим статистику (6) для X €= Р, где Ρ отлично от Р\.
Одно из распределений Pi или Ρ мы можем, не ограничивая общности, считать
равномерным. Пусть это будет Р. Относительно F предположим для простоты, что
существует непрерывная плотность /(£) = F'{t), сосредоточенная на [0,1]. Тогда
для X €= Uo,i главная часть пМп будет равна
n-f-l
ηΣ[/(χ(*+ι))(Χ(*+ΐ) "х(*))12 =ηΣυ^Κη+ι)&Κη+ι]
(8)
fc=0
fc=l
По усиленному закону больших чисел k l(k —> 1 при к —> оо. Поэтому главная
п.н.
часть (8) в свою очередь будет равна
Ё/2(*/»)й/п·
(9)
к=1
396
Гл. 3. Теория проверки гипотез
Используя снова закон больших чисел (или неравенство Чебышева), получим, что
это выражение сходится по вероятности к
2 I f2(t)dt>2\ I f(t)dt\ = 2.
\Jf2(t)dt>2U
о \о
Здесь знак неравенства строгий, если f(t) ^ 1. Это значит, что при Χ ^ Ρ
= U0,i φ Ρι и при η -> оо
ν~η(ψ-ή
> 00,
Ρ
что влечет за собой в силу теоремы 3 состоятельность критерия Морана любого
фиксированного уровня 1 — ε. <
Будучи состоятельным, критерий Морана не различает, однако, близких
гипотез. Предположим, что Χ ^ Ρ = Uo,i,
F(«)=t + p(i)n-1/2, ί e [ο, ι],
ρ(0)=ρ(1) = 0
и что функция p(t) непрерывно дифференцируема. Тогда
n3/2Mn = n3/2X>(ifc+1)-x(fe))2 +
η η
+ 2n53(x(fc+1) -x(fc))(p(x(fc+i))-Mx(fc))) + \/^5Z(p(x(Jfc+i) -P(x(fc)))2· (H)
fc=0 fc=0
η
Главная часть второй суммы здесь равна 2n YJp/(x^))(x(fc+i) ~ x(fc))2 или в силу
тех же соображений, что и в (9),
k=0
ι
2£j/(*/n)#/n -у 4 /V(0 Λ = 0.
*=1 η
Последнее слагаемое в (11) также сходится по вероятности к нулю, так как имеет
главную часть, совпадающую по распределению с
4=f>(*/n)]2tf/n
Tnim]
или с —j= / [ρ (ί)] dt -> 0. Изложенное означает, что для функции F вида (10)
о
статистика п3/2Мп/2 — у/п будет иметь то же предельное распределение Фо,ь что
и для F(t) — t. <
Следует отметить, что из этого факта нельзя делать поспешных выводов о том,
что критерий Морана плох. Дело в том, что, не различая близких гипотез вида
(10), критерий Морана различает гипотезы (также в известном смысле близкие),
§ 53. Асимптотически оптимальные критерии
397
которые другие критерии, рассмотренные в этом параграфе, различить не могут.
Речь идет о гипотезах для плотностей.
Рассмотрим гипотезу Н2 = {Χ ί= Ρ}, где распределение Ρ имеет плотность
Г 2 при 2Α:Δη ζ * < (2k + 1)Δη,
/U \θ при (2Α:+1)Δη^ί<(2Α: + 2)Δη,
k = 0,1,.. .,Ν - 1, где Δη = 1/27V, N = Nn > 0 целое. Тогда при Δη = о{рГ1'2)
функция распределения Fp(t), соответствующая распределению Р, будет обладать
свойством
sxip\FP(t)-t\ = o{n-^2).
t
Это значит, что гипотеза Н2 как гипотеза для функции распределения будет
настолько близкой к Hi = {X ^ Uo,i}, что критерии Колмогорова и и;2
асимптотически их различать не будут (предельное значение мощности в точке Ρ будет
совпадать с предельным уровнем критерия). Однако как гипотезы для плотностей
гипотезы Н\ и Н2 существенно различны, так как sup|/(£) - 1| = 1. Поскольку
Х(о) = 0, Х(п+1) = 1> то Для X €? Ρ статистика Мп будет превосходить величину
Δ^Ν = Δ„/2. Стало быть, при η/Ν = 2пАп -> оо с Р-вероятностью, равной 1,
будем иметь
пМп -» оо.
Фиксировав критическое множество Ω2 — {пМп > 3}, получим Ρι(Ω2) —> 0.
Это означает, что при Δη = ο(η-1/2), Δηη -* оо критерий Морана с вероятностью,
близкой к 1, будет различать гипотезы Hi и Н2. Другими словами, статистика Мп
чувствительна к отклонениям в плотности, а сам критерий Морана можно
рекомендовать как критерий для проверки гипотез, относящихся к плотностям. С другой
стороны, мы знаем из § 10, что скорость сближения эмпирических плотностей с
истинной медленнее, чем п"1/2. Поэтому «неразличимость» гипотез о плотностях,
отличающихся друг от друга на величину порядка п"1/2 (см. (10)), не является
удивительной.
В связи с критерием Морана и некоторыми другими критериями,
рассмотренными ранее, можно сделать одно общее замечание. Если сравнивать два критерия
одного фиксированного уровня, первый из которых предназначен для отбраковки
большего числа альтернатив, чем второй, то мощность первого критерия для каждой
фиксированной альтернативы (отвергаемой обоими критериями) будет, как
правило, меньше, чем мощность второго. Наиболее простой пример, иллюстрирующий
это обстоятельство, читатель может получить, рассмотрев критерии |χι| > λε/2 и
χι > λε, предназначенные соответственно для проверки гипотез {а ф 0} и {а > 0}
против {а = 0} по наблюдению χι ί= Фад. Здесь Хе есть квантиль распределения
Фод порядка 1 — ε. Мощности в точке а > 0 будут равны соответственно
1 - Фод {-К/2 - ос, Х£/2 - а) < 1 - Φ(Χε - а).
§ 53. Асимптотически оптимальные критерии.
Критерий отношения правдоподобия
как асимптотически байесовский критерий
для проверки простой гипотезы против сложной
1. Асимптотические свойства к. о. п. и байесовского критерия.
Рассмотрим задачу проверки простой гипотезы Н\ = {X €= РяЛ против сложной
альтернативы Η<ι = {X €= Р#; θ φ 0χ, θ Ε Θ} в параметрическом случае.
398
Гл. 3. Теория проверки гипотез
В предыдущих параграфах мы видели на примерах, что р. н. м. к. в этом
случае, как правило, не существует.
Будем рассматривать «частично байесовскую» постановку задачи,
которая была описана в §44, 49. Она состоит в предположении, что θ выбирается
на 02 = Θ \ {θχ} случайно с распределением Q2 = Q. Можно считать, что
Q задано на Θ, Q({#i}) = 0. В этом случае распределение выборки X будет
определяться «усредненной» плотностью
fQ(x) = J ft(x)Q(dt). (1)
Таким образом, если Q известно, то гипотезу Hq2 = #q, в силу которой X
имеет распределение с плотностью (1), вместе с Hi можно рассматривать как
простую гипотезу и пользоваться леммой Неймана-Пирсона для построения
наиболее мощного критерия.
Оказывается, что в этом случае для «почти всех» гладких Q наиболее
мощные критерии будут асимптотически совпадать с критерием отношения
правдоподобия
sup MX) ( .
R{X)- MX) -i^m>c (2)
и, стало быть, не зависеть от Q. Этот факт позволяет считать найденный
критерий асимптотически оптимальным по крайней мере в тех случаях,
когда можно предполагать, что θ в ©2 выбирается случайно, но его
распределение Q нам неизвестно.
Прежде чем формулировать соответствующую теорему, напомним
некоторые нужные нам результаты и докажем одно вспомогательное
утверждение. Главную роль в нем будут играть уже известные нам асимптотические
свойства отношения правдоподобия. Будем сразу рассматривать случай
многомерного параметра; все необходимое для этого имеется в § 36, 37.
Итак, пусть 0 Ε θ С К*1, к ^ 1, и выполнены условия регулярности (RR),
формулировка которых дана в §36. Пусть, кроме того, Q имеет плотность
q(t) относительно меры Лебега X(dt) = dt.
В соответствии с леммой Неймана-Пирсона наиболее мощный
нерандомизированный критерий π<22 = ttq для проверки Н\ против Hq будет иметь
следующий вид: ttq(X) = 1, если
n{c) = {x:juχ)>c}, Iq{x) = /«μλλ*)**'
где с = сп выберем позже по заданному уровню критерия.
Такой же вид будут иметь и байесовские критерии для проверки Н\
против Hq.
Вероятности ошибок первого и второго рода равны соответственно
(4)
§ 53. Асимптотически оптимальные критерии
399
где P{ttq) = / /(3(χ)μη(άχ) есть мощность наиболее мощного
{fQ(xKcfei(x)}
критерия.
Аналогичные выражения сможем записать для к. о. п. π, который
принимает Hq при выполнении (2):
ai(7r)=p4tw>cJ'
α2(π) = У 9(t)Pt (|^|y < с) <ft = J Μχ)μη(άχ).
(5)
{/?.(*)<«!/·!(■)}
Положим I = 1{θ\) (значение информационной матрицы Фишера в
точке 6>ι),
Тогда критические области критериев 7Гди? (см. (3), (2)) можно записать
соответственно в виде
T(X)>cQ, T(X)>c. (7)
Лемма 1. Пусть выполнены условия (RR) §36, Χ ^ Р#1? θ\ —
внутренняя точка Θ. Тогда
2Т(Х) = 2Т(Х)(1 + εη(Χ)) @. Hfc) en{X) -^ 0.
Доказательство. Утверждение леммы есть очевидное следствие
теорем 36.4, 36.5. Надо лишь заметить, что Т(Х) в обозначениях теоремы 36.4
есть не что иное, как Y(u*) (при θ — θ\). <
2. Асимптотическая байесовость к. о. п. Перейдем к формулировке
основного утверждения. Напомним, что когда мы изучаем асимптотические
свойства критериев, на самом деле имеем в виду не один, а целую
последовательность критериев π = πη, где πη есть критерий, основанный на выборке Хп.
Такую же ситуацию мы имели, рассматривая асимптотические свойства
оценок. Таким образом, здесь и в дальнейшем — везде, где это потребуется —
под критерием π мы будем понимать последовательность функций πη(Χη),
определенных при каждом η и Хп = [Χοο]η·
Определение 1. Критерий π для проверки гипотезы Н\ == {Θ £ Θι}
против Ή.2 = {θ Ε Θ2} принадлежит классу Κε критериев
асимптотического уровня 1 — ε, если
limsup sup Έβπ(Χ) ^ ε. (8)
π->οο 0£θι
400
Гл. 3. Теория проверки гипотез
В нашем случае, когда гипотеза Н\ является простой и θ ι = {0ι},
соотношение (8) превращается в неравенство
limsupE^^(X) ^ ε.
гс-юо
Пусть h£ есть квантиль порядка 1 — ε распределения χ2 с А; степенями
свободы (Hfc((/ie, оо)) = ε). Тогда из леммы 1 вытекает, что kq Ε Ке, т? €
Ε Ке, если cq = ? = Ле/2.
Определение 2. Положим eg = Λε/2, так что πρ Ε ife. Критерий
π £ Κε называется асимптотически байесовским критерием (а. б. к.) в
Ке для проверки гипотезы Н\ = {0 = #ι} против Яд, если для
вероятностей ошибок второго рода, вычисленных при гипотезе Hq, справедливо
соотношение
lim sup 2; \ = lim sup -£-*- = lim sup —^ V^T = L
Мы использовали в этом определении отношение (а не разность)
вероятностей ошибок второго рода, так как с*2(я"д) —> 0 при η —> оо.
Теорема 1. Пусть выполнены условия (RR), точка θ\ является
внутренней точкой Θ. Тогда критерий отношения правдоподобия π (см. (2),
(7)) при с = h£/2 принадлежит Ке и является а. б. к. в Κε для проверки
Н\ против Hq при любом распределении Q, плотность q(t) которого
непрерывна и положительна в Θ. При этом
где I = I(#i), Vk — объем единичного шара в Шк.
Доказательство. Принадлежность π Ε Ке при с = h£/2 нами уже
доказана. Рассмотрим теперь ошибки второго рода. В силу (4), (7) имеем
«2(π<?) = J ία{χ)μη{άχ) = Εβι {^fy! 2T(X) < Λε} =
= &) ^^;2Τ(Χ),Μ·
Здесь под знаком математического ожидания стоит ограниченная функция
от 2Г, непрерывная п. в. относительно предельного распределения Н^. По-
§ 53. Асимптотически оптимальные критерии
401
этому при η —> оо, χ1 €= Η*
Εθι(βΓ(χ);2Γ(Χ) < he) -> Ε{β^2;χ2 ^ hg} =
= (2π)^/2 I e5M24lvl2d2/1...d2/, = (27r)-^/2Ffe.
{lvla*M
Найдем теперь асимптотическое поведение агО?). Положим Ап = {X : kq φ
Φ π}. В силу леммы 1 P^j (An) -> 0. Поэтому из теоремы 37.5 вытекает, что
при любом фиксированном N
sup Ρθ+η/νϋ(Αη) ~> °· (9)
Воспользуемся представлением (см. (5))
a2(n)=Jq(t)Pt(f(X)^c)dt =
f + j ^fq(t)Pt(T(X)^c)dt +
+ j q(t)Pt(An) dt + j q(t)Pt(T(X) < c) dt.
\ί-θι\^Ν/^/η \t-0i \>N/y/E
В силу (9) мы получаем
lim sup гг^аг (π) < lim nfc/2a2(7rg) +
п-юо n^°°
+ max q(t) lim sup / Ρ Л {*' J < eA dt
1 n-юо J \;θι{Λ) }
|«-0ι|>ΛΓΛ/η
Но вероятность под знаком интеграла не превосходит
Ρ
Ч^(Ж^е J^exp\2—— у (10)
Здесь мы использовали теорему 36.L Следовательно, сам интеграл не
превосходит
1 ес/2 [ e-\uf9,2du^0
yjn J
\u\>N
при Ν —> оо. Отсюда следует, что
lim sup η^α^π) < lim пк/2а2{^). (11)
п-юо n~>oo
Очевидно, это равнозначно тому, что π есть а. б. к.
402
Гл. 3. Теория проверки гипотез
Нам осталось установить только, что α2(π) ~ a<z(nQ) или, что то же в
силу (11),
liminfn*/2a2(7r) ^ lim пк/2а2Ып)> (12)
Для этого заметим, что построенный нами критерий kq является
байесовским, соответствующим априорной вероятности q\ гипотезы Н\,
определяемой из уравнения (ср. (3), (6))
1-91 V"/ V\I\
Это означает, что вероятность ошибки ttq будет вести себя асимптотически
как
eqi + (1 - <7i)a2(7TQ) ~ eqi + α2{πς).
Если допустить, что (12) неверно, то мы получим критерий π, для которого
вероятность ошибки будет меньше. Так как это невозможно, (12) доказано.
Теорема полностью доказана. <
Из приведенных рассуждений видно, что основной вклад в
вероятности ошибок второго рода вносят случайные значения 0, попадающие в
п~*/2-окрестность точки θ\ (этим обуславливается порядок малости п~к12
этих вероятностей).
Незначительные изменения в рассуждениях доказательства теоремы 1
позволяют получить также следующее утверждение.
Теорема 2. Критерии π' и π" с критическими областями
Ω' = {χΕΧη: η(θ* - θχ)Ι{θι)(θ* - 0Х)Т > /ιε},
Ω" = {xeXn: L,{x,01)rl(0l){L'(x,e1))T > he)
являются наряду с π а. б. к. в Ке. Это свойство сохранится, если в (13)
1{θι) заменить на 1(0*).
Критерии (13) получаются, если воспользоваться разложением
1п 7*Щ = L[x^]~ЦХЛ)
в ряд около точки Θ* (см. теорему 36.4). Форма критерия 7? в известном
смысле более удобна, так как она с размерностью не связана.
Доказательство теоремы 2 мы предоставляем читателю.
В одномерном случае критическое множество Ω' (при замене 1{β\) на
/(#*)) имеет вид
Ω!=1\θ·-Θι\>\ \ \, (14)
§ 53. Асимптотически оптимальные критерии
403
где, очевидно, he = λ2,2, Φο,ι((-λε/2, λε/2)) = 1 — ε. Мы видим, что
соответствующий (14) критерий π', асимптотически эквивалентный π, можно
интерпретировать так: π'(Χ) = 1, если θ\ не попало в доверительный
интервал асимптотического уровня 1 — ε для параметра 0, построенный
с помощью о. м. п. Θ*.
Такая же интерпретация сохранится, очевидно, и в многомерном случае;
доверительные множества при этом будут иметь форму эллипсоидов:
(Θ*-Θ)Ι{Θ*)(Θ*-Θ)Τ <п~Ч.
Мы видим, таким образом, что о. м. п. тесно связаны с а. б. к.
Пример L Пусть X €= Пд и проверяется гипотеза Н\ = {λ = λι}
против #2 = {λ Φ λι}. Β этом случае λ* = χ, Ι(Χ) = λ-1, и а.б.к. будет
иметь вид
η '
где Ηι((/ιε,οο)) = ε.
Пример 2. Пусть X ^ Φα,σ2 и проверяется гипотеза Н\ = {(α,σ2) =
= (c*i,ctj)} против дополнительной альтернативы. Здесь а* = χ, σ2* =
= 52 = ~Σ(χ« ~^)2' /(α'σ2) = (^ a-4/2j (СМ· §26)· П09Т°МУ a-6,K-
имеет вид
(х-α,)2 (S*-a?K he
σ\ + 2σ| η '
где H2((/ie,oo)) = ε.
3. Асимптотическая несмещенность к. о. п. В заключение этого
параграфа установим, что к. о. п. (2) является асимптотически несмещенным.
Напомним предварительно, что критерий π для проверки Н\ = {θ Ε Θχ}
против Ή.2 = {θ Ε Θ2} называется несмещенным, если
inf Ε#π — sup Ε#π ^ 0.
Определение 3. Критерий π называется асимптотически
несмещенным^ если
lim inf ( inf Ε^π — sup Ε^π) ^ 0.
п-юо \ве®2 ве&1 '
Теорема 3. К. о. π. π (см. (2), (6), (7)) для проверки Н\ = {θ = θχ}
против Ή.2 — {θ Φ θχ] является асимптотически несмещенным.
Доказательство. Так как в нашем случае θχ = {θχ} и lim Έ$.π = ε,
71-ЮО
то достаточно убедиться, что
__ t 'Μα**,*
?Aoo ike l n^oo ike ъ \fe1{X)
lim inf inf Ε*π = lim inf inf Pt ( f ,~v[ > e° ) > ε> (15)
где сГ = h€/2.
404
Гл. 3. Теория проверки гипотез
Из оценки (10) следует, что существует N > 0 такое, что
Ш§>')
inf Ρ, [ Ч^тг > ес ) > ε.
\t-9i\ZN/y/E
Остается доказать, что inf Ε^π —> ε.
\t-0i\^N/y/E
Но в силу теорем 36.4, 37.3 при X ^ T?t равномерно по гх, \и\ ^ ЛГ,
и = v/n(t — #ι),
f(x)^^(e-U)/(e-u)T, ^φ0ι/-ι,
Е47г^р{^(е-и)де-«)т>с = ^).
Правая часть здесь достигает своего наименьшего значения при и = 0. Это
значение равно Έ*(ξΙξτ > h£) = ε. <
§ 54. Асимптотически оптимальные критерии
для проверки близких сложных гипотез
1. Постановка задачи и определения. В §43 мы обсуждали два
асимптотических подхода в задаче о проверке двух простых гипотез Н\ и Щ. Если
эти гипотезы считать фиксированными, т. е. неизменными при растущем
объеме η выборки Л"п, то мы приходим при вычислении вероятностей
ошибок к задаче о вероятностях больших уклонений, так что по крайней мере
вероятность одной из ошибок сходится к нулю. Согласно другому подходу
гипотезы Н\ и Ή.2 рассматриваются как элементы последовательности
«сближающихся» гипотез, при этом скорость сближения подбирается так, чтобы
вероятности ошибок первого и второго рода сходились к собственным
(отличным от нуля и единицы) пределам. Мы видели, что в параметрическом
случае значения параметра θ\ и #2> соответствующие близким гипотезам Н\
и i?2, должны отличаться на величину порядка п-1/2. Каждый из этих
подходов может быть оправдан в зависимости от конкретных условий.
В предыдущем параграфе мы рассматривали не зависящее от η
распределение Q для альтернативного значения θ и, как это естественно было
ожидать, получили, что вероятность ошибки второго рода сходится к нулю
как п-/с/2. Это обусловлено тем, что основной вклад в эту вероятность вносят
близкие гипотезы, для которых θ удалено от θ\ на расстояние порядка п"1/2
(объем области, содержащей такие 0, и будет иметь порядок малости n~k'2).
В этом параграфе мы рассмотрим задачу о проверке близких сложных
гипотез, когда альтернативные значения параметра сближаются при η —>
—> оо. Оказывается, что в этом случае задачу проверки гипотез можно в
известном смысле редуцировать к значительно более простой задаче для
нормального распределения.
Перейдем к более точным формулировкам. Пусть по выборке X €= Р#
проверяется гипотеза Hi = {θ Ε Θι} против Η<ι — {θ Ε 02}. Фиксируем
какую-нибудь внутреннюю точку θ\ множества Θ и положим
θ = θχ+Ίη-χΙ2. (1)
§ 54. Близкие сложные гипотезы
405
Предположим теперь, что множества Θ; имеют вид
Эг-^+ГгП"1/2, (2)
где Гг от η не зависят. Запись (2) означает, что θ £ θ; тогда и только тогда,
когда в (1) 7 € IV Гипотезы Щ = {Θ Ε Θ*} при условии (1) мы будем,
как и в §43, называть близкими (на самом деле это последовательность
гипотез — своих для каждого п).
Задачу проверки близких гипотез Hi по выборке X €= Р# будем называть
задачей А.
Рассмотрим теперь другую задачу. Пусть У €= Φ7,/-1 есть выб°Рка
единичного объема из нормальной совокупности Φ7/-ι с вектором средних
значений 7 и матрицей вторых моментов 1~1 = /_1(0ι), где Ι(θι) есть
информационная матрица Фишера для задачи А в точке θ\. Обозначим
через \)i гипотезы {7 £ 1\}. Задачу проверки гипотез fo по одному
наблюдению У €= ^7,/-1 будем называть задачей В.
Замечательный факт, позволяющий делать упомянутую выше редукцию,
состоит, грубо говоря, в следующем. Пусть π(Υ) есть оптимальный в том
или ином смысле критерий (р. н. м. к., байесовский, минимаксный) для
проверки 1)ι против 1)2 в задаче В. И пусть 0*, как обычно, есть о. м. п. в
задаче А, 7* = (Θ* — в\)у/п. Тогда критерий π(7*) для проверки Н\ против #2
в задаче А будет асимптотически обладать теми же свойствами
оптимальности, что и критерий π (У) в задаче В.
Таким образом, чтобы найти асимптотически оптимальный критерий в
задаче А, Мы должны рассмотреть более простую задачу В и найти в ней
(если это возможно) критерий π, обладающий нужным свойством
оптимальности. Если теперь взять в качестве наблюдения У значение 7* и подставить
его в π, то мы получим искомый критерий в задаче А.
Этот факт можно было бы назвать предельным признаком
оптимальности. Смысл его довольно прост. Ведь мы знаем из результатов главы 2, что
при X ^ Р#
νη(β*-0)/1/2(0)θ>Φο,β
равномерно по Θ. Стало быть, для θ = θ\ + ηη~ιΙ2
λ/ϊ{θ*-θ1)--γ&Φθ9ΐ-4θι)
или, что то же,
7* ©>Φ7ι/-ι.
Таким образом, Φ7,/-ι — распределение, присутствующее в задаче В, есть
не что иное, как предельное распределение для 7*· Поэтому предельный
признак оптимальности является весьма естественным: он сводит задачу
проверки гипотез к «предельной» задаче. Замечательным во всем этом является
тот факт, что при такой редукции никакой существенной потери
информации относительно θ не происходит: критерий, оптимальный в задаче В,
сохраняет эту оптимальность и для задачи А.
Чтобы придать изложенному точный смысл, введем теперь основные
понятия асимптотической оптимальности критериев для проверки близких
гипотез в задаче А.
406
Гл. 3. Теория проверки гипотез
Определение класса КЕ критериев π асимптотического уровня 1 — ε дано
в предыдущем параграфе (определение 53.1). Для π £ Κε справедливо
limsup sup Еетг(Х) < ε.
η->οο θ€Θι
Определение 1. Критерий πι Ε Κε называется асимптотически
р. м. м. к. (а. р. н. м. к.) е K£j если для любого η Ε Γ2 и любого π € Ке
liminf(E*7ri(X) - Εβπ(Χ)) > 0,
где б = 01 + jn~1/2 e &2 при 7 £ Г2.
Пусть на Fi заданы распределения Пг. Эти распределения индуцируют
на ©г некоторые другие распределения (сосредоточенные в
п~^-окрестности точки 01), которые мы обозначим через Qi, i = 1,2. Гипотезы о том,
что 0 выбирается случайно с распределением Qi, как и прежде, обозначим
через #q..
Через Κε будем обозначать класс критериев π, для которых
HmsupEg^(X) ^ ε,
тг-юо
где Eq. означает безусловное математическое ожидание по совместному
распределению 0 и X, 0 €= Qi, X €= Р#. Очевидно, что ife С К£ при любом Q.
Определение 2. Критерий πι £ Ке для проверки #φχ против Hq2
называется асимптотически байесовским критерием (а. б. к.) в Κε , если
для любого другого критерия π Ε
liminf(Eg27riPO - Ед2тгрО) > 0. (3)
η—>оо
Можно дать эквивалентное определение асимптотической байесовости, в
котором вместо (3) требуется, чтобы
liminf(Egain(X) - Eq2kQiQ2(X)) > 0, (4)
71—>00
где TtQxQ2 — байесовский критерий из Κε для проверки гипотез Hq1
против Hq2 (или, что то же, н. м. к. критерий для проверки Hq1 против Hq2
асимптотического уровня 1 — ε).
Следует отметить, что определение 2 несколько отличается от
определения а. б. к., которое было дано в предыдущем параграфе (см.
определение 43.2; там фигурирует отношение вероятностей ошибок, а не разность).
С точки зрения последующего изложения эти определения эквивалентны, но
последнее из них нам будет удобнее.
Определение 3. Критерий πι Ε Κε называется асимптотически
минимаксным в КЕ критерием для проверки Н\ против Нъ, если для любого
другого критерия π Ε Κε выполняется
liminf( inf Ε0πι(Χ) - inf ΕΘπ{Χ)) ^ 0. (5)
n-юо ν0<=θ2 0€θ2
§ 54. Близкие сложные гипотезы
407
Как и при рассмотрении обычных минимаксных критериев (см. §49),
множества Θι и 02 во избежание малосодержательных рассмотрений
разумно разделить некоторой промежуточной зоной так, чтобы они не
соприкасались. В противном случае оба нижних предела в (5) могут оказаться
равными ε для любого асимптотически несмещенного критерия π.
Из приведенных определений видно, что свойство той или иной
асимптотической оптимальности отличается от обычного свойства той же
оптимальности лишь тем, что перед соответствующей разностью появляется знак
liminf вместо inf.
Наряду с асимптотически байесовскими и минимаксными критериями
в классах Κε и К?1 можно изучать обычные асимптотически байесовские
и минимаксные критерии. Пусть на θ = Θι U ©2 задано распределение
Q = g(l)Qi + g(2)Q2, q(l) + q{2) = 1. Тогда критерий πι называется
асимптотически байесовским для априорного распределения Q, если для
любого другого критерия π
liminf [g(l)E0lщ(Χ) + g(2)Eg2(l - щ(Х))-
-9(1)Εριπ(Ζ)-ς(2)Ερ2(1-π(Χ))]<0. (6)
Усредненная по Q вероятность ошибки критерия π, присутствующая в этом
неравенстве, может быть записана с помощью вероятности α(π,0) ошибки
в точке θ в виде Ες>α(7Γ,0), где
( θ)^ίΈ^(Χ) при β€θι,
а[7Г' ] \Ε*(1-π(Χ)) при 0ев2.
Тогда неравенство (6) примет вид
liminf Εη[α(πι(Χ),θ) -α(π(Χ),0)] < 0.
п-юо
Критерий πι будет асимптотически минимаксным, если
liminf [sup α(πι, θ) — 8ΐιρα(π,0)] < 0
для любого другого критерия π.
Изучение асимптотических байесовских (в Κε) и асимптотически
минимаксных (в Κε) критериев и просто асимптотически байесовских и
минимаксных критериев, по существу, представляет собой одно и то же.
Например, байесовский критерий в есть обычный байесовский критерий
при соответствующем q(l). В этом параграфе мы будем изучать критерии
из классов Κε, Κε; обычные асимптотически байесовские и минимаксные
критерии будут рассмотрены в главе 6 при исследовании более общей
постановки задачи.
2. Основные утверждения. Чтобы максимально упростить дальнейшее
изложение, введем одно предположение, которое с существом дела никак не
связано и которое при желании может быть убрано — все необходимые для
этого результаты имеются. Именно, будем предполагать, что множества 1\
ограничены, т.е. существует N > 0 такое, что 1\ С {7 : |т| ^ Ν}.
408
Гл. 3. Теория проверки гипотез
- определение 4. Критерии πι, π2 для проверки близких гипотез Нх =
= {Θ € θι), Я2 = {0 Ε Θ2} по выборке X называются асимптотически
эквивалентными, если
lim sup \Εθπχ(Χ) - Εθπ2(Χ)\ = 0. (7)
При сделанном предположении можем под знаком sup в (7) поставить
область |0 — 0i| ^ N/y/n.
Асимптотически эквивалентные критерии πι, π2 обладают следующими
свойствами: _ _ _ _
1) если πι Ε ΛΓε (шш К?1), mo π2 Ε ί?ε (if?1);
2) если πι обладает одним из свойств асимптотической
оптимальности в определениях 1-3, то тем же свойством будет обладать
критерий π2.
Первое утверждение вытекает из (7) и неравенства
sup Ε^π2(Χ) ^ sup Ε$πι(Χ) + sup |Ε#(π2 - πι)|.
0€θι θβθι θ£θι
Второе утверждение доказывается аналогично. Если, например, πι
является асимптотически минимаксным, то асимптотическая минимаксность π2
будет следствием (7) и неравенства
inf Εθπ2(Χ) ^ inf E^i(A") - sup |Ε^(π2 - πι)|. <
0€θ2 9еВ2 θ€θ2
Условия асимптотической эквивалентности критериев устанавливает
Лемма 1. Пусть в окрестности точки θ\ выполнены условия (RR),
щ(Х) = I{Tn(X)+eni(X)>c}i * = 1,2, где для X €= Р^ имеют место
соотношения eni(X) —> 0, Тп(Х) ©■ G, распределение G непрерывно. Тогда
критерии πι, π2 асимптотически эквивалентны.
Доказательство. Имеем |Ε^πι(Χ) - Ε*π2(Χ)| ^ Pt(An), где для
события Ап = {ττι(^) т^ К2{Х)} выполняется Р^(АП) = Ρβ1(Τη(Χ) +
+ εη1(Χ) > с, Тп(Х) + εη2(Χ) ζ с) + Ρ$ι(Τη{Χ) + εη1(Χ) < с, Т„(Х) +
4- еП2{Х) > с) -> 0 при η -> оо, так как предельное распределение Тп
непрерывно. Стало быть, в силу теоремы 37.5
sup P*(An) -> 0. <
i*-0itetf/^/n
Байесовский критерий уровня 1 — ε в задаче В для проверки гипотез
1)п< о том, что 7 выбирается случайно с распределением П; на Г^, г = 1,2,
обозначим через ππ1π2(^)· Он имеет вид
fexp{-l(Y-u)I(Y-u)T)n2(du)
r(Y) = Lr И > с, (8)
у ехр |--(У - «)/(У - u)T J Πι (Αι)
§ 54. Близкие сложные гипотезы
409
где с = се выбирается из условия
/^(7,c)n1(d7) = ε, φ{Ί,6) = Р(г(У) > с), У ^ Ф7|/-ь (9)
Это соотношения означают, очевидно, что ЕщтгщПгОО — ε·
Заметим, что г(у) есть аналитическая функция от у. В силу
аналитичности эта функция не может принимать постоянное значение на
множестве положительной меры Лебега или меры Φ7ί/-ι (в противном случае она
была бы постоянной всюду, что возможно лишь при Πι = Пг). Значит,
Р(г(У) = с) = 0 при любом с и распределение r(Y) непрерывно.
Пусть, как и прежде, 7tq1q2(X) обозначает байесовский критерий
асимптотического уровня 1 — ε в задаче А.
Теорема 1. Пусть условия (RR) выполнены в окрестности точки θ\.
Тогда критерий гг(Х) = 7τπιΠ2(7*)5 7* = (#* ~~ 0ι)ν™> асимптотически
эквивалентен критерию ^qxq2 Щ стало быть, является
асимптотически байесовским.
Кроме того,
sup \Εθι+Ί/νήπ(Χ) - <р{Ъс)\ -> 0 (10)
\ίΚν
при η —> оо, где <£>(7>с) = Ε7ππ!Π2(^) определено в (9).
Доказательство. Рассмотрим байесовский критерий π^^2 в
задаче А. Он имеет вид
тт ... f/*+u/vs(*)n2W . г
1 J //^μγΡΟΠι^Γ '
Если X ^ Р#15 то в силу теоремы 36.5
Т(Х)=г(1*)(1+е(Х,в1))
(7* = и* при б = θ\). Так как распределение r(Y) непрерывно, 7* =>■ У €=
^ Фо,/-1 и так как критерий π имеет вид г(7*) > с, то в силу леммы 1
первое утверждение теоремы доказано.
Соотношение (10) следует из представления
Ε*ι+7/ν^π(Χ) = E*i+7/v^7M7*)>c} -> РМУ) > С),
У ^ Φ7?/-ι, и теоремы 37.4. <
Теорема 2. Пусть в окрестности точки θχ выполнены условия (RR),
7* = (**-0i)V".
Пусть, далее, существует минимаксный критерий πι (У) уровня 1-е
для проверки \}\ против 1)2 β задаче В w этот критерий является
байесовским
πι00=πΠιιι2(η (И)
410
Гл. 3. Теория проверки гипотез
при априорных распределениях Πι, Пг, удовлетворяющих условиям
ΕΠιπι(Κ) = suPE77r(Y),
76Γι
(12)
Еп2тг1(У) = inf ΕΊπ(Υ), Υ (= Φ ,_ι
(ср. с условиями теоремы 49.1). Тогда критерий π(Χ) = ππιΠ2(7*) будет
асимптотически минимаксным в классе Ке критериев для проверки Н\
против #2 в исходной задаче А.
Доказательство. Так как πι есть критерий уровня 1 — ε, то
sup Ε7πι(Γ) = ΕΠιπ(Υ) = ε.
7€Γι
В силу (10), (12) отсюда получаем
lim sup E,1+ 7/v/^rQlQ2(X) = lim EQlnQlQ2{X) = ε.
η—^°°7^Γι η—>οο
Это означает, что ^qxq2 € Κε, πς^ Ε /С?1.
Надо доказать теперь, что для любого критерия π* £ ΛΓε
lim inf [ inf ΈΘπ(Χ) - inf Έθπ*(Χ)]) > 0.
n->oo Ug02 0€02 -I
Имеем
limsup inf ΕΘπ*(Χ) ^ HmsupE^*(X) < limsupEg^Q^JX). (13)
Последнее неравенство справедливо в силу байесовости kq1q2 (т.е.
минимальности qi1^Q17tQ1Q2 + (1 - 5i)Eq2(1 - nQ1Q2) при соответствующем gi) и
того, что limsupEQ17r*(.X') < ε, ΙϊτηΈςιπςις2 = ε.
Далее, в силу (10), (12) и теоремы 1 правая часть в (13) равна
lim Eq2tti(7*) =Επ2ππ1π2(^Γ) =
η—>оо
= ^2Ε7πΠιΠ2(^) = п1|ш^ mf Εβι+7/^πβιί}2(Χ). <
Теорема 3. Пусть существует р.н.м.к. πι (У) уровня 1-е для
проверки f)i против f)2 β задаче В. Предположим, кроме того, что для
любого 72 € Гг существует распределение Πι wa Γχ такое, что
πι(Υ) = *ηιη2(Υ) (14)
есть байесовский критерий для проверки ()Πι против f)n2 {здесь U2 со-
средоточено в точке 72)· Тогда критерий π(Χ) = πι(7*) является
а.р.н.м.к. (асимптотического уровня 1 — ε) <?лл проверки Н\ против
#2 б исходной задаче А.
§ 54. Близкие сложные гипотезы
411
Отметим, что для задач §45-47 условие (14) всегда выполнено. Это
следует из самого построения р. н. м. к. в этих параграфах.
Доказательство теоремы 3. Принадлежность πι(7*) Ε Κε следует
из теоремы 1, так как
lim sup Ε07Γΐ(7*) = sup lim Ε^πι(7*) = sup φ{η, с) ^ ε.
>0€θι 0€Θιη·^°° 7€Г
Пусть теперь π* — любой другой критерий из К£. Тогда
limsupEQ^*(X) ^ lim sup sup Ε^π*(Χ) ^ ε,
η->οο η-ϊοο θζΘι
и, стало быть, π* можно рассматривать так же, как критерий из Κε для
проверки Hq^ против Hq2, где Qi индуцировано распределением Π χ (см.
формулировку теоремы), a Q2 сосредоточено в точке 02 = #ι +72^-1^2· Если
nQiQ2 — байесовский критерий асимптотического уровня 1 — ε для этих
распределений, то
lim Ee2nQlQ2(X) ^ limsupE027r*(X).
П-+00 П-+00
Но левая часть этого неравенства совпадает в силу теоремы 1 со значением
lim Ε02πΠιπ2(7*) = Ит Е^тг^*). <
η—>оо η—юо
Аналогичным образом можно искать асимптотически р. н. м. к. в классе
асимптотически несмещенных критериев.
Замечание 1. Если распределения Πι, Пг сосредоточены
соответственно в точках 71 и 72> то
г(У) =
ехр|~(У-72)/(Г-72)Т}
exp|-|(r-7i)/(r-7i)T}
Стало быть, критическая область ππιΠ2(^) будет иметь вид
У/(72-71)т = (У/,(72-71))>с
В одномерном случае мы получаем отсюда а.н.м.к. (43.21), изучавшийся
нами в §43.
Замечание 2. Если распределение Πι сосредоточено в точке и = 0, а
распределение Пг является равномерным в шаре \и\ < iV, то знаменатель
функции r(Y) будет равен ехр < —~YIYT > , а числитель при больших N и
\у\ < N — у/N будет близок к у/\Г\(2к)к/2. Стало быть, критическая область
для 7ΓΠιΠ2 ПРИ таких Πχ, Пг будет близка к внешности эллипсоида
ΥΙΥΤ > с,
412
Гл. 3. Теория проверки гипотез
а критическая область асимптотически байесовского критерия 7гп1п2(7*)
будет близка к
7*/7*Т > с.
Это есть не что иное, как асимптотическая форма к. о. п., изучавшегося в
предыдущем параграфе (ср. с теоремой 43.2).
Замечание 3. В теоремах 2, 3 присутствуют условия о том, что
минимаксный критерий (теорема 2) или р.н.м.к. (теорема 3) для задачи
В являются байесовскими при некоторых распределениях Π; на IV Мы
увидим в главе 6, что эти условия излишни — класс всех байесовских
критериев содержит в себе все «неулучшаемые» критерии, в том числе р. н. м. к.
и минимаксные.
§ 55. Свойства асимптотической оптимальности
критерия отношения правдоподобия,
вытекающие из предельного признака оптимальности
В этом параграфе мы рассмотрим некоторые следствия результатов § 54,
связанные с критерием отношения правдоподобия. Мы установим, в
частности, асимптотические равномерную наибольшую мощность и
минимаксность к. о. п. для некоторых важных конкретных задач, связанных с
проверкой близких гипотез.
Везде в дальнейшем предполагается, что в окрестности точки θ\
выполнены условия (RR). Для сокращения выкладок нам будет удобно, как и в
предыдущем параграфе, считать, где это потребуется, что множества Г^
ограничены.
1. А.р.н.м.к. для близких гипотез с односторонними альтернативами.
Пусть параметр 0 одномерный и проверяется односторонняя гипотеза Н\ =
= {Θ < 01 + 7ι™~1//2} против гипотезы #2 = {0 > 02 = #1 4- 72™~1//2}>
71 < 72·
Теорема 1. Критерий отношения правдоподобия π(Χ) с
критической областью
sup fe(X)
RW Ξ tfnfm > c Μ
sup fe[X)
θββι
при Θι = {0 : 0 ^ 0ι + 7ι™~1/2}, Θ2 = {0 : 0 > θχ + 72™~1/2} w подходящем
с асимптотически эквивалентен критерию
Ί* = (θ*-θ1)^>οε = \εΓ1'2 + >η, Φ0,ι(λε) = 1-ε (2)
и является а.р.н.м.к. асимптотического уровня 1-е для проверки
Hi = {0 < 01 + 7irc"1/2} против Н2 = {0 > 01 + 72™~1/2}· В формулах (2)
I означает информацию Фишера /(0ι) в точке 9\ для семейства /#.
Доказательство. Из §45 следует, что для выборки У €= Φ7,/-ι
единичного объема из нормальной совокупности с известной дисперсией /_1
существует р.н.м.к. для проверки гипотезы f)i = {7 ^ 7ι} против 1)2 =
= {7 > 72} вида Υ > с£, где се определено в (2). Так же будет выглядеть,
§ 55. Свойства асимптотической оптимальности критерия 413
очевидно, байесовский критерий для вырожденных распределений,
сосредоточенных в точках 7ι и 72 (или в точках 71 и 7 > 7ь если 71 = 72)·
На основании этого из теоремы 54.3 следует, что асимптотически р. н. м. к.
асимптотического уровня 1-е для проверки Н\ против #2 существует и
имеет вид (2).
Нам осталось доказать, что критерии (1) и (2) асимптотически экви-
f (X)
валентны. По теореме 36.4, полагая Z\(t) = ^ ? будем иметь при
X
ВД =
/*(*)
sup Ζχ{ηη-χΙ2)
Ц>72
sup Z\{un~ll'1)
sup exp
U>72
sup exp
u<7i
|_Ι(7._„)2/+ε(2)ρο|
|_i(r_u)2/ + £a)w|
= Tn(X)+eW(X),
.«
гдееХ'(Х)—>0, i = 1,2,3,
Ρβι
Tn(X) = r(Y)
sup exp
U>72
{-i(7·-«)·/}
sup exp
u^7i
|exp{-2(7*-72)2-fj
72)2/ + ^(7*-7i)2/
при
при
7* <7Ь
71 < 7* < 72,
|exp|2(7*-7i)2^}
при 7* > 72.
Это есть непрерывная, монотонно возрастающая функция от 7*· Стало быть,
неравенство ТП(Х) > с эквивалентно неравенству 7* > с' при некотором с7.
Так как, кроме того, 7* =^ Υ €= Фо,/-Ь то распределение r(Y) абсолютно
непрерывно. Условия леммы 54.1 для критериев (1), (2) выполнены. <
2. А. р. н. м. к. для двусторонних альтернатив. Пусть параметр θ
по-прежнему одномерный, а задача А состоит в проверке гипотезы Н\ =
= {(Θ - 9i)y/n <£ (71,72)} против #2 = {(0 - 0i)<y/n G (7ь7г)Ь 72 > 71-
Положим
_ 71+72
7= —η—>
Δ =
72-7ι
414
Гл. 3. Теория проверки гипотез
Теорема 2. Критерий отношения правдоподобия тг(Х),
определенный в (1) при соответствующем с и Θχ = {θ : (θ — #ι)\/η ^ (71,72)},
©2 = {θ : (6 — в\)у/п G (7ъ72)}> имя w критерий
l7*-7l = l(0*-0i)\/^-7l<ce, (3)
где се определяется из уравнения Φο,ΐ-1^0 — Δ, с — Δ) = ε,
являются а. р. н. м. к. асимптотического уровня 1 — ε для проверки Н\ =
= {(0-0i)V™£ (7b72)} против #2 = {(0-0ι)\ΛΪ€ (71,72)}.
Доказательство этой теоремы вполне аналогично доказательству
предыдущей. Из §45 следует, что для задачи В, состоящей в проверке
по наблюдению Υ €= ^J"1 гип0тезы 1)1 = {7 Φ (7ь72)} против fo =
== {7 € (7ь72)}, существует р. н.м. к. вида с7 < F < с", где с7, с77
подбираются так, чтобы
Ф7ь/-1((с',с")) = Ф721/-1((с',с")) = £.
Нетрудно видеть, что мы удовлетворим этим соотношениям, если положим
с' = 7 — οε, с77 = 7 + се, так как
Φ7ι,/-ι((7 " се,7 + Се)) = Ф0|/-1((-се + А,се + Δ)) = ε,
^г,/"1 ((7 - се,7 + сс)) = Фо,/-1 ((-се - Δ, се - Δ)) = ε.
Кроме того, мы видели в §45, что для любого 7о € (71,72) существует g G
G (0,1) такое, что байесовский критерий тгщпг Для проверки гипотезы ()Πι
для распределения Πι: Πι({71}) = q, Πι({72}) = 1 — g, против гипотезы
Ьп2 — {7 = 7о} будет иметь вид
с' <Y< с".
Это означает, что условия теоремы 54.3 будут выполнены и критерий (3)
будет а. р. н. м. к. для проверки Н\ против #2·
Рассмотрим теперь к. о. п. (1) для областей Θ^, определенных в теореме,
и покажем, что он асимптотически эквивалентен (3). Как и в доказательстве
теоремы 1, из теоремы 36.4 получаем, что при X €= Р^
sup ехр\-1(Г-и)21 + е^(Х))
Ц£(71,72) t l )_ _
sup ехр\-1(Г-и)21 + е^(Х))
«£(71.72) I ^ J
= Τη(Χ)+ε£Ηχ),
sup Ziiun'1/2)
Ц€ (7Ь72)
sup Zi(un~1/2)
u£ (7l>72)
§ 55- Свойства асимптотической оптимальности критерия 415
гдее^РО—Ю, г
Р»1
1,2,3,
Т(Х) = г(7·) =
sup exp
«€(<*! ,72)
{-;(τ·-)»/}
sup S-r(7*-")2^l·
u^(71,72) I ^ J
exp
exp
-7i)2/
7i)2/}
{|(7--72)2/}
|exp{-i(7--72)2i}
при
при
при
7* <7b
7ι <7* <7ι>
7 < 7* < 72,
при 72 < 7*
Из этих равенств видно, что г(7*) есть непрерывная монотонно убывающая
функция от |7* — 7| (она симметрична относительно точки 7* == 7)· Поэтому
неравенство r(j*) > с эквивалентно неравенству |7* — 71 < с'· Так как 7* =>
=> Υ ^ Φ0/-ι, то условия леммы 54.1 выполнены. <
3. Асимптотически минимаксный критерий для близких гипотез,
касающихся многомерного параметра. Рассмотрим теперь многомерный
параметр 0. В этом случае а. р. н.м. к. для проверки гипотезы Н\ = {θ Ε ©ι}
против #2 = {Θ € ©2}j как правило, не существует, и мы рассмотрим задачу
построения асимптотически минимаксных критериев.
Сначала сделаем одно общее замечание, которое упростит дальнейшие
рассуждения. Оно состоит в том, что рассматриваемую задачу проверки
гипотез всегда можно «перепараметризировать» (т. е. ввести новый параметр)
так, чтобы информационная матрица I — ϊ{β\) в точке θ\ стала единичной.
Для этого достаточно сделать линейное преобразование и ввести новый
параметр β равенством
θ = βΓ1'2.
Тогда информационная матрица Фишера J(P) для параметрического
семейства Р/3/-1/2 будет равна в точке β\ = θ\ΙιΙ2
J(fa) = I-Wir1'2 = Ε.
В этом пункте иногда нам будет проще иметь дело с параметром β.
Вернуться к исходному параметру всегда можно с помощью обратного линейного
преобразования.
Итак, пусть / = 1{β\) = Ε. Рассмотрим задачу А, состоящую в проверке
по выборке X €= Р# гипотезы
Hi = {\θ - θχ\ ζ arC1/2} против #2 = {\θ - θχ\ > 6η"1/2}, α < 6. (4)
416
Гл. 3. Теория проверки гипотез
Теорема 3. Критерий отношения правдоподобия π, определенный
в (1) при соответствующем с и Θι = {θ : \θ — θ\\ ^ αη~ιί2}, ©2 =
= {θ : \θ — θ\\ ^ 6η-1/2}, асимптотически эквивалентен при любых
0 < α < b < оо критериям
%т>* (5)
|7Ί = |(δ'·-βι)^|>6ε, (6)
гс?е с2 есть решение относительно с уравнения
Рс(а) = Ρ((ξ! + α)2 + £ + ... + ξΐ > с2) = ε, (7)
и является асимптотически минимаксным критерием
асимптотического уровня 1 — ε для проверки гипотез Hi и Η<ι, определенных в (4).
Случайные величины ξι в (7) независимы, ξι ^ Φο,ι· Гарантированная
предельная мощность критериев π, (5), (6) равна pCe(b).
Доказател ьство. Задача В здесь будет состоять в проверке по
наблюдению Υ ^ Φη,Ε гипотезы 1)ι = {|7| ^ а] против 1)2 = {|т1 ^ Ь}. В
примере 49.1 мы видели, что в этой задаче существует минимаксный критерий
уровня 1 — ε, который имеет вид
\Υ\ > Се.
При построении этого критерия мы пользовались теоремой 49.1. Это
означает, что условия теоремы 54.2 выполнены. Следовательно, критерий
будет асимптотически минимаксным критерием асимптотического уровня
1 — ε для задачи А.
Критерий отношения правдоподобия (1) здесь будет иметь вид
sup Zi{un-ll2)
RW = Ш\( -im > с· (8)
sup Zi{un ι//·)
\u\^.a
Следуя в точности рассуждениям в доказательствах теорем 1, 2, мы
получим, что ЯрО = Тп(Х) + εη{Χ), εη{Χ) —► О, где
sup exp
Тп(Х)=гЮ=]^—
sup exp
{-\\τ-ηή
{-\\γ-«ή
Как и прежде, отсюда следует абсолютная непрерывность распределения
r(Y) и асимптотическая эквивалентность критериев R{X) > с и Тп(Х) > с.
Последний эквивалентен критерию
17*1 > с',
§ 55. Свойства асимптотической оптимальности критерия 417
который при с' = с£ будет критерием уровня 1 — ε. По теореме 54.1
(см. (54.10)) он будет иметь гарантированную предельную мощность,
равную рС5 (Ь) (см. теорему 49.2). <
Замечание 1. Если вернуться к первоначальному параметру (до
параметризации, переводящей 1{θχ) в единичную матрицу), то получим, что
утверждение теоремы будет справедливо относительно гипотез Щ = {θ Ε
£ ©i}, где (ср. с примером 49.2 при σ2 = Ι~ι)
θχ = {θ:(θ- 0ι)/(0ι)(0 - 0ι)Τ < ^η"1},
Θ2 = {θ : (θ - 0ι)/(0ι)(0 - 0ι)Τ ^ Λι"1}.
Критерий (6) примет форму
Τ„ ^ „2
(0* - βι)/(βι)(0* - βι)' η > с;
'ε
или (см. теорему 53.2)
L'(X,9l)r1(e1)(L'(X,e1))T>c2£. (9)
Критерий отношения правдоподобия, очевидно, не изменится, так как
величина максимума fe{X) в области θ{ не зависит от замены переменных (при
соответствующем преобразовании областей ©i).
Отметим также, что форма критерия (9) иногда более удобна, чем (5), (6),
^+*
так как не связана с вычислениями Θ*. Аналогичные замены можно сделать
для критериев (2), (3) в теоремах 1, 2. Мы предоставляем это читателю.
Замечание 2. Совершенно аналогично теореме 3 можно построить
асимптотически минимаксный критерий для таких задач А, которые
могут быть редуцированы к задаче В, рассмотренной в примере 49.5.
Замечание 3. В §53 мы построили а.б.к. для проверки гипотезы
{β — θ\} против {θ Φ 01}, который имеет вид к. о. п.
Таким образом, этот критерий, являясь а. б. к., обладает также свойством
асимптотической минимаксности при проверке гипотезы {θ = θ\} против
{{β ~ θι)Ι{θι)(θ - 0i)T ^ b2n~1} при любом Ъ > 0.
4. Асимптотически минимаксный критерий о принадлежности выборки
параметрическому подсемейству. Рассмотрим теперь к. о. п. в несколько
более сложной задаче о проверке гипотезы Н\ = (θ Ε ©ι} против Ή.2 =
= {θ Ε ©2}, когда размерность / множества θ ι положительна, но меньше
к > 1. Именно, пусть дана гладкая функция θ = g(a) от ί-мерного (/ < к)
параметра α Ε А\ С Ш1. Образ множества А\ в 0, порожденный
отображением #, обозначим через ©ι. Задача состоит в проверке гипотезы Н\ =
= {θ Ε ©ι} о том, что параметр θ принадлежит «кривой» ©ι (или о том, что
Χ ^ Ρρ(α) при некотором a £ А\), против дополнительной альтернативы
{X ^ Ря; θ £ ©ι}, так что в этом случае ©2 = θ \ ©ь Другими словами,
418
Гл. 3. Теория проверки гипотез
это есть задача о проверке принадлежности выборки X параметрическому
подсемейству распределений [Рд(ау,а £ Αι}.
К этому классу задач относятся, например, уже известные нам задачи
о проверке гипотезы {X €f Φαο>σ2} против {Χ ^ Φα,σ25 α Φ αο} ПРИ
данном ао и неизвестном о2 или о проверке гипотезы {X €= Φασ2} против
{Χ ^ Φα,σ25 σ Φ σο} ПРИ данном σο и неизвестном α и другие.
Относительно кривой θ = д(а) в Θ мы будем предполагать, что
она является дважды непрерывно дифференцируемой и что матрица G =
= {dgi{a)/dotj\\ {% = l,...,fc; j = 1,...,ί; ^г(«), «г суть координаты д(а)
и α соответственно) имеет ранг /. Это значит, что мы можем произвести
дифференцируемую взаимно однозначную замену параметра
(перепараметризацию задачи) так, чтобы первые / координат (можно положить их, не
ограничивая общности, равными α = (αχ,.. .,aj)) определяли положение
точки θ на кривой Θι, а остальные (обозначим их β = (/?ι,.. .,/?£_{))
определяли положение θ в «плоскости» (подпространстве), скажем,
ортогональной (это не обязательно) к «кривой» д(а) в точке а. Тогда задача сводится
к проверке гипотезы {β = 0} против {β φ 0} при наличии неизвестного
«мешающего» подпараметра а.
При этом будем рассматривать близкие гипотезы, положив β = η"η~ιΙ2,
и проверять гипотезу {7" = 0} против {7" φ 0} или против
{7"Μ2(α)7"Τ ^ Ь2} (10)
при Ь > 0 и некоторой положительно определенной матрице М2(а).
В исходных координатах последняя задача будет соответствовать
проверке гипотезы Н\ = {θ Ε θι} против близких альтернатив, когда
параметр θ располагается в п~^-окрестности кривой Θι и находится вне
некоторой «трубки», содержащей Θι и соответствующей множеству (10).
Возможен и другой вариант постановки задачи о проверке близких гипотез,
исходящий из того, что параметр θ «локализован», и мы знаем, что он
располагается в окрестности некоторой точки #о = 9ia°)i <*° € А\. Тогда новый
параметр τ = (β,α — α°) будет локализован около точки то = (0,0).
Положим α — α° = η'ηΓ1!2, β = ηηη~ιΙ2 и будем проверять гипотезу {7" = 0}
против {7" φ 0} или против {77/М2(а°)7//Т ^ Ь2} при наличии мешающего
параметра η1'.
Интересующие нас результаты в этих двух постановках задач
практически совпадают. Но нам удобнее будет иметь дело со второй постановкой,
поскольку в этом случае мы располагаем всеми необходимыми
предварительными результатами. Предположение о локализации параметра θ носит
условный характер, и форма утверждений, полученных ниже, от #о зависеть
не будет.
Итак, будем считать, что новый параметр τ = (а — а°,/3) имеет вид
г = 7п-1/2, 7 = (7/,7//)>
и будем проверять гипотезу Ηι = {7" = 0} против Η<ι = {ηπΜ2η"τ ^ Ь2}, где
в качестве Mq = M2(a°) мы возьмем информационную матрицу Фишера для
§ 55. Свойства асимптотической оптимальности критерия 419
параметрического семейства {Ρ$(ο,β)} в точке β = О, где θ(τ) = 0((α-αο), β))
есть функция, восстанавливающая θ по значению г = (τ^τ").
Теорема 4. Пусть θο — д{оР) является внутренней точкой Que
окрестности этой точки выполнены условия (RR). Пусть, далее,
функция д(а) дважды непрерывно дифференцируема в точке а0, а матрица
G = \\dgi(a)/daj\\a=ao имеет ранг I. Тогда к. о. п. (1) при определенных
выше θι, ©2 и при соответствующем с асимптотически эквивалентен
критериям
RUX)^J^^>eh''\ (11)
ф*-9{а*))1{д{а*))$*-д{а*)У>Кп-\
(12)
(θ* - 9(α*))Ι(θ*)(θ* - <7(ά*))τ > Λ,η-1
w является асимптотически минимаксным критерием
асимптотического уровня 1 — ε для проверки гипотезы Hi = {0 £ θι} = {7" = 0} против
я2 = {7"м27"т > ь2}.
Распределение статистики 21ni?i(X) при X ^ Рр(а°) (m· е· nPu ги~
потезе Н\) сходится при η —> со к распределению χ2 с к — I степенями
свободы (и, стало быть, от f$ и о0 не зависит). В соответствии с
этим h£ в (11), (12) означает квантиль порядка 1 — ε распределения
Гарантированная асимптотическая мощность к. о. п. равна
Р((£1 + ь)2 + £22 + ..- + £Ь>М,
где ξί ^ Φο,ι и независимы.
Мы видим, что асимптотически минимаксные критерии (11), (12) со
значениями а0 никак не связаны.
Замечание 4. Гипотезу #2 в терминах исходного параметра θ можно
записать в виде
#2 = {inf(θ - g(a° + 7V-1/2)) J(5(a°))(0 - g(a° + -/гГ1'2))1" > Ъ2п~1}.
У
Напомним, что мы считаем множества 1\ ограниченными, так что здесь
(0 - θο) < Νη~1/2, |У| ^ N при некотором N > 0.
Замечание 5. Как будет видно из доказательства, утверждение
теоремы полностью сохранится, если гипотезу Н\ = {η" = 0} заменить на
Н\ — {7/7М27//Т ^ а2}> а <Ь, при .соответствующей замене множества θι.
Доказательство теоремы 4. Здесь в качестве «основного» мы будем
рассматривать критерий (11), эквивалентный (1) и более удобный по своей форме.
Установим его асимптотическую эквивалентность асимптотически минимаксному
критерию, а затем его асимптотическую эквивалентность (12).
Рассмотрим распределения Р# и Р5(а) как зависящие от параметров г = {т'} г")
и a = τ' -f a° соответственно. Положим τ = jn-1/2, 7 = (7,,7,,)> так что г' =
= 7,π~1/2, г" = η"η~ιί2, и будем проверять гипотезу #ι = {7" = 0} против
420
Гл. 3. Теория проверки гипотез
#2 = {7"М27"Т ^ &2}, где Л^2 — информационная матрица Фишера для
семейства Р5(а) в точке а0. Сделаем теперь еще одно преобразование над параметром,
подобное тому, которое проводилось нами в примере 49.4 и которое превращает
информационные матрицы в единичные. Именно, положим ρ = τΛ и соответственно
η = 7^ (ρ = ηη""1/2), где Л — треугольная матрица, подробно описанная в примере
49.4 и обладающая свойствами
J"1 = ЛТМ"1Л = Е, J2_1 = AjM2_1A2 = Я,
где J, Μ, J2, Μ2 есть информационные матрицы в точке θο соответственно для р,
г, р", г" (верхние штрихи у обозначений имеют тот же смысл, что у г', г", 7', 7 )>
Л2 — матрица порядка (& — Ι) χ (А: — /), образованная последними k — l строками и
столбцами матрицы Л, так что р" = т"Л2, 77" = 7"^2-
В новых параметрах гипотезы Н\ и Я2 запишутся в виде
#1 = {»/' = 0}, Я2 = {|Ч"| £ Ь).
Из свойств произведенных преобразований ясно, что θ = 0(р) есть взаимно
однозначная функция от ρ и что все рассматриваемые нами параметрические
семейства (в том числе с параметрами р, р") удовлетворяют условиям (RR). Положим
р0 = θ~ι(θο) (это есть решение уравнения θ(ρ) = θο),
Воспользуемся теоремой 37.3. Мы получим при |w| ζ Цпу/п, Ρ = Ро + τ/η-1/2,
Χ ^Ρ^(ρ), что
Yo(u) = (ίη + r?,u) - ±(ti,u) + (N2 + M2)e„(*,u,q), (13)
где |εη(-Χ",гг,77)| ^ εη(Χ) —> 0 равномерно по η при |г/| ^ г/пЛ/п, г/п — произ-
РНй)
вольная последовательность, сходящаяся к нулю. В этих равенствах мы
использовали тот факт, что информационная матрица для параметра ρ является
единичной. Вектор ξη есть вектор производных функции 7i-1/2Z/(X, 0(p)) no pj в точке
Ρ = Ро +Г/П""1/2, так что £„ ©► Фо,я равномерно по ρ (по η) при |г/| ζ r\ny/n. (Ввиду
предположения об ограниченности (В - 6о)у/п равномерность сходимости здесь и в
дальнейшем достаточно устанавливать для Μ ^ Ν при произвольном
фиксированном N. Однако ничто не мешает нам устанавливать требуемую равномерность и в
более широкой области \η\ ζ f)ny/n -л оо.)
Положим теперь в (13) и = (υ,',υ,"), и" = 0. Мы сможем записать тогда при
прежнем соглашении относительно обозначений со штрихами
Ко((«',0)) = {C + V',u')-^(u',u') + (\uf + \V\2)en(X,u',V). (14)
Из (13), (14) следует, что максимальные значения Yo(u) и УЬ((^',0)) достигаются
соответственно при
η=(ξη+η)(Ε + εη(Χ,η)), и' = (& + η')(Ε + ε£\Χ,η)), (15)
§ 55. Свойства асимптотической оптимальности критерия 421
где εη(Χ,η) —> О, βη (Χ,η) —> О равномерно по η, \η\ < ηη>/η/2. Надо лишь
РНр) РПр)
заметить, что вероятность больших значений |ξη -f т?| равномерно мала, так как
ξη + V & Φη,Ε равномерно по τ], \η\ < ηη\β"> и Pfldfn + f?! > r]ny/n) -> 0 равномерно
по 77, \η\ < j]nyjnj2.
Обратимся теперь к к.о.п. Имеем при θ — 0(р), X €= Р#, ρ — ро 4- ηη~1/2,
Ri(X)~ θ
sup/* (X) supey°<")
supfg{a){X) supeyo((^,o»
α u'
exp ] xl^n + »?|2 +εη{Χ,η)\ .
где функции en с различными индексами сходятся к нулю по Ρ ^-вероятности
равномерно при |т7| < ηη\/η\
21пД!(*)=НУ" + »Л2, У^*о,Е, (17)
равномерно по 77.
Так как при θ — g(a) с необходимостью 77" = 0, то отсюда следует утверждение
теоремы относительно статистики 21ni?i(X).
Вспомним теперь, что (см. теорему 36.4) ξη = u*(E + εη(Χ, 77)), где u* =
= (ρ* - р)у/п, ρ* — ο. μ. п. для параметра р. Отсюда и из равенства р% = 0,
полагая 77* = (р* — Ро)у/п, получим
ξη + 77 = >/п(р* -ρ + ρ-ρ0) + υ,*εη(Χ,η) = >/п(р* - ρΌ) + ί**εη(Χ,77) =
= 77*+^εη(Χ,77) &Φη,Ε,
Стало быть, правая часть в (16) может быть записана также в виде ехр < -|(f7*)"|2 4-
-f ε'η(Χ,η) ?, ε'η(Χ,η) —> 0. Это означает, что критерий
IfoTI2 > he (18)
и к. о. п. асимптотически эквивалентны, т. е.
lim βιιρΡί(ο)(Λι(.ϊ) > eft</2) = lim supPi(e)(|(f?*)"| > h,)=e,
n—►oo q τι—►oo q
lim suPPe(i?ipO>eA'/2)= lim sup Pe(|(i?')"|2 > Л.) =
n-Уоо ee02 n-t-oo 0€©2
= sup Р(|У" + ^|2>^)=Р((У1-|-6)2-|-у^... + уЬ>^).
где yi Φ Фод независимы.
422
Гл. 3. Теория проверки гипотез
Докажем теперь, что критерий (18) является асимптотически минимаксным
критерием асимптотического уровня 1 - ε. Воспользуемся теоремой 54.2. В нашем
случае η* = (ρ* — po)y/n & $7,£- Задача В для Υ €f Φ-у,ε рассматривалась нами в
примерах 49.3, 49.4. Мы установили там, что критерий
\Y'f > he
является минимаксным уровня 1 —ε. Следовательно, по теореме 54.2 критерий (18)
является асимптотически минимаксным.
Чтобы завершить доказательство, нам осталось установить асимптотическую
эквивалентность (11) и (12). Эта эквивалентность легко следует из результатов §36
и леммы 54.1. <
Пример 1. Пусть X ^ Фд^2, где λ, и а2 — скалярные параметры. (Мы
используем здесь обозначение А вместо традиционного а, чтобы не
возникло путаницы с аргументом функции <7(а).) Требуется проверить гипотезу
{А = λο} против {λ φ λο} или против {|λ — λο| ^ 6n-1/2}, b > О, когда σ
неизвестно. Мы знаем, что о. м. п. в этом случае имеют следующий вид. Если
обе компоненты λ и а2 вектора θ = (λ, σ2) неизвестны, то о. м. п. для θ есть
Θ* = (λ, σ2)* = (х, S2), S2 = - V> - x)2.
Если λ = λο, то о. м. п. для σ2 имеет вид (<?2)* = S2 = — /~^(χϊ ~~ λο)2, так
что д{а*) = (Ao,S2). Так как
/β(ΛΓ) = (^σ)-"βχρ{-(2σ2)-1^(χι·-λ)2},
то критерий отношения правдоподобия (11) будет иметь вид
52
В силу равенства S2 = S2 4- (χ — λο)2 этот критерий эквивалентен критерию
^ > С (19)
Но это есть хорошо известный критерий Стьюдента, рассматривавшийся
нами ранее (об оптимальных свойствах этого критерия см. (48.10) и § 47, 48).
Нетрудно проверить, что такую же форму будет иметь критерий (12).
Действительно, в §26 мы видели, что матрица Ι(θ) для семейства Φχσ2
имеет вид
В нашем случае Θ* — д(а*) = (х — λο, S2 — 52) = (χ — λο, —(χ — λο)2),
§ 56. Критерий хг и сгруппированные данные
423
Так как в левой части (12) стоит квадрат нормы \{g{a*) — б*)/1/2(0*)|2, то
критерий (12) будет иметь вид
(х - Ар)2 (х - Ар)4
S* + 254 >С2'
который, очевидно, эквивалентен (19).
Если вместо /(б*) здесь использовать I(g(Si*))1 то мы получим
асимптотически эквивалентный критерий
Пример 2. Пусть X €= Ф\)(Т2. Требуется проверить гипотезу {σ = σο}
против {|σ2 — o"q J ^ 6η-1/2}, когда λ неизвестно. Здесь, очевидно, о. м. п. Θ*
для θ = (λ, σ2) будет той же, что и в предыдущем примере. Если σ = σο, то
А* = х, так что 0(3*) = (χ, <rg), 0* - g(8*) = (θ, 52 - σ2).
Критерий (11) (или, что то же, критерий отношения правдоподобия)
будет иметь вид
(&-<Ί)2.,. .-ι
> 2h£n
эквивалентный, очевидно,
S2
°2о
-1
>
\j2hen-
где Φο,ι((^ε >°°)) ^ ε/2· Этот критерий также уже рассматривался в §47.
Дальнейшие примеры использования теоремы 4 см. в § 57.
§56. Критерий χ2. Проверка гипотез
по сгруппированным данным
1. Критерий χ2· Свойства асимптотической оптимальности. Сам по себе
«исходный» критерий χ2 предназначается для проверки по выборке X из
полиномиального распределения В#, θ = (0ι,..., 0r), Y^ fy = 1, простой ги-
потезы ifi = {θ = ρ} против дополнительной альтернативы Щ — {θ φ ρ},
ρ = (pi,..-,Pr)· Полиномиальное распределение В# описывается
вероятностями 0i = P(Ai), г = Ι,.,.,γ, появления в отдельном испытании одного
из непересекающихся г событий Αι,..., Аг. Элемент Xj выборки X из этого
распределения можно представлять себе как один из векторов βχ,..., ег с г
координатами. У вектора е^ (г — 1) координата равна нулю, а координата
с номером к равна единице; при этом xj = e&, если произошло событие А^.
424
Гл. 3. Теория проверки гипотез
Обозначим через v^ число наступлений события А^ъп независимых испы-
п
таниях. Тогда ν = (^i,...,^r) = /,хг есть достаточная статистика для 0,
г=1
так как функция правдоподобия fe{X) имеет вид
г
Л(*) = ПС· (1)
Статистика χ2 есть по определению
2/гм _ V^ {Щ-nPiY
X
!ро = Σ
ί=ι npi
а критическое множество критерия χ2 (область приема Яг) имеет вид
х2(Х) > с,
где с выбирается по заданному уровню значимости.
Рассмотрим более внимательно сформулированную выше задачу о
проверке гипотезы Н\ = {Θ = р} против #2 = {# 7^ ρ].
Ясно, что распределения {В#} образуют параметрическое семейство,
зависящее от к = (г — 1)-мерного параметра (θχ,.. .,0r_i); значение 0Г опре-
г-1
деляется равенством 0Г = 1 — У~]^г· Вектор (#ι,.. .,0r_i) так же, как и
г=1
(01,..., 0Г), будем обозначать буквой б. Недоразумений от этого не возникнет.
г-\
Область Θ представляет собой симплекс θ{ ^ О, г = 1,...,г — 1, У^бг ^ 1.
Логарифмическая функция правдоподобия Σ(Χ,Θ) равна
г η
Ь(-М) = £>1п0* = Σ ί (*,*). (2)
Семейство {Β#} удовлетворяет условиям (Ао), (Αμ), (Ас), а также условиям
регулярности (RR) в любой внутренней точке из Θ, т.е. в любой точке 0,
для которой все θ{ > 0. Действительно, в нашем случае
ί(χι,0) = lnfy при χι = ej\
(3)
δΙ(χί,θ) Ι
щ ]
d2l(xu0)
dOiddj
-Θ71
, ο
UiUj
Ι -*r-2
lo
при
при
при
при
при
при
χι = е,·,
χι = ег,
χι φ ej, χι ^ er,
χι == e,·,
xi = er,
xi ^ e,, χι Φ er,
(4)
§ 56. Критерии χ2 и сгруппированные данные
425
где 5{j — символ Кронекера. Из этих формул видно, что
д21(хив) ^ д1(хи0)д1(хив)
дв{щ двг d0j ' г'^г '
Часть условий (RR), связанных с существованием математических
ожиданий, здесь выполняется очевидным образом, так как множество X в нашем
случае конечно.
Из (3) или (4) находим
|Fd2/(xi,0)|
W) = №#)ll
двгдв0
i,j = Ι,...,γ-I.
(5)
Если в этой матрице первую строку вычесть из всех остальных, а затем
воспользоваться разложением по элементам первой строки, то мы получим
-1
г-1
I'WI
г-1
ι+Σ? ΙΚ1- П«<
i=i
Г
U = 1
Таким образом, 0 < |/(0)| < оо, если ТТ^А; > 0, т.е. если точка θ является
А;=1
внутренней точкой симплекса Θ.
Итак, мы видим, что вправе воспользоваться результатами § 53, 54 об
асимптотически оптимальных критериях. Из этих результатов вытекает,
что для проверки гипотезы i/ι = {# = р} против Н2 = {θ Φ ρ} существует
а. б. к., совпадающий с критерием отношения правдоподобия
fp{X)
> с.
(6)
Этот же критерий будет асимптотически минимаксным для проверки Н\
против гипотезы {{θ-ρ)Ι{θ)(θ-ρ)τ > Ρη'1} (см. теорему 55.3).
Чтобы найти в более удобной форме критическую область (6), вычислим
значение /^. (X). Дифференцируя (2) по θ\,..., 0Γ_ι, получим
дЦХ,в) = щ νΤ . = 1 г_х
Οθι Ό{ ΘΓ
Приравнивая эти производные к нулю, получим, что о. м. п. равна
Θ* = п"1!/,
так что θ\ = n~lVi.
Таким образом, переходя к логарифмам, критерий (6) можно записать в
виде
</>2(Х) = У>Ш-^>С1. (7)
426
Гл. 3. Теория проверки гипотез
(9)
Согласно теореме 53.1 (см. также лемму 53.1) статистика 2ψ2(Χ) при
гипотезе Н\ имеет предельное распределение χ2 с г — 1 степенями свободы.
Поэтому мы получим критерий асимптотического уровня 1 —ε, если положим
d = /ιε/2, где h€ — квантиль распределения ΗΓ_ι порядка 1 — ε.
Что же собой представляет в наших условиях асимптотически
эквивалентный (6) критерий π', полученный в теореме 53.2 и имеющий вид
η(θ*-ρ)Ι(ρ)(9*-ρ)τ>Ηε1 (8)
г-1
При t = (ίχ,.. ,,tr_i), s = /]U, получим
tl(p) = (— + —,..., + —
\Pl pr Pr-l Ρτ
где
г
ir = -e, ^i< = 0· (ίο)
i=l
Полагая t = θ* — ρ и замечая, что условие (10) выполнено, мы получим в
качестве (8) критерий
£istz«a>!>v („,
Это есть не что иное, как критерий χ2. Из цитированных утверждений
вытекает, что х2(Х) ©■ Hr_i.
Критерий π" в теореме 53.2, асимптотически эквивалентный (7) и (11),
будет иметь вид
J2^zm^>htm (12)
t=l Щ
Учитывая также теорему 55.3 и замечание 55.1, мы можем резюмировать
изложенное в виде следующего утверждения.
Теорема 1. Критерий (7) при с\ = h£/2, а также критерий χ2
(11) и критерий (12) имеют асимптотический уровень 1 — ε и
являются а. б. к. для проверки по выборке Χ €= 3$ гипотезы {Θ = р}
против {θ φ ρ}. Они же являются асимптотически минимаксными
критериями для проверки гипотезы {Θ = р} против близкой альтернативы
/]{0j —Pi)2/pi > Ь2 /η > при любом Ь > 0.
.i=l
§ 56. Критерий хг и сгруппированные данные 427
Асимптотическую эквивалентность критериев (7), (11), (12) можно было
щ
бы установить и непосредственно, пользуясь разложением в ряд In — =
npi
= ln(l + ^^W).
V nPi J
Эти критерии являются асимптотически непараметрическими, так как
предельное распределение используемых в них статистик является
«абсолютным», т.е. с природой исходного распределения никак не связано.
2. Применения критерия χ2. Проверка гипотез по сгруппированным
данным. Критерий χ2 является очень распространенным, и значение его
выходит за пределы задачи, рассмотренной в предыдущем пункте.
Обратимся к общей задаче о проверке гипотезы Н\ = {X ^ Pi} против
Hi = {X §Р, Р^ Pi}, изучавшейся в § 52. Так как сколько-нибудь
развитая теория об оптимальных критериях существует лишь в параметрическом
случае, то естественно пытаться как-то «параметризовать» эту задачу*).
Наиболее простым и естественным способом сделать это в общем случае
является группировка данных. Она состоит в следующем. Область
возможных значений наблюдаемых величин (т. е. пространство X) разбивается на
г непересекающихся областей Δι,..., ΔΓ и вместо наблюдения xj
указывается лишь тот интервал Δ&, в который это наблюдение попало.
Другими словами, мы огрубляем наблюдения, и те Xj, которые попали
в Δ*, можем заменить каким-нибудь одним значением ^ G Δ^, Ясно, что,
выбирая достаточно богатое разбиение, мы можем приблизить наблюдение Xj
с помощью Zk сколь угодно точно.
Итак, группировка приводит к тому, что наблюдение Xj заменяется
вектором е&, если произошло событие Ак = {xj Ε Δ&} (векторы е* были
определены в начале предыдущего пункта). Но новая выборка, полученная в
результате такой операции, очевидно, есть не что иное, как выборка из В#,
вк = Р(ху £ Δ^). Мы уже знаем, что в этом случае вектор ν = {у\,.. .,vr)
частот попаданий в интервалы Δ,,..., ΔΓ будет достаточной статистикой.
Произведенная редукция выборки X к вектору ν и называется
группировкой данных.
Ясно, что группировка связана с некоторым «обеднением» выборки X и
частичной потерей информации.
На произведенную параметризацию возможен и несколько иной взгляд.
Допустим для наглядности, что X = К, и все рассматриваемые
распределения сосредоточены на конечном интервале и имеют плотность, т.е.
удовлетворяют условию (Αμ), где μ — мера Лебега. При данном разбиении
Δ, ...,ΔΓ наряду с плотностью f(x) рассмотрим кусочно-постоянную
плотность
fe^) = ^^ = XiJf^)dx = ^: при xeAi. (13)
*) Имеется в виду конечномерный параметр. Любую задачу можно считать
параметрической, если допускать бесконечномерный параметр, так как его можно отождествить с
распределением Р, X ^ Р.
428
Гл. 3. Теория проверки гипотез
Здесь Δι обозначает также длину интервала Δ;. Это есть параметрическое
семейство распределений Р#, Р^(5) = / fe(x)dx.
в
Мы получим выборку Υ из Р#, если для каждого к соберем все
наблюдения из X €= Р, попавшие в Δ&, и затем случайно и равномерно «разбросаем»
их по Δ&. По существу, это то же самое, что мы делали раньше, так как
сведения о том, в какой точке интервала Δ& находится наблюдение у;, никакой
информации в себе относительно параметра θ не содержит: функция
правдоподобия fe(Y) при «перемещении» наблюдений в пределах своих интервалов
не меняется. Таким образом, достаточно лишь знать количества ^i,...,^r
наблюдений, попавших в Δι,..., ΔΓ.
Ясно, что если f(x) — гладкая функция, то /я (я) будет хорошо
приближать f(x) при достаточно «мелком» разбиении {Δι,..., ΔΓ}.
Соотношения (13) означают другой способ параметризации,
эквивалентный первому. Эквивалентность следует из совпадения с точностью до
множителя, не зависящего от параметра, функций правдоподобия. Для
распределения (13) она равна
г=1 г=1
где первый множитель представляет собой функцию правдоподобия выборки
из Βθ (см. (1)).
Следует отметить, что группировка наблюдений возникает часто и сама
по себе, не для целей параметризации, а просто как удобный и часто
более экономный способ записи информации, содержащейся в выборке. Если,
например, η = 104, а точность измерений, наблюдаемых значений на [0,1]
сравнима с 0,1, то ясно, что практически бесполезно знать все 104
наблюдений, а достаточно указать 10 частот ι>ι,...,ΐΊο попадания в интервалы
Δϊ = ((г — 1)/10,г/10), г = 1,...,10, т.е. знать лишь гистограмму
выборки.
Вернемся к задаче проверки гипотезы Н\ = {X ^ Pi} против Ή.2 =
= {X €= Ρ φ Ρι}. Мы будем предполагать произведенную группировку
наблюдений такой, что значимое для нас отклонение распределения Ρ
выборки X от Pi обязательно скажется на распределении сгруппированных
данных. Тогда нашу задачу можно рассматривать как задачу проверки
гипотезы {Θ = р}, где ρι — Ρι(Δϊ), против {θ φ ρ} для параметрических
семейств В^ или (13). Как мы уже знаем, критерий χ2 (как и критерии
(7), (12)) будет асимптотически оптимальным в этой задаче в смысле,
сформулированном в теореме 1.
Кроме того, критерий χ2 является асимптотически
непараметрическим, так как предельное распределение статистики χ2{Χ) при гипотезе Н\
от исходного распределения выборки X не зависит.
Отметим при этом, что проверка гипотезы {Θ = р} для семейств (13) или
В# все же не равнозначна проверке гипотезы {X ^ Pi}, хотя при
некотором разбиении {Δι,..., ΔΓ} может быть и близка к ней. На самом деле, для
выборки X проверяется гипотеза Χ ^ Ρ, Ρ(Δ^) = pi = Ρι(Δί). Это делает
§ 56. Критерий χζ и сгруппированные данные
429
критерий χ2 несостоятельным относительно альтернатив Ρ φ Pi, для
которых Θϊ = Ρ(Δϊ) = Ρι(Δ^) = pi. Поэтому еще раз отметим, что критерий
χ2 есть критерий, обладающий рядом свойств асимптотической
оптимальности, но он действует лишь против альтернатив, меняющих вектор 0, т. е.
против альтернатив, для которых {Ρ(Δί)} φ {Pi (Δ;)} = {pi}.
Сделаем несколько замечаний, касающихся применений критериев χ2,
(7), (12). Мы будем говорить при этом в основном лишь о критерии χ2,
так как, с одной стороны, названные критерии близки друг к другу, а с
другой — критерий χ2 исторически (отчасти ввиду своей наглядности) получил
значительно более широкое распространение.
Уровень значимости критерия Х2(Х) > hE равен 1 — ε лишь «в пределе».
Опыт показывает, что для ε ^ 0,01 истинный уровень значимости этого
критерия удовлетворительно приближается значением 1 — ε лишь при ηρι ^
^8, % = 1,...,г.
При большом числе групп г, скажем, при η > г > 30, можно пользоваться
нормальным приближением как для распределения —■= (χ2 — г), χ2 ^ Нг
(см. §12), так и для распределения при гипотезе Н\ статистики χ2(Χ),
нормированной моментами
ЕХ2(Х) = г-1,
Όχ2(Χ) = 2(г - 1) + £ [Σ,ΡΪ1 - г2 - 2г + 2 J .
Часто используют также нормальное приближение Фод для
распределения случайной величины (см. § 12) ^2χ2 — \/2г — 1, χ2 €= Нг.
Отметим также, что при увеличении числа групп улучшается
приближение плотности f(x) с помощью ступенчатой функции, построенной по
значениям Ρι (Δι) = / f(x) dx. Это значит, что возрастает число альтернатив,
не согласующихся с Н\, и критерий χ2 все более становится критерием для
проверки гипотез о плотности. В связи с этим мощность критериев χ2
фиксированного уровня при увеличении числа групп будет убывать (ср. с
замечаниями предыдущего параграфа о критерии Морана; подробнее об этом
см. [14, 135]).
К недостаткам критерия χ2 следует отнести тот факт, что в ряде случаев
разбиение {Δι,...,ΔΓ} приходится устанавливать статистику. Здесь
следует проявлять осторожность, так как при этом вносится элемент
субъективизма в «обеднение» выборки X. Кроме того, иногда это разбиение выбирают
в зависимости от выборки X, что, вообще говоря, не всегда допустимо, так
как при этом Δ* становятся случайными (подробнее об этом см. [50], §30, 31).
Пример 1*). Некто в городе N обследовал показания 500 часов,
выставленных в витринах различных часовых мастерских. Результаты на-
*) Пример заимствован из [58].
430 Гл. 3. Теория проверки гипотез
блюдений были разбиты на 12 групп (в зависимости от положения часовой
стрелки на циферблате). Приведем полученную таблицу наблюдений:
Промежутки
на циферблате
Число
наблюдений
0-1
41
1-2
34
2-3
54
3-4
39
4-5
49
5-6
45
6-7
41
7-8
33
8-9
37
9-10
41
10-11
47
11-12
39
Проверяется простая гипотеза Н\ — {распределение положения
стрелки по часовым группам на циферблате равномерно} против сложной
дополнительной альтернативы.
В этом примере η — 500, pi = 1/12, г = 1,...,12; npi « 41,67. На
основании теоремы 1 можно приближенно считать, что χ2{Χ) €= Нц. В
нашем примере непосредственным подсчетом убеждаемся, что χ2{Χ) ~ 10
и фактически достигаемый уровень критерия χ2 приближенно равен
1 — Нц((10,оо)) « 0,47 (см. табл. III). Это означает, что результаты
эксперимента согласуются с гипотезой Н\ с точки зрения критерия χ2 любого
уровня 1 — ε, заключенного между 0,47 и 1.
Мы уже отмечали, что критерий χ2 имеет широкое распространение.
При этом сфера его приложений не ограничивается проверкой лишь простых
гипотез. Один из таких примеров будет рассмотрен в следующем параграфе.
§ 57. Проверка гипотез о принадлежности выборки
параметрическому семейству
Рассмотрим задачу о проверке сложной гипотезы Н\ = {X § PQ, a G Л}
о том, что распределение выборки принадлежит параметрическому
семейству {Ра}а€А против дополнительной альтернативы Ή.2 = {X € Ρ, Ρ φ
£ {Ра}аел}· Примером такого рода гипотез могут служить утверждения о
том, что X есть выборка из какой-нибудь нормальной совокупности
(гипотеза #ι), и утверждение, дополнительное к этому (гипотеза Щ).
Другим примером может служить проверка гипотезы о том, что X ^
^ Bfl(a), где размерность α меньше размерности Θ. Эту задачу можно,
конечно, трактовать и как задачу о проверке гипотезы о принадлежности X
параметрическому подсемейству (см. §55), однако верной будет и первая
трактовка, поскольку в том случае, когда в результате эксперимента
наступает лишь конечное число возможных исходов (см. определение В# в § 12),
семейство В# содержит в себе все мыслимые распределения выборки.
В следующем пункте мы рассмотрим задачу о проверке гипотезы X €=
^ Bfl(a) и покажем, что общая задача о принадлежности параметрическому
семейству может быть редуцирована к этой задаче путем группировки
данных.
1. Проверка гипотезы X € В^(а). Группировка данных. Рассмотрим
сначала общую задачу, сформулированную в начале параграфа, в случае
произвольного пространства X. Возьмем разбиение пространства X на области
(«интервалы») {Δι,...,ΔΓ} такое, что число «интервалов» г больше I + 1,
§ 57. Принадлежность параметрическому семейству 431
где / есть размерность параметра а. Произведем группировку наблюдений
по этим интервалам. Если гипотеза Н\ — {Χ ^ Ρα} верна, то вероятности
попадания наблюдений в интервалы Δ; будут равны
ρ<(α)=Ρα(Δί).
Это означает, что в этом случае вектор θ = (#ι,..., θτ) вероятностей
попадания наблюдения в Δ* должен лежать на кривой θ = ρ(α) = (ρι(α),.. .,pr(^))·
Таким образом, по полученной при группировке выборке Υ ξ= Bq мы
должны проверить гипотезу Н\ о принадлежности Υ параметрическому
подсемейству Вр(а) против альтернативы {Υ €= В^}, где θ не располагается на
кривой θ = ρ(α), α Ε А Эта задача рассматривалась нами в §55, где был
найден асимптотически минимаксный критерий для проверки Н\ против
близкой альтернативы
Я2 = {У#В„; inf|6-p(ao + 7n~1/2K1/2b(«o + 7n~1/2))T|>^"1/2} (1)
7
(см. замечание 55.3 к теореме 55.4; точка ао означает «локализованное»
значение параметра такое, что альтернативы располагаются в окрестности
точки #о = р{&о))· Критерий отношения правдоподобия (55.11) в нашем
случае имеет вид
г г ,
InR\(Χ) == max22 V{ lnfy — max \\ Vi lnpi(a) > -^
или, что то же,
j=/iln^(^)>T'
где α* есть о. м. п. параметра α по выборке У (или по вектору ν =
= (ζ>Ί,.. .,z/r)). Этот критерий асимптотически эквивалентен (см.
теорему 55.4) критерию
(р(а*) - г/п"1)/^))^^) - ^гГ1)7 > Лс.
Так как вид матрицы 1(9) нам известен (см. (56.5)), то, пользуясь (56.9),
мы получим из теоремы 55.4
Следствие 1. Если г —I > I и функцияр(а) удовлетворяет условиям
теоремы 55.4, то критерий отношения правдоподобия
асимптотического уровня 1 — ε для проверки по сгруппированным данным гипотезы
Ρα? Ρα £ {Ра}абд} против дополнительной альтернативы
Ή.2 является асимптотически минимаксным [для проверки гипотезы Н\
против (1)) и имеет вид
5>Ш-^->^, (2)
££ npi{a*) 2
432
Гл. 3. Теория проверки гипотез
где he — квантиль порядка 1-е распределения χ2 с г — 1 — 1 степенями
свободы. Этот критерий асимптотически эквивалентен критерию
№)=Σ(ι/ί-"?!Τ))2>^· о
Последний критерий называют также критерием χ2, но в случае, когда
неизвестные «мешающие» параметры оцениваются по выборке.
Распределение статистики χ2(Χ), как это вытекает из следствия 1, сходится при
гипотезе Н\ к распределению χ2 с г - / - 1 степенями свободы (число степеней
свободы г — 1 в предельном распределении статистики χ2{Χ) уменьшилось
на число скалярных параметров αχ,.. ,,α/, оцениваемых по выборке).
Пример 1. В примере 35.3 был описан механизм наследования групп
крови 0 (ноль), А, В, АВ. Он управляется генами трех типов: А, В, 0.
Вероятности появления этих генов в данной популяции обозначим через р,
д, г = 1 — ρ — q. Вероятности Pi(a), α = (ρ, g), того, что человек будет иметь
г-ю группу крови, найдены в примере 35.3 и приведены в табл. 1 из § 35.
Нам дана выборка X с частотами V{, г = 1,2,3,4 (см. табл. 1), появления
г-й группы крови, полученная в результате обследования η = 353 человек.
В примере 35.3 для этой выборки были найдены приближенные значения
о.м.п. а* = (р*,<7*) = (0,246; 0,173). Это дает нам значения Рг(#*),
приведенные в табл. 1.
Таблица 1
Распределение людей по группам крови
Pi = щи"1
Pi(a*)
0
121
0,343
0,337
А
120
0,340
0,347
В
79
0,224
0,231
АВ
33
0,093
0,085
Всего
353
1
1
Мы получаем возможность воспользоваться следствием 1 для проверки
гипотезы о том, что описанный выше механизм наследования крови имеет
место. С помощью табл. 1 находим, что статистика χ2(Χ) (см. (3)) в нашем
случае равна примерно 0,44. Это дает хорошее согласование с гипотезой, так
как критическое значение he, соответствующее распределению χ2 с одной
степенью свободы и значению ε = 0,2, равно /io,2 ^ 1564.
Пример 2. Задача о сопряженных признаках. Допустим,
что выборка X есть результат обследования некоторых объектов, каждый из
которых характеризуется признаками А и В. Первый признак может
принимать значения А\,..., As, второй — Βχ,..., Bt. Спрашивается, зависимы
ли эти признаки? Например, мы можем проводить некоторый эксперимент
G с исходами B\,...,Bt в разных условиях j4x,...,j4s. Задача состоит в
том, чтобы выяснить, зависят ли результаты эксперимента G от условий, в
которых он производится.
Эту задачу можно рассматривать также как задачу о проверке
независимости двух случайных величин ξ и η по сгруппированным наблюдениям
над парой (£, 77).
§ 57. Принадлежность параметрическому семейству 433
Результаты экспериментов в нашем примере представляют собой
матрицу значений ||^||, где u\j есть число появлений исходов с признаками А{
и Bj в выборке X объема η (каждый элемент выборки есть пара признаков
обследуемого объекта).
t s
Положим pij = P(AiBj), pi. = 2_"pij, p.j = 2_]Pij· Тогда гипотеза Hi о
j = l i=l
независимости признаков будет иметь вид Н\ = {ρυ = рг.р.3}. Нетрудно
видеть, что это есть гипотеза о принадлежности распределения выборки
параметрическому подсемейству, где роль параметра α играет (s + i — 2)-мерный
вектор α = (ρι·,. · .,ps-i.;p.i,.. .,ρ.^ι) (значения ps. и p.t определяются из
s-l ί-1
равенств ps. = 1 - ^p*., p.t - 1 - Σ,Ρ-j)·
i=l 3=1
Функция правдоподобия выборки X при гипотезе Н\ равна
t s
ij i j j=l i=l
Из результатов §56 (ср. с (56.1)) следует, что о. м. п. а* для такой функции
правдоподобия имеет вид
η J η
Итак, критерий χ^ в нашем случае принимает вид
s^-E^-***3''
»Σ
(^j
П
Wv.jf
>h£,
i,J г 3 i,3 J
где he — квантиль порядка 1—ε распределения χ2 с числом степеней свободы
st-l-{s + t-2) = (s — 1)(ί — 1).
Можно указать много прикладных задач, где используется построенный
нами критерий сопряженности признаков. Рассмотрим в качестве
иллюстрации одну из них — задачу социологического обследования о связи между
доходом семей и количеством детей в них (см. [58, с.481]).
Пример 2А. Пусть признак А означает количество детей и принимает
значения 0, 1, 2, 3, ^ 4. Признак В указывает, какому диапазону (0-1),
(1-2), (2-3), (^3) (за единицу принято 1000 шведских крон) принадлежит
зарплата. По результатам η = 25 263 обследований были получены
следующие данные, приведенные в табл. 2.
Таблица 2
Признак А
0
1
2
3
^4
I/.j
Признак В
0-1
2161
2755
936
225
39
6116
1-2
3577
5081
1753
419
98
10928
2-3
2184
2222
640
96
31
5173
>г
1636
1052
306
38
14
3016
V{.
9558
НПО
3635
778
182
25263
434
Гл. 3. Теория проверки гипотез
В этом примере χ2{Χ) = 568,5, что значимо больше критического
значения h£ для распределения χ2 с (5 — 1)(4 — 1) = 12 степенями свободы даже
при достаточно малых ε. Так что мы вынуждены признать
несостоятельность гипотезы Η ι = {А и В независимы (несопрлжены)}.
Отметим, однако, что более тонкий анализ указывает на очень слабую
зависимость признаков А и В.
2. Общий случай. Критерий χ2, примененный в задаче этого параграфа,
обладает теми же недостатками, которые отмечались нами применительно к
задачам предыдущего параграфа.
Задача проверки гипотезы {X €= Ρ в] о принадлежности X
параметрическому семейству {Рв}ве<Э допускает, конечно, и более широкий подход,
аналогичный тому, который излагается в §52. Выберем некоторое
расстояние d(P,Q) в пространстве распределений. Далее, найдем точку Р$+ из
{Р#}, ближайшую к Р£ в смысле расстояния d. В качестве Р#* можно брать
также Р^,, где Θ* есть о. м. п. (см. § 15) или какая-нибудь другая разумная
оценка. Если гипотеза Ηγ верна, то d(P^*,P*) не должно быть большим,
и наоборот, если верна i?2, то d(P^*,P*) будет значимо. Это соображение
дает нам следующую конструкцию критерия: мы отвергаем гипотезу i/i,
если d(P^*,P*) > с, и принимаем в противном случае.
Число с следует выбрать так, чтобы
supPe(rf(P^,P;) >c) <ε
или чтобы это соотношение выполнялось асимптотически. Следствие 1
предлагает в качестве расстояния d(P^*,P*) взять статистики в (2), (3). Среди
других они обладают еще и тем достоинством, что являются асимптотически
непараметрическими: при гипотезе Н\ = {X ^ Р#} предельное
распределение χ2(Χ), например, от θ не зависит.
Рассмотрим реализацию изложенного выше общего подхода в двух важных
частных случаях, когда параметрические семейства образованы параметрами сдвига и
масштаба.
1. Пусть мы проверяем гипотезу X ^ Р#, θ € R, где Ре(А) — Р(А - 0), А С К.
Обозначим через F(x) функцию распределения, соответствующую Р, и положим
Fg{x) = F(x — θ). В качестве d возьмем расстояние, использованное нами в
критерии Колмогорова.
Теорема 1. Пусть X ^ Р#, Fo(x) = F(x — θ), функция F(x) имеет огра-
иичеииуп РаеноМеРио пепРеРЫеиуЮ плотность /(«) = F>(x), /' *»/(*) * < оо.
Если обозначить / xf(x) dx = о, θ* = χ — о, то пРи любом θ
lim Pe(supv^|F^(x) -F„.(x)| > с) =
η—юо Ν χ ■ ' '
= Ρ (sup
\w°(F(x)) 4-/(χ) fw°(F(t))dt\ > с]
где w° — стандартный броуновский мост.
§ 57. Принадлежность параметрическому семейству 435
Правая часть в этом соотношении от θ не зависит. Вычисляя ее для заданной F
и выбирая с = се так, чтобы она равнялась ε, мы получим критерий
Dn = supy/ii\F*{x) - F(x - 0*)| > ce
X
асимптотического уровня 1 — ε для проверки гипотезы Hi о принадлежности
выборки X параметрическому семейству {Р#}, где θ — параметр сдвига.
Доказательство теоремы 1. Рассмотрим процесс
Wn(x) = v^ (Fn*(x) - F$.(x)) = wn(x) - y/ii(Fo.(x) - F9(x)),
где wn(x) = y/n (F*(x) - Fe(x)). Имеем при t -> θ
Ft(x) - F$(x) = -(* - 0)(/(x - β) + ε(ί,β,χ)),
\ε(ί,θ,χ)\ $W|t-fl|,
где о;д — не зависящий от χ модуль непрерывности функции /, о;д —> 0 при Δ —> 0.
Так как Θ* —> Θ. то, полагая t = б* и принимая, не ограничивая общности, α = 0,
Ρθ
получим
>/ВД.(*)-Я(з»^
= -/(ж-0) [tdwn(t)+e(e*,e,x),
\ε(θ*,θ,χ)\ ζ ω(θ* - 0) = у^|0* - 0|w|,._fl| —> 0.
Далее, функционал
HN(wn) = sup
ρ*
TV
WnW - /(я -β) / wn(t)dt
-Ν
при любом N > 0 является непрерывным в равномерной метрике. Замена
переменной χ на F^~1(y) = 0 + F~1(y)i которую естественно сделать для применения
теоремы 6.3, этого факта не меняет. Поэтому в силу названной теоремы
HN{wn) => sup
w
Ν
'(Fix - θ)) + /(χ - 0) У ™°(F(* - 0))
Л
Чтобы доказать требуемое соотношение
Dn => sup
w°(F(x - 0)) + /(χ -θ) ί w°(F(t - θ)) at
436
Гл. 3. Теория проверки гипотез
(сдвиг на θ аргумента в правой части значение последней не меняет), нам в силу
соотношений
\Όη-ΗΝ{υ)η)\^ω{θ*-θ)+ο I wn{t)dt,
№>*r (4)
ω(θ* - θ) —> О,
Ρθ
остается убедиться, что интеграл в (4) вместе с интегралом / w°(F(t))dt (
\t\^N
ложим для простоты θ = 0) сходятся по вероятности к нулю при η —> оо, N —> оо.
Оценки обоих названных интегралов проще всего, по-видимому, провести,
доказав малость их дисперсий и воспользовавшись неравенством Чебышева. Так как
первые два момента подынтегральных выражений в обоих интегралах ведут себя
одинаково, то мы можем ограничиться оценкой лишь одного из этих интегралов.
Рассмотрим, например,
по-
/ w°(F(t))
dt.
В силу соотношений Ew°(s)w°(и) — min(s,u) + su ζ. 2min(s,u) при s ^ 1,
и ζ 1 имеем
-TV \ * -Ν -ΛΓ
—оо —оо
-ΛΓ -Ν
ί w°(F(t))dt\ ζ2 ί f mm(F(t),F(s))dtds =
-ΛΓ
= 4 ί(-ί- N)F(t) dt <C -8 ί tF(t) dt-+0
—оо —оо
при N —> оо, так как / ί dF(t) < оо. Аналогично рассматриваются остальные
интегралы. <
2. Пусть теперь проверяется гипотеза Χ ξ= Ρ#, θ £ Ε, 0 > 0, где Рв(А) —
— Ρ (А/0), А С К. Обозначим снова через F функцию распределения,
соответствующую Р, и положим
Теорема 2. Пусть X €= Р#, F#(:r) = F(x/9), существует ограниченная
непрерывная плотность f(x) = F'(x) такая, что
j xAf(x) dx < оо, xf(x) -> О (5)
§ 57. Принадлежность параметрическому семейству
437
при χ —> 0. Тогда при любом θ
lim Pflisupv^lF^z) -F(x/0*)| > с) =
n-»co χ
= Ρ (sup
ιυ°№)) +xf{x) ftw°{F{t))dt
>c .
Доказательство этой теоремы совершенно аналогично доказательству
теоремы 1. Имеем
^„(«) = VS(Fn'(x)-F(^)) =«,„(«)-^(f(^)-f(D),
При t —► oo
ад - ад = (f - ^) (/(f)+ε(ί,Μ)),
где в силу соотношения /(х) = о(1/|х|) и равномерной непрерывности / на любом
конечном интервале выполняется sup \χε{ί,Θ,χ)\ ^u\t_e\ -> 0. Полагая £ = Θ* —> 0,
получим
где sup второго слагаемого сходится по Р^-вероятности к нулю. Нам остается
χ
воспользоваться рассуждениями предыдущей теоремы ί малость интегралов
/ tw°(F(t))dt и / twn(t)dt обеспечивается условием (5)) и заметить, что
|«|>ЛГ \t\>N
главная часть Wn(x) равна (примем, не ограничивая общности, σ2 = 1)
wn{x)
θθ*{θ + θ*) *\θ)
= Wn{x) ~ Έ^φ^) It2dWn{t)Wn{x) = Wn{x)I^e^)jtWn{t)dt'
где θ*(θ + θ*) —> 202. Поэтому
sup I Wn (x) | =$► sup
'('(!))+«Мг)М'(г))*
-■ykK!))+!'(f)/«»p™>*
Так как преобразование сжатия по χ под знаком sup ничего не меняет, то теорема 2
X
доказана.
Аналогичные результаты читатель может получить и для статистик
J{F*n{x)-Fe.{x))dFe.{x).
438
Гл. 3. Теория проверки гипотез
§ 58. Устойчивость статистических решений (робастность)
1. Постановка задачи. Качественная и количественная характеризации
робастности. При построении различных статистических процедур в
предыдущих параграфах — в задачах оценивания или проверки гипотез — мы
исходили каждый раз из некоторой совокупности условий. Эти условия
касались, в частности, независимости наблюдений и их одинаковой
распределенности, предположений о характере распределения Ρ элементов выборки.
Невыполнение этих условий делало бы соответствующие утверждения
(например, о характере предельного распределения или об оптимальности той
или иной статистики), вообще говоря, неверными.
С другой стороны, на практике обсуждаемые условия есть, как правило,
результат аппроксимации и неизбежной идеализации. Стало быть, в точном
виде эти условия обычно не выполнены, и возникают опасения, связанные
с правомочностью рекомендаций, сделанных с помощью той или иной
выбранной статистической процедуры.
Следовательно, как и в любой другой области математики, касающейся
приложений, здесь необходимо на последней стадии перед применениями
разработанных методов выяснить, как велики должны быть отклонения от
принятых условий, чтобы это заставило нас изменить сформулированные
выводы.
С математической точки зрения это есть задача очень близкая к
проблеме устойчивости. В англоязычной литературе для этого круга задач
принят термин «robustness»*). В связи с этим в русской литературе наряду с
«устойчивостью» используется также слово «робастность».
Робастность статистических процедур в широком понимании есть малая
чувствительность этих процедур к малым отклонениям от исходных
предположений.
Наиболее распространенные отклонения от упомянутых выше условий
состоят в следующем.
1. Распределение х^ не в точности равно Р, а лишь приближенно.
2. В серии наблюдений X присутствует малая доля «выбросов», т.е.
наблюдений, вызванных грубыми ошибками измерений или записи или
порожденных каким-то другим «мешающим» механизмом, отличным от
исследуемой системы. Отделить эти наблюдения, как правило, невозможно.
Вместо этого ищут процедуры, которые были бы мало чувствительны к
таким «засорениям» выборки.
3. Элементы выборки X не являются независимыми, а лишь слабо
зависимы.
Задача состоит в том, чтобы построить решающие правила для
основных задач математической статистики, которые были бы близки по своей
эффективности к оптимальным и в то же время были бы нечувствительны
к перечисленным отклонениям от принятых условий или хотя бы к тем из
них, которые для нас существенны. Эту задачу, которая является весьма
трудной и не всегда точно поставленной, нельзя считать изученной в полном
объеме. Результаты здесь носят пока еще разрозненный характер.
Остановимся несколько подробнее на названных видах отклонений от
исходных предположений. В задачах из практики эти отклонения могут
*) Robust — крепкий, здоровый.
§ 58. Устойчивость статистических решений
439
присутствовать, конечно, все одновременно. Здесь мы рассмотрим их
влияние по отдельности.
1. Пусть на самом деле выборка X принадлежит не распределению Fo, a
распределению FE = (1 — e)Fo + eF\, где ε мало. Мы будем рассматривать
оценки подстановки неизвестного параметра θ (мы видели в главе 2, что
все разумные оценки являются таковыми). Другими словами, если θ есть
значение функционала G(Fo) от распределения Fo, то мы будем пользоваться
в качестве оценки значением Θ* = G(F^), где F£ — эмпирическая функция
распределения, построенная по выборке X.
Возможны как качественная, так и количественная характеризации
робастности таких оценок.
a) Качественная робастность. Оценку Θ* = G(F*) мы будем
называть робастной (относительно замены Fo на близкое распределение F£),
если функционал G(F) непрерывен в точке Fo относительно слабой
сходимости распределений (слабая сходимость, по-видимому, лучше других
описывает интуитивное понимание близости распределений). Если считать для
простоты, что функция распределения Fo непрерывна, то слабая сходимость
будет эквивалентна равномерной сходимости. Все статистики (оценки)
второго типа, рассмотренные β § 3, 8, являются робастными оценками.
Если Θ* = G(F*) есть статистика второго типа и X €= F£ = (1—e)Fo+eFi, то
G(F*) будет близко при больших η к значению G((l — s)Fq 4-eFi), которое,
в свою очередь, будет близко при малых ε и любом F\ к G(Fo) = 0.
Статистики первого типа (см. §3) не являются, вообще говоря,
робастными оценками. Пусть, например, θ = G(Fo) = / g(x)dFo(x) < оо,
g{x)dF1{x) = оо, Χ €= Fe = (1 - e)F0 + eFi. Тогда 0* = G(F*) будет
близко при больших η (см. § 7) к (1— ε) I д(х) dFo(x)+e / д(х) dF\(x) = оо.
b) Количественная характеризация робастности. Степень
близости G(F£) для X ^ F£ и θ = G(Fo) можно характеризовать и
количественно. Для этого нам придется предполагать, что функционал G является
достаточно «гладким». Именно, мы будем считать, что функционал G
дифференцируем (см. определение 8.1 и замечания в конце §8), что означает в
нашем случае существование
limОд)-од) _,.тод-мп-^-ОД) _ _
ε-уО ε ε->Ό ε
Тогда
G{F*) - G(F0) = {G(K) ~ ОД)) + (G(Fe) - G(F0)). (1)
Первое слагаемое здесь согласно § 8 можно представить приближенно при
больших η в виде
-±=G'(FE,wnFe)
\Jn
/
440
Гл. 3. Теория проверки гипотез
(это в свою очередь близко к η l/2G'(Fo,w°Fo) при наличии свойств
непрерывности G'). Второе слагаемое в (1) при малых ε близко к
eG'iFcF.-Fo). (2)
Из сказанного видно, что суммарная погрешность в (1) имеет тот же
порядок малости, что и
n-l'2G'{F0,w°F0) + eG'{F0,F1-Fo).
Здесь к задаче робастности имеет отношение лишь второе слагаемое,
которое и характеризует робастность оценки количественно. Если оно мало по
сравнению с гг"1'2, то влиянием отклонений в предположениях о
распределении X можно пренебречь. Заметим, что малость (2) может быть
обусловлена и близостью F\ к Fo, так как G'(Fq,Fi — Fq) = 0 при F\ = Fq. Это
имеет место, например, когда некоторые элементы выборки известны лишь
приближенно (огрублены) и интервалы приближения малы. Если
произведение (2) не мало по сравнению с п-1/2, a F\ и ε известны, то значение
sG^FojFi — F*) можно использовать как «поправку» κθ* = G(F*),
уменьшающую смещение оценки.
При оценке параметра θ по выборке X из параметрического семейства
{Р#} следует проявлять осторожность в связи с тем, что значение G(Fe)
при F£ φ {Ρе} не обязано иметь смысл параметра этого семейства.
с) Устойчивость статистик. Возможны и несколько иные по
сравнению сп. а), Ь) подходы к задачам робастности, не связанные с методом
подстановки и анализом функции G(F£), где G(Fq) = θ есть оцениваемый
параметр. Пусть в некоторой статистической процедуре используется
статистика S(X). Тогда анализ робастности этой процедуры можно проводить,
используя свойства регулярности функции S. Будем предполагать здесь, что:
(Ci) Статистика S(X), X ^ Fq, асимптотически нормальна:
a^vMSPO - 0) е> Фод
(в правой части здесь может стоять и любое другое распределение).
(Сг) Для любого ε > 0 найдется множество Ωε и постоянная LE такие,
что
Ρο(Ωε) > 1 - ε, \S(X) - S(Z)\ < — Υ) |* - z<|,
где Ζ = (zb...,zn), zj <^ Fi.
Предположим теперь, что Fi и Fq обладают свойствами:
(Сз) Функции F{ непрерывны,
\Ful{FQ{t){l + Δ)) - ί| < c\Af, β > 0.
(C4) Справедливо
Fi{x) = FQ{x){l+ei{x)),
§ 58. Устойчивость статистических решений
441
где Si(x) = eiin(x) -> 0 при η —> оо таким образом, что
Таким образом, мы имеем дело здесь со схемой серий, когда Fi = Ff>n
зависят от гг.
Лемма 1. Пусть хг· ^ i<o, zz ^ F{ и выполнены условия (Ci)-(C4).
Тогда выборки X и Ζ можно так задать на одном вероятностном
пространстве, что {S(X) — S(Z))yfn —> 0. Это означает, что наряду с
условием (Ci) справедливо также
a-l^{S{Z)-e)&*0il. (3)
Сходимость (3) означает, что статистические выводы, основанные на
статистике S в предположении х^ €= Fq, сохраняются и в случае х^ €= F{.
Применение этого подхода проиллюстрировано в задаче об оценке хвостов
распределения в § 68.
Отметим, что все статистики I типа S(X) = h I — #(xi) 1 удовлетворяют
\n )
условиям (Ci), (C2) при подходящих условиях на /г, д. Например, если
Т?{д{Х) Ε [а,Ь}) -> 1, P{g{Z) е [а, 6]) -> 1 при η -+ оо, где д{Х) =
= — ; jfxj), и если h непрерывно дифференцируема на [а, 6], д удовлетво-
п ^—' _ _
ряет условию Липшица, то на множестве Ω = {д{Х) £ [а, Ь], #(<£) € [а>&]}
получаем
|5(Х) - S(Z)| = \h(g(X)) - h(g(Z))\ = |Λ'®)&(*) - g(Z))\ <
< |Λ'№-1 Σ Ι^(χί) - ^1 < Wmn-'cY^ \xi - 2i|,
где 5 G [α, 6].
Доказательство леммы 1. Пусть zj (= i^. Так как Fi
непрерывны, то
Далее,
|х< -2,·| = ^(Fifa)) -Zi\ = iFo^FoiziWl+eiizi))-*] < c\£i(zi)f.
Для любых ε > 0, 7 > 0 имеем
P{y/H\S(X) - S(Z)\ > 7) < ε + P(xfo\S{X) - S(Z)\ > -у,X е Ωβ) ^
< ε + Ρ (Len-1^ ^ |Xi - ζ,.| > 7) ^ ε + Ρ (η'1'2 £ Μ*)!* > ^Λ .
Правая часть здесь выбором ε и η может быть сделана сколь угодно малой.
Лемма доказана.
442
Гл. 3. Теория проверки гипотез
2. Рассмотрим теперь второй тип отклонений от предположения X ^ jFq,
когда известно, что доля ε = εη = τη/η > 0 элементов выборки X €= Fq
заменена на значения уь ■ · -,Ут5 τη = εη, относительно которых ничего не
известно. Другими словами, мы располагаем выборкой Хп, состоящей из
выборки Xn-m и выборки Υ = (yi,.. .,ym), которую выделить из Хп
невозможно. Эмпирическую функцию распределения F* для выборки Хп можно
представить в виде F£ — (1 — s)F^_m 4- £i*7y\ при очевидном толковании
обозначения FTyy Наша задача по-прежнему состоит в оценке θ = G(Fq).
Имеем согласно (6.6)
G{F*n) = G{{\-e)FZ_m+eF{Y)) =
1-е
\/n — m
= G ( (1 - еЩ + -j=^=wn-m(F0) + εΡ{γλ =
« ОД) + bnG' (Fo, J^f- ^-™(F0) + f (F(V} - F0) V
где предполагается, что
6n = max [ ε, , Ι = — max (га, y/n — m) —> 0
\ y/n — ra/ η
при η —> oo. Здесь опять важно сравнение величин ε и (п — га)-1/2, но не
только это, поскольку в рассматриваемой ситуации нам ничего не известно
относительно Fj*Yy
Пусть, например, G'(Fq,v) есть линейный функционал относительно и.
Тогда при Ьп = у/п — m/n (при га < л/п — га) имеем
- 771
= G^Fo^-iFo)) + 7^EG'(F°'FL· ~ *Ь), (4)
где F/* ч (я) = 0 при χ ^ у, i*?x (ж) = 1 при χ > у. Влияние второго слагаемого
в (4) будет мало, если Gf(Fo, F?, — Fq) равномерно ограничено по у. Однако
это не всегда имеет место. Например, если
G'(F0,v)= fl(x)dv(x),
то
G'{F0,F{y)-FQ) =l(y)-Jl(x)dF0(x). (5)
§58. Устойчивость статистических решений
443
Это значение может быть сколь угодно большим, если функция 1(у) не
ограничена (считаем, что / l(x)dFo(x) < оо).
Отсюда видно, что функция от у
I(F0,y) = G'{F0,F{y)-Fo)
играет важную роль для характеризации робастности функционала G. Ее
называют функцией влияния (влияния наблюдения у на изменение
функционала G(-F*); подробнее об этом см., например, в [122, 127-130]).
Итак, второе слагаемое в (4) будет иметь порядок гп(п — т)-1/2 при
всех У, если sup/(Fo,y) < оо и, следовательно, при m = о(у/п) будет пре-
у
небрежимо малым по сравнению с первым слагаемым, которое описывает
«естественный» разброс значений G(F^_m) около значения Θ. В этом
случае оценка G (F*) будет робастной.
3. Рассмотрим теперь третий тип отклонений от предположения X €= Fo,
состоящий в том, что наблюдения х^ €= Fq не являются независимыми.
Чтобы рассматривать задачу устойчивости относительно этого допущения,
мы должны предполагать, что зависимость между наблюдениями х$ и х;+А;
ослабевает с ростом к или равномерно мала при всех &. Остановимся на
первом варианте и будем характеризовать ослабление зависимости весьма грубо
через убывание коэффициентов корреляции. В отличие от п. 1, 2 здесь ро-
бастными оказываются статистики обоих типов, рассмотренных в § 3. Как
мы увидим, это связано с тем, что закон больших чисел и центральная
предельная теорема устойчивы относительно появления небольшой
зависимости между наблюдениями.
Пусть Θ* = G(F*), G есть функционал I типа G(F) = h I g(x) dF(x) 1 ,
где функция h непрерывна в точке до = Е^(х^) = / д(х) dFo{x). Положим
Δ,- = g{xi) - до, р{к) = EAiAi+k,
так что р(0) = D^(xf), и будем считать, что р(к) от г не зависят.
Теорема 1. Если
оо
0<p{0)+2j2p(k) -σ2 <οο, (6)
fc=l
mo для выборки X из зависимых наблюдений Х{ €= Fq выполняется
G{F*) -^ h(g0) = G(F0).
444
Гл. 3. Теория проверки гипотез
Доказательство. Имеем
(п \ 2 η—Ι п—к
t=l / fc=l t=l
где rn = о(1),
η —1 7ΐ-1
= ηρ{0) + 2 ]Γ(η - k)p(k) = ησ2 - 2 ^ A/o(fc) + rn,
*=1 fc=l
n—1 n—In—1
Λ=1 *=lj=fc
при η —> oo. Поэтому для эмпирической функции распределения F£,
построенной по выборке из зависимых наблюдений, в силу неравенства Че-
бышева будет выполняться
(I/
9{x)dF*{x)-g0
> ε
= ε~2η~1(σ2 + ο(1)) ->0
при η —> οο. Остается воспользоваться теоремой непрерывности.
Аналогично обстоит дело с функционалами II типа. Обозначим через
1а{х) индикатор множества Л, д(х) — Ι^^^χ).
Теорема 2. Пусть для введенной функции g выполнено (6) при
любом ζ. Тогда если функционал G непрерывен в равномерной метрике в
точке Fo, то G(F*) —> G{F0).
Доказательство. Нам достаточно доказать, что для выборки X из
зависимых наблюдений справедливо
8ир|^п*(а:)-ВД|—>0.
X Г
Это следует из того, что в силу теоремы 1 F*(z) —> Fo(z) при любом ζ и
из рассуждений, аналогичных доказательству теоремы 2.2. <
Нетрудно провести и количественную характеризацию робастности в
условиях этого параграфа. Для статистик I типа предельное распределение
у/п I / g(x)dF^(x) — go) в широких предположениях будет нормальным
Φ0σ2, так что влияние зависимости будет осуществляться лишь через
параметр σ2, определенный в (6). Таким образом, появление зависимости
наблюдений сказывается лишь на степени разброса Θ* около θ (для
независимых xj выполняется а2 = р(0)). Для статистики II типа эта картина
в целом сохраняется, хотя изучение предельного распределения G{F£) для
§ 58. Устойчивость статистических решений
445
функционалов второго типа и зависимых наблюдений выглядит сложнее
(качественно все результаты §8 в этом случае сохраняются).
Рассмотрим теперь несколько примеров. Первый из них будет связан
главным образом с анализом влияния выбросов (второй тип отклонений от
предположения X €= Fo).
2. Оценка параметра сдвига. Пусть по выборке X €= Ρα, Ρα(Α) =
= Т?(А — а) оценивается параметр сдвига а. Мы рассмотрим здесь два типа
оценок: М-оценки (как мы видели в § 14; они ведут себя в известном смысле
как аддитивные статистики) и L-оценки (основанные на порядковых
статистиках; см. §8).
При рассмотрении М-оценок наиболее интересными являются два
случая, когда функция д(хг,а), участвующая в построении М-оценок (см. § 14),
имеет вид д(х,а) = д(х) (метод моментов) и д{х,а) = д(х — а). В первом
случае истинное значение ао параметра α определяется как решение
уравнения
а{а) = / g{x)Pa{dx) = / g{x)PaQ{dx),
так что М-оценка а* в этом случае (являясь оценкой подстановки) имеет
вид
a* = a-1^J9(x)dF:(x)y (7)
Во втором случае для д(х,а) = д{х — а) получим уравнение (считаем для
простоты, что 0 € Θ)
ί д{х - a)Pao{dx) = f д{х - θ)Ρα(άχ) =
= I д{х- a)P(dx - а) = / g(x)P(dx) = α(0).
Таким образом, если решение уравнения
д(х - a) dF(x) = α(0)
/'
обозначить через G(F), то М-оценка а* в этом случае будет иметь вид а* =
— G{F^). К этому второму случаю относятся, очевидно, и о. м. п. Достаточно
положить д(х — а) = ί'(α;,α), где 1(х,а) = lnfa(x) = In/(я — α).
Если д(х) = х, то а(а) = а(0) +а и оценки а* в обоих рассматриваемых
случаях будут совпадать:
α* =χ-α(0).
Очевидно, эта оценка является а.н. оценкой с параметрами (0,σ2), σ2 =
= ί x2V{dx).
Для g(x) — χ, как и для произвольной неограниченной функции д, в
обоих случаях М-оценки не являются робастными относительно
присутствия выбросов. В первом случае это видно непосредственно из формы
446
Гл. 3. Теория проверки гипотез
оценки (см. (7)), во втором — из того, что производная функционала G
(см. § 14) равна
G'(Fao,v) = -b-1 Jg(x - α0) dv{x\ b = Jg'(x)I>(dx),
так что в этом последнем случае в обозначениях (5)
Ку) = -b~lg{x-a0).
Чтобы сделать рассматриваемые М-оценки робастными, можно вместо д
использовать ограниченную функцию
gN{x) = min[max{g{x),-N),N].
Следует отметить, что при этом вычисления функции α(Θ) и функционала
G(F) могут усложниться, а коэффициент разброса оценок увеличиться
(напомним, что для ряда задач линейная функция д(х) = χ дает эффективные
оценки). Число N следует выбирать исходя из специфики задачи, а также
в зависимости от η и от величин выбросов (они не превосходят крайних
значений выборки). В связи со сказанным отметим также, что сам класс
М-оценок был введен в [127] как такое расширение класса о. м. п., в котором
можно искать робастные оценки, не слишком теряя при этом в
эффективности.
Рассмотрим теперь L-оценки (см. § 8), связанные с функционалом
(см. (8.2))
ι
G(F)= JV(t)g(F-1(t))dt-b, (8)
о
при д(х) = χ, φ(ί) = ^ /(7>1_7)(г), где 7 Ξ (ОД/2), IA(t) —
индикатор множества А, постоянную b мы выберем так, чтобы G{Fq) = θ. Имеем
Fjj~l{t) = F^~l(t) + θ (будем считать для простоты, что О Ε Θ),
1—7 1—7
G(Fe) + b=T^ J FfHt)dt = e+T^ J F0-l(t)dt
У 7
Поэтому нам следует положить
1-7
ъ=т^! F«X{t)dt-
Ί
При таком Ь мы можем пользоваться оценкой подстановки (L-оценкой)
, [(l-7)n]
§ 58. Устойчивость статистических решений
447
Предположим, что функция распределения Fq(x) имеет плотность Fq(x) =
= f(x — θ). Тогда согласно §8 оценка Θ* является а. н. с параметрами
ι
12
О, I A2{t)dt-Az | ,где
ι ι
A(t) = Ja(t)dt, A = JA(t)dt, a(t)= ^
t о
Производная функционала G здесь равна (см. § 8)
1-7
«™-ϊ-*Ι№
Ml*.
7
При ν = F/* ч — F0O получим функцию влияния
I(FBo,y)=G'(Feo,F^y)-Feu) =
WW)
1—7 1—7
1 /" <ft 1 Г tdt
f dt 1 /"
1 f(FzHt)) + l-2rYJ
1-27 ,i ,„>№(*)) ι-*{ /WW)'
max(7,^0(2/)) 7
Очевидно, что она ограничена по у и, стало быть, оценка (9) является ро-
бастной (относительно выбросов; см. пп. 2 из п. 1). Об оптимальности (в
известном смысле) выбора функции φ в (8) см. в [66, 102] и § 17.
Если 7 сближаются с 1/2, то оценка (9) сближается со «сдвинутой»
выборочной медианой ζ* — b I или с оценкой — \^ x{[n/2-k]) ~~ b I, которой в (8)
соответствует обобщенная ^-функция с единичной массой в точке t = 1/2. В
нечувствительности ζ* к появлению выбросов yi,...,ym (см. пп. 2 из п. 1)
можно убедиться и непосредственно. Действительно, ζ* будет располагаться
между значениями х^) и Х(&2), где
*1 =
п + 1
— m
А;2 =
п + 1
— Ь m
x(fc)> fc = 1,.. .,n —m, образуют вариационный ряд выборки Xn-m €= i^0. Но
асимптотические свойства х^), х(к2) одинаковы и совпадают со свойствами
выборочной медианы (см. §8, 12).
Если 7 ·""> 0> то оценка (9) сближается с χ — 6. Таким образом, при
7 Ε (0,1/2) оценки (9) заполняют весь «промежуточный спектр» оценок,
лежащий между ζ* — b и χ — b. Если оценка χ — b оптимальна, то выбирая
7 > 0 достаточно малым, мы получим робастную оценку, близкую к
эффективной. В связи со сказанным отметим следующее. Свойства оценки Θ* = χ
448
Гл. 3. Теория проверки гипотез
мало зависят от изменений Р, сохраняющих дисперсию &i= t2f{t) dt и,
в частности, от локальных изменений f(t) в точке t = 0. В этом смысле она
устойчива. Но свойство оптимальности этой оценки, имеющее место для
Ρ = Φασ2, неустойчиво. Действительно, пусть при малом ε > О
Ρ = {1-ε)ΦΘΛ + ευΘ-εΜε.
Тогда /(0) = (1 - ε)/\/2π + 1/2 > 1/2 и, как показывают соотношения
Г ε3
(χ - 0)ν^ θ> Φ0,σ?. σ? = у *2/(«) Λ = (1 - ε) + у,
<C-*)v^ *„,„!, .? = ^=(1 + ^)
-2
оценка С* будет лучше, чем χ (σ2 < σι), для ε < εο, где εο > 0 легко
вычислить.
Сказанное означает также, что распределение статистик ζ* неустойчиво
относительно малых изменений Fg0 в окрестности точки F^l{l/2) (значение
/(0) в приведенных выше рассмотрениях может при этом сильно меняться).
Соображения об устойчивости оценок параметра сдвига, приведенные в
этом пункте, нетрудно переформулировать применительно к статистическим
критериям, относящимся к проверке гипотез о параметре сдвига, например
к несмещенным р. н.м. к. |х — ао| > с для проверки по выборке X €= Фа,1
гипотезы #ι = {а = ао} против #2 = {\<* — ао| > d > 0}.
3. Статистики Стьюдента и S%. Рассмотрим теперь вопрос относительно
устойчивости статистических процедур (оценивания и проверки гипотез),
связанных со статистиками
t- g , 50-п_12^(Хг Χ)·
г=1
На этих статистиках, как мы знаем (см. § 47, 48), основаны оптимальные
критерии соответственно для проверки гипотез относительно среднего α и
дисперсии σ2 нормальных совокупностей в случае, когда второй параметр
(σ2 или а) распределения Фа?(Т2 неизвестен.
Статистики t и Sq ведут себя по-разному относительно нарушений
условия X €= Φα,σ2. Допустим, что η велико, aJi §Р, где Ρ — любое
распределение со средним а и конечной дисперсией. Тогда распределение t так же,
как и в случае Χ ^ Φα,σ2> будет сближаться с нормальным распределением
Фод. Это следует из теорем непрерывности (§5) и того, что
(х — θί)\/η , г> ^
Сказанное означает, что размер критерия Стьюдента при больших η
будет мало отличаться от заданного, если даже распределение Ρ выборки X
существенно отличается от нормального.
§ 58. Устойчивость статистических решений
449
Этого нельзя сказать относительно критериев, построенных по
статистике Sq . Это обстоятельство связано с тем, что предельное распределение Sq
зависит от значения Ех*. Действительно, из рассмотрений главы 1 следует,
что
(S2 - σ2)Λ ©- Фо^. d2 = Е(х2 - σ2)2 = Dx2.
Стало быть, размер критерия, построенного по статистике Sq для
нормальной совокупности, может существенно отличаться от заданного, если X €= Ρ
и Ρ отличается от Φα?σ2 (разницы не будет при совпадении четвертых
моментов Ρ и Φα>σ2).
Обе статистики t и Sq чувствительны к отказу от предположения о
независимости наблюдений в выборке X. Если, например, все наблюдения в
выборке коррелированы друг с другом и коэффициент корреляции равен /9,
то, принимая, не ограничивая общности, a = 0, получим
Е502 = -Е
п — 1
Σχ*2-"(*)2
.i=l
п-1
по1
\*=1 У
= -\ησι - σ\\ - ρ) - ησ'ρ] = σ2(1 - ρ).
η — 1
Таким образом, здесь нарушается даже свойство несмещенности Sq , хотя
при малых ρ отклонение будет небольшим. Отыскание распределений t и Sq
при появлении зависимости обычно представляет собой значительные
трудности.
4. Критерий отношения правдоподобия. Этот критерий обычно весьма
чувствителен к наличию выбросов и даже к малым отклонениям в
предположениях о распределении X. Пусть, например, проверяются две простые
гипотезы Н\ = {X €= Фод} иЯг = {X ^ и_1д}. Ясно, что при использовании
н. м. к. Неймана-Пирсона появление хотя бы одного наблюдения χ вне
отрезка [—1,1] при идеальном соответствии остальных наблюдений
равномерному распределению U_i}i заставит нас (с нулевой вероятностью ошибки!)
принять гипотезу Н\. Это значит, что наличие хотя бы одного выброса или
появление даже малых отклонений от распределения U_ii могут вынудить
нас принимать ложное решение.
В этом отношении критерий Колмогорова, например, является
значительно более устойчивым (хотя и менее мощным относительно #2)· Вообще,
непараметрические критерии, как того и следовало ожидать, в целом
значительно более устойчивы, чем «индивидуальные» критерии, обладающие
свойством оптимальности в той или иной конкретной задаче.
Что касается рассматриваемой задачи о проверке нормальности (Hi)
против равномерности (Щ) выборки X, то отыскание мощных и в то же время
устойчивых относительно выбросов критериев можно произвести,
используя по-прежнему отношение правдоподобия, но для «усеченных» выборок
(ср. с (9)). Можно также идти по пути подбора какого-нибудь другого
критерия. В этом отношении наличие достаточно большого запаса различных
критериев и оценок представляется весьма полезным. Это связано зачастую
не только с соображениями устойчивости, но и с вопросами удобства
вычислений.
Глава 4
СТАТИСТИЧЕСКИЕ ЗАДАЧИ С ДВУМЯ И БОЛЕЕ ВЫБОРКАМИ
В § 59, 60 рассмотрены задачи об однородности двух выборок.
В § 61 рассмотрены задачи регрессии.
В §62 излагаются основные результаты дисперсионного анализа.
В § 63 рассмотрены задачи распознавания образов.
§ 59. Проверка гипотез об однородности
(полной или частичной) в параметрическом случае
1. Рассматриваемый класс задач. В предыдущих главах основным
объектом всех рассмотрений была выборка X объема η из полностью или частично
неизвестного распределения Р. Мы переходим теперь к статистическим
задачам, где фигурирует не одна, а две или более выборок.
Один из основных классов задач, которые при этом рассматриваются,
составляют задачи о проверке однородности (полной или частичной) двух
выборок.
Сюда относятся следующие основные три типа задач.
I. Проверка «обычной» однородности. Задача здесь состоит в
проверке гипотезы о том, что две выборки X и Υ извлечены из одного и
того же неизвестного распределения. Такие задачи возникают, например,
при сравнении двух способов обработки в каком-нибудь технологическом
процессе или в сельском хозяйстве. Основой для сравнения обычно служат
числовые характеристики конечного продукта (выборки), которые носят
случайный характер. Такого же рода задачи возникнут, если мы по состоянию
больных будем проверять воздействие нового лекарства, сравнивая
подопытную группу пациентов с контрольной.
К задачам об однородности относится пример 3 из введения.
В этом параграфе мы будем рассматривать параметрический случай.
Пусть дано параметрическое семейство распределений {Ре}веэ и даны две
независимые выборки X = (χχ,...,хП1) и Υ — (уι,..., уИ2) объемов щ и П2
соответственно, относительно которых заранее известно, что они относятся
к семейству {Р#}:
Х<=Рв1, Υ^Ρθ2, (1)
при некоторых #ι, 02- Обычная задача об однородности состоит в
проверке гипотезы Н\ = {θ\ = 02} против дополнительной альтернативы H<i ==
= {01 Φ 02}· Очевидно, что здесь обе гипотезы Н\ и Ή.2 являются сложными.
П. Проверка однородности при наличии мешающего
параметра. Здесь предполагается, что размерность к параметра 0 больше
§ 59. Проверка гипотез об'однородности
451
единицы. Запишем вектор θ в виде набора θ = (u, v) двух «подвекторов» и
и г; и обозначим через Uj} Vj подвекторы векторов 0j в (1), j — 1,2.
Пусть нам заранее известно, что «подпараметр» г; у обеих выборок хотя
и неизвестен, но является общим: г;ι = ν2 = v. Проверяется гипотеза Hi =
= {щ = U2} ПРОТИВ Н2 — {Щ φ U2}.
Это и есть задача об однородности при наличии мешающего параметра г>.
Она отличается от обычной задачи об однородности тем, что альтернатива
для гипотезы Н\ = {θ\ = θ2} имеет вид Н2 = {г^ φ и2, v\ = v2}.
Можно привести следующий пример возникновения такого рода задач.
Допустим, что нас интересует состояние некоторого объекта, которое
характеризуется вектором а. Но измерить а непосредственно нельзя. Нам
доступны лишь измерения, при которых на а накладывается случайный шум.
Природа шума при разных наблюдениях остается неизменной. Надо
проверить гипотезу о неизменности а в двух сериях наблюдений X и У.
Если, скажем, измерения имеют вид х* = αϊ +&, где & ^ Φλσ2
определяют роль шума, и такой же характер имеют наблюдения у; с заменой
αϊ на а2, то мы можем записать X ^ Φαι+λ,σ2> Υ ^ Φα2+λ,σ2· Мы ПРИ~
шли к задаче о проверке равенства средних {αϊ = а2} двух нормальных
совокупностей Φαι σι и Φα2 σι при общем неизвестном значении σ2.
III. Проверка частичной однородности. Здесь проверяется
гипотеза Н\ лишь о «частичном» совпадении θ\ и θ2. Именно, проверяется
гипотеза Н\ = {г^ = и2} (в обозначениях предыдущего пункта) против
Н2 = {щ φ и2}. Значения ν\, υ2 для каждой из выборок Χ, Υ могут быть
свои.
Допустим, например, что в лаборатории оценивается результат
воздействия нового способа обработки на урожайность какого-нибудь злака.
Наблюдения представляют собой суммарный вес зерен в отдельных колосках.
Предположим, что χ; ^ Φαι σ2, i = 1,.. .,ηι, для опытной партии колосков
и у ι ^ Φ σ2 для контрольной партии. Естественно допустить, что
«разброс» сг2 в результате изменения обработки мог измениться. Для нас же
существенно, изменился ли главный показатель а, определяющий
урожайность культуры. Мы приходим к задаче о проверке гипотезы Н\ = {а\ = а2}
против Н2 = {αϊ φ α2} для нормальных совокупностей, дисперсии которых
могут быть разными. Это задача, хорошо известная в литературе под
названием проблемы Беренса-Фишера*).
В этом параграфе мы произведем редукцию всех трех типов задач для
произвольных параметрических семейств к задаче, рассмотренной в §55,
о принадлежности одной выборки параметрическому подсемейству и
найдем вид асимптотически минимаксных критериев в предположении близо-
*) Поиску ее оптимальных решений посвящена довольно обширная литература (см.
библиографию, например, в [65, 66]). Значительный вклад в исследование проблемы Беренса-
Фишера, оказавшейся весьма трудной, принадлежит Ю. В. Линнику и его ученикам. Эти
исследования требуют введения новых понятий и использования весьма сложного
математического аппарата. Это делает невозможным цитирование и доказательство (в рамках
настоящей книги) полученных результатов. Положение в задачах об обычной однородности и об
однородности при наличии мешающего параметра для нормальных совокупностей несколько
лучше (в ряде задач удается найти равномерно наиболее мощные (р. н. м.) инвариантные
несмещенные критерии, однако необходимые для этого построения также оказываются
довольно сложными; подробнее об этом см. [65, 66]).
452
Гл. 4. Задачи с двумя и более выборками
сти проверяемых гипотез. Это будут критерии отношения правдоподобия,
которые для нормальных совокупностей будут совпадать с критериями,
построенными в поисках той или иной точной оптимальности (если таковые
имеются; ср. с [65, 66]).
Статистический критерий π для проверки Ηχ против Η<ι в нашем случае
будет функцией π = π(Χ, У) двух выборок X и Υ и будет, как и ранее,
означать вероятность приема #2 при данной объединенной выборке (Χ, Υ)
(см. гл. 3). Определения асимптотического уровня и асимптотической
оптимальности критерия π здесь остаются теми же, что и в § 43.
Определение 1. Будем говорить, что критерий π имеет
асимптотический уровень 1 — ε (принадлежит классу Κε), если
limsup sup Έ$ιβ2π(Χ, Υ) < ε,
»£Ξ (*ιΛ)€5ι
где Ε0Χ02 означает математическое ожидание по распределению Р^ χ Ρ#2,
Θι есть множество значений (61,62), при которых выполнена гипотеза Н\
(например, множество всех точек (61,62)? лежащих на «биссектрисе» θ\ — 02
в задаче об обычной однородности).
Определение 2. Критерий πι €= Κε называется асимптотически
минимаксным в Κε для проверки Н\ против #2, если для любого критерия
π Ε Κε выполняется
liminff inf _ ЕМ27Г!(Х,У) - inf _ Εθιθ2π(Χ,Υ)) > О,
nj-юо 40ι,02)6Θ2 (01,02)€θ2 '
П2~-юо
где ©2 есть множество значений (61,62)? соответствующих альтернативам
ИЗ #2.
2. Асимптотически минимаксный критерий для проверки близких
гипотез об обычной однородности. Введем новый параметр θ = (61,62),
характеризующий «объединенную» выборку (X, У). Функция правдоподобия этой
выборки равна fg{X,Y) = fei(X)fe2{Y)·
Допустим для простоты, что объемы выборок совпадают: п\ = п,2 —
= п. Тогда выборку (Χ, Υ) можно представлять себе как выборку объема п,
образованную наблюдениями (xi,yi),..., (xn,yn) из распределения Р^ =
= Ρ#; χ Pfl2, имеющего плотность /θι(χ)ίθ2(ν)· Мы приходим к задаче,
рассмотренной в §55, о проверке по выборке (Χ, Υ) гипотезы Н\ о том, что
параметр 6 располагается на «кривой» 6ι = 62. В обозначениях §55
гипотеза Н\ в нашем случае имеет вид θ = #(α), где α = #i, g(a) = (α,α). Оче-
т^Ч L i = 1,...,2A;; j = 1,..., fe, имеет вид (E),
где Ε — единичная матрица fc-го порядка, так что ранг G равен к.
Будем считать параметр θ локализованным, т. е. будем считать, что
значения 6ι и 62 близки и, стало быть, возможные значения θ
располагаются в окрестности точки 6q = (6o,6q) при некотором фиксированном 9q.
видно, что матрица G =
§ 59. Проверка гипотез об однородности
453
Если следовать §55, то нам будет удобнее ввести новый параметр τ =
= (τ', т") = (т7>/п, 7/;Л/й) = Ί/y/n, где τ' = 0ι - 0О, τ" = 02 - 0ь так что
отображение θ = 0(т) взаимно однозначно: θ\ = τ' 4- 0о, #2 = т;/ 4- τ' + 0ο·
В терминах параметров г и 7 гипотеза Н\ об однородности примет вид
Н\ = {τ11 = 0} = \η" = 0}. В качестве альтернативы мы рассмотрим
«отделенную» гипотезу
Н% = {7"/7"Т ^ б2}, 6>0, (2)
где / = Д0о) есть матрица Фишера для семейства {Р#} в точке 0о-
Теорема 1. Пусть β окрестности точки 0о семейство {Рв}
удовлетворяет условиям (RR) (см. §36). Тогда критерий отношения
правдоподобия
sup Л, (X)/fc(r)
Ri (Χ, Υ) = '"* f,yw,Vx > J*'2 (3)
вирЛ(Х)Л(У)
θ
является асимптотически минимаксным критерием асимптотического
уровня 1 — ε для проверки Н\ = {0χ — θ2} против Н% = {(0ι — Θ2)Ι(Θ\ —
■~ #2)Т ^ Ь2/п} при любом Ъ > 0, где /ιε есть квантиль порядка 1-е
распределения χ2 с к степенями свободы (такое предельное
распределение при гипотезе Н\ имеет статистика 21ni?i(X, У)).
Пусть θ*χ, θγ, θ* есть о.м.п. параметра θ = θ\ = θ2
соответственно по выборкам X, У, (X, У). Тогда критерий
(θ*χ - 0*)/(0*)(0χ - £*)Т + (0у - 0*)/(0*)(0к - 0*)Т > — (4)
ТЬ
будет асимптотически эквивалентным критерию (3).
Доказательство. Приведенное утверждение является прямым
следствием теоремы_55.4. Нам надо лишь выяснить, что собой представляет
матрица Фишера Ι{θο) = /(0о,#о) Для «объединенного» параметра θ = {θχ,θ2)
и матрица М2 для параметрического семейства {Р(0о,0о+0)} B т0чке /5 = 0.
Имеем
ln^l(x)/fc(y)=i(xjei) + i(y,e2).
Обозначим через U, г = 1,..., 2&, координаты вектора 0. Тогда если через Е^
обозначить математическое ожидание по распределению Р^, то элементы
I%j{9) матрицы 1(9) будут равны
7 т тг ί9ι^ιΛ) , д1(уъв2)\ (Щхив^ д1(уив2)\
454
Гл. 4. Задачи с двумя и более выборками
Отсюда в силу независимости χχ и ух получаем
W'-y о ΐ(θ2))·
Поэтому критерий (4) есть не что иное, как критерий (55.12) в теореме 55.4.
Аналогичные вычисления показывают, что Μ<ι = /(#о)5 так как при β =
= (Α, ■■·.&) = о
dl(xlte0) , dl(yi,e0 + fi) ЩУ1,в0) ._
ад + ад " dti ' t-1'·-·'*· <
Замечание 1. Утверждение теоремы 1 мы получили в предположении,
что ni = П2- Однако это ограничение совершенно несущественно.
Рассмотрим, например, случай, когда п\ —> оо, щ -> оо так, что отношение nijn^
равно рациональному числу г\/г2 (π, τ*ι — произвольные целые
фиксированные числа, щ = пгг, η —> оо). Мы введем опять новый параметр
θ = (0χ,#2) и будем рассматривать объединенную выборку (X,У) как
выборку объема η с наблюдениями (χχ,.. .,хГ1;ух,.. .,уГ2), (хп+ъ .. .,X2ri»
Уг2+ь · · ч У2г2)>. · · из распределения
Р^Р^х-'-хР^хР^х-'-хР^,
N ν ' Ν ν '
τ\ раз Г2 раз
зависящего от параметра Θ. Функция правдоподобия здесь вновь будет иметь
вид
Если ввести, как и прежде, новый параметр г = (г1, т") = (0χ — 0о> ^2 — ^ι) и
положить г = ύ/у/п = (т'/чАь 7"/\/™ )> т0 рассматриваемая задача состоит
в проверке i/χ = {7" = 0} против Н^ — {7"Л^27"Т ^ б2}, где Мг — матрица
Фишера для Р(0О,0О+/?) в точке /3 = 0. Легко видеть, что в нашем случае
Μ<ι = Г2/(^о), так что множество альтернатив сохраняет свою форму (2):
*5 = {7"/7"Т>£}·
Матрица Фишера Ι(θ) будет иметь вид
(rim) о \
V о r2m)j ·
Остается воспользоваться теоремой 55.4. Получим тогда утверждение
теоремы 1, в которой критерий (4) следует заменить на
ηι(θ*χ-θ*)ΐ(θη(θ*χ-θ*)τ + η2(θ^-θ*)ΐ(θη(θ*γ-θ*)>Ηε. (5)
С помощью теоремы 55.4 можно указать также гарантированную
асимптотическую мощность критериев (3)-(5).
§ 59. Проверка гипотез об однородности
455
Утверждение теоремы остается справедливым и в общем случае, когда
п\ —> со, ri2 —> со, n\/ri2 —> с, где с — произвольное число из (0,1). Однако
доказательство этого факта требует дополнительных рассмотрений.
Замечание 2. Утверждение теоремы 1 сохранится, если гипотезу Hi =
= {θ\ — Θ2} заменить гипотезой (см. §55)
Я? = ί (βι - 02)/(0ι - 02)т < тг} . О < α < ft.
Замечание 3. Форма асимптотически минимаксных критериев в
теореме 1 от #о не зависит. Значение 0о входит только в определение
гипотезы Н% через / = J(0o) (см· (2)), хотя и этого появления 0q можно было
бы избежать, заменив / в (2) на (0χ + 02)/2. Это дало бы нам
«асимптотически эквивалентную» /Г^ гипотезу Н\^ для которой утверждение теоремы 3
полностью сохраняется. Появление в (2) значения 0о есть следствие
использования наиболее простого пути редукции рассматриваемой задачи к
результатам § 55.
Пример 1. Пусть ХиУ есть выборки объемов щ, η<ι из
полиномиальных распределений X €= В^, Υ €= В^2, 0j G R*, 0; = (fti,.. .,0»*)»
i = 1,2. Векторы частот ^ = (&ί, ..., ζ/&) и μ = (μι,..., μ^) появлений
событий Αι,..., Afc (см. § 12) образуют достаточные статистики,
/*(*) = ПС /*(у) = ГК·
О. м. п. имеют вид Q*x = ζ//ηι, 0^ = μ/^2> 0* = [у + μ)/(ηι + ™2)·
Матрица /(0) определена в (56.5), так что (см. (56.9))
Итак, в силу теоремы 1 и замечания 1 асимптотически минимаксный
критерии асимптотического уровня 1 — ε для проверки Hi — {βι — 02}
против
имеет вид
А; А;
~^ П1 ~[ П2 П! + П2 2
456
Гл. 4. Задачи с двумя и более выборками
где h£ — квантиль порядка 1 — ε распределения χ2 ck — 1 степенями свободы.
Согласно (4), (5) асимптотически эквивалентным будет критерий
к
г=1
ηχ
ν% + μ%
ηχ + η2
2 , k /
ηι + η2 , ν^ / μι
+ η2 > —
к
-Σ(
» — 1
Щ + μ%
ηχ +Π2
КПХ П2)
'П\ +Π2
Щ + μι
2
Πχη2
щ + μ%
>h£. (6)
Пример ΙΑ. В примере 35.3 был описан механизм наследования групп
крови, которые были обозначены как 0 (ноль), А, В, АВ. Он управляется
с помощью генов трех типов А, В, 0. Вероятности появления этих генов
в данной популяции обозначим соответственно через р, q, г = 1 — ρ — q.
Вероятности pi(a), a — (ρ,g), того, что человек будет иметь г-ю группу
крови, выражаются через α по формулам, приведенным в §35, табл. 1.
Нам даны две выборки X и Υ с частотами щ и μι, г = 1,.. .,4,
появления г-й группы крови, полученные в результате обследования ηχ = 353 из
общины I и п2 = 364 человек из общины И. Распределение людей по группам
крови приведено в табл. 1.
Таблица 1
Община I
Община II
Всего
0
121
118
239
А
120
95
215
В
79
121
200
АВ
33
30
63
Всего
353
364
717
Надо проверить гипотезу о принадлежности обследуемых общин одной
популяции, т. е. гипотезу о равенстве вероятностей ρ и q для этих групп
или, что то же, о равенстве вероятностей Pi{a). Это есть, очевидно, задача
об однородности, рассмотренная в примере 1.
Если проверять совпадение вероятностей четырех групп крови, то
статистике (см. (6))
4 / ч 2
2 V^ I Ui μί\ ГЬхП2
i=l
rci п2 ) Щ + μι
будет соответствовать распределение χ2 с тремя степенями свободы. В
нашем случае значение χ2 составляет 11,74. Фактически достигаемый (см. § 44)
уровень полученного уклонения превосходит 0,99. Это значит, что гипотезу
об однородности следует забраковать с точки зрения критерия χ2 > /ΐο,οι
уровня 0,99.
Отметим, что примененный критерий не полностью отвечает природе
рассмотренного явления, так как мы должны проверять совпадение
вероятностей ρ и д, а не вероятностей р\ появлений групп крови. Если следовать
в точности теореме 1, то мы должны методами §35 вычислить о. м.п. а^,
<5у и а* параметра α = (ρ, q) соответственно по выборкам X, У, (Χ, Υ) и
§ 59. Проверка гипотез об однородности
457
воспользоваться статистикой
Xl = 2[L(a*x,X) + L{a^Y) - L(a\(X,Y))} =
= 2
]Г щ InPi(a*X) + Σ Vi ^Рг(3у) - Σ (Уг + Pi) lnP*(S*)
.i=l
<=1
i=l
имеющей при больших η распределение, близкое к распределению χ2 с
двумя степенями свободы. Если провести необходимые вычисления (см.
пример 35.3), то мы получим χ| ~ И>04, что для двух степеней свободы
дает более значимое уклонение, чем 11,74 для трех.
О проверке самой гипотезы о принадлежности X и Υ параметрическим
подсемействам Вр(а), где р(а) — (ρι(α),.. ,,р4(<*))? смотри пример 57.1. Обе
выборки хорошо согласуются с этой гипотезой.
Пример 2. Пусть Χ ^ Φαΐι(Τ2, Υ €? *α2,σ2, где точки θχ = (α^,σ?)
располагаются в окрестности точки θο — (αο,σο). Здесь
-2
Ό
О
О 2σο
(см. §26), и мы будем рассматривать задачу о проверке гипотезы Н\ =
= [θ\ — 62} против
- ' Η — > — > , п = щ+п2.
Щ =
ση
2σ04
П2
1 _П1_
Имеем θ*χ = {x,S2x), S2X = — ]Г(х; -χ)2, /f. (Χ) - (2πβ5^)~ηι/2. Ана-
ηι i=i x
логичные формулы справедливы для выборки У. Далее,
0*=М|,у), Ζ =
Til ГС2 \
Σ хг + Σ Уг
,г=1 t=l /
Щ +П2
= ах+ (1 -а)у,
гг2
ni +п2
щ
712
Σ (χί -z)2+Σ fo -г)
i=l t=l
= а<& + (1 - a)S2 + (1 - а)а(х - у)2, (7)
где а = щ/(щ + п2), /?. (*)/?. (П = (2πε5^)-(ηι+"2)/2.
Таким образом, асимптотически минимаксным для проверки Н\
против #2 будет критерий
Х-У ^ pheHni+Tl2)
ς2ας2(1-α) ^е
;ХиУ
458
Гл. 4. Задачи с двумя и более выборками
где h£ — квантиль распределения χ2 с двумя степенями свободы. Мы
предлагаем читателю в виде упражнения найти асимптотически эквивалентный
критерий вида (5).
3· Асимптотически минимаксные критерии для задачи об однородности
при наличии мешающего параметра. В этом и последующих пунктах мы
будем считать для простоты, что объемы выборок X и У совпадают: щ = П2-
Это ограничение несущественно. В случае n\jri2 = T\jr*i (ri, τ<ι целые)
читатель может избавиться от него самостоятельно так же, как это было
сделано в замечании 1 к теореме 1.
Итак, пусть даны две выборки X ^ Р#15 У ^ Р#2, θ% = (г^,г>г), г = 1,2,
объемов щ = П2 = п. Проверяется гипотеза {г^ = гхг} против {щ φ η<ι\
в предположении, что v\ = г>2 = ν и ν нам неизвестно. Размерность щ
обозначим через г, г < к.
Введем новый параметр θ = (ui9U2,v). Объединенную выборку (X,У)
представим как выборку объема η с наблюдениями (xi, yi),..., (xn, yn),
плотность распределения которых равна f§{x,y) = f(Uuv){x)f{u2,v)(y)- Для этого
параметрического семейства рассматриваемая нами задача эквивалентна
задаче о проверке гипотезы Н\, состоящей в том, что значение θ лежит на
«кривой» θ = g{9\) = (τχχ,Tii,г?), против дополнительной альтернативы.
Матрица G =
%
ΘΘ
У
Ε О
г = 1,...,А+г; j = !,...,&, имеет форму ( ' J , где
сверху стоит единичная матрица порядка г, а внизу — единичная матрица
порядка &, так что ранг G равен к.
Как и в предыдущем пункте, будем считать параметр θ
локализованным около точки #о = {щ>щ)· Введем параметр τ = τ(θ) = (тг)т",тгп) =
= (u\ —uo,U2 —υ,ι,ν — νο). Обратное отображение θ = θ(τ) всегда существует
и имеет координаты щ = т' + щ, U2 = τ" + τ' + зд, ν = τ'" + νο. Положим
r = 7/>/n, 7= (У,7", У")·
Для нового параметра τ (или 7) гипотеза об однородности имеет вид
Н\ = {7" = 0}. В качестве альтернативы рассмотрим «отделенную»
гипотезу #2 = Wh{0oWT ^ &2}> где 1\{θ) есть подматрица исходной
информационной матрицы Фишера 1(9), образованная ее первыми г строками и
столбцами.
Теорема 2. Пусть β окрестности точки θο семейство {Рв}
удовлетворяет условиям (RR). Тогда критерий отношения правдоподобия
sup f{uiiV)(X)f{u2yV)(Y)
является асимптотически минимаксным критерием асимптотического
уровня 1 — ε для проверки Н\ = {щ = U2} против
Е\ = |(«ι - u2)/i(0o)(ui - «2)Т > ^} (9)
§ 59. Проверка гипотез об однородности
459
при общем значении V\ = V2 = ν и при любом Ь > 0. Здесь he — квантиль
порядка 1 — ε распределения χ2 с г степенями свободы. (Таким будет
предельное распределение 21nJf?i(X, Y) при гипотезе Н\.)
Обозначим через θ значение параметра Θ, при котором достигается
максимум числителя в (8), и Θ* = (гх*,г>*) — значение 0, при котором
достигается максимум знаменателя. Представим матрицу Ι(θ) в виде
()~\Ыв) /22(0)7"
(ιΛ«>·))/(Ο(0* - (u»*))T > -, (Ю)
η
Ш) 0 /21(βι)
Ο Ιι(θ2) Ι2ι(θ2) | , (11)
Λ2(0ΐ) Д2№) /22(βΐ) + /22№)>
будет асимптотически эквивалентным (8).
Доказательство. Эта теорема также является прямым следствием
теоремы 55.4. Нам надо лишь выяснить структуру матрицы Ι(θ) для
выборки (X, У) и «объединенного» параметра θ и матрицы Мг. Имеем
I = lnfg(x,y) = 1(х,(щ,у)) + l{y,(u2,v)).
Обозначим через fj, г = 1,..., к + г, координаты вектора Θ. Тогда
(dl{x,{u\,v))
dti ~^
dti
dl(y,(u2,v))
dti
0 < г < г,
г < г < 2г,
ЩМ^^ + ΟΚνΛ^ν))^ 2г<<<* + г;
отсюда без труда получается (11).
Матрица Μ<ι для параметрического семейства Р^одо) = P(uo,uo+/?,i>o) B
точке /3 = 0 вычисляется аналогично, равна Л(0о) и соответствует средней
подматрице матрицы Ι(θο). <
В примерах объемы выборок πι и пг мы будем считать произвольными.
Пример 3. Пусть Χ ^ Φαι σ2, Υ ^ Φα2<72. Надо проверить
гипотезу Н\ — {а\ = с*2}, когда σ2 неизвестно. Для отыскания с помощью
теоремы 2 асимптотически минимаксных критериев нам надо найти
статистику R\(X, Υ) в (8), где в нашем случае щ = α;, ν = σ2, θ = (αι,α2,σ2).
460
Гл. 4. Задачи с двумя и более выборками
Имеем
ln-/W2)PO/(a2,ff2)00 =
= --(ηι+η2)1η(2πσ2)-
1 п\
i=l
-«!)2-
-ι ™2
- 2^2 Σ (У* - <*?·
г=1
Обращая в нуль производные этой функции по αϊ, α.% и σ2 и решая
полученные уравнения, находим (в обозначениях примера 2)
Θ* = (x,y,aS£ + (l-a)S2.), a =
«ι
Щ+П2 (12)
/r (X,Y) = [JhreCaSe + (1 - a)5f )]"(ni+7l2)/2.
Поступая таким же образом с функцией
In fe(X)MY) = 1η/(Ω,σ2)(Χ)/(Ω>σ2)(Υ),
получим (см. пример 2)
e* = (z,SlY),
(13)
Ы*)ЫП = (2™s|>y)-(ni+n2)/2.
Таким образом, асимптотически оптимальный критерий имеет вид
Sx'Y > Jw/(ni+n2)
aS% + (1 - a)52
или (см. (7))
y/a(l - a) \x - y| / /i£
JaS2x + (l-a)S$- > V^+na'
где Де — квантиль порядка 1 —ε распределения χ2 с одной степенью свободы,
так что χ/^ε можно заменить значением Αε/2> Для которого Фод (—λε/2> ^ε/2)~
= 1 — ε. Нетрудно видеть, что левая часть неравенства
v/g(l-fl)(n1+n2)|x-y|
~" > Λε/2, {Щ
^aS2x + {l-a)S\
определяющего асимптотически минимаксный критерий, после замены
|х — у | на χ — у будет асимптотически нормальной с параметрами (0,1)
случайной величиной.
Но этот критерий можно сделать точным (т.е. имеющим в точности
наперед заданный уровень). Действительно, в силу результатов §40 при
§ 59. Проверка гипотез об однородности
461
гипотезе Н\
^П\П2 Х-у
п\ + П2 σ
Фо,ь
(Я1+п,)'^-ЛЕ^-^*д-
σ2 σ* .
•ь
(ni+n2)(l-Q)Sy _ 1
σ2 α-1
= ^г1](У*-"У)2е:Нп2-1·
Так как все три случайные величины независимы, то отношение
,-1/2
Vni + n2 [nl+n2-2K х к } Υ}
(x-y)>/a(l-a)(ni + fi2-2)
"" ^ -»-П1+П2-2
У^ + (Г^)^
имеет распределение Стьюдента с ηι + ^2 ~~ 2 степенями свободы. Таким
образом, критерий (ср. с (14))
(х - у) y/a{l -a)(ni + п2 - 2)
> те,
^aS£ + (1 - a)S£
где τε такое, что ТП1+П2_2(—τε,τε) = 1 — ε, будет иметь уровень
значимости, в точности равный 1 — ε, и его можно использовать при любых (а не
только больших) значениях ηι, η<χ. Этот критерий называется критерием
Стьюдента. Он обладает также некоторыми свойствами точной (а не только
асимптотической) оптимальности (см. [65, 66]).
Пример 4. Пусть ЛГ^Фа 2, Υξ=Φασ2. Проверяется гипотеза {σ\=θ2\,
когда а неизвестно. Поступая аналогично предыдущему, придем к
значению R\ в (8), у которого знаменатель тот же, что и в предыдущем примере,
а числитель равен
sup /Κσ?)(Χ)/Κσ!)(η (15)
(α,σι,σ2)
Выписывая уравнения для точки максимума, получим
ηιέΐ
ι П2
η2ΊΞί
-5(x-a) + -5(y-a) =0.
σι σ2
462 Гл. 4. Задачи с двумя и более выборками
Отсюда, полагая
σ\ ' α/σ\ + (1 - α)/σ|
"^■„/^п-^и^0-1)' ^
находим
a = рх + (1 - р)у,
^ = 5| + (1-Ρ)2Δ2, σ2 = 52+ρ2Δ2,
где мы для краткости положили Δ = χ — у; ρ можно рассматривать как
решение уравнения (16) или
pss "(^+Г2А2)
a[S$ + р2А2) + (1 - a) (Sx + (1 - ρ)2A2)'
Так как максимум в (15) равен
(27ге)-(П1+П2)/2(^ + (1 -p)2A2)-ni/2(5f +ρ2Δ2)_η2/2, (17)
то, сравнивая это с (13), (7), мы получим асимптотически минимаксный
критерий
aS2x + (l-a)SY + a(l-a)A2 > еЛе/(п1+П2)
(£% + (1 -ρ)2Δ2)β(5£ +ρ2Α2γ-α
или
где
aS2x + (1 - a)S^ не/(П1+п2) л-i
ο2ας2(1-α) > е '
α(1 - α)Δ2
+ α6%. + (1 - 0)5^
" {l + (l-p)2A2/S2x)a(l+p2A2/SY)
(18)
(19)
1-α»
he есть квантиль распределения χ2 с одной степенью свободы. Здесь Δ2 =
= {σ2/η1 + σ2/η2)ξ2, ξ © Φο,ι, S2x/a2 -^ 1, S2Y/o2 -у 1, σ2/σ2 -+ 1,
ρ —> α (можно считать для простоты, что a = η\/(ηι +П2) фиксировано),
In A —> 0 для каждой из рассматриваемых близких гипотез. Стало быть,
правая часть в (19) имеет вид
1 + ; , 7п -г> 0.
πι + п2 Ρ
Левая часть (19) представляет собой отношение среднего арифметического к
среднему геометрическому величин S\ и 5у. Если обозначить S^/Sy = Ζ2,
то неравенство, обратное к (19), можно записать в виде
aZ2 + (\-a) _ he + ln
Ζ2α 1ίζη1+η2· (20)
§ 59. Проверка гипотез об однородности 463
В левой части здесь стоит выпуклая вниз функция от Ζ (можно для
определенности считать о ^ 1/2)? имеющая в точке Ζ = 1 кратный нуль. Так
как правая часть этого неравенства мала, то решение удобно искать в виде
Ζ2 = 1 + С ПРИ малом ζ. Пользуясь разложением в ряд по степеням ζ и
отбрасывая члены третьего и более высоких порядков малости, мы получим
для границ ζι, ζ2 интервала, в котором справедливо (20), значения
Cl _ . / 2(^ + Уя) ,_ _ . I 2(ft, + Tg)
I о(1 — a)(rii + п2)' у а(1 — α){ηι + п2)'
у —ι π У —>► 0
Это означает, если вернуться к исходным переменным, что область
/
-о(1 -α)(ηι + га2)
Si
> y/hs = λε/2 (21)
(λε определено в примере 3) определяет критерий, асимптотически
эквивалентный (18) и, стало быть, асимптотически минимаксный.
Здесь, как и в примере 3, мы можем сделать полученный критерий
точным, поскольку нам известно точное распределение статистики S'x/Sy.
Действительно,
niSX - хх n*SY - τχ
2 ^ Γίηι— 1) 2 Х1П2 —1
σ1 σ2
и при гипотезе Ηχ = {σι = σ<ι\
nxS\
n2Sl
F
7li~ 1,П2 — 1»
где Fni_i)7l2_i есть распределение, введенное нами в § 12 и табулированное в
руководствах по математической статистике. Напомним (см. §12, п. 6), что
если пользоваться таблицами распределения Фишера, то надо для
отыскания квантилей f£ распределения Fklyk2 порядка 1-е вводить поправочный
множитель. Если κε — квантиль порядка 1 — ε распределения Фишера с
(&ъ&2) степенями свободы, то }е = — хе.
Сказанное означает, что можно вычислить точный уровень значимости
критерия (21) и применять его при любых п\ и п2 (о свойствах точной
оптимальности этого критерия см. [65, 66]). Если п\ и п2 велики, то левая
часть в (21) (без знака абсолютной величины) асимптотически нормальна с
параметрами (0,1).
4. Асимптотически минимаксный критерий для задачи о частичной
однородности. Пусть Χ ^ Ρ015 Υ ^ Ρ#2, θι = {щ,У{), i = 1,2. Проверяется
гипотеза {ui = u2} против {^ι φ гх2}, когда значения ν\ и г>2 в выборках X
и Υ могут быть любыми. Размерность щ, как и прежде, обозначим через г,
г < к.
464
Гл. 4. Задачи с двумя и более выборками
Введем новый параметр θ = (#ι,02) = (^ъ^ъ ^2^2) размерности 2к>
Как и раньше, выборку (Χ, Υ) (при п\ = η<ι = η) представим как выборку с
наблюдениями (xi,yi),..., (хп?Уп)5 имеющими плотность
fefay) = f(uuvi)(x)f(u2,v2){y)·
Для этого семейства исходная задача о частичной однородности
эквивалентна задаче о проверке гипотезы Н\, состоящей в том, что θ лежит
на «кривой» θ = g(a) = (ιΐι,νι, 1*1,02)? где α = {ui,v\,V2) есть
«подпараметр» размерности 2к — г. Мы предлагаем читателю, следуя рассуждениям
Π II &9г II ■ ι о/
двух предыдущих разделов, выписать матрицу G = —— , г = 1,...,2«;
\\даз\\
j = 1,..., 2к — г. Ее ранг будет равен 2к — г.
Как и в п. 2, 3, мы будем считать задачу «локализованной» около точки
Введем наряду с θ параметр г = т(0) = (τ/,τ//,τ///,τΙν) = (ui — wo,
г?1 — г?о, W2 — г/1, V2 — vq). Обратное преобразование θ = 0(т) имеет
координаты
щ = τ' + uo, υχ = г" 4- υο5 ^2 = τ'" + τ' + Щ, V2 = τιν + vq.
Если положить τ = ύ/у/п) 7 — (l*->l"->l'U·>Ί™)·> τ0 гипотеза Η\ будет иметь
вид #ι = {η911 = 0}. В качестве альтернативы будем рассматривать
«отделенную» гипотезу #! = {7'"Л(0о)7///Т ^ ^2}> гд-е ^ι(^) имеет тот же смысл,
что и в теореме 2.
Теорема 3. Пусть β окрестности точки #о семейство {Pq}
удовлетворяет условиям (RR). Тогда критерий отношения правдоподобия
sup ЛЛ-ВДЛУ)
* (Х'у) = "^Т ппТ (V\ > 6"ε/2 W
sup f{UiVl){X)f{UiV2){Y)
{u,Vl,V2)
является асимптотически минимаксным критерием асимптотического
уровня 1 — ε для проверки Н\ против гипотезы Н^ определенной в (9),
при произвольных значениях ν\ и г>2- Значение h£ здесь то же, что и в
теореме 2.
Доказательство этой теоремы повторяет рассуждения предыдущих
разделов и тоже полностью основано на теореме 55.4. Отыскание
информационной матрицы Фишера Ι(θ) для параметра θ и матрицы Мг для
семейства с плотностью /^ο,ο,β,ο) = /(uo.vo.uo+frvo) в точке Ρ = ° мы предоставляем
читателю. _ ^ ^ ^ ^
С помощью матрицы ΐ{{θχ,θγ)) и вектора (#х50у) — (и*,г^,гг*,г>2),
где (#х>0у) и (и*,^*,^) суть векторы, в которых достигаются максимумы
числителя и знаменателя в (22), мы можем, как и прежде, с помощью
теоремы 55.4 (см. (55.12)) построить асимптотически эквивалентный критерий,
использующий квадратичную форму от введенных оценок. <
§ 59. Проверка гипотез об однородности
465
Пример 5. Сравнение дисперсий нормальных
совокупностей. Пусть Χ ^ *αι>σ2, Υ ^ *Q2j(T2, Hi = {σι = σ2}^ Здесь
вычисления значительно проще, чем в примере 4, поскольку значение числителя
в (22) (как и вектор (θ*χ,θγ) = (χ, S\, у, Sy)) нам известно, а значение
знаменателя найдено в примере 3 (см. (12)). Неравенство (22) здесь будет
иметь вид
aS2x + (1 - a)Sfy ehe/(m+n2)
q2aq2(l-a)
Сравнивая это с (19) и с последующими рассмотрениями, мы придем к
тем же критериям и выводам, что и в примере 4.
Пример 6. Проблема Беренса-Фишера о сравнении двух
нормальных совокупностей. Пусть
Х ^ *αι,σ2> Υ ^ Φα2,σ22> Η1 = ial = α2>,
значения σι и σ2 произвольны. Для этого примера числитель в (22) тот же,
что и в предыдущем примере, а знаменатель найден в примере 4 (см. (17);
там это был числитель для (8)).
Асимптотически минимаксный критерий, стало быть, будет иметь вид
т + (1-р)2Д»у/Д«+^А'у-в>Л/,И|+И9,.
(23)
здесь Δ = χ — у представимо в виде
, 2 2
Δ = (αι _ α2) + J_L + -2 £ ξ (= Φ0,ι,
]j Πι П2
$χ ν ι ^V ν Ί
σ{ ρ σ$ ρ
так что Δ —>► 0 при гипотезе Η\. Это соотношение сохранится, очевидно, и
ρ
для каждой из близких альтернатив. Чтобы найти более простой по форме
критерий, асимптотически эквивалентный (23), выделим в обеих частях
неравенства (23) главные части. Получим
S\ S2, ™ П1+П2 V(«l+«2)2
где pn —>· ρ = const. Учитывая, что
Ρ=α^+Ω(1-α)5|+Δ4' "ή^Ρ^ const,
мы получим
о(1 - a)2S2xA2{m + п2) + а2(1 - a)S$А2(щ + п2)
(aS2, + (1 - a)S2x)
2 +
+ Д4(щ + n2)p"n >hE + 0 (—ί—
466
Гл. 4. Задачи с двумя и более выборками
где рпп —> р" = const, Δ4(ηι 4-пг) —> 0. Это неравенство можно
эквивалентным образом записать в форме
Δ2(ηι +η2)
Sfy/a + Sfy/il-a)
Отсюда вытекает, что критерий
> К + 7ηι Ίη —> 0.
и-я,дгн» > Λι _ (24)
JSila + g>Y /(1-о)
является асимптотически эквивалентным (23) и, стало быть,
асимптотически минимаксным для проблемы Беренса-Фишера. Здесь Αε/2 имеет тот же
смысл, что и в примере 4. В отличие от примеров 2-4 здесь допредельное
распределение статистики в левой части (24) зависит при гипотезе Н\ от
неизвестных параметров σ^, σ\.
5. Некоторые другие задачи. Мы отметим здесь еще два класса задач,
асимптотическое решение которых может быть найдено с помощью
теоремы 55.4.
1. Первый класс задач составляют задачи, обобщающие задачи п. 2-4
на случай, когда проверяются гипотезы вида \β\ = /(0г)} (например,
{01 = α + Ьв2}) в условиях п. 2 и вида \и\ = f{u2)} в условиях п. 3,4.
Нетрудно видеть, что проведенные в п. 2-4 рассмотрения переносятся на этот
более общий случай.
2. Второй класс задач составляют задачи с тремя и более выборками.
Рассмотрим, например, задачу об однородности для трех выборок. Пусть
X €= Р#15 Υ €= Р#2, X €= Pfl3· Проверяется гипотеза Н\ = {θ\ — θ2 = #з}
против дополнительной альтернативы. Предположим для простоты, что
объемы выборок πι, П2, щ равны: щ = П2 = пз = п. Рассмотрим
объединенную выборку (Χ,Υ,Ζ) как выборку объема η с наблюдениями (χι,γι,ζι),...
•.., (хщУти zn), имеющими плотность fj(x, у, ζ) - ίθι [x)fe2(ν)ίθ3(ζ)ι r^e θ =
= (0ь02>#з)· Гипотеза Н\ тогда будет эквивалентна тому, что θ лежит на
«кривой» θ = g(a), α = θ\) g(a) = (α, α, α). Мы видим, что проблема вновь
сводится к задаче, рассмотренной в теореме 55.4.
§ 60. Задачи об однородности в общем случае
1. Постановка задачи. В этом параграфе мы будем рассматривать две
выборки X и Υ объемов rii и п2 соответственно, не предполагая, что они
относятся к какому-либо параметрическому семейству.
Задача об однородности выборок X и Υ в общем случае выглядит
следующим образом. Обозначим через Pi и Р2 распределения выборок X
и Y: X €= Ρι, Υ €= Р2. Проверяется гипотеза Н\ = {Pi = Р2} против
Н2 = {Ρι φ Рг}· Обе гипотезы, очевидно, являются сложными.
Распределения Pi, P2 могут выбираться из заданного семейства V или быть
произвольными. Общий принцип построения статистического критерия для
проверки Н\ против Н2 остается тем же, что и в главе. 3. Разница, как и
в § 59, состоит лишь в том, что здесь он основан на объединенной выборке
§ 60. Задачи об однородности в общем случае
467
(X, У), так что π = π(Χ,Υ) есть вероятность принять Ή.2 при данной
выборке (Χ, У). В нерандомизированном случае (π равно нулю или единице)
критерий π определяется критической областью Ω С ХП1+П2 такой, что при
(Χ, У) Ε Ω принимается #2- Число
1-ε= inf Pi xPi((X,y)gfi)
называется уровнем значимости, а значение
Αγ(Ρι,Ρ2) = ΡιχΡ2((*,1Ί€Ω), Ρι€7>, Р2 е V,
— мощностью критерия π в «точке» (Ρι,Ρ2).
Критерий π называется состоятельным, если /?π(Ρι,Ρ2) -4- 1 при
щ -* оо, П2 ~> оо и при любых Pi т^ Р2, Pi GP, Р2 Ε P.
Мы уже знаем, что с ростом ηι, П2 эмпирические распределения Р^, Ру,
соответствующие выборкам X и У, неограниченно сближаются с Pi, P2
соответственно. Поэтому естественной основой для построения критериев
однородности является использование разного рода «расстояний» d(P^,Py)
между Р^ и Ру, где d удовлетворяет тем же общим условиям, которые
описаны в § 52. При этом особый интерес представляют непараметрические и
асимптотически непараметрические критерии, которые определяются
следующим образом.
Пусть d(P, Q) — некоторое расстояние (не обязательно метрика) в
пространстве распределений. Если вероятность
P1xP1(d(Px,P^)>c)=£ (1)
не зависит от выбора Pi, то критерий π, определенный равенствами
„(Χ,Υ) = (°· еСЛИ <<ρ*·ρ!'> <«■ (2)
[1 в противном случае,
называется непараметрическим. Очевидно, построенный
непараметрический критерий будет иметь уровень 1-е.
Аналогичным образом определяются асимптотически непараметрические
критерии, когда (1) сохраняется асимптотически, при добавлении в левой
части операции lim . В этом случае критерий (2) будет иметь асим-
711—> 00,712—Ю°
птотический уровень 1 — ε. При отсутствии непараметричности (точной
или асимптотической) строить критерии проверки однородности заданного
уровня весьма трудно.
Рассмотрим некоторые основные критерии проверки однородности.
2. Критерий Колмогорова-Смирнова. Пусть Pi, P2 принадлежат классу V
всех непрерывных распределений на прямой, и пусть F%- и Fy —
эмпирические функции распределения, соответствующие Р^ и Ру. Критерий
Колмогорова-Смирнова в качестве расстояния d(P*x, Ру) рассматривает
статистику
/?П1>П2=8иР|^(*)-^у(<)|·
468
Гл. 4. Задачи с двумя и более выборками
Критерий £>71ЬП2 > с? построенный с помощью статистики £)ПьП2,
является непараметрическим. Действительно, пусть верна гипотеза Н\ и F(t)
есть общая функция распределения для X и У. Статистику Dnii7l2 можно
записать в виде
Dnun2=sup\G*x(F(t))-G*Y(F(t))\, (3)
где Gx(u) = Fx(F~l(u)) есть эмпирическая функция распределения,
соответствующая равномерному на [0,1] распределению (см. §6, 52). Но в
силу (3) Dnii7l2 = sup|G^(u) — Gy(u)|, так что распределение Dnu7l2 от F
U
никак не зависит.
Можно найти точное распределение статистики DniiTl2. Например, при
Πι = П2 = П
[n/k]
Έ>(ηΌη,η >k) = 2(С%ПУ1 £>1)'Ч1С2^, (4)
k = 1, 2,.. .,n. Этот факт был установлен Гнеденко и Королюком сведением
задачи к простой проблеме для случайных блужданий (см. [111])-
В §6 мы видели, что распределение niG*x(u) совпадает с
распределением пуассоновского процесса ζι(η) при условии (ι(ί-) = п\. Так как G*x(u)
и Gy(u) независимы, то распределение G*x(u) — ΰγ(υ,), u E [0,1],
совпадает с распределением сложного пуассоновского процесса С(гх), в котором с
интенсивностью щ происходят скачки величиной 1/ηι и с интенсивностью
П2 — скачки величиной — 1/гг2,* распределение надо брать при условии, что
произошло η\ + П2 скачков и что ζ(1) = 0. Поэтому
P(Aii П2 < х) — Ρ (sup \C{u)\ < —— = 0; произошло п\ + П2 скачков).
Ки<^1 CU) '
На основании этого факта в приложении II наряду с теоремой 6.2 о
сходимости процесса wn(u) = yjn{ (G*x(u) — и) к броуновскому мосту w°(u)
доказано также утверждение о сходимости к броуновскому мосту и процесса
V П\ +П2
Точнее, для любого измеримого и непрерывного в равномерной метрике
функционала / распределение f{wnii7l2) сходится к распределению f{w°).
Отсюда сразу вытекает следующее утверждение, называемое теоремой
Смирнова.
Теорема 1.
lim p(J П1"2 Dnun2<x) =p(sup\w°{u)\<x) = К{х),
где К(х) — функция Колмогорова (см. §8, 52)).
§ 60. Задачи об однородности в общем случае
469
Так как функция К(х) табулирована, то теорема 1 дает удобное средство
для приближенного вычисления уровня значимости критерия Колмогорова-
Смирнова.
Предоставляем читателю убедиться, что критерий
Колмогорова-Смирнова является состоятельным.
3. Критерий знаков. Пусть п\ = П2 = п. Тогда из наблюдений выборок X
и Υ можно составить η разностей
Х1-Уь---,Хп-Уп· (5)
Если верна гипотеза Н\ и Ρι χ Ρι(χι — yi = 0) = 0 при всех Pi Ε V (это,
очевидно, всегда так, если V — множество непрерывных распределений), то
Pi х Ρι(χι - yi > 0) = Pi χ Ρχίχι - yi < 0) = -.
Статистика ν критерия знаков представляет собой число положительных
разностей в (5) *). Сам критерий можно построить, взяв в качестве
критического множества
n = {(X,Y):\u-^\>c}.
Так как распределение ν от Pi не зависит,
PixPi(i/ = *) = C*2-n,
то этот критерий является непараметрическим.
Число с по заданному уровню 1 —ε критерия выбирается из соотношения
£ С*2- * 1 - е. (6)
k:\2k—п\^.2с
Так как левая часть здесь возрастает с ростом с дискретно, то в качестве
решения следует взять наименьшее с, при котором левая часть в (6)
превосходит 1-е.
Мы видим, что здесь используется критерий для проверки гипотезы о
том, что вероятность успеха в схеме Бернулли равна 1/2. С точки зрения
исходной задачи проверяется не гипотеза об однородности, а более широкая
гипотеза о том, что
Pi х P2(xi - yi < 0) = У Fi(<) dF2{t) = |, (7)
где Fi соответствуют Ρ;, г = 1,2. Соотношение (7) означает, что медиана
распределения χι — yi равна нулю.
Критерий знаков асимптотического уровня 1 — ε будет иметь вид
/wx ι 2|ι/-η/2|
π(Χ, Υ) = 1, если - -fJ-1 > λε/2,
ν^ ' (8)
Φο,ι(-λε/2,λε/2) = 1-ε.
*) Если в выборках Χ, Υ из-за огрубления данных окажется, что некоторые разности
Хг — yi = 0, то их следует просто выбросить, а в качестве η взять число разностей, отличных
от нуля.
470
Гл. 4. Задачи с двумя и более выборками
Этот критерий не является состоятельным, так как для Ρι φ Р2,
удовлетворяющих (7), /?π(Ρι,Ρ2) —> ε < 1 при п\ -> оо, П2 -> оо.
4. Критерий Вилкоксона. Этот критерий весьма распространен при
проверке гипотез об однородности.
Объединим выборки X и Υ в одну выборку (Χ, Υ) и построим из нее
вариационный ряд, т. е. расположим все наблюдения в порядке возрастания.
Получим последовательность вида
У(1),У(2),х(3),У(4),х(5),..·, (9)
где верхний индекс означает номер наблюдения в общем вариационном
ряде, а буква указывает на принадлежность к выборке. Пусть ri,r2,.. .,гП1
означают номера элементов выборки X в вариационном ряде (9). Для
выписанной в (9) последовательности г\ = 3, τ<ι = 5. Статистикой Вилкоксона
называется функция
υ = υ{Χ,Υ) = Σ(η-ί),
г=1
где г% — г есть число элементов выборки Υ, меньших чем х^у
Так как порядок наблюдений в (9) инвариантен относительно
монотонных преобразований над переменными (порядок для F^(t), Fp(t) будет тем
же, что и для Fx(F~l(t)), -Ру(^-1(£)), где F — функция распределения),
то критерий, построенный по статистике U, будет непараметрическим.
Теорема 2. Пусть X €= Ρι, Υ €= Р2, F{ Ε T суть функции
распределения, соответствующие Р^, г = 1,2; Τ есть класс всех непрерывных
функций распределения. Предположим также, что а = ^1/(^1+^2) —> ао
при п\ —> оо, П2 -> оо. Тогда
£/-ηιη2Ε^2(χι)
^/ηιη2(ηι +η2)
*ο,σΊ (Ю)
где σ2 = (1 - a0)DF2(xi) + a0DFi(yi).
Если Fi = F2 = F, mo ^(xi) ^ U01, i*i(yi) ^ Uo 1 w, стало быть,
EF2(Xl) = 1/2, DF2(xi) = DFi(yi) = 1/12.
Следовательно, критерий Вилкоксона асимптотического уровня 1 — ε
будет иметь вид
rcin2|
t/-
K/2\/nln2{ni +П2)
> 2ν/3 ' (И)
2
φο,ι(-λε/2,λε/2) = 1-е
Из (10) видно, что этот критерий нацелен главным образом на проверку
гипотезы (ср. с (7))
J' F2{t)dFx{t)=l- или J(F2(t)-F1(t))dFl(t) = 0. (12)
§ 60. Задачи об однородности в общем случае
471
Если принять, не ограничивая общности, что Fi(t) = t, t € [0,1], и
предположить, что ^(0) = 0, ^(1) = 1, то в силу равенства
ι
f{l-F2(t))dt = Eyl
о
проверяемая гипотеза примет вид Eyi — 1/2.
Это значит, что критерий Вилкоксона, как и критерий знаков,
чувствителен главным образом к сдвигам распределений одно относительно другого.
Для таких сдвинутых альтернатив мощность их бывает достаточно большой
(см. пример 1). Если же F2 ^ F\ и выполнено (12), то согласно критерию
Вилкоксона гипотеза {F2 = F\} будет приниматься с вероятностью, близ-
/ λε/2 λε/2 \
кой к Фод I /=—ч —7=~ ) > Это означает, что критерий Вилкоксона будет
\ 2ν3σ 2ν3σ/
не со стояте л ьным.
Доказательство теоремы 2. Статистику U можно записать в виде
U = Y,n2Fp(xi) = ЩП2 / Ft(t)dF*x(t).
i=l J
Положим
wx{t) = >/nT(Fi(i) - Fi(0), wY(t) = y/rZ (FY(t) - F2(t)).
Тогда очевидно
U = тцп2 I F2(t)dFl(t) +
+ γ Πι7l2(71i + 712
+ х/ад wY(t)dwx{t). (13)
Так как здесь / F2(t)dwx(t) = / wx(t) dF2(t) и, стало быть, второй и третий
интегралы в (13) имеют одну и ту же форму и независимы, то для доказательства
теоремы нам достаточно убедиться, что
JwY(t)dFl(t)0'9o,a»l, oi = OF1(yi), (14)
и что
> \п [wY(t)dwx(t) —> 0. (15)
у/Щ +П2 J P
В силу теоремы 6.2
y*iuy(i)dFi(i) e> Jw°(F2(t))dFl(t), (16)
472
Гл. 4. Задачи с двумя и более выборками
где w°(u) есть броуновский мост. Чтобы найти распределение последнего
интеграла, заметим, что траектории винеровского процесса w(u) с вероятностью 1
непрерывны (см. [17, §16.2]) w°(u) = w(u) — uw(l) и что, следовательно,
интеграл (16) есть по определению результат почти наверное сходимости при N —> ос
сумм
N
^(^O^Fi-m^l), (17)
г=1
где 771!=/ F2{t)dF\(t)i {ti)iL0 образуют разбиение вещественной оси, Δ^ρ =
г N
= g{U) - giU-г), w{F2{U)) = ]>>/4F2), w{l) = ^Δ^).
В силу преобразования Абеля
N / г \ N / Ν \
Σ Σ* * = Σ Σ4*·
t=l \/ = l / i=l \l=i J
Поэтому (17) равно
Ν
Σ (1 - ίΊ(*«_ι) - mi)Aiti;(F2). (18)
i=l
Здесь 1 — 777-1 ^ / F\(t) dF<2(t) = Ш2, a А»и;(.Р2) суть независимые нормально
распределенные случайные величины с параметрами (О, Δ^). Поэтому распределение
(17), (18) будет нормальным с нулевым средним и дисперсией
Ν Г
Σ (™2 - Fi(ti-i))2AiF2 -+ / (m2 - Fx(i))2 dF2(i) = DFi(yi).
t=l ^
Соотношение (14) доказано.
Чтобы доказать (15) *), проще всего оценить дисперсию интеграла в (15).
Приближая интеграл снова с помощью конечной суммы, можно убедиться, что
дисперсия
2
Ώχ,γ =еП wY{t)dwx{tyJ
ограничена при п\ -> оо, п^ —У оо. Отсюда и из неравенства Чебышева следует (15).
Доказательство ограниченности D^y мы опускаем ввиду громоздкости и рутинного
характера вычислений. <
По поводу критериев знаков и Вилкоксона см. также [34].
Пример 1. Мы отмечали, что критерии знаков и Вилкоксона
наиболее чувствительны к сдвигам. Поэтому интересно сравнить их мощности с
мощностью оптимального критерия в задаче, где однородность проверяется
*) Интеграл в (15) сходится по распределению к / w°(F2(t))dw°(Fi{t)).
§ 60. Задачи об однородности в общем случае
473
для семейства V распределений, отличающихся лишь сдвигами. Именно,
пусть
Ρ = {Φα,ΐ}, Ρΐ=Φαι,1, ?2 = *а2|Ь П1 = П2 = П.
В этом случае согласно теореме 59.1 для проверки гипотезы Н\ = {Ρχ —
= Р2} = {«ι = а2} против #£ = {\ol\ — а2| ^ Ь/у/п} существует
асимптотически минимаксный критерий πο уровня 1 — ε, имеющий вид
|х-у| >λε/2γ~> *ο,ι((-λε/2,λε/2)) = 1-ε
(то, что это неравенство в нашем примере эквивалентно (59.3), (59.4),
читатель может проверить сам). Примем этот критерий за эталон для
сравнения с другими критериями и рассмотрим альтернативу (Ρι,Ρ2), где а2 =
= ai+c/y/n (мы рассматриваем близкие альтернативы, чтобы не иметь дела
с задачей о больших уклонениях). Очевидно, что в этом случае (х — у) €=
^ ф-с/у^,2/п· Стало быть>
/3π0(Ρι,Ρ2) = ΡιχΡ2Μχ-7|>λε/2^] =1-Ф.с/^|1(-Ае/2,Ае/2) =
= 1 - Фо.1 (-λε/2 + -^, λε/2 + -^j = Д,(с). (19)
Рассмотрим теперь критерий знаков (8) и обозначим его через πχ.
Пользуясь разложением в ряд по степеням с/у/п, находим {Φα^σι{χ) =
= *αισ*((--°0>&)))
р. * р,(« - у, < о). ф„,2 (-£.) = I + -^ + о (I).
Поэтому в точке (Ρι,Ρ2)
2 / η Су/п\ _
Стало быть, для критерия знаков πχ асимптотического уровня 1 — ε
/ΜΡΐ,Ρ2)=ΡΐΧΡ2(2|ΐ/-^|>λε/2Λ/ϊϊ) -*·
-> 1 - Фо.1 (-\/2 + -^ λε/2 + -£=) .
Обратимся, наконец, к критерию π2 Вилкоксона (см. (11)), имеющему в
нашем случае вид
и~2
n2L Αε/2η3/2
ν/6
474
Гл.4. Задачи с двумя и более выборками
Очевидно, что статистика U инвариантна относительно преобразования
сдвига элементов выборок 1иУ. Поэтому можно считать, что Ρ ι = Фо,ъ Рг =
= Фс/у^,1 и> стал0 быть'
EF2(xi) = JF2(t)dF1(t) = |*o,i (t- Αλ <ίΦο,ι(ί) =
Так как DF2(xi) -> DFi(xi) = 1/12, DFi(yi) ->· DFi(xi) = 1/12, то по
теореме 2
Αγ2(Ρι,Ρ2) = ΡιχΡ2
и_гЦ>К1^
Vg
ι3/2.
-1-PlXp,^ + ^^n^^-^ + ^j<
-> 1 - Φ0|ΐ -λε/2 + С
Заметим теперь, что βο{ό) (см. (19)) есть монотонно возрастающая
функция от с и что при больших η
/MPi,P2)«A)h/-c · ^(РьРг)*^)
Таким образом, при каждом с > 0 наиболее мощным среди πο, πι, π2
оказывается, как этого и следовало ожидать, критерий πο· Затем идут критерий
Вилкоксона и критерий знаков; при этом критерий Вилкоксона уступает
критерию πο совсем немного, так как y/3/π « 0,977.
Если мы при том же смещении ot^ — ot\ = с/у/п рассмотрим выборки X7
и У объема п' > п, то для того чтобы с помощью проведенных
вычислений получить мощность в точке (Р^Рг) критериев Kj(Xr,Yr), мы должны
рассмотреть прежнюю задачу при новом значении с, равном с' = суп'/у/п
(тогда с*2 — d\ можно будет записать в виде d/vn')· Стало быть, мощности
πι(Χ',Υ') и π2(Χ',1//) в той же точке (РьРг) будут равны приближенно
ι / π / π
= 1, мы получим значения η = — η, η = — η
πη πη J 2 ' 3
(они от с не зависят) для числа наблюдений, которые надо проделать, чтобы
соответственно с помощью критериев πι и π2 получить ту же мощность, что
и для критерия πο с η наблюдениями. Например, для η = 100 наблюдений
§ 60. Задачи об однородности в общем случае
475
с критерием πο нам потребуется для получения тех же результатов п' и 105
наблюдений с критерием π2 и п' « 157 наблюдений с критерием π\.
Совсем другие результаты мы получили бы, если бы проверяли
однородность для семейства V = {Ф0)(72}. В этом случае критерии знаков и Вилкок-
сона оказались бы несостоятельными. Более того, критерий знаков уровня
1 — ε был бы, по существу, равнозначен критерию π ξ ε, не зависящему от
выборок, так как Ε(χχ— yi) = 0 и Pi xP2(xi— yi > 0) = 1/2 для любой пары
распределений Pi и Ρ 2 из V. Для этой задачи можно было бы рассмотреть
другие непараметрические критерии, использующие статистики г$, напри-
m
мер критерий \_\ (ri+i — г%) > го = 0, гП1+1 = ^25 напоминающий по своим
г=0
свойствам критерий Морана (§52).
5. Критерий χ2 как асимптотически оптимальный критерий проверки
однородности по сгруппированным данным. В этом пункте мы будем
предполагать, что данные в обеих выборках X и У объемов соответственно п\
и П2 сгруппированы (см. § 56). Тогда вместо выборок X, У можно
использовать векторы ν = [у\,..., ντ) и μ = (μι,.. .,μΓ) частот наблюдений
соответственно из выборок X и У, попавших в интервалы Δι,..., ΔΓ, определяющие
группировку.
Обозначим через 9\ = (#α, - ·-,0гг)5 г = 1,2, векторы вероятностей
попадания наблюдений соответственно из первой и второй выборок в интервалы
Δι,...,ΔΓ, так что 9ц — P(xj £ Δ/), θ2ι = P(yj £ Δ/)· Огрубленные
выборки X и У можно рассматривать тогда как выборки из параметрических
семейств В^х и В^2 соответственно.
Таким образом, задача становится параметрической и мы можем
использовать результаты, изложенные в примере 1 предыдущего параграфа. Из
этого примера следует, что если мы проверяем гипотезу об однородности
Hi — {θι = 92} в случае, когда параметр 9 локализован, т.е. значения 0χ,
#2 располагаются в окрестности точки #о == ($оъ · · ·» #0г)> т0 асимптотически
минимаксный критерий асимптотического уровня 1 — ε для проверки Hi
против
имеет вид
... #0г гг2 .
^ \™ι п2/ щ + μ%
где /ιε есть квантиль порядка 1 — ε распределения χ2 с г — 1 степенями
свободы. Это и есть критерий χ2 для проверки однородности по
сгруппированным данным.
В качестве асимптотически эквивалентного можно рассматривать
критерий
г г г
Υ] vi1п — + У] Pi 1п — - У2 {"г + Pi) ln -J—--L > ~.
f-f ni f-f ra2 f-f ni 4- n2 2
г=1 г=1 г=1
476
Гл. 4. Задачи с двумя и более выборками
§ 61. Задачи регрессии
1. Постановка задачи. В приложениях часто возникают задачи,
относящиеся к наблюдениям, распределение которых меняется в разных
экспериментах при изменении некоторых параметров, характеризующих эти
эксперименты. Набор значений указанных параметров в г-м эксперименте,
г = 1,..., п, обозначим через
хг == 1хг,Ь · · ·> xi,rJ
(так что г есть размерность векторов xj. Значения хг·^ определяются либо
экспериментатором, либо природой изучаемого явления. Вектор (xi ^, · · ->χη k)
(ΧΑ
мы обозначим через Х^, а матрицу ( -·· I = (χχ~,...,χΧ) — через X.
Таким образом, здесь в отличие от предыдущего X является матрицей порядка
г χ η и может быть произвольным неслучайным набором чисел, природа
которых нас интересовать не будет. Вектор наблюдений обозначим через
У = (Уъ>",Уп)>
Задачи регрессии связаны с предположением, что наблюдения у^ в
зависимости от набора параметров Хг — (хг,ь · · >>хг,г) имеют вид
У г = αΐχζ,1 + · " + <*гхг,г + ξί, г = 1, . . ., ГС, (1)
где α = (αχ,.. .,o:r) — неизвестные нам постоянные, ξι & Φ0 σι и
независимы.
Постоянная ос\ часто играет особую роль, так как в ряде случаев она
выделяет в представлении (1) постоянное слагаемое, что соответствует тому,
что в матрице X заранее полагается Х\ = (1,...,1) (хгд = 1). Мы этим
предположением пользоваться не будем. Случайные величины £г*
обуславливаются шумами, флуктуациями или ошибками измерений.
В матричной форме соотношения (1) можно записать в виде
Υ = αΧ + ξ. (2)
Регрессия вида (1), (2) называется линейной (как по а, так и по X). В
качестве задач регрессии могут рассматриваться как задача оценки неизвестных
параметров α, σ2, если известно, что справедливо (1), (2), так и задача
проверки самой гипотезы о том, что представление (1), (2) имеет место.
Исходными данными в обоих случаях служит «выборка» (Χ, Υ). Термин «выборка»
здесь используем уже в более широком, чем прежде, смысле, обозначая им
набор результатов наблюдений, не обязательно имеющих одинаковую
природу. Кроме того, напомним, что первая из двух «выборок» X и Υ может
быть неслучайной. Матрицу X называют иногда регрессором, а вектор Υ —
откликом.
Модель регрессии (1), (2) является весьма общей, если иметь в виду
зависимость уг* от набора параметров. Полагая, например, х^ = фь^г),
где φι,.^,ψτ — заданный набор функций, a Zj — значения одномерного
§61. Задачи регрессии
477
параметра, мы получим модель
Уг = aiV>i(zi) + ... + ar?/v(zi) + £, i = Ι,.,.,η,
(3)
у = Qx 4- a2z
регрессии по произвольным функциям φι,..., фт (и по-прежнему линейной
по а). Если V>i(z) = 1, ^2(ζ) ξ ζ, г = 2, то мы получим модель простейшей
(одномерной) линейной регрессии (рис. 6).
В отличие от простейшей, общую модель (1), (2) иногда называют
множественной регрессией. В целом задачи регрессии, как мы видим, связаны
с изучением (с наличием)
функциональной зависимости у = φ(χ) для заданного
класса функций φ в тех случаях, когда у^[
наблюдения над переменной у при
данном χ «зашумлены» случайными
отклонениями.
Строки Xi,...,Xr матрицы X в (2)
обычно выбирают таким образом, чтобы
они были линейно независимы (иначе
координаты α нам не удастся оценить). Мы
тоже будем следовать этому соглашению, означающему, что ранг матрицы X
равен г.
Иногда бывает удобнее иметь дело с ортогональными векторами
Χι,...,Хг, т.е. удовлетворяющими условию (Xi,Xj) = 0, i ф j, где (а,Ь)
означает скалярное произведение. Если исходный набор линейно
независимых векторов {.XV;} таким свойством не обладает, то его можно ортогонали-
зировать, введя новые векторы
Рис. 6
Х[ = Хи
Х'2 = Х2 + α2,ι-Χ"ι,
(4)
Х'г = Хт + 0,т%г-\Хт-\ + · ■ ■ + Αγ,Ι-ΧΊ-
Коэффициенты akj легко определяются из условий ортогональности
Х'к _L Хр к Φ j, так что, например, а^\ = — {XuX2)/{Xi,Xi)·
Соотношения (4) можно записать в виде X' = АХ, где А — треугольная
обратимая матрица (с единицами по главной диагонали). Отсюда получаем
X = Α~ιΧ'', Υ = αΑ~ιΧ' + ξ. Мы пришли к задаче регрессии с
коэффициентами β = аА~1. Вектор α очевидным образом восстанавливается по β
с помощью равенства a = β А.
Для простейшей линейной регрессии предположение об ортогональности
Х\ = (1,..., 1) и Хч — (ζι,..., zn) означает предположение \^ Ъ{ = 0,
которое очевидным образом может быть удовлетворено путем изменения начала
отсчета переменной ζ.
2. Оценка параметров. Везде в дальнейшем будем предполагать, что
г < η и что векторы Х^, к — 1,.. .,г, линейно независимы. Функция прав-
478
Гл. 4. Задачи с двумя и более выборками
доподобия наблюдения У при данном X для регрессии (1), (2) равна
LAY) = {tL·) ехр\~άέ (*-Σ>χ^
> =
1
ехр<--
\Y-aX]
2σ2
(5)
,y/2na
Функция (5) зависит от параметра θ = (α,σ2). Отметим, что если (5)
рассматривать как функцию правдоподобия не одного наблюдения Υ (или
(X, У)), а п наблюдений yi,..., уп, то она не будет соответствовать выборке
из какого-нибудь одного параметрического семейства. Наблюдения у^ отно-
г
сятся к разным распределениям Ф7{)(72> Ъ = У^о^х^, зависящим от х^.
*=1
Поэтому те рассмотрения глав 1-3, в которых использовалась одинаковая
распределенность элементов выборки, здесь непосредственно неприменимы.
(О статистике неодинаково распределенных наблюдений см. гл. 5.)
Итак, будем рассматривать (5) как функцию правдоподобия наблюдения
(X, У). Воспользуемся методом максимального правдоподобия.
Непосредственно из (5) видно, что оценка максимального правдоподобия а* = а*,
максимизирующая fe{Y) по а, есть оценка, минимизирующая \Y — аХ\2.
Поэтому в нашем случае метод максимального правдоподобия совпадает с
«методом наименьших квадратов».
Обозначим через С[Х] подпространство, натянутое на векторы Х\,..., Хт.
Это есть совокупность точек вида аХ, когда α пробегает значения из W. Это
пространство имеет размерность г и содержит единственную точку β = α*Χ,
Υ
Рис. 7
наименее удаленную от Υ (рис.7). Значение β однозначно определяется
условием ортогональности Υ — β и С[Х] или, что то же, условиями
(Υ - а*Х,Хк) = (Υ - a*X)Xj = О, к = 1,.. .,г.
В матричной форме эти условия можно записать в виде (У — а*Х)Хт = 0.
Отсюда находим
a* = YXT(XXT)-K (6)
§61. Задачи регрессии
479
Здесь обратная матрица (XX ) 1 (порядка г χ г) существует, так как
матрица D = XX является положительно определенной. Действительно, мы
видели, что существует невырожденная матрица А такая, что строки
матрицы X1 — АХ ортогональны. Стало быть, матрицу D можно записать в
виде
ХХТ = А-1Х,(Х,)Т(А"1)Т = Α-ιΒ(Α-χ)τ,
где В = Х'(Х')Т — диагональная матрица с элементами
(х>,х>) = {№2>° при i = j>
[О при ъф].
Следовательно, В положительно определена, aBa > 0 для любого а Е W,
а ф 0. Полагая Ь = аА, получим bDbT = аЛХХтАтат = аВат > 0 при
любом Ь Ε П£г, 6 φ 0, что и требовалось доказать.
Если Xfc ортогональны, то из (6) находим а*к = (Y,Xk)l(Xk->Xk)·
Результат (6) мы могли бы получить и другим путем —
дифференцируя (5) по ak и приравнивая производные нулю.
Разность У — а*Х называют иногда остатком. Эта разность
ортогональна С[Х], а вместе с этим и любому вектору ηΧ Ε С[Х], η Ε W. Если
взять 7 — <** — а5 то из равенства У — аХ — У — а*Х + (а* — а)Х будет
следовать
\Υ - аХ\2 = |У - а*Х|2 + |(а* - а)Х|2. (7)
Найдем теперь о. м. п. для σ2. Из (5) видно, что это будет та же оценка,
что и для нормального семейства (можно заново продифференцировать (5)
по σ и приравнять производную нулю), так что
(а2)* = -|У-а*Х|2. (8)
п
Положим
^ = ^γ - а*х? = ^7(52)*· (9)
п — г п — г
В дальнейшем Е[ будет означать единичную матрицу порядка Ι, σ*=\/(<72)*.
Теорема 1. Оценки (6) w (9) являются независимыми несмещенными
эффективными оценками параметров а и σ2. Кроме того,
{а* - a)Dll2 S= Ф0^Ег, D = XXT, (10)
(n-r)(a2)* |Υ-α*Χ|2
σ2 σ2
H„_r. (11)
£7сли Xk ортогональны, то а£ независимы,
(а1-ак)\Хк\<=Ф0>(т2. (12)
480
Гл. 4. Задачи с двумя и более выборками
Следствие 1. Из (10), (11) вытекает, что
{а* - а)Р{а* - а)Т \{а* - а)Х\2
(n-r){a2Y ~ \Y-a*X\2
Ξ Fr>n_r. (13)
Пусть α, α* — тодвекторы» размерности I ^ г векторов а и а*,
составленные из координат с фиксированными номерами к\,..., ki, и пусть
X — матрица, составленная из строк Х^,.. .,Xkr Тогда если Х^, к =
= 1,...,г, ортогональны, то
(3* - а)(ХХУ е Φ0,σ2£„ (а*-°*)'^' е тп_г. (14)
Доказательство теоремы 1. Так как ΥΧΤ = аХХТ + ξΧτ, то
α = {YXr - ξΧτ)Ό-1, α* -α = ξΧτϋ^1. (15)
Матрица вторых моментов вектора (а* — a)D1'2 равна
ЕД1'V - <>)Τ(α* - a)D1'2 = Ό^ϋ^Χ^ξ^7 D^D1'2 = σ2ΕΓ.
Так как компоненты этого вектора нормальны, то они независимы и
-ί|(α* - α)!)1/2!2 g= Hr. Далее, в силу (7), (9)
σ2
(η - ν){σ>γ = \Υ- α*Χ\ι = \ξ\2 - \{α* - α)Χ\\
Убедимся теперь, что векторы α* и Υ — а*X (а стало быть, а* и σ*)
независимы. В силу их нормальности достаточно проверить, что коэффициенты
корреляции между их компонентами равны нулю или, что то же, что
матрица центральных вторых моментов Е(а* — α)ι (У — а*Х) равна нулю.
Заметим, что в силу (6)
а*Х = ΥΧτ{ΧΧτ)-ιΧ = YXTD~1X
и вектор а*Х получается из Υ путем проектирования Υ на С[Х]. Оператор
проектирования, определяемый матрицей Π = XTD~lX, обладает
очевидными свойствами: П2 = П, BXU = ВХ для любой матрицы В, имеющей г
столбцов. Поэтому в силу (15)
Е(а* - а)т(У - а*Х) = ΕΒ~ιΧξτ{ξ - ξΧΎΌ~ιΧ) = Β~ιΧσ2{Εη - Π) = 0.
Докажем теперь (11). В силу (7)
\Υ - а*Х\2 = \ξ\2 - |(α* - а)Х\2 = \tf - |(α* - a)Dll2\2,
где ^|ξ|2 ш Η„, -^|(α* - a)Dl'2\2 # Hr (см. (10)). Утверждение (11)
будет следствием этих соотношений и леммы 1.
§61. Задачи регрессии
481
Лемма 1. Если η = 771 +т)2, где щ и т/2 независимы, η €= Нп, 771 €= Нг,
то 772 ^ Нп_г.
Доказательство. Если обозначить через φ(ί) характеристическую
функцию распределения Ηχ: ψ(ί) = (1 + 2ζί)-1'2, то
Ее** = φ{ί)η = <p{t)r · Ее*72'.
Так как φ(ί) Φ 0 на вещественной оси, то Еег7?2* = (p(t)n~'r. Лемма доказана.
Несмещенность оценок α*, (σ2)* с очевидностью следует из (10), (11)
(Е77 = /, если 77 ^ Hj).
Нам осталось доказать эффективность оценки θ* = (α*, (о-2)*). Для этого
заметим, что параметрическое семейство (5) относится к экспоненциальному
типу, так как (5) представимо в форме (см. (25.1))
ΜΥ)={тЬУехр{-^т2 - 2{γ·αΧ)+|а*|2)}=
= ЫУ) ехр \ V <ц(в)0-»(У) + У(в) 1,
7 У
.Jk=l
где
Л(У) = (2π)""/2, 7(0) = -ηίησ - ^2 |«Х|2,
а*(0) = ^, С/к(У) = (Г,Хк), А; = 1,...,г,
or+i(6) = -^> 17Г+1(У) = |Г|2.
Так как условия теорем 25.1, 25.2 здесь выполнены, то статистика U =
= ({/ι(.ΛΤ),..., ί/Γ4-ι(^)) (а вместе с ней и Θ*) является минимальной полной
достаточной статистикой). Отсюда следует (см. следствие 25.1)
эффективность 0*.
Утверждение (12) с очевидностью следует из (10), так как для
ортогональных Хк матрица D1!2 диагональна с элементами \Xk\ по диагонали.
Теорема доказана.
Замечание 1. Хотеллинг (см. [101]) доказал, что Da£ ^ а2/\Хь\2
и равенство достигается только в том случае, когда Xk ортогональны.
Таким образом, при планировании эксперимента при заданных значениях \Xk\
оптимальный выбор регрессора X состоит в том, чтобы сделать Xk
ортогональными.
Замечание 2. Интересно сравнить матрицу вторых моментов
оценки 0* с нижней границей для несмещенных оценок, определяемой в силу
многомерного неравенства Рао-Крамера матрицей /_1(0), где 1(9) —
информационная матрица Фишера:
/(Ι?) = ||^·(0)||, 'i#)=E*f^fp L = Ц¥;в) = In fe(Y).
482
Гл. 4. Задачи с двумя и более выборками
Здесь мы приняли θ^ = α^, k = 1,..., г; 0r+i = σ2. Пусть для простоты Х^
ортогональны. Из независимости 0£ следует, что матрица Έβ(θ* — θ)τ(θ* — θ)
будет диагональной с диагональными элементами
2
Е«(а*-«)2 = ГГ12> k = l,...,r,
\Xk\
Eq
((σ2)* - σ2)2 = Ε (^^ _ Α 2 = ^_Ε(χ2 - ΐ)2 = —,
где xf <Ξ Н^.
С другой стороны, для матрицы Ι(θ) в силу того, что
яг л п I г \ 1
dL η 1 А / А \ 1 (\Υ-αΧ\2 \
находим при к = 1,..., г
Ы0) = еАх*(У - аХ)т(У - aX)XfeT =
74
= ^ΕΧ^ξΧΪ = -^EfcX*)* =
ί5
2 |Xfc|2E|£|2 \Xk\2
Ir+i,r+i{6) = -^μ Ε
при г / j. Так что
Lt=l
η
/ *2
/-Α(β) =
\*ι\2
ο ο
2^, ΐν(θ) = ο
\
\
ο
ο
\ΧΑ2
2σ4
~7Γ/
Таким образом, в неравенстве Рао-Крамера
ΈΘ{Θ*-Θ)Τ{Θ*-Θ)^Γ1{Θ)
(16)
для первых г компонент 0* достигается равенство. Для (г 4- 1)-й оно
достигаться не может (хотя асимптотически при η —> оо обе части (16) ведут
§61. Задачи регрессии
483
себя одинаково), так как необходимое и достаточное условие теоремы 26.1 А
здесь не выполнено.
Замечание 3. Предположение о нормальности ξ{ становится
малосущественным для утверждений (10)—(12), если η велико (в (11) лучше
произвести нормировку и утверждать близость к нормальному закону).
Замечание 4. Сам термин «регрессия» относится к совместному
распределению двух случайных величин ξ и η и означает кривую
9{χ)=Ε{η/ξ = χ),
которую называют также регрессией η на ξ. Например, если (ξ, η) €= Φ7,σ2,
7 = (7b72)i σ2 = \Wij\l hj = 1Д то, как мы видели в §20, д(х) =
О1 9
= 72 + —{х — 7ι)· Это есть простейшая линейная регрессия.
Я"22
Замечание 5. Предположение ξι Ε Φο,σ2 °б одинаковой
распределенности ξί при известном σ2 может быть ослаблено. Мы можем считать, что
ξί ξ= Ф0 σ2, если σ% различны и известны. В этом случае, обозначив че-
Г Ί
рез σ диагональную матрицу σ = '., I и введя новые
переменно aj
ные ξ' = £<7~\ -Χ"' = Χα"1, Υ' = Уа-1 (так что ξ2· = &Л^? χί = х^/а,·,
yj = yj/^i), мы придем к задаче регрессии
в которой вектор наблюдений У и регрессор X7 нам известны, £' €= *o,£n-
Легко проверить (мы предоставляем это читателю), что в этих условиях
справедлив следующий аналог теоремы 1.
Теорема 2. Оценка
а* = Ya-2XT{D')-\ & = Χσ~2Χτ,
является несмещенной эффективной оценкой а,
п ( Уг - Σ OfcX»* )
\У - а*Х'\2 = £ -^ *=L '— ш Hn_r.
Обратимся снова к теореме 1. Соотношения (10)—(12), установленные в
ней, дают возможность строить доверительные множества как для
отдельных координат 0, так и для вектора θ в целом. Например,
Р.|<^<^<£#|-1-., (.»>
Αε/2 Αε/2
484
Гл. 4. Задачи с двумя и более выборками
и если Х^ ортогональны, то
р* (к
где Tn-r((-ic/2iie/2)) = 1 -£, Ηη-Γ((Λ[/2'Λί/2)) = Х ~ 6'
Пусть Xk ортогональны. Обозначим через α «подвектор» вектора а,
определенный в следствии 1. В силу теоремы 1 доверительное множество для a
естественно строить с помощью соотношения
|(ά-α*)Χ|2
(η — г)(а2)*
< /ε· (19)
Значение /ε, соответствующее заданному уровню 1 — ε, определяется
известным образом (см. гл. 3) с помощью распределения F/jn_r с числом степеней
свободы 1>п — г.
Если σ2 известно, то доверительное множество будет определяться
соотношением
|(α-α*)*|2<σ2/ιε, (20)
где he соответствует распределению Н/.
В задачах регрессии может понадобиться также оценить значение
поверхности регрессии у = αζτ в новой, наперед заданной точке ζ = (ζι,..., zr) E Rr.
Положим у* = α*ζτ. Тогда, как и раньше, находим
у* - у = (а* - α)ζτ = ξΧτΌ~ιζτ €= ФМ2,
d2 = σ2ζί)-1ζτ, ^f/- ί= Τη_Γ.
ασ*
Это дает возможность строить доверительные интервалы для у.
Следует отметить, что отыскание доверительной области для поверхности
регрессии «в целом» есть задача более трудоемкая (ср. с [101]).
Совокупность поверхностей, входящих в доверительное множество, будет
определяться доверительным множеством для 0, построенным, например, с
помощью (10), (11) (см. §48). Подробнее об этом см. [101].
3. Проверка гипотез относительно линейной регрессии. Коснемся здесь
двух типов задач.
1. Пусть известно, что представление (1), (2) имеет место. Требуется
проверить гипотезу о том, что θ равно заданному значению Θ' или что набор
координат 0fci>.. .,0^ равен набору 0J. ,.. .,0Ц. , в то время как остальные
координаты неизвестны.
Критерии для проверки таких гипотез удобно строить с помощью
доверительных множеств (17)—(20) (см. §48). Пусть, например, требуется
проверить гипотезу Н\ о независимости Υ от X для простейшей линейной
регрессии, т.е. гипотезу Н\ — {с*2 = 0}. Тогда из (18) (или из (14)) получим
критерий уровня 1 — ε, отвергающий Н\, если
И > %■ (21,
§61. Задачи регрессии
485
В общем случае регрессии (1) с ортогональными Х^ гипотеза о
независимости Υ от X будет иметь вид Н\ = {а = 0}, где а = (с*2,.. .,сО> Χΐΐ = 1»
и для ее проверки можно воспользоваться критерием
(n-r)(a2)*
где X и /е определены в (19) при ί = г — 1_
Можно использовать также подходы §55, где рассматривалась проверка
принадлежности выборки параметрическому подсемейству. Мы придем
тогда к критерию отношения правдоподобия, который будет в известном
смысле близок к (22). Если σ2 известно, то к. о. п. для проверки Н\ = {а = 0}
будет иметь вид
σ~2\α*Χ\2 > he,
где he есть квантиль ΗΓ_ι порядка 1 —ε. Этот критерий будет минимаксным
(см. § 49, 50) для соответствующим образом отделенных альтернатив.
2. Проверка гипотезы о наличии в выборке (Χ, Υ) самой регрессии (1),
(2). Под этим мы понимаем гипотезу о том, что при каких-нибудь α, σ имеет
место представление (1), (2), т.е. что при каких-нибудь α, σ справедливо
σ~ι(Υ — аХ) €= Фо Еп- Это есть задача о принадлежности Υ
параметрическому семейству. Но, как уже отмечалось, наблюдения в Υ неодинаково
распределены. Чтобы свести задачу к случаю одинаково распределенных
наблюдений (см. §57), мы воспользуемся следующим утверждением,
дополняющим теорему 1. Будем считать Х^ ортогональными.
Теорема 3. Пусть С — любая ортогональная матрица порядка
η χ η, содержащая θ качестве первых г столбцов столбцы матрицы
X1D~1/2. Тогда вектор η = (Υ—а*Х)С имеет независимые координаты,
обладающие свойством 71 = · · > = Ъ = 0, 7г €= Фо,<72> « = г + 1,..., п.
Таким образом, задача сводится к проверке гипотезы о принадлежности
выборки 7г-ъЬ"ч7п объема п — г семейству Φο,σ2 (Γ наблюдений ушло,
грубо говоря, на оценки для а). Эта задача рассматривалась в §57. Чтобы
получить значение 7ь надо по выборкам Χ, Υ вычислить последовательно
значения α*, Υ — а*Х и применить к Υ — а*Х любое преобразование С,
обладающее отмеченными в теореме 3 свойствами.
Если σ известно, то мы придем к задаче о проверке простой гипотезы
о принадлежности Ф0 σ2. Однако в этом случае для проверки интересующей
нас гипотезы можно использовать и теорему 1, в силу которой
(n-r)(a2)*
о ^ **П —Г·
σΔ
Доказательство теоремы 3. Если Ζ _L C[X\, то первые г
координат вектора ZC образуют вектор ZXTD~1/2 = 0. Так как (Y — а*Х) ± С[Х]
и 7 = (Y — а*Х)С, то отсюда следует, что 7ι = · ■ · = 7г = 0· Далее,
7 = {Y - аХ)С - (а* - а)ХС = τ/ - ηΌ~1/2ΧΟ,
486
Гл. 4. Задачи с двумя и более выборками
где η = £С, η = (ηι,. ..,ηΓ) = (α* - α)!)1/2 = £XTD ll2 и, стало быть,
7 есть результат линейного преобразования над η,
г=1 г=г+1
η η
так что 2_] 7i = 2-1 ^i* ^т0 В03М0ЖН0 только в том случае, когда
i=r-fl г=г+1
(7r-fb · · ·>7π) есть результат поворота вектора (т/г+ь · · -iVn) или> чт0 т0
же, результат ортогонального преобразования над (^Γ+ι»···^η)- Так как
σ_177 €= Фо,яп> то теорема доказана. <
Пример 1. В этом примере мы опишем математическую сторону
физического эксперимента, с помощью которого был обнаружен эффект распада
(^-мезона на два π-мезона (см. [103]). Полученный результат носит
статистический характер, и в нем, по существу, использовалась модель регрессии.
Исследование относится к изучению взаимодействия электронов (еГ) и
позитронов (е+) на встречных пучках. Если суммарная энергия этих
частиц 2Е находится в окрестности точки 2Ео = 1019,6 МэВ (рис. 8), то при
100-
V
6
5
4
3
2
i
<
-
r-JLj^
"iSj"~y^U3
e"c+ -
Ι τ
—►
О 1,00 1,01 1,02 1,03 1,04 2Е
Рис. 8. Кривые изображают оценки линий регрессии при гипотезах Н\ и Яг
их «столкновении» в результате взаимодействия образуются (наряду с
другими) частицы двух типов: (^-мезоны и пары π-мезонов. Вероятность воз-
,+
никновения пары π-мезонов при взаимодействии е-*", е~ в зависимости от
энергии Ε описывается с большой точностью линейной функцией, которую
представим в виде (гипотеза if ι)
рГ
(Ε) = αο + α\χ, χ = Ε - Ε0,
(23)
где αο> &1 неизвестны.
Было выдвинуто предположение (гипотеза Н2) о том, что при распаде
родившихся (^-мезонов также могут появляться пары π-мезонов. Обнаружить
непосредственно этот эффект практически невозможно, так как было
установлено, что это явление, если оно происходит, то происходит очень редко,
§61. Задачи регрессии
487
не чаще чем один раз на 104 распадов (^-мезонов. Однако благодаря эффекту
интерференции этого дополнительного канала рождения π-мезонов с
основным каналом вероятность возникновения этих частиц будет равна не (23), а
pY(E) = {a0 + alx]
1 +
b0 + b\x + b2x1
Χ4
+ d2
(24)
(как и (23), это есть весьма точное приближение несколько более сложной
формулы, основанное на том, что рассматриваемый диапазон изменения
χ = E — Eq мал по сравнению с Eq). В этом равенстве коэффициенты fy, как
и аг·, неизвестны, d известно.
Чтобы установить, какое из двух соотношений (23) или (24) на самом
деле имеет место, было проведено η — 20 экспериментов при различных
значениях энергии ϋ?χ,..., i?2o·
Таблица 1
Таблица экспериментальных данных
Номер
эксперимента i
\ 1
2
3
4
5
6
7
8
9
10
- -
Ei, МэВ
497,75
500,65
503,65
505,40
506,62
507,66
508,40
508,90
509,40
509,90
Ni
6960
7908
8102
22 259
16938
21728
14014
13793
14 075
14867
Vi
384 Ι
435
432
1080
765
951
603
545
615
691 j
Номер
эксперимента i
11
12
13
14
15
16
17
18
19
I 20
Ei, МэВ
510,40
510,92
511,39
512,17
513,20
514,62
516,58
518,64
520,61
522,88
Ni
14 322
13470
12008
23951
27 796
37 771
25 902
27857
23228
26482
Vi
716
568
569
1117
1185
1539
1036 j
1057 i
989
1066 ;
Результатами экспериментов (см. табл. 1, рис. 8) являются количества
iVi, i = 1,...,20, взаимодействий е+, е~ и количества щ родившихся пар
π-мезонов при энергии Е{. В каждом из проведенных экспериментов
числа Ni и щ достаточно велики (Ni имеют порядок 104). Так как при
фиксированном Ni число пар π-мезонов щ имеет распределение Бернулли В^*
(pi = p^n(Ei) при гипотезе Hi npi = ρψ(Εΐ) при гипотезе i?2)> то, пользуясь
нормальным приближением, мы вправе считать, что имеет место
представление
■ο,σ?
(в слагаемое ξι входят также случайные помехи (фон)),
мы будем иметь два возможных варианта регрессии:
ι
В силу (23), (24)
Pi = Y^akipk{xi), фк(х) = хк, к = 0,1
*=о
(гипотеза Н\) и
° к
ΣΧ
(ХкФк{щ), Фк{х) = η , м, к = 0,1,2,3
к=о Х +(Р
(25)
(26)
(гипотеза #2)·
488
Гл. 4. Задачи с двумя и более выборками
Значения σ2 при изменении гипотез меняются очень мало; они могут
быть весьма точно оценены, и их можно считать известными. Тогда на
основании теоремы 2 статистика
х2 =
к
<=1
σχ
будет иметь распределение Нп_г, где г — число оцениваемых параметров
ак (г = 2 при гипотезе Н\ и г = 4 при гипотезе #2).
Проводя необходимые вычисления в соответствии с рекомендациями
теоремы 2, мы получим для статистики (27) значения: в первом случае (г = 2)
χ2 = 36,8, во втором (г = 4) χ2 — 19,0. Фактически достигаемые уровни
значимости (см. §44) критерия χ2 > с для проверки (в качестве
основных) гипотез Н\ и #2 составят соответственно Ηιβ((0, 36,8)) = 0,9944,
Н1б((0, 19,0)) = 0,731.
Другими словами, предположение об отсутствии дополнительного канала
рождения пар π-мезонов отвергается критерием, основанным на
статистике χ2, с уровнем значимости, равным, например, 0,99. В то же время
предположение о наличии этого канала хорошо согласуется с экспериментальными
данными.
Если быть более точным, то в этой задаче мы должны были бы
проверять две сложные параметрические гипотезы, соответствующие
предположениям (25), (26) для значений вероятностей появления пар π-мезонов. Если
использовать критерий отношения правдоподобия, то он, как нетрудно
проверить, будет основан на разности статистик χ2, соответствующих моделям
(25), (26), и, стало быть, результаты его будут примерно теми же.
4. Оценивание и проверка гипотез при наличии линейных связей.
Рассмотрим, как и прежде, линейную регрессию (1), (2), но в предположении,
что координаты вектора α связаны s < г линейными соотношениями
Σ·
,OLkQ>kl =Qi ' = 1, ...,5.
В матричной форме эти соотношения можно записать в виде
осА = с, (28)
где А — матрица порядка г х 5. Мы будем предполагать, что А имеет ранг 5.
В этом случае мы могли бы выразить s переменных (скажем, ar_s+i,..., ar)
через остальные (т.е. через αχ,.. .,ar_s), подставить полученные значения
в (1), (2) и получить снова стандартную задачу линейной регрессии (но с
измененным регрессором).
Однако для дальнейшего нам будет удобнее подойти к решению этой
задачи несколько иначе. Обратимся к доказательству теоремы 1.
Подпространство Л значений а, определяемое соотношениями (28), выделяет
в С[Х] подпространство размерности r — s значений аХ, которое обозначим
через £л[^1· Очевидно, что оценивание a G А можно вести теперь теми же
§61. Задачи регрессии
489
приемами, которые мы использовали в теореме 1. Нужная оценка a*A Ε Л
будет определяться, как и в теореме 1, с помощью проекции а*АХ вектора У
на £д[Х]. Таким образом, наряду с соотношением (У — а*Х) J_ C[X] будем
иметь соотношение (Y — a*AX) ± СА[Х], которое однозначно определяет а*А.
Для получения самого значения а*А удобнее воспользоваться аналитическим
подходом — применить метод неопределенных множителей Лагранжа для
отыскания min|y — аХ\2 при условии аА = с. Для этого мы должны
реек
шить уравнения
аА = с, —[|У - аХ\2 + Х(аА - с)т] = 0 (29)
да
(мы используем множители λι,..., As, образующие вектор А и
соответствующие условиям (28)). Так как \Y — аХ\2 = (У — αΧ)(Υ — аХ)т, то второе
из уравнений (29) примет вид
Отсюда
находим
<**А =
-2ΥΧΤ
= YXTD~1 -
- 2аХХт
■\ы
+ ХАТ ■■
1 = а* -
= 0.
\^D-K
В силу (29) с = ос\А = a*A — -\ATD lA. Так как матрица D положительно
определена, А имеет ранг s, то В — D~ll2A также будет иметь ранг 5, а
матрица ВтВ = ATD~lA будет также положительно определенной (см. п. 1).
Следовательно,
-Ιλ = (с - аМ)2?л, а*А=а* + {с- a*A)DAATD-\ (30)
где мы положили для краткости 1)д = [А7!)-1^!]-1.
Читатель может проверить, что это есть о. м. п. параметра а при
условии аА = с. Тот же результат (30) можно получить и из геометрических
соображений, используя соотношения а\Х Ε £д[Х] и ортогональность
(Υ - а*АХ) ± СА[Х),
{а*А - а*)Х = [(Υ - а*Х) - (У - а\Х)] 1 СА[Х].
Обратимся теперь к задаче проверки линейных гипотез. Гипотезу if ι
относительно параметра а будем называть линейной, если она имеет вид
Н\ = {аА = с}, где матрицы А и с определены выше.
Сразу же можно отметить, что, введя новый параметр β = аАс, где Ас —
любая невырожденная матрица, у которой первые s столбцов совпадают с А,
мы сведем задачу к регрессии
Υ = βΧ' + ξ, Χ' = Α-ιΧ, (32)
и к проверке гипотезы β = с, β = (/?ι,..., /?5) (см. п. 2).
490
Гл. 4. Задачи с двумя и более выборками
Естественно также исходить из следующих соображений. Чем больше
α А отличается от с, тем аХ удаленнее от £д[Х] и тем больше точки аХ,
а*Х будут отличаться от о*АХ G £λ[-Χ"]. Поэтому в основу критерия для
проверки Н\ естественно положить расстояние ot*AX от а*Х. Если гипотеза Н\
верна, то в силу (31)
| (а*А - а*)Х\2 = |У - а*АХ\2 - |У - а*Х\2. (33)
В силу (30) (с заменой с на аА) а*А — а* есть результат линейного
преобразования над α — α*. Поэтому (а*А — а*)Х не зависит от У — а*Х (см.
теорему 1).
Далее, в силу (30)
|К - а*)Х\2 = К - а*)ХХт(а*А - а*)Т =
= (с - аМ)£>Л(с - а*Л) = (а* - a)ADAAT(a* - а)т. (34)
Так как
{а* - а)А = ξΧτϋ'ιΑ (= Φ0^Ατο-ιΑ = *0iffa£>-i,
то в силу (34) и § 12 (п. 4)
^|(а*д-а*)Х|2€=Н4. (35)
Из сказанного и из теоремы 1 следует, что
\{<Ъ-*)х£_\у^я£_1т (36)
\Y-a*X\2 \Y -a*X\2
Соотношения (35), (36) дают нам возможность строить критерии
(основанные на использовании удаленности а*Х от а.*АХ) для проверки гипотезы Н\
соответственно в случаях, когда а2 известно и неизвестно (см. гл. 3).
Важно отметить, что гипотеза Hi есть гипотеза о принадлежности а
параметрическому подсемейству (при наличии мешающего параметра σ2, если
σ2 неизвестно), а статистики (35), (36) есть не что иное, как статистики
отношения правдоподобия (см. §50, 55). Действительно, пусть, например, σ2
неизвестно. Тогда (см. (5), (8))
вщ>Л(У) =sup(N^a)-nexp{-^-^-) =
-(^r-p{-E^C}.(^^2f^..
Значение sup /#(У) вычисляется точно так же. Надо лишь заметить, что
α€Α}σ
о. м. п. для а в случае α Ε Λ будет равна а*А, а о. м.п. для σ2 будет равна
§ 62. Дисперсионный анализ
491
аналогично (8) -\Y-a*AX\ . Поэтому
-71
sup MY) = Ι ^2π'- α^Χ| Ι -""Ζ2
sup/e(r) "|У-а^Г
и, стало быть, статистика критерия отношения правдоподобия
эквивалентна (36).
Если σ2 известно, то в основу критерия для проверки Н\ можно положить
соотношение (35). Читатель может аналогично предыдущему убедиться, что
это тоже есть критерий отношения правдоподобия. Так как этот критерий
инвариантен относительно замены параметра (см. § 50), то в силу замечания
и утверждений §49, 50 можно утверждать, что к. о. п.
\{a*A-a*)X\2>a2hE,
где h£ — квантиль порядка 1 — ε распределения Hs, будет минимаксным
критерием уровня 1 — ε для проверки Н\ против отделенных
соответствующим образом альтернатив.
Изложенное выше и результаты глав 2, 3 (см., в частности, §55) дают
основание считать, что критерий (36), как и оценка (30), также будут
обладать свойствами оптимальности. Подробнее на этом мы останавливаться не
будем. Весьма полное изложение задач регрессии можно найти в [101].
§ 62. Дисперсионный анализ
Задачи дисперсионного анализа, излагаемые ниже, по своему существу
относятся к задачам регрессии. В последних изучалась зависимость
наблюдений от числового фактора х, который мог принимать любые
наперед заданные значения χχ,...,χη и каждому из них соответствовало одно
наблюдение. В задачах дисперсионного анализа обычно изучается
воздействие лишь дискретных факторов (одного, двух или более), которые могут
принимать лишь конечное число значений. При каждом из этих значений
мы располагаем набором наблюдений (выборкой). Дисперсионный анализ
объединяет группу статистических приемов, основанных на анализе сред-
неквадратических уклонений и предназначенных для проверки различных
гипотез и оценки параметров, связанных с воздействием факторов. Основы
дисперсионного анализа были заложены Фишером.
1. Задачи дисперсионного анализа как задачи регрессии. Случай одного
фактора. Пусть дано г независимых выборок
У\ = (У1Ъ---,У1П1),···,^ = (Уг1,--мУгпг)
объемов ni,...,nr из нормальных совокупностей У^ €= Фаь(Т2.
Предполагается, что наблюдения YJt, k = 1,...,г, проводились при разных значениях
492
Гл. 4. Задачи с двумя и более выборками
некоторого фактора, роль которого нас интересует, и что влияние этого
фактора сказывается на значении среднего ak. Значение дисперсии σ2
предполагается одним и тем же для всех выборок и, как правило, неизвестным.
Задачи дисперсионного анализа включают в себя проверку гипотез,
относящихся к значениям αι,...,αΓ, и, в частности, гипотезы об однородности
αχ = ... = αΓ = α (эта последняя задача рассматривалась нами в §59), а
также оценки параметров ak и их изменчивости.
Дисперсионный анализ, как и задачи регрессии вообще, имеет
чрезвычайно широкое поле применений, особенно в социологии, сельском
хозяйстве, биологии, медицине. В качестве весьма типичной задачи для
применения методов дисперсионного анализа можно назвать, например, проблему
о выяснении зависимости содержания холестерина в крови человека от его
профессии.
Сформулированные выше задачи дисперсионного анализа есть частные
случаи задач линейной регрессии. Действительно, наблюдения уы можно
представить в форме
Уki = otk + £*;г, £ki <Ξ Φ0>σ2
0,σ2>
1,
,r,
ι,-
,ra*·
(1)
Образуем вектор
, yim; У211 · · · > У2п2; · · ·; Уп, · · ·, y™r)
и вектор ξ по тому же правилу. Тогда соотношения (1) можно записать в
матричной форме Υ = αΧ + ξ, где X есть матрица размера г χ η, η =
= ηχ + ... + nr, вида
Χ =
/1 1 ..
/0 0 ..
0 0..
\ό о ..
. 1
. 0
. 0
. 0
0 0..
1 1 ..
0 0..
0 0..
. 0
. 1
. 0
. 0
0 0..
0 0..
0 0..
1 1 ..
• °
• °
■ ι/
Очевидно, что строки этой матрицы (векторы Xj) ортогональны. Гипотезу
Ηχ = {αϊ = OL2 = ■. · = otr} можно записать в виде
olA = 0,
где А есть матрица размера г χ (г — 1)
(2)
1 °
1 0
\-1
0 ..
1 ..
0 ..
-1 ..
: t\
i
• -ι/
А =
Очевидно, что А имеет ранг г — 1.
Мы видим, что проверка основной гипотезы Ηχ дисперсионного анализа
есть не что иное, как задача о проверке линейной гипотезы для регрессии.
Выясним, что собой представляют эффективные оценки для α и σ2,
найденные в теореме 61.1. В нашем случае \Хк\2 = Пк, матрица D = ХХТ
§62. Дисперсионный анализ
493
°'-Щл)-*£>-у'·· <3)
г пк
(n-r)(a2r = \Y-a*X\2 = ^2^2(yki-ykf^Q2(Y).
к=1 г=1
При этом α*,...,α*, (σ2)* независимы. Доверительные интервалы для
параметров α, σ2 и функций от них строятся так же, как и в § 61.
Для проверки линейной гипотезы (2) нам нужно вычислить также о. м. п.
а*А при наличии условия (2) (см. п. 4 предыдущего параграфа). Простейший
путь здесь — использовать подход, изложенный в начале п. 61.3, и выразить
αι,...,αΓ через независимые переменные. В нашем случае независимая
переменная лишь одна — пусть это будет αΓ = μ,Ηή = (μ*,..., μ*), где μ*
минимизирует
Г Пк
|Γ^(μ,...,μ)Χ|2 = Χ;^(Υ,^μ)2.
Л=1<=1
Очевидно, что
1 г пк
*=1 г=1
г njfe
\Υ -α*ΑΧ\2 = ΣΣ>« "У)2 Ξ W =
*=1 i=l
Г Пк Г Пк Г
= Σ Σ (у** - у+у*- - у*-)2 = Σ Σ ^ki~ у*·)2 + Σ n*(y*·~ у)2
Ar=l i=l Jb=l г=1 jfe=l
(сумма смешанных произведений равна нулю, так как \_\ (Укг "** Уь) ^ 0)·
•=1
Если гипотеза Ηχ верна, то в силу (61.33), (3) и только что полученного
равенства
| [а\ - а*)Х|2 = Q(Y) - Q2(y) = £ пк(ук. - у)2 Ξ Q^Y).
Jc=l
Ha основании (61.36) при выполнении Н\ получаем Qi(Y)/Q2{Y) €=Fr_ijn_r,
что дает нам возможность строить критерий Qi{Y)/Q2{Y) > ίε if ε —
квантиль Fr_i,n_r порядка 1 — ε) для проверки ifi, который будет к.о.п. Если
494
Гл. 4. Задачи с двумя и более выборками
σ2 известно, к. о. п. будет иметь вид
Ql(Y)>a2he
[he — квантиль Hr_i) и будет минимаксным критерием при
соответствующим образом отделенных альтернативах (см. §49).
2. Влияние двух факторов. Элементарный подход. В задачах этого
раздела исследуется влияние на результаты эксперимента факторов двух видов.
Применительно, скажем, к сельскому хозяйству это может быть изучение
влияния на урожайность состава почвы (фактор А принимает г значений)
и способа обработки (фактор В принимает s значений).
Здесь наблюдения можно представить в форме
Ykli — Oikl + £>kli, Ыг €= 3>0,<72>
к = 1,...,г, Ζ = l,...,s, г = 1,...,п)н,
и рассматриваемая модель, по существу, ничем не будет отличаться от
модели (1), рассмотренной в п. 1. Стало быть, здесь также применимы все
результаты §61, но прямое их применение становится более громоздким.
Громоздким является уже само присутствие тройных индексов. Чтобы
несколько упростить задачу, положим пы = 1, это избавит нас от одного
индекса (индекса г в (4)). Кроме того, мы предложим в этом пункте несколько
иной, элементарный подход, который независимо от теорем §61 позволит
получить утверждения, необходимые для проверки основных гипотез.
Итак, будем рассматривать выборки Yki = уы единичного объема, так
что набор экспериментальных данных Υ здесь будет представлять собой
матрицу г х s чисел у^, определяющих результат эксперимента под
воздействием к-то значения фактора А и 1-го значения фактора В. Эту матрицу
можно трактовать как г выборок (строк) объема s, соответствующих разным
значениям фактора Л, или как s выборок (столбцов) объема г,
соответствующих разным значениям фактора В. В соответствии с этим в дальнейшем и
будет происходить группировка наблюдений. Положим
Is 1 г 1
у*·= 5 Σ у**» у·*= - Σ у«> у= — Σ у«-
1-1 к=1 к>1
Справедливо тождество
Q(Y) = Σ (У« - У)2 = £i(y) + £*(y) + £з(П (5)
Qi(y) = s£ (У*· " У)2' Оа(У) = г^(у, - у)2,
к I
£з(п = Е(у*<-уь-у./+у)2·
kjL
Предположим, что влияние факторов аддитивно, т. е. существуют a*, bi
такие, что
Oikl ^CLk+bi, к = 1, . . ., Г, I = 1, . . ., 5. (6)
где
§ 62. Дисперсионный анализ
495
Очевидно, что Q\ определяет изменчивость значений ак (т.е. связано с
фактором A), Q2 определяет изменчивость 6/ (фактор £?), a Q$ есть сумма,
создаваемая всецело случайностью. Очевидно также, что
Qi(Y + a) = Qi(Y), г = 1,2,3. (7)
Теорема 1. 1) Справедливо
σ2 ^ W(r-l)(s-l)· W
2) Если верна гипотеза На = {а\ = ... = аг = а}, то Qi(Y) не
зависит от Q2{y) и Qs(Y), Qi(Y)/a2 €= Hr_i. Аналогичное утверждение
имеет место относительно Qi и гипотезы Нв = {Ь\ = ... = bs = b}.
3) Если справедлива гипотеза Н\ = {ак1 — «}> ™>° все три
квадратичные формы Qi, Q2i Фз независимы.
Доказательство. Положим, не ограничивая общности, σ2 = 1. Тогда
_ (akiaij, если (i,j) ^ (&,/)>
У*'УУ"Ы, + 1, если (i,j) = (fcl0.
Отсюда следует, что
е(Еу«) (Еу«) = (Σα«) (Σ°«)+m-
где m — число одинаковых слагаемых в суммах \J и YJ · Пользуясь этим
I II
равенством, легко получить теперь, что
Е(У*. - У)(У.; - у) = (а*. - а){оц - а) = {ак - а)(6^ - 6) (9)
при естественных соглашениях относительно обозначений ак., а.^, а, а,
6. Если верна гипотеза На = {с*1 = ... = аг = а}, то математическое
ожидание в (9) равно нулю. Так как при этом Е(уд.. — у) = ак. — α = 0, то
установленный факт означает, что набор случайных величин {укт — у} не
зависит от {у,ι — у}*
Аналогично устанавливаем, что при любых А;, I, г
Е(У«-У*.)(У<.-У) =0.
Это значит, что совокупность {ук,— у} не зависит также от {уы—Уь*-Ул+у}.
Это означает в свою очередь, что Qi{Y) при выполнении На не зависит
от Q2{Y) и Qz{Y). Тот факт, что Q\{Y) €= Hr_i, вытекает из леммы Фише-
ра(§40).
Аналогично обстоит дело, если выполнена гипотеза Η в- Если же
справедлива гипотеза Н\ (т.е. справедливы На и Нв), то, очевидно, все три
названных выше набора случайных величин будут независимы. Это
означает независимость Qi(Y), QziX), Qz(Y)·
Нам осталось найти распределение Q^(Y). Так как это распределение
от а&, bi не зависит, то мы можем считать, что ак = Ь[ = 0 для всех &, /
496
Гл. 4. Задачи с двумя и более выборками
и что, стало быть, выполнена Н\. Тогда из определения Q{Y) следует, что
Q{Y) ^ Hrs_i. Кроме того, справедливо (5), где Q\{Y) ^ Hr_i, Q2{Y) ^
€= Η5_ι· Остается воспользоваться независимостью Qi{Y) и леммой 61.1.
Теорема доказана. <
Аналогичный подход может быть применен и к задачам п. 1.
Из теоремы 1 вытекает возможность построения следующих
статистических процедур.
1. Оценка параметров а& — а*, 6/ — 6j, σ1 (числа α*;, 6/ в (6)
определены с точностью до последнего слагаемого) с помощью оценок yk, — yio
У./ ~y.j> (°"2)* = Qs{Y)/{r - l)(s — 1)· Так как, по существу, проведенные
выше рассмотрения совпадают с тем, что мы делали в § 61 и в п. 1
настоящего параграфа, то названные оценки будут эффективными. Доверительные
интервалы для σ2, α^ — аг можно строить с помощью соотношений (8),
У*. ~ Уг- - (в* - аг) ^ *0,2σ2/5'
/ ^ ±(r-l)(s-l)
2д3(У)
У 5(г-1)(5-1)
(для 6^ — bj все происходит аналогично).
2. Проверка гипотезы На с помощью критерия Q1/Q3 > /ε·
Критерий будет иметь уровень 1 — ε, если /ε есть квантиль порядка 1 — ε
распределения Fr_lj(r_1)(5_1).
Аналогичный вид будет иметь критерий для проверки Нв- Q2/Q3 > /ε5
где /ε — квантиль порядка 1 — ε распределения Fe—i,(r—1)(д—ι)· <
3. Проверка гипотезы i/χ с помощью критерия
Уз
уровня 1—ε, где /ε — квантиль порядка 1—ε распределения Fr+e_2,(r-i)(e-i)·
Более подробно задачи дисперсионного анализа рассмотрены в [101, 136].
§ 63. Распознавание образов
В этом параграфе мы коснемся кратко круга задач, для обозначения
которого наряду с названием «распознавание образов» иногда используются
также термины «классификация» и «дискриминантный анализ»*).
В § 41 мы рассматривали следующую задачу о проверке г простых
гипотез. Даны распределения Pi,...,Pr и выборка X объема п. Требуется
определить, какая из гипотез
Я, = {Х#Р;} (1)
верна.
*) Следует отметить, что последние два термина употребляются также и для обозначения
иных задач, например задач, в которых распределения Р, в (1) известны.
§ 63. Распознавание образов
497
Однако в практических задачах распределения Pj часто неизвестны, и
судить о них мы можем опять-таки лишь по выборкам.
Итак, пусть дано г выборок Х{ = (χ;ι,.. .,XjnJ, г = 1,...,г, объемов
πι,..., пг соответственно, отвечающих г различным неизвестным нам
распределениям Pi,.. .,РГ, и пусть, кроме того, дана выборка X. Надо решить
все ту же задачу: определить, какая из гипотез (1) верна. Другими словами,
надо установить, продолжением какой из выборок ΑΊ,...,ΧΓ является
выборка X. Это и есть задача распознавания образов.
Для простоты мы ограничимся рассмотрением случая г = 2.
1. Параметрический случай. Предположим сначала, что Pi принадлежат
некоторому семейству {Ря}, удовлетворяющему условию (А^), т.е. Χι €=
^ Рви Х2 €= Ря2, Χ ^ Ρ в при некоторых θγ φ θ2 и θ = θ\ или θ — 02.
Первое из этих равенств соответствует гипотезе Н\ = {X ^ Р^}, второе —
гипотезе Н2 = {X ^ Р#2}.
Предположим, далее, опять-таки для простоты, что объемы выборок ηι,
П2, η равны: щ = η2 = η.
Рассмотрим объединенную выборку (Χι,Λ^-Χ") и представим ее как
выборку объема п, образованную наблюдениями (хн,Х2г,Хг) и относящуюся к
распределению Р^ χ Р#2 х Р#, имеющему плотность /^ {χι)/θ2{χ2)Ιθ{χ)ι за-
висящую от параметра 0 = (0ι,02»0)· Очевидно, что функция правдоподобия
выборки (ΧΊ,Λ^ϊ-Χ") будет равна
/д(Хг,Х2,Х) = /θι(Χ1)/θ2(Χ2)ΜΧ).
Мы приходим к задаче о проверке гипотезы Hi о том, jjito параметр θ
лежит на «кривой» θ = #ι, против гипотезы Н2 о том, что θ располагается
на другой «кривой» θ = #2- Это есть задача проверки гипотезы о
принадлежности параметрическому подсемейству (см. §55), однако в том случае, когда
конкурирующая гипотеза означает принадлежность другому
параметрическому подсемейству. Рассмотрение этой задачи происходит аналогично § 55,
но по своей технической трудности выходит за рамки настоящей книги.
Мы ограничимся здесь тем, что для случая одномерного параметра θ
опишем вкратце существо результата. Оно вполне аналогично содержанию § 55:
если параметр θ локализован, т. е. точки 0ι, 02 располагаются в окрестности
некоторой точки 0о, |#1 — θ2\ > b/y/n, и если семейство {Р#} удовлетворяет
в точке во условиям регулярности (RR), то критерий отношения
правдоподобия
3ηρ/θι(Χι)/θ2(Χ2)/θ2(Χ)
*£ > с (2)
supfei(Xl)fe2(X2)f$l(X)
01,02
будет при η —У оо асимптотически минимаксным для проверки Н\
против Н2.
Ограничение щ = η2 = η несущественно. Оно устраняется так же, как
и в рассмотрениях § 59.
2. Общий случай. В общем случае, когда у нас нет оснований
предполагать, что Χι связаны с параметрическим семейством, возможен общий
подход, в основе которого лежат те же соображения, которые использовались
498
Гл. 4. Задачи с двумя и более выборками
нами при построении в § 60 критериев однородности. В этом случае
критерий π для проверки #ι против i/2 будет функцией трех выборок, так что
π = π(Χι,Χ2)Χ) есть вероятность принять #2 ПРИ данных (Х\,Х2,Х).
Как и прежде, нерандомизированный критерий определяется критической
областью Ω С #П1+П2+П в пространстве значений (Χι,Χ2,Χ). Уровнем
значимости критерия естественно называть число
1 - ε = inf Pi х Р2 х Pi{{XuX2jX) t Ω),
где V есть класс допустимых распределений. Значение
Дг(РьР2) = Ρι χ Ρ2 χ р2(№,-*2,х) е Ω),
Pi G?, Р2 Ε Ρ,
есть мощность критерия в точке (Ρι,Ρ2).
Критерий π называется состоятельным, если /3π(Ρι, Р2) —> 1 при η ι —> оо,
п2 -> оо, η ->· оо при любых Ρι φ Р2, Pi eV, Р2 Ε V.
В качестве основы для построения состоятельных критериев можно
использовать хорошо известный нам факт о сближении эмпирических
распределений Р^ и Р^2 для выборок Х\ и Х2 с Pi и Р2 соответственно.
Если d(P, Q) есть некоторое расстояние между распределениями, то при
гипотезе i/2 расстояние d(P*X2,P*x) должно быть меньше, чем d(jP*Xi,Px).
Поэтому в качестве критерия можно использовать неравенство
d(PX2,Px)-d{PXl,Px)<c,
при выполнении которого принимается #2. Расчет такого рода критериев
(вычисление их уровней значимости и мощности) связан обычно с
большими трудностями (ср. с более простыми задачами, изложенными в §60).
Используя группировку наблюдений, мы можем в общем случае
применять асимптотически оптимальный критерий (2). Предположим, что
группировка по областям Ai,...,Am произведена и (упч-.^Щт) и (^ъ · · м ^т)
есть частоты попаданий в эти области наблюдений выборок Χι, г = 1,2,
и X соответственно. Пусть, кроме того, θ{ — (вц,.. .,#гт) есть вероятности
(Ρϊ(Δι),.. .,Рг(Дт)) попаданий в области Δι,..., Δ™ для распределений
Pi, г = 1,2. Так как для сгруппированной выборки Х{, г = 1,2, функция
771
правдоподобия /θ{{Χϊ) равна fe^Xi) = JJ &"£, то критерий (2) будет иметь
вид
т т
SUp Σ ("Μ + Vk) Ь 02fc + SUp 53 *Ί* ln #1* ~
6,2 Λ=1 Ul *=1
771
- sup V) (i/lfc + z/fc) In θιΗ - sup V ^2jk In 02jfc > In с
§ 63. Распознавание образов
499
или
т т
^2A: + ^A: Ш ; + > Z/iA; In >
m m
έί ηι+η έί П2
Аналогичные рассмотрения могут быть проведены и для г > 2.
Глава 5
СТАТИСТИКА РАЗНОРАСПРБДЕЛЕННЫХ НАБЛЮДЕНИЙ
В §64 приведены примеры задач, которые помогают сформулировать общую
постановку проблемы.
В § 65, 66 излагаются основные методы построения оценок в случае разнораспре-
деленных наблюдений. Изучаются асимптотические свойства М-оценок и
устанавливается асимптотическая оптимальность оценок максимального правдоподобия в
классе М-оценок.
Параграф 67 посвящен достаточным статистикам и построению эффективных
оценок на их основе.
В § 68 рассмотрена задача об оценке «хвостов» правильно меняющихся
распределений.
В § 69 установлены аналоги неравенства Рао-Крамера для случая разнораспре-
деленных наблюдений. Найдены критерии эффективности оценок, основанные на
этом неравенстве.
Параграф 70 посвящен анализу отношения правдоподобия и уточнению
асимптотических свойств оценок максимального правдоподобия.
В § 71 рассмотрены задачи проверки гипотез для разнораспределенных
наблюдений.
Параграф 72 посвящен задаче о разладке.
§ 64. Предварительные замечания. Примеры
В этой главе мы будем рассматривать задачи математической
статистики, для которых экспериментальные данные представлены в виде
выборки X = (χχ,...,χη), состоящей, в отличие от глав 1-3, из наблюдений
Xi разной природы. В какой-то мере мы уже сталкивались с такими
задачами в гл. 4, например в задачах линейной регрессии об оценке
параметров (αϊ,.. ·,αΓ) по выборке У, состоящей из наблюдений γι = αιχ^ι + ·..
... + arXi>r 4- ξί, г = 1,...,η, где векторы х^ = (х^д,.. .,х^г) различны
при разных г, ξι ^ Φο,σ2· Эти задачи оказалось возможным в
значительной мере редуцировать к традиционным подходам, изложенным в гл. 1-3.
Такая редукция возможна и в ряде других задач, внешне формулируемых в
терминах разнораспределенных (неоднородных) наблюдений, но далеко не
всегда.
Рассмотрим несколько примеров, которые с разных сторон
характеризуют рассматриваемые в этой главе задачи.
Пример 1. Пусть надо оценить параметры (α,σ2) по выборке X =
= (χι,.. .,хп), где Xi €= Φα£;,σ2^ρ U, щ известны, г = 1,...,п. Если α
известно и надо оценить лишь σ2, то можно рассмотреть преобразованные
Xi — ati
наблюдения —— €= 3>οσ2> которые позволяют все свести к стандартной
у/Щ
§ 64. Предварительные замечания. Примеры
501
задаче об оценке σ2 по однородным наблюдениям. Если σ2 неизвестно и
надо оценить а, то такого сведения, вообще говоря, осуществить не удается,
так как Хг/ау/щ при α φ 0 и щ φ t\ имеют разные распределения. Если
щ = £2, г = 1,..., п, то Xi/л/щ ^ Φα>σ2 и сведение вновь возможно.
Для пуассоновских наблюдений Xj €= Пд^, где U известны,
использование линейных преобразований не позволяет получить требуемую редукцию
к случаю однородных наблюдений, так как тц/и ί Ε— = λ ] не имеют
распределения Пуассона (эти значения даже не обязаны быть целочисленными).
Пример 2. Нелинейная регрессия. Так называются задачи об
оценке неизвестного параметра θ (или о проверке соответствующих
параметрических гипотез), когда наблюдения xj имеют вид
Xi = <p(0,Zi)+& (l)
или
Χί^β,ζΟίΙ+ξΟ, (2)
где φ(θ,ζ) — известная функция; 21,22,... — суть значения «регрессора»,
при которых проводятся наблюдения; распределения & известны или
ξί €= Pfl. В простейшем случае в задаче (1) предполагается, что & €= Φο,σ2
(σ2 может быть неизвестным). Если xj > 0, φ(θ,Ζί) > 0, то путем
логарифмирования задача (2) может быть сведена к (1). Линейная регрессия,
рассмотренная в § 61, является, очевидно, частным случаем задачи (1).
Вместо φ(θ,Ζ{) в (1), (2) можно писать также ψί{θ), где функции ψ{ известны.
Пусть, например, в пространстве движутся прямолинейно и равномерно
два тела АиВ, сближаясь друг с другом. Тело А может в моменты времени
t{ = id, г = 1,.. ,,η, зондировать с помощью локатора расстояния до тела В,
которые получаются «зашумленными» из-за наличия ошибок ξι. По данным
локации надо оценить расстояние /ι, на котором тело А пройдет мимо
тела В. Не ограничивая общности, мо- „
жно считать, что тело В неподвижно; ^
тело А движется со скоростью υ, ко- ,у/ \ h
торая также может быть неизвестной /''/ *
(см. рис.9). Тогда наблюдение х^ бу- /'/.Ζ
дет иметь вид
Xi = y/{\-ivd)2 + h2+tu
г = 1,...,п, Рис. 9
где неизвестными параметрами могут быть в лучшем случае /г, λ, в
худшем — /ι, λ, ν и σ2 = Όξϊ (можно считать, например, что & ^ Φ0>σ2,λ
определяет расстояние, на котором начинается зондирование).
Пример 3. Усеченные и зашумленные наблюдения. Пусть
У = (Уь — чУп) есть выборка из распределения Р# с плотностью fe(y)
относительно некоторой меры μ. Наблюдателю доступны лишь значения
Xi = min(yi,5i), где si,...,sn — заданная последовательность чисел
(возможно, случайных). Требуется, как и в исходной задаче, оценить параметр #.
502
Гл. 5. Статистика разнораспределенных наблюдении
Отображение χ = min (у, s) не имеет обратного, и восстановить по хг-
значения γι невозможно. Чтобы охарактеризовать распределение хг·, введем в
рассмотрение меры μ·, сосредоточенные в точках S{\
//m ί1' если sieB>
если Sitf: Β,
и положим μ·χ = μ + μ[. Тогда очевидно, что распределение xj имеет
следующую плотность /0,г(я) относительно μι\
(fe{x) При X < 5i,
ίθ,ι{χ) = { ί1 + ΑΦΟΓ^Ο?, 5г) При X = Si,
0 при χ > si,
где Q(0,s) = Р*(У1 ^ 5) = ! }θ{χ)μ{άχ).
Возможны ситуации, когда при больших η значения si таковы, что
Р#(Уг<5г) малы. В этом случае следует рассматривать схему серий, когда
для каждого η имеем свой набор значений Si = slj7l такой, что Р#(уг < £г,п) ->
—> 0 при η —> оо.
Встречаются также ситуации, когда наблюдателю доступны лишь
значения Хг = Уг + sj, где Si — случайные помехи (при тех же, что и прежде, у$).
Если Si имеет распределение G\, то плотность хг относительно μ будет равна
ЛДя) = / dGi{u)f9{x - и).
Пример 4. Статистика случайных процессов. Пусть ξ(ί) —
случайный процесс, заданный на [0,Т], распределение которого зависит от
неизвестного параметра Θ. Будем различать три вида статистических
данных.
(a) Рассматриваются η независимых реализаций ξι (£),..., ξη(ί) этого
процесса, относительно которых нам известны значения хг· = &{щ) в известные
моменты времени щ = 0, гхх,..., ип.
(b) Мы рассматриваем одну реализацию ξ(ί) этого процесса, и нам
известны значения x$ = £(щ) этой реализации в моменты щ = Ο,τχι,.. .,гхп.
(c) Нам полностью известна одна реализация процесса ξ на [0,Т].
Конечно, возможны и другие виды статистических данных. Для
процессов с независимыми приращениями при £(0) = 0 виды данных п. (а),
(Ь) в известном смысле совпадают, так как реализации £(щ + t) — £{щ),
t Ε (0, щ+ι — щ), г ^ 0, независимы при разных г.
Если обозначить через Р^ распределение £(£), то в условиях п. (а) мы
будем иметь выборку X = (xj,.. .,хп), состоящую из независимых
наблюдений xi €= Рб,иг В условиях п. (Ь) мы также будем иметь xj ^ P0,ui5 но
значения Xj будут, вообще говоря, зависимы. Для процесса с независимыми
приращениями из выборки X можно получить выборку из независимых
наблюдений уг = Xi: - Xi-i ^ ^в.щ-щ^ , i ^ 1.
§ 64. Предварительные замечания. Примеры
503
В условиях п. (с) нам доступны данные, предусмотренные п. (Ь) при
любых η и iii, · · -,ип· Однако к этому обстоятельству, предъявляющему
повышенные требования к точности измерений £{щ) при малых щ — Щ-ι, надо
подходить с осторожностью (об этом см. ниже) в связи с тем, что точность
наблюдений в экспериментах всегда ограничена и, стало быть, абсолютно
точные значения ξ(ί) в реальных задачах знать невозможно. Одна из
возможностей построения математических моделей, более точно описывающих
эксперимент, состоит в предположении, что нам даны не «точные» значения
£(£), а значения ξ(ί) + Δ(£), где A(t) — процесс «ошибок» с независимыми
значениями, Δ(ί) ^ U-δ,α или Δ(£) €= Φο,Δ, где Δ определяется условиями
эксперимента.
Если ξ(ί) — диффузионный процесс с коэффициентами сноса и
диффузии (α, σ2) (см. [17, §18.4]), то в условиях п. (a), (b) мы будем иметь
выборку X = (χι,.. .,xn), Xi ^ Фащ,а2щ-> рассмотренную в примере 1.
Если £(£) — пуассоновский процесс со сносом α и параметром λ и если
Tii мы можем выбирать произвольно малым, то с высокой вероятностью
значение α определяется по одному наблюдению: при малых щ с вероятностью
e~Xui имеем хг = αηι, α = х\/щ. Если известно, что ащ не целые, то
можно использовать также арифметические соображения. В силу этого
будем считать, что а известно. Тогда в условиях п. (а), (Ь) мы будем иметь
выборку со значениями хг· = £г(^г) — &Щ ^ Н\щ (см. пример 1).
Если ξ(ί) — диффузионный процесс с неизвестными переменными
коэффициентами сноса и диффузии а{х), σ2(χ) (см. [17, § 18.4]) и нам надо
оценить по траекториям процесса эти функции, то мы придем к задаче об оценке
«бесконечномерных» параметров (α(ζ), σ2(χ)). При оценке таких
параметров приходится сталкиваться с качественно новыми явлениями, которые
при оценке конечномерных параметров, по сути, не возникают, но о
существовании которых можно догадываться. Например, мы встречались с
фактом, что если число оцениваемых параметров велико (сравнимо с объемом
выборки или превосходит его), то нельзя надеяться на существование
«хороших» оценок. То же происходит с бесконечномерным параметром: когда
параметрическое множество очень богато, то все известные нам регулярные
методы оценивания, в том числе метод максимального правдоподобия, как
правило, утрачивают свою эффективность. Это можно проиллюстрировать
на примере оценки функции плотности f(x) (ее можно отождествить с
неизвестным бесконечномерным параметром) по выборке X из распределения
с этой плотностью (см. §10). Функция правдоподобия в этом случае равна
η
f{X) = ТТ/(хг)· Если не накладывать никаких ограничений на множество
i=l
«допустимых» значений параметра / ^ 0, / /(χ)μ(άχ) — 1, то максимум
f(X) будет равен оо и будет достигаться на всех /, для которых /(х;) = оо
хотя бы при одном Xi, /(xj) φ 0 при остальных Xj, j φ г. Чтобы
получать здесь более содержательные результаты, надо вводить ограничения на
множество допустимых / (например, существование вторых производных,
см. § 10). Случай, когда / принадлежит параметрическому множеству, нами
во многом изучен в гл. 2.
504 Гл. 5. Статистика разнораспределенных наблюдений
При переходе к изучению статистики случайных процессов появляется и
другое важное обстоятельство. При рассмотрении в качестве наблюдений не
конечной выборки, а всей траектории процесса на [Ο,Τ], Τ < оо (см. п. (с)),
может оказаться, что относительно некоторых параметров (скалярных или
конечномерных) эта траектория несет в себе «бесконечное количество
информации», что позволяет определить этот параметр точно (детерминированно).
Это будет проиллюстрировано ниже на примере оценки параметра диффузии
σ2 = const (но не сдвига!) по конечному отрезку траектории диффузионного
процесса.
В целом задачи об оценке параметров случайных процессов часто
существенно отличаются от аналогичных задач, изложенных в гл. 2. В то
же время подходы к задаче проверки гипотез (те, что не связаны с
размерностями; см. также элементы общей теории статистических решений
в гл. 6) во многом остаются прежними, а некоторые результаты, не
связанные с параметрическими гипотезами, полностью сохраняют свою силу.
Например, в задаче о проверке двух простых гипотез оптимальный критерий
(байесовский, минимаксный, н.м.к) по-прежнему будет основан на
статистике отношения правдоподобия — ведь наблюдаемую траекторию процесса
можно рассматривать как выборку объема 1 в соответствующем
пространстве X. Наиболее трудным элементом этой задачи становится отыскание в
явном виде плотностей распределения (если они существуют) этих
наблюдений относительно какой-нибудь меры.
Разработка общей теории статистических выводов для случайных
процессов является делом технически весьма сложным и выходит за рамки
настоящей книги. Представление о некоторых основных результатах этой
теории можно получить, например, по книгам [6, 8, 61, 70]. Отдельные
простые примеры, упомянутые выше и относящиеся к случайным процессам
(см. также пример 6), будут рассмотрены позже в качестве иллюстраций.
До сих пор в примерах шла речь в основном об оценке параметров.
Рассмотрим теперь примеры задач о проверке гипотез по разнораспределенным
наблюдениям. К ним можно отнести, конечно, все задачи о проверке
параметрических гипотез в примерах 1-3. Приведем здесь также пример иного
рода.
Пример 5. Проверка двух простых гипотез. Пусть нам
известно, что возможна лишь одна из двух гипотез Н\ или Н^ относительно
природы наблюдений χι,...,χη. В соответствии с гипотезой Н\
наблюдение Xi имеет распределение с плотностью ц (х) относительно некоторой
меры μι\ по гипотезе Н^ распределения х$ имеют плотности ц \х)
относительно той же меры μχ. Задача состоит в построении критериев (желательно
оптимальных) для проверки гипотез Н\, Η<χ по выборке X и в вычислении
вероятностей ошибок этих критериев.
Как было установлено в §42, оптимальные критерии (в том числе
наиболее мощный критерий) для проверки Н^ г = 1,2, имеют критическую
область вида
г=1 J i \хг)
§ 64. Предварительные замечания. Примеры
505
построенную с помощью отношения плотностей (относительно меры μι χ ...
... χ μη) наблюдения X при гипотезах Н{. Как и в §43, мы можем здесь
рассматривать два асимптотических подхода к исследованию критерия (4):
a) считать гипотезы Hi фиксированными, т.е. плотности f\
фиксированы;
b) считать гипотезы Щ близкими, т. е. ц = ц3^ зависят от η и
сближаются при η —¥ оо. Если ограничиться рассмотрением параметрических
гипотез, т.е. считать, что Ц (х) = fi{x,0j), θ\ = 02, то предположение о
близости будет означать предположение о близости θ\ и 02*. 02 = 02,η = #ι + ε(η),
ε(η) —>> 0 при η —> оо. В этих случаях мы будем иметь дело со схемой серий
для разнораспределенных наблюдений. Более подробно об этом см. §71.
Приведем теперь пример, относящийся к статистике случайных
процессов, в котором естественным образом применимы оба подхода: с позиций
теории оценивания и с позиций теории проверки гипотез. Речь идет о
задаче о разладке, упомянутой в примере 2 введения.
Пример 6. Задача о разладке. Пусть дана совокупность
наблюдений X = (χι,.. .,хп) объема η, η ^ оо, устроенная следующим образом.
Первые 0 — 1 наблюдений, 1 < 0 < п, независимы и имеют плотность
распределения gi (χ) относительно некоторой меры μ. Последующие η — θ
наблюдений также независимы, но имеют плотность распределения д2{х) φ 9ι{χ)>
Требуется найти или оценить момент 0, называемый моментом разладки.
Это есть задача оценки дискретного параметра θ случайного процесса X.
Одновременно ее можно рассматривать как задачу о проверке η простых
гипотез Hj — {θ — j} по единственному наблюдению X.
Вернемся к задачам, связанным с оценкой параметра скалярных
наблюдений. Следующий пример иллюстрирует редукцию задачи о
разнораспределенных наблюдениях при наличии мешающего «бесконечномерного»
параметра к однородным наблюдениям в схеме серий.
Пример 7. Оценка «хвостов» распределений. Эта задача
представляет интерес в теории страхования (см., например, [59, 87]).
Пусть ух,уг,..., уп — наблюдения над случайными величинами с
плотностями (относительно меры Лебега)
Лм (У) = 7i (а, у)у"а~ \ У > О,
где α > 0. Относительно функций 7г(а,у) известно лишь, что 7г(<^,у) —► 7
при у —¥ оо при всех г. Требуется оценить параметр а. Предел 7 может быть
любым. Поэтому можно рассматривать в известном смысле эквивалентную
задачу об оценке параметра 0 = (а, 7) по выборке из распределения с
плотностью
fe,i{y) = f{an)Av) = 7(1 + ^г(а,у))у"а"1, е4(а,у) -> 0, (5)
при у —> оо.
Сделаем сначала упрощающее предположение, что при достаточно
большом N и всех у ^ N слагаемые Е{{а,у) пренебрежимо малы (т.е. можно
считать, что ε* (α, у) = 0 при у > N). Введем в рассмотрение наблюдения
Xi = max(iV,yi)
(6)
506
Гл. 5. Статистика разнораспределенных наблюдений
и положим μΝ = μ + μ'Ν, где μ — мера Лебега, μ'Ν — мера,
сосредоточенная в точке N (ср. с примером 3). Тогда х$ будут иметь распределения с
плотностью }q{x) относительно μρι\
{7#~Q_1 при χ > Ν,
1-р при χ = Ν, (7)
0 при χ < Ν,
где
00
ρ = ρ(θ,Ν) = ίΊ-α~ιάχ^^-^.
Ν
Мы получили вполне «регулярную» задачу для однородных
наблюдений Xi, которая согласно §36 при η -> оо допускает а.н. оценки (а*,7*)
(например, о.м.п. а*, 7*)> имеющие точность при фиксированном N
порядка го"1'2. Это значит, что при больших го основная погрешность при
оценке α может быть связана не с разбросом оценок а*, 7*> a co сделанным
выше упрощающим предположении о замене еДа, у) при у > N на нуль.
Чтобы уменьшить эту вторую погрешность, естественно рассматривать
значения N = iV(n), растущие вместе с п. Мы вновь получим задачу в схеме
серий. С ростом N доля р(#, N) «нетривиальных» наблюдений хг- (отличных
от N) будет уменьшаться. Остается выбрать скорость роста N(n) так, чтобы
слагаемыми ε^α, у) при у > N действительно можно было пренебречь, что
возможно, если известны оценки для скорости убывания 6i(a<y) < е(у).
Подробнее об этом см. в § 68.
Аналогичным образом может быть рассмотрена задача об оценке
«экспоненциальных хвостов», в которой предполагается, что плотность
наблюдений γι имеет вид
/«,*(!/) = 7i(a,v)e-<4', У > О,
где функции 7г обладают теми же свойствами, что и прежде. Если вместо
наблюдений у$ рассмотреть наблюдения ъ-х = eyi, то плотность этих новых
наблюдений будет иметь вид
UAZ) = /а,г(тф-1 = 7«(α,1η*)ζ"α"1, ζ > 1,
так что задача сводится к предыдущей.
В последующем изложении в качестве основного объекта в этом
примере будем рассматривать задачи об оценке параметра θ = (α, 7) по выборке
X = (χι,.. .,хп) с плотностями (5) (задача А) и по выборке X с плотностью
наблюдений (7) в схеме серий при N —> оо (задача В).
Приведенные примеры будут более подробно рассмотрены в последующих
параграфах либо в качестве иллюстрации, либо в качестве объектов
изучения, представляющих самостоятельный интерес. Эти примеры позволяют
заметить следующее.
1. В каждом из них мы могли выборку X = (χΐ5...,χη) рассматривать
как одно n-мерное наблюдение и применять к нему качественные результаты
глав 1-4, 6. Это позволяет нам перенести на случай разнораспределенных
§ 65. Основные методы построения оценок. Μ-оценки 507
наблюдений результаты, связанные с принципами сравнения оценок и
критериев, с понятиями эффективных оценок и оценок максимального
правдоподобия, оптимальных критериев, достаточных статистик, с неравенствами
Рао-Крамера и др.
2. При этом, как правило, оказывается невозможным использовать
основные асимптотические результаты глав 1-3, поскольку для разнораспределен-
ных наблюдений отсутствует сам исходный объект этих глав — выборка X
из одного и того же распределения Р. Такие фундаментальные факты,
как теорема Гливенко-Кантелли и другие теоремы об асимптотическом
поведении эмпирических распределении и статистик, остаются в стороне от
рассматриваемых задач, а вместе с ними и такой фундаментальный
принцип построения оценок, как метод подстановки.
3. В связи с этим желательно выработать более общие подходы,
позволяющие сохранить аналоги тех асимптотических результатов глав 2, 3,
которые допускают обобщение на случай разнораспределенных наблюдений.
В последующих разделах мы реализуем в какой-то мере программу,
намеченную в п. 1, 3. При этом мы будем придерживаться той же
последовательности изложения, которая была принята в гл. 2, 3.
§ 65. Основные методы построения оценок. Μ -оценки.
Состоятельность и асимптотическая нормальность
1. Предварительные замечания и определения. Как уже отмечалось, в
условиях этой главы отсутствует, вообще говоря, какое-то одно
распределение, характеризующее выборку, и задача оценки этого распределения или
функционалов от этого распределения не возникает. Понятие оценки здесь
будет относиться только к параметрическому случаю, когда известно, что
Xi €= Ря,ь г = 1,.. .,гг, где Р^д,Р^,25· · · — данная последовательность
распределений (разного типа, вообще говоря), зависящих от параметра Θ. Из
всех подходов к построению оценок, изложенных в гл. 2, естественным
образом переносятся на случай разнораспределенных наблюдений лишь метод
М-оценивания (см. § 14) и, в частности, метод моментов и метод
максимального правдоподобия. Оценки подстановки как собирательный класс оценок,
выражающий некоторый общий подход к их получению, здесь во многом
теряют свой смысл.
Как и в гл. 2, нам понадобятся понятия состоятельности и
асимптотической нормальности оценок. В дальнейшем мы будем писать X ^ Р#, если
Хг ί= Р0,г, понимая под Р# набор распределений {Ρ^,ΐ}. При этом часто мы
будем иметь в виду схему серий, т. е. будем считать, что распределения Р^^,
г = 1,2,..., вообще говоря, зависят и от п.
Свойство состоятельности оценки Θ* параметра θ определяется, как и
в §13 (см. определение 13.1), соотношением
Ρ(|0*-0|>ε) ->0
при η -> оо для X ^ Р# и для любого ε > 0, которое можно записать также
в виде
Θ* —>θ
Р
при X ^ Р#, η —> оо. (Сходимость Θ* по вероятности к постоянной θ не
требует задания Θ* при разных η на одном вероятностном пространстве.)
508 Гл. 5. Статистика разнораспределенных наблюдении
Если мы не имеем дело со схемой серий и выборка X образована
первыми η элементами данной бесконечной последовательности Л^, Х{ €= Р#,г,
то можно рассматривать также сильно состоятельные оценки
0* —> θ при η —)- оо.
п.н.
Понятие а. н. оценок здесь несколько иное, чем в гл. 2.
Определение 1. Оценка Θ* = (0?,...,0£) к -мерного параметра 0 =
= (01,..., Ok) называется асимптотически нормальной с разбросом σ2(0, η),
где σ2(0,η) — положительно определенная матрица, если при X ^ Р#,
η —> оо,
(θ*-θ)σ'1(θ,η)^Φ0>Ε,
где ϋ7 — единичная матрица. Часто σ2(0,η) удается представить в виде
σ2(0)&_1(η), где σ2(θ) — матрица вторых моментов. При этом здесь Ь(п) в
отличие от определений § 13, вообще говоря, не равны у/п. Разброс σ2(0, η)
часто совпадает с матрицей вторых моментов (0* — 0).
Для пуассоновских наблюдений х^ €= Пд^. оценка
λ* = 6-ι(η)χ;χί, 6(η) = £ί,-
t=l
η
является а. н. с разбросом ХЬ 1{п), так как X*b(n) = YJ х,- ^ Пд6(п) и, стало
г=1
быть,
ί^» = (λ._λ)6(η)ι/2λ-ι/2θ>Φθι1.
>/λ&(η)
2. М-оценки. Как уже отмечалось, в случае разнораспределенных
наблюдений основной общий метод получения оценок связан с М-оценками.
Базой для построения М-оценок являются функции 3г(я,0), обладающие
свойством
Гдг(х,в)Рв,г(ах) = 0. (I)
/
Везде ниже в этом параграфе будет предполагаться, что функции д%{х^ 0)
этим свойством обладают. Получить функцию gi{x,9) с таким свойством
можно из любой интегрируемой функции <7г(я,0), положив
9ί{χ,θ) = &(χ,0) - / ft(z,0)P0,i(dz).
Фиксируем теперь некоторое 0о 6 Θ и положим
Si{9) = j gi{x,e)V9o^dx). (2)
§ 65. Основные методы построения оценок. Μ-оценки 509
Тогда 0о можно рассматривать как решение уравнения Si(6) = 0.
Эмпирическим аналогом правой части в (2) в случае X ^ Р#0 является значение
<7i(xi,0). Эти факты и лежат в основе следующего определения.
Определение 2. Любое решение уравнения
η
5>(χ*>0) = ° (з)
i=l
называется М-оценкой параметра 0, соответствующего выборке X.
Если θ — fc-мерный параметр, то в качестве дг следует брать ^-мерную
вектор-функцию с линейно независимыми координатами, так что (3) будет
представлять собой систему из к уравнений.
Если
gi{x, θ) = gi(x) - mi((9), τηι{θ) = / ρι(χ)Ρθιί(άχ),
то М-оценки по аналогии со случаем однородных наблюдений можно
называть оценками по методу моментов, хотя прозрачность этого подхода
здесь значительно меньше, чем в однородном случае.
η
Если считать, что θ — скалярный параметр, πι(θ) = 2_]гпг{^) — моно-
i=l
тонная функция, то оценка по методу моментов единственна и определяется
равенством
г = ш-1(5>(х'))
(здесь и ниже, если не указаны пределы суммирования, имеется в виду
суммирование от единицы до п). Подобрать функции д%{х) так, чтобы πΐί(θ)
(а следовательно, и т(в)) были монотонными, возможно, если исходить из
«физического» смысла параметра Θ. Например, если θ — параметр сдвига,
то 9ί{χ) следует брать линейными, если θ — параметр масштаба, то
квадратичными.
Пример 1. Пусть Р; — известные распределения, θ = (α,σ2), χ* €=
€= Р#г> Ρθί{Β) = Ρ г ί 7=^ Ι · Предполагается, что Pi имеют конечные
моменты второго порядка,
щ= xPi{dx) = 0, h= x2T?i(dx) = 1.
(Случай произвольных α;, b{ также может быть рассмотрен с той лишь
разницей, что уравнения (3) для α и σ2, рассматриваемые ниже, в этом случае
будут немного сложнее.) В примере 64.1 в качестве Р^ фигурировали
нормальные распределения Φο,ι·
Положим д{(х) = (&,i(z),0i,2(z))> * = 1,2; ft,i(z) = vtx, д^{х) = WiX2,
где vi, Wi выберем позже. Тогда
τηίΛ{θ) = Eflffi.ifci) = atiVi,
mia{9) = E^i|2(x) = Wi[E(xi - ati)2 + a2t?] = Юг(а2щ + α2*?).
510 Гл. 5» Статистика разнораспределенных наблюдений
Оценки по методу моментов будут определяться уравнениями (см. (3))
Y^Vi{xi - at-t) = 0, Y^wifa? - що1 - α2ή) = О,
которые дают
* ЕъУг /2ч» Σ^(χ?-(<**Κ?) (Αλ
Σ t'i»i Σ uiwi
Рассмотрим сначала оценку α*. Имеем
α·.α= £«■(*-<*), Е(а*-<*)2 = ^%
Σ to (Σ to)2
Стало быть, если
М") = ξ^ ^оо, (5)
το α* — состоятельная оценка. В силу центральной предельной теоремы
(см. приложение IV) а* будет а.н. с разбросом σ2(α,η) = а2Ъ^1{п), если
суммы 2_2vi(xi ~~ а^г) удовлетворяют условию Линдеберга или условию
Ляпунова:
(Σ<-.?»0"3/2Σε|
Хг — at{]3
—> 0 при η —> оо.
Отметим, что выбор V{ в (5) может влиять не только на постоянный
множитель, но и на саму скорость роста 6г(п). Естественно выбрать v\ так, чтобы
максимизировать &ι(η). Так как (/_^αΛ) ^ 7>а* У"^, то
(ς42«(ς|)(ς«?-0· »·<»>< ς*.
где правая часть от v% не зависит. Эта верхняя граница для &ι(η), очевидно,
достигается при Vi = и/щ> Для таких значений νι получаем «оптимальную»
в классе (4) оценку
α =
Σ:1
ί? '
для которой
t?
Μη) = Σ5:
Как уже отмечалось, оценка а* будет состоятельной, если bi(n) —^ оо. Это же
условие необходимо для асимптотической нормальности а*. В примере 64.4
§ 65. Основные методы построения оценок. Μ-оценки 511
об оценке параметров диффузионного процесса t% = щ и условия Ъ\{п) —> оо
эквивалентно у tj —> оо.
Аналогичным образом может быть рассмотрена оценка (4) для σ2. Здесь
оптимальными будут значения wi = u,"1. Читатель без труда может
убедиться в этом аналогично предыдущему. Мы опускаем здесь эти
рассмотрения еще и потому, что оптимальность выбора Wi — u^1 будет независимым
образом подтверждена ниже (как, впрочем, и выбора v% = U/щ). В
результате будем иметь дело с оценкой
J.
(χ» - <***<)*
так что
((σ2Γ-σ2)^=^^
\/Й
(xi - aij)5
(a*-a)2b!(n)
4=(a*-a)2bi(«)·
(6)
Так как E(a* - a)2bi(n) = σ2, то последнее слагаемое в правой части
сходится по вероятности к нулю (если α известно, то это слагаемое будет от-
σ2
сутствовать). Первое слагаемое можно представить в виде —γ= у. (£* ~~ 1)>
у τι *-~*
v. at'
ξι = ——=^·, где Е£г = 0, D& = 1. Оно будет асимптотически нормально
οφΐχ
с параметрами (0,a4d4), d4 = - ^Ε(ξ? - l)2 = - ^Εξ^ - 1 в предполо-
/J 7i
жении, что выполнено условие Линдеберга или условие Ляпунова:
„-1-7/2^^14+27^0, 7>0-
(7)
Итак, при выполнении (7) и d4 = const оценка (σ2)* будет а.н. с
разбросом a4d46^1(n), b2{n) = η, который, очевидно, не зависит от
последовательностей {ίχ,ιΐχ}. Кроме того, нетрудно видеть, что, как и в однородном
случае, а* и (σ2)* будут асимптотически независимыми
(некоррелированными), т.е. оценка Θ* = (а*, (а2)*) для θ = (а,а2) будет а.н. с разбросом
а2{9,п) = а2(0)Ъ-1{п),тце
σ2(0) = ΐΜ0)ΙΙ> *(η) = IIMn)||, *«W = Mn) = o при *^i.
σι1(0) = σ2, σ22(0) = a4d4, bn{n) = 6χ(η), Ь22(п) = Ь2(п) = η.
Отметим, что здесь соотношение между b\(n) = ^J -L и 62(n) = п может
быть любым.
Ъ.
Щ
512 Гл. 5. Статистика разнораспределенных наблюдений
Отметим также, что из асимптотической нормальности (σ2)* с разбросом
a4d4n_1 следует состоятельность
при η —> оо, хотя условия состоятельности могут быть, конечно, и более
слабыми (см. п. 4). Далее, названные выше условия (см. (7)) выполнены в
примерах 64.1 и 64.4 об оценках параметров диффузионного процесса. В
последнем примере в условиях п. (с) мы располагаем реализацией процесса ξ(ί)
на [0,Т] и, взяв разности наблюдений в точках щ = г'Т/п, мы можем по ней
ПОСТРОИТЬ выборку X = (Χι,...,Χη), Хг = ξ(*Δ) - ξ((ί - 1)Δ) €? Φ(αΔ,σ2Δ)
любого объема η, где Δ = Τ/η (здесь ti = щ — Δ). В соответствии с
предыдущим мы будем иметь здесь оценки
* Σ** ξ(τ)
τ τ '
(о2 = £ Σ Κ2 - («*)2д2) = ψ Σ*2- ^·
Здесь (а* — а) €= Ф0)(Т2/Т и оценка а* при фиксированном Τ и растущем η
несостоятельна; при этом лучших оценок не существует (см. §67 или §25).
Для оценки (σ*)2 имеем
(о2 = ψ Σ (χ< -αΔ)2 - («- «*)2д'
α*)2Δ —>> О при η —> оо, Τ ^ const. Так как по закону больших
то (σ*)2 —► σ2. Это означает, что, пользуясь траекторией ξ (Γ) лишь на
малом отрезке [О, Г], мы можем выбором η восстановить любой заданной
точностью параметр σ2. Как уже отмечалось в примере 64.4, процедура
построения оценок (σ*)2 при этом требует знания траектории ξ(Τ) с неограниченной
точностью (в связи с этим к сделанному выводу надо относиться с
осторожностью). Чтобы избежать затруднений, связанных с этим обстоятельством,
можно предположить, например, что мы имеем в качестве наблюдений в
моменты гА не ξ(ζΔ), а значения ξ(ίΑ) + щ, где ошибки наблюдений щ
независимы и одинаково распределены, Ет/г = О, Е772 = ε/2, г ^ 1. Число ε
будем считать малым. В этом случае мы будем иметь дело с выборкой
Xi = ξ(ίΔ) - ξ{{ι - 1)Δ) + щ - m-u ξ(0) = щ = 0.
Метод моментов приводит к оценке
где (а
чисел
§ 65. Основные методы построения оценок. Μ-оценки 513
которая, как и прежде, несостоятельна при фиксированном Т, Da* =
2σ2Τ + ε2
= ^ ' и °Ценке
ю2 = ψ Σχ2 - χ - (°*)2д = ψ Σ fc - «Δ)2 - к ~(α - α*)2Δ·(8)
Считая для простоты a = 0 известным, получим
При каких Δ разброс Ε((σ*)2 — σ2)2 будет минимальным? Предположим,
что Ε ί — 1 < const, Τ ^ const. Тогда получим
.2ч2
η
Va
τ-*
^c
λ ε4
Δ+Δ
с = const. Наименьшее значение правой части достигается при Δ = ε2, так
как разброс (наименьший) оценки (σ*)2 будет иметь порядок ε2. Очевидно,
это сохранится и в общем случае (8). Точный подсчет наименьшего значения
Ε((σ*)2 — σ2)2 предоставляем читателю.
Пример 2. Пусть xj €= H\tr Здесь параметр λ не является ни
параметром сдвига, ни параметром масштаба. Тем не менее ясно, что при
gi(x) = νιχ мы получим монотонную линейную функцию тп(Х) и, стало быть,
можем, как и в примере 1, найти оценку по методу моментов в явном виде.
Действительно, здесь
Так как
77ij(A) = ЕЛ^Хг = \tiVi, m{\) = A^tfT;», λ* =
У j Щц
λ*-λ =
Σ щи
то разброс λ* равен Ε(λ* — λ)2 = Aft-1 (n), b(n) = г9г—. Здесь мы имеем
ту же задачу минимизации, что и в примере 1, но при щ = t\. Поэтому
оптимальные коэффициенты равны v% = 1,
η
Очевидно, что эта оценка будет а. н. (с разбросом А6_1(п)), если V^i —> ο°·
Вернемся к общим определениям. Как и в § 14, здесь можно
рассматривать несколько иной подход к определению М-оценок. Пусть ψι(χ,θ)
обозначают заданные функции на Χ χ Θ.
514 Гл. 5. Статистика разнораспределенных наблюдений
Определение 2А. М-оценкой параметра θ по выборке X €= Ρ я
называется значение 0, при котором достигается максимум по t (или минимум)
]Г>г(х*,*). (9)
i=l
В качестве ipi(x,t) естественно брать такие функции, для которых
/ ψ^χ,ήΡο^άχ) достигает своего максимума (соответственно минимума)
при t = θ.
Например, если Р^^(Б) = T?i(B — вщ), где Р; известны, / xPi(dx) = щ
(см. пример 1), то среднее значение для Р^ равно а\ — вщ и при t = θ
достигается min / (χ — αι + tui)2Pej(dx), так что М-оценкой θ будет
значение, минимизирующее (9) при ψι(χ,ί) = (χ — а,{ + tui)2. Таким образом,
Оценки по методу наименьших квадратов есть М-оценки.
В примере 64.2 о нелинейной регрессии
х- = <^(0)+£, £е Ρ*, Ε£ = 0.
Оценка Θ* по методу наименьших квадратов минимизирует У", (xi ~
— ψι{θ))2 и будет М-оценкой. Другим важным примером М-оценок является
о. м.н., о которых речь пойдет ниже. Связь М-оценок и М-оценок здесь та
же, что и в случае однородных наблюдений. Она обсуждалась в § 14.
3*. Состоятельность М-оценок. Как и в однородном случае, мы будем
предполагать здесь выполненным условие
(Ас) Множество Θ компактно.
Комментарии по поводу этого условия см. в § 14. Естественно
предполагать также выполнение условия
(Ао) Функции ψΐ(χ,θ) таковы, что / φ{(χ,ί)Ρο^(άχ) достигает
максимума в единственной точке t = 0, так что при t φ θ
l·
{фг{х,Ь) - 1>i(x,e))Pofi{dx) = Eo^i{t) < 0,
где
τ/<(ί)=^(Χή*)-^<(χ<,β) (10)
(Ее,г есть среднее относительно Р^,г)·
В дальнейшем мы будем допускать, что рассматривается схема серий,
т.е. что функции φι, щ и распределения P^j могут зависеть также от п.
Нам понадобятся дополнительные условия. Обозначим
1^0М)= sup ^ifot + u), η£(ί) =1^0Μ)-^·(Μ).
§ 65. Основные методы построения оценок, Μ-оценки 515
Наряду с семейством {Р#,г} через Р# будем обозначать также
распределение Р#д χ ... χ Pflj7l на Хп и через Е# — математическое ожидание
относительно этого распределения, так что Έβ^ηί(ϊ) можно записывать и в
виде Е07?;(£). Через (θ)δ мы будем обозначать (^-окрестность точки Θ.
Введем в рассмотрения условия
(Af) Для любых δ > О u t £ (θ)δ, ί G θ, существуют Δ = Α(δ)
u Ν > О такие, что при некотором ε = ε(£, ί, Ν) > 0
limsup-^-rf^E^f (t)rf(θ) > -Ν) < -ε,
где
bn(t) = XXfof (t)|;qftt) > -^) -> °°· (И)
(A^) Для любых τ > О, £ Ε Θ выполняется
limsup г^тт Σ E^ W^)i ^) > Tb"(*)) = °-
2 = 1
Из (A^) следует, очевидно, что
£р(т£(<)>тм«))-ю (12)
при η -* оо.
В качестве Ьп = 6η(ί) можно брать также bn = -^jE^rjf (ί) или fcn =
= — V^EflTft^), если эти суммы имеют «тот же порядок», что и (11). Это
возможно, если они не содержат бесконечно больших отрицательных
слагаемых (больших положительных слагаемых они содержать не могут в силу
(А^)). Об условиях, достаточных для выполнения (Af), (А^), см. ниже.
Теорема 1. При выполнении (Ас), (Af), (А^) М-оценка
состоятельна.
Доказательство. Обозначим
η
φ*(ί) = Σ(^(χΐ,*)-^(χ<^))·
χ=1
Если θ* — М-оценка, то
Ρ*(|0*-0|>ί)=Ρ*( sup **(*)> sup Φ*(ί))<Ρ*( sup Φ*(ί)>0).
|*-0|><ί |t~0|$* |t-0|>*
Пусть J фиксировано, А и N удовлетворяют (Af). Покроем множество
Θ \ (0)* окрестностями Δ,- = (*/)Δ, j = 1,.. .,m, t» 6 θ \ (0)*. Тогда
sup Φ*(t) ^ max sup Φ*(ί) ^
|t-0|><i J ί€ΔΛ·
η η
^maxV^ftxijij) -^(хг-,(9)) = maxVr/f (t,-).
г=1 г=1
516 Гл. 5. Статистика разнораспределенных наблюдений
Отсюда следует, что
m / η \
ρ.(ΐ0*-0ΐ>ί)^ΕρΜΣ^Δ(^·)>ο ,
j=\ \i=\ J
и нам достаточно доказать, что для ί ^ (Θ)
рЛ ί>Δ(ί) > о)-* о.
Обозначим
rilt) = rt?W{n?(t)>-N),
где 1{А) — индикатор А, Тогда
= ρ* (Σ tiN) - *(-*)) > - Σ α*-Νή -
где
щ(-М) = Εθη\Ν) = E(i^(t);^(t) > -Ν).
По условию (А^)
-Τ-ΣΜ-Ю > ε-
Поэтому нам достаточно убедиться, что
Воспользуемся следующим законом больших чисел (см. приложение IV).
Теорема А. Пусть &?п, г — 1,...,п, независимы и удовлетворяют
условиям
Е&,п = о, Σ Е&>1 < с> Σ Ε(Ιί<.πΙ; lif.nl > г) -+ о
при любом τ > 0 и η —> оо. Тогда Ρ ( /_^£г> > ε) —> 0 при η —ϊ оо и
любом ε > 0.
Нам надо проверить, что величины ξ{ίΤΙ = — удовлетворяют
On
условиям теоремы А. Первое и второе условия выполнены очевидным
обрати IгЬп\
зом. Далее, имеем — Ν < αι{—Ν) < —- + сц ( -—- 1 , где по условию (А^)
di I —— ) = o(bn). Поэтому при достаточно больших η
-Ν < ai(-N) < ψ, η^ - at(-N) >-Ν-ψ> -тЪп
§65. Основные методы построения оценок. М-оценки 517
и событие {η\ — аг( —Ν) < — rbn} невозможно. Следовательно, при
достаточно больших η
E{\riN)-ai{-N)\i\ri^-ai{-N)\>rbn) =
= Ε{η\Ν) - ai(-N);^N) - oi(-N) > rbn) <
<лпр(ч{ло>^)+в(ч!ло;ц(ло>^)!
ΓΣ4ΗΝ) -<чЫ0|; ΗΝ) -aii-N)\ > rbn) <
Jn t=l
N
при η —> oo в силу (А^) и (12). Теорема доказана. <
Перейдем к выяснению условий, достаточных для выполнения (А^),
(А^). Обозначим
& = Ί^Γ> f+=max(0,«
Μ*)
и рассмотрим условие
(L2) Яри каком-нибудь s выполняется
η
limsup^Efl min (ξ+, (ξ+)') = 0.
η-»οο 1
г=1
Так как Ε min (ξ+, (ξ+) ) < E(f/") > то это условие можно рассматривать
как ослабление условия типа Ляпунова.
Условие (L2) достаточно для выполнения (Arj )·
Действительно (т ^ 1),
и,(з£Ш;5еш>г)<1(,№,</>1)+
+ r'-B.itO'iT < {?· < 1) ί τ'-Β, min (ξ+, ({+)').
Из условий (Af), (А^) следует, что они не предполагают ограничений в
области отрицательных значений η^(ί) того же типа, которые
предполагаются условием (А^) в области положительных значений η^{ί). Однако если
такие ограничения ввести, то условия, достаточные для выполнения (А^),
(А^), можно сделать более симметричными.
518 Гл. 5. Статистика разнораспределенных наблюдении
Обозначим в ближайших рассмотрениях
η
(это соответствует N = со в (11)) и введем условия
(Lq) При t £ (θ)δ выполняется
bn(t) -> oo, limsupV^E^· < — ε < 0.
η—юо . 1
г=1
(Li) #pu 5 > 1 выполняется
η
limsup^Eemin(|&|,|£i|s) = 0.
η—>oo . 1
г=1
Условие (Li) эквивалентно условию (см. приложение IV): при любом
г >0
limsup£E0(|a&i>^)=O. (14)
Условия (Lo), (Li) влекут за собой (Af), (А^).
Действительно, условие (Li) влечет (L2) и, следовательно, (А^). Условие
(Af) при N = оо вытекает из (Lo)»
Неудобство рассмотренных выше условий состоит в том, что они
выражены в терминах величин т?^№> (V^(xi>*))> a не ^(ί) WKxi>*))· Этого
неудобства можно избежать, если потребовать, чтобы функции ^(χ^,ί) были
в известном смысле непрерывны по t. Обозначим
ω?(x,t) = sup \i/>i{x,t + u)-ilH{x,t)l ω£(t) = E^f (χ,,*),
η η
βη{ΐ) = 5>w(i), Μ*) = Х>*|*к(«)|.
Может быть полезной
Лемма 1. Пусть при t £ (θ)δ, с < оо
-βη№ > d>n(t)-> oo, £u;f(*) = o(M*)) при Δ-Ю.
Тогда выполнено условие (А^) при TV = 00.
Доказательство леммы 1 носит чисто технический характер и основано
на неравенстве |^W ~~ ^гМ) ^ а;г^(х^^)· Мы предоставляем его читателю.
Отметим, что наиболее важным «качественным» элементом
рассмотренных выше условий, обеспечивающих состоятельность М-оценок, является
сходимость при t φ θ
η
/Ш = ^Ев%(<)->-°°· (15)
i=l
§ 65. Основные методы построения оценок, Μ-оценки 519
Асимптотическая нормальность М-оценок требует выполнения
условий дифференцируемое™ ψ{(χ,ί) по t. Поэтому ее естественно изучать в
рамках п. 5, посвященного асимптотической нормальности М-оценок.
4. Состоятельность М-оценок. Чтобы упростить изложение,
ограничимся здесь в основном рассмотрением одномерного случая, когда θ —
скалярный параметр. Комментарии по поводу многомерного случая см. в конце
параграфа. Как и в предыдущем пункте, мы будем предполагать, что
выполнено условие компактности (Ас). Кроме того, нам понадобится ряд условий
на исходные функции gi{x,6) (см. определение 2), которые в схеме серий
могут зависеть от п.
(Μι) Функции gi(x, θ) интегрируемы и удовлетворяют условию типа
Линдеберга в следующем смысле:
8ΐιρ|#(ζ,ί)| = 7i(z) < оо, 7г = / 7ΐ(χ)Έ>Θιί(άχ) < оо,
*€Θ J
Γ^^έ / 7i(^)Pw(^)->0, Г(гг) = £7г,
Ι=17ί(*)>τΓ(η) i=1
при η —> оо, где θ — «истинное» значение параметра, соответствующее
выборке Χ, τ > 0 — любое фиксированное число.
(М2) Функции gi(x, θ) непрерывны по θ «в среднем» в следующем
смысле. Пусть
UA,i{x) = sup \gi{x,t + u)-gi{x,t)\
есть модуль непрерывности gi wa9, luaj = Е^о;д,г(хг) = / MA,i{x)T?e,i{dx).
Мы будем предполагать, что
при Δ —> О, где о>д от η не зависит (в лемме 14.1 было показано, что
ωΔ,ι -^ 0 при Δ -* 0).
(Мз) ί Ε θ является единственным решением уравнения S(t) = О,
где 5(i) = ^5i(t), Si(t) = / ffi(s,i)Pt,i(daO (см. (2)). Кроме того,
функция s(t) = Γ_1(η)5(ί) удовлетворяет условию: для любого достаточно
малого ε > 0 найдется δ > 0 такое, что
inf |*(ί)|>ε (16)
*€0,|0-*|><Г
гари всея η (ε, £ от η ме зависят).
Теорема 2. Дри выполнении условий (Mi)-(Ms) М-оценка θ*
состоятельна.
520 Гл. 5. Статистика разнораспределенных наблюдений
Положим
Для доказательства теоремы 2 нам понадобится
Лемма 2. Если выполнены условия (Μι), (Μ2), mo*)
sup\s*n(t)-S(t)\—>0
te& p
при η —> oo, функция s(t) непрерывна.
Доказательство. Имеем
η
ωΑ{Χ) = sup \s*n{t + u) - <(t)| < Τ-1 {η) YWitxi) =
ί€θ,ί+α€θ,|α|ζΔ i=1
η η
= Γ"1 (η) £>Δ,, + Γ"1 (η) ]Γ (ωΔ,.-(χί) - ωΔ><). (17)
i=l i=l
Покажем, что второе слагаемое здесь сходится по вероятности к нулю.
Это следует из закона больших чисел (теорема А) и следующего почти
очевидного утверждения, которое означает, что слагаемые ξί?η = Γ"1 (η) χ
χ(^Δ,ΐ(χί) — <*>Δ,ί) удовлетворяют условиям теоремы А.
Лемма 3.
η
Ε&,η = О, ^Е|Ы < const, £>[(Ы; I6.nl > г) -> 0 (18)
<=1
при η —> oo w любом τ > 0.
Из этой леммы и из (17) следует, что о;д(Х) ^ о;д + εη(Χ), εη(Χ) —> 0.
Дальнейшее доказательство леммы 2 ничем не отличается от
доказательства леммы 14.1 (надо лишь сходимость п.н. заменить на сходимость по
вероятности).
Непрерывность s(t) очевидна, так как
β(ί + Δ) - s(t) ζ T-'in) Σ Ы* + Δ) " *(*)) < г~Чп) £>Δ,ζ < ωΔ. (19)
Нам осталось доказать лемму 3. Имеем
η
£е|£|П| = T-^n^EluA^Xi) - u*,i| < гГ-^^^ыл,,· ^ 2ωΔ.
г=1
Это доказывает неравенство в (18). Чтобы доказать сходимость в (18),
заметим, что из (Μι) и комментариев к теореме 1 приложения IV следует
*) Здесь и в дальнейшем для краткости мы используем запись ζη —> 0 вместо Ρ(|ζη| >
> ε) —> 0 для любого ε > 0.
§ 65. Основные методы построения оценок. М-оценки 521
(см. там (6), (Si)), что
Г-1{п)тахц ~> 0, ^P(7i(xi) > εΤ{η)) -> 0 (20)
при η —> оо. Отсюда получаем
тахо;д,г ^ 2тах7г = о(Г(п))
г
и следующие вложения для области интегрирования Β^η = {|&,η| > τ} в (18)
при достаточно больших п:
BiiU = {|^Д,г(Хг) " ^А,г| > тГ(п)} С
С |«;д,г(Хг) > уГ(^)} С |7г(Хг) > ^^J^] = Ai,n.
Следовательно, последняя сумма в (18) не превосходит
Σηΐξί,ηϊ,Αί,η) < Γ^Η^ωϊ,ΔΡ^,η) +
2r-1(n)X;E(|7i(xi)|;7i(x«)>
Здесь правая часть в силу (20), (Μι) и неравенств с^дг £Ξ ш&Г(п) сходится
к нулю при η —> оо. Лемма 3, а вместе с ней и лемма 2 доказаны.<
Доказательство теоремы 2 почти ничем не отличается от доказа-
тельства теоремы 14.3. Надо лишь сходимость п.н. заменить на
сходимость по вероятности. Неравенства (14.14), используемые в доказательстве
теоремы 14.3, вытекают из условия (Мз) (см. (16)).
5. Асимптотическая нормальность М-оценок. Здесь нам потребуются
условия (М1)-(Мз) и аналоги условий (Μι), (Мг) для производных д\(х,Θ)
по (9.
(Μι) Функции gi(x,t) непрерывно дифференцируемы по Θ,
sup k'(z,*)| ξ η[{χ) < оо, 7г( = / 7i(z)P0,i(cte) < оо,
ее© J
ί==17ί(χ)>τΓι(η)
η
при η -> оо, где Γι (η) = /_^7г'> ^ — истинное значение параметра,
г > О — любое фиксированное число.
Положим
wk,i(s) = SUP |^ОМ + и) -0i(M)|>
ί€θ,ί+α€θ,|α|$Δ
ыд|4 = Е^д^(хг) = / ω^^Ρ^ώ?).
522 Гл. 5. Статистика разнораспределенных наблюдении
(М2) Г1 ι(η) 2ΖωΔ>* ^ ωΔ ~^ 0 при Δ -> оо, где ω'Α от η не зависит;
\з'{в)\ >δ>0.
Заметим, что в силу (М2) законно дифференцирование интегралов Si(t)
по параметру, так что
η
s'(t) = T-1(n)Y^Eeg'i(xht).
2 = 1
Кроме того, мы будем предполагать выполненным условие Линдеберга
(М4) Ό-Ηη)ΣΜ9Ϊ(*>0)Μ*Μ >rD(n)) ->0,
edeD{n) = ^E^i^^·
Условия (Μι), (Μ2) (они тоже будут нам нужны), как и в § 14, во многом
являются следствиями условий (ΜΊ), (М2). Однако для краткости
изложения не будем выделять минимальные требования, а будем предполагать
(Μι), (М2) выполненными наряду с (M'J, (М2). Если состоятельность
М-оценки Θ* будет установлена каким-либо другим способом (см. §68), то
нужда в условиях (Mi)-(Ma) в следующей теореме отпадает.
Теорема 3. При выполнении условий (Μι)-(Μ4), (М'х), (М2) М-оцен-
ка Θ* асимптотически нормальна с разбросом
σ2(θ,η) = D(n)(s'(0))-2T^(n) = D(n) (^Еед'^ив))'2.
Доказательство теоремы 3 аналогично доказательству теоремы
14.4. Условия теоремы 3 влекут за собой условия теоремы 2 и,
следовательно, Θ* —> θ> Функция
непрерывно дифференцируема и допускает представление
о = W) = <(*) + (0* - *)«(*))', θζ [βχι
где0 —>0.
ρ
В силу условий (Mi), (M2) функция (s^(t)) удовлетворяет условиям
леммы 2 и, следовательно,
sup|«(i))'-S'(i)|—>0.
tee p
Кроме того, аналогично предыдущему (см. (19)) получаем
sup \s'(t + и) - s'{t)\ ζ ω'Α -> О
§ 65. Основные методы построения оценок. Μ-оценки 523
при Δ -> 0. Из этих соотношений и (М'2) следует, что
(3*η(θ))'-8'(θ)-^0, 8'(θ)-8'(θ)-^0,
«(?))'= β'(6Ι)(1 + ε„), εη-^0.
Это дает нам
(θ*-θ) = -8*η(θ)(8,(θ)Γ1(1 + εη)-1,
где в силу центральной предельной теоремы (см. приложение IV) и
условия (М4) сумма Γι(η)θ*(0) асимптотически нормальна с параметрами
(О, D(n)r^2(n)(s'(e))~2). Остается воспользоваться теоремой
непрерывности. Теорема 3 доказана. <
Изучение асимптотических свойств М-оценок в многомерном случае
происходит аналогичным образом, но технически сложнее. Поэтому, как и
в § 14, ограничимся здесь краткими комментариями по поводу
асимптотической нормальности. В многомерном случае функции gi являются /г-мерными
векторами gi(x,6) = (#г- ,.. .,д\ ') и М-оценки суть решения системы из к
уравнений (в векторной форме)
]Г#(х;,0)=О.
Характер условий на функцию gi остается прежним. Роль величины D(n)
в условии (М4) может играть теперь минимальное собственное значение
матрицы
η
D(0,n) = £>;, Ог = \\Евд?{ъ,вЫъ,в)\\.
Роль матрицы пз'(9) в § 14 будет играть сумма
i=l
где 8[{ί) — матрица, составленная из столбцов (grads^(i)) ,...
...^grad^i))7", з\г)(в) = Е^г)(х;,0). Основное асимптотическое
соотношение для Θ* — θ остается прежним:
(б· _ в) « -S*n(9)(S'(e,n))-\ S*n(e) = £>(*,*).
Отсюда при выполнении соответствующих условий можно получить, что Θ*
будет асимптотически нормальна с разбросом
[(3'(θ1η))-1]τΌ(θ,η)(3,(θ,η))-1. (21)
524 Гл. 5. Статистика разнораспределенных наблюдений
§ 66. Оценки максимального правдоподобия.
Основные принципы сравнения оценок.
Оптимальность о.м. п. в классе М-оценок
1. Оценки максимального правдоподобия. С методами М-оценивания
тесно связан общий метод построения оценок, называемый методом
максимального правдоподобия (ср. с гл.2).
Предположим, что X €= Р#, распределения Р^ имеют плотности fe.iix)
относительно некоторой меры μ^, не зависящей от 0.
Определение 1. Функцией правдоподобия (относительно меры μι χ ...
... χ μη) выборки X = (χι,.. .,χη) называется функция
η
лро = Пл,<(*)·
t=l
Логарифмической функцией правдоподобия называется функция
L(X,e) = \nfe(X) = y£h(xi,e),
где Ιί(χ,θ) = 1η/05ΐ(ζ). Оценкой максимального правдоподобия Θ*
параметра θ называется значение 0, при котором достигается тах/^(Х) по Θ.
Очевидно, что о.м.п. Θ* является М-оценкой при ψι{χ,θ) — 1{(χ,θ).
Читатель без труда может построить функции правдоподобия в примерах
64.1-64.7. Например, в условиях примера 64.1 θ = (α, σ),
(1)
Логарифмическая функция правдоподобия L(X,0) здесь имеет вид
«*.«_*-„*,-£ &£*!>!,
где сп от θ и X не зависит.
В более общей постановке, относящейся к схеме серий (см. примеры
64.3-64.7), мы должны предполагать, что распределения Р^^ наблюдений
Xi зависят также и от п: Pqj = Р^ . Зависеть от η могут также меры
μι,.. .,μη и, несомненно, плотности /о\{х) относительно меры μζ- .
В дальнейшем верхний индекс (п) для краткости мы будем опускать.
Если рассмотрения исключают схему серий, это будет оговариваться особо.
Если функции Дг(#) (или li(x,t)) непрерывно дифференцируемы по t —
= (ίχ,.. .,£&), то точка максимума L(X}t) удовлетворяет уравнениям
dL{X,t) A3,, ч Λ Λ
J i= 1 J
§ 66. Оценки максимального правдоподобия
525
Так как, кроме того, / Ιί{χ,ϊ)$ο^(χ)μι{(Ιχ) достигает максимума при t = θ
(см. § 16), то в случае законности дифференцирования этих интегралов по t
получаем
/
Q^k{x,0)f9)i{x)fr{dx)=0. (2)
Это означает, что при выполнении названных условий о. м. п. является
М-оценкой. Равенство (2) также можно получить, дифференцируя
тождество / ίθ,ίκ^βικ^χ) = 1, если законно дифференцирование под знаком
интеграла.
Для выборки X из нормальных распределений в примере 64Л эти усло-
вия выполнены, и о. м. п. является решением уравнений —— = 0, тг~ = О
σα σσ
или, что то же,
γ^ (xi - atj)t% _ ^ (χ, - atj)2 _ η
так что
a —
2 = 1 ^ (χ, - aHtf _ 1 /у, χ? - (S*)2*?
(3)
Для пуассоновских наблюдений χ$ €= Пд^ функция правдоподобия и
о. м. п. λ* соответственно имеют вид
г=1 Xi< ^Ц
Мы сразу получили здесь оценки, оптимальные в классе оценок по методу
моментов и найденные нами в п. 65.2.
Отметим, что других общих «регулярных» методов построения оценок
для разнораспределенных наблюдении, помимо Μ-оценивания и метода
максимального правдоподобия как важнейшего частного случая, по существу,
нет. Поэтому большое значение приобретает метод последовательных
приближений при отыскании о.м.п., изложенный в §35.
Среди немногих других методов можно указать подходы к построению
оценок, связанные с некоторыми частными предположениями. Допустим,
например, что при каждом г можно построить несмещенную оценку Θ*
параметра 0, построенную по одному наблюдению х$: Е#0* = θ (имеется
в виду математическое ожидание по распределению Р#,г). Тогда оценка
η
θ* = У^Рг0*\ У^Рг — 1 также будет несмещенной и может обладать хо-
г=1
рошими асимптотическими свойствами.
526 Гл. 5. Статистика разнораспределенных наблюдений
2. Асимптотические свойства о. м.п. Рассмотрим сначала одномерный
случай Θ С К. Как уже отмечалось, при выполнении некоторых условий
регулярности о.м.п. являются М-оценками. Это дает возможность
воспользоваться результатами предыдущего параграфа (теоремы 65.1-65.3), в
которых следует положить
ψί{χ,θ) = k{x,0), 9i{*i,0) = /|(xi,0).
Из теоремы 65.1 вытекает
Теорема 1. Пусть функции ψι(χ,θ) = 1{(χ,θ) удовлетворяют
условиям теоремы 65.1. Тогда о.м.п. Θ* состоятельна.
Условие (65.15) для о. м. п. превращается в условие неограниченного
роста при t φ 0 сумм расстояний Кульбака-Лейблера
Σ //*,i(z)ln^M<te)-*oo. (4)
i=1 J Ιί,ι\χ)
Пример L Рассмотрим пример 64.2, в котором хг· = ψι{θ) + ξ{ (мы
положили здесь </?(#, ζζ) — ψί(θ))} и предположим, что £г- имеют всюду
положительную плотность / относительно меры Лебега. В этом случае
/«,-(*) = Я* - <PiW)), </Ф,0) = Ιχ{χ,θ) = lnf(x - ¥>t(0))·
Пусть Ρί{θ,ί) — расстояние Кульбака-Лейблера между /β^ и Дг-:
/н(в, t)=( f(x - Ψ№) ь ττΗγττΙτ dx
J /{χ - ww)
/
/(*)b/(*-wW+ <«(*))**·
Предположим, что для t φ (θ)δ при любом фиксированном δ > О и η —> оо
тг
МО = ]£«(*,*)-►<»· (5)
i=l
Пусть, кроме того, при η —» оо и некотором 7 > О
έ/Η-τ^Λ^Γ*-·^· <6)
£ [/(хЫх^А^ах^о^) (7)
г=1 ^
и для любого ε > 0 найдется Δ = Δ(ε) такое, что
η -
Σ I f(x)ri(x,t,A)dx ^ ebn, (8)
i=l
§ 66. Оценки максимального правдоподобия
527
где
п(х, t, Δ) = sup
In
/(a;-¥4(i + u) + ¥>i(0))
/(x-ViW + ViW)
(9)
6n = inf bn{t) -* oo.
Тогда условия теоремы 65.1 выполнены. Чтобы убедиться в этом,
проверим выполнение условий (Lo), (Li) из §65.
Из (5), (8), (9) следует (Lo) при любом ε £ (О,1) (определения bn(t) в (5)
и (Lo) близки, но не совпадают). Условие (Li) следует из (7). Стало быть,
о. м.п. Θ* при выполнении (6)-(9) состоятельна.
Асимптотическая постановка задачи в той конкретизации примера 64.2,
которая дана в § 65, приводит к схеме серий, когда в (64.3) вместо φ%(Χ, h) =
= у/(Χ - ivd)2 + h2 (здесь θ = (λ, h)) следует рассматривать <^η(λ,/ι) =
= \/Х2{1 — ίβ/η)2 + h2, β < 1 (интервал d между наблюдениями мал и
равен Χβ/νη). Если, кроме того, в этом примере ξι Ш Фо ь т0 мы получим
(см. (9))
ri(x,i,0) = sup
\u\<A
x(ipi(t + u) -<Pi{t)) -
1
1
2(Ψί(ί + ti) - φ№)2 + ^{φι{ί) - φ{(θ)γ
< Ci|a;|A 4- c<i
при всех i. Отсюда очевидно выполнение (6)-(9) при Ьп = сп.
Перейдем теперь к асимптотической нормальности. Сначала опять
ограничимся рассмотрением одномерного случая Θ С R. Аргументы у
функций gi(x,6), /0,i(z), h{x,0) иногда для краткости будем опускать.
Теорема 2. Пусть некоторый набор функций {gi} и функции 1\
удовлетворяют условиям теоремы 65.3. Пусть, кроме того, законно
дифференцирование под знаком интеграла в равенствах
У"/(М = о, Jgife,i = o, Ji'ife,i = o
(последнее получено дифференцированием первого). При выполнении этих
условий М-оценка 0*, соответствующая функциям {gi}, и о. м.п. Θ*
асимптотически нормальны. Разброс σ2(θ,η) оценки Θ* удовлетворяет
неравенству
σ2(0,η) = (Х><7г?(х,-,0)) (]ГЕ^(хь0))~2 > (5>(β))_1, (Ю)
где 1г(в) — информация Фишера наблюдения щ:
ΐΛθ) = Έθ(ι[(*,θ))2,
528 Гл. 5. Статистика разнораспределенных наблюдений
и достигает своего нормального значения, равного f/_^-fi(0)) при
В этом утверждении нуждается в доказательстве лишь та его часть,
которая связана с неравенством (10). Так как
|Εβώ(*,0)| = \f gi(x,t)f'ej(x)n(dx)\ < [EegUxi,e)Ii(e)]l/2,
TO
(Σ,Έ,ά(*,θ))2 < [£ (Ев9Пщ,в))1/211<2(в)]'
^
(Σ iWfc, *))(£/<(*))
В силу условий теоремы все сказанное применимо и к функциям gi = ^,
для которых в (10) достигается равенство. Теорема 2 доказана.
В многомерном случае при выполнении соответствующих условий
регулярности на вектор-функции # = (g\l\...,g\k)) и 1\ = ί ^-,...,^-J
М-оценка 0* и о. м.п. Θ* будут а.н., при этом разброс М-оценки Θ*
(см. (65.21)) будет удовлетворять неравенству
[(S'(e,n))-1]TD(ein)m0,n))-1 > Γ'ίθ,η),
где 1{θ,η) = /J/i(0), /i(0) — информационная матрица г-ro эксперимента
/*w =
ed9rd9j
, /f = k{x,0) = ]nf9ii(x).
При gi = /f в этом неравенстве .0(0, η) = /(θ,η), £'(0,η) = 1{θ,η) и оно
превращается в равенство.
В примере 64.2 при гладких функциях ^j(0) все требуемые условия бу-
дут выполнены, так что о. м. п. Θ* будет асимптотически оптимальной (см.
ниже) в классе М-оценок и иметь разброс Ι~ι(θ,η). При & €= Φο,ι будем
иметь
^-(-«(ВД^. '-!.-.*■
Поэтому здесь
Ш = |1'Г>)||, 4Г» =
м,
#Vi cfy>»
30r W, '
О приближенном вычислении о. м. п. в многомерном случае см. § 35.
§ 66. Оценки максимального правдоподобия
529
Отметим, что иногда приближенное представление функции
правдоподобия может подсказать удобную явную форму оценок, а асимптотические
свойства этих оценок проще устанавливать непосредственно, исходя из их
явного вида (а не через весьма громоздкие условия теорем 1,2).
Проиллюстрируем это на следующем примере.
Пример 2. Рассмотрим пример 64.3 в случае, когда у, неотрицательны;
Si малы (s{ -> 0 при η —> оо), μ — мера Лебега. В этом случае плотность
fe,i{x) относительно меры μ2, введенной в примере 64.3, будет иметь вид
t ι ϊ ίίθ{χ)
fe'iix) = \l-Q(e,Si
при χ < Si,
) при χ = Si,
Q{9,s) = j fe{x)dx.
0
Будем считать, что fe{x) непрерывна по х в точке χ = 0, и рассмотрим
два случая:
a) /я(0) = αο(θ) монотонно зависит от 0;
b) αο(θ) = αο > 0 не зависит от Θ, fe{x) дифференцируема по χ в точке
х = 0:
fe(x) = α0 + χαι(θ) + о{х),
где αϊ (θ) =
монотонно зависит от Θ.
х=0
Эх _ _
В первом случае для простоты отождествим ао(0) и Θ. Тогда Q{9,s) =
= 9s + o(s) и логарифмическая функция правдоподобия будет приближенно
равна
η η
L{X,9) = ^ J(Xi < 5i)ln0 + J^/(xj = 5j)ln(l - 540).
г=1 t=l
Приравнивая к нулю производную
1гл , \ NT4 Sil(xi = 5i)
^,№β) = έΣ^<*)-ΣίίτΓ^
и решая приближенно (при малых s^) полученное уравнение, получим
значение
£/(Хг <Зг)
Σ *г ДХг = *) '
которое дает нам основание в качестве оценки Θ* рассмотреть значение Θ* =
"р Их- < s)
= ^ г —, близкое к (11). Покажем, что если
η
5η = Σ si ~* °° nPw n ■"* °°> (12)
i=l
530 Гл. 5. Статистика разнораспределенных наблюдений
то оценка Θ* состоятельна (условие (12) соответствует (65.15)).
Действительно, в этом случае
η η
S~l Σ ?θ(χϊ < si) = S"1 Σ (08i + o(si)) = θ + ο{1)
г=1 г=1
и, стало быть,
η
0*-0 = 2>)П + о(1),
г=1
где
6,n = S~l(Ji - E^Ji), Ji = J(xi < si).
η
В силу закона больших чисел (см. приложение IV) 2Ζ£i,n —> 0, что дока-
i=l
зывает состоятельность Θ*.
Чтобы установить, что Θ* является а. н. оценкой, предположим
дополнительно, что функции fe(x) дифференцируемы по χ в точке χ = 0, Σ5^ =
= o(v^), ^ 7^0. Тогда
D,£ji = 0S„ + o(5„)
и, стало быть,
где распределение первого слагаемого в правой части сходится при η —> оо
к Фо,0. Итак, 0* — а.н. оценка с разбросом 9S~l.
Рассмотрим теперь случай Ь), в котором мы положим, не ограничивая
общности (с точки зрения последующих выводов), ао = 1 и отождествим
9s2
αχ(θ) с θ. Тогда Q(6,s) = s + —- + o(s2) и логарифмическая функция прав-
доподобия с точностью до величин более высокого порядка малости будет
иметь вид
ЦХ,в) =^2Ып(1 + вХг) + ^1(ъ = Si)\n(l - Si - &θ).
В этом случае приближенное решение уравнения L'(X,6) — 0 показывает,
что естественно использовать оценку
§ 66. Оценки максимального правдоподобия
531
η
Нетрудно видеть, что если ]T^s? -> оо при η -> оо, то из закона больших
i=l
чисел будет следовать состоятельность Θ*. Мы предлагаем читателю найти
условия, при которых эта оценка будет асимптотически нормальна.
О приближенном вычислении о. м. п. в общем случае см. § 35.
3* Основные принципы сравнения оценок. Асимптотическая
эффективность о.м.п. в классе М-оценок. Принципы сравнения оценок для раз-
нораспределенных наблюдений остаются, по существу, теми же, что были
рассмотрены в гл. 2: это среднеквадратический и асимптотический подходы
(более общие подходы см. в гл. 6).
Понятие эффективной оценки в классе Кь оценок с фиксированным
смещением Ь(в) (и, в частности, в классе Ко несмещенных оценок)
сохраняется полностью. Сохраняется и утверждение теоремы о единственности
эффективных оценок, так как его доказательство с объемом выборки
никак не связано и, стало быть, применимо к выборке, состоящей из одного
наблюдения X.
Асимптотический подход к сравнению оценок естествен в классе Кф всех
а.н. оценок. Определение а.н. оценок было дано в начале §65. Главной
характеристикой а.н. оценки является ее разброс σ2(0,η). Класс Кф а.н.
оценок здесь в известном смысле шире, чем в однородном случае, так как он
включает в себя а. н. оценки с разными скоростями убывания σ2(0,η) (а не
только σ2(η)(0,η) = σ2η-1, как это было в гл. 2).
Если 0£, к = 1,2, суть две а. н. скалярные оценки с разбросами σ2(0,η),
к = 1,2, соответственно, то, очевидно, оценка 0* будет асимптотически
предпочтительней, если σχ(θ)η) < σ2(0,η) при всех достаточно больших η и всех
θ ев.
Определение 2. Оценка 0* Ε К называется асимптотически
эффективной (а. э.) в К, если для любой другой оценки Θ* £ К
limsup σ1^'η\ < 1 при всех θ Ε Θ, (13)
σ2(θ,η)
где σ2(0,η) и σ2(0,η) суть разбросы оценок 0* и Θ* соответственно.
Мы можем в качестве К взять, например, класс Км М-оценок,
построенных по функциям #ή удовлетворяющим условиям теоремы 65.3. Тогда из
теоремы 2 будет вытекать следующее утверждение.
Следствие 1. При выполнении условий регулярности, приведенных
в теореме 2, о. м. п. Θ* является а. э. оценкой в Км-
Роль этого утверждения для разнораспределенных наблюдений
представляется более значительной, чем в однородном случае, так как здесь М-оце-
нивание, как уже отмечалось, по сути, исчерпывает все общие «регулярные»
методы получения оценок. Тем не менее представляет интерес и другой
подход к отысканию асимптотически оптимальных оценок, изложенный в § 18
и состоящий в построении а. э. оценок во всем классе а. н. оценок Кф, лишь
532 Гл. 5. Статистика разнораспределенных наблюдений
незначительно суженном до класса Кф$ оценок, для которых сходимость
(θ* — θ)σ~1(θ,η) @> Фод имеет место вместе с двумя первыми моментами:
τ, (θ*-θ) Л „ (0*-0)2 Λ
Ед- -+ 0, Ел- > 1
9 σ{θ,η) ' θ σ2(0,η)
(здесь Eg означает интегрирование по распределению Ряд χ ... χ Р#)П
выборки X).
Аналогично § 18 асимптотическая эффективность оценки Θ* Ε К С Кф^
в классе К (согласно определению 18.2) будет эквивалентна неравенству
Εθ(θϊ-Θ)2
для любой другой оценки θ* Ε К и при всех θ Ε θ.
Сохраняет свою силу аналог теоремы об асимптотической
единственности а. э. оценок: если θ\ и θ\ — две а. э. оценки в К С Кф$ такие, что
-(θ* +θ%) Ε К, то они асимптотически совпадают, т.е.
Доказательство повторяет рассуждения теоремы 18.2.
Переход к многомерному случаю выглядит так же, как в § 18. Однако
здесь возникают и некоторые усложнения, связанные в тем, как понимать
соотношение (13) определения 2 в многомерном случае. Наиболее
естественный аналог этого определения в многомерном случае выглядит следующим
образом. Оценка Θ* называется асимптотически эффективной в К Ε Κφ$,
если для любой другой оценки θ* Ε К и для любого а = (αϊ,..., α&)
τ Σ<?υ(θιη)αΐαί ^ ι (Λλ\
hmsup^ / ^ 1, (14)
где σ2 = (σ^·) и σ2 = (σ^·) — матрицы разброса соответственно оценок θ*
и θ*).
В классе Кф^ неравенство (14) эквивалентно неравенству
Понятия байесовской и минимаксной оценок с объемом выборки никак не
связаны (см. также гл. 6) и потому в условиях этой главы полностью
сохраняются. Сохраняются также все основные определения и утверждения § 21
о байесовских и минимаксных оценках.
§ 67. Достаточные статистики. Эффективные оценки 533
§ 67. Достаточные статистики. Эффективные оценки.
Экспоненциальные семейства
Определение достаточной статистики, утверждение основной факториза-
ционной теоремы 22.1 и остальные утверждения §22 для разнораспределен-
ных наблюдений полностью сохраняются (они не связаны с объемом
выборки).
В примере 64.1 функция правдоподобия имеет вид 66.1, и, стало быть,
достаточная статистика равна [ >^ —, > ""^ ) · Для пуассоновских наблю-
дений χ; ^ ΐΙ\ί{ достаточная статистика остается той же, что и в однородном
случае, и равна /Jxj-
В примере 64.2 для & €= Φο,σ2 нетривиальная достаточная статистика
отсутствует. В задаче В примера 64.7 функция правдоподобия имеет вид
/,(*) = (ι-ρ)"-" Π Ί^-^^-ρτίτζ-Υ Π χΓα_1 =
i:Xi>N ^ P' i:xi>N
= ^-p)Na+r({1_J)Na+1JU-r-\ (i)
где ρ = ρ(θ,Ν) = , ν — число наблюдений Xi, отличных от N. Стало
α
быть, достаточная статистика здесь равна ( ν, |J xj J или \v, JJxi) ·
^ i:Xi>N '
Процедура построения эффективных оценок с помощью достаточных
статистик остается без изменений.
Определения, связанные с экспоненциальным семейством, здесь также
выглядят аналогично. Пусть 0 = (0ι,. ..,0*) — fc-мерный параметр. Будем
говорить, что выборка X соответствует экспоненциальному семейству,
если ее функция правдоподобия (относительно некоторой меры) представима
в виде
MX) = exp {(a(0), S(X)) + V{0)}h(X), (2)
где а(0) = (αι(0),.. .,afc(0)), S(x) = {Si{x),..., Sk{x)), под х понимается
вектор (χι,.. .,хп)5 функции ао(0) = 1, αχ(0),.. .,α^θ) линейно независимы.
В примере 64.1 0 = (α,σ2), функция правдоподобия определена в (66.1),
так что в этом случае
НХ) = Л(27гщГ^2, αι{θ) = -\σ-\ α2(θ) = ασ~2,
* χ* χ-ί· (3)
t*X l*j ΐΛ<ι
534 Гл. 5. Статистика разнораспределенных наблюдении
Для распределения Пуассона 0 = λ,
Аг- Аг- М)
αι(λ)=1ηλ, ν(λ) = -λΣ>, 5i(X) = 2xi·
В примере 64.7 θ = (α, 7), функция правдоподобия определена в (1).
Здесь в представлении (2)
h(X) = l, ν(θ) = [ηΙη(1-ρ(α,Ί,Ν))}, a№ = ]n £
α2(θ) = -а - 1, 5ι(Χ) = ι/ = J] /(χ,- > ЛГ),
S2(z)= 2 1пхг = 5^1nXi/(xi >ЛГ).
г:х;>ЛГ
Так как результаты § 25 с объемом выборки никак не связаны, то они для
разнораспределенных наблюдений полностью сохраняются. В частности,
справедливы следующие утверждения.
Теорема 1. 1. Если ао(0) = 1, αχ(0),.. .,α&(0) линейно независимы,
mo статистика S в представлении (2) является минимальной
достаточной статистикой.
2. Если, кроме того, α(θ) зачеркивает кгмерный параллелепипед в Шк,
когда θ пробегает Θ, то S — полная достаточная статистика.
Отсюда вытекает
Следствие 1. Если X соответствует экспоненциальному
семейству, выполнены условия п. 2 теоремы 1 и 0* Ε К^ то оценка 0£ =
= Е(0* | S) является эффективной в К^.
Если выполнены условия п.2 теоремы 1, то о.м.п. 0* является
эффективной в классах с соответствующим им смещением.
Последнее утверждение вытекает из того, что о.м.п. измеримы
относительно S.
Вернемся к примерам §64. В примере 64.1 несмещенная оценка
«·=(ς^)(ς!Γ
в силу следствия 1 является эффективной. Напомним, что такую же оценку
мы получили в п. 65.2 путем варьирования коэффициентов Vi в оценках по
методу моментов. Найдем теперь несмещенную оценку для σ2. Для этого
вычислим смещение оценки
(х, - cftj)3 I v^ (*? ~ (а*)2*?)
,2ч* = I у^ (х» - (**иУ _ I у
* ' Π ·<£-' 71.· Π t—J
η ■<—' щ η *—' щ
η
E(Xi fi)2-(^-a)%(n)\, ш-Σ
t
2
i_
Щ
§ 68. Эффективные оценки в задаче оценивания «хвостов» 535
(см. (65.6)). Так как Е(а* - а)2Ъ\(п) — а2 (см. (65.5)), то мы получаем
E(a2)* = ifVa2-a2l=^—К2.
Отсюда, из (3) и следствия 1 вытекает, что несмещенная оценка
является эффективной для оценки σ2. Таким образом, относительно
смещения и эффективности оценки (σ2)* здесь сохраняется полная аналогия с
однородным случаем (ср. с §17). Оценка (5) отличается постоянным мно-
п
жителем от оценки, найденной в п. 65.2.
η — 1
Для пуассоновских наблюдений оценка λ* = (У^хг) (/\^г) будет,
очевидно, также эффективной.
Отметим, что оценки α*, (σ2)*, λ* в этих примерах являются также
о. м.п.
Примерам 64.6, 64.7 мы посвятим специальные параграфы, которые
служат иллюстрацией того, как решать нестандартные задачи оценки
параметров и проверки гипотез, как иметь дело, например, с бесконечномерными
мешающими параметрами, как изучать сложные статистики и использовать
схему серий.
§68. Эффективные оценки в задаче
оценивания «хвостов» распределений (пример 64,7).
Асимптотические свойства оценок
В этом параграфе мы рассмотрим применение результатов предыдущих
разделов к «идеализированной» задаче об оценке параметра θ — (α, 7) B
примере 64.7 с функцией правдоподобия (67.1) (задача В). Будут найдены о. м. п.,
которые, будучи измеримыми относительно достаточных статистик от
выборки экспоненциального типа, будут эффективными оценками в классах
с соответствующими смещениями. Далее будут найдены асимптотические
свойства этих оценок -- доказана их асимптотическая нормальность (это
можно установить и с помощью общих результатов §66; для одномерных
неизвестных параметров а или η это следует из теоремы 66.1). Будет
выяснено, при каких условиях мы можем пользоваться оценками, найденными в
задаче В, для оценивания параметров в исходной задаче А с плотностями
наблюдений хг (64.5) при хг > N. При этом рассматриваются два подхода.
Первый основан на изучении условий, при которых задачи А и В оказываются
асимптотически эквивалентными. Второй использует построение
наблюдений и нужных нам статистик в задачах А и В на одном вероятностном
пространстве. Условия, при которых нужные нам статистики становятся
асимптотически эквивалентными, оказываются более широкими, чем при
первом подходе.
1. Оценки максимального правдоподобия. Функция правдоподобия
выборки X в задаче В имеет вид (см. (67.1))
Л№ = (1-рГ/п-а-1)
536 Гл. 5. Статистика разнораспределенных наблюдений
где
„ = 5^/(χί > ЛГ), In Π = £/(Хг > ΛΓ)1ηΧί, ρ = -ί .
Логарифм L = Σ(Χ,Θ) этой функции правдоподобия примет вид
£ = (η-ι/)1η(1-ρ) + ι/1η7- (а + 1)Ы1. (1)
Для отыскания о. м. п. нам понадобятся частные производные
выражений, присутствующих в (1). При очевидных соглашениях относительно
обозначений имеем
P'a = -p(inN + ±y P; = ^,
т. . ,p(lniV + Ι/α) , _ τΙ . . ρ ν
L'a = {n-v)^— ^-ΙηΠ, ϋΊ = -{η-ν) ./ +-■
1-ρ 7 7(1-Ρ) 7
Уравнение L' = О дает
ν ναΝα
η η
Из уравнения L' = 0 получаем равенство р(п — i/)lniV Η =
α
= (1 — ρ) In Π, которое при подстановке ρ = ι//η дает
-* " _ ^t ,«ч
где
& = /(xi>iV), w = /(Xi>JV)ln^.
Отметим, что оценка а* определена лишь на множестве \у > 0}. Если
ζ/ = 0, то а* можно положить равной любому числу из множества возможных
значений. В силу (2) имеем также
γ = — Na\ (4)
η
По следствию 67.1 оценка θ* = (а*,7*) эффективна в классах оценок с
соответствующим смещением. Если 7 известно, то о. м. п. а* будет решением
весьма сложного уравнения. Проще пользоваться оценкой (3), которая, как
мы увидим ниже, будет асимптотически эффективной. Если α известно, то
о. м. п. для 7 имеет вид 7* = ανΝα/η. Эта оценка в соответствии с
теоремой 67.1 будет а. н. и а. э. в классе М-оценок. Мы будем рассматривать
лишь случай двух неизвестных параметров.
§ 68. Эффективные оценки в задаче оценивания «хвостов» 537
2. Асимптотическая нормальность Θ* в задаче В. Начнем с оценки а*.
Для представления (3) имеем
Щг=р, Εξ?=ρ, Όξί=ρ{1-ρ),
J Να
Ν
(5)
2ρ ρ2 ρ(2-ρ)
Ότα = ~2 —2 = —2—
(для вычисления последних двух интегралов следует воспользоваться
интегрированием по частям). Поэтому
Е(& - ащ) = О, Е(& - ащ)2 = Εξ? - 2аЕщ + α2Έ,η} = р.
Мы будем рассматривать схему серий, когда Ν = Ν(η) —> сю так, что
пр —> ос. Воспользуемся представлениями (см. (5))
\/прСз
δ·-α=ΣΜ_
(6)
a \ у np
где
Ci =
Σ(ξΐ-Ρ) ^*o,i,
Vnp-(l-p)
С2=7^Е^-^Фод'
(7)
Сходимость к нормальному распределению здесь имеет место, так как
условие Линдеберга очевидным образом выполнено.
Отсюда и из теоремы следует, что
(а* - а)
у/пр
Сз
α (1 + ζ2^/(2-ρ)/ηρ)
и, стало быть, а* а.н. с разбросом а2/пр. Далее,
Сз
= Сз 1 + О
у/пр
(8)
а = а
1 +
у/пр
Ы%))
, 7* = -&№ ,
η
538 Гл. 5. Статистика разнораспределенных наблюдений
In7* = lnz/ - lnn + ΐηα* +a*lniV =
= In rap + In 11 + J -ζχ j - Inn 4- In a 4-
^+ζιβΞΙ+^ + α-ψί+ο(^), (9)
V np y/np yjnp \ np J
где ζ есть случайная величина (не всегда одна и та же в последующих
формулах), распределение которой слабо сходится к некоторому собственному
распределению. В итоге в силу (7) получаем
1пГ = 1п7 + — Υ](ξί(1 + Α)-αΑτΗ-ρ) + θ(^£*ί),
np *—' \ np )
(10)
где А = 1 4- a In iV, слагаемые под знаком 2_\ независимы, одинаково
распределены и имеют нулевое среднее. Кроме того, непосредственный подсчет
с помощью равенств ξ? = &, ηιξι = щ и (5) дает
Β(ξί(1 + Λ) » ατκΑ -ρ)2 =ρ(Α2 + 1 -ρ).
Поэтому
г., 1+^+0
(^))·
(и)
С4 = [пр(А2 + 1 -р)]"1/2 Σ (6(1 + Л) - «Л»к -р) ©- Фод.
Это означает, что 7* также является а.н. оценкой с разбросом А2(А2 +
+1 —р)/пр.
Покажем, что и Θ* = (а*,7*) является а.н. оценкой. Предположим на
время, что Ν, а вместе с ним и А — фиксированные числа. Введем в
рассмотрение вектор (а,7)j где α, η — главные части оценок а*, 7* B
представлениях (8), (И), являющиеся линейными функциями от £з» С4> Но совместное
распределение (з> С4 сходится, очевидно, к нормальному с коэффициентом
корреляции
ЕСзС4 = (W^2 + l-p)"1/2E(£i - atfc)(e<(A + 1) - аАщ -р) =
А
y/Al + 1-p
(он стремится к единице при А -> оо). Отсюда следует, что Ε(δ—a)(j—7) =
= ajA/np и, стало быть, матрица вторых моментов ((а — a), (j — 7)) имеет
вид
2( s _ 2_ { °? °ПА \ _ М_ , .
σ [ϋιП) ~ np \αΊΑ A2(A2 + l-p))=n~p'· {Щ
§ 68. Эффективные оценки в задаче оценивания «хвостов» 539
(Если показать, что α* Ε if φ,2, 7* 6 #ф,2, то это будет также главная часть
матрицы вторых моментов (а*— а)(7*~7)0 Эта матрица имеет определитель
Deta2(0,n) = (np)~2aV(l -ρ) > 0
и обратную матрицу
/Л2 + 1-р Л\
1 -ρ
α2 α7
_Λ -Ι
\ «7 72 /
Это означает, что матрица вторых моментов вектора ((α—α), (7—7))σ * (#>п)
равна единичной матрице Ε, ((α — а), (7 — η))σ~ι{θ^η) ©► Фо,£· Эти
соотношения сохранятся, очевидно, и в случае N —> оо, а вместе с ними и
сходимость
((а* - а), (Г - 7))<7-1(0,") θ· Φο,Β. (13)
Как уже отмечалось, асимптотическая нормальность (а*,7*) может быть
установлена также с помощью общих теорем об асимптотической
нормальности о. м. п. (ср. с п. 70.4 или с §36, модифицированным на случай схемы
серий). В соответствии с этими результатами оценка (а, 7*) будет а.н. с
разбросом (nJ(e))""1, где Ι(θ) — информационная матрица Фишера; при этом
сходимость
(g* - α,Г - Ί){ηΙ{θ))1'2 & Ф0,Е (14)
имеет место вместе с моментами любого порядка. Матрицу Ι(θ) можно
подсчитать непосредственно исходя из определения, при этом в соответствии
с (13) окажется, что ηΙ{θ) = σ~2(0,η). Действительно, в нашем случае
функция I — Ι(χ,θ) (θ = (α,7)) равна
Ίπ7 - {θί + 1)1ηα: при χ > Ν,
ΊΝ-<*
1η(1 — ρ) при χ = Ν, ρ =
α
так что
■In x,
(1-ρ)α'
Отсюда находим элементы матрицы 1{θ):
Е,(£)2 = -ВД Р
Ρ ™ ,/ и _ та,л _ Ρ
ΕΘ(1'Ί) =-Εθ1'^ --^-—^, ^θΙ'αΙ'Ί--Έ.Ι'άΊ--γ^· —
540 Гл. 5. Статистика разнораспределенных наблюдений
Дальнейшей нашей целью является установление асимптотической
нормальности Θ* в задаче А и отыскание N, при котором задачи А и В будут
в некотором смысле асимптотически эквивалентными.
3*. Асимптотические нормальность и оптимальность в задаче А.
Рассмотрим теперь вопрос о том, в каком соотношении находятся
«идеализированная» задача В и исходная задача А. Этот вопрос можно
рассматривать как проблему робастности (ср. с § 58) в задаче В относительно малых
возмущений функции плотности наблюдений (ср. (64.5) и (64.7)) в области
χ > N. Переход от наблюдений у, к х; (см. (64.6)) означает отбрасывание
«неинформативных» наблюдений у; ^ ΛΓ, поскольку функция плотности этих
наблюдений начинает больше зависеть от неизвестных функций 7ι(α>2/) и,
стало быть, содержит меньше информации о 0. Задача здесь состоит в
оптимальном выборе Ν, который возможен, очевидно, лишь в случае, когда
«мешающие» функции £г(а,у) в (64.5) допускают оценку скорости убывания,
например
Ыа,у)\^е(у)у-р, р>0, (15)
где е{у) —> 0 при у —> оо, или
\£i(a,y)\^e(y)e-Py, ρ > 0. (16)
Мы должны выбрать возможно меньшее iV, которое позволяло бы
статистические выводы в задаче В переносить на исходную задачу А.
Рассмотрим два подхода к задаче о выборе N.
(а) Первый подход связан с таким выбором N, при котором задачи А и В
оказываются в известном смысле асимптотически эквивалентными.
Теорема 1. Если выполнено (15) и N = п^а+Р\ то любая a. w.
оценка (а*,7*) для задачи В имеет то же самое предельное
распределение в задаче А (исходной), и наоборот. В частности, оценка (а*,7*)>
определенная в (3), (4), является а. w. в задаче А с разбросом σ2(0, η),
определенным в (12). Такое же утверждение справедливо при N = - Inn,
Ρ
если выполнено (16).
Если N = nl/(p+CL\ то пр = — пр/(р+а) и разброс σ2(0,η) будет иметь вид
(см. (12))
σ2(6,η) = -η-^^+α)Μ, (17)
7
ex.
при этом A = l + aln7V=lH Inn. Аналогичным образом
выписываем +/э
ется матрица разброса в случае N = - Inn.
Ρ
^»
Замечание 1. Утверждение теоремы означает, что оценка 0*, будучи
асимптотически оптимальной (в известном смысле, см. § 66) в задаче В,
будет таковой и в задаче А. Более точно, пусть класс оценок К Ε Кф таков,
что принадлежность Θ* классу К С Кф в задаче А означает принадлежность
§ 68. Эффективные оценки в задаче оценивания «хвостов» 541
θ* Ε К в задаче В. Тогда если Θ* — а. э. оценка в К в задаче В, то эта оценка
будет а. э. в К в задаче А.
Действительно, если Θ* — а. э. оценка в К в задаче В, то для любой
другой оценки Θ* £ К выполнено (66.12). Так как матрицы разброса σ2
и σ2 этих оценок в задаче А сохраняются (с точностью до асимптотической
эквивалентности), то Θ* будет а. э. в К и в задаче А.
(Ь) Второй подход связан с таким построением наблюдений х^ в
задачах А, В на одном вероятностном пространстве, что имеет место
асимптотическая эквивалентность оценок Θ* в этих задачах. Статистики Θ* и Θ** мы
называем здесь асимптотически эквивалентными, если они а. н. с разбросом
σ2(0,η) и {θ*-θ**)σ-ι{θ,η) —> 0 (или (θ*-Θ**)σ-2(θ,η){θ*-Θ**)τ —► 0).
Теорема 2. Пусть выполнено (15) и N = nV(2p+°). Тогда оценка
(а*,7*), определенная формулами (3), (4), является а. к. в задаче А с
разбросом σ2(0,η), определенным в (12). Такое же утверждение спра-
Inn
веоливо при N = -——, если выполнено (16).
2р
Отметим, что значение N в теореме 2 меньше, чем значение N в
теореме 1. При выполнении (15) и N = п1^2^4*^ разброс σ2(0,η) будет иметь
вид
a2(efn) = 2n-2p/(2/H.a)Me
7
Ясно, что этот разброс меньше, чем (17), и достигается это за счет
возможности выбора меньшего N.
Доказательство теоремы!. Напомним, что функция
правдоподобия в задаче А имеет вид (ср. с (64.5))
feiX)= Π a-Pi) Π 7хГв_1(1+*(«,*)),
iiXi^N i:xt>N
oo (18)
Pi =Pi(e,N) = У 7(1 + ei{a,y))y-°-1 dy.
N
Функция правдоподобия f^(X) в задаче В приведена в (67.1). Обозначим
через РД Pf соответственно распределения выборок в задачах А, В (это
суть распределения с плотностями /^ и jf). Допустим, что мы можем
выбрать N = N(n) так, что f(f{z)/fp{x) -* 1 равномерно на множестве Ωη
при каждом θ £ Θ, где
ΡΒ(Ωη)->1, ΡΛ(Ωη)->1
при η —>· оо. Тогда все утверждения о предельном распределении
статистик (а*,7*) в условиях задач А, В будут совпадать. Действительно, в
542 Гл. 5. Статистика разнораспределенных наблюдении
этом случае
ρθΛ(χ ес) =
= f tf(xMdx)+PeA(Cnn)= Ι !θΒ(χ)(1 + Α(θ,χ))μ(άχ) + ο(1) =
= ρθβ(χ e cn„)(i + γΔ(6)) + o(i) = pf(x e c) + 0(i), (19)
где r ^ 1, Δ(0) = sup Α(θ,χ) —> 0 при η —> оо. Это означает, в частно-
сти, что асимптотическая нормальность (а*,7*) B задаче В влечет за собой
асимптотическую нормальность (а*, 7*) с теми же параметрами в задаче А:
= νΒ{{α*,Ί*)σ-\θ,η) Ε С2) + о(1) -> Ф0,я(С2), (20)
где С2 С R2. (Вместе с тем (19), (20), вообще говоря, не влекут за собой
сходимость моментов (а*, 7*)·)
Нам осталось выяснить, при каких N возможно (19). Положим
Ωη = {и < 2рп}. (21)
Согласно результатам п. 1, 2 Ρ^(Ωη) —у 1 при η —> оо. Аналогично в
задаче А имеем и < ζ/χ, ν\ ^ 5^, ρ\ = р(1 + Δ) при достаточно малом Δ > 0.
Отсюда при Δ < 1 следует Ρ^(Ωη) —> 1. (Нетрудно видеть, что на самом деле
справедливы экспоненциальные оценки, например 1 — Ρ^(Ωη) < ехр(— рп)
(см. [17, §5.5]).) Утверждение теоремы 1 будет вытекать из следующего
предложения.
Лемма 1. Если Ν = гг1/^*"^) и Ωη определены в (21), то выполнено
(19). В случае (16) надо положить N = -Inn.
Ρ
Доказательство. Сравнивая (18) и (67.1), получаем
1 -Р%
ill
i:Xi>N i:xi^.N
lnfgA(X)-lnfB(X)= ]Г 1η(1 + ε,·(α,χ,·))+ £ lnT^· (22)
Будем считать, не ограничивая общности, что (ε* (α,х)\ I 0. Тогда при
выполнении (15) первая сумма в (22) на множестве Ωη не превосходит
Σ £г(с*,хг) ^ νε{Ν)Ν~ρ < 2ρηε{Ν)Ν-ρ. (23)
i:*i>N
§ 68. Эффективные оценки в задаче оценивания «хвостов» 543
Во второй сумме при ρ —> О, щ —> О
оо
Pi^P + Ί <ч(а, У)у~а~1 dy,
Ν
оо I oo
Jei(a,y)y-a-1 dyU Je(y)y-a-P~1 dy < ε(Ν)
N I N
ε(Ν)α
p + a j(a + p)
pN-t,
ln^=p_Pi + 0(|p2_p2|),
Поэтому
In
I-Pi
l-p
ε(Ν)α
a + ρ
ρΝ-Ρ{1 + ο(1)).
^—' 1-й
v.s' AT г
i:xi^N
< I JWap\ N-P(i + 0(i))n ^ CpnN-pe{N). (24)
Эта оценка вместе с (23) означает, что разность (22) будет сходиться
к нулю на множестве Ωη, если в качестве N взять значение N — ηι/α+ρ,
при котором ηρΝ~ρ = α/η и правые части в (23), (24) сходятся к нулю.
Аналогичные выводы можно сделать в случае (16) при N = Inn/p. Лемма 1
доказана.
Обратимся теперь ко второму подходу, связанному с построением
наблюдений и статистик в задачах А, В на одном вероятностном пространстве.
Доказательство теоремы 2. Обозначим
pB(i)=min(l,VQ-1), PA>i(t)=T?f(yi>t). (25)
Очевидно, что pe(t) = Pf (xi > t) при t > Ν,
Ρ«,<(<)=ΡΒ(ί)(1 + Δ<(<)),
где
pB(T)\Ai{t)\ =
7
00
Je^y)-"-1
dy
-y\ei{a,t)\t a
^ = PB(t)\ei(a,t)\.
a
Будем считать для простоты, что функции Рд,г(£) непрерывны. Зададим
случайные величины хг· в задачах А, В на одном вероятностном
пространстве следующим образом. В качестве исходного возьмем вероятностное
пространство (Rn, 53мп, Р^) в задаче А и рассмотрим наряду с наблюдениями у*
(с плотностью (64.5)) наблюдения ζ,- = РдЧ-РаЛу»))-
Очевидно, что щ имеют распределение рв и, следовательно, значения
xf = max(iV, Zi) можно рассматривать как наблюдения х* в задаче В.
544 Гл. 5. Статистика разнораспределенных наблюдении
Рассмотрим теперь статистики, на которых строятся основные части
оценок a*, 7*S*, и выясним, чем они отличаются в задачах А и В. Начнем со
статистики
5(Г) = чДфСз = Х;&-с^), ti = I(yi>N), m = I(yi>N)ln^.
В задаче В аналогичная статистика на том же вероятностном пространстве
имеет вид
3Β(Υ) = Σ,{ξ?-αη?), & = I(*i>N), η? = /(* > iV)ln^,
так что
s(Y) - sB(Y) = Σ (& - tf) - « Σ (w - ч?); (26)
Σ fc - tf) = Σ ('fa > N) - '(* > ")) =
= Σ /(у,- > ЛГ, Zi < iV) - J] /(у,- < JV, z< > n). (27)
Рассмотрим сначала первую сумму в правой части (27) и предположим
для определенности, что Ai(N) > 0. Событие {у* > N, Zj ^ N} возможно,
если yi = Ν + Δ, Δ > 0, ζ* = р^СРдДу»)) < N или, что то же (см. (24)),
Р51(«) = Ит)-1/а,
^=(2)1/β(^'β(1+ΔίΜ"Ι/β=
= yi(l + ^(yi))"1^ = (ЛГ + Δ)(1 + Δ«(ΛΓ + Δ))"1/0 < Ν. (28)
Это, в свою очередь, возможно, если (|Δί(ί)| и |£j(a, ί)| монотонно убывают)
ΛΓΔ<(ΛΓ)>οΔ(1 + ο(1)),
Δ<ίΜΏ(1+ο(1))<ίΜ^(1 + <ι(1)).
a a
Изложенное означает, что первая сумма в (27) не превосходит
Σ/(*φ*(ΐ + Μ(1+<>(1))))). (29)
Среднее значение этой суммы при достаточно больших N не превосходит
2nMN)^i^U ς 3η7ΛΓ»2^ ^ ΪΒε{η)Ν-ο-«. (зо)
a a a
Аналогично происходит оценка второй суммы в (27) в случае Δ < 0.
Оценим теперь вторую сумму в (26):
Σ (* - О = Σ^1 - tf) - Σ^1 - ω+Σ fa - tfteef ■ (31)
§ 69. Неравенство Рао-Крамера
545
Здесь первые две суммы оцениваются так же, как суммы в (27), с той лишь
разницей, что оценку (29) надо еще домножить на малый множитель, не
, iV + Δ Δ
превосходящий In—■-— ζ —.
Последняя сумма в (31) согласно (28) по абсолютной величине не
превосходит
Σ|1η|| = -Σι1η(1+Δ^))ΐ^«ΣΐΔ^)ΐ<
Среднее значение этой суммы не превосходит
00
α^—'у a(a + p)
Ν
Мы получили здесь ту же оценку, что и в (30). Это означает в силу
неравенства Чебышева, что с вероятностью, сходящейся к единице,
\S(Y) - SB(Y)\ < cnell2{N)N-f>-*,
(см. (6)); постоянные с здесь различны; а*в есть о. м.п. для а в задаче В,
построенная на наблюдениях у^.
Если выбором N мы сделаем квадрат правой части неравенства (32)
меньше разброса оценки а*в, равного (пр)-1, то оценки а* и а*в будут
асимптотически эквивалентными (иметь то же самое предельное распределение).
Требуемое неравенство будет выполнено, если мы положим N~2p = — {пр)"1
а
или, что то же, N = п1^2р^°^.
Сравнение в задачах А и В статистик вида Σ(ζί{1 + А) — аАщ — р),
определяющих оценку 7*> проводится аналогично, как и анализ оценок Θ*
при выполнении (16). Остальные члены для (а* — а) и (7* — 7) B
представлениях (8), (9), (11) имеют в задаче А то же асимптотическое поведение,
что и в задаче В (надо использовать центральную предельную теорему в
приложении IV). Теорема 2 доказана.
§ 69, Неравенство Рао-Крамера
Вернемся к изучению свойств оценок в общем случае. Пусть, как и
прежде, Χ ^ Έ>θ = {Ρ0,ι,...,Ρ0η}5 feti(x) ~~ плотность распределения Р^
относительно меры μι, Кь — класс оценок со смещением Ь{9) (см. § 66). Мы
будем предполагать, что выполнено условие
546
Гл. 5. Статистика разнораспределенных наблюдений
(R) Функции у//в,г{х) для η. в. [μι] значений χ непрерывно
дифференцируемы по 0. Информации Фишера 1%(0) = Е^[^(хг·,^)] существуют,
положительны и непрерывны.
Если Θ — компакт (выполнено (Ас)), то непрерывность Ц(0) в
условии (R) эквивалентна условию
8ирЕ,(^(^^)]2|^(Хг^)|>^)^0
Θ
при N —> со (см. приложение V, теорема 3).
Неравенство Рао-Крамера для неоднородных наблюдений естественным
образом обобщает неравенства для однородного случая, полученные в § 26.
Теорема L Если θ* Ε Кь, выполнено условие (R) и Έο(θ*)2 < с < оо,
то
D^T^T' Ηθ,η) = Σ,ΐ№· (ΐ)
ιφ,η) ^
Если в этом неравенстве достигается равенство на некотором отрезке
θ £ [61,62] С θ и Oq0* > 0 на этом отрезке, то функция правдоподобия
fe{X) Щи 0 Ε [0ь#2] представима в виде
MX) = ехр {Θ*Α{Θ) + В(в)ЩХ), (2)
где А(0), В(0) от X не зависят.
Обратно, если0* = const или если справедливо представление (2), то
в неравенстве (1) достигается равенство.
Доказательство теоремы 1 почти полностью повторяет
рассуждения в доказательстве теоремы 26.1 с той лишь разницей, что применительно
к новым условиям в (26.9) надо подставить
(п \ 2 η
ΣΜχί,θ) =J2Ml'i(xi,9)Y = Ι(θ,η).
t=l / i=l
Здесь полностью сохраняет свою силу следствие 26.2 о том, что для
достижения нижней границы в неравенстве Рао-Крамера необходимо и
достаточно, чтобы оценка 0* была достаточной статистикой, а функция
ф(0*,0) в факторизационном равенстве имела вид
^(0*,0)=ехр{0*Л(0)+Я(0)}.
Сохраняется также следствие 26.3 о том, что если θ* Ε Кь и в
неравенстве Рао-Крамера достигается равенство, то 0* — эффективная в Кь
оценка.
Сохраняют свою силу и другие утверждения и определения § 26 (с
заменой 1(0) на 1(0,п); многие из них с объемом выборки не связаны).
В многомерном случае изменения аналогичны. Под (R) следует
понимать условие
§ 70. Неравенства для отношения правдоподобия
547
(R) Функции ^/fe,i{%), г = 1,.. .,η, непрерывно дифференцируемы по 9j,
j = 1,..., к, для п. в. [μ*] значений х. Матрицы Фишера 1{(θ) = ||./TS(0)||,
/Г(^) = Е-
двг Θθζ
п
непрерывны по 0, определитель |/(0,п)|, 7(0, п) = У^Л(0), отличен от
нуля.
В неравенстве (16.14) теоремы 26.1А вместо (ηΙ(θ))~ι следует поставить
матрицу 7(0, п)-1.
Интегральное неравенство Рао-Крамера также сохраняется при
естественной модификации формулировок и доказательств. Утверждение
теоремы 30.1 для скалярного параметра θ в условиях этого параграфа будет
иметь вид
h{ey2
Ε(θ* - θ)2 Ζ
Ε
Q(0)
2 /и/о\\ 2'
-Ч$)"($)
При h{9) = g(0)/7(0, n) в предположении, что эта функция является
финитной и дифференцируемой, получаем
е<*--^>л+е|(9м/4п))ч-ч*)Г л-"-1"·-'·
Это значит, что для гладких д(0) и 7(0, п) средний разброс Е(0* —0)2
(усреднение Ε берется по совместному распределению 0 и выборки X с плотностью
q(t)ft(x)) имеет тот же порядок малости, что и Jn. Если 7г(£) при разных г
соизмеримы и I(t,n) -> оо, то Jn будет сходиться к нулю.
Важным следствием интегральных неравенств Рао-Крамера является
возможность устанавливать тот факт, что а. Я-э. оценки являются
асимптотически байесовскими (см. §30). Это означает, что «в среднем» никакие
другие оценки не дают выигрыша по сравнению с а. 72-э. оценками.
§ 70. Неравенства для отношения правдоподобия
и асимптотические свойства о.м. п.
Этот параграф является аналогом §33, 34 и содержит результаты о
свойствах асимптотической оптимальности о. м. п.
1. Неравенства для отношения правдоподобия и состоятельность о.м.п.
Как и прежде, отношением правдоподобия мы называем функцию
(предполагаем выполненным условие (Αμ))
Z(u) = /ί?.+"^) = exp {L(X, θ + u)- L(X, θ)}, Χ ί= Ρβ.
Je{X)
548 Гл. 5. Статистика разнораспределенных наблюдений
Рассмотрим сначала одномерный случай (многомерный случай будет
рассмотрен в п. 4). Обозначим через ri(u) расстояние Хеллингера между Р#+и ι
П{и) = p(Pe+U)UPGii) = / (yjfe+u,iix) ~ yfoA*)) Vi(dx)·
В этом и последующих разделах будем предполагать, что выполнены
условия (Ао) {ft,i{x) φ fe,ilx) ПРИ t φ θ) и (Ас) (множество θ — компакт).
Кроме того, будем предполагать, что функции y/fetiix) дифференцируемы
ff'$i{xi)\2
для п. е. \pi\ значений х\ информация Фишера 1{{θ) = Е# —%——- по-
ложитпелъна и ограничена на Θ. (Это есть условие (R) без свойств
непрерывности.) При выполнении этих условий в §31 было установлено, что
inf^^X), (1)
9,и иг
где gi при \и\ ^ щ и малых щ может быть выбрано сколь угодно близким к
-1{(θ). Нам будет удобнее использовать свойство (1) в его равномерном по
отношению к частному gi/Ii(6) виде. Именно, мы будем предполагать, что
выполнено условие
(Аи) Существуют g > 0, с\ < оо такие, что при всех 0, θ + и Ε θ
ЩгЪяШ, Ii(9 + u)<ciJi(0).
Обозначим, как и в §33, р(и) = Z3/4(u).
Теоре ма 1. При выполнении сформулированных выше условий
EeZV2(u) <ехр |-£рГ(0,п)|, ЕвР(и) < ехр |-^-/(^п)},
Έθ\ρ'(η)\ < ^1/2(^ + u,n)exp|-^/(^n)}.
Доказательство аналогично доказательству теоремы 33.1. Из
результатов §31 следует, что
EoZ^(u) = fl[l-
Ti{u)
*=1
Правая часть здесь не превосходит в силу (Аи)
exp|^2^ri^)f <exp j-^/(0,n)j.
§ 70. Неравенства для отношения правдоподобия 549
Далее, в силу неравенств Коши-Буняковского (ср. с §33)
Eep(u) < [EiZ1/2(«)EeZ(u)]1/2 = [Щг112{и)]112 <ехр{-^/(0,п)},
Ев|р'(и)| = -AKe\L'{X,e + u)\Zll2{u)Zll\u) <
^ |{Εβ[4(^^ + «)]2^(«)Εβ^1/2(«)}1/2 <
<^{E9+u[^№^ + «)]2}1/2exp{-^,n)}.
Теорема 1 доказана.
Теорема 2. При всех ζ,η ^ 1
Р# ί sup Ζ{νΓιΙ2{θ,η)) >ехрИ <сехр< -у I ехр < -^- I,
где с = 1 + 3^/ci/g, ci — постоянная из условия {Аи).
Доказательство. Оценим функцию Я (ε) = Е# sup ρ (υ). Будем счи-
\v\>e
тать, что Θ = [α, Ь]. Тогда для w Ε [0 + ε, 6]
IU-0 U7-0
р(ге; - 0) = ρ(ε) + p,{u)du^p{e)+ / |р'(и)|Л*,
ε ε
#+(ε) = supp(u) <ρ(ε) + / \p'{u)\du.
u^e J
Пользуясь теоремой 1 и условием (Аи), получаем (ср. с §33)
#+(εΚβχρ{-^/(Μ)} + | f 11/Ч0 + и,п)ехр(-^1(в,п))аи
^ ехр (-^/(Α,η)) + ^-/1/2(0,п) | ехр (-^-Ι(θ,η)^άη <
<
Ч-х/(ЧИУ?)
Вместе с аналогичной оценкой для Я-(ε) = sup p(u) это дает такое же
u^—ε
неравенство для Н(е) = max (Η-(ε), Η+(ε)). Остается, как и в теореме 33.2,
550 Гл. 5. Статистика разнораспределенных наблюдений
воспользоваться неравенством Чебышева для оценки
Ρθ [ sup Ζ(υΓ1/2{θ,η)) > exp z J = Ρ Л sup p(v) > exp \ -%■ \ ) <
\M*« / \>l£«'-1/a(*.O I 4 J /
< exp [-^Н(п1-У\в,п)) < (l + 3^|) exp {-f } exp {-^}.
Теорема 2 доказана. <
Из теоремы 2 вытекает
Теорема 3. Существуют значения с < оо, # > 0 такие, что
Έ>θ(\θ* - βΙ/^^,η) > «) < сехр {-^}·
Доказательство. Как и в §33, следует воспользоваться включением
{\θ* - θ\ < ε} D < sup Ζ(ί) ^ 1 > , в силу которого и теоремы 2 получаем
[те J
утверждение теоремы. <
Следствие 1. 2?сли 7(0,п) —► оо при η —► оо, шо оценка Θ*
состоятельна.
Более того, теорема 3 дает оценки вероятностей уклонений |0* — θ\^ ε.
Она позволяет также утверждать, что справедливо
Следствие 2. При любом а ^ g/Ъ существует сч < оо, не зависящее
от пив, такое, что
Е^ехр{а(и*)2} < с2,
где , Λ
(ср. с §33).
Теорема 3 и следствие 2 представляют собой значительно более сильные
утверждения, чем утверждение о состоятельности о. м. п., приведенное в § 66.
Они означают, в частности, существование второго момента 0* — 0,
убывающего, как Ι~ι(θ,η). Утверждения §66 такого вывода делать не позволяли.
2. Асимптотическая нормальность о.м.п. Как и в однородном случае,
доказательство асимптотической нормальности требует более
ограничительных условий на гладкость функций /г(а;,0). Эти условия можно найти в
теоремах 65.3, 66.2. Воспроизведем здесь эти условия.
(RR) 1. Выполнены условия (Ао), (Ас), (Αυ), (R).
2. Функции Ιί(Χ)θ) дважды непрерывно дифференцируемы по 0, при
этом
sup|i"(z,0)| ^ *t(я), U = / Цх)/вАх)м(ах) < °°·
вее J
§ 70, Неравенства для отношения правдоподобия
551
Сходимость интегралов здесь предполагается равномерной в следующем
смысле: при η —> оо и при каждом τ > 0
r-V) ]Г [li(x)fe,i(x)Vi(dx)->0, Γ(η) = ]Γ>.
li{x)>rT(n)J t=l
Обозначим
t€0,t+u€0,|u|$A
ωΔ,ί = Е^о;д,г(хг).
3. Функции I"(χ, θ) непрерывны в среднем:
Γ"1(η)Σα;Α,^^Δ -+0
при η -> оо, где о>д от гг ме зависит.
4. Дри гг —> оо
η
О</(0,п) = £]/*(0)-Юо,
i=l
/-^,^ΣΜΟΚ*^))2; |г<(х*,^)| >τ7(^,η)] -*ο.
5. Законно дифференцирование по θ под знаком интеграла в
равенствах
Jfe,i = l, fl'ife,i = 0.
В формулировке теоремы 66.2 присутствуют также условия (М1)-(Мз),
нужные для доказательства состоятельности Θ*. Так как состоятельность
в силу следствия 1 уже доказана, то необходимость в этих условиях здесь
отпадает.
Из теорем 65.3, 66.2 вытекает
Теорема 4. При выполнении условий (RR)
(Θ* - θ)Ι^2(θ,η) = ξη(1 + εη(Χ,θ)), (2)
где
η
εη(Χ,θ) -^ 0, ξη = Γ1ί2(θ,η)Σ1'άχ"θϊ ®· ф°-ь
г=1
Это утверждение в силу п. 1 можно дополнить следующим образом.
Теорема 5. Сходимость
η* = (θ*-θ)ΐν2(θ,η)&Φ0Λ, (3)
552 Гл. 5. Статистика разнораспределенных наблюдений
вытекающая из (2), имеет место вместе со сходимостью моментов
любого порядка, т. е. вместе с (3) при любом к > О выполняется
Щи*)к ->ЕтД г/^Фод.
Более того, для любой непрерывной функции w(t) такой, что \w(t)\ <
< egt /6 (см. следствие 2), Eqw(u*) -> Ειυ(η), η €= Φο,ι-
Доказательство этого утверждения повторяет доказательство
теоремы 33.5.
3. Асимптотическая эффективность. Асимптотическая эффективность
о. м. п. в классе Км М-оценок была доказана в § 66. Совершенно аналогично
однородному случаю можно установить теперь, что о. м. п. обладает всеми
другими возможными свойствами асимптотической оптимальности из тех,
что были введены нами в рассмотрение в п. 66.3 и в § 18, 21.
Предварительно следует заметить, что
1. О.м.п. Θ* принадлежит классу Кф$ оценок 0*, для которых имеет
место сходимость со вторыми моментами (см. п. 66.3):
(0* - θ)σ-\θ,η) & Φο,ι, Е*(0* - 0)2σ"2(0,η) -+ 1.
В этом классе среднеквадратический и асимптотический подходы к
сравнению оценок совпадают. _
2. О. м. п. Θ* принадлежит классу Ко асимптотически несмещенных
оценок, для которых 6(0) = ο(σ(θ,η)), b'{9) = о(1).
Это доказывается точно так же в § 33, 34. Аналогично § 33, 34
доказываются и следующие утверждения.
Теорема 6. Если выполнены условия (RR), то
1) о. м> п. 0* является a.R-э. оценкой]
2) о. м. η. 0* является а. э. оценкой в Ко;
3) о. м. п. Θ* является асимптотически R-байесовской и
асимптотически байесовской оценкой для любого априорного распределения Q,
имеющего плотность относительно меры Лебега (см. теоремы 33.8, 30.5).
Все изменения, которые надо внести в доказательства § 33, 34 при
переходе к неоднородным наблюдениям, сводятся к замене nl{9) на 7(0, п), a
также к некоторым другим не менее очевидным модификациям.
Утверждение об асимптотической минимаксности о. м. п. требует
введения элементов равномерности по 0 в условиях (RR) (ср. с условиями (RRu)
в § 34). Установление свойств минимаксности при таких равномерных
условиях безусловно возможно, но требует предварительных рассмотрений,
аналогичных тем, что были проведены в § 37. Читателю, хорошо усвоившему
результаты и доказательства §33, 34, это под силу.
4· Замечания об о.м.п. для многомерного параметра. В многомерном
случае 0Cifc, к > 1, наиболее широкие условия состоятельности о.м.п.
можно получить из теоремы 66.1 (условия этой теоремы с размерностью 0,
по существу, не связаны).
§71. Замечания о проверке гипотез
553
Доказательство асимптотической нормальности о. м. п. в
многомерном случае возможны путем использования как подходов, близких к тем, что
изложены в § 65 при изучении М-оценок, так и подходов, изложенных в § 34
и 70. При этом доказательство и сама формулировка условий регулярности
(условий типа (RR)), обеспечивающих эту нормальность, оказываются более
громоздкими и трудоемкими. Изменится вид тех компонент условий (RR)
(ср. с теоремами 67.5 и 36.6), которые содержат отношения сходимости
и неравенства (например, условия (RRu), (36.3) и др.). Вместо условия
/(0, п) —> оо в одномерном случае здесь надо предполагать Λι(0, η) —> со, где
η
Λι(0,η) — минимальное собственное значение матрицы Ι(θ,η) = y^Ij(9).
При этом минимальное и максимальное собственные значения 7(0, п) могут
сходиться к оо, вообще говоря, с разной скоростью (см., например,
значение /(0, п) в §68). «Качественный» вид основного утверждения остается
прежним:
(0*-0)/1/2(0,η)θ'Φ<Μϊ,
где Ε — единичная матрица; при этом сходимость имеет место и для мо-
^+*
ментов любого порядка; о. м. п. Θ* является асимптотически эффективной в
том же смысле, что и в теореме 6.
§ 71. Замечания о проверке гипотез
по неоднородным наблюдениям
Все основные принципы построения критериев для проверки
статистических гипотез, изложенные в гл. 3, при переходе к статистике неоднородных
наблюдений полностью сохраняются.
Пусть дана выборка X = (χι,...,χη) ^ Ρ = Pi x ... х Рп и по ней
проверяется некоторая гипотеза Η относительно распределения Ρ этой выборки.
В этом случае наблюдение X можно рассматривать как выборку объема 1
из распределения Ρ и применять все выводы и результаты гл. 3. (Отметим,
что это замечание справедливо и для зависимых наблюдений χχ,.. .,хп; ср.
также с гл. 6.)
Рассмотрим простейший пример (см. пример 64.5), когда проверяются
две простые гипотезы Hj = {X €= Р^}, j = 1,2, при выполнении
условия (Ад) о том, что распределение элемента выборки х^ имеет плотность
относительно некоторой меры μ,·. Обозначим через Д (ж) эту плотность при
гипотезе Hj, j = 1,2, и через f^(X) — функцию правдоподобия f^\X) =
η
= ТТ fi(xi), так что fW(X) есть плотность распределения Р^ выборки X
t=l
при гипотезе Hj относительно меры μι χ ... χ μη. Пусть, далее, Ζ(Χ) есть
отношение правдоподобия Z{X) = /(2)Р0//(1)(*)·
Тогда согласно теореме 42.1 все оптимальные критерии (байесовские,
минимаксные, н. м. к.) будут основаны на статистике Z(X), и в том случае,
когда распределение Z(X) при обеих гипотезах непрерывно, будут иметь вид
554 Гл. 5. Статистика разнораспределенных наблюдений
5С(Х) = I(Z(X) > с) при надлежащем выборе с. Если Ί?^(Ζ(Χ) = с) > О,
то необходимо рандомизировать критерий (обозначим его через 7гс(Х)),
положив пс(Х) = р{Х) > 0 на множестве {Ζ(Χ) = с}; 7гс(Х) = Ι(Ζ(Χ) > с)
при других X. Пусть для простоты Ρ^^(Ζ(Χ) = с) = 0 при всех с.
Тогда о. м. к. ic(-X") будет иметь вероятности ошибок первого и второго рода
равными соответственно
ai(6c)=pM(Z(X)>c), a2(6c) = pM(Z(X)<c). (1)
Стоящее под знаком вероятности в (1) событие можно записать в виде
" /·(2)(χΛ
У2т> In с, щ = In-7ТТ——,
где случайные величины ητ независимы. Если рассматривать н. м. к.
уровня ε, то надо выбрать с так, чтобы Р'1^ У^% ^ lnc J = е.
Положим
в! = ЕРМЩ = ί ^(χ^η^-^-μ^άχ) = -Р1(Р{Х>,Р{2>),
J fi '\x)
k = Epwm = f tf\x) Ini^-Mdx) = р^рЗД1)),
J fiW
где распределения Р^ соответствуют плотностям fr\ pi(P, Q) —
расстояние Куль бака-Лейблера между Ρ и Q (см. замечание 31). Положим далее
(σ?>)2 = Я0>*, (2#>)2 = Σ (σ?>)2, , = 1,2.
г=1
В дальнейшем мы не будем исключать схему серий, когда
распределения Р\ (плотности д ') зависят от гг. Мы можем теперь во введенных
обозначениях записать ai(6c) в виде
При выполнении условия Линдеберга
η
Σ>ρ(ι) (»/?; Ы > тв!1)) -> о, г > о,
и при с таком, что fine— /Ja0 /^η = ^ε> гДе ^ε> как и прежде, —
квантиль нормального распределения порядка 1 — ε, мы будем иметь в силу
центральной предельной теоремы
§71. Замечания о проверке гипотез
555
так что при выбранном с критерий 8С будет иметь асимптотический уровень
1 — ε. Этот критерий имеет следующую вероятность ошибки второго рода:
«зад = t"·' ι "·"„, " < --~Σ<" 1 _
r(2)
On
_ Р(2) / Σ fa - Μ < Σ (&i - Qt) + λ ^
(1)'
Μ2) ^ 5<2) T S<2\
Здесь
Σ * - «d - Σ (ΛίρΡ,ρί")+л(И,,.рР)» =
= Λ(Ρ(2»,Ρ<Ι>) +ρ,(Ρ'1>,Ρ<2)) =/,(Ρ"),Ρ<2))
является «симметризированным» расстоянием Куль бака-Лейблера
между Р^1) и Р(2). Если выполнено условие Линдеберга
ΣΕρ(2,(4?;|77ί|>τβΡ))->0, τ>0,
то здесь также применима центральная предельная теорема и соотношение
<*2(^с) -> /? ^ 0 эквивалентно тому, что
p(P(i)tpW) дМ
"(5) + λε-^λ1_/?. (2)
Поэтому малые значения β (или β = 0) возможны лишь в случае, когда при
больших η велико значение
ρ(ρ(1))Ρ(2))/5(2).
Будем говорить, что гипотезы Hj фиксированы, если /^ (а
следовательно, и распределение ηι) от η не зависят. В этом случае необходимым
условием состоятельности критерия 5С (не ограничивая общности, можно
считать, что σ^ > 0) является неограниченный рост вместе с π расстояния
р(Р^\р(2)). Если (Вп ) растет с той же скоростью, что и р(Р^),р(2)), как
это имеет место в случае однородных наблюдений, то условие р(Р^, Р^2)) ->
-* оо является и достаточным для состоятельности 6С.
Будем называть гипотезы Hj близкими (но различимыми), если ц3'
зависят от п, р(Рг· ,Рг· ) 4 Ои имеет место (2) при \\~β Φ —оо, β <
< 1 — ε. Сюда будет относиться, в частности, случай параметрических
гипотез Hj = {X ^ Ρθ.}, j = 1,2, когда ΡΘ = Р^д χ ... χ Р$|П, Р^ от η
не зависят, 02 = #ι + ^/_1/2(#ι,η), информационное количество Фишера
η
/(0ьп) = xj^(^i) обладает свойством Ι(θχ,η) —> оо при η —> оо (пара-
метр 0 для простоты считаем скалярным). Если выполнены условия
регулярности типа (RR), то, пользуясь результатами §70, читатель без труда
556 Гл. 5. Статистика разнораспределенных наблюдений
сможет получить приближенные значения otj(Sc) (ср. с (43.20))
β1(ίβ)«1-Φ^-^ у а2(5с)«(^ ^ J.
Изучение асимптотического поведения ау(£с) в случае фиксированных
гипотез оказывается более трудной и менее исследованной задачей (за
исключением случая однородных наблюдений; ср. с §43).
Используя аналогичные модификации, можно перенести на случай
неоднородных наблюдений и результаты §53-55 об асимптотически
оптимальных критериях для проверки близких сложных гипотез. При этом при
необходимости следует использовать результаты об асимптотическом
представлении отношения правдоподобия, приведенные в § 70.
§ 72. Задача о разладке (пример 64.6)
Обратимся теперь к примеру 64.6 и несколько уточним постановку
задачи. Пусть дана последовательность X независимых наблюдений X =
= (χι,Χ2,.. .,X0_i,X0,...), первые Θ — 1 из которых имеют распределение
Gi, остальные — распределение G*i Φ G\. He ограничивая общности, можно
считать, что G\ и G<i имеют плотности (абсолютно непрерывны)
относительно некоторой меры μ. В качестве μ можно взять, например, μ = G1 + G2.
Параметр θ < оо неизвестен, и задача, которую мы будем рассматривать,
состоит в том, чтобы по возможности точно «угадать» или оценить этот
параметр по наблюдению X. Двойственный характер этой задачи состоит в
том, что, с одной стороны, ее можно рассматривать как задачу о проверке
конечного или счетного числа гипотез Hj = {θ = j}, j = 1,2,.. .,η; η ^ оо,
и тогда естественно рассматривать задачу об отыскании оптимального
критерия δ(Χ), который минимизировал бы вероятность ошибки или, что то
же, максимизировал бы вероятности Ρ^(ί(Χ) = .Я^) «угадывания»
неизвестного параметра. Через Ρ г мы здесь обозначаем аналогично предыдущему
распределение в пространстве последовательностей X в случае θ = t.
С другой стороны, параметр θ носит количественный характер и, стало
быть, естественно рассматривать задачу об оценке параметра θ и об
отыскании такой оценки Θ* = Θ*(Χ), которая минимизировала бы среднеквадрати-
ческие уклонения Е#(0* — 0)2. Ниже мы рассмотрим оба этих подхода в их
асимптотической форме, предполагая параметр θ большим.
Задаче о разладке посвящена обширная литература (см., например, [41,
53, 71, 79, 90, 138]); некоторые из известных результатов мы будем
использовать.
1. Задача о разладке как задача проверки гипотез. Мы уже отмечали,
что θ является количественным параметром. Поэтому в этом разделе
наряду с термином «критерий £(Х)», принимающим значения в множестве
{#ι,#2,...}, нам будет удобно использовать также термин «оценка Θ* =
= Θ*(Χ)», где Θ* принимает значения 1,2,... Функцию Θ*(Χ), как и δ(Χ),
в рамках этого раздела можно также называть критерием.
Обозначим
( \ к"г
гг = ^7, Дк = Я(*,Х) = 11г*. (1)
92[хг) . ..
§ 72. Задача о разладке
557
Определение 1. Критерием (оценкой) максимального
правдоподобия называется такое наименьшее число θ* = Θ*(Χ), что
R(9\X) >R{t,X)
при всех t ^ η -f 1, где η ^ оо — число наблюдений.
Если η < оо, то θ = 0* максимизирует функцию правдоподобия
θ-ι η
Л(*) = 1Ы*)1Ы*)· (2)
i=l г=0
Определение 2. Критерий Θ* = 0*(Х) называется асимптотически
однородным, если
Pt(0* = t)->p>O (3)
при t —> оо.
Если мы имеем дело с ограниченной последовательностью η < оо
наблюдений, то в (3) предполагается также, что η —> оо, η — t —> оо.
Покажем, что о. м. п. 0* является асимптотически однородной и найдем
соответствующее ей значение ρ = р. Нам понадобятся следующие
обозначения. Рассмотрим две независимые друг от друга последовательности {&}
и {£i} независимых случайных величин, определенных равенствами
92 (Xt)
0 = In р—г, Хг ^ G2.
Очевидно, что
Щг = ~ ί9ι(χ)\η^\μ(άχ) = -P1(GUG2) < О,
ЕСг = ί92(χ)1η^\μ(άχ) = -pi(G2,Gi) < О,
У saw
где pi — расстояние Кульбака-Лейблера, введенное в §31. Оба расстояния
pi(Gi, G2) и p(G2, Gi) мы будем предполагать конечными. Обозначим далее
η η
»Ьп = / ^ Цг> ^η = χ ^ Cz'j
f=l t=l
5 = sup 5fc, Ζ = sup Zfc.
fc>l A:>1
558 Гл. 5. Статистика разнораспределенных наблюдений
Так как Е& и Е^ отрицательны, то в силу усиленного закона больших чисел
S и Ζ — собственные случайные величины,
Р(5 < 0) > О, Ρ(Ζ < 0) > 0
(см., например, [12]; [17, §11.3]).
Распределения S и Ζ могут быть найдены в явном виде в терминах
компонент факторизации функций 1 — ζφ(\) и 1 — ζφ(λ) соответственно,
где φ(Χ) = Ее^1, ^(λ) = Ее^1 (см. [12]; [17, § 11.3])- Отметим, что
ψ{\) = φ(1 — λ) и φ(Χ) ^ 1 при λ £ [0,1]. Действительно,
*А>-/*<*> (£$ГМ,,,)"
= / Si Χ(χ)92{χ)μ(άη) < II ςχάμ\ ί / ρ2άμ)
1.
(5)
Такое же неравенство справедливо для ψ(λ). Кроме того, производные φ'{\) =
= — ψ'(1—А) в силу сделанных предположений конечны на всем отрезке [0,1],
φ'{0) < 0, ^(1) > 0.
^+*
Теорема 1. Оценка максимального правдоподобия Θ* является
асимптотически однородной,
Pt(e* = t)ip = P(S<0)P(Z^0) (4)
при ί|οο (и η — ί t со» если η < οο). Кроме того,
Pt(9* >t)^P{Z>S;Z> 0),
Pt(9* <t)^P{Z^S;S^ 0),
Pt(0* >t + k)^ 2/, Pt{0* <t-k)^ 2/, (6)
где
<p = minEeA£ < 1.
λ
Более полные сведения о предельном Ре-распределении разности Θ* — t
содержатся в приложении VII.
Доказательство. Имеем
{i-l Jfc-l
Пг* > Π Т{ при всех ^' ι ^ ^ < *;
г=1 t=l
t-1 k-\ \
Π Ti ^ Π Ti при всех ^' n+ 1 ^ k > t\
<=1 t=l J
§ 72. Задача о разладке
559
Поэтому в силу независимости х^
Pt(0* = t) = P(-& - ... - 6-х > 0 при всех Л, 1 < А; < t) х
χ P(£t + ... + Ofc-i < 0 при всех fc, i<fe^n + l)t
tP(S<0)P(Z<0)
при 11 сю, η — 11 oo. Аналогично находим
(*-l 5-1 ϊ
г=1 г=1 J
Pt(0* > <) = Р ( max (Ct + · · · + Ofc-i) > max (£4 + ... + &-i) J =
= Ρ ( max Z; > max S\ ) -> P(Z > 5; Ζ > 0).
\1^^η-ί 0<^*-l /
Далее,
{θ* > t + A;} = < max TT V{ > max TT r\ > ;
Ч г=1 г=1 J
Pt(0* > ί + k) = Ρf5t_i + Zk + max Z(* >
V ΙζΙζη—t—k
> max (5b..., S*_b u-i + Сь ■ · ·, u-i + ^)), (7)
где последовательность {Ζ*} имеет то же распределение, что и
последовательность {£/}, и не зависит от нее. Так как последний max под знаком
вероятности в (7) больше или равен S^-i, то вероятность (7) не превосходит
оо
p(zfc + ζ* > о) ^ P(zk > о) + ί P(zk e dv)P{z* > -v).
—oo
Так как ^(λ) = Ee^1 = 1 при λ — 1 (см. ниже), то
Ρ(Ζ* > и) < еЛ P(Zk>0)^ipk(\)
при любом λ, 1 ^ λ ^ 0 (см., например, [12, 17]). Поэтому
оо
Pt(0* > t + k) < фк{\) + ί evXP{Zk e dv) < фк{\) + фк{\) = 2φ*
—oo
при λ = λο, φ = ψ{λο) = min^(A) < 1. Второе неравенство в (6)
доказываем)
ется аналогично. Теорема доказана. <
560 Гл. 5. Статистика разнораспределенных наблюдений
Класс if(o) асимптотически однородных критериев, введенный в
определении 2, следует считать весьма естественным, поскольку он состоит из
критериев (оценок), ведущих себя «симметричным образом» по отношению
к разным большим значениям параметра 0. Аналогичное свойство
симметричности в теории оценивания и в теории проверки гипотез вводилось,
например, понятиями несмещенности или инвариантности. Если мы не
имеем дело с байесовской постановкой задачи, то у нас нет оснований
выделять те или иные значения 0, так что для разумных оценок Θ* значения
Pt(6* = t) должны быть примерно одинаковыми при всех больших
значениях ί (и η - ί, если η < оо). Теорема 1 показывает, что класс К^ не
пуст.
Покажем теперь, что о. м. п. Θ* обладает свойством оптимальности в К^у
Теорема 2. Пусть Θ* — любая оценка из К^\
Pt{e* = t)->p>0
при t —> оо (и η — ί —> оо, если η < оо). Тогда ρ ^р.
Доказательство. Рассмотрим байесовскую постановку задачи,
когда на множестве {1,...,п} задано априорное распределение Q с
вероятностями q{k) = l/n. (Точнее, мы будем рассматривать последовательность
Q = Q(n) распределений, зависящих отп-^ оо.) Байесовский критерий 6q
выбирает в качестве θ значения &, при котором максимизируется
апостериорная вероятность
Я («/·*) = = -ц ·
ZqWMX) Efi(x)
t=l t=l
Это означает, что 9q = 0*. Далее, для вероятности ошибки olq(6*) =
η
= y^(?(&)Pfc(0* Ф к) асимптотически однородного критерия θ* будем иметь
1 п
р= lim -Vp*(0* = fc) = lim (l-aQ(0*)K
71=1
1 n
^ lim (l-ag(0*)) = lim TP#^)=p.
n=l
Теорема доказана. <
Можно выделить еще один класс критериев (оценок), в котором о. м.п.
будет асимптотически оптимальной. Это класс байесовских критериев с
«плавно меняющимися» априорными вероятностями q(h).
Чтобы ввести этот класс, рассмотрим произвольную последовательность
δ -+ 0. Если η < оо, то мы будем считать, что η = η(δ) -* оо при δ -+ О
(можно отождествить, например, δ с 1/гг).
§ 72. Задача о разладке
561
Обозначим через Q класс распределений Q на {1,...,η}, η < оо,
зависящих от параметра δ и обладающих следующим свойством: для любых
kx = &i(<S) < fc2 = /c2(i) таких, что k\ -* оо, η - Лг -* оо при £ -* О,
выполняется
ς(Ατ +1) ε f ^7
—— < е ПРИ «ι ^ А; < п,
(8)
v /ух У <ее при 2 < А; < Лг2,
где ε = e(fci, fo) ~~* О ПРИ ^ -* 0.
Очевидно, что для любого фиксированного /
при ί -> 0, А; —> оо, η — к —> оо.
Равномерное распределение q{k) = 1/п на множестве {1,..., п}
принадлежит Q при ε = О, ί = 1/п. Геометрическое распределение q(k) = р(1 — р)*"""1,
А; = 1,2,..., также принадлежит Q при 5 = ρ -> 0, ε = — In (1 — ρ).
В обоих этих примерах соотношения (11) выполняются и без условия
роста к\ и η - ^2·
Названные два примера можно обобщить следующим образом. Пусть,
как и прежде, £ — произвольная последовательность, сходящаяся к нулю,
и ρ(ί) — плотность, непрерывная и положительная внутри отрезка [0, а] и
равная нулю вне его, α < оо. Тогда при широких условиях на поведение p(t)
на концах интервала (0, а) последовательность
,(*)= / *>*, *-!,...,§
(fc-l)i
(считаем для простоты, что δ нацело делит а), будет принадлежать Q. Можно
взять, например,
, , Jc(a,/3)U°(1-U)«, и €[0,1],
ρ(") = 1ο, uiio.i],
при любых α ^ 0, /3^0, где с(а, /3) — нормирующая постоянная.
Для определенности будем называть байесовским критерием 9q = 0q(X)
функцию, которая выбирает минимальное значение А:, для которого q{k/X) =
= maxg(j/X).
Теорема 3. £7сли Q Ε Q, то
Pt{e*Q -*>*)< 2(^0)*, Pt(ej -< < -Λ) ^ 2(<^ελ°)*, (9)
562 Гл. 5. Статистика разнораспределенных наблюдений
где, как и прежде, λο — точка, в которой достигается minV'(A), φ —
= -0(λο). Если Q Ε Q, P{Sj = 0) = P(Zj = 0) = 0 при всех j, mo
Pt(9*Q^9*)-+0 (10)
при t —> oo, η — ί —> oo.
Очевидно, что наряду с (10) имеет место также сходимость Р(0д Φ
Φ θ*) -> 0 относительно распределения Ρ пары (Q,X), θ €= Q Ε Q.
Вместе с теоремой 2 утверждение (10) означает, что все байесовские
критерии, соответствующие Q Ε Q, асимптотически эквивалентны о. м. п. 0* и
имеют в пределе одну и ту же вероятность ошибки, равную 1 — р.
Так как о. м. п. Θ* является байесовским критерием (для равномерного
априорного распределения), а Ре(Θ* = t) асимптотически не зависит от t, то
нетрудно установить также, что Θ* является асимптотически
минимаксным критерием при соответствующем естественном определении этого
понятия (ср. с §53).
Доказательство теоремы 3. Доказательство неравенств (9)
вполне аналогично доказательству неравенств (6) в теореме 1. Имеем
{e*Q>t + k} = j max 9(i) ГЬ > Й&^ШГ<|'
Совершенно аналогично с (7) имеем
Pt(0g > < + к) = p(St_i + Ζ* + max(Ζ,* + lng(i + к + I)) >
> max (Si + lng(2),..., St-i + lng(<);
St-i + Zi+ lnq{t + 1),..., St-i + Zk + ]nq(t + Λ))) <
^ Ρ (st_i + Zk + ek + пшх (Zf + ε/) > 5t_i) ^
о
< P(Zfe + ek > 0) + A P(Zfe + ek € <fo)P(max (Z,* + el) > -v).
-00
Пусть s > 0 — решение уравнения Εελ^+1+ελ = ^(λ)βίλ = 1. Очевидно, что
s < 1, s -> 1 при ε —> 0. Поэтому при любом фиксированном λ е (0,1)
о
Pt(9*Q >t + k)< (ф(\ух)к + ί esvP{Zk + ek € eft;) < 2(^(λ)βελ)/:.
— OO
Отсюда следует первое утверждение теоремы. Второе неравенство в (9)
получается аналогично.
§ 72. Задача о разладке
563
Докажем (10). Событие 9q φ 0* наступает в том случае, когда макси-
k-i
мум последовательности q(k) II Т{ достигается в точке А:, отличной от точки
максимума JJn· В силу неравенств (6), (9) мы можем ограничиться рас-
<=1
смотрением значений Л;, \t — k\ < JV, при достаточно большом, но
фиксированном N. Но в этих пределах
. ?(*) t ?(*) t
mi = mm —τ -> 1, m? = max —У-f —* 1
\b-t&N q{t) \k-t\^N q{t)
при t —> oo, η — £ -> oo. Стало быть, P*(#q 7^ β*) оценивается Р^-вероят-
ностью того, что Sr и Zs при некоторых г < JV, s ^, Ν попадут в интервал
в окрестности нуля, шириной не превышающей 1птп2 — In mi -> 0. Так
как распределения 5Г и Zs непрерывны в точке 0, то Ргвероятности этих
событий сходятся к нулю. Теорема доказана. <
2. Задача о разладке как задача оценки параметра. Бели число ρ в
теореме 1 невелико, то шансы точно угадать параметр θ тоже невелики.
Поэтому подходы предыдущего раздела, максимизирующие вероятность
точного угадывания, не всегда являются наиболее естественными. Часто целью
является не точное угадывание 0, а определение значения 0*, которое было
бы по возможности близко к 0, например в среднеквадратичном смысле.
Отметим при этом, что мы оцениваем целочисленный параметр случайного
процесса χχ,Χ2,... по одному наблюдению X (в гл. 2 мы оценивали
параметры распределений Х{ и, как правило, по многим наблюдениям). Так как
мы имеем лишь одно наблюдение X, то невозможно рассчитывать получить
оценки, которые обладали бы свойством состоятельности (это видно и из
содержания предыдущего раздела). Мы опять будем рассматривать
асимптотическую постановку задачи.
Определение 3. Оценка Θ* называется асимптотически однородной
(в среднеквадратичном), если
ВД* - t)2 -> σ2 < oo (11)
при t —> 00 (и η — ί -> оо, если η < oo). Класс таких оценок обозначим
через Кру Из теоремы 1 следует, что о. м. п. 0* Ε К^), при этом σ2 = σ2 =
= EJ?2, где D — случайная величина, определенная в приложении VII.
Определение 4. Оценка 0*, определенная равенством
*тЪт· (12)
называется оценкой среднего правдоподобия.
564 Гл. 5. Статистика разнораспределенных наблюдений
Ясно, что эта оценка не обязательно целочисленна. Наряду с Θ* можно
рассматривать эквивалентную ей в известном смысле
рандомизированную целочисленную оценку 0**, принимающую значение [Θ*] с вероятностью
1 — {#*} и значение [Θ*] + 1 с вероятностью {б*}, где [х] и {х} — целая и
дробная части χ соответственно.
Введем в рассмотрение случайные величины
ОО ОО ОО 00
fc=l A;=l *=1 *=1
Так как по усиленному закону больших чисел S& < — ск < О, Z^ <
< — ск < О с вероятностью 1 при некотором с > 0 (с < — Εξι, с < —Ed)
и при всех &, начиная с некоторого, то рассматриваемые ряды сходятся, а
введенные случайные величины являются собственными (заметим, что при
этом EeSk = EeZk = 1, EEi = оо). Более детальные сведения о
распределении Ej см. в приложении VII.
Теорема 4. V ^-распределение Θ* — θ слабо сходится при θ —> оо
(и п — θ —> оо, если η < оо, η —> оо) к распределению -—~ —-.
I + JSi + J>2
Эта сходимость имеет место вместе со сходимостью моментов лю-
(Е1 — Ε' \ 2
-—~ ~- ) < °°· Оценка среднего правдоподо-
1 + Е\ + Е2/
бия Θ* является асимптотически оптимальной в К(2)'· для любой оценки
Θ* Ε If(2) с предельным разбросом σ2 (см. (11)) выполняется σ1 ^ σ2.
Кроме того, для любого Q Ε Q байесовская оценка 9q и оценка Θ*
асимптотически эквивалентны:
Pt{\e*Q-0*\>e)->O (13)
при t —► оо, η — t —> оо.
Во избежание недоразумений напомним, что байесовский критерий 0£,
фигурирующий в предыдущем разделе, и обозначаемая тем же символом
байесовская оценка 9q определяются по-разному.
Доказательство. Докажем сначала, что θ* Ε К^)· Имеем
при k ^ 0,
V ' ' -с" ι+ζ*-· при fc:>0.
§ 72. Задача о разладке
565
Умножим числитель и знаменатель в (12) на es$~l . Тогда
Θ* - θ = ]£ {к - 0)е5·-*-5*-! + ^ (fc - 0)ez*-< x
ik<9
к>в
-1
_ Е'2}П-в
Е\
1,0
Χ Σ^^+Σ^Ι 7 14-F + F '
<k<0
где
$-1
e+1
i-1
£μ = Σ(
A
e+l
/b=l
Ясно, что Е[ s
fc=l fc=l
£?j-, г = 1,2. Очевидно далее, что
fc=i
ΈΆ
ι,*
Ε[
1 + E\fi + E2in-e 1 + Ει + Ε2
0
при 0 —» οο, η — θ —> οο. Кроме того, согласно лемме 1 из приложения VII
момент любого фиксированного порядка величин
ΕΊ,θ
>
Е1в
E\fi 1 + Eij + i?2,n-0
чен. Отсюда следует сх
с моментами любого порядка. Такое же утверждение спра-
равномерно по θ ограничен. Отсюда следует сходимость распределений
ΕΊ,θ
1 + Eij + Ε2ιπ-θ
ведливо для
Ε2,η-Θ
1 + #1,0 + #2,n-0
Это доказывает сходимость Р^-распределения
EL-Ei
θ* — θ к распределению
вместе с моментами любого порядка.
1+Ei+Eb
Рассмотрим теперь байесовскую постановку задачи и равномерное на
{1,...,п} априорное распределение Q. Тогда, очевидно, что Θ* совпадает с
байесовской оценкой 0q. Обозначая через Ε = Eq математическое ожидание
относительно распределения (0,Χ), θ G Q, получим, что для любой оценки
θ* Ε lf(2) с предельным разбросом σ2 (см. (11)) справедливо
η—>οο τι
1 П
о2 = lim - У ВД* - t)2 = lim Е(0* - θ)2 >
1 η
^ lim Ε(0£ - θ)2 = lim - V Ε,(02 - *)2 = σ
566 Гл. 5. Статистика разнораспределенных наблюдений
Нам осталось убедиться, что байесовская оценка 0д = Е(0/Х) для
любого априорного распределения Q £ Q асимптотически эквивалентна 0*, т.е.
что выполнено (13). Имеем
E(b-G)R(k)q(k) £(fc-0)i?(fc)
°*Q ~θ*= Е*(*)ВД ЕВД ' (14)
к к
Из доказательства первой части теоремы мы видели, что второе слагае-
2 N — 1 N
мое в (14) будет сколь угодно близким к = =— при достаточно
1 + E\%pf + &2,N
большом Ν, т.е. близким к слагаемому того же вида, в котором, однако,
суммирование в числителе и знаменателе ведется лишь по значениям fc,
|Λ - 0| < N.
То же самое справедливо, очевидно, и для первого слагаемого в (14), и
q(k)
для их разности. Но для Q £ Q выполняется —т-гг —> 1 при \к — 0| < TV,
0 —> оо, η — θ —> оо. Поэтому разность (14), в которой суммирование ведется
по &, \к — 0| ^ ΛΓ, сходится к нулю при 0 —> оо, η — 0 -* оо. Другими
словами, при 0 = £ Pf(|0g — 0*| > ε) —> 0 при ί —> оо, η — ί —> оо. Теорема
доказана. <
Утверждение, аналогичное теореме 4, можно получить и для
целочисленной рандомизированной оценки 0**. При этом под классом К^) надо будет
понимать класс асимптотически однородных рандомизированных
целочисленных оценок,
ВД** - 0)2 = Et(0* - 0)2 + Et(0* - 0**)2
будет отличаться от Е^(0* — 0)2 на величину
ВД* - 0**)2 = 2Е,{0*}(1 - {0*}) < \.
Отметим также, что оценка среднего правдоподобия, являясь
асимптотически байесовской и однородной (Ег(0* —t)2 асимптотически от t не зависит),
будет также асимптотически минимаксной оценкой при соответствующем
естественном определении этого понятия (ср. с §21).
3· Последовательные процедуры. Последовательные процедуры
представляют интерес в тех случаях, когда существует необходимость принять
решение о наличии разладки и ее локализации в возможно короткие сроки (по
минимальному числу наблюдений). Сокращение числа наблюдений
естественно проводить с помощью следующей процедуры. Обозначим через 0^
наименьшее значение А;, при котором R(k) > R(j) при всех j ^ т + 1,
так что 0* = 0*, если мы располагаем η наблюдениями. В дальнейшем
для определенности будем считать η = оо. В качестве момента ν
остановки наблюдений естественно выбирать такое т, при котором разность
§ 72. Задача о разладке
567
lni?(0^) — InR(m) достигнет достаточно большого значения, которое мы
обозначим через N + b(m). (Нетрудно видеть, что если Ъ(т) = о(га), то при
т — θ -> оо это произойдет с вероятностью 1. Если же т < 0, то θ^ будет
расти вместе с т и рассматриваемая разность будет оставаться
«ограниченной».) Итак, мы положим
z/ = min{m: \пЯ(в^) -1пД(т) ^iV + 6(m)}. (15)
Технически, чтобы упростить вычисления и не запоминать все наблюдения,
можно воспользоваться следующей эквивалентной процедурой. Рассмотрим
последовательность {wn}, определенную рекурсивными соотношениями
wk = [wk-\ +7fc)+> k > !>
+ m χ ι ι gi(xn) (16)
x^ = тах(0,ж), 7n = — lnrn = -in—:—-.
52 (Xn)
Основные свойства последовательности wn мы сформулируем в виде леммы.
Лемма 1. Уравнение (16) имеет решение
wn = тах(гУо + Гп, та,х(Гп-Гл)) = Гп + тах (ΐϋ0,Γη),
где
η
Γη = Уль Г~ = max (-Г*).
Если 7^ независимы и одинаково распределены, как 7, Е7 < 0> шо Рас~
пределение цепи Маркова wn сходится к стационарному распределению
величины w = Г^ = sup (—Г^).
Если уравнение φΊ{\) = Ее*7 = 1 имеет решение μ > 0, то
P(w > χ) < β~μχ.
.Бели дополнительно φ'Ί(μ) < оо, то
P(u> > χ) ~ ce_/iX, 0 < с < 1.
Утверждение леммы вытекает из результатов глав 1, 4 в [12].
Из леммы при wq = 0 получаем, что wm = lni?(0^) — 1пД(га), а 0^
совпадает со значением т — s(m), где s(m) — наименьшее значение s, при
котором wm-s = 0.
Итак, наряду с (15) мы можем положить также
и = i/(JV) = min {m: wm^ N + b{m)}. (17)
Такой момент остановки называют моментом, полученным методом
кумулятивных сумм (CUSUM). Этот метод в случае Ь(т) = 0 был предложен
в [71, 90]. Ясно, что Ρ\ν < оо) = 1, так как при т > θ в силу усиленного
568 Гл. 5- Статистика разнораспределенных наблюдений
закона больших чисел wm+k > ck, 0 < с < — Έζχ, при всех достаточно
больших к. __
Если к < Θ, то распределение Wk совпадает с распределением Sk-i =
= max Sj, которое монотонно сходится к распределению 5+ = sup 5,.
ο^α-ι J i^o 3
Поэтому если N + b(m) — const, a θ велико, то событие {wm ^ N + b(m)}
рано или поздно произойдет, так что вероятность Ρ#(ζ/ < θ) близка к 1 и
момент остановки ν с высокой вероятностью будет «ложным». Стало быть,
для того чтобы избежать этого, мы должны выбирать растущие
последовательности 6(m) t со (по возможности медленно растущие, чтобы ν — θ было
не очень велико). Пусть b(m) t оо так, что
00
к=1
(Можно взять, например, Ь(к) = In к 4- (1 4- β) In In к, β > 0 при к ^ 3;
6(1) = 6(2) = 0. Любая такая последовательность будет верхней для {wk}
при θ = оо, а последовательность Ь(к) = lnfc + (1 — β) In In/с, β > О, —
нижней последовательностью.)
Свойства момента остановки ν = ν(Ν) ({ζ/ ^ η} Ε σ(χι,.. .,χη)),
определенного в (17), описываются следующим утверждением. Чтобы упростить
рассуждения, мы будем предполагать, что распределение —& непрерывно в
области (0, оо). Каким образом обойти технические трудности, возникающие
при нарушении этого условия, отражено в замечании 2 к теореме 8.
Обозначим P(t) = P{t,N) = Pt{v{N) < ί).
Теорема 5. Пусть β > О,
оо
b(fc) = lnfc+(l+/3)lnln(fc), 6 = 2 + 5^fc"1(ln(A;)r(1+«.
з
Тогда при всех t
P{t) < feT*. (18)
Если распределение —ξ{ непрерывно в (0, оо), то P(t) и Р(оо) непрерывно
зависят от N и для любого ε < во существует Ν = Ν(ε), являющееся
решением уравнения Р(оо, Ν) = ε, так что P(t) t -P(oo) = ε при t —> оо,
где £о = Роо { Μ {wk ^ &(&)} ] · Кроме того, для нерешетчатых ζι
\k=i J
Εί{^1>1)^Έ1{-Ρ(ζ -^(^)+^-^Етах(5+^+) + Ех)+о(1),
(19)
где ρ = ρ — l(G2,Gi), S+ и Z+ независимы, χ есть величина перескока
через бесконечно удаленный барьер последовательности сумм —Ζ^. Если
Ε
ζί решетчаты, то слагаемые —^ 4- о(1) в правой части (19) следует
Ρ
заменить функцией, ограниченной известной постоянной.
§ 72. Задача о разладке
569
Доказательство. Оценка (18) вытекает из очевидного соотношения
ft-\ \ t-\
P(t) = Pt(i/ < ί) = Ρ* ( {J{™k >N + b(k)} ζ £P(S+ > N + b(k)) <
оо
<е-ЛГ£е-^)=Ье"Лг. (20)
Далее, если распределение —& непрерывно на (0, оо), то непрерывными
будут и распределения Wk на (0, оо). Стало быть, P(t) и Р(оо) в силу (20)
будут непрерывно зависеть от /V, так как вероятность скачка в точке N оце-
00
нивается суммой \JP(wfc = N + b(k)). Далее,
P(t) = Poo(\J{wk>N + b(k)}j fP(oo).
Таким образом, функция Р(оо) = P(oo,iV) с ростом N > 0 монотонно и
непрерывно убывает от εο до 0. Положив Ν(ε) равным решению уравнения
P(oo,iV) = ε, мы получим утверждение теоремы, касающееся Ν(ε).
Докажем теперь (19). В силу (16), (17), (20) и леммы 1 мы имеем
представление
Et ίι/-- >ί) = Ет/,
где τ/ есть марковский момент
rj = min{fc: - Zk ^ JS(i,fc)},
S(i, k) = b{t + k)+N- max (г^, Ζ*),
(21)
Ζλ = max Ζ,·, ω* = 5*-1 и {Z^} независимы.
0<j<k d
Η)
Пусть для простоты /3^1. Тогда при t > max ( 3, - ) выполняется
b(t + k) <31n(i + fc) ^31ηί + 3- <31ηί+-^. Поэтому
η < min{fc: - Zk ^ ft(i + Α;) + Ν} < τ/ο =
= min|fc: -Zfc>31nt + iV+γ|, (22)
61ηί
Ετ/ ^ Erjo ^ Η const.
570 Гл. 5. Статистика разнораспределенных наблюдений
Кроме того, E|0t| < оо. Поэтому к мартингалу —Z£ = — Z^ — pfc
применима теорема Вальда-Дуба (см., например, [17, § 14.2]), в силу которой
Ε{-Ζη - μη) = 0,
1 - (23)
Εη = -Ε[6(ί + η) + Ν - max {wu Ζη) + χ*],
Ρ
где χι = — Ζη — Β{ί,η). Мы опускаем здесь доказательство того, что
supExi < оо (для ограниченных ^ это очевидно), и того, что для нерешет-
t
чатых ζί выполняется Е%е —► Εχ. Доказательство этих утверждений можно
найти в [23]. Далее, распределения Wt и Ζη сходятся вместе с
экспоненциальными моментами соответственно к распределению S+ и Z+. Кроме того,
в силу (22)
Ε6(ί + η) = Ш + О (^] = Ιηί + 0(1).
Изложенное вместе с (23) доказывает (19). Теорема доказана. <
Если вернуться к исходной задаче оценивания θ с помощью
последовательной процедуры, то из сказанного выше следует, что в качестве
приближений для Θ* естественно взять значение
0** = ι/-θ(ι/),
а в качестве приближения для Θ* — значение
Σ kR(k)
л** k=v-2s{v)
V ~ ν ·
Σ ад
k=v-2s{v)
Теорема 6.
θ** < θ*,
(24)
Кроме того, для любого ε > О
Ρί(|0*-0**)Ι>ε)->Ο (25)
при Ν —> оо, t —> оо.
Доказательство. Первое утверждение теоремы очевидно. Далее,
ΡΛΘ** < Θ*) = Р<(0** < 0*; ν > t) + Р<(0** < θ*· ν < ί). (26)
Событие {#** < 0*; ζ/ ^ £} означает, что в области k ^ t траектория InR(k)
будет иметь по крайней мере еще один максимум, превосходящий Θ**. Стало
§ 72. Задача о разладке
571
быть, Р^вероятность этого события не превосходит P(Z > N + b(t)) ^
Вторая вероятность в (26) не превосходит (см. (20))
Pt(i> < *К be"".
Доказательство последнего утверждения теоремы (25) мы предоставляем
читателю. Все необходимое для этого уже подготовлено. <
Вернемся к теореме 5. Из нее следует, что при фиксированной
вероятности ложной тревоги J*t(v < t) « ε среднее значение «задержки» с объявле-
1 л.
нием тревоги Щ{у — θ/и > Θ) имеет при больших θ порядок —. Оказы-
Р
вается, что в широких предположениях улучшить (уменьшить) величину
этой задержки в классе произвольных моментов остановки г ({г ^ η} Ε
£ σ(χ,..., хп)) с той же вероятностью ложной тревоги Р*(т < t) невозможно.
Чтобы сформулировать более точное утверждение, введем в рассмотрение
классы асимптотически «однородных» (ср. с определениями 2, 3)
марковских моментов.
Определение 5. Момент остановки г называется асимптотически
однородным, если существует
limEt(r-*/0<) o<«<oo. (27)
Класс таких моментов, для которых Pt(v < t) -+ ε при t —> ос, обозначим
через -К"(с).
Теорема 7. Для любого момента остановки г G К^ выполняется
ν > 1/р.
Если не требовать существования предела (27), то из доказательства этой
теоремы, приведенного в приложении VII, будет следовать, что
г Ее (г - t/r > t) ^ 1
lim sup г—£ > -.
t-+oo In t p
Итак, из теорем 5 и 7 вытекает, что для момента остановки ι/,
определенного в (17), нижняя граница 1/р возможных значений υ достигается.
В этом смысле момент и является асимптотически оптимальным. В
приложении VII будет построен еще один асимптотически оптимальный момент
остановки, который в ряде случаев может быть более предпочтительным.
Приведем теперь утверждение об оптимальном байесовском моменте
остановки в задаче о разладке, на которое мы будем опираться при
доказательстве теоремы 7 в приложении VII и которое представляет самостоятельный
интерес.
Итак, пусть задано априорное распределение Q — {q{n) = Ρ (θ = η)}.
Обозначим Хп = (χι,. ..,χη). Тогда определено апостериорное распределе-
572 Гл. 5. Статистика разнораспределенных наблюдений
ние
?№) = #«
q(k)R(k)
Σ qWWn) Σ 4(i)R(i) + Щп + l)Qn
(28)
i=l
i=l
где fk{Xn) и R(k) определяются так же, как в (1), (2), Qn = \^ q{%).
i=n+1
Положим
Q (η/ΛΓ„) = Ρ (0 ^ η/Χη) = £ ς (Λ/Χη)
/ Ν"1
д(п + 1)дп
fc=l
Е?(0ВД
\ ί=1
/
и определим момент остановки
Σ в(0Д(0
r(A) = min{n ^ 1: Q [n/Xn) ^ A} = min < η ^ 1:
f=l
^
u(n + i)gn i-л
Вероятность ложной тревоги Pq(t(A) < б) равна
00
a(A) = Pq(t(A) <Θ) = Σ Q(n)Pn(r(A) < η).
(29)
71=1
Обозначим через i^(£)g) класс всех моментов остановки т, для которых
Pq(t<0)<6.
Теорема 8. Пусть Αε — решение уравнения а(А) = ε. Тогда
момент остановки τ(Αε) G -K(£,q) является оптимальным в Кит в
следующем смысле: для любого τ G Кид) выполняется
Вя(г-в)+>Ед(т(Ае)-в)+. (30)
Если Pq(t < θ) = ε, mo (30) эквивалентно неравенству
Доказательство этой теоремы для геометрического априорного
распределения
g(n) = (l-p)"-1p, n = 1,2,..., (31)
содержится в [138]. В этом случае мы и будем пользоваться этой
теоремой для доказательства теоремы 7 в приложении VII, хотя ее утверждение
остается справедливым для любого априорного распределения.
§ 72. Задача о разладке
573
Замечание 1. Нетрудно видеть (ср. с теоремой 5), что
Pt(r(A) < t) = Pt Ш {Q (k/Xk) > A})
будет непрерывно зависеть от А, если распределения & (и, стало быть, R(i))
непрерывны. В этом случае а(А) в (29) также непрерывно зависит от А.
Так как, кроме того, а(А) монотонно убывает по А,
а{А) = Р{т{А) < Θ) = 1 - Р(0 < τ{Α)) =
= 1-ΕΈ>(θ<^-) <1-Λ, (32)
V Χτ(Α))
то для любого ε Ε (0,1) существует единственное решение Αε уравнения
α(Α) = ε. Отметим также, что если все q(n) малы, то «перескок» через
уровень А будет тоже мал и наряду с (32) будет справедливо приближенное
равенство а(А) « 1 — А. Например, если в (31) ρ —> 0, то а(А) —> 1 — А,
Αε -* 1 - ε.
Замечание 2. Предположение о непрерывности распределения ξ^ (в
области (—оо,0)) делалось нами также в теореме 5, чтобы обеспечить
непрерывность функции Р(оо, Ν)> Эти предположения о непрерывности ξ{ в
теоремах 5, 8 не носят принципиального характера и могут быть обойдены
путем следующей рандомизации процедуры принятия решения. Пусть,
например, мы находимся в условиях теоремы 5 и монотонно убывающая по N
функция
Р(оо, Ν) = РооИ^) < оо) = Ρ I \J{wk > b(k) + Ν} J
такова, что уравнение Р(оо, N) = ε для заданного фиксированного ε > 0 не
имеет решения. Это означает, что найдется точка Ν(ε), в которой Р(оо, iV)
имеет скачок,
Р(оо, Ν{ε) - 0) = ει > ε, Р(оо, Ν {ε) + 0) = ε2 < ε.
Введем случайную величину ζ/(Ν(ε),ρ), которая при первом попадании w^
в область (b(k) + Ν(ε), оо) ведет себя как ν{Ν). Если же Wk = £>(&) + Ν(ε),
то «тревога» о разладке объявляется с вероятностью ρ независимо от Х\
с дополнительной вероятностью 1 — ρ испытания продолжаются по той же
схеме: либо до первого попадания w^ в {b(k) + Ν(ε),οο) (и тогда
объявляется тревога), либо до следующего попадания Wk в точку b(k) + Ν(ε), и
тогда повторяется процедура «случайного розыгрыша» решения, описанная
выше. Очевидно, Ροο(^(Ν(ε), 1) < оо) = Ρ00(ι^(Ν(ε)) < оо) = εχ > ε,
Ροο(ζ/(Λί(ε),0) < оо) = Ρ00(ι/(Ν(ε) + 0) < оо) = ε2 > ε. Кроме того,
Poo {ν {Ν (ε), ρ) < оо) непрерывным и монотонным образом зависит от р.
Поэтому найдется ρ(ε) Ε (0,1) такое, что Έ>00(^(Ν(ε),ρ(ε)) < оо) = ε.
Далее, ν(Ν,ρ) есть вновь момент остановки, но уже относительно
последовательности (χχ,ωι),..., (χη,α;η), где ω\ принимают значения 1 с
вероятностью ρ и 0 с вероятностью 1 — ρ независимо от X и других значений ω^.
574 Гл. 5. Статистика разнораспределенных наблюдений
Нетрудно проверить, что все остальные рассмотрения в доказательстве
теоремы 5 сохранят свою силу применительно к v{N,p).
Аналогичные модификации можно осуществить и относительно момента
остановки т(А) в теореме 8, после которых уравнение &{А) = ε всегда будет
иметь решение.
Таким образом, мы можем считать, что предположения о
непрерывности ξί в теоремах 5, 8 не ограничивают общности.
Теоремы 2-8 (см. также теорему 2 из приложения VII) дают нам вид
асимптотически оптимальных статистик, которые следует использовать в
задачах о разладке при больших 0. Однако теорема 5 оставляет
существенный произвол в выборе статистической процедуры. Речь идет о выборе
взаимосвязанных компонент N и b(k) криволинейной границы b{k) + N. Если
0 очень велико, то, видимо, предпочтение следует отдавать «пологим»
границам с функцией 6(A), рассмотренной в теореме 5. Если же 0 не очень
велико, то для таких границ слагаемое Ν(ε) в оценке (19) может оказаться
существенно больше 6(0). Поэтому для уменьшения Ν(ε), возможно, следует
выбирать более быстро растущую функцию 6(£), например (1 + /?)1п£ или
даже βί. Отыскание оптимального соотношения между b(t) и N представляет
собой трудную задачу, так как явный вид зависимости Ν(ε) от ε и функции
b(t) нам неизвестен.
Глава б
ТЕОРЕТИКО-ИГРОВОЙ ПОДХОД К ЗАДАЧАМ
МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
В § 73-75 вводятся понятия обычной и статистической игр, выделяются
основные классы оптимальных стратегий.
В § 76, 77 рассмотрены методы отыскания оптимальных статистических
решений.
Материал § 78-80 посвящен построению асимптотически оптимальных
решающих правил.
§ 73. Предварительные замечания
В предыдущих главах было рассмотрено большое количество
разнообразных статистических задач. Всех их объединяет то обстоятельство, что
статистик на основании экспериментальных данных должен принять некоторое
решение. В теории оценок эти решения могут иметь форму точечных
оценок 0*, которые мы должны принять в качестве неизвестного параметра 0, в
теории проверки статистических гипотез — форму утверждений, в которых
говорится, какие предположения относительно природы исследуемого
объекта являются верными, а какие — нет. Эти решения, если они ошибочны,
сопряжены с последующими потерями. Например, ошибка в лабораторной
оценке (производимой с помощью выборки) содержания различных
компонент в руде может привести к нарушению оптимального режима плавки
и ухудшению качества выплавляемого металла. Это означает, что мы
понесем материальные потери, которые будут зависеть от величины ошибки.
Ошибка, касающаяся эффективности действия медицинского препарата,
который проверяется на выборочной группе больных, очевидно, тоже может
привести к потерям, которые мы для единообразия подхода также будем
считать возможным исчислять в некоторых единицах. Такое же
соглашение мы примем и относительно других задач статистики, в которых потери
не носят ясно выраженный материальный характер.
Изложенное позволяет нам в задачах математической статистики
выделить следующие четыре общих элемента. Эти элементы, собственно, и
определяют сущность каждой конкретной задачи. Для простоты в
последующем изложении мы будем снова, как и в гл. 1-3, иметь в виду лишь
задачи с одной выборкой X фиксированного объема гг. (Это не мешает
успешно применять полученные результаты к выборкам объема 1 в задачах
гл. 4, 5.) Эти элементы таковы.
1. Множество Θ, элементы которого 0 £ Θ определяют состояние
исследуемого объекта. Если θ известно, то необходимость построения
статистического решения отсутствует. Множество θ называют также
множеством параметров, хотя θ могут допускать и более широкое толкование (на-
576
Гл. 6. Теоретико-игровой подход
пример, множество Θ может быть очень богатым и совпадать с множеством
всех распределений на некотором пространстве X).
2. Чтобы получить информацию о неизвестном Θ, статистик ставит
эксперимент и производит наблюдения над некоторой случайной величиной,
распределение которой зависит от Θ. Другими словами, статистик
располагает выборкой X из распределения Р#. Как мы уже знаем, из выборки X
можно извлечь информацию о Р# и, стало быть, о 0. Можно считать, что
выполнено условие (Ао) (см. § 16) о взаимно однозначном соответствии между θ
и Ρ*.
3. В задачах статистики всегда определено множество D = {δ}
решений, которые может принимать статистик. В теории оценивания
множество D обычно совпадает с Θ, в задачах проверки гипотез множество D
конечно, а число его элементов равно числу проверяемых гипотез. Если θ
известно, то решение δ = φ(θ) определяется однозначно. Если θ неизвестно,
то решение δ желательно выбрать в известном смысле оптимально. Но
оптимизация решений требует, чтобы мы имели возможность их сравнивать.
Для этого будем предполагать, что задана функция потерь, определяющая
количественно последствия принятия решений.
4. Функция потерь ζν(δ,θ) определена на β χ θ и указывает, какие
потери мы будем нести, если примем решение δ, а исследуемый объект, к
которому относится решение, находится в состоянии 0. Будем считать, что
ιυ{δ,θ) > О при δ ф φ{θ), υ){φ{θ),θ) = 0.
Если из перечисленных четырех элементов убрать п. 2 об
экспериментальных данных, то мы получим объект, представляющий собой обычную
игру двух лиц, игру, в которой роль первого игрока играет статистик
(исследователь), а второго — природа.
§ 74. Основные понятия и теоремы, связанные
с игрой двух лиц
1. Игра двух лиц
Определение 1. Игрой двух лиц называется тройка (D, Θ, w),
составленная из множеств D и Θ и функции ю, отображающей DxQ в полупрямую
[0,оо). Элементы δ множества D называются стратегиями (действиями)
I игрока, элементы 0 £ θ — стратегиями II игрока, a w есть функция
потерь I игрока (или функция выигрыша второго игрока), определяющая
потери νύ{δ,θ), которые будет нести I игрок, если он выберет стратегию δ, а
II игрок — стратегию 0.
Основная задача теории игр двух лиц состоит в выборе оптимальной
стратегии I игрока, которого мы часто будем отождествлять с собой. Для
этого множество стратегий нужно как-то упорядочить. Сделать это
непросто, так как потери w{6, θ), с помощью которых мы должны производить
упорядочение, зависят от двух аргументов, так что для каждого 0
стратегия δ, минимизирующая w(6, θ), будет, вообще говоря, своя.
Определение 2. Будем говорить, что стратегия δ\ лучше, чем#2, если
η)(δι,θ) ^ш(62,в) при всех 0ев (1)
и существует по крайней мере одно значение θ\ £ θ, при котором η)(δ\, θ\) <
<ιι/(<*2,0ι).
§ 74. Основные понятия и теоремы, связанные с игрой двух лиц 577
Если выполнено лишь (1), то мы будем говорить, что стратегия δ\ не
хуже, чем #2-
Стратегию #о, для которой
ю($о,в) ^ w(6,9) при всех δ и 0,
будем называть равномерно оптимальной (или равномерно наилучшей).
Равномерно наилучшая стратегия обеспечивает наименьшие потери при
всех 0. Однако, как правило, такие стратегии не существуют.
Отметим следующие три подхода к исследованию оптимальных
стратегий I игрока:
— отыскание равномерно оптимальных стратегий в подклассах;
— отыскание байесовских и минимаксных стратегий;
— изучение совокупности всех неулучшаемых стратегий (так
называемого полного класса стратегий).
2. Равномерно оптимальные стратегии в подклассах. Применительно к
задачам математической статистики часто используется следующий прием
(см. §77). Из некоторых соображений, не связанных непосредственно с
потерями (соображения симметрии, естественность процедуры, простота
вычислений и др.), иногда оказывается возможным сузить класс
рассматриваемых стратегии. Если это сужение оказывается таким, что после него
существует равномерно оптимальная стратегия, то тем самым проблема выбора
стратегии решается. Этот подход необходимо сопровождать исследованиями
вопроса о том, не утратили ли мы путем сужения класса стратегий
возможности получения существенно лучшего результата. Примеры использования
такого подхода, относящиеся, правда, к более сложному объекту —
статистическим играм, будут приведены в последующих двух параграфах. Читатель
уже знает о них по гл. 2, 3, где рассматривались наилучшие (эффективные)
оценки в подклассе несмещенных оценок и равномерно наиболее мощные
критерии в подклассах всех инвариантных или несмещенных критериев.
3. Байесовские стратегии. Они возникают в тех случаях, когда второй
игрок выбирает свою стратегию случайным образом, с некоторым
распределением (известным или неизвестным) на Θ.
Чтобы иметь возможность рассматривать в дальнейшем «случайные»
стратегии, мы будем предполагать, что на Θ и D выделены некоторые
естественные σ-алгебры подмножеств #θ и 3χ>. Тогда на (Θ,^θ), {D,$d)
можно определить распределения Q и π соответственно, так что (e,#e,Q),
(D,$d,k) будет вероятностными пространствами.
Задание распределений π и Q индуцирует вероятностное пространство
(D χ Θ,37)χθ5π χ Q)> где $Dxe есть σ-алгебра, порожденная прямыми
произведениями множеств из #d и #θ· Выбор σ-алгебр #d и #θ должен быть
таким, чтобы выполнялись следующие два условия.
1· 3d и 5ό содержат одноточечные множества {δ} и {Θ}.
2. Функция потерь w(6,9) измерима относительно $Dxe-
Определение 3. Распределения π на {D,$d) и Q на (θ,#θ) мы
будем называть смешанными или рандомизированными стратегиями
соответственно I и II игроков.
578
Гл. 6. Теоретико-игровой подход
Распределение Q мы часто будем называть априорным. Смысл этого
термина должен быть ясен из гл. 2, 3. Он будет пояснен дополнительно в
следующем параграфе.
Множества всех смешанных стратегий I и II игроков (т.е. множества
всех распределений на (£>,3т>) и (Θ,#θ)) обозначим через D и Θ. Так как
5d и #θ содержат одноточечные множества, то D и Θ будут содержать
распределения, сосредоточенные в одной точке, и, стало быть, мы можем
считать, что D и Θ содержат в себе стратегии δ и 0, которые, чтобы иметь
возможность их выделить, мы будем называть чистыми стратегиями.
Соглашение, по которому мы будем распределения из D и Θ, сосредоточенные
в одной точке δ или 0, обозначать соответственно теми же символами δ и 0,
нигде к недоразумениям не приведет.
Определим теперь потери χν(π, Q) при использовании смешанных
стратегий равенством
tZ/(7r, Q) = MnxQw{6,9) = J w{u,t)n(du)Q{dt). (2)
Таким образом, наряду с исходной игрой мы можем рассматривать игру
(Ό,Θ,ίν) с функцией потерь (2), которая называется усреднением или
рандомизацией игры (D,Q,w).
В соответствии с принятым соглашением мы будем писать
*>(π(δ)> Q) = ™№ Q)> ™(π, Q(0)) = г5(тг, 0),
ΰ(δ,θ) =w(i,0),
если Arm и Q(0\ есть распределения, сосредоточенные соответственно в
точках δ и 0.
Очевидно, что рандомизация игры (D, 9,ги) означает переход к игре с
более богатыми множествами стратегий, по отношению к которой исходная
пара является «вложенной» — она получается, если рассматривать лишь
чистые стратегии обоих игроков. Задачи упорядочения стратегий в играх
(D, Э,гу) и (D, Θ, гу), как мы увидим, тесно связаны.
Определение 4. Стратегия π = πς>, для которой
w(ttq,Q) = inftt;(7r,Q),
π
называется байесовской, соответствующей априорному
распределению Q.
Таким образом, байесовская стратегия есть не что иное, как наилучшая
стратегия π при данном Q в усредненной игре.
Стратегия δη G D, для которой w(6n,Q) = inf iu(7r,Q), называется чи-
π
стой байесовской.
Теорема 1. Если для данного Q существует смешанная
байесовская стратегия πη, то существует и чистая байесовская стратегия δη
такая, что
§ 74. Основные понятия и теоремы, связанные с игрой двух лиц 579
Доказательство почти очевидно. Обозначим a = w(kq,Q). Ясно,
что
w(<5,Q) ^ infi?(7,Q) >a.
δ
Если допустить, что ύΊ(δ, Q) > α при всех ί, то, производя усреднение по δ
с помощью 7гд, получим
a = / w{u, Q)kq(cIu) > a.
Это противоречие доказывает теорему. <
Таким образом, если inf {5(π, Q) достигается, то он достигается и на чис-
π
тых стратегиях.
Если inf w(6, Q) не достигается, то байесовские стратегии не существуют.
δ
В этом случае полезным оказывается понятие ε-байесовской стратегии,
которая существует всегда и определяется как стратегия ig, для которой
tf(iQ,Q) <infu(£,Q)+£ (3)
δ
для заданного ε > 0. Однако в дальнейшем для упрощения изложения мы
будем обычно ограничиваться теми задачами, в которых байесовские
стратегии существуют. В связи с этим везде, где это понадобится, мы будем
считать существование байесовских стратегий обеспеченным. Это имеет
место, например, во всех случаях, когда множество D конечно или когда D
есть метрический компакт, а функция w(g, Q) непрерывна «снизу» по 6:
liminftt;(£fc, Q) = w(#o><2)· Последнее свойство означает, что если 8^ —> 8о
и w(8k,Q) |, то w(8k,Q) I w{8o,Q)· В нашем случае всегда найдется
последовательность стратегий 8'k такая, что w(8'k,Q) I infu;(£, Q). Так как
δ
D — компакт, то из нее можно выделить подпоследовательность 8^
такую, что 8^ —> δο G Ό. Β силу изложенного выше получаем w(8k,Q) J,
I £>(#o,Q) = inf (£, Q). Это означает, что существует байесовская стратегия
δ
6q = J0. Можно приводить также и другие условия, обеспечивающие
существование байесовских стратегий, связанные, например, с выпуклостью
функции г5(£, Q)>
Вопрос о практическом использовании байесовских стратегий является
довольно тонким. Если наличие априорного распределения обусловлено
некоторым реальным физическим механизмом, то этот подход бесспорен. Но
байесовский подход можно оправдывать и в тех случаях, когда его
связывают с наличием некоторых, быть может, даже субъективных и не всегда
достаточно полных представлений, которые тем не менее сбрасывать со счета
нельзя. Более подробное обсуждение вопроса об использовании байесовского
подхода см. в п. 4.
4. Минимаксные стратегии. Если априорная информация относительно θ
отсутствует, то при упорядочении стратегий можно ориентироваться на
«наихудшую» стратегию противника. Если мы выберем стратегию δ, то макси-
580
Гл. 6. Теоретико-игровой подход
мальные потери составят
supw(i,0) = u;(i,t). (4)
Θ
Это количество зависит лишь от δ и так же, как и значения ιυ(δ, Q),
позволяет упорядочить δ.
Определение 5. Стратегия δ называется минимаксной, если
n;(i,t) =infu;(i,t) = «>*· (5)
δ
Термин «минимаксный» образован из соединения наименований
операций в правой части соотношения
w(i,t) — minmaxw(6, θ),
δ θ
Очевидно, что минимаксные стратегии так же, как и байесовские, могут,
вообще говоря, не существовать. В этом случае аналогично (3) можно ввести
понятие ε-минимаксной стратегии. В последующих рассмотрениях будем
исходить из того, что sup и inf в (4), (5) достигаются.
Так как при любом θ
ιυ(δ,θ) <w(i,t) =ti7*,
то минимаксная стратегия δ характеризуется тем, что обеспечивает потери
I игрока в размере, не большем чем w*.
Определение 6. Значения
w* =infw(£,t) (w(i,t) = supw(<5,0)),
δ θ
iu* = supw(4, Θ) (гиЦ,0) = Ίηΐιυ(δ,θ))
Θ δ
называются соответственно верхней и нижней ценой игры. Если w* — w*,
то говорят, что существует цена игры, равная общему значению w* и гд*.
Из сказанного выше и соображений симметрии ясно^ что II игрок,
действуя аналогично первому и выбирая свою стратегию θ из тех же
минимаксных соображений, может всегда обеспечить себе выигрыш не меньше,
чем ги*. (Такую стратегию θ было бы правильнее называть максиминной,
но мы будем использовать для нее тот же термин: минимаксная стратегия.)
Стало быть, если существует цена игры, то, выбирая минимаксную
стратегию δ, мы обеспечим себе неулучшаемый результат в том смысле, что
если противник выберет 0, то никакая другая стратегия не даст нам потери,
меньшие, чем w* = w*. Очевидно, что w(S,0) = w* = iu*.
В общем случае всегда w* ^ w+, так как при всех δ и θ ιυ{δ, ΐ) ^ w(6, θ) ^
^ w(l,0) и, следовательно,
w* = inftu(£,t) > supii;(4,0) = w*. (6)
δ θ
§ 74. Основные понятия и теоремы, связанные с игрой двух лиц 581
Если w* > w*, то минимаксную стратегию δ можно улучшить, вводя
смешанные стратегии. В этом состоит одно из главных назначений
последних.
Минимаксные стратегии для усредненной игры (если они существуют)
обозначим соответственно символами π и Q и положим
w* = infsupu;(7r, Q), w* = supinf w(n,Q).
* Q Q ^
Покажем сначала, что при усреднении игры верхняя и нижняя цены
игры сближаются.
Теорема 2. Всегда справедливо
w* ^ w* ^ w* ^ w*.
Доказательство этой теоремы, как и теоремы 1, очень просто. Так
как усреднение игры можно производить в два этапа: сначала по
множеству D, а затем по Θ, то для доказательства достаточно рассмотреть лишь
частичное усреднение (Ρ,Θ,ΰ;) игры (Ζ),Θ,ΐί;). Имеем
w* = infsupu;(7r,0) ^ infsupw(5,0) = w*.
* θ δ θ
Так как при всех π
νί(π,θ) = [w{u,0)n(du) ^ infw{6,0) = w(|,0),
το ίηί{ϋ(π, θ) ^ ги(4,0),
π
ίδ* = supinf ΰ5(π,6) ^ supw(|,0) = ги*.
tf π θ
Неравенство w* ^ г?* доказано в (6). <
Фундаментальным фактом теории игр является так называемая теорема
о минимаксе, которая утверждает, что при весьма широких предположениях
усредненные игры имеют цену w* = w* и для них существуют
минимаксные стратегии.
Более точно это утверждение будет сформулировано в следующем
параграфе в более общей ситуации применительно к статистическим играм.
Исходная игра (£>, Θ, iu), особенно в случае, когда D πθ конечны, цены,
как правило, не имеет.
Пример 1. Рассмотрим простейшую игру, когда множества D и θ
двухточечные, D = {#ъ#2л ® = {^ь^}· Значения функции потерь w(S,9)
определяются матрицей ||tu(Ji,^)l|5 hj = 1,2, которую положим равной
10 II ^
L J . Это соответствует, например, игре с угадыванием, когда I игрок
угадывает, в какой руке II игрок спрятал монету. Угадывание означает нулевой
582
Гл. 6. Теоретико-игровой подход
проигрыш (ιν(δι,θι) = ^(#2,02) = 0), ошибка — проигрыш в размере 1
рубля (w(£i,02) = w(#2,0i) = 1)· Очевидно, что здесь w(^,t) = 1, w* = 1,
w(l,9i) = 0, w* = 0, так что игра не имеет цены, а I игрок не может себе
гарантировать проигрыш меньше чем 1 рубль. Само понятие минимаксной
стратегии здесь бесполезно.
Рассмотрим теперь усреднение этой игры. Здесь классы стратегий D
и Θ представляют собой совокупность всех распределений на двухточечном
множестве. Очевидно, каждое из распределений на D и Θ описывается одной
вероятностью ρ и q соответственно выбора стратегий δι ив\. Поэтому можно
считать, что D = [0,1], Θ = [0,1]. Потери I игрока в этой игре равны
™(р, ч) = Р(1 - ч) + 9(1 - Р) = Ρ + Ч - 2рд,
{р + 1 — 2р = 1 — ρ при 2р < 1,
ρ при 2р ^ 1,
Я* = 1/2.
Аналогично находим, что ΰ5* = 1/2. Таким образом, усредненная игра
уже имеет цену, и первый игрок, выбирая δχ и 6% с вероятностью ρ = 1 —ρ =
= 1/2, может гарантировать себе проигрыш не больше 1/2. Улучшить эту
стратегию нельзя, так как такой же выигрыш может гарантировать себе
II игрок, выбирая q = 1/2. Таким образом, стратегия ρ = 1/2 будет
минимаксной, соответствующей стратегии q = 1/2 второго игрока.
Если все же окажется, что усредненная игра не имеет цены (это может
быть только в играх специальной сложной конструкции), то повторное
усреднение не даст никаких результатов, поскольку это повторное усреднение по
существу будет совпадать с одинарным.
Байесовский и минимаксный подходы к решению игровых проблем
весьма распространены в повседневной человеческой деятельности. Байесовский
подход ориентирован на наличие некоторых представлений, хотя бы
приближенных, о поведении второго игрока. Минимаксный подход оправдан в тех
случаях, когда необходимо гарантировать себя от большого проигрыша.
Пример 2. Студент готовится к экзамену. Будем считать, что это не
идеальный студент и что у него не оказалось достаточно времени для того,
чтобы хорошо подготовить к сдаче весь материал. Кроме того, целью этого
студента является получение возможно более высокой оценки.
В описанных условиях студент может выучить на отлично лишь часть
материала. Поэтому для него возможны по крайней мере два пути: 1)
выучить на отлично лишь те разделы, которые по имеющимся сведениям чаще
всего спрашивает экзаменатор; 2) выучить все понемногу, чтобы
гарантировать себе хорошую или удовлетворительную оценку. Первый вариант будет
соответствовать байесовскому, второй — минимаксному подходу.
Ясно, что равномерно оптимальной стратегией здесь было бы выучить
весь материал, но по условию задачи она невозможна.
Минимаксные стратегии в конкретных ситуациях выглядят не всегда
разумными.
§ 74. Основные понятия и теоремы, связанные с игрой двух лиц 583
Пример 3. Пусть Θ = [0,1], а множество D = {^ь^г} состоит из двух
элементов. Функция потерь
определяется соотношениями (см. рис. 10)
™(£2,0)=4(1+ε)0(1-0).
Здесь tu(Ji,t) = 1, Ц*2?Т) = 1 + ε,
w* = 1, и минимаксной стратегией
будет ίχ, хотя при малых ε > 0 для
«большинства» значений θ
стратегия 02 будет лучше: τυ(<?2>0) < 1 при 0
11
«; = Ц£1? Θ)
из области
0-
1
>2
«/ = Ц<52, 0)
1 + ε
. Для
Рис. 10
«большинства» распределений Q на Θ = [0,1] (чья масса не
сосредоточена в окрестности точки θ = 1/2) байесовские стратегии также будут
совпадать с <$2·
Понятия байесовской и минимаксной стратегии тесно связаны между
собой. Следующее утверждение дает способ отыскания минимаксных
стратегий с помощью байесовских.
Определение 7. Стратегия π называется уравнивающей на
множестве Эо^С Θ, если
1) ζ/;(π,0) = с = const при Θ Ε Θο,
2) {υ(π, θ) ^ с при всех θ.
Теорема 3. Пусть существуют априорное распределение Q и
соответствующая ему байесовская стратегия 7Tq-, которая является
уравнивающей на носителе Nq распределения Q. Тогда π = Kq является
минимаксной стратегией.
Если Nq = Θ, то уравнивающая стратегия π делает игру второго игрока
«безразличной» — от него не зависящей (ср. с примером 1).
Доказательство теоремы 3. Обозначим
supw(n,0) = supu>(7r, Q) = ΰ;(π,|),
θ Q
inf t5(i, Q) = inf ад(тг, Q) = £5(4, Q).
S π
Нам надо убедиться, что
tf(*o>t) = inftS(7r,t)·
^ π
Это вытекает из следующих неравенств, справедливых для любого π:
г5(тг,Т) ^ t2(7r,Q) ^ u(ttq, Q) = / w(iCQ,t)Q(dt) = с > г5(тг^,Т). <
Иногда бывает полезным следующее небольшое обобщение теоремы 3.
584
Гл. 6. Теоретико-игровой подход
Теорема ЗА. Пусть существуют последовательности Q п, 7Tq
такие, что w{kq , Qn) ~* с· Пусть, кроме того, существует стратегия π,
обладающая свойством w(tt, θ) ^ с при всех 0. Тогда π — минимаксная
стратегия.
Доказательство столь же просто:
Это может быть только тогда, когда infi5(7r,t) ^ с. Так как с ^ ί^π,Ι), то
π
теорема доказана. <
Распределение Q в теореме 3, определяющее байесовскую минимаксную
стратегию 7Tq, обладает одним замечательным свойством: оно будет
наихудшим в том смысле, что для него байесовские потери w{7Tq,Q) будут
максимальными.
Определение 8. Распределение Q называется наименее
благоприятным или наихудшим, если
wfeQ) =supw^Q,Q)
Q
или, другими словами, г5Ц, Q) = supu;(i, Q).
Q
Последнее соотношение означает, что определение наихудшего
распределения в наших условиях совпадает с определением минимаксной (макси-
минной) стратегии Q.
Теорема 4. Пусть игра (D,®,w) имеет цену, а оба игрока имеют
минимаксные стратегии ?uQ. Тогда распределение Q является
наихудшим, α π является байесовской стратегией π = tTq, отвечающей Q.
Замечание 1. Из того, что в силу теоремы 1 наряду с ttq существует
чистая байесовская стратегия Sq, вовсе не следует, что последняя также
будет минимаксной.
Замечание 2. В силу фундаментальной теоремы о минимаксах
условие теоремы 4 о существовании цены усредненной игры и минимаксных
стратегий не следует рассматривать как существенное ограничение.
Замечание 3. Из соображений симметрии и_теоремы 4 следует, что
распределение π также является «наихудшим», a Q является байесовской
стратегией, отвечающей π.
Нам понадобится следующее вспомогательное утверждение, которое мы
сформулируем в терминах исходной (не усредненной) игры.
Лемма 1. Пусть игра (ϋ,Θ,ζν) имеет цену и минимаксные
стратегии δ, θ обоих игроков
w(5,t) = inf ω(ί,Τ)ι «/Ц,ё) = supw(4,0).
δ θ
§ 74. Основные понятия и теоремы, связанные с игрой двух лиц 585
Тогда
w(SA)=w(S,e)=w(l9), (7)
w* =w(6,e)=w*. (8)
Обратно, если при некоторых δ, θ выполнено (7), то справедливо (8),
α δ, θ являются минимаксными стратегиями.
Доказательство. При всех δ и θ имеем
ια(δΛ)>υ>(δ,θ)2υ>(ΐ,Θ).
Отсюда следует, что
w* = w{Srf) ^ υ)(δ,θ) ^ w{i,9) = w*. (9)
Так как по условию w* = w*, то в (9) все знаки неравенства надо
заменить равенствами. Это доказывает (7), (8).
Обратно, если справедливо (7), то
w* = infiu(<5, t) ^ w(i,t) = w(l)0) ^ supw(i, θ) = ги*.
δ θ
Так как всегда w* ^ w+, то приведенные неравенства означают, что w* = u>*,
а стратегии δ, θ являются минимаксными. Лемма доказана. <
Точка {δ,θ), обладающая свойством (7), называется седловой точкой, а
лемма 1 — критерием наличия седловой точки неулучшаемых минимаксных
стратегий.
Доказательство теоремы 4. Тот факт, что Q является
наихудшим распределением, следует непосредственно из определения 8. Применим
теперь лемму 1 к усредненной игре (D,U,w). Получим тогда, что
Отсюда следует, что π есть байесовская стратегия, соответствующая Q.
Теорема доказана. <
Из леммы 1 вытекает также следующий критерий минимаксности
стратегий в игре (D,<d,w).
Теорема 5. Пусть стратегии 7r^Q таковы, что π является
байесовской относительно Q: π = 7Tq\ Q является оптимальной
относительно π: Q — Qtt. Тогда π и Q — минимаксные стратегии,
гй* = ΰ)(π, Q) = w*.
Доказательство немедленно следует из леммы 1, так как π, Q
удовлетворяют соотношениям
w{W, Q) = й(ттд, Q) = w{i, Q), w{n, Q) = w{n, Qw) = τ2(π, t),
которые влекут за собой (7). <
586
Гл. 6. Теоретико-игровой подход
Содержание приведенных утверждений можно резюмировать (с
некоторыми дополнениями) в виде следующего предложения, которое весьма полно
описывает связь минимаксных и байесовских стратегий. Введем в
рассмотрение следующие условия.
А. Игра (Ρ,Θ,ί?) имеет цену и минимаксные стратегии.
1. Стратегия π является минимаксной.
2. Стратегия π является байесовской и уравнивающей.
3. Стратегия π является байесовской и соответствует наихудшему
распределению Q: π = 7Tq. Стратегия Q является байесовской по
отношению к π.
Теорема 6. Справедливы следующие импликации:
1,А^З; 3=>2,А; 3=>1,А, 2 => 1.
Отсюда следует, что при выполнении А условия 1-3 эквивалентны.
Доказательство. Первое, третье и четвертое соотношения доказаны
соответственно в теоремах 4, 5 и 3 (см. также замечание 3). Оставшаяся
вторая импликация доказана в теореме 5 лишь частично. Чтобы показать,
что справедливо 3 => 2, надо доказать, что байесовская стратегия,
соответствующая наихудшему распределению, является уравнивающей. Так как π
в условии 3 в силу теоремы 5 является минимаксной стратегией, то мы
будем иметь
ίίί* = ΰ;(π, Q) = / ΰ5(π, t)Q(dt) < supu;(7r, t) = ΰ>(π,|) = infz5(7r,t) = w*.
Это означает, что / ΰ;(π, t)Q(dt) = supui(7f, t) и, стало быть,
w(W,t) = t5(7r,t) п. в. [Q].
Так как, кроме того, всегда ΰί(π, t) ^ w(n,ΐ), то π является уравнивающей
стратегией. Теорема доказана. <
Вернемся к вопросу о применении рассматриваемых классов стратегий.
Допустим, что мы не можем выделить удовлетворяющий нас подкласс
стратегий, среди которых существовала бы равномерно наилучшая. Допустим,
далее, что мы располагаем некоторыми представлениями о поведении
второго игрока (т.е. об ожидаемых значениях 0), недостаточными, однако,
для применения байесовского подхода в его чистом виде. Минимаксный
подход в этих условиях будет означать пренебрежение имеющейся у нас
информацией. В такой ситуации можно использовать промежуточный подход,
который выглядит следующим образом.
1. Сначала нужно оградить себя от высоких потерь, т.е. рассматривать
лишь те стратегии δ, для которых ги(£, 0) < w* + а при подходящем
значении а > 0 и при всех Θ. Множество стратегий, удовлетворяющих этому
неравенству, обозначим символом Da.
2. В этом подмножестве (т.е. в игре (2}α,Θ,ΐϋ)) уже можно
применять байесовский подход с использованием доступных нам приближений
для априорного распределения Q.
§ 75. Статистические игры 587
Такой смешанный подход также постоянно используется в
повседневной человеческой деятельности. В условиях примера 2 этот подход будет
означать, что студент совсем немного (чтобы избежать
неудовлетворительной оценки) выучит весь материал, а затем получше выучит то, что чаще
спрашивают.
Математически использование смешанного подхода должно
сопровождаться исследованиями устойчивости байесовских потерь в игре (£)а,0,ги)
при допустимых изменениях Q.
5. Полный класс стратегий. Если все описанные выше подходы не дают
возможности однозначно выбрать стратегию, то решение задачи
ограничивают описанием так называемого полного класса стратегий.
Определение 9. Класс стратегий Dc С D называется полным, если
для любого π £ Dc существует стратегия πο £ Dc, которая лучше, чем π.
Класс Dq называется минимальным полным классом, если Dq есть
полный класс, но никакой его собственный подкласс полным классом не
является.
Другими словами, минимальный полный класс состоит из одних неулуч-
шаемых стратегий.
Польза построения минимального полного класса или полного класса,
который существенно меньше, чем D, очевидна. Это позволяет
редуцировать игру (Ζ),Θ,ΰ>) к игре (Dc, Θ,ΰ;), которая может иметь более простую
структуру.
Вторая фундаментальная теорема теории игр состоит в том, что при
широких предположениях класс всех байесовских стратегий {πρ}, QE0,
является полным классом. Точная формулировка этой теоремы будет
приведена в следующем параграфе. В некоторых случаях полные классы можно
строить и непосредственно, используя структуру игры. Допустим, например,
что существует разбиение пространства D на подмножества Df^ D = \) J2&,
ье в
£)6ι φ Db2 при Ь\ Φ &2 такое, что в каждом из этих подмножеств (т. е. для
игр {Db, Θ, w)) существует равномерно оптимальная стратегия 8ь £ D^. Ясно,
что в этом случае класс Dc = {6ь}ьев будет полным. Такой подход к
построению полного класса будет проиллюстрирован в § 75.
§ 75· Статистические игры
1. Описание статистических игр. Основные элементы статистической
игры образуются той же тройкой (ΐ),θ,ΐί;), которая рассматривалась нами
в предыдущем параграфе. Однако к ним добавляется следующее.
1. В статистических играх роль I игрока играет статистик
(исследователь), роль II игрока — природа (точнее, природа того явления, которое
исследуется). Последняя выбирает (или «загадывает») параметр (стратегию) 0,
который нам неизвестен и который определяет состояние исследуемого
объекта. Большинство задач математической статистики так или иначе связано
с принятием таких решений δ, которое как можно более точно «угадывали»
бы это неизвестное 0. При этом следует иметь в виду, что природа как игрок
не стремится к максимальному выигрышу (т.е. не стремится причинить
588
Гл. 6. Теоретико-игровой подход
нам максимальные потери) и в этом смысле является игроком,
«беспристрастным» к выбору своих стратегий.
2. В статистических играх мы имеем возможность «разведывать»
стратегию природы с помощью экспериментов, которые дают нам в виде выборки
X €= Р# «наводящие» указания на то, каким может быть значение Θ. Итак,
элементом статистической игры является выборка X объема *) η из
распределения Р#, зависящего от 0.
В этих условиях наше решение δ мы должны выбирать, очевидно, в
зависимости от X. Стало быть, стратегиями статистика становятся теперь все
функции δ(Χ), отображающие Хп в D. Эти функции δ(Χ) называются
решающими функциями или решающими правилами, или просто решениями.
Мы ограничимся рассмотрением лишь функций δ{Χ), осуществляющих
измеримое отображение (Afn,55^) в (ДЗЪ). Множество всех таких функций
обозначим через 2λ
Множество стратегий II игрока (природы) Θ остается прежним.
Если мы воспользуемся решением δ(Χ), а природа выберет 0, то наши
потери составят ν)(δ(Χ),θ). Это есть случайная величина. Чтобы избежать
этого неудобства, естественно в качестве потерь для стратегий δ = δ(·) Ε V
и 0 £ Θ принять значение математического ожидания
\ν(δ(-),θ) = Εθτν(δ(Χ),θ) = f χν(δ(χ),θ)Ρβ(άχ), (1)
которое называется функцией риска (появление слова «риск» здесь
естественно, так как применение δ(·) дает случайный результат). Если
выполнено условие (Αμ) о наличии плотности fe(x) распределения Р#
относительно некоторой σ-конечной меры μ, то функцию риска можно записать в
виде
W(S(-),0) = J\ν(δ(χ),θ)Μχ)μη(άχ).
Мы можем дать теперь следующее
Определение 1. Статистической игрой называется тройка
(Х>, Θ, W), где Θ есть множество стратегий природы, Т> — множество всех
измеримых отображений пространства Xй в множество D, W определено
в (1). Для более полной характеризации статистической игры вместе с
тройкой (ϋ,Θ, W) можно считать также заданной пару (X, Р#), где X ^ Р#.
Пример 1. Пусть θ Ε [0,1] определяет содержание некоторой
химической компоненты руды, приготовленной для плавки. Если мы примем
решение, что доля этой компоненты равна δ φ 0, и в соответствии с этим
решением будет организован весь процесс плавки, то в результате качество
выплавленного металла будет хуже, чем при δ = 0, а расходы энергии выше.
Другими словами, мы будем нести потери ν)(δ, 0), которые будут тем больше,
*) В построениях этого параграфа мы могли бы, не ограничивая общности, считать, что
η = 1. Однако мы сохраним понятие выборки объема η с тем, чтобы, сохранить простые
связи с предыдущими результатами и с последующими рассмотрениями (§78-80).
Более общая и более сложная концепция статистической игры имеет дело с
неограниченной выборкой Хоо = (xi,X2,.. .)> использование элемента хп которой сопряжено с затратами
сп > 0 (см. [3, 112]).
§ 75. Статистические игры
589
ίοδ2
[с(1-
= W
при
- δ)2 при
кгЧ^а-
'4
ι4
чем больше £ отличается от 0. Предположим для простоты, что ιυ(δ,θ)
пропорциональна квадрату отклонения δ от 0:
υ)(δ,θ) = с(£-0)2.
(Если функция τν(δ, 0) гладкая и если рассматривать окрестность прямой
δ = 0, то упрощающим предположением здесь будет лишь независимость с
от 0.) В результате получим игру (D, Θ, w), у которой £> = [0,1], Θ = [0,1],
w(i,t) = supiu(£,0)
Таким образом, стратегия δ = 1/2 является минимаксной и гарантирует
потери не больше с/4. Так как ги* = 0, то эта игра цены не имеет.
Рандомизация игры минимаксную стратегию δ = 1/2 не улучшает (она дает
г5+ = с/4). Предоставляем читателю убедиться, что байесовская
стратегия ig здесь имеет вид ig = Eg0 = / tQ(dt) (это вытекает из равенств
w(6, Q) = cEg(£ - 0)2 = cEg(0 - Eg0)2 + cEg(£ - EQ0)2) и что наихудшее
распределение Q будет иметь вид Q({0}) = Q({1}) = 1/2. Очевидно, что
соответствующая ему байесовская стратегия есть 6q = 1/2.
Предположим теперь, что руда неоднородна и что мы имеем возможность
брать η проб руды. Эти пробы организованы так, что результаты
лабораторных анализов для содержания упомянутой компоненты в пробах будут
случайны и дадут нам независимые значения (χι,...,хп) = X, относительно
которых известно, что Exj = 0, Dx^ = 6(0). В этом случае решениями δ(Χ)
будут всевозможные оценки 0* = δ(Χ) параметра θ по выборке X. Риск
решающей функции δ(Χ) будет равен
\Υ{δ,θ) = όΕθ{δ{Χ)-θ)2,
и мы приходим к задаче отыскания оценки 0* = δ(Χ), минимизирующей в
том или ином смысле этот риск. Если положить, например, δχ(Χ) = χ, то
получим
*№,»>-£*а. (2)
П
Наибольшее значение 6(0) равно 0(1 — 0) и достигается на
распределении χι, сосредоточенном в точках 0 и 1. Так как такую возможность можно
исключить, то
6(0) < 0(1-0)*Л W{6ue)<j-.
4 4п
Таким образом, даже при η = 1 и при использовании, возможно, не
наилучшей стратегии мы получим результат, лучший чем для минимаксной
590
Гл. 6. Теоретико-игровой подход
стратегии в игре без выборки. Соотношение (2) показывает также, что риск
сходится к нулю при η —> оо и будет тем меньше, чем меньше Ъ{9). <
Из приведенного выше определения статистической игры видно, что
последняя обладает значительно более богатым множеством стратегий V и по
сравнению с исходной игрой (D,Q,w).
Как и в §74, наряду с игрой (Ρ, Θ, W), стратегии которой будем
называть чистыми, можно рассматривать рандомизированные или
смешанные игры (2?, θ, W). Здесь множество V является множеством отображений
π(Χ): Хп —> D. Эти отображения должны быть такими, чтобы значения
ϋί(π(Χ),θ)= fw{u,0)n{X,du)
Ό
были случайными величинами (7г(Х, А) есть вероятность множества А С D
в соответствии с решающим правилом π в точке X). Тогда по определению
полагаем
W{n{-),Q) = f f I'w{u,t)ic{x,du)Pt(dx)Q{dt).
θ Χη Ό
Стратегия π(Χ) называется рандомизированным решающим правилом.
Отношения частичного порядка между стратегиями, равномерно
наилучшие стратегии, байесовские и минимаксные стратегии, полные классы
стратегий для статистических игр определяются точно так же, как для игр
обычных (с заменой множества D на V, а функций w, w — на W, W).
На статистические игры полностью переносятся утверждения
теорем 73.1-73.6, так как последние с природой множества D никак не
связаны.
2. Классификация статистических игр. С природой множеств D и Θ
связана следующая классификация, выделяющая основные виды
статистических игр.
1. Если Θ = A, D = А, где А есть «телесное» подмножество в R*
(например, параллелепипед), w(t, t) = 0, w(t,u) > 0 при t φ и, то мы получим
задачи теории точечного оценивания неизвестного параметра Θ.
2. Если множества θ = [θ\,..., 0Г}, D = {ίι,..., δΓ} конечны и содержат
одинаковое число элементов, ιν(δ{,θί) = 0, w(6i10j) > 0 при г φ j, то мы
получим задачи проверки конечного числа простых гипотез.
3. Если Θ есть «телесная» область в R*, D = {ίι,^} состоит из двух
элементов, w(S\,θ) = 0 при θ Ε Θι, w{S<2,θ) = 0 при θ £ Θ2 (Θι U Θ2 пусто)
и w(Si,9) > 0 в остальных случаях, то мы приходим к задаче проверки
гипотез {Θ £ Θι} и {Θ £ Θ2}.
Возможны, конечно, и другие классы задач. Мы выделили эти три типа,
поскольку они рассматривались нами в гл. 2, 3. Мы рассматривали эти
задачи с чисто «статистических» позиций, что соответствует специальному
выбору функций w(S, θ): в первой группе задач потери определялись
среднеквадратичным уклонением, что соответствует функции потерь ιυ(δ,θ) = {δ — 0)2;
§ 75. Статистические игры
591
во второй группе задач потери определялись вероятностью ошибиться, что
соответствует функции
««,«,>-β;
То же относится и к третьей группе задач, в которой мы использовали
функцию потерь
/О при 0евь /1 при 0бвь
v ь ' \l при 0€θ2, V J \θ при 0<Εθ2.
Эти функции потерь, соответствующие чисто статистическому подходу к
проблемам, будем называть статистическими.
Приведенная классификация показывает, что никакой принципиальной
разницы между задачами теории оценивания и проверкой статистических
гипотез нет. Все дело в природе множеств θ и D и виде функций потерь.
На примере этой классификации можно отметить еще одно своеобразие
статистических игр (в дополнение к п. 1, 2 в начале этого параграфа); оно
состоит в том, что множество D в статистических играх либо совпадает с Θ,
либо представляет собой множество, более бедное, чем Θ.
3. Две фундаментальные теоремы теории статистических игр.
Сформулируем теперь основные результаты теории статистических игр. Мы уже
отмечали, что утверждения теорем 73.1-73.6 для статистических игр
полностью сохраняются, так как они с природой игр не связаны. Чтобы получить
две фундаментальные теоремы, упоминавшиеся в § 74, введем некоторые
предположения. Это далеко не самые общие предположения (иначе
формулировки и доказательства чрезвычайно усложнились бы), но они достаточно
широкие, чтобы охватить наиболее интересный и содержательный круг
задач и, в частности, задачи, рассмотренные в гл. 2, 3.
Условие (А). Каждое из множеств Θ и D либо конечно, либо
представляет собой компактное множество в Шк.
Как уже отмечалось, случай, когда θ конечно, a D С Шк, можно не
рассматривать. В остальных трех случаях мы будем предполагать, что функция
потерь ιυ(δ,θ) удовлетворяет следующему условию.
Условие (В). 1. Если D С Шк, Θ С R*, то функция w{8,9)
непрерывна на D χ Θ.
2. Если Θ С R*, a D = {δ\,.. ·,#Γ} конечно, то каждая из τ функций
w(Si,0), i = 1,.. .,τ, непрерывна на θ.
Если θ = {0ι,.. .,0Г} и D = {δχ,.. .,δΓ} конечны, то значения w(5i,9j),
i,j = l,...,r, могут быть произвольными.
Кроме того, мы потребуем, чтобы выполнялось
Условие (С). Мы располагаем выборкой X €= Р# из
распределения Р#, абсолютно непрерывного при всех θ относительно некоторой
592
Гл. 6. Теоретико-игровой подход
σ-конечной меры μ. Если θ С КЛ, то плотность --.— (х) = fe(x)
непрерывна в £ι(Λ\93;τ,μ) относительно Θ, т. е. при 9т —> θ
I
\/вп(х) - Μχ)\μ(άχ)-Ю. (3)
Нетрудно проверить, что обычная непрерывность fe(x) по θ для [μ] п. в.
влечет за собой непрерывность (3).
Следующие две теоремы носят название фундаментальных теорем
теории статистических игр.
Теорема L Если выполнены условия (А), (В), (С), то усредненная
игра (Ζ>, Θ, W) имеет цену и минимаксные стратегии π(Χ) и Q:
W(*(-)A) = infW(7r,at), WUQ) =supWUQ).
π Q
Из теорем 73.4-73.6 предыдущего параграфа мы знаем, что Q есть
наихудшее распределение,
W(*»(0,Q) =supWfyrQ(.),Q) =supWa,Q)>
4 Q Q
и π(Χ) = πο"(Χ) является байесовской стратегией, соответствующей Q.
Мы знаем также (см. теоремы 74.3-74.5), что для того чтобы стратегия
π(Χ) была минимаксной, необходимо и достаточно, чтобы она была
байесовской: π(Χ) = ttq(X) для некоторого априорного распределения Q и
Й?(тг(-),в) = с = const п. в. [Q], ^(7г(0,ёКс.
Этот последний критерий минимаксности мы уже неоднократно
использовали в различных частных ситуациях (см. §21, 41, 45, 49).
Теорема 2. При выполнении условий (А), (В), (С) класс всех
байесовских стратегий является полным.
В приложении VIII мы приводим доказательства теорем 1, 2 в их более
общей форме, когда D и θ — произвольные компактные метрические
пространства (условие (А)); функция ιυ(δ,θ): D χ θ —> R непрерывна по δ и θ
в соответствующих метриках (условие (В)); распределение Р# непрерывно
относительно θ по вариации (условие (С)).
Доказательства теорем 1, 2 при некоторых дополнительных
предположениях можно извлечь из [30]. Доказательства для случая конечных D и θ
можно найти в [9, 109]. В этих же монографиях можно найти сравнительно
полное изложение элементов общей теории статистических игр (и, в
частности, обсуждение для некоторых случаев конструкции минимального полного
класса; см. [109]).
Теоремы 1, 2 показывают, насколько важной является задача описания
класса всех байесовских решающих правил. Этой задаче посвящен
следующий параграф.
§ 76. Байесовский принцип. Полный класс решающих функций 593
§ 76. Байесовский принцип. Полный класс решающих функций
Мы видели, что по своей конструкции статистическая игра является
объектом более сложным, чем исходная игра (£>, Θ, w). Для последней, особенно
в случае простых множеств D и Θ (например, конечных), отыскание
байесовских и минимаксных стратегий может оказаться делом сравнительно
простым. В то же время даже простейшие статистические игры имеют
весьма сложную природу множества £>, и это заметно усложняет их
изучение, если подходить к ним как к обычным играм.
Пример 1. Пусть множества D — {δι,δ2}, Θ = {θ\,θ2} двухточечные,
w(5ii6j) = Wij, wu = 0, i,j = 1,2. Пусть Q = (g, 1 — q) есть априорное
распределение на Θ. Тогда
й(й, Q) = qwn + (1 - q)wi2.
Стало быть, байесовская стратегия ttq имеет вид
если w{Su Q) < w{S2, Q) (qw2i > (1 - q)w12),
если w(52l Q) < w(Si,Q) {qw2i < (1 - q)wi2)
ttq{52) = <!'
(ttq(U) есть вероятность принятия δ{).
Если
w(S1,Q) = w(62,Q) (2)
или, что то же, q = q = wi2/(wi2 + w2i), то в качестве kq можно взять
любое распределение π на множестве {δι,δ2). Точно так же всегда можно
найти распределение π = (ρ, 1 — ρ) такое, что
ΰ;(π,0ι) — ΰ)(π,θ2) или pw\2 = (1 — p)w2\.
Решение этого уравнения ρ = w2\/(w2i + w\2), очевидно, отвечает
байесовской уравнивающей стратегии 7Tq-, Q = (g,1 — q), которая в силу теорем
73.2, 73.5, 73.6 будет минимаксной. Распределение Q (минимаксная
стратегия «природы») будет наихудшим.
Мы видим, что «решение» этой игры осуществляется довольно просто.
Если же перейти к статистической игре, то даже в простейшем случае w\2 =
= w2\ = 1 мы получим задачу о байесовских и минимаксных критериях,
для рассмотрения которой нам потребовались § 41, 42.
Замечательный факт, которому посвящен настоящий параграф, состоит
в том, что задача отыскания байесовских стратегий (а стало быть, полного
класса и минимаксных стратегий) для статистических игр может быть
редуцирована в известном смысле к той же задаче для исходных игр (Ρ,Θ,ΐϋ).
В основе этой редукции лежит следующее утверждение, которое назовем
байесовским принципом. Пусть, как и прежде,
η
есть функция правдоподобия выборки Х\ она же — плотность X в Хп
относительно μη. Пусть, кроме того, априорное распределение Q на (θ, #θ) имеет
594 Гл. 6. Теоретико-игровой подход
плотность q(t) относительно некоторой меры λ (очевидно, это не есть
ограничение). Тогда согласно §21 функция /(#,£) = q{t)ft{x) будет плотностью
совместного распределения (Χ, Θ) в Χη χ Θ. Это означает, что функция
q (t/x) = ^ч*р /(*) = / g(t)ft(x)X(dt), (3)
определяет условную плотность распределения θ при условии X = х. Эта
плотность соответствует апостериорному распределению Qx случайной
величины θ при условии X = х. Соотношение (3) носит название формулы
Байеса (см. §20, 21).
Теорема 1 (байесовский принцип). Пусть выполнено условие (Αμ),
априорное распределение на θ имеет плотность q(t) и Qx означает
апостериорное распределение с плотностью (3), соответствующее
априорному распределению Q. Пусть, далее, исходная игра (D,Q,w) для любого
априорного распределения Q имеет байесовскую стратегию nQ. Тогда
статистическая игра (V, Θ, W) имеет байесовскую стратегию ttq(X),
соответствующую распределению Q, которая совпадает с kqx —
байесовской стратегией исходной игры, соответствующей апостериорному
распределению Qx.
Утверждение этой теоремы можно выразить одним равенством
kq{X) =7tqx>
Оно сводит поставленную задачу к нахождению апостериорного
распределения Qx и к отысканию байесовских стратегий для исходной игры.
Теорема 1 очень существенна для понимания механизма влияния
информации, полученной от выборки, на выбор оптимальной стратегии.
Априорная информация, представленная распределением Q на Θ, под влиянием
экспериментальных данных постоянно меняется. Оптимальной стратегией
будет та, которая учитывает эти изменения следующим образом: надо взять
оптимальную стратегию в исходной игре, но стратегию, соответствующую
уже не Q, a Qx.
Доказательство теоремы 1. Имеем
W(*('hQ) = J J u(Ax),t)ft(x№(dx)q(t)X(dt) =
θ Хп
= ί ί{χ)μη{άχ) fu(K(x),t)q{t/x)\(dt). (4)
Χη Θ
Здесь мы воспользовались (3). Изменение порядка интегрирования законно
в силу неотрицательности подынтегральной функции. Второй интеграл в
правой части (4) есть не что иное, как w(n(x)^Qx). Но при любом χ
w{tt(x),Qx) ^w(7rQlB,Qx) = / w(nQm9t)q(t/x)\(dt).
Θ
§ 76. Байесовский принцип. Полный класс решающих функций 595
Подставляя это неравенство в (4) и возвращаясь к исходному порядку
интегрирования, получим
Щ<-\ Q) > J f(*)vn(dx) J й(тгда, t)q (t/x) λ(Λ) = W(*Qu, Q).
xn θ
Так как π{χ) здесь произвольна, то это означает, что
7Tq(x) = KQm. <
Замечание 1. Аккуратности ради мы должны в проведенных
рассмотрениях оговаривать измеримость относительно 53η χ#θ функции ΰ^πς^,ί).
Эти оговорки мы опускаем, так как они носят чисто технический характер,
а при выполнении условий (А), (В), (С) из §75 они заведомо излишни.
Последнее утверждение читатель может проверить самостоятельно, пользуясь
тем, что для дискретных D и Θ эта измеримость устанавливается
очевидным образом, и тем, что произвольная игра при условиях (А), (В) может
быть сколь угодно точно «приближена» к дискретной.
Возвращаясь к примеру 1, мы можем теперь на основании теоремы 1
сразу указать вид байесовских стратегий для соответствующей
статистической игры. Именно, из (1) получаем
п g/giPO ^ Wi2
0, если qx = ,ν,^η w ,у> > ; ,
1, если qx <
/
Если
W\2 + 1021
W12 ,-v
qx = —τ—. (6)
W12 + 1021
то в качестве nQx можно брать любое распределение на (#ι,#2)·
Неравенство (5) можно переписать в виде
/θ! РО o(l-g) = wi2 m
fe2{X) g(l-a)' w12 + w2i' ()
Это знакомый нам критерий отношения правдоподобия.
Далее,
WX*tq.i0j) = «7πΕ^π4χ(ίι) +W2jEejnQx(52), j = 1,2.
Допустим для простоты, что равенство (6) имеет место с Рд.-вероятностью О,
так что байесовская стратегия с Ρ ^.-вероятностью 1 будет чистой, j = 1,2.
Тогда
596
Гл. 6. Теоретико-игровой подход
Отсюда уже нетрудно найти значение q, соответствующее наихудшему
распределению Q, при котором 7Tq будет уравнивающей стратегией, т. е.
стратегией, при которой
W(n^,9l) = W(^>e2).
Эта стратегия согласно теоремам 74.4, 74.6 будет минимаксной.
Распространение описанной процедуры отыскания минимаксной
стратегии на общий случай, когда Р^- или Р^2-распределения fel(X)/f02(X)
содержат дискретную компоненту, мы предоставляем читателю.
Пользуясь теоремой 1, мы можем аналогичным образом получить
обобщение результатов §41, 42 на случай произвольных конечных D и Θ и
произвольной функции потерь w(6i,6j) = Wij, которую в этом случае можно
называть также матрицей потерь ||u>(#i,0j)ll· (В §41, 42 мы рассматривали
частный случай wij = 1 при i φ j.) При произвольных w^ байесовское
решающее правило будет иметь следующий вид. Пусть Q = (g(0i),. · -,q(0r)),
Qx = (?x(0i),...,<7x(0r)),
„ (й) g(W*(*)
Тогда w(6i, Qx) = ^Jtyygx^) и, стало быть,
kqx (ί*) = 1, если w(6k, Qx) < w(6i, Qx) при всех i
или, что то же, если
г г
Если существует несколько значений &, обладающих этим свойством
(обозначим их через fci,..., ks), то байесовской стратегией 7Tqx будет также
любое распределение на δ^,.. ·, <^θ.
Отыскание минимаксной стратегии происходит следующим образом.
Предположим опять для простоты, что Р^.-распределения w(Si,Qx) не
имеют дискретных компонент. Тогда
W(*Q.>0j) = 5^^A-(^№,Qx) < minui(iz>Qx)).
В силу теоремы 75.1 существует Q = (<ζ(#ι),.. .,<z(0r))> при котором
стратегия 7Tq будет уравнивать значения W(ttq ,0j) при всех j. Эта стратегия
и будет минимаксной.
Из проведенных рассмотрений и теоремы 75.2 нетрудно получить
также вид полного класса стратегий статистической игры (Х>, 0,W) в случае
конечных D и Θ.
§ 76. Байесовский принцип. Полный класс решающих функций 597
Рассмотрим стратегии 7tqx, представляющие собой произвольное
распределение на тех ί^,..., ifce, для которых
min I Y^(wkiJ - ь)ц)/в;(Х)д(ву) J = 0.
Класс таких стратегий (байесовских), который получится, если g(0i),...
..., q{6r) будут пробегать все возможные значения, и будет полным классом.
Мы видели, что в случае г = 2 этот класс оказывается весьма простым и
узким (см. (7)): он состоит из решающих функций π(Χ) — (π(Χ, ίχ),π(Χ, ^2)),
где π(Α", δι) суть вероятности принятия решения с^,
Γΐ, если R{X) > с,
π{Χ,δι) = 1ρ£ [0,1], если R(X) = с,
[θ, если R(X) < с. (8)
ВД = ^1)' О^с^оо.
В играх с континуальными множествами D и θ для некоторых важных
конкретных функций потерь также можно найти в явном виде форму
байесовских решений. Пусть, например, D и Θ — области из Kfc, а функция
потерь является квадратичной:
к
ιν(δ,θ)=β\δ-θ\2 = οΣ&-θί)2> (9)
где £;, θί — координаты δ и Θ. Тогда
w
(δ, Q) = с ί\δ - t\2Q(dt) = cEQ\6 - θ\2.
Мы знаем, что минимум этого выражения достигается при δ = Eq0 =
= / tQ(di). Это и есть, очевидно, байесовская стратегия <5q = Eq0. Отсюда
и из байесовского принципа следует, что байесовская стратегия 6q(X) = ΘΧ
в статистической игре будет иметь вид
0Q = *Qx = ftQxidt) = ftq(t/X) λ(Λ). (10)
Rk Rk
Этот результат нам уже известен по гл. 2.
Риск стратегии 0q равен W(0q,0) = cEfl|0Q — θ\ . Априорное
распределение Q, для которого Efl|0Q — θ\ = const, дает нам минимаксную оценку
598
Гл. 6. Теоретико-игровой подход
0 = Sq(X). Примеры построения минимаксных оценок на этом пути
содержатся в §21.
Класс оценок (10), где Q пробегает значения в классе всех распределений
на Θ, представляет собой полный класс.
Рассмотрим теперь другой частный случай функции потерь
ω($,0) = φ-0| (11)
и предположим, что Θ = R, D = Ш. Тогда
δ 00
u?(i,Q) = cEQ|i-0| = ci\6- t\Q(dt) = с Г (δ- t)Q{dt)+c / (ί - i)Q(cft).
-00 δ
Пользуясь интегрированием по частям и положив F(t) = Q((—оо,£)),
находим
δ 00
w{6, Q)=c ί (δ-t) dF{t) -с f(t- S)d(l - F(t)) =
δ oo
f F(t)dt+ f{l-F(t))dt
L-oo δ
Производная этого выражения по δ существует п. в. и равна c[2F(6) — 1].
Эта функция монотонно возрастает и меняет знак в точке £, равной медиане
распределения F: F{6 — 0) < 1/2, F(i + 0) ^ 1/2. Отсюда следует, что
г5(£, Q) будет выпуклой по ί и в точке 5 будет иметь минимум.
В силу байесовского принципа это означает, что байесовской оценкой
0q = 6q(X) для априорного распределения Q и функции потерь (11)
будет медиана апостериорного распределения Qx. Это дает возможность,
как и в случае (9), найти минимаксную решающую функцию и полный
класс.
Аналогичным образом можно рассмотреть случай
ιυ{δ,θ)=β\δ-θ\α, α>0.
В заключение этого параграфа отметим, что квадратичная функция
потерь (9) при с = 1 для континуальных множеств D и θ и функция потерь
для конечных D и θ играют в теории статистических игр особую роль.
Для них функции риска превращаются соответственно в сумму дисперсии
и квадрата смещения оценки для континуальных D и Θ и в вероятность
ошибиться — для конечных Ри0. Эти характеристики, являющиеся
естественными сами по себе, служили нам основой для выбора оптимальных
правил в гл. 2-5. Если статистическая задача не содержит прямых
указаний на форму функции υ)(δ, θ), то чаще всего в качестве w(6, θ) выбираются
именно эти две функции (9) или (12). Мы условились называть их
статистическими функциями потерь.
§ 77. Достаточность, несмещенность, инвариантность 599
§ 77. Достаточность, несмещенность, инвариантность
Принципы достаточности, несмещенности, инвариантности служат для
сужения класса решающих правил. Они состоят в том, чтобы
использовать в качестве решающих функций лишь соответственно достаточные,
несмещенные и инвариантные решающие правила. Использование одного из
этих принципов, двух из них или всех трех (если это оказывается
возможным) позволяет в ряде случаев настолько сузить класс рассматриваемых
стратегий, что его пересечение с полным классом оказывается состоящим
из одной-единственной решающей функции. Это означает, что в
выделенном подклассе существует равномерно наилучшая стратегия (ср. с п. 73.1),
и это решает проблему выбора решения.
Все три принципа представляются довольно естественными и уже
обсуждались нами в разных конкретных задачах в гл. 2-5.
Наиболее бесспорным из них является принцип достаточности, который
часто представляет собой не что иное, как способ описания полного класса.
1. Достаточность. Предположим, что выполнено условие (Αμ) и что
существует достаточная статистика 5, т. е. (см. § 22)
Mx) = tl>(e,s)-h(x).
Пусть, далее, априорное распределение Q имеет плотность q(t) относительно
некоторой меры λ. Тогда в силу байесовского принципа байесовская
стратегия будет полностью определяться апостериорной плотностью
,(ί!Ύλ_ QWt(X) _ q(tmt,S)
ЧКЪ'Л) f q(u)fu(X)X(du) /g(u)^(«,5)A(du)' ^ ;
зависящей лишь от 5. Так как любое распределение Q имеет плотность
относительно подобранной соответствующим образом меры λ (можно положить,
например, λ = Q, q(t) ξ 1), то сказанное означает, что все байесовские
решающие правила kq (X) будут функциями лишь от S:
kq(X)=Pq(S).
Другими словами, любая байесовская стратегия ttq(X) не зависит от X при
фиксированной S.
Пусть теперь выполнены условия (А)-(С) из § 75. Тогда высказанное
утверждение будет относиться и к минимаксным стратегиям. Оно будет
означать также, что все решающие правила, построенные как функции лишь
от S (т. е. все измеримые отображения S —> D, где S есть пространство,
в котором лежат значения 5), образуют полный класс T>s- Это следует из
того, что V$ содержит в себе все байесовские стратегии, образующие, как
мы знаем, полный класс. Очевидно, класс T>s будет наименьшим для
минимальной достаточной статистики 5.
Ясно, что в минимальный полный класс входят далеко не все функции
от S (со значениями вЙ), а лишь узкая их часть. Это подтверждает
формула (1), из которой следует, например, что для двухточечных множеств D
и Θ (см. (76.8)) полный класс образуют функции π(Χ), у которых
вероятность π(Χ,δ\) принятия решения δ\ имеет форму индикатора множества
{R{X) > с}, где R(X) = tl>{euS)/tp{e2,S) (точнее см. (76.8)).
600
Гл. 6. Теоретико-игровой подход
Если D С R*, Θ С R*, а функция потерь ιυ(δ,θ) имеет вид ιυ(δ, θ) =
= w(S — θ), где w(u) — выпуклая функция в R*, то принципу достаточности
можно придать очень конструктивную форму, позволяющую эффективно
характеризовать полный класс. Именно, имеет место следующее обобщение
теоремы 24.1.
Теорема 1 (Блекуэлл). Для любой решающей функции (оценки) Θ* =
= δ(Χ) существует оценка
θ*8 = Е, (|)
(θ$ от θ не зависит, так как S — достаточная статистика), которая
не хуже, чем Θ*. Именно, для всех 0 G Θ
Eew(e*s-e) *ζΕθιυ{θ* -θ).
Доказательство. Имеет место следующее неравенство Иенсена
(см. § 19): если g — выпуклая функция в Rfc, ξ — случайная величина со
значениями в Rk, а # — какая-нибудь σ-подалгебра основной σ-алгебры, то
■(f) >»(■(!))■
В соответствии с этим неравенством
> Bjto (в, (** - |) ) = Е»и>№ - в). <
Если достаточная статистика S является полной, то теорема 1 вместе
с принципом несмещенности позволяет однозначно определить равномерно
наилучшую оценку. Действительно, рассмотрим класс Ко всех
несмещенных оценок Θ* = δ(Χ):
Εθθ* = θ для θ* Ε Κ0·
Тогда, следуя в точности рассуждениям §24 (теорема 24.3), убеждаемся, что
9*s = Е#(0*/S) для всех θ* Ε Ко совпадают и, стало быть, пересечение Ко и
полного класса состоит из одной-единственной оценки у?(5), которую
естественно называть эффективной.
Из сказанного видно, что эффективные оценки, если они существуют,
будут одни и те же для произвольной выпуклой функции потерь ιυ(δ—θ).
Это позволяет использовать для любой такой функции потерь все
утверждения соответствующих теорем гл. 2, полученных для w(u) = и2.
Приведенные рассуждения иллюстрируют совместное применение
принципов достаточности и несмещенности.
2. Несмещенность. Мы только что видели, какую роль может играть
принцип несмещенности в теории оценок. В § 46 было установлено, что
§ 77. Достаточность, несмещенность, инвариантность 601
аналогичный эффект (существование равномерно наиболее мощных
несмещенных критериев) может быть получен при использовании несмещенных
критериев в теории проверки статистических гипотез.
В общем случае определение несмещенности выглядит следующим
образом. Допустим, что проблема статистического решения состоит в
«определении» неизвестного значения θ и что, следовательно, множества D и Θ
совпадают. Функция потерь νι(δ,θ) может быть произвольной.
Определение 1. Решающая функция δ(Χ) называется несмещенной,
если
Eew{S{X),e)^Eew{S{X),tf)
при любых 0, θ' φ θ.
Другими словами, при ν = θ достигается minE^w;(i(X), v). Это означает,
V
что δ(Χ) в среднем находится ближе всего к неизвестному 0, чем к какой-
нибудь другой точке.
Легко видеть, что данное ранее определение несмещенных оценок
является частным случаем этого определения.
Если проверяются две сложные гипотезы Н\ = {θ Ε Θι} и Η<ι = {θ Ε Θ2},
то множество D = {£1,^2} может существенно отличаться от Θ. В этом
случае определение несмещенности будет формально несколько иным, хотя
смысл его остается тем же. Именно, определение 1 можно модифицировать
так (см. [65, 66]), что оно перейдет в следующее определение.
Определение 1А. Решающая функция δ(Χ) называется несмещен-
ной если
Εβυ)(δ{Χ),θ) ^Eew{S{X),#)
при любых θ е θι, θ1 е ©2 или θ е ©2, & € ©ь
Пусть для простоты w(ii,0) = гУ] = const при θ Ε ©25 νο{δ2,θ) = W2 =
= const при θ Ε ©ι; δι = 0, δι = 1 и δ (Χ) означает вероятность (1 или 0)
принятия #2. Тогда
Έ*ο(δ(Χ),θ) ={WiPMx)=0) при 6£θ2>
ΕΜδ{Χ)'θ)-\ν*Ρβ{δ(Χ) = 1) при 0 6θ2, 0'€0Ь
и неравенства в определении 1А означают, что
ιυ2Ρβι MX) = 1) ^ «;ιΡβι {δ{Χ) = 0) при θλ £ ©ь
ωιΡβ2(ί(Χ)=0)<τϋ2Ρβ2(ί(Χ) = 1) при 6>2 е Θ2
или, что то же,
u>i + u;2 ωι + гу2
602
Гл. 6. Теоретико-игровой подход
Отсюда следует, что
sup Εθδ{Χ) ζ inf Εθδ{Χ)
и что, стало быть, критерий δ будет несмещенным в смысле определений § 46.
Наоборот, если справедливо последнее неравенство, то критерий δ будет
несмещенным в смысле определения 1А при подходящем выборе функции
потерь ΐϋ(δ,θ), например при w\/{w\ + к^) = sup Έθδ(Χ).
0€θι
Дополнительные примеры использования принципа несмещенности
(помимо результатов §46) можно найти в [65, 66].
3. Инвариантность. Мы видели, что пересечение полного класса,
порожденного «достаточными» решениями, с классом несмещенных решений
может состоять из единственной стратегии. Еще одним естественным
классом стратегий, в котором может оказаться единственное неулучшаемое
решение, является класс инвариантных решающих правил (ср. с §28,29,47).
Определение инвариантной проблемы статистического решения связано
с группами преобразований во всех трех пространствах, которые участвуют
в определении статистической игры: в пространствах 0, 0и выборочном
пространстве Хп. В основе определения лежат измеримые взаимно
однозначные преобразования g пространства Хп в себя, образующие некоторую
группу G с групповой операцией, определенной как композиция: если g\ G G,
#2 € G, то #2<7i определяется как преобразование χ —> 32(01 ж), которое снова
обязано принадлежать G. Тождественное преобразование обозначим через е.
Обратное к g преобразование g~l определяется как преобразование, для
которого g~lg - е. Измеримость g G G означает, что дХ вместе с X будет
случайной величиной в Хп.
С введенной группой G тесно связано понятие инвариантности
семейства Р#, которое было определено нами в §29 и 47. Оно означает, что для
каждых д £ G и θ £ θ найдется элемент θ9 G θ такой, что
Рв(дХеА) = Р9д(ХеА). (2)
Преобразования 7j пространства Θ в себя, определенные равенством
дв = Од, при выполнении условия (Ао) образуют группу G (см. §29).
В терминах математических ожиданий условие (2) означает, что для
любой интегрируемой функции φ
Εθφ(9Χ)=Ε<;Θφ(Χ). (3)
Определение 2. Проблема статистического решения, связанная со
статистической игрой (ϋ,Θ,ΐϋ), (Χ,Ρ^), называется инвариантной
относительно группы G, если семейство Р# инвариантно относительно G и
функция потерь w инвариантна относительно G в следующем смысле: для
любых δ G D, g G G найдется единственное δ1 G D такое, что
ν){δ,θ) = %о{8\дв) при всех θ G Θ. (4)
Значение £', однозначно определенное по #, обозначим через д'6.
Лемма 1. Преобразования д' пространства D в себя, порожденные
группой G, образуют группу G'.
§ 77. Достаточность, несмещенность, инвариантность 603
Доказательство. Покажем, что совокупность G' всех
преобразований д' замкнута относительно композиции, причем справедливо равенство
Μ = (0201 )'■
Действительно,
ιυ{δ,θ) = w(g[6,gie) = ^{g^S^g^) = w((g2gi)'S, ЩГ)0).
Так как (гвдГ) = 0201? то в СИЛУ единственности (дъдх)' = gf29v Лемма
доказана. <
Итак, с основной группой G преобразований д пространства Хп в себя
связаны еще две группы G и G' преобразований пространств θ и D в себя.
Применение одновременно всех трех преобразований g,7j и д1 оставляет
проблему решения неизменной (инвариантной). Поэтому естественно выбирать
такие решающие правила, которые не менялись бы при переходе от одной
эквивалентной проблемы решения к другой. Естественность такого подхода
нами обсуждалась весьма детально в §28, 29, 47.
Определение 3. Решающая функция δ(Χ) инвариантной проблемы
решения называется инвариантной, если
δ(9Χ)=9'δ(Χ).
Рандомизированное инвариантное правило π(Χ) определяется как
любое распределение, сосредоточенное на инвариантных решающих правилах.
Примеры использования принципа инвариантности содержатся в уже
цитированных нами § 28, 29, 47, где рассматривались эквивариантные оценки
и инвариантные критерии. Отметим некоторое своеобразие с точки зрения
общего подхода этих двух частных случаев.
В проблеме оценивания группа преобразований G' не вводилась вовсе.
В этом случае множества D и θ совпадают, и с самого начала
предполагалось, что g'S = 7}δ. Поэтому эквивариантные оценки определялись с помощью
равенства в*{дХ) = дв*{Х).
В теории проверки гипотез преобразование д' полагалось равным
тождественному д1 = е, так что инвариантный критерий π определялся
соотношением тг(дХ) — 7г(Х).
В этом случае для инвариантности проблемы проверки двух гипотез
{θ Ε Θι} и {θ Ε ©г} нужно предполагать также (см. (4)), что дЭ{ = Θ;.
Наличием некоторой разницы в этих двух подходах и объясняется в
какой-то мере использование двух разных терминов: «эквивариантность»
(для оценок) и «инвариантность» (для проверки гипотез) для обозначения
инвариантных решающих правил. Дополнительно к примерам
инвариантных проблем решения, рассмотренным в гл. 2 и 3, приведем еще один.
Пример 1. Пусть Χ ^ Φα,σ2· Здесь Θ есть полуплоскость {θ = (α,σ):
σ ^ 0}. Пусть D есть вещественная прямая R и пусть ιυ(δ, θ) = (δ — α)2/σ2.
Рассмотрим группу G преобразований да,ьХ = а + ЬХ = (а + 6χι,...
..., а + Ьхп), где Ъ φ 0. Случайную величину да,ъХ в Хп можно
рассматривать, очевидно, как выборку из Φα+6α,62σ2· Следовательно, семейство Ф0)(Т2
604
Гл. 6. Теоретико-игровой подход
инвариантно относительно G, если положить gab9 = (а + &α, |6|σ). Функция
потерь будет инвариантной, если мы положим g'abS = а + 6£, поскольку
Таким образом, имеем инвариантную относительно G проблему
решения. Инвариантные решающие функции δ(Χ): Χη —ϊ Ж должны обладать
свойством
δ(α + ЬХ) = S(ga,bX) = gfaJb5{X) = а + Ы(Х). (5)
Далее, нетрудно установить, что рассматриваемая проблема решения
является инвариантной и относительно группы F всех перестановок /
координат вектора X; при этом / и /' будут тождественными преобразованиями.
Поэтому если потребовать, чтобы функция δ(Χ) была инвариантным
решением и относительно F, то должно выполняться также
δ(/Χ)=δ(Χ). (6)
Отметим, что класс функций, удовлетворяющих (5), (6), все еще
достаточно широк: в него входят, например, все линейные формы
η η
где X(i),.. .,Χ(η) — вариационный ряд выборки X. Если использовать
принцип несмещенности, то получим еще одно условие на коэффициенты ак:
η
Y^akEe{x{k)-a) = 0. <
При построении оптимальных инвариантных решений в теории
оценивания и теории проверки статистических гипотез важную роль играют
понятия, в известном смысле близкие друг другу: понятие орбиты в теории
оценок и понятие инварианта в теории проверки гипотез. Напомним, что
орбитой в пространстве Θ называется множество {дво, д Ε G}, где во есть
некоторая точка из ©^Другими словами, θ\ и #2 принадлежат одной орбите,
если существует # G G такое, что θ ι = двъ.
Аналогично можно определить орбиты в Хп. Тогда инварианты по
определению есть статистики, постоянные на орбитах в Хп.
Понятие орбиты сохраняет свое значение и в общем случае.
Лемма 2. Функция риска инвариантной проблемы решения для
инвариантного решающего правила постоянна на орбите:
\ν(δ(·),θ) = \ν(δ(-),ςθ)
при всех θ £ θ, g E G.
§ 78. Асимптотически оптимальные оценки
605
Доказательство. В силу инвариантности соответственно функции
потерь, решающего правила и семейства Р$ (см. (3), (4)) имеем
Ψ(δ{.),θ) = Eew(S(X\9) =Eew(g'5(X),ge) =
= Eew(S(gX),g0) = Щеы{6(Х),дв) = W{S{.),e). <
Постоянство на орбите риска для рандомизированных инвариантных
решающих правил следует из их определения и леммы 2.
Из леммы 2 вытекает, что в том случае, когда все пространство Θ
является орбитой (т.е. Θ = {дво,7} Ε G} при каком-нибудь 0о*> это имеет место,
например, для преобразований сдвига), инвариантное решающее правило
становится уравнивающим. Поэтому из леммы 2 и теорем 74.3-74.6
получаем немедленно следующее утверждение, устанавливающее важную связь
между инвариантностью и минимаксностью.
Теорема 2. Пусть пространство θ является орбитой и
существует априорное распределение Q, для которого байесовская стратегия
kq(X) является инвариантной. Тогда πς}(Χ) — минимаксная
стратегия.
Из теоремы 75.3 вытекает также, что имеет место следующее обобщение
теоремы 2.
Теорема 2А. Пусть существует априорное распределение Q,
сосредоточенное на одной из орбит во, такое, что байесовская стратегия
ttq(X) является инвариантной. Тогда если при всех θ
W(irQ(-),e)^W(irQ(-),e0), θοΕθο,
то kq(X) является минимаксной.
Этим критерием мы пользовались в §49.
§ 78. Асимптотически оптимальные оценки
при произвольной функции потерь
Многие из результатов гл. 2 об асимптотически оптимальных оценках и
гл. 3 об асимптотически оптимальных критериях допускают обобщения на
функции потерь весьма общего вида.
В этом параграфе остановимся на задачах теории оценивания и
предположим, что w(6,9) = w(S — θ).
Сделаем сначала одно общее замечание. В гл. 2 мы видели, что в
регулярном случае (X €= Р#, Р# удовлетворяет условиям (RR); см. §34,36) все
разумные оценки θ* = δ(Χ) параметра θ «сосредоточены» в 1/\Лг-окрест-
ности точки Θ. Так, например, для асимптотически нормальных оценок
(Θ* — 9)у/п & ΦΟσ2(0). Отсюда следует, что при широких предположениях
относительно функции w(t) асимптотическое поведение риска Eew(9* — θ)
будет определяться свойствами функции w(t) в окрестности точки t = 0.
Если w(t) дважды непрерывно дифференцируема в нуле, w" > 0, то при
W(t) = ^t* + o(t>). (1)
606
Гл.6. Теоретико-игровой подход
Это значит, что в интересующей нас области значений t (порядка 1/\/п)
функция w(t) будет вести себя так же, как квадратичная функция потерь
wo(t) = ct2 при с = ΐί/'(0)/2, для которой были установлены результаты
гл. 2. Если к тому же w(t) < eQl*' при достаточно малом а > 0 (см.
теорему 36.6), то все эти результаты останутся в силе — перенесение их на
случай функции w(t) вида (1) — дело несложной техники, вполне доступной
читателю.
В этом параграфе мы рассмотрим значительно более содержательное
обобщение. Мы предположим, что функция потерь ιυ(δ,θ) зависит от η и
представима в виде
W{S, θ) = ιυη{δ - θ) = w{y/ii{δ - 0)), (2)
где функция w(t) ^ 0 определена во всем пространстве R*. Очевидно, что
в этом случае будут существенными значения w(t) во всей области
значений £. Предположение (2) означает, что величина потерь чувствительна даже
к небольшим отклонениям δ от 0. Мы будем предполагать, что функция w
в (2) удовлетворяет следующим условиям.
1. w(t) ^ ес1*1 при некотором с > 0.
Такая форма условия 1 несколько упрощает выкладки. На самом деле
все результаты сохранятся, если потребовать, чтобы w(t) ^ ciett'*' при
достаточно малом а > 0.
В дальнейшем существенную роль будет играть функция
νσ2{8) = fw{s- u)e-*w2uT du,
где σ2 — некоторая положительно определенная матрица вторых моментов.
Функцию Va2 (s) можно интерпретировать как
(2π)Α;/2
Так как
Υσ2{8)= ίw{v)e-^s-v^2^v^r dv,
то эта функция будет аналитической функцией переменных s и σ2.
Нам понадобятся следующие условия.
2. Функция Va2(s) достигает своего минимального значения по s в
единственной точке, которую мы обозначим через bw.
3. bw = 0.
4. Функция w(t) непрерывна.
Условие 2 будет заведомо выполнено, если w(s) φ const есть выпуклая
вниз функция. В этом случае, очевидно, Va2(s) также будет выпуклой и не
будет содержать «линейных» участков (т.е. матрица вторых производных
будет всюду положительно определенной).
§ 78. Асимптотически оптимальные оценки
607
Условие 3 будет выполнено, если
у;2(0) = - /' uw{u)e-*u"2uT du = 0,
что всегда имеет место для симметричных функций w(u) = w(—u).
Значение bw можно было бы назвать смещением функции потерь w. Оно
удовлетворяет уравнению V^2{bw) = 0. Условие 3 о том, что bw — 0, не
является существенным и лишь упрощает изложение, которое читатель может
без труда перенести и на случай bw φ 0. Изменения в формулировках
теорем, которые при этом произойдут, будут проиллюстрированы в замечании 2
к теореме 1.
Напомним теперь, во что перейдут здесь определения оптимальных
стратегий § 74, 75. Оценка 0q будет байесовской относительно априорного
распределения Q с плотностью q относительно меры Лебега (и функции
потерь гип), если
/W(9*Q,t)q{t)dt = min i W{6%t)q{t) dt, (3)
где W(6*,t) = Etwn(9* -t). Здесь интеграл в правой части (3) можно
записать в виде безусловного математического ожидания Ewn(9* — 0), где
усреднение берется по распределению с плотностью ft{x)q(t).
Оценка θ будет минимаксной, если для любой другой оценки Θ*
supW(0*,t) <supW(0*,t).
t t
Изложенное делает естественными следующие определения, совершенно
аналогичные определениям §21.
Определение 1. Оценку Θ* будем называть асимптотически
байесовской, если
limsup [Ειυη(θ* - 0) - Ewn(e*Q - θ)] < 0, (4)
η—>οο
где 0q — байесовская оценка.
Определение 2. Оценку 0* будем называть асимптотически мини-
максной, если для любой другой оценки 0*
limsup [sup W{e\,t) - sup W{9\t)] < 0, (5)
π-юо teQ0 teQo
где Θο — любое замкнутое подмножество, лежащее внутри Θ.
При изучении асимптотически оптимальных оценок в этом параграфе мы
будем оперировать лишь понятиями, введенными в определениях 1 и 2. Это
составляет некоторое отличие от гл. 2, где присутствовали также
асимптотически эффективные оценки. Их отсутствие здесь объясняется тем, что для
произвольных функций потерь w мы не располагаем неравенствами типа
Рао-Крамера для inf W(9*, θ) (Kq есть класс несмещенных оценок), с
608
Гл. 6. Теоретико-игровой подход
помощью которого можно было по значению W(6*,6) судить о качестве Θ*
и выделять, в частности, эффективные (и асимптотически эффективные)
оценки, т.е. оценки, равномерно наилучшие в классе
последующие утверждения устанавливают, что оценка максимального
правдоподобия является, как и в условиях гл. 2, асимптотически байесовской и
асимптотически минимаксной. Кроме того, мы получим асимптотическую
нижнюю границу для функции риска при произвольной функции потерь w
(неравенство Рао-Крамера дает точную нижнюю границу). Во всех
последующих трех теоремах мы предполагаем, что выполнено условие (RR).
Теорема 1. Пусть X €= Р#, Θ* есть о.м.п., a 0q есть байесовская
оценка, соответствующая функции потерь w (см. (2)),
удовлетворяющей условиям 1-3, и априорному распределению Q с ограниченной
плотностью q относительно меры Лебега, Тогда
|^-0·|^-^Ο, (6)
{e*Q-e)V^^ Φο,ι-49) (7)
равномерно по θ £ Θο, Θο — любое замкнутое подмножество, лежащее
внутри Θ, на котором q(9) > qo > 0 непрерывна.
Если, кроме того, функция w удовлетворяет условию 4, то
E™n(0Q - θ) = ЕЦ^ (0q - Θ)) -+ Εν(ηθ) = Ε^25ν>(β)(0), (8)
где ηβ £f Фо,/-1^)' ^ €= Qi E, как и прежде, означает безусловное
математическое ожидание с плотностью ft{x)q{t) [Χ ^ Ρ#, θ ^ Q).
Замечание 1. Наряду со сходимостью (6) можно установить также
сходимость почти наверное относительно Р#.
Замечание 2. Если w таково, что смещение bw φ 0, то утверждение
теоремы 1 полностью сохранится, если 0q в (6)-(8) заменить на 9п — Ьги/у/п.
Таким образом, bw имеет смысл асимптотического смещения величины
(^-e)Vn.
Теорема 2. Пусть функция w удовлетворяет условиям 1-4. Тогда
для любой оценки Θ*
liminf sup Etwn(9* - t) ^ sup Ew(fy),
n-+°° te&o tee0 /g\
Любая оценка θ*, для которой
Etwn{6* -t) ->Ε<ω{ηι) (10)
равномерно по t, является асимптотически минимаксной.
§ 78. Асимптотически оптимальные оценки
609
Теорема 3. Пусть Х€=Р# и функция w удовлетворяет условиям 1-4.
Тогда оценка максимального правдоподобия Θ* является
асимптотически минимаксной и асимптотически байесовской для любого априорного
распределения Q с непрерывной положительной в точке θ плотностью q.
Все эти утверждения вполне аналогичны соответствующим
утверждениям гл. 2. Они делают правдоподобным предположение, что и для
произвольной функции потерь w, удовлетворяющей условиям 1-4, о. м. п. является
асимптотически равномерно наилучшей в классе асимптотически
несмещенных оценок (ср. с §33, 34, 36).
Доказательство теоремы 1. Байесовская оценка определяется в
силу байесовского принципа как значение 0q, обладающее свойством
/ Μηίθη - t)q (t/X) dt = min f wn(u - t)q {t/X) dt =
J wG0 J
= min fw{y/ii(u - 0) - Vn (t - в))ТЩ^§— dt.
Это значит, что в качестве (0q — в)у/п = Uq можно взять любое значение s,
при котором достигается min/7(s),
s
где, как и прежде, Z(t) = fo+t(X)/fe{X)>
Нам понадобятся утверждения об асимптотическом поведении U(s).
В § 36,37 было установлено (теорема 36.5), что при выполнении условий (RR)
Щи*) = eY^q(e*)(Vm(0)+en(X,9)), (12)
(2тг)*/2
где εη(Χ,θ) —> 0 равномерно по θ (мы заменили здесь —, Έυ)(η) на
Vm(0); g(0) на <#))
Заметим теперь, что
P(Vu\e*Q-e*\>e)=P(\u*Q-u*\Ze)<-p( min U(s)<U(u*)). (13)
Поскольку асимптотическое представление для U(u*) мы имеем, то нам
надо оценить здесь значение U(s). Из теорем 36.4, 37.3 следует, что для
произвольной последовательности еп —> 0 при \v\ < епу/п выполняется
InZ [vy/n) = Y(u*) - ^(v - u*)I{0){v - u*)T(l + εη(Χ,0, и)),
\εη{Χ,&,и)\ ^ 6η {Χ,θ) —> 0 равномерно по 0. Но
U(s) > Un{s) = ί w(s- v)q (θ + -^ J Ζ (-j=} do.
\v-u'\^en\/n
610
Гл. 6. Теоретико-игровой подход
Рассмотрим множество
Αη = ίε^(Χ,θ)<ρ inf q(e+^=)>q(e*)(l-p)\,
P>0,
обладающее очевидным свойством
Ρθ(Αη) -> 1. (14)
Равномерно по θ на этом множестве
Un(s)Z(l-p)q(e*)eY^x
χ J w(s-v)expl--{v-u*)I(e)(v-u*)T(l + p)\dv =
= (1 - ρΜ^^ν,ο,χ^ - «*) - rn(s)}, (15)
где по условию 1
rn{s) = J w{s- ν)exp l--{ν - η*)Ι{θ){ν - u*)T{l + p)\ dv ζ
\v-U*\>€nVn
< ес^7Щ^Р(1»?1 > εηλ/£), τ/ ё Φ0,/(*)(ΐ+/>)>
d — диаметр области Θ. Аналогично лемме 33.1 нетрудно убедиться, что
Ρ(Μ>εη^Κβ-αηε«, а>0.
Выбирая εη = η-1/9, мы получим, что при всех 5 и достаточно больших η
ги(5К е-"3/\ (16)
Воспользуемся теперь условиями 2, 3, в силу которых
min Vm(s - и*) ^ V7(0)(0) + 4т, τ = т(е) > 0.
В силу аналитических свойств Vai (s) мы получим, что при достаточно
малых ρ
, ^η V/(e)(i+p)(5 - u*) > Vm{0) + 3r,
\s—u*\^e
и в силу (15), (16) при X Ε Αη и достаточно больших η
min t/n(s) £ (1 - pMOe^Vr^O) + 2r].
s-u* >e
§ 78. Асимптотически оптимальные оценки
611
Используя (12), (13), окончательно находим
P*(^|0Q-0*|>e)^P*( min Un(s)^U(u*))^
\\s-u*\^e /
< Έ>Θ(Χ i Αη) + Ρβ((1 - p)[Vm(0) + 2т] < Vm + εη(Χ,θ)).
Выбирая дополнительно р столь малым, чтобы выполнялось (1 — р)2т —
"" pVi(9) (0) ^ т, получим
Р{уД\в*я-в*\ > ε) < Р*(Х £ Λη) + Ρ*(εη(Χ,0) > г) -> 0
при η —> со. В силу (12), (14) утверждение (6) доказано.
Из (6) и теорем §37 вытекает (7). Докажем теперь соотношение (8).
В силу (7) и свойства 4
w(y/n (0q - θ)) =» w(r/0), % е Φο,/-ΐ(^)-
По лемме Фату
liminfEtu>(vfi(0Q - *)) > Ею(т/4),
liminf Ew(y/n (0q - 0)) > / g(i)Eu;(r;t) rfi = Вш(зд).
С другой стороны, по определению 0q
Ew(y/K(0*Q - {Θ)) ζ Ew{yfti(9* - θ)) -> Ею{щ).
Последнее соотношение вытекает из равномерной сходимости Е$ги х
х(у/п(в* — £)) —> Etu(r/t), доказанной в §37. Теорема доказана. <
Доказательство теоремы 2. Возьмем распределение Q,
сосредоточенное на во, с ограниченной плотностью ςτ(ί) > 0 при t E ©о, и пусть
0q — байесовская оценка, отвечающая Q. Тогда для любой оценки Θ*
sup Εθν)η{θ* - ί) > /*Ε*™η(0* - i)9(t) Л ^
^ У Etwn (0*Q - t)q(t) dt = Ewn (^ - β).
t€0o
θ0
θο
По лемме Фату в силу (8)
liminf sup Ε^η(0* - ί) ^ liminf Ewn(0?) - 0) ^ Вад(ад) = / Ew{qt)q{t) A.
Θο
612
Гл. 6. Теоретико-игровой подход
Так как функция Ew(rft) = xfc^^wW непрерывна относительно t, то
выбором q(t) интеграл
Jy/mVm(0)q(t)dt
Θο
может быть сделан сколь угодно близким к sup y/I{t) Vjm(0) = sup Ew(fy).
tee0 ί€θ0
Это доказывает (9).
Пусть теперь оценка 0* обладает свойством (10) и Θ* — любая другая
оценка. Тогда в силу (9) и равномерности сходимости (10)
limsup [sup Etwn(e{ — t) — sup Etwn(0* — t)] <
п-юо teQ0 ί€θ0
< sup lim Etwn(0l — i) — sup Ег^(^) = 0.
tee0 n-+°° teeQ
Неравенство (5) определения асимптотической минимаксности, а вместе с
ним и теорема 2 доказаны. <
Доказательство теоремы 3. Асимптотическая минимаксность Θ*
следует из того, что для о. м.п. Θ* по теореме 37.4 справедливо (10).
Асимптотическая байесовость Θ* следует из того, что при θ* = Θ*
выполнено (4), ибо для Θ* имеет место равномерная сходимость (10) и, стало
быть,
lim Ειυη(θ* - θ) = lim [Etwn{()* - %(*) eft =
n—>oo x ' n—>oo J
= Ew(77„) = lim Eu)n(0?, - 0).
Последнее неравенство вытекает из (8). Теорема доказана. <
Утверждение теоремы 1 можно усилить, если потребовать дополнительно,
чтобы функция w(t) росла достаточно быстро. Именно, положим гидг =
= min w(t), Wm = max w(t) и рассмотрим условие
5. Существует 7 < 1 такое, что w^ > 2\¥ίν при всех достаточно
больших N.
Если w(t) растет при \t\ —» со как степенная или экспоненциальная
функция, то условие 5 выполнено.
Теорема 4. Если выполнены условия 1, 5, q(t) > qo > 0 на
замкнутом множестве ©о и q(t) ^ qm < со, то при некоторых с < со, а > 0,
не зависящих от £,
Pt W^ (0q - «) > ЛГ) ^ се"лЛг2, t Ε Θ0.
§ 78. Асимптотически оптимальные оценки
613
Отсюда и из теоремы 1 следует, что для любой непрерывной функции
v(t) такой, что \v(t)\ < e~~aN /2, справедливо
Etv(Vn {0*Q - ή) -> Ev(rfe), ί Ε θ0.
Доказательство теоремы 4. Обозначим
(это есть часть интеграла (7(0) по области \v\ ^ г). Для доказательства теоремы 4
нам понадобится
Лемма 1. Если w(t) удовлетворяет условию 1, gm = maxg(u) < оо, то при
и
некоторых β > 0, α < оо, не зависящих от 0, и всех 0 < ε < 1
*-/*·»
ε
Это неравенство сохраняется при w(t) = 1.
Доказательство. Имеем
Р*(«(г) > ε)< Ρ*ί sup Ζ f-^Λ > 1J + P* lu(r) > ε, sup Ζ ί^=\ ζ 1J .
Оценка для первого слагаемого дана в теореме 33.2, в силу которой это слагаемое
не превосходит с\е~Т &, β > 0. Второе слагаемое не превосходит
р'(/"<-*('+Зг)г,/,Ш*>')· (17>
\vfer
Так как в силу теоремы 33.1
ΕθΖΐ/2 {ja) ^ e~2lv{20' β>0'
то математическое ожидание интеграла в (17) не будет превосходить (см.
лемму 33.1)
Ят ! есНе-2Иа*А; ζ с2егЧ
Ы>г
Поэтому в силу неравенства Чебышева вероятность (17) не превосходит с2е r ^/ε.
Лемма доказана. <
Обозначим через и\(г) значение интеграла и(г) при w(t) = 1:
*"("-^*('+^)гШ*·
614
Гл. 6. Теоретико-игровой подход
Лемма 2. Если q(6) > О на замкнутом множестве ©о, то при некотором
b < оо, не зависящем от 0, любом ε > 0 и всех достаточно больших η
Ρ*(ΜΟ)<εΚ&ε2, θ G0O.
Доказательство. При всех достаточно больших η имеем
^q0 J expJL Ιχ>Θ+ -j=) -L(X,0) |cfo = ς0 / exp j (v,Cn) + -^νηηυτ \dvy
\v\^l \v\^l
где
qo = mmq(t)>0, ζη = -±=L'(X,t), Ίη = ±||L£(X,0)||,
0 = 0 + ρυη"1/2, \p\ ^ 1. (Здесь Ζ/ есть вектор производных логарифмической
функции правдоподобия, L^- — частные производные второго порядка.) Так как
|(^>Сп)| ^ М|Сп| и так как в СилУ условий (RR)
η
где Ln = /~/(χΐ)> т0 на множестве А = {\ζη\ ^ Ι/ε, Ln ^ n/e2k} справедливо
wi(0) ^ go / exp | -^ - j^L υυ ^ go£ / exp J _|5| _ i£L bs ^ Cl^
Это означает, что имеет место вложение {^i(0) < cie} С А. Так как
ΡΘ(Α) ζ Ρθ(\ζη\ ϊ ε""1) + Р* (L„ > ^) ^ ε2Ε,Κη|2 + ^EffLn>
E*|Cn|2 = 5>;(0), E,Ln = nE,Z(Xl),
TO __
Pe(A)^c2e2.
Лемма доказана. <
Доказательство теоремы 4. Обозначим через Мп множество точек s, в
которых достигается mmU(s) (т.е. множество точек (0q — 6)у/п;ш. (11))*). Тогда
= \mmU(s) < mmUIs) \
{Mn С D} = ^ min t/(s) < min t/(s) l. (18)
*) Вместо Mn можно было бы рассматривать, например, наименьшую по норме точку, в
которой достигается mmU(s).
§ 78. Асимптотически оптимальные оценки
615
Стало быть,
{V^\0q - θ\ > 2Ν\ = ί min U(s) < min 17(e)} С min U(s) < 17(0)}.
Здесь
ВД^«>п | 9^ + ^ζΓ^ώ = ^(^(0)--^(7ν)),
mm
\s\>2N
\u\<N
wn = min wis — u) = min w(£).
\s\>2N \t\>N
\u\<N
Далее,
U(0) = Jw(-u)q (θ+±\ζ ί^\ du ζ (tii(0) - tii(Af ))Wm 4- u(M),
где Wm = max tu(£). Отсюда получаем
{^ |0q -θ\> 2Ν} С W(^i(0) - m(N)) < WM{ui(P) - txi(M)) + u(M)} С
В силу условия 5 выберем Μ = 7-Ν, 7 < 1» так> чтобы wyv > 2Wm при всех
достаточно больших N. Кроме того, воспользуемся неравенствами Wm > 2 (при
достаточно большом М), wn < w(N) < ecN. Тогда, очевидно,
{yfc\0Q-0\> Щ С К(0) < η(ΊΝ) +Ul(N)ecN}. (19)
В силу леммы 1 находим
Ре (η(ΊΝ) > \е-°»Л <: 2ae^N^+aN\
Ре (щ(М) > Ιβ-«"-«"Λ ^ 2ae-eN2+aN2+cN.
Выбирая α < -/?72> мы получим, что при достаточно больших N из (19) следует
Ρβ(ν^ Κ -θ\> 2Ν) < 4ae-aN2 + Pfl(Ul(0) < е~а"2).
Нам остается лишь воспользоваться леммой 2, в силу которой
P9M0)<e-a"2K6e-2""2.
Теорема доказана. <
616
Гл. 6. Теоретико-игровой подход
§ 79· Оптимальные статистические критерии
при произвольной функции потерь.
Критерий отношения правдоподобия
как асимптотически байесовское решение
1. Свойства оптимальности статистических критериев при произвольной
функции потерь. Мы видели в предыдущих двух параграфах, что многие
главные результаты теории оценивания качественно сохраняются при
переходе к более общим задачам статистического решения с потерями ги(£, 0),
δ £ D cRk, б G θ С tf, отличными от квадратичных.
Такая же картина имеет место и в теории проверки гипотез. Мы видели
в § 76, что оптимальные решающие правила для игр с конечными
множествами D и θ и произвольной функцией потерь имеют ту же форму, что
и оптимальные критерии для проверки конечного числа простых гипотез,
рассмотренные в §41. Результаты §45, 47, 49, 51, 53-55 также в
основном сохранятся. В частности, теоремы о р. н. м. к. в § 45-47 перейдут в
утверждения о равномерно наилучших стратегиях в соответствующих
статистических играх (Θ С R*, D = {#ь#2} двухточечно), в которых, однако,
функция потерь w(S{, 0) = Wi(0), Wi{9) — 0 при 0 € Θ*, г = 1,2, уже будет не
обязательно статистической (г^(0) = 1 при 0 ^ Θ;), а будет лишь
удовлетворять некоторым весьма общим условиям (например, свойствам монотонного
возрастания г^(0) при удалении θ от Θ;). Роль классов Κε, в которых мы
искали р. н. м. к., будут играть теперь классы решающих функций π(Χ) с
фиксированным максимальным значением ε «потерь первого рода»:
ε = sup ИЧтг(-), 0) = sup ιυ2{θ)Εθπ{Χ, J2). (1)
0€θι 0€θι
Минимизироваться будет значение «потерь второго рода»:
\ν{π(·),θ)=ν)1{θ)Εθπ{Χ,δ1) при 0 Ε θ2. (2)
Здесь π(Χ,δί) означает вероятность принятия решения δ{ критерием π.
Для сокращения записи положим, следуя гл. 3, π(Χ, δ2) = тг(-Х"), так что
π(Χ,δχ) = 1 — π(Χ). Обозначение одним символом π(Χ) критерия и числа
π(Χ, δ2) удобно и, как мы видели в гл. 3, к недоразумениям не приводит.
В (1), (2) ищутся экстремумы выражений, которые отличаются от
соответствующих выражений для статистических функций потерь лишь не
зависящими от π{Χ) множителями. Если эти множители обладают
естественным свойством монотонности, то изложение §45-47, 49, 51 при переходе к
задаче, определяемой (1), (2), существенно не изменится.
По существу мало изменятся и результаты асимптотического характера
в §53-55. В этом параграфе мы остановимся более подробно на обобщении
на случай произвольной функции потерь результатов § 53 и убедимся, что
это обобщение действительно не требует никаких дополнительных усилий.
2. К. о. п. как асимптотически байесовский критерий. Рассмотрим
статистическую игру (Х>, 0,W), в которой множество θ континуально и есть
выпуклое компактное множество в R*, а множество D стратегий статистика
§ 79. Оптимальные статистические критерии
617
двухточечно: D = {^ь^г}· Функция потерь w(£, 0) имеет вид
где 0ι — фиксированная внутренняя точка Θ. При w2 = wi(0) = 1 это
соответствует задаче проверки простой гипотезы #ι = {0 = 0χ} против
дополнительной альтернативы Н2 = {0 φ θι}.
Чтобы, пользуясь байесовским принципом, найти вид байесовского
решения, рассмотрим обычную игру (£), Θ, w) и предположим, что на Θ задано
распределение Q такое, что q = Q({0i}) > 0 (полная байесовская постановка
Q - <βθ\
задачи). Обозначим Q2 = —: , где 1^ есть вырожденное распределение,
1-q
сосредоточенное в точке 0. Тогда
;(ibQ) = (1 -q) [wi{t)Q2{dt), w{S2,Q) = qw2.
Это означает, что байесовская стратегия 7Tq(S2) = 1, если
(1-9) ί w1{t)Q2{dt) > qw2l (3)
и 7tq(6i) = 1, если имеет место обратное неравенство. Соотношение 3 можно
записать в виде
wi
/■
w(t)Q(dt) > О,
где
;(ί) = {
В силу байесовского принципа байесовское решающее правило kq{X)
имеет вид kq(X) = 1, если
wx{t) при ίφθχ,
-гУ2 при г = 01.
/
Mi)Qx(di)>o,
где Qx — апостериорное распределение. Пусть X(dt) = dt при t φ θχ,
Α({0Χ}) = 1 и распределение Q2 имеет плотность q2(t) относительно меры
Лебега. Тогда априорное распределение Q имеет плотность q(t)
относительно λ, равную (1 — q)q2{t) при t φ θχ и q(t) = q при t = θχ. Это означает,
что апостериорная плотность относительно меры А будет равна
д(г/Х) = Л™*}, f(X) = Jfu(X)q(u)\(du).
Следовательно, байесовское решающее правило πς}(Χ) имеет вид πς}(Χ) = 1,
если
{l-q)Jwi(t)ft(X)92{t)dt > w2qfei(X)- (4)
618 Гл. 6. Теоретико-игровой подход
Риск этого правила равен
WWO.Q) ^ qw2Pei(nQ(X) = l) + (l-q) Jw1(u)q2(u)Pu(7rQ(X) =0)du.
Сравнивая эти соотношения с содержанием § 53, мы видим, что область (4)
приема решения δ2 имеет здесь тот же вид, что и область Q(c) в (53.3) при
с = W2q/{1 — q) и при замене функции q(t) в (53.3) на Wi(t)q2{t). Другими
словами,
fl, если tq2(X) > с,
ttqW = < 7, если tq2{X) = с, (5)
[θ, если rQ2(X) < с,
где
!у>1{ЩЩХ)А w2q
Г*{Х) = Щ) ' C=—q
Далее, мы можем, следуя рассуждениям § 53, поступить следующим
образом. Из совокупности байесовских правил (5) путем изменения числа q
выбрать такое решение 7vq(X)^ которое имело бы фиксированное значение
«потерь первого рода»:
w2[Pei(7rQ(X) = 1) +ΊΡθι(πο(Χ) = 7)] = а.
Тогда среди всех правил π(Χ), для которых
αι(π) = ^2Εβιπ(Χ) < α, (6)
решение ttq(X) будет минимизировать «потери второго рода», равные
α2(π)
= iw1(u)q2(u)Eu{l-n{X))du. (7)
Это есть прямое следствие байесовости решения π<2« Сравнение
значений (6), (7) с величинами вероятностей ошибок первого и второго рода
(53.4) показывает, что мы снова имеем дело с несущественными
отличиями, главное из которых состоит в замене функции q(u) в (53.4) на функцию
wi(u)q2{u). Числа с и 7 в (5) определяются по а.
Изложенное позволяет нам, в точности следуя рассуждениям § 53,
сформулировать следующие определения и утверждения.
Определение 1. Решающее правило π(Χ) принадлежит классу Κε
(имеет асимптотический уровень 1 — ε), если
limsupE^^(X) < ε.
n-юо
Это определение, по существу, ничем не отличается от определения 53.1.
§ 79. Оптимальные статистические критерии
619
Покажем теперь, что выбором q мы можем добиться того, чтобы ttq € Κε.
Положим
гяЛХ) = Ш) "Uv vffi '
где / = Ι(θ\) есть информационная матрица Фишера в точке θ\.
Предположим, далее, что выполнены условия (RR) и что θ\ есть внутренняя точка Θ,
функция Wi(t)q2{t) непрерывна в точке θ\ и положительна,
Тогда в силу леммы 53.1 для функцииpt(c) = ~Pt(rQ2(X) > с) получаем
ρθι (с) = Pfll (Т(Х) >z)^ Hfc((2*, oo)).
Следовательно, полагая q = с/(с + г^), где с определено в (8), ζ = Ле/2, h£
есть квантиль порядка 1-е распределения χ2 с к степенями свободы, мы
получим
lim p0l = ε,
η~>οο \l-qj
и, стало быть, ttq(A') Ε Κε.
Определение 2. Для данного априорного распределения Q
решающее правило π(Χ) называется асимптотически байесовским в Κε, если
limsup— г = 1.
n-юо «2(ttq)
Теорема 1. Пусть выполнены условия (RR), точка θχ является
внутренней точкой Θ. Тогда в Κε существует асимптотически
байесовское решающее правило π(Χ) — одно и то же для любых
распределений Q2 и любых функций w\(t) таких, что функция w\(t)q2(t) непрерывна
и положительна в точке θ\ и ограничена на Θ. Критерий π
определяется соотношением
ЗД = 1, если !f^>eh*l\ (9)
Теорема доказывается точно так же, как теорема 53.1, с точностью до
замены функции q(t) на w\(t)q2(t). Теорема 53.1 позволяет также найти
значение «потерь второго рода» (см (7)) критерия π.
Критерий (9) есть не что иное, как критерий отношения правдоподобия.
620
Гл.6. Теоретико-игровой подход
§ 80. Асимптотически оптимальные решения
при произвольной функции потерь
в случае близких сложных гипотез
В этом параграфе мы рассмотрим обобщение на случай произвольной
функции потерь результатов § 54. Это обобщение будет более
содержательным, чем в предыдущем параграфе, так как функции потерь будут
зависящими от η (ср. с §78).
Пусть (Ρ, Θ,ΡΓ) — статистическая игра, в которой θ С R*, множество
D = {5ι, ^2} двухточечно, νο(δΐ,θ) = Wj(0), где Wi{9) = 0 при Θ Ε Θ;, i = 1,2,
пересечение Θ ι Π 02 пусто.
Если Wi(9) = 1 при θ £ Θ;, то мы получим задачу о проверке гипотез
Н{ = {θ Ε Θΐ}, i = 1,2, рассмотренную в §54, 55.
Найдем байесовскую стратегию для игры (Ζ), Θ,ΐϋ). Пусть Qj —
распределения на ©г,
Q = 9iQi + 92Q2, 9ι + 92 = 1>
если
Тогда, очевидно, iJ(ij,Q) = / Wi(t)Q(dt) и πρ^) = 1,
jw2{№{dt) < f wx{t)Gl{dt),
или
9i/t^(i)Qi(rfi) <?2/ti;i(t)Q2(rfi)-
Следовательно, в силу байесовского принципа байесовское решающее
правило будет иметь вид kq(X) = 1, если
iw2(t)Qx{dt) < [wi(t)Qx{dt). (1)
Допустим, что распределения Qj имеют плотности <ft(i), г = 1,2,
относительно меры λ. Тогда Q и апостериорное распределение Qx будут иметь
плотности соответственно q(t) = qiqi{t) 4- 9292(0 и
i(t/X) = i7^p, /W =fq(u)fu(X)\(du).
Это значит, что соотношение (1) можно переписать в виде
91 f w2(t)qi(t)ft{X)X(dt) < q2 J w1(t)q2(t)ft(X)X(dt). (2)
Θι Θ2
Риск байесовского правила kq(X) равен
W(irQ(-),e) = w^EenciiX) + χν2(θ)(1 -Ееп^Х)),
W(nci№) = Jw(nQ(.),t)q(t)\(dt).
§ 80. Асимптотически оптимальные решения
621
Перейдем теперь к рассмотрению близких альтернатив. Пусть θ\ —
какое-нибудь фиксированное значение параметра 0. Как и в § 54, мы будем
предполагать, что множества Θζ имеют вид
Bi = 4 + ^L, (3)
где Γί от η не зависят. Относительно Qz будем предполагать, что они
индуцированы некоторыми распределениями П*, сосредоточенными на Ι\ и
от η не зависящими. Если множества 1\ ограничены, то стратегии
природы θ располагаются в 6/\/га-окрестности точки #i, b < оо. Поэтому если
Wi(£), W2{t) непрерывны, W{(t) > с > 0, г = 1,2, соответственно на
множествах ©2, θι, то статистическая игра (Ρ, Θ, W) для такой функции потерь
практически не будет отличаться по своим свойствам от игры со
статистической функцией потерь W{(t) = 1 при t ^ θ*, рассмотренной нами в § 54, 55.
Рассмотрим здесь более содержательное обобщение, аналогичное
тому, которое проводилось нами в §78. Будем считать, что функция потерь
w(5i,6) = wi{9) зависит от η так, что
Wi(9) = щ9П{в) = ViWii (θ - θι)), (4)
где V{(t) — ограниченные измеримые функции, не зависящие от п. Как и
в § 78, предположение (4) означает, что функции потерь очень чувствительны
к отклонениям θ от θ\.
Следуя § 54, мы будем задачу отыскания по выборке X €= Р# решения
игры (£>,6,W), описанной выше, называть задачей А. Если выполнено
(3), (4), то будем говорить о задаче А для близких гипотез с функциями
потерь V{(t).
Рассмотрим теперь другую статистическую игру (£>#, Г, V), относящуюся
к выборке Υ ^ Ф7^-1 еДиничн0Г0 объема, где / = Ι(θ\) есть
информационная матрица Фишера для семейства Р# в точке θ\. Эта игра имеет
двухточечное множество решений Ό в = (с/ъ^г) и множество стратегий природы
(параметрическое множество) Г = Γι иГг. Функция потерь v(d, 7): Db χ Γ —> R
определяется соотношениями
v{di,j) = ^(7), щЫ=0 при 7^ Гг.
Таким образом, в этой игре Т>в есть класс всех решений d(Y): Rk -> Db,
функция риска равна
V(d(-),y) = υι{Ί)ΦΊ>Ι-ι(ά(Υ) = ά1)+ν2(7)ΦΊίΙ-ι(ά(Υ) = d2)
(одно из слагаемых в правой части равно нулю). Аналогично
выписываются потери для рандомизированных стратегий π(Υ) в терминах Επ(Ι^),
Υ ^ Φ7?/-ι. Сформулированную задачу будем называть задачей В»
Между задачами А и В существует то же соотношение, которое было
установлено между этими задачами в §55. Пусть π{Υ) есть решение задачи В,
оптимальное в том или ином смысле (байесовское, минимаксное). И пусть
Θ* есть о. м. ц. в задаче А, 7* = Ф* — #ι)\/η. Тогда решение π(7*) будет
асимптотически оптимальным (в том -же смысле) решением задачи А.
622
Гл. 6. Теоретико-игровой подход
Сформулированный «предельный признак оптимальности» позволяет
редуцировать задачу А к более простой задаче В.
Чтобы придать изложенному точный смысл, дадим следующие
определения. Пусть на Г{ заданы распределения П^. Положим Π = ςχΤΙχ + фПг,
Qi + 42 — 15 и обозначим через Q распределение на Θ, индуцированное
распределением Π и преобразованием θ = θ\ + j/y/n-
Определение 1. Решение πι{Χ) называется асимптотически
байесовским, если
limsup[WM0,Q)-W^Q(-),Q)KO.
ге->оо
Здесь, как и прежде,
W{n(-),0) = w^EgiriX) + w2{0)(l - Εθπ(Χ)),
W(n(-),e)=Jw(n(-),t)Q(dt),
7tq — байесовское решающее правило.
Определение 2. Решение -к\(X) называется асимптотически
минимаксным, если для любого другого решения π(Χ)
lim sup
sup W{n(·),#) - sup Ψ{π{·), Θ)
П-+00 ΙθζΘ ΘβΘ
<0.
Если следовать определению 1, то мы могли бы здесь сравнивать πι с
минимаксным правилом π.
Аналогично § 54 мы могли бы рассматривать также асимптотически
байесовские и минимаксные решения в классе Κε решений с фиксированными
асимптотическими «потерями первого рода»:
ε = lim sup sup ιυι(θ)Εθπ(Χ).
п-юо 0£Θι
Чтобы получить соответствующие результаты, достаточно будет сравнить
содержание этого параграфа с § 54.
Обозначим через кп(У) байесовское решение игры (Х>в,Г, V) (т.е.
задачи В), соответствующее априорному распределению П, и предположим для
простоты, что множества 1\ ограничены.
Теорема 1. Пусть в окрестности точки θ\ выполнены условия (RR),
о функции V{ и распределение П, таковы, что
О < / v1(u)U2(du) < оо, 0 < / v2(u)Ili(du) < оо.
Тогда во введенных обозначениях критерий
πι(Χ)=7ΓΠ(7*), 1* = (θ*-θι)^,
будет асимптотически байесовским решением игры (U,Q,W) (т. е.
задачи А), соответствующим априорному распределению Q.
§ 80. Асимптотически оптимальные решения
623
Теорема 2. Пусть в окрестности точки θ\ выполнены условия (RR)
и в задаче В существуют минимаксное решение тг(У) и
соответствующее ему наихудшее распределение П. Тогда критерий π\{Χ) = π (7*)
будет асимптотически минимаксным решением задачи А.
Замечание 1. Условия теоремы о существовании π и Π в силу
теорем § 75 будут выполнены, если νι — непрерывные функции.
Доказательство теоремы 1 вполне аналогично доказательству
теоремы 54.1. Из (2) следует, что байесовское решающее правило ttq имеет
вид ttq(X) = 1, если
fw1(t)g2(t)ft(X)X(dt) ъ
fw2(t)qi(t)ft(X)X(dt) > q2- U
f (Χ)
Полагая Z\(t) = -1 , ч и учитывая, что
«(ί)λ(Λ) = Q<(di), Qi U + 4=) = ВДи),
мы можем неравенство (5) с помощью замены £ = θ\ -\-ujy/n преобразовать
к виду
Jvi{u)Zl(u/y/n)Ti2{du) = fZi(u/y/n)H*(du) = ft , .
/«2(ιχ)Ζι(τχ/>/η)Πι(^) /Ζχ (иД/n) ni(du) C' C ?2'
обобщенные распределения П[(Л) = / Vi+\(u)Ili(du) {vs{u) = v\(u),
A
i = 1,2) можно превратить в вероятностные перенормировкой, введя
распределения ТЩА) = Π·(Α)/Π'ί(Γΐ) (по условию 0 < П-(Г;) < оо). Получим
тогда в качестве (5) неравенство точно того же вида, как в § 54.
Последующие рассуждения доказательства отличаются от
соответствующих рассуждений в § 54 лишь упрощениями. Мы предоставляем провести
их читателю. В основе этих рассуждений лежит равномерная по η
сходимость (Θ = θι+ j/y/n)
W(*q(-),0) -> VW-),7), WW),*) -> П*п(-),7), (7)
где щ(Х) = 7гп(7*)· <
Для доказательства теоремы 2 нам понадобится
Лемма 1. Пусть Q — априорное распределение и πι —
соответствующее ему асимптотически байесовское решение такое, что
limsuptV(7ri('),Q) =сь limsupsupW(7Ti(-),0) ^ с. (8)
тг-юо п-юо θ€θ
Тогда π χ — асимптотически минимаксное решение.
где
624
Гл. 6. Теоретико-игровой подход
Доказательство. Обозначим, как и прежде, через ttq байесовское
решение. Тогда для любого решения π имеем
limsupsup\¥(π,θ) ^ HmsupVF(7r, Q) > HmsupW^QjQ) >
п-юо 0£θ n->oo п-юо
^ limsupi^^i,Q) = с ^ limsupsup Η^(πι,0). <]
n-*oo n—юо 0£0
Доказательство теоремы 2. Пусть П — наихудшее
распределение на Г, так что тг(У) = πγ[(Υ) есть минимаксное решающее правило в
игре (Vb,T,V). Тогда по теореме 1 ъ\(Х) — 7Tjj(7*) будет асимптотически
байесовским решением для распределения Q, соответствующего П, и для
доказательства теоремы нам достаточно убедиться, что Q и πχ удовлетворяют
условиям леммы 1.
Обозначим через iVjj- носитель распределения П. Тогда в силу теорем § 75
V4*n(-)>7) = c при 7€J%, supF(7Tn(.),7) < с. (9)
Но для б = θ\ 4- j/y/n имеет место (см. (7)) равномерная по j сходимость
W(7ri(-),0) -> νΓ(πυ(·),7)· Отсюда и из (9) следует (8). Теорема доказана. <
Табли
Таблица I. Нормальное распределение Φ0,ι
В таблице приведены значения
оо
Ф(ж) = Ф0,1((ж,оо)) = -j= fe-t2/2dt.
Χ
Таблица I
χ
0^0
од
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
ι,ο
1Д
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
χ =
Щх) =
0
0,5000
,4602
,4207
,3821
,3446
,3085
,2743
,2420
,2119
,1841
,1587
,1357
,1151
,0968
,0808
,0668
,0548
,0446
,0359
,0288
,0228
,0179
,0139
,0107
,0082
,0062
,0047
,0035
,0026
,0019
ЗД)
0,0013
1
0,4960
,4562
,4168
,3783
,3409
,3050
,2709
,2389
,2090
,1814
,1562
,1335
,1131
,0951
,0793
,0655
,0537
,0436
,0351
,0281
,0222
,0174
,0136
,0104
,0080
,0060
,0045
,0034
,0025
,0018
зд
0,0010
2
0,4920
,4522
,4129
,3745
,3372
,3015
,2676
,2358
,2061
,1788
,1539
,1314
,1112
,0934
,0778
,0643
,0526
,0427
,0344
,0274
,0217
,0170
,0132
,0102
,0078
,0059
,0044
,0033
,0024
,0018
зд>
0,0007
3
0,4880
,4483
,4090
,3707
,3336
,2981
,2643
,2327
,2033
,1762
,1515
,1292
,1093
,0918
,0764
,0630
,0516
,0418
,0336
,0268
,0212
,0166
,0129
,0099
,0075
,0057
,0043
,0032
,0023
,0017
3J3
0,0005 |
4
0,4840
,4443
,4052
,3669
,3300
,2946
,2611
,2297
,2005
,1736
,1492
,1271
,1075
,0901
,0749
,0618
,0505
,0409
,0329
,0262
,0207
,0162
,0125
,0096
,0073
,0055
,0041
,0031
,0023
,0016
3^4
0,0003
626
Таблицы
Таблица I (окончание)
X
ОД)
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
X =
?(*) =
5
0,4810
,4404
,4013
,3632
,3264
,2912
,2578
,2266
,1977
,1711
,1469
,1251
,1056
,0885
,0735
,0606
,0495
,0401
,0322
,0256
,0202
,0158
,0122
,0094
,0071
,0054
,0040
,0030
,0022
,0016
3^5
0,0002
6
0,4761
,4364
,3974
,3594
,3228
,2877
,2546
,2236
,1949
,1685
,1446
,1230
,1038
,0869
,0721
,0594
,0485
,0392
,0314
,0250
,0197
,0154
,0119
,0091
,0069
,0052
,0039
,0029
,0021
,0015
3^6
0,0002
7
0,4721
,4325
,3936
,3557
,3192
,2843
,2514
,2206
,1922
,1660
,1423
,1210
,1020
,0853
,0708
,0582
,0475
,0384
,0307
,0244
,0192
,0150
,0116
,0089
,0068
,0051
,0038
,0028
,0021
,0015
3J
0,0001
8
0,4681
,4286
,3897
,3520
,3156
,2810
,2483
,2177
,1894
,1635
,1401
,1190
,1003
,0838
,0694
,0571
,0465
,0375
,0301
,0239
,0188
,0146
,0113
,0087
,0066
,0049
,0037
,0027
,0020
,0014
3,8
0,0001
9
0,4641
,4247
,3859
,3483
,3121
,2776 |
,2451
,2148
,1867
,1611
,1379
,1170
,0985
,0823
,0681
,0559
,0455
,0367
,0294
,0233
,0183
,0143
,0110
,0084
,0064
,0048
,0036
,0026
,0019
,0014
3^9
0,0000
Таблица II. Квантили нормального распределения
В таблице приведены значения Х€ такие, что
Φ(λ*) = Φο,ι((λ*,οο))=ε.
Таблица II
100ε
50
45
40
35
30
25
λ*
0,0000
0,1257
0,2533
0,3853
0,5244
0,6745
' 100ε
1 20
15
10
5
2,5
1
λε
0,8416 Ι
1,0364 J
1,2816 Ι
1,6449
1,9600
2,3263
100ε
0,5
од
0,05
0,01
0,005
λ.
2,5758
3,0902
3,2905
3,7190
3,8906 !
Таблицы
627
Таблица III. Распределение хи-квадрат Н&
В таблице приведены значения (см. § 2.2)
оо
Нк(Х) = Н*((*,оо)) = ^^ ft^e-^dt
X
при 1 ^ к ^ 20. При больших к можно пользоваться приближением (см. § 12, табл. I)
Нк(х) « Ф(л/2^ - V2k - 1) = Нк{х). (1)
Последний столбец таблицы содержит значения Нк(х) при к — 20. Путем сравнения
с предыдущим столбцом можно оценить степень точности приближения (1). С ростом к
погрешность уменьшается.
Таблица III
X
о7~
>2
'4
,6
,8
1,0
,5
2
3
4
5
6
7
8
9
10
11
12
! 13
1 14
15
j 16
17
18
19
20
21
22
23
24
25
1
0,7518
,6547
,5271
,4386
,3711
,3173
,2207
,1573
,0833
,0455
,0254
,0143
,0082
,0047
,0027
,0016
,0009
,0005
,0003
,0002
,0001
,0001
Объем выборки
2 ~~~~
0,9512
,9048
,8187
,7408
,6703
,6065
,4724
,3679
,2231
,1353
,0821
,0498
,0302
,0183
,0111
,0067
,0041
,0025
,0015
,0009
,0006
,0003
,0002
,0001
,0001
,0001
3
0,9918
,9776
,9402
,8964
,8495
,8013
,6823
,5725
,3916
,2615
,1718
,1116
,0719
,0460
,0293
,0186
,0117
,0074
,0046
,0029
,0018
,0011
,0007
,0004
,0003
,0002
,0001
,0001
к
4
0,9988
,9953
,9825
,9631
,9385
,9098
,8266
,7358
,5578
,4060
,2873
,1992
,1359
,0916
,0611
,0404
,0266
,0174
,0113
,0073
,0047
,0030
,0019
,0012
,0008
,0001
,0003
,0002
,0001
,0001
,0001
5
0,9998
,9991
,9953 1
,9880
,9770
,9626
,9131
,8492
,7000
,5494
,4159
,3062
,2206
,1562
,1091
,0752
,0514
,0348
,0234
,0156
,0104
,0068
,0045
,0030
,0019
,0013
,0008
,0005
,0003
,0002
,0001 J
628 Таблицы
Таблица III (продолжение)
X
0,5
1,0
,5
2,0
,5
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
1 23
24
! 25
26
27
28
29
30
Объем выборки к
б
0,9978
,9856
,9595
,9197
,8685
,8089
,6767
,5438
,4232
,3204
,2381
,1736
,1246
,0884
,0620
,0430
,0296
,0203
,0138
,0093
,0062
,0042
,0028
,0018
,0012
,0008
,0005
,0003
,0002
,0002
,0001
,0001
7
0,9995
,9948
,9823
,9598
,9271
,8850
,7798
,6600
,5398
,4284
,3326
,2527
,1886
,1386
,1006
,0721
,0512
,0360
,0251
,0174
,0120
,0082
,0056
,0038
,0025
,0017
,0011
,0008
,0005
,0003 ;
,0002
,0002
,0001
8
I 0,9999
,9983
,9927
,9810
,9617
,9344
,8571
,7576
,6472
,5366
,4335
,3423
,2650
,2017
,1512
,1119
,0818
,0592
,0424
,0301
,0212
,0149
,0103
,0072
,0049
,0034
,0023
,0016
,0011
,0007
,0004
,0003
,0002 !
9
1,0000
,9994
,9972
,9915
,9809
,9643
,9114
,8343
,7399
,6371
,5342
,4373
,3505
,2757
,2133
,1626
,1223
,0909
,0669
,0487
,0352
,0252
,0179
,0127
,0084
,0062
,0043
,0030
,0020
,0014
,0010
,0007
,0004
10
1,0000
,9998
,9989
,9963
,9909
,9814
,9474
,8912
,8153
,7254
,6288
,5321
,4405
,3575
,2851
,2237
,1730
,1321
,0996
,0744
,0550
,0403
,0193
,0211
,0151
,0108
,0076
,0054
,0037
,0026
,0018
,0013
,0009
Таблицы 629
Таблица III (продолжение)
X
2
3
4
5
6
7
8
9
10
12
14
16
18
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
11
0,9985
,9907
,9699
,9312
,8734
,7991
,7133
,6219
,5304
,3636
,2330
,1411
,0816
,0453
,0334
,0244
,0177
,0127
,0091
,0065
,0046
,0032
,0023
,0016
,0011
,0008
,0005
,0004
,0003
,0002
,0001
,0001
,0001
Объем выборки
12
! 0,9994
,9955
,9834
,9580
,9161
,8576
,7852
,7029
,6160
,4457
,3007
,1912
,1157
,0671
,0504
,0375
,0277
,0203
,0148
,0170
,0077
,0055
,0039
,0028
,0020
,0014
,0010
,0007
,0005
,0003
,0002
,0002
,0001
,0001
13
0,9998
,9979
,9912
,9752
,9462
,9022
,8436
,7729
,6939
,5276
,3738
,2491
,1575
,0952
,0729
,0554
,0417
,0311
,0231
,0107
,0124
,0091
,0066
,0047
,0034
,0024
,0017
,0012
,0009
,0006
,0004
,0003
,0002
,0001
к
Η
0,9999
,9991
,9955
,9858
,9665
,9347
,8893
,8311
,7622
,6063
,4497
,3134
,2068
,1301
,1016
,0786
,0603
,0458
,0346
,0259
,0193
,0142
,0105
,0076
,0055
,0040
,0029
,0021
,0015
,0010
,0007
,0005
,0004
,0003 !
15
1,0000
0,9996
,9977
,9921
,9798
,9577
,9238
,8775
,8197
,6790
,5255
,3821
,2627
,1719
,1368
,1078
,0841
,0651
,0499
,0380
,0287
,0216
,0161
,0119
,0088
,0064
,0047
,0034
,0025
,0018
,0013
,0009
,0006
,0005
630 Таблицы
Таблица III (окончание)
X
4
5
6
7
8
9
10
12
14
16
18
20
22
24
26
28
30
31
32
33
34
35
36
37
38
39
40
41
42
43 '
44
45 !
16
0,9989
,9958
,9881
,9733
,9489
,9134
,8666
,7440
,5987
,4530
,3239
,2202
,1432
,0895
,0540
,0316
,0180
,0135
,0100
,0074
,0054
,0040
,0029
,0021
,0015
,0011
,0008
,0006
,0004
,0003
,0002
,0001
Объем выборки
1 ^
0,9995
,9978
,9932
,9836
,9666
,9403
,9036
,8001
,6671
,5238
,3888
,2742
,1847
,1194
,0745
,0449
,0264
,0200
,0151
,0113
,0084
,0062
,0046
,0034
,0025
,0018
,0013
,0009 ι
,0007
,0005
,0003
,0002
18
0,9998
,9989
,9962
,9901
,9786
,9597
,9319
,8472
,7291
,5926
,4557
,3328
,2320
,1550
,0998
,0621
,0375
,0288
,0220
,0167
,0126
,0095
,0071
,0052
,0039 !
,0029
,0021
,0015
,0011
,0008
,0006
,0004
lk
I ^
0,9999
,9994
,9979
,9942
,9867
,9735
,9530
,8856
,7837
,6573
,5224
,3946
,2843
,1962
,1302
,0834
,0518
,0404
,0313
,0240
,0184
,0140
,0106
,0080
,0059
,0044
,0033
,0024 ι
,0018
,0013
,0009
,0007
20
1,0000
0,9997
,9989
,9967
,9919
,9829
,9682
,9161
,8305
,7166
,5874
,4579
,3405
,2424
,1658
,1094
,0699
,0552
,0433
,0337
,0261
,0201
,0154
,0117
,0089
,0067
,0050
,0037
,0028
,0020 '
,0015 ,
,0011
Я20(х)
0,9997
,9990
,9973
,9938
,9876
,9774
,9619
,9109
,8298
,7218
,5968
,4683
,3489
,2472
,1670
,1078
,0667
,0517
,0396
,0301
,0227
,0169
,0125
,0092
,0067
,0048
,0035
,0025
,0017
,0012
,0010
,0006
Таблицы
631
Таблица IV. Распределение Стьюдента Тк
В таблице приведены значения
™-™~»-^/И)
-(fc + l)/2
dt
при 1 ^ к ^ 20. При больших значениях к можно пользоваться приближением (см. § 12,
табл. I)
ГЛ(ж)«Ф(я) = Фод((х1оо)). (2)
Точность приближения (2) при к = 20 можно оценить путем сравнения последнего
столбца таблицы с табл. I.
X
0,0
5
1,0
2
4
6
8
2,0
2
4
6
8
3,0
2
4
6
8
4,0
2
1
0,5000
,3524
,2500
,2211
,1974
,1778
,1614
,1476
,1358
,1257
,1169
,1092
,1024
,0964
,0910
,0862
,0819
,0780
,0744
Объем выборки
2
0,5000
,3333
,2113
,1765
,1482
,1253
,1068
,0917
,0794
,0692
,0679
,0537
,0477
,0427
,0383
,0346
,0314
,0286
,0261
3
0,5000
,3257
,1955
,1581
,1280
,1039
,0848
,0697
,0576
,0479
,0402
,0339
,0282
,0247
,0212
,0184
,0160
,0140
,0123
Τ
к
4
0,5000
,3217
,1869
,1482
,1170
,0924
,0731
,0581
,0463
,0372
,0300
,0244
,0200
,0165
,0136
,0114
,0095
,0081
,0068
а б л и ц а IV
5
0,5000
,3191
,1816 !
,1419
,1102
,0852
,0659
,0510
,0395
,0308
,0241
,0190
,0150
,0120
,0096
,0078
,0063
,0052
,0045
632
Таблицы
Таблица IV (продолжение)
X
4
6
8
5,0
2
4
6
8
6,0
2
4
6
8
1 7,0
2
4
6
8
8,0
1
0,0711
,0681
,0654
,0628
,0605
,0583
,0562
,0543
,0526
,0509
,0493
,0479
,0465
,0452
,0439
,0428
,0416
,0406
,0396
Объем выборки
2
0,0240
,0221
,0204
,0199
,0175
,0163
,0152
,0142
,0133
,0125
,0118
,0111
,0105
,0099
,0094
,0089
,0086
,0080
,0076
3
0,0109
,0097
,0086
,0077
,0069
,0062
,0056
,0051
,0046
,0042
,0039
,0035
,0033
,0030
,0028
,0025
,0024
,0022
,0020
к
4
0,0058
,0050
,0043
,0037
,0033
,0028
,0025
,0022
,0019
,0017
,0015
,0014
,0012
,0011
,0010
,0009
,0008
,0007
,0007
5
0,0035
,0029
,0024
,0020
,0017
,0015
,0012 Ι
,0011 ι
,0009
,0008
,0007
,0006
,0005
,0005
,0004
,0004
,0003
,0003
,0002
Таблица IV (продолжение)
X
0,0
5
1,0
2
4
6
! 8
I 2,0
2
! 4
I 6
! 8
I 3,0
1 2
4
6
8
4,0
2
4
6
8
5,0
6
0,5000
,3174
,1780
,1377
,1055
,0804
,0610
,0462
,0350
,0266
,0203
,0156
,0120
,0093
,0072
,0057
,0045
,0035
,0028
,0023
,0018
,0015
,0012
Объем выборки
7
0,5000
,3162
,1753
,1346
,1021
,0768
,0574
,0428
,0319
,0237
,0177
,0132
,0100
,0075
,0057
,0044
,0034
,0026
,0020
,0016
,0012
,0010
,0008
8
0,5000
,3153
,1733
,1322
,0995
,0741
,0548
,0403
,0295
,0216
,0158
,0116
,0085
,0063
,0047
,0035
,0026
,0020
,0015
,0011
,0009
,0007
,0005
Jfe
9
0,5000
,3145
,1717
,1304
,0975
,0720
,0527
,0383
,0277
,0199
,0144
,0104
,0075
,0054
,0039
,0029
,0022
,0015
,0012
,0009
,0006
,0005
,0004
10 ,
0,5000 |
,3139 :
,1704
,1289
,0959
,0703
,0510
,0367
,0262
,0186
,0132
,0094
,0067
,0047
,0034
,0024
,0017
,0013
,0009
,0007
,0005
,0004
,0003
Таблицы
633
Таблица IV (продолжение)
X
0,0
5
1,0
2
4
6
! 8
! 2,0
2
4
6
8
3,0
2
4
6
8
4,0
Объем выборки к
11
0,5000
,3135
,1694
,1277
,0945
,0689
,0496
,0354
,0250
,0176
,0123
,0086
,0060
,0042
,0030
,0021
,0015
,0010
12
0,5000
,3131
,1685
,1266
,0934
,0678
,0485
,0343
,0241
,0168
,0116
,0080
,0055
,0038
,0026
,0018
,0013
,0009
13
0,5000
,3127
,1678
,1258
,0925
,0668
,0475
,0334
,0232
,0160
,0110
,0075
,0051
,0035
,0024
,0016
,0011
,0008
14
0,5000
,3124
,1671
,1250
,0916
,0660
,0467
,0326
,0225
,0154
,0105
,0071
,0048
,0032
,0022
,0014
,0010
,0007
15
0,5000
,3112
,1666
,1244
,0909
,0652
,0460
,0320
,0219 1
,0149
,0100
,0067
,0045
,0030
,0020
,0013
,0009
,0006
Таблица IV (окончание)
X
0,0
5
1,0
2
4
6
8
2,0
2
! 4
6
8
3,0
2
4
; 6
8
4,0
16
0,5000
,3119
,1661
,1238
,0903
,0646
,0454
,0314
,0214
,0145
,0097
,0064
,0042
,0028
,0018
,0012
,0008
,0005
Объем выборки
17
0,5000
,3117
,1657
,1233
,0898
,0640
,0448
,0309
,0210
,0141
,0093
,0061
,0040
,0026
,0017
,0011
,0007
,0005
18
0,5000
,3116
,1653
,1228
,0893
,0635
,0443
,0304
,0205
,0137
,0090
,0059
,0038
,0025
,0016
,0010
,0007
,0004
к
19
0,5000
,3114
,1649
,1224
,0888
,0630
,0439
,0300
,0202
,0134
,0082
,0057
,0037
,0024
,0015
,0009
,0006
,0004
20
0,5000
,3113
,1646
,1221
,0884
,0626
,0435
,0296
,0199
,0131
,0086
,0055
,0035
,0022
,0014
,0009
,0006
,0003
Приложения
Приложение I
Теоремы типа Гливенко-Кантелли
В этом приложении будут доказаны утверждения, из которых будут вытекать
теоремы 4.1, 4.2. Обозначения § 4, в котором эти теоремы сформулированы, мы
будем использовать без пояснений. Докажем сначала один общий вспомогательный
вариант теоремы Гливенко-Кантелли.
Определение. Класс Я множеств из 93 # = 93т будем называть конечно
аппроксимируемым (относительно распределения Р), если, каково бы ни было
ε > 0, для него существует другой класс множеств 6(ε), состоящий из конечного
числа Ν = Ν(ε) элементов 5i,...,Sw, Si Ε 58m, такой, что для любого В Ε Я
найдутся множества А\ и А 2 из б (ε) со свойствами
Αι СВс Л2,
Ρ(Α2-Α1)<ε. (1)
Определим над классами множеств операции сложения, умножения и
дополнения. Классами Я\ + Я2 и Я\Я2 будем называть соответственно классы множеств
вида A U В и А П В, где А € Я\, В € S^. Дополнением Я будем называть класс
множеств, составленный из дополнений А, А € Я.
Теорема 1. 1) Пусть Хп = [Хоо]п5 -ΧΌο €= Р, а класс Я является конечно
аппроксимируемым. Тогда
sup|P;(*)-P(B)|—>0. (2)
вея Π·Η·
2) Совокупность конечно аппроксимируемых классов замкнута
относительно введенных операций.
Доказательство. Первое утверждение получается с помощью тех же
соображений, которые применялись нами в одномерном случае в теореме 2.2. Для
заданных В Ε Я и ε > 0 найдутся Ν = Ν(ε) и множества Αι, Л2, обладающие
свойством (1). Для них имеем
р;(в) - р(в) < ρ;μ2) - р^о < р;(а2) - р(а2) + е,
Р* (£) - Р(В) £ Ρ· (Αι) - Р(Л2) > Ρ^ΛΟ - Ρ(Λι) - ε.
Поэтому
f]{K(Sk) -Р(5*)| <ε} С (sup |Р;(В) -Р(В)| < 2ε Ι,
где 5ι,...,5η — элементы 6(ε). Так как P*(S*) —> Р(5*)> то отсюда уже без
п.н.
труда получаем (2) (ср. с доказательством теоремы 2.2А).
Приложение I
635
Второе утверждение теоремы 1 почти очевидно. Пусть дано ε > 0 и пусть 61 (ει)
и 62(ε2) — аппроксимирующие классы для Я\ и Л2 соответственно. Пусть, далее,
А и В — любые множества из Я\, Л2. Из соотношений ει -f ε2 = ε,
Αι С Л С Л2, Р(Л2 - Αι) < ει (Λ; е 6ι(ει)),
В1СВсВ2, Ρ(Β2-Β1)<ε2 №6 62(£2))
получаем
ΑλΒι С ABC А2В2,
А2В2 - ΑλΒγ С (А2 - ЛО U (В2 - ВО,
Ρ(Λ2£2-Λι£ιΚε.
Таким образом, класс Я\Я2 конечно аппроксимируем. Сумма Я\+Я2 и дополнение
Я рассматриваются аналогично. <
Следствие!. Пусть X = Жт, Хп = [Χ<χ>]η & F. Тогда
euplF^O-FWl—>0
t п.н.
при п —> оо, где F^(£) — эмпирическая функция распределения.
Доказательство. Из доказательства теоремы 2.2А видно, что классы
множеств Я] = {у € Mm: 2/j· < tj}, -00 < £_,· < 00, при каждом j = 1,.. .,т являются
конечно аппроксимируемыми. В качестве системы 6(ε) достаточно взять
полупространство {yj < Zk}n {yj ^ Zk}, к = 1,..., iV, где ζ* определены в (2.6).
По второму утверждению теоремы 1 класс углов Я = Я\Я2 ... Л^ также будет
конечно аппроксимируемым. Нам остается воспользоваться первым утверждением
теоремы 1. <
Следствие 1 есть не что иное, как теорема 4.1.
Рассмотрим теперь классы множеств Л, которые удовлетворяют следующему
условию (Г). Пусть Км есть куб
Км = <У = (У1,...,Ут): max \ук\ ζ Μ L
(Г) Все множества В £ Я обладают свойством: ε-окрестностъ Гев границы
Гв = 9(В П Км) имеет меру Лебега (объем) μ(ΓεΒ) ^ </?(ε, Μ), где </? зависит
только от своих аргументов и при любом Μ φ(ε, Μ) —> 0 при ε —> 0.
Теорема 2. Пусть X = Мт, 1§Ри распределение Ρ абсолютно
непрерывно относительно меры Лебега. Тогда класс Л, удовлетворяющий
условию (Г), конечно аппроксимируем и, следовательно, для него справедливо (2).
Доказательство. Заметим прежде всего, что задачу с пространства Rm
можно редуцировать к кубу Км в следующем смысле. Допустим, что при любом
фиксированном Μ найдется класс Θ подмножеств из Км такой, что для любого
В' € Л и В — В' Π Км выполнено (1). Тогда Л будет конечно аппроксимируем.
Действительно, для ε > 0, выбранного в (1), найдем Μ = Μ(ε) такое, что Р(Км) ^
^ 1 - ε, и положим А[ = А\, А2 = Α2Ό Км, где Αχ — множества из (1), Км —
дополнение до Км· Тогда, очевидно,
А[сВгсАг2, Ί>{Α'2-Α'1)^2ε.
636
Приложения
Итак, мы можем считать, что Р(Км) = 1, Я составлено из подмножеств Км-
Рассмотрим в качестве Θ фигуры Д,, образованные различными
объединениями замкнутых кубов с ребрами длиной J и с вершинами в точках
/•Г · CN Μ ^ . Μ
(можно считать для простоты, что δ нацело делит М). Определим множества Αχ,
Ά2 соответственно как объединения всех кубов, принадлежащих и задевающих В.
Очевидно, что
Αι СВсА2,
μ(Α2 - Аг) ζ μ(Γ^) ζ <p(2SJm,M).
Выбором δ правая часть этого неравенства может быть сделана сколь угодно малой.
Далее, Ρ абсолютно непрерывна относительно μ. Поэтому для заданного ε
можно найти 7 = Ί(β) такое, что sup Ρ (Α) < ε. Если теперь δ выбрать так,
д(Л)<7
чтобы φ(2δ\/τη,Μ) < 7, то получим
Р(Л2 -Αι) <ε. <
Следствие 2. Класс С всех выпуклых множеств конечно аппроксимируем
щ следовательно, для абсолютно непрерывных Ρ
sup|p;(B)-P(£)|—>0.
вес1 ' и.н.
Действительно, максимальная «площадь» поверхности выпуклого множества
в Км составляет 2га(2М)т~1, что есть «площадь» поверхности Км, а
максимальный объем μ((ΘΚΜ)ε) ε-окрестности дКм не превосходит 2ε · 2m(2M)m~1. Это
означает, что условие (Г) выполнено. <
Следствие 2 совпадает с теоремой 4.2. Замечание о существенности условия об
абсолютной непрерывности Ρ содержится в § 4.
Нетрудно видеть, что условие (Г) будет выполнено и для классов невыпуклых
множеств с достаточно гладкими границами.
Приложение II
Функциональная предельная теорема
для эмпирических процессов
Мы докажем здесь следующее утверждение (теорему 6.3). Пусть
есть эмпирический процесс, определенный в §6, и w°(t) — броуновский мост.
Теорема 1. Если f есть измеримый функционал D(0,1) -* R, непрерывный
в точках пространства (7(0,1) в равномерной метрике, то при η —> оо
f(wn) =» f(w°).
Для доказательства теоремы нам понадобятся две леммы.
Лемма 1. Конечномерные распределения процессов wn слабо сходятся при
η —> оо к соответствующим распределениям процесса w°.
Доказательство. Рассмотрим случайные (га + 1)-мерные векторы
wn = (A0wny...,Amwn)y
где Ajg9 как и в § 6, обозначает разности
Ajg — g(tj+i) -g(tj), tj+i>tj, j = 0,...,m, ίο=0, tm+i = 1.
Через w° обозначим аналогичный вектор для процесса w°(t). В силу второй
теоремы непрерывности для доказательства леммы нам достаточно показать, что
wn => w°.
Найдем характеристические функции wn и ги°. Для вектора и = (щ,.. .,ит)
имеем
Eeiw°uT = Еехр J i^UjAjW0 \ = Еехр li^UjiAjW - m(l)Ai) [,
где Aj = tj+ι — ij, j = 0,.. .,m, w(t) — стандартный винеровский процесс.
Представим показатель у экспоненты как сумму независимых величин. Обо-
т
значив для краткости 2_\uj^j ^ U, получим
^UjiAjw - w(l)Aj) = £ (uj - ί/)Δ^.
i=o j=o
638
Приложения
Так как Еехр {iuw(s)} = ехр {-и2$/2}, то
Eexp{iw°ur} =
= ехР{-\Σ(«i - ^} = ^р{~\ (ί>;Δί - ^2) }· (ι)
Рассмотрим теперь Еехр{ш"ит}. Пусть, как и прежде (см. §6),
тг„(*)=пВД.
Тогда, как мы уже знаем (см. (6.1)),
Ρ(Δ0πη = fc0, · · -, Дт7гп = km) = ' ,Δ*°... Δ{£>.
В правой части стоят члены разложения полинома (Δο + ... + Дт)п. Используя
этот довод, получаем
Ε ехр j г £^Δ,-τγ„1 = £ £-ρηρ[ (ехр[ш0]Л0)*°. ..(ехр[шт]Дт)*т =
= (ехр [iu0]Ao + ... + ехр [гит]Ат)п.
Так как
Δ,*» = Гп (F*(tj+1) - ЪЪ) - Δ,·) = ^""^,
TO
(m I J . m
-ί^Μ^>/ηΔ^ >Eexp< -^=]^ϊζ;Δ;πη
i-o J l^i=0
= exp {iVfiCO I £exp { ?J|}Δ' ) '
Отсюда для фиксированного и, пользуясь равенствами
2 2
ехра = 1 + а + ^- + 0(а3), 1п(1 + а) = а - ^- + 0(а3)
Приложение II
639
при α = о(1), находим
1пЕехр{ггипит} = -iUy/n + nln
'-£('—ШЬ
= —iUy/n + nln
ι+Σ
j=o
Vn 2n
+ 0(n~3/2) Δ,
гС/ 1 Л о A t/2 л/ _о/оч
Ч-ОСп-1/2).
(2)
Сравнивая с (1), мы видим, что при η -* оо
Еехр{ггапг*т} -► Еехр{гги°ит}.
Остается воспользоваться теоремой непрерывности для характеристических
функций многомерных распределений (см. [17, §7.6]). <
Лемма 2. Для любого ε > О
lim sup Ρ {ωa {wn) > ε) -> 0 (3)
η~*οο
при Δ -)> 0, где и>д(2/) есть модуль непрерывности функции у € D(0) 1):
wa(|/)= sup |y(fi)-y(*2)|.
0^ti<t2^l
Доказательство. Не ограничивая общности, мы можем рассматривать
лишь двоично-рациональные Δ = 2~К Имеем при т > I
где
τη
ω\ ' = max
Δ |(*-,·)/2»|<Δ
ω(-5^Γ'^)= SUP Fn(^)-U,n(u)
V 2m 2"»,/ ((k-i)/2«^tt<fc/2·» I \2my
Чтобы доказать (З), рассмотрим
Ρ(«Δ(«;») £3ε) <Ρ(ωΜ >e) +pf |J {ω (^τ·£) > «}Υ (4)
640
Приложения
Возьмем здесь первое слагаемое. Нетрудно видеть, что при / > 3 событие
влечет за собой {с^д < ε}. Поскольку для дополнительных событий имеет место
обратное включение, то
ΡΙ4"1».) <р (у U {|»" (£) -»" (*^)|» £}) · и
Но
где
-Ш-*Ш
есть частота попадания элементов выборки в интервал длины 2 г. Другими
словами, это есть сумма Sn случайных величин в схеме Бернулли с η испытаниями и
вероятностью исхода 1, равной ρ = 2~г. Так как (см. [17, §5.1])
Е(5П - τιργ = п(р(1 - р)4 + (1 - р)р4) + Зп(п - 1)р2(1 - ρ)2 ^ ηρ + 3η2ρ2,
то по неравенству типа Чебышева
(h»(i)-(¥)M) =
= Ρ [\Sn - пр\ >
£у/п\ (np + 3n2p2)r8 _ г8 3r8
ε42Γη ε422Γ"
Следовательно, правая часть в (5) не превосходит
-=- Г г8 Зг8
r=/ L
ε4η ε42Γ
^ , m9 Ζ8
ε*π ε
42< J '
(m oo
У^ r8 ~ m9/9 при m —► oo, Y^ r82~
~ 2Z82~' при Ζ -> со ). Полагая m = 31og2 η, получим, что
г ι Ζ8
limsupP(c^j^)^c—-
n->oo ε ζ
Это выражение может быть выбором Ζ (или Δ) сделано сколь угодно малым.
Приложение II
641
Оценим теперь второе слагаемое в (4), не превосходящее
«К4^· £)>*)■ (б)
Событие, стоящее здесь под знаком вероятности, означает при выбранном га, что на
интервале ((А;-1)/п3, к/п3) шириной п~3 отклонение η(F*(u)-и) от n(F^(k/n3) -
— к/п3) превзойдет y/ηε. Так как у/пе ^ 3 при достаточно большом п, то для
этого в интервал ((к - 1)/гг3, к/п3) должно попасть по крайней мере два элемента
выборки X, т.е. должно произойти событие {Sn ^ 2}, если воспользоваться снова
обозначениями для схемы Бернулли при ρ = η"3. Но так как
1 = (1 -р + р)п = (1 -р)" + пр(1 -р)п~1 + 0(п2р2),
то
Р(5П ^ 2) = 1 - (1 -р)п - ηρ(1 -ρ)"-1 = 0(п2р2).
Таким образом, (б) не превосходит п30(п~4) = (^(п""1) = о(1). Это заканчивает
доказательство леммы. <
Доказательство теоремы 1. Для любого χ G D(0,1) положим
|Н| = sup |ζ(ί)|, /+(*) = sup /(у), /е"(а:) = inf /(у)
и обозначим через хд непрерывную ломаную с узлами в точках (кА,х(кА) =
= £δ(&Δ)), к — О,..., 1/Δ, где Δ нацело делит 1. Заметим, что
||я;-жд|| ζωΑ(χ) (7)
и что /*(хд) суть непрерывные функции от вектора (χ(0),χ(Δ),χ(2Δ),.. .,х(1)).
В силу леммы 1 и второй теоремы непрерывности
при η —> оо. Кроме того, из непрерывности w° и функционала / следует, что
||и&-ш°|| $и;д(ш0)—Ю при Δ -> 0, (9)
/±(ш°)->/(ш°) при ε-Ю. (10)
Из определения /е~ следует, что /е_(у) ^ /(ж) на множестве ||у-а;|| ^ ε. Поэтому
р(/(ш") < «к ρ (/Г К) < *; ΙΚ - ω"|| ^ ή +
+ Р(|« - Ш"|| > ε) ^ Ρ (/Γ Κ) ^ ί) + Р(«д(«»я) > ε).
Переходя здесь к пределу при п -» со и используя (8), (9), получим
limsupP(/(iun) ^ ί) ^ Р(/е-(и£) ^ <) +limsupP(cjA(u;n) > ε). (11)
642 Приложения
Аналогично находим
Р(Л"К) ^ <) ^ Р(/2~>°) ^ 0 + Ρ(«Δ(ω°) > е).
Подставим теперь последнее выражение в (11) и перейдем к пределу при Δ -> оо.
Из (9) и леммы 2 получим тогда, что
limsupP№n) < <) < Р(/2->°) < t).
П->00
Отсюда и из (10) вытекает, что
limsupPt/K1) < t) < Ρ(/(ω°) ^ t).
П-400
Аналогично устанавливается обратное неравенство
limsupP(/(wn) < t) > P(/(w°) < 0-
n-юо
Полученные неравенства означают, очевидно, что f(wn) =» f(w°). <
Рассмотрим еще одну функциональную предельную теорему для эмпирических
процессов, весьма близкую к теореме 1.
Пусть наряду с выборкой X объема ηι нам дана независимая от нее выборка Υ
объема П2 из того же равномерного на [0,1] распределения. В условиях этого раздела
нам удобнее будет эмпирические функции распределения выборок X и Υ обозначать
соответственно через Fx(t) и .Ру(£). Положим
Теорема 2. Если функционал f удовлетворяет условиям теоремы 1, то
при ηι -> оо, П2 -> оо
f(wx<Y) => f(w°).
Доказательство. Докажем эту теорему при упрощающем предположении,
что
α = —^ ► а0 е [0,1]
Щ + 712
при η = min (711,712) -► 00. Имеем
WxAt) = \/^k №x{t) ~ *> ~ (W) " *)] = ^Wx{t) + ν/ΓΓ^^«). (12)
где wx(t) и wy(t) — эмпирические процессы, соответствующие выборкам X и У.
Так как и&(х + у) ^ cja(x) + cja(j/), to из (12) и леммы 2 сразу вытекает аналог
леммы 2 для процесса iux,y(£): для любого ε > О
limsupPiu^iux^ > ε) -> 0.
n-юо
Приложение II 643
Сходимость конечномерных распределений ιυχ,γ и w° также вытекает из (12).
Действительно, обозначим через Wxyy, Wx, wy векторы, построенные по
процессам wxtY (£), wx(t), wy(t) точно так же, как строился вектор wn по процессу wn(t).
Тогда, используя независимость X и Υ и доказательство леммы 1, получим
Eexp{itujv,yiiT} = Eexp{iy/awxuT}Eexp{Vl - агюуит) ->
= Еехр{гги°ит}.
В остальном доказательство теоремы 2 ничем не отличается от доказательства
теоремы 1. <
Приложение III
Свойства условных математических ожиданий
В § 19 перечислены основные свойства у.м. о. Ниже приводятся доказательства
этих свойств, расположенных в том же порядке, что и в § 19.
1а. Е(с£/Я)=сЕ(^/Я).
lb. Е(& + 6/Я) = Е(&/а) + Е(6/Я).
1с. Ясли ξι < 6 π. м., mo Ε(ξι/21) ζ Е(£2/Я) η. κ.
Чтобы доказать свойство 1а, надо убедиться согласно определению 19.2, что
1) сЕ(£/Я) есть Я-измеримая функция,
2) Е(сЕ(£/Я); А) = Е(с£; Л) для любого ЛЕЯ.
Выполнение первого свойства очевидно. Второе свойство вытекает из свойств
линейности обычного математического ожидания (или обычного интеграла):
Е(сЕ(£/Я); Л) = сЕ(Е(£/Я);Л) = сЕ(£Л) = Е(с£; Л).
Свойство lb доказывается точно так же.
Чтобы доказать свойство 1с, положим для краткости £j = Е(^/Я). Тогда для
любого Л Ε Я
A A A
Отсюда вытекает, что £2 — f ι ^ 0 п. н.
2. Неравенство Чебышева. Ясли ξ ^ 0, χ > 0, то
P(i>l/a)<HIZS.
Это свойство вытекает из 1с, так как Р(£ ^ х/Я) = Е(/^^х}/Я), где Ια —
индикатор события А и справедливо неравенство 1{ξ^χ} ζ ξ/χ·
3. Если Я w σ(ξ) независимы, то Е(£/Я) = Εξ.
Так как ξ = Εξ является Я-измеримой функцией, то нам остается проверить
лишь второе условие определения 19.2: для любого ЛЕЯ
Ε(ξ;Λ)=Ε(ξ;Λ).
Справедливость этого равенства вытекает из независимости случайных величин Ια
и ξ и соотношений
Ε(ξ; Α) = Ε(ξΙΑ) = Εξ ■ ША = ξΡ(Α) = Ε(ξ; Α).
Приложение HI
645
4. Теорема о монотонной сходимости. Если О $С ξη | ξ η. к., то
Е(ея/а)|Е(£/а)я.н.
Действительно, из ξη+ι ^ £п п.н. следует ξη+ι^ ξη п.н., где ξη = Ε(ξη/21).
Поэтому существует 21-измеримая ξ такая, что ξη t ξ п. н. В силу обычной теоремы
о монотонной сходимости для любого А £ 21
JtndP->j$dP, jtndP-> jidP.
Так как левые части этих соотношений совпадают, то совпадают и правые. Это и
означает, что ξ = Ε(ξ/21).
5. #с/ш τ] вещественна и Чк-измерима, то
Е(!гё/Я) = i?E(£/a). (1)
Если η = 1в (индикатор множества В £ 21), то утверждение справедливо, так
как при любом A £ 21
/Ε(/Βξ/α) dP= [ΙΒξ(ϊΡ= [ ξ<ΙΡ= [ E(£/a) dP = / 'вЕ(£/И) dP.
л л лв лв л
Отсюда и из линейности у. м. о. следует, что утверждение справедливо и для любых
простых функций η.
Если ξ ^ О, 77 ^ 0, то, взяв последовательность простых функций 0 ^ г\п ΐ 77 и
пользуясь теоремой о монотонной сходимости в равенстве
Е(ч»*/а) = ъЕК/щ,
получим (1). Переход к случаю произвольных ξ и η осуществляется обычным
образом — путем рассмотрения положительных и отрицательных частей случайных
величин ξ и η. При этом для того чтобы полученные разности и суммы имели
смысл, нужно требовать существования Ε|ξ| < оо, Έ\ξη\ < оо.
6. Неравенство Коши-Буняковского
Е&б/И) ζ [E(tf/И)Е(Й/И)]
1/2
доказывается точно так же, как для обычных математических ожиданий (см.,
например, [17, §4.7, 4.8]), поскольку доказательство не использует других свойств
математических ожиданий, кроме линейности.
Неравенство Йенсена
5(Ε(ξ/21)) ^ Е(0(О/Я) (2)
для любой выпуклой вниз функции g вытекает из следующих соотношений (ср.
с [17]). В силу выпуклости д(х) для каждого у найдется число д\{у) такое, что
9(х) ^9(y) + {x~y)9i(y)·
646
Приложения
Положим здесь χ = ξ, у = ξ = E(f/2l) и возьмем у.м. о. обеих частей этого
неравенства. Так как в силу свойства 5
Ε[(ξ - ОЫЙ/и] = л(ОЕК - Ы = о,
то мы получим (2).
7. Формула полной вероятности следует из свойства 8, если в
качестве 21 взять тривиальную σ-алгебру.
8. Если 21 С 2ti С 5, то справедлива формула «последовательного
усреднения»
E({/a) = E(E(f/ai)2).
Действительно, для любого А 6 21 в силу того, что А Е 211
/Έ(Ε(ξ/Βι)/α)<ίΡ= ί Ε(ξ/Λχ) dP= [ξ*Ρ= /*E(£/2l)dP.
В заключение отметим, что свойство 5 при широких предположениях допускает
следующее обобщение.
5А. Если η измерима относительно 21, φ(ω,η) есть измеримая функция
переменных ω € Ω и η € R*, πιο
Ε(φ{ω,η)/*) = 1>(ω,η), (3)
где ф{ш,у) = E(<p(u,y)/f&).
Докажем это свойство в предположении, что существует последовательность
простых функций ηη такая, что φ{ω>ηη) | φ(ω,η), ψ(ω,ηη) | Ψ (ν, η) п. н.
Действительно, пусть 77η = yk при ω € Ak С 21. Тогда
к
В силу свойства 5 отсюда следует выполнение (3) для функций ηη. Остается
воспользоваться теоремой о монотонной сходимости (свойство 4) в равенстве
Ε{φ(ω%ηη)/1&) = 1>(ω9ηη).
Приложение IV
Закон больших чисел и центральная предельная теорема.
Равномерные варианты
1. Закон больших чисел в схеме серий. Рассмотрим последовательность
произвольных серий ξι,η,.. .,ξη,η» η = 1,2,..., независимых случайных величин, где
распределения ξ^,η могут зависеть от п.
η
Обозначим ζη = /j£fc,n· С точки зрения последующих результатов можно
к=1
считать, не ограничивая общности, что
Е&,„ = 0. (1)
Предположим, что выполнено условие
η
Dj^^Emind^i.^n-^O (DO
k=l
при η -» οο.
Теорема 1 (закон больших чисел). При выполнении условий (1), (Di) для
любого ε > О
Ρ(|ζη|>ε)->0
или, что то же, ζη —> 0.
Рассмотрим внимательнее условие (Di). Очевидно, что его можно записать
также в форме
η η
d1 = £ E(|€*,nl; Ifc,»! > ι) + Σ E(lfc.nl2; Ι&.»1 < ι) -»о.
Если
η
Afi=$3E|6bin|^c<oo (2)
при η —У оо, то для выполнения (Di) необходимо и достаточно выполнение условия
η
мх(г) ξ £Е(1&.»1;1&,»1 > r) -» ° (Μι)
при любом г > 0 и η -4 оо, которое можно назвать условием типа Линдеберга
(условие Линдеберга (Мг) будет введено в следующем разделе. Действительно
648
Приложения
(т<1, £?1(ж) = min(|x|,|a;|2)),
η η η
Ζ?! = ΣΈ9ι(ξΗ,η) ζ Χ)Ε(|ξΜ|; |&,η| > τ) + £e(|&,„|2; |&,„| $ τ) £
η
^ Μ^τ) +t£e(|£m|; |fcfn| ^ r) ^ Μχ(τ) +τΜι(0). (3)
Так как Μχ(0) = Λίχ ^ с, а г может быть произвольно малым, то D\ —у 0 при
η —У оо.
Обратно (здесь условие (2) не требуется), при τ ^ 1
η η
Afi(r) ^ Σ>(|&,η|;|&,η| > 1) + Т-1 £Ε(|&,η|2;τ < &,„| ^ 1) ^ τ"1/?! -» О
(4)
при п-4оои при любом τ > 0.
Каждое из условий (Di), (Mi) влечет за собой равномерную малость Е|£*,п|:
max E|fc,n| -> 0 при η -> оо. (5)
Действительно, (Μι) означает, что существует достаточно медленно убывающая
последовательность тп -у О такая, что Μι(τη) -У 0. Поэтому
maxE|fc,n| ^ max[rn + Ε(|&,„|; |&,„| > r„)] ^ rn + Mi(r„) -> 0. (6)
Из (5) следует, в частности, свойство пренебрежимой малости слагаемых ξ^η·
Будем говорить, что ξι^η пренебрежимо малы или, что то же, обладают
свойством (S), если при любом ε > О
тахР(|&|П|>е)->0. (S)
к^п
Свойство (S) можно было бы назвать также равномерной сходимостью fc>n no
вероятности κ нулю. Свойство (S) сразу следует из (5) и неравенства Чебышева.
Оно следует также из более сильных соотношений, вытекающих из (Μι):
Ρ (maxlfc.nl > ε) = Ρ(1){|&,„| > ε}) ^
\к^п J
< Σ ρ(Ιί*.»Ι > ε) ζ ε~ι Σ E(lb.nl; lb.nl > ε) -> ο. (SO
k^n k^n
Доказательство теоремы 1. Положим
tpk%n(t) = Ее'**-, ΔΛ(ί) = Vfctn(i) - 1.
Надо доказать, что при каждом t и при η —У оо
¥>Сп(0=Ее«<- = Π ?*,„(*)-►!.
*=ι
Приложение IV
649
Нам понадобятся следующие неравенства (см., например, [17, § 7.5, леммы 2, 3]).
Если Re/З ^ 0, то
Если |α*| ζ 1, \bk\ ^ 1, к = 1,.. .,п, rrao
*-!-*-£
I/3I3
Πα*~Πδ*
^Σ>*-Μ·
(7)
(8)
В силу (8)
Ινα(0-ΐ| =
П^-о-П1
*=1
*=1
Σ>*(«)Ι =
Л=1
= £ |Е(ей«*- - 1)| = Σ |Ε(β«€»- - 1 - <ί&.„)|.
A=l
*=1
В силу (7) (gi(x) = min (|я|,х2))
'2*2
|eiix - 1 - ite| ^ min f 21**1, *-γ- 1 ^ 2^ι(te) ^ 2Л(*Ы*)>
где /&(£) = max (|ί|, |ί|2). Поэтому
η
|y>Cn (ί) - 1| ^ 2h(t) Σ Ел(&,п) - 2Λ(ί)Α -> 0. <
Замечание 1. Если {£*} есть заданная фиксированная (не зависящая от п)
η
последовательность случайных величин, 5n = /j£fc> Щк — а*> то для нее мы
будем изучать поведение сумм
к=1
η Sn - Σ ак
Ьп
где ξΐζ,η = (& —a>k)/bn удовлетворяют (1), 6n -* со. Если положить, не ограничивая
общности, a,k = 0, то условия (Di), (Mi) будут в этом случае иметь вид
650
Приложения
Если ξΐι одинаково распределены, то из теоремы 1 вытекает в качестве частного
случая «обычный» закон больших чисел: если Ε|ξ*| < оо (в этом случае выполнено
Μι (г) при Ьп = п), то ζη —> 0.
Для выполнения (Di) достаточно также выполнения следующего условия: при
некотором $, 2 ^ 5 > 1,
η
£>|&,n|e^0. (L.)
Это утверждение очевидно, так как д\(х) ζ \x\s при 2 ^ s > 1. Условие (Ls)
можно было бы назвать условием типа Ляпунова (ср. с условием Ляпунова (Ls)
в следующем разделе.
Замечание 2. Теорему 1 можно доказывать и иначе, используя не
характеристические функции, а так называемые срезки случайных величин и оценки их
дисперсий. Такое доказательство приведено в первом издании книги.
2. Центральная предельная теорема для сумм произвольных независимых
случайных величин. Как и в п. 1, мы будем рассматривать серии случайных величин
Sl,nj · · ·» ζη,η
и их суммы
η
Cn = J>,n. (9)
Будем предполагать, что ξ*,η имеют конечные вторые моменты σ\η — D^)U < оо,
и считать, не ограничивая общности, что
η
Е*м=0, 5>2,„ = DC„ = 1. (Ю)
k=l
Введем в рассмотрение условие: при некотором s > 2
η
^2 = ^Emin(^n,|^nr)^0, (D2)
которое будет играть важную роль в дальнейшем. При этом многие рассмотрения,
связанные с условием (D2) и с условиями (М2), (Ь5), вводимыми ниже, будут
вполне аналогичны рассмотрениям, связанным с условиями (Di), (Mi), (Ls) в п. 1.
При выполнении (10) необходимым и достаточным для выполнения (D2)
является условие Линдеберга
η
М2(г) = Σ Ε(Κ*,η|2; Ifik.nl > г) -+ 0 (М2)
при любом г > 0 и η —► оо. Действительно, положим
g2(x) = min(s2,|z|*).
Приложение IV
651
Тогда (ср. с (3), (4); τ < 1)
п п п
Λ=1 *=1 Λ=1
^ M2(r) + r*-2M2(0) = M2(r) + r'-2.
Так как т произвольно, то D2 -► 0 при η -> оо.
Обратно, при г ^ 1 (условие 10 здесь не требуется)
η
Af2_ ,"
Л=1 ' Л=1
при любом τ > 0 и η —^ оо. <
Итак, при выполнении (10) условие (D2) инвариантно по s > 2,
Условию (D2) можно придать более общую форму:
ί3(τ) ^ £ Е(£»; &.»! >х) + ;έϊ Σ Е(КмГ; г < Км1 < ι) < ^d2 -> о
ΣΕ£„Λ(ω->ο,
Л=1
где Л(х) — любая функция, обладающая свойствами h(x) > 0 при χ > 0, Л(х) t»
/i(a;) -> 0 при χ -> 0, Л(х) -> с < оо при я; -> оо. При этом все основные свойства
условия (D2) сохранятся. Условие Линдеберга выясняет существо условия (D2) с
несколько иной точки зрения. В нем h(x) = /(r,oo)» Т € (О? 1)·
Аналогично тому, как это было сделано в п. 1 относительно условия (Μι), легко
проверить, что условие (М2) влечет за собой сходимость (см. (б))
maxD&>n->0 (11)
Λ^η
и пренебрежимую малость £k,n (свойство (S)). Очевидно также неравенство
Мг(т) ζ -Μ2(τ).
τ
Если {£*} есть заданная фиксированная (не зависящая от п) последователь-
п
ность независимых случайных величин, Sn = У^£л, Щк = ал, Щл = v\% то для
Л=1
нее мы будем изучать поведение нормированных сумм
η
Sn - Σ ак η
которые, очевидно, также имеют вид (9), где £*,„ = fa - a,k)/Bn.
Условия (D2), (M2) для ξΐς будут иметь вид
м^т) = -L· Σ Е((& -α*)2! Ι& - α*ι > τβ«) ->· °·
п *=1
(12)
652
Приложения
Теорема 2 (центральная предельная теорема). Если последовательности
независимых случайных величин {£л,п}]ь=1> τι = 1,2,..., удовлетворяют, уело-
виям (10), (D2), то Р(Сп < я) -> Ф(я) равномерно по х.
Доказательство. Достаточно убедиться, что
^п(*) = П^.»(*)-+е-'2/2.
*=1
В силу неравенств (8)
l*U')-e-t2/2| =
IW)-IKtVil
/2
*=1
к=\
<Y,WkAt)-e-t2"lJ2\<
*=1
«Σ
fc=l
¥>*,»(*) ~ 1 + 2*4"
+ Σ
rt2<"/2 -1 +i*4n
(13)
Так как в силу (7)
егх - 1 - гх + —
^ min
in U2'"^" ) ^ 02(a),
(при s ζ 3), то первая сумма в (13) не превосходит
f2c2 *
к-l
Ε ett«"·»-!-«&,„ + ■
^ £ел(1%,я1) ^ λ(0Σελ(Ι&.»|) ^ Λ№ -> ο.
jfe=l
k=l
где /ι(ί) = max(£2, \t\8). Вторая сумма в (13) (снова в силу 7) не превосходит
(см. (10), (11))
τΣσ1η^τ-ηι^σ^η->0 при п->оо. <
8
к=1
Иногда утверждение теоремы 2 бывает удобным в следующей форме.
Следствие 1. Пусть Е^)П = 0, Όζη -> σ2 > 0 и выполнено условие (D2)
Sn — an
или (М2), тогда ζη & Φο,σ2·
ЗамечаниеЗ. Утверждение об асимптотической нормальности ζη = -- ,
oyjn
когда £* одинаково распределены, следует из теоремы 2. Условие Линдеберга
выполнено, так как в этом случае В2 — ησ2, и (12) примет вид
М2(т) = — Е((& - α)2; |& - α| > τσγ/τϊ) -> 0 при η -> оо
для любого τ > 0.
Приложение IV
653
Замечание 4. Достаточным условием для выполнения (D2), (М2) является
более ограничительное условие Ляпунова. Проверять его в ряде случаев легче.
Предположим, что выполнено (10). Величину
L. = £E|fc,n|
k=l
при некотором s > 2 называют отношением Ляпунова порядка s. Условие
Ls -> 0 (L.)
называют условием Ляпунова. Величина Ls получила название отношения
потому, что для ξ^η = {£k - ак)/Вп (ак = Е&, В2п = Όζη, ξΗ от η не зависят) Ls
имеет вид
ΣΕΙί*-β*|·
Если ξ/c одинаково распределены, ак = a, D£* = σ2, Ε|ξ* - a\s = /χ < сю, то
σ*η(*-2)/2
0.
Достаточность условия Ляпунова вытекает из очевидных неравенств #2(я) ^ \х\8
при любом s, D2 ζ Ls.
3. Закон больших чисел и центральная предельная теорема в многомерном
случае. В этом пункте мы будем предполагать, что f i,n,..., ξη,η есть случайные векторы
в схеме серий, Е&,„ = 0, ζη = ^ &,η·
Закон больших чисел ζη —> 0 получается немедленно из теоремы 1, если
предположить, что условиям теоремы 1 удовлетворяют координаты ^)П. Поэтому ничего
не мешает считать, что теорема 1 сформулирована и доказана для векторов.
Чуть сложнее обстоит дело с центральной предельной теоремой. Здесь мы будем
предполагать, что Е|£*>п|2 < оо, где \х\2 = (х,х) есть квадрат нормы х. Обозначим
σ\η = E£j£n&,n, σ1 = ζ2 σ^η
(индекс Т означает транспонирование, так что ξ£η есть вектор-столбец).
Введем в рассмотрение условие
η
^Emin(|6>n|2,|6,nle)->0, s>2, (D2)
fc=l
и условие Линдеберга
η
ΣΕ(ΐ^.«ΐ2;ΐ^.ηΐ>^)-^ο (м2)
fc=l
654
Приложения
при η -» оо и любом τ > 0. Как и в одномерном случае, легко убедиться, что
условия (М2) и (D2) при trcr* < с < оо равносильны.
Теорема 3. Если σ\ —> σ2, где σ2 — положительно определенная матрица,
и выполнено условие (D2) {или (М2)), то
ζη @> *0,er
2.
Следствие 2 («обычная» центральная предельная теорема). Если ξι, £2,... —
последовательность независимых одинаково распределенных векторов, Εξ* = О,
η
σ2 = Εξ£ξι<, Sn = ^2 &> mo nPw n ~* °°
1
5„
y/n
^*0,σ2.
Это утверждение является следствием теоремы 3, так как случайные величины
£*,п = ik/y/n удовлетворяют ее условиям.
Доказательство теоремы 3. Рассмотрим характеристические функции
η
<pktn(t) = Ее^Ч Vn(t) = Εβ««-) = Π W,n(t).
Для доказательства надо убедиться, что при любом t и при η -> оо
<рп(*)->ехр|--*<72*т
Воспользуемся теоремой 2. Функции <£*,п(0 и <£п(0 можно рассматривать как
характеристические функции
<Pk,n(v) = EexP («Ό» tf» = Еехр (г<;)
случайных величин ξ£η = (£fc,n>r)> С£ = (Cmг), где г = ί/|ί|, ν = |t|. Покажем,
что скалярные случайные величины ££ п удовлетворяют условиям теоремы 2 (или
следствия 1) для одномерного случая. Очевидно,
Σ Ε(€ίιΒ)2 = Σ Ε(ξ*,„,Γ)2 = ra»rT -► ra2rT > 0.
Выполнение условия (D2) следует из очевидных неравенств
(fc.»,r)2 = |«,„|2 < |Ь.„|а,
Приложение IV
655
где д2(х) = min(x2,\x\8), s > 2. Таким образом, для любых υ и г (т.е. для
любых t) в силу следствия 1 теоремы 2
φη(ή = Еехр{»Х^} -> exp | --v2ra2rT i = exp j --*σ2Γ Ι. <
В теореме 3 остается вне поля зрения случай, когда элементы матрицы σ\
неограниченно растут или ведут себя так, что ранг предельной матрицы σ2 становится
меньше размерности векторов ξ^η. Такое может происходить, когда дисперсии
разных координат £k,n имеют разные порядки убывания (или роста). В этом случае
вместо ζη следует рассматривать преобразованные суммы ζ'η = ζη^ΰ1· По существу
теорема 3 является следствием следующего более общего утверждения, которое в
свою очередь вытекает из теоремы 3.
Теорема ЗА. Если случайные величины £к п = ξ^,η^"1 удовлетворяют
условию (D2) (или (М2)), то ζ'η & Фо,я, где Ε — единичная матрица.
4. Равномерные предельные теоремы для сумм случайных величин, зависящих
от параметра. Мы докажем в этом пункте теоремы 37.1, 37.2.
Пусть X €= Р#, α(χ,θ) — заданная измеримая функция Λ'χθ-^ΐ',
η
*„(0) = £а(хя0).
i=i
Будем говорить, что интеграл α(θ) = / о(х,θ)Ρ$(άχ) сходится равномерно по θ в
области ©о С Θ, если
sup / \α(χ,θ)\Ρθ(άχ) -► О
?€θ0 J
θςβο
\α(χ,θ)\>Ν
при Ν -> οο.
Теорема4 (равномерный закон больших чисел). Если интеграл α(θ) =
= / а(х,θ)Υβ(άχ) сходится равномерно по θ в области ©о С Θ, то
ζη(θ) = 8-^-α(θ)->0 (14)
П Ре
равномерно по θ € ©о -* 0.
Доказательство. Допустим, что (14) не имеет места. Тогда найдутся ε > О,
δ > О и последовательность θη £ ©о такие, что
при всех п.
(\ΨΠ
> ε > δ (15)
656
Приложения
Рассмотрим случайные величины
_ a(xj,gw) -α(θη)
4j'n " η
Нетрудно видеть, что они удовлетворяют условиям теоремы 1. Действительно,
положим Ап = {χ: \α(χ,θη) - α(θη)\ > τη}. Тогда
ήΕ0η\ξ;9η\ ζ 2α = 2 sup / |α(χ,0)|Ρ*(ώ) < οο,
eee0J
пЕвп(\ЬА\&п\ > τ) = У |α(*,0η) - α(0η)|Ρ*«(ώΟ -► 0.
Последнее соотношение следует из равномерной сходимости интеграла α(θ) и
неравенства Чебышева
P..(An)<5bJ^<--+0.
Г ТП
Сказанное означает, что последовательность £jiTl удовлетворяет закону больших
чисел
Ё^> >ε) ->°
для любого ε > 0. Это противоречит (15) и доказывает теорему. <
Перейдем к центральной предельной теореме. Пусть Ε$α(χ\,θ) = 0.
Положим σ2(θ) = ||σ^·(0)|| = Ε^ατ(χι,β)α(χι,ί) и обозначим через оу(ж,0),
j = 1,..., Ζ, координаты векторов α(χ, Θ).
Теорема 5 (равномерная центральная предельная теорема). Пусть
интегралы o-jj(0) = E0a^(xi,0) сходятся равномерно в ©о С Θ, т. е.
SUp<7jj(0) < ΟΟ,
во
8ирЕ*(а?(х1,0);|а,-(хь0)| > iV) -> 0
θ0
при Ν -* οο. Тогда
8η(θ)
?0,σ2(9)
(16)
(17)
npw η -* οο равномерно по θ € ©ο·
Доказательство. Невыполнение (17) будет означать существование
последовательности θη € ©о, для которой суммы случайных величин ξjyn = a(xj,6n)/y/n
не будут по распределению сближаться с Фо,<г2(0„)·
В силу компактности замыкания {σ2(θ),θ € ©о} последовательность θη можно
считать выбранной так, что для некоторой матрицы σ2
a2(9n)=:nEeJl^Un^a2.
(18)
Приложение IV
657
Тогда наше допущение о невыполнении (17) будет означать, что У^ £j,n не будет
сближаться по распределению с Фо,*2- Но это невозможно в силу теоремы 3, так
как ξ_;?η удовлетворяют условиям этой теоремы. Действительно, в силу (18)
достаточно проверить условие Линдеберга. Для множеств А{,п — {|aj(xi,0n)| > Ту/п/1}
находим
supP0(Ai>nK sup ^p->0
θ€θ0 θ£θο ПТ
I
при η -> оо. Используя тот факт, что {|£ι,η| > т) с U ^г'п' полУчаем
ι
nEflfl (lii.nl2; Ki.nl >г) ^ Σ Ε^(α?(χιΑΜΛ,η). (19)
г,к=1
Здесь Efln (α?(χι, θη)\ A{iTl) —> О в силу равномерной сходимости интеграла σ„(0).
Если г ^ /с, то, полагая Β^ν — {|ai(xi,0n)| > TV}, получим
Εβ«(α?ΜΛι„) =Ε0η(α?; ЛА,ПБ^) + Ε0η (a?; AM2?lfJV).
Здесь для заданного ε > 0 можно выбрать N так, что первое слагаемое в силу (16)
будет меньше ε. Второе слагаемое не превосходит N2Vgn{Ak^n) ->■ 0 при η ->· оо.
Это означает, что (19) сходится к нулю при η -> оо. <
Приложение V
Некоторые утверждения, относящиеся
к интегралам, зависящим от параметра
1. Теоремы о сходимости интегралов, зависящих от параметра. Пусть
{il>(t,y)} — семейство измеримых функций, заданных на измеримом пространстве
(У> ®у) с мерой ν на нем. Нас будут интересовать условия, при которых
JШУ)"Ш -+ J ф{в,у)и{ау) при ί^θ. (1)
Пусть {A(t) — A{t,0),t € Θ} есть некоторое семейство множеств из Ъ$у.
Обозначим через /д(г)(х) индикатор A(t) и через A(t) — дополнение к A(t).
Следующее утверждение является некоторым обобщением известной теоремы
Лебега.
Теорема 1. Пусть семейство {A(t)} таково, что
1) ip(t,y)lA(t)(y) —> ф(в,у) при t —> θ для η. β. [и] значений у, для которых
2) sup \tp(t,y)lA(t){y)\ ^ Ф{у)ч где Φ — интегрируемая функция
/■
/·
Ф(у)"(ау) < оо.
Тогда для выполнения (1) необходимо и достаточно, чтобы
^y)h{t)(y)v(dy) -► 0 при t-юо. (2)
Доказательство. В силу теоремы Лебега
/ ^(t,y)lA{t)(y)v{dy) -> I ф{0,у)и(ау).
Так как
то (1) эквивалентно (2). <
Если / ф{9,у)и(ау) существует, то в качестве множества A{i) для п. в. [и]
непрерывных ф(Ь,у) можно использовать множество
A(t) = {y:mt,V)\^2\W,v)\},
как это делается, например, в следующем утверждении.
Приложение V
659
Следствие 1. Пусть π(χ) — любая измеримая ограниченная функцияХп
R, fe{x) непрерывна по θ для п. в. [μη] значений χ € Хп. Тогда функция
Е9тг(Х)= f π(χ)Μχ)μη(άχ
)
непрерывна по Θ.
Доказательство. Используем теорему 1 при У = Хп, у = х, и = μη,
ψ(ί,χ) = n(x)ft(x), A(t) = {χ: ft(x) ^ 2fe(x)}. Очевидно, что условия 1), 2)
теоремы 1 выполнены. Так как для π(χ) = 1 функция Εθπ(Χ) = 1 непрерывна, то
выполнено (см. (2))
J Μχ)μη(άχ)^0
x<£A(t)
при t —> 0. Но по теореме 1 отсюда следует непрерывность Έβπ(Χ) для любой
ограниченной функции π. <
Если речь вести лишь о достаточном условии для сходимости (1) в случае
Ф{1,у) ~* Ψίβ,ν) Π·Β· при t ->· 0, то в качестве такового можно использовать
равномерную сходимость интегралов в (1). Последнюю можно определить как
существование конечной меры λ такой, что неравенство Х(А) < δ = δ(ε) влечет за
собой sup / \tl>(t,y)\v(dy) < ε для заданного ε > 0.
А
Если существует интегрируемая мажоранта ф(у) = sup^(£, у), то такая мера λ
t
всегда существует: достаточно положить Х(А) = / i/>(y)v(dy).
А
2. Следствия условий (R). Докажем здесь лемму 26.1 и равномерную сходимость
интеграла Ι(β):
8ирЕ,(|Г(х1^)|2;|^(х1^)1 >Ν) ^0 (3)
θ
при N —> оо (именно такая равномерность имеется в виду в §33, 34, 36, 37).
Так как рассмотрения для одномерного и многомерного параметра практически не
отличаются, то мы в этом и следующем пункте ограничимся изучением одномерного
случая.
Теорема 2 (лемма 26.1). Пусть выполнено условие (R) и S = S(X) есть
любая статистика, для которой E#S2 < с < оо при θ € Θ. Тогда в равенстве
α8(θ) = Eo{S) = J S(x)fe(x№(dx)
возможно дифференцирование под знаком интеграла:
°Ш = J S(x)ti(x)Mn(dx) = EeSL'(X, θ), (4)
при этом функция α'3(θ) непрерывна.
660
Приложения
Доказательство. Заметим предварительно, что из (4) при S(x) = 1 и η = 1
следует, что
/
/'θ(χ)μ(άχ)=0. (5)
Так как в этом случае L'(X,6) = Y~,Z'(xi,0) есть сумма независимых случайных
величин с нулевым средним (см. (5)), то
ВвЬ'(Х,в} = Ев(Ь'(Х,в))2 = nEfl(/'(xi,0))2 = ηΙ(θ). (6)
Предположим теперь, что функция
Ιη(θ) = Εβ(Σ'(Χ,θ))2 = 4 J {s/~h(x)')\n(dx)
непрерывна по θ (мы еще не можем пользоваться (6)) и докажем непрерывность
интеграла в (4). Воспользуемся теоремой 1 при У = Хп, ν = μη, tp(t,x) =
A(t) = Ai(r) =
= {х: sup y/fv(x)<2y/fe(x), sup \y/fv(x) Ί ζ 2 I >//*(*) Ί }. (7)
L ν:\θ-ν\<\τ\ ν:\θ-υ\<\τ\ ' ' ' ' J
Условия 1), 2) теоремы 1 при ψ(χ) — 2φ(θ,χ) в силу непрерывности функций yffe
и у/Υθ выполнены. Поэтому из сходимости In(t) к Ιη(θ) при t —> оо получаем
(см. (2)), что при £ ->· б
ε(0= / (x/7^)')V(d*)->0. (8)
Аналогично тому, как это делалось в следствии 1, мы получаем отсюда
непрерывность / 3(χ)/'θ(χ)μη(άχ). Чтобы убедиться в этом, надо воспользоваться
теоремой 1 «в обратную сторону» при тех же множествах A{t) и ψ(ί, χ) = S(x)f[(x).
Условия 1), 2) теоремы 1, очевидно, будут выполнены (ψ(χ) = 2\S(x)f'9(x)\1
Выполнение (2) обеспечивается (8)
и только что приведенным неравенством, в котором интегрирование надо вести по
множеству χ ^ А\{т).
Обратимся теперь непосредственно к доказательству (4). Заметим, что
ι ι
i (J S/*+T/zn - J S^A = j j Sf9+UT άημη = J J 25y/f^{y/fo^)' άημη.
о о
Воспользуемся снова теоремой 1 при У = К х Хп, у = (и, ж), ν = λ χ μη (λ —
мера Лебега), ф(т,у) = S{x)f'e+ur{x), τ -> 0, А(т) = Ах(г), где -Αι(г) определено
Приложение V
661
в (7). Опять из непрерывности y/fe(x) и \Jfe(x) следует выполнение условий 1), 2)
теоремы 1
1>(T>v)lA(T)(x)->S(x)fi(x) = il>(0iy) при τ-►(),·
sup№(r,y)IA{T)(x)S(x)\ ζ 4S(x)\f'e(x)l
где в силу неравенства Коши-Буняковского
J 4S\f^^ 4 IJ S2/*m» J ^μ»
1/2
< CO.
Таким образом, для доказательства (4) нам надо проверить условие (2). Оно
вытекает из неравенства Коши-Буняковского и соотношения (8):
1
**Λι(τ) 0
,1/2
J J32/θ+ητάημη\ J J (ν/β+ητ'γάημη
[?(Mi(r) Ο
1/2
<cJ/2
1
JeiO
+ ur) (iw
1/2
при τ -> 0.
Итак, мы доказали (4) в предположении, что Ιη(β) непрерывно. Но Ιη(θ) = 1{θ)
при η = 1, и это предположение выполнено в силу условий (R). Стало быть, (4) верно
при η = 1 и, стало быть, верно (5). Но из (5) следует соотношение (6), означающее
непрерывность Ιη(θ). Теорема доказана.
Теорема 3. Если множество Θ компактно, функция y/fe(х) для [μ] η. β.
значений χ непрерывно дифференцируема по 0, то непрерывность Ι(θ) имеет
место тогда и только тогда, когда выполнено (3).
Теорема означает, что непрерывность Ι(θ) в условии (R) можно заменить
условием (3).
Доказательство. Допустим, что Ι(θ) непрерывна, а (3) не выполнено.
Тогда существует 7 > 0 и последовательности £->#£©, Nt —► со, такие, что
m(i) = Et[|/l(x1,i)r;il(xbO>^]>7
(9)
"'\2
при всех t из выбранной последовательности.
Воспользуемся теоремой 1 при У= X, и = μ, ψζί,χ) = (\/ft(x) У
= -{l'(x,t))2ft{x), A(t) = {χ: J у/ft (χ) Ι ^ 2\\//θ(χ) |}. В силу непрерывности
662
Приложения
y/fe(x) условия 1), 2) теоремы 1 выполнены и, следовательно, из непрерывности
I{t) будет вытекать, что
"и(0= / |\/ЛЙТм^)-^о
x£A(t)
при t -> θ. Но m(t) ζ mi(t) + ra2(05 где
m2(t)= J (,/Κ')2μ, B{t) = {x:2\y/K(x)'\>Nty/f^)}·
B(t)nA{t)
Из вида множества A(t) следует, что
m2(0^4 J |v7*'|V
B(t)
Используя опять сходимость (y/ft(x))' ~> Wfe{x))', y/ft(x) -* \/fe(x) при t ->
-> 0, мы получаем, что B(t) сходится к множеству μ-меры нуль. Это значит, что
μ(Β(ί)) -> О, 7П2(0 ~* 0> m(0 ~^ 0 ПРИ ^ -^ оо. Мы получили противоречие с (9).
Соотношение 3 доказано.
Путь теперь выполнено (3). В силу теоремы 1 для доказательства
непрерывности I(t) нам достаточно убедиться, что при том же, что и выше, множестве A(t)
выполняется га ι (t) -> 0 при t -+ оо. Но
™i(*K J \1'\2Λμ + Ν2 J Λμ,
1ί'|>ΛΓ *tA{t)
где первый интеграл выбором N может быть сделан в силу (3) сколь угодно
малым. Для оценки второго интеграла заметим, что μ{Α(ί)) -> 0 и что при C(t) =
= {χ: ft(x) ^ 2fe(х)} выполняется / /^μ —> О при t -> θ (см. доказательство
*tc(t)
следствия 1). Поэтому
J /,μ^2 J /*μ + j Λμ->0
x£A{t) x£A(t) x£C(t)
при t -> Θ. <
3. Следствия условий (RRU). Условия (RRU) были введены в §34.
Теорема 4. Если выполнены условия (RRU)} то / /β(χ)μ(άχ) = 0.
Вместе с теоремой 2 это обеспечивает выполнение нужных нам в § 33, 34
условий (RR), 3.
Доказательство. В силу теоремы 2 при всех θ е θ
/
/ί(χ)/ι(ώ) = О
Приложение V
663
и нам достаточно доказать, что при t -> О
J(i) = -±-9 [| Λ'μ - J /ίμ] -> У /ί'μ.
Заметим, что ^{П - ,<) = ψιίι + Д/L·* где ^t = -L (| - |). Поль-
зуясь этим равенством, мы можем J(t) представить в виде суммы четырех
слагаемых J(t) = Ji + J2 -l· J3 + t/4, где
J\ = Ι φιίβμ, h = / ν^ί(Λ - ίβ)μ,
J*= J φ№-ίθ)μ, J^jjJ-JZT^
1>Ν
Ι = 1(χ) есть мажоранта для /"(χ, t) в условиях (RRU)· В силу теоремы 2 при η = 1,
S(x) = Ι'(χ,θ) получаем
1
J4 = —т(Е/(хь0) - Е^(хьв)) -* E,(/'(xlf0))2 = 7(6).
ί-0
Далее,
ы </
и, стало быть, по теореме Лебега
limJi= []im<ptfo = [ΐ"/θμ= [ίθ'μ-Ι(θ).
t->9 J t->9 J J
Используя опять (11), получаем в силу условий (RR)
(10)
(И)
(12)
ш$
/ 4ιμ\ + / ΐίβμ
при Ν -» οο. Наконец, в силу неравенства Коши-Буняковского
t ί
|е/2| ^ N J\ft - Λ|/ζ ^ N j j\fu\dw ^N J у/Щаи -> О (13)
при £ -> 0. Сопоставляя (10)—(13), мы получим, ч*то 0 = J(t) -> / /^'μ. <
Приложение VI
Неравенства для распределения отношения
правдоподобия в многомерном случае
В этом приложении будет доказана следующая теорема (теорема 36.2;
обозначения см. в §31, 33, 36).
Теорема 1. Пусть выполнены следующие условия:
inf^>
inf
9{θ) > О,
Εθϊ(χ1,θ)=0,
7 = supEe|/'(x1,l9)|s <oo
θ
(1)
(2)
(3)
при некотором s > к. Тогда при любых ζ,η^ 1
Рв С sup Z (-j=) > ελ < n(e-z/2+e-2)e-M^\
где β > О зависит лишь от к и s, с < оо зависит от к, s и д(в) и может быть
выбрана не зависящей от 0, если д{в) > д > О при всех Θ.
Нам понадобятся несколько вспомогательных утверждений *). Через ce, Ck,s мы
будем обозначать различные постоянные, зависящие лишь от своих индексов.
Лемма 1. Пусть ξ*, к = 1,2,..., независимы и одинаково распределены,
Εξι = 0, Ε|£ι|5 < 7 < оо, s ^ 2. Тогда
Ε
Σ*
ζ cs7ns/2.
Доказательство. Для упрощения рассуждений ограничимся
рассмотрением случая, когда s — 2т есть целое четное число**). В этом случае достаточно
рассмотреть скалярные величины ξ^. Имеем
Ε
jfe=l
(4)
") Другой вариант доказательства теоремы 1 предложен в испанском издании этой
книги [19].
**) Доказательство в общем случае см., например, в [49, с. 255].
Приложение VI
665
где суммирование ведется по всем целым fci,-..,An таким, что /Jfcj = s, к{ φ Ι
г
(А:г· = 1 исключаются, так как Εξ* =0). По неравенству Гёльдера
|Ε#|^(Ε&|·)*'/· = 7*'/·
и, стало быть,
i=i i=i
Нам осталось оценить У^ 1. Обозначим через (/ι,...,/ρ) ненулевые эле-
ρ
менты (Zi ^ 2) набора (fci,...,fcn) (/J'i = sj. Тогда оцениваемая сумма будет
i=i
равна Σ Лр, где Лр есть число расположений элементов 1\,...,/р по η местам.
(Ί 'р)
Очевидно, что Ар ^ п(п — 1)... (п — ρ + 1). Самое большое возможное значение ρ
равно m = s/2 (оно соответствует набору (2,2,.. .,2)), так что Ар ^ Лт ζ пт. Но
число различных наборов (/ι,.. .,/р) зависит только от s. Следовательно,
оцениваемая сумма не превосходит с8пт. <
Положим р(и) = Z1//s(u).
Лемма 2. Яри выполнении условий (2), (3)
Е„|р'(и)|8 < cs7ns/2.
Доказательство. Имеем
Е9\р'(и)\8 = Ε*
-L'(X,e + u)Zl'8(u)
s
8—Έ9\ν(Χ, θ + u)\8Z{u) = e-E*+tt|L'(X, 0 + u)|'.
Остается воспользоваться леммой 1, применив ее к случайным величинам ξα
Лемма 3. При выполнении условий теоремы 1
E*|p(u + t/) -р(г/)|5 ^ |ν|·^7ηβ/2,
где cs то же, что и β лемме 2.
Доказательство. В силу неравенства Гёльдера и леммы 2
Ев\р(и + ν) - р(и)\8 = Ее
/('Ю-й)*
1 " 1
[ (p'(u + hv),-^\ dh\ ^\v\s iEe\p'(u + hv)\sdh^\v\scBjna/2. <
666
Приложения
Обозначим через KU}& куб в Шк со стороной длины Δ и с вершиной в точке
u = (txi,...,iife):
KuA = {ν £ Rk:ui ^ Vi ^ щ + Δ, t = 1,..., *}
и положим Δ = e-l"!20(0)/(4*).
Лемма 4. Яри выполкекии условий теоремы 1
Ρ Л sup s(-^^e*l ^crA^e-^+e-'Je-l^'W,
где постоянные с < оо и β > 0 зависят только от к и s.
Такая же оценка будет верна для любого куба со стороной длины Δ,
содержащего точку и.
Доказательство. Точку ν £ Ки,& представим в виде ν = и + ίΔ, где
£ € /£ο,ι· Для координат £i вектора £ воспользуемся двоичным разложением
оо ,
, __ \^ Oir
г=1 Z
где все 6{Г равны либо единице, либо нулю. Положим
771 jr
Τ = Σ#' *m = («Г, ···.*?), «° = 0, (5)
r=l
так что tm есть двоичное приближение t: \t - tm\ < 2~my/k.
Положим
Тогда
оо
v(i) = v(o) + ^Mr)-Vp(r-1)).
Точки £?К и ££v назовем соседними, если их представления (5) отличаются
лишь одним из чисел #im,..., £*т. Ясно, что если для любых двух соседних точек
И*ю)-?(«5))|<^. (6)
то |<p(£m) -<£(£m~1)| < cm. Стало быть, если (6) выполнено для всех соседних точек
при всех 771 и при ст = а(1 - q)qm, q < 1, и, кроме того,
р(0) < а(1 - 9), (7)
то
оо
ψ(1) <^α(1- g)gm = а,
т=о (8)
sup <ρ(ί) < α.
teAO.i
Приложение VI
667
Обратимся теперь непосредственно к утверждению леммы. Нам надо оценить
Р* ( sup Ζ ( 4= ) 2* ez j = Ρ Л sup <p(t) > a) (9)
\v£KUtA WnJ J \teK0ti J
при а = e2/s. Неравенство, стоящее под знаком вероятности, означает
нарушение (8) и, стало быть, влечет за собой нарушение одного из неравенств (6), (7).
Следовательно, вероятность (9) оценивается суммой вероятностей
Ρβ(φ(0) £ α(1 - q)) + f; £ Ρ* (|p(tft) - ν(*5))| £ α(1 ^)gT") , (10)
где последняя сумма образована к(2т)к слагаемыми, соответствующими всем
возможным парам соседних точек №* и Щу Так как [ίΤΚ — tjiL | = 2~~т, то для каждой
такой пары в силу леммы 3 и неравенства Чебышева
Р, (М,;у -,Ш > ^) < (^)'с^ (^)~.
Следовательно, двойная сумма в (10) будет оцениваться значением
оо
Δ*β8Ί[α(1 - ϊ)]"·*1-·/2 £ 2-то<'-*>9-то'. (11)
m=l
Выберем q = 2(к~8^28 < 1. Тогда ряд в (11) будет сходиться и все
выражение (11) будет иметь вид Ck,sl&8cr8. Первое слагаемое в (10) оценивается в силу
теоремы 36.1 и неравенства Чебышева:
Р,(„(0) £ a(l-g)) = Ρβ (ζ1'3 (-^) £ (a(l - 9))«/2) ^ (a(l-9))—/2e-l-la*W/2.
Полагая Δ = e~lu' p(fl)/(4*)) учитывая, что а~8 = е~2, и считая, не ограничивая
общности, что s ^ 2A:, мы получим для (9) оценку
см7ДЛе-|и|2^)(5-Л)/(4Л)(е"2 + е"*/2).
При β = (s — к)/4к получим первое утверждение леммы.
Справедливость второго утверждения очевидна, так как в доказательстве вместо
<£?(0) мы смогли бы взять значение φ(ίο) в любой фиксированной точке ίο £ Код
(первая сумма в (10) соответствует значению в точке, а вторая — полному
возможному изменению φ(ί) в -Код)· Лемма доказана.
Доказательство теоремы 1. Покроем все пространство Жк системой
кубиков -Ки,д> У которых координаты точек и кратны А. Число таких кубиков,
пересекающихся со слоем Sr = {ν G Шк:г ^ |ν| ζ г + 1}, ограничено количеством
668
Приложения
скгк *Δ к. Следовательно
Ρ,
sup z(^=) > еЛ ^ скгк-1ск,Ме-г/2 + е-')е^^'\
I sup Ζ (jJ) > e* U ckckiMe~z/2 + e~z) f](r + j)k~l e~W
'■β№
Так как sup (г + ,-)*-1е-Л(*)(г+Ла/2 и £ в-Л(в)[(г+Ла-г»]/а < £ e-fiM?f2 огра.
rJ i i
ничены постоянной ο(βρ(θ)), зависящей от Рд(в), то полученное выражение не
превосходит cfc,s7c(/fy(0))e-r2/?s(9)/2(e-;i/2 + е-2), где с(0д(в)) < с{0д) < со, если
9{θ) ^ 9 > 0 при всех Θ. <
Приложение VII
Задача о разладке.
Вспомогательные предложения
и теоремы об асимптотически оптимальных
моментах остановки
Везде ниже мы будем использовать обозначения § 72, как правило, без
напоминаний.
1. Теорема о предельном распределении оценки максимального правдоподобия.
В этом пункте мы получим утверждение, обобщающее теорему 72.1 о предельном
Ρί-распределении разности Θ* — t при t —> оо, где Θ* — оценка максимального
правдоподобия. Обозначим через n(S) момент последнего достижения
неотрицательного максимума 5, так что Sn(s) = S, если S ^ 0, и через n(Z) — момент
первого достижения Ζ ^ О, £η(Ζ) = %· Если S < О, Ζ < О, то полагаем n(S) = О,
n(Z) = 0 соответственно. Определим на одном вероятностном пространстве две
независимые пары (S,n(S)) и (Ζ,η(Ζ)) и случайную величину
D
—n(S) < О на множестве Ζ ^ 5, 5^0;
0 на множестве S < 0, 2^0;
η(Ζ) > 0 на множестве Ζ > 5, Ζ > 0.
Если P(Sfc = 0) = 0 при всех к, то моменты первого и последнего достижения
максима S совпадают с вероятностью 1 (см. [12]). То же справедливо для Z, если
V{Z\z = 0) = 0 при всех к. В этом случае распределение D совпадает с
распределением
(-n(S) < 0 на множестве Z+ ζ S+, S+ > 0;
Do = < 0 на множестве S+ = Z+ = 0;
[n(Z) > 0 на множестве Z+ > S+, Z+ > 0.
Совместные распределения пар (5+,п(5)) и (Ζ+,π(Ζ)) (точнее, двойные
преобразования Ezn(5)eA5 и Ezn^eAZ ) могут быть найдены в явном виде в терминах
компонент факторизации функций 1 — ζφ(λ) и 1 — ζψ(Χ) соответственно (см. [12]).
Если ϊΌζ+(ν) — положительная компонента канонической факторизации функции
1 — ζφ(ίν), т.е. функция, аналитическая в верхней полуплоскости, непрерывная,
включая границу Im v = 0, и обладающая свойствами
inf |юг+(г;)| > 0, tOz+(ioo) = 1,
lmu>0
(подробнее см. § 14, 15 в [12]; гл. 11 в [17]), то
Ezn(S)eivS+ = *ι+(°)
tOz+(v)
670
Приложения
В широких предположениях справедливо асимптотическое представление
Р(п(5) = к) ~ ^j, с = const > 0
(см. [12, §21]). Аналогичные соотношения верны для Ez
n{Z)eivZ+ и p(n(Z) = к).
Теорема 1. Pt-распределение Θ* — t сходится κ распределению D:
Pt(0*-t = *)-*P(O = ib)
при £ -> оо.
В силу оценок (72.6) эта сходимость будет иметь место вместе со сходимостью
моментов любого порядка.
Доказательство теоремы следует доказательству теоремы 72.1 и
отличается лишь большей детализацией. Поэтому мы предоставляем его читателю.
2. Оценки распределений, связанных со случайными величинами Е{. В этом
пункте мы получим оценки для «хвостов» распределений случайных величин -=р и
Ei
1пЕ{, г = 1,2, где Ei и Е\ определены в теореме 72.4. Эти оценки использованы в
доказательствах теоремы 72.4 и теоремы 2 этого приложения.
Так как величины & и £, определенные в п. 1 §72, обладают одними и теми
же свойствами (Е& < О, Е& < 0; ^(1) = Ее*' = 1, ^(1) = Ее*' = 1), то можно
ограничиться рассмотрением лишь случайных величин, ассоциированных с ξι (т.е.
с Е\). При этом мы несколько расширим наши допущения и будем считать, что ξι —
произвольные независимые случайные величины, распределенные как ξ, Εξ < О,
<^(λ) = ЕеЛ* < оо при некотором λ > 0.
Как и прежде, обозначим
3 8
Ει>8 = Σβ8\ El8 = Y^kes\
fc=l k=l
оо
так что Ει = £?ι|00, Ε[ = £{)00. Обозначим Ь"1 = 3 + ]Г AT1 In"2 к.
к=1
Лемма 1. При всех достаточно больших χ справедливо неравенство
х)х ( у/Ьх Л ^
ехр т= 1η ψ
φ \]пу/Ъх j
где λ > 0 есть значение аргумента, при котором достигается min<^(A) = φ < 1.
/Ε' \
Такое же неравенство справедливо при всех s > 3 для Ρ ( —— > χ ).
\Ε1,8 )
Ε'
Таким образом, случайная величина -=~ имеет моменты любого порядка. Из
Е\
доказательства леммы будет видно, что полученная оценка может быть улучшена.
Приложение VII
671
Однако истинная асимптотика Ρ ( —г > х ) ПРИ х ~* °° остается неясной.
Возможно, что она имеет тот же вид, что и Р(п(5) > х) (см. выше).
Доказательство. Обозначим через η значение *, при котором достигается
максимум последовательности 5£, S£ = Sk + 2 In A: -f 2 In In A, A: ^ 3; 5q = 0,
S* = 5ь SJ = S2. Обозначим Λ^ = {τ/ = n,5* G <&;}, Б = < -=f > χ >. Тогда
оо °°
Р(В) = Σ / P(^nd,). (1)
На событии Ап,^ выполняется
оо оо / оо \
k=l к=3 \ к=3 )
Ει ζ ev-2Inn-2Inlnn = ev(n\nn)-2; § ζ b'^nlnn)2.
Εχ
Поэтому произведение BAn^v не пусто лишь при п таких, что η In n ^ y/bxi
Л V5x 1
5ЛП^„ С An4v 1<п^ -—-= > .
Следовательно, в силу (1)
вд<,Й)- <2>
Но {q = k} С {5* + 21η* + 21η1η*;>0},
Р(ту = к) ^ P(Sk > -21η* - 21nIn*) ^ ^(A)eM2inM-2inin*) = ^(fclnfc)2A?
где под λ > 0 мы понимаем значение, при котором достигается πήηφ(Χ) = φ < 1.
Следовательно, при достаточно больших *
Р(0*К^(*1п*)2\
и в силу (2)
n/m 2 / л/te , \ / л/te , Vte \2λ
Р(В) ^ ехр ,—lny? -Ц== In-^-7==
У 1 - ^ \lnVfa / \1п>/5я 1пл/Йж/
Очевидно, что при bx ^ e последний множитель не превосходит (Vbx)2X. Это
доказывает первое утверждение теоремы.
672
Приложения
Второе утверждение доказывается точно так же. Надо лишь вместо η
рассмотреть значение щ8) = min(s,7;), при котором достигается максимум S£, к ζ s.
Теорема доказана. <
В следующем утверждении изучается асимптотика P(\nEi > χ) при χ -* оо.
Лемма 2. Пусть s = sup {λ: φ(λ) ^ 1}. Тогда
1ηΡ(1ηΕι >ж) = -ва:(1 + о(1)). (З)
Если
φ{μ) = 1, iff {a) < оо, (4)
то
Ρ(1ηΕλ>χ) = cie~8X(l + o(l)), о < а < оо. (5)
Доказательство. Рассмотрим последовательность
Wn = In (e*" + е*»**—1 + ... + ein+-+€l). (6)
Очевидно, что она удовлетворяет рекурсивным соотношениям
Wn = W„-i+i„ + ln(l + e-w-0
(7)
и является цепью Маркова. Распределение Wn при любом начальном значении W\
(не обязательно Wi = ξι) сходится к распределению W = Ιηϋα, которое будет
стационарным распределением цепи, так что цепь {Wn} является эргодической.
Приращение этой цепи ξ(χ) = Wn - Wn-\ при условии l/Fn-i = х имеет вид £(х) =
= ξη -f 1п(1 4- е~х). Это означает, что цепь {Wn} является асимптотически
однородной (в пространстве; см. [20, 21]) и к ней применима теорема 3 из [21], в силу
которой выполнено (3). Чтобы применить теорему 4 из [21] о точной асимптотике
P(W > χ) (из которой будет следовать (5) при 0 ^ с\ < оо), наряду с условиями
(4) требуется также выполнение условий
оо
/
est|P(£ + In(1 + е-У) > t) - Ρ(ξ > t)\dt ζ l(y), (8)
где 1 (у) — правильно меняющаяся функция такая, что
l(y)dy <оо. (9)
/'
Разность под знаком интеграла (8) неотрицательна, и поэтому нам достаточно
оценить разность интегралов
оо оо
[ ε8ΐΡ(ξ >t)dt=- ί est άΡ(ξ <t) =
<?(*)
Приложение VII
673
ОО
/
е'еР(£ + h(y) >t)dt = ^ , h(y) = ln(l + β"»),
s
—oo
равную
-φ(8)(1 - e8h^) ^ -v>(e)(l - (1 + е~Уу) ζ <p(8)e~*.
s s
Это гарантирует выполнение условий (8), (9). Положительность с\ в (5) следует
из неравенства ΧτιΕι ^5и асимптотических представлений в лемме 72.1. Лемма
доказана. <
Доказательство теоремы 72.7. Чтобы разгрузить само доказательство
от технических деталей, мы начнем со вспомогательных утверждений.
Лемма 3. Если ρ > О, ρ ->· 0, то
ОО
ρ ]Г С1 - P)k~l In A; = - lnp + с + o(l),
где \с\ < oo, с от ρ не зависит.
Доказательство. Положим Δ = — 1п(1 — р) = р+0(р2) и воспользуемся
представлением
fc+l JH-1
/ e-xAlnxdx = e^Alnik / (1 + 0(Δ)) (ΐ + θ(-Υ\άχ =
к к
= e-kA]nk(l + 0(b) + o(±Y\.
Из него следует, что
Ρ Σ (χ -Ρ)*""1 lnk = Pi1 "Ρ)"1 IVA*lnx /Ί + 0(Δ)+0 [-^ dx =
oo
Δ
= (1 + ο(1)) ί [e-ylnydy-\nA+o(l) J .
Лемма доказана. <
Рассмотрим теперь последовательность геометрических априорных
распределений Q (72.31) при ρ -> 0. Рассмотрим байесовский момент остановки т(А),
определенный в теореме 72.8, и для заданного ε > 0 выберем А так, чтобы Р(т(А) < Θ) —
= Pq(t(A) < 0) = ε. Это будет означать, что т(А) G ^(e,Q) (см. п.З из §72). Как
уже отмечалось в п. 3 из § 72, при малых q(n) = р(1 — р)п~1 выполняется А « 1 — ε.
674
Приложения
Нам понадобится асимптотика Е(т(А) - Θ)* при р-^0.
Лемма 4.
Е{Т{А) _,)+ = (l-e)(-lnp-l + V) + % + о(1))
(10)
где
V = ln- -Ε\η(ί + Ει + Ε2), supup<c<oo.
1 — -Л. ρ
Если распределение ζι нерешетчато, то ир —> (1 —ε)Έχ < оо, где χ — перескотс
'через бесконечно удаленный барьер в блуждании {—Ζ^}.
Доказательство. Имеем
я(т(Л) -<?)+ =ρ]Γ(ι -рГ^ил) -*)+ =
= ρΣ i1 "Ρ)'"1 P'(r(A) ^ *)E« (r(A) - ^ £ i) . (11)
Наша ближайшая цель — найти асимптотику Et(r(A) - t/r(A) ^ t) при t -> оо.
Рассмотрим более внимательно момент остановки
т(А) = min < η ^ 1:
Ε(ι-ρ)*-1^)
fc=l
где
(1-р)»Л(п + 1) р(1-Л)
Λ = 1η-
> = min {n ^ 1: Mn ^ eh},
(12)
P(l - 4)' (13)
Мп = (1 -р)^1 + (1 - ^(ΓηΓη-ιΓ1 + ... + (1 - P)n(rn .. .η)-1.
В нашем случае
r^1 = e^fc при А; < t,
r^1 = e"^fc при fc ^ £.
Поэтому, полагая Δ = — In(1 -ρ) = ρ + 0(ρ2), получим
Μη = е-^-л + β-<»-<»-*-2Δ + ... + e-C«-...-C.-(n-t+i)A +
+ ^Cn-.-.-Ct-in-t+VA+tt-x-A + . . . + β-^-.--ζ·-(η-ί+1)Δ+ξ,-ι+...+ξι-(ί-1)Δ =
__ e-Cn-...-Ct-(n-i-f-l)Ar1 + eCt+A 4. ... 4- CCt+-+C»-i + (n-t)A +
+ eCt-i-A 4- . .. + e£t-i+...+£i-(*-l)Ai
Пользуясь независимостью {&} и {&} и сдвигая индексы у £# на ί — 1, получим
т(А) - t 4-1 = г = min{* ί> 1: - ΖΔ + In [l + Д£,_1 + *£*-ι] £ Λ}>
Приложение VII
675
где
Ζ? = Zk + *Δ, S£ = Sk- *Δ,
η η
Таким образом, величина т(Л) — t + 1 при условии т(А) ^ ί имеет такое же
распределение, как момент остановки г для мартингала {—Ζ£—к(р—Δ)}. Нетрудно
видеть, что здесь, как и для величины η в доказательстве теоремы 72.5, применимо
тождество Вальда-Дуба, в силу которого —ΈΖ^ = Ет(р - Δ). Отсюда вытекает
р-А
где
-ΖΤΔ = h - In [1 + E*t + £2Ar_i] + Xt-
Здесь «перескок» \t имеет тот же смысл, что в доказательстве теоремы 72.5, и для
Ех^ справедливо то же утверждение, что в теореме 72.5. Кроме того, Е^к | Е^ <
< оо и в силу леммы 2 Ε In [l + Е^^ 4- Е^^] < оо при достаточно малых Δ;
Eftn -> Ei при Δ -> 0, г = 1,2.
Поэтому
Er = h-E]n[l + El+E2]+EXt +
Ρ
где supE^t < с < оо и для нерешетчатых £* выполняется Εχ* = Εχ 4- о(1) при
£ -► оо, Δ -> 0 (см. [23]). Остается заметить, что в силу (11)
Щт(А) -<?)+ =ρΣ(1-ΡΫ-1?ΜΑ) Ϊ i)Er =
= - 1Р*(т(Л) ^ ί) + up + о(1) =
- In ρ + In j - Eln [1 + Ει + £*]
= L~A (1 ~e) + up + o(l),
где sup up < oo, Up = (1 - ε)Εχ + o(l) для нерешетчатых С*· Лемма доказана. <
ρ
Мы можем обратиться теперь непосредственно к доказательству теоремы 72.7.
Возьмем произвольный асимптотически однородный момент остановки г Ε
Ε Κ(€ι), ει < ε (см. п. 3 из §72). Тогда Р*(т < t) -¥ ει при £ -> оо и, стало
быть, Pg(r < θ) -* ει при ρ ->· 0. Это означает, что г € K(eyQ) ПРИ всех достаточно
676
Приложения
малых р. Имеем в силу леммы 3
оо
E(r-Q)+=p^(l-p)t-1Et(r-i)+ =
оо
= ρΣ,0- -ρ)*-ιΡι(τ > φ1ηί(1 + ο(1)) = -ν(1ηρ)(1 - £ι)(1 + ο(1)).
Следовательно, в силу теоремы 72.8 при А = Αε и леммы 4
„(1 _„,. lim MlzDI > lim *МЛ)-Г . Οζω,
р-ю —In ρ р-ю —In ρ /9
(l-£l)/>
Так как ει — произвольное число, меньшее ε, то мы получаем ν ^ 1/р. Теорема
доказана. <
Из теоремы 72.5 видно, что полученная нижняя граница 1/р достигается для
момента остановки ι/, построенного в (72.17). Сказанное выше означает также,
что ν асимптотически эквивалентно (в смысле приведенных утверждений)
байесовскому моменту т(А) относительно априорного распределения Q (72.31) при ρ -* 0.
Нетрудно убедиться, что это останется справедливым и для других распределений Q
из класса Q, описанного в п. 2 из § 72.
4. Еще одна конструкция асимптотически оптимального момента остановки.
Эта конструкция возникает естественным образом из приведенных в
доказательстве теоремы 72.7 (см. также лемму 4) рассмотрений, из которых видно, что
оптимальное правило строится на последовательности статистик Мп (см. (12), (13)),
которые асимптотически близки при ρ -> 0 к последовательности
Мп = Г*1 + (ГпГп-ΐΓ1 + . . . + (Г„ . . .Γι)"1.
Из доказательства леммы 2 видно, что статистики Wn = 1пМ£, допускающие
рекурсивное представление
Wn+1==-brn+i+ln(l + ew-) = W„ + 7n+i+ln(l + e-w"), (14)
очень близки по своим свойствам к последовательности {wn}, определеннной в
(72.16). Аналогично тому, как это делалось в п. 3 из §72 мы можем определить
момент остановки
1/1 = ui(N) = min{k^l:Wk^ b(k) + Ν], (15)
где функция b(k) имеет тот же вид, что и в теореме 72.5.
Момент остановки ν\ при Ь(к) = 0 был предложен в [97]. Относительно него в
[92,93] установлено, что он является асимптотически оптимальным в следующем
смысле: он минимизирует главную часть асимптотики supEt(i/i — t/v\ ^ t) при
t
В -¥ оо в классе моментов т, для которых EqqT ^ В.
Для v\ справедлив следующий аналог теоремы 72.5.
Приложение VII
677
Теорема 2. При всех t
Ρί(*Ί < t) ^ C\be~N, οχ = const < oo. (16)
Если распределения ξk непрерывны, mo P\(t) = Pi(t,N) — Ρ*(&Ί < t) и Р\(оо)
/oo \
непрерывно зависят от N и для любого ε < εο — Ρ ί Μ {Wk ^ b(k)} Ι суще-
\k=i J
ствует Νι = Νχ(ε) такое, что Pi(t) t Ρι(οο) = ε при t -* oo. Кроме того,
Et (* - 1. > ,) = b(t)+N-Eln(l + E1 + E2) + EX + ^ (χ?)
где χ для нерешетчатых ζΐε имеет тот же смысл, что и в теореме 72.5. Для
нерешетчатых ζk значение Εχ следует заменить функцией, ограниченной
известной постоянной (той оке, что и в теореме 72.5).
Как и в теоремах 72.5, 72.8, условие о непрерывности распределения £k здесь
не является существенным.
Доказательство теоремы 2. Если 0 = оо, то 7* = £* и
последовательность Wn образует эргодическую цепь Маркова, рассмотренную в доказательстве
леммы 2. Распределение Wn монотонно сходится к распределению W = In М£> =
= 1η£ι.
d
Очевидно, что в нашем случае η = ξ выполнены условия второй части леммы 2
при s = 1 и, стало быть,
Ρι(ί, Ν) = Ρι («/ι < ί) = Ρ ί (J {Wk> b(k) + N}W
OO OO
^Σ P(H^6(fc) + iVK]£ cie-6(fc)-^(i+0(i))=ClteAr(i + 0(i)).
Jk=l *=1
Это доказывает (16) при, возможно, несколько ином значении постоянной с\.
Непрерывная зависимость P\(t,N) от N доказывается так же, как в теореме 72.5.
Если Θ = t, то V\ — t при условии v\ ^ t распределено так же, как время г
первого прохождения уровня b(t + к) + N блужданием Wk при 7j = ~Cj и с
начальным значением Wo, распределение которого монотонно сходится при t —> oo к
распределению 1пЕ\. В этом случае приращения ξ(χ) = Η^+ι — ^fc превосходят
-Cfc+i, а в области Wk ^ Μ допускают мажоранту £(я) ^ -Ofe+i + е~м. Отсюда и
из рассмотрений [23] нетрудно получить существование предельного значения Εχ в
нерешетчатом случае и ограниченность соответствующей функции в общем случае.
Далее,
ewn = ezn+w0 + ezn + ezn-^ + _ + ezn-zn-r _ ezn(! + El + E2 + £n^
где εη -> 0. Таким образом, Wn ведет себя асимптотически как Zn+\n (1 + Εχ + £2),
где ϋα и #2 независимы. С помощью тождества Дуба-Вальда находим, как и
прежде,
Ет = —- = ρ-ΐΕ[6(ί + г) + ΛΤχ - 1η(1 + £ι + £2) + EXt] =
= ρ"1 [&(<) + ΛΓΧ - Ε In (1 + Εχ + Ε2) + EXt + ο(1)],
678 Приложения
где xt имеет прежний смысл величины перескока, Εχ* -> Εχ в нерешетчатом
случае. Теорема доказана. <
Представляет интерес сравнение средних значений задержек моментов
остановки ν и ν\ в условиях теорем 72.5 и 2 (см. правые части в (72.19) и (17))
при фиксированной вероятности ложной тревоги ε. Однако сделать это довольно
трудно, так как вид функций Ν(ε) и Νχ(ε) в этих теоремах нам неизвестен. Мы
может лишь высказать некоторые соображения, которые позволят хотя бы
приближенно понять природу этих функций. Заметим, что для функции Р(оо, Ν) в
теореме 72.5 вместо (72.18) при больших N можно использовать в силу леммы 72.1
более точную оценку
P(oc,N)ncbe-N, (18)
где постоянная с из леммы 72.1. Слабая зависимость событий Ап = {wn < b(n) + Ν}
и An+k при больших к и сравнение с некоторыми близкими результатами о
распределении maxWj позволяют сделать предположение, что асимптотическое поведение
P(oOjiV) отличается от (18) лишь постоянным множителем К, так что
P(oo,N)*Kcbe-N. (19)
Такое же замечание справедливо относительно функции
Pi(oo,tf)»tfiCite-N, (20)
где с\ из леммы 2, при этом в силу большого сходства в устройстве
последовательностей {wk} и {Wk} значения множителей К и Κι близки друг другу. Из
соотношений (19), (20) следует, что при малых ε выполняется
Νι{ε) - Ν(ε) « lnci - Inc.
Взяв разность между правыми частями в (72.19) и (17), мы получим, что
«выигрыш» при использовании v\ по сравнению с ν будет измеряться величиной
Eln(H-Ei+£;2)-Emax(5+,Z+)-ln—. (21)
с
Если эта величина окажется значимой положительной, то момент остановки v\
следует считать более предпочтительным. Относительно разности (21) заметим,
что в ней, очевидно,
1η(1 + £ι) >5+, 1п(1 + £?1+Ег) >max(5+,Z+), cx > с.
Приложение VIII
Доказательство двух фундаментальных теорем
теории статистических игр
Мы будем предполагать здесь, что выполнены следующие условия.
Условие (А). Множество решений D и множество параметров (чистых
стратегий природы) Θ представляют собой компактные метрические
пространства соответственно с метриками рп и р&.
Условие (В). Функция потерь w(5,6)\D χ Θ -> TSL непрерывна no δ и θ в
метриках pd и Ρθ соответственно.
Свойство w(S,6) ^ 0 нам не потребуется, и мы не будем предполагать, что оно
имеет место.
Далее, мы располагаем выборкой X & Р$ из распределения Р#. Ее объем п, не
ограничивая общности, можно считать равным единице.
Условие (С). Распределения Р$ непрерывны по вариации относительно Θ,
т. е.
sup \Р$т(В)-Рв(В)\-+0,
если ре(вт,6) -> 0 при т -> оо.
Если выполнено условие (Ад), т.е. Р# имеет плотность fe(x) относительно
некоторой σ-конечной меры μ на (Χ,*Βχ)\
fe{x) = fr(х)'
то условие (С) будет эквивалентно непрерывности fe{x) в L\(X,*&x^)\
если ре{9т,в) -> 0 при т -> оо.
Условия (А)-(С) допускают, конечно, возможность множествам D или Θ быть
конечными.
Если D конечно и состоит из точек <5χ,.. .,<Sr, то условие (А) относительно D
будет выполненным (выбор ро не играет роли), а условие (В) будет означать
непрерывность относительно ре функций ιυ(5ι, 0),...,χν(δΓ,θ).
Если оба множества D и Θ конечны, то условия (А)-(С) автоматически
выполнены.
Обозначим через ση, && соответственно σ-алгебры борелевских множеств из D
и из Θ. Следуя § 75, обозначим через (Ζ>, Θ, W) усредненную статистическую игру,
где элементами Θ являются распределения Q на (Θ, σβ), а элементами V являются
распределения π(χ) = π(χ, ·) на (ϋ,ση) (для каждого χ € #), где π(χ, А) для
каждого A G ση есть функция, измеримая по х.
Функция риска W(n, Q) определяется равенством
W(tt,Q) = J J [w(u,t)n(x,du) ft(xMdx)Q(dt).
θ Χ D
680
Приложения
Если вместо аргумента Q подставить Θ, то W(ny9) будет означать W(n,Ie), где 1в
есть распределение, сосредоточенное в точке Θ. Такое же соглашение будет
действовать относительно замены π Ε D на δ Ε V. Нам будет удобнее также вместо W
писать W. Это нигде не приведет к недоразумениям.
Лемма 1. Если выполнены условия (А)-(С), то функция \¥(π,θ)
непрерывна по θ для любой стратегии π(χ).
Доказательство. Имеем при θη -> θ
\Щ*,вп) - W(n,e)\ ζ \Ε0Ε[ν(π(Χ),θ) -υ>(π(Χ),θη)/Χ]\ +
+ \E$E[w{n{X)ten)/X]^E$nE[w(n(X)99n)/X]\ ζ
ζ ί Iwinix)^) -w(n(x),en)\Pe(dx)^snp\w(Sie)\ [\P$n(dx)-P$(dx)\. (1)
J δ,θ J
Первый интеграл здесь сходится к нулю в силу непрерывности функции w по Θ.
Сходимость к нулю второго интеграла вытекает из условия (С). Действительно,
пусть f$n (x) есть плотность Р#п относительно меры
и пусть Вп = {х: fen{x) ^ fe(x)}· Тогда второй интеграл в (1) равен
/ \fen (х) - fe(x)Hdx) = 2 J (/,„(χ) - ίθ(χ))μ(άχ) = 2(Ρ*η (Βη) - Ρ, (Βη)) -> 0.
Βη
Лемма доказана. <
Теорема 1 (первая фундаментальная теорема). Если выполнены условия
(А)-(С), то игра (£>, Q,W) имеет цену и минимаксные стратегии обоих
игроков. Другими словами, существуют наименее благоприятное распределение Q
и минимаксное решающее правило π(χ):
W* = supinf W(tt,Q) = W(W9Q) = inf supWfaQ) = W*. (2)
Q π π Q
В силу леммы 74.1 утверждение (2) эквивалентно тому, что
W(W,t) = supW(7T,Q) = W(W,Q) = inf (π, Q) = W(4,Q). (3)
Q
Теорема 2 (вторая фундаментальная теорема). Если выполнены условия
(А)-(С), то байесовские решения ttq(x) образуют полный класс. Другими
словами, для любого πο Ε V найдутся Q Ε Θ, ttqGP, такие, что
2) W(kq,0) ζ Ψ(π0,θ) при всех Θ.
Доказательство теоремы 2. Вторая фундаментальная теорема является
следствием первой. Действительно, рассмотрим произвольную стратегию тгобРи
Приложение VIII
681
игру (V, Θ, Wo), где W0 построена по функции w0(6)θ) = χν(δ,θ) - W(7ro,0), так
что
^о(7Г,0)=Щ7Г,0)-Щ7ГО,0). (4)
Функция υ(θ) = W(ko,9) в силу леммы 1 непрерывна по θ и, стало быть, функция
потерь τνο(δ,θ) ~ ιν(δ,θ) — ν(θ) вместе с ги(<5,0) удовлетворяет условию (В). Это
означает, что к игре (V, 0,Wo) применима теорема 1. Так как Wo(7i"o,t) — О
(см. (4)), то верхняя цена этой границы удовлетворяет неравенству W£ ^ 0. Из
(2), (3) следует тогда, что существуют π, Q такие, что
sup W0(π, Ρ) = sup W0(π, θ) ^ 0, π = π^.
ρ θ ν
Эти два соотношения эквивалентны утверждениям 2, 1 теоремы 2, если положить
Q = Q, π = nQ. Теорема доказана. <
Доказательство теоремы 1 будет вытекать из следующих двух лемм.
Лемма 2. При выполнении условий (А)-(С) существует распределение Q
такое^ что W(|, Q) ^ inf W(7r,f) = W*.
π
Лемма 3. При выполнении условий (А)-(С) существует стратегия π
такая, что W(7f,t) ^ W*.
Из неравенств лемм 2, 3 следует соотношение
W* > W(7f,t) £ W(7T,Q) J> W(4.,Q) £ W,
эквивалентное (3) и, стало быть, (2). Это доказывает теорему 1. <
Леммы 2, 3 разделяют доказательство теоремы 1 на две части. Первая из них
(лемма 2) очень мало связана с тем, что игра является статистической. Эта часть
доказательства проводится примерно так же, как для обычных игр (ср. с [73]).
Доказательство леммы 2. Пусть V есть множество функций Θ -> R,
представимых в виде ν(θ) = W(n,0), π € Ό. В силу леммы 1 все функции из V
непрерывны, так что V С С(Э), где С(0) — пространство всех непрерывных
функций на Θ. Далее, пусть υχ(θ) = W(7ri,0), ^(0) = W(n2,0). Так как при
ρε [ο,ι]
υ{θ) = μι>ι{θ) + (1 -ρ)ν2(β) = W(pm + (1 -ρ)π2,0),
π = ρπχ + (1 - ρ)π2 € Ρ,
το ν Ε V и, стало быть, множество V выпукло.
Заметим теперь, что W* = infW(7r,f) = inf supv(0). Нам будет удобнее
π veV q
* д. /χ m ж w(i,0) -υ0 + 1
вместо исходной функции ινίό,θ) рассматривать функцию —— , ν0 =
ру * — ^о + 1
= inf inf ν{θ). Обозначая новую функцию снова через «;(£,Θ) (задача при этом
остается неизменной), мы получим, что для нее
W = l, ϋο>0. (5)
Пусть теперь U есть множество непрерывных функций ν(θ): Θ -> Μ таких, что
supv(9) < 1. Очевидно, что U — выпуклое открытое множество из С(0). Кроме
682
Приложения
того, из (5) следует, что пересечение V Π U пусто. Поэтому в силу теоремы Хана-
Банаха (см., например, [140, с. 171, 200-206]) существует линейный функционал
L(v):C(Q) -> Ε такой, что
L(v) < 1 при ν G i/, L{v) ^ 1 при υ € V. (6)
Этот функционал с необходимостью обладает свойством L(v) ^ 0, если ν{\) ξ
= ϊηίν(θ) ^ 0. Действительно, допустив существование элемента vq £ С(0),
б/
^ο(4-) ^ 0, для которого L(vo) < 0, мы получим, что v8 = —svq £ U при любом
s > 0, L(t;s) = -sL(vo) > 1 при достаточно большом s. Это приводит к
противоречию с (6).
Но неотрицательный функционал L в силу теоремы Рисса (см. [120, с. 240])
допускает представление в виде интеграла
L(t/)= ίυ(θ)λ(άθ)1
θ
где λ — конечная мера. Так как 1 ^ supL(i;) = λ(Θ), то, полагая Q(A) =
veu
= λ(Α)/λ(Θ), мы получим при v eV
L(v) = ί\ν(π,θ)λ(άθ) = A(0)W^,Q),
Лемма доказана. <
Доказательство леммы 3. Так как функция W(n,6) при каждом π € V
непрерывна по θ (см. лемму 1J, то нам достаточно построить стратегию π, для
которой при всех к = 1,2,...
WfrflfcUW, (7)
где 0& суть точки некоторого счетного всюду плотного в D множества Τ = {θ\, #2, · · ·}■
По определению верхней цены W* существует последовательность стратегий 7ГП =
= πη(χ, ·) такая, что
W(7rn,0fc)<W*+- (8)
η
при всех fc.
Построим теперь с помощью распределений πη последовательность специально
подобранных случайных элементов ζη и выделим из нее сходящуюся
подпоследовательность. Для этого обозначим через fek{%) плотность распределения Рвк
оо
относительно вероятностной меры μ = \j2~fcP^fc) так что
ИЧтгпА) = if w(u&)nn(x,du)fek(xMdz). (9)
Приложение VIII
683
Рассмотрим пространство DxlT, где RT есть пространство значений
элементов f{x) = {ΙθΛχ)ιΙθ2(χ)ι· ··} с σ-алгеброй 93т, порожденной цилиндрическими
множествами. Каждой стратегии π поставим в соответствие вероятностное
пространство (D χ Χ, σο х 2$,*,Ρ), где распределение Ρ определяется равенством
Ρ{δ <ЕА,ХеВ)= f μ(άχ)φ, A), A€aD, ВеЪх. (10)
в
На этом пространстве определим случайные элементы
ζ = ζ(δ;Χ) = (δ;/θ,(Χ)Λθ2(Χ),...) = (δ;ΗΧ))
и обозначим через ζη элементы, соответствующие πη, так что ζη есть случайные
величины на выборочном вероятностном пространстве (D χ Мт, σο х 5*т, Пп), а
распределение Пп порождено πη, формулой (10) и отображением ξ(δ, x):D χ Λ* ->
->L> x RT.
Обозначим через П^ сужения распределения НПа на D χ Шк (это есть
совместное распределение (<5; /^(Х),..., fek(X)) и через λ — распределение /(X) на
(Λ*, ©,ν,μ). Нам понадобится
Лемма 4. Существуют такое распределение Π κα излеергисол*
пространстве (D χ IRT, σ/) χ 93τ) и такая подпоследовательность {πη*} С {7гп}, -что
П^ => П(Л) (11)
при любом к (Π cz/гаь сужения Π),
П(1)хС)=А(С), СеЯЗТ. (12)
Доказательство леммы 4 проведем позже.
Обозначим через ζ = (5, /) случайный элемент с распределением П.
Соотношение (12) означает, что распределение / совпадает с λ (вторая «координата» ζη
при изменении η распределения не меняет). Так как пространство D есть
метрический компакт, то оно сепарабельно и, стало быть (см. [35, с. 191]), существует
условное (регулярное) распределение δ относительно /(X), которое мы обозначим
через Π(·//(χ)).
Рассмотрим стратегию π (ж, А) = П(£ Ε A/ f(X)) и докажем, что для нее
выполняется (7).
Заметим предварительно, что
Ew(S,ek)7e„ = E7*kE №ψύλ = j f6h{x) jw(u,ek)W(u,dx)M(dx) = W(W,0k).
(13)
Далее, в силу леммы 4 распределение (5n*,/^fc(X)) слабо сходится к
распределению (δ,/вк(Х)). Поскольку функция w непрерывна, то совместное распределение
{ιν{δη*,0*), fek(X)) слабо сходится к распределению (w(6,0*),/^(Х)). Но
функция g(u,v) = w(u,6k)v непрерывна по и и ϋ и мажорируется функцией g(v) = cv,
684
Приложения
с = maxw(u,0fc), такой, что Eg(fek(X)) = с / /βίί(χ)μ(άχ) = с. Поэтому по теореме
непрерывности для моментов (см. теорему 5.4)
Jim Ед(6п.,/вк(Х))=Ед(5,Увк(Х)),
или, что то же,
lim Ew(Sn.,9k)f0h(X) = Ew(5,6k)Jek(X).
η*—>οο *
В силу (9), (13) это дает нам сходимость
lim W{*n.,ek) = W{%eh).
Так как левая часть этого равенства (см. (8)) не превосходит W*, то лемма 3
доказана. <
Доказательство леммы 4. Фиксируем какое-нибудь к ^ 1 и рассмотрим
D χ R* как полное метрическое сепарабельное пространство относительно метрики,
порожденной евклидовой метрикой в R* и метрикой ро. Для любого ε > 0 в Шк
найдется компакт К€ такой, что Р((/^1(Х),.. .,/^fc(X)) £ Ке) ^ 1 - ε. Так как
D х К€ есть компакт в D x Rk и так как
Ρ(ί„ е Д (/в1 (X),..., Λ, (X)) € *«) £ 1 - е,
то последовательность распределений П^' является плотной (см. [7]).
Следовательно, по теореме Прохорова [7] существуют распределение Τί^ и
подпоследовательность п^ = (п[' ,т4 ,..·) такие, что ΐΙηλ\ =>· П^*К Но распределения
П(*\ очевидно, согласованы и, следовательно, по теореме Колмогорова на (DxRT,
σ£> χ 05т) существует распределение П, для которого П^^ являются сужениями на
(D х R*, σΌ χ Β*).
С другой стороны, можно считать, что п^+1^ С п^кК Положив п* =
= (^ι \щ. >пз »·■·)» получим подпоследовательность, для которой П„/ => П^
при всех А;.
Докажем теперь (12). Пусть С Ε 2$т есть цилиндрическое множество такое, что
П-мера его границы равна нулю. Обозначим через множество
из R*, образованное первыми А: координатами точек из С, и положим С^ = С^ х
χ Кт~* G ®т. Тогда А(£<*>) = Π^(Ζ? χ С<*>) -> П<*>(£> χ С<*>). Так как
со
C(*+i) сСС», С= П <?(*>, то
А(С) = lim А(С(*>) = lim П<*>(1> χ C(fc)) = lim П(£> χ C(fc)) = U(D χ С).
fc—too Λ—юо fc-*oo
Лемма 4 доказана. <
БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
Ниже приводятся библиографические комментарии, в которых делается попытка
проследить историю появления основных идей и результатов, излагаемых в книге. Эти
комментарии не претендуют на полноту и часто будут содержать ссылки не на оригинальные
труднодоступные статьи, а на учебники, монографии или обзорные статьи, в которых
нужные результаты найти проще. Более обширные библиографические указания и исторические
справки содержатся, например, в [48, 65-67].
Некоторые основные понятия математической статистики возникли еще в начале
прошлого века и связаны с именами Лапласа и Гаусса. В конце прошлого века работы Пирсона
положили начало периоду интенсивного развития этой науки. Оно было обусловлено
фундаментальными работами Р.Фишера, Ю.Неймана, А.Н.Колмогорова, А.Вальда. В нашей
стране развитие математической статистики связано прежде всего с именами А. Н.
Колмогорова и Н. И. Смирнова.
Глава 1
§2-4. Теорема Гливенко-Кантелли была установлена в 1933 г. (Гливенко принадлежит
доказательство для непрерывного распределения, Кантелли — для общего случая).
Доказательство теоремы 2.2 близко к доказательству, приведенному в [72, с. 28] и
представляет собой частный случай использования более общего подхода, основанного на
«конечной аппроксимируемости» рассматриваемого класса множеств. В полном виде этот подход
изложен в приложении I, где доказана теорема 4.2. Независимо аналогичный подход был
рассмотрен в [43]. Закон повторного логарифма (теорема 4.3) установлен в [52].
Статистики вида G(F„) иногда называют также статистическими функциями. Их
систематическое исследование было начато фон Мизесом (см. [75, 76, 115]).
М-статистики были введены Хьюбером в [127] (см. также [128, 129, 122, 102, 67]) как
обобщение оценок максимального правдоподобия. Об L-статистиках см. в [67, 102, 139].
§ 5. Теоремы непрерывности, изложенные в § 5, встречаются в качестве вспомогательных
утверждений во многих работах; о некоторых из них см., например, [102].
§6. Теоремы 6.1, 6.2 о распределении nF^it) содержатся в книге Феллера [111, т. 2,
гл. III, §3]. Теорема 6.3 о сходимости процесса y/n{F^{t) — F(t)) к броуновскому мосту,
доказанная в приложении II, была установлена Донскером в [44]. Несколько иное по сравнению
с приложением II доказательство теоремы 6.3 можно найти в книге Биллингсли [7].
§7. Утверждение примера 7.3 о предельном распределении статистики χ2(Χ) (хи-квад-
рат) впервые получено Пирсоном (см. [58, с. 454]).
§8. Исследование предельного распределения статистик второго типа или
«статистических функций» по Мизесу было начато в [75, 76]. Ближе других к теореме 2 находятся
результаты Филипповой [115], которая изучала статистические функции специального вида.
При доказательстве теорем 8.2 и 6.3 реализован так называемый аппроксимативный метод
изучения сходимости случайных процессов, изложенный в [11]. Утверждение следствия 8.2
составляет содержание теоремы Колмогорова, а следствия 8.3 — теоремы Смирнова. По-
1
следняя включает в себя также явный вид распределения / [w (t)]2 dt, который ввиду его
о
сложности мы не приводим (см. [105]).
О предельном распределении L-статистик см. [139, 102].
§ 10. Оценки плотности, рассматриваемые в этом параграфе, были введены Парзеном [89]
и Розенблаттом [98]. Обзор результатов в этом направлении и библиографию см. в обзорной
работе Розенблатта [99] и в §25 книги Ченцова [131].
686
Библиографические замечания
Глава 2
§ 12. Некоторые другие параметрические семейства описаны в книге Уилкса [109]. Весьма
полное исследование распределений членов вариационного ряда выполнено Гнеденко. Полное
изложение результатов и обширную библиографию по этому поводу можно найти в книге
Дейвида [42].
§ 14. Метод моментов исторически является первым регулярным методом
построения оценок. Он был предложен Пирсоном в 1894 г. М-оценки были введены Хьюбером
(см. [127-129]). Об асимптотической нормальности М-оценок см. также [67, 102].
§ 15. Метод минимума χ2 был предложен Фишером в 1922 г.
§ 16. Метод максимального правдоподобия в частных случаях применялся еще Гауссом.
Как общий метод получения оценок он был предложен Фишером в краткой заметке в 1912 г.
Позднее, в 1925 г. в классической работе [117] им же были изучены асимптотические свойства
о. м.п.
Исследование состоятельности о.м.п. было начато в 30-40-х годах прошлого столетия
в работах Дуба [45], Вальда [28], Вольфовица [33], Крамера [58]. Основные условия
состоятельности в [28] включают в себя (помимо условий (Αμ), (Ас), (Ао)) принадлежность ft(x)
классу Do и интегрируемость
j\nf?{x)fe{xMdx).
В монографии [49] получены условия состоятельности, использующие сходимость
/ sup {y/ft+u(x)- v7f(s))V {dx) -> 0 при Δ -> 0.
J \uKA
Результаты теорем 14.1, 14.3 и их следствий 16.1-16.5 являются более общими. Метод
доказательства близок к [28]. Достаточность условий (Aq) и (7) была замечена Саханенко.
Асимптотическая нормальность оценок максимального правдоподобия изучалась во
многих работах (см., например, [49, 67, 102, 117]). Условия асимптотической нормальности в
теореме 16.3 близки к минимальным (ср. также с результатами в §34). Оптимальность
оценок максимального правдоподобия в классе М-оценок отмечена в [102].
§ 17, 18. Излагаемые подходы к сравнению оценок являются общепринятыми.
Доказательство леммы 17.3 заимствовано из [58]. Понятие эффективной оценки было введено
Фишером в 1922г. в [116].
В существующей статистической литературе один и тот же термин «эффективность»
используется в двух разных смыслах. Эффективными оценками называют: (а) оценки с
минимальными дисперсиями и (Ь) оценки, для которых достигается нижняя граница в
неравенстве Рао-Крамера. Классы оценок (а) и (Ь), вообще говоря, не совпадают. В настоящей
книге для оценок (Ь) используется термин «Я-эффективность» (см. §26).
§ 19, 20. Фундаментальное понятие условного математического ожидания было введено
Колмогоровым в 1933г. в классической работе [56]. Свойства условных распределений
детально изучены в [35, 46, 137].
§21. Байесовский подход широко использовался еще в прошлом веке Лапласом. Этот
подход подвергался критике со стороны Фишера, и в 20-30-х годах прошлого столетия
центр тяжести исследований переместился на эффективные и асимптотически эффективные
оценки. Затем по мере того, как стала осознаваться фундаментальная роль байесовского
подхода, интерес к нему вновь стал возрастать.
Понятие минимаксной оценки вошло в математическую статистику вместе с теоретико-
игровым подходом, развитым в работах Бореля (1921) и Дж. Неймана (1928), теоремы 21.1-
21.3 были получены Ходжесом и Леманом [124].
§22. Фундаментальное понятие достаточной статистики было введено Фишером в [116]
в 1922г. Фишер [116] и позже Ю.Нейман [82] предложили простой критерий,
обнаруживающий существование и вид достаточной статистики. Этот критерий носит название фактори-
зационной теоремы Неймана-Фишера и представлен в теореме 22.1. Строгое теоретико-
множественное доказательство теоремы Неймана-Фишера было получено лишь в 1949 г.
Халмошем и Сэвиджем [121].
Более простое доказательство этой теоремы, приведенное в книге и основанное на
теореме 22.1В, автору предложил В.В.Юринский.
Библиографические замечания
687
§ 23. Понятие достаточной σ-алгебры шире, чем понятие достаточной статистики.
Необходимые и достаточные условия для их совпадения приведены в [48]. Конструкция
достаточных разбиений и теорема 23.1 связаны с работой Лемана и Шеффе [68], посвященной
выяснению условий существования и построению минимальных достаточных статистик.
Краткое изложение этой статьи можно найти в [48]. Доказательство теоремы 23.2 было
предложено И. С. Борисовым.
§24. Теорема 24.1 была получена независимо Блекуэллом [8] (1947), Рао [95] (1945), [96]
(1949) и Колмогоровым [55] (1950). Теорема 24.3 принадлежит Рао [96] (1949) и Блекуэллу [8]
(1947).
§ 25. Экспоненциальное семейство упоминалось еще Фишером в [116]. Теоретическое
значение этого семейства было осознано в 30-х годах в работах Питмена, Купмена, Дармуа.
Именами последних иногда и называют экспоненциальное семейство. Теорема 25.2
доказана Леманом [65, с. 183; 66].
§ 26, 27. Неравенство Рао-Крамера иногда называют также неравенством информации.
Оно принадлежит, по существу, Фишеру [119], хотя в приводимой форме оно было получено
независимо Фреше [119] в 1943 г., Рао [94] в 1945 г. и Крамером [57] в 1946 г.
Условия регулярности, нужные для выполнения неравенства, в руководствах по
математической статистике трактуются не всегда аккуратно. Мы имеем в виду условия,
обеспечивающие законность дифференцирования по параметру под знаком интеграла. Доказательство
этой законности часто содержит пробелы (см., например, [48]) либо отсутствует вовсе
(например, в [31]). В ряде случаев она оговаривается в виде условия [31], что неудобно для проверки
в реальных задачах.
Условия регулярности, принятые в книге, весьма просты, хотя, по-видимому, не
являются наиболее общими (ср. с [49]). Тот факт, что при этих условиях можно
дифференцировать под знаком интеграла, доказан в приложении V, написанном на основе результатов
А. И. Саханенко.
Различные обобщения неравенства Рао-Крамера см. в [48, 131]. Понятие информации
(Фишера) было введено в [117]. При доказательстве теорем 26.1 А и 27.1 мы следуем
книгам [48, 49].
§28, 29. Идея использования инвариантных соображений принадлежит Хотеллингу и
Питмену. Значительный вклад в разработку теории внес Стейн. Основное содержание
теоремы 28.1 принадлежит Питмену. При ее доказательстве мы использовали изложение
в [48, 49]. Минимаксность оценки Питмена была установлена Гиршиком и Сэвиджем.
§30. Результаты этого параграфа были получены автором совместно с Саханенко [24].
Некоторые неравенства при более жестких ограничениях можно получить также из работ
[39, 130].
§31. Расстояние Кульбака-Лейблера в параметрическом случае называется также
функцией информации Кульбака-Лейблера. К этому расстоянию независимым образом пришел
И. Н. Санов при описании вероятностей больших уклонений эмпирического распределения.
Идея широкого использования расстояния Хеллингера для изучения свойств отношения
правдоподобия нами заимствована из книги Ибрагимова и Хасьминского [49]. На
результатах этой книги базируются и доказательства основных теорем § 33. Доказательство теоремы
31.3 было существенно упрощено Саханенко.
§32. Теорема 32.1 была установлена Чепменом и Роббинсом в 1951г. в [132] и Кифером
в 1952 г. в [51].
§ 33, 34. Излагается материал лекций, значительно усовершенствованный после
появления книги Ибрагимова и Хасьминского [49]. Основные усовершенствования связаны с
систематическим использованием расстояния Хеллингера для оценки ΈιθΖι^2{η). Предложение
использовать / Εβ|(Ζ ' (u))f\du для оценки supZ(u) (см. теоремы 33.1, 33.2)
принадлежит А. И. Саханенко. Асимптотическая нормальность и асимптотическая эффективность
о. м. п. была установлена еще Фишером [117]. Весьма общие условия асимптотической
нормальности о. м. п. получены в [49].
Асимптотическая нормальность апостериорной плотности (или отношения
правдоподобия) была обнаружена С. Н. Бернштейном в 1927г. Теорема 33.8 принадлежит Бахадуру [2].
Асимптотическая байесовость и минимаксность о. м. п. легко получаются благодаря
результатам § 30. Ранее асимптотическая байесовость о. м. п. устанавливалась при более жестких
ограничениях на плотность априорного распределения.
688
Библиографические замечания
При доказательстве теорем 34.1, 34.2 мы использовали некоторые усовершенствования,
предложенные А. И. Саханенко.
§35. Излагается один из вариантов численного метода Ньютона-Рафсона отыскания
экстремума функции. Более подробное изложение см. в [48]. Пример 3 заимствован из книги
Рао [96].
§36, 37. См. комментарии к §33, 34. Пример 36.3 заимствован из книги Ван-дер-
Вардена [31]. В изложении параграфов внесен ряд усовершенствований, предложенных
А. И. Саханенко (в частности, добавлена теорема 37.5). Эти изменения позволили упростить
текст в §43-45 гл. 3.
§38. Подробнее о последовательном оценивании см., например, в [48].
§ 39, 40. Впервые доверительные интервалы встречаются, по-видимому, у Лапласа. Еще
в 1812 г. он показал, что можно обратить относительно ρ утверждение о степени
расхождения наблюдаемой частоты и биномиальной вероятности ρ с тем, чтобы найти интервал для
возможных значений р. Правильная интерпретация доверительных интервалов (не
предполагающая случайность параметра) дана в 1927 г. Вилсоном.
Общий метод отыскания точных доверительных интервалов для вещественного
параметра был предложен Фишером в 1930г. в [118]. В 1937-38г. Ю.Нейманом была развита
общая теория доверительных утверждений и установлена их связь с теорией проверки
гипотез. Весьма полное современное изложение вопроса можно найти в книге Лемана [65]. Это
изложение использовано нами в § 47.
Теорема 40.1 и лемма 40.2 принадлежат Фишеру.
Глава 3
Первые отдельные применения статистических критериев восходят к Лапласу (конец
XVIII в.). Систематическое использование критериев для проверки гипотез начинается с
работ Пирсона, предложившего в 1900 г. критерий χ2. Фундаментальные понятия ошибок
первого и второго рода были введены Нейманом и Пирсоном в 1928 г. в [84]. Этими же
авторами впервые была осознана роль альтернатив для рационального выбора критерия.
В итоговой работе Неймана и Пирсона [85] развита теория р. н. м. к.
Систематическое изложение теории проверки гипотез содержится в книге Лемана [65].
§41-43. Фундаментальная лемма Неймана-Пирсона получена в [85]. Теоремы 41.1, 41.2
можно извлечь из книги Блекуэлла и Гиршика [9]. Теорема 42.1 содержится в книге
Лемана [65]. Теорема 43.1 о больших уклонениях принадлежит Крамеру (см. [17]). Оценка
качества критериев, связанная с вероятностями больших уклонений, легла в основу понятия
эффективности критерия по Бахадуру. Итоги исследований в этом направлении изложены
в [4, 22].
Роль статистики эффективного вклада была отмечена еще в 1925 г. в работе Фишера [117].
В дальнейшем подход, связанный с рассмотрением близких гипотез, интенсивно развивался
в работах Ле Кама, Русаса, Чибисова (см. также комментарии к §44, 45).
§44. Излагаемая общая концепция статистических критериев является общепринятой
(см. [58, 65]). Понятие р. н.м. к. было введено Нейманом и Пирсом в [85]. Байесовский
подход использовался еще Лапласом в XIX в.
§45-48. Основные результаты этих параграфов взяты из книги Лемана [65]. Изложение
также близко к этой книге, но отличается тем, что основано на байесовском подходе, а не на
обобщенной лемме Неймана-Пирсона (лемма 45.2, см. также [65]). Это упрощает изложение
и делает его более цельным.
По поводу доверительных множеств см. комментарии к § 39, 40.
О возможности перенесения основных результатов на случайные процессы см. книгу
Гренандера [37].
§49. Теорема 49.1 принадлежит Ходжесу и Леману [124].
§50. Фундаментальная роль отношения правдоподобия в математической статистике
была выяснена в работах Неймана и Пирсона [84, 85]. К. о. п. посвящена обширная
литература. Попытки установить те или иные свойства асимптотической оптимальности этого
критерия содержатся в работах [3, 28, 88, 109, 123].
§51. Основной вклад в развитие теории последовательного анализа принадлежит Валь-
ду [29]. Наиболее компактное изложение главных результатов, которому мы следуем в книге,
можно найти в [65].
Библиографические замечания
689
§ 52. По поводу критериев Колмогорова и ω2 см. § 8 и комментарии к нему. О некоторых
модификациях критерия Колмогорова, дающих наибольшую возможную мощность, см. [26].
Критерий Морана был предложен в [80]. Его мощность для близких альтернатив изучалась
в [32, 133].
§53. Асимптотическая байесовость к. о. п. установлена в работе автора [13]. Результаты
о предельном распределении отношения правдоподобия при основной гипотезе принадлежат
Уилксу [108] и Вальду [27] (см. также книгу Уилкса [109]). Идея замены сложной
гипотезы усредненной использовалась Вальдом. Асимптотический вид байесовских критериев
содержится в [69]. См. также комментарии к §36, 37 гл. 2.
§54, 55. Основные идеи, связанные с отысканием асимптотически оптимальных тестов
для близких гипотез, изложены в работах Вальда [27], Ле Кама, Русаса (см. книгу Ру-
саса [100]), Чибисова [134]. О возможности перенесения основных результатов на случай
бесконечномерного параметра (на случайные процессы) см. [25]. Форма изложения §54, 55
с цитированными работами связана мало. Редукция исходной задачи А к задаче В для
параметра нормального распределения при отыскании оптимальных критериев для основных
типов задач, рассмотренных в §54, содержится в работе Вальда [27]. Утверждение теоремы
55.4 о распределении статистики 2 In Ri (X) при гипотезе Hi можно найти в [109]. См. также
комментарии к § 36, 37 гл. 2.
§ 56. 57. Критерий χ2 был предложен Пирсоном в 1900 г. Ему посвящена обширная
литература (см., например, специальную монографию Ланкастера [62]). Обсуждение различных
свойств оптимальности см. в [27, 88, 109, 123] и др. О поведении мощности критерия χ2
при увеличении числа групп см., например, [14, 135]. Примеры 56.1, 57.2 заимствованы из
книги Крамера [58], пример 57.1 — из книги Рао [96].
§ 58. Начальный этап в изучении устойчивости статистических решений проследить
трудно. Более поздние исследования имеют в своей основе работы Тьюки, Ходжеса, Лемана.
Обстоятельный обзор этого направления представлен в работе Хьюбера [128].
Глава 4
§59. Критерий χ2 в задаче примера 59.1, критерий Стьюдента в задаче примера 59.3
и критерий Фишера в задачах примеров 59.4, 59.5 используются очень часто. О других
свойствах оптимальности этих критериев см. книгу Лемана [65]. Пример 59.1 А заимствован
из [96]. По проблеме Беренса-Фишера (пример 59.6) имеется обширная литература (см. [65]).
§60. Точное распределение статистики Dn,n найдено Гнеденко и Королюком (см. [111]);
предельное распределение статистики Dtlx^tl^
— Смирновым. Теорема 60.2 доказана впервые
в [74] методом моментов. О критериях знаков и Вилкоксона см. также [34].
9 61, 62. Подробнее задачи регрессии и дисперсионного анализа изложены в специальных
монографиях Себера [101] и Шеффе [136]. См. также [58, 65, 96].
§63. Замечание об асимптотической оптимальности критерия (63.3) содержится в [13].
Глава 5
§ 64. Изучению задач регрессии (пример 2) посвящена обширная литература (см.
комментарии к § 61, 62 гл. 4, а также [101, 136]). Теория статистических выводов для случайных
процессов (пример 4) является технически весьма сложной и, по-видимому, окончательно
еще не сформировалась. Некоторые важные элементы этой теории можно найти в
монографиях [1,38,61,70]. Пример 7 индуцирован работами, ссылки на которые содержатся в [59,87].
§о5, 66. Асимптотические свойства оценок максимального правдоподобия в
неоднородном случае изучались в [114, 113, 125].
§68. Основные результаты и библиографию, относящиеся к задаче об оценке хвостов
распределений, см., например, в [59, 87]. Некоторые результаты §68 близки результатам
этих работ.
§ 70. См. комментарии к § 65, 66.
§72. Задаче о разладке посвящена обширная литература (см., например, [41, 53, 71, 79,
90, 138]). Использование последовательности {wn}, определенной в (72.16), было предложено
в [71, 90]. Теорема 72.7 об оптимальном байесовском моменте остановки получена в [138].
Основные результаты § 72 и приложения VII об асимптотически однородных оптимальных
процедурах были получены автором специально для предлагаемой книги.
690
Библиографические замечания
Глава 6
В математике теоретико-игровое направление возникло с появлением работ Бореля
1921 г. и фон Неймана 1928 г. В математической статистике исходной работой,
подготовившей использование теории игр, можно считать классическую работу Неймана и Пирсона [86],
в которой были высказаны многие основные идеи теории статистических решений.
Фундаментальный вклад в развитие общей теории статистических решений принадлежит Вальду.
Основные положения этой теории изложены в его завершающей книге [30].
Общематематическая теория игр получила свое полное развитие в книге фон Неймана и Моргенштерна [81].
Доступное изложение основ теории статистических игр можно найти в книгах Блекуэлла и
Гиршика [9] и Фергюссона [112].
§ 74. Сравнительно полным введением в обычную теорию игр является книга Мак
Кинси [73].
§75, 76. Более полное описание основ теории статистических игр см. в [9, 112]. В этих
книгах две фундаментальные теоремы теории статистических игр доказаны лишь в частном
случае для дискретных множеств D и Θ. Объясняется это большой сложностью изложения в
общем случае (см. [30]). В приложении VIII приведено наиболее простое из известных нам
доказательств этих теорем. Оно было предложено А. И. Саханенко.
Роль байесовского подхода в разное время оценивалась по-разному. Он широко
использовался в прошлом веке Лапласом. Затем байесовский подход был подвергнут критике со
стороны Фишера, и в 20-30-х годах прошлого столетия центр тяжести переместился на
эффективные оценки и наиболее мощные критерии. Затем по мере того, как стала осознаваться
фундаментальная теория байесовского подхода, интерес к нему стал вновь возрастать. Эта
фундаментальная роль выясняется в теоремах 75.1, 75.2.
§77. Фундаментальное понятие достаточной статистики было введено Фишером в [116]
в 1922 г. Фишер [116] и позже Ю. Нейман [82] предложили простой критерий,
обнаруживающий существование и вид достаточной статистики. Этот критерий носит название фактори-
зационной теоремы Неймана-Фишера и представлен в теореме 22.1. Строгое теоретико-
множественное доказательство теоремы Неймана-Фишера было получено лишь в 1949 г.
Халмошем и Сэвиджем [121].
Понятие достаточной σ-алгебры шире, чем понятие достаточной статистики.
Необходимые и достаточные условия для их совпадения приведены в [48]. Теорема 77.1 (сначала для
квадратической функции потерь) была получена независимо Блекуэллом [8] (1947), Рао [94]
(1945), [95] (1949) и Колмогоровым [55] (1950). Обобщения на случай произвольной функции
потерь связаны с именами Лемана и Шеффе [68].
Идея использования инвариантных соображений принадлежит Хотеллингу и Питмену.
Значительный вклад в разработку теории внес Стейн (см. [48, 49]).
О несмещенности подробнее см. [48].
§ 78. Результаты, близкие к теоремам этого параграфа, можно найти в книге Ибрагимова
и Хасьминского [49].
§79. Асимптотическая байесовость к. о. п. установлена в работе автора [13]. Результаты
о предельном распределении отношения правдоподобия при основной гипотезе принадлежат
Уилксу [108] и Вальду [27] (см. также книгу Уилкса [109]). Идея замены сложной
гипотезы усредненной использовалась Вальдом. Асимптотический вид байесовских критериев
содержится в [69].
§ 80. Основные идеи, связанные с отысканием асимптотически оптимальных тестов для
близких гипотез, изложены в работах Вальда [27], Ле Кама, Русаса (см. книгу Русаса [100]),
Чибисова [134]. О возможности перенесения основных результатов на случай
бесконечномерного параметра (на случайные процессы) см. [25]. Форма изложения §80 и §54, 55 с
цитированными работами связана мало. Редукция исходной задачи А к задаче В (для
параметра нормального распределения) при отыскании оптимальных критериев для основных
типов задач содержится в работе Вальда [27].
Приложения
Доказательство двух фундаментальных теорем теории статистических игр из
приложения VIII можно найти в [30] (см. также [9, 112]). Это доказательство технически очень
сложно и сопровождается ограничительными условиями (предполагается, например, что
распределение наблюдений либо решетчато, либо имеет плотность относительно меры Лебега
Библиографические замечания
691
в Rk). Другой значительно более общий подход был предложен Гошем [36] и Ле Камом [63,
77, 110]. Однако в этих работах требуемые доказательства также труднодоступны, так как их
приходится извлекать из громоздких и весьма общих утверждений (включающих в себя
критерии последовательного анализа, к тому же в предположении неограниченности функции
потерь; см. [63, ПО]).
В настоящей книге излагается более короткое и обозримое доказательство, занимающее
менее шести страниц в детальном изложении. Оно подготовлено Саханенко и близко по
смыслу идеям Ле Кама. Центральной его частью являются леммы 2, 3. Лемма 2, по существу,
не связана со статистическим характером игры, основана на теоремах Хана-Банаха и Рисса
и близка по своей идее рассуждениям, использованным, например, в [140]. Доказательство
леммы 3 основано на теоремах Колмогорова [56] и Прохорова [7].
При составлении таблиц I-IV использовалась книга Болынева и Смирнова [10].
СПИСОК ЛИТЕРАТУРЫ
1. Басава И., Пракаса Рао Б. (Basawa I. V., Prakasa Rao В.) Statistic inference
for stochastic processes. — N.Y.: Acad. Press, 1980.
2. Бахадур P. (Bahadur R.R.) On Fisher's bound for asymptotic variances /Ann.
Math. Statist. 1964. V. 35, X* 4. P. 1545-1552.
3. Бахадур Р. (Bahadur R.R.) An optimal property of the likelihood ratio
statistic /Proc. 5-th Berkeley sympos. math, statist, prob. Berkeley; Los Angeles, 1965. V. 1.
P. 27-40.
4. Бахадур P. (Bahadur R.R.) Some limit theorems in statistics. — Philadelphia:
SIAM, 1971.
5. Бахадур Р., Леман Э. (Bahadur R.R., Lehman E.L.) Two comments on
«Sufficiency and statistical decision functions» /Ann. Math. Statist. 1955. V. 26. P. 139-141.
6. Биллингсли П. (Billingsley P.) Statistical inference for Markov processes. —
Chicago: Univ. Chicago Press, 1961.
7. Биллингсли П. Сходимость вероятностных мер. — Μ.: Наука, 1977.
8. Блекуэлл Д. (Blackwell D.H.) Conditional expectation and unbiased sequential
estimation /Ann. Math. Statist. 1947. V. 18. P. 105-110.
9. Блекуэлл Д., Гиршик М.А. Теория игр и статистических решений. — М.: ИЛ,
1958.
10. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. — М.: Наука,
1965.
11. Боровков А.А. Сходимость распределений функционалов от случайных
процессов /Успехи мат. наук. 1972. Т. 27, № 1. С. 3-41.
12. Боровков А. А. Вероятностные процессы в теории массового обслуживания. — М.:
Наука, 1972.
13. Боровков А.А. Асимптотически оптимальные тесты для проверки сложных
гипотез /Теория вероятностей и ее применения. 1975. Т. 20, № 3. С. 463-487.
14. Боровков А. А. О мощности критерия χ2 при увеличении числа групп /Теория
вероятностей и ее применения. 1977. Т. 22, № 2. С. 375-379.
15. Б оровков А. А. Математическая статистика. Оценка параметров. Проверка гипотез. —
М.: Наука, 1984.
16. Боровков А. А. Математическая статистика. Дополнительные главы. — М.: Наука,
1984.
17. Боровков А. А. Теория вероятностей. 3-е изд. перераб. и доп. — М.: Эдиториал УРСС,
1999.
18. Боровков A. A. (Borovkov A. A.) Statistique mathematique. — Moscow: Mir, 1987.
19. Боровков A. A. (Borovkov Α. Α.) Estadistica matematica. —Moscow: Mir, 1988.
20. Боровков А. А. Эргодичность и устойчивость случайных процессов. — М.: Эдиториал
УРСС, 1999.
21. Боровков Α. Α., Коршунов Д. А. Вероятности больших уклонений одномерных
цепей Маркова. I /Теория вероятностей и ее применения. 1996. Т. 41, вып. 1. С. 3-30.
22. Боровков Α. Α., Могульский А. А. Большие уклонения и проверка статистических
гипотез. — Новосибирск: Наука, 1992.
Список литературы
693
23. Боровков Α. Α., Φ о с с С. Г. Оценки для перескока случайного блуждания через
произвольную границу и их применения /Теория вероятности и ее применение. 1999. Т. 44,
№ 2. С. 245-277.
24. Боровков Α. Α., Саханенко А.И. Неравенства типа Рао-Крамера для байесовского
риска /Теория вероятностей и ее применения. 1980. Т. 25, № 1. С. 207-209.
25. Боровков Α. Α., Саханенко А. И. Об асимптотически оптимальных тестах для
проверки сложных близких гипотез /Тр. Ин-та математики им. С. Л. Соболева СО АН СССР.
1982. Т. 1. С. 79-89.
26. Боровков Α.Α., Сычева Η.Μ. О некоторых асимптотически оптимальных
непараметрических критериях /Теория вероятностей и ее применения. 1968. Т. 13, № 3.
С. 385-418.
27. Вальд A. (Wald A.) Tests of statistical hypotheses concerning several parameters
when the number of observations is large /Trans. Amer. Math. Soc. 1943. V. 54, № 3.
P. 426-482.
28. Вальд A. (Wald A.) Note on the consistency of the maximum likelihood
estimate /Ann. Math. Statist. 1949. V. 20. P. 595-601.
29. Вальд А. Последовательный анализ. — Μ.: Физматгиз, 1960.
30. Вальд А. Статистические решающие функции /Позиционные игры. — М.: Наука,
1967. С. 300-522.
31. Ван-дер-ВарденБ. Математическая статистика. — М.: ИЛ, 1960.
32. Вейс Л. (Weiss L.) The asymptotic power of certain tests of fit based on sample
spacings /Ann. Math. Statist. 1957. V. 28, № 3. P. 783-786.
33. Вольфовиц Дж. (W о 1 f о w i t ζ J.) On Wald's proof of the consistency of the maximum
likelihood estimate /Ann. Math. Statist. 1949. V. 20. P. 601-602.
34. Гаек Я., Шидак 3. Теория ранговых критериев. — М.: Наука, 1971.
35. Гихман И.И., Скороход А.В. Введение в теорию случайных процессов. — М.:
Наука, 1977.
36. ГошМ. (Ghosh M.N.) An extension on Wald's decision theory to unbounded weight
functions / Sankhya. 1952. V. 12. P. 8-26.
37. Гренандер У. Случайные процессы и статистические выводы. — М.: ИЛ, 1961.
38. Гренандер У. (Grenander U.) Abstract inference. —N.Y.: J. Wiley, 1981.
39. Гусев С.И. Асимптотические разложения, связанные с некоторыми статистическими
оценками в гладком случае. II /Теория вероятностей и ее применения. 1976. Т. 21, № 1.
С. 16-33.
40. Дакуна-Кастелли Д., Дюфло М. (Dacunha-Castelle D., Duflo M.) Proba-
bilites et statistique. T. 1, 2. — Paris: Masson, 1982, 1983.
41. Дарховский B.C., Бродский Б.Е. Непараметрический метод скорейшего
обнаружения изменений среднего случайной последовательностью / Теория вероятностей и ее
применение. 1987. Т. 32, № 4. С. 703-711.
42. Д ей вид Г. Порядковые статистики. — М.: Наука, 1979.
43. Де Хард τ Дж. (De Hardt J.) Generalizations of the Glivenko-Cantelli
theorem /Ann. Math. Statist. 1971. V. 42. P. 2050-2055.
44. Донскер Μ. (Donsker Μ.) Justifications and extensions of Doob's heuristic approach
to the Kolmogorov-Smirnov theorems /Ann. Math. Statist. 1952. V. 23. P. 277-281.
45. Дуб Дж. (Doob J.L.) Probability and statistics /Trans. Amer. Math. Soc. 1934. V. 36,
№ 4. P. 759-775.
46. Дуб Дж. Вероятностные процессы. — Μ.: ИЛ, 1956.
47. Ефрон Б. (Efron В.) Bootstrap methods: another look at the jacknife /Ann. Statist.
1979. V. 7, № 1. P. 1-26.
48. Закс Ш. Теория статистических выводов. — Μ.: Мир, 1975.
694
Список литературы
49. Ибрагимов И.Α., ХасьминскиЙ Р.З. Асимптотическая теория оценивания. —
М.: Наука, 1979.
50. Кендалл М., Стьюарт А. Статистические выводы и связи. — М.: Наука, 1973.
51. Кифер Дж. (Kiefer J.) On minimum variance estimators /Ann. Math. Statist. 1952.
V. 23. P. 627-629.
52. Кифер Дж. (Kiefer J.) On large deviations of the empiric D. C. of vector chance
variables and a law of the iterated logarithm /Pacific J. Math. 1961. V. 11, № 2. P. 649-
660.
53. Кличене Η., Телькснис Л. Методы обнаружения момента изменения свойств
случайных последовательностей / Автоматика и телемеханика. 1983. J№ 10. С. 5-56.
54. Кокс Д. Р., Хинкли Д. В. Теоретическая статистика. — М.: Мир, 1978.
55. Колмогоров А.Н. Несмещенные оценки /Изв. АН СССР. Сер. мат. 1950. Вып. 14,
JY* 4. С. 303-326.
56. Колмогоров А.Н. Основные понятия теории вероятностей. — М.: Наука, 1974.
57. Крамер Г. (Cramer H.) A contribution to the theory of statistical
estimation / Aktuariestidskrift. 1946. V. 29. P. 458-463.
58. Крамер Г. Математические методы статистики. — Μ.: Мир, 1975.
59. Ксерго С, Дехувельс П., Масон Д. (Сsorgo S., Deheuvels P., Mason D.M.)
Kernel estimates of the tail index of a distribution /Ann. Statist. 1985. V. 13, № 3.
P. 1050-1077.
60. Кульбак С, Лейблер P. (Kullback S., Leibler R. A.) On information and
sufficiency /Ann. Math. Statist. 1951. V. 22. P. 79-86.
61. Кутоянц Ю. А. Оценивание параметров случайных процессов. — Ереван: Изд-во АН
Арм. ССР, 1980.
62. Ланкастер Г. (Lancaster Η.) The chi-squared distribution.—N.Y.: J.Wiley, 1969.
63. Ле Кам Л. (Le Cam L.) An extension of Wald's theory of statistical decision
functions /Ann. Math. Statist. 1955. V. 26. P. 69-81.
64. Ле Кам Л. (Le Cam L.) Asymptotic methods in statistical decision theory. — N.Y.;
Berlin: Springer-Verl., 1986.
65. Леман Э.Проверка статистических гипотез.—Μ.: Наука, 1979.
66. Леман Э. (Lehmann Ε. L.) Testing statistical hypotheses. Second Edition. — N.Y.:
J. Wiley, 1986.
67. Леман Э. Теория точечного оценивания. — Μ.: Наука, 1991.
68. Леман Э., Шеффе Г. (Lehmann E.L., Scheffe H.) Completeness, similar regions
and unbiased estimation. I /Sankhya. Ser A. 1950. V. 10. P. 305-340.
69. Линдли Д. (Lindley D.) The use of prior probability disributions in statistical
inference and decision /Proc. 4-th Berkley sympos. math, statist, prob., Berkeley; Los Angeles,
1960. V. 1. P. 453-468.
70. Липцер Р.Ш., Ширяев А.Н. Статистика случайных процессов. — Μ.: Наука, 1974.
71. Лорден Г. (Lorden G.) Procedures for reacting to a change in distribution /Ann.
Math. Stat. 1971. V. 42, JY* 6. P. 1897-1908.
72. Лоэв M. Теория вероятностей. — Μ.: ИЛ, 1962.
73. Мак Кинси Дж. Введение в теорию игр. — М.: Физматгиз, 1960.
74. Манн Г., Уитни Д. (Mann Η.В., Whitney D.R.) On a test whether one of two
random variables is stochastically larger than the other /Ann. Math. Statist. 1947. V. 18.
P. 50-60.
75. Мизес Р. (Mises R. von) On the asymptotic distribution of differentiable statistical
functions /Ann. Math. Statist. 1947. V. 18. P. 309-348.
76. Мизес P. (Mises R. von) Mathematical theory of probability and statistics. — N.Y.:
Acad. Press, 1964.
Список литературы
695
77. Ми л л ар П. (Millar P.) The minimax principle in asymptotic statistical
theory /Lecture Notes in Math. 1981. V. 976. P. 76-267.
78. Миллер P. (Miller R.) The jacknife: a reviev /Biometrica. 1974. V. 61. P. 1-16.
79. МонстакидесГ. (Monstakides G.V.) Optimal stopping times for detecting changes
in distributions / Ann. Stat. 1986. V. 14, JY* 4. P. 1379-1387.
80. Моран П. (Moran P.A.P.) The random division of an interval /J. Roy. Statist. Soc.
Ser. A. 1947. V. 9. P. 92-98.
81. Нейман Дж. фон, Моргенштерн 0. Теория игр и экономическое поведение. —
М.: Наука, 1970.
82. Нейман Ю. (Neyman J.) Sur un theorems concerente le cosidette statistische
sufficient! /Inst. Ital. Atti. Giorn. 1935. V. 6. P. 320-334.
83. Нейман Ю. Вводный курс теории вероятностей и математической статистики. — М.:
Наука, 1968.
84. Нейман Ю., Пирсон Э. (Neyman J., Pearson E. S.) On the use and
interpretation of certain test criteria /Biometrika. Ser. A. 1928. V. 20. P. 175-240, 263-294.
85. Нейман Ю., Пирсон Э. (Neyman J., Pearson E.S.) On the problem of the
most efficient tests of statistical hypotheses /Phil. Trans. Roy. Soc. Ser. A. 1933. V. 231.
P. 289-337.
86. Нейман Ю., Пирсон Э. (Neyman J., Pearson E.S.) The testing of statistical
hypothess in relation to probabilities a priori /Proc. Camb. Phil. Soc. 1933. V. 34. P. 492-
510.
87. Нова к С.Ю., Утев С. А. Об асимптотике распределения отношения сумм случайных
величин /Сиб. мат. журн. 1990. Т. 31, JY* 5. С. 92-101.
88. Оостерхов Дж., Цвет В. ван (Oosterhoff J.W.R., van Zwet W.R.) The
likelihood ratio test for rhe multinomial distribution /Proc. 6-th Berkley sympos. math,
statist, prob., Berkeley; Los Angeles, 1970. V. 1. P. 31-50.
89. Парзен Ε. (Parzen Ε.) On estimation of a probability density function and
mode //Ann. Math. Statist. 1962. V. 33, № 3. P. 1065-1076.
90. Пей дж Ε. (Page E.S.) Continuous inspection schemes /Biometrica. 1954. V. 41, № 1.
P. 100-115.
91. ПитменЕ. (Pitman E.J.G.) The estimation of the location and scale parameters of
a continuous population of any given form /Biometrika. 1938. V. 30. P. 391-421.
92. ПоллакМ. (Pollak M.) Optimal defection of a change in distribution /Ann. Statist.
1985. V. 13, № 1. P. 206-227.
93. ПоллакМ. (Pollak M.) Average run length of an optimal method of defecting a change
in distribution /Ann. Statist. 1987. V. 15, JV* 2. P. 749-779.
94. Pao С (Rao C.R.) Information and accuracy attainable in estimation of statistical
parameters /Bull. Calcutta Math. Soc. 1945. V. 37. P. 81-91.
95. Pao С (Rao C.R.) Sufficient statistics and minimum variance estimates /Proc. Camb.
Phil. Soc. 1949. V. 45. P. 213-218.
96. Pao С. Линейные статистические методы и их применения. — М.: Наука, 1968.
97. Роберте С. (Roberts S.W.) A comparison of control chart,
procedures / Technometrics. 1966. V. 8. P. 411-430.
98. Розенблатт Μ. (Rosenblatt Μ.) Remarks on some nonparametric estimates of a
density function /Ann. Math. Statist. 1956. V. 27, № 3. P. 832-837.
99. Розенблатт Μ. (Rosenblatt Μ.) Curve estimation /Ann. Math. Statist. 1971.
V. 42, № 6. P. 1815-1842.
100. Ρ уса с Дж. Контигуальность вероятностных мер. — Μ.: Мир, 1975.
101. Себе ρ Дж. Линейный регрессионный анализ. — М.: Мир, 1980.
102. Серфлинг P. (Ser fling R.J.) Approximation theorems of mathematical statistics. —
N.Y.: J. Wiley, 1980.
696
Список литературы
103. Сидоров В.A. (Sidorov V. A.) Measurement of the φ —> π+π branching
ration //Phys. Lett. В. 1981. V. 99. P. 62-65.
104. Скороход А.В. Случайные процессы с независимыми приращениями. — М.: Наука,
1964.
105. Смирнов Н.В. О распределении ω2 Мизеса /Смирнов Н.В. Теория вероятностей и
математическая статистика. Избранные труды. — М.: Наука, 1970.
106. Теребиж В.Ю. Максимально правдоподобное восстановление изображений. I.
Основные соотношения /Астрофизика. 1990. Т. 32, № 2. С. 327-339.
107. Тьюки Дж. (Тикеу J.W.) Bias and confidence in non-quite large samples /Ann.
Math. Statist. 1958. V. 29, № 2. P. 614.
108. У и л кс С. (Wilks S. S.) The large sample distribution of the likelihood ratio for testing
composite hypotheses /Ann. Math. Statist. 1938. V. 9. P. 60-62.
109. Уилкс С. Математическая статистика. — Μ.: Наука, 1967.
ПО. Фаррел P. (Farrel R. Η.) Weak limits of sequences of В ayes procedures in estimation
theory /Proc. of V-th Berkeley sympos. math, statist, prob., Berkeley, 1965. V. 1. P. 83-
111.
111. Феллер В. Введение в теорию вероятностей и ее приложения. — М.: Мир, 1967. Т. 1,
2.
112. Фергюсон Т. (Ferguson Th.S.) Mathematical statistics: A decision theoretic
approach. — N.Y.; London: Acad. Press, 1968.
113. Филипп Α., Руссас Дж. (Philippou A.N., Roussas G.G.) Asymptotic
distribution of the likelihood function in the independent not identically distributed case / Ann.
Statist. 1973. V. 1, № 3. P. 454-471.
114. Филипп Α., Руссас Дж. (Philippou A.N., Roussas G.G.) Asymptotic
normality of the maximum likelihood estimate in the independent not identically distributed
case /Ann. Inst. Statist. Math. 1975. V. 27, JY* 1. P. 45-55.
115. Филиппова А. А. Теорема Мизеса о предельном поведении функционалов от
эмпирических функций распределения и ее статистические применения / Теория вероятностей
и ее применения. 1962. Т. 7, № 1. С. 26-60.
116. Фишер P. (Fischer R.A.) On the mathematical foundations of theoretical
statistics /Phil. Trans. Roy. Soc. Ser. A. 1922. V. 222. P. 309-368.
117. Фишер P. (Fischer R.A.) Theory of statistical estimation /Proc. Camb. Phil. Soc.
1925. V. 22. P. 700-725.
118. Фишер Р. (Fischer R.A.) Inverse probability /Proc. Camb. Phil. Soc. 1930. V. 26.
P. 528-535.
119. Фреше Μ. (Free he t Μ.) Sur l'extension de certains evalutions statistiques au cas de
petits echantillons /Rev. Inst. Internat. Statist. 1943. V. 11. P. 182-205.
120. Халмош П. Теория меры. — Μ.: ИЛ, 1953.
121. Халмош П., Сэвидж Л. (Halmos P. R., Savage L.J.) Application of the Radon-
Nikodym theorem to the theory of sufficient statistics /Ann. Math. Statist. 1949. V. 20.
P. 225-241.
122. Хам пел ь Ф., Рончетти Э., Рауссеу П., Штаэль В. Робастность в
статистике. — М.: Мир, 1989.
123. Хеффдинг У. (Hoeffding W.) Asymptotically optimal tests for multinomial
distributions /Ann. Math. Statist. 1965. V. 36, № 2. P. 369-401.
124. Ходжес Дж., Леман Э. (Hodges J., Lehman Ε.) Some problems in minimax
estimation /Ann. Math. Statist. 1955. V. 21, № 2. P. 182-197.
125. Ходли Б. (Hoadley В.) Asymptotic properties of maximum likelihood estimators for
the independent not identically distributed case /Ann. Math. Statist. 1971. V. 42, № 6.
P. 1977-1991.
Список литературы
697
126. Хотеллинг X. (Hotelling H.) The generalization of student's ratio /Ann. Math.
Statist. 1931. V. 2. P. 360-378.
127. Хьюбер П. (Huber P.J.) Robust estimation of a lokation parameter /Ann. Math.
Statist. 1964. V. 35. P. 73-101.
128. Хьюбер П. (Huber P.J.) Robust statistics: a review / Ann. Math. Statist. 1972. V. 43.
P. 1041-1067.
129. Хьюбер П. Робастность в статистике. — Μ.: Мир, 1984.
130. Ченцов Η. Η. Об оценке неизвестного среднего многомерного нормального
распределения /Теория вероятностей и ее применения. 1967. Т. 12, Ν* 4. С. 619-633.
131. Ченцов Н.Н. Статистические решающие правила и оптимальные выводы. — М.:
Наука, 1972.
132. Чепмен Д., Роббинс Г. (Chapman D.G., Robbins Η.Ε.) Minimum variance
estimation without regularity assumptions /Ann. Math. Statist. 1951. V. 22. P. 581-586.
133. Чибисов Д.Μ. О критериях согласия, основанных на выборочных
промежутках /Теория вероятностей и ее применения. 1961. Т. 6, JY* 1. С. 354-358.
134. Чибисов Д.М. (Chibisov D.Μ.) Transition to the limiting process for deriving
asymptotically optimal tests /Sankhya. Ser. A. 1969. V. 31, № 3. P. 241-258.
135. Чибисов Д.Μ., Гванцеладзе Л.Г. О критериях согласия, основанных на
сгруппированных данных /III Советско-японский симпозиум по теории вероятностей. —
Ташкент: Фан, 1975. С. 183-185.
136. Шеффе Г. Дисперсионный анализ. — М.: Фиэматгиз, 1963.
137. Ширяев А. Н. Вероятность. — М.: Наука, 1980.
138. Ширяев А.Н. Статистический последовательный анализ. — М.: Наука, 1976.
139. Шорак Дж., Веллнер Дж. (Shorack G.R., Wellner J.A.) Empirical processes
with applicatons to statistics. — N.Y.: J. Wiley, 1986.
140. Эдварде Р. Функциональный анализ. — Μ.: Мир, 1969.
СПИСОК ОСНОВНЫХ ОБОЗНАЧЕНИЙ*)
а. б. к. —- асимптотически байесовский
критерий, 400, 406
а. н. оценка — асимптотически нормальная
оценка, 85
а. р. н. м. к. — асимптотически равномерно
наиболее мощный критерий, 406
а. э. оценка — асимптотически эффективная
оценка, 131
а.Л-э. оценка — асимптотически Я-эффек-
тивная оценка, 191
к. о. п. — критерий отношения
правдоподобия, 375
н. м. к — наиболее мощный критерий, 303,
310
о. м.п. — оценка максимального
правдоподобия, 103
р. н. м. к. — равномерно наиболее мощный
критерий, 332
у. м. о. — условное математическое
ожидание, 140
(Ао) — условие взаимнооднозначного
соответствия между параметрическим
множеством θ и семейством
распределений V = {Ρθ}θ£θ (Ρ*! Φ Pfl2> еСЛИ
0ι Φ ft), 100
(Ас) — условие, состоящее в том, что
параметрическое множество θ компактно,
233
(Αμ) — условие, в силу которого все
распределения семейства V = {Ре} домини-
руются мерой μ (существует плотность
U =άΡθ/άμ), 101, 102
б, 6(0) — смещение, 116, 129
Вр — полиномиальное распределение (в том
числе распределение Бернулли), 82
*В — σ-алгебра борелевских множеств на
прямой R, 24
93* — σ-алгебра в фазовом пространстве X
(борелевских множеств, если X = Rm),
21
C(a,b) — пространство непрерывных на
[а, Ь] функций, 45
D(a,b) — пространство функций на [а, 6],
непрерывных слева (в точке а справа)
и имеющих лишь конечное число
скачков, 45
Όθ — дисперсия по распределению Р#, 128
*) Обозначения расположены в
алфавитном порядке: сначала русский алфавит,
затем латинский, готический и греческий. В
конце помещены математические символы.
Ε — единичная матрица, 195
Ε — экспоненциальное семейство
распределений, 178
Έθ — математические ожидание по
распределению Р$, 128
Е(£/21) — условное математическое
ожидание ξ относительно σ-алгебры 21, 141
Έι(ξ/η) — условное математическое
ожидание ξ относительно случайной
величины 77, 143
}в{х) —- плотность распределения Р#
относительно меры /i, 102
}θ{Χ) — функция правдоподобия, равная по
η
определению Π /е(хг), 105
ι = 1
F(x) — как правило, функция,
распределения, соответствующая распределению Р.
22
Fn(x) — эмпирическая функция
распределения, 25, 34
Ρχ(χ) — эмпирическая функция
распределения, соответствующая выборке JV, 467
Fjfe^fcj — распределение, ассоциированное с
распределением Фишера, 74
G — группа преобразований X в себя,
соответствующая инвариантному семейству,
215
Ηε — квантиль распределения χ2, 296, 400
Ηг — гипотеза, 301
Нк — распределение χ2, 73
7(0) — информация Фишера, 186, 200, 201
Ια — индикатор множества А, 141
ΗΘ) = \\ТгЛв)\\, /ч(0) = Εβ^ίίχι,β)^ х
χ ί(χι,0) — информационная матрица
Фишера, 204
1Х — распределение, сосредоточенное в
точке я, 24
Кь — класс оценок со смещением Ъ = Ь(в),
131
Ко — класс несмещенных оценок, 130, 139
Ко — класс асимптотически несмещенных
оценок, 192
К0 — класс асимптотически центральных
оценок, 250
Кф,2 — класс асимптотически нормальных
оценок 0*, для которых Ебп(0* — Θ)2 —>
—> <72(0), где σ2(θ) — дисперсия
предельного для у/п(в* — 0) нормального
распределения, 137
Список основных обозначений
699
Ке — (в гл. 3) класс критериев размера ε
(уровня 1-ε), 312, 330
Ке — класс несмещенных критериев
размера ε, 345
Ке — класс критериев асимптотического
уровня (1 -ε), 400
К с1 — класс критериев размера ε для
частично байесовского подхода, 364
К?1 — класс критериев асимптотического
размера ε для частично байесовского
подхода, 406
Και Qr_j — класс критериев с
фиксированными значениями аи вероятностей
ошибок г-го рода, г = 1,..., г — 1, 303
Κα,σ — распределение Коши, 80
Ζ(χ,0) = 1η/0(ζ), 105
L(X, 0)= In /β (Χ) — логарифмическая
функция правдоподобия, 105
L0)ir2 — логнормальное распределение, 80
η — объем выборки, 22
Νρ, Νρ — носитель распределения Ρ с
функцией распределения F, 29, 228
V — семейство распределений, 70
Ρ — символ распределения, употребляемый
в разных смыслах, указанных на с. 22,
23
Р* — эмпирическое распределение, 24
Рх — эмпирическое распределение,
соответствующее выборке X, 467
Ρ я — распределение, зависящее от
параметра 0, 81
Р(В/у) — условное распределение, 146
Q — рандомизированная стратегия
[[природы]] (априорное распределение 0), 578
Qx — апостериорное распределение, 150,
_ 304
Q — наихудшее распределение 0
(минимаксная стратегия «природы»), 581
q(t/X) — плотность апостериорного
распределения, 150
R — вещественная прямая, 21
Rm — m-мерное евклидово пространство, 21
R-э. оценка — Д-эффективная (регулярно-
эффективная) оценка, 191
(R) — условие регулярности
параметрического семейства, в силу которого
функция yjfe (χ) непрерывно
дифференцируема по 0, а информация Фишера
положительна и непрерывна, 186, 194
(RR) — условия регулярности
параметрического семейства, требующие
выполнения условий (Ао), (Ас), (R), а также
непрерывной дифференцируемости
второго порядка функции /(ж, 0) и
существования мажоранты l(x) ^ |/;/(х>01> для
которой интеграл Е$1(х\) сходится
равномерно в Θ, 247, 271
5 = S(X) — статистика, 29
S2 — эмпирическая дисперсия, 28
S02 = -^-rS2, 119
η — 1
Tfc — распределение Стьюдента, 75
u* = y/n (0* — 0) — нормированная оценка
максимального правдоподобия, 253, 282
иа,ь — равномерное распределение на [а, 6],
78
w(t) — (не везде) винеровский процесс, 44
w°(t) — броуновский мост, 44
wn(t) — эмпирический процесс, 44
Xi — элемент выборки, 22
X(t) — г-й элемент вариационного ряда, 25
х = (ει, · · ·, Хп) — элемент Xni 23
χ — эмпирическое среднее, 28
X = Хп = (xi, · · ·, Хп) — выборка объема п,
22
[-^оо]п = Хп — часть бесконечной выборки,
состоящая из первых η ее элементов, 24
X — пространство, которому принадлежат
наблюдения (фазовое пространство
выборки), 21
(Л^ЯЗд^Р) — выборочное вероятностное
пространство, соответствующее одному
наблюдению, 21
(Λ'η,ί8^,Ρ) — выборочное вероятностное
пространство, соответствующее выборке
объема π, 23
аг(7г) — вероятность ошибки г-го рода
критерия π, 306
β(δ) — мошность критерия J, 311
β* (β) — функция мощности критерия π, 330
Βλι,λ2 — бэта-распределение, 77
Γα,λ — гамма-распределение, 72
δ — стратегия I игрока, 576
6 = δ(Χ) — (в гл. 3) решающее правило
(критерий), 302
δ = δ(Χ) — решающая функция, 588
ζρ — квантиль порядка р, 28
ζρ — выборочная квантиль порядка р, 29
0 — параметр (стратегия «природы»), 69, 81,
576
0* — оценка параметра 0, 70
0д — байесовская оценка параметра 0,
соответствующая априорному
распределению Q, 150
0 — границы доверительного интервала
для параметра 0, 285
0 — минимаксная оценка параметра 0, 151
0* — оценка максимального правдоподобия
параметра 0, 103
700
Список основных обозначений
θ — множество возможных значений
параметра θ (пространство стратегий
«природы»), 70, 81, 576
Θ* — доверительное множество, 295
Хе — квантиль нормального распределения,
469
π = π(Χ) — (в гл. 3) рандомизированный
критерий, 306, 329
π = π(Χ) — рандомизированное решающее
правило (критерий), 590
π° — равномерно наиболее мощный
критерий, 332
kq — байесовский критерий,
соответствующий априорному распределению Q, 332
π<?ι<?2 — байесовский критерий для
частично байесовского подхода, 333
π — минимаксный критерий, 308, 333
π — критерий отношения правдоподобия, 375
Па — распределение Пуассона, 81
Φα>σ2 — нормальное распределение, 71
Ф(х) — функция стандартного нормального
распределения, 74
= —- знак, означающий совпадение распре-
d
делений выборок или случайных
величин, 22
—> — знак сходимости почти наверное (с
п.н.
вероятностью 1), 25
—ϊ — знак сходимости по вероятности, 35
=> — знак слабой сходимости
распределений (употребляется как между
случайными величинами, так и между
распределениями, 36
^ — знак, употребляемый между
обозначениями выборки (или случайной
величины) и распределения и означающий,
что выборка извлечена из данного
распределения (случайная величина имеет
данное распределение), 22
€> — знак слабой сходимости. Соотношение
ξη ©> Ρ означает, что распределение ξη
слабо сходится при η —> оо к Р, 36
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Асимптотический доверительный интервал,
287
— подход к сравнению оценок, 119, 125, 131
Асимптотическое доверительное множество,
295
Байесовский подход полный, 332, 363
частичный, 332, 364
— принцип, 593
Беренса-Фишера проблема, 465
Близкие гипотезы, 320, 404, 555
Броуновский мост, 44
Бэта-распределение, 77
Вариационный ряд, 25
Вероятность ошибки г-го рода, 302, 306
первого рода, 329
Винеровский процесс, 44
Выборка, 22
Выборочная квантиль, 29
— медиана, 28
Выборочные моменты, 28, 35
— характеристики, 28, 35
Выборочный коэффициент корреляции, 35
Гамма-распределение, 72
Гипотеза основная, 311, 329
— простая, 301
— сложная, 329
Границы доверительных интервалов, 287
Группировка данных, 427
Доверительное множество, 295, 354
инвариантное, 360
наиболее точное, 355
несмещенное, 359
Доверительный интервал, 285
Достаточная оценка, 172
— статистика, 157
— σ-алгебра, 165
Закон повторного логарифма для
эмпирических распределений, 34
Игра двух лиц, 576
— рандомизированная (смешанная), 577
— статистическая, 588
Инвариантное семейство, 349
Интервальное оценивание, 285
Информация Фишера, 186, 200
Источник излучения, 213
Квантиль, 28
Классификация частиц, 264
Критерий, 302
— асимптотически байесовский, 400, 407
минимаксный, 407
наиболее мощный, 322
несмещенный, 403
равномерно наиболее мощный, 406
эквивалентный, 322, 408
— асимптотического уровня, 316, 399
— байесовский, 304, 332, 364
— Вилкоксона, 470
— знаков, 393, 469
— инвариантный, 349
— Колмогорова, 390
— Колмогорова-Смирнова, 467
— минимаксный, 308, 333
— Морана, 393
— наиболее мощный, 303, 310
— непараметрический, 393
— несмещенный, 345
— отношения правдоподобия, 375
— проверки однородности, 451, 467
асимптотически минимаксный, 452
непараметрический, 468
состоятельный, 469
χ2, 475
— равномерно наиболее мощный, 332, 333
— состоятельный, 389
— Х\ 423
— ω2 (Мизеса-Смирнова), 392
Критическая область, 311
Лемма Неймана-Пирсона, 312
обобщенная, 341
Логарифмическая функция правдоподобия, 105
Максимальный инвариант, 352
Медиана, 28
Метод максимального правдоподобия, 101
— минимального расстояния, 99
— моментов, 87
— подстановки, 83
Минимальная достаточная σ-алгебра, 165
Монотонное отношение правдоподобия, 333
Мощность критерия, 311, 330
Неравенство Иенсена для у.м.о., 144
— Коши-Буняковского для матриц, 196
у. м. о., 144
— Рао-Крамера, 186
интегральное, 218
разностное, 238
Нормальность асимптотическая, 519, 527
Носитель распределения, 29
702
Предметный указатель
Орбита, 217
Отношение правдоподобия, 243, 269
Оценка, 69, 82
— асимптотически байесовская, 156,226,607
минимаксная, 156, 227, 607
нормальная, 85
эффективная, 131, 531
Д-байесовская, 226
/^-эффективная, 291
— байесовская, 150, 156
— достаточная, 171
— максимального правдоподобия, 103, 529
— минимаксная, 151, 156
— недопустимая, 129
— несмещенная, 116
— параметра масштаба, 207
сдвига, 207
— параметров, 504
— Питмена, 209
— плотности, 65
— подстановки, 83
— сильно состоятельная, 85
— состоятельная, 85
— суперэффективная, 219
— эквивариантная, 208, 217
— эффективная, 130, 138, 531
— /^-эффективная, 191
Оценки по методу моментов, 509
Плотность апостериорная, 150
— априорная, 150
— условная, 147
Полное семейство распределений, 174
Полный класс стратегий, 587
Последовательное оценивание, 284
Последовательный анализ, 378
— критерий, 379
Приближенное вычисление о.м.п., 261
Принцип достаточности, 207
— инвариантности, 207
— несмещенности, 207, 345
Проверка однородности, 450
ПуассоновскиЙ процесс, 40
Равномерная сходимость интеграла, 260
по вероятности, 278
распределений, 279
— центральная предельная теорема, 280
Равномерный закон больших чисел, 278
Размер критерия, 311, 329
Распределение, 21
Распределение апостериорное, 150, 304
— априорное, 150, 304
— Бернулли, 81
— вырожденное, 81
— Коши, 80
— логнормальное, 80
— наименее благоприятное (наихудшее),
309, 344, 365, 584
— наихудшее, 152
— нормальное, 71
— полиномиальное, 81
— Пуассона, 81
— равномерное, 78
— Стьюдента, 75
— Фишера, 74
— экспоненциальное, 74
— χ2 (хи-квадрат), 73
Расстояние Кульбака-ЛеЙблера, 229, 316
— Хеллингера, 229
— X2, 229
Регрессия, 483
— линейная, 476
Регрессор, 476
Решающая функция (решающее правило,
решение), 588
асимптотически байесовская, 619, 622
асимптотически минимаксная, 622
инвариантная, 603
несмещенная, 601
рандомизированная, 590
Риск (функция риска), 588
Робастность, 439
Смещение, 116
Среднеквадратический подход к сравнению
оценок, 116, 125
Статистика, 29
— достаточная, 157
— минимальная достаточная, 165
— непараметрическая, 63
— полная, 174
— тривиальная достаточная, 164
— Х\ 49, 53
Статистики I и II типов, 29, 30
Стратегия, 576
— байесовская, 578
— минимаксная, 580
— равномерно оптимальная, 577
— рандомизированная (смешанная), 577
— уравнивающая, 583
— чистая, 578, 590
Сужение метода подстановки, 84
Теорема Гливенко-Кантелли, 25, 34
— Неймана-Фишера (факторизационная), 158
Теоремы непрерывности, 35
Уровень доверия, 286
— значимости критерия, 330
Условие (Ао), 100, 101
— (Ас), 233
— (АД 101
— R), 186, 194
— (RR), 247, 271
Условная вероятность, 143
— плотность, 147
Условное математическое ожидание, 142
— распределение, 146
Предметный указатель
703
Устойчивость статистических решений, 438
Фактически достигаемый уровень, 331
Формула Байеса, 150
— полной вероятности, 144
Функционал непрерывно дифференцируемый,
51
Функционалы I и II типов, 29
Функциональная предельная теорема для
эмпирических процессов, 45
Функция логарифмическая, 105
— правдоподобия, 105, 524
логарифмическая, 524
Цена игры, 580
Эквивариантное оценивание, 215
Экспоненциальное семейство распределений,
178
Эллипсоид рассеивания, 126
Эмпирическая функция распределения, 25,
34
Эмпирический процесс, 44
Эмпирическое распределение, 24, 33
сглаженное, 64
Ядерные оценки плотности, 68
Александр Алексеевич БОРОВКОВ
МАТЕМАТИЧЕСКАЯ
СТАТИСТИКА
У ч еб ни к
Издание четвертое, стереотипное
ЛР №065466 от 21.10.97
Гигиенический сертификат 78.01.07.953.П.004173.04.07
от 26.04.2007 г., выдан ЦГСЭН в СПб
Издательство «ЛАНЬ»
lan@lpbl.spb.ru; www.lanbook.com
192029, Санкт-Петербург, Общественный пер., 5.
Тел./факс: (812)412-29-35, 412-05-97, 412-92-72.
Бесплатный звонок по России: 8-800-700-40-71
ГДЕ КУПИТЬ
ДЛЯ ОРГАНИЗАЦИЙ:
Для того, чтобы заказать необходимые Вам книги, достаточно обратиться
β любую из торговых компаний Издательского Дома «ЛАНЬ» :
по России и зарубежью
«ЛАНЬ-ТРЕЙД». 192029, Санкт-Петербург, ул. Крупской, 13
тел.: (812) 412-85-78, 412-14-45, 412-85-82; тел./факс: (812) 412-54-93
e-mail: trade@lanpbl.spb.ru; ICQ: 446-869-967
www. lanpbl. spb. ru/price.htm
в Москве и в Московской области
«ЛАНЬ-ПРЕСС». 109263, Москва, 7-ая ул. Текстильщиков, д. 6/19
тел.: (499) 178-65-85; e-mail: lanpress@ultimanet.ru
в Краснодаре и в Краснодарском крае
«ЛАНЬ-ЮГ». 350072, Краснодар, ул. Жлобы, д. 1/1
тел.: (8612) 74-10-35; e-mail:lankrd98@mail.ru
ДЛЯ РОЗНИЧНЫХ ПОКУПАТЕЛЕЙ:
интернет магазины:
«Сова»: http://www.symplex.ru; «Ozon.ru»: http://www.ozon.ru
«Библион»: http://www.biblion.ru
также Вы можете отправить заявку на покупку книги
по адресу: 192029, Санкт-Петербург, ул. Крупской, 13
Подписано в печать 20.10.09.
Бумага офсетная. Гарнитура Школьная. Формат 70 хЮО 716.
Печать офсетная. Усл. п. л. 57,20. Тираж 1500 экз.
Заказ №
Отпечатано в полном соответствии с качеством
предоставленных материалов в ОАО «Дом печати — ВЯТКА»
610033, г. Киров, ул. Московская, 122