М. Е. ДОЙНО
КУРС ГИДРАВЛИКИ
ГЛАВНАЯ РЕДАКЦИЯ СТРОИТЕЛЬНОЙ ЛИТЕРАТУРЫ
Москва	1 9 3 6	Ленинград
Редактор мнж. А. М, Латыше нк о в Техн, редактор Д. М. Судак
Книга представляет собой, учебное пособие по курсу гидравлики. Она излагает все основные законы гидравлики и в кратком виде охватывает важнейшие ее практические применения.
Книга рассчитана на тех студентов строительных втузов, для которых гидравлика не является ведущей дисциплиной.
ОГЛАВЛЕНИЕ	Стр.
От автора.............................................. 7
Введение
§ 1.	Определение гидравлики как науки..; . « ............ 9
§ 2.	Внешний контур жидкости...........................И
§ 3.	Силы внутри жидкости ........................    •	12
§ 4.	Понятие о единичном гидромеханическом давлении и единичной силе трения.................. .........................—
§ 5.	Избыточное давление и вакуум...........,............13
§ 6.	Основные физические свойства жидкостей	.	•	.	•......14
§ 7.	Понятие об идеальной жидкости	.....................  19
§ 8.	Основные свойства единичных сил	в	идеальной	жидкости : • • . 20
Гидростатика
Глава I. Единичное гидростатическое давление
§ 9.	Определение величины единичного гидростатического давления 23
§ 10.	Закон Паскаля .......................................   24
§ И.	Поверхности равного давления ............................—
§ 12.	Приборы для измерения давления .........................25
§ 13.	Механический смысл основного уравнения гидростатики.....27
§ 14.	Удельная потенциальная энергия ........................ 28
§ 15.	Энергетический закон в покоящейся жидкости .............29
Глава II. Суммарное давление на поверхности
§ 16.	Аналитическое определение суммарного давления на плоскую стенку 32
§ 17.	Графоаналитическое определение суммарного давления.....34
§ 18.	Давление жидкости на криволинейные поверхности..........38
Глава III. Равновесие погруженного в жидкость тела
§ 19.	Закон Архимеда......................................... 44
§ 20.	Условия равновесия тела, полностью погруженного в жидкость . . 45
§ 21.	Равновесие тела, частично погруженного в жидкость...... • 46
Глава IV. Гидравлические машины § 22. Гидравлические машины . < ..................  .	• . . 53
Гидродинамика Глава V. Общие понятия
§ 23.	Установившееся и неустановившееся движение . ....... 58
§ 24.	Кинематические элементы движения	59
| 25	. Схема движения . .  « ...........	. • . .  . • .........60
§ 26.	Медленно изменяющееся движение ..............................63
§ 27.	Расход и средняя скорость ..............................«...	64
§ 28.	Понятие о равномерном движении ...............................—
§ 29.	Понятие о напорном и свободном движении....................  65
§ 30.	Методы изучения законов движения жидкости ..................  —
§ 31.	Применение аналитического метода в гидродинамике ............67
Глава VI. Основные законы гидродинамики
§ 32.	Уравнение расхода для элементарной струйки и потока.......69
§ 33.	Уравнение Бернулли для элементарной струйки идеальной жидкости 70
§ 34.	Механический смысл уравнения Бернулли....................72
§ 35.	Энергетический смысл уравнения Бернулли ... .............74
§ 36.	Гидравлический смысл членов уравнения Бернулли ......... 75
§ 37.	Определение размерности членов уравнения Бернулли • . .	. . —
§ 38.	Графическое изображение уравнения Бернулли для идеальной жидкости .......................................................  76
§ 39.	Уравнение Бернулли для реальной жидкости ................77
§ 40.	Уравнение Бернулли для потока при медленно изменяющемся движении ..................................................... 	. . 79
Глава VII. Гидравлические сопротивления
§ 41.	Два режима движения ..................................  83,
§ 42.	Факторы, определяющие тип движения	85
§ 43.	Определение критической скорости ........................86
§ 44.	Число Рейнольдса ...................... .................88
§ 45.	Физический смысл числа Рейнольдса .....................  90
§ 46.	Область практического применения ламинарного и турбулентного движения ..................................................    91
§ 47.	Осредненные скорости..........................  .	• . • . 94
$ 48.	Распределение скоростей при турбулентном движении ..... 96
§ 49.	Силы сопротивления при ламинарном и турбулентном движении . 97
Глава VIII. Потери энергии € 50. Классификация видов потерь ...............*..............  104
§ 91.	Определение видов потерь по длине при равномерном движении жидкости ...	. ..........................................—
§ 52.	Законы ламинарного движения в цилиндрической трубе..........106
§ 53.	Вид основного уравнения для случая турбулентного движения . 108 | 54. Вывод основного уравнения методом размерности.............	111
§ 55.	Коэфициенты основных формул турбулентного движения . ... 113
§ 56.	Определение коэфициента К методом размерности	114
§ 57.	Эмпирические формулы для определения коэфициента К .... — | 58. Выбор расчетной формулы .................................  120
| 59.	Виды местных потерь...............*....................  .121
$ 60.	Определение потерь при внезапном расширении (теорема Борда) 121
§ 61.	Случай внезапного сужения .............................    123
§ 62.	Комбинированный случай поворота с расширением ....... 124
§ 63.	Обобщение полученных формул ..............................125
§ 64.	Значения коэфициента сопротивления С для отдельных случаев . 126
Глава IX. Истечение через отверстия и насадки § 65. Истечение через малые отверстия в тонкой стенке при постоянном
уровне ....	.............................................130
§ 65.	Определение скорости и расхода при истечении струи в атмосферу 131
§ 67.	Случай истечения из затопленного отверстия..................134
§ 68.	Влияние близости стенки на истечение из отверстия ............—
§ 69.	Истечение через большие отверстия при постоянном уровне . . 136 4
§ 70.	Истечение при переменном горизонте	i . . 137
§ 71.	Случай затопленного отверстия при переменном горизонте . • . 138
§ 72.	Типы насадок ...........................................   143
| 73.	Истечение через внешнюю цилиндрическую насадку................—
I 14. Внутренние цилиндрические насадки > . .  ...................145
I 75. Конически сходящиеся насадки . . . . •....................  146
§ 76.	Конически расходящиеся насадки............................    —
§ 77.	Коноидальные насадки ...................................... 147
§ 78.	Практические случаи применения насадок . .....................—
Глава X. Движение жидкости по трубопроводам
§ 79.	Классификация водопроводов..................................149
§ 80.	Виды расходов .	    150
§ 81.	Модуль расхода в трубах	. ...............................  151
§ 82.	Случай простого водопровода ................................153
§ 83.	Эквивалентные водопроводы ..................................154
§ 84.	Случай расхода по пути .....................................  —
§ 85.	Расчет сифона ............................................  155
§ 86.	Сложные водопроводы ........................................157
§ 87.	Гидравлический удар ........................................160
§ 88.	Гидравлический таран ...................................    165
Глава XI. Равномерное движение жидкости в открытом русле
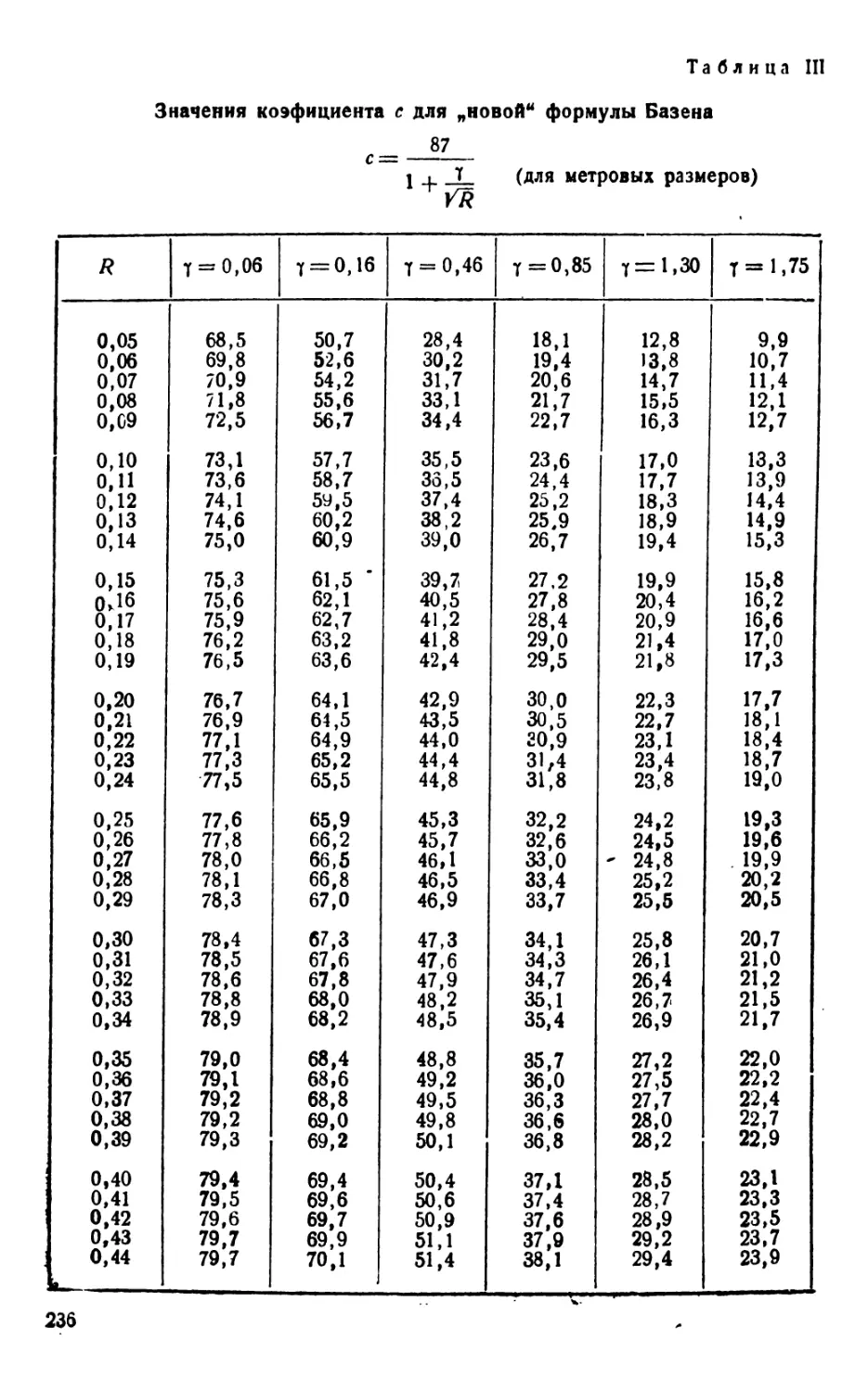
§ 89.	Эмпирические формулы для коэфициента С ........... 167
| 90. Условия осуществления равномерного движения в открытом русле 170
§ 91.	Модуль расхода в открытых руслах....................... . . —
§ 92.	Определение функциональной зависимости между К и h для разных типов русел..............................................  .	... 171
§ 93.	Задачи при проектировании каналов..........................173
§ 94.	Гидравлически наивыгоднейший профиль.......................174
§ 95.	Определение наивыгоднейших размеров для трапецоидального русла с заданными откосами.............................................175
§ 96.	Понятие об удельной энергии сечения........................178
§ 97.	Определение критической глубины для сечения произвольной формы 180
Глава ХП. Движение воды через водослив
§ 98.	Классификация водосливов . . . ............................182
§ 99.	Водосливы с острым порогом ..............................  185
§ 100.	Водослив с широким порогом...............................  190
§ 101.	Гидравлический расчет отверстий малых водопропускных сооружений в земляном полотне (мосты, малые отверстия и безнапорные трубы).................... .	. ................................193
§ 102.	Водосливы практического профиля............................197
Глава Х1П. Неравномерное движение в открытых руслах
§ 103.	Общее понятие..............................................200
§ 104.	' Определение кривой свободной поверхности в искусственных руслах 201
§ 105.	Случай прямоугольного русла большой ширины ................204
§ 106.	Построение кривой свободной поверхности для естественных русел 207
§ 107;	Определение сопряженных глубин при прыжке..................208
§ 108.	Случай прямоугольного русла •..............................210
§ 109.	Расчеты сопряжения бьефов из гидротехнической практики ... 211
Глава XIV. Движение грунтовых вод
§ ПО	. Основная характеристика фильтрационных свойств грунтов . . . 217
| 111. Основные гидравлические понятия....................  .	. 219
§ 112.	Основной закон фильтрации ..............................220
§ 113.	Определение коэфициента фильтрации . ..............  .	. 221
§ 114.	Фильтрация через земляные плотины на непроницаемом основании. 222
§ 115.	Решение системы фильтрационных уравнений................226
§ 116.	Движение к водосборным колодцам.......................  228
Приложения (таблицы).	............... 233
ОТ АВТОРА
Прохождение курса гидравлики в строительных втузах в настоящее время сильно затруднено отсутствием учебника, который, придерживаясь программы, утвержденной для этих специальностей, излагал бы сжато, в достаточной степени научно и в то же время в ясной форме все законы современной инженерной гидравлики и ее практическое применение.
Настоящая работа ставит своей целью восполнить вышеуказанный пробел. Работа построена соответственно программе, утвержденной Всесоюзным комитетом по высшему техническому образованию при СНК СССР для втузов строительных специальностей, и охватывает все указанные в этой программе разделы.
Автор заранее выражает благодарность всем лицам, которые пожелают прислать свои замечания.

ВВЕДЕНИЕ
)
§ 1. Определение гидравлики как науки
Гидравликой называется наука, изучающая законы равновесия и движения жидких тел, или, иначе говоря, гидравлика является механикой жидких тел Практическое значение этой науки очень велико, так как она'является основой при расчетах в области водоснабжения, водных путей, гидросиловых установок и целого ряда машин и приборов, имеющих самое широкое применение в инженерной практике.
Аналогично механике других тел гидравлика делится на две части: 1) гидростатику, изучающую законы равновесия. жидкостей, и 2) гидродинамику, изучающую законы движения жидкостей.
Развитие гидравлики шло исторически весьма сложным путем. Хотя история указывает на существование еще в древние времена в Египте, Сирии, Риме весьма интересных гидротехнических сооружений в виде водопроводов, каналов, плотин, однако никаких указаний на какие-либо гидравлические расчеты, связанные с этими сооружениями, мы не имеем, и нужно полагать, что они были выстроены на чисто эмпирических основах. Поэтому за начало гидравлики нужно считать открытие Архимедом (287 — 212 гг. до нашей эры) его известного закона.
Далее, в связи с известным застоем науки, характеризовавшим вообще средние века, дальнейшее развитие гидравлики начинает проявляться только в эпоху возрождения.
Так, в XVI в. Паскаль дал свой известный закон передачи давления в жидкостях, а Стевен определил величину давления воды на стенки сосуда. Все эти исследования относились однако к области гидростатики, которая вообще является вполне ясной в своем методе и базируется на общих законах механики.
Если обратип ся к истории развития гидродинамики, то XVII в. дает нам законы истечения жидкости из сосудов (Ньютон и Торричелли). XVIII в. дает фундаментальную фсрмулу гидравлики — уравнение Бернулли и весьма важную формулу Борда.
Если однако отвлечься от этих отдельных, хотя и крайне важных основных законов, а рассмотреть целые исторические шко-лы. пытавшиеся разными методами изучить законы движения жидкостей, то развитие гидродинамики с XVIII в. пошло двумя различными путями.
С одной стороны, поскольку жидкость, как и всякое материальное тело, должна подчиняться общим законам механики, казалось возможным применить общие уравнения механики к специальным особенностям, отличающим жидкость от других тел природы.
Развившаяся таким образом часть теоретической механики, занимающаяся специально изучением жидких тел, получила название теоретической гидромеханики. Отцом этой науки с полной справедливостью можно считать Леонарда Эйлера, давшего в 1755 г. уравнения движения и равновесия жидкостей.
Теоретическая гидромеханика, разработанная в дальнейшем трудами Навье, Стокса, Гельмгольца и др., развилась в науку, преследующую строгость и точность постановки задач и общность полученных решений. В своих исследованиях она пользовалась чисто аналитическими методами и мало прибегала к помощи эксперимента. Кроме того ввиду крайней сложности проблем, возникающих при движении вязких жидкостей, теоретическая гидромеханика вынуждена была оперировать главным образом с так называемой „идеальной* жидкостью (см. § 7), что сильно снижало практическую ценность полученных результатов.
Благодаря этим своим особенностям теоретическая гидромеханика, давшая ряд очень интересных научных обобщений, оказалась весьма серьезно оторванной от решения вопросов и задач, поставленных в области гидромеханики стремительным развитием техники в XIX в., и ее результаты плохо совпадали с действительностью даже для того небольшего круга вопросов, для которых ею были найдены окончательные решения.
Одновременно с этим, а отчасти даже предшествуя этой школе, создавалась другая школа (Шези, Дюбуа и др.), пытавшаяся другими методами удовлетворить запросам практики. Эта школа, наиболее видными представителями которой в XIX в. можно назвать Вейсбаха, Дарси, Базена, Буссинеска и др., создала науку, которую в настоящее время принято называть гидравликой в собственном смысле этого слова. Гидродинамика как часть гидравлики, будучи применена к той же научной области, что и теоретическая гидродинамика, стала сильно от нее отличаться как поставленными перед собой целями, так и методами разрешения задач. Конечная цель, которую ставит перед собой гидравлика, — это дать ответ (хотя бы и неполный в смысле своей точности и общности) на отдельные вопросы, выдвигаемые инженерной практикой. В качестве метода решения этих задач гидравлика, опираясь на общие законы теоретической механики и физики (в особенности на упоминавшееся уже выше уравнение Бернулли), всегда создает некоторые теоретически упрощающие предпосылки, на этой базе строит физический образ изучаемого явления и далее корректирует полученные выводы на основе результатов опытов. Вообще эксперимент занимает в гидравлике исключительное место. Произведенный опыт дает основу для теоретических исследований. Опыт же, корректируя ю
полученные теоретическим путем вывоты, дает представление об их правильности.
Над опытным изучением гидравлических явлений работали сотни ученых, в результате чего к настоящему времени накопился громадный экспериментальный материал.
Поскольку специфические свойства жидкости, затрудняющие приложение к ней аналитических методов, проявляются главным образом при ее движении, обе эти науки различны в основном только во 2-й части—гидродинамике. Гидростатика как часть теоретической гидромеханики и гидростатика как часть гидравлики между собой почти совпадают.
Достоинством гидравлики как науки является то, что она сравнительно удовлетворительно отвечает запросам практики. Недостаток же ее заключается в отсутствии достаточной идейной строгости в ее выводах и достаточной общности получаемых решений, вследствие чего все отдельные изучаемые ею проблемы не получили должной внутренней увязки между собой.
Гидравлика и теоретическая гидромеханика довольно продолжительное время развивались самостоятельно и независимо друг от друга, однако в конце XJX в. под влиянием развития авиации и гидротехники между ними намечается весьма серьезное сближение. С одной стороны, теоретическая гидромеханика начинает уделять значительно больше внимания вопросам движения вязких жидкостей, а также отдельным практическим проблемам, а в качестве метода исследований она начинает применять эксперименты; с другой стороны, и гидравлика развивается в науку, пред'являющую больше требований к идейной строгости своих методов и к обобщению получаемых опытным путем результатов. Этот синтез теоретической гидромеханики и гидравлики делает все более крупные успехи, и хотя трудности, стоящие на этом пути, еще очень велики, но все же развитие этих наук позволяет надеяться на создание в будущем единой синтетической науки, соединяющей в себе строгость и законченность теоретической мысли одновременно с живым практическим духом.
§ 2. Внешний контур жидкости
Рассматривая какую-нибудь жидкость, находящуюся в состоянии движения или покоя, мы видим, что она по своему контуру ограничена какими-то поверхностями. Эти внешние поверхности бывают двух родов:
1) Наружные стенки сосуда, в котором жидкость содержится. Давление, оказываемое на них жидкостью, и обратная реакция стенок определяются из условия задачи и заранее, вообще говоря, неизвестны. Положение же стенок заранее задается и от свойств жидкости не зависит.
2) Во многих встречающихся в практике случаях жидкость граничит по какой-то поверхности не с твердой оболочкой, а
с какими-то другими жидкостями или газами. Эти поверхности называются свободными.
В качестве примера такой свободной поверхности может служить поверхность соприкосновения жидкости с атмосферой при движении в открытых каналах или реках. Силы, приложенные к свободной поверхности, обычно заранее заданы и известны (для приведенного примера это будет, очевидно, атмосферное давление). Вид же и положение свободной поверхности являются следствием механических свойств данной жидкости.
§ 3.	Силы внутри жидкости
Рассматривая всякую жидкость как совокупность материальных частиц, мы должны аналогично общим представлениям механики разделить все силы, действующие на нее, на 2 категории: 1) внутренние силы взаимодействия между частицами, причем согласно 3-му закону Ньютона (действие равно противодействию) две соседние частицы действуют друг на друга двумя равными и прямо противоположно направленными силами; 2) внешние силы, характеризующие механическое воздействие на жидкость каких-то посторонних тел.
Все внешние силы в свою очередь делятся на: 1) поверхностные силы, приложенные к граничным поверхностям жидкого об£ема, и 2) об‘емные силы, приложенные ко всем точкам жидкости в данном об'еме. Примером поверхностных сил могут служить силы, действующие на свободную поверхность, а также реакции стенок сосуда. Примером же об'емных сил может служить сила тяжести или сила инерции.
§ 4.	Понятие об единичном гидромеханическом давлении и единичной силе трения1
Аналогично существующему в механике твердых тел понятию «напряжение* в гидравлике вводится понятие „единичная сила*, под которой понимается предел, к которому стремится сила, приложенная к площадке внутри жидкости в том случае, когда эта площадка стремится к нулю. Для уяснения этого понятия рассмотрим какой-то жидкий об'ем, находящийся под действием системы внешних сил (атмосферное давление, реакции стенок, собственный вес и т. д.). Разделим мысленно этот об-'ем плоскостью MN на две части, причем первую часть будем считать отброшенной (фиг. 1). Для того чтобы состояние частиц второй части после отнятия от нее первой осталось без изменения, необходимо приложить ко всем точкам сечения MN силы, производящие точно такое же действие, какое оказывали отброшенные частицы.
‘ Нами сохраняются эти термины, поскольку они уже укоренились в гидравлике, хотя в интересах унификации следовало бы ввести в гидравлике те же термины—-„нормальные и касательные напряжения*, которые применяются в строительной механике.	*	 г
12
Определим, какая часть этих сил придется на произзольную очку жидкости А. Для этого выделим в плоскости сечения Л/Л/ т зле точки А элементарную площадку Дш. Пусть сила Д7? представляет равнодействующую сил, приходящихся на эту площадку. Рассматривая случай движения жидкости, мы должны считать силу эту наклоненной под некоторым углом а к нормали. Разложим эту силу на две составляющие: на нормальную составляющую ДР, прижимающую частицы друг к другу и тангенциальную составляющую ДГ, препятствующую сдвигу одних частиц по другим (сила трения). Разделив величину ДР на соответствующую ей площадку Лш, получим среднее напряжение сжатия по площадке Дш, или, как принято называть в гидравлике, среднее гидромеханическое давление. Очевидно, чем меньше будет взята площадка, тем ближе окажется величина среднего давления к истинному давлению.
Если площадка Дш будет взята бесконечно-малой, то в пределе среднее давление совпадает с истинным. Таким образом, обозначив среднее давление через а истинное давление через ра, имеем:
(1)
(2)
ДР
Дш->0
Для того чтобы подчеркнуть, что ра — это величина, приходящаяся на единицу площади, ее называют единичным давлением, в то время как давление, приходящееся на всю площадь ш, называется суммарным давлением.
Д
Совершенно аналогичным образом найдем, что = tep представляет среднюю единичную силу трения, приходящуюся на площадку Дш, a 11m	= т представляет истинную единич-
Дш->0 ную силу трения в точке А.
В случае, если внешние силы действуют на жидкость равномерно, средние значения сил давления и сил трения будут равны истинным. Так как в дальнейшем изложении мы практически эти обе величины будем считать одинаковыми, то нами сохраняются для обоих случаев обозначения ра и t.
§ 5.	Избыточное давление и вакуум
В рассмотренном выше примере к свободной поверхности жидкости были приложены какие-то единичные силы р0. Если
13
среднее, или истинное, гидромеханическое давление, как это указано на фиг. 1, включает в себя давление р0, оно называется полным, или абсолютным, единичным давлением и имеет при себе индекс а. В большинстве случаев практики давление по свободной поверхности бывает атмосферным (барометрическим) давлением, которое обозначаем через рь. Поскольку однако атмосферное давление приложено не только к точкам жидкости, но и ко всем другим телам, окружающим жидкость, оно часто при учете давления в жидкости во внимание не принимается. Единичное давление в жидкости в этом случае называется избыточным. Обозначив его через р, получим:
|Р=Л—А-|	(3)
В практике встречаются также случаи, когда единичное давление в жидкости становится меньше атмосферного. Такое разреженное состояние жидкости называется вакуумом. Величиной вакуума называется разность между атмосферным и абсолютным давлением в жидкости.	\
Обозначив величину вакуума через р„, получим:	\
\Р, = Рь-Ра-\	(4)
Резюмируя все вышесказанное об единичных давлениях в точках жидкости, мы видим, что нами здесь введены следующие понятия:
1.	Если взять точки на свободной поверхности, то в самом общем случае единичные давления, действующие на эти точки, могут быть и неатмосферными (например давление от сжатого воздуха, пара и т. д.). Эти единичные давления нами обозначены через р0. В частном случае, когда по свободной поверхности действуют силы атмосферного давления, они нами обозначены через рь.
2.	Если взять точки внутри жидкости, то вычисленное в них единичное давление в самом общем случае называется абсолютным и обозначается через ра. В частном случае, когда по свободной поверхности приложены силы атмосферного давления, они часто во внимание не принимаются. Единичные давления жидкости в этом случае называются избыточными и обозначаются через р. Таким образом избыточное давление жидкости во всех случаях бывает больше атмосферного.
3.	В тех случаях, когда единичное давление в жидкости меньше атмосферного (например во всасывающей трубе насоса или в сифоне), вводится данное выше понятие вакуума, обозначенного через р,.
§ 6. Основные физические свойства жидкостей
В физике принято делить тела на твердые, жидкие и газообразные, причем признаком, характеризующим твердые тела, является сохраняемость их формы при действии на них внешних 14
сил- Жидкими же и газообразными телами называются тела, легко изменяющие свою форму или совсем ее не имеющие. Опыт однако показывает, что строгого разграничения между телами по данному признаку нельзя провести, так как одно и то же тело при различных обстоятельствах может вести себя то как твердое, то как жидкое тело. В качестве примера может служить асфальт, который, если разбить его молотком на части, будет вести себя, как твердое тело; если же этот самый асфальт при той же температуре поместить в бочку с открытым боковым отверстием, то он со временем под влиянием собственного веса начнет вытекать из сосуда наподобие очень вязкой жидкости. Разница в обоих случаях будет заключаться только в скорости происходящей деформации (в первом случае деформация происходит очень быстро, во втором случае она протекает очень медленно).
Можно отметить и ряд других промежуточных по своим физическим характеристикам тел, обладающих большей вязкостью, чем это принято предполагать у жидких тел (смола), или большей пластичностью, чем это принято считать у твердых тел (воск).
Таким образом деление различных тел на категории становится возможным только на основании наиболее характерных особенностей их деформаций и вызываемых ими внутренних сил.
Переходя с указанной точки зрения к определению важнейших свойств жидкости, рассмотрим следующие возможные в ней деформации и их связь с действующими силами.
1. Сжимаемость. Как известно, молекулы жидкости оказывают сильное сопротивление их взаимному сближению. Так, если первоначальный об'ем жидкости обозначим через wlt затем приложим к ней сжимающие силы, создающие давление на поверхности д= 1 кг/см?, то жидкость сожмется до об'ема да4.

Отношение
-ft
называется, как известно, коэфици-
ентом об'емного сжатия. Для воды величина {V^-a. ппа-4W 1 \ZkzV
Было бы однако ошибкой думать, что жидкие тела оказывают большее сопротивление сжатию их, чем твердые. Так например, сталь при аналогичных условиях сжимается только на 2oqqqqq своего перь'оначального об'ема, т. е. примерно в 95 раз меньше.
В большинстве практических вопросов, в которых приходится иметь дело с движущейся жидкостью, ее сжимаемость оказывает настолько ничтожное влияние на происходящее явление, что ею пренебрегают. Существуют однако случаи (например гидравлический удар), когда сжимаемость жидкости должна весьма точно Учитываться (см. § 87).
2. Температурное расширение. Повышая температуру жид-°сти, мы обычно заставляем ее молекулы удаляться друг от Друга. Если обозначим попрежнему первоначальный об'ем жид
кости через Wj, а затем нагреем ее на 1°, то жидкость займет новый об'ем
w2 — w. „ Отношение —1----1 = В.
Wj	r‘
называется, как известно, коэфици-
ентом температурного расширения.
Эта величина зависит вообще от первоначальной температуры жидкости и от давления, под которым она находилась. В частности при температуре воды от 0—10° и при наличии давления в 1 кг/см2 3 4 * *, = 0,000014, что практически может быть оставлено без внимания.
Вышеуказанные оба свойства оказывают влияние на изменяемость плотности и об'емного веса жидкостей.
Плотностью жидкости, как известно, называется количество массы, содержащейся в единице ее об'ема. Обозначив плотность жидкости через р, а вес единицы об'ема (об'емный вес) через ?, мы имеем между ними следующую зависимость:
l = ?g’
где g— ускорение силы тяжести.
Поскольку, как это указано было выше, об'ем жидкости при обычных в инженерной практике колебаниях температуры и давлений изменяется незначительно, то плотность и об'емный вес жидкости практически следует считать очень мало изменяемыми.
(Следует различать понятие об'емного веса жидкости от понятия удельного веса, так как удельный вес жидкости представляет отношение веса некоторого об'ема к весу такого же об'ема воды при температуре, равной 4°С, и является отвлеченным числом, в то время как об'емный вес 7 имеет размерность сила \	" "
длина* /
3. Сопротивление растягивающим, силам. Молекулы жидкости оказывают совершенно ничтожное сопротивление силам, стремящимся их оторвать друг от друга. Достаточно сказать, чго для разрыва жидкости достаточно напряжения в 3,6 кг/м2, что по сравнению с железом дает величину, в 107 раз меньшую. Капиллярные же силы и силы поверхностного натяжения в гидравлике обычно не рассматриваются.
4. Сопротивление сдвигающим силам. Опыт показывает, что если под действием' внешних сил две частицы жидкости начнут двигаться с разными скоростями, то между этими частицами появятся силы сопротивления движению, или, иначе, силы трения. Эти внутренние силы будут зависеть, с одной стороны, от относительной разности скоростей перемещающихся частиц, а с другой стороны, — от свойств самой жидкости. Свойство жид-
кости, обусловливающее сопротивление сдвигу ее частиц друг относительно друга, называется вязкостью. Вязкость для каждой
жидкости характеризуется некоторой величиной •»], называемой
абсолютным коэфициентом вязкости.
рассмотрим два слоя жидкости, двигающихся на расстоянии ДУ ДРУГ от друга (фиг. 2). Слой А движется со скоростью «, слой В— со скоростью	Благодаря существующей
пазности скоростей слой В сдвигается относительно слоя А Р едивицу времени на величину Ли. Следовательно величина Ли а	л	о Д«	<
является абсолютным сдвигом А по слою В, а , очевидно, бу-
дет относительной деформацией сдвига в единицу времени. Появляющееся при этом движении напряжение обозначим через т. Тогда аналогично явлению сдвига в твердых телах мы получим следующую зависимость между напряжением и деформацией:
(5)
или если слои будут бесконечно близки друг к другу, то
du
Как видно из этого выражения, коэфициент вязко-
“1---------
ъ,
-----—
и*4 и
Фиг. 2
сти ») играет здесь роль, аналогичную роли коэфициента сдвига в твердых телах, т. е. характеризует сопротивляемость жидкости сдвигу.
В твердых телах напряжение сдвига, как известно, выражается формулой t=G&, где О — модуль упругости при сдвиге, &—относительная деформация.
Сравнивая эту формулу с формулой (5), мы видим различие в деформационных свойствах твердых и жидких тел: так, в твердых телах всякой возникающей при сдвиге деформации соответствует вполне определенное напряжение. В жидкостях же эти напряжения будут зависеть от скорости происходящей деформации; так, если деформация будет происходить бесконечно медленно, то и возникающие напряжения сдвига окажутся бесконечно-малыми. Исходя из характерных для жидкости свойств, проф. Прандль в своем труде указывает, что жидкостями могут называться такие тела, у которых при бесконечно-малой скорости деформации силы, необходимые для этой деформации, будут тоже бесконечно-малы (проф. Пр а н дл ь, Гидро- и аэромеханика, 1932 г.).
Из формулы (5) можно определить размерность величины ц. оная, что -с как напряжение является силой, деленной на площадь, и заменяя силу через массу и ускорение, получим:
н
Г идравлика
массахдлина масса
В итоге имеем:
_ М [А.У] . масса [Ли] =длинахвремя ’
В системе CGS единица абсолютной вязкости называется пуазом.
Величина, обратная абсолютной вязкости, называется в гидравлике текучестью. Обозначим эту величину через 5, тогда е = -i-.
Вязкость жидкости меняется с изменением ее температуры.
Для пресной воды закон этого изменения был найден французским ученым Пуазейлем и представлен в виде следующей эмпирической формулы:
71	0,0178
р “1 +0,0337 Г + 0,0002217^*
(6)
где р — плотность воды, имеющая размерность
Т—температура в градусах Цельсия.
Величина у, встречающаяся часто в гидравлике, называется кинематическим коэфициентом вязкости и обозначается буквой у.
Это название вытекает из того, что в размерности этой величины силы отсутствуют. В самом деле, подставив размерность величин ») и р, получим:
' т) ~|___массахдлина3	длина2
. Р J — длинахвремяхмасса время
В приведенной формуле (6) у- имеет размерность см?) сек.
В нижеследующих табл. 1 и 2 приводятся данные для кинематического коэфициента вязкости различных жидкостей, а также вычисленные значения кинематического коэфициента вязкости для воды при различных температурах.
Резюмируя все вышесказанное о физических свойствах жидкостей, можем отметить следующие:
1) «з перечисленных первых двух свойств (малая сжимаемость и малое температурное расширение} мы в качестве следствия имеем малую изменяемость об'ема жидкостей и 2) из указанных последующих двух свойств жидких тел вытекает легкоподважность их частиц.
Как известно, большой легкоподвижностыо своих частиц отличаются и газы, но в отличие от жидких тел они оказывают 18
Таблица 1
Величины кинематического коэфициента вязкости некоторых жидкостей .
Наименование жидкости	Г° С	Кинематич. коэфициент вязкости V см'/сек	Примечание
Бензин			18	0,0065	В таблице указаны
Спирт винный . .	18	0,0133	средние значения ве-
Керосин 		18	0,0250	личины v; надо пом-
Нефть 		18	0,2500	нить, что для разных
Нефть тяжелая . .	18	1,4000	сортов бензина, керо-
Глицерин . * .	20	8,7000	сина и нефти коэфици-
Вода		0	0,0178	ент вязкости различен
Таблица 2
Зависимость кинематического коэфициента вязкости пресной воды от температуры Т°С
Т°	v см'/сек	г	v см'1сек	Г°	м см^сек
0	0,0178	12	0,0124	30	0,0080
' 5	0,0152	15	0,0114	50	0,0055
10	0,0131	20	0,0101	100	0,0028
ничтожное сопротивление всякой силе, стремящейся уменьшить их об‘ем. В тех случаях, когда силы давления изменяются незначительно, жидкости и газообразные тела подчиняются одним и тем же законам движения. Благодаря этому иногда жидкости и газы об‘-единяются общим наименованием жидкости (в широком смысле этого слова) и тогда обычные жидкости называются капельными, или неупругими, жидкостями, а газы называются газообразными, или упругими, жидкостями. Так как в гидравлике рассматриваются только капельные жидкости, то в дальнейшем будем иметь в виду только такие жидкости, а полученные выводы не будут распространяться на газы.
§ 7. Понятие об идеальной жидкости
При изучении законов движения жидкостей бывает полезным введение понятия идеальной жидкости. Это понятие, широко используемое теоретической гидромеханикой и имеющее сравнительно небольшое применение в гидравлике, воплощает в себе свойства жидкости в их крайнем выражении и облегчает в некоторых случаях доследующее изучение реальных жидкостей.
Идеальная, или совершенная, жидкость, представляющая собой, вообще говоря, абстракцию, наделяется следующими свойствами: *	19
1) абсолютной несжимаемостью; 2) полным отсутствием температурного расширения; 3) абсолютным отсутствием сопротивления растяжению и 4) абсолютным отсутствием сопротивления сдвигу.
Из первых двух свойств вытекает полная неизменяемость об‘-ема, а из двух других свойств — абсолютная подвижность частиц идеальной жидкости.
При сравнении идеальной жидкости с реальной видно, что пртктически в большинстве случаев, изучаемых в гидравлике, реальная жидкость может с точки зрения 1-го, 2-го и 3-го свойств считаться идеальной; в гидростатике же, где скорость, а следовательно и силы трения отсутствуют, все свойства реальной жидкости практически совпадают со свойствами идеальной.
§ 8. Основные свойства единичных сил в идеальной жидкости
1. Единичные силы в идеальной жидкости всегда действуют по направлению внутренней нормали к площадке своего действия.
Это свойство вытекает из представления о свойствах идеаль
Фиг. 3
Фиг. 4
ной жидкости, данного в § 7. В самом деле, рассматривая возможное направление силы в точках жидкости, взятых на произвольной плоскости MN (фиг. 3), видим, что направление I по внешней нормали невозможно, поскольку оно соответствует случаю растяжения: направление II под углом к нормали также невозможно, поскольку приложенная сила дает тангенциальную составляющую, производящую сдвиг в жидкости; следовательно единственно возможным является направление III по внутренней нормали, соответствующее случаю сжатия жидкости.
2. Единичное гидромеханическое давление в точке идеальной жидкости не зависит от угла наклона площадки, по которой оно действует.
Докажем, что в движущейся идеальной жидкости единичное гидродинамическое давление не зависит от угла наклона площадки, по которой давление приложено. Этим же свойством обладает давление в жидкости, находящейся в равновесии (гидростатическое).
20
Для этого выделим из жидкости частицу в форме призмы высотой dz и основанием в виде прямоугольного треугольника, катеты которого обозначим dy и dx (фиг, 4).
Для равновесия выделенной частицы к ней необходимо приложить все действующие на нее силы, которые в рассматриваемом случае разбиваются на следующие категории:
1. Силы давления по всем граням выделенного об'ема (поверхностные), каждая из которых равна произведению из среднего давления по грани на величину площади грани; так, сила давления на вертикальную грань:
Рх =	= P\dz dy.
Сила давления на горизонтальную грань:
Ра =	= pt dx dz.
Сила давления на наклонную грань:
Р = />ш; или, так как	-
о) — —dz dy cos a cos а ’ то р р dz dy> cos а
где а—угол между направлением Pt и Р (силы Р3 и Pi впоследствии из рассмотрения выпадают, поэтому выражения для них здесь не приводятся).
2. Сила веса выделенного об'ема (об'емная сила).
Обозначив вес об'ема через G, а массу через dm, получим,
G = gdtn = g ~pdxdydz, *
где g—ускорение силы тяжести, р—плотность, а у dxdy dz представляет, очевидно, об'ем нашей призмы.
К категории об'емных сил относятся и силы инерции, которые по правилу д'Аламбера необходимо приложить к движущемуся телу для того, чтобы привести его в состояние равновесия.
Обозначив силу инерции через J, получим что
J = jdm =	dx dy dz,
£ *
Где/•—'ускорение движущейся частицы.
Сравнивая полученное выражение для сил обеих категорий, “Видим, что об'емные силы являются бесконечно-малыми ве-"Чйгнами более высокого порядка, чем поверхностные, поэтому пренебрегаем.
Напишем теперь для оставшихся поверхностных сил условие равновесия, для чего спроектируем их на горизонтальную ось.
Имеем: F\ = Р cos а или, подставляя вместо Pt и Р их значения, получим:
A<ei=P<e cos а;
вставив в это уравнение значение:
ш — ----,
cos а’
после сокращения получим:
Pi=P-
Проектируя аналогичным образом все силы на ось К, можем
также получить:
Следовательно:
Р1 = Р2==Р,
что и требовалось доказать.
Г ИДР О СТ А ТИКА
ГЛАВА J
ЕДИНИЧНОЕ ГИДРОСТАТИЧЕСКОЕ ДАВЛЕНИЕ
§ 9. Определение величины единичного гидростатического давления
Нами уже установлены специфические свойства единичного давления в покоящейся жидкости. Для определения величины этого давления выделим из жидкости прямоугольный параллелепипед с гранями, параллель-
ными координатным плоскостям, и приложим все действующие на него силы (фиг. 5). Эти силы, очевидно, сведутся к следующим:
1. Силы, приложенные к граням параллелепипеда. Таких сил по количеству граней имеется всего шесть, и они попарно направлены параллельно координатным осям. Величина каждой из этих сил равна произведению из среднего гидростатического давления на соответствующую площадь грани.
2. Собственный вес:
G = у dx dy dh,
где у — об'емный вес жидкости.
Так как рассматриваемый элемент находится в равновесии, то, применяя к нему известные уравнения статики, получим;
1)	Л-Р, = 0;
2)	Р3-Р4=0;
3)	Ps4-G-Pe = 0.
Из первых двух уравнений получим:
Pl=Pj и Pg в Р1>
а иэ третьего уравнения после подстановки значений Р6 — р^к dy и ^t—Psdxdy получаем:
Ptdx dy + у dx dy dh — ptdx dy = 0.
После сокращения на dx dy и замены разности рв — ръ через dpa получим:
dpa = ^dh.
Интегрируя это уравнение, найдем:
Ра == ih -|- С.	(а)
Произвольная постоянная С определяется из условия давления на свободной поверхности. Подставив в уравнение (а) значение h — 0, и ра = Ро> получим С = р0> откуда окончательно имеем:
I Л=Ро + ^- I	(7)
Если в частном случае давление на свободную поверхность рй равно атмосферному ръ, формула (7) примет вид:
Ра=Рь+1к, а избыточное давление: 
|/> = Т^-1	(7а)
Полученное уравнение (7) называется основным уравнением гидростатики.
§ 10. Закон Паскаля
Из полученной формулы видно, что в любой точке жидкости, находящейся в состоянии равновесия, давление определяется двумя факторами:
1) давлением р0, приложенным к ее свободной поверхности;
2) глубиной h ее погружения под свободной поверхностью.
Если мы возьмем в жидкости ряд точек, расположенных на разных глубинах, и вычислим в них давление по формуле (7), то переменной величиной, влияющей на величину давления в этих точках, явится только глубина А, величина же р0 будет для всех точек фигурировать как постоянная величина. Вывод, который отсюда можно сделать, заключается в том, что давление, приложенное к свободной поверхности жидкости, передается внутри ее всем точкам одинаково.
Кроме того, как нами уже раньше было установлено, в одной и той же точке давление по всем направлениям одинаково. В физике это свойство жидкости называется законом Паскаля.
§ 11. Поверхности равного давления
Зная из предыдущего закон распределения единичного давления в жидкости, находящейся в состоянии равновесия, рассмотрим вопрос о так называемых поверхностях равного давления, т. е. о поверхностях, на которых расположены точки с одинаковым единичным давлением. Уравнение этих поверхностей находится из условия рЛ = const, или, вставив значение ра, имеем р0 + f А = = const, что для однородных жидкостей возможно только при условии А — const. Таким образом все точки жидкости, распо-24
ложенные по поверхности одинакового давления, должны отстоять на одинаковом вертикальном расстоянии от свободной поверхности, откуда вытекает, что поверхности одинакового давления в этом случае представляют собой горизонтальные плоскости. Необходимо отметить, что это будет верно лишь для случая, когда жидкость находится под влиянием только одной об'емной силы — ее собственного веса, так как только для этого случая была получена формула (7). В случае действия других об'емных сил поверхности равного давления могут быть другими.
Во всех случаях однако эти поверхности обладают следующими свойствами:
1, Равнодействующая внешних сил перпендикулярна к поверхностям равного давления. Для случая действия одной только силы тяжести это вытекает из того, что эта сила вертикальна, а поверхности давления, как мы только что Это же свойство сохраняется и для случая других внешних сил.
2. Поверхности равного давления не могут между собой пересекаться. Это свойство тоже весьма понятно, так как в случае, если бы эти поверхности пересекались, мы по линии пересечения имели бы ряд точек, принадлежащих одновременно разным поверхностям и обладающих при этом одинаковым давлением, что невозможно.
В качестве примера случая, когда поверхности уровня не горизонтальны, рассмотрим положение жидкости в цистерне, движущейся по горизонтальному пути с одинаковым ускорением (фиг. 6).
Если исключить из рассмотрения моменты, когда ускорение изменяется, то жидкость в цистерне будет находиться в состоянии относительного равновесия. Если приложить к частице силу инерции mj и силу ее тяжести mg, то из равновесия этих сил следует, что давление на частицы направлено к вертикали под постоянным углом а, который определяется из равенства tga =
так как согласно сказанному выше поверхности равного давления перпендикулярны к направлению равнодействующей сил давления, то они, очевидно, наклонены под тем же углом к горизонту, т. е. являются уже не горизонтальными плоскостями, а наклонными.
видели, горизонтальны.
фиг. 6
§ 12. Приборы для измерения давления
Для измерения единичного гидромеханического давления гидравлика располагает различного рода приборами, основанными либо на Упругих свойствах тонких пластин либо на возможности измерять давление высотой столба жидкости. К числу первых относятся пружинные манометры, устройство которых показано
на фиг. 7. Жидкость, поступая в манометры, производит давление на полую пружину, которая, частично распрямляясь с помощью зубчатки, приводит в движение стрелку. Отсчет давления производится по градуированной шкале. Второй тип приборов распадается на следующие категории:
А) Пьезометрические трубки, представляющие тонкие стеклянные трубки, соединенные с пространством, где должно быть измерено давление (фиг. 8). Жидкость под влиянием давления поднимается в трубке на какую-то высоту Л. Единичное давление в точке М может быть определено по общей формуле:
А^Л + Й, откуда
Фиг. 7
Фиг. 8
Если вообразить эту трубку сверху закрытой, а воздух из нее выкачанным, то жидкость в ней поднимется на другую высоту ha>h. Давление в точке М определится по формуле ра = т ha (так как рь = 0). Отсюда:
(9)
следовательно величина ha характеризует полное единичное давление ра, а величина Л характеризует избыточное давление р. Величины haH h называются пьезометрическими высотами (полной. и избыточной).
Пьезометрические трубки являются весьма простыми и удобными приборами, однако они могут быть применены лишь при малых давлениях, так как большие давления требовали бы слишком большой их высоты.
Б) Ртутные манометры, представляющие собой U-образные стеклянные трубки (фиг. 9). Давление измеряется по предыдущей формуле:
Ра— Рь = Ък,
где очевидно, должна быть взята как об'емный вес ртути. Имея в виду, что 7 ртути в 13,6 раз больше, чем у воды, получим, что высота под'ема жидкости в ртутном манометре при одном и том же давлении окажется в 13,6 раз меньше, чем в пьезометре. Несмотря на это, при очень больших давлениях трубки ртутных манометров тоже оказываются слишком высокими, и тогда применяются описанные выше пружинные манометры .
В) Диференциальные манометры, употребляемые при определении разности давлений в двух сосудах (фиг. 10).
Фиг. 9	Фиг. Ю
где h — разность уровней в коленах трубы, — об'емный вес жидкости, находящейся в сосудах А и В, уа — об'емный вес жидкости, наполняющей трубку.
§ 13.	Механический смысл основного уравнения гидростатики
Рассмотрим две частицы жидкости, заключенные в каком-то сосуде (фиг. 11): частицу А, давление в которой равно р0, и частицу В, взятую на расстоянии h от А и давление в которой равно ра, Вес обеих частиц принимаем равным единице. Напишем основное уравнение гидростатики в следующем виде:
Ра— Ро = ^.	(10)
Левая часть этого уравнения представляет приращение давления точки В, а правая часть является работой, совершаемой частицей л при ее опускании на высоту А. Таким образом с механиче-б°и стороны уравнение (7) представляет собой уравнение ра-^Пы.' Указывающее, что при переходе частицы жидкости us ной точки пространства в другую приращение давления воз-
27
можно только при затрате на это определенной работы внешних сил. Эта работа может быть положительной, если ее совершают внешние силы, или отрицательной, если она совершается внутренними силами давления.
Таким образом находящаяся в равновесии жидкость оказывается работоспособной, т. е. должна обладать каким-то запасом энергии.
§ 14.	Удельная потенциальная энергия
Выберем в жидкости произвольную точку А весом G и на расстоянии z от нее зададимся произвольной плоскостью MN, которую назовем плоскостью сравнения (фиг. 12).
Энергия нашей частицы Е складывается из двух частей: 1) из энергии £,, обусловливаемой весом частицы и ее расстоянием до плоскости MN (энергия положения), и 2) энергии £р, обусловливаемой давлением соседних частиц (энергия давления).
Следовательно:
Фиг. п
Определим оба вида энергии в отдельности.
Так как энергией называется способность тел совершать какую-то работу, то, очевидно, частица при ее опускании до плоскости сравнения под влиянием силы G совершила бы работу, равную Gz. Следовательно эта величина и представляет энергию положения точки А, т. е.
Е, = Gz.
Для-определения энергии давления вообразим в точке А закрытую пьезометрическую трубку. Если такая трубка в действительности была бы здесь поставлена, то под влиянием давления точка поднялась бы на высоту:
а работа, совершенная при этом под'еме, равнялась бы:
G • h = О—,
7
откуда
Е =G—. р т
Из уравнения (а) имеем, что вся потенциальная энергия точки:
\ Т /
Для того чтобы иметь возможность сравнивать между собой энергию разных точек жидкости, необходимо, очевидно, выбирать эти точки так, чтобы они обладали одинаковым весом, или, что еще проще, сравнивать между собой энергию, отнесенную к единице веса данных точек. Назовем энергию, отнесенную к единице веса точки, удельной энергией, и обозначим ее через е. Очевидно, что для жидкости, находящейся в равновесии;
или, иначе,
(П)
Таким образом удельная потенциальная энергия в точке жидкости представляет сумму двух высот — геометрической вы-
соты z и пьезометрической высоты
§ 15.	Энергетический закон в покоящейся жидкости
Сравним удельную потенциальную энергию двух точек, находящихся на расстоянии и г.2 от условной плоскости сравнения (фиг. 13). Обозначим их расстояния от свободной поверхности через hi и йа, а расстояние между свободной поверхностью и плоскостью сравнения через Н. Тогда согласно предыдущему удельная потенциальная энергия обеих точек будет:
энергия обеих точек
Pi
Т
а
А Т
Подставив вместо аиА величины А + 'Г^и/’о+'^г» получим: ei = z, + *,=H+^,
откуда имеем:
е,---ег,	(Па)
т. е. что в покоящейся жидкости удельная потенциальная энергия во всех точках—величина постоянная и от положения точки не зависит.
Задача. Закрытый резервуар А соединен коленчатой трубкой с открытым пьезометром В (фиг. 14). Вся система заполнена водой и ртутью. Отметка свободной поверхности воды в резервуаре =10 м, отметка горизонта воды в пьезометрической трубке Н3 = 15 м. В среднем колене соединительной трубки находится ртуть; отметки раздельных поверхностей между ртутью и водой //,--= 9 м и /У4=Г2лг. Требуется определить абсолютное давление в воздушном пространстве сосуда А, если удельный вес ртути—13,6.
Фиг. 14
Фиг. 15
Решение.
1.	Определяем давление в точке, принадлежащей раздельной поверхности воды и ртути на отметке Н<:
Р1=^04-тй = 1+0,001 (Я4 — Я4) = 1 +0,001 (15 — 12)100 = = 1,3 кг/см1.
2.	Определяем давление на второй раздельной поверхности в соединительной трубке на отметке Н3:
р, = Ро+ 1ft =Pi + 0,0136 (Ht — Ht) = 1,3 + 0,0136 (12 — 9) 100 = = 5,38 кг/см3.
3.	Определяем искомое давление на свободной поверхности воды в резервуаре А:
р* = Ро +	= Pi + 0,001 (Ht — Н^ = 5,38 - 0,001 • 100 =>
= 5,38 — 0,1 =5,28 кг! см2.
Задача. Какой груз нужно приложить к поршню цилиндра А (фиг. 15), чтобы вода в пьезометрической трубке В поднялась на высоту Л = 4,75 м, если площадь поршня 30 см2.
Решение. Единичное давление под поршнем:
р -	- 0,001-4,75 = 0,475 кг'см\
отсюда вся сила давления:
Р = шр = 0,475 • 30 = 14,25 кг.
Задача. Прибор, известный под названием „герснов фонтан*, состоит из трех резервуаров А, Б и В (фиг. 16). Закрытые резервуары А и Б соединены между собой воздушной трубкой а, резервуары же Б и В—трубкой б. Резервуар А имеет кроме того трубку в, верхний конец которой снабжен фонтанным насадком. Требуется определить давление на свободной поверхности воды в резервуаре А в начале и в конце работы фонтана
при указанных на чертеже геометрических размерах прибора и отметках горизонтов воды в сосудах в начале опыта йх = 100 см, Ла = 20 см, Л3 = 150 см. Цилиндрические резервуары А и Б одного и того же диаметра, Б = 25 см и 1 о см.
Решение, душной трубки
высота резервуара отметка дна его
Ввиду наличия воз-ж _ а давление воздуха Г резервуарах А и Б будет одинаково. Давление это вследствие наличия трубки б будет обусловливаться горизонтом воды в сосуде В. Пренебрегая весом воздуха, получаем избыточное давление в сосудах А и Б в начале работы прибора: рА=рБ = =(ht — ht) у = (150 - 20) 0,001 = 0,013 кг'см2.
В процессе работы прибора горизонт воды в сосуде Б будет медленно повышаться, пока весь сосуд Б не будет заполнен водой и последняя
не начнет поступать в воздушную	Фиг« 16
трубку а.
Имея в виду, что горизонт воды в сосуде В остается все время постоянным, найдем, что давление в сосудах А и Б в
этот момент будет равно;
р'А = р’Б = [А, — (Л4 + 25)] т = (150 — 40)0,001 = 0,011 кг[см\
Рассмотренный момент и будет практически окончанием нормальной работы прибора, так как заполнение трубки а водой ввиду незначительности ее сечения происходит весьма быстро, обусловливая и быстрое падение давления.
Работа прибора окончательно прекратится в момент наступления равновесия, т. е. когда уровень воды в трубке а достигнет горизонта воды в сосуде А. Давление в резервуаре А в этот момент будет обусловливаться разностью горизонтов воды в сосудах А и В.
Пренебрегая об'емом воды, идущим на заполнение трубки а, имея в виду, что диаметры сосудов А и Б одинаковы, имеем
отметку горизонта воды в сосуде А при наступлении равновесия:
Л5 = Aj — (Л4 + 25 — А2) = 100—20 = 80 см.
Давление в сосуде А при наступлении равновесия:
рА = (Л8 — йБ)у = (150 — 80) 0,001 = 0,007 кг/см*.
,чг.о
Фиг. 17
Задача. Основание кессона запроектировано на отметке — 32,0 м. Отметка уровня воды в реке -|-12,0 м. Требуется определить максимальное избыточное давление в кессоне в момент достижения им проектной отметки (фиг. 17).
Решение. Глубина погружения нижнего края кессона под уровень воды в реке составляет:
й = 12— ( — 32) = 44 м.
Для того чтобы вода из реки не стала проникать в кессон, необходимо, чтобы давление воздуха в кессоне было равно гидроста
тическому давлению.
Отсюда единичное давление воздуха в кессоне определится по формуле избыточного давления:
р = уй = 1,0 • 44 = 44 т1м2= 4,4 кг/см2.
ГЛАВА II
СУММАРНОЕ ДАВЛЕНИЕ НА ПОВЕРХНОСТИ
§ 16. Аналитическое определение суммарного давления на плоскую стенку
Суммарное давление, как всякая сила, характеризуется тремя данными: величиной, направлением и точкой приложения. Направление этой силы определяется из того обстоятельства, что она является равнодействующей единичных сил давления, параллельных между собой и нормальных к стенке в каждой ее точке; отсюда следует, что и суммарное давление на плоскую стенку направлено нормально к ней; остается следовательно определить только величину суммарного давления и точку его приложения.
Рассмотрим некоторую фигуру на плоской стенке, наклоненной под углом а к горизонту (фиг. 18).
Пусть точка С—центр тяжести фигуры, а точка d—точка приложения суммарного давления (центр давления), ® — площадь фигуры.
Возьмем на фигуре произвольную точку А Единичное избыточное давление в ней по формуле (7а) (см. § 9) будет:
р = уЛ	sin а;
если выделить возле точки А элементарную площадку Дф, то на нее будет дейавовать элементарное суммарное давление:
Д Р = р Дф = р] sin оДф.
Все суммарное давление:
Р = /р (fa = у sin a J* = 7 sin ат]еФ	(а)
Ш	(О
или, заменив величину sin а через Ас, получим:
I Р = т/гсш. |	-	(12)
Но Ае есть глубина погружения центра тяжести фигуры, а yZte—единичное гидростатическое давление в нем.
Следовательно аналитически
величина суммарного давления на плоскую фигуру определяется как произведение площади этой фигуры на единичное давление в ее’центре тяжести.
Для определения координат центра давления ворьмем сумму моментов всех элементарных единичных сил относительно оси §.
М = f dPq == у sin a f к]2 d<a = а>	ш
= у sin а Л,
где Д — момент инерции фигуры относительно оси $ и может быть выражен через центральный
Фиг. 18
момент инерции:
п .	Л = /о + ше -
Следовательно:
М = у sin а (/0 -|- ф щ2).
С другой стороны, согласно уравнению (а):
М = Ptjj — у sin л т% ф
Приравнивая оба значения Л1, получим:
откуда:
(/о + ш V) — V Чг.
+	-^+А-
(13)
Аналогичным образом могут быть найдены и другие координаты центра давления.
2 Гидравлика	33
§ 17.	Графоаналитическое определение суммарного давления
Если во всех точках стенки отложить в определенном масштабе величину единичного давления и концы отложенных отрезков соединить между собой, то площадь полученной фигуры будет представлять собой величину суммарного давления. Эта площадь называется эпюрой , единичного давления.
t Построение эпюр давления
1.	Случай полного давления. Проведем через точку А координатные оси (фиг. 19).
Применим уравнение (7):
Ра=Ро+Й.
В точке A—h=0, и следовательно ра-=р0 В точке В—h - H и ра=чН', отложим обе величины в соответствующих точках в одном
и том же масштабе. Так как величина ра как функция от h изменяется по закону прямой линии, то для построения эпюры давления соединим обе ординаты прямой линией. Площадь полученной трапеции ш будет суммарным давлением на единицу ширины стенки, а ее центр тяжести определяет положение равнодействующей; проведя через центр тяжести равнодействующую и найдя точку ее пересечения со стенкой, получим центр давления.
2.	Суммарное давление от избыточного гидростатического давления. Для этого случая имеем формулу (7а) р = fA. В точке А—h. = 0, поэтому р = 0. Для точки В— h = Н и р = уН.
Полученная эпюра имеет форму треугольника (фиг. 20).
3.	Случай наклонной стейк и. Вычисления производим аналогично предыдущему, но при построении эпюры величины р откладываются нормально к стенке (фиг. 21).
Задача. Каменная прямоугольная стенка поддерживает разность горизонтов воды слева Н = 3,6 м и справа h — 1,0 м. Определить коэфициент запаса стенки на опрокидывание, если 34
размеры сечения стенки а 2 м, b ~ 4,0 м и об'емный вес кладки 1,8 гп/м3 (фиг. 22).
Решение. Расчет ведем на пог. метр длины стенки. Момент, опрокидывающий стенку, обусловлен давлением воды слева и равен:
Н2	Н	Н3
Л/«.Р = 4— 4-Г 1	7, 146/плс.
лл	о	о
Момент удерживающий равен сумме моментов силы веса стенки G и давления воды справа: а	аз л	/ ath	h? \
Л^ = с4 + 4-.4-г1= ® +-£_ т.1=8,о+о, 167=8,167тч.
Z	л» О	у £	О ]
Кбэфициент запаса:
А=^-=И^=1’14-M„„f 7,146
Задача. На вертикальной плоской стенке выделена часть в виде круга (фиг. 23) диаметром d Центр круга лежит на расстоянии -= d от свободной поверхности. Найти величину
Фиг. 22
суммарного давления и центр давления.
Решение. Задача решается аналитически.
Для силы давления имеем:
7j = ‘“A0 = -1-7D=
Положение центра давления определяется по формуле:
г.  г । Л,  nt к 7^4,4	_ Г) । 7) _ 17 ~
Ад-Лс + а>Л0 ~D + q4-kD<D~ 16 “ 16 D'
Задача Определить горизонтальную силу, стремящуюся сднч-нуть каменную плотину 'фиг. 24), если дана длина логины L ~ 5,0 м.
Глубина воды Н = 4,0 м.
Решение. Обозначив силу давления через Р, а ее гори* °нтальную проекцию через Рх, получим, что
Рх = Р cos а.
Р аналитически находится по формуле: Р = А»,
Отсюда;
р .	.
2 cos а’
D у№А 1 • 4,02 • 5,0	..
*Р*=2~ =---------2------= 40 т'
Задача. Определить усилие, необходимое для под'ема наклонного щита А (фиг. 25), если дано, что глубина воды перед щитом //= 3 м, глубина воды за щитом = 1 м., ширина щита В = 2 м.
Коэфициент трения щита о каменные пазы/=0,2. Угол наклона щита к горизонту а = 30°. Собственным весом пренебрегаем.
Решение. Сила F, необходимая для под'ема щита, должна равняться силе Т трения щита о пазы. Сила Т, как известно, равна
силе, прижимающей щит к пазам, умноженной на трения.
щита
нормальной коэфициент
где P = Pt — Р2 представляет результирующую сил ческого давления на щит.
Аналитическим способом находим: р ш	1-3,0
1	1	2 t in а 2
'	г,	у/7, Н.,В
2 sin а
гидростати-
3,0-2,0' ,Q о?.
2 /п.
Отсюда:
Р = 18 —2 = 16 tn;
F =	16 • 0,2 = 3,2 tn.
Задача. Плоский щит А (фиг. 26), служащий затвором у плотины, может вращаться в шарнире (затвор Шаноана).
Определить: 1) коэфициент устойчивости щита в тот момент, когда вода достигнет его верхней кромки, если шарнир расположен в середине щита;
2) положение шарнира, при котором щит начнет опрокидываться в тот момент, когда вода над верхней кромкой щита будет иметь толщину А = 0,90 м.
Дано Н =2,5 м, а = 45°. Ширина щита В = 1 м.
Решение. Для решения 1й части задачи разобьем эпюру давления воды на две части. Обозначив расстояние от шарнира
Фиг. 26
до краев через I, силы давления верхней и нижней части воды через Pj и Р2, а расстояния центров тяжести до шарнира через at и а., получим:
~ 2 2	1 * * ~ 4 **
I
Л1 ~ 3:
отсюда опрокидывающий момент: .. п Мтр =	= —12-;
р--К''"4
at находим как центр тяжести трапеции:
_ I w+i'i 5,
3 Н . Н' ~ 9 L
1-
2-й части задачи воспользуемся условием, что когда щит начинает опрокидываться, удержива-должен равняться опрокидывающему моменту.
Отсюда удерживающий момент:
Муд =Р2аа=^1 I =	1\
коэфициент устойчивости:
8 —=	-г//, Л = 5.
Для решения в тот момент, ющий момент
для чего необходимо, чтобы сила давления на весь щит проходила через шарнир или, иначе говоря, чтобы шарнир совпадал с центром давления. Отсюда положение шарнира графоаналитически находится из трапеции.
Крайние ординаты трапеции:
pi — yh = 0,9 т/м*;
+	3,4 т]м*,
отсюда:
1	2,5	2-3,40 + 0,90
Х~ 3 ’ sin 45° ’ 3,40 + 0,90 ,П
§ 18. Давление жидкости на криволинейные поверхности
В общем случае решение задач о давлении неподвижной жидкости на поверхность произвольного вила всегда приводится к определению величины и момента суммарною давления. Если
решать эту задачу как пространственную, то по правилам статики придется определить три составляющие суммарного давления по координатным осям и три момента вокруг координатных осей. Такой случай однако в практике встречается крайне редко; в большинстве же случаев поверхности имеют какую-нибудь ось симметрии, что превращает задачу из пространственной в плоскую. Мы ограничимся здесь изложением именно этого случая.
Рассмотрим какую-нибудь цилиндрическую поверхность.
Учет давления на нее приходится производить в двух случаях практики.
1) Эта поверхность может представлять собой сосуд, в который помещена жидкость (фиг. 27).
2) Этой поверхностью может являться какая-нибудь стенка, часто применяемая в гидротехнике: плотина, затвор и т. д. (фиг. 28).
Расположение жидкости в обоих этих случаях различно: так, если провести через крайние точки А и В поверхности вертикальную и горизонтальную плоскости, то для данного в фиг. 27
1-го случая жидкость будет расположена внутри об'ема О АВ, для случая же 2-го, изображенного на фиг. 28, жидкость расположена вне этого об'ема.
Рассмотрим 1-й случай. Суммарное давление Р легко может быть определено, если будут известны его проекции Рх и Ри на две координатные оси, так как его величина легко
определяется по правилу треугольника: Р = у/Р^ + Ру\ а точка приложения может быть определена из условия, что равнодействующая сила должна пройти через точку пересечения обоих составляющих сил Рх и Ру.
Определение величины Рх и Ру может быть произведено аналогично случаю плоской стенки на основании следующих соображений. Возьмем на поверхности какую-нибудь произвольную точку (фиг. 29). Единичное давление в ней определится по общей формуле:
(Давление будем принимать избыточным). Выделим возле точки очень малую площадку Д<о, которую ввиду ее малости будем считать плоской. Элементарная сила давления на эту площадку ДР = рДш и направлена по нормали к поверхности.
Обозначим угол, составленный нормалью и осью х, через а, проекцию силы ДР на координатные оси через ДРХ и Д Ру. Тогда, очевидно, Д Рх = Д Pcos а. = р Дш cos а. Или ввиду того, что Дшсо8а = Дша., будем иметь:
Д Рх = р £н»х = -|'Л Дшх, отсюда:
Р„ = 2ДРХ= tffid<ox. UJ
Как известно, .fhd<s>x представляет статический момент пло-ш
Щади ш* относительно оси А'-ов. Обозначив расстояние от центра тяжести этой площади до оси через hc, получим:
=	(14)
Но эта величина по формуле (12) представляет собой суммарное Давление, приходящееся на площадь о>х. Поэтому полученная Нами формула (14) может быть сформулирована следующим образом: величина горизонтальной составляющей суммарного
давления на криволинейную поверхность равна суммарному давлению жидкости на вертикальную проекцию данной поверхности.
Перейдя теперь к определению вертикальных проекций Ру, имеем:
Д Ру = Л Р sin а = р Да> sin а.
Подставив вместо Дш81па величину Д<и„ получим:
ш
Как видно из фиг. 30, величина hd^y представляет об'ем беско-нечно малого цилиндра, имеющего основанием площадь dwy и высотой величину h. Поэтому f hda>y может быть рассматриваем
U)
как об'ем тела О А 3, Обозначив об'ем этого тела через W, а вес через G, получим:
или, иначе,
(15)
что может быть словами сформулировано следующ:м образом: вертикальная составляющая суммарного давления на криволинейную поверхность равна весу жидкости, заключенной в об'еме, ограниченном самой поверхностью, двумя вертикальными плоскостями, проходящими через верхнюю и нижнюю образующие, и свободной поверхностью жидкости. При избыточном давлении точка приложения силы Рх будет, очевидно, на одной трети Н, а точка приложения Ру совпадает с центром тяжести об'ема О АВС. Пересечение сил Рх и Ру дает нам точку, через которую должна пройти сила Р, а пересечение направления силы Р с данной поверхностью будет центром давления.
Приведенные формулы могут быть получены и другим способом без интегрирования. В самом деле, выделим об'ем ОАВ и рассмотрим его как одно целое (фиг. 31). Приложив все действующие на об’ем силы, получим из условия равновесия непосредственно:
^ = — ^=7^0),
И
Рассмотрим 2 й случай (фиг. 32). Если мы возьмем точно такую же поверхность, как и в предыдущем случае, но с жидкостью, давящей извне, то давление в произвольно взятой точке а с координатой h по величине -останется тем же и выразится той же формулой:
Элементарное давление на площадке Дш выразится аналогично предыдущему:
Д Р - у АД ш.
Проектируя ДР на координатные оси, получим:
Д Рх = 7 АД шх, а
ДРу = —7АДшу
(знак минус взят потому, что ДРу направлено в сторону отрицательных у-ов).
Фиг, 32	Фиг. 33
Проинтегрировав оба выражения, получим:
^» = ТАеш« и Р„ = — 7 ^= — G.	(16)
Таким образом горизонтальная проекция суммарного да' вления получена во 2-м случае точно такая же, как и в 1-м. Вертикальная же проекция по величине равна весу в об'еме О АВС, выделенном точно так же, как и в первом случае, и называемом „телом давления*, по направлению же эта проекция противоположна весу, т. е. она направлена вверх.
Задача. Определить суммарное давление на цилиндрическую часть стенки, если ширина ее В = 0,5 м, г= 1,5 м и /У = 5,0 м (фиг. 33).
Горизонтальная составляющая суммарного давления находится по эпюре давления на вертикальную проекцию цилиндрической части стенки:
Р, = ^В = Н ~ГеЛН-гВ^ = ^-1,5-0,5-1 =3,1875 т. £ £
Вертикальная составляющая направлена вверх и равна:
Р — о о / и	о /с 1 с 3,14-2,25 \Л _
I Hr — ~г~ I °7 ~ 5-1,5-----:i------10,5	1,7 т.
\	4 /	\	4	/
Задача. Определить силу давления воды на единицу длины плотины параболической формы (фиг. 34), если дано, что глубина воды Н = 4- м, уравнение параболы х2 = 9у.
Решение. Обозначив силу давления через R, найдем обе ее составляющие. Как известно, Rx равна силе давления на вертикальную проекцию стенки, откуда:
Rt равна весу воды в об'еме ОАВ, отсюда:
Rs = • 1,
2 где ® как площадь параболы равна -^-ЬН.
О
Отрезок b определяется из данного выше уравнения параболы. Определив из этого уравнения х = 3}/у, имеем:
д = 3/4 = 6л<;	|-6-4 = 16 м\
О
а
Я,= 116 = 16от; давление
R =	= /82 + 162 = 17,89 т.
Задача Определить давление воды на ось секторного затвора водоспуска плотины, имеющей пролет / = 4,0лг, если центральный угол сектора а = 45° и радиус сектора г = 2,0 м (фиг. 35).
Решение. Применяя графоаналитический метод решения, строим эпюры давления воды для горизонтальней составляющей суммарного давления, имея в виду, что величина суммарного давления, направленного по радиусу сектора, представляет собой искомое давление на ось затвора.
Проектируя цилиндрическую поверхность на вертикальную плоскость и строя для полученной проекции эпюру давления abc, получаем величину горизонтальной составляющей /?„:
/?г = пл-abc-fl = ------=----• 1,0-4 — 4,0 т.
Вертикальная составляющая характеризуется площадью Мт и направлена снизу вверх. Величина ее составляет:
(-ТГ	\
~—-V- ГН = 0,57-1-4 - 2,28 т.
о 4 J
Равнодействующая суммарного давления найдется по формуле:
R ---/RJ 4- Я/ = /4,02 + 2,282 = 4,6 т.
Следовательно давление на ось секторного затвора плотины будет составлять 4, 6 т.
Задача. Определение прочности стенок цилиндрического сосуда.
Пусть цилиндрический сосуд заполнен жидкостью (фиг. 36). Единичное давление в разных сечениях стенки определяется по общей формуле:
В результате действия этого давления в стенках сосуда возникают растягивающие напряжения. Определим зависимость между этими напряжениями и между единичным давлением р. Для
этого выделим из сосуда двумя горизонтальными сечениями MN и MlNi кольцо высотой dh., разрежем это кольцо диаметральной плоскостью на две части и рассмотрим равновесие одной его половины. Обозначив растягивающие силы в кольце через Т, а суммарное давление, производимое жидкостью на полукольцо, через Р, мы из условия проекции всех сил на вертикальную ось имеем ^ = 0, а из условия проекции на горизонтальную ось Р1 = 27', где согласно уравнению (12):
Рв^= p<o, — p2rdh.	(а)
Обозначив напряжения в материале стенок трубы через k, а толщину стенок через 3, получим T=kbdh. Подставляя значения Рх и Г в формулу (а), получим:
2pr dh = 2kldh,
откуда определяем напряжение k:
и деформацию стенок:
k рг
~Ё= Ж
(17)
(18)
Так как величина р зависит от глубины погружения под водой данного сечения, то напряжения в материале стенок будут возрастать с глубиной.
ГЛАВА П1
РАВНОВЕСИЕ ПОГРУЖЕННОГО В ЖИДКОСТЬ ТЕЛА
§ 19. Закон Архимеда
Пользуясь выведенными выше формулами, можно определить давление, производимое жидкостью на погруженное в нее тело. Рассмотрим первоначально для простоты призматическое тело, ограниченное вертикальными и горизонтальными гранями (фиг. 37),
Применим формулы, полученные в § 16.
Тогда:
Pj _ у Qj Zti — Р8;
Р3 = у2й3;
P4 = y2A4;
откуда:
Р4-Р8---ТЛ2(Л4-А3)=у^,
(19)
(20)
Фиг. 37	где W—об'ем данного тела, a yUZ—
вес жидкости, содержавшейся в этом об‘еме. Следовательно при погружении в жидкость призматического тела горизонтальные силы давления, производимого жидкостью на тело, взаимно уничтожаются, а вертикальные силы дают равнодействующую, направленную кверху и равную по величине весу жидкости, взятой в об'емЬ данного тела (закон Архимеда), Эта равнодействующая называется под'ем-ной силой, об'ем вытесненной жидкости (для случая воды) называется водоизмещением, а точка приложения под'емной силы называется центром водоизмещения. Полученный закон нетрудно распространить также на тело произвольной формы.
В самом деле, рассматривая тело какой угодно формы и об'ема W (фиг. 38), разобьем его на ряд бесконечно-малых тел, которые будем считать призматическими.
44
Обозначив об'ем каждог» элемента через dW, а под'емную силу, действующую на него, через dP, получим по предыдущему: dP='(dW\
проинтегрировав это уравнение, получим:
P=^fdW а пи	w
I Р = Т^.|	(21)
Все приведенные выводы остаются справедливыми для случая, когда тело погружено в жидкость не полностью, а частично. Очевидно, что при этом под об'емом W приходится понимать об'ем не всего тела, а только той ча-сти» которая погружена в жидкость.
§ 20. Условия равновесия тела, полностью погруженного в жидкость
Пусть в теле, полностью погруженном в жидкость, центр тяжести находится в точке С, а центр водоизмещения в точке D (фиг. 39). Очевидно, что для случая, когда рассматриваемое тело все однородно, обе эти точки совпадут. Для неоднородного же тела эти точки будут различны.
Ось 00, проходящая через эти обе точки, называется осью плавания.
Для того чтобы погруженное тело сохранило свое равновесие, приложенные к нему силы должны, очевидно, удовлетворять общим уравнениям статики. Эти уравнения дают величину и положение силы Р. *
1. Из условия проекции на вертикальную ось имеем G = P, т- е. что под'емная сила должна быть равной весу погруженного тела. При несоблюдении этого условия погруженное тело приходит в движение.
При этом, если G>P, — тело тонет,	1 122)
, G <Р, — тело всплывает на поверхность.] ' '
2. Из условия равенства нулю моментов сил G и Р относительно любых координатных осей вытекает равенство плеч этих
сил, что в свою очередь возможно только при расположении точек С и D на одной вертикальной оси.
Если оба указанных условия выполнены, т. е. силы G и Р равны между собой, а точки С и D находятся на одной вертикали, тело будет находиться в равновесии.
Устойчивость этого равновесия зависит от взаимного расположения точек С и D.
В самом деле, пусть тело, находившееся первоначально в равновесии, под действием внешних сил наклонилось на какой-то угол а (фиг. 39).
Силы Р и G при этом должны образовать пару. В зависимости от направления этой пары здесь могут встретиться следующие три случая:
Фиг. 40
1)	Точка С находится ниже точки О (случай яа“), образовавшаяся пара стремится вернуть тело в первоначальное положение. Следовательно в этом случае равновесие будет устойчивым.
2)	Точка С находится выше точки D (случай ,,б“). В этом случае пара вращает тело'в том же направлении, что и опрокидывающая сила. Ривновесие следовательно будет неустойчивым.
3)	Точки С и D совпадают (случай ,в“). В этом случае никакой пары не образуется; тело остается в том положении, в которое ее приведет внешняя сила. Равновесие будет безразличным.
§	21. Равновесие тела, частично погруженного в жидкость
Пусть тело частично погружено в жидкость (фиг. 40). Линия LL' пересечения свободной поверхности жидкости с поверхностью тела называется ватерлинией, а площадь, ограниченная ватерлинией, как контуром, называется площадью ватерлинии.
Переходя к условиям равновесия данного тела, вообразим аналогично тому, как нами было сделано ранее, что тело под влиянием внешних сил наклонилось на какой-то угол а, при этом часть OKL выйдет из жидкости, а часть OK'L' погрузито 46
в жидкость; центр тяжести тела при этом повороте останется на прежнем месте, но центр водоизмещения переместится уже р новое положение Dv Продолжив направление под'емной силы р до пересечения с осью 00, мы получим новую точку М, которая, как мы увидим дальше, играет важную роль при определении остойчивости равновесия тела‘. Точка эта называется метацентром, а расстояние между метацентром и центром водоизмещения называется метацентрическим радиусом. Таким образом тело, частично погруженное в жидкость, «имеет три характерные точки:
1) Центр тяжести тела, не изменяющий своего положения при любом положении тела.
2) Центр водоизмещения, перемещающийся при повороте тела.
3) Метацентр, который при небольшом повороте тела (не больше 15°) может считаться неперемещаю-щимся. При нормальном положении тела все эти точки расположены на оси плавания.
Обозначим метацентрический радиус через р, а расстояние между центром тяжести и центром водоизмещения через а. Остойчивость равновесия тела зависит от относительного расположения точек М и С (метацентра и центра тяжести). Так, если точка М лежит выше точки С, направление пары указывает на остойчивость равновесия (фиг. 40, случай ва“), если точка М находится
ниже точки С, равновесие будет нео-
стойчивым (случай „6“). Если обе точки совпадают, равновесие будет безразличным. Нетрудно видеть, что первому условию соответствует условие а < р, второму условию а > р, а третьему условию а = р.
Таким образом для определения вида равновесия необходимо знать величину метацентрического радиуса. При определении этой величины воспользуемся известной в механике теоремой Гульдена, согласно которой, если имеется составное тело, в котором какая-нибудь часть перемещается, то перемещение центра тяжести ?той части относится к перемещению центра тяжести всего тела обратно пропорционально их об'емам. Применив эту теорему к нашему случаю, мы можем рассматривать в качестве составного об'ема водоизмещение погруженного тела, в котором часть OKL переместится в положение OK'U (фиг. 41). Если обозначить об'ем
* Г1₽и рассмотрении равновесия плавающих тел обычно применяется термин .остойчивость* вместо .устойчивость*.
всей вытесненной воды (все водоизмещение) через UZ, а об'ем клина через w, то получим:
w  D d
откуда:
. vol	. .
ур- >	(®)
где d — горизонтальная проекция отрезка а
/—горизонтальная проекция отрезка В^В,.
Из треугольника MDD2 находим величину метацентрического радиуса:
(вследствие малости угла sin а заменен через а).
Выражение wl, равное представляет двойной статический момент одного из клиньев относительно оси 00. Для определения этого момента разобьем об'ем клина на ряд элементарных об'емов dw, причем из фиг. 42 видно, что dw = dwh, где dw площадь бесконечно узкой полосы вдоль тела, a h = уа — ее высота. Обозначив момент такого элементарного об'ема относительно оси 00 через dM, получим:
dM = dwy = ay2 dw,
а сумма таких моментов: ♦
М = №-^- = л£ у* dw,
О)
fy^dw представляет собой момент инерции половины пло-ш	* „
щади ватерлинии относительно оси 00 (продольная ось судна). Обозначив величину момента инерции всей площади ватерлинии через /, получим:
= или WI - а/.
Подставив это значение в выражение (б), получим окончатель» но значение метацентрического радиуса.
»=Ж	'	<23>
После определения величины р мы с помощью данных выше неравенств можем судить об остойчивости плавающих тел.
Задача. Определить глубину погружения h ареометра размеров, указанных на фиг. 43, в пресной и в морской воде, если рее ареометра с грузом 0 = 38 г, и об‘емный вес морской воды 1,02.
Решение. Площадь поперечного сечения широкой части ареометра:
2 =	—Lyjl в 7 07 см2
4	4
Площадь шейки ареометра:
3,14 0,25
= 0,196 см*.
Фиг 42
Фиг. 43
Для первого случая:
. _ 38-5-7,07
* ~	0,196-1
Для второго случая:
38-5-7,07
Ла- 0,196-1,02
Условие равновесия плавающего тела даст:
О = Р; 38 = (5 2 -f- ш Л)у.
2,65
О, 196
= 13,5 см.
4^-= 13,25 см. U, ХЬ
Задача. Определить остойчивость плавающего деревянного параллелепипеда в положении, указанном на фиг. 44, если размеры ребер параллелепипеда а = 60 см, 6 = 30 см, с = 20 см и об'емный вес дерева уд = 0,8 г[см\
* Г идравлика	49
Решение. Условие равновесия плавающего тела дает: Р= G,
где вес тела:
G = 60 • 30 • 20 • 0,8 = 28 800 г.
Под'емная сила'
Wf = 60 • 20 • 1 • / = 1200t.
Поэтому осадка t найдется из уравнения:
1200 /=28800,
откуда:
,	28800	о.
t	1200	24 СМ'
Переходим к определению остойчивости.
Условие остойчивости.
р > а,
где р— метацентрический радиус, а — расстояние между центром тяжести и центром водоизмещения.
Находим а:
Определяем р:
/ ас3 с3 202 _ 400
р “ W ~ 12 • act ~ 12£ “ 12 • 24 “ 12 • 24 1,,ЗУ СМ‘
Так как 1,39 < 3, то параллелепипед будет неостойчив.
Задача. Плоскодонная шаланда весом G = 3 т, имеющая длину L—10 м и ширину В — 3,0 м при высоте борта h — 1,4 м, предназначена для перевозки песка (фиг. 45).
Определить осадку шаланды t и проверить ее остойчивость при условии, что шаланда будет загружена слоем песка об'ем-ного веса у„ = 1,8 т/м3, толщиной </ = 0,60 м. Положение центра тяжести пустой шаланды составляет 55 см над дном шаланды. Длиной носовой части пренебрегаем.
Решение. Осадку t найдем из условия равновесия плавающего тела P = G, где Р—под'емная сила, определяемая по формуле:
Р = BL^ = 3 • 10 • 1 • t = 30 /;
G =	+ Gt = Gt + BLd-[u = 3 + 3 • 10 • 0,6-1,8 = 35,4 m.
Имеем:
30/ = 35,4, откуда:
.  За,4	. -
w=1,18 м
Таким образом высота борта над уровнем воды:
1,4 — 1,18 0,22 м.
Для проверки остойчивости шаланды определим величины дир. Для определения а найдем центр тяжести нашей системы из условия статических моментов относительно оси, проходящей через дно шаланды.
Имеем:
Gi • *ie +	• 4- 3 • 0,55 + 32,4 • 0,30
Л ПО'
Расстояние от дна до центра водоизмещения:
Метацентрический радиус:
р = W’
где 1—момент инерции площади ватерлинии относительно продольной оси:
водоизмещение: W = LBt— 10.3-1,18 = 35,4.и3.
Отсюда: л	22,5 Л««
р = ~35Д “ 0)63 м‘
Сравнивая полученные значения аир, видим, что р> а, т. е. что шаланда удовлетворяет условию остойчивости.
Задача. Пешеходный пловучий мостик запроектирован на понтонах (размеры указаны на фиг. 46). Расстояние между понто-4»	51
нами принято равным 3 м. Вес понтона 200 кг, положение его центра тяжести принято в геометрическом центре его сечения.
Заданная нагрузка от толпы вместе с настилом составляет 350 кг]ма, положение центра тяжести ее над дном понтона принято 2 м.
Проверить пловучесть и остойчивость мостика.
Решение. Для рассмотрения выделяем один понтон с частью настила, нагрузка от которой передается понтону. Длина этой части настила, очевидно, будет L = 3,0 м.
Определяем передаваемый понтону вес настила и толпы:
Gt = 350 • 2-3 = 2100 кг.
Осадку понтона определяем из условия:
G = P,
где G — вес понтона с нагрузкой:
0 = 0,24-0,35 • 2 - 3=2,3 т.
Под'емная сила:
D / , «к о . 2-1,25-0,9 \ ,	___.
Р=у-1 1,25-2 4-----—х-----1г = 3,75г,
\ /
откуда имеем:
2,3 = 3,751,
9 Ч
*=-^ = 0,61 м.
о,/о
Следовательно борт понтона возвышается над уровнем воды на величину:
0,8 —0,61 = 0,19 м.
Для определения остойчивости мостика определим положение его центра тяжести из условия статических моментов относительно оси, проходящей через дно понтона.
Имеем:
Центр водоизмещения находится над дном понтона на расстоянии = 0,305.
Расстояние между центром тяжести и центром водоизмещения: a=zc--------------£-=1,86 — 0,305 = 1,555 м.
Определим величину.
/
,1^. + 2 + , ,3<) = 277
Водоизмещение:
W = 1,25 • 2 • 0,61 + —1,25 °’90’61 = 2>2 л/3, 2*
отсюда: 1 _ 2-77	1 ол
р~ w “ 2,2 “ ,24 М‘
Из полученных значений для аир видно, что р < а, следовательно понтон будет неостойчив.
ГЛАВА IV
ГИДРАВЛИЧЕСКИЕ МАШИНЫ
§ 22. Гидравлические машины
Гидравлические машины вообще, т. е. машины, действующие с помощью жидкости, могут быть двоякого рода: 1) машины-двигатели, приводимые в движение действием протекающей через них воды (водяные колеса, тараны, турбины и т. д.), 2) машины, основанные на принципе Паскаля, которые мы и рассмотрим вкратце в настоящей главе.
Способность жидкости передавать почти мгновенно во все стороны единичное давление, производимое на нее в каком-то определенном месте, послужило основанием для применения жидкости как работающего агента в особом роде механизмах гидравлического типа. Жидкость, вступая в эти механизмы с единичным давлением р, сохраняет это давление и по существу находится в покое, перемещаясь лишь временами с небольшой скоростью с целью достижения тех равновесных условий, которые отвечают рабочим состояниям механизмов. Ввиду значительной величины действующих гидромеханических усилий собственным весом воды при этом пренебрегаем. К числу таких механизмов можно отнести гидравлический пресс, гидроаккумулятор, гидравлический под'емник и прочие машины, нашедшие себе самое широкое применение в разных областях техники.
Ниже приводим технические схемы некоторых гидравлических механизмов. Все эти машины, как уже сказано выше, основаны на одном и том же принципе, поэтому их схемы по сути дела однотипны.
1. Гидравлический пресс является одной из наиболее распространенных гидравлических машин и применяется там, где требуются большие концентрированные сдавливающие усилия (для прессования различных материалов, ковки железных болванок, штамповки разных изделий и д.). Состоит он из
двух частей: насоса и собственно пресса (фиг. 47). Насос состоит из малого цилиндра А, в котором движется вверх и вниз ныряло В, приводимое в движение рычагом ghk. Вода поступает в цилиндр через всасывающую трубу, на конце которой помещен клапан. При обратном движении ныряла клапан закрывается, и жидкость через клапан R поступает в прессовальный цилиндр К. В этом цилиндре вверх и вниз движется поршень D, к которому прикреплена платформа или прессовальный стол. Работа пресса происходит следующим образом: прикладывая к концу рычага насоса силу Q, мы оказываем на жидкость давление Р, причем по закону рычага:
Фиг. 47
п_ Q L I ’
откуда:
Сила Р распределяется по площади поршня со, вызывая единичное гидростатическое давление:
_Р 4Р
& ш ъср *
Это давление, передаваясь на поршень прессовального цилиндра, оказывает на него суммарное давление:
..p-D2 -р D*
4 ~ d* '
R D2 отсюда	отношение это характеризует передаточное
I и
число гидравлического устройства пресса. Полный эффект действия пресса выясняется при сравнении силы R с приложенной к насосу силой Q:
Q Qrf2 Id2 •
Полученная формула имеет приближенный характер, поскольку здесь не учтено трение, возникающее при движении поршней, и вес поршней. При учете этих факторов величина R. получится меньше и формула получит следующий вид:
R _ LD-Q ~~ 71 № ’
(26)
где коэфициент показывающий уменьшение полезной силы R, одновременно может быть принят за к. л. д. пресса. Величина его равна 0,75 — 0,80.
Из полученной формулы видно, что гидравлическим прессом достигается громадное увеличение давления. Так например, имея пресс с величинами d = 2 см,
D=20 см; ф= 10;	= 0,75,
4
получим:
/?	1п400 „Л
5=г — 0,75* 10—— = /50. Q	4
Развиваемые гидравлическим прессом силы достигают весьма значительной величины (существуют прессы, дающие усилие до 4000 и даже до 7000 т).
2. Вызываемые давлением воды в поршнях цилиндра силы могут быть применены не только для операций сжатия, но и для
других технических целей, в соответствии с чем и машины получили другое наименование.
Так например, гидравлический кран, служащий для под'ема грузов, по существу представляет соединение гидравлического пресса с полиспастом (фиг. 48). В цилиндре пресса Л движется поршень В со штоком С. Неподвижные блоки укреплены при этом ко дну цилиндра (на чертеже показан один такой блок Е'), а подвижные блоки Е соединены со штоком С (на чертеже показаны дватаких блока). Цепь, служащая для перемещения груза, укреплена концом а в станину, поддерживающую цилиндр. Затем она идет на первый подвижный блок Е, откуда на неподвижный блок Е', далее опять на подвижный блок и т. д. и наконец через блок Е к грузу Q. Если по трубке впустить в цилиндр сжатую воду, то поршень, двигаясь, тянет за собой Цепь и следовательно поднимает груз Q. Как известно из теории полиспаста, при числе подвижных блоков п, числе неподвижных блоков п’ и при ходе поршня I путь груза увеличится в (п + д') раз и следовательно под’ем груза	I.
Работа, совершаемая при движении поршня, равна РI, где »)— к. п. д.
Работа, совершаемая грузом, равна Q (п + п') I.
Приравнивая оба эти выражения, получим:
Q =	(27)
4 n-f-n
Следовательно применение блоков, увеличивая высоту под’ема в п + п! раз, одновременно уменьшает вес поднимаемого груза в то же число раз. Для того чтобы возвратить поршень в первоначальное положение, воду впускают по
Фиг. 50
Фиг. 49
3. В качестве третьего примера механизма, основанного на гидростатическом давлении, приведем гидравлический аккумулятор. Назначение этого механизма, как следует уже из его названия, — аккумулировать, т. е. запасать в какие-то определенные моменты времени энергию с тем, чтобы впоследствии по мере надобности ее расходовать. Надобность в таком аккумуляторе встречается, когда одним каким-нибудь большим двигателем приходится обслуживать ряд механизмов (так, в порту могут одновременно работать ряд гидравлических кранов, гидравлические машины для открывания и закрывания шлюзов и т. д.), причем работа этих механизмов в большинстве случаев происходит неодновременно. Работа гидравлического аккумулятора сводится тогда к тому, что, принимая в себя всю воду из насосов, он отдает только ту часть воды, которая необходима для обслуживания работающих в данное время механизмов. Устройство гидравлического аккумулятора видно из фиг. 49. Это опять аналогичный предыдущим механизм. Имеется цилиндр, в котором движется поршень, к верхней части которого присоединена доска, поддерживающая нагрузку (ящик с ломом 56	х	'
чугуна, плиты и т. д.). Вода подается в цилиндр из насоса по трубе. При этом поршень с доской и нагрузкой поднимаются кверху. Давление, оказываемое на жидкость, будет при этом О — Т
р = —-—, где О — вес поршня и груза, /—сила трения.
Если при этом открыть кран на трубке, идущей к гидравлической машине (гидравлическому прессу, крану и т. д.), то вода из цилиндра будет притекать к этим машинам и производить полезную работу. В зависимости от того, будет ли вода уходить из аккумулятора в количестве, большем или меньшем, чем притекать от насоса, поршень аккумулятора либо поднимется либо опустится. Из приведенной выше формулы видим, что давление р в аккумуляторе получается тем больше, чем меньше площадь его поршня. В случае необходимости очень больших давлений площадь эта может оказаться столь малой по сравнению с грузом, что поршень окажется ненадежным в отношении своей прочности. В таких случаях поршень часто устраивается с кольцевым уступом и хвостом, имеющим меньший диаметр. Посту-
пающая жидкость оказывает давление на площадь этого кольцевого уступа, т. е. на площадь ш = шх — <оа.
Такой аккумулятор, в котором единичное давление получается значительно больше обыкновенного, называется диференциаль-ным (фиг. 50).
Задача. Пренебрегая трением, определить силу, необходимую для удержания поршня, если дано, что Лх=2,0 м, А4=3,0 м, D=30 см и й=5сле(фиг. 51).
Суммарное избыточное давление на поршень с левой стороны
равно:
/	D \ к D3
Рмв = р 2 = 7 /ц + Аа +	) -f-=0,001 -515 х
\ / *
3,14 • 900 осо о_ X —-—-------= 363,85 кг.
4
Давление с правой стороны равно:
=Л(В-»)» Т (л, + 'а)- 0,001 • З15х X 3,14(900 — 25) д216|3), кг
Для удержания поршня в равновесии необходимо приложить силу Q, равную Q = Рлел Рnpat — 363,85 — 21636 = 147,49 кг.
ГИДРОДИНАМИКА
ГЛАВА V
ОБЩИЕ ПОНЯТИЯ
§ 23. Установившееся и неустановившееся движение
Переходя к вопросам гидродинамики, мы об'ектом своего изучения*будем иметь какое-то пространственное поле, внутри которого помещены движущиеся частицы жидкости, каждая из которых обладает скоростью и единичным давлением.
Эти факторы движения распределены непрерывно во всех точках поля, т. е. между двумя точками, взятыми бесконечно близко друг к другу, они должны отличаться на бесконечномалую величину.
Фиг. 52
Возьмем в движущемся потоке частицу а и проследим за ее движением (фиг. 52).
Пусть за промежуток времени t она последовательно пройдет’ положения /, 2, 3, имеющие различные координаты. При этом скорость и единичное давление в точке а должны все время изменяться, т. е. они являются функциями координат точки. Рассмотрим теперь другую точку Ь, движущуюся по той же траектории 1, 2, 3 вслед за точкой а. Таким образом точка b будет попадать в те же места/, 2,3 и будет иметь те же координаты, что и предшествующая ей точка а, только время ее прохождения будет другим.
Если при этом единичное давление и скорость точки Ь окажутся другими, чем в предшествующей точке а, то движение называется неустановившимся, если же они сохраняют те же значения, движение называется установившимся.
Таким образом установившееся движение это такое, пои котором скорость и единичное дав ение в точках жидкости являются только функциями координат точек и непосредственно от ере-58
мена не зависят. Неустановившимся движением называется такое, в котором скорость и единичное давление в точках жидкости являются функциями не только координат точек, но и времени. При установившемся движении жидкости частицы ее бегут одна за другой по траекториям, имеющим неизменяемую форму во все время движения. При неустановившемся движении, поскольку изменение скорости происходит не только по величине, но и по направлению, траектории движения частиц непрерывно меняются со временем.
В качестве примера установившегося двйжения может служить истечение жидкости из отверстия в сосуде, когда горизонт воды в этом сосуде держится постоянным. Если же этот горизонт начинает со временем меняться, то скорость и единичное давление в частицах начнут тоже меняться; из сосуда начнет выходить струя различной формы (так называемое „биение” струи), т. е. движение станет неустановившимся (фиг. 53).
§ 24, Кинематические элементы движения
В гидростатике мы занимались изучением сил, действующих в жидкостях, находящихся в состоянии равновесия. Переходя к изучению законов, связывающих эти силы с движением жидкости, мы кроме вопроса о напряжениях должны еще изучить кинематические элементы движения, т. е. перемещения и скорости частиц. В самом общем случае движения перемещения частицы жидкого тела могут быть разделены на поступательное и вращательное, причем поступательное движение может быть тоже разделено на два вида: 1) движение, при котором происходит перемещение частицы как целого с одинаковой скоростью, присущей ее центру, и 2) движение, перемещающее точки этой частицы друг относительно друга (деформационное движение).
Движение, в котором имеет место только поступательное перемещение частиц, называется безвихревым, а движение, в котором имеет место вращательное перемещение частиц, называется вихревым.
Рассматривая более подробно оба вида движения, выделим для этого из жидкости частицу в форме прямоугольного параллелепипеда со сторонами dx, dy, dz и приложим все действующие скорости. При этом можно говорить о трех возможных случаях:
1.	Если скорости действуют по всем параллельным граням частиц, то частицы, перемещаясь, изменяют свое положение относительно всех трех координатных осей. Такое перемещение является наиболее общим и называется пространственным. 
2.	Если по каким-нибудь двум параллельным граням скорости частиц равны нулю, то частицы уже не будут перемещаться относительно оси, перпендикулярной к эГим" граням, и движение тогда будет происходить в плоскости, проходящей через две остальные координатные оси. Такое движение называется плоским,
3)	Если скорости действуют только по двум параллельным граням, а по остальным четырем равны нулю, то движение будет происходить по направлению оси, перпендикулярной к этим двум граням. Такое движение называется одноразмерным.
§ 25. Схема движения
Установив кинематические элементы отдельной движущейся частицы, мы в порядке постепенного усложнения должны перейти
к рассмотрению движения целой массы совместно движущихся частиц. Подобное движение, как об этом ниже подробно будет
изложено, во многих случаях является крайне сложным, поэтому для облегчения изучения этого движения оно заменяется ка-
кой-то схемой, расчленяющей движение на его составные части.
Рассмотрим отдельные части указанной схемы.
1. Линия тока. Возьмем в жидкости произвольную точку А и отложим ее вектор скорости ut (фиг. 54). На этом векторе возьмем вторую точку В и, построив соответствующий ей вектор
выберем на нем третью точку
Если полученные таким образом точки взяты бесконечно близко одна от другой, то ломаная линия ABCD превратится в кривую, называемую линией тока. Следовательно линией тока называется кривая, проведенная через ряд точек так, что направление скоростей в этих точках является к ней касательным.
Очевидно, что в установившемся движении линии тока совпадают с траекториями движения точек. При неустановившемся же движении эти кривые будут различны.
2. Элементарная струйка. Если в жидкости провести элементарную площадку Д«>, затем через все точки, находящиеся как внутри этой площадки, так и на ее контуре, провести линии тока, то получим об'емный пучок линий тока, называемый элементарной струйкой (фиг. 55). При установившемся движений элементарная струйка обладает следующими свойствами:
а)	Так как при установившемся движении линии тока, из которых состоит струйка, не меняют своей формы со временем, то и форма всей элементарной струйки остается неизменной во времени.
б)	Так как контур элементарной струйки ограничен линиями тока, к которым, как известно, скорости касательны, то приток 60
от остальной жидкости к струйке и отток от струйки к остальной жидкости являются невозможными.
в)	Имея в виду незначительность поперечного сечения элементарной струйки, скорости во всех точках одного и того же поперечного сечения струйки можно считать одинаковыми.
количество жидкости, протекающее в единицу времени через поперечное сечение струйки, называется элементарным расходом.
Обозначим этот элементарный расход через q, тогда, имея в виду указанные свойства струйки, получим следующее выражение для элементарного расхода:
(28)
п I
3. Вихревая линия и вихревой шнур. Если частицы жидкости помимо поступательного движения находятся еще во вращательном движении, в нашу схему необходимо ввести еще понятие о вихревых линиях и вихревых шнурах. Для уяснения этих понятий возьмем в жидкости частицу А, ось вращения которой является линией 7—2 (фиг. 56). Выбрав на этой оси другую точку В, построим соот- б ветствующую ей ось вращения 2—3.	Арч
Возьмем на этой оси новую частицу С и, а> AjZ сделав аналогичное построение для ряда других частиц, получим ломаную линию 1—2—3—4, которая, в случае если ча- зОмГэ стицы взяты бесконечно близко друг к другу, превратится в кривую, назы-ваемую вихревой линией.
Таким образом вихревой линией назы-вается кривая, у которой каждый бес- д конечно-малый отрезок служит в дан- *' ный момент временной осью вращения фИГе 55 определенной жидкой частицы.
Если через все точки бесконечно-малого контура провести вихревые линии, то совокупность совместно
щихся вокруг этих линий частиц жидкости называется элементарным шнуром, а боковая поверхность его образует так называемую вихревую трубку.
Из приведенных построений вполне очевидна аналогия между линией тока и вихревой линией, с одной стороны, и между элементарной струйкой и элементарным вихревым шнуром—с другой стороны.
4. Поток. Потоком называется совокупность элементарных струек, движущихся в данном русле (при наличии вращательного Движения в схему потока пришлось бы включить и вихревые трубки). В потоках помимо жидких частиц имеются также и граничные линии твердого тела, оказывающие значительное влияние на движение жидкости. Таким образом в потоках различают следующие гидравлические элементы.
Фиг. 57
(фиг. 57) вращаю-
а)	Живым сечением потока называется часть поверхности, проведенной нормально к потоку и заключающаяся в его пределах (фиг. 58). Строго говоря, эта поверхность должна быть криволинейной. Так например, если рассматривать поток со сходящимися или расходящимися в плане струйками (фиг. 59), мы, очевидно, в качестве живы* сечений будем иметь криволинейные поверхности (на фиг. 58 они представлены кривыми MN). Однако в большинстве практических случаев для упрощения изучения гидравлических явлений струйки считаются параллельными (см. далее § 26 о медленно изменяющемся движении). Живые сечения в этом случае будут, очевидно, плоскими. Площади живых сечений обозначим через ш,
б)	Смоченным периметром называется линия соприкосновения жидкости с твердыми границами потока. Так как по этой линии происходит трение жидкости о твердые стенки, то величина смоченного периметра является одной из характеристик
Фиг. 58
Фиг. 59
сопротивления жидкости движению. Величину смоченного периметра обозначаем через X.
в)	Если возьмем два русла различной формы, но со стенками одинаковой шероховатости, то при пропуске одного и того же расхода мы в обоих случаях получим различные величины смоченного периметра. Для того чтобы получить возможность сравнивав между собой сопротивления этих русел движению, мы должны в обоих случаях взять отношение площади живого сечения к смоченному периметру. Это отношение,показывающее, ' какая величина площади живого сечения приходится на единицу длины смоченного периметра, называется гидравлическим радиусом. Обозначая ее через R, получим выражение:
(29)
R= — X
Гидравлический радиус имеет самое широкое применение в различных гидравлических формулах. Особенное значение он имеет при изучении движений в руслах некруглой формы, где он играет роль, аналогичную роли диаметра при напорном движении в круглых трубах. В последнем случае гидравлический радиус выражается через диаметр следующим образом:
п nD2 D
от«уда:	Д ” Йо " Г
D = 4R.	(29а)
§ 26. Медленно изменяющееся движение
выделим иэ жидкости какую-
Фиг. 60
Установив в нашей схеме понятие о потоке, мы имеем дело, вообще говоря, с явлением весьма сложного движения жидкости. Для облегчения изучения этого движения гидравлика вводит некоторые упрощения, одним из которых является введение понятия о медленно изменяющемся движении.
Под медленно изменяющимся движением гидравликой понимается движение, очень близкое к паралЛелеструйному, оно, очевидно, должно удовлетворять следующим условиям:
1. Кривизна струек должна быть весьма незначительна, или, иначе, радиус кривизны должен быть очень велик.
2. Угол расхождения между струйками должен быть очень мал (фиг. 60),
Из указанных свойств медленно изменяющегося движения следует, что оно практически может быть рассматриваемо как движение, при котором скорости и ускорения всех частиц направлены параллельно друг другу и нормально к плоскости живого сечения. Поэтому, если мы частицу abed (фиг, 61) и рассмотрим ее равновесие согласно принципу д'Аламбера, т. е. если мы приложим к ней внешнюю силу в виде ее собственного веса G, силы связи в виде давления сосед
них частиц Р и силу инерции, равную mj, то эта сила инерции тоже будет направлена нормально к плоскости живого сечения (так как по предыдущему в плоскости живого сечения / = 0). Поэтому, если мы, рассматривая равновесие частицы, будем проектировать все силы на вертикальную ось, то сила инерции в сумму проекций не войдет; следовательно равновесие частицы в плоскости живого сечения ничем не будет отличаться от равновесия точки, находящейся в состоянии покоя; поэтому' и силы связи (давления) частицы в этой плоскости ничем не будут отличаться от давления в точка, находящейся в состоянии покоя. Отсюда вытекает следующий важный вывод: при медленно изменяющемся движении жидкости распределение давления по живому сечению происходит по гидростатическому закону.
Поэтому графическое изображение этих напряжений в точках одного и того же живого сечения дает нам эпюру в форме трапеции.
На фиг. 62 показаны случай А — распределение давлений при медленно изменяющемся движении и случай В—распределение Давлений в криволинейном потоке. Пример .распределения давления в криволинейном потоке приводится также далее при изучении движения жидкости через водослив (см. гл. XIII).
Следующее важное свойство потока при медленно изменяющемся движении заключается в том, что удельная потенциаль-
пая энергия во всех точках данного живого сечения — величина постоянная. В самом деле, обращаясь к сказанному в § 15 об удельной потенциальной энергии покоящейся жидкости, мы видим для случая медленно изменяющегося движения, что данные там законы полностью сохраняют свою силу.
§27. Расход и средняя скорость
Расходом называется количество жидкости, протекающее в единицу времени через данное живое сечение.
Обозначив расход для элементарной струйки через q, получим для элементарного расхода:
q = и Дш , а в полном потоке расход:
Q = и dw, ш
Назовем средней скоростью потока воображаемую скорость, с которой должны дыли бы двигаться все струйки при условии, что расход оказался бы равным расходу при движении с истинными скоростями.
Заменив следовательно истинную скорость и в струйках потока средней скоростью V, получим:
Q = fv dw = vf dw ID	Ш
или, иначе,	__________
I Q = ш x>, I	(30)
m. e. расход в потоке равняется произведению площади его живого сечения на среднюю скорость.
§ 23. Понятие о равномерном движении
Это понятие для потоков может быть сформулировано двояко:' 1 Если назвать «соответствующими точками" точки пересечения одной и той же струйки с разными живыми сечениями потока, то для осуществления равномерного движения должны быть соблюдены два условия: во-первых, должно существовать равенство скоростей в соответствующих точках потока и, ва-
вторых, должна существовать неизменяемость живых сечений по длине русла (т. е. русло должно быть призматичным). Таким образом это понятие о равномерности базируется на равенстве истинных скоростей в струйке.
Ввиду затруднительности определения для каждого отдельного случая величины „соответствующей скорости" в практике при определении равномерного движения обычно исходят из равенства средних скоростей в живом сечении.
В этом случае равномерным движением потока называют такое, при котором средние скорости во всех его живых сечениях равны между собой.
§ 29. Понятие о напорном и свободном движении
В зависимости от источника силы, действующей на жидкость и приводящей ее из состояния покоя в состояние движения, все виды потоков могуть быть разделены на следующие категории:
1) Напорным движением потока называется такое, при котором движение совершается под влиянием давления, сообщаемого каким-либо внешним источником. При этом жидкость заполняет полностью сосуд, в котором она движется. Примером такого движения может служить движение воды в водопроводных трубах.
2) Свободным движением потока называется такое, при котором жидкость перемещается только под влиянием собственного веса. Такое движение характеризуется наличием так называемой своболной поверхности, т. е. поверхности с заранее известным и одинаковым во всех ее точках давлением (обычно это давление является атмосферным). Примером такого движения может явиться движение в реках, каналах и канализационных трубах.
§ 30. Методы изучения законов движения жидкости
Установив, какие величины нас должны интересовать при изучении движения частиц жидкое и, необходимо перейти к изучению законов, связывающих эти величины с величинами, наперед заданными и известными (т е. с внешними силами, действующими на жидкость). Зная эти законы, мы сумели бы определить в каждой частице движущейся жидкости ее скорость и давление, что было бы достаточным для разрешения всех проблем, связанных с движением частицы. Инженерных же проблем подобного рода существует большое количество: сюда относятся движение жидкости в разного рода машинах (насосах, турбинах), ее движение в водопроводных трубах, каналах, реках, разного рода гидротехнических сооружениях и т. д. Во всех этих случаях мы имеем Дело с движением значительных по своему об'ему количеств жидкости или то, что мы назвали потоком.
Получение формул, безупречных в научном отношении и надежных в практическом смысле, оказалось задачей крайней сложности, и наука вынуждена была пойти к ее разрешению не-Б Гидравлика	65
сколькими различными методами, которых мы здесь вкратце коснемся.
1.	Самым логичным и выдержанным с научной точки зрения методом явилось бы изучение потока путем расчленения его на отдельные составные элементы — струйки и линии тока. Начав рассмотрение с первичного бесконечно-малого элемента, приложив к нему все действующие силы и применив к нему общие законы механики, получим диференциальные уравнения, характеризующие состояние этого элемента.
Интегрирование этих уравнений по длине струйки должно дать законы распределения давлений и скоростей в точках, взятых вдоль струйки. Интегрирование же по поперечному сечению потока должно дать эти же величины, распространяемые на целый поток. Такой чисто аналитический метод является наиболее всеоб'емлющим и научно выдержанным, однако сложность решения подобным методом задач оказалась настолько велика, что для большинства практических вопросов этот метод окончательного ответа на сегодняшний день не дает.
2.	Сущность другого метода заключается в том, что рассматриваются не диференциальные элементы движения жидкости, а какие-то конечные об'емы. К этим конечным об'емам больших или меньших поперечных размеров применяются общие законы механики и физики в виде уравнений равновесия или закона сохранения энергии. Взаимодействие отдельных частей жидкости при этом из рассмотрения выпадает, что весьма упрощает рассмотрение вопроса. Для искомых величин (скорости и давления) даются не точные аналитические выражения, характеризующие их состояние в каждой частице, а некоторые средние величины, получаемые приближенным способом. Естественно, что этот метод, сильно упрощающий решение задач, страдает в смысле строгости и точности получаемых решений.
3.	При изучении ряда вопросов гидравлики смог быть весьма плодотворно применен метод размерности, сущность которого заключается в нижеследующем: как известно, всякая физическая величина характеризуется своей размерностью, которая отражает ее природу и ее физическую сущность. Если у нас имеется уравнение, связывающее аналитически между собой какие-нибудь физические величины, то, очевидно, это уравнение не просто устанавливает числовую связь между входящими в нее величинами, а по существу запечатлевает физическую сущность явления. Отсюда понятно, что такое уравнение между физическими величинами возможно только в том случае, если эти величины имеют одну и ту же размерность или, иначе выражаясь, если уравнение однородно. Как известно из теории измерений, все единицы меры могут быть сведены к трем основным единицам, за которые обычно принимаются единица длины, массы и времени. Следовательно размерность любой физической величины может быть выражена через эти три основные единицы. Если какая-нибудь величина выражается через несколько основных единиц меры, то измерение в этом случае называют составным, или сложным. 66
Равенство между сложными размерностями двух физических величин предполагает также равенство между основными единицами меры, из которых составлена эта сложная размерность. Таких равенств по количеству основных единиц, очевидно, может быть три. Таким образом если у нас имеются две физических величины, из которых размерность одной содержит 7\ единиц времени, /Иг единиц массы и £, единиц длины, а размерность второй содержит Тг, Мг и £2 этих единиц, то равенство размерности, характеризующей эти физические величины, может быть представлено в виде следующей системы трех уравнений.
= 72; Д = М2:	= Z2.	(31)
На этих трех уравнениях и основан метод размерности, дающий возможность установить аналитическую зависимость между несколькими заранее заданными физическими величинами.
В самом деле, пусть нам известно, что какая-то физическая величина А зависит от каких-то других физических величин В, С, D, и т. д. Допустим для начала, что этих величин только три. Задаемся при этом следующей формой функциональной зависимости между этими величинами.
А АОВХ Cv D*. |	(32)
Далее, зная размерности величин А, В, С, D, мы составляем три уравнения и из них определяем значение трек показателей х,у, иг. Если неизвестных величин четыре и более, то решение включает уже в себе один или более неопределенных показателей, которые находятся другими способами. Величина Ло является при этом безразмерным числом, которое, очевидно, определяется тоже только опытом.
4.	Четвертый метод, широко применяемый гидравликой и неразрывно связанный с предыдущими методами, заключается в получении искомых законов на опытном изучении вопросов. Опыты, применяемые в гидравлике, бывают двух типов: с одной стороны, это могут быть опыты над отдельными гидравлическими явлениями, проводимые в естественных условиях; тогда полученные результаты после их обобщения распространяются на аналогичные встречающиеся в практике случаи. Другой тип опытов — это опыты, производимые в лабораторной обстановке, в которой явления воспроизводятся в уменьшенном масштабе. Для того чтобы иметь право распространения полученных результатов на явления, происходящие в естественных условиях, необходимо, очевидно, знать законы, связывающие величины, полученные в лабораторной обстановке, с величинами, получаемыми в естественных условиях. Такие законы называются законами подобия.
§ 31.	Применение аналитического метода в гидродинамике
Приступая к изучению движения жидких тел первым чисто аналитическим методом общих законов, мы в качестве заданных величин имеем внешние силы, действующие на жидкость. Результатом воздействия этих внешних сил являются внутренние силы возникающей в каждой точке жидкости (единичное в*	67
давление и трение), а также скорость, представленная своими тремя компонентами по координатным осям. Так как определение сил трения является особенно сложной задачей, то первоначально на\ка пошла по пути упрощения явлений, рассматривая жидкость идеальной (см. § 7). При введении подобного упрощения в каждой точке останутся 4 величины, подлежащие определению (гидродинамическое давление и 3 проекции скорости). Эти величины в разных точках жидкости различны и при установившемся движении являются функцией только координат точек. Для определения вида этой функциональной зависимости механика распечатает ч< тырьмя уравнениями. Если мы к выделеннсму элементу жидкости приложим все действующие силы, включая сюда согласно принципу д'Аламбера также силу инерции, спроектируем затем все эти силы на три координатные оси и приравняем су^му этих проекций нулю, мы получим три искомых уравнения; 4-е уравнение может быть получено без особых трудностей, если учтем, что жидкость нами принимается неразрывной и несжимаемой и что через ее поперечное сечение проходит все время одинаковое количество частиц.
Выразив аналитически это условие, мы можем получить 4 е уравнение, называемое уравнением неразрывности. Применив > казанные законы к движению частицы, Эйлер в 1755 г. вывел уравнения, связывающие в диференциальной форме заданные внешние силы, силу давления и скорости1.
Эти диференциальные уравнения мо. ут быть проинтегрированы для случая установившегося движения. Если на жидкость действуют только силы тяжести, частный вид интеграла, взятого по длине какой-то струйки, получает следующий вид:~
(33)
п	Ц2
z 4- £-5 4.	— const,
Т	2g
где г — текущая координата точек струйки, р и iz— давление и скорости в них. Павье, приняв эту зависимость и выразив силы трения как функцию от ско-
рости, дополнил уравнения Эйлера и представил их в форме, учитывающей также эти силы.
Таким образом Навье дал уже три совокупных диференциальных уравнения для вязкой жидкости, которые впоследствии удалось проинтегрировать для некоторых простейших случаев движения. Между прочим этим методом удало ь теоретически найти величину скорости и давления в частицах жидкости, движущейся параллельно в трубе. Однако при проверке полученных результатов опытным путем оказалось, что они справедливы только для трубок с очень маленьким диам« тром и решительно отличаются при движении в трубах с более или менее значительными диаметрами.
Дальнейшие исстезования показа ш существование принципиального отличня в законах движения очень маленьких и более зн1чите1ьных об'емов жидкостей. Особенно значительную роль в исследованиях этих законов сыграл английский, ученый Осборн Рейнольдс (см. далее § 41).
ГЛАВА VI
ОСНОВНЫЕ ЗАКОНЫ ГИДРОДИНАМИКИ
Сложность проблемы движения жидкостей сильно ограничивает применение к ее изучению чисто аналитических диференциальных методов, указанных в § 30. Гидравлика для изучения явлений, имеющих место при движении жидкостей, воспользовалась другими методами, указанными в том же параграфе, на основании которых ею были получены два основных закона (уравнение расхода и уравнение Бернулли), являющихся главным
1 Подробный вывод этих диференциальных уравнений и их интегрирование
приводятся в разных курсах. См. например проф. Павловский, Гидравлика, изд. 1928 г.
орудием для изучения всех практических случаев движения жидкостей.
К изложению этих законов мы сейчас и перейдем.
§ 32.	Уравнение расхода для элементарной струйки и потока
Рассмотрим элементарную струйку ABCD (фиг. 63).
Пусть через промежуток времени Д( частицы из сечения А В перемещаются в сечение А'В', а из сечения CD — в сечение CD'. Обозначим пройденные пути через и Д$2> где = = «jA t, а Д s4 = иа Д t, обе'м АВ А'В' = Д (Oj Д Sj = До»! их Д t, а об'ем
CDCD' = До>2 Д $2 = иа
Из условия неразрывности и несжимаемости жидкости, а также из второго свойства элементарной струйки (см. §25) следует что эти об'емы должны быть равны друг другу.
Об'ем АВА'В' равен об'ему -CDCD', откуда:
Д «>! их Д t = Д и>2 и.х A t
Фиг. 64
или
Д и, их — Д u.t = q = const.	(34)
Следовательно элементарный расход через любое сечение струйки есть величина постоянная.
Уравнение расхода для потока. Разбивая поток на ряд струек (фиг. 64), мы для любой струйки можем по предыдущему написать:
Д (Bj их = Д о>2 и2.
Проинтегрировав обе части этого уравнения, получим:
,fux du>l = f ua d<s>a или Qj = Q2 =const, U>1	U)|
fn. e что расход через все живые сечения потока является постоянной величиной.
Выразив расход через средние скорости, получим уравнение расхода в следующем виде:
(Dj Vx — «>2 Vt.
(35)
69
§ 33	Уравнение Бернулли для элементарной струйки идеальной жидкости
Возьмем на оси элементарной струйки движущейся идеальной жидкости точку / и на бесконечно-маюм расстоянии ds от нее другую точку Г (фиг. 65). Проведем через эти обе точки нормальные к струйке сечения и выделим из струйки элементарный об‘ем aba’b'. Элементарные площадки ab и а'Ь' вЭяты бесконечно близко друг к другу и отличаются между собой на бесконечно малую величину 2-го порядка. Поэтому с достаточной степенью точности считаем их одинаковыми.
Обозначим эти элементарные площадки через Дш, а вертикальное расстояние их центров тяжести до произвольно взятой
оси X через z и z', Так как с увеличением $ ордината z убывает, то приращение z будет отрицательной величиной; поэтому для выбранных точек имеем:
dz = г'— z = — (z—z').
Применим к выделенному об'ему основное уравнений движения, согласно которому каждое движущееся тело если приложить к нему внешние силы и силы инерции, находится в равновесии. Рассмотрим в отдельности каждую из этих сил.
1.	К частицам сечения ab приложено давление отброшенных слева частиц жидкости. Обозначив единичное давление в точке /через ра, суммарную силу, действующую на сечение ab, через Р, получим:
Р = Ра Дш.
2.	На частицы сечения а'Ь' действуют аналогичные силы отброшенных справа частиц. Единичное давление в точке /’ равно (ра + Фа). а суммарное давление по сечению a'b' Р'= (pa-\-dp^ 4®.
3.	На боковую поверхность струйки действуют нормальные силы рп (касательные силы по этой поверхности здесь не рассматриваются, так как жидкость считается идеальной).
4.	Собственный вес выделенного об'ема G = ^mds, проекция этой силы на ось струйки равна:
G cos а = уДа» ds Zl , -- = — “уДш dz.
аь
5.	Силы инерции, как известно, равны произведению из массы данного об'ема на его ускорение; обозначив эти силы через J, а массу через dm, имеем:
1 j du
J dm—jT, at
где
dm = -2- Дш ds, g
а
du _ du ds du
~dt~ ds dt “•
Подставляя эти значения в выражение для сил инерции, получим:
J= —^wds-u^ = — bnudu. g ds g
Так как все эти силы согласно принципу д'Аламбера должны находиться в равновесии, то сумма их проекций на любую ось должна равняться нулю. Выберем за ось проекций ось струи.
Имеем:
Р — Р + G cos а — J = 0.
Подставив вместо сил полученные для них раньше выражения, имеем:
ра&м—раЬ<в — dpa^ — y^(xidz —-~^<Dudu = 0.
Разделив все уравнения на величину -уД® и переменив знаки на обратные, получим:
<а)
Так как a у </(«’), то все величины, входящие в уравнение (а), представляют собой диференциалы каких-то перемен-71
них, и уравнение виде:
может быть переписано в следующем
зная, что только постоянные величины имеют диференциалы, равные нулю, получим:
п и2
z — 4-	= const.
7 2g
Точка 1 в жидкости была выбрана совершенно произвольно, поэтому полученный результат будет, очевидно, верен и для любых двух точек, взятых на оси. Выбрав поэтому какие-то две точки 1 и 2 на оси струи, мы Вправе для них написать следующее уравнение1:
(36)
Полученное уравнение называется уравнением Даниила Бернулли по имени известного итальянского гидравлика, давшего его вывод.
Как явствует из самого вывода, это уравнение дает связь между скоростью, давлением и координатами точек элементарной струйки. Необходимо обратить внимание на то, что это же уравнение, как указано в § 31, получено как один из интегралов диференциальных уравнений Эйлера. Кроме того, сравнивая уравнение с данной выше в § 15 формулой (11) (энергетический закон в покоящейся жидкости), мы видим, что последняя представляет собой частный случай уравнения Бернулли и может быть непосредственно из него получена, если скорость приравнять нулю.
§ 34. Механический смысл уравнения Бернулли
Ввиду особой важности, которую имеет уравнение Бернулли, рассмотрим его механическую трактовку.
Представим первичное уравнение в немного измененном виде: iz Z) i Pi-P*
и определим механический смысл каждого из стоящего в скобках двучлена. Для этого будем рассматривать по предыдущему элементарную струйку, ограниченную по бокам сечениями, проходящими через точки 1 и 2 (фиг. 66k Как известно, на эти сечения действуют нормальные силы Р, = ру* и Ра = р^ь. Пусть за элементарный промежуток времени струйка ABCD пере-
* Индекс а для краткости письма мы здесь опускаем и также поступаем далее при применении уравнения Бернулли.
72
местилась в положение А1 В'CD1. Так как конечные результаты этого перемещения равносильны перемещению об'ема АВА'В' в положение CDC'D', то все изменения, происшедшие с элементарной струйкой, должны быть взяты именно для этого перемещения.
Механический процесс, происходящий при этом, сведется, очевидно, к тому, что, с одной стороны, приложенные к об'ему силы совершают какую-то работу а, с другой стороны, вследствие изменения своей скорости струйка изменяет свою живую силу.
Определим в отдельности работу, совершаемую каждой силой.
1. Работа, совершаемая силой тяжести об'ема ABCD, при перемещении струйки, будет, очевидно, равна произведению G fa — z2), где fa — z2)—разность координат точек 1 и 2 представляет собой вертикальное перемещение силы О.
Разделив эту работу на вес об'ема G, получим работу, совершаемую единицей веса об'ема жидкости. Обозначив эту единичную работу через F, получим:
F = z1 —za.
2. Определим работу, совершаемую силами Pj и Р2. Обозначив эту работу через 7\ и Т2, найдем, что
Fj - PiSi - А<М1-
Умножив и разделив правую часть уравнения на у и зная, что вес O = ps, найдем:
7 ~Р'° 1 I ’
а работа, отнесенная к единице веса, равна -у-; аналогично этому можем получить, что работа силы P2t отнесенная к единице веса:
т* = — •
Суммируя всю работу, совершаемую при перемещении струйки, найдем, что эта работа равна:
G(Zl-Zi)^GP-^,
а отнеся эту работу к единице веса, получим, что эта единичная работа равна:
Изменение живой силы струйки при этом перемещении равно: и2 ти^_ G (и/ — и2)
т~2~ 2 “У 2
Относя по предыдущему это изменение к единице веса жид-«а2 — и,2 _
кости, получим, что это изменение равно ——Так как со-
гласно известному в механике уравнению живых сил, работа, совершаемая силами при перемещении какого-нибудь тела, равна изменению его живой силы, то
(	\ . I Pi—Рь\ (Ui—uSX
+ ИН/1 = НЧ/- •
Следовательно уравнение Бернулли может быть рассмотрено как специальное применение закона живых сил к случаю уста-носившегося движения элементарной струйки.
§ 35. Энергетический смысл уравнения Бернулли
Уже в § 14 было выяснено энергетическое значение величин z и , входящих в уравнение Бернулли; как там было указано, z представляет собой удельную энергию положения, — удельную энергию давления жидкости, а сумма z +у-представляет собой удельную потенциальную энергию частицы жидкости в данной .	, т	.	«2
струйке. Нетрудно показать также энергетический смысл члена В самом деле, кинетическая энергия жидкости массы т равна ти2 „
—Если же взять частицу весом, равным единице, то ее масса 1	и?	и2
будет — а кинетическая энергия . Следовательно величина является удельной кинетической энергией, т. е. кинетической энергией для частицы единичного веса.
р и2
Весь трехчлен z + —+ к- представляет собой сумму удель-ной потенциальной и кинетической энергии, т. е. полную удельную энергию е в данной частице жидкости. Следовательно с энергетической стороны выведенное нами уравнение Бернулли для идеальной жидкости может трактоваться как равенство удельной энергии во всех частицах элементарной струйки идеальной жидкости и является частным выражением общего закона сохранения энергии.
Обозначив полную удельную энергию через е. из уравнения (36) имеем:
ei ~ e const
При этом необходимо подчеркнуть, что это равенство удельной энергии верно лишь для точек одной и той же элементарной струйки. Если взять точки разных струек, то величина удельной энергии может в них оказаться различной, так как переход частицы из одной струйки в другую может сопровождаться вихрями, в которые превратится часть нашей энергии. Если же движение безвихревое, то уравнение Бернулли окажется верным для всех точек данного потока.
§ 36. Гидравлический смысл членов уравнения Бернулли
1)	z — координата движущейся точки.
2)	— — высота поднятия жидкости в закрытой пьезометрической трубке.
3.	Для определения гидравли-иа , ческого смысла члена вообразим в данной точке две трубки, из которых одна представляет собой обыкновенную пьезометрическую трубку, а другая имеет изогнутый против движения конец (фиг. 67— трубка Пито).
Если высота поднятия в обычной пьезометрической трубке будет то в изогнутой трубке жидкость должна подняться на добавочную высоту hx‘.
Рассмотрим жидкость, находящуюся в изогнутой трубке, как элементарную струйку и напишем уравнение Бернулли для точек 1 и 2:
(а)
г1 + А+£11==2а+А1 + ^; 1 7 2g 8 у 2g’
-h ;	= Zt +	+ hi ;	= 0;	= 0;
вставим эти значения в уравнение (а):
*i + Ai + ^ =	+ Ai или
т. е. третий член уравнения Бернулли равняется дополнительной высоте поднятия жидкости в изогнутой трубке по сравнению с ее поднятием в обычной пьезометрической трубке.
§ 37.	Определение размерности членов уравнения Бернулли
1)	z как высота измеряется в единицах длины.
л Ра сила/длива«
у =
л\ U? ___длинаУвремя1	л
2g длина/нремя1 e ДЛИНЯ*
Следовательно все члены уравнения Бернулли имеют одну и ту же размерность длины.
§ 38.	Графическое изображение уравнения Бернулли для идеальной жидкости
Отложим в одном и том же масштабе по вертикали вели
чины z, (фиг. 68).
Соединив концы отрезков —, получим линию, называемую пье-
Y н2 зометрической, а соединив получим линию, называемую напорной.
Пьезометрическая линия характеризует изменение удельной потенциальной энергии по длине струйки.
Напорная линия характеризует изменение всей удельной энергии по длине струйки
Для идеальной жидкости напорная линия всегда горизонтальна.
Фиг. 69
Задача. По круглой трубе переменного сечения движется жидкость об'емного веса у ••• 2,0 г{см' (фиг. 69). Найти, пренебрегая сопротивлениями, разность уровней воды в пьезометрах А, если диаметр узкой части трубы rf = 0,l ли широкой части D — 0,25 м, а расход Q = 100 л!сек.
Решение. Скорость в узкой части:
127,4 nd* 3,14-1	'
Скорость в широкой части:
и = Q__ Q-4	100-4 п. д ,
111	= 3,14-6,25	20,4	'
Составляем уравнение Бернулли для точек 1 и 2: Получаем:
Pl । ц12 _ P'l I цг2
Т 2g Т 2g’
откуда:
Т I 2g 2g’
т. е.
. uf — u/ 12,74s — 2,04»
Л~~ 2g~ =--------ВД2-----8Л
§ 39.	Уравнение Бернулли для реальной жидкости
В реальной жидкости при перемещении точки из первого положения в положение второе должна будет произойти некоторая потеря энергии, поэтому et ф е% или et = e2-}~ 'E.h, где Ъй называется удельной потерянной энергией и с физической стороны представляет собой количество энергии, теряемое единицей веса движущейся жидкости при ее перемещении из первого во второе положение.
Уравнение Бернулли для реальной жидкости на основании того же энергетического закона примет следующий вид (вместо ех и подставляем их значения):
1*. + ^-,+^+ I (37) __I __I XS_
Так как в полученном уравнении шесть членов измеряются в единицах длины, то и 7-й член уравнения — 2Л тоже должен измеряться в единицах длины
Графическое изображение уравнения Бернулли для реальной жидкости (фиг. 70). Абсолютное изменение удельной потенциальной энергии между точками 1 и 2 будет, очевидно:
(*i +jy)~(*s+Jy) ’
а относительное изменение (на единицу расстояния) будет:
L
Эта величина называется средним пьезометрическим уклоном и обозначается через J.
Абсолютное изменение всей удельной энергии между точками / и 2 будет, очевидно:
\	7	2g/	\ Т 2g-/
а относительное изменение будет -г-.
П	,
Величина -j- называется средним гидравлическим уклоном и обозначается через Jb.
П	и18
При равномерном движении отрезки и равны между собой, поэтому J = Jh.
Если жидкость взята в .свободном* движении, то кроме указанных двух уклонов будут существовать еще следующие два уклона (фиг. 71):
Ч Уклон свободной поверхности потока:
2. Уклон дна потока:
CL\ CLa l= L
«,® и? предыдущему
Если движение равномерное, то по далее, на свободной поверхности давление р = pv Следовательно
J=J,.
Кроме того для осуществления равномерности движения при постоянном расходе необходимо равенство глубины во всех живых сечениях потока, т. е. hY = /z2, откуда J, — I. Таким образом в свободном потоке, находящемся в равномерном движении, имеем:
= 4 = J =
(38)
Для получения истинных значений уклонов необходимо точки
1 и 2 брать бесконечно близко друг к другу; тогда
d ( z + — \ Y
J (истинное) =
а
J д (истинное) —	•
При равномерном движении истинные значения уклонов, очевидно, совпадают со средними.
§ 40. Уравнение Бернулли для потока при медленно изменяющемся движении
При выводе уравнения Бернулли для потока будем исходить из энергетического толкования этого закона.
Рассмотрим модель медленно изменяющегося движения в форме сочетания протекающих друг возле друга продольных струек жидкости, подчиненных каждая выведенному нами ранее уравнению Бернулли (фиг. 72). При идеальной жидкости мы имеем равенство удельной энергии для двух элементарных сечений каждой струйки потока, а следовательно и равенство полной энергии Для жидкости, протекающей в единицу времени через два живых сечения потока.
Обозначив величину этой полной энергии через Е, мы для двух произвольно выбранных сечений в потоке можем написать Et =£<,. Разделив величину Е на вес жидкости, протекающей в тот же промежуток времени через сечение, получим среднюю величину удельной энергии в данном сечении, т. е. энергию, приходящуюся на единицу веса жидкости, протекающей через данное сечение. Обозначив эту среднюю удельную энергию через еср, получим для каждого сечения:
Е
Так как по условию постоянства расхода величина Q = const и имея в виду также равенство величин Et и Еа, получим:
YQi“*rQa
или

(а)
79
Для определения величины еер возьмем в каком-нибудь сечении потока произвольную струйку; удельная энергия этой струйки:
а энергия жидкости, протекающей в единицу времени через поперечное сечение струи:
(л //2 \
Z + ~ + О- I и> Т 2gl « отсюда полная энергия жидкости в этом сечении:
£= / ( Z ldWU' U>
Так как при медленно изменяющемся движении величина z 4- — в каждом сечении является неизменной (см. § 26;, го, 7 вынося его за знак интеграла, получим:
Д = Т ( z + у) J* ndw и* ш	ш
Разделив же величину Е на величину ?Q, получим среднюю удельную энергию:
=Кz + fud<u + W fu'dm‘ (б) ш	ш
Перейдем к определению обоих интегралов.
1, J* udw, как известно, представляет собой расход через ш
данное живое сечение (см. § 27). Поэтому, произведя сокращение на величину Q, получим:
где величина г-|-у может быть взята для любой точки сечения.
2. Для решения интеграла J" u3da> надо знать закон распре-ш
деления скоростей по площади поперечного сечения. Такая аналитическая зависимость для случая турбулентного движения (см. § 41) пока не установлена, поэтому решение этого интеграла достигается следующим приближенным способом.
80
Умножим и разделим интеграл на с»2, где г,—средняя скорость:
1 С , , v2 Г и3 do> v2 Г и3 rfio	. .
2gQ j U <0 “ 2g J v3Q 2g j
<o	to	U)
Так как в подинтегральном выражении числитель и знаменатель имеют одну и ту же размерность, то этот интеграл является отвлеченной величиной и может быть выражен ка некоторый коэфициент. Обозначив этот коэфициент через а, мы из выражения (в) получим:
2Fq/“1‘z" =
го
V2
2g'
Подставив полученные значения обоих интегралов в выражение для еср в формуле (б), получим:
еср z г 7 -г а 2g '
Рассмотрим теперь два сечения потока. Среднюю удельную энергию в первом сечении определим по только что найденной формуле:
е ^1+А +а^.
Аналогично этому средняя удельная энергия во втором сечении:
е - z I А , a ^2_2
е2ер ~ гаТ ? т » 2g-
Принимая во внимание сказанное выше о равенстве этих двух величин, получим уравнение Бернулли для потока идеальной жидкости:
\zi + у + a 2> г+Т+ ~2g	(39)
Для реальной жидкости в это уравнение прибавится, очевидно, член ЕЛ, представляющий некоторую среднюю удельную энергию, теряемую от сечения 1 до сечения 2. Подставив эту величину в уравнение (39), получим уравнение Бернулли для потока реальной жидкости:
I •_ 4- Д. a	? 4- Д- Л ЕЛ
j *1 + у + a	г2 + у + а 2^+ i-Л.
/* и3 д
Для уяснения сущности коэфициента a = -——
6 Гидравлика
(40)
умножим
81
р числитель и знаменатель на , где р — плотность жидкости, и
представим его в следующем виде:
v3 ш	v2
Произведение ри d<o = р dQ = dm представляет собой массу жидкости, проходящую в единицу времени через сечение эле-ментарной струйки, a puda> = dm -% представляет собой л»	L
С j а2
живую силу этой массы, следовательно I ра аш — является жи-
вой силой жидкости, проходящей в единицу времени через данное сечение потока, причем эта живая сила взята как сумма живых сил отдельных струек.
Аналогично этому paw = Af представляет собой массу всей жидкости, протекающей в единицу времени через живое сече-
Т>2	..V2	, .
ние потока, a p^v -g-=представляет собой живую силу, которую имела бы жидкость, если бы она вся двигалась со средней скоростью V.
Таким образом
f а3
ш	истинная живая сила
v3 ш средняя живая сила
что представляет собой некоторое исправление той неточности, которая получилась в выражении для живой силы при замене истинных скоростей струйки средней скоростью. Среднее значение этого коэфициента, полученное опытным путем, приблизительно 1,1. Очевидно, что если бы все струи потока двигались бы с сред-,.ней скоростью, то а равнялась бы единице. На практике часто пренебрегают этим коэфициентом и считают его равным единице* 1.
При этом точки 1 и 2 в каждом сечении могут быть взяты совершенно произвольно. Тогда уравнение Бернулли для потока выражается совершенно аналогично с выражением для струйки:
 Z' +Y+2i“Z< + T+2i+ -k-
1 В последующем мы будем учитывать коэфициент только при неравномерном движении в открытых руслах. Во всех же остальных случаях принимаем
ГЛАВА VII
ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ
§ 41. Два режима движения
На полученном выше урдвнении Бернулли для реальной жидкости базируются буквально все гидравлические расчеты. В состав этого уравнения входит однако величина -/г, определение которой является весьма сложной задачей. Сложность этой задачи становится понятной, если вспомнить вообще сложность всей проблемы движения и если принять во внимание то разнообразие инженерных случаев, при которых приходится иметь дело с движением жидкостей. Понятно, что при определении потерь энергии приходится прибегать к введению ряда упрощающих предпосылок и широко использовать данные опытов.
Потери энергии при движении жидкости являются следстви м возникающих при этом движении сопротивлений, причем под силами сопротивления между движущимися частицами следует понимать силы взаимодействия, которые проявляются между этими частицами при их движении, в результате которых происходят замедление движения и потеря частицами части их энергии.
Фиг. 73	Фиг. 74
•
Исследования вопроса о возникающих при движении жидкости сопротивлениях указали на существование двух разных, резко различных по своей сущности типов движения.
1. При одних обстоятельствах имеет место такое движение жидкой массы, при котором перемещение каждой частицы происходит за счет непрерывной деформации как ее самой^ так и окружающей ее среды. Частицы при этом движутся совершенно правильными ярко очерченными струйками (фиг. 73). Такое движение называется ламинарным.
2. При известных обстоятельо вах, о которых будет сказано ниже, мы имеем резко выраженные индивидуальные движения отдельных частиц жидкости.
При этом отдельные частицы, отрываясь от всей массы жидкости, начинают двигаться по самым разнообразным и причудливым траекториям, все время сталкиваясь друг с другом до тех пор, пока они не потеряют своей энергии и не смешаются с остальной жидкостью (фиг. 74). Такое движение называется турбулентным.
Существование этих двух режимов движения реальной жидкости было впервые в 1883 г. экспериментально доказано Рей-t*	83
нольд^ом. Сущность его опытов заключается в следующем (фиг. 75). Имеется бак А со стеклянной трубой /?, снабженной на входном конце плавно очерченной воронкой С. У выходного конца труба имеет кран К, открывая который можно регулировать скорость движения воды. Величина средней скорости в трубе определяется об’емным способом, для чего имелся калиброванный сосуд емкостью w. Наполнив этот сосуд за время t, полу-
~ w	Q w
чим расход Q = ^-, а средняя скорость =
Над баком установлен небольшой сосуд Е, содержащий краску, которая по трубке Т поступает в воронку С. Краном К1 в трубке Т можно регулировать скорость притока краски. Процесс производства опытов заключался в постепенном открывании крана, измерении расхода и наблюдении за движением краски,. Поведение этой краски давало возможность судить об имеющемся типе движения. Так, при ламин <рном движении поступающая в трубу краска образует внутри движущейся жидкости устойчивую, резко очерченную нить; остальная часть жидкости остается неокрашенной, что указывает на отсутствие обмена частиц между струйкой и остальной жидкостью. Очевидно, что все остальные частицы жидкости в трубе при этсм тоже движутся отдельными струйками, т. е. что все движение носит струйчатый характер
или, иначе говоря, что в трубе имеет место ламинарное дви-
жение.
Если, постепенно открывая кран К, увеличить скорость движения в трубе, то при каком-то значении этой скорости движение внезапно изменяет свой характер, окрашенная нить исчезает, отдельные частицы расплываются во всем жидком об'еме трубы и вся жидкость оказывается равномерно окрашенной.
Если подмешать в поток какие-либо мелкие твердые частицы с удельным весом, равным удельному весу жидкости, то при турбулентном движении перемещение этих частиц изображает наглядно общее движение частиц жидкости в трубе и показывает появление ряда неустойчивых вихрей и те сложные зигзагообразные, пронизывающие весь поток траектории, которые характеризуют турбулентное движение. Переход из ламинарного движения в турбулентное становится возможным только после того, как скорость движения в трубе достигает какого то значения vk, твердо фиксированного для данного опыта. До тех пор, пока скорость была менее этого значения движение было всегда ламинарным. Даже если путем предварительного перемешивания жидкости в сосуде искусственно создать ее турбулентное состояние и в таком турбулентном состоянии впустить ее в трубу, она при входе в трубу успокаивается и двигается дальше ламинарно.
Величина vk названа была Рейнольдсом нижней критической скоростью.
Когда скорость в трубе становится больше нижней критической скорости, движение могло либо полрежнему оставаться ламинарным либо перейти в турбулентное состояние в зависимости от внешних чисто случайных обстоятельств (сотрясение трубы, спокойное состояние жидкости в сосуде и т. д.). Движение таким образом приобретает в этом случае неустойчивый характер. Подобное неустойчивое движение прекращается после того, как скорость в трубе достигает какого-то нового, вполне определенного для данного опыта значения vk, называемого верхней критической скоростью.
Когда скорость в трубе переходит за передел vk, движение становится устойчивым и при любых обстоятельствах турбулентным.
Таким образом в этих опытах движение проходит через три стадии. Условие существования каждой из этих стадий может быть аналитически сформулировано следующим образом. Если по предыдущему обозначим через v среднюю скорость движения в трубе, то
при v < vk —ламинарное движение „ vk < v <vk — неустойчивое	„
я v> vk — турбулентное	и
(41)
§ 42.	Факторы, определяющие тип движения
Анализируя вопрос об обстоятельствах, при которых жидкость движется ламицйрно или турбулентно, мы должны преж ie всего установить, какие факторы влияют и определяют разные типы движения. Таких факторов можно установить пять.
а)	Первым фактором является средняя скорость этого движения. Влияние этого фактора достаточно выявлено в описанных выше опытах, из которых видно, что увеличение средней скорости способствует переходу из ламинарного движения в турбулентное.
б)	Следующим фактором, влияющим на тип движения, является вязкость жидкости.
Совершенно очевидно, что жидкости, обладающие большой вязкостью (например нефть, глицерин и т. д.) и оказывающие вследствие этого большое сопротивление отделению одних частиц от других, будут при прочих равных условиях переходить в турбулентное движение при больших скоростях, чем жидкость с малой вязкостью (вода).
в)	Третьим фактором, оказывающим влияние на тип движения, является плотность жидкости Это слияние однако действует совершенно противоположно влиянию вязкости. Как мы видели выше, вязкие жидкости стремятся дольше сохранить ламинарный режим по сравнению с менее вязкими, более плотные же жидкости, наборот, при прочих одинаковых условиях
переходят в турбулентное движение при меньших скоростях, чем менее плотные.
г)	Четверты м фактором, от которого зависит тип движения, являются поперечные размеры потока. В очень тонких трубах жидкость, двигающаяся даже со значительной скоростью, сохраняет ламинарность. При увеличении диаметра трубы жидкость начинает переходить в турбулентное состояние даже при незначительных скоростях. Следовательно близость стенок трубы действует на частицы жидкости направляющим образом и способствует струйчатости движения. То же явление будет иметь место и в сечениях некруглой формы, где вместо диаметра будет фигурировать гидравлический радиус, играющий в этом смысле для сечения роль, аналогичную той, которую играет в
круглых сечениях диаметр.
д)	В качестве последнего фактора можно указать на влияние самого русла на тип движения. Это влияние оказывает , ,	прежде всего форма русла.
Далее, значительную роль играет шероховатость стенок, способствующая переходу жидкости в турбулентное движение. Наконец можно указать на влияние, которое оказывают изменение поперечных сечений потока и возникаю-
Фиг. 76	щая вследствие этого нерав-
номерность движения. Так, в опытах Рейнольдза установлено, что в сходящемся потоке ламинарность движения сохраняется при ббльших скоростях, чем при расходящемся потоке. Это обстоятельство дало возможность английскому ученому Гибсону, применившему при опытах стеклянную трубу сходящегося и расходящегося очертания, демонстрировать одновременно в первой половине трубы ламинарное движение, а во второй половине — турбулентное движение (фиг. 76).
§ 43.	Определение критической скорости
Решение вопроса о типе движения в каждом отдельном случае может быть получено помощью данного выше неравенства (41). для чего необходимо знать входящие туда величины vk и vk. Рейнольдс подошел теоретически к определению vk, пользуясь методом размерности.
Зная, что тип движения, а следовательно и величина критической скорости для случая круглой трубы заданной шероховатости обусловливаются данными выше факторами, напишем для величины vk общую формулу метода размерности (см. § 30):

(а)
где Л4— какой-то коэфициент, а показатели степени х, у, z должны быть определены из условия одинаковой размерности обеих частей уравнения.
Обращаясь к размерности каждой величины в отдельности, видим, что:
г_. 1 __ длина, г -J __ ____масса______, г -i______ масса
L W время’ 1'J длина х время ’ I Р J длина8 *
Подставив эти величины в уравнение, получим: длина _ / масса V/ масса V z время \алина х время / Удлина* / Длина
ИЛИ
длииаХвремя ’ = масса* + X длина г~х X время *•
Приравнивая показатели степени в обеих частях уравнения, получим:
1)	х + .у=0;
2)	z — х — Зу = 1;
3)	— х = —1, откуда:
х = 1; у = — 1; z — — 1.
Подставив полученные значения в уравнение (а), имеем:
* pD
(41а)
Проделанные Рейнольдсом для проверки этой формулы опыты вполне подтвердили ее правильность.
Величина коэфициента Nk была получена из экспериментов над гладкими трубами и оказалась равной приблизительно 2000. Для определения верхней критической скорости тем же Рейнольдсом предложено считать, что она в шесть раз больше нижней критической скорости, т. е. что

6.
Однако ряд опытов, производившихся впоследствии, такое соотношение не подтвердил и дал для величины vk совершенно другие значения.
Так например, новейшие опыты проф. Шиллера в Геттингене, подтвержденные недавно произведенными опытами лаборатории промысловой механики ГИНИ, показали, что при гладких трубах достаточной длины значения обеих критических скоростей сильно сближаются и
Подобная неопределенность в величине верхней критической скорости для практики не является особенно существенной, так как жидкость, находящуюся в неустойчивом состоянии, надо считать по наиболее неблагоприятному в практическом отношении случаю, т. е. по случаю турбулентного движения; поэтому, как то 1ько скорость перейдет за пределы движение практически следует считать турбулентным. Тогда вместо неравенства (41) практически приходится считаться с следующим неравенством, в котором vk не фигурирует:
1)	если v < vk — движение ламинарное;!
2)	»	—	» турбулентное./	(42)
§ 44. Число Рейнольдса
К вопросу об условиях перехода жидкости из одного типа движения в др\гое можно подойти еще по-иному. Из сказанного в § 42 видно, что для трубы заданной формы и шероховатости ламинарность и турбулентность потока определяются четырьмя факторами, из которых три (плотность р, средняя скорость v и диаметр D) способствуют переходу жидкости из ламинарного в турбулентное движение, а четвертый фактор — вязкость—способствует ламинарности движения. Зная влияние каждого из этих факторов на тип движения, мы можем составить какой-то один об'единенный фактор, который сконцентрировал бы в себе свойства всех четырех факторов в единое выражение. Такой об‘единенный фактор легко составить в виде
кг	.	*
выражения N = —— , в котором факторы, способствующие турбулентности движения, находятся в числителе в виде произведения, а фактор, способствующий ламинарности, помещен в знаменателе.
Вставив в полученное выражение размерность всех его величин, получим:
« ,  м 'сса длина длина х длина х время ~ длина3 х время	масса	’
что после сокращения даст безразмерное выражение.
Таким образом размерность величины (Vпоказывает, что это— какое-то отвлеченное число, что создает большое удобство при пользовании им.
Эго число играет громадную роль во всей теории современной гидравлики и по имени известного гидравлика называется числом Рейнольдса. Оно имеет своими предельными значениями величины Nk и Nk’, отделяющие ламинарное движение от неустойчивого, а неустойчивое от турбулентного (величина Nk встречалась нам уже в § 43).
Определив значение числа Рейнольдса для данного состояния движения, достаточно сравнить его с критическим значением. При этом получим следующие неравенства: 88
1)	если AZ < Nk—движение ламинарное;
2)	Nk< N < Nk' — движение неустойчивое;
3)	„ AZ>Af/-— , турбулентное.
(43)
Справедливость этого неравенства можно непосредственно получить из формулы (41а).
Определив из нее величину Nk= мы получим, что при
v>vk, N> Nk, v <vk, N <Nta
что делает неравенство (43) вполне эквивалентным неравенству (41).
Из сказанного в § 43 о верхней критической скорости должно быть очевидно, что величина Nk практически играет незначительную роль. Главное 31?ачение при определении типа движения имеет величина Nk, которая, как сказано там же, при гладких трубах равна приблизительно 2000.
Что же касается величины Nk, то она определяется из отношения:
1,3.
N* vk
Опыты Рейнольдса были произведены главным образом с водой, но дальнейшие исследования распространяют полностью все полученные выводы на все другие жидкости, причем величины Nk и Nk остаются при этом неизменными.
Дальнейшим обобщением формулы Рейнольдса должно явиться ее распространение и на случай движения жидкости в открытых руслах (свободное движение), при этом формула (41а) принимает следующий вид:
V -Р Я’
(43а)
где R—гидравлический радиус. Значение же Nt в этом случае будет другим.
Так, если воспользоваться данным выше в формуле (29а) выражением диаметра через гидравлический радиус D = 4Я и подставить это значение в формулу (41а), то получим:
vk — —гг> Т. е. Nk = 500. р R
Однако достаточного количества опытов, дающих значение Nk для свободного движения в различных руслах, на настоящий день еще не проведено. В качестве примера опытов, дающих значение Nk для одного частного случая, могут служить опыты Хопфа над движением жидкости в гладком прямоугольном канале. Эти опыты подтвердили полную справедливость формулы (43а), а для величины Nk дали значение, равное 300.
§ 45. Физический смысл числа Рейнольдса1
Рассмотрим какой-то движущийся поток, например жидкость в напорной трубе или канале. В этом потоке числу Рейнольдса может быть придан определенный физический смысл, если для всех входящих в поток величин мы вместо обычно принятой системы единиц измерения (сантиметры^ граммы, секунды) воспользуемся другой, специально приспособленной для данного случая системой единиц. В этой новой системе единиц примем за единицу длины любое линейное измерение, связанное с размерами потока (так, в трубе удобно будет за единицу длины выбрать радиус или диаметр, в канале — глубину или гидравлический радиус).
Выбрав указанную единицу длины, мы все остальные линейные измерения будем выражать через нее. Так например, если в трубе координаты какой-нибудь тонки выражались раньше через х, у, z, то в новой системе единиц они будут выражаться х у z	х у z
через	или через у, — в зависимости от того,
что нами принято за единицу длины (в дальнейшем мы за таковую будем считать величину D). Далее, вместо единицы времени введем единицу скорости, за которую мы можем принять какую-то постоянную скорость в потоке (удобнее всего принять среднюю скорость потока v). Тогда скорость в отдельных струйках, выражаемая в обычной системе единиц через и см/сек, в новой системе единиц выразится через отношение -. Полученные в новой системе единицы длины и скорости будем называть приведенными. Очевидно, что эти величины представляют собой безразмерные числа.
Задавшись двумя основными единицами — длиной и скоростью, мы можем получить сразу единицы измерения для других интересующих нас величин. Так, зная что в обычной системе единиц единица времени может быть выражена через единицу длины и скорости в виде отношения: единица времени = едДскорости' _	i	D ,
мы в нашей системе для единицы времени имеем —.	Анало-
гично этому, зная, что в обычной системе единиц единица ускорения выражается через единицу длины и времени в виде отношения: единица ускорения = ^чДр"м^-=еДеГОд7ИныИ1> мы в нашей системе за единицу ускорения получим величину Деля на эту единицу величину ускорения в струйке потока, получим приведенное ускорение этой струйки в виде безразмерного числа.
1 Подробнее см. проф. Великанов, .Обобщенная формула гидравлических зависимостей для стационарных потоков вязкой жидкости". Ленинград. 1926 т. 90
Рассмотрим теперь в нашей системе единиц вязкость потока. Так как в обычной системе единиц размерность вязкости выражается В виде отношения ^Гх^ремя	= плот-
ность х скорость х длина, то в нашей системе единиц единицей вязкости является величина vDp. Деля вязкость нашей жидкости на эту величину, мы, очевидно, получим приведенную вязкость. Обозначим ее через тогда:
g —	= 1
5 pW N’
откуда обратно:
"“Т
(44)
Так как величина, обратная вязкости, называется текучестью, то полученное выражение говорит о том, что число" Рейнольдса в каком-нибудь потоке является иначе его „приведенной текучестью", т. е. текучестью, выраженной в определенной системе единиц. В этом и заключается физическая трактовка числа Рейнольдса.
§ 46. Область практического применения ламинарного и турбулентного движения
Для того чтобы ответить-на вопрос о том, в каких случаях практики приходится иметь дело с ламинарным движением и в каких случаях с турбулентным, вернемся к основной формуле:

Рассмотрим в качестве примера движение воды по трубе.
Величина может быть определена из формулы Пуазейля (§ 6). В практике при этом пользуются данными таблицы, приведенной в том же параграфе. Подставим его значение из этой формулы; тогда:
2000-0,0178
Vk (1 + 0,0337 Т+0,000221 V)-D см'<сек‘
Если принять в качестве средней температуры t = 10° и вычислить значение vk, то получим:
25	,
v*=-g сл/сеж,
из которой непосредственно видна зависимость критической скорости от диаметра трубы.
Так например, если возьмем случай движения в 4" трубе (D = 10 см), то
25 о , vk = уф = 2,5 см1сек,
т. е. является совершенно ничтожной величиной. Движение в этом случае должно быть бесспорно турбулентным
Обратно, если задано vk — 1,0 MiceK, то диаметр трубы получится:
О-^=0.4^,
т. е для того, чтобы движение было в этом случае ламинарным, необходима труба ничтожно малого диаметра.
Если вместо движения воды будем иметь дело с вязкой жидкостью, то, подставив в предыдущую формулу соответствующие значения >) и р, можем получить достаточно большие значения критических скоростей и следовательно можем встретиться со случаем ламинарного движения.
Из приведенных примеров видно, что в обычных случаях при движении воды в трубах, каналах, реках и т. д. имеет место всегда турбулентный режим. Ламинарный режим имеет место только при движении воды в очень узких капиллярных трубах, что практически встречается в движении грунтовых вод; ламинарный режим может иметь место также при движении вязких жидкостей, из которых наиболее интересным в практическом отношении представляется движение нефти.
Задача. Определить минимальную скорость, при которой будет иметь место устойчивый турбулентный режим движения воды в канале прямоугольного сечения шириной b = 1,0 м и глубиной 0,6 м при Т = 5°С.
Решение. Верхняя критическая скорость
, т) 300-1,3	ЗЭО-1,3 Л„„	,
vk = -----R— = 0,0152--~— = 0,02 см сек.
kpR	27
Эта величина, очевидно, будет искомой минимальной скоростью.
Задача. Определить, какой режим (ламинарный или турбулентный) будет иметь место в одной и той же трубе диаметром D = 10 см при движении в ней воды, сурепного масла, патоки и нефти, считая температуры их Т= 20° и скорость v— = 1 м)сек.
Решение, а) для воды по таблице § 6 (при Т — 20°; v = = 0,0101 см2[сек	0,01 см21(ек, так что
N	=25000.
г 0,01
б) Для сурепного масла v= 1,97 см'! сек, а потому
v 1,97
'в) Для патоки v = 430 см2/сек, а потому
vR 100 2,5 __
Л "	“ 430----ft6;
г) Для нефти v = 0,3 см2/сек, а потому
Следовательно при движении воды и нефти имеем N>NJ, т. е. турбулентный режим; при движении же патоки и сурепного масла имеем 7V<7V/, т. е. режим ламинарный.
Задача. Найти рейнольдсовы числа для следующих водных потоков:
а)	для р. Сены при средней скорости v = 1,4 м/сек и гидравлическом радиусе R = 5 м;
б)	для р. Миссисипи при v — 1 м/сек и R = 22 м;
в)	„ „ Сыр-Дарьи при v = 1 м/сек и R = 2 м;
г)	„ водопроводной трубы диаметром 200 мм.
vR
Во всех случаях будем пользоваться формулой М = —, полагая в ней для воды v = 0,01 см.2/сек (температуру воды принимаем 20°).
Решение, а) Для р. Сены находим, что число
ЛГ-^- '•41О°-,51ОС-7.Ю-.
v	0,01
б)	Для р. Миссисипи находим:
= 1  100  22  100 v 0,01
в)	Для р. Сыр-Дарьи находим:'
N = loo 2иоо V	0,01
г)	Для водопроводной трубы диаметр D = 200 мм, а потому м D D 200 _л с
гидравлический радиус 7? = -£ = -£-= 50 л<л< = 5 см, имея в виду обычную скорость v = 1 м/сек, находим:
Д5.1ОЧ
1 v 0,01
Сопоставим полученные в этом примере значения:
р. Сена...................=	7-10е,
„ Миссисипи...........Af=22-10°,
„ Сыр-Дарья...........7V = 2 10е,
водопроводная труба . N = 5-10‘.
§ 47.	Осредненные скорости
После приведенной выше характеристики турбулентного движения возникает вопрос, возможно ли при том хаотическом перемещении частиц жидкости, которым характеризуется турбулентное движение, подойти к определению скоростей в этих частицах с какими-нибудь аналитическими формулами. В самом деле, многочисленные наблюдения над движением воды в реках и каналах показывают, что даже в случае, если внешние условия движения не меняются, движение все-таки, строго говоря, не может быть принято установившимся, так как оно в каждой данной точке пространства сопровождается постоянным изменением скоростей по величине и направлению. Так например, наблюдая за какой-нибудь точкой А пространства в области движущегося потока (фиг. 77), мы можем заметить, что две частицы, попадая в эту точку в разные промежутки времени, будут обладать различными скоростями. Обозначив эту переменную во времени скорость через и (так называемая мгновенная скорость), мы можем разложить ее на три составляющие: одну продольную составляющую (их) и две поперечные составляющие (иу, и,). Вопрос об устойчивости и закономерности этого движения получает положительный ответ, если принять во внимание, что обычно в гидродинамике рассматривается только движение сплошной жидкости, т. е. жидкости, внутри которой не образуется пустот, а следовательно не происходит разрыва струй. Поэтому в каждой точке пространства средний расход через элементарную площадку Дш за какой-то промежуток времени является постоянной величиной, и следовательно результатом действия переменных во времени скоростей является какая-то вполне устойчивая неизменная величина. В качестве аналогии с описанным явлением можно привести пример с давлением газов на твердые тела. Как известно из кинетической теории газов, давление газа на стенки сосуда рассматривается как результат весьма большого числа отдельных ударов, производимых беспорядочно движущимися во всех направлениях частицами газа. Несмотря на произвольность движения этих частиц, среднее количество ударов на единицу площади сосуда за некоторый промежуток времени считается постоянной величиной и принимается за величину удельного давления в сосуде.
Подробный анализ этого факта по отношению к жидкостям становится возможным при использовании понятия осредненной скорости, введенного еще Сен-Венаном и подробно затем разработанного Буссинеском. С введением этого понятия мгновенные скорости частиц при турбулентном движении рассматриваются 94
как результирующие двух величин: а) основной скорости движения, являющейся вполне устойчивой величиной, и б) добавочной скорости колебательного и беспорядочного характера, обусловленной ударом данной частицы о другие частицы, врывающиеся при турбулентном движении из других слоев жидкости.
Изменение мгновенных скоростей (так называемую пульсацию скоростей) можно изобразить графически, если на оси абсцисс отложить продольную составляющую мгновенной скорости в данной точке А, а на оси ординат — время наблюдений (фиг. 78). Опыт, полученный в результате многочисленных наблюдений, позволяет заключить, что уклонения мгновенных скоростей от основных скоростей на протяжении достаточного промежутка
времени взаимно компенсируются и уничтожаются.
Эти основные устойчивые скорости, называемые иначе осредненными скоростями, являются следовательно какими-то среднестатистическими величинами и представляют собой
такие постоянные скорости, с которыми через данную элементарную площадку в /печение определенного промежутка вре
мени Т должны были бы двигаться частицы жидкости при условии, чтобы расход оказался равным расходу, получаемому в среднем за этот же промежуток времени при истинных мгновенных скоростях.
Если обозначить осредненную скорость через иср, то расход через площадку d<o, вычисленный по мгновенной скорости, равен т
£ utfadt. Тот же расход, вычисленный по средней статистической скорости, равен u^d® Т, откуда, сокращая на d&, получим:
fudt ач> ~~ р "
При уяснении понятия „осредненной скорости" надо иметь в виду, что осреднение скоростей здесь происходит во времени и что это понятие нельзя смешивать с введенным ранее понятием .средней скорости", которое производит осреднение скоростей в разных точках живого сечении.
Буссинеск в своих исследованиях показал возможность оперирования с .осредненными" скоростями так же, как если
бы они были истинными, что послужило первым средством по пути изучения турбулентного движения. Очевидно, и другие гидромеханические элементы должны при этом рассматриваться как некоторые осредненные величины. Так можно говорить об осредненных давлениях, ускорениях и т, д. Также следует иметь в виду, что, говоря о линиях тока и струйках в турбулентном движении, мы имеем в виду тоже какие-то среднестатистические величины, построенные для осредненных скоростей.
В заключение необходимо указать, что обычные приборы, измеряющие скорости и давления в определенных точках сечения, дают как раз их осредненные значения, что придает этим величинам вполне реальный смысл.
§ 48.	Распределение скоростей при турбулентном движении
Усыновив понятие об осредненной скорости при турбулентном движении, перейдем к вопросу о том, как распределяются эти скорости в поперечном сечении потока. Ввиду большой сложности турбулентного движения установить аналитически законы распределения этих скоростей пока не удалось, и наши знания об этих законах базируются на весьма богатом экспериментальном материале, накопившемся еще с начала XIX в.
Если обратиться к истории этого вопроса, то увидим, что уже издавна внимание крупнейших гидравликов, занимавшихся экспериментами в этой области, привлекало следующее обстоятельство: измерение скоростей в поперечном сечении потока показывало, что скорости в точках жидкости, расположенных вблизи стенок и дна русла, достигают весьма больших значений, в остальных же точках живого сечения скорости в общем меняются весьма незначительно. Так как указанные эксперименты проводились в первой половине прошлого столетия, когда еще отсутствовали приборы, позволяющие измерить скорость у самих стенок, tq соображения о скоростях в этих точках базировались на повседневных наблюдениях о передвижении наносов. Исходя из того несомненного обстоятельства, что частицы, находящиеся у самих стенок, прилипают к ним и участия в общем движении не принимают; экспериментаторы в прошлом приходили к выводу, что у стенок и дна русла всегда имеется мертвый слой жидкости, по которому вся остальная масса жидкости движется со значительными скоростями; следовательно согласно этим взглядам непосредственно у стенок происходит сразу возрастание скоростей от нулевого до какого-то конечного значения или, иначе говоря,- что там имеет место разрыв скоростей. Эта идея была долгое время доминирующей в гидравлике и продержалась почти все XIX столетие, пока трудами знаменитого ученого проф. Прандля не была создана другая теория. Согласно этой теории, являющейся основой современного научного мировоззрения в гидравлике, принимавшийся прежде неподвижным „мертвый слой' в действительности находится в движении, но движение это происходит по ламинарному закону.
Таким образом всякое турбулентное движение потока сопровождается ламинарным движением тонкого пограничного слоя и турбулентным движением остальной массы жидкости, называемой иначе ядром.	(
Распределение скоростей в пограничном слое и турбулентном ядре дано на фиг. 79, где кривая АВ дана для ламинарного слоя, кривая ВС (в другом масштабе)—для турбулентного ядра, линия же AD относится к случаю ламинарного движения во всем потоке. Из сравнения кривых АВ и ВС видим, что при турбулент
ном движении происходит выравнивание скоростей и значение скоростей в отдельных точках приближается к среднему значению.
Благодаря исследованиям той же школы Прандля удалось также подойти к выяснению механизма турбулентного движения. Причина возникновения турбулентного движения может, быть представлена в следующем виде (фиг. 80).
При движении частиц по прилипшему слою между неподвиж- ---------------------—
ными и движущимися частицами возникают силы трения т. Подобные же касательные силы возникают между движущимися частицами М2 Mv Эти касательные силы, приложенные внецен-тренно к частицам, создают пары, благодаря которым частицы переходят во вращательное движение. Вихри, передаваясь от одной частицы к другой, образуют вихревые трубки, и таким образом пограничный слой пронизан такими поднимающимися от стенок вихрями.
Попадая в предельный слой пограничной зоны, находящейся уже в неустойчивом положении, вихри становятся сами неустойчивыми, начинают отделяться от ламинарной зоны и проникать в турбулентную зону, где правильность их движения нарушается, вихри как организованная система исчезают, а отдельные вихри, разлетаясь по*всем направлениям, создают картину беспорядочности и хаотичности, которыми характеризуется турбулентное движение.
§ 49.	Силы сопротивления при ламинарном и турбулентном движении
При движении жидкостей, как сказано было уже выше, между ее частицами возникают силы сопротивления, препятствующие этому движению. Эги силы по своей природе различны для 7 Гидравлика	97
разных типов движения: так в ламинарном движении это, очевидно, будут силы трения между отдельными слоями жидкости, причем единичная сила трения определяется согласно формуле (5) § 6:
du
Где т]— абсолютная
du
вязкость, а^-—относительное изменение
скорости перемещения двух слоев.
Таким образок при ламинарном движении силы сопротивления прямо пропорциональны вязкости жидкости и относительному изменению скорости. Так как последняя величина в свою очередь прямо пропорциональна средней, скорости потока, то при ламинарном движении единичная сила трения прямо пропорциональна средней скорости. При турбулентном движении к силам трения присоединяются сопротивления от ударов частиц между собой и о стенки сосуда. Благодаря этим добавочным сопротивлениям, а также благодаря тому, что при турбулентном движении частицы движутся по более длинным и извилистым траекториям, потери энергии при турбулентном движении всегда значительно больше, чем при ламинарном движении.
Переходя к определению этих сил сопротивления, определим сначала их зависимость от определяющих их факторов. Отвлекаясь пока от факторов, характеризующих свойства жидкости, т. е. считая пока, что мы имеем дело с одной и той же жид
костью, рассмотрим влияние, которое оказывают на сопротивление средняя скорость движения потока, его поперечные размеры и шероховатость стенок русла.
1) Влияние средней скорости на сопротивление.
Зависимость сил трения от средней скорости при ламинарном движении уже вь ражена выше. Как известно, силы трения пропорциональн'ы 1-й степени скорости. Произведенные исследования для турбулентного движения установили, что и в этом
случае существует степенная зависимость между силами сопротивления и средней скоростью, но показатель степени в этом случае оказывается больше единицы.
Эту зависимость можно для обоих видов движения выразить в виде формулы:
— = bvn, _Х_________
(45)
где п, как было выше сказано, при ламинарном движении равно единице, а при турбулентном движении — больше единицы.
Если на основании опытов того же Рейнольдса изобразить графически эту зависимость (фиг. 81), то до тех пор, пока скорость не достигнет своего критического значения, т. е. пока имеет место ламинарное движение, график изменения -- от v 98
представляется в виде прямой АВ\ начиная же от точки С, где скорость достигнет верхнего критического значения и где движение принимает турбулентный характер, линия СЕ становится кривой.
Участок между нижней и верхней критическими скоростями представляет неустойчивый режим, поэтому он изображен в виде кривой ВС и прямой BD со скачком DC в точке D.
Эту же зависимость можно графически представить еще в другом виде (фип. 82). Так, если прологарифмировать данное выше уравнение, то получим
1 г	1
1g—E = «lg v-by-b  ь
Откладывая теперь значения логарифмов по координатным осям, мы получим графическую зависимость между логарифмами
обеих переменных. Подобная зависимость изображается прямой линией, причем тангенсы углов наклона прямой к оси абсцисс представляют/ собой показатели степени. Для части АВ ламинарного движения tga = l и угол = 45°. Для части CD угол оказывается больше 45°. Многочисленными исследованиями установлено, что для прямой CD, представляющей турбулентный участок движения, tg а зависит от степени шероховатости стенок трубы и колеблется от 1,79 до 2,0; так, по опытам Рейнольдса можно составить следующую таблицу значений этого показателя (см. табл. 3).
Таблица 3
Значения показателя степени п для труб различной шероховатости
Вид трубы	Свинцовые трубы	Стеклянные трубы	Асфальтированные трубы	Новые чугунные трубы	Вычищенные чугунные трубы	Старые чугунные трубы
п	1,79	1,79	1,82	1,88	1,91	2,0
7*
99
Из этой таблицы видно, что для наиболее распространенных случаев практики /1^2.
Кроме того и необходимость известного запаса прочности также требует в сомнительных случаях принимать наиболее неблагоприятные условия. Поэтому в большинстве случаев практики п принимается равным двум, хотя существует ряд формул, в которых величина п имеет меньшие значения.
2) Влияние шероховатости на сопротивления. Под шероховатостью стенок русла подразумеваются их неровности, благодаря которым стенки представляют собой не гладкие поверхности, а образуют ряд выступов и впадин (фиг. 83). Эти неровности, обусловленные свойствами материала и продолжительностью службы стенок, распределены неодинаково по длине стенки и для периметра одного и того же поперечного сечения тоже различны. Если взять в каждом поперечном сечении среднюю длину соответствующей ,	।	3 неровности д0, то эту
~ТГ —~4 —~ величинУ можно назвать LllSitu	—гК~ ’ абсолютной шерохова-
ирлт*	1]у-- тостью Абсолютная шеро-
5	ховатость сама по себе не
фиг- 83	может являться полной ха-
рактеристикой влияния стенки на сопротивления, так как очевидно, чго стенка одной и той же шероховатости при потоках малых поперечных размеров (например при трубах небольшого диаметра) будет оказывать гораздо ббльшее сопротивление, чем при потоках больших поперечных размеров. Поэтому кроме понятия абсолютной шероховатости вводится понятие относительной шероховатости, под которой понимается отношение абсолютной шероховатости к величине, характеризующей поперечные размеры потока (к гидравлическому радиусу или к диаметру).
Столь очевидная на первый взгляд зависимость между шероховатостью и силами сопротивления не сразу однако завоевала себе признание в гидравлике.
Так, примерно до 50-х годов XIX в. среди самых авторитетных гидравликов господствовал взгляд, что сопротивление не зависит от рода стенки. Взгляд этот в наиболее отчетливой форме был высказан в 1804 г. знаменитым инженером и директором Французского института путей сообщения Прони. Предложенная им формула имеет следующий вид:
av _|_ bv2,	(46)
где а и b — какие-то постоянные величины (для нормальных труб а 0,00017, а b = 0,00034).
Идейное обоснование этой формулы вытекает из представления о существовании у стенок „мертвого слоя* (см. § 48).
Так как по взглядам того же Прони остальная масса жидкости движется именно по этому слою, а не по материалу самой 100
стенки, то этот слой им рассматривался как истинная стенка, и отсюда делался вывод, что материал самой стенки в движении никакой роли не играет.
Из значений коэфициентов а и Ь видно, что хотя Прони и не принимал квадратичной зависимости между т и V, но что при сколько-нибудь значительной величине скорости второй член формулы начинает превалировать над первым и формула приближается к квадратичной. Немецкий ученый Вейсбах, производивший самостоятельно опыты над движением в трубах; нашел, что первый член формулы Прони неправильно отражает влияние скорости на сопротивление, поэтому им была предложена следующая исправленная формула:
v*
+ Ь
2g’
(47)
где а и b — какие-то постоянные величины.
В идейном отношении формула Вейсбаха по сравнению с формулой Прони ничего нового не дала; поэтому в настоящее время она считается устаревшей.
Жизнь однако требовала ревизии этих неудовлетворявших практику взглядов, и в 1837 г. главный инженер Парижского водопровода Дарси предпринял свои знаменитые опыты над движением воды в водопроводных трубах.
Опыты эти были закончены уже после его смерти его бывшим помощником Базеном, и их результаты совершенно опрокинули господствовавшую до того времени теорию Прони.
Первым выводом этих классических опытов явилось признание весьма серьезного влияния состояния стенки (ее шероховатости) на сопротивление движению частиц. Так, из опытов Дарси выяснилось, что для чугунных труб при одной и той же длине, одном и том же диаметре и расходе сопротивление может увеличиваться почти в два раза при замене новых труб старыми.
Вторым выводом из этих опытов явилось признание того факта, что поперечные размеры потока несомненно влияют на сопротивление движению.
Наконец третий вывод, к которому пришли эти ученые, заключался в том, что отклонение от квадратичного закона является незначительным, и поэтому в формуле Прони первый член является излишним.
Предложенная вначале Дарси, а потом Базеном формула (она так и называется формула Дарси-Базена) имеет следующий вид:
— =
7
(48)
где коэфициент должен, очевидно, заключать в себе факторы, определяемые шероховатостью стенок и поперечными размерами
потока. Для этого коэфициента ими била предложена следую* щая эмпирическая формула:
*‘мв(1+1)’	(49>
где а и £ — коэфициенты, имеющие различные численные значения для стенок различной шероховатости, a R — гидравлический радиус.
(Для новых чугунных труб значение л ^0,0005 а 0,000013.)
Идейное обоснование этой формулы может быть схематически представлено в следующем виде1. Не отказываясь от взгляда о существовании мертвого слоя и разрыва скоростей у стенок, авторы этой теории (т. е« Дарси, Базен) считают однако этот сл »й настолько тонким, что он не закрывает собой всех выступоз и впадин, образуемых шероховатостью стенки, а только обволакивает их.
Фиг. 85
Пусть поток равномерно движется по какому-нибудь руслу, неровности стенок которого обусловливаются его шероховатостью фиг 84) Обозначим высоту выступов через д2, а3 и т. д., причем, так как по ширине сечения эти неровности распределяются неравномерно, то под величиной а надо понимать какую-то среднюю по периметру данного сечения шероховатость (фиг. 85 \ Русло разбиваем на участки равной длины I. Сложим теперь сумму высот неровностей, приходящихся на каждый участок, и отложим их в виде прямых тонких выступов К (фиг. 86), В полученном схематически русле частицы типа М, лежащие ниже личин ВВ, ударяются о стенки и теряют полностью свою живую силу. Частицы же М\ лежащие выше линии ВВ, вследствие ударов и трения друг о друга теряют свою силу лишь частично. Так как в действительных потоках стенки обладают более плавным очертанием своих неровностей и частицы при ударе о них теряют только часть своей живой силы, то сделанное выше допущение о том, что эти частицы теряют свою живую силу полностью, должно дать в нашем случае схематического русла преувеличенное значение потерь. Поэтому делается второе допущение, согласно которому частицы типа М\ лежащие выше линии ВВ, при движении никаких потерь не испытывают, так что преуменьшение потерь в одном случае компенсируется преувеличением потерь во втором случае.
Найдем выражение для потерь живой силы слоя ААВВ. Масса этого слоя: А т = рХХа/, ’ а живая сила
t/2	V1 «
=	(а)
где vcp обозначает среднюю скорость, a W представляет собой по указанной схеме полную потерю энергии рассматриваемого слоя жидкости.
1 См. Проф Н. Н. Павловский «Гидравлика*, изд. 1928 г. 102
Для получения удельной потери необходимо полную потерю разделить на вес этого об'ема G = I. Разделив величину W на и и заменив величину р
через j, мы из уравнения (а) получаем:
тХЕд./.у2ср __ lav'f,
2gy»l R2g
С другой стороны, по формуле (52) (см. далее § 51) имеем:
приравняв оба эти выражения, получим:
± = la'Vlcp = Т 2gl 2g
(б)

-L -- V —* —
. so
где b =: — представляет собой высоту выступов, приходящихся на единицу
длины потока. Эта величина называется приведенной шероховатостью.
Введем теперь вместо vcp — средней скорости у стенок — вели-чину v—среднюю скорость потока. -------
Обозначим отношение этих ско- ------
ростей через ф, тогда из урав- 2ZZZZ. нения (Ь) получим;	—в
х и it v* «. — = 5ф2 -5- = b.—t T	2^	1 2g
где через 5t обозначим выражение b ф2.
Из равенства
В
— к

Фиг. 86
. Хаф3 ^1= —
(50)
видно, что если представить себе русло, высота которого будет увеличена в масштабе ф3, то Ьх представит собой приведенную шероховатость этого русла.
Приведенное здесь идейное обоснование формулы ~ = b^v* дает довольно простое схематическое изображение явления, но целью его является не получение каких-то количественных соотношений, а только некоторые попытки об‘-яснения структуры самой формулы.
Разработанная за последнее время школой Прандля новая теория турбулентного движения дает со ершенно другое физическое об'яснение процессу движения жидкостей (<м. § 48).
Роль пограничного ламинарного слоя, движение вихрей и т. д. дают совершенно другие основы для создания модели движения. Состояние гиаравлики на настоящий день еще не позволяет считать окончательно установленной модель турбулентного движения. Существуют разные теории по этому вопросу1.
1 См: статью Лойцянского (, Известия научно-исследовательского института гидротехники* № 11).
ГЛАВА VIII
ПОТЕРИ ЭНЕРГИИ
§ 50. Классификация видов потерь
Рассмотренные в предыдущей главе сопротивления жидкости при ее движении вызывают потери энергии. Эти потери, обозначенные в уравнении Бернулли через SA, будут, очевидно, различны для ламинарного и турбулентного движения. В обоих типах движения однако потери энергии могут быть разделены на два вида: а) потери, происходящие во всех сечениях Жидкости вследствие трения (а при турбулентном движении и ударов) частиц друг о друга и о стенки сосуда; эти потери называются потерями по длине и обозначаются через б) потери, происходящие в том случае, когда жидкости приходится в каком-либо из своих сечений внезапно изменить скорость по величине или направлению (например при резком изменении направления движения, при наличии в одном из сечений крана, задвижки и т. д.). Эти потери имеют место в некоторых отдельных сечениях и называются местными потерями.
§ 51. Определение потерь по длине при равномерном движении жидкости
Выделим из движущейся жидкости призматический отсек DCEM с живым сечением площадью ® (фиг. 87).
Движение при этом может быть и ламинарным и турбулентным. Оно может также быть и напорным и свободным (сечение А соответствует случаю напорного движения, а В—случаю свободного движения). Таким образом единственным ограничением в рассматриваемом случае является условие равномерности движения.
Жидкость слева и справа от отсека, а также дно и стенки сосуда считаем отброшенными и их действие заменяем следующими силами:
1.	Силами Ра, заменяющими действие отброшенных частиц на частицы в сечениях CD и ME. Если равнодействующие этих сил обозначим через Pj и Р2, а через pt и р., обозначим единичные давления, приложенные в центрах тяжести сечений, то Pi =А“ и Р2 =р2о>.
2.	Силой трения жидкости по стенкам. Обозначим через т силу трения, приходящуюся на единицу площади боковой поверхности стенки (при турбулентном движении сюда прибавляются указанные выше добавочные сопротивления, но для упрощения мы их включаем в эту же величину т), а через Т — суммарную силу трения, приходящуюся на боковую поверхность. Тогда T=x%L (где х — смоченный периметр).
3.	Нормальные силы давления жидкости на стенки. Если обозначить аналогично предыдущему единичную силу давления на боковую поверхность через рп, а всю силу давления через М то N = pn%L.
4.	Сила веса О = ©Lf (где — об'ем).
Зная, что все силы находятся в равновесии, спроектируем их на ось потока 0 — 0.
Разделив полученное уравнение на величину <оу, получим:
7	7	7®	8
откуда:
2LL = Zl +El_z^Pi. Т	I
Напишем теперь уравнение Бернулли для точек 1 и 2:
2,4 7 +2g“*a+ т ’r2i+A’-
Так как движение равномерное, то = и.г и
Л, = + — — г2—	.
7	7
(б)
Сравнивая полученные уравнения (а) и (б), заметим, что
(51)
V	1
или, заменив через где R — гидравлический радиус, получим эту же формулу в другом виде:
(52)
Уравнение (51), и соответственно (52), называется основным уравнением равномерного движения.
Полученная формула верна как для ламинарного, так и для турбулентного движения. Приступая к изучению какого-нибудь из этих типов движения, необходимо, очевидно, заменить вели
чину — соответствующим выражением.
§ 52.	Законы ламинарного движения в цилиндрической трубе
Пользуясь выведенным выше уравнением, мы можем получить все интересующие нас законы ламинарного движения жидкости в цилиндрической трубе. Ниже мы последовательно рассмотрим вопрос о распределении скоростей по живому сечению, далее дадим формулу для расхода и средней скорости и наконец выведем формулу для потери энергии.
1.	Для определения закона, по которому распределяются скорости в точках живого сечения, рассмотрим ламинарное движение жидкости в круглой трубе радиусом г (фиг. 89), тогда
X 2иг 2 ® к Г* Г
В ламинарном движении, как известно, силы трения выражаются следующей формулой:
где знак минус взят вследствие того, что скорость убывает от середины к стенкам, что при данном расположении координатных осей делает du отрицательными.
Подставив значение т в основное уравнение, получим:
r^du 2
{dy г
откуда:
du =
Отсюда определится скорость и в произвольной точке А жидкости:
/*>---l,o-u = -^Lir'-y'y
а	у
Так как скорость у стенки и0 = 0, то окончательно
что дает распределение скоростей по параболическому закону.
Максимальная скорость, очевидно, получится при значении v - 0; отсюда:
2,	Для определения расхода при ламинарном движении выделим из жидкости (фиг. 90) кольцо толщиной dy и площадью
</и> = fyty dy.
Расход через это кольцо:
rfQ = и d<o
Отсюда полный расход:
^ht( г1 гП	1	yht
27]£\2	4	8 Г
или, иначе,
Q =
1 г М 128
О‘,
(55)
а средняя скорость:
=	(56)
к U o4T\L
3.	Из полученной формулы для средней скорости легко можем получить зависимость между потерей энергии и определяющими ее факторами. Определив из этой формулы величину й,, получим:
T'32W'	|56а)
откуда видим, что при ламинарном движении потери энергии прямо пропорциональны средней скорости и кинематической вязкости и обратно пропорциональны квадрату диаметра. От шероховатости трубы эти потери не зависят (эта зависимость впервые была установлена Пуазейлем).
Формула (56а) может быть еще представлена в другом виде. Для этого умножив и разделив правую часть на 2v и заменив у через pg, получим;
hy 64 тр!
L = р vD l 2g ’
а заменив выражение
- через -jy- (где W—число Рейнольдса),
получим:
ht _ .	6 4 v1
T h=^ ~N2g ’
(57)
откуда видим, что при ламинарном, движении потери прямо пропорциональны удельной, кинетической энергии и обратно пропорциональны числу Рейнольдса.
§ 53.	Вид основного уравнения для случая турбулентного движения
Подставив в формулу (51) вместо величины — указанную выше
величину получим уравнение:
, _ h vlL h'~bl R ’
(58)
пользуясь которым мы, зная геометрические элементы потока (длину и гидравлический радиус R), среднюю скорость v и коэфициент можем вычислить и потери энергии по длине потока.
В практике однако основное уравнение в том виде, в котором оно представлено в выражении (58), не привилось и подверглось еще некоторым дополнительным преобразованиям. При 108
этих преобразованиях из основного уравнения могут быть полу, чены три распространенные в настоящее время формулы, коте» рые приводятся ниже.
1-й вид основного уравнения при турбулентном движении (формула Шези), Рассмотрим свободный поток, находящийся в равномерном движении. Пусть нам заданы уклон дна i, гидравлический радиус R и шероховатость стенок; требуется определить среднюю скорость v.
Вопрос этот занимал умы гидравликов с давних времен, и известный исследователь Шези еще в 1775 г. на основании весьма элементарных соображений предложил в качестве решения этой задачи следующую формулу:
V = С у /?/,
в которой коэфициент с считался им постоянной величиной. Нетрудно видеть, что эта же формула может быть получена непосредственно из основного уравнения равномерного движения.
В самом деле, из формулы (58) имеем:
•	1	ж
откуда, заменив величину .—: другим коэфициентом с и зная, У
что представляет гидравлический уклон потока (§ 89), получаем:
v = cy'RJh-	(59)
Учитывая еще, что при равномерном движении в открытых руслах JK i, получаем тот же вид формулы:
\v — c \(Ri, |	(59а)
которая сохранила название формулы Шези и является по настоящее время важнейшей и распространеннейшей формулой. Данный в выражении (59) вид этой формулы обобщает ее применение и для случая напорного движения.
Величина же с определяется, очевидно, без всяких трудностей, если известен коэфициент bv
Нетрудно видеть, что, пользуясь формулой Шези, можно определить и другие неизвестные величины в движении потока. Так, возведя обе части уравнения в квадрат, можно получить и величину потерянной удельной энергии при напорном движении:
-	(60)
2-й вид основного уравнения при турбулентном Д в и ж е н и и (применяется только при напорном движении). При
109
(a)
напорном движении в круглых трубах диаметр трубы выражается через гидравлический радиус следующим образом:
_ пО2 _D
Н'~ 4*D 4
Подставив это значение /? в формулу (58), получим: , 4btL & й,= -ь—
Полученная формула может быть представлена еще в более удобном виде, если в качестве множителя в правой части войдет представляющий удельную кинетическую энергию. Подобные предложения, насколько известно, были в разное время сделаны Вейсбахом и Эйтельвейном. Умножив и разделив согласно этому правую часть уравнения (а) на 2g, получим:
или
L v2
(61)
и гидравлический уклон:
L D2g'
где величина 8b}g представляет произведение из основного коэфициента на какое-то постоянное число; для краткости обозначим его через X.
Формула эта названа формулой. Вёйсбаха и имеет также очень широкое распространение при гидравлических расчетах.
3-й вид ос н о в н о г о у ра в н е н и я при турбулентном движении. При расчетах водопроводных сетей приходится всегда иметь дело со следующими величинами:
а) с напором, или, что то же, с удельной энергией, которой обладает жидкость в разных точках сети и которая обусловливает высоту и дальность ее подачи;
в) расходами жидкости, пропускаемыми через каждый из имеющихся участков;
с) диаметрами труб на этих участках;
d) с длинами отдельных участков.
Наиболее удобной расчетной формулой, очевидно, является такая, которая все эти величины об'единит вместе.
Для получения подобного рода формулы выразим в формуле (58) скорость через расход и площадь живого сечения.
Так, из формулы расхода имеем:
Q « 16 Q2
«'==-, a ^2 = -573l-
ш	1сгЦ*
(61a)
НО
Подставив это выражение в формулу (58) и заменив также по предыдущему R через получим:
_ 64b^L кЧ) ' *
(а)
Так как величина -=- является каким-то постоянным числом, то
тг
646, выражениепо предыдущему для краткости может быть обо-
значено другим коэфициентом.
' Тогда окончательно формула (а) представится в следующем
виде:	_____________
h -	& Г
—	(62)
где:
,__ я2
7 =б4б?
Называется эта формула водопроводной по вполне понятным причинам.
§ 54.	Вывод основного уравнения методом размерности
В § 51 мы получили для равномерного движения жидкости зависимость между потерянной энергией и основными факторами движения в виде формулы (51).
Получена была эта формула на основании общих законов движения в применении к жидким телам.
Рейнольдсом был дан другой, очень интересный способ определения той же зависимости методом размерности, приведенным уже выше в § 30. В самом деле, обращаясь снова к фиг. 87 для случая напорного движения в трубе, мы видим, что потеря энергии в этом случае сводится к затрате какого-то давления Др на участке длины L. Эта затрата, отнесенная к частице единичного веса, будет зависеть, очевидно, от следующих факторов:
1)	от свойств жидкости, т. е. от ее вязкости и плотности, 2) от длины участка £, 3) от средней скорости движения vt 4) от диаметра и абсолютной шероховатости трубы.
На основании этого мы можем написать, что
Др = 76).
где f представляет пока неизвестную функцию.
Представив эту функцию в показательной форме аналогично проделанному выше (см. § 43), получим:
pe vnL, где величина k явится безразмерным коэфициентом.
Вставив размерность всех величин, входящих в это уравнение, получим:
массяхдлин._ =	/-----масса--ух /_м«са \\	х длина;
время* х длина*	\ длинах время ) \длина») \ время )
или
масса _________
-------------— --ДЛИНА длина х время*
у + <г	—л—у
х масса у х время
(а)
Приравняв показатели в обеих частях уравнения, получим систему трех уравнений:
D x — y — 3z\-n + l=s— 1;
2)	у 4-^=1;
3)	-0'4- п} = -2.
Решение этих уравнений дает:
х = п — 3;j/ = 2 — л; z=*n- 1.
Подставив эти значения в уравнение (а), получим;
Др гпЛ-З 2 —л п—1 п
-X = kD	р v ,
откуда гидравлический уклон:
Л = / = А£ =
, r^n—З 2 — п п — 1 п kD Ц р V
7
(63)
Или, заменив у через pg, а коэфициент k другим коэфицпентом k' = 2k, получим:
4 =
2 — п п
V
3— п * Р
(63а)
Входящ й в эти формулы показатель степени п зависит от шероховатости трубы, Как сказано уже выше (см. § 49), этот показатель зависит от типа движения (при ламинарном движении п = 1, при турбулентном движении л = 1,75 —2,0).
Нетрудно убедиться, что полученные нами ранее формулы для потери напора при ламинарном и турбулентном движении (56а) и (61а) могут рассматриваться как частные случаи формул (63) и (63а). В самом деле, подставив в формулу (63; значение л=1, имеем:

(64)
что вполне совпадает с формулой (56а).
Если же подставить в формулу (63а) значение л = 2, то получим: рз
4 = D2g' •	<64а)
что совпадает с формулой (61а).
Таким образом полученная Рейнольдсом формула по сравнению с полученными ранее формулами имеет гораздо более общий вид.
1) Она применима к обоим видам движения, 2) она включает в себя величину Y] и р. зависящие от свойств жидкости, и может быть применена не только для движения воды, но и для движения любых других жидкостей.
И* этих же формул видно влияние, оказываемое вязкостью жидкости, на ее сопротивление. В самом деле, из формулы (64) видно, что при ламинарном движении потери энергии прямо пропорциональны вязкости жидкости. Из формулы же (64а) видно, что при турбулентном движении в трубах значительной шероховатости вязкость жидкости никакого влияния на потерю энергии не оказыв ает. Если же формулу (63а) применить для совершенно гладких труб. т. е для значения л = 1.75, то получим:

К [ 7) \ 0,25^1,75
7‘" f О/ £1,25 -
(65)
из которой видно, что в этом случае вязкость уже оказывает некоторое влияние на потерю энергии, хотя в общем это влияние весьма незначительно.
§ 55. Коэфициенты основных формул турбулентного движения
Полученные из основного уравнения равномерного движения три формулы (Шези, Вейсбаха и водопроводная) содержат три коэфициента, причем, как это ясно из самого вывода, все они представляют собой в преобразованном виде основной коэфициент bt; поэтому любой из этих коэфициентов легко может быть выражен через blt р также через другие коэфициенты.
Так например из формул (62), (61), (59) можно непосредственно получить:
1 с = ~7=
(66)
• X = 8gdi: _1	64
у1	i&bt
Размерность этих коэфициентов различна. Так из формулы Шези имеем размерность коэфициента с:
(67)
(68)
Id =
длина ’/• время
Из формулы Вейсбаха имеем размерность коэфициента К:
X
Г htDg 1
L ^2 J
длина x длина х длина х время» длинахдлинаахв( емя’
что после сокращения дает безразмерное выражение. Из водопроводной формулы имеем:
Г h,D' 1
. id L^q2 J“
__ длина х длина1 х время* _____ впемя* длинах длина*___________________длина ’
Таким образом из данных трех коэфициентов только X получился в виде отвлеченного числа. Это обстоятельство представляет известное практическое удобство при пользовании им и, что еще гораздо важнее, представляет определенный теоретический интерес. Вообще в современной теории гидравлики этот коэфициент занимает значительное место, поэтому в следующих параграфах мы несколько подробней остановимся на нем.
Сведения же о коэфициентах с и-Сбудут даны в соответствующих главах о напорном и свободном движениях жидкости.
Входящий в формулу (61) коэфициент X может быть определен тремя разными путями:
1)	Самым старым способом, применяемым для определения X и всех остальных коэфициентов, является экспериментирование. Этим путем разные исследователи получили огромное количество различных формул, наиболее важные из которых будут приведены ниже.
8 Гидравлика	ЦЗ
2)	Следующим способом, давшим теоретическое выражение для коэфициента X, является примененный нами уже ранее метод размерности.
3)	В самое последнее время проф. Лейбёнзон дал теоретическое выражение коэфициента X, базирующееся на рассмотрении движения жидкостей по схеме проф. Прандтля (см. проф. Лей-бензон „Руководство по нефтепромысловой механике”, 1931 г.).
§ 66. Определение коэфициента X методом размерности
Из данного Рейнольдсом методом размерности формулы для гидравлического уклона:
. _ k' f т) \2 — п уп
к~ ^S\P~) D3-n
можно путем небольших преобразований получить выражение для X. Д^я этого перепишем это уравнение в следующем виде:
-	(jlV-я gn~2 vl
* 2g \ р '	Dn~~2 &
или, иначе, ,	/ fvD\n — l 1 v1 и^,п~2 1
J* — k \ г, / ~D'2g~kN D ‘ 2g'	<69>
где	как известно, является числом Рейнольдса. Если сравнить это
выражение для Д с выражением, данным в формуле (61а), то получим:
'	X = k'Nn~2-	(70)
Полученная формула имеет одночленный вид; ее теоретический интерес заключается в том, что X здесь представлен в виде--функции числа Рейнольдса, т. е. в*виде функции наиболее общей характеристики движения.
§ 57. Эмпирические формулы для определения коэфициента X
История гидравлики за последние столетия — это в значительной степени история различных опытов, ставивших своей целью получить правильные формулы для коэфициентов, характеризующих потери энергии при движении жидкости.
Опыты эти производились в очень большом количестве и в настоящее время существует уже ряд формул, применяющихся с достаточным успехом на практике.
Приведем из них некоторые наиболее известные.
1) Формула Дарси. Эта формула в ее более общем виде уже дана в § 49 под названием формулы Дярси-Базена, где а и £ — коэфициенты шероховатостей. Произведенные весьма тщательные опыты над 21 трубой различного материала, в которых диаметр варьировал от 0,12 до 0,5 м, а скорость изменялась от 0,16 -5 м1сек. позволили Дарси предложить для новых труб значение а = 0,0005, а р = 0,000013. Тогда выразив через X, т. е. 114
X	Ч	/ г> Щ
bt = -g ,а гидравлический радиус через диаметр I R =-4j • по" лучим формулу: _______________________ _____
X-0,°2(1+^jy
(71)
где D должно быть взято в метрах.
Для старых труб коэфициент X следует по Дарси увеличить в 1,5—2 раза, что конечно является весьма грубым приближением.
Для более точного учета влияния загрязнения трубы на коэфициент X немецкий ученый Зонне предложил учесть то обстоятельство, что влияние этого загрязнения отражается гораздо значительнее при небольших диаметрах труб (см. об относительной шероховатости § 49); на этом основании им предложено включить в формулу Дарси поправочный множитель 5. Формула Дарси при этом напишется следующим образом:
Х~0,02а(1-|-^-),	(72)
где значение о может быть взято из следующей таблицы:
Таблица 4
D в м	0,1	0,2	0,4	0,6	0,8	1,0
7	2	- 1,8	1,6	1,4	1,2	1,1
Формула Дарси по своей размерности теоретическим требованиям не удовлетворяет, так как в ней X не является отвлеченным числом. Вытекает это из того обстоятельства, что X здесь представлена he в виде функции числа Рейнольдса, а в виде функции только диаметра трубы.
Несмотря на это, формула Дарси достаточно широко используется в настоящее время на практике.
2) Формула Лянга. Немецким ученым Лянгом была предложена следующая формула дли коэфициента X:
X - а ______
у/ vD'
(73)
где а зависит от шероховатости трубы; 0 — величина, зависящая от температуры (для £=10° 0 = 0,0020, при £ = 20° ₽ = 0,0018).
Значения коэфициента а могут быть взяты по следующим опытным данным:
а) для новых труб с весьма гладкой поверхностью (оловянных, свинцовых) а = 0,009 — 0,010, Ь) для новых или очен|> хорошо очищенных труб с весьма незначительными шероховатостями «•	115
(новые чугунные) а = ’0,020, с) для труб негладких, бывших в / D \6
употреблении, a = 0t;2l-^— I где D — первичное значение диаметра, a Do—диаметр после загрязнения.
Формула Лянга, построенная на основе большого опытного
материала (кроме учета опытов своих предшественников Лянгом было проделано около 300 самостоятельных опытов, при которых скорость варьировала от 0,004 до 53 м[сек), получила в настоящее время весьма обширное распространение.
По входящим в формулу величинам она приближается к теоретически правильному виду, который, как мы знаем, требует,
чтобы X была функцией от величины (число Рейнольдса).
г с-
Формула Лянга в написанном выше виде предназначена исключительно для воды, где вязкость является функцией только
температуры; поэтому X в ней выражена как функция произведения vD, температуры t и шероховатости. Влияние загрязнения труб учтено двояко: с одной стороны, изменение шероховатости, имеющее место из-за замены первоначальной гладкой
поверхности стенок неровными поверхностями осадков, учитывается коэфициентом а. Кроме того Лянг предложил учесть также увеличение сопротивлений, возникающее благодаря сужению сечения трубы осадками и уменьшению ее полезного диаметра. Это прогрессирующее со временем сужение сечения Лянг предлагает учесть тем, что полученные значения X умножаются на (D-У величну ^-1 .
Подобный учет сужения трубы однако большого практического применения не получил, так как при этом требуется на
перед гнать толщину слоя осадка, что весьма затруднительно.
3) Формула Биля. Эта формула, опубликованная в 1907 г., явилась новой интересной попыткой охватить одной аналитической зависимостью потери энергии в любой жидкости (поэтому она называется универсальной). Для труб круглого сечения она имеет такой вид:
X = 0,001
+ i + — /Я vf R I/
(74)
а
где v должно быть взято в метрах, а—постоянное число, равное 0,12, b и с коэфициенты шероховатости, определяемые по табл. 5.
По своей структуре формула Биля относится к многочленным, причем второй член отражает влияние на коэфициент X так называемой относительной шероховатости. Третий же член, который может быть представлен в виде:
cyf R  iq _cy~R g ?vR~ gN '.
должен дать зависимость коэфициента X от числа Рейнольдса. 116
Таблица 5
Степень шероховатости		с
1) Для очень гладких стенок (медь, стекло и т. д.)		0,0064	0,95
2) Для гладких стенок (оцинкованные трубы, строганые доски и т. д.)		0,018	0,71
3) Лля негладких стенок (обыкновенные чугунные трубы, деревянные трубы, по-крытые пылью) . . 			0,036	0,46
4) Для нестроганых досок, гладкого камня бетона 		0,054	0,27
5) Для кладки обыкновенного камня, кнр-пича	.	. .	0,072	0,27
К числу недостатков формулы следует отнести ее громоздкость и тот теоретический дефект, что в ней не соблюден закон размерности.
4) Формула Мизеса. Эта формула, появившаяся в 1914г., представляет видоизменение формулы Биля.
Она имеет следующий вид:
X.O.O1+J/J+
(75)
где k — величина, пропорциональная абсолютной шероховатости, которая может быть взятой из следующей таблицы:
Таблица 6
Материал	10е k
Стекло 	 Тянутые латунь, свинец, медь . . Цемент шлифованный ...... п	необработанный . . . . . Резиновые рукава обыкновенные . .	„ шероховатые . Железо . . 		 Чугун асфальтнров. .	 . новые трубы	 . старые .	....... Жесть		 Дерево ............. Каменные стены из тесаного камня Бутовая кладка, скала 	 .	от	6,4 до	25,6 .	6,4 .	*32,0 .	240	.	4Я0 .	640	.	1 280 .	200	.	400 .	480	.	960 ,	640	.	1600 .	950	.	1900 .	3 200	.	6400 .	8 000	.	16 000 .	6400	.	16000 .	1 600	.	3200 .	6 400	.	12 000 .	6400	.	120000
Сравнивая эту формулу с формулой Биля, мы видим между ними формально большое сходство: по своей структуре она также трехчленна, причем первый ее член является тоже посто-117
яяным числом, второй член в явном виде выражает влияние относительной шероховатости, а третий член может быть представлен в виде 1,771 / 2_ и дает явную зависимость коэфициента X
V N
от числа Рейнольдса.
Следовательно с теоретической стороны эта формула построена уже совершенно правильно, и в этом смысле недостаток, присущий формуле Биля, здесь устранен. Громоздкость формулы сохранилась однако и здесь, что для применения ее в практике представляет неудобства. Интересно также отметить, что благодаря тому, что в обе вышеуказанные формулы входят различные числовые величины, они могут давать при подсчетах весьма различные результаты.
5) Формула Фламана и Блязиуса. Во всех вышеприведенных формулах X представлен в виде суммы нескольких членов.
Наряду с этим существует и много одночленных формул для X', построенных по типу формулы Рейнольдса. К числу их относится данная Фламаном формула, по которой
1 ™
где а для чугунных новых труб принимается равным 0,00074, а для труб, бывших в употреблении, а—0,00092.
Если подставить это значение X в формулу (61а), то, получим:
_ а 1 1>г _ a v1’75 Jh= v 0,25
(77)
Полученная формула позволяет сделать следующее заключение;
1) Поскольку формула не содержит в себе коэфициента вязкости, она пригодна для воды и то при весьма ограниченном колебании температуры (около 15° С).
2) То обстоятельство, что показатель п, входящий в эту формулу, равен 1,75, в соответствии со сказанным в § 49 должно ограничить применение этой формулы только для гладких труб; во всяком случае применение одного и того же показателя п для труб разной шероховатости находится в противоречии со взглядами Рейнольдса и других исследователей.
Немецкий ученый Блязиус в 1912 г. опубликовал работу, в которой он, опираясь на новейшие опыты (Саф и Шодер) и используя закон подобия, дал для случая совершенно новых труб следующую формулу для х:
. 0,3164
А = ——=-
(78)
И»
Формула эта по внешнему виду весьма напоминает формулу Фламана. Если аналогично предыдущему раскрыть величину |/N, то получим:
0,3164
а гидравлический уклон:
(Qxo,2s
If) «1,75
(79)
(80)
Л —
2g D1'25
Сравнивая эту формулу с формулой Фламана, мы видим, что в ней избегнуты недостатки последней:
а)	Формула дана только для гладких труб, что вполне согласуется с показателем при скорости 1,75,
б)	Наличие коэфициента позволяет эту формулу применить не только для воды, но и для вязких жидкостей; с теорети-ческой, стороны эта формула также обоснована безукоризненно.
6) Формула Маннинга. Эта формула,получившая в настоящее время широчайшее распространение, была первоначально получена из опытов над движением воды в естественных руслах. Она дает следующее выражение для коэфициента с:

(81)
где п — коэфициент шероховатости, для которого автор берет значения по Гангилье-Куттеру (см. приложения, табл. II).
В применении к трубам, имея в виду соотношение между с и X, (X = Ц) и заменив R через —, получим:
4*	4
(82)
Таким образом аналогично формуле Дарси для трубы определенной шероховатости х является функцией толькд диаметра.
В настоящее время инженерная практика очень охотно пользуется формулой Маннинга благодаря тому, что вычисления по этой формуле (помощью таблиц и графиков) получаются крайне простыми, а результаты весьма хорошо совпадают с данными практики.
§ 58.	Выбор расчетной формулы
Суммируя все вышесказанное об эмпирических формулах для коэфициента X, мы видим, что все они могут быть классифицированы по следующим признакам.
А.	По своей конструкции формулы делятся:
1)	На одночленные показательного типа, к которым относятся формулы Маннинга, Фламана, Блязиуса. Существует также и много других, не приведенных в настоящем курсе.
2)	На многочленные, к которым относятся формулы Дарси, Лянга, Биля и Мизеса.
В.	По аргументам, входящим в эти формулы, они делятся на:
1)	формулы, в которых аргументом является диаметр трубы; сюда относятся формулы Дарси и Маннинга;
2)	формулы, в которых аргументом является произведение v'd, куда относятся формулы Лянга, Фламана;
3)	формулы, в которых аргументом является число Рейнольдса; сюда относятся формулы Блязиуса, Мизеса.
'Кроме того эти формулы различаются еще в зависимости от учета или шероховатости. Так, формула Блязиуса шероховатость совершенно не учитывает, формула Дарси (без поправок Зонне) учитывает шероховатость довольно грубым коэфициентом. Формулы Биля и Мизеса вводят уже относительную шероховатость явным образом.
На вопрос о том, какой же из этих формул (приведенных здесь далеко еще не в исчерпывающем виде) следует пользоваться при инженерных расчетах, одного мнения на настоящий день не существует. Положение осложняется тем, что часто условия движения жидкости по трубе зависят от многих с большим трудом учитываемых факторов (тщательность производства сборки, характер отложений в трубе и пр.). Однако некоторые руководящие указания в выборе расчетной формулы вполне возможны. Уже в данных выше характеристиках отдельных формул вырисовывались области, в которых целесообразно применение той или иной формулы. Так, очевидно, что формулы Фламана и Блязиуса теоретически правильны только для новых очень гладких труб и именно при расчетах таких труб их и следует применять. Формулу Блязиуса целесообразно применять также для жидкостей, отличных от воды (опять-таки при условии совершенно гладких труб). В случае же движения вязких жидкостей в старых покрытых осадками трубах целесообразно пользоваться формулой Биля (очень популярной среди работников химической промышленности) и формулой Мизеса.
V При расчете водопроводов не утратила своего практического значения еще формула Дарси (хотя вообще ее можно считать устаревшей), но целесообразнее ограничить ее применение только для случая труб, диаметр которых меньше, чем 0,5 м, так как формула Дарси получена именно из опыта над подобными трубами. При трубах же большого диаметра в настоящее время наибольшей популярностью пользуется формула Маннинга, кото-120
рая, несмотря на ее теоретические недочеты, все же показала себя в условиях практики весьма удобной и заслуживающей доверия. Для водопроводных труб (особенно железных) можно рекомендовать также формулу Лянга.
§ 59. Виды местных потерь
Разобрав в предыдущем вопрос о потерях по длине, перейдем к рассмотрению других видов потерь. Как известно, при изменении конфигурации трубы или русла в тех местах, где скорость меняет свою величину или направление, происходят потери энергии, называемые местными потерями.
В качестве примера разных случаев местных потерь здесь приведено движение жидкости по трубе переменного сечения (фиг. 91). В сечении 1 происходит внезапное расширение, в сечении 2—внезапное сужение, в сечении 3—поворот.
Кроме того местные потери происходят в местах расположения кранов, задвижек, клапанов и т. д.
§ 60. Определение потерь при внезапном расширении (теорема Бордй)
Пусть жидкость при своем движении переходит из сосуда М в сосуд N большего диаметра. Частицы жидкости, вынужденные внезапно изменить свою скорость, будут находиться, с одной стороны, под влиянием сил инерции и следовательно стремиться сохранить свое первоначальное направление, а с другой стороны, давление соседних частиц заставит их двигаться по направлению к боковым стенкам (фиг. 92). Под влиянием этих двух факторов движение на переходном участке будет происходить по кривым и в сосуде N образуется кольцеобразная полость, заполненная жидкостью, находящейся в медленном вихревом движении, постепенно затухающем по направлению к стенкам. Эти вихревые движения, вызываемые силами трения по раздельной поверхности ас, сопровождаются выделением тепла и потерей энергии. Потери энергии обозначим через hyd (А удара), так как в этом случае имеется аналогия с ударом двух твердых тел, движущихся в одном направлении с различными скоростями .
Для определения величины hyd выделим из жидкости отсек ABCD и приложим все действующие на него силы (фиг. 93).
1)	По грани АВ отброшенные связи сведутся к силам гидростатического давления, так как по стенкам А и В жидкость находится почти в состоянии покоя, а давление по слою ab, считая движение медленно изменяющимся, принимаем также гидростатическим (см. § 26). Равнодействующая этих сил Р1 = р^.
2)	По грани CD силы давления распределяются также по гидростатическому закону. (Движение и здесь считается медленно изменяющимся.) Их равнодействующая Рг=р2м2,
3)	Давление боковых стенок направлено нормально к жидкости (силы трения по этим стенкам принимаем равным нулю ввиду наличия «мертвого слоя”, не участвующего в общем движении).
4)	Собственный вес отсека G = 7<»4 L.
Для определения величины потери на удар воспользуемся известным в динамике уравнением количества движения, согласно которому при движении тела проекция на
любую ось изменения его количества движения равна сумме проекций импульсов всех приложенных к нему сил на эту же ось. Так как количество движения равно произведению из массы тела на его скорость, то в нашем случае изменение количества движения равно tn — vt).
Рассмотрим движение жидкости за время dt. Пусть жидкость при этом переместится в положение а{ Dt Это перемещение равносильно перемещению об'ема abat в положение cdCtDi. При этом произойдет изменение количества движения:
у Q (v2— vt).
S
Проекция на ось потока импульса сил за это время будет: (Рх — Р2-[-О cos a) dt.
На основании закона количества движения получим:
Pt — Р, + G cos а ) dt
или, заменив Q через ®2va и подставив значения для сил, получим:
, z, — z,	V
Pi —Pi + T<“4 L -+	= v2 —	.
Разделим все уравнение на <»ат и сократим на L:
Напишем теперь уравнение Бернулли для точек 1 и 2:
+	+ y’ + % + Aj'd:
откуда, сравнивая оба уравнения, получим:
V,*— v* .	. А—Pt	А2— Vi2 , v„ /	\
2g + г»~^ +£-~~= ' 2g
_ V2 — A*+ 2Уа* — 2t\ vi _ (V1 — vt) 2 2g	“ , 2g
Полученный конечный результат: ,	— i»a )г
hyd== 2i	(83)
называется уравнением Бордй. vt— vt представляет собой потерянную скорость. Обозначив ее через w, получим: . w’ hvd~2g
При оценке полученной формулы необходимо учесть, что при выводе нами сделаны следующие допущения: 1) мы полностью пренебрегаем силами трения по стенке, 2) мы считаем движение медленно изменяющимся, 3) мы применили здесь уравнение Бернулли, взятое для струйки, в то время, как ввиду неравномерного распределения скорости по поперечному сече нию следовало бы применить уравнение Бернулли для потока. Вследствие этих допущений полученная формула дает некоторое увеличение потерь; учитывая однако, что это увеличение идет в запас прочности и что точный учет этих обстоятельств крайне сложен, выведенную выше формулу оставляют без изменений.
2-й вид,уравцения Борда. Из уравнения расхода имеем:
______	^2^2 о»! А = А; А = ~г-»
подставим это выражение в формулу (83), откуда:
(84)
§ 61. Случай внезапного сужения
Жидкость при выходе из широкого сосуда в узкий сначала сжимается, а потом, подвергаясь расширению, заполняет, все сечение узкой трубы (фиг. 94). Следовательно все явление можно разбить на две части: 1) от входного сечения до сечения
123
•car потери происходят из-за сжатия жидкости и неравномерного распределения скоростей по поперечному сечению, 2) от сечения и>сж до сечения потери происходят вследствие внезапного расширения жидкости.
Опытами установлено, что первые потери по сравнению со вторыми незначительны и ими можно пренебречь. Таким образам, применяя второй вид уравнения Бордй, получим:
(85)
Степень сжатия сечения характеризуется отношением которое обозначим через г (коэфициент сжатия). Следовательно
(1	\2 Г/ 2
1 - т)	(86)
Так как определение величины е для данного случая затруднительно, то при практических подсчетах пользуются не этой формулой, а таблицей, полученной на основании экспериментальных данных.
Фиг. 94
§ 62. Комбинированный случай поворота с расширением (фиг. 95)
Применим и к этому случаю формулу Бордй (1-й вид):
"КОмб 2^>
где w— потерянная скорость и по величине по направлению найдется из треугольника скоростей:
да2 = v? + т>аа — 2 vt cos (3;
cos P = 1 — 2 sin*
&
отсюда:
w2 = t'124-T'a2—2Vi vt+4vt T»asin2-|-=	— v2\ + 4-o1v2sin2
откуда:
A	2
пКОмв “ 2g H 2g
Для случая простого поворота а», = <о2, следовательно vt — va; тогда:	йяов = 4 sin2-^-	.	(87)
§ 63. Обобщение полученных формул
Выпишем последовательно формулы, полученные для трех рассмотренных случаев:
-2Н1	<» J ’
3)
h -£Msln2JL 11'ПОв	15111 2 *
Все три формулы представляют собой произведения, в которых один из множителей является кинетической энергией для скорости, взятой за данным местным препятствием, а второй множитель является каким-то коэфициентом. Этот коэфициент характеризует степень теряемой энергии в данном местном сопротивлении; называется он коэфициентом сопротивления и обозначается £ Следовательно:
Все остальные виды местных потерь (кран, задвижка и пр.) выражаются также аналогичным образом, причем -значения С берутся на основании опытных данных из таблиц.
Выразим аналогичным образом потери по длине по формулам Вейсбаха:
L v2 v*
где
- Л — л D.
Если поэтому при движении жидкости в трубе просуммируем все потери энергии, то получим какую-то алгебраическую сумму, могущую быть представленной в следующем виде:
Величина S£ представляет сумму коэфициентов сопротивления и называется иначе коэфициентом сопротивления системы и обозначается через тогда вся потеря энергии может быть определена по формуле:
ЕА = Сс^;	(87а)
полученное уравнение называется законом наложения потерь.
§ 64.	Значения коэфициента сопротивления £ для отдельных случаев
1.	Случай внезапного сужения (фиг. 94). Значения коэфициента сопротивления даны в табл. 7.
2.	Потери при входе из резервуара в трубу (фиг. 96). Этот случай можно рассчитывать по предыдущей таблице, причем так как -^-<0,10, то ^о<?о = 0,50.
3.	Случай поворотного крана (фиг. 97). Сопротивление поворотного крана зависит от угла поворота ? (см. табл. 8).
Таблица 8
	10°	20*	30*	40°	50е	60°
с	0,29	1,56	5,4?	17,3	52,6	206
4.	Потери на закруглениях (фиг. 98) при плавном повороте на 90° (см. табл. 9)
Таблица 9
D d	0,2	0,3	0,4	0,5	0,6	0,7 '	0,8	4 0,9	1,0
с	0,138	0,158	0,206	0,294	0,440	0,661	0,977	1,408	1,979
5.	Потери в задвижках (фиг. 99). Потери энергии при протекании жидкости через задвижки зависят главным образом от соотношения между высотой поднятия задвижки h и диаметром трубы D.
Кроме того на величину сопротивления влияют абсолютные размеры трубы.
Зависимость коэфициента сопротивления задвижки в круглой трубе от соотношения высоты поднятия задвижки к диаметру
трубы дана в табл. 10 (по Вейсбаху для малых труб D < 0,5 м и по Кихлингу для больших труб D > 0,5).
Таблица 10
h D	13 72	7 36	5 24	_1_ 4	1 3	оо |оо	5 12	11 24	1 2	7 12	2 3
Малые трубы С Большие трубыС	43,0 41,21	35,0 35,36	28,0 31,35	17,0 22,68	7,92 11,89	5,52 8,65	3,97 6,33	2,89 4,57	2,06 3,27	1,Н 1,55	0,57 0.77
6.	Потери в диафрагмах (фиг. 100). При наличии диафрагмы потери зависят от отношения площади диафрагмы к площади живого сечения трубы.	*
Зависимость коэфициента сопротивления при протекании че-(D
эез диафрагму от соотношения -д-дана в табл. 11 (по Вейсбаху).
7.	Сопротивление сетки и обратного клапана. Зсли на конце трубы поставлена сетка, то в зависимости от эода сетки коэфициент сопротивления колеблется от 1 до 5. Цля обратного клапана в зависимости от его конструкции вели
чина коэфициента сопротивления колеблется от 2 до 5; поэтому, если имеется всасывающаяся коробка с сеткой и обратным клапаном, величина коэфициента сопротивления может колебаться от 3 до 10.
Таблица 11
1 э |о	0,10	0,20	0,30	0.40	0,50	0,60	0,70	0,80	0,90
'D	225,9	47,8	17,5	7,8	3,8	1,8	0,8	0,3	0,06
Задача. Вода из закрытого резервуара А (фиг. 101), в котором давление выше атмосферного, переходит по трубе переменного сечения в вышележащий резервуар В, в котором имеется вакуум. Требуется определить скорость v2 в широкой трубе.
Даны: показание манометра (избыточное давление на свободной поверхности сосуда Д)/?ш = 0,1 кг/см2-, показание вакууметра pv ='0,6 «г/сл2;/,, = 20 м; £а=40лс; Dt~Q, 1 ж;Ра = 0,2 л; //=2,50 м\ d «I радиус закругления -у = 0,1 м.
Решение. Напишем уравнение Бернулли для точек 1 и 2.
Фиг. 100
Фиг. 101
Т	I
Pl = Ро + Р» = 1 > 1 кг\см2-, pt = pQ —р, = 0,4 кг/см2-,
отсюда:
“ _ г^-н = -Ц__М _2,50 = 4.5 х.
Переходим к определению ЕЛ.
ЕЛ — h вх 4" Ац 4- Л уд 4- Ли 4“ h закр + л вых.
или
2A-^x2g+>.^ 2i + 2g^1 .r ^ + r + >. закр T '•зых 2g •
_L*
2g
Найдем значения всех коэфициентов. Имеем С«х = 0,5; х находим по формуле Дарси;
л-°.°3( I + то^от) =адз75;
:>=°-03 (1 + ToW)~ °’031;
Слокр находим по таблице —Сзажр 2; = I (из формулы Борда).
Подставив эти значения, получим:
(9О\ «з	40	п.г
0,5 + 0,0375^ .^ + (9 + 0,034^+ 2 + l)-^-
= 8	18,8	.
2g 2g
Из уравнения расхода имеем:
1*1	<0,
—’ = —? = 4; V, = 4 Vo,
va ш, 1	**
откуда:
2А = 81^+ 18,8^=146,8^.
Подставив найденное раньше значение — 4,5 .и, получим:
77^
4,5= 146,8+?, 2g
откуда:
v.2 =	i^^6 =0,78 м)сек.
® Гидравлика
12»
ГЛАВА IX
ИСТЕЧЕНИЕ ЧЕРЕЗ ОТВЕРСТИЯ И НАСАДКИ
Рассмотрев в предыдущих главах общую теорию движения жидкостей, мы в дальнейшем перейдем к применению полученных зависимостей к отдельным гидравлическим явлениям.
Первоначально рассмотрим движение жидкости через отверстия и насадки, относящееся к числу явлений, в которых трение жидкости о стенки играет незначительную роль и в которых потеря энергии может быть отнесена к виду местных потерь.
§ 65. Истечение через малые отверстия в тонкой стенке при постоянном уровне
Общее описание явления. Если в стенке или дне сосуда, содержащего жидкость, сделаем небольшое отверстие, то вытекающая из этого отверстия струя обнаруживает определенную закономерность (фиг, 102). Прежде всего обращает на себя внимание цвет струи. После выхода из отверстия струя на своем начальном участке имеет гладкую, кристаллически прозрачную поверхность. Если ввести на этом участке в жидкость какое-нибудь подкрашивающее вещество, то оно выделяется отчетливо из всей жидкости в виде отдельной правильной струйки, что указывает на ламинарность движения на этом участке. После этого участка характер движения меняется. Так, при мгновенном освещении можно обнаружить распад всей массы жидкости на отдельные, друг с другбм не связанные и движущиеся самостоятельно частицы, поэтому движение здесь относится к типу свободного.
После выхода из отверстия жидкость меняет свою форму. Так, если в сосуде имеется отверстие круглой формы, то струя после выхода имеет эллиптическое очертание. При отверстии квадратной формы происходит изменение вида сечения жидкости вдоль струи. По наблюдениям Понселе и Лебро струя в этом случае, выходя из отверстия сосуда, сначала имеет форму восьмиугольника abcdefgh (фиг. 103) ив дальнейшем получает крестообразную форму klmn. Это интересное явление называется инверсией струи, и об'яснение ему следует искать в том, что частицы, находясь на различной глубине, вытекают вследствие этого с различной скоростью. Траектории частиц, находящихся в одной вертикальной плоскости, должны пересечься между собой, благодаря чему происходят столкновение частиц, сжатие струи в одном направлении и ее расширение в другом направлении. Поверхностное натяжение между частицами однако препятствует их рассеиванию и собирает расходящиеся частицы к оси струи. Совместное действие этих факторов и приводит, с одной стороны, к изменению формы струи, а с другой стороны, к тому, что струя после своего выхода уменьшает площадь своего поперечного сечения. Опыты показывают, что при круглом отверстии участок, на котором происходит сжатие поперечного 130
сечения, равен приблизительно 0,5 диаметра отверстия. В сечении, взятом на расстоянии 0,5 диаметра, жидкость уже разбивается на отдельные струйки и движение становится свободным. Это сечение принято называть сжатым сечением, так как после этого сечения благодаря освобождению частиц создается представление как бы об обратном расхождении внешнего контура струи
Таким образом под сжатым сечением следует понимать гра яичное сечение, в котором движение переходит в свободное. В этом сечении частицы, перестав прижиматься друг к другу, движутся параллельно. Отношение площади сжатого сечения к площади выходного отверстия называется коэфициентом сжатия и обозначается через е
ш сж ----= 6, (D
откуда со сж = ео).
Опытами установлено, что величина е меняется незначительно и в качестве среднего значения ее можно принять е - 0,64.
§ 66. Определение скорости и расхода при истечении струи в атмосферу
При изучении истечения жидкости через отверстие на первом плане обычно стоит вопрос о скорости истечения и расходе, проходящем через отверстие. При выводе аналитических зависимостей для этих величин исходим из следующих предположений: 1) уровень жидкости в сосуде считаем постоянным и движение следовательно установившимся; 2) принимаем, что размеры отверстия сравнительно с поперечным сечением сосуда невелики; 3) центр тяжести отверстия считаем достаточно глубоко погруженным под свободной поверхностью, так что на этой поверхности не будет заметно движения частиц, и истечение будет происходить совершенно спокойно; 4) отверстие считаем в достаточной мере удаленным от примыкающих стенок и дна, близость которых могла бы влиять направляющим образом на условия истечения. Обращаясь теперь снова к фи г.=38j напишем уравнение Бернулли для двух сечений потока, причем сечение 1 выберем на свободной поверхности, где начальные участки
траекторий гсех частиц перпендикулярны к сечениям и поэтому между собой параллельны. За сечение 2 возьмем сжатое сечение (шедг;, за которым частицы начинают двигаться свободно и их траектории также могут считаться параллельными. Жидкость принимаем идеальной. Скорость при этом обозначим через vm (v теоретическое); тогда имеем:
н । А , А ।
+ 7 + 2Я 7 + 2g •
Выражением
и0
2g
ввиду его незначительности пренебрегаем,
откуда:
^=/2^77
(закон Торичелли).
Напишем это же уравнение вторично для случая реальной жидкости. Потери энергии при этом будут, очевидно, отнесены к типу местных.
Скорость обозначим vn (v,практическое).
Н+ \ v ° — Рь I Уя 21 Л + 7 +2g“ 7 + 2g+hom‘-
Или, пренебрегая попрежнему величиной имеем:
^-2 + С^ = ^(1+С) 2g'* 2g 2gIU+'*-’’
откуда:
Обозначив отношение vn 1 /ГТС через 9, имеем:
’"/ттг откуда:	_________
(88)
(88а)
(89)
Коэфициент <р, показывающий, насколько уменьшается действительная скорость по сравнению со случаем, идеальной жидкости, называется коэфициентом скорости; величина его определяется опытным путем и в качестве среднего значения может быть принята равной 0,97. 132
Зная величину коэфициента скорости, нетрудно также определить и величину коэфициента сопротивления; так, из данного 1 выше отношения —-----= о имеем:
/1 + ?
C=4i-1-	(89а)
В нашем случае С —	1 = 9.06.
Перейдем теперь к определению расхода. При существовании сжатия струй расход найдется в виде произведения скорости vn на площадь сжатого сечения.
Q = vnwC3K или, подставив вместо vn и их значения, получим:
Q = ? vme<o = |М1> vm,	(90)
где |i =
Q ">Vm
показывает, насколько истинный расход, пропус-
каемый отверстием, уменьшается по сравнению с идеальным случаем; называется он коэфициентом расхода. Как видно из предыдущего, коэфициент расхода может быть выражен через коэфициенты сжатия и скорости по формуле:
р = ер.	(91)
Понятие о коэфициенте расхода может быть применено и для других случаев движения жидкости; так например, при движении жидкости по трубе теоретический расход (считая жидкость идеальной) определился бы по формуле:
Qm= “у4 2gH.
Действительный же расход благодаря наличию потерь окажется меньше. Обозначив действительный расход через Q„, получим:
=	(91а)
где р.в—учитывающее влияние, оказываемое на расход всеми сопротивлениями, называется коэфициентом расхода системы. Так как при истечении из трубы сжатия струи не бывает (е = 1), то И» = Ч =
<рв по формуле (88а) равняется *	, откуда коэфициент
У 1 I ч
расхода системы выражается через коэфициент сопротивления системы £ формулой:

(886)
Выпишем теперь значения всех четырех коэфициентов для случая истечения из отверстия в тонкой стенке.
е = 0,64; <р = 0,97; у = 0,62; С = 0,06.
В действительности эти коэфициенты не являются постоянными величинами, а зависят от величины Н. Результаты опытов, характеризующие эту зависимость, приведены в табл. 1 (в приложениях).
§ 67. Случай истечения из затопленного отверстия (истечение под уровень) (фиг. 104)
= const;
Нг = const.
Этот случай отличается от случая истечения в атмосферу только тем, что в выходящей из отверстия струе давление отлично от атмосферного.
Напишем уравнение Бернулли для точки на свободной поверхности в первом сосуде и для точки, находящейся на оси во втором сосуде, считая жидкость идеальной:
величина рх определяется по формуле:
А=А4-Т^-
Подставим полученные значения pt в формулу (а):
н,Ръ Ръ + ^Н^ vm2
,+ Т-------7	+V'
откуда:
^ = H1-Hi = h-,
\/2gh.\	(92)
Из полученного выражения видно, что все формулы, выведенные для случая истечения в атмосферу, верны также и для истечения под уровень, если вместо величины Н подставить величину h—разность уровней в обоих сосудах.
§ 68. Влияние близости стенки на истечение из отверстия
Здесь возможны три случая:
1	Отверстие так далеко расположено от краев стенки, что т^г=3а и п^ЗЬ (фиг. 105). Этот случай называется случаем полного совершенного сжатия, и предыдущие выводы даны именно для него.
131
2.	Указанные условия полностью не соблюдены, так что края отверстия лежат близко к краям стенки, не совпадая однако с ними.
Этот случай называется случаем несовершенного сжатия, и коэфициент расхода может быть взят на основании экспериментальных данных по следующим формулам:
для круглых отверстий	И — Но U + 1}	(93)
и для прямоугольных отверстий н = Но(1+4)>	(94)
где коэфициент расхода для случая совершенного полного сжатия, а величины I и могут быть взяты по табл. 12.
Таблица 12.
ш £Г	0,10	0,20	0,30	0,40	0,50
/	0,014	0,034	0,059	0,092	0,134
/1	0,019	0,042	0,071	0,107	0,152
ш — площадь сечения отверстия
2 — площадь сечения сосуда
3.	Отверстие своим одним или несколькими краями совпадает с краями стенок или дна сосуда. Этот случай называется случаем неполного сжатия. Коэфициент расхода для этого случая вычисляется по формулам Бидона:
Н-Но (1+0,152	(95)
для прямоугольных отверстий и
Н “ Но (1 +0,128 -А-)	(95а)
для круглых,
где п — часть периметра, на котором устранено сжатие, р — полный периметр отверстия.
Задача. Вода из резервуара М поступает в резервуар N через круглое отверстие А площадью <о0 =0,4 дм2 и квадратное отверстие В, расположенное у дна резервуара с площадью
135
ав -=0,25 дм9. Из второго резервуара вода сливается чере; стенку высотою Л2 = 2 м. Определить расход волы, если глубина воды в первом резервуаре h = 6 м и напор воды над отверстием А составляет hx = 1,5 м (фиг. 106).
Решение. 1) Определяем расход через отверстие А:
Q = |1®д/2ёлГ = 0,62-0,4	196,2-15= 13,4 л\сек.
2) Определяем расход через отверстие В. Коэфициент расхода определяем по формуле Бидона:
р- Но(1 +0,152 -yj=O,62 (1 +0,152	=
= 0,62(1 +0,031)=0,64.
Напор для отверстия В:
hB = h — h2 = 6 — 2 = 4 м.
QBusV.u>By2gAB = 0,64-0,25}Л196,2-40 -=14,3 л]сек.
Суммарный расход:
Q = Qa 4- Qa - 13,4 + 14,3 = 27,7 л!сеч.
169. Истечение через большие отверстия при постоянном уровне
В случае, когда жидкость выходит из отверстия значительных размеров, отдельные частицы, находящиеся на разных глубинах, должна двигаться с разными скоростями. С точки зрения врименения основных законов гидравлики это означает, что применить к этому случаю уравнение Бернулли для элементарной струйки здесь нельзя и необходимо применить то же уравнение, взятое для потока (см. § 40) с введением поправочного коэфициента а. Если включить этот коэфициент в общий коэфициент /*, характеризующий различие между теоретическим и истинным расходом, то общее выражение расхода останется то же, что и для случая истечения через малое отверстие*. Таким образом и для случая большого отверстия имеем ту же формулу:
,	Q=mw^2gH,	(96)
где коэфициент расхода т учитывает помимо двух предыдущих факторов (е и 9), характеризующих сжатие струй и уменьшение скорости, также и третий фактор а, характеризующий неравномерное распределение скоростей в поперечном сечении. Коэфи-цяент расхода т определяется эмпирически.
Случай большого прямоугольного отверстия. При истечении из больших отверстий особый практический интерес представляет собой случай большого прямоугольного отверстия, так как через такое отверстие вытекает жидкость в разных гидротехнических сооружениях.
136
При вычислении расхода через эти отверстия можно пользоваться данной выше формулой (96). Кроме того в гидравлике часто пользуются для вычисления этого же расхода следующим выводом.
Выделим из площади сечения струи элементарную площадку (фиг. 107) Д 2 = BdH на расстоянии Н от свободной поверхности (где Н переменная величина). Элементарный расход через эту площадку будет равен:
d Q = н dQ y/lgH = р* BdH / 2gH,
а общий расход:  
Q = y.B]/2g f Н* dH J	о	\
3 = m0B /2g [н1— H* J
(97)
Указанный вывод страдает двумя недостатками:
1. Условия истечения струйки, ограниченной другими частицами жидкости, конечно отличаются от условий истечения струйки, ограниченной твердыми стенками, поэтому непосредственное применение формулы малого отверстия к этому случаю теоретически не вполне правильно.
2. С другой стороны, опытом установлено, что коэфициент I* не является постоянной величиной, а зависит от напора Н и поэтому, строго говоря, не может быть вынесен за значение интеграла.
Указанные теоретические погрешности компенсируются тем, что значения коэфициента расхода т0 определяются всегда экспериментальным путем, а не по указанному отношению:
2
§ 70. Истечение при переменном горизонте
Движение является неустановившимся, поэтому, строго говоря, уравнение Бернулли не может быть к нему применено; однако при значительном соотношении площади сечения сосуда 2 к 137
площади отверстия ш (5® 100) может быть с достаточной точностью сделано допущение, согласно которому выходная скорость равна скорости, которая имела бы место в данный момент времени при установившемся движении.
Задача заключается в определении времени, в течение которого, жидкость опустится от положения Zj до положения z3 (фиг. 108). Возьмем промежуточное положение уровня с ординатой z\ пусть за время dt он опустится на величину dz. Об'ем жидкости, прошедший через сосуд, при этом будет равен — 2 dz.
С другой стороны, об'ем жидкости, прошедший через отверстие, будет равен	___
W = Qdt = 2gz dt.
Приравнивая оба выражения для об'ема, получим:
2gzdt = — 2 dz,
откуда:
dt —-----т^=—dz,
•	p<»V2gz
отсюда:
t==_ [_____р____ =	1 С Q
J |л 04/ 2gz dz у 2g J }/z dz
Для интегрирования этого уравнения необходимо знать функциональную зависимость межу 2 и z. В частном случае, если 2 = = const = 20, получим:
t = —( z~2dz |ia>/2g J
2,
ИЛИ
рыу !
(98)
В случае опорожнения сосуда Z2 = 0, тогда:
(99)
§ 71. Случай затопленного отверстия при переменном горизонте (фиг. 109)
Пусть первоначальное положение уровней в сосудах АВ и
Bi при разности между ними й0, а конечное положение CD и С( Д с разностью уровней hv
Возьмем какое-то промежуточное положение уровней FE и и Fi Ev Отметки горизонтов при этом обозначим z0 и zx. За 138
время dt уровень в первом сосуде понизится на dz0 и во втором поднимется на dz}. Обозначим площади поперечных сечений сосудов через е0 и Аналогично предыдущему выводу имеем:
— 20 dz0 = н ш /2gh dt;
dt —------' dz° •
2gh
Для интегрирования hjjkho выразить dzQ через dh. Имеем h = Zq Zp
откуда:
dh = dz0 — dzt,
имеем:
— Qodzo-= Q^dz^dz^
Тогда:
/S< + йЛ \
dh = dzQ -|—g dz0 — dzQ (	— j,
откуда:
dz0^ -[-Qodfl• тогда:
• Q,
dt = — ——— — dh.
<2o+st) И1*»/ %gh
______
too/2g J (20 4-2t)|//i
В частном случае, когда £20 = const; £2, - const, тогда:
ho
(£20 4- Ot)!*® /2g J 'h
В случае, если £20 величина бесконечно-большая (реки), для определения времени t разделим и помножим правую часть на величину £20; тогда получим:
2 0	90
(,01>
Аналогичным образом поступают, когда — величина бесконечно-большая.
Задача. Камера шлюза длиной L = 50 м и шириной b = 10 м с вертикальными стенками наполняется через отверстие А,расположенное на глубине Л, = 1 м, считая от уровня воды в реке выше шлюза, и опорожняется через отверстие В, расстояние до центра которого от горизонта воды в реке ниже шлюза й2 = 0,5 м. Определить время наполнения и опорожнения шлюза, если площади отверстий шд = о>в =0,5 ж2 и напор Н составляет 2,£ м (фиг. ПО).
Решение. Определяем время наполнения.
Первая стадия. От горизонта нижнего бьефа до центра отверстия А наполнение идет путем свободного истечения воды через отверстие А при постоянном напоре. Расход при этом:
Qi = ju<o j/2gAj= 0,62-0,5]/19,62 • 1 = 1,37 м3[сек.
Количество воды, поступающей в камеру при этой стадии, составляет:
w = L-b{H—hl) =50-10-1,5 = 750 м\
Время первой стадии наполнения:
. w 750	_
~~ Q, “ 1,37-60 ~9,1 МИН‘
Вторая стадия. Истечение происходит при изменяющемся напоре от hx до 0.
Время определяется по формуле:
, _ 2 £2]4/ц
2	И- ®/2g
где £2 •= 7^ = 500 л2
Подставляя наши данные, имеем: .	2-500	_ 1000	1о_
* 0,62 • 0,5/iW- 60 1,37-60 122 мин-
Время, потребное на наполнение камеры:
t=tx + /2 = 9,1 + 12,2 = 21,3 мин.
Определим время, потребное на опорожнение камеры.
Весь процесс происходит путем истечения при переменном напоре, изменяющемся от Н до 0.
Время t опорожнения определяем по формуле:
	22/77
^“/2£
где 2 имеет то же значение.
. 2 • 500 • /2£	,, _
г =-------1——-- — 11,5 мин.
0,62-0,5-60/19,62
Фиг. ПО
Задача. Круглый резервуар диаметром D, = 12 м (фиг. 111) наполняется водой из реки при помощи трубы длиной £ = 100 м и диаметром D = 150 леи.
Труба имеет два закругления и предохранительную сетку. Определить время наполнения резервуара, если hx — 2,0 м и = 3,5 ж.
Решение. Наполнение резервуаоа до отметки будет происходить при постоянном напоре Н —hvH время наполнения до отметки определится из формулы:
1 Р-сш
где £1 —сечение резервуара, ® — сечение трубы, н-с—коэфициент
Л 1 расхода системы, равный-^.
Принимаем: для сетки £= 10 и для закруглений С—0,25.
Согласно формуле Дарси имеем:
С по длине = >£= 0,03 ( 14- 40.0 15 )бЛ5= 23,3
Отсюда коэфициент сопротивления системы:
~ С сетки + 2f закр + ^дл + С вых = 10 + 0,5 + 23,3 4” 1 ~ 34,8,
/С /3+8 5,9 и>1л
Искомое время будет равно:
_ Р^А,_________________________144-2___________
1- НСО1 2 /2g(Ai—A1) • 60 ~ 0,17-0,0225/49,62 • Т,5 • 60 “ МИН’
С отметки Ai до отметки А2 наполнение резервуара будет происходить при переменном напоре, изменяющемся от Н = = А2 — Ах до Н = 0.
Время, потребное для этой операции, найдется из формулы:
.	2 2/77	2-144-/L5
Ч —--------7=----= а i~7 A none , -- = 347 мин.
H«®/2g	0,17-0,0225)/19,12
Полное время наполнения резервуара будет:
t = tx 4~ К = 236 + 347 ^5 580 мин. 9 ч. 40 м.
Задача. Дана система, состоящая из двух баков и трубопровода длиной £ = 20.и и диаметром D = 200 мм (фиг. 112).
Определить, через сколько времени уровень в баке // повысится с отметки А, = 10 м. до А2 = 5 м, если горизонт воды в баке / остается неизменным и диаметр бака 11 Dt = 2 м.
Решение. Так как истечение будет происходить при переменном напоре, то искомое время определится по формуле:
t = 22(/а~х-/а;)=гогс/А,-/^) t = Не “ / 2g	|*с D2 V2g
Определяем коэфициент сопротивления системы:
1 + 40-0,2 ) *
вых
4s — Чвж -J- ЧЛ» Т закр Т 20
X-^ + 2.0,25 4-1 = 5,38; v,
1
Не =
1
= 0,43.
Находим искомое время: 2-4(/1о_/5->_ 8(3,16-2,23> 7-44	38с
0,43-0,04 /19,62	0,43 • 0,04 • 4,4<3	0,и76	« <*к. - IM. б» С.
§ 72.	Типы насадок
Если к отверстию в сосуде приделать коротенькую трубочку, то условия истечения изменяются весьма существенно. Такие короткие трубки, длина которых I = (3,5 — 4)D (где D—внутренний диаметр трубки), называются насадками.
Фиг. 113
Наиболее распространенными в практике типами насадок являются следующие:
1.	Цилиндрические насади и. Они бывают двух типов: а) внешняя насадка (Вентури) (фиг. 113), б) внутренняя насадка (Борда) (фиг. 114).
2.	Конические насадки. Они бывают тоже двух типов: а) конические сходящиеся (фиг. 115), б) конические расходящиеся (фиг. 116).
Фиг. 114
3.	Коноидальные насадки, под которыми в гидравлике принято понимать насадки криволинейного очертания по форме вытекающей струи (фиг. 117).
§ 73.	Истечение через внешнюю цилиндрическую насадку
При истечении из насадок можно говорить о двух сжатиях: о внутреннем сжатии (при входе струи в насадку) и наружном сжатии (при выходе струи из насадки).
В цилиндрической насадке наружного сжатия нет, а внутреннее сжатие примерно такое же, как для случая истечения из отверстия в тонкой стенке.
® нар — 1,	^ьн 0,64.
Движение жидкости в насадке может быть расчленено hi следующие этапы (фиг. 118).
1. От входного сечения аа до сжатого сечения bb будет имет! место сжатие струй. Обозначив скорость в сжатом сечении мере: Vi, а скорость в сечении сс и dd через v, можно из уравнение расхода получить:
__	v v
Ш СЖ е 8Н 0,64
Потери на первом участке обозначим через hex.
Учитывая данные выше значения для коэфициента сопротив ления при отверстии в тонкой стенке, получим:
. _nn«vi2 0,06 -v*	n,^2
Авж 0,06 Q б48.2g - 0,1462£-
Фиг. 118
2. От сечения bb до сечения сс имеет место внезапное рас
ширение. Потери энергии при этом определяются по формуле Борда:
А _ / »	t \2 z>a f 1_iYji_от Ji
hya U*	/ 2g \0,64	J 2g ’31 2g*
3. От сечения сс до сечения dd движение происходит, как в трубе; ввиду незначительной длины этого участка потерями на трение пренебрегаем.
Напишем уравнение Бернулли для точек, взятых на свободной поверхности и в сечении dd:
Y 2g у 2g 2g 2g
Пренебрегая величиной
Vo2
?g-
ПОЛуЧИМ:
/7= 1,457 J-, 2g’
откуда:
(102)
Следовательно для цилиндрической насадки 9 = 0,82, С = 75?82^ “ 1 ~0’49'	(ЮЗ)
Определение коэфициента расхода. Согласно найденному раньше выражению
р. = е® = 0,82.	(104)
Сравнивая полученные коэфициенты расхода для насадок с полученным ранее значением р- для истечения из отверстий, подучаем:
t* нас	0,82	4
Ноте	0,62	3
Следовательно, пропуская жидкость через цилиндрическую насадку, мы увеличили расход в отношении около 4/3. 06‘ясне-ние этого явления следует искать в том, что при истечении через цилиндрическую насадку в мертвой полости аа — сообразуется вакуум, и жидкость, вытекая при пониженном давлении, увеличивает свою скорость.
Величина вакуума в этой полости может-быть определена следующим образом: напишем уравнение Бернулли для точек в сечениях bb и dd;
I 2g Y 2g
заменив попрежнему через a hyg через 0,31^., получим: 1 ! 031\_ 112^.
1 Y 2g\0,642	°’31;- 1’122g’
так как v = 0,82yf2gH, то окончательно
= 1,12-0,822//^ 0,75//.
-Y
(105)
§ 74.	Внутренние цилиндрические насадки (фиг. 114)
Вследствие наличия у входа струй встречного направления сопротивления в этих насадках, а следовательно и потеря энергии в них больше, чем в насадках Вентури. Условия истечения зависят от длины насадки следующим образом:
а) Если длина насадки /<1,50, струя вытекает, не касаясь стенок насадки. Коэфициент сжатия в при этом равен приблизительно 0,5, а коэфициент скорости ? в этом случае близок к единице, б) При длине насадки /=2,5£> струя протекает внутри насадки, образуя внутреннее сжатие и вакуум.
Коэфициент наружного сжатия при этом равен единице, а коэфициент скорости <р = 0,71 (вследствие увеличения сопротивлений при входе).
И = «? = 0,71, а С—gyp- — 1 = 1.	(Ю6)
При длине между 1,5 и 2,5 D характер движении зависит от условий производства опыта.
§ 75.	Конически сходящиеся насадки (фиг. 115)
При входе в насадку происходит сжатие струи, хотя и меньшее, чем у цилиндрической насадки. При выходе происходит второе сжатие, после чего жидкость течет ровной струей. Благодаря незначительности внутреннего сжатия и расширения потери в этих насадках незначительны и вытекающая струя обладает относительно большой живой силой.
Все коэфициенты истечения (в, 7, у-, С) являются функциями от угла конусности 0.
Максимальный коэфициент расхода оказался при Р = 13°.
При этом имеем е = 0,982; <р = 0,963; y=0,946.
Однако необходимо учесть, что коэфициент у относится к выходному сечению насадки.
Если же отнести этот коэфициент к отверстию в стенке, к которой приделана насадка, то он окажется значительно меньше.
Поэтому конически сходящиеся насадки при больших выходных скоростях дают меньшую величину расхода по сравнению с цилиндрическими насадками.
§ 76.	Конически расходящиеся насадки (фиг. 116)
При входе в насадку жидкость испытывает сжатие и затем довольно быстрое расширение, следствием чего являются довольно большие потери на удар, а в мертвом пространстве образуется значительный вакуум.
При выходе из насадок сжатия струи не замечается, однако жидкость не вытекает ровной струей и в ней замечается стремление к разрывам. При угле конусности больше 8° происходит срыв струи и истечение происходит, как из отверстия в тонкой стенке. При углах конусности меньше 8° можно указать на следующие средние значения коэфициентов: е=1; <р=у=0,45; С -3,93.
В этом случае также необходимо учесть, что коэфициент ц не может служить для сравнительной оценки расхода, протекающего через конически расходящуюся насадку, так как он относится к выходному сечению значительной величины. Если же отнести /л к входному сечению, то значение его достигнет величины 2 — 3, что указывает на увеличение расхода, пропускаемого такими насадками.
$ 77. Коноида льные насадки (фиг. 117)
В этих насадках внутреннее сжатие значительно уменьшается, поэтому коэфициенты скорости и расхода увеличиваются.
Коэфициент расхода колеблется от 0,92 до 0,98 в зависимости от тщательности выполнения закруглений.
В среднем р, = 0,95; тогда коэфициент скорости 9 = 0,95 (так как енар= 1) и С = 0,10.
Из всего сказанного о насадках следует, что в тех случаях, когда желательно получить наибольшую скорость вытекающей струн, при данном напоре следует брать конически сходящуюся насадку, там же, где важен наибольший возможный расход, следует брать конически расходящуюся насадку.
Сводные данные о коэфициентах для разобранных выше случаев даны в табл. 13.
Таблица 13
Коэфициенты для истечения из отверстий и разных насадок
Тип истечения	Коэфициенты			
	t		Р	с
Отверстие в тонкой стенке .........	0,64	0,97	0,62	0,063
Насадка Вентури			1	0,82	0,82	0,487
, Бордй	  .	......	1	0,71	0,71	~1,0
Конически сходящаяся при р = 13° ..... .	0,98	0,97	0,95	0,063
» расходящаяся при р <8°		1	0,45	0,45	3,938
Коноидальная 				1	0,95	0,95	0,010
§ 78. Практические случаи применения насадок
Инженерная практика применяет насадки в весьма разнообразных и многочисленных приборах, устраиваемых с целью поднятия жидких, а иногда и твердых сыпучих тел, или с целью их разбрызгивания под большим давлением. Сюда относятся водо-и пароструйные насосы, брандспойты в пожарных насосах, форсунки для распыления нефти в топках и т. д.
Изложим вкратце устройство некоторых подобных приборов.
1. Водоструйный на сое, или водогон, представляет собой систему конически сходящихся и конически расходящихся насадок, расположенных вместе в коробке (фиг. 119). Вода поступает из напорного резервуара первоначально в конически сходящуюся насадку, далее направляется в конически расходящуюся насадку, а оттуда удаляется по трубе С. В месте перехода из одной насадки в другую вода движется с большой скоростью и образует вакуум. Если соединить всасывающую коробку помощью трубы с местом, откуда желательно удалить воду (например с затопленным подвалом), то под влиянием атмосферного давления вода из подвала поднимется кверху и вместе с напорной водой будет удаляться по трубе Q "
-	ну
Отношение работы, совершаемой весом поднятой воды* к работе, совершаемой весом напорной воды, называется к.п.д’ водогона Этот коэфициент вообще невелик и колеблется от 0,15 — 0,30, но зато эти насосы отличаются большой простотой устройства, автоматичностью действия и не нуждаются в особом присмотре.
2. Пароструйный насос, или инжектор. Этот прибор служит для питания водой паровых котлов. Аналогично предыдущему, мы здесь имеем систему двух насадок (фиг. 120). Горячий пар поступает из ксггла в конически сходящуюся насадку, а оттуда с очень большой скоростью поступает в камеру М. Благодаря образованию в этой камере вакуума вода под действием атмосферного давления из питательного резервуара поднимается по трубе К камеры 2И; здесь происходит конденсация частиц пара, а далее смесь горячей воды с паром проходит че
Фиг. 120
рез насадки b и е в котел. Происходящий при этом нагрев воды является полезным попутно достигаемым эффектом. Поэтому в данном случае инжектор является весьма экономичным прибором.
Насадки для пожарных рукавов. Эти насадки имеют важное значение в вопросе тушения пожаров, так как в этом случае из вытекающей из брандспойта струи требуется, чтобы она обладала максимальной живой силой при возможно большем расходе и кроме того чтобы она возможно дальше сохраняла свою форму не разбрызгиваясь. Наиболее подробные исследования таких насадок были произведены американским инженером Фриманом, который установил, что наилучшие результаты дают конически сходящиеся насадки с цилиндрической короткой направляющей трубкой на конце. Возможны также и другие типы насадок. Высота поднятия струи определяется по формуле Фримана:
где Н—статический напор при входе в брандспойт; /70 = Н+ *v $
+"^ —гидродинамический напор; а—коэфициент, равный 0,000113.
Задача. Вода из водохранилища выпускается трубами (фиг. 121). Требуется определить число и диаметр труб, если напор Н = 5 м и расход Q должен составлять 50 м^сек. Толщина стенки плотины на уровне расположения труб L = 4,8 м.
Решение. Определим диаметр труб, исходя из соотношения для насадки. Для насадки отношения должно быть 3,5—4.
Принимаем ~ = 4. Тогда:
д=4._«=1,2л.
4	4
Площадь сечения трубы: = 1,13 м2.
4
Расход через одну трубу составит:
(О =
Я =	2gH = 0,82-1,13/19,62-5 = 8,7 м3.
Число труб, очевидно, составит:
принимаем 6 труб.
ГЛАВА X
ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБОПРОВОДАМ
§ 79. Классификация водопроводов
В изученных ранее случаях с насадками, представлявшими трубы очень небольшой длины, намй учитывался только один вид потерь энергии—так называемые местные потери. При удли-нении этих труб к местным потерям прибавляются еще потери по длине. Соотношение этих обоих видов потерь зависит от длины трубы: так, принято считать, что в трубах длиной примерно до 100 м (домовые водопроводы, сифоны, дюкера) местные потери должны учитываться точно по данным ранее формулам. Такой случай называется случаем короткого водопровода. В длинных трубах местные потери уже играют незначительную роль в общей балансе потерь, поэтому в этом случае они обычно учитываются суммарно в 5 —10% от потерь по длине. Рассмат-149
ривая водопроводы как способ передачи жидкости на расстояние, их можно разделить на два типа:
1. Простыми водопроводами называются трубы, передающие воду из одной точки в другую (из одного резервуара в другой или к отверстию в конце водопровода, через которое вода вытекает в атмосферу).
2. Сложными водопроводами называются системы труб, подающих воду сразу в несколько точек. Таким образом при сложном водопроводе у нас имеется сеть труб, состоящая из магистральной трубы и ответвлений. В зависимости от движения воды по этой сети сложные водопроводы делятся на следующие виды:
Фиг. 122
а)	разветвленными (разомкнутыми или тупиковыми) водопроводами называются такие, в которых жидкость от разветвлений больше на магистраль не попадает (фиг. 122);
б)	кольцевыми водопроводами называются такие, когда жидкость из магистрали поступает в замкнутую сеть (фиг. 123).
в)	параллельными называются водопроводы, с разветвлениями, которые опять все сходятся в одной точке магистрали (фиг. 123а).
§ 80.	Виды расходов
При передаче жидкости по водопроводу могут встретиться разные способы расходования воды, в зависимости от чего различают разные виды расходов: 1) если поступающая в трубу жидкость передается полностью в другую точку, то такой расход называется транзитным; 2) если часть этого расхода по пути забирается какими-нибудь расходными пунктами, то забираемый расход называется попутным. При этом в зависимости от близости расположения расходных пунктов различают следующие виды попутных расходов: а) еспи расходные пункты расположены достаточно далеко друг от друга, то мы имеем случай сосредоточенного расхода (фиг, 124); б) если расходные пункты расположены очень близко друг к другу, расход называется непрерывным (фиг. 125).
Типы задач. Задачи,решаемые при расчетах водопровода, бывают трех типов:
1)	при заданном диаметре трубы D и расходе Q найти необходимый напор И;
2)	при заданном D и напоре Н найти расход Q, пропускаемый через трубопровод;
3)	при заданном напоре Н и расходе Q найти необходимый диаметр трубы D.
Первые два типа задач решаются непосредственным применением уравнения Бернулли и уравнения расхода. Третий же тип задач представляет ббльшую сложность и решается методом подбора.
При решении всех задач для определения потерь напора по длине пользуются обеими формулой Вейсбаха:
и водопроводной:
А,=
1-Q*
№ L'
формулами, приведенными в § 53, т. е. h^rg
в
Я Фиг. 124
'Qi
Фиг. 125
§ 81.	Модуль расхода в трубах
При пользовании водопроводной формулой мы имеем коэфи-циент у, который, как известно, может быть выражен через коэфициент К (см. § 55). Если при определении коэфициента X мы воспользуемся формулой Маннинга, в которой К для трубы определенной шероховатости является функцией метра, то и коэфициент у представится в виде диаметра:
Только ее диафункции этого
Следовательно ,Lt-будет тоже функцией от
шероховатости
у-/Ю)-для трубы заданной D.
Обозначим эту функцию через = № (К берется во второй О2
степени для того, чтобы в формуле Л, = придать ему одинаковую размерность с Q). Вставив это значение в водопроводную формулу, мы получим:

(Ю7)
где коэфициент К называется модулем расхода. Он, как сказано выше, для трубы данной шероховатости зависит только от **	151
диаметра трубы; поэтому для разных значений D он может быть заранее вычислен.
Определим значение К из этой формулы:
или Q = /С/45
(108)
формула
Л,
Q2
= -^-А употребляется при отыскании потери напора, К
a Q = употребляется для определения расхода. Так как Jh величина отвлеченная, то К имеет размерность расхода.
При JK, равном единице, — Q — К, т. е. модуль расхода представляет собою расход для трубы, имеющей гидравлический уклон, равный единице.
Если имеем ряд труб одинаковой длины при одном и том же напоре, но разных диаметров, то вследствие равенства у них величины Jh величина Q будет прямо пропорциональна величине К.
Так, для трубы диаметром Dt имеем (фиг, 126).
Q1 = A'1/7“
Для трубы диаметра Dt:
Qi = А2/ 4, откуда:
Qh_K1
Q»4‘
Следовательно модуль расхода характеризует пропускную способность труб. Значения модуля расхода для труб различных диаметров даны В табл. 14.	Таблица 14
			Значения модуля расхода /Сдля нормальных чугунных труб, вычисленных по формуле Маннинга		
*	111,|| I’ll 1		D в дш	К в л)сек	К1 в {л/сек)1
			40 50 75 100 125 150 175. 200 225 250 300 350 400 450 500 750 1000	4,66 8,46 24,94 53,72 97,40 158,4 238,9 341,1 467,0 618.5 1006 1517 2166 2 965 3 927 11 580 24 930	21,77 71,58 622,2 2 886 9487 25090 57 080 116 400 218 100 382 500 1 ОН 000 2301 00J 4 691 000 8 792 000 15 410 000 134 100 000 621 700000
			д			
				 1			
					
1 -*	1 гг 1II л				
1		-	D,				
!	’ Фиг 125					
§ 82.	Случай простого водопровода
Установив возможные виды задач, могущих встретиться при движении жидкости по трубам, перейдем к рассмотрению способов их решения.. При этом начнем рассмотрение с наиболее простого случая — простого водопровода с постоянным диаметром (фиг. 127).
Пусть два резервуара А и В с установившейся разностью уровней Н соединены трубой длиной L с диаметром D. Роль верхнего резервуара может выполнять насос, производящий в начале трубы давление, которое соответствует пьезометрической высоте Н.
Напишем уравнение Бернулли для точек на обеих свободных поверхностях:
+ + (а)
сокращая на — и пренебрегая
весьма малыми величинами
2L
2g
/V
Фиг. 127
и , получим:
Zi — zl = 'Lh.
Величина EA = hM 4- At, где hM ~
T-представляет местные
.	, rv2
потери, a A, = X £ представляет zg
потери по длине. Вставив эти значения лучим:
в формулу (а), по-
L\ v2 ~D]Tg'
из которого можно по заданному Н определить скорость v, и наоборот. Задача усложняется в том случае, если требуется определить диаметр, так как величина D входит также в выра
жение для А. В этом случае приходится действовать методом подбора, заключающемся в том, что задаются постепенно вели-
чиной X и проверяют затем правильность подобранного значения.
Задача решается проще, если воспользоваться данными ранее значениями модуля расхода. В этом случае можно по вычисленному значению К подобрать из таблицы соответствующее значение D.
В водопроводе часто бывает необходимо определить давление в сечении трубы (например для расчета прочности трубы, выяснения высоты поднятия жидкости в данном месте и т. д.). Для
определения этих давлений строится напорная линия, в которой путем вычитания ординат получаем ординаты пьезометри-
ческой линии. Построение напорной линии производится весьма просто путем вычитания из горизонтальной линии величин потерь энергии для соответствующих сечений.
§ 83.	Эквивалентные водопроводы
При расчете водопроводов с трубами разного диаметра эквивалентной трубой называется такая фиктивная труба постоянного диаметра, потеря напора в которой при одинаков >м расходе равна потерям напора в данном водопроводе.
При определении размеров эквивалентной трубы можно поступать двояко.
1.	Задаемся произвольным диаметром эквивалентной трубы Do. Фиктивную длину трубы обозначим через £0.
Из самогоеловия эквивалентности имеем:
1 Q* г
Г °
1 z 4-_L_£L/
/ D? 1 r' DJ L1
7'
1
Коэфициент y* принимаем приближенно всегда одинаковым. Тогда после сокращения получим:
(109)
2.	Задаемся условием, что длина эквивалентного трубопровода £0 равна длине истинного трубопровода L. Тогда из предыдущего после сокращения имеем:
L __	।	^2 .
D5
(НО)
§ 84.	Случай расхода по пути
1.	Случай сосредоточенного расхода (фиг. 128). Пусть даны сосредоточенные расходы qv q.lt q3-, тогда на участке АВ расход равен q, + q.t на участке ВС проходит уже меньший расход а на участке CD только расход qz. Соответственные потери напора на участках равны:
h _ + + .
ПЦ—	Д' 2 2
2	^2 И Т. Д.
Пьезометрическая линия выразится при этом в виде ломаной линии.
2. Случай непрерывного расхода. Пусть дана труба длиной L (фиг. Л29); расход распределен непрерывно, так что на каждый 154
пог. метр вытекает расход q. В сечении, взятом на расстоянии х от начального сечения, протекает расход:
Q — qx = q(L—х).
На бесконечно-малом участке dx этот расход можно считать постоянным. Потеря напора при этом равна:
,, q2(L — х)2 .
ал,= ~—К2-----'
Отсюда видно, что потеря напора происходит по параболическому закону. Полная потеря напора: ,
L
Таким образом потеря энергии при непрерывном расходе получилась в три раза меньше потерь, которые имели бы место в случае, если бы расход был сосредоточен в конце водопровода.
§ 85.	Расчет сифона
Сифоном называется труба, передающая жидкость из одного резервуара в другой помощью созданного в ней вакуума. Резервуары при этом должны быть расположены на разных уровнях (фиг. 130); передача жидкости будет происходить всегда из верхнего резервуара в нижний.
Определение расхода, пропускаемого сифоном при заданной разности горизонтов сосудов и заданном диаметре, производится совершенно аналогично со случаем обыкновенных труб. Точно так же и определение диаметра сифона при заданном расходе и разности горизонтов в сосудах ничем не отличается от обычного способа определения в трубах. Специфическим вопросом для сифона является определение предельной высоты под'ема жидкости в сифоне.
Для решения
/ 2
точек 0 и 1 (
этой задачи пишем уравнение Бернулли для при этом пренебрегаем):
— 1 + hi,
т т
откуда:
Т 2g ° т 2g 1
Теоретический предел для —, как известно, равен 10,33 м,
а практически он не превосходит 7 м. Для под'ема жидкости на данную высоту Лх при условии возможно меньшего вакуума
и ЕА0—1- Так как умень
необходимо уменьшать значение
шение скорости возможно только при увеличении потерь энергии, то очевидно, что увеличение потерь может пройти только за счет участка 1 — 2. Таким образом для уменьшения вакуума в верхних частях сифона необходимо увеличить сопротивление на спускной части трубы.
Для второго случая задач может быть применена предыдущая формула. Величина диаметра, как и во всех остальных случаях, определяется подбором.
Задача. Вода подается из водонапорной башни А по трубе переменного сечения (фиг. 131). В точках 1 и 2 имеются сосредоточенные расходы. Требуется определить необходимый напор Н,
если дано, что
Dt = 300 мм
Г>а = 250 „ /4 = 200 „ qv 20 л[сек;
4 = 400 м
4 = 200 „
4 = 400 „ q.2 — 20 л/сек,
q} = 30 л]сек.
Решение. Пишем уравнение Бернулли для точек 0 и 3:
//+А + = А + + I 2g т 2g
Пренебрегая величинами
V2
-у-, получим,
что Н = Sh,
Величина 1/z определяется по водопроводной формуле:
Переходя к отдельным участкам, имеем: Потери на участке 0—Г.
h	70*-400
Kf юооюоо — 1,у
Потери на участке 1 — 2: _Q2l3	50*-200
'	К2 374 000 * 1,33
Потеря на участке 2 — 3:
К32
302-400
116000
= 3 10 м,
Потеря же по всей длине 0—1 — 2 — 3 равна:
Aj +	+ h3 = 1,96 + 1,33 + 3,10 = 6,39 и.
Прибавив 5% на местные сопротивления, получим, что общая потеря SA = 1,05-6,39 = 6,71 м, откуда требуемый напор /7^6,7 м.
§ 86.	Сложные водопроводы
Из сложных водопроводоз в настоящем курсе приводится только расчет параллельного и тупикового (разветвленного) водопроводов, причем для большей ясности задачи эти решаются в числовом виде.
Задача. Пусть дан водопровод с тремя параллельно включенными ветвями (фиг. 132). Размеры элементов трубопровода указаны на чертеже. Определить напор Н, необходимый для пропуска указанных на схеме расходов, если в точках В и D имеются сосредоточенные расходы ^в = 20 л1сек и qD = 30 л/сек и в точке D вода изливается в атмосферу.
Дано: Z.J = 600 м, L3 = 700 м, L3 = 400 м, Lt = 800 м, L3 = 1000 м\ Dx = 200 мм, D3 = 100 мм, D3 = 150 мм, Dt« 175 мм, Dk =225 мм.
г	157
Решение. 1. Составляя уравнение Бернулли (расположенной на свободной поверхности воды имеем:
^О2
Пренебрегая членом кинетической энергии лости, имеем:
для точек б в баке) и D,
ввиду его ма-
(а)
Н = Ы.
Фиг. 132
I
2.	Для определения расходов в параллельных ветвях имеем 4 уравнения:
Qz + Q# + Qi — qo •	(в)
Из уравнений (б) имеем:
0,237
1,07 Q3.
(г)
Значения модуля расхода К берем из таблиц для нормальных труб.
Подставляем значения Q2 и Q4 из равенств (г) в уравнение (в): 0,257 Q3+ Q3-H ,07 или
2,327 Q3 = 30 л1сек, откуда:
Уз = 9^7 = 12>9 л1сек‘
3.	Определяем расход на участке ЛЛ
Q, = qB + qD = 20 + 30 == 50 л[сек.
4.	По известным расходам Q3 и qa определяем потери на участках АВ, ВС и CD:
=^Л>=П6™ 600j=i2'9a
О 2	166
=^з =-24600-400 = 27’0Л-
а 2	900
5.	Суммируя потери, находим величину напора Н:
Н = Ей = йдв + h-вс 4* hcD = 12,9 + 27,0 + 4,2 — 44 м.
Задача. Определить диаметры труб для участков а — b; b — т и Ь—п, если расход в точке т равен 80 л1сек, а в точке п=12 л/сек, а напор Н как для точки т, так и для точки п равен 7 -м. Длины участков показаны на фиг. 133.
Рассматриваем наиболее длинный участок.
Полагая потери напора рав- -номерной на длине 700 жкимеем потерю напора на 1 м или гидравлический уклон
•1'400-
Фиг. 133
Jh ~ “700	0,01
По этой потере подбираем диаметры. Тогда для участка а — Ь:
К =
Q 80 + 12 _ 92 _ /4-/+оГ о-1
Согласно таблице (§ 81) наиболее подходящим диаметром является D = 300 мм.
Для определения диаметра трубы на участке b—п предварительно определяем возможную потерю напора на этом участке.
Для этого находим потерю напора на участке а — b при найденном диаметре 300 мм. Потеря напора на этом участке:
. Q2 , _92М00 о._ h'~ К^1	10002 -3,4° м‘
Следовательно на участке Ь — п возможная потеря напора равна 7,00—3,40 = 3,60 М.
Возможная потеря на 1 м или гидравлический уклон:
» /
hi 3,60
W0,018,
Тогда:
_ Q____________
/л ~ К °>°18
12	= 95.
По той же таблице ближайшим диаметром является D=125.mjh.
§ 87. Гидравлический удар
Общее понятие. Если движущаяся в трубе жидкость по каким-либо причинам (например вследствие внезапного закрытия крана) мгновенно рстанавливается, то наблюдаемое при этом явление называется гидравлическим ударом. Теряемая при этом живая сила жидкости трансформируется в работу внутренних сил. Поэтому при ударе резко уве-Г1-------=1	личивается давление внутри жидко-
ГЗ_Т_~	сти и у стенок трубы, которые под
---- —	действием этого давления увеличи-
—	с	е,	а,	а	а,	вают свой первоначальный	радиус г
~! j j j j № на величину Дг. Это увеличение дав> —	!	I	!	t—k-T ' ления обозначим через р.	Под влия-
~	~	|	-j	i	j	’I ,J	нием резкого возрастания	давления
------------------с/	<л	у	происходит сжатие частиц	жидкости. ___________________________________________________________ Это сжатие, как и в любом упругом
ф ]34	теле, подчиняется закону Гука:p=Ei,
г‘	где Е— модуль упругости воды, рав-
ный приблизительно 21 000 кг/см2.
Благодаря этим двум обстоятельствам (сжатие частиц жидкости и увеличение поперечного сечения трубы) произвольно взятое сечение ab (фиг. 134) переместится в новое положение а'Ь' и длина столба жидкости уменьшится до длины /2.
Аналогичное явление произойдет и с сечением cd, которое, перемещаясь, пройдет с одной стороны путь, проходимый сечением ab, и кроме того дополнительный путь сжатия столба cdab. По окончании сжатия частицы жидкости в трубе обладают большей энергией в трубе, чем частицы в сосуде, и начинают двигаться по трубе в обратном направлении. При этом частицы а^, пройдя по инерции сечение ab, попадут в новое сечение а2д2. Аналогично этому сечение cxdv попадет в сечение c2rf2 и столб жидкости окажется разреженным. Вследствие этого под влиянием давления частиц в сосуде начнется снова движение жидкости в первоначальном направлении и пройдет новая волна сжатия. Таким образом частицы жидкости в трубе будут совершать колебательное движение, причем вследствие трения эти колебания будут затухающими. Это колебательное движение, передающее сжатие частиц от одного сечения к другому, про-160
исходит с какой-то скоростью, причем эта скорость, как скорость звуковой волны, определяется по формуле Ньютона:
где р — плотность жидкости, Е — модуль упругости, соответствующий сложной деформации, который может также быть определенно по закону Гука:
Е-'T-	(а)
Определение величины Е. Возьмем столб жидкости длиною I, площадью ® и об'ема чю (фиг. 135).
Обозначим относительное уменьшение величины I, происходящее вследствие сжатия частиц жидкости через ilt а относительное уменьшение этого же столба вследствие увеличения
Фиг. 135
радиуса трубы через z2; обозначим также через Ц и /2 соответствующие длины столба жидкости.
Величину z2 получим из условия равенства об'ема жидкости до и после увеличения радиуса трубы:
л гЧ = к (г + Д г)2/2,
откуда:
I (г + Д г)2 г2
или
_ (г4-Дг)2-г2
С-)- h--------7*
г
Эта же величина Л может быть выражена через модуль упругости трубы, Для этого рассмотрим поперечное сечение трубы, причем это сечение предполагаем рассеченным на две части, (ф К°136)ЫХ ПРаВУЮ часТЬ 0Т^Расываем и заменяем силами Т И Гидравлика	161 1
Если обозначить напряжение в материале трубы через k, модуль упругости трубы через Eit а относительное удлинение трубы через im, то будем иметь:
. _ 2it (г + Д г) — 2 it г
1т---------5Т7-------
2 к Г
или
• _^г. 1т----
Г сравнивая значение 1т с полученным ранее значением /2, мы
2Дг .
видим, что х2 = —— = 2 im.
С другой стороны, согласно выводу, данному в задаче § 18 об определении прочности стенок цилиндрического сосуда, нами получена формула (18):
i т~ 8£2 •
Определив в отдельности оба вида деформаций, напишем теперь выражение для полной деформации i. i-i . i _ Р , ^рг
С другой стороны, согласно выражению (а), имеем:
‘=f-
Приравнивая оба выражения для i, получим, что
Ег Т 8Е2“ £’
откуда определяем величину Е:
Е=------
1 4- 2	
Определив величину Е, мы можем найти скорость волны из выражения:
(112)
движения
а =
(ИЗ)
Таким образом при заданной жидкости, т. е. заданной величине плотности р и модуля упругости Elf скорость распространения ударной волны по трубе зависит от поперечных размеров 162
трубы, толщины 3 стенок и коэфициента упругости материала, из которого эта труба сделана. Зависимость эта такова, что с увеличением диаметра трубы скорость а убывает; с увеличением же толщины стенок и модуля упругости материала трубы (или, иначе говоря, с увеличением ее жесткости) скорость а увеличивается.
Определение величины давления/?. Возникающие при ударе внутренние силы давления в точках жидкости совершают при их перемещении какую-то работу. Величина этой работы, отнесенная к единице об'ема жидкости, может быть определена по формуле строительной механики и равна , р
В самом деле, если отложим по оси абсцисс величину t = -g-,
а по оси ординат величину р, то, имея в виду, что напряжение р с возрастанием i
само возрастает, мы закон изменения р по-
лучим в виде прямой линии (фиг. 137). Работа, совершаемая при этом, очевидно,
выразится площадью треугольника и бу-/ /’Мл
дет равна р	. Отсюда полная ра-
дет равна Р~^ = ^
бота, совершаемая частицами в данном р2
об'еме, W = ~p4>L. Так как эта работа
совершается за счет исчезновения живой силы, то по закону живых сил обе эти величины, т. е. работа внутренних сил об'ема и его живая сила, должны быть друг другу равны. Обозначив эту живую силу через Wb имеем:
-ршГ-у.

А из равенства W= Wx имеем:
р* , .чР 2EmL = ^L^-
или, сокращая, получим:
р\= т’И’р^.
Выразим величину Е из формулы Ньютона:
Е = агр, тогда получаем:
IP = vap-l	(114)
формула Жуковского.
Здесь v — средняя скорость движения воды в трубе;
а — скорость волнообразного движения воды при ударе; ₽ — плотность воды;
р— искомое давление.
Приближенно можно принять, что р кг]см2 = (10— 13) v м]сек. Из полученной формулы видно, что для жидкости заданной плотности величина единичного давления при гидравлическом ударе пропорциональна двум величинам: 1) скорости движения жидкости в трубе и 2) скорости распространения ударной волны а. Отсюда понятно, что при наличии опасности гидравлического удара в трубах, не могут быть допущены большие скорости; кроме того из данной выше формулы (113) для величины а видно, что гидравлический удар опасен для труб малого диаметра и что действие его значительно ослабевает при уменьшении модуля упругости материала труб.
В качестве предохранительных мер против гидравлического удара применяются приспособления, допускающие только медленное закрытие водовыпускных кранов или задвижек.
Другим способом, предохраняющим от вредных последствий гидравлического удара, является устройство предохранительных клапанов и воздушных колпаков, являющихся как бы воздушными буферами, воспринимающими на себя возникающее давление.
Зависимость повышения давления в трубах от быстрого закрытия крана дана экспериментальной формулой Спарра:
ЧФа ______
g ' at—I
(115)
где I—длина трубы, t—продолжительность ее закрытия.
Задача. Определить величину давления (единичного) в чугунной водопроводной трубе диаметром 100 мм при быстром закрытии задвижки, если скорость течения воды в трубе 2,5 м)сек, толщина стенок трубы 10,5 мм и давление в трубе до закрытия задвижки было равно 3 ат.
Решение. Давление от гидравлического удара определяется по формуле:
г р= pva = -^- va,
где 7 = 0,001 кг/см?-, ^ = 250 см/сек-, g = 981 см)секг;
где г= 10 см1, Еч (чугун) = 1000000 кг/см?-,
1g 981
Р у 0,001
981 000;
8 = 1,05 см\ Ei (вода) = 21 000 кг [см*
Следовагельно:
< 981 /	21 000
I/ 0,001 .	2-10-21000
'	\ 1 + 1,05 • 10е
= 120900 см[сек
1209 м[сек.
в
981
Следовательно давление от гидравлического удара:
= 0,001-250-120900 _ g	981
Так как согласно условию гидростатическое давление равно 3 ат, то полное давление равно:
30,84-3 = 33,8 кг/см9.
Задача. Определить длительность закрытия задвижки в трубе при данных предыдущей задачи из условия, чтобы единичное давление воды, возникающее вследствие гидравлического удара, не превысило двух атмосфер. Дано: v — 2,5 м[сек, длина трубы /= 3627 м, а = 1209 м!сек.
Решение. По формуле Спарра:
„ vva I g ‘at — Г
откуда:
gP a
, 0,001 • 250 • 362 700 , 362 700 ,, _ , _ .n _ t. e. t	-----+ -120900-46.2 + 3 - 49,2 сек.
981 • 2
§ 88. Гидравлический таран
Происходящее при гидравлическом ударе резкое повышение давления представляет собой во многих случаях весьма опасное явление. Однако техническая мысль нашла возможным это явление использовать в полезном смысле. Так, в 1796 г. братья Монгольфье изобрел» водопод'емную машину „Гидравлический таран", основанную на действии гидравлического удара и представляющую собой соединение в одной машине двигателя и насоса. Машина эта отличается крайней простотой своей конструкции и состоит из следующих частей (фиг. 138): 1) питательной трубы
С, имеющей ударный клапан 2) воздушного колпака D, внутри которого помещается нагнетательный клапан и 3) напорной трубы В. Труба С соединяется с резервуаром А, откуда вода может поступать под напбром Клапан соединен со стержнем k, на который свободно надета пружина, упирающаяся в гайку 7V и клапан (фиг. 139). Для пуска в ход тарана необходимо пустить воду по нагнетательной трубе; если одновременно с этим помощью гайки N открыть клапан С, то вода начнет вытекать через образующиеся вокруг оси клапана зазоры. Давлением воды клапан Wj однако тотчас же захлопнется, движение воды мгновенно прекращается и в трубе происходит гидравлический удар. Возникающая при этом волна повышенного
давления достигает клапана и приподнимает его кверху; тогда
вода под действием этого повышенного давления начинает вте-
кать в воздушный колпак. Следующая за волной сжатия волна разрежения создает у клапана и пониженное давление. При этом клапан да2под влиянием собственного веса опустится и не даст воде вытечь обратно из колпака в трубу, а клапан под действием пружины М откроется и даст снова возможность движению воды через свои зазоры. При этом движении вода снова прижимает кдапан wx к седлу, происходит новый удар и явление повторяется. Входящая в воздушный колпак с каждым новым ударом новая порция воды
Фиг. 139
сжимает в колпаке воздух, который в свою очередь оказывает давление на жидкость, заставляя ее подниматься по нагнетательной трубе В на желательную высоту Аа. Необходимо иметь в виду, что подаваемый по трубе полезный расход qx составляет только часть полного расхода Q, подающегося из резервуара А, так как другая часть этого расхода q2 выливается через зазоры ударного клапана и представляет собой потерянный расход. Коэфициент полезного действия тарана может быть определен по следующей эмпирической формуле Эйтельвейна:
(115а)
где Но представляет выраженное высотой столба воды давление в воздушном колпаке, a hx — напор, создаваемый резервуаром А.
ГЛАВА XI
РАВНОМЕРНОЕ ДВИЖЕНИЕ ЖИДКОСТИ В ОТКРЫТОМ РУСЛЕ
Понятие .открытое русло" охватывает все реки, искусственные каналы, акведуки, лотки и даже трубы в тех случаях, когда они работают неполным сечением, как это имеет например место в канализации. Таким образом открытые русла могут быть разбиты на две категории: 1) русла естественные (реки, ручьи), представляющие собой неправильные и постоянно меняющие свое очертание профили, и 2) искусственные русла, имеющие обычно правильную и относительно постоянную форму сечения.
Сравнивая движение в открытых руслах с рассмотренным ранее нами движением в напорных трубах, мы видим, что с теоретической стороны движение в трубах является более простым. В самом деле, напорные трубы, представляющие для потока жесткие и неизменные стенки по всему периметру, заранее предопределяют живое сечение потока, а следовательно и его расход и среднюю скорость. Движение может быть отнесено при этом к типу одноразмерного.
При движении в открытых руслах эти обстоятельства, облегчающие изучение законов движения, уже отпадают: поток на своем протяжении может принимать разные глубины, а вместе с этим меняются и площади живых сечений, скорости и т. д. В особенности это относится к случаю естественных русел, где движение почти всегда бывает неравномерным и почти всегда неустановившимся. Поэтому говоря о равномерном движении, мы имеем в виду искусственные русла и то для весьма ограниченного числа случаев практики.
§ 89. Эмпирические формулы для коэфициента с
При решении различных задач, связанных с движением воды в открытых руслах, основной расчетной формулой является выведенная выше в § 53 формула Шези:
v — ctf Ri,	(62)
для пользования которой необходимо знать коэфициент с.
Говоря об эмпирических формулах для этого коэфициента, необходимо вернуться к сказанному уже в § 55, где мы видели что этот коэфициент является лишь некоторым изменением основного коэфициента bv Опыты, ставившиеся для определения основного коэфициента, должны были, очевидно, дать результаты, пригодные и для искомого коэфициента с. Первоначально поэтому была сделана попытка представить его в виде какого-то постоянного, не зависящего от шероховатости русла коэфициента (в частности Шези в 1775 г. предложил дать значение с — 50). Упоминавшаяся уже формула Дарси-Базена стала уже
учитывать зависимость коэфициента с от шероховатости русла и гидравлического радиуса.
В 1869 г. швейцарские инженеры Гангилье и Куттер, использовав все произведенные до того времени опыты, предложили следующую формулу:
23+2+адо155 г 0,00155 ХУ"*
i //Я
с =--------—
1+ (23
где I—уклон потока, а п — коэфициент шероховатости стенок русла; для разных материалов стенок были получены различные значения величины п (см. приложения, табл. VII).
Формула Гангилье-Куттера употребляется также для движения в трубах. Несмотря на сложность ее конструкций, она получила очень широкое распространение; особенностью этой формулы является то, что в ней коэфициент с ставится в зависимости от уклона дна потока, что в настоящее время подвергнуто весьма серьезным сомнениям. При значении i >0,0005 членом, зависящим от I, пренебрегают, и тогда формула приобретает более простой вид:
23 +-п
с =------------------
1 + 23 -"
(П6)
и в этом виде она носит название сокращенной формулы Куттера.
В 1897 г. Базен снова пересмотрел вопрос о наиболее рациональном виде формулы, использовав при этом весь накопившийся за это время материал.
Предложенная им новая формула для с имеет следующий вид:
87
(Н7)
где у — коэфициент шероховатости. Значения т приведены в табл. 15, а значения с по этой формуле в табл. III (приложения).
Характерным в этой формуле является то, что с увеличением гидравлического радиуса влияние шероховатости на скорость падает; в самом деле, чем больше R, т. е. чем глубже река или канал, тем меньше должно сказываться влияние шероховатости его стенок и дна на скорость. При R — оо, с по формуле Ба-зена превращается в постоянное число с = 87.
Формула Базена наряду с приведенной выше формулой Гангилье-Куттера является основной расчетной формулой для коэфициента с. По сравнению с формулой Гангилье-Куттера она отличается своей простотой, но зато формула Гангилье-Куттера 168
Значения у для формул Базена
№	Род стенки	Коэфициент шероховатости у		
		Для метр.	Для саж.	Для фут.
I	Очень гладкие стенки (строганые доски, гладкая цементная штукатурка и т. д.).	0,06	0,04	0,11
11	Гладкие стенки (нестроганые доски, тесовая и кирпичная кладка, бетонные и чугунные трубы, весьма хорошая бето-нировка и др.)		0,16	0,11	0,29
III	Негладкие стенки (хорошая бутовая кладка, посредственная бетонировка). . . . Промежуточная категория (грубая бутовая кладка; весьма грубая бетонировка по скале; замощение булыжником; стенки в плотных землистых грунтах, притом весьма хорошо содержимые; стенки, чисто высеченные в скале)		0,46	0,315	0,83
Ша		0,85	0,58	* 1,54
IV	Земляные стенки в обычном состоянии (сюда же — мощеные, но несколько заросшие и т. п.)		1,30	0,89	2,35
V	Земляные русла, оказывающие особенно сильное сопротивление (при плохом содержании; значительных водорослях; скалистом с валунами или крупногалечном дне и пр.)		1,75	1,20	3,17
имеет гораздо более обширную шкалу значений коэфициента шероховатости, причем эти значения хорошо подтверждены эпытами.
Существует еще целый ряд формул, в которых зависимость коэфициента с от гидравлического радиуса и шероховатости русла представлена в одночленной форме. Наиболее известной из них является приведенная уже в § 57 формула Маннинга:
п
(118)
где п — коэфициент шероховатости, имеющей те же значения, что и в формуле Гангилье-Куттера. Если подставить его значение в формулу Шези, то получим:
2
V = J- /< 3 л 5
п
одночленное уравнение показательного типа.
Подобного вида формул существует в настоящее время довольно много. В общем же виде эти формулы могут быть представлены так:
Л/?1 Д |	(119)
где ? обычно принимается равной 0,5, А — величина, зависящая только от абсолютной шероховатости; для значения а разные авторы предлагают различные значения.
§ 90.	Условия осуществления равномерного движения в открытом русле
Из формулы Шези v = cyfRi, где с зависит от шероховатости русла и его гидравлического радиуса, вытекают три основные условия, необходимые для существования равномерного движения в открытом русле.
1.	Неизменность шероховатости русла во всех его сечениях (7 = const).
2.	Постоянство гидравлического радиуса (/? = const).
3.	Неизменяемость уклона дна (i — const).
Кроме того из условия постоянства расхода имеем еще два дополнительных условия:
4.	Q = const, (отсутствие притока жидкости от каких-нибудь внешних источников и оттока от русла к посторонним источникам).
5.	Из выражения v = при условии Q = const мы получаем еще условие <о — const.
Из условий постоянства живых сечений и гидравлических радиусов по длине потока с неизбежностью вытекает и равенство смоченных периметров, а также глубин во всех живых сечениях. Таким образом при равномерном движении мы во всех живых сечениях имеем одинаковые глубины; свободная поверхность при этом представляет плоскость, параллельную дну, что является характерным признаком для данного вида движения. Глубину потока при равномерном движении, так называемую нормальную глубину, мы в последующем будем обозначать через hnl.
§ 91.	Модуль расхода в открытых руслах
При решении задач на движение в открытых руслах весьма полезным бывает применение данного уже выше понятия о модуле расхода (см. § 81).
Как известно, модуль расхода /С=-^=.
V Л
Так как при равномерном движении в открытом русле Jh = i, то в этом случае
^=^=>	(120)
т. е. модуль расхода является расходом, пропускаемым данным руслом при уклоне дна его, равном единице.
1 Обозначение '»то дано в ОСТ 6126.
Подставив в выражение для расхода величину скорости из формулы Шези v = с y7Ri, можно получить:
| Q = o>cK/?Z; |
(121)
следовательно:

Из полученного выражения видно, что модуль расхода зависит от трех факторов:
а)	от типа данного русла, характеризуемого величиной /?;
б)	шероховатости его стенок и дна;
в)	площади живого сечения ш или, как это часто бывает удобнее, глубины заполнения Л.
Для русла заданной формы и шероховатости/(является функцией одной величины h.
§ 92. Определение функциобальной зависимости между Kuh для разных типов русел
1.	Прямоугольное русло (фиг. 140).
В этом случае:
ш Bh\ 7 = В 4- 2Л;
„ Bh _ h
К —	~ 2h ’
B + 2h 1+^-
D
большой ширины
Для русел большой ширины величиной можно прене-з
бречь; тогда R^h; K=Bhc y^R = Bch2’
Задаемся двумя глубинами и Л4; тогда зависимость модуля расхода от глубины заполнения выразится следующим образом:
з	з
Ki _ Bchy - _ / Л] \ 2 з~ I h I
К9 Bchi^ ' 4'
(122)
2.	Параболическое русло большой ширины (фиг. 141). Условие большой ширины выражается в том, что принимают В = X. Из общего уравнения параболы имеем:
х2 = 2ду =р>;
при х = у = А, откуда 1-п~) = р' А;
о п /“ТЕ п ш 25/2	2 ,
в = 2/ЛЯ-т/--за—
9	4	___
<u = -5~ Bh. = -~-h. yp'h. (j	о
Отсюда модуль расхода:
К = Я = _£ h y/p’h • cl/^-h =4-1/^Р' di2 = Ach\ o	f о о У о
где через А обозначаем выражение
Задаемся по предыдущему двумя наполненными А, и А2. Тогда д’ * Ach.2	/ А \2
отношение модулей расхода -тЛ = >  / 2 = -Л) •	(123)
Z\2 ДСП* \ /1% /
3.	Любое русло правильной формы. В обоих рассмотренных выше случаях мы видели, что между модулями расхода и глубиной заполнения существует степенная зависимость.
Исследованиями проф. Бахметева установлено, что эта степенная зависимость между К и А имеет место и для других типов русел, т. е. что для русла любой формы
fk-lhxX Kt U J ’
(124)
где р называется гидравлическим показателем русла.
Для определения величины гидравлического покаЛтеля задаются двумя значениями глубин hv А2 и вычисляют соответствующие им значения и /Са.
Величина р может быть затем определена путем логарифмирования.
Задача. Определить величину гидравлического показателя для земляного трапецеидального русла (фиг, 142).
Имеем tg а = ~.
Ширина понизу равна 5 м. Задаемся = 3 ht = 5 м, находим площади «о* = 33 л<2;	= 75 м2.
Находим смоченный периметр:
X, = 18,4; Х2 = 27,4;
р  Ш1 _ 33 _ 1 д. р _ ю2	75	» jл.
^"Х,	18,4	,9, Х2	27,4 2‘74,
87	87	87 .ос.
Ci —	. п 45; с2 1 ч — 48,6,
1+4= 1 + 1L 1+-Д= //?!	1,38	/2,74
7С1 = <л/Я1 = 33-45 /Ё9 = 2049,3;
Д', = ш2 crfR* = 75 • 48,6 /274 = 6050,7;
Ki _ ( А, V. 2049,3 _ (3_\р 1g3 = 0,477;
К, \hj’ 6050,7	5 ) ' 1g 5 = 0,699;
1g 2049,3 — 1g 6050,7 - р lg	;
□
_ lg 2049,3 — lg 6050,7 _
P Ig3-lg5
§ 93. Задачи при проектировании каналов
Существует три типа задач, приведенные в табл. 16 (стр. 174).
Задача. Определить расход в канале с обычными земляными стенками трапецоидального профиля, если уклон дна канала i = 0,002; т = tg а = 2, ширина понизу b =5 м, глубина наполнения h = 2 м.
Решение. Величина расхода определится по формуле Q = = v ш = ш с ^Ri.
Определяем входящие в формулу величины:
= tH»±2ta).4_5+13.2=184i,
р №______18	— I 29 м'
К X “5+2 • 4,47“ ’ М'
87
Тип	Задано	Требуется определить	Решение
I	1.	Русло (форма, шероховатость, основные размеры) 	 2.	Глубина заполнения h 3.	Уклон дна 1 . .  , .	Пропускаемый расход Q	Q=<*cV~RJ, где шс и R определяются по заданным величинам и по коэф, шероховатости
II	1.	Русло 2.	Глубина заполнения h 3.	Расход Q, который должно пропустить русло	Уклон 1	Решается аналогично
III	1.	Дан расход 2.	Допускаемый уклон дна 1 3.	Шероховатость дна и стенок	Живое сечение	При пользовании прежней формулой туда войдут две неизвестных о» и /?; поэтому задача допускает множество решений и для ее определенности необходимы какие - то дополнительные условия. Одним из дополнительных условий является нахождение гидравлически наивыгоднейшего русла
принимаем 7 для обычных земляных стенок равной 1,30» тогда:
/1,29
и величина расхода:
Q = 18 • 40,5 /1,29 • 0,002 = 37 м*1сек.
§ 94. Гидравлически наивыгоднейший профиль
Понятию о гидравлически наивыгоднейшем профиле может быть дано следующее определение:
Гидравлически найвыгоднейшим профилем называется такой профиль, который дает наименьшую площадь живого сечения для пропуска заданного расхода при одной и той же шероховатости и одном и том же уклоне дна. Из этого определения вытекает, что при заданной площади живого сечения и при одной и той же шероховатости и уклоне дна гидравлически наивыгоднейшим профилем будет тот, который пропустит наибольший расход.
При определении гидравлически наивыгоднейшего профиля нужно установить: а) наивыгоднейший тип русла, б) при данном типе русла—наивыгоднейшую комбинацию его размеров.
Определение наивыгоднейшего типа русел. Имеем основную формулу:
где с нами дано по формуле Базена.
При заданных ?, <», i максимальный расход получится при п “ максимальном гидравлическом радиусе, или так как к = -у, то максимальному расходу соответствует минимальный смоченный периметр.
Как известно, из всех геометрических фигур наименьшим периметром обладает круг. Поэтому в открытом канале гидравлически наивыгоднейший профиль будет полукруглым.
Непосредственно за полукругом следует правильный многоугольник, который, очевидно, будет тем выгодней, чем больше число его сторон. Отсюда ясно, что при трапецеидальном профиле (половина шестиугольника) гидравлически наивыгоднейшим будет тот случай, когда угол а = 60°, а откос ctg а =0,5.
Из прямоугольных профилей гидравлически наивыгоднейшим будет тот, где А = 0,56, т. е., тот, который является половиной квадрата.
§ 95. Определение гидравлически наивыгоднейших размеров для трапецеидального русла с заданными откосами
В большинстве практических случаев земляные каналы имеют трапецоидальную форму, причем откос задан из свойств грунта.
Рассмотрим каким условиям должно в этом случае удовлетворить русло, чтобы соблюсти требования гидравлически наивыгоднейшего профиля.
Обозначим через b ширину русла понизу (по дну); h глубину заполнения, т уклон откоса /п=с!§а(фиг. 143).
Тогда, исходя из геометрических соображений, получим:
1)	ш = bh -J- mh2, откуда:
b - -^- — mh; h
2)	Х=6 + 2А или, подставив b из предыдущего выражения, получим:
X =-у — mh -f- 26)/1 4- /п2;
3)	R = ш = bh mtl* * b + 2A/ITOT5’
Так как при гидравлически наивыгоднейшем профиле, как известно, X должно быть минимальным, то:
^ = 0 dh и’
откуда:
— т + 2|/1 4- т"- = О,
что после замены ® через bh 4- mh2 дает:
откуда:
b -|- mh = h (2 1 4- /га2 — т),
(125)
Это и есть гидравлически наивыгоднейшее соотношение между шириной канала по дну и глубиной воды в нем. Если обозначить -д- через 0, то уравнение (125) можно получить в следующем виде:	______
Р = 2	1 4- т2 — т ).
Задаваясь различными значениями т, получим соответствующее значение р (см. табл. 17).
Таблица 17
Наивыгеднейшие соотношения ширины канала по дну и глубины воды
Уклон откоса т = ctg а	0	74	7»	’/4	'1	17.	2	3	4
Соотношение ширины канала по дну и глубины А b воды Р = £	2	1,56	1,24	1	0,83	0,61	0,47	0,32	0.2S
Если подставить в данное выше выражение для гидравлического радиуса R полученные значения Ь, то после соответству-176
jomero сокращения нетрудно убедиться в том, что R — 0,5Л, т. е. что гидравлический радиус должен в этом случае равняться половине глубины заполнения русла.
Задача. Пункты А и В, отстоящие друг от друга на расстоянии 4000 м с разницей отметок в 2 лс.-необходимо соединить каналом (фиг. 144). Грунт песчано-глинистый; т=1,3 по Базену. Откосы необходимо сделать двойными. Профиль трапецеидальный. Уровень воды должен совпадать с естественной поверхностью грунта. Определить наивыгоднейшие размеры сечения канала для пропуска расхода Q=4m3/cck.
Определим модуль расхода:
воспользуемся установленной зависимо-
Для решения задачи стью между А и К',
Al
К.
М’.
задаемся ht = 1; А4 = 2 по условию т = 2.
Зная, что К = “сR, заменим ш, с и R через А, используя за* висимость, выведенную выше, получим:
А = 2А()Л1+/п2 — /п) = 2-(|Л5 — 2)=0,47 м,
отсюда;
ю, = h{b + mh) = 1(0,47 + 2 • 1) = 2,47.
^=1/ -4-= ]/"-}- = 0,71;
12
Гидравлика
177
Для А = 2 имеем:
А = 2-2(/5 — 2 )= 0,92; ша = 2(0,92+ 2-2) = 9,84;
с,=-----------= 37,8.
1 + -^-
Кх _	_2,47-30,7-0,71 _0144.
9,84-37,8.1
^0Д4£ = Р 1g 0,5
Воспользуемся тем же отношением между А и Ар где одну из глубин возьмем из задания, и, зная, что Kt = 179, а /Са=376, получим:
179 _ / Ai \2,7
376	\ h ) *
откуда:
А=1,54 м,
А = 2-1,54 (/б-— 2)=0,72 м.
Остальные размеры легко могут быть найдены из геометрических соотношений.
§ 96. Понятие об удельной энергии сечения
При изучении движения воды в открытых руслах, поскольку при таком движении в большинстве случаев приходится иметь дело с целым потоком, является весьма полезным введение понятия об „удельной энергии сечения*.
Рассмотрим какой-либо поток при медленно изменяющемся движении (фиг. 145).
В любой точке d, взятой в каком-либо поперечном сечении потока, удельная энергия выражается по предыдущему:
+ Т +2g-*+ 7 + 2g •
где и — истинная скорость струйки, a v — средняя скорость потока.
Так как атмосферное давление действует во всех точках потока одинаково, то оно никаких изменений в условиях движения потока не вызывает и может быть при рассмотрении энергетического состояния отдельных сечений русла принято равным нулю.
178
Давление р в точке жидкости определится по формуле избыточного давления р = -\hd.
Если принять за условную плоскость сравнения плоскость АВ, проходящую через самую низкую точку в сечении, то при указанных допущениях величина удельной энергии в произвольной точке d выразится:
. lAd , ат/2 . , , az/2 , , az/2
e-z* + -	+-7—2</4-Ad+-—= А+
Эта величина характеризует энергетическое состояние потока в данном живом сечении и называется удельной энергией сечения. Обозначать ее будем через Э.
Следовательно:
(126)
Фиг. 145 формулы aQ* 2g ®2 величина Э зависит от
Э = А-|--у—. ______ 2g
Изменение удельной энергии сечения при изменении глубины потока. Из данной выше ~ l । B-V* li Э - h-\—= h 4-
видно, что при постоянстве расхода Q
величины Ан®. Так как величина ® может быть представлена в свою очередь как функция от А, то в конечном счете Э является функцией одной только величины А.
Рассмотрим изменение величины Э в зависимости от разной глубины наполнения русла при условии постоянства расхода. Все явление при этом разделим на следующие части:
1. Пусть А % 0; тогда ш 0 и Э = со.
2. А возрастает, имея все время конечные значения. Величина В, представляющая собой сумму двух членов, из которых первый увеличивается, а второй уменьшается, будет при этом изменяться двояко:
\ n	a Q2 -
а)	Первоначально уменьшение величины -^g^' °Удет пРева' лировать над увеличением А, в результате чего Э будет уменьшаться. Явление будет протекать в такой форме пока глубина « не достигнет какой-то определенной величины А*.
б)	Когда величина А получит значение, большее At, увеличение l	а О*
« начнет превалировать над уменьшением величины ,
в результате чего величина Э начнет увеличиваться.
Величина hk называется критической глубиной.
3.	При возрастании А до бесконечно-больших значений, т. е. при Н = сю и Э = сю. Полученная зависимость между удельной энергией сечения и глубиной заполнения русла может быть изо-
17j
бражена графически. Для этого откладываем по оси абсцисс величину А, а по оси ординат величину Э (фиг. 146). В полученной кривой левая ветвь асимптотически приближается к оси ординат, а правая ветвь асимптотически приближается к прямой, наклоненной под углом 45* (так как в бесконечности Э = h).
Левая ветвь соответствует движению при малых глубинах и больших скоростях и называется ветвью бурного течения, а правая, соответствующая большим глубинам и малым скоростям, называется ветвью спокойного ’течения. По этому признаку потоки делятся на бурные и спокойные. Следовательно бурным называется поток, у которого уклон больше критического, а следовательно глубина при равномерном движении меньше кри
тической, а спокойные потоки это те, у которых уклон меньше
критического, а глубина при равномерном движении больше
критической. Если обозначить уклон дна у потока с критической глубиной через 1к (критический ук-<Н	лон), то условие для обоих видов
Фиг. 146
выразится следующим обра-
Фиг. 147
при i<ikn следовательно npHAn>At—спокойный поток; 1
ри i>ik, а следовательно приА„<А*— бурный поток.;
| 97. Определение критической глубины для сечения произвольной формы
Пусть попрежнему изменяется глубина А; тогда каждому значению А соответствует свое значение В, ® и Э (фиг. 147). Кроме того при изменении А также изменяется величина
Так
dd	,	2а	О2	d а> __ а Q2 ~
dh	~l	2g	ш*	dh ~	1 —
как величина hk соответствует Эпцп, то при этом
dh	Я ш *
где <0* и Вк—значение ширины и площади для значения h=^hki

или
(128)
что и является условием для определения критической глубины 180
Для русел сложной формы величина А* из полученного выражения определяется методом подбора.
Определение At для прямоугольного русла. 0 этом случае имеем Вк В; шк = Bhk (фиг. 148). Подставляя в формулу (128) эти значения, получим:
53А/ _ а<?2 В g ’
откуда:
(129)
В случае, если задана скорость для глубины А4, т. е. vk, величину Л* можно выразить следующим образом:
Q = u)ivt = BAJk^;
3
А/ = —А/и/
* g * *
и окончательно:	__________
Пример. Дан поток а прямоугольного сечения, ширина которого 5 = 5 ^.^Пропускаемый расход Q = 2 м2)сек.
Надлежит определить критическую глубину.
з  з
Решение. Л,-	-0.242 *
Второе определение понятия о критической Глубине. Допустим, что уклон русла, а следовательно глубина его заполнения меняются, а энергия данного сечения останется неизменной. Естественно, что при этом расход, пропускаемый руслом, тоже будет меняться (так как для одного расхода возможна только одна глубина с одинаковой удельной энергией сечения).
Для простоты примем русло прямоугольным. Удельная энергия сечения:
77 2
Э = А + а	»
отсюда:
а расход:
q = hv — h "|/^y-(3 — h).
(1296),
Полученная формула даст закон изменения q в зависимости от глубины Л (закон полукубической параболы) (фиг. 149).
Из формулы (1296) видно, что при Л = 0 q = 0,
. Л = Э q = 0.
Для получения максимального расхода имеем условие:
Л1/1£	,__
/2g/q	,/1 =о ,
dh у h) 2^9 — h У «\2/Э —Л/
откуда:
9
23 ЗА или А =--- 3.
о
Скорость
Фиг. 149
(130)
,	v2	.
а л в свою очередь равно а—,т. е- является совершенно такой же, что и в предыдущем случае. Отсюда понятно двойное определение для критической глубины.
1. Критической глубиной называется такая глубина, при которой живое сечение для поопуска заданного расхода обладает
наименьшей удельной энергией.
2. Критической глубиной называется такая глубина, при которой живое сечение русла при одной и той же величине удельной энергии пропустит максимальный расход.
ГЛАВА ХИ
ДВИЖЕНИЕ ВОДЫ ЧЕРЕЗ ВОДОСЛИВЫ
§ 98. Классификация водосливов
Если жидкости при своем движении приходится переливаться через стенку или вырез в стенке, то происходящее при этом гидравлическое явление называется движением через водослив.
Верхняя грань стенки называется ребром, или порогом, а толщина переливающегося слоя называется напором. При этом в зависимости от формы водосливной части стенки имеются три типа водосливов: а) водослив с острым порогом (фиг. 150); б) водо-182
слив с широким порогом (фиг. 151); в) водослив практического профиля (фиг. 152).
Стенка, преграждая путь потоку, делит его на две части: часть, лежащую выше стенки, — верхний бьеф и часть, лежащую
за стенкой, — нижний
бьеф. При переливе через стенку жидкость .попадает из верхнего бьефа в нижний, причем здесь на практике встречаются два случая:
W//W/W//Z
77777,
7777777,
Фиг. 151
Фиг. 150
1. Если нижний бьеф не оказывает никакого влияния на условия истечения, то водослив называется незатопленным (фиг. 153).
При водосливе с острой стенкой и водосливе практического профиля уровень воды непосредственно за стенкой должен 'быть
Фиг. 153
при этом ниже ребра водослива. Так, если принять горизонтальную линию, проходящую через порог, за координатную ось, то этот случай имеет место при А<0. Если уровень нижнего бьефа оказывает влияние на истечение, то водослив называется затопленным (фиг. 154). Очевидно, что при этом h > 0.
777777
Фиг. 154
Фиг. 155
Имеются однако случаи, когда при А > 0, водослив считают незатопленным. Это происходит при значительной толщине переливающегося слоя по сравнению с глубиной нижнего бьефа (фиг. 155). В подобных случаях может иметь место отгон нижнего бьефа на некоторое расстояние, и истечение происходит, 183
как для случая незатопленного водослива (случай отогнанного прыжка). Приближенно такой случай можно принять при условии
Фиг. 156
Фиг* 157

> 0,7. Следовательно для случая затопленного водослива необходимо принять, что 1) h > 0 и 2) у< 0,7.
tZZZZZZZZZZ/ZZZ
Фиг. 158
zzzz/zz/zzzzzzz/z
*7777/77777/77^777,
Фиг. 159
Кроме указанных основных признаков классификации водосливы могут быть разделены по следующим признакам.
'/////////////////,
777777777777777777
Фиг. 160
777777777^77777/
Фиг. 161
В зависимости от расположения водосливной части стенки по отношению ко всей стенке: а) водослив без бокового сжатия (фиг. 156); б) водослив с боковым сжатием (фиг. 157).
Фиг. 162
Фиг. 163
В зависимости от расположения водослива в плане могут быть следующие случаи: а) прямые (фиг. 158), б) косые (фиг, 159), в) ломаные (фиг. 160), г) криволинейные (фиг. 161).
Фиг. 165
Фиг. 164
Водосливы с острым порогом в зависимости от наклона боковых граней подразделяются на: а) прямоугольные (фиг. 162), б) треугольные (фиг. 163) в) трапецеидальные (фиг. 164), г) параболические (фиг. 165).
§ 99. Водосливы с острым порогом
Общее описание явления. Для того чтобы разобраться
в физической стороне явления, рассмотрим механизм того взаимодействия струек, который дает переливающейся жидкости
устойчивую форму (фиг. 166). Несомненным с самого начала является то, что скорость отдельных частиц по закону Бернулли
будет возрастать сверху книзу. Если бы кажцая струйка могла двигаться самостоятельно и независимо от других, мы имели бы дело со свободным движением, при котором траектории каждой частицы представляли бы собой параболу тем большей кривизны, чем меньше скорость частицы. Так как при таком движении неизбежно
Фиг. 166
столкновение частиц между собой, то не-
зависимое движение струек является вообще невозможным, а вся переливающаяся жидкость образует единую сомкнутую струю. При этом необходимо различать струи типа а, движущихся только под влиянием своего веса, и струи типа Ь, вынужден-
ных менять направление своего движения на противоположное. Верхние струйки типа а, опираясь под влиянием собственного веса на нижележащие частицы, вызывают в них возрастание давления, причем это давление будет меньше гидростатического вследствие того, что нижележащие струйки обладают большей скоростью, чем верхние. Нижние струйки типа b ведут себя уже по-иному: меняя при истечении свое направление на диаметрально противоположное, они приобретают кривизну, бблыпую той, которая им соответствовала бы при их свободном движении. Каждая нижележащая струйка передает при этом свое давление верхним и давление возрастает снизу вверх. Таким образом давление в переливающейся жидкости идет, возрастая снизу вверх с одной стороны, и сверху вниз с другой стороны, достигая в какой-то точке своего максимума, причем очевидно, что проходящая через эту точку струйка движется уже по нормально искривленному пути, соответствующему ее скорости.
Французским исследователем Базеном были произведены крайне тщательные опыты над изучением формы переливающейся струи. Результаты этих опытов видны из фиг. 167, из которых вытекает нижеследующее: 1) начало искривления струй можно считать примерно на расстоянии ЗН от порога (ордината струи равна 0,003/7); 2) над порогом ордината струи равна 0,15/7; 3) в сечении а>1, проведенном через место наивысшего под‘ема нижней струйки, этот под'ем у = 0,11/7, а ордината верхней струйки равна 0,22/7; 4) сечение ч>еж, расположенное примерно на расстоянии 1,09/7 от стенки, характеризуется тем, что струйки в нем становятся параллельными друг другу. Толщина потока в этом сечении А = 0,435/7.
Распределение давлений и скоростей в сечении видно из фиг. 168.
Определение расхода. При определении расхода через
зодослив с тонкой стенкой в гидравлике поступают двояко:
6
Фиг. 167
1) Одни гидравлики уподобляют движение через водослив с тонкой стенкой движению через боль* шоепрямоугольноеотвер
^/7/А7/77777/7777777/.
Фиг. 168
стие. Разница между этими обоими видами движений принимается только" в том, что в водосливе вытекающий поток не имеет жесткого стеснения (ребра) с верхней стороны; при таком подходе формула для водослива получится как частный случай формулы для большого прямоугольного отверстия. Поэтому, подставив в формулу (97) Нг = 0 и /72 - Н, получим:
з
Q = mb yT2gH7.
(131)
что и является основной расчетной формулой расхода для водослива.
2) Приведенный подход страдает однако тем недостатком, что он не отражает в себе физической картины движения жидкости через водослив.
Поэтому для данной выше формулы применяется и другой метод, заключающийся в нижеследующем: напишем уравнение Бернулли для двух сечений изучаемого потока: для сечения АВ 186
перед стенкой в том месте, где понижение уровня уже незначительно, и для вертикального сечения ®t* взятого так, что его средние струйки находятся на уровне порога водослива.
Как видно из фиг. 167, в этом сечении касательные к общим граням направлены под одним и тем же углом к горизонту и струйки поэтому между собой параллельны.
Так как при применении уравнения Бернулли для потока точки, для которых составлены эти уравнения, выбираются в обоих сечениях независимо друг от друга (см. § 40), то за точку 1 возьмем точку на свободной поверхности сечения АВ, а за точку 2—точку на оси сечения шсж. Первоначально сделаем следующее допущение: 1) скоростью v0 в сечении АВ пренебрегаем, 2) давление в струйках сечения а>сж считается равным атмосферному и 3) потерей энергии по пути пренебрегаем (эти потери являются крайне незначительными, ими можно в действительности пренебречь).
При этих допущениях уравнение Бернулли напишется в еле* дующем виде:
откуда:
l’ = j/2F"7T-
Так как сделанные выше допущения в той или иной степени отражаются на величине v, то действительная средняя скорость в сечении ab:	____
где <р — коэфициент, включающий в себя кроме влияния указанных выше трех допущений также и коэфициент а, учитывающий влияния неравномерного распределения скоростей в струйках.
Для получения расхода мы должны среднюю скорость умножить на перпендикулярную к ней площадь (проекцию площади а>сж).
Тогда Q = bh' vp, где Ь — ширина порога, а Л' = h cos р =0,75Л.
Вставив вместо v_ полученное выше значение и обозначив h
— через 6, получим:
Q =	2g?77
Обозначив произведение е? аналогично тому, как это сделано при истечении через отверстие, через т (коэфициент расхода для водослива) получим:
з
Q = mb-\f~2gH 2,
что совпадает с данной выше непосредственно формулой (131).
187
Коэфициент расхода т получен Базеном на основании его экспериментов и дан им в виде следующей формулы:
0,405
0,003 \ + Н /
0,55№
+ (/7+Ла
(132)
где Н и Т должны быть взяты в метрах.
Структура этой формулы такова, что второй ее множитель учитывает влияние, оказываемое на расход наличием в сечении АВ скорости, а первый множитель учитывает влияние всех остальных факторов.
Кроме формулы Базена существует и ряд других экспериментальных формул для коэфициента т (формула Ребокка, швейцарских инженеров), которые за краткостью данного курса здесь не проводятся.
ж
Фиг. 169
Фиг. 170
Фиг. 171
Влияние вакуума на форму струи. В случае, когда пространство между падающей струей и стенкой изолировано от внешней атмосферы, струя, увлекая за собой воздух, создает там разреженное пространство. Понижение давления в струе влечет за собой: 1) возрастание скоростей, а следовательно и увеличение расхода; 2) поднятие уровня воды в разреженном пространстве, 3) прижатие к стенке водослива, причём такая струя называется отжатой (фиг. 169). С возрастанием напора вакуум возрастает, причем струя может принять двоякую форму:
а)	при сравнительно медленном разрежении пространство окажется полностью заполнено жидкостью, что называется случаем подтопленной струи (фиг. 170),
б)	при быстром разрежении струя может примкнуть к стенке— случай прилипшей струи (фиг. 171).
Влияние вакуума на увеличение расхода показано в табл. 18.
Таблица 18
Влияние вакуума на увеличение коэфициента расхода
Род струи	Свободная	Отжатая	Прилипшая	Подтопленная
т % увел и ч.	0,428 0	0,460 7	0,497 16	0,547 28 —
Влияние затопления струи на расход. В случае, когда водослив затоплен, расход жидкости через него, очевидно’ должен измениться. Это изменение было предложено Базеном учесть путем введения в обычную формулу для расхода нового коэфициента 8 (коэфициент затопления).
Следовательно при этом _ з Q =	(133)
где:
(134)
При обычных значениях z величина в скобках, а следовательно и вся величина 8 меньше 1. Следовательно для большинства случаев практики расход воды для затопленного водослива меньше, чем для незатопленного.
Фиг. 173
Фиг. 172
Влияние бокового сжатия на расход. Боковое сжатие струй в водосливе, как и в случае истечения из отверстий, понижает пропускаемый расход. В этом случае в формулу расхода вместо ширины b приходится вводить величину сжатого сечения Ьх (фиг. 172). Следовательно формула расхода будет иметь следующий вид:
Q = mb^^g Н2.	(135)
Величина Ьх по формуле Френсиса определяется так:
—O,lntfo,	(136)
где п — число сжатий по бокам.
Задача. Прямоугольный канал оканчивается мерным водосливом с острым порогом (фиг. 173).	'•
Длина водосливной стенки равна ширине канала b = 0,5 м. Определить расход, если напор Н—0,6 м и высота порога 7=0,4 м.
Решение. Так как длина порога равна ширине канала, то боковое сжатие отсутствует. Расход определится по формуле: _______________________________ _з
Q — mb]f 2g Н 2 
Коэфициент расхода т определяем по формуле Базена:
'« = (о,405 +	• [1 +0,55(7^р?];
т® (о,405 +	Y (14-0,55	=0,41 (1 4- 0,198) = 0,491
\	Цо / \	l,UU /
и далее:
Q = 0,491 • 0,5 у/19,62 /0,6* = 0,505 м3[сек.
§ 100. Водослив с широким порогом
Общее описание явления. Встречая на пути своего движения широкую стенку, жидкость поднимается на какую-то дополнительную высоту, накапливая при этом потенциальную энергию.
Фиг. 174
Фиг. 175
В отличие от случая водослива с острым порогом жидкость при этом не переливается свободно через порог, а первоначально ударяется о его поверхность и далее течет по нему. При этом вследствие потерь энергии скорость меняет свою величину, и движение, вообще говоря, является неравномерным; однако при незначительной длине потока потери эти настолько незначительны, что ими можно пренебречь. Движение тогда рассмат-ривается как равномерное, и поверхность воды на пороге будет при этом параллельна порогу. В зависимости от положения уровня воды за порогом могут иметь место следующие случаи:
1.	Уровень воды в нижнем бьефе ниже уровня порога (фиг. 174). Если принять условно ось порога за координатную ось, то случай этот выразится следующим образом:
А, <0.
2.	Уровень воды в нижнем бьефе выше уровня порога, но ниже уровня воды на пороге (фиг. 175):
h>hi>Q.
Оба эти случая по своим гидравлическим свойствам совершенно одинаковы, так как истечение в нижний бьеф происходит под атмосферным давлением и в обоих случаях будут существовать 2 перепада и z4. Называются эти случаи незатоплен-ным водосливом.
190
3.	Уровень нижнего бьефа выше уровня h, устанавливаемого при незатопленном водосливе (фиг. 176).
В этом случае движение уже будет носить другой характер; здесь будет иметь место только один перепад z и на пороге Йстановится глубина А', соответствующая уровню нижнего бьефа, [азывается этот случай затопленным водосливом.
Определение расхода для случая незатоплен-ного водослива. Напишем уравнение Бернулли для точек О и 1 (фиг. 175):
V *
Обозначив сумму
через получим:

а расход на единицу ширины порога:
Фиг. 176
Фиг. 177
Фиг. 178
где ? — коэфициент скорости — зависит от очертания входного ребра и может быть принят равным для острого входного ребра 0,85 (фиг. 177), а для округленного входного ребра — 0,92 (фиг. 178).
Полученное уравнение для расхода может быть приведено к виду, обычному для других типов водосливов. Для этого умножим и разделим величину h на /70:

Нй
2gtf0(l- А) =Ф \	"о/
з
з
откуда:
q — т
где:
т —
(137а)
О
что представляет собой коэфициент расхода для водослива с широким порогом.
Из полученной выше формулы видно, что расход через во-дослив с широким порогом зависит от глубины h на пороге. Эта глубина может быть определена из следующих соображений. Как известно, всякой глубине движущегося потока соответствует определенное значение энергии (см. § 96). При пропуске существующего в русле расхода через горизонтальный участок, каковой представляет собой водослив с широким порогом, эга глубина в силу естественных свойств жидкости установится так, чтобы количество энергии, соответствующее этой глубине, оказалось минимальным или, говоря иначе, чтобы при данной глубине через водослив прошел максимальный расход. Такая глубина, как сказано было выше, называется критической (см. §97) и для прямоугольного русла находится по формуле:
А> = ,7^
I/
или, приняв приближенно а — 1 и обозначив попрежнему через q, получим:
Q в
3
h
 отсюда:
|/ h3g.
Сравнивая полученное из формулы 137 значение q с только что полученным значением, имеем:
VW = ?A/2g(tf0-A),
отсюда: А = 2?» (7/0 —А).
Разделим обе части уравнения на Нй'.
h / А\ А/ \	А 2?2
2т> (1 -^(1 +	) - V и	(138)
Формула (138) позволяет при известных значениях ? находить искомую глубину на пороге А в виде функции Н„. Так, если никакого уменьшения скорости при движении через водослив не произошло бы, т. е. если бы мы имели <р = 1, то из формулы
А 2
(138) получим:-ту-= —-% 0,66. /7 о	О
При данных же выше значениях <₽ имеем для порога с острым краем = 0,85 и
^=0,59.
Для порога с закругленным входом
<Р = 0,92
и	^ = 0,63.
л»
Из полученной формулы q — уГ h?g можно получить выражение для скорости движения жидкости на водосливе. Так, из формулы расхода q = hv= у h-g получаем непосредственно:
I v =	(138а)
Отсюда также обратно имеем:
h = g
Затопленный водослив с широким порогом.
Расчетная формула расхода остается та же:
q -= ?А 2g(H0—А),	(139)
где величина А определяется по имеющимся данным об уровне нижнего бьефа.
§ 101. Гидравлический расчет отверстий малых водопропускных сооружений в земляном полотне (мосты, малые отверстия и безнапорные трубы)
Одним из весьма важных применений теории истечения через водослив с широким порогом является применение выведенных выше формул к расчету отверстий малых мостов и труб, служащих для пропуска весенних или ливневых вод через насыпи железных или шоссейных дорог, каналов и пр.
На фиг. 179 изображена	х *
схематически такая труба. Основание трубы предпо-ложим горизонтальным.Оче- . видно истечение через по*	X	\
добное сооружение одина-	FE7 X; :4а*
ково с истечением через водослив с широким поро- W. -гом; разница заключается	фиг-179
лишь в том, что в случае водослива стеснение русла достигнуто возвышающимся над дном канала порогом, тогда как в рассматриваемом случае русло стеснено в плане насыпью.
Пройдя через трубу, вода течет далее так же, как текла до устройства трубы, т. е. ниже1 трубы устанавливается глубина h&, соответствующая бытовым условиям, так называемая бытовая глубина.
В конце трубы, как и в водосливе с широким порогом, устанавливается глубина А, равная критической.
И Гидравлика	1W
Если величина отверстия равна Ь, а расход Q, то, считая отверстие прямоугольным, получаем глубину в конце трубы (А == = At) на основании § 100 равной:
А = А,
(а)
Обычно при расчете отверстий для пропуска вод приходится считаться с тем, что при очень больших скоростях существует опасность размыва дна лотка, трубы или мостика, поэтому для каждого вида материала устанавливается наибольшая допустимая средняя скорость, значения которой даны в табл. 19.
Таблица 19
Наибольшие допустимые средние скорости в зависимости от рода русла
№ п/п	Род русла	Наибольшая допустимая средняя скорость В MjCCK
1	Илистый грунт	0,15
2	Мелкий песок		0,35
3	Крупный песок, лесс, одиночная дерновка	
	плашмя	\	.	0,80
4	Суглинки, супески		0,55 — 0,95
5	Гравий и мелкая галька диам. до 25 мм .	1,25
6	Хрящеватый грунт, галька, крупная . . .	1,50
7	Глина плотная, твердая, дерновка в стенку	1,80
8	Каменистый грунт, одиночная мостовая . .	2,50
9	Скальный грунт, двойная мостовая ... .	3,50
10	Кирпичная кладка на цементе		4,50
11	Бетон, бутовая кладка 		5,00
12	Деревянный лоток 			6,50
Из выражения (а) непосредственно получаем:
Qg. V*
(б)
А =
Эта формула предложена Брессом для определения ширины отверстия малого моста или трубы при заданном расходе Q и допустимой скорости V.
Полученное значение b не учитывает однако возможности бокового сжатия потока при трубах небольшой длины и мостиках. Учет этого сжатия достигается введением в формулу ширины не A, a bt = е Ь, где е — коэфициент сжатия. Вставив это значение в формулу (б), получим:
<140)
коэфициент е принимается для малых мостиков и для труб с откосными крыльями равным 0,85 — 0.95 (в среднем 0,9) и для труб без откосных крыльев — е = 0,75.
194
о р
Необходимо помнить, что формула Бресса Ь = •—j соответ-© V
ствует случаю свободного истечения: истечение не будет свободным, если бытовая глубина he больше критической, т. е.
если
Л, ,1’/?
или если

~g
Что касается глубины Н до трубы, то, пренебрегая скоростью подхода, получаем из § 100:
откуда: з ----------------
Н - 1/- Qi
V m22gb2
(141)
2н 1чение коэфициента т для различных случаев даем в табл. 20-
Таблица 20
№	Тип трубы	т
1 2	Трубы без оголовка	 „ с расходящимися крыльями	0,32 0,35


Фиг. 180
Если бытовая глубина Л<г больше критической, т. е. если , v2	,
Лб >—-, то в этом случае надлежит применить формулу затопленного водослива в предположении, что глубина внутри трубы установится равной бытовой he (фиг. 180).
Скорость в трубе или под мостом в этом случае равна:
13»
v = 2gz = ^yr2g(H - h6).
195
V* 2 * * * * * В
(141а)
2g®r
Перепад же:
z =
Значения коэфициента ? для различных случаев даны в табл. 21.
Таблица 21
Значения коэфициента <р при мостах и трубах разного типа
Тип моста или трубы
1
2
3
Мосты с конусами и трубы с расходящимися откосными крыльями......................0,90
Мосты без конусов и трубы без расходящихся откосных крыльев, а также трубы, срезанные в плоскости откоса насыпи . . . 0,80
Трубы с выпущенными из тела насыпи кон-
цами, а также арочные мосты с затоплен-
ными пятами ............................0,75
Все вышеизложенное относилось к сооружениям с горизонтальным дном; если же дно сделано с уклоном, то здесь надлежит различать два случая:
1. Уклон незначительный (менее критического).
В этом случае все вышеприведенные формулы в практических расчетах вполне применимы.
2. Уклон велик (более критического). Формулы неприменимы: расчет труб сводится к рассмотрению истечения через „короткий лоток* крутого уклона.
Задача. Определить отверстие каменной трубы (с откосными крыльями) для пропуска 7 м^/сек при предельной скорости 3 м/сек-, бытовая глубина he = 0.6 м.
Решение. Определим критическую глубину: т.2	02	'
А‘=1=^й=0’92-“>0'6 м-
Следовательно истечение свободное; ширина отверстия:
* = ^ = 7Пг|г = 2,85 м. бтМ 0,9-3®
Задача. Определить отверстие трубы, пропускающей расход Q = 25 м3 при глубине перед насыпью Н = 2,75 м и бытовой глубине 2 м. Скоростью подхода пренебрегаем.
Решение. Определяем критическую глубину из условия: h 2	9. Г> ОЧ2
Н- - ГЙ? - Г,-7Ж? * 0.64 Wo: 4, _ 0,64 • 2,75 - 1,76 1,76 < 2, поэтому водослив будет затопленным, и ширина отверстия определится из уравнения Q =<fbhyr2gz, где z=H—h= — 0,75 м.
Отсюда:
b =
и =------
?A|/2g-z ’
_________25__________25
0,95 • 2 /19,62 • 0,75 7,29^ ’ М’
Задача. Отверстие мостика b = 4 м, расход, пропускаемый этим отверстием,—15 м3[сек. Определить скорость под мостом и глубину воды выше моста, если бытовая глубина h6 = 1,0 м (фиг. 14).
Решение. Определяем критическую глубину, принимая коэфициент сжатия е = 0,90:
1,21 > 1, поэтому водослив	Фиг. 181
считаем незатопленным.
Глубина перед мостом Н и скорость определяются по формулам: Н = 1,56; Л* = 1,21 • 1,56 = 1,89 м;
V=yhg=]/1,21 • 9,81=3,38 м]сек.
§ 102. Водосливы практического профиля
Движение воды через водосливы практического профиля1 имеющее громадную область применения в практике (водосливные плотины), в гидравлическом отношении представляет нечто промежуточное между водосливом с острым порогом и водосливом с широким порогом. Поэтому основная формула расхода Q = 3
= mby~2gHJ t данная для тех двух типов, остается верной и здесь; большое затруднение представляет только правильный выбор коэфициента т ввиду большого разнообразия применяемых в практике форм очертания таких плотин.
Наиболее общая классификация таких водосливов дана акад. Н. Н. Павловским (см. «Учебный гидравлический справочникэ 1931 г.).
По этой классификации все такие водосливы могут быть разделены на следующие два класса:
1) водосливы криволинейного очертания;
2) водосливы неплавного очертания (трапецеидальные, поли-Г9дадьмые, прямоугольные и др.).
Фиг. 182
Водосливы криволинейного очертания удобно разделить на три типа (фиг. 182): а) высокие, б) средние, в) низкие (растяну, тые).
По этомуже признаку удобно делить и трапецоидальные профили (фиг. 183). Прямоугольные профили удобно делить на: а) чистый прямоугольный, б) прямоугольный с закруглением входного ребра, в) прямоугольный с наклонным верхом (фиг. 184). Не останавливаясь на точных значениях коэфициента расхода для всех этих случаев (подробнее см. в указанной выше работе Н. Н. Павловского), отметим лишь, что в качестве первого приближения при незатоп-ленврм водосливе можно взять следующее значение коэфициента /п:
1) для криволинейного профиля /п = 0,45;
2) для'профиля некриволинейного очертания /п = 0,40.
При затопленном водосливе эти значения следует умножать на коэфициент затопления (см. § 99).
Влияние бокового сжатия учитывается тем, что вместо. геометрической ширины водослива b вводится уменьшенная ширина blt где bi вычисляется по формуле Криджера:
bi^b — О,1п?Яо.	(1416)
Эта формула отличается от данной выше в § 99 формулы (136) Френсиса только тем, что здесь включен коэфициент учитывающий плавность очертания водослива.
Значения этого коэфициента согласно указаниям акад. Н. Н. Павловского могут быть следующие в зависимости от очертании головы опор:	т
1.	Прямоугольное I «1,0,	**
№
2.	Полуциркульное или* заостренное (равносторонний треугольник) £ = 0,7.
3.	Заостренное криволинейное 5 = 0,4.
Задача. Найти ширину отверстия водослива практического профиля для паводкового расхода Q = 300 м*[сек. Толщина переливающегося слоя через водослив принята Н=3м (фиг. 185). Скоростью подхода пренебрегаем.
Решение. Имеем формулу расхода через незатопленный водослив:
________________________________ _з Q = mb/ 2gH0 2, откуда:
/п/ 2gH0 2
Принимая т = 0,45, имеем:
------------------з 0,45 • /Ж • 3~2
Задача. Каменная водосливная плотина (фиг. 186) состоит из двух пролетов отверстием b = б м. Отметка гребня плотины 5,0 м, отметка горизонта воды верхнего бьефа равна 7,6 м. Отметка нижнего бьефа — 0,3 м. Определить расход через плотину, пренебрегая скоростью подхода.
Решение. Определение расхода производим по формуле расхода для незатопленного водослива, так как отметка гребня нижнего бьефа ниже отметки порога, и плотина будет работать как незатопленный водослив. Ввиду наличия береговых устоев и промежуточного бычка струя при входе на водослив будет испытывать сжатие, и потому в формулу для расхода необходимо ввести ширину порога, исправленную на сжатие. Тогда расход определится по формуле:
Q = 2тЬУ^Н^>
Пренебрегая скоростью подхода, имеем:
= /7-7,60-5,0 = 2,6 м,
Ширина пролета, исправленная на сжатие, определится из формулы Криджера:
bt = b — 0,1 пЬН.
Принимаем п = 2 и 5 = 0,4;'
= 6 — 0,1 • 2 • 0,4 • 2,6 = 6 — 0,208 = 5,792 м.
Принимаем ^=5,8 м.
Коэфициент расхода т принимаем для плавного очертания оголовка т = 0,45.
Окончательно имеем:
Q = 2 • 0,45 • 5,8 • 2,6 У 19,62 • 2,6 = 98 м3/сек.
ГЛАВА XIII
НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ В ОТКРЫТЫХ РУСЛАХ
§ 103. Общее понятие
Согласно сказанному в § 90 равномерное движение в откры-
тых руслах характеризуется тем, что живое сечение потока должно быть везде одинаковым, а линия свободной поверхности должна быть па-
раллельна линии дна. При несоблюдении этих условий движение становится неравномерным. Отсюда понятно, что неравномерное движение в открытых руслах всегда сопро-
Фиг. 187
вождается изменением глубины по длине потока. Следовательно свободная поверхность почти всегда при этом должна быть криволинейной. Приведем несколько примеров.
1.	В канале, в котором происходило равномерное движение с глубиною А„, поставлена плотина (фиг. 187); при этом на участке ab глубины станут переменными, а движение неравномерным.
Кривая ab пересечения свободной поверхности с вертикальной плоскостью в этом случае называется кривой подпора.
2.	В канале, в котором происходило равномерное движение с глубиною h„, произведено углубление дна (фиг. 188). При этом движение на участке ab будет также неравномерным, а кривая свободной поверхности в этом случае называется кривой спада.
3.	Все реки представляют собой пример неравномерного движения, поскольку в них постоянно меняются величины ш, Q, h, /? и т. д.
В приведенных выше примерах свободная поверхность представляла собой непрерывную кривую. В практике однако встречаются случаи, когда кривая свободной поверхности в каком-то сечении терпит разрыв непрерывности, и в этом сечении происходит резкое изменение глубины с увеличением ht до величины (фиг. 189). Глубины hx и h2 называются сопряженными, а все явление называется прыжком.
В качестве примера прыжка приведем случай, когда поток, первоначально двигавшийся с глубиной, меньшей критической, встречая на своем пути препятствие в виде стенки, получает возле нее глубину больше критической. Поток при этом разбивается на две части: одна часть, находящаяся до кривой подпора, относится к типу бурных потоков, другая же часть потока, находящаяся возле стенки на кривой подпора, представляет собой спокойный поток (см. § 96). В спокойной части потока
вследствие уменьшения его глубины происходит уменьшение удельной энергии сечения, поэтому в каком-то сечении поток переходит из одной глубины hx в другую глубину Аа, затрачивая на это часть своей энергии.
§ 104.	Определение кривой свободной поверхности в искусственных руслах
Рассмотрим случай искусственного русла с поставленной в нем плотиной Подпор, вызываемый ею, распространяется вдоль потока на какой-то участок ab.
До этого участка движение равномерное с постоянной скоростью 1*0 и с постоянной глубиной h„. На участке ab имеем переменную глубину h и переменную скорость v (фиг. 187).
Для определения вида свободной поверхности на этом участке выделим из него бесконечно-малый элемент длиной ds (фиг. 190).
При выводе сделаем следующие упрощения:
1)	примем, что дно канала лежит на прямой, т. е. i — const;
2)	угол а очень незначителен;
3)	русло считаем призматическим;
4)	величину коэфициента с из формулы Шези при неравномерном движении считаем одинцдовой с коэфициентом для равномерного движения
Из второго допущения следует, что т’р tri b cos а^т’Ь.
Кроме того ввиду малости участка величину dl считаем приблизительно равной ds.
Переходя к выводу, имеем непосредственно из чертежа;
. kb _ km' m’b _ km’ m'p _dh dz
i— ga=* ~ ds ds ~~ ds + ds ~ ds + ds'
отсюда:
dh dz
1 ~dT
(a)
Для решения полученного диференциального уравнения с двумя различными производными необходимо освободиться от одного dz
из них. Для исключения величины напишем уравнение Бернулли для сечений т и т’:
г +А+ = + 7 + 2g
Отсюда, произведя _ adv2 брегая величиной -
dz = 2vdv dh, = ad (	) + dh,.
2g	‘	\2g/	1
Для определения величины dht напишем уравнение [см. § 53, формула (59)]:
z_dz+^+‘л^+dk„ приведение подобных членов и получаем;
прене-
v = с
\ = c
dA, ds ’
отсюда^
(6)
Шези
(142)
dz =* ad
= c2R ds‘
Из уравнения (б) теперь имеем;
v2 dz d (v2 v2
c2R ’ ds ~ adF[2g) + ~^-
Из полученного выражения видно, что кривизна свободной поверхности зависит от двух факторов;
d tv2 \
а)	член « э- s— I характеризует зависимость этой кривизны **s \^g /
от изменения кинетической энергии по длине потока;
х d,h,
б)	членравный - характеризует влияние на кривизну потерь энергии, вызываемых силами трения по длине потока, 803
Подставим значение т— в уравнение (а, U&
dh _ . d (v2 \ v2
ds~t~'ads\2g) c^R"	W
Полученное диференциальное уравнение имеет только одну производную. Для решения этого уравнения необходимо выразить все его члены либо через постоянные величины либо через явные функции от А.
о	Q
Заменим поэтому v через тогда имеем:
о2 Q* d ( vi\^ d ( Q* \ Q2 2 da> (\ c2R u>2c2R' d s \2g ) ds \ <o82g / = 2g <os ds	r'
Величина 4^, характеризующая изменение живого сечения по as	длине потока, может зависеть
от двух факторов: 1) от непосредственного изменения живого сечения вследствие раз-
Фиг. 191
линия его формы в разных местах потока; 2) от изменения живого сечения вследствие изменения глубины потока. Аналитически это изменение представится в следующем виде:
d<o дш дш dh ds ~ ds 'dh ’ds'
Так как русло по третьему допущению изменять своей формы не может, то-^-= 0. Определим теперь член ds~' Изфиг.191 имеем:	<Ь. _ Bdh- % - в,
dh
откуда:
d<a _ п dh ~ds~ & ds'
Подставив полученное выражение в уравнение (г), имеем:
</ / у2 \	Q* 2
(/s \ 2g ]	2g
5-^-. ds
Подставим теперь полученное значение в уравнение (в):
или
отсюда:
= _ aQ2	dh Q2
ds ~ l~gw‘	ds	w2c2R
db( i	i____
ds\ gw3 ) w!c2R'
Q1 dh = 1 ^c3R ds t aQ2 g*»3
(143)
Полученное уравнение называется диференциальные уравнением свободной поверхности. Интегрирование этого уравнения, дающее функциональную зависимость между h и $, должно быть произведено отдельно в каждом случае для русел различных форм.
При интегрировании этого основного уравнения всегда делаются следующие преобразования: 1) <о и R выражаются как функции от h, 2) Q выражается через гидравлические элементы потока, взятого на участке с равномерным движением. В данном курсе мы интегрирование произведем только для одного случая русла.
§ 105. Случай прямоугольного русла большой ширины (фиг. 192)
Эта задача была решена Брессом.
Имеем: 1) Здесь гидравлический радиус примерно равен глубине R^h.;
2) со = Bh;
3) Q =	<?2 = B2c2h2 i.
Подставим полученные значения в уравнение (143):
B2c2hn3i , Лпз
dh_ B2c2h3	. h1
ds ~	a.B2c2hnHB	1 , gc2V
gB3h2	gh3 1
Разделив эту дробь на величину получаем:
Заменив величину -г- через a dh = hndri, имеем: h = nds
h
новую переменную -q, т. е. — =
. -- 1
I J---------
т)3 — —А g
Произведем разделение переменных и и отнимем dr):
(vf — — сЧ) dr[
—----------------\-dri — dti =
кроме
т)3 — — c2i g
. , стц	. а	\
= d-ц + —г 1----сЧ ;
¥—1 \ g	I
интегрируя это уравнение, получаем:
-И
i hlS
1 решается циентов и выражается:
f ..bn (71~1)2
I .з-i 6шт2 + т1+1	;
интеграл
того прибавим
Фиг. 192
методом неопределенных коэфи-
1 х 2т) +1 ,	, ч .
= arc tg —==---------|-с-= ?(г))4-с,

где величина 9 (-ц) заранее высчитана и помещена в таблице функций Бресса. Таким образом имеем:
4-s=1l + ( 1— -7	ЪоО + л	(144)
/Ln	X	Ь	/
Зависимость между ц и $ получена нами в виде неопределенного интеграла, в котором величина с зависит от положения начала координата.
Если искать не всю длину кривой s, а только расстояние между двумя какими-либо ординатами, то величина с может быть исключена следующим образом (фиг. 193). Задаемся двумя значениями Sj и з2;. получим следующие два уравнения:
. i	/ . а , ,\ , . ,
1)-т—Si = ’h+ 1 —?(»!.)
2) J + ( 14-Ph) + с.
Вычитая почленно уравнения, имеем формулу Бресса:
l-r-L = (i)a — Th)-( 1	?W — ?0li) ,	(145)
Значения <р даны в табл. 22.
Таблица 22
Значения у (к)) по Брессу
*1	ч» (ч)		<? (1)		V (Т)	*1	| <р (ч)
		0,960	0,940	1,15	0,561	3,0	*0,0550
0 01	-0,595	0,970	1,040	1,20	0,479	4,0	0,0310
0,05	— 0,555	0,980	1,178	1,25	0,420	5,0	0,0200
0,10	— 0,505	0,990	1,412	1,30	0,373	10,0	0,0J50
0,20	— 0,404	0,999	2,183	1,35	0,335	20,0	0,0013
0,30	— 0,303	1,(00	00	1,40-	0,304		
0,40	— 0,198	1,001	2,183	1,50	0,257		
0,50	— 0,088	1,005	1,647	1,60	0,218		
0,60	4-0,032	1,010	1,416	1,70	0,190		
0,70	+ 0,171	1,020	1,191	1,80	0,166		
0,80	+ 0,346	1,030	1,060	1,90	0,146		
0,85	0,460	1,050	0,895	2,00	0,132		
0,90	0,614	1,и70	0,783	2,20	0,108		
0,95	0,862	1,100	0,676	2,50	0,082		
Задача. Определить, на каком расстоянии L от плотины, (фиг. 194) подпоруг = 0,35 м, если глубина^ плотины // = 4,20 .и, уклон дна i = 0,00033, нормальная глубина hn = 2,00 м, русло прямоугольное, коэфициент шероховатости по Базену у = 1,75;
Фиг. 193
Фиг. 194
Решение. Находим расстояние L из формулы Бресса:
iL
—7li
fOh) — ?0li) .
где i = 0,00033; Л„=2л; L — искомое расстояние;
2,10;
_A«+ji 2 + 0,35 , 175
а» 1,1;
и взятые по таблице, равны <р(т)2) =0,120 и = - 0,517 (по интерполяции),
Коэфициент с определим по формуле Базена:
с =
87	87
= 38,9.
Подставив эти значения, получим:
0,00033	2.10 — 1,175 — (1— 1,1 •38’^-0-0.0033\ (од20-0,517
2	\	9,81	/ \
откуда:
L = 7879 м.
§ 10В. Построение кривой свободной поверхности для естественных русел
Метод приближенного интегрирования. Пусть для реки на данном отрезке известны продольный профиль дна ABCD, а также профиль по-
верхности воды в ее естественном состоянии abed.
В подпертой состоянии—уровень воды а' Ь1 с (фиг. 195). Пусть известна одна из глубин, например z4'; требуется построить линию свободной ПО
Фиг. 195
верхности.
Для решения этой задачи производятся некоторые вспомогательные построения: 1) русло разбивается на ряд участков I, II, III и т. д. так, чтобы на каждом из них линии ab, be, cd с достаточной точностью можно было бы принять за прямые; 2) для точек А, В, С и D вычерчиваем поперечные профили; 3) в каждом из этих сечений вычисляются величины В (ширина), ® и с при разных глубинах наполнения. Для построения кривой, свободной на каждой поверхности, на каждом участке воспользуемся диференциальным уравнением, причем начнем с участка, в котором нам известна подпертая глубина.
Из уравнения (142) имеем:
dz d (у* \ у* ds ** * ds\2gj "гс2/?'
Это уравнение приближенно применяем к участку конечной длины. Тогда имеем для участка III:
fv1 \ _v4* и/*
dz = z^ zz; ds — L$\ d / 2g 2g''
Подставим эти значения в предыдущее уравнение: а / ,г_ ,2 \ v*
L3 2g£3\ 4	3 /+с;Я
или
,	!	01 (	,9	,9	\	.
*• z‘ ‘-v ’• )+И?’
где "V, с и R— средние величины на участке III, т. е.:
4- с»', р Rt' 4- /?3'
2	’ Н “	2
Заменив v через	R—через ^-или приближенно R —
получим:
V
2	’ С
<0
В'
— Zt' = а
1 \ , <УЛ> а>3'2/ о>2 Са R
(146)
В полученном уравнении
Фиг. 196
неизвестными являются как z3’, так и все величины, от нее зависящие. Решается это уравнение методом подбора. Для этого задаемся величиной zt', вычисляем все от нее зависящие величины и подставляем в ур’авнение (146). При правильном подборе уравнение (146) тождественно удовлетворяется. Аналогичным образом строится линия на других участках.
§ 107. Определение сопряженных глубин при прыжке
Выделим из жидкости, находящейся в состоянии прыжка (см. § 103), об'ем abed и рассмотрим перемещение этого об'ема при прыжке (фиг. 196). Через промежуток времени dt об'ем abed переместится в положение а’, Ь’, с’, d\ причем dlt = vYdt, а dli = vidt. Рассмотрим изменение количества движения при этом перемещении: так как об'ем a'b'cd входит как в об'ем abed, так и в об'ем a’b'c'd', то изменение количества движения об'ема abed будет равно разности между количеством движения с'd' cd и a'b’ ab. Если обозначим количество движения a'b’ab через kit а количество движения c'd'cd—через kit то:
,	т Qdt
= mxVi =• a
,	7 Qdt
а Л3= а — vit &
где коэфициент а вводится вследствие того, что количество движения вычислено здесь не по истинной скорости в струйках, а по средней скорости потока.
Этот коэфициент не намного отличается от введенного нами ранее коэфициента, корректирующего живую силу (см. §40), поэтому мы здесь для него сохраняем то же обозначение.
Определим теперь изменение количества движения: .	, т Qdt.	.
=	(v4 —г»!),
б
Рассмотрим импульс всех сил, действующих на выделенный об'ем. Эти силы сводятся к нижеследующим:
1.	Давление жидкости справа и слева. Так как рассматриваемое движение медленно изменяющееся, то давление это распределяется по гидростатическому закону.
Пусть yt и уа — расстояние центров тяжести сечений от поверхности жидкости. Суммарное давление на грани ab равно
<»i суммарное давление на грани а/ равно /?a = «aTJa, импульс этих сил:
/?а = со, уу8 rft
2.	Силы трения по дну и боковой поверхности. Этими силами пренебрегаем.
3.	Сила веса (приближенно принимаем наклон этой силы к основанию равным 90°).
4.	Нормальная составляющая реакции дна.
Спроектируем все эти силы на ось потока.
Проекции импульсов 3-й и 4-й сил на ось потока дадут нуль. Поэтому уравнение количества движения примет следующий вид:
подставив значения k и R, получим:
-- т Qdt (?, — vx) = у dt («V!— ®ауа) или а _	а _	.	О
- — Qt'a-|-®a<ya; заменив v через — , g	S	®
получим:
(H7)
a Q2	a Q2
--------(-со. у. =--------------(- а>.,у.>
— основное уравнение прыжка.
Так как ®1(У1 являются определенными функциями от глубины Л, (до прыжка), а ®а и уа— функциями от глубины Ла (после прыжка), то можно написать FfAJ = F(Aa).
Построим график этой функции (фиг. 197).
Имея этот график, можно определить сопряженную глубину.
Построив дополнительно еще кривую удельной энергид сечения, можно определить потерю энергии при прыжке.
14 Гидравлика	*	209
Для этого по известной глубине hr определяем по графику функции прыжка глубину Л4. Затем на графике удельной энергии разность ординат покажет потерю энергии при прыжке (фиг. 198).
§ 108. Случай прямоугольного русла
Обозначим погонный расход через q\ тогда:
Q = Bq\ ш = Bh\ у =	.
Подставим все это в основное уравнение прыжка: aB2q2 Bh2 _ aB2q- Bh2 gBht + 2 ~ gBh2 + 2 >
gq U, A.J 2 или
	Д j__(^2	^1) (^2~l~ ^1) ^2	. £_________________________2
й1Л22+й12Аа-2-|^ = 0, откуда:
^*"’±'|Z4>‘ + 8y?!*i_-A.!±V|/'l+Y5 h* =	2ht	2^
Следовательно:
(148)
что и является расчетной формулой для определения сопряженной глубины.
§ 109. Расчеты сопряжения бьефов из гидротехнической практики
1. Случай водосливных плотин. Задача при этом распадается на две части:
1. Определение расхода, пропускаемого данной плотиной.
2. Определение сопряжения падающей струи с нижним бьефом.
Первый вопрос решается просто по известной формуле:
3
Q = mb}/ 2gHo2
При решении второго вопроса могут встретиться 3 случая:
а)	Струя сопрягается с нижним бьефом без образования прыжка. Этот случай называется затопленным прыжком (фиг. 199).
Фиг. 199
Фиг. 200
б)	Струя сопрягается с образованием прыжка, расположенного за подошвой плотины. Этот случай называется отогнанным прыжком (фиг. 200).
в)	Струя сопрягается с нижним бьефом, образуя прыжок у самой подошвы плотины. Этот случай называется случаем надвинутого п р ы ж ка (фиг. 201).
При определении типов сопряжений вычисляется сначала глубина у начала подошвы (глубина Ах), затем вычисляется ее сопряженная глубина Л2. Эта глубина Л2 сравнивается с глубиной нижнего бьефа Ло. При этом, если Л2 < Ао, прыжок будет затоплен, при Л2 > Ло прыжок будет отогнанный и при /г2 = й0 прыжок будет надвинутый.
Следовательно для решения вопроса о типе сопряжения нужно знать величину Ах, которая определяется следующим образом.
Напишем уравнение Бернулли для точки на свободной поверхности в верхнем б'ефе и для точки в сжатом сечении (фиг. 200):
(Н4-Т\4-Рь -h 4-р» J-*4* -I-(Н+Т)+ у +2g _й1+-- + —+ С— .
Обозначим:
14*	2И
тогда:
2^1 +f) = tf0+ T—hx\
v* = ^77^1/2^0 + T-hJ = ? ДШГ-Л,).
Расход на единицу ширины:
Я = ? Ауг^СНо+Г-ЛО;
с другой стороны, по общей формуле водослива имеем: _____________________________	2_
q = т.^2g^o2 •
Сравнивая эти формулы, получим:
<ih^2g(H0+T-hi) = т^Нй~ нли
m2 Н 8
А1’(//о+Г-А1) = -^-;
т?Н 3
V-Ах«(//о + Т) +	=• 0,	(149)
откуда и находится искомая величина ЛР
Если при расчетах обнаружится, что прыжок не затоплен, то для его затопления устраивается либо водобойная стенка либо водобойный колодец.
Глубина d водобойного колодца определяется методом подбора (фиг. 202).	4
Задаваясь величиной d, определяем:
r = r + d,aft'0, = A0 + rf.
Тогда величина hf найдется из формулы:
^=?A1'/2g(/70 + r-A1’);	(150)
сравниваем ее с величиной Ло' и определяем, будет ли здесь прыжок. Если прыжка не будет, тогда глубина d удовлетворяет условиям.
Второйспособ определения со пряжения бьефов (способ проф. Бахметева). Этот метод основан на следующем. При заданном напоре Н тип сопряжения зависит от положения нижнего бьефа, который может быть определен величиной перепада z.
Обозначим через z0 положение, соответствующее надвинутому прыжку (фиг. 201). Если заданный по условию задачи z>z0, то прыжок будет отогнанным, а при z < z0 — прыжок будет затопленным. Следовательно для определения типа сопряжения неоС-.412
ходимо знать z0, которое может быть заранее вычислено следующим образом.
Имеем два уравнения: 1) уравнение, вытекающее из равенства расходов в верхнем и нижнем бьефах:
з
m /2g Яо ’ = Т Лх /2g(H0+ Т— ht) = q-
2) уравнение, вытекающее из условий надвинутого прыжка:
= Ло,
где Л2 —глубина, сопряженная глубине	а Ло —глубина ниж-
него бьефа, или, подставив значение из формулы (148), получим:
Фиг. 201
Фиг. 202
Так как
А0 = Я+Т-д0, то второе уравнение перепишется так:
_	8 а Д’’
Заменим во втором уравнении через величины из пер-вого уравнения; имеем в первом уравнении:
?,Ai22g(^0 + T-A1) = ^
или
8а^г 16/а
___ = __(//°+Г_А1).
Практически удобно бывает искать отношение у; поэтому разделим второе уравнение на величину Т:
Т + 1"Т-57[/ 1 + Т2-(т + 1-7)-1]-
Отсюда!
?=4+1 -	1+16-W -ь > - 44 -1 ] • 1151>
л, н
Из первого уравнения выразим через ?:
mytyH2 =^hiy2g(H-\-T—hi)\ т2 2g И3 = ? h2 2g(H+T—hi).
Деля левую и правую часть на 2g и Г3, получим:
т2
г) ‘
,, А1
Из полученного уравнения, зная ? и т, можно -у. выразить Н через у .
Таким образом из уравнения (151а) величину у можно по-,	н
лучить как функцию от величины -у .
Если построить график (фиг. 203), в котором по оси абсцисс Я	hx z0
отложить величины у, а по оси ординат — величины у и у , то он представит большие практические удобства.
В графике 7 принято равным 0,95, а для т взято несколько значений, в соответствии с чем получено несколько кривых.
Этими графиками пользуются так: пусть заданы величины Н, Т, Ао, т; тогда находим z — Н + Г — Ао и вычисляем величину z	//
-у; затем по заданному у и т берем по графику соответствующее значение у и сравниваем полученное по графику Zo	Z
отношение -у с вычисленным у .
Задача. Определить вид сопряжения бьефов, если даноН Зм, Т = 10 м, Ло = 5 м и т = 0,48.
Решение. Имеем: у = 0,3 и 4 ~ °>8’ п0 графику для
т — 0,48 и у — 0,3 находим:
у—0,76.
Так как
Фиг. 204

то прыжок будет отогнанным,
2. Случай вытекания из-под щита. Струя при выходе подвергается сжатию. В сжатом сечении струйки двигаются параллельно, причем глубина в сжатом сечении й^еа, где с — коэфициент сжатия в зависимости от очертания нижней кромки щита меняется от 0,65 до 0,75.
Сопряжение струи с нижним бьефом здесь тоже бывает троякое:
1) затопленный прыжок (фиг. 204); 2) отогнанный прыжок (фиг. 205); 3) надвинутый прыжок (фиг. 206).
Для определения типа сопряжения поступают аналогично случаю водосливной плотины, т. е. находят сопряженную глубину Л, и сравнивают с Ло (глубиной нижнего бьефа).
Фиг. 206
ГЛАВА XIV
ДВИЖЕНИЕ ГРУНТОВЫХ ВОД
Движение грунтовых вод относится к специальному типу движений жидкости, изучаемых современной гидравликой. Вода, попадая в поры грунта различными способами: путем ли просачивания части атмосферных осадков, или путем конденсации поднимающихся из глубины земли водяных паров, или путем сгущения паров подземного воздуха (теории образования грунтовых вод изложены в специальных курсах), образует там водоносные
Фиг. 207

Фиг. 208
пласты, расположение которых зависит от геологической структуры породы в данном месте. При наличии известного уклона этих пластов вода под влиянием собственного веса приходит в движение, образуя подземные потоки, причем на отдельных участках это движение может происходить исключительно под влиянием собственного веса, что сопровождается образованием свободной поверхности и соответствует случаю безнапорного движения надземных потоков (фиг. 207); на других участках это движение обусловливается давлением вышележащих частиц и соответствует случаю напорного движения. Такое движение может иметь место, когда водяной пласт заключен между двумя 21в .
водонепроницаемыми слоями, расположенными достаточно близко друг к другу и образующими нечто вроде трубы с водонепроницаемыми стенками (фиг. 208).
Для случая, когда грунт представляет собой однородную песчаную среду, вода заполняет все поры этого грунта и образует почти сплошной поток. В горных же породах, образующих значительные трещины, это движение происходит довольно значительными по своим поперечным размерам разобщенными друг от друга струйками.
Если пробурить в почве скважину и соединить водоносный пласт с атмосферой, то мы получим своего рода пьезометрическую трубку, в которой вода поднимется на соответствующий уровень. Подобного рода скважины, как известно, называются артезианскими колодцами.
В качестве другого примера напорного движения можно привести случай движения воды под фундаментами плотин (фиг. 209). В этом случае вода под влиянием разности напоров в верхнем и нижнем бьефах протекает в грунт и медленно движется в его толще, переходя в основании плотины из верхнего бьефа в нижний.
Фиг. 209
Фиг. 210
§ НО. Основные характеристики фильтрационных свойств грунтов
Из всего вышесказанного очевидно, что движение грунтовых вод сильно зависит от свойств самого грунта. В каждом грунте его фильтрационные свойства определяются следующими характеристиками:
1. Пористость. Так как грунт представляет собой совокупность частиц (зерен) самой неправильной и разнообразной формы, то очевидно, что и геометрические очертания пор, т, е. каналов, по которым проходит движение воды, и их размеры в поперечном направлении являются переменными по длине.
При определении суммарной площади конечного сечения пор в грунте исходят из некоторой условной модели, так называемого «идеального грунта", представляющего собой твердое тело с цилиндрическими порами, оси которых совпадают с направлением движения воды (фиг. 210). Для такого «идеального грунта" сум-
марная площадь пор a>t для любого поперечного сечения гручта 1—1 будет величиной постоянной и равной:
т
О)1
(а)
где — об'ем пор в рассматриваемом об'еме грунта, а I—размер этого об'ема в продольном направлении.
Переходя далее к модели так называемого „фиктивного грунта*, более близкого по своим свойствам к действительному (фиг.211) и состоящего из правильных шаровых зерен, мы видим, что суммарное сечение пор в этом случае уже не является величиной постоянной для любого сечения грунта, а поэтому величина <ох должна исчисляться здесь как некоторая средняя величина, определяемая тем же выражением (а).
Очевидно, что и при переходе к действительному грунту, отличающемуся от фиктивного лишь непртвильностью форм частиц, вышеприведенные рассуждения могут быть полностью применены.
Таким образом под суммарной площадью пор следует понимать отношение об'ема пор к длине рассматриваемого об'ема грунта:
Аналогично для суммарной площади сечения зерен служит отношение:
где — об'ем зерен, содержащихся в рассматриваемом об'еме грунта. Очевидно, что полное сечение грунта:
, W, + Ш, ISO
<0 = ^ + ^ = —-t-----= z-,
где w — полный об'ем грунта.
В соответствии со сказанным коэфициент пористости представляет собой отношение об'ема пор данной породы к ее полному об'ему или отношение средней площади сечения пор ш, к площади сечения об'ема о>. Обозначая этот коэфициент через т, имеем:
_<ОХ _	О»!
/7Г	“	—	—	•	(о)
ш 0)1 4-	v 7
2. Механический состав грунта. Он определяется путем механического анализа грунта, на основании которого строится гранулометрическая кривая (фиг. 212).
218
По оси абсцисс откладывают диаметры зерен, взятые через определенные интервалы, а по оси ординат откладывают в процентах суммарный вес всех фракций зерен, диаметр которых меньше данной отложенной на оси абсцисс величины. При этом диаметр того зерна, меньше которого в данном грунте содержится 10%, называется действующим диаметром и обозначается через dr.
Действующий диаметр играет весьма значительную роль в вопросах фильтрации, так как по исследованиям американского ученого Газена каждый разнородный грунт по своим фильтрационным свойствам может быть приравнен к однородному грунту, состоящему из зерен, имеющих диаметр, равный по величине действующему диаметру.
Если взять отношение диаметра зерна, меньше которого в грунте содержится 60%, к диаметру, меньше которого содержится 10%
Фиг 212
(т. е. к действующему диаметру), то это отношение является характеристикой однородности состава грунта и называется коэфициентом однородности.
§111. Основные гидравлические понятия
Поскольку движение грунтовых вод является только частным случаем движения воды, то все основные понятия, данные в общей части гидравлики, остаются и здесь в силе. Небходимо только иметь в виду, что мы здесь имеем дело с движением в очень узких трубках и с очень малыми скоростями, поэтому в большинстве случаев движение грунтовых вод является ламинарным. Далее необходимо иметь в виду, что здесь под живым сечением потока понимается не сумма пор, находящихся в данном поперечном сечении, а вся величина и, включающая в себе как поры, так и твердые частицы.
Деля расход на живое сечение, мы получаем так называемую скорость фильтрации:
которая, очевидно, представляет какую-то уменьшенную скорость по сравнению с истинной. Как нетрудно однако убедиться, переход от этой средней скорости к истинной совершается без всякого труда при введении пористости грунта.
В самом деле, обозначив скорость фильтрации струйки через Q и и считая эти скорости одинаковыми в потоке и равными
мы из формулы (б) § НО имеем:
ш -— т
откуда:
Движение грунтовых вод может быть равномерным или неравномерным, причем характеристика этих случаев такая же, как и в случае поверхностных потоков.
Так, при безнапорном движении грунтовых потоков свободная поверхность потока представляет собой плоскость, параллельную плоскости нижнего подстилающего слоя. При неравномерном же движении свободная поверхность в большинстве случаев криволинейна. Для плоской задачи эта поверхность превращается в линию, называемую кривой депрессии. Примером такой кривой депрессии может служить случай фильтрации воды через тело земляной плотины или случай движения воды к водосборным колодцам, устраиваемым в толще грунта.
§ 112. Основной закон фильтрации
Французский ученый Дарси в средине XIX в. на основании ряда опытов установил закон, по которому вода движется через поры грунта. Для своих опытов Дарси воспользовался прибором, показанным на фиг. 213. Имелся цилиндрический сосуд, заполненный песком, через который пропускалась вода при постоянном напоре Н.
Изменяя в этих опытах вид песка, толщину слоя Н и расход Q, Дарси нашел такое постоянное соотношение:
® L
О
или, имея в виду, что ~ = г' (скорость фильтрации), а разность показаний манометра Н представляет собой потерянный при фильтрации напор Л(, получим формулу:
, hi v
или иначе:
1	,1	(152)
где как известно, называется гидравлическим уклоном и в нашем случае может быть принят равным пьезометрическому уклону J, аА -является коэфициентом, характеризующим водопроницаемость грунта. Определяется он опытным путем и называется коэфициентом фильтрации.
Таким образом закон Дарси дает зависимость между скоростью фильтрации, водопроницаемостью грунта и теряемой при движении энергией.
По входящим в формулу (152) величинам эта формула сходна с формулой Шези, данной для движения поверхностных вод.
Главное различие между обеими форму-
лами состоит в том, что, в то время как в формуле Шези скорость пропорциональна корню квадратному из гидравлического уклона, в формуле Дарси между этими величинами существует линейная зависимость.
Это различие может быть достаточно легко об'яснено, если учесть, что изучавшееся Дарси движение в песках представляет собой движение в очень маленьких трубках капиллярного типа и должно быть поэтому отнесено к ламинарному типу движения, а в этом случае мы как раз
имеем линейную зависимость между ско-
ростью движения и гидравлическим уклоном [см. § 52, формула (56)]. Отсюда также понятно, что если при движении грунтовых вод скорости достигнут большого значения и перейдут за предел vt, т. е. если движение хотя бы частично турбулентное, то применение закона Дарси в этом случае нарушается.
§ 113. Определение коэфициента фильтрации
Существует большое количество экспериментальных формул, дающих зависимость коэфициента фильтрации от механического состава грунта. Из них в настоящем курсе приводятся две:
1. Формула Хазена:
~Ь=АМГ2, |
(153)
где Л — коэфициент, зависящий от размерности, в которой выражены скорости фильтрации, причем для скорости, выраженной в м/сутки, Л = 1; с — некоторая постоянная, зависящая от чистоты песка.
Для чистых песков с = 1000, для песков с примесями с = 700; t—температурный коэфициент, определяемый формулой:
(=0,7 + 0,037, где Т—температура в градусах Цельсия; dr—действующий диаметр зерна (определяется по гранулометрической кривой).
По входящим в формулу Хазена величинам видно, что фильтрационные свойства грунта в ней даны как функции только действующего диаметра и температуры. Пористость грунта формулой Газена не учитывается, что надо отнести к числу ее недостатков.
При пользовании формулой Хазена необхбдимо иметь в виду, что ее применение ограничено, с одной стороны, требованием, чтобы коэфициент однородности не превышал бы 5, а также требованием, чтобы действующий диаметр зерен находился в пределах от 0,1 до 3,0 мм
2. Формула Слихтера (в этой формуле дана зависимость коэфициента фильтрации от трех величин: от действующего диаметра, температуры и пористости грунта).
Формула имеет следующий вид:
| k = Ad^At]	(153а)
где А — коэфициент, зависящий от принятых единиц измерения (так для k Mjсутки — А 5000);
т — поправка на температуру по Пуазейлю, причем приближенно: г = 1 -|~ 0,0337 Т [см. § 7 формулу (6)], М—коэфициент, зависящий от коэфициента пористости т, значение которого может быть взято из табл. 23
Таблица 23
т°/о	М	т %	Я		М		м
26	0,01187	31	0,02122	37	0,03808	43	0,06267
27	0,01350	33	0,1'2601	39	0,04524	45	0,07295
29	0,01694	35	0,03163	41	0,05339	47	0,08455
§ 114. Фильтрация через земляные плотины на непроницаемом основании
В качестве примера движения грунтовых вод рассмотрим случай фильтрации воды через тело земляной плотины, находящейся на непроницаемом основании (фиг. 214). Пусть нам заданы геометрические размеры этой плотины: высота Н, ширина поверху b и углы откоса ? и <р, (или сами откосы т и /п,), а также положение воды в обоих бьефах Нх и h0 и коэфициент фильтрации k.
Задача заключается: 1) в определении фильтрационного расхода q, 2) в определении положения кривой депрессии 7И, Мй, дающей верхнюю границу движущегося грунтового потока.
Решение этой задачи дано акад. Павловским в следующем виде (Н. Н. Павловский „О фильтрации через земляные плотины”, Ленинград 1?32). Разбиваем фильтрационный поток на три характерные части /, //, ///, которые назовем „верхним клином", „средней частью" и „низовым клином", и рассмотрим движение потока в каждой из этих частей в отдельности.
Для определения кривой депрессии необходимо, очевидно, знать положение точекЛ/, ТИр/Ио, атакже закон изменения кривой депрессии на участке между этими точками.
Положение точки М нам задается самим условием (величиной для точки A4i неизвестна ее координата hi, а для точки 7И0 неизвестны ее две координаты $ и _у0. Характер изменения кривой между этими точками, как буд*т указано в последующем, тоже сможет быть определен. Таким образом задача заключает в себе всего четыре неизвестных — q, hiS,ya.
Для определения этих неизвестных мы располагаем известным нам условием равенства расходов на всех трех фильтрационных участках, что дает систему трех уравнений, включающих искомые геличины.
Недостающее же четвертое уравнение может быть найдено из следующих геометрических соотношений: из фиг. 214 имеем
Ь 4- Щ Н = $ + /П1(а0 + Ао),
Переходим теперь к составлению уравнений для расхода во всех трех частях плотины.
1. Рассмотрим сначала расход в верховом клине /. При изучении движения воды в этом клине для упрощения этого изучения струйки считаем прямыми и горизонтальными.
Такое предположение, вообще говоря, не соответствует истине, поскольку как аналитически, так и экспериментально установлено, что струйка при входе направлена нормально к откосу. Однако замена ноинных струек типа ab воображаемыми струйками типа а'Ь большого значения для явления не имеет, поскольку плотины < бычно возводятся почти горизонтальными слоями, а гидравлические сопротивления на более коротком криволинейном пути ab приближаются к сопротивлению на более длинных горизонтальных путях а'Ь.
Перейдем теперь к определению сопротивлений такой струйки Из фиг. 215 видим, что длина этой струйки:
/ = (4, + z) ctg ? = m(d0 Н- z).
Напор, теряемый струйкой на этом пути, равен а. Следовательно гидравлический уклон: а _ а I ~m{d^z}'
Скорость же фильтрации:
v = kJ*=k /n(rfo + 2;) •
а полный фильтрационный расход через верхний клин: л+Л<	o+ftg
Г 1	* ka I « f t । \
q =-----1 —j—;---dz =---- n (d0 4-z) =*
4 mJ d^-j-z m I	v 1 '
a	a
a ka	d^a-\-hx
a m Jo + a
или, заменяя d0 + a + через H, а d0-|-a через Н—Дополучим: ka , Н
»- v ta Н=к;-	(1Иб>
2. Перейдем к среднему участку II (фиг. 216).
Выделив из него бесконечно-малый участок ААВВ, имеем падение напора на этом участке, равное - dy (знак минус взят вследствие того, что ось г направлена кверху), а гидравлический уклйн
J = “ * dx ’
o'; сюда:
V = kjh = —t
* dx а расход на единицу ширины
или
dx = —ydy.
Проинтегрировав это уравнение, получим:.
{х = - 4-+^	(е)
Произвольную постоянную с найдем из условия, что для х = 0; y = hx.
Подставив эти значения в уравнение (е), получим:
следовательно это уравнение может быть переписано в следующем виде:
(ж)
Фиг. 217
что является уравнением параболы.
Для построения кривой депрессии на среднем участке при известном q мы будем задаваться значениями у, лежащими в пределе между At, и а0 + й0, и определим соответствующие им значения х. Подставив в уравнение (ж) вместо х всю длину средней части s, а вместо у соответствующее значение _у0, получим:
откуда находим выражения для расхода:
=	(154 в)
хо
3. Рассмотрим теперь движение через нижний клин ///. Этот клин в общем случае мы должны разбить на две зоны: треугольник, в котором жидкость вытекает в атмосферу, и трапецию, в которой жидкость вытекает под уровень нижнего бьефа (фиг. 217).
Рассматривая, как и в верхнем клине, струйки горизонтальными, получим длину струйки:
х — z ctg ft = mvz.
15 Гидравлика
225
Отсюда в первой зове гидравлический уклон: j —— — z — * ~ х ~ mtz = mi
скорость:
.. k
v - kJh = —• " mi Элементарный расход;
dq, = vdz —— dz, nil
До + Ло
а весь расход:
= I — dz = —
I71 J т1 т1 л»
Для струек второй зоны имеем по предыдущему: "	х = m,z;
однако потерянный напор здесь равен: z—гг = а0,
следовательно:
J =— — к X niiZ *
Элементарный расход:
• dz,
41 m-iZ
а полный расход:
=ka0 °C°dz_ka0 1д п0+Л0,
?2 nii J z	а0
Оо
Отсюда весь фильтрационный расход в низовом клине опре-деляется как сумма расходов qt + q.^
(164г)
§ 115. Решение системы фильтрационных уравнений
В предыдущем параграфе нами были получены следующие 4 уравнения:
1)	$ = b 4- mi [Н — («о + Ао)1-	(154а)
<7 _ а Н .
2)	¥	“ т In Н— й/	(1546)
ox q	hi —yQ\	(154в)
3)Т='^—’
4)	£	= flo /1  1п	ао	+ Ло	V	<154г)
' Й	nil \	ао	/
Для решения поставленной задачи, заключающейся в определении фильтрационного расхода q и в построении кривой депрессии, мы должны из данной системы уравнений определить искомые величины q, ht, s, у0.
Вид этих уравнений позволяет сделать одно важное заключение: так как величины у0, s, At даны здесь как функции вели-q чины то и вся кривая депрессии будет зависеть также от ве-/v
личины -? но, как известно из формулы Дарси, величина q сама /v
пропорциональна коэфициенту k.
Поэтому при изменении коэфициента k в п раз отношение |-остается неизменным, а отсюда следует, что вид кривой депрессии в земляной плотине не зависит от фильтрационных свойств грунта.
Решение указанных выше уравнений может быть произведено аналитически методом подстановки. Однако результаты получаются при этом очень громоздкими и сложными, поэтому в указанном выше труде акад. Н. Н. Павловским предложено следующее приближенное решение этих уравнений. При этом решении до--пускаются некоторые упрощения, заключающиеся в том, что пограничные вертикали между 1-й и 2-й частями фильтрационного потока проводятся не через верхнюю „бровку" плотины, как это было сделано раньше, а через точку М на урезе воды (как показывают подсчеты, расхождения при этом получаются незначительными).
Не входя в подробности указанного решения, дадим лишь его окончательные результаты. Так, для определения величины а0 выведена следующая формула:
а0 = аМ-$Ь,	(154д)
где аир — коэфициенты, зависящие от коэфициентов откосов т и mit а также от отношения глубин в обоих бьефах, т. е. от вели-
Ао ЧИНЫ -7J-.
Эти значения могут быть определены по приводимым ниже графикам (фиг. 218 и 219).
Найдя по формуле (154д) величину а0, мы без всякого труда можем определить искомые величины:
Уо=«о + Ао и s = Ь^-т^Н— у0).
Подставив эти же величины а0 в уравнение (154г), мы найдем искомый расход q, после чего из уравнения (154в) найдем также величину
Определив основные элементы депрессионной кривой, мы можем приступить к построению этой кривой, для чего, расположив ось у-ов, как это уже указано на фиг. 214, мы от нее 15*	227
начинаем построение 2-й части кривой, как это уже было указано ранее.
Затем, зная, что в точке М линии токов перпендикулярны к откосу, а также, что части кривой должны быть между собой соединены плавным образом, сопрягаем точку М с построенной 2 й частью депрессионной кривой.
Фиг. 218
§ 116. Движение к водосборным колодцам
В качестве другого примера неравномерного движения грунтовых вод рассмотрим движение грунтовой воды к водосборным колодцам.
Пусть уровень грунтовых вод в водоносном пласте однородной структуры стоит на отметке тп (фиг. 220).
Предположим, что поверхность подстилающего водонепроницаемого слоя горизонтальна. Грунтовая вода будет тогда находиться в статическом состоянии и ее свободная поверхность будет также горизонтальна. Если мы теперь в грунт опустим трубчатый колодец и будем производить из него откачку воды, то в водоносном слое начнется движение к колодцу, свободная поверхность по мере приближения к колодцу будет все более понижаться, поэтому, начиная с некоторого расстояния R от колодца, называемого радиусом влияния колодца, свободная поверхность будет криволинейной, и следовательно на этом участке мы будем иметь неравномерное движение. Кривая свободной поверхности в этом случае, как известно, называется 228
кривой депрессии. Так как структура грунта принята однородной, то приток воды со всех сторон будет совершенно симметричен, струйки будут двигаться по радиальным направлениям, и сечения потока, движущегося к колодцу, представляют поверхности цилиндров переменной высоты, вертикальная ось которых совпадает с вертикальной осью колодца.
Если нам известны радиус влияния колодца R, мощность водоносного пласта Н и глубина воды в колодце Л, то вся кривая депрессии, а также расход воды в колодце могут быть определены следующим образом.
Выделим из жидкости цилиндрический слой, взятый на расстоянии х от оси колодца. Площадь живого сечения этого слоя ш = 2кху, где у представляет, очевидно, высоту цилиндра. Возьмем теперь на бесконечно близком расстоянии dx от выделенного цилиндра другой цилиндрический слой высотой yt=y— dy.
Фиг. 220
Потеря удельной энергии жидкости, проходящей расстояние dx между обоими цилиндрами, будет, очевидно, равна dy, а относительная потеря энергии или, иначе, гидравлический уклон:
I - dy
J*' dx
Отсюда по формуле Дарси можем определить скорость движения воды на этом участке:
v-kJh- k£,
после чего может быть определен расход:
Q=u>.v=2“Xy k dx
Производим разделение переменных в полученном диферен-циальном уравнении.
Имеем:

=ydy.
Проинтегрировав это уравнение от г0 до любого значения х, мы можем получить значение у, представляющее собой соответствующую ординату кривой депрессии.
Это интегрирование даст нам выражение:
Q rdx 2~k J х
Г*
У fydy, Л
откуда:
кА г0 л	(155)
Задаваясь в полученном выражении различными значениями х, мы можем определить из него соответствующее значение у и построить кривую депрессии, которая, очевидно, представляет параболу. Подставив вместо х его предельное значение R и вычислив у, соответствующий значению Н, мы уравнение (155) получим в следующем виде:
Я In — = №—Л2, ий г0
откуда можно определить величину расхода:
Q	—•
(156) го
ПРИЛОЖЕНИЯ
ТАБЛИЦЫ

Величины коэфициентов расхода рь через прямоугольные отверстия в тонкой стенке по опытам Понсле и Лебро
Напор в л над верхним ребром отверстия h	Ширина отверстия В = 0,200						В = 0,600	
	Высота отверстия h				в м е		h в м	
	0,01	0,02	0,03	0,05	0,10	0,20	0,02	0,20
0,01	0,701	0,650	0,630	0,607	—	—	0,644	—
0,02	0,694	0,659	0,634	0,615	0,596	0,572	0,643	—
0,03	0,688	0,659	0,638	0,620	0,600	0,578	0,642	0,593
0,04	0,683	0,658	0,640	0,623	0,603	0,582	0,642	0,595
0,05	0,679	0.658	0,640	0,625	0,605	0,585	0,641	0,597
0,06	0,676	0,657	0,640	0,627	0,607	0,587	0,641	0,599
0,08	0,670	0,656	0,638	0,629	0,610	0,589	0,640	0,601
0,10	0,666	0,654	0,637	0,630	0,611	0,592	0,639	0,602
0,14	0,660	0,651	0,635	0,630	0,613	0,595	0,637	0,603
0,20	0,655	0,648	0,633	0,630	0,615	0,598	0,635	0,605
0,30	0,650	0,644	0,632	0,629	0,616	0,600	0,633	0,607
0,50	0,644	0,640	0,630	0,628	0,617	0,603	0,630	0,607
1,00	0,632	0,633	0,628	0,626	0,615	0,605	0,626	0,605
1,50	0,615	0,619	0,620	0,620	0,611	0,602	0,623	0,602
2,00	0,611	0,612	0,612	0,613	0,607	0,601	0,620	0,602
3,00 1 1 । 	 1	0,609	0,610	0,608 । 1	0,606 I	0,603	0,601	0,615 i	0,601 i
Значения коэфициента с по формуле Гангилье-Кутгера
го ,	1 L 0,00155
20 ' Т —I—
е = Л 0,00155 \ 7Г~ <для метР°в“* РазмеР°в)
1+(23+-т-Н
Значения коэрици-ента п	Гидравлич. радиус в м	•	Уклоны			t		
		0,0000'5	0,000050	0,0001	0,0002	0,0034	0,001	0,01
	0,05	38	44	51	51	56	57	58
	0,10	49	56	61	65	68	70	71
	0,20	63	70	74	77	78	79	80
	0,30	72	77	81	84	85	86	86
	0,50	83	86	88	90	91	91	91
	1,00	100	100	100	100	100	100	100
0,010	2,00	115	Ш	109	107	106	105	105
	3,00	124	117	113	111	ПО	109	108
	5,00	134	123	118	115	113	112	111
	15,00	151	135	125	121	118	117	116
	0,05	28	31	35	38	40	41	42
	0,10	36	41	44	47	49	50	51
	0,20	46	50	53	56	58	59	59
	0,30	53	57	60	63	64	64	65
	0,50	62	65	67	69	69	70	70
0,013	1,00	77	77	77	77	77	77	77
	2,60	90	87	85	84	83	82	82
	3,00	99	94	89	88	87	86	85
1	5,00	108	100	93	91	90	89	88
I	15,00	125	114	102	98	96	94	92
	0,05	19	22	24	26	28	29	29
	0,10	25	29	32	34	35	36	36
	0,20	34	37	39	41	42	42	43
	0;30	' 40	43	45	46	47	47	48
	0,50	47	49	50	51	51	52	52
л Л1 7	1,00	58	58	58	58	58	58	58
	2,00	71	69	67	66	65	64	64
	3,00	'	78	74	71	70	69	68	68
	5,00	87	79	75	73	72	71	70
	15,00	105	90	83	79	77	76	75
	0,05	15	18	20	21	23	23	24
	0,10	21	23	25	28	29	29	30
	0,20	28	30	32	34	35	36	36
	0,30	33	35	37	38	39	40	40
	0,50	40	41	42	43	43	44	44
	1,00	50	50	50	50	50	50	50
0,020	2,00	61	59	57	56	56	55	55
	3,00	69	64	61	59	59	58	58
	5,00	76	70	66	63	62	61	61
	15,00	94	81	74	70	68	67	66
Значения	Гидравлич.	У клоны				i		
коэфициента п	радиус в м	0,000025	0,0и0050	0.С001	0,0002	0,0004	0,001	0,01
	0,05	12	13	15	16	17	18	18
	0,10	17	18	19	20	21	22	22
	0,20	22	23	24	25	26	27	27
	0,30	26	28	29	30	30	31	31
	0,50	31	32	33	। 34	34	35	35
0,025	1,00	40	40	40	40	40	40	40
	2,00	50	48	47	46	45	45	45
	3,00	56	53	51	49	48	48	47
	5,00	64	«59	54	53	52	51	50
	15,00	81	71	63	59	57	56	55
	0,05	10	* 11	12	13	13	14	14
	0,10	13	14	15	16	17	18	18
	0,20	18	19	19	20	21	22	22
	0,30*	21	22	23	24	24	25	25
	0,50	25	26	27	27	28	29	‘ 29
0,030	1,00	33	33	33	33	33	33	33
	2,00	42	41	40	40	39	38	38
	3,00	48	45	43	42	42	41	41
	5,00	56	51	47	45	44	43	43
	15,00	72	62	55	52	51	49	48
	0,05	8	9	9	10	10	11	И
	0,10	11	12	12	13	13	14	14
	0,20	15	16	16	17	17	18	18
	0,30	18	19	19	20	20	21	21
0,035	0,50	22	23	23	23	24	24	24
	1,00	29	29	29	29	29	29	29
	2,00	36	35	34	34	33	33	33
	3,00	42	40	38	37	36	36	36
	5,00	49	45	43	42	41	40	39
	15,00	65	56	51	47	45	44	43
	0,05	6	7	7	8	8	9	9
	0,10	9	10	11	11	12	12	12
	0,20	13	14	14	15	15	16	16
	0,30	15	16	17	18	18	18	18
0,040	0,50	19	19	20	20	21	21	21
	1,00	25	25	25	25	25	25	25
	2,00	32	31	31	30	30	29	29
	3,00	37	35	34	33	33	32	32
	5,00	44	41	39	38	37	36	35
1 !	15,00	59 *	52	46	43	42	41	40
Значения коэфициента с для „новой" формулы Базена
87 с=--------
1 । Т (для метровых размеров)
R	Т = 0,06	7 = 0,16	7 = 0,46	7=0,85	7 = 1,30	7 = 1,75
0,05	68,5	50,7	28,4	18,1	12,8	9,9
0,06	69,8	52,6	30,2	19,4	13,8	10,7
0,07	70,9	54,2	31,7	20,6	14,7	11,4
0,08	71,8	55,6	33,1	21,7	15,5	12,1
0,09	72,5	56,7	34,4	22,7	16,3	12,7
0,10	73,1	57,7	35,5	23,6	17,0	13,3
0,11	73,6	58,7	36,5	24,4	17,7	13,9
0,12	74,1	5У,5	37,4	25,2	18,3	14,4
6,13	74,6	60,2	38,2	25.9	18,9	14,9
0,14	75,0	60,9	39,0	26,7	19,4	15,3
0,15	75,3	61,5 ‘	39,7,	27,2	19,9	15,8
0к16	75,6	62,1	40,5	27,8	20,4	16,2
0,17	75,9	62,7	41,2	28,4	20,9	16,6
0,18	76,2	63,2	41,8	29,0	21,4	17,0
0,19	76,5	63,6	42,4	29,5	21,8	17,3
0,20	76,7	64,1	42,9	30,0	22,3	17,7
0,21	76,9	64,5	43,5	30,5	22,7	18,1
0,22	77,1	64,9	44,0	20,9	23,1	18,4
0,23	77,3	65,2	44,4	31,4	23,4	18,7
0,24	77,5	65,5	44,8	31,8	23,8	19,0
0,25	77,6	65,9	45,3	32,2	24,2	19,3
0,26	77,8	66,2	45,7	32,6	24,5	19,6
0,27	78,0	66,5	46,1	33,0	' 24,8	. 19,9
0,28	78,1	66,8	46,5	33,4	25,2	20,2
0,29	78,3	67,0	46,9	33,7	25,5	20,5
0,30	78,4	67,3	47,3	34,1	25,8	20,7
0,31	78,5	67,6	47,6	34,3	26,1	21,0
0,32	78,6	67,8	47,9	34,7	26,4	21,2
0,33	78,8	68,0	48,2	35,1	26,7	21,5
0,34	78,9	68,2	48,5	35,4	26,9	21,7
0,35	79,0	68,4	48,8	35,7	27,2	22,0
0,36	79,1	68,6	49,2	36,0	27,5	22,2
0,37	79,2	68,8	49,5	36,3	27,7	22,4
0,38	79,2	69,0	49,8	36,6	28,0	22,7
0,39	79,3	69,2	50,1	36,8	28,2	22,9
0,40	79,4	69,4	50,4	37,1	28,5	23,1
0,41	79,5	69,6	50,6	37,4	28,7	23,3
0,42	79,6	69,7	50,9	37,6	28,9	23,5
0,43	79,7	69,9	51,1	37,9	29,2	23,7
0,44	79,7	70,1	51,4	38,1	29,4	23,9
в							
R	7 = 0,06	7 = 0,16	7 =0,46	7 = 0,85	7 = 1,30	7 = 1,75
0,45	79,8	70,2	51,6	38,4	29,6	24,1
0,46	79,9	70,4	51,8	38,6	29,8	24,3
0,47	80,0	70,5	52,0	38,8	30,0	24,5
0,48	80,0	70,6	52,3	39,1	30,2	24,7
0,49	80,1	70,8	52,5	39,3	30,4	24,8
0,50	80,2	70,9	52,7	39,5	30,6	25,0
0,55	80,4	71,5	53,7	40,5	31,6	25,9
0,60	80,7	72,1	54,6	41,4	32,5	26,7
0.65	80,9	72,6	55,4	42,3	33,3	27,4
0,70	81,1	73,0	56,1	43,1	34,1	28,1
0,75	81,3	73,4	56,8	43,9	34,8	28,8
0,80	81,5	73,8	57,4	44,6	35,5	29,4
0,85	81,7	74,1	58,0	45,2	36,1	30,0
0,90	81,8	74,4	58,6	45,9	36,7	30,6
0,95	81,9	74,7	59,1	46,5	37,3	31,1
1,00	82,0	75,0	59,6	47,0	37,8	31Л
1,10	82,2	75,4	60,5	48,0 '	38,8	32,6
1,20	82,4	75,9	61,3	48,9	39,7	33,5
1,30	82,6	76,3	62,0	49,8	40,6	34,3
1,40	82,8	76,6	62,6	50,6	41,4	35,1
1,50	82,9	76,9	63,2	51,3	42,2	35,8
1,60	83,0	77,2	63’8	52,0	42,9	36,5
1,70	83,1	77,5	64,3	52,6	43,6	37,1
1,80	83,2	77,7	64,8	53,2	44,2	37,7
1,90	83,3	77,9	65,2	53,8	44,8	38,3
2,00	83,4	78,2	65,6	54,2	45,3	38,9	“
2,20	83,6	78,5	66,4	55,3	46,4	39,9
2,40	83,7	78,8	67,1	56,2	47,3	40,8
2,60	83,8	79,1	67,7	57,0	48,1	41,7
2,80	83,9	79,4	68,2	57,7	48,9	42,5
3,00	84,0	79,6	68,7	58,3	49,7	43,3
3,20	84,1	79,8	69,2	58,9	50,4	44,0
3,49	84,2	80.0	69,6	59,5	51,0	44,6
3,60	84,3	80,2	70,0	60,1	51,6	45,2
3,80	84,4	80,4	70,4	60,6	52,2	45,8
4,00	84,4	80,5	70,7	61,0	52,7	46,4
4,50	84,6	80,9	71,5	62,1	53,9	47,6
5,00	84,7	81,2	72,1	63,0	55,0	48,8
5,50	84,8	81,4	72,7	63,8	56,0	49,8
6,00	84,9	81,6	73,2	64,6	56,8	50,7
Значения, коэфициента с по формуле Маннинга
1	1
с = — о (для метровых размеров)
Гидравлический радиус в м	Величины п							
	0,010	0,013	0,017	0,020	0,025	0,030	0,035	0,040
0,05	60,7	46,7	35,2	30,4	24,3	20,2	17,6	15,2
0,06	62,6	48,2	36,3	31,3	25,0	20,9	18,2	15,6
0,07	64,2	49,4	37,2	32,1	25,7	21,4	18,6	16,0
0,08	65,6	50,5	38,0	32,8	26,2	21,9	19,0	16,4
0,10	68,1	52,4	39,5	34,0	27,2	22,7	19,7	17,0
0,12	70,2	54,1	40,7	35,1	28,1	23,4	20,4	17,5
0,14	72,1	55,6	41,8	36,0	28,8	24,0	20,9	18,0
0,16	73,6	56,7	42,7	36,8	29,4	24,5	21,3	18,4
0,18	75,2	57,9	43,6	37,6	30,1	25,1	21,8	18,8
0,20	76,5	58,9	44,4	38,2	30,6	25,5	22,2	19,1
0,22	77,7	59,8	45,1	38,8	31,1	25,9	22,5	19,4
0,24	78,8	60,7	45,7	39,4	31,5	26,3	22,9	19,7
0,26	79,9	61,5	46,3	39,9	32,0	26,6	23,2	20,0
0,28	80,9	62,3	46,9	40,4	32,4	27,0	23,5	20,2
0,30	81,8	63,0	47,4	40,9	32,7	27,3	23,7	20,4
0,35	83,9	64,6	48,7	42,0	33,6	28,0	24,3	21,0
0,40	85,8	66,1	49,8	42,9	34,3	28,6	24,9	21,4
0,45	87,5	67,4	50,7	43,8	35,0	29,2	25,4	21,9
0,50	89,1	68,6	51 >7	44,6	35,6	29,7	25,8	22,3
0,55	90,5	69,7	52,5	45,3	36,2	30,2	26,2	22,6
0,60	91,8	70,7	53,2	45,9	36,7	30,6	26,6	22,9
0,65	93,1	71,7	54,0	46,6	37,2	31,0	27,0	23,3
0,70	94,2	72,5	54,6	47,1	37,7	31,4	27,3	23,6
0,80	96,4	74,2	55,9	48,2	38,6	32,1	28,0	24,1
0,90	98,3	75,7	57,0	49,1	39,3	32,8	28,5	24,6
1,00	100,0	77,0	58,0	50,0	40,0	33,3	29,0	25,0
1,10	101,6	78,2	58,9	50,8	40,6	33,9	29,5	25,4
1,20	103,1	79,4	59,8	51,5	41,2	34,4	29,9	25,8
1,30	104,5	80,5	60,6	52,2	41,8	34,8	30,3	26,1
1,50	107,0	'82,4	62,1	53,5	42,8	35,7	31,0	26,7
1,70	109,2	84,1	63,3	54,6	43,7	36,4	31,7	27,3
2,00	112,0	86,2	65,0	56,0	44,8	37,3	32,5	28,0
2,50	116,5	89,7	67,6	58,2	46,6	38,8	33,8	29,1
3,00	120,0	92,4	69,6	60,0	48,0	40,0	34,8	30,0
3,50	123,2	91,9	71,5	61,6	49,3	41,1	35,7	30,8
4,00	126,0	97,0	73,1	63,0	50,4	47,0	36,5	31,5
5,00	131,0	100,8	76,0	65,5	52,4	43,7	38,0	32,7
10,00	147,0	113,1	85,3	73,5	58,8	49,0	42,6	36,7
15,00	157,0	120,9	91,1	78,5	62,8 I	52,3	45,5	39,4
Значения коэфициента расхода т для водослива с тонкой стенкой по формуле Базена
Напор Н в м	Высота стенки водослива Т в м									
	0,20	0,30	0,40	0,50	0,60	0,80	1,00	1,50	2,00	00
0,05	0,458	0,453	0,451	0,450	0,449	0,449	0,449	0,448	0,448	0,448
0,06	0,456	0,450	0,447	0,445	0,445	0,444	0,443	0,443	0,443	0,443
0,08	0,456	0,447	0,443	0,441	0,440	0,438	0,438	0,437	0,437	0,436
0,10	0,459	0,447	0,442	0,439	0,437	0,435	0,434	0,433	0,433	0,432
0,12	0,462	0,448	0,442	0,438	0,436	0,433	0,432	0,430	0,430	0,429
0,14	0,466	0,450	0,443	0,438	0,435	0,432	0,430	0,428	0,428	0,427
0,16	0,471	0,453	0,444	0,438	0,435	0,431	0,429	0,427	0,426	0,425
0,18	0,475	0,456	0,445	0,439	0,435	0,431	0,428	0,426	0,425	0,423
0,20	0,480	0,459	0,447	0,440	0,436	0,431	0,428	0,425	0,423	0,421
0,22	0,484	0,462	0,449	0,442	0,437	0,431	0,428	0,424	0,423	0,420
0,24	0,488	0,465	0,452	0,444	0,438	0,432	0,428	0,424	0,422	0,419
0,26	0,492	0,468	0,455	0,446	0,440	0,432	0,429	0,424	0,422	0,419
0,28	0,496	0,472	0,457	0,448	0,441	0,433	0,429	0,424	0,422	0,418
0,30	0,500	0,475	0,460	0,450	0,443	0,434	0,430	0,424	0,421	0,417
0,35	—	0,482	0,465	0,455	0,447	0,437	0,431	0,424	0,421	0,416
0,40	—	0,489	0,472	0,459	0,451	0,440	0,433	0,424	0,421	0,414
0,45	—	0,495	0,477	0,464	0,455	0,442	0,435	0,425	0,421	0,413
0,50	—	—	0,482	0,468	0,459	0,445	0,437	0,426	0,421	0,412
0,60	—	—	0,490	0,476	0,466	0,451	0,441	0,427	0,421	0,409
0,70	—	—	0,498	0,484	0,473	6,456	0,446	0,430	0,423	0,408
Значения коэфициента затопления б для водослива с тонкой стенкой по опытам Базена
Z	/ / т	0,00	0.05	0,10	0,15	0,20	0,30	0,40	0,50	0.60	0,70	0,80	0,90	1,00	1,10	1,20	„1,30	1,40	1,50
0,05	1,00	0,80	0,70	0,65	0,61	0,55	0,51	0,49	0,48	0,46	0,45	0,44	0,43	0,43	0,42	0,42	0,42	0,41
0,10	1,00	0,88	0,81	0,76	0,72	0,67	0,63	0,61	0,58	0,57	0,55	0,54	0,54	0,53	0,52	0,52	0,51	0,51
0,15	1,00	0,91	0,86	0,82	0,78	0,73	0,70	0,67	0,66	0,64	0,63	0,62	0,61	0,60	0,60	0,59	0,59	0,58
0,20	1,00	0,93	0,89	0,86	0,83	0,78	0,75	0,72	0,70	0,68	0,67	0,66	0,66	0,66	0,65	0,65	0,64	0,64
0,25	1,00	0,95	0,91	0,87	0,86	0,82	0,78	0,76	0,74	0,73	0,71	0,71	0,70	0,69	0,68	0,68	0,68	0,67
0,30	1,00	0,96	0,92	0,89	0,87	0,84	0,81	0,79	0,77	0,76	0,75	0,74	0,73	0,73	0.72	0,72	0,71	0,71
0,35	1,00	0,96	0,93	0,91	0,89	0,86	0,84	0,82	0,80	0,79	0,78	0,77	0,76	0,76	0,75	0,75	0,75	0,74
0,40	1,00	0,97	0,94	0,92	0,90	0,87	0,86	0,84	0,83	0,81	0,80	0,80	0,79	0,78	0,78	0,78	0,77	0,77
0,45	1,00	0,97	0,95	0,93	0,91	0,89	0,87	0,86	0,85	0,83	0,83	0,82	0,81	0,81	0,80	0,80	0,80	0,80
0,50	1,00	0,98	0,96	0,94	0,93	0,90	0,88	0,87	0,86	0,85	0,85	0,84	0,83	0,83	0,83	0,82	0,82	0,82
0,55	1,00	0,98	0,96	0,95	0,93	0,91	0,89	0,88	0,87	0,86	0,86	0,86	0,85	0,85	0,84	0,84	0,84	0,84
0,60	1,00	0,98	0,97	0,95	0,94	0,93	0,91	0,89	0,88	0,87	0,87	0,86	0,86	0,86	0,86	0,86	0,86	0,85
0,65	1,00	0,99	0,97	0,96	0,95	0,93	0,92	0,91	0,90	0,88	0,88	0,88	0,87	0,87	0,87	0,87	0,86	0,86
0,70	1,00	0,99	0,97	0,96	0,95	0,94	0,93	0,91	0,91	0,90	0,89	0,89	0,89	0,88	0,88	0,88	0,88	0,87 i
Значения коэфициента п к формуле Гангилье-Куттера
№	Род стенки	п	п
1	Поверхности, покрытые эмалью или глазурью. Весьма тщательно остроганные доски, хорошо	0,009	111,1 •
2	Строганые доски. Штукатурка из чистого це-мента .		0,010	100,0
3	Цементная штукатурка (Vs песку). Чистые (новые) гончарные, чугунные и железные трубы, хоро-шо уложенные и соединенные		0,011	90,9
4	Нестроганые доски, хорошо пригнанные. Водопроводные трубы в нормальных условиях без заметной инкрустации; весьма чистые водосточные трубы, весьма хорошая бетонировка . . •	0,012	83,3
5	Тесовая кладка, весьма хорошая кирпичная клад* ка. Водосточные трубы в нормальных условиях; несколько загрязненные водопроводные трубы. Нестроганые доски, не вполне тщательно пригнанные 		0,013	76,9
6	.Загрязненные* трубы (водопроводные и водосточные); средняя кирпичная кладка; бетонировка каналов в средних условиях 		0,014	71,4
7	Грубая кирпичная кладка; каменная кладка (не тесовая) с чистой отделкой поверхностей при ровном постелистом камне. Чрезвычайно загрязненные водостоки. Брезент по деревянным рейкам . 				0,015	66,7 1
8	Обыкновенная бутовая кладка в удовлетворительном состоянии; старая (расстроенная) кирпичная кладка; сравнительно грубая бетонировка. Гладкая, весьма хорошо разработанная скала .	0,017	58,8
9	Каналы, покрытые толстым, устойчивым илистым слоем; каналы в плотном лессе и плотном мелком гравии, затянутые сплошной илистой пленкой (все притом в безукоризненном состоянии)	0,018	55,6
10 j	Очень грубая бутовая кладка; сухая кладка из крупных камней; булыжная мостовая. Каналы, чисто высеченные в скале. Каналы в лессе, плотном гравии, плотной земле, затянутые илистой пленкой (в нормальном состоянии) 		0,020	50,0
1* Гидравлик.
241
№	ч	- — 		 	 	 - 		 Род стенки	п	£ п
11 •	Мостовая из крупного рваного камня с резко выступающими углами; каналы в скале при посредственной обработке поверхности; каналы в плотной глине. Каналы в лессе, гравии, земле, затянутые несплошной (местами прерываемой) илистой пленкой. Большие земляные каналы, находящиеся по условиям содержания и ремонта выше средних 		0,0225	44,4
12 i 1	Большие земляные каналы в средних условиях содержания и ремонта и малые — в хороших. Реки и ручьи в благоприятных условиях (со свободным течением без засорения и значи-тельных водорослей)		0,025	40,0
13	Земляные каналы: большие — в условиях ниже среднего/малые — в средних			0,0275	36,4
14	Каналы и реки в сравнительно плохих условиях (например местами с водорослями и булыжником или заметно заросшие травой, с местны-мы обвалами откосов и т. д.)			0,030	33,3
15	Каналы и реки, находящиеся в весьма плохих условиях, с неправильным профилем, значительно засоренные камнями и водорослями и пр.	0,035	28,6
16	То же — в исключительно плохих условиях (обломки скалы и крупные камни по руслу, густые корни, значительные промоины й обвалы, заросли камыша)	  .	0,040	25,0 	Л
Учета. № 5248. Индекс С-55-5-2. Тираж 3000. Пр. № 17 от 27/II 36 г. Сдано в пр-во с матриц 2/V11 1936 г. Подл, в печ. 8/VII 1936 г. Формат бумаги 62 X 94. Уч.-авт. л. 18. Бум. лист. 7®/в. Печ. зн. в бум. листе 101.000 Заказ № 1135.
Уполном. Главл. № В-23820. Выход в свет август 1936 г.
3-я тип. ОНТИ им. Бухарина. Ленинград, уд. Моисеенко, 10.
ОПЕЧАТКИ
в книге Дойно «Курс гидравлики*
Стр.
77
91
116
119
119
131
181
ШЗ
188
Строка	Напечатано	Следует читать
1 сверху
8 сверху
П
4
6
3 снизу
17 снизу
Фиг. 155 4 сверху
и? -
p/?D
h =
pvD
— vD 1
Заказ
1135
фиг. 93 a vk? g g
размер T должен быть только до уровня порога. Н и Т	Н и Т (фиГ 173)
3 руб. Пер. 60 къп.
С-55-5-2
М. Е. ДОПНО
К У I’ с
ГИДРАВЛИКИ
онти
1936