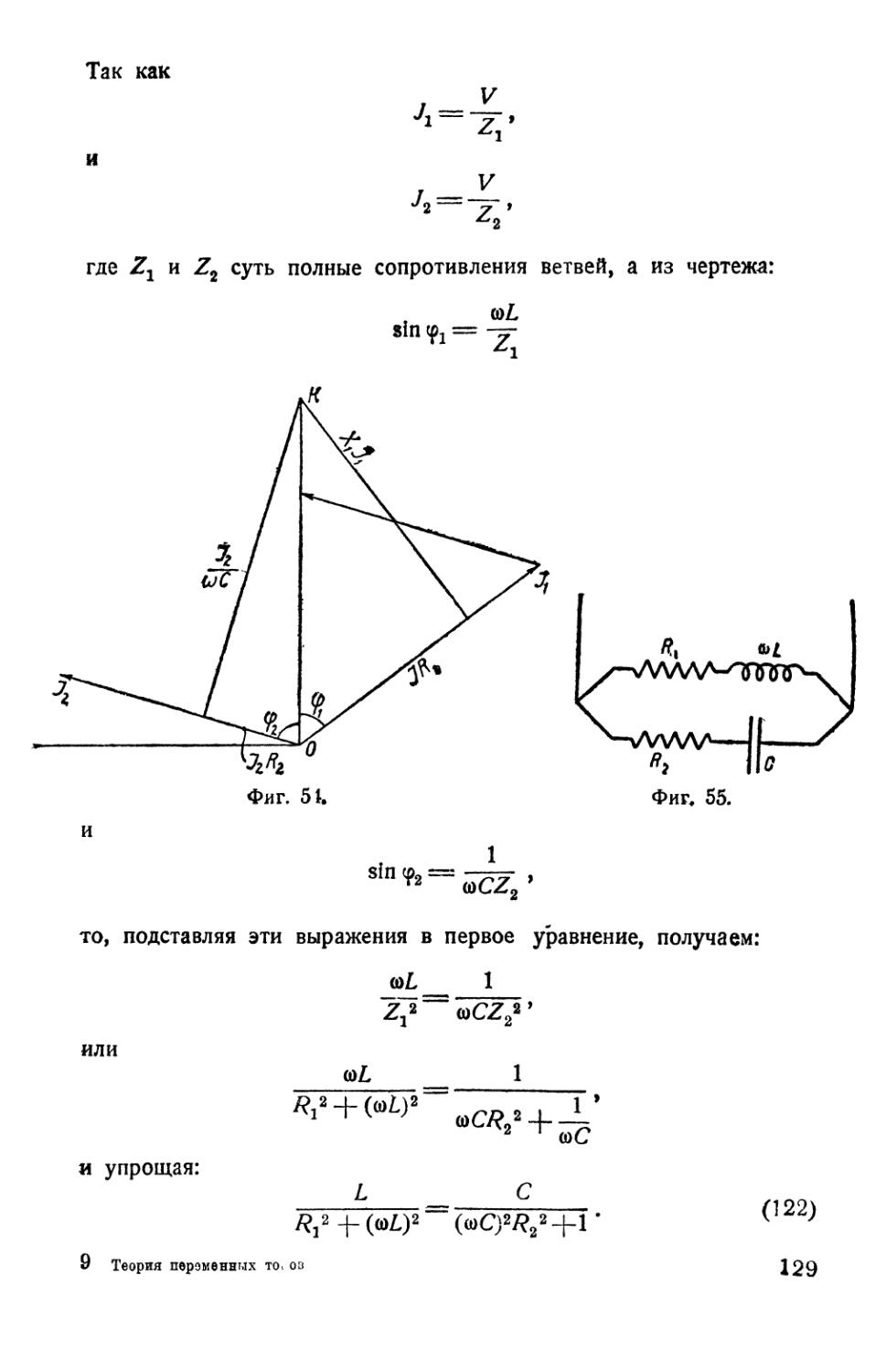
Similar
Text
Проф, И. А. ЧЕРДАНЦЕВ
ТЕОРИЯ
ПЕРЕМЕННЫХ TOKG
Издание третье
ГОСУДАРСТВЕННОЕ
ЭНЕРГЕТИЧЕСКОЕ ИЗДАТЕЛЬС МОСКВА * 1932 * ЛЕНИНГРАД
ТЕ
Проф. И. А. ЧЕРДАНЦЕВ
ТЕОРИЯ
ПЕРЕМЕННЫХ ТОКОВ
ИЗДАНИЕ ТРЕТЬЕ, ПЕРЕРАБОТАННОЕ И ДОПОЛНЕННОЕ, С ЗАДАЧАМИ И ПРИМЕРАМИ
Scan AAW
ГОСУДАРСТВЕННОЕ ЭНЕРГЕТИЧЕСКОЕ ИЗДАТЕЛЬСТВО МОСКВА • 1 9 3 2 * ЛЕНИНГРАД
Редактор Энергоиздата А. Д. Смирнов.
Технический редактор С. В. Вишневский.
ПЕРВАЯ ТИПОГРАФИЯ ОГИЗА РСФСР «ОБРАЗЦОВАЯ». МОСКВА, ВАЛОВАЯ, 28.
★
Уполномочен. Главлита Б-16239. НЗ-1 ГНТИ 3176. Зак. 3517. Тираж 10 000 екз. 311/* п. л.
ПРЕДИСЛОВИЕ К ТРЕТЬЕМУ ИЗДАНИЮ
Третье издание отличается от второго значительными дополнениями, главным образом в главах о многофазных токах, векторных уравнениях, круговых диаграммах и линиях мощностей на них, а также и несколько измененным распределением материала: сложная форма кривых и ряд Фурье вводятся непосредственно перед разбором вопроса о влиянии железа на цепь переменного тока, а метод комплексных величин перенесен ближе к началу курса, дабы читатель имел возможно больше случаев упражняться в его применении.
В этом издании введено около пятидесяти примеров и задач.
Означенными изменениями и исчерпываются те пожелания, которые были мне высказаны лицами, преподающими теорию переменных токов во втузах разных городов
Вычисления в решениях задач на расчет трехфазных систем и линии передачи и точные графические построения в этих и некоторых других задачах с большой тщательностью проделаны инж.-электриком А. А. Сорокиным, которому я и выражаю здесь мою глубокую благодарность.
Печатание книги производилось необыкновенно спешно, что, к сожалению, могло повести за собой появление некоторых опечаток.
22/Х11—1931.
Проф. И. Черданцев.
ОГЛАВЛЕНИЕ
ВВЕДЕН И Е Стр.
Технические способы получения периодической электродвижущей силы. Основные понятия
§ 1. Принцип устройства генератора переменного тока........ 9
§ 2. Электродвижущая сила генератора; графическое изображение ее изменений.................................................. 10
§ 3. Период, частота, число оборотов и число полюсов...... 15
ГЛАВА I
Кривые магнитного поля и электродвижущей силы
§ 4. Предварительные понятия.............................. 17
§ 5. Кривые поля и электродвижущей силы................... 20
глава II
Цепь переменного синусоидального тока, содержащая самоиндукцию и ваттное сопротивление
§ 6. Синусоидальный ток. Электродвижущая сила самоиндукции . . 27
§ 7. Закон Ома для всей цепи и для части ее................ 31
§ 8. Сопротивления ваттное, безваттное и полное............ 35
глава III
Геометрическое представление соотношений в цепи переменного тока посредством векторов
§ 9. Введение понятия вектора . ;........................... 39
§ 10. Сложение векторов...................................... 41
§ 11. Векторная диаграмма напряжений в цепи переменного тока . . . 45
§12. Диаграмма синхронного генератора....................... 51
§ 13. Векторная диагра *ма напряжений для последовательно соединенных участков цепи............................................ 53
§ 14. Вектор электродвижущей силы индукции в контуре при синусоидальном изменении магнитного потока......................... 54
глава IV
Действующие значения силы тока и напряжения. Мощность переменного тока
§ 15. Показания приборов. Действующие или эффективные значения силы тока и напряжения....................................... 57
4
Стр.
§ 16. Среднее значение. Длина вектора и масштаб................. 61
§ 17. Средняя за период мощность в цепи переменного тока......... 63
§ 18. Кривые мгновенных мощностей............................... 66
§ 19. Зависимое ть cj едней м щ ости от других величин в цепи ... 72
§ 20. Диаграмма Беделя и Крехора................................ 77
§ 21. „Падение* напряжения и „потеря* напряжения в проводах линии передачи энергии.................................................. 78
глава V
Емкость в цепи переменного тока
§ 22. Закон Ома для цепи, содержащей ваттное сопротивление и емкость...................................................... 81
§ 23. Мощность в цепи с емкостью............................. 87
§ 24. Закон Ома для цепи, содержащей ваттное сопротивление, самоиндукцию и емкость......................................... 83
§ 25. Резонанс напряжений ................................... 93
§ 26. Разложение силы тока на ваттную и безваттную составляющие. Проводимости............................................... 101
ГЛАВА VI
Метод комплексных величин или символический
§ 27. Основные понятия.......................................105
§ 28. Симво ическое обозначение векторов и действия с ними .... 109
§ 29. Простейшие примеры приложений метода . ................114
§ 30. Замечания о выражении мощности, cos<p, о дифе^енцировании векторов и о символических обозначениях, отличных от описанные ......................................................118
глава VII
Сложные цепи переменного тока
§ 31. Соотношения в синхронном генераторе.......................122
§ 32. Разветвляющиеся цепи......................................123
§ 33. Значение компенсации сдвига фаз.........ч................% 125
§ 34. Резонанс токов............................................127
§ 35. Точное ешенре вопроса о компенсации сдвига фаз.............128
§ 36. Общий вид задачи о параллельных ветвях.....................133
§ 37. Продолжение исследования резонанса токов...................135
§ 38. Потери в диэ гектрике емкости...........• • ..............138
§ 39 Решение одной задачи....................*..................149
§ 40 Приближенная векторная диаграмма длинной линии передачи энергии . . . •.......................................•..........142
§ 41. Измерение мощности тремя вольтметрами или тремя амперметрами .........................................................115
§ 42. Получение токов или напряжений, сдвинутых в фазе на четверть периода ..........................................................147
§ 43. Первый и второй законы Кирхгофа. Принцип наложения .... 150
§ 44. Схемы Бушеро.........................................152
§ 45. Некоторые мостики переменного тока...................155
§, 46. Геометрические места. Работа синхронной машины генератором
и двигателем Диаграмма Блонделя.......................159
§ 47. Топографический метод................................163
5
Стр,
ГЛАВА VIII
Многофазные токи
148. Двухфазный ток.............................................
49. Трехфазный юк............................................
50. Соединение звездой.......................................
51. Соединение треугольником............................... • •
52. Мощность трехфазного тока и измерение ее.................
§ 53. Применение топографического метода — включение нагрузки тре-УГО 1ЬНИКОМ................ ....................................
§54. Применение топографического метода — вк печение нагрузки звездой ... ..............................
§ 55. Применение симвотического метода к трехфазному току ....
§ 56. Определение сил токов и напряжений при включении фаз генератора и нагрузки звездой ..............................
§ 57. Определение сил токов и напряжений при нагрузке треугольником (способ непосредственный) . . ....................
§ 58. Эквивалентные звезда и треугольник........................
§ 59. Графический способ перехода от треугольника к звезде и наоборот .........................................................
§ 60. Определение напряжений и сил токов при включении нагрузки звездой (второй способ) ........................................
§ 61. Графический способ решения той же задачи ................
§ 62. Наиболее общий случай расчета трехфазной цепи .....
§ 63. Графический способ решения задачи, когда даны три линейные напряжения...................... ....
§ 64. Пример аналитического и графического расчета трехфазной системы ..........................................................
§ 65. Нулевая точка нагрузки и ее потенциал....................
§ 66. Вращающееся магнитное поле Случай I: симметричные составляющие ........................................................
§ 67. Вращающееся магнитное поле. Случай II: несимметричные составляющие ........................................................
§ 68. Многополюсное вращающееся-поле............................
§ 69. Разложение несимметричной трехфазпой системы на две симметричных ......................................................
167
169
171
174
175
181
183
188
189
192 197
200
201
204 2J7
209
210 215
221
224 228
232
ГЛАВА IX
Сложная форма кривых электродвижущей силы и силы тока
§ 70. Основные понятия........................................242
§ 71. Разложение в ряд Фурье..................................248
§ 72. Графический метод анализа кривых 257
§ 73. Сложная форма кривых ЭДС и силы тока.................. 262
§ 74. Эквивалентный синусоидальный ток........................268
§ 75 Резонанс для составляющих различных порядков............271
§ 76. Влияние самоиндукции и емкости на форму кривой тока а . . . 272
§ 77 Разветвление тока.......................................273
§ 78. Очищейие тока...........................................274
§ 79. Составляющие высших порядков в трехфазном токе..........275
глава X
Влияние железа на явления в цепи переменного тока
§ 80. Переменный ток, намагничивающий железо. Потери в железе . . 277
§ 81. Векторная диаграмма катушки с железным сердечником .... 281
6
Стр,
§ 82. Самоиндукция четырех катушек с общим или отдельными сердечниками .......................................................288
$ 83. Аналитические выражения соотношений в катушке............291
§ 84. Феррорезонанс. Опрокидывание фаз.........................294
глава XI
Трансформатор
§ 85. Векторная диаграмма трансформатора.......................298
§ 86. Баланс мощностей........................................3 )4
§ 87 Приближенное построение диаграммы........................306
§ 88. Изображение cooiношений в цепи переменного магнитного потока посредством векторов.....................................309
§ 89. Автотрансформатор........................................313
§ 90. Аналитические выражения для соотношений в трансформаторе . 314
§ 91. Аналитический вывод круговой диаграммы тока..............318
§ 92. Эквивалентная схема, первый вид ее.......................321
§ 93. Другой вид эквивалентной схемы...........................323
глава XII
Метод обращений, приложения его к выводу диаграмм тока и напряжения
§ 94. Взаимнообратные кривые................................ 324
§ 95. Основная теорема . . . ,...............................325
§ 96 Координаты центра и радиус обращенной окружности .... 329
§ 97. Обобщение предыдущего на случай пространства трех измерений. 330
§ 9^. Примеры приложения метода обращении...................... —
§ 99. Круговая диаграмма транс юр^атора и асинхронного двигателя.
Первая эквивалентная схема ............................. 336
§ 100. Пример построения круговой диаграммы тока для первой эквивалентной схемы.............................................. 344
§ 101. Круговая диаграмма второй эквивалентной схемы . ........347
глава XIII
Векторные уравнения и круговые диаграммы
§ 102. Выражение прямой линии и окружности векторными уравнениями .......................................................350
§ 103. Применение метода векторных уравнений к первой эквивалентной схеме 358
§ 104. Экспериментальное построение окружности тока..360
§ 105. Векторные соотношения между разными величинами в круговой диаграмме. Третий вид эквивалентной схемы......................364
§ 106. Окружности падения напряжения, первичной ЭДС/ вторичного напряжения и др.............................................. 368
§ 107. Вычитание одной окружности из другой....................372
§ 108. Пример на нахождение окружностей различных переменных величин первой эквивалентной схемы................... . *........373
глава XIV
Линии мощностей на круговых диаграммах
§ 109. Линии потерь мощности на круговой диаграмме.............376
§ 110. Линии первичной мощности, потерь и полезной мощности на круговой диаграмме первой эквивалентной схемы..................381
7
Стр.
§ 111. Масштабы для линий мощностей и коэфициент полезного действия................................................. . . 387
§ 112. Линии мощности на круговой диаграмме второй эквивалентной схемы........................................................391
ГЛАВА XV
Неустановившийся режим в цепи тока
§ 113. Теория разряда конденсатора.................................399
§ 114. Наиболее общая форма уравнения цепи переменного тока . . . 410
§ 115. Неустановившийся режим тока. Включение постоянного тока . 411
§ 116. Включение переменного тока..................................415
глава XVI
Теория длинных линий передачи энергии
§ 117. Диференциальные уравнения цепи с равномер о распределенными емкостью, самоиндукцией, ваттным сопротивлением и утечкой.................................................... 423
§ 118. Исследование уравнений линии передачи энергии...............425
§ 119. Волны в линии...............................*...............429
§ 120 Телеграфные и телефонные кабели.............................434
§ 121. Замеч ние об электрическом расчете линии . . ,..............437
§ 122. Гиперболи лес ие функции.............................—
§ 123. Уравнения линии пер дачи в гиперболических функциях . . . 442
§ 124. Формулы для приближенного расчета линий. Замечания о расчете трехфазной линии. Примеры.............................,444
§ 125. Определение постоянных линий................................450
§ 126. Эквивалентные схемы линии передачи..........................454
§ 127 Замечания о влиянии трансформаторов.........................457
§ 128. Собственный период колебаний линии без потерь...............458
глава XVII
Наиболее общая форма уравнений электрического тока
§ 129. Общие уравнения и исследование их...........................462
§ 130. Случай постоянного тока.....................................471
§ 131. Стоячие волны...............................................473
§ 132. Упрощенное решение основных лиференциальных уравнений . . 475
§ 133. Отр. жен <е волл в точках соединения двух проводов с различными волновыми сопротивлениями...............................477
глава XVIII
Теория поверхностного эффекта при переменном токе и переменном магнитном потоке
§ 134. Диференциальное уравнение плотности тока в проводнике . . . 480
§ 135. Интегрирование уравнения плотности тока..............482
§ 136 Интегрирование уравнения плотности тока — другой способ . . 486
§ 137. Уравнение плотности магнитного потока ..................... 490
§ 138. Вывод формулы Стефана для сопротивления проводника при переменном токе.............................................492
Ответы к примерам.....................................498
Некоторые литературные указания.......................500
ВВЕДЕНИЕ
ТЕХНИЧЕСКИЕ СПОСОБЫ ПОЛУЧЕНИЯ ПЕРИОДИЧЕСКОЙ ЭЛЕКТРОДВИЖУЩЕЙ СИЛЫ. ОСНОВНЫЕ ПОНЯТИЯ
§ 1. Принцип устройства генератора переменного тска
Всякий меняющийся с течением времени по величине или по направлению ток есть ток переменный; для электрического освещения и электрических двигателей употребляется такой переменный ток, при котором все значения величин электродвижущей силы
(ЭДС) и силы тока периодически повторяются через одни и те же промежутки времени, называемые периодом тока — при этом в течение периода ток имеет в цепи сначала одно, потом другое направление.
В дальнейшем мы ознакомимся и с другими видами переменных токов, например с токами при разряде конденсаторов и др., а теперь соср доточимся на изучении только что указанных периодических токов, получивших исключительное значение при передаче электрической энергии на расстоя
Фиг. 1.
ние.
Источниками такого переменного тока являются особые машины — генераторы переменного тока.
Существенные части такого генератора (фиг. 1) следующие: во-первых, вращающаяся часть А, называемая ротором, которая делается из стали и несет на себе сердечники электромагнитов В с их катушками: в катушках электромагнитов, соединенных так, чтобы полюса северные и южные чередовались, течет постоянный ток, подходящий к ним от источника постоянного тока, т. е.
&
особой машины постоянного тока или батареи аккумуляторов, через щетку С, нажимающую на медное кольцо D на валу рот< ра, соединенное проводом с началом первой катушки, — и уходящий из последней катушки через другое такое же кольцо Е и щетку F; во-вторых, неподвижная часть /И, называемая статором, изготовляемая из листового железа и имеющая на внутренней цилиндрической поверхности углубления—„пазы", в которых заложены проводники (по одному или нескольку в пазе), прово ники, лежащие в разных пазах, соединяются друг с другом последовательно, составляя обмотку генератора переменного тока. При вращении ротора магнитные поля его электромагнитов проходят сквозь витки обмотки, вызывая в них своим изменением ЭДС.
Расстояние pq между осями двух соседних электромагнитов или тп — между двумя соседними нейтральными линиями, измеренное по окружности, проходящей через центры паз< в статора, назовем полюсным делением.
Вследствие того, что конструкция электромагнитов совершенно одинакова, поля их тоже все совершенно одинаковы: магнитные индукционные линии под одним полюсом имеют ту же конфигурацию и густоту в различных местах поля, что и под другим полюсом, только направление их под южным полюсом прямо противоположно направлению под северным.
Представим теперь себе, что мы обмотку на статоре выполним так: наметим те из пазоб, которые отстоят друг от друга на расстояние, как раз равное одному полюсному делению, заложим в эти пазы по проводнику и соединим эти проводники все последовательно соединительными проводниками попеременно на передней и задней стороне статора, но при этом не будем соединять последнего проводника с первым, с которого начали обмотку; таким образом получится незамкнутая обмотка, схематично изображенная на фиг. 1. Остальные пазы статора все оставим пустыми.
§ 2. Электродвижущая сила генератора; графическое изображение ее изменений
Обозначим через Вг радиальную, т. е. перпендикулярную к направлению относительного движения проводника в магнитном поле слагающую магнитной индукции в том месте поля, которое сейчас проходит через проводник, пересекая его, через I — длину проводника в сантиметрах; через D — диаметр вышеупомянутой окружности, проходящей через центры пазов или, в данном случае, через центры поперечных сечений проводников; через пт — число оборо-тов ротора в минуту и через •——— — скорость движения поля о0
* ds
относительно обмотки, иначе равную —, где 5 есть длина соответствующей дуги.
10
При вращении ротора магнитный поток Ф, проходящий сквозь контур каждою витка из двух проводников, указанного на фиг. 2, будет меняться, причем его изме» ение за беско ечно-малый промежуток времени dt, т. е. при бесконечно-малом продвижении ds поля, выразится так:
d<D = 2Br-l-dst
так что ЭДС в витке равна (отбросим знак минус, как ненужный в данном случае)
4J-10-8^2Br./-^.10-8=2B,-Z-^®.10-8 вольт. dt ' r dt г 60
Явление индукции ЭДС описывают часто иначе: говорят, что при относительном перемещении магнитного поля и проводников происходит пересекание магнитных линий проводниками и что в каждом отдельном проводнике индуктируется ЭДС,
тг Г)1!
60
Проводники разделены расстоянием в одно или несколько полюсных делений; поэтому они все находятся во всякий момент, вследствие упомяну! ой выше полной одинаковости полей всех электромагнитов, в полях или, точнее, в местах полей с равным для всех их £>г, так что и все ЭДС в отдельных проводниках во всякий момент равны. Применив правило правой руки сначала к одному проводнику, находящемуся под северным полюсом, потом к другому, соединенному с первым, проводнику, находящемуся под южным полюсом, мы найдем, что ЭДС отдельных проводников будут суммироваться, как при последовательном включении источников тока Слагаясь, эти ЭДС дадут результирующую ЭДС всей обмотки
е — 2 е1 =
где N—число всех проводников, или,
e = N-B10-8 вольт, (1)
г 60 '
которая и создаст на концах Н и К нашей обмотки разность потенциалов, равную в отсутствие тока, т. е. при незамкнутой обмотке, этой ЭДС е.
Теперь заметим, что Вг есть величина переменная вдоль по дуге окружности под полюсом: под серединой полюса она имеет наибольшую величину, — индукционные линии здесь густы и перпендикулярны к цилиндрической поверхности статора, — по середине
11
между полюсами, на нейтральной линии она равна нулю, так как индукционные линии здесь направлены по касательной к поверхности статора.
Так как Вг есть величина переменная, то и е является величиной переменной. В зависимости от того, какой своей частью поле электромагнита пересекает проводник и следовательно каково Вг% будет получаться и величина е. Из формулы (1) видно, что еспи число оборотов машины пт будет постоянно, — а это мы отныне и будем пр дполагать всегда имеющим место, — то все множители при Вг дадут постоянную величину, и следовательно ЭДС е будет пропорциональна радиальной составляющей индукции, величине Вг, в тех точках окружности статора, в которых нах одятся в данный момент пр водники обмотки.
Так как для появления электродвижущей силы индукции определенной величины и направления необходимо лишь то или другое относительное движение проводника и магни«ного поля, то мы можем с одинаковым правом говорить и о прохождении поля через проводник при движении электромагнита и о прохождении проводника в противоположном направлении через поле, как будто бы двигалась обмотка со статором, а электромагнит оставались неподвижными.
В этом смысле мы будем говорить, что в некоторый момент времени проводники находятся например в.е на нейтральных линиях /и, в другие моменты проводники бучут занимать дру-
гие1'положения в полях полюсов, однако же так, что Вг для всех проводников будет иметь одну и ту же величину, меняющуюся для всех проводников одинаково по мере продвижения обмотки в магнитном поле полюсов.
Для того чтобы изобразить наглядно ход изменения Вг и следовательно ЭДС е по мере продвижения проводников в поле, прибегают к графическому способу представления магнитного поля посредством кривой.
Возьмем прямоугольную систему координат. Будем откладывать по оси абсцисс расстояния, измеренные по известной нам уже окружности, проходящей через центры пазов, — от точки нахождения проводника до какой-нибудь нейтральной линии, например до той соседней, от которой проводник удаляется, — а по оси ординат будем откладывать значения Вг в точках нахождения проводника, причем под северным полюсом будем считать Вг положительным и откладывать вверх, а под южням— отрицательным и откладывать вниз. Проведя затем через концы ординат одну непрерывную линию, мы получим 1ак называемую кривую поля; кривая, изображенная на фиг. 2, дает нам пример такой кривой поля. Эту кривую можно толковать двояким образом.
Во-первых, нетрудно видеть из построения, что в какой-нибудь определенный момент времени эта кривая представляет нам вели-12
нины индукции Вг вдоль по окружности статора в этот момент. Если один из проводников обмотки в этот момент на>оди?ся например под серединой северного полюса в точке / фи). 2, ю с ним непосредственно соединенный проводник находится под серединой ю киот о полюса в точке 2. Часть кривой ОС представит тогда распределение индукции Вг, ее величины влево от проводника /, вдоль по окружности статора, часть же С А— вправо.
Еще раз заметим, что, на сколько при вращении роюра переместится в поле одного полюса за какой-ни> удь промежуток времени один какой-нибудь проводник, на столько же передвинутся и остальные проводники под своими полюсами, так что можно говорить о поле с индукцией определенной величины Вг< в котором находится вся вообще обмотка. (Это яв.»яе1ся следствием отсутствия в такой обмотке, как принятая нами в этой
главе, сдвига в магнитном поле при каждом шаге по обмотке, как 'это есть в обмотках постоянного тока.)
В.орое толкование кривой Вг фиг. 2 таково: так как вращение ротора равномерно, то абсциссы на этой фигуре,—длины дуг окружности, — пропорциональны времени, протекш. му с того момента, когда приводних, расстояния которого до некоторой нейтральной линии нами приняты за абсциссы, находился на этой нейтральной линии; поэтому ординаты кривой предсга ят нам значения Вг для определенного места, именно — ме^та нахо-ждепия угого проводника, в различное время.
Иначе: если крив я фиг. 2 даст нам значения Вг в различных точках окружности, то ясно, что- при вращении ротора и движении полюсов ог»’осител1 но проводников веяний проводник с теч нием време» и побыв ет в магнитном поле со всяким значением величины индукции Вг, даваемым этой кривой, и та»-им образом та же кривая фиг. 3 представит все значения индукции Вг в каком-ниб.дь любом месте статора, например в месте нихожде ия любого проводника, принимаемые индукци< й с течением времени.
Для всякого просодии а эти значения начинают с-ова повторяться в точности каждый раз по прошествии ioio промежутка
13
времени, в течение которого мимо проводника проводит двойное полюсное деление Этот промежуток времени называется периодом. Пока мимо проводника, например р (фиг. 1), идет северный полюс, т. е. в течение половины периода, ЭДС в нем одн01 о направления; ЭДС всей обмотки направлена при этом н обмотке от одного ее конца к другому, например от Н к К', когда же мимо этого проводника пойдет южный полюс, т. е. в течение всей следующей поло-ины периода, ЭДС в этом проводнике переменит свое направление, но и все остальные проводники в это время будут под другими полюсами, чем "'были раньше; все ЭДС будут противоположного направления, чем раньше, и ЭДС всей обмотки будет направлена в самой обмотке в сторону, обратную прежнему ее направлению, т. е от К к Н. Таким образом пол-периода Н имеет высший потенциал, чем /<, т. е. Н есть плюс-за
Фиг. За.
Фш. 36.
жим обмотки нашего источника тока, а К есть минус-зажим, и полгириода наоборот, К имеет высший потенциал, чем Н, и следовательно К есть плюс, а Н—минус.
Так как ф-ла (1) показывает, что е про орнионально при постоянной скорости, то та же самая кривая фиг. 3 в ином масштабе для абснисс и ординат дает нам электродвижущую силу е в зависимости от времени; масштаб для ординат при этом будет в п
2V./.251^.10-8
60
раз меньше, чем раньше, так как численно е во столько раз больше, чем Вг; масштаб для абсцисс будет в
*Dnm 60 раз больше, так как длины дуг численно в
---2L 60
раз больше протекшего времени.
14
Положим в основу дальнейших рассуждений кривую фиг. 2 как кривую ЭДС во всей обмотке в зависимости от времени. При э ом ОА будет выражать пр межуток времени в полпериода, и ЭДС все это время одного направления, которое мы условно назовем положительным АЗ есть другая половина пер иол а; ЭДС в течение ее действует в другом направлении, отрицательном; ОВ есть целый период. За точкой В и раньше точки О кривая повторяется Heoi раниченно Итак: ЭДС обмотки генератора переменного тока есть периодическая функция времени.
Вследствие „одинаковости“ полей под северным и южным полюсами часть кривой ОСА симметрична с частью ADB\ если часть ADB сдвинуть влево на полпериг да вд ль по оси абсцисс и перегнуть по оси абсцисс чертеж, то обе части ОСА и ADB совпадут всеми своими точками. Следовательно кривая электродвижущей силы симметрична относительно оси абсцисс.
На фиг. 3 (а и Ь) приведены два примеря кривых: а) симметричной о нэсительно оси абсцисс и Ь) несимметричной. Отступления от этой симметрии у существующих машин переменного тока так редки и незначительны, что мы от них отвлечемся в дальнейшем изложении.
§ 3. Период, частота, число оборотов и число полюсов
Выведем теперь одно основное соотношение величин для генератора переменного тока, именно: определим прод )лжи ельность одного полного периода его электродвижущей силы. Обозначим число всех полюсов у машины, как число четное, через 2р; продолжительность одного периода — через Т. пт секунду -2- один ЬО
это время мимо
все полюсов, или
оборот
любого
р пар
делается за
проводника
полюсов;
При числе оборотов в
, пт 60
1: —~ сек. =— сек ; за
60 пт
обмотки статора прохолят
одна пара полюсов, т. е. двойное полюсное деление, проходит мимо проводника за время, в р раз меньшее, i*. е. за
1 60
— сек.;
m
Р
это и есть продолжительность
периода; следовательно
Т
60
----- сек.
P'ti
* m
(2)
15
Величина, обратная продолжительности периода,
/=У (3)
выражает ч и с л о полных периодов, заключающееся в одной секунде,—эта величина называется частотой ЭДС переменного тока.
Подставляя выражение (2) в ф-лу (3), получаем:
f=P'nm
60
(4)
Ф-лу (4) можно вывести и не из ф-лы (2), а непосредственно: за один оборот мимо проводника пройдет р пар полюсов, следовательно протечет р полных периодов; так как зз ri
одну секунду ротор сделает оборотов, то число периодов,
протекших в течение одной секунды, будет
р, т. е. будет равно:
<Р'пт
60 ’
в раз
больше, чем
Двойное число — 2/—есть число перемен направления ЭДС в секунду.
В современных турбогенераторах, т. е. генераторах переменного тока, соединенных с паровыми турбинами, делают обычно только два полюса, т. е. делают р=1; тогда из последних формул имеем /2^ = 3 000; таково число оборотов вала паровой турбины.
Пример 1. Сколько попюсов должен был иметь в прежнее время генератор, предназначенный работать с пазовой машиной, делавшей «^=150 оборотов в минуту, чтобы давать ток с/==50 периодов в секунду?
Когда несколько таких машин работают вместе на одну и ту же сеть, т. е., как принято говорить, работают „параллельно", то очевидно, число периодов их ЭДС должно быть строго одно и тоже; самая малая разница в числе периодов сделала бы параллельную работу машин невозможной, ибо были бы промежутки времени, когда знак^ у соответственных полюсов двух или нескольких генераторов были бы разные, а это было бы равносильно короткому замыканию машин.
Вс машины должны работать поэтому со строго одним и тем же числом периодов, меняя знаки у своих полюсов одновременно; от этого машины переменного тока называются еще синхронными машинами.
16
ГЛАВА I
КРИВЫЕ МАГНИТНОГО ПОЛЯ И ЭЛЕКТРОДВИЖУЩЕЙ СИЛЫ
§ 4. Предварительные понятия
Предположим, что мы к зажимам Н и К обмотки генератора подключаем некоторое сопротивление и таким образом замыкаем цепь; тогда по всей этой цепи потечет ток; так как ЭДС переменна по величине и по направлению и периодична, то и этот ток будет также переменным по величине и по направлению и периодичным. При этом сила тока определяется не только величиной ЭДС е в обмотке и сопротивлением цепи, так как раз ток изменяется, то изменяется и создаваемое им магнитное поле, а при этом, как известно, в цепи тока появляется ЭДС самоиндукции; величина силы тока Z в каждый отдельный момент определится отношением алгебраической суммы двух ЭДС в цепи — индукции в магнитном поле полюсов е и самоиндукции
— к сопротивлению всей цепи Z?:
(5) *\
Могут быть случаи, когда магнитное поле, создаваемое этим током, очень слабо, — это будет тогда, когда в цепь тока не включено никаких соленоидов или катушек, когда проводники в цепи не образуют витков, — хотя в некоторых случаях, например при большой длине проводников, может оказывать влияние магнитное поле даже и прямолинейных* проводников с током и вызывать заметную ЭДС самоиндукции.
Здесь мы воспользуемся только что употребленным выражением заметная ЭДС, чтобы остановиться на вопросе о величине переменных ЭДС и силы тока. На кривой фиг. 3 мы видели, что когда проводники обмотки находятся в нейтральных линиях, ЭДС в равна нулю. Вблизи этого положения она мала и лишь по удалении от нейтральной линии возрастает до максимума, потом 2 Теория переменных токов. 17
опять постепенна убывает до нуля при подходе к следующей нейтральной линии, меняет направление и т. д. Сила тока тоже, перед тем как ток меняет направление, приближается к нулю, делается на один момент равной нулю, потом растет в противоположном направлении до максимума, убывает и т. д.
Когда мы в дальнейшем будем говорить, что в цепи течет переменный ток небольшой силы или большой, что ЭДС самоиндукции незначительна или велика, то мы будем понимать это так, что незначительны или велики те наибольшие значения, максимумы, которых соответствующие величины, например сила тока, вообще достигают за полпериода.
Таким образом выражение „ток в несколько сотых долей ампера" обозначает ток, наибольшая сила которого достигает лишь нескольких сотых долей ампера; также не забудем и того, что ЭДС „в десять тысяч вольт" или сила тока „в сто ампер" кроме этих наибольших значений проходит и через все меньшие значения и через нуль.
Когда желают ЭДС самоиндукции сделать возможно меньшей, тогда проводники цепи, по которым ток идет в разных направлениях, — например провод, подводящий ток, и провод, уводящий, ток от какого-нибудь прибора,-— помещают рядом, возможно ближе; при этом магнитные действия одного тока будут во внешнем (не между проводниками) пространстве ослабляться противоположными магнитными действиями другого. Для этой жЪ цели служит известная из курса физики бифилярная обмотка.
Подобными расположениями при отсутствии катушек в цепи достигается то, что ЭДС самоиндукции во внешней части цепи делается очень малой, так что ею, даже при точных измерениях, можно пренебречь. Такой случай называют случаем безиндук-ционной нагрузки машины.
Нужно однако же заметить, что и в этом случае собственное магнитное поле проводников обмотки машины будет существовать и вызывать некоторую ЭДС самоиндукции в той же самой обмотке; ее мы назовем „внутренней" ЭДС самоиндукции, т. е. индуктирующейся в самой обмотке; если величина ее будет гС1, то при безиндукционной нагрузке машины
В общем случае ЭДС самоиндукции ес в формуле (5) распадается на две слагаемых: есе индуктирующуюся в самой обмотке машины, где индуктируется и г, и гС|, индуктирующуюся в разных частях внешней цепи, подключенной к зажимам машины.
Если мы включим где-либо в цепь какую-нибудь катушку, то около нее появится более или менее значительный переменный магнитный поток, и следовательно в ней самой, в ее проводниках
13
появится ЭДС самоиндукции Сила тока в цепи будет в л& бой момент равна частному от деления алгебраической суммы величин в этот момент всех трех ЭДС: et и е^, на сопротивление всей цепи (ф-ла 1). Это есть случай индукционной нагрузки машины.
Если в случае безиндукционной нагрузки мы возьмем внешнее сопротивление R достаточно большим, то получим ток I очень малым (например сотые доли ампера); тогда его магнитное поле будет очень слабо, и вызываемая изменениями этого поля внутренняя ЭДС самоиндукции ес< будет сравнительно с ЭДС е от поля полюсов так мала, что ею можно будет свободно пренебречь и написать для этого случая очень небольшого тока ф-лу (6) так:
Этот ток мы можем пропустить через петлю осциллографа и получить его кривую; а так как из ф-лы (7) следует, что
* = /•/?, (8)
где R постоянно, то та же кривая в масштабе в R раз более мелком представит нам ход изменений величины ЭДС е.
Чем больше будет сила тока Z, которым мы нагружаем генератор переменного тока, тем менее точной будет становиться ф-ла (7) и тем менее точно кривую силы тока можно будет счесть за кривую (в ином масштабе) ЭДС генератора.
Пусть в цепи течет переменный ток Z, уже не слабый, а какой0 угодно. Выделим такой участок А—В цепи, чтобы около него магнитное поле было слабо и чтобы электродвижущей силой самоиндукции в нем можно было пренебречь; тогда для этого участка цепи будем иметь для всякого момента, обозначив переменную разность потенциалов на концах его, или напряжение на нем, через V^q, а сопротивление участка через R^:
(9)
^АВ
Следовательно
= (Ю)
и кривые напряжения и силы тока (ср. с ф-ЛЪй 8) при отсутствии самоиндукции отличаются лишь масштабом.
Чтобы иметь возможность производить точные расчеты как самих генераторов переменного тока, так, в* особенности, и различных приборов, потребляющих электрическую энергию, а также и для расчета всех явлений в цепи переменного тока, надо знать аналитическое выражение для этих кривых, т. е. аналитическое ВЫ-ражение зависимости ЭДС машины от времени (или от положения 2* 19
обмотки под полюсами) как периодической функции этого послед-него (времени или положения); то же -* и относительно силы тока и ЭДС самоиндукции.
§ 5. Кривые поля и электродвижущей силы
Что касается формы кривой ЭДС генератора, то мы ее можем сильно изменить, меняя форму полюсных наконечников или, объяснение чему увидим далее, систему соединения проводников в обмотке; например, делая воздушный прослоек между полюсом и железом статора неодинаковым вдоль под всем полюсом, а уве-।__________________________личивая его по мере удаления
< х от середины полюса в стороны
к нейтральным линиям фиг. 4, мы можем кривой поля придать Фиг* вид очень близкий к желаемой
аналитической кривой, например к синусоиде (фиг. 5). Обратным изменением формы наконечников (фиг. 6) можно придать кривой поля вид близкий к прямоугольнику (фиг. 7). Вместе с кривой поля будет изменяться и кривая ЭДС.
В современных больших (в 20, 40 тысяч kW и больше) генераторах переменного тока, вращаемых паровыми турбинами с большим числом (1 500—3 000) оборотов в минуту, в так называемых
Фиг. 5.
„турбогенераторах", ротор делается без выступающих полюсов1, чем достигается и большая прочность, необходимая при большой скорости, и большее приближение формы кривой поля ротора к синусоидальной.
Следует заметить, что прежде думали, что всего желательнее иметь для ЭДС и силы тока форму кривых, приближающуюся к прямоугольнику, ибо при этом лампы накаливания большую часть
* См. проф. 3. В. Черданцева и И. А. Черданцев, JKype ебщей электротехники", 1931 (фиг. 2о1 и 262).
20
полупериода, именно АВ (фиг. 8), горят с достаточно сильным накалом, и лишь в течение незначительной части периода ВС накал их ослабевает, пока ток быстро уменьшается до нуля и
потом с нуля растет в противоположном направлении, — тогда как например при синусоидальной форме кривой ЭДС и силы тока ток сравнительно мен шую часть периода имеет большие величины И лампа заметно затухает около
Фиг. 6.
при частоте в 50 периодов
Фиг. 7.
нулевого значения сиды тока на больший промежуток времени. Однако в секунду, обычно употребляющейся теперь, когда переменный ток служит целям электрического освещения, это явление перестает быть ощутимым для глаза. Из других соображений в пользу плоских форм кривой можно было бы указать на желательность таковой при работе ртутного выпрямителя, но это соображение недостаточно, чтобы определять желательность формы кривой поля и прочее для всех вообще машин.
Форма кривой бо -
лее острая, чем синусоида, вызывает, как увидим далее, большие
потери в цепи и в некоторых случаях опасна для изоляции проводников и приборов; в настоящее время считается, что наиболее удобной во всех отношениях является форма кривой поля в
Теперь следует обстоятельно уяснить себе, как можно осуществить конкретно сравнение кривой поля с синусоидой; остановимся подробнее на этом вопросе.
21
Из геометрии известен способ построения синусоиды. Выбираем условно некоторый отрезок прямой линии за единицу длины и описываем им, как радиусом, из любой точки, как центра, окружность (фиг. 8). ОМ есть подвижная сторона переменного угла АОМ, вращающаяся, как обычно, против часовой стрелки. Обозначим переменный угол через а. На ab — продолжении диаметра М2А— от некоторой точки а будем откладывать длины дуг от неподвижной точки А до перемещающейся по окружности точки ЛГ, так что ат = АМ, ат1 — АМ1 и т. д., до ab = АМ2М2М2А = 2п; в точках т, mv... восставляем перпендикуляры к ab и откладываем на них величины NM, т. е. синусы переменного угла. Соединив вершины отрезков п, nv... непрерывной линией, получим синусоиду ап^п^Ь. Наибольшая из ее ординат — т1п1 — называется ее „амплитудой*. Она равна единице.
Пусть теперь на фиг. 9 кривая 1—2—3—4—5—6 есть кривая поля, полученная нами с исследуемой нами машины тем или иным путем, — например мы могли ее построить в произвольном масштабе по точкам, снятым с помощью шайбы Жубера, или получить фотографическим путем с помощью осциллогра ра. Основание этой кривой, отрезок оси абсцисс 1—6, есть в масштабе длин двойное полюсное деление, в масштабе времени — полный период Т. Перенесем синусоиду фиг. 8 на фиг. 9, т. е. изменим основание синусоиды. Для этого мы радиус ОМ на фиг. 8 представим себе вращающимся равномерно и описывающим один полный оборот за время Г, т. е/как раз в течение периода переменного тока. Угловая скорость его вращения при этом выразится очевидно так:
2п
® == === 2п/, (11)
угол же АОМ=а через переменное время выразится так:
a —at. (12)
Что касается времени /, то условимся на фиг. 8 отсчитывать его с того момента, когда подвижная сторона угла ОМ начинает свое движение, отделяясь от стороны ОА, а на фиг. 9 — с того момента, когда обмотка проходит нейтральные линии, т. е. когда ЭДС или индукция Вг равны нулю, или по оси абсцисс, начиная от точки /, для которой /=0.
Время которое соответствует любому значению угла а, мы определим из соотношения (12) так:
, a al ,=^=й-7'’ <13>
что можно словами выразить просто: какую долю а составляет от 2п, такую долю I составляет от Т.
22
Полученную из формулы (13) величину t отложим на фиг. 9 от точки 1 в виде абсциссы 1—7, в точке 7 проведем ординату 7—S, равную 2ИМ=;г/п на фиг. 8, т. е. синусу угла а. Повторив это построение для достаточно большого числа отдельных моментов времени за период Т и соединив одной линией полученные точки 8, мы получим кривую 1—8—10—5—11—6, кото-
рую тоже назовем синусоидой, так как ее ординаты равны:
sin а — sin со/.
Ее амплитуда, т. е. наибольшая из ординат 9—10, равна единице; основание ее теперь, 1—5, новое.
Умножим все ординаты этой синусоиды на некоторое число а2, определяемое по способу, который будет изложен далее, и мы получим кривую 1— —Р—q~5—S—6. Эта кривая называется Синусоидальной кривой и выражается уравнением, показывающим, что ее ординаты в а2 раз больше синусов переменного угла, меняющегося пропорционально времени
по ф-ле (12), т. е.
у = а .-sinw/. (14)
Для краткости речи и эту кривую называют синусоидной и с ней-то и сравнивают экспериментально полученную кривую поля.
При конструировании современных машин стараются придать кривой поля, а следовательно и электродвижущей силе, форму, наиболее приближающуюся к этой последней полученной нами синусоиде (10).
Составим и раз навсегда усвоим следующую таблицу значений времени /, аргумента синуса и самой функции у (14) для наиболее важных или бросающихся в глаза моментов времени в течение периода (см. стр. 24).
Допустим, что машина сконструирована так, что кривая поля есть точная синусоида, т. е. можно подобрать или вычислить аг так, чтобы кривая (14) точно совпала с кривой поля. Тогда при известном уже нам изменении масштаба ординат та же кривая даст нам величины электродвижущей силы
e=£'1-sln со/, (15)
23
Время t Аргумент mt sin mt Функция У
0 0 0 0
V 4»^ 1 6 II ю| я + 1 +
II Э 0 0
W । 4*1 w 6 II кэ| w й -1 — aj
Т <1>Г=2к 0 0
где Ej есть „амплитуда* ЭДС, т. е. отрезок а19 измеренный в масштабе ЭДС.
Введем следующее название: любое значение периодической функции, какое только может она получить, мы будем называть мгновенным ее значением. Амплитуда есть тоже одно из мгновенных значений ее, именно — наибольшее. В дальнейшем, чтобы применить средства анализа к исследованию этих функций, мы часто будем пред юлагать, что эю мгновенное значение удерживается функцией в течение бесконечно малого промежутка времени di9 после которого функция принимает другое значение, отличающееся от предыдущего на бесконечно малую величину dy
Если ЭДС машины выражается точно ф-лой (15), т. е, кривая ее есть точная синусоида, расчет явлений в ее цепи очень прост; когда же форма кривой ЭДС отступает от синусоиды, как например на фиг. 9, расчет несколько усложняется; теорией этого случая мы займемся после, ближайшие же главы (II — VIII) посвятим изучению явлений в цепи, в которой действует синусоидальная ЭДС.
В современных машинах переменного тока кривая ЭДС обыкновенно очень близка к синусоиде.
Кроме придания полюсным наконечникам соответствующей формы, средством для получения такой кривой является еще и усложнение обмотки машины против показанного на фиг. 1. Кривая поля и в этом случае может быть такой же, как на фиг. 2, и следовательно кривая ЭДС всей обмотки будет отступать по форме от кривой поля.
Обмотку статора машины выполним в этом случае следующим образом.
Назначим для закладывания проводников обмотки не по одному пазу на каждое полюсное деление длины окружности, а по нескольку соседних пазов, например по три паза, как на фиг. 10, за-24
лежим во все эти пазы проводники (оставив остальные пазы пустыми), перенумеруем их по порядку слева направо так: 7, 2 и 3 — одна группа, 4, 5, 6 — следующая, 7', 2\ З1— следующая, и т. д., и соединительными проводниками соединим их, последовательно в обмотку; пунктиром показаны соединительные проводники на задней стороне статора; таким образом от проводника 7 пойдем по передней стороне статора к проводнику 6, от 6 — по задней стороне к проводнику 2, от 2 — по передней стороне к 5, от 5— по задней к 3, от 3 — по передней к 4, от 4 — по задней к новой группе, к проводнику Г и там повторим соединение подобно предыдущему. Совокупность проводников 1—б—2—5—3—4 составляет катушку обмотки, проводник между 4 и Г соединяет одну катушку с другой. Проводники 7, 2 и 3 составляют одну сторону катушки, проводники 4, 5 и 6 — другую. Заметим, что середины сторон катушек, у нас проводники 2 и 5, 5 и 2\
Фиг. 10.
отстоят друг от друга на полюсное делание. Обыкновенно в современных машинах сторона катушки заполняет от трех до пяти пазов.
Когда середины сторон катушек находятся на нейтральных линиях, тогда в проводниках, принадлежащих к одной половине стороны катушки и находящихся в сфере действия одного полюса, у нас проводник 7, индуктируются небольшие ЭДС одного направления, — в проводниках же другой половины стороны катушки, у нас проводник 3, лежащий уже в сфере действия другого полюса, — электродвижущие силы противоположного направления; результирующая ЭДС равна в этот момент нулю. По мере перехода сторонами катушек и следовательно всей обмоткой нейтральной линии, ЭДС в каждой сторона растер от двух причин: во-первых, проводники, удаляющиеся ог нейтральной линии, вступают во все более усиливающееся поле, во-вторых, увеличивается число проводников, на |ример три, четыре, пять —► при пяти проводниках в стороне катушки,—находящихся по одну сторону нейтральной линии, и уменьшается число проводников, остающихся еще по
25
другую сторону нейтральной линии, ЭДС которых вычитаются из ЭДС первых.
Если бы все проводники каждой стороны каждой катушки были сосредоточены в однам пазу, что тоже выполнимо, и паз не был бы очень широким, ЭДС всей обмотки изменялась бы по кривой индукции различаясь только масштабом и от этой последней величины от ЭДС обмотки, изображенной на фиг. 1, где каждая сторона катушки состояла из одного проводника. Значения ЭДС были бы при этом больше чем для обмотки фиг. 1 во столько раз, сколько проводников в стороне катушки. Наибольшее значение ЭДС мало изменится, именно несколько
уменьшится, если мы в сторону катушки разместим в нескольких пазах, как на фиг. 11, но при вступлении стороны катушки в поле какого-нибудь полюса рост ЭДС в такой стороне будет совершаться медленнее, чем при сосредоточении всей стороны катушки в одном узком пазу. Подобное же явление будет иметь место и при выходе стороны катушки из-под полюса. Кривая ЭДС будет в начале и конце каждой половины периода изменяться медленнее при распределенной в нескольких пазах стороне, чем при сосредоточенной в одном пазу,кривая ЭДС станет более пологой при росте и уменьшении ЭДС. Следствием этого будет то, что кривая очень приблизится по форме к чистой синусоиде. На фиг. И кривая изображает поле и в некотором другом масштабе ЭДС обмотки с несколькими проводниками в одном пазу под каждым полюсом; кривая б дает ЭДС обмотки при том же числе проводников в стороне, но распределенных в нескольких пазах под каждым полюсом.
26
ГЛАВА П
ЦЕПЬ СИНУСОИДАЛЬНОГО ПЕРЕМЕННОГО ТОКА, СОДЕРЖАЩАЯ САМОИНДУКЦИЮ И ВАТТНОЕ СОПРОТИВЛЕНИЕ
§ 6. Синусоидальный ток. Электродвижущая сила самоиндукции
Пусть мгновенные значения ЭДС, измеренные в вольтах, выражаются ф-лой (15):
e = 5OTsln(<o/), (16)
где Ет есть амплитуда, наибольшее, максимальное значение ЭДС, что и должно указываться значком т.
Если эта ЭДС действует в цепи, самоиндукцией которой мы можем пренебречь (ф-ла 7), то мгновенные значения силы тока будут определяться по закону Ома:
Чг
где Я есть сопротивление всей цепи. Подставляя сюда ф-лу (16), имеем:
р
I—sin (wQ = J sin (®0. (17)
Здесь J' =есгь амплитуда силы тока, т. е. наибольшая Г\
сила тока; она получается в тот момент, когда ЭДС е имеет наибольшее значение Ет. На фиг. 12 представлены кривые ЭДС и силы тока, достигающие максимумов и проходящие через нулевые значения одновременно. Ординаты кривой е отложены в масштабе ЭДС, ординаты кривой i — в масштабе для силы тока.
Остановимся теперь на более общем и сложном случае, когда в цепи переменного тока создается настолько значительная ЭДС самоиндукции, что пренебречь ею уже нельзя.
27
Электродвижущая сила самоиндукции ес выражается так:
(18)
где L есть самоиндукция в цепи в практических единицах, т. е.
в генри.
Очень важно представлять себе хорошо то условие, при кото* ром это выражение для ЭДС самоиндукции точно; это условие
состоит в следующем: в магнитном полб данного тока не должны иметь места явления магнитного насыщения железа и явления гистерезиса. Вообще ведь ЭДС самоиндукции, индуктирующаяся от изменения потока Ф, создаваемого током Z,
в каком-нибудь контуре, состоящем в общем случае из п щитков,
выражается так: </Ф /Я0~8)
<* ==----~/И0’8 вольт ----------~----- вольт. (19)
с sit пт. х
Мы всегда можем положить Фп 10”8 —Д-/, вводя новук* величину L — самоиндукцию цепи.
Если насыщения и гистерезиса нет, то магнитный поток всегда точно пропорционален току, а потому L есть величина постоянная; тогда
— d(Li\ — т &
~ dt'
Если же есть насыщение, т. е. имеется в магнитном поле сильно намагничивающееся железо, то поток не пропорционален току, а растет, чем дальше, тем медленнее сравнительно с силой тока; поэтому L тогда уже не постоянно, а убывает с ростом тока и потока, и в ф-ле (19) следовало бы диференцирование производить, как у произведения функций.
Так как кривая намагничения железа не выражена еще точно каким либо уравнением, то диференцировать L по t мы можем лищь каким-либо приближенным способом. В технике переменных токов поэтому пользуются ф-лой (18?) даже и то!да, когда имеется намагничивающееся данным переменным током железо. Другим оправданием применения этой формулы служит то обстоятельство, что наибольшие значения магнитной индукции в железе машин 28
и приборов переменного тока обыкновенно из-за соображений о потерях на гистерезис и токи Фуко не бывают очень велики,— их допускают не выше 10 000 линий на 1 см2; при таких величинах индукции перегиб кривой намагничения еше только начинает проходиться, так что допущение пропорциональности между величиной индукции, а следовательно и ее потока Ф, и мгновенной величиной силы тока, т. е. допущение постоянства L, является Приближением приемлемым вполне.
С приведенными оговорками примем ф-лу (18),
При существовании ЭДС самоиндукции сила тока выразится ф-лой (5):
.__е 4-
l~ R ’
Далее мы увидим, что при синусоидальной ЭДС е сила тока отступает от точной синусоидальной формы только в том случае, когда в магнитном поле тока есть явление гистерезиса, т. е. тогда, когда и ф-ла (18) делается лишь приближенной. Этот случай мы разберем потом подробно, пока же исследуем тот случай, когда сила тока изменяется тоже по синусоиде.
Зададимся выражением для такого тока, начав отсчет времени с момента прохождения его через нулевое значение,
sin (о/)- (20)
Найдем прежде всего ЭДС самоиндукции, подставив в ф-лу (18) вместо силы тока ее выражение (20) и произведя диференцирова-ние. Будем считать при этом L данным. г
Затем решим следующую задачу: какую ЭДС е надо приложить к нашей цепи с данными сопротивлением ее R и самоиндукцией £, чтобы по ней шел переменный ток с амплитудой которой мы задались в выражений (20). При этом мы воспользуемся ф-лой (5) и получим уравнение или формулу, связывающее амплитуды силы тока Jw, ЭДС пока искомой, с величинами R, L и числом.периодов. Потом же мы сможем из этой формулы просто находить любую из этих всех величин, когда остальные все будут даны. Итак переходим к первому вопросу — о нахождении выражения ЭДС самоиндукции. Подставив выражение I из (20) в (18), имеем:
ее = — L sin (о)/)] = — ®Un cos (<о0 =
= <»LJmsin -£-1. (21)
Сравнивая выражения (20) и (21), мы замечаем, что максимум ЭДС самоиндукции наступает на четверть периода позже, чем
29
максимум силы тока, так как в (20) sin(®/) достигает значения 4~ 1 , 1 ~ «\
в момент времени /=— Т, a sinl®/—— 1 достигает того же
значения 4-1 в момент, когда , к п 2 = 2‘
т. е.
I f 1 \
вообще, если sin(w^) равен какой-нибудь величине, то sin I со/2 — 1
приобретает такую же величину на четверть периода позднее, так как если
(тс \
<о/2--5" I ,
то
«>*1=4—7-,
Таким образом синусоиду, изображающую ЭДС самоиндукции, надо чертить сдвинутой относительно кривой силы тока вправо, в сторону возрастания времени, на четверть периода и с амплитудой
^ст ~ (22)
измеряемой в масштабе ЭДС.
На фиг. 18 изображены обе синусоиды-*силы тока и ЭДС самоиндукции.
30
ЭДС самоиндукции положительна все время от момента i=OA = 4-T 4
3
до момента fs=OC=—T, т. е. пока ток уменьшается в положительном или растет в отрицательном направлении (не забудем, что положительное и отрицательное направления тока — понятия условные, просто обозначающие два противоположных направления), остальные полпериода она отрицательна. В каждый отдельный момент она стремится противодействовать изменению тока согласно закону Ленца.
dl
Ф-ла (18) дает непосредственно, что в момент /, когда —saxО, лъ
т. е. когда *с = 0, сила тока I имеет максимум; наоборот, в мо-di
менты времени О, В и D величина —, тангенс угла наклона к оси абсцисс касательной к синусоиде, делается наибольшей, и поэтому в эти моменты ЭДС самоиндукции достигает максимума в том или другом направлении.
§ 7. Закон Ома для всей цепи и для части ее
Перейдем теперь к решению задачи, поставленной нами: найти ЭДС е. Если бы не было в цепи ЭДС самоиндукции, кривая ЭДС е, необходимой для создания данного тока Z, была бы кривой е на фиг. 12, причем e = iR.
Теперь же
и следовательно e~lR — ес. (23)
Это последнее соотношение показывает, что мы можем представлять ЭДС е состоящей во всякий момент из двух слагаемых; вторая слагаемая — ес уравновешивает, компенсирует ЭДС самоиндукции ес в цепи, в сумме — ес и ес в каждый момент дают нуль; первая слагаемая IR тратится на преодоление сопротивления R при токе I. На фиг. 14 начерчены следующие синусоиды: 1) тока /, 2) //?, полученная из первой простым умножением ее ординат на /?, 3) ЭДС самоиндукции ес (пунктиром), 4) обратной по знаку величины — яс; затем ординаты второй синусоиды IR и четвертой — ес сложены, и получена пятая синусоида, изображенная на фигуре жирной линией, — синусоида ЭДС е.
Как видим из чертежа, ЭДС е достигает максимума или нулевого значения не в те моменты, когда достигает таких значений
31
сила тока, и не в те, когда их достигает ЭДС самоиндукции. Например е имеет положительный максимум в момент времени t— ОМ, на промежуток времени AM = -у Т— ОМ раньше, чем достигает положительного, т. е. в том же направлении максимума сила тока.
На фиг. 14 мы имеем разные синусоидальные функции, или кривые, которые началом отсчета положительного времени застигнуты в разных стадиях своего изменения, или, как принято говорить в теории переменных токов, — в разных фазах. Фазой синусоидальной величины называется та часть периода, которая протекла уже с начала периода этой величины до начала отсчета положительного времени, причем началом периода для единообразия условно считают момент прохождения функции через то нулевое значение, после которого она принимает положительные значения.
Таким образом фазы величин на фиг. 14 будут таковы: сила тока и составляющая IR ЭДС имеют фазу 0; ЭДС самоиндукции ez фазу----составляющая ЭДС — ес фазу4--|‘7'; ЭДС е фазу
Г — ОМ=МА. О синусоидальных величинах, имеющих одинаковые фазы, говорят, что они совпадают в фазе, например I и Z/?; о величинах, имеющих разные фазы, говорят, что они имеют разность фаз; например I и ez имеют разность фаз в четверть периода, причем сила тока i опережает в фазе ЭДС самоиндукции на четверть периода, или, иначе, ЭДС самоиндукции отстает в фазе от силы тока на четверть периода; сила тока отстает в фазе от ЭДС ? на величину МА, и т. д. Разность фаз двух синусоидальных величин А и В равна промежутку времени 32
выраженному в долях периода, протекающему с момента, когда А имеет какую-либо величину, например положительную максимальную, или две трети от максимальной, до момента, когда В имеет соответствующую величину, т. е. свою максимальную, или две трети от нее, и т. д.
Все вышеизложенное получим теперь аналитическим путем, который приведет нас к точному выражению функциональной зависимости всех величин в цепи тока друг от друга.
Подставим в формулу (23) для ЭДС е значения i из формулы (20) и ЭДС самоиндукции q из формулы (7):
/ тг \
е = JmR sin (©/) — sin of---— L
\ " /
или
e = JmR sin (of) 4“ cos (co/).
Чтобы упростить это выражение, вынесем сначала за скобки величину Jm V + (coL)2:
е
=JmV&A-W
sin (co/)
(oL
COS (»/)
R
У R^(^L^
Введем вспомогательный угол ср, определяемый условием:
tg(?==^-. (24)
откуда получается, что
sin ф = z .—= и cos ф = -1 = . (25)
У ^ + («)L)3 /7?2 + (0)L)3
Теперь ____________
е = Jm УR2 (©Z,)2 [cos ф • sin (ш/) -[- sin ф • cos (<of)],
<? = ]/> -f- (wZ.)2 sin (со/ -f- ф). (26)
Так как ш=^, то формулу (26) можно представить еще
^ = ^m'K^i4-(“A)2sin[<o (z + ф^
I \ ^ТГ
и так:
(27)
Сопоставляя это выражение ЭДС с выражением (20) для силы тока i = Jm sin (о)/), мы видим, что одни и те же величины синуса получаются для sin(o)f) позднее, т. е. для большего значения времени, чем для sin
/ Т
(01 / _1_ ф
I ‘ f2n
3 Теория переменно токов .
33
так как если
то
sin
= sin (ш/2),
e>01+'f>s=o>^ и (28)
Выражение (14) дает нам разность фаз между ЭДС и силой тока, причем последняя запаздывает относительно первой; в момент времени /=0 сила тока равна нулю, а* ЭДС равна:
e=JOT//?2 + (®£)2sin (а>.<р.^==
Эта разность фаз на фиг. 14 представлена отрезком по оси абсцисс, равным МА, следовательно
(29)
Правая часть формулы (29) имеет, как видим, размерность времени.
Разность фаз двух синусоидальных величин называют еще сдвигом в фазе, или сдвигом фаз этих величин.
Сообразно формулам (21) и (27) нужно считать отставание отрицательным сдвигом, опережение — положительным.
Итак сдвиг фазы силы тока относительно ЭДС равен
Т &L
чг ± 0)1 .
Угол <p = arctg— называется фазовым углом, 1\ углом сдвига фаз.
Рассматривая формулы (26) или (27), мы видйм, что амплитуда
ЭДС равна:
или чаще
£ет=4Г/?2-Н^)2-
(30)
Формулы (24) и (26) представляют вместе полное решение задачи, поставленной нами: какую надо иметь в цепи с данными /?, L и числом периодов, т. е. с данной со, ЭДС, чтобы сила тока имела амплитуду Jm?
После того, как эти соотношения установлены, мы можем любую величину счесть неизвестной, а остальные — данными, и ее определить. Неизвестной может быть только одна величина, так как хотя
34
у нас два уравнения (12) и (10), но (10) служит для определения другими словами, эти два уравнения можно заменить одним, которое и будет представлять самое краткое решение задачи; подставим в (26) вместо <р его выражение из (24) и мы получим:
или:
e = Jmy/?2 4-(<o£)2sin
arctg-g-l, *\ /
e = £msin
' . , <о£\
e>/ + arctg-D • К /
(31)
(32)
Если нам даны Ет, R, L н <и (т. е. f или Г), то из формулы (30) мы можем определить амплитуду силы тока:
п ]//?* +(<о£)2’
(33)
Соотношение (33) называется законом Ома для цепи переменного тока. Оно определяет амплитуду силы тока, фаза же ее определяется из сботношения (24).
Когда самоиндукции в цепи нет, тогда £ = 0, и формула (31) переходит в
е = JmR sin (Ы) = Ет sin (Ы),
уже известное нам соотношение.
Ф-ла (33) есть закон Ома для всей цепи, поэтому в нее входит ЭДС, сопротивление /? всей цепи и самоиндукция L тоже всей цепи, т. е. включая и самую обмотку машины переменного тока. Часто бывает нужно решить другую, хотя и подобную задачу. При данных сопротивлении и самоиндукции LAB участка цепи от точки А до точки В требуется узнать, каково должно быть переменное напряжение, или разность потенциалов, на этом участке, чтобы „прогнать* через него ток с амплитудой JРешение подобно предыдущему, только исходить мы будем из закона Ома для мгновенных значений не в форме (5), а в форме
1= vab+JsAb t (34)
^АВ
где vAB обозначает напряжение, или разность потенциалов, между точками А и В, что дает аналогичную (23) формулу:
vab — Шав есАВ* (35)
Само собой понятно, что и ezAB есть ЭДС самоиндукции на участке АВ. равная
еьлв~ ^ав-д}- (36)
35
Дальнейший ход построения кривых и аналитических выводов ничем уже решительно не отличается от предыдущего и приводит нас к формуле:
= VKab' + ^ab^ (Warctg^A = \ lxAB /
= VABmM^+^ (37)
Угол сдвига фаз между силой тока и опережающим ее напряжением
?AB = arCtg (38)
КАВ
Амплитуда напряжения равна:
VАВт== (39)
Из последнего мы получаем: j V АВ т____
т
что и представляет собой закон Ома для части цепи АВ, или участка АВ цепи при переменном токе.
§ 8. Сопротивление ваттное, безваттное и полное.
Обратимся к знаменателю выражений (33) и (40), который по-видимому аналогичен простому сопротивлению при постоянном токе.
г 2ir г
Величина имеет такую же физическую размерность, как
и сопротивление. Затем из ф-л (33) и (40) видим, что и физическое действие самоиндукции L на силу тока похоже в некотором отношении на действие увеличения сопротивления: именно амплитуда силы тока меньше тогда, когда есть в цепи £, чем тогда, когда L нет. Поэтому величину
zVc = <o£ (41)
называли прежде „индуктивным сопротивлением" (Reaktanz) в цепи переменного тока; величину же R называли „омическим сопротивлением" (Resistanz); вся величина знаменателя
Z = //?2_|_(e)£)2) (42)
тоже имеющая размерность сопротивления, прежде называлась „кажущимся сопротивлением" (Impedanz).
Эти величины мы будем в дальнейшем называть так: величину R — ваттным сопротивлением всей цепи или части ее, величину X—безваттным сопротивлением цепи или части ее и наконец величину Z — полным сопротивлением всей цепи
36
или части ее. Смысл названий яваттное" и „безваттное" сопротивления выяснится позднее, когда мы выясним вопрос о мощности в цепи переменного тока.
Следует особенно обратить внимание на то обстоятельство, что для получения полного сопротивления цепи из сопротивлений ваттного и безваттного служит ф-ла (42) и что нельзя просто сложить эти два последние сопротивления, чтобы получить полное.
Пусть например мы имеем напряжение на участке цепи с амплитудой VABm— 110 вольт; частота переменного тока /=50 периодам в секунду, так что по ф-ле (И) <о = 314; ваттное сопротивление /?лд = 3 омам; самоиндукция участка АВ равна LAB = 0,0128 генри. Какова будет при этом сила тока в цепи? Находим прежде всего безваттное сопротивление:
XzAB = о)£лв = 2тг«50«0,0128 = 4 омам;
далее по ф-ле (42) полное сопротивление
Z4b = 5 омам и силу тока в цепи (амплитуду ее)
Ля——22 амперам. £ав
Соотношения между полным сопротивлением, с одной стороны, и ваттным и безваттным — с другой, таковы же, как между гипотенузой прямоугольного треугольника и его катетами; формулу (42) можно строить графически, откладывая по сторонам прямого угла в некотором одинаковом масштабе отрезки R и X и соединяя конечные точки их прямой; длина этой прямой между этими точками — гипотенуза полученного прямоугольного треугольника — определится как квадратный корень из суммы квадратов R и X9
следовательно по ф-ле (42), и даст поэтому величину Z (фиг. 15)
Умножив все стороны этого треугольника на силу тока J, т. е. увеличив его линейно в J раз, мы получим треугольник напряжений, все значение которого выяснится в следующей главе.
При этом очевидно угол ср между катетом R и гипотенузой Z есть тот же самый угол из фиг. 14 видно, что
R
Фиг. 15.
ср, который был введен нами выше, ибо
cp = arctg—.
фигурах мы изображали синусоидальные
До сих пор на всех величины, пользуясь прямоугольными координатами; в следующей главе мы применим для той же цели полярные координаты, что
37
позволит нам соотношения в цепи переменного тока представить еще более наглядно.
Пример 2. Определить амплитуду силы тока Jmt если дано: Ет~ ==135 вольт, /?==3 ома, £ = 0,0124 генри и /=50 пер/сек.
Пример 3. Определить величину самоиндукции L цепи, если R = = 80 омов и при £ж = 6000 вольт течет ток с амплитудой Jm — 60 ампер и /=50 пер/сек.
Пример 4. Какова частота тока, если сила тока в цепи Jm = 25 ампер, а напряжение на участке АВ цепи с /?дв = 6 омам и LAB — 0,0244 генри равно Vab/h = 250 вольт. Какова будег сила тока при часюте/= 50 пер/сек.?
33
ГЛАВА Ш
ГЕОМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СООТНОШЕНИЙ В ЦЕПИ ПЕРЕМЕННОГО ТОКА ПОСРЕДСТВОМ ВЕКТОРОВ
§ 9. Введение понятия вектора
Любую синусоидальную величину, мгновенное значение которой выражается формулой а можно представить геомет Проведем под углом ср, входящим в ф-лу (43), к вертикальной оси OY (фиг. 16) прямолинейный отрезок ОА по длине равный в известном масштабе величине Ат
ОА = Ат.
Затем представим себе прямую линию NONa непрерывно вращающуюся около точки О, через которую она проходит, по направлению движения часовой стрелки с пос
тоянной скоростью и именно такой, что полный оборот линия эта делает точно за один период изменения рассматриваемой, синусоидальной величины А.
Таким образом угловая скорость вращения этой линии выразится, как
2тг Т’
39
следовательно будет равна со, входящей под знаком синуса в выражение синусоидальной величины а. Линия NONA называется линией времени. Переменный угол NOX = а, составляемый с горизонтальной осью ОХ, пропорционален времени t, протекшему с того момента, когда линия времени совпадала с горизонтальной осью:
a = ®t.
Момент, когда линия времени совпадала с осью ОХ, примем за начало отсчета времени.
Отрезок О А называется вектором рассматриваемой синусоидальной величины.
Вектор имеет таким образом величину и направление.
Докажем, что проекция вектора синусоидальной величины на линию времени в любом ее положении, т. е. в любой момент времени, равна мгновенному значению этой синусоидальной величины в этот именно момент.
Проведем линию ОК под углом ср к горизонтальной оси ОХ ниже ее; тогда / КО А — ср 4~ / ХОА — / ХО Y — и OK I О А.
&
Берем произвольное положение линии времени ON\ ^/_NOX = ant\ £KON= ^NOX-\-y = ®t-\-y, опускаем из точки А перпендикуляр AM на линию времени; отрезок ОМ есть проекция вектора ОА на линию времени.
Далее имеем:
0М = 0А-$1п (/ ОАМ).
£ОАМ и X.KON равны как углы с перпендикулярными сторонами; следовательно
/ О AM = ant ср;
поэтому
ОМ — О А • sin (ant 4- ср) или
ОМ = Ат sin (ant 4“ ср), т. е.
ОМ = а и теорема доказана.
Таким образом проекции вектора на линию времени в разные моменты являются здесь тем же, чем были на прежних фигурах ординаты синусоид.
Геометрическое место точек М в разные моменты времени, т. е. при вращении линии времени, есть окружность, описанная на векторе как на диаметре.
Следует заметить, что на фиг. 12, 13, 14, где начерчены синусоиды и применены декартовы координаты, линия времени тоже легко может быть представлена и именно следующим образом: это 40
есть прямая, всегда остающаяся параллельной оси ординат, движущаяся поступательно с постоянной скоростью вдоль оси абсцисс.
Отрезок ее от оси абсцисс до синусоиды есть мгновенное значение синусоидальной величины; на фиг. же 16 мгновенные значения равны отрезкам от полюса О до окружности, описанной на векторе как на диаметре.
На фиг. 12 — 14 время пропорционально длине абсциссы места нахождения линии времени, на фиг. 16—углу поворота ее.
Когда угол а = (о/ ставится больше тс — ср, тогда в формуле (43) sin (tot ср) становится отрицательным; отрицательным становится псэтому и а; вместе с тем при а^>тг — ср, как легко видеть из фиг. 16, величина а, как проекция вектора ОД, откладывается от точки О не по самой линии ON, а по ее продолжению за точку О — по линии ONr Поэтому будем считать, что линия времени состоит из двух частей — положительной ON и отрицательной ON2', когда проекция вектора приходится на положительной части линии времени, тогда зта проекция есть величина положительная; когда же линия времени повернется так, что проекция вектора откладывается на ее отрицательной части, эта проекция — величина отрицательная. Таким образом за один полный период Т точка М два раза опишет окружность ОМА, построенную на О А как на диаметре, — один раз при пересечении окружности положительной частью линии времени, другой — при пересечении отрицательной.
§ 10. Сложение векторов
Предположим, что мы имеем несколько синусоидальных величин, амплитуды которых и фазы не равны, а действия суммируются алгебраически. Такие синусоидальные величины можно все заменить одной новой, результирующей их синусоидальной величиной, действие которой в каждый момент будет тождественно с действием их всех вместе. Посмотрим, как найти эту новую величину, результирующую, т. е. как определить ее амплитуду и фазу.
Как пример таких величин могут служить электродвижущие силы в отдельных проводниках обмотки, изображенной на фиг. 10. Рассмотрим сначала ЭДС в одной катушке. Так как в катушке шесть проводников: 1, 2, 3, 4, 5 и 6, то и ЭДС мы имеем шесть. Максимума и нулевых значений они достигают не все одновременно, а парами, сначала (при вращении полюсов по часовой стрелке) пара проводников 1 и 4, затем пара 2—5 и после всего 3—6; таким образом ЭДС будут обладать разностью фаз. Амплитуды же их будут одинаковы.
41
Мгновенное значение результирующей ЭДС сложится из мгновенных значений всех шести ЭДС:
== “F ^2 + *3 ^4 ^5 “Ь ^в»
или, так как они попарно обладают одинаковыми фазами (et во всякий момент равно ev тоже е2 и е5 и тоже е8 и ев, как ЭДС проводников, отстоящие ровно на одно полюсное деление),
е = 2(^ + *з)-
Будем считать, что в фо мулах, выражающих эти ЭДС как синусоидальные функции времени, моментом начала отсчета времени является момент прохождения через нейтральную линию проводников 1~4, тогда
d = q -f- е4 = 2ег = sin С<о/)> (а)
где Е' есть у военная амплитуда ЭДС в каждом отдельном проводнике .
ЭДС проводников 2 и 5 запаздывают на время т, составляющее такую долю периода, какую от двойного полюсного деления составляет расстояние 1—2 или 4—5, поэтому
e* = ea + eB = 2ea = E^sin[®(Z — т)]; (0)
время т вошло сюда со знаком минус, чтобы выразить, что е2 за-п а з д ы в а е т * сравнительно с время t должно иметь большее значение в ф-ле (0), чем в ф-ле (а) для равных значений е2 и е2. Преобразуем (£):
2е2 = Е'тsin (со/ — сот) = Е'тsin(<о/— ср). (у)
Здесь <р есть фазовый угол, определяемый соотношением:
сот = ср, и, наоборот, имеем:
(о 2п ’
формулу, нам уже знакомую.
ЭДС проводников 3 и 6 запоздают на вдвое большую часть периода против ev поэтому
е!11 = е3 eQ = %еа = & sin [со (t — 2т)] = Е^ sin (<f)t — 2ср). (S)
Чтобы пример и дальнейшие пдстроения уяснить полнее, конкретизируем задания еще полнее Зададимся числом пазов, умещающихся на двойном полюсном делении Пусть это число будет 18, т. е. расстояние между центрами двух соседних пазов, например 1 и 2, равно одной восемнадцатой от двойного полюсного деления, 42
Тогда и
ф Т 1
Т~ 18*
и следовательно
2л 1
в градусах ср = 20°.
Применим построение фиг. 16 к этим ЭДС. Для е9 угол ср фиг. 16 раген нулю; поэтому (фиг. 17) амплитуду OA1 — E9fn откладываем прямо по вертикальной оси OY. Для е” угол ср фиг. 16 отрицателен (ф-ла у) и равен — л; отложим его вправо от оси У
ОУ, т. е. по вращению линии времени; на стороне его откладываем ОЛ2 = Е^. Линия времени позднее совпадает с ОЛ2, чем, с ОЛР и максимум е” наступит позднее,-чем е9.
2
Для е9" угол отрицателен и равен —тс согласно ф-ле (8). От-х 4 2
кладываем вправо же, на стороне этого угла, от-
кладываем ОА3 = Е'т.
При каком-нибудь положении ON линии времени, т. е. в произвольный момент времени /, мгновенные значения ЭДС выразятся проекциями векторов OAV ОА3 и ОА3 на линию времени:
ОМг = ОАг • sin (со/) =
ОМ2 = ОА2 • sin (со/ — <р) = е”, ОМ3 = ОА3 - sin (<о/ — 2ср) = е™.
Нас интересует величина
Известно, что алгебраическая сумма проекций отрезков, произвольных величин и направлений равна проекиии геометрической суммы этих отрезков. Приложив к ОАг отрезок А2А^ равный по величине и по направлению вектору ОЛ3, видим, что его проекция на линию времени MjM3 равна О7И3. Отложив отрезок А^А^ по величине и направлению равный вектору ОЛ2, имеем, что его проекция М'.М2 равна ОМ2. Таким образом для любого и следовательно для всякого момента времени мгновенное значение результирующей ЭДС
1 г
проекиии геомет> ической суммы векторов ЭДС OAV ОЛ2> ОА3, или проекции результирующего вектора ОА'Т
43
Когда линия времени повернется так, что совпадет с линией ОА2, тогда сумма ЭДС е9 е1' -^-е?9' имеет свой максимум, достигает своей амплитуды, равной отрезку ОА'2. Заметим, что из чертежа очевидно, что эта амплитуда меньше Если мы все три проводника каждой стороны катушки поместим вместе в одном пазу, то все углы ср станут равными нулю, и амплитуда результирующей ЭДС станет З/j^. Из фиг. 17 легко видеть, что при увеличении углов ср, т. е. при увеличении расстояния меж у соседними пазами, амплитуда ОА'2 будет уменьшаться, и, наоборот, она будет расти до предела, равного при умешшении углов ср до нуля, т. е. при сближении пазов.
Те же результаты можно получить и аналитическим путем, преобразовав выражение мгновенного значения результирующей ЭДС:
е = е' е” + е"' = Е^ {sin (otf) + sin (ад/ — <₽) 4~ sin (Ы — 2ср)}.
Складывая сначала в скобках первый член с третьим, преобразуя их как сумму синусов и вынося затем sin (со/ — ср) за скобки, имеем е = Е'т(1 + 2 cos ср)-sin (<о^ — ср). (44)
Амплитуда результирующей ЭДС равна:
= Е' (1 4- 2 cos ср) = Е' 4- 2Е' cos ср. т т' * т * т *
Это есть выражение для величины отрезка ОА2 на фиг. 21, так как
А’А' = Е' а ОА\ — 2Е' cos ср. о л т1 з т *
Фаза результирующей ЭДС по ф-ле (44) есть — ср, что является также и фазой вектора ОА'2.
Если бы векторы OAV ОА2 и ОА3 имели физическое значение
другое, например представляли бы силы токов, наши рассуждения и выводы величины результирующего вектора или вектора результирующей физической величины нисколько бы не изменились.
Таким образом имеем окончательно: по величине и фазе вектор результирующей нескольких синусоидальных величин тождествен с вектором геометрической суммы векторов этих величин.
Чтобы придать рассмотренному примеру законченность, заметим, что ЭДС всей обмотки машины выразится вектором в р раз большим ОА2, так как ОА2 есть вектор ЭДС одной ка
тушки, а катушек столько, сколько пар полюсов, т. е. р.
44
Рассмотрим еще один пример.
Пусть даны две синусоидальные величины, которые все время в действии своем суммируются
6i = 5i«sin(<B/ + (Pi) и 62 = S2msinfa*—Тг);-требуется найти амплитуду Вт и фазу ср результирующей синусоидальной величины Ь.
Вт и ср должны быть таковы, чтобы в каждый момент
Ь = bx -I- b2 = sin (ш/ 4- cpj) 4- В2т sin (<о/ -|- <р2). Преобразуем это выражение так, разлагая синусы сумм:
£ = (Blm cos <pj 4- В2т cos <₽2) sin <s>t 4- (Blm sin 4- B2m sin <p2) cos <ot.
Вводим вспомогательный угол (p, который определим известным образом:
, В, m sin ф, -4- В9„ sin И = arc tg -----Y1 У D2gl--i-2.
Тогда, вынося за скобки в правой части корень квадратный из суммы квадратов коэфициентов при sin со/ и cos ©А получаем:
(45)
£ = ]/(Bjmcos<f>i + B2mcos<p2)24-(Blmsin<p14-B2msin(p2)!!sin(<o/4-(p)-=
= /ВШ2 + В2т2+ 2Blm COS — (?,) Sin (ш/ 4- <р). (46)
На фиг. 18 построены векторы: OAV представляющий по ампли-
туде и фазе величину &2; ОА2, представляющий Ь2, и их геометрическая сумма, вектор ОА Нетрудно
видеть, что длина ОА выразится точно так же, как амплитуда в ф-ле (46), а фазовый угол Л ОУ определится так же, как ср в ф-ле (45).
Следовательно О А по амплитуде по фазе и представит искомую результирующую.
Когда мы будем иметь несколько различных синусоидальных величин, то найдем сначала результирующую двух из них, потом, прибавив третью величину, найдем новую результирую-
щую и т. д., как поступают при сложении сил.
В отдельных случаях задача может вследствие соотношений амплитуд и.фаз составляющих упрощаться (фиг. 17).
После уяснения сложения векторов остановимся на вычитание их.
Пусть дана синусоидальная величина
Так как
al=?1msin(<B/ + 'F)-
sin (а Чг тг) = — sin а,
45
то синусоидальная величина
fl2 = 4Bsin(0>/ + '?±n)
с амплитудой той же, что и у av но с фазовым углом, отличающимся на -4-тг от угла величины а2, будет всегда равна и противоположна по знаку величине av т. е.
или
Amsin (<о/ 4“ ? ± к) *= — Ат sin (<о/ -}- ср). (47)
Поэтому мы всегда можем — аг заменить 4“ а2» т* е* заменить вычитание синусоидальной величины сложением с новой синусоидальной величиной, с амплитудой такой же, как и у вычитаемой величины, но с фазовым углом, отличающимся на Ч^тг.
Вектор, изображающий величину а2, будет иметь длину такую же, как и вектор, изображающий величину а2, по направлению же он будет отличаться от него на разность фазовых углов ±тг, т. е. будет ему прямо противоположен.
Вычесть какой-нибудь вектор — значит прибавить прямо противоположный по направлению вектор той же длины.
Заметим, что чертеж, на котором нанесено несколько векторов, приведенных в некоторую связь друг с другом, называется „векториальной", или „векторной диаграммой" тех физических величин, которые этими векторами представлены.
Пример 5. Построить в масштабе четыре вектора ЭДС:
100 sin (vt + , 100 sin (vt + , 100 sin (<of) и 50 sin (W + к)
и сложить их графически.
§11. Векторная диаграмма напряжений в цепи переменного тока
Ту задачу о нахождении ЭДС по данным ваттному и безваттному сопротивлениям цепи и амплитуде силы тока, которую мы аналитически решили в главе второй, можем теперь решить, применяя метод изображения синусоидальных величин векторами.
Построим векторную диаграмму напряжений в цепи переменного тока.
В основу рассуждений, как и прежде, положим формулу
e — iR — ес. (48)
Пусть отсчет времени начат так, что на фиг. 16 угол ср для силы тока J равен нулю; в таком случае вектор силы тока OA — Jm откладываем по оси Y (фиг. 19). Величина iR очевидно имеет ту же фазу, что и Z, и отличается от последней лишь амплитудой. 46
Поэтому, умножив Jm на /? и переведя на масштаб напряжений, получим вектор OB=JmR, который представит нам величину iR.
ЭДС самоиндукции согласно ф-ле (21) имеет амплитуду ®LJm и отстает в фазе на четверть периода; поэтому ее следует преДста-_ тг __
вить вектором 0£>, направленным под углом—~ к оси У, т. е.
At вправо от О по горизонтальному направлению. Ясно, что линия времени совпадает с 0D на четверть периода позднее, чем с О А и ОВ. Длина 0D= ®LJm.
Так как согласно ф-ле (23) ЭДС, приложенная к цепи, распа-нам надо ввести в чертеж
Г
то
дается на две слагаемых: iR и — ес, еще вектор синусоидальной величины— ес, т. е. равной, но противоположной по знаку величине ЭДС самоиндукции; это есть вектор 0/7, отложенный в противоположную сторону, чем OD, и равный ему по длине.
По ф-ле (23) мгновенное значение ЭДС е равно сумме мгновенных значений IR и — ес, т. е. проекция на линию времени вектора ЭДС равна сумме проекций векторов ОВ и ОН\ следовательно вектор ЭДС согласно предыдущему равен по величине и направлению геометрической с^мме этих двух векторов. Складывая геометрически ОВ и 0/7, находим вектор ОС. Найдем из прямоугольного треугольника ОВС его величину — амплитуду Ет фазовый угол ВОС\
X
\ I
\ D
или
ос2=о^2 + вс2,
bjLJm
Фиг. 19.
ЭДС —и
откуда
^2=(^)2+(^4)2>
И
Em=JmV& + №,
р т _
что представляет уже известий нам закон Ома. Далее
ВС inL
что тождественно с ф-лой (24) и /_ВОС — у.
47
Таким образом задачу об определении амплитуды и фазы приложенной к цепи ЭДС мы решили здесь геометрическим путем при помощи представления синусоидальных величин векторами.
Треугольник ОВС носит название векторной диаграммы напряжений в цепи переменного тока.
Вектор ЭДС ОС представлен здесь как геометрическая сумма двух составляющих его векторов, которые называются так: вектор ОВ— вектором ваттной составляющей ЭДС, вектор ОН— —ВС— вектором безваттной составляющей ее. Смысл этих названий, как и смысл соответствующих названий сопротивлений R и (о£, выяснится позднее, когда мы будем разбирать зопрос о мощности в цепи переменного тока.
Если бы в только что изложенном построении R и L были ваттным сопротивлением и самоиндукцией не всей цепи, а лишь одного ее участка, то вектор ОС представил бы нам не ЭДС/?^, а напряжение Ym на этом участке согласно с формулой (39) Векторы ОВ и ОН=ВС были бы векторами ваттной и безваттной составляющих напряжения ОС на участке цепи.
Обратим внимание на следующее обстоятельство. Очевидно, что на соотношения различных величин в цепи переменного тока не может иметь никакого влияния то, с какого момента мы начнем отсчет времени — с момента ли прохождения через нулевое значение силы тока, или же с момента его максимума, или с момента прохождения через нулевое значение приложенной к цепи ЭДС.
Положим, что отсчет времени взят такой, что представит общий случай, и сила тока выразится так:
i =Jn sin (ш/ + а). (А)
Тогда ЭДС самоиндукции выразится так:
ez — — L %' = — <oL/OTcos (<о/ -|- а) = ®LJm sin (at -f- a — £), at \ /
следовательно, попрежнему отстает на четверть периода. Далее, ЭДС ___________
c = lR — сс = Jm УR2^(®L)2 sin (art-J-а<?)>
где определится той же самой ф-лой (24).
Как видим, существа соотношений между сопротивлениями, электродвижущими силами и силой тока тот или иной отсчет времени совсем не затрагивает и сказывается лишь введ нием во все формулы для синусоидальных величин под знаком синуса угла а. На векторной диаграмме напряжений (фиг. 1$) тот или иной отсчет времени скажется лишь поворотом всех векторов на угол а Если угол а в формуле (А) положителен, то вектор силы тока О А повернется на него влево, т. е. в сторону опережения или более ран-
48
йего времени; если а отрицателей, — вектор О А повернется вправо, в сторону более позднего времени. Вместе с вектором ОА повернется в ту или другую сторону и весь треугольник напряжений ОВС. Таким образом тот или иной отсчет времени скажется на чертеже только поворотом треугольника ОВС около точки О. В зависимости от удобства или частных, конкретных, условий задач, мы будем чертить векторы различных величин, треугольники напряжений и пр. в различных случаях различно, т. е. под разными углами к оси ОХ, в разных положениях относител но точки О, и читателю следует поэтому теперь же проделать вычерчивание всей фиг. 19 для нескольких различных случаев начала отсчета времени, чтобы узнавать все элементы этой фигуры впоследствии без труда, независимо от положения треугольника напряжений около точки О.
Выразим теперь еще раз в виде четырех положений главнейшие результаты предыдущего относительно фаз различных величин в цепи переменного тока:
1) ЭДС самоиндукции отстает в фазе от силы тока на четверть периода, вектор ее „отстает*, т. е. сдвинут по направлению вращения линии времени относительно вектора силы тока на тг
Угол
2) ЭДС, приложенная к цепи, в случае существования в цепи ср самоиндукции опережает силу тока в фазе на ~~ Т; вектор ее
„опережает* вектор силы тока, т. е. сдвинут относительно его навстречу вращения линии времени на угол ср, определяемый формулой (24);
3) обратно второму, — сила тока отстает от приложенной
ЭДС в фазе на Г, и вектор 2п
ее отстает от вектора ЭДС на
угол ср;
4) если рассматривается не вся цепь, а лишь некоторая часть ее, то во втором и третьем положениях, вместо приложенной к цепи электродвижущей силы надо взять приложенное к рассматриваемой части цепи напряжение (или разность потенциалов).
Прежде чем перейти к изложению некоторых подробностей о векторной диаграмме напряжений, остановимся на следующем.
После того как мы построили векторы, результирующие из нескольких других векторов, мы получили треугольники ОА2А3 на фиг. 17, ОАгА нафиг. 18 и ОВС на фиг. 19; на эти треугольники можно взглянуть еще с новой точки зрения.
Линии Л^з, ЛзХ на фиг. 17, /ЦД на фиг. 18 и ВС на фиг. 19 (или НС) представляют соответствующую синусоидальную
4 Теоржя переменных токов
49
величину (например ВС—величину, противоположную ЭДС самоиндукции) так же полно, как если бы они были построены из точки О, так как длина их равна амплитуде, а угол с осью Y есть фазовый угол соответствующей синусоидальной величины, ибо эти линии параллельны соответствующим векторам, построенным из точки О. Проекции этих линий на линию времени во всякий момент равны проекциям соответствующих векторов и представляют поэтому мгновенные значения соответствующих синусоидальных величин.
Таким образом при суждении о той или иной синусоидальной величине безразлично, от какой точки построить вектор этой величины; проще всего при выборе точки начала вектора руководиться тем, с каким например другим вектором рассматриваемый вектор должен складываться или из каких других векторов и какими действиями он получается. При этом на основании предыдущего для всякого вектора характерным для него является не фазовый угол его сам по себе, а разности фазовых углов, — углы его с другими векторами диаграммы (фиг. 19).
Из вышеизложенного следует правило условно го обозначения вектора, когда вектор обозначается буквами, стоящими у начала 47 и у конца его; при таком обозначении сначала называется буква, стоящая у начала вектора, например вектор OZ>, вектор ВС и т. д. Принимая же во внимание, что поворот вектора на угол Чк л изменяет знак соответствующей синусоидальной величины, получаем, что вектор фиг. 19
ВС=— СВ, и вообще вектор
NM = — NM. (49)
Как не изменяет зависимости между величинами поворот диа-С граммы около точки О, так не изменит этой за-
висимости и перенос всей диаграммы в другую \ ч\ точку, как начало, каковой перенос все же мо-\ \ жет иметь свой обычный физический смысл.
\ 1 Для того чтобы легко отличить начало и
\ ! п конец вектора в сложных диаграммах, часто на U конце вектора ставят стрелку. Мы тоже иногда
УЧ * будет делать это, но не всегда, для того что-
^у / бы читатель в простых случаях приучался „ви-
деть" направление вектора и без стрелки, так как и в журнальной литературе он встретит Фиг. 20. часто векторы без стрелок.
Пример 6. Построить в масштаб^ треугольник напряжений ОВСдля5 примеров 2, 3 и 4 § 8.
На фиг. 20 произведено это построение. Для примера 2 выбран масштаб 1 мм~2 вольта; отложен отрезок ОС = 67,5 лм« = 13э вольт; на нем как на диаметре начерчена полуокружность, так как угол В прямой; умноже-50
ййем Jm на R получена величина вектора JmR = 27,3 = 81 вольт; при выбранном масштабе ОВ = 40,5 мм, наконец точка В соединена с С,
Если нам нужно представить и силу тока, откладываем по направлению ОВ отрезок OD, выбрав масштаб для силы тока, например 1 мм = 0,5 аМпер. Тогда 00 = 51 мм = 27 ампер.
Читатель должен продела!ь подобные построения для примеров 3 и 4, выбрав другие масштабы.
§12. Диаграмма синхронного генератора
Обратимся к тому, что мы назовем детализацией основной диаграммы напряжений генератора переменного тока. На фиг. 21 мы
имеем снова треугольник ОВС фиг. 19, расположенный на чертеже так, что с вертикальной осью Y совпадает гипотенуза его; вектор, приложенный к цепи ЭДС Jm, есть вектор силы тока, отстающий от ОС на угол СОВ, который мы прежде обозначали через ср, а теперь обозначим через Je. Далее, вектор О В = JmR, где есть ваттное сопротивление всей цепи. Обозначим сопротивление самой обмотки генератора через 7?вну, а сопротивление внешней части цепи через /?вне, так что R — ЯВНу + #вне ; тогда очевидно ОВ разлагается на сумму двух величин:
ОВ = JmR = Jm{Rmy + /?вне) = Ля^вну “Ь* Ли^вне*
Пусть
Фиг. 21.
£^~Ли^вне И &В—Ля^вну
Далее, аналогично только что изложенному, и самоиндукцию можно разложить на сумму:
^вну 4~ ^вне ’
Вспоминая рассуждения по поводу ф-лы (6), мы видим, что самоиндукция обмотки машины £виу всегда не равна нулю; самоиндукция же внешней части цепи £вне в случае безиндукционной нагрузки равна нулю.
Вектор ВС разлагается на сумму:
ВС = (0 (Лвну 4“ ^вне) = Ю £вну 4“ ^вне Ли ~ где
FC — й)£вну Jm И BF~ Ф^вне т*
Вектор DB назовем вектором ваттного падения напряжения внутри машины, вектор FC назовем вектором безваттного падения напряжения там же; название „падение напряжения* следует здесь
4*
51
из полной аналогии с падением напряжения в источнике постоянного тока. Если мы из ЭДС ОС вычтем оба падения напряжения, то получим то напряжение, которое остается для внешней части цепи, или напряжение на зажимах машины. Вычесть вектор FC— значит согласно предыдущему прибавить вектор С/7, а вычесть
—значит прибавить BD. Прикладываем к ОС от точки С вектор Cf, затем FK равный BD, и получаем результирующий вектор ОК, вектор напряжения на зажимах; его величину обозначим через Ит. Так как линия FK равна и параллельна линии BD, то и DK равно и параллельно BF, и ОК представляется результирующим вектором из двух: во-первых, вектора О£>, равного и, во-
вторых, DK) равного Можно было построение начать с
проведения DK, вектора, равного BF\ тогда мы сначала получили бы вектор напряжения на зажимах ОК, а вектор КС потом, — как разность между ОС и ОК
В вышеприведенном обозначении можно вычитание вектора напряжения ОК из вектора ЭДС ОС представить в виде таких операций:
ОС— ОК= ос+ко==ко-\-ос==кс.
Как видим, действия с векторами синусоидальных величин совершенно подобны действиям с векторами в механике.
Из фиг. 21 видим, что напряжение на зажимах запаздывает относительно ЭДС на угол СОК- Назовем угол запаздывания силы тока против напряжения / ВОК через ; значки при у и указывают, что в первом случае угол берется между векторами силы тока и ЭДС е9 во втором же — между векторами силы тока и напряжением v. Угол сдвига фаз между ЭДС и напряжением, / СОК обозначим через 0:
0 = <ре—<р„.
Пример 7. Проделаем один пример построения диаграммы. Пусть будет дано, что напряжение на зажимах машины имеет амплитуду: 1/^ = 2 000 вольт; сила тока в цепи имеет амплитуду, Jm = 100 амперам ваттное сопротивление обмотки машины /?вну=1 ому; самоиндукции обмотки £вну = 0,0095 генри; затем дано, что угол таков, что cos ^ = 0,8. Как увидим далее, из непосредственных измерений в цепи переменного тока можно вычислить именно прежде всего cos а затем уже узнать самый угол.
Затем дана еще частота переменного тока: /=50 пер/сек, так что <о = 2я/ = 314 (ф-ла 11). Требуется по этим данным построить диаграмму напряжений генератора и, в частности, узнать его ЭДС. На фиг. 22 проделаны все относящиеся к задаче построения.
Прежде всего чертим две линии под углом одна к другой таким, косинус которого равен 0,8 Для этого из произвольной точки О проводим в произвольном направлении линию ОК- Откладываем на ней отрезок 01, равный 50 мм\ из точки 1, как из центра, описываем радиусом 10 окружность О2К\ затем из точки О радиусом, численное значение которого в миллиметрах равно значению косинуса в сотых долях единицы, т. е. в данном случае радиусом в 80 мм> зачерчиваем дугу окружности, пересекающую 62
первую окружность в точке 2; проводим прямую 02; угол К02 имеет косинус требуемой величины 0,8.
Откладываем по линии 02 отрезок ОЛ, равный 50 мм, представляю-
щий в масштабе 1 мм = 2 амперам силу тока с амплитудой в 100 ампер Для напряжений выбираем масштаб 1 лме^20 вольтам.
Отложим вектор O^=^000 вольт, значит длина отрезка ОК равна 100 мм
Приложим к нему, как на фиг. 21, вектор KF = = 100*1 вольт, представляемый
отрезком в 5 мм, параллельным линии 02.
Перпендикулярно к нему строим отрезок FC длиной в 15 мм, представляющий вектор безваттного падения напряжения
(о£вну • = 314 • 0,0095 • 100 = 300 вольт.
Отрезок ОС есть вектор ЭДС машины. Дли на его 1132/3 мм\ следовательно
Ет = 11 З2/з -20 = 2 263 вольта.
Предлагаем читателю для упражнения достроить диаграмму до вида фиг. 21, т. е. найти точки В и D, и вычислить /?впе, £вце и cos <ре.
Пример 8. Построить всю диаграмму снова для случая, когда £вне==0.
§ 13. Векторная диаграмма напряжений для последовательно соединенных участков цепи
Перейдем к другому примеру.
Дана часть внешней части цепи, подразделяющаяся еще на три
участка, последовательно,соединенные один с другим; допустим, что каждый участок представляет собой например катуцщу с сердечником. Даны ваттные и безваттные сопротивления каждого из трех участков, г. е. каждой из этих последовательно соединенных катушек: Ry — 3, = 4,
/?> = 2, g>L2 — 2, /?3 = 5, 0)L3 = 1; сила тока, текущего через цепь, равна (амплитуда) Jm=5 А. На фиг. 23 построены, в масштабе 1 мм =1,5 вольта, векторы OAfj = R ко-
торые дают вектор ОКг напряжения на участке первом, далее, векто-
ры KjM2= т и ^2^2 ~
дают вектор КУК2 напряжения V2 на участке втором; наконец векторы К2М3 — R3Jm и
М3К = дают вектор К2К
напряжения V3 на участке третьем. Сложив все три вектора на-
пряжений на участках, получим вектор ОК напряжения V на всей
53
рассматриваемой части цепи. Измерив в миллиметрах длины OD и KD мы найдем сдвиг фаз во всей цепи по формуле
А KD
Мы видим, что напряжения на разных участках имеют разные фазы, которые совпадают в том случае, когда углы ср имеют одну и ту же величину для разных участков, т. е. если
Ф1=¥2 = сРз’:==--->
или пользуясь известным соотношением (67):
(dLj__Ч- L2 Ч~ -|“ • • •)________________________
-----/?! + /?2+/?3+• • • ~~R’
или наконец, сокращая на со:
Л-1 Ln . Ln Li -т- Ln ч— Ao"?-... L
где L и R есть самоиндукция и ваттное сопротивление всей рассматриваемой части цепи. При выполнении такой пропорциональности все V, включая и результирующие, имеют одну и ту же фазу; для получения результирующего напряжения на нескольких участках частичные напряжения нужно при этом сложить просто арифметически.
Треугольник напряжений участка цепи, как например OM1KV или КгМ2К2, или ODK и т. д., есть один из всего чаще встречающихся элементов векторных диаграмм, а потому читателю рекомендуется освоиться с ним как можно лучше путем вычерчивания для различных частных случаев.
Пример 9. Построить в масштабе векторную диаграмму напряжений на участках цепи и определить все напряжение v на ней и угол у сдвига фаз между v и силой тока J, если 7=6 ампер и
#4=10 2, #2 = 22, #3 = 52, #4=152, = 22, Х2 = 42, Х3 = 02, Л4 = 32.
§ 14. Вектор электродвижущей силц индукции в контуре при синусоидальном изменении магнитного потока
ЭДС самоиндукции представляет частный случай индукции ЭДС при синусоидальном изменении магнитного потока, проходящего через какой-либо контур.
Магнитный поток через контур может измениться только от двух причин: или контур движется в магнитном поле соответствующим образом (движение понимается как относительное), или магнитный поток создается переменным током.
64
Рассмотрим сначала первый случай.
Синусоидальность изменения потока в этом случае может осуществиться следующим образом.
Представим, что в однородном магнитном поле (фиг. 24) вращается равномерно около перпендикулярной к направлению индукционных линий оси прямоугольный контур из проводников.
Обозначив угол поворота плоскости контура от направления индукционных линий через со/, мы будем иметь, что площадь $ проекции контура на плоскость, перпендикулярную к индукционным
линиям (например торцевую поверхность полюса), выразится через площадь контура 5 и время так:
s = S sin (cof).
Так как поле однородно, то поток, проходящий через, контур,
где В есть магнитная индукция. Поэтому ф — В • Ssin (cd/) = Ф/72 sin (со/), где — В • S есть амплитуда синусоидально изменяющегося потока через контур; Фт есть поток, проходящий через контур при
ЭДС, индуктируемая в каждом витке контура при этом изменении потока,
е=— ^== — <o’Fmcos(<oO = “-’Pmsin (®/—J). (51)
Эта ЭДС, как видим, отстает от индукционного потока в фазе на четверть периода. Физически это можно пояснить элементарно так, что когда со/ — и поток ф достигает максимума, тогда про-£
55
водники а и b контура движутся вдоль индукционных линий и ЭДС равна нулю, и т. д.
Переходим ко второму, более важному случаю.
Пусть мы имеем два контура, первый и второй, и пусть магнитная проницаемость пространства, где они находятся, есть величина постоянная.
Если в контуре 1 будет течь синусоидально меняющийся ток, то магнитный поток от контура 7, как весь фртак и та часть его ф1, которая проходит через контур 2, будет изменяться как синусоидальная функция времени. Вводя величину М, равную взаимной индукции контуров 1 и 2, будем иметь
ф1 = 7Ич\ .
Положим
h = Amsin(^4-a);
ЭДС индукции в контуре 2 выразится так: е = =
2 dt dt
= (О • 7И • J1Z72 sin
Здесь амплитуда ЭДС равна
^2т — ,
тс ~, 1. С. <?2 Wi'VldCT В ipdcse
на четверть периода, а вектор ее
ет от вектора силы тока Гг на~. На фиг. 25 нанесены: О А — вектор силы тока ; O/V — вектор всего магнитного потока ф1, совпадающий в фазе с током; ОМ — вектор потока ф^ проходящего через контур 2, совпадающий в фазе со всем потоком .фх; OD— вектор ЭДС е2, отстающий от векторов тока и потоков на тс
угол -•
Этот случай индукции представ----- ----- ------, __л трансформатора и поэтому очень важен, так же как и изображающая его векторная диаграмма фиг. 25. С нею нам придется еще не раз встретиться.
со • М • Jlfn cos (<oZ + а) =
/
(52)
и фазовый угол равен а — т. е. ЭДС е2 отстает в фазе дуктирующего ее тока
ОТ ин-
отста-тг „
X
в
Фиг. 25.
2
ляет собой основу идеи
56
ГЛАВА IV
ДЕЙСТВУЮЩИЕ ЗНАЧЕНИЯ СИЛЫ ТОКА
И НАПРЯЖЕНИЯ. МОЩНОСТЬ ПЕРЕМЕННОГО ТОКА
§ 15. Показания приборов. Действующие или эффективные значения силы тока и напряжения
До сих пор мы считали, что мы знаем все, что нужно, о синусоидальной величине, если нам известны ее амплитуда и разность фаз с другими величинами. Но как узнать амплитуду силы тока или напряжения в действительности, имея перед собой цепь переменного тока? Если известны сопротивления цепи, то одну из этих величин можно вычислить по другой, например напряжение по силе тока, на основании закона Ома, но эту другую, в примере — силу тока, — надо узнать непосредственным измерением в цепи тока. Как измерить амплитуду силы тока? Ведь сила тока имеет значение Jm (амплитуду) лишь в течение бесконечно-малого промежутка времени; поэтому отклонения или показания теплового амперметра, включенного в цепь переменного тока, не могут быть равны Jm, иначе выходило бы, что сила тока все время Jm. Вообще же тепловой амперметр должен давать какие-то отклонения или показания, если через него идет переменный ток, так как отклонения стрелки обусловлены нагревом и удлинением от нагрева проволочки, по которой проходит ток, а нагрев происходит и при переменном токе (лацпы накаливания).
Если бы мы включили в цепь амперметр не тепловой, а типа Депре-Дарсонваля, с постоянным магнитом и подвижной катушечкой, связанной со стрелкой, то такой прибор ничего не показал бы при частоте в 50 пер/сек, ибо катушка и стрелка не успевали бы преодолевать свою инерцию. При очень малой частоте, например один период в секунду, она качалась бы вправо и влево (если на шкале нуль предположить по середине) сообразно с изменениями направления тока, но все же и тут мы не могли бы решить, успевает стрелка показать амплитуду силы тока или нет.
Как известно, осциллографы являются такими гальванометрами, у которых инерция подвижной системы очень мала, период соб
57
ственных колебаний тоже мал (тысячные доли секунды), так что с помощью их можно проследить ход изменений например силы тока за весь период. Но для повседневных измерений, для практики эти приборы дороги, громоздки и неудобны по сложности измерений. Поэтому займемся решением вопроса, что покажет в цепи переменного тока тепловой амперметр?
Когда через тепловой амперметр с сопротивлением проволочки Ra протекает постоям ный ток силы J, то количество теплоты, развивающейся в прово очке, одинаково в юбые одинаковые промежутки времени t и выражается через J2Rat в джаулях; при этом стрелка отклоняется на постоянный угол, указывая на шкале силу тока J.
При переменном токе количество развивающегося тепла в проволочке будет за одинаковые промежутки времени, но в разные моменты, разное, так как сила тока i переменна. За бесконечномалый промежуток времени dt} в течение которого силу тока I можно рассматривать как неизменяющуюся, разовьется количество тепла, равное в джаулях
Температура проволочки и ее удлинение не смогут следовать за всеми мгновенными значениями величины мощности i'2Ra, превращающейся в тепло в разные моменты, — не смогут потому, что проволочка обладает известной теплоемкостью; температура и удлинение установятся соответственно среднему количеству тепла, развивающемуся за целый период переменного тока.
Все количество тепла, развивавшееся в проволочке за целый период, равно: т т
\i*Radt = Ra^?dt.
О о
Среднее количество тепла, выделяемое за единицу времени, равно всему, разделенному на время Г:
фрл.
и
При развитии в проволочке в среднем такого тепла стрелка как-то отклонится и покажет на шкале деление J; такое же точно отклонение при постоянном токе будет в том случае, когда количество тепла за единицу времени будет такое же; раз стрелка опять покажет то же J, то значит сила постоянного тока равна J, а из условия равенства средних количеств тепла в обоих случаях имеем:
т J*Ra=A^dt,
О
58
откуда мы получаем, что та величина J, которая на шкале будет показана стрелкой, выражается следующим образом:
(53)
Вычислим правую часть этой формулы ной силы тока I. Так как вообще
для случая синусоидаль-
Г If al
| sin2a-da = - | (1 —cos 2a) a — -sin2a,
J 2 J 2 4
TO T T T
J /2 dt — J sin2 (cd£) . J sin2 (co/) d (co/) =
oo о
T J 2 (0/ 1 1 J 27
= “ -7Г — Tsin(2(0/) =^-.
co L 2 4 J 2
0
Следовательно, подставляя в ф-лу (53), имеем:
r /2
(54)
(55)
Таким образом то, что покажет тепловой амперметр, в /2 раз меньше амплитуды силы тока. Пусть например в цепи переменного
тока амперметр показывает 15 ампер. Согласно ф-ле (55) мы нахо-
дим, что амплитуда силы тока равна
4 = 15/2=15.1,4 = 21 ампер.
Величина J, показываемая тепловым амперметром, в корень квадратный из двух раз меньшая амплитуды, называется действующей, или эффективной, силой тока. Мы будем обозначать ее той же большой буквой J, что и амплитуду, только без значка /п, в отличие от последней.
Нужно помнить, что в действительности такая сила тока (в примере— 15 ампер) существует только бесконечно-малый промежуток времени, появляясь четыре раза за полный период, остальное время сила тока или больше или меньше; но среднее количество тепла, развивающееся в проволочке при переменном токе, точно таково, какое получится, если все время <ила тока была бы постоянной, равной J, — поэтому прибор и покажет эту величину.
Далее, следует помнить и то, что при большой продолжительности периода, например две-три секунды, проволочка
59
будет успевать нагреваться сильнее, когда сила тока близка к максимуму, и остывать, когда сила тока близка к нулю, и стрелка будет показывать то бдльшую, то меньшую чем J силу тока.
Так как вольтметр есть не что иное, как амперметр с очень большим сопротивлением и со шкалой, на которой нанесены произведения из силы тока, идущего через него, на это сопротивление, то и для случая измерения напряжения или ЭДС (последнее-приближенно) тепловым вольтметром мы получим подобное же соотношение. Обозначая действующую силу тока через вольтметр JB, амплитуду ее через JBT, сопротивление вольтметра через /?в, имеем, что прибор покажет
JB/?B = ^/?B = -^ = V,
/2 V 2
где V есть действующее значение напряжения.
Рассмотрим, что покажет прибор электродинамический, т. е. с двумя катушками.
В амперметре через неподвижную катушку течет весь измеряемый ток Z, а через подвижную, обычно шунтированную, только i часть его — = i.
s
Если мы задержим подвижную катушку в каком-нибудь положении, так что взаимодействующие стороны катушек будут все время в одинаковом положении друг относительно друга, то вращающий момент, действующий на подвижную катушку, будет зависеть только от сил токов i и ?, именно будет им пропорционален:
m — C'i-t,
где коэфициент С зависит от чисел витков в катушках, их размеров и от положения их друг относительно друга.
Так как токи переменны, то вращающий момент будет принимать разные значения в течение периода, средняя величина его за целый период выразится так:
т т
/ИВ. = 4С ( i-i' dt—— /Цг = С J2. вр Т J sy/j у 5
о о
Пропустив через прибор постоянный ток силы J ампер, мы найдем, что его постоянный вращающий момент равен:
C-J- — = — А
т. е. тот же самый, следовательно и отклонение будет то же самое. Тот же результат получим и при вольтметре.
60
В практике приборы для переменного тока, например электромагнитные, градуируются по электродинамическим, последние же градуируются при постоянном токе.
Подвижная катушка снабжена спиральной пружиной, сила противодействия которой кручению пропорциональна углу кручения а. Этому углу пропорционален и момент D этой силы относительно оси вращения:
D — c-a.
При равновесии средний момент вращающий (от взаимодействия токов в катушках) и момент противодействия (пружины) равны:
M=D. или са— — S и
a = k-J*.
Таким образом угол отклонения подвижной катушки и связанной с ней стрелки был бы пропорционален квадрату силы тока, если бы К было постоянно. Но К зависит от С и следовательно от положения катушек и с ростом угла а уменьшается, поэтому удается достигать довольно равномерной шкалы подбором размеров катушек.
§ 16. Среднее значение. Длина вектора и масштаб
Кроме амплитуд и действующих, или эффективных, значений синусоидальных величин есть еще их средние значения, в которых впрочем редко встречается надобность.
Среднее значение синусоидальной величины а = Ат sin (©/) за целый период очевидно равно нулю, так как обе половины синусоиды, положительная и отрицательная, одинаковы; среднее значение ее за полпериода равно:
С a-dt
J А С 2
Аср = \ sin (а>0 • d (Ы) = - Ат, (56)
± т — Гц) \
2 2 J
о
В предыдущем примере среднее значение силы тока за полупериод равно: 2
— .21 = 13,3 ампера.
61
В дальнейшем мы увидим, что можно значительную часть расчетов явлений переменного тока производить, оперируя лишь с действующими значениями силы тока и напряжения.
Возьмем формулу (26) § 7, выражающую закон Ома для части цепи, и разделим обё“'части ее на У 2; тогда и в левой и в правой частях вместо амплитуд войдут действующие значения:
Уав .
У^АВ "t
(57)
аналогично получим для всей цепи:
У /?2 + ((ОА)2 ’
Если у нас имеется какая-нибудь векторная диаграмма, т. е. фигура более или менее сложная, элементами которой являются векторы и их фазовые углы, то, уменьшив все линейные размеры в У2 раз, мы не изменим соотношений между ними по законам геометрического подобия; примером этого может служить только что приведенный закон Ома в связи с фиг. 23, из которой можно вывести формулы (33) и (40). Можно не изменять в У2 раз линейные элементы чертежа, а увеличить в У2 раз масштабы для силы тока, напряжения и ЭДС. Тогда прямолинейный отрезок, выражавший своей длиной амплитуду какой-нибудь величины, выразит в ]/2 раз меньшее значение ее, т. е. действующее. На фиг. 23, 24 и других в этом легко убедиться вполне. Таким образом можно на всякой векторной диаграмме считать длиной вектора не Ат — амплитуду, а А — действующее значение.
Например мы желаем начертить вектор силы тока. Амперметр показывает 15 ампер. Нам нужно было бы изобразить длиной вектора амплитуду, равную 21 амперу; но мы, назначив масштаб, например 1 мм^=Л амперу, чертим отрезок длиной \Ъ мм, подразумевая, что если надо знать амплитуду или любое мгновенное значение, то масштаб должен быть другой, именно \ мм^еее^У 2 ампер (1,4). Этим достигается то упрощение, что величины, полученные на чертеже, именно и будут показаны приборами без предварительного перевычисления, т. е. деления их на У2\ и наоборот, измеренные величины прямо наносятся на чертеж без предварительного умножения их на У2.
Условимся также называть и обозначать вектор его действующей величиной: вектор J, вектор Е, вектор JR и т. д.
62
§ 17. Средняя за период мощность в цепи переменного тока
Разберем вопрос о мощности в цепи переменного тока, в которой имеется ЭДС
е = Ет • sin (со/ + а 4- <ре) (А)
и сила тока
Z=/OT-sin((o/ + a). (В)
Угол сре, согласно предыдущему, есть угол сдвига фаз между ЭДС и силой тока, угол между их векторами.
Если вместо всей цепи рассматривается только часть ее, то вместо е, Ет и во всех следующих выводах следует только поставить Ti, Vm и соответственно.
Мощность при синусоидальном токе есть величина переменная. Ее мгновенное значение равно, по определению мощности,
p = ei. (58)
Работа тока за бесконечно-малый промежуток времени dt> в течение которого можно считать е, i и р неизменяющимися, равна:
dw = pdt — eidt. (59)
Работа, совершаемая переменным током за целый период, очевидно выразится интегралом от dw.
т
w — J e>i*dt. о
При всех расчетах величины машин, количества энергии, затрачиваемой при том или ином процессе, главную роль играет понятие мощности; например работа пара при расширении его в цилиндре паровой машины неодинакова за равные малые промежутки времени, взятые в разные моменты; работа за весь ход поршня, деленная на время — продолжительность его, дает нам „индикаторную" мощность, с которой дальше и ведут расчеты. Аналогично, если мы работу переменного тока за целый период разделим на продолжительность периода, мы получим среднюю мощность тока. Она оказывается очень удобйой для всевозможных расчетов, в чем мы впоследствии и будем часто убеждаться; к тому же, что чрезвычайно важно, и прибор, служащий для измерения мощности, — ваттметр — показывает именно ее — среднюю мощность. Обозначим бе величину большой буквой Р. Итак
т
^e-i*dt. (60)
о
63
Подставим вместо е и i их выражения (А) и (В) и произведем вычисление интеграла:
• Л=
о т
^^J[sin(<o/ + a)
0 г
=| jsin2 (<o14- a) d(mt) 4-
r °
Jsin a) cos (cd/ + a) d (©/) | —
0
E*Jn, coscp^F 1 . , . . 4 z , . x 1 <
— ----— — — sin ((о/-j-a) cos (ю/+ a)+
T У L 2 - j0
, E-J^ sin co, 1 Г . „ z . . /lr E м сояф <dT . A + -----~--7T sin2((»)/+a) = -^—“*v + 0^
1 T a) 2 I I Ta) 2
u Jo
Z: • Jm
= ~V25cos<Pr
cos <ре 4- cos (mt -f- a) sin у J • sin (mt4~ a) dt ~
т
Таково выражение средней мощности через амплитуды электродвижущей силы и силы тока и угол сдвига фаз между ними. Чтобы ввести не амплитуды, а действующие значения, преобразуем последнее выражение, пользуясь тем, что 2 = У 2 • /2, так
Е -J
Р = -Д cos сре — EJ cos срй.
/2J/2 Те
(61)
Если мы рассматриваем только часть цепи с напряжением V, то мощность в этой части
р = cos у" yj cos (62)
Итак величина средней мощности в цепи переменного тока зависит не только от величин силы тока и ЭДС (или напряжения), но и от сдвига фаз их, или от разности фаз. Чем больше этот сдвиг фаз, чем больше та часть периода, на которую одна из величин в цепи опережает другую, чем следовательно больше угол <р, представляющий угол между векторами этих величин, тем меньше cos ср и тем меньше мощность Р.
64
Таким образом при одних и тех же значениях V и J мощность может иметь самые разнообразные значения, в зависимости от величины множителя cos ср, и, наоборот, при одной и той же мощности и том же напряжении с^ла тока может быть самой различной величины в зависимости от cos ср: чем cos <р меньше, тем больше нужна сила тока, чтобы при данном напряжении получить данную мощность. Это чрезвычайно важно заметить для дальнейшего.
Произведение VJ часто называется „кажущейся* мощностью; она равна „средней", т. е. действительно развиваемой, только тогда, когда cos ср = 1 (см. конец § 26)
Прибор, измеряющий среднюю мощность, называется ваттметром; электродинамический ваттметр состоит из двух катушек: неподвижной— из более толстой проволоки, включаемой в цепь тока последовательно (при больших силах тока с шунтом), так что через нее и идет ток z, и подвижной, из тонкой проволоки, включаемой последовательно с большим сопротивлением в цепь, как вольтметр, т. е. параллельно; через нее идет ток\ пропорциональный напряжению v. Если самоиндукцией подвижной катушки можно пренебречь, то ? находится в фазе с напряжением обозначим сопротивление подвижной катушки с подключенным к ней сопротивлением через /?'; тогда
Вращающий момент, действующий на подвижную катушку, будет зависеть только от сил токов i и именно будет им пропорционален:
т ~ C'i'i1.
Так как токи переменны, то вращающий момент будет принимать разные значения в течение периода, будет становиться даже отрицательным, — если токи не совпадают в фазе, — на то время, пока они разно направлены в катушках. Средняя величина вращающего момента за период выразится так:
Т
т т
-C^i-i'-dt=y р
О о
' dt
согласно формуле (60), вводя величину средней мощности.
Подвижная катушка снабжена спиральной пружиной, сила противодействия которой кручению пропорциональна углу кручения а.
Теория переменных токов. АК
Этому углу пропорционален и момент D этой силы относительно оси вращения:
D = c-a.
При равновесии средний момент вращающий (от взаимодействия токов в катушках) и момент противодействия (пружины) равны:
M = D, или
и
а = ^Р=КР. С
Коэфициент К стараются делать посредством подбора размеров катушек возможно более постоянным для получения более равномерной шкалы. Таким образом угол отклонения подвижной катушки и связанной с ней стрелки пропорционален величине Р, так что ваттметр показывает нам среднюю мощность тока. Мы можем толстую катушку включить в цепь одного источника переменного тока с действующим значением силы тока J и неизвестным напряжением, а тонкую подключить к другому источнику переменного тока с тем же числом периодов и с действующим значением напряжения V. Раз число периодов одинаково, строго одинаково, то J и V будут все время сохранять постоянным некоторый сдвиг фаз ср (в частном случае равный нулю), как будто бы т
они принадлежали к одной цепи. В последней формуле о даст тогда ту же величину И‘7‘созср^, и ваттметр укажет эту величину, но это будет фиктивная, не существующая в действительности мощность. При некоторых измерениях с переменными токами часто бывает нужно знать, не сдвинуто ли то или иное напряжение относительно какого-нибудь тока (даже и в другой цепи, но при условии одинаковости числа периодов) на четверть периода; тогда подключают, как только что описано, ваттметр, и если он отклоняется, то заключают, что сдвиг фаз не достигает четверти периода, так как cos ср не равен нулю. Если же ваттметр не отклоняется, то значит cos ср = 0, и V и J сдвинуты на четверть периода. Заметим теперь же, а докажем это впоследствии в главе девятой, в § 73, что при разной частоте в цепях толстой и тонкой катушек ваттметр не отклонится вообще.
§ 18. Кривые мгновенных мощностей
Для понимания явлений в цепи переменного тока крайне важно усвоить не только понятие о средней мощности, но и весь ход
66
изменения мощности, мгновенных значений ее, в течение периода. К исследованию этого хода изменений мощности за период мы теперь и обратимся.
Построим кривую мгновенных значений мощности
Р = Ч (С)
где V есть напряжение на любом участке цепи; вместо v, понятно, может быть взята ЭДС источника, — это нисколько не изменит хода последующих рассуждений. На фиг. 26 начерчены синусоиды силы тока и напряжения для случая опаздывания тока на угол сравнительно с напряжением. Затем, согласно ф-ле (С), ординаты v
Фиг. 26.
и i перемножены, и получена кривая р мгновенных мощностей. Мы видим, что р положительны и кривая расположена выше оси абсцисс все то время, пока v и i имеют одинаковые знаки, т. е. или оба положительны — промежуток От, — или оба отрицательны — промежуток nk, пока же v и i имеют разные знаки, — промежутки тп, kl и т. д., — мощность р отрицательна, и кривая ее идет ниже оси абсцисс.
Выразим аналитически кривую р\
p = V'i—Vmsia (a>f <р„) • Jm sin (ш/).
Преобразуем это выражение, пользуясь известным тригонометрическим соотношением:
cos а -- cos р = — 2 sin —r sin —. (А)
5*
67
Полагаем здесь
—I_r^(D/4-<p И —^— = <0/.
Отсюда, складывая и вычитая, получаем: а = 2<^-|-<ро и ? = <₽„.
Подставляем эти значения в (А):
cos (2(0/ + (pw) — cos <pv — 2 sin (со/ 4~ <?J sin (co/).
Следовательно
sin (a)/ 4- <po) sin (<o/) = — [cos — cos (2w/ -f- cpv)] и наконец
p = vi = [cos <pv ~ cos (2(0/ 4- <p J] —
= VJ cos <pw — VJ cos (2(0/ 4- tpj ==
= P — yjcos(2(o/4-<pJ (63)
Таким образом ординаты кривой мгновенной мощности складываются из постоянной величины Р средней мощности и ординат синусоиды с двойной частотой (пунктирная линия): значения р колеблются около средней мощности Р, причем наибольшие положительные и отрицательные значения ее в моменты, когда
cos (2(о/ 4- ± L
равны (фиг. 26)
P±JV.
Если на фиг. 26 за ось абсцисс взять линию АВ, проведенную параллельно оси / на расстоянии Р от нее, то уравнение кривой р будет:
р = cos (2(0/ -I- (рД
Возьмем прежнюю ось абсцисс / и посмотрим, какова работа, производимая током в цепи?
Напомним, что выводы наши относятся к тому случаю, когда (ф-ла 18) L — самоиндукция цепи — постоянна. Если L непостоянна в течение периода, то, значит, имеется магнитное насыщение железй (мы исключаем случай искусственного изменения L посредством например изменения формы цепи, числа витков и пр.), и имеются потери энергии на перемагничивание (на гистерезис). Этот случай разберем позднее.
68
Элемент площади между кривой р и осью абсцисс t выразится через р dt, а это же согласно ф-ле (59) есть элементарная работа, производимая током. Интегрируя за любой промежуток времени, мы получим, что площадь между кривой и осью абсцисс равна работе в цепи' тока. При этом одни площади, над От, nk, положи [ельны,
значит работа в эти промежутки действительно совершается, энергия тратится в цепи; другие площади, как под тп, kl, отрицательны, значит’ за эти промежутки энергия возвращается в цепь; в эти про-
межутки генератор переменного тока не производит работы, но, наоборот, сам поглощает ее.
Откуда возвращается энергия в эти промежутки?
Из магнитною поля вокруг цепи тока, где она была запасена. Чтобы яснее представить себе процесс обмена энергией между цепью и средой, — причем передаточным механизмом является ЭДС самоиндукции, — произведем еще следующие построения.
Разложим напряжение V на две составляющие (фиг. 27), JZ? и (i)LJ, чему соответствует разложение
Фиг. 27.
мгновенной величины, нам уже известное, выражаемое фор-
мулой:
iR— ес.
Из последней формулы, умножив левую и правую ее часть на Z, имеем:
p — PR—ezL. (64)
Величину JR мы раньше назвали ваттной составляющей, a (oLJ— безваттной составляющей напряжения; смысл этих названий теперь и выяснится. Обозначим iR через vB, указав значком „ва ваттный характер составляющей, a ez— чер<з -убв, со значком „бв“, указывающим безваттный ее характер. Тогда
®=®в + г’«в
= + (65)
Представим это разложение v на две составляющие на чертеже синусоидами, начертив синусоиды vB и ^бв (фиг. 28). Синусоида vB совпадает в фазе с синусоидой тока; ординаты ее равны iR; синусоида ^бв = — vc опережает в фазе на четверть периода силу тока (вспомним кривую — ес фиг. 14) ординаты ее равны o>L, по-множенному на силы тока, имеющие быть еще четверть периода спустя. Умножим ординаты той и друюй синусоиды на I, и мы получим, во-первых, кривую pj^= i2R ~ ivB расположенную всегда выше оси абсцисс, т. е. с ординатами всегда положительными (ибо мясовпадают в фазе); эги ординаты дают мгновенные значения мощности, переходящей в тепло в проводниках (джаулев
89
эффект); во-вторых, мы получим кривую р2 = ^бв» четверть периода (промежутки Oqy rs и т. д. — когда i и т>бв имеют одинаковые знаки), имеющую ординаты положительные и расположенную поэтому сверх оси абсцисс, а четверть периода (промежутки qry st и т. д.— когда i и ?бв имеют разные знаки) — имеющую ординаты отрицательные и расположенную ниже оси абсцисс: ее ординаты дают мгновенные значения мощности, запасаемой в магнитном поле, когда или получаемой из него цепью,
когда
Плошади кривой рг всегда положительны, проводники всегда нагреваются, и с течением времени энергия, ушедшая на их нагревание (джаулев эффект), непрерывно растет, как растет площадь, ограниченная кривой р1У по мере продвижения вдоль по оси t.
Фиг. 28.
Площади, ограниченные кривой р2, попеременно положительны и отрицательны, по абсолю!ной же величине они равны между собой. За целый период сумма их равна нулю, и потерь в магнитном поле, например на перемагничивание железа, нет. Положительная площадь представляет энергию, запасенную в магнитном поле около цепи за ту четверть периода, пока сила тока растет в том или другом направлении, — промежутки Oq, rs\ отрицательная площадь представляет энергию, возвратившуюся в цепь из магнитного поля при его исчезновении, когда ток с максимума убывал до нуля в течение четверти периода, — промежутки gr, st. ЭДС самоиндукции ес представляет тот „механизм", посредством которого энергия передав тх я из цепи в среду, в магнитное поле, и возвращается из него в цепь. Если ес направлена одинаково с током, а это бывает всегда, когда сила тока убывает, то в выражении (64) (—ej) 7Q
отрицаельно, т. е. мощность р, посылаемая в цепь от зажимов с напряжением v9 меньше мощности Z2/?, переходящей в этст момент в тепло в сопротивлении /?; недостаток ezi покрываете я мощностью, возвращающейся из поля. Вычислим одну из площадей, чтобы узнать, какое количество энергии запасается в Mai нитном поле за время роста силы тока.
Эта энергия
4 4 4
/7M==J Pidt= [ iviAdt = - J ieadt.
° о о
Так как
, di e^~~Ldt'
тэ
f Um П —L\ idi=—?. м 1 2
о
Выражение
LJ2
Пы----f (66)
для энергии магнитного поля известно нам и из курса физики.
Когда ez и i имеют разные знаки, т. е. когда / возрастает, такое количество энергии запасается в магнитном поле; в выражении (64) (—ezi) югда положительно, и источник тока доставляет мощность не только /*/?, переходящую в тепло в цепи, но еще и р2 = — ej9 идущую в магнитное поле.
Кроме того фиг. 26 нам показывает, что в течение промежут-Ф
ков времени тп = -~ Г, меньших четверти периода, вся мощность р отрицательна; следовательно мощность eQi, возвращающаяся в цепь, не только покрывает потери на джаулев эффект в цепи в это время, но и превышает их на некоторую величину, разную в разные моменты внутри этих промежутков времени mtr. Это превышение и есть ординаты отрицательной части кривой р под mn9 kl и т д. Эта мощность идет к генератору, который в эти промежутки времени берет таким образом мощность из сети, работает двигателем. Любая катушка, включенная в цепь, возвращая запасенную в ее поле магнитную энергию в цепь, посылает в эти промежутки электрическую мощность в генератор переменного тока: она, катушка, есть сейчас генератор, а он является приемником, двигателем. В эти промежутки времени напряжение v
71
у зажимов и сила тока I имеют разное направление; направление силы тока определяется сейчас ЭДС самоиндукции. Если мы сравним фиг. 26 с фиг. 14, то увидим то же самое в промежутке NB и т. д.
Таковы соотношения мощностей и энергий в цепи переменного тика, обладающей самоиндукцией.
Так как сумма площадей кривой p2 = iv63 за целый период равна нулю, то можно сказать, ?то при учете средней мощности составляющая дает с своей стороны среднюю мощность, равную нулю; вся средняя мощность обусловлена составляющей v3:
p^dt = v3i • dt — PR • dt.
Поэтому и назвали величину
= — <4 = — ^Jln Sin (mt — у )
безваттной составляющей напряжения, вектор ОН—ВС на фиг. 19 — вектором безваттной составляющей, величину v3 — ваттной составляющей напряжения, вектор ОВ — вектором ваттной составляющей.
Далее, так как
= и
^бв = -^с,
то сопротивление R назвали ваттным сопротивлением, a coL, входящее в ес, — безваттным сопротивлением. В дальнейшем при изучении зависимости величины средней мощности Р от этих величин правильность таких названий еще более уяснится.
§ 19. Зависимость средней мощности от других величин в цепи
Теперь мы можем опять обратиться к средней мощности Р и рассмотреть, как меняется ее величина в зависимости от изменения различных других ве шчин в цепи.
Из фиг. 19, 21 и 27 мы видим, что ваттная составляющая ЭДС или напряжения есть проекция вектора ЭДС или напряжения на направление вектора тока. Будем в дальнейшем говорить лишь о части цепи и о напряжении на этой части, помня, что все выводы без всякого изменения могут быть отнесены и ко всей цепи и ее ЭДС. Для упрощения не будем при V и R ставить значков, указывающих границы участка цепи. Тогда
или
= l^COS
JR~ V COS
(67)
72
Теперь в формулу (62) подставим вместо Vcoscp^ величину J/?, и мы получим,
P—J2R, (68)
это есть второй вид выражения средней мощности, показывающий, между прочим, известный уже нам факт, что вся средняя мощность переходит в тепло. (Нужно заметить, что если в цепи включен двигатель переменного тока, то большая или меньшая часть средней мощности перейдет в механическую мощность; двигатель имеет про-тивоэлектродвижущую силу, которую всегда можно заменить сопротивлением так, чтобы сила тока в цепи по величине и по фазе не изменилась; тогда механическая мощность двигателя будет заменена равной ей мощностью, превращающейся в тепло в сопротивлении. На такой замене основаны все способы теоретического рассмотрения и учета работы, например асинхронного двигателя и др., так что эта замена представляет для электромеханики очень важный прием.)
Теперь в выражение (68) подставим вместо J его величину, определяемую из закона Ома, и мы получим:
V*R
/?2 4- (coL)2 ’
(69)
это есть третий вид выражения мощности.
Исследуем изменения мощности в цепи переменного тока в зависимости от изменения различных условий. Предположим, что
частота постоянна, и напряжение, приложенное
к цепи, постоянно
V = const, а величины R и L изменяются. В зависимости от изменения этих величин будет изменяться и мощность по ф-ле (69).
Разберем сначала случаи, когда R и L изменяются не одновременно. Пусть L постоянно, а R изменяется.
На фиг. 29 опять произведено обычное построение составляющих каковы бы ни были изменения /?, L и связанного с ними законом Ома J, векторы JmR и Мт составляют прямой
Фиг 29
угол, а следовательно при всех этих изменениях
точка М движется по окружности, построенной на Vm как на диаметре. При изменении R мощность имеет максимум, усло-
вия которою можно найти, приравняв первую производную от (69)
нулю; но мы найдем их иначе.
73
Площадь треугольника ОАМ равна:
-1-. ОМ• AM = -i- JmRu>LJm = <s>LJ*R=®LP. Л it
Так как co и L по условию постоянны, то очевидно для Р будет тогда максимум, когда левая часть формулы, площадь треугольника, будет иметь максимум. Последнее наступит, когда точка М будет в Жо, посредине полуокружности ОМА; при этом
или
т. е.
ОМ0 = М0А,
R = со 7.
(70)
Таким образом, когда L в цепи дано, мощность в цепи достигнет максимума при выполнении условия. При значениях мощность будет меньше, и чем больше будет неравенство между этими величинами, тем ближе к диаметру переместится точка Л4,
тем меньше будут площадь треугольника и мощность.
Теперь посмотрим, что будет с мощностью, если R остается по-
стоянным, a L изменяется. Формула (69) дает непосредственно, что
V2 7? ПрИ
с увеличением L мощность уменьшается от величины Р==
£ = 0 непрерывно до величины Р=0 при L — QQ.
Это влияние величины самоиндукции на величину мощности следует представлять себе так: увеличение самоиндукции вызывает уменьшение силы тока по закону Ома, а уменьшение силы тока обусловливает притомже/? уменьшение мощности по ф-ле (68). Увеличение самоиндукции можно представить себе конкретно напри
мер как результат вдвигания железного сердечника в катушку, включенную в цепь тока, или замыкания ее разомкнутой магнитной цепи. Таким образом мы видим, что влияние изменений R и L на ве
личину мощности неодинаково.
В случае одновременного изменения R и L мощность будет изменяться в зависимости от того, как и в каком отношении друг к другу изменяются величины R и L; рекомендуем читателю обсудить несколько случаев возможных комбинаций изменений этих величин.
Теперь нам надо исследовать еще, как будет изменяться мощность при изменении R и L в цепи, в которой не напряжение, а сила тока постоянна.
Итак полагаем J== coast.
Сначала опять разберем случай, когда L постоянно, а Р изменяется. Построим для какого-нибудь значения R треугольник век
74
торов ОАМ (фиг. 30). В этом треугольнике, при условии постоянства J и Л, сторона AM будет постоянна по величине; с изменением
будет пропорционально ему изменяться сторона ОМ] пропорционально ей будут изменяться площадь треугольника и следовательно мощность. При каком-нибудь будет OM' = JmR'] А'М'= ®LJm = AM] OA'= V'm — новому напряжению, и наконец ^AfOMf— <р^, и cos <p^>cos<p0, так как <f/ < <pv.
При росте /? в формуле Р= VJcoscp^, где J теперь постоянно, растет ваттная слагающая напряжения V cos <pw = JR, представляемая векторами ОМ, ОМ', .. в; при этом уменьшается угол cpw.
Посмотрим, что будет с мощностью, если R будет постоянно при постоянном J, а изменяться будет Л. При этом сторона ОМ = JmR будет оставаться постоянной; пропорционально L будут
изменяться сторона AM и площадь треугольника ОА"М, так что, согласно соотношению:
площадь /\OAM = ®LP,
мощность Р будет оставаться постоянной.
Иначе: при означенных условиях ваттная составляющая напряжения не будет изменяться и с постоянной силой тока даст. постоянную мощность.
Может быть еще случай, когда даны (т. е. считаются за постоянные) и напряжение, и сила тока; тогда мощность будет изменяться пропорционально cos <ро, т. е. величине выражения (25):
R
COS CpT, ~ .г ==• .
Так как cos ср является множителем, отличающим выражение мощности при переменном токе от выражения ее при постоянном,— то иногда его называют еще коэфициентом мощности. Это название в особенности уместно, когда кривые v и i не синусоиды, а сложной формы. Об этом подробнее будет сказано ниже, когда будет изучаться влияние формы кривых v и L
Остается сказать еще о влиянии на мощность изменения частоты, которую до сих пор мы предполагали по условию постоянной. Формула (69) показывает, что с ростом частоты, при прочих равных условиях, мощность непрерывно уменьшается до нуля при /=±=ОО. Закон Ома показывает, что и сила тока при этом тоже уменьшается до нуля.
76
Этим мы закончим обсуждение вопроса о влиянии на величину средней мощности различных величин в цепи переменного тока.
В виде примера приложим изученное нами понятие средней мощности к диаграмме генератора переменного тока (фиг. 21), где вместо амплитуд представим теперь действующие значения, чтобы иметь упражнение в таком переходе.
Здесь мы будем иметь прежде всего мощность:
PM = EJcos(pe>
которую назовем механической мощностью генератора и отметим буквой „м“. На такую величину мощность машины-двигателя (например паровой турбины), вращающей наш генератор, должна быть при нагрузке, т. е. когда мы берем от генератора ток, — больше, чем при холостом ходе, т. е. когда цепь, подключенная к генератору, разомкнута и J = 0.
Из чертежа видим, что
Рм=Е cos <ре • J = ОВ • J = J2 (А>вну /?8не). (71)
Далее, мы имеем мощность
Р9== K/costp,,, (72)
которую мы назовем электрической мощностью генератора и отметим буквой „э“. Такую мощность генератор отдает во внешнюю цепь, ибо
Р9= Vcos^J = OD.J = J4^. (73)
Разность этих двух мощностей
Л< ^2^вну
представляет потерю мощности в самом генераторе на нагревание его обмотки.
В примере, к которому относится фиг. 22, был в числе данных назван cos ср^, равный 0,8. Теперь мы видим, что он мог быть узнан следующим путем. Ваттметром могла быть измерена электрическая мощность Р9 (ф-ла 72), амперметром измерена сила тока, действующая, в 71,4 ампера, что дает амплитуду 71,4 • ]/2 — 100 амперам; вольтметром измерено напряжение, действующее, в 1 428 вольт, что дает его амплитуду 1 428-J/2 = 2 000 вольт. Разделив согласно ф-ле (72) электрическую мощность на произведение действующих силы тока и напряжения, мы и получим coscp^.
Предлагаем читателю для упражнения вычислить в этом примере Рм, Р9 и разность между ними.
76
§ 20. Диаграмма Беделя и Крехора
Рассмотренный в предыдущем параграфе первым случай цепи, состоящей из постоянного X и переменного R, включенных последовательно, имеет следующую аналогию в практике.
На фиг. 31 изображена воздушная линия передачи энергии. Точки АВ есть ее начало, здесь провода AM и AN подключены к генератору; напряжение V в АВ постоянно; между точками М и N подключены лампы, т. е. осветительная нагрузка. При практических подсчетах часто считают лампы накаливания за чисто ваттное сопротивление; обозначим его через /?н как сопротивление нагрузки. Кроме него в цепи есть ваттное сопротивление проводов проводов Апров. Строго говоря, эта самоиндукция распределена равномерно вдоль всей длины проводов, но при расчетах, в особенности линий небольшой длины (10 — 30 /см), можно получить достаточно точные результаты, если действительно существующую величину самоиндукции линии считать сосредоточенной в одном месте, например в середине линии, символизируя ее на чертеже катушкой ^пров ^^Пров’
Построим (фиг. 32) треугольник напряжений ОАМ, причем гиповертикали. Здесь катет ОМ — = -/(ЯПр0В + ^н) = ЛЛ где и Jm и R переменны; R может стать равным бесконечности при разомкнутой цепи и может уменьшиться до величины /?пров, если в конце линии произойдет короткое замыкание, и даже стать меньше /?0, если короткое замыкание случится не в самом конце линии, а где-нибудь по ее длине. Катет AM — = где^пров постоян-но, исключая случай короткого замыкания не в конце линий. Так совпадает в фазе с величиной JR=OM. Разделим ОМ на 7? и в масштабе силы тока отложим величину J от О по ОМ\ пусть ON=J.
Проведем из точки N линию NB | ON, она пересечет горизонтальную ось в точке В. Тогда /\ONB будет подобен ДЛЛЮ, так как они прямоугольны и углы АОМ и NBO равны.
3
в
м
---------------
В проВ Я*
J bi
Фиг. 31.
7?Пров» затем есть самоиндукция
тенузу О А = V направим по
В
Фиг. 32
77
Поэтому
ОВ _0М
ОА AM
или
OB = OA-°~ = V
AM
V\ X'
так как V и X постоянно, то и ОВ имеет для разных положений и величин вектора ОМ, т. е для разных нагрузок, постоянную ве-V
личину —; разделив напряжение в вольтах на X в омах, получен
ную величину отложим в масштабе силы тока по горизонтали в виде отрезка ОВ.
Так как угол ONB прямой, то, описав на ОВ, как на диаметре полуокружность, будем в ней иметь геометрическое место концов вектора силы тока при различных нагрузках. В самом деле для любой точки N' имеем:
ОМ _ AM1 ОВ ~ОА'
откуда
ON' — OB-
AM ОА
V /X х9 V
ОМ равно новому значению J силы тока в цепи. При коротком замыкании линии в конце ее = и сила тока есть ONk. Когда R = 00, т. е. цепь разомкнута, точка М находится в О, при этом 0N=0.
Мощность в цепи достигает максимума, как изложено в начале предыдущего параграфа, когда R=X; £±0МА чюда становится равнобедренным; таким же делается и подобный ему £±BN0.
§ 21. „Падение" напряжения и „потеря" напряжения в проводах линии передачи энергии
Построив (фиг. 33) еще раз треугольник напряжений ОАМ для линии передачи энергии, поступим с его катетами аналогично тому, как мы поступали с ними в фиг. 21; именно выделим падения напряжения в ваттном сопротивлении проводов линии передачи — вектор KM=^NP—JR^k и в безваттном — вектор DA = JXnpon. Предположим для общности, что йагрузка индукционна, так что кроме 2?н существует и Л'1| = <оАн (нагрузки).
Вектор №4=JZnp0B=J]/^~+:^4^ есть вектоР паления напряжения в проводах. Вычитая его из OA = Vv по* 78
О Фиг. 33.
Далее
МУ= и
РТ так что
лучим вектор ОМ== У2 напряжению на конце линии, на нагрузке. Обычно это последнее напряжение поддерживается постоянным по величине при разных нагрузках посредством регулирования напряжения У1. Но для машин и ламп в месте нагрузки важна величина а не его фаза относительно V\, поэтому для практики важно, насколько арифметически У2 меньше Vv или больше V2.
Продолжим линию ОМи опустим AQ | OQ. Приближенно примем OQ = О А, что возможно во многих случаях по малости угла а. Тогда
Vx — V2 = OQ — ОМ= MQ.
NQ разлагаем на два отрезка:
NQ = MS-|- SQ = МУ+ РТ.
= NP. cos <р2 = J/?np0B cos <р2
= РА - sin <р2 = Z¥np0B sin <j>2,
У, — У2 = NQ === J/?np0B cos <р2 4- Z¥npaB sin <р2.
Эта арифметическая разность двух напряжений, учитываемая легко с помощью двух вольтметров, называется потерей напряжения в проводах.
Пример 10. К линии передачи энергии с Япров = 0»6 ома и ЛГпров = 0,8 ома подключен асинхронный двигатель, полезная мощность которого Ра равна 304 киловатт, коэфициент полезного действия его т) равен 0,95; при этой мощности cos?a = 0,8, напряжение Уа на его зажимах должно быть 2000 вольт. Вычислить „потерю* напряжения в проводах, мощность, берущуюся в линию от генератора, коэфициент полезного действия всей линии передачи энергии, напряжение cos?! в начале линии и построить векторную диаграмму.
Потеря напряжения равна согласно последней формуле:
У( — У2 = (Л?пров cos <ра 4- *пров‘ sin <р,);
надо следовательно прежде всего узнать J.
Мощность, берущаяся линией передачи от генератора*
Р = ^ = ^21 = 320 киловатт = 320 000 ватт, 0,09 так как в формуле
Р= VJ cos ?9
Р должно быть выражено в ваттах и
. Р 320 000 ОЛП
J~~ Vc'os?2 — 2 600-0,8 ~ 200 аМпер‘
79
Теперь вычисляем
- V2 = 200 (0,6-0,8 + 0,8.0,6)== 200-0,96 =192 вольта,
что соответствует около 10% от Vb которое равно 2 192 вольта.
В проводах тратится
^пров = 2002-0,6 = 24 000 ватт = 24 киловатт.
Мощность Рь берущаяся из генератора, равна:
Р{ = 320 + 24 == 344 киловатт = 344 000 ватт.
Коэфициент полезного действия всей установки равен:
ll~Pt~ 344 — °’88’
В начале линии имеется
_ Pt 340 003 _л„„
cos ft — ViJ - 2 192.2(W — °.77-
Фиг. 34. На фиг. 34 построена векторная диаграмма на-
пряжений и тока.
Пример 11. Проделать весь пример 10 с измененными данными: cos?2 = 0,6 и -Кировв 1,2 ома-
80
ГЛАВА V
ЕМКОСТЬ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
§ 22. Закон Ома для цепи, содержащей ваттное сопротивление и емкость
Переменный ток может течь в цепи, в которую включен конденсатор; последний будет при этом заряжаться переменно, то в одном направлении, то в другом.
Обозначим для дальнейшего, как и раньше, ваттное сопротивление цепи через /?, емкость конденсатора в практических единицах (фарадах) через С, разность потенциалов, или напряжение, на его обкладках — мгновенное значение — через vk, амплитуду — через Vkfn, действующее значение — через V*, все напряжение или ЭДС, приложенные к цепи, как и раньше, — через V, V или е.-Е.
Количество электричества qy собравшееся к произвольному моменту времени на обкзадках конденсатора, может быть выражено через емкость его и существующую в этот момент на его обкладках разность потенциалов так:
q = Cvk. (74)
За следующий бесконечно-малый промежуток времени dt в конденсатор притечет количество электричества dq\ значит, сила тока в этот момент была равна:
Если dq положительно, т. е. если заряд увеличивается, то и dq -37 положительно и сила тока t положительна. dt
Подставляя в формулу (75) вместо q его выражение (74) и диференцируя последнее по /, получаем:
^dv.
l==c~dt' (76)
6 Теория переменных токов.
81
Зададимся тем, что напряжение vk есть синусоидальная функция времени при произвольном начале отсчета времени, выражающаяся так :
®*=Vt„sin(e/-|-f). (А)
Тогда, подставляя вместо это последнее выражение в формулу (76) и производя диференцирование, имеем:
/= cos (и/ + ₽) = <oCVkm sin L/ -j- £ -j- (77)
\ /
Синусоидальная функция sin Iо)/£ -f-, как известно, one-режает на четверть периода функцию sin (о>/-|~ Р)-
Таким образом сила тока, проходящего через конденсатор, опережает напряжение на его обкладках на четверть периода; на векторной диаграмме поэтому вектор напряжения на конденсаторе надо чертить повернутым относительно вектора силы тока в сторону более позднего времени, т. е. по вращению линии времени, на п
Угол т.
Амплитуда силы тока из формулы (77) получается в виде:
Jm = ^Vkm, (78)
и напряжение на конденсаторе через силу тока и емкость:
(79)
Это выражение аналогично выражению (22) для амплитуды ЭДС самоиндукции через силу тока и самоиндукцию, хотя, как видим, полного сходства в строении обеих формул нет.
Быть может, у читателя явится вопрос, почему в главе второй при выводе соотношения (22) между ЭДС самоиндукции и силой тока мы задавались тем, что сила тока есть синусоидальная функция времени [формула (20)], а теперь задавались аналогичным выражением для напряжения у конденсатора [формула (А)]?
Мы* сделали так просто потому, что этим путем скорее получается результат, выражаемый формулой (77). Следует заметить, что и здесь, при выводе соотношения между силой тока и напряжением на конденсаторе, мы могли поставить условием существование в цепи синусоидального тока с данной амплитудой
z = JOTsin((<oO (В)
и искать, как будет через силу тока выражаться напряжение vk. Итак допустим, что формулу (113) мы незнаем.
82
Из формулы (76) следует, что
= Р'^’
(С)
но поставить здесь у интеграла нижний предел для читателя, незнакомого с действием емкости в цепи переменного тока, представит трудности, так как для указания этого предела необходимо уже знать, что сила тока опережает напряжение не четверть периода. Однако узнать этот предел можно путем следующих рассуждений, которые мы приведем для того, чтобы читатель мог узнать подход с разных сторон к этому вопросу.
Установим сначала такое положение: интегрируя синусоидальную функцию между пределами, один из которых переменен, мы получим тоже синусоидальную функцию того же периода; таким образом vk должно быть, по (С), синусоидальной функцией того же периода, что и L
Далее, из формулы (76) имеем, что когда /=0, то -^ = 0
и следовательно vk равно положительному или отрицательному максимуму (амплитуде) Vkm. До этого момента напряжение^ росло,— следовательно электри-
чество текло в конден- м
сатор; после этого момента vk, оставаясь
по знаку таким же, X ш\/ X \
как и раньше, будет d------------у---------г
уменьшаться, следова- / х. \
тельно ток будет течь /
из конденсатора. По- У этому силу тока после момента положитель- фиг- 35.
ного максимума напряжения нужно счесть отрицательной. Сообразно этому синусоиды vk и i чертим так, как на фиг. 35; гри этом сила тока опережает напряжение на четверть периода Таким образом, когда i = Jm, тогда vk = 0\ поэтому интегрировать между моментами, когда vk— 0 и когда оно имеет некоторую величину vk,— значит интегрировать как раз между моментами, когда i=Jm и когда i — i.
Таким путем мы приходим к величине нижнего предела в интеграле (С) x — Jm и пишем:
р*л-
(80)
83
Подставляя вместо i его выражение (В) и ставя пределы для переменной /, имеем: t
= J sin(<o/)-rf(a>0=^sin (81)
Тг
Формула (81) по содержанию одинакова с (77); из нее вытекают также и формулы (78) и (79)
Заметим, что нижний предел в формуле (С) пишется очень часто неверно, именно, как i=Q (например Arnold Wechselstrom-techmk, Bd. I, S, 47, 2 Aufl.). Предлагаем читателю убедиться, что можно поставить нижним пределом /=0, если выражение для vk взять не (С), а иное, именно: i=»t
J 1 dt~Vkm
1=0
и что в результате вычислений получится тоже формула (81).
Перейдем теперь к решению следующей задачи.
Требуется определить амплитуду и фазу напряжения, или ЭДС, которые надо приложить к цепи с ваттным сопротивлением R и емкостью С, включенной в цепь, чтобы получить силу тока данной амплитуды
Возможны два способа решения: аналитический и геометрический или, лучше сказать, графический, как и при решении задачи о цепи с самоиндукцией
Основанием для того и другого хода решения является разложение напряжения v, которое надо приложить к цепи, на два слагаемых— первое /7?, необходимое для того, чтобы силу тока i „прогнать" через сопротивление /?, и второе vk — напряжение у конденсатора, необходимое для силы тока L
Итак
v = iR-\-vk. (82)
Для аналитического решения положим
i = Jm sin (ш0 и
. I л п \
Vk — ~~Мш 1(1)/-— ,
* (оС \ 2 /
где Jm нам задано. Подставляем эти величины в формулу (82):
v=4 sln (®о + sin ( —-J ) в
84
== Jm Г7? si» (®0 — COS (Wf) 1 =
Последнее соотношение справедливо и для действующих значений J и V; оно называется законом Ома для цепи, содержащей емкость.
Величина
к ©С
(86)
по физической размерности своей представляет сопротивление, аналогично величине XC=&L и называется безваттным сопротивлением. Разница между ними та, что вызывает своим присутствием 1
в цепи отставание тока от напряжения, а — вызывает опережение
током напряжения
Графическое решение состоит в следующем.
Отложим вектор силы тока J (фиг. 36). Введем для упражнения в выводы и построения не амплитуды, а действующие значения. Вектор J есть ОА\ ОВ представляет величину JR OD есть вектор напряжения на конденсаторе [формула (79)]
отстающего от силы тока на четверть периода.
Отрезок ОС есть результирующий вектор напряжения в цепи V. На основании теоремы Пифагора легко получаем соотношение (85) для действующих значений
85
Сравнивая фиг. 36 с фиг. 23 или 30, мы видим, что угол ср
при самоиндукции
откладывается влево от вектора силы тока, а при емкости — вправо. Будем считать углы <р, откладываемые в одном направлении, положительными, откладываемые в другом — отрицательными Условимся, что положительные ср мы откладываем влево, отрицательные — вправо; значит формула (24) дает положительные <р, а формула (84) — отрицательные; такое условие есто просто, в свою очередь, следствие из формул (26) или (37) и (83). Если мы желаем найти соотношение мощности и других величин в цепи, то мы в формулу (А) начала параграфа 17 должны поставить вместо 4- сре, угла запаздывания тока, из формулы (83) —угол его опережения Дальнейшие выводы величины средней
мощности от этого нискол> ко не изменятся, и мы получим те же формулы (61) и (62), так как при изменении
знака угла косинус его не меняет знака.
Итак, от чего бы ни происходил сдвиг фаз межлу силой тока и напряжением (или ЭДС), т. е будет ли он положительным
или отрицательным, средняя мощность выражается формулами (61) и (62).
Затем заметим, что при изменении С или R точка В движется
по полуокружности (фиг. 37); чем больше угол у (фиг. 37) и формула (84); когда С=оо, тогда <р = 0, и из формулы (85):
емкость С, тем- меньше
Фиг. 37.
Таким образом не следует думать, что когда источник пер менного тока замкнут на одно лишь ваттное сопротивление /?, то емкость в цепи равна нулю, — наоборот, тогда емкость бесконечна. Когда же цепь совсем разомкнута и части ее в месте размыкания у^лены одча от другой так, что электрическое поле между ними равно нулю, тогда и емкость в цепи
равна нулю, т. е. С=0, и по формуле (85) 7=0.
Вектор ОВ есть вектор ваттной составляют# напряжения, вектор OD есть вектор безваттной составляющей напряжения. Анало
гия и во всем остальном тому случаю, когда в цепь включена
самоиндукция, — полная, только угол имеет теперь другой знак, сила тока опережает напряжение.
86
§ 23. Мощность в цепи с емкостью
Мы могли бы повторить все рассуждения, приведенные в главе четвертой по поводу фиг. 26 и 28 о ходе изменений мгновенных
значений мощ ости, с той лишь разницей, что безваттная составляющая напряжения'на фиг. 27 и 28 опережала силу тока, а теперь (фиг. 37) она будет отставать от силы тока Эти кривые изображены на фиг 38 О кривой мощности p^^PR ничего нового нельзя сказать Наоборот, умножив ордина>ы кривой v^3 = vk на i и получив кривую p2 = ^fez, мы
видим, что ординаты ее положительны, т. е. источник тока тратит мощность или энергию, — тогда, когда сила ток1 убывает по своей величине, — промежуток времени qr\ в это время vk растет до максимума, следовательно происходит заряд конденсатора, накопле
Фиг. 38.
ние в нем энергии в виде энергии электрического поля; продолжительность этого накопления — четверть периода; в следующую четверть периода vk убывает до нуля, и электричество течет из конденсатора по цепи (от одной его обкладки через всю цепь к другой обкладке), — здесь нет нужды в особом „механизме", каким была ЭДС сам индукции для возвращения запасенной в э/ектрическом, поле энергии в цепь. Сумма всех площадей за целый период равна нулю, следовательно происходит лишь простой обм н энергией между цепью и диэлектриком конденсатора без потерь. Строго говоря, существует явление диэлектрических
потерь при циклическом изменении электрического поля, но это явление так слабо и потери так малы, что ими в большинстве случаев можно пренебречь; в конце этой главы мы покажем, как их учесть, когда это оказывается необходимым.
Вычислим энергию, запасаемую в диэлектрике конденсатора за четверть периода qr (фиг. 36):
^/с= Ут n3 = \vkidt,
или, принимая во внимание выражение (76) для i:
Vk-cVlan CV*
(87)
87
Формула (87) представляет известное из курса физики выражение для энергии заряженного до разности потенциалов Vkm конденсатора, вывод ее не зависит от закона изменения vk и I во время заряда.
§ 24. Закон Ома для цепи, содержащей ваттное сопротивление, самоиндукцию и емкость
Перейдем теперь к общему случаю, когда к цепь переменного тока вклю ены ваттное сопротивление 7?, самоиндукция L и емкость С. Какое надо приложить к этой цепи напряжени (или ЭДС), чтобы сила тока в ней была данной амплитуды (или дейс вующего значения)?
Для мгновенных значений имеем, что
v = iR-e<.-\-vk,
(88)
т. е. в каждый момент часть vk всего напряжения сосредоточивается на конденсаторе, час1ь ес компенсирует ЭДС самоиндукции и часть IR тратится на проведение тока через сопротивление 7? цепи.
Подставляя сюда вместо i его выражение i = Jm sin (wt) и связанные с этим выражением выражение (21) для ес и выражение (81) для vk получаем:
v — JmR sin (со/) — sin
Выносим Jm за скобки и соединяем два последних члена в од-.
ночлен:
v — jl R sin (ft)/) — ( (j)L sin ( ~ И — I \ \ 2 / J = Jm 17? sin (co/) 4- f ft)L — j cos (co/) |.
Совершенно аналогично выволу соотношения (26) вводим вспомогательный угол
r 1
ft)L — —
<f> = arc tg--(89)
и получаем:
1
^с) .sin^ + <p).
(90)
Отсюда для
амплитуд и для действующих значений имеем ф; рмулу:
1 со С
(91)
88
которую и назовем законом Ома в общем случае цепи переменного тока.
Здесь уже
Х=в>А— ±- = Хс — Xk (92)
(оС с Л
есть безваттное сопротивление.
В векториальной форме решение виде.
Откладываем вектор OB = JR фиг
во — вектор OD = Vb = —- , пер-* со С
пендикулярно влево—ве тор ОН= = — Ez — — (bLJ> складываем векторы, сначала например ОН и OD, где сложение сводится к вычитанию из ОН отрезка HF = = ODt разность — вектор OF — складываем с ОВ и получаем ОС, вектор результирующий из всех трех, а потому представляющий все напряжение v согласно формуле (88).
Величина вектора OF равна
---J | -о)С \
представится в следующем
39); перпендикулярно впра-
Применив к треугЬльнику ОВС теорему Пифагора, получим опять формулу (91) закона Ома.
Средняя мощность выражается прежней формулой Р= JVcos где угол <pv определяется из формулы (89); ординаты кривой мгновенных мощностей разлагаются на сумму ординат трех кривых: Z2/? — ezi и vki, к которым и применимо все сказанное о них выше.
Если мы измерили амперметром J, вольтметром V и ваттметром Р, то, разделив Р на JV, мы получим coscpv, причем однако мы не будем знать, ‘ положителен или отрицателен сам угол ср^, другими словами, чем вызван сдвиг фаз — емкостью или самоиндукцией, или, — при существовании и той и другой в цепи,— влияние которой больше, каков знак X в формуле (92)? Если Xz^>Xh, то берет верх самоиндукция, X положительно, ср положительно, и сила тока отстает от напряжения; если же Xz< Xk, то берет верх емкость, X и ср отрицательны, и сила тока опережает напряжение. Таким образом мы приходим к необходимости как бы приписать безваттным сопротивлениям знак: сопротивлению
Xc=vL знак плюс, а сопротивлению Xk= — — знак минус; он
89
я стоит в формулах (89), (90) и (92). „Результирующее" сопротивление Х = ХС — Хк тоже получает знак. Для определения этого
знака и, следовательно, знака угла экспериментально нужны другие еще приборы, например осциллограф
Нам надо теперь для дальнейшего условиться в способе обозначения на схеме ваттного и безваттных сопротивлений. Будем ваттное сопротивление обозначать зигзагообразной линией, как на фиг. 40 между точками а и Ь\ безваттное сопротивление самоиндукции будем обозначать витой линией, как на той же фигуре между точками с и так же будем обозначать и всякую катушку с небольшим ваттным
сопротивлением; наконец емкость обозначим двумя парал-
лельными линиями одинаковой длины, как на фиг. 40 между точками b и с.
На схеме (фиг. 40) изображена цепь переменного тока, присоединенная к зажимам А и В источника переменного тока; в цепь включено ваттное сопротивление 7?, емкость С (конденсатор) и самоиндукция L (катушка) Конечно провода Аа, Bd и соединительные провода между R и С и между С и L тоже обладают и ваттным сопротивлением и самоиндукцией. При решении
Фиг. 40. многих задач однако этими величинами
можно пренебречь ввиду их чрезвычайной малости в сравнении с ваттным сопротивлением R какого-нибудь реостата или т. п., и самоиндукцией L катушки. В других случаях можно через R обозначить ваттное сопротивление всей части цепи от А до В, включая и провода и ваттное сопротивление проволоки, свитой в катушку, а через £ обозначить самоиндукцию всей части АВ цепи. Наконец можно все эти величины учесть и порознь, считая, что участок cd кроме самоиндукции L обладает еще и некоторым ваттным сопротивлением, так же как и все остальные участки. В последующем мы будем иметь случаи разного подхода к этому вопросу сообразно конкретным условиям каждой задачи, соотношениям в ней всех этих величин.
Между прочим, следует заметить, что если мы подключим по вольтметру на каждый участок цепи и „главный" вольтметр к самим зажимам ЛВ, то, в противоположность случаю цепи постоянного тока, показание этого „главного" вольтметра вообще не будет равно сумме показаний всех вольтметров на участках, так как все напряжения на участках складываются в результирующее напряжение не арифметически, а геометрически (вспомним фиг. 23, где было несколько участков, каждый с разным отношением своего о)Л к своему Rf и фиг. 32).
90
Проделаем небольшой пример.
Пример 12. Пусть на фиг. 40 катушка самоиндукции сделана из небольшого числа витков очень толстой проволоки, так что ее ваттным сопротивлением мы можем пренебречь, самоиндукция же ее L = 0,31 генри; ваттное сопротивление какого-то приемника электрической энергии /? — — 10 омам; емкость конденсатора С = 20 микрофарадам, или 20-10~б фарадам; сопротивлением ваттным и безваттным коротких соединительных проводов пренебрегаем ввиду их малости. Сила тока J равна 5 амперам. Что покажут все четыре вол тметра?
Вольтметр покажет напряжение
Л? = 5. Ю = 50 вольт.
Вольтметр В2 покажет напряжение [формула (79) отнесенная не к амплитудам, а к действующим значениям]
Vk = 800 вольт.
* ыС 314-20
Вольтметр В3 покажет напряжение, равное ЭДС самоиндукции, так как на этом участке мы положили 7? = 0 (формула 39, отнесенная тоже к действующим значениям), т. е. величину
Ус = <o£J = 314-0,31-5 = 500 вольт.
Вольтметр же главный покажет напряжение [формула (125)]:
V = J — 2-)* — 5 Y102 4-(100—160)2сд304 вольта,
т. е. даже меньше, чем В2 и В$.
Закончим этот параграф построением векторной диаграммы длй
случая более сложного. На фиг. 41 дана схема цепи переменного тока, разделяющейся на три последовательно соединенные участка Аа, ab и ЬВ. Каждый участок представляет последовательное соединение ваттного сопротивления, самоиндукции и емкости. Нас интересуют напряжения на отдельных целых участках, но не от
91
дельно на каждом сопротивлении, конденсаторе и т. д., так как этот последний случай мы только что уже изучили. Как все напряжение на зажимах А и В разложится на участковые напряжения? Мы пойдем обратным путем и построим все участковые напряжения, сложив которые затем получим все напряжение на зажимах А и В. Пусть (фиг. 42) О А есть вектор силы тока J, а ОВЛ — вектор JRy падения напряжения в ваттном сопротивлении первого участка; отложим по известным уже правилам, ана. огично фиг. 39, векторы OD^= Vk и ОНЛ = — Е^, сложив все три вектора, получим ОСУ = вектор напряжения на первом участке; переходя ко второму участку, заметим, что напряжение на нем придется потом геометрически складывать с напряжением Vlt а потому для упрощения и строить его будем не oi точки О, а от т< чки Cv построение аналогично предыдущему: C}B2 = JR2^ C1D2~Vk2, СгН2= — и ^1^2= ^2 Точно также поступим и с напряжениями третьего учас ка: С2С8=У3. Величины векторов Ez и Vk для участков таковы, что, как изображено на векторной диаграмме, на первых двух участках самоиндукция берет верх над емкостью и сдвиг фаз <pw получается положительным, на третьем же участке, емкостный эффект сильнее эффекта самоиндукции, и ср3 отрицательно. При изображенных на диаграмме соотношениях для всей части цепи от А до В угол получился положительным.
Если все участковые равны, то напряжения на участках сложатся арифметически в полное напряжение V; лля этого, аналогично случаю, рассмотренному в § 14, и согласно формуле (89), должно быть:
т 1 г 1 г 1
(0L.------ о)£2------— — r
.. (94)
где L есть самоиндукция всей части цепи от А до В, С—ее емкость, a R — ваттное сопротивление. Как известно из формулы (50)
£=^1 + + + • • • + • • •
Что ваттное сопротивление R выразится таким же образом через сопротивления участков, — очевидно.
Как связано С с величинами емкостей в участках?
Легко видеть, что построение фиг 40 можно изменить следующим образом: построим сначала все векторы —Eze — £ср —Ес* и, сложив их, получим —Ес—вектор слагающей напряжения, уравновешивающей ЭДС самоиндукции для всей части АВ цепи; так же построим и сложим Vki, Vk* и Vk ; очевидно, что, вычтя их из предыдущего вектора —Ес, мы потучим ту же самую безватт
92
ную слагающую, равную C3B, что и прежде; и окончательный результат будет тот же самый — вектор ОС3 — V; но
или
и, обобщая,
_L + J_+J_=_L, (oCj ’ о)С2 о)С3 <оС
1
A=1+_L+_L
с с^сг^с3
Итак, когда мы имеем в цепи последовательно соединенные емкости (непосредственно соединенные или с промежутками из L и А?,—это безразлично, как явствует из всего хода рассуждений), то емкость все * рассматриваемой части цепи опред ляется из емкостей участков этой части по формуле (95).
Формула (95) известна и‘из курса физики.
Таким образом при нескольких участках имеем:
(95)
т. е.
(i)L = o)L1 4- g)L2 + o>L3 4-
o)C (oC, ©C2 (i)C3
Пример 13 Построить последнюю векторную диаграмму для случая: /?4 = 3 ома; £4 = 0,01 генри, С4 = 100 микрофарад; /?2 = 10; £2 = 0,1; С2 = 200; 7?3 = 5; £2 = 0,05: С3 = 50
§ 25. Резонанс напряжений
Может случиться, что в формуле (91) АГ = О, т. е. что
o)L
1 о)С’
(96)
Тогда на фиг. 39 вектор OD = OH, FG = CB = Q и V~JR9 т. е. вектор ОВ сливается с вектором ОС по величине и по фазе, угол (р становится равным нулю.
При всяком другом ср, при , будет ОС^>ОВ, поэтому
при выполнении равенства (96) необходимое для создания данной силы тока напряжение является при данном 7? наименьшим. В ф-ле (91) знаменатель получается при этом наименьшим, так что можно из этой формулы вывести и другое за
93
ключение, именно — что при данном напряжении V и при данном R сила тока J будет наибольшей при выполнении равенства (96). Эта сила тока равна:
как будто 'в цепи нет ни самоиндукции, ни емкости, а есть только одно ваттное сопротивление.
Описываемый случай носит название резонанса напряжений емкости и самоиндукции.
Резонанс может случиться от разных причин, например при постоянной самоиндукции L цепи может изменяться емкость так, что станет равной
1 (i)2L’
или же при постоянной емкости С может изменяться самоиндукция так, что станет равной
1 (1)2С’
или же изменения обеих величин приведут к выполнению равенства (96); наконец может изменяться в некоторых случаях практики и число периодов в секунду так, что получится
<о= —= , (97)
Vlc V 7
что опять приводит к равенству (96).
Теперь следует остановиться на следствиях из равенства (96), на различных сторонах этого явления „резонанса".
Для этого обратимся к тому численному примеру, который мы рассматривали в § 24.
Мы из него видели, что напряжения на отдельных участках могут значительно превосходить все напряжение в цепи — такова особенность явлений в цепи переменного тока.
Посмотрим, что будет, если мы, оставляя Напряжение V неизменно равным 304 -вольтам, будем увеличивать самоиндукцию в цепи (например заменяя одну катушку другой или вдвигая в них железные сердечники и т. п.) до того, чтобы наступил резонанс напряжений.
В примере —=160 омам, так что для резонанса должно быть и 0)1=160 омам, и следовательно £ = 0,5 генри.
94
Тогда у 304
J — — — -17- — 30,4 ампера, R 1 и
а напряжения будут:
К = V_ = 160*30,4— 4 864 вольта!
Мы вычислили действующие значения напряжений на емкости и на самоиндукции, т. е. на конденсаторе и на катушке, а амплитуды будут- в 2 раз больше.
Эти два напряжения достигают на £ и С своих амплитуд и других равных значений в одно и то же время, тольк - направления их в цепи всегда прямо противоположны (проекции на линию времени векторов OD и ОН на фиг. 39 при равенстве величин OD и ОН)\ например на схеме фиг. 40. в тот момент, когда потенциал точки b оказывается выше потенциал точки с на 3 00Q вольт, на столько же выше потенциала точки с и потенциал точки d\ точка же d имеет тот же потенциал, что и зажим В (мы ведь считаем сопротивление между В и d равным нулю), следовательно зажим или конец b вагп ого сопротивления R{ab) всегда имеет тот же потенциал, что и зажим В, другой же конец а ваттного сопротивления R имеет очевидно тот же потенциал вЬ всякий момент, что и зажим А. Таким образом сопротивление ab и R подключено к напряжению V на зажимах АВ Кроме того имеется точка с, потенциал которой то становится ниже на тысячи вольт, чем потенциал b или В, то выше на такие же величины Вольтметры В2 и В3 эти напряжения покажут (действующие их значения , а вольтметр ж главный" В4 их совсем никак не отметит и покажет только JR
Эти отдельные напряжения могут быть и опасны, например конденсатор может не выдержать напряжения около пяти тысяч вольт, и диэлектрик его может быть пробит искрой, так же как и изоляция в катушке самоиндукции.
Таким образом, включая эти приборы в цепь с напряжением, для них не опасным (в примере 304 вольта), не подсчитав заранее частичных напряжений, не посмотрев, не имеет ли места соотношение (96), можно как раз получить случайно резонанс, причем высокими частичными напряжениями могут быть пробиты и испорчены включенные приборы При включении в цепь переменного тока емкости и самоиндукции нужно поэтому предварительно проверять возможность резонанса по ф-ле (96).
Может быть еще и следующий случай.
Пусть в нашем примере изменится R и станет вместо десяти равным одному ому. Пока резонанса не было, сила тока при изменившемся R была следующая:
304
J=—— .. .. ^2 5 амперам;
у Р + (100 — 160)2
95
сильное изменение — с десяти до одного ома — ваттного сопротивления не привело к заметному изменению силы тока, что является следствием того, что безваттное сопротивление осталось прежним и что оно велико в сравнении с ваттным.
Пусть теперь при изменившемся R наступит резонанс; тогда сила тока будет:
304
J = —р=304 ампера!
Смотря по обстоятельствам, может быть тот или иной вред от неожиданно большой силы тока; всего легче может попортиться от нагрева изоляция и быть затем пробита большим частичным напряжением, которое теперь, при уменьшенном R и увеличенном V, будет:
Vk= Vc = o)LJ= 160-304 = 48 640 вольт!
Само собой разумеется, что можно получать произвольно резонанс напряжений в цепи переменного тока, подсчитав предварительно, какое напряжение V к ней надо приложить и какую силу тока установить в цепи, чтобы частичные напряжения при резонансе и сила тока не были опасны; можно соответствующим абра-зом подбирать и самые величины L и С.
Теперь следует сказать несколько слов о смысле самого названия описанного явления—„резонанс напряжений".
Мы уже раньше условились отвлечься пока от потерь на гистерезис (перемагничивание) в магнитном поле переменного тока и считать, что вся средняя мощность Р идет на нагрев сопротивления R
Разберем следующий абстрактный случай, к которому однако мы практически очень близко можем подойти.
Пусть R = 0; тогда
и при резонансе У
J= — = oo. (А)
Последнее выражение показывает, что при отсутствии в цепи ваттного сопротивления достаточно самого небольшого напряжения, чтобы в случае резонанса вызвать ток бесконечно большой силы.
Отделив провода аА и dB от зажимов Л и В и соединив их, эти провода, друг с другом, мы делаем все напряжение У, приложенное к а — d, равным нулю, и тОгда получается из (А) сила , 0
тока J=—, что представляет неопределенность; значит сила тока
может иметь разную величину.
96
Объяснение мы найдем в следующем.
Присоединим конденсатор С к зажимам некоторого источника постоянного тока, например аккумуляторной батареи, на короткое время; конденсатор зарядится; при этом в нем запасется электрическая энергия; затем отделим конденсатор от батареи, вставим его на место между b и с и провода аА и dB соединим друг с другом; конденсатор теперь окажется замкнутым через ваттное сопротивление R и самоиндукцию L и будет разряжаться. В том случае, о котором мы условились выше перед ф-лой (А), т. е. когда /? = 0, разряд будет колебательным. Дальше, в § 113, посвященном разряду конденсаторов, мы разберем теорию этого явления подробнее, пока же ограничимся лишь самым существенным.
Условием существования колебательного разряда является выполнение неравенства
что в нашем случае очевидно имеет место, так как мы приняли /? = 0. Колебательный разряд состоит в том, что конденсатор, разрядившись до напряжения, равного нулю, тотчас же уже сам собой заряжается до прежнего напряжения, однако в направлении, противоположном прежнему, обкладка, которая была раньше „плюсом", теперь станет „минусом" и наоборот, после чего опять разряжается и затем заряжается в первоначальном направлении. При таком разряде все время происходят превращения энергии из электрической в магнитную и обратно. Когда конденсатор заряжен в том или ином направлении до полного напряжения вся
энергия цепи есть энергия в нем
V? С
П =
9 2 .
по ф-ле (87); когда напряжение на обкладках нуль, тогда сила тока в цепи максимум, — вывод этого мы увидим при изложении теории разряда конденсатора, — и вся энергия Пэ теперь превратилась в энергию магнитного поля
по ф-ле (66). В в виде суммы:
промежуточные моменты
Т’
энергия представляется
(В)
Т
равной каждому из предыдущих выражений энергии. Наложим фиг. 38 на фиг. 28; запасенная за время Oq в магнитном поле энергия, равная площади кривой над (фиг. 28), затем начи-
7 Теория переменных токов. 97
нает возвращаться в цепь в течение времени qr, но в цепи она идет вся в конденсатор, — площадь кривой р2 = vki над qr (фиг. 38). Так как /? = 0 и траты энергии на джаулев эффект в цепи нет, то количество ее постоянно, распределение же ее между электрическим и магнитным полями изменяется по ф-ле (В). Равенство П9 и /7М нетрудно доказать. Так как у нас имеется резонанс, то
умножая на Jmt получим:
(D) т соС
что впрочем следовало и из известного уже нам равенства векторов напряжений:
— или — К .
ст кт ст кт
Преобразуем одно из выражений энергии, например П9, следующим образом:
V*C (^LJm)2C
rj __ кт ___ ст ____4 т*
9 ~ ~1Г ~ 2
подставляя сюда выражение для С из условия резонанса (ф-ла Q, получаем окончательно:
Здесь однако можно возразить следующее: так как источника— генератора — переменного тока больше нет в цепи, то как можно говорить о выполнений условия резонанса (С), где входит величина 2тг „=-?
Как определяется теперь Г?
Упомянутая уже нами изложенная ниже теория разряда конденсатора дает выражение для периода колебательного разряда, периода возникающего при нем переменного тока в цепи конденсатора, именно следующее:
7'=2п/Щ
откуда тотчас же получается:
2тг со = — —- ——.
Т Vlc
т. е. соотношение (97), а отсюда сейчас же имеем соотношение (С) или (96). Случай, когда R не равно нулю и когда при колеба-тельном разряде происходит за каждые полпериода трата энергии
98
(98)
1
на нагревание проводов, мы сейчас разбирать не будем и отнесем разбор его к изложению всей теории разряда в § 113.
Какая же сила тока будет в рассматриваемом случае разряда? Так как
^9 — П# то
_VlmC 2 2
И
7» (99)
и действующее значение силы тока
J=v -\/"ё-
Vftm у 2L'
Не забудем, что здесь Vkm есть амплитуды напряжения на конденсаторе, равные тому напряжению, которое первоначально было на eiо обкладках, равные следовательно напряжению постоянного тока (аккумуляторной батареи) при заряде конденсатора.
V
Теперь возвратимся к формуле (A) J = — == оо и замечанию, следующему за ней.
Пусть при /? = 0 и колебательном разряде в цепи действует какая-нибудь переменная ЭДС, например индукции, в одном из соединительных в схеме проводников, хотя бы и очень незначительной величины. При отсутствии траты энергии на нагрев проводника колебательный разряд продолжается до бесконечности; если эта ЭДС имеет период, в точности совпадающий с периодом переменного тока при разряде [ф-ла (133)], то она все время своим действием будет усиливать силу тока в цепи и увеличивать при этом запас энергии в полях .цепи. Через бесконечно большой промежуток времени сила тока возрастет до бесконечности. Такой случай имеет себе механическую аналогию в явления раскачивания до очень большой амплитуды колебания тяжелого маятника легкими толчками, следующими в такт за качаниями маятника,— толчками, разделенными друг от друга одинаковыми промежутками времени, равными половине периода качания маятника, если толчки следуют попеременно то в одну, то в другую сторону, или же целом > периоду при одинаковом направлении всех толчков. Подобные явления известны и из акустики и носят везде название резонанса. Поэтому и вышеописанному явлению переменного тока в цепи с дано название резонанса, и именно — жрезо-
о)С нанса напряжений".
7* 99
Достаточно немного изменить частоту припоженного к цепи внешнего напряжения К, как равенство *96) уже не будет имет.ь места, и сила тока очень сильно уменьшится.
В общем случае, когда цепь обладает и ваттным сопротивлением /?, а сила’тока определяется ф-лой (91), это уменьшение силы тока будет разное при разных /?, что можно обнаружить аналитически следующим образом.
Возьмем производную от J по о) [ф-ла (91)]:
Если мы в прямоугольной системе координат абсциссами будем откладывать разные (о (равные 2п/, как известно), а как ординаты будем откладывать J, вычисляемые но ф-ле (91) при постоянных
К L, С и R, то выразит тангенс угла наклона к оси абсцисс du
касательной к кривой J Рассмотрим влияние величины /?
dJ
на величину этого угла. Из выражения для — мы видим, что при данном со и данных К L и С эта производная имеет тем меньшую величину, следовательно касательная и кривая тем положе,
г. . 1 г 1
чем /? больше, и нао орот, при (о = --______ или <оь =— выра-
j/ LC шС
жение для производной обращается в нуль, кривая достигает ма-ксумума и перегиба; при отступлении о г этой величины со изменение в силе тока тем больше, чем меньше в цепи /?, т. е. при малом R в цепи явление резонанса сказывается на силе тока резче — достаточно малого изменения со или частоты, чтобы сила тока изменилась сильно.
Как сказано в начале этого параграфа, резонанс может получиться при изменении любой из ве шчин L, С и / (или при комбинации их изменений); оказывается, что при наличии в цепи R сила тока и частичные напряжения на конденсаторе и на самоиндукции достигают максимума не все одновременно.
Читателю предлагается самому исследовать вопрос математически. Ход рассуждений при этом должен быть таков: пишем выражение силы тока по закону Ома и подставляем его в выражения частичных напряжений, которые получают такой вид:
100
и
где /?0 есть ваттное сопротивление самой той части цепи, где содержится самоиндукция и на зажимах которой мы меряем или исследуем напряжение. Далее уславливаемся, какая величина из трех (L, Си/) переменна, растет от нуля до величин, соответствующих резонансу и далее, — и ищем, когда Vk, Vc и J достигают максимума.
§ 26. Разложение силы тока на ваттную и безваттную составляющие. Проводимости
В предыдущем мы разлагали напряжение (или ЭДС) на две составляющие— ваттную и безваттную; сила тока определялась при этом законом Ома по формуле:
V
J=Z' (А)
где Z обозначало по ное сопротивление, равное ]//?2 -f- А2, 7? — ваттное, а X—безваттное сопротивление, определяемое ф-лой (92).
При расчетах передачи электрической энергии и всех явлений, связанных с ней, удобнее исходить из представления о постоянстве напряжения в сети или у генераторов и оперировать все время с одной величиной этого напряжения при всяких изменениях нагрузки, а потому введено разложение силы тока на ваттную и безваттную составляющие. Пусть на фиг. 43 вектор ОК есть напряжение, вектор ОА есть сила тока; разложим последний вектор на составляющие ОВ — по направлению ОК и ОС — по перпендикулярному к ОК направлению. Составляющая ОВ называется ваттной составляющей силы тока, а ОС—безваттной. Обозначим первую через JB, а вторую через /бв.
Аналогично тому, что ваттная составляющая всего напряжения V равняется произведению всей силы тока на ваттное сопротивление J7?, мы выразим теперь ваттную составляющую силы тока JB произведением всего напряжения на некоторый множитель^, который назовем ваттной проводимостью
4= (100)
Аналогично же безваттной составляющей напряжения JX выразим безваттную составляющую
силы тока при помощи безваттной проводимости Ь так:
(Ю1)
101
Фиг 43
Так как из фиг. 43 следует, что
то, подставив сюда ф-лы (100) и (101), имеем: /= = УУ.
(102)
Здесь Y мы назовем полной проводимостью данного участка цепи.
Сравнив ф-лу (102) с ф-лой (А), мы видим, что
(103)
т. е. что полная проводимость есть величина, обратная полному сопротивлению, аналогично этим величинам в учении о постоянном токе.
За единицу проводимости принята полная проводимость проводника, полное сопротивление которого равно одному ому. Эту единицу проводимости иногда обозначают словом „мо“.
Следует особенно заметить, что ваттная проводимость и ваттное сопротивление не являются величинами друг другу обратными, тоже и безваттные проводимость и сопротивление.
Из фиг. 43 имеем:
Je = Jcos<pe, или на основании второй из ф-л (25): J —1 Я • //?24-Х2
и, заменяя J по закону Ома: j — у___________________________—____
в /?2-|-X2,
Сравнивая последнее выражение с ф-лой (100), видим, что
ё~Xi==Z*' <104)
Таково выражение ваттной проводимости через сопротивления ваттное и безваттное.
Аналогично, на основании фиг. 43, первой из ф-л (25) и закона Ома, z т • v Х т/ х
J.^=J sin = -7-”—г1 = • -у== = V-----------;
68 т" + /?2-|-х2
102
сравнивая это с ф-лой (101), получаем выражение безваттной про-
водимости через сопротивления
ь /?24-хг z2‘
(105)
Разделив на фиг. 44 все стороны треугольника ОАВ на V, мы получим треугольник проводимостей, с гипотенузой Y и катетами О и В, фиг. 44, подобный треугольнику сопротивлений, фиг. 15.
Из ф-л (104) и (105) можно, наоборот, выразить сопротивления через проводимости:
R=gZ^=^-, (106)
X = bZ^-^. (107)
Перейдем к мощности:
Р = VJcos^= VJB. (108)
Мощность переменного тока зависит таким образом при данном V только от JB, но не от всего J и следовательно не от /бв, почему JB, составляющая силы тока, совпадающая в фазе с напряжением, и называется ваттной, а Убв, имеющая разность фаз в четверть периода (на фиг. 43 /бв отстает, но ясно, что если в цепи емкостный эффект больше индукционного, то /бв будет опережать напряжение на четверть периода), — безваттной.
Подставляя в ф-лу (108) ф-лу (100), получаем:
P=V*g. (109)
Подставив сюда вместо g его выражение (104), получим уже известную ф-лу (69), с тем обобщением, что X определяется ужё ф-лой (92).
В дальнейшем читатель будет иметь случай
менении понятий о проводимостях и о разложении тока к различным примерам.
В заключение заметим, что понятие о безваттной составляющей силы тока, или просто „безваттном токе", является понятием чисто формальным, под которое не нужно подводить определенного физического содержания или обоснования сверх, того, что заключается в ф-ле (108): p=VJ,
упражняться в при-
т. е. что мощность можно выразить произведением всего напряжения на часть тока. Это выражение и это разложение тока
103
есть лишь прием расчета. Физически всякий ток в проводнике есть ток ваттный, так как при всяком гоке развивается тепло в проводнике, причем мощность, переходящая в тепло, выражается так*
р=^=(^+-/б2в)я
Физически ваттно или безваттно — напряжение, для расчетов же мы множитель coscp в ф-ле (108) относим не к IZ, а к J.
Заметим, что аналогично треугольникам сопротивлений, фиг.—15 и проводимостей — фиг. 44, мы можем построить прямоугольный треугольник мощностей с гипотенузой JV (кажущаяся мощность) и катетамм JV cos ср (действительная мощность) и JV sin ср (реактивная или безваттная мощность). Последняя величина служит выражением базваттной нагрузки сети.
ГЛАВА VI
МЕТОД КОМПЛЕКСНЫХ ВЕЛИЧИН ИЛИ СИМВОЛИЧЕСКИЙ
§ 27. Основные понятия
Векторные диаграммы дают очень наглядное представление о соотношениях между различными величинами в цепи переменного тока, — соотношениях, существующих при данной нагрузке или вообще при каких-нибудь определенных условиях, для случая выполнения которых и построена диаграмма, но, чтобы найти численные значения тех или иных величин, нужно векторную диаграмму чертить в подходящем масштабе с достаточной точностью и для новых условий чертить ее вновь. Это требует много времени, что еще важнее, часто случается, что нельзя и построить чертеж, когда неизвестным является какой-нибудь особый элемент диаграммы. Все это заставляет искать особого алгебраического метода, позволяющего геометрические соотношения на диаграмме выразить алгебраически, т. е. в общей форме, охватывающей все частные случаи данной диаграммы, чтобы затем из алгебраических формул и уравнений вычислять искомые величины в разных частных случаях. Алгебраический метод может быть поле* зен и для нахождения геометрических мест концов тех или иных векторов когда соотношения на чертеже сложны. Самым удобным методом приложения алгебры к векторным диаграммам является нижеследующий.
Всякий вектор начерченный на плоскости, может быть разложен на дви составляющие его вектора по двум произвольным осям, причем разложение это лишено всякого физического характера или смысла — это просто операция с прямолинейным о резком на чертеже; если и вестны эти составляющие, то известны и величина и направление вектора.
Поэтому надо ввесги в теорию явлений переменного тока понятие о векторе как геометрической сумме двух составляющих его по некоторым осям, одним и тем же, постоянным дня всех рассма
105
триваемых, входящих в соотношения векторов; тогда путем чисто алгебраических операций над этими составляющими всех векторов можно будет получать величины неизвестных составляющих, а вместе с тем величины и направления неизвестных векторов.
То обстоятельство, что надо ввести ческую сумму, заставляет прибегнуть
в вычисления геометри-к какому-нибудь искусственному сгГособу обозначения или различения составляющих по двум различным осям. Яснее все это представится при изложении самого метода
Пусть нам дан какой-__нибудь вектор ОМ (фиг. 45), величину которого обозначим через А. Проведем через его начало О как через начало координат две взаимно перпендикулярные оси, одну вертикальную — О Y и другую горизонтальную — ОХ.
Начертим затем векторы ОМ2 и ОЛ43,
по величине равные первому, но повернутые относительно его „ тс 3
против движения часовой стрелки на углы — , тс и — тс соот-£
ветственно (или по движению ее на углы, следующие в обратном порядке).
Спрашивается, нельзя ли найти такой алгебраический множитель, чтобы можно было умножением на него вектора повернуть последний в положение, перпендикулярное прежнему, т. е. повер-
тс
нуть на угол —, л
например против движения часовой стрелки.
Допустим, что такой множитель есть; обозначим его через 1. Тогда по определению этого множителя вектор ОМ2 = вектору ОМ -X-
Заменим здесь слова „вектор*, которые указывают на определенную направленность отрезков ОМг и ОМ, особым знаком,— чертой над буквами, обозначающими вектор. Таким образом ОМ означает „вектор ОМ“, а ОМ без черты означает только длину отрезка ОМ.
Итак __ _____
ОМ^ОМЛ.
106
Но по тому же определению к как множителя, п о в о р а ч и-тг
в а ю щ е г о вектор на угол — против движения часовой стрелки, имеем
OAf^OAf^k.
Подставляя вместо OAf, его предыдущее выражение, получаем: ОА?2 = О7ЙЛ2.
В конце предыдущего параграфа мы установили, что вычесть какой-нибудь вектор — значит прибавить вектор той же длины, но прямопротивоположный, следовательно во всех вычислениях надо полагать:
— бМ = ^ОМ2.
Мы имеем для ОМ2 два выражения, они дают нам
— 0М = 0М-1*
или
откуда
V = —1, х==±/^Т.
В дальнейшем будем V—1 обозначать буквой / Остановимся пока на положительном корне:
Х = +/.
Итак ____
OAf^-f-y-OAf; (а)
— ОМ. (Ь)
Очевидно и ____ _________ _______
OAf3=+/. ОМ2 = — ОМ19 (с)
но можно написать и так на основании (Ь):
ОМ3— + у • ОМ2= —J-ОМ.
Вектор ОМ3 перпендикулярен к OAf, но сдвинут относительно
вектора ОМ на
не против, а по движению часовой стрелки.
Такой поворот на прямой угол выражается алгебраически, как видим, умножением на (—У).
Итак умножение любого вектора на выражает поворот его
п
на — против &
движения, а на — j по движению часовой
стрелки.
107
Однако можно было с самого начала искать множитель, nosopi-чивающий вектор ОМ в положение ОМ3, и мы, проделав те же самые рассуждения, тоже нашли бы -4-/ как ответ; таким образом является условным — с поворотом в какую сторону соединить умножение на +/ и — в какую сторону — умножение на —/. В этом и заключается смысл двух знаков у ]/ —1, когда мы находили 1
Мы остановимся на вышеприведенном первом варианте.
Обратимся к разложению вектора ОМ на два составляющие вектора. Прежде всего-можем написать:
ОМ =
Пусть длина CW=10 и длина ОР—5. Спрашивается, как написать последнее равенство, перейдя к числовым значениям векторов.
Возьмем отрезок OQ, по величине равный ОР, а по направлению вертикальный Очевидно, что
Если один из этих двух векторов мы сочтем или сделаем величиной действительной, то другой будет мнимой и наоборот. Пусть
OQ==4-5, тогда
ОР = 4-/.5.
Так как ON —10, то
ОМ = 02V-J-‘dP= 10 +/. 5.
При таком написании формулы разложения вектора на два составляющие его вектора, направленные по двум осям, нельзя смешать эти компоненты. Для дальнейшего нужно условиться, какое направление из двух или четырех ОУ, ОХ, ОУг и ОХг считать основным, а остальные считать полученными из него путем поворота.
Примем за такое основнсе направление OY верхнюю половину вертикальной оси.
Компоненты по оси OY бужм представлять действительными числами, например:
ON=10,
где над буквами ON помещаем черту, чтобы показать, что речь идет не о величине, а о направленном отрезке.
Компоненты по горизонтальной оси выразятся при этом мнимыми числами, например:
OP = -\-j. 5.
108
Вниз от О по вертикальной оси будут откладываться компоненты действительные — отрицательные и вправо О по горизонтальной оси — мнимые — отрицательные. Таким образом:
ОМ = 10 Ц-/.5,
ОМг = 4-/.олГ= — 5 -]-/• ю, где
0ЛЛ1 = +7 10 и = —5;
67и2 = 4-7.0^ = — ом =—1о —/.5, и
ОМ3=5 — /10.
§ 28. Символическое обозначение векторов и действия с ними
Величину вектора ОМ (фиг 45) мы обозначили через А; обозначим величину или длину каждого из его составляющих какой-нибудь одной буквой, например так:
ON—m и ОР = п.
Можно и самый вектор обозначить одной той же, которой обозначили его величину, нос
0М = А\ тогда
А — т /я, далее очевидно
ОМг — -[-jA — — и /ю;
ОМ2 = — А = — т —jn и
ОМ3 — — jA =п — jm.
Сделаем в ф-ле (I) такое преобразование:
буквой, например чертой наверху:
(I)
Из чертежа фиг. 46 видно, что т п
— = и —=sinj, А А
где а есть угол вектора А с вертикальной осью. Тогда
А — A (cos a -j- j sin а)
109
Фиг. 46.
(П)
В анализе доказывается теорема, принадлежащая Эйлеру, которая дает нам следующее равенство, связывающее триюнометрические функции с показательными:
cos а sin а = е “ •
Поэтому _
Д = (III)
Такое выражение вектора будем называть „символическим". Величина А вектора А называется его модулем, а угол а — его аргументом.
Заметим, что угол а для первого вектора, с которого мы начинаем строить какую-нибудь векторную диаграмму, произволен; он зависит от того, как мы на чертеже направим оси координат или как направим первый вектор.
Рассмотрим различные математические операции с комплексами, выражающими векторы, и исследуем геометрический смысл результатов этих операций.
Пусть даны два вектора А = -|-/Л2 и В = Вг /В2; сложим
их геометрически, что алгебраически выразим так:
А + В = А, +/Л2 + В, +/В8 = (Л! 4- Bj) +7 (А3 + Ва).
Результатом сложения является новый вектор с составляющими по горизонтальной оси A2-j-B2 и по вертикальной оси Длина нового вектора равна:
Ко-ч+вр’+с^+в,)*, направление его определяется тангенсом угла его с вертикальной осью:
__Л2 -|- В2
Ai ’
Этот результат можно обобщить на какое угодно число слагаемых векторов, а также и на случаи вычитания одного вектора из другого. Ввиду элементарности этого вопроса мы на нем долее не останавливаемся. Переходим к умножению.
Умножим вектор А на вещественную величину т:
mA = шАг 4“/^Л2;
результат представляет новый вектор того же направления, что и прежний, так как тангенс угла его наклона к вертикальной оси равен
110
длина же нового вектора равна (тАг)2 (тА2)2 = т-УА2-\- А2 = mA,
в т раз больше длины прежнего.
Тот же результат получается скорее, если применить символическое обозначение вектора:
А = А&к, mA = тАе\ откуда сразу видно, что аргумент, т. е. направление вектора, не изменилось, а длина его увеличилась в т раз.
В дальнейшем нам придется множить и делить векторы на комплексы.
Пусть даны вектор
А == Ае^
и какой-то комплекс, о физическом значении которого в различных случаях мы скоро узнаем:
Требуется умножить или разделить вектор на этот комплекс.
Придадим ему прежде всего форму, аналогичную с формой выражения вектора
* — К*2 +.У2 f ~7 4~ / —=- ----Л =
1 1 \]/x2-hJ2 У *2+.У2/
= и (cos ср-[-/sin <р), где
<P = arctg-£, так что
х • У
COS ср = - и S1H ф = г ' .
]/*2+>2 У&-^у2
Окончательно
x-^jy = ue^ — и.
Далее
А • и = А • ei* • и • = (Au)e^a+?).
Таким образом получился новый вектор, величина которого в и раз больше величины первоначального вектора А, и направление его составляет с вертикальной осью угол а -1- ср, т. е. оно отклонено от прежнего на угол ср.
Если <р > 0, то отклонен новый вектор в сторону против движения часовой стрелки, так как a-j-cp>a. Если ф<0, то ® 4~ <р < а, и отклонение произошло п о часовой стрелке.
111
Рассмотрим деление:
А :и =
Ае* А „ . ____ —_____ £/(«-ф) ие^ и
Величина нового вектора в и раз меньше величины первоначального вектора, и с вертикальной осью он с ставлчет угол а — ср, так что по нап авлению он отклонен обратно, сравнительно с предыдущим случаем умножения, а именно если <р>0, ю по часовой стрелке, так как а — <р < а, и если <р > О, то против часовой стрелки, так как а — <р>*а
До сих пор мы вектором называли прямолинейный отрезок, представляющий ту и пи иную синусоидально меняющуюся с течением времени величину; мы проектировали иногда вектор на вращающуюся линию времени и получали мгновенное значение этой величины. Назовем эти векторы векторами первого рода. Как увидим далее, полные сопротивления и проводимости удобно буде! представлять в виде комплексных чисел; эти комплексные величины мы тоже будем изображать прямолинейными отрезками, например комплекс и — х jy мы представим отрезком, имеющим компонент по вертикальной оси X и по мнимой К. Такие отрезки мы назовем векторами второго рода; они представляют постоянные величины, и проектировать их на линию времени не имеет смысла.
Если мы умножим вектор А на комп пеке, у которого модуль равен единице, т. е. на комплекс
"Т /ф
е~ = cos ср ±/sin ср = £ ±/т),
то величина вектора не изменится, а изменится лишь его направление, — его угол с вертикальной осью, — на величину угла ± ср. Мы будем такой комплексный множитель называть поворачивающим множителем.
Когда этот множитель дан в виде Е±/т] мы будем говорить, что он дан в раскрытой форме; когда же он дан в виде мы будем говорить о символической форме.
Пример 14. Дан множитель
1 . 1
У~2 ’
требуется узнать, изменит ли он величину вектора и на какой угол повернет его
Так как модуль его равен /(>>'• то это только поворачивающий множитель.
112
Угол поворота равен:
arc tg (~L=:: -~=Л = аге tg 1 = 4- 45°; \у 2 /2/
поворот происходит в сторону против движения часовой стрелки; множитель можно представить в символической форме, как е^45°
1 , . 1 /45°
-=+/ = е •
у 2 V 2
Пример 15. Дан множитель
__ J__ У 3 .
2 ' 2 ’
узнать, есть ли это только поворачивающий множитель и на какой угол он поворачивает вектор.
Модуль его равен
поэтому множитель есть только поворачивающий.
Угол поворота поворачивающего множителя\удобнее всего определять не по тангенсу, как мы сделали в предыдущем примере, а строя вектор, изображающий этот множитель, т. е. откладывая его компоненты по осям. Эту операцию следует приучаться производить мысленно, воображая оси и отрезки на них без помощи карандаша и бумаги
Так как в данном примере оба компонента отрицательны, то вектор находится в правом нижнем квадранте, угол ? поворота отрицателен и равен —
Отложив компоненты, мы видим, что 3 = 30°, ? = — 120°= — -х-. Пово-«5
рот происходит по вращению часовой стрелки на угол 120°.
Таким образом:
Г— i2K
1 Vз
~г-' —= е
Примеры. Определить, является ли множитель и только поворачивающим и на какой угол в следующих случаях:
16)“=FT_JVT’ 17’“=4+'т^ 18>
Примеры. Перевести из символической в раскрытую форму множители
19) е+} s’, 20) 2, 21)/", 22) е~^* , 23) /75°, 24)
Пример 25. В цепи переменного тока при индукционной нагрузке приборы дают следующие показания:
вольтметр —120 вольт,
амперметр — 20 ампер,
киловаттметр —1,68 киловатта.
Для введения напряжения и силы тока в некоторые расчеты требуется придать им комплексную форму выражения.
& Теория переменных токов. 113
Прежде всего определяем косинус угла сдвига фаз между напряжением V и силой тока J: так как мощность Р = 1,68 киловатта = 1 680 ватт, то
1 680 Л7
C0S 7 == 12JT20 = °’7-
Из таблиц находим угол у:
? = arc cos 0,7 = 45°35F.
Вектор напряжения, если нет других условий, вытекающих из данных задачи, подлежащей решению, расчету, можно направить по вертикальной оси и положить _
У= V= 120 вольт.
Сила тока 7 отстает от Уна?, лежит в правом верхнем квадранте, поэтому
7= 20е “'45°35'.
§ 29. Простейшие примеры приложений метода
Приложим теперь изложенные правила обозначений векторов и комплексов и действий над ними к действиям над векторами величин в цепи переменного тока.
На фиг. 47а отрезок О А есть вектор силы тока, OA—J. Выразим вектор ЭДС'самоиндукции ОС = Ес с помощью J через 7 Известно, что величина ЭДС самоиндукции
£c = G)AJ. (ПО)
Вектор ОС9 — uLJ по величине равен вектору ЭДС самоиндукции, но по направлению не совпадает с ним, так как вектор (oLJ получается от умножения вектора J на действительную величину <oL, а
потому совпадает по направлению с J. Вектор
тг сдвинут на —
в сторону вращения линии времени, поэтому если мы вектор (oLJ умножим на —у, то как раз и получим вектор Ez. Итак
£с=—Л/J, (111)
114
или
E=-jXJ.
Перейдем к току через конденсатор.
Как известно, сила тока через конденсатор и напряжение на нем связаны соотношением их величин:
Jk=*>CVk л К
и соотношением фаз: вектор силы тока опережает на вектор
напряжения. Вектор ®CVk (фиг. 476) совпадает по направлению с вектором умножим его на 4~7» и мы получим вектор силы
тока
или
или еще удобнее
(112)
где bk есть величина безваттной проводимости самого конденсатора.
Вспомним, что мы безваттное сопротивление обозначаем буквой X с индексом „с“ при самоиндукции, с индексом k — при емкости и без индекса — в общем случае.
Известно, что вектор напряжения V на участке, содержащем ваттное сопротивление /? и безваттное Хс, можно разложить на два составляющих: один, равный по величине и совпадающий в фазе с током, т. е. того же направления, — обозначим его согласно предыдущему — и другой — противоположный и равный по величине ЭДС самоиндукции £с,— мы его обозначим (ф-ла 111):
Таким образом
V = /?7 +/лгс7= (7? +/Л-С)7. (113)
Мы видим, что вектор силы тока надо помножить на комплекс Z[=/?-^jXc, (114)
чтобы получить вектор напряжения. Так как модуль этого комплекса
Zc = /
есть просто полное сопротивление участка цепи, то и весь комплекс Z мы назовем полным сопротивлением и представим отрезком из О длины Z, направленным под углом
Л
(р = arc tg
115
впево к вертикальной оси. Таким образом мы ввели в наши методы представление сопротивления посредством прямолинейного отрезка определенной длины и направления.
На фиг. 43 нами была разложена сила тока J на две составляющие: Vg и J6B—Vb. Выразим теперь соотношения в этом
случае при помощи изложенного метода. JB совпадает в фазе с V, поэтому (мы предположим для общности результатов, что вектор напряжения не совпадает с вертикальной осью)
тг
7бв отстает в фазе от V на —; поэтому
J6B=-JVb.
Далее, вектор силы тока J есть геометрическая сумма этих двух составляющих; поэтому
4+тбв = Vg-jVb=(g-jb) V.
Здесь сила тока получается от умножения напряжения на комплекс
Y=g-jb, (115)
который есть полная проводимость. Ее мы теперь тоже представим отрезком длиной r_y g' + P,
проведенным из О под углом
. / Ь\
ср = arc tg I-I
\ /
к вертикальной оси.
Полная проводимость участка есть величина обратная полному сопротивлению; следовательно произведение их должно равняться единице; проверим это на выражениях проводимости и сопротивления через комплексы (114) и (115)-
ZY = (/? +JXJ (g-Jb) = gR + bXe +J(gXc - bR).
Подставляя сюда значения g и b из ф-л (104) и (105), получаем: £7? + k¥c=l, gXz — bR = 0 и
Z-Y=l.
Не нужно забывать, что если безваттное сопротивление в цепи будет обусловлено емкостью, то выражение для полного сопротивления будет содержать знак минус'перед мнимым членом
Zk = R-JXk, |
а проводимость выразится }• (116)
Y=g±jb\ '
116
в общем случае, когда в цепи есть и самоиндукция и емкость*, имеем:
Z = R+j\Xz-Xk) = R+JX. (117)
Формулы (115) и (117) можно, согласно предыдущему, напи
сать и так:
Y= Ye*, или
У = + • e~J arc tg ( ? ) >
и _
Z=Z-«A
ИЛИ г. /Хс-Х/Л z= у R2 (лс - Х^ eM(—R~) •
(И8)
Представляя любой вектор ОМ (фиг. 45) выражением
А = Ае^,
мы вводим в показатель у е тот самый угол ф = / MON, который фигурирует как фазовый угол в аналитическом выражении данной синусоидальной функции времени:
а = Ат sin (а)/ 4“ ф) = Ат sin + / MON).
При последовательном соединении нескольких участков с сопротивлениями
Z2 = R2 -|- ]Х2
и т. д.
Полное сопротивление всей цепи выразится как
Z = Zj +Z2+. . .= /?! +^2 +• • •+/(^1 +^2 +• • •)•
Читателю предлагается для упражнения вывести это соотношение из диаграммы фиг. 42 и найти Z и ср в формуле:
Z = Z^,
для того численного примера, который был дан после этой фигуры.
Для вектора ОМ3 (фиг. 45), представляющего, скажем, силу тока, напишем:
где ф есть угол, составляемый вектором ОМ3 с вертикальной осью; но можно здесь и не писать минуса в показателе, если считать ф величиной алгебраической и ^вспомнить, что углы вправо от вертикальной оси мы условились считать отрицательными.
117
§ 30. Замечания о выражении мощности, cos ср, о дифе-ренцировании векторов и о символических обозначениях, отличных от описанных
Следует при пользовании методом комплексных величин помнить, что величина мощности не получается простым перемножением комплексных выражений Е = Е*е^ и J = в таком произве-
дении будет, во-первых, мнимая часть, а во-вторых, чтобы ввесш в действительной части угол между векторами Е и J, а не сумму их фазовых углов, как эго получается из
приходится вводить дополнительные соображения о двойной частоте изменений мгновенной мощности (сравни ф-лу 63) и положить = оставляя в стороне только что написанное выражение произведения через е.
Хотя Штейнмецом подобные векторы мощности и были введены 3) в теорию переменных токов, мы, ввиду того, что пользование ими не несет за собой никаких особых удобств в вычислительных операциях, заниматься ими здесь не будем.
Когда даны напряжение вектором I/=V1-|-/V2 и сила тока вектором J—J14-/V2, то косинус угла между ними определится так:
cos <р = cos (ф^ — ф7) = cos ф^ • cos ф7 -j- sin ф^ • si п ф7=
Ziц_А ,11{П
~ J * V "I J * V ~ JV ’ ' }
Эт? формула имеет еще и тот смысл, что в числителе стоит мощность в нашей цепи, слагающаяся из двух мощностей ^ибо с V2, так же как и J2 с Vv не дают мощности, так как
те \
сдвинуты друг относительно друга на —I, а в знаменателе — так
называемая „кажущаяся" мощность JV.
Разумеется, аналогично мы можем определить косинус угла между двумя любыми векторами, уже не придавая физического смысла действиям с их составляющими, и т. д.
Когда векторы выражены в символической форме
у=Уе1ъ и J = Je^^
то очевидно ср = — <р2 и cos ср = cos (<р2 — <р2).
В дальнейшем, в особенности в главах о длинных линиях передачи, нам встретился необходимость в диференцировании векторов.
Когда нам дан вектор (фиг. 48)
ой=л=л14-/л2> (А)
118
причем оба его компонента являются функциями некоторой переменной х, в векторную диаграмму даже не входящей, то для некоторого значеня этой переменной x-\-dx значения компонентов
будут:
АН" ^1
и
^2 — А 4“ ^2»
и сам вектор л7=Л1'+/д;. (в)
Вычитая (А) из (В), имеем вектор
Д7 — A = dA1+/dA2
с бесконечно-малыми компонентами; этот вектор мы и будем считать диференциалом
вектора А. Итак
dA = dA-i jdA2.
(С)
Производной вектора А по х назовем отношение
dA__dA, , . dA2
— = —-4- /----
dx dx ' dx
Можно выражению диференциала вектора придать и другую форму, чем (С); продиференцируем символическое выражение вектора
А = А * eft, получим
dA = dA • eft-\- j-A- eftdtf. (D)
Здесь диференциал вектора представлен тоже в виде геометрической суммы двух бесконечно-малых векторов, только других, чем в уравнении (С), теперь уже не совпадающих по направлению с осями фиг. 49. Первый вектор dA • eft имеет направление самого вектора А и равен приращению его величины; второй век-Фиг. 49. тор j*A-eftdy имеет величину Д • Лр,
т. е. дуги, на которую повернется конец вектора А при увеличении угла^ср на диференциал tfp, и направлен перпендикулярно к вектору А, что показывает множитель j*eft) в сторону увеличения угла <р.
119
Формула (D) и фиг. 49 справедливы с точностью до бесконечномалых второго порядка.
Из ф-лы (D) легко получить ф-лу (С) выражения диференциала вектора; в самом деле, подставляя в ф-лу (D) вместо его обычное разложение, получаем:
i/Д = zM-coscp— A sin ср • —|— Дб/Х • sin ср -р cos ср • dcp),
что представляет диференциал выражения
A -cos ср +/-Л -sin ср, т. е. выражения
Далее, следует упомянуть, что изредка пользуются еще иначе комплексными выражениями, именно операции с мгновенным значением синусоидальной величины
a = 71-sin (о)/-}"?) заменяют операциями с выражением
Д = Л-е7(ш''+<р). (120)
Это выражение разлагается в такое:
A — A-[cos (со/ + ср) -|-/sin (со/ Ц- ср)]. (М)
Формуле (Aty можно дать следующее простое геометрическое толкование
Отложив по оси .ординат вверх A cos (со/ 4~ Т), а по оси абсцисс влево A sin (со/ -|- ср), мы получим из этих двух составляющих вектор, величина которого очевидно есть А, а угол с вертикалью ф = Ы 4” ср изменяется пропорционально времени Таким образом формула (М) представляет вращающийся против часовой стрелки вектор А.
Линию времени мы должны теперь считать неподвижно й, иначе период изменений величины а был бы иной, чем нужно.
Полагая линию времени совпадающей например с вертикальной осью, мы вводим в наши расчеты функцию Л cos (о)/-|“ ?)•
Возьмем производную от функции а по t.
— = jwAe = о)Д[/ cos (ш/ + ср) — sin (со/ 4~ ср)].
То же самое конечно получим диференцированием формулы (М).
Для изображения этой функции, вектором надо вниз отложить &А sin (со/ -|“ <р) и влево соД cos (со/4" ?)>’ величина вектора есть соД,
он составляет с вертикалью угол ф' = о/ 4“ 4" тг» т- е- опере-
120
жает вектор величины а на —. Величина ( — —- I будет оче*
А у (It J
п
видно отставать от А на — ; все соотношения получаются таким &
образом совершенно такими же, как мы имели их раньше.
При выкладках не нужно и переходить к тригонометрической форме, так как оперирование с показательной функцией много ускоряет дело.
Иногда употребляют такой прием: когда после различных преобразований мы получаем какую-либо окончательную формулу, ее можно опять написать с помощью тригонометрических функций, просто отбросив в разложении показательной функции мнимую часть.
Пусть например т. е.
Z== J.cos (со/),
если мы отбросим мнимую часть, ЭДС самоиндукции выразится так* с at at
или
ez == —
с таким выражением мы можем оперировать и дальше. Если же это была бы окончательная наша формула, то мы раскрыли бы ее так:
ez~ — jwLJ • <nt -|- J sin wf) =
= w£J(sin co/ — i cos co/), или
£c = o)Z,7 • sin co£ — wZJcos( (о/— V )• \ £ /
Последнее выражение мы написали лишь для уяснения того, что получается правильное соотношение между фазами силы тока I ЭДС самоиндукции ez, вообще же оно ненужно. В последней главе о поверхностном эффекте мы тоже сделаем употребление из этого способа условного, символического обозначения синусоидальных величин.
Выражение мощности и при этом способе не получается без добавочных условий.
121
ГЛАВА УП
СЛОЖНЫЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА
§ 31. Соотношения в синхронном генераторе
Применим изложенный метод к выражению соотношений на диаграмме фиг. 21. Вектор ЭДС Е машины переменного тока распадается на сумму трех векторов: напряжения на зажимах V, падения напряжения в ваттном сопротивлении обмотки машины RwyJ и вектора, противоположного ЭДС самоиндукции в обмотке машины — Ес=/ ^LwyJ =JXwyJ. Таким образом
£=У+(/?вну4-УХвну)Л (А)
или
E=V+ZmyJ.
Пример 26. Проделаем пример на вычисления с комплексными величинами. -
Даны (фиг. 21)/?вну = 0,1 ома, Хвну = <о£вну = 0,3 ома, V= 115 +/-20 вольт. 7= 100+/-30 ампер. Требуется вычислить все остальные величины. Подставляем данные в формулу (А):
115 + /-20 + (0,1 + У-0,3)(100 +/-30) == 116 + /-53 вольт.
Е = V1162 4- 53* & 128 вольт.
У= ]/115* 4- 20* — 116,7 вольта.
J= j/li0*4"30*= 104 ампер.
По формуле (113) V=ZBHe7 следовательно
? —V 1154-/.20
— J 100 + у.зб-1,11 —^’°’22 ° '
Следовательно
/?вне=1Д1 ома, Хвне =— 0,22 ома; значит во внешней цепи имеется емкость, и ее влияние сильнее влияния самоиндукции.
Определить величину емкости нельзя, пока неизвестна величина самоиндукции внешней части цепи.
122
:,-^=0,98.
vx*вне 4“ ^2вне
Далее, имеем: cos =
Сила тока опережает напряжение, что ясно из самих заданий обеих величин.
Полезная мощность
Р, =VJcos = 116,7-104*0,98 =11 894 ватта 11,9 киловатт.
Продолжая вычисления, можно найти cos <ре, всю мощность машины, по* тери в ней и коэфициент полезного действия.
§ 32. Разветвляющиеся цепи
При рассмотрении вопросов о разветвлении токов следует прежде всего помнить, что напряжение на всех ветвях, выходящих из одной общей точки и в другую общую точку сходящихся, одно и то Же и представляется поэтому одним и тем же вектором, какую бы из ветвей мы ни рассматривали; силы же токов отдельных ветвей будут суммироваться геометрически, давая силу тока главного до и после разветвления.
о
Фиг. 51.
При последовательных соединениях различных сопротивлений ваттных и безваттных, которые мы до сих пор исключительно рассматривали, было обратное: мы силу тока и ее вектор принимали для всех участков и сопротивлений одними и теми же и складывали геометрически напряжения.
Пусть мы имеем между точками М и N (фиг. 50) цепи переменного тока две ветви, одна с ваттным сопротивлением и безваттным <о£1, другая только с ваттным сопротивлением /?2; силу тока в первой ветви обозначим через J19 а во второй — через J2.
Напряжение между точками ЛГиЛ^представим вектором OB2=V (фиг. 51). Так как в ветви второй сила тока определится просто, как
123
то V J2R2 и тот же вектор ОВ2 представит нам и J2Rr Разделив его величину на /?2, мы получим в масштабе силы тока вектор
OA2=J2, представляющий силу тока во второй ветви Перейдя к первой ьетви, мы тот же самый вектор V разлагаем
на две составляющих, причем фаза силы тока в первой ветви
, о)Л1 определяется из обычной формулы <p = arctg — строим
угольный треугольник на______гипотенузе ОВ2 с острым
прямо-
углом
В2ОВх = у. Деля катет ОВХ на /?3, получаем силу тока в виде вектора ОАГ В цепи до и «осле разветвлений М и N текут оба тока ОА1 и ОА2, которые, складываясь геометрически, дают результирующую силу тока OA=J.
Заметим, что сдвиг фазы эюй всей силы тока против напряже-
ния V меньше, чем сдвиг фазы силы тока (но больше, чем J2, для которого сдвиг в фазе равен нулю).
Разберем теперь другой случай, имеющий большое значение для практики. На фиг. 52 изображена схема цепи, состоящей из двух длинных проводов, между концами М и N которых включены две ветви, первая — содержащая и L, с силой тока Jv и вторая, содержащая только емкость С; пусть мы можем пренебречь ваттным сопротивлением проводов в этой второй ветви по его малости.
На фиг. 53 построена векторная диаграмма для разветвленияMN. Напряжение V—OK разложено в ветви первой нз две составляющих— 0^=/^ и КВг — при помощи построения прямоугольного треугольника на ОК с острым углом = arc tg —раз-
____
делив ОВХ на получим в масштабе силы тока вектор ОАХ силы тока Для ветви второй нужно построить лишь вектор силы тока J2; он будет перпендикулярен к напряжению (как вектор OA = J перпендикулярен к OD=VK на фиг. 39) и будет опережать на пря-124
мой угол его,— вектор ОА2 есть /2. Теперь, сложив векторы ОА2 и ОА2, мы узнаем силу тока до и после ра ветвлений J, — вектор OD представляег ее. Из того обстоятельства, что к отстающему току О А1 мы прикладываем опережающий напряжение ток ОЛ2, следует, что результирующая сила тока будет сдвинута в фазе или на меньший угол, чем ср3, если и J будет отставать от У, или на угол, мог щий принимать разные значения, если J будет опережать напряжение. Сила тока J2 определяется ьедь по известной фопмуле:
/2=У(оС,
и стоит только выбрать емкость С достаточно большой, чтобы A2D = J2 было например больше AyDA и точка /Показалась влево от линии ОК, т. е. чтобы вектор OD опережал напряжение. При соотношениях, как на фиг 53, главный ток OD имеет меньший сдвиг фаз, чем ток Jv и меньшую величину, чем оба тока в ветвях.
Подобрав * одходящую величину емкости, мы получим для J2 вектор ОА'2 и для главного тока вектор OD^—J, совпадающий в фазе с напряжением V. В этом случае главный ток J имеет наименьшую величину при данных /?3 и А3. Это явление мы назовем компенсацией сдвига фаз. Влиянием емкости в одной ветви мы компенсируем влияние самоиндукции в другой.
Чтобы получить напряжение в начале проводов, надо к вектору ОК приложить вектор ^/?пров,— где 7?пров означает сопротивление проводов, — который совпадает в фазе с вектором ОК в том случае, когда ток представляется вектором ODV Если самоиндукция проводов значигелгна, легко и ее принять в расчет, прибавив вектор со/ пров J, перпендикулярный к OK (L пров есть самоиндукция проводов).
§ 33. Значение компенсации сдвига фаз
При достижении минимального значения главного тока, — причем мощность в ветви первой и сила тока в ней остаются без изменения (мы меняем ведь только J2f меняя емкость),— достигают наименьшей величины, и потеря напряжения, и потеря энергии в проводах, и в отношении опасности их сильного нагрев <-условия изменяются; раз сила тока J наименьшая, то очевидно и поперечное сечение проводов, подсчитанное на основании допустимою из-за юображений экономических падения напряжения в них и потери энергии, становится наименьшим и следовательно стоимость этих проводов — наименьшей. Таким образом, когда мы имеем на конце двух проводов сильную индукционную нагрузку,— что вызывает большой сдвиг фаз между током и напряжением, малый cos ср и силу тока, большую, чем нужно для
125
получения той же мощности присозср=1,— то подключением параллельно к нагрузке там же на концах проводов подходящей величины емкости можно улучшить cos ср и уменьшить ток в проводах, сделав установку более экономичной со стороны потери энергии на нагрев проводов или со стороны стоимости меди этих
проводов.
Кроме изложенного здесь имеется и еше одна сторона дела, именно экономичность работы самой станции в начале проводов.
Представим себе, что на электрической станции имеется несколько агрегатов, состоящих каждый из двигателя внутреннего сгорания (или паровой машины) и генератора переменного тока. Пусть на конце двух проводов, идущих от станций, подключен ряд приборов, представляющих сильно индукционную нагрузку, со средним cos ср = 0,8, но при некоторых условиях cos ср может доходить до 0,6.
Пусть каждый агрегат на станции имеет напряжение на зажимах в 2 000 вольт и рассчитан на электрическую мощность /\ = = V cos cpw в 800 киловатт, или 800 000 ватт, и именно для cos(pv = 0,8, как это теперь всегда делается при расчете генераторов переменного тока, т. е. обмотка его может выдержать в ——=1,25 раз большую силу тока, чем нужно для полной безиндукционной нагрузки генератсра. В данном случае каждый генератор может выдержать следовательно длительно без опасного
нагрева силу тока J=
р9 Vcostp0
800 000
2 000-0,8
= 500 ампер,
тогда как при cos<p0==l сила тока достигла бы для той же мощ-800 000
ности величины - - = 400 ампер.
ЛUUU•1
Предположим, что нагрузка такова, что cos <р^ = 0,6 при силе тока .7=600 ампер, т. е. мощность, требуемая от генераторов станции, равна:
2 000 *600 *0,6 ватт = 720 киловатт.
Такая мощность меньше мощности одного агрегата, но сила тока в 600 ампер больше, чем предельная длительно допустимая сила тока в 500 ампер для каждого генератора, в 1,2 раза. Если сила тока больше в 1,2 раза, то тепла выделится в обмотке больше в 1,22 = 1,44 раза (по формуле J2R). Такая длительная перегрузка опасна, поэтому придется пускать в ход второй агрегат машин на станции в помощь первому и распределять между ними мощность, которой мало и для одного, с тем, чтобы и сила тока распределилась между ними приблизительно поровну — по 360 киловатт и 300 ампер. При таких малых нагрузках, меньших половины нор
126
мальной, двигатели внутреннего сгорания и .паровые машины работают с плохим коэфиниентом полезного действия, и вся установка,, включая сюда и линию передачи с большими потерями энергии в ней, работает неэкономично.
В практике подобные случаи бывают например с трехфазным током и асинхронными двигателями в виде нагрузки (на заводе или на руднике). Тогда все наши электрические расчеты должны относиться к одной фазе, и при переходе к машинам на станции все мощности должны умножаться на три. Читателю рекомендуется после прочтения главы о трехфазном токе возвратиться к этому примеру и пере-вычислить все величины, исходя из данной мощности агрегата и линейного напряжения.
Если мы включением конденсатора доведем cos ср до единицы и тем уменьшим силу тока в проводах и в генераторе, то коэфи-циент полезного действия всей установки сильно увеличится; в нашем примере с нагрузкой в 720 киловатт и 360 ампер, т. е. в условиях, близких к полной нагрузке, будет работать один агрегат, и при этом потери в линии будут меньше.
Применение конденсаторов для этой цели упрочивается по мере улучшения их конструкции в отношении их прочности и пр. Но чаще в подобных случаях применяют „перевозбужденные" синхронные двигатели. Об них будет сказано в следующей главе.
В последнее время начали применяться также так называемые асинхронные генераторы безваттной мощности.
§ 34. Резонанс токов
Определим величину емкости, необходимой для того, чтобы довести cos ср до единицы.
Из фиг. 53 имеем:
ОА'2 =41D1 = 041*sin<p1, или J2 = ./1*sin (рг
Из Д ОВгК имеем:
Sin ф. = . 1 г=.
Затем имеем два выражения для напряжения V, одно — для одной ветви, другое — для другой, которые и приравниваем
Подставляя сюда выражения для J2 и sin фр получаем после сокращения:
^ = /?12 + (<oL1)2,
127
откуда искомое
Когда величина емкости, подключенной параллельно другой ветви с 7?! и Lv удовлетворяет этому соотношению, говорят, или что мы имеем компенсацию сдвига фаз, или что мы имеем резонанс токов.
Разберем тот случай, когда 7?1 = 0; тогда из ф-лы (121)
с= йёц ’
ИЛИ т 1
уртвнение уже знакомое нам нз явления резонанса напряжений. При 7?1 = 0 имеем sin ср, = 1 и ср, =5, a J2 = Jr Главный ток а
при этом получается:
J—J1 cos (р2 = 0!
Таким образом в этом случае в обеих ветвях идут во всякий момент токи равные, но противоположные по фазе: если один из них (фиг. 52) в данный момент идет например по ветви первой слева направо, то в это в*, емя другой идет по ветви второй справа налево, и т. д. Они представляют собой просто один переменный ток, циркулирующий только по обеим ветвям; наружу ток не выходит: 7 — 0 Такое явление опять представляет тот же колебательный разряд конденсатора при 7? = 0, который мы уже начали разбирать в предыдущей главе
§ 35. Точное решение вопроса о компенсации сдвига фаз
Исследуем более общий случай, когда сопротивлением в ветви, содержащей емкость С, нельзя пренебречь; обозначим его величину через Т?2 фиг. 55. Очевидно, что векторная диаграмма фиг. 53 изменится для этого случая лишь в том, что напряжение ОК будет иметь составляющую, направленную по вектору тока J2 и выражающую потерю напряжения в ваттном сопротивлении Т?2. Приняв обозначения, указанные на фиг. 54, мы можем выразить условие компенсации, т. е. что результирующий ток совпадает в фазе с напряжением V (вектор ОК), таким уравнением:
= J2sin(p2.
128
Так как
и
где Zx и Z2 суть полные сопротивления ветвей, а из чертежа:
со/, sin ^=-7-
то, подставляя эти выражения в первое уравнение, получаем:
или
<oL 1
~ (»cz229
со/, 1
и упрощая:
L _ С (<о£)2 — (шС)2/?22-|-1"
(122)
9 Теория порэмеииых то. оз
129
Это уравнение может служить для определения емкости С при остальных известных величинах и, наоборот, для определения £, когда известно С и все остальное.
Пусть L дано, так же' как и Rx и /?2.
Введем обозначение
Тогда
0)2С2/?22 -|- 1 = F' или
0)2/?2/7С2 + F— С=0, или еще
c!-^?c+i47“0' <в>
откуда
= 1±/ 1 — 4О)27?22^2
С1>2 WR^F
Таким образом получаются для С два решения, следовательно и векторов J2 будет два и соответственна два угла <р2, так как на основании (А) мы можем написать, что
/2—021 __________
2 ^2 ‘ <о2С2 <o2CF’
и
1 1А
sin ср2 ——— = 1/
Т2 wCZ2 у С
и следовательно каждому из двух С соответствует свой <р2. Эти углы ср2г и tp2* дополняют друг друга до прямого. В самом деле, составим и преобразуем выражение суммы квадратов синусов этих углов:
sin2 <рз' + sin2 = -£ + £ = F. (•
^2 \ /
Вместо суммы и произведения и С2 (корней квадратного уравнения) подставим их выражения из уравнения (В):
sin2 4“ sin2 <р2"= F-
Таким образом мы видим, что
utfR^F 2
'Р2'+'?2'=^
130
Оба вектора и J2", соответствующие двум возможным значениям С, представлены на фиг. 5.6 Из нее мы ясно видим, что решение с Ср обусловливающим ток J2', невыгодно, ибо этот ток очень велик, а также велик, хотя и нахсдится в фазе с напряжением, и ток в линии; эти токи тем больше, при прочих равных условиях, чем меньше 7?2, как нетрудно видеть и из формул для Сг и С2 Но мало того, что это решение невыгодно, оно в про-
мышленных установках и технически почти невыпол! имо вследствие большой величины емкости Сг Рассмо»рим пример.
Пример 27. Моторы рудника поглощают 2 000 киловатт при 6 000 вольт напряжения и cos ^ = 0,6, что cooi.ei-ствуег силе тока
. 2000 000 ссс
Jl = 6000^6 = 555 ампер-
sin», при этом равен 0,8;
. 6000-0,8 __
“£=-555- = 8’6:
Г ППО-7 „ 6000-0,6 __
L = 0,027 генри; — 6,5 ома.
ООО
Введенное выше F равно 0,00023.
Допустим, что R* = 0,01 ома; тогда
4®2/?/F2 = 2blO-l
Ввиду малости этой величины положим радикал равным приближенно единице. Тогда
2
C1 = 2«>a/?a?=438 ФаРадам-
56.
Фиг.
Получается, как видим, совершенно неудобная для осуществления на практике величина. При больших могут получиться и выполнимые величины для
Что касается С2, то ввиду близости величины радикала к единице и малости числителя нам лучше для суждения о величине С2 преобразовать выражение для него — именно, помножив числитель и знаменатель на сумму единицы и радикала; тогда мы получаем:
2 1 4-]/ 1—
положив здесь при малом R2 радикал, равным приближенно единице, получим
с2=Л
т. е., принимая во внимание значение F, мы получаем то же самое выражение для емкости, что уже было получено выше в виде ф-лы (121).
9* 131
Теперь предположим, что в уравнении (122) нам дано С и требуется наити L, т. е. мы имеем, задачу, обратную прежней.
Обозначим правую часть уравнения через К9 т. е. положим
(0)С)2/?2Ч- 1
Тогда
(С)
«ЛИ
А’=у- Ф)
Решая ур-ние (С), получим:
1±/1-4<о2/?г№
т. е. тоже два решения и для самоиндукции, которым соответствуют и два угла ср* и <р"г
Так как
wL (oL 1Z—
sin ср. = — = —-— = o) у LK,
z' /I TO
sin2 cp\ -j- sin2 = <o2-f- L2).
В скобках стоит сумма корней, которая очевидно равна
а поэтому
sin2 ср’ 4" sin2 ср" — 1,
т. е. углы <р' и ср* дополняют друг друга до прямого.
Предлагаем читателю самому рассмотреть вопрос о сравнительной величине обоих корней, и L2, аналогично предыдущему.
Можно предыдущую задачу видоизменить следующим образом.
При данных сопротивлениях и Т?2 в двух параллельных ветвях и данных L и С найти частоту, при которой наступит резонанс токов.
Из уравнения (122) предыдущего параграфа получаем:
(о2С27?22£ 4- L = 2 4- Со)2/.2,
откуда
о)9С£,(/?22С— L) = R*C — L
132
и
(123)
Частота / в 2тг раз меньше.
Очевидно, что если под корнем числитель и знаменатель имеют разные знаки, т. е. если
то корень из дроби получается мнимый, и нет такой частоты, пр» которой возможен был бы резонанс или компенсация фаз.
Если — то корень из дроби обращается в единицу и
величина, нам встречавшаяся уже дважды. Если наконец
то дробь под корнем
О превращается в неопределенность —,
и для
а) нет определенного значения, т. е. резонанс есть при всяких частотах, обе параллельные ветви вместе взятые представляют только ваттное сопротивление. Выясним это еще другим пугем^ применяя метод комплексных величин.
§ 36. Общий вид задачи о параллельных ветвях
Предварительно решим в общем виде задачу о нахождении полного сопротивления, эквивалентного нескольким параллельным ветвям. Пусть между точками А и В цепи мы имеем п параллельных ветвей с сопротивлениями
z;=/?2+/^2,..., ~zn=Rn\jxn.
Сопротивление, эквивалентное совокупности всех этих параллельных ветвей, обозначим через Z = R-\-j-X, обратная ему величина есть проводимость Y=g— как при включении
вместо п ветвей одного сопротивления Z напряжение между А и В должно остаться прежним РАЗ, а сила тока должна равняться
133
геометрической сумме сил токов в ветвях, т. е. равняться силе тока до и после разветвления, то должно быть:
или
= I I Л4В I I г z, z, z, z,'
i-i+X+i+...+i, Z ^2 Z3 Хп
(124)
или еще
_ 1 1 । 1 . , 1
S 1 Ъ *2 + 7^2 *3 + ’ “‘X +JX„'
Освобождаясь от мнимостей в знаменателях, имеем:
откуда:
е 7 Z,2 Т- Z2
^n—jXn
R и X определяются по ф-лам (106) и (107)
/г’+*2’
^2+*2’
Таким образом основной формулой для расчетов эквивалентных нескольким ветвям сопротивлений является формула (124), аналогичная формуле для подобных расчетов при постоянном токе.
Пример 28. Даны четыре параллельные ветви:
74 = 20+/30, 22 = 1О+4 Z3 —5—/3 и Z4 —30;
дано, что сила тока через третью ветвь /З = 3 амперам.
Вычислить, какова сила тока до и после разветвления и каков весь cos в цепи.
Всю силу тока мы получим, если напряжение на ветвях разделим на эквивалентное сопротивление или, что то же самое, умножим на эквива-. лентную проводимость; напряжение же, которое нам неизвестно, узнаем умножением силы тока в третьей ветви на сопротивление этой ветви.
134
Вычисляем
Z^=1300, Z22=101, Z32 = 34, Z42=900.
= — 0 015- _^2 — J£—or - = -5—-014?
Z,2 1300 u,u10' Z22"“101” Z32 34 ’ ’ Zt2 900’“W-
У ^ = 0,295,
Й=п»=+ода: 5=пг=+ад1; ^=-й=-»« §=»• £^ = -0.OSS.
так как J п о л y-из V умножением V на У, сдвига фаз между V и J
Y = 0,295 + >0,055 = О.ЗООе710’35'.
Очевидно, что чается то угол
и есть аргумент У, т. е. ? = arg У= = 10°35', откуда cos ? — 0,982.
Теперь вычисляем напряжение, полагая J$*
Фиг. 57.
V= 73zs = 15 —/9 = 17,5<?-/31°.
Вся сила тока до и после разветвления
J= VP— (15 —/9)(0,295 + /0,055) = 4,920 —/1,830 = 5,15е-^6'
На фиг. 57 начерчены оба вектора J и V.
Найдем cos ср еще иначе, именно по формуле (119) § 30:
4,95.15 + 1,83.9
JV ~ 5,25-17,5 ’ ’
COS <p
Пример 29. Найти У, J, V и cos <р для случая, когда
Z| = 4 + j*2, Z2 — 5 + /-3 и Z3 == 1 —у,
если сила тока через вторую ветвь равна 10 ампер. Начертить векторную диаграмму.
Вычислить, какой величины емкость надо включить в третью ветвь, чтобы cos ср равнялся единице.
§ 37. Продолжение исследования резонанса токов
Перейдем опять к задаче о резонансе токов. Полные сопротивления ветвей на фиг. 55' выражаются так:
ZT — Ri~\-j(j)L и Z2—R2 j —.
135
Общая проводимость обеих ветвей равна: £ , 1_ 1 1 = ^+/^ 0-/4;' ' (оС
1 7 2
^2
/?п —/<о£ 7 2
^1
(А)
Для того чтобы получить резонанс токов, или, иначе, компенсацию одним током сдвига фазы другого, необходимо, чтобы эквивалентное полное сопротивление Z или эквивалентная полная проводимость Y обеих ветвей не содержала в себе мнимого члена; ибо тогда, умножив напряжение V на действительное число У, мы получим ток J, н е сдвинутый в фазе от напряжения. Это равносильно требованию, чтобы в символическом выражении
У= Уе^
угол ср равнялся нулю, тогда
сила тока будет совпадать в фазе с напряжением.
Итак мнимая часть в выражении для У должна быть равна нулю, т. е.
1
(oL . о)С
Z~2 1 7 2 °’
^2
ИЛИ
0)L _ 1
V+W~e-^T? (В>
что представляет собой уже полученное нами другим путем условие резоанса (122)
Теперь выясним, при каких условиях наступление резонанса не будет зависеть от частоты.
Преобразуем последнее уравнение и получим опять
о)2С27?22 + L = СИ* 4- C(o2ZA
Это есть условие резонанса в несколько другой только форме; оно должно выполняться при всяких значениях (о. Очевидно, что это возможно только тогда, когда порознь равны между собой 136
члены правой и левой части, содержащие о, и тоже — члены не содержащие о, т. е.
£ = <?/?, 2
и
откуда и получается:
C2R22 = CL?, я,=ъ=]/%.
(С)
уже знакомое нэм условие резонанса при всяких частотах.
Какова же при выполнении этого условия величина эквивалентного сопротивления всего разветвления?
Так как мнимая часть в Y равна нулю, то остается только действительная, равная
& Г*
Подставляя сюда значения /?р /?2, Z2 и Z2, получаем:
Итак эквивалентное сопротивление обеих ветвей вместе при условии (С) равно ваттному сопротивлению каждой ветви в отдельности.
При невыполнении условий резонанса (В) эквивалентное сопротивление разветвления представляет величину, сильно меняющуюся с частотой. __ __
Это сопротивление Z мы получим как величину обратную К в ф-ле (А).
Пример 30. Пусть на фиг. 55 £ = 0,01 генри, а (7=100 микрофарад.
137
Тогда для независимости величины сопротивления разветвления от частоты надо взять
0 01 ,Л
ТбоЛ<Р«==10 омам'
Если /?< = /?2, но не равно 10 омам, то резонанс наступает при частоте /=—. *— = 15,92 пер/сек.
2к VLC
Если ^t=3 и /?2 = 3 омам, то резонанс наступает при частоте {ф-ла (J23)]: _______
/=15,92]/g±Ct = 25,3 пер/сек.
Если /?/ =5, а /?а = 12 омам, резонанс вообще невозможен.
Предлагаем читателю для двух последних случаев значений и и для /=50 вычислить Z=Z^/?, т. е. определить, исходя из формулы для Y, величину Z эквивалентного сопротивления и вызываемый им сдвиг тока в цепи относительно напряжения, и построить диаграмму напряжений, если У= 120 вольтам.
§ 38. Потери в диэлектрике емкости
Вернемся к тому, что в диэлектрике конденсатора от изменений в нем электрического поля происходят потери энергии, которыми во многих случаях по их ма юсти пренебрегают; в некоторых случаях их необходимо однако принять во внимание. Таков например случай кабеля, в котором провод и наружная оболочкаг или если в нем два или три провода, то и эти провода друг относительно друга представляют емкость, диэлектриком же является гуттаперча или другое изолирующее вещество. Когда имеются в емкости потери в диэлектрике, тогда ток через емкость сдвинут
относительно напряжения на ее зажимах на угол срэ, меньший —. £
Кроме того обыкновенно в емкости есть еще потери от так на ываемой „утечки", т. е. от того, что кроме токов смещения
Фиг. 58.
в диэлектрике имеется еще, хотя нормально и слабый, ток от одной обкладки емкости к другой, вследствие того, что диэлектрик не является идеальным, непроводящим. Когда имеются эти потери энергии, тогда мы можем представить себе их как происходящие в некотором ваттном сопротивлении, заменяя таним образом явлением выделения в этом ваттном сопротивлении мощности в виде
тепла явление потерь мощности в диэлектрике (или так называе-
мого диэлектрического гистерезиса), тоже разумеется переходящей
в тепло.
138
Есть два способа представить себе включение этого ваттного сопротивления. По первому способу (фиг. 58) предполагают, что перед емкостью включено сопротивление R9i. Тогда все напряжение на емкости Vk можно разложить на две составляющие, как показано на фиг. 59, сдвинутые в фазе на , — одну, равную JR3^
и другую,
равную
J
при этом оче-соС
ВИДНО J
tg!?9 = <oC7?9 ' Э|
Полное сопротивление конденсатора имеет очевидно выражение:
Z1 УшС
Однако вследствие того, что, во-первых, напряжение» электрического поля и диэлектрическое смещение в нем пропорциональны всему напряжению на емкости Vk, что от него же зави-
сит и потеря энергии и что, во-вторых, ему же при прочих рав-
ных’условиях пропорционален и ток утечки, лучше представлять себе, что ваттное сопротивление подключено параллельно к емкости
(фиг. 60). В этом случае мы имеем разветвление тока, как показано на векторной диаграмме фиг. 61. Сила тока - через емкость есть V^wC, она опережает напряжение Vk на четверть периода; сила тока через ваттное сопро-~Vk тивление есть
этот ток находится в фазе с Vk. При этом действительно существующий ток
MW
Фиг. 60.
равен их геометрической сумме. __
Здесь полное сопротивление Z2 мы сможем определить, вычис-
лив сначала полную проводимость, так как имеются две парал-
;г. с
лельные ветви; итак _______ i
13»
и
z2= =
1 ___ /? _/?—jmCR
1 . . “ 1+уй)СЯ~ 1 + «>2Сг
+/<»с
Далее имеем:
tg<p9 = <oC/?9j.
генсов дополнительного
В таблицах справочных книг дают обыкновенно величины тан-угла, т. е. угла о = —---------------------<р9, называемого
&
углом потерь.
Для парафина tg 5 —150-10-4, для стекла для резины (каучука) 300-10"4—700-10-Ч
равен 0,8-10“ для бумаги 30-10~4— 30.10-4—180- IO-4, для фарфора 500- Ю-4, 200-Ю-4 — 400-10-4 и для гуттаперчи
§ 39. Решение одной задачи
Решим символическим методом следующую задачу.
Дана цепь переменного тока, изображенная на фиг. 62, состоящая из ваттного сопротивления /?3, самоиндукции L и емкости С с параллельно к ней подключенным сопротивлением R2
Фиг. 62
Как было пояснено в предыдущем параграфе, сопротивление /?2 может заменять утечку и диэлектрический гистерезис и должно быть переменно, если С переменно. Но мы сейчас не будем придавать такого толкования или значения сопротивлению /?2 и формулируем задачу так: при постоянных /?р £ и /?2 найти такое С, чтобы сила тока совпала в фазе с напряжением на АВ
Найдем результирующую проводимость параллельно включенных С и /?2; она равна той величине, на которую надо умножить на-140
пряжение VMN между точками MN, чтобы получить силу тока в главной цепи. Сила тока через /?2 равна
Т'__ ^MN .
*2 ’
сила тока через конденсатор [формула (112)], выражается так:
Сумма этих сил токов есть сила тока в главной цепи
следовательно проводимость цепи между точками 2И и W равна
Введя для нее обозначение
^MN = &MN ~Ь имеем:
_ 1 &MN — q
И
^MN=(dC-
Сопротивление цепи между точками М и равно .
^MN
Полное сопротивление всей цепи очевидно выразится так:
1 F--
/?j -j- -------=/?! 4-/ю£ + у2--------.
+/1ОС +„!С-Л &
Чтобы сила тока совпадала в фазе с напряжением на всей цепи, безваттное сопротивление в ней должно равняться нулю; следовательно в последнем выражении должна равняться нулю сумма мнимых членов, или должно быть
. юС
----1-------• = 0.
141
Таким образом для С получаем квадратное уравнение: c,-^c+^b=o-
Отсюда
^2±//?22 -4ш«£2
С== 2ш3Л/?2 *
Решение возможно, если
/?2 > 2<о£.
§ 40. Приближенная векторная диаграмма длинной линии передачи энергии
Рассмотрим соотношения в цепи из двух длинных проводов с нагрузкой на конце, но, в отличие от рассуждений по поводу фиг. 31 и 32, принимая во внимание емкость этих проводов. Два параллельных провода или две жилы кабеля представляют собой между прочим две обкладки конденсатора; изоляция, разделяющая
нечно-малой емкости.
эти жилы или воздух между двумя свободными проводами, есть диэлектрик этого конденсатора. На всем протяжении двух жил или проводов между ними существует электрическое поле, обусловленное разностью потенциалов точек того и другого провода. Каждый бесконечно-малый элемент длины одного провода с другим проводом составляет конденсатор беско
Кроме того надо принимать во внимание при
построении векторных диаграмм и ваттное сопротивление и самоиндукцию проводов, как было указано по поводу фиг. 53.
Таким образом следовало бы провода разделить на бесконечнобольшое число бесконечно-малых элементов и представить себе, что между проводами с R и L включены все эти элементы, как обкладки бесконечно-малых конденсаторов Качественно исследовать явление мы можем, взяв не бесконечно-большое, а просто доста
точное количество конденсаторов, включенных между проводами параллельно друг другу (фиг. 63). На этой фигуре А и А суть зажимы генератора, от которых идут два длинных провода АВ и АВ, между концами В и В которых включена нагрузка. Емкость этих проводов друг относительно друга мы заменим не
которым числом параллельно включенных конденсаторов с емкостями Ср С2, C3i...
142
Точки присоединения этих конденсаторов разделят всю цепь на участки 1-й, 2-й, 3-й и т. д.
Назовем через /? и L со значками 1, 2, 3 и т. д. ваттное со
противление и самоиндукцию каждого отдельно участка в целом, т. е. обеих его частей, например km и In для участка второго. Соответствующими значками, как показано на фиг. 63, снабдим ц силы токов в проводах Jj, J2,... и в конденсаторах Jce в ветвях тп, kl и т. д. нет уже ни самоиндукции, ни ваттного сопротивления: эти ветви фиктивные и представляют собой исключи
тельно действие емкости проводов друг относительно друга.
Пусть дано, что между точка-
ми В и В имеются напряжение V2 и сила тока J1 с данным сдвигом фаз <р0. Требуется найти построением напряжение у генератора. Строим на фиг. 64 векторы
и под углом ср0 друг к другу. Найдем теперь напряжение между точками т и я, или — что то же самое ввиду условия, сделанного нами только что о »• етвях тп} kl (их 7? и L равны нулю), — напряжение на конденсаторе Сг Приложим к вектору У2 векторы: параллельный Jlf и перпендикулярный к Jr и мы
получаем требуемый вектор напряжения V1 межд^ тип. Сила тока в конденсаторе равна JCi = ИшС* и опережает напряжение на у, что и изображено на фиг. 64. Сложив два тока
и J , мы получим ток дальше точек разветвления т и л, т. е. ток J2 на участке km и In.
После этого приложим к вектору V' векторы: J2R2, параллельный J2, и (o/2J2, перпендикулярный к J2, и получим У", вектор
143
напряжения между точками kl или на конденсаторе С2. Теперь при-
ложим к вектору J2 вектор Jc*= V"(t>C2 по направлению, оперетт *
жающему V9 на — ,и получим вектор J3 силы тока в проводах на а
очевидно то же самое,
Фиг. 66.
третьем участке. Продолжая так построение до участка, примыкающего к Л и Л, мы найдем напряжение V1 в АА и силу тока у АА.
На этой диаграмме мы замечаем, что напряжение у генератора больше, чем где-нибудь между проводами, — напряжение убывает по мере удаления от генератора, сила же тока в проводах, наоборот, растет по мере удаления от станции Это явление есть что и рассмотренное выше уменьшение тока в главной цепи при подключении параллельно нагрузке конденсаторов.
Предположим, что цепь между В и В разомкнута. Вследствие существования емкости проводов ток будет циркулировать в проводах и при разомкнутой цепи. В предыдущей диаграмме надо положить при этом равным нулю и перестроить диаграмму, как показано на фиг. 65. При J1==0 имеем и Vf=V2; V" отличается от V' на падение напряжения в участке km — In от тока J = == J2.
Строим вектор J и проводим из конца векто а У2 вектор JCR2 параллельно ему
я вектор ®L2J перпендикулярно и получаем вектор Vn. Затем отроим вектор = V"(t)C2. Складываем его с J и получаем вектор J3. Строим от конца вектора V" вектиры 1J3R3 и ®L3J3 и получаем вектор 0ГГ, и т. д. На этой диаграмме мы замечаем обратное тому, что было на фиг. 64. Сила тока в проводах уменьшается по мере удаления от генератора; напряжение же, наоборот, по мере удаления от генератора растет— таково действие емкости проводов в незамкнутой цепи. Увеличение напряжения по мере удаления от станции носит название „явления Ферранти", по имени инженера, открывшего его впервые на опыте с длинным концентрическим кабелем в Лондоне
В нашей схеме, когда мы емкость проводов, распределенную по всей длине их непрерывно, заменили емкостями, сосредоточенными лишь в известных точках т, п, ky Z и т. д, сила тока и напряжение изменялись скачками от участка к участку, тогда как в действительности эти величины изменяются непрерывно. Однако эта разница между схемо^ и действительностью часто не имеет значения, если важны лишь наибольшие и наименьшие величины сил токов, напряжения и падения напряжения Чтобы приблизиться в этих величинах к действительности, следует лишь взять достаточное количество делений на участки и соответствую
144
щие величины С, X? и L. Точную теорию распределения напряжения и сил токов в длинных проводах мы найдем в главе шестнадцатой.
§ 41. Измерение мощности тремя вольтметрами или тремя амперметрами
На схеме фиг. 66 участок MN есть та часть цепи, в которой нам желательно узнать потребляемую мощность. Пользуясь ваттметром, следовало бы его тонкую катушку подключить к Л! и параллельно к участку MN, а толстую включить последовательно с MN. Можно измерить мощность без ваттметра при помощи трех вольтметров 4). Обозначим напряжение на MN через Vj, силу тока в MN через J, угол сдвига фаз между этими величинами через Искомая мощность равна:
Р= V^cos (рг
Включим последовательно с некоторое ваттное сопротивление Х?2 и увеличим все напряжение, приложенное к цепи, так, чтобы напряжение на MN и теперь, после включения Х?2, оставалось прежним V}, тогда и мощность в MN останется прежней. Подключим три вольтметра: Вг к MN, В2 к ваттному сопротивлению Х?2 и В3 к зажимам А и В всей цепи. Самоиндукцией и ваттным сопротивлением про-
водов в цепи пренебрежем. Величину Х?2 выберем Фиг. 67. так, чтобы напряжение на этом участке, IZ2 = JX?2, у было. приблизительно равно напряжению Так как J = ,
то мощность выразится так:
О ^2 Р = -^СО5(рг
Начертим диаграмму напряжений в цепи (фиг. 67). Векторы V4 и J составляют угол ср2; приложим к Уг вектор У2 = /Х?2, совпадающий в фазе с J, и мы получим вектор всего напряжения У31 причем из полученного косоугольного треугольника имеем:
V32 = +
откуда
Уг V3 cos к - у ( У3» - VS - V,’).
Это выражение подставим в выражение мощности и получим:
10 Теория переиешых токм.
145
Таким образом, зная Т?2 и измерив вольтметрами означенные три напряжения, мы сможем вычислить Р. Из того обстоятельства, что для большей точности определения величины V2 cos cpj надо, чтобы в треугольнике напряжений сторона V2 была приблизительно той же длины, что и и следовательно все напряжение после включения R надо повысить почти в два раза до величины V3, вытекает неудобство этого метода для практики. Удобнее в этом, отношении способ трех амперметров измерения мощности, который заключается в следующем 5).
Не будем изменять напряжения в цепи* и включим параллельно участку AW некоторое ваттное сопротивление /?2. Затем включим в обе параллельные ветви по амперметру, как показано на фиг. 68, а также в цепь за разветвлением один амперметр. Для ветви Р2 имеем V1—J2R2i так что выражение мощности мы можем теперь преобразовать так:
Р= V1J2cos^1=J1J2R2cos<fr
Так как J2 совпадает в фазе с то (фиг. 69) проводим из конца вектора вектор J2, параллельный вектору^ напряжения Vv и, складывая J1 и J2, получаем вектор J3 силы тока за разветвлением.
Из треугольника токов следует, что
A2 = /12+J2»4-2J1J2cos<P1,
откуда
A A cos w - - J&.
Л!
Подставляя в выражение для мощное!и, получаем:
Способ трех вольтметров был предложен Эйртоном, Сван-бурном, Сэмпнером, а трех амперметров — Флемингом.
146
§ 42. Получение токов или напряжений, сдвинутых в фазе на четверть периода
Рассмотрим теперь задачу о получении сначала двух токов, затем двух напряжений со сдвигом фаз в четверть периода, когда дано на зажимах АВ (фиг. 70 и 71) напряжение V.
Для получения таких двух токов служит способ Гуммеля, схема включения которого изображена на фиг. 70. К зажимам А и В подключена цепь, состоящая из катушки некоторого сопротивления Z3, с небольшим ваттным сопротивлением /?3 и большим безваттным — соL3, и последовательно к нему присоединенных двух параллельных ветвей — одной из ваттного сопротивления и другой из катушки сопротивления Z2 с ваттным
сопротивлением /?2 и с безваттным (оЛ2. В обе ветви и в главную цепь включено по амперметру; кроме того W обозначает ваттметр, Толстая катушка которого включена в ветвь 2, а тонкая подключена к зажимам АВ (или, что то же самое,—AD\ т. е. к данному напряжению V. Изменением Z2, Z3 и можно достичь того, чтобы сила тока J2 была сдвинута на четверть периода относительно V и следовательно относительно любого тока в
какой-нибудь другой цепи, присоединенной к тем же зажимам АВ, находящегося в фазе с V (т. е.
идущего лишь через ваттное сопротивление, подключенное к АВ). Что такой сдвиг фаз достигнут, узнают по ваттметру, который при этом покажет нуль, так как косинус угла сдвига фаз между токами в катушках его будет равен при этом нулю. О таком употреблении ваттметра было уже сказано в главе четвертой после описания ваттметра.
Векторная диаграмма (фиг. 71) начерчена для случая осуществления требуемого сдвига фаз.
Сила тока J3, главного, имеет сдвиг фаз относительно напряже-
ния УАЗ, равный <р3; сила тока имеет меньший сдвиг фаз,
а сила тока J2 — больший, именно равный Напряжение между л
10*
147
С и D представлено вектором J^R^ сила тока J2 отстает от на-пряжения между С и D по общему правилу на угол
получаем J3 со сдвигом фаз промежуточным
Разность между VAB и J1R1 есть
Суммируя Jj и между сдвигами фаз и J2. вектор VAC напряжения между А и С; угол между векторами VAC и Л определяется как arctg^S. и при малом 7?3 приближается к прямому.
Упражнение. Вывести аналитическое условие перпендикулярности к VAB. _
Указание. Направить VAB по вертикальной оси, так что мнимая часть комплекса УдВ равна нулю, и вывести условие, когда Л не будет иметь действительной части.
Фиг. 72. Фиг. 73.
Сдвиг фаз в четверти периода между двумя напряжениями получается по способу Гергесса, схема включения которого дана на фиг. 72. На зажимах А и В или М и N имеется данное напряжение V; на фиг. 73 оно представлено вектором MN. Главный ток J, измеряемый амперметром Ло, отстает от напряжения и представлен вектором J. В участках МС и DN включены регулируемые катушки (с выдвижными сердечниками) с малым R и большим L; в участках же MD и CN включены лишь ваттные сопротивления, так что токи и совпадают в фазе с напряжениями на MD и C7V соответственно. Между С и D включено то же ваттное сопротивление; в эту ветвь включена и толстая катушка ваттметра, тонкая катушка которого подключена к зажимам М и Nf т. е, к напряжению V. Шестью амперметрами мы можем измерить все
148
шесть токов; вольтметром же, не изображенным на чертеже, можем измерить все шесть напряжений, т. е. на участках MB, CN, MD, DN, CD и главное — на MN.
Сила тока главного J может быть представлена двояким образом: или как сумма и J3, причем меньше отстает от напряжения, чем J, a J3 — больше; или как сумма и J4, причем J4 меньше отстает от напряжения, чем J, a J3 — больше. Напряжение на MD совпадает в фазе с J1 и представлено вектором MD\ разность между MN и MD — вектор DN—есть напряжение на участке DN; сила тока J2 сильно отстает от этого напряжения. Вектор AfC, параллельный вектору J4, есть напряжение на участке Ж?, а вектор МС представляет напряжение на МС. Наконец разность векторов MD и МС есть вектор CD напряжения на участке CD, диагональ четырехугольника MCND. Векторы CD и J5 параллельны.
Изменением всех сопротивлений, ваттных и безваттных, можно достичь того, чтобы вектор CD был перпендикулярен к вектору MN\ что требуемый сдвиг фаз в четверть периода достигнут, на опыте узнается из того, что ваттметр при этом показывает нуль, так как сила тока J& в толстой катушке находится в фазе с напряжением CD.
Очевидно, что изменение частоты, хотя бы и небольшое, повлечет за собой нарушение требуемого сдвига фаз в в обеих разобранных схемах.
Ответ к упражнению настоящего параграфа.
Сопротивление всего включения Z равно:
Z3 4- * = za 4- =/?з+JX3+
4-7*4
Напряжение VAq направим по вертикальной оси, так что ^лв— ^ав>
Далее, __
^=УлС=Й=1/ла А;
149
V2 = VCO= УЛВ - У AC- У AB -УАВ-^г=
2
^2 ___ у __
Z2 AB (R'+Za)Z'
Это выражение не должно содержать действительной части; следовательно не должна ее иметь и дробь
1 (R^zjz’ а это возможно только тогда, когда знаменатель не имеет действительной части (доказать это!); итак:
(Ъ + ZJZ не должно иметь действительной части. Раскроем это выражение: (/?! 4- Z2) Z=R£Ra -I- JXZ) + (/?! + Ra 4- JX2)(R3 4-/x3),
откуда получаем, что должно удовлетворяться условие: ад++^2) - ад=°-
§ 43. Первый и второй законы Кирхгофа. Принцип наложения
Из последних трех задач мы замечаем следующее: векторы сил токов, притекающих к одной точке (или утекающих от нее),— в наших задачах их было три,— \ составляют замкнутый много-
Д^УД^****/* угольник. Это положение являет-
у ся геометрической формой закона
Кирхгофа для переменного тока:
—О, что при переходе к век-у. / торам от мгновенных значений оз-
X. / начает, что результирующий век-
тор равен нулю (его проекция на ось времени, равная всегда Фиг- 74* равна нулю), так что векторы
сил токов, притекающих к одной
точке (или утекающих от нее), образуют всегда замкнутый много-
угольник (в наших примерах — треугольник).
Второй закон Кирхгофа применительно к замкнутому контуру (фиг. 74) выводится способом, совершенно подобным тому, которым
150
этот закон доказывается в учении о постоянном токе. Для каждой стороны контура мы имеем:
= VA — ^ + *1 + < + <+••• ^2=VA — ^ + *2+ *2+ *2 +
где ev е[, означают все возможные ЭДС одного и того же числа периодов с токами, действующие в стороне I; е2, е', е2 — то же в стороне II и т. д.
Складывая эти равенства, мы получим:
т. е. формулу, выражающую 2-й закон Кирхгофа для мгновенных значений.
Здесь под ек мы подразумеваем все ЭДС, действующие в сторонах, т. е. в том числе и ЭДС самоиндукции. Перенеся их в левую часть с обратным знаком и переходя к векторам и действующим значениям, получим:
где Ек означает действующие в сторонах контура ЭДС индукции от других токов, в том числе и от других сторон контура и пр.
Может случиться, что ЭДС, действующие в сторонах контура, не все одинаковой частоты; спрашивается, как тогда вести расчет.
Такой случай подойдет под очень общее правило или принцип расчета, который называется принципом наложения.
Принцип наложения мы формулируем так: если в цепи электрического тока причина А (например некоторая ЭДС) вызывает явление М (например некоторую силу тока), а причина В (пусть—другая ЭДС) вызывает явление N (силу тока, отличную от прежней), то при совместном действии А и В вызываются явления М и AZ (если обе ЭДС при этом одной частоты, они геометрически суммируются и оба тока тоже), и только они, если связь между А и М и между В и N математически выражается линейным уравнением. В скобках мы привели пример этого. Приведем обратный пример Сила тока постоянного (причина 4) вызывает тепло Jj2 7? (явление М) в цепи; связь здесь выражается не линейно, а с помощью второй степени; сила, тока J2 (причина В) вызывает тепло J22/? (явление N). Когда существуют обе причины А и В, т. е. токи и /2, то тепло будет не J22# (явления М и Л/), а другое, именно: (J2 Л)2^*
Таким образом все те явления, которые связаны ЭДС линейно, например сила тока, а через нее магнитное поле, можно рассчитывать отдельно для каждой из ЭДС, а затем результаты сложить
151
геометрически или алгебраически и получить то результирующее явление, которое в действительности будет при наличии нескольких первопричин, например ЭДС.
Исключаются те явления, которые с причиной (силой тока или ЭДС) связаны не линейно, например выделение тепла в меди, магнитное поле в железе при заметном его насыщении, потери на гисте-грезис, токи Фуко и пр.
Далее при исследовании несинусоидальных токов как периодических, так и непериодических мы воспользуемся принципом наложения для вывода теории явлений этих токов.
Упражнение, Составить уравнения для схемы Гёргеса.
§ 44. Схемы Бушеро
Рассмотрим теперь, как дальнейший случай применения символического метода, предложенные Бушеро особенные схемы включений, служащие для того, чтобы от источника переменного тока с напряжением, действующее значение V которого постоянно, получить в цепи нагрузки ток, действующая сила которого не зависит от сопротивления4 этой цепи, а всегда одна и та же; задача устройства такого включения кратко формулируется так: преобразовать постоянное напряжение в постоянную силу тока (не смешивать с постоянным током).
Первое из включений Бушеро изображено на фиг. 75, где Zo символизирует нагрузочную цепь; на практике это может быть ряд последовательно включенных ламп накаливания или дуговых для освещения коридоров, туннелей, к ZQ подключена емкость С и последовательно
с этими обеими ветвями самоиндукция L. Сила тока JQ не должна зависеть от величины Zo. Ветвь с емкостью С и участок с самоиндукцией L пусть имеют такое малое ваттное сопротивление, что им можно пренебречь.
Напряжение между точками А п В можно выразить двояким образом — по ветви Zo или по ветви С; для последнего выражения нам служит в преобразованном виде (теперь напряжение должно быть выражено через силу тока) ф ла (112), таким образом получаем:
х к и х х м—
3q Zq Фиг. 75.
садов; параллельно
Далее, имеем:
Уд —jmCJ^Z^.
152
V=ju>LJQi
Сила тока главного
М + А = Л>( 1 +/®CZ0).
Все напряженйе на зажимах
V=70Z0 —£с, или на основании ф-лы (111):
V=.7gZ,+/7«L
Подставляем вместо силы тока главного его выражение
V=70[Z0 +/«£ (1 +/«с-С)1=(1 - ®2^Q
Теперь мы сделаем
(А> тогда и
Таким образом сила тока ?0 оказывается не зависящей от Zo.
Если ветвь Zo разомкнута, то цепь состоит из последовательно включенных L и С при выполнении условия резонанса (равенство А); так как ваттное сопротивление ничтожно, — мы положили его равным нулю, — то сила тока J будет при этом бесконечно велика; таким образом выключение цепи нагрузки равносильно короткому замыканию всей цепи; наоборот, при коротком замыкании цепи нагрузки, т. е. между точками А и В, сила тока будет:
Второе включение Бушеро получается из первого переменой мест L и С, а потому соотношения при нем подобны вышенапи-санным.
Третье включение представлено на фиг. 76.
Опять предполагаем, что ваттные сопротивления равны нулю для четырех сторон ADBC.
Затем мы делаем емкости в ветвях AD и СВ равными, а также делаем равными самоиндукции в ветвях АС и DB.
Вследствие этого силы токов будут в ветвях попарно одинаковы. В диагонали CD включена нагрузка — сопротивление Zo — с током Jo.
153
о
о
D
J
3,
С
А1
Фиг. 76.
Для составления уравнений применим, во-первых, первый закон Кирхгофа к любой точке разветвления. Так как нас интересует ток Уо, то естественно постараться прежде всего и ввести его в уравнения, а для этого следует взять или точку £>, или точку С. Пусть мы останавливаемся на второй. Выберем совершенно произвольно на схеме вдоль всех пяти ветвей тока направления, которые будем считать за направления сил токов, когда последние имеют положитель-В ные значения. Пусть эти направления отмечены / стрелками на чертеже. На основании первого закона Кирхгофа сумма притекающих к С токов равна нулю: положительные силы токов все как раз, согласно нашему выбору, притекают к С, поэтому все токи надо взять с плюсами; иначе: многоугольник векторов должен дать результи-равный нулю, — геометрическая сумма векторов
Zo
Jo
рующий вектор, сил токов, притекающих к С, равна нулю:
Л + Л + —°-
(В)
За второе уравнение возьмем выражение напряжения VAB между точками А и В через силы токов и сопротивления. Имеем:
Vab = Vac+Vcb-
На основании ф-лы (111), обозначая через Ес(ЛС) ЭДС самоиндукции на участке АС, имеем:
^ас — Ez(ac) —JvLJr
Далее __
У св= ^вс-
По ф-ле (112)
vBc—
следовательно
v4B=/®z.724-/A. (С)
Из уравнения (В)
У1 —— JQ Jg,
подставляем это выражение в (С):
V. =/7 (<о£—Ц —у А.
лв * \ <йС/ »С
154
Теперь сделаем в нашем включении, как раньше, (оС тогда
70=7v«c-;^. О»
Мы видим, что, как и в первом включении, JQ не зависит от сопротивления Zo цепи нагрузки.
Согласно правилам умножения вектора на 4”У> вектор JQ опереть те
жает вектор напряжения V на —, или сила тока опережает напря-жение на четверть периода; при этом однако надо иметь в виду, что мы за положительное направление для Jo совершенно произвольно приняли направление от D к С; если, бы мы приняли за положительное направление от С к D, то получили бы, что
70 = — yVwC,
т. е. что JQ отстает от V на четверть периода; оба результата очевидно утверждают одно и то же.
Первый закон Кирхгофа в последнем случае надо было бы на-
писать-в таком виде:
Л+Л-Л=о-
Когда мы имеем на зажимах напряжение переменного тока, то от нашего произвола зависит, в каком направлении считать его положительным.
Мы можем условиться, что напряжение имеет положительное значение, когда потенциал А выше, чем потенциал В. Из основных понятий о разности потенциалов и силе тока вытекает, что сила тока тогда положительна, когда ток течет тоже от Л к В. Но когда считать силу тока Jo в ветви CD положительной — когда он течет от С к D, или наоборот? — в этом надо снова условливаться, так как связать этот выбор с выбором положительного направления для VАВ в общем случае нельзя. Когда даны численные значения С и L, тогда можно судить, потенциал которой точки, С или £), ближе в среднем к потенциалу точки А, и тогда установить положительное направление силы тока в ветви CD. В рассматриваемом случае, при выполнении условия резонанса, ток Jo сдвинут на четверть периода относительно напряжения, но в какую
155
сторону — в сторону опережения или отставания? — на этот вопрос можно ответить лишь условно, выбрав сначала какое-нибудь из направлений JQ за положительное.
В заключение разбора третьего включения Бушеро заметим, что когда ветвь CD разомкнута, мы имеем в каждой из ветвей ADB и АСВ резонанс, и сила тока в каждой из них, а потому и в главной цепи, бесконечно-велика. Когда же ветвь CD замкнута на короткое, т. е. Zo = O, проводимость включения равна нулю, и главный ток равен нулю.
Доказывается это просто: проводимость части AD по формулам (112) равна +/<оС; проводимость АС по ф-ле (111) равна / . 1 \
| — / — I, так как
\
7лс=-£с=/а>2.7;
сумма этих двух проводимостей равна нулю:
j(»C---LU°.
Практического значения включения Бушеро не получили вследствие малого costp.
§ 45. Некоторые мостики переменного тока
Фиг. 77.
В практике электрических измерений часто употребляется мостик Уитстона, при переменном токе; таким способом меряют емкости, углы потерь в диэлектриках емкостей, самоиндукции и взаимные индукции. Гальванометр при этом употребляется вибрационный (употребляется также телефон). Стороны мостика содержат ваттные и безваттные (индукционные или емкостные) сопротивления (фиг. 77). Когда в ветви гальванометра
нет тока, тогда очевидно падения напряжения в сторонах схемы попарно равны:
Azi = */2Z3»
откуда
•*1^2--•/2Z4»
z2 z4
Z3Z4 = Z2Z8.
или
156
Если комплексы равны, то равны их модули и равны их аргументы, поэтому условиями равновесия мостика являются уравнения:
= z2z3 и
<Р1 + ?4 = + <РЗ-
Приведем еще два примера мостиков переменного тока.
Одним из самых точных и удобных способов измерения самоиндукции является способ Андерсона, в котором самоиндукция сравнивается с емкостью. Схема включений приборов приведена на фиг. 78.
Здесь L обозначает измеряемую самоиндукцию, г0 — ее ваттное сопротивление, и R с разными значками суть величины сопротивлений в магазинах, С есть эталон емкости; между точками b и f включен вибрационный гальванометр.
Зажимы а и с присоединяются к источнику переменного тока с возможно более чистой синусоидальной формой кривой напряжения, например очищенной по описанному в § 78 способу. Введем обозначение г0 Л = Rv Меняя сопротивления и
емкость, будем менять распределение потенциала.
Когда гальванометр покажет отсутствие тока, тогда потенциалы точек Ъ и / равны. Для этого состояния мы можем написать следующие три уравнения, каждый член которых выражает изменение потенциала в той или другой части включения:
«/<#£) == *4^5»
4^5— и четвертое:
157
Подставляя в "первое уравнение выражение J3 из последнего, имеем:
^(/?i +/«£)== 47?8+4/?3 4- Д/?6.
Подставим сюда выражение из третьего:
Деля это уравнение на второе, получаем:
g,+/.L +*+*
/?3 . 1
~J^C
Отсюда цо упрощении имеем:
Вторым примером возьмем мостик Кэри — Фостера для измерения взаимной индукции тоже сравнением ее с емкостью.
Фиг. 79.
Фиг. 79 показывает схему включения. Здесь М есть величина взаимной индукции между двумя катушками или контурами, L — самоиндукция той катушки (или контура), которая входит в сторону четырехугольника abed, остальные обозначения понятны без пояснений.
Для того состояния, когда вибрационный гальванометр покажет отсутствие тока и следовательно потенциалы точек а и с будут равны, будут иметь место следую
щие очевидные соотно
шения:
+Ъ +/®О - (Л + Л)/®^=°.
158
Подставляя в первое уравнение выражение для J2 из второго, имеем:
М (^1 + ^2)^3 +JaL#3——J®MR — — = 0.
Приравнивая порознь нулю действительную и мнимую части* получаем:
-^ + (^ + ^3 = 0.
откуда
Ж = С/?3(/?1+/?2) и
L/?3 —Ж(/?3 + /?4) = 0, откуда
§ 46. Геометрические места. Работа синхронной машины генератором и двигателем. Диаграмма Блонделя
Решение предыдущих вопросов заключалось каждый раз в построении одной единственной векторной диаграммы, выражавшей соотношения между величинами графически.
Во многих случаях бывает важно знать, как будут меняться некоторые величины, например напряжение на каком-либо участке* цепи’ или сила тока через какую-либо ветвь цепи, при изменении других величин. В особенности подобные вопросы важны при рассмотрении работы электрических машин при разных нагрузках или других меняющихся обстоятельствах. Как пример можно указать на работу синхронного генератора при постоянной нагрузке, но при меняющейся силе тока в цепи возбуждения его. В таких случаях* чтобы получить ответ на поставленный вопрос, надо было бы построить целый ряд векторных диаграмм для отдельных частных случаев и смотреть, как изменяется на них по величине и фазе интересующий нас вектор в зависимости от меняющихся условий в цепи, — в упомянутом примере, скажем, ток в статоре при изменении возбуждения.
Вместо построения большого количества диаграмм, — что и утомительно, да и само по себе, без геометрических выводов, все равна не приведет к точной формулировке закона изменений рассматриваемого вектора — идут другим путем.
Анализируя векторную диаграмму, выводят геометрически, как будет измёняться один вектор при изменении других. Чаще всега в таких случаях ищут, какое геометрическое место будет
15»
описывать конец вектора интересующей нас величины при изменении тех или иных условий в цепи.
В главах XI и XII рассматривается работа нагруженного трансформатора и асинхронного двигателя и доказывается, что конец вектора первичного тока, который трансформатор или асинхронный двигатель берет из первичной сети, будет при изменениях нагрузки перемещаться по окружности, причем и выводятся формулы для положениях центра и для величины радиуса этой окружности. Таким образом дается закон, как изменяется с нагрузкой сила тока из сети по своей величине и фазе.
Когда для той или иной машины, для определенных условий ее работы, такое геометрическое место найдено, уже легко судить, какое состояние, какой режим работы ее наиболее выгоден или удобен, что можно ожидать при изменениях его и т. д.; на одной такой диаграмме с начерченным на ней геометрическим местом можно легко обозреть все состояния работы машины, недогрузку, нормальную работу, перегрузку и пр.
Сейчас мы покажем, как эта идея прилагается к изучению работы синхронной машины.
Каким вектором при этом „ заинтересоваться геометрическое место концов какого вектора искать, какие величины считать не-изменяющимися, какие считать изменяющимися, — на эти вопросы иногда может быть и не один, а два и три ответа, смотря по тому, с какой точки зрения мы подходим к задаче исследования работы машины. Обыкновенно напряжение сети переменного тока, к которой подключена машина, считают постоянным и ищут, как будет изменяться при тех или иных условиях сила тока в машине. Иногда же поступают иначе.
Обратимся к исследованию работы синхронной машины и зададимся следующими условиями: пусть на ту же сеть работает параллельно с рассматриваемой машиной еще так много других «синхронных генераторов, что наша машина никакого влияния на напряжение сети не оказывает; это напряжение можно таким образом принять постоянным. Говорят в таких случаях, что машина подключена к бесконечно-сильной сети (если бы оказалось необходимым, поправку на колебания напряжения в окончательный наш результат мы сможем ввести после).
Затем пусть будет постоянным возбуждение генератора и следовательно его ЭДС.
Обращаясь к векторной диаграмме генератора фиг. 22, мы видим, что при таких условиях точка С будет при изменениях нагрузки генератора, т. е. при различных по величине и фазе силах тока, перемещаться по окружности, описанной из О радиусом, равным ОС.
На фиг. 80 эта диаграмма начерчена для трех следующих случаев: OKFC, когда ЭДС ОС совпадает в фазе с напряжением ОК;
160
напряжение, значит наша ма-
ток в этом случае отстает в фазе, от напряжения, и вектор силы тока есть ОД; затей — ОЛТ^С^ для случая, когда сила тока — вектор ОДа—опережает напряжение, и наконец ОЛГГ2С2, когда ток — вектор ОД2 — имеет сдвиг фазы относительно напряжения больший . В последнем случае произведение К/cos ср отрица-тельно; это показывает, что теперь уже наша машина не посылает мощность в сеть, а берет ее из сети, т. е. она работает как синхронный двигатель. Что касается силы тока, то можно сказать, что машина посылает в сеть ток ОД2 или берет из сети ток ОВ =—ОД2. Этот ток оп шина действует не просто как двигатель, но и оказывает влияние на сеть как конденсатор.
Читателю нетрудно заметить, перечерчивая четырехугольник OKF2C2 для разных величин ЭДС ОС2, что по мере увеличения ее « при уменьшении / КОС<> вектор KF2 будет поворачиваться против движения часовой стрелки около точки ТС, чтобы при некоторой величине ^/_КОС2 стать перпендикулярным к ОК.
Такое же положение век-
тор KF2 может получить и Фиг. 80.
при той же величине
ЭДС ОС2, если уменьшать силу тока ОД2, а следовательно пропорционально ОА2 и все стороны Д?С^2С2, причем опять будет уменьшаться /_КОС2 и Д KF2C2 — поворачиваться.
Состояние машины, когда ТСА2_|_О7С, является как бы переходным от работы ее двигателем к работе генератором, так как при этом VJcos<p^ = 0, т. е. она ни берет из сети, ни посылает сама в сеть мощности.
Синхронные двигатели часто употребляются вместо конденсаторов, как уже было упомянуто; при этом механическая мощность, развиваемая ими, £7cos<ptf, а следовательно и мощность, берущаяся из сети, Wcos'fn, бывает очень невелика — последняя покрывает потери на трение и гистерезис. Необходимым условием работы синхронного двигателя в качестве конденсатора является „перевозбуждение" его, т. е. чтобы ЭДС ОС2 была больше напряжения ОК—и тем больше, чем больший опережающий ток должен взять из сети двигатель.
11 Теория переменных тотов.
161
Читатель легко выведет из рассматриваемой векторной диаграммы? и второе следствие, именно следующее: если уменьшать ЭДС ОС2, т. е. уменьшать возбуждение двигателя, оставляя, допустим, / КОС2 постоянным, то треугольник KF2C2 будет поворачиваться около точки К по направлению движения часовой стрелки; при некоторой величине ОС2 вектор KF2 перейдет вертикаль ОК и затем будет располагаться уже влево от ОК, Ь это будет значить, что ток, который двигатель „берет* из сети (направление вектора которого есть направление от F2 к К), будет теперь уже отставать от напряжения ОК. При этом двигатель будет, как говорят, недовоз-бужден. Разумеется подобный же результат получится, если мы одновременно с уменьшением ОС2 будем уменьшать и / К0С9.
Такова роль возбуждения в синхронных двигателях. Ввиду важности этого вопроса читателю усиленно рекомендуется проделать построение векторных четырехугольников OKFC для всевозможных частных случаев, чтобы закрепить в воображении изложенное
выше.
Далее отметим следующую важную деталь. Как видим из фиг. 80, когда машина работает генератором, она, в зависимости тоже от величины ее ЭДС, т. е. от ее возбуждения, может посылать ток в сеть или опережающий или отстающий от напряжения. У читателя может явиться вопрос, как это может быть, если при этом не происходит соответствующих изменений с нагрузкой, т. е. если во внешней цепи не происходит замены самоиндукции на емкость или наоборот, а нагрузка остается постоянной и следовательно постоянным остается и соотношение между ваттным и безваттным ее сопротивлением?
Ответ на этот1 вопрос следующий. Если все генераторы, работающие параллельно на сеть, одинаковы и нагружены и возбуждены одинаково, т. е. их мощности и ЭДС равны, то coscpv для всех их один и тот же и зависит исключительно от отношения
(X \ по формуле если же возбуждение и
''вне/
ЭДС какой-нибудь машины изменяются, то изменяется и сдвиг фазы
тока в этой машине относительно напряжения, причем оказывается, что часть этого тока не идет от собирательной машины во внеш
нюю цепь, а направляется в другие генераторы, там прикладывается геометрически к их току и затем возвращается в наш генератор.
Вопрос осложняемся, когда генераторы неодинаковы, другими словами, когда их конструкции разнятся настолько между собой, что кривые электродвижущих сил получаются у них разные. Тогда вообще нельзя подобрать такого возбуждения у них, чтобы не было этих внутренних „уравнительных* токов между самими машинами.
Примем для дальнейшего, что возбуждение постоянно.
Обратимся к выводу других следствий из нашей векторной диаграммы и обратим внимание на то, что концы С, С2 и т. д.
162
векторов электродвижущей силы при изменениях нагрузки перемещаются по окружности, описанной из О радиусом, равным ЭДС Е. Переходя к полным внутренним падениям напряжений представленным векторами КС. КСг. КС2 и т. д., можем сказать, что концы этих векторов С, Сг. С2 движутся по окружности с радиусом Е. причем центр ее лежит на продолжении линии КС (т. е. вектора полного падения напряжения для случая, когда ЭДС и напряжение совпадают в фазе, т. е. когда уе — <р^ = 0) на расстоянии ОК= V от точки К. Концы векторов силы тока Д, Д1# Д2 и т. д. поэтому опишут дугу окружности с радиусом в ZBHy раз меньшим, но измеренным в масштабе тока и с центром, лежащим
на продолжении линии ОА (т. е. вектора силы тока для случая, V
когда — (рда = 0) и на расстоянии —— от точки О. вну V
Наносим на продолжение О А отрезок ООг = у— , причем оче-Е ВНУ
видно все О1А = ——, и радиусом О1Д описываем окружность, ^впу
которая и будет геометрическим местом концов вектора силы тока
при данном напряжении, данном возбуждении и переменной нагрузке.
В теории машин переменного тока эта окружность, называемая диаграммой Блонделя по имени французского ученого, введшего ее
в теоретическую электротехнику, служит для изучения многих здесь не упомянутых свойств синхронных машин. Один из диаметров определит на окружности две точки, которые являются границами устойчивости работы машины, одна точка для работы ее генератором, другая — двигателем. Между этими двумя точками и перемещается конец вектора J с изменением нагрузки машины, другая же половина окружности значения не имёет.
Заключим эту главу замечанием общего характера.
Не всегда искомое геометрическое место оказывается кругом.
Например в теории машин синхронных известны так называемые „линии мощностей" Гёргеса 6, немецкого ученого, которые, как и диаграмма Блонделя, имеют целью представить геометрически работу синхронных машин. Это ряд параллельных прямых, каждая из которых является геометрическим местом концов вектора ЭДС при различных возбуждениях и постоянной, соответствующей данной линии электрической мощности VJcostp^.
При исследовании работы других машин или их соединений
геометрические места получаются иногда в виде весьма сложных
кривых.
§ 47. Топографический метод 7
При решении некоторых задач может оказаться весьма полезным по своей наглядности так называемый топографический метод, который в краткой формулировке заключается в том, что мы рас-
11*
163
Фиг. 81. для упрощения вопроса
стояния между двумя любыми точками на векторной диаграмме считаем за векторы разностей потенциалов между этими двумя точками, как точками цепи.
Поясним эту идею на примере. Пусть нам дан один провод линии передачи энергии, состоящий из трех участков (фиг. 81) ОА0, AqBq и BqCq, провод продолжается и далее, или быть может в Со к нему подключена нагрузка, но мы рассмотрим именно только показанную на фиг. 81 часть его ОС0. Сопротивление R и самоиндукция L распределены вдоль по каждому участку равномерно, как было уже пояснено раньше, но на разных участках имееют разную вели»-чину, и фазовый угол между силой тока J и участковым напряжением Кол, Клд, VBC получается разным.
На фиг. 81 дана диаграмма этих напряжений.
Емкостью самого провода относительно другого мы в данном примере ренебрегаем.
Если на всем участке ОА0 теряется напряжение О А, то на части его ОМ0 потеряется напряжение О2И, причем ОМ совпадает в фазе с ОА, так как мы имеем равенство:
вследствие равномерного распределения сопротивления и самоиндукции вдоль провода.
По той же причине и по величине
ОМ _ OMQ О А ~ OAq ’
где OMQ и OAq могут выражать прямо длины частей провода.
Таким образом расстояния точки М до О дадут нам прямо напряжения на участках ОМ0.
То же самое относится очевидно и к участку А0В0. Например вектор AW даст нам напряжение между точками Ао и MQ.
Соединив М с М, мы получим отрезок ММ, который векто-р и а л ь н о представит нам разность потенциалов между точками М9 и Мо, складывающуюся из двух векторов. ЛМ — напряжения на участке М0А0 и AM—напряжения на участке AqMq.
164
Фиг. 82.
Rk, Рядом построена
Итак, соединив между собой отрезком любые две точки ломаной ОАВС, мы получим вектор, дающий напряжение между двумя соответствующими точками цепи.
В данном примере мы должны обе точки брать на линии ОАВС9 должны оставаться на этой линии; но могут быть случаи, когда отрезок между любыми точками площади фигуры и точками даже целой плоскости дает напряжение между этими точками. С такими примерами мы встретимся в следующей главе при изучении явлений трехфазного тока.
Рассмотрим другой пример.
На фиг. 82 дайы две параллельные ветви, в одной включено только сопротивление /?2, в другой сопротивление и катушка с самоиндукцией L и сопротивлеш векторная диаграмма.
Здесь
ОА^Т^, = + OC=J^.
Возьмем в ветви / какую-нибудь точку р, например, „электрическую* середину ее, делящую сопротивление /?2 пополам; такую же точку возьмем на сопротивлении Rp ветви //. Тогда напряжение между этими точками представится вектором qp9 соединяющим на векторной диаграмме середины (или иные соответствующие точки) векторов ОА и ОС.
Здесь в обоих примерах мы чертили рядом схему и векторную диаграмму. Обычно схемы и не чертят в таких случаях, а на векторной диаграмме отождествляют векторы напряжений на участках цепи с самими участками.
Конечно здесь нужна известная осмотрительность. Например середине катушки будет соответствовать середина вектора ЛС, а не АВ или ВС и т. д.
Остановимся еще на Одном весьма важном для последующего примере.
На статоре генератора переменного тока помещена вторая обмотка, совершенно одинаковая с первой, но смещенная относительно ее на одну треть двойного полюсного деления. ЭДС в ней имеет поэтому ту же самую амплитуду, как и в первой обмотке, но запаздывает (или опережает, смотря по направлению сдвига обмотки) относительно нее на одну треть периода. Эти ЭДС предста-
— — 2п
влены на фиг. 83 векторами 01 и 02, угол между которыми равен
165
Фиг. 83. или
или 120°. Тут же схематическими, — витками, — изображены и обе обмотки.
Начала обоих обмоток соединены вместе, в одну точку О; спрашивается, каково будет напряжение между двумя оставшимися свободными концами обмоток?
Здесь нельзя сложить геометрически векторы ЭДС, ибо катушки нельзя рассматривать, как соединенные последовательно; последнее имело бы место, если бы конец первой обмотки, ее последний проводник, соединили с первым проводником второй обмотки,— с ее началом.
Конец 1 первой обмотки имеет потенциал, отличающийся от потенциала начала ее на разность потенциалов, изображаемую вектором ЭДС 07, или, короче, — на вектор О??
Конец 2 второй обмотки имеет потенциал, отличающийся от потенциала в О на вектор 02.
Отсюда мы заключаем, что к потенциалу 2 точки 2 надо приложить вектор 27, чтобы получить потенциал точки 7, т. е.
К.
^-V2=V12=27,
и конечно наоборот
V2-17=72.
С подобными соотношениями мы встретимся в трехфазном токе. Для последующего полезно определить величину вектора 27.
Так как /207 = 120° и £±201 равнобедренный, то
/027 =/072 = 30°, и
(27) = 2-(07). cos 30° или
(2/) = (О/)./3.
166
ГЛАВА VIII
МНОГОФАЗНЫЕ ТОКИ
§ 48. Двухфазный ток
В устройство генератора переменного тока, имеющего обмотку, подобную изображенной на фиг. 10, может быть внесено существенное улучшение следующего рода.
Так как большая часть пазов по окружности статора при этой обмотке осталась незанятой, то можно в этих пазах поместить еще одну или несколько таких же обмоток, как уже существую* щая.
Предположим сначала, что мы не хотим заполнять всех пазов и помещаем еще только одну обмотку так, что „стороны" ее катушек приходятся как раз по середине между „сторонами" катушек уже Существующей обмотки. Таким образом в то время как проводники одной обмотки находятся например все как раз под серединами полюсов и в них ЭДС достигла максимума, — другая обмотка находится как раз на нейтральных линиях, и в ней ЭДС равна нулю. Когда первая обмотка через четверть периода попадет в нейтральные линии и ЭДС в ней будет равна нулю, тогда вторая обмотка будет находиться под серединами полюсов, и в ней ЭДС достигнет максимума.
Обмотки эти всегда делаются совершенно один а ко* вы ми, т. е. в сторонах их катушек имеется одинаковое число проводников, и размещены они в одинаковом числе пазов у обеих обмоток; поэтому амплитуды и следовательно эффективные значения электродвижущих сил обеих обмоток равны. Вследствие сдвига одной обмотки относительно другой на половину полюсного деления будет существовать таким образом сдвиг в фазе в четверть периода между электродвижущими силами этих обмоток, по амплитуде равными.
У статора теперь имеются четыре зажима: два,— от концов одной обмотки и два другие — от концов другой обмотки. Каждую обмотку мы можем нагружать любым током независимо от того,
167
какой ток берется от другой обмотки; единственным ограничивающим произвол обстоятельством при этом является нагревание машины. Нагрузив обе обмотки до наибольшей, допустимой из соображений о нагреве машины силы тока, мы получим от машины мощность, почти вдвое большую прежней — ири одной обмотке; мы говорим „почти*, так как при двух обмотках допустимая наибольшая сила тока получится для каждой обмотки меньше, чем при одной единственной обмотке, — иначе в статоре выделится слишком много тепла и получится перегрев. Конечно и машина, приводящая во вращение генератор переменного тока (т. е. вращающая его ротор), называемая „первичным двигателем*, должна быть теперь вдвое большей мощности.
Такцм образом небольшим повышением стоимости генератора от наложения второй обмотки вдвое увеличивается мощность, кото-
рую можно получить от него.
К месту потребления электрической энергии идут от генератора четыре провода — по два от каждой обмотки; между концами проводов, принадлежащих одной и той же обмотке, и включается нагрузка. Заметим, что нельзя обе обмотки вклю
чить на одну и ту же нагрузку, например группу ламп, потому что такое параллельное включение двух источников электродвижущих сил при переменном токе только в том случае не представляет опасности, если эти ЭДС имеют не только равные амплитуды, но совершенно одинаковые фазы; при выполнении этого условия два источника тока в параллельном включении имеют ЭДС, направленные (внутри замкнутой цепи, состоящей из этих двух источников) во всякий момент навстречу одна другой, — ни одна из них не может послать тока через другую обмотку. В вышеописанном случае ЭДС двух обмоток различаются в фазе на четверть периода; на фиг. 84 нанесены две соответствующие синусоиды 1 и 2; мы видим, что ЭДС направлены будут друг по отношению к другу навстречу только в течение двух четвертей периода, АВ и CD, причем равны они при этом только в моменты т и /»'; следовательно за исключением этих моментов в течение всего периода в цепи из двух обмоток будет действовать переменная ЭДС в будет циркулировать ток короткого замыкания.
168
Система двух токов, сдвинутых в фазе на четверть периода^ называется двухфазным током, соответствующий генератор — генератором двухфазного тока.
В настоящее время двухфазный ток встречается крайне редко,, а потому в дальнейшие подробности этой системы и ее видоизменения мы не будем входить.
§ 49. Трехфазный ток
Переходим к получившей всеобщее распространение трехфазной системе, при которой генератор имеет на статоре три.
обмотки, так что использование машины получается еще более
полным: при трех обмотках можно ими занять уже всю окружность статора, не оставляя пустых пазов, и повысить мощность машины приблизительно в три раза.
На фиг. 85 изображена схематично обмотка трехфазного тока, состоящая из трех одинаковых обмоток, сдвинутых по окружности статора, — вторая относительно первой и третья относительно. второй, — на одну треть двойного полюсного деления. След-
ствием этого сдвига яв- фиг< 35.
ляется то, что ЭДС во
второй обмотке запаздывает относительно ЭДС в первой на одну треть периода, а ЭДС в третьей — на одну треть периода относительно ЭДС во второй.
Векторы, изображающие эти три ЭДС, будут составлять углы о
в — тг, или 120°. о
На фиг. 85 первая обмотка, или, как обыкновенно ее называют, хотя и не совсем правильно, „первая фаза", начинается у
верхнего северного полюса, и ее начало отмечено подходящим к нему от зажима проводом с буквой /н („начало"). Обмотка, как и остальные, имеет два паза на каждый полюс, занятые ее проводниками; это выражают словами: обмотка имеет два (или вообще паза на полюс и на фазу. Конец первой фазы присоединен к проводу /ж („конец"), идущему к другому зажиму.
169
Вторая фаза имеет начало //н и конец //к, и третья фаза — начало III* и конец — ///к.
ЭДС всех фаз могут быть представлены векторами фиг. 86а. Заметим, в предупреждение обычных ошибок начинающих, что если бы мы вторую и третью фазы передвинули из теперешнего
положения на окружности статора и поместили начало второй фазы ® паз, в котором сейчас лежит проводник, отмеченный через III* <(т. е. сдвинув относительно начала первой фазы лишь на одну треть полюсного деления простого, не двойного), а начало третьей — соответственно в паз, где сейчас находится //н, то ЭДС этих трех
обмоток представились бы векторами фиг. 866; такая система не употребляется. Если мы начертим синусоидальные кривые электродвижущих сил в трехфазной обмотке, согласно фиг. 86а, то получим фиг. 87. Предлагаем читателю нарисовать синусоиды для неправильной обмотки, только что описанной и соответствую* •щей фигуре 866.
170
От машины трехфазного тока таким образом идут шесть проходов; мы имеем три независимые друг от друга цепи, в которых «действуют ЭДС с равными амплитудами:
е1=Ет sin (®0 , 2п
e2 = 5msin at---
\ &
_ . / . 4тг
*3 = £mSlnl — “з
(12b)
отстающая каждая от предыдущей на одну треть периода.
Оказывается, что число проводов можно сократить по крайней мере до четырех, а в некоторых случаях и до трех. Почему это возможно, — объясняется дальше.
Названия „конца" и „начала" у обмоток конечно условны, относительны; можно на фиг. 85 все „концы" назвать „началами" и наоборот.
§ 50. Соединение звездой
Разберем теперь случай, когда все три обмотки — все три фазы нагружены одинаково, т. е. сила тока и сдвиг фаз между силой тока и ЭДС во всех трех цепях одинаковы. Тогда силы токов могут быть выражены так:
i2==J_sin <о/---г + т
2 т \ 3 1 т/ (126)
‘з=Ля!51П(®/ — у+ ?)
Из тех шести проводов, которые идут от машины к месту потребления электрической энергии, выделим три провода „одноименных*, т. е. идущих от трех „начал" или от трех „концов" обмоток, и соединим их вместе в один провод; что от этого произойдет? Какова прежде всего будет сила тока в этом проводе? Ясно, что она будет равняться сумме трех токов в отдельных проводах. Чтобы найти ее, сложим эти токи, т. е. сложим уравнения (126). Легко доказать (предоставляем это проделать читателю самому), что в правой части мы получим нуль, ибо при всяком а
sin а 4- sin [ а —
Итак при одинаковой нагрузке, т. е. одинаковой амплитуде силы тока, во всех трех фазах сумма мгновенных значений сил токов в них равна нулю.
171
Но если сила тока в этом проводе, сложенном из трех прово
дов, равна нулю всегда, то и провод этот не нужен, и его можно выбросить, оставив только соединение трех концов обмоток в одну точку у самого статора. Таким образом, когда можно иметь уверенность, что нагрузка всех трех фаз всегда будет одинакова, тогда можно обойтись при трехфазном токе только тремя проводами; когда же этой уверенности нет, четвертый провод надо оставить, чтобы по нему и шел ток, равный сумме трех токов в
фазах.
Если мы в случае разной фазовой нагрузки попробуем обойтись без четвертого провода, то силы токов автоматически дол ж-н ы будут установиться такими, чтобы их сумма была равна нулю, а при этом, как будет ясно из дальнейшего, напряжения распределятся на фазы не одинаково, и нагрузка, например лампы, будет находиться в разных фазах под разными напряжениями.
Четвертый провод на-
зывается „нулевым", или „нейтральным".
Описанное соединение фаз обмотки машины и нагрузки изображено схематически на фиг. 88. Здесь представлены условно три фазы обмотки машины переменного то-
Фиг. 88.
ка, концы которых присоединены к общему „нулевому" проводу. Далее изображено включение ламп в сеть в разном числе на каждую фазу. Точка А, в которой соединяются все три фазы обмотки машины и нулевой провод, называется нулевой точкой, или нейтральной. Возможно, как увидим ниже, и иное соединение фаз для той же цели, чтобы сэкономить в количестве проводов; поэтому данное соединение носит особое название в отличие от другого, — оно называется соединением фаз „звездой".
Рассматривая правую часть фиг. 88, мы видим, что она по способу включения нагрузки похожа на левую; точка В — место соединения всех трех „фаз" нагрузки и подключения нулевого провода — называется нулевой точкой, а все соединение — соединением, или включением нагрузки звездой.
Остановимся на некоторых обозначениях и соотношениях при этом включении фаз обмотки машины.
Прежде всего заметим, что справедливость того, что ток в нулевом проводе при одинаковой, или, как принято говорить, с и м~ метричной нагрузке фаз равен нулю, мы можем доказать, пользуясь диаграммой векторов токов в фазах, а не тригонометрическими формулами (126). Каждый из этих токов сдвинут относительна
172
своей ЭДС в фазе на одну и ту же величину, следовательно век-
о 2тг торы этих токов составляют углы между собой —. Геометрическая о
сумма таких векторов равна нулю; эти векторы составляют замкнутый треугольник, следовательно и сумма мгновенных значений этих токов, или ток в нулевом проводе равен всегда нулю.
Введем далее такие обозначения.
Силу тока в одной фазе обмотки машины обозначим через Л; силу тока в проводах, идущих от машины к нагрузке, — через }л (ток в „линии" передачи энергии); напряжение между началом и концом фазы — через 1/ф; напряжение между двумя проводами (исключая нулевой) у машины, — напряжение в линии, — через Ул,
Для соединения звездой мы очевидно будем иметь
*^Ф — Л»
(127)
так как ток, идущий по „фазе" машины, не разветвляясь, вступает в провод, в „линию".
Каково будет напряжение Ул например между проводами 7 и 2 фиг. 88 в точках М и N? Такую задачу мы уже решили в конце § 47 и нашли, что VJ2 = 01-]/3; решим здесь ту же задачу несколько иным путем.
Мгновенная величина этого напряжения складывается из мгновенной разности потенциалов от точки М до точки Л, т. е. от конца к началу фазы 7/, и мгновенной разности потенциалов от А до N, т. е. от начала к концу фазы 7. Первое слагаемое есть мгновенное значение напряжения в фазе 77, взятое с обратным знаком, второе слагаемое есть мгновенное значение напряжения в фазе 7 с неизмененным знаком. Поэтому, чтобы получить вектор напряжения между точками М и N, или вектор Ул, надо сложить
геометрически вектор напряжения в фазе 7 и вектор, обратный по направлению вектору напряжения в фазе 77. Это сложение произведено на фиг. 89, где вектор 02'—— 02, Складывая 02' с 07, получаем вектор О А напряжения между точками М и N. Длина этого вектора из Д07Л получается равной O7-J/3.
Следовательно при соединении звездой
(128)
Напряжение Ул называется еще также „междуфазовым", а 1/ф— „фазовым".
173
Такое же соотношение существует и между напряжениями ^us~ и ^ит~ ^ф>
§ 51. Соединение треугольником
Перейдем теперь к другому возможному соединению фаз обмотки генератора трехфазного тока.
Сложив уравнения (125), мы получим в сумме нуль. Следовательно сумма мгновенных значений трех ЭДС трехфазной обмотки всегда, во всякий момент, равна нулю. Поэтому все фазы можно соединить так: конец 7 с началом 77, конец 11 с началом III и конец III с началом 7. Такое соединение изображено на фиг. 90.
Здесь все три фазы
Фиг. 90.
соединены так, что каждая включена навстречу двум остальным; в этом треугольнике из трех „фаз" сумма ЭДС всегда равна нулю; поэтому это соединение подобно параллельному соединению источников
тока: пока внешняя цепь не подключена к обмотке, тока в обмотке быть не может.
Нагрузка — лампы — изображена на фиг. 90 включенной тоже аналогичным образом.
Такое включение называется включением или соединением фаз „треугольником*.
I »ри этом включении имеются только три провода, нулевого провода и нулевой точки совсем нет.
Рассмотрим соотношения напряжений и сил токов при включении фаз треугольником.
Напряжение между началом Л! и двух проводов „линии" 7 и 2 есть напряжение между началом и концом одной фазы — 7; поэтому здесь
Гл=уф. (129)
Ток в линии, т. е. например в проводе 2, складывается из двух токов: тока, текущего по одной < фазе — по 7 — от начала N к концу М и дальше по проводу 2, и тока, текущего по другой фазе — по II—от конца К к началу М (в точке М мы имеем ведь конец одной фазы и начало другой), т. е. тока фазы 77, взятого с обратным знаком. Такое сложение токов может быть
174
представлено той же фиг. 89. Здесь О2Г = — 02 представляет ток обратный току в фазе //. ОА есть ток в линии Ja. Таким образом для включения треугольником
Л-А/з. <1зо>
Сравним теперь оба соединения — звезду и треугольник.
На фиг. 88 лампы в каждой фазе нагрузки присоединены нулевым проводом к концу одной фазы обмотки машины и соответствующим проводом /, 2 и 3 к началу ее, так что, пренебрегая падением напряжения в проводах, можно считать, что лампы находятся под фазовым напряжением 1/ф. Если мы отбросим нулевой провод, то* напряжение на лампах не изменится только в том случае, когда общее сопротивление ламп в каждой фазе нагрузки одинаково для всех трех фаз, т. е. общее сопротивление ламп, включенных между 5 и Q, такое же, как и между U и Т и между X и Y. Рассматривая цепь, составленную из таких частей: фаза I—фаза II—провод 2 — лампы 5Q— точка В — лампы TU—провод /, мы найдем, что все напряжение Ул между /И и N распределится при этом поровну между SQ и TU ^разлагаясь на геометрические слагаемые VSq—Vq и Vw—Vq по амплитуде равные, по фазе* 2гс\ сдвинутые на — I.
Если же сопротивление ламп в SQ не равно сопротивлению их в TU, то это напряжение Ул разделится на два геометрических слагаемых уже не равных амплитуд, а пропорциональных общим сопротивлениям этих частей цепи.
В результате лампы в SQ окажутся под другим напряжением, чем лампы в TU, и горение тех и других будет неправильное.
При включении же как фаз обмотки машины, так и ламп треугольником (фиг. 90) лампы в каждой фазе нагрузки будут всегда находиться под фазовым напряжением, независимо от отношений между сопротивлениями отдельных фаз нагрузки. В этом отношении включение треугольником удобнее включения звездой: первое требует и при неравномерной нагрузке фаз всего трех проводов.
Преимуществом включения звездой является более высокое напряжение в линии. Для уяснения этого вопроса надо сначала определить величину мощности при трехфазном токе.
§ 52. Мощность трехфазного тока и измерение ее
Каково бы ни было соединение фаз, при симметричной нагрузке' вся мощность машины Р в три раза больше мощности одной
175
фазы. Обозначим через срф угол сдвига фаз между напряжением фазовым Уф и силой тока через фазу /ф. Тогда
^=З.Уф/фС05¥ф. (131)
В случае соединения звездой
К,-Иф/3 И Уф = /Л, следовательно:
Р—/ЗУЛ«>8?ф- (132)
В случае соединения треугольником
и 4=4/3, поэтому:
Р=/зУл4соз<рф.
Таким образом, введя величины „линейного* напряжения Ул и „линейной* силы тока Ул, в обоих случаях мы получили одно и пго же выражение для мощности (132).
Пусть мощность Р и напряжение фазовое в машине Уф даны. Определим силу тока в линии при передаче этой мощности в двух случаях — при включении фаз машины треугольником и звездой.
Из ф-лы (132) имеем:
/ЗУлсоз<рф’
при соединении треугольником
/ЗУфсоз(рф*
При соединении звездой
^=/зУф И
4 ЗУфсоз<?ф
Таким образом при передаче одной и той же мощности сила тока в линии при соединении фаз машины звездой в раз меньше, чем при соединении треугольником, следовательно соответственно меньше потребуется и поперечное сечение проводов. Вот в каком отношении соединение звездой выгоднее соединения треугольником.
176
Следует заметить, что соединение обмотки в машине может ,быть одного рода, а соединение нагрузки — другого. Пусть например у нас имеются лампы накаливания на 220 вольт и генератор трехфазного тока, ЭДС которого достигает в каждой фазе величины всего лишь в 130 вольт. Включим фазы обмотки машины звездой; тогда напряжение между проводами будет = 130 • ]/3 = = 225 вольт — величина, подходящая для ламп, принимая во внимание падение напряжения в проводах. Лампы включим треугольником; тогда все они будут находиться под напряжением приблизительно в 220 вольт.
Для дальнейшего следует заметить, что вся изложенная в предыдущих главах теория переменного тока применяется к каждой фазе в отдельности. При симметричной нагрузке во всех фазах
можно ограничиться построением векторных диаграмм только для одной фазы; для остальных фаз диаграммы получатся в точности такие же. Диаграммы трех фаз будут повернуты друг относительно
2тг 4тг
друга на углы — и —. о о
В случае же несимметричной нагрузки
фаз, например при разном сдвиге фаз между Уф и Уф, необходимо вычерчивать диаграммы и вести расчеты для всех фаз по отдель
Фиг. 91.
точка, тогда ватт-включается в лю-
ности.
Теперь рассмотрим способы измерения ваттметрами мощности трехфазного тока; здесь могут быть разные случаи, в зависимости от того, симметрична или нет нагрузка, имеется или нет, доступен или нет нулевой провод или нулевая точка.
Обратимся сначала к случаю, когда нагрузка симметрична.
Тогда достаточно измерить мощность в одной фазе, чтобы простым умножением ее на три получить всю мощность трехфазного тока.
Если имеется нулевой провод или нулевая метр включается так: толстая катушка (фиг. 91)
бой провод — кроме нулевого — последовательно; один зажим тонкой катушки присоединяется к этому же проводу, а другой зажим — к нулевому- проводу или к нулевой точке; тогда тонкая катушка находится как раз под напряжением одной фазы, и ваттметр меряет мощность Иф/ф cos <рф. Умножая его показание на три, получим всю мощность. Если нулевого провода нет, то можно искусственно создать нулевую точку на основании следующих соображений.
Подключим к трем проводам трехфазного тока в точках т — п — — k (фиг. 92) три равных ваттных сопротивления, O'N\ О'М' и О'К\ и соединим их друг с другом звездой. Так как сопротивления равны, то и токи по ним равны, мы имеем симметричную
12 Теория иеременных токов.
177
нагрузку фаз при включении и нагрузки звездой. Если мы нулевые точки генератора О и нагрузки О1 соединим проводом, то этот провод и будет нулевым, ток в котором при данных условиях будет равен нулю. Если же ток в каком-либо проводе равен нулю, то потенциал вдоль этого провода не меняет своей величины, следовательно потенциал в О' всегда равен потенциалу в О. При отсутствии провода 001 это равенство очевидно не нарушится. Отсюда и вытекает такое следствие: если мы к трем проводам
трехфйзного тока подключим звездой три равных ваттных сопротивления, то общая всем им точка будет обладать тем же потен-
циалом во всякий момент, что и ну-
накова.
левая точка. Включим тонкую катушку ваттметра вместо одного из этих сопротивлений, например О 'ЛГ; уравняем два другие сопротивления с сопротивлением этой катушки; если напряжение таково, что необходим реостат для включения тонкой катушки, то включим его и учтем его сопротивление. Цепь тонкой катушки теперь у нас будет включена между нулевой точкой и точкой т\ если мы толстую катушку включим в провод Л4/п, то мы измерим мощность фазы ОМт\ утроив ее, получим всю мощность трехфазного тока.
Заметим, что нельзя было бы тонкую катушку ваттметра включить между О1 и tn параллельно с
включенным уже сопротивлением О'М\ равным сопротивлениям OW и О'К\ так как тогда нагрузка фаз не была бы оди-
Перейдем к случаю, когда нагрузка фаз различна.
Если имеется нулевой провод, то, включив три ваттметра толстыми катушками последовательно в три главных провода линии и присоединив тонкие катушки к нулевому и соответствующему главному проводу, мы смэжем измерить все три фазовые мощности по отдельности и, сложив их, получим всю мощность.
Если • нулевого провода нет, то можно измерить только всю мощность, а не отдельные фазовые мощности, и для этого достаточно только двух ваттметров. По первому закону Кирхгофа мы имеем и в общем случае при какой угодно нагрузке фаз в случае отсутствия нулевого провода:
h + *2 + 4 — откуда . __
12 li 1з
178
Величина мгновенной мощности во всех трех фазах такова: где v с индексами означают мгновенные значения фазовых напряжений; подставляя сюда вместо /2 его последнее выражение, получаем: р = -o2) + z2(c3—^г)- (133>
Один ваттметр включим так, чтобы он измерил среднюю за период величину первого слагаемого, для чего его тонкая катушка должна находиться под разностью напряжений двух фаз, перовой и второй; другой ваттметр включим так, чтобы он измерил среднюю за период величину второго слагав- .-----------
мого, для чего его тонкая катушка должна j л|\ л______________
находиться под разностью напряжений третьей 1 v \|V
и второй фаз. Такое включение представлено 2-----------1------
на фиг. 93 Сложив показания обоих ваттмет- 3 д!4- -> ров, мы получим всю мощность всех трех | j
фаз.
Большей частью при этом обе слагаемые Фиг. 93.
мощности положительны, но если нагрузка сильно индукционна, хотя и не во всех фазах одинакова, то возможен другой случай.
Представим себе, что на фиг. 89 векторы О/, 02, 03 представляют фазовые напряжения. При сильно индукционной нагрузке ток Jj может отстать от своего фазового напряжения 01 на угол, больший 60°, и следовательно от напряжения междуфазового У1 — V3 = ОА (при неравномерной нагрузке фаз не составляющего уже впрочем с 01 угла равного 30°) на угол, больший 90°, или —, а тогда средняя мощность этого тока Д с напряжением £
О А = Vj 2, равная I/, 2Д cos (Д О А), будет отрицательна; при этом другой важный’ нам (см.’ формулу 133) вектор напряжения У3 г= 03 4“ 02’, наоборот, приблизится к вектору Д— в чем читатель легко убедится, начертив векторы токов для описываемого случая индукционной нагрузки, — так что другая слагаемая мощность будет положительна (по абсолютной же величине больше первой)
Если одно из двух слагаемых делается при этом отрицательным, то ваттметр, показывающий отрицательную мощность, надо переключить, чтобы можно было эту отрицательную мощность отсчитывать (конечно если у ваттметра нуль находится по середине шкалы, так что можно пользоваться отклонениями в обе стороны, то в переключении нет нужды), и затем его показания вычитают из показаний другого, чтобы получить всю мощность в цепи. 12 * 179
Начинающие часто думают, что в том случае, когда нулевого провода нет, а нагрузка фаз симметрична, можно узнать мощность и не образуя искусственной нулевой точки, а включив один лишь ваттметр так, как включен любой из ваттметров на фиг. 93. Покажем, как при таком включении и упомянутых условиях величина всей мощности связана с показаниями ваттметра. Пусть тонкая катушка включена между проводами 1 и 2, а толстая включена в фазу /, как на фиг. 93
Очевидно, что при симметричной нагрузке фаз вектор Vj 2 = с® Уд составит угол в 30° с вектором Уг и что ваттметр измерит и покажет мощность
Р'= Vj cos (<?„, + 30°),
где <рф есть угол сдвига фаз между фазовым током J~ и фазовым напряжением
Так как
cos С?ф + 30°) = cos <рф — у tg ,
то, принимая во внимание выражение (132) для мощности Р трехфазного тока, имеем:
г(А)
откуда, называя Р показанием ваттметра,
21/^ р— - х (показание ваттметра).
/з-tg^
Так как в случае индукционной нагрузки при подобном измерении угол срф неизвестен, то и узнать мощность Р из показаний одного только ваттметра при такой нагрузке нельзя.
Читателю нетрудно будет вывести самому, что в случае подключения второго ваттметра его показания будут:
Вычитая (А) из (В), имеем:
откуда
(134)
180
Фиг. 94.
Не забудем, что формула эта для определения угла срф выведена для случая симметричной нагрузки трех фаз (например трехфазными двигателями). При отступлении кривых тока или напряжения от синусоидальности она перестает быть точной.
Из выражения (А) для Р* мы опять видим, что когда tg^ станет больше |Лз, т. е. когда срф станет больше 60°, множитель в скобках станет отрицательным, и ваттметр надо будет переключить.
Описанное включение двух ваттметров неприменимо для цепи с нулевым проводом.
Остановимся еще на употреблении способа двух ваттметров в том случае, когда фазы нагрузки соединены треугольником.
Обозначив через Zp Z2 и Z3 мгновенные значения фазовых токов в нагрузке, через vv v2
и — напряжения в фазах нагрузки, они же линейные напряжения в данном случае, мы будем иметь прежде всего
vi + ^4-уз=°> откуда
Преобразуем выражение мгновенной мощности:
hVl + '2 V2 4" 1з»3 = 4- из('з — 4)'
Подключив тонкую катушку из первого ваттметра под напряжение а толстую, как показано на фиг. 94, в линейный провод, подводящий ток к фазам 1 и 2, мы измерим первую слагаемую правой части последнего выражения.
Вторым ваттметром, показанным на фигуре, измерим вторую слагаемую.
§ 53. Применение топографического метода — включение нагрузки треугольником
Для представления соотношений в цепи многофазного тока посредством векторных диаграмм очень удобен топографический метод. Мы поясним его приложение на примере трехфазной цепи, нагруженной несимметрично.
181
«Л
Фиг. 95.
Пусть фазы генератора включены звездой, а фазы нагрузки треугольником, как изображено на фиг. 95. причем нагрузка несимметрична. Силам токов в линии и в треугольнике нагрузки придадим обозначения, указанные на чертеже Фиг. 96 представляет векторную диаграмму для электродвижущих сил, напряжений и сил токов в этой трехфазной цепи. ЭДС трех фаз генератора представлены векторами О/, ОН и OHI соответственно обозначениям самих фаз генератора. Вернувшись к фиг. 89, мы видим, что вектор СМ, результирующий из 01 и О2' =—02, мы могли получить, просто соединив точки 2 и 7, так как О А = 21. Поэтому на фиг. 96 из 01 и — О//; он представит
ЭДС, действующую в контуре ОН 2110 (фиг. 95); подобным же образом (777, П) есть вектор ЭДС в контуре ОН231ПО\ (7, 777) есть вектор ЭДС в конту Далее, на фиг. 96 на» в сторонах треугольника составляют разные углы сдвига фаз с ЭДС контуров, в которые входят эти стороны треугольника. По этим силам токов можно найти и силы токов в линии Jv J2 и J3. Перенесем все три вектора У12, У23 и Jgj параллельно самим себе в центр фигуры О, так что Оа== J12, Ob = J23 и Ос — 731. Тогда вектор ab — Ob — О а = J23 — — Л2 = Л ( Лг ВХ°ДИТ здесь в левой части с ми
есть
е 0HI31I0
;рчены векторы J]2 У23 и 731 сил токов нагрузки; силы этих токов различны и
Г
нусом, так как мы силы токов считаем положительными, когда они текут в фазе нагрузки от „начала" к „концу", а при треугольнике „начало" одной фазы соединено с „концом" другой; хотя для нагрузки понятие „начала" фазы и „конца" еще более условно и произвольно, чем для обмотки генератора, но оно необходимо, чтобы считать, что три тока в сторонах треугольника сдвинуты друг от-
182
. 2п 4п\
носительно друга в фазе в среднем приблизительно на — и — ;
" о У далее, получаем bc~J3 и ca = Jr Силы токов в фа ах генератора составляют, как видим, разные углы сдвига фаз с электродвижущими силами в фазах генератора О/, ОН и ОШ
Мы можем теперь получить напряжения, под которыми нахо-
дятся стороны треугольника нагрузки.
Вычтем ЭДС 7 фазы 01—вектор падения напряжения в ваттном сопротивлении как самой фазы, так и провода 7—7, при силе тока ca==Jv именно — вектор Л7У1/?1, и прибавим ЭДС самоиндукции фазы и провода Al — JyXv причем А1 | са, и мы получим вектор 01 напряжения между точками О и 7 фиг. 95. Все построение совершенно подобно нахождению напряжения ОК на фиг. 24. Проделав то же с другими фазами, найдем векторы 02 — напряжения между точками О и 2 и ОЗ — напряжения между точками О и 3 (фиг. 95). Соединяя точки 7 и 2, мы получим вектор 27, представляющий напряжение У12 от точки 7 до точки 2 по фазе 12 нагрузки; аналогично 32 есть У23— напряжение от 2 до 3 и 13 есть У31 —напряжение от 3 до 7.
Если сопротивления проводов и фаз и их самоиндукции одинаковы, что и нормально, то треугольники 7Л/, 2BI1 и ЗСШ подобны.
Заметим теперь следующее. Допустим, что потенциал точки О фиг. 95 равен нулю. Изобразим его на фиг. 96 точкой О. В фазе 01 действует ЭДС 01. Чертим на фиг. 96 вектор 01 и считаем, что конец фазы 01 в отсутствие тока имеет потенциал, изображаемый точкой 7, т. е. его потенциал отличается от нуля потенциала точки О на величину 01 фиг. 96; то же самое имеет место относительно фазы 011 и вектора ЭДС 011 Концы фаз 7 и 11 фиг. 95 имеют разность потенциалов, представленную на фиг. 96 вектором 77 7; вообще расстояния между двумя точками фиг. 96 представляют собой разности потенциалов между двумя соответствующими точками фиг. 106. В этом и заключается, как было уже сказано, идея топографического метода.
§ 54. Применение топографического метода — включение нагрузки звездой
Рассмотрим другой пример.
Пусть нам подано напряжение трехфазного тока от мощной станции по достаточно толстым проводам, так что нагрузки, подключаемые нами к сети, не изменяют заметно линейных напряжений, как бы несимметрична нагрузка ни была.
Треугольник линейных напряжений 123 фиг. 96 повторен на фиг. 97 и 98.
183
Для последующего очень важно раз навсегда заметить, что векторы трех линейных напряжений всегда составляют замкнутый треугольник, если мы их начертим не из одной точки, а приложим один к другому последовательно, причем совершенно безразлично, как включен генератор и как — нагрузка.
Доказательство этого весьма просто.
Обозначим буквой V1 с чертой и штрихом потенциал одного из проводов или зажимов трехфазного тока (например относительно земли), через V" потенциал другого провода или зажима и V919— третьего; тогда очевидно линейное напряжение^между проводом или зажимом первым ме ду вторым и третьим:
К и между третьим и первым:
1 вторым равно:
= И —И
— у" у919
= ут yf.
Складывая эти три равенства, мы в правой части получим нуль а следовательно
^ + V23+V31 = 0;
если сумма векторов равна нулю, это значит, что многоугольник их замыкается, результирующая его сторона равна нулю.
В далг нейшем мы не раз будем говорить о замкнутости или незамкнутости треугольника, составленного из тех или иных векторов.
Включим (фиг. 97) между тремя зажимами /, 2 и 3 симметричную нагрузку звездой, например в виде трех реостатов без ну евого провода. Из предыдущего ясно, что напряжения в каждой фазе или „луче" звезды нагрузки выразятся векторами 011 02 и ОЗ;, они в/З раз меньше линейных напряжений и составляют д^уг с другом углы 120°.
Будем теперь изменять нагрузку в одной из фаз, например уменьшать сопротивление в луче 01. Тогда и векторы фазовых 184
напряжений будут изменяться по величине и награвлению. Геометрическая разность двух векторов должна быть при этом прежней, должна выражать по величине и фазе все то же линейное напряжение, т. е. концы векторов фазовых напряжений остаются попрежнему в точках /, 2, 3, а общее начало их перемещается.
Так как нагрузка в фазе.02 остается равной нагрузке в фазе ОЗ* то и напряжения на этих фазах равны по величине; поэтому при изменении нагрузки в луче 01 общее начало векторов перемещается по перпендикуляру 1 — М9 опущенному на сторону 23; при этом напряжение в первой фазе может принимать весьма разные значения. При некотором уменьшенном сопротивлении напряжение в первой фазе равно N1, причем два других фазовых напряжения будут N2 и N3.
Если сопротивление в первой фазе равно нулю, т. е. между нулевой точкой О нагрузки и проводом или зажимом 1 имеется короткое замыкание, то напряжение в этой фазе равно нулю; точка N теперь находится в точке 1; две другие фазы нагрузки естественно попадают под полное линейное напряжение каждая; напряжения на фазах нагрузки будут теперь вместо N3 вектор 13 и вместо N2 вектор 12.
Состояния симметричной нагрузки мы теперь можем охарактеризовать или символизировать нахождением точки общего начала векторов фазовых напряжений как раз в центре тяжести О треугольника линейных напряжений 1—2—3.
Будем теперь сопротивление в луче 01 увеличивать, тогда точка О будет переметаться вниз, например в положение М1.
Разомкнем фазу 01; тогда у нас нагрузка будет состоять из двух равных сопротивлений, включенных последовательно одно за другим между зажимами 2 и 3.
Подходя к этому состоянию как к пределу, мы можем считать за среднюю точку нагрузки точку Ж, и за фазовое напряжение в фазе первой, теперь разомкнутой, вектор Ml.
Если мы между зажимом 1 и точкой соединения двух упомянутых равных сопротивлений включим электростатический вольтметр, он покажет напряжение, по величине равное Ml, т. е. в j/*3 раз большее, чем напряжение М2 или М3 на каждом из двух сопротивлений, так как
Ml = М2-УЗ.
Если мы подключим не электростатический вольтметр, а какой-нибудь другой, то этим самым между серединой нагрузки и точкой 1 мы включим некоторое, хотя и большое, но все же не равное бесконечности сопротивление, и средняя точка нагрузки будет символизироваться точкой Mf; напряжения будут Л1'2 и М'З на двух сопротивлениях и Mfl — на вольтметре.
185
Теперь представим себе, что все три сопротивления различны; тогда и все три фазовые напряжения тоже будут различны и по величине и по фазе и изобразятся векторами Plt Р2 и РЗ (фиг. 98).
Конечно, если сопротивления безиндукционны, то те же векторы представят в другом масштабе и силы токов в фазах нагрузки. Очевидно, что, подбирая различные величины фазовых сопротивлений, мы можем точку Р общего начала векторов фазовых напряжений перенести в любую точку внутри треугольника 123.
Точка Р своим положением дает уже потенциал средней точки нагрузки, и мы теперь каждой точке внутри треугольника 123 приписываем потенциал, разнящийся от потенциалов зажимов /, 2, 3 на разность потенциалов, или на напряжение, представляемые вектором из Р в точку /, 2 или 3
Это и есть то дальнейшее развитие идеи топографического метода, о котором было упомянуто в § 47.
Выразим рассматриваемые соотношения аналитически, остановившись в этом параграфе ha том частном случае, когда отношение сопротивлений ZA и Z2 в фазах 01 и 02 (или Р1 и Р2) есть число действительное, т. е. оба сопротивления вызывают одинаковый сдвиг фаз тока от напряжения и в одинаковом направлении.
Итак
Zj= т Z2.
Тогда, обозначая фазовые напряжения в нагрузке через Vv V2 и V3, по первому закону Кирхгофа имеем, что
i+K+s=0
Z3
(сумма фазовых токов равна нулю, следовательно их векторы составляют замкнутый треугольник).
Подставляя выражение Zv имеем:
Z2 \т ?з
откуда
1 _ __ 7 —
у2=—£1-и8.
т Z3
Если фаза третья разомкнута, то Z3 = оо и
— + =
т 1 1 2
186
следовательно
^ = -^2,
т. е. Уг и У2 прямо противоположны по направлению, так как т — число действительное, или, иначе, лежат на одной прямой; а так как концы их 1 и 2 даны, то очевидно они лежат на прямой 12, и
Q7=Vp a Q2 = y2 = --Lyi2,
при этом
21 = Q1 4 2Q = Qj - Q2 = У. - V2 = У.2.
Далее длины Q1 и Q2 относятся как т к 1:
Q7 =
Q2
т.
Напряжение q$ между точкой Q и 3 есть напряжение на третьей
разомкнутой фазе. Однако такое определение имеет смысл только
при подходе к точке Q, после того, как фаза третья стала разомкнутой, точка соеди* нения фаз первой и второй теряется, любую точку на всем том сопротивлении, которое включено между зажимами 2 и 7, можно счесть за точку, бывшую раньше средней точкой нагрузки, а потому вектор из любой точки стороны 21 до точки 3 может быть рассматриваем, как вектор напряжения между зажимом 3 и этой точкой.
В § 65 мы продолжим это исследование и увидим, что точка Р может и выйти за
Фиг. 99.
пределы треугольника.
Решим задачу, предложенную в свое время Кенелли, о получении из трехфазной системы двухфазной, т. е. двух напряжений, сдвинутых на четверть периода Как мы видели на фиг. 97, вектор ОМ перпендикулярен к векторам М3 и Л42, но лишь в отсутствии тока в фазе Ml, т. е. когда Z1 = oo.
На фиг. 99 величина Z3 такова, что при равенстве Z3 = Z2 имеем Уг = У2 и V2 | V2, Во все три фазы предполагаем включенными только ваттные сопротивления, так что токи совпадают с напряжениями; на фиг. 110 нанесены токи
— У - У — У
j — _ j — —?_ и J — —— ГА)
причем
187
так что
А = А>
далее, ___ __
73= J Jt
по первому закону Кирхгофа. _ __ __ _
Из чертежа ясно, что вектор -J- J2 по величине равен 2,
следовательно и J3 = 2; далее
У =У2 = ^— или У1==У =УЛ4=, 1 2 у 2 У 2
у 1/"q 1 1/"^__ 1
Р5=25=х=ул; P3 = S3-PS=V3^-Vjiy = VjlL_--------------
или
V3 = 0,365 Ул.
Подставляем эти величины J3 и У3 в третью формулу (А):
а/-2- = 0^5
из первой же формулы (А) имеем:
J=-^ 1 ЪУ2‘
Деля последние полученные равенства одно на другое, получаем:
/2 : Л’365^ ^3
откуда
/?1:/?3 = 2,73.
§ 55. Применение символического метода к трехфазному току
Обратимся к тому, как применить метод комплексных величин для выражения трех электродвижущих сил трехфазного тока (фиг. 86а). Вектор Ег направим по оси действительных величин, поэтому его выражение будет h — E. Для вектора Е2, составляющего угол в 30° вниз с отрицательной осью мнимых величин, выражение очевидно будет таково;
а для Е3:
Лз -14-7/3 Р
2 ~~ 2
(135)
1
2
188
Отметим, что комплекс
-1-JV*
2
= — 0,5 —у‘0,866,
имеющий модуль, равный единице, выражает поворот вектора Et относительно вектора Ег Если мы, далее, умножим вектор Е2 на этот же комплекс, то получим вектор E3i так как
/-1 -7/з\«_-1_|_7/з
\ 2 / 2
По общему правилу символического изображения комплексов
- 1 -уУЗ _
Эти выражения нам известны уже из задачи.
Таково выражение множителя, поворачивающего векторы на 120° по направлению вращения линии времени. Итак
,2тс 4п
Ё1=Е, E2 = Ee~J^ и E3 = Ee~J\
Такие же выражения для напряжений можно написать очевидно только для случая симметричной нагрузки; при несимметричной — падения напряжений будут для разных фаз разные, и напряжения будут и по величине отличаться друг от друга и по фазе будут 2п
сдвинуты друг относительно друга не на —-, как это показано на о
фиг. 96. +/-
Множителю е 3, поворачивающему векторы на 120°, навстречу линии времени, т. е. Ё3 в положение Е2 и Е2 в положение Ev присвоено в литературе особое обозначение — буквой а, так что 1 1Zo
a = e+i =-2_4-уКг== —0,5 4-/0,866. (136)
Л л
Черты над буквой а не будем ставить ввиду полной определенности значения этого символа.
Примеры 31 и 32. Чему равно а9 и 1 4- а + а9 и какой геометрический смысл имеет тот и другой результат.
§ 56. Определение сил токов и напряжений при включении фаз генератора и нагрузки звездой
Рассмотрим тот случай, когда генератор и нагрузка включены звездой (фиг. 100), но без нулевого провода, и составим уравнения, выражающие соотношения между всеми величинами в такой цепи
189
Обозначим силы токов в фазах через Jn J2, J3; за положительные направления их возьмем направления, совпадающие с электродвижущими силами; полные сопротивления каждой фазы генератора через Zr—проводов линии Zp Z2, Z3 (обыкновенно Zj = = Z2 = Z3) и фаз нагрузки Z1If, Z2h, Z3h; ЭДС, как обычно, £3.
Применим второй закон Кирхгофа поочередно к контурам О—I—I—O'—2—И—О, О—II—2—0'—3—III—О и О—Ш—З— —О1—I—I—О и мы получим уравнения:
(A)
^2 = Л + Л 4” Л ^1н Л ^2Н Л Л £г>
^2 ^3 А —г 4~ —2 4" 7* ^2н А ^Зн £з ^3 А ^г’
£*з Ег = J3 Zr -j- J3 z3 + /3 z3h Z1h J3 z3 Zt.
Фиг. 100.
Здесь одно из уравнений есть следствие двух других Эти уравнения можно упростить, положив
zt-\-z.l=zT-}-zi=zr-\-z3=z и заметив, что
4i?ih=2jo'> ]
Л ^Зн = ^30' > ) или Ту ____________________Ту — у
12_2Н -Л12>
17 ____ 17 — \7
±2н 13 _3н--_23 ’
1 7 ___ 17 V
(В)
(С)
где V12, Vgg и У31—линейные или междуфазовые напряжения. Таким образом получаем:
~ 7*2 7з 2 4" J^23 »
Ез-E^J.Z-J.Z+V,..
190
Кроме того имеем еще уравнение:
Л + <D)
Два из уравнений (А) и уравнение (D) составляют систему трех уравнений с тремя неизвестными токами, которые из уравнений и определяются.
Могут быть конечно неизвестны и три сопротивления нагрузки Z1H, Z2H, ^зн» когда известны три тока. Последние должны непременно удовлетворять уравнению (D), но при решении задачи об определении сопротивлений нагрузки уравнение (D) бесполезно, оно есть условие правильности задания трех токов. Поэтому кроме двух уравнений (А) нужно еще третье уравнение, которое может быть разной формы, например может быть дано одно из фазовых напряжений в звезде нагрузки (Б).
Пример 33. Даны: величина ЭДС Е = 130 вольт,
Z= 3 + у 0,4, Z1H = 4 -|- /2, Z2h = 3 + /2, Z3h = 3 4- /•
Вычисляем отдельные выражения В уравнении (А):
Ё, — = Е + Е-_ £.1+ = 195 +/-65 / 3 =
= 130 КЗ е = 225г7300.
£, — — Е. — - В-—- +2?= — EjV3 = — /130]/! =
= 225г_/7 = 225г~^°.
Решим систему уравнений (А) и (D) в общем виде и найдем например 7L Из (D):
— Л — Л 4~
Преобразуя несколько первое уравнение (А) и подставляя во второе вместо —J3 его выражение, имеем:
£*4 Е% = («А — /з) Z 4~ A Z1H /2 ^2н»
^2 — ^s— 1 + 2Za) Z + 4^(^ 1 + Л) z3„ =
= Ji (Z 4- Zijh) 4~ h (?Z 4- Z2h 4- Z8H).
Из первого _________ _
_ ^(Z+Z^)-^^)
J 9 = ----— —------------
Z + Z2H
подставляем во второе и получаем:
Ei-Et = Jl(Z+ Z3H) + Л _
Z + Z2H
— (4“ ^2h 4* Z3H)
191
7=(£» - 5>) (£+£2н) + (£« - jfi) (2 z + z2H + g,H) (2- + Z3H) (Z + ^2н) + (Z + ZlH) (2Z + Z^ +
Производим необходимые вычисления:
Z + Z2h = 6 + /2,4 = 6,5^21050», 2Z + Z^ + Zjh = 12 + /3,8 = 12,6^17°зз;
z + Z3H = 6 + /1,4 = 6,^/13°10\ Z + Z1H — 7 + /2,4 = l,5e№7,
(F2 — £,)(Z + Z2h) = 225 • 6,5^-/68010' = 1 462^-/68010' = 544 357,
— Ё~2) (2Z + Z2H + Z3H) = 225 - 12,6e/47°33’ = 2 835г/47<>зз' = 1 900 + /2 070, (Z 4- Z2rf) (Z + Z3H) = 40,3e/35o = 33+ /22,3 (ибо cos 35° = 0,820.)
(Z + Z1H) (2Z + Z2H + Z3H) = 94,5^/36026' = 75,6 + /55.
Знаменатель равен:
Ю8,б + /77,3 = 133^35025’.
Числитель равен:
2 444 + /705 = 2 540г/1бо10».
Производя деление, получаем:
^=19,8^-/190154
Далее для вычисления J2 узнаем:
7t (Z + Z1H) = 19,8е- /19°15'. 7,5е/18°53' = 148,5г-/о°22' = 148 —/0,9.
Числитель в выражении
J2 = — 195 -/112,45 + 148 —/0,9 = — 47 —/113 = 123^/(б7°35+180°),
Разложив /( и /2 в комплексные двучлены и взяв сумму их с обратным знаком, получим J3.
§ 57. Определение сил токов и напряжений при нагрузке
треугольником
(Способ непосредственный)
1. Для того случая, когда фазы генератора включены звездой, а нагрузка треугольником (фиг. 95), определим теперь аналитически силы токов и напряжений.
Даны: три ЭДС генератора Ev Е2 и Ё3; полные сопротивления каждого провода линии вместе с той фазой генератора, к которой провод подключен: Zp Z2 и Z3; полные проводимости каждой стороны треугольника нагрузки (если известны сопротивления их, переходим к проводимостям) У12, Y23l Y3V
192
Тогда
£ “Лз £з1» £й = £28 Л 2» А вЛ1 Лз -
(А)
составят первые три ур-ия из нужных нам.
Заметим, что сложив их, получим:
Л+Л + Л®0-
Для напряжений на нагрузке имеем:
У12 — £2 ££т “F £^2»
^23 = £2 ’ £з ^2^2 А£з>
V3i = E3-E1-J323 + J1Z1
Эти уравнения есть не что иное, как алгебраическое выражение геометрического определения напряжений, сделанного на фиг. 96, именно вычитания вектора Е2 — J2Z2 из вектора Et—JyZt и т. д. Уравнения (В) получаются так же легко и применением второго закона Кирхгофа.
Последними, необходимыми нам для решения, являются ур-ия:
£12--- ^12^12'
j ==17 г _23 2_23_28»
Л1 в ^31 ^31*.
(С)
В девяти уравнениях (А), (В) и (С) содержится девять неизвестных Jj, J2, J8, /12» *^23> 731> ^12’ ^23’ V3P
Так как все они имеют комплексные выражения и всякое уравнение распадается поэтому на два ур-ия, выражающие равенства действительных членов в правой части действительными членами в левой и тоже относительно мнимых членов, то можно говорить и о 18 неизвестных и 18 уравнениях.
Можно решать эту систему уравнений в общем виде, причем получаются чрезвычайно длинные формулы, можно вести решение уравнений в каждом частном случае, когда «данные» (5Р Е2,... Zv Z2.,.) известны в числах, производя все необходимые переделки и сокращения с самого начала.
Определим прежде всего напряжения на нагрузке.
Подставляем из (С) в (А):
£i= Х12312 1
£2 = ^23^23 — ^12 ^12 ( (®)
А = ^31^31 ^23 Кз’ J
3 Теория переменных токов.
193
Полученные выражения подставляем в (В):
Yii ~ — ^2 — 4~ 4*
——з—^sj^23—2 4* 4*Zsi2jn?i
^31 = ^3 А ^81 ^81^3 4“ ^23 ^28^8 4" ^12 *12 А ^31 *81 А’
Решив эти ур-ия и найдя напряжения V12, Ри и И81, вычисляем затем по (D) силы линейных токов.
Пример 34.
Даны! __
Е ==240 воли; Z пРов. = 1,7 +/0,2; = 0,3-j-/;
Zi3 — Ю +/ 6; 2Гад = 5 ~\~J 4; Z3^ = 8 +/ 5.
Из этих данных находим:
£< = 240; Fs= —120 (1 ±J VjY, F8 = 120 (— 1 +J /3).
7=2, = Z2 = Z3 = 2 +j 1,2;
У14== 0,0735—/0,0441; Км = 0,1220—/0,0975; P8i = 0,0899—/0,0362;
yu= 0,0868 Ги = 0,1601 e-JW>W-, У31 = 0,106
так как FI = F8 = Z8=^ то ур-ия для напряжений на нагрузке напи-шутся следующим образом:
7а = Ei - Ё3 - Vuria2+ ”81У817+ VnY*Z- ?aYaZ.
Преобразуя, получим следующее:
Via (1 + 2 PflZ) - ЙмГиг- V8IT81T- Et + Fs =. О (1)
и аналогично два других ур-ия:
- ^Л£+ ^a + 2^Z)-V8178^-F8+F8 = 0, (2)
- VaY^Z- V„Y*Z + У8| (1 + 2 Y3lZ) -£, + £, = 0. (3)
Вычитая ур-ие (3) из ур-ия (1), получаем:
Va (1 + 3 r«Z) - V8I (1 + 3 r81Z) —2 F, + F8 + F8=о,
а так как F2 + £3 = — to __ ___
v y8<H +3r8,Z) + 3£1
1 +3 KiaZ
Вычитая ур-ие (3) из ур-ия (2) и преобразуя, получаем:
v ^V3i(1^3y.tZ) ^3F3 “ 1 + 3 YnZ _
Складывая два последних ур-ия и замечая, что Из + Цй = *-получим; ___ __________ ________ __
_^31 (1 + 3 У3^ +3^ У31 (1 + 3- ЗЕ3
~ “ 1 + згиг -* 1+згяг
Отсюда по упрощении:
V —^1(1 4“3 -jb+3^22?)
W 1 + 2г(Уа +Yn+Yu)+'3Z*+ КЮР81 + YtlYa) ’
194
Разделим числитель и знаменатель на Z и обозначим X через У; тогда
V -_ _ ^Y+3Ya)-EtjY+3Y^^____________________
У + 2 (Кц -f- Kgj) 3 Z (У&Y4- Y№Yи -j- ¥цУв) ’
аналогично
V -_ _ КУ4-ЗУгз)-_Ку+3^1)_
13 Г 4- 2 (Уй 4- Y„ 4- Ув1) 4- 3 Z (УвУа + УаУ814- У31УЙ) ’
К+ 2 (У12 + Уэд +У31) + 3 Z (К12У23 + Ки + Л
Вычислим знаменатель:
У= ~ о 4 „ = * 2“+ = 0,368 —/0,221 z 2 4-71,2 5,44 '
2 (УИ 4- Кз 4- Ki) = 2(0,0735 —/0,0441 4-0,1220 —j0,09754-0,0899 — —j 0,0562) = 2 (0,2854 —j 0,1978) = 0,5708 —/ 0,3956.
Yl2Y^ = (0,0735 — J 0,044) (0,1220 —/ 0,0975) = 0,00467 — j 0,01255. KsKt = (0.1220 — j 0,0975) (0,08999 —j 0,0562) = 0,00549 —/ 0,01427. KtKa = (0,0899 —/ 0,0562) (0,0735 —/ 0,0441) = 0,00113 —j 0,00810.
______YaY^ 4- W + КЛз = 0,01429 —J 0,03492.
3^(KiKt 4- УМУ314- KtK2) = 3(24-J 1,2)(0,01429 —/0,03492) = = u, 2115— /0,158.
Знаменатель равен: 0,368 — / 0,2214- 0,5708 —/ 0,3956-|- 0,2115 — / 0,158= = 1,15 -/0,775= 1,387 e-7«°.
£. (74- 3 Кз) = 240 (0,368 —/ 0,221 4- 0,3660 —/0,2925) = = 240 (0,734 -/0,5135) = 176 — j 123.
£, (Y+ 3 Ki) = (- 120 - j 208) (0,361 - / 0,221 4- 0,2697 —/ 0,1682) = — (_ 120 — J 208) (0,6377 - / 0,3892) = —157,5 —/ 86.
Ё, (У4- 3 Ka) = ( - 120 4-7'208) (0,368—/9,221 + 0,2205-/0,1323) = = (- 120 4-/ 208) (0,5885 - 0,3533) = 3 4-/164,7. p _ 176-/1234-157,54-/86_ 333,5-/37 Va~ 1,15-/0,775 1,15 -/0,775 я*
з^^ =242.е/ио^ 1,387
« - 157,5 -/ 86 - 3 - /164,7 — 160,5 - / 250,7
Г 23 —• 1 __ А> I nm .* al ’ 353
1,387 e~Jtl ~ 1,387 e-7«*J
297 7 e~i т~зо' 5 j— 215 -y WO80r
1,367 e~J »*°
« 3+/164,7— 176+/123 —173+/287,7
И81 =---------------—-------------------------
1,587 e~7s»J 1,387 е-№“
335,7 г 7 «1° яля tma "" =242*1
1,387
T1S = Vir Va = 242* е 7 «°«' -0,0868 e-i^ = 20,75 e-i»’»' = 20,73 -/1,17.
Лв= KtrKa = 215.е-788°ао'.о,160-е~7в8ЧО- -» 34,4 e-i ap.v = = -20,76-/27,4.
13*
195
73( = = 242-е/ «в°-0,106 e"M° = 25,62 ei™> = 13,95 + j 21,5.
J. == ja — Л, = 20,73 — /1,17+13,95 —j 21,5 = 34,68 -j 22,67 = — 41,5 e~! «pis'.
7.=7» - Ла = - 20,76 — i 27,4 - 20,73 +/1,17 = - 48,49 —j 2\27 = = 53,7e-/‘M°»’.
= Л1 — Лз = —13,95 +/ 21,5 + 20,76 + j 27,4 = 6,81 + / 48,9 = 49,4 e! ^P«.
II. Включение фаз генератора треугольником встречается крайне редко, а потому в курсах, посвященных теории переменных токов, обычно не содержится. Дадим здесь для полноты представления соотношений в трех разных цепях теорию и этого случая.
Фиг. 101.
На фиг. 101 дана схема включения треугольником и генератора
и нагрузки.
Обозначения ясны из чертежа.
Применяя второй закон Кирхгофа поочередно к 1—11—2—1—1, II—III—3—2—II и III—1—1—3—III,
контурам получаем
уравнения:
Здесь
£1= 4? Л 2^1 г + Л А Л1^зр
^2 = + Лз£гз ”Ь Л^2 £12^J 2, ►
*8 ~ Л^8 "Ь 41Z31 + Лз^28-
(М)
(N)
напряжения на сторонах треугольника нагрузки. Далее
(Р)
откуда
106
т. е. силы токов в линейных составляют замкнутый треугольник.
Напряжения __________ ___ _____
^21» V32 И ^13
на нагрузке очевидно тоже составляют замкнутый треугольник; тот же результат получается и применением второго закона Кирхгофа к контуру нагрузки 2 —1 — 3.
7^+^ + ^=°. (Q)
Так как электродвижущие силы в генераторе тоже составляют замкнутый треугольник _ ___
£,+£,+£3=0,
то, сложив ур-ния (М), получим, как легко видеть,
JjZj ^2^2 + =
т. е. паления напряжений внутри генератора составляют замкнутый треугольник.
Но в генераторе _____ _ _____
Zj = Z2 = Z3,
поэтому, вынося Zj за скобки, получаем:
Л А + Л =
т. е. силы токов в генераторе, соединенном треугольником, составляют замкнутый треугольник.
Читателю следует особенно заметить, что силы токов в треугольнике нагрузки не составляют в общем случае замкнутого треугольника, ибо из ур-ния (Q) следует* что равенство
возможно не при всяких значениях сопротивлений нагрузки.
§ 58. Эквивалентные звезда и треугольник8
Итак, если нагрузка включена треугольником, то при расчете линейные токи приходится вводить в виде разностей фазовых токов, что делает расчет длинным и не наглядным. А. Е. Кенелла Показал, что с большим удобством можно нагрузку, включенную треугольником, заменить натрузкой, включенной звездой, причем все токи напряжения в линии остаются теми же, что были при треугольнике. Такая замена называется переходом с треугольника
197
на эквивалентную звезду. Выведем формулы для определения полных сопротивлений „лучей" звезды, т. е. трех ее фаз, если даны полные сопротивления „сторон" треугольника, т. е. трех фаз действительной нагрузки (фиг. 102).
Эквивалентность очевидно требует, чтобы полное сопротивление между каждыми двумя зажимами было в обоих включениях одно и то же. Между зажимами 1 и 2 в звезде сопротивление равно Zj-J-Zg; в треугольнике надо взять результирующее сопротивление двух ветвей 1 — 2 и 1 — 3 —2.
Поэтому
откуда получаем: аналогично:
Складывая эти уравнения по два и вычитая третье, найдем:
(137)
198
Эти формулы дают возможность от данного треугольника перейти к эквивалентной звезде
Если сопротивления сторон треугольника равны друг другу:
—^2----------^3-------”3"^’
Если, наоборот, требуется перейти от данной звезды к эквивалентному треугольнику, то математически задача сводится к определению Z12, Z23 и 2^ из вышеприведенной системы ур-ний, т. е. к выражению их через Zp Z2 и Z3 Однако в таком виде решение привело бы к неудобным по сложности их алгебраи веским выкладкам.
Последние очень упрощаются, если мы перейдем во всех ур-ниях от сопротивлений к проводимостям. Первая из вышеприведенных систем напишется в проводимостях так:
2 11 = 1 = к;+5;_______________=
у- . 1 ^Лз+ПзХи+«2
__2 Пз + ^1.
X
1 1
У. Г. X Л а
1 I
где _ _ _ _
X = У„ у28 + Кз у»! + Гм. (А)
По умножении на X ур-ния эти напишутся так:
199
Сложим их и разделим на 2:
Вычитая из этого ур-ния каждое из трех последних (В) поочередно, получим:
^-*=; ?.,=*=• >;>=*= го r3 Г2
Подставим эти выражения Г12, У23 и У31 в выражение (А) для X и мы получим, вынося в правой части X за скобки:
откуда
х=х*(4- — 4-—\ = х2 • dz IktГз, \Y&Y^ Y2yJ Y.YJ Y1Y3YJI
и вследствие собтношений (С)
(138)
Формулы эти совершенно аналогичны формулам, выражающим сопротивления.
В § 62 будет объяснено, почему нам важно уметь совершать переход не только от треугольника к звезде, но и обратно.
§ 59. Графический способ перехода от треугольника к звезде и наоборот
Графические способы значительно облегчают работу, так как сводят вычисления к минимуму.
Графический метод перехода от треугольника к звезде и наоборот настолько прост, что мы поясним его прямо на числовом примере.
Пусть даны в треугольнике
z12 = 104-/4, 2;,—154-/10,
200
Строим эти три вектора (фиг. 103)
OA = ZU, OB=Z., и
и затем строим их результирующий вектор
OD — Z12 -|- Z23 Дн*
Из ф-л (137) предыдущего параграфа имеем:
А____,__ Ai _______
Аз Аз 4” Аз4~ Ai
Соединяя D с С, получаем Л DOC, затем на О А строим п о-д о б н ы й ему Л AOF, по углам: £AOF=^DOC и ^/ОЛГ= — £ODC\ сторона OF удовлетворяет пропорции:
Аг Аг 4“ Аз 4~ А1 следовательно OF=Zj и в принятом масштабе
Фиг. 103.
Z1 = 2,5-/0,75.
Совершенно аналоги чно
ре-
щается задача и о нахождении
проводимостей сторон треугольника по данным проводимостям звезды.
§ 60, Определение напряжений и сил токов при включении нагрузки звездой
(Второй способ)
Представим себе теперь, что генератор, фазу которого соединены звездой, как это обыкновенно и делается, нагружен несимметрично, причем нагрузка включена звездой.
В таком случае между его нулевой точкой и нулевой точкой нагрузки существует разность потенциалов, которую мы обозначим Вектором Vo. __
Далее, обозначим через Zo полное сопротивление нулевого провода, если таковой имеется, от нулевой точки генератора до нулевой точки нагрузки; через Zp Z2 и Z3 обозначим полные сопротивления каждой фазы, т. е. суммы сопротивлений одной фазы
201
нагрузки, одного линейного провода и соответствующей фазы генератора. Линейные токи пусть будут Jv J2 и J3 и в нулёвом проводе Jo; пишем закон Ома для каждой фазы и нулевого проводя:
= A
^2--Хр = ^2 ^2’
^3 ” ^0 ==== А ^3*
O-V0^JQZQ
или, вводя проводимости:
A = (5~Vo) ур ^=(£2-^) г2, {з — (£з_Г_Ув> Гз, Jo=—voyo.
(139)
Сложив эти ур-ния, в левой части получим нуль; затем опреде-
лим Уо:
V =Щ+Д2д+ДХз
° Го+^ + ^+Г,
(140)
Подставляя VQ в последнее ур-ние, найдем все четыре тока. Если нулевого провода нет, то надо положить
г0=о.
В этом выводе совершенно не предполагается, что Ev Е2 и Е3 должны иметь одинаковые амплитуды и быть сдвинуты в фазе на
2п
Т
поэтому весь вывод приложим и к тому случаю, когда нам
даны три напряжения генератора, уже нагруженного несимметрично, Кр V2 и V3i не равные по амплитуде (фиг. 104), причем нагрузка включена звездой и нулевая точка ее соединена особым нейтральным проводом ;U| с нулевой точкой генератора.
Если выполняется условие, что три напряжения генератора не изменяются заметно нашей новой нагрузкой, то можно для расче- V; та применить только что выведенные форму-l/з лы, подставив в них вместо электродвижу-
Фиг. 104. щих сил Е напряжения V, т. е.
(141)
и т. д.
202
Конечно в этих формулах Уг У2 и Y3 не те, что были в предыдущем случае, ибо в соответствующие сопротивления
^ = =L, z;==, Z = 1
1 F, 2 У2 8 У8
теперь не входят сопротивления фаз генератора.
Проделаем следующий пример.
Пример 35.
У<=?240 вольт, 17а = 230г—/0»7я Vg = 210г-Н№;
Z± хя 10 /5 омов, =s 8 -|- j6, == 10 —*• /4j
35=10+/.
По данным сопротивлениям вычислим проводимости лучей звезды:
Yi == = == —j— = -~у5 — !2~/5 — 0,08— /0,04 = 0,0895г-/г^зз', «2Г* 10 +/5 103 4- 5» 125
Yi = i = —5— = = 0,08 —/0,06 = 0,10г -/36052'.
Zs 84-/6 100
Yt = X = —— = — = 0,0862 + /0,0345 — 0,0928г/21’48'.
Z, 10-/4 116
П = — = —1— = — 0,099 —/0,0099 = 0,0996г - /5’43-.
Ze Ю+/1 111
2УР= Yt + Yi + Ys = 0,08 —/0,04 + 0,08 —/0,06 + 0,0862 +/0,0345 + + 0,099 —/0,0099 = 0,3452 —/0,0754 = 0,3539г -/ISMS', —
это будет знаменатель выражения для Vj. Теперь вычислим числитель:
У1 = 240.0,0895г-/2в«зз' = 21,45-г-/2вчз' = 19,2—/9,6..
Vt-Ya — 230г-/о.?»-0,10г -/зб«52' — 230г-/126°. 0,10г -/36’52' в = Se-'jietpsr = — 21,97 —/6,78.
V8. 210е/о>. 0,0928г/21’48' = 19,49г/129’48' — _ 12,48 + /14,96.
V, -F/+ • У, + к-у; = 19,2 —/9,6 — 21,97 —/6,78 - 12/48 + +/14,96 = —15,25 —/1,42 =в 15,32г -/1W.
НаЙдеу Vo:
F -х Г| YL+ -’= К + Уа+П + П
15,32г-/174’41'
0,3539г -/12°18' =
43,3г-/1в2°23'=
-41,3-/13,1.
Зная VJ, найдем токи в каждой фазе пр формуле:
= (V, — = (240 + 41,3 + /13,1).0,0895е - /26’33'^281,1 +
+/13,1) 0,0895г-/2б°зз' = 231г5г/2°4о' .0,0895г -/26^3’= 25,2г —/23953'.
^==(У4— 14). У7= (230г-/0,7к + 41,3+/13,1). 0,1г-/зв®52’ = — (—135 _/186,1 + 41,3 + /13,1).0,1г -/Зб’зг'—
= (— 93,7— /173)-0,1г - /36°52 = 196,8-/118^4'. 0,1г -/36®52’ = = 10,7г - /155’16’.
203
Jt = (V8 — Vn) Y3 = (21Ог/о> + 41,3 + /13,1)-0.0928г/21°48( = = (— 65 +J 99,5 4- 41,3 + /13,1)-0,0928г/21<’48 — = (— 23,7 + /212,6)-0,0928-е/21°48' = 214-г/9бО20'.0,0928.г+/21в48' = = 19,9г+/11808’.
J5 = (0—<T) Vi = —43,3г-/162023'.0,0996г-/5®43'= _4,3e-/16806' =a = 4,3<?/H°54’.
§ 61. Графический способ решения той же задачи
Графический способ может быть применен здесь различными приемами; наиболее простым является представление VQ [ф-ла (141)] как суммы трех векторов:
и
каждый из которых строится как четвертый, пропорциональный к трем данным векторам, например:
и т. д.
На фиг. 105 представлено графически решение числовой задачи предыдущего параграфа.
После TorojcaK построены векторы Ад и их геометрическая сумма VQ, мы находим векторы 72 —70 и т. д,
и затем силы токов Jv J2 и J3 подобным же построением, на
пример:
где вектор 1 откладывается по вертикали.
ГРАФИЧЕСКОЕ РЕШЕНИЕ ПРИМЕРА П Р Е Д Ы Д У Щ Е Г О ПАРАГРАФА. Выбираем подходящие масштабы для проводимостей напряжений, в нашем примере: 1 лл/=^гмо и 1 мм =s= 2 вольта и - ООО
~ Т
строим в этих масштабах векторы заданных проводимостей Yt, Уз и У3 и напряжений 72 и V3 (фиг. 105).
Затем строим вектор ОА, результирующий всех векторов проводимостей:
204
9
Соединяем точку А с концами векторов У2 и F8.
На векторе У2 строим треугольник OCD, подобный треугольнику ОАВ по углам /_OCD = £ОАВ и £DOC — £ВОА\ из этих подобных треугольников получаем:
— ОС<ОВ_ OD_ ОВ
~ ОА К + + ОС~ОА'
следовательно вектор OD в масштабе напряжений изображает Хг Аналогично найдем и векторы, изображающие Х2 и Х39 строя подобные треугольники на векторах V2 и V3.
Складывая графически Xv Х2 и Х3, получаем вектор ОЕ, изображающий потенциал нулевой точки нагрузки. Соединяя концы векторов Уг V2 и У3 с точкой Е, получаем векторы у;=^-й0, F2=v2-v0 и у’=у3-у0, и перемещаем их параллельно самим себе таким образом, чтобы их начала попали в точку О.
^Следовательно ~OF= V\ — OG = V2 — VQ) OH=^—~VQ
и OK—О — Vo.
Для определения токов по вертикали откладываем вспомогательный единичный вектор OL такой длины, чтобы получился удобный масштаб для силы тока.
Так как
.(V;-у~о)К 1
то, подставляя J1:=l ампер, —Уо=1 вольту = 0,5 мм, и У^=1 мо = 500 .ил и единица в' знаменателе = 50 ЛЛ, получаем: , 0,5-500 е
1 ампер = ——— = 5 мм ои
или
1 мм = 0,2 ампера.
Точку L соединим с концами векторов проводимостей. На векторе OF построим треугольник ОЛИ, подобный треугольнику OLB по углам
£FOM~*£LOB и ^OFM= тогда
ОТИТОВ OF OL ’
306
следовательно вектор ОМ в масштабе 1 ампер изобра-
жает по величине и фазе ток Jr Таким же образом найдем и токи •^2» /з И Л>* ____ ___
Измеряя длины векторов ОМ, CW и ОР и углы их с вертикалью, получаем, что:
0М = 126 мм, £ M0L & — 24°, следовательно
= 25,2е~^24°,
O2V=98,5 мм, £NOL & — 155°15\
ОР -=99,5 мм, /РО1^118°Ю7 /8= 19,9^+/118010',
т. е. результаты вполне совпадают с аналитическим решением.
§ 62. Наиболее общий случай расчета трехфазной цепи
Чаще всего задача расчета трехфазной цепи встречается в следующем виде.
Представим себе, что генератор нагружен несимметрично. Часть нагрузки включена в виде нескольких’ треугольников, а часть — в виде нескольких звезд без нейтрального провода.
Для того чтобы воспользоваться только что выведенными формулами, надо всю нагрузку привести к одной звезде.
У нас имеется в нагрузке несколько параллельно подключенных звезд; если бы они были совершенно симметричны, то потенциалы их нулевых точек были бы равны, и все эти звезды можно было бы привести к одной з* езде простым алгебраическим сложением полных (комплексных) проводимостей соответствующих лучей как параллельных ветвей, находящихся под одним и тем же напряжением; но в общем случае звезды не симметричны, и нам задано, что нулевого провода нет; мы должны поэтому каждую звезду превратить в эквивалентный треугольник, пользуясь ф-лами (138), затем комплексные проводимости соответствующих, т. е. соединяющих одни и те же линейные провода, сторон всех треугольников,— т. е. не только полученных из звезд, но и заданных непосредственно, как часть нагрузки, — сложить и получить таким образом один единственный треугольник нагрузки, эквивалентный прежде заданным звездам и треугольникам всем вместе.
После этого, пользуясь ф-лами (137), мы должны перейти к эквивалентной звезде и определить по ф-лам (139) и (140) и
207
все токи, после чего будет уже крайне просто найти например па-
дения напряжения в генераторе, в линии, мощности и т. д.
При подобных расчетах в практике чаще бывает, что заданы не
электродвижущие силы генератора, а три линейных напряжения у места подключения нагрузки, причем в общем случае эти напря-
жения уже несимметричны, т. е. по величине не равны и в фазе
2п сдвинуты друг относительно друга не на —. о
Решение задачи и в этом случае очень несложно, если допу-
стить, что вновь подключаемая нагрузка не увеличит несимметричности напряжений.
Итак пусть нам даны линейные напряжения У12, И28 и У81 (фиг. 104) и сопротивления нагрузки Z19 Z2 и Z3, включенные звездой без нулевого провода.
Обозначим через V2 и У8 фазовые напряжения в нагрузке. Тогда
(А)
Сложив эти три уравнения, получим, что векториальная сумма трех линейных напряжений равна нулю, что, как известно, означает, что эти векторы составляют замкнутый треугольник.
Так как нулевого провода нет, то сумма трех фазовых токов нагрузки равна нулю, т. е.
Vi V, к, гаЯ=«о.
Выразим V2 и И8 через данные линейные напряжения и и
мы получим ур-ние с одним неизвестным Vv которое и определим
из него. Имеем, что
^Yi-^Л
(142)
поэтому
КК+(- V12) (Уп + V1) =о.
откуда
1 У1+Л+г3г
(143)
а затем по ф-лам (А) определяем Р, и У8.
Пример 36.
ss 120 вольт; VM =159^-/0,77.; V81 з* 105е+Лг = /105.
Х = 0,1— /0,05; = 0,2+/0,08; ^ = 0,3—/0,1.
208
• Га — 120- (0,2 4- /0,08) = 24+ /9,6.
V31 • Yj=./105-(0,3 -/0,1) = 10,5 + /31,5.
^ + K2 + Г, = 0,1 —/0,05 + 0,2 + /0,08 + 0,3 —/0,1 = 0,6 —/0,07.
Подставляя в ф-лу (143), определяем V4:
_ 24 + /9,6 - l'\5 - /31,5 _ (13,5 — 21,9/ (0,6 + /0,07) __
1 — 0,6 - /0,07 — 0,0* + 0,07» ""
8,1—/13,14 + уО,945 + 1,533 9,633-/12,185 ,
=-----------7Г-------------=-------А о А с- = 20,4 —/00,4 =
0,Зсэ 0,365
= 42,6г-/5Г4О».
Уа и У8 находим по ф-лам (142):
26, —/33,4 — 120 = — 93,6 —/33,4 = 99,4^-/1б(Р2о;
У3 = У81 4- Vt=/1 и5 + 26,4 -/33,4 = 26,4 + /71,6 = lbt3ejW>W.
Умножая фазовые напряжения на соответствующие проводимости, получим линейные токи:
J\ = Vr Y{ = 42,6^-/51040'.(0,1 —/0,05) = 42,6^-/51040'.0,112^-/26034» = = 4,77г-/78°14',
= ?2-?2 = 99,4^-/160020'.(0,2 + /0,08) = 99,4^-/160020».0,216^/2Р48’= = 21,5^— /38032»,
J3 = V3 . Y3 = 76,3^/69°45».(0,3 —/0,1) = 24,1^/51°20'.
§ 63. Графический способ решения задачи, когда даны три линейные напряжения
Величины Vp V2 и V3 строятся графически на основании определяющих их ф-л (142) и (143) предыдущего параграфа.
Вектор строили, как разность двух векторов: __________ ____ + __ у~ V. = V12 ---------------------------2--=. — V31 -=-_.
12у,.у2+у3 y1+ys+r8
Сначала найдем вектор У, -f- У2 -f- У3, ‘затем найдем вектор Л такой, чю _ ___
А— Г»
V “ К + у2+*7
Так же найден и второй вектор и наконец взята их разность.
Графическое решение предыдущей задачи (фиг. 106, см. вклейку).
Берем масштаб для проводимостей 1 мм^ 0,005 мо, строим в этом масштабе векторы проводимостей О А =^ = 0,1—/0,05; ОВ=Т2 = 0,2+/0,08 и ОС= У3 = 0,3— /0,1.
14 Теория пэрвменных токов. 209
Затем в масштабе 1 вольт =1 мм строим векторы напряжений: OD= У12 = 120 вольт и ОЕ = 1/31=/105.
Складывая О А, ОВ и ОС, получаем вектор OF— Yx ^4“ При точке О строим / DOG = / FOB, а при точке D — / ODG = / OFB. Полученный Д ODG очевидно подобен Д OFB и следовательно:
OD~ of’ OG = X, = У12 • =—2л
Аналогично построим f\OEH подобный /\OFC, из которых
получаем:
0Н—Х2 = У31
_ _
гх + га+г8
Вектор НО действительно
в принятом масштабе изобразит напряжение V/
Построим при точке О вектор O/C=//G=V1: О/С=43 мм, а / DOK=^2,1Q, следовательно:
Vx = 43е->52040'.
Вычитая из вектора ОК вектор OD, получим вектор DK или равный ему OL, который и изобразит напряжение У2. Измеряя OL, находим, что:
172 = 99,5^“>160020’.
Складывая векторы ОЕ и ЕМ — ОК, получим вектор ОМ, очевидно изображающий напряжение V3.
Измеряя длину ОМ и / РОМ, найдем, что:
73 = 76,5-^69°45'.
§ 64. Пример аналитического и графического расчета трехфазной системы
Нам заданы линейные напряжения: - - -
V12 = 240 вольт, У23 = 220 е 4 , У31 = 177
и нагрузка в виде одного треугольника с сопротивлениями
Zlz = 20 4-/10, z23 = 30 4-/8, Z31 = 30—/10
210
и двух звезд с сопротивлениями
z; = io4-/4, z;=8+/3, z;=io-]-/5
И
z;=2o+/8, z;=i2-/5, ^=124-/4.
Требуется найти тли линейных тока, результирующих для всей нагрузки
Приведем всю нагрузку к одному эквивалентному треугольнику. Для этого обе звезды приведем -к эквивалентным треугольникам, а затем проводимости одинаковых фаз всех нагрузок сложим. Для приведения звезд к треугольникам воспользуемся ранее выведенной формулой, преобразовав ее следующим образом; ввиду того, что даны сопротивления лучей звезды:
Вычислим проводимости треугольника, эквивалентного первой звезде.
Для простоты расчета вычислим знаменатель формул отдельно:
z;z;+ z;Zj + z’z; = (io 4-/4)-(8 4-/3)4-(8 4- /3) (io4-/5)4-(1 о 4-/5) (10 4-/4) = 80 4-/32 4-/30 — 12 4- 80 4-/30 4-/ 40 — —154-1004-/504-/40 — 20=2134-/222.
г _ 10+/5 = (10 4-/5)(213—/222) 3240—/1155
Г12—213-|-/222 2132-|-222? 94653 “
= 0,0342-/0,0122.
218Д%2 = 00250 ~/0.0>20-
14*
211
Таким же образом приведем вторую звезду:
z;^ + z;z;4-z;z;=(2o+/8)(i2—/5)4-(i2-/5)(i2-f-/4)4-4- (12 4-/4) (20 -|-/8) = 652 4- j 160.
=65?+/^~181)188+j'(,'0°'5-г1=ий^=0’М18+''00015-^=a/f^o=0/)1S6~;0>0:15-
Вычислим проводимости треугольника:
уп=JL=—?—=о.оззз 4- j o.oi оо Z31 30-/10
Треугольник, эквивалентный всей нагрузке, должен иметь следующие проводимости:
J12, = + ^12 + S = 0-0930 ~j °>0307-^Зэ = ^23 + 5з + 1J=0.0948 /0,- 183.
Г31э= Г31+ ^4-^ = 0,0706-/0,0135.
Теперь можем вычислить линейные токи, придав выражениям напряжений такой вид:
-
У1а = 240; Уаз = 220<? 1 4 = 220 e-i^ = — 155,5 —j 155,5;
PL = 177 в/о,бб1== 177 е/и^в1 = _ 84,5 4- / 155,5. ах 9 I J 9
В данном случае нет необходимости переходить к общей эквивалентной звезде, ибо известны напряжения у самой на! рузки. Поэтому ур-ния (А) § 57
А = А2 -Л1 = ^12^2 - V31 й31 = 240 (0,0930 -/0,0307) -— (— 84,5 4- / 155,5) (.0,0706 —/0,0135)= 22,32 —/7,37 4- 5,96 — _ —/1,15_—j 10,98^-2,10 = 26,18 — j 19,50 = 32,64 в ~J 36° Л = Лз - Лз = Яз Г23 — ^12^2 = (— 155,5 — j 155,5) (0,0948 —
—/ 0,0183) — 240 (0,0930 —j 0,0307) = — 39,91 —j 4,54 = = 40,1 е-Уиаозо;
Т3 = — 7, —7а = 13,73 4-/24,04 = 27,68 ei 800i8'.
212
Графическое решение Прежде всего произведем графическое приведение звезд к эквивалентным треу» ольникам Для этого (фиг. 107, см. вклейку) построим векторы: О А — изображающий проводимость
F; = = 0,08 62 —j ®,0345;
OB=Y’= i =0,1095—/0,0412 2 7'
И
ОС=>=Д =0,0800-/0,0400.
Масштаб для проводимостей выбираем 1 мм = 0 001 мо. Суммируя векторы ОЛ, ОВ и ОС, получаем вектор OD, в принятом масштабе представляющий У* -|- У' -|- У^.
Далее поступаем, как было показано в § 59. Соединяем точку D с точками А, В и Си строим подобные треугольники:
ДОЛСс/эДСЮЯ, ДОВСслДООС и__Д OCFoo Д ODA.
Как было доказано ранее, векторы ОС, ОЕ и OF в принятом масштабе по величине и фазе изобразят проводимости сторон эквивалентного треугольника; измеряя их проекции hi оси, находим:
OG = У;2 = 0,0342 —у 0,0122; ОЕ = К23 = 0*0319 —j 0,01 45;
OF= = 0,0250 —j 0,0120.
Совершенно так же находим проводимости треугольника, эквивалентного второй звезде.
Построив векторы OK, (5L и ОМ, имеем, измеряя составляющие:
ОК= У"2 = 6,0180 +/ 0,015; OL = Y23 = 0,0318 -f- j 0,0045 и ом— у" = 0,0156—/о,оь 5.
Для нахождения проводимостей между фазами суммируем соответствующие проводимости всех трех треугольников, — одно! о данного и двух эквивалентных. Чтобы не загромождать чертежа, сложение проводимостей произведено отдельно (фиг. 108, см. вклейку).
Из диаграммы находим, что:
712э= Г12 + 0,0930-/0 0307,
> = ^3 + ^3 + У23 = °>0948 —700183,
Гз> ^>0,0176-/0,0135.
213
Для определения линейных токов находим сначала произведения
Уц == Аг> ^23 ^яз == Аз1 Ум = У81,
т. е. токи в сторонах эквивалентного треугольника.
Строим (фиг. 109, см. вклейку) векторы напряжений в масштабе 1 мм=2 вольта,
04 = Vw ОВ=У28 и ОС=Уа1, XX7 40 О17
и переносим на эту диаграмму в прежнем масштабе найденные значения проводимостей сторон треугольника
OD = F12, О£ = К3 и О?=У31. Гл9 Хо ох
Строим вспомогательный единичный вектор OG = -J-1.
, Точку О соединяем с точками О, Е и F. На векторе О А строим Л ОАНоп Л OGD по углам: £OGD = /_ОАН и ^А0Н= — / GOD, из подобных треугольников находим:
ОН OD — OA-OD
-7 7" — --- \Л1 -- •
ОА 00 00
Так как О А Vlt • 0,5 мм; OD= К12 • 1000 мм и OG = = 1100 мм, то
— Р,2.0,5. 1000 т _
0Я= 1.100------= Ji2 • 5 мм,
следовательно ОН изображает ток в масштабе 1 мм = 0,2 ампера.
Строя Л ОВКЛ OGE, находим вектор ОК, изображающий ток J23, и из Л OCL, подобного Д OGF, находим вектор OL, соответствующий току J3r Вычитая из вектора ОН вектор OL (или равный ему МН), находим вектор ОМ, соответствующий току Jr Соответственно ток J2 изобразится вектором ON—ОК—ОН, и J8 — вектором OQ = OL — ОК.
Измеряя векторы ОМ, ON и OQ, находим, что
4 = 32,64 36О45’;
•4 = 40,1 е“71тз°зг;
Т3 = 27,68 *5’.
Определять углы при графическом решении можно с достаточной точностью хорошим транспортиром, позволяющим отсчитать четверть градуса или 151.
214
§ 65. Нулевая точка нагрузки и ее потенциал
В этом параграфе остановимся подробнее на исследовании вопроса о потенциале нулевой точки нагрузки, включенной звездой, без нулевого провода.
Рассмотрим сначала частный случай, когда
Zj = Z2 == Z3, как это бывает при включении в виде нагрузки трехфазных двигателей.
Так как сумма трех токов в звезде без нулевого провода равна нулю, то
7 7 7
а вследствие равенства Z-ов, и
(A)
(В)
Из ур-ий (А) мы имеем:
= 5-v3i>
Сложив и приняв во внимание ур-ие (В), получим:
и аналогично
(^3-^12) ^.=4
(С)
соотношения читатель должен для упражнения
Последние два вывести сам.
Отложим на фиг. ПО AD =—У31 =— АС', тогда на основании первой из ф-л (С) получаем, что
OA = ~-BD,
О
т. е. О А || BD до пересечения
аналогично — и
и О А =4“ •££>, а в таком случае, продолжив АО о
в М с ВС, имеем:
ВМ = МС и АО=~АМ;
О
для других векторов.
215
Следовательно точка О есть центр тяжести треугольника линейных напряжений АВС, __
Перейдем к общему случаю, когда Zv Z2 и Z3 не равны.
Вычисление и в этом случае надо начать с определения , V'2 и 1/д для одинаковых Z во всех фазах. Действительно существую
щие при заданных Z-x напряжения обозначим через
У3 и vs.
На основании ур-ний (А) все напряжения объединены в векторной диаграмме фиг. 111.
Между нулевой точкой О' действительной нагрузки и нулевой точкой О нагрузки при
равных Z существует разность потенциалов ООг = Уо, и мы мо-
жем написать:
(D)
^0=^3- V3
216
Умножим каждое из этих ур-ий на проводимость соответствующей фазы нагрузки и сложим; так как сумма трех фазовых токов нагрузки без нулевого провода ра ша нулю, то
^Г1 + Й2Г,+ У3Т3 = 0,
и мы получим окончательно:
Vq--- ---=----—-----------.
Перейдем к другому способу исследования потенциала нулевой точки нагрузки.
Этот потенциал отличается от потенциала одного из проводов линии, например первого, на разность потенциалов И7 = О/.
Вектор совершенно определяет положение точки О, и потому можно исследовать изменения этого положения, исследуя изменения вектора при различных состояниях нагрузки. Законы перемещения точки О весьма разнообразны и зависят от того, что и как в нагрузке изменяется.
Исследуем например такой случай.
Пусть У2 и Уд постоянны, а переменно; рассмотрим, какие положения при этом может занимать точка О. Так как
1 у, - У2 + У3 ’
(А)
то, вводя комплексные выражения для векторов, мы очевидно будем иметь:
Y2-[-Ya = a Yjb, (В)
v12r2-v31 = (С)
Следует заметить, чго здесь а существенно положительная величина (ваттная проводимость); величины же Ь, с и d могут быть положительными и отрицательными.
Далее
Y1 = т -j- /л,
где т и п переменны, но т тоже положительно. Наконец
^ = ^+/(7. (D)
где X и U мы принимаем предварительно за величины, которые могут быть положительны и отрицательны.
Поместим (фиг 112) начало координат в точку 1, а положение точки О будем определять вектором 10 = — = — X—jU\
217
тогда величины — X и —U являются координатами точки О в той же системе осей действительной и мнимой, к которой мы относим все наши векторы.
Итак
X+jU = , (F)
ci —|— m -j— j (b —j— /2)
откуда
(Z>4-rt)Ar4-(a + >n)£7==tZ. J
Фиг. 112.
Из этой системы ур-ий следует, что каждому = т jn соответствует свой комплекс X -J-JU, ибо X и U определяются из этих ур-ний по данным^ т и п\ а, наоборот, задаваясь положением точки О на плоскости, т. е. задаваясь величинами X и U, мы можем определить т и п, т. е. узнать, каковы должны быть ваттная и безваттная проводимости в фазе 7, чтобы напряжение в ней было заданным по величине и по фазе.
Однако последняя задача не всегда возможна. Разберем этот вопрос.
Определим из ур-ний (Н) т и п9 считая X и U данными:
_сХ — aX2 + dU— aU* X*±U2
dX—bX* — cU — bU*
Л2Н-7/2
Так как т должно быть положительным, то должно выполняться условие этого:
cX+dU^a(X^U2y,
так как, как указано выше, а тоже положительно, то
— Х + — и^Х*4-и\ а * а 1
(К)
Обратимся к числовому примеру.
218
Примвр 37. Пусть даны три симметричных линейных напряжения
= 60 /3 4- j 60 = 103,8 + j 60,
V» = — /120, ^ = -103,8 4-/60.
Далее задано Z3 = 2£=l00; следовательно У2 = У, = р,01; вычисляем
Ка Г,- У,< Y9= c+Jd = ?'6^p- = 2,076.
откуда
с =2,076; d = 0.
KJ + ?i = a+;^ = 0,02, откуда
а = 0,02; £ = 0.
Условие (К) принимает теперь вид:
60/3
Так как правая часть есть сумма квадратов, а потому всегда положительна, то и левая часть положительна, это значит, что X отрицательно быть не может, т. е. точка О не может лежать выше горизонтальной оси 4- j 1ЛГ, не забудем, что координаты точки О нами представлены как (— X) и (— О), так что если X < 0, то эта ордината положительна.
Положим, что мы ищем, куда может удалиться точка О вниз по вертикальной оси 1— М\ для этой оси 0 = 0, и неравенство (К) получает вид
103,8 ^Х.
Так как высота треугольника равна 60 / 3 = 103,8, то следовательно: в этом направлении точка О' не выходит из треугольника 123.
Возьмем точку S с координатами
iS=_A=_!q2 . QS=-I/=“p.
Условие (К) при этом удовлетворяется, ибо
60/3. “13 = («ЦТ)’+(“£!)’;
при этом получается
т = 0, л= + 100-
Таким образом, чтобы точка О, нулевая точка звезды нагрузки, пришла в точку S, надо в фазу 01 включить нагрузку чисто емкостную, на что указывает знак плюс у п.
Читателю предлагается проверить, что при чисто емкостной нагрузке в фазе 01 точка О может занимать любое место на левой полуокружности, описанной на высоте треугольника 1Л4 как на диаметре, в зависимости от соотношений между величиной емкости и величиной сопротивлений в фазах 2 и 3.
219
Если переменить последовательность фаз 2 и 3, т. е. если переменить направление вращения линии времени, то точка О будет помещаться на правой половине окружности На этом принципе основан один прибор — указатель последовательности фаз.
Таким о разом точка О может всходить за границы площади треугольника 123
Остановимся еще на одном примере.
Пусть Y2 и У3 удовлетворяют следующим усювиям:
Y = const, const, К ~ var; J 1 А 'О'
их углы (рр (р2 и ф3 равны всегда:
<?|=<Рз = %-
Тогда из ур-ний (В) и (D) имеем:
b п
। , а т
или b п= т—. а
Подставляем это выражение п в ур-ние (F):
УД.П1 —_________
. b\ (а + j b) (a 4- m) ’
Преобразуем*
{c-\-jd)a__(c-[-Jd}(a—jb')a_ ,
—«TA
и следовательно X-\-JU=h^}k, а-\-т
откуда и=—~ а~\-т a -f- in
поэтому — У h k
или x=^u. к
220
Это есть ур-ние прямой линии (фиг. 112), проходящей через начало координат, т. е. точку 1 Слеювательно при указанном изменении /3 и равенстве фазовых уг^ов точка О перемещается по указанной п ямой.
Конечно при этом должно выполняться условие аналогичное (К), которое и ставит пределы изменениям положения точки О.
В зависимости от знаков h и k величины X и U могут быть или одинаково-о знака или противоположного, и может быть несколько разных случаев в направлении этой прямой и проч.
Разо рать эти случаи на основании вышесказанного не может представить никаких трудностей для читателя, но явится весьма полезным упртжнением.
Пример 38 Доказать, что если
К2 — const, = const, fА = const, но ?£ не равно <p2 и ?з> a = var, то нулевая точка описывает окружность.
§ 66. Вращающееся магнитное поле 9. Случай I: симметричные составляющие
С помощью многофазных юков можно получать вращающееся в пространстве магнитное поле и именно следующим способом
Возьмем столько одинаковых катушек, сколько фаз имеет многофазная система; расположим их под равными углами одна к другой (фиг. 113) (далее мы увидим, что можно катушки расположить и под неравными углами, что однако приведет к необходимости выполнить другие условия) и через каждую катушку пропустим ток соответствующей фазы одинаковой силы. В пространстве около катушек мы получим вращающееся магнитное поле.
Так как направ -ение поля от катуш-
ки всего проще определяется около се* редины ее, где поле направлено по ее оси, то мы в дальнейшем и будем исследовать поле именно около точки О, являющейся для всех катушек общим центром. На фиг. 113 цифрами /. //, /// обозначены три одинаковых катушки, через которые идут токи zi=7OTsin(“0, , . / , 2тг\ i2=4sly/-jb z3=4sin'kwZ“- j ) s\ \ 4» а «я 1 В а •1 \s ч Ф^г. 113.
221
Векторы OZ, 02 и ОЗ дают направления магнитных полей катушек.
Магнитодвижущие силы катушек имеют равные амплитуды, так как катушки одинаковы, —обозначим их через Fm, и фазы — одинаковые с фазами токов в катушках.
Узнаем величину Лр — магнитодвижущей силы результирующей. Возьмем произвольное направление £—£и вычислим, каково будет мгновенное значение /р этой результирующей в этом направлении. Для этого надо сложить проекции всех трех магнитодвижущих сил на направление S, составляющее углы: с катушкой / а,
.. . 2п ггг , 4п
с катушкой II a -f- -г- и с катушкой III а 4- —: о о
/ = Л I sin (<о/) cos а 4" sin (Ы —
Преобразуя произведения синуса на косинус по формуле
, . Л . т-+-н т — п sin т sin л = 2 sin —— cos —-— Л Л
получаем:
1
2 Si
sin (wf -|-а)-|--i-sin (w/ — а) -}- 4-sin((o/-|"a)H_ Z £
4п\ . 1 . 1 . / 8тг\
— у )+ysin (®^ + а) +ysinl <о/ —а —у )
а так как
8тг о 2тг
__ = _2к—
то в скобках члены второй, четвертый и шестой представляют сумму синусов трех углов, отличающихся на 120° друг от друга, — а та-ьан сумма равна нулю, как известно уже; суммируя остальные три члена, имеем:
3
/р=у ^mS'nC^ + a).
Таким образом амплитуда результирующей магнитодвижущей силы, а потому и магнитного потока (если о - создается в железе,
состояния насыщения), больше
то последнее должно быть далеко от 3 амплитуды составляющих в — раза.
Рассмотрим изменение этого поля во времени и пространстве.
Для одного и того же направления S—5, т. е. для одного и
222
того же а мгновенное значение / представляет синусоидальную функцию времени.
Далее замечаем, что для одного и того же момента времени i величина /р по различным направлениям будет синусоидальной функцией угла а.
Для любого а, т. е. для любого направления, .можно найти та* кое /, т. е. такой момент, что
со/ -j- а = 4” п£,
£
где k — целое число; тогда
sin (со/ + а) = ± 1
и
т. е. амплитуде. Для
Л 4 Т 4 ! я
а = 0 ив момент / = —, со/ -f~ a =
4 л
к Т 1 1Г .
а=у . . . t==~2’ <^ + а=2- + *,
3 к
а = * „ , „ t = — T, ш/-|-а = у4-21Г,
а=4" ” » • t=T, ®/4-a = y-f-3n>
a = 2ix „ » . t = ®/4-a==-^--f-4ir,
т: &
и т. д.; с ростом а на — возрастает необходимое для достижения в э т о м месте амплитуды у / в р е м я, и именно возрастает на ве-Т личину —.
Отсюда видно, что результирующее поле за время одного периода повертывается на угол, равный 2тг, т. е. д е-лает один полный оборот.
Вращающееся в пространстве поле можно с большим удобством представить посредством вращающегося вектора
3
'р 2 1 in' »
о котором было сказано в § 30. При этом линии времени не нужно себе и представлять, а угол со/ отсчитывается от вертикальной оси при положительном значении со в сторону против часовой стрелки.
223
Линию времени впроче^м можно и здесь ввести, но представлять ее надо неподвижной и совпадающей с вертикальной осью.
Пусть нам даны два вектора: Fe^* и Fe~^\ первый вращается против часовой стрелки, согласно вышесказанному, второй — по часовой стрелке.
Сложим эти два вектора и применим формулу Эйлера:
_ cos s;n • получим:
Fe№ Fe~№ = 2F cos (со/) = 2/:’sin ((of 4“ .
Таким образом, если мы возьмем два поля, вращающиеся в разные стороны, но имеющие одинаковую величину, и сложим их действие, то получим просто переменное синусоидальное поле, или, как обычно говорят, пульсирующее поле, вдвое более сильное Как оно будет .направлено?
Из формулы видно, что направлено оно будет по действительной оси, иначе, по оси, от которой отсчитывается время для обоих вращающихся векторов; это есть направление, в котором совпадают на один момент оба вращающиеся вектора, или оба поля.
Разумеется, в прямо противоположном направлении оба поля тоже совпадут, когда придут туда через полпериода.
Для теории машин важен бывает обратный переход: когда дано пульсирующее в пространств поле, его разлагают на два поля, вдвое меньшей силы каждое, вращающиеся в разные стороны с одинаковой ^скоростью, именно делающие один оборот за один период Такое разложение было впервые введено Феррарисом, так же как и получение вра нающегося поля с помощью многофазных токов.
§ 67. Вращающееся магнитное поле. Случай II: несимметричные составляющие
Рассмотрим теперь более общий случай сложения трех полей, именно, когд! амплитуды их не равны, фазы не симметричны, т. е. сдвинуты эти поля в фазе друг относительно друга не на 120°, и в пространстве поля составляют друг с другом углы тоже не в 120°.
Таким образом пусть нам даны три магнитодвижущих силы или три поля
Fj sin (со/ 4- cpj, F2 sin (со/ 4* 2) и sJn № 4~ ?J’
найдем их результирующую по некоторому направлению X, составляющему углы а2 и а3 с осями этих трех полей. Обозначим эту результирующую через х.
224
Задача сводится опять к преобразованию суммы:
х = /\ sin (со/ + <pj) cos 4~ sin W 4“ Т2) cos +
Ц- F3 sin (со/ -J" cos аз-
Каждый из членов этой суммы заменяем по следующей формуле двучленом:
F F
Fsin (<о/ 4“ Т) cos а sin 4~ <? + я) + v sin (<о/ + ¥ ~ а)
и получаем:
л=3 л=3
* = у J] sin + Тл + ал) + у 2 Fn Sin + <Рл ~ Л = 1 Л = 1
Вычислим теперь результирующую по направлению У, перпендикулярному к Х\ обозначим ее величину через у.
Очевидно
у = F1 sin (со/ 4“ )sin ai 4“ ^2sin 4~ ¥2) s*n а2 4-4- F3 sin (wt 4- <Рз) sina3.
Преобразуем члены по формуле: F F
FsMybt + <р) sin a=cos (со/ —j— ср — а) — cos (со/ 4~ ¥ 4~а)
2# 2t
и получаем: л=? л=3
У = у S Л. cos (“'+ ?л — «л) — у J] Fn cos (<*+ <Рл + «»)• Л=1 Л=1
В выражениях для х и у разлагаем sin и cos суммы, выделяя sin(<o/) и cos (со/), и получаем: л=3
*=у 2 ря sin (“0 cos (<?„ + aj + n=l л=3 л=3
+т SF»cos sin +ал+т Е f« sin c°s + л=1 л=1
п м3
+у S F"cos (<oZ) sin — л»1
Читатель должен написать сам соответствующее выражение для у и после нижеследующего преобразования этого выражения получить уравнение (В2).
15 Теория переменных токовс 225
Обозначим:
л=3
У S Fn COS (<?« + = т> п=1
п=3
y2F-s,n{<p«+a',):=:A
Л = 1
л=3
2“SFncos(<?« — aJ = n> /1 = 1
л=3
2*2 F«sin(<?«—«») = ?• /1=1
!> (А)
Величины tn, nt р и как видим, постоянны.
Таким сбразом
х== (т -{- п) sin (со/) 4“ (Р 4“ Q) cos (со/) (BJ
у — {р — q) sin (a)f) — (т — п) cos (со/)* (В2)
В ур-иях (В) величины х и у дают сумму проекций всех составляющих на направления х и у, а потому являются проекциями
всего результирующего поля на эти два перпендикулярные на
правления.
Все результирующее поле равно очевидно их геометрической сумме.
Следовательно х и у можно рассматривать как координаты точки конца вектора результирующего поля F .
Если мы из ур-ний (В) исключим время, го получим одно ур-ие между х и у, дающее геометрическое место, по которому будет двигаться конец вектора результирующего поля при изменении х и у, т. е., другими словами, с течением времени.
Определим для этого из ур-ий (В) sin (а)/) и cos(toZ):
sin ((Of)
cos ((Of)
— n) x(pq) у m2 — n2 4~ P2 — Я2 * _(p — q)x — {m + n)y m2 — n2 -f- p2 — q2
(C)
Возведя правые и левые части обоих ур-ий в квадрат и сложив, мы получим в левой части единицу и время таким образом исключим. После приведения к целому виду и соединив члены, содержащие х2, у2 и ху, получим:
[(/и — л)2 + (р — q)2]x2 — п)(р -Н) ~ (« + Я)(Р — <?)1ХУ
+ [(« + «)’ + (/’ + ?)2] У2 = т2 — »2 +р2 — 92- (D)
Таково ур-ие искомого геометрического места в общем случав. Оно может представлять окружность с центром в начале координат, что будет обозначать, что результирующ е поле вращается и сохраняет при этом постоянную величину, равную радиусу круга г = /х2 4”У2*
226
Это ур-ие может представлять и эллипс, что в свою очередь будет обозначать, что результирующее вращающееся поле в разных направлениях имеет разную величину и в одном направлении .наименьшую, а в другом, перпендикулярном первому, наибольшую величину. Такое поле называется эллиптическим.
В машинах стараются всегда получать круговое вращающееся поле' Выведем условия получения его, т. е. условия того, чтобы ур-ие (D) представляло окружность с центром в начале координат.
Для этого, как известно, необходимо, чтобы коэфициенты при х2 и у2 были равны, а коэфициент при ху был равен нулю, т. е.:
(т — л)2 (р — ?)2 = (т + л)2 -]-(/» + q)1, (т — п) (рq) — (тя) (р — q).
Из этих ур-ий легко получается:
тп — — pq mq — пр.
Если мы попробуем разделить полученные теперь ур-ия одно на другое, то получйм результат:
q т
что очевидно невозможно, так как ни одна из четырех величин /и, л, р и q не может быть мнимой по самому определению их.
Остается предположить, что некоторые из них равны нулю. Ур-ия удовлетворяются, если
ш=р = 0 или если п = ^=0.
Второе условие по существу ведет к тем же результатам, что и первое, а потому остановимся только на первом.
Оно означает, что
F, sin (<р, 4- -f- F3 sin (<р2 4- а2) 4» F3 sin (<р3 4- а3) = 0,)
и (Е)
Fj cos (cpj 4- aj 4“ cos (?2 + аг) + cos (?з + аз) = °- '
Вернувшись к тому, что тако? представляют собой углы ая и фя, мы увидим, что всегда можем положить = 0 и ^ == 0; первое будет обозначать, что мы находим результирующую х, по направлению оси первой катушки, второе — изменение отсчета времени. Тогда вышеприведенные ур-ия (Е) упрощаются.
15* 227
Рассмотрим пример. Пусть у нас будут две одинаковые катушки и мы имеем в распоряжении зажимы трехфазного тока, 2
от которых можем взять два тока с разностью фаз в —те. Следо-2
вательно мы имеем ср2 = — те. Ур-ия (Е) дадут нам: о
^8 =°.
(2 \
— тг 4- аг) — О, О /
/2 \
Л + cos ( ) =°>
откуда следует, что (2 \
у те + а2 ) = °>
т. е.
, 2 Оз4-уЯ=1Г
И
ае = л — v к=4~п = 60°; О о
а также, что
F2 = Fr
Таким образом, расположив данные две катушки под углом в 60° друг к другу и пропустив" по ним токи одинаковой силы (так как катушки одинаковы, т. е. имеют одно и то же число витков) от двух линейных напряжений трехфазной сети, мы получим круговое вращающееся поле.
Если у нас в распоряжении имеется двухфазный ток, т. е. те те
если ср2 = — , то должно быть и а2 = —, и катушки надо рас-положить под прямым углом друг к другу.
Таким именно способом впервые экспериментально и получили круговое вращающееся поле Н. Тесла и Г. Феррарис.
§ 68. Многополюсное вращающееся поле
Перейдем к последнему вопросу, именно к многополюсным вращающимся магнитным полям.
Представим себе трехфазную обмотку стдтора машины переменного тока с одним пазом на полюс и фазу.
228
Если мы на фиг. 1 нанесем еще две обмотки, то и получим как раз то, что нам сейчас надо, так как на фиг. 1 на один полюс приходится три паза.
Разрежем мысленно статор вдоль по его образующей и развернем его окружность в прямую линию, как показано на фиг. 114, где изображена только часть его 1—3\ именно двойное по- уч, Lx люсное деление / — Р— 1Г и S''*/*'
еще одна шестая часть его / \
Г—З9. Длину простого полюс-ного деления обозначим через т.
Введем магнитные поля, со-
здаваемые каждым из трех то- фиг. ц4
ков в отдельности.
Подробное исследование формы кривой такого поля делается в теории электрических машин; эта форма зависит от конструкции обмотки и других деталей, нам же здесь для выяснения принципа получения вращающегося поля достаточно принять, как это делается и в учении о машинах, что в первом, достаточно точном для решения некоторых вопросов приближении можно считать это поле распределенным вдоль по окружности синусоидально, как это и изображено на фиг. 113. Физическое значение ординат таких синусоид просто; всякая ордината представляет магнитную индукцию В в этом именно месте окружности статора. Амплитуда такой синусоиды пропорциональна мгновенному значению силы тока в соответствующей фазе обмотки.
Таким образом, если мы обозначим амплитуду синусоиды от фазы / или от обмотки /—— 1Г через В„ то будем иметь:
В1== С sin (со/)
и соответственно для фаз II и III:
B2 = Csinf со/—(а) \ /
/ 4п\
B3 = Csinl со/ — — ).
Какая-нибудь ордината В\ поля первой фазы, ордината, определяемая расстоянием х от места амплитуды поля, выразится как
п I х \
В. = & cos — тг.
1 1 \ т J
Здесь мы вводим отсчет х от амплитуды, а не от нулевого значения, и потому берем косинусоидальную зависимость в формуле.
229
Ординаты кривых поля второй и третьей фаз выразятся так:
Df о Iх 2тг
Я2 = В2соз I у тс----у
о, о (х 4п'
В = В cos — и — —
3 8 \ т 3,
Результирующее поле от всех трех фаз будет: в'=в;+в;+ в’3> или, подставляя вместо амплитуд их выражения (а):
В' = С sin (со/) cos I —
/ х 4тг\ cos — тс---------— )
\ Т о /
-f- С sin
Преобразуя каждый член подобно тому, как это мы сделали в начале этого параграфа, мы получаем:
-J-sin
Здесь сумма первого, третьего и пятого членов равна нулю, как синусов трех углов, разнящихся на 120°, и окончательно
о / X '
В' — ~Cs\n I ®t--п
2 \ т
(?)
Итак и в общем случае амплитуда результирующего поля 3
в — раза больше амплитуды составляющих полей.
Мы видим из этой формулы, что результирующее поле синусоидально и в зависимости от времени в любом данном месте, т. е. при данном х, синусоидально для любого момента t вдоль по дуге окружности, т. е. в зависимости от переменного х.
Следовательно в разные моменты времени в разных местах В' может иметь одно и то же значение. Исследуем этот вопрос подробнее.
Если в формуле ([J) t и х увеличатся так, что весь угол под знаком синуса останется той же самой величины, то и значение Вг будет то же самое.
230
Возьмем момент времени на Д/ более поздний, чем какой-то момент /, тогда вместо х надо взять абсциссу, на какую-то величину Дх бдльшую, чтобы угол остался прежним. Итак
. х /4 । дл х4- Дх
---------------------— п = со (t-j- ДО------—г тг, откуда, перенося члены с t в одну часть, а с х— в другую, получаем :
или Дх________________________шг___2т
Д/—V-Т’
Дх
Величина — = v есть скорость продвижения одинаковых значений В1 вдоль дуги окружности, т. е. это есть скорость движения поля.
За период проходится путь
vT = 2т,
т. е. проходится двойное полюсное деление.
Таким образом по окружности статора движется, или вращается, поле, причем за один период оно передвигается на двойное деление.
Если таких делений на статоре р, то один полный оборот поле делает за р периодов, а не за один, как было в случае фиг. ИЗ.
Если мы внутрь такого статора вставим ротор не с электромагнитами постоянного тока, как у генератора, а с какой-нибудь замкнутой обмоткой, то вращающееся поле будет пересекать проводники этой обмотки ротора и индуктировать в них электродвижущие силы, а следовательно при замкнутой обмотке и токи, которые по закону Ленца всегда будут противодействовать причине, вызвавшей электродвижущие силы, т. е. будут, взаимодействуя с полем, увлекать ротор с обмогкой за полем, как бы стремясь нагнать его, будут создавать вращающий ротор момент. Ротор будет вращаться всегда с несколько меньшим (на 1—3°/0) числом оборотов, чем поле, ибо поле должно пересекать обмотку, чтобы в ней появился ток.
Таков принцип асинхронного двигателя.
Следует заметить, что когда мы нагрузим симметрично трехфазный генератор и в трех фазах его обмотки потекут токи, мы получим как раз картину, изображенную на фиг. 114, — трехфазный ток в обмотке статора создаст вращающееся поле.
231
Так как ротор с электромагнитами постоянного тока, как нам уже известно из первых страниц курса, проходит за период тоже двойное полюсное деление (на этом бы по основано самое определение „период"), то получается, что поле от трехфазной обмотки статора вращается с той же самой скоростью, что и ротор, или, иначе, — синхронно с ним.
Если нагрузка генератора несимметрична, то амплитуда поля периодически изменяется.
§ 69. Разложение несимметричной трехфазной системы на две симметричных 10
В предыдущих параграфах были изложены методы аналитического и графического расчета трехфазных систем также и в том случае, когда система токов и напряжений несимметрична.
Однако в случае несимметричности вышеизложенными способами трудно получить суждение о влиянии самой этой несимметричности на явления в трехфазной цепи. Кроме того расчеты всех трех фаз часто могут быть длинны.
В последние годы весьма развились такие специальные отрасли электротехники, как например расчет токов коротких замыканйй трехфазных систем, где мы можем сильно сэкономить работу, прилагая метод, принципы которого излагаются в этом параграфе и который позволяет даже и при несимметричности токов и напряжений свести задачу к расчету только одной фазы.
В учении об электрических машинах метод этот чрезвычайно облегчает и ускоряет рассмотрение работы различных синхронных и асинхронных машин в случае несимметричности линейных напряжений и облегчает суждение о влиянии этой несимметричности на работу их.
Идея этого метода впервые была высказана американским ученым Фортескью 10.
Мы будем различать здесь два случая: первый, когда даны три вектора, составляющие замкнутый треугольник, например векторы трех линейных напряжений или токов в системе без нейтрального провода, и второй, — когда даны четыре вектора, составляющие замкнутый четыреугольник, например три фазовых тока и ток в нейтральном проводе. Остановимся сначала на первом случае.
Любую несимметричную систему трех замыкающихся в треугольник векторов можно разложить на две симметричные системы, причем у одной величина векторов будет меньше, чем у другой, и последовательность фаз у векторов будет обратная.
Сначала покажем, что сложением соответствующих векторов таких двух систем получается несимметричная система, образующая однако замкнутый треугольник.
232
первой фазы на —, а век-о
п
- вектор Вг первой фазы.
называют так: систему
На фиг. 115 Av Л2, А3— три симметричных вектора, относящиеся к трем фазам; В2, В3— другие три симметричные век-
тора, однако с обратной последовательностью, именно в.ектор А* второй фазы отстает от Аг—вектора
2 тор В2 второй фазы опережает на -
<
Эти системы векторов обычно At — А2 —А3 — системой прямой или положительной последовательности векторов, а систему — В2 — В3 — системой обратной или отрицательной последовательности векторов (вместо слова „векторов* здесь можно употребить и слово „фаз").
Сложим геометрически векторы одних и тех же фаз, т. е. Аг с Bv А2 с В2 и А3 с В3, и мы получим векторы Ср С2, С3, которые составят непременно замкнутый треугольник. Доказательство последнего утверждения очень просто, — именно ’мы имеем, что так как
системы и т. д. и В1 и т. д. системы симметричные, то
Л1+Л2 + ^3 = 0 и
^+^+^=.0,
а следовательно, сложив эти два ур-ия:
А + + ^2 + ^2 + ^3 + 0)
т. е.
^ + ^ + ^ = 0,
т. е. треугольник векторов Ср С2 С3— замкнутый. Следует заметить, что многоугольник из этих шести векторов А и В замкнется при всяком порядке сложения их, ибо в ур-ии (I) конечно члены можно группировать и переставлять как угодно.
Система векторов Cv С2 и С3 несимметрична. Далее мы покажем, каким способом данную нам несимметричную систему можно разложить на две таких симметричных, т. е. при данных векторах системы С найти векторы системы А и В,
Физический смысл такого разложения тоже очень прост. Сравнивая например вектор Ct и его составляющие с вектором С2 и его составляющими, мы находим, что большая по величине составляющая вектора опережает равную ей соста
233
вляющую Д2 вектора С2 на , а меньшая составляющая Вг вектора С| отстает на такой же угол от такой же составляющей второго ьектора С2.
Таким образом векторы системы положительной или прямой последовательности по величине больше векторов системы отрицательной или обратной последовательности.
Применим символический метод для выражения всех векторов.
__ __ ,2ге _ , ,2к
Д1=Д, А2 = Ае 1 3, А3—Ае 13,
В1 = Ве+^а, В2=Ве'(’+1\ В3 = Be ,
С3 = АВе>л,
Сг = Ае~ з_|_Ве+'Г+з^ (Ц)
, 2п / 2к \
C3 = Ae^1 *-\-Be+jV .
Если нам заданы эти три вектора Ср С2 и С3, то из трех ур-ий (II) мы можем определить три неизвестные Д, Виа. Начнем л +j2i
с определения Д, для чего умножим второе ур-ие на е %
а третье на е 3, тогда коэфициенты при А везде будут равны единице, а коэфициенты при В будут:
+л +/(«+*) +'(«-£)
сумма их, как трех векторов, равных по величине, сдвинутых на 120°, равна нулю.
Поэтому, сложив три полученных из (II) ур-ия, будем иметь:
_ _ __________
с1+с2^ 3 + С3^ 3=ЗА
(III)
л
В этом ур-ии умножение вектора С2 на е 3 означает поворот вектора С2 на 120° против вращения линии времени или иначе в сторону возрастания положительных фазовых углов, а умножение вектора С8 на е 3 означает поворот его в обратную сторону на 120°.
На фиг. 116 нам даны три вектора Cv С2 и С3, сумма которых равна нулю.
234
Производим построение, выраженное ур-ием (Ш). Вектор С8 поворачиваем по часовой стрелке на 120° в положение Ok и, прикладывая к Clt получаем вектор 01.
Затем поворачиваем вектор С2 против часовой стрелки на 120° в положение Oh и, прикладывая к 01, получаем вектор ОР=ЗА. Проводим линию Ор под некоторым углом к ОР, откладываем на ней три равные отрезка, соединяем последнюю точку р с Р и проводим mS [] рР. Вектор 05 = Л. _ _
Далее, вычитая из С2 вектор OS, находим вектор Вг Угол между В* и OS есть угол а.
На фиг. 117 данные векторы С19 С2 и С3 начерчены уже в виде треугольника. Тогда построение еще проще, нужно только С2 и С3 повернуть на 120° в разные стороны в положение 2Р и JO, и линия ОР 2 даст нам вектор ЗА. Деля его на 3, получаем OS — А Вычитая OS из Ср находим Вг Можно вектор Вг = = Ве^л найти путем, аналогичным нахожде-
нию вектора А. Для фиг этого умножим второе . 2* + / "o’ л
третье на е и, сложив, будем иметь:
Cj + Cae 7 2 4- cse+i 3 = 3Br
Для графического выполнения этой операции вектор С2 вращаем по линии времени или по часовой стрелке на 120°, а вектор С3 — в противоположном направлении, в остальном поступаем, как выше описано.
Метод разложения несимметричной системы на две симметричные составляющие системы позволяв» быстро получить решение весьма сложных задач. Как пример, рассмотрим влияние несимметричности линейных напряжений на работу асинхронного двигателя.
235
Магнитодвижущие силы различных фаз обмотки статора пропорциональны силам токов, а потому при включении этих обмоток треугольником пропорциональны линейным напряжениям.
Разложим эти магнитодвижущие силы на две симметричные системы. Система положительной последовательности создает вращающееся магнитное поле, которое и увлечет ротор за собой.
В системе отрицательной последовательности ток в фазе второй опережает ток в фазе первой вместо того, чтобы отставать от него (фиг. 115), а ток в фазе третьей опережает ток во второй.
Поэтому роли обмоток второй и третьей фазы переменились, и в то время как в системе положительной последовательности магнитное поле перемещается вдоль обмоток в порядке номеров 1—2—3—1 — 2—3..., в системе отрицательной последовательности поле перемещается по обмоткам в порядке 3—2—1—3—2— 1..., т. е. в порядке обратном Это вращающееся ма< нитное поле вызовет и соответствующий вращающий момент, ^В3 действующий на ротор, но так как это второе поле слабее первого (ибо векторы системы отрицательной после-7 довательности меньше векторов положительной последовательности), то его вращающий момент будет только вычитаться из вращающего момента первого поля и уменьшать таким образом коэфициент полезного действия. Исходя из векторной диаграммы, как на фиг. 115, можно всем этим соотношениям выражение.
A
A
Фиг. 118.
дать и аналитическое
Остановимся теперь еще на том случае, когда векторы системы В отрицательной последовательности равны по величине векторам системы А положительной последовательности.
На фиг. 118 изображен этот случай.
Мы видим, что в этом случае векторы С\, С2 и С3 лежат на одной прямой, делящей углы межд/ каждой парой слагающих векторов пополам. Сумма их равна нулю. Они представляют собой однофазную систему.
Если эти векторы пропорциональны полям трех обмоток, то их надо расположить пространственно по осям обмо'ок, тогда они дадут некоторое результирующее пульсирующее, а не вращающееся поле.
Таким образом мы опять приходим к результату, уже однажды нами полученному, именно, что пульсирующее поле можно разло-236
жить на два вращающиеся в противоположные стороны, равные по амплитуде друг др\гу.
Такие два поля дважды за оборот совпадают по своему направлению, причем амплитуды их складываются и дают амплитуду поля пульсирующего. Поэтому для представления таких полей надо положить
А —В —1
и угол
а = 0.
Теперь перейдем к исследованию того случая, когда данные три вектора не составляет замкнутого треугольника, а дают геометрическую сумму, отличную от нуля.
На фиг. 119 мы имеем три вектора D2 и D3, которые в сумме дают вектор Do, так что
+ D2 + — Дг
Разделим вектор Do на три равные части по — DQ и, пере-о
неся их в левую часть последнего ур-ния, вычтем из каждого данного вектора по этой трети от Do, применив для наглядности скобки:
*
( D. -1 Do ) + ( D, - Do ) 4- (Ьа 4-1 Do) = 0. (IV)
\ о / \ о / \ о /
На чертеже векторы
sr = rq = пр — ~тп —~ Do. (V)
О О
Обозначим
^-1^0=^.
На фиг. 119 это есть вектор тг — sr=ms= nq\ далее
D2---— D^ — С2,
на чертеже это есть вектор rt— rq = qtt и наконец
£>3--Dq = С3
237
на чертеже представляется как
1р — пр = tn.
сумма которых равна нулю по вляют замкнутый треугольник.
Таким образом мы получили три новых вектора Ср С2 и С3, (IV), которые следовательно соста-Систему векторов С2 и С3 мы можем, как раньше показано, разложить на две симметричные системы,’ Ak положительной и Bk отрицательной последовательности.
Три равных вектора со-о
ставляют так называемую систему нулевой последовательности.
В практике такими токами являются токи, текущие по нейтральному проводу, или, если его нет, то в случае короткого замыкания двух фаз на землю, — ток заземления, ток, идущий по земле от места короткою замыкания к другой заземленной точке линии.
Вы азим аналитически
2* разложение векторов D19 D2 и D3 на векторы Ak, Bk и £>0, для чего воспользуемся соотношениями (136), выведенными в § 55, и при-Меним их к фиг. 119:
Af=aAv А2=аА3—сРА^
Фиг. 120.
В2=аВи B3 = aB2 = a2Bv
и далее из фиг. 115 и ф-л (IV), (V) и др.
3
— a*At aBj 4~ — Z)o, о
Dt = аА1 -|- й«в, + у Do-
238
Если нагрузка соединена звездой, то может оказаться необходимым разложить на две симметричные системы не только линейные напряжения, но и напряжения фазовые.
На фиг. 120 дано такое разложение: векторы О1\ 02' и ОЗГ представляют систему прямой последовательности, векторы О1"?О2", ОЗ"—обратной последовательности. Из них получаются действительные фазовые напряжения 01, 02, 03 и линейные 72, 23, 31.
Возьмем любой из векторов линейных напряжений, например 23; построим на нем равносторонний Д/И23 и соединим точку М с точкой 7, т. е. с той вершиной треугольника напряжений, которая не вошла в равносторонний треугольник (М23). Оказывается, что Л47 = 3«О7\ что и дает возможность путем такого простого построения ДМ23 из данных линейных напряжений находить векторы симметричных систем фазовых напряжений п.
Докажем, что Ml = 3«01". Имеем:
О?= V; = 01" =V\ =
O2'=F'=yi'^(e"‘3'), oz= v"==
X 1 A 1
03’= vT= V'.ey(?+ r), 03’=
О 1 7 о 1
Очевидно, что
Ml =31 — ЗМ.
ЗТ= ОТ’-\- 6Т"— 03'— 03"= V{e^ 4-
ire/(«+₽) __ у\е} ( 3 ) — V[e1 ( “+₽“ ¥ ).
__ —• _/Л
Вектор ЗМ получается из вектора 32 умножением его на е 3, т. е. поворотом на 60°, а вектор 32 = 02— 03; поэтому
~ЗМ = 32-е~^~
Выражая Ml через все эти компоненты, сгруппируем их следующим образом:
~Mi={v{e^— уу(₽+з)_ vy^+D-f-
-f- 17"е;(’+Р-'з )— V"e/(“+₽+3’)4-
239
В первых скобках стоят четыре вектора, которые дают: ЗУ^, т. е. 3-67'
(фиг. 121); четыре вектора во вторых скобках дают нуль, что читатель должен доказать сам, построив их, подобно фиг. 121.
Упражнение. Доказать, что, перевернув Л М23 в положение Р23, мы будем иметь __ _____ _
Р1 = 3-ОР=3-У[.
Проделать графическое построение и проверку для других сторон.
В действительности может и не быть нагрузки, включенной звездой.
Построив вектор Ж/, мы можем и не строя векторов О1\02\ О3\ сразу узнать величину междуфазового или линейного напряже-
1
Фиг. 121.
Фиг. 122.
яия прямой системы, так как по величине
Г2' = О/'./3 = ^1 = 0,577-Ml.
/3
Узнать линейное напряжение обратной системы по формуле
~Т"2"==72 — Т7?'
мы, не построив векторов 01', 02', не можем, ибо неизвестна фаза вектора 1'2' относительно 12. Поэтому строим Л Р23 и, измерив Р1, вычисляем 0,577 *Р1 = 1 ”2" или Г'З".
240
Таким образом построением двух треугольников Л423 и Р23 и двумя умножениями на 0,577 мы узнали длины векторов Г29 и Г2”.
Пример 9. На фиг. 122 проделано это построение: найдены точ^и М и Р описыванием из точек 2 и 3 дуг радиусом, равным 23\ длины Ml и Р1 умножены на 0,577; и из линии /2, Г2' и У? построен треугольник 12К. На стороне 1К, как на большей, построен равносторонний треугольник с той же последователь остыо фаз, что и 123, а на стороне К2 построен треуготьник с обратной последовательностью.
При этом мерилом точности вы ,ерчивания служит проверка, выполняются ли равенства векторов (т. е. равны ли их длины и параллельны ли направления):
КЗ* =33 И КЗ =3*3.
Следует заметить, что так как вектор Ml параллелен фазовому вектору 01' (действительном \ или воображаемому), то Ml _L2,3 на фиг. 120 и М1_1_КЗ' на фиг. 122, т. е £ М1К= 30°. Эго заме ание служит для того, чтобы построить Л 1К2 фиг. 122 в правильном положении, ибо ведь дуги, описан 1ые из ючки 1 радиусом ГЗ и из точки 2 радиусом /"2", пересекаются в двух ючках.
16 Теория переменим* токов.
211
ГЛАВА IX
СЛОЖНАЯ ФОРМА КРИВЫХ ЭЛЕКТРОДВИЖУЩЕЙ СИЛЫ И СИЛЫ ТОКА
§ 70. Основные понятия
Когда форма кривой электродвижущей силы отступает от синусоиды, расчет усложняется; теорией этого случая мы и займемся теперь; сначала остановимся на общем приеме для получения аналитического выражения электродвижущей силы.
Если кривая электродвижущей силы и синусоида [ф-ла (14) § 5] не совпадают, то надо посмотреть, нельзя ли прибавлением к синусоиде (14) других периодических функций получить функцию, кривая (графйк) которой будет ближе к кривой поля, чем чистая синусоида (14).
За такие функции возьмем синусы и косинусы с периодами в 2, 3, 4...п раз меньшими, чем Т—период функции (14) (тангенсы и котангенсы неудобны, так как принимают бесконечно-х п 3 \
большие значения при значениях аргумента — и — п 1.
А Л» J
Сначала разберем несколько примеров.
Посмотрим, что за кривая получится от сложения с ординатами синусоиды (14) ординат синусоиды с периодом Т3, в три раза меньшим, и с некоторой амплитудой а3. Значками „три* мы указы-гаем условно, что у этой новой синусоиды период составляет одну треть прежнего, т. е. что
(А)
Новую синусоиду мы можем выразить аналогично ф-ле (14); ее ординаты равны
А'3 = а3-5ШС08Л
Здесь
е8= =- = 2w:-|- Т= 3-^=3®, л 3 О 1
242
тому же спосооу, изложенному далее, по
сначала одну, потом другую синусоиды, а
и поэтому
у3 = a3.sin3(o/. (В)
Ординаты результирующей кривой выразятся ур-нием:
у = ♦ sin ш/ 4“ аз •sJn 3^- (С)
Что касается величины a3i то она при решении конкретных задач определяется по которому определяется и аг Мы пойдем обратным порядком, именно.— зададимся величиной а3, например положим
1 аз— з ai
и построим кривую, выражаемую формулой (С), для чего построим
затем сложим их ординаты алгебраически и начертим по точкам результирующую кривую.
На фиг. 123 все это построение и выполнено, причем здесь кривая б есть синусоида с амплитудой а3 и с периодом в три раза менее периода синусоиды а, а кривая в есть результирующая.
Можно было бы не складывать ординат кривых, а вычитать Ординаты второй синусоиды из ординат синусоиды а; тогда получили бы кривую, аналитическое выражение которой было бы таково:
у — Oj’Sin со/— — а3-sin Зю/ (D) и которая графически представлена кривой в на фиг. 123.
Построим теперь кривую, выражающуюся ур-нием:
фиг- 124- j^aj-sin (о/4-Лз*
•sin3o>/-}-а&-sin5(o< (Е) в котором зададимся соотношениями:
Лз = з av —If
243
и где очевидно период функции
sin5(i)Z = sin(o6f
по аналогии с (В) в пять раз меньше периода- Т.
На фиг. 125 представлены все три синусоиды и кривая а, полученная алгебраическим сложением их ординат. Синусоиды, ординаты которых мы алгебраически складываем для получения результирующей кривой, называются „составляющими" синусоидами для этой кривой или просто „составляющими". Коэфициент под знаком синуса при со/ называется „порядком" синусоиды. „Составляющая л-го порядка® означает синусоиду с периодом Тп в п раз меньшим, чем период Т самой периодической функции или изображающей ее кривой, результирующей из нескольких синусоид Амплитуду
составляющей л-го порядка мы будем обозначать разными буквами с значком я, а аргумент ее через (оя^, где
2тг 1 2те
т =2п:у = (G)
п
Может случиться, что, сложив с основной синусоидой (14) или синусоидой первого порядка несколько синусоид высших порядков, мы поучим кривую, которая оч^нь близко подойдет к экспериментально полученной с машины кривой поля или электродвижущей силы. Эго буает означать, что вопрос об аналитическом выражении этой ЭДС решен Выражение (Е) или другое, подобное, в котором буд/т сод ржаться члены, выражающие все составляющие, и будет требуемым аналитическим выражением.
Заметим еще, что все полученные нами до сих пор от сложения различных синусоид кривые симметричны относительно оси абсцисс.
Может случиться одн ко, что придется для подходящего представления кривой ЭДС анатитическими периодическими кривыми привлечь еще и косинусоиды.
Сначала опять обратимся к примеру.
244
На фиг. 126 сложены ординаты синусоиды первого порядка и косинусоиды третье! о порядка (применяя понятие „порядка* к косинусоиде совершенно таким же образом, как и к синусоиде), причем в нашем примере принято, что амплитуда косинусоиды
^3=3- а1>
и начерчена результирующая кривая.
Аналитически ординаты кривой выражаются так:
или:
y==a1.sin(o/-|-Z>3‘Cos3 /, у = ^-310a)/-|-^3‘sin
(Ц>
Из фиг. 126 мы видим следующее.
Во-первых, перв я и вторая четверти периода между собой не одинаковы, тоже — третья и четвертая между собой, т. е. х(®я кривая симметрична относительно оси абсцисс, $о она несимметрична относительно точки перехода через нулевое значение. Взяв на одинаковом расстоянии от точки 02 вправо и влево по ординате, мы увидим, что они цо абсолютной величине не равны; отметим, что в предыдущих кривых этого не было; следовательно вхождение в число составляющих косинусоиды влечет за собой асимметрию относительно точки перехода через нуль.
Во-вторых, если результирующая кривая подходит по форме к кривой ЭДС достаточно, то из фиг. 126 i идно, что, написав выражения (Н), мы тем самым счет времени (/ = 0) начинаем не с того момента, ко да ЭДС равна нулю, т. е. не с точки О3, а позднее на промежуток времени т, с точки О.
_ Так как однако отсчет времени с момента нулевого значения ЭДС часто бывает желательнее, то мы выражения (Н) для соста-
245
ваяющих должны изменить. Введем отсчет времени от точки О3: тогда новое время
где т— постоянная величина, равная ОО8.
Подставив в уравнение (Н) вместо / его выражение через новое время, т. е. величину f—т, получим:
у == • sin ((i>f — шт) 4~ • sin 3(о/г — Зшт 4“
Введя для постоянных величин сокращенные обозначения: — от =
— 3®T-f-y = <ps, мы имеем:
у = аг - sin (o)f -|“ Ti) + ^з *sin (К)
или же, преобразуя и развертывая:
у — аг cos <р2 sin sin <р2 cos го/' 4" cos ?з s*n 3w/' “F 4~^з sin ср3 cos Зсо/'.
Произведя дальнейшее сокращение обозначений постоянных величин и положив
аг cos = Др аг sin cp-j = Vos Тз = А>. £3 sin (р3 = Z?3>
а также упразднив теперь значок при tt как уже не нужный, — раз другого счета времени, кроме нового, у нас нет, — получим окончательное выражение:
у = Aj sin со/ 4” cos 4~ A3 sin 3(0/ 4” ^3 cos 3<oZ. (L)
После всех этих примеров нам нетрудно будет перейти и к более общему исследованию вопроса об аналитическом выражении электродвижущей силы.
Фурье (Fourier) показал, что всякая периодическая функция может быть представлена аналогично L разложением в некоторый ряд, состоящий из отдельных синусоидальных (и „синусов" и „косинусов") функций с периодами в 2, 3, 4, 5,... п раз меньшими основного периода Тис амплитудами, определяемыми по особым правилам. Число членов этого ряда, называемого рядом Фурье, различно для различных видов периодических функций.
246
В общем случае его можно считать бесконечным и представить поэтому периодическую функцию у так:
У =s. Aq sin Ci)/ 4“ C0S + ^2 S*n 2(0/ 4“ ^2 cos 2(о/ 4“ 4-Л3 sin 3(о/4“ В3 cos Зсо/ 4~.. -4“ Ais*n Л(о/4~
4~ВЯ cos/гео/-j-... (144)
Прежде чем перейти к изложению способа вычисления коэфи-циентов этого ряда, т. е. амплитуд отдельных составляющих, остановимся на двух общих свойствах этого ряда для того случая, когда 4о = О.
Во-первых, нетрудно видеть, что если кривая, изображающая рассматриваемую периодическую функцию, симметрична относительно точки перехода через нуль, то косинусоиды входить в число составляющих не могут, а потому все коэфициенты при них — В2,...ВЯ...— равны нулю.
Во многих случаях практики кривая означенной симметрией не обладает, а потому будет иметь в числе составляющих косинусоиды различных порядков.
Обратимся ко второму свойству.
На фиг. 127 сложены: синусоида а основная, или первого порядка, и синусоида & второго порядка с некоторой амплитудой и получена кривая в, изображающая уравнение:
у =s А1 sin (о/ 4~ s*n 2®^
Мы видим, что кривая в несимметрична относительно оси абсцисс.
Далее, пунктиром г изображена косинусоида второго порядка, и сложением ее с а получена кривая д, изображающая уравнение:
у — Ах sin (о/ 4“ cos 2©/.
Эта кривая тоже несимметрична относительно оси абсцисс.
247
Нетрудно видеть, что и вообще всякая составляющая четного порядка вводит нарушение такой симметрии, а потому кривая, симметричная относительно оси абсцисс, не может иметь в числе составляющих таковые четного порядка. Так как кривая электродвижущей си «ы вследствие одинаково ти полюсов бо ;ыпей частью обладает это^ симм трией, то обыкновенно она не содержит четных составляющих.
При построении электрических машин идут таким путем. По пучив экспериментально у построенной машины кривую электродвижущей силы, исследуют, какие конструктивные и иные соотношения содействуют уменьшению амплитуд состав яющих высших порядков,— причем под словом „высший" будем подразумевать всякий „больший единицы" порядок, — а затем строят согласно полученным результатам машины так, чтобы их ЭДС была возможно ближе к чистой синусоиде. Тогда можно было бы считать для ЭДС применимой формулу (15).
Операция нахождения величины амплитуд всех отдельных составляющих какой-нибудь эмпирически данной периодической функции называется анализом ее. Для анализирования ЭДС служат особые методы: арифметические, когда кривая уже получена, и экспериментальные без предварительного снятия самой кривой ЭДС,— а также особые приборы — анализаторы, применяющиеся тоже при имеющейся уже кривой.
В современных машинах переменного тока кривая ЭДС обыкновенно очень близка к синусоиде и содержит, кроме основной синусоиды первого порядка, синусоиды высших порядков, только с оч^нь малыми амплитудами.
§ 71. Разложение в ряд Фурье
Обратимся теперь к аналитическому определению коэфициентов в ряде Фурье (144):
у = Ло-|- sin со/ -}- Вг cos со/ -{-Я2 sin 2 со/ -|-B2cos2q)/-|-» • • (144)
Будем производить следующие действия: сначала умножать обе части уравнения (144) на
sin • d(®t) ) или на > fa)
COS (/ZCO/) • б/(СО/) J
придавая n целые и положительные значения, — начиная с нуля, — и затем интегрировать обе части между пределами
/ = 0 или со/= О и
t=T или (о/ = 2п
248
При этих операциях у нас в правой части будут получаться от умножения членов правой ч сти уравнения (144) на одно из выражений (а) члены следующего вида:
2п
J sin (m®f) sin (nut) • d ((of) о 2к
J sin (yitot) cos («(of) • d (of) > о 2n
J cos (mcof) cos • d(of) о
умноженные еще на амплитуды Ат или Вт, и ксоме того еще члены вида:
2к 2к
Ао У sin («(of) d(cof) и Aq У cos («(of) d(of).
о 0
Последние интегралы, как читателю нетрудно доказать самому, все равны нулю.
Переходим к первым трем.
Преобразуем первый интеграл, пользуясь соотношением:
cosy/ — cos z = — 2 sin'-—— sin a i
(?)
Полагая
-1— = /77(0/ И — = ЛО/, 2*
имеем:
у = (m —}—/г)(о/, z — (m— ri)wt
и, подстагляя в (p), получаем:
sin (mof) sin (/zof) =f=-{cos [(m -f- ri) of] — cos [(m — ri) of] }.
Подставляя это выражение в первый из трех вышенаписанных интегралов и производя интегрирование, получаем выражение:
---{ J C°S — J C°S — П _________________________________________ sin '(m ri) of] ( sin \(т — ri)wt 2(m-\-ri) ' 2 (т — ri)
(1>
24&
Далее, пользуясь формулой v “4“ z у______________________________________z
sin у -|- sin z = 2 sin —5— cos —-— Z Z
найдем, что второй интеграл дает выражение:
cos \(т 4- п) (00 cos \(т — п) со/]
2 (лг -f~ Л) 2 (лг — л) ‘
наконец на основании разложения
у -4- z у — z
cos у 4~ cos z — 2 cos —5—cos<—5—~ z z
для третьего интеграла получаем выражение:
sin [(лг 4-л)(о0 . sin (лг—л)(о0 .
2 (т -\-п) * 2</л— л) ‘
(И)
(III)
Возьмем разность значений выражений (I), (II) и (III) между пределами (of=O и со/=2п, чтобы перейти к определенным интегралам. Ингеграл (II) для всех значений т и л обращается в нуль; интегралы (I) и (III) обращаются в нули для /л^л; только при т — п второй член этих интегралов
sin [(лг— л)2п] 2 (лг —- л)
О дает неопределенность —, которая раскрывается так:
(sin \(т — л)2тг1) (sinr(^ — л)21т]) ZT_^
предел|. =«.предел|-(и_)|)2|1 | «=к, (IV)
от=л т=п
так как предел отношения синуса к его дуге при уменьшении ее до нуля есть единица.
Таким образом после умножения уравнения (144) на то или другое из выражений (а) и интегрирования между указанными пределами, в правой части останется только тот член, для которого т = л и который получился или от перемножения синусов (I) или косинусов (III). Например при умножении на
sin (5 со t)*d ((00,
все, кроме одного, члены после интегрирования дадут нули, в том числе и член
В5 cos (5(00 »sin (5(o0«^f(o0, и лишь член
А5 sin (5(00. sin (5(00 • d(g>0
даст после интегрирования величину согласно (IV):
Д5п.
250
При умножении же ряда (144) на
COS (5(dt)-d((i)t)
не даст нуля после определенного интегрирования только член
В5 cos (5со/) cos (5(0/) • (/(со/), от которого мы получим на основании (IV):
В6п.
В левой же части мы будем иметь определенные интегралы от произведения функции у на ту величину, на которую мы множили обе части; таким образом
<о/=2к
у sin (mat)-d(wf)==Amn (145)
w/=o
И
<о/=2к
J^cos(/n<o/)-d(a>0==£«in- (146)
a)/=0
Что касается Ао, то его мы определим так: умножим обе части ряда (144) на d(®t) и проинтегрируем между пределами 0 и 2тс. В правой части получим только Л02п, так как остальные интегралы будут равны нулю, а в левой части получим площадь между кривой у и осью абсцисс за период. Разделив обе части на 2п, будем иметь: 2к т т
AQ = ^yd^t) = ^y.dt=^^y.dt, 0 0 0
т. е. Ло есть „среднее" значение ординаты кривой за период.
В дальнейшем мы будем иметь в виду исключительно переменный ток, получающийся от описанных выше генераторов; среднее значение его за период равно всегда нулю, другими с. овами, для него Ло = О;’ читателю ясно, что это . является следствием упомянутой уже не раз симметрии его кривой относительно оси абсцисс.
Ф-лы (145) и (146) дают нам возможность вычислить значения всех коэфициентов ряда (144) и кроме того дают нам общие математические доказательства правильности тех соображений относительно составляющих четного и нечетного порядков, а также синусоид и косинусоид, которые были развиты выше и иллюстрированы фиг. 125—127.
Выразим аналитически условие симметрии кривой у — /(/) относительно оси абсцисс.
251
Так как эта симметрия означает, что на фиг. 2
ab = — hg,
то, обозначая Оа через /, имеем, что Oh = t —- Г, и следова-тельно условие симметрии кривой относительно оси абсцисс выразится так:
= + (147)
Введем это условие в выражения (145) и (146) путем следую-
щего рассуждения.
Пусть кривая, выражающая функцию у, обладает этой симметрией, и для нее поэтому имеет место соотношение (147). Подста-j им в ур-ние (145) вместо буквы у выражение /(/) и сгруппируем
бесконечно-малые слагаемые под интегралом для значений времени, 1
отличающихся одно от другого на — Г, попарно, после чего получим: Ц)/ = ТС
sin^/жо
со/=0
^ + yT)]W).
Интегрирование теперь производим между пределами со/=0 и (о/=п, так как все бесконечно-малые слагаемые второй половины периода, от <о/=тг до (о/ = 2тг, уже сами собой вошли в
суммирование под знаком интеграла в виде второго члена в кривых больших скобках; если бы мы не изменили иределов интегриро-
вания, а оставили бы их старыми, нужно было бы перед' интегра-1
лом поставить множителем —, чтобы не нарушить равенства. 2*
В последнем выражении вынесем /(/) за большие скобки, пользуясь соотношением (147), тогда получим:
Ц)/ = К
Лт-п== J /(/) | sin (mat) — sin |j7Z(o ^+"5" d(prf).
<D/ = 0
Раскрывая прямоугольные скобки под знаком синуса и помня, что — (оГ=- тт, получаем: 2/
U)/ = 7t
Лт-п = J /(/) |sin(m®*) —cos(mir)— wZ = 0
— cos (wo/) sin (/wtt) 1
252
sin(лтгтг) = 0 для всякого целого т\ далее, для т четного имеем cos (mir) = 1; выражение в скобках под интегралом обращается
при этом в нуль, следовательно и Ат для т четного равны нулю; сделав аналогичные подстановки и преобразования (146), убедимся, что Вт для т четкого тоже равны нулю; следовательно составляющие четных порядков не могут иметься (выражаясь математически: их амплитуды равны нулю), если кривая симметрична относительно оси абсцисс.
Выразим аналитически условие симметрии относительно точки перехода функции через нуль. Эта симметрия дает равенство cd — =— hg (фиг. 2); полагая Cc — t, имеем: Ac —Ah. hB = Oc = t. и Oh = OB — hB—T—t; поэтому условие означенной симметрии можно аналитически выразить так:
Я0 = -/(Г-0. (148)
Подставим это в уравнение (146) и проделаем преобразования, аналогичные предыдущему,
(О/ = к
Вт-тг = J j/(0 cos (zraco/) /(Г — 0 cos [/м(о(Г — | d (со/), ш/ = О
Так как
cos [/ясо(Т — f)] = cos (/жоТ) cos (mcof) sin (mwT) sin (z/zo>Z) —
= 4~ cos (mart)
для всякого целого m. ибо а)Г=2тс, то
О)/ = к
j /(04~/(^—cos(zwa>/)-^(a)/)==0, w/ =E 0
так как выражение в больших кривых скобках под интегралом для всякого момента t согласно соотношению (148) равно нулю.
Подставив ур-ние (148) в ур-ние (145) и проделав преобразования, ничего нового не найдем.
Таким образом при симметрии относительно точки перехода функции через нуль косинусоиды в .число составляющих входить не могут.
Пример 40
O6pai имея теперь к одному примеру вычисления коэфициентсв в ряде ь урье для случая, когда кривая может быть хотя бы по частям вы-
р окена ана'л ити ч ес к и.
Пусть функция у =f(t) представлена графически равнобокой трапецией (фиг. 1/8,. В течение времени т функция растет, в течение времени
А Г •— 2t — остается равной постоянной величине С, затем в течение времени
т убывает до нуля и т. д. Так как кривая обладает обоими видами симметрии, то ряд Фурье должен содержать только синусоиды нечетных порядков. Интеграл (145) разобьем на шесть частей, от 0 до т, от т до
253
Т — т и от н- Г—t до Т и т. д., причем достаточно вычислить пер-X А £л
1 я
вые три и сумму их удвоить или приравнять
Для первой и третьей части имеем:
/М = /г(47’-^) (»)
и далее
sin Г—/)] = sin (ттс — mco/) = — sin (mtn f) cos (/ля) =
= -|- sin (m<o0> (?)
так как m нечетное и cos (mn) = — 1.
Таким образом интегралы вдоль первой части и вдоль третьей будут равны вследствие (а) и (?):
4 *** = 2]
Поэтому вместо (145) имеем:
2
/(/) sin (mntyd (to/) -|- J /(f)sin (mto/)*rf (<о/). (a)
О т
В первой части функция растет пропорционально времени:
/(/):С = /:?, (Ь)
и поэтому, подставляя из (Ь), получаем:
t
/ (0 sin (m со/) d (со/) = у J t sin (mw/) • d (oaf) = о
С Г T«cos(m<OT) sin /и(отУ|
254
Во второй части функция постоянна, и потому второй интеграл в (а) равен:
- Г—т
2
j* С sin • d (со/) = — cos т® Т — j — cos (mwt) | =
t
C I 1 2C
=------\ cos (mit — mu>f) — cos (/n<or) > = — cos (man), (d)
так как sin(mit) = 0 и cos(mic) =—1, ибо m нечетное.
Удвоив выражение (с) и сложив с (d), получим правую часть для (а):
1 2С 2С 2С
Л -я =--------cos (w<or) -|---sin (/ясот) -4---cos (теот),
2 m m ' ' ' vnfa ' ’ 1 tn v
откуда:
. _____4Csin (mcor)
m /w2<d:ic
(e)
Подставляя сюда вместо m нечетные числа, начиная с единицы, мы и вычислим все Лот. Конечно для вычисления нужно знать еще и величину т; пусть например т = -|- Г; тогда (/иск) приобретает для различных m вели* 15 1
чины -х- к (/я = 1), тс (т = 3), -у к (/и = 5) и т. д.; сот = ~ я; вычислив си-о о и
нусы и затем все Ат, мы получим ряд:
У = 6 [sin (“0 — sin (5<о0 + sin (7®0 — Sin (11«0 + •••]•
Если т = -^- Г, то трапеция превращается в равнобедренный треуголь-м 1
ник с высотой С; при этом сот = у тс, и
8Csin (у
Ат— ^3 ’
и далее
у = [sin (»0 —к- sin (3«0 + X sin (5W) —.. .1.
1С1 L J
Наконец при т = 0 трапеция превращается в прямоугольник; при этом sin (ттт)___________________________
тшт ’ и
т /ИЯ и ряд будет таков:
у = — [sin (a»0 4- 4 sin (3a>0 + -1 sin (5<oA я l * о j
В разобранном примере амплитуды составляющих убывают с ростом порядка составляющей, в разных случаях по разному закону» Далее мы встретим случаи, например в кривой силы тока при
255
включении емкости в цепь, когда амплитуды составляющих могут и расти с ростом порядка составляющей, что, вообще говоря, всегда представляется нежелательным и вызывает различные осложнения при работе цепи переменного тока.
Представить кривую в виде ряда (144) с известными уже коэ-фициентши значит дать анализ ее.
Полученные экспериментально, например с помощью осциллографа, кривые переменного тока не могут быть выражены аналитически даже по частям, как это было возможно в только что проделанном примере, вследствие их эмпирического происхождения; поэтому анализировать их посредством интегрирования левых частей ур-ний (145) и (146) нельзя. В этих случаях приходится прибегать к другим способам определения коэфициентов ряда (144)* или к арифметическому анализу путем замены интегрирования суммированием достаточного количества членов вида
у -sin (/по)/)
и деления суммы уже не на тг, как это следовало бы из ф-л (145) и (146), а на число слагаемых, или к чисто графическим методам, один из которых описан в следующем параграфе, или наконец к особым приборам — анализаторам *.
Остановимся еще на оаном формальном прео'разовании, которому можно подвергнуть ряд (144). Соединим попарно члены одинаковых порядков, синусы и косинусы, и преобразуем эти двучлены в одночлены, пользуясь тригонометрическими функциями. Например возьмем двучлен
А1п sin (/wcoZ) -|- B^cos (wo>/),
помножим его и разделим на 1/Д2 4-В2, r т ’ th*
получим:
1/Д2 1 £2
V m I tn
VГ l r m ' m
А В 1
— -----sin (mat) --I—5 ; = cos (mat) .
r m । m J
Затем введем вспомогательный угол ат, такой, что
Вт tn
= sinaw
(И9)
♦ Описание этих способов ч .татель найдет в русском переводе (в дополнительной статье) книги Линкера, Электротехнические измерения, И5Д. Маки*, 1927.
256
или, что по существу то же самое,
Ь д'
Тогда наш двучлен представится так:
sin (moi) -]- sin aOT cos (/ww/)] =
= /^ + B«sin(OT(oZ +“/»)• (150)
Положим
и тогда ряд (144) можем представить в такой форме:
у = sin (со/ ai) + ^2 sin (2(0^ + Л2) 4~ sin С3(0^ + аз) + ••• (151)
В дальнейшем такая форма разложения периодической функции нам будет очень полезна.
§ 72. Графический метод анализа кривых
Выведем некоторые соотношения между мгновенными значениями и суммами определенного числа их.
Возьмем несколько, например /?, мгновенных значений синусоидальной величины, отделенных друг от друга во времени промели
жутком в —где т и п — целые числа, и сложим их, обозначив
сумму через 5:
5 = ?lsin (со/) + A sin + sin |^(о
Д sin ^(о —1) ~ j
или символически
Здесь может быть два случая. Первый случай, когда —<? 1,— п
рассмотрим его.
Все члены суммы s можно рассматривать как проекции п векторов, сдвинутых в фазе на друг относительно друга. Множитель, поворачивающий один вектор в положение другого, например предшествующего, выразится как 2кт
17 Теория переиеиныи тот ов.
267
Геометрическая сумма п таких векторов равна нулю, т. е. многоугольник из них замыкается. Докажем это.
Эта геометрическая сумма, — обозначим ее через большое S,— выражается так:
[ 2пт ~2хт 2пт 2irml
1-l-е'2— 4-^3— J.
Выражение в скобках представляет сумму п членов геометрической прогрессии; эта сумма равна:
• е'~ - 1 ,2кт --°’
е!~ — 1
так как
е!2пт _ 1 .
Итак
<9=0,
а потому равно нулю и S, мгновенное значение 5 или проекция его на линию времени:
Перейдем к тому случаю, когда — равно целому числу. Тогда
sin I со Г t-\-k — Т\ = sin со/
L \ п )] в
s = nA sin (®f). (jj)
Очевидно, что повернув все векторы навстречу линии времени на угол —, мы не изменим по существу соотношений (а), а по-&
тому можем написать, взяв для общности другую амплитуду:
$' = B^cos I со (/-}-& — Т\ =0, (а')
л=о L Л / J
m 1
если — <1 и п
/ = пВ cos (со/), (рг)
иг когда — равно целому числу.
258
В выражениях (,3) и (£') величины A sin (со/) и В cos (со/) суть первые ординаты в ряду суммирующихся, иначе — начальные ординаты.
Соотношения (а) и (f) и положены в основу одного из самых простых графических методов анализа кривых, метода Фишер-Хиннена.
Обратимся к случаю кривых переменного тока наиболее важному, именно когда нет четных составляющих и постоянной составляющей, так что
у = sin (о>/) -}- cos (со/) -|- Л3 sin (Зсо/) В3 cos (Зсо/) +
+ Аа + 1 sin [(2А -f- 1) <ot] -f- ... (у>
На фиг. 129 изображена такая кривая, причем взят некоторый произвольный момент за начало О отсчета времени.
Если мы в ф-ле (у) положим / = 0, то получим ординату у = s0 в точке О; при этом в правой части все синусы обратятся в нули, а косинусы в -fl, и мы будем иметь:
i0 = fil + 53+'>-52A + l4"---i (О таким образом эта начальная ордината дает нам сумму амплитуд всех косинусоид.
Теперь разделим основание кривой, т. е. длину, представляющую полный период Г, на три равные части; построим ординаты в этих точках и сложим их, при* нимая во внимание их знаки; обозначим сумму через s3.
Разберем, что войдет в эту сумму как в ней будут участвовать составляющие различных порядков.
Для синусоиды первого порядка в ф-ле (а) величина — равна п
так как взят один период (zn = l) и разделен на л = 3 части, о
Поэтому алгебраическая сумма ординат синусоиды первого порядка дает по (а) величину 0. Эго впрочем ясно и из элементарных соображений: первая ордината равна нулю, а две остальные равны и по знаку противоположны, как sin 120° и sin 240°. Далее, для си-
нусоид 5, 7, И и т. д. порядка число — будет хотя и больше
259
£ JL 1L\ 3"’ з ’ з /
единицы
, но дробным, так
окружностей (или 2п или Т) под знаком т’
мы получим остаточный множитель — при
что, отделив целое число синуса в формуле (а), kTм е н ь ш и м единицы,
так что сумма 5 всегда будет равна 0.
ш
Для синусоид порядков 3, 9, 15 и т. д., кратных трем, —будет целым числом (1, 3, .5...), так что результат будет получаться по формуле 0), т. е. алгебраическая сумма ординат этих синусоид даст трехкратную (п = 3) начальную ординату; эти же ординаты для всех синусоид равны нулю, поэтому и для этих порядков s равно нулю. Таким образом в сумме синусоиды не войдут совсем.
Обращаясь к косинусоидам, мы, повторяя предыдущие рассуждения, находим, что только косинусоиды порядков 3-го и кратных трем дадут в сумме по формуле ({}’) трехкратную начальную ординату; она для косинусоиды любого порядка равна амплитуде, поэтому окончательно для суммы всех косинусоид
ss = 3(b3 + b9 + z?i5 + ...); (П)
Разделим теперь основание кривой на 5 равных частей и сумму ординат в соответствующих точках обозначим через $5.
Рассуждения относительно синусоид остаются прежними, с той разницей, что ф-лу (jj) надо будет применить к синусоиде не 3-го, а 5-го порядка. Синусоиды не войдут в s5.
Косинусоиды войдут только порядков 5-го и кратных пяти и по формуле ({}') дадут пятикратную сумму их амплитуд, так что
^6 = 5(Вв4-Д184-585 + ...). (Ш)
Аналогично, разделив на 7, 9 и 11 частей, получим суммы ординат, равные
s7 = 7(B7+B21 + ...) (IV)
s9 = 9(B9 + B274-...) (V)
= 11 (Z?n + B33+ ...). (VI)
Остановившись например на 11-м порядке при разложении кривой, мы будем иметь шесть уравнений с шестью неизвестными Bv B3i В^ B7t BQ и В119 причем из (III) имеем:
из (IV)
260
из (V) и (VI)
из (II)
В = и В =^1
^9 9 ” 11’
+ з3-
Вычитая отсюда В9, находим В3 и наконец, вычитая сумму найденных Bk из (1), найдем Вг
Чтобы определить амплитуды синусоид, передвинем начало
координат из О в О, на (фиг. 130). При таком новом отсчете времени все синусоиды станут косинусоидами, хотя не все они будут находиться в одной и той же фазе, — именно в начале координат О' будем иметь для 1-го порядка, 5-го, 9-го и т. д. положительные амплитуды (ибо синусы углов it _ тг Л тг
— , 5 —, 9 —,.. положитель-£ £
ны) и для порядков 3-го, 7-го, 11-го отрицательные ам-
плитуды (синусы углов 3,
£
четверть периода вперед
таким образом для f = 0, для на-
7 Л 11 Л...
2 ’ 2
отрицательны);
чала координат, получим:
—Л+А—лт +л9 •••
Разделиз на три части основание кривой, начиная с нового на-чала координат О', получим:
S3 = 3 (-Л8 + Л9-Л15 4; • •
Разделив на 5, 7, 9 и 11 частей, получим совершенно аналогично:
«5=5(Л5 — ли + ’-')
s^ = 7 ( Л7 Л31 ...)
< = 9(Л9-...)
^ = 11 (- Лп + . ..)•
Пример 41. На фиг. 131 (см. вклейку) дана кривая, которую надо анализировать.
261
На чертеже проведены все необходимые ординаты и получена
а0 = 36; s9 = 35 +60.5 —6Ч,9 = 27.6;
ss = 36 + 67,3 + 48 — 61 — 59,8 = 30,5;
s, = 36 + 68,5 + 59,9 4- 29 - 53 — 65,4 — 58,5 = 16,5;
а9 = 36 + 63,5 + 64,5 + 60,5 + 12,5 - 50 — 68,9 - 59,8 — 51,5 = 6,8;
sH 35 + 58,7 + 68,5 f 60 + 57,5 — 1,5 — 48,2 — 68 — 63,8 — 69,2 — — 43,5 = -4,5.
Отсюда
BH=|L‘ = -0,41; Si = -J = 0,76; S7 = ^ = 2,36;
Bs = = 6,1; B3 = -g’ — Л9 = 9,2 — 0,76 = 8,44;
Bt = 36 — 8,44 — 6,1 - 2,36 — 0,76 + 0,41 = 18,75.
Передвинем начало координат О (фиг. 132, см. вклейку).
= 61,1; $з = 61,1 - 5«,2 — 3%0 = - 34,1;
% = 61,1 + 5,6 — 68,6 — 59,4 4- 49,0 = — 12,3;
= 61,1 + 51 — 47,0 — 68,5 — 60,5 + 12 + 62,9 = 11,0;
s' = 61,14-58— 18,1 — 56,2 — 67,8 — 6^,0 — 39,0 + 45,3 4- 68,0 = — 8,7. = 61,1 + 60,2 4- 26,8 — 44,2 - 63,9 — с6,8 — 59,7 — 52,4 + 22,5 + + 52,5 + 68,9 = 5;
откуда
Sa а 5 Sa
Лп = - + =-тт = -0.45; Л9 = 4 = -0,Э7; f Г F
=-----г- = - 1,57; Л5 = 4- = - 2,46; А3 =------- =
< о о
^1—0,97=19,4;
Л = 72,91.
Таким образом данная кривая может быть представлена аналитически следующим рядом:
у = 72,91 sin (ю/) + 18,75 cos (<о/) + 10,4 sin (Зю/) + + 8,44 cos (Зю/) — 2,45 sin (5ю/) + 6,1 cos (5ю/) — 1,57 sin (7ю/) + + 2,36 cos (7ю/) — 0,97 sin(fW) + 0,76 cos (9ю/)—0,45 sin (1 1ю/)—0,41 cos (И ю/);
§ 73. Сложная форма кривых ЭДС и силы тока
Пусть ЭДС разложена в ряд Фурье, причем члены четных порядков не будем писать, считая кривую ЭДС симметричной относительно оси абсцисс:
е ~ Elm' s*n 4~ «1> 4" Е3п • sin (Зю/ аз) 4"
4-fiSm.^n(5o>/4-ab) . (152)
262
Действие такой ЭДС в цепи равносильно с одновременным действием всех этих составляющих ЭДС, мгновенные значения которых мы будем обозначать буквой е со значком 1, 3, 5,..., равным порядку составляющей.
Поэтому, если цепь представляет только ваттное сопротивление /?, то сила тока в цепи будет:
4- • sin (3®/ 4- а8) sin (и/ 4- аг) 4»
4-J3„-sin (3®/4- а3) 4-...,
где J1OT, 73zn, Jnm суть амплитуды составляющих силы тока различных порядков—1-го, 3-го, л-го и т. д.
Если в цепи есть самоиндукция, то появляется ЭДС самоиндукции, каждая с частотой соответственно одному из токов; тогда
/— | g3"bgCs | e5^eci |
/? /? R
Здесь мгновенные значения составляющих силы тока суть:
откуда мы получаем ф-лы для составляющих каждого порядка, совершенно подобные ф-ле (23):
е1 = *1 * есе е3 ~ 4 ’ ес9» ^5 = 4 * • • •
Все дальнейшие выводы из них таковы же, как и из ф-лы (23), и в результате мы получим для составляющей любого порядка п формулу, выражающую закон Ома для нее:
J ____
яя,~/я24-(чЛ)а’
Принимая во внимание соотношение
<оя = п • (О, мы перепишем предыдущую ф-лу так: . р
Jnm^—=^====^. (153)
Если в цепи есть и емкость, то для любой составляющей по-лучим:
/яж = — Еп'п . (154)
Л/П Г 1 I 2
1/ --------------
Г 1 \ п<йС]
263
Сила тока Jn, составляющая силы тока л-го порядка, сдвинута в фазе относительно своей ЭДС Еп, составляющей электродвижущей силы П’ГО порядка, на угол который определяется из соотношения: j
ло)Л------
<pn = arctg---------. (1о5)
Вывод всех этих формул тождествен с выводом закона Ома в главе второй и далее.
Нужно теперь же заметить, что на одной векторной диаграмме не могут фигурировать величины, относящиеся к составляющим разных порядков, так как для каждого порядка синусоидальных величин продолжительность периода своя особая, в три, пять, п раз меньшая основного; следовательно у нас векторных диаграмм должно быть столько (для каждого рассуждения о цепи), сколько различных порядков имеется у составляющих электродвижущей силы, причем на каждой диаграмме линия времени вращается с особой скоростью, в три, пять, п раз быстрее, чем на диаграмме составляющих первого порядка.
Таким образом сила тока теперь выразится рядом
Z = Jlnlsin +(Р?+7Зт.5’П(3<0/ + аз + 'Рз) + -
пт sin(«(oZ + a„ + <pn) + ... (156)
Понятно, что в ф-лы (153) и (154) вместо электродвижущих сил можно поставить напряжения на участках цепи, и тогда L и С будут обозначать соответствующие величины на этих участках.
Перейдем теперь к вопросу, какие величины будут -измеряться тепловыми амперметром и вольтметром и ваттметром при сложной форме кривых ЭДС и силы тока.
Средняя мощность, переходящая в тепло в сопротивлении /?, равна отношению всей электрической энергии, перешедшей в тепло в течение целого периода, к продолжительности периода
т
— J i2dt. (А)
о
Тепловой амперметр покажет величину J, которая попрежнему будет с этой средне ! тепювой мощностью связана соотношением:
т
j* Pdt, О
или: ! т
Jf (В)
264
Средняя мощность в цепи и показание ваттметра выразятся, как и раньше:
т
P=i^eidt. (С)
О
Подставим в (В) и (С) вместо е и I их выражения (152) и (156); тогда получим вместо (В):
У JkmJim sin + <** + Фл) sin (/и*+а(+<?м (D)
I
где стоящее под знаком суммы 2 выражение символизирует квадрат ряда (156) Индексам k и I (и множителям при ю/) нужно придать всевозможные имеющиеся в ряду (156) для порядков составляющих значения, например 1, 3, 5 и т. д.
Вместо (С) мы будем иметь:
т
Р = У ( У sin sin (/о)/ + «/+?/) Л- (* Е * * *>
Выражен ie под знаком суммы 2 символизирует произведение ряда (152) на ряд (156) при тех же всех возможных значениях k и /.
Таким образом ишегралы в (В) и (С) разбиваются на сумму интегралов вида:
для (В):
т
J JkmJl>n sin + a'k + sin № + «/ + fl) dt (F) 0
и для (С):
т
j Ekmdlm Sin (kat + ak) sin (/(o/ + ai + fl) dt> (Q)
0
что ввиду того, что Ekrn, Jkm и т. д. суть амплитуды, т. е. величины постоянные, сводится к нахождению ряда интегралов вида:
т
sin (Ахо/ 4“ (У * s*n 4“ fy) ’ (Н)
о
265
Преобразуем подинтегральное выражение, пользуясь известным уже приемом и равенством:
О • У~Ьг у —z
Cos у — cos г = — 2 sin —у- • sin —— . £> и
Здесь
у = (k 4- /) (о/
г = (Л —/)(о/4"?л“”
интеграл (Н) теперь преобразуется в т т
—fcos 4“ —Jcos ((^ — 0 4-
0 о
I р ? 1/7/1— 1 Fsin Г(^ Ч-0 <«>/4-
sin f(A> —/)(0/+Pfe —{jy (k — Z) co ] 0’
Выражение в скобках при обоих пределах дает одну и ту же величину, если &^Z, а потому интеграл (Н) равен нулю во всех случаях, крс ме того, когда k — I и разность значений второго члена в скобках при пределах Г и 0 отлична от нуля. Вычислим ее, для чего преобразуем выражение
£ [sin [(fe-/)«>/+?,-$,] 1 г
"г 2 L (* — /)«> Jo ' '
следующим образом, беря разность значений его при пределах:
1 sin [(Л — /) — 3,) — sin (pft —3<)
2 * (k — I) <o
2-cospA — + — 4'sin ]
= _ _ Z) (|) =
Г Г1
т г T 1 sin P!—/)(0,-2
= o'-cos (fe-/) «-x-H-P* — 3, ------------xr-J.
L J (*-o«4
Теперь полагаем & = Z, причем дробь на конце последнего выражения дает нам единицу по теореме о пределе отношения синуса бесконечно-малого угла к этому углу, и все выражение (К) дает:
Icos(pft—S^TcosC^ —s^). (М)
266
Итак интеграл (Н) для тех случаев, когда Л = /, дает величину (М), для всех остальных случаев он равен нулю. Что означает это условие равенства k и /? Оно означает, что из интегралов (F) и (G), которые входят в величины J и Р, только те не равны нулю, для которых Ли/ одинаковы, т. е. например
т
EVn • Jlm • J sin (<o* 4- сц) • sin(w/ -f- a, 4- <?,) • dt, 0
T
A4 • Jsin2 + Vi) • dt> 0
T
E3n ’ J3m • Jsin (3<0' + «3^ * S,« (3<0/ + «3 + ?з)' dt>
° T
0
и т. д.
Для интегралов (F) при k = l под знаком интеграла стоит квадрат синуса, т. е. в ф-лах (Н) и = и cos(^A — 5Л)=1, Т а сами интегралы все равны произведению — на квадрат ампли-
туды соответствующего порядка. Поэтому ф-ла (В) превращается в
= + (157)
после деления квадратов амплитуд на два и введения действующих значений.
Для ф-лы (С) мы имеем в ф-лах (G), (Н) и (М): = ak9
= и cos (£л—= cos а потому ф-ла (С) принимает вид:
1 Т
Р—~Т ’ ~2 C0S 4” ^3/и*Л/л C0S Тз + • • • +
4” ^ntn * nm COS rfn 4“ • • •) »
или, произведя тот же переход к действующим значениям:
Р = ЕгJr cos 'Pi 4~ Е3J3 cos (р3 -|-1- EnJn cos 'p„ - (158)
Следует особенно подчеркнуть, что из вышеизложенного и в особенности из ф-лы (158) ясно, что составляющая силы тока некоторого порядка или некоторой частоты со всеми
267
составляющими электродвижущей силы (или напряжения) других порядков или других частот дает среднюю за период мощность, равную нулю, и только с составляющей электродвижущей силы (или напряжения) той же самой частоты (k — l) дает среднюю мощность, величина которой отлична от нуля и определяется, как видим из ф-лы (М) или из (158), той же ф-лой;
£Лсозь-
Меряя напряжение тепловым вольтметром, мы получим показание I/, которое равно произведению действующего значения силы тока через него J на его сопротивление; выражая J ф-лой (157), умножая обе ее части на сопротивление и подводя последнее под корень, мы сможем написать, что
У = 1/у2+1/2_Ь..+ у2+... (159}
§ 74. Эквивалентный синусоидальный ток
Производить различные расчеты, разлагая силу тока и напряжение на их составляющие и вычисляя мощность по формуле (158)г где различные определяются из ф-лы (155), представляет много неудобства и сложно; поэтому введено понятие об эквивалент-
ном синусоидальном токе, при котором действующие сила
тока и напряжение такие же точно, как и существующего действительно тока сложной формы, т. е., значит, равны J и V [ф-лы (157) и (158)], и мощность которого равна в точности мощности существующего тока, т. е. Р в ф-ле (158). Так как .произведение V и J в общем случае отличается от Р и именно больше
ж Р
его, то введено понятие о коэфициенте мощности, равном и v J
по аналогии с действительно синусоидальным током, называемым косинусом ср. Итак
р=х= jycoscp
Таким эквивалентным синусоидальным током заменяют данный ток с сложной формой кривых напряжения и силы тока, с ним ведут расчеты и для него строят векторные диаграммы. Для такого тока применяют и все остальные известные уже нам формулы и соотношения.
Теперь же заметим, что есть много вопросов и задач, где отвлечься таким образом от действительной несинусоидальной ф р ?ы ю ивых силы тока и напряжения нельзя, и тогда приходится оперировать с рядами, в котор >е эти величины можно разложить.
Для характеристики той или иной кривой иногда пользуются понятием о так называемом коэфициенте формы кривой
268
(Formfactor); его определяют как отношение действующего значения к среднему.
Для чистой синусоиды он равен
для прямоугольника 1 и для треугольника 1,15.
Построив обычную диаграмму напряжений (фиг. 23) для эквивалентного тока, будем иметь величину коэфициента мощности
J-R
COS(p = ~.
Подставим вместо J и V их выражения (157) и (159) и преобразуем полученное
_ _ /(Л^2 + (-W 4-... + (Л/?)2 4-... _ у ин-ун-т-
V^cos2^ -|- Узcos2(р3... 4“ V2cos2(pn4“ • • •
И+^-Н-’- + ^4-...
Иногда бывает удобна еще следующая формула: так как cos ср7 =
Л 7? г. VjCOS^
= -|у- и следовательно /? = ————, то, подставляя это выраже-«Л
ние в ф-лу для cos ср, получим:
cos ср = C0S ’
В примере 12 § 24 мы считали, что вольтметр, присоединенный к зажимам катушки с ничтожным ваттным сопротивлением, покажет величину
Vc=uLJ,
откуда можно очень просто определить самоиндукцию катушки, если она нам неизвестна, а известны Vc1 J и частота по формуле
При токе сложной формы последним соотношением пользоваться для определения L нельзя, величина L будет отличаться от правой части этого выражения некоторым множителем, который мы сейчас и определим. Для отдельных составляющих мы имеем:
z=Zl z=Z3. j .
1 wL’ 3 3<oZ’ n /?©£*
269
подставим эти выражения вместо Jk в ф-лу (157):
Умножим правую часть на V, разделим ее на правую часть ф-лы (159), от чего равенство не нарушится, и переменим местами L и J, так как мы определяем
у_. (oJ
или еще иначе:
Радикал и представляет искомый множитель; смотря по соотношениям между амплитудами высших порядков и первого, этот радикал может очень отступать от единицы, и следовательно определение L по ф-ле (а) делается ошибочным. Если например мы имеем кроме составляющей первого порядка еще только составляющую третьего, все же остальные отсутствуют, причем пусть V3 = — Vv то радикал равен 0,96, т. е., вычисляя L по ф-ле (а), мы сделаем ошибку в 4°/0.
Значительно больше будет ошибка, если мы станем определять величину емкости по показаниям вольтметра и амперметра и по ф-ле:
J=VuC и из нее следующей;
где V есть напряжение на конденсаторе. Именно для отдельных составляющих мы опять имеем:
/ = У о)С, Л= КЗшС, ..., J ...
1 1 'о о ’ 1 П П »
и, вставляя в ф-лу (157), получаем:
J — шС- /У?4-9’72-J-... ...
270
Отсюда определяем С, деля затем правую часть на V и умножая на правую часть ф лы (159):
Если мы теперь будем иметь опять только V2 и У3> причем V3=-i- то радикал в последнем выражении будет равен 0,75; о
следовательно, определяя величину емкости из ф-лы (£), мы сделаем ошибку в 25°/0 Таким образом определение L по (а) много точнее, чем С по (р).
Эги результаты между прочим показывают, что самое применение векторных диаграмм к эквивалентному току очень условно и должно всегда производиться с известной осмотрительностью и что построение даже основного треугольника напряжений при сложной форме кривых тока является лишь приближенным решением.
§ 75. Резонанс для составляющих различных порядков
Далее, следует остановиться на явлениях резонанса.
Так как теперь кроме частоты основной /, есть еще частоты 3/, 5/,..., то и резонанс может наступать при разных
L и С, лишь бы выполнялось условие:
1 (0я=^=--= • V LC
Таким образом могут возникнуть явления резонанса для такой* составляющей, которая была очень слабо выявлена в кривой ЭДС или силы тока, пока условия резонанса не выполнялись; при резонансе эта составляющая может выявиться более или менее в опасных формах.
Явление резонанса дает нам средство измерить емкость при по мощи переменного тока, если имеется регулируемая самоиндукция Именно, устанавливают такую величину самоиндукции, чтобы наступил резонанс напряжений (при последовательном включении емкости и самоиндукции) для составляющей 1-го порядка; тогда будет:
,
юС
271
откуда определяем С через с» и £; если L неизвестно, то мы его можем определить из ф-лы (а) и затем по нему вычислить С, что и будет много точнее, чем определение С по ([}).
§ 76. Влияние самоиндукции и емкости на форму кривой тока
Нужно заметить, что когда мы говорим о цепи тока сложной формы, ю данной и от нас независимой является только форма кривой ЭДС генератора; формы же кривой силы тока и напряжения на участках зависят от того, что мы в цепь вообще и в эти участки включим. Пусть f ам дана ЭДС с кривой сложной формы. Подключим цепь с ничтожно малым ваттным сопротивлением, которым пока и пренебрежем, и самоиндукцией. Из ф-лы (153) с едует, что составляющая силы тока любого л-го порядка определится при этом так:
Е J e пт n®L'
(А)
Отсюда получается, что отношение амплитуды силы тока к амплитуде ЭДС, — ДЛЯ Различных составляющих различно:
оно тем меньше, чем порядок п составляющей выше. Таким образом составляющие высших порядков в кривой силы тока выражены слабее (при самоиндукции), чем в кривой ЭДС; при включении самоиндукции кривая силы тока становится ближе к чистой синусоиде, чем кривая ЭДС.
Теперь включим в цепь емкость, а самоиндукцию выключим. Полагая в ф-ле (154) /? = 0 и Л = 0 получаем, что составляющая любого /г-го порядка силы тока определится так:
Jnm = n^CEn^ (В)
откуда следует обратное предыдущему: чем выше порядок составляющей, тем больше отношение амплитуды этой составляющей силы тока к амплитуде ЭДС, Jnm>Enni — пмС. Таким образом при включении в цепь емкости кривая силы тока дальше отходит в форме от чистой синусоиды, чем кривая ЭДС.
На фиг. 133,а представлена кривая ЭДС е, состоящая из синусоиды 1-го порядка и 5-го, причем Е5т = -^ Ег • на фиг. 133,# начерчены составляющие кривой силы тока при самоиндукции в цепи, 119 первого порядка, причем масштаб для силы тока для наглядности выбран такой, что отрезки, изображающие на фиг. 133, а и на фиг. 133, b равны; одна и та же синусоида изображает таким образом et и согласно с ф-лой (А} 272
амплитуда составляющей силы тока пятого порядка взята в пять
раз меньше отрезка, выражающего Е5т; сложением получена кри-
вая z, очень мало отступающая от синусоиды.
На фиг. 133,67 при емкости в цепи начерчена та же самая си-ну оида для Zj (что не обозначает, что сиза тока в амперах теперь та же самая, что при самоиндукции, так как мы могли масштаб переменить и чертить одну и ту же синусоиду для наг. ядности) и синусоида z5 с амплитудой, согласно ф-ле (В), в пять раз больше, чем отрез.к Е~т на фиг. 133,а. Сложением получена кривая сила тока z, не только далеко оiступающая от синусоиды, но и обладающая тем очень интересным свойством, что она несколько фаз в течение периода пересекает ось абсцисс, т. е. сила тока z несколько раз за период делается
Фиг. 133.
равной нулю через разные промежутки вре-
мени.
Присутствие в цепи ваттного сопротивления умеряет эти влияния самоиндукций и емкости, но качественно явления остаются
теми же.
§ 77. Разветвление тока
Все это нам показывает, что формы кривых напряжений на разных участках цепи и сил токов в разных ветвях при разветвлении тока могут очень разниться между собой в зависимости от того, что в эти участки или ветви включено. Это иногда делает построение векторных диаграмм для эквивалентного тока не точ-18 Теория переменных токов. 273
ним. Таким образом например следует прибегать к вычислению, а не к графическому построению при сложении разветвленных токов, когда ветви разным образом влияют на форму кривой тока, особенно когда одни не содержат емкости, а другие содержат. При точном вычислении здесь нужно проделать сложение разветвленных токов сначала для каждого порядса составляющих, а затем уже переходить к эквивалентному току.
§ 78. Очищение тока
На аналогичных соображениях основано так называемое „очищение" тока. Предположим, что нам для целей лабораторной измерительной практики необходимо иметь ток по возможности более близкий к чистому синусоидальному. Тогда мы к источнику его
С
Фиг. 134. Фиг. 135
подключаем, как показано на фиг. 134, самоиндукцию и емкость. При этом, обозначая через 2)я и 1/(2 напряжения между точками 1 и 2 или 2 и 3 соответственно для составляющей л-го порядка, им ем:
1 ^Г<2,з)л = ^’/га>С’
Полагая /? = 0, пэлуч im отношение: ^(2.3)л__________________________ 1
^(1,2)я n'®2CL которое показывает, что составляющие высших порядков вырзжены в кривой напряжения на ем<ости слабее в /г2о)2СА раз, чем в кривой напряжения на самоиндукции.
Подключив к зажимам 2 и 3 снова самоиндукцию и емкость, можем еще более заглушить составляющие высших порядков и про-274
до икать так и дальше, пока не поучится ток, форма кривой которого будет для наших целей уже достаточно чистой
Если кривая первоначального напряжения содержала составляющую постоянного тока Ло в ряде Фурье, то при вышеизложенных включениях эта составляющая пройдет через подключенные нами самоиндукции и появится в окончательном напряжении; поэтому, чтобы избавиться от нее, надо или пропустить ток сначала через трансформатор, а потом его очищать, или воспользоваться схемой фиг 135.
§ 79 Составляющие высших порядков в трехфазном таке
Остановимся в заключение этой главы на том случае, когда при трехфазном токе не выполняется условие, положенное нами в начале главы в основу наших рассуждений, именно условие строгой синусоидальности кривых ЭДС сил. Пусть эти кривые имеют сложную форму.
Оказывается, что при этом форма кривой ншряжения (возьмем случай безиндукционной нагрузки, или холостой х д) будет разная для напряжений фазового и междуфазового (при включении фаз генератора звездой).
Прежде всего заметим, что высшие составляющие ЭДС сил порядка 3-го, 9-го и вообще ЗЛ-го, где k — целое, нечетное число, будут во всех трех обмотках генератора в каждый момент иметь одинаковую величину, т. е. будут находиться в одной и той же фазе во веек трех обмотках, так как разность фаз в одну треть периода трех ЭДС этих обмоток для упомянутых составляющих представляет или „период", их собственный, или целое число периодов (для 9-й и т. д.).
Поэтому при соединении фаз генератора звездой, когда ЭДС одной фазы в ыч итаются из ЭДС другой фазы, эти составляющие друг друга компенсируют, дают результирующую, равную нулю, по формуле:
Еак sin (3ko>t <|>3ft) — E3k sin [з Aw (t—-J) -|- <|>3A j = 0.
Таким образом в междуфазном или линейном напряжении не будет составляющих синусоид порядков ЗЛ, тогда как фазовое напряжение, т. е. напряжение между одним из трех главных проводов и нулевым, буд-^т их иметь.
Отсюда получается следующее соотношение.
Фазовое напряжение генератора равно:
линейное же при соединении фаз звездой не будет содержать третьей составляющей, но всякая другая составляющая линейного 18* 275
напряжения будет в ]/ 3 раз больше соответствующей составляющей фазовой, поэтому:
=V3(^4- v4+^+...),
Откуда следует, что отношение Ул: Уф не равно для этого случая / 3, а несколько меньше; деля под корнем все члены на Иц, , получаем:
Далее, сила тока в нулевом проводе даже и при точно одинаковой нагрузке фаз будет теперь равна не нулю, а сумме всех токов высших составляющих порядка 3-го, 9-го и т. д. (составляющие например 9-го порядка для трех „фаз" генератора будут отличаться друг от друга в фазе на три целых периода и суммироваться поэтому будут арифметически).
В случае соединения „фаз" генератора треугольником мы будем иметь новое явление. Сумма электродвижущих сил внутри треугольника теперь уже не будет равной нулю, ибо теперь ЭДС 3-го порядка будут суммироваться арифметически, как имеющие одну и ту же фазу; то же — ЭДС 9-го и т. д. порядков, а потому в соединенных треугольником трех обмотках генератора будет течь ток даже и при разомкнутой внешней трехфазной цепи. Для этих ЭДС генератор при соединении его „фаз" треугольником явится замкнутым на короткое, и они не будут иметь никакого влияние на напряжение на зажимах генератора.
Если мы разомкнем треугольник, то вольтметром сможем измерить результирующую из этих ЭДС.
Измерение мощности трехфазного тока, например двумя ваттметрами, остается правильным независимо от формы кривой, как -показывает ф-ла (133), в которую входят мгновенные значения.
276
ГЛАВА X
ВЛИЯНИЕ ЖЕЛЕЗА НА ЯВЛЕНИЯ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
§ 80. Переменный ток, намагничивающий железо. Потери в железе
В настоящей главе мы прежде всего исследуем одно явление, которое является следствием гистерезиса при перемагничивании пе еменным током железа, именно — искажение синусоидальной формы кривой намагничивающего тока.
Пусть к зажимам источника переменного тока с синусоидальным напряжением
v = Vm sin (<о/)
подключена катушка, которая намагничивает циклически, т. е. то в одну сторону, то в другую, при постепенном изменении силы тока в течение периода, железный сердечник. Катушка с сердечником может иметь например форму цилиндрического кольца — тороида.
Если ваттное сопротивление катушки равно 7?» то v — iR — ez.
Всегда можно так подобрать поперечное сечение и длину проволоки катушки, чтобы R было мало и чтобы величиной iR можно было, в сравнении с величиной гс, пренебречь. Тогда v =— ес; следовательно ЭДС самоиндукции будет синусоидальной функцией и выразится так:
ее= —£cmsin (<о/),
хотя, как увидим далее, сила тока i не будет синусоидальной функцией.
Так как при п витках в катушке и мгновенном значении магнитного потока ф
б/ф
ее —— /г-тг10~8 вольт, с dt
277
то мы имеем, что магнитный поток ф есть тоже сину-п соидальная функция, опережающая ес на
t 108.F Г ф = I sin((o/)^/;
п J 4г
магнитный поток синусоидален, хотя сила тока не синусоидальна. Нанесем на чертеж (фиг. 136) синусоиду fb3h с амплитудой, равной амплитуде магнитного потока Ч;^.
Фиг. 136.
Затем начертим кривую силы тока Z, причем строить ее придется по точкам, так как сна уже не является синусоидой. Построим ее следующим образом.
Начертим кривую намагничения для железа в катушке за полный . цикл, т. е. так называемую петлю гистерезиса, причем масштаб для значений магнитной индукции В выберем такой, чтобы наибольшая ордината петли гистерезиса Z?max на чертеже представилась отрезком, равным амплитуде синусоиды магнитного потока. Обозначив чесез S площадь поперечного сечения железа, мы имеем ф = В.£ и 4rffl = Bmax«S; таким образом в новом, в 5 раз меньшем-масштабе, ординаты петли гистерезиса представят значения потока ф в зависимости от намагничивающей силы Н катушки; как известно
Н =
1
где i есть мгновенные значения I—средняя длина сердечш ка; в
силы намагничивающего тока, а . 0,4пя
масштабе в —-— раз большем
278
абсциссы петли гистерезиса представят нам уже не /7, а самую силу тока /. Таким образом петля гистерезиса представит нам зависимость потока ф от силы тока I. Пользуясь этой кривой и кривой ф в зависимости от времени (уже начерченная синусоида), мы и сможем начертить кривую i в зависимости от времени.
Возьмем на синусоиде ф точку, например а3; проведем прямую а3а2, параллельную оси абсцисс, до пересечения с той ветвью петли, которая соответствует возрастанию потока, так как точка а3 взята на части синусоиды-при возрастании ф. Затем найдем соответствующее значению ф = а4а3 = а1а2 значение силы тока 1=Оаг и отложим на ординате ф = я4а3, т. е. для соответствующего момента времени ty это значение i как ординату кривой силы тока, так что а^аь = Оа1Уи так поступим для возможно большего количества точек.
Таким образом мы по точкам построим кривую силы тока с а5 d...
Следовательно, если поток индукции в железе меняется с течением времени по синусоиде /—д3— Ь3— h,,.y то сила тока, производящего этот поток, меняется по кривой с — а5 — Ьь—d. Эта кривая, во-первых, не является чистой синусоидой, а во-вторых, она сдвинута влево относительно кривой ф на cf=dh, следо-
. cf
вательно сила тока i опережает поток ф на долю периода (ординаты синусоиды ф в точках с и d равны между собой, так
как они равны остаточному магнетизму, поэтому равны и промежутки вг вмени cf и dti).
Выделим из кривой силы тока синусоиду первого порялка с действующим значением остающаяся совокупность каких-то составляющих высших поряд-ков будет иметь действующую величину J2. Эти составляющие силы тока Е9 ЕЫСШИХ порядков С ЧЙСТО синусоидаль- Фиг. 137.
ным напряжением первого порядка -у
дадут мощность, равную нулю; мощность же в цепи выразится так:
V* cos ср = W1B,
П Cf n где ф= —-------на основании того, что у =— и что
т 2 2-/Й с с
отстает от ф на Д- (фиг. 137). На этой фигуре а — угол опере-£
cf жения током магнитного потока — равен —= -2тг.
2-/А
279
J]B есть ваттная составляющая тока Jr Эта мощность превращается вся в тепло в железе, ибо /? = 0; мы будем обозначать ее через Ph, так что Pft=V-J3B; так как V=EZ по абсолютной величине, то можно написать:
Ph=EzJya. (160)
Мы вводим вместо V величину Ez потому, что если R не равно нулю, то в наши предыдущие рассуждения должна входить составляющая напряжения, равная и противоположная ЭДС самоиндукции, а не все напряжение. Однако тогда и ez уже не будет строго синусоидальной функцией, но будет отступать от синусоиды тем больше, чем больше R. Явление всегда сложно, и расчет здесь возможен всегда лишь с тем или иным приближением.
Мы можем заменить теперь несинусоидальный намагничивающий ток эквивалентным с составляющими — ваттной JB = J]B и безваттной
На фиг. 137 изображены поток Фт, ЭДС самоиндукции £‘с’ напряжение V = — Ezf эквивалентный ток J и его составляющие-
Угол а, на который вектор тока опережает вектор потока, называется кратко углом гистерезиса.
Как только что упомянуто, когда’ R не равно нулю, явления усложняются.
Разберем этот случай.
Из обычного уравнения
мы видим, что если v синусоидально, а I несинусоидально, то и ez несинусоидально; из этого ур-ния мы имеем, умножая все члены его на i-dt и интегрируя за целый период, соотношение для энергий или работ;
т т т
J vi-dt= J ez'i-dt-\- P-R-dt.
ООО
В левой части здесь стоит вся энергия, полученная за период от источника тока; в правой части последний член выражает энергию, обратившуюся за период в тепло в сопротивлении /?, а первый член — энергию, не возвратившуюся из магнитного поля, пошедшую на нагревание железа в магнитном поле через гистерезис. Если гистерезиса нет, то ez и I синусоидальны (при синусоидальном ^), сдвинуты в фазе на четверть периода, и первый член правой части равен нулю. Если имеется гистерезис, то ez и I несинусоидальны, и за время убывания силы тока магнитный поток (фиг., 136) изме-280
няется меньше, вообще говоря, иначе, чем за время его возрастания, т
а потому и ЭДС е& будет различна и J e^i-dt будет иметь ко-о
нечную величину.
Нужно заметить, что к гистерезису присоединятся еще токи Фуко в железе, и этот интеграл будет иметь, вообще говоря, величину ббльшую, чем потери на гистерезис, вычисленные по площади кривой — петли гистерезиса.
Математическое решение вопроса здесь возможно лишь приближенное; один из способов такого решения изложен далее.
§ 81. Векторная диаграмма катушки с железным сердечником
Введем эквивалентные токи и построим векторную диаграмму,.
а затем исследуем соотношения мощностей для того случая, когда
к зажимам с напряжением V приключена сердечником (фиг. 138) и с ваттным сопротивлением /?, коим нельзя пренебречь. При построении векторной диаграммы мы заменяем намагничивающий ток эквивалентным синусоидальным, а следовательно и ЭДС, индуктируемую в катушке, синусоидальной ЭДС,—хотя теперь’уже R и не равно нулю, — и для этих эквивалентных величин силы тока и ЭДС и применяем ф-лы предыдущей теории.
Затем мы теперь введем в векторую диаграмму еще некоторое уточнение, именно мы разделим весь магнитный поток,* все
катушка с железным
количество линий, создаваемых катушкой,
на две части или два по-
тока, — один поток пусть состоит из тех магнитных линий, которые весь свой путь проходят по железу (фиг. 138),— назовем этот поток через — поток в железе, — другой поток должен заключать в себе все остальные линии, из которых одни часть пути идут по железу, а часть — по воздуху, а другие весь свой путь совершают
в воздухе; внутри катушки эти последние проходят в пространстве между сердечником и витками катушки; выходя из катушки, все они загибаются вокруг края катушки и идут по воздуху вне катушки к другому ее концу, где и входят в нее. Некоторые линии оцепляют не всю катушку, а только несколько витков и т. д.
Назовем этот поток потоком рассеяния и обо значим через Фрасс. все количество подобных линий, охватывающих однако все витки катушки. Поясним это примером: пусть имеется в некотором месте,.
281
например около середины катушки, сто линий, охватывающих пять
витков, всех же витков у катушки пятьсот; тогда мы можем считать, что в отношении величины ЭДС, индуктируемой этими линиями в катушке, они эквивалентны одной линии, сцепляющейся со всеми пятьюстами витков, и таким образом включаем в число Фрасс одну линию; так же поступаем и со всеми другими линиями; в результате получаем некоторое число линий Фрасс, которое индуктирует ту же самую ЭДС, что и действительные линии рассеяния.
Векторная диаграмма построена на фиг. 139. За длины векторов примем здесь, как обычно, действующие значения вели
чин, за исключением векторов магнитных потоков, для которых возьмем амплитуды. ОК есть вектор напряжения V на зажимах; под углом КОА, равным ср, к4 нему проведен вектор О А силы тока J.
Магнитный поток в железе Фж представлен вектором О/7. по величине равным амплитуде потока, по фазе отстающим на угол а от вектора силы тока согласно предыдущему. Поток рассеяния идет главным образом по воздуху, в поле этого потока нет явления гистерезиса, во всяком случае, мы им пренебрегаем по незначительности самого объема железа, затрагиваемого этим потоком (фиг. 138). поэтому этот поток Фрасс находится в фазе с производящим его током J; на диаграмме поток рассеяния изображен вектором OD. Поток .в железе индуктирует в катушке ЭДС
Е, представленную вектором ОС, отстающим на — от вектора потока OF\ мы не будем называть эту ЭДС
электродвижущей силой самоиндукции, чтобы распространить наши рассуждения и на тот общий случай, когда поток в железе является результатом действия не одной рассматриваемой катушки, а также и других, — с подобным случаем мы дальше встретимся при построении диаграммы трансформатора и тогда уясним необходимость отказа от слова псамоиндукция “ полнее. Мгновенные значения этой ЭДС выразятся формулой, подобной формуле (19), только вместо Ф должно стоять Фж-51п((о/):
П di
Ю-8 —2тг//гф 10-8sin I со/-£
ж \ 2
282
Действующее значение будет в раз меньше амплитуды, а так как 2п:У^2 = 4,44, то
£ = 4,44-/*л-Фж-10’8 вольт. (161)
Это и есть формула ЭДС трансформатора. Поток рассеяния индуктирует ЭДС, представленную вектором OG, отстающим на “ от век-тора потока OD, Поток OD создается только рассматриваемой катушкой, а потому OG можно назвать ЭДС самоиндукции, но лучше называть ее ЭДС от потока рассеяния, — она пропорциональна силе тока: OG = J-X.
Вектор напряжения V должен разлагаться на три составляющие: ON, равную по величине и противоположную по фазе ЭДС ОС, затем 7VQ, равную по величине и противоположную по фазе ЭДС OG, и наконец 0К= J • /?, тратящуюся на преодоление сопротивления ЭДС ОС и QN, а также и NQ и 00 попарно уравновешиваются и дают в сумме нуль, — остается лишь величина QK, которая и прогоняет ток J через сопротивление /?.
Если бы вектор напряжения не был начерчен, то построением трех его составляющих мы всегда могли бы получить его, подобно построению его в основной диаграмме напряжений (фиг. 19 и 21).
Теперь, когда векторная диаграмма вся построена, перейдем к мощности. Вся мощность, берущаяся катушкой от зажимов, есть
Р = V. J-coscp;
это выражение мы преобразуем так:
P=(Vcos (₽)•/== =
= (ON-cos£NOH-\-QK)-J = рcos (у — «)+/•/?] J = = £• J-sina-|-J2/?. (162)
Здесь буква E означает только величину вектора ON.
Таким образом вся мощность представилась в виде суммы мощностей, одной J2/?, идущей на нагревание проводников, — „меди, — и другой Е- J* з1п'а = РЛ> идущей на перемагничивание железа и переходящей в нем в тепло, идущей на нагревание железа.
Представим себе, ч о мы подходим к изучению катушки, отвлекаясь от присутствия железа, т. е. с той точки зрения, с которой подходили к построению диаграммы фиг. 19, 21, 27 и т. д.; однако величины, требуемые для диаграммы, берем прямо из опыта. Мы измеряем следовательно амперл етром силу тока J, вольтметром —
283
напряжение V и ваттметром — мощность Р, Деля затем Р на произведение V на J, мы получаем cos ср и строим векторы V и J под углом ср, как на фиг. 139. Затем, проводя /С/И ОД, находим ваттную составляющую напряжения ОМ — V cos ср и полагаем ее равной произведению силы тока J на ваттное сопротивление цепи. Последняя величина есть в таком случае величина фиктивная,— такой величиной должно было бы быть ваттное сопротивление катушки, чтобы, не учитывая потерь на перемагничивание железа, мы все же имели мощность в цепи равной Р, тратящейся теперь. Обозначим это фиктивное „результирующее* сопротивление через /?рез. Тогда ___
Подставляя вместо ОМ его истинное выражение, как суммы ОН и НМ, мы имеем:
J-/?pe3 = £-sina4“‘/-/?, откуда получаем:
= + (163)
Если мы не знаем, что у катушки есть сердечник, то мы и будем считать, что 'ее ваттное сопротивление есть это /?р23, и следовательно преувеличим истинное ваттное сопротивление. „Самоиндукцию* катушки (кажущуюся, если есть действие еще и других катушек, увеличивающих поток Фж) мы получим, разделив вектор КМ (измеренный в масштабе напряжений) на со-Л
Вся векторная диаграмма представится тогда треугольником напряжений ОМК; две ЭДС от потока — в железе NO и в воздухе QN — не будут в нашем представлении разделены, а заменятся вектором КМ, который есть безваттная составляющая вектора QO — суммы обеих ЭДС. Ваттная составляющая суммы ЭДС — вектор ОН — Esina, входит таким образом и вектор J• Rрез = ОМ; эта ваттная составляющая и вызывает увеличение ваттного сопротивления сравнительно с истинным его значением.
Не следует забывать, что разложение ЭДС в катушке на две ОС и 00 есть лишь метод представтения или изображения явлений и что в действительности физически (поскольку представлению электродвижущей силы в действительности соответствует некоторое явление) существует в катушке во всякий момент лишь одна ЭДС, численно равная сумме мгновенных значений ЭДС, нами введенных, ОС и OG.
Обратимся к экспериментальному построению этих ЭДС.
284
Когда мы, произведя действительно измерения с катушкой, узнаем, что она имеет железный сердечник, и хотим разложить ЭДС QO на две слагаемые QN и NO (OG и ОС), мы встречаем затруднение в том, что нельзя точно определить величину X, а потому и величину J*X—OG — QN.
Так как по предыдущему
Ph — P — J'£R = Е • sin а • J, то
. P—J2R £-sin а=------у--,
т. е. если мы отдельно измерим R (одним из способов измерения сопротивлений), то из последней формулы мы будем знать проекцию ЭДС Е на одно направление (ОА); но проекции E-cosa^NH этой ЭДС на другое, перпендикулярное к первому направленье, мы не можем определить из данных измерений (т. е. из величин Р, V, J и R). Следует прибегнуть к другим методам; например навьем на сердечник подальше от катушки несколько витков проволоки — ЭДС в них будет иметь ту же фазу, что и Е=ОС—и посредством двойного осциллографа определим затем разность фаз между с^лой тока J и ЭДС в этих витках (потоком рассеяния в них от их собственного тока — ср. работу трансформатора — мы при этом пренебрегаем) и следовательно определим угол NOA, а тем самым и точку N на перпендикуляре, восставленном в точке Н к О А. Однако ввиду малости угла АОР=а и такие измерения лишь приближенны.
Несмотря на только что описанные трудности экспериментального построения диаграммы фиг. 139, она послужит нам в дальнейшем основой для изучения работы трансформатора.
С/едует упомянуть о способе непосредственного измерения величины потерь в железе EJsina.
На сердечник навивается вторая катушка с тем же точно числом витков, что у первой катушки. Очевидно, что в ней будет индук-т, роваться ЭДС; если эта катушка помещена на сердечнике далеко от первой, то эта ЭДС есть E=ON\ если она намотана вокруг первой, то ЭДС есть векторная OQ или несколько меньшая, но имеющая конец на линии NQ.
К зажимам этой катушки подключим катушку напряжения ваттметра, катушку тока которого включим в цепь тока J. Показания ваттметра и дадуг нам EJcos(EyJ) = EJsina.
Нужно заметить, что величина Ph= E*J•sin а включает в себе не только мощность, тратящуюся на перемагничивание железа, но и мощность токов Фуко, индуктирующихся в железе при переменном магнитном потоке по этому железу. Таким образом и угол а,
285
получаемый на диаграмме фактический угол, есть угол не только гистерезиса, но и токов Фуко. Мощность и силу токов Фуко можно ослабить, утончая листы железа, и вместе с этим утончен чем листов будет уменьшаться и угол а между векторами J и Уж, стремясь к „истинному" yr iy гистерезиса; при этом, чтобы величина потока не изменялась, нужно общую площадь поперечного сечения сердечника увеличивать, т к как будет увеличиваться площадь, занятая немагнитными прослойками между листами железа. Это влияние токов Фуко в железе окончательно может быть уяснено лишь после рассмотрения работы трансформатора, так что мы к нему еще вернемся в следующей главе, посвященной диаграмме трансформатора.
В заключение вв дем несколько новых понятий и величин, которые впосзедствии помогут упрощать математические выкладки, касающи ся цепей переменного тока, намагничивающих железо.
Обратимся к фиг. 139.
Вектор силы тока ОА можно разложить на составляющие самыми разнообразными способами. Спроектируем О А на направления ОК и к Н:му перпендикулярное. Проекция на ОК равна /•cosср; это есть ваттная составляющая силы тока по отношению к напряжению; безваттная составляющая равна проекции на второе направление /-sin ср Полагая
/•cosср = V^g I /•sinср = V-b j
(164)
как это было введено уже нами в § 26, и называем g ваттной проводимостью цепи, а b — безваттной проводимостью цепи. Возводя в квадрат, складывая и извлекая корень, имеем:
J= v- + (165)
где У= j/g2-4-£2 назовем полной проводимостью цепи.
Из ур-ний (165) и (164) имеем, что
и
£-=Усоз(р и 6 = У sin ср.
Теперь проектируем вектор / на наравление ЭДС ON перпендикулярное. Проекция на ON равна /-sinа; это есть ная составляющая силы тока по отношению к ЭДС Е\
беззаттная составляющая равна проекции на направление OF\ перпендикулярное к ON, и выражается через /»cosa
По агая г .
J-sin a. = E-ga J • cos a = E*ba
(166)
к нему в а т т-
(167)
и называем ga ваттной проводимостью „намагничения", подразумевая под этим то обстоя ельетво, что эта величина зависит исклю
286
чительно от намагничения железа и ваттное сопротивление цепи 7? в нее уже не вхэдит; величину Ьа аналогично называем безваттной проводимостью „намагничения* и наконец величину
называем полной проводимостью намагничения данной цепи. Понятно, что
и что Г (168)
ga=Yaslna и ba=Yacosa /
С помощью символического метода расчета явлений переменного тока мы сможем по шее выяснить соотношения между проводимостями в:ей цепи и проводимостями намагничения.
Если при соз 1ании переменно, о магнитного поля током J нет гистерезиса, например при отсутствии железа, и следовательно ваттная относительно ЭДС слагающая силы тока равна нулю, то из ф-лы (167) вытекает, что £^ = 0
Если есть потери на гистерезис, но максимальные значения (за каждый период) магнитной индукции невьиоки, так что магнитного насыщения железа нет и коэфициент магнитной проницаемости ц— постоянная величина, — можно считать, что, изменив реостатом силу тока J в катушке, мы изменим пропорционально ей и магнит-
/ .. , . 0,4тт n-J „ \
ный поток 1по известной формуле Фтах =-------------—-p-S I и
ЭДС индукции Е. При этом Ya в ф-ле (168) есгь постоянный коэфициент пропорциональности между J и Е, a ga и Ьа суть постоянные ьоэфициенты п опорциональносги между составляющими силы тока и Е по ф-ле (167) Однако и Ya и его составляющие ga и Ьа постоянны, при этом лишь между некоторыми пределами изменения J, при сильном же изменении J скажется влияние насыщения в ф-ле для Фтах и изменения р, отчего изменится и соотношение между J и Е, т е. величины Ya. ga и ba.
Воспользуемся введенным нами понятием проводимости н магничена, чтоб j дать иное выражение мощности, тратящейся на перемагничивание железа.
По ф-ле (160)
Ph=E-Jt,
подставляя сюда выражение JB из ф-лы (167), получаем:
Ph = E?ga, (169)
важное соотношение, которое нам впоследствии будет полезно
287
§ 82. Самоиндукция четырех катушек с общим или отдельными сердечниками
Рассмотрим следующую задачу.
Даны (фиг. 140) четыре одинаковые кагушки, надетые на один общий железный сердечник, представляющий замкнутую магнитную цепь; требуется определить, как будет изменяться самоиндукция L такого прибора при различных включениях катуиь к, а именно,—
П
Ж
Фиг. 140.
во-первых, когда все катушки включены параллельно, во-вторых, когда они включены все последовательно, и в-третьих, когда катушки по две соединены последовательно, а обе пары между собой — параллельно.
При решении этой задачи нам придется прежде всего разобрать вопрос о разнице между включением в цепь двух катушек, не имеющих общего сердечника, т. е. не имеющих-общей магнитной цепи, и катушек с общим сердечником, т. е. с общей магнитной цепью.
На фиг. 141, а изображены две параллельно включенные между точками А я В цепи катушки *, каждая с своей собственной магнитной цепью и с самоиндукцией £г Если напряжение VAB между точками А я В постоянно, то ясно, что если сила тока через катушку, когда она одна включена в цепь, раьна то сила тока в цепи, когда включены две катушки параллельно, равна 2JP т. е. сила тока через каждую катушку такая, какая шла прежде через одну катушку. Сила тока через катушку не
изменится, если мы подключим параллельно еще несколько катушек. Если их четыре, то сила тока в цепи J==4Jr Раз сила тока возросла в четыре раза, то значит полное сопротивление Z между А и В уменьшилось в четыре раза; а так как ваттное сопротивление при параллельном соединении четырех одинаковых катушек уменьшилось в четыре раза, то значит и безваттное уменьшилось тоже в четыре раза, следовательно общая самоиндукции четырех (л) параллельно включенных одинаковых катушек в четыре (п) раза меньше такового одной катушки —
* Самоиндукция катушки выражается так:
L = —-----10 э генри,
где п есть число витков катушки, ц — магнитная проницаемость сердечника, S — площадь поперечного сечения его в см\ I — длина его в см, — средняя — в случае замкнутого сердечника; при незамкнутом сердечнике однако и сама формула, только что написанная, перестает быть сколько-нибудь точной.
288
Пусть теперь такие же точно параллельно включенные катушки навиты на о б щ и й сердечник (фиг. 141, Ь) Здесь может быть два случая; рассмотрим сначала первый, когда катушки навиты так, что действуют навстречу друг другу при создании магнитного потока в сердечнике; вследствие од шаковости катушек их магнитоле 1жущие силы во всякий момент будут уравновешиваться для
сердечника, и поэтому общего магнитного по-
тока в сердечнике совсем не будет, а будут лишь потоки или поля, похожие на поля или потоки пр !мого соленоида, окружающие лишь одну катушку и часть пути—идущие по железу, а часть—по воз • духу; из-за последнего обстоятельства эти потоки много слабее патака, создаваемого одной катушкой при том же токе и на том же
сердечнике, т. е. на сердечнике, п эедзтавляю-щем замкнутую магнитную цепь; раз маг-НИ1НЫЙ поток слабее, значит самоиндукция каждой катушки стала меньше, чем через каждую катушку идет половина всего тока,
т. е обе -они пропускают силу тока вдвое большую, чем каждая из них при этих условиях, — следовательно общая их самоинлукция на основании рассуждения, подобного предыдущему,
вдвое меньше самоиндукции каждой из них при этих условиях, т. е. окончательно — она меньше половины
Перейдем ко второму случаю, когда катушки навиты так, что их магнитодвижущие силы складываются и магнитный поток в сердечнике является результатом действия их обеих. Для упрощения рассуждений примем, что рассеяния магнитных линий нет и что все
линии, создаваемые катушками, проходят весь путь по сердечнику, и отвлечемся от влияния магнитного насыщения железа, т. е. от переменности величины pt Весь магнитный поток можно представить себе состоящим из двух половин, причем одна половина
19 Теория переменных токов.
289
создается одно*! катушкой, другая — другой. При этом в каждой катушке будут индуктироваться две ЭДС: одна ес1 —самоиндукции от потока, создаваемого этой катушкой, другая ем — взаимной индукции — от потока, создаваемого другой; из сказанного следует, что ес1 = ем. Обе эти ЭДС в каждой катушке сложатся в одну ЭДС ес, отстающую от силы тока на Выразим соотно
шения во всей части цепи между А и В аналитически Обозначим ваттное сопротивление одной ~ катушки через /?3; две параллельно
включенные катушки представят сопротивление Силу тока, те
кущего через прибор (т. е. обе катушки), как целое, обозначим через через каждую катушку течет следовательно Взаимную индукцию двух катушек обозначим через М. Тогда:
или, так как еи = ес1,
£,с = иЛГ--^-4*в)£.1- = =
Л л л
п из закона Ома
Подставляя вместо Ez его выражение, получаем:
72 . D2 Г / р \ 2 ~1
П = 4- <0^2 J2 = £ + J*
Ай Д j \ & 1 j
Отсюда видим, что прибор, как целое, представляет ваттное сопро-тивление -1 и безваттное <о£3, т. е. обладает той же самоиндукцией, £
что и каждая катушка в отдельности (на том же сердечнике).
Аналогично докажем, что если мы соединим параллельно все q четыре катушки, то ваттное сопротивление прибора будет , а
самоиндукция — попрежнему А3.
Посмотрим теперь, что будет, если мы будем соединять катушки последовательно. На фиг. 141, с представлено последовательное
соединение двух катушек с независимыми магнитными потоками. Ясно, что ЭДС самоиндукции обеих катушек сложатся, давая ЭДС самоиндукции Ec — 2®L1J=m(2L1)J. Общая самоиндукция таким образом L = 2LV как это нам уже известно из последовательного соединения самоиндукций в цепи переменного тока; для четырех катушек Z, —4£3.
290
Соединим теперь последовательно две катушки с общей магнитной цепью (фиг. 141, d).
Не будем останавливаться на том случае, когда катушки включены навстречу одна другой, — самоиндукция поибора тогда невелика,— а перейдем прямо к тому случаю, когда магнитный поток является общим и создается обеими катушками. Здесь в каждой катушке мы опять имеем по две ЭДС #С1 и ем, которые, слагаясь, дают ес, причем Ес == 2(оА2J, так как опять гс7=ем. Обе катушки, включенные последовательно, дают в цепи ЭДС силу самоиндукции (и индукции), равную 2ЕС в 4(0^ J ==(!)• (4 т. е. при-
бор обладает самоиндукцией L — 4А].
Этот же результат можно получить и проще, если заметить, что на фиг. 141, d две катушки, / и //, представляют собой просто одну катушку с вдвое ббльшим числом витков, и вспомнить, что самоиндукция катушки пропорциональна квадрату числа витков ее и следовательно при увеличении числа витков вдвое увеличится в четыре раза.
Аналогично докажем, что если мы соединим все четыре катушки последовательно, то получим:
L==16Lj.
Не следует забывать, что во всех предыдущих рассуждениях мы считали, что магнитная проницаемость pt железа сердечника величина постоянная, что магнитного насыщения нет; поэтому в зависимости от большего или меньшего отступления от этого на практике могут получиться некоторые отступления в соотношениях между £ и Lr
Третий из намеченных случаев, именно когда катушки включены по две последовательно, а обе пары параллельно, решается на основании предыдущего просто: самоиндукция L при параллельном включении (с общим сердечником) не меняется, следовательно она равна 4L3.
§ 83. Аналитические выражения соотношений в катушке
Применим символический метод для алгебраического выражения тех соотношений между различными электрическими величинами в цепи катушки, которые геометрически выражены векторной диаграммой фиг. 139; при этом нам понадобятся понятия о проводимости намагничения и проводимости всей цепи, введенные нами в § 81.
Прежде всего переведем на язык символического метода соотношение (168) J = EYa. Это есть соотношение между величинами двух векторов J и Е и модулем Ya комплекса Ya—ga — jba. Как написать соотношение между самими векторами и комплексом?
19* 294
Разберем, что представит собой произведение EYa
По правилу, изложенному в предыдущей главе, это произведение есть иозый вектор, получающийся из вектора Е так, как комплекс Ya получается из положительной единицы; следовательно новый вектор будет иметь величину EYa и будет повернут относительно вектора Е (вектор ОС на фиг. 139) в сторону вращения часовой стрелки, так как комплекс Ya, обладающий отрицательной мнимой частью, изображается отрезком, повернутым в эту сторону относительно вертикальной оси, т. е. оси положительных действительных величин; угол поворота нового вектора
_
относительно вектора Е равен arctg —; берем его абсолютную ве-£>а
личину, ибо направление уже известно. На основании соотношений (168)
-а = ctg а,
а потому
, Ьа П arctg -^ = -5 — а; ©а
таким обр зом новый вектор, представляющий произведение Е Ya, займет на фиг. 139 положение в виде продолжения линии АО за точку О влево; он будет по величине равен вектору силы тока J, ибо J=^E'Ya, а по направлению ему прямо противоположен; если мы возьмем его со знаком минус, т. е. два раза умножим на -4-/, то получим как раз вектор силы тока; следовательно в векториальной форме, даваемой символическим методом, соотношение между всеми тремя рассматриваемыми величинами будет таково:
/ = -£Уя.
(170)
Вводим вектор ON=— Е (фиг. 139) и обозначаем его через Ё1; тогда
7=£%. (171)
Переходим к самой диаграмме фиг. 139.
Вектор NK выразится алгебраически вполне подобно ф-ле (113)
AW'==(/?+/Ar)7-=ZJ.
Таким образом то обстоятельство, что вектор напряжения на зажимах ОК — V является результирующим из ON и /W, — равен их геометрической сумме, — алгебраически и в символической форме выразится соотношением:
V=E' + JZ. (172)
292
Подставляя из ф-лы (171) сюда величину Е\ получаем:
<173>
\ 1 а /
С формальной математической стороны катушка, согласно ф-ле (173), представляет собой просто сопротивление
Ya
мы будем обозначать это сопротивление через Z с индексом „все* или „рез* от слова результирующее:
ZBCe,=y + Z (174)
Это сопротивление имеет ваттную и безваттную части, или „составляющие* (употребляем последний термин аналогично применению его к векторам), по ф ле
^рез ^рез ”1” 7^рез*
Определим /?рез и Хрез. Для этого подставим в ф-лу (174) вместо Ya и Z их выражения:
оа j а или
*рез + /^рез =4 + / 4 + * + /*•
1 а 1 а
Чтобы это равенство было возможно, должны быть порознь равны действительные части между собой и мнимые между собой, т. е.
^=4+*’ а
*рез = 4 + * а /
(175)
Сравнивая выражение для 7?рез в ф-лах (175) с выраххнием (163) мы виаим, что одно из них легко переходит в другое, так как
Е sin а __ Е sin а Уа s?n а __
293
Формулами (164) и (165) мы ввели понятие о проводимости цепи Y—g—jb< очевидно, что эго есть величина, обратная результирующему сопротивлению, так что
V — 1 -
^рез' или ^все*
^рез
Найдем выражения для g9 b и Y. Имеем:
Отсюда:
За । р
ва + ЯП
8~ /^+ fl V+ (4й 2 Z2 Га + 1 + ’
\ / \ У а /
^-Д-Х
. УГ _ Ьа + *У1
Ма _|_И2+ (4 + хГ Z2 1 + 2№ + ^’
\ / \ У а /
и наконец на основании соотношения K2=^2-|-Z>2
У*
Для упражнения применим ф-лу (106) для определения фиктивного ваттного сопротивления катушки; по этой ф-ле оно равне
g
; подставляем вместо g и
Y их значения:
g ga + R-Уа _Sa
У1 ~ У2а Ч
таким образом опять получается выражение (175).
§ 84. Феррорезонанс. Опрокидывание фаз
Явления резонанса в цепи, где самоиндукция представлена катушкой с железным сердечником, представляют весьма интересные особенности, хотя пока еще мало использованные практически, так что мы ограничимся здесь в описании их лишь самым существенным.
294
Пусть к цепи, содержащей конденсатор и такую катушку, приложено напряжение, котирое мы можем изменять по' произволу; частота же пусть будет постоянна; далее — ваттным сопротивлением катушки, потерями в железе и искажением кривой тока пренебрежем— качественную сторону картины это не изменит, тлда как учет этих обстоятельств делает теорию в высшей степени с, ожной.
Резонансом мы называем то состояние, когда напряжение на катушке равно напряжению на конденсаторе, т. е.
т (оС
В выражении напряжения на катушке L теперь, в присутствии железа, не будет величиной постоянной; произведение LJm равно амплитуде потока Фот, умноженной на /г-10“8, где п есть число витков; следовательно, если 5 есть площадь поперечного сечеция железа сердечника,
10’8 = ®«5 10’8-5И-
Таким образом если мы возьмем кривую намагничения ОР железа
ного сердечника (фиг. 142) и применим к ней масштаб в со*п*S* 10”8
раз меньший прежнего, то ’эта кривая даст нам напряжения на катушке в зависимости от силы тока, которую мы сможем изменять, меняя все приложенное к цепи напряжение.
Поведем на той же фигуре прямую OQ под углом
/QCW==arctg^,
к оси абсцисс. Ее ординаты дадут нам напряжения на конденсаторе.
Прямая OQ и кри вая ОР пересекутся в точке М*> это и будет состояние резонанса при данной частоте, так
как напряжения на катушке и на конденсаторе теперь равны.
Таким образом в нашей цепи наступление резонанса зависит or силы тока, в цели, т. е. от приложенного напряжения.
Однако экспериментально это состояние резонанса мы не сможем получить именно по следующим причинам.
Представим себе, что мы увеличиваем приложенное к цепи напряжение, начиная от нуля. При условии, что ваттное сопротивление равно нулю, это на ’ряжение будет все безваттно и равно разности напряжений на катушке и на конденсаторе. При какой-нибудь его величине OS в цепи будет течь ток On, напряжение на катушке будет пт, на конденсаторе nq, причем пт — nq — OS, Ток при этом отстает от всего напряжения.
Проводя касательную Згтх к кривой Отт^М, параллельную прямой Oqq^Q, ю пересечения с осью ординат, мы получим на последней отрезок OSX — m^qv который представит нам наибольшее напряжение, при котором еще возможно иметь в цепи отстающий ток, ибо малейшее повышение напряжения перенесет всю работу цепи на совсем другие части кривых.
Именно между точками О и М отрезок т дг есть наибольшая разность ординат тп и qn, бдльшую разность мы сможем иметь лишь на кривых вправо от точек Q и Р, где точка Р получается так: отложим 0^ = 05^ вниз по оси ординат и проведем прямую Т\Р || 0Q. Отрезок ординаты QP=z 07\ = ОЗр всякий отрезок ординаты между прямой 0Q и кривой ОМР вправо будет больше. При каком-нибудь напряжении 0S2 > 0S2, делая такое же построение, получим 0Т2 = 0S2 = Q^Pj и в цепи установится режим, характеризующийся точками Ру и Qv Сила тока при этом будет O/Vf, она будет опережать все напряжение Q-^PV ибо теперь напряжение на конденсаторе стало больше напряжения на ка
тушке.
Если сила тока изменила свою фазу относительно всего напряжения на п, то также изменяют свои фазы на прямо противополож-
Фиг. 143.
ные и напряжения на конденсаторе и катушке. Это явление часто называется опрокидыванием фаз. Сопровождается это явление ростом тока скачком от величины Опг до величины OXj и напряжения на конденсаторе от величины п^ до величины в то время как напряжение на катушке
возрастет сравнительно немного вледствие влияния насыщения
железа.
В практике подобные случаи наблюдались например при обрыве одного провода линии, ведущей к трансформатору, и заземлении конца его у трансформатора, как показано на фиг. 143. Так как
296
провода линии обладают емкостью по отношению к земле, то у нас образуется цепь с последовательным соединением емкости и самоиндукции, как описано выше, с большими перенапряжениями в линии относительно земли.
Опрокидывание фаз, как нетрудно видеть, можно получить и при постоянном напряжении и переменной частоте. При этом только очевидно после опрокидывания напряжение на катушке будет расти почти пропорционально частоте.
297
ГЛАВА XI
ТРАНСФОРМАТОР
§ 85. Векторная диаграмма трансформатора
Если мы на замкнутый железный сердечник намотаем не одну, а две катушки, то при подключении одной из них, которую мы при этом назовем к другой, которую мы
первичной", к зажимам переменного тока назовем „вторичной", будет индуктироваться переменная ЭДС того же числа периодов, какое имеет ток в первичной катушке; от вторичной катушки мы можем взять переменный ток, как от обычного источника переменного тока — генератора. Такой прибор называется трансформатором, так как с помощью его можно изменить ге-личину напряжения переменного тока, прежде чем приложить его к данной цепи. На фиг. 145 схематически представлен такой трансформатор. Цифрой I обозначена первичная катушка, цифрой II — вторичная. Обратимся прежде всего к рассмотрению магнитных потоков в трансформаторе и вызываемых этими потоками ЭДС. Пока вторичная катушка не замкнута на какую-либо цепь (или на она не оказывает никакого влияния
и
короткое), в ней тока нет, на явления. Мыч имеем при этом случай, рассмотренный в предыдущей главе.
Состояние трансформатора, когда вторичная катушка не замкнута, называется „холостым ходом", или „холостой работой" его.
Диаграмма фиг. 139 есть векторная диаграмма холостой работы трансформатора.
Предположим теперь, что вторичная катушка замкнута и сила тока в ней и в цепи, подключенной к ней, J2. Силу тока в первич
298
ной катушке обозначим через Jv мгновенные значения сил токов— через и /2.
Состояние трансформатора, когда от вторичной катушки берут ток, называется состоянием „нагрузки", или просто' „нагрузкой* трансформатора.
Итак изучим его состояние при нагрузке.
В отличие от случая холостой работы (фиг. 139) здесь будут действовать магнитодвижущие силы двух катушек, и магнитный поток 1РЖ, идущий весь свой путь по железу и проходящий таким образом сквозь обе Kai ушки, будет являться результатом действия обеих катушек.
Магнитодвижущая сила первичной катушки теперь должна преодолевать не только магнитное сопротивление пути магнитного потока в железе, но и магнитодвижущую силу вторичной катушки, так как ток, индуктирующийся в последней, хотя в фазе своей и зависит от соотношений ваттного и безваттного сопротивлений, подключенных ко вторичной катушке, в общем по закону Ленца противодействует вызвавшей его причине, и общее действие вторичной катушки будет противоположно действию первичной.
Пусть на фиг. 144 вектор OF есть вектор потока Фж, общего* обеим катушкам. В первичной катушке этим потоком индуктируется ЭДС Ev во вторичной—ЭДС Е2. Эти ЭДС относятся, как,числа витков /Zj и п2 первичной и вторичной катушек:
• Е2 = /Zj• п2»
Ег есть для нас противоэлектродвижушая сила в первичной катушке, а Е2 есть ЭДС „источника* — нового — для получения переменного тока. -В зависимости от соотношений ваттного и безваттного сопротивлений цепи, подключенной к этой ЭДС Е2,сила тока J2 в этой „вторичной цепи* будет более или менее сдвинута в фазе относительно Е2. Нанесем J2 на чертеж в виде вектора ОЛ2» отстающего на угол у2е от вектора Е2. Умножив J2 на /?2, получим вектор ОВ2 магнитодвижущей силы вторичной катушки.
* „Первичную* силу тока мы получим из того соображения, что первичная магнитодвижущая сила должна слагаться из двух составляющих: первой — равной и противоположной J2zz2, т. е. вектора OD, уравновешивающего магнитодвижущую силу, или лучше сказать, размагничивающее действие вторичной катушки при нагрузке ее (т. е. когда от нее берем ток), и второй составляющей, создающей магнитный поток Фж; как увидим далее, этот поток не постоянен при разных нагрузках трансформатора, т. е. при разных силах тока J2, а меняется — при малых нагрузках мало, а при больших — сильно. Магнитодвижущая сила, необходимая для создания потока OF, пусть будет ОС, так что, разделив ОС на число витков в первич
299
ной катушке nv мы получим вектор ОН той силы тока, которая должна была бы течь в первичной катушке, чтобы при холостом ходе, т. е. когда во вторичной катушке тока нет, создать такой же поток в железе OF, какой создается теперь.
Так как теперь есть размагничивающее действие вторичной катушки, то первичная магнитодвижущая сила должна быть представлена суммой OD и ОС, т. е. вектором ОВГ Разделив ОВу на nv получаем вектор ОЛ2 „первичной" силы тока Jr
Заметим, что треугольник ОАуН подобен треугольнику ОВуС^ стороны первого в Пу раз менее сторон второго, а потому
А?Н= B7C:n,=J,N 1 11 2 Пу
Далее, естественно, в соответствии с изложенным в предыдущей главе, угол COF равен углу а гистерезиса (и токов Фуко).
Теперь следует уяснить себе, пока без особых математических выкладок, характер физического процесса при нагрузке трансформатора, особенно при ее росте, г. е. при росте тока J2.
Увеличим сравнительно с предыдущим состоянием силу тока J2 (уменьшив сопротивления, подключенные к зажимам вторичной катушки). При этом увеличится размагничивающее действие вторичной катушки, ослабнет поток Ч;.к, уменьшится от ослабления потока противоэлектродвижущая сила первичной катушки Еу (вектор ON на фиг. 139), увеличится разность между У3 и Еу, т. е. вектор на фиг. 139; а так как . J/^2 == Л\2, причем Ry и ^ по-
стоянны, то увеличится сила тэка Jt до такой величины, чтобы Ч1 стало почти прежней величины. Однако Фж не сможет стать в точности равным своему прежнему значению, ибо тогда Еу было бы прежним, и разность между Vy и Еу не была бы больше прежней, следовательно и ток Jy не мог бы быть больше. В этом объяснении процесса при росте нагрузки мы не учитываем влияния изменения сдвига фаз различных век оров друг относительно друга, но это влияние качественной стороны вопроса не меняет, а в дальнейшем мы найдем и математические выражения для всех этих только что описанных зависимостей.
Итак с ростом нагрузки, т. е. силы тока J2, растет соответственно и Jyf и уменьшается общий поток Фж.
Ток холостого хода есть поэтому обыкновенно наименьший ток в первичной катушке, хотя ciporoe математическое исследование показывает, что могут быть такие соотношения в величинах, характеризующих трансформатор (все сопротивления и проводимости намагничения), что при малых нагрузках, т. е. при малом Л, первичный ток Jy сначала немного уменьшается, а потом уже начинает расти. Технического значения это явление не имеет.
300
Теперь обратимся к магнитным потокам (фиг. 145) и построению векторной диаграммы (фиг. 146).
Так же, как в обыкновенной катушке (фиг. 145, а), здесь будет существовать поток рассеяния около первичной катушки, пропорциона 1ьный первичной силе тока Z3 и находящийся в фазе с ней; мгновенную величину этого потока обозначим через ф3р и назовем его первичным потоком рассеяния. Введя в рассмотрение ЭДС, индуктируемую этим потоком в первичной катушке, мы можем теперь построить диаграмму напряжений первичной катушки.
Начертим (фиг. 146) по о разцу фиг. 144 снова векторы:
ОМ = Е2, OB2 = J2n2, ОН, ~OC,~OA.=JV
Ж7 6 л 1 J а.1 ' 7 Л 47
— и наконец вектор ON = — Ег подобно вектору ON ni
на фиг. 139. З.’тем о ложим OD = Ф1р, амплитуде первичного потока рассеяния, и 00 — вектор, равный ЭДС от этого потока.
Так как вектор ф]р пропорционален току /3 и фазе с ним, то можно положить
ф1р = /1 X (постоянная величина), и ЭДС от него
dfcb- dL dL
-^10-=-(^Xnoer. =
3 есь коэфициент не есть величина самоиндукции первичной катушки, так как им учитывается только поток рассеяния, а не весь поток, производимый первичным током. Sj правильнее называть здесь величиной рассеяния или другим подобным названием.
Таким образом вектор OG представляет ЭДС с действующим значением Е1р — = JxXr
Приложив к вектору ON вектор NQ=—OG и вектор QK^ *7?^ мы. получаем ОК—вектор всего напряжения V3, приложенного к первичной катушке трансформатора.
Можно сложить векторы ODX и OF и получить вектор Ф3 всего первичного потока, которому соответствует вся первичная ЭДС QO, причем вектор QO перпендикулярен к вектору Фг
Так как векторы Е2 и J2 у нас уже на чертеже есть, то очень просто теперь достроить диаграмму для вторичной цепи. Треугольник OLM есть обычный треугольник напряжений; в нем ОМ = Е2, OL —- J%R.2 (^2вну ^2вне) ZLAf (&S2J2 (I) (^bhv "
— X2J2-(X2my-[-X2BHe)J2, здесь к CO значками означают ваттные сопротивления самой вторичной катушки (/?2вну) и цепи на~ грузки, подключенной к ней (Т?2вне); ^2вне означает самоиндукцию
301
этой цепи нагрузки, т. е. внешней части вторичной цепи, а 52виу есть величина рассеяния вторичной катушки, совершенно аналогичная по своему значению и происхождению коэфициенту только что нами введенному. Остановимся на этом вопросе подробнее и
обратимся опять к магнитным
потокам (фиг. 145).
Кроме потока Фж общего обеим катушкам, во вюричной катушке около витков ее будет существовать еще вторичный поток рассеяния О/)2 = Ф2р (фиг. 146), производимый током J2 и находящийся с ним в одной фазе ка к идущий в воздухе (фиг. 145,6). Так как ток J2 вообще противодействует току то и ф2р внутри катушки направлено навстречу но в одном месте не могут существо зать два разных потока, а потому потоки фж и ф2р сложатся внутри катушки в результирующий вторичный поток ф2 (фиг. 146), а вне катушки в воздухе поток ф2р останется (фиг. 145,а). Введем коэфициент 52вну и ЭДС от потока ф2р выразим так:
_____ *^2р 1П_Я___ Q е»р“ ""^dt 10 “ di '
Откладываем на линии LM от-резок ТМ = (oS2BHV. J2 = J2 • Х2 вну. Тогда вектор ОТ представит всю ЭДС во вторичной катушке от всего вторичного потока ф2 и еледо* вательно будет перпендикулярен к вектору Ч;2,
Можно представить себе дело
Фиг. 145.
и так, что из всего потока только часть ф2 проходит сквозь вторичную катушку, а часть — ф2р (прямо противоположная по фазе току J2 и мгновенному значению OD2 = Ф2р) вследствие противодавления вторичных ампер-вигков оттесняется и огибает вторичную катушку по воздуху,
как изображено на фиг. 145, а. При таком представлении и вто-
ричный поток рассеяния создается первичной катушкой, но находится он в фазе не с первичным, а со вторичным током: чем
мгновенное /2 больше, тем (в эют момент) большее число линий ф2р оттесняется из катушки наружу.
302
Конечно не следует упускать из виду, что будет промежуток времени (пока линия времени близка к направлению, перпендикулярному к -73), когда будет в магнитной цепи доминировать вторичная магнитодвижущая сила. Тогда все потоки создаются вторичным током, в том числе и первичный поток рассеяния ф1р (фиг. 145, Ь) создается током J2, хотя находится в фазе с током Jv
Фиг. 1:6.
Чтобы закончить построение диаграммы, надо получить вектор напряжения на зажимах вторичной катушки, или „вторичного напряжения". Для этого из вектора полной ЭДС ОТ вычтем вектор падения напряжения в ваттном сопротивлении катушки ST — и получим вектор OS— V2 вторичного напряжения. Угол между Е2 = ОМ и J2 = OA2 обозначим через <р2е, а угол между V^—OS и J2 — через <р2„. Далее, UL = ST = У2/?2аяу) OU = J2R2Bai и US= == ®^2вне "4 == *4 ‘ ^2вне"
303
§ 86. Баланс мощностей
Перейдем теперь к соотношениям мощностей в трансформаторе, причем введем предварительно обозначения: угол NOBy между Еу и Jy обозначим через а угол КОВу между У3 и Jy обозначим через
Обозначим далее мощность, получаемую первичной катушкой от зажимов с напряжением Vv через Рг Она равна:
Л = FiAC0S(Pi.- (А)
Отнеся здесь косинус множителем к У3, заменяя проекцию вектора V3 на вектор тока через сумму проекции векторов, составляющих Vlf и приняв во внимание, что один из составляющих векторов, именно Л/Q, перпендикулярен к вектору тока, мы получим:
Р1 = /1 ( A cos Т1Р = А <Е1 cos <Ple + А • ^1) =
= + (В)
Здесь JZR.} есть потеря на джаулев эффект в первичной катушке, a *ЕУ cos ср3е представляет мощность, передающуюся из первичной катушки в магнитное поле посредством противоэлектро-движушей силы —Еу. Выражение этой мощности можно преобразовать так:
ри = А • Еу cos <р1е = Еу • (Jy cos сртД =sЕу • (ОАу cos <pu) = = Еу • [ОН cos (/_ NOH) 4- HAy . cos (ВгОМ)], принимая во внимание, что НАу || ОВТ
Далее, так как </_NOH—^r— а, то, обозначая величину ОН Л
через Ja, получаем:
Ри = Еу-(Ja sin а + Jt • cos <f>2e) =
= Еу • Ja sin а + Еу • J2 cos <р2е. (С)
Здесь первый член в правой части представляет потери на гистерезис в железе (и токи Фуко) при потоке Фж данной величины (амплитуды), так как Ja ест , как выше было указано, та сила тока, которой должна иметь место в первичной катушке при холостом хо »$, чтобы поток этот был такой же точно, как и теперь.
Итак =
Второй член представляет мощность, передающуюся из магнитного поля во вторичную катушку, что ясно обнаруживается, если
304
множитель — ni
отнести не к силе тока, а к ЭДС; тогда мы будем
иметь:
£jJ2 Jcos<p2e=(£i ni \
«1/
J2cos<p2f = £2-J2costp2e,
(D)
так как Ег :Е2 = пА :п2, как было указано в начале этой главы.
Последнее выражение может быть опять представлено в виде суммы, именно следующим образом:
£2 J^cos (f J2 (Е2 cos <p2e) = J2 (ОМ • cos <p2e) =
= Л(5Г+ 03 •C0S = ЛСАЛвну + v2 •cos ?2О) =
= -/2/?2вну4- V2J2 C0S Фго- (Н)
Первый член в правой части /^гвну представляет потери на джаулев эффект во вторичной катушке, а второй
Р2= V2J2cos<p2, уже полезную вторичную мощность, — мощность, тратящуюся во внешней части вторичной цепи.
Сопоставляя теперь формулы (А), (В), (С), (D) и (Н), мы имеем:
==::: *^1^1 *^2^2вну 4" ^2A C0S ^2»»
ИЛИ
Л = ^1+^ + 4^ 4-^-
Отношение Р2 к Р1 есть коэфициент полезного действия трансформатора.
Если при всевозможных изменениях нагрузки трансформатора угол сдвига фаз между током и напряжением во вторичной цепи остается постоянным, то вектор первичной силы тока изменяется с нагрузкой по величине и фазе (углу с вектором 1/3) так, что его конец Аг описывает окружность; центр этой окружности лежит вправо от О несколько выше линии ОЕ Такая окружность называется круговой диаграммой тока. Доказывается то положение, что At описывает окружность, различными способами. С двумя из них мы ознакомимся ниже. Особенно интересен тот случай, когда (р2^ = 0, т. е. когда Х>вне = 0, так как тогда одна и та же векторная диаграмма и одна и та же круговая диаграмма тока получаются и для трансформатора и для асинхронного двигателя.
От холостого хода, когда вектор мал и составляет с V*
большой угол, до полной нагрузки вектор тока J3 все время растет и поворачивается к вектору У3, так что угол cplv все время уменьшается.
20 Теория переменных токов. 305
Добавим, что трансформаторы и асинхронные двигатели обыкновенно рассчитываются так, что при полной их нагрузке вектор тока является касательной к окружности. При перегрузке вектор Jt растет далее, но поворачивается понемногу в сторону к О/7, т. е. при этом угол <p3w растет. Таким образом при полной нагрузке этот угол наименьший, a cos<p3v наибольший — при полной нагрузке машина или трансформатор работают при этом с наилучшим коэ-фициентом мощности, наилучшим cos ср.
§ 87. Приближенное построение диаграммы
Теперь следует обратиться к вопросу, как построить диаграмму трансформатора (фиг. 146) для определенной нагрузки, т. е. для определенных значений силы тока J2 и cos<p2e экспериментальным путем.
Из фиг. 146 мы видим, что для построения диаграммы нам надо знать следующие величины: J3, и Р3 (откуда получается и угол ф1а), 7?3 и Xv которые дают возможность построить треугольник KQN и вместе с тем вектор CW; далее, необходимо знать если
/г не самые числа витков, то по крайней мере их отношение —, что-
бы получить вектор Е2 = ОМ=^Е1-~^ \ затем необходимо знать /?2вну и -^2вну> что в связи с подразумеваемым нами уже известным данным J2 дает возможность определить по величине вектор MS = *4* V^2BHy ^2вну’ напРяжение V2=O5 измеряется непосредственно, и в пересечении двух дуг с радиусами OS из О и SM из М получаем точку 5 и вектор V2; наконец надо знать полезную мощность Р2, что дает нам угол и направление вектора J2.
Величины Jj, Vv Р3, J2, V2 и Р2 мы меряем амперметром, вольтметром и ваттметром. Величины 7?3 и Т?2вну можно измерить одним из способов измерения сопротивлений, причем однако надо иметь в виду (как и при определении ваттного сопротивления всякой простой катушки), что переменный ток не использует так всего поперечного сечения проводника, как ток постоянный: чем ближе к центру поперечного сечения, тем „плотность" тока меньше, понимая под плотностью тока силу тока через единицу площади поперечного сечения в том или другом месте этого поперечного сечения. Эффект этот растет с рортом частоты переменного тока. Вопросу этому посвящена в этом курсе последняя глава.
Таким образом величины /?3 и Р2вну, полученные из измерений при постоянном токе, надо несколько увеличить сообразно с частотой переменного тока, чтобы получить действительные значения ваттных сопротивлений обмоток при переменном токе.
306
Остается определить экспериментально лишь Х2 и X2Kgyi для чего мы применим следующий приближенный способ.
Замкнем вторичную катушку на короткое. Так как J2 при этом
будет иметь наибольшее значение, то и вектор МТ (фиг. 146), равный J2 • .ЛГ2вну, где ?f2BHy есть постоянная величина, тоже получит наибольшее значение и превратится в вектор ML (фиг. 147). ЭДС Е2 раз
ложится на две составляющие ОА — У2*/?2вну и LM = J2'X2my, перпендикулярные друг к другу. Треугольник ампервитков ОВгС примет
вид, изображенный на фиг. ших сил токов J2 и обмотки, первичное напряже-ние при этом понижают, доводя его приблизительно до-трети или четверти от первоначальной величины, причем руководствуются именно тем, чтобы силы токов J2 и были приблизительно» таковы по величине, какими они должны быть при нормальной, полной нагрузке трансформатора При этом векторы ОВг иВ1С(фиг. 147) имеют ту же длину, что и
147. Чтобы не перегрелись от боль
Фиг. 147.
на фиг. 146, если предположить, что фиг. 146 на-
черчена для нормальной нагрузки, но направление их на фиг. 147
не то, что на фиг 146; при коротком замыкании они почти совсем
противоположны друг другу; вектор ОС равнодействующих ампервитков поэтому получается небольшим, небольшими будут и поток Фж и ЭДС Ег и Е2 (несколько процентов от прежних значений).
Примем приближенно, что ОВг || ВгС и что OB1 = B1Ci т. е. что
•/•j • /Zj —J2 *
(А)
О в
Построить по вектору J± = —1 треугольник NQK мы еще не мо-п1
УША, ибо не знаем Xv но пока допустим, что этот треугольник и
вектор E1 — ON=E2' — у нас на чертеже уже имеются. УВеЛИ-^Я
чим треугольник OLM в — раз линейно, отчего его гипотенуза П2
ОМ переводится в ОМ- — = Е2*— , т. е. станет равной ОМ, и пе
307
ренесем его в положение OpN так, чтобы гипотенуза его совпала с ON. Так как мы приняли, что || J2, то имеем, что и pN || QK и Ор || NQ. Продолжим Ор и QK до пересечения их в точке q. Тогда вектор первичного (пониженного) напряжения представится в виде геометрической суммы двух векторов Oq и qK, .причем величины этих двух катетов прямоугольного треугольника OqK таковы:
П2
Oq — J1X1 4“ Л^2вну’ТГ •
Л2
При помощи соотношения (А) преобразуем эти выражения так:
^аГ^+^вну^)2!.
L \ а2 / J
L \ п2 / J
Ход экспериментальных измерений и построения таков. Измеряем значения /?2 и /?2вну ПРИ постоянном токе и вычисляем их значения при переменном токе сообразно с его частотой, пользуясь
таблицами. Затем переходим к измерениям с переменным током. Замыкаем на короткое вторичную катушку при пониженном пер-
вичном напряжении. Меряем величины V19 Jv Pv откуда опреде-
ляем угол KOBV равный OKq. Наносим на чертеж ОК = и линию Kq, на которую опускаем перпендикуляр Oq. Находим точку
Q, делящую линию Kq в отношении KQ'. Qq = Rx :/?2вну
/чу
\«2/ ’
До-
пуская приближенно, что /?,: /?2вну = Хл :АГ2ш1у, проводим линию QN || Oq до пересечения с ОК в точке N и линию Np || Kq. Раз-/ п \2
делив затем отрезки pq на и Ор на 1 , мы получим Xt \ П2 /
и АГ2вну соответственно. Таков приближенный способ нахо
ждения этих величин, зная которые можно построить
векторную диаграмму трансформатора.
Строить эту диаграмму для каждой возможной нагрузки трансформатора было бы слишком обременительно; поэтому свойства векторной диаграммы были обобщены, и была выработана особая диаграмма, — диаграмма работы, — которая представляет состояния трансформатора при изменениях нагрузки в самых широких
пределах, с единственным условием постоянства при этих изменениях величины coscp2w. Ее построение по данным опыта много точнее
308
построения простой векторной диаграммы; теория ее изложена далее в следующих главах.
Обратимся теперь к вопросу, намеченному нами в конце предыдущей главы, именно к вопросу о токах Фуко в железе.
Если бы токов Фуко в железе не было, то при холостом ходе угол а между векторами тока и потока был бы чистым углом гистерезиса.
Токи Фуко в железе являются по существу вторичными токами. Можно заменить в расчетах токи Фуко в железе током в некоторой обмотке с подходящими числом витков и ваттным сопротивлением.
При нагр/зке трансформатора токи Фуко будут таким образом увеличивать действие вторичного тока J2. Так как мы из диаграммы фиг. 146 видели, что с ростом нагрузки угол B^OF растет (до полной, нагрузки), то ясно, что и действие токов Фуко при холостой работе трансформатора скажется также. Чем толще листы железа, тем сильнее эти токи, тем больше их размагничивающее действие,, тем больше мощность их, переходящая в тепло, и т. д. и тем больше угол COF на фиг. 146 или A OF на фиг. 138.
С этой точки зрения вообще чисто холостого хода трансфор' матора не может быть, ибо всегда есть токи Фуко, по существу являющиеся вторичными токами, но условно мы считаем холостым ходом состояние трансформатора до тех пор, пока нет тока в его вторичной катушке.
Этим мы и закончим пока изучение явлений в нагруженном трансформаторе, чтобы позднее вернуться лишь к чисто математической обработке результатов, в частности к выводу круговой диаграммы тока.
§ 88. Изображение соотношений в цепи переменного магнитного потока посредством векторов
Мы уже и раньше, например на векторной диа рамме трансформатора, вводили векторы магнитодвижущих сил и магнитных потоков. В настоящем параграфе мы несколько расширим область применения векторов к изобра кению соотношений между величинами в цепи переменного тока.
Рассмотрим магнитную цепь, изображенную на фиг. 148. Железное кольцо намагничивается переменным током iv текущим через катушку / с числом витков пг Переменную магнитодвижущую силу этой катушки обозначим буквой Л43, ее амплитуду—через М1т> так что
М, m = 0,4пя, .Л = lm 1 1 I tn 1 im
Кроме катушки I на кольце есть еще катушка // с числом витков п2 и катушка III, к которой подключен вольтметр с очень
30 &
большим сопротивлением или, еще лучше, электростатический. Переменный магнитный поток Фр. амплитуду которого мы обозначим через Ф1да, индуктирует в кааушке /// ЭДС, измеряемую вольтметром. Так как ток через вольтметр или очень мал или, при электро
статическом вольтметре, практически равен нулю, то магнитодви-
жущую силу катушки III мы можем положить равнс й нулю. Опыт показывает, что ЭДС катушки ПЦ даваемая показаниями вольтметра, много больше в том случае, когда катушка II разомкнута, чем в том, когда катушка // замкнута на короткое. Объяснение этого факта после ознакомления с теорией трансформатора легко. В коротко замкнутой катушке // индуктируется ЭДС и течет большой силы ток короткого замыкания; поэтому магнитодвижущая сила ее велика, но направлена почти прямо противоположно магнитодвижущей си-
ле катушки /; результирующая магнитодвижущая сила теперь меньше, чем при незамкнутой катушке 1Ц магнитный поток в железе меньше, меньше и ЭДС катушки III. Переведем это объяснение на язык математики.
Обозначим магнитное сопротивление пути магнитного потока по кольцу через R , причем
V.S'
где I — длина магнитных линий, S—площадь поперечного сечения железа, а ц—магнитная проницаемость железа.
Как известно, между постоянной магнитодвижущей силой М от постоянного тока, постоянным магнитным потоком Ф и ма нитным сопротивлением /?м существует соотношение, в котором видят некоторую аналогию с законом Ома для тока:
Для переменного потока и для переменной магнитодвижущей силы Мг от переменного тока такое соотношение мы можем принять, лишь пренебрегая тем, что Ф2 отстает в фазе от на угол а гистерезиса.
Итак с этим приближением пусть пока для мгновенных значений М
Ф1 = ~Б1> или (А)
810
и для амплитуд
(В)
Подобное же соотношение будет существовать и для результирующей магнитодвижущей силы -(-• М2 двух катушек I и II и результирующего магнитного потока Ф в том случае, когда катушка // замкнута на короткое. ЭДС, индуктируемая общим или результирующим потоком Ф в этой катушке, равна:
йФ
*2 =— л9- —тг‘10”8 вольт; л 2 di ’
если ваттное сопротивление катушки II равно /?2, то сила тока в ней
, е2 га,10~8 <УФ '=/<--------ИГ' л-а”™р;
магнитодвижущая сила катушки II равна: Л/гПО"8 ЛФ <1Ф
M2~kn2ia=* — ~ =ss — N. — t
(9.
причем
АлИО"8
О,4тсп|’1О-8
(D)
Применяя формулу (А) для результирующих величин ствии двух катушек, имеем для мгновенных значений:
^1 + ^2 = Ф^м.
при дей-
но для амплитуд этих величин такого ур-ния, аналогичного соотношению (В), мы однако не можем написать, так как Мг и М2 сдвинуты в фазе. Вставив в последнее ур-ние вместо М2 его величину
(С), получим:
йФ ^~N-dT^R№,
откуда
(Е)
Если мы в параллель к (D) . напишем ур-ние (23) в таком виде:
ТО сразу увидим полную аналогию (D) (23).
S11
Если мы примем для простоты, что магнитный поток изменяется, как синусоидальная функция времени, то можем ншисать:
Ф = Ф^-sin (о)/)
и, вставив это выражение потока в (D), получим:
Ml = sin (“0 + шМФт sin ( + 4 )• (F)
Из этого ур-ния вытекает, что Л42 изменяется тоже синусои-может быть разложено на две составляющие величины. Ур-ние (F) можно представить векториально, как это сделано на фиг. 149.
Здесь вектор О А = Фот7?м; проекция его на линию времени даст первое слагаемое в правой части ур-ния (F); вектор ОВ — ®МФт опережает на четверть периода первый вектор, его проекция на линию времени даст второе слагаемое в правой части ур-ния (F). Результирующий из О А и ОВ вектор ОС представит магнитодвижущую силу 7И1/и, которую надо иметь катушке /, чтобы в цепи с данным железом, т. е. величи
ной /?м, и данной катушкой //, т. е. величиной N, создать магнитный поток с амплитудой Фт. Очевидно, что из треугольника О АС мы имеем:
М, 2 = 02/?24-(l)W202 1/и т м I т
и далее
ф — _ т V
Последняя формула напоминает по форме закон Ома для переменного тока.
Так как токи Фуко в железе, как было указано в конце предыдущего параграфа, подобны току во вторичной катушке, то ясно, что их влияние можно учесть коэфициентом N.
Из фиг. 149 имеем, что угол запаздывания в фазе потока Ф относительно магнитодвижущей силы равен:
<pM = arctg—. (177)
Так как гистерезис действует в tgm же смысле, что и коэфи-циент N, т. е. сдвигая Ф относительно в сторону запаздыва-312
ния, то и его можно учесть коэфициентом W или следующим образом.
Разделив вектор ОА на /?м, получим вектор 0О=Фт магнитного потока. Теперь повернем вектор ОА на угол а гистерезиса влево относительно вектора OD в положение ОА'. Вектор ОА' есть вектор магнитодвижущей силы, необходимой для того, чтобы создать в магнитной цепи с сопротивлением /?м поток Фт при отсутствии вторичных токов, т. е. при условии М=0. Прибавим к О А' вектор ОВ = А'СГ, получим Вектор ОС магнитодвижущей силы, необходимой для создания того же потока Фт при данном N.
Фиг. 150.
Разделив ОС на /?м, получим вектор OF, представляющий магнитный поток,- который при усливии пренебрежения гистерезисом и насыщением появится в цепи, если при той же магнитодвижущей силе ОС величина N сделается равной нулю.
Мы можем теперь перейти к более общему случаю, когда в цепи катушки II есть самоиндукция £2. На фиг. 150,а представлены соотношения в катушке // для этого случая, и получена магнитодвижущая сила ее ТИ2/Я; на фиг. 150,# произведено сложение векторов — магнитодвижущей силы ОА = ФтН1Л и АС—— ОВ —— М2т— и получен вектор ОС = М1т, так что удовлетворяется соотношение
М1^М2 = Ф-^.
§ 89. Автотрансформатор
Представим себе, фиг. 151, что в случае /^>/*2 все витки вторичной кату пки совпали и слились с п2 витками первичной Тогда в этих п2 витках будет течь ток, равный геометрической.
313
сумме токов и J2, в остальных же п1 — п2 витках сила тока будет Магнитодвижущая сила всего трансформатора, которая раньше выражалась через тепеРь выразится так:
(A -|- J2) ^2 A
что однако дает прежнюю же величину Ап14“ Ал2*
Таким образом от такого слияния вторичной обмотки с частью первичной действие трансформатора в общем не изменится. Уменьшатся только потери на джаулев ’ * т 3 7 эффект, который раньше изме-
* gi * рялся* величиной J2Rt а
g теперь будет значительно меньше,
о так как теперь нет совсем вторич-
g____________ ной обмотки, а в части первичной
g течет ток не Jv а А4~А» кото"
_____________g) рый вообще меньше Jv
фиг> 151. Такой трансформатор называет-
ся автотрансформатором и употребляется часто при сравнительно небольших мощностях для небольших (редко более чем в три раза) понижений или повышений напряжений. Повышение достигается, разумеете^, присоединением к первичному напряжению п2 витков, а к нагрузке тот же результат получим, полагая пг < п2 и считая, что после слияния обмоток в п,2 — пг витках течет ток а в ток А 4" А*
Область применения автотрансформаторов весьма невелика; подробности об этом следует искать в книгах, посвященных трансформаторам.
Заметим, что любая реактивная катушка может в известных пределах служить автотрансформатором.
§ 90. Аналитические выражения для соотношений в трансформаторе
Перейдем теперь к алгебраическому выражению соотношений в трансформаторе, представленных геометрически диаграммой фиг. 146.
Основным яв/яется соотношение:
оТс=д^4-лда,
или, аналогично ф-ле (172):
= Ж + (178)
В нагруженном трансформаторе ЭДС Ех индуктируется потоком в железе Фж, который сам создается ампервитками (магнитодвижущей силой), результирующими из первичных и в оричных, -\~J2n2. 314
Другими словами, при отсутствии тока во вторичной катушке в одной первичной должен был бы течь ток силы
(179)
чтобы создавался тот же самый магнитный поток и индуктировалась та же самая ЭДС Ev что и теперь, при нагрузке трансформатора. Тогда мы не имели бы вторичного тока, и явления были бы подобны явлениям в простой катушке.
Поэтому проводимость намагничения есть коэфициент пропорциональности между Et и этим фиктивным током /Л, который мы назовем намагничивающим током:
7O=-V3=^ (180)
Прибавим к трем ур-ниям — (178), (179) и (180) — четвертое, служащее для определения J2:
__ Е ~
j
*/п =3= —fc- -
7 Z
^2 ^2
или, положив где и называют коэфициентом транс-
формации:
В этих четырех уравнениях величина первичное напряжение, дана, — она постоянна и известна; величина Zx определяется конструкцией первичной катушки, величина Z2 определяется как конструкцией вторичной катушки, так и нагрузкой, т. е. сопротивлениями ваттным и безваттным цепи, подключаемой ко вторичной катушке; при переменной нагрузке эта величина есть независимая переменная в той своей части, которая относится к этой внешней части вторичной цепи; таким образом
^2 ^2вну Ч” ^2вне Ч~/(^2вну Ч" ^2 вне)’
где/?2внв иХ2вне меняются как независимые переменные: их изменение есть изменение нагрузки трансформатора и вызывает изменение силы тока J2 и по величине и фазе.
Величина Ya при условии постоянства магнитной проницаемости, как выяснено в конце § 81, т. е. при небольших колебаниях нагрузки, при небольших изменениях величин Ег и Jai может считаться величиной постоянной.
315
D п2
Величина и — — есть отвлеченное чиспо, постоянное для дан-/21 ного трансформатора.
Остальные величины J2, Ja, Ег суть величины, меняющиеся с изменением нагрузки. Из них обыкновенно наибольший практический интерес предс!авляет первичный ток, т. е. его величина и фаза, затем вторичный; величины же Ja и Ег суть величины характера математического или расчетного, а потому и важны лишь при расчетах.
Исключим из написанных нами четырех уравнений три величины— J2, Ja и Ev после чего мы получим одно уравнение, связывающее при помощи постоянных величин, упомянутых только что, переменные Z2 и .
Подставив из формулы (181) выражение для J2 в формулу (179), а затем полученное выражение для Ja в формулу (180), получим:
__ _________ 7/2
F' . V — 1 ____ F' ___
1а — у •
___ Z2
Z —
Обозначим через Z'2 и назовем эту величину сопротивлением вторичной цепи, приведенным к первичной цепи; тогда
откуда
__________ Е
Z2
от
1 1+^4’
Подставляя это выражение в формулу (178) получаем:
4__\
1+^4/
(182)
Соотношение (182) чрезвычайно важно: как указывается в теории машин переменного тока, оно распрос’раняется не только на трансформатор, но и на асинхронный двигатель и другие машина; далее мы увидим, что такое же соотношение получается и для любой линии передачи энергии.
В случае асинхронного двигателя, коэфициент трансформации и равен отношению произведений из чисел витков на соответствующие обмоточные коэфициенты ротора и статора.
316
Далее, у асинхронного двигателя Х'вне = 0, а /?'вне эквивалентно его механической нагрузке.
Выражение в скобках дает величину того сопротивления, которое нагруженный трансформатор или асинхронный двигатель представляет для тока Jr Можно по аналогии с прежним назвать эгу величину фиктивным сопротивлением первичной катушки трансформатора или обмотки статора асинхронного двигателя.
Изменяя по своему произволу величину Z'2 в формуле (182), т. е. изменяя нагрузку, мы будем изменять и силу тока по величине и фазе, К случаю безиндукционной нагрузки, т. е. когда во внешней части вторичной цепи самоиндукции нет и потому Х2вне = 0, мы вернемся позднее.
В последующем нам встретятся два предельных значения сопротивления, представляемого выражением в скобках в формуле (182).
При холостом ходе трансформатор (или асинхронный двигатель) подобен простой катушке, для которой мы вывели формулы (173) и (174). Формула (173) получается из формулы (182), если мы подставим в нее то значение Z'2, которое оно приобретает при холостом ходе, т. е. когда вторичная цепь разомкнута,—тогда /?2вну = ОО, а следовательно и Z2 = OO; при этом из формулы (182) имеем, обозначая через jT, значение первичного тока при холостом ходе:
\ 7
т. е. формулу (173).
Полагая
(183)
* а получаем:
= (184)
Zo есть сопротивление, представляемое трансформатором или двигателем при холостом ходе.
Второе интересующее нас значение сопротивления в формуле (182) получится, когда нагрузка возрастет до своей максимальной величины, т. е. когда /?2вне уменьшится до нуля; это есть случай короткого замыкания при полном первичном напряжении при этом Z2 = Z2BHy, и сопротивление в скобках формулы (182) получает величину:
Z7
zi + . , <85>
1 Т ‘а ^2вн v
317
формулу (182) мы для этого случая напишем так, обозначая первичную силу тока при коротком замыкании и нормальном первичном напряжении через
Й-4Л- <186)
Заметим, что асинхронный двигатель характеризуется часто названием „всеобщий трансформатор" на том основании, что в роторе его тран формируется не только напряжение и сила тока, как в обыкновенном трансформаторе, но и частота. Обыкновенный трансформатор является в своей области — трансформирования напряжения и силы тока — аппаратом более совершенным, чем асинхронный двигатель в той же роли, ибо в последнем есть воздушный прослоек и намагничивающий ток в нехМ поэтому больше. Главным его применением является его работа двигателем, т. е. трансформирование же электрической мощности в механическую. Кроме этого он употребляется еще в качестве фазорегулятора и потенциал-регулятора, но в измененных включениях, которых мы касаться здесь не будем.
Работа обыкновенного трансформатора при Jf2BHe = 0 с математической стороны может быть совершенно уподоблена работе асинхронного двигателя, последний воображают заторможенными стоящим неподвижно, причем в цепь его ротора введено такое сопротивление /?2вне, что сила тока Л в роторе та же самая, что при некоторой механической нагрузке его в о время хода. Таким образом механическую нагрузку и ток J2 частоты а/, где s — скольжение, заменяют электрической нагрузкой и током той же силы Ja, но частоты /.
§ 91. Аналитический вывод круговой диаграммы тока
Если AT2BHe = O, то, как указано выше, работа трансформатора со стороны математической ее теории совершенно подобна работе асинхронного двигателя. Если мы при этом будем менять /?2вне, т-е-на-рузку, то первичная сила тока будет изменяться по величине и фазе, причем конечная точка вектора будет занимать различные положения на плоскости чертежа по отношению к вектору напряжения Vr Как было уже сказано, геометрически местом положений этой конечной точки является окружность. Докажем это. Исходным пунктом нашего доказательства явится соотношение (182). Для упрощения дальнейших выкладок диаграмму 146 представим себе начерченной так, чтобы вектор первичного напряжения V* совпадал по направлению с вертикальной осью, т. е. с осью действительных величин. Общности дальнейших заключений такой вы. бор направления вектора нисколько не затрагивает, как было 318
разъяснено раньше. Тогда составляющая вектора по оси мнимых величин равна нулю, и мы имеем:
Вектор первичной силы тока мы представим в комплексной форме; __
А = /В;
так как А есть проекция вектора на вертикальную ось, т. е. на направление Vv то А равно ваттной составляющей силы тока (относительно напряжения), Д=/в> а В как проекция на направление перпендикулярное, равно безваттной составляющей, B = J6^ мы ввели буквы А и В вместо JB и /бв для того, чтобы облегчить рассматривание следующих далее алгебраических выкладок.
После этого мы переписываем соотношение (182) в таком виде;
(V, 1 + Ya z?=(л + z;+Ya Z^).
Подставляя сюда комплексные выражения всех величин:
Ya = Sa— Jba>
__Zg ^2 ~Ь М'гвну ^2 , . ^2 в ну । .у
2 U2 U2 К2\'Л2ыу
и получаем:
v,[i+^+^B„y *в+/(^вНУ£,-я; *0)ь=
= (Л -jB) {+ jX. + /?' +;• х2вну 4-g, (ЭД + Х^2вт) 4-+ + W +J {ga Мвну + ед? -
-^ед-ед^п-
Приравнивая друг другу действительные части, а также мнимые, получаем два уравнения:
v/14-R'2ga4-х, РНА)=А [Я,+/?; 4- ga(R^2-Х.Х' у+
+*в(ед.иУ+ед?] + +едг) - ba{R^2 -
~I- •‘^гвнуЬ
^(^вну ga - /???=ед+*;вну++ед? -- UR& - Хгх:^)] - ед 4- /?’ + g^R.R, - едВН¥) 4-+*а(ед;вну+ед?]
В этих двух уравнениях переменны составляющие силы тока А и В и сопротивление /?2> включающее в себя переменную нагрузку;
31»
исключим эту последнюю величину из этих двух ур*ний, и мы получим одно ур-ние с двумя переменными А и В. Затем мы можем истолковать А и В как координаты конечной точки вектора и посмотреть, какое геометрическое место в координатах А и В полученное ур-ние выражает.
Для исключения переменной нагрузки мы в обоих ур-ниях переносим все члены, содержащие R'2, в левую часть, а остальные члены в правую, после чего получаем:
#2 - * 1 + + W + B(R.ba - ад] =
= Л Pl + X’2my(R,ba - X,gn)} + + X.ba +
+ад]-^1+^В1Л);
- Щ>а + B(1 + Rtga + X.ba) + А(Ъ-Ьа-Xlga)] = =- ад+х2т^ьа - x,gay\4- ад 4- ^BHy(i + х,ьа 4-
4“ — ^l^iwySa-
Деля одно ур-ние на другое, после приведения к одному знаменателю и упрощений получаем:
{Хг 4- baz\+ад I ад Z* 4- 2(ад + ад)]} (д* 4- -
- 2(адвну4-baRx + v.a - г[ад 4- ад) +
4- адЛну + у]^ = - V^ba + X2myY^. (А)
Ур-ние это выражает круг, так как может быть> приведено к виду:
Половины коэфициентов при А и В, деленные на коэфициент при A2 -j- В29 как раз представят координаты центра круга Е и гр прибавив к первой части уравнения (А) квадраты этих координат, мы получим квадрат радиуса круга.
В уравнение (А) кроме напряжения V2 входят пять постоянных величин, вполне характеризующих трансформатор (и асинхронный двигатель): Rv Xv Х'вну, ga и ba.
В действительности они постоянны лишь между некоторыми пределами изменения нагрузки; с ростом последней, т. е. с ростом токов J2 и растет температура трансформатора , а с ее ростом растет сопротивление /?р которое таким образом при сильных изменениях нагрузки уже не окажется постоянной величиной; далее, потоки рассеяния в некоторой своей части идут ту или иную часть пути в железе, как было в свое время указано; при больших величинах сил токов Jj и У2 эти пути потоков могут перейти в со-320
стояние магнитного насыщения, и тогда потоки не будут расти пропорционально токам, а это будет обозначать, что коэфициент и 52вну, а следоват льно и величины в а) раз бо «ыиие— и ^2вну ^СвнР бУДУт уменьшаться с ростом нагрузки; наконец с ростом нагрузки будет расги и падение напряжения в первичной обмотке (хотя и из^-е яясь по фазе), и будет уменьшаться ЭДС злотому — и магнитный поток (физически — первопричиной яв яется соответствующее изменение результирующих ампервитков), и проводимость нама1ничения может при этом несколько измениться, скорее всего увели‘Ш1ься из-за уменьшения насыщения. Таким образом совершенной точностью круговая диаграмма не обладает Кроме непостоянства означенных пяти величин оказывает влияние и то обстоятельство, что напряжение и сила тока на диаграммах являются синусоидальными величинами, лишь „эквивалентными" действительно существующим.
В наши задачи, в теории переменных токов, не входит исследовать, какие указания относительно целесообразного конструирования трансформаторов и асинхронных двигателей можно извлечь из свойств только что полученного круга, — это задача электромеханики, т. е. учения об электрических машинах; заметим лишь, что в истории электротехники эта круговая диаграмма тока имела большое значение.
§ 92. Эквивалентная схема, первый вид ее12
для вывода круговой диаграммы — называемым методо.м обращений
Возможны и другие пути особым геометрическим методом, и методом векторных уравнений, которые мы изложим в следующих главах. Для того чтобы метод обращений при менить к трансформатору или асинхронному двигателю, эти последние заменяются* или изображаются особой искусственной комбинацией сопротивлений и проводимостей, называемой эквивалентной схемой; для нее имеет место ур-ние (182); схема эта представлена на фиг. 152 и заключается в последовательном включении сопротивления Zj = RA -f-/Хг и двух параллельных ветвей: одной, в ко-21 Теория переменных токов. 321
торой дана проводимость Ya=ga—равная проводимости намагничения трансформатора, и другой с сопротивлением Z'T Напряжение V3 на зажимах АА то же, что у трансформатора (или асинхронного двигателя).
Проводимость двух параллельных ветвей равна сумме их проводимое) ей: __
у- , 1 +
e'1~ z; z'
их эквивалентное сопротивление есть величина обратная:
l±KflZ2’
полное сопротивление включения от 4 до В есть:
т. е. точно такое же, какое, по формуле (182), представляет нагруженный трансформатор. Если мы будем давать величине Z'2 те же значения, что и в случае трансформатора, то сила тока будет одна и та же по величине и по фазе в обоих случаях и из* меняться будет по одному и тому же закону.
После того как J3 прошел сопротивление Zv произошло падение напряжения JjZp и осталось напряжение между точками Л4 и N, равное:
^mn~ Л А»
что, в свою очередь, по формуле (178), равно — Сила тока в ветви с проводимостью Уа равна:
т. е. равна силе Сила тока в
тока намагничивающего Ja (формула 180).
ветви с сопротивлением Z' равна:
у___ Клглг__
2~ Z1 ~ ’
2 _ 2 —
Последняя величина равна (—J2-«)> если J2 есть вторичный ток трансформатора при том же 2^, так как, согласно формуле (181),
2
822
Таким образом в эквивалентной схеме сила тока разветвляется на две по уравнению:
Л = Та + (— 4-«) = 4 + ^» (187)
что опять находится в полном согласии с разложением тока в трансформаторе и формулой (179). Таким образом между работой трансформатора и работой эквивалентной схемы существует полное подобие. ___
Изменяя в эквивалентной схеме ваттную часть сопротивления Z^ мы будем изменять первичный ток совершенно так же, как он изменяется при безиндукционной нагрузке трансформатора (или при механической нагрузке асинхронного двигателя).
Можно изменять и ^чне и ^2вне> и в будущем мы будем рассматривать как наиболее общий и этот случай, с одним лишь ограничением, именно, чтобьГ при этом coscp2BHe оставался постоянным.
§ 93. Другой вид эквивалентной схемы18
Уравнению (182) может удовлетворить и другая схема, которая получается следующим образом.
Введем вместо полного сопротивления нагруженного трансформатора (или асинхронного двигателя и пр.) его полную проводимость; она равна:
у
“е Z^Z'2-\-Z,Z'2Ya (I + ^ZJZ'+Z, '
Произведем здесь деление числителя на знаменатель, но только до первого члена частного, прибавив остаток:
— ___ к I 1
Гвсе“ 1ТВД+(1 + уа А)24 + (1 + К ЗД •
Введем для большей краткости _ обозначения:
1 + К^-с;
тогда
— К 1
у = -4^7 4- =-----=-==.
все с CiZ2-\-CZ1
Таким образом проводимость
всего включения представлена как фиг# 153
сумма двух проводимостей, следова-
тельно эквивалентная схема должна иметь две параллельные ветви, они и изображ ны на фиг. 153, где показаны сопротивления ветвей.
На этой схеме переменными могут быть и R'2 и Х'2, это случай более общий, чем безындукционная нагрузка, когда Х’> — Л^вну — пост.
21*
323
ГЛАВА XII
МЕТОД ОБРАЩЕНИЙ, ПРИЛОЖЕНИЯ ЕГО К ВЫВОДу ДИАГРАММ ТОКА И НАПРЯЖЕНИЯ
§ 94. Взаимнообратные кривые
Две кривые ММ2 и МГМ\ (фиг. 154) называются взаимнообрат-ными относительно некоторой точки О, если произведения длин радиусов-векторов, совпадающих по направлению, от этой точки О до кривых представляют величину постоянную, т. е.
ом- ом'= омгом\ =
Величина К называется и М\ Mi и М\ называются
степенью обращения; точки М соответствующими, всякой точке одной кривой соответствует при этом некоторая точка другой; точка О, из которой проводятся радиусы-векторы к кривым, называется центром обращения.
Из определения взаимнообратных кривых следует, что если дана какая-либо кривая, то, приняв некоторые величины, пропорциональные обратным величинам радиусов-векторс в и^ произвольной точки О до данной кривой, за величины радиусов-векторов от той же точки О по тем же на-
правлениям до новой кривой, мы по-
лучим эту новую кривую как горциональности при этом есть центр обращения.
В основе приложения идеи
обратную данной; коэфициент про-степень обращения, а точка О есть
обратных кривых к явлениям пере-
менного тока лежит следующая
элементарная теорема.
324
§ 95. Основная теорема
Коивой, обратной данной окружности, является другая окружность, причем центр обращения является центром их подобия, а бтношение подобие ее к первой равно частному от деления степени
обращения на произведение длин наибольшего и наименьшего радиусов-векторов из центра обращения до первой кривой.
Докажем эту теорему отдельно для трех случаев: 1) когда центр обращения лежит вне пер-вой окружности, 2? О когда он находится на ней и 3) когда он находится внутри нее.
Фиг. 15х
е р в ы й с л у-
чай. Пусть нам да-
на окружность с гентром в Сг и центр обращения в О вне
окружности (фиг 155). Построй окружность M2Q2N2 с центром С2 на продолжен, и прямой ОСГ подобную данной, г е. с общей ка-сател»ной, так, тобы отношение сходственных линейных элементов
о _ q2c2 _ ом2 = on2
Ьсг QjCj ОЛ/, ОМ1 рав' ялось
К
ОМг ONX'
При эюм условии имеем.
ом2_ К ONX OM^ON^
откуда омх-ом2=к (А)
и on2 к
OMj OMj-ON/
откуда ON2-ONj = K. (В)
Для некоторого произвольно взятого луча ОРХР2 б демиме.ь. ОР, _ ОМ, OS2~ON2
и OP2-OS2 = OM2-ON2.
А А А А
325
Перемножив два последние равенства, получим для этого произвольно взятого луча:
ОР1-ОР2 — ОМУ^ОМ2,
а следовательно по (А):
OPrOP2 = K> (С)
и аналогично докажем, что
OSVOS2 = IC (D)
Соотношения (С) и (D) показывают, что вторая окружность действительно является обратной первой. Следует заметить, что для точки Рг соответствующей точкой является Р2, в то время как при рассмотрении одного лишь подобия окружностей ей соответствовала бы точка S2. При повороте луча ОРуР2 около центра О соответствующие точки Pj и Р2 или и 52 движутся по их окружностям в противоположных направлениях. Для построения окружности С2 всего лучше исполкзовать именно соотношения (А) и (В), т. е. найти точки ТИ2 и Д/2 — концы диаметра искомой окружности.
Очевидно, что чем ближе центр обращения О будет находиться к окружности Cv тем больше при одной и той же степени обращения буд-.т радиус окружности С2 и тем больше будет становиться расстояние ОМ2, свя данное с уменьшающимся ОМг со-огношением (А). Когда центр обра
щения О будет находиться на окружности, т. е. в Mv мы будем иметь второй случай, подлежащий. исследованию.
Второй случай. При этом ОМ2 равно нулю, и ОМ2 равно из (А) бесконечности, тогда как из (Б)
°N* ONT /Wj/Vj ’
(Е)
Окружность С2 с бесконечно-большим диаметром есть прямая, проходящая через точку N2 на расстоянии
очевидно
/< ----- от ж.л/,
центра обращения и направленная перпендикулярно к линии диаметра
На йиг. 156 изображена такая прямая. Из чертежа ясно, что
для любого луча OSyS2
OS^ _ ON2 ~ OS. 9
326
и следовательно, принимая во внимание (Е):
OSrOS2 = ONVON2 = K.
Когда центр обращения передвинется еще, он окажется уже внутри данной окружности» и мы будем иметь:
Третий случай. Строим, как и в пе ^вом случае, окружность с центром С2 на продолжении линии С1М1 с отношением ее ли-
нейных элементов к сходственным элементам первой данной окруж-
ЛГ OM^ON/
ности, равным
и с центром подобия в О.
На фиг. 157 M2P2N2S2 представляет такую окружность. Проводим произвольный луч P2OS2. По подобию окружностей относительно точки О имеем следующий ряд равных отношений:
Соединяя четвертое отношение с самым последним, получаем:
ОТИ2_ К
ONy ~ OM1-ONy 9
пли ОМ1-ОМ2 = К. (А)
Соединяя с последним — пятое, получим:
ONVON2^K. (В)
327
Езяв пятое и шестое отношения:
ON. OS.
ОМА~ОР^
Умножим это равенство на равенство
OMvONy = OS1 ОРи
после чего получим:
ON^ON2 = OSVOSV или
OS2-OS2 = K
А так как третье и шестое отношения дают:
ОР2 OS.
OSr ~ ОРг ’ то и
ОРг-ОР2 = К.
В этом случае соответствующие точки Рг и Р2 (или и S2) при повороте луча движутся по своим окружностям в одинаковых направлениях.
Равенства-(А) и (В) представляют простое средство для построения искомой окружности и в этом случае.
Очевидно, что, увеличивая степень обращения К, мы будем удалять во всех трех случаях окружности друг от друга, уменьшая ее,— сближать их, причем при некотором значении величины К они коснутся, затем при дальнейшем уменьшении ее будут пересекаться.
При K—OM1*ON1 в первом случае окружности сольются, в третьем случае будут равны и симметрично расположены относительно центра обращения О.
Далее, необходимо заметить, что, если центр обращения находится внутри одной окружности, он при всякой степени обращения будет находиться и внутри другой.
Все геометрические выводы, связанные с изложенным выше, читателю рекомендуется проделать со всей полнотой и во всех деталях.
Все разобранные три случая можно объединить в одной, так сказать, кинематической картине: при данной степени обращения по мере приближения центра обращения к первой окружности диаметр второй растет и делается бесконечностыд, т. е. окружность становится прямой, когда центр обращения доходит до первой окружности; при дальнейшем его продвижении уже внутрь эта прямая изгибается опять в окружность сначала большого, потом все меньшего радиуса, но уже в противоположную сторону.
328
Эта же картина получается весьма просто из случая первого тем способом, который носит название „приложения алгебры к геометрии
Очевидна справедливость и следующей теоремы, обратной вышерассмотренному второму случаю: дана прямая (фиг. 158) ВМ' и точка О вне ее; кривой, обратной прямой относительно О, являе ся окружность OMAV проходящая через О, с центром Сг на перпен-
дикуляре из О на прямую и с диаметром, равным частному от деления степени обращения на длину этого перпендикуляра, т. е.
Нужно заметить, что й окружность ОМ"Л2, проходящая через О, с диаметром ОЛ2=ОЛ1 и центром в С2 обратна прямой В/И', а пот >му при обращении окружности в прямую или прямой в окружность возможны всегда два
решения — следует выбирать их,
сообразуясь со смыслом решения илц удобством.
Мы в последующем будем всегда поступать так: строить сначала окружность Ср т. е. с центром в той же стороне от центра обращения О, в которой находится и обращаемая прямая, а затем рассматривать, удовлетворяет ли эта окружность физическому смыслу задачи и не нужно ли ее заменить окружностью С2.
§ 96. Координаты центра и радиус обращенной окружности
Далее, нам нужно будет уметь выразить координаты центра и радиус обращенной окружности и степень обращения.
Пусть радиус первой окружности будет г, координаты ее центра т и п\ соответствующие величины для второй окружности обозначим через И, ni и nf.
На основании только что изложенной теоремы
т' _ К т ~OMVON^
а та< как ______
= ]//п2 -|- п2 — г
и
ON1 = У т2 4* «2 + Л
329
то
Г is М
т ^‘w2 + «2—г2
и аналогично
-> __ у п /п2Н-л2 —г2’
? =/<’/л24-л2 —г2 •
(188)
§ 97. Обобщение предыдущего на случай пространства трех измерений
Очевидно, что изложенную выше для трех случаев теорему можно перенести без всякого изменения из плоскости в пространство трех измерений на случай обращения сфер одной в другую: стоит только представить себе вращение окружностей во всех трех случаях около оси ОС^ окружности образуют тогда сферические поверхности, а прямая линия в случае втором опишет плоскость.
Формулы (188) претерпят изменение, соответствующее введению трех координат вместо двух.
Метод обращений в пространстве трех измерений широко применяется при решении задач электростатики.
Вернемся опять к методу обращений на плоскости.
§ 98. Примеры приложения метода обращения
Перейдем к приложению идеи обратных кривых к изображению соотношений в цепях переменного тока14.
Пример 42. Пусть мы имеем цепь, схематично представленную на фиг. 159, состоящую из последовательно включенных безвапного сопротивления X постоянной величины, на-О---пример 3 ома, и ваттного сопротивления /?,
X-3Q меняющегося от 0 до 00. Оказывается, что
<> конец вектора тока J при изменении опи-сывает окружность. К доказательству этого <> мы и переходим.
3 На фиг. 160 точка О есть начальная точ-
Q- ..иг, UAi.igyQ
ка координатных осей, вертикальной и гори-Фиг. 159. зонтальной. Выбираем масштаб для сопроти-
вления, например 1 м]м = ~ ома, откладываем отрезок О А = -j- X о
(на чертеже X = 3 омам) и проводим через А вертикальную линию. Эта линия есть геометрическое место конечных точек отрезков ОМ, представляющих комплекс
z = /?+yx
330
знаме-
мощности откуда-то из другого источника,—никак генератор, а не как приемник электрической мы можем расширить наше представление об
на напряже-
на действительную, а не на комплексную дело.
при постоянном X и переменном /?. Мы видим, ^то эта линия естественно продолжается ниже горизонтальной оси, но там ния R становятся отрицательными Каков физический смысл этого? Если R отрицательно, то мощность J2R тоже отрицательна, следовательно физически мы имеем на месте R не сопротивление, а подвод электрической ша цепь работает энергии. Поэтому
изменяемости R и положить, что R изменяется от —00 до -|-00.
Если мы знаем значения переменной проводимости какой-нибудь цепи, то, умножив эти значения
ние V, приложенное к цепи, получим соответствующие значения силы тока. Вектор напряжения V мы направим по вертикальной оси, так что комплексное выражение его превращается в V = V; таким образом проводимости нужно множить величину, что упрощает
Проводимости обратны соответствующим сопротивлениям, поэтому при всяком состоянии цепи
Y-Z= 1.
Отрезки, изображающие проводимости У, в случае безваттного сопротивления X, обусловленного самоиндукцией (а не емкостью), откладываются от той же точки О в правом верхнем квадранте. Выберем масштаб для проводимости, например 1 сл = ^- мо, и обра-
У
тим прямую AM относительно центра О, взяв степень обращения равную единице; мы получим окружность 0М1В1 с диаметром, со-
ответственно всему изложенному, равным ~ = —мо, или 30мм. Ра-X о
диусы-векторы 0М2 представят величины, обратные величинам ОМ, * 1 V
и будут равняться-^, следовательно — как раз проводимостям г, только отложенным в левом верхнем квадранте Таким образом геометрическим местом концов отрезков, изображающих проводи
331
мости данной цепи, является окружность. Перевертываем ее около вертикальной оси, проходящей через О, из положения ОМУВ2 в положение ОМ" В, иначе — переносим центр ее из Сг в С, т. е берем второе из возможных решений, тогда отрезки, изображающие У, попадают на свое на лежащее место — в правый верхний квадрант, те, которые пол чились и отрезков Z с положительным/?, т. е содержащие положительное g,— в нижний же — те, которые получились из отрезков Z с отрицательным /?, а потому содержащие в себе отрицательное g Умножив все Y на I/, получим значения силы тока. Окружность при этом представит геометрическое место концов вектора силы тока. Те же отрезки ОМ" мы будем отсчитывать или измерять в масштабе силы тока, а этот масштаб возгмем в V раз мельче, чем выбранный нами раньше масштаб проводимости, тогда отрезки ОМ" прямо ;адут силу тока J для соответствующих величин сопротивления OM = R f jX
Заметим, что, когда цепь разомкну!а, /?=-|-ОО, - назовем это состояние цепи холостым ходом,— точка М находится при этом вверху на бесконечности, линия ОМ параллельна AM, и отрезок ОМ", а с ним и проводимость равны нулю; О есть точка холостого хода; ток холостого хода рачен нулю при уменьшении R точка М снижается, приближается к А; линия ОМ при этом поворачивается все вре^я влево, приближаясь к горизонтальному положению О А отрезок ОМ" поворачивается вправо, приближаясь к положению ОВ". Когда /? = 0, — будем называть это состояние коротким замыканием цепи,— Z — OA, a Y—OB"\ отре-з ж ОВ", измеренный в указанном масштабе силы тока, даст величину тока короткого замыкания цепи; точка В" есть точка короткого замыкания.
При всех обращениях геометрических мест концов вектора Z в геометрические мес^а концов вектора 4 Y следует иметь в ^иду следующее основное соотношение.
Так как
~Z^ZeJ\
то
Y= X = — е~К, Z Z
следовательно, Z и Y всегда наклонены по вертикальной оси под равными, но и противоположными по знаку углами. На это соотношение мы обращаем особое внимание чи>ателя.
Обращая кривую (или прямую), нужно всегда находить на обратной кривой характерные точки, соо ветствующие характерным
332
точкам на первой кривой, каковы например точки холостого хода и короткого замыкания.
Чтобы упростить умножение Y на I/, мы V направили по вертикальной оси и тем избавились от мнимой части в его выражении, что’ в свою очередь сводит умножение Y на V к умножению лишь длины переменных отрезков Y на постоянное число V без поворота их, как это было бы при умножении на комплексное выражение. В последующе мы будем вы ирать направление V так же, так что всякая диаграмма для величин Y будет в масштабе в V раз более мелком являться диаграммой силы тока.
На диаграмме фиг. 160 непосредственно для каждой величины силы тока J мы можем отсчи ать или измерить и угол ср сдвига фаз тока с напряжением V
Рассмотрим другой пример.
На фиг. 161 дана схема включения, где /? постоянно, а Х=
, 1
= (о£,— —переменно и может быть положительно, когда в цепи
доминирует самоиндукция, и отрицательно, когда емкостный эффект больше индукционного.
Фиг. 161. Фиг. 162.
На фиг. 162 прямая SQ есть геометрическое место векторов полно- о сопротивления Z = /? 4 jX\ при X = 0 имеем Z = ОД; если X=-|~OO» т- е- когда L — QO, а С конечно или тоже бесконечно-велико (последнее означает, что цепь замкнута и конденсаторов, последовательно с L включенных в цепь, н е т), тогда Z = оо и совпадает с левой оложительной осью абсцисс; если Х=— 00, т. е. когда L конечно или равно нулю, а С = 0 или бесконечно-мало (если конденсатора в цепи нет, а цепь просто разомкнута посредством рубильника, то две части рубильника— нож, с одной стороны, и щеки, куда он врубается, с другой стороны, представляют весьма'малую емкость, — пусть читатель оценит порядок величины этой емкости), тогда Z =— СО и 'совпадает с правой отрицательной осью абсцисс.
Обращая прямую SQ относительно точки О, получаем окружность ОВ Остановимся подробнее на вопросе о масштабах.
333
Если для сопротивлений взят масштаб Хмм^т омов, то О А (измеренное в миллиметрах) y^m = R\ масштаб для проводимостей пусть будет 1 мм = п мо; тогда ОВ (измеренное в миллиметрах) 1 /? 1 1
X п = —; или О А ~ мм и ОВ ~ -=г- мм, так что О А • ОВ=--.
R т Rn т^п
Следе 1вием этого является, что произведение и всех других, соответствующие друг другу радиусов-векторов тоже будет равно величине т. е- величине, обратной произведению масштабов.
Итгк степень обращения на чертеже (когда меряется в миллиметрах длина линий) равна:
К=—. т-п
Какой-нибудь величине Х~АМ, или, иначе, вектору Z = ОМ, соотве ствует вектор проводимости У=ОМ". По величине он равен отрезку ОМГ, а углы наклона их к вертикальной оси равны,
Фиг. 163.
Проводимость части 4W цепи, фиг.
но противоположны по знаку.
Левой половине прямой SQ соответствует правая половина окружности, а правой половине прямой — левая половина окружности.
Как следующий пример применения мето-_да обращений, рассмотрим задачу, решенную в параграфе 39 аналитически: те же два значения для С в случае отсутствия сдвига фаз между током и напряжением на всей цепи мы можем найти и графически.
62,
при изменяющемся С есть величина переменная. Геометрическое место концов векторов, представлющих эту переменную провэди-
334
мость, есть на фиг. 163 прямая линия AQt параллельная мнимой оси и проходящая от нее на расстоянии
OA=g=~-.
Интересной особенностью ее является то, что она, будучи бесконечной в сторону возрастания положительных мнимых величин, имеет начало на оси ординат, чему соответствует значение
6 = 0, С=0.
Если бы нам было задано, что параллельно с /?2 включено вообще безваттное сопротивление, то нам следовало бы эту линию считать бесконечной в обе стороны, но так как задано, что в параллельной с Т?2 ветви включена именно емкость и мы не считаем, что вместо нее может оказаться надобность в самоиндукции, то и упомянутую прямую линию мы будем считать имеющей начало в Л
Обратив эту прямую относительно точки О, найдем геометрическое место концов векторов, представляющих сопротивление между М и N. Эго будет окружность
На основании сказанного выше о масштабах и степени обращения имеем:
и
ОВ = ---= Цг- мм,
ОА-т-п nR2
так как пл 1
О А = —— мм. mR2
Обратим внимание на следующее. Так как прямая не имеет* другой половины от А вправо (т. е. эта половина не имеет для нас смысла), то и окружность будет иметь для нас только одну половину OS2S2B. ___
Но если какой-нибудь вектор ОЛ11 есть проводимость Y2 при емкости, то соответствующее ей сопротивление Z1 = Od1 должно быть отложено в правом квадранте, согласно с изложенным выше.
Следовательно, решив задачу геометрически, т. е. найдя половину окружности мы сообразно физическому смыслу дол-
жны ее повернуть в правый квадрант в положение ON^N^B.
Ко всем векторам из О в точки этой дуги, представляющим сопротивления части цепи 'MN, надо прибавить сопротивление
835
т. е. постоянный вектор, идущий из О в левом квадранте, что сдвинет всю полуокружность влево.
Вместо перечерчивания полуокружности проще перенести начало координат вправо на ту же длину
(<о£)2
по противоположному направлению, т. е. перенести его в точку Ог, причем
ОО2 — — (/?! + J&L).
Радиусы-векторы из в точки полуокружности дадут сопротивления всей цепи.
Чтобы сила тока совпала в фазе с напряжением, надо, чтобы сопротивление не имело безваттной части, т. е. чтобы вектор его не имел горизонтальной составляющей. Проводим линию OtN2 || ОВ и находим точки и М2 пересечения ее с полуокружностью O-lN1 и Ог№2 будут те сопротивления, которые имеют только ваттную часть. Переносим точки и Л72 на левую половину окружности в Sj и S2 и в пересечении направлений радиусов*векторов OSt и OS2 с прямой AQ наводим точки Мг и М2.
ОМ2 и ОМ2 будут проводимости части цепи MN фиг. 62 для этого случая
Проектируя эти точки на ось мнимых величин, находим точки D1nD2, Отрезки OD1 и OD2 дают нам величины безваттной проводимости to С, деля их на <о, получаем два решения для С.
Геометрическое условие возможности решения задачи очевидно заключается в том, чтобы вертикальная прямая OTN2 пересекла окружность или коснулась ее, следовательно решение возможно, если ТОг меньше радиуса окружности, или
То же самое условие было нами получено и в конце § 39.
§ 99. Круговая диаграмма трансформатора и асинхронного двигателя. Первая эквивалентная схема 15
Переходим к более сложному случаю.
Фиг. 152 изображает схему включения, эквивалентного трансформатору при безиндукционной нагрузке и асинхронному двигателю Сила первичного тока для этого включения изменяется с нагрузкой совершенно так же,— как было выяснено,— как и в трансформаторе или двигателе. Найдем, как изменяется проводимость 336
йСего включения с изменением нагрузки, т. е. величины сопротий* ления /?2вне» Умножая, как выше, проводимость на постоянную величину напряжения V или уменьшая масштаб для силы тока в V раз сравнительно с проводимостью, мы получим закон изменения силы тока.
Выберем прежде всего масштабы для сопротивления и проводимости, затем построим (фиг. 164) линию AM, параллельную вертикальной оси на расстоянии ЛО2 = Л^ВНу от нее» радиусы-век-торы О2М представляют сопротивления „ветви нагрузки*
Z2 =“= #3 вну + $2 вне +/-^2 вну .
при переменном /?2вне. Когда зажимы вторичной катушки трансформатора замкнуты накоротко, во вторичной цепи трансформатора имеется сопротивление
^2 ^2 вну ^2 вну Н* J^2 вну ’
такое же сопротивление будет и в „ветви нагрузки* эквивалентной схемы, и это состояние всего эквивалентного включения мы назовем коротким замыканием. При работе асинхронного двигателя такое сдстояние получается, когда ротор, замкнутый накоротко, заторможен вполне.
Радиус-вектор О2К представляет ^вну, и точку К назовем точкой короткого замыкания.
Когда точка М спустится ниже К, мы будем иметь введенным в ветвь Z'2 отрицательное сопротивление /?2 вне, т. е. будем иметь здесь ввод электрической энергии в наше включение, оно будет работать при этом генератором и передавать энергию в первичную цепь.
Когда ветвь Z2 разомкнута, тогда /?2внв = оо,и точка М удалена на бесконечно-большое расстояние, при этом радиус-вектор О2М принимает положение вертикальное и по величине бесконечно велик.
Обратим прямую AM относительно точки О2 со степенью обращения, равной и мы получим окружность O2M"Mk^ с
центром в С2 и диаметром, равным —?—. Радиусы - векторы ОМ" А2вну
представят проводимости „ветви нагрузки", отложенные однако не в надлежащем еще квадранте. Точке К соответствует точка —*
это есть тбчка короткого замыкания; точка О2 соответствует бесконечно-удаленной точке М и есть точка холостого хода, когда ветвь нагрузки разомкнута. Между точками М и /V включения 22 Теория веретенник токов. Я Я 7
фиг. 152 кроме ветви нагрузки есть еще ветвь е постоянной про* водимостью Ya=ga — jba\ прибавив ее к радиусам-векторам О2ЛГ, мы получим всю проводимость между М и N; чтобы прибавить Ya, откладываем O2N==ga и №г—Ьа\ тогда ОгМ№ есть вся проводимость между М и N (обеих ветвей) при соответствующей нагрузке (некоторой величине КМ переменного сопротивления #2 вне)*
Следует хорошо уяснить следующее: жвектор* проводимости намагничения должен был бы быть отложен в правом верхнем квад-
Фиг. 164.
ранте, т. е. ga вверх от О2, Ьа вправо от О2; такой вектор следовало бы приложить к вектору проводимости нагрузки, представленному зеркальным изображением в правом верхнем квадранте вектора О2ЛГ (ср. фиг. 160); мы же оставляем пока О2М" в левом квадранте, а потому и проводимость намагничения должны'пока изобразить вектором тоже в левом квадранте, т. е. ga вверх от О2, Ьа влево от О2; но приложить такой вектор к О2М"— значит приложить вектор ОгО29 как и сделано на фиг. 164.
Обратим окружность С2 относительно точки Ог со степенью обращения ““jp где 0^=® новый масштаб для сопротивлений (конечно можно выбрать и = и мы получим окружность М£М*
338
С центром в Cj как геометрическое место точек, расстояния до кб-торых от Oj представляют величины, обратные величинам О1Л1", т. е. представляют сопротивление (при разных нагрузках) цепи между точками М и N. Точке короткого замыкания соответствует точка которая на этом круге есть точка короткого замыкания; точке О2 соответствует точка M’Q — точка холостого хода на этом круге. Прибавим к этому переменному сопротивлению сопротивление , для чего отложим О15=7?1 и SO — X1; тогда радиусы-векторы окружности С7 из точки О представят сопротивление всего включения фиг. 152.
Обратим окружность относительно точки О со степенью обращения —-— и мы получим окружность MQMkT с центром Z7Z j * /Zj
в С, радиусы-векторы которой из О представят переменную проводимость всего включения. Точке М'о соответствует точка 7И0 — точка холостого хода; величину OMQ проводимость включения имеет тогда, когда ветвь нагрузки Z'2 разомкнута; точке M'k соответствует точка Mk— точка короткого замыкания; величину OMk проводимость включения имеет тогда, когда ветвь нагрузки имеет сопротивление вну вну, когда /?2вне = 0.
Так как проводимости цепи без емкости надо откладывать в правом квадранте, то повернем окружность С около вертикальной оси, проходящей через О; тогда мы получим фиг. 165.
Как и раньше, положим V— У, т. е. направим вектор V по вертикальной оси, а масштаб для силы тока Jj выберем в V раз меньше, чем для проводимостей; тогда круг MQM1Mk фиг. 165 явится геометрическим местом концов вектора первичного тока Jlt т. е. мы получаем круговую диаграмму тока. ОЖ0 есть ток холостого хода — такова сила тока в первичной катушке трансформатора, когда вторичная цень разомкнута и тока от вторичной катушки не берется; OMk есть ток короткого замыкания— такова сила тока в первичной катушке, когда вторичную катушку мы замкнем накоротко.
Наименьший угол сдвига фаз между первичным током и напряжением получается тогда, когда вектор силы тока касается окружности (на фиг. 165 положение ОЛ^). Трансформатор рассчитывается обыкновенно так, что его полная нагрузка соответствует точке и току ОЛ12 (то же — и для асинхронного двигателя).
Часть окружности в круговой диаграмме лежит ниже оси абсцисс ОХ; для точек этой части угол между вектором тока и вертикальной осью, вдоль которой направлен вектор напряжения, будет больше прямого, a cos ср будет отрицательным, т. е. и мощность y/jcoscp будет отрицательной; при этом следовательно наше 22$ 339
включение работает генератором, посылает электрическую мощность в первичную сеть. Для случая трансформатора это возможно, понятно, лишь тогда, когда ко вторичной катушке подключен генератор переменного тока (с тем же числом периодов), т. е. когда /?2 внв — отрицательно.
Как экспериментальным путем построить круговую диаграмму15, излагается в следующей главе (путем непосредственной нагрузки трансформатора или вообще включения фиг. 152 и измерения силы тока , напряжения V и мощности VJ1 cos ср, — откуда вычисляется ср, — этим путем можно получить только
часть MqMl круга, так как дальше наступают перегрузка и с ней перегрев, ниже же точки Мо эксперимент хлопотлив; часть круга обычно яв-
ляется, — вследствие своей небольшой величины и отступления экспериментально полученных точек от теоретической линии окружности, вследствие разных осложняющих обстоятельств — недостаточной для построения целого круга). На круговой диаграмме особым приемом можно отсчитать первичную и вторичную мощности, потери и коэфициент полезного действия всего включения.
Круговая диаграмма со вспомогательными построениями для этих отсчетов называется также диаграммой работы цепи переменного тока.
Чтобы видеть, какое влияние на диаграмму оказывают постоянные схемы замещения, полезно иметь выражения радиуса круга и координат его центра в функции этих постоянных, которые в построение диаграммы входят все время как координаты тех или иных точек. Воспользуемся ф-лами § 96. При неоднократном последовательном обращении эти ф-лы очевидно перепишутся в таком виде:
- ___is г\
'"k+l == К ч -------------5 ,
____„ пх
840
В разбираемом случае, полагая для упрощения письма ^2 вну =S ^2 ’
для окружности Ся имеем:
л1=°-
После переноса начала координат будет:
r=J_ т_______2 _1+2»Ла
s 2Х' 1~~2хЛ°а~~ 2Х.
Л Л &
«2=&,;
Я12 4"/г2 — ,2 =
' ^2
После обращения этой окружности получим для окружности Сг:
_ 1
Г* 2(^+ВД;
т —_!__а_±- •
8 2(*a+W
и —_
* ba+W, *
Последний перенос начала координат дает:
_____. v-'+^ + ^+W. г*~т, — т, + Х,—
v а • а а/
+ ba+Y^X2
2. 2 2 ^ + ^ + ^{1 + ^ + 2^+^)]
«4 + «4 “ Г1=-------£ J- Y‘X-------- ’’
а Г a 2
1
Г’ “ +V? +^2[1 + + 1
m. = r5 [1 + 26Л + 2Xi(ba + %)];
%-2rl(rA+^1+
подставляя r5 в выражения m5 и лб для сокращения письма.
Предлагаем читателю убедиться, что р, $ и 7], получаемые из ур-ия (А) § 91, отличаются от г5, тъ и п5 лишь множителем Vlf так как они относятся не к кругу проводимостей, а уже к кругу силы тока.
341
Эквивалентная схема фиг. 152, положенная в основу получения круговой диаграммы тока методом обращений, так же как и аналитический вывод § 91, относилась к случаю, когда ^2вне = ^» т* е* к случаю безиндукционной нагрузки трансформатора. Положим в основу дальнейшего несколько более общее условие: именно, пусть во внешней части вторичной цепи имеется постоянный по величине сдвиг фаз между током J2 и напряжением V2, т. е. постоянное отношение двух переменных величин и 2 вне частный случай, когда
; на фиг. 152 и 164 мы имеем тот = 0. Эквивалентную схему мы теперь будем изображать в виде, представленном на фиг. 166, где ВВ суть зажимы, к которым подключается внешняя часть вторичной ным рых ние зажимы вторичными.
Согласно с рассу-в конце § 92, силу тока (—J2u) вторичной силой тока, „приведен-для краткости же мы дальше эту
^2 вне ’
<?2v
цепи с постоян-<p2w и на кото-имеется напряже-V2. Назовем эти
ждениями перед ф-лой (187) обозначим через и назовем ной" к первичной части цепи; величину будем называть просто вторичным током.
Аналогично напряжение на зажимах ВВ, равное р — р 7 7 Ту7 и 2— 2^2 вну»
назовем вторичным напряжением, „приведенным" к первичной части цепи или — для краткости — вторичным напряжением, хотя не будем забывать, что в действительности вторичное напряжение, как ясно видно из фиг. 146 (вектор OS), равно:
^2 вну = а *4^2 вну ~ (у1 J2Z2 вну =
________ Z \ _
_r F
Комплекс Z^= есть вторичное сопротивление, приведенное к первичной части цепи.
„Приведение" величин вторичной части к первичной обусловлено существованием коэфициента трансформации и (в который у асинхронных двигателей входят еще и обмоточные коэфициенты) и может быть резюмировано в следующих правилах: приведенный
542
ток равен действительному, помноженному на и (отвлекаясь от знака); приведённое напряжение равно действительному, деленному на и (тоже отвлекаясь от знака), и приведенное сопротивление равно действительному, деленному на и2.
На фиг. 147 увеличение Д MLO линейно в — раз было
приведением вторичной части цепи к первичной.
Из вышеизложенного ясно, что выражения вторичной мощности
как в „приведенных" величинах, одну и ту же величину этой мощности.
Далее очень важно заметить, что включение фиг. 166 эквивалентно не только отдельному трансформатору или асинхронному двигателю, но, как легко видеть, и целой сети с подключенными к ней трансформаторами, двигателями, не только асинхронными, но и всякими другими двигателями переменного тока, умформерами, лампами и пр. Линия передачи энергии тоже эквивалентна схеме фиг. 166. Провода, передающие энергию и имеющие на своих концах нагрузку, по своей длине имеют равномерно распределенную емкость (ср. фиг. 63), каковую
так и в действительных дают
Фиг. 167.
можно заменить сосредоточен-
ной в оеном месте, что будет доказано в § 96, а это равносильно существованию ветви MN с положительным Ьа, т. е. с проводимостью ga-\“jb^ трансформатор^ и двигатели на конце проводов в этом случае представляют просто индукционную нагрузку между вторичными зажимами ВВ. При этом « = 1, и кроме того отпадает разница в знаке между приведенной силой тока и действительной, тоже для приведенного напряжения и действительного. При условии постоянства <р210 при изменении этой нагрузки для всех таких Сетей имеют место и эквивалентная схема фиг. 166,
и последующие выводы, и диаграммы.
Круговая диаграмма для случая ср2г,, не равного нулю, методом обращений получается следующим образом.
Построим (фиг. 167) вектор OK=*Z'2my9 отложив С^4=^2Вну и AK=R' Затем отложим любое значение = и со-Л ВИу Л
843
ответстаующее ему значение К2 = МИ; отрезок КМ изобразит одно из значений переменного z* вне, а радиус-вектор ОМ представит все Zj. При изменении Z'2 внв угол <p2v остается постоянным и точка М перемещается по прямой ЗГ, проходящей через точку К и наклоненной под углом ср2т, к вертикальной оси. Обратив прямую ST относительно точки О, мы получим окружность, изображенную на фиг. 167, с центром С на перпендикуляре, опущенном из О на прямую ST, Радиусы-векторы ОМ' будут величинами, обратными радиусам-векторам ОМ, т. е. представят проводимости ветви MBBN эквивалентной схемы фиг. 166, т. е. всей вторичной части цепи. Когда вторичные зажимы ВВ замкнуты накоротко, тогда Z’2 = Zg вну = ОК\ соответствующая точке К точка M'k есть точка короткого замыкания; точка О есть точка холостого xoia. Отложив OB = ga и ВО1 — Ьа, мы получим, что радиусы-ве кторы О2М' представят проводимости обеих ветвей вместе между точками М и М эквивалентной схемы. Далее вывод не будет отличаться от изложение го выше.
Для построения круговой диаграммы для существующей и работающей цепи переменного тока, которая может быть представлена эквивалентной схемой фиг. 166, при помощи метода обращений нужно знать Z' вну, Ya и Zjj определение этих „постоянных" экспериментальным путем оказывается весьма сложным. Построение круговой диаграммы или диаграммы работы цепи изложенным в следующей главе способом оказывается практически более удобным. Наоборот, для такой цепи (трансформатора, двигателя, линии передачи), которая только еще рассчитывается, проектируется, метод обращений бывает удобен; в особенности он удобен для теоретического исследования работы двигателей, основанных на новых принципах, новых схемах включения.
§ 100. Пример построения круговой диаграммы тока для первой эквивалентной схемы
П р и м в р 43. Требуется построить круговую диаграмму тока для цепи со следующими данными (фиг. 168):
Zi = 5 + /10; Z2 впу = 3 + /9; Ya = 0,004 + /0,020, Vi = 2 000 вольт; cos = 1.
Обращаем внимание _читателя, что в этом примере безваттная соста-. вляющая проводимости Ya положительна, что означает, что в Ya находится не самоиндукция, как в схеме трансформатора, а емкость, что и показано на фиг. 167.
Таким образом рассматриваемый пример может относиться не к трансформатору, а к линии передачи энергии во всяком случае по характеру зависимостей.
344
Фиг. 1С8.
Выберем масштабы: для сопротивлений 1 лмг = 7И = О,4 ома, и для проводимостей 1 мм = п = 0,00£ мо.
Строим (фиг. 169) вектор Z2BHy, откладывая 9 3
0^4 = — = 225 мм и АВ == — == 7,5 мм. 1 0,4 0,4
Продолжая отрезок АВ в обе стороны, получаем прямую FFi — геометрическое место концов вектора сопротивления Z2 = Z2 вну + вне-
Точка В есть точка короткого замыкания, когда /?2вне = 0, а бесконечноудаленная точка D есть точка холостого хода, когда /?2 внв == оо.
Обратив прямую FF{ относительно (?!, получим окружность проводимостей
Степень обращения равна;
К= — = Л . = i wv.
тп 0,4-0,001
Поэтому
_ _ К 2 500 ,,, , 0,0 = 7^-7 = 7^-=- = 111,1 мм
1 OiA 22,5 и О1С1==55,5 мм.
Продолжив линию O^Bt найдем в точке Mk точку короткого замыкания круга проводимостей. __ __
К кругу проводимостей У2 надо теперь прибавить Ya.
843
Не забудем, что проводимости Y2 должны были бы быть отложены jio правую сторону от вертикальной оси через О1 (фиг. 170); прибавляя]^, проводимость емкостного характера, т. е. с положительным Ь, мы, как видно из фиг. 170, передвинули бы всю окружность в новое положение; но проще передвинуть' в обратном направлении на ту же величину начало координат, т. е. поместить его в точку О2, причем О1О2 = -Л- Ya. Перевернув чертеж опять на левую сторону от вертикали получим то, что начерчено уже в масштабе на фиг. 169, где
0,001 . 0,02
°‘°=6Ж1=4 мм и 00а=бЖ1 мм-
Обратим круг Y2 относительно точки О2 и мы получим круг сопротивлений двух параллельных ветвей схемы.
Для этого вычисляем:
пкг К 2 500
0N* ~ ~ 19J5 ~126,7 мм
И
°"-=<я?;=29СТ=27'3"'
O2V2 4- ОМ2 = 154 мм
есть диаметр нового круга и
Л42С2 = 77 мм его радиус.
Продолжая линию О2ОЬ находим точку холостого хода М& а проводя О2Л4^, находим точку короткого замыкания ЛГ*.
Прибавляем к кругу С2 сопротивление Z{ = 5 + ДО, откладывая
ОаЯ=А=12,5 мм и
ЯО8 = ^ = 25 мм,
и получаем точку О3. Замечаем, что безваттное сопротивление НО3 мы отложили вправо от вертикали через О2, так как оно положительно и будет увеличивать безваттные составляющие всего сопротивления Z всего включения.
Чтобы найти проводимость Y всего включения, обращаем окружность С2 относительно точки О3, для чего находим:
п п __ К 2 500 ~лл
O3Qa ~ 102,5 ~ 24,4
Ло _ К _2 500 .
°8₽s ~ О3Р3 ~~ 51,5 “ 48,4 ММ
и P3Q3 = 72,8 мм\ это есть диаметр нового круга С3, радиус его
С3Р3 = 36,4 мм.
Если мы повернем весь чертеж (фиг. 171) около вертикальной оси через О3, то получим окружность проводимостей в правильном положении; большая часть ее будет находиться при этом справа от этой вертикальной оси.
346
Направим вектор напряжения по вертикали; тогда векторы от О8 до любых точек М окружности Y дадут нам силу тока в масштабе р, который определяется из соотношения:
(длина О3М)'П*2 000 = (длина ()$№)• р или
р = л-2 ООО = 2 или
1 мм = 2 ампера.
Выразим символически токи при холостом ходе и коротком замыкании. Проще всего нанесем на окружности тока (фиг. 171) точки Mq" и Измерением находим, что О3М^ = 44,4 мм, следовательно
Jlk = О3м£ • р = 44,4 • 2 = 88,8 ампера.
Меряем по транспортиру угол между М*'О9 и вертикалью через О3 или вычисляем его по компонентам отрезка О3м£, этот угол равен 64°18г. Следовательно
= 88,8е—•/64°18’ или
Л^вв^-'64’30.
Отрезок О37И0” = 24,5 мм, следовательно J10 = 49 ампер. Аргумент его получаем равным -f- 69°, так что
7w = 49e+'89°(
т. е. в данном примере ток холостого хода есть ток, опережающий напряжение.
§ 101. Круговая диаграмма второй эквивалентной схемы
В этом параграфе возвратимся ко второй эквивалентной схеме, представленной на фиг. 153, и на получении для нее круговой диаграммы.
347
Для вывода последней можно воспользоваться фиг. 167. Отложим согласно схеме фиг. 153 вектор
w=czx + c>Z;w
и проведем линию MKS под таким углом <р2 к вертикальной оси, что
<р2 = arc tg .
^2 вне
Обратив ее, получим окружность С. Любой вектор ОЛг до этой окружности дает проводимость ветви с нагрузкой (конечно не в надлежащем еще квадранте). К этой проводимости надо прибавить постоянную проводимость второй ветви, т. е. векгор
Уд С
= Yae-*
для чего и строим его зеркальное изображение, вектор
ОгО =
отложив отрезок ОВ равным ваттной составляющей вектора Уо и ВО3 равным безваттной его составляющей.
Повернув всю фигуру около вертикальной оси, проходящей через Ор получим окружность проводимости всего включения уже в надлежащем квадранте^ после изменения масштаба это будет и окружность тока.
Как видим, для этой схемы вывод получается много быстрее, чем для первой эквивалентной схемы. Что касается эксперименталь-
ного определения постоянных величин, положенных в основание обеих эквивалентных схем, то оно много проще при схеме второй. При холостом ходе,
и отсюда вычисляются
Jsincp
—у» очевидно, что
когда Z2BHe = oo, меряются V, J и Р, Р . Jcostp -
cos<p=pj, sin ср и величины ——- и
J cos ср
^sin(P____
V ~ с 0
равно проводимости включения при разомкнутой внешней цепи, К
т. е. проводимости ветви
348
При коротком замыкании, когда Z2BHe = 0, проделывается измерение тех же величин, обозначим их V, Jk и Рю и вычисляется
4C0S?fe AslntPft у v J v
проводимость всего включения при коротком замыкании. Из этой проводимости вычитается первая и получается проводимость ветви нагрузки при коротком ее замыкании:
У. — 70 = .
Величина обратная этой есть вектор ОК (фиг. 167): w=cZ,+az;
Таким образом имеются оба элемента, ОК и ОгО> необходимые для построения круговой диаграммы.
Заметим, что опыт короткого замыкания проделывается при пониженном первичном напряжении во избежание слишком большого перегрева трансформатора или асинхронного двигателя от большого тока короткого замыкания, причем изменились бы и сами „постоянные" #'2 вну, Xv Ya, и результат перевычисляется на нормальное напряжение.
349
ГЛАВА ХШ
ВЕКТОРНЫЕ УРАВНЕНИЯ И КРУГОВЫЕ ДИАГРАММЫ1*
§ 102* Выражение прямой линии и окружности векторными уравнениями
Мы можем в некоторых случаях по одному виду выражения одного вектора в функции других известных постоянных и переменных векторов судить о том, какое геометрическое место описывает конец этого вектора при изменениях его; в других, более сложных случаях требуется исследование того уравнения, которое связывает один вектор с другими.
Начнем с того, как выразить посредством векторов ур-ие неко-торой произвольно проведенной прямой линии MN (фиг. 172).
Проведем некоторый вектор OK=A=tAe^ из начала координат до некоторой точки К прямой. На прямой возьмем отрезок KL и назовем его вектором Положение точки L теперь
определяется суммой векторов А В, она есть конец этого результирующего вектора. Какая-нибудь другая точка М на прямой MN определяется вектором ОК-\-КМ, но KM = mKL=mBi где т— некоторое действительное число,, поэтому
^^'КМ = А^тВ.
Для точки N вектор KN имеет направление обратное вектору В:
A7V = —«В,
поэтому положение точки N определяется вектором
— пВ.
Нетрудно видеть, что общий вид выражения вектора U из О до точек прямой MN будет такой:
U=A-±xB, (I)
где х есть переменное действительное число. 350
Следовательно конец вектора U9 выражающегося согласно ур-ию (I), описывает прямую линию.
Рассмотрим пример.
Сопротивление цепи состоит из постоянного ваттного сопротивления /?0 и переменного сопротивления Z1 = R1 причем величины /?2 и X} меняются одна пропорционально другой, так что
tg<p=^- = COnSt (II)
и угол ср остается постоянным.
На фиг. 173 отложены Оа = /?0 и угол <р при точке а такой, что
ag^=Z1 = R1
Ур-ие прямой ар получается в виде:
O^=U=H0 + /i1-{-jX1, (III)
или, так как R1=cX1 из ур-ия (П), то
t7=/?o+(*+/)*!, (IV)
где переменно только Хг Если мы введем вектор
который, как читатель ^должен сам доказать, параллелен прямой линии ар или вектору ад, то ур-ие (IV) превращается в
и=7?04-вхр
в котором легко видеть частный случай ур-ия (I).
351
и1
(V)
Теперь рассмотрим, какое геометрическое место будет описывать конец вектора, выражающегося ур-ием:
z 1
Д-|~хВ
Построим (фиг. 174) два частных значения вектора U', именно: при х==0, которое отметим индексом k:
U'=~ = OMk к А
и при х = оо, отметив его индексом 0:
Ц=о.
Представим положительном
/ /
Фиг. 174.
себё теперь вектор U' при некотором произвольном значении х, пусть это будет вектор ОМ. Соединим
М с Mk и определим угол е между продолжением ОМ и MMk; окажется, что его величина будет постоянна и незави-сяща от х.
Определение его произведем следующим образом.
Угол е есть разность углов, составленных с вертикальной осью векторами ОМ и МК9 т. е. разность аргументов этих векторов.
На чертеже эти углы отрицательны (находятся в правом квадранте), поэтому, если мы вектор ОМ разделим на вектор
MMki то аргумент частного и будет угол е, что мы обозначим так:
е = arg
Вычисляем
ОМ
MMk
ММ' = ОМ.-ОМ=^-~ _
к * А А-{-хВ А(А^-хВ)
ОМ 1 хВ А А ,,
_—_= ______; ____=— —=----е1' ₽ >.
А±хВ А(А-}-хВ) хВ хВ
Итак ^МлМ^=^е = а —
т. е. действительно равен постоянной величине. 352
Отсюда мы делаем следующее важное заключение: при всех п о-ложительных значениях х конец вектора выраженного ур-ием (V), описывает дугу окружности ОММ& вмещающую угол
тг — s = тг — (а — р).
Рассмотрим, что будет, если х будет принимать отрицательные значения. Поставим вместо знака плюс знак минус перед х и будем давать ему всевозможные положительные значения, при этом некоторый новый вектор
ОМ' = ~ 1 >
А — хВ
тгг, х&
М'МЬ == -=-—----— = — =-=------=
к А А — хВ А(А — хВ)
и
Авл.-В,
M'Mk хВ а так как — 1 =cosn4z7sln н —
то, беря в показателе знак минус, чтобы не вводить углов больших 180°, имеем:
ОМ1 А н к
-----— —--- М'Мк хВ
следовательно
—тг4-б
или по абсолютной величине
/ МкМ'О = ъ.
Таким образом при отрицательных х конец Mf вектора U1 описывает дугу, вмещающую угол е; обе дуги вместе соста-вляют очевидно окружность. Ее легко построить: вектор OMk известен; из середины его т восставляем перпендикуляр тп, и при О строим угол
/М*ОС=&=-£- —е;
точка С встречи стороны ОС этого угла с тп и есть центр круга.
Можно было бы доказательство того, что вектор, выражающийся ур-ем
(7'==Д-^=,
А + хВ
23 Теория переменных, токов.
353
опишет окружность, построить и иначе, именно на основании известных нам уже теорем об обращении прямой в окружность.
Так как из ур-ий (I) и (V)
Z7-Z7'= 1,
то U и U суть взаимнообратные величины в том расширенном смысле, в каком взаимнообратны векторные величины, например Z и 7, так как
U=^UeJt, a Z7'=»-X- = —е-Л,
U U
квадрантах.
Согнем чертеж по оси ординат, тогда U* совпадет по направлению с U.
Если мы будем из-х менять х в ур-ии (I), то U опишет своим концом прямую линию, пусть это будет прямая MN (фиг. 175); отрезки £?, обратные по величине отрезкам £7,
Фиг. 175. опишут своими конца*
ми при этом окружность OPQ, проходящую через начато координат, которое, являясь началом всех радиусов-векторов, будет и центром обращения; для любого радиуса-вектора ОР будет
и следовательно
ОР-Ор = 1
0P=^TJ = U'
Сам вектор U* не есть однако ОР, а согласно предыдущему наклонен к оси ординат под таким же углом, но с другим знаком, т. е.
Геометрическое место концов вектора U при изменении х есть окружность ОР с центром в Со.
Таким образом ур-ие (V) выражает окружность.
Необходимо уметь находить на обращенной кривой точки, соответствующие точкам данной или первообразной кривой.
354
Допустим, что вектор А есть Ор> а В направлено от р к М; тогда при х>0 концы вектора U будут находиться на части pN, а при х<^0— на части рМ. Точка Рг {йзделит окружность ОР на две части: х^>0 соответствует дуге Р'тО, а х<0 — дуге PSO. Точка О соответствует значению т. е. обоим
бесконечно-удаленным концам прямой MN*
Далее рассмотрим ур-ие
1 А-\-хВ
Очевидно, что всякое Ц получается из некоторого (7 умножением последнего на один и тот же комплекс С=±СеЛ; при таком умножении U1 увеличивается в С раз и поворачивается против часовой стрелки на угол у. Поэтому все концы векторов Uf иЛи иначе вся окружность ОР (фиг. 175) будут увеличены в С раз и повернуты относительно этого начала на угол у.
Таким образом, если вектор U, определяемый ур-ием (I), есть Ор, то вектор Up определяемый ур-ием (VI), есть OPV
Возьмем теперь вектор, определяемый таким ур-ием:
Сравнивая ур-ие (VII) с ур-ием (VI) видим, что
т. е. если к любому Ц прибавить один и тот же вектор D, то получится соответствующее значение вектора Ц; другими словами, концы векторов U2 все сдвинуты на D относительно концов векторов Ur Поэтому геометрическим местом концов , (7а будет окружность того же диаметра, что и для векторов Uv но сдвинутая на D. _
Для ее получения нужно сдвинуть на D центр Cj прежней окружности ОРХ фиг. 175, оставив радиус без изменения.
Ур-ие (VII) можно преобразовать, приведя правую часть к общему знаменателю:
_ AD + хВР + С _ ЛТ-Н xN.
А-\-хВ А-\-хё'
где ________
и _ __
(УШ)
23* 355
Таким образом мы приходим к результату, что если переменный вектор имеет выражение (отбросим индекс 2 у t/2, теперь ненужный)
17=^+^ (IX)
А 4- xN
где A, В, М и N суть постоянные комплексы, ах переменное действительное число, то конец этого вектора описывает окружность, не проходящую через начало координат.
Чтобы эта окружность прошла через начало координат, должно быть D = 0 в ур-ии (VII), а это означает, что 0 в ур-ии (VIII) и (IX) и U приводится к виду (VI).
Когда дано ур-ие, выражающее вектор в форме (IX), окружность, которую описывает его конец, можно легко построить не переводя это ур-ие в формы (VII), (VI) и (V), а непосредственно, и именно вполне аналогично предыдущему случаю.
Дадим переменному множителю х в ур-ии (IX) два частных значения х—О и х==оо.
Им будут соответствовать два частных значения вектора U, которые мы обозначим, как и раньше:
при х=0, U—Uk и при х = оо, U—Uq.
Из ур-ия (IX) находим, что
Uk = ^-^ — ei^ (X)
А А
И
Здесь в правых частях все величины даны, поэтому векторы Uk и UQ легко вычислить.
Начертим векторы (фиг. 176)
ОЙ0 = Ц) и OMk=Uk.
На чертеже вектор Uk взят больше £/0, — в наиболее важных для нас дальше случаях так именно и будет, но при других физических значениях векторов U может быть и обратное.
Отрезок ОМ представляет вектор U, соответствующий некоторому положительному значению х между 0 и оо, это есть любой вектор U. Соединим между собой точки М и Мк,
356
7И0 и М и наконец MQ и Mk; продолжим линию ЛТ0/И за точку М в виде МК.
Угол £MkMK есть постоянная величина, обозначим его опять через е, и докажем, что е от переменной х не зависит.
Угол в есть угол, на который надо повернуть вектор MMk навстречу линии времени, чтобы он совпал по направлению с вектором MQM, это есть угол опережения вектором вектора MMk. Представим себе, что мы делим комплексное выражение опережающего вектора MQM на ком-
плексное выражение отстающего фип
вектора MMk\ при этом аргументы их вычитаются, и очевидно, что аргумент частного и есть угол s.
Произведем указанное вычисление, для чего сначала выразим векторы MMk и MQM через данные,и вектор ОМ.
УТлл М М±хК (BM — AN}x
k k A A-\-xB (A^xB)A
M+xN* N BM-AN /VTT4
ALM = ОМ — ОМЛ — —--= =- — . (XII)
0 A^xB В (A±xB)B
Теперь разделим второй результат на первый: S-=A=AeA.-(>, ММЛ хВ хВ
откуда следует, что б = а —р. (XIII)
Так как углы аир нам известны, ибо известны A — AeJ* и В = то и s определится, и окружность мы построим по углу
Пример 44.
Л==3^70°, В = 5^10°, Л? = 60е--'5°> N = 25e-^°°, так что
-7_60е--'5° -Ьх?5е--'70°
Зе^ 4- х5е/1и°
357
Построим окружность, являющуюся геометрическим местом концов
этого вектора £7. Вычисляем
Z7,=4- = 5e-'809, В
л А • = «-^60*
a sb <— t == 30°.
Л
Откладываем (фиг. 177) под углом — 75°, т. е. вправо от вертикали, отрезок OMft=100 мм, выбирая таким образом-ма^ штаб 1 мм~ 0,2 еди-
ницы той физической величины, которую представляет собой £7; затем под углом —80° отрезок ОМ9 = 25 мм, т. е. представляющий величину 5 указанных единиц.
Откладывая при Af0 угол & = 30° и проводя его сторону, находим в пересечении ее с перпендикуляром, восставленным из середины центр С искомой окружности.
Если при таких построе-
ниях угол а получится отрицательным, его надо отложить вверх от линии а не вниз.
Предлагаем читателю проделать цостроедие для следующего случая:
Пример 45.
А=*3е 12 ", ~ff=s2, М —100, N=20e Т
й проверить местонахождение концов вектора £7 для некоторых значений величины х, например одной положительной (верхняя дуга М^ММ^) и другой — отрицательной (нижняя большая дуга как в этой задаче,
так и в предыдущей.
§ 103. Применение метода векторных уравнений к первой эквивалентной схеме
Уравнение, которое послужило нам основанием для создания первой эквивалентной схемы, было следующее (182):
Выразим отсюда ток через напряжение и проводимость всего включения:
(189)
858
Полагая, как и раньше, V=Vv мы можем геометрическое место концов векторов Увсе считать за геометрическое место концов вектора силы тока Jv
Перейдем к исследованию выражения вектора
Прежде всего разложим Z'2 на два слагаемых: постоянный вектор 2^ и переменный вектор Z'2 вне = га +/а;2. Затем введем условие постоянства угла <р21?:
Т- = fg <?2о в C0I1St = k>
rt
так что
Х8=еГяА.
Тогда
Вектор 1 4” jk имеет угол ср, равный (р2о, ибо tg(p==A = tg<p21>
(отличаться же на и эти углы не могут); таким образом
1 -\~Jk = H—He^w
(190)
Будем здесь г3 считать отвлеченным числом, а размерность сопротивления отнесем к вектору Н.
Преобразуем теперь выражение yLe, стараясь придать ему один из изученных в предыдущем параграфе видов.
у ______
“ +г; + w;
В знаменателе первые три члена группируем следующим образом:
+ ^2 вну вну = %>2 вну 4“ -2^(1 4~ вну) e
-a+i?,„p fe+. Af—)• (isi)
1 г 1<Г'2 вну'
Здесь выражение в больших скобках представляет величину сопротивления всего включения при коротком замыкании, когда Двне=0, и поэтому ^2=^'ВНу’ что Уже было указано в § 90, где это выражение обозначено через Zk, ф-ла (185).
359
Введем следующие обозначения, частью уже встречающиеся и
раньше: 14-Ув^=с, (192)
(193)
— V с °’ (194)
Z2 (195)
Из ур-ния (191) получаем: Z1 + Z2BHy + Ya Z1 Z2BHy — Ck Zk- (196)
Тогда FBCe можно представить в таком виде: (197)
ВСе CkZk + r2CH
В этом выражении в правой части переменна только одна величина г2, так что ур-ние (197) есть векторное уравнение типа, данного ур-нием (IX) Если мы в ур-нии IX считали х за отвлеченное число, то и в ур-нии (197) г2 мы сделали числом отвлеченным, отнеся размерность сопротивления к Н.
Таким образом на основании результатов предыдущего параграфа мы заключаем, что конец вектора YQZ^ а следовательно и Jv описывает окружность.
Когда г2 = 0, мы имеем короткое замыкание, и из ф-лы (197) у =—•
все k ’уГ9
когда г2 = оо, мы имеем холостой ход и, деля числитель и знаменатель на г2 и полагая затем его равным оо, получаем:
F —~Y
* все О л О’
§ 104. Экспериментальное построение окружности тока
Следует остановиться на экспериментальном построении окружности тока.
Из опыта холостого хода мы находим три величины V19 J10 и Ро, где через обозначена первичная сила тока при холостом :оде. Отсюда мы вычисляем
360
и, отложив под углом (— ср0) к вертикали отрезок длиной J10, получаем точку Мо холостою хода на искомой окружности (фиг. 178). Из опыта короткого замыкания мы находим опять три величины: Vt (оставшееся без изменения), и Pk.
Раз навсегда заметим, что опыты короткого замыкания обыкновенно приходится производить при пониженном напряжении, во избежание слишком большого перегрева включения от тока ко
роткого замыкания, а потом в расчет вводить нормальное напряже
ние и пропорционально увеличенную
силу тока; мощность же для введения в расчет при определении угла сдвига фаз нужно увеличить пропорционально квадрату отношения напряжений нормального к пониженному.
Вычислив
C0S(P*=y7-’
строим вектор тока короткого замыкания Jlk и получаем точку Mk короткого замыкания ца окружности (фиг. 178).
Чтобы построить всю окружность,
надо, как известно уже, найти угол е, Фиг. 178.
равный пр ур-нию (XIII) разности а — [J.
Вектору Я yjp-ния (IX) соответствует в ур-нии (197) вектор
СИ, а вектору А — вектор CkZk. Поэтому
= «= -===•
в сн
Нас интересует не модуль этого отношения, а только его аргумент. Соединяя и С в одну группу, можем написать:
__ __
s == arg =1 arg Zk — arg H. (198)
С
Что мы соединяем Ck и С в одно комплексное выражение, оправдывается дальнейшим. Для определения аргумента комплекса = необходим третий опыт, кроме описанных выше двух, именно опыт холостого хода „обратного", т. е. такой «опыт, когда напряжение прикладывается ко вторичным, а не первичным зажимам; при этом первичные зажимы остаются незамкнутыми, ни к чему не присоединенными.
На соотношениях, получающихся при этом опыте, следует остановиться подробнее.
361
Силу тока, текущего при этом через це ъ из 2*виу и Уа, обозначим J20.
Чтобы написать закон Ома для этого случая, надо принять во внимание, что ^2виу и Уа суть величины, приведенные к первичной цепи, и нам надо „перевести* их на вторичную. Очевидно, что первая величина дает при этом -я2; что же
касается второй величины, то соотношения здесь уяснит следующее рассуждение. __
Мы имели проводимость Ya=ga—jba и соотношение при холостом хоДе Jo = — Еу • Уа или Jo = Еу • УЛ, причем потери в железе выражались так: Ph = E?xga\ если ветвь MN схемы фиг. 166 означает не проводимость намагничения, а что-нибудь другое, например емкостную проводимость линии передачи энергии, т. е. емкость проводов линии друг относительно друга и относительно земли, то согласно ф-ле (109) получим для потерь на участке MN опять выражение
Слагающая тока Etga обусловливает потери РА, а слагающая ЕуЬа создает магнитный поток.
Пропустим теперь намагничивающий ток холостого хода через вторичную катушку трансформатора или вообще через вторичную часть включения и срегулируем, чтобы упростить дальнейшие рассуждения, его силу так, чтобы магнитный поток был такой же, как и при намагничении с первичной стороны. Потери в железе будут при этом те же, что и прежде, но выразятся теперь через ЭДС Е2 и проводимость намагничения со вторичной стороны У^—g^— так: Рл= E%ga2; Сравнивая с прежним их выражением, получаем:
= (199)
Так как магнитный поток равен прежнему, равны и магнитодвижущие силы
=3 Е2Ьап^ откуда
<20°)
Из соотношений (199) и (200) имеем, что
(201)
362
Закон Ома для случая холостого хода со вторичной стороны напишется следовательно так:
или
_ _ f1 + ^20 в Ло ' ^а2
Подставляя ур-ние (2Q1), получим:
или
_ , \ _ С*_____________
^20 в Ло^2 “ J = Ло^2 ’ Т= = Ло ^02» (202)
* а где ___
Zm<=Z0,e^. (203)
Измеряя силу тока, напряжение и мощность при этом опыте, мы вычисляем и угол сдвига фаз между напряжением и силой тока <₽20.
Таким образом из опыта обратного холостого хода мы узнаем
<Pw = arg
Подставляя вместо Ya его выражение из ур-ния (194), получаем, что __
’»=агг(^)-
Очевидно, что
/ёЛ । v-
arg М) = f го + arg Уо =• <Р,о — Фо-
\ Сг /
Обращаем внимание читателя на минус, который мы поставили перед углом <р0. __
Это мы сделали потому, что Zo и Fo, сопротивление и проводимость всего включения при холостом ходе, суть величины обратные и <р0 для Zo положительно, а для Уо отрицательно. (Пусть
393
читатель разберет вопрос, что будет, если в ветви Ya включена не самоиндукция, а емкость.)
Обращаясь теперь к ф-ле (198), имеем, что
argZ*==+<p4
и из (190):
arg77= + <₽2o,
и таким образом получаем искомую величину.
е = ?20 — <Ро + <Ра —(204)
Для асинхронного двигателя
?2О = 0 и
8 = <Р2О —<Ро + 'Рй-
§ 105. Векторные соотношения между разными величинами в круговой диаграмме. Третий вид эквивалентной схемы
На фиг. 178 дана круговая диаграмма тока.
Остановимся на векторе /Ио/И; выяснить его значение всего проще можно следующим образом.
Подставим вместо его вы ажение (189), а вместо^ получаемую из (189) величину, когда 2^ = 00, и мы будем иметь:
___ _ <_1±ЛЗ_ К А
М°М - Ц + z2 + Ya Z, Z,f 1 + Ya zj
« • --==.- - 1 . (205)
(Z1+Z/+FeZ1Z’)(l+yaZ1)
Вычислим теперь величину вторичного тока
гг
Приняв во внимание выражение (182) для V^, получаем, что
Л=Л—Д-=7-2 1 1 4- Y Z
1 I га ^2
364
Подставляя же сюда вместо J2 его выражение (189), имеем:
1 z1+z,+ rez1z'
(206)
Сравнивая (205) и (206), видим, что
M0M = f2
или
1
1+^Л
м^м
(207)
Таким образом векторы, проведенные из точки холостого хода Мо в любую точку М окружности, пропорциональны вторичной силе тока, причем коэфициент пропорциональности есть комплексное число С.
Перейдем теперь к вектору вторичного напряжения V2. Выражение его, получаемое непосредственно на основании первой эквивалентной схемы, таково:
v2=v;-^^-^z’BHy.
Подставим сюда выражение
72=луй-с= (Г,-тогда
”7L'^+ezu+
+/>сг;..,= '> <А+<у+ r.z, z^+j,cz,^.
Выражение в скобках преобразуется на основании ф-л (191) и (196) в CkZk, так что
^=^-те^+лё^В11у-
Вместо То подставим __
С»
тогда __ ___ _____ ____________
^=^а + ^Лвну)-А^^
и окончательно _________________
(208)
Выведем еще выражения Vt и Jx через Уг и Т2.
365
Из ф-лы (206) имеем, принимая во внимание ф-лы (102), (193) и (195):
5(a +ъ+г. а 25=4 <5++
+r.^+ VZj -T!z;„.c+^^^+^y)=
-y,S+J;c,Z, (209)
Далее
^=^+^=^+(^ + ^^^ = ^ + ^(1 + ^^)= =^л+^.
или по соотношению (194):
Л = г2УоС4-^^. (210)
Представим себе теперь, что мы проделываем опыт холостого хода; при этом мы регулируем первичное напряжение и именно так, чтобы вторичное V2 имело свою нормальную величину, какую оно должно иметь при нагрузке (У3 надо очевидно для этого несколько понизить до величины V10). Соотношения здесь будут следующие:
(311) так как напряжение на ветви Уа будет в этом случае, когда JJ=O, равно и
(212)
Теперь перейдем к опыту короткого замыкания, при котором будем опять регулировать первичное напряжение (тоже понижать его до У\Л), так, чтобы вторичная сила тока Забыла нормальной величины, например как при полной нагрузке; тогда V2== «а 0; напряжение на ветви Ya равно J^Z^^ и ток в этой ветви
^2 Ъвиу 1 а-
Первичный ток короткого замыкания
^“^ + ^=^(1 + Чну (813)
и наконец первичное напряжение
Л* А Л ^2Вну 4" Л» А 4 (^вну 4~ ~
(214)
366
Сравнивая выражение (209) с (211) и (214), мы видим, 4to правая часть выражения (209) равна сумме правых частей выражений (211) и (214), т. е. любое
^1=»^о+к;.
если .соблюдены вышеуказанные условия регулирования первичного напряжения при обоих опытах.
Точно так же, сравнивая (210) с (212) и (213), находим
Аг
Таким образом мы приходим к результату, который могли бы получить и при помощи принципа наложения, т. е. сложения двух состояний цепи, — одного, при котором нормально и j^s=O, и другого, при котором J'2 нормально, а 1/8 = 0.
Остановимся еще на одном преобразовании основных ур-ний (209) и (210)., Умножив (210) на ZK и вычтя из (209) получим ^-J.Z^CV^-Y.ZJ.
Определяя отсюда Vs и подставляя его выражение в (210), а также в выражение
и результат подставляя опять в (210), получим
У _1_ _
..,..
А r0ZK
Это выражение силы тока позволяет представить эквивалентную схему в третьем виде: ток проходит сначала сопротивление ZK, а затем разветвляется по двум параллельным ветвям, — одной с ло-стоянной проводимостью
и другой ветви с переменной проводимостью , _____________________Gs____-.3= у
(1-тЛ)с4и. ’
Этот третий вид эквивалентной схемы тоже можно применить для вывода круговой диаграммы. Сравнительно со второй схемой эта схема менее удобна.
367
§ 106. Окружности падения напряжения, первичной ЭДС вторичного напряжения и др.
Относительно эквивалентной схемы фиг. 166 следует остано* виться еще на следующем.
Так как ____
Ег = J1 Zv
где Vt постоянно, а вектор изменяется, описывая своим концом окружность, то и Ег будет изменяться так, что конец вектора Еу опишет окружность. Эту последнюю мы получим так.
Когда мы будем умножать векторы силы тока J1 на комплекс Zj = то все эти векторы увеличатся числейно в Z1 раз и повернутся навстречу вращению линии времени на угол р, что мы можем представить себе так, что вся окружность тока Со (фиг. 179) сначала увеличится в Zt раз, оставаясь подобной себе относительно начала координат, затем повернется около этого начала на угол р. Само собой разумеется, что надо сделать еще перевод на масштаб напряжений на нашей диаграмме. На фиг. 179 окружность Cj и есть круговая диаграмма впадения напряжения в первичной части цепи. Вычтя эти падения напряжения из вектора ОА~ == Vv т. е. перенеся окружность в положение С2, причем OCt = = ДС2 и ОС2 || АС2, получим круговую диаграмму для составляю-368
щих ОМ напряжения, уравновешивающих электродвижущую силу в первичной части цепи Е2 при разных нагрузках
УмножиВ—Векторы —J2Z2 на Ya, мы получим векторы тока Ja в ветви Ya. Для этого достаточно окружность С2 увеличить и удалить от О в Ya раз и повернуть на угол, равный аргументу Уа> выражаясь короче, окружность С2 умножить на Ya. На фиг. 183 это есть окружность С4.
В последующем нам будет полезен другой способ представле ния окружности (—Е2), основанный на следующем.
Возвратимся к окружности сопротивлений всею включения, т. е. к окружности M'QQM’k фиг. 164.
На фиг. 180 она начерчена вновь. Возьмем на ней произвольную точку М'. Вектор ОМ' представит собой сопротивление всего включения ZBce при некоторой величине Z2BHe. Далее обозначим эквивалентное сопротивление двух параллельных ветвей Ya и Z'2 через ZO/2, так что
Тогда ___ _____ ______
ОМ'=ОО2 + 6^М', или
ZBce = -Zl +^«.2- _
Задавшись какой-либо постоянной силой тока J2 и изменив в J2 раз масштаб, так что 1 мм^п вольт, мы в этой же окружности будем иметь геометрическое место концов вектора первичного напряжения V2, которое надо прилагать к цепи при различных значениях Z2BHe, чтобы под держивать эту силу тока Jv
Тогда _________ ______
n-OOJ = J1Z1,
24 Теория пореи^виих токов.
369
т. е. падение напряжения в Zt; и
п-ОуМ — Jy Za,2 —— т. е. напряжение на двух параллельных ветвях.
Переходя к окружности проводимостей, найдем и ту точку О8 плоскости чертежа, которая соответствует точке Ои т. е. для которой
О^= = ; (а)
8 ООг
мы знаем, что она должна находиться в правом квадранте.
Таким же образом и
О7Й = = . (8)
ом'
Так как векторы ОО3 и ОО3 наклонены к оси ординат под углами одинаковой величины, тоже и векторы ОМ и СШ, то / О,ОМ' = £ О3ОМ.
Из двух последних отношений (а) и (р) следует пропорция модулей:
ОО3 _ ОМ
ОМ'~ООг'
что при равенстве углов при О указывает на подобие Д ОгОМ' и ДО3ОЛ1. Поэтому
ОО3 _ОМ _О3М ОМ^ОО^О^''
В масштабе тока 1 мм = т ампер ОМ есть или
т*ОМ = JU поэтому
Л
ОМ___ т __ 1 д .
OOi-W п
Из (у) и (8) получаем:
О3М _ 1 п 0гМ~ Z^m
и
370
таким образом О3М в масштабе силы тока дает величину в Z3 раз меньшую, чем Е^ в масштабе же 1 мм = вольт этот же отрезок О3/И дает прямо величину Ev
Следует отметить, что отрезки от точки 03 до окружности дадут согласно вышеизложенному Еу только по величине, но не по фазе.
Далее мы можем получить геометрическое место концов вектора вторичного напряжения 1/2 Для • этого удобнее всего воспользоваться ур-нием (208) настоящей главы
Умножаем окружность тока Со на комплекс CkZk фиг. 181, получаем окружность С3; затем умножаем ОА = У2 на Ckt получаем
вектор ОЕ. Переносим окружность С3 в положение С2. Окружность С2 и есть геометрическое место концов вектора вторичного напряжения У2.
Ее можно получить и другими комбинациями действий, например вычитанием из —Е3 векюра J2Z2 , см. § 108.
Наконец мы можем из круговой диаграммы первичного тока получить окружность тока вторичного и именно на основании того, что вектор
____ ~Г2
MQM = ^
С
описывает ту же окружность, что и Jv
24* 871
Векторы М02И надо увеличить в С раз и повернуть влево около MQ на угол у (C—Cety или, короче, /И0Л1 C=J'2.
Чтобы получить сразу всю окружность, мы множим на
С и из нового положения С4 центра радиусом Л/0С4 описываем окружность.
Упражнение. Найти на новой окружности точку короткого замыкания.
§ 107. Вычитание одной окружности из другой
Можно было бы находить окружность на основании соотношения = — Jat но здесь возникает новый вопрос о вычи
тании одного геометрического места из другого
или в частности о вычитании одной окружности из другой (или сложении их).
Для того чтобы такая задача была определенной, должен
быть задан закон соответствия точек одной окружности
точкам другой, иначе будет неизвестно, из какого именно вектора надо вычитать тот или иной вектор Ja В различных случаях после вычитания могут получиться разные кривые; остановимся на частном случае, когда центральные углы дуг, описываемых соответствующими точками на двух окружностях, равны; в этом случае вычитание одной окружности из
другой (и сложение их) дает тоже ^окружность.
Возьмем на окружности С2 тока J1 две точки М' и АГ, соот-
ветствующие значениям тока и J' (фиг. 182).
После умножения на Zx вся диаграмма изменится линейно, оставшись сама себе подобной. ____
Вычитаем окружность J1 Zx из У1; диаграмма вид изменит, но угол останется равным углу Л4ГСЛГ; после умножения
окружности С2 на Ya мы получаем окружность С3 тока Jа, причем / остается равным углу М'СМ".
Таким образом имеется выполнение поставленного нами условия о равенстве соответствующих друг другу центральных углов двух окружностей.
372
Обозначим радиусы-векторы и? О в центры окружностей через ОСг и ОС3 и радиусы-векторы из центров и С3 в точки М”, М’3, М3 — через р[, pj, р3, pjj Тогда
~ ^3 + Рз’ = 4" Рз-
Произведем требующееся вычитание векторов:
А ^а~ 0Сз + Pi Рз»
Длины векторов р', р3 и т. д. постоянны; наклонены р* и р* друг к другу под таким же углом, как и р' и р3, причем точка Af3 переходит в положение Л4", двигаясь по часовой стрелке, т. е. в том же направлении, в каком движется точка Af, переходя в положение АГ. Поэтому
р>=р?~Л и и
р[-р1=<л — рХл
Таким образом вообще
А А=== °С3 + (Р ?з^
или
А==А А=^ч4“Р** » что очевидно представляет ур-ние окружности;
OQ = OC\ — дает положение ее центра, а геометрическая разность двух друг другу соответствующих (один из них произволен) радиусов-векторов р2 и р3 дает радиус новой окружности. Разумеется при этом по величине р = ОС4, так как новая окружность проходит через начало координат при этом способе построения.
§ 108. Пример на нахождение окружностей различных переменных величин первой эквивалентной схемы
Построим эти окружности для примера, разобранного в § 100. Окружность первичного тока дана на фиг. 183 в масштабе вдвое более крупном, т. е. 1 мм — 1 ампера; на ней показаны и точки Mq холостого хода и Mk — короткого замыкания.
373
Фиг. 183.
Умножаем круг С{ на комплекс Z{" 5 + /10, т. е. умножаем ОС4 на 4~ Ю2= 11,18 и поворачиваем его на угол
?4 = arc tg ^ == + 63°25'. о
Масштаб для напряжений возьмем 1 мм ~ 10 вольт. Поэтому ОСЬ равное 24 мм или 2* амперам, умноженное на Z4 = 11,18, дает 268 вольт или 26,8 мм. Таким образом
О(?2 = 26,8 мм.
Вычтя круг С2 из У4 = 2 000 вольт ~ 200 мм, получаем круг С3 напряжения на ветви Ya.
Умножаем круг С3 на == 0,004+/0,02. Для этого ОС3 = 181,5-10 вольт умножаем на Ya == 0,02, получаем 36,3 и, деля на масштаб силы тока, равный единице, получаем отрезок ОС\ — 36,3 мм', положение его находим по углу
__ 0 02
Z С.ос, = arg Ya = arc tg = 7840'.
Радиус круга С4 получаем таким же умножением радиуса круга С& равного 81 мм, на Кд = 0,02 с переводом на масштабы:
81-10-0,02
----------= 16,2 мм.
Вычитая круг С4 из круга С4, для чего из ОС4 вычитаем ОС^, получаем круг С3, геометрическое место концов вектора вторичного тока J3.
Умножив круг С5 на комплексJZikhj = 3 +/9, получим круг С3 падения напряжения в сопротивлении Z2BHy.
Напряжение У2 совпадает в фазе с J2. Окружность У2 находим проще всего вычитанием круга Св из круга С3, причем получается круг Су.
Читателю необходимо проделать следующее упражнение.
1. Определить на всех кругах точки холостого хода и короткого замыкания: они даны на чертеже, необходимо проследить, как их получить.
2. Задавшись каким-нибудь током J2 на круге С5, найти соответствующие ему величины V2, Jb Ja и т. д.
3. Разобрать вопрос, почему имеется такая часть окружности напряжения V* а) где У2 больше У4, б) где У2 опережает Уь в) где отстает от К
375
ГЛАВА XIV
ЛИНИИ МОЩНОСТЕЙ НА КРУГОВЫХ ДИАГРАММАХ”
§ 109. Линии потерь мощности на круговой диаграмме
На круговой диаграмме тока можно провести такие прямые линии, что расстояния до них от переменной точки М окружности будут пропорциональны различным мощностям: первичной мощно-
сти, потерям в первичной части цепи, потерям в железе, полезной
мощности. Прежде всего остановимся на линиях потерь. Теория этих линий основывается на следующих теоремах геометрии.
На фиг. 184 дана прямая линия KN, делающая на осях координат отрезки а и Ъ (ось х направлена влево, т. е. отлично от того, как принято в геометрии, но это не . вносит в рассуждения никакого изменения)
Ур-ние прямой KN есть:
Опустим из начала координат О перпендикуляр Oq на A7V и обозначим длину его через р0, и угол, составленный им с осью х, через а. Тогда
а = b = cos a sin а
Подставим эти выражения в ур-ние прямой и мы получим*
х cos а 4- У sin а — — (I)
Эта форма ур-ния прямой называется нормальной.
Когда ур-ние прямой дано в форме:
Лх4-Ву4-С=0, (II)
376
то можно привести его к нормальной форме на основании следующих соображений.
Очевидно, что при данной форме ур-ния получаются отрезки на осях координат
Далее
и
В sin а = --==, V А* + В* а
• А cos а = г.
]/ л2 -f- в2
Таким образом, разделив ур-ние (II) на ]^А2 В2, мы получим
коэфициенты при х и у равными cos а и sin а, следовательно третий член, равный
С
Уа2-+ в2’
выразит длину pQ перпендикуляра из О на прямую. Итак ур-ние прямой (II), приведенное к нормальной форме, будет:
ARC
у-2.-.^4- —...............= о. (III)
Va2-\-b2 Va2^\-b2 Va2-\-b2
Возьмем теперь произвольную точку М с координатами х1 и уА на плоскости чертежа и определим длину рм перпендикуляра из М на прямую A7V, фиг. 184.
Из чертежа видно, что рм можно представить так:
рм = Мт = Мп 4~ гО — Oq — у2 sin a -f- cos а — р0
или
Рм ~ xi cos а 4”Л sin а — Ро- (IV)
Для формы ур-ния прямой (II)
Рм--
С
Уа*±в*
(V)
Следовательно пока мы в ур-ние (I) или (III) подставляем координаты точек самой прямой, мы получаем величину в левой части, равную нулю; если же мы подставим в эти уравнения координаты точки, не лежащей на прямой, то левая часть даст нам величину перпендикуляра из этой точки на прямую.
377
Читателю предлагается доказать, что для расположения, данного на фиг. 185, получим:
Рм = — (Х1cos « +Л sin « — Ро)» так что знак у рм зависит от положения точки М.
Пусть на фиг. 186 окру> какого-ю включения в масштабе 1 мм т ампер, причем в этом включении этот ток J проходит через со
есть окружность тока / для
Фиг. 186.
вопрос о том, как нам ввести в диа-
противление /?; рассмотрим грамму учет потерь мощности J2/? на нагревание этого сопротивления.
Обозначим координаты любой точки М окружности через х, yt координаты ее центра С — через £ и 7], радиус ее — через р и расстояние ОС центра ее от начала координат—через X.
Тогда мы будем иметь, во-первых:
J = тУх2 или
<VI)
и, во-вторых, ур-ние окружности:
(х — S)2 + О — ч)2 = Р2.
или, раскрывая скобки:
х2 +у2 — 2£х — 2 v + S2 + г2 = р*. (VII)
Соединим центр С с началом координат О и на линии ОС, как на диаметре, построим окружность (фиг. 186) Координаты ее
центра Cj суть и радиус ее 0С2 равен £» и
378
и ур-ние ее таково:
Х2 У2 _ v _|_ 1 52 _|_ 1 Г(2 = X. £2 _|_ ± е
ИЛИ
X2 -J- у2 — & — у = °. (VIII)
Когда мы из ур-ния одной кривой вычитаем ур-ние другой, мы получаем ур-ние некоторой третьей кривой, проходящей через точки пересечения первых двух.
Вычитаем из ур-ния (VIII) ур-ние (VII): при этом вторые степени координат исчезнут, так что мы получим ур-ние прямой линии:
Sx-bv — S2 — т)«+р2 = 0, (IX)
проходящей через точки пересечения обоих кругов, т. е. прямой HL (фиг. 186).
Введя для краткости обозначение:
£2 + ч2 —р2=$2>
приводим ур-ние прямой HL к форме:
-Ну —82 = o. (X)
Эта прямая называется полярой окружности MQS относи-тельно точки О или полюса О.
Теперь перейдем к выражению потери на нагревание в R. Из ур-ния (VII) окружности MQS имеем:
х2 -|-у2 = 2 ( gx -|- ijy — - + 713 ~ И \ ** /
или
X2 + у2 = 2 I -|- V — —)
\ £» ]
и на основании ур-ния (VI) потеря J2/? представится в виде:
/ 82\
PR = 2т2 R $х -|- 1]у — — ). (XI)
Сравнивая выражение в скобках этого последнего ур-ния с ур-нием (X) поляры, видим, что, если мы его приравняем нулю,—
5x4-v—у=о, (ХП)
то получим ур-ние прямой, делающей на осях коораинат вдвое меньшие отрезки, т. е. находящиеся вдвое ближе к началу координат, чем поляра, и параллельной поляре Такая прямая называется полуполярой, на фиг. 1Ьб это есть прямая /<М
379
Разделив, согласно ур-нию (III) все члены ур-ния (XII) на + 7)3» получим ее ур-ние в нормальной форме.
Но ]/Gz-j-= ОС, так что это ур-ние будет таково:
$ Т)
-1-+т^-и=°- (ХШ>
Если мы сюда вместо хну координат точек прямой подставим координаты х и у точек М окружности тока, то получим в левой части величину, отличную от нуля и, согласно ур-нию (V), равную длине перпендикуляра, опущенного из М на полуполяру,—
+ v — 4-S2
Рм =--------х-------• (X1V)
Сравнивая последнее выражение (XIV) с выражением потерь на нагревание (XI;, видим, что
J*R = <2m?R\pM (XV)
Таким образом отрезки Mq пропорциональны потерям J2R или выражают эти потери в масштабе: единица длины отрезков рм представляет <2m2R\ ватт.
Может случиться, что точка О начала координат лежит на окружности тока (фиг. 187) или внутри нее (фиг. 188) В первом случае поляра и полуполяра совпадают с касательной в точке О Во втором случае проводим через О линию тп JL ОС и в точке т строим касательную к окружности; через точку G пересечения касательной с продолжением линии ОС проводим линию HL GC; прямая HL есть поляра для точки С; полуполяра KN будет лежать вдвое ближе к точке О,
Сравнивая фиг. 186 и 188, видим, что теперь точки О и G поменялись ролями, и поляра HL, занимающая на фиг. 186 то положение, которое на фиг. 188 занимает прямая тп, перешла на фиг. 188 в такое положение, какое занимала бы на фиг. 186 не 380
начерченная на ней прямая, параллельная поляре и проходящая через О.
Прямые тп и HL фиг. 188 суть сопряженные поляры.
Эти свойства поляр являются легко выводимыми следствиями их определения: если дана кривая второго порядка (у нас окружность AMQS) и точка О вне ее, то геометрическое место точек, гармонических точке О, есть прямая линия; эту прямую называют полярой точки О.
Поясним сказанное: на фиг. 186 гармонической для точки О является например точка G; точки О и G дечят диаметр AD окружности AMQ^ в гармоническом отношении:
OD_GD
OA~AG *
Точки О и любая точка поляры делят в гармоническом отношении находящуюся внутри окружности часть луча, идущего из О через эту точку поляры.
Мы рассмотрели вопрос о пред тавлении на диаграмме тока потерь J2/?; теперь следует остановиться на представлении потерь в том случае, когда* нам дана окружность напряжения, как например окружность, описываемая вектором — Е., способ получения которой изложен в начале предыдущего параграфа и на фиг. 180; в этэм случае мощность, теряемая в той ветви, напряжение на которой представлено каким-то вектором — Ev изменяющимся по окружности, определяется аналогично предыдущему.
Введем проводимость
Y=g—jb\
величина потери мощности равна V2g*, т. е. выражается через V и g совершенно аналогично потерям, выраженным через J и /?.
Поэтому способ построения линии потерь теперь ничем не будет отличаться от рассмотренного выше: длины перпендикуляров, опущенных из точек окружности напряжения на полуполяру точки О, начала координат, дадут нам величины, пропорциональные этим потерям. Если масштаб напряжений 1 мм^п вольт, то подобно (XV):
У^ё=2п^р'м^ (XVI)
§ НО. Линии первичной мощности, потерь и полезной мощности на круговой диаграмме первой эквивалентной схемы
Ко всему включению подводится мощность
Рг = У, Jj cos <pr (XVII)
Здесь J, cos (р., есть ваттная составляющая силы тока, т. е. ордината точки М— конца вектора первичного тока; поэтому в мас
381
штабе 1 мм= Vxm ватт ордината любой точки дает нам величину всей подведенной, или иначе первичной, мощности. Ось абсцисс при этом является линией первичной мощности. Полезная мощность Р2 получается как разность между первичной мощностью и всей суммой потерь.
Остановимся на случае всеобщего трансформатора и именно на первой эквивалентной схеме его, как на случае наиболее сложном из часто встречающихся.
На фиг. 189 мы имеем окружность первичного тока Jr Чтобы учесть первичные потери мощности „в меди", т. е. Q1 = J2/?1, проводим полуполяру KN\ тогда, опуская из любой точки М перпендикуляр Mq на полуполяру, будем по ф-ле (XV) иметь:
Qi = j2/?i = 2/«2 R^-Mq.
Далее следует учесть потери в железе фж, которые по ф-ле (169) §81 можно выразить как:
Q^^ga.
Так как величины Ел изменяются (фиг. 180), как расстояние от О3 до точек окружности тока, то величинам Е2 будут пропорциональны длины перпендикуляров, \ опущенных из этих точек окружности на полуполяру точки О3. Находим точку О3, такую чтобы
чертим ее полуполяру и опускаем из М перпендикуляр Mqy\ тогда
Qx=E>qa~2n*gaV-Mqv
где n — mZv как доказано в § 106.
Теперь следует просуммировать потери первичные „в меди* и „в железе"; в асинхронном двигателе эта сумма даст потери в статоре.
Сложив потери, мы получим двучлен, у которого каждый член будет иметь вид выражения (XIV), помноженного для одного члена на <2m2R^k и для другого на Ът2 Z2ga)!, причем величины Е, т), й и 1 будут в обоих членах разные. Так как (XIII) есть ур-ние прямой, то, приравняв нулю сумму, мы получим то же ур-ние некоторой прямой:
2m*R1\-------г-------Ь 2niiZ\g}!--------------=0. (XVIII)
Л Л
Эта прямая проходит через точку пересечения первых двух уже полученных нами прямых — полуполяр.
382
Если в это ур-ние подставить координаты х и у точки, не лежащей на этой новой прямой, то левая часть будет не равна нулю, а будет пропорциональна длине перпендикуляра, опущенного на нее из этой точки, а если мы приведем ур-ние (XVIII) к нормальному виду, то равна ей.
Итак эта прямая проходлг через точку пересечения A7V и и расстояния любой точки окружности М до нее в некотором масштабе представляют сумму „двух потерь*. Чтобы Зачертить ее, надо найти какую-нибудь вторую точку, через которую она должна проходить.
Такую вторую точку найдем путем следующих рассуждений.
Обозначим через Р'2 мощность, передающуюся во вторичную цепь (ср. сказанное о мощностях в § 86 „Баланс мощностей"), и через ф1+ж сумму потерь Q1 и QM в статоре асинхронного двигателя или в первичной катушке и в железе трансформатора, так что
И
+ ж ИЛЯ
(xix>
Полезную мощность мы обозначаем через Р2, — это есть мощность, тратящаяся во внешней части вторичной цепи (или эквивалентная механической мощности ротора асинхронного двигателя); очевидно, что
Р2= ^Л003^
И
р;=р1+Л1'г;.„-
Когда мы имеем Z2 вне = 0, т. е. короткое замыкание, тогда
Р2 = 0 и =
Остановимся на том, когда Р2 может стать равным нулю.
В случае трансформатора очевидно, во-первых, тогда, когда 7^ = 0, т. е. при холостом ходе, и, во-вторых, когда /?2 вне будет отрицательно, т. е. когда, как было пояснено уже, во вторичной цепи будет включен генератор, подающий мощность, как раз равную вторичным потерям J'2 /?2 вну, покрывающую их, так ЧТ0 Я28не= — Я2вну-
В случае асинхронного двигателя Р'2 будет равно нулю, во-первых, тоже, когда J2 = 0, т. е. при синхронном вращении ротора (или при идеально-холостом ходе) и, во-вторых, при бесконечно-большом
383
IV
Фиг. 189.
скольжении (при g=qo). Эту точку на окружности отметим буквой ЛГоо-
Найти эту точку легко методом обращений, исходя из соотношения, что для нее
^2 вне == ^2 вну’
В теории электрических машин доказывается, что величина Т?2в?|е сопротивления, которое надо включить в цепь неподвижного ротора для замены механической нагрузки его при некотором скольжении с нагрузкой электрической, равна:
р ______1 § р
^2 вне q v2 вну*
При 3 = 0, ^?2внв = СО, и мы имеем идеально-холостой ход или синхронизм; при а=1, /?2внв = 0, и мы имеем короткое замыкание; и наконец при а = СО,Т?2 внв = (i — 1) /?2 вну = — /?2 вну и Pi = 0; практически последний режим не осуществим точно, ибо при нем надо вращать ротор с бесконечно-большим числом оборотов.
334
На диаграмме фиг. 164 это будет точка А на прямой Л/ОИ сопротивлений при этом
На круге проводимостей С2 ей соответствует тот конец диаметра О2С2, у которого нет буквы.
На круге сопротивлений С3 соответствующая точка будет находиться немного ниже точки и наконец на круге проводимостей С она будет находиться тоже несколько ниже Mk, точки короткого замыкания. На фиг. 189 тоже нанесена эта точка /Иоо«
Из ур-ния (XVIII) мы заключили, что потери Q1+jK выражаются линейно, т. е. через первые степени координат точки х, у\ то же самое имело место относительно мощностей подведенной или первичной (XVII); поэтому и из ур-ния (XIX) следует, что и Р2 выразится тоже через первые степени хи у. Другими словами, ур-ние (XIX) превратится в ур-ние прямой линии, если приравнять Р' нулю. Для точек этой прямой Р2 = 0; для других точек, т. е. для других х и у, это ур-ние, приведенное к нормальной форме, даст величину перпендикуляра, опущенного из точки х, у на эту прямую; длина этого перпендикуляра даст нам величину Р2 — Q1 + ж. Эту прямую назовем линией всей вторичной мощности (или передаваемой во вторичную цепь мощности).
Мы имеем две точки, 7И0 и ТИоо, для которых
следовательно прямая, проходящая через 2И0 и A/qo, и есть линия всей вторичной мощности. Она пересекает ось абсцисс в точке 5. Так как ур-ние (XIX) можно написать и так:
<?1+ж=Л-^« (XX)
то очевидно, что линия мощности Qj +ж проходит через точку пересечения линии мощности Рг (или оси абсцисс) и линии мощности Р2, т. е. через точку
Таким образом мы имеем, что линия потерь мощности ф3+ж проходит через точку 5 и точку пересечения прямых KN и
Последняя точка W обыкновенно находится ’довольно далеко и выходит за пределы чертежа, поэтому для построения искомой линии потерь Р1+ж воспользуемся тем, что
и AW^AW» так что
fg _ gh SL~ LLy'
W ибо оба отношения порознь равны ^7*
хб Теория переменных токов. 385
Задаваясь gh, ищем fg как четвертую пропорциональную к трем данным отрезкам. Для этого переносим gh в положение проводим Lg* и находим Kv точку пересечения с соединяя Кг с 5, получаем отрезок fg?=fg\ отложив fg на продолжении gh, проводим линию Sf, это и есть искомая линия потерь ф1 + ж.
Переходим к построению линии вторичных потерь мощности
Мы знаем, что отрезок
Л М0М~=-*.
Следовательно в масштабе 1 мм = тС ампер отрезки MQM представляют по величине вторичную силу тока. Поэтому вторичные потери будут даны длинами перпендикуляров из М на полуполяру точки 2И0 (начало векторов J^9 а согласно фиг. 187 это будет касательная в точке Мо к окружности линии 7И0Т.
Далее, так как полезная мощность
(хи)
то, подобно тому, как мы из ур-ния (XIX) заключили, что Р2 выражается линейно через координаты х, у и затем нашли линию этой мощности, так и теперь на основании того, что в ур-нии (XXI) Р'2 и ^22^?2вну выражаются длиной отрезков прямых, т. е. линейно относительно координат х и у, заключаем, что и Р2 тоже может быть выражено линейно через них.
Если мы выражение
приравняем нулю, то получим ур-ние прямой линии (ибо х и у входят сюда в первой степени), — назовем ее линией полезной мощности. Приведя это ур-ние к нормальной форме и подставляя вместо х и у координаты точки, не лежащей на этой прямой, получим длину перпендикуляра, опущенного из точки на эту прямую; по ур-нию (XXI) эта длина пропорциональна Р2 полезной мощности.
Чтобы построить линию Р2, найдем две точки, через которые она проходит, т. е. найдем две точки, для которых Р2 — О
Первая точка есть точка идеально-холостого хода асинхронного двигателя или, иначе, точка синхронизма, а у трансформатора просто точка холостого хода УИ0, — вторая точка есть точка короткого замыкания в первой J^O, а в0 второй Уа = 0, так что
Р3 = lZ2'4COS<f?We0
в обоих случаях.
Следовательно линия полезной мощности есть линия Продолжим ее до пересечения ее с осью абсцисс в точке U.
386
Построим теперь линию всех потерь:
4*i+£?«i+7М.,.=р, -
Очевидно, что это будет прямая линия, проходящая, с одной стороны, через точку пересечения линии, для которой Pj —О, с линией, для которой Р2 == 0, т. е. через точку £7, с другой стороны, — через точку пересечения линии первичных потерь Sf и линии вторичных потерь Л40Т.
Проведя линию, параллельную оси абсцисс на некоторой высоте, отрезок ее гр между линией Sf ,и М0Т переносим вниз в положение ггр\ здесь делим пропорционально SU и UTQ и, перенеся точку деления на гр, проводим через нее и U прямую UQ\ это и есть искомая линия всех потерь.
Теперь мы имеем на чертеже линии всех мощностей и всех потерь в отдельности и в сумме.
§ 111. Масштабы для линий мощностей и коэфициент полезного действия
Следует остановиться еще на вопросе о масштабах для линий ^2^2» + ж И Фвсе *
Эти масштабы можно определить, исходя из ур-ния (XVIII), из которого можно вывести масштаб для первичных потерь, и затем переходить к другим линиям до последней. О
Этот путь сложен и утомите-лен; гораздо проще определение \ масштабов на основании одной i теоремы, которую мы сейчас и докажем. ’П *1
На фиг. 190 снова начерчены линия первичной мощности Pv у р ~ *
совпадающая с осью абсцисс" UX, *
линия UMk вторичной полезной Фиг. 190.
мощности и линия UQ всех потерь.
Возьмем точку, например Mk, для которой Р2 = 0. Если полезная мощность равна нулю, то вся первичная мощность обращается в потери:
= QBCe.
Пусть масштаб для Рг будет 1 мм~т1 ватт; масштаб же потерь 1 MM = mq ватт. Тогда
Mkr • m1 as Mks • mq.
25*
387
Подставляем вместо и Mks их выражения через гипотенузу обоих треугольников MkU и синусы углов при £7;
MU- sin (MkUX) • тг = MU- sin (MkUQ) - tnq, откуда m1 sin (MkUQ) 7nq^s\n(MkUXy
Обозначая линии мощностей кратко буквами Plt Р2 и QBCe, как показано на фиг. 190, имеем:
• Sin (Рр Р^) Мд • SIH (Т^2, Qece^* (А)
Возьмем теперь произвольную точку М на окружности (фиг. 191). Обозначим отношение величины первичной мощности к величине потерь через А?, так что и
Ра== (А а
Р, k
Проведя MF и AfGJ_P3, мы имеем в длинах этих перпендикуляров меры мощностей РА и Р3, но в разных масштабах; масштаб для Pt обозначим через /и3.
Перенесем отрезок MF параллельно самому себе так, чтобы вершина его легла на линию Q, пусть это будет в точке N; тогда NK # МР. То же самое сделаем с отрезком MQ, так что получим:
МО # LH.
Теперь мы можем написать очевидные равенства:
рг = NK- тг = NU- sin (Pj, <2тсе). тг = k - MS-mq,
Р2 = LH-т2 — LU-з\п(Р^ QBCe)-/w2 = (A — \)-MS-mq, откуда делением получаем:
M7-sta(Pp k
£l/-sin(P2, QecJ./Wa k — 1
Проведем линию Ml || QBce; тогда M\—NU и M2=eeLU, следовательно
4fl-sin(Pr
/И2-8!п(Р2, 4?юе)-«2
388
Отсюда мы видим, *1то при начальным масштабе, и именно
измененном сравнительно при одном общем:
с перво-
М2 будут находиться в том же отношении,
что
отрезки 7И1 и и мощности
М2
889
В этом общем новом масштабе отрезки прямой, проведенной параллельно линии потерь, заключенные между точкой М и линиями Pj и Р2, и дадут нам величины этих мощностей, а отрезок 12 = 7141—М2 даст все потери.
Новый масштаб можно выразить еще так:
Выведем еще некоторые соотношения.
Проведем линию NT, параллельную оси абсцисс, через точку М-
P2 = MG’/n2 = Mr-sin(P1, P2)-w2,
Q^=MS’mg = MN^m{Pu QBJ-ma, и так как
P2 = (A-l)QBoel
ТО
4fr-sin(Pp P2).m2 = (k — l)-MN-sin(Pv QBQ<j-mg, откуда следует, что в новом масштабе, равном
ma-sin(P1, Р2) = «уsin(Pj, QBce), (С)
отрезки МТ и MN представляют величины полезной мощности и всех потерь, а следовательно отрезок NT— NM -J- МТ представит всю первичную мощность.
Сравнивая равенства (А), (В) и (С), мы находим, что, проведя из точки М прямую, параллельную одной из трех линий Рр Р2 или QBce, мы в трех отрезках ее между этими линиями будем иметь измеренными в одном общем масштабе все три величины мощностей Pv Р2 и QBce.
Находить масштаб мощности всего проще можно следующим путем. Проведем из точки Mk линию в желательном направлении, например параллельно линии потерь; отрезок ее от Mk до оси абсцисс представляет всю мощность Plk при коротком замыкании, нам известную или из опыта или из расчета (при проектировании); отсюда вычисляется и масштаб.
Из (С) получается удобный способ графического определения коэфициента полезного действия
так как из фиг. 191
_ МТ _МТ NM^-MT~ NT'
390
Продолжим линии MkU и QU за точку U и проведем АВ || ОХ так, чтобы АВ =100 мм. Продолжение MU пересечет АВ в некоторой точке IF. Очевидно, что
МТ AW Г*~ NT^AB’
и число миллиметров в AW прямо даст нам величину коэфициента полезного действия.
§112. Линии мощности на круговой диаграмме второй эквивалентной схемы 18
Построение линий мощностей и потерь для круговой диаграммы второй эквивалентной схемы всеобщего трансформатора значительно проще, чем для первой.
Соотношения здесь следующие:
При нагрузке весь ток есть тот же самый, что и в действительности.
Ток в ветви -=^ есть ток холостого хода Jlo, ток в ветви z12=cz;+c*z;, который мы обозначим через 7^, равен их разности pss-T______________________7
иначе же из схемы
В действительном трансформаторе вторичный ток
а так как из основного ур-ния напряжений в трансформаторе
(?)
Деля (а) на (£), получаем:
j' j, c(cz;+z,)’
391
Подставляя сюда выражение для через Jv получаем:
Z 1 /;=с’
ИЛИ
Перейдем к мощностям.
Первичная или подведенная к схеме мощность равна:
Р\ = cos
она та же самая, как и в действительности.
Мощность холостого хода равна:
С/
где знаком мы обозначаем действительную часть следующего затем выражения, т. е. в данном случае действительную или ваттную часть всей проводимости холостого хода.
Эта мощность имеет тоже такую же величину, как в действительности.
Вторичная полезная мощность Р'2 будет во второй схеме равна:
^2 = ~£2 вне»
где __
Z ' = Z' •
2 вне 2 вне 9
а
С= Ceh.
Вычислим правую часть выражения Р'2.
С2==С»еЛт
C2Z' = C2Z' e^f>v+Sf) 2 вне 2 вне
И
J’2
р;= = + (у)
В действительности же полезная мощность равна:
^2 33 Л2^2 вне'
или
Р2 = ^2^2 вне C0S ^2?• (8)
392
Отсюда получаем:
Р3 cos <f2„ “ ’
где k может быть^ I, смотря по значениям <рао и 2у.
Потери в ветви Z12 равны:
<2'=^^(СА + ^ВИ>
(&)
и так как, как выше указано и ясно из схемы,
1?
~С
(фиг. 192), то QF представляется расстоянием от М до полуполяры точки Мо, т. е. до касательной Ж0Г к кругу в точке /Ио.
Все потери в схеме равны P0-|*-Qr и представляются расстояниями от М до прямой t/lF, параллельной MQT и отстоящей от нее на расстояние, выражающее в том же масштабе Ро
Как и раньше, на основании того, что РА и P04“Qr линейны, находим, что и линейно и линия Р'2 проходит через точки 2И0 и Mk, где Р2 —0. Очевидно, что и линия P0 + Qr проходит через точку U встречи линий Рх и Р2; так она и проведена на чертеже.
Пусть, напр., Р'2 получилось (&) меньше, чем истинная полезная мощность Р2, это значит, что потери слишком велики; от них надо отнять что-то, чтобы получить истинное Q.
393
Проведем MS || UMk\ тогда по теореме о масштабах в некотором общем масштабе
MK = P0-[~Q’, М5^Рг и RS—P'2 = kP2.
Где-то между М и К лежит точка £, для которой sl=p2 и ml^q, т. е. ML представляет истинные вторичные потери.
Из схемы получается:
р0+<?4-лр8-р1,
а в действительности
л>+<?+^=л.
откуда
Qr-Q + (A-l)P2 = o, или
Q'_Q = 7<£ = (1—Л)Р2 = (1—А).5£.
Отсюда следует, что при изменении нагрузки Р2 точка L двигается по некоторой прямой UR.
Проводим KN || UR и тогда будем иметь:
KL _NU_SU—SN SL SU~ SU =
откуда
SN .
(X)
Таким образом, чтобы построить линию всех потерь, мы: 1) чертим UW параллельно Л40Г, касательной к кругу в /Ио, 2) проводим некоторую прямую SM || MQMky 3) делим отрезок SU в отношении, даваемом ф-лой (X), 4) соединяем точки N и К и 5) проводим UR || NK\ эта линия UR и есть линия всех потерь.
На фиг. 193 дано построение линии потерь для примера, рассмотренного в § 100 и 108.
Так как в этом примере
С<=* 1 + Ya Z>= 1 + (0,004 +/ 0,020) (б +/ 10) = 0,820 0,14,
то
— 0 14
у = arg С= arc tg = 9°45', V,OX5
и
Л = со8 2у=0,943;
на фигуре и отложено .JW = 0,943 • SU.
394
395
Такой же результат получим и в том случае, когда у<0 и if2т — 0, как это имеет место у асинхронного Двигателя, ибо и тогда k<\. У асинхронного двигателя 2у впрочем настолько мало, что можно k положить приближенно раьным единице.
Рассмотрим случай, когда В этом случае из (9) полу-
чаем, что Р'2> Р2> т. е. потери Q1 меньше, чем в действительности, и где то, между /С и S лежит точка для которой ML^^Q и SLl^=»P2 (фиг. 192); при этом, очевидно
Q-Q' = (*-1)P2
ИЛИ =
Проводим Ь1А71 [| UW и получаем
KL1_^U _SU—SNt_SU SLt ~ Sty ~ — ~
Исследу м графические способы определения из диаграммы коз* фициента полезного действия ц.
На фиг. 194 построены касательная Д40Г, затем линия Ul\ || М^Т и линия истинных потерь, з шсь обозначенная буквами UW. Проведем MF || C71F; то да т] может быть выражена через отношение отрезков тремя способами, прежде всего
£5 MQ
398
Проводим MH~MQT и МВ±ОХ.
Имеем, что в одном и том же масштабе
MD = Р2 и
МН=РГ
Так как из (&) вытекает, что
Р = р С03 К*
2 2cos(<p2„+2Y)’
ТО
= Л = ^2C0S?2O __ Р2
4 Л Picos(<f>2,-j-2f) р cos (уг„4> 2 у)*
1 cos <pav
(В)
И< построения окружности тока методом обращения (§ 101 и фиг. 166) ясно, что У MqCH-i == <p2tr 4~ следовательно, имеем, что
Z вмн= Z маснх = <ра„.+ 2у.
Строим / ЕСН, = <р1г и проводим линию МА ЕС, так что
тогда и
поэтому из (В)
£ВМА~^
Л1В = Л1Я. cos (<р2в 4- 2у)
... МВ МА =* ----,
cos<pa.
MD ’I-МА'
Соединяя (А) и (С), можем написать
__ LS _ МО _ MD T>~MS~ME~ МА'
(С)
(D)
Фиг. 195 дает построение для быстрого отсчета 7], когда его надо определять для многих точек: продолжаем Ж0/ИЛ в виде Up, через U проводим Uq || 7И0Г; на некотором расстоянии от UX проводим pq || UX\ строим /qpr — cp2v 4~ 2у, проводим qrj^pr и затем откладываем £rps ~ cp2v; в пересечении ps и qr находим точку радиусом, равным полученному ps, засекаем дугу и находим точку t на линии pq или на ее продолжении; отрезок pt делим на 100 равных частей или проводим линию, параллельную pt и равную 100 лл, внутри угла pUt\ тогда, проводя из любой точки окружности М луч Мт, будем им ть, что рт численно равно ц.
397
Доказательство этого следующее:
поэтому
/\mUqcr>^ UMH,
mq UH . qU~MH’
(Е)
далее
откуда
&pUqcs>&UDH,
(F)
pq _UH qU DH’
Деля (E) на (F) и образуя производную пропорцию, получаем = (G)
pq МН’ W
а так как
pr = pq-cos Cf2, + 2Y), И
. рг — па. C0S + 2у)
Р ps cos<p2o cos <рао
то, умножив знаменателей в (G) на это отношение косинусов, будем иметь
___MD____тр Л~'МА~~~Н'
398
ГЛАВА XV
НЕУСТАНОВИВШИЙСЯ РЕЖИМ В ЦЕПИ ТОКА
§ 113. Теория разряда конденсатора19
В практике нам приходится встречаться с явлением особого переменного тока при разряде емкости. Любая линия передачи энергии представляет собой, как мы уже знаем, между прочим, и определенную емкость; обмотки любой машины относительно друг друга и корпуса машины обладают емкостью, хотя- и небольшой; поэтому явление разряда емкости встречается весьма часто.
Ознакомимся с теорией этого явления, при котором возможно получение частоты переменного тока во много раз большей, чем в машинах.
Конденсатор можно зарядить от любого источника постоянного тока (например от аккумуляторной батареи); и если мы обкладки конденсатора, заряженного до не- £ которой разности потенциалов и отделенного затем от источника тока, соединим одну с другой каким-либо проводником, то произойдет s''"’ разряд конденсатора: через этот проводник по- Z \
течет ток, причем напряжение на обкладках будет h rV
уменьшаться, потенциалы обкладок будут стре- I J
миться выравняться. ./
Обозначим через С емкость конденсатора, че-рез /? — ваттное сопротивление цепи разряда А (включая сопротивление того воздушного проме- фиг 195. жутка, в котором проскакивает искра при разряде, когда мы проводник, соединенный с одной обкладкой, приближаем к другой обкладке, или, при двух „разрядниках", соединенных с обкладками, — промежутка между ними, на фиг. 196 помеченного буквой Л); далее обозначим: через L — самоиндукцию цепи разряда; через VK — разность потенциалов, или напряжение на обкладках конденсатора перед началом разряда; через vK— переменное напряжение на них в течение разряда: через q — переменное количество
399
электричества на положительно заряженной обкладке и наконец через i — переменную силу тока в цепи разряда.
Закон Ома, примененный ко всей цепи, дает для произвольного момента времени /:
или
= + (215)
Сила твка выражается, как известно, так:
. dq
di ’
причем q = Cv, следовательно
dv
(216)
Подставляя вто выражение силы тока в ур-иие (215), получаем:
— LC
d7V-~dP
dvK dt
к>
или
dlvK , /? dv„ , v* „ dP “ L dt ~LC
(217)
Частный интеграл этого ур-ния есть vK = А • ет\
А есть произвольная постоянная, а т можно определить, подставив эту величину vK в ур-ние (217) и получив так называемое „характеристичное" ур-ние:
m2 4--у-m 4-^=0.
Отсюда имеем:
«1,2
_R_ , ,/>L____L
= 2L — У 4L2 LC'
Соответственно этим двум значениям т мы получаем два частных интеграла ур-ния (217):
ок = Де'"*/ и рк = Вея’«/,
сложив которые, получим полный интеграл этого уравнения:
_ Л t I , i/Т?» Г , 1/ я1 1 \ ок = <? 2i \Ае‘ У Й7_7^4-^~Тс). (218)
400
Теперь могут представиться три случая: корни тл и т2 могут быть мнимыми, действительными и равными.
Разберем сначала первый случай.
В этом случае
^<гс"™ *<2]/4- <219>
Положим:
LC 41*
и > (220)
Ур-ние (218) мы можем теперь представить так: = e~bt(AeiaJ + Be~ial), где j = V—1. Применяя формулы Эйлера, мы получим: vK— e~bf[(A + В) cos at(А — В) j sin at], или, вводя новые постоянные:
Д4-В = С1 и (A — B)J=C2 = cos at C2 sin at). (221)
Произвольные постоянные получат определенные значения, если мы примем во внимание начальные усяовия: в момент t=Q мы dv имеем п = VL I = 0, и следовательно —~ — 0.
к к dt
Подставляд эти значения t и v в (221) и в производную от (221), получаем:
Сг = у, аС2 — ЬСг = 0, откуда
Мы видим, что прежние произвольные постоянные А и В должны были быть сопряженными комплексными величинами:
А = т 1п и В = т — jn,
А-\- В = <2т — С1
А — В= j2n и
/?)/ = -—2я== С2.
26 Теория переченнлх то ов. 401
Таким образом:
= e~b*Vd cos at-\---sin at
к hi ’ a
Умножим и литель отнесем
разделим правую часть на
/1 i *
1 + причем де-
к скобкам; затем, полагая ~- = tg5, получим:
= e-wVl/ 1 4- sin (at + $).
(222)
При /=0 из этого ур-ния имеем ик= VK, так как
Г а2 sin5=1/ -2, .2. у а£ -f- b*
Если бы здесь не было множителя e’w, синусоидальную функцию с амплитудой V фазой $ и периодом
мы имели бы простую
Ь*
14- — , начальной 1 а2
v к
(223)
но этот множитель e~bt изменяет вид кривой, превращая синусоиду в кривую фиг. 197.
Амплитуды этой кривой уменьшаются с каждым периодом в еьг раз. Если некоторая амплитуда есть Vkn, то следующая за ней одинаковая по знаку амплитуда есть Vkn+1 = Vkne~bT. Отсюда мы получаем:
у = ЙГ=1п (224)
Величина у = ЬТ называется логарифмическим декрементом затухания колебаний.
Величина г*г=еТ = Д носит название просто декремента колебаний.
Самый процесс разряда конденсатора в рассматриваемом случае мнимых корней характеристичного уравнения является процессом колебательным, с чем мы уже встречались в параграфах, посвященных резонансу напряжений или токов. Так как амплитуды колебаний с каждым периодом убывают, то колебания называются затухающими, в отличие от того случая, когда 4 = 0 и е~ьт=з 1 и когда амплитуды остаются все время одинаковыми, равными V. В последнем случае колебания будут незатухающими: они возможны лишь, когда 6 = 0, а последнее условие означает, что 402
/? = 0. Следовательно в действительности колебания всегда будут затухающими, ибо как ни было мало /?, сопротивление разрядников и искры, оно всегда отлично от нуля.
Так как по предыдущему
di ’
то из ур-ння (222) мы получаем выражение для силы тока:
/Ь2 Г
1 ~
1 а2 [
Ь sin (at -|- $) + «<*s (fit + £) ’
или после преобразования:
вз 4- ьз
I = Се~ы sin (at 4- тг). (225)
Таким образом сила тока опережает в фазе напряжение на угол к — S = arctg — — . В том случае, когда можно хотя бы при-
ближенно имоисить 7?=0,
, А w
мы имеем Ь — Ь и <р=—, т. е. сдвиг л
фаз между током и напряжением в отсутствии иотерь достигает четверти периода.
Из сказанного следует, что кривые VK и i строятся следующим образом (фиг. 197): сначала строится синусоида
— пунктирная кривая, — затем ее ординаты умножаются на переменный множитель и получается кривая Ук — черная кривая. Ординаты я^нктирной кривей растут еще некоторое время послё момента / = 0, ординаты же черной кривой непрерывно с момента /~0 уменьшаются, начиная со значения
sin$=y;
26*
403
в самом деле, так как
at
T
в течение времени от /=0 до / = — отрицательно, кондеи-л»
сатор разряжается!
"di
т. е. уменьшается в течение того же промежутка времени, становясь в конце его отрицательным.
Кривая I строится аналогично кривой т>к.
Заметим, что vK имеет максимумы положительные и отрицательные, когда / = О, поэтому у кривой одна четверто периода несимметрична относительно другой четверти.
При Z? = 0 нет траты энергии (потери на магнитный и диэлектрический гистерезис можно ввести уже известным нам образом в величину J2/?, расширяя как бы величину 7?) есть только постоянный переход энергии из электрической в магнитную, и наоборот Ранее нами были уже даны некоторые соотношения между электрическими величинами; при этом был описан и самый физический процесс этих колебаний.
Так как при /? = 0, Ь — 0 и а = из ур-ния (220), то, подставив эти величины в ур-ние (225), мы получаем для силы тока выражение:
»= {at),
И III
Jm=VK^
т. e. уже известную нам ф-лу (99).
Из ур-ния (223), подставив значение а, мы получаем для продолжительности периода в общем случае величину
Т = ,22(226)
\/ LC Ю
и для идеального случая /? = 0,
Т=2к VTC,
т. е. ф-лу (98), известную под названием „формулы В. Томсона*.
404
Перейдем к тому случаю, когда
1Р>Гс
и корни характеристического уравнения действительны.
Введем обозначение
и, как прежде,
*=ь.
2L
Тогда
/и12==— Ь + а,
и полный интеграл ур-ния (148) фгдет:
vK = Ae(~b+aV-[- Ве~(ь*аК.
Далее
— (— b 4- а)Ле<-6+в)'—(а 4- Ь)Ве~^аК
Постоянные А и В определим опять из условий, что при /= О,
dv
v = V. а — к- = 0. к к’ dt
Эти условия дают:
A-\-B=VK,
(а — Ь)А — (а 4- Ь)В = 0.
Отсюда
В
а-=±.у
2а к
Так что
(a -f" b)eat 4- fa — Ь)е ** 2а
(227)
Подставляч в выражение производной вместо А и В их значения, получаем:
Так как
Ь^> а,
405
то эта производная всегда отрицательна:
иг<*
следовательно напряжение непрерывно уменьшается, стремясь к нулю при /=оо. Разряд конденсатора происходит в этом случае без колебани и
Для случая равных корней (т1 — т3) имеем:
1=0
Ш LC
или
в = 0.
Преобразуя выражение (227) для v, получаем:
4 = VKe~*l=Ике~"(1+«). (228) ( Jud cd = 9
Далее для этого случая di *
эта производная тоже все время отрицательна. В обоих последних случаях сила тока .
di
начинаясь с нуля имеет, в чем читателю предлагается убедиться самому, отрицательный максимум в некоторый момент времени, стремясь затем к нулю при f = GO (фиг. 198).
Оба случая, т. е. когда вообще корни действительны, носят название случая „апериодического" разряда.
Практически напряжение и сила тока в этих случаях перестают быть доступными по величине для измерений по истечении весьма небольшого промежутка времени.
При разряде конденсаторов в проводнике, соединяющем обкладки, обычно делается так называемый „искровой" промежуток некоторой постоянной длины, о котором мы уже упоминали выше. Он может появиться и оттого, что разряд происходит не при прикосновении проводника к обеим обкладкам, а уже при некотором минимальном расстоянии его от их обеих или от одной из них, если он к другой уже присоединен.
При цепи электрических колебаний с искровым промежутком сопротивление искры входит как часть, обычно главная, в сопротивление /?.
40S
По мере затухания колебаний сопротивление искрового проме-жутка растет, отчего растет и продолжительность периода Г, а
также увеличивается и само затухание, вследствие роста декремента колебаний ЬТ. Вследствие затухания амплитуда напряжения наконец достигнет такой величины, что не сможет поддержать ток через искровой промежуток, искра прервется, разряд не сможет продолжаться. От этого колебания прерываются на некоторой стадии,
а не идут до конца, т. е. в конденсаторе остается некоторый остаточный заряд, некоторая энергия Э1у энергию можно снова заста-
вить колебаться, замкнув на короткое искровой Разобранный нами в этой главе колеба-
тельный разряд есть случай так называемых свободных электрических колебаний, т. е. таких, • период которых определяется только через /?, L и С сам эй цепи, или „контура" колебаний, и общим выражением которых является ф-ла (222). Кроме того бывают колебания несвободные, или вынужденные, период и затухание которых зависят и от постоянных другого контура и которые индуктируются этим последним. Явления во вторичной цепи трансформатора представляют пример вынужденных колебаний.
Из формулы для периода колебаний мы видим, что, уменьшая /?, L и С контура, мы будем уменьшать продолжительность периода и следовательно увеличивать частоту колебаний.
промежуток.
Фип. 198.
Пример 43. Вычислим частоту колебаний / в следующем примере.
Плоский стеклянный конденсатор с толщиной стекла в 0,1 см и площадью каждой обкладки в 20 X 20 = 40Э см* разряжается медным проводником, согнутым по кругу с радиусом в 25 см\ диаметр поперечного сечения проводника равен 1 см Вычислим сначала емкость С конденсатора по приближенной формуле — g'jgH ФаРаД> где 6 есть диэлектрическая постоянная стекла (равная приблизительно трем), S — площадь обкладки, d — толщина диэлектрика. Подставляя вместо этих величин их значения, получим С = 1//6-10—9 фарад.
Самоиндукцию круглого, согнутого по кругу, проводника вычислим по формуле Кирхгофа:
L = 4яа (jn — 1,75^ 10-9 генри,
где а есть радиус круга, а b — диаметр поперечного сечетия проводника. Подставляя а —25 и £ = получаем £ = 1,33-10~6 генри.
Как мы увидим из последней главы, сопротивление R при токе большой частоты больше, чем при обычной частоте, вследствие поверхностного эффекта, т. е. того, что ток при большой
407
частоте идет главным образом по наружным слоям проводника, осевая же часть проводника остается почти совсем без тока и площадь поперечного сечения проводника не используется полностью, отчего и возрастает сопротивление. В разбираемом примере оценим все ваттное сопротивление , цепи, т. е. и проводника, и искрового промежутка, в 3 ома.
При указанных значениях всех величин имеем:
1 R2
^=7,5.10’4 и — = о,О1 • 1С14.
Пренебрегая второй величиной, имеем из ур-ния (226):
2тг 1
Т---_---------------------- СРК
V 7,5.10>4 0,43.10’ •
и частоту
— = 4,3’106 колебаний в секунду.
З.Юв
Декремент колебаний равен:
Y = 6Г== 2L’Т = 2-1,33.0,43.10’ ~ °’26’
Таким образом амплитуда каждого периода составляла бы при этом в ~0,26 0,77 от амплитуды предшествовавшего периода,
если бы затухание не увеличивалось, т. е. если бы 7? оставалось постоянно равным 3 омам.
Искровой промежуток в самом колебательном контуре не является Неизбежным, без него можно обойтись например в том случае, когда энергия сообщается контуру не зарядом конденсатора, как было описано выше, а путем индукции от другого колебательного контура, уже содержащего искровой промежуток. В подробности о таких „связанных" колебательных контурах в общем курсе теории переменных токов мы входить не можем.
Рассмотренный нами колебательный контур называется обыкновенно „замкнутым вибратором".
Представим себе, что от начального момента прошло время , 1 t = ~г ; тогда b
е~ь1 = — е 9 1 тг напряжения равна — V*.
~ называется „постоянной времени" контура; она
показывает время, когда амплитуда колебаний уменьшится в Е раз. 408
и амплитуда
Величина
Положим, что от начального момента прошло время i = tnt> когда заряд стал очень уже мал (например 0,01 первоначальной величины).
Тогда
v'max=e-^y==o,oi V, откуда е-*'>н = 0,01, ^ = 1п 100, t 1П100^5 т~ ь ~ ь'
Через промежуток tm конденсатор может снова заряжать.
При периодически повторяющемся заряде, когда
„ I
снабжение энергией производится т — — раз в секунду, имеем, что в течение секунды подведена энергия:
CV2
2
которая превр щается в тепло J2/?; здесь / называется действующей силой тока, и величина ее определяется из выражения:
ад-
Представим себе теперь два металлических шара или две большие металлические пластины, соединенные прямолинейным проводником (с искровым щ омежутком или без не о) Здесь шары или пластины составляют вместе емкость, и в такой системе, называемой „открытым" вибратором, будет возможен совершенно такой же колебательный разряд, как было описано.
Отличается открытый вибратор от замкнутого тем, что в первом появляется новая потеря энергии, не имевшая места в Зг'мкнутом^ а именно — излучение электромагнитной энергии. Часть энергии тратится каждый период на нагревание проводника, а часть в отрывающихся от Проводника и шаров электрических индукционных трубках и связанных с ними магнитных уносится со скоростью света от вибратора во все стороны.
Если мы шары или пластины на концах проводника станем уменьшать, то все большее относительное значение будет приобретать емкость частей проводника друг относительно друга. В пределе, в случае простого прямого провода, вся емкость в системе есть емкость самого провода, — таким образом теперь емкость равномерно распределена по длине провода, т. е. так же, как самоиндукция.
409
В этом случае мы, аналогично описанным далее в главе XVII, волнам в проводах с равномерно распределенными емкостью и самоиндукцией, получим в вибраторе волнообразное распределение тока и напряжения, или потенциала. Потенциал имеет наибольшие значения, по знаку противоположные, на концах, нулевое значение — по середине провода, сила тока наоборот.
Теория колебаний в открытом вибраторе и излучения иМ электромагнитной энергии составляет предмет специального учения об э ектромагнитных колебаниях и вотнах и служит основой для радиотехники, но в конце главы XVI, в § 128, мы вернемся к во-прозу о5 этих так называемых „свободных*, или „собственных", колебаниях в длинных линиях передачи энергии, где емкость и самоиндукцию будем считать равномерно распределенными по длине проводов.
§ 114. Наиболее общая форма уравнения цепи переменного тока
Рассмотрим цепь переменного тока с самоиндукцией ваттным сопротивлением /?3 и последовательно включенной емкостью Cf, пусть в ней действует ЭДС ei9 в общем случае переменная, кроме нее будет существовать, тоже в общем случае, ЭДС самоиндукции, и закон Ома для мгновенных значений напишется так:
(229)
где через vK мы обозначили напряжение, тратящееся или существующее на емкости.
Из ур-ния (229) получаем:
ei= 4" 4~
или, заменяя т>к его выражением через 1г:
е, = + (230)
Jitn
Последнее уравнен те является достаточно общей формой „уравнения цени переменного тока". Но можно сделать в нем еще следующее добавление.
Предположим, что ЭДС в рассматриваемой цепи индуктируется магнитным потоком второй цепи с током /2, так что
л < ^^2
410
где * М есть коэфициент взаимной индукции обеих цепей. Если существует относительное движение обеих цепей, то М п ре-менно, и его нельзя выносить из-под знака диференцирования, и
(А)
а ур-ние (230) превращается в Ulf <*-*’ 1
Jim
В частном случае i2 может быть и постоянным током, например током возбуждения в обмотке электромагнитов синхронного двигателя; в форме, аналогичной (А), может быть представлена и ЭДС генератора переменного тока и т. д.
Продиференцировав последнее ур-ние по t9 получим:
di <Р1Х , , 1
^'dt'T'^d^^ •
или dh j 1 f- 1 ,2,n
dfl ' I, ' dt ’+‘£1C1 1 Lj dt* * < '
Такова наиболее общая форма уравнения цепи переменного тока при последовательном соединении емкости, самоиндукции и ваттного сопротивления.
Предлагаем читателю составить уравнение для участка цепи, где включен синхронный двигатель, а конденсатора нет.
§ 115. Неустановившийся режим тока. Включение постоянного тока
Рассмотренный в предыдущей главе колебательный разряд конденсатора с затуханием является одним из случаев переменного тока с изменяющимися амплитудами напряжения и силы тока. Такой ток называется неустановившимся током; часто употребляются также выражения — неустановившееся состояние тока или неустановившийся режим тока.
При таком неустановившемся режиме следует различать два случая.
Первым случаем назовем тот, когда во всех частях цепи мгновенное состояние тока (величины и фазы напряжения и силы тока) — одно и то же; изменение его происходит одновременно во всех частях цепи одинаковым образом.
Вторым случаем назовем тот, когда изменение состояния тока неодинаково в разных частях цепи, т. е. когда имеет значение
411
время, необходимое для того, чтобы измененное состояние распространилось с одной части цепи на другую
Практически последний случай имеет большое значение при возникновении в достаточной длинной цепи (линии передачи) собственных, или свободных, колебаний. В этой главе мы остановимся на первом случае неустановившегося режима тока.
Введем следующее условие: „постоянные" цепи — ее сопротивления, емкость^ самоиндукция — не изменяются
Рассмотрим случаи включения и выключения тока; в этих случаях заранее видно, что неустановившеёся состояние тока есть переходное от одного установившегося состояния (например работа цепи при определенной нагрузке) к другому (например отсутствие тока и напряжения). В течение переходного времени, т. е. пока режим тока не установился, точ можно рассматривать как состоящий из суммы двух токов — установившегося, или вынужденного, и так называемого свободного. На последующем примере эти понятия уяснятся конкретнее.
Сначала рассмотрим включение источника постоянного тока, например аккумуляторной батареи, в цепь, содержащую сопротивление R и обладающую самоиндукцией L. Напряжение источника обозначим через V.
В переходное гремя, пока растет сила тока i и вместе с ней растет магнитное noie тока, будет существовать ЭДС самоиндукции, на уравновешение которой потратится часть напряжения; для этого-состояния таким образом мы будем иметь при изменяющемся Z:
V=Ri-\-L~.
Так как V— const, то уравнение интегрируется разделением переменных:
откуда, не забывая ввести произвольную постоянную, имеем: 1 1 /• v\ &
п С V R ) L ’
и дагее
Постоянную интегрирования С определим из начального уело* вия, что при /=0 сила тока Z = 0, откуда
—
412
Подставляя окончательно:
это значение С в предыдущее ур-ние, получаем
У У -Ф-l~ R ' Re
(232)
В этом ур-нии второй член правой части с ростом t, т. е. с течением времени, уменьшается, стремясь к нулю при / = ОО; поэтому сила тока приближается с течением времени к пределу
. _JZ гв— % >
(233)
т. е, к величине, определяемой по закону Ома для постоянного тока. Величину /в, определяемою ф-лой (233) мы назовем вынужденной, или установившейся, силой тока, а величину
у _~
= L (234)
назовем силой тока свободного, и таким образом урние (232) может бьпь переписано еще и так:
i=iB + ‘c-
На фиг. 199 представлена кривая силы тока I.
Если Д = 0, то второй член в ур-нии (232) обращается в нуль для всякого t, и поэтому для всякого t
(235)
V l~ R ’
т. е. сила тока „устанавливается" мгно- фиг-
венно в той цепи, где нет самоиндукции,
т. е. нет запасания энергии в магнитном поле. В период неуста-новившегося тока будем иметь для мощности
V-i^R-P4-L~-i-, 1 dt
второй член правой части здесь выражает мощность, идущую в магнитное поле.
Энергия, запасенная за период неустановившегося состояния в магнитном поле, равна:
/ = 0О / =
f r di . Г г .
I — *i'dt— I L-i'dt — — ,
у dt ] 2
/=о / = о
413
что представляет уже известное выражение энергии магнитного поля.
Практически влияние второго члена, т. е. тока /с, в ур-нии (232) перестает быть заметным по истечении некоторого промежутка времени — от долей секунды при слабых магнитных полях, до нескольких минут при очень сил ных.
Из уравнения (234) мы имеем, что при / = 0
а при
т после включения свободный ток падает
t. e. что через время
до —, или своей начальной величины. Величина т назы-
в Z,/1q2o
вается „постоянной времени" данной цепи тока.
При включении постоянного тока, напряжения V, в цепь, содержащую 7? и С, т. е. например для заряда конденсатора, будем из закона Ома:
иметь
vK=V — iR.
(236)
Сида тока выразится теперь через положительную иэводную от vK, так как пока ток есть, vK растет, так что
про-
1 = С^ = - CR^r. at at
Отсюда
*_______Lz//
i ~~ CRdt
и
l = A-e CR.
V
Когда /=0, тогда фк = 0и из уравнения (236) I- — } следо-
ват ель но окончательно
7?
Уцножив уравнение (236) на l-dt и интегрируя, найдем известное уже нам выражение энергии, запасаемой в конденсаторе.
414
§ 116. Включение переменного тока
Рассмотрим теперь включение источника синусоидальной ЭДС в цепь, содержащую R и L.
В этом случае будем иметь:
£„,sin(o)/) = /?Z + L^-. (237)
Не будем теперь задаваться, как делали это в § 7, выражением для силы тока, а определим I интегрированием уравнения (237),— это будет общее решение вопроса о токе при переменном напряжении в цепи, содержащей и L
Интегралом уравнения (237) является
__ f
— ср) 4-Л2.£ l . (238)
и ср определим, подставив выражение (238), вместо i в уравнение (237):
Ет sin (wf) =Лг R cos ср • sin (<о/) — /ЦТ? sin ср • cos (ш/) -f-cos ср cos (of) -f- ФАЛ jSin ср • sin ((of) -|-
/ R\
+ (л2/?-л2д^р * .
Последний член здесь равен нулю; далее, отсюда имеем, приравнивая сумму коэфициентов в правой части при sin (of) вели--чине Emi а при cos (of) — нулю:
Аг$ cos ср (nLA1 sin ср = Ет, — ATR sin ср mLA1 cos <p = 0. Отсюда получаем известные соотношения:
х (t)L
•ST—R.
=s
1 7? cos cp-j-o)£ sin cp j//?'*-f-(co/j з жв?
есть амплитуда установившегося тока ZB, и таким образом^ из уравнения (238) имеем опять:
/ = ZB + Za» где
-5/
/С = + Л2е .
Постоянная А2 определяется из начальных условий, например так.
Из уравнения (237) ясно, что счет времени нами начат с момента, когда напряжение v равно нулю. Пусть оно включено в цепь
41&
8 момент /==/,; в этот момент сила тока i равна еще нулю; подставляя значения i и t в уравнение (238), получаем:
4в8‘п(<Ц — <р) + 4е L =°> откуда
А2 = — Jm3eL 1 sin — ср). (239)
Из этого уравнения ясно, что если включение напряжения прэ-язошло в такой момент /г что co/j — <р = 0, или /3 = ~ , то А2 — О, а потому и Zc = 0 для всякого момента времени, т. е. второго •члена в уравнении (238) совсем нет.
Ф
Указанный момент *1= соответствует прохождению тока /в через нулевое значение.
При включении напряжения в Какой-нибудь другой момент имеется ток zc, быстро — в обыкновенных случаях в течение не-сколькик периодов — уменьшающийся практически до нуля.
Теперь следует поставить вопрос о силе тока в более общем случае, именно, когда в цепи кроме /? и L имеется и С и соединены /?, L и С последовательно.
Для такой цепи имеет место соотношение (230): e=7?z+£^ + f~?- (А)
l&L j Lx
Полагаем опять, — осциллограммы это подтверждают,
так как zB есть ток при установившемся режиме в цепи, то для него одного уравнение (А) тоже имеет место, приводя к общему случаю закона Ома, а потому, вычитая из общего уравнения (А) частный его вид для zB, получим уравнение для одного zc:
/?Zc + £SC+fL?=0- {В)
> Диференцируя, имеем:
+ =о. dt* L dt 1 LC с (С)
Подставляя в уравнение (В) величину — где qc обозна-
чает заряд емкоси С от свободною тока, получим:
1 Я j l-п (D)
416
Оба последние ур-ния (С) и (D) вполне подобны ур-нию (217) для разряда конденсатора и интегрируются так же. Поэтому
ic = AemU-± Be™*,
а = Г L dt= — emlt 4- — J
(E)
где и имеют прежние значения (см. § ИЗ).
Если R > 2 то пг1 и т2 действительны, Zc уменьшаете»
апериодически с течением времени вследствие существования мно-жителя е L , все время складываясь алгебраически с током ZB; по истечении нескольких периодов Zc становится практически незаметным, и остается в цепи один ток ZB, для которого по соотношению (А) имеет место закон Ома в общей форме (фиг. 200).
Фиг. 200.
То же будет при , т. е. при т1 — т2.
Если R < 2 , то и w2 мнимы, и мы получаем, ввмя
опять величины а и Ь\
тг =— b-\-ja и т2 —— b—ja\ ic = e~bi (Cj cos at C2 sin at). (240)
Произвольные постоянные Q и C2 мы определим из начальных условий. Будем считать время с момента включения тока. Так как включение застает напряжение в какой-то фазе, то выражение напряжения сети будет:
e = Ems\n (о)/ + ф).
Обозначим добавочным индексом О значения всех величин в момент включении, т. е. при / = 0;
27 J еория переменных то -ов. л i у
тогда
Zo — О, или
*во + 1оо — °> откуда
*со = — Zbo = — 4fsin (+ Ф — <?)] t=о = “ Jm Sin (Ф — <р),
Далее
(°)
Так как и
v — v -4- v . к кв I КС’ и при
/=0 vKO = 0,
ТО
®ксо = Чсо — ®кво = — ®кво = —[sin [(!)/-]- ф — <р — у)j
Итак
V “° = feC0S (Ф ~ <₽) = VK«C0S (Ф “ 'Р)- W
Возвратимся к определению С3 и С2 в уравнении (240).
При t = 0 из уравнения (240) и (F) имеем:
Zco=Cl = — Л.5111 (ф — <₽)•
Для определения С2 уравнение (240), уравнение тока, как видим, не может служить, перейдем к уравнению напряжений (В) и подставим в него выражение (240) для /с, причем последний член можем писать просто, как VK, ибо
J?^”W(C1 cos at-j— С2 sin at) Le~b\— bCy cos pt— bC2 sin at —
— aCy sin at aC2 cos at) + vKZ = 0.
При / = 0 получаем, принимая во внимание уравнение (Н):
RCX + L(aCa — bCy) = — VKm cos (ф — <p), откуда r _ (- R + Lb)C. - VKm cos (Ф - <₽) 2~ La
418
или, нодставив значение С* и VKm,
с*=^rrJm sin (^_ <f) ~i cos —»>•
Таким образом постоянные С7 и С2 нами определены, остается несколько упростить получающееся из уравнения (240) сложное выражение для /с:
iz = e~bt £—Ляsin (Ф—tp)cos at
, (/? — Lb)Jm sin (ф — <р) - Укт cos($ — <р) sjn Л ,
‘ La J *
Так как
те
затем, соединив вместе члены, содержащие Jmt получим:
Jm sin (ф — ср) ( sin at—cos а/) —
_кю СОЗ (Ф
La т
Так как
к вводя уже известный нам угол Е, такой, что
2La а
~R~~T9
получаем окончательно:
27*
е~ь‘
sin (ф — ср) sin(0/ — £) — VKm cos (ф — ср) sin at
419
Величина
есть период собственных затухающих колебаний в цепи. Эти колебания, как видим, разлагаются на два ife и сдвинутых по фазе, на Е и с разными амплитудами колебания.
Если включение произошло в тот момент, когда ZB = 0, то ф = (р, и первое колебание исчезает, так что в этом случае
<=-----г—
с La кт
Если включение произведено на четверть периода раньше или позднее, то
н исчезает второе колебание, так что
Г — —sin (at — g). c aVLC m
Ток Zc в особо неблагоприятных случаях, т е. яри некоторых значениях /?, L и С, а также при неблагоприятной фазе ф, может, слагаясь t ZB, обусловить колебательный ток в цепи, изображенный на фиг. 201, по временам достигающий большой силы и обусловливающий большие напряжения на емкости и самоиндукции.
Примером может явиться включение генератора в цепь, содержащую трансформатор с подключенным к нему разомкнутым кабелем.
Дабы уменьшить Zc, подобное включение производится так, что выключатель замыкает цепь сначала через добавочное сопротивление, а затем уже без него; это сопротивление увеличивает декремент колебаний, увеличивает затухание.
Другим способом является включение в цепь генератора сначала при пониженном напряжении.
Остановимся еще на выключении перем иного тока, причем возьмем случай, представляющий большой практический интерес,— именно выключение длинной, т е представляющей известную емкость, линии, замкнутой в конце на короткое. Допустим, что разрыв цепи произошел как раз в момент максимума силы тока Jm Запасенная при этом в магнитном поле всей цепи магнитная энергия, равная
4 20
должна превратиться в
так что приближенно, водов и пр. за Первую
энергию электрического ноля,
__ CV* 2 ’ пренебрегая потерями на нагревание прочетверть периода, имеем:
формулу, аналогичную формуле {99); до такого напряжения варя* дится линия; далее • роцесс исчезновения энергии будет иттж знакомым нам путем затухающих колебаний.
<21
В дальнейшем, после ознакомления с теорией длинной линии
передачи, мы еще раз вернемся к неусталовившемуся режиму, именно
к упомянутому в начале главы второму случаю и в частности к вопросу, с какой часто!ой будут совершаться в такой линии свободные колебания.
Пример 47. Начертить кривую всего тока z = fB-|-fc по кривым /в и /е для цепи, в которой /?= 10 омам, £ = 0,01 генри,
С= 0,0001 микрофарады для трех случаев:
1) когда ф = —
2) ф -=<₽ и 3) ф = <р
422
ГЛАВА XVI
ТЕОРИЯ ДЛИННЫХ ЛИНИЙ ПЕРЕДАЧИ ЭНЕРГИИ20
§ 117. Диференциальные уравнения цепи с равномерно распределенными емкостью, самоиндукцией, ваттным сопротивлением и утечкой
Нам уже приходилось упоминать, чго всякая линия передачи энергии обладает емкостью, равномерно распре деленной по ее длине; при этом могут представиться разные случаи Если два провода, передающие электрическую энергию, идут над землей, то их емкость, обусловленная их положением и рассюянием друг относительно друга и относительно земли, сравнительно невелика, и за ядный ток (ср. фиг. 63) и связанные с ним явления (большее падение напряжения и пр.) оказывают значительное влияние лишь при высоких напряжениях, когда присоединяется и еще новое явление,— разряд через воздух, так называемый „тихий разряд", в темноте создающий явление „короны*; К|.оме тихого разряда при высоком напряжении существует уже при всяком напряжении вдоль всех проводов утечка от провода к проводу через плохую изоляц1 ю на столбах линии.
Другой случай получим, когда провода, передающие энергию, представляют собой жилы кабеля, проложенного под землей, как это имеет место во всех городских сетях как сильных токов (т. е. для освещения и моторов), так и слабых (телефонных и телеграфных), а также и в некоторых других случаях, например в подводных телеграфных кабелях.
Здесь емкость проводов становится значительной, и ее влияние необходимо уметь учесть точно во всех случаях С ростом частоты это влияние увеличивается, что ведет к очень важным следствиям для техники слабых токов. В дальнейшем мы отметим главнейшие пункты этого влияния.
Заметим, что всякие «провода обладают еще и распределенной по длине их самоиндукцией, которую тоже следует учесть при общем расчете явлений в лин^и передачи энергии, так же как и распределенное по д >ине их ваттное сопротивление.
423
Сделаем следующее допущение: пусть емкость, самоиндукция, ваттное сопротивление, утечка через изоляцию и утечка в воздух тихим разрядом распределены по линии равномерно, т. е. величина их на единицу длины провода постоянна по всей длине линии; затем введем обозначения: пусть /?0 означает ваттное сопротивление единицы длины, именно — одного километра, л и-нии, т. е. того и другого провода вместе, Ло = о>Ао — безваттное сопротивление (обусловленное самоиндукцией) одного километра, Z = /?0 -4-JXQ — полное его сопротивление; далее, через Ов обозначим ваттную проводимость между проводами на один километр длины линии; если мы умножим на GQ-dx напряжение между проводами в любом месте линии, то получим ваттную силу тока, слагающуюся из тока утечки через изоляцию и через воздух и из ваттной составляющей, если таковая есть, заряжающего провод тока (или иначе—его продолжения — т ка смещения между проводами) в этом месте, через Во = (оСо обозначим безваттную проводимость от провода к проводу на один километр; умножив ее нанапряжение,получим безваттную составляющую зарядного тока; UQ=a = Gq есть полная проводимость (берем перед JBQ плюс, так как безваттный ток есть ток емкостной) между проводами на один километр длины линии. Ве-
личины /?0, £0, (70, Со называют постоянными линии. Всю длину линии обозначим I На конце линии у вюричных зажимов напряжение пусть будет сила тока первичных зажимов в начале линии: Vj и (фиг 202)-
Условимся положение элемента линии определять его расстоянием х от конца линии.
Падение напряжения в элементе dx длины линии выразится так: du = Z/?o dx -j- Lq dx,
HI а изменение мгновенной силы тока:
di—vGodx -f- Co dx.
В векторной форме эти соотношения представятся так: dV = jZQ dx
Фиг. 202.
(241)
(242)
d J = V Uo dx,
и
424
или
dx
= J Z„
и
^-^VUQ. dx °
(243>
(244>
Уравнения (241) и (242) не предполагают какой-либо частгой формы зависимости i и v от времени и поэтому приюдны для исследов^ния любого случая тока.
В уравнениях (243) и (244) нами введены векторы; этим самым, мы уже предполагаем, что v и1—синусоидальные функции времени, следовательно предполагаем, что приложенное к линии напряжение синусоидально и что кривая тока не искажается влиянием железа; кроме того мы расширяем область приложения законов разве 1вления токов и пр. на бесконечно-большое число бесконечно-малых элементов, содержащих все виды сопротивлений и составляющих в совокупности, линию передачи.
§118. Исследование уравнений линии передачи энергия
Диференцируя эти уравнения еще раз по х9 получим: d?V_dJ у dx2 ~dx °’
dx2 dx °’
Подставляя сюда из уравнения (243) и (244) выражения первык
производных, получаем такие уравнения:
d2V dx2
= VZ0Ua
аЧ--------
d^ = j Z°U°
(J45>
Мы получили для тока и напряжения уравнения одного и тоге же вида, что показывает, что напряжение и сила тока распределены, в проводах одинаково.
Частный интеграл например второго уравнения есть
(246)
где е есть основание натуральных логарифмов, постоянная А пома, произвольна, а т определяется из уравнения, получаемого подстановкой решения уравнения (246) в уравнение (245) (первое).
«5
а
Так как
dV -
— пг A emxi dx
d2V
—-==zm2Aem* dx2
то из уравнения (245) получаем:
т2 = Zo UQ
или
= ztz V(RQ + + /^o)
(247)
Подставляя два полученные значения т в уравнение (246) и делая постоянные для общности различными, получаем общий интеграл первого из уравнений (245) в таком виде:
= А^е* 9^(Яо+/Ао) (Go+/Bo) _|_ "*•* (0>+/Д|\ (248)
или, обозначая через т арифметическое значение корня в уравнении (247):
У = ^е+тх 4- А2е-*“ (249)
J =-Х- т (А^тх — Аге~тх
Чтобы получить J, обратимся к уравнению (243), из которого имеем:
j____1 dV
ZQ dx ’
или, на основании уравнений (249) и (247):
(А^** — (250)
~0 “0
Из уравнения (247) следует, что т есть отвлеченное комплексное число; полагая
т = а -|~ jb
и подставляя это выражение вместо т в уравнение (247)^ возвышения в квадрат находим:
- *2 + 2jab = ад - Х0В0 + j(R0BQ + X0GJ, откуда, приравнивая сначала действительные, затем мнимые «Случаем:
а*-^ = ад-ад 1
(251)
ловле
чмти,
(252)
426
Решая эту систему уравнений относительно а и Ь, получаем:
*• a==V у(/?0с0-ед+К(^Н-хо)(^+ор1 ................................ — /(253)
Hl Ь^У т1ЗД-/?0Оо+/(^ + ХЬ(^ + °о>1 J
Так как по формулам Эйлера
е+тх _ ea^jbx _ ^(cos Ьх -f- J sin bx),
e~mx = = e-ax(cos bx — J sin bx),
то уравнения (249) и (250) приобретают такой вид:
V = Агеах [cos (bx) /sin (bx)] -f“
-j- A2e~ax [cos(bx) — /sin(bx)]
{Axeax [cos (bx) +- j sin (bx)] —
— A2e~ ax [cos (bx) — J sin (#x)]}.
(254)
Для определения постоянных Л, и А2 могут служить данные для какой-нибудь определенной точки линии величины V и J; всего удобнее исходить из „вторичного" напряжения, т. е. напряжения У2 в конце линии у нагрузки и нагрузочного тока J2, каковые значения величины V и J получают при х = 0; при этом мы из ур-ния (254) получаем: __ .
й2=л14-л2,
откуда и определяем
А)
А)
-Л),
(255)
Подставляя эти выражения А1 и А2 в уравнения (249) и (250) и вводя следующие обозначения:
UO=UO<^,
427
причем
j Л, ) ^3 = arctg^
g ।
<J>4 = arctg—0 I
(25»)
нолучаем:
V=А^а+^х+^1 + A2e~ +/ф, _ = АгеахеК bx~ > -j- ^7(" bx+
1 /”Ц)ГЛ ** /(&х+*<+^7^) A ~ax
= 1/ ^[Ate e v 2 ’ — A2e e v 2
r zo
>(257)
Перейдем в уравнениях (257) от символического выражения напряжения и силы тока к выражению их мгновенных значений.
Из последних уравнений мы видим, что для любой точки х с течением времени и v и i изменяются синусоидально. Если мы отвлечемся от множителей еах и положив например а равным нулю и эти множители следовательно равными единице, то, рассматривая значения v и i для какого-нибудь момента, т. е. полагая /= const, мы видим, что они изменяются вдоль линии синусоидально в зависимости от переменного х. Если мы возьмем две точки х* и х2, причем расстояние между ними х2—хг будет таково, что
Ьх2 = Ьхх 4- тт, или п х2 хА = — ,
то значения v в этих двух точках будут по фазе точно противоположны, так же как и значения z, потому что
sin (а п) = — sin а.
428
Таким образом получается такой совершенно новый для наэ результат исследования уравнений (258): при достаточной длине проводов, в них в различных точках будут действовать в один н тот же момент напряжения в противоположных направлениях и течь в противоположных направлениях токи.
Из предыдущего следует, что в любых двух точках, отстоящих 2тг „
друг от друга на расстоянии —, фазы и напряжений и сил токов
будут одинаковы, хотя величины напряжений и сил токов при этом будут в этих точках разные, ибо в уравнения (258), дающие величины и фазы v и /, входят множители еах и е-**, которые и показывают, что амплитуду v и i изменяются непрерывно от точки к точке вдоль проводов.
Величина
(259)
называется длиной волны в проводе.
§ 119. Волны в линии
Из уравнений (258) следует, что процесс изменения о и / вдоль проводов и с течением времени можно представить себе, вообразив движение вдоль проводов двух синусоидальных кривых навстречу одна другой. Для напряжения -о:
4- sin (со/ 4" + Ф1)
есть синусоидальная кривая, двигающаяся от начала линии к концу, причем амплитуды ее по мере продвижения уменьшаются, приближаясь к пределу при х = 0;
4* А^ах sin (Ы — Ъх 4" ФР
есть синусоидальная кривая, двигающаяся в обратном направлении тоже при уменьшении амплитуд по мере продвижения до величины Эти результаты легко получить, полагая сначала
sin (о>/ 4“ &х 4“ Ф1)=
где k — некоторая постоянная величина, например амплитуда синуса, т. е. единица, и рассуждая, где получится эта величина во время так как при этом должно быть
sin (о)^ 4“ Ьхг 4“ ФР = то очевидно
со/ 4“
429
и, если /j > t, то Xj <х, следовательно в более поздний момент времени /1 кривая оказывается смещенной к концу линии
Подобным же образом получим направление движения второй кривой.
Действительно существующее в любой точке в любой момент напряжения v получается суммированием значений ординат этих двух кривых для этой точки и в этот момент.
Аналогичное получаем и для силы тока; только действительно существующая в любом элементе длины провода в любой момент сила тока Z, согласно ур-нию (258), получается вычитанием из ординаты кривой, идущей от начала к концу, ординаты второй, идущей навстречу кривой Кривые, идущие от конца к началу, называются отраженными волнами; кривые, идущие от начала к концу, называются главными волнами.
Рассмотрим, с какой скоростью перемещаются вдоль линии значения синусов ур-ний (258) Из условия, что по прошествии времени dt
sin [о)(/ 4“ ^0 + + dx) + Ф1 ] = sin(o>/ + dx' 4“ Ф1)>
находим:
откуда
®dt -j- bdx — 0,
dx
<W~ dt
(0
~b'
Знак минус и показывает, что главная волна идет от начала к концу (в сторону убывающих х-ов) То же абсолютное значение скорости получим и для отраженной волны.
За период волна пройдет расстояние
2п___2п___
т. е. ту же самую длину волны X Таким образом скорость
движения волн в проводах равна:
X со
w = — = —.
Т b
(260)
Эта скорость, как видим, имеет конечную величину и зависит только от числа периодов тока и „постоянных" линии передачи.
Допустим, что все потери энергии в линии так ничтожны, что ими можно пренебречь; это значит, что /?о = 0 и Go = O Подставляя эти значения в ур-ния (253), получаем, что а = 0; это обозначает, что амплитуды волн не изменяются по мере продвижения 430
волн по линии, — множители еах и е~ах при этом равны единице; далее, из ур-ний (253) имеем, что
Так как Х0 = а>£0, а Во —а)С0 (ибо емкостной, зарядный ток Jc~toCQV на единице длины провода, и следовательно о>Со есть проводимость Во), то
= <о
Подставляя это значение b в ур-ние (260), получаем:
w = ~=L= километров в секунду; (261)
Г ^0^0
что w действительно есть скорость в километрах в секунду, вытекает из того, что самоиндукция имеет размерность длины, емкость же — размерность времени в квадрате, деленного на длину, a А и Со суть самоиндукция и емкость, отнесенные к одному километру длины.
В линиях с воздушными проводами величины Ло и Со, вообще говоря, меньше, чем во всех других случаях, и скорость w при этом получается наибольшёЦ.
В курсах электричества и магнетизма выводятся формулы для определения величины самоиндукции и емкости двух параллельных проводов. Эти формулы дают с достаточной точностью
г * . D » генри L =4 In — 10-4 ——, ° г км
и
__ 1 1 фарад
0— ~~D ‘ 9-Ю6 ~км~ ’
4 In — г
где D ъетъ расстояние между осями проводов, а г—радиус их поперечного сечения.
Таким образом, подставляя эти выражения в ур-ние (261), получаем:
w = = з. ю5 км сек,
т. е. скорость, равную скорости света в пустоте.
Полагая приближенно для воздушных проводов w равной скорости света, из ур-ния (260) получим длину волны для обычных линий передачи энергии при числе периодов пятьдесят в секунду:
1 = w Т= 6 000 километров.
431
Таким образом глина даже наибольших линий передачи, по
строенных до настоящего времени, есть только часть длины волны тока. Например при длине линии в 200 километров на линии уме-1
стится только — доля волны, т. е. напряжение в начале линии и <50
напряжение в конце ее будут иметь сдвиг в фазе —«2ТГ, или 12°. <50
То же конечно имеет место и для силы тока.
В кабелях, где Со значительно больше, чем в воздушных линиях, скорость w движения волн получается в 3—5 раз меньшей, так же как и длина волны при одинаковом числе периодов.
Остановимся на случае холостой работы линии, т. е. положим /^=0. Тогда ур-ния (255) дают нам:
2
Ф1 = Фз-
Поэтому первое из ур-ний (258) может быть в этом случае преобразовано следующим образом:
»= [sin (<о/ + ф2) cos bx -|- cos (©/-f- ф2) sin bx] -f-
-|- Aye~ax [sin (©/ -f- фг) cos bx — cos (tat -ф- фх) sin bx].
Введем для упрощения дальнейших рассуждений предположение, что потери в линии ничтожны, а потому можно положить а = 0. При этом последнее ур-ние упрощается следующим образом:
v = 2Аг cos bx sin (о>/ -|- ф2) (262)
Последнее выражение показывает, что амплитуды (2ЛТ cos bx) напряжения растут к концу линии, достигая максимума 2^4j = И, ар и х = 0, т. е. у вторичных зажимов. Это явление повышения напряжения в линии по мере удаления от станции или от генератора есть то же самое явление Ферранти, которое было уже приближенным образом описано в § 41.
Обратимся ко второму ур-нию (258), сделанное нами допущение, что а = 0, так как потери ничтожны, равносильно утверждению, что 0 и 0 = 0, и следовательно Uo — BQ = <dC0, а = = (nLQt а потому из ур-ний (г56) мы получаем, что фа =
ж= = о > и втоРое ур-ние (258) преобразуется поэтому так: At
i = 24, р/"sin bx cos (wt -|- Ф,) =
= 2Aj ^°sintasin(26Э)
432
Из этого ур-ния мы видим, что амплитуда 2А2 sin bx силы к £°
тока уменьшается по мере приближения к концу линии, и на самом конце, где х = 0, сила тока равна нулю. По фазе сила тока
опережает напряжение везде на четверть периода.
Ур-ния (262) и (263) суть уравнения стоячих волн в проводах. На таких расстояниях х от конца линии, что cos#x = 0, амплитуды напряжения равны нулю; в этих точках все время напряжение равно нулю; эти точки суть узлы для напряжения; в тех точках, для которых 4 cos bx = 1, амплитуды напряжения будут
иметь наибольшую величину 24j = V2,— эти точки суть пучности; во всех промежуточных между узлами и пучностями точках амплитуды имеют величины 241cos/?x по ур-нию (262).
Там, где cos#x = 0, sinZ?x — 4^1 и наоборот; поэтому в тех точках* где находятся , узлы напряжения, будут находиться пучности силы тока по ур-нию (263), и в точках, где находятся пучности напряжения, будут находиться узлы силы тока.
На конце линии таким образом при холостой работе мы имеем
пучность напряжения и узел тока.
В точках, где находятся узлы напряжения, мы можем оба провода линии передачи соединить друг с другом без всяких последствий от этого.
Стоячие же волны с узлом напряжения и пучностью тока на конце мы получим при коротком замыкании конца линии, конечно при том же условии, что а = 0. При этом условии стоячие волны получатся вообще всегда, • когда вторичная мощность равна нулю, например и тогда, когда сдвиг фаз (p2w между J2 и У2 есть таков случай подключения конденсатора к концу
линии; доказательство сказанного предоставляем провести самому читателю, заметив лишь, что для доказательства нужно принять во внимание следующее. При ср2гг = ^- векторы У2 и J2 перпендику-лярны один к другому; так как потери равны нулю и
Ц = 4-/В0= +/*о = +Мо.
ТО
есть цействительное, а не комплексное выражение, а потому в ур-ниях (252) векторы
% и Л1/
/ 2 у 7
28 Теория переменных токов.
433
составляют прямой угол. Отсюда вытекает, что величины комплексов (модули) Aj и А2 равны:
Л1 = Л2
и что ср! = — ф2-
Если вторичная мощность или потери в линии имеют величину, отличную от нуля, образуются волны — главная и отраженная, — идущие вдоль проводов со скоростью порядка скорости света.
При низкой частоте (например 50 периодов в секунду) длина волны получается настолько большой, как мы видели выше, что длина линии передачи составляет только небольшую часть ее, а потому в таких линиях нельзя наблюдать пучности и узлы тока. Но при высокой частоте, например при токах от разряда конденсатора, волна обладает небольшой длиной (например в несколько метров), и в линии, состоящей в этом случае из дв\х проводов в воздухе, можно наблюдать хорошо выраженные стоячие волны с пучностями и узлами напряжения и тока. Место пучности напряжения находится при этом легко следующим образом. Внесенная в пространство между проводами линии гейслерова трубка начинает ярко светиться там, где имеется пучность напряжения, т. е. где переменное электрическое поле между проводами имеет наибольшую амплитуду.
§ 120. Телеграфные и телефонные кабели
Обратимся к линиям с потерями и рассмотрим один частный случай.
В телеграфных и телефонных кабелях самоиндукция и утечка так малы, что ими можно пренебречь, положить выражающие их величины Хо и О0 равными нулю и считать, что кабель обладает только ваттным сопротивлением /?0 и емкостью Со или проводимостью Во = (оСо.
В этом случае из ур-ний (253) получается, что
Таким образом при увеличении частоты переменного тока а растет пропорционально корню квадратному из частоты.
Предположим, что переменный ток имеет составляющие высших порядков. Для такой составляющей /z-го порядча вместо а будем иметь: _
следовательно составляющие „затухают" относительно тем сильнее, чем выше их порядок. Сильное „затухание" ограничивает расстояние для передачи по кабелю различных сигналов, например речи в
434
телефонных кабелях, ибо сильное затухание обертонов делает речь неясной.
Если к концу линии подключен аппарат, в котором отношение — — /~ А
между У2 и равно как раз |/ = , то и в этой линии по-
V щ
всюду устанавливается это же самое постоянное отношение между напряжением и силой тока, и отраженная волна исчезает, ибо, как нетрудно видеть из ур-ний (255), числитель в выражении для А2 равен при этом нулю.
Величину
+ 7 е0 о
(265)
часто называют * волновым" сопротивлением линии.
Величина а характеризует или определяет величину затухания и, как показывает ур-ние (253), I, — где. BQ и Xq зависят от частоты, — тоже зависит от нее, и именно — с ростом частоты растет; однако а изменяется и в зависимости от соотношений между величинами /?0, XQt GQ и Во, при этом, что особенно важно, наименьшая величина, которую а может иметь, не зависит от частоты.
Исследуем вопрос подробнее. Так как /?0 и О0 должны быть вообще возможно ценьшими, насколько это позволяет стоимость производства, то изменять в широких пределах мы можем только BQ и Хо. Эти величины входят в формулу для а совершенно симметрично. Найдем, при каком значении Xq и следовательно Lq, имеет минимум величина а, или, что проще, подкоренное выражение в ур-нии (253), I. Для этого производную от него по Xq приравниваем нулю, что дает:
откуда
о*-]-в*
и наконец
или
Bq Oq
^0__^0
Cq Oq
(266)
28*
435
Такому соотношению должно удовлетворять или £0, чтобы а имело минимум, — а что это будет именно минимум видно из того, что вторая производная, равная
^+со и + о; ijf, И I - ~ Л I и — I.» ? .v I «тяж »-
У/гГМЗ e/(^-t-^3 Z<A 4
положительная (ибо Jf0<Z0). Преобразуя ур-ние (253) I, на основании ур-ний (266), получаем следующие выражения для минимального а, не зависящие от частоты:
Так как обыкновенно в телефонных кабелях О0 очень мало, /?0 довольно значительно и Сь тоже значительно, a Lq, как уже указывалось, очень мало, то для удовлетворения условия (266) надо увеличить искусственно.
Значение величины а для ясности речи и необходимость искусственного увеличения £0 выяснил впервые Хивисайд Пу пин предложил для увеличения самоиндукции включать в кабель катушки и дал расчет необходимого числа их. По его теории, яодтверженной практикой, число катушек на длине одной волны не должно быть меньше шести; увеличение числа их свыше десяти на длине волны не приносит уже пользы. Таким образом в среднем одна катушка приходится на 1,5—3 километра длины кабеля. Для воздушных проводов катушки располагаю ?ся реже ввиду меньш-й емкости этих про одов сравнительно с кабелем. Описанным способом Пупин достиг значительного уменьшения затухания высших составляющих тока и увеличения ясности речи.
При подключении к кабелю воздушных проводов нарушается указанное выше постоянство отношения между напряжением и силой тока, так как емкость кабеля больше таковой воздушного провода; включение катушки Пупина в кабель восстанавливает приблизительно постоянство этого отношения и тем улучшает работу линии.
Того же искусственного увели ения Lo в кабеле Краруи предложил достигать обмоткой телефонного провода или жилы железной проволокой. Этот способ является невидимому не столь удобным ввиду добавочных потерь в железной проволоке, токов Фуко, искажающих ее действие, и пр»
436
§ 121. Замечание об электрическом расчете линий
Остановимся теперь на расчетах явлений в длинных линиях.
Если мы желаем по данным величинам, — во-первых, нагрузки ( У2, J2 и ср2) и, во-вторых,—постоянных линии (см. ур-ния (253), — вычислить V и J по величине и фазе в любой точке линии, например в начале, то мы должны будем обратиться к ур-ниям (257), которые для этого перепишем, освободившись от мнимости в показателе, как уже мы привыкли это делать. Ограничимся ур-нем для V:
V — X^fcos (bx 4- Ф0 -j-/sin (hx 4~ Ф])1 +
4- A^~ax [cos(— bx -j- ф2) +/sin(— bx + <J>2)].
Здесь сначала мы должны вычислить Av А2, и ф2 по ур-ниям (255); затем, возвышая в квадрат действительную часть и множитель при у, складывая эти квадраты' и извлекая из суммы квадратный корень, найдехм амплитуду V, а деля множитель при J на действительную часть, найдем тангенс фазового угла V (относительно У2).
Подобным же образом определим J.
В настоящее время для расчетов с длинными линиями часто употребляются гиперболические функции. Покажем кратко их происхождение, выведем основные зависимости для них и соотношения межау ними и тригонометрическими функциями и наконец применим их для выражения соотношений в линии передачи.
§ 122. Гиперболические функции
X2 у2
В ур-нии гиперболы —2— = 1 положим b — а\ ур-ние приобретает простой вид: х2 —у* = а2. Пусть кривая АВ на фиг. 203 есть именно такая, такая называемая равнобокая, гипербола; здесь ОЛ = а, ОС=х и ВС=у. По обычным правилахМ вычисления площадей криволинейных фигур определим заштрихованную на чертеже площадь ОВ^АВО как разность между площадью треугольника ОВгВ и гиперболы; обозначая эту площадь через ср, имеем:
х—х х=х
ср = ху— 2 J у *dx = ху — 2 J х—a2-dx. х-а х<=а
437
Так как
Удваивая это выражение и вычитая его из ху, получаем:
т а
Положим теперь а равным единице, т. е. пусть ОД = 1, тогда
<? = In
Отсюда следует, что
хЦ-у=е'?. (I)
Определим из последнего ур-ния х и подставим его выражение в ур-ние гиперболы х1—у2 = 1, после чего решим это ур-ние относительно у и получим:
Отношение ВС к ОА называется гиперболическим синусом площади ср. Так как у нас ОА = 1, то ВС=у и есть численно сам этот синус, подобно линии синуса в круге с радиусом, равным единице. Обозначение введем такое:
y = sinh(p. (Ill)
Сопоставляя (II) и (III), получаем первое основное соотношение: е?— е-ч
sinh <р =--------. (IV)
4
438
Отношение ОС к ОА называется гиперболическим косинусом площади ср; у нас ОС — х численно и представляет этот косинус:
х = cosh ср. (V)
Сопоставляя (III) и (V) с ур-нием гиперболы, имеем:
cosh2 ср — sinh2 ср = 1, (VI)
второе основное соотношение.
Из (1), (III) и (V) имеем:
sinh ср 4- cosh ср = е*. (VII)
Наконец из (VII) и (IV) получаем:
cosh ср = —. (VIII)
£
Отношение ВС к ОС называется гиперболическим тангенсом пдощади ср; на основании предыдущего
(IX)
Величину ср назовем и здесь, аналогично теории тригонометрических функций, аргументом.
Расширим понятие тригонометрических и гиперболических функций и введем мнимые аргументы — углы для первых, площади для вторых.
Нужно заметить следующее: при радиусе круга, равном единице, двойная площадь сектора с углом а равна а, поэтому и тригонометрические функции можно считать функциями площади а, — аналогия с гиперболическими функциями получается совершенная.
Связь между обоими видами функций можно установить с помощью формул Эйлера:
cos ср 4~ J sin ср = cos ср — j sin <р =
из которых получаем:
sin (р = ег? (М)
cos ср = е ? 2 (N)
439
Сопоставляя последние два выражения (М) и (N) с выражениями (IV), (VIII) и (IX), можем написать следующие соотношения:
sin ср = — / sinh (/ф) (X)
cos ф = cosh ( /ф) (XI)
tg<p = —/tgh(7<p) (XII)
sin (/ф) = j sinh ср (XIII)
cos (/ф) = cosh <p. (XIV)
Последние две формулы мы получим, введя в левых частях ур-ний (М) и (N) мнимые аргументы, преобразовав соответственно их правые чисти и сравнив затем последние с (IV) и (VIII).
Рассмотрим еще, как выражаются гиперболические синус и косинус суммы двух аргументов.
Составим выражения:
е?< — £ - <р1 еъ _1— —«г» sinh ср, • cosh <р2=---------------=
— £-<Р« + ф1 £<Р1-Ф1 — £-(<Pi + <Ps)
= 4 ’
и cosh • sinh <р2 = —------------------------------=
_|_ £” ф< + Ф1 £ф< -Ф1 Qг (ф< + Ф1) “ 4 •
Сложив левые и правые части, будем иметь в правой части:
2 ’
что очевидно может быть представлено как sinh (<р7 -J- Тг)» приравнивая последнее сумме левых частей вышенаписанных выражений, имеем:
sinh (<р2 4- ср2) = sinh cpj • cosh <р2 cosh • sinh <р2, выражение, вполне соответствующее разложению синуса суммы двух углов в тригонометрии.
Составим далее выражения:
cosh ср, • cosh cp2=------------2----
+ Tt + Ti _|_ “Ts (cpl + ^s)
= 4
440
и . . е?*—
sinh <р, - sinh <р2 ==-----------2----:
£?< + <pi — e“<pi+?i — tf'pt-’pi ^“('pi+'pi)
= 4
Сложив, получим в правой части:
e?t+<pi j- e-(<pi+<pi) 2 9
т. е. cosh (eft (ft); таким образом получаем:
cosh (cpj -j- (ft) = cosh (ft • cosh (ft -f- sinh (ft • sinh ft, формулу, отличающуюся от соответствующей тригонометриче* ской знаком плюс пред произведением синусов.
Один или оба аргумёнта в этих формулах могут быть и мнимыми, как ф-лах. (XI) — (XII).
А. Е. Кенелли разработал очень простые приемы геометрического построения гиперболических синуса и косинуса комплексных аргументов; существуют и таблицы для этих величин, которые помогают упростить вычисления.
Гиперболические синус и косинус комплексного аргумента можно представить и в виде комплексов, именно следующим образом.
Пусть нам приходится оперировать с величиной
sinh (p+/q).
Преобразуем это выражение
sinh (р -\-Jq) = sinh р • cosh (Jq) -J” cos^ P *sln^ (/?)>
или, принимая во внимание ф-лы (X) и (XI):
sinh (р 4~ Jq) = sinh р • cos q 4~/ cosh p • sin q.
Последнее выражение есть комплекс, модуль которого выразим, принимая во внимание (VI), так:
У sinh2 р • cos2 q 4- cosh2 р • sin2 q = У sinh2 p 4- sin2 q — У cosh2p — cos2 q.
а аргумент есть
cosh p- sin q S sinh p'cosq *
Таким образом
sinh(p4“A) = V<sinh2P4“sin2^’e 7*arcts[ctghp’tg^== 1 (967) = У cosh2 p — cos2/* e 7'arc Ict« h
441
Аналогично найдем:
cosh (р 4~ jq) — cosh р • cosh (jq) sinh p • sinh (/7) = = cosh p • cos q-j-/•sinhp«sin7 =
= ]/cosh2p — sin27- с /,агс te11 рл°=
= /sinh2p cos2 q-e ^arc рл*
.(268)
§ 123. Уравнения линии передачи в гиперболических функциях
С помощью предыдущих формул мы можем ввести в теорию линии передачи гиперболические функции.
Обратимся к ур-ниям (254); подставим в первое из них вместо ’Ла и А2 их выражения (255) через вторичное напряжение и вторичную силу тока и преобразуем уравнение, как следует ниже:
__ __рах _ /7 рак ___ рак
V —V2 — • cos bx -J- Л1/ =--cos bx 4- V2-j sin bx 4-
2 f Uq 2 2
4-771/" — ~—j-sinbx-^- V2>--cosbx—
т 2 V Щ 2 2
__ /7 a-ax ___ e~ax
— J,]/ —----------cosfoc—V,------J-sinbx4-
F u0/ 2 = 2 2
/7” p-ax =------------/-sin foe.
Uo
Группируя здесь члены — первый с пятым, третий с седьмым, второй с шестым, четвертый с восьмым, пишем:
еах I е-ах еах_е-ах ~|
-г I ---------у Sin ^ 4-
v=y2|- 2
• cos bx 4-
-e~ax . . t 1 ------j sin bx .
Z I
J_7 i / za\e“x- e~ax ! I
+ Л1/ -=2 -------5----cos foe 4
г t/0L 2
Принимая же во внимание ф-лы (IV), (VIII), (X) и (XI), введем сюда гиперболические функции:
V = V2 [cosh (ах) cosh (jbx) 4~ sinh (ах) sinh (jbx)] 4-
[sinh (ax) cosh (jbx) -J- cosh (ax) sinh (jbx)}, Uq
442
или окончательно
^•sinh {тх).
(269)
Заметив, что ур-ние (254) „второе" отличается от первого
лишь множителем I/ и знаками перед членами, содержащими ' Zo
е~а*> сразу можем написать:
7— V 1/— е~ах и , ea*-\-e~ax . . и , J — к2 |/ -у- ------2----C0S bx !----2------7 Sin Ьх \ +
, - t , еах_е~ах 1
+ А -------5----cos “х I------о------/sin °х •
L 2 2 J
или
J — J2 [cosh (дх) cosh {fox) -|- sinh {ax) sinh {fox)} -J-
+ ^2 1/ [sinh {ax) cosh {fox) cosh {ax) sinh {fox)}, V Zo
и окончательно:
J=J2 cosh {mx) -f- V2 1/ *==^ sinh (mx\ (270) r Zq
Ур-ния (269) и (270) являются наиболее часто встречающейся формой выражений V и J.
Sinh (/их) и cosh {тх) должны быть вычисляемы при этом по формулам (267) и (268).
В некоторых случаях могут быть нам даны не 1Z2 и J2, а соответствующие первичные величины V, и Jr
В этом случае, очевидно, удобнее исходить из отсчета расстояния х не от конца линии, а от начала.
Ур-ния (241) и (242) § 117 в этом случае, как легко видеть, будут иметь каждое знак минус перед одной из частей; после же исключения из каждого уравнения одного из неизвестных путем диференцирования и подстановки, мы получим ур-ния, тождественные с ур-ниями (245)
Дальнейший ход решения, преобразований и исследования совершенно подобен изложенному выше; единственная разница будет вызвана упомянутым отличием новых форм/л для dv и di от прежних в знаках, вследствие чего J определится, как
1 dV
ZQ dx
443
Поэтому вместо ур-ний (254), будем иметь:
V = Аа ёах [cos (bx) -f-jsin (bx)] -|- Aa e-ax[cos (bx) — /sin (bx)],
J=1/ — XjC®* [cos(^x)-|-/sin(^x)] -f-
A3e~ax [cos (bx) — /sin t
Для определения постоянных A3 и A3 будут служить условия у начала линии, т. е. где х=0; поэтому
й1=3+^>
4=1/^Ч4»-А)-zo
Окончательный результат в гиперболических функциях будет таков:
V = Vj cosh (тх)— А|/ sinh (/их),
J = cosh (тх) — 1/ • sinh (тх).
Ур-ния (269) и (270) обычно полагают в основу расчета длинных линий передач.
Часто довольствуются и приближенным расчетом, разлагая в этих уравнениях гиперболические функции в ряды, как показано ниже, и беря из этих рядов лишь первые члены.
§ 124. Формулы для приближенного расчета линий.
Замечания о расчете трехфазной линии. Примеры
При расчетах с линиями передачи, например когда нам нужно найти первичное напряжение и первичную силу тока по данным вторичным, мы можем или найти cosh (ml) и sinh (ml) в таблицах, или вычислить их по ф-лам (267) и (268), или наконец, когда можно ограничиться приближенным подсчетом, заменить их приближенными выражениями на основании разложения этих функций в ряды, как мы и покажем теперь.
Так как
Т Т "Г 2 Т 3! 4! п- 6! *Г • • •
444
и
то
.и/ ч етх_е-тх (тх)3 ^тху,
sinh (тх) =-2-= тх + v—-f-L_...
и
и/ ч етх-\-е~тх , , (тх)2 ( (тх)4 , cosh (тх) =»---------= 1 Ч-----— + —4- ...
Подставляя вместо tn его значение
V и^, а вместо тх величину
где U и Z есть проводимость и сопротивление всего участка линии длиной х от конца ее, получим вм сто ур-ния (269) следующее:
UZ (UZ)* 2'4!
>5
V=V2
и вместо (270) — соответствующее уравнение для силы тока Л Вынося из вторых прямых скобок UZt получаем: uz , (uz)\ , 1 '
2 * 4! * ’
uz I (uz)3 1
3! * 5! ‘ ’ *
И
2
uz Лиг)3 2 4!
иг Лиг)3 31 + 5!
(270 А)
Обычно при расчетах возможно ограничиться приведенными членами, вследствие малости остальных.
Следует напомнить читателю, что вся изложенная здесь теория линии передачи энергии основана на допущении, формулированном в начале—именно, что емкость, самоиндукция, утечка и пр. распределены по линии равномерно. В действительности эго усло
445
вие осуществляется лишь с большим или меньшим приближением; в частности, все места линий, где находятся опоры для проводов, представляют места нарушения, большего или меньшего, указанной равномерности.
Пример 48. Дана линия с постоянными: Ло —2 1-10-3 генри/хсн, /?о=О,2 ом//си, Со—0,0053* 10-6 фа рад//си, G9 = 1 • 10-8 мо/км, /—50 пер/с^к, ; = 250 км, ==_110_000 вольт, и cos?2 = 0.3 (нагрузка индукци нна).
Определить Vh Jlt cos? в начале линии и коэфициент полезного действия т) в зависимости от вторичной мощности Р2.
В начале линии __
У\ = V2 cosh {ml) 4 J2 sinh (mZ),
Л = J2 cosh {ml) 4 V21/ = sinh {ml).
r Zb
Вычисляем:
X0 = (o£0 = 314.2,1*10-3 = 0,66; Zo = /?0 4/Z0 = 0,2 4- /0,66 = 0,69e№ Bq = <oC0 = 314*0,0053* 10-e = 1,67* 10-6; Uq = Gq 4-/Bo = 0,01 * 10-e 4 4 /1,67 • 10 - 6 = 1,67 * 10 - 6 /89,650.
0,69 e i 73,3°
1,67*10-6^7 89,650
0,69 ---------- e
1,67*10-6
1
Zq 643*e"'j8*18°
2
. 73,3° — 8 V5°
’ = 643 e“^8’18°’
= 1,551* 10'3.'8’18°
a = у у (0,2* 10'8 — 0,66* 1,67* 10"6 4 0,69* 1,67* 10'e) =
j/"у *5,21* 10"8== 0,1615* 10'3,
£ = j/"y (0,66* 1,67* 10'6 —0,2*20’8 4 0,69* 1,67* 10~e) = = j/* у *2,252*10'6 = 1,061*10'3. m = a +jb = (0,1615 4/1,061) 10'3, mZ= (0,1615 + / 1,061) * 10-3* 250 = 0,0404/ 0,2652.
По номограммам гиперболических функций находим:
cosh (ml) = cosh (0,0404 + J 0,2652) = 0,9655 + j 0,0107 = 0,9655 e j 0.68° sinh (ml) = sin i (0,0404 + /0,2652) = 0,0395 4- J 0,2600 = 0,263 eJ 8J.5°.
Vt = 110- Юз-0,9655-е/0.68° + /^643-e-\ 8,18°.0,263• e 81’5° = 106 200 e i 0.68° + J2 -169 e i 73,32°.
T, = 72• 0,9655 e0168° + 110-103 1,554• 10-з•« 7 0,18°.0>263.e j81,5° _ == 45 e189’68° + 72 • 0,9655 e J °’s8°.
446
Выразим через вторичную мощно ть
ср2 = arc cos 0,8 = 36,87°.
Направляем V2 по вертикальней оси, тогда
= -J^ = Pr п,3б. 10’6-е'36'87’.
V4= 106 200 <?7°'S8°+ Pr 11,36- 1О_в.е-7'36-870.160г/.73-32°= 106 2С0 ^°168° -|-+ Р2.1920.10“вг736-45°.
= 45-е7 89168° + Р2.11,36- 10~6-г ~7 36,87°.0,9655-е 7°-с8° = 45е 7 89’68°
+ Pi • 10,98 • 10_* • е ~ 7 36Д9°.
Подставляя в эти формулы различные значения Р2 и вычисляя модули Vv и получим таблицу зависимости Vv Jv Pv cos^ и т). Читателю следует проверить несколько точек графика, данного на фиг. 204.
Предыдущая теория относится к двум проводам, по которым течет простой переменный ток. В настоящее время передача энергии ^совершается исключительно трехфазным током. Если три провода линии удалены друг от друга на одинаковое расстояние, т. е. расположены в вершинах правильного треугольника, то самоиндукция, взаимоиндукция и емкость относительно друг друга всех их одинакова, только емкость их по отношению к земле несколько разная.
В этом случае представляют себе четвертый нейтральный провод и изложенную выше теорию прилагают к линии, состоящей из одного фазового провода и нейтрального, беря соответствующие этому расположению постоянные 7?0, 70, Со и О0.
Когда линия еще только рассчитывается, мы определим сначала эти постоянные по правилам, излагаемым в специальных курсах (исключая Go—утечку, которой приходится задаться на основании эмпирических Данных), затем из формул (272) и (274) вычисляем и Zk и, принимая во внимание соотношение (281), определяющее С, по формулам (287) и (288) вычисляем элементы эквивалентной схемы.
В случае несимметричной нагрузки трехфазной линии мы соединяем в звезду три эквивалентных схемы, и, отбросив нейтральный провод, решаем задачу о напряжениях, силах токов и пр., так как указано в главе о трехфазном токе.
Пример 49. Дача трехфазная линия длиной 7 = 500 км с симметричным расположением проводов по углам равностороннего треуголь-
447
дика. Расстояние между проводами £> = 430 см. В качестве провода взят медный кабель, внешний диаметр которого равен 2г =15,8 мм. Сопротивление кабеля = 0,12 ом/клг. Линейное напряжение в конце линии V2 = = 220 kV, мощность, потребляемая приемником Тока, при начале эксплоа-
гации линии, составляет лишь Р2 = 49 000 клв. п^и cos <?2 = 0,85. Частота J —50 пер/сек. Определить режим у генератора и на конце лилии при холостом ходе и указанной нагрузке.
448
Постоянные линии определим по следующим формулам (см. на приме» СЭТ. III. Отд. 19, стр. 21, форм. 26 и стр. 24 форм. 37):
Ze= ^2In у+0,5yiO-< генри/кж = ^2-1п-^^ + 0,5^. 10-« =
= (2 • 6,3 + 0,5) • 10-* = 1,31 • 10-» генри/км,
Со = —‘сГТт фарад/л:л= -^^ = 0,00883-10-е фарад/от.
21п— ’
Таковы величины самоиндукции и емкости на 1 км длины для каж* дого отдельного прохода (не для двух, как в предыдущем примере).
Таким образом для каждой, фазы линии имеем:
/?0 =^0,12 omIkm, Х9 = (о£а = 314* 1,31.10~в = 0,412 omJkm,
ZQ = 0,12 + J 0,412 = 0,429 е 7 73045'-
Ваттной проводимостью (или утечкой) вследствие ее малости пренебрегаем, так .что Go = O,
В9 = <оС0 = 314-0,00883.10-« = 2,77- 10-в.
U9 = О0 + J Вл =J 2,77-10-» = 2,77- 10-в е' 90°-
омов.
МО.
Далее для всей длины линии
Z= Zel = (0,12 + J0,412).500 = 60 + J206 = 214,5 e<73O4S' If = U* I =J 2,77 • 10-e. 500 =/1;r385 • 10-» = 1,385 - 10-8. e i 900
Фазовое напряжение в нагрузке (или в приемнике) равно
„ 220000 1ГГ7ЛЛЛ
VkA ==---= 127 000 вольт,
/з
Линейная сила тока у приемника
. Pt 40000
= _ =—7=-----------— 123,7 ампер.
/3/2cos<?2 КЗ 220-0,85
Направим Ргф по вертикали, тогда = 127 000, и 72 = 123,7 е ~ j arc cos °’85 = 123,7 е ~ 31°47'*
Для определения фазового напряжения и силы тока JJ в начале линии воспользуемся приближенным методом расчета и вышеприведенном разложением V и J в ряды.
7) Z= 1,385-10-3.eJ 900.214,5е7 73°45' = 0,297-^ 163°45' (Z7. Z)2 = 0,0883. е ~ j 32030%
так как 2-163°45'= 327°30'=360° —32°30'.
В разложении ограничимся лишь тремя членами.
Вычислим выражения, стоящие в ква.ратных скобках в форм. (270 А):
~А — 1 4-— I - 1 ! . 0.0^83 _/32Р30* Д
1 т 2 4! — -г2 ‘г 2-3-4
= 1 — 0,1425 + j 0,0416 + 0,0031 —j 0,3020=0,8606 + j 0,0396 = 0,861 е/2«40’.
29 Теория переменных токов. 44$
Д 1 UZ - 1 -U °’297 . °’°883 й -/32*30'
в = 1 + -зГ + ~5Г-1+~ГГ* + Гз^5*
== 1 — 0,0475 + j 0,0139 + 0,0006 — / 0,0004 = 0,9531 -h j 0,0135 = 0,953 еJ ™ и1ф= й2фЯ-4- ^ZB=127 000.0,861 e/2°40' 4.
4- 123,7 е - / 31*47'. л 214,5 е J • 0,953. е / 48' == 109 200 • е / 2°4О' 4-
+ 25 300. еi42*46' = Ю9 200 4- j 1720 4- 18510 4- j 17 180 = 127 610 +
+J 18 900 = 128 500 е J 8*28'.
Jt = J^A 4-"У2ф UB = 123,7 г? - /31о 47' .0,861 е/ 2*<0' 4.
+ 127003-1,3^5.Ю-з.е/эо°.0,953.e/o°48' = 107,2e-/2907' + 167,2 е/90о48'=» == 9зэб —jb^l — 2,34 + j 167,2 = 91,3 +/ 115 = 146,8 el 51*35'.
При холостом ходе J2 = О и Ike вычисленные величины
Хоюсюй ход:
д1ф = 109 200 е / 2*40' Р2ф = 127 000 Л = 167,2е/90°48' /2-0 ®2 — ?1== + 88°8' cos ? 4= 0,0325 Р£ = 1 760 клз.
. 1ф = 109 200 е 12°40', a Л = 167,2 е i «ОЧ»-. можем свести в таблицу.
Нагрузка 'Р, = 40 000 клв.
У1ф = 128,5 е/8028' у2ф = 1'27 000 /, = 116,8 <?/5Р35' Jt =123,7 е/ЗР47' ?г = — 31 47' <Pi = Ц- 43°7* cos >?| =0,73 Pt — 41 300 клв. n = 96,8«/0.
Как видим и при указанной нагрузке ток J£ в начале линии опережает напряжение.
Читателю предчаг< ется проделать вычисление всех этих же величин при нагрузке Р2 = 80 000 клв.
§ 125. Определение постоянных линий
Перейдем теперь к опытному исследованию линии передачи энергии.
Аналогично тому, как в предыдущей главе для экспериментального исследования были введены новые постоянные, введем новые постоянные и здесь для удобства экспериментального исследования лшрш передачи. Само это исследование состоит из двух опытов — холостого хода и короткого замыкания.
О ратимся сначала к холостому ходу.
Зададимся величиной вторичного напряжения К; при этом J2 = 0. Измерим первичную мощность Ро, первичное напряжение У10 и первичную, т. е. у начала линии, силу тока J10.
Положив в ур-ниях (269) и (270) х = 19 получим:
VI0 = V2 cosh (ml), Ъ
- -./'и } <271>
Ao = V2]/ sinh (ml)
r ^0 J
450
Введем, как и дрежае, величину Fo:
p_r .e/Tt_A.= .sjnh(^.i/ ro— roeT — v10 cosh (ml) V z0
= 1/ tgh (ml).
J °
Здесь Уо = -^-, a tp0 определяется из соотношения!
Ио
(272)
cos ?0 =
ПоАо
таким образом Уо нам вполне известно.
Переходим к опыту короткого замыкания.
В этом случае V2 = 0, a J2 — сила тока у конца линии — имеет заданную величину. Измеряем У1Д> Jlk и мощность Рд.
Из ур-ний (269; и (270) имеем при этом:
Jlk = J2 cosh {ml)»
(273)
Введем опять величину Zk\
Zk — Z.e^k = X~ К Як ]
Jlk
(274)
у
причем Zk — -~-9 а срд определяется из соотношения: Ал
C0ST*=v"j~
vikJik
Из ур-ний (272) и (274) перемножением получаем:
tgh(w/) = / Y0Zk, (275)
а после деления ур-ния (274) на (272) имеем:
ио го 10
Теперь можно поставить задачу об определении m — a-\-jb.
Применяя ф-лу (IX), получаем из ур-ия (275):
/=г-=- emi — e~ml e2ml — 1 И Yo Z„ — eml \e-ml = eunl 1 ’
29*
451
откуда
etml — ~Ь А :
(277)
Раскроем символическую форму:
/rozA=/yozA
/(<Го4- <pfc) е
<=У Y0Zh cos ^-° у---+/sin j •
Подставим это выражение в ур-ние (277) и избавимся от мнимости в знаменателе:
1 - % -F 2/]/Т^ sin (&±Ь )
е2т/ _----------------------}-------' . (278)
1 + % - 2 cos ^±1* )
Так как
е2т1 = е2{а^]Ь)1 = еы1 [cos(2W) + у ski (2W)], (а)
то можно приравнять друг другу мнимые части на правой и левой сторонах ур-ния (278) и действительные.
Делением первого равенства на второе получим очевидно
^откуда
2]/y0ZA sin (^о ~4~ <Ра) tg (2W) =-------:---= k,
1 zoz'A
(279)
. 1 . , b= gjarcig^.
Так как eZal есть модуль выражения e2ml, что видно из разложения (а), то, возводя в квадрат и складывая действительную часть и множитель при j в правой стороне ур-ия (278), мы получим квадрат этого модуля; поэтому
1/(1 - K0ZA)* + 4 YQZk sin* (j '--1 + y0Zk - 2 V Y^z; cos (
(280)
откуда
452
*=4>n/
(281)
На основании известного нам уже принципа наложения мы можем из состояний холостой работы линии и короткого замыкания получить состояние любой нагрузки, так как уравнения (271> и (273) линейны.
Из этих ур-ний прежде всего находим:
^1- = = cosh (ml) = С.
У2
Сравним эти отношения с ур-ниями (211) и (213).
Мы видим, что первое из отношений (281) равняюсь С, а второе СЛ; для линии передачи энергии получается С=СЛ, как будта имеет место равенство:
= ^2вну
Определить С всего проще можно так: из ур-ния (275)
V? х LO7 Л sinh2 (/«/)
К Zb = tgh2 (^0 = —Loк • 0 k & \ / cosh2 (ml)
(282)
имеем:
Пользуясь соотношением (VI), можем написать:
--- cosh2 (ml) — 1 1
0 k tG$№(ml) cosh2(/nZ)
или
Y0Zk = l — 4-, * (С)2
откуда
(283)
Таким образом по известным уже Ко и Zk определяем Из ур-ния (281) мы имеем:
=Jlkzk=J.CZ^
и С.
из (274):
из (272):
На основании принципа наложения: V,
Л’
(284)
453
Сравнивая ур-ния (284) с ур-ниями (209) и (210), видим, что полученные нами ур-ния (284) для линии передачи являются частным случаем ур-ний (209) и (210), имеющим место при условии (282) и при коэфициенте трансформации, равном единице. Трансформаторы и асинхронные двигатели, подключенные к напряжению на конце линии, мы рассматриваем теперь ведь просто как индукционную нагрузку.
§ 126. Эквивалентные схемы линии передачи
Из сказанного вытекает, что для линии передачи энергии мы можем дать эквивалентную схему в виде, изображенном на фиг. 205.
На основании ур-ния (282) сопротивление „первичной" части взято равным сопротивлению
Zj до
вторичной"; каждое мы обозначим через Zr В ветви Ya показаны включенными параллельно емкость и ваттная проводимость, — это выражает то обстоятельство, что в линии, кроме емкостного, есть ток утечки.
Как Zv так и проводимость Уд, подключенную по середине между двумя Zj, нужно выбрать так, чтобы при холостой работе эквивалентной схемы и при коротком замыкании ее получить те же самые величины напряжений и сил токов, что и ; тогда по принципу наложения и при на-
фУа
N
Фиг. 205.
i-o
, 3,
в действительной линии;
грузке схема и линия будут эквивалентны.
При холостой работе схема представит собой сопротивление, как видно из фиг. 205, равное ____ j
а
* 1
а это должно быть равно ——; поэтому
• Y,
(285)
4
1 К
При коротком замыкании схема представит сопротивление, которое мы определяем из фиг. 205 и приравниваем ZA, как это следует из ур-ния (274):
г2—+ 2- =
Определяем из ур-ния (285) Zr*
z
(286)
464
подставляем это выражение вместо Zx в ур-ие (286) и после упро* щений получаем:
1 _____ у 7
1
откуда, принимая во внимание ур-ние (283), получаем:
(287)
Далее, из ур-ния (286) имеем:
1 + УЛ
Подставим сюда из ур-ний (285) и (287)
1 + УЛ = ^=с
__ г°
я вынесем Zj за скобки:
и наконец
-М 1 + с
(288)
При значениях Za и Уа, согласно ур-ниям (287) и (288), схема фиг. 205 эквивалентна действительной линии, т. е. при одних и тех же значениях У2 и J2 мы получим в обоих случаях, и в линии и в схеме, одни и те же значения У, и j, и одни и те же значения мощностей и потерь в линии. Таким образом эквивалентная схема заменяет линию во всех вопросах, не касающихся распределения напряжения и силы тока вдоль линии, их мгновенных значений, образования волн и пр., одним словом, исключая те вопросы, для решения которых необходимо учесть время, нужное для распространения вдоль линии любого значения напряжения.
Нетрудно видеть, что, во-первых, при этих условиях для эквивалентной схемы, а потому и для линии передачи, имеет место ф-ла (182), а во-вторых, для изменений силы тока в начале линии у первичных зажимов при изменении нагрузки при постоянном coscp2 имеет место круговая диаграмма тока или диаграмма работы, которая получается подобно тому, как и раньше, с тем только
455
отличием, что проводимость Ya берет теперь опережающий ток, а не отстающий, как в трансформаторе или асинхронном двигателе.
Однако в линии передачи постоянным поддерживается не первичное, а вторичное напряжение.
Упражнение. Читателю предлагается исследовать, как будут изменяться Vi и (у_нач<1ла линии): 1) если V2 = const и ?2 = const и 2) если V2 —const, а для имеет место круговая диаграмма; как будут в оэоих случаях и ,меряться на диаграммах первичная и вторичная мощности.
Следует упомянуть, что иногда вместо эквивалентной схемы фиг. 205 употребляется другая, изображенная на фиг. 206. Указанные на ней величины Y и Z мы найдем из того же условия, как и при определении соответствующих величин в первой схеме, именно что при холостом ходе и коротком замыкании схема должна представлять те же сопротивления, что и действительная линия передачи. Поэтому имеем:
и
T-Lz=^- (В)
= 4- Y Z
Из (В) получаем:
Z 1
подставляя в (А) величину -=* вместо ----—. мы имеем
Z 1 -р YZ
Foz. z=zft+PzzA,
у__.
zzh ’
или
Из (С) получаем: или
(D)
456
подставляя последнее выражение вместо Y в (D), получаема
Z — Z? . Z —Z? ——
—* Ч-------=—- — Уп Z,
zk z
ъгмуж __ __________
Z2(l-F0Zft) = Z2.
Следовательно
2=.-^, Kl-r.z,
или
Z = ZAC.
Из (D) имеем далее:
1 Z
Схема фиг. 205 называется иногда Т-схемой а фигуры 206 — П-схемой. Чаще пользуются первой.
§ 127. Замечания о влиянии трансформаторов
В начале и конце всякой линии передачи стоят трансформаторы,, так что Vj и являются вторичным ^напряжением и силой тока в трансформаторе у генератора, a V2 и J2 — первичными — в трансформаторе у нагрузки.
Цель первого трансформатора — повысить напряжение для передачи энергии, цель второго — понизить его для распределения энергии.
Обозначим через Zrl' полное первичное, т. е. обмотки более низкого напряжения, подключаемой к генератору, — сопротивление повысительного трансформатора, приведенное ко вторичной цепи, через Zr2 — вторичное сопротивление того же трансформатора; ¥а — его приведенная проводимость намагничения, ZH2—сопротивление вторичное, т. е. обмотки низкого напряжения понизительного трансформатора, приведенное к первичной части; приведение таким образом делается у обоих трансформаторов ксамой линии, т. е. к части цепи высокого напряжения.
Напряжение в начале линии есть Vv—ток намагничивающий ток выразится при этом так:
457
Сила тока в генераторе (приведенная) будет:
я напряжение у генератора (приведенное):
К =А+-Л А» + {А + Уа( К + А или
к==К(1+^л;)+А(^+^з+^а;к)-
Стоящие здесь Vt и выражаются ур-ниями f269) и (270) через V2 и J2.
Читателю не будет трудно выразить последние величины через напряжение и силу тока самой нагрузки, т. е. за понизительным трансформатором, и связать напряжение и силу тока у генератора с напряжением и силой тока у нагрузки.
§ 128. Собственный период колебаний линии без потерь
Представим себе, что в линии передачи у конца ее (х — 0) произошло длительное короткое замыкание, вследствие которою сила тока возросла до ненормальной величины, отчего предохранители в начале линии (х = /) перегорели и линия оказалась отсоединенной от трансформатора у генератора и именно приблизительно в момент максим ма силы тока, чему соответствует и максимальное магнитное поле около проводов. В главе восьмой о неустановившемся режиме в цепи переменного тока уже упоминалось, что энергия, запасенная в этом поле, будет колебаться, превращаясь то в энергию электрического поля, заряжая линию до высокого напряжения, то опять в энергию магнитного поля. Колебания будут затухать вследствие траты энергии на нагревание проводов и на утечку.
Рассмотрим, с каким периодом бу пут происходить эти колебания в линии с распределенными постоянными, причем для упрощения задачи рассмотрим незатухающие колебания, т. е. отвлечемся от потерь в линии, положив 7?о = О и Go = 0.
При этом условии
а = 0 и * = ]/вд;
и ур-ния (254) приобретают такой вид:
v=(А, + Щ) cos (bx) +/ (л, — Та) sin (bx),
7=1/ ^ | (А, — Щ) cos (bx) + j (лг л^) sln (bx) 1,
Zo L J
Введем обозначения:
Aj + A2 = C,
458
и
так что
^2----^2»
V = Q cos (bx) -\-jC2 sin (bx),
Ct cos {bx) -f- J Cj sin {bx) .
-o I- J
Заметим, что при x — 0
V = Va = 0, а при x = l, т. e. у генераторного конца
J=J1==O.
Из первого условия, при х = 0, имеем:
так что
V==/Casin(&x), 7=1/ ^C^cos(ftx).
(289)
(290)
С2 должно определяться или по данному V = Vj при х = / или по ванному J=J2 при х = 0.
При х = 1 сила тока, как указано, равна нулю, т. е.
С2 cos (bl) = 0.
, Если бы мы здесь С2 положили равным нулю, то тогда V и J по всей линии равнялись бы нулю; поэтому надо положить
cos (bl)= О, откуда
И«(2Я-1)* (А)
Л
где л = 1, 2, 3,... любому целому числу.
Так как ____
ь=ух^а, то, подставляя сюда вместо Хо и Во величины
(оЛ0 = 2п/л£0 И
(оСо = 2тг/л(?0,
459
где /л есть число периодов уже не генератора, который отсоединен, а того переменного тока, который будет теперь — при колебаниях энергии, т. е. число периодов колебаний в лини и,— будем иметь:
Ь = 2тг/л ]/"LqCq
и из равенства (А):
2п/л//£^=(2л-1)у.
Вводя I под радикал, обозначая через L и С самоиндукцию и емкость всей линии, получаем:
_2л —1 /л~ 4|/fc’
Первое решение получим, положив п — 1; тогда f = У 1 4/LC
Если бы L и С были сосредоточены, а не распределены по всей длине равномерно, мы имели бы из формулы Томсона:
f —_____*__
1 2n/LC’
Подставляя для п значения 2, 3, 4, 5,..., будем получать частоты в 3, 5, 7, 9,... раз большие; таким образом эти колебания имеют высшие составляющие нечетных порядков.
Из ур-ния (290) мы видим, ч о значения V и J изменяются вдоль линии как sin и cos от аргумента, пропорционального расстоянию рассматриваемой точки от конца линии. Для составляющей первого порядка вся линия соответствует значению этого аргумента, равному 4г• Поэтому эти колебания называются колебаниями л четвертью волны.
Наибольшая длина волны, которая может свободно возникнуть в линии, равна учетверенной длине линии.
У составляющей (2л — 1)-го порядка по длине линии располагается (2л—1) четвертей волны, причем у всех составляющих напряжение и сила тока сдвинуты друг относительно друга на четверть волны, т. е. где V имеет максимальное значение, там J равно нулю, и наоборот.
Введем такие величины:
L' = — L ir
(291)
460
тогда
n2 LC = 4 L'C 4
и
Д = —1= =---------. (292)
1 4^ LC 2nVL'C
Введя величины £' и С1, мы получаем таким образом возможность пользоваться формулой Томсона, подставляя в нее эти величины. Lf и называются иногда „действующими" значениями самоиндукции и емкости.
Представим теперь себе другой случай. Пусть каким-либо образом колебания возникли в линии, отсоединенной от обоих трансформаторов, т. е. как у генератора, так и у нагрузки.
Тогда в ур-ниях (239) мы будем иметь, при х = 0 и при х = 1,
7 = 0.
Первое условие дает, что
С2=-0 и что следовательно
J=7’l/ • С\ sin (Ьх)\
* Zq второе условие дает, что
sin (Ы) = 0, откуда
Ы = тгп,
где п — любое целое число. Производя те же самые подстановки, что и в предыдущем случае, получаем:
л 2Д/ЬС
Эти колебания могут содержать таким образом и четные составляющие. Сила тока на обоих концах линии равна нулю, а напряжение есть максимум; поэтому эти колебания называются колебаниями полуволной.
461
Г Л АБА XVII
НАИБОЛЕЕ ОБЩАЯ ФОРМА УРАВНЕНИЙ ЭЛЕКТРИЧЕСКОГО ТОКА
§ 129. Общие уравнения и исследование их
В главе пятнадцатой мы занимались интегрированием диферен-циальных ур-ний тока и напряжения для цепей с сосредоточенными постоянными (/?, С и £), причем там было указано, что разница по существу между этим приемом исследования переменного тока и приемом, которым выводился закон Ома в главе второй, заключалась в том, что в главе второй мы заранее задавались функциональной зависимостью тока или напряжения от времени, именно считали их синусоидальными функциями последнего, а в главе пятнадцатой мы этого предположения не делали, а потому и получили решение более общее, охватывающее два тока, свободный и вынужденный.
То же самое сделаем мы в настоящей главе по отношению к днференциальным ур-ниям тока в цепи с распределенными постоянными, в отличие от предыдущей главы, где мы с самого начала исследования ввели векторы, т.- е. синусоидальные токи.
При выводе ур-ний (241) и (242) было указано, что они приложимы к любому случаю тока в цепи с распределенными постоянными. Из них мы имеем:
и
di dx
(293)
=^+c«Tt
Сделаем, как и раньше, допущение, что 7?0, £0, О0 и Со постоянны вдоль линии.
Диференцируем первое ур-ние по х, второе по t и подставляем в первое место di d*i dx dt-dx
462
их выражения из второго; после этого получаем.*
dX2 — RoPov 4" (^Со 4“ W 4“ Л)£*о ^2 (294)
и аналогично получим:
/У 2; di d2i
^2 = W + Wo + W ~ + £0C0 (295)
Таким образом диференциальные ур-ния для силы тока и напряжения одинаковы; следовательно и сами эти величины — сила тока и напряжения — выражаются ур-ниями, отличающимися только постоянными интеграции; последние определяются из начальных и конечных услбвий
Так как в ур-ниях (294) и (295) линейно связаны функции с их первыми и вторыми производными, то интегралом их является экспоненциальная функция, т. е. для силы тока например:
i = A'e~mx~nt. (296)
Можно было бы вначале поставить у т и п плюсы, тогда минусы, выражающие „затухание", выявились бы после.
Подстановка этого выражения в диференциальное ур-ние для I дает соотношение между т и я:
«2 = - (^о + W« + =.
= (л£0-/?0)(/гС>0-О0); (297)
подстановка же (296) в первое из ур-ний (293) дает:
^ = (7?0 —л£0)Д.е-»«-« ху у* 4 U Uz
и после интегрирования:
V =. HLq----^0 е - тх - лг
т
или
V= —---------I.
tn
откуда
/г£0 — /?0
i т 9
(298)
или, принимая во внимание ур-ние (297),
- = 2 = 1/ nL0—^0
i у пс0 — о0'
(299)
463
Величину Z называют, аналогично ранее разобранному случаю, h волновым сопротивлением".
Таким образом v = iZ. (300).
Ур-ния /= A-e~mx~nt 1
и nL0 — Ro . тх м ( <301> v — —о о A'e~mx~nt т 1
•и являются наиболее общей формой выражения меняющихся как во времени, так и в пространстве (вдоль линии) напряжения и силы тока в цепи с равномерно распределенными /?, G, L и С; А, т и п суть постоянные интеграции, определяемые из условий задачи, причем jn и п связаны соотношением (297).
Заметим теперь же, что, положив х = 0, мы простым преобразованием можем получить ур-ния для цепей с сосредоточенными R и L.
От величин т и п зависит самый характер изменения v и i во времени и пространстве; читателю на основании всего предыдущего ясно, что для того, чтобы в изменениях v и I во времени была периодичность, величина п должна быть мнимой; далее, чтобы и и i были периодичны и в пространстве, величина т должна быть мнимой.
Из предыдущего мы также знаем, что всякий неустановившийся процесс или режим переходит в тот или иной установившийся, причем происходит затухание колебаний большего или меньшего запаса энергии; что периодичность в пространстве даже в установившемся режиме, как изложено в предшествовавшем, связана с некоторым затуханием; таким образом еще до исследования ур-ний (301) неустановившегося режима мы можем уже предположить, что самой общей формой для величин т и п будет комплексная.
Положим
т = a -j- jb
и выразим с помощью этого соотношения и ур-ния (297) величину л.
(а 4-/Й)» = /?0О0 — (₽0С0 + O0L0) п + LoCon\
п2__“Ь „ । *0о0 Ч~jb)2_______________~
ЛА L0C0 “°’
или еще
й2 _ п + g0GO^.^.+#)2 _ 0.
\ Ар О) / AqCq
464
Отсюда
п~
'О
Введем такие обозначения:
о
А _2о_=е 2L0 -I" 2С0 ®’
2 R$GQ — (аjb)2
(302,
L ф °о V -'о 2С0/
где сами 8 и [} — действительные величины. Таким образом
л = 8±(5+/р).
Возвысим (А) в квадрат и приравняем друг другу обе , тельные части и- также мнимые, после чего получим:
У __^o-^+£2_S2_g2 )
2Cj LqC. Р
(А)
(303)
действи-
(301)
0
и
Положим
ь0^0
2
/ । _9о_ \2__ ( Л___________@о
\ 2А0 LqCq \ 2Z,0 2С0
Тогла мы получим вместо двух последних ур-ний для следующие:
(305)
Д2___ А2
£oGo
(306)
S и £
В выражениях v и i переменным является множитель
p-mx-nt.
Подставляя сюда вместо т и п их комплексные выражения, мы получим два множителя:
е— ах — (е-]-8)/ e~<jbx + $t\
Здесь второй множитель разлагается в тригонометрические функции от аргумента bxAzfy и выражает периодичность во времени и пространстве, а первый множитель выражает затухание тоже и во времени и в пространстве. Если второй множитель для точки х' 30 Теория переменных токов. 465
и момента t имеет ту же величину, что и для точки х в момент/» то мы и говорим о движении волны вдоль линии со скоростью
Так как очевидно при этом
то скорость движения волны
™ = (307)
Для определения этой скорости решим систему ур-ний (306). Подставляя из второго ур-ния 8 в первое, получаем после пре-
образования:
а2 — Ь2\ 09
L С / Р L2C^
Отсюда
tr — ^2\2 ।
£0С0 ) + L2C2
k2
= 0
CL2 — Ь2 \ 1 v-гг- (308) ьоьо /J
Перед вторым радикалом, под корн м, мы берем знак плюс, потому что р должна быть действительной величиной по условию.
На основании последней формулы для имеем, что скорость движения волны
а2—Ь2\2 , 4а Ь*
/ а2______Ъ2 \
<309>
V ь0ь0 /-
Если мы имеем в линии выполненным условие (266) предыдущей главы минимума затухания, то &=0. Если мы пренебрегаем потерями, то и k и а равны нулю.
В обоих случаях из последней формулы для w получаем уже знакомую нам формулу:
, 1 w = Ч----=.
~Vloco
Из условия р/ = 2тг
получаем время, в течение которого напряжение и сила тока претерпевают весь цикл изменений, возвращаясь затем, если отвлечься от затухания, к прежним значениям,
_ 2тг
Т^= —
436
Из условия же
Ьх ~ 2п
получаем
2тт b ’
длину, на которой происходит весь цикл изменений, т. е. длину волны.
Чем больше Ь, тем короче волна, и наоборот.
Перейдем теперь к интегралу, выражающему*/:
i — A-e-mx~nt.
Здесь может быть несколько частных случаев в зависимости от знаков при дейс |В1Тельчых и мнимых частях т и л, ибо может быть и
т — + a
и
п = е± § ±7?-
Однако ур-ние (306) ab
вносит сюда то ограничение, что если а и b имеют одинаковые з 1аки, то и S и р должны иметь одинаковые знаки, и если а и Ь имеют разные знаки, то и J и тоже имеют разные знаки.
Не забудем, что s известно и определяется ур-нием (302). Таким образом возможны следующие восемь комбинаций величин а, & и jj с разными знаками, одинаково удовлетворяющие исходному диференциальному уравнению:
1.
2.
3.
4.
5.
6.
7.
8.
т — + а + jb. а — jb
— а — jb — a-]-jb — a -\-jb — а — jb -{-a—jb + а
п = е — 5—у? 8-5+/? е-S-/?
е + §—
е 4 J — j$ е + 54-У₽
(310)
Подставим эти значения т и п в наш интеграл и сгруппируем полученные таким образом частные интегралы, каждый с его осо-30* 467
бой произвольной постоянной Д, попарно, так что получим четыре таких пары. Первый и второй случаи значений тип дают:
1Х = Дд^-(а-/&)--(б-“8+/р)/ =
_ g-ax-(e-5)r{ —
£-(е-8)/{Д5 cos(p/— bx) -{- jAy sin (Р/ — bx) -|-
4- A2 cos ($t — bx) — JA2 sin (p/ — bx)} =
— cav • ^-(£~8)z{ (Д2 -j- Д2) cos (p/— bx) 4-7 (Д3 — Д2) sin (р/ — bx)} ==
= е~ах-е~^~ъ^{Ву cos (р/ — bx) 4- % sin (P? — bx)} =
— e-ax.e-(8-S)/. sin | p/ — bx-\- фх), (I)
где
4>j==arctg^ °2
c^V^bi,
a
— A + Л 1
Я } (я)
52=/(А-Л) J
Третий и четвертый случаи значений т и п дают:
— Дз . ^.е(а /&)x-(s-5+/p)^
или после подобных же преобразований, полагая
А3 ~Ь А* ^з
/ (Д3 Д4) = Вр
а затем
c2=rBpbsi и т. д.:
Z2 = еах ‘ С2 sin (р, 4- Ьх 4- ф2). (II)
Пятый и шестой случаи дают:
= еах • е- <6+5)'. С3 sin (р/ — Ьх + ф3), (III)
при аналогичных заменах.
Последняя пара частных интегралов дает:
—Д7 .е-(л-/^)х-(е + 6-/р)/_|_ дЯ.е-(а+/^)д;-(6 + 8+/Р)/_
= ^-^.^-“(6+5)^C4sin(pZ 4 6х4-ф4). (IV)
Складывая все четыре выражения, получим полный интеграл: — e“(e'“8)/{C1e“axsin(p/— bx-\ (bj 4- С2еах sin (р/4- Ьх 4- $2)}~T + e-(‘+»)<{C8ee*sin(^—ф3)4-С4г-^81п(р4^+Ф4)} (3U) 468
Все четыре члена здесь представляют каждый движущуюся волну.
Постоянные С и величины a, b, f и 8 определяются из условий задачи или так называемых „пограничных условий"; кроме того мы имеем два ур-ния. (306), связывающие последние четыре величины.
Из только что полученного выражения для I получается легко и его вы ажение при установившемся режиме, например для случая включения переменного тока на линию. Последние два члена имеют множитель £-(6+8)/, где е и § — положительные числа, так что этот множитель при всяком значении 8 выражает затухание во времени двух последних волн; чтобы первые две волны не затухали во времени, должно быть __g q
или
8 = е.
Далее, [J должно быть равным со приложенного к нашей линии переменного тока
Таким образом после того как затухнут последние две волны, сила тока в линии выразится первыми двумя членами, т. е. тем же ур-нием (258-).
Подобно тому как первая волна в полном выражении i называется отраженной волной для второй, третья волна есть отраженная для четвертой.
Из выражения (311) мы видим, что в то время как обе волны, представляющие устойчивый режим, имеют амплитуды, убывающие по мере продвижения волны по экспоненциальному закону, обе волны, представляющие преходящий ток, имеют амплитуды, растущие по тому же закону по мере продвижения каждой волны.
Чтобы выражение для I было пригодно для любого случая функциональной зависимости тока от времени при пограничных условиях или при установившемся режиме, мы должны сделать последнее обобщение и представить i в виде ряда Фурье, т. е. так:
/ = £ {Спе~^х sin ($nt — bnx 4 фЯ() 4
+ Сп.еааХ sin (М +• ьпх 4- ф„3} 4-
4 е-(е+8Л)/ {спеа»х sin $nt — bnx 4 ф„9) 4»
4 cn/“anX sin (У 4 bnx 4- <|>„4) }.
Теперь следует получить выражение для напряжения.
Ур-ние (298) теперь после разложения нами т и п примет восемь различающихся комбинацией знаков форм.
Группируя их по два, получаем:
v = (е~? л е-(а+/»)*-(е-8-/Р)< 4
1 a -\-jb 1 1
I (е 4~/7J 1 ^0 #0 д
~ а—jb 2
469
Освобождаясь от мнимости в знаменателе и вводя тригонометрические функции вместо показательных, имеем:
v _ е~ах~ (•-&)/ ( J Ие ZQ ^о] а _______
1 \ I a2 -f- b2
_ / [fs - Ln~^ b + a^ [а2 [cos (₽/ - bx) 4-/sin С?/ - bx)] 4-
"i~ | a2 4- b2 ‘
। .[fs — 8iz0— /?п]ъ4“I r й . и \
4-/v-------a~----------- J A* [C0S (— bX^ Sin ’
Сделаем подстановку:
[(e —- S)Z,0 — Z?o] a — ^Z,o _ „
a2 + b2 ~ Ъ
[(8-§)£0-/?0]^4-4£0^ a24~Z>2
раскроем скобки, сгруппируем члены с cos и с sin и примем во внимание соотношения (а), после чего выражение для vt представится так:
= е~ах~ ^^{{NB2 — MBJ cos ($t — bx) — — (МВ2 4- MBJ sin (₽/ — bx)}.
Подобным же обравом из Z2 получаем v2; при этом, так кам третий и четвертый (310) случаи значений т отличаются от первого и второго только знаком минус перед всем т, а п то же самое, то мы получим те же самые величины М и Л/, и v2 выразится так:
v2 = еах~{ (JNB± — МВ3) zqs ф 4- Ьх) — _ (ЛШ4 4- NB3) sin (₽/ 4- bx) }.
Пятый и шестой случаи в (310) отличаются от первого и второго переменой знака у а и 5; поэтому при преобразовании у нас получатся выражения:
r(e + i)A0_/?ja + ^0 _
a*-Yb* '
[(е-18)£0-/?0]&-4£0_______
а? + Ь* тюсле чего будем иметь:
= eaje“ <•+«)*{ (ЛГ^в — ЛГ'55) cos $/— bx) —
— (М'36 4- N'B6) sin 0/— bx}
470
и подобным же образом находим:
г4 = е~ах-<8+ *)' {(Л'В8 — ЛГВ7) cos (Р/ 4- Ьх) —
— (ЛГВ8 -j- Л/'В7 sin (fi/ 4" } •
Сумма всех этих четырех vn и дает нам все напряжение *0.
В общем случае в правой части будет стоять сумма составляющих разных порядков.
§ 130. Случай постоянного тока
Не всегда удобно брать ур-ния (311) для тока и аналогичное для напряжения за исходную точку при исследовании различных случаев, иногда лучше исходить из первоначальных ур-ний:
i = A-e-mX-nt,
v=nL"~^оде-тх-ги = д/ Ae — mx~nt=ZL
т у пс0 — Gq
т2 = /?0) (nC0 Go).
Предс1авим себе, что на линию с равномерно распределенными ностоянными включен источник постоянного тока, и мы рассматриваем установившийся режим; тогда в этих формулах надо положить:
п = 0,
ибо во времени никакого изменения теперь нет. В этом случае из соотношения (297), связывающего тип, получаем, что
т = ±/£/F0 И
7__^0_________2TZ 1
« -+|/ <V
Следовательно
I = А1е~хУ^Г° + А 2е+хУ^,
J (312)
Таковы ур-ния цепи постоянного тока с равномерно распределенной утечкой.
Всякий подводный или подземный кабель, питаемый постоянным током, или рельсы электрическо о трамвая, работающего на таком же токе, представляют такую цепь.
Рассм01рим лишь один случай из различных возможных при исследовании этих ур-ний.
471
Пусть линия замкнута в какой-нибудь точке на расстоянии х — хА от конца линии на сопротивление /?р тогда
или
Отсюда
или
А2 = Д^"2*1 г/?о<7о
таким образом
(313)
При расчетах с линиями постоянного тока с равномерно распределенной утечкой тоже часто употребляются гиперболические функции. Переход к ним в ур-ниях (312) совершенно аналогичен переходу к ним в случае переменного тока.
Пусть нам даны напряжения и сила тока J2 на конце линии, т. е. при х = 0. Из ур-ний для i и v имеем, при х = 0:
4“ ^2=
Л2-Л1= V2]/^
472
Отсюда
Подставляя эти значения и Д2 в ур-ния для I и v и группируя надлежащим образом члены, получаем:
/ — J2
е + х е-х¥К& Г
2
£> + X V RqGq ___ V R^G^
2
ИЛИ
i = J2 cosh (X //?0O0) + v2 у w sinh (x ^oGo) и аналогично
v=V1 cosh (x + J2 /sinh С* /Я(А)-
(315>
§ 131. Стоячие волны
Если мы в ур-ниях (311) и других положим а = 0, то получим ур-ия стоячих волн в линии.
Из ур-ния
ab
в этом случае мы имеем, что или 5 = 0 или [5 = 0. Обращаясь к ур-нию (308) для р, мы видим, что при а = 0 будет [5 равняться нулю или нет, зависит от того, какой знак имеет второй член под общим радикалом, так как мы условились уже для первого радикала брать лишь его арифметическое значение. Таким образохМ здесь могут быть два случая:
Во втором случае [5 = 0, и волны не являются периодическим явлением во времени, а затухают апериодично.
473
Случай, когда
L0C0
называют критическим; для него
« длина волны
Ь k]fLqCq, ___ 2тт
Как читатель может легко убедиться, взяв постоянные для любой линии передачи и подставив их в эту формулу, эта длина во много раз больше, чем длина существующих линий передач; а наибольшая длина волны, котор 1Я может установиться в линии без посте роннего источника тока, в четыре раза больше длины линии и оказывается много меньше Таким образом эти волны не м тут существовать в линии, если к ней не приложен посторонний источник тока.
В случае же
Ь*
мы имеем:
и следовательно 5 = 0.
Ур-ние (311) для силы тока принимает теперь такой вид:
I = { Сг sin (0/ — Ьх 4- ф1) + С2 sin (р/ -|“ Ьх 4" Фз) }5
что касается третьей и четвертой составляющих волн в ур-нии (311), то, как легко видеть, вследствие обоих условий а = 0 и 5 = 0 они тождественны с первой и второй соответственно. Аналогично получаем ур-ние для напряжения.
Эти ур-ния суть ур-ния стоячих волн в линии, затухающих с течением времени
Мы ограничимся данным выше приложением общих ур-ний линий с распределенными постоянными к нескольким случаям, вообще же область их применения весьма широка — они охватывают и импульсы тока, и б ’уждающие волны, и свободные колебания и находят поэтому мастое применение в технике высоких напряжений для анализа перечисленных явлений.
474
§ 132. Упрощенное решение основных диференциальных уравнений
Неустановившийся режим исследуют часто при помощи следующего упрощенною решения.
ПреобразуехМ ур-ния (294) и (295) § 129 так, чтобы исчезла первая производная по времени; для этого пр жде всего положим
где и есть какая-то функция времени и расстояния. Тогда
d2? d2u . п du f , п . at2 dt2 dt 1 ’
d'-v d2u - . . О “ QU
dx2 dx2
Ур-ние (294) вместе с этим приобретает вид:
d2u
— = [/?0О0 - а(/?0С0 4- А0О0) 4- a?L0C0] • и 4-
+ [/?о^о + L'0Gq - 2aL0C0] .^4-L0C0~ CLL CL L
Чтобы первая производная исчезла из этого ур-ния, нужно чтобы
RqCq 4” W — 2а£0С0= откуда
JL (। £о\
2 Uo О)/’
т. е. а должна равняться е, введенному нами ур-нием (302): а —г.
Полагая а равным не комплексу, мы тем самым, как читателю должно быть ясно после сказанного в начале § 129, ограничиваем решение случаем неустановившегося режима.
Множитель при и становится равным теперь
R а _ сад+адр+<ад±ад)!=_ адад _ w
00 2L0C0 4Л0С0 4 \L0 СJ ’
что, принимая во внимание ур-ние (305), равно:
-W2.
475
Здесь делают допущение, что в рассматриваемой линии имеет место соотношение (266):
Л) Со
Для воздушных линий высокого напряжения, где Со невелико, a Lq больше, чем в кабелях, это соотношение можно считать приближенно имеющим место в действительности.
В этом случае
£ = 0,
и ур-ние для и принимает вид:
d2u__ d2u
d^~L^'di*'
Вводя уже знакомую нам величину
1
J/£060 можем написать;
d2u _ d2u — = w2 —. dt2 dx2
Решением этого уравнения является:
«=f-i<x — wt) -|- /2(х -j- wf),
где вид функций Д и /2 определяется из заданных условий. Таким образом
^ = ^“е/[/1(лг — wt +/2(х + ^/)]; (316)
= — S • e-‘Vi (•* — + /2(х 4- да0] +
। „-./RM*—। W* -
±e L 1 it J*
Выражение в последних квадратных скобках очевидно можно заменить следующим:
Ъх ЪХ ’
таким образом, отбрасывая при писании промежуточных ур-ний скобки (х— wf) и (x-|-w/) как ненужные, имеем из (293) — второго:
^. = О0.е^(Л +/2) - C0.S.e~^ +/2) +
4- Co e~tf( — 4- w- —) ,
'° \ дл ‘ дх ’
476
или
£ = e-f(G0 - еС0)(/, +/2) - е~**> w• CQ (g -g). Ь*-* \0Х OX ]
Здесь вследствие условия & = 0
Изменим отсчет расстояния х на обратный: будем отсчитывать его не от конца линии, а от начала; тогда dx войдет в ур-ние с обратным знаком, подставляя затем вместо w его величину и интегрируя, получим:
i = е~* |/^[/,(х — ®»/) — /2(х -j- w/)]. (317)
Величина 1/ , обратная коэфициенту перед скобками, е^ть
г Ч) волновое сопротивление линии, как читателю нетрудно вывести самому, приняв во внимание условие, что k — О. Эту величину называют также „характеристикой" линии
После всего изложенного в настоящей и предыдущей главах читателю ясно, что мы в ур-нии для v и i имеем дело с двумя волнами, движущимися в противоположных направлениях по линии со скоростью w и не меняющими своего вида при движении, но с течением времени затухающими.
Эти ур-ния в технике высоких напряжений часто полагают в основу при рассмотрении вопросов о вк ючении и выключении линии, о блуждающих волнах от атмосферных влияний и т. д.
§ 133. Отражение волн в точках соединения двух проводов с различными волновыми сопротивлениями
Приложим к исследованию данного вопроса только что полученные ур-ния неустановившегося режима.
Диференциальные ур-ния должны удовлетворяться и для одного и для другого проводов, но постоянные этих проводов различны, поэтому и скорости волн и затухания их будут различны в этих проводах.
Процесс в каждом проводе мы можем представить посредством двух движущихся навстречу волн; поэтому, обозначая римскими
477
цифрами I и II величины, относящиеся к одному и другому проводу, мы будем иметь следующие ур-ния:
Vj = е-а‘'[/и(х — Wjt) /12(х 4- w,/)] = vn -|- vlit
= e-a"Vni(* — WnO +/п2<Х + = ®U1 + иП2>
h 1/ = «'“VnC* — w/) — fl2(x4- да/)],
Г С01
zn 1/ F5- = Vin(* — «’ц) — W* + ®п0]-г соп
Так как в месте соединения происходит переход напряжения и силы тока из состояния, обус овленного первым проводом, в состояние в другом проводе, то должно быть:
^11 + ^12 = ^П1+^П2
1 /"^01 V___1 f £рп f . k (А)
\/ ^12) — 1/ 7 (vni vna)-
Г Ь01 r ьоп
Если волна впервые с начала процесса проходит место соединения двух линий, то конечно волны г>П2 еще нет, а есть только как идущая дальше, теперь уже по второму проводу, волна, и ф12 — отраженная от места соединения волна в первом проводе. Полагая vIh2 = 0 и обозначая характеристики или волновые сопротивления проводов через zx и zw находим:
^11—^12 ЧП }
z\ zu ]
Деля первое на второе, получаем:
^ll+^l2./ll
Vn~ *12 *1 ’
откуда отраженная волна в первом проводе
гп г\
Подставляя это выражение в первое из ур-ний (В), имеем идущую дальше, по второму проводу, волну
2гп
478
После того как волна -пП1 дошла до конца линии II, получается и волна т/П2, отраженная от конца линии.
Теперь нужно решать ур-ния (А), куда входят четыре величины; если мы будем за данные считать г>п и г>112, тогда сможем из этих двух ур-ний (А) выразить остальные две величины так: проходящею дальше волну
. z\ zn zl =---------v -I---------х/П9,
Zj t 2ц z\~]~ ZU
отраженную от места соединения в первом проводе*.
гп zY 2zj
ЯЛ2 “ i i ~ I ~i~~" ^П2'
Таким образом из двух волн и г>П2, идущих к мест/ соединения, проходят его только определенные части, остальная же часть каждой волны отражается назад в тот провод, из которого волна пришла.
zu z\
Величину -------- называют коэфициентом отражения.
479
ГЛАВА XVIII
ТЕОРИЯ ПОВЕРХНОСТНОГО ЭФФЕКТА ПРИ ПЕРЕМЕННОМ ТОКЕ И ПЕРЕМЕННОМ МАГНИТНОМ ПОТОКЕ
§ 134. Диференциальное уравнение плотности тока в проводнике
В предыдущем мы не раз упоминали о том, что переменный ток распределяется по площади поперечного сечения проводника неравномерно, а именно — сила тока, приходящаяся на единицу этой площади, так называемая „плотность" тока, убывает по мере приближения к центру площади или к оси проводника. Если мы возьмем цилиндрический проводник, то из соображений о симметрии ясно, что в элементах площади поперечного сечения, одинаково удаленных от оси, мы будем иметь одинаковую плотность тока.
Далее оказывается, что и фаза силы тока в различных слоях проводника различна. Рассмотрим весь вопрос математически.
Рассечем мысленно цилиндрический проводник плоскостью, проходящей через его ось О(У (фиг. 207), и в плоскости разреза выделим элементарный прямоугольник на расстоянии х от оси 00'. Длину двух его сторон, параллельных оси, возьмем равной единице длины — одному сантиметру; длину же двух других сторон возьмем равной dx.
Далее обозначим: через I— силу тока в цилин ре радиуса х с осью ОО\ через и—плотность тока на i асстоян и и х от оси, через Н—напряжение магнитного поля, производимого этим током, там же; Z, и и Н суть мгновенные значения соответствующих величин.
По закону Био и Савара
77—0,2-—, или Hx — Q^L х
Дифе1 енц^руя по х, получаем:
х^-|-Я=0,2.~. (А)
dx ' dx у '
480
Величина есть сила тока, проходящего через кольцевую площадь поперечного сечения стенки цилиндрической трубка с радиусами х x-\-dx. Площадь эту, отбрасывая бесконечно-малые в . личины второго порядка, мы мо ем выразить через 2/nxdx, а потому силе тока через ее можем дать и такое выражение: 2ттхи^х, откуда, сравнивая с первым сражением для этой силы тока, имеем:
^-—Ъъхи. (В)
/V v 4 '
Подставляя (В) в (А), получаем:
dH , п л х ——к Н=0,4пхи.
dx 1
(С)
Обозначим через я величину, результирующую из напряжени , приложенного на единицу длины провода извне, и ЭДС само-
индукции, тоже отнесенной к единице длины. Вследствие того, что всякий элемент площади сечения проводника осевой плоскостью, всякий прямоугольник mnsr, пронизывается магнитным потоком, в сторонах его индуктируются ЭДС. - оследние в сторонах тг и ns .равны и противоположны, в сторонах же тп и rs обусловливают изменение величины v\ псследняя на стороне тп равна v и на сгсрое rs dv
равна v-\- — dx. Таким образам окон-
чательно в контуре mnrs действует ЭДС dv , ~ „
— dx. Она равна про зводной по вре-
Фиг. 207.
мени от магнитного потока, пронизывающего этот контур ^H*dxy где g есть магнитная пр ницаемость вещества проводника.
Отсюда имеем:
dv dH
dx dt
10-8
Ф)
Из фиг. 207 м »i видим, что, задавшись направлением мгно ен-ной силы тока, как на чертеже, мы получим магнитный поток, идущий через прямоугольник mnrs от нас за плоскость чертежа. dH
Если > 0, т. е. поток возрастает, то ЭДС в контуре направлена по правилу Максвелля против вращени правог) винта, т. е. в стороне rs направлена снизу вверх, а это означает, что 31 Теорит переменных токов 481
dv . — лх положительно; это правило знаков и удовлетворяется
ур-нием (D).
Далее, с б значив через р удельн>е сопротивление в омо-санти? метрах, т. е. сопротивление, измеренное в омах и отнесенное к ку-. dv du
бическому сантиметру, имеем v=pu и —Ртг** ах dx
Сравнивая с (D), получаем:
dt р dx
Диференцируем (С) по времени:
d2H , dxdt r dt
~ 0,4ях
du
~dt'
(Е)
(F)
х
Диференцируем (Е) по х и подставляем в (F):
108 d2u , 108 du л л du
Хр--- -г-^ + р--- °’4™ - >
г р dx2 1 г р dx dt
или
dhi । 1 __ОЛгсц du
dx2 ‘ x dx plO8 dt9
Таково диференциальное ур-ние для плотности тока.
§ 135. Интегрирование уравнения плотности тока
В исследовании полученного ур-ния пйдем следующим путем. Прежде всего полежим
и = F(x) • sin (со/ f ф), (Н)
где амплитуда um^=F(x) и фаза ф суть функции расстояния от оси. Разложив синус суммы, получим:
и = Fx sin (ш/) -р F2 cos (со/), где
/71 = Г(х)созф, F2 = F(x) sin ф, I так что амплитуда
+ и '}> = arctg^2.
У)
482
Находим производные от ut входящие в ур-ие (G):
du dF* . dFn
~ sin (со/) 4- cos (®0»
dx dx 1 dx v 7
d2u d*Fr . f „ . d2F, .
du
— = co^ cos (co/) — wF2 sin (co/).
Подставляем эти выражения производных в ур-ние (G), группируя члены, содержащие cos (со/); получаем:
М2Л I 1
\ dx2 ‘ х ,[d2F2 \_ dF2
sin (со/), отдельно от членов, содержащих
cos (со/) = 0.
dF, . 0,4тш \ ,
—1J------. (и Р । gm (со/) -+-
dx ^р-108 ’) 1
0,4пр dx~~^
Так как ур-ние это справедливо для произвольного /, то множители при синусе и косинусе должны быть равны нулю, так что мы получаем, полагая для
краткости 0,4 тс’ко а~ р- 108 ’
1
следующие два ур-ния:
dx2 1 х
dx2 ‘ x
dF. . „ Л
vf'—’Л1 = ° dx 1
(К)
Затем полагаем, что Ft и F2 можно выразить бесконечными рядами:
Л = А) + А1Х + А2Х' + • • • + А«хП + •••
Ft - в0 4- Вгх + в2хг 4-...+Впх“ +...
Определим коэфициенты в этих рядах. Для этого подставим в ур-ния (К) производные от этих рядов. Имеем:
= А1 + 2Л2х 4- ЗА3х* 4-...4- пАпхп-’ 4-...
Т л’ + 2л’ + ЗА*Х +’ • •+пА*хП~2 +• • •
Л Л
5§=2Д2 + 2.зл3х4-...4-(«-1)^,,-2+...
32 Теория переменных токе».
483
Заменив здесь всякое Ат на Вт, получим соответствующие выражения для функции В2, затем подставляем все полученные выражения в ур-ния (К). Первое из них дагт:
2А2 4- 2 • ЗАах+... + (п - 1)яА„х»-» +.. <+
+а1.14-2а2+за3х+...4-йаях"-1+...+ >
+ а(во + В1х4-В2^4-...4-Вя^ + ...) = О. , Второе дает:
2В2 + 2 -ЗВ8х +...+(я - 1)яВях"-«+... + + В, • А- + 2Ва + ЗВ8х 4-... 4- пВ^с-У 4-... -
(L)
(М)
-а(Л0 + А2х4- А2х«4-.. .4-Лях»+.. .) = 0.
Теперь рассуждаем так: каждое из этих двух ур-ний (L) и (М) справедливо для произвольного х, лишь бы х не превосходило радиуса поперечного сечения проводника; поэтому должна равняться нулю всякая сумма коэфициентов при одинаковых степенях х.
Таким образом получаем ряд ур-ний, приравнивая нулю сначала сумму коэфициентов при х~\ затем при х°, при х и т. д.
Ур-ние (L) дает:
А1==0 2-2А8 4~а50 = О
4.4А44-аВ2 = 0
A2AA4-«^ft_s = 0
Ур-ние (М) дает:
2-2В2 — аАо = 0
3-ЗВ8 —аА2 = 0
4-4В4 —аА8 = 0
Л2ВА —аАЛ_2 = 0
На каком бы номере п в разложениях Рг и мы ни остановились, мы всегда получим п таких ур-ний между Л и В из ур-ния (L) и п из ур-ния (М); итого будем иметь 2п ур-ния, неизвестных же у нас ибо нумерация у А и В начи-
нается с нуля. Таким образом два каких-нибудь А и В приходится считать как бы известными, — выберем за таковые До и BQ, как их определить, мы увидим дальше, — и выражать все остальные А и В чегрез эти Ао и Во.
484
Таким образом получаем:
Л1 = °, .
А-------— В
71 а — 22 °о»
Л- = 0, а ct2
42 ^2 = 22-42 А°’
А = о, л __ а я _ а3 я лв------62 — 22.42-о» °’
Л7 = 0, а а4
^8 = gJ~ 22.42.52.^2^о»
В1 = 0,
В — а А п2 — 22
Bq = 0, а а2
4И2 3 22«42
Вб = 0, а а3
^в = б2 ^4 = 22-42«62 ^°’
В7 = 0, а а4
^8 = g2 Лв~ 22.42-62-82
и т. д.
Что касается величин До и Во, то мы зададимся их величиной следующим образом. На оси проводника, т. е. при х = 0, имеем из разложений и /у
^10 = А) И ^20 = ^0> так что на оси
«о=/ ло+В1 •sin (®*+Фо);
будем отсчитывать фазы и относительно этого я0; тогда надо
считать
Фо = О.
и следовательно по формуле для F2 из (J) и
В0 = F20 = F(°) ’Sin Фо = °, так что
tto = /o-sin(o)/), и амплитуда плотности тока на оси проводника % = ло-
Подставим в формулы для А и В значения Во±=О и А^^и^ и мы получим:
^о=аот»
Д1==0, В1 = 0,
. Л „ а
Л2 — 0> В2— 22W0w>
Л, = 0, ^4 = 0^
О ' о *
Л2 ^4 —~ То О,
* 22 • 42 и,Л *
Л5 = 0, Въ = о,
32*
485
2^•42•6a*ЙOm,
Д7 = 0, B7 = 0,
8“22«42.62-82 *U°^ и т. д.
Fj и Г2 представятся теперь следующими рядами:
( а2 \
F (а х> а3 хв । «5 хю_ \
г “о»^22х (2.4-6)2 ^(2-4-6-8-Ю)2
Ряды эти сходящиеся, так как отношение (л-|-1)-го члена к л-му стремится к нулю при возрастании п.
Отсюда мы можем вычислить для любого х, т. е. в любом месте поперечного сечения провода, сначала Fx и а затем по ур-ниям (J) амплитуду плотности тока w w = /7 и фазу ф.
Если а мало, то можно ограничиться для Ft первыми двумя членами, а для F2 — только одним первым. Тогда легко видеть, что с ростом х растет и ф (от нуля), и следовательно сила тока в слоях большего радиуса опережает силу тока в слоях радиуса меньшего. То же конечно имеет место и при больших а, только тогда нужно взять для вычисления больше членов.
Определяя F, найдем, что оно растет с х, т. е. в наружных слоях плотность тока больше.
Таким образом, резюмируя, видим, что плотность тока все более уменьшается по величине, по мере того как мы переходим к слоям все меньшего радиуса, и все более запаздывает в фазе.
Изложенное решение вопроса принадлежит автору, оно пригодно для всяких значений а и х. Приведем другое решение, данное в 1900 г. Коном, чтобы показать читателю, каким, часто весьма искусственным, путем приходится итти при решении некоторых задач, чтобы получить удобные формулы.
§ 136. Интегрирование уравнения плотности тока — другой способ
Делаем такую подстановку
(N)
Вспомним сказанное в конце § 30 о таких подстановках. Множитель пусть при этом выражает только то, что и есть синусоидальная функция времени. ПодСтавляя (N) в (G), получаем:
<Р/(х) । 1 df(x) 0,4пц<о dx* + х' dx ==‘J р10«
486
или
^/(x) 1 df(x)
^ + x-dr-/3/(x) = 0’
где опять __________________________0,4пца>
а~ "pros'*
Делаем еще подстановку, полагая -
j/ = x/=7a
и следовательно
1
X =------ у
V-Ja
(Р)
(Q)
после чего получаем, обозначая искомую функцию одной буквой /,
dx dy dx dyv J
^7^17
dx2 dy2
(—.fa)
и, подставляя в (Р):
dy2~^~ у dy
(319)
Частными интегралами этого ур-ния являются бесселевы функции первого и второго рода; так как бесселева функция второго рода при j = 0 принимает значение, равное бесконечности, то она по смыслу нашей задачи не является решением ее (так как ^/3=0 означает, что х —0, и следовательно в точках на оси проводника плотность тока и — ф-ла (N) — была бы при этом бесконечно большой), решение же дается только бесселевой функцией первого рода, которую обозначим через JQ(y), причем
у2 . у4 у* у%
^o(j)=1 — 777-2 + 24.(1.2)2 — 26(1 *2’ 3)2+ 28-(Г-2-3-4)2 R)
Найти это частное решение ур-ния (319) мы очевидно легко можем путем, совершенно подобным решению ур-ний (J) и (К), приведенному выше: т. е., разложив функцию / в ряд по степеням j>, мы можем определить коэфициенты этого ряда из ур-ний, полученных подстановкой f и ее производных в ур-ние (319) и приравниванием коэфициентов в нем при различных степенях у нулю.
Вообще же о бесселевых функциях и об интегрировании ур-ний посредством рядов следует смотреть в курсах анализа.
487
Таким образом из (N) получаем, вводя произвольную постоянную Л:
u = A>JQ(y)-e№. (320)
Введем такое обозначение:
тогда по (Q)
Подставив это выражение для у в ур-ние (R), получим после преобразований:
/ В2 В* \ / В8 \
ЛСу)=(1 — (^ — зб + ---)-
Из ур-ния (320) мы видим, что амплитуда и равна модулю правой части, или, иначе, амплитуда отношения и к А равна модулю J0(y); последний определяем приближенно для того случая, к о г д a [J мало, ограничиваясь в (Т) членами второй степени:
^~ModJ0oo=»|/ (1_^2 + р2=«1+£... (и)
Наибольшая величина f, а следовательно и левой части, получается для х = г, радиусу цилиндрического проводника, так как это есть наибольшее значение х, так что по ур-нию (S) наибольшая величина
R __аг2__тгрсог2
Т— pio9 *
Подставив в (U) значение {5 из (S) и введя при и, индекс для обозначения места, где мы рассматриваем величину плотности тока, имеем:
а для центра проводника, т. е. его оси, где х = 0:
— 1-
\ f т
таким образом, деля первое на второе, получаем для отношения амплитуд плотностей тока:
U хт и0т
(321)
488
Для х=^г получаем отношение амплитуды плотности тока на периферии к амплитуде плотности тока в центре:
(322)
Не забудем, что это соотношение справедливо при условии, введенном перед ур-нием (U), что мало.
Сравнивая а с мы видим, что для того чтобы было мало, нужно, чтобы были малы g и © и велико р. Для медного проводника g = l, для железного — g большая величина, поэтому для медного проводника при низкой частоте, например обычной в 50 периодов в секунду, можно применять ур-ние (322), а для железного — нельзя.
Если же частота тока велика, например сотни тысяч периодов в секунду, то соотношения будут совсем другими; то же и при большом g.
При этом а, а следовательно и у будут велики, а для больших у имеем вместо (R) приближенное решение:
е»
Из ур-ния (Q) имеем:
у2 = —
или
- У2 = (1 -1 + 2/) *2 • 4,
(323)
(Z)
Возьмем отношение значений амплитуд и в точках х = г и х = г— так как отношение модулей комплексов равно модулю отношения самих комплексов, то нам надо найти:
Mod =-Mod \ «г /
^О^У^х—г
489
Подставляя вместо J0£y) только что полученное выражение (Z), а в него вместо х один раз г — 5, другой раз г, получаем после сокращения:
Соотношение (324) справедливо, если i не очень близко к г, так как иначе х, равное г—5, а следовательно и у по ур-нию (Q), становятся малыми, и ур-ние (323) не имеет места.
Если i мало сравнительно с г, то приближенно
Mod ( = е~8 . (325)
„ > 1 Z’2
На расстоянии ^—1/ — от поверхности проводника ампли-
1 туда плотности тока уменьшается до — ее величины на поверхности.
Вообще же, каковы бы ни были [J и х, из ур-ний (320) и (Т) мы всегда можем вычислить ихт, задаваясь постоянной А, т. е. плотностью и(]т на оси.
§ 137. Уравнение плотности магнитного потока
Выводы настоящей главы нетрудно распространить и на переменный магнитный поток.
Внесем в обозначения фиг. 207 следующие изменения: будем считать, что вместо цилиндрического проводника с переменным током мы имеем цилиндрический „магнитопровод" с переменным магнитным потоком вдоль него; материал сердечника магнитопровода пусть будет электропроводен (т. е. не диэлектрик, а например металл); вместо прежнего результирующего напряжения v введем магнитодвижущую силу т на единицу длины; вместо плотности тока и — магнитную индукцию В\ вместб Н по направлению, отмеченному крестиками или навстречу ему, — плотность тока и\ этот ток индуктируется переменным магнитным потоком Ф, который займет теперь положение прежнего тока /; этот поток проходит через площадь радиуса х.
490
Тогда будем иметь:
и, диференцируя по х:
dm_ dx р dx 9
с другой стороны, есть приращение магнитодвижущей си-
ах
лы на стороне ее на стороне п через Q^Ttudx. rs прямоугольника mnrs сравнительно со значением пп\ это приращение можно выразить и иначе, именно Поэтому d/w л л dx
и следовательно 1 ав А — •— = О,4тги« ц dx
Отсюда: i /в m U 0,4 тгр. dx ’ * '
и затем: du 1 d?B dx 0,4пц dx2'
ЭДС в круговом контуре, оцепляющем поток Ф, может быть выражена, с одной стороны, через Ф, с другой стороны,— через силу тока и сопротивление в этом круговом контуре следующий образом:
d<D , 2ттхр о
—- 108 = zz^x«—г-5- = 2прх. dt dx г
На основании соображений, аналогичных приведенным после ур-ния (D), отбрасываем в левой части знак минус, считая, что и положительно, когда индуктированный ток помогает внешней магнитодвижущей силе, и отрицательно — в обратном случае; диференцируя затем по ху получаем
d /ЛФ\ dt\dx)
10“8 = 2ттр [х^ 4" И • г \ dx ' /
(III)
d<t>
Но — • dx есть приращение потока, равное г отоку через кольцо
2irxrfx; поэтому:
</Ф о
—2пх dx
В.
491
Подставляя это выражение в левую часть ур-ния (III), получаем:
10“8 = 2тгр )•
dt г \ dx 1 /
Подставляя в это ур-ие вместо и их выражения (I) и (II), имеем:
dB 1Л-8 Р d2B I Р dB dt 0,4 яр, \/х2^0,4пр dx1
или окончательно:
&В , 1 ^В_0,4яр dB dx2'х ' dx~ plO8 ‘ dt
Это ур-ние совершенно подобно ур-нию (G), а потому для значений В в различных точках поперечного сечения магнитопровода имеют место те же соотношения, что и для и в проводнике.
Таким образом переменный магнитный поток распределяется по плошади неравномерно, а убывая в своей плотности от периферии к центру с увеличением при этом запаздывания в фазе.
Следствием этого является между прочим и то, что при токах высокой частоты, проходящих через катушку с железным сердечником, магнитного потока в железе практически совсем не будет,— магнитный поток будет иметься только в промежутке между сердечником и катушкой.
Если материалом сердечника магнитопровода будет служить диэлектрик, то эффект будет обратный: магнитная индукция будет больше у оси, чем у периферии, но количественно это явление крайне слабо.
<§ 138. Вывод формулы Стефана для сопротивления проводника при переменном токе
Следует отметить, что часто утверждается, что при явлении поверхностного эффекта ток оттесняется из центра проводника к его поверхности; таким утверждением вызывается иногда неправильное представление о величине плотности тока у поверхности. Нужно помнить, что плотность тока в поверхностном слое при этом явлении имеет величину не большую, чем определяемая сопротивлением и величиной ЭДС самоиндукции для поверхностного слоя и приложенным напряжением, но чем глубже в проводнике находится точка, плотность тока в которой мы определяем, тем ЭДС самоиндукции больше, а потому эта плотность тока становится все меньше по величине и все более запаздывает по фазе.
492
Из предыдущего следует, что вследствие неравномерного распределения переменного тока по поперечному сечению провод представляет для переменного тока сопротивление больше, чем для постоянного тока.
Для определения величины /?' сопротивления провода при переменном токе служит формула Стефана, которую мы теперь и выведем, слегка лишь изменив вывод, данный им.
Будем рассматривать случай не слишком малого радиуса г поперечного сечения провода и частоты достаточно большой, чтобы приближенно можно было принять, что при х < г плотность тока и становится настолько малой, что ею можно пренебречь и положить ее равной нулю. При этом условии в ур-нии (G) множитель 1 du 1
—- при — можно заменить через —; как увидим в конце, несмотря на большую ограничительность условий, вывод дает формулу, применимую во всех случаях практики с достаточно большой точностью. Ур-ние (G) теперь напишется так:
d2u f 1 du 0,4пц du dtf+'r ’ dx~ plO« ‘ ~di *
Интегралом этого ур-ния будет
и = А • ekx• sin (<о/ -|- тх). (Ь)
Постоянные k и т определим следующим образом.
Подставим в ур-ие (а) выражения производных, полученные из ур-ния (Ь), и сгрупируем члены с sin (<о/ -|-тх) и с cos 4" тхУ Ввиду произвольности t и х коэфициенты при этих sin и cos должны быть равны нулю; отсюда мы получаем два ур-ния:
АЗ-/И2 4-—= 0 * г
о , I т 2mk Ч---= а
1 г
(с)
Здесь через а обозначена, как и ранее, величина Решая эти уравнения, находим:
Перед радикалами берем знаки плюс, чтобы ур-ние (Ь),выражало уже известное нам обстоятельство уменьшения плотности тока и запаздывания ее в фазе с уменьшением х.
493
Умножив основное ур-ние (G) на x*dx, получим:
du --'X>dx. dt
Выделим в правой части группу множителей 2nxt/x, что представит собой площадь кольца; тогда
, / du\ a d , ч
d х— -----------— (2тшх dx)\
у dx] 2тпо dt
теперь проинтегрируем в пределах от х==0 до х = г du a di
г — =-------- —;
dx х _г 2тго) dt
здесь I означает всю силу тока через поперечное сечение провода, т. е.
X = г
i = J 2тгих dx.
х = о
Полученное нами ур-ние перепишем так: di 2no)r du
dt a dx
и подставим в него значение производной от и при х = г, которое определим из ур-ния (Ь); получим:
~ деьт sin тг} т cos (q)/ mf)\.
Интегрируя, имеем:
2тг/*
i = —— Aekr [ т sin (<of -f- mr) — k cos (w/ 4” mr)].
Умножим первое ур-ние на k, а второе — на т® и результаты сложим, получится:
т со/ 4“ &ekr (^2 ~Ь ^2) sin “И тг\
или, обозначая через иг плотность тока в поверхностном слое, т. е. при х — г:
. , , di 2тго)г . «ч
(е) QrL Gt
Выделим теперь мысленно в проводе, в поверхностном слое его, прямолинейную нить бесконечно-малого поперечного сечения ds и составим для нее уравнение напряжений на единицу длины.
494
Так как сила тока в нити равна u1»dst сопротивление единицы длины нити равно р: ds, то мгновенное значение ваттного падения напряжения равно ^«р.
Весь ток в проводе, распределенный вокруг оси концентрически, действует индуктирующим образом на все внешнее пространство, в том числе и на эту нашу нить так, как будто бы весь он был сосредоточен на оси.
Поэтому, пренебрегая бесконечно-малой ЭДС „самоиндукции" нити, находим, что мгновенное значение, безваттного падения
напряжения в нити равно М — , где М есть „величина взаимно-индукции" оси и нити на единицу длины, равная, как известно . Л Л 2/ , . г \ ,
из курса электричества, приблизительно 2 I log—-1 —f— -j- 1, где I
есть длина провода.
Таким образом, обозначив через мгновенное значение приложенного извне напряжения на единицу длины, будем иметь:
di = +
Вставим сюда вместо иг его выражение из ур-ния (е); тогда получим:
/пар . , / бар . \ di
V1 “ 2пг-j- /и2) ~t“ \2mor(fe2 т } dt' W
В последнее ур-ние вошла вся сила тока i через поперечное сечение провода; ур-ние напряжений через ваттное сопротивление R на единицу длины и самоиндукцию L1 то же на единицу длины пишется так:
поэтому в ур-нии (/) коэфициент при I есть /?, а коэфициент Л .
при — есть L .
Итак
2яг(Л2 Ф /п2) ’
или, после подстановки вместо а его выражения:
2ягр® 10»/-(Л2 4-/п2) *
495
Это выражение преобразуем следующим образом.
Пренебрегая в ур-нии (d) величиной в сравнении с , по-лучим:
и
Тогда приближенно т . __ 1 __ 1 . 1
/•(Л2 + «2) ~’ г/2а — 1 ~ г У 2а ‘ 2^а'
Подставляя это выражение в ф-лу для 7?г, а вместо а вставляя его значение, получаем:
Стоящий перед скобками множитель есть сопротивление 7? единицы длины провода при постоянном токе. Обозначим отношение 7?г к 7? через /С, затем заменим г перед радикалом через — , 4^ где d есть диаметр поперечного сечения провода, и введем эту величину под корень; тогда для отношения сопротивлений имеем:
К
№
0,4р
1
4 *
Это соотношение и называется формулой Стефана.
Госпиталье вычислил К как функцию fd* для круглого проводника из чистой меди, исходя из других формул, именно— В. Томсона; эти значения К сведены в нижеследующую таблицу:
л*» к к к
20 1,0000 720 1,3180 2 880 2,3937
80 1,0001 980 1,4920 5120 8,0958
180 1,0258 1 280 1,67’78 8000 3,7940
820 1,0805 1620 1,8628 18000 5,5732
500 1,1747 2 000 2,0430 32000 7,3250
496
Из таблиц мы видим, что для обычной частоты в 50 периодов в секунду в медных проводах до 1 см диаметром влияние поверхностного эффекта еще незаметно.
Формула Стефана дает величины К несколько меньшие, чем приведенные в таблице: при jtaf2 = 500 на 6%, при /^2 = 2 000 на 3,5%; с ростом fd2 ошибка все более уменьшается; вычисление к и т по ур-ниям (d) тоже несколько уменьшает ошибку. Для магнитных материалов формула вообще приближенна, ибо точное значение ц, которое надо в нее подставить, нам никогда неизвестно.
Заметим, что предыдущая теория не учитывает влияния обратного провода.
Из ур-ния (f) мы можем вывести заключение об изменении самоиндукции провода под влиянием поверхностного эффекта. С ростом частоты L! уменьшается, приближаясь к М.
В заключение заметим, что с влиянием поверхностного эффекта не нужно смешивать влияние токов Фуко в массивных проводниках (например в обмотках машин), индуктируемых посторонними полями, например какими-нибудь полями рассеяния. Эти токи Фуко тоже вызывают неравномерное распределение тока и увеличение сопротивления, часто большое — до 50% и более; существенную роль в этом вопросе играют конструктивные детали, определяющие величину и направление магнитных потоков; учитывается влияние неравномерного распределения тока в этом случае главным образом по эмпирическим данным.
497
ОТВЕТЫ К ПРИМЕРАМ
1. 2р = 40. 2. Jm = 27 ампер. 3. £=0,191 генри. 4./= 52; Jm = 25,6.
16. u = <?_/45°. 17. й=г+/60°. 18. н = 4-в-73О°. 19. е+7Т = —4- +
Z Z
20. е+/Т = +/. 21. #'*«= —1. 22. в~'т = +/=г+'Г.
23. е 7 75 ° = 0,259+/0,966. 24. е-7500 =0,643-/0,766. 29. Г=
= 0,903г+720°15'; У=58,5г+'31°; / = 52,8г751°и'; cos f = cos 20*4 5'= = 0,938.
Искомая емкость в третьей ветви, необходимая для получения cos? = = 1, находится следующим путем. Если cos? = l, то
а так как
^=^| = 0,1, д2=—* = 0,088,
Zj z2
то
&3 = || = _ 0,188,
51ЛИ
/?з=1, поэтому получаем ур-ние:
Л|+5,ЗХ»+1 = 0, откуда xj = — 0,195 и Уз = — 5,105.
Полагая абсолютное значение X равным , получаем:
—j = 0,0163 фарады = 16 300 микрофарад.
с2 = —1-7, = 0,00062 фарады = 620 микрофарад.
<4Л3
Как видим, необходимая емкость получается чрезвычайно большой!
498
31. a’= 4-1. Умножив вектор например Е± три раза на а, мы переведем его через положения сначала E3t затем £2 снова в первоначально^ положение, другими словами, повернув три раза на 120°, всего повернем его на 360°, т. е. оставим без изменения.
32. 1 4- а 4- а2 = 0, — что является символическим выражением той геометрической теоремы, что геометрическая сумма трех векторов, сдвинутых в фазе на одну треть периода, равна нулю. Уравнения
14-a4-a2 = 0 и
sin (<о/) 4" sin ^<0/4- у) + sin (ш^4"
выражают одно и то же, первое в символической, второе в тригонометрической форме.
38. Воспользуемся ф-лами (В), (С), (D) и (F):
Y I ЦТ_______С _______
а + гп+М + пУ
а 4- jb = 4- У3 = const,
с +jd=:VaT^V3iY3= const, m 4/л =s Ур Так как = const, то , п . .
tg «. = — = k = const, 6 T1 tn ’
n = tnk, Y I ЦТ_______c Jd_____
'J a + m+j(b + km) *
Приравнивая отдельно мнимые и действительные части, получаем:
(а + т) X — (Ь 4- km) и=с, (Ь 4- km) X 4- (а 4- т) U = dt или
т (X - kU) + аХ - b U - с = 0, (1)
т (kX 4- U) 4- ЬХ 4- a U - d = 0. (2)
Из последнего определяем пг.
___.bX—aU+d т~ kX+U подставляем в (1):
_ ЬХ* — aXU 4- dX 4- kbXU + kaU* — kdU 4- kaX* + 4- aXU — kbXU — bU*—ckX— cU~ 0,
по преобразовании:
X* (ak -b)-\-U* (ak-b) + X(d-ck)—U(c+ kd) 0, что представляет ур-ние круга, проходящего через начало координат.
499
Некоторые литературные указания
1. Векторы введены в теорию переменных токов английским электриком Т. Г. Блекслеем, в книге „Papers on alternating currents of electricity*, содержащей статьи, опубликованные им в английских журналах за 1880 г. Эта книга издана на русском языке в переводе В. К. Лебединского— Блекслей, „Переменные электрические токи“, изд. К. Риккера, 1894. Далее много содействовали введению векторов Ф. Бедель и А. К рехор статьями и книгой „The alternating currents*, 1892. Книга издана на русском языке — Бедель и Крехор, „Переменные токи", перевод под ред Н Булгакова, изд. Суворина, 1911.
2. Комплексные числа применены впервые для решения задач переменного тока Гельмгольцем, в статье: „Ober Telephone und Klangfarbe“, 1878. Систематически этот метод развит С. Штейнметцом и А. Кене л л и в статье в „Trans. Amer. Electr. Eng.*, т. 10, стр, 175, 1893 и в книгах Штейнметца: „Theoretical Elements of Electrical Engineering*, 4-е изд.. 1915; „Theory and Calculation of alternating current phenomena*, 5 e изд., 1916 (Me. Graw. Hill Book C°) и других.
3. См. указанные сочинения Штейнметца.
4. Этот способ предложен был английскими электриками Айртоном и Сумйнером „Electrican*, т. 26, стр. 736, 1891, и С в и н б у р н о и „Industries*, т. 10, стр. 306, 1891.
5. Предложено английским ученым Флемингом „Electricin*, т. 27, стр. 9, 1891.
6. Г. Г е р г е с, El. Zeitschrift, стр. 189, 1900.
7. См. указанные сочинения Штейнметца и Г. Гергеса, „Е1. Zcitschrift“, стр. 164, 1898.
8. А. Кен не л л и, „Electrical Worled*, т. 34, стр. 413.
9. Г. Феррарис и Н. Тесла.
10. Фортескью, Proc. Am. Inst. El. Eng., June 1918. К. Мюллер, „Е1. Zeitscnrift*, № 35, 1918.
11. Этот способ указан Цахриссоном, „Е1. Zeitrschrift*. 1923, стр. 897.
12. Первая схема дана Лакуром и Брагштадом в книге: „Wech-selstromteciinik* (von Е. Arnold) т. 1, 2-е изд., 1910 (1-е изд. 1904).
13. Дана впервые проф. Г. Н. Петровым в статье „К теории асинхронного двигателя*. Труды Гос. экспер. электр. инет., вып. 8, 1925.
14. Метод обращений развит Лакуром и Брагштадом в указанной книге: „Wechselstromtechnik".
15. Метод построения круговой диаграммы по данным опытов холостого хода и короткого замыкания развит впервые Лакуром в книге: „Leerlauf und kurzschlussversuche", 1902, и также вместе с Брагштадом в „Wechselstromtechnik*.
16. Теория векторных уравнений подробно разработана в книге О. Блоха: „Die Ortskurven der Graphischen Wechselstromtechnik*, 1917.
17. Теория линий мощности развита впервые в „Wechselstromtechnik* Лакуром и Брагштадом.
18. Вывод линий мощности второй эквивалентной схемы дается здесь впервые.
19. Теория разряда конденсатора дана впервые В. Томсоном (Кельвин) в 1854 г.
20. Теория длинных линий с приложением к ней гиперболических функций впервые развита английский электриком О. Хивисайдом в книге: „Electromagnetic Theorie*, тт. I, II и III, 1899.
Цена 4 р. 60 к.
Переплет 40 к.