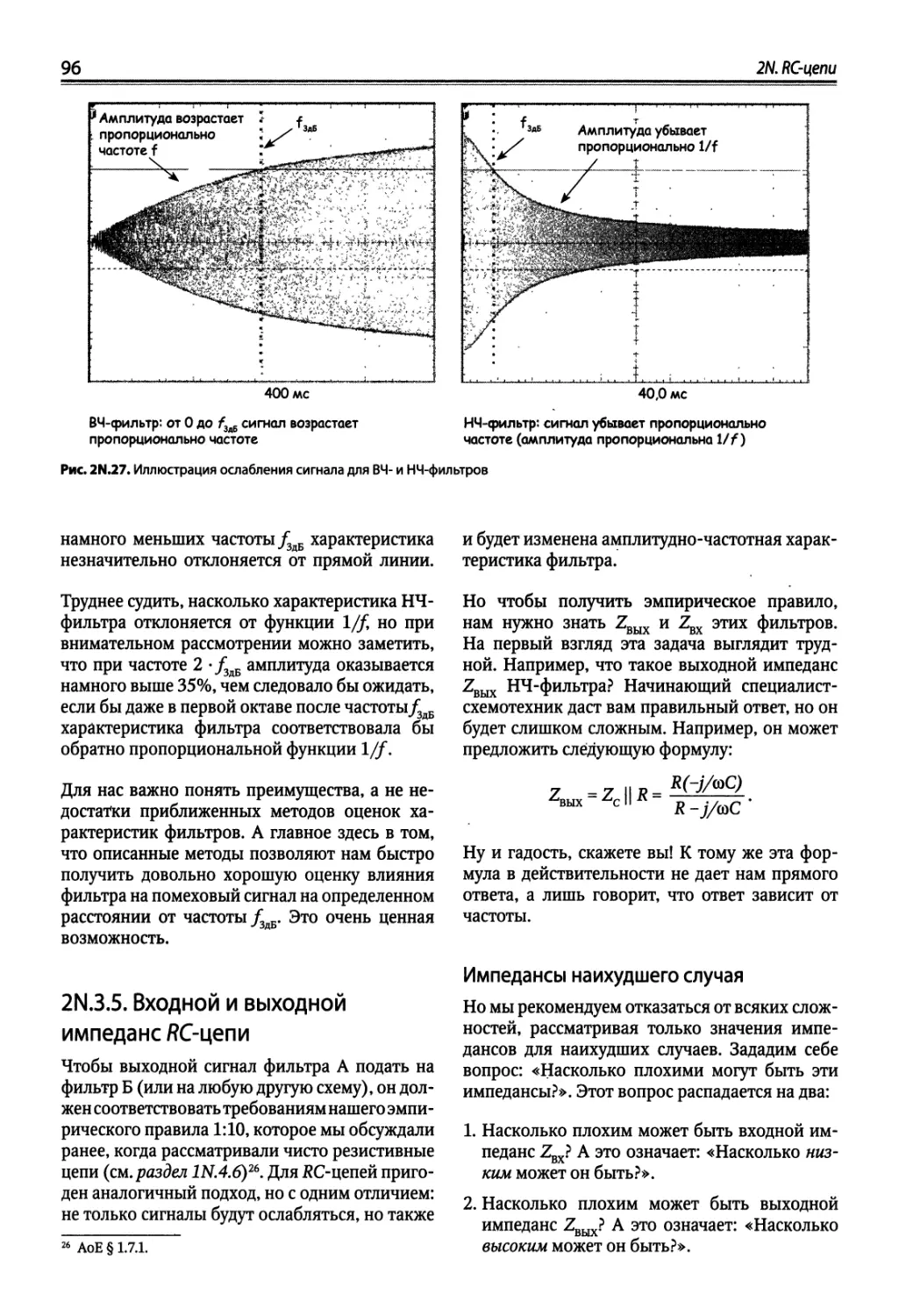
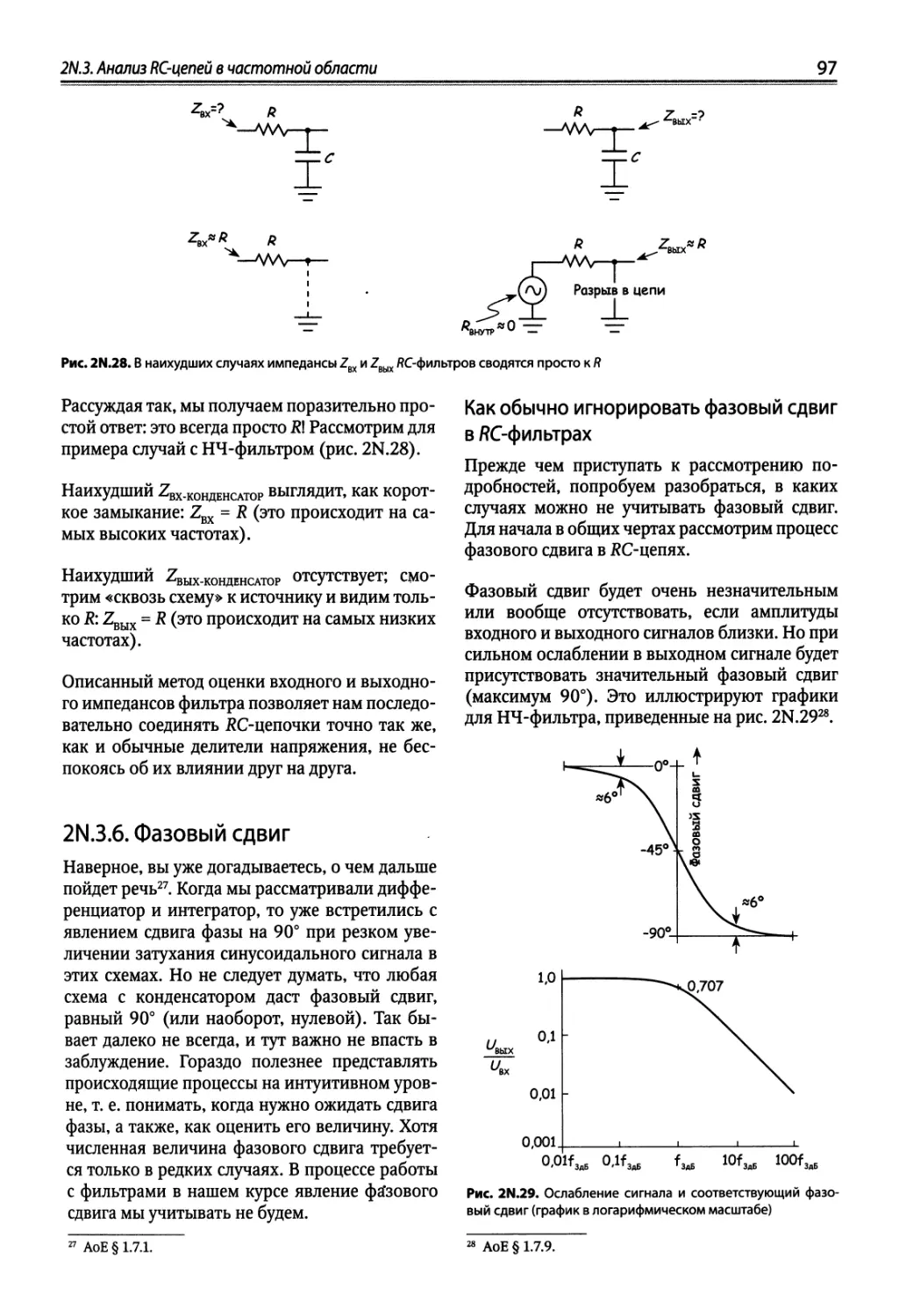
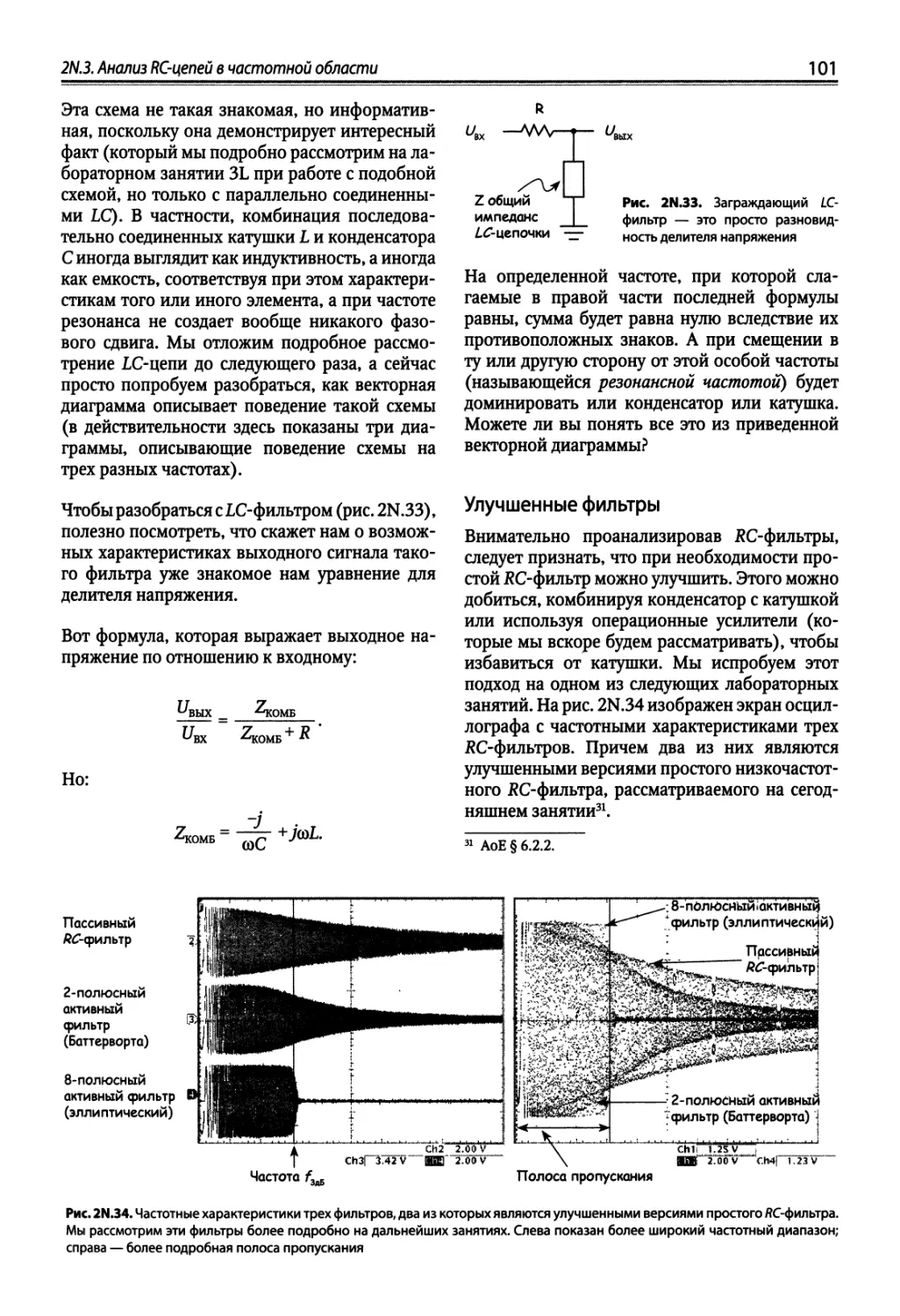
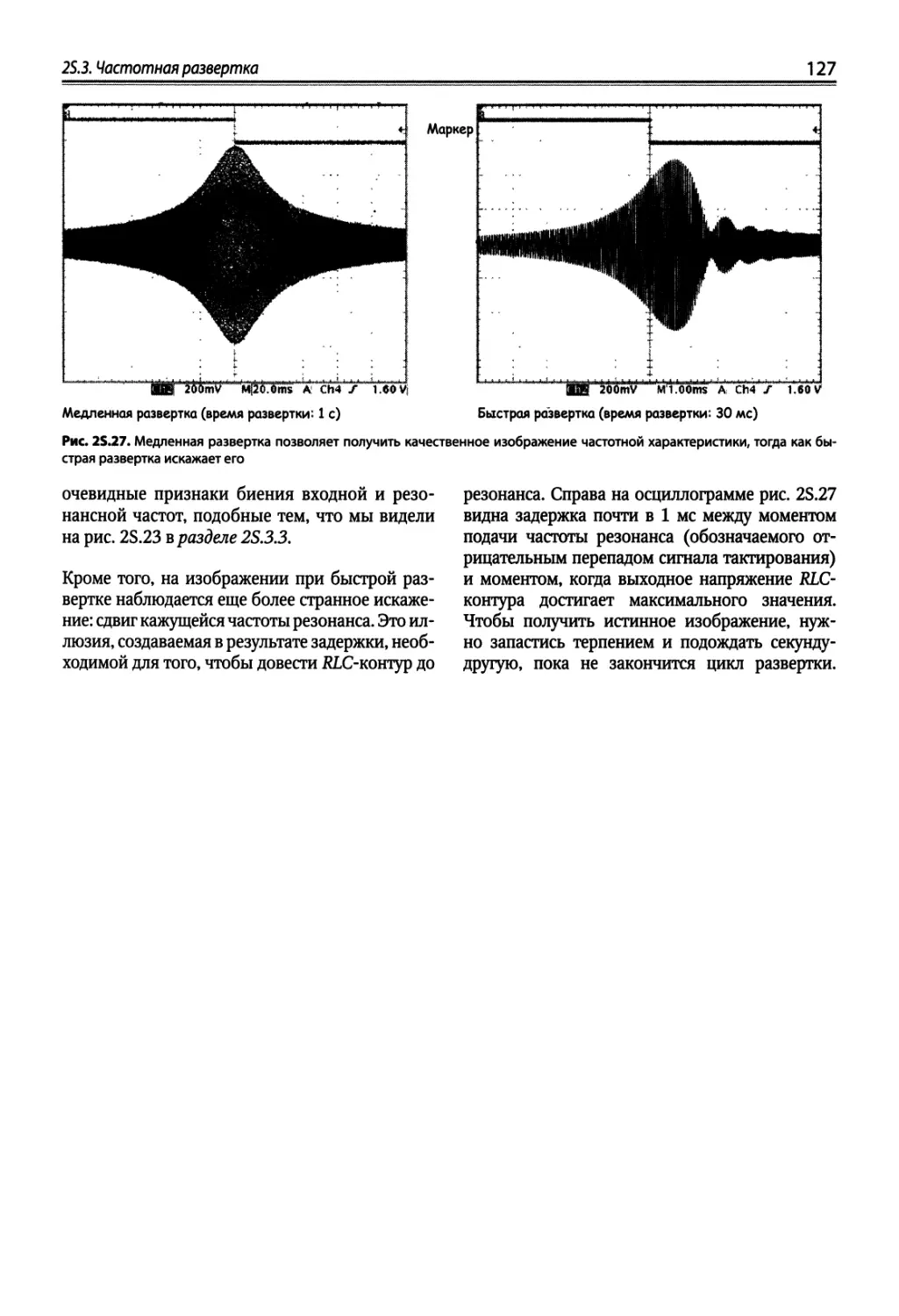
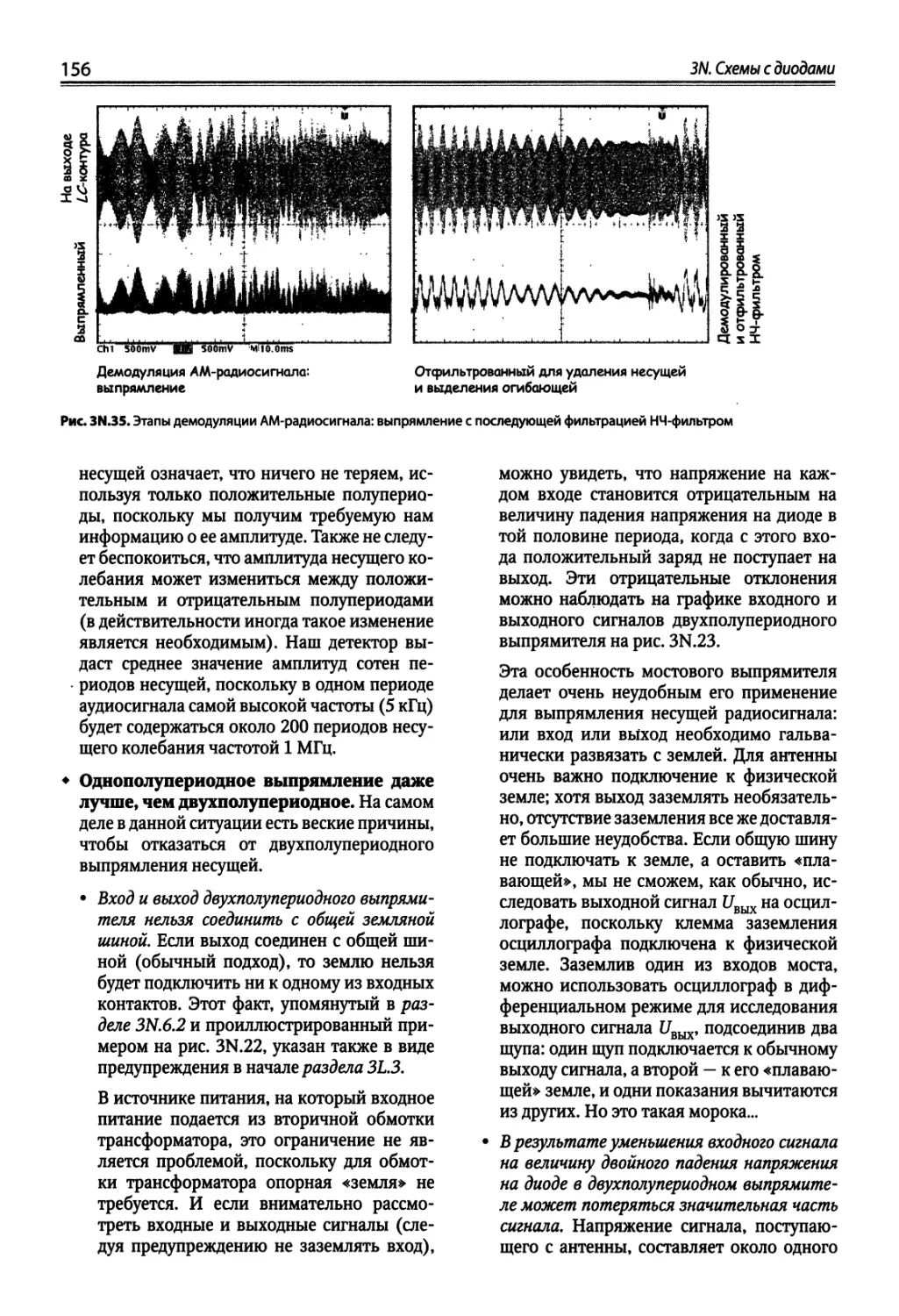
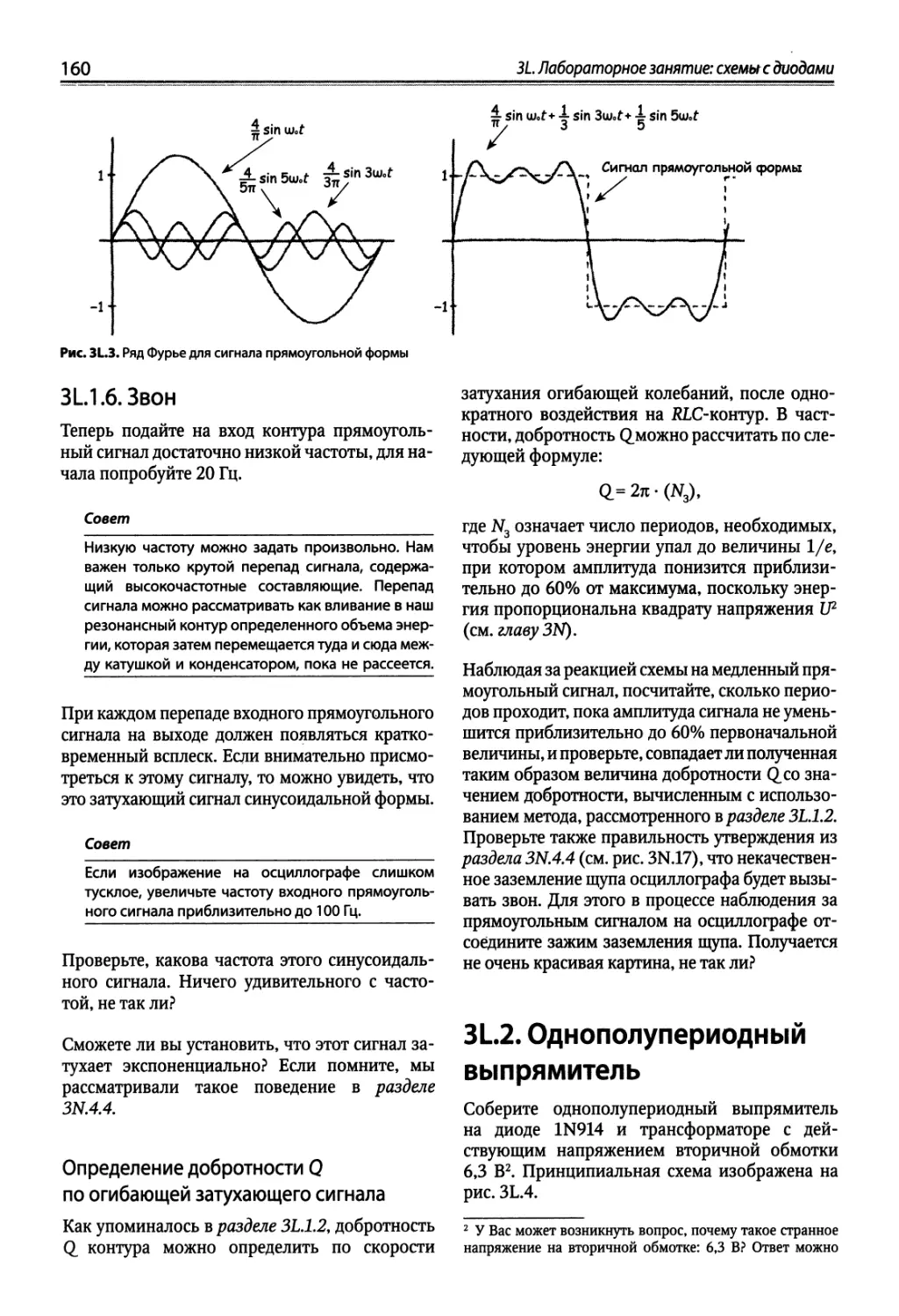
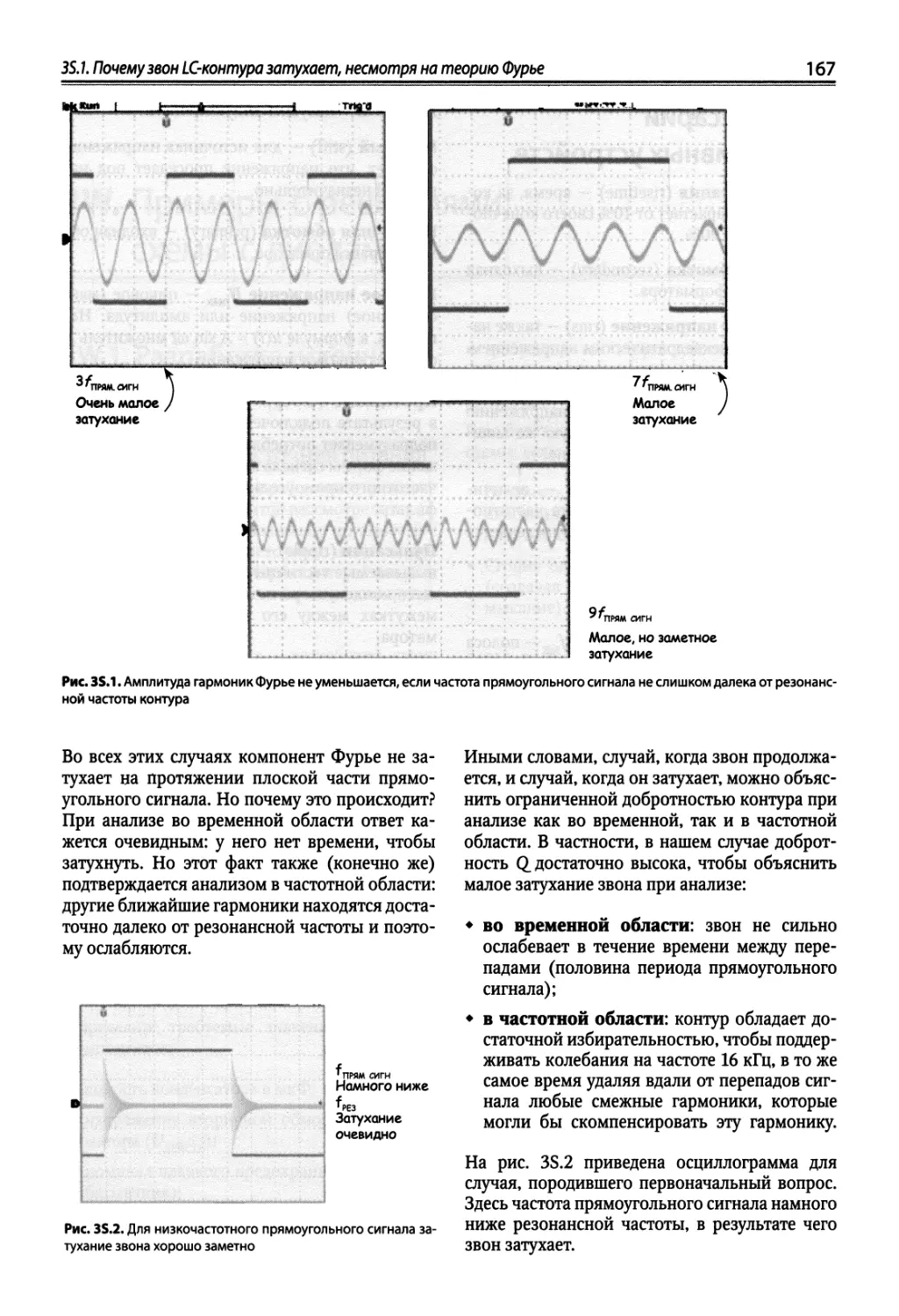
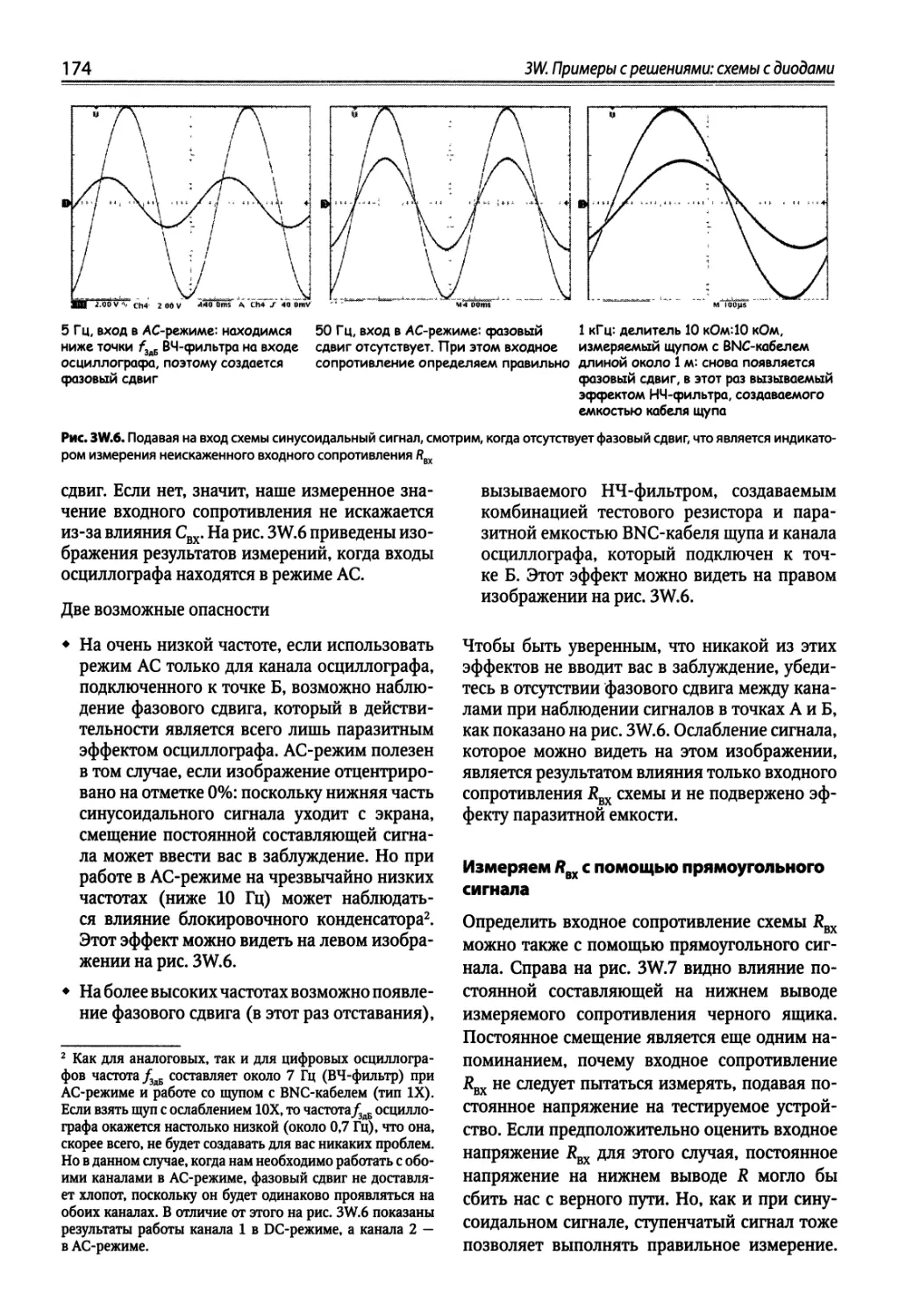
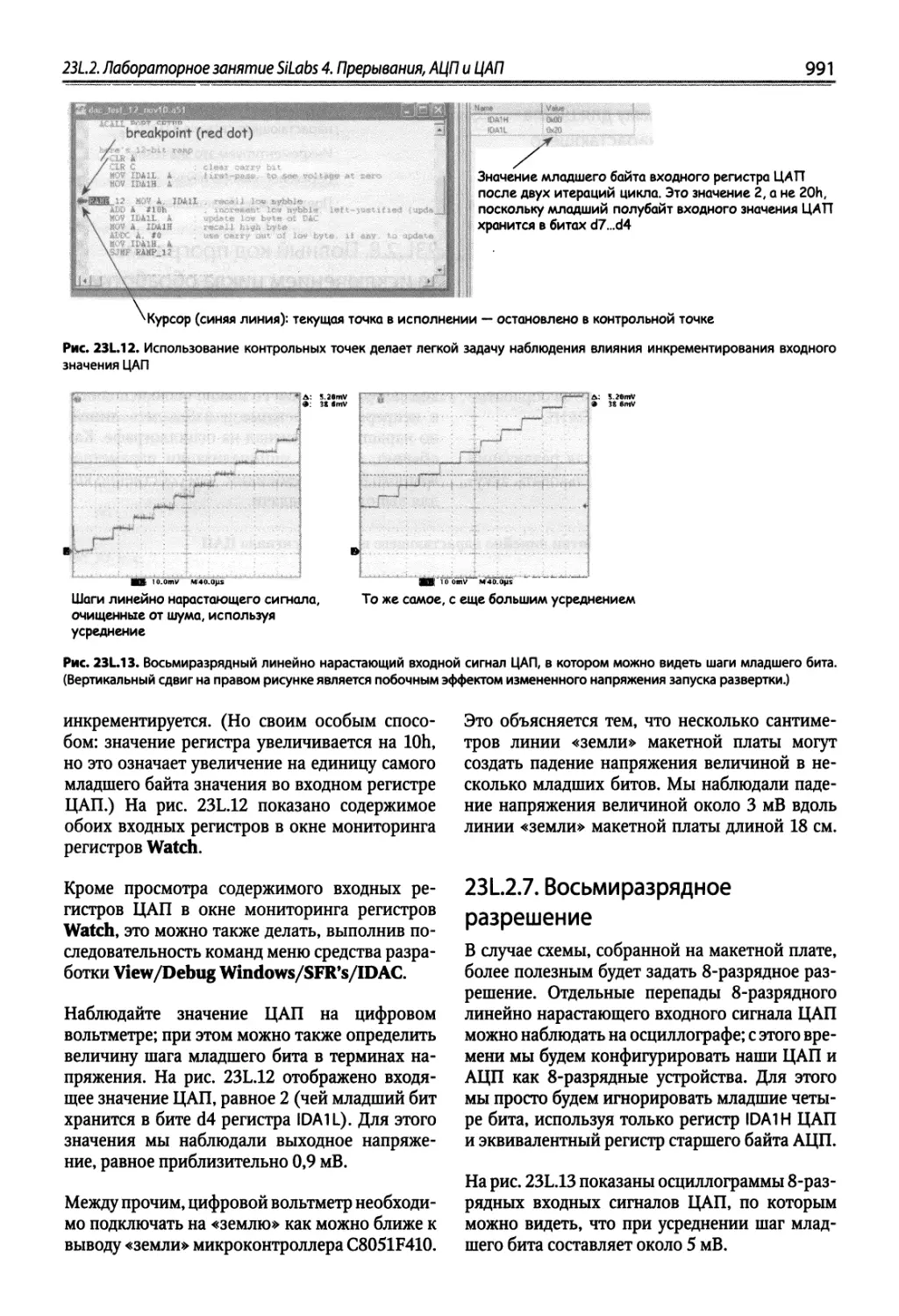
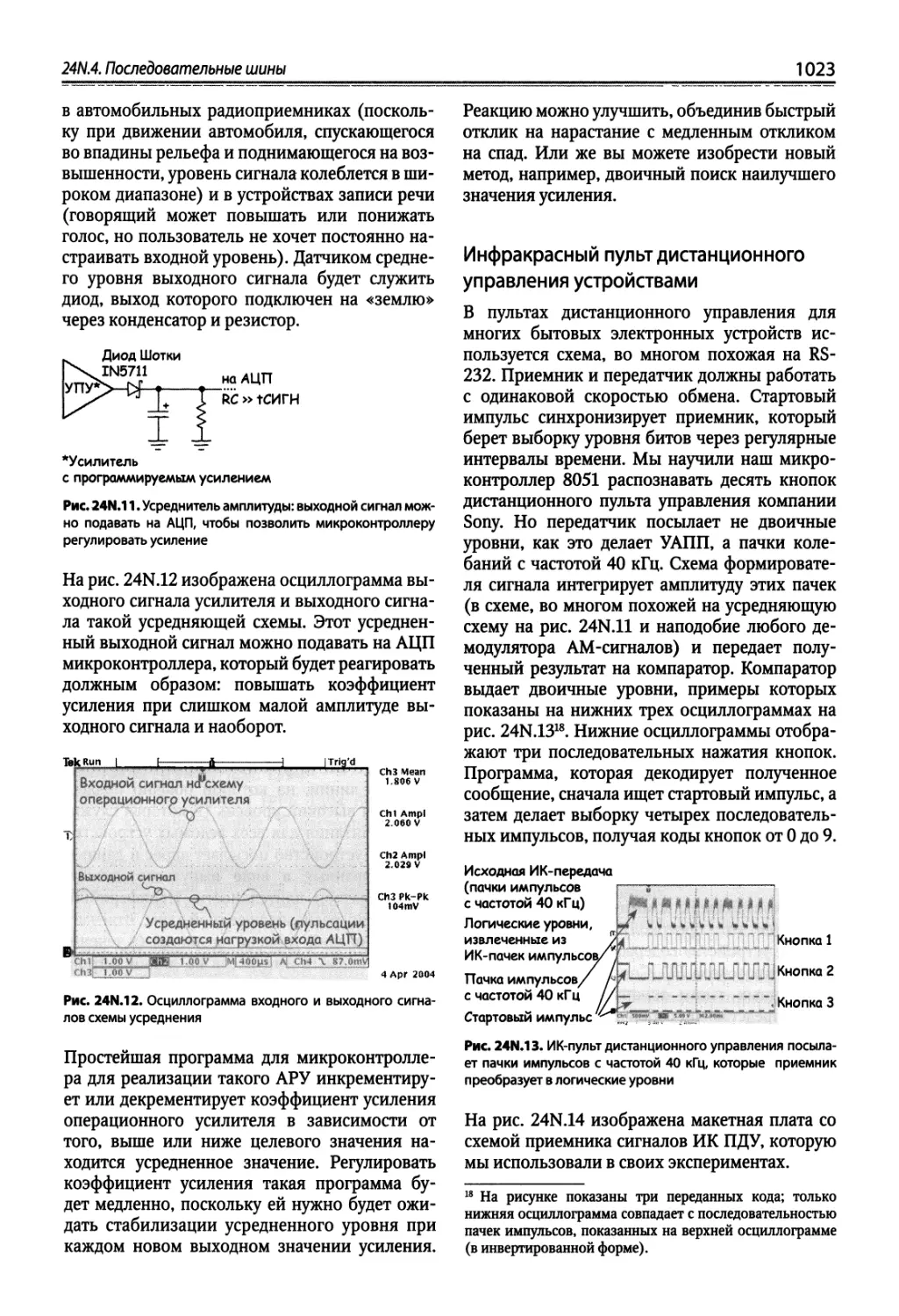
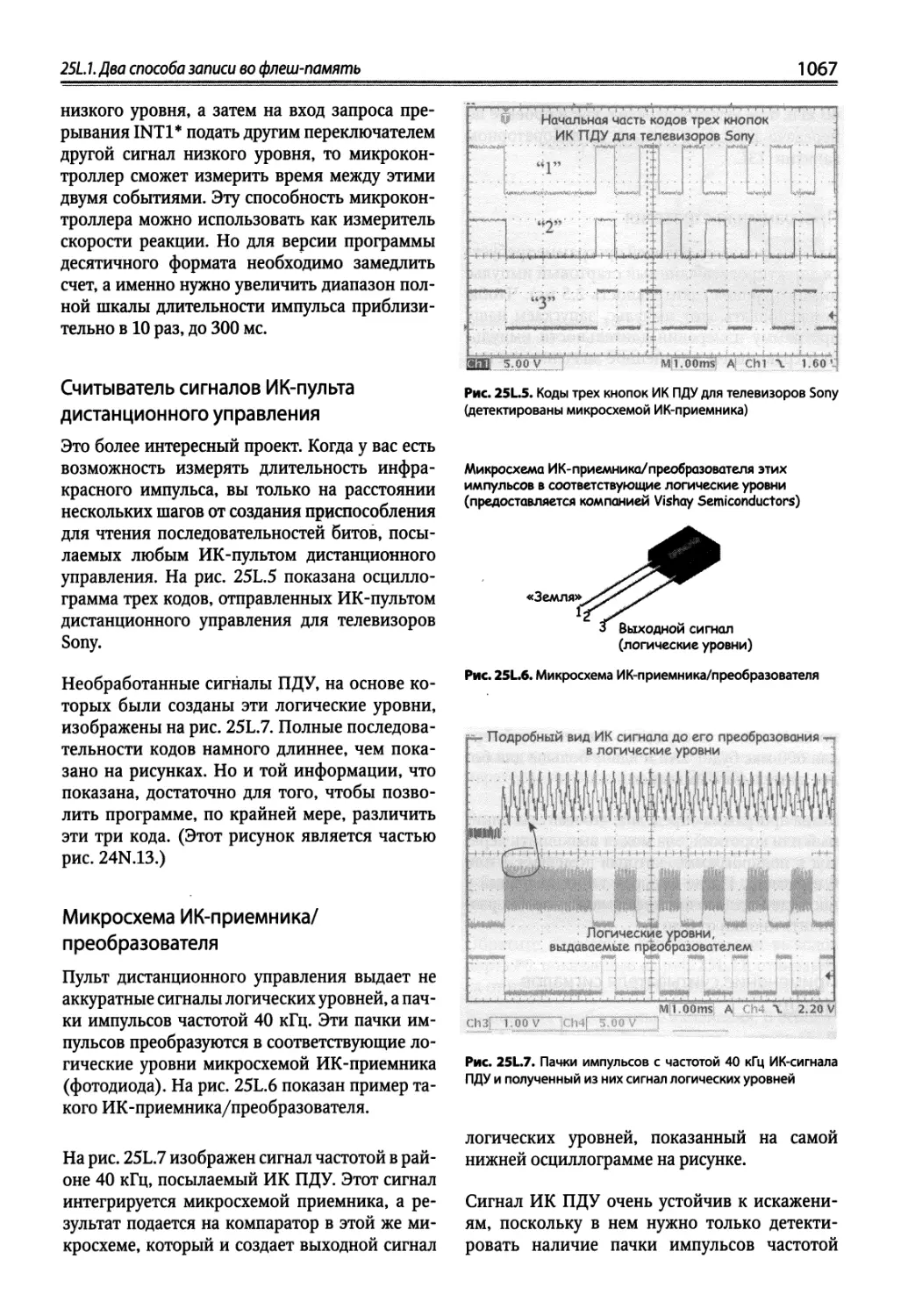
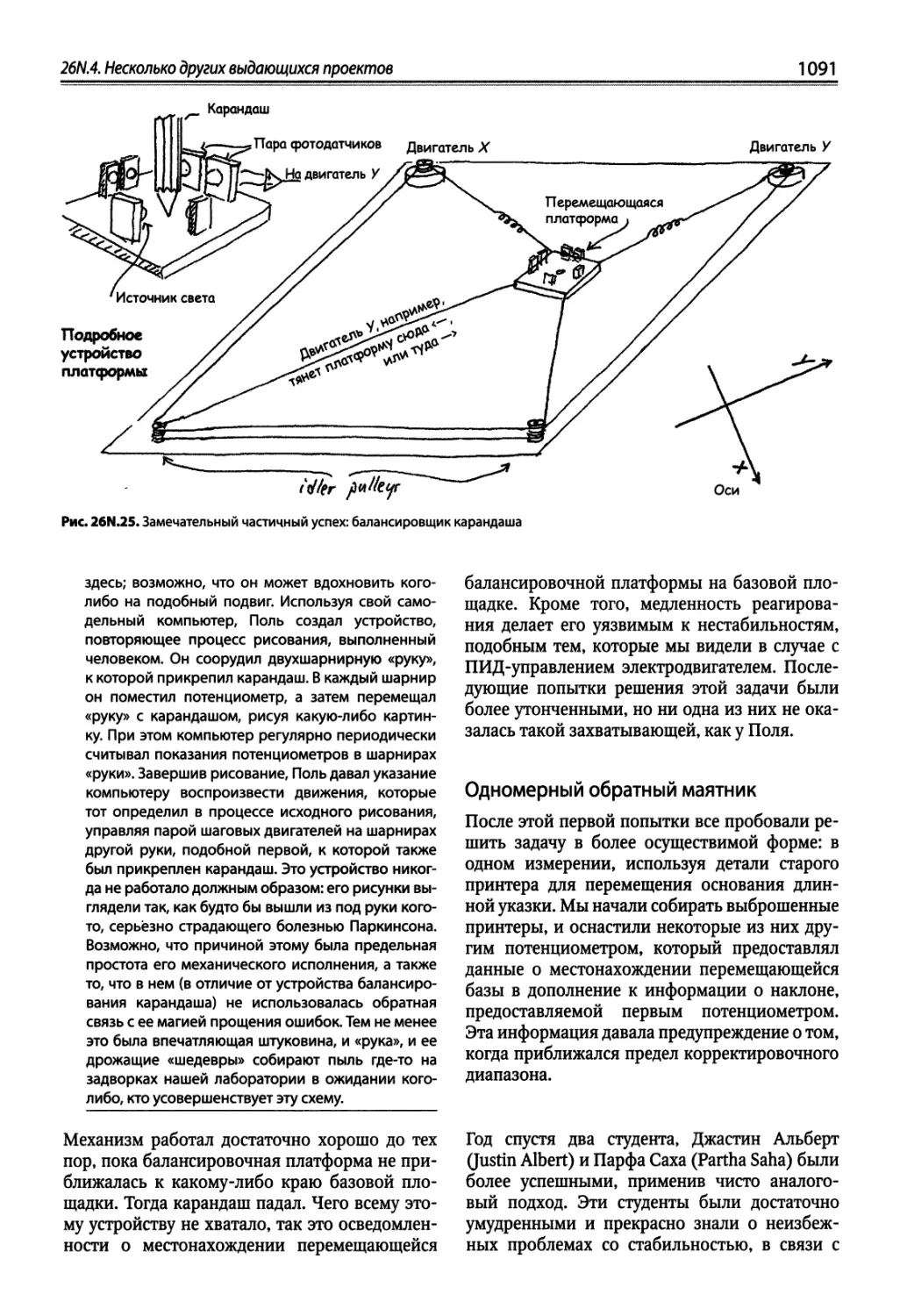
Author: Хоровиц П. Хейс Т.К.
Tags: компьютерные технологии электроника схемотехника
ISBN: 978-5-9775-6689-6
Year: 2022
Text
Learning the Art of Electronics
A Hands-On Lab Course
Thomas С Hayes
with the assistance of Paul Horowitz
ТОМАС К. ХЕЙС
ПОЛ ХОРОВИЦ
ИСКУССТВО
СХЕМОТЕХНИКИ
ТЕОРИЯ И ПРАКТИКА
Санкт-Петербург
«БХВ-Петербург»
2022
УДК 681.325.65
ББК 32.85
Х35
Хейс,Т.К.
Х35 Искусство схемотехники. Теория и практика: Пер. с англ. / Т. К. Хейс, П. Хоровиц. —
СПб.: БХВ-Петербург, 2022. - 1200 с: ил.
ISBN 978-5-9775-6689-6
В этой уникальной книге по схемотехнике содержится не только теоретический материал, но и пол-
ноценный курс лабораторных работ. Подробно рассмотрено применение аналоговых устройств (пассив-
ных элементов, транзисторов, операционных усилителей), цифровых устройств (логических элементов,
триггеров, счетчиков, ПЛМ, памяти, АЦП, ЦАП, ФАПЧ) и микроконтроллеров. Каждое из 25 занятий
содержит две части: теоретический конспект и лабораторную работу. Занятие начинается с рассмотрения
той или иной схемы, после чего предлагается реализовать ее на практике и изучить работоспособность.
Занятия включают примеры с решениями и дополнительными пояснениями. Рассматривается язык опи-
сания аппаратных средств Verilog. В приложениях представлена общая информация по осциллографам,
линиям связи, цоколевке микросхем, программам и т. п., а также даны советы по выбору деталей и обо-
рудования. В книге очень мало математики, основной упор делается на интуитивный подход и практиче-
ские навыки.
Для радиолюбителей, студентов и преподавателей
УДК 681.325.65
ББК 32.85
Группа подготовки издания:
Руководитель проекта Игорь Шишигин
Зав. редакцией Людмила Тауль
Компьютерная верстка Людмилы Тауль
Оформление обложки Зои Канторович
© Cambridge University Press 2017
This translation of Learning the Art of Electronics is published by arrangement with Cambridge University Press.
Перевод издания Learning the Art of Electronics опубликован по соглашению с Cambridge University Press.
Подписано в печать 30.12.21.
Формат 60х901/8. Печать офсетная. Усл. печ. л. 150.
Тираж 1500 экз. Заказ № 22.
«БХВ-Петербург», 191036, Санкт-Петербург, Гончарная ул., 20.
Отпечатано в ООО «Типография «Миттель Пресс»
Адрес: 127254, г. Москва, ул. Руставели, д. 14, стр. 6.
Тел./факс: +7 (495) 619-08-30,647-01-89.
E-mail: mittelpress@mail.ru
ISBN 978-0-521-17723-8 (англ.) © Cambridge University Press, 2017
ISBN 978-5-9775-6689-6 (рус.) О Перевод на русский язык, оформление,
ООО «БХВ-Петербург», ООО «БХВ», 2022
Искусство схемотехники. Теория и практика
Эта книга по схемотехнике необычна в несколь-
ких отношениях.
Прежде всего, в ней содержится не только тео-
ретический материал, но и полноценный курс
лабораторных работ. Каждое из 25 ежеднев-
ных занятий начинается с рассмотрения той
или иной схемы, после чего предлагается реа-
лизовать ее на практике и посмотреть, как она
работает. Таким образом, студенты лучше вос-
принимают теорию и глубже понимают работу
схемы, чем если бы просто изучали ее функцио-
нирование по соответствующим формулам.
Во-вторых, в данной книге рассматриваются
схемы, которые при традиционном подходе к
изложению схемотехники изучаются на более
поздних этапах. Например, уже на третий день
мы знакомимся со схемой радиоприемника, а
на пятый — создаем операционный усилитель
из нескольких транзисторов. Внимание в циф-
ровой части курса концентрируется на исполь-
зовании микроконтроллеров, но здесь попутно
рассматривается мощный язык описания аппа-
ратных средств Verilog.
В-третьих, переход от простого материала к
более сложному происходит довольно бы-
стро, но при этом никаких предварительных
знаний электроники от читателя не требуется.
Благодаря успешному погружению в разработ-
ку схем студенты воспринимают материал на
интуитивном уровне.
♦ Каждое занятие содержит две части: теоре-
тический конспект и лабораторную работу,
а многие также включают примеры с реше-
ниями и дополнительные пояснения.
♦ В приложении А приведено введение в язык
Verilog.
♦ В отдельных приложениях предоставлена
общая информация по осциллографам, элек-
тронным компонентам компании Xilinx, ли-
ниям связи, цоколевке микросхем, програм-
мам и т. п., а также даны советы по выбору
деталей и оборудования.
♦ В книге очень мало математики, основное
внимание уделено интуитивному подходу и
практическим навыкам.
♦ В последней главе продемонстрировано не-
сколько проектов, созданных студентами,
которые изучали курс схемотехники в раз-
ные годы.
Томас С. Хейс (Thomas С. Hayes) пришел в
электронику извилистой дорогой, которая на-
чалась на юридическом факультете института
и, в конце концов, привела его к преподава-
нию электроники с практическим уклоном
в Гарвардском университете, чем он и зани-
мался в течение последних 35 лет. Кроме того,
он преподавал электронику на летних и допол-
нительных курсах в этом университете, а так-
же в течение 17 лет на кафедре физики Бостон-
ского университета. Томас Хейс является со-
автором патента на устройство для контроля
времени воздействия яркого света в лечебных
целях. Совместно со своими коллегами он хо-
чет запустить это устройство в производство
в стартапной компании Goodlux Technologies.
Том разрабатывает схемы по мере того, как
в них возникает надобность в его курсе по схе-
мотехнике. Среди его разработок универсаль-
ный дисплей, последовательный интерфейс
и программатор для микрокомпьютера, со-
зданного студентами.
Поль Хоровиц занимает должность профес-
сора по научно-исследовательским работам
в области физики на кафедре электротехники
в Гарвардском университете, где он в 1974 г. по-
ставил курс практической схемотехники, кото-
рый послужил основой для его книги «The Art
of Electronics» («Искусство схемотехники»).
Для Дебби (Debbie), Тессы (Tessa),
Тюрнера (Turner) иДжейми (Jamie).
В память моего любимого друга
Джонатана (Jonathan)
СОДЕРЖАНИЕ
Искусство схемотехники. Теория и практика 5
Введение.....................................................................................................
И книга, и учебный курс , 21
Что нового в данной книге? - 21
Кому подойдет эта книга 22
Основа: книга «The Art of Electronics» 23
Аналоговая и цифровая части: варианты подхода к изучению 23
Люди, которые помогли в работе над этой книгой « ■. 24
Юридическое уведомление 25
Замечание относительно первых занятий..........................................................26
Часть I. Аналоговая электроника: пассивные устройства ...............................29
1N Цепи постоянного тока .................................................................................31
1N.1. Краткая сводка 31
»|^V> . ■»«.«> WV^IIW
1 N.2. Три основных закона электротехники 34
1N.3. Первая практически важная схема: делитель напряжения 40
1 N.4. Нагрузка и «выходной импеданс» 43
1 N.5. Материал для чтения из АоЕ ~ 52
1L Лабораторное занятие: цепи постоянного тока 53
1L1. Закон Ома 53
1L2. Делитель напряжения 55
1L3. Использование закона Ома для преобразования гальванометра в вольтметр и амперметр 56
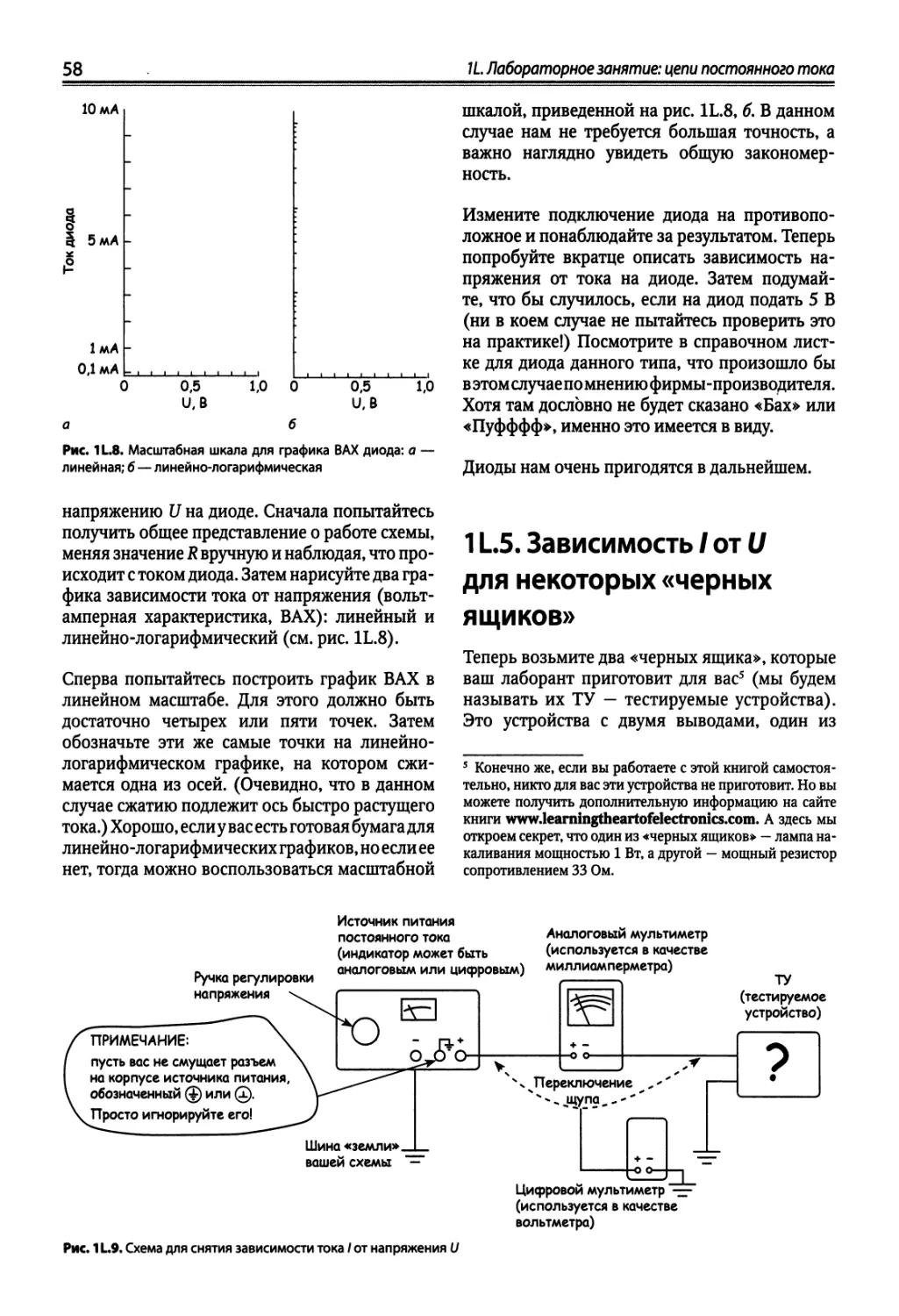
НАДиод ., 57
1 L.5. Зависимость / от U для некоторых «черных ящиков» 58
1 L.6. Осциллограф и генератор сигналов 60
1S Дополнительный материал: резисторы, напряжение, ток ...................64
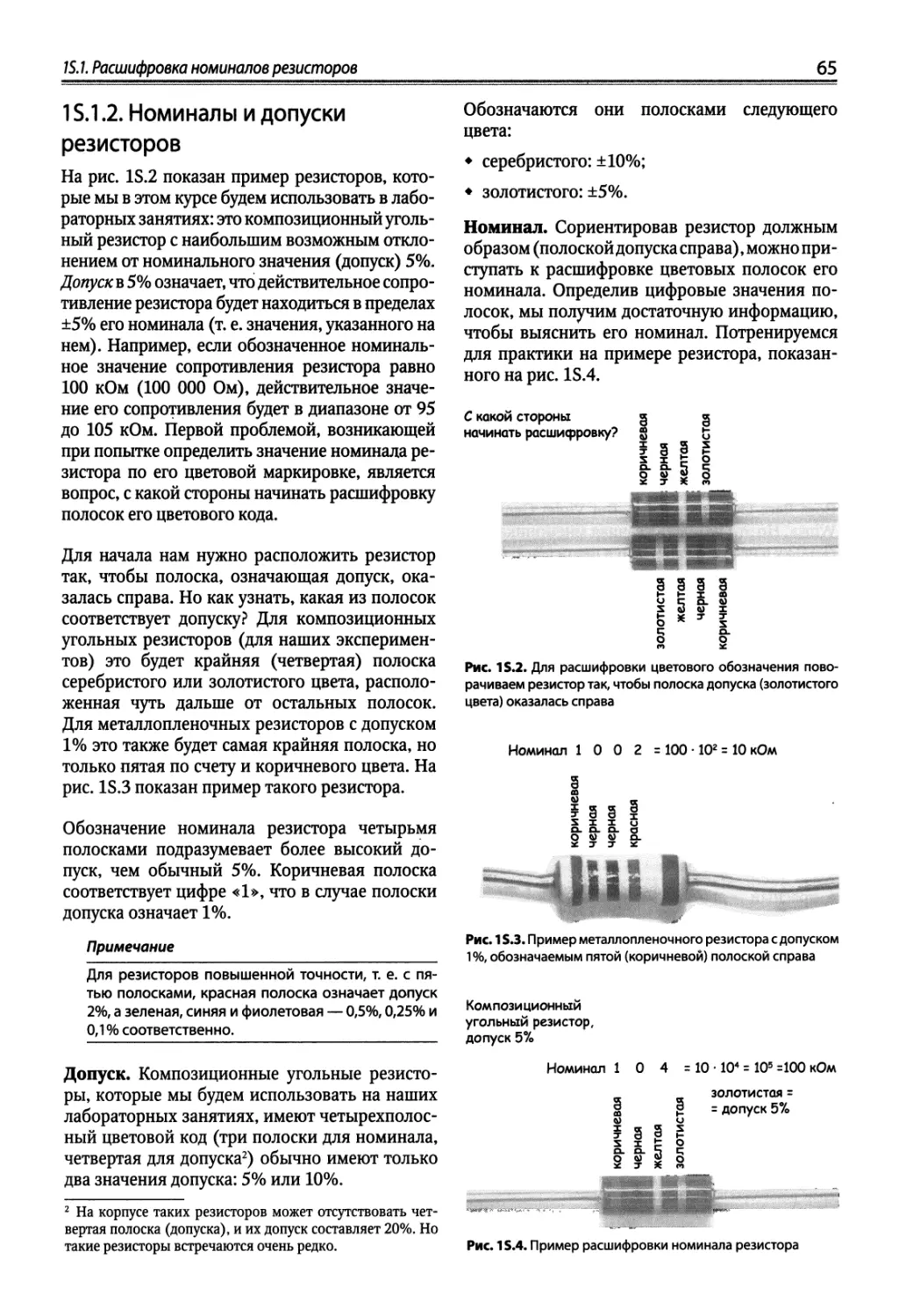
1 S.1. Расшифровка номиналов резисторов 64
1S.2. Напряжение и ток 67
1W Примеры с решениями: цепи постоянного тока 71
1 W.1. Разработайте схему вольтметра и амперметра 71
1W.2. Рассеивание мощности резисторами 73
1 W.3. Обходное решение проблемы неточности инструментов 74
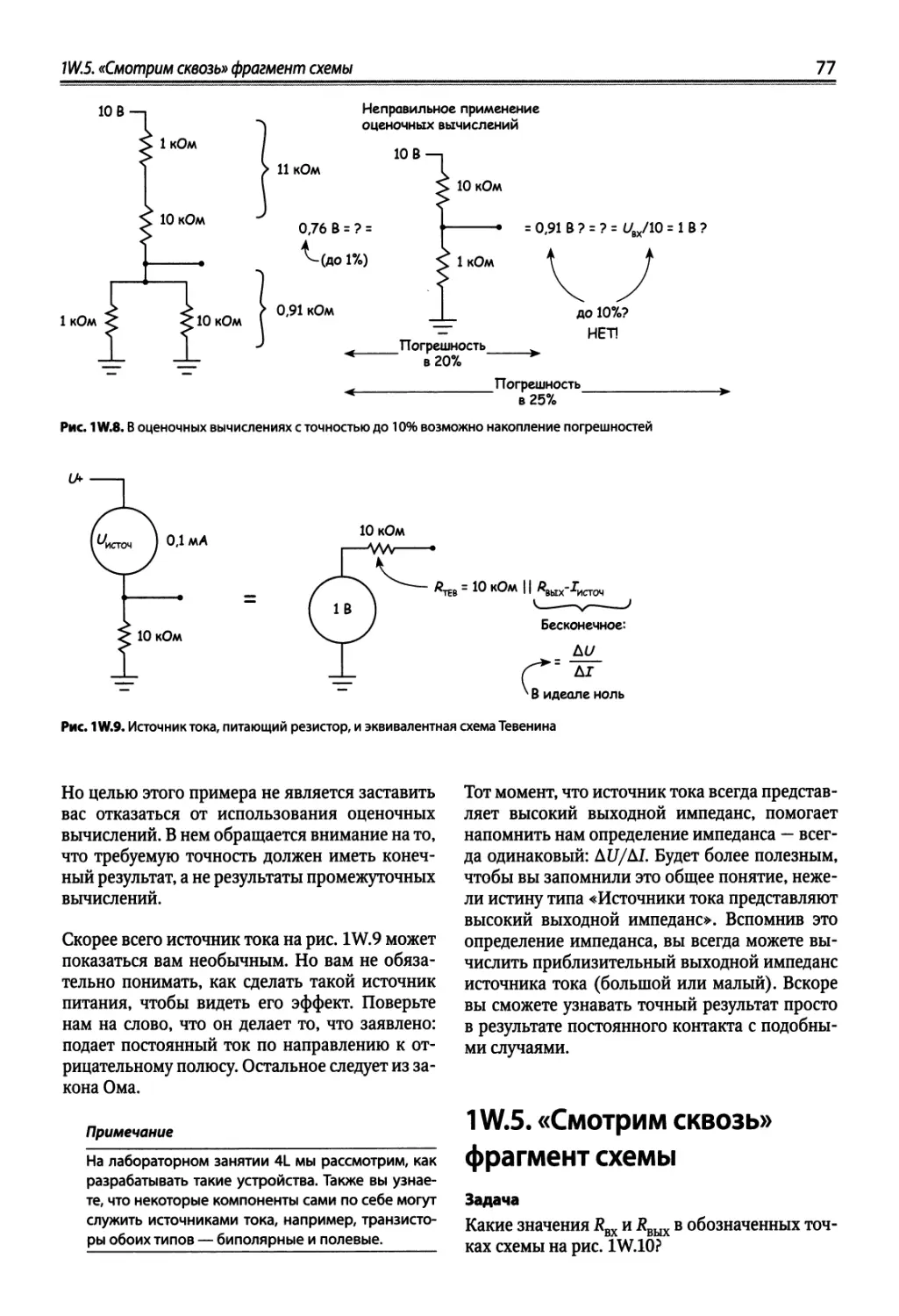
1 W.4. Эквивалентные схемы Тевенина 76
1 W.5. «Смотрим сквозь» фрагмент схемы м 77
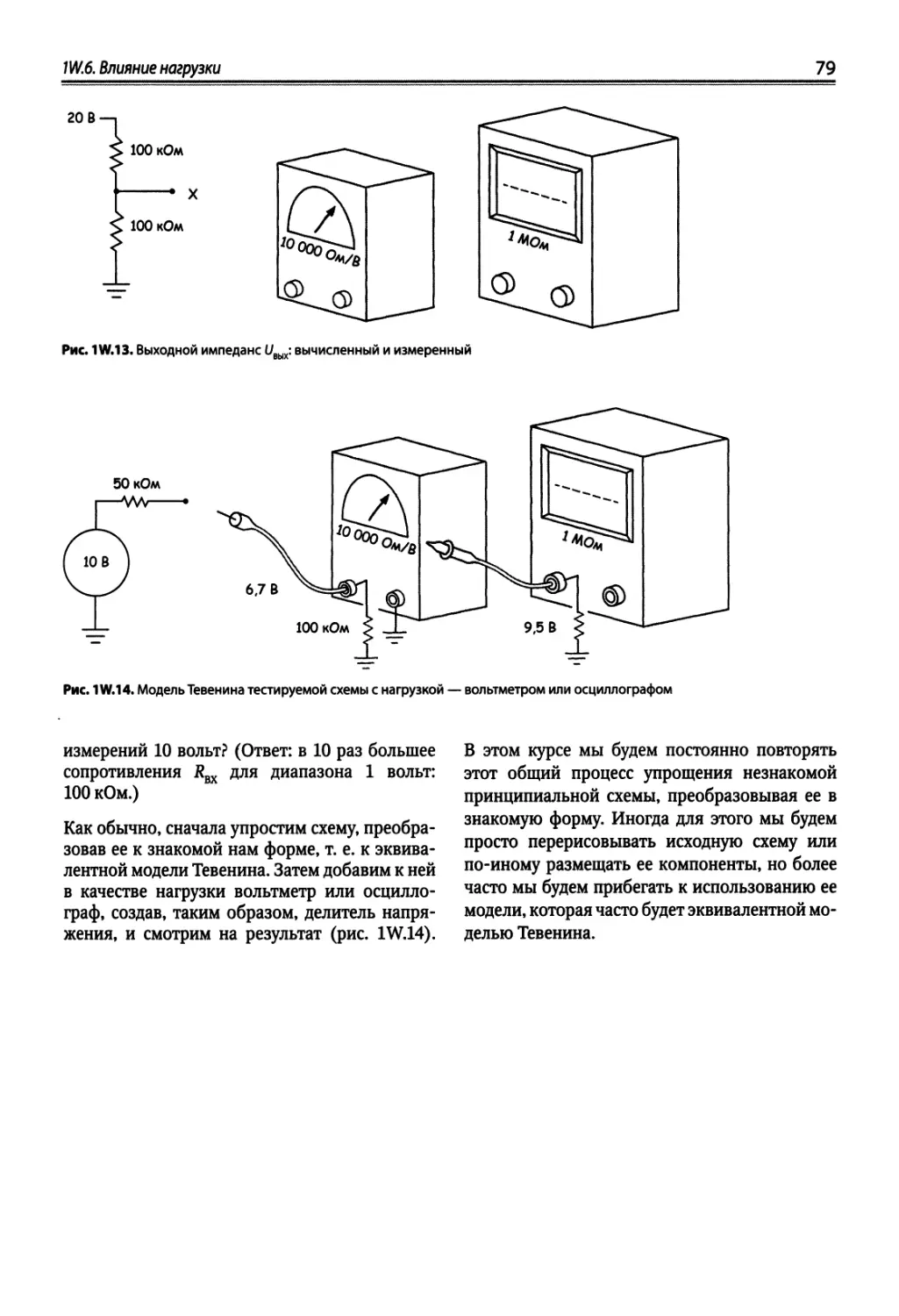
1W.6. Влияние нагрузки 78
2N
2N.1. Конденсаторы 80
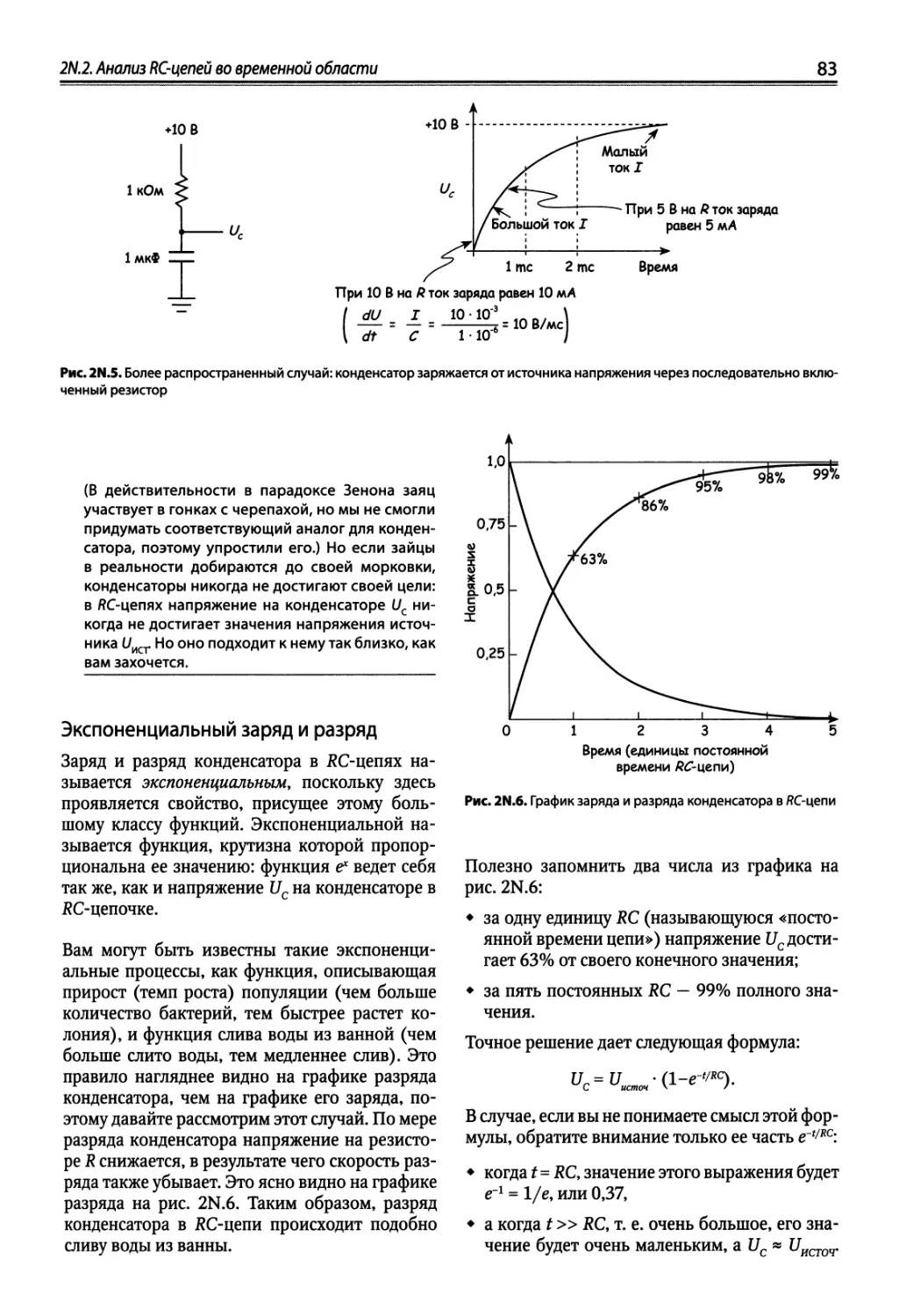
2N.2. Анализ /?С-цепей во временной области ~ 82
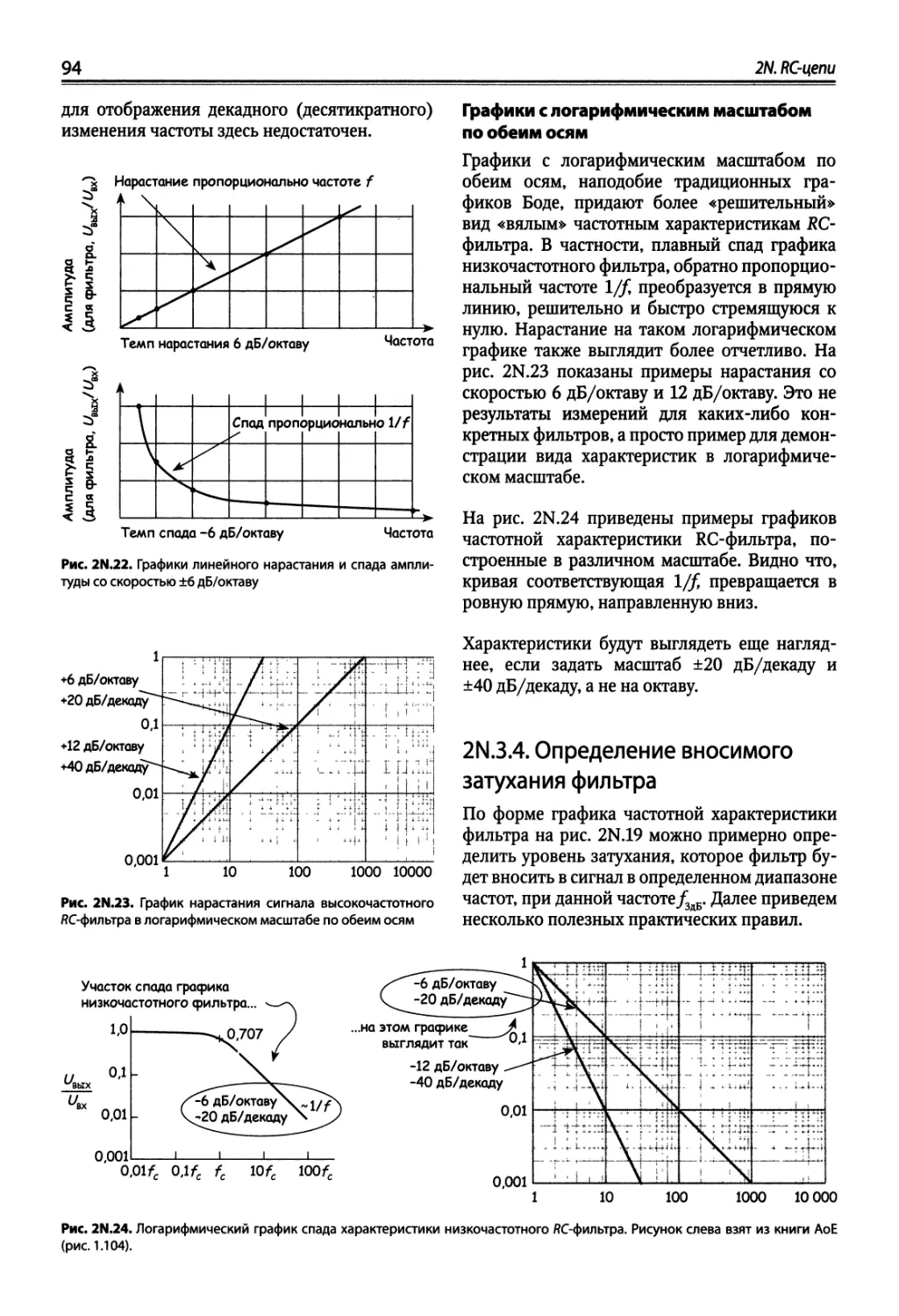
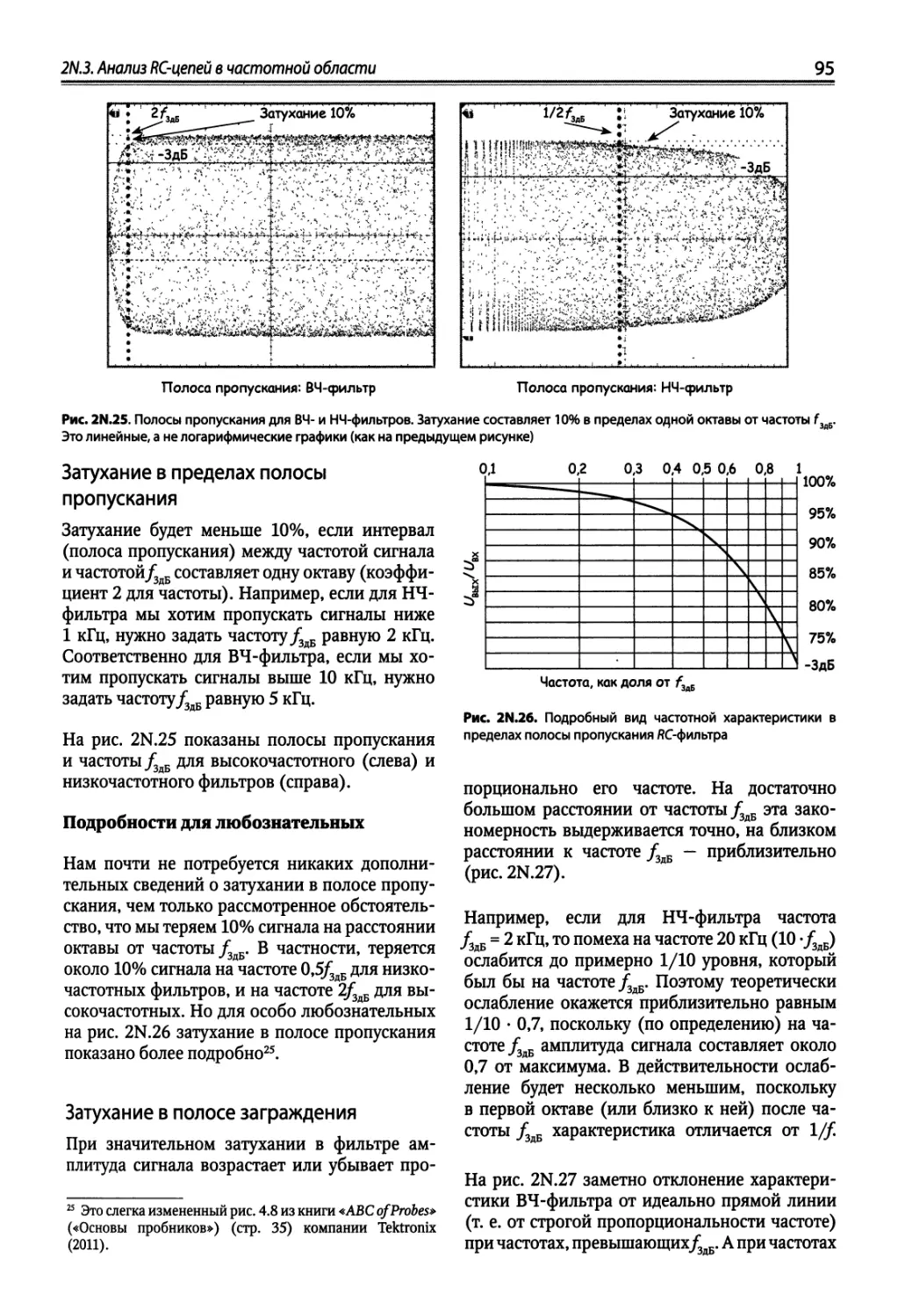
2N.3. Анализ г?С-цепей в частотной области 87
2N.4. Два простых, но важных варианта применения конденсатора: блокировка и развязка 102
2N.5. Математический взгляд на ЯС-фильтры , 105
2N.6. Материал для чтения в АоЕ 106
10 Содержание
2L Лабораторное занятие: конденсаторы...................................................107
2L1. Анализ во временной области 107
2L2. Анализ в частотной области 109
2S Дополнительный материал: ffC-цепи .••••....•..•....•.•••••..•••••...•.•....•..•...•••...Л 13
25.1. Определение номиналов конденсаторов 113
25.2. Заметки в помощь интуитивному пониманию поведения конденсаторов 118
25.3. Частотная развертка 121
2W Примеры с решениями: /?С-цепи ..............................................................128
2М1.ЯС-фильтры 128
2W.2. Переходная характеристика RC-цепи 132
С ДИОДвМИ ••••••••••••••••••••^•••••••••••••••••••••••••••••^••••••••••ф#«»»*§««««««««*0«*««#««««* 15Э
3N.1. Сильно нагруженный фильтр: еще одна причина, по которой следует придерживаться
правила 1:10 ......................... 135
3N.2. Щуп осциллографа 136
3N.3. Индуктивности .........139
3N.4. Резонансный LC-контур '. 140
3N.5. Схемы с диодами 145
3N.6. Самое важное применение диода: выпрямление переменного тока 146
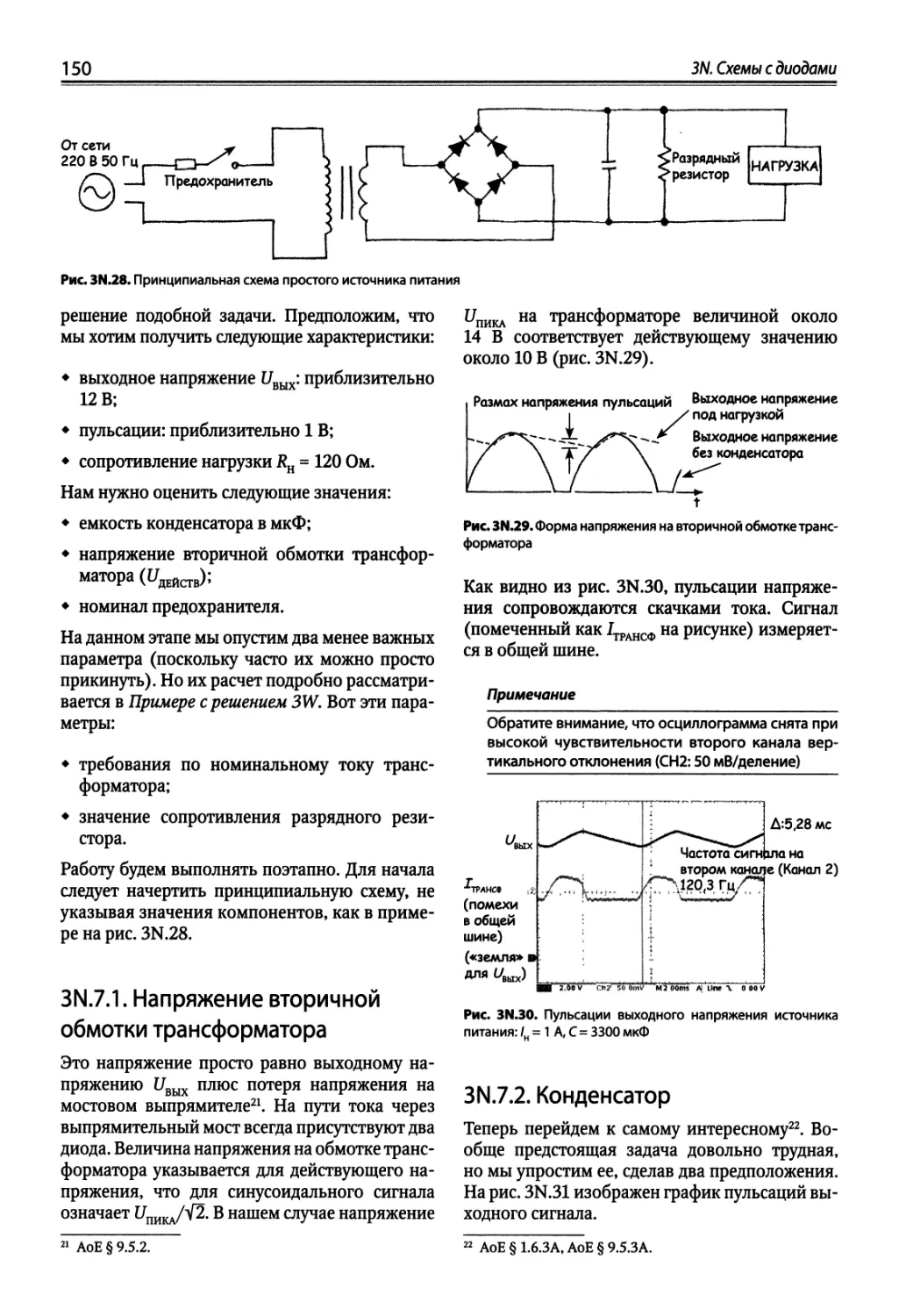
3N.7. Самое важное применение диода: источник питания (нестабилизированный) 149
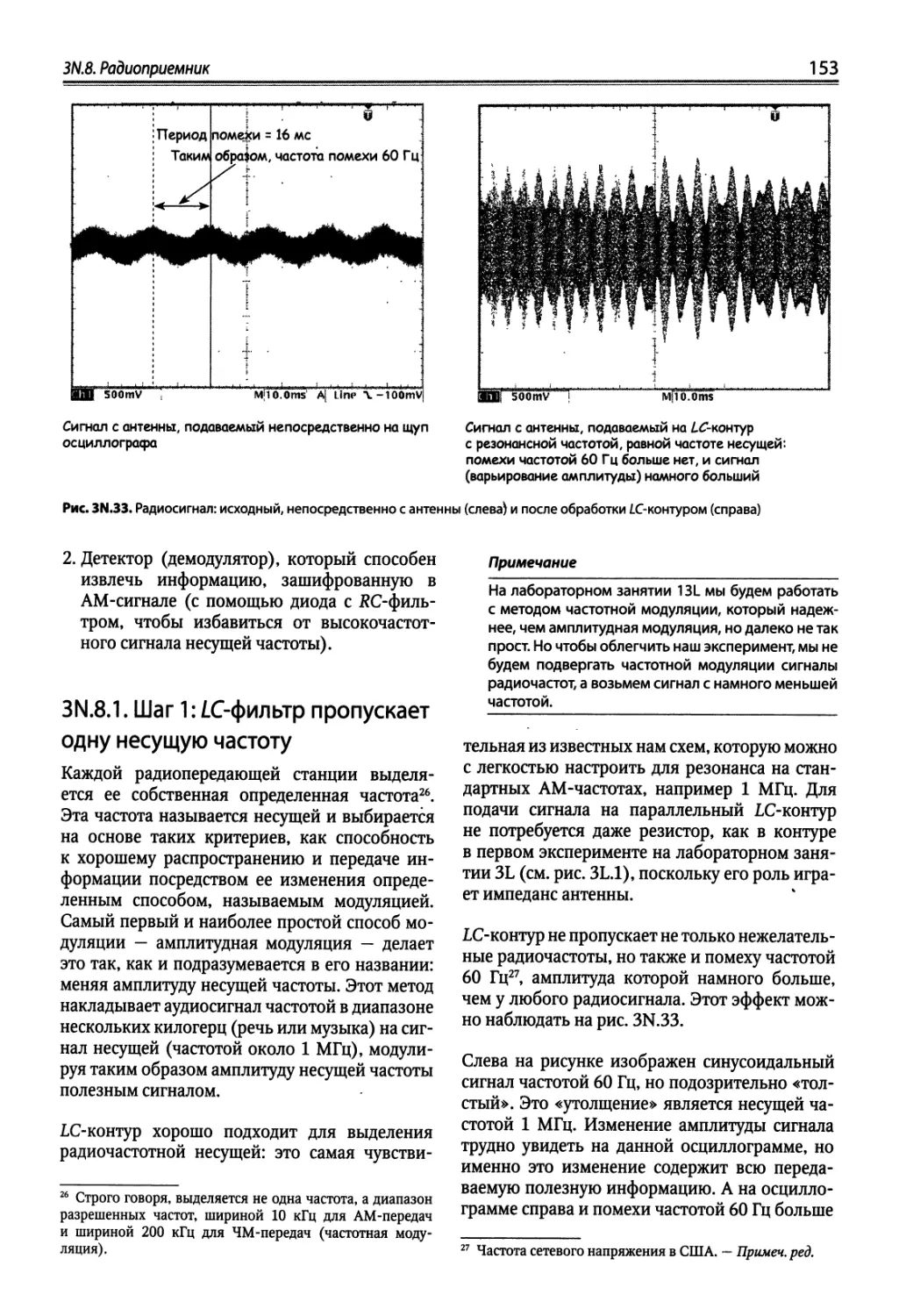
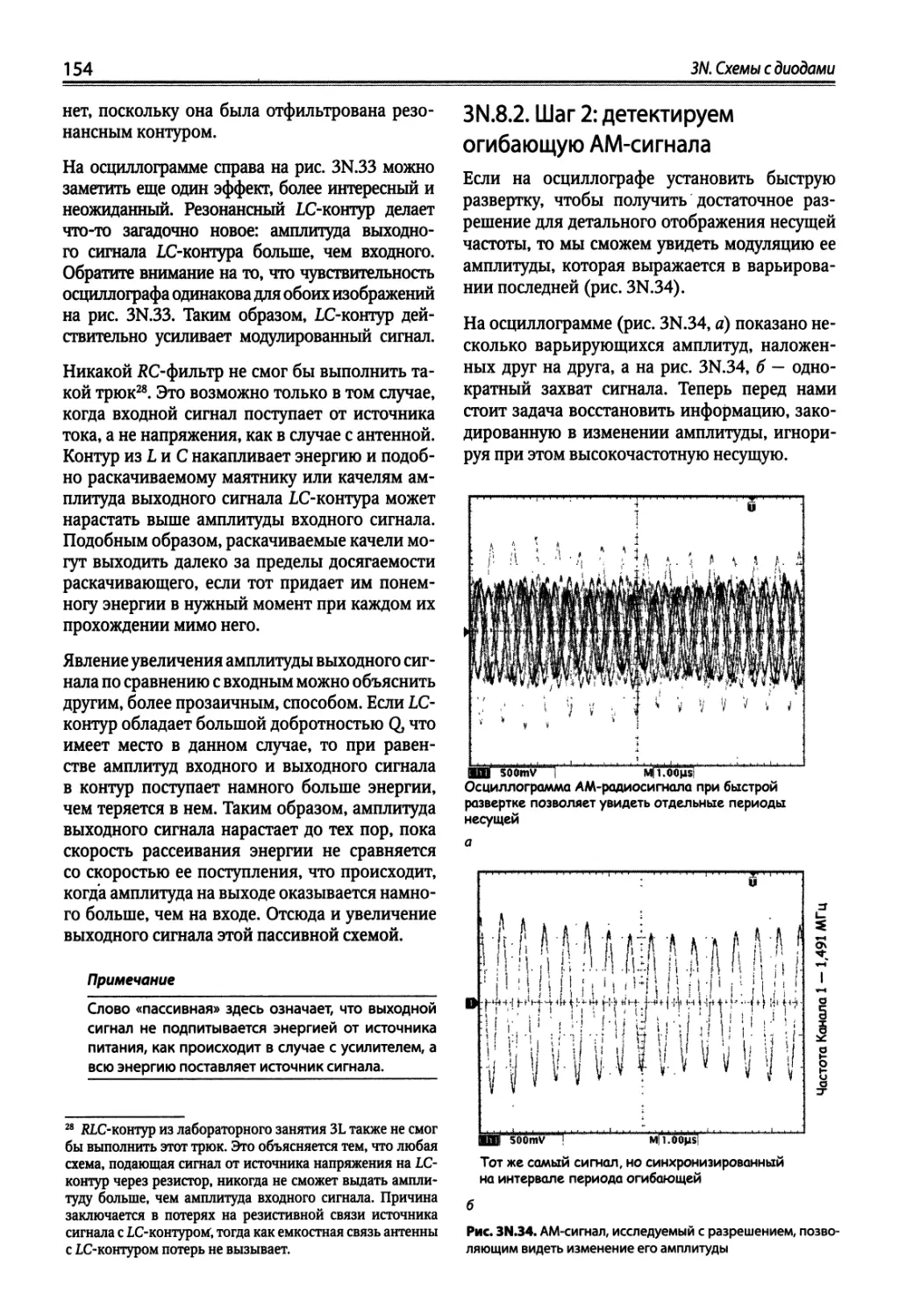
3N.8. Радиоприемник « * 152
3N.9. Материал для чтения в АоЕ 157
3L Лабораторное занятие; схемы с диодами ..............................................158
3L1. Резонансный LC-контур 158
3L2. Однополупериодный выпрямитель..... ..........160
3L3. Двухполупериодный мостовой выпрямитель 161
3L.4. Упражнение по разработке: АМ-радиоприемник 162
3L5. Сигнальные диоды ., 164
3S Дополнительный материал и глоссарий.................................................166
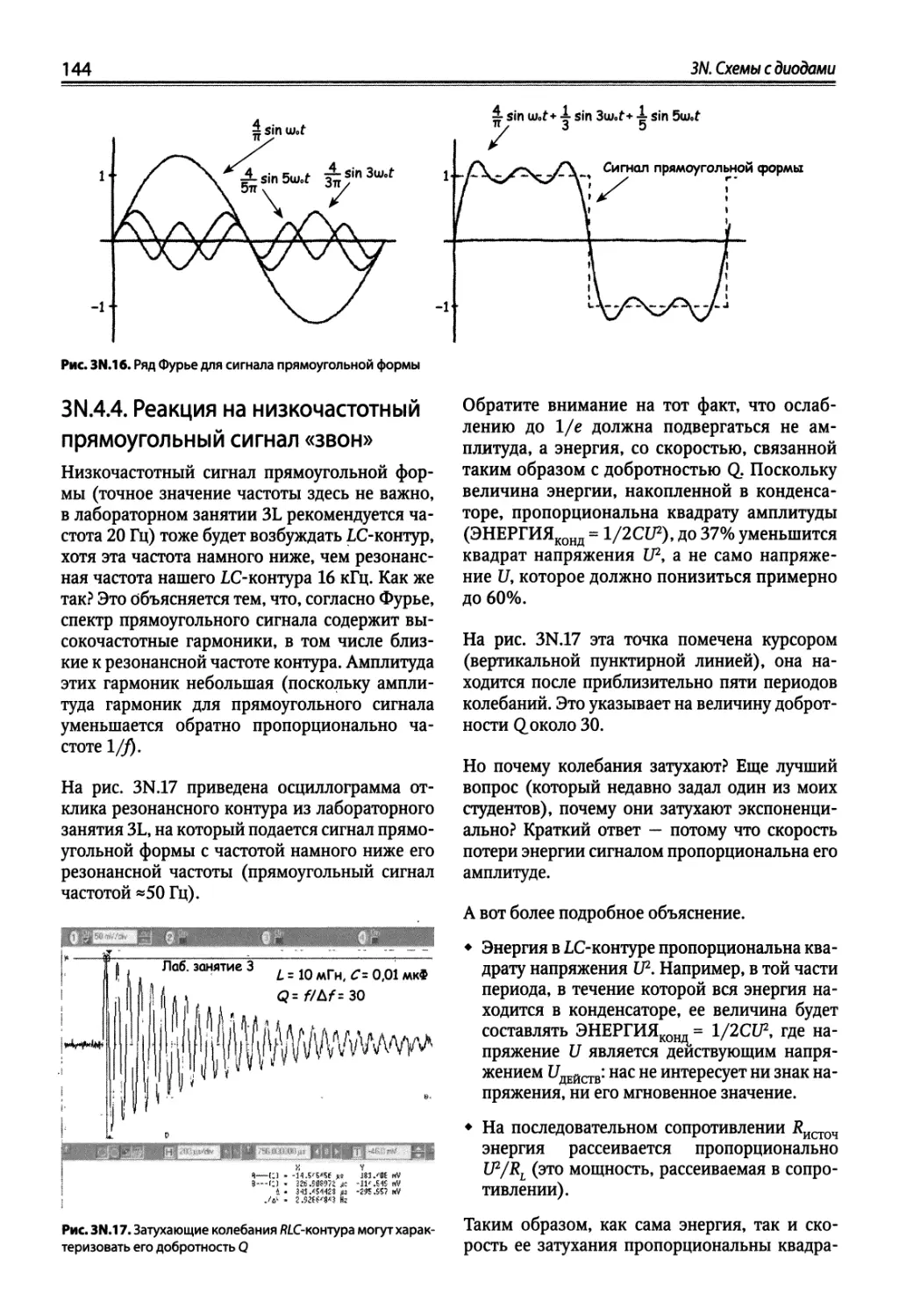
35.1. Почему звон LC-контура затухает, несмотря на теорию Фурье 166
35.2. Глоссарий для пассивных устройств 168
3W Примеры с решениями: схемы с диодами 169
3W.1. Разработка источника питания 169
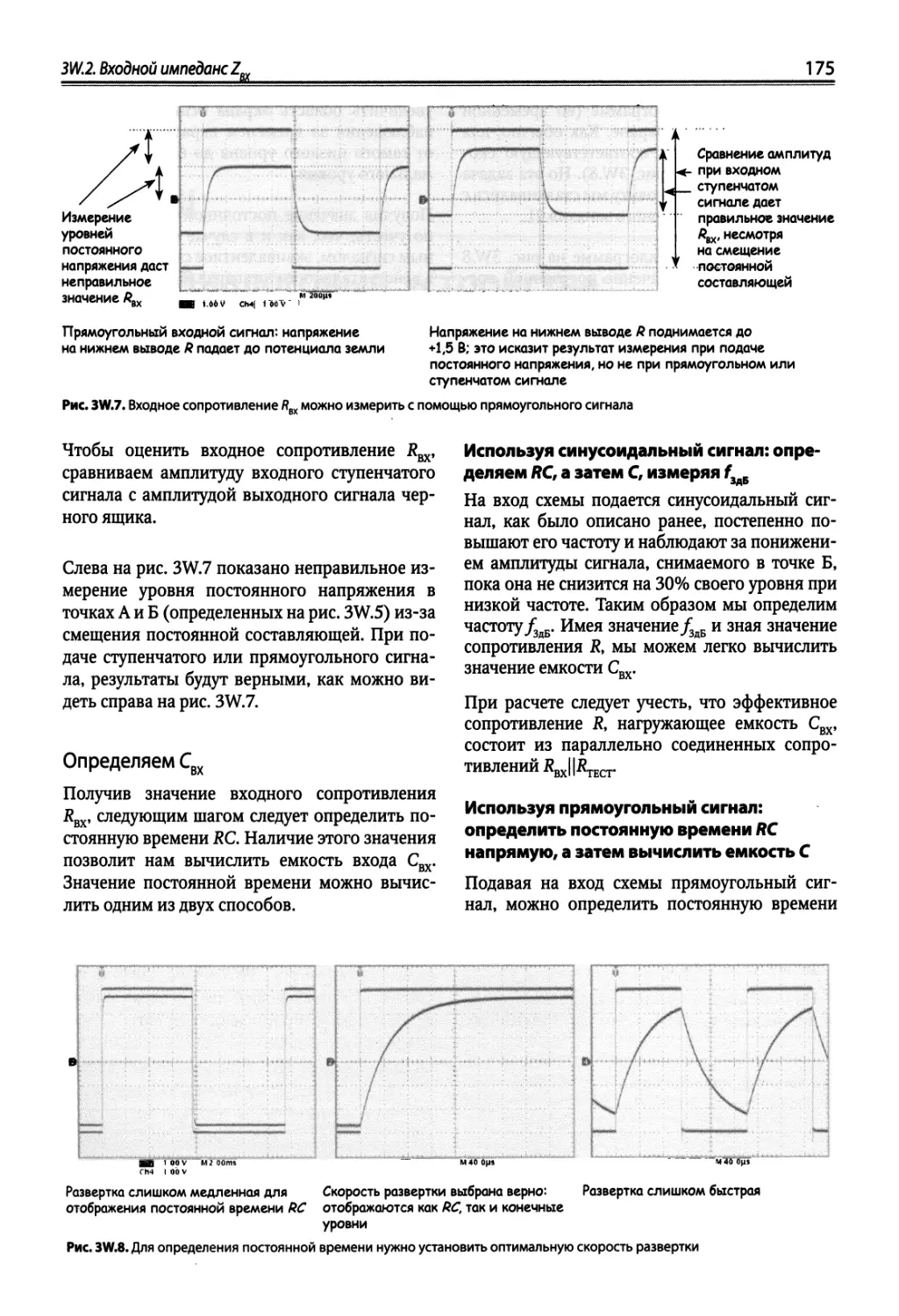
3W.2. Входной импеданс Z 173
Часть II. Аналоговые устройства: транзисторы ...•••••••..••...•••.••••.•••.....•••..•......•177
4N Транзисторы 1 179
4N.1. Краткий обзор рассматриваемого материала 179
4N.2. Предварительная информация 181
4N.3. Простое представление без (J 182
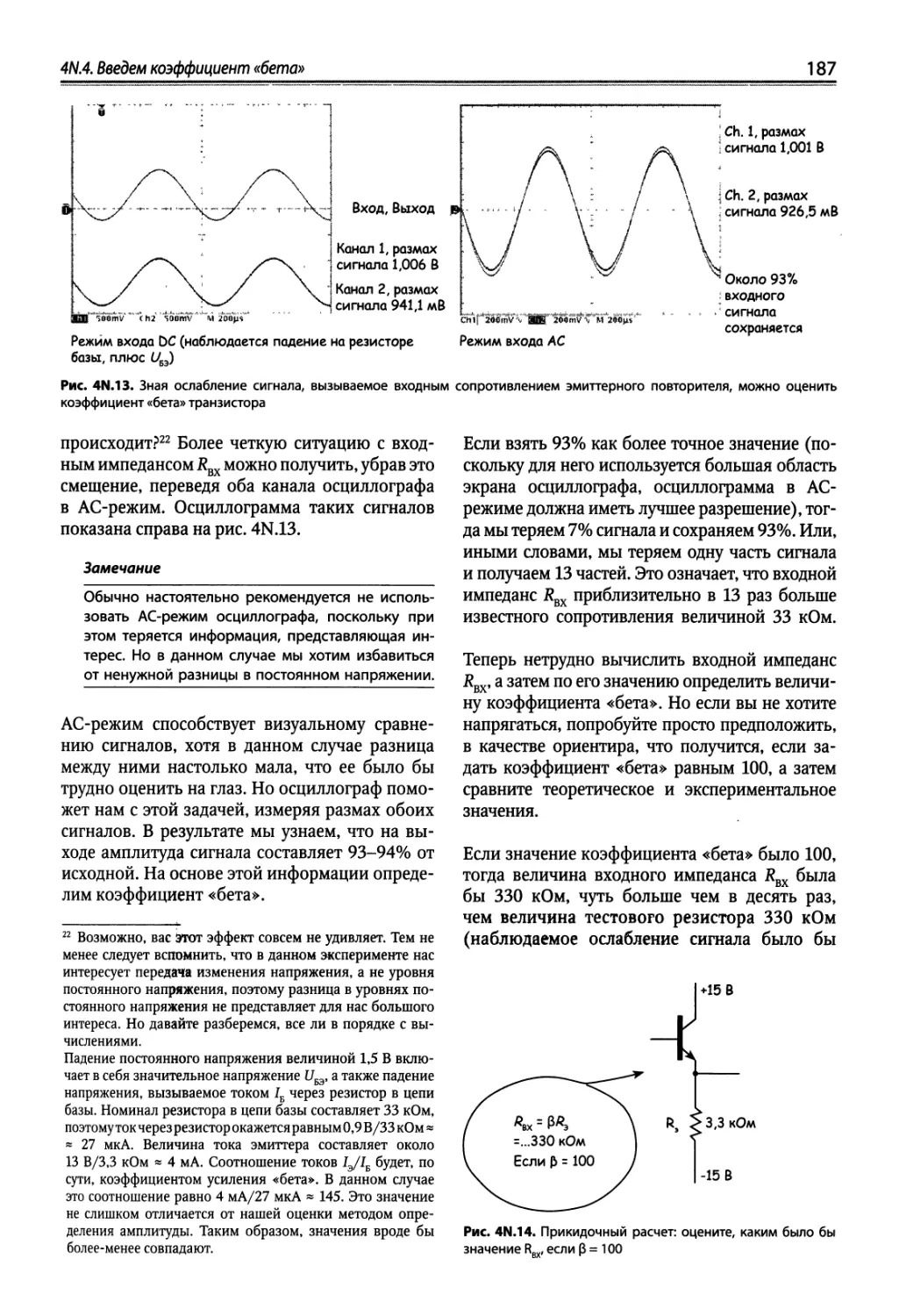
4N.4. Введем коэффициент «бета» 185
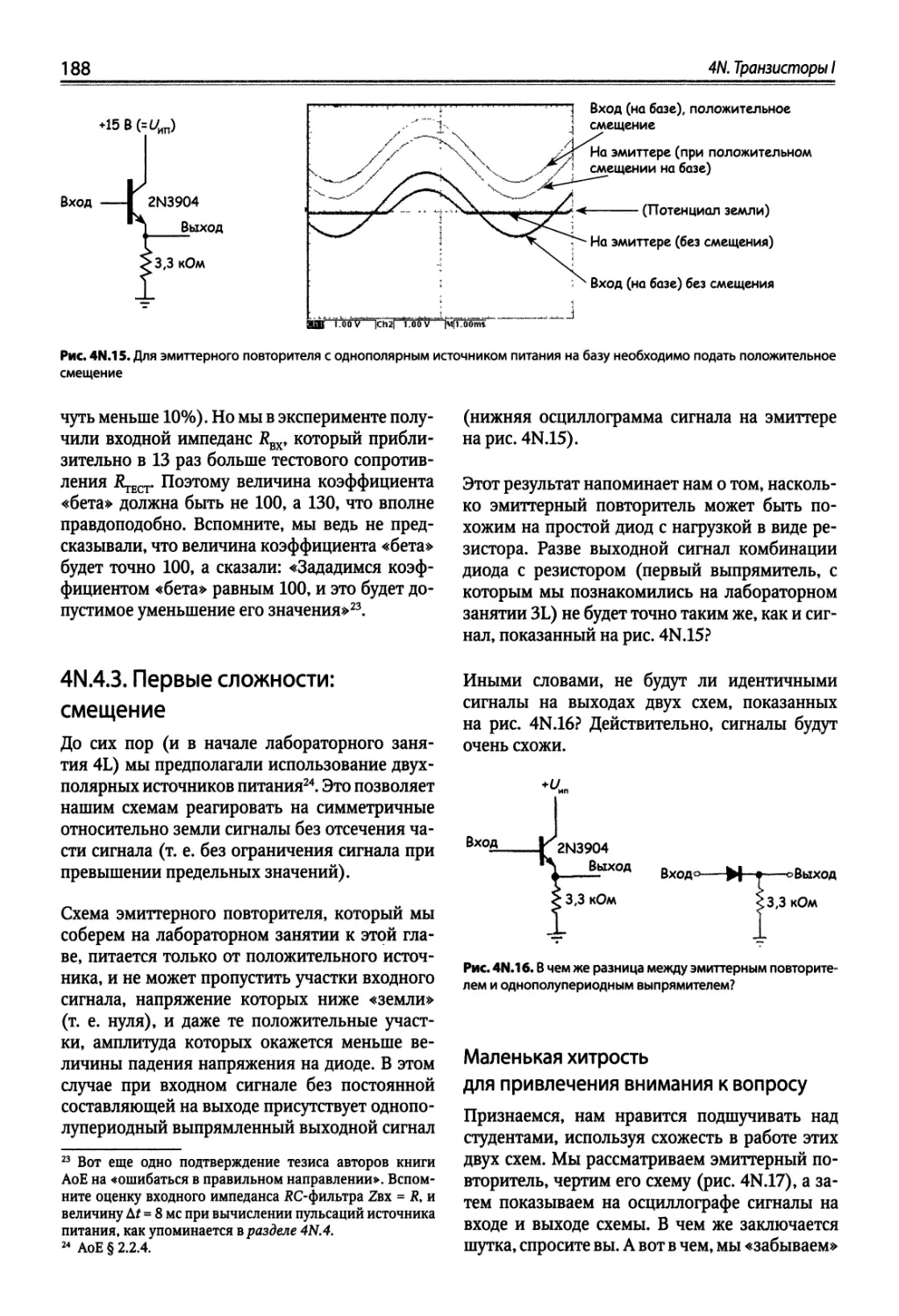
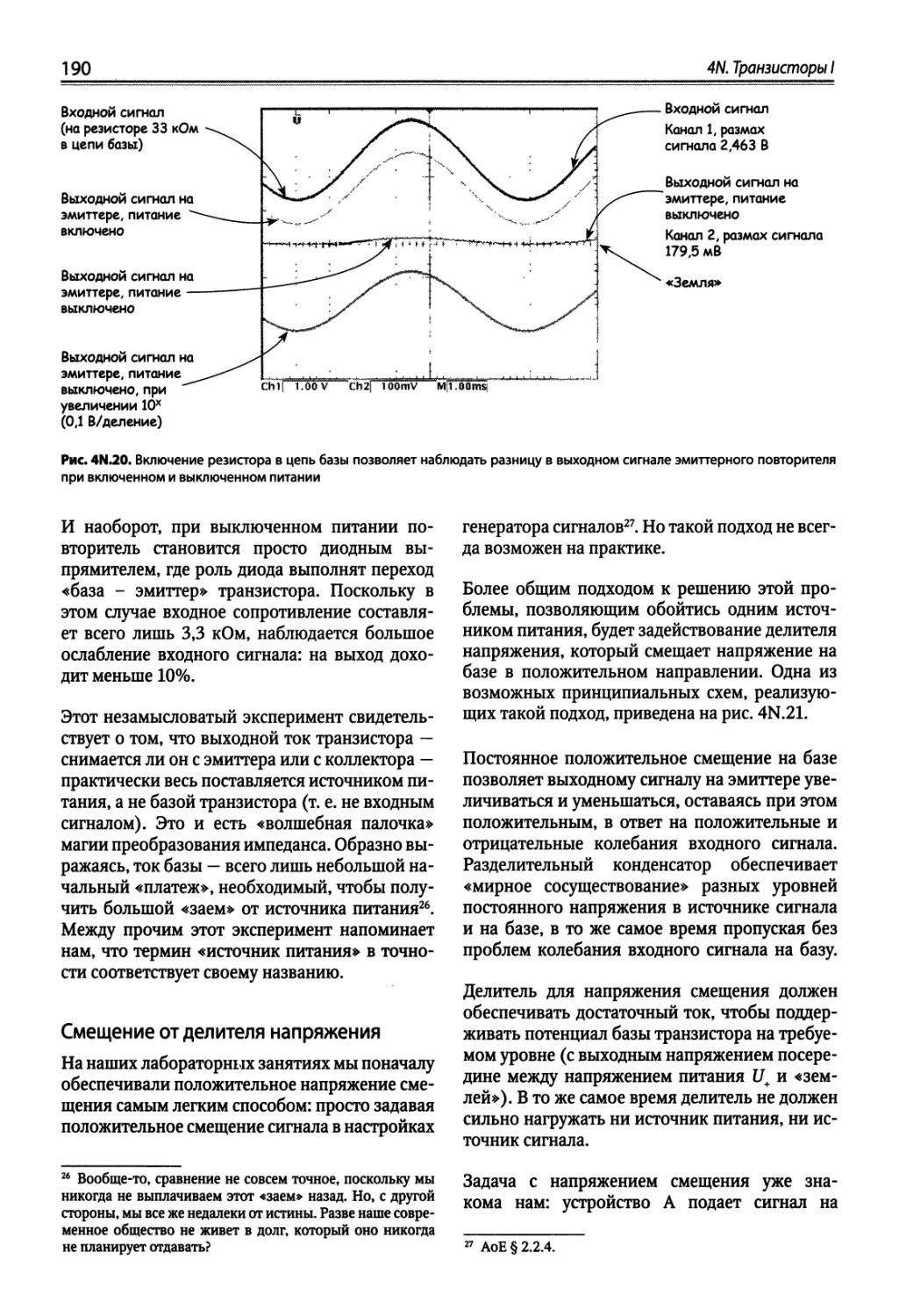
4N.5. Переключатель: транзисторная схема особого типа 194
4N.6. Краткий обзор основных транзисторных схем для закрепления пройденного материала 194
4N.7. Материал для чтения в АоЕ 195
4L Лабораторное занятие: транзисторы .....•••.......•..••.....•••.••••.•..•.•••••....••..•Л 96
4L1. Предварительное знакомство с транзисторами м 196
4L.2. Эмиттеоный повторитель 197
4L.3. Источник тока 199
Содержание 11
4L4. Усилитель с общим эмиттером „ 200
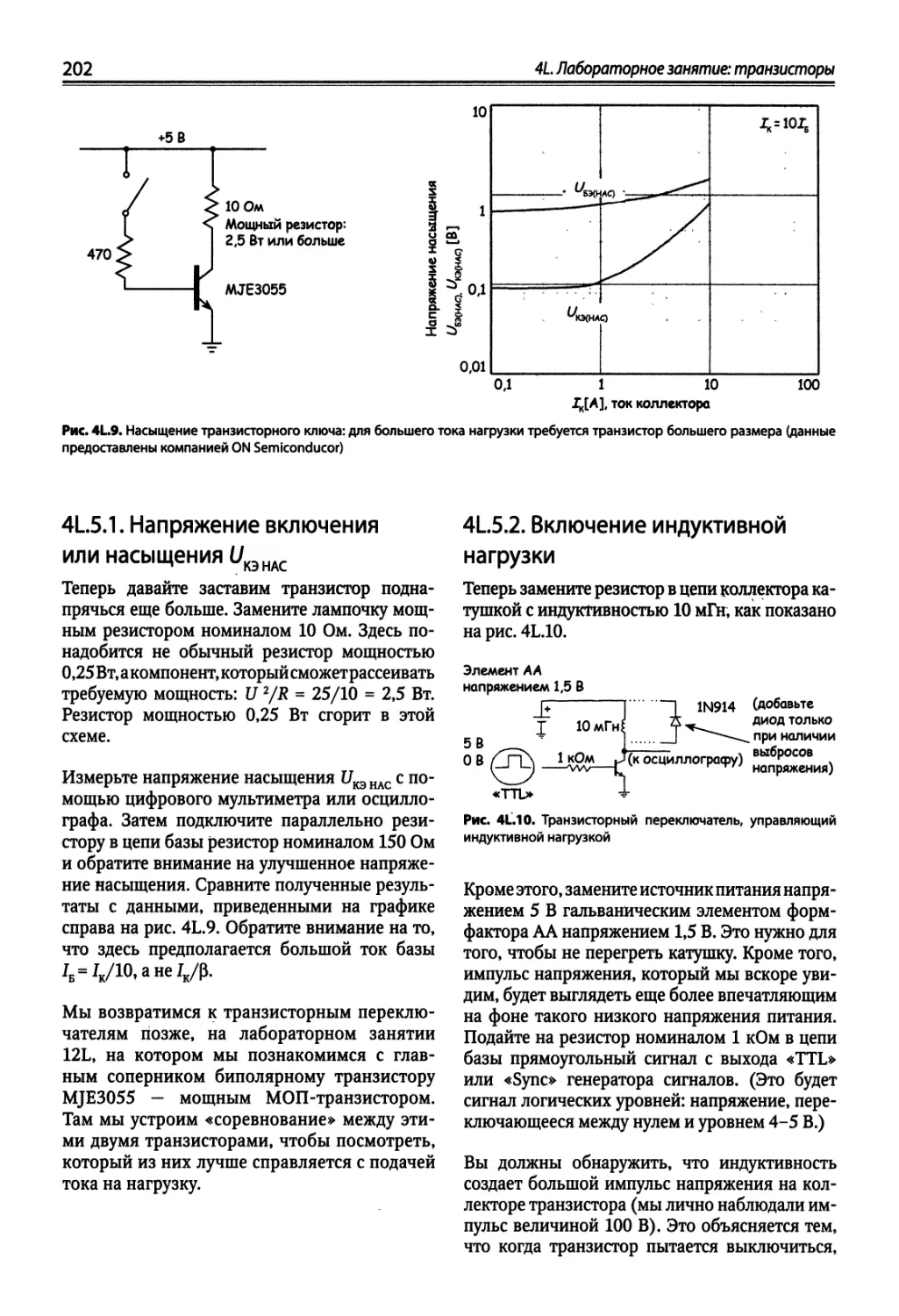
4L5. Транзисторный переключатель 201
4L6. Проблема помех источников питания 203
4W Примеры с решениями: транзисторы I ...................................................205
4\Л/.1.Эмиттерный повторитель *..... 205
4W.2. Фазорасщепитель: входной и выходной импедансы транзисторной схемы 208
4W.3. Транзисторный переключатель 213
5N Транзисторы II •••••••••••••••••••••••••••••••••••••••«••••••••••••••••••••••••••••••••••••••••••••••••••••••215
5N.1. Новое не отменяет старого 215
5N.2. Вкратце снова о фазорасщепителе 216
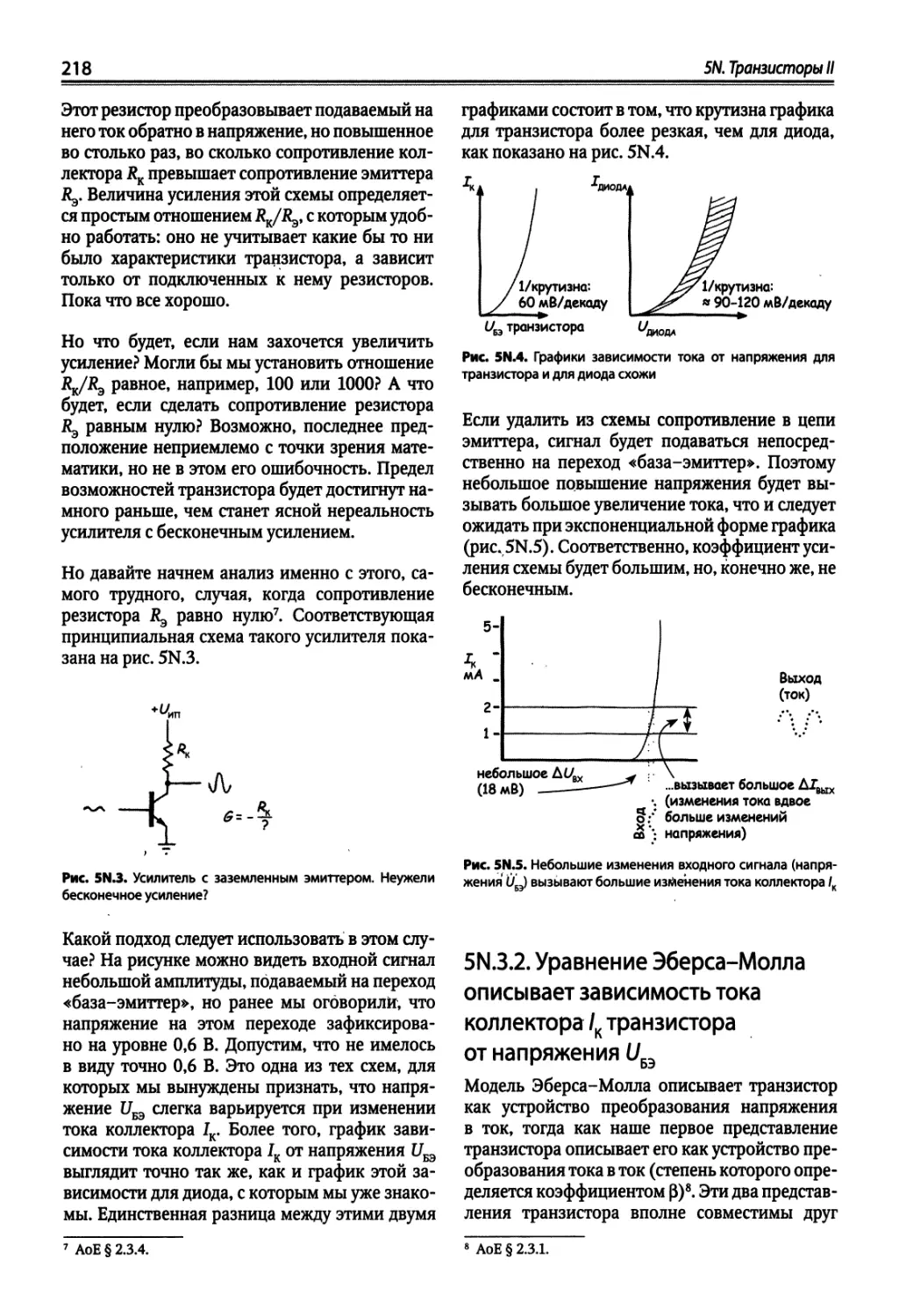
5N.3. Модель Эберса-Молла транзистора ; 217
5N А Искажения в усилителе с высоким коэффициентом усиления 221
5N.5. Искажения, вызываемые температурной неустойчивостью 222
5N.6. Согласование модели Эберса-Молла с моделью /к = Р • /Б 227
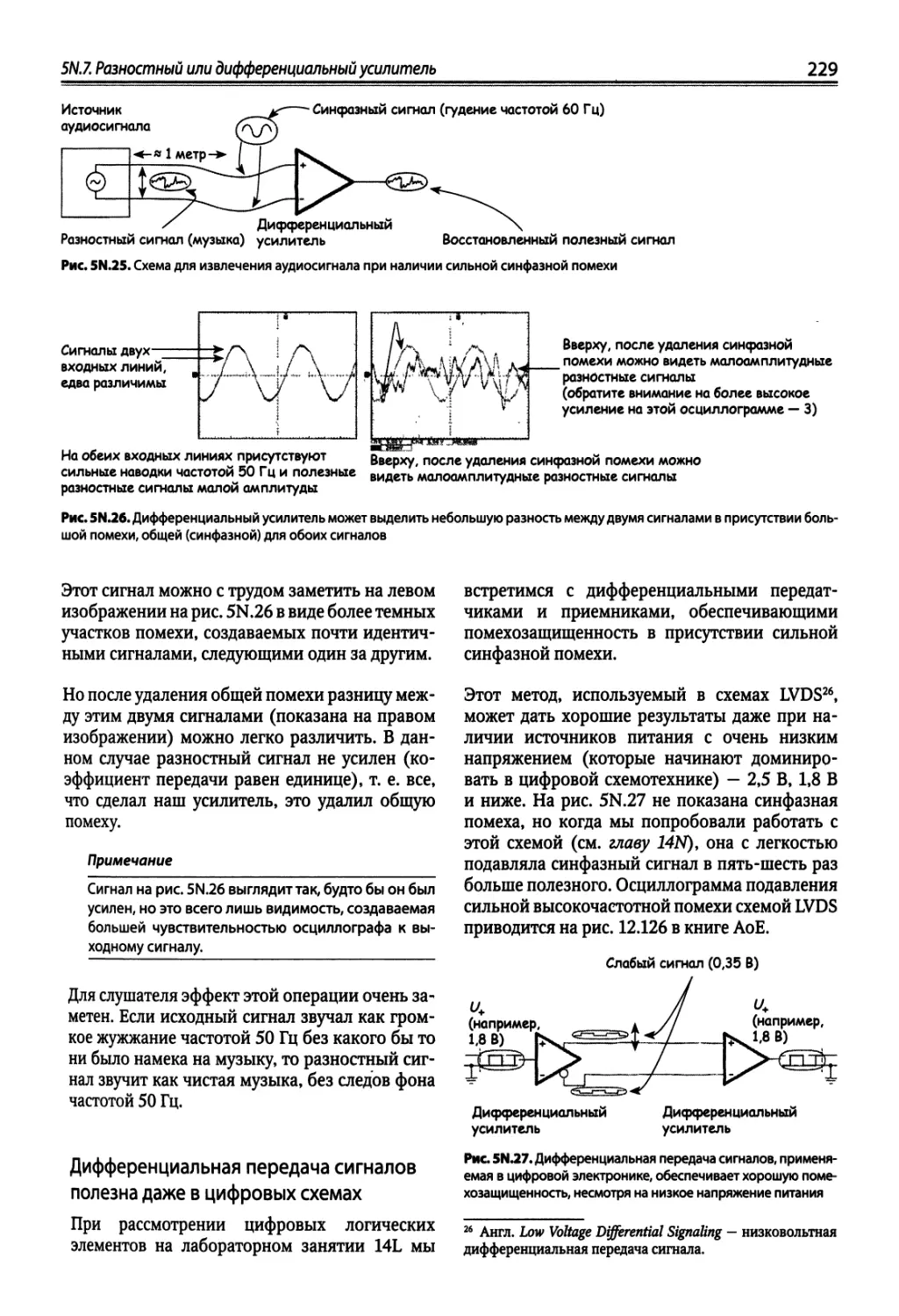
5N.7. Разностный или дифференциальный усилитель 227
5 N.8. Послесловие м 232
5N.9. Материал для чтения в АоЕ 233
5L Лабораторное занятие: транзисторы II ...................................................234
5L.1. Разностный или дифференциальный усилитель „ 234
5S Дополнительный материал и глоссарий: Транзисторы II 244
55.1. Два новых эффекта в поведении дифференциального усилителя 244
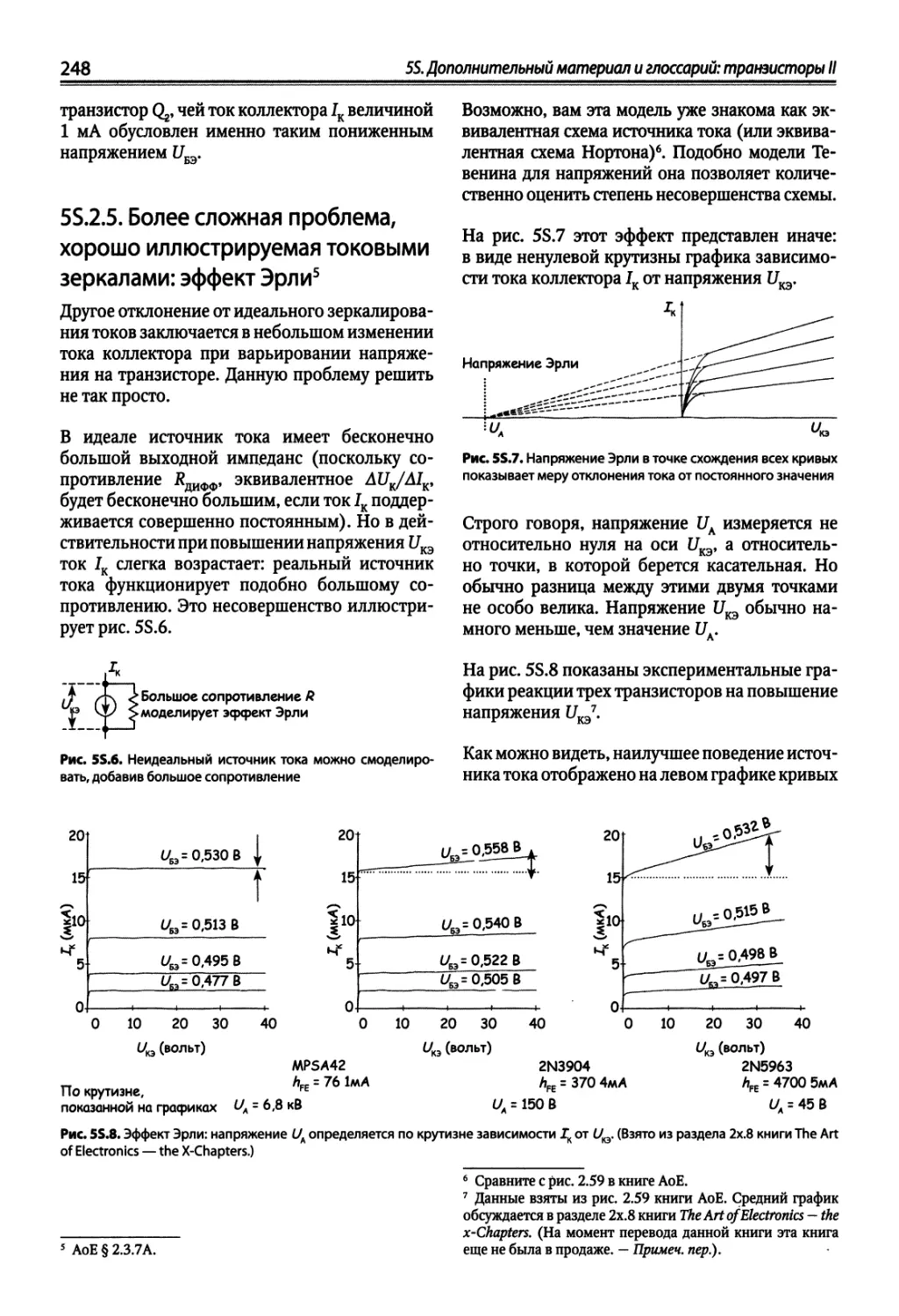
55.2. Токовые зеркала и эффект Эрли 246
55.3. Резюме по транзисторам 254
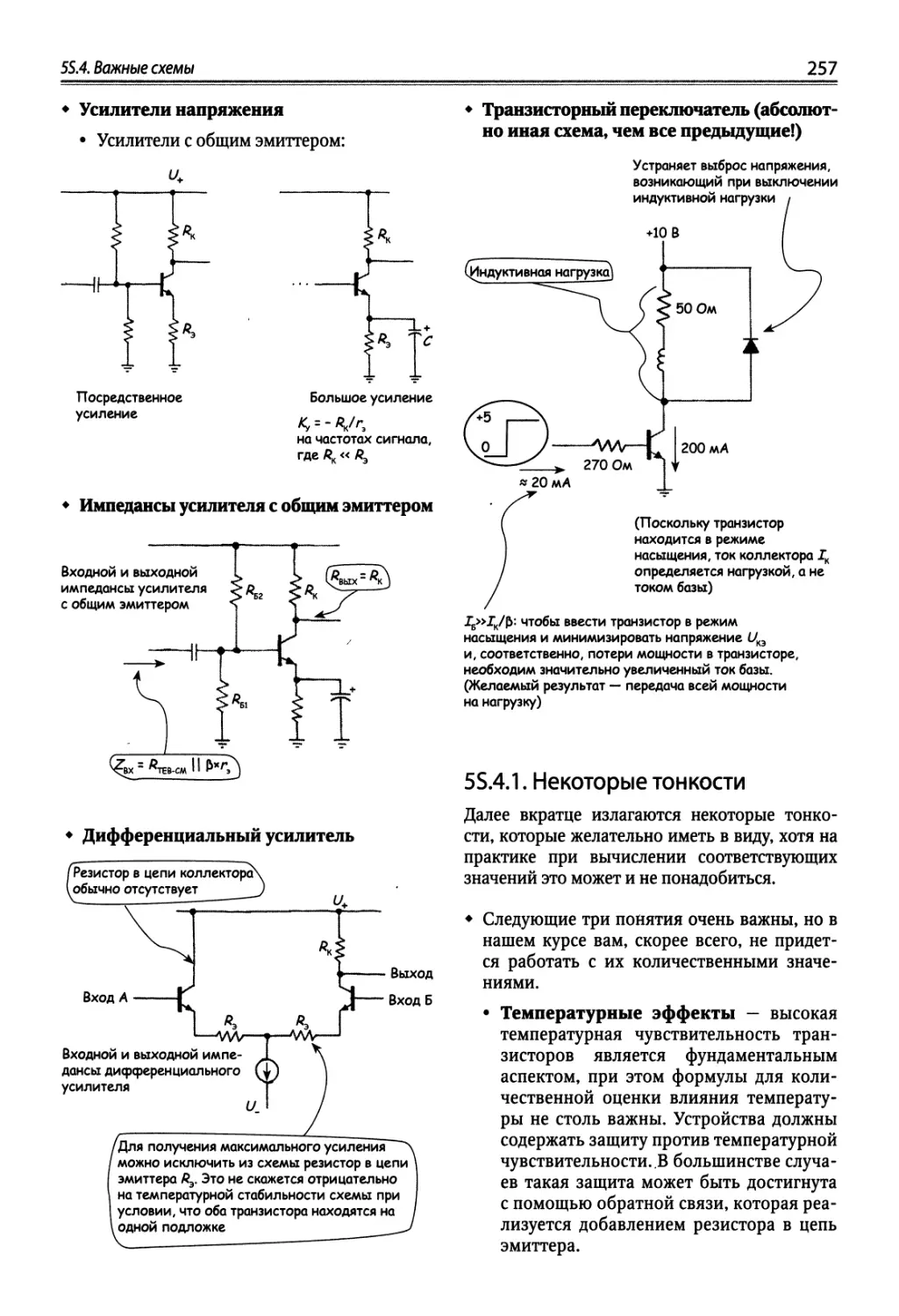
55.4. Важные схемы 256
55.5. Глоссарий по биполярным транзисторам 258
5W Примеры с решениями: транзисторы II 260
5W.1. Усилители с высоким коэффициентом усиления 260
5W.2. Дифференциальный усилитель „ 261
5W.3. Дифференциальный усилитель в микросхеме операционного усилителя 262
Часть III. Аналоговые устройства. Операционные усилители
и их применение 267
6N Операционные усилители 1 269
6N.1. Общие сведения об обратной связи 269
6N.2. Сущность отрицательной обратной связи 272
6N.3. Обратная связь в электронике « 273
6N.4. «Золотые правила» для работы с операционными усилителями 275
6N.5. Применение операционного усилителя 276
6N.6. Усилители двух типов 277
6N.7. Инвертирующий усилитель 278
6N.8. Когда применимы «золотые правила»? 280
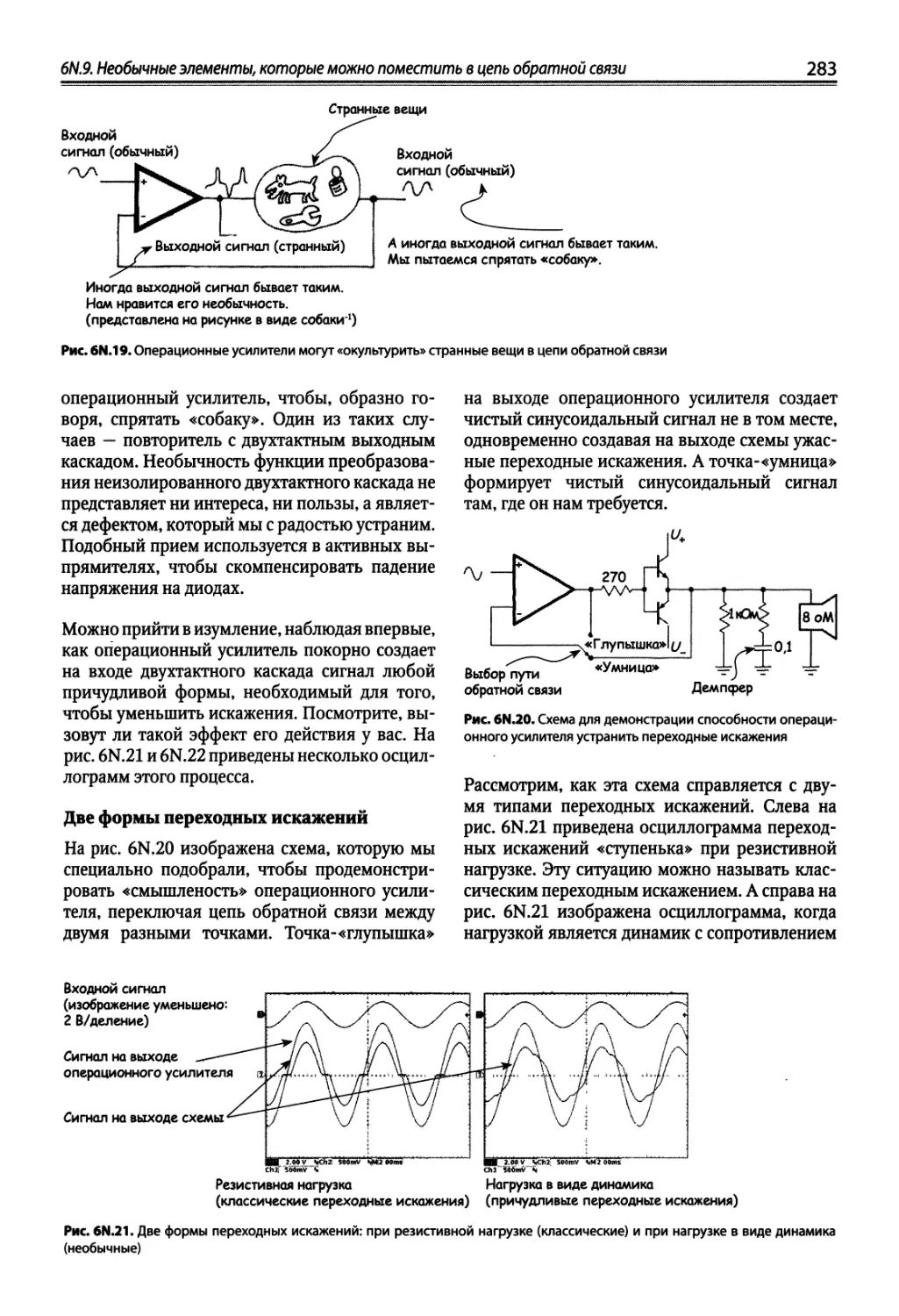
6N.9. Необычные элементы, которые можно поместить в цепь обратной связи 282
6N.10. Материал для чтения в АоЕ 285
6L Лабораторное занятие: операционные усилители 1 286
6L1. Предварительные сведения , 286
6L.2. Экспериментальная схема с операционным усилителем без обратной связи 287
12 Содержание
6L3. Вводим обратную связь, получаем повторитель 287
6L.4. Выходной импеданс ~ , 287
6L5. Инвертирующий усилитель м 289
6L6. Суммирующий усилитель 289
6L7. Разработка фазовращателя с единичным усилением , 290
6L8. Двухтактный 6v6eo м *......« 292
П / *" »...■».»■ •— J ^-mmf^ ................................................................................. .... .... ............................................................._«- _
6L9. Преобразователь «ток —напряжение» » 293
6L.10. Источник тока 294
6W Примеры с решениями: операционные усилители I............................296
6W.1. Простой разностный усилитель на операционном усилителе 296
6W.2. Более интересный разностный усилитель — микросхема IN A149 с широким диапазоном
входных напряжений синфазного сигнала 299
6W.3. Необычная суммирующая схема..- » 300
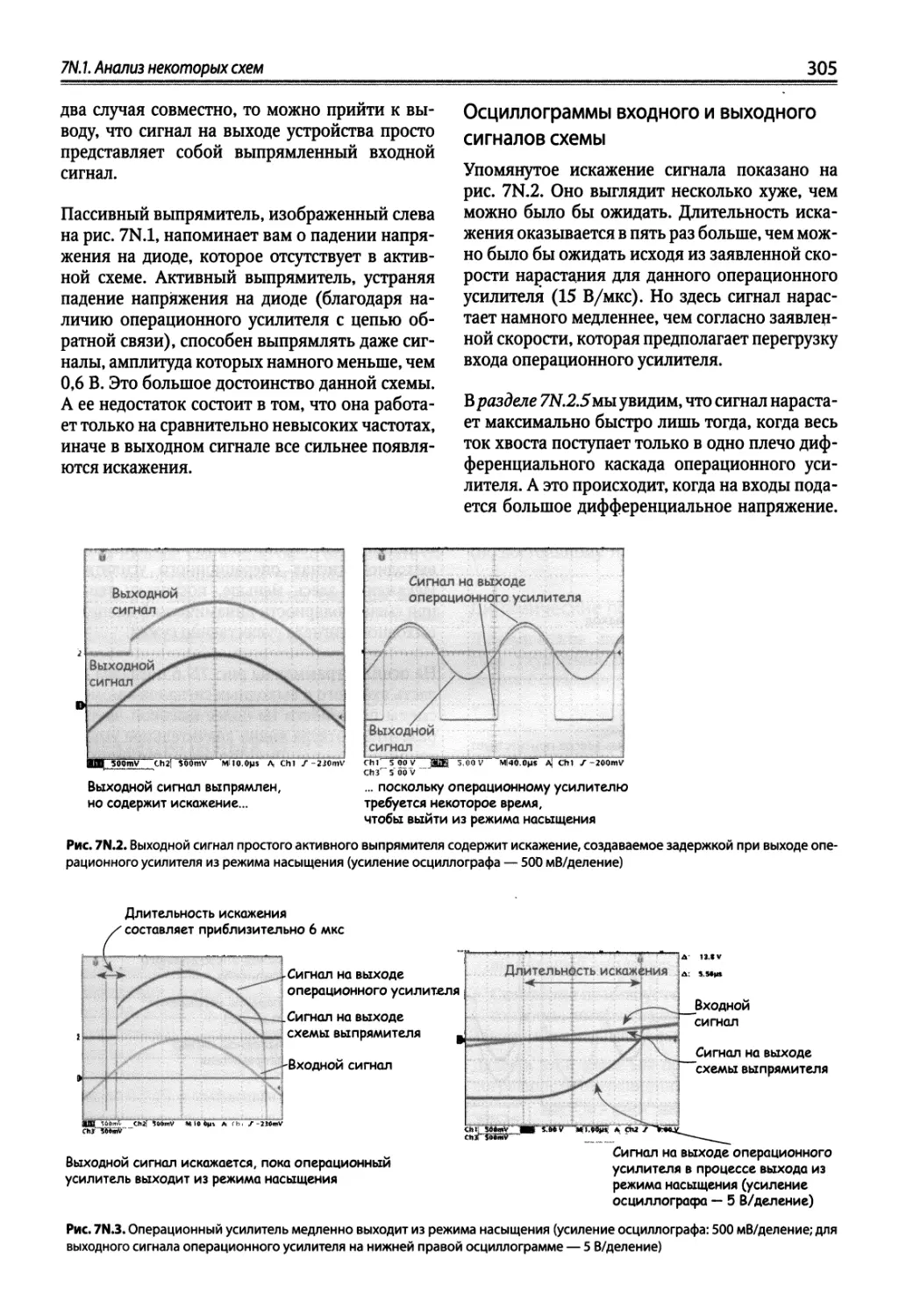
7N Операционные усилители II: отклонения от идеальности ..................303
Основные моменты ранее рассмотренного материала 304
7N.1. Анализ некоторых схем м 304
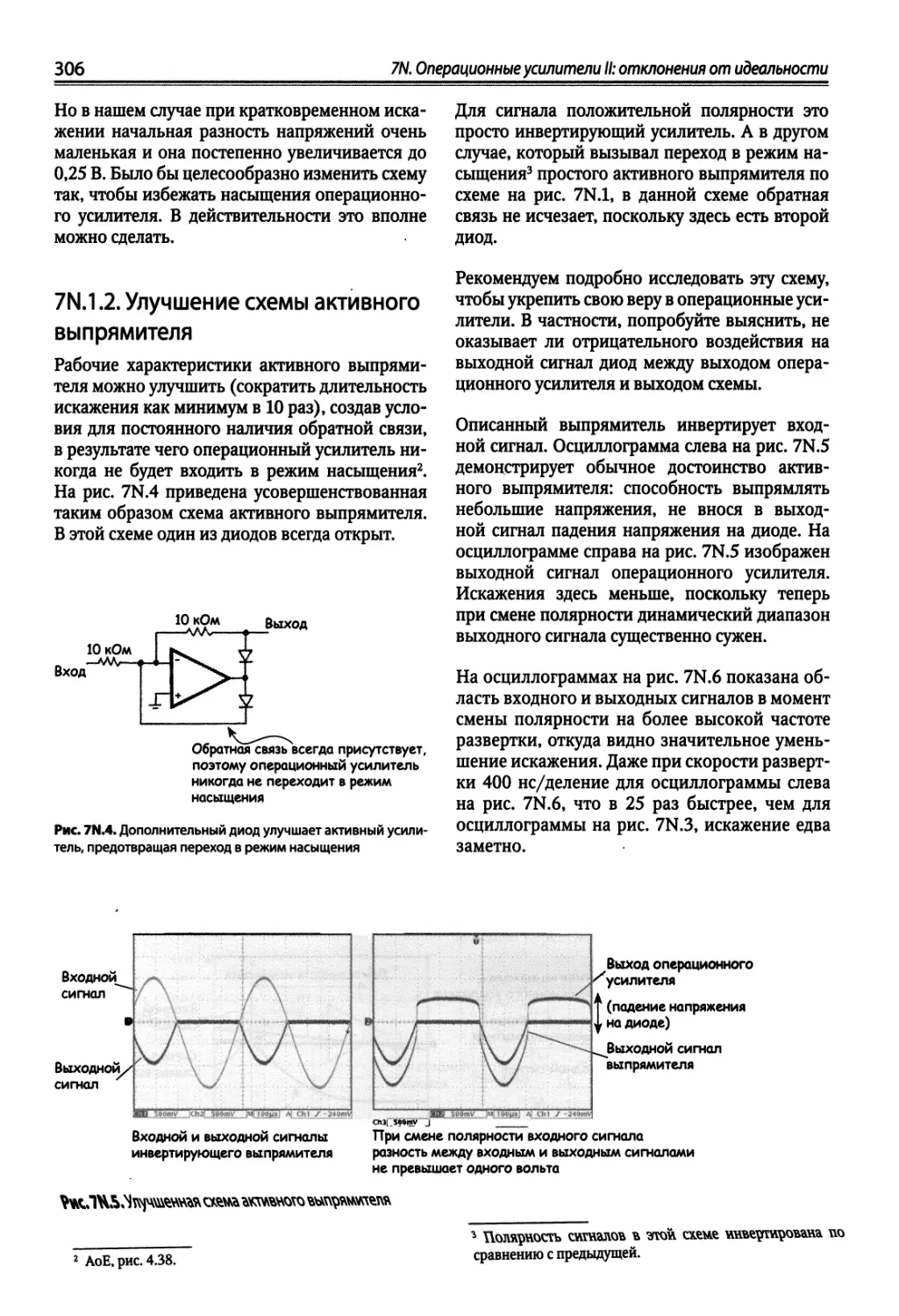
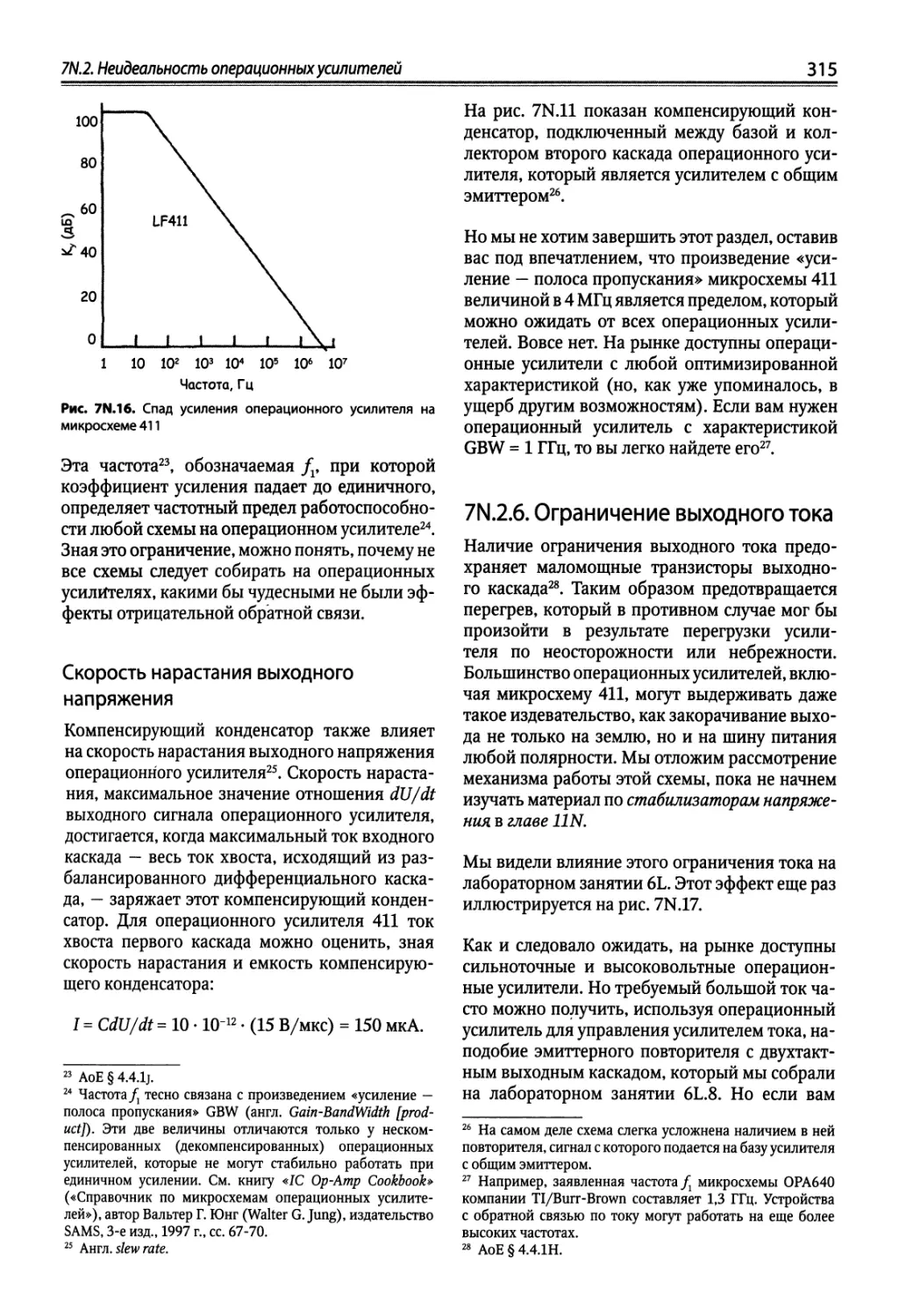
7N.2. Неидеальность операционных усилителей 307
7N.3. Еще несколько вариантов применения: интегратор, дифференциатор, выпрямитель,
разностный усилитель, усилитель по переменному току 320
7N.4. Дифференциатор................... .....................,...................«W...M.».«................................« 325
7N.5. Разностный усилитель на операционном усилителе 326
7N.6. Усилитель переменного тока: хороший способ минимизировать влияние погрешности
по постоянному току операционного усилителя 327
7N.7. Материал для чтения в АоЕ 328
7L Лабораторное занятие: операционные усилители II 329
7L.1. Интегратор 329
7L2. Дифференциатор 333
7L3. Скорость нарастания выходного напряжения 334
7L.4. Микрофонный усилитель переменного тока 335
7S Дополнительный материал: глоссарий
по операционным усилителям 337
7W Примеры с решениями: операционные усилители II 339
7W.1. Задача „ 339
7W. 1.1. Решение «..«м„.«.^..,«.«.......«..........%.м..««..........................*...........« 339
7W.2. Милливольтметр на операционном усилителе 342
8N Операционные усилители III: положительная обратная связь •••••••
8N.1. Полезная положительная обратная связь 348
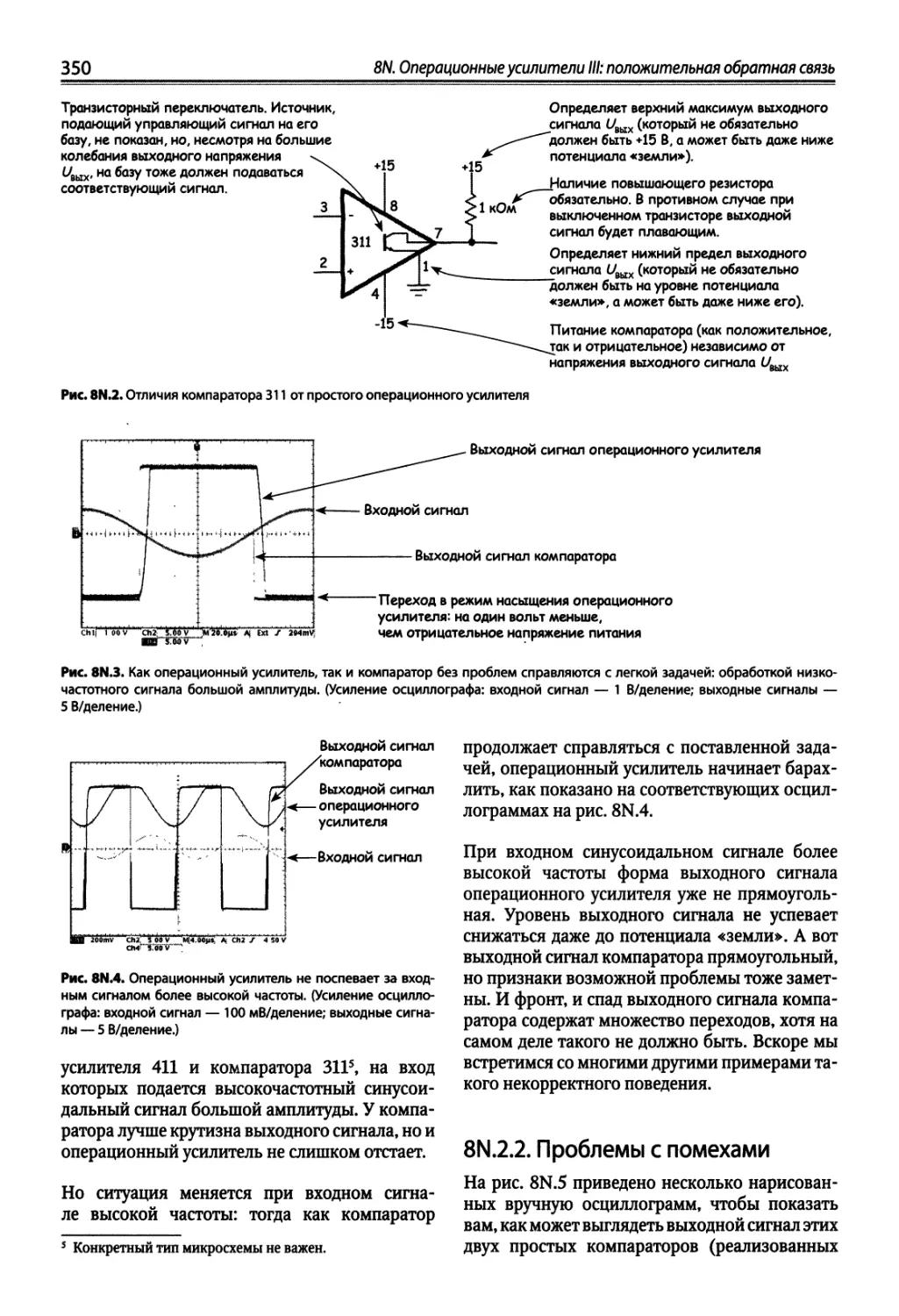
8N.2. Компараторы « « 349
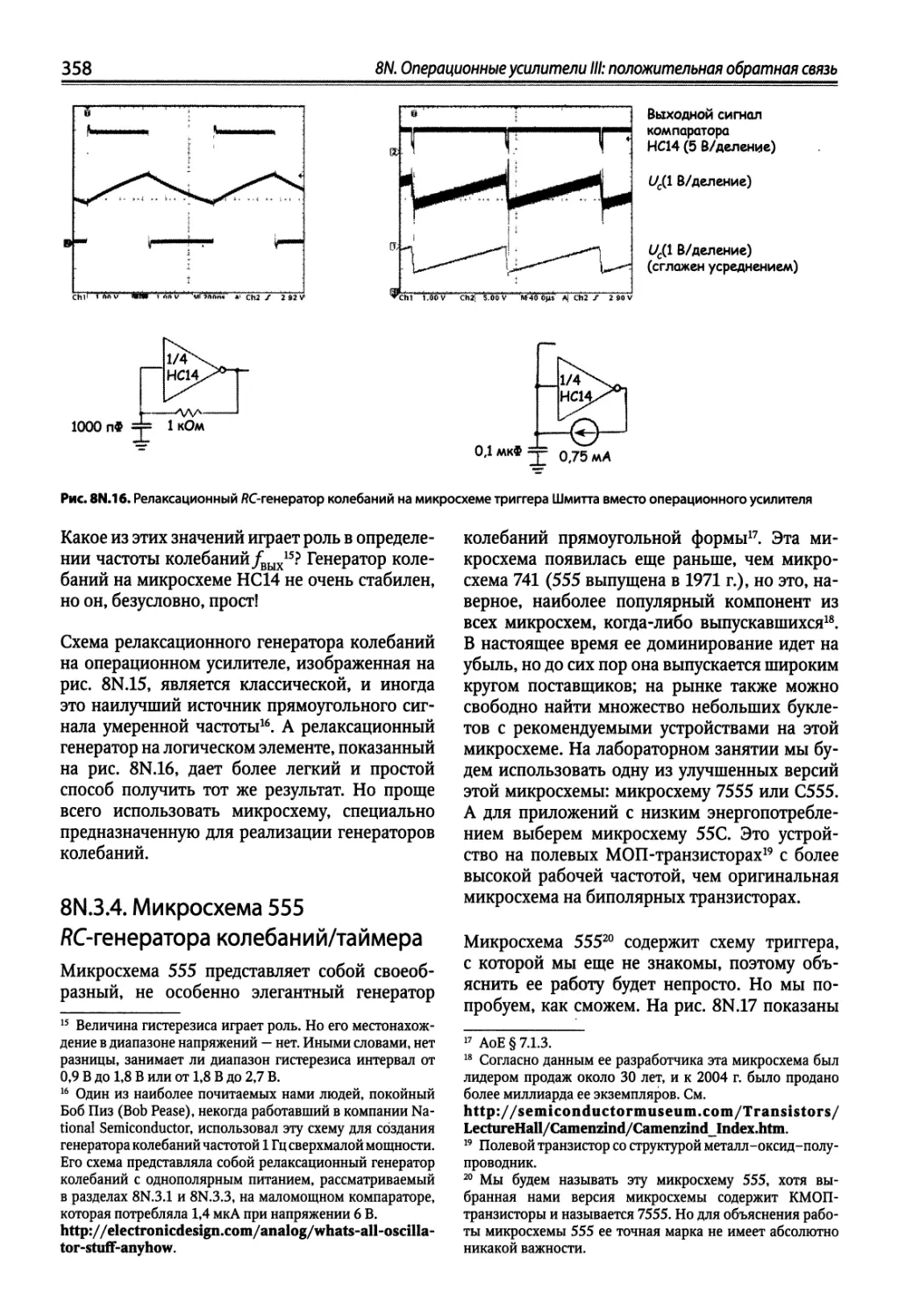
8N.3. Релаксационный ЯСтенератор колебаний 357
8N.4. Генератор синусоидальных колебаний на мосте Вина 360
8N.5. Материал для чтения в АоЕ ., „364
8L Лабораторное занятие. Операционные усилители III ..........................365
8L1. Две схемы компаратора 365
8L2. Релаксационный /?С-генератор колебаний на операционном усилителе 367
8L3. Самая простая схема ЯС-генератора колебаний на триггере Шмитта 368
8L.4. Использование пилообразного сигнала для ШИМ-питания электродвигателя 369
Содержание 13
8L5. Релаксационный /?С-генератор колебаний на микросхеме 555 370
8L7. Генератор синусоидальных сигналов на мосте Вина 372
8W Примеры с решениями: операционные усилители III 374
8W.1. Советы по разработке схем с триггером Шмитта 374
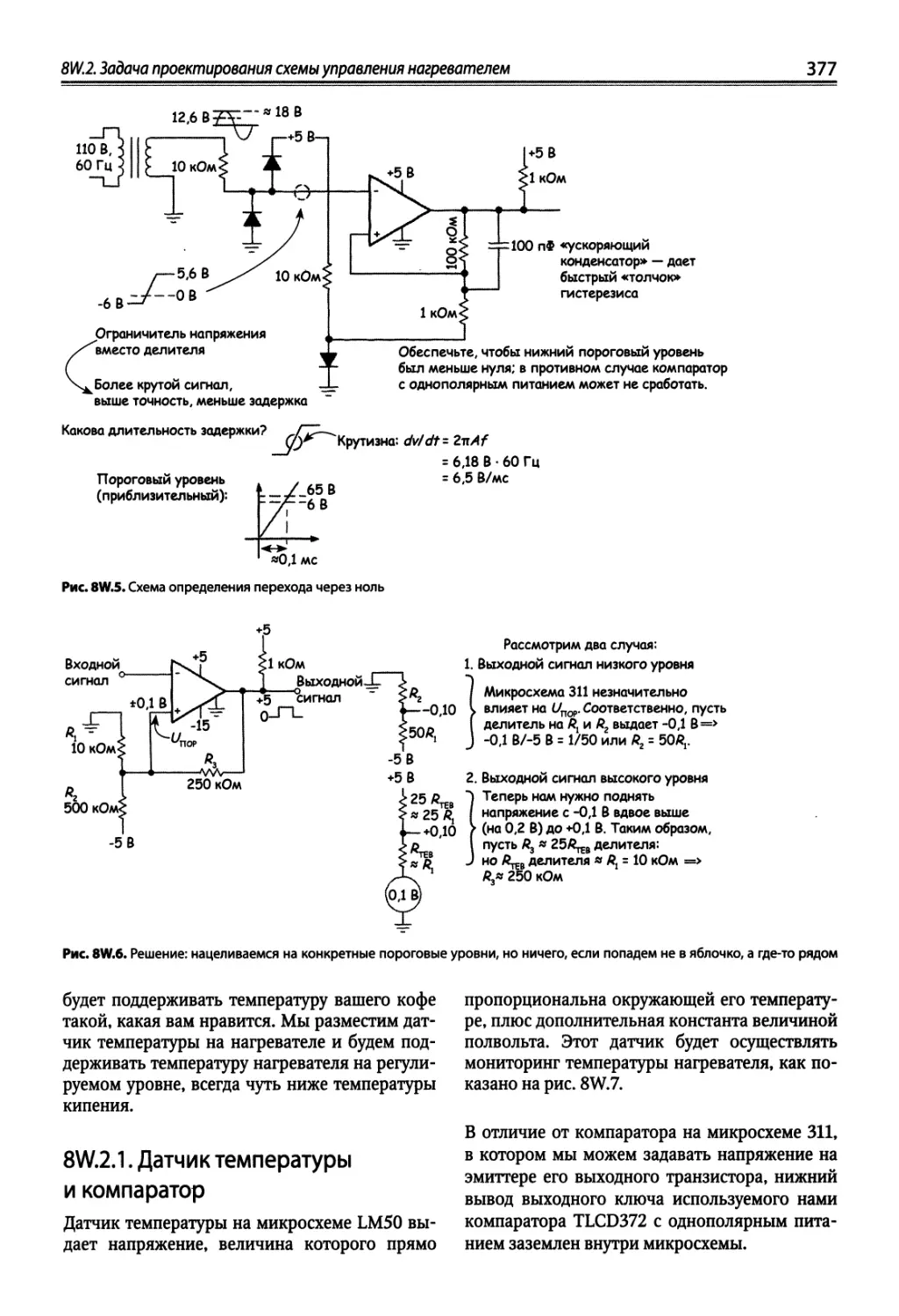
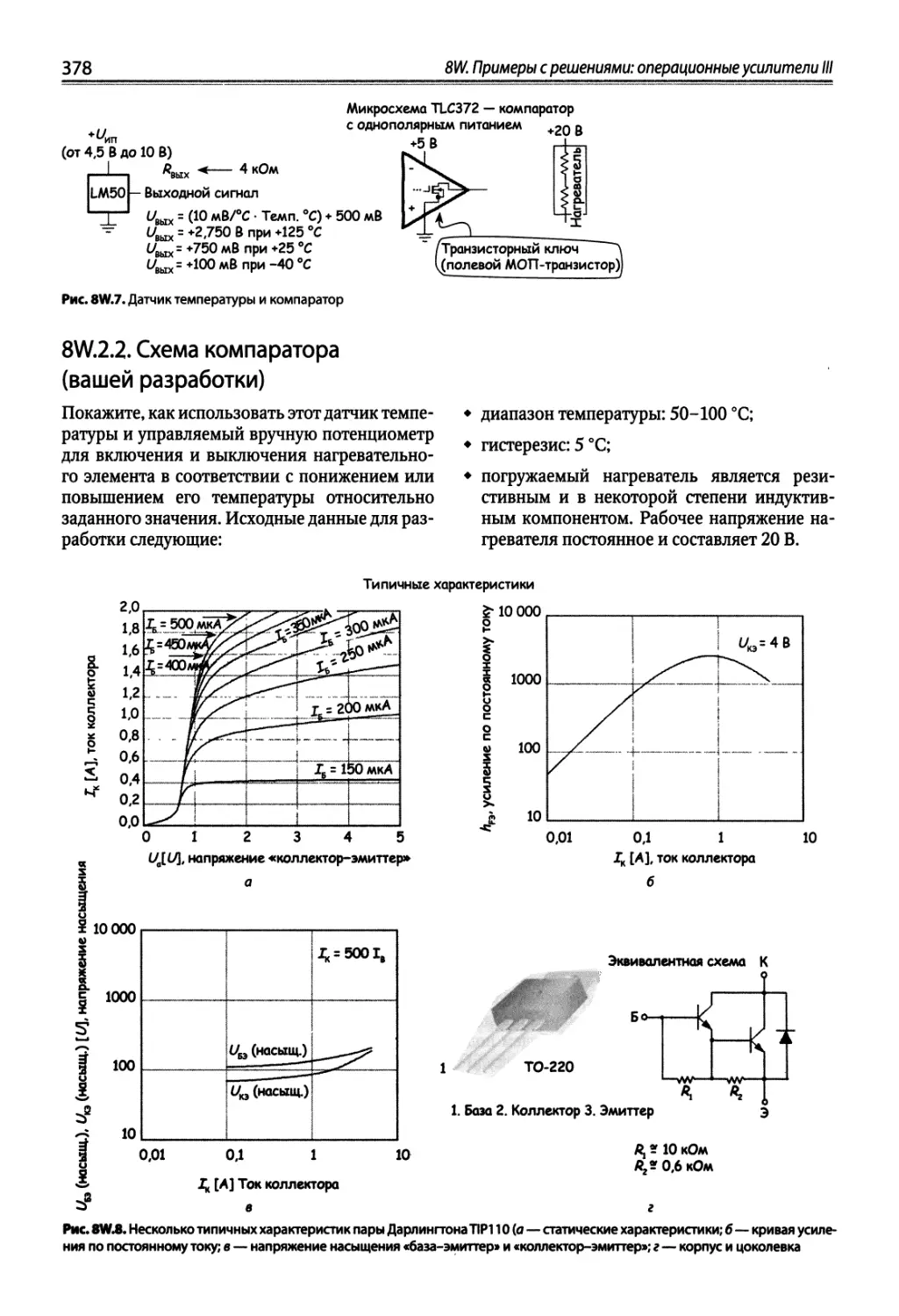
8W.2. Задача проектирования схемы управления нагревателем 376
9N Операционные усилители IV: паразитные колебания
и активный фильтр.,......,..,.....^
9N.1. Введение ~~ * 382
9N.2. Активные фильтры 383
9N.3. Общий взгляд на проблему паразитных колебаний 385
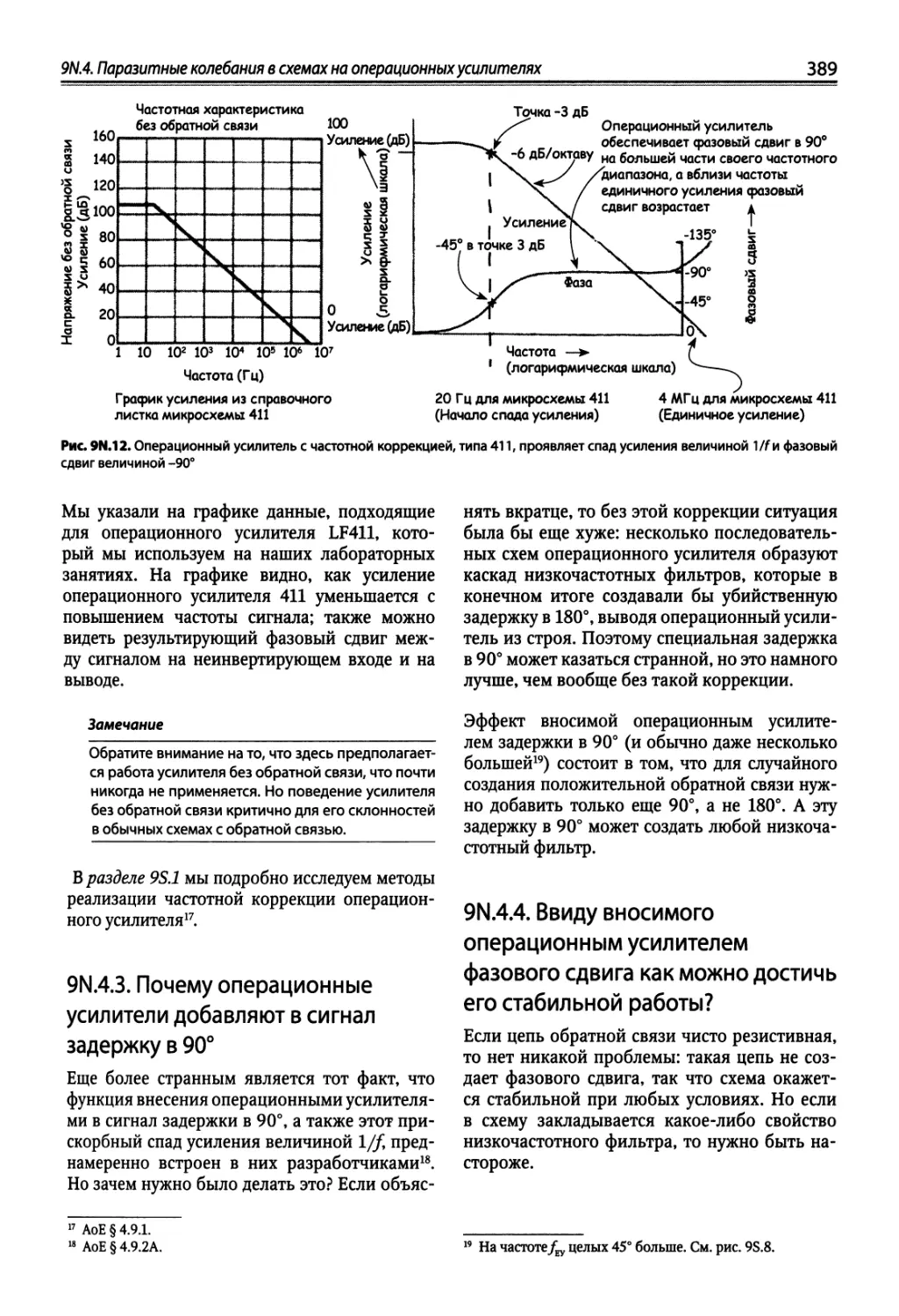
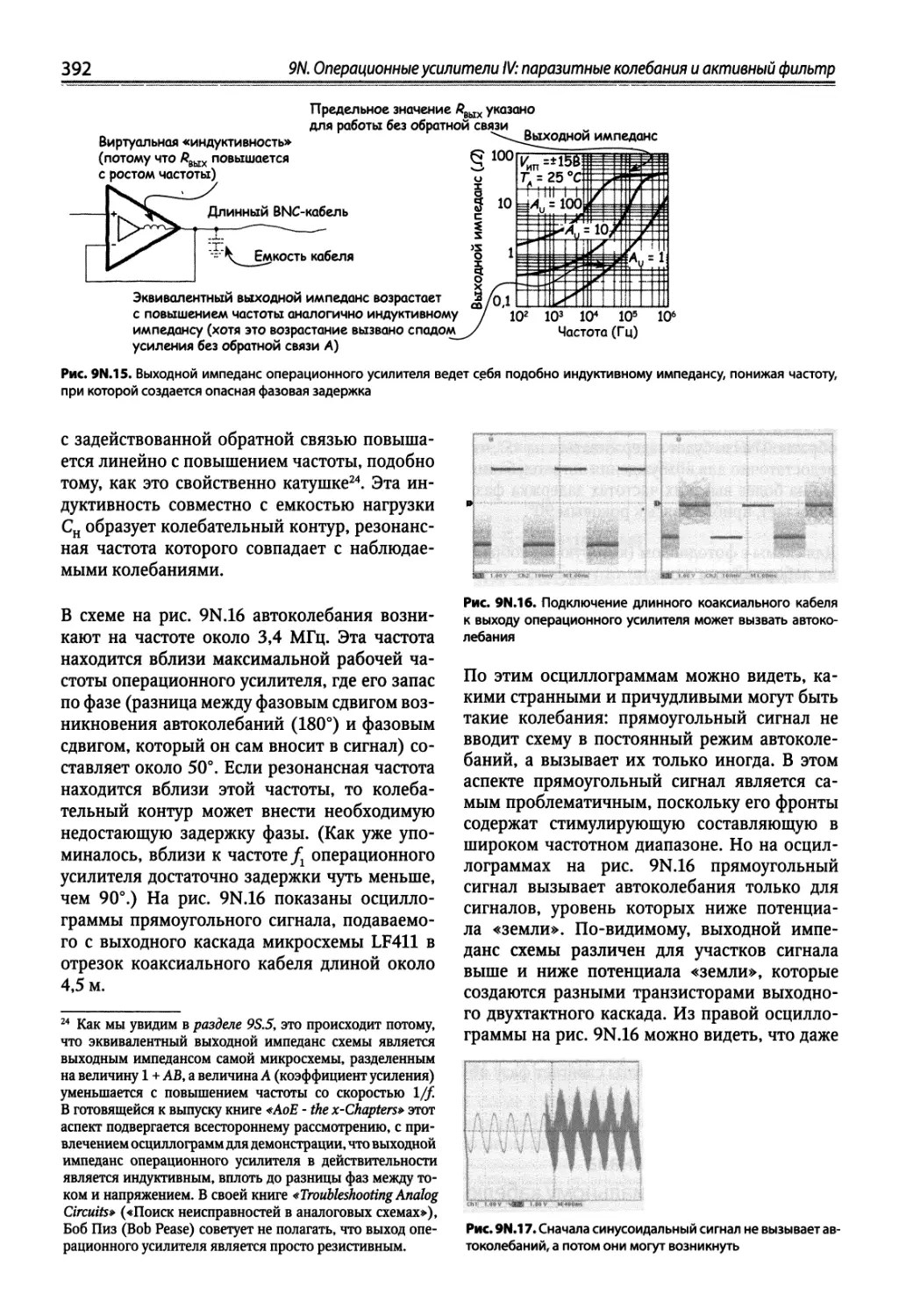
9N.4. Паразитные колебания в схемах на операционных усилителях 385
9N.5. Решения для стабилизации работы операционных усилителей 390
9N.6. Общий критерий стабильности: петлевое усиление, когда фазовый сдвиг
приближается к 180°........ ........ 395
9N.7. Паразитные автоколебания в схемах без операционного усилителя 397
9N.8. Решения для проблемы паразитных автоколебаний 399
9N.9. Подведение итогов по вопросу стабилизации схем 401
9N.10. Материал для чтения в АоЕ 401
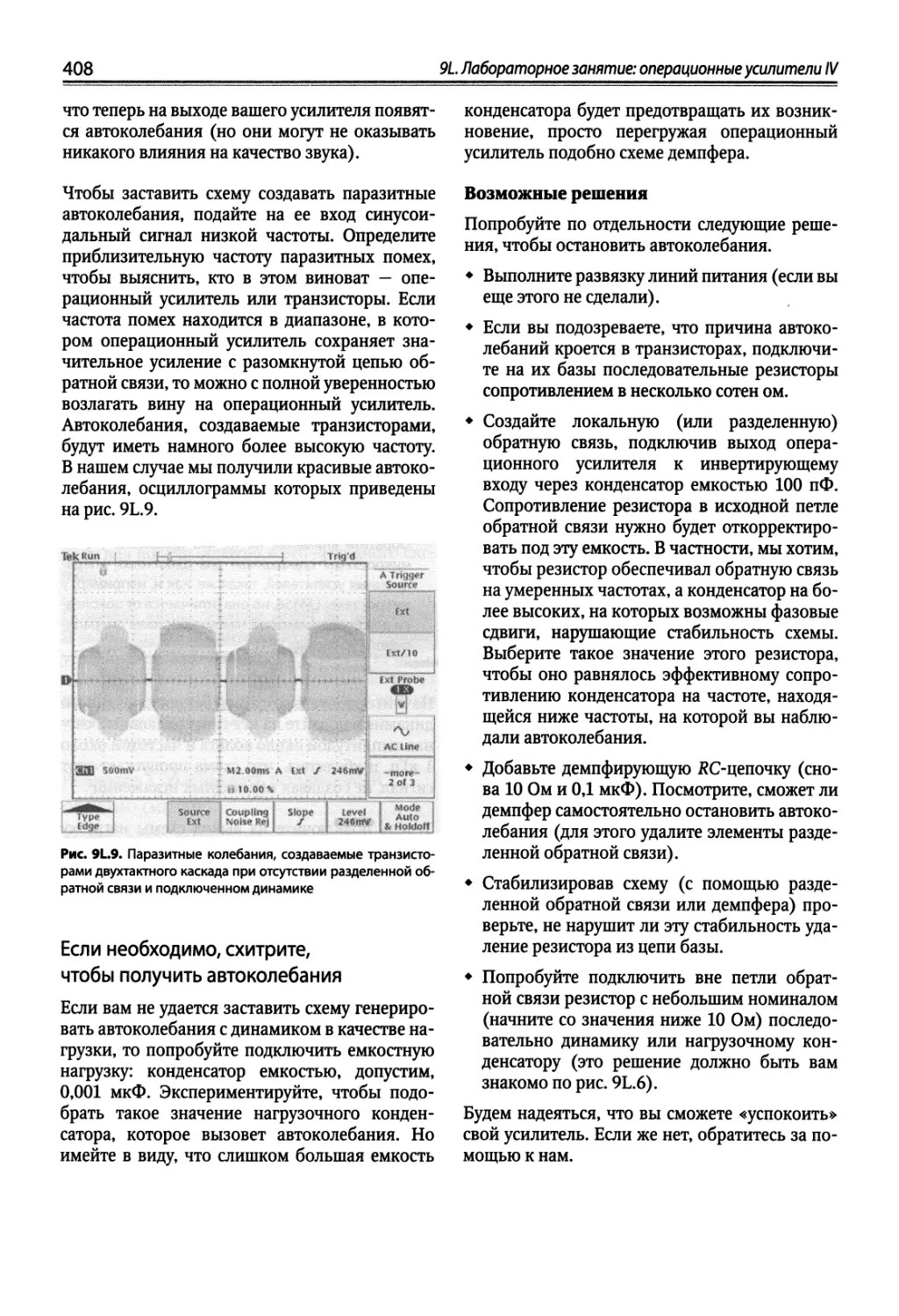
9L Лабораторное занятие: операционные усилители IV 402
9L1. Активный VCVS-фильтр 402
9L.2. Эмиттерный повторитель на дискретных элементах 404
9L3. Нестабильность операционных усилителей: фазовый сдвиг может вызывать
автоколебания в операционном усилителе 405
9L.4. Операционный усилитель с буфером в петле обратной связи 407
9S Дополнительный материал: операционные усилители IV .......409
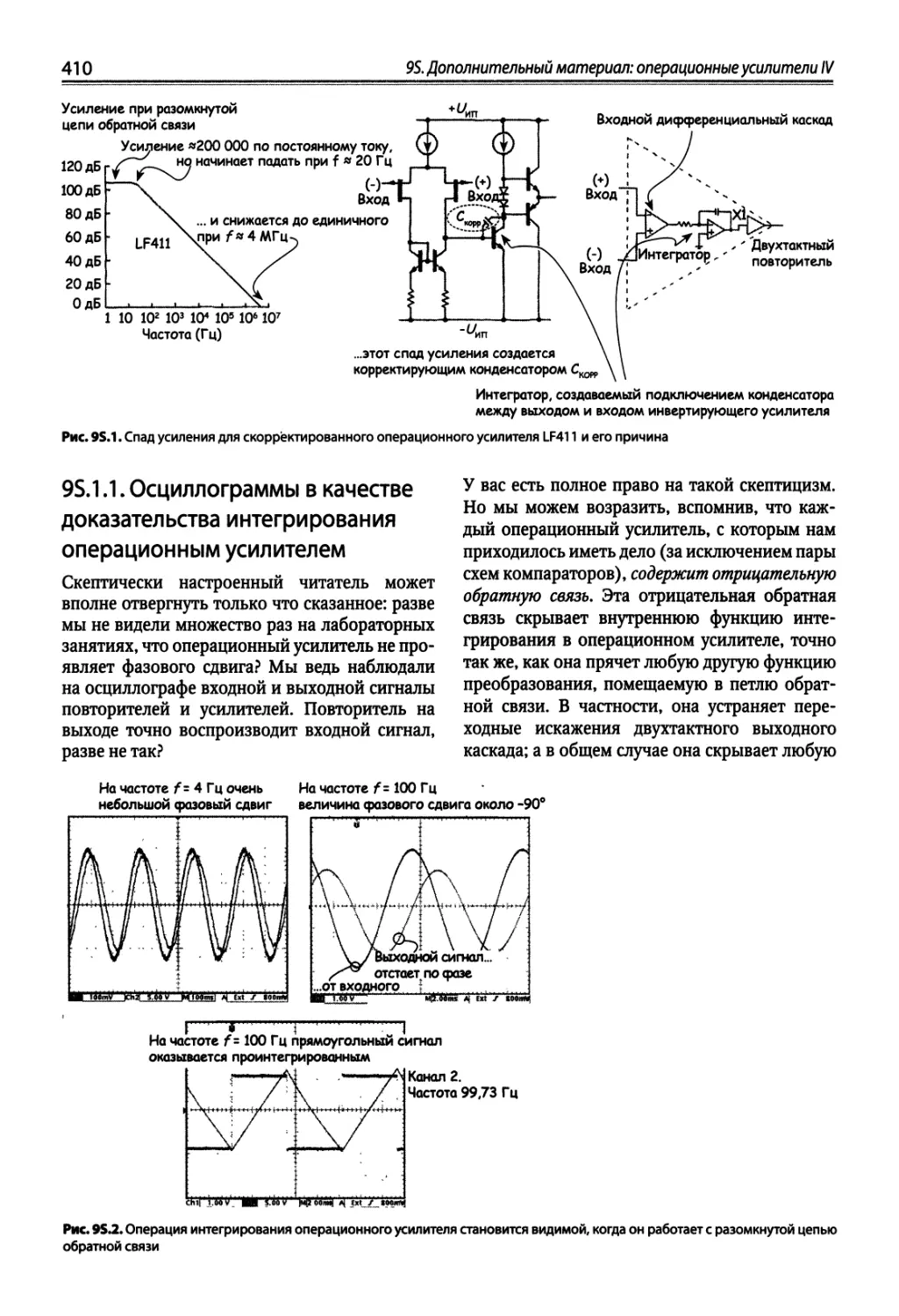
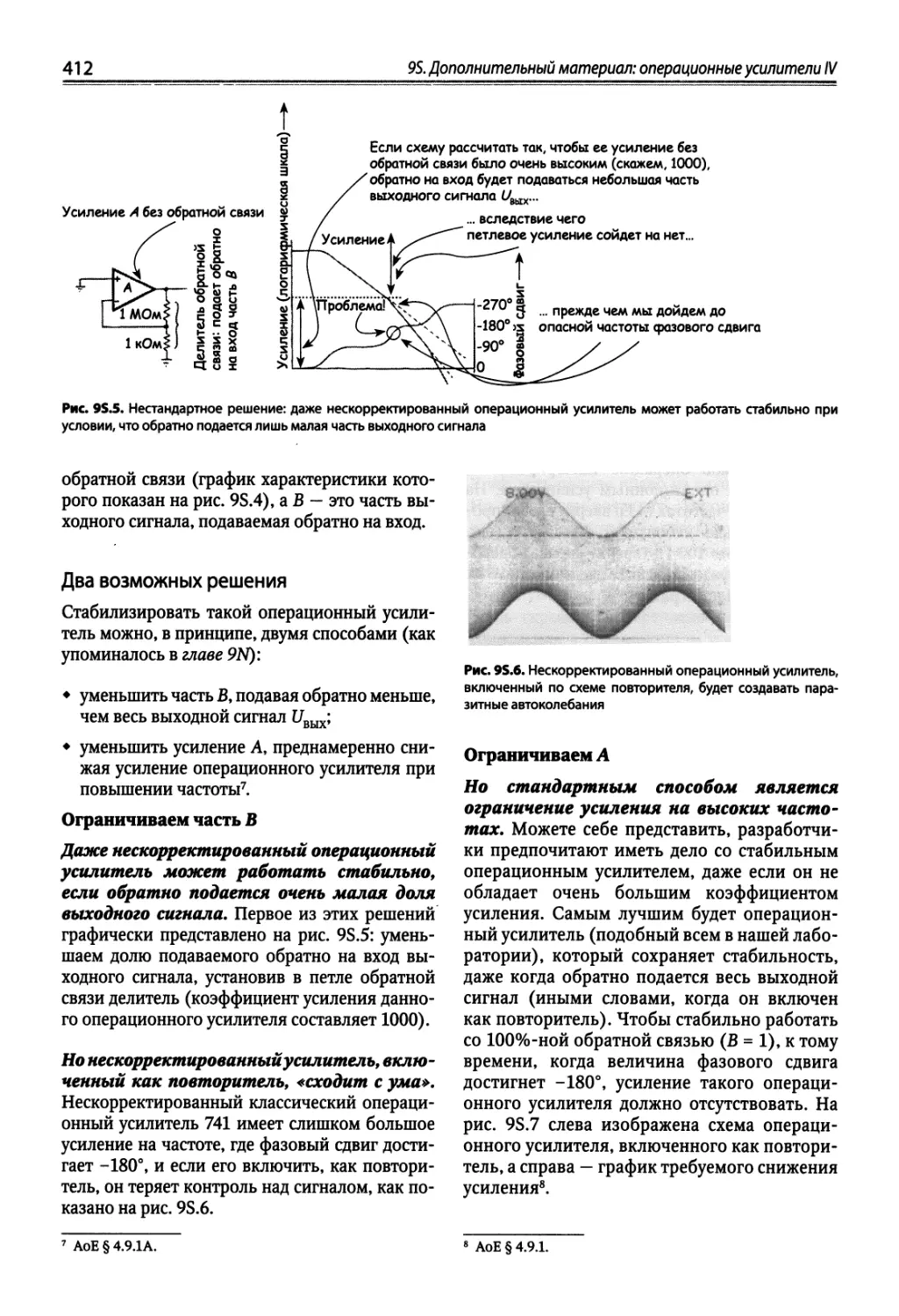
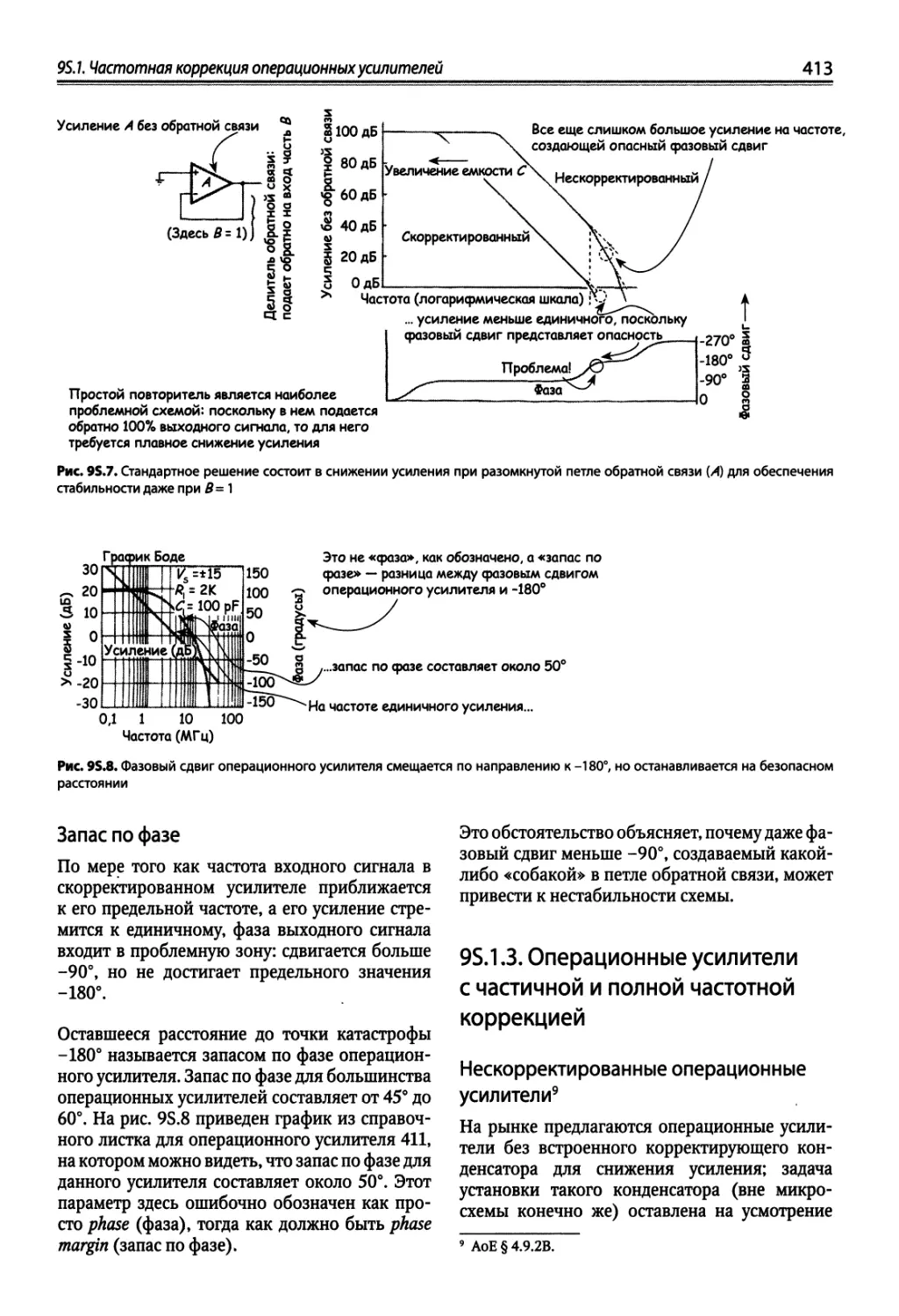
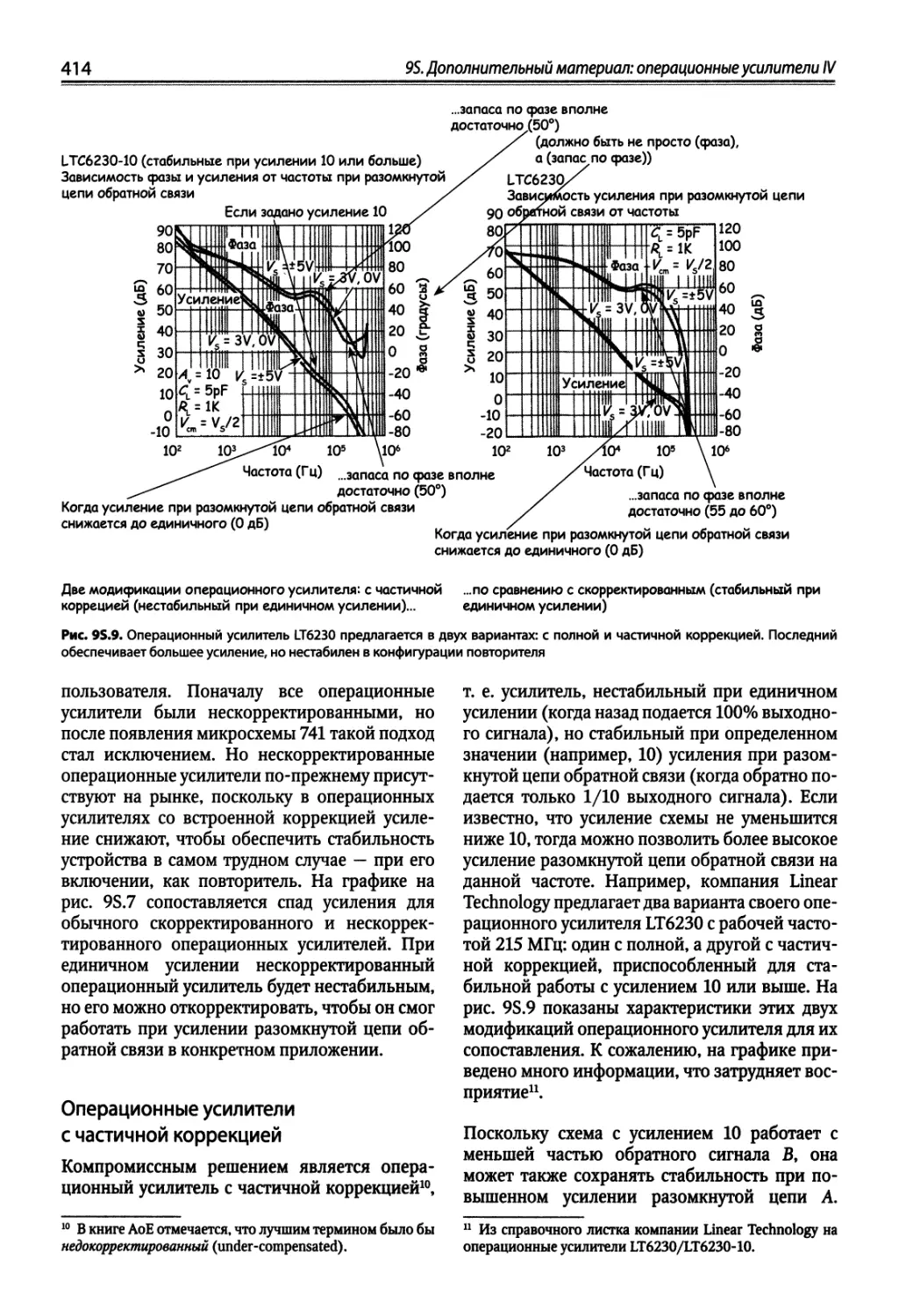
95.1. Частотная коррекция операционных усилителей 409
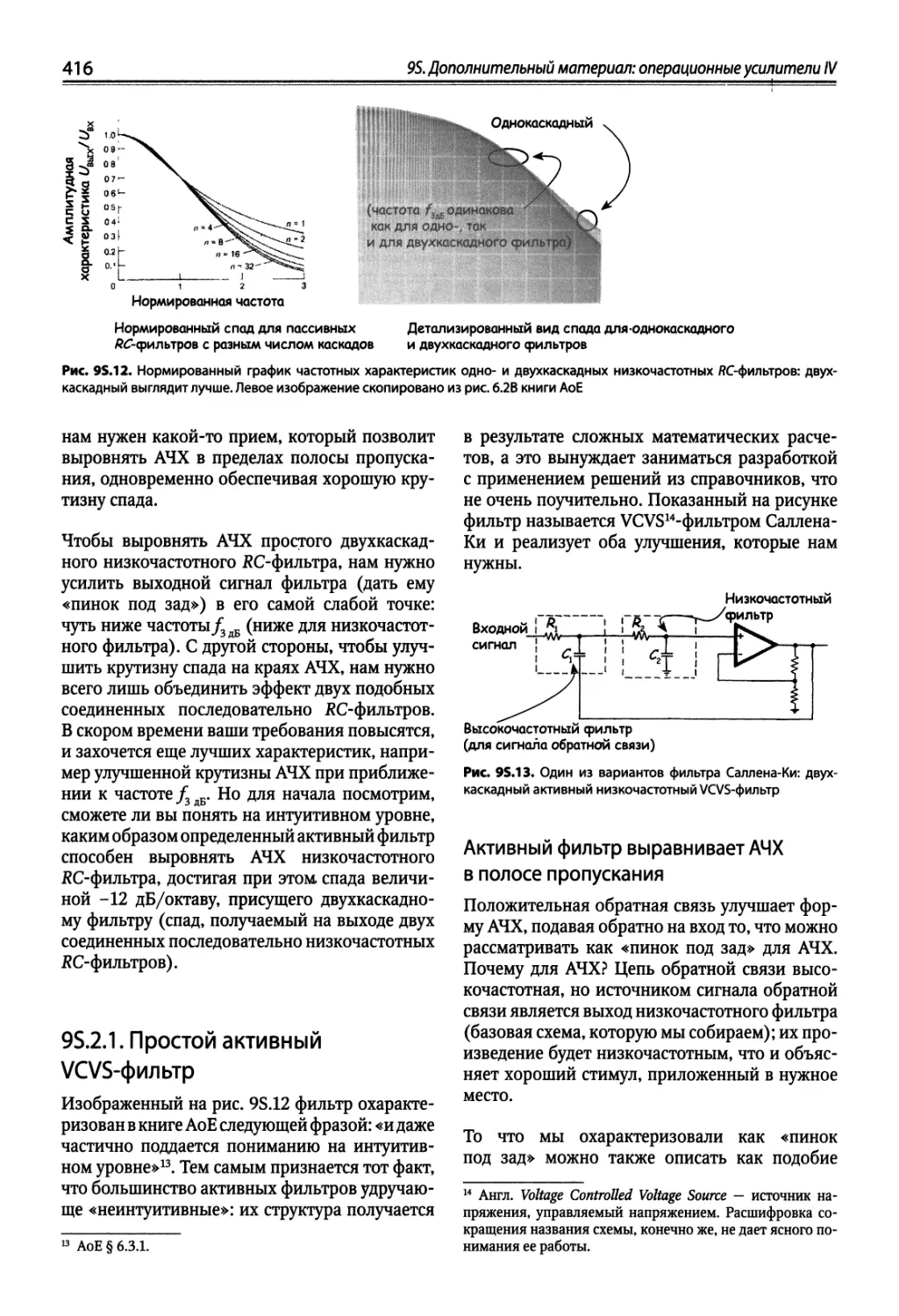
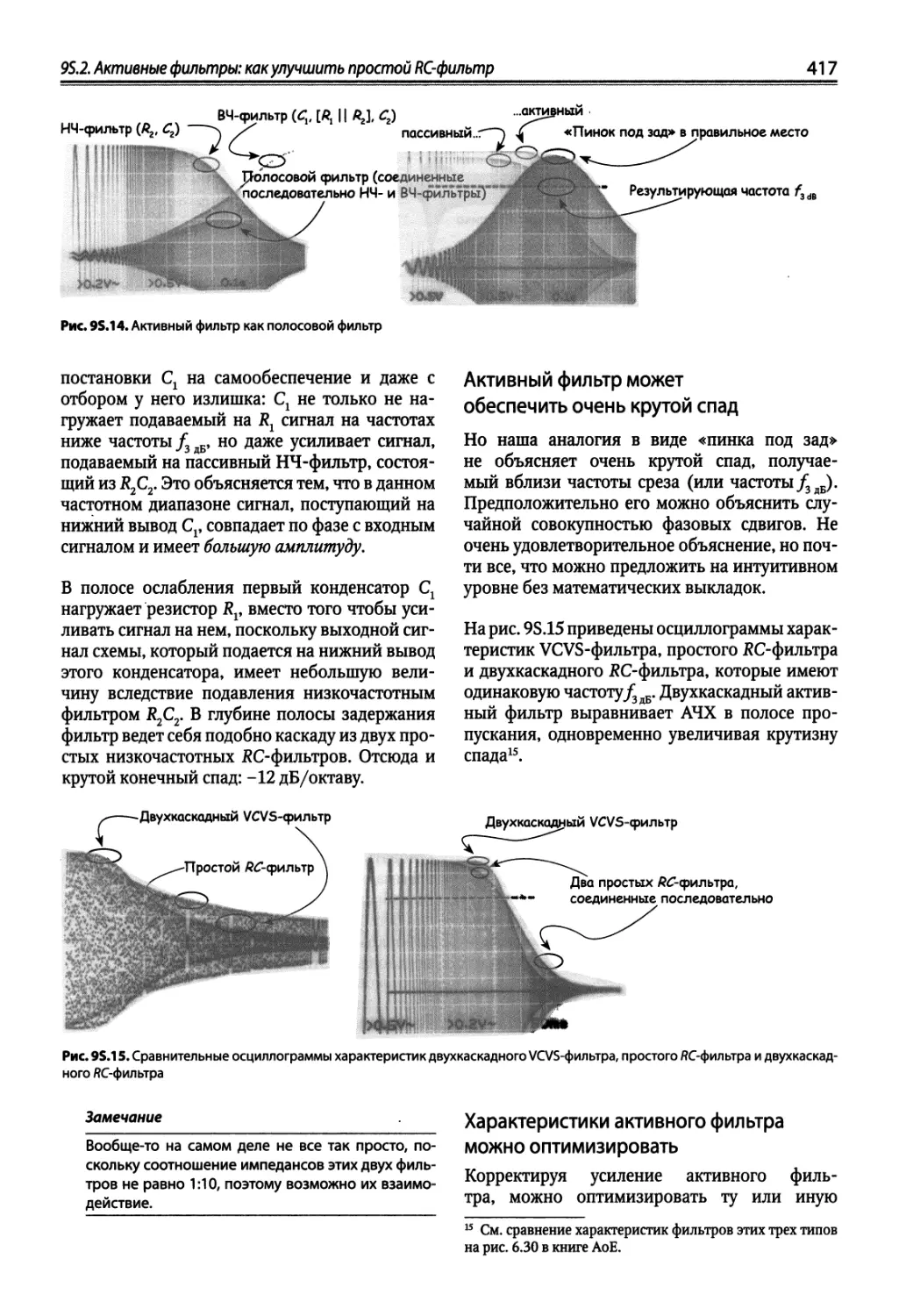
95.2. Активные фильтры: как улучшить простой ЯС-фильтр 415
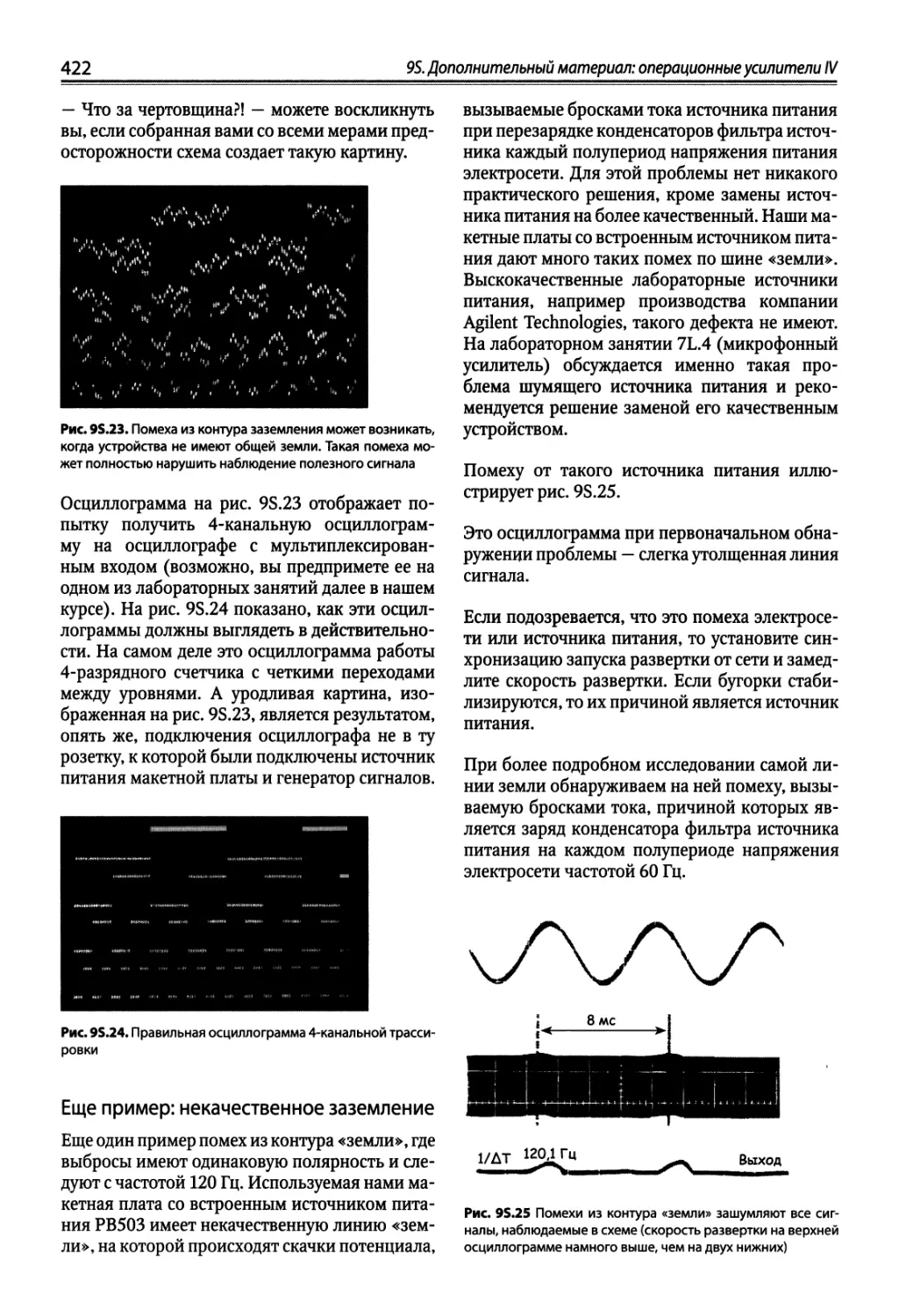
95.3. Диагностирование помех 419
95.4. Схема операционного усилителя LF411 425
95.5. Количественное описание обратной связи 426
9W Примеры с решениями: операционные усилители IV 430
9W.1. Польза, получаемая от усиления операционных усилителей 430
9W.2. Воп росы стабил ьности 431
10N Операционные усилители IV: ПИД-регулятор
для электродвигателя .....•.......^^^
10N.1. Примеры реальных задач, требующих такого решения ; 437
101Ч.2.ПИД-цепь управления электродвигателем 437
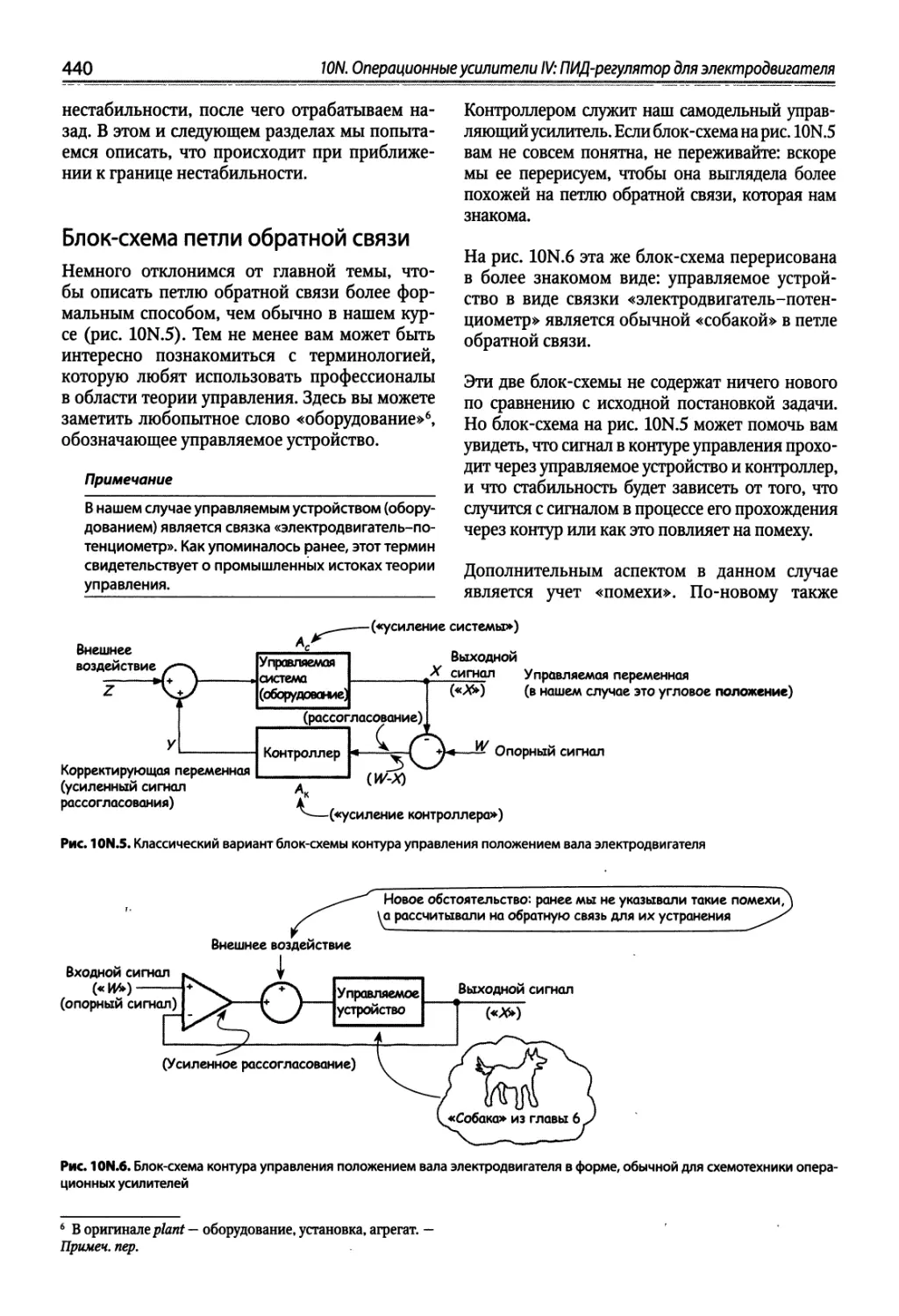
10N.3. Проектирование контроллера (специализированного операционного усилителя) 439
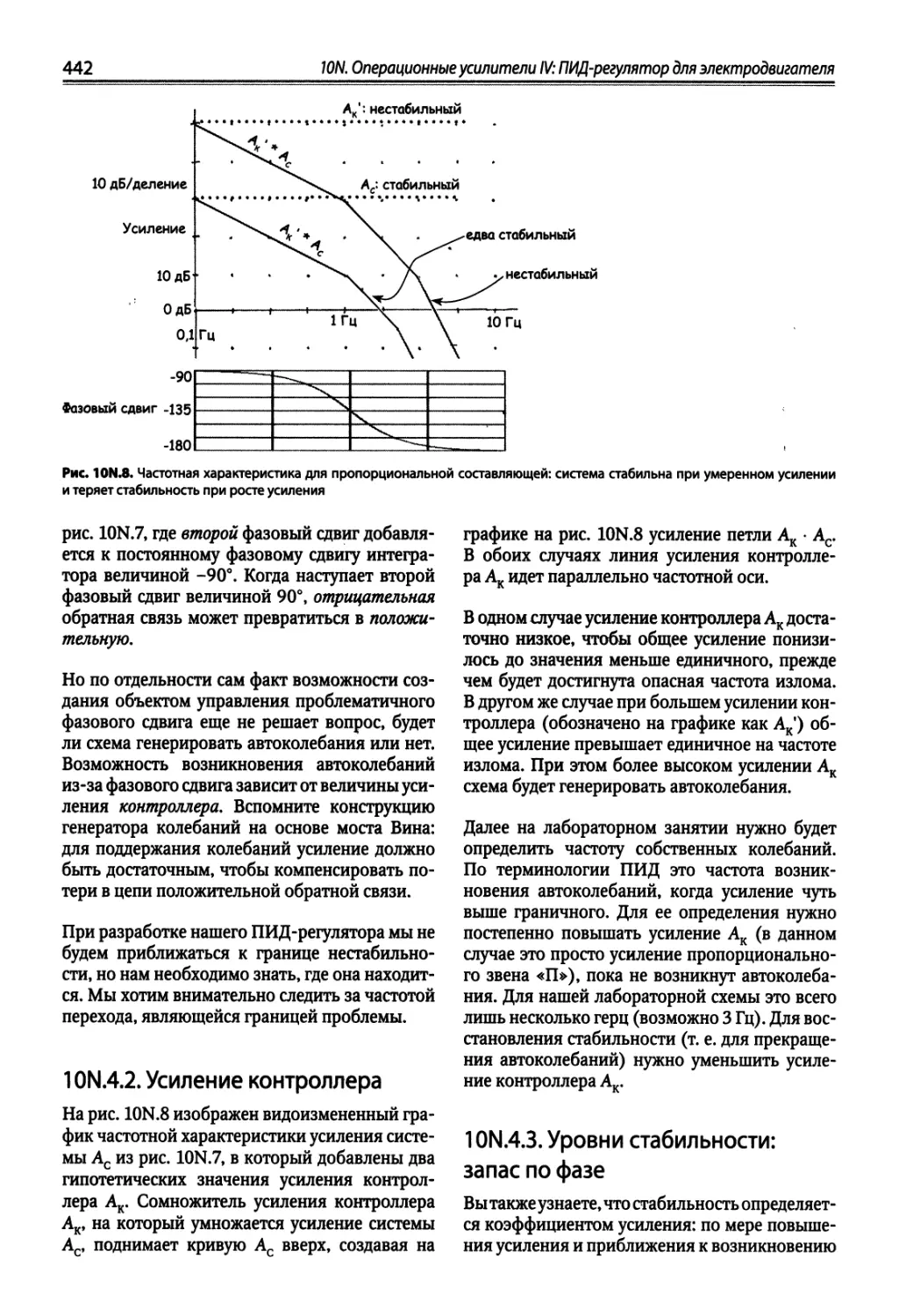
10N.4. Схема только для пропорциональной составляющей П: расчет усиления 441
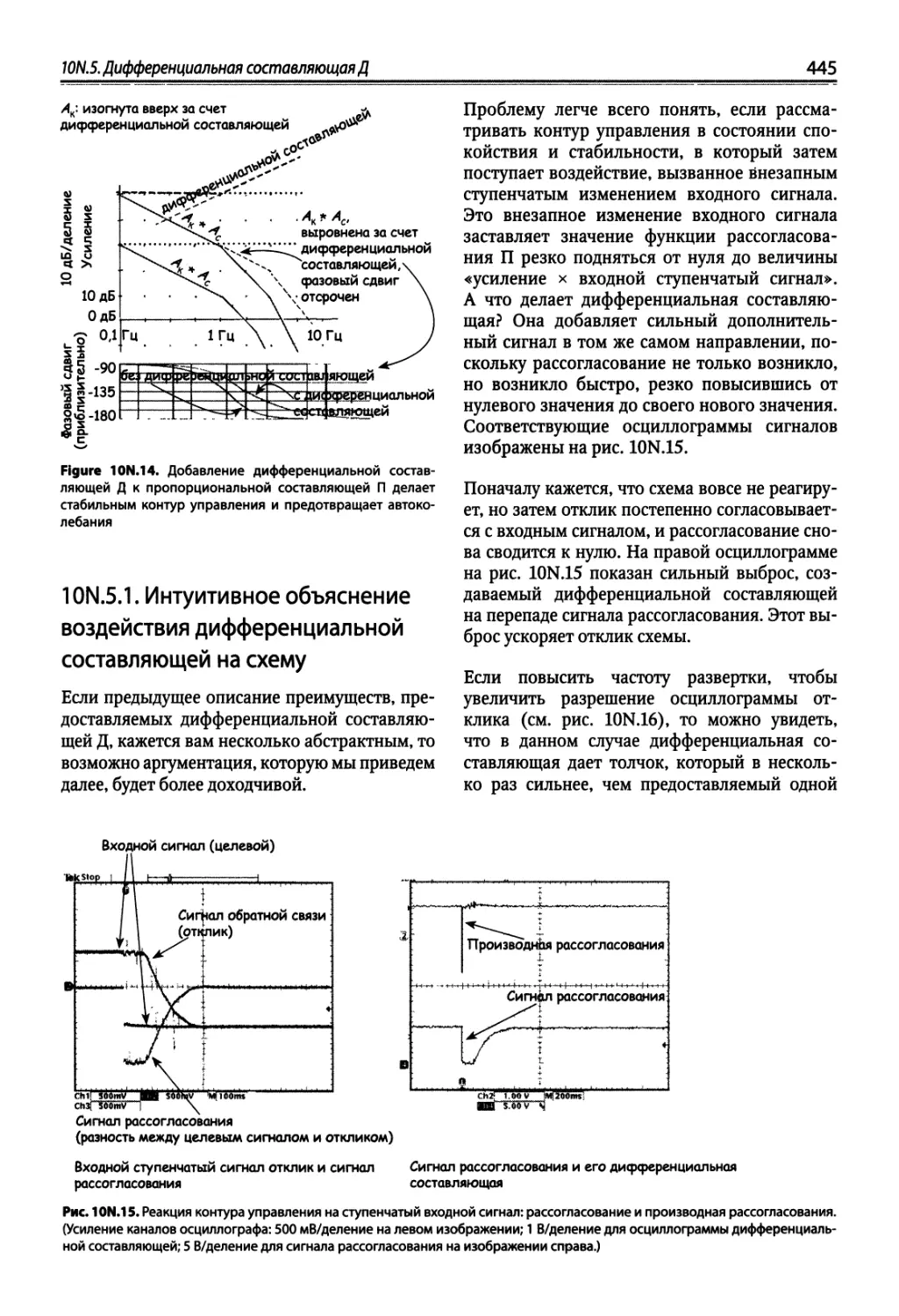
10N.5. Дифференциальная составляющая Д 444
10N.6. Материал для чтения в АоЕ 450
10L Лабораторное занятие. Операционные усилители V ...........................451
10L1. Какая польза от ПИД-регулятора? < 451
10L.2. ПИД-контроллер электродвигателя 452
10L.3. Добавляем дифференциальную составляющую i 459
10L.4. Добавляем интегральную составляющую 461
10L5. Осциллограммы 462
14 Содержание
11N Стабилизаторы напряжения ......................................................................464
11N.1. Эволюция стабилизированного источника питания 465
11N.2. Более простые интегральные стабилизаторы - 469
11 N3. Проектирование с учетом тепловой защиты 471
11N.4. Источники тока 472
11 N.5. Защита от перенапряжения посредством автоматического шунтирования на землю 474
11 N.6. Импульсные стабилизаторы напряжения 474
11 N.7. Материал для чтения в АоЕ 480
11L Лабораторное занятие: стабилизаторы напряжения 481
11L1. Линейные стабилизаторы напряжения 481
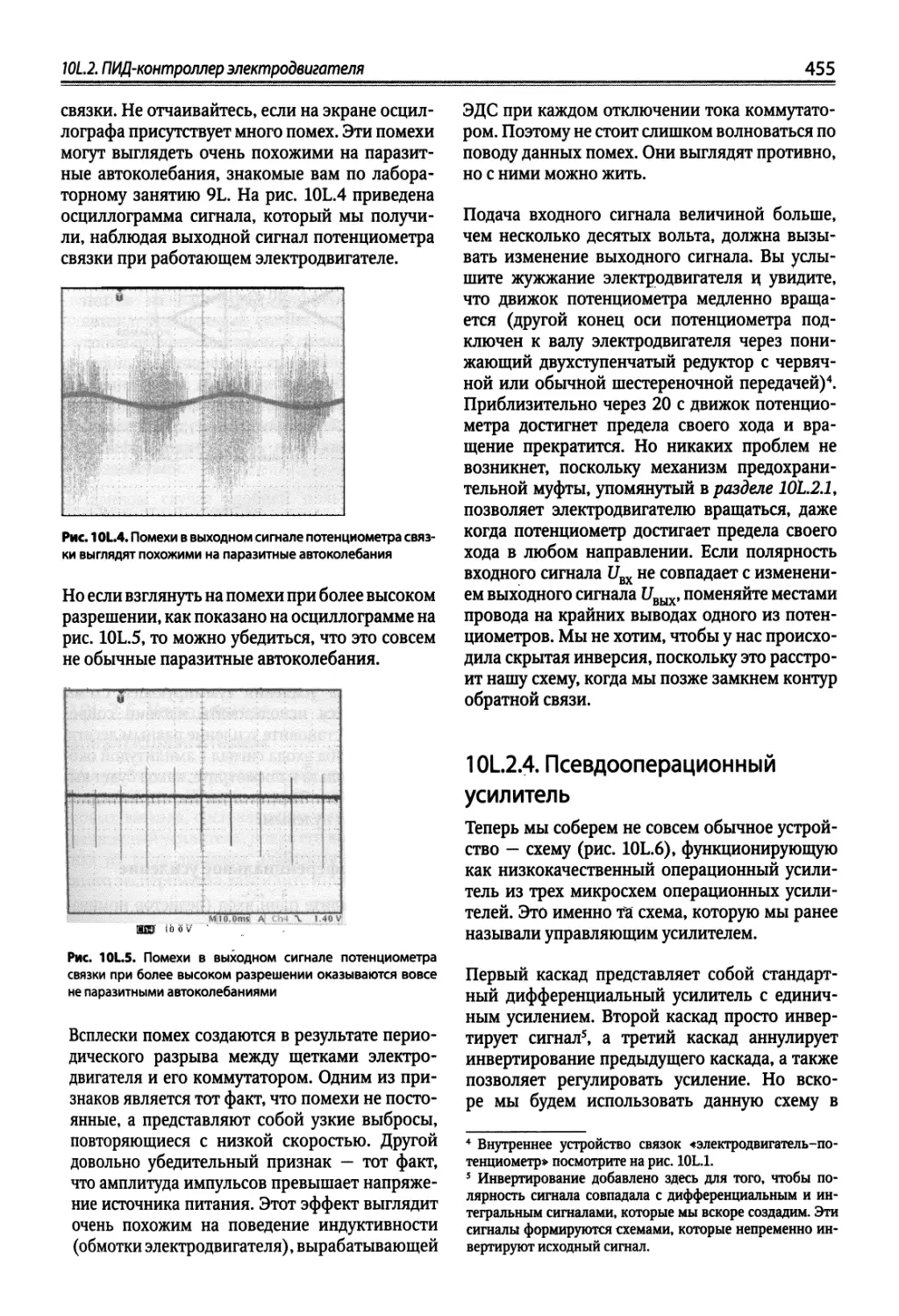
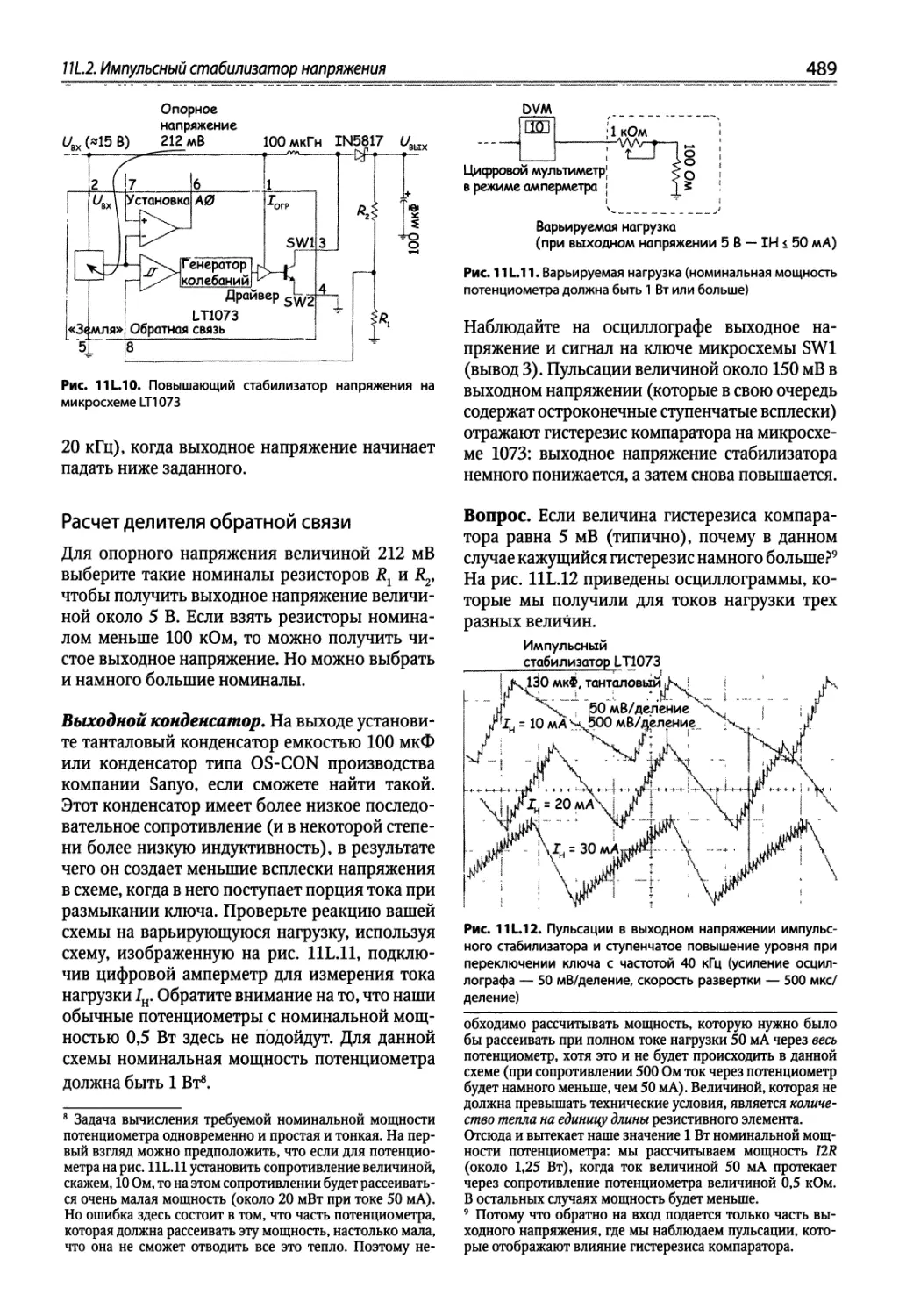
11 L.2. Импульсный стабилизатор напряжения 488
11W Примеры с решениями: стабилизаторы напряжения..........................491
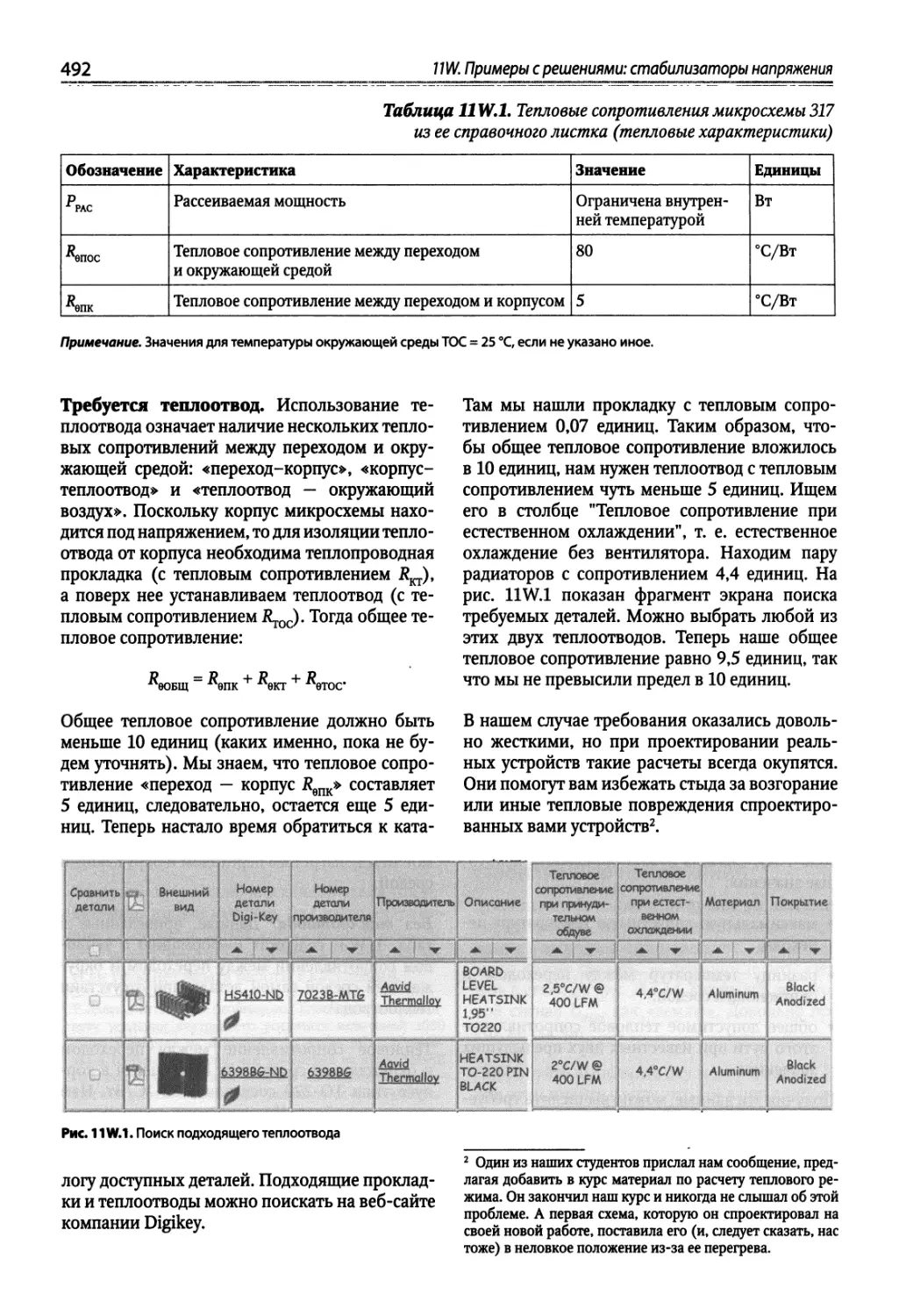
11W.1. Выбор теплоотвода 491
11 W.2. Применение микросхемы-источника тока 493
12N Ключи на полевых МОП-транзисторах 494
12N.1. Почему мы отводим полевым транзисторам всего лишь одно занятие 494
12N.2. Включение и выключение устройств большой мощности 498
12N.3. Применение силового ключа: усилитель звуковой частоты 500
12N.4. Логические вентили 502
12N.5. Аналоговые коммутаторы 503
12N.6. Применение аналоговых коммутаторов , 504
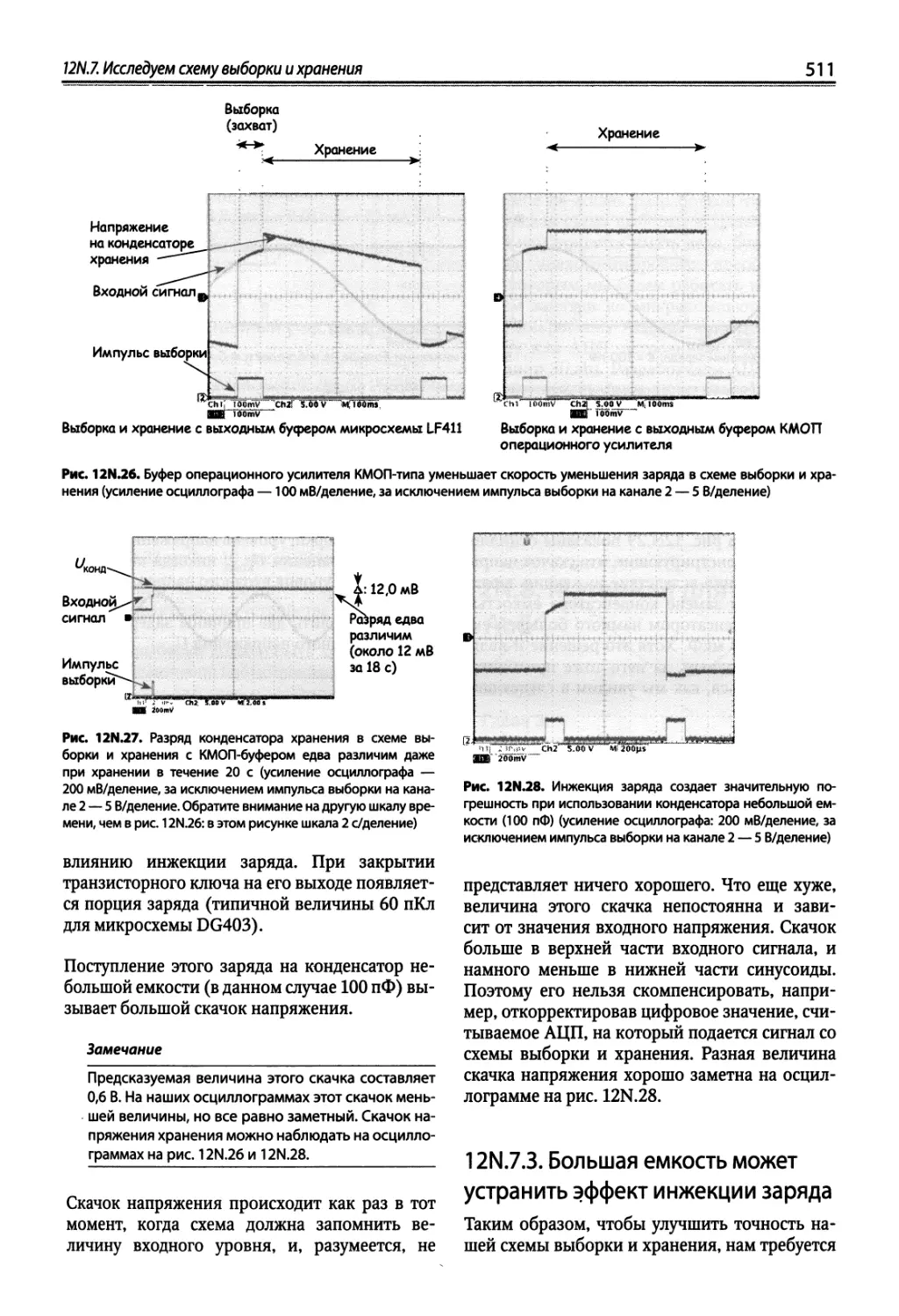
12N.7. Исследуем схему выборки и хранения 509
12N.8. Материал для чтения в АоЕ * 513
12L Лабораторное занятие: ключи на полевых МОП-транзисторах.........514
12L1. Мощный полевой МОП-транзистор 514
12L2. Аналоговые коммутаторы 517
12L.3. Импульсный усилитель звуковой частоты 523
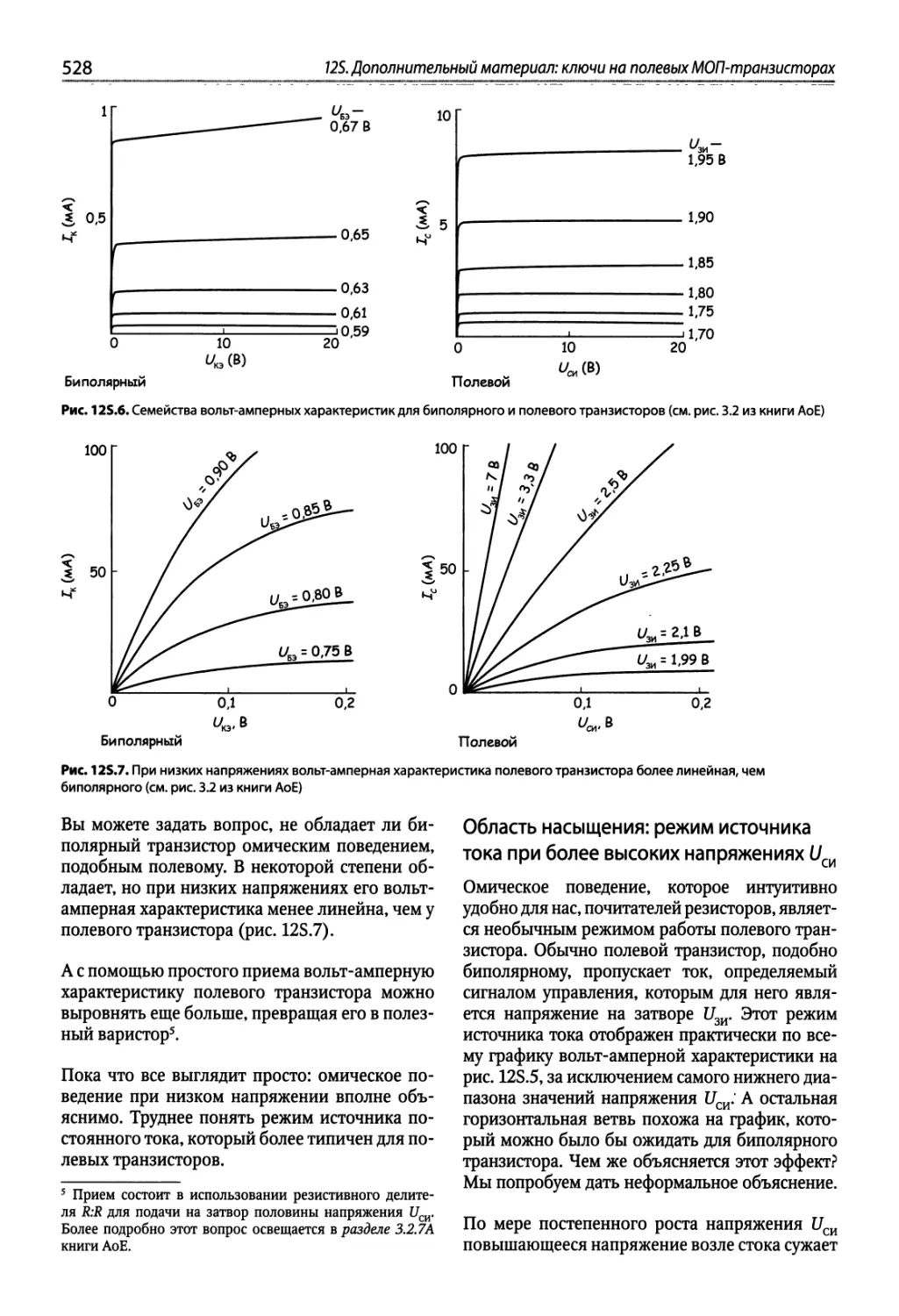
12S Дополнительный материал: ключи на полевых МОП-транзисторах....525
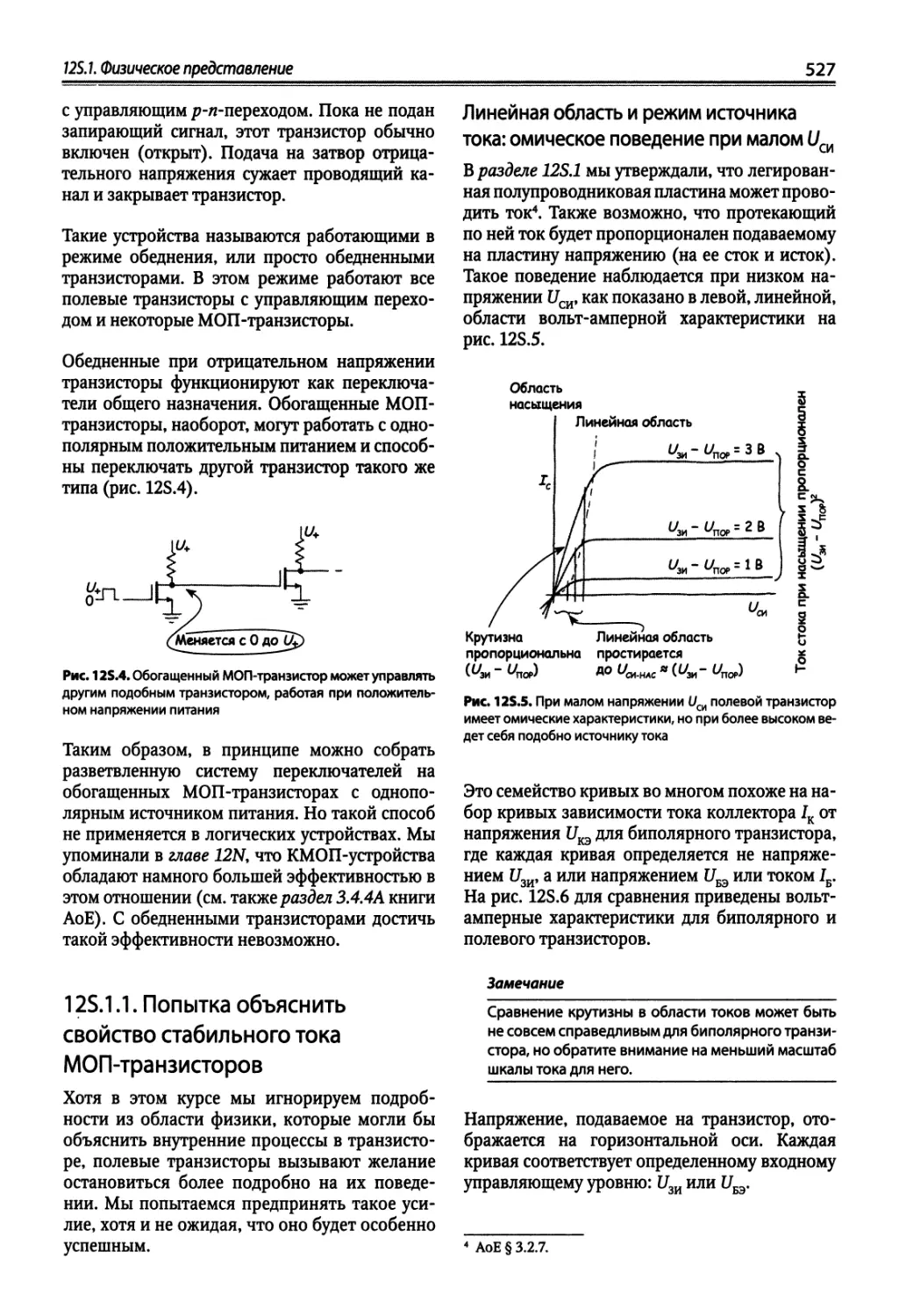
12S.1. Физическое представление 525
13N Совместный аудио проект .........................................................................531
13N.1. День совместных усилий ; 531
13N.2. Общая проблема обеспечения стабильности 535
13N.3. Параметры светодиода и фототранзистора 535
13L Лабораторное занятие: совместный аудиопроект ...•.•.••.•.••..•••••••.••.•
13L1. Типичные сигналы 536
13L2. Стратегии поиска и устранения причин неполадок 536
Часть IV. Цифровые устройства: логические элементы, триггеры,
счетчики, ПЛМ, память ........................................................................539
14N Логические устройства ...............................................................................541
14N.1. Аналоговые и цифровые системы 542
14N.2. Двоичная система счисления 545
14N.3. Комбинационная логика 547
14N.4. Реализация цифровой логики с помощью программируемых матриц 553
Содержание 15
14N.5. Логические элементы типа ТТЛ и КМОП ;...« 555
14N.6. Помехоустойчивость 557
14N.7. Дополнительные сведения о типах логических вентилей 560
14N.8. Материал для чтения в АоЕ , 563
14L Лабораторное занятие: логические устройства ••..••••.••.•.•••••••.•••..•••.•••..564
14L.1. Предварительная информация « 564
14L2. Входные и выходные характеристики микросхем ТТЛ и КМОП 567
14L3. Аномалии м 568
14L4. Использование вентилей микросхем для создания определенных логических функций 570
14L5. Исследуем внутреннее устройство логических элементов КМОП 571
14S Дополнительный материал: глоссарий по цифровой электронике ....575
14W Примеры с решениями: логические устройства .•••••....•••.•••••••...•.••.•.•••.578
14W.1. Общие сведения о мультиплексировании 578
14W.2. Двоичная арифметика 582
15N Триггеры •• •••••••••••••••••••••••••••••••••••••••••••••••••••••••••••594
15N.1. Реализация комбинационной функции 595
15N.2. Снова о сигналах с низким активным уровнем 596
15N.3. Вентили как функции «Делай это/делай то» 600
15N.4. Функция Исключающее-ИЛИ в качестве функции Инверсия/Пропуск* 601
15N.5. Функция ИЛИ в качестве функции Установка/Пропуск* 601
15N.6. Последовательные схемы в общем и триггеры в частности 601
15N.7. Применение триггеров в схемах устранения дребезга контактов 608
15N.8. Счетчики 609
15N.9. Синхронные счетчики 610
15N.10. Сдвиговый регистр на триггерах 612
15N.11. Материал для чтения в АоЕ 613
15L Лабораторное занятие: триггеры .............................................................614
15L1. Самый простой триггер: RS-защелка 614
15L2. D-триггеры 614
15L3. Счетчики со сквозным переносом и синхронные счетчики 617
15L4. Дребезг контактов переключателей и три схемы устранения дребезга 618
15L.5. Сдвиговый регистр 620
15S Дополнительный материал: триггеры.....................................................623
15S.1 Программируемые логические устройства 623
15S.2. Приемы работы с триггерами 625
16N Счетчики......................................................^
16N.1. Краткое повторение пройденного материала 629
16N.2. Аномалии и опасности схем на триггерах 633
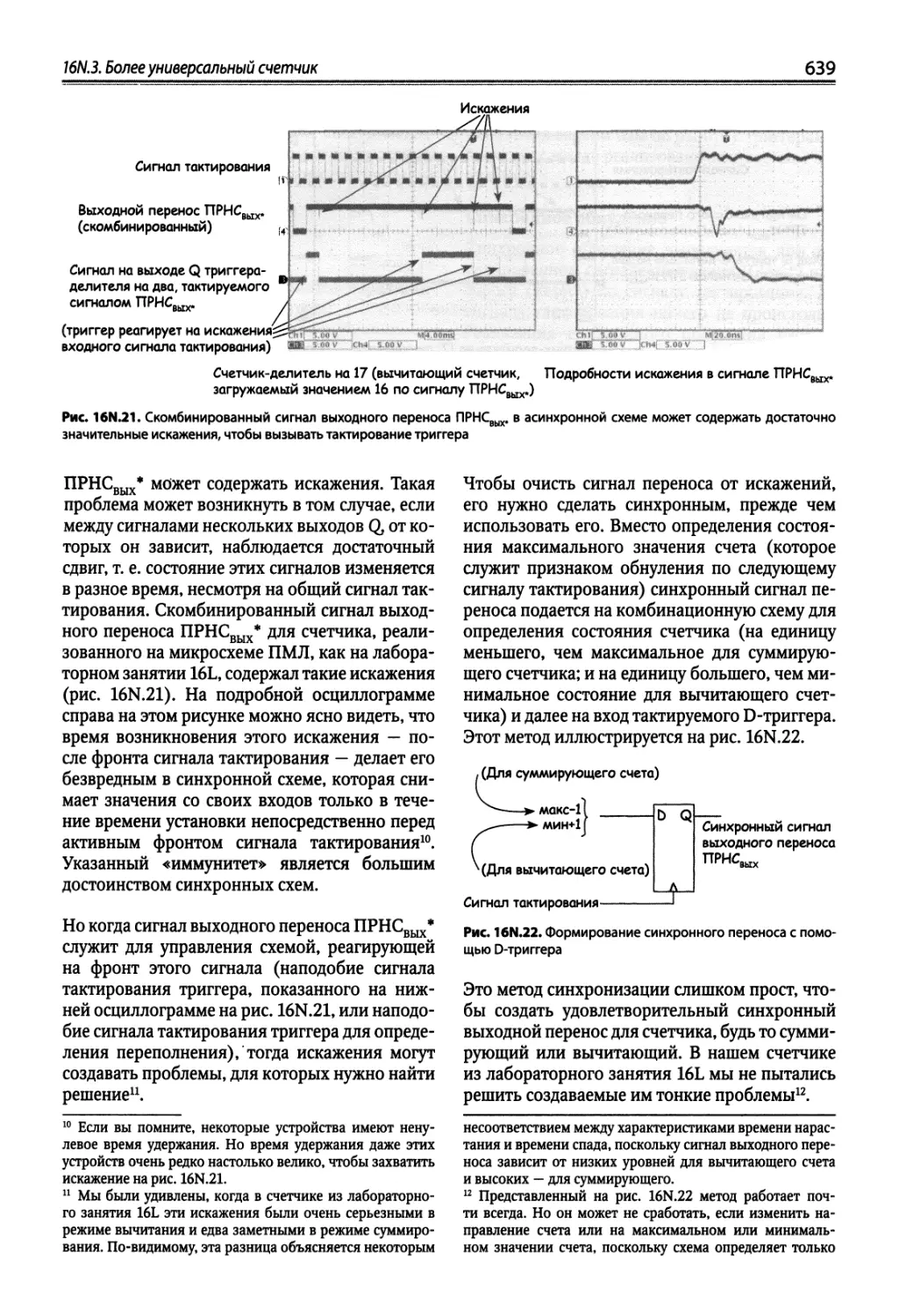
16N.3. Более универсальный счетчик 636
16N.4. Выводы относительно функций счетчиков 640
16N.5. Счетчик-делитель на N из лабораторного занятия 16L 641
16N.6. Счет как стратегия проектирования цифровых схем 642
16L Лабораторное занятие: счетчики .•.••••.•••.•.•..•••••.•••.•.••••..•.•..••••••.•.••...•••••••644
16L1. Два пути к микроконтроллерам ~ 644
16L2. Лабораторное занятие по счетчикам 647
1 б Содержание
16L.3.16-разрядный счетчик 648
16L4. Создаем ужасную музыку „ 657
16L5. Применение счетчика: секундомер * .'. 659
16W Примеры с решениями: применения счетчиков...................................662
16W.1. Счетчики с необычными модулями „ 662
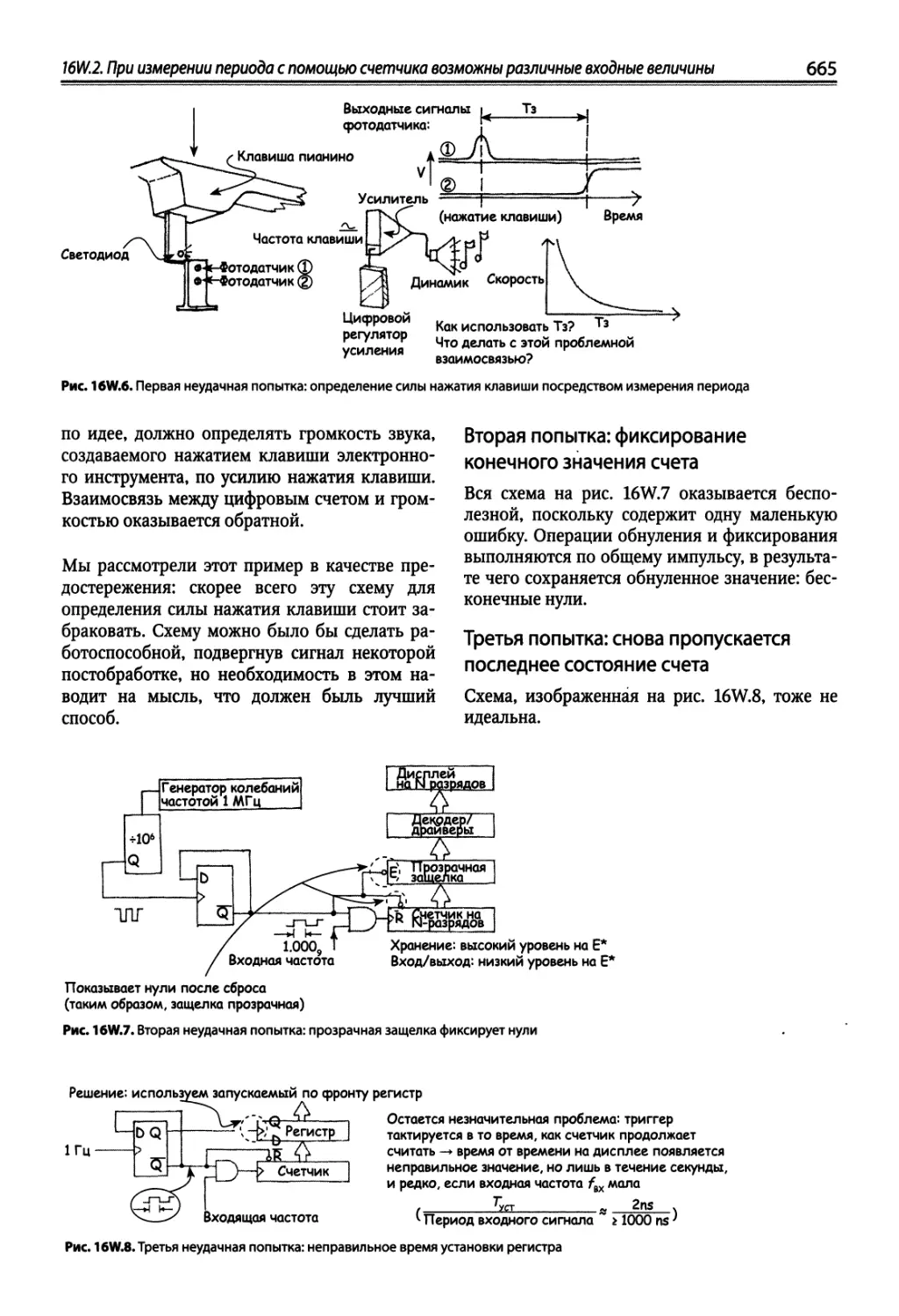
16W.2. При измерении периода с помощью счетчика возможны различные входные величины 664
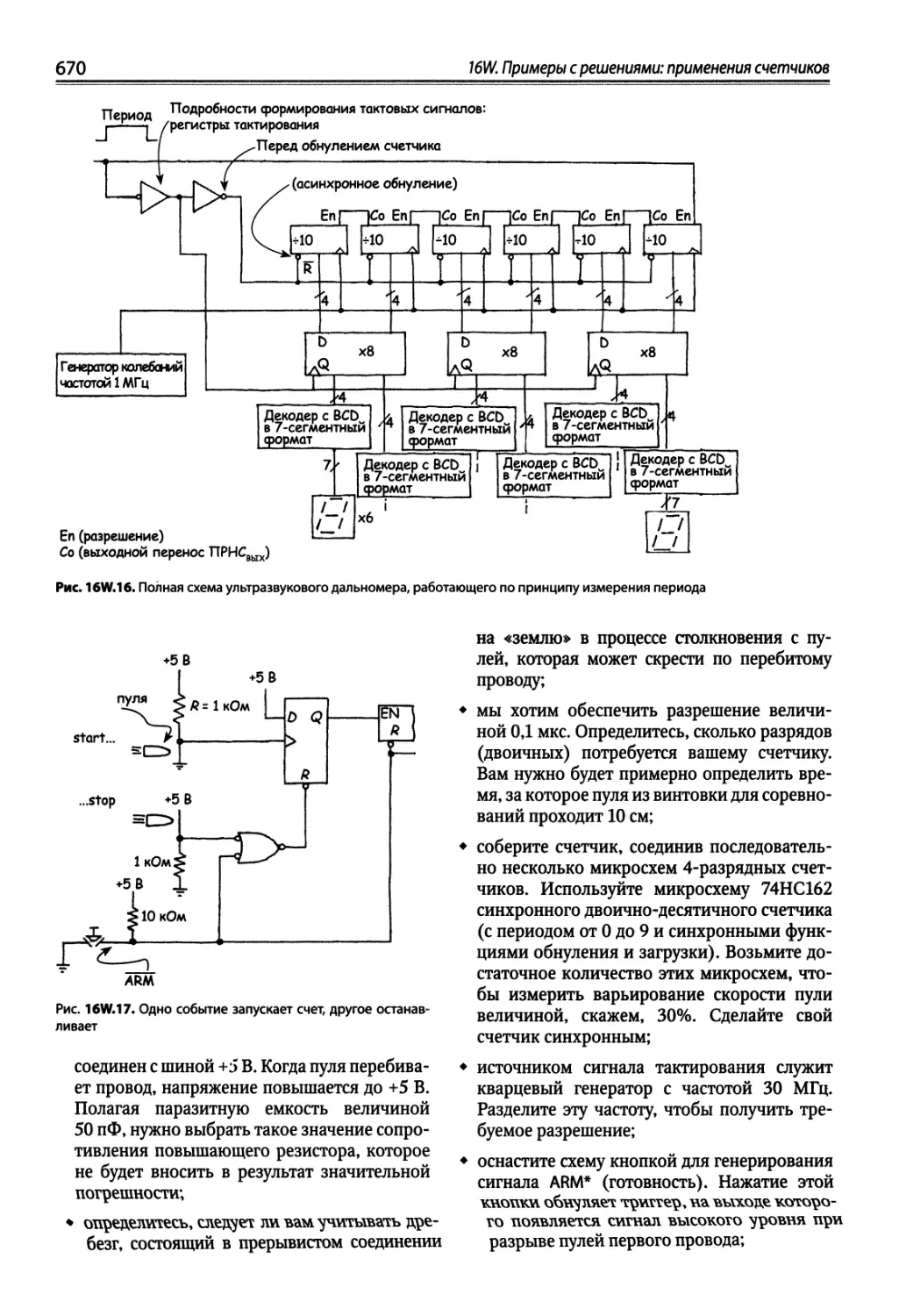
16W.3. Измеритель скорости пули « 669
17N
17Ы.1.Шины 675
17N.2. Память 678
17N3. Конечный автомат: новое название старого устройства 683
17L Лабораторное занятие: память......................................................,...,......689
17L1. Память RAM „ . „„ 690
17L2. Конечные автоматы 691
17L3. Создание конечного автомата с помощью программирования микросхемы
ПМЛ логическим компилятором Verilog... 698
17S Дополнительный материал: диагностика цифровых схем
и декодирование одресов•»•••§••••»••••••••••••••♦>••••••••••••<•••••♦•••••»••>—»••••»•»«#•>»#>/\м\з
17S.1. Советы по диагностированию цифровых схем i 700
17S.2. Декодирование адресов 705
17W Примеры с решениями: память........................................ 708
17W.1. Цифровая последовательностная схема управления замком -. 708
17W.2. Решения 710
Часть V. Цифровые устройства: АЦП, ЦАП, ФАПЧ 717
18N Аналоговые и цифровые преобразования; ФАПЧ 719
T8N.1. Сопряжение устройств разных логических семейств 719
18N.2. Общие сведения о цифроаналоговых и обратных преобразованиях 723
18N.3. Методы цифро-аналоговых преобразований 728
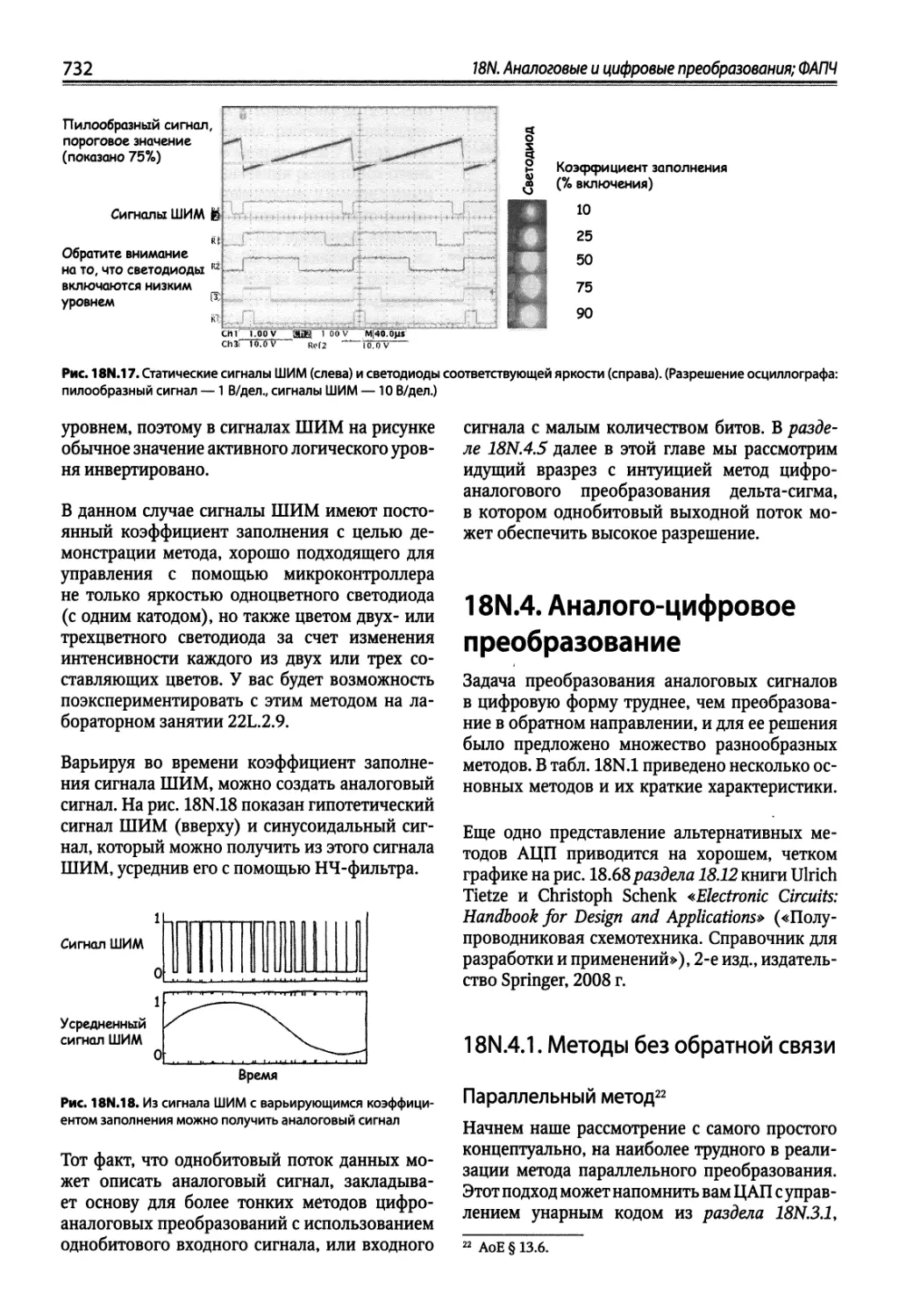
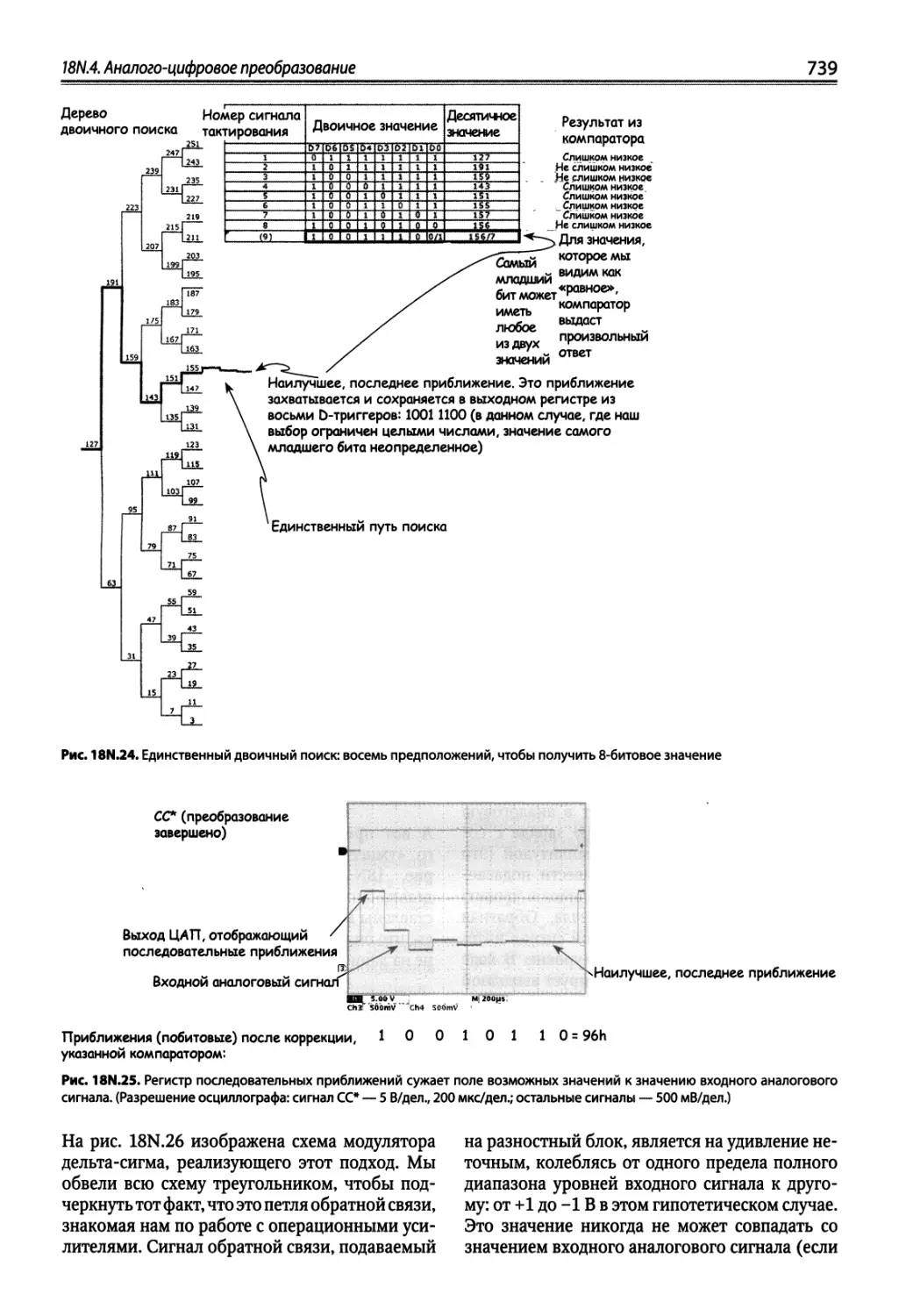
18N.4. Аналого-цифровое преобразование 732
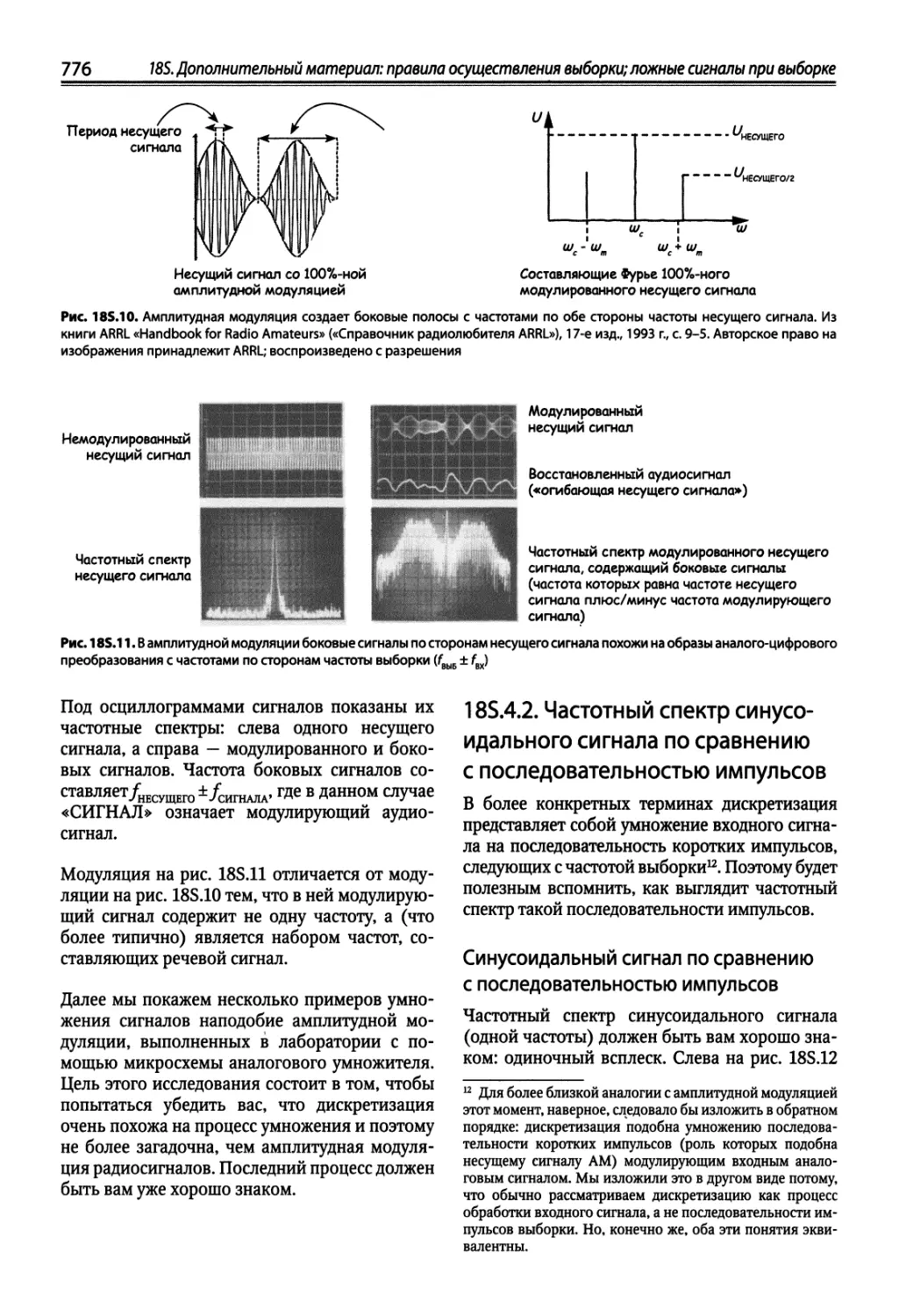
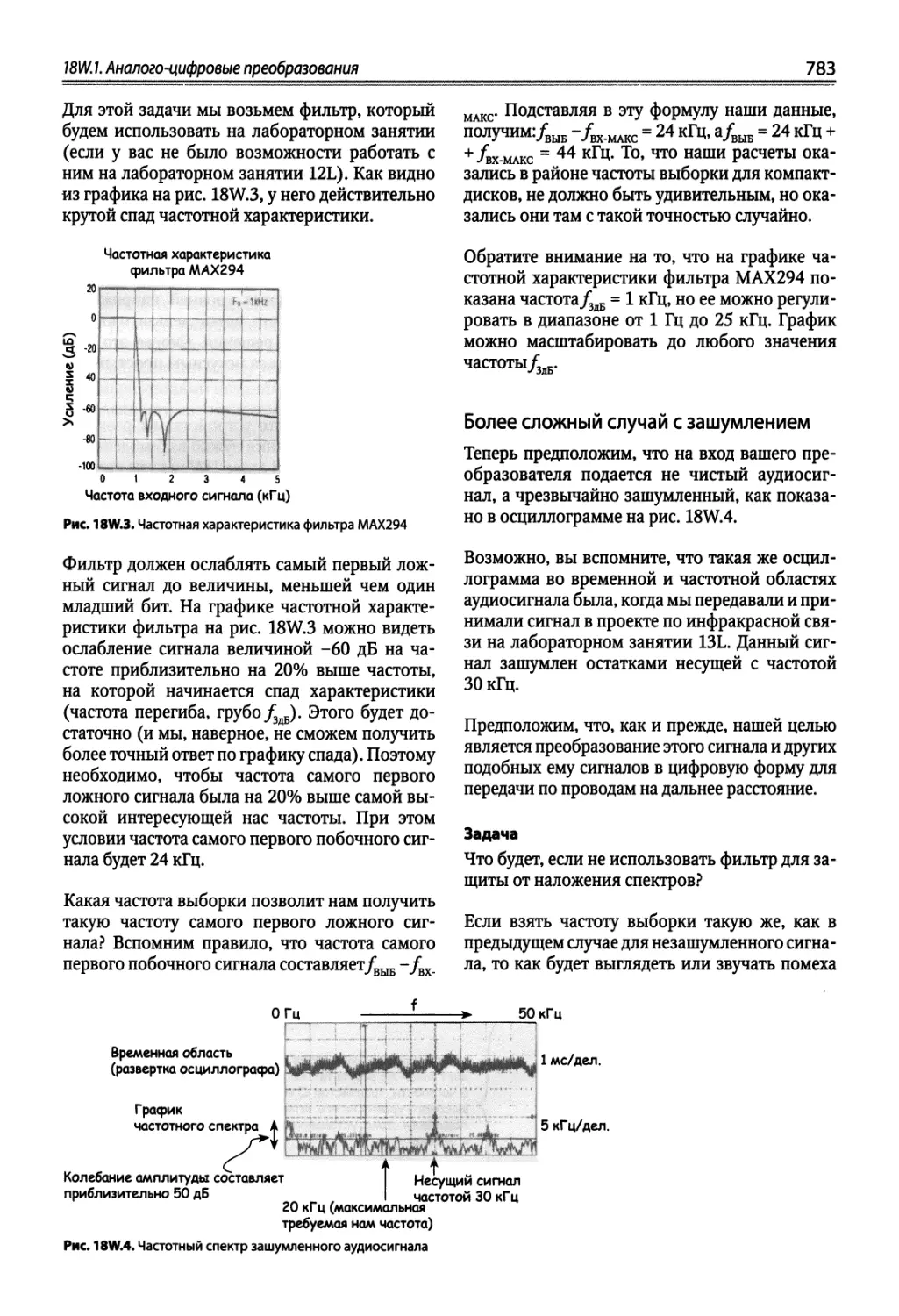
18N.5. Ложные сигналы в процессе выборки 745
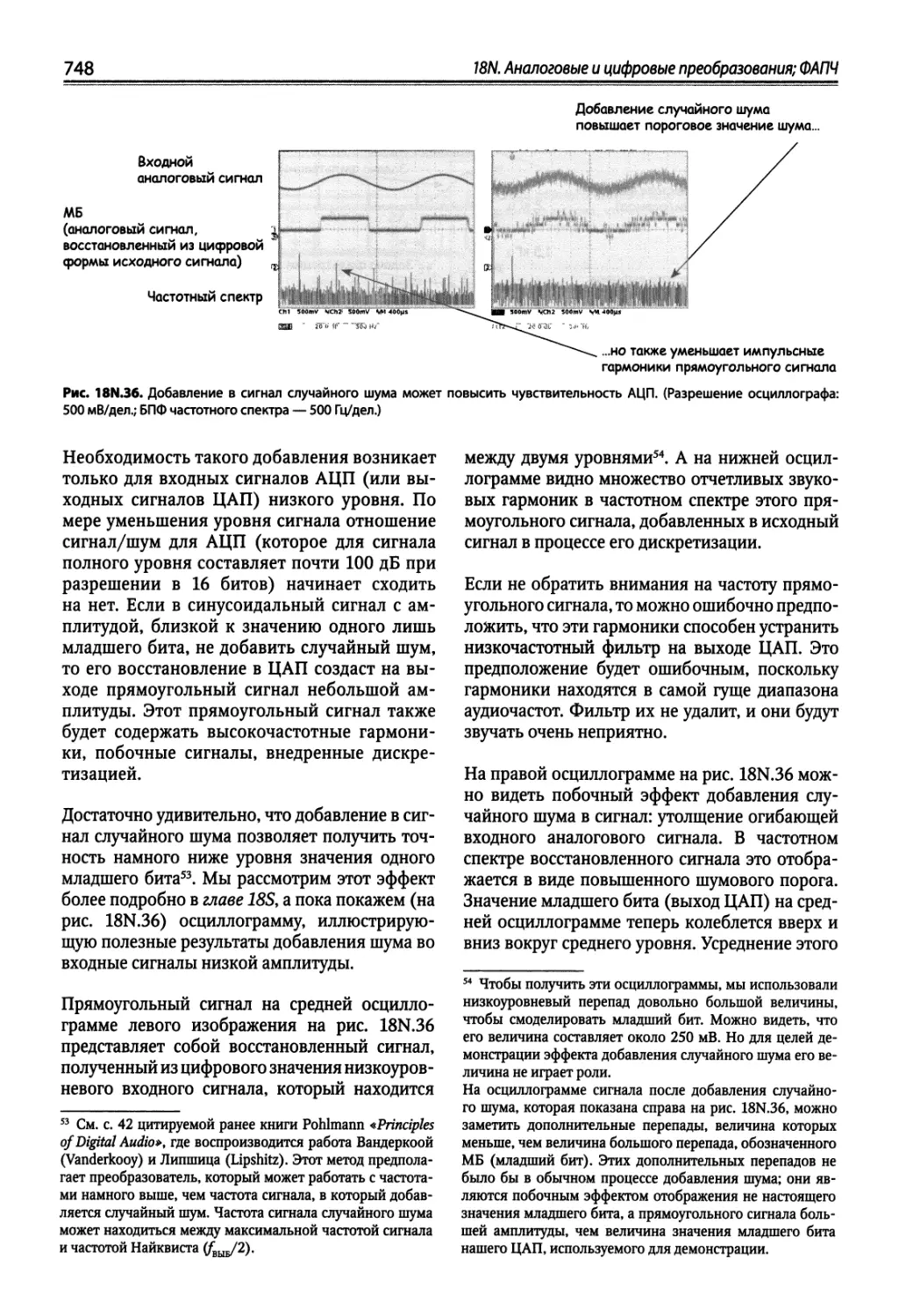
18N.6. Добавление случайного шума 747
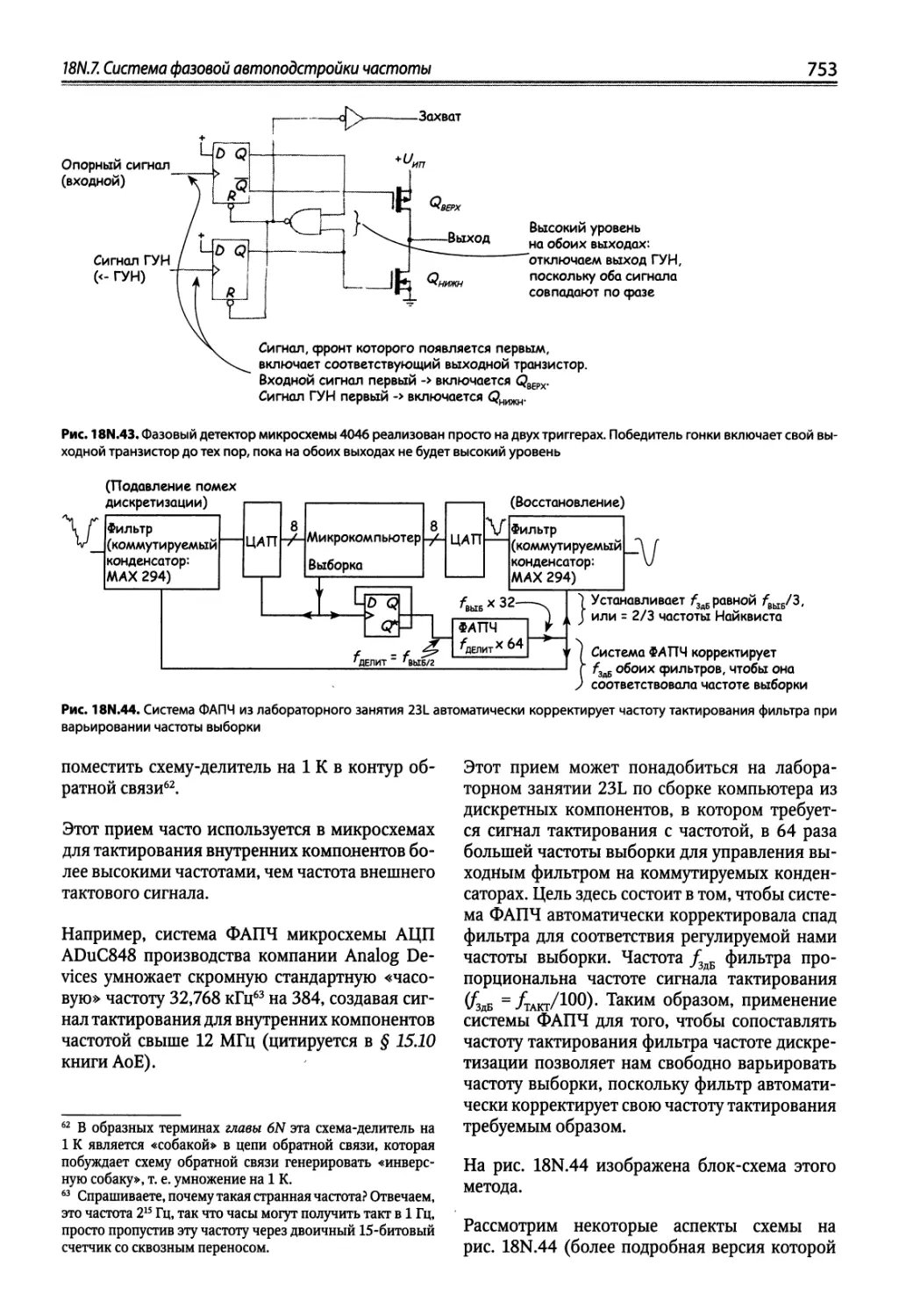
18N.7. Система фазовой автоподстройки частоты 749
18N.8. Материал для чтения в АоЕ 756
18L Лабораторное занятие: аналоговые и цифровые
преобразования; ФАПЧ 757
18L1. Аналого-цифровой преобразователь 757
18L.2. Система фазовой автоподстройки частоты: умножитель частоты 763
18S Дополнительный материал: правила осуществления выборки;
ложные сигналы при выборке 769
185.1. Содержимое этой главы 769
18S.2. Дискретизация создает предсказуемые ложные сигналы 769
185.3. Примеры побочных сигналов во временной и частотной областях 770
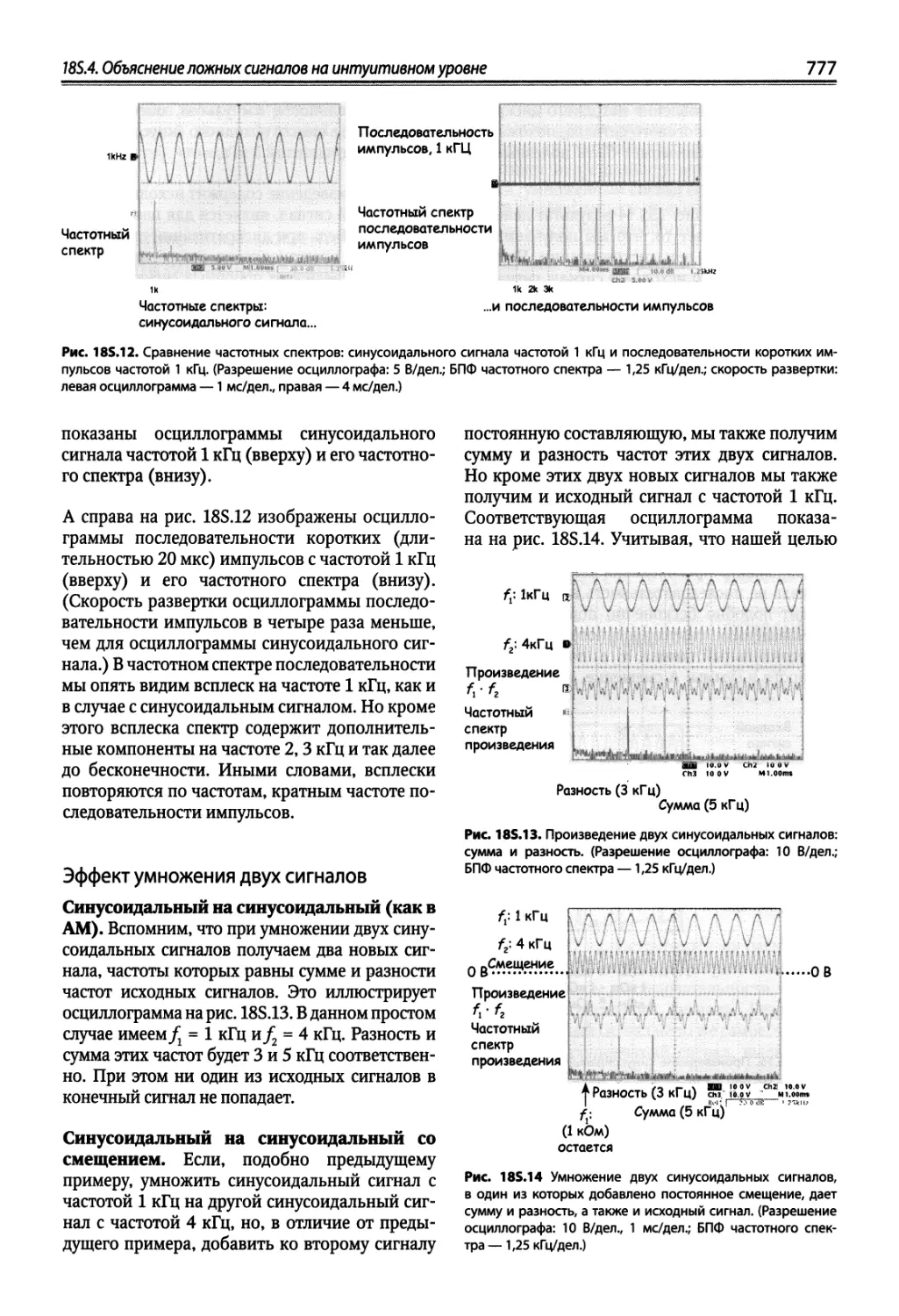
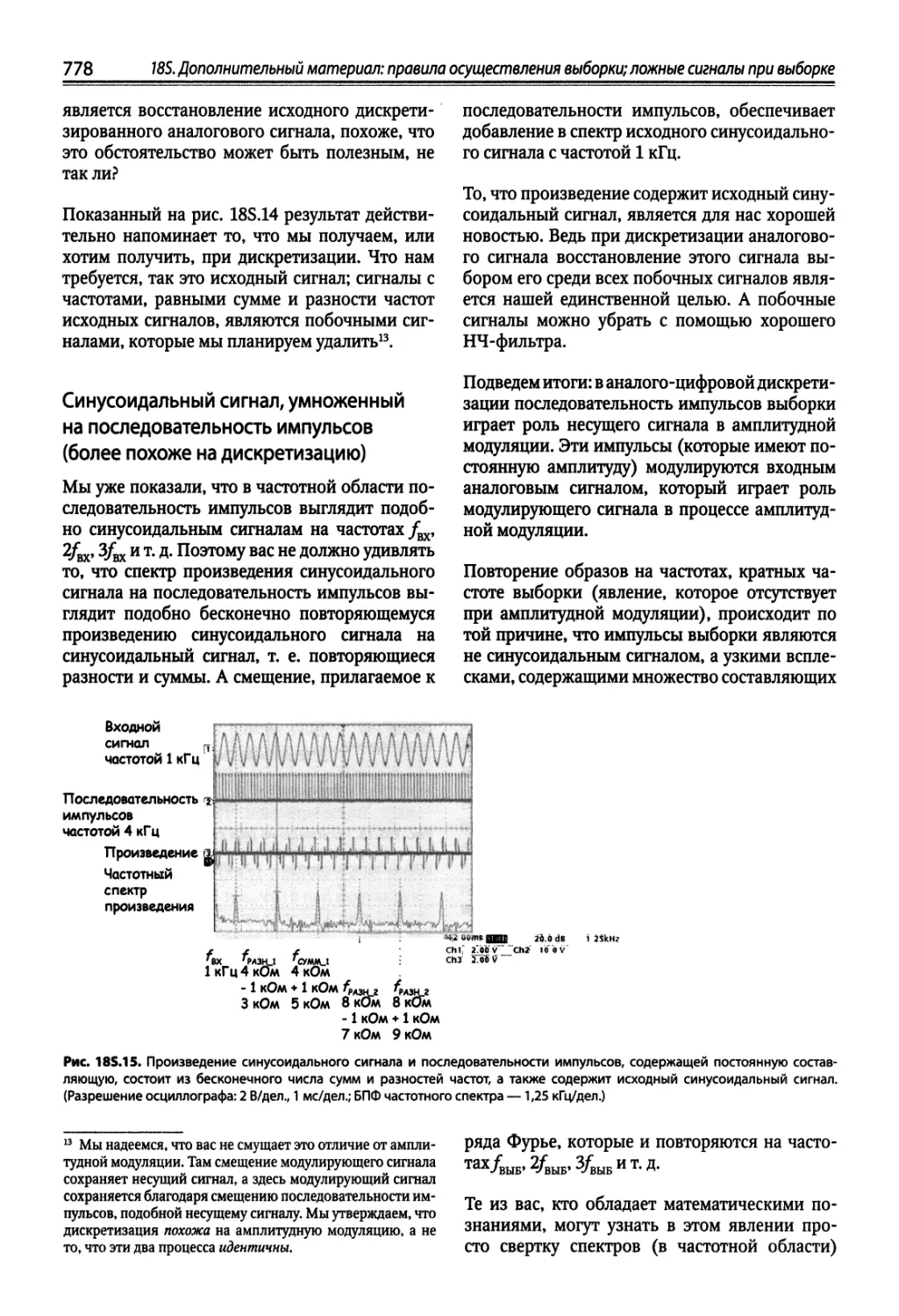
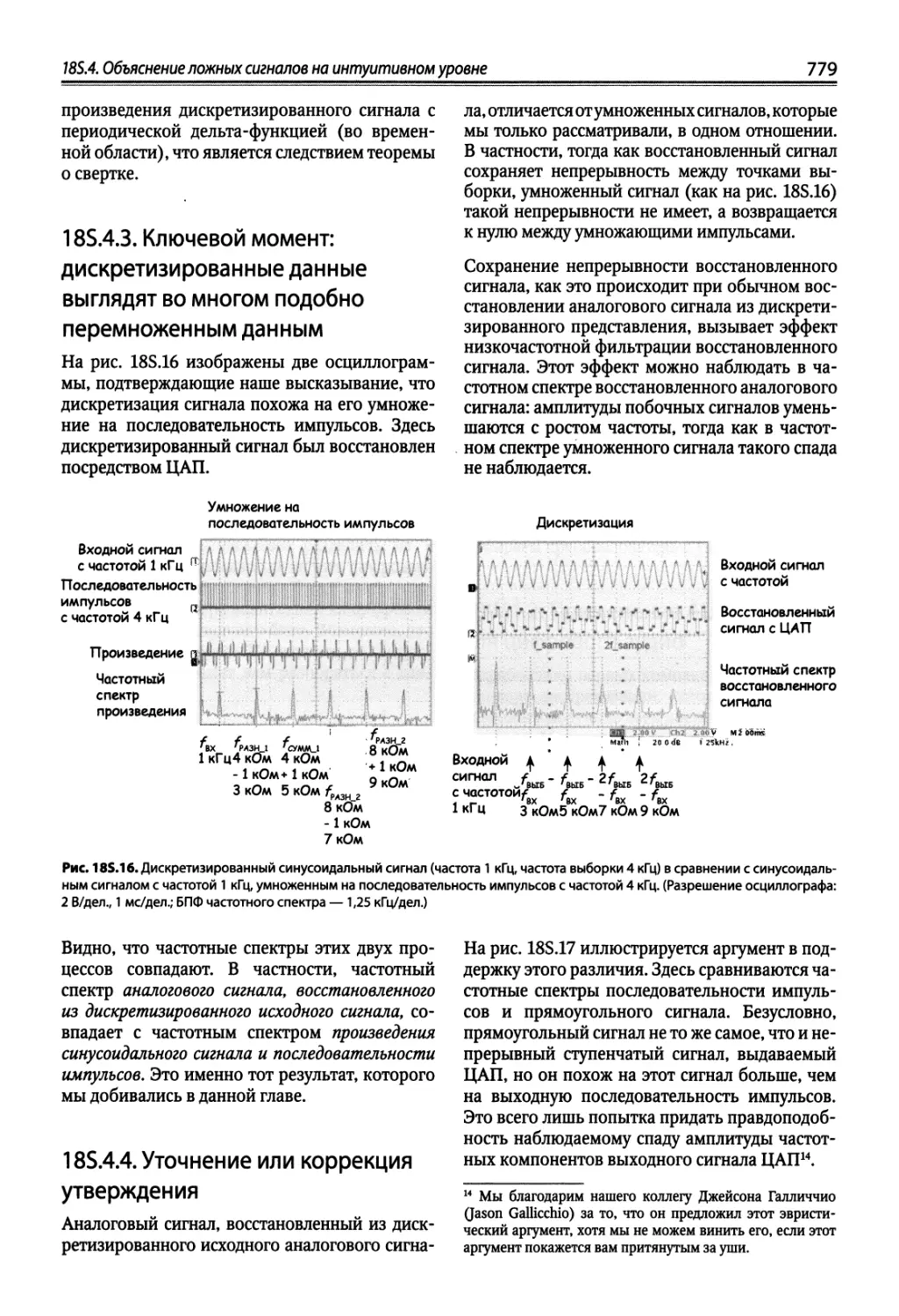
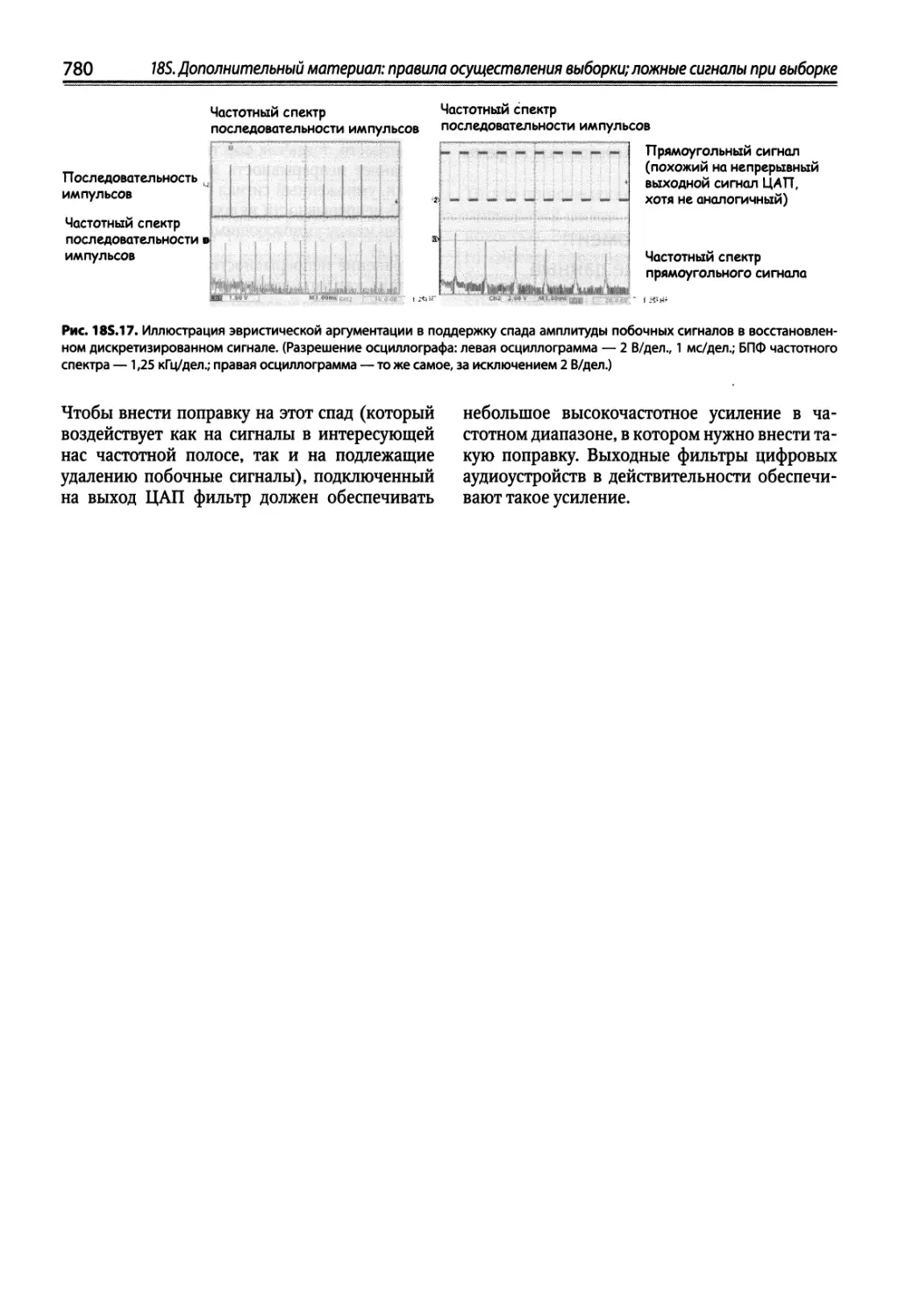
185.4. Объяснение ложных сигналов на интуитивном уровне 774
Содержание 17
18W Примеры с решениями: аналоговые и цифровые
преобразования ••••••••••••• 781
18W.1. Аналого-цифровые преобразования 781
18W.2. Преобразователь логических уровней 784
19L Лабораторное занятие по цифровым схемам 786
19L.1. Цифровой проект 786
Часть VI. Микроконтроллеры 791
20N Микропроцессоры I 793
20N.1. Основные сведения о микрокомпьютерах м 793
20N.2. Минимальные необходимые компоненты компьютера 797
20N.3. Выбор микроконтроллера 799
20N.4. Возможные основания для выбора более трудного пути сборки компьютера
из дискретных компонентов 801
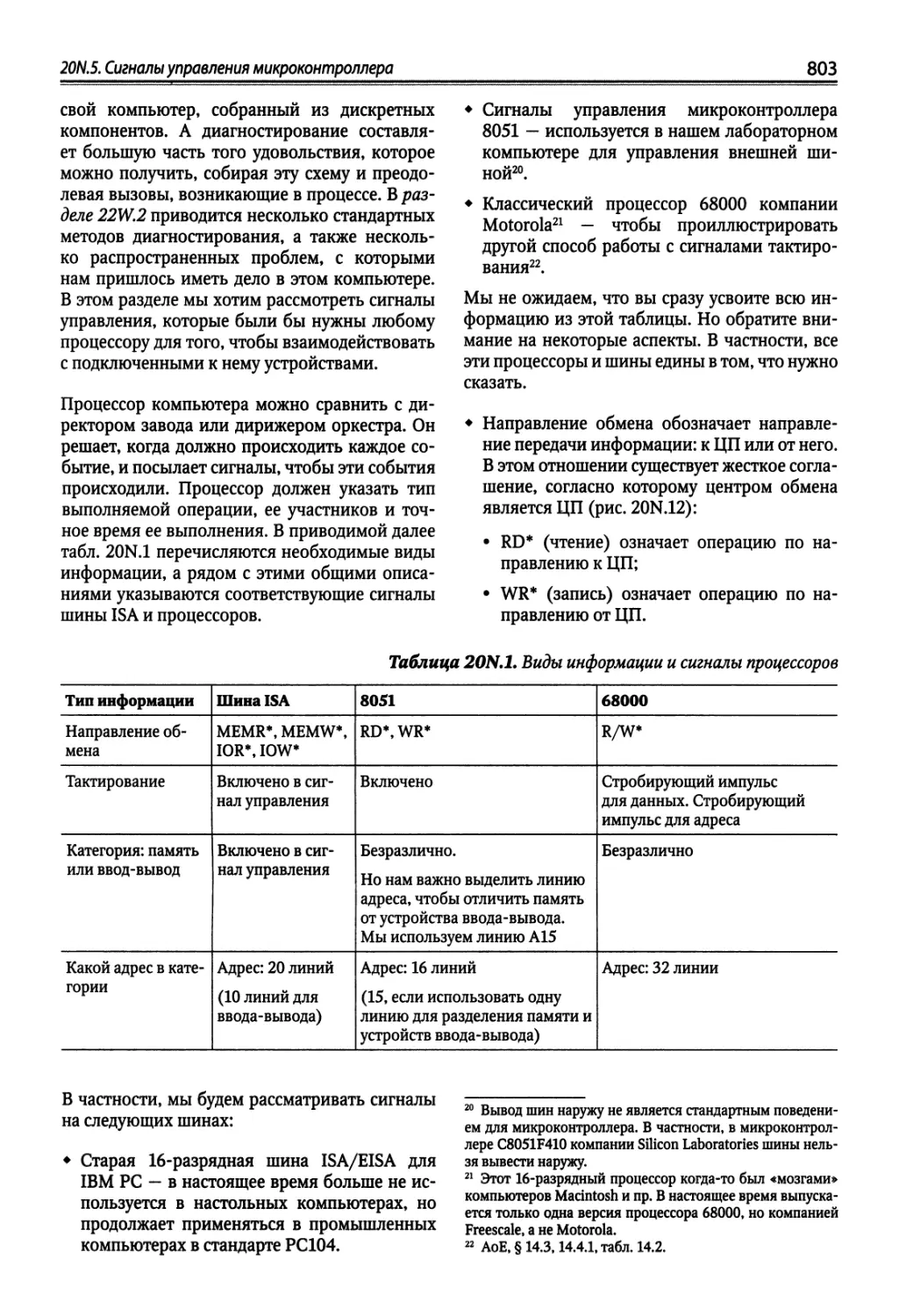
20N.5. Сигналы управления микроконтроллера « 802
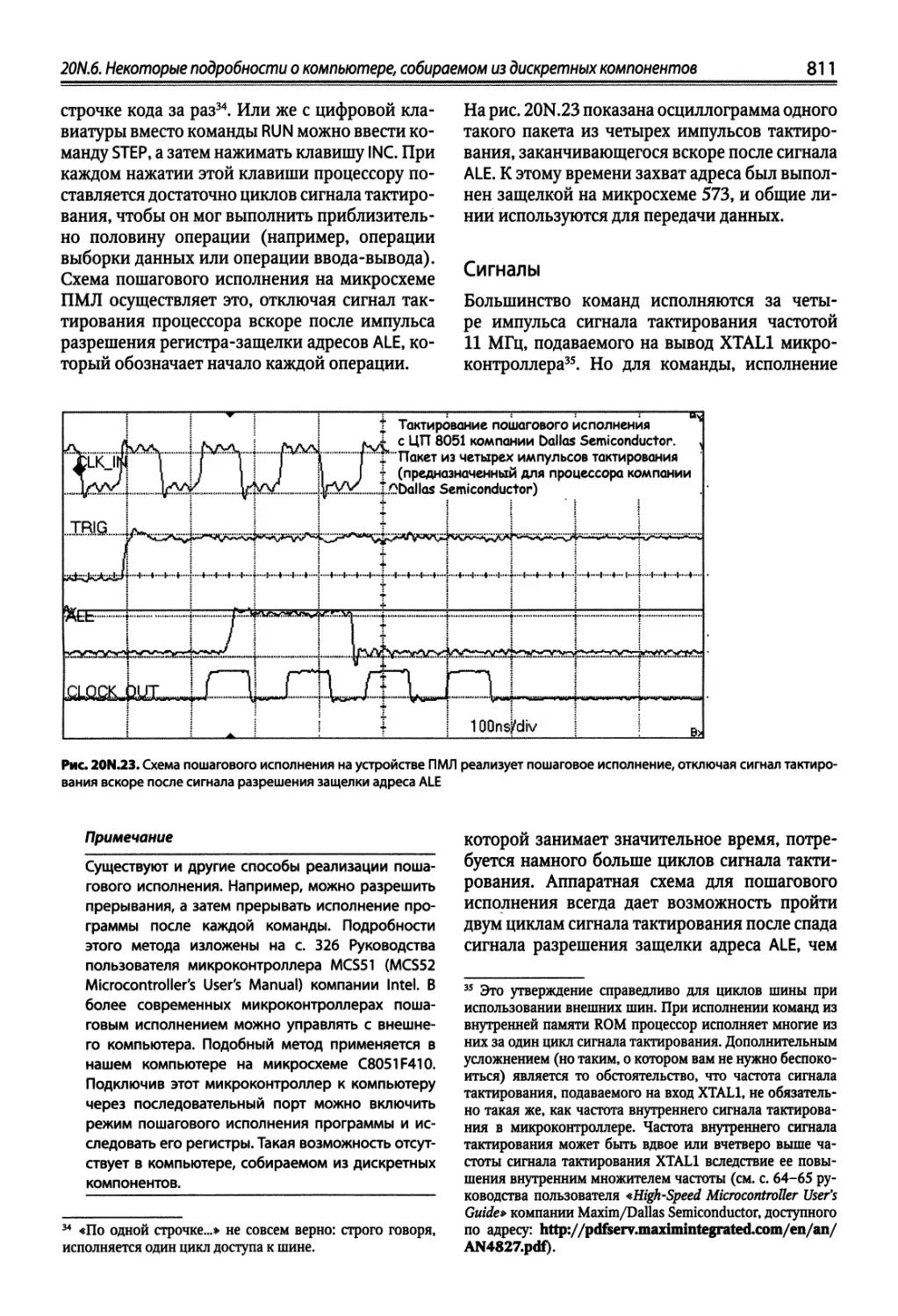
20N.6. Некоторые подробности о компьютере, собираемом из дискретных компонентов 809
20N.7. Первое занятие с компьютером на одной микросхеме 812
20N.8. Материал для чтения из АоЕ 816
20L Лабораторное занятие: микропроцессоры I .818
20L1. Микрокомпьютер из дискретных компонентов 818
20L.2. Устанавливаем GLUEPAL и выполняем частичный монтаж 819
20L.3. Начальный этап пути SiLabs 831
20S Дополнительный материал: микропроцессоры I... 844
205.1. Устройство ПМЛ для микрокомпьютеров ~ 844
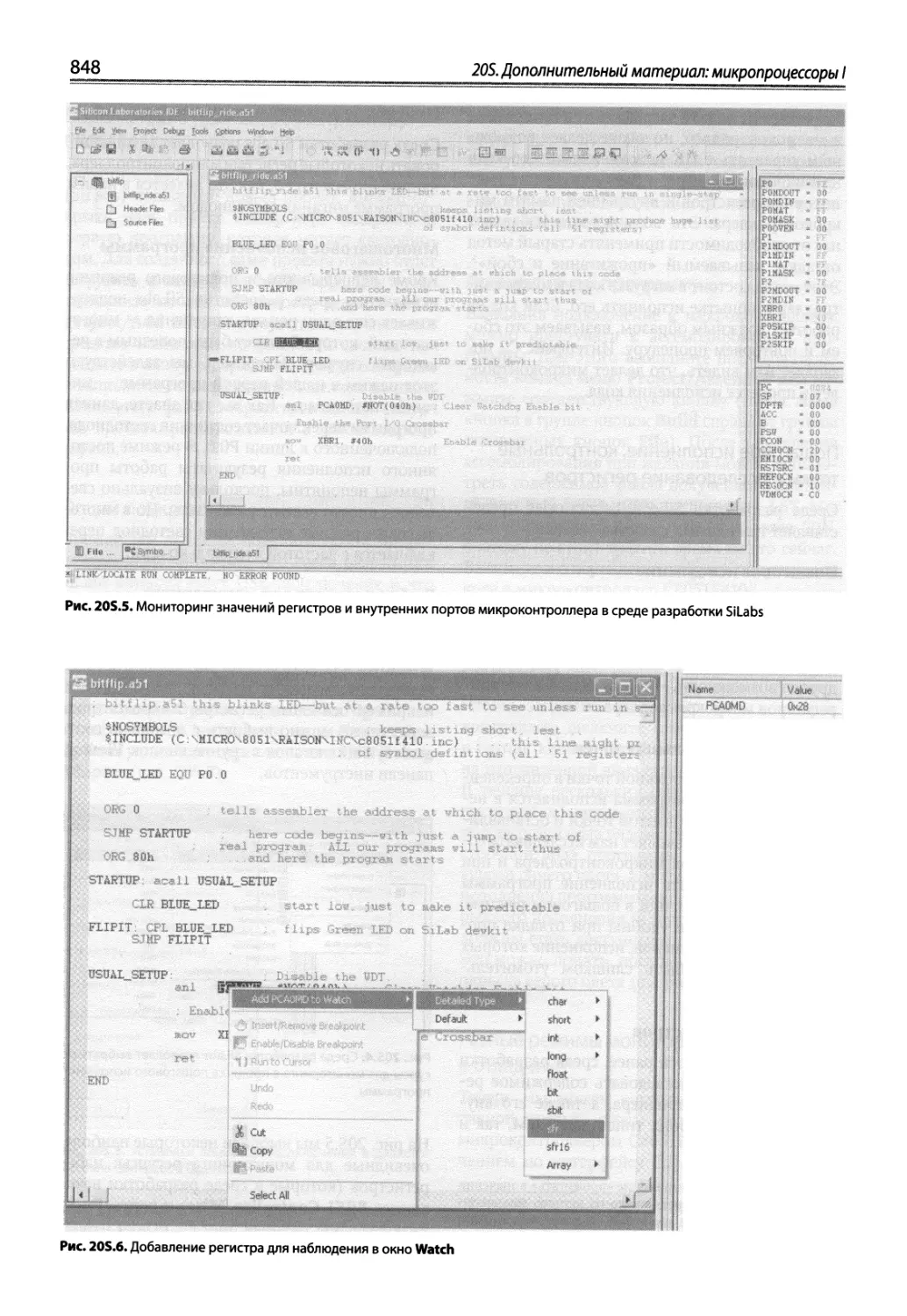
205.2. Примечания о среде разработки Silicon Labs IDE м 845
20W Примеры с решениями: «Инсектарий» 850
Баг № 1. Микроконтроллер отказывается выполнять команды 851
Баг № 2. У нас разногласия с микроконтроллером относительно содержимого RAM 851
Баг № 3. При попытке использовать кнопку Ready происходит фатальный сбой компьютера 852
Баг № 4. При попытке АЦП выложить данные на шину данных возникает конфликт 853
Баг № 5.АЦП работает при пошаговом исполнении программы, но не при непрерывном 853
21N Микропроцессоры II. Ввод-вывод и первая программа
на ассемблере 855
21 N.1. Язык ассемблера и причины для его использования 855
21 N.2. Снова о декодировании 861
21 N.3. Код ввода-вывода для дискретного компьютера 863
21 N.4. Сравнение версий на ассемблере и на языке С программы вывода на дисплей значений,
вводимых с цифровой клавиатуры 866
21 N.5. Вызов подпрограмм 867
21 N.6. Расширение операций до 16 разрядов 871
21 N.7. Материал для чтения из АоЕ 872
18 Содержание
21L Лабораторное занятие: микропроцессоры II .........................................873
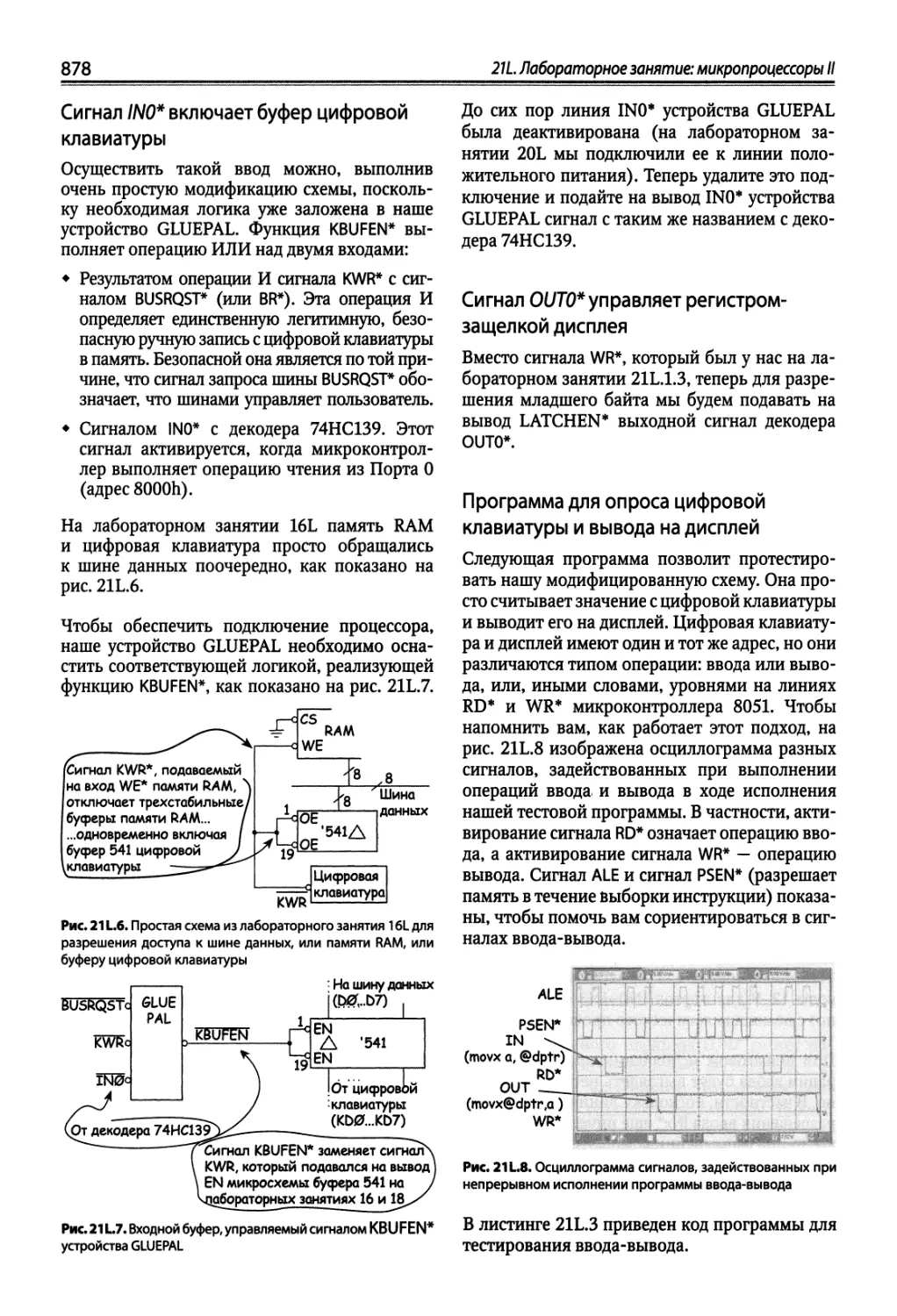
21L1. Ввод-вывод на большом компьютере 873
21L.2. Байтовые операции ввода в малом компьютере. . 887
21S Дополнительный материал: режимы адресации
микроконтроллера 8051.............................................................................901
21 S.1. Знакомство с режимами адресации микроконтроллера 8051 901
21S.2. Некоторые режимы адресации с иллюстрацией «... 912
22N Микропроцессоры III: операции с битами ..............................................914
22N.1. Операции с битами 914
22N.2. Условные переходы 919
22L Лабораторное занятие: микроконтроллеры III.
Операции с битами; таймерыв............^........................,........................,...927
22L.1. Компьютер из дискретных компонентов. Операции с битами; прерывание ~ 927
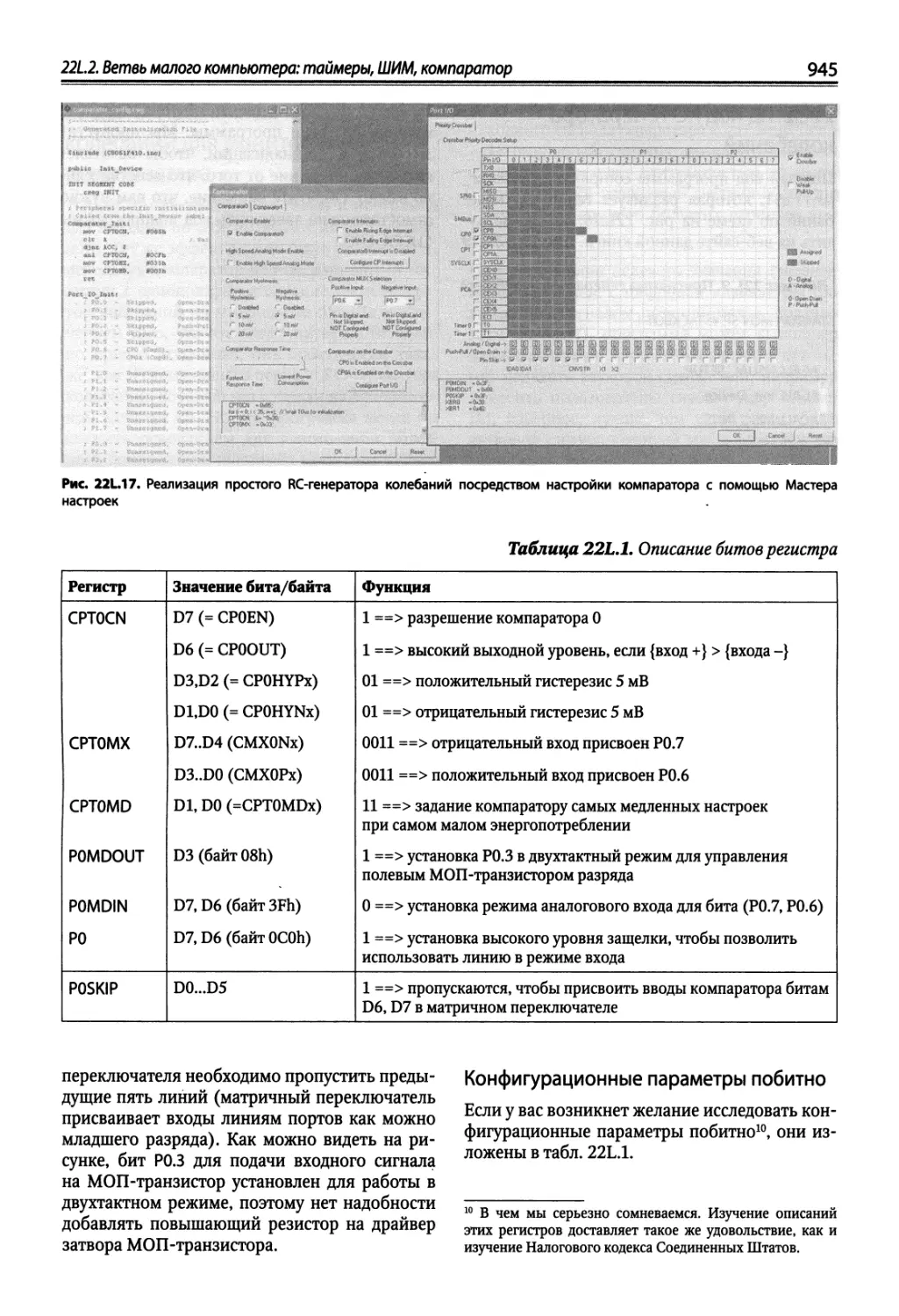
22L2. Ветвь малого компьютера: таймеры, ШИМ, компаратор 933
22W Примеры с решениями. Битовые операции: раздолье ошибок ........949
22W.1. Задача « 949
22W.2. Множество плохих и одно хорошее решение 949
22W.3. Другой способ реализации функции кнопки Ready........................... 952
23N Микропроцессоры IV: прерывания; АЦП и ЦАП....................М..............953
23N.1. Основные моменты ранее рассмотренного материала 953
23N.2. Прерывания м 953
23N.3. Обработка прерываний в языке С 960
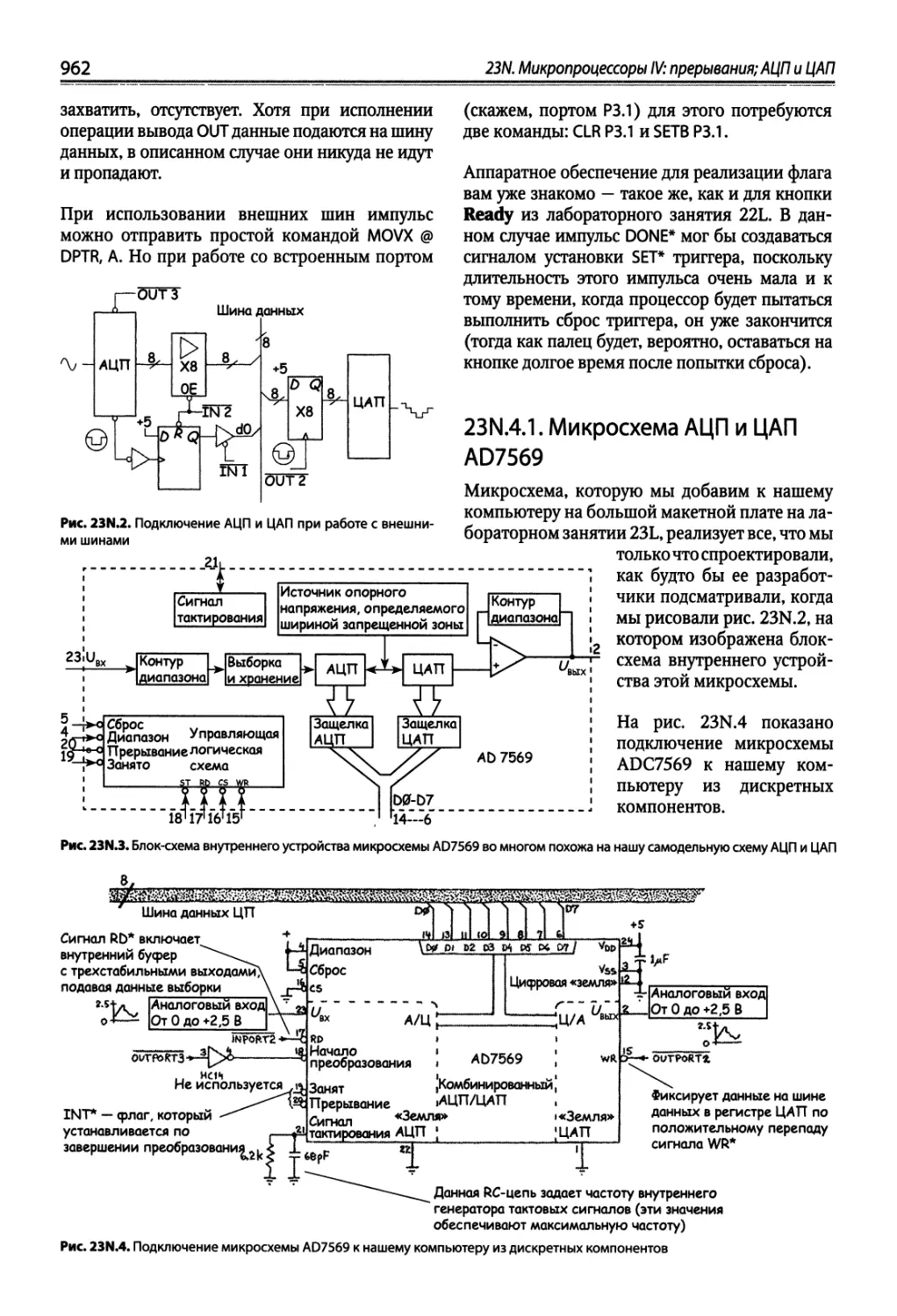
23N.4. Сопряжение АЦП и ЦАП с микроконтроллером 961
23N.5. Некоторые подробности о лабораторных занятиях по АЦП/ЦАП 967
23N.6. Предлагаемые лабораторные задания при экспериментах с АЦП и ЦАП 970
23L Лабораторное занятие: микроконтроллеры 4.
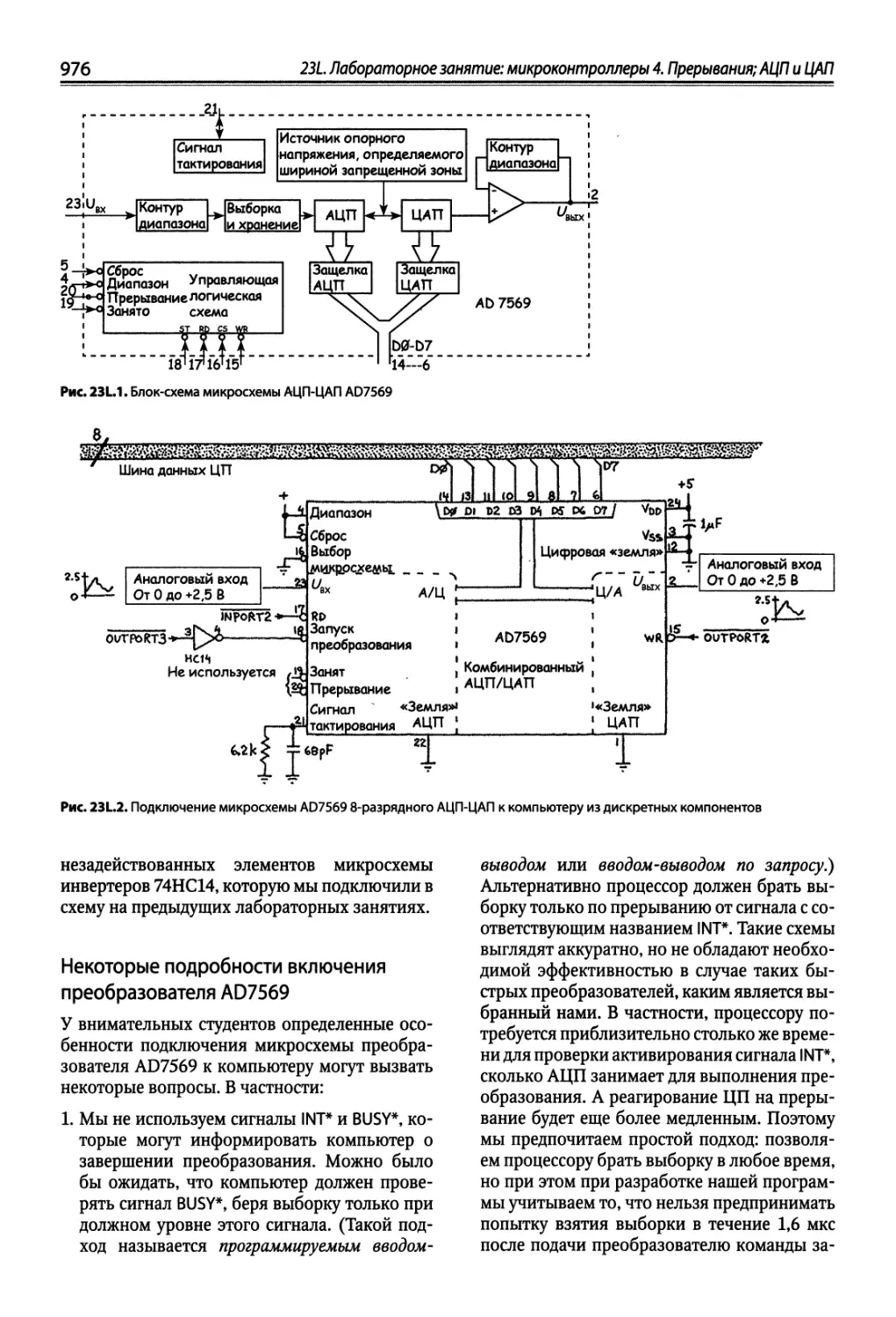
Прерывания; АЦП и ЦАП .•.....•••.•.•••••.••.••.•••...•.........•...••......•••.••.•••...•.•....•..975
23Ы.ЦАПиАЦП 975
23L2. Лабораторное занятие SiLabs 4. Прерывания, АЦП и ЦАП 981
23S Дополнительный материал: микроконтроллеры 4 •...•.•..••.••............•.•.998
235.1. Использование ассемблера/компилятора и симулятора RIDE 998
235.2. Отладка 1003
235.3. Изменение (Ьоомы сигнала 1006
■^ ^"^ ^* ^" ^^f»"1»»» ^»ri« ■■*«#•*■...».....»....«.....»...........................................»........................................«........................... ■ www
24N Микроконтроллеры V. Перемещение указателей,
последовательные шины ........................................... 1010
24N.1. Перемещение указателей 1010
24N.2. Регистр DPTR также может быть полезным и для микроконтроллера С8051F410 1015
24N.3. Определение достижения конца таблицы 1015
24N.4. Последовательные шины 1017
24N.5. Материал для чтения в АоЕ 1025
24L Лабораторное занятие: микроконтроллеры V.
Перемещение указателей, последовательные шины....................... 1026
Содержание 19
24L1. Таблица данных, шина SPI, таймеры 1027
24L2. Последовательные шины микроконтроллера C8051F410 1034
Общие сведения о последовательных шинах 1035
Двунаправленный последовательный интерфейс м 1039
24S Дополнительный материал. Загрузчик программ
для микроконтроллеров компании Dallas Semiconductor 1044
245.1. Загрузчик программ « 1044
■»*"■ rJ" '"" "■Г***' f *••»"»" ••••••••• w
245.2. Оборудование 1044
245.3. Два способа использования загрузчика -1045
245.4. Диагностика проблемы с записью во флеш-память программой Loader420 1049
245.5. Диагностирование проблем присвоения порта СОМ 1050
24W. Пример с решениями. Четыре способа копирования таблицы...... 1053
24W.1. Несколько способов скопировать таблицу „ 1053
25N Микроконтроллеры VI. Таблицы данных......... 1056
25N.1. Устройства ввода и вывода для микроконтроллера 1056
25N.2. Задача для пользователей компьютера из дискретных компонентов:
работа с автономным микроконтроллером 1058
25N.3. Задача для пользователей компьютера на основе автономного микроконтроллера:
использование внешней памяти RAM 1059
25L Лабораторное занятие: микроконтроллеры VI.
Автономный микроконтроллер 1062
25L.1. Два способа записи во флеш-память 1062
25L.2. Лабораторное занятие SiLabs6: память RAM с интерфейсом SPI 1068
25L.3. Ссылки на листинги программ 1072
26N Потенциальные проекты. Игрушки на любой вкус .........•........••.••.•.. 1073
26N.1. Еще один микроконтроллер, который может быть вам интересен 1074
26N.2. Проекты: приглашение и предостережение ~ 1076
26N.3. Несколько примеров впечатляющих проектов 1077
26N.4. Несколько других выдающихся проектов 1080
26N.5. Игры 1093
26N.6. Датчики, приводы, другие приспособления 1094
26N.7. Драйвер шагового двигателя 1101
26N.8. Идеи для проектов 1103
26N.9. Две потенциально полезные программы: драйвер ЖКД и сканер цифровой клавиатуры.... 1104
26N.10. Множество других примеров в книге АоЕ 1104
26N.11. А теперь вперед, к новым приключениям 1105
ПРИЛОЖЕНИЯ 1107
Приложение А. Язык HDLVerilog..................................................................... 1109
А.1. Проектный файл Verilog «« 1109
А.2. Созданная Verilog схема может пригодиться при отладке 1110
A3. Эмуляционный файл Verilog testbench 1111
А.4. Проверочный файл эмуляции 1114
А.5. Триггеры в Verilog.................... .« - 1115
А.6. Поведенческое и структурное описание схемы 1119
А.7. Verrlog позволяет иерархические проекты 1120
20 Содержание
А.8. Счетчик ДДК „ м » 1123
А.9. Два альтернативных способа создания экземпляра субмодуля 1125
А. 10. Конечные автоматы 1125
А.11. Устройство, более подходящее для реализации в виде конечного автомата: арбитр шины.... 1128
А.12. Среда ISE Xilinx предлагает помощь в разработке 1130
А.13. Блокирующие и неблокирующие присваивания 1131
Приложение Б. Работа с логическим компилятором Xilinx 1134
Б.1. Краткий обзор Xilinx, Verilog и ABEL 1134
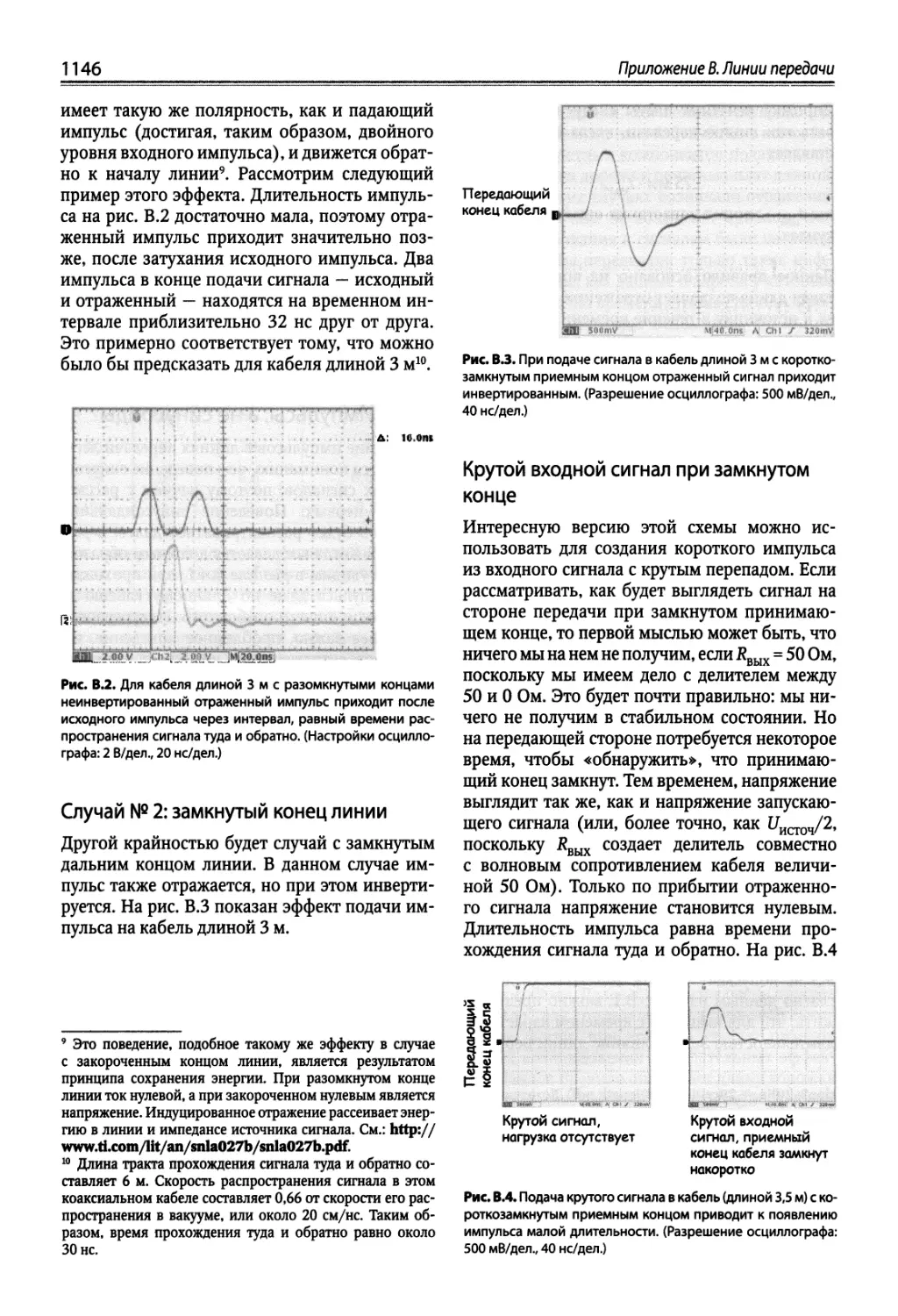
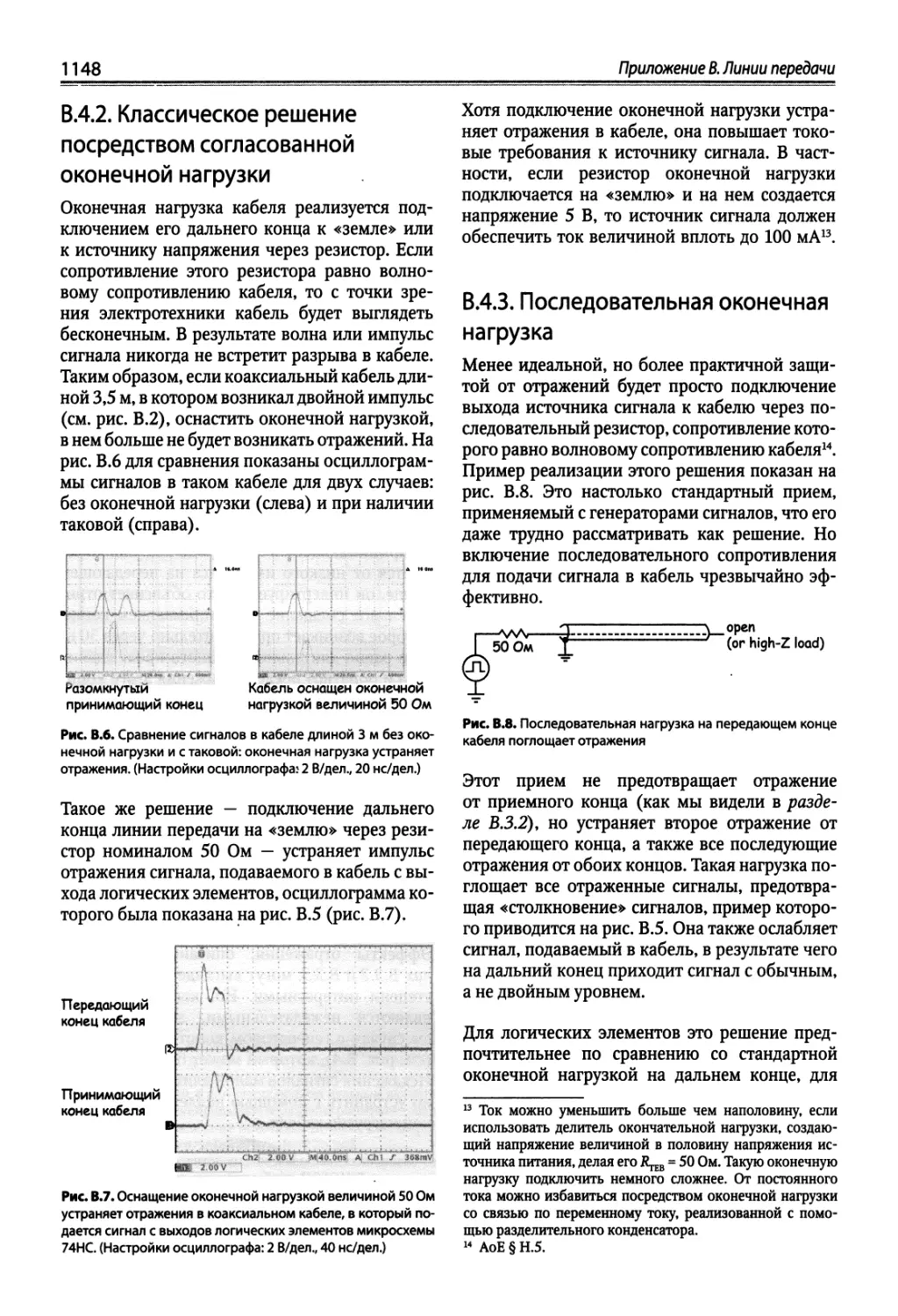
Приложение В. Линии передачи....................... 1142
8.1. Тема, от которой мы до сих пор уклонялись 1142
8.2. Линия передачи 1143
8.3. Отражения ." 1145
B.4. Почему мы беспокоимся об отражениях? 1147
В.5. Влияние линии передачи для синусоидальных сигналов 1150
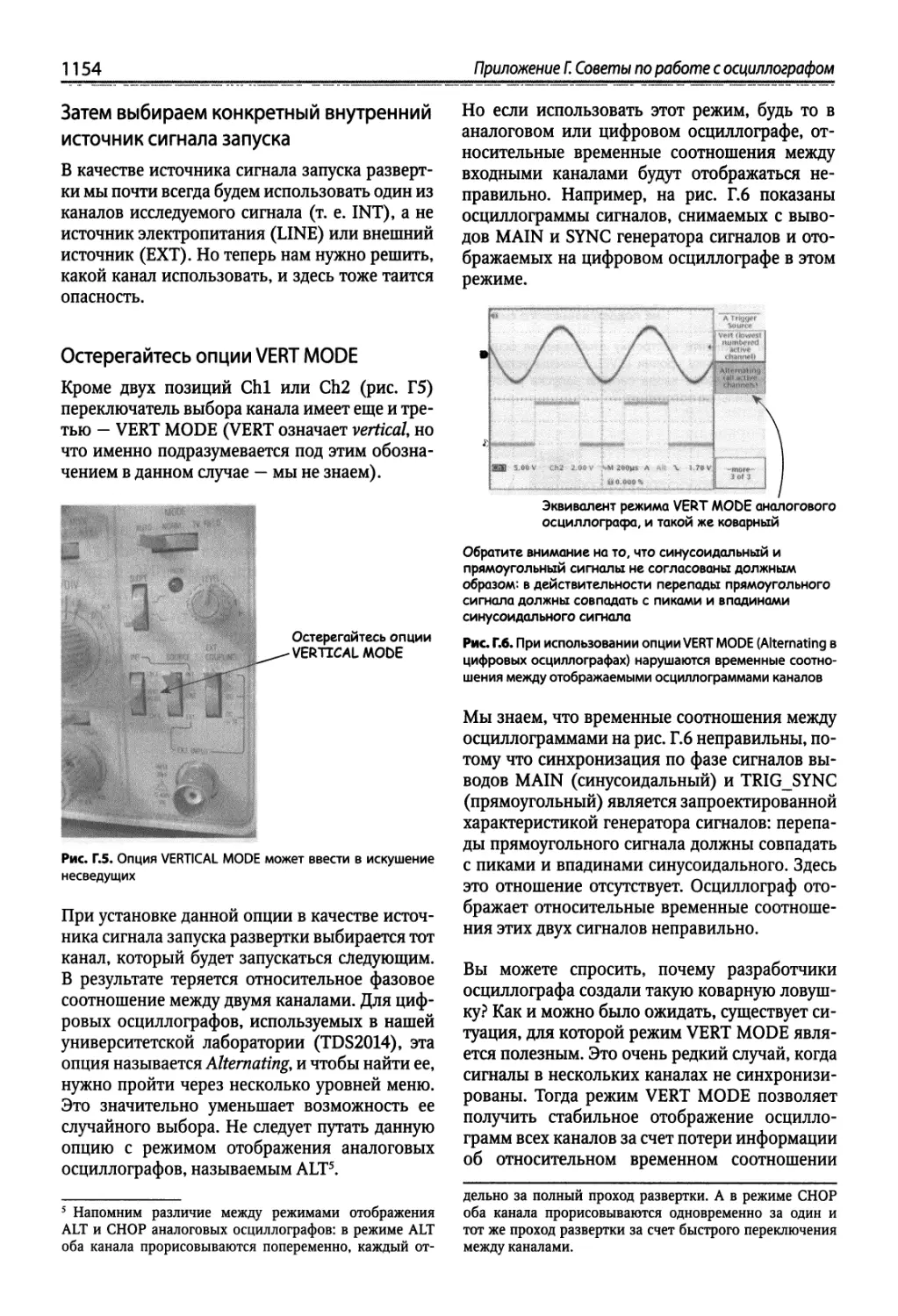
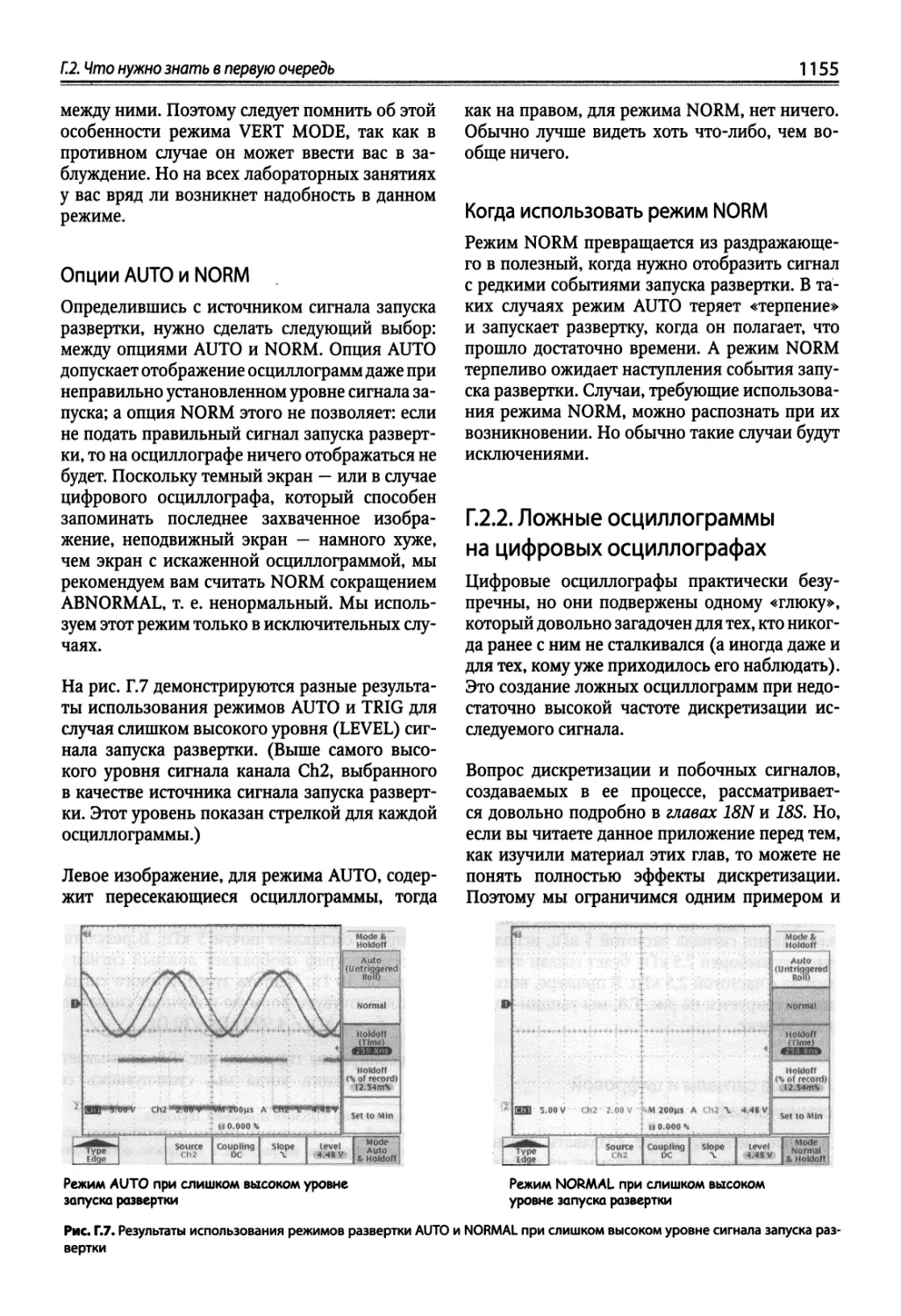
Приложение Г. Советы по работе с осциллографом .................................... 1152
Г.1. Что не следует делать 1152
. . w . .<«. w.4.^%.. n<w •«•№»< ^т.
Г.2. Что нужно знать в первую очередь.. ~ 1152
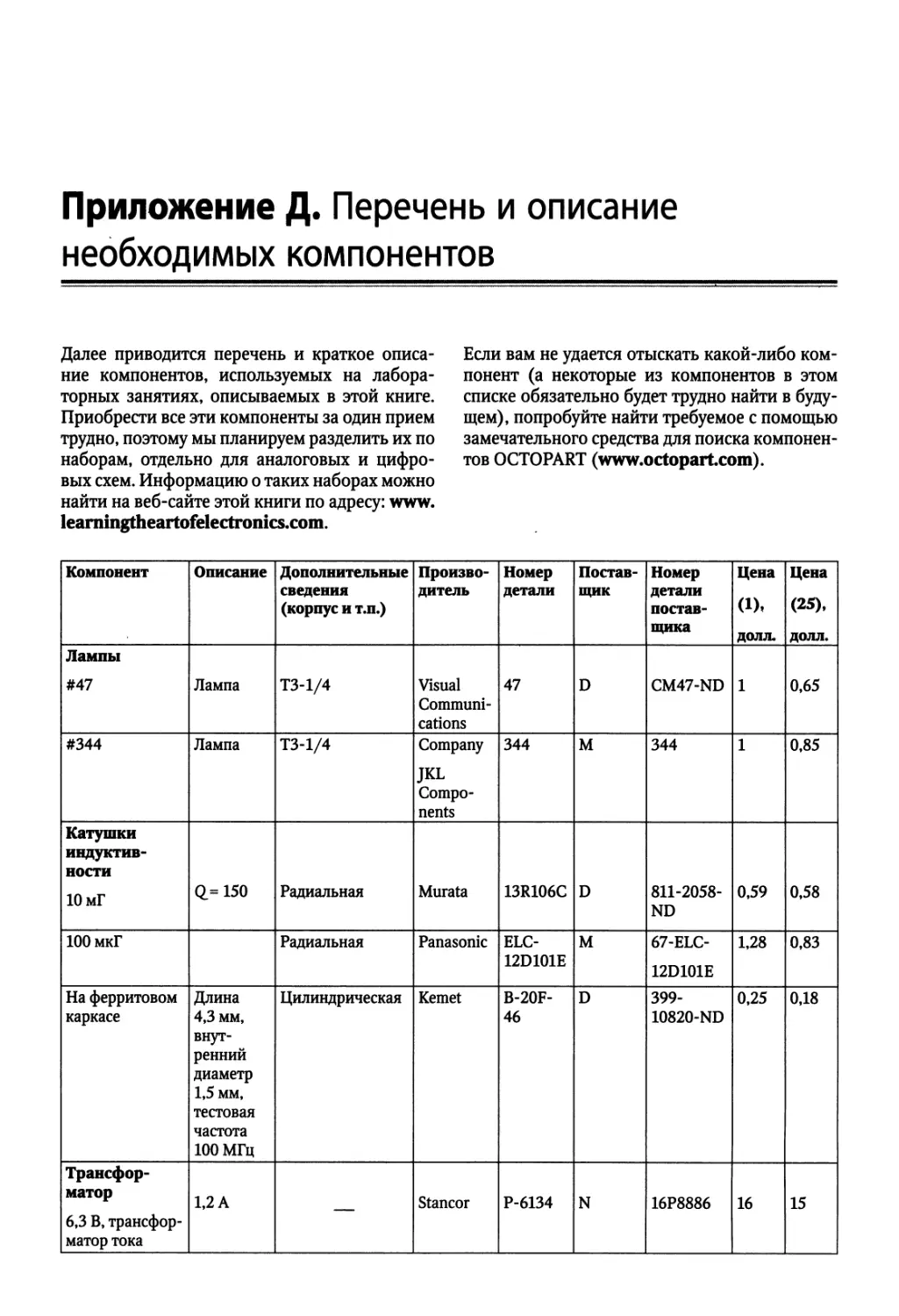
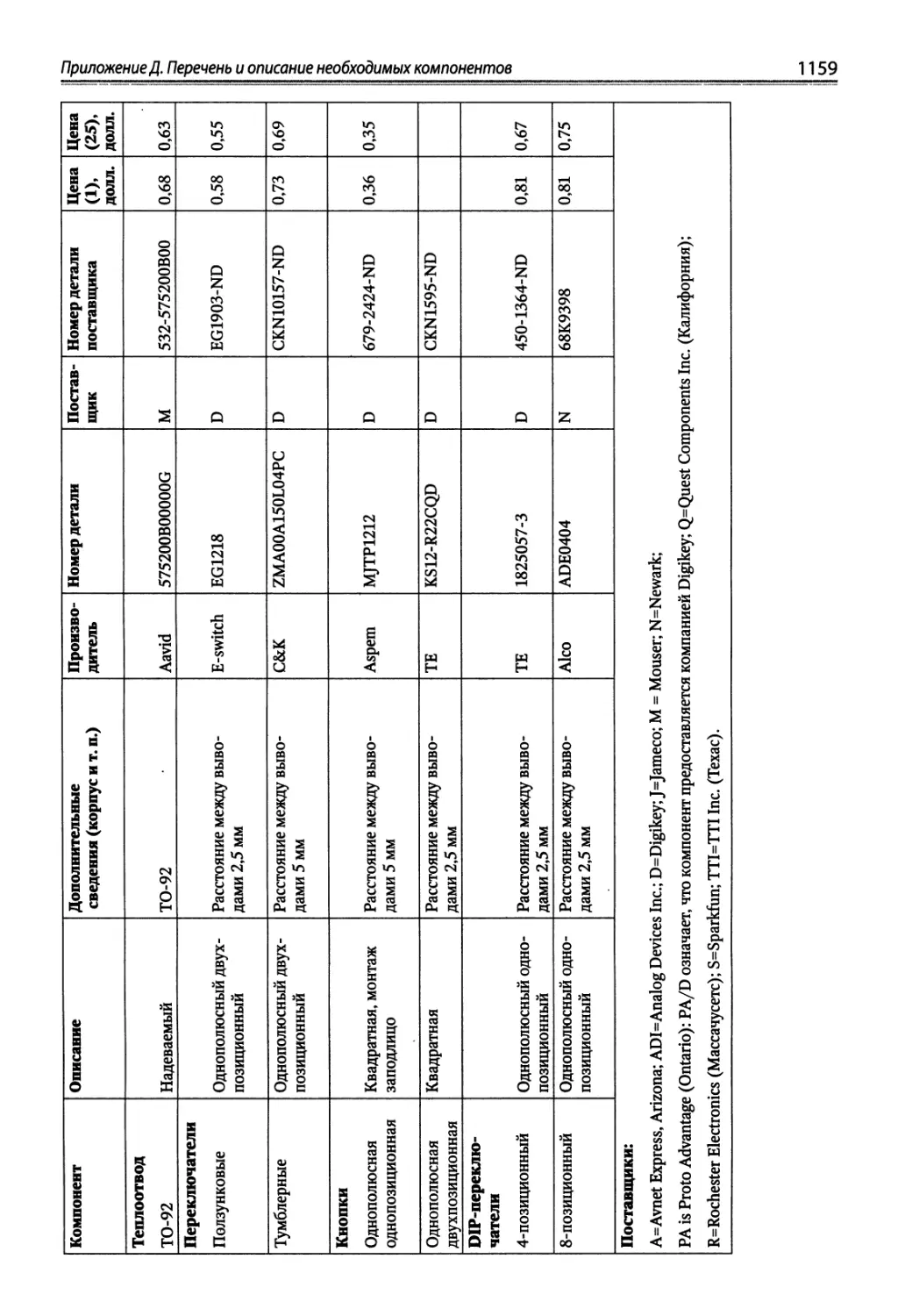
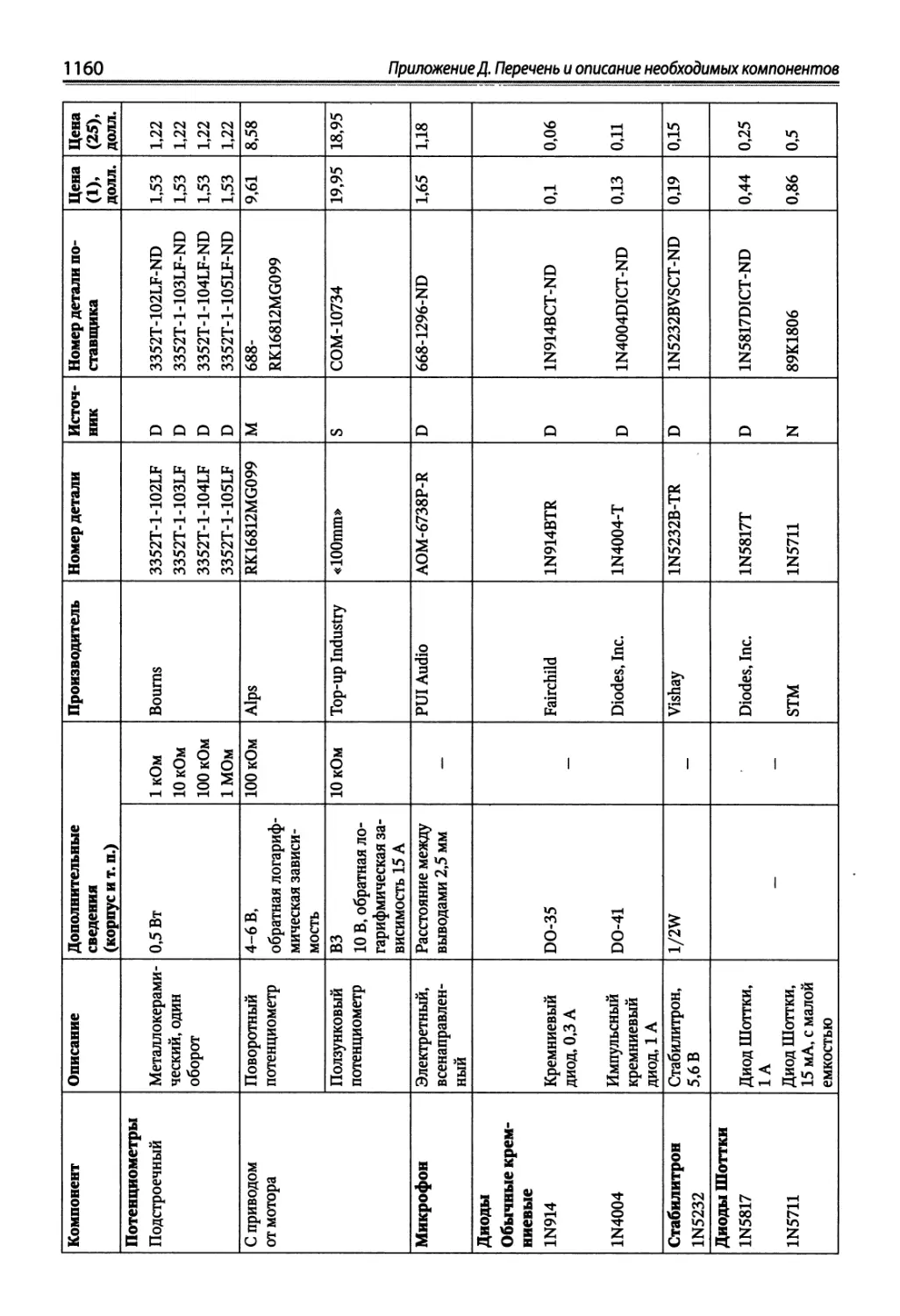
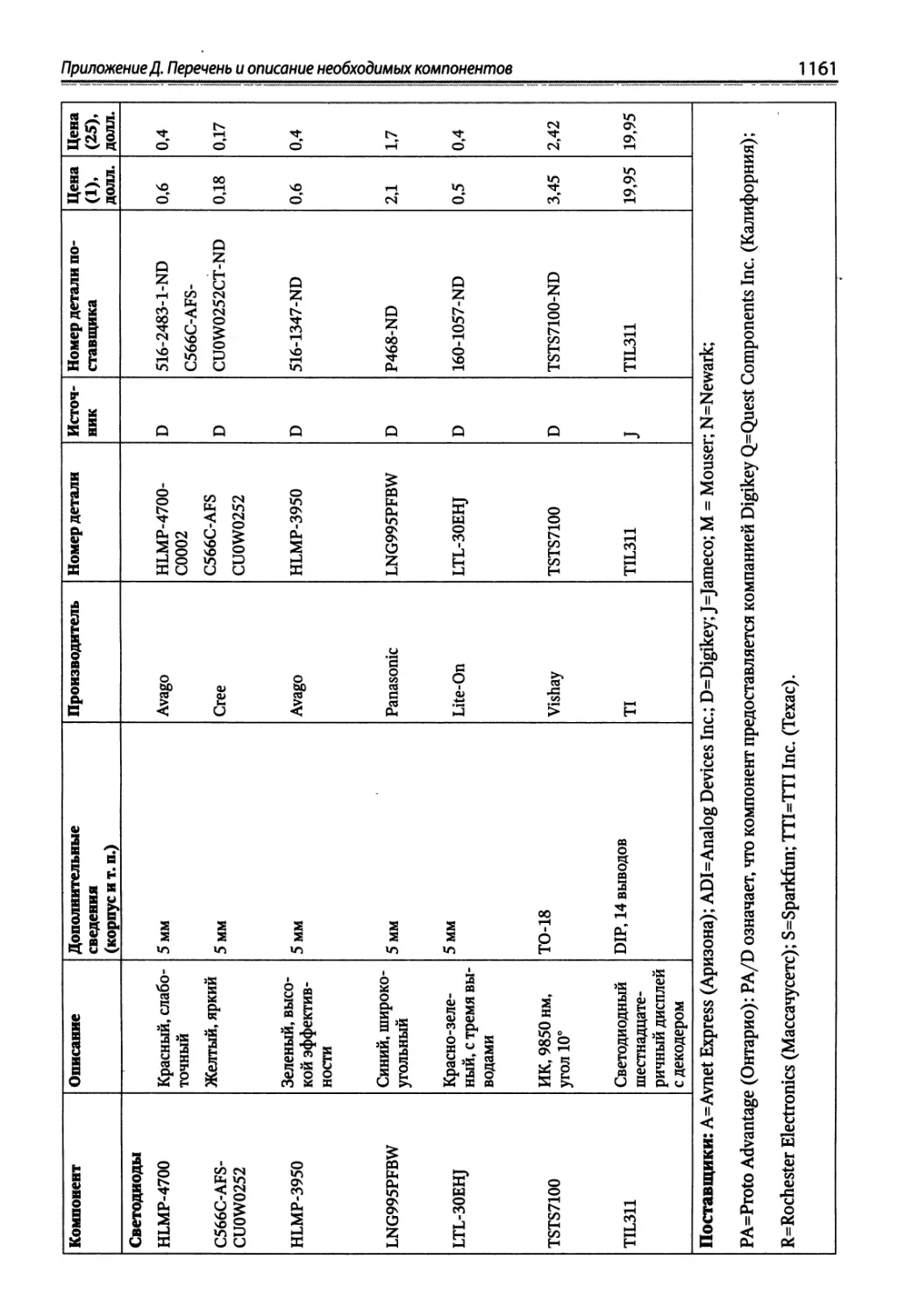
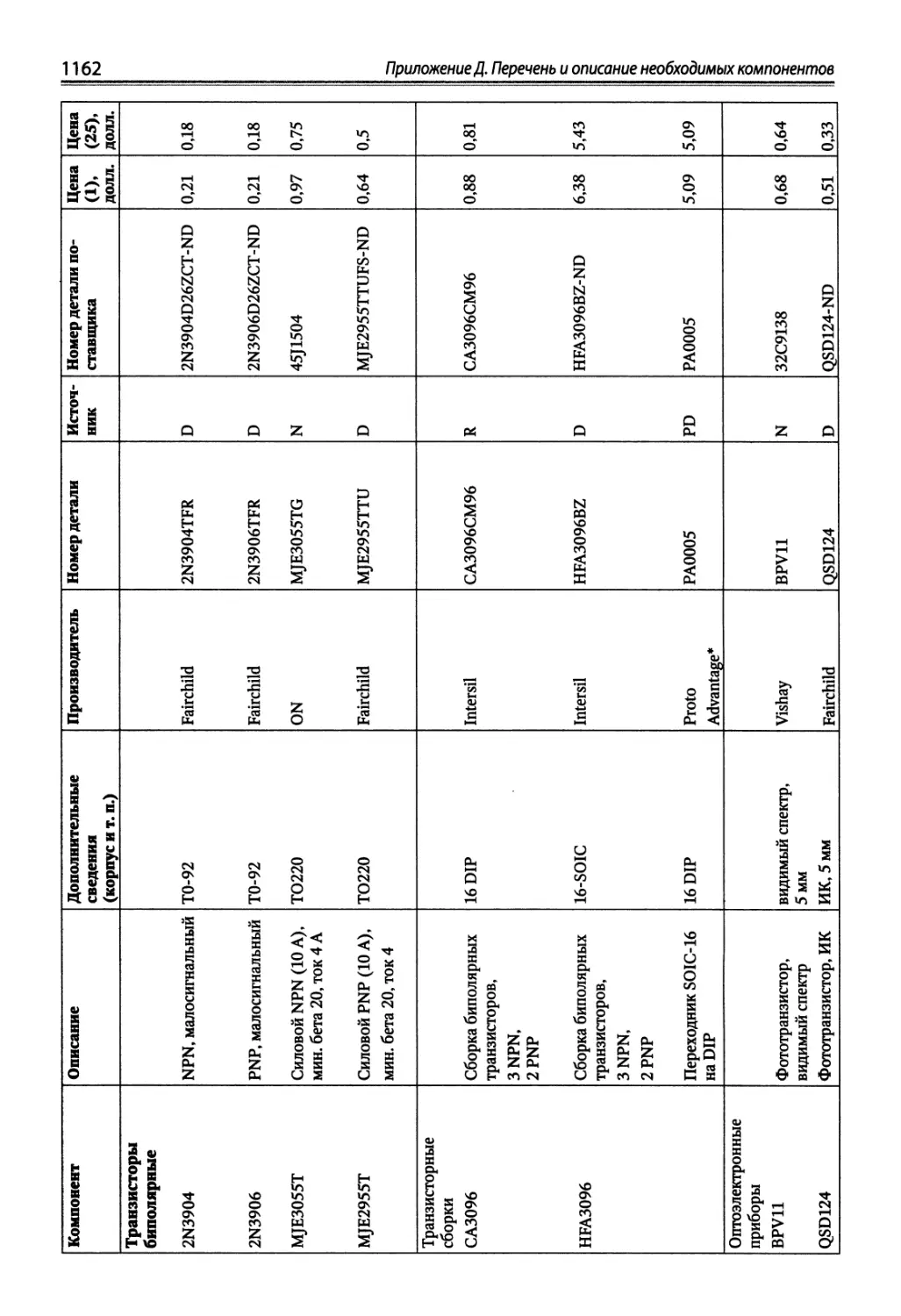
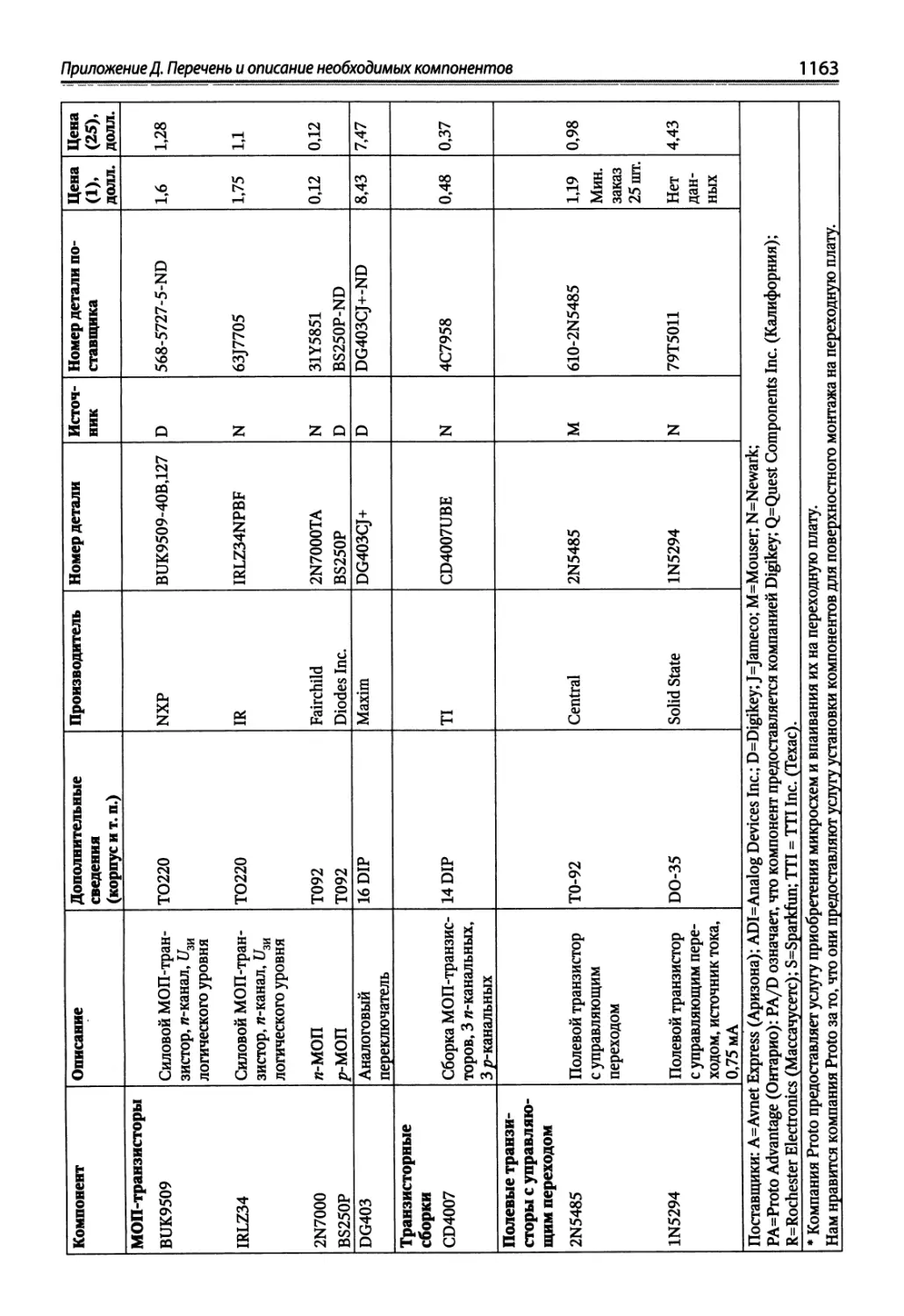
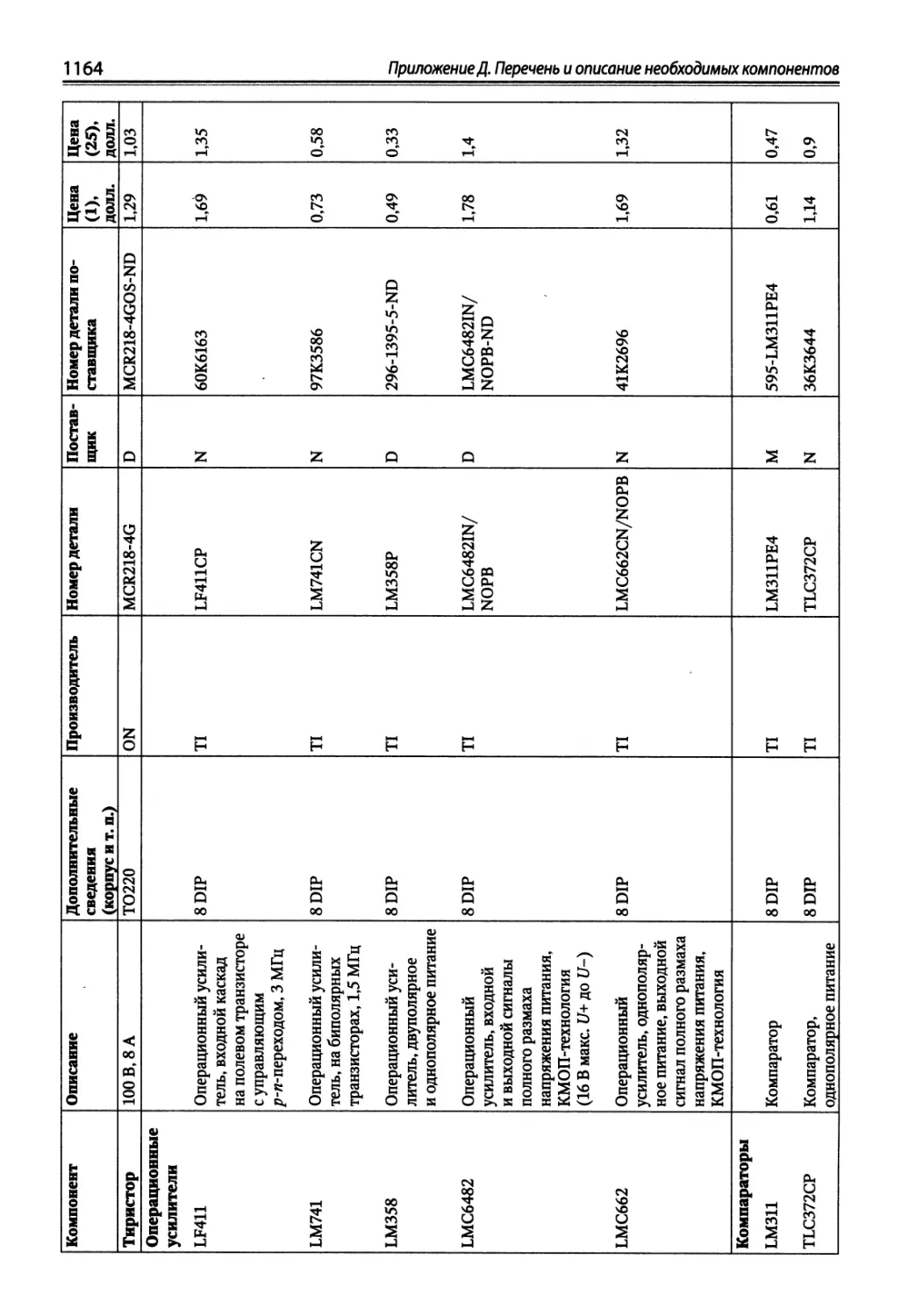
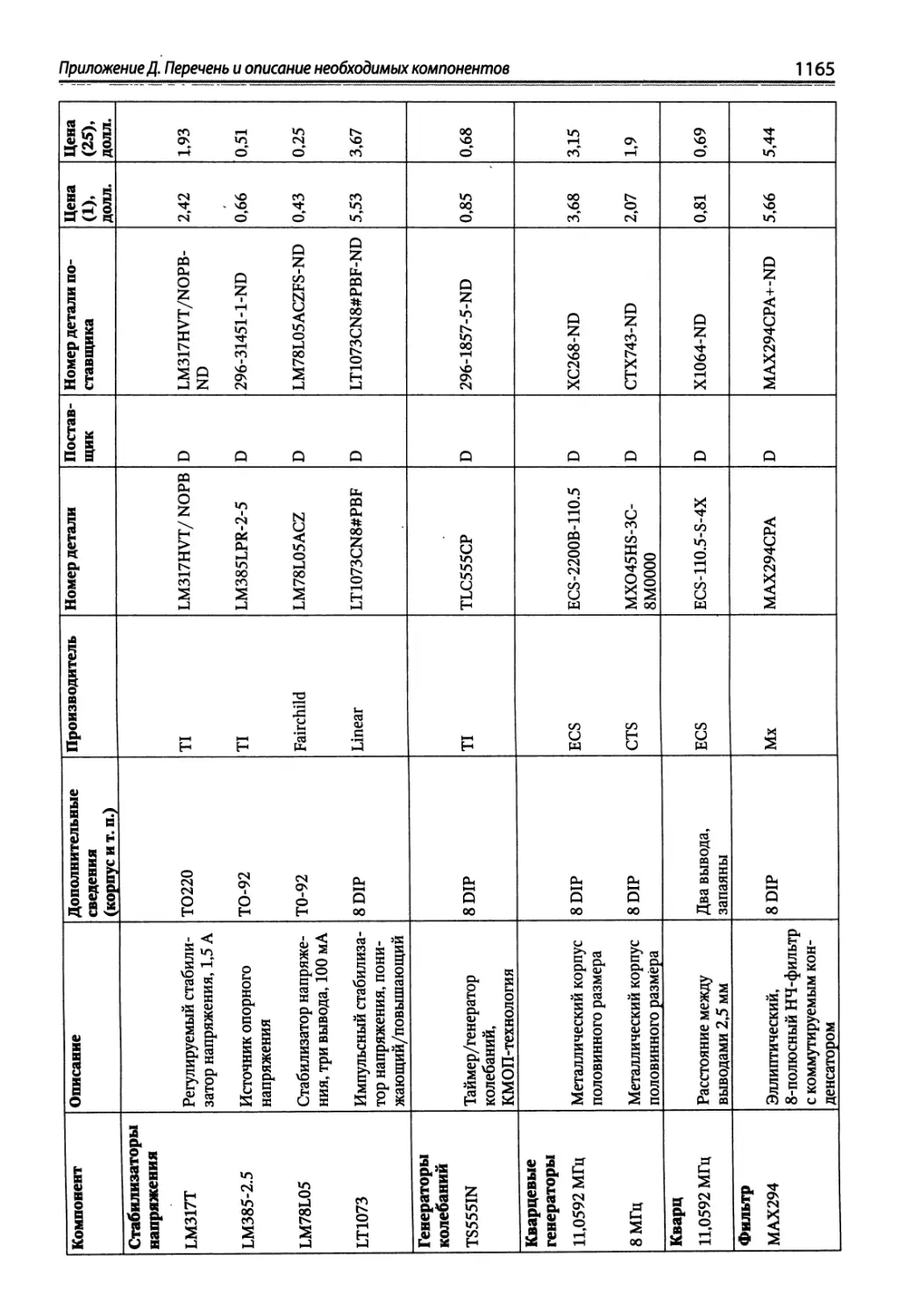
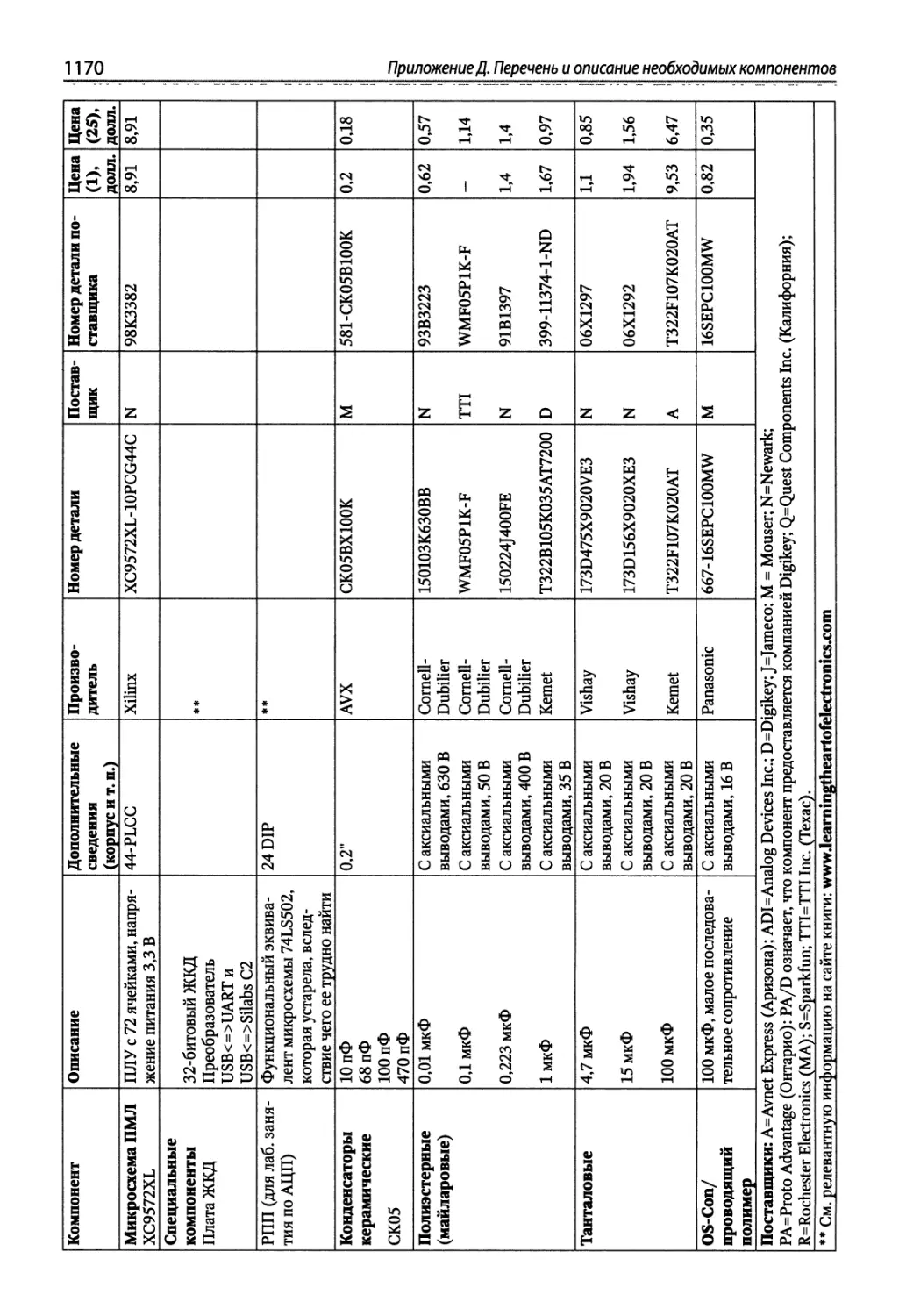
Приложение Д. Перечень и описание необходимых компонентов.......... 1158
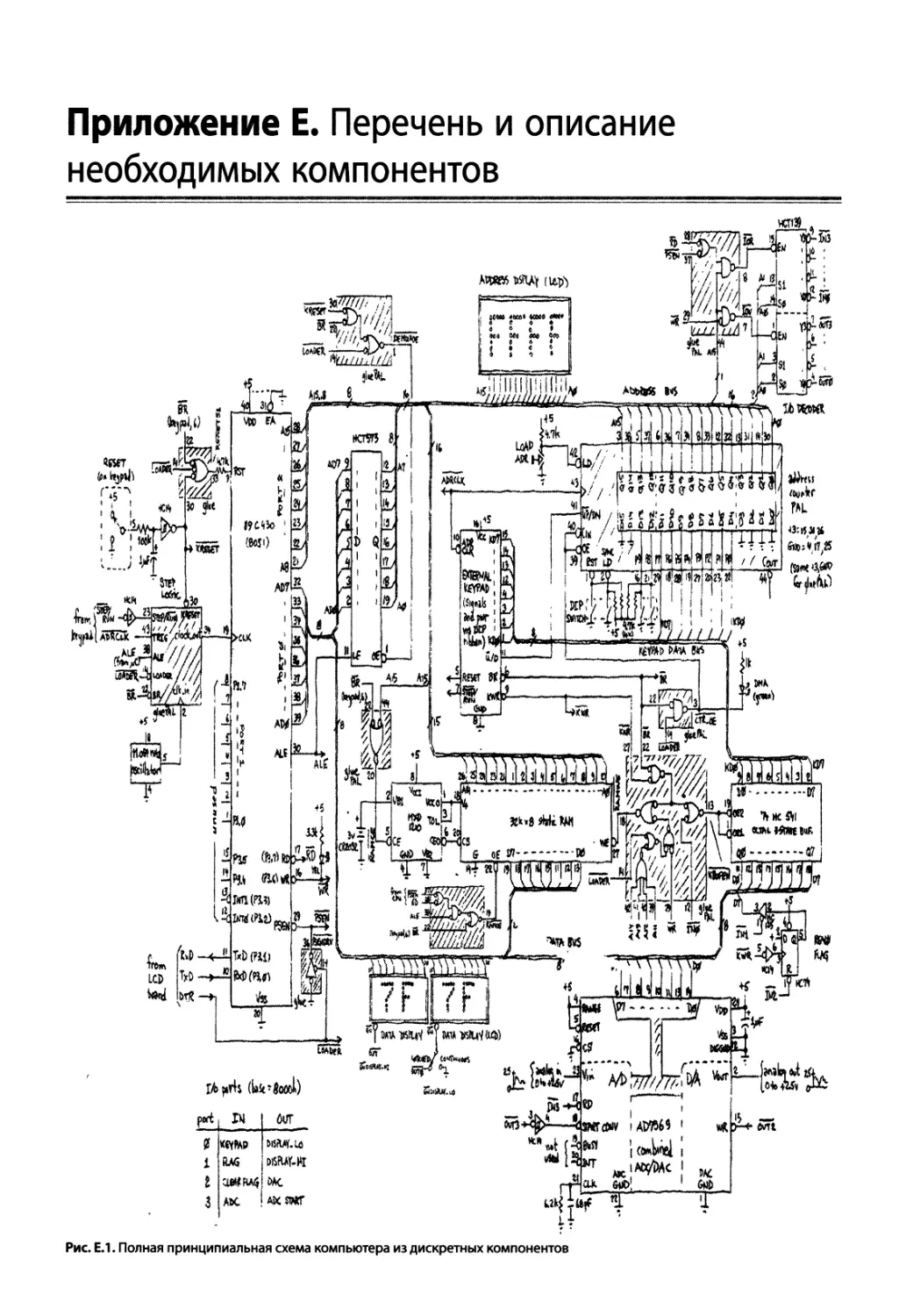
Приложение Е. Перечень и описание необходимых компонентов.......... 1172
Приложение Ж. Где приобретать электронные компоненты?................... 1174
I По почте и чеоез Интернет м .«. -.. ». . .; 1174
II. Каталоги и поисковые системы 1175
III. Местные источники , 1175
IV. Прочее .,... 1175
Приложение 3. Программы, доступные на веб-сайте книги...................... 1176
Приложение И. Оборудование......................................................................... 1178
И.1. Для кого будет полезна эта информация 1178
И.2. Осциллограф «м 1178
И.З. Генератор сигналов 1179
И.4. Макетная плата со встроенным источником питания 1179
И.5. Авометр и цифровой мультиметр 1180
И.6. Источник питания 1180
И.7. Логический пробник 1180
И.8. Магазин сопротивлений 1180
И.9. Модуль программирования ПЛУ и FPGA .....м.............м. 1181
И.10. Ручные инструменты 1181
W. J .».<«. ШШШ •<«. f*y •»•<«.■ М- • W
И.11. Провода . 1181
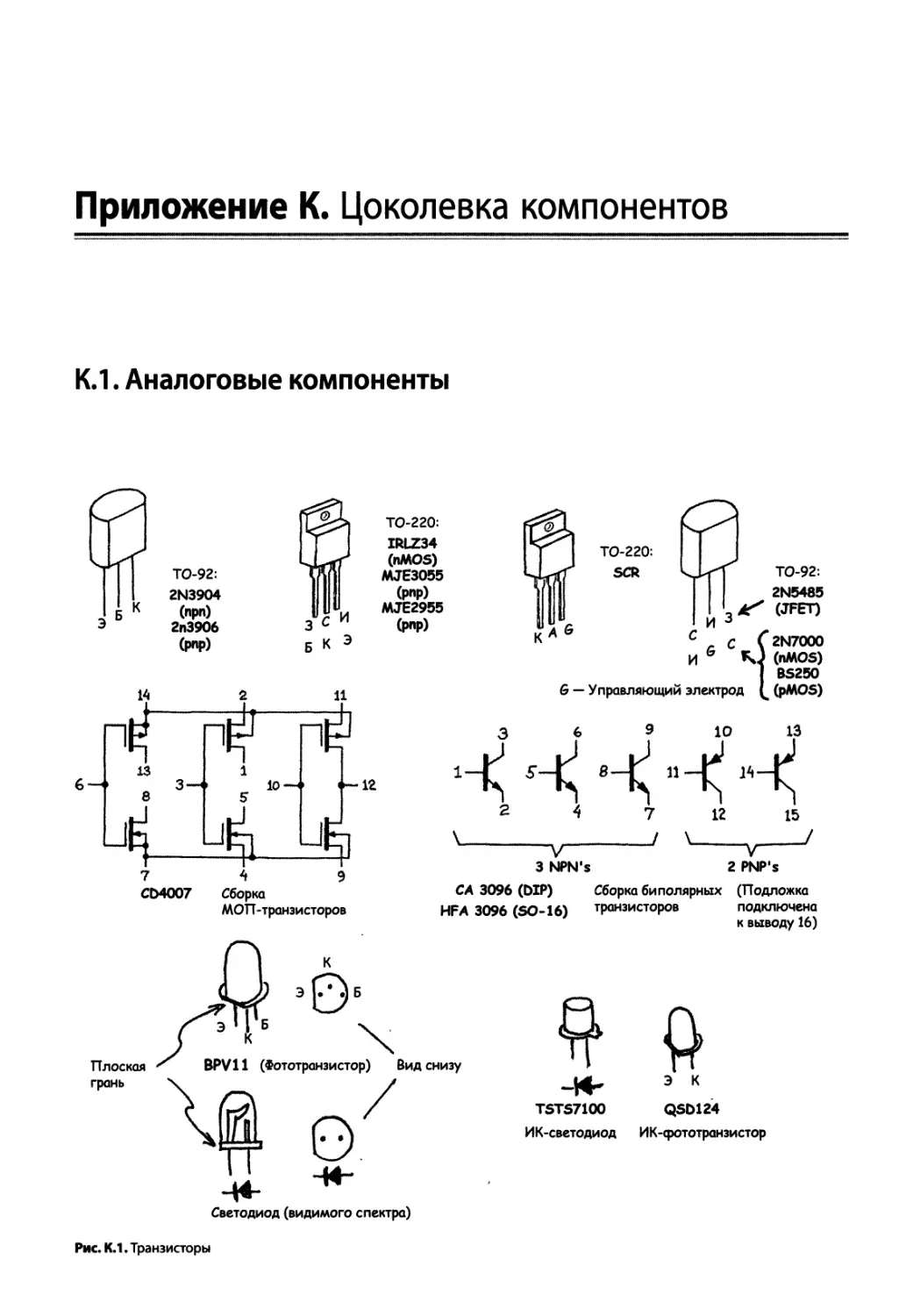
Приложение К. Цоколевка компонентов........................................................ 1182
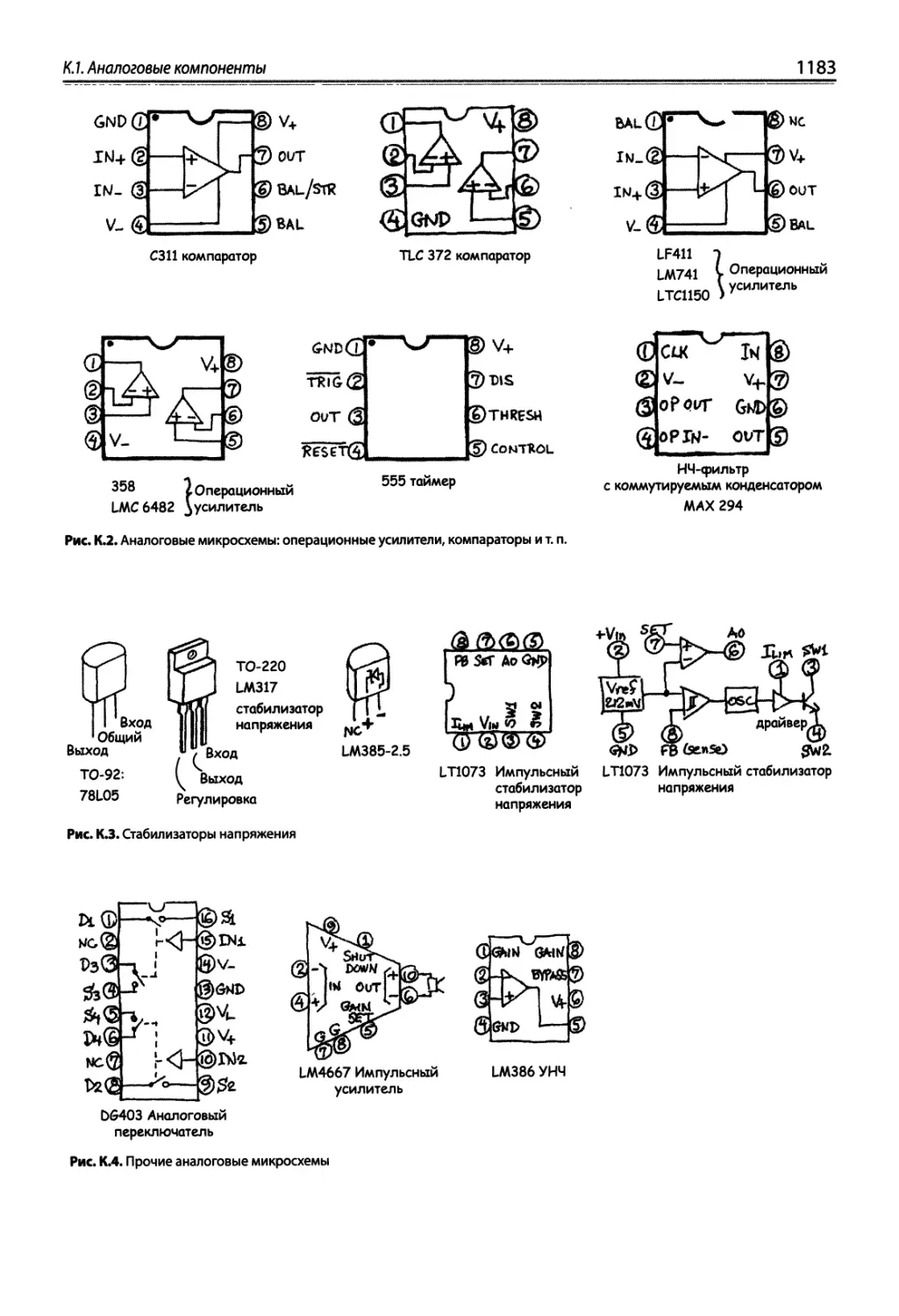
К.1. Аналоговые компоненты 1182
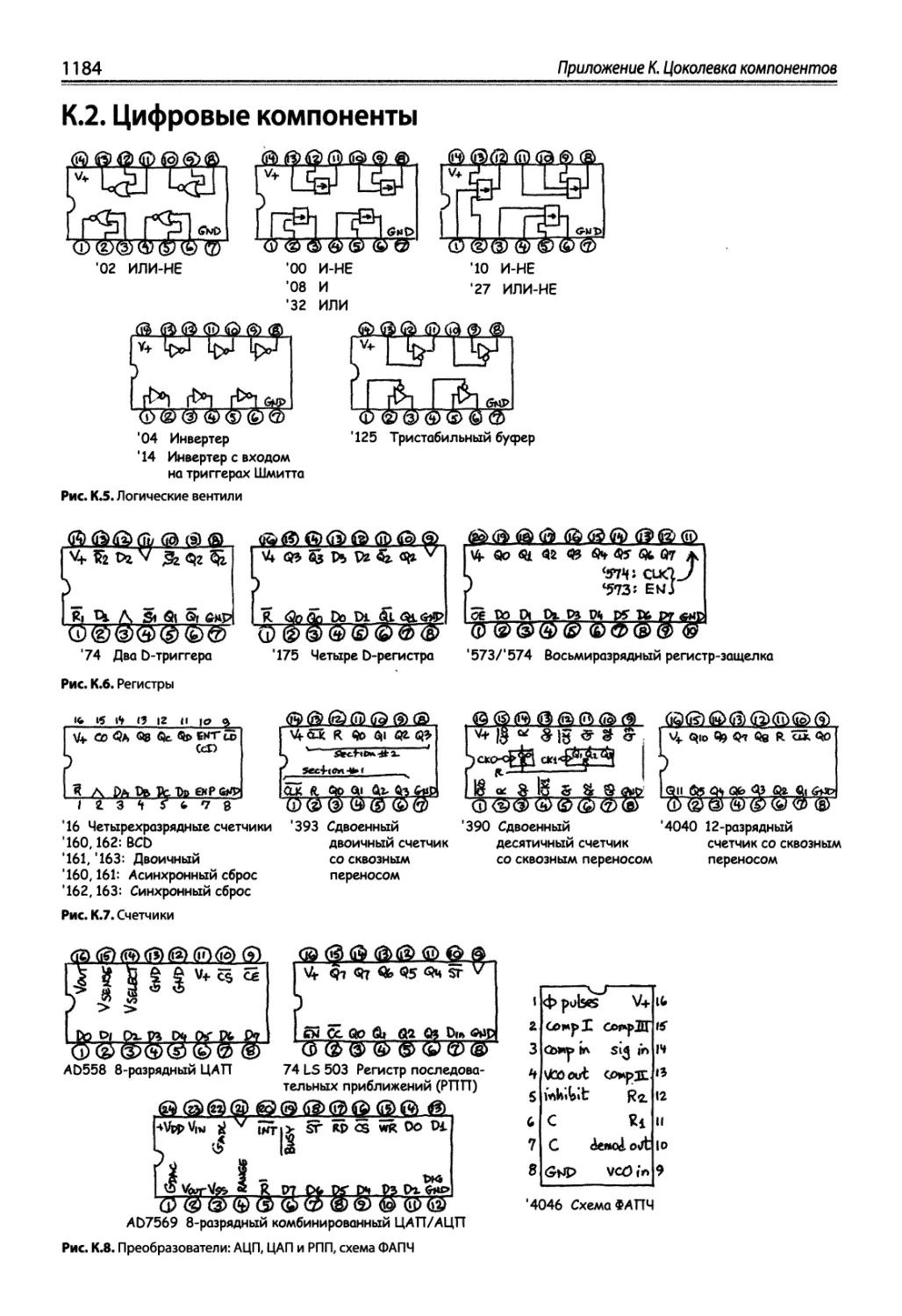
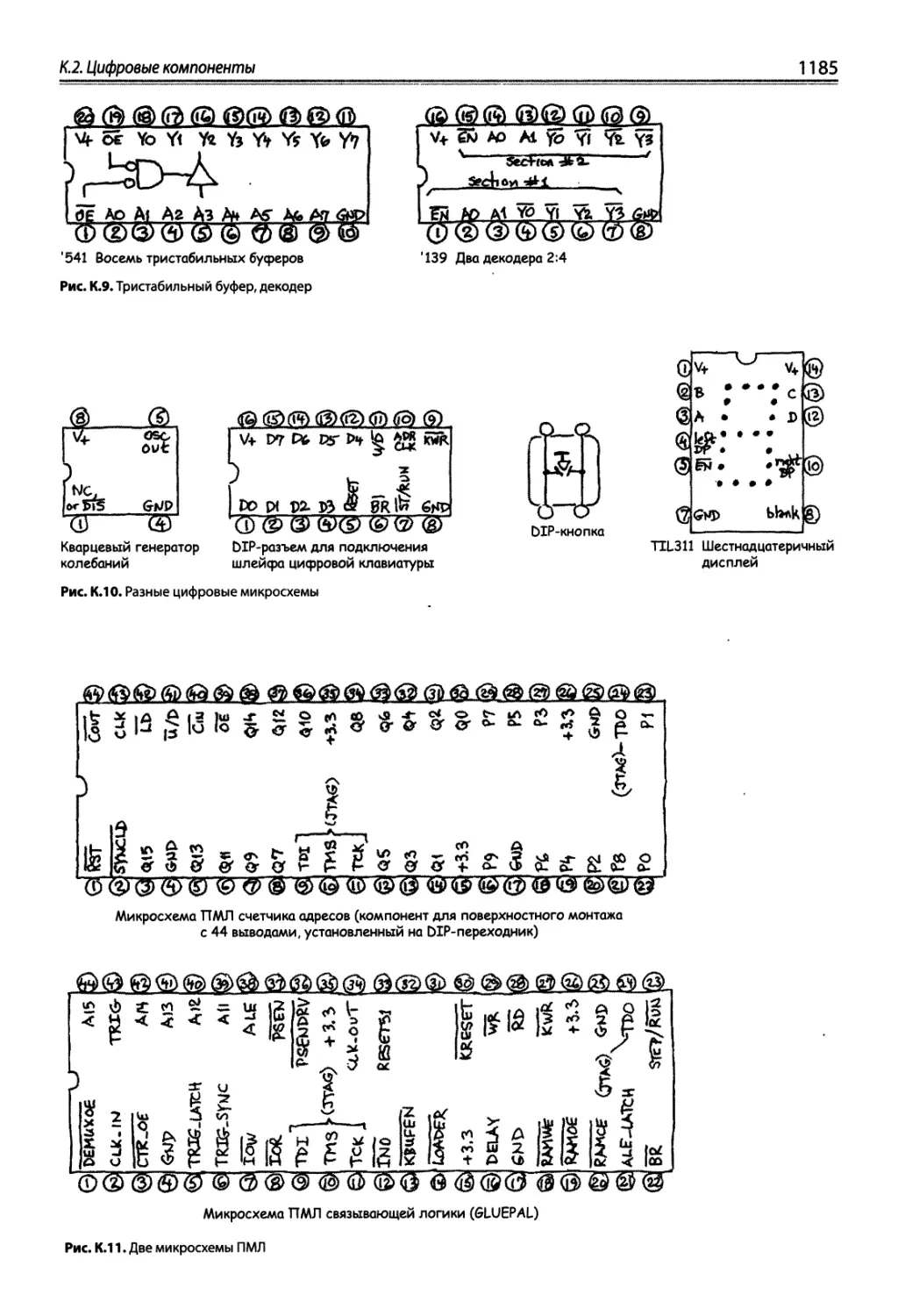
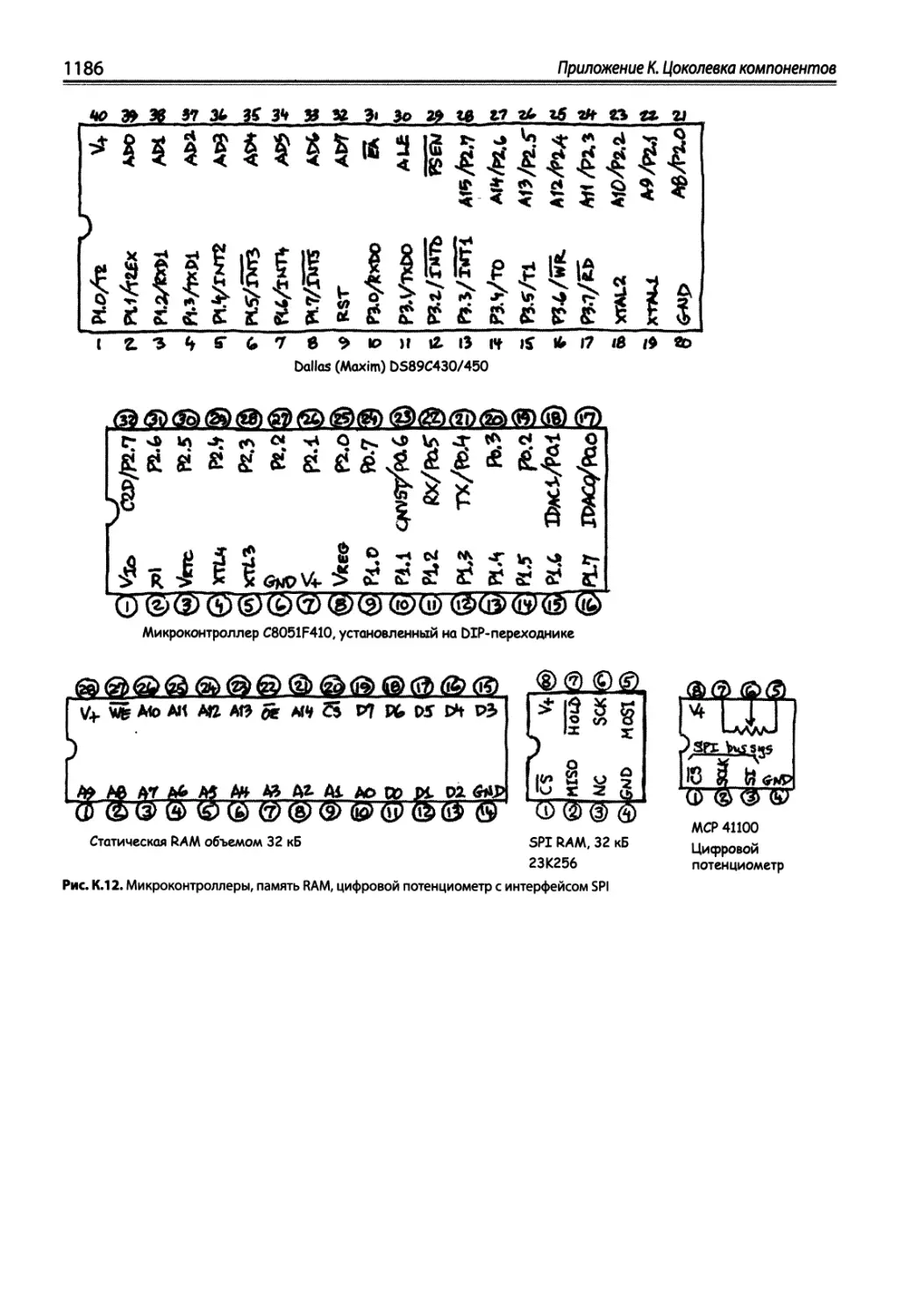
К.2. Цифровые компоненты .' 1184
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ 1187
ВВЕДЕНИЕ
И книга, и учебный курс
Эта книга предназначена для нетерпеливых.
Для тех, кто горит желанием начать получать
удовольствие и восхищение от практическо-
го применения электроники. В данном учеб-
ном курсе за 25 дней занятий читатель усвоит
то, что мы шутя называем «всей электрони-
кой». Конечно же, это далеко не вся электро-
ника, но мы надеемся, что предоставленного
материала будет достаточно, чтобы каждый
желающий смог освоить азы схемотехни-
ки и начать разрабатывать схемы, работаю-
щие в полном соответствии с поставленной
задачей.
Книга одновременно является лабораторным
практикумом и учебником. Это объясняется
тем, что содержащийся в ней материал соот-
ветствует учебному курсу, который мы вместе
с Полем Хоровицем преподавали в Гарвард-
ском университете в течение свыше 25 лет. Но
форма подачи материала такова, что изучать
его мы рекомендуем по одному уроку последо-
вательно день за днем.
Однодневное занятие: немного
теории, лабораторная работа,
практические задания и
дополнительные материалы
В каждое ежедневное занятие входит не толь-
ко обычное содержимое учебника по электро-
нике — описание и объяснение новых схем, но
также и лабораторная работа, позволяющая
применить на практике полученные теорети-
ческие знания, собирая схемы, воплощающие
теоретические концепции. Мы убеждены, что
сборка схем позволит вам приобрести знания,
которые не получить, просто читая описание
их работы.
Кроме того, почти каждое занятие содержит
практическое задание (с решением), а зача-
стую и дополнительные справочные сведения.
Этот материал, например, как расшифровы-
вать маркировку резисторов и конденсаторов,
не обязателен для всех читателей, поскольку
некоторые из вас уже знакомы с ним. А другие
могут пропустить его, если не хотят тратить
на него время при первом прочтении книги.
С этим нет никаких проблем. Данный мате-
риал потому и называется дополнительным:
он (подобно витаминным добавкам) может
быть полезным, но без него вполне можно и
обойтись.
Что нового в данной книге?
Если некоторые из вас уже имели возмож-
ность ознакомиться с изданной в 1989 г. кни-
гой «Пособие студента» ко второму изданию
книги «The Art of Electronics» («Искусство
схемотехники»)1, стоит обратить внимание
на основные различия между тем пособием
и этой книгой. Прежде всего, данная кни-
га написана как законченная и самодоста-
точная, тогда как пособие предназначалось
для использования вместе с сопутствующей
основной книгой. Перечислим наиболее важ-
ные различия между содержимым этих двух
книг.
♦ Аналоговая часть:
• в настоящей книге мы выделяем один день
занятий интересной и непростой теме па-
разитных колебаний и способам их устра-
нения;
• также одно занятие посвящено сборке схе-
мы типа ПИД для стабилизации цепи об-
ратной связи, управляющей вращением
двигателя. В такой схеме используются
сигналы, представляющие три функции
сигнала рассогласования, т. е. разницы
между требуемым и имеющимся напряже-
ниями: пропорциональная (П), интеграль-
ная (И) и дифференциальная (Д).
♦ Цифровая часть:
• в этой книге рассматриваются програм-
мируемые логические устройства (ПЛУ
или ПАЛ — программируемая матрич-
ная логика), программирование которых
1 Имеется перевод книги «The Art of Electronics» на рус-
ский язык, причем эта книга переиздавалась многократно.
См. напр. Хоровиц П., Хилл У. Искусство схемотехники:
в 3 т.: пер. с англ. — 4-е изд. перераб. и доп. - М.: Мир,
1993. - Примеч. ред.
22
Введение
осуществляется с помощью высокоуров-
невого языка описания аппаратных средств
(HDL2) Verilog;
• в части по компьютерам, завершающей
данную книгу, внимание концентрируется
не на микропроцессорах, а на микрокон-
троллерах. В отличие от микропроцессо-
ров, для работы микроконтроллеров либо
вообще не нужны дополнительные компо-
ненты, либо их требуется очень немного,
что делает микроконтроллеры наиболее
подходящими для создания прикладных
устройств, а не компьютеров.
♦ Веб-сайт:
• веб-сайт книги (https://learningtheartof-
electronics.com) содержит намного боль-
ше материала, чем пособие, в частности
там приведен машинный код программ.
Список этих программ дается в прило-
жении 3.
Стиль изложения материала
Подобно учебнику для студента, материал дан-
ной книги подается в предельно неформальной
манере. Многие рисунки специально нарисова-
ны от руки, обозначения могут быть разными,
а пояснения направлены на развитие интуи-
тивного понимания работы схем, а не на точ-
ное математическое представление. Внимание
концентрируется на разработке, а не на анализе
схем. Кроме того, для сборки мы старались вы-
бирать схемы, с которыми было бы интересно
работать — нам нравится, когда наши устрой-
ства издают звуки (в удачный день они могут
проигрывать музыку), и нам доставляет удо-
вольствие наблюдать за вращением электро-
двигателей.
Кому подойдет эта книга
Чтобы извлечь максимальную пользу из дан-
ной книги, вам не обязательно быть похожим
на студентов, которые проходят этот курс в
университете, но вам может быть интерес-
но знать, кто они такие, поскольку курс схе-
мотехники создавался специально для них.
Схемотехника преподается в трех разных
вариантах. Большинство наших студентов
изучают ее в течение осеннего и весеннего
Англ. Hardware Description Language.
семестров дневных занятий. Около полови-
ны слушателей курса работают над дипло-
мом бакалавра технических наук, а вторая
половина уже прошла этот этап, и работают
над дипломом магистра. Также обычно при-
сутствуют несколько студентов из программы
обмена с Массачусетским технологическим
институтом, которые хотят получить уско-
ренное (и, надо сказать, менее подробное)
введение в электронику, чем предлагается
в их институте. (Студенты, работающие над
дипломом специалиста в области электротех-
ники в этом институте, не изучают наш курс.
Его обычно предпочитают студенты, которые
хотят получить менее формальное введение
в эту область.)
Вечернюю версию курса в большинстве случа-
ев изучают студенты более старшего возраста.
Многие из них уже трудятся в этой области и им
интересно узнать о содержимом «черных ящи-
ков», с которыми они работают. Большинство
этих «ящиков» — просто компьютеры, а сту-
денты — программисты. Иногда «ящиком»
является лабораторное оборудование или си-
стема управления технологическим процессом,
а студенты обслуживают эту технику и хотят
глубже понять ее работу.
Ну а в летней версии курса около половины
студентов являются учащимися предвыпускно-
го класса средней школы. Наиболее способные
из них доказывают наше постоянное утвержде-
ние, что научиться разрабатывать схемы вполне
можно, не зная большой объем теоретической
физики или высшей математики. Некоторые из
первокурсников нашего университета, изучаю-
щих обычную версию курса, также доказывают
это утверждение (хотя большинство этих сту-
дентов на два-три года старше студентов летней
версии).
И мы не можем удержаться, чтобы снова не
упомянуть, как мы хвастались во введении в
Пособие студента, что от случая к случаю наш
курс берут профессора, или, по крайней мере,
посещают наши занятия. Один из них недав-
но поймал одного из наших преподавателей
за пуговицу в коридоре, когда он был в нашем
университете, чтобы прочитать лекцию. «Ну,
Том, — сказал он — из одного из твоих студен-
тов наконец-то получился толк». Таким обра-
зом он скромно высказался о факте недавнего
вручения ему Нобелевской премии. Сказать,
что мы помогли ему получить премию, мы,
Введение
23
к сожалению, не можем, но приятен сам факт,
что он был нашим студентом3.
Возможно, один материал в книге покажется
вам слишком элементарным, а другой — чрез-
вычайно сложным. Но это вполне допустимо,
поскольку рассматриваемые темы знакомы
вам в различной степени. Для некоторых из
вас, например, для опытных программистов,
программирование на ассемблере, рассматри-
ваемое под конец курса, не будет представлять
никаких трудностей, тогда как для других это
будет тяжелой задачей. Но это не представляет
никаких проблем. Учебный курс, на котором
основана данная книга, слывет занимательным
и легким с одной стороны, но трудным с другой.
Нетрудный он благодаря простым концепциям
и малому количеству абстракций. Но студентам
сразу предоставляется весьма большой объ-
ем информации за короткое время, и ожида-
ется, что они ее за это время усвоят. Наш курс
во многом похож на начальный курс изучения
иностранного языка, и мы хотим использовать
в нем метод обучения, который иногда назы-
вается погружением. Самый лучший подход
к обучению — выполнение лабораторных работ.
Мы надеемся, что эта книга поможет сделать
такие упражнения полезными. Но, учитывая
склонность современного общества к решению
многих проблем в судебном порядке, я хочу ре-
комендовать вам обратить внимание на юриди-
ческое уведомление в конце введения.
Основа:
книга «The Art of Electronics»
Когда Поль Хоровиц поставил курс схемотехни-
ки 40 с лишним лет назад, вместе с Уинфильдом
Хиллом (Winfield Hill) они написали книгу, раз-
ные издания которой служили в качестве учеб-
ника. Книга «The Art of Electronics» («Искусство
схемотехники») сейчас уже многократно пере-
издана (мы будем сокращенно называть ее да-
лее АоЕ), она остается справочным материа-
лом, на который мы полагаемся в нашем курсе.
Но для изучения нашего вводного курса схемо-
техники эта книга несколько избыточна. В ней
3 Это был Франк Вильчек (Frank Wilczek). Он действи-
тельно некоторое время посещал наш курс и тихо сидел
на задних рядах, надеясь получить какие-либо озарения
по теме, над которой он работал. Если это и удалось, то,
скорей всего, не у нас.
охватывается настолько много материала и так
подробно, что она может вызвать «интеллекту-
альное несварение» у студентов, только начи-
нающих изучать электронику. Но мы убеждены
в том, что некоторые наши студенты и читатели
захотят взглянуть более подробно на предметы,
излагаемые в нашей книге, и чтобы помочь та-
ким энтузиастам мы далее будем ссылаться на
книгу АоЕ. Читатели, у которых есть доступ к
книге АоЕ, могут извлечь из нее дополнитель-
ную информацию.
Аналоговая и цифровая
части: варианты подхода
к изучению
В стандартной версии учебного курса мы прохо-
дим весь материал книги за один семестр в тече-
ние 13 недель. В вечерней версии курса студен-
ты посещают занятия раз в неделю, мы прохо-
дим этот же материал за два семестра. В первом
семестре (занятия 1-13) изучается аналоговая
часть, а во втором (занятия 14-26) — цифро-
вая. Мы знаем, что некоторые другие учебные
заведения применяют такой же подход, разби-
вая материал на аналоговую и цифровую ча-
сти. Но вполне можно изучать цифровую часть
материала перед аналоговой. Только в первом
занятии по цифровой части (когда мы собира-
ем логический элемент из МОП-транзисторов)
студенту потребуются некоторые дополнитель-
ные сведения в аналоговой схемотехнике. Но,
по большому счету, при изучении цифровой
части курса устройства рассматриваются как
«черные ящики», для работы с которыми нет
надобности изучать их внутреннюю структуру
и принцип действия. Все что нужно знать — это
свойства их входов и выходов, но для этого не
требуется никаких особых знаний аналоговой
электроники.
При необходимости учебный курс можно не-
сколько сократить. Исключение любого ла-
бораторного занятия из курса было бы неже-
лательным, но в летней версии курса, которая
длится чуть больше шести недель, десятое ла-
бораторное занятие (по ПИД-контроллеру для
электродвигателей) является факультативным.
Также в летнем курсе отсутствует интересное,
но не обязательное цифровое лабораторное
занятие 20L, на котором студенты собирают
устройство собственной разработки.
24
Введение
Люди, которые помогли
в работе над этой книгой
Самым первым и наиболее очевидным из таких
людей будет Поль Хоровиц, мой старый учи-
тель, с которым я также совместно преподавал
в течение многих лет и который всегда был тре-
бовательным и компетентным критиком книги
на всех этапах ее подготовки. Большинство на-
рисованных от руки рисунков в этой книге яв-
ляются его работой. Без Поля и его поддержки
эта книга не появилась бы на свет.
Далее я хочу выразить признательность не-
скольким друзьям и коллегам, которые тща-
тельно просмотрели разделы книги, исправили
и улучшили их. Это Стив Морс (Steve Morss)
и Джейсон Галличио (Jason Gallicchio) — два
моих друга, с которыми я однажды препода-
вал, и которые поэтому являются не только
экспертами по электронике, но также хорошо
знают наш учебный курс. Я работал вместе со
Стивом почти 30 лет тому назад, и он помогал
мне собирать новые схемы и разбираться с их
функционированием. Затем он ушел с должно-
сти преподавателя, чтобы создать собственную
компанию, но мы продолжали поддерживать
контакты, и когда в нашем курсе начал исполь-
зоваться логический компилятор (Verilog), я
воспользовался его опытом. Стив дал подроб-
ные рекомендации, а затем тщательно вычитал
материал. Поскольку это мое первое знаком-
ство с довольно большим объемом возмож-
ностей компилятора Verilog, было очень по-
лезным получить консультацию у опытного и
знающего специалиста.
А Джейсон очень помог мне с изложением мате-
риала по дискретизации аналоговых сигналов.
Привлекательной, но также пугающей чертой
его характера является его неспособность ми-
риться даже с мелкими недочетами. Так, когда
я попросил его оценить качество изложения
материала, он с готовностью взялся за это дело
и возвратил мой черновик весь красный от по-
меток. Я совсем не ожидал получить такой ре-
зультат, но в итоге это только улучшило каче-
ство изложения материала.
В процессе написания книги у меня всегда была
возможность обратиться за советом к очень
сведущим людям по какому-либо трудному для
меня вопросу. Джим Макартур (Jim MacArthur)
заведует лабораторией электроники в нашем
университете и всегда сильно загружен рабо-
той. Зачастую он проводил в лаборатории даже
выходные дни, и даже в таком случае он не воз-
ражал оторваться от своих дел, чтобы ответить
на практические или сложные вопросы. Другой
мой коллега, Дэйвид Абраме (David Abrams),
также высококвалифицированный специалист,
и дважды он помог мне объяснить студентам
результаты, которые мы никак не могли понять.
Благодаря опыту работы в промышленности и
одновременно в преподавании схемотехники
помощь Дэйвида при работе над книгой невоз-
можно переоценить.
Куртис Мид (Curtis Mead), один из студентов
магистратуры Поля Хоровица, щедро поде-
лился своими знаниями и опытом в области
разводки схем, чтобы помочь нам сделать пе-
чатную плату для жидкокристаллического дис-
плея, который мы рассматриваем в цифровой
части курса. Ассистент преподавателя Джейк
Коннорс (Jake Connors) помог в изготовлении
плат для дисплея, разводку которых выполнил
Куртис. Другой из бывших ассистентов препо-
давателя, Рэндалл Бриггс (Randall Briggs) осно-
вательно и тщательно вычитал этот раздел.
Должен особо подчеркнуть, что если, несмо-
тря на всю полученную мною помощь, в этой
книге встретятся какие-либо огрехи, то это моя
собственная вина, мой, так сказать, вклад, а не
кого-либо из моих помощников.
Очень важную помощь в трудоемком процессе
создания наглядных иллюстраций, которых в
книге насчитывается свыше тысячи, мне оказа-
ли два человека. Мой сын, Джэйми Хейс Qamie
Hayes), сначала нарисовал, а затем улучшил ка-
чество цифровых изображений отсканирован-
ных рисунков. А высококвалифицированный
иллюстратор Рей Крейгхед (Ray Craighead4),
которого мы нашли в Сети, преобразовал наши
вчерне нарисованные от руки картинки в каче-
ственные компьютерные изображения. Причем
он смог сделать все это так, чтобы конечные
изображения ло смыслу не особо отличались
от нарисованных исходных оригиналов. Мы не
смогли найти никого другого, кто бы справился
с этой задачей лучше, чем Рей.
А после того, как рукопись объемом около
1000 страниц была подготовлена, потребо-
валась изнуряющая работа по доводке, обнару-
жению противоречий и повторений, удалению
См. веб-сайт http://www.raycraighead.com.
Введение
25
ссылок на изъятые рисунки, приведению ма-
териала к некоему единообразию (например,
Umr а не Ueux или ивых, по крайней мере, хотя
бы на одной и той же странице, и тому подоб-
ное), которую проделал мой редактор, Дэйвид
Тран (David Tranah). Он не высказал никаких
нареканий не только на качество исходного ма-
териала, который он привел в порядок, но также
и на необходимость постоянно выполнять мел-
кие изменения вплоть до самого конца работы
по подготовке книги к печати. И всю эту работу
он выполнил сразу же после редактирования
предыдущей книги «The Art of Electronics».
Я восхищаюсь его неутомимым трудолюбием
и очень благодарен ему за это.
Наконец, я должен поблагодарить свою жену
Дебби Миллс (Debbie Mills) за то, что она стой-
ко терпела унылое и раздражающее зрелище
моей непрерывной работы над правками к кни-
ге, отрешенного от всего окружающего и везде
и повсюду — дома на крыльце, на террасе на
отдыхе в Италии, снова дома у камина. Я не со-
мневаюсь, что она бесконечно рада, что книга,
наконец, завершена.
Юридическое уведомление
В этой книге мы предпринимаем попытку обу-
чить методам разработки электронных схем,
используя для этого примеры схем и данные,
которые мы считаем верными и точными. Но
все эти примеры, данные и прочая информация
предназначены исключительно в качестве обу-
чающих пособий и не должны служить каким
бы то ни было иным целям без предваритель-
ного независимого тестирования и проверки
лицом, разрабатывающим конкретное устрой-
ство. Независимое тестирование и проверка
особенно важны для любого практического
приложения, в котором неправильная работа
схемы может повлечь телесные повреждения
или материальный ущерб.
По этим причинам мы не даем никаких гаран-
тий, прямых или косвенных, в том, что опи-
санные в книге примеры, данные или прочая
информация не содержат ошибок, что они со-
ответствуют промышленным стандартам, или
что они отвечают требованиям какого бы то
ни было приложения. АВТОРЫ И ИЗДАТЕЛЬ
ПРЯМО ОТКАЗЫВАЮТСЯ ОТ ПОДРАЗУ-
МЕВАЕМЫХ ГАРАНТИЙ ТОВАРНОЙ ПРИ-
ГОДНОСТИ ИЛИ ПРИГОДНОСТИ ДЛЯ ЛЮ-
БОГО КОНКРЕТНОГО ПРИМЕНЕНИЯ, даже
если авторы были осведомлены о каком-либо
конкретном применении и даже если в книге
указывается какое-либо конкретное примене-
ние. Авторы и издатель также снимают с себя
всю ответственность за прямые, непрямые, по-
бочные и косвенные убытки, возникшие в ре-
зультате использования примеров, данных или
иной информации в книге.
Кроме того, мы не делаем никаких заявлений
касательно возможного нарушения прав интел-
лектуальной собственности других лиц, вклю-
чая патенты США и других стран, возникшего
вследствие использования примеров, данных и
другой информации в этой книге. Читатель не-
сет полную ответственность за обеспечение не
нарушения им каких бы то ни было прав интел-
лектуальной собственности, даже для приме-
нений, которые считаются экспериментальны-
ми. Фактом использования любых примеров,
данных или прочей информации из этой книги
читатель соглашается принять на себя всю от-
ветственность за любые убытки, возникшие в
результате или связанные с таким использова-
нием, независимо от того, основана ли такая
ответственность на нарушении прав интеллек-
туальной собственности или на любом другом
основании для иска, и независимо от того, яв-
ляются ли убытки прямыми, непрямыми, по-
бочными, косвенными или любого иного типа.
Авторы и издатель отказываются от любой та-
кой ответственности.
ЗАМЕЧАНИЕ ОТНОСИТЕЛЬНО
ПЕРВЫХ ЗАНЯТИЙ
Схемы, рассматриваемые на первых трех за-
нятиях, не так сложны, как последующие.
Изучаемые на этих занятиях устройства будут
в большей степени известны вам, чем такие
устройства, как транзисторы, операционные
усилители, не говоря уже о микропроцессо-
рах. Вряд ли кто-либо из читателей не знает
закона Ома, а формула I = CdU/dt тоже будет,
вероятно, по крайней мере, хотя бы смутно
знакома вам.
Но рассматриваемые на первых занятиях ком-
поненты, которые называются пассивными
устройствами, всегда присутствуют в более
сложных электронных схемах на дальнейших
занятиях. Поэтому, если вы решите пропустить
второе лабораторное занятие, то вам придется
как-то наверстать его. Это объясняется тем, что
вторая лабораторная работа является самой
важной во всем курсе, поскольку в ней иссле-
дуются ДС-цепи. Пропуск этого лабораторного
занятия не позволит вам закрепить свое по-
нимание ДС-цепей, особенно фильтров, в ре-
зультате чего вы будете постоянно испытывать
трудности с пониманием остального материала
аналоговой части курса.
С резисторами у вас не будет никаких про-
блем, а диоды тоже будут казаться достаточно
простыми, по крайней мере, с используемой
нами точки зрения на эти устройства, как одно-
направленные вентили. Но функционирова-
ние конденсаторов и катушек более сложное.
Индуктивности присутствуют в учебном курсе
в очень небольшом количестве схем, но кон-
денсаторы встречаются гораздо чаще. Чтобы
хорошо усвоить основные свойства конден-
саторов — они пропускают переменный ток,
препятствуют протеканию постоянного тока
и в некоторых случаях вызывают сдвиг по
фазе — вам, скорей всего, потребуется немало
попрактиковаться с этими устройствами.
Мы также убеждены, что вы сможете успеш-
но пройти наш учебный курс, даже если у вас
нет ни малейшего понятия, что означает «-/»
в формуле для вычисления значения импедан-
са конденсатора. Если у вас есть книга АоЕ и
если после попытки разобраться с материалом
по полным импедансам в довольно сложном
Математическом обзоре (Приложение Б этой
книги) вы чувствуете себя полным тупицей, не
переживайте. Если даже у вас появится мысль,
не следует ли замедлить темп изучения всего
курса, то советуем потерпеть до тех пор, когда
мы начнем изучать транзисторы. Одно из са-
мых замечательных свойств этой книги — от-
каз от сложностей во всех случаях, когда хо-
рошую схему можно создать с помощью более
простого решения. Хороший пример подоб-
ного подхода — рассмотрение транзисторов, и
вам следует продержаться хотя бы до этого эта-
па, чтобы воочию убедиться в этом: хотя глава
по транзисторам довольно трудная, изложение
материала по предмету в ней намного проще,
чем в большинстве других книг. Вы увидите,
что сможете начать разрабатывать полезные
схемы на транзисторах с первого же дня заня-
тий по этой теме.
На первых трех лабораторных занятиях мы
также рассмотрим применение измерительной
техники и особенно наиболее важного прибо-
ра — осциллографа. Это сложное устройство,
и научиться грамотно работать с ним можно
только на практике. В этом отношении не сле-
дует совершать распространенную ошибку,
думая, что работающий рядом с вами студент
вращает ручки, щелкает тумблерами, нажимает
кнопки и выполняет настройки с такой уверен-
ностью сразу же на первом или втором занятии
потому, что он умнее вас. Это совсем не так,
просто он уже имеет опыт работы с данным
прибором. Где-то после двух недель вы буде-
те взаимодействовать с осциллографом так же
уверенно. Но только при условии, что в течение
этих двух недель вы не переложите всю работу
на плечи напарника, который и так уже доста-
точно опытный.
Изображения на экране осциллографа (кото-
рые называются осциллограммами) делают не-
видимые события видимыми, но при этом так-
же придают им странную абстрактность. Эти
осциллограммы позволят вам осознать про-
цессы, происходящие в схеме. Таким образом,
осциллограф будет играть роль своеобразного
микроскопа времени, позволяющего увидеть
Замечание относительно первых занятий
27
события, длящиеся несколько наносекунд —
интервал, за который свет проходит расстояние
между вами и студентом, сидящим за соседним
лабораторным столом. Может случиться, что вы
будете эмоционально реагировать на фигуры на
экране осциллографа, получая удовольствие от
плавных, красивых синусоид, испытывая бес-
покойство при виде отсечения верхушек волны
или искажения ее формы, и раздражение, когда
ее четкая линия становится размытой.
Чтобы расположить вас к получению удоволь-
ствия от предстоящей работы, когда микро-
скопические события проявляются на экране
осциллографа, мы предлагаем вам взглянуть
на несколько осциллограмм. Эти осциллограм-
мы хоть и не отражают процессы в электрон-
ных схемах, тем не менее, выглядят как на-
стоящие — как события окружающего нас мира
могли бы отображаться на осциллографе, если
бы он имел такую возможность. Рисунок этих
«осциллограмм» годами висел на двери мое-
го кабинета, и при виде его проходящие мимо
студенты останавливались, смотрели на него
более внимательно и задумывались, как будто
бы стараясь создать мысленную рамку для этих
причудливых изображений. Иногда кто-либо
спрашивал, настоящие ли это осциллограммы?
Конечно же, нет. Этот полет фантазии о способ-
ностях осциллографа нарисовал художник Саул
Стайнберг (Saul Steinberg), который любезно
разрешил нам поместить его иллюстрацию
в этой книге. Мы надеемся, что она вам понра-
вится. Возможно, это поможет вам смотреть на
более прозаичные настоящие осциллограммы
с толикой того уважения и восхищения, кото-
рое у вас вызывают «осциллограммы» на при-
веденном далее рисунке.
28
Введение
ШММММЮ^^
ж^ж^ж ж ж^ж ж ж ж ж ж,
SS///&////////,
♦ИWtmWtttttWtWtmWtttt
^
■•■•.•>•>•'
■•>•■
Звонок телефона
Звонок телефона в телевизионном сериале
Звонок телефона в доме напротив
Звук работающего холодильника
Шум газонокосилки
Рокот небольшого самолета
1уЛ пассажирского самолета
Ж ж Звук сверчка
Тиканье часов
Шум легкового автомобиля
Гудение грузовика
Шелест листьев по мостовой
———_ циск комара
Скомканный лист бумаги распрямляется в урне
Шелест веток вербы
Крик енота?
Скрипение комода
Кваканье лягушки
щуд! дождя по крыше
Д5ш дождя по террасе
<Д» >
М?"
Крик голубой сойки
Неизвестный звук
— Саул Стайнберг
Рисунок Саула Стейнберга; авторские права принадлежат Фонду Саула Стайнберга (Saul Steinberg
Foundation); оригинал опубликован в 1979 г. в журнале «The New Yorker Magazine». Репродукция
с разрешения.
Часть I
Аналоговая электроника:
пассивные устройства
IN. Цепи постоянного тока
Содержание
1N.1. Краткая сводка
1N.1.1. Зачем это нужно?
1N.1.2. Что такое «искусство схемотехники?»
1N.1.3. Что мы не будем изучать в этом курсе
1N.1.4. Что мы будем изучать в этом курсе: обработка информации
1N.2. Три основных закона электротехники
1N.2.1. Закон Ома: t/ = IK
1N.2.2. Законы Кирхгофа для напряжения и тока
1N.3. Первая практически важная схема: делитель напряжения
1N.3.1. Исследуем делитель напряжения
1N.4. Нагрузка и «выходной импеданс»
IN.4.1. Вычисление выходного напряжения нагруженного делителя
1N.4.2. Объяснение метода Тевенина
1N.4.3. Применение модели Тевенина
1N.4.4. Какой мультиметр лучше: аналоговый или цифровой?
1N.4.5. Несколько слов о «земле»
1N.4.6. Основное правило для соотнесения ДВЫХ_А с R^B
1N.5. Материал для чтения из АоЕ
31
31
32
32
33
34
34
38
40
42
43
44
44
46
49
49
50
52
1N.1. Краткая сводка
Наш курс начинается с рассмотрения схем, со-
стоящих исключительно из компонентов двух
типов:
♦ источников напряжения постоянного тока
(т. е. источников, выдающих напряжение, не
меняющееся в течение времени, например,
таких как батарея или лабораторный источ-
ник питания);
♦ резисторов.
Если эта задача кажется вам простой, так оно и
есть. Мы попытаемся упростить ее еще больше,
показав эффективные способы работы с этими
знакомыми компонентами.
При этом мы рассмотрим только один тип схе-
мы — делитель напряжения.
1 N.1.1. Зачем это нужно?
В начале каждого занятия даются краткое опи-
сание задачи и теоретические сведения для ее
решения.
Это делается для того, чтобы дать ответ на во-
прос, который может возникнуть у любого кри-
тически мыслящего студента: Ну хорошо, есть
некоторая схема. Но для чего она предназначе-
на, что она делает? Зачем мне требуется то или
другое? Например, вот это схема интегратора,
но зачем мне нужен интегратор?
Попробуем привести пример применения де-
лителя напряжения.
Задача. Имея в наличии источник питания по-
стоянного тока, создайте источник с меньшим
напряжением (но достаточно мощный) для
подключения к нему определенной нагрузки.
32
1N. Цепи постоянного тока
Формулировка задачи простыми словами.
Создайте делитель напряжения, выдающий на-
пряжение ишх заданной величины, которое
при увеличении тока нагрузки до максималь-
ного не должно меняться больше заданного
значения (в процентах).
1 N.12. Что такое «искусство
схемотехники?»
В данном случае, это не тот тип искусства, ко-
торое выставляется на обозрение в музеях1,
но искусство в более старом значении слова:
мастерство2. Вполне может быть, что при вы-
боре названия книги «The Art of Electronics»3
(в дальнейшем просто АоЕ) сыграло какую-то
роль чувство, что рассматриваемому предмету
присуще определенное волшебство, и, возмож-
но, что такое название это намек на «искусство
черной магии»4.
В самой книге АоЕ предмет излагаемого в ней
курса определяется таким образом:
Предмет нашего курса — законы, практические
правила и приемы, которые составляют искусство
схемотехники, как мы его видим.
Если вы уже бегло просмотрели текст данной
книги, то поняли, что наш курс отличается от
обычного учебного курса электронной техни-
ки тем, что основное внимание в нем уделяется
«практическим правилам» и «приемам». Мы
будем стараться научить вас применять такие
практические правила и проверенные приемы,
не особо заботясь о доказательстве их правиль-
ности. С помощью таких правил и приемов вы
оставите далеко позади начинающего инжене-
ра, не способного ни шагу сделать без своего
калькулятора.
1 Но если вам доведется побывать в Мюнхене, посетите
не имеющий равных во всем мире научно-технический
музей Deutsches Museum. Там вы увидите удивительные
машины, демонстрирующие секреты таких процессов,
о существовании которых вы даже не подозревали, на-
пример, историю изготовления резьбовых крепежных
деталей.
2 «Требующее специальных навыков промышленное за-
нятие, дело, профессия» Оксфордский словарь английского
языка (1989).
3 Искусство схемотехники.
4 АоЕ § 1.1.
1 N.1.3. Что мы не будем изучать
в этом курсе
Сделать электропроводку в квартире?
Починить телевизор?
Выпускников нашего курса иногда просят
оказать помощь, выходящую за пределы их
знаний и навыков. Например, установить
электрические розетки в квартире. Но в на-
шей книге вы не найдете сведений, чтобы
должным образом справиться с этой каза-
лось бы простой задачей. Сложность здесь
заключается в том, что требуются подробные
знания электротехнических правил и норм:
какой диаметр проводов выбрать, с какой
изоляцией должен быть провод, где устанав-
ливать автоматы защиты и т. п. Также вы, ско-
рее всего, не сможете починить вышедший из
строя телевизор своего приятеля, поскольку
большая часть его блоков будет выполнена на
загадочных специализированных интеграль-
ных схемах. Для ремонта, при условии, что он
будет финансово оправдан, вам, скорей всего,
придется целиком заменить какой-либо боль-
шой модуль, а не перегоревший резистор или
транзистор, как это было в телевизорах ваше-
го детства.
Подача электропитания
Также необходимо сделать еще одно замеча-
ние: в этом курсе мы будем только в некото-
рых случаях пытаться подавать электропита-
ние на что-либо (это «что-либо» обычно на-
зывается «нагрузкой»). Иногда, конечно же,
энергоснабжение нагрузки будет представлять
интерес, например, когда мы хотим обеспе-
чить громкий звук из динамика или привести
во вращение вал электродвигателя. Но гораздо
чаще желательно свести потребление электри-
чества к минимуму; вместо этого нас намного
больше интересует поток информации.
На стене в вестибюле здания электротехниче-
ского факультета Массачусетского технологи-
ческого института (МТИ) висит огромная фо-
тография, снятая где-то в 30-х годах прошлого
столетия (рис, 1N.1), на которой несколько
инженеров института стоят возле электротех-
нического оборудования (видимо это генера-
торы или электродвигатели, каждый из кото-
рых размером с большого теленка).
1N.1. Краткая сводка
33
Рис. IN.l.TaK выглядела электроника в 30-х годах прошлого столетия [Воспроизведение с разрешения МТИ]
В те времена заниматься электроникой в
основном означало иметь дело с подобными
большими устройствами, обеспечивающими
электропитание. Больше всего возможностей
трудоустройства в те времена (один мой дядя
закончил МТИ где-то около 1936 г.) предлага-
ли компании — производители электроэнергии.
Плотина Гувера (Hoover Dam), строительство
которой было завершено в 1935 г., была чудом
инженерной мысли того времени. Девизом того
времени было «Большое — значит хорошее».
(Даже сейчас на сайте плотины Гувера гордят-
ся ее весом. Это 6,6 миллионов тонн, если вам
интересно.)
11МЛ А Что мы будем изучать
в этом курсе: обработка
информации
Но, как вы уже догадываетесь, сейчас насту-
пило другое время. Теперь хорошим считается
маленькое, а размеры из области нано — во-
обще прекрасным. А задачей современной
электроники в основном является обработка
информации5.
5 Мы полагаем, что возможное исключение — продолжа-
ющаяся борьба за создание эффективного и экономически
выгодного электромобиля. Того, кому удастся успешно ре-
шить эту задачу, ожидает большая слава.
Таким образом, нам нравятся устройства, ко-
торые обрабатывают и передают сигналы, вы-
деляя при этом очень небольшие объемы тепла,
т. е. потребляют очень мало электроэнергии.
Например, цифровые микросхемы, собранные
на полевых транзисторах, функционирующих
как переключатели, весьма экономичны. Такие
электронные компоненты имеют низкое входное
и очень высокое выходное сопротивление, а также
близкий к нулю ток покоя. Можно сказать, что
такие схемы не преобразуют, не потребляют
и не передают электроэнергию. Они обрабатыва-
ют только информацию. В нашем курсе мы поч-
ти всегда будем иметь дело с таким типом схем*
Чтобы не перегружать вас в первый же день
занятий, мы отложим на потом рассмотрение
связанной темы: какие именно формы ин-
формация может принимать в электронных
схемах — в виде напряжения или тока? Ответ
может удивить вас, или вы можете посчитать
вопрос бессмысленным, поскольку знаете, что
давным-давно некий Ом доказал, что напря-
жение и ток в устройстве очень тесно связаны
между собой. В следующий раз мы попытаем-
ся убедить вас, что вопрос далеко не праздный,
и выясним различие, представлен ли сигнал на-
пряжением или током (также см. заметку IS по
этой теме). Ну а теперь перейдем к менее аб-
страктной теме и нашей первой полезной схе-
ме: делителю напряжения.
34
IN. Цепи постоянного тока
1 N.2. Три основных закона
электротехники6
Далее мы будем постоянно полагаться на три
основных закона электротехники: закон Ома
и законы Кирхгофа для напряжения (ЗКН) и
тока (ЗКТ). Поэтому рассмотрим вкратце эти
три закона.
Законы Кирхгофа мы редко употребляем явно,
используя их косвенным образом. В отличие от
этого закон Ома встречается на практике по-
всеместно и проявляется наглядно. Пока еще
никому не удалось осуществить требование,
которое мы часто видим на бамперных наклей-
ках на кампусе МТИ: «Требуем отменить закон
Ома!»
1№2.1.3аконОма:(У = /Д.
Рассмотрим величины, входящие в формулу из
заголовка, пользуясь аналогией водяного стол-
ба (рис. 1N.2). Тогда:
♦ U — будет аналогом давления, оказываемого
водяным столбом;
♦ R — обозначает сопротивление потоку;
♦ I — соответствует скорости потока (объем/
единица времени).
Сопротив-
ление
потоку R
Давление
водяного
столба: U
Скорость
потока I
Море
Рис. 1N.2. Водяная аналогия: напряжение представляется
давлением водяного столба, и т. д. Эта аналогия может быть
полезной для понимания взаимосвязи между основными
электрическими величинами
Такая простая аналогия с водяным столбом
работает достаточно хорошо, если только не
слишком увлекаться с ее применением, а также,
если вы не возражаете против такого подспорья
для своей интуиции.
Что такое «напряжение» и другие
сложные вопросы
В основном мы будем избегать таких слож-
ных вопросов в нашем курсе. Что касается уже
сформулированного вопроса о напряжении,
нас подмывает ответить на него фразой типа:
«О, вольт это то, что проталкивает ампер через
ом». Но это будет звучать как ответ гарвард-
ского студента, и мы не будем кичиться своим
остроумием, а дадим более традиционное опре-
деление: Напряжение — это объем потенциаль-
ной энергии на единицу заряда. Можно также
привести эквивалентное определение, но более
простыми словами: напряжение — это работа
по перемещению единицы заряда против элек-
трического поля (надеемся, что этот термин
не смутит вас; в любом случае, рекомендуется
привыкнуть к нему, даже если на данном этапе
вы сомневаетесь, что от этого будет какая-либо
польза7) от одного электрического потенциала
(наподобие одной точки на холме) к другому,
более высокому, потенциалу (к более высокой
точке на холме).
Разность напряжений между двумя уровнями
холма (или лестницы, как показано на рис. 1N.3)
можно описать, как разность электрических
потенциалов, или вольтаж. Электрическое поле
Единица
заряда
Высота
подъема
заряда
Рис. 1 N3. Напряжение — это работа, которую нужно выпол-
нить, чтобы поднять единицу заряда с одного уровня (или
потенциала) на другой, более высокий, уровень.
АоЕ § 1.2.1.
7 Возможно, подобно автору одной замечательной книги,
вы зададитесь вопросом: «... что такое поле? Это что-то
действительно существующее или же просто член урав-
нения, который нужно умножить на что-либо другое,
чтобы получить числовое значение измеряемой в экспери-
менте силы?» Е.М. Пурсел (Е.М. Purcell) и Д. Дж. Морин
(DJ. Morin) Электричество и магнетизм (Electricity and
Magnetism), 3-е издание (2013), § 1.7. Далее он приводит
убедительный аргумент о полезности понятия поля.
/W.2 Три основных закона электротехники
35
будет стремиться оттолкнуть этот заряд обрат-
но, подобно тому, как сила тяжести пытается
вытолкнуть воду из цистерны вниз. Наконец,
вам может быть интересно узнать, что единица
измерения напряжения вольт определяется как
работа, выполняемая при присоединении одно-
го джоуля потенциальной энергии к одному ку-
лону заряда8. Но дальше мы не будем использо-
вать такие термины, которые больше подходят
для физики, чем для искусства схемотехники.
Понятие «земли»
Иногда мы рассматриваем напряжение отно-
сительно какого-либо опорного уровня, воз-
можно, относительно планеты Земля. Но более
практичным будет выбрать в качестве такого
опорного уровня потенциал в том месте, в ко-
тором в землю закопан медный штырь, на-
пример, в подвале здания, где вы занимаетесь
экспериментами по электронике. Если возвра-
титься к нашей водяной аналогии напряжения,
для нее абсолютным нулевым уровнем может
быть уровень моря. Но нас чаще интересуют
только относительные напряжения: разница
потенциалов, замеренная относительно произ-
вольного опорного уровня, а не относительно
планеты Земля.
Хотя закон Ома очень полезен, он применим
только к элементам, которые ведут себя по-
добно сопротивлению. Какие же это элементы?
Как раз те, к которым применим закон Ома!
(Хотите, обижайтесь, хотите — нет, но это бу-
дет самое подробное изложение данного во-
проса в нашем курсе9.)
Почему закон Ома работает?
Элементы схемы, которые называются рези-
сторами10, оказывают сопротивление протека-
нию тока через них (чему можно противопо-
ставить намного более легкое протекание тока
8 См. Пурсел и Морин, §2.2.
9 Если этого объяснения вам недостаточно, можете посмо-
треть его в обычной книге или учебнике по электричеству
и магнетизму. В частности, этот вопрос хорошо освещен в
упомянутой ранее книге Пурсела и Морина, а также в кни-
ге «Принципы электронных схем» («Principles of Electronic
Circuits»), авторы С. Берне (S. Burns) и П. Бонд (P. Bond),
1987 г. издания.
10 Или сопротивлениями. В данной книге термин «рези-
стор» служит для обозначения собственно устройства, а
«сопротивление» — для обозначения характерных свойств
этого устройства. Таким образом мы избегаем таких выра-
жений, как «значение сопротивления сопротивления».
в отрезке проводника11). Это объясняется тем,
что несущие заряд электроны, которые пере-
мещаются под воздействием электрического
поля, сталкиваются с преградами (вибрация-
ми в атомной решетке) после краткого бес-
препятственного перемещения, и нуждаются
в повторном ускорении в направлении поля.
Хорошие проводники (это, в основном, ме-
таллы) обладают значительным количеством
электронов, не привязанных к атомной решет-
ке, которые вследствие этого могут свободно
перемещаться под действием электрического
поля. Величина проводимости металла зави-
сит от плотности носителей заряда, которыми
обычно являются свободные электроны. Это
объясняется тем, что повышение температуры
вызывает повышение амплитуды колебаний
атомной решетки, в результате чего свобод-
ные электроны проходят меньшее расстояние
из-за более частых столкновений с решеткой.
Вы сможете наглядно убедиться в этом на ла-
бораторном занятии 1L, если выполните экспе-
римент правильно. (Чтобы убедиться в реаль-
ном существовании этого эффекта, вам нужно
будет немного пораскинуть мозгами, посколь-
ку в описании к этой лабораторной работе не
указывается, как все происходит.) Чем сильнее
электрическое поле, тем выше скорость движе-
ния электронов. Напряженность поля зависит
от разности напряжений между двумя точками
проводника, а скорость движения электронов
определяет величину тока. Так что закон Ома
вполне обоснован.
Чем определяется величина
сопротивления резистора?12
Резистор, конечно же, также является и провод-
ником. На первый взгляд может показаться
странным называть резистором (т. е. сопротив-
лением) устройство, добавляемое в схему для
того, чтобы создать возможность для протека-
ния тока. Но название этого элемента говорит
о том, что он вставляется в участок цепи вместо
идеального проводника, например, простого
отрезка провода. Существуют два основных
типа резисторов: угольные композиционные и
металлопленочные. Угольные резисторы (на-
подобие тех, которые мы будем использовать
в наших лабораторных занятиях, поскольку их
значения сравнительно легко определяются)
11 Или еще лучше, в сверхпроводнике, сопротивление ко-
торого не просто очень мало, но вообще равно нулю.
12 АоЕ § С.4.
36
1N. Цепи постоянного тока
создают, смешивая порошкообразные изоля-
тор и уголь в пропорциях, необходимых для по-
лучения требуемого удельного сопротивления13.
А металлопленочные резисторы (более рас-
пространенные в настоящее время) создают,
напыляя тонкою пленку металла на керамиче-
скую подложку, а затем удаляя некоторый объ-
ем напыления до получения требуемого сопро-
тивления.
Как обычно применяется закон Ома?
Практически с самого начала мы начнем стал-
киваться с устройствами, не подчиняющимися
закону Ома (например, электронная лампа или
диод в лабораторном занятии 1L). Закон Ома
описывает лишь один из возможных вариан-
тов взаимоотношений между напряжением (U)
и током (Г) в компоненте, но существуют и дру-
гие типы взаимоотношений этих величин.
В книге АоЕ наш интерес в различных функ-
циональных взаимосвязях между напряжени-
ем и током объясняется следующим образом:
«Мы хотим создавать и использовать устрой-
ства с интересными и полезными функциями
зависимости тока /от напряжения U».
В резисторе ток и напряжение связаны точ-
ной линейной зависимостью: увеличив на-
пряжение вдвое, мы получим вдвое больший
ток. Таким образом, для резисторов закон Ома
справедлив. Но не ожидайте того же самого от
любого другого компонента. Даже обычная
лампочка, нить накаливания которой пред-
ставляет собой простой кусочек металла, так
похожий на резистор, не подчиняется закону
Ома, как мы увидим в лабораторном занятии
1L. Постарайтесь самостоятельно догадаться,
почему это так14.
Расширение области действия закона
Ома15: дифференциальное сопротивление
В дальнейшем нам редко придется использовать
устройства с обычными резистивными свой-
ствами. Как уже упоминалось, даже обычная
лампочка, нить накала которой похожа на рези-
стор, не говоря уже о диоде (мы познакомимся
с обоими этими устройствами в лабораторном
занятии 1L), не подчиняются классическому
закону Ома. Расширенная формулировка, ко-
торую мы будем называть законом Ома для
дифференциального (динамического) сопротив-
ления, позволит нам применять этот закон в
ситуациях, когда классическая формула не ра-
ботает. Эта формулировка закона основана на
понятии дифференциального сопротивления,
которое определяется как крутизна кривой в
данной точке графика зависимости [/-/для не-
которого устройства:
13 Удельное электрическое сопротивление, или просто
удельное сопротивление вещества — физическая вели-
чина, характеризующая его способность препятствовать
прохождению электрического тока.
14 Подсказка: лампочка подчинялась бы закону Ома, если
температура нити накаливания оставалась постоянной.
15 АоЕ § 1.2.6.
Это определение позволит нам рассматривать
эффективное сопротивление диодов, тран-
зисторов или источников тока (схема, под-
держивающая выходной ток неизменным).
На рис. 1N.4 изображен график зависимости
тока /диода от напряжения £/, где напряжение
U отложено по вертикальной оси. Благодаря
такой ориентации крутизна кривой измеря-
ется в обычных единицах — Омах, а не в об-
ратных — 1/Ом16, как на стандартном графике
такой зависимости17.
Возможно, вам больше нравится простая и точ-
ная прямая линия графика зависимости I- U для
резистора. Но понятие дифференциального со-
противления Я., хорошо своей универсально-
стью, поскольку оно позволяет описать график
зависимости I-U для любого устройства, будь
то транзистор или какой-либо экзотический
электронный компонент. Вертикальная линия
для источника тока на рис. 1N.4, означающая
гигантское внутреннее сопротивление Ru.., бу-
дет очень важной в дальнейшем для понимания
работы транзисторов.
Мощность резисторов18
Если вы помните, в курсе механики мощность
была связана со скоростью выполнения ра-
боты. В электронике это понятие встречается
наиболее часто при попытке определить спо-
собность компонента безопасно рассеивать
подаваемую на него электрическую мощность.
Большая мощность создает значительный
объем тепла, и компонент должен быть в силах
сбросить или рассеять это тепло. На рис. 1N.5
16 Или в Сименсах, что является официальным названием
единицы, обратной Ому.
17 Ее часто называют «Вольт-амперной характеристи-
кой» — Примеч. ред.
18 АоЕ § 1.2.2С.
7Л/.2. Три основных закона электротехники
37
Источник
тока
150 Ohh при 0,2 мА
1(мА)
Несколько графиков зависимости
тока Гот напряжения U
Только один график с линейной
зависимостью
1(мА)
Подробный вид графика для диода
Рис. 1 N.4. Иллюстрация дифференциального сопротивления, определяемого для устройств с неомическими19 характеристи-
ками, как крутизна кривой в заданной точке графика
наглядно проиллюстрирована примерная
взаимосвязь между номинальной мощно-
стью рассеивания резисторов и их размером:
резисторы большего размера обычно имеют
большую площадь контакта с окружающей
средой, что обеспечивает более эффективный
отвод тепла.
Указанная номинальная мощность рассеива-
ния является максимальной, которую резистор
может безопасно выдержать. Миниатюрный
резистор для поверхностного монтажа слева на
рисунке (его размер 0805 достаточно велик по
меркам поверхностного монтажа) рассеивает
довольно большую мощность (0,125 Вт), чем
можно было бы ожидать, если сравнить его
размер с габаритами угольного резистора с но-
минальной мощностью 0,25 Вт (мы используем
резисторы этого типа в наших лабораторных
проектах). Это объясняется тем, что он при-
паивается непосредственно на печатную плату,
медные дорожки которой эффективно отводят
и рассеивают тепло.
На последующих лабораторных занятиях нам
иногда нужно будет определить, смогут ли те
или иные компоненты выдержать подводимую
к ним мощность. Обычные резисторы, кото-
рые мы будем использовать на этих занятиях,
имеют номинальную мощность рассеивания
равную 0,25 Вт. На такие резисторы можно
безопасно подавать напряжение 15 В (обычное
максимальное напряжение питания), при усло-
вии, что номинальное сопротивление резисто-
ра не превышает 1 кОм. Потребляемая устрой-
ством мощность рассчитывается по формуле
Ю Вт
0,125 Вт
0,25 Вт
19 «Омический» — означает подчиняющийся обычному
закону Ома.
Рис. 1N.5. Три резистора (и монета из никелево-медного
сплава)
Заменив U на I • R (согласно закону Ома, где
U= I- R), получим следующую формулу:
Р = Й?,
а поскольку I = U/R,
тогда
P=U2/R.
В данном случае наиболее полезной является
последняя формула. 0,25 Вт = 152/#min. Таким
образом, Rmin = 225/(0,25) = 900 Ом. Так что
значение 1 кОм достаточно близко к минималь-
ному безопасному значению сопротивления
при напряжении 15 В (значение 910 Ом также
безопасное, но не будем мелочиться и остано-
вимся на сопротивлении 1 кОм).
До сих пор мы рассматривали мощность для
резисторов. Но понятие мощности применимо
не только к резисторам, и формула:
P=U-I
справедлива для любого электронного компо-
нента.
Более подробное рассмотрение, что мы обозна-
чаем через U и I, поможет сделать эту формулу
более очевидной:
38
/Л/. Цепи постоянного тока
♦ ток представляет собой отношение заряд/
время;
♦ напряжение представляет собой отношение
работа/заряд.
Таким образом, произведение U • I = работа/
заряд х заряд/время = работа/время, т. е. ра-
бота, выполняемая за единицу времени, или
скорость выполнения работы, что и соответ-
ствует нашему определению мощности, приве-
денному в начале этого раздела. В дальнейшем
заботиться об ограничении мощности нам при-
дется в тех исключительных случаях, когда мы
работаем с относительно большими напряже-
ниями (например, с напряжением 30 В на вы-
ходе «компаратора» в лабораторном занятии
8L) или с большими, чем обычно токами (на-
пример, для питания динамика в лабораторном
занятии 6L, светодиода в лабораторном заня-
тии 13L и в стабилизаторах напряжения в ла-
бораторном занятии 11L).
1 N.2.2. Законы Кирхгофа
для напряжения и тока
Скорее всего эти два закона только подтверж-
дают то, что вы считаете общеизвестными фак-
тами:
♦ сумма напряжений в замкнутом контуре
(цепи) равна нулю (рис. 1N.6, слева);
♦ алгебраическая сумма токов, входящих в узел
и исходящих из него, равна нулю (рис. 1N.6,
справа).
Применение этих законов для элементов, со-
единенных последовательно и параллельно
(рис. 1N.7):
Последовательно: /
общий
Параллельно: 7общий = 1г +12
Рис 1N.7. Применение законов Кирхгофа для элементов,
соединенных последовательно и параллельно
Последовательно: Г70бщее = иг + U2
Параллельно: [7общее = Ц = £/2
Вопрос
Кстати, что это за «замкнутый контур», о котором
идет речь в правиле Кирхгофа для напряжений?
Ответ
Замкнутый контур (или замкнутая цепь) стано-
вится очевидным, если источник питания изобра-
зить в виде элемента схемы, подключив оба его
вывода к резисторам (рис. 1 N.8).
Обычно на принципиальных схемах источник
напряжения не изображают полностью, вме-
сто этого напряжения указывают в некоторых
точках схемы, подразумевая, что пользователь
при необходимости может сам представить всю
цепь замкнутой.
Чтобы не заскучать, давайте-ка займемся менее
абстрактными схемами, пригодными для прак-
тического применения. Но сначала рассмотрим
несколько приемов, облегчающих расчеты в
схемах.
+ [
А
**•
L
В
+
Л-
С
Рис. 1N.6. Законы Кирхгофа для напряжения и тока. Слева: Закон Кирхгофа для напряжения — сумма напряжений в замкну-
том контуре равна нулю; справа: закон Кирхгофа для токов — алгебраическая сумма токов, входящих в узел цепи и исходящих
из него, равна нулю
7Л/.2 Три основных закона электротехники
39
+30 В
Это не похоже
на замкнутый
контур...
...а здесь все наглядно видно;
но обе схемы электрически -Z- ^0 В
эквиваленты.
Рис. 1N.8. Схема делителя напряжения в стандартном варианте (слева) и нарисованная в виде замкнутого контура (справа)
Вычисление эквивалентного
сопротивления параллельно
соединенных резисторов
Общая проводимость схемы с параллельными
резисторами равна сумме проводимостей каж-
дого резистора (рис. 1N.9):
Проводимостьобщая= Проводимость^ +
+ Проводимость^ = 1/RX +1/R2.
Это правило легко запомнить, но оно обычно
не очень удобно, поскольку на практике мы
редко оперируем проводимостями. В подавля-
ющем большинстве случаев используется по-
нятие сопротивления, и формула для вычисле-
ния общего сопротивления двух параллельно
соединенных резисторов выглядит следующим
образом:
Но даже эта формула слишком сложна для на-
шего курса. Поэтому опишем несколько при-
емов для упрощения расчётов. Для этого рас-
смотрим три случая параллельного соединения
двух резисторов, показанные на рис. 1N.10.
Рис. 1N.9. Свойства параллельных резисторов: проводимо-
сти складываются, но сопротивления, к сожалению, нет
Особый интерес представляют первые два слу-
чая, поскольку они позволяют быстро опреде-
лить общее сопротивление в подобных схемах.
Приемами для упрощения расчетов не следует
пренебрегать, так как они экономят время и
дают практически верный результат. Но если
получение ответа кажется трудным, то вам бу-
дет просто лень это делать. Типичным приме-
ром является ситуация, когда студент думает:
«О, я вычислю это позже, как-нибудь сегодня
вечером, когда запущу Excel на компьютере20».
Такой студент никогда не выполнит даже этого
простейшего расчета! Чтобы определить об-
щее сопротивление схемы на рис. 1N.10, а, не
нужно никаких формул: общее сопротивление
20 АоЕ § 1.2.2В.
10/?
а б
Рис. 1 N.10. Три простых примера параллельного соединения двух резисторов
40
1N. Цепи постоянного тока
двух параллельных резисторов с одинаковым
номиналом равно половине сопротивления
каждого из них: 1?общ = R/2. Еще проще выпол-
нить прикидку для средней схемы (рис. 1N.10,
б), если допустить погрешность не более 10%,
то 2?общ « R. (С другой стороны, если нужно
уменьшить значение R на 10%, это можно лег-
ко сделать с помощью этого метода.) Для самой
правой схемы (рис. 1N.10, в) нужно немного
интуиции: резистор с сопротивлением R можно
рассматривать как два параллельных резистора
с одинаковыми сопротивлениями: 1/1? = 2/21?.
Тогда всю схему можно рассматривать как три
параллельных резистора каждый с сопротивле-
нием 21?, а общее сопротивление схемы будет
В данном курсе для нас обычно приемлемы
ответы с точностью до 10%. Поэтому, если
значения одного из двух параллельных рези-
сторов больше другого в 10 раз или больше,
можно спокойно игнорировать этот больший
резистор.
Давайте сформулируем наше первое эмпири-
ческое правило для двух параллельных рези-
сторов, а заодно и эквивалентное правило для
двух последовательно соединенных резисторов
(рис. 1N.11).
1 N3. Первая практически
важная схема: делитель
напряжения
Прежде всего зададимся вопросом, зачем во-
обще нам нужны делители напряжения?21
Почему мы не можем просто сразу подавать
необходимое напряжение? Потому что, как вы,
скорее всего, знаете, в типичной схеме присут-
ствуют напряжения разных величин, и иметь
отдельный источник питания для каждого из
них непрактично (слишком дорого). Мы вско-
ре будем заниматься разработкой источников
питания, и тогда вы сможете самостоятель-
но оценить, насколько делитель напряжения
проще (и дешевле) полноценного источника
питания.
Для демонстрации практической важности де-
лителей напряжения предлагаем вам рассмо-
треть принципиальную схему довольно слож-
ного устройства — генератора сигналов, кото-
рый скоро понадобится на лабораторном заня-
тии 2L. На рис. 1N.12 изображена часть схемы,
преобразующая сигнал треугольной формы
в синусоидальный.
Правило
При параллельном соединении доминирует ре-
зистор с намного меньшим сопротивлением, чем
другие. При последовательном соединении доми-
нирует резистор с намного ббльшим сопротивле-
нием, чем другие.
Малое
сопротивление
Большое
сопротивление
Большое со-
противление
Малое сопро-
тивление
Регулируемые делители напряжения,
или «потенциометры»
Прежде чем приступить к подробному рас-
смотрению обычного делителя напряжения,
обратим ваше внимание на разновидность де-
лителей, которая встречается довольно часто:
регулируемый делитель напряжения. Эта схема
также существует в виде готового устройства,
называемого потенциометром.
Название устройства достаточно хорошо со-
ответствует его функции: потенциометр «от-
меряет»22 потенциал. Отсюда следуют два при-
менения этого устройства:
♦ собственно в качестве потенциометра;
♦ в качестве переменного резистора.
Рис. 1N.11. Быстрая оценка общего сопротивления двух
резисторов, соединенных параллельно (слева) и последова-
тельно (справа)
21 АоЕ § 1.2.3.
22 Англ. meter (out).
/Л/.З. Первая практически важная схема: делитель напряжения
41
Регулируемый дели-
тель напряжения
Несколько обыч^
ных нерегулируе^
мых делителей
напряжения
Регулируемый дели-
тель напряжения
(делает выходной сиг-
нал положительным
или mm
отрицательным) /^—^
Еще не-
сколько
обычных
делителей
напряжения
V
Рис. 1N.12. Делители напряжения, используемые в генераторе сигналов: как видим, делители нужны не только для обучения
новичков [Генератор сигналов Krohn-Hite 1400]
Потенциометр в качестве переменного
резистора
Потенциометр (устройство с тремя выводами)
можно использовать в качестве переменного
резистора (устройства с двумя выводами).
Для этого к схеме подключают один из крайних
выводов потенциометра и средний вывод пол-
зунка (рис. 1.N13); кроме того, вывод ползунка
часто соединяют с другим крайним выводом,
что несколько лучше (рис. 1N.14)23.
23 Разница между этими двумя подходами довольно тон-
кая. Если значение сопротивления потенциометра равно,
например, 100 кОм, диапазон значений переменного рези-
стора будет от 0 до 100 кОм при любом из этих двух под-
ходов. Разница (и причина предпочтения второго спосо-
ба) становится заметной, когда со временем путь ползунка
загрязняется. Если вследствие этого ползунок временно
теряет контакт с постоянным резистором, то во втором
варианте (ползунок соединен со вторым выводом) ре-
зультирующее значение сопротивления окажется равным
100 кОм. В первом же случае при потере ползунком кон-
такта с постоянным резистором образуется разрыв в цепи
и результирующее значение сопротивления будет бес-
конечно большим. Поскольку ничего не стоит соединить
ползунок с одним из крайних выводов, мы советуем вам
всегда так и делать.
Потенциометр
Выводы
постоянных
резисторов
Выход
Ползунок
Рис. 1N.13. Устройство потенциометра (слева) и его обозна-
чение (справа)
Переменный резистор
Рис. 1N.14. Потенциометр можно использовать в качестве
переменного резистора
42
IN. Цепи постоянного тока
Постоянный резистор
(неизолированный) Ползунок
Выводы ^^0^^
постоянного
резистора \^
Вывод ' >^
ползунка
Крупногабаритный (мощный)
потенциометр старого образца
Постоянный
резистор ^^^
. ^Л
Миниатюрный подстроенный
потенциометр
(вид сверху; 012 мм)
Внутренности
подстрочного
потенциометра
Контакт ползунка
/
Ползунок
(обеспечивает
контакт между
ползунком
и постоянным
резистором)
Рис. 1N.15. Конструкция потенциометра
Конструкция потенциометра
Для работы с потенциометром будет полезным
знать его конструкцию. На рис. 1N.15 показа-
ны два образца потенциометра. Конструкцию
и принцип действия потенциометра, изобра-
женного слева, понять легко. Вдоль внутрен-
ней окружности корпуса расположен неизоли-
рованный постоянный проволочный резистор,
образующий контактную дорожку. К нижней
части этого резистора прижат скользящий кон-
такт, который может перемещаться от одного
конца дорожки к другому.
На рис. 1N.15 слева ползунок потенциометра
находится на расстоянии примерно 70% между
нижним и верхним выводами постоянного ре-
зистора. Если теперь верхний вывод подклю-
чить к напряжению 10 В, а нижний к «земле»,
то на выводе ползунка окажется напряжение
около 7 В.
Потенциометр, изображенный посредине и
справа на рис. 1N.15, имеет, по существу, анало-
гичное устройство, как и первый потенциометр,
зов
но он более компактный (на рисунке он показан
увеличенным по сравнению с первым потенци-
ометром). Кроме того, дорожка его постоянно-
го резистора сопротивлением 1 кОм выполнена
не из проволоки, а из кермета
,24
1 N3.1. Исследуем делитель
напряжения
На рис. 1N.16 показан простой пример более
распространенного обычного нерегулируемого
делителя напряжения. Этот делитель выдает на
выходе требуемое напряжение ишх меньшей
величины, чем на входе.
Прежде всего одно замечание по обозначению:
буква «к» в «кОм» означает кило-, т. е. 103,
но вы, наверное, это уже знаете.
Выходное напряжение [7ВЫХ делителя можно
вычислить несколькими способами, но мы
порекомендуем наиболее простой из них, по-
зволяющий легко провести все вычисления
в уме.
Три способа вычисления выходного
напряжения делителя
Первый способ. Сначала определяем ток, про-
текающий по соединенным последовательно
резисторам (рис. 1N.17).
Получаем:
1=30В/20кОм=1,5мА.
Рис. 1 N.16. Обычный делитель напряжения
24 Композитный материал из керамики и металла.
IN.4. Нагрузка и «выходной импеданс»
43
Кн.
Рис. 1N.17. Первый способ вычисления выходного напря-
жения делителя
Рис. 1 N.18. Второй способ вычисления выходного напряже-
ния делителя
Получив общий ток, рассчитываем напряжение
на нижнем резисторе делителя:
или:
= 15mA-10kOm =
Но этот способ занимает слишком много вре-
мени.
Второй способ. Воспользуемся тем обстоя-
тельством, что через оба резистора протекает
одинаковый ток (рис. 1N.18).
Используем косвенный метод расчета и соста-
вим алгебраическое уравнение:
или
В итоге получим
ишх = 17К. (10 кОм/20 кОм) = UBX/2.
Это намного лучше, и мы будем использовать
формулу (1N.1) довольно часто. Но хотелось
бы избавиться от необходимости составлять
уравнение и еще более упростить вычисления.
Третий способ. Попробуйте описать слова-
ми работу делителя. Получится примерно так:
«поскольку через оба резистора протекает оди-
наковый ток, падение напряжения на каждом
из них пропорционально сопротивлению25 со-
ответствующего резистора».
25 В дальнейшем мы будем оперировать не сопротивле-
ниями, а более общим понятием импеданса, что позволит
нам работать с устройствами иными, чем резисторы.
Поскольку в данном случае нижний резистор
составляет половину общего сопротивления,
падение напряжения на нем будет также равно
половине общего входного напряжения.
А если, например, сопротивление нижнего
резистора будет, скажем, в 10 раз больше чем
верхнего, то напряжение ишх на нем будет со-
ставлять 90% от входного напряжения (говоря
точнее, выходное напряжение составит 10/11
от входного, но мы принимаем величину 90%,
находящуюся в пределах допускаемой нами по-
грешности).
1 N.4. Нагрузка и «выходной
импеданс»
Теперь, когда мы знаем, как вычислить выход-
ное напряжение ишх простого делителя, пред-
положим кто-то «нагрузил» этот выход, под-
ключив к нему еще один резистор, как показа-
но на рис. 1N.19. Как это скажется на выходном
напряжении? (Вы считаете, что имеете полное
право негодовать, поскольку так нечестно?26)
Как и в случае с простым делителем, выходное
напряжение нагруженного делителя можно вы-
числить несколькими способами, один из кото-
рых более легкий, чем другой.
26 Мы считаем, что у вас нет причин для негодования, ну
разве что для легкого расстройства. Подключение какого-
либо потребителя питания (называемого нагрузкой) к вы-
ходу нашей схемы — обычное дело. Ведь мы же и создали
эту схему в качестве источника питания. Но, и мы это бу-
дем постоянно повторять в будущем, у вас есть право ожи-
дать, что эта нагрузка не будет слишком обременительной,
т. е. не потребляет слишком большой ток. В схемотехнике
зачастую нагрузка в 10 кОм слишком велика. Почему это
так мы увидим чуть далее.
44
1N. Цепи постоянного тока
зов
I Чых
ЮкОм
i ^ ^10 кОла
| I Нагрузка
Рис. 1N.19. Делитель напряжения с нагрузкой
ЗОВ
ЮкОм
5кОм
(ЮкОм || ЮкОм
кОм >
U
>кОм>
0кОм<
Две вертикальные черточки между резисторами означа-
ют параллельное соединение этих резисторов.
Рис. 1N.20. Делитель напряжения с нагрузкой. Совмещаем
два нижних сопротивления
1N.4.1. Вычисление выходного
напряжения нагруженного
делителя
Трудоемкий способ. Рассматриваем два ниж-
них сопротивления (резистора), как одно, и вы-
числяем выходное напряжения ишх для этой
модификации делителя (рис. 1N.20).
Таким образом, выходное напряжение UBUX на-
груженного делителя будет составлять 1/3 от
входного 17К. Это вполне разумный метод, но
он требует создания отдельной модели схемы
для каждой возможной нагрузки.
20 В
Лучший способ27. Применяем модель Теве-
нина (рис. 1N.21).
Два элемента модели Тевенина вычисляются
следующим образом. Заменяем исходную схе-
му (без нагрузки) более простой схемой (назы-
ваемой моделью Тевенина), которая представ-
ляет собой идеальный источник напряжения,
включенный последовательно с резистором.
Теперь легко понять, как эта преобразованная
схема будет вести себя с разными нагрузками.
В частности:
♦ напряжение [7ТЕВ будет равно просто напря-
жению 17^, т. е. напряжению холостого хода,
когда к делителю не подключено никакой на-
грузки;
♦ а сопротивление RTEB часто представляет-
ся в виде дроби ^тевДсз- Ток короткого за-
мыкания 1КЗ — это ток, который протекает
при соединении выхода схемы напрямую
с «землей».
Но на практике мы редко определяем #ТЕВ таким
опасным методом. В подавляющем большин-
стве случаев закорачивание выхода на «землю»
крайне нежелательно, поскольку это может по-
вредить или полностью вывести из строя схему
и иногда представляет опасность для экспери-
ментатора. Представьте себе результат такого
эксперимента, например, с автомобильным ак-
кумулятором! А если у нас есть принципиаль-
ная схема устройства, то можно применить на-
много менее трудоемкий способ (рис. 1N.22).
1N А2. Объяснение метода Тевенина
Быстрый метод вычисления сопротив-
ления Тевенина R^. При наличии принци-
пиальной схемы, проще всего вычислить со-
противление #ТЕВ, если рассматривать его как
АоЕ § 1.2.5.
Обратите внимание,
что нагрузка не является
частью модели Тевенина
U^ (холостой ход; S I
без нагрузки) ""
Рис. 1 N.21. Модель Тевенина: идеальный источник напряжения, подключенный последовательно к выходному сопротивлению
1N.4. Нагрузка и «выходной импеданс»
45
несколько параллельно соединенных сопро-
тивлений, подключенных к выходу.
Примечание
Кстати, такая постановка задачи предполагает
идеальные источники напряжения; в противном
случае необходимо также учитывать их выходное
сопротивление. Но на данном этапе мы будем иг-
норировать это усложнение.
При быстром методе определения #ТЕВ, про-
иллюстрированном на рис. 1N.22, утвержда-
ется, что значение этого сопротивления равно
общему значению параллельных сопротивле-
ний (Rpgg = -RJI^)» H0 данный результат может
показаться вам несколько необычным: почему
сопротивление Rv подключенное к положи-
тельному полюсу источника питания, должно
считаться параллельным сопротивлению R2?
Ну, предположим, что напряжение положи-
тельного полюса равно нулю. Тогда эти сопро-
тивления, несомненно, были бы соединены па-
раллельно, не так ли?
Проведем другой мысленный эксперимент, пе-
реопределив положительный полюс питания,
как О В. Тогда напряжение на полюсе, который
мы называем «землей» и нулем, будет равным
-30 В (см. обозначения на рис. 1N.16). Теперь
важную роль играет верхний резистор, подклю-
ченный к «новой земле»; а нижний резистор Rr
подключенный к -30 В, кажется несуществен-
ным. Но, конечно же, схема «не знает» и ей «все
равно», как мы, люди, определяем нашу «зем-
лю», или нулевой провод.
Суть этого манипулирования определения-
ми «земли» заключается в том, что относи-
тельно выхода схемы напряжения на других
+20 В
ЮкОм
+20 В
Рис. 1 N.22. Сопротивление /?ТЕВ = /?J| /?2
концах резисторов не играют никакой роли.
Единственно важен тот факт, что эти напряже-
ния постоянные28.
Рассмотрим делитель напряжения с другими
параметрами: входное напряжение 20 В по-
дано на два резистора по 10 кОм. Определить
выходной импеданс можно обычным методом
(который мы будем постоянно упоминать и
применять):
Стандартная процедура определения
импеданса в точке
Чтобы узнать значение импеданса в точке:
Задаем ALT и А/.
Определяем импеданс, разделив первую
величину на вторую.
Иллюстрации на рис. 1N.23 являются просто
демонстрацией дифференциальной или дина-
мической формулировки закона Ома.
В данном случае перед небольшим изменением
напряжения на выходе делителя ток составлял
Конечно же, они совпадают!
Просто ты доплачиваешь разницу
ЮкОм
Без нагрузки
ЮкОм
Подаем LU- +1 В на выход
Эй! Балансы не совпадают! I
Рис. 1 N.23. Гипотетический делитель: ток = 1 мА; подаем на
вход небольшое напряжение Л С/ и смотрим, какой получится
соответствующий ток Л/
28 Позже мы ослабим и это требование. На самом деле
модель Тевенина применима для определения выходного
сопротивления как при постоянном, так и при переменном
напряжении.
46
1N. Цепи постоянного тока
1 мА. После того как мы поднимем выходное
напряжение на 1 В, токи в резисторах делите-
ля перестают совпадать: ток через верхний ре-
зистор равен 0,9 мА, а через нижний — 1,1 мА.
Разницу должен возместить тот, кто обеспечи-
вает изменение выходного напряжения. В ре-
зультате:
Импеданс = Д U/AI = 1В /0,2 мА = 5 кОм.
И, ко всеобщему удовлетворению, это и есть об-
щее сопротивление двух параллельно включен-
ных сопротивлений. Облегчает ли приведенное
объяснение понимание данного результата29?
Возможно, вы задаетесь вопросом, что делает
эту модель полезной. На рис. 1N.23 проиллю-
стрирован лишь один вариант ответа на этот
вопрос, хотя, возможно, у вас останутся сомне-
ния, пока вы не познакомитесь с другими при-
мерами.
Простое объяснение метода Тевенина
для параллельных сопротивлений.
При нагрузке неидеального источника напря-
жение на нем падает. Величина падения напря-
жения зависит от выходного импеданса источ-
ника. Модель Тевенина об эквивалентном пре-
образовании путем введения J?TEB описывает
это свойство одним числом.
1N A3. Применение модели
Тевенина
Сначала удостоверимся в надежности модели
Тевенина: убедимся, что ее поведение эквива-
лентно поведению моделируемой схемы. Ранее
мы установили, что без нагрузки выходное на-
пряжение делителя напряжения из двух рези-
сторов по 10 кОм с входным напряжением 30 В
составляет 15 В, и падает до 10 В при нагрузке
в 10 кОм (рис. 1N.24). Дает ли модель Тевенина
такой же результат?
Действительно, напряжение в модели Тевенина
падает точно так же, как и в реальной схеме до
10 В. Данная модель обладает свойством, от-
сутствующим у исходной схемы: она характе-
ризует степень падения выходного напряжения
через одно число — Rj,EB.
ЮкОм
ЮкОм
ЮкОм
Рис. 1N.24. Модель Тевенина при наличии нагрузки: напря-
жение в эквивалентной схеме падает, как и в исходной
Благодаря этому при изменении сопротивле-
ния нагрузки модель Тевенина облегчает
определение соответствующего изменения вы-
ходного напряжения делителя. Если же как
обычно вычислять значение нижних двух па-
раллельных сопротивлений, то потребуется не
только больше времени, но и не удастся полу-
чить практически удобный результат.
Давайте попробуем применить описанную мо-
дель к нескольким источникам напряжения,
отличающимся только Rj.EB. Одновременно вы
сможете понять влияние входного импеданса
измерительного инструмента (вольтметра) на
выходное напряжение.
Для этого рассмотрим несколько делителей
напряжения, на которые подано одинаковое
входное напряжение 20 В (рис. 1N.25).
Предположим, что резисторы в делителях имеют
погрешность номинального значения, равную
1% (т. е. действительные значения отличаются
не более чем на ±1% от номинала). Очевидно,
что напряжение UTEB будет одинаковым во всех
случаях, а импеданс 1^ЕВ — разным.
Предположим, что мы хотим измерить выход-
ное напряжение UBUX каждого делителя. Если
вольтметр идеальный, то напряжение во всех
случаях будет равно 10 В. (Кстати, подумайте,
с какой точностью 10 В? 10 000 В? 100 В?30)
Но если проводить замеры реальным лабо-
раторным вольтметром, то на результат будет
влиять входной импеданс RBX этого прибора.
Давайте проведем измерение сначала аналого-
вым, а затем цифровым мультиметром.
29 АоЕ § 1.2.6.
30 Это напряжение может быть равным точно 10,0 В, но
также может быть и немного меньше, чем 9,9 В, или не-
много больше, чем 10,1 В при условии, что погрешность
напряжения 20 В источника питания и номиналов резисто-
ров находится в пределах 1%. Все элементы неидеальны.
IN А. Нагрузка и «выходной импеданс»
47
20 В
20 В
Ббльшие сопротивления
20 В
20 В
Меньшие сопротивления
Рис. 1 N.25. Несколько делителей напряжения с одинаковым иш, но разными R
+20 В
100 кОм
Рис. 1N.26. Показания реального аналогового
вольтметра отличаются от идеального. По ним
можно судить о входном импедансе Явх измери-
тельного прибора
100 кОм
По этому показанию
можно вычислить £вх
I Аналоговый
вольтметр
Начнем измерять с правого (на рис. 1N.25) де-
лителя с резисторами по 1 кОм. В таблице 1N.1
приведены результаты замеров для трех дели-
телей.
Таблица 1N.1. Результаты измерений
аналоговым вольтметром
Значение
R
1к0м
ЮкОм
100 кОм
Замеренное
"вых
9,95
9,76
8,05
Заключение
В пределах
погрешности R
Влияние входного
импеданса вольтметра
заметно
Вольтметр сильно
влияет на результат
измерения
Показание 8,05 В свидетельствует об очевид-
ном влиянии входного импеданса измеритель-
ного прибора, и если мы округлим значение
до 8 В, то сможем без большого труда вычис-
лить входное сопротивление RBX мультиметра
(рис. 1N.26).
Как обычно, у нас есть выбор — мы можем во-
оружиться калькулятором и формулой или же
попытаться вычислить входное сопротивление
нашего вольтметра с помощью карандаша и ли-
ста бумаги. Попробуем второй способ.
Прежде всего мы знаем, что сопротивление #ТЕВ
равно общему сопротивлению двух параллель-
ных резисторов по 100 кОм, т. е. 50 кОм. Далее
обсудим способ получения решения (приблизи-
тельного, поскольку мы округляем измеренное
выходное напряжение делителя ишх до 8 В).
Прибор показывает 8 частей из 10; остальные
2 части, должно быть, падают на импедансе
RTEB (или можно назвать его #вых) делителя.
Относительные величины наших двух сопро-
тивлений пропорциональны этим двум паде-
ниям напряжения — 8 к 2, поэтому входной
импеданс вольтметра RBX должен быть равным
4 х RJEB или 200 кОм.
Замечание
Если мы посмотрим на переднюю панель на-
шего вольтметра, то обнаружим надпись —
20 000 Ом/В.
Это значит, что при установке вольтметра на
предел 1 В (т. е. таким образом, чтобы при
входном напряжении в 1 В стрелка вольтме-
тра отклонилась на всю шкалу), его входное
сопротивление будет составлять 20 кОм. Но
мы-то получили значение 200 кОм. Что пошло
не так? Все правильно, нужно только принять
во внимание, что для выбора диапазона изме-
рений напряжения в аналоговом вольтметре
48
IN. Цепи постоянного тока
предусмотрен набор последовательно соеди-
ненных резисторов31. Наш ответ 200 кОм пра-
вильный для диапазона измерений 10 В, кото-
рый мы установили для этого эксперимента.
Теперь, наверное, самое время разобраться с
внутренним устройством мультиметров, как
аналогового, так и цифрового.
Внутреннее устройство мультиметра
По принципу работы мультиметры делятся
на два типа: аналоговые приборы определя-
ют ток, цифровые — напряжение (рис. 1N.27,
1N.28). Но оба прибора можно настроить
для измерения любой из этих величин, что и
объясняет, почему они называются мульти-
метрами.
Техническая характеристика аналогового
мультиметра — 20 000 Ом/В — характеризует
чувствительность гальванометра, являющего-
ся центральной частью прибора. Гальванометр
довольно значительно снижает входное сопро-
тивление аналогового мультиметра для опреде-
ленного диапазона измерений.
Стрелка
Шкала
Вращающаяся
катушка
Постоянный^
магнит . J
Входные клеммы
Предположим, что выполнив те же самые за-
меры выходного напряжения делителей с по-
мощью цифрового вольтметра, мы получили
следующую таблицу 1N.2.
Таблица 1N.2. Результаты измерений
цифровым вольтметром
Значение
R
100 кОм
1М0м
ЮМОм
Замеренное
"вых
9,92
9,55
6,69
Заключение
В пределах
погрешности R
Влияние входного им-
педанса мультиметра
заметно
Мультиметр сильно
влияет на результат
измерения
Как и раньше рассмотрим случай с очевидным
падением напряжения и обсудим способ полу-
чения решения.
Решение
На этот раз сопротивление /?та составляет 5 МОм;
падение напряжения на входном импедансе Явх_циф
цифрового мультиметра составляет 2/3 части
общего напряжения, а на сопротивлении ЯТЕВ —
1/3 часть. Поэтому входной импеданс /?вхциф циф-
рового мультиметра оказывается равным 2 х /?ТЕВ
или ЮМОм.
Если мы посмотрим в технический паспорт для
данного цифрового мультиметра, то обнару-
жим, что для его входного импеданса указано
что-то типа «10 МОм на всех диапазонах». Так
что наши измерения снова оказываются пра-
вильными.
Рис. 1N.27. Механизм аналогового вольтметра реагирует на
изменение тока
вход
. датчик напряжения
(very high Rin)
(с очень высоким /?вх)
индикатор
Рис. 1N.28. Механизм цифрового мультиметра основан на
определении напряжения
31 Вы сможете лучше разобраться с этим вопросом, решив
задание 1.8 из АоЕ; пока же просто поверьте мне на слово.
+20 В
ЮМОм
ЮМОм
Цифровой
j ? % мультиметр
Рис. 1 N.29. Показания реального цифрового вольтметра от-
личаются от показаний идеального. По ним можно судить о
его входном импедансе Явх
1N.4. Нагрузка и «выходной импеданс»
49
1 N.4A Какой мультиметр лучше:
аналоговый или цифровой?
Анализируя материал предыдущего раздела,
можно сделать вывод, что цифровой мульти-
метр будет лучше, по крайней метре, с точки
зрения входного импеданса RBX. С ним так-
же удобнее работать. Но для измерения тока
он ничем не лучше, чем аналоговый мульти-
метр. Падение напряжения на нем составляет
1/4 полной шкалы, как и в аналоговом вольт-
метре. Ток в цепи с помощью мультиметра из-
меряют, просто замеряя падение напряжения на
встроенном резисторе небольшого номинала!
1NA5. Несколько слов о «земле»
Понятие «земли» в электронике играет очень
важную роль, и кроме того, оно в действитель-
ности оказывается многозначным. Попробуйте
понять значение этого термина, изучив пока-
занные на рис. 1N.30 примеры.
Вопрос
Какое будет сопротивление между точками А и Б?
(На этот вопрос легко ответить, если не слишком
углубляться в общие рассуждения.32)
Мы знаем, что означает символ «земли» на элек-
трической схеме, — нижние выводы обоих рези-
сторов соединены электрически друг с другом.
Играет ли какую-либо роль то обстоятельство, что
каждый вывод также соединен с планетой Земля?
Как оказывается, не играет ни малейшей.
А теперь скажите, где же присутствует «земля»
в схеме на рис. 1 N.31 ?
Две разновидности «земли»
«Земля» в смысле общей опорной точки
В большинстве случаев для нас важна только
«земля» в смысле общей точки цепи, потенци-
ал в которой условно считается равным нулю
32 Не так и легко, если вы не знаете, что показанная на
рис. 1N.30 «земля» является общим узлом цепи, потенциал
которого условно принимается за ноль, и все напряжения
в схеме отсчитываются от потенциала этого узла. В таком
случае общая «земля» означает, что резисторы 10 кОм и
22 кОм соединены последовательно. Но если под «землей»
понимать планету Земля с одним резистором, соединен-
ным с ней в Нью-Йорке, а другим в Чикаго, то ответить на
вопрос будет на так просто. К счастью, к такому обозна-
чению «земли» (по крайне мере, как в данном примере)
прибегают в схемотехнике чрезвычайно редко.
>22кОм
10 кОм
ЮкОм
Рис. 1 N30. Два понятия «земли»
Источник питания
Рис. 1 N31. Две разновидности «земли»
и относительно которого измеряются все дру-
гие напряжения в схеме. Такая «земля» также
часто называется «общим» (проводником)
или сигнальной землей. Эта общая точка может
быть подключена к планете Земля посредством
соединения с забитым в землю металлическим
штырем.
«Земля» в смысле заземления
Но иногда встречаются ситуации, когда устрой-
ство необходимо подключить собственно к
земле, например заземлить специальный про-
вод на щупе осциллографа. Такая «земля» на-
зывается заземлением.
Хороший пример заземления можно найти
здесь:
http://en.wikipedia.org/wiki/
File:HomeEarthRodAustralial.jpg.
Для обозначения этих двух разных понятий
«земли» на принципиальных схемах суще-
ствуют два различных символа, показанные на
рис. 1N.32.
50
1N. Цепи постоянного тока
Сигнальная земля
(общий провод)
±
Физическое
заземление
Рис. 1N.32. Символы для обозначения разных типов «земли»
К сожалению, на практике разница между эти-
ми двумя обозначениями «земли» сплошь и
рядом не соблюдается, и сигнальную «землю»
обозначают символом заземления. Этим также
грешат авторы книги АоЕ и настоящей кни-
ги. В данной книге мы в подавляющем боль-
шинстве случаев подразумеваем сигнальную
«землю» (общий провод или шину), но для ее
обозначения применяем символ заземления
(справа на рис. 1N.32). В редких случаях, когда
нужно обозначить заземление, т. е. физическое
соединение с землей, об этом будет сказано
в тексте словами.
1N А6. Основное правило
для соотнесения /?ВЫХ_А с Rms
Делители напряжения, выходное напряжение
которых мы пытались измерить в предыдущем
разделе, обладают недостатком, с которым мы
будем постоянно сталкиваться. При подклю-
чении нагрузки напряжение на выходе делите-
ля изменяется. Мы должны уметь рассчитать
это изменение и по возможности уменьшить
его. Для этого нам нужно, прежде всего, пони-
мать сущность входного импеданса RBX (с этим
обычно все ясно), а также суть #вых (а вот что-
бы разобраться с этим понятием, обычно тре-
буется некоторое время). В дальнейшем, когда
мы познакомимся с частотно-зависимыми це-
пями, мы будем обобщенно обозначать эти ха-
рактеристики как полные импедансы Zbxh Zbhx
соответственно.
А сейчас мы сформулируем еще одно эмпи-
рическое правило, которое немного облегчит
Вход
Рис. 1 N.33. Выход схемы А подключен ко входу схемы Б
вашу работу разработчика схем. Начнем с по-
становки задачи разработки: когда выходной
сигнал схемы А подается на вход схемы Б, нуж-
но сделать так, чтобы нагрузка схемы Б на схе-
му А была достаточно небольшой и сигнал под-
вергался лишь незначительному ослаблению.
Отсюда следует эмпирическое правило, проил-
люстрированное на рис. 1N.33.
Эмпирическое правило разработки
Пусть выход схемы А подключают ко входу
схемы Б.
Тогда желательно обеспечить, чтобы Явыхдля А
не превышало 1/10 Двх для Б.
Как же объяснить справедливость данного пра-
вила? Обратимся к уже знакомой нам задаче о
нагрузке делителя напряжения. Если #ВЫХ_А на-
много меньше, чем #ВХ_Б, тогда на выходе дели-
теля исходный сигнал почти не претерпевает
изменений. В частности, при соотношении этих
сопротивлений 1:10 делитель выдает 10/11 ис-
ходного сигнала, т. е. ослабление сигнала со-
ставляет чуть меньше 10%, что вполне прием-
лемо для наших целей.
Такая ситуация нравится нам не просто пото-
му, что нам по душе сильные сигналы. (Если
бы это было единственной проблемой, мы
всегда могли бы просто усилить выходной сиг-
нал.) Самое важное для нас состоит в том, что
в данном случае можно рассматривать части
схем (звенья или каскады) независимо друг от
друга, т. е. мы можем сначала разработать ка-
скад А, затем каскад Б, и т. д. Иными словами,
нам не требуется рассматривать объединенные
звенья схем А и Б, как одну большую схему.
Такой подход очень хорош, поскольку намно-
го облегчает нашу работу по анализу и синтезу
схем по сравнению со случаем, когда каждая
большая схема представляется в виде общего
целого.
Рассмотрим следующий пример двух таких
каскадов делителей напряжения, показанный
на рис. 1N.34. Требуется определить, каким
должно быть ЯТЕВ, чтобы ослабление сигнала
было меньше 10%. Соответственно, нужно
рассчитать, какими должны быть значения
резисторов JR.
Это эмпирическое правило становится еще бо-
лее наглядным, если увеличить число звеньев
1N.4. Нагрузка и «выходной импеданс»
51
с сигналом, передающимся с делителя А на Б,
а с Б на В, как показано на рис. 1N.35.
Каким должно быть значение RTEB для звена Б,
чтобы добавить звено В? Будет это просто два
сопротивления по 10 кОм, соединенных парал-
лельно? Этого было бы достаточно, если рас-
сматривать звено Б само по себе, подразумевая
обычные упрощающие допущения: идеаль-
ный источник (Двых = 0) и идеальную нагрузку
Но допустимы ли такие упрощения на са-
мом деле? Если признать, что верхняя
ветвь в действительности выглядит как
10 кОм + 2 кОм = 12 кОм, разница составит
20%. Означает ли это, что все наше решение
рушится? Не придется ли нам начать вычисле-
ния заново со входа схемы, чтобы разработать
следующий каскад? Иными словами, нужно
ли нам рассматривать всю схему, как одно це-
лое, а не только звено Б, как мы изначально
надеялись?
Расслабьтесь, ничего этого делать не придется.
Предполагаемая погрешность в 20% умень-
шается в два раза: ДТЕВ для Б состоит из парал-
лельных сопротивлений величиной 10 кОм и
12 кОм, т. е. равно чуть меньше 5,5 кОм. Так
что нам не нужно выходить за пределы звена Б,
и мы действительно можем рассматривать схе-
му, как мы надеялись: каждый каскад делителя
по отдельности.
Если вы еще не устали от этой дискуссии, то
можем подвергнуть наше утверждение даль-
нейшему испытанию, рассматривая еще один
вопрос: сильно ли (>10%) изменяет звено В
входное сопротивление звена Б? Мы конечно
заранее знаем ответ, но его доказательство
позволит вам проверить свое понимание
данного эмпирического правила и его след-
ствий.
Два важных исключения из правила:
сигналы в виде токов и линии передачи
Правило в разделе 1N.4.6 для соотношения им-
педансов чрезвычайно важное и полезное. Но
следует знать два класса схем, к которым оно
неприменимо:
♦ Источники, выдающие сигналы в виде тока,
а не напряжения. Скорее всего, на данном
этапе подобное утверждение озадачит вас.
Выход, А
Каким должно быть R^B,
чтобы ослабление сигнала
не превысило 10%?
Соответственно, какими
должны быть значения рези-
сторов Л?
ЮкОм
Выход, Б
ЮкОм
Рис. 1N.34. Выход одного делителя напряжения соединен
со входом другого — хорошая возможность применить
наше эмпирическое правило
Рис. 1N.35. Несколько соединенных последовательно зве-
ньев делителей напряжения: проверяем утверждение, что
наше эмпирическое правило позволяет рассматривать каж-
дую часть схемы по отдельности
Но источники напряжения (которые встре-
чаются чаще всего) и источники тока сильно
различаются по своим свойствам33.
♦ Высокочастотные цепи (длинные линии), в
которых пути сигнала необходимо рассмат-
ривать как «линии передачи» (см. приложе-
ние В)34.
Но это относится только к частотам, более вы-
соким, чем те, с которыми бы будем работать
в этом курсе. Это такие частоты (или спек-
тральные составляющие, поскольку, соглас-
но учению Фурье, «крутые» фронты и спады
сигналов содержат высокочастотные состав-
ляющие — см. главу 3N), при которых период
сигнала сравним со временем, требуемым на
33 Вы можете возразить, что ток можно преобразовать в
напряжение и наоборот. В дальнейшем мы соберем нашу
первую схему с выходным сигналом в виде тока на лабо-
раторном занятии 4L, а на занятии 6L мы рассмотрим наш
первый преобразователь тока в напряжение (фотодиод).
34 АоЕ § h.l.
52
IN. Цепи постоянного тока
передачу сигнала по линии. Например, время
прохождения сигнала по кабелю длиной око-
ло 2 м будет порядка 9 не, что соответствует
синусоидальному сигналу с частотой 100 МГц.
С сигналами прямоугольной формы дело об-
стоит еще сложнее. Например, прямоугольный
сигнал с частотой всего лишь в несколько мега-
герц содержит довольно интенсивную состав-
ляющую на этой частоте, которая при отсут-
ствии согласованной конечной нагрузки будет
искажаться таким кабелем. В действительности
трудности на высоких частотах еще больше,
поскольку согласованную нагрузку необходи-
мо предусмотреть на каждом отрезке прово-
дников, если путь сигнала туда и обратно пре-
вышает 1/10 длины волны.
Но сейчас нам нет надобности беспокоиться
об этих двух моментах. Источники тока чрез-
вычайно редко встретятся в нашем курсе, и нам
вряд ли придется столкнуться с проблемами
длинных линий передачи. Но имейте в виду,
что' вы столкнетесь с указанными проблемами
в будущем, если решите работать с сигналами
более высокой частоты.
1 N.5. Материал для чтения
изАоЕ
И напоследок мы посоветуем вам прочитать
определенные разделы из книги «The Art of
Electronics». Та книга, конечно же, приходит-
ся сестрой (или матерью?) книге, которую вы
читаете сейчас. Чтение этого факультативного
материала не обязательно. Но если вы решите
изучать эти две книги параллельно, указанные
далее разделы наиболее близки по тематике.
Материал для изучения
Глава 1, разделы 1.1-1.3.2.
Приложение С по типам резисторов: цветовой
код резисторов и прецизионные резисторы.
Приложение Н по линиям передачи.
Задачи
Задачи в тексте.
Упражнения 1.37,1.38.
1L Лабораторное занятие:
цепи постоянного тока
1L1. Закон Ома
Замечание по ходу работы
Основная задача данного лабораторного заня-
тия состоит в том, чтобы просто ознакомиться
с беспаечной макетной платой и методом под-
ключения к ней оборудования. Мы не считаем,
что закон Ома будет для вас чем-то совершен-
но неизвестным. Главное сейчас — практика в
сборке электронных схем на макетной плате.
Новички часто начинают с того, что просто
«подвешивают» резистор между зажимами
«крокодил» на проводах питания и мульти-
метра. Пытайтесь применять более грамот-
ный подход: вставьте проводники, идущие от
тестируемого устройства, в гнезда макетной
платы. Затем подсоедините к макетной плате
источник питания и измерительные прибо-
ры, используя для этого проводники с одним
концом, зачищенным от изоляции для встав-
ки в гнезда макетной платы и с разъемом типа
«банан» на другом конце. На рис. 1L.1 при-
веден пример неправильного и правильного
подхода к монтажу схем.
Цветовая маркировка проводников
и сборка устройств согласно
их принципиальным схемам
Теперь самое время познакомить вас с опреде-
ленными принципами монтажа, облегчающи-
ми работу с электрическими схемами. Для при-
мера рассмотрим один из типовых модулей для
макетирования со встроенными источниками
питания (рис. 1L.2). В данном макете напря-
жение от разъемов питания (в правом верхнем
углу модуля) подается на необходимые ряды
контактных гнезд платы путем подключения
провода одним концом к требуемому разъему
питания, а другим концом — в гнездо в требуе-
мом ряду контактных гнезд макетной платы
(рис. 1L.3).
«Земля»
(общий
провод)
Выход,
к осциллографу
Выход,
к осциллографу
Вход
Шина «земли» (общий провод)
Рис. 1L1. Неправильный и правильный методы монтажа схем. Слева: неопрятный и ненадежный висящий монтаж. Справа:
Аккуратный и надежный монтаж на макетной плате
54
7L Лабораторное занятие: цепи постоянного тока
Две секции горизонтальных рядов гнезд соединены
проволочной перемычкой
Вертикальные шины
питания подключены
к двум встроенным
источникам питания
Плюс вертикальной
шины питания подклю-
чен к горизонтальной
шине питания каждой
отдельной макетной
платы
Делитель напряжения;
верхний вывод под-
ключен к +(/шины
питания, а нижний —
к «земле»
Положительный щуп циф-
рового мультиметра под-
ключен к средней точке
делителя напряжения
Три источника постоянного напряжения (но напряжения ±15 В
можно регулировать)
Разъемы питания разного цвета: +15 — желтого, +5 — красно-
го, «земля» — черного, -15 — синего
Придерживайтесь данной цветовой маркировки напряжений
питания при работе с другими источниками питания и макет-
ными платами
v
Встроенные источники питания под-
ключены к горизонтальным шинам
питания
Эти горизонтальные и вертикальные
шины питания соединены между собой
Вольтметр измеряет напряже-
I ние в средней точке делителя
1 (относительно «земли» макет-
I ной платы, к которой подклю-
* чен щуп «земли» прибора)
Отрицательный щуп цифро-
вого мультиметра подклю-
чен к «земле»
Вертикальные и горизонтальные
шины питания каждой отдель-
ной макетной платы соединены
между собой
Рис. 1L.2. Разводка питания на шины макетной платы
ВИД СВЕРХУ
Все пять гнезд столбца
соединены металличе-
ским контактом снизу
под макетной платой
ВИД СНИЗУ
Разрыв посередине горизон-
тальных шин питания
- Горизонтальные шины
питания
Верхний и нижний столбцы
гнезд разделены выемкой
в плате
Рис. 1L3. Конструкция макетной платы: вид сверху и снизу на гнезда и соединения между ними
Внимание!
Ни в коем случае не подавайте внешнее напряже-
ние на цветные разъемы питания (красный, жел-
тый и синий) на модуле для макетирования. Это
разъемы для вывода напряжения со встроенных в
модуль источников питания, которые подключены
к соответствующим встроенным схемам модуля.
Поэтому, даже когда питание модуля выключено,
подача внешнего питания на эти разъемы может
вывести из строя электронные схемы модуля. То же
самое касается и трех белых горизонтальных шин
питания вверху макетной платы: они подключены
к тем же самым внутренним источникам питания,
что и разъемы питания на модуле. (Относительно
цветовой маркировки разъемов питания: красный
соответствует постоянному напряжению +5 В, а на-
пряжение на желтом и синем разъемах можно ре-
гулировать, но обычно оно установлено на плюс и
минус 15 В для соответствующих разъемов.)
1L2. Делитель напряжения
55
Обратите внимание, что напряжения измеря-
ются между двумя точками в схеме, тогда как
токи измеряются в одной точке схемы. Поэтому,
чтобы измерить ток в требуемой точке, необ-
ходимо разорвать цепь в данной точке и под-
ключить щупы амперметра к образовавшимся
точкам разрыва.
1L2. Делитель напряжения
Соберите на макетной плате делитель напряже-
ния, принципиальная схема которого показана
на рис. 1L.4. Подайте на делитель постоянное
входное напряжение 17ВХ величиной 15 В и за-
мерьте напряжение на выходе делителя [7ВЫХ
(без нагрузки). После этого подключите к вы-
ходу делителя нагрузку величиной 7,5 кОм и
посмотрите, какой эффект это окажет на вы-
ходное напряжение.
Далее измерьте ток короткого замыкания.
Примечание
Это означает «закоротите выход делителя на зем-
лю через амперметр». Не пугайтесь этого страшно-
го слова «закоротите», поскольку ток в этом случае
будет очень незначительный. Мы знаем, что корот-
кое замыкание электропроводки выбивает предо-
хранитель, но в электронике это часто не так.
Зная ток короткого замыкания 7КЗ и напряже-
ние холостого хода (без нагрузки) U^ делите-
ля, можно вычислить параметры эквивалент-
ной схемы Тевенина.
Теперь соберите эквивалентную схему Теве-
нина, используя регулируемый источник по-
стоянного напряжения в качестве источника
питания, и проверьте, совпадают ли напряже-
ние холостого хода и ток короткого замыкания
модели с соответствующими характеристиками
моделируемой схемы. После этого подключите
к выходу модели нагрузку величиной в 7,5 кОм,
как и в первоначальной схеме делителя, и про-
верьте, ведет ли модель себя таким же самым
образом, как и исходный делитель.
Замечание по практическому
применению моделей Тевенина
В дальнейшем мы больше не будем так делать:
закорачивать выход схемы на «землю», чтобы
Рис 1 L.4. Делитель напряжения
определить ее Л^ (или выходной импеданс, как
мы будем называть этот параметр). Это слиш-
ком опасный способ для лабораторных опытов
и слишком трудоемкий, когда нам всего лишь
нужно вычислить R^g.
В лабораторных условиях ток короткого за-
мыкания /^ может повредить тестируемую
таким образом схему (подобно короткому за-
мыканию электропроводки с перегоранием
предохранителя). Мы вскоре познакомимся с
более безопасным способом. Самый быстрый
способ найти RTEB для принципиальной схемы
делителя — рассчитать эквивалентное сопро-
тивление всех параллельных сопротивлений
делителя, полагая источник питания идеаль-
ным, т. е. ]?ип = 0 Ом. Этот случай иллюстрирует
рис. 1L.5.
Замечание
Поначалу это может показаться трудным, но нужно
просто выявить все параллельные пути, идущие
к любому фиксированному напряжению, а не толь-
ко к «земле». Объяснение этого результата иллю-
стрирует рис. 1 N.23.
+15 В
15к0м
7,5 В
Рис. 1 L.5. Параметр /?ТЕВ представляет собой общее значение
параллельных сопротивлений относительно выхода схемы
56
1L Лабораторное занятие: цепи постоянного тока
1 L3. Использование закона
Ома для преобразования
гальванометра в вольтметр
и амперметр
Эквивалентная схема Тевенина чрезвычайно
полезна как теоретическая концепция, но мы
больше пользоваться ею не будем. Собранная
нами в предыдущем разделе схема полезна
только для подкрепления теоретических зна-
ний на практике. А сейчас мы применим закон
Ома для решения почти практической зада-
чи — создания вольтметра, а затем и ампер-
метра.
Исходным оборудованием у нас будет обычный
гальванометр. Это, по сути, устройство для из-
мерения тока: отклонение стрелки пропорцио-
нально вращающему моменту, создаваемому
катушкой, расположенной в поле постоянного
магнита, а сам момент прямо пропорционален
протекающему через катушку току. На рис. 1L.6
изображено схематическое устройство гальва-
нометра1.
В основе аналогового мультиметра или аво-
метра2 лежит именно такой механизм, к кото-
рому добавлен набор переключаемых рези-
сторов. В качестве упражнения попытайтесь
самостоятельно придумать конструкцию ана-
логового мультиметра.
Возвратная
пружина
Стрелка
Подвижная
катушка
Постоянные
магнить!
Возвратная
пружина
Рис. 1L.6. Устройство гальванометра
1 L3.1. Внутреннее сопротивление
гальванометра
Чтобы создать вольтметр из гальванометра
(чем мы займемся в следующем разделе), мож-
но просто предположить, что его внутреннее
сопротивление пренебрежимо мало. Это на са-
мом деле так, 1?внг«1 кОм. Но давайте для уточ-
нения все же замерим его. Обратите внимание,
что мы работаем просто с гальванометром, а не
с мультиметром. (Начинать с исходной точки
всегда интереснее.)
Внутреннее сопротивление гальванометра
можно измерить по-разному, используя регу-
лируемый источник питания, цифровой муль-
тиметр или аналоговый авометр. Если вы со-
бираетесь измерить ток цифровым мультиме-
тром, то имейте в виду, что при этом можно
легко сжечь внутренний предохранитель при-
бора, так как в момент прикосновения к источ-
нику питания через прибор будет протекать по
сути неограниченный ток. Самое неприятное,
что факт перегорания предохранителя никак не
отображается на цифровом мультиметре, про-
сто на экране появится нулевое значение тока.
Но эту проблему можно решить несколькими
способами.
Механизмы аналоговых мультиметров осна-
щены защитой3, поэтому не беспокойтесь,
что вы сожжете прибор, даже если соверши-
те какую-либо ошибку при измерении. Даже
при «зашкаливании» стрелки прибор не будет
поврежден, как мы обнаружили в нашем экс-
перименте, но все же следует избегать таких
ситуаций и не подвергать аналоговые прибо-
ры измерению значений, превышающих их
диапазон. Все приборы в нашей лаборатории
оснащены диодами, защищающими их от пере-
напряжения в обоих направлениях. Но следует
иметь в виду, что при этом показания прибора
при превышении допустимого диапазона изме-
рений будут неправильными. (Несомненно, вы
можете догадаться, подобно какому устройству
аналоговый прибор ведет себя в таком случае.)
Поэтому отбрасывайте данные, полученные
при замерах, превышающих диапазон измере-
ний прибора.
1 По изображению из файла Google analog meter movement
(аналоговый гальванометр). Источник неизвестен.
2 Сокращение от Амперметр/Волътметр/Омметр.
3 Совет для экспериментаторов: подсоедините к выводам
гальванометра два параллельных, встречно включенных
кремниевых диода, например, 1N4004. При напряжении
около 0,6 В эти диоды откроются, обеспечивая защиту
гальванометра при превышении диапазона измерений.
1 LA Диод
57
+5 В
«Земля» о
Цифровой вольтметр с диапазоном
измерений 0*1 В
Полярность диода
—М—
Рис. 1L.7. Принципиальная схема подключения оборудования для измерения тока и соответствующего напряжения на диоде
Зарисуйте принципиальную схему, исполь-
зуемую для измерения RBH г, определите и за-
пишите это значение и значение тока полной
шкалы I
тшг
со шкалой измерений 10 мА. (Эта задача будет
несколько сложнее, чем создание вольтметра.)
Нарисуйте принципиальную схему прибора,
соберите и испытайте ее в действии.
1 L3.2, Вольтметр с пределом 10 В
Теперь на базе гальванометра, добавив к нему
другие необходимые компоненты, создайте
вольтметр со шкалой измерений в 10 В (это
означает, что стрелка прибора должна откло-
няться на всю шкалу при подаче на вход схемы
напряжения 10 В). Нарисуйте принципиальную
схему своего прибора.
Примечание
Сейчас настало самое время применить ваши
навыки оценочных вычислений требуемых зна-
чений сопротивлений в процессе разработки.
Рассчитывая значение сопротивления, которое
нужно добавить к базовому гальванометру, не за-
бывайте, что мы работаем с резисторами с допу-
ском 5%, т. е. их действительное значение может
отличаться на ±5% от номинала.
Подумайте, приводит ли внутреннее сопротив-
ление гальванометра к появлению значитель-
ной ошибки измерений?
Совет
Прежде всего нужно понять, что именно означает
слово «значительную»? Можно, например, срав-
нить влияние внутреннего сопротивления /?вн г
с влиянием погрешности номинала подключенно-
го резистора.
1 L3.3. Амперметр с диапазоном
10 мА
Покажите, как из гальванометра и других не-
обходимых компонентов создать амперметр
1LА Диод
Диод — один из электронных компонентов, ко-
торые не подчиняются закону Ома. На данном
этапе от вас не требуется понимание принципа
работы диода. Мы просто хотим поскорее по-
знакомить вас с этим электронным компонен-
том, чтобы вы убедились в том, что закон Ома
выполняется далеко не для всех элементов.
Для работы с диодом нам придется несколь-
ко модифицировать эксперимент, поскольку
на диод нельзя просто так напрямую подать
напряжение, как на резистор или лампочку4.
Причина станет ясной после того, как мы за-
мерим напряжение на диоде и сопоставим его
с соответствующим током. Схема подключения
оборудования для опытов с диодом изображе-
на на рис. 1L.7.
В отличие от предыдущих экспериментов, где
мы подавали на устройство напряжение и заме-
ряли протекающий ток, в этой схеме мы подаем
на диод ток и замеряем соответствующее на-
пряжение. Резистор номиналом 1 кОм служит
для ограничения тока до безопасных значений.
Резистор R является обычным потенциометром
номиналом 100 кОм, включенным как пере-
менный резистор (см. раздел ШЗирис. IN.14).
Переменный резистор можно также заменить
магазином сопротивлений или просто набо-
ром постоянных резисторов разных номина-
лов. Меняйте сопротивление jR и наблюдайте,
какое значение тока I соответствует текущему
4 В принципе, можно, но больше одного раза на один и тот
же диод не получится.
58
/L Лабораторное занятие: цепи постоянного тока
10 мА
0,5
и, В
1,0
Рис. 1L8. Масштабная шкала для графика ВАХ диода: а —
линейная; б—линейно-логарифмическая
напряжению U на диоде. Сначала попытайтесь
получить общее представление о работе схемы,
меняя значение R вручную и наблюдая, что про-
исходит с током диода. Затем нарисуйте два гра-
фика зависимости тока от напряжения (вольт-
амперная характеристика, ВАХ): линейный и
линейно-логарифмический (см. рис. 1L.8).
Сперва попытайтесь построить график ВАХ в
линейном масштабе. Для этого должно быть
достаточно четырех или пяти точек. Затем
обозначьте эти же самые точки на линейно-
логарифмическом графике, на котором сжи-
мается одна из осей. (Очевидно, что в данном
случае сжатию подлежит ось быстро растущего
тока.) Хорошо, если у вас есть готовая бумага для
линейно-логарифмических графиков, но если ее
нет, тогда можно воспользоваться масштабной
шкалой, приведенной на рис. 1L.8, б. В данном
случае нам не требуется большая точность, а
важно наглядно увидеть общую закономер-
ность.
Измените подключение диода на противопо-
ложное и понаблюдайте за результатом. Теперь
попробуйте вкратце описать зависимость на-
пряжения от тока на диоде. Затем подумай-
те, что бы случилось, если на диод подать 5 В
(ни в коем случае не пытайтесь проверить это
на практике!) Посмотрите в справочном лист-
ке для диода данного типа, что произошло бы
в этом случае по мнению фирмы-производителя.
Хотя там дословно не будет сказано «Бах» или
«Пуфффф», именно это имеется в виду.
Диоды нам очень пригодятся в дальнейшем.
1L5. Зависимость / от U
для некоторых «черных
ящиков»
Теперь возьмите два «черных ящика», которые
ваш лаборант приготовит для вас5 (мы будем
называть их ТУ — тестируемые устройства).
Это устройства с двумя выводами, один из
5 Конечно же, если вы работаете с этой книгой самостоя-
тельно, никто для вас эти устройства не приготовит. Но вы
можете получить дополнительную информацию на сайте
книги www.learningtheartofelectromcs.com. А здесь мы
откроем секрет, что один из «черных ящиков» — лампа на-
каливания мощностью 1 Вт, а другой — мощный резистор
сопротивлением 33 Ом.
Источник питания
постоянного тока Аналоговый мультиметр
(индикатор может бить (используется в качестве
Ручка регулировки анал0Г0ВЬ1М или Цифровым) миллиамперметра)
напряжения
ТУ
(тестируемое
устройство)
ПРИМЕЧАНИЕ:
пусть вас не смущает разъем
на корпусе источника питания,
обозначенный @ или
Просто игнорируйте его!
4 n Переключение „ *
Шина «земли»
вашей схемы "^
Цифровой мультиметр -=-
(используется в качестве
вольтметра)
Рис. 1L9. Схема для снятия зависимости тока / от напряжения U
7L5. Зависимость I от U для некоторых «черных ящиков»
59
которых является обычным резистором, а дру-
гой более интересным компонентом. В нашей
лаборатории корпуса «черных ящиков» пред-
ставляют собой кассеты для 35-миллиметровой
фотопленки. Подавайте на эти устройства на-
пряжение от нуля до двух вольт (используя для
этого регулируемый источник питания) и на-
блюдайте за напряжением и током (рис. 1L.9).
В диапазоне от 0 до 1В увеличивайте напряже-
ние с шагом 0,1 В (в этих пределах нам требует-
ся детальная картина).
Отобразите на графике несколько точек зави-
симости, чтобы получить общее представление
о ее поведении. Медленно вращайте ручку регу-
лировки напряжения и постарайтесь выяснить,
какие участки графика требуют более высокой
точности (т. е. больше точек).
Определите тип каждого устройства: какое из
них обычное (соответствует закону Ома), а ка-
кое — нет.
Внимание!
Не подавайте на устройства напряжение выше 7 В,
поскольку это может вывести их из строя.
Несколько усложним задачу — измеряйте одно-
временно напряжение и соответствующий ток
в процессе выполнения эксперимента. Таким
образом вы сможете установить, как оба при-
бора влияют на измерения.
Рассмотрим несколько практических вопросов
о влиянии измерительных инструментов на ре-
зультаты измерений, возникающих даже в этом
простейшем эксперименте.
Измеряет ли вольтметр напряжение в требуе-
мом месте, т. е. на самом тестируемом устрой-
стве? Или же на показания вольтметра влияет
подключенный амперметр? Насколько важно
это учитывать? При точном измерении напря-
жения на устройстве измеряете ли вы только
его ток, или также и ток, протекающий через
цифровой мультиметр? Если не удается полу-
чить точные показания одновременно с обоих
приборов (а оно и не получится) и нужно вы-
брать одну из двух погрешностей, какой вари-
ант схемы обеспечит меньшую погрешность?
Сравните два возможных варианта подключе-
ния вольтметра, приведенных на рис. 1L.10.
Если известно, что эквивалентное сопротив-
ление нагрузки не превышает 1 кОм, то по-
пробуйте предположить, какая из двух схем на
рис. 1L.10 позволит получить более точные по-
казания/и U. Соберите эту схему и снимите не-
сколько показаний I и U, а затем попытайтесь
оценить значение сопротивления нагрузки R.
Аналоговый
мультиметр
Цифровой мультиметр
(Двх = 10 Ом)
Измеряем ток
Внутреннее сопротивление
прибора
VW
Диапазон измерений
составляет 1/4 В
Аналоговый
мультиметр
Внутреннее f ч^
сопротивление ( / \
прибора \ I / )
vw—
■ Измеряем ток
Цифровой мультиметр
(Явх =
Диапазон измерений
составляет 1/4 В
► 10 МОм
Рис. 1L.10. Одновременное измерение тока и напряжения: точные показания выдает только один из приборов
60
1L Лабораторное занятие: цепи постоянного тока
1 L5.1. Оценка погрешности
измерительного прибора
Получив наилучшую оценку значения R, оце-
ните погрешности, вызываемые приборами.
В частности, когда диапазон измерений ампер-
метра составляет 10 мА, оцените погрешность
значения R, вносимую:
♦ амперметром при измерении напряжения,
если вклад в погрешность вносит амперметр;
♦ вольтметром при измерении напряжения,
если амперметр не вносит погрешность.
Ответив на эти вопросы, вы можете сказать,
какое влияние должен оказывать идеальный
вольтметр (или амперметр) на тестируемую
схему? Каким должно быть его внутреннее со-
противление?
Теперь по полученным экспериментальным
точкам начертите графики. Не пытайтесь быть
особенно точными, нас интересует лишь об-
щий ход зависимости. График для резистора
(независимо от его номинала) будет не очень
интересный, а вот для другого загадочного
устройства зависимость окажется более интри-
гующей.
Мы надеемся, что вы уже построили график.
Чем, по вашему мнению, является это загадоч-
ное устройство? Самое интересное, что оно сде-
лано почти из такого же материала, как и ре-
зистор. Почему же графики вольт-амперных
характеристик этих двух устройств так отлича-
ются друг от друга? Забегая вперед, скажем, что
излом в ходе кривой может быть полезен: да-
лее, на лабораторном занятии 8L, мы восполь-
зуемся этим свойством, чтобы заставить схему
управлять своим усилением. Проделав все до
конца, можете теперь открыть корпус кассеты
и узнать, что же за загадочное устройство на-
ходится внутри ее.
1 L5.2. Куда подключать цифровой
мультиметр и амперметр
при большом /?н?
Выполнив предыдущее упражнение, вы те-
перь знаете, куда подключать вольтметр,
чтобы получить наиболее точные показания
тока и напряжения. Но, чтобы вы не слишком
зазнавались6, попробуйте предположить, что
тестируемое устройство имеет очень высокое
сопротивление (RH = 10 МОм). Допустим, что
входное сопротивление JRBX цифрового мульти-
метра составляет 10 МОм. (От вас не требуется
проделать этот эксперимент на практике, а про-
сто попробуйте предсказать, каковы были бы
его результаты.)
Если подключить цифровой мультиметр к на-
грузке, он окажется включенным параллельно
ей. Какую погрешность в процентах это вы-
зовет при одновременном измерении тока?
И наоборот погрешность измерения напряже-
ния, вызванная размещением вольтметра перед
амперметром, в этом случае будет не больше,
чем в предыдущем лабораторном опыте.
Теперь вы можете сделать общее заключение,
в каких случаях необходимо учитывать вну-
треннее сопротивление RBX цифрового мульти-
метра.
1 L.6. Осциллограф
и генератор сигналов
В этом разделе мы вкратце расскажем об осцил-
лографе, чтобы подготовить вас к работе с этим
прибором (осциллографы и работа с ними рас-
сматриваются более подробно в приложении А
этой книги и в приложении О книги АоЕ). Чуть
позже, на лабораторном занятии 2L, мы будем
интенсивно использовать этот прибор.
С этого момента осциллограф и генератор сиг-
налов7 понадобятся нам практически на каж-
дом лабораторном занятии. На этом лабора-
торном занятии нам было вполне достаточно
мультиметров, которые здесь даже удобнее
осциллографа, поскольку напряжения и токи в
схемах менялись довольно медленно. Если вы
уже знакомы с осциллографом, то можете сразу
же перейти к первому настоящему упражнению
в лабораторном занятии 2L, или отложите на
время книгу и отдохните.
Вскоре, когда мы начнем исследовать не ста-
тические сигналы (называемые сигналами
6 Шутка.
7 Измерительный прибор, вырабатывающий сигналы раз-
ной формы (варьирующееся во времени напряжение) —
синусоидальной, треугольной и прямоугольной.
1L6. Осциллограф и генератор сигналов
61
постоянного тока на электронном жаргоне), а
динамические, т. е. сигналы, меняющиеся во
времени, осциллограф станет нашим излюб-
ленным инструментом. В лабораторном заня-
тии 2L и, за редкими исключениями, во всех
дальнейших экспериментах мы будем работать
исключительно с динамическими сигналами.
На экране осциллографа можно наблюдать гра-
фик изменения напряжения (отображаемого на
вертикальной оси) во времени (отображаемом
на горизонтально оси).
Для первого знакомства с осциллографом и
генератором сигналов подайте сигнал синусои-
дальной формы частотой 1 кГц с генератора и
наблюдайте его на экране осциллографа.
Подключите выход генератора сигналов непо-
средственно ко входу осциллографа посред-
ством кабеля BNC8, а не с помощью щупа.
Если поначалу вас приведет в недоумение мно-
жество различных тумблеров и ручек на этих
инструментах, не волнуйтесь. Это сложные
приборы и, соответственно, их панели управле-
ния также сложны. Вам потребуется несколько
лабораторных занятий, чтобы ознакомиться с
их назначением. Может оказаться, что даже к
концу занятий с некоторыми органами управ-
ления вы так и не познакомитесь. Например,
вам долго не понадобится функция ждущего за-
пуска или одноразовый режим развертки (если
ваш осциллограф оснащен этими возможно-
стями).
Поэкспериментируйте с элементами управ-
ления разверткой и запуском осциллографа.
Большая часть рассматриваемой здесь инфор-
мации касается только аналоговых осцилло-
графов. В цифровых осциллографах некото-
рые функции, например, такие как запуск или
установка коэффициента усиления, можно при
желании автоматизировать. Не рекомендуется
начинать знакомство с осциллографом с раз-
личных экзотических возможностей, в частно-
сти, остерегайтесь кнопки с «магическим» обо-
значением AUTOSET9.
8 Англ. BNC (Bayonet Neill-Concelman) - тип разъема для
коаксиального кабеля. (См. АоЕ § 1.8). Мы обычно будем
так называть сам кабель, хотя, строго говоря, этот термин
обозначает его разъемы.
9 Здесь и далее оставлены авторские обозначения органов
управления приборов, функция AUTOSET означает «Воз-
врат к заводским настройкам» и приводит к сбросу всех
пользовательских установок. — Примеч. ред.
Рекомендуем вам начать знакомиться с осцил-
лографом, исследуя такие элементы управ-
ления:
♦ Переключатель коэффициента верти-
кального усиления — этот переключатель
задает значение вольт/деление (volts/div).
Обратите внимание, что одно деление соот-
ветствует одному сантиметру на шкале, а не
делению в 0,2 см.
♦ Ручка установки скорости горизонталь-
ной развертки — задает интервал времени
на деление (sec/div).
Обе эти ручки необходимо установить в
режим CAL, а не VAR10. Для этого обычно
меньшую ручку в центре главной ручки нуж-
но провернуть по часовой стрелке до щелчка.
Если этого не сделать, измеренные величины
не будут соответствовать откалиброванным
значениям.
♦ Элементы управления запуском раз-
вертки. Не переживайте, если вам не удается
сразу обеспечить правильный режим запуска
развертки. Запуск развертки — это, безуслов-
но, самая хитроумная функция управления
осциллографом. Схема запуска указывает
осциллографу, когда начинать перемещать
луч развертки по экрану, т. е. прорисовы-
вать на нем график сигнала. Если вы решите,
что полностью овладели искусством запуска
развертки, пригласите кого-либо из одно-
курсников доказать вам, что это не так: пусть
он установит органы управления в произ-
вольные позиции, а вы затем попытайтесь
вернуть их обратно, чтобы привести осцил-
лограф к нормальному рабочему режиму.
(Советуем однако вашему однокурснику не
особо усердствовать.)
Не поддавайтесь искушению установить так
называемый «нормальный» режим запуска
развертки (обычно обозначается NORM).
Это далеко не всегда помогает, и более того,
может причинить много хлопот. Лучше для
начала считайте, что «нормальный» на самом
деле означает «ненормальный». Прибегайте
к этой настройке только в тех редких слу-
чаях, когда вы определенно знаете, что она
вам требуется. В большинстве случаев луч-
шим выбором будет автоматический режим
запуска (обычно обозначенный AUTO).
10 На панели управления отечественных осциллографов
обычно имеется обозначение «Не калибр.» - Примеч. ред.
62
7L Лабораторное занятие: цепи постоянного тока
Это объясняется тем, что осциллограф ожи-
дает какого-либо сигнала, чтобы запустить
развертку. В режиме автоматического запу-
ска развертка запускается или специальным
сигналом, или самостоятельно, когда ей «на-
доест» ждать этого сигнала. Таким образом,
в режиме автоматического запуска вы всегда
будете видеть, по крайне мере, хотя бы луч
развертки.
В отличие от этого, в режиме запуска NORM
осциллограф обладает «безграничным» тер-
пением: он будет ожидать бесконечно, не вы-
водя ничего на экран, пока не получит дей-
ствительный сигнал запуска развертки. Тем
временем вы будете наблюдать лишь темный
экран, что, как можно догадаться, не очень
информативно.
Еще один элемент управления, с которым
следует быть аккуратным, — переключатель
источника сигнала запуска (для аналоговых
осциллографов это обычно ручка, обозна-
ченная SOURCE в группе элементов управле-
ния TRIGGER). В качестве такого источника
можно выбрать или один из двух входных
каналов (СН1 или СН2)11, или внешний сиг-
нал, который подается на BNC-разъем, обо-
значенный ЕХТ.
Настройте генератор сигналов на выдачу сиг-
нала прямоугольной формы и с помощью
осциллографа замерьте время нарастания сиг-
нала (период времени, за который амплитуда
сигнала переходит от 10% до 90% его полной
амплитуды).
Вы сразу же можете усомниться: «Время на-
растания? Прямоугольный сигнал нарас-
тает моментально, откуда и его название».
Осциллограф, при правильном его использова-
нии, покажет вам, что это не так.
Рекомендация касательно запуска развертки
Очень полезно наблюдать на экране осциллогра-
фа фронт сигнала, который запускает развертку,
а не запускать развертку одним событием, а на-
блюдать другое. Такке желательно установить
высокую скорость развертки, чтобы изображение
не «убегало» с правой стороны экрана. Таким об-
разом, чтобы измерить время нарастания сигнала,
подаваемого на разъем СН1, задайте СН1 в каче-
стве источника сигнала запуска и укажите вид за-
пуска положительный перепад, или нарастающий
фронт (rising edge).
А что же за сигнал присутствует на разъеме
SYNC OUT (или TTL12) генератора сигналов?
Исследуйте этот сигнал на одном канале осцил-
лографа одновременно с наблюдением за пря-
моугольным или треугольным сигналом на
другом канале. Данный сигнал предназначен
для внешней синхронизации запуска разверт-
ки осциллографа. Чтобы увидеть, насколько
это полезно, попробуйте запускать развертку
на вершине синусоидального сигнала, сначала с
внутренней, а затем с внешней синхронизацией.
Вы воочию убедитесь, насколько легче осущест-
влять запуск развертки во втором случае.
Запуск развертки в строго определенный мо-
мент особенно полезен при измерении сдвига
по фазе двух сигналов, что мы будем выполнять
несколько раз на следующем лабораторном за-
нятии. Развертку можно запускать по переходу
через нулевой уровень (среднюю точку размаха
сигнала) или, используя вспомогательный сиг-
нал запуска SYNC, по пику или впадине сигнала.
А для чего служит разъем осциллографа, обо-
значенный CALIBRATOR (или CAL)? Он при-
меняется для выдачи сигнала для калибровки
щупа (или пробника) осциллографа. Этот сиг-
нал понадобится только на лабораторном за-
нятии 3L, на котором рассматриваются устрой-
ство и работа щупов. На данном этапе просто
имейте в виду, что такой сигнал доступен вам.
Не пользуйтесь щупами осциллографа, пока вы
не узнаете их устройство и принцип работы.
Щуп с коэффициентом 10х представляет собой
нечто большее, чем просто отрезок коаксиаль-
ного кабеля с разъемом «крокодил» на конце.
Если ваш генератор сигналов обеспечивает воз-
можность смещения сигнала по вертикали (off-
set), проделайте это, подавая сигнал на осцил-
лограф, а затем посмотрите, что делает пере-
ключатель (или кнопка) AC/DC осциллографа
(обычно она находится возле входного разъема
канала вертикального отклонения).
Здравый смысл13 может подтолкнуть вас в
большинстве случаев использовать положе-
11 Разумеется, это справедливо только для двухканальных
осциллографов. — Примеч. ред.
12 Сокращение TTL расшифровывается как не менее зага-
дочная фраза транзисторно-транзисторная логика (ТТЛ),
которая более подробно рассматривается в главе 14N.
В данном контексте ТТЛ можно просто понимать, как пря-
моугольный сигнал логического уровня, т. е. сигнал пря-
моугольной формы, амплитуда которого меняется в ин-
тервале от 0 до примерно 4 В.
13 Полагаем, вы знаете, что DC означает direct current -
постоянный ток, а АС означает alternating current — пере-
менный ток.
//..б. Осциллограф и генератор сигналов
63
ние «АС» переключателя: ведь, в конце концов,
все исследуемые вами меняющиеся во време-
ни сигналы являются сигналами переменного
тока. Воздержитесь от этого кажущегося ло-
гичным, но в действительности ошибочного
предположения. При установке переключателя
в положение «АС» к входу канала вертикально-
го отклонения осциллографа последовательно
подключается конденсатор (рис. 1L.11), что
может вызвать заметные искажения сигнала.
(Посмотрите, как будет выглядеть прямоуголь-
ный сигнал частотой 50 Гц в режиме АС, если
вы не верите.) Кроме того, при этом из сигнала
удаляется постоянная составляющая, как вы,
возможно уже заметили, если провели указан-
ный выше опыт. В частности, при работе в этом
режиме смещение сигнала по вертикали совер-
шенно не видно. Но удаление какой-либо ин-
формации о сигнале нежелательно, за исключе-
нием тех случаев, когда это делается осознанно
с какой-либо конкретной целью. Например,
иногда необходимо исследовать синусоидаль-
ный сигнал без его постоянной составляющей;
но в общем случае мы должны знать, что сигнал
содержит эту составляющую, и просто инфор-
мация о ней была скрыта.
Установите частоту сигнала на генераторе сиг-
налов приблизительно посередине рабочего
диапазона, а затем попытайтесь точно изме-
рить эту частоту посредством осциллографа.
Вход
«DC»
«АО
К каналу
вертикального
отклонения
осциллографа
SIMOaa
Рис. 1L.11. Схема переключателя AC/DC канала вертикаль-
ного отклонения осциллографа
(В действительности, необходимо, конечно же,
измерять период сигнала, а не его частоту14.) На
протяжении курса схемотехники вам придется
выполнять эту операцию сотни раз и вскоре вы
овладеете данным приемом в совершенстве.
При различии показаний на осциллографе и
на генераторе сигналов доверяйте первым, по-
скольку индикация частоты выдаваемого сиг-
нала генератора сигналов довольно грубая15.
14 Вообще то, если используется цифровой осциллограф,
можно прибегнуть к «нечестному» приему, настроив его
на измерение частоты. Но не стоит начинать изучение
электроники, используя такие приемы.
15 Утверждение верно для генераторов сигналов с аналого-
вой шкалой, современные цифровые приборы обеспечи-
вают достаточно высокую точность индикации частоты. —
Примеч. ред.
IS. Дополнительный материал:
резисторы, напряжение, ток
1S.1. Расшифровка
номиналов резисторов
На лабораторных занятиях вам потребуется
быстро определять номиналы резисторов по их
цветовой маркировке, а не измерять их сопро-
тивление с помощью омметра (некоторые от-
чаявшиеся студенты иногда прибегают к таким
крайним мерам). Поначалу расшифровка но-
минала резистора может показаться слишком
трудной, но вскоре вы привыкнете, по крайней
мере, к наиболее распространенным номина-
лам резисторов и сможете понимать многие
цветовые обозначения с первого.взгляда. Мы
будем использовать резисторы достаточно
большого размера, чтобы их маркировку мож-
но было различать без проблем. Современные
резисторы для поверхностного монтажа на-
столько малы, что зачастую не маркируются
вообще. При этом не нужна (да и невозможна)
их расшифровка. Но если случайно просыпать
и перепутать несколько таких резисторов, при-
дется или брать новые, или измерять сопротив-
ление каждого из них.
1 S.1.1. Ассортимент резисторов
с номиналом 10 кОм
На рис. 1S.1 изображены резисторы с номина-
лом 10 кОм, изготовленные в разных корпусах.
В наших экспериментах мы применяем ком-
позиционные угольные резисторы (пример
такого компонента изображен на рис. 1S.1 пер-
вым сверху). В настоящее время этот тип ре-
зисторов почти не употребляют, поэтому они
сравнительно дорогостоящие. Но они хорошо
подходят для лабораторных занятий, посколь-
ку их номинал можно с легкостью определить
(при наличии соответствующего опыта) по их
цветовой маркировке. Другие типы резисторов
плохо подходят для монтажа на беспаечной
макетной плате. Резисторы, номинал которых
указан цифрами, могут быть вам больше по
душе, если вы не желаете изучать цветовую
маркировку. Но с ними могут возникнуть дру-
гие трудности, поскольку в случае их установки
значением вниз вы не сможете быстро опре-
делить их номинал.
Угольный резистор RC07,1/4 Вт, допуск 5%
Метоплопленочный резистор, допуск 1% (последняя коричневая
полоска соответствует 1%)
Металлопленочный резистор RN55D, допуск 1%
Резистор для поверхностного монтажа, размер 0805 (размеры
в 10 милов1 = 0,01 дюйм, таким образом, размер составляет
0,08*0,05 дюйма или 2,032x1,27 см)
0603
0402
0201
Рис. 1S.1. Несколько резисторов разных типов номиналом по 10 кОм
Мил (англ. mil) — единица длины, равная 0,001 дюйма.
/5./. Расшифровка номиналов резисторов
65
1 S.1.2. Номиналы и допуски
резисторов
На рис. 1S.2 показан пример резисторов, кото-
рые мы в этом курсе будем использовать в лабо-
раторных занятиях: это композиционный уголь-
ный резистор с наибольшим возможным откло-
нением от номинального значения (допуск) 5%.
Допуск в 5% означает, что действительное сопро-
тивление резистора будет находиться в пределах
±5% его номинала (т. е. значения, указанного на
нем). Например, если обозначенное номиналь-
ное значение сопротивления резистора равно
100 кОм (100 000 Ом), действительное значе-
ние его сопротивления будет в диапазоне от 95
до 105 кОм. Первой проблемой, возникающей
при попытке определить значение номинала ре-
зистора по его цветовой маркировке, является
вопрос, с какой стороны начинать расшифровку
полосок его цветового кода.
Обозначаются они полосками следующего
цвета:
♦ серебристого: ±10%;
♦ золотистого: ±5%.
Номинал. Сориентировав резистор должным
образом (полоской допуска справа), можно при-
ступать к расшифровке цветовых полосок его
номинала. Определив цифровые значения по-
лосок, мы получим достаточную информацию,
чтобы выяснить его номинал. Потренируемся
для практики на примере резистора, показан-
ного на рис. 1S.4.
С какой стороны § g
начинать расшифровку? § £
Для начала нам нужно расположить резистор
так, чтобы полоска, означающая допуск, ока-
залась справа. Но как узнать, какая из полосок
соответствует допуску? Для композиционных
угольных резисторов (для наших эксперимен-
тов) это будет крайняя (четвертая) полоска
серебристого или золотистого цвета, располо-
женная чуть дальше от остальных полосок.
Для металлопленочных резисторов с допуском
1% это также будет самая крайняя полоска, но
только пятая по счету и коричневого цвета. На
рис. 1S.3 показан пример такого резистора.
Обозначение номинала резистора четырьмя
полосками подразумевает более высокий до-
пуск, чем обычный 5%. Коричневая полоска
соответствует цифре «1», что в случае полоски
допуска означает 1%.
Примечание
Для резисторов повышенной точности, т. е. с пя-
тью полосками, красная полоска означает допуск
2%, а зеленая, синяя и фиолетовая — 0,5%, 0,25% и
0,1 % соответственно.
Допуск. Композиционные угольные резисто-
ры, которые мы будем использовать на наших
лабораторных занятиях, имеют четырехполос-
ный цветовой код (три полоски для номинала,
четвертая для допуска2) обычно имеют только
два значения допуска: 5% или 10%.
2 На корпусе таких резисторов может отсутствовать чет-
вертая полоска (допуска), и их допуск составляет 20%. Но
такие резисторы встречаются очень редко.
i I
I 1
1
О-
S
Рис. 1S.2. Для расшифровки цветового обозначения пово-
рачиваем резистор так, чтобы полоска допуска (золотистого
цвета) оказалась справа
Номинал 1 0 0 2 = 100 • 102 = 10 кОм
Рис. 1 S3. Пример метал л оп лен очного резистора с допуском
1%, обозначаемым пятой (коричневой) полоской справа
Ком поз и ционный
угольный резистор,
допуск 5%
Номинал 1 0 4 = 10 • 104 = 105 =100 кОм
золотистая =
= допуск 5%
5 § 5
§ 3 $
Рис. 1S.4. Пример расшифровки номинала резистора
66
IS. Дополнительный материал: резисторы, напряжение, ток
Коричневая, черная и желтая полоски пред-
ставляют, соответственно, цифры 1, 0 и 4; чет-
вертая3, золотистая полоска обозначает допуск
±5%. Первые две цифры составляют обычное
десятичное число, а четвертая соответствует
степени числа 10. Значение номинала опреде-
ляется, умножая число, полученное из первых
двух полосок, на степень числа 10, обозначае-
мую третьей полоской. Таким образом, значе-
ние номинала данного резистора составляет
10 • 104 = 100 000 Ом, или 100 кОм.
Цветовой код номинала. Полоски разно-
го цвета соответствуют различным цифрам.
Чтобы запомнить, какие цифры какому цвету
соответствуют, было придумано множество
мнемоник, большинство из которых являются в
той или иной степени неприличными4. Одна из
более приличных мнемоник следующая: «Big
Boys Race Our Young Girls, But Violet Generally
Wins». Но это не очень удачная мнемоника, по-
скольку в ней не различаются цвета black, brown
и blue и green и gray. Запомнить соответствие
черного (black) цвета нулю можно, вспомнив,
что черный цвет является отсутствием цвета;
а следующий за черным коричневый (brown)
цвет в действительности очень близок к черно-
му; ну а значение серого (gray) цвета можно за-
помнить, ассоциируя его, как близкий к белому
(white). Но ни один из этих приемов не слишком
хорош. Поэтому в нашей лаборатории на стене
всегда висит таблица цветовой маркировки.
Приведем перечень цветовых кодов:
♦ черный — ноль
♦ коричневый — один
♦ красный —два
♦ оранжевый — три
♦ желтый — четыре
♦ зеленый — пять
♦ синий — шесть
♦ фиолетовый — семь
♦ серый — восемь
♦ белый — девять
3 На корпусе таких резисторов может отсутствовать чет-
вертая полоска (допуска), и их допуск составляет 20%. Но
такие резисторы встречаются очень редко.
4 Речь идет, конечно же, об английских мнемониках. По-
иск в Интернете русских мнемоник не увенчался успе-
хом — Примеч. пер.
Следующие два цвета используются только для
множителей и встречаются очень редко:
♦ золотистый — ОД
♦ серебристый — 0,01
1 S.1.3. Ряды номиналов
с 10-процентным допуском
Стандартные номиналы резисторов поначалу
могут вызвать недоумение. Это непонятные
округленные значения, которые кажутся слу-
чайными и произвольными. Но эта кажущаяся
странность полностью обоснована. Поскольку
вследствие погрешности мы не знаем действи-
тельное значение сопротивления любого рези-
стора, нецелесообразно располагать номиналы
слишком близко друг к другу, поскольку дей-
ствительные значения сопротивлений могут
перекрываться. Чтобы избежать этого, рези-
сторы изготавливают с номинальными значе-
ниями, расположенными на достаточном «рас-
стоянии», и тем самым минимизируют возмож-
ность перекрытия действительных значений
смежных номиналов.
Например, действительное значение резисто-
ра номиналом 10 Ом с допуском 10% может
быть целых 11 Ом. А действительное значе-
ние резистора номиналом 12 Ом при таком
же допуске может оказаться меньше 11 Ом.
Таким образом, не имеет смысла изготавли-
вать резисторы номиналом 11 Ом, а целесоо-
бразно, чтобы следующим после 10 Ом был
номинал 12 Ом. Аналогичный принцип при-
меняется и к другим номиналам, только по
мере увеличения номиналов увеличивается и
шаг между ними, в результате чего получают-
ся такие странные номиналы, как 27, 39, 47
и т. д. Далее приводится ряд номиналов для
резисторов с 10-процентным допуском (так
называемый ряд Е12, содержащий 12 значе-
ний в декаде):
10,12,15,18,22,27,33,39,47,56,68,82,100.
Более подробную информацию на эту тему
см. в приложении С книги АоЕ.
Резисторы с номиналом из ряда Е12 будут
использоваться в большинстве наших схем
(с соответствующими множителями: нам
редко нужны резисторы 10 Ом, но довольно
JS.2 Напряжение и ток
67
часто номиналом 10 кОм). При этом допуск
резисторов в нашей лаборатории обычно
равен 5%.
1S.1 А Мощность
Обращать внимание на номинальную мощность
компонентов, используемых на наших лабора-
торных занятиях, приходится не так часто. Это
объясняется тем, что мы работаем с низкими
напряжениями (менее ±10 В) и малыми токами
(несколько десятков миллиампер). Таким обра-
зом, наши компоненты не рассеивают большую
мощность, поскольку мощность является про-
изведением этих двух величин: U • /. Например,
10 В • 10 мА дает 100 мВт, или ОД Вт. Но наши
стандартные резисторы не в состоянии выдер-
жать большую мощность: максимум, что они
могут выдержать в течение продолжительного
времени — 0,25 Вт. Не забывайте об этом огра-
ничении, чтобы обожженные пальцы не на-
помнили вам о нем.
Важно постоянно помнить, что возможность
перегрева вероятнее всего будет у резисторов
малого номинала. Например, резистор номи-
налом 1 кОм и мощностью 0,25 Вт выдержит
подключение к источнику напряжением 10 В
без каких бы то ни было проблем. Но прикос-
новение к резистору такой же мощности и под
таким же напряжением, но номиналом 100 Ом
уже может привести к ожогу.
1 S.2. Напряжение и ток
В этом разделе мы хотим обсудить следующие
два вопроса:
1. Что именно «протекает» в большинстве на-
ших схем, напряжение или ток?
2. Что нас больше интересует в курсе схемотех-
ники, передача информации или энергии?
1 S.2.1 • Насколько необходимо
это примечание?
Я надеюсь, что вы не слишком обидитесь, читая
данное примечание, поскольку в нем скрыт на-
мек, что вы можете спутать ток с напряжением.
Давайте предположим, что мы обращаемся не к
вам, а к вашему слегка сбитому с толку напарни-
ку по лабораторным занятиям. Таким образом,
мы пытаемся изложить некоторые аргументы,
которые помогут вашему смышленому, но слег-
ка озадаченному напарнику понять истинное
положение дел.
Глядя на рис. 1S.5, даже толковые студенты не
всегда могут уяснить различение между током и
напряжением. Эту схему нарисовал один очень
знающий студент при ответе на экзамене. Ответ
хороший, но содержит потрясающую ошибку,
показывающую, что студент думал о токе, ког-
да работал с напряжением.
Два усилителя, каждый
с коэффициентом
+15 В усиления 2 Здесь будет высокий
У логический уровень,
/еслиСвх>Ц
£4,7 кОм
Вот где ошибка: 1/2 от Ц
/1/2 от Ц
I МОЖНО +j
Ч усилить ± \hU=UfU
\ в два раза ^ s^
Логический
элемент И
5В
Напряжение в этой
точке:
= Ц
Рис. 1S.5. Эскиз схемы в ответе на экзаменационный вопрос. Ток и напряжение перепутаны?
68
1S. Дополнительный материал: резисторы, напряжение, ток
Вам ясно, где студент, похоже, перепутал ток и
напряжение? Чтобы вникнуть в суть пробле-
мы, вам не нужно полностью понимать схему:
вам лишь необходимо знать, что два фрагмента
данной схемы (эти усилители выделены на схе-
ме) обеспечивают коэффициент усиления по
напряжению, равный двум. Теперь вам, навер-
ное, понятно, что даже смышленый студент, об-
ладающий хорошим пониманием электроники,
все равно может совершить ошибку касательно
таких фундаментальных понятий.
Ошибка кроется в наличии здесь двух усили-
телей с двукратным (2х) коэффициентом уси-
ления и несколько загадочной надписи с ле-
вой стороны: «1/2 от их можно усилить в два
раза». Обратите внимание, что обозначение V1
снова появляется на выходе верхнего усилите-
ля. Автор, видимо, думал, что напряжение Ux
с движка потенциометра номиналом 10 кОм
должно разделиться пополам, поскольку оно
идет в два разных места — по горизонтали
в верхнюю часть схемы, и по вертикали —
в нижнюю.
Но это неправильное рассуждение: оба усили-
теля имеют очень высокий входной импеданс.
А, как известно, напряжение можно подавать
на несколько входов с высоким импедансом,
и на каждом входе оно будет одинаковым.
Высказывание «при подаче сигнала на два
одинаковых входа, на каждом из них окажется
только половина сигнала» более соответствует
поведению тока, а не напряжения. На рис. 1S.6
приводится эскиз схемы, которой, мы предпола-
гаем, руководствовался студент в своем ответе.
Наверное, у вас еще остались сомнения, так
что продолжим рассмотрение этого сложного
вопроса.
Рис. 1S.6. В отличие от напряжения, токи действительно де-
лятся пополам при наличии двух путей с одинаковым сопро-
тивлением
1S.2.2. Что именно «протекает»
в большинстве наших схем?
С точки зрения здравого смысла вы, наверное,
захотите ответить на этот вопрос, что проте-
кает ток, поэтому сигналы, обрабатываемые и
передаваемые в схемах, скорей всего, являют-
ся токами. Хотя этот аргумент звучит правдо-
подобно, но в лучшем случае он окажется не
вполне верным, а обычно является вообще не-
правильным.
Несомненно, ток протекает, тогда как напря-
жение определенно нет. Разумеется, это не-
преложная истина, и многим студентам при-
ходится избавляться от заблуждения в первые
недели занятий, когда они обнаруживают, что
они говорят о «протекающем в резисторе на-
пряжении».
Но — и это более тонкий нюанс — хотя напря-
жения не «протекают» по схемам, мы часто
говорим о прохождении через них сигналов.
В действительности, все наши схемы предна-
значены для обработки сигналов, и практиче-
ски всегда обрабатываемые сигналы являются
напряжениями, а не токами.
Как же совместить два истинных утвержде-
ния: (1) протекают токи, а не напряжения,
но (2) сигналы, интересующие нас в процессе
разработки и анализа схем, почти всегда явля-
ются напряжениями, а не токами? Это вполне
возможно, и мы надеемся, что некоторые по-
следующие примеры помогут нам убедить вас
в этом.
Но прежде выясним главный вопрос: нужно
ли нам вообще затрагивать эту тему? Разве, в
любом случае, напряжения и токи не пропор-
циональны друг другу? Важно ли, что мы будем
иметь в виду, если преобразовать одну величи-
ну в другую можно простым умножением ее на
постоянную? Неплохой вопрос, но в нем скрыт
подвох. И дело вовсе не в том, что некоторые
устройства не являются омическими (хотя это,
конечно же, и так, но это неважный момент).
Самая большая ошибка в том, что в зависимо-
сти от типа сигнала, который мы хотим пере-
дать (ток или напряжение), стратегия разра-
ботки схемы будет вестись в противоположных
направлениях.
Сигнал в виде напряжения. Предположим,
что наш сигнал содержит информацию в виде
1S.2. Напряжение и ток
69
А
ллл
Б
i
Чтобы предотвратить
искажение сигнала,
нужно ЯВХ_Б»/?ВЬГХ.А
Сигнал в виде напряжения —
Рис. 1S.7. Соотношение импедансов схемы А по отношению к схеме Б при неискаженной передаче напряжения
Странная
нагрузка...
с
)
Е
Сигнал в виде тока
Допустимая
нагрузка...
Да, весьма странная нагрузка:
мы замыкаем выход на «землю» лишь для того, чтобы
обеспечить идеальный входной импеданс для сигнала
в виде тока
Что-либо, что реагирует на ток.
В данном случае, за отсутствием
лучшего, мы используем просто
амперметр
Рис. 1S.8. Сохранение сигнала в виде тока подразумевает совсем иное соотношение импедансов схемы А по отношению
к схеме Б
напряжения, а не тока. Что из этого следует? То,
что, во-первых, при его прохождении из одной
части схемы в другую он проходит через дели-
тель напряжения. Но главное состоит в том,
что для предотвращения искажения такого сиг-
нала схемой нужно, чтобы входной импеданс
#ВХ_Б был больше выходного импеданса RBHX_A.
В идеале мы хотим, чтобы импеданс.
бесконечным (рис. 1S.7,1S.8).
гвых-Абыл
На практике данная ситуация встречается очень
часто. Так было в главе IN, где мы вывели эм-
пирическое правило.
Сигнал в виде тока. Правила разработки схе-
мы для передачи сигнала в виде тока будут со-
всем иными. В частности, мы хотим, чтобы схе-
ма Б оказывала минимальное влияние на выход
схемы А. Это означает, что схема Б должна вы-
глядеть для схемы А, как короткое замыкание.
В идеале мы хотим, чтобы импеданс ЯВЫХ_А был
нулевым!
Описанный случай в нашем курсе встречается
очень редко (тем не менее мы будем сталкивать-
ся с ним время от времени; например, см. схему
с фотодиодом на лабораторном занятии 6L).
Общий случай? Сигнал в виде мощности5.
Иногда из точки А в точку Б нам требуется пе-
редать мощность, например, когда мы хотим
получить громкий звук из динамика. При этом
нам потребуется подать на вход динамика как
напряжение, так и ток. Задача будет невыпол-
ненной, если любая из этих составляющих бу-
дет недостаточной, поскольку мощность в дина-
мике определяется произведением напряжения
и тока. Для заданного выходного импеданса
Двых значение входного импеданса Двх, которое
максимизирует мощность в нагрузке, оказыва-
ется в точности равным значению #ВЫХ_А , т. е.
значения этих двух импедансов (#ВЫХ_А и ДВХБ)
должны быть одинаковыми*.
Но, опять же, это исключительный случай для
нашего курса. Почти всегда нас интересует об-
5 АоЕ Exercise 1.10.
6 Обратите внимание на тонкий нюанс здесь: мы изложи-
ли правило (впервые озвученное ученым Якоби) для опре-
деления значения импеданса R^^ для заданного значения
импеданса Двых. Обратная задача - определение выход-
ного импеданса RBUX для заданного входного импеданса
R^ — дает другой результат. Для такого случая максималь-
ная мощность, подаваемая на нагрузку с импедансом RBhlx,
равна нулю.
70
IS. Дополнительный материал: резисторы, напряжение, ток
работка и передача информации, а не мощности,
и эту информацию мы почти всегда кодируем в
виде напряжения.
Наглядный пример: низкочастотный
фильтр (предварительное знакомство)
С частотно-зависимыми ЯС-фильтрами мы
познакомимся на следующем занятии. Но мы
полагаем, что приведенный здесь пример по-
может вам разобраться по существу дела.
Низкочастотный фильтр иллюстрирует главный
аспект для нас — передача с помощью сигнала
некоторой информации. Нам вовсе не нужно,
чтобы фильтр передавал ток с входа на выход.
Этот пример особенно замечателен тем, что
в частотном диапазоне, в котором передается
сигнал, входной ток минимален, и наоборот.
Интересующее нас определение
децибела
Поскольку мы заинтересованы в обработке на-
пряжений, расчеты в децибелах следует выпол-
нять по формуле:
= 201о§10и2/[/1.
(1S.1)
Формула для расчета в виде соотношения мощ-
ностей не подходит для наших целей:
= 101оё10Р2/Р1.
(1S.2)
Разница между этими двумя формулами отра-
жает тот факт, что мощность в резистивной на-
грузке варьируется пропорционально квадрату
напряжения.
1S.2.3. Главный вывод: в курсе
схемотехники нас интересует
информация, а не энергия
Таким образом, хотя электроэнергия продол-
жает пользоваться большим спросом (а хра-
нение, доставка и управление электроэнер-
гией для автомобилей — особенно популярная
тема), в курсе схемотехники наибольший инте-
рес представляет использование электрических
сигналов для обработки и передачи инфор-
мации.
Входной сигнал
Значительный Гвх на высоких
частотах: это НЕ то, что нас
интересует!
Выходной сигнал
АЛ
Низкие частоты
(колебания напряжения)
проходят
Рис. 1S.9. Рисунок иллюстрирует, что в данном случае мы считаем сигналом напряжение, а не ток
. Примеры с решениями:
цепи постоянного тока
1 W.1. Разработайте схему
вольтметра и амперметра
Внутреннее сопротивление гальванометра с
пределом шкалы 50 мкА составляет 5 кОм1.
Каким должно быть сопротивление шунтирую-
щего резистора, чтобы сделать из него ампер-
метр с диапазоном измерений 0—1 А? Каким
должно быть сопротивление последователь-
ного резистора, чтобы получить из этого галь-
ванометра вольтметр с диапазоном измерений
0-10 В?
Цель данного упражнения — объяснить вам
принцип работы этого прибора, но оно также
позволит вам на практике выяснить, какая точ-
ность вычислений требуется в том или ином
случае.
Амперметр с диапазоном измерений 1 А.
Фраза «гальванометр с пределом шкалы
50 мкА» означает измерительный прибор,
стрелка которого отклоняется на всю шкалу,
когда через его катушку (см. устройство галь-
ванометра на рис. 1L.6) протекает ток величи-
ной 50 мкА. При подаче на вход амперметра
тока, превышающего 50 мкА, избыточный ток
должен обходить катушку, но показания галь-
ванометра должны быть пропорциональны
входному току.
Такое длинное объяснение может сделать раз-
работку амперметра сложной задачей. Но в
действительности, как вы, наверное, догады-
ваетесь, задача предельно проста: нужно про-
сто подключить резистор (который мы назы-
ваем шунтирующим в постановке задачи) па-
раллельно катушке гальванометра (рис. 1W.1).
Осталось выяснить, каким должно быть значе-
ние сопротивления такого резистора?
50мкА
АоЕ 1.2.3, Multimeters, ex. 1.8.
—► 1 А - 50 мкА ►
Рис. 1W.1. Шунтирующий резистор позволяет чувствитель-
ному гальванометру измерять токи до 1 А
Хорошо, что еще мы знаем на данном этапе?
Нам известно внутреннее сопротивление галь-
ванометра. Этот параметр вместе с предельным
током катушки позволяет нам вычислить паде-
ние напряжения на гальванометре при макси-
мальном токе:
иГАЛЬВ 1МАКС ^ГАЛЬВ
= 50 мкА • 5 кОм = 250 мВ.
Теперь мы можем определить значение Дш, так
как мы знаем значения тока и напряжения, ко-
торые должны быть при параллельном вклю-
чении этих двух элементов. Дальше нужно ре-
шить, выполнять ли точные вычисления или
будет достаточно приблизительной оценки.
Этот выбор связан с необходимостью получить
ответ на вопрос, какой ток должен проходить
через шунтирующий резистор.
Возможны два ответа: «1 А минус 50 мкА, или
0,99995 А» или просто «1 А».
Какой из вариантов вам нравится больше? Если
вы недавно изучили раздел физики, связанный
с электричеством, то наверное склоняетесь к
выбору первого ответа. В таком случае нам по-
требуется следующее сопротивление для шун-
тирующего резистора:
72
1W. Примеры с решениями: цепи постоянного тока
и,
полн. шкалы
*полн. шкалы
250 мВ
0,99995 А
= 0,2500125 Ом.
С точки зрения теории это может быть и хоро-
ший ответ, но не для нашей задачи. В наших об-
стоятельствах это очень глупый ответ. Глупый
потому, что полученное значение сопротивле-
ния должно быть с точностью до миллионных.
Если бы такие резисторы вообще существова-
ли, использовать их в приборе, всего лишь от-
клоняющем стрелку, на которую мы хотим по-
смотреть, было бы нелепо.
Поэтому мы должны пойти вторым путем: видя,
что ток 50 мкА гораздо меньше по сравнению с
током 1 А, следует уяснить насколько меньше
(в дробном или процентном виде). Ответ бу-
дет 50/1 000 000. Эта дробь настолько мала в
сравнении с действительными погрешностями
резистора и гальванометра, что током 50 мкА
можно пренебречь.
Избавившись от тока гальванометра, мы уви-
дим, что сопротивление шунтирующего рези-
стора будет всего лишь:
250 мВ /1А = 250 мОм (0,250 Ом).
Как видим, задача очень легкая, если у нас до-
статочно здравого смысла, чтобы не усложнять
ее. В курсе схемотехники мы будем постоянно
сталкиваться с такими ситуациями: если вы за-
вязли «в трясине математики», особенно, если
результаты ваших вычислений содержат слиш-
ком много цифр после десятичной запятой,
значит вы, скорее всего, прошли мимо «брода»
легкого решения. Нет никакого смысла учиты-
вать все эти цифры в дробной части значения
компонента, а затем использовать резистор
с 5-процентным допуском или конденсатор
с 10-процентным. Хотя в данной задаче раз-
работки амперметра мы рекомендуем выбрать
несколько более точный резистор с допуском
1%, все равно имеет смысл вычислять лишь его
приблизительное значение.
Вольтметр. В этой задаче мы хотим сделать из
базового гальванометра вольтметр с диапазо-
ном измерений 10 В, т. е. с отклонением стрел-
ки на полную шкалу при подаче на вход 10 В.
Как мы должны рассматривать причину этого
отклонения — как ток в 50 мкА, протекающий
через катушку, или как напряжение в 250 мВ,
подаваемое на катушку?
Любой из этих вариантов будет приемлемым.
Но рассматривая задачу с точки зрения напря-
жения, можно лучше понять, что падение боль-
шей части 10 В должно происходить на допол-
нительном резисторе, поскольку падение на-
пряжения на самом гальванометре будет всего
лишь 0,25 В. Исходя из этого можно составить
принципиальную схему прибора (рис. 1W.2).
юв
975 В
0,25 В
Рис. 1W.2. Для создания вольтметра последовательно с ка-
тушкой гальванометра подключаем резистор
Снова возникает вопрос, какой должна быть
величина этого подключаемого последователь-
ного сопротивления? Можно предложить два
равнозначных метода решения:
1. При протекании через это сопротивление
тока величиной 50 мА падение напряжения
на нем должно быть 9,75 В из максимально
возможного 10 В. Отсюда R = 9,5 В / 50 мкА =
= 195 кОм.
2. Общее сопротивление резистора и гальвано-
метра должно быть 10 В / 50 мкА = 200 кОм.
В постановке задачи в начале раздела со-
общается, что внутреннее сопротивление
гальванометра составляет 5 кОм; вычитая
его из общего, получаем искомое значение —
195 кОм.
Если вы попали впросак с ответом типа
0,2500124 Ом в предыдущей задаче с амперме-
тром, то ход ваших мыслей может быть при-
мерно таким: «О, 50 мкА очень малый ток,
гальванометр деликатный, поэтому я просто не
буду принимать его в расчет. Подключу после-
довательный резистор номиналом 200 кОм, и
получу лишь небольшую погрешность».
Ну, чтобы вы не слишком расслаблялись, у нас
для вас есть противоположный аргумент: на
этот раз, хотя ток 50 мкА и невелик, он все же
не пренебрежимо мал, поскольку он не сравни-
вается с каким-либо намного большим током.
Наоборот, теперь это критически важный пара-
метр, который нам обязательно нужно учиты-
вать: он определяет значение добавочного ре-
зистора. Также не следует говорить «значение
1W.2. Рассеивание мощности резисторами
73
200 кОм достаточно близкое», несмотря на
полученную точную величину 195 кОм. Хотя в
данном случае разница составляет 2,5%, что на-
много меньше, чем обычно будет встречаться в
нашем курсе (поскольку обычный допуск на но-
минал компонентов составляет 5% и 10%). Но
для прецизионного измерительного прибора,
несомненно, стоит немного поистратиться на
резистор с допуском 1% и номиналом 196 кОм.
1 W.2. Рассеивание мощности
резисторами
В следующих примерах2 по вычислению мощ-
ности резистора, если полученное значение от-
сутствует в перечне значений ряда Е12, выбира-
ем из этого ряда наиболее близкое безопасное
значение. Для справки приведем вторую декаду
ряда:
10; 12; 15; 18; 22; 27; 33; 39; 47; 56; 68; 82.
Задача
Каким должно быть минимально допустимое
сопротивление резистора мощностью 0,25 Вт,
чтобы на него можно было безопасно подать
напряжение 5 В?
Решение
Р = IP/R; Я = 25 B2/0,25 Вт = 100 Ом.
Задача
Каким должно быть минимально допустимое
сопротивление резистора для поверхностного
монтажа мощностью 0,125 Вт, чтобы его можно
было безопасно подключить между двумя точ-
ками с потенциалами -15 В и +15 В?
Решение
P=IP/R;
R = 900 В2/0,125 Вт = 7200 Ом * 7,5 кОм.
Ближайшим значением из ряда Е12 (10% до-
пуск) будет номинал 8,2 кОм.2
Задача
Какое максимальное напряжение можно пода-
вать на резистор сопротивлением 10 Ом и мощ-
ностью 10 Вт?
Решение
P=U2/R;U =
- R =V 10Вт• 10Ом = 10В.
Задача. Передача электроэнергии. Эффект повы-
шения напряжения
Для передачи электричества на большие рас-
стояния применяются высокие напряжения,
чтобы свести к минимуму потери в линиях пе-
редачи. Если энергокомпания сможет повысить
напряжение в линии передачи с 100 000 вольт
до 1 миллиона вольт, во сколько раз уменьшат-
ся потери в линиях электропередачи? (Пред-
полагается, что энергокомпания должна до-
ставить клиенту определенный объем электро-
энергии, одинаковый в обоих случаях.)
Решение
Потери мощности в линиях электропередачи
пропорциональны произведению напряже-
ния и тока U • I в линии, или, что равнозначно,
Р • U, где R представляет собой сопротивление
единицы длины провода (которые хотя и боль-
шого диаметра, но, тем не менее, не с нулевым
сопротивлением3).
Повышение напряжения в десять раз снижает
ток на столько же (при заданном количестве
электроэнергии). Поскольку потери мощности
пропорциональны квадрату тока, рассеивае-
мая мощность уменьшится до (1/10)2 = 1/100.
Так что повышение напряжения выглядит
разумным. Но при очень высоком напряжении
нужно позаботиться о тщательной изоляции,
поэтому значение 1 MB будет на практике поч-
ти предельным.
Задача
Почему в большинстве случаев электроэнер-
гию намного лучше передавать в виде перемен-
ного напряжения, а не постоянного, как пред-
лагал один из первопроходцев в этой области —
Томас Эдисон?
Решение
Причина заключается в том, что переменное на-
пряжение довольно просто повысить или пони-
зить с помощью трансформаторов. Повышение
или понижение постоянного напряжения тре-
бует гораздо более сложного оборудования.
Тем не менее высокое постоянное напряжение
используется для передачи электроэнергии в
особых случаях, когда потери при передаче на
переменном напряжении оказываются слиш-
ком высокими, например, в подводных кабелях.
2 АоЕ § 1.2.2С.
3 По крайней мере, до тех пор, пока в линиях электропере-
дач не будут использоваться сверхпроводники.
74
Ш Примеры с решениями: цепи постоянного тока
Но, по большому счету, использование высоко-
го переменного напряжения для передачи элек-
троэнергии преобладает благодаря простоте
и низким потерям этого метода.
1 W.3. Обходное решение
проблемы неточности
инструментов
В разделе 1L.5 была поставлена задача под-
твердить на практике справедливость закона
Ома. Но здесь мы сразу же сталкиваемся с труд-
ностью, заключающейся в том, что эту задачу
экспериментально невозможно выполнить:
одновременно точно измерить значения тока I
и напряжения U для резистора. Посмотрите на
рис. 1W.3. Одно из возможных мест для под-
ключения цифрового мультиметра очевидно,
а вот второе предлагаем вам определить само-
стоятельно.
Качественный подход
Поразмышляйте пару минут, и вы догадае-
тесь, что при сборке предлагаемой схемы по-
казания вольтметра будут не совсем точными.
Подключение вольтметра непосредственно к
резистору повышает точность измерения на-
пряжения, но... увеличивает погрешность по-
казаний амперметра.
Количественный подход
Теперь рассмотрим данную проблему более
подробно.
Задача. Оценить погрешности показаний, вызы-
ваемые взаимным влиянием измерительных при-
боров
Возьмем характеристики авометра из раздела
1W.1 и определим погрешность показаний на-
пряжения при подключении вольтметра, как
показано на рис. 1L.10, а, для следующих зна-
чений сопротивления резистора:
♦ Д = 20кОм;
♦ Д = 200 Ом;
♦ Я = 2МОм.
Примем напряжение питания 20 В и диапазон
измерений амперметра, позволяющий полу-
чить отклонение стрелки прибора на полную
шкалу.
Решение
Эта задача легче, чем кажется на первый взгляд.
Погрешность вносится вследствие падения на-
пряжения на амперметре, ранее мы уже вычис-
лили величину этого падения: 0,25 В при от-
клонении на полную шкалу. Поэтому номина-
лы резисторов не имеют значения. Показания
вольтметра всегда будут завышены на четверть
вольта, если стрелка амперметра отклоняется
на всю шкалу. Итак, сопротивление резистора,
на котором измеряется напряжение, не влияет
на результат.
Когда цифровой вольтметр показывает 20 В,
действительное напряжение (на выводах ре-
зистора) составляет 19,75 В. Таким образом,
показания вольтметра оказываются выше дей-
ствительного на 0,25 В /19,75 В или приблизи-
тельно на 0,25/20 = 1/80 или 1,25%.
Регулируемый
источник
питания
0-20 В
0-20 В
Цифровой
вольтметр
Авометр
20кОм
Рис. 1 W.3. Схема для эксперимента из раздела 1L5. Измерительные приборы влияют на показания друг друга
ШЗ. Обходное решение проблемы неточности инструментов
75
Примечание
При меньшем напряжении питания погрешность
показаний вольтметра могла бы возрасти при
условии, что стрелка амперметра также откло-
няется до максимального значения шкалы (этого
можно добиться, изменив диапазон измерений
амперметра).
Задача
Аналогичная задача, но касательно погреш-
ности показаний амперметра при подключе-
нии вольтметра непосредственно к резистору
и тех же номиналах резисторов, что и раньше.
Входное сопротивление цифрового вольтметра
примем равным 20 МОм.
Решение
Если подключить цифровой вольтметр непо-
средственно к резистору (рис. 1W.4), его по-
казания напряжения на резисторе будут со-
вершенно точными. Но теперь показания ам-
перметра окажутся несколько завышенными:
он измеряет не только ток через резистор, но
также и ток, протекающий через параллельно
подключенный цифровой вольтметр.
Величина этой погрешности непосредственно
зависит от номинала резистора R, на котором
выполняется измерение. Вычислить величину
погрешности для каждого номинала, можно
даже в уме:
♦ при R = 20 кОм и внутреннем сопротивлении
цифрового вольтметра 20 МОм через прибор
протекает одна тысячная часть всего тока,
следовательно, показание амперметра будет
завышено на 0,1%;
♦ при R = 200 Ом через вольтметр протекает
одна стотысячная часть общего тока, и пока-
зание амперметра окажется завышено всего
лишь на 0,001%;
ЦИФРОВОЙ
МУЛЬТИМЕТР
Рис. 1W.4. Подключение цифрового вольтметра вызывает
погрешность показаний амперметра, величина которой
пропорциональна отношению Я//?ЦИФР вольт
♦ а при R = 200 МОм погрешность показаний
амперметра будет большой, поскольку че-
рез вольтметр протекает одна десятая часть
общего тока.
Какой из всего этого можно сделать вывод? На
вопрос, какой из двух способов подключения
цифрового вольтметра в схему лучше, нет одно-
значного ответа. Ответ зависит от значения со-
противления R, подаваемого напряжения и уста-
новленного диапазона измерений амперметра.
Прежде чем завершить рассмотрение этого во-
проса, мы хотим обратить ваше внимание на
последнюю составляющую: погрешность зави-
сит от выбранного диапазона измерений ана-
логового амперметра. Почему? Здесь действует
принцип, который мы в шутку называем «элек-
тронная справедливость» или «жадность будет
наказана». Поскольку вы раньше не слышали
об этих понятиях, объясним их более подробно.
Суть заключается в том, что если вы хотите по-
лучить меньшую цену деления шкалы аналого-
вого амперметра, за это придется «заплатить»4,
так как прибор внесет в показания большую
погрешность, чем при установке диапазона
с большей ценой деления шкалы (рис. 1W.5).
Отсюда и понятие «цены деления шкалы». - Примеч. ред.
1/10 полной шкалы
s ч
Низкая точность...
<—► ...и малая вносимая
0,25 В погрешность
0,25 В
Рис. 1W.5. Компромисс между ценой деления и погрешностью. Аналоговый или цифровой амперметр: чем выше точность,
тем больше вносимая погрешность. Аналоговый вольтметр: чем больше отклонение стрелки при заданном 1/вх, тем ниже
входной импеданс
76
Ш Примеры с решениями: цепи постоянного тока
Если вы хотите, чтобы стрелка амперметра от-
клонялась почти на всю шкалу (что дает наи-
лучшее разрешение, поскольку небольшие ко-
лебания тока вызывают сравнительно большие
отклонения стрелки), соответствующее падение
напряжения на амперметре будет составлять
1/4 вольта. То же самое касается и цифрового
амперметра, для которого отклонение полной
шкалы означает заполнение всех 3,5 цифр его
дисплея (символ 0,5 цифры может отображать
только значения 0 и 1). Таким образом, точ-
ность показаний, например, таких как «0,093»
будет плохой (около 1%). А при установке дру-
гого диапазона измерений, при котором тот же
самый ток отображается в виде «0,930», будет
лучше в десять раз, чем в предыдущем случае.
Но при этом пропорционально увеличивается
падение напряжения на приборе, поскольку,
подобно аналоговому прибору, падение на-
пряжения при «отклонении» на полную шкалу
составляет 1/4 вольта и пропорционально сни-
жается для меньших отклонений (для аналого-
вого прибора) или меньших долей диапазона
полной шкалы (для цифрового).
ЮВ
20 В
-5 В
I I
> 10 кОм
Рис. 1 W.6. Схемы для сведения к моделям Тевенина
1 W.4. Эквивалентные схемы
Тевенина
Задача
Начертите модель Тевенина для схем на
рис. 1W.6. Дайте ответы с точностью до 10%
и 1%.
Некоторые из этих схем содержат типичные
трудные моменты, которые могут усложнить
вашу работу по созданию их модели, пока у вас
нет большого опыта по созданию моделей
Тевенина.
Модель для левой схемы легче всего создать,
временно переопределив «землю», что преоб-
разовывает схему в полностью знакомую фор-
му (рис. 1W.7).
Единственная проблема в средней схеме возни-
кает при попытке оценочных вычислений. То
есть для варианта с точностью до 1% проблем
нет, но вариант с точностью до 10% мудреный.
Если вы уделяли внимание нашим наставлени-
ям использовать приблизительные вычисления
с точностью до 10%, у вас может возникнуть
искушения смоделировать каждый из блоков
резисторов, используя доминантное сопротив-
ление R: малое в случае параллельного соеди-
нения и большое в случае последовательного
(рис. 1W.8).
К сожалению, это тот редкий случай, ког-
да погрешности накапливаются; нам нужно
применять большую точность вычислений
для двух составляющих делитель элементов.
Сопротивление RTEB также нужно вычислять
с большей точностью: приблизительное зна-
чение 0,84 кОм общего сопротивления парал-
лельных резисторов 0,91 кОм и 11 кОм непри-
емлемо близко к обычному приблизительному
значению в 1 кОм.
20 В —, 25 В
► 15 кОм
бкОм
•\ 2/5 общего ... возвращаем [ 5 В
ЛОкОм <Л0кОм (падения первоначальную «землю»
1и ким Г напряжения: Ю В —► 5 В
J ЮВ
-5 В -I 0 В
Рис. 1 W.7. Слегка необычная задача сводится к знакомой форме временным переопределением «земли»
1W.5. «Смотрим сквозь» фрагмент схемы
77
10 В
1 кОм
1 кОлл
Неправильное применение
оценочных вычислений
ИкОм
10 В
ЮкОм
ЮкОм
076 В = ? =
Мдо1%)
0,91 кОм
1 кОм
Погрешность
в 20%
= 0,91 В ? = ? = (Увх/10 = 1 В ?
до 10%?
НЕТ!
Погрешность
в 25%
Рис. 1 W.8. В оценочных вычислениях с точностью до 10% возможно накопление погрешностей
"источ ОДмА
ЮкОм
Бесконечное:
v В идеале ноль
Рис. 1 W.9. Источник тока, питающий резистор, и эквивалентная схема Тевенина
Но целью этого примера не является заставить
вас отказаться от использования оценочных
вычислений. В нем обращается внимание на то,
что требуемую точность должен иметь конеч-
ный результат, а не результаты промежуточных
вычислений.
Скорее всего источник тока на рис. 1W.9 может
показаться вам необычным. Но вам не обяза-
тельно понимать, как сделать такой источник
питания, чтобы видеть его эффект. Поверьте
нам на слово, что он делает то, что заявлено:
подает постоянный ток по направлению к от-
рицательному полюсу. Остальное следует из за-
кона Ома.
Примечание
На лабораторном занятии 4L мы рассмотрим, как
разрабатывать такие устройства. Также вы узнае-
те, что некоторые компоненты сами по себе могут
служить источниками тока, например, транзисто-
ры обоих типов — биполярные и полевые.
Тот момент, что источник тока всегда представ-
ляет высокий выходной импеданс, помогает
напомнить нам определение импеданса — всег-
да одинаковый: AU/AI. Будет более полезным,
чтобы вы запомнили это общее понятие, неже-
ли истину типа «Источники тока представляют
высокий выходной импеданс». Вспомнив это
определение импеданса, вы всегда можете вы-
числить приблизительный выходной импеданс
источника тока (большой или малый). Вскоре
вы сможете узнавать точный результат просто
в результате постоянного контакта с подобны-
ми случаями.
1 W.5. «Смотрим сквозь»
фрагмент схемы
Задача
Какие значения RBX и #вых в обозначенных точ-
ках схемы на рис. 1W.10?
78
1W. Примеры с решениями: цепи постоянного тока
Рис. 1 W.10. Определение значений сопротивлений /?вх и Явых:
нужно решить, что находится за пределами схемы, к которой
вы подключаетесь
Решение А
Входное сопротивление R^. Ясно, какое значе-
ние Двх должен показывать делитель: просто
Rx + Rr Но будет ли это ответом на правильный
вопрос? Разве питание с выхода делителя не
будет подаваться на что-то, подсоединенное к
нему далее? Если нет, какой смысл в создании
этого делителя?
Ответ, конечно же, да, напряжение с выхода
делители будет подаваться на что-то — на на-
грузку. Но это что-то должно предоставлять до-
статочно высокое входное сопротивление 1?вх,
чтобы оно не изменяло существенно результат,
который мы получили, когда не принимали на-
грузку во внимание. Если следовать нашему эм-
пирическому правилу 10-процентного ослаб-
ления (см. раздел 1N.4.6), наш результат не
будет слишком далеким от этой идеализации:
менее чем 10%. Вкратце можно просто сказать,
что мы предполагаем идеальную нагрузку, т. е.
нагрузку с бесконечно большим входным импе-
дансом.
ЮкОм
£Нлгр: бесконечное,
или «громадное»
ЮкОм
Рис. 1W.11. Чтобы определить значение /?вх, нужно какое-
либо предположение о нагрузке, питаемой схемой
Решение Б
Выходное сопротивление, Двых. Здесь возникает
такая же проблема, которую мы решаем таким
же образом: предполагая идеальный источник.
Но трудность опять состоит в том, что для того,
чтобы определить #вых, нам нужно сделать
определенное предположение касательно того,
что подключено к входу делителя (рис. 1W.12).
Чкточ
Ноль О/а
Рис. 1W.12. Чтобы определить Явых, нам нужно сделать
какое-либо предположение относительно источника пита-
ния схемы
Предположение, принимаемое при определе-
нии сопротивления Явых, знакомо вам по мо-
делям Тевенина: мы предполагаем импеданс
источника настолько низким, что им можно
пренебречь, считая его равным нулю. Таким
образом, если сопротивление каждого рези-
стора равно 10 кОм, выходной импеданс будет
равным 5 кОм.
1 W.6. Влияние нагрузки
Задача
Для схемы на рис. 1W.13 определите напряже-
ние в точке X в следующих случаях:
1. Без подключенной нагрузки.
2. При измерении этого напряжения аналого-
вым вольтметром с обозначенной на нем ха-
рактеристикой 10 000 Ом/В.
3. При измерении этого напряжения с по-
мощью осциллографа с входным импедан-
сом 1 МОм.
Возможно, вы распознали, что этот пример
обобщаетутверждение,встречающеесянесколь-
ко раз в главе IN. Вспомним: характеристика
«Ом/вольт» обозначает входное сопротивле-
ние измерительного прибора в диапазоне из-
мерений в 1 вольт (т. е. когда 1 вольт на входе
прибора вызывает отклонение стрелки на пол-
ную шкалу). Каким будет входное сопротив-
ление прибора при установленном диапазоне
1W.6. Влияние нагрузки
79
20 В-
100 кОм
100 кОм
Рис. 1W.13. Выходной импеданс 1/вых: вычисленный и измеренный
50кОлл
Рис. 1 W.14. Модель Тевенина тестируемой схемы с нагрузкой — вольтметром или осциллографом
измерений 10 вольт? (Ответ: в 10 раз большее
сопротивления R^ для диапазона 1 вольт:
100 кОм.)
Как обычно, сначала упростим схему, преобра-
зовав ее к знакомой нам форме, т. е. к эквива-
лентной модели Тевенина. Затем добавим к ней
в качестве нагрузки вольтметр или осцилло-
граф, создав, таким образом, делитель напря-
жения, и смотрим на результат (рис. 1W.14).
В этом курсе мы будем постоянно повторять
этот общий процесс упрощения незнакомой
принципиальной схемы, преобразовывая ее в
знакомую форму. Иногда для этого мы будем
просто перерисовывать исходную схему или
по-иному размещать ее компоненты, но более
часто мы будем прибегать к использованию ее
модели, которая часто будет эквивалентной мо-
делью Тевенина.
2N. /?С-цепи
2N.1.
2N.2.
2N.3.
Конденсаторы
2N.1.2. Устройство конденсатора
Анализ ЯС-цепей во временной области
2N.2.1. Интеграторы и дифференциаторы
Анализ ЯС-цепей в частотной области
2N.3.1. Импеданс, или реактивное сопротивление конденсатора
2N.3.2. ДС-фильтры
2N.3.3. Децибелы
2N.3.4. Определение вносимого затухания фильтра
2N.3.5. Входной и выходной импеданс #С-цепи
2N.3.6. Фазовый сдвиг
2N.3.7. Векторные диаграммы
Два простых, но важных варианта применения конденсатора:
2N.4.
2N.4.1. Блокировочный конденсатор
2N.4.2. Развязывающий конденсатор
2N.5. Математический взгляд на ДС-фильтры
2N.6. Материал для чтения в АоЕ
80
81
82
84
87
87
89
92
94
96
97
99
102
103
103
105
106
2N.1. Конденсаторы
Теперь мы приступаем к изучению более сложно-
го, но и более интересного материала: частотно-
зависимым схемам. Основной компонент таких
схем — конденсатор, обладающий свойством
«запоминать» свое недавнее состояние.
Благодаря этому свойству мы можем создавать
схемы тактирования (или таймеры на профес-
сиональном жаргоне), т. е. устройства, которые
позволяют происходить определенным событи-
ям по истечении заданного периода времени по-
сле другого события. Наиболее важные из этих
схем — генераторы колебаний, которые выраба-
тывают незатухающие колебания с заданной ча-
стотой выходного сигнала. Свойство «памяти»
конденсатора также позволяет создавать схемы,
реагирующие на изменения сигнала (диффе-
ренциаторы) или на средние значения сигнала
(интеграторы). На основе конденсаторов также
можно создавать наиболее важный для нас тип
ЯС-схем: фильтр, т. е. устройство, которое отде-
ляет сигналы определенной частоты.
Примечание
Чтобы вы окончательно убедились в исключитель-
ной полезности свойства памяти конденсатора,
заметьте, что далее в этом курсе, в материале по
цифровым технологиям, мы познакомимся с боль-
шими массивами конденсаторов, единственной
целью которых является запоминание. Различные
типы цифровой памяти (динамическая RAM1, флэш-
память, EEPROM2 и EPROM3) используют миллионы
или миллиарды крошечных конденсаторов для
хранения информации в виде электрических заря-
дов. В последних двух типах памяти эта информа-
ция может сохраняться в течение долгих лет.
Все сложные электронные схемы можно раз-
бить на более простые составляющие, чем мы
1 Random Access Memory — память с произвольным до-
ступом, ОЗУ (оперативное запоминающее устройство).
2 Electrically Erasable Programmable Read-Only Memory —
электрически стираемая программируемая постоянная
память, ЭСППЗУ (электрически стираемое программи-
руемое постоянное запоминающее устройство).
3 Erasable Programmable Read-Only Memory - стираемая
программируемая постоянная память, СППЗУ (стираемое
программируемое постоянное запоминающее устройство).
2N.L Конденсаторы
81
и будем заниматься далее. А с фильтрами мы
будем иметь дело больше всех остальных ти-
пов схем, практически постоянно, когда мы
начнем работать с другими аналоговыми схе-
мами. Схемы фильтров применяются почти так
же повсеместно, как и делители напряжения на
резисторах, с которыми мы познакомились на
нашем первом занятии (см. главу IN и сопут-
ствующие материалы).
Ранее мы уже упоминали несколько примене-
ний #С-схем. На сегодняшнем занятии мы рас-
смотрим как с помощью этих схем можно ре-
шить две задачи:
♦ поменять уровень напряжения выходного
сигнала по истечении определенного перио-
да времени после изменения напряжения
входного сигнала;
♦ разделить сигналы различных входных ча-
стот (задача фильтрации сигнала).
2N.12. Устройство конденсатора
На рис. 2N.1 приводится устройство конден-
сатора, напоминающее бутерброд: металличе-
ские пластины вместо хлеба, а вместо начин-
ки — диэлектрик между пластинами (керами-
ческие конденсаторы действительно устроены
так просто). Но чаще для увеличения площади
пластин (а значит, и емкости) исходная форма
«бутерброда» модифицируется в «рулет». Для
этого между двумя длинными лентами метал-
лической фольги помещается диэлектрик, а за-
тем все это сворачивается в трубку. Так устрое-
ны конденсаторы, изготовленные, например,
из майлоровой пленки.
Статические свойства конденсатора4
Функционирование конденсатора в статиче-
ском случае выглядит следующим образом:
Q,= CU.
Здесь Q.— общий заряд; С — мера емкости кон-
денсатора (насколько большой заряд он может
хранить при данном напряжении: С = Q/U);
U — напряжение на выводах конденсатора.
Приведенная формула просто определяет поня-
тие емкости. Это подход для описания поведения
ИЗОЛЯТОР
Это может быть вакуум, но обычно
используется какой-либо диэлект-
рический (т. е. непроводящий или
изолирующий) материал — керами-
ка, пластмасса или оксид металла,
который позволяет получить боль-
шую емкость на единицу площади
ТОКОТТРОВОДЯЩИЕ ПЛАСТИНЫ
Рис. 2N.1. Устройство конденсатора в виде «бутерброда»
конденсатора согласно законам физики, но нам
он в дальнейшем потребуется редко.
Динамическое описание поведения
конденсатора
Вместо этого мы будем использовать динами-
ческое описание — формулу изменения харак-
теристик во времени:
1=С
dU
dt
Эта формула получается из формулы статиче-
ского описания введением производной по вре-
мени. Составляющая Сне меняется во времени,
а I определяется, как скорость протекания за-
ряда. Суть формулы понять несложно: если ток
через конденсатор оказывается больше, значит,
напряжение на нем изменяется быстрее.
«Водяная» аналогия конденсатора
Аналогия с потоком воды может помочь с пони-
манием сути конденсатора: его (с заземленным
одним из выводов) можно рассматривать как
емкость, которая способна накапливать заряд
(рис. 2N.2).
X"
Путь
заряда
\
**- - -
\ Высота
соответствует
напряжению U
<
'-Л
Путь
разряда
Объем воды
соответствует
заряду Q
\ Размер емкости
р^? (площадь)
соответствует С
Йй,
4 АоЕ § 1.41.
Рис. 2N.2. Конденсатор, один вывод которого заземлен,
функционирует во многом подобно емкости с водой
82
2N. RC-цепи
Емкость большого размера (конденсатор) со-
держит определенный объем воды (заряд) при
данном уровне (U). Если наполнять/опорож-
нять емкость через тонкий шланг (малый ток
I), уровень воды (напряжение V) будет подни-
маться/падать медленно. Но если взять шланг
большого диаметра (большой ток), емкость
будет наполняться/опорожняться (конденса-
тор заряжаться/разряжаться) быстрее. Чем
больше объем емкости (конденсатор большей
емкости), тем больше времени потребуется,
чтобы ее заполнить/опорожнить, чем мень-
шую емкость. Отличная аналогия, не так ли?
2N.2. Анализ /?С-цепей
во временной области
Оставим теперь в стороне емкости с водой и
попробуем предположить, что получится, если
подать на конденсатор напряжение, изменяю-
щееся во времени. Наблюдать сигнал удобнее
всего с помощью осциллографа, как мы и будем
делать на лабораторном занятии 2L.
Простой частный случай: постоянный ток
На рис. 2N.3 приведена схема для этого экспе-
римента (слева) и осциллограммы напряжения
на конденсаторе для малого и большого тока
Большой ток Г
Ur ис / Малый ток I
~ Время
Рис. 2N.3. Простой случай: постоянный ток I —> постоянная
производная dil/dt
Разряд
Рис. 2N.4. Использование конденсатора для создания сигна-
ла треугольной формы с линейным нарастанием и убывани-
ем амплитуды
(справа). Мы видим простой и понятный гра-
фик линейно изменяющегося напряжения, ко-
торый является, в чем вы в дальнейшем не раз
убедитесь, характерной особенностью данной
цепи: конденсатора, на который подается ста-
бильный во времени ток (от источника тока)5.
Рассмотренная цепь служит основой схемы для
создания треугольного (пилообразного) сигна-
ла, как показано на рис. 2N.4.
Но линейно изменяющийся сигнал встречается
сравнительно редко, поскольку источники тока
тоже довольно редки. Намного более распро-
странен следующий случай.
Более трудный, но и чаще
встречающийся случай:
источник постоянного напряжения
с последовательно включенным
резистором (экспоненциальный
заряд емкости)
В данном случае значение напряжения на кон-
денсаторе Uc приближается к значению напря-
жения источника, но по мере приближения Uc
к конечному значению скорость его нарастания
стремится к нулю6. На рис. 2N.5 можно видеть,
как напряжение на конденсаторе Uc начинает
бодро повышаться, двигаясь к значению вход-
ного напряжения UBX (при токе заряда вели-
чиной 10 мА начальная скорость повышения
напряжения конденсатора составляет 10 В/мс),
но по мере приближения к своей цели начинает
терять свою «прыть». Когда до цели остается
1 В, скорость нарастания падает до 1/10 на-
чальной скорости.
Замечание
В данном случае конденсатор ведет себя во мно-
гом подобно зайцу из парадокса Зенона: пом-
ните такого? Зенон развлекался, задавая сво-
им афинским согражданам каверзные задачи.
Одной из них была задача о зайце, который дви-
гается по коридору к стенке, где его ждет мор-
ковка. Он проходит полпути по направлению к
морковке, затем половину оставшегося расстоя-
ния, и т.д. Сможет ли он таким образом добрать-
ся до морковки, если до нее всегда остается такое
же расстояние, как и только что пройденное?
5 АоЕ § 1.4.4А.
6 АоЕ § 1.4.2А.
2N.2. Анализ RC-цепей во временной области
83
+10 В -
1 кОм
1 ллкФ
При 5 В на R ток заряда
I равен Г
1 тс 2 тс
При 10 В на £ ток заряда равен 10 мА
Время
dU _ I
dt ' С
10 • 10"
= 10 В/мс
Рис. 2N.5. Более распространенный случай: конденсатор заряжается от источника напряжения через последовательно вклю-
ченный резистор
(В действительности в парадоксе Зенона заяц
участвует в гонках с черепахой, но мы не смогли
придумать соответствующий аналог для конден-
сатора, поэтому упростили его.) Но если зайцы
в реальности добираются до своей морковки,
конденсаторы никогда не достигают своей цели:
в ЯС-цепях напряжение на конденсаторе Uc ни-
когда не достигает значения напряжения источ-
ника 1/исг Но оно подходит к нему так близко, как
вам захочется.
Экспоненциальный заряд и разряд
Заряд и разряд конденсатора в #С-цепях на-
зывается экспоненциальным, поскольку здесь
проявляется свойство, присущее этому боль-
шому классу функций. Экспоненциальной на-
зывается функция, крутизна которой пропор-
циональна ее значению: функция е* ведет себя
так же, как и напряжение Uc на конденсаторе в
ДС-цепочке.
Вам могут быть известны такие экспоненци-
альные процессы, как функция, описывающая
прирост (темп роста) популяции (чем больше
количество бактерий, тем быстрее растет ко-
лония), и функция слива воды из ванной (чем
больше слито воды, тем медленнее слив). Это
правило нагляднее видно на графике разряда
конденсатора, чем на графике его заряда, по-
этому давайте рассмотрим этот случай. По мере
разряда конденсатора напряжение на резисто-
ре R снижается, в результате чего скорость раз-
ряда также убывает. Это ясно видно на графике
разряда на рис. 2N.6. Таким образом, разряд
конденсатора в ДС-цепи происходит подобно
сливу воды из ванны.
12 3 4
Время (единицы постоянной
времени £<Г-цепи)
Рис. 2N.6. График заряда и разряда конденсатора в /?С-цепи
Полезно запомнить два числа из графика на
рис. 2N.6:
♦ за одну единицу RC (называющуюся «посто-
янной времени цепи») напряжение [^дости-
гает 63% от своего конечного значения;
♦ за пять постоянных RC — 99% полного зна-
чения.
Точное решение дает следующая формула:
В случае, если вы не понимаете смысл этой фор-
мулы, обратите внимание только ее часть е~t/RC:
♦ когда t = RC, значение этого выражения будет
е~г = 1/е, или 0,37,
♦ а когда t» RC, т. е. очень большое, его зна-
чение будет очень маленьким, a Uc « UHCT04.
84
2N. RC-цепи
Небольшой совет по оценке постоянных вре-
мени в ЯС-цепях:
• постоянные для сопротивлений в ме-
гаомах и емкостей микрофарадах будут
в секундах;
• для сопротивлений в килоомах и емко-
стей в микрофарадах постоянные вре-
мени будут в миллисекундах.
Второй случай (кОм и мкФ) встречается очень
часто. В ранее рассмотренном примере посто-
янная времени ДС-цепочки является произве-
дением 1 кОм и 1 мкФ и равна 1 мс.
Постоянная времени, RC
Поначалу для вас может оказаться непривыч-
ным частое упоминание «постоянной време-
ни» даже в таких случаях, когда в схеме явно
не присутствуют резисторы и конденсаторы,
например, в генераторе колебаний. На самом
деле постоянная времени служит в качестве
ориентира для оценки быстродействия эле-
ментов. Таким образом, если, например, вы
видите на экране осциллографа сигнал помехи
с частотой 1 МГц, то сразу можете исключить
JRC-цепочку с постоянной времени в милли-
секундном диапазоне из числа возможных
виновников.
Прием для вычисления погрешности
без калькулятора
Экспоненциальное выражение e~t/RC9 описыва-
ющее погрешность, может казаться довольно
трудным для вычисления вручную. Но в дей-
ствительности приблизительно оценить по-
грешность совсем не трудно. Для этого обра-
тите внимание на следующую закономерность:
в конце интервала величиной в одну постоян-
ную времени погрешность уменьшается при-
близительно до 40% от значения, которое она
имела в начале.
Таким образом, через интервал времени, рав-
ный двум постоянным #С-цепи, погрешность
уменьшается до 0,4 х 0,4 или около 0,16. Если
прибавить к этому интервалу еще одну по-
стоянную времени, то погрешность умень-
шится до приблизительно 0,06. И так далее
в том же духе.
2N.2.1. Интеграторы
и дифференциаторы
Из формулы I = С можно получить еще
dt
много полезных результатов. Например, с ее
помощью мы можем установить, при каких
условиях схемы, изображенные на рис. 2N.7,
функционируют как интегратор и дифферен-
циатор.
- Выход
Выход
Интегратор ли это?
Дифференциатор ли это?
Рис. 2N.7. Оценка параметров дифференциатора и интегра-
тора с помощью формулы l=C{dU/dt)
Дифференциатор
Рассмотрим сначала более простую схему, изо-
браженную на рис. 2N.8.
и 1 ч
Рис. 2N.8. Бесполезный «дифференциатор»?
Ток, протекающий через конденсатор, про-
порционален отношению dUBX/dt, поэтому, с
одной стороны, данная схема в полной мере
осуществляет дифференцирование входного
сигнала: ток пропорционален крутизне входно-
го напряжения 1/вх. Но довольно очевидно, что
схема совершенно бесполезна. Она не дает ни-
какой возможности измерить ток. Если приду-
мать какой-либо способ для измерения тока, то
мы бы получили идеальный дифференциатор.
Посмотрим на рис. 2N.9, здесь снова приводит-
ся первоначально предложенная (см. рис. 2N.7,
схема справа) схема дифференциатора. Будет
ли она работать ожидаемым от нее образом?
И да, и нет. Да, поскольку Uc = UBX (и, отсю-
да, dUKOim/dt - dUBX/dt)9 следовательно, схема
работает как дифференциатор. Но, поскольку
2Л/.2 Анализ RC-цепей во временной области
85
UBhSX меняется, схема несовершенна, так как
вследствие этого изменение напряжения Uc от-
личается от напряжения UBX.
Так что схема дает погрешность, поскольку на-
пряжение выходного сигнала смещается отно-
сительно нулевого потенциала (но, конечно же,
оно должно отличаться от нуля, чтобы образо-
вался некоторый выходной сигнал). Как видим,
данная схема дифференциатора неидеальна.
Нетрудно понять, что простой ДС-интегратор
тоже функционирует неточно. Почти идеальные
интеграторы и довольно хорошие дифферен-
циаторы мы сможем создать лишь, когда начнем
работать с операционными усилителями.
В книге АоЕ этот аспект излагается следующим
образом:
♦ для дифференциатора7:... значения R и С
должны быть достаточно малыми, чтобы
dUBUX/dt«dUBX/dt...
♦ для интегратора8: ...обеспечьте, чтобы ишх
«Ubx...q*-RC»19.
Эту ситуацию можно описать простыми слова-
ми, хотя и менее изящно.
Определение
Пусть у нас входной сигнал синусоидальной фор-
мы. Тогда /?С-дифференциатор (и интегратор тоже)
функционирует достаточно хорошо в том случае,
если он очень сильно ослабляет сигнал, чтобы вы-
ходное напряжение С/вых (а также сКУвых) было очень
низким: чуть выше нулевого потенциала.
dt
Чьгх
J*x \ Погрешность!
Дифференциатор ли это?
Рис. 2N.9. Возможная схема дифференциатора
Отсюда заодно вытекает10, что дифференциа-
тор и интегратор вносят во входной синусо-
идальный сигнал смещение по фазе на 90°. Этот
результат, очевидный в данной ситуации, дол-
жен помочь вам в дальнейшем предсказывать
величину смещения по фазе в ДС-цепочках,
рассматриваемых как фильтры.
Исследуем дифференциатор
На рис. 2N.10 показано, как выглядит вы-
ходной сигнал дифференциатора, подобного
тому, который мы создадим на лаборатор-
ном занятии 2L, при прямоугольном входном
сигнале. Выходной сигнал формируется при
каждом перепаде прямоугольного входного
сигнала и вследствие медленной развертки
выглядит просто как выброс (импульс) на-
пряжения (рис. 2N.10, а). На рис. 2N.10, б де-
тально показана форма выходного сигнала
Паб. занятие 2.'Дифференциатор
(Лх(желый) $
Цых (Теоретически
это производная от UBX)
а б
Рис. 2N.10. Осциллограммы сигналов на входе и выходе дифференциатора: общий вид {а); детальное изображение (б)
7 АоЕ § 1.4.3.
8 АоЕ § 1.4.4.
9 Здесь мы впервые встречаемся с символом со (омега).
Этот символ обозначает частоту не в циклах в секунду, или
герцах, а в радианах в секунду. Поскольку полный цикл со-
держит 2я радиан, то со = 2л£
10 Когда мы говорим «отсюда вытекает», мы предполагаем,
что вы соглашаетесь с утверждением, что производная или
интеграл синусоидального сигнала является другим сину-
соидальным сигналом, смещенным по фазе на 90° отно-
сительно исходного сигнала. Если это утверждение непо-
нятно для вас, подождите немного. Вскоре мы увидим, как
это происходит, на лабораторном занятии для этой главы.
86
2N. RC-цепи
ДС-дифференциатора11 (здесь постоянная вре-
мени RC равна 100 Ом • 100 пФ = 104 • 1012 =
= 10-Ю-9 = 10нс).
Дифференцирование входного сигнала прямо-
угольной формы весьма впечатляет: сигнал на
выходе мало похож на входной. Входной сигнал
синусоидальной формы вызывает более уме-
ренную реакцию дифференциатора: на выхо-
де получается другой синусоидальный сигнал,
просто со сдвигом по фазе. Обратите внимание,
что в этом случае амплитуда выходного сигнала
меньше, чем входного (рис. 2N.11).
Выходной сигнал выглядит более-менее пра-
вильным: он соответствует крутизне входного
8Х . Лоб. занитие 2. Дифференциатор
V .у. ■-/...■■./;
* Чих (теоретически
это производи» от С/|х)
Рис. 2N.11. Реакция /?С-дифференциатора на синусоидаль-
ный входной сигнал: видно, что выходной синусоидальный
сигнал искажен (обратите также внимание на разные ампли-
туды входного и выходного сигналов: входной сигнал пода-
ется на первый канал вертикального отклонения)
сигнала. Но бросается в глаза также одна стран-
ность: форма синусоиды неидеальна. Но это
вина не дифференциатора, а входного, якобы
синусоидального, сигнала, который выраба-
тывает генератор сигналов. Синусоидальная
форма этого сигнала не совсем настоящая, ее
создают посредством срезания вершин тре-
угольника. Дифференциатор разоблачает эту
подделку: на выходном сигнале можно раз-
личить участки постоянной крутизны там, где
исходный треугольный сигнал переходит че-
рез ноль.
Интегратор12
Схема на рис. 2N.12, а представляет собой
идеальный интегратор, но с входным сигна-
лом в виде тока. Когда входной сигнал по-
дается в виде напряжения, как в схеме на
рис. 2N.12, б, JRC-интегратор становится не-
идеальным. Ограничения #С-интегратора и
ЯС-дифференциатора схожи. Для простоты
представьте, что на вход подается ступенчатый
сигнал; задайте себе вопрос, какой формы вы-
ходной сигнал вы ожидаете увидеть и, следова-
тельно, как бы себя вел ток13.
Интегратор работает только при условии, что
1/вых « 17ВХ или, образно выражаясь, если он
«уничтожает» входной сигнал. Это достигает-
ся тем, что конденсатору не дается достаточ-
ного времени, чтобы зарядиться в интервале
между сменой полярности входного сигнала:
например, когда RC » {полупериода входного
прямоугольного сигнала}.
Предполагается постоянное Uw
Ток Г не постоянный, поскольку ишх меняется
—тг^ должно быть постоянным
at
Но так ли это?
Идеальный интегратор Интегратор ли это?
а б
Рис. 2N.12. Снова интегратор, но тоже неидеальный
11 В данном случае картина отличается от случая медлен-
ной развертки, поскольку здесь показана реакция на по-
ложительный перепад в 4 В (передний фронт прямоуголь-
ного ТТЛ-сигнала). Передний фронт такого сигнала круче,
чем у сигнала, показанного при медленной развертке. Бо-
лее крутой фронт позволяет получить форму ответного
импульса, близкую к идеальной.
12 АоЕ § 1.4.4.
13 Мы бы хотели видеть линейно нарастающий выходной
сигнал: постоянная производная dUmx/dt для постоянно-
го Uw.
2N.3. Анализ RC-цепей в частотной области
87
Лоб. занятие 2; интегратор
1 ;
Um (желтый)! . |
'Щш (теоретически
это ЛЬ
Лаб. занятие 2: интегратор
/тхр
„у это интеграл от С/8Х)
Рис. 2N.13. Реакция ЯС-интегратора на прямоугольный (а) и синусоидальный (6) сигналы. (Обратите внимание на разные ам-
плитуды входного и выходного сигналов: входной сигнал подается на первый канал вертикального отклонения.)
Исследуем интегратор
Как и в случае с дифференциатором, интегра-
тор легче всего протестировать сигналом пря-
моугольной формы, поскольку очень вероятно,
что такой сигнал должен заряжать и разряжать
конденсатор с почти постоянной скоростью,
создавая линейно нарастающий и убываю-
щий выходной сигнал. На рис. 2N.13 показана
реакция ЯС-интегратора на прямоугольный
(рис. 2N.13, а) и синусоидальный (рис. 2N.13, б)
сигналы.
Обратите внимание, что этот интегратор очень
сильно уменьшает амплитуду входного сиг-
нала, что и требуется для ДС-интегратора: на
рис. 2N.13 коэффициент усиления второго ка-
нала вертикального отклонения в десять раз
больше коэффициента усиления первого.
Кстати, чтобы лучше понять суть происходя-
щих процессов, испробуйте такой прием: вы-
полните обратное действие. Убедитесь, что
входной сигнал отображает крутизну выходно-
го; иными словами, что входной сигнал явля-
ется производной выходного, функцией, обрат-
ной интегралу.
2N.3. Анализ /?С-цепей
в частотной области
Теперь мы перейдем к рассмотрению тех же
самых ДС-цепей иным способом, описывая не
отображение сигналов на экране осциллогра-
фа (так называемый анализ во временной об-
ласти), а поведение схемы при изменении ча-
стоты. Этот тип анализа называется анализом
в частотной области (или спектральным анали-
зом). Не пугайтесь этого определения: это все-
го лишь способ обозначения содержимого оси
абсцисс (подобно области определения мате-
матической функции, которая, если вспомните,
определяет ее исходные данные).
2N.3.1. Импеданс, или реактивное
сопротивление конденсатора
Значение импеданса конденсатора зависит от
частоты входного сигнала. Импеданс — это
общее название свойства, аналогичного сопро-
тивлению для резисторов, а термин «реактив-
ное сопротивление» применяется для обозна-
чения сопротивления конденсаторов и катушек
индуктивности. Индуктор14 обычно представ-
ляет собой катушку из изолированного прово-
да, часто намотанную на железном сердечнике.
Очевидно, что конденсатор не может проводить
постоянный ток: просто вспомните его внутрен-
нее устройство — две пластины из токопроводя-
щего материала, разделенные изолятором. Это
устройство и определяет импеданс конденсато-
ра постоянному току: ясно, что он бесконечный
(или по крайней мере очень большой).
Но подача на конденсатор изменяющегося во
времени напряжения вызывает протекание
тока через него. Этот факт, мы надеемся, четко
установлен при рассмотрении дифференциато-
ров в разделе 2N.2.1.
14 Здесь сохранен авторский термин «индуктор», в отече-
ственной литературе по схемотехнике он мало распростра-
нен и заменяется в зависимости от контекста терминами
«индуктивность», «дроссель» или «катушка индуктивно-
сти». — Примеч. ред.
88
2N. RC-цепи
Но при рассмотрении фильтров нас интересует
другой, хотя и взаимосвязанный, вопрос: мы
бы хотели понять, почему быстро меняющееся
переменное напряжение может проходить че-
рез конденсатор. Данный эффект имеет место,
и нам нужно уяснить этот процесс, чтобы мы
поняли работу высокочастотного фильтра. Но
если вы уже знаете ответ, можете пропустить
этот раздел.
Когда мы говорим, что сигнал переменного тока
проходит через фильтр, мы имеем в виду лишь
то обстоятельство, что колебание амплитуды
напряжения слева вызывает соответствующее
изменение амплитуды справа (рис. 2N.14).
сигнал на входе...
... « сигнал на выходе
Через резистор протекает
небольшой ток, но недостаточно
долго, чтобы напряжение Uc
значительно изменилось
Рис. 2N.14. Переменный ток проходит через конденсатор
Переменный сигнал проходит через конден-
сатор при условии, что напряжение на нем не
успевает значительно измениться до оконча-
ния колебания, т. е. прежде чем напряжение из-
менит направление. Иными словами, быстрые
колебания проходят, а медленные — нет.
Обратите внимание, что мы только что описали
прохождение сигнала в виде напряжения через
фильтр. Это не одно и то же, что протекание
тока через конденсатор — процесс, который не
может быть непрерывным. Ток может прохо-
дить только при условии изменения разности
потенциалов на пластинах конденсатора, на-
пример, при непрерывном входном синусои-
дальном сигнале.
Но если вы предпочитаете точные математиче-
ские формулировки вместо интуитивных вы-
сказываний15, то импеданс конденсатора мож-
но выразить следующей формулой:
Zc= -7
= -j/2nfC.
Сразу видно, что импеданс конденсатора обрат-
но пропорционален частоте подаваемого сиг-
нала и его емкости С. Но что означает символ
«/»? Это всего лишь принятое в электронике
условное обозначение математического симво-
ла мнимой единицы «/» или V-T16. Такой ответ
может вызвать недоумение из-за того, что для
большинства людей в здравом уме выражение
V-1 выглядит очень странно. Можно еще до-
бавить, что символ «/» предоставляет матема-
тически удобный способ описывать фазовые
сдвиги. Но мы не будем использовать этот под-
ход в нашем курсе, а обычно обойдемся без него
и даже без самого фазового сдвига (как далее в
этом разделе).
Формула для импеданса конденсатора (которая
показывает, что импеданс плавно изменяется
соответственно частоте) позволяет уяснить,
как конденсаторы будут вести себя в делителях
напряжения.
Несколько слов о вычислении Zc
Если предыдущий материал вам понятен, то
можете пропустить этот раздел. Он предназна-
чен для тех, кому недостаточно формулы, для
которой не был приведен ее вывод.
Почему, собственно говоря, формула Zc =
= -j/(oC = -j/2nfC справедлива? Мы ответим
на этот вопрос, используя приблизительные
вычисления (в стиле нашего курса).
Суть выражений «импеданс конденсатора» и
«импеданс резистора» одинакова: это частное
от деления U/L Заменив U и I их несколько не-
обычными выражениями для конденсатора, мы
должны получить упомянутую формулу для Zc.
Поскольку нас интересует реакция конденсато-
ра на изменяющиеся во времени сигналы и си-
нусоидальный сигнал является самым простым
их представителем17, мы будем считать напря-
жение на конденсаторе Uc не постоянным, а си-
нусоидальным:
Uc = Asin(cof).
Поскольку ток, протекающий через конден-
сатор, представляет собой производную по
15 В разделе 2S.2 мы снова попытаемся помочь вам понять
на интуитивном уровне это математическое выражение.
16 Инженеры-электротехники не используют букву «/», по-
скольку она выглядит, как буква для обозначения тока J.
17 Как вы, вероятно, помните, теорема Фурье гласит, что
сигнал любой формы, не только синусоидальный, напри-
мер, прямоугольный или треугольный, можно получить,
сложив синусоидальные сигналы. Отсюда вытекает, что
для понимания поведения схемы в общем случае нам доста-
точно рассмотреть ее реакцию на синусоидальный сигнал.
2N3. Анализ RC-цепей в частотной области
89
времени напряжения на конденсаторе (см. раз-
дел 2N.1), то выражение для тока через конден-
сатор, на который подается напряжение Uc бу-
дет следующим:
1С= С
2
= САсо cos(Grf)>
и импеданс конденсатора Zc будет частным от
деления U/I:
U uc Asin(w/)
с j ic A(ocos(<ot)C
Чтобы воспользоваться этой формулой для
расчета, нам придется иметь дело с тем непри-
ятным обстоятельством, что синус и косинус
сдвинуты по фазе. Этот факт удобно (но зага-
дочно для тех, кто еще не привык к комплекс-
ным величинам) отображается символом «-/►>,
который входит в классическую формулу импе-
данса конденсатора Zc. Но на данном этапе мы
предпочитаем не иметь дела с этим неудобным
обстоятельством и игнорировать как -j, так и
фазовый сдвиг.
Игнорирование фазового сдвига18
Если мы не учитываем фазовый сдвиг, то мо-
жем упростить дробь:
Asin(atf)
A(dcos(cq£)C
В частности, мы можем рассматривать только
максимальные значение функций синуса и ко-
синуса (т. е. 1), а затем сократить амплитуду (А)
вместе со значениями синуса и косинуса, кото-
рые мы принимаем равными единице, чтобы
получить следующую очень простую формулу:
Вертикальные черточки «|» означают здесь
«амплитуда, без учета фазы»19. Таким образом,
реактивное сопротивление описывает только
амплитуды напряжения и тока. Хотя это, оче-
видно, не точное выражение, поскольку в нем
игнорируется фазовый сдвиг, но оно достаточно
хорошо описывает поведение импеданса кон-
денсатора, и его также нетрудно воспринимать.
Из этой формулы следуют два важных фак-
та, которые мы уже заметили, когда впервые
встретились с импедансом Zc:
1. Импеданс конденсатора обратно пропорцио-
нален емкости С.
2. Импеданс конденсатора обратно пропорцио-
нален частоте входного сигнала.
Второе обстоятельство, конечно же, чрезвы-
чайно интересно: у нас есть устройство, ко-
торое позволит создать новый тип делителя
напряжения, более сложный, чем делитель
на резисторах. Такие делители могут быть
частотно-зависимыми, что звучит очень ин-
тересно.
Далее в курсе мы еще возвратимся к теме фазо-
вого сдвига, но пока обойдемся без него.
2N.3.2. /?С-фильтры
Создание НС-фильтров — наиболее важная об-
ласть применения конденсаторов. Эти схемы
представляют собой просто делители напря-
жения, наподобие делителей на резисторах, с
которыми мы уже познакомились. Делители на
резисторах реагируют на сигналы постоянного
и переменного тока одинаково. Возможно, это
для вас очевидный факт и упражнение в конце
лабораторного занятия 1L, в котором вам нуж-
но было подтвердить, что для делителя на рези-
сторах нет никакой разницы между сигналами
постоянного и переменного тока, казалось из-
лишним. Делители на резисторах обрабатыва-
ют постоянное и переменное напряжения оди-
наковым образом потому, что резисторы не мо-
гут «помнить», что было с напряжением даже
мгновение назад. Они «живут» только насущ-
ным моментом (имеются в виду, конечно же,
££-цепочки
похожи
* на фильтры
для ко<ре
Низкочастотный
Высокочастотный
18 АоЕ § 1.7.1А.
19 В математике это «модуль комплексного числа». - При-
меч. ред.
Рис. 2N.15. Самым важным применением ЯС-цепей явля-
ются фильтры, функционирующие наподобие фильтров для
кофе
90
2Л/. RC-цепи
идеальные резисторы). На рис. 2N.15 в шутку
изображена аналогия между ДС-цепочками и
фильтрами для кофе.
Редкий, но простой случай:
емкостной делитель
Мы уже знаем, как делитель напряжения обра-
батывает синусоидальный сигнал. А теперь по-
думайте, как делитель на конденсаторах будет
обрабатывать сигнал, изменяющийся во вре-
мени? В действительности, чисто емкостной
делитель трудно реализовать на практике, по-
скольку он обычно содержит значительные па-
разитные сопротивления, которые усложняют
его работу. Но рассмотрение такого делителя
(рис. 2N.16) полезно в качестве исходной точки
в изучении фазовых сдвигов.
Входной синусоидальный
сигнал
Входной
синусоидальный
сигнал
(Л.
Рис. 2N.16. Два делителя, выдающие 1/2 входного напряже-
ния 1/вх без фазового сдвига
Вы, наверное, уже немного испугались при
мысли о фазовых сдвигах. Но в данном случае
никаких проблем не возникнет: выходной сиг-
нал совпадает по фазе со входным.
Замечание
Если вас не пугают операции с комплексными ве-
личинами, напишите Zc = -;/шС, и вы увидите, что
все множители -] сократятся.
Но что будет в комбинированном случае, когда
делитель содержит как резистор, так и конден-
сатор? Это именно та ситуация, которая обычно
нас интересует. Данная задача окажется потруд-
нее, но все равно по сути не выходит за рамки
делителей напряжения. Давайте немного обоб-
щим эту схему, как показано на рис. 2N.17.
Качественное представление частотной
характеристики фильтра
Поведение делителей напряжения, которые мы
называем фильтрами, когда рассматриваем их
с точки зрения частоты, поскольку отдельные
устройства пропускают или высокие, или низ-
кие частоты, легко поддается анализу, по край-
ней мере, приближенному:
1. Смотрим, какой эффект фильтр оказывает на
частоты в противоположных концах диапазо-
на. Исследование пределов диапазона явля-
ется полезным приемом, который мы вскоре
снова используем для определения значений
ZBX и ZBbIX фильтров для наихудших случаев.
2. В одном конце диапазона одна схема филь-
тра почти не пропускает входной сигнал, а
другая пропускает весь сигнал, и наоборот.
3. Теперь выясните два вопроса:
• Какие частоты не пропускаются при нуле-
вой частоте?
• Какие частоты не пропускаются при очень
высокой частоте?
Как показано на рис. 2N.18, каждый из изо-
браженных фильтров на одном конце частот-
ного диапазона пропускает весь входной сиг-
нал, но не пропускает сигнал с частотой дру-
гого конца диапазона. Причем проходящие и
не проходяйще сигналы для обоих фильтров
имеют частоты, расположенные на противо-
положных концах частотного диапазона.
Обобщенный делитель напряжения
Рис. 2N.17. Обобщенный делитель напряжения (слева) и делители напряжения с R и С (справа)
2N.3. Анализ RC-цепей в частотной области
91
Высокочастотный конец диапазона: результаты для двух схем противоположны
Хс очень велико
Хс очень мало
Низкочастотный конец диапазона:
опять противоположные результаты для двух схем
Рис. 2N.18. Устанавливаем предельные точки частотной характеристики для каждого фильтра, испытывая каждый из них на
низкой, а затем на высокой частоте
Низкочастотный фильтр
Высокочастотный фильтр
Рис. 2N.19. Графики частотных характеристик ЯС-фильтров
И наконец, определите точку, в которой харак-
теристика пересекает критическое значение (ее
расположение может определяться произволь-
но20), как частоту входного сигнала, при кото-
рой выходной сигнал на 3 дБ меньше, чем вход-
ной. Эта точка всегда называется просто «точка
Лдб*21 (МИНУС подразумевается).
Определив граничные частоты, по которым
можно судить, является данный фильтр низ-
кочастотным или высокочастотным, и зная
точку/3дБ, можно начертить кривую частот-
ной характеристики для каждого фильтра
(рис. 2N.19).
ТочкаУздБ, т. е. частота среза фильтра, определя-
ется следующей формулой:
Л
ЛдБ =
Остерегайтесь более элегантной формулы, в
которой частота обозначена через ю:
3дБ 2nRC
20 На самом деле не совсем произвольно: ослабление мощ-
ности выходного сигнала на 3 дБ соответствует половине
мощности исходного сигнала.
21 Употребляется также термин «частота среза». — При-
меч. ред.
RC
Хотя эта формула с виду проще, ее результаты
будут отличаться от действительных в шесть
раз, поскольку на наших лабораторных заняти-
ях мы будем измерять период и обратную ему
величину, т. е. частоту, в герцах, а не в радианах.
Поэтому избегайте обозначения © при вычис-
лении частоты.
Внимание!
Не путайте графики в частотной области с рас-
смотренными ранее графиками переходных ха-
рактеристик ЯС-схем, которые отображаются во
временнбй области. На рис. 2N.20 приводятся при-
меры графиков обоих типов.
Не только сами графики выглядят похожими
друг на друга, но даже подробности кажутся
специально придуманными, чтобы ввести бед-
ного студента в заблуждение.
92
2N. RC-цепи
ис
Рис. 2N.20. Обманчивая схожесть графиков временной (слева) и частотной (справа) характеристик RC-схем
Временная область. За время RC (постоянная
времени) напряжение Uc повышается до при-
близительно 0,6 подаваемого напряжения (это
будет (1-1/е))
Частотная область. При частоте /3дЪ, которая
определятся ДС-схемой, отношение UBUX/UBX
фильтра составляет около 0,7 (это будет 1/V2).
Остерегайтесь этой ловушки. Не путайте эти
два полностью разных графика.
Замечание касательно логарифмических графиков
Возможно, у вас возник вопрос, почему графики на
рис. 2N.19, графики в разделе по фильтрам (раздел
1.7.8) книги АоЕ22, а также графики частотного сиг-
нала на экране осциллографа отличаются от более
плавных графиков, приводимых в большинстве
книг, рассматривающих частотные характеристи-
ки, например в главе 6 книги АоЕ. Наши графики
для НЧ-фильтров приближаются к нулю постепен-
но, а кривые в других книгах сразу плавно падают
к нулю. Это эффект логарифмического сжатия осей
на традиционных графиках. Наши графики линей-
ные, а другие упомянутые графики выполнены
в логарифмическом масштабе. См. примеры на
рис.21Ч.21.
В следующем разделе, после краткого знаком-
ства с децибелами, мы проиллюстрируем раз-
ницу между графиками в линейном и логариф-
мическом масштабах.
2N3.3. Децибелы
Децибел2324 выражает отношение значений
двух величин. Поскольку это отношение выра-
жается его десятичным логарифмом, оно может
описывать очень большой диапазон значений.
Поскольку децибел выражает отношение, он
должен всегда соотноситься с каким-либо на-
чальным уровнем отсчета. Кроме электроники,
децибел используется для выражения уровня
или громкости звука относительно уровня, со-
ответствующего самому тихому слышимому
22 АоЕ § 1.7.8.
23 АоЕ § 1.3.2А.
24 Децибел — это одна десятая бела. Эта единица была
введена Лабораторией Белла для измерения затухания
сигнала в телефонных кабелях и названа в честь изобре-
тателя телефона Александра Грэхема Белла. Но, подобно
другой единице, фараде, бел оказался слишком велик для
практического применения и вместо него используется его
десятая часть — децибел. Если желаете, дополнительную
информацию по децибелу можно найти в разделе 2.18
книги «The Art of Digital Audio» («Искусство цифрового
аудио»), автор Джон Уоткинсон (John Watkinson), 3-е из-
дание, 2001 г.
ш
2
Частота
Частота (логарифмический масштаб)
Рис. 2N.21. Сравнение графиков частотной характеристики в линейном (слева) и логарифмическом масштабе
2N.3. Анализ RC-цепей в частотной области
93
звуку. Децибел очень хорошо подходит для из-
мерения уровней звука, поскольку звук, вос-
принимаемый человеческим ухом, занимает
очень большой диапазон: самый громкий звук
может быть в три миллиона раз громче самого
тихого (в терминах уровней звукового давле-
ния). Эту огромную величину трудно выразить
напрямую, но в децибелах она имеет разумный
и наглядный вид: 130 дБ. А уровень самого ти-
хого звука, выбранный в качестве точки отсче-
та, будет соответствовать 0 дБ.
В электронике децибел тоже описывает отно-
шение, но это отношение может быть между
уровнями других величин: мощности, напря-
жения или амплитуды. Поскольку мощность
пропорциональна квадрату напряжения, опре-
деления децибела для мощности и амплитуды
отличаются друг от друга:
дБ =
(2N.2)
где Р — мощность, а А — амплитуда. Для нас
интерес представляет определение децибела
для амплитуды.
Иногда к обозначению «дБ» добавляется сим-
вол, указывающий опорную величину, с кото-
рой выполняется сравнение. Например, обо-
значение «дБм» (децибел на милливатт) озна-
чает, что опорным значением служит 1 милли-
ватт (с некоторым предполагаемым нагрузоч-
ным импедансом). Но в курсе схемотехники
мы в основном будем с помощью децибелов
описывать затухание, вносимое фильтром. При
этом нам придется постоянно сталкиваться
с некоторыми числовыми значениями, краткое
описание которых приведено далее.
Некоторые часто встречающиеся
значения величин в децибелах
♦ -3 дБ — отношение амплитуд, равное
1/V2. Это отношение встречается постоян-
но, особенно часто в формуле частоты, где
фильтр вносит такое затухание в сигнал,
что можно сказать, что кривая имеет пере-
гиб (хотя этот перегиб иногда настолько за-
кругленный, что его трудно так назвать, как
можно видеть, например, на рис. 2N.27).
♦ -6 дБ - отношение амплитуд, равное
1/2. Это отношение встречается в описании
крутизны затухания сигнала в ДС-фильтрах.
Выражение «-6 дБ на октаву» описывает
спад частотной характеристики низкоча-
стотного фильтра, что обычными словами
означает уменьшение амплитуды наполови-
ну при каждом удвоении частоты.
♦ +3 дБ и +6 дБ, конечно же, описывают уси-
ление, а не ослабление, т. е. умножение ам-
плитуды на V2 и 2 соответственно.
♦ 20 дБ — отношение амплитуд, равное 10.
Это отношение встречается, как одно из воз-
можных описаний крутизны кривой частот-
ной характеристики RC-фильтров. Например,
крутизна низкочастотного фильтра падает в
темпе«-20дБнадекаду»,чтоозначатослабле-
ние амплитуды в 10 раз при каждом 10-крат-
ном умножении частоты.
Нарастание и спад на линейных
и логарифмических графиках
Линейные графики
Наблюдая на осциллографе ослабление сигна-
ла фильтром, мы видим и, возможно, подраз-
умеваем линейную зависимость амплитуды от
частоты.
Замечание
Некоторые генераторы сигналов можно настроить
на создание логарифмического сигнала развертки,
который будет сжимать горизонтальную ось. Такой
полулогарифмический график выглядит иначе, чем
обычные графики в учебниках или справочниках,
которые используют логарифмический масштаб
по обеим осям. Но мы обычно не применяем такие
генераторы.
Можно видеть, что график характеристики низ-
кочастотного фильтра падает довольно плавно
и описывается выражением 1/f. На графике
с обеими осями в логарифмическом масшта-
бе (стандартная форма графиков в литературе
по электронике) этот плавный спад выглядит
в виде прямой линии, как показано слева на
рис. 2N.24.
Чтобы освежить вашу память, на рис. 2N.22
приводится пример нарастания и спада графи-
ка со скоростью ±6 дБ/октаву. Оси этих графи-
ков обозначены «UBUX/UBX» и «Частота», как
для фильтра.
Как упоминалось ранее, крутизна графика мо-
жет также составлять ±20 дБ/декаду. Этот слу-
чай не показан на рис. 2N.22, так как диапазон
94
2N. RC-цепи
для отображения декадного (десятикратного)
изменения частоты здесь недостаточен.
^ Нарастание пропорционально частоте f
-о
i
Темп
\
\
\
HQpQC
>
ч
тания
6дБ/
Спад
октав
проп<
У
эрцис
налы-
Част
ol/f
ота
Темп спада -6 дБ/октаву
Частота
Рис. 2N.22. Графики линейного нарастания и спада ампли-
туды со скоростью ±6 дБ/октаву
+6 дБ/октаву
+20 дБ/декаду
ОД
+12 дБ/октаву
+40 дБ/декаду
0,01
0,001
1000 10000
Рис. 2N.23. График нарастания сигнала высокочастотного
/?С-фильтра в логарифмическом масштабе по обеим осям
Графики с логарифмическим масштабом
по обеим осям
Графики с логарифмическим масштабом по
обеим осям, наподобие традиционных гра-
фиков Боде, придают более «решительный»
вид «вялым» частотным характеристикам RC-
фильтра. В частности, плавный спад графика
низкочастотного фильтра, обратно пропорцио-
нальный частоте 1/f, преобразуется в прямую
линию, решительно и быстро стремящуюся к
нулю. Нарастание на таком логарифмическом
графике также выглядит более отчетливо. На
рис. 2N.23 показаны примеры нарастания со
скоростью 6 дБ/октаву и 12 дБ/октаву. Это не
результаты измерений для каких-либо кон-
кретных фильтров, а просто пример для демон-
страции вида характеристик в логарифмиче-
ском масштабе.
На рис. 2N.24 приведены примеры графиков
частотной характеристики RC-фильтра, по-
строенные в различном масштабе. Видно что,
кривая соответствующая 1/f, превращается в
ровную прямую, направленную вниз.
Характеристики будут выглядеть еще нагляд-
нее, если задать масштаб ±20 дБ/декаду и
±40 дБ/декаду, а не на октаву.
2N.3A Определение вносимого
затухания фильтра
По форме графика частотной характеристики
фильтра на рис. 2N.19 можно примерно опре-
делить уровень затухания, которое фильтр бу-
дет вносить в сигнал в определенном диапазоне
частот, при данной частоте/3дБ. Далее приведем
несколько полезных практических правил.
Участок спада графика
низкочастотного фильтра...
^вых
^вх
1,0
од
0,01
0,001
-6 дБ/октаву\^
^-20 дБ/декаду
-6 дБ/октаву
-20 дБ/декаду
..на этом графике
выглядит так
-12 дБ/октаву
-40 дБ/декаду
c 0,lfc fc 10fc 100fc
0,001
10
100
1000 10 000
Рис. 2N.24. Логарифмический график спада характеристики низкочастотного flC-фильтра. Рисунок слева взят из книги АоЕ
(рис. 1.104).
2N.3. Анализ RC-цепей в частотной области
95
■"У *■ " !
;. - * % *
I
#
•
•
[^ Затухание 10% ;
/ 4S<;
t
Затухание 10%
Полоса пропускания: ВЧ-срильтр
Полоса пропускания: НЧ-фильтр
Рис. 2N.25. Полосы пропускания для ВЧ- и НЧ-фильтров. Затухание составляет 10% в пределах одной октавы от частоты г*3дБ.
Это линейные, а не логарифмические графики (как на предыдущем рисунке)
Затухание в пределах полосы
пропускания
Затухание будет меньше 10%, если интервал
(полоса пропускания) между частотой сигнала
и частотойУздБ составляет одну октаву (коэффи-
циент 2 для частоты). Например, если для НЧ-
фильтра мы хотим пропускать сигналы ниже
1 кГц, нужно задать частоту ^ равную 2 кГц.
Соответственно для ВЧ-фильтра, если мы хо-
тим пропускать сигналы выше 10 кГц, нужно
задать частоту/3дБ равную 5 кГц.
На рис. 2N.25 показаны полосы пропускания
и частоты/3дБ для высокочастотного (слева) и
низкочастотного фильтров (справа).
Подробности для любознательных
Нам почти не потребуется никаких дополни-
тельных сведений о затухании в полосе пропу-
скания, чем только рассмотренное обстоятель-
ство, что мы теряем 10% сигнала на расстоянии
октавы от частоты/3дБ. В частности, теряется
около 10% сигнала на частоте 0,5^дБ для низко-
частотных фильтров, и на частоте 2^дБ для вы-
сокочастотных. Но для особо любознательных
на рис. 2N.26 затухание в полосе пропускания
показано более подробно25.
Затухание в полосе заграждения
При значительном затухании в фильтре ам-
плитуда сигнала возрастает или убывает про-
25 Это слегка измененный рис. 4.8 из книги «ABC of Probes»
(«Основы пробников») (стр. 35) компании Tektronix
(2011).
ОД
0,2
0,3 0,4 0,5 0,6 0,8 1
—
\
ч
\
\
S
V
s
\
100%
95%
90%
85%
80%
75%
-ЗдБ
Частота, как доля от
ЗдБ
Рис. 2N.26. Подробный вид частотной характеристики в
пределах полосы пропускания ЯС-фильтра
порционально его частоте. На достаточно
большом расстоянии от частоты /3лЕ эта зако-
номерность выдерживается точно, на близком
расстоянии к частоте f3RE — приблизительно
(рис. 2N.27).
Например, если для НЧ-фильтра частота
/3дБ = 2 кГц, то помеха на частоте 20 кГц (10 -/3пЪ)
ослабится до примерно 1/10 уровня, который
был бы на частоте /3дБ. Поэтому теоретически
ослабление окажется приблизительно равным
1/10 • 0,7, поскольку (по определению) на ча-
стоте^ амплитуда сигнала составляет около
0,7 от максимума. В действительности ослаб-
ление будет несколько меньшим, поскольку
в первой октаве (или близко к ней) после ча-
стоты Уздб характеристика отличается от 1/f.
На рис. 2N.27 заметно отклонение характери-
стики ВЧ-фильтра от идеально прямой линии
(т. е. от строгой пропорциональности частоте)
при частотах, превышающих/^. А при частотах
96
2N. RC-цепи
* Амплитуда возрастает I
пропорционально
частоте f
1
•
'■ f
у
ЗдБ
Амплитуда убывает
пропорционально 1/f
/ Г: -
j
400 мс
ВЧ-аэильтр: от 0 до fm сигнал возрастает
пропорционально частоте
40,0 мс
НЧ-срильтр: сигнал убывает пропорционально
частоте (амплитуда пропорциональна 1/f)
Рис. 2N.27. Иллюстрация ослабления сигнала для ВЧ- и НЧ-фильтров
намного меньших частоты /3яБ характеристика
незначительно отклоняется от прямой линии.
Труднее судить, насколько характеристика НЧ-
фильтра отклоняется от функции 1/f, но при
внимательном рассмотрении можно заметить,
что при частоте 2 -/3дЪ амплитуда оказывается
намного выше 35%, чем следовало бы ожидать,
если бы даже в первой октаве после частоты^дБ
характеристика фильтра соответствовала бы
обратно пропорциональной функции 1/f.
Для нас важно понять преимущества, а не не-
достатки приближенных методов оценок ха-
рактеристик фильтров. А главное здесь в том,
что описанные методы позволяют нам быстро
получить довольно хорошую оценку влияния
фильтра на помеховый сигнал на определенном
расстоянии от частоты f3
возможность.
ЗдБ*
Это очень ценная
2N3.5. Входной и выходной
импеданс /?С-цепи
Чтобы выходной сигнал фильтра А подать на
фильтр Б (или на любую другую схему), он дол-
жен соответствовать требованиям нашего эмпи-
рического правила 1:10, которое мы обсуждали
ранее, когда рассматривали чисто резистивные
цепи (см. раздел 1N.4.6)26. Для UC-цепей приго-
ден аналогичный подход, но с одним отличием:
не только сигналы будут ослабляться, но также
и будет изменена амплитудно-частотная харак-
теристика фильтра.
Но чтобы получить эмпирическое правило,
нам нужно знать ZBbIX и ZBX этих фильтров.
На первый взгляд эта задача выглядит труд-
ной. Например, что такое выходной импеданс
ZBbIX НЧ-фильтра? Начинающий специалист-
схемотехник даст вам правильный ответ, но он
будет слишком сложным. Например, он может
предложить следующую формулу:
R -)
26 АоЕ § 1.7.1.
Ну и гадость, скажете вы! К тому же эта фор-
мула в действительности не дает нам прямого
ответа, а лишь говорит, что ответ зависит от
частоты.
Импедансы наихудшего случая
Но мы рекомендуем отказаться от всяких слож-
ностей, рассматривая только значения импе-
дансов для наихудших случаев. Зададим себе
вопрос: «Насколько плохими могут быть эти
импедансы?». Этот вопрос распадается на два:
1. Насколько плохим может быть входной им-
педанс ZBX? А это означает: «Насколько низ-
ким может он быть?».
2. Насколько плохим может быть выходной
импеданс ZBHX? А это означает: «Насколько
высоким может он быть?».
2N.3. Анализ RC-цепей в частотной области
97
k-A/VW—
—VW-1—
х=*
Рис. 2N.28. В наихудших случаях импедансы2 и Z /?С-фильтров сводятся просто к R
Рассуждая так, мы получаем поразительно про-
стой ответ: это всегда просто 1?! Рассмотрим для
примера случай с НЧ-фильтром (рис. 2N.28).
Наихудший ZBX.K0HflEHCAT0P выглядит, как корот-
кое замыкание: ZBX = R (это происходит на са-
мых высоких частотах).
Наихудший ZBHX.K0HflEHCAT0P отсутствует; смо-
трим «сквозь схему» к источнику и видим толь-
ко R: ZBHX = 1? (это происходит на самых низких
частотах).
Описанный метод оценки входного и выходно-
го импедансов фильтра позволяет нам последо-
вательно соединять ЯС-цепочки точно так же,
как и обычные делители напряжения, не бес-
покоясь об их влиянии друг на друга.
2N.3.6. Фазовый сдвиг
Наверное, вы уже догадываетесь, о чем дальше
пойдет речь27. Когда мы рассматривали диффе-
ренциатор и интегратор, то уже встретились с
явлением сдвига фазы на 90° при резком уве-
личении затухания синусоидального сигнала в
этих схемах. Но не следует думать, что любая
схема с конденсатором даст фазовый сдвиг,
равный 90° (или наоборот, нулевой). Так бы-
вает далеко не всегда, и тут важно не впасть в
заблуждение. Гораздо полезнее представлять
происходящие процессы на интуитивном уров-
не, т. е. понимать, когда нужно ожидать сдвига
фазы, а также, как оценить его величину. Хотя
численная величина фазового сдвига требует-
ся только в редких случаях. В процессе работы
с фильтрами в нашем курсе явление фазового
сдвига мы учитывать не будем.
Как обычно игнорировать фазовый сдвиг
в /?С-фильтрах
Прежде чем приступать к рассмотрению по-
дробностей, попробуем разобраться, в каких
случаях можно не учитывать фазовый сдвиг.
Для начала в общих чертах рассмотрим процесс
фазового сдвига в ЯС-цепях.
Фазовый сдвиг будет очень незначительным
или вообще отсутствовать, если амплитуды
входного и выходного сигналов близки. Но при
сильном ослаблении в выходном сигнале будет
присутствовать значительный фазовый сдвиг
(максимум 90°). Это иллюстрируют графики
для НЧ-фильтра, приведенные на рис. 2N.2928.
-45° V
-90°-
«6°
Р707
и*.
0,01 -
0,001
o,oif
Рис. 2N.29. Ослабление сигнала и соответствующий фазо-
вый сдвиг (график в логарифмическом масштабе)
27 АоЕ § 1.7.1.
28 АоЕ § 1.7.9.
98
2N. RC-цепи
Очевидно, что в пропускаемый фильтром сиг-
нал не вносится большого фазового сдвига. Но
выходной сигнал все же сдвинут по фазе от-
носительно входного, и полезно знать, в какой
мере. Если предположить, что точку/3дБ можно
расположить на частоте, вдвое больше наивыс-
шей, которую мы хотим пропускать (назовем
ее максимальной частотой сигнала), то сигнал
будет немного ослаблен (около 10%) и его фа-
зовый сдвиг не превысит 25°. Как ослабление
сигнала, так и его фазовый сдвиг будут меньше
на низких частотах.
Но вы можете возразить, что на протяжении
большей части диапазона входных частот фа-
зовый сдвиг намного больше, что явно видно
на рис. 2N.29. Действительно, фазовый сдвиг
ощутим на многих частотах: начиная с -45° на
частоте^дБ, он увеличивается по мере повыше-
ния частоты, приближаясь к -90°. Почему эти
сдвиги не должны нас волновать?
Потому что они вносятся в ту часть сигнала,
которую мы не считаем полезной, а рассма-
триваем как помеху, и нас не особо интересует,
какие нехорошие вещи происходят с помехой.
Мы считаем важным лишь ослабление помех,
нам важна величина этого ослабления, и мы
в некоторой степени заинтересованы в этом.
Но только потому, что мы хотим избавиться от
нее. Нас не волнуют подробности искажения
помехового сигнала, в том числе и его сдвиг
по фазе.
Причина фазового сдвига
Почему происходит фазовый сдвиг? Попробуем
дать рациональное объяснение этому явлению:
♦ как вы уже знаете, в последовательных RC-
цепях напряжения на сопротивлении R и ем-
кости С сдвинуты по фазе на 90°;
♦ в любой данный момент сумма напряжений
на сопротивлении R и емкости С должна
быть равна входному напряжению U^
♦ выходное напряжение фильтра 1/вых пред-
ставляет собой напряжение или только на
резисторе R (для ВЧ-фильтра), или на кон-
денсаторе С (для НЧ-фильтра);
♦ при изменении частоты соответствующая
доля общего напряжения 1/вх на резисторе
R и конденсаторе С меняется, и поэтому вы-
ходное напряжение [7ВЫХ может в той или
иной мере отличаться от входного. Иными
словами, фазовый сдвиг между входным на-
пряжением UBX и выходным напряжением
^вых меняется в зависимости от частоты.
Рассмотрим для примера НЧ-фильтр. Если
большая часть входного напряжения UBX на
выходе передается на конденсатор, то фаза вы-
ходного напряжения Uc будет близка к фазе
входного напряжения (которое образуется на
последовательной ДС-цепи). Иными словами,
сопротивление R играет незначительную роль,
а выходное напряжение ивых приблизительно
совпадает с входным напряжением UBX как по
амплитуде, так и по фазе. Но разве мы просто
не повторили наше более раннее утверждение?
Похоже, что почти да.
Теперь давайте представим это наглядно.
На рис. 2N.30 иллюстрируется ожидаемая си-
туация: небольшой фазовый сдвиг на частоте,
пропускаемой фильтром, и большой сдвиг в
На высоких частотах
значительно выше частоты
На низких частотах
значительно ниже частоты
ЗдБ
He пропускает Пропускает
Рис. 2N.30. Входное напряжение распределяется между резистором и конденсатором по-разному на разных частотах
2N.3. Анализ RC-цепей в частотной области
99
пределах полосы заграждения. В следующем
разделе мы рассмотрим еще один прием, об-
легчающий интуитивное понимание фазового
сдвига: векторные диаграммы.
2N.3.7. Векторные диаграммы
Эти диаграммы позволяют нам сравнивать
фазу и амплитуду на входе и выходе схем, сдви-
гающих фазы (схемы, включающие емкость С
и индуктивность L)29. Они делают расчет на-
глядным и позволяют нам получить приблизи-
тельные результаты, используя геометрические
методы, а не манипулируя комплексными вели-
чинами.
На горизонтальной оси такой диаграммы от-
ложены импедансы, подобные резисторам —
действительные (реальные, Re), и импедансы,
подобные конденсаторам или катушкам индук-
тивности — мнимые (воображаемые, Im). Пусть
второе название вас не смущает; оно означает
всего лишь, что напряжения на таких элементах
сдвинуты по фазе на 90° относительно напря-
жений на резисторах. Такие диаграммы также
называют чрезвычайно страшным термином —
векторы на комплексной плоскости (что для не-
привычного уха может звучать как что-то типа
«плоскости, слишком сложные для понимания»).
Но не стоит впадать в отчаяние, поскольку все
это легко понять и использовать. Впрочем, если
вы не хотите, то можно вообще обойтись без
изучения данного предмета. В нашем курсе мы
будем очень редко использовать векторы, вме-
сто этого всегда непосредственно манипулируя
комплексными величинами. Векторы на самом
деле очень удобная штука, но если вам кажется,
то это не так, забудьте о них.
29 АоЕ § 1.7.12.
Векторная диаграмма ЯС-схемы
На рис. 2N.31 изображена векторная диаграмма
ЯС-фильтра в точкеУздБ, где, как можно видеть,
величина импеданса конденсатора такая же, как
и резистора. Стрелки, или векторы, отобража-
ют фазу и амплитуду (обратите внимание, что
это амплитуда сигнала: пиковое значение, а не
варьирующееся во времени напряжение); они
направлены под углом 90° друг к другу, указы-
вая на то, что напряжения на резисторе и кон-
денсаторе сдвинуты по фазе на 90° друг относи-
тельно друга.
Фаза. Будем считать, что в течение периода
подачи входного сигнала векторы вращаются
против часовой стрелки. Таким образом, рас-
сматривая входное напряжение как направ-
ленное по гипотенузе, можно видеть, что на-
пряжение на резисторе опережает напряжение
на входе (что верно для схемы этого типа: ВЧ-
фильтр, выходной сигнал которого снимается
с резистора). Мы также можем видеть, что на-
пряжение на конденсаторе отстает от входного
напряжения (что верно для схемы этого типа:
низкочастотный фильтр, выдающий выходной
сигнал на конденсаторе).
«Напряжения?» — можете протестовать вы.
«Но разве не было сказано, что эти стрелки
представляют импедансы?». Все верно. Но в
схеме из двух последовательно соединенных
элементов, где через них протекает одинако-
вый ток, напряжения пропорциональны импе-
дансам. Так что обе интерпретации диаграммы
одинаково приемлемы.
Общий импеданс, цепи из резистора JR и кон-
денсатора С для источника сигнала не равняет-
ся 21?, а выражается суммой векторов: это длина
гипотенузы — V2R. По векторной диаграмме мы
15кОм
Мнимая ось: реактивное сопротивление
или напряжение на С\лп\л L
I
\ZC\ = 15 кОм
или
^Вещественная осы сопротивление или напряжение
на сопротивлении
Zc = -15 кОм
(мнимый)
Общий импеданс (последовательный)
или напряжение на £+ С
Рис. 2N.31. Векторная диаграмма: комплексная плоскость, отображающая импеданс /?С-цепи на частоте f
100
2N. RC-цепи
теперь можем вывести две знакомые истины о
поведении ДС-фильтров в точке 3 дБ:
♦ амплитуда выходного сигнала относительно
входного ослаблена на 3 дБ (на 1/Y2), что
соответствует длине вектора R или С относи-
тельно гипотенузы;
♦ выходной сигнал сдвинут на 45° относитель-
но входного: угол между векторами для R и
С и гипотенузой равен 45°, что соответствует
фазе входного напряжения. Опережение или
отставание выходного сигнала от входного
зависит от точки, которая служит выходом
схемы, как уже было сказано ранее.
Пока что мы только что повторили то, что мы
уже знаем. Но чтобы получить какую-либо до-
полнительную информацию с помощью диа-
граммы, попробуйте несколько раз последо-
вательно удвоить частоту входного сигнала и
понаблюдайте за результатами: при каждом
удвоении длина вектора Zc сокращается напо-
ловину от предыдущей длины.
Но при первом удвоении также значительно
меняется длина гипотенузы, поэтому амплиту-
да выходного сигнала относительно входного
(предположим, мы имеем дело с НЧ-фильтром)
сокращается меньше, чем на 50% (на 6 дБ).
Видно, что выходной сигнал ослабляется на-
много больше, чем в точке /3дБ, а также то, что
фазовый сдвиг между входным и выходным
сигналами также значительно увеличился.
Xc = половина предыдущего: R/2
Векторная диаграмма RC-аэильтра после первого
удвоения частоты по сравнению с рис. 2N.31
После второго удвоения частоты длина векто-
ра Zc снова сокращается наполовину, но на этот
раз длина гипотенузы изменяется меньше, чем
в предыдущем случае. Так что теперь ситуация
упрощается: выходной сигнал сокращается
почти на столько, на сколько и вектор Zc — т. е.
почти на 50%. Здесь мы приближаемся к пре-
дельной крутизне графика спада сигнала филь-
тра: -6 дБ/октаву. В то же самое время фазовый
сдвиг между выходным и входным сигналами
также нарастает, приближаясь к граничному
значению 90°.
Я=15кОм
Хс = малое (« 15 кОм)
Векторная диаграмма &£-<рильтра на частоте, вдвое
большей по сравнению с предыдущей диаграммой
В рассмотренных примерах предполагался низ-
кочастотный фильтр. Если же взять высокоча-
стотный фильтр и рассмотреть его векторные
диаграммы, то мы обнаружим, что из них тоже
можно извлечь всю необходимую информа-
цию. Ничего удивительного, но отметить дан-
ное обстоятельство все же приятно.
Векторная диаграмма для ЛС-фильтра
Теперь рассмотрим векторную диаграмму за-
граждающего LC-фильтра (рис. 2N.32)30.
Замечание
Это просто беглый взгляд на схему, с которой мы
еще не знакомы, и компонент, с которым мы по-
знакомимся на следующем лабораторном занятии.
Но, говоря о векторных диаграммах, невозможно
удержаться, чтобы не упомянуть данную схему.
АоЕ § 17.14.
Чх -ЛЛА^Г— 4
Z общий
импеданс
/.^-цепочки
Заграждающий ££-фильтр
Рис. 2N.32. Схема заграждающего LC-фильтра (слева) и его векторная диаграмма (справа)
со > 1/JiC: Xl доминирует
(подобно индуктивности)
ZL при частоте резонанса
ZLc-uenn ПРИ частоте резонан-
са где Zc нейтрализует ZL
Zc при частоте резонанса
со < 1//Ес~: Хс доминирует
(подобно конденсатору)
2N3. Анализ RC-цепей в частотной области
101
Эта схема не такая знакомая, но информатив-
ная, поскольку она демонстрирует интересный
факт (который мы подробно рассмотрим на ла-
бораторном занятии 3L при работе с подобной
схемой, но только с параллельно соединенны-
ми LQ. В частности, комбинация последова-
тельно соединенных катушки I и конденсатора
С иногда выглядит как индуктивность, а иногда
как емкость, соответствуя при этом характери-
стикам того или иного элемента, а при частоте
резонанса не создает вообще никакого фазо-
вого сдвига. Мы отложим подробное рассмо-
трение LC-цепи до следующего раза, а сейчас
просто попробуем разобраться, как векторная
диаграмма описывает поведение такой схемы
(в действительности здесь показаны три диа-
граммы, описывающие поведение схемы на
трех разных частотах).
Чтобы разобраться с LC-фильтром (рис. 2N.33),
полезно посмотреть, что скажет нам о возмож-
ных характеристиках выходного сигнала тако-
го фильтра уже знакомое нам уравнение для
делителя напряжения.
Вот формула, которая выражает выходное на-
пряжение по отношению к входному:
'вых
"
Но:
Z общий
импеданс
/.^-цепочки it-
Рис. 2N.33. Заграждающий LC-
фильтр — это просто разновид-
ность делителя напряжения
Zkomb -
На определенной частоте, при которой сла-
гаемые в правой части последней формулы
равны, сумма будет равна нулю вследствие их
противоположных знаков. А при смещении в
ту или другую сторону от этой особой частоты
(называющейся резонансной частотой) будет
доминировать или конденсатор или катушка.
Можете ли вы понять все это из приведенной
векторной диаграммы?
Улучшенные фильтры
Внимательно проанализировав ЯС-фильтры,
следует признать, что при необходимости про-
стой ЯС-фильтр можно улучшить. Этого можно
добиться, комбинируя конденсатор с катушкой
или используя операционные усилители (ко-
торые мы вскоре будем рассматривать), чтобы
избавиться от катушки. Мы испробуем этот
подход на одном из следующих лабораторных
занятий. На рис. 2N.34 изображен экран осцил-
лографа с частотными характеристиками трех
JRC-фильтров. Причем два из них являются
улучшенными версиями простого низкочастот-
ного ДС-фильтра, рассматриваемого на сегод-
няшнем занятии31.
31 АоЕ § 6.2.2.
Пассивный
/?£-срильтр
2-полюсный
активный
фильтр
(Баттерворта)
8-полюсный
активный фильтр
(эллиптический)
: 8-полюсный «активный i
^фильтр (эллиптический)
Пассивный
Частота
Полоса пропускания
Рис. 2N.34. Частотные характеристики трех фильтров, два из которых являются улучшенными версиями простого ЯС-фильтра.
Мы рассмотрим эти фильтры более подробно на дальнейших занятиях. Слева показан более широкий частотный диапазон;
справа — более подробная полоса пропускания
102
2Л/. RC-цепи
Между прочим: отображение сигнала на
осциллографе с «разверткой» по частоте
На экране осциллографа на рис. 2N.34 по гори-
зонтальной оси отображается частота, а не вре-
мя, как при обычной развертке сигнала. Этот
метод развертки, при желании, можно приме-
нить на лабораторном занятии 2L, а на лабо-
раторном занятии 3L его использование будет
практически незаменимым (поскольку он обес-
печивает наглядную демонстрацию чрезвы-
чайно интересной частотной характеристики
резонансного ЯС-контура). В разделе 2S3 при-
ведено подробное описание этого метода раз-
вертки. Но на данном этапе достаточно сказать,
что частота практически нулевая в левой сторо-
не экрана осциллографа и линейно возрастает
по направлению к правой границе экрана (где
в данном примере она достигает значения око-
ло 3,8 кГц). Частота/^ для всех трех фильтров
составляет около 1 кГц.
1. Самая верхняя из трех характеристик на
рис. 2N.34 соответствует пассивному RC-
фильтру. Видно, что она довольно плоская в
диапазоне, в котором фильтр должен пропу-
скать сигналы, и плавно спадает (ослабляет
сигналы) при увеличении частоты.
2. Посередине на рис. 2N.34 показана харак-
теристика для активного 2-полюсного32 RC-
фильтра. Даже для такой не слишком слож-
ной схемы график лучше, чем для пассивного
фильтра. Это достигается благодаря хитро-
умному применению усилителя и обратной
связи.
Примечание
Если выражение «обратная связь» вам незнакомо,
сильно не переживайте. На данном этапе вам нет
необходимости его понимать, а когда будет нужно,
возможно, на лабораторном занятии 6L, мы разбе-
ремся, что это такое.
Характеристики активного ЯС-фильтра
лучше пассивного в трех отношениях: по-
лоса пропускания более равномерная, спад
(ослабление сигнала с повышением частоты
за пределы полосы пропускания) более кру-
той. С фильтром этого типа мы близко по-
знакомимся на лабораторном занятии 9L.
32 Выражение «2-полюсный» в данном контексте означа-
ет приблизительно следующее: ведет себя подобно двум
обычным ДС-фильтрам, соединенным каскадом (т. е. по-
следовательно).
3. Внизу на рис. 2N.34 изображена частотная
характеристика более замысловатого актив-
ного #С-фильтра: 8-полюсного. Подобно
2-полюсному фильтру, этот фильтр пред-
ставляет собой восемь обычных низкоча-
стотных ЯС-фильтров, соединенных по-
следовательно, но здесь применена опти-
мизация для значительного улучшения его
работы, чем при простом последовательном
соединении звеньев. С фильтром данного
типа мы близко познакомимся на лабора-
торных занятиях 12L и 23L. Очевидно, что
крутизна спада этой частотной характери-
стики довольно велика.
Но мы не хотим, чтобы вы смотрели свысока на
обычные ДС-фильтры. В рамках нашего курса
совсем не обязательно добиваться превосход-
ной передаточной функции фильтра. В боль-
шинстве случаев для целей нашего курса будет
достаточно простого ДС-фильтра. Но всегда
полезно помнить, что в тех случаях, когда тре-
буется лучший фильтр, реализовать его тоже
можно.
2N А Два простых,
но важных варианта
применения конденсатора:
блокировка и развязка
Отчасти мы упоминаем эти области применения
конденсаторов, чтобы познакомить вас с неко-
торыми техническими терминами, которые мо-
гут вызвать у вас ошибочное представление об
этих компонентах. На первый взгляд термины
«блокировочный конденсатор»33 и «развязы-
вающий конденсатор» могут заставить вас по-
думать, что речь идет о конденсаторах особых,
специализированных типов. Но это совсем не
так. Данные термины просто обозначают две
разновидности применения конденсатора, на-
подобие термина «нагрузочный резистор».
Этот термин встречался в главе IN, где он обо-
значал не резистор специального типа, а просто
резистор, играющий роль нагрузки для рассма-
триваемой схемы.
33 Его также называют «разделительным конденсато-
ром». — Примеч. ред.
2N.4. Два простых, но важных варианта применения конденсатора: блокировка и развязка
103
2NA1 Блокировочный конденсатор
Название конденсатора хорошо соответствует
его функции: он блокирует постоянное напря-
жение, одновременно пропуская сигнал пере-
менного тока. Например, конденсатор в схеме
на рис. 2N.35 препятствует прохождению через
схему постоянного напряжения 10 В, не мешая
при этом входному сигналу, симметричному
относительно нулевого потенциала.
Можно возразить, что блокировочный кон-
денсатор одновременно является и пропуска-
ющим. Это так, но элементы, пропускающие
сигнал, встречаются повсеместно (например,
резистор), а разделительный конденсатор от-
личается от проводника именно своей блоки-
рующей функцией.
Можно привести еще один аргумент, что та-
кая комбинация конденсатора с резистором не
представляет ничего нового: это просто высо-
кочастотный фильтр, в котором резистор R яв-
ляется просто RTEB для делителя. Да, схема дей-
ствительно ведет себя подобно ВЧ-фильтру.
Главное назначение разделительного конденса-
тора — блокирование постоянного напряжения,
в то время как для обычного высокочастотного
фильтра основной функцией будет ослабление
низкочастотных помех.
Когда мотивом является блокировка, выбор
частоты Уздб перестает быть критичным: про-
сто задаем эту частоту достаточно низкой, что-
бы могли проходить все частоты, которые мы
считаем сигналом. Если целью является только
воспрепятствовать прохождению постоянного
напряжения, то большая емкость вполне при-
емлема. Более того, никакое значение емкости
не будет слишком большим, хотя не совсем
разумно использовать емкость большей вели-
чины, чем необходимо, поскольку, чем боль-
ше емкость конденсатора, тем он дороже и тем
больше места он занимает в схеме. Кроме того,
конденсаторы большой емкости обычно имеют
полярность и дольше заряжаются до установ-
ления конечного напряжения.
Знакомый пример: разъем «АС»
осциллографа
Когда мы переключаем вход осциллографа в
режим «АС» (что, как уже упоминалось, следует
0В
Блокировочный
конденсатор
Рис. 2N.35. Блокировочный конденсатор, блокирует посто-
янное напряжение, но пропускает переменное
делать только в очень редких случаях), мы до-
бавляем в путь сигнала блокировочный конден-
сатор. Таким образом, в результате блокирова-
ния постоянной составляющей сигнала инфор-
мация о ней теряется. Поэтому рекомендуется,
как правило, выбирать режим работы «DC» для
входа канала вертикального отклонения, за ис-
ключением редких случаев, когда нужно убрать
большое смещение из-за постоянной состав-
ляющей, чтобы иметь возможность исследо-
вать переменный сигнал малой амплитуды, по-
скольку при большом коэффициенте усиления
осциллограмма сигнала с постоянной состав-
ляющей вышла бы за пределы экрана.
2NA2. Развязывающий конденсатор
Очень простой, но очень важной областью
применения конденсатора является уменьше-
ние пульсаций напряжения источника питания.
Источники питания неидеальны, и шины пита-
ния содержат определенную паразитную ин-
дуктивность (или сопротивление, хотя обычно
больше проблем связано с индуктивностью).
Если потребление тока в какой-либо части схе-
мы резко возрастает, это вызывает так называ-
емые скачки тока в шине питания, которые при
протекании через паразитную индуктивность
шины приводят к всплескам напряжения. Эти
помехи по питанию могут передаваться от ча-
сти схемы, которая их вызывает («преступник»
на рис. 2N.36), в другие части схемы («жертва»
на рис. 2N.36), с которыми первая часть связа-
на общей линией питания.
Подключение развязывающего конденсато-
ра в шину питания способствует стабилиза-
ции напряжения от источника питания. Такой
конденсатор служит локальным источником
питания для «преступника», когда тому тре-
буется дополнительный большой «глоток»
тока, вследствие чего не весь требуемый ему
104
2N. RC-цепи
Неидеальный
источник питания
Скачки тока вызывают
всплески напряжения
Источник
питания
«Жертва»
о
Рис. 2N.36. Конденсатор, используемый для сглаживания пульсаций напряжения источника питания, развязывает части схе-
мы одну от другой
Импульсный сигнал
(логические уровни: 0-5 В)
Источник питания (+5 В)
ОД мкФ пленочный
ОД мкФ керамический
Максимальная амплитуда
выбросов помех составляет
примерно 0,9 В
т *
Chi SOOmV \ М 400ns
Рис. 2N.37. Подключение конденсаторов параллельно шине питания способствует стабилизации питающего напряжения
ток будет поставляться источником питания
по более длинным шинам питания. Установка
развязывающего конденсатора на шине пита-
ния вблизи «жертвы» способствует поддержа-
нию амплитуды питающего напряжения. На
рис. 2N.37 показана осциллограмма напряже-
ния питания, на которой отображается влия-
ние цифрового генератора колебаний («пре-
ступник») на напряжение питания, измеряемое
осциллографом возле «жертвы» на другом кон-
це макетной платы на расстоянии около 15 см
от «преступника».
Небольшие по размеру конденсаторы мо-
гут иметь на удивление большую емкость
(ОД мкФ). Самые дешевые конденсаторы — ке-
рамические, которыми пренебрегают для дру-
гих целей, отлично работают в качестве раз-
вязывающих. Более того, как можно видеть на
рис. 2N.37, в этой роли они даже чуть лучше,
чем более дорогие пленочные конденсаторы,
которые предпочтительнее в фильтрах. Часто
параллельно керамическому конденсатору не-
большой емкости (0,01—0,1 мкФ) устанавлива-
ют другой конденсатор большой емкости (на-
пример, 4,7 мкФ, танталовый).
Наилучшая защита от таких проблем пита-
ния — уменьшить собственную паразитную
индуктивность шины питания (или дорожки)
на печатной плате. На более качественных пе-
чатных платах под «землю» и положительную
шину питания отводят по целому слою. Но даже
в таких случаях умный разработчик непремен-
но добавляет развязывающие конденсаторы
(иногда несколько десятков).
Еще одно распространенное применение кон-
денсаторов — шунтирование элементов схем.
Пример такого шунтирования резистора кон-
денсатором мы увидим в усилителе с большим
коэффициентом усиления в разделе 5N.5.2.
Также мы познакомимся с подобным использо-
ванием конденсатора для разделения пути об-
ратной связи в главе 9L, например, в усилителе
на рис. 9L.8.
2N.5. Математический взгляд на RC-фильтры
105
2N.5. Математический
взгляд на ЯС-фильтры
В этом курсе мы прилагаем все возможные уси-
лия, чтобы избежать использования математи-
ки для объяснения поведения схем. Математика
часто идет вразрез с интуицией. Но в данном
случае мы предлагаем посмотреть, не поможет
ли немного математики лучше понять частот-
ную характеристику ЯС-схемы. Надеемся, что
да, но если нет, то можете просто игнорировать
этот материал.
Высокочастотный фильтр
как делитель напряжения
На рис. 2N.38 изображена принципиальная схе-
ма простейшего высокочастотного фильтра (сле-
ва) и его частотная характеристика (справа).
Если рассматривать этот фильтр как делитель
напряжения, то отношение его выходного на-
пряжения к входному выражается следующей
формулой:
Цвых _ R_
UM R + 2
1
(Zc/ R)
Давайте попробуем разобраться, какую пользу
можно извлечь из этого выражения.
В этой формуле наибольший интерес представ-
ляет выражение -y(l/col?C). В зависимости от
частоты его значение может быть следующим:
♦ очень малым;
♦ очень большим;
♦ равным единице.
Это не единственные возможные значения
этого выражения, но они определяют три раз-
ные области в поведении фильтра, которые на
рис. 2N.38 обозначены «блокирует», «пропу-
скает» и «/здБ». Давайте поочередно рассмотрим
эти три случая.
♦ Если значение -j(l/(oRC) очень мало, что
означает co»l/JRC, то частота сигнала будет
значительно выше частоты /3яБ и отношение
UBUX/UBX «1. Это соответствует области «про-
пускает». Почти полное отсутствие у в выра-
жении (поскольку его коэффициент очень
мал) означает отсутствие фазового сдвига.
Блокирует Пропускает
ис
Рис. 2N.38. Высокочастотный фильтр
Это соответствует результатам лаборатор-
ного занятия 2L, согласно которым фазовый
сдвиг в ЯС-фильтре сопутствует ослаблению
сигнала.
♦ Если значение -j(l/(oRC) равно единице, что
означает ю = 1/2?С, то частота сигнала находит-
ся в точке/3дБ и отношение UBhsx/U^ = 1/(1-;).
Это соответствует величине 1/V2, что обыч-
но указывается как -3 дБ.34
Наличие j в выражении намекает на фазо-
вый сдвиг. Векторная диаграмма, наподобие
изображенной на рис. 2N.31, может наилуч-
шим способом проиллюстрировать, почему
величина этого фазового сдвига будет 45°.
Фазовый сдвиг — это угол между гипотену-
зой (17ВХ) и вектором, представляющим на-
пряжение на резисторе R. Это напряжение
опережает входное напряжение [7ВХ на 45°.
Соответствующая векторная диаграмма при-
ведена на рис. 2N.39.
♦ Если значение -j(l/(oRC) очень большое, что
означает со«1/#С, то частота сигнала будет
значительно ниже частоты /ЪяБ и отношение
^вых/^вх s l/(-j(l/(oRC)) =j(oRC. Это выра-
жение очень информативное: наличие мни-
мой единицы; означает фазовый сдвиг вели-
чиной +90°, а присутствие круговой частоты
со — возрастание амплитуды пропорциональ-
но повышению частоты.
Импедансы
Напряжения
Рис. 2N.39. Векторная диаграмма наглядно иллюстрирует
фазовый сдвиг в 45° в точке f3fl5 для ЯС-фильтра
34 этот результат можно получить, умножив 1/(1-j) на его
соответствующее комлексно-сопряженное число 1/(1 +j).
Произведением этих чисел будет значение в квадрате, ко-
торое является действительным числом равным 1/2. Из-
влекая его квадратный корень, получим 1/VZ что более
привычно выглядит как 0,7 или -3 дБ.
106
2N. RC-цепи
2N.6. Материал для чтения
вАоЕ
Материал для изучения
Разделы 1.4-1.7.12 за исключением разделов
1.5—1.6.8 и 1.7.2 по индуктивностям, транс-
форматорам и диодам (мы будем разбираться с
этими элементами на дальнейших занятиях).
Чтение разделов 1.7.3-1.7.9 по комплексным
импедансам оставляем на ваше усмотрение. Эти
разделы насыщены математикой, что противо-
речит характеру нашего курса. Многие студен-
ты, испытывавшие отвращение к математике,
позже обнаружили, что могут прекрасно раз-
бираться в материале курса схемотехники без
такого строгого подхода. Математический ап-
парат в этих разделах не характерен даже для
самой книги АоЕ, и совершенно не похож на
подход, используемый в данной книге.
Приложение А — сводка математических пра-
вил (Math Review). Наиболее краткая справка
по высшей математике, если вы чувствуете,
что вам необходимо-освежить свои знания
в этой области. Но в любом случае вы смо-
жете справиться с нашим курсом без такого
повторения.
Упражнения
Упражнения в тексте.
Дополнительные упражнения 1.39—1.42.
2L Лабораторное занятие: конденсаторы
2L1. Анализ во временной
области
2L1.1. /?С-цепи: постоянная
времени
Чтобы, как и ранее в нашем курсе, сделать ла-
бораторные занятия более интересными, на-
полненными новыми открытиями, мы пред-
лагаем вам решить первую задачу — измерить
постоянную времени ДС-цепи (рис. 2L.1) и
вычислить номиналы резистора и конденсато-
ра. Чтобы освежить свои знания о постоянной
времени ЯС-цепочки, обратитесь к рис. 2N.6,
на котором иллюстрируется экспоненциаль-
ный характер заряда и разряда емкости.
о улдл
Вход
Выход
Т JL
Рис. 2L.1. Определение номиналов элементов /?С-цепи
Измерьте постоянную /?С-цепи
Подайте на вход схемы сигнал прямоугольной
формы частотой 500 Гц или чуть ниже и наблю-
дайте на экране осциллографа выходной сиг-
нал. Отрегулируйте частоту входного сигнала
так, чтобы измерения по осциллограмме были
удобными. Слишком высокая частота не даст
вам достаточно места на экране, чтобы наблю-
дать за графиком всего сигнала, а при слишком
низкой частоте увидеть выходной сигнал цели-
ком можно, но только на небольшом участке
экрана, в результате чего результаты замеров
времени будут неточными. Сказанное иллю-
стрирует рис. 2L.2.
Не забудьте убедиться в том, что установлен
режим «DC» для входа канала вертикального
отклонения осциллографа, несмотря на то,
что подается переменный входной сигнал.
(См. Комментарий касательно переключате-
ля AC/DC входа осциллографа в конце разде-
ла 1L.6.)
Определение постоянной времени данной RC-
цепи не представляет никакой трудности. Для
этого нужно просто измерить время, за кото-
рое амплитуда выходного сигнала понизится
до37%(=1/е).
Рекомендация
Обозначения процентов, нанесенные на левый
край экрана осциллографа, сделаны как будто бы
специально для этой задачи: установите нижний
край графика сигнала напротив обозначения 0%,
а верхний — напротив 100%. Затем повысьте ско-
рость развертки, чтобы наблюдать падение ампли-
туды со 100% до 37% на большей части экрана.
Теперь измерьте интервал времени, в течение
которого амплитуда сигнала возрастает с 0% до
63%, и сравните его с предыдущим измерением
(время падения амплитуды до 37%). Если эти
две величины окажутся разными, значит, вы
делаете что-то не так. Попробуйте поменять
частоту прямоугольного сигнала.
1 > i 1 s j \ s
Побор, зон. 2. Пара частот, не подходящих
-для измерения постоянной времени RC-схемы
Рис. 2L.2. Неудачный выбор частот при измерении постоян-
ной времени /?С-цепи
108
2L Лабораторное занятие: конденсаторы
Вычислите номиналы Я и С
Сопротивление резистора легко можно было
бы узнать с помощью омметра, но на данном
занятии так сделать нельзя. Вместо этого сле-
дует использовать наши знания о предельных
значениях входного импеданса ЯС-цепи и опре-
делить номинал резистора экспериментальным
путем. Зная это сопротивление, можно вычис-
лить емкость конденсатора. Чтобы облегчить
вам решение задачи, приведем несколько под-
сказок.
Подсказки
♦ Сначала попытайтесь определить значе-
ние сопротивления резистора, несмотря
на присутствие конденсатора. Соберите
схему делителя напряжения с резистором
известного номинала, подключенным по-
следовательно к входу RC-цепи (рис. 2L.3).
Рекомендуется взять резистор с номиналом
1 кОм. Подайте на этот резистор сигнал си-
нусоидальной формы и наблюдайте за сиг-
налом на входе и выходе резистора, как по-
казано на рис. 2L.3.
Канал 1 (осциллографа)
Канал 2
Рис. 2L.3. Схема с дополнительным резистором для опреде-
ления значения сопротивления резистора R
♦ Как узнать, что мы наблюдаем влияние имен-
но резистора R, а не какой-либо комбинации R
и Хс? Подсказка: посмотрите, есть ли фазовый
сдвиг между сигналами на первом и втором
каналах осциллографа («Канал 1» и «Канал 2»).
Примечание
Не увеличивайте частоту входного сигнала fBX
выше 1 МГц, чтобы влияние паразитной емкости
кабеля не усложняло вам задачу. Эта емкость (со-
ставляющая около 30 пф/фут1) играет важную роль
на высоких частотах, образуя совместно с сопро-
тивлением Йш НЧ-фильтр в точке, обозначенной
«Канал 2» на рис. 2L3. Поэтому ваши старания
устранить фазовый сдвиг на слишком высоких ча-
стотах могут не увенчаться успехом.
♦ Подумайте, что произошло со значением Хс,
если фазового сдвига нет.
♦ Получив значение сопротивления R, можно
считать, что мы практически решили задачу.
2L1.2. Дифференциатор
Соберите схему JRC-дифференциатора, изобра-
женную на рис. 2L.4. Подайте на ее вход сиг-
нал прямоугольной формы частотой 100 кГц
и уровнем 20 дБ (последний устанавливается
на генераторе сигналов). Наблюдайте за вы-
ходным сигналом на осциллографе. Сделайте
вывод о работе дифференцирующей цепочки.
Выполните аналогичные эксперименты с сиг-
налами треугольной и синусоидальной формы.
1 1 фут я 30 см — Примеч. ред.
Рис. 2L.4. Принципиальная схема /?С-дифференциатора
Входной импеданс
Здесь у нас есть еще один шанс попрактико-
ваться с быстрым вычислением импедансов
предельных случаев вместо того, чтобы зани-
маться точными вычислениями частотной ха-
рактеристики (результаты которых практиче-
ски бесполезны).
Определите входной импеданс схемы относи-
тельно генератора сигналов (предполагая от-
сутствие нагрузки на выходе схемы). Выясните,
какой будет импеданс при:
♦ /=0
♦ /= ОО ?
Подобные оценки особенно важны в случаях,
когда характеристики источника сигнала не
такие идеальные, как у вашего лабораторного
генератора.
2L1.3. Интегратор
Соберите схему ДС-интегратора, изображен-
ную на рис. 2L.5. Подайте на ее вход сигнал
прямоугольной формы частотой 100 кГц с
212. Анализ в частотной области
109
максимальным уровнем 0 дБ (устанавливается
на генераторе сигналов).
ЮкОм
Вход о \ЛЛЛ-
-о Выход
~. 0,01 ЛАК*
Рис. 2L5. Принципиальная схема ЯС-интегратора
Уменьшите частоту сигнала до минимума
(нуля) и выясните, какой импеданс наблюда-
ется в этом случае. Подумайте, каким он будет
при бесконечно большой частоте. Подайте на
вход сигнал треугольной формы и посмотрите,
какой формы окажется выходной сигнал.
Замечание
Вам не кажется, что эта схемка обладает собствен-
ным интеллектом? Похоже, что она знает высшую
математику лучше, чем вы, или, по крайней мере,
вспоминает ее быстрее.
Чтобы убедиться, что исследуемая схема явля-
ется только приблизительным, неидеальным
интегратором, уменьшите частоту подаваемо-
го на нее сигнала. Подумайте, не нарушается
ли здесь условие, изложенное в разделе 2N.2.1:
ишх«ивх?
Рассмотренный ранее дифференциатор также
неидеальный и хорошо работает только при
условии, изложенном в разделе 2N.2.1:
dUmx/dt«dUBX/dt
Слишком большая постоянная времени диф-
ференцирующей цепи нарушает ее работу. Если
у вас есть желание, вы можете возвратиться
к эксперименту с дифференциатором в разде-
ле 2L.1.2, но на этот раз увеличив постоянную
времени, например, в 1000 раз. Производная
прямоугольного сигнала будет уродливой, что
не должно вас удивить, но ухудшение про-
изводной треугольного сигнала будет не так
очевидно.
Когда мы начнем рассматривать операционные
усилители в главе 3N, то узнаем, как создать
идеальные дифференциаторы и интеграторы,
т. е. свободные от ограничений, налагаемых на
ЯС-цепочки.
2L2. Анализ в частотной
области
2L2.1. Низкочастотный фильтр
Соберите низкочастотный фильтр, принципи-
альная схема которого показана на рис. 2L.6.
Замечание
— Позвольте! — можете запротестовать вы, —
но разве это не схема интегратора, который мы
только что собрали в предыдущем упражнении?
Действительно, это точно такая же схема. Так за-
чем же собирать ее снова? Мы надеемся, что вы
постепенно придете к ответу на данный вопрос
самостоятельно, по мере продвижения в этом экс-
перименте. Один из этих экспериментов можно
назвать частным случаем другого. Завершив экс-
перимент, попытайтесь определить, кто есть кто.
15кОм
Вход о \ЛЛЛ-
-о Выход
""^ 0,01 мкФ
Рис. 2L.6. Низкочастотный ЯС-фильтр
Подумайте, что нужно сделать, чтобы узнать
частотуУздБ для этого фильтра? Чтобы понять
свойства данного фильтра, подавайте на его
вход синусоидальный сигнал в широком диа-
пазоне частот. Наиболее полезными для это-
го будут диапазоны частот в области 1 кГц и
10 кГц.
Определите частоту /3дБ экспериментальным
путем: измерьте частоту, на которой фильтр
ослабляет сигнал на 3 дБ (выходное на-
пряжение [7ВЫХ составляет 70,7% от полной
амплитуды).
Примечание
В дальнейшем мы будем употреблять выражение
«точка 3 дБ», а не «f Б», «-3 дБ» или «f Б» Поначалу
это может выглядеть непривычно, но поскольку
это общепринятый термин, рекомендуем начать
привыкать к нему.
Проверьте, каким будет предельный фазо-
вый сдвиг как на очень низких, так и на очень
высоких частотах?
110
21. Лабораторное занятие: конденсаторы
Лоб. занятие 2 с использованием:
1. Внешнего запуска- развертки
2. Масштаба в 8 клеток на период
Вход Это облегчает измерение фазового сдвига
Вмход (сигналы сдвинуты
почти на 2 деления: фазовый
сдвиг почти 90°)
Рис. 2L.7. Правильный выбор масштаба развертки облегча-
ет определение фазового сдвига
Рекомендация
При измерении фазового сдвига подключите выход
синхросигнала (SYNC или TTL) генератора сигна-
лов к разъему внешнего сигнала запуска разверт-
ки осциллографа (обычно обозначен как ЕХТ или
сходно). Это позволит более точно определить фазу
входного сигнала. Затем (если используется анало-
говый осциллограф) выберите режим плавно регу-
лируемой частоты развертки2 и настройте разверт-
ку так, чтобы полный период входного сигнала ото-
бражался точно на восьми основных делениях (или
восьми сантиметрах). Таким образом, при одновре-
менном наблюдении входного и выходного сигна-
лов фазовый сдвиг хорошо заметен (рис. 2L.7).
Проверьте, ослабляет ли наш низкочастотный
фильтр сигнал на 6 дБ/октаву на частотах на-
много выше точки 3 дБ. В частности, измерьте
амплитуду выходного сигнала в точках 10 -f3nB
и 20 • /3дБ. Попутно определите зависимость
фазового сдвига от частоты. В частности, про-
верьте фазовый сдвиг для частот/«^дБ,/=^дБ,
Наконец, измерьте и запишите ослабление сиг-
нала на частотах/= 2 -/3дБ, 4 -/3дБ, и 10 -/3дБ.
Частотная развертка
С помощью рассмотренной схемы можно экс-
периментально получить зависимость ампли-
2 На большинстве осциллографов эту настройку можно
выполнить, провернув против часовой стрелки маленькую
ручку в центре большой ручки настройки развертки, что-
бы она вышла из защелкнутого положения, которое обыч-
но обозначается CAL. Но в этом режиме временной мас-
штаб по оси X не соответствует обозначенному на панели
прибора. Поэтому, завершив измерение фазового сдвига,
поверните эту ручку обратно до щелчка.
туды от частоты вместо обычной зависимости
амплитуды от времени. Если у вас есть время и
желание, рекомендуем выполнить этот экспе-
римент, подав на осциллограф сигнал разверт-
ки от генератора. Но если время вас поджима-
ет, отложите эту задачу до следующего занятия,
когда мы будем рассматривать резонансную
LC-схему, которая также предоставляет хоро-
шую возможность для работы с частотной раз-
верткой.
Подробно процесс частотной развертки описан
в разделе 2S3, но вкратце его можно изложить
следующим образом.
Чтобы создать график амплитуды выходно-
го сигнала 17ВЫХ в зависимости от частоты,
пилообразный сигнал развертки подается от
генератора сигналов на вход X канала гори-
зонтального отклонения осциллографа, на ко-
тором включен режим работы «X-Y». В этом
режиме внутренний генератор горизонтальной
развертки осциллографа отключен и развертка
осуществляется внешним сигналом.
При этом скорость развертки задается управле-
нием временем линейного нарастания сигнала
развертки, подаваемого от генератора сигна-
лов. Эта скорость должна быть небольшой,
тогда изображение на осциллографе будет не-
много мерцать, но останется удобным для на-
блюдения и измерения.
2L2.2. Высокочастотный фильтр
Из компонентов только что рассмотренного
НЧ-фильтра соберите ВЧ-фильтр, принципи-
альная схема которого изображена на рис. 2L.8.
Определите точку 3 дБ для этого фильтра.
Посмотрите, как этот фильтр обрабатывает
синусоидальные сигналы: выясните, пропор-
циональна ли амплитуда выходного сигнала
частоте на низких частотах (значительно бо-
лее низких, чем частота^); Подумайте, каким
будет предельный фазовый сдвиг как на очень
низких, так и на очень высоких частотах?
0,01 мкФ
Вход о 1 |
о Выход
Рис. 2L.8. Высокочастотный ЯС-фильтр
2L2. Анализ в частотной области
111
2L2.3. Первое применение
фильтров: определение искажений
Схема на рис. 2L.9 позволяет установить на-
личие искажений напряжения в электрической
сети 220 В 50 Гц. Для этого нужно подключить
осциллограф к вторичной обмотке трансфор-
матора в точке А. Сигнал здесь должен иметь
более или менее классическую синусоидаль-
ную форму.
Замечание
Напомним, что трансформатор выполняет две за-
дачи — он понижает переменное сетевое напря-
жение 230 В до более разумных 6,3 В, а также галь-
ванически изолирует схему.
Переменное
напряжение
6'3 в
0,01 мкФ
Переменное
напряжение
220 В
Переменное
напряжение 6,3 В
Трансформатор
Рис. 2L.9. подключение ВЧ-фильтра к шине питания 6,3 В
50 Гц
Чтобы наблюдать помехи типа всплесков или
проседания напряжения, посмотрите с по-
мощью осциллографа сигнал на выходе ВЧ-
фильтра в точке Б. Здесь должны присутст-
вовать разного рода интересные явления, и
главное, некоторые из них будут меняться во
времени. Выясните, каким будет ослабление,
вносимое фильтром на частоте 50 Гц?
Совет
Ответ на этот вопрос не потребует сложных вы-
числений. Подсказка: подсчитайте октавы или вос-
пользуйтесь установленным ранее фактом, что
при частотах намного ниже частоты f3fl5 амплитуда
линейно возрастает с повышением частоты.
2L2A Второе применение
фильтров: отделение сигнала
от помех
Теперь мы попробуем использовать снача-
ла высокочастотный, а затем низкочастот-
ный фильтр, чтобы выделить один частотный
Выход
Переменное
напряжение
220 В 50 Гц
Рис. 2L.10. Сеема для формирования составного сигнала,
состоящего из двух синусоидальных
диапазон, а затем другой из смеси сигналов в
схеме, показанной на рис. 2L.10. Здесь комби-
нируются два сигнала: к выходному сигналу
генератора добавлен синусоидальный сигнал
большой амплитуды с частотой 50 Гц от транс-
форматора. Сначала установите частоту на ге-
нераторе сигналов около 10 кГц.
Чтобы выбрать номинал резистора R для на-
шего фильтра, нам нужно определить значение
выходного импеданса3 созданного нами источ-
ника сигнала (генератор сигналов и трансфор-
матор). Выходное сопротивление #вых генера-
тора сигналов равно 50 Ом; на интересующих
нас частотах последовательное сопротивление
катушки трансформатора незначительное. Ре-
зистор номиналом 1 кОм подключен между
генератором сигналов и трансформатором для
защиты генератора от короткого замыкания
выхода схемы.
Задание I: высокочастотный фильтр. Раз-
работайте ВЧ-фильтр, который пропускает
большую часть полезного сигнала и подавляет
большую часть помехи частотой 50 Гц. Частота
сигнала может находиться в диапазоне от 2 до
20 кГц. При разработке фильтра примите во
внимание следующие факторы:
♦ Какой будет подходящая частота^ для это-
го фильтра?
♦ Каким будет подходящий входной импеданс
2вхдля фильтра?
Подайте на вход созданного фильтра состав-
ной сигнал, состоящий из полезного сигнала и
помехи.
3 Хотя мы абсолютно правильно называем эту харак-
теристику выходным импедансом Z^, она не является
частотно-зависимой, поэтому правильнее называть ее вы-
ходным сопротивлением #вых.
112
2L Лабораторное занятие: конденсаторы
Каково ваше мнение о выходном сигнале этого
фильтра? Отвечает ли вашим ожиданиям вели-
чина ослабления сигнала частотой 50 Гц (по-
мехи)?
Примечание
Со временем вы убедитесь, что электрические ли-
нии с частотой 50 Гц являются самым распростра-
ненным и проблематичным источником помех в
лаборатории. Создаваемые ими помехи часто на-
зывают наводками по сети.
Задание И: низкочастотный фильтр. Теперь
изменим техническое задание: предположим,
что сигнал частотой 50 Гц является полезным
сигналом, а сигнал частотой 10 кГц, созда-
ваемый генератором, — помехой. Разработай-
те НЧ-фильтр, который пропускает полезный
сигнал и значительно ослабляет помеху.
Подайте на вход созданного вами фильтра со-
ставной сигнал и посмотрите, хорошо ли он рабо-
тает. Если результат вам не понравится, внесите
в схему фильтра необходимые корректировки.
2S. Дополнительный материал: /?С-цепи
2S.1. Определение
номиналов конденсаторов
25.1.1. Почему эта информация
важна для вас
Большинство студентов довольно быстро раз-
бираются с системой обозначения номиналов
резисторов. Но определение номиналов конден-
саторов оказывается более сложной задачей1.
Решить эту задачу трудно, потому что изгото-
вители конденсаторов не заботятся о том, что-
бы пользователи могли определять их номина-
лы по маркировке. Прочитав этот раздел, вы
согласитесь со мной. Международный комитет
разработал маркировку конденсаторов так, что
на практике пользоваться ею непросто. Но мы
дадим вам несколько советов, которые помогут
обойти эти препятствия и научиться расшиф-
ровывать маркировку номиналов конденсато-
ров. Давайте же приступим.
25.1.2. Конденсаторы большого
размера: электролитические
Эти конденсаторы имеют сравнительно большие
размеры, что позволяет наносить их номинал,
включая единицы измерения, обычным текстом.
Также обозначается максимальное напряжение,
которое можно подавать на конденсатор, не под-
вергая его риску повреждения. Отрицательный
вывод таких конденсаторов обозначается зна-
ком минус (-) и направленной вниз стрелкой.
Конденсаторы емкостью более 1 мкФ
обычно полярные
Конденсаторы большой емкости (1 мкФ и бо-
лее) полярные. Это значит, что для накопления
положительного и отрицательного заряда ис-
пользуются материалы с разными свойства-
ми2. Поэтому неправильное подключение
конденсатора к цепям питания может вывести
конденсатор из строя3. Чтобы избежать этого,
потенциал на положительном выводе (это вы-
вод, противоположный отрицательному, см.
рис. 2S.1) должен быть, как минимум выше, чем
на противоположном выводе. В результате не-
соблюдения полярности при подключении кон-
денсатор иногда может взорваться, но чаще его
обкладки просто закорачиваются внутри. При
низких напряжениях несоблюдение полярно-
сти может не вызвать никаких отрицательных
последствий. Тем не менее экспериментировать
не следует.
Рис. 2S.1. Пример понятной маркировки благодаря большо-
му размеру конденсатора
Один из наших студентов4 принес на занятие
конденсатор, который он случайно включил, не
соблюдая полярность. Результат иллюстрирует
рис. 2S.2.
Было бы хорошо, если неправильно подклю-
ченные конденсаторы всегда реагировали та-
ким образом, поскольку тогда остальная часть
схемы могла бы при этом уцелеть. К сожалению,
АоЕ § 1.4.1.
2 Диэлектриком в этих конденсаторах служит тонкий слой
оксида на поверхности металлической ленты, которая яв-
ляется положительным электродом. Эта лента свернута в
рулон и залита электролитом (жидким, твердым или геле-
вым), который служит отрицательным электродом.
3 Это относится к продолжительному действию посто-
янного напряжения; кратковременная смена полярности,
недостаточная для создания значительного обратного на-
пряжения на конденсаторе, будет безвредной.
4 Это был Рик Монтесанти (Rick Montesanti), который
и принес нам конденсатор. Он также рассказал нам, что
конденсатор отреагировал на неверную полярность
взрывом, выбросившим его внутренности на расстояние
около 7 метров.
114
2S. Дополнительный материал: RC-цепи
Рис. 2S.2. Последствия подключения электролитического
конденсатора с неправильной полярностью
неправильно подключенный конденсатор обыч-
но прячет свою «обиду», внутренне закорачивая
электроды и не проявляя никаких внешних при-
знаков. В результате схема не функционирует, а
вы не можете понять, почему.
2S.1.3. Конденсаторы сравнительно
большого размера: танталовые
По мере того, как размеры конденсаторов
уменьшаются, начинают возникать трудности
с расшифровкой их маркировки. Танталовые
конденсаторы обладают сравнительно большой
емкостью и часто достаточно большими разме-
рами для нанесения отчетливой маркировки.
Внешне танталовые конденсаторы имеют вид
цилиндров серебристого цвета. Подобно элек-
тролитическим конденсаторам они также по-
лярные, при этом положительный вывод обо-
значается знаком плюс (рис. 2S.3)5. Поверхность
танталового конденсатора, изображенного на
рис. 2S.3, достаточно велика и его характери-
стики обозначены дважды, двумя разными
способами.
Рис. 2S.3. Танталовый конденсатор
5 В конденсаторах данной серии положительный вывод
можно также определить по металлической оболочке, в
который он заключен при выходе из корпуса. Ее намного
легче заметить, чем маленький знак «+», для обнаружения
которого конденсатор необходимо повернуть в единствен-
но правильное положение. К сожалению, это не является
общепринятой практикой среди производителей.
Маркировка 4R7, по большому счету, легко
поддается расшифровке, если знать, что буква
R означает radix point, т. е. десятичную запятую:
емкость 4,7 мкФ, предельное напряжение 50 В.
А вторая маркировка, 475М под CS13B (что
означает тип конденсатора), обозначает но-
минальное значение емкости конденсатора
в экспоненциальном формате, подобно ре-
зисторам: 47х105 М. А что означает буква М?
Микрофарады? (Ведь не может же это быть
мегафарады.)
Но не следует поддаваться искушению принять
правдоподобное предположение, что буква «М»
означает единицу измерения, поскольку это не
так. Она обозначает величину допустимого от-
клонения от номинального значения (допуск),
а именно 20%. Мы же говорили вам, что из-
готовители конденсаторов не заботятся о том,
чтобы пользователи могли с легкостью расшиф-
ровывать их обозначения. Угадайте, какой бук-
вой они обозначают другое значение допуска?
Правильно, буквой «К», которая по всем прави-
лам должна соответствовать приставке «кило»,
а в действительности обозначает допуск 10%.
У вас еще остались какие-либо сомнения в на-
мерениях производителей конденсаторов?
Какие же единицы емкости
использовать?
Если буква «М» означает не единицу измере-
ния, а допуск, какая же единица используется?
ДО5 чего? 105 чего-то очень маленького. Вам
придется постоянно сталкиваться с такой си-
туацией, поэтому нужно сразу же прояснить
данный вопрос. Это можно сделать, исходя из
практических соображений. Для маркировки
конденсаторов наиболее часто используется
следующие единицы емкости:
♦ микрофарады: 10~6 фарады;
♦ пикофарады: 1012 фарады.
Промежуточная единица — нанофарада, нФ:
10~9 фарад — встречается на принципиальных
схемах, но к счастью, не в маркировке конден-
саторов. К счастью потому, что разница между
нФ и пФ очень велика, а обозначения похожи
и трудно определить, какая единица имеется в
виду в маркировке конденсатора.
Единица мФ (миллифарада — 10~3 фарады)
выглядит разумным вариантом, но не исполь-
2S.7. Определение номиналов конденсаторов
115
зуется; емкость конденсаторов в этом диа-
пазоне измеряется в тысячах микрофарад.
Например, емкость конденсатора будет обо-
значена 4000 мкФ, а не 4 мФ. Странно, но так
сложилось исторически.
Фарада — громаднейшая единица емкости.
Самый большой номинал конденсатора, кото-
рый встретится в нашем курсе, составляет не-
сколько сотен микрофарад (мкФ). Конденса-
тор такой емкости имеет большие габариты.
В нашей лаборатории мы держим конденсатор
емкостью 1Ф, но только для разных демонстра-
ционных целей6. Таким образом, если малога-
баритный конденсатор обозначен только циф-
рами, например, 680, знайте, что это 680 пФ7.
А пикофарада, наоборот, очень маленькая еди-
ница емкости. В курсе схемотехники нам не
понадобятся конденсаторы такой малой емко-
сти, как 1 пФ8. Таким образом, если вам в руки
попадет конденсатор с дробной маркировкой,
но без единицы измерения, например 0,01, эта
единица будет микрофарада (мкФ), т. е. номи-
нал данного конденсатора равен 0,01 мкФ.
Но не подумайте, что пикофарада лишь нена-
много меньше микрофарады. Величина пико-
фарады не 10~9Ф (т. е. не 10~3 мкФ), а 10~12 Ф:
в миллион раз меньше микрофарады.
Таким образом, возвращаясь к нашему конден-
сатору на рис. 2S.3, его маркировка 475 означа-
ет 4,7хЮ6 пФ. Это просто иной способ обозна-
чения емкости величиной 4,7хЮ"6 Ф.
Здесь мы заранее знали ответ до того, как при-
ступили к последнему упражнению по расшиф-
ровке маркировки. Хотя такой способ марки-
ровки действительно несколько замысловатый,
6 Эти огромные конденсаторы используются вместо ак-
кумуляторов в калькуляторах, планшетных компьютерах
и даже мигалках для велосипедов. Их преимущество над
аккумуляторами состоит в эксплуатационной долговечно-
сти: поскольку при их заряде и разряде нет никаких хи-
мических реакций, они выдерживают большое количество
циклов заряда/разряда.
7 За исключением, конечно же, случаев, когда использует-
ся экспоненциальная маркировка (см. раздел 2S.1.5).
8 И легко объяснить причину: паразитная емкость в на-
ших схемах на макетной плате соизмерима по величине.
Например, паразитная емкость между двумя смежными
столбцами гнезд на плате составляет около 2 пФ. А вход-
ная емкость пробника х10 осциллографа (с которым мы
познакомимся на лабораторном занятии 3L) составляет
около 10 пФ. Наконец, емкость соединительного кабеля
с разъемом BNC длиной около одного метра будет при-
мерно 90 пФ.
но по крайней мере, он однозначный. Хорошо,
если бы он использовался шире. Еще один
пример экспоненциальной маркировки в слу-
чае керамических конденсаторов серии СК05
встретится нам в разделе 2S.1.5.
2S.1 А Конденсаторы меньшего
размера: с диэлектриком
из полиэстеровой (майларовой —
лавсановой)пленки
Эти конденсаторы имеют цилиндрический кор-
пус желтого цвета и довольно разборчивую мар-
кировку. Пример такого конденсатора показан
на рис. 2S.4.
Рис. 2S.4. Майларовый конденсатор: все еще достаточно
большого размера для понятной маркировки
Маркировка .01К, конечно же, означает про-
сто 0,01 мкФ. Мы уже упоминали ранее, что
«К» означает не «кило», а допуск в 10%, по-
добно тому, как «М» в маркировке танталового
конденсатора, рассмотренного выше, означает
допуск 20%. Эти конденсаторы неполярные;
черная полоска обозначает внешний конец ру-
лончика фольгированной пленки (рис. 2S.5).
Не беспокойтесь насчет этой тонкости и под-
ключайте их в схему любым способом.
Рис. 2S.5. Размотанный пленочный конденсатор. Можно ви-
деть металлическую фольгу, слои которой разделяются май-
ларовой пленкой
2S.1.5. Конденсаторы малого
размера: керамические
Керамические конденсаторы — это «рабо-
чая лошадка» конденсаторного мира: трудя-
ги, без благородных манер, непредсказуемые,
неточные, но в трудных условиях тянут свою
116
2S. Дополнительный материал: RC-цепи
лямку без нареканий9. Наиболее часто они
применяются для развязки по цепям питания.
Керамические конденсаторы обычно выпол-
нены в корпусах в виде небольших кирпи-
чиков или оранжевых таблеток (устаревший
тип) и выпускаются электронной промышлен-
ностью в колоссальных количествах10. Они со-
храняют свои характеристики даже на высоких
частотах. Секрет в расшифровке маркировки
этих конденсаторов заключается в игнори-
ровании обозначений, которые не относятся
к номиналу. Как мы вскоре увидим, нужно так-
же иметь в виду возможность нестандартной
маркировки.
Конденсаторы типа СКО5
Эти конденсаторы выполнены в корпусе ква-
дратной формы с выводами на расстоянии око-
ло 5 мм друг от друга. Благодаря этому свой-
ству их удобно устанавливать на печатной пла-
те (правда, в настоящее время они вытеснены
миниатюрными конденсаторами для поверх-
ностного монтажа). На рис. 2S.6 показана мар-
кировка такого конденсатора на двух сторонах
корпуса.
♦ К — на этот раз это не допуск, а обозначение
фирмы-производителя: Kemet;
♦ 9902 — не номинал, но год и неделя изготовле-
ния конденсатора: вторая неделя (19)99 года.
Все это не представляет интереса для нас. По-
смотрим на обратную сторону корпуса. Здесь
мы видим:
♦ СК05 — тип конденсатора;
♦ ВХ — обозначение типа корпуса;
♦ 680К — а вот это, наконец, и есть обозначе-
ние номинала: 680 в экспоненциальном виде;
здесь символ «К» обозначает допуск (10%).
Таким образом, номинал этого конденсатора
равен 68 пФ (68x10° какой-то очень малой еди-
ницы, а именно, пикофарад).
Возможная неопределенность:
устаревшие дисковые конденсаторы
Время от времени вам могут встречаться кера-
мические конденсаторы с маркировкой старого
образца. Корпус таких дисковых конденсаторов
сравнительно большого размера. На рис. 2S.7
показан пример такого конденсатора по срав-
нению с конденсатором типа СК05.
Рис. 2S.6. Маркировка конденсатора типа СК05 на двух сто-
ронах корпуса
Давайте расшифруем номинал этого конденса-
тора, определив не относящиеся к этой задаче
части маркировки и игнорируя их.
♦ 200V — в точности как и написано: макси-
мальное рабочее напряжение конденсатора
(200 В);
9 Согласно книге АоЕ некоторые керамические конденса-
торы имеют хорошие характеристики, в частности, кон-
денсаторы типа C0G (класс I).
10 Согласно английской Википедии (http://en.
wikipedia.org/wiki/Ceramic capacitor) в год произ-
водится около одного триллиона (1012) керамических
конденсаторов.
Рис. 2S.7. Некоторые дисковые конденсаторы старого об-
разца имеют не экспоненциальную маркировку
Познакомившись с маркировкой конденсато-
ров типа СК05, вы можете предположить, что
номинал обоих конденсаторов на данном ри-
сунке равен 56 пФ. На самом деле, этот номи-
нал только у конденсатора справа, а номинал
устаревшего дискового конденсатора слева со-
ставляет 560 пФ. Неприятно, конечно, но тако-
ва жизнь. Но нет худа без добра, и можно уте-
шиться тем, что дисковый корпус и его схема
маркировки устарели и почти не встречаются.
2S.7. Определение номиналов конденсаторов
117
2S.1.6. Конденсаторы слишком
малого размера для внятной
маркировки: за ними будущее!
Ранее мы рассмотрели примеры маркировки
конденсаторов, с которыми вам, скорее всего,
придется столкнуться при выполнении лабора-
торных занятий в нашем курсе. Но при сборе
схем на печатных платах вы, вероятно, будете
работать с компонентами для поверхностного
монтажа. Нанести маркировку в данном случае
можно только на экземпляры самих больших
размеров. Компоненты меньшего размера ни-
как не маркируются, и вам придется помнить,
из какой партии каждый такой компонент был
взят. Если вы запутаетесь в номиналах несколь-
ких таких компонентов, единственным выхо-
дом будет взять новые из пакета или ячейки с
обозначенным номиналом.
Конденсаторы для поверхностного
монтажа: достаточно большого размера
для маркировки
На рис. 2S.8 приведен пример конденсатора,
емкость которого достаточно велика (4,7 мкФ),
поэтому ему требуется сравнительно большой
корпус по меркам поверхностного монтажа.
Таким образом, хотя он и миниатюрный, но
все же достаточного размера для нанесения
маркировки.
Рис. 2S.9. Увеличенное изображение конденсатора для по-
верхностного монтажа: маркировка 475К обозначает его
номинал
Сверхминиатюрные конденсаторы для
поверхностного монтажа слишком малы
для нанесения маркировки
Но по мере того, как размеры конденсаторов
для поверхностного монтажа становятся все
меньше и меньше, прекращаются даже попыт-
ки наносить на них какую бы то ни было мар-
кировку. На рис. 2S.10 показано несколько
примеров таких конденсаторов.
0805
0603
0402
0201
Рис. 2S.10. Маркировка сверхминиатюрных конденсаторов
для поверхностного монтажа даже не обсуждается
Рис. 2S.8. Конденсатор для поверхностного монтажа доста-
точно большого размера для нанесения маркировки
На увеличенном изображении этого конденса-
тора (рис. 2S.9) можно различить маркировку
475К, как и следовало ожидать на конденсаторе
емкостью 4,7 мкФ.
2S.1.7. Обозначение допусков
Чтобы ничего не упустить, а также потому, что
эту информацию не всегда легко найти, далее
в табл. 2S.1 приводятся обозначения допуска
номинала в маркировке компонентов. Эти обо-
значения применимы как к конденсаторам, так
и к резисторам; но обозначения малых допу-
сков применимы только к резисторам; а символ
«z» относится только к конденсаторам.
118
25. Дополнительный материал: RC-цепи
Таблица 2S.1. Обозначение допуска компонента
Обозначение
допуска
z
М
К
J
G
F
D
С
В
А
Z
N
Допуск
+80%,
-20%
±20%
±10%
±5%
±2%
±1%
±0,5%
±0,25%
±0,1%
±0,05%
±0,025%
±0,02%
Примечания
Для конденсаторов большой емкости, используемых в фильтрах, где возможны
проблемы из-за несимметричного отклонения номинала: конденсатор
слишком малой емкости будет пропускать слишком много пульсаций. Эта тема
рассматривается более подробно в главе 3Nn на лабораторном занятии 3L
Прецизионные резисторы. Очевидно, что ассиметричная погрешность
(как z для конденсаторов) здесь не имеет смысла
2S.2. Заметки в помощь
интуитивному пониманию
поведения конденсаторов
25.2.1. Конденсаторы, конечно,
отличаются от резисторов
Здесь мы попытаемся изложить несколько
очень простых аргументов в надежде, что они
помогут улучшить ваше интуитивное пони-
мание поведения конденсаторов. Не теоре-
тические выкладки с формулой Zc = -//юС,
а мысленный эксперимент, представляющий
процесс изменения напряжения на пласти-
нах конденсатора при подаче на него вход-
ного сигнала. Прежде всего заметим, что ре-
зисторы «живут текущим моментом», кон-
денсаторы же, наоборот, по своей природе
«консервативны», как образно иллюстрирует
рис. 2S.11.
Я живу сегодняшним днем, старина...
В самом деле, что может быть важней
чем настоящее?
А я всегда думаю о былых временах..
Я размышляю о событиях милли-
и микросекундной давности...
Рис. 2S.11. Вверху: резистор-хиппи: живет одним днем. Внизу: конденсатор-почитатель Марселя Пруста1:... убежден, что про-
шлое важно
Французский писатель. Автор семитомной эпопеи «В поисках утраченного времени».
2S.2. Заметки в помощь интуитивному пониманию поведения конденсаторов
119
Напряжение на конденсаторе не меняется рез-
ко, и ДС-схемы могут быть достаточно инер-
ционными11. Давайте поразмышляем, что же
нам в результате ожидать от конденсаторов и
на что они способны.
25.2,2. Низкочастотный фильтр
Низкочастотный фильтр ослабляет вы-
сокие частоты. При быстро изменяющемся
уровне входного сигнала напряжение на кон-
денсаторе не может изменяться в том же темпе,
как и входное напряжение, что можно видеть
на рис. 2S.12.
Выходное напряжение Uc начинает меняться
вслед за входным, но уровень входного напря-
жения тоже меняется, выходное за ним не успе-
вает. В результате на выход фильтра поступает
только часть входного сигнала.
Низкочастотный фильтр пропускает низ-
кие частоты. Если у вас есть достаточно
11 Как вы вскоре убедитесь (если еще не знаете этого),
свойство инерционности больше всего подходит для низ-
кочастотных устройств.
терпения (вернее, если у сигнала есть доста-
точно терпения) и вы дадите конденсатору
достаточно времени, чтобы зарядиться или
разрядиться почти до уровня входного напря-
жения, тогда практически весь входной сигнал
проходит на выход фильтра. Иными словами,
фильтр пропускает сигнал низкой частоты
(см. рис. 2S.13).
2S.2.3. Высокочастотный фильтр
Высокочастотный фильтр пропускает бы-
строменяющееся напряжение с входа на
выход. Процесс прохождения крутого перепа-
да входного напряжения на выход фильтра по-
нять несколько труднее. Я считаю, что процесс
понимания можно облегчить, рассматривая
поведение схемы во временной области (т. е.
представив изображение входного и выходного
сигнала на экране осциллографа), а не в более
абстрактной частотной области.
Обратитесь к схеме высокочастотного RC-
фильтра и представьте себе подачу на его вход
сигнала с перепадом напряжения, как показано
на рис. 2S.14.
Низкочастотный фильтр Вход
ослабляет высокие
частоты
\ЛЛЛ-
Быстро изменяющееся
напряжение
Выход
Не поспевает
Напряжение Uc начинает повышаться
или понижаться, но вскоре направление
входного сигнала меняется на обратное.
В результате (УВЬЕХ « UBX
Рис. 2S.12. НЧ-фильтр ослабляет быстро меняющийся входной сигнал. Выходной сигнал не поспевает за изменениями
входного
НЧ-фильтр пропускает
низкие частоты
Вход
Выход
Медленно меняющееся
напряжение
Большая часть (Увх,
поэтому фаза здесь
не сильно отличается
от фазы UBX
Есть время, чтобы
поспеть за UB
вх
Нет ни большого ослабления,
ни большого сдвига по фазе
Рис. 2S.13. НЧ-фильтр пропускает низкие частоты, поскольку у выходного сигнала есть достаточно времени, чтобы поспеть
за входным
120
2S. Дополнительный материал: RC-цепи
Начнем с рассмотрения
поведения сигнала
во временной
области
Перепад напряжения
10 В
Выход
10 В
10 В
В первый момент ВЫХОДНОЙ сигнал должен
совпадать с ВХОДНЫМ сигналом, поскольку
конденсатор не может зарядиться моментально.
Соответственно, перепад напряжения проходит
Рис. 2S.14. В первый момент ВЧ-фильтр должен пропускать перепад сигнала; только по истечению некоторого времени
выходной сигнал начинает расходиться с входным
Прямоугольные импульсы проходят. Сиг-
нал в виде меандра с перепадами вверх и вниз
представляет собой высокочастотный импу-
льсный сигнал прямоугольной формы, как по-
казано на рис. 2S.15. Подобно быстрому еди-
ничному перепаду напряжения такой сигнал
также будет проходить через фильтр, при усло-
вии, что частота следования достаточно вели-
ка. Но если входной сигнал будет находиться
на высоком или низком уровне слишком долго,
выходной сигнал может начать затухать.
остается неизменным слишком долго, то у вы-
ходного напряжения недостаточно времени,
чтобы отклониться от входного напряжения.
Таким образом, большая часть выходного сиг-
нала проходит на выход фильтра и, опять же,
если амплитуда выходного сигнала похожа на
амплитуду входного, тогда и его фаза похожа на
фазу входного сигнала. Иными словами, отсут-
ствие ослабления означает отсутствие и фазо-
вого сдвига (то же самое наблюдается и в слу-
чае с НЧ-фильтром).
Прямоугольные импульсы
с быстрым перепадом
Вход
Быстрый
перепад
Выход
Синусоидальный сигнал
с малым периодом
Вход
Выход
Если перепады уровней входного -
сигнала происходят быстро,
конденсатор не успевает
полностью зарядиться/разрядиться
Высокочастотный
входной сигнал
Рис. 2S.15. ВЧ-фильтр пропускает прямоугольный сигнал
с малым периодом между перепадами уровней
Также проходит высокочастотный сину-
соидальный сигнал. Синусоидальный сиг-
нал с малым периодом также проходит по тем
же самым причинам12: если уровень сигнала не
12 Если вы знакомы с теоремой Фурье, то это, вообще, оче-
видно для вас: то, что мы называем быстрым перепадом,
согласно Фурье можно описать, как совокупность синусо-
идальных сигналов, некоторые из которых являются
Рис. 2S.16. ВЧ-фильтр пропускает «быстрый» (т. е., высоко-
частотный) синусоидальный сигнал
Но высокочастотный фильтр не пропуска-
ет низкие частоты. Это не кажется каким-то
сюрпризом: если перепады чередуются медлен-
но, выходное напряжение располагает доста-
точным временем, чтобы начать расходиться с
входным. Таким образом, перепады входного
высокочастотными. Таким образом, выражение «крутые
перепады проходят» эквивалентно выражению «высоко-
частотные синусоидальные сигналы, составляющие пере-
пад, проходят». Эта тема рассматривается более подробно
на лабораторном занятии 3L.
25 J. Частотная развертка
121
сигнала не смогут заставить выходной сигнал
следовать ему в значительной мере. В этом
случае фаза сигнала, которому удастся достичь
выхода, будет значительно отличаться от фазы
входного сигнала. Последнее обстоятельство
мы еще не доказали, но оно выглядит правдо-
подобным, не так ли?
Но входной синусоидальный сигнал с медленными
перепадами дает возможность конденсатору зарядиться
в течение каждого периода.
Таким образом, конденсатор поглощает большую часть
входного сигнала UBX.
Очень малая часть входного сигнала достигает выхода
в виде ишх.
Вход
Выход
Медленные
перепады
Рис. 2S.17. ВЧ-фильтр плохо пропускает сигнал с медлен-
ными перепадами, поскольку время между перепадами
достаточно большое, чтобы конденсатор успел зарядиться
или разрядиться
2S.3. Частотная развертка
С помощью осциллографа мы можем ис-
следовать частотные характеристики схемы.
В частности, осциллограф может отображать
график зависимости амплитуды от частоты,
а не от времени, как при обычных измерени-
ях13. Но для этого необходимо иметь в своем
распоряжении генератор, который способен
создавать сигнал с качающейся частотой, т. е.
с регулярно меняющейся частотой. В нашей
лаборатории есть такие генераторы сигналов.
Способ развертки зависит также от типа ваше-
го осциллографа: аналоговый или цифровой.
Студенты нашего курса начинают обучение с
аналогового осциллографа, поэтому рассмо-
трение частотной развертки мы также начнем
с обзора характеристик осциллографов этого
типа.
13 Строго говоря, даже в режиме X-Y осциллограф строит
график зависимости амплитуды от времени, когда раз-
вертка по оси X осуществляется сигналом повторяющей-
ся формы типа пилообразного сигнала. Но когда частота
изменяется во времени и осциллограф должным образом
синхронизирован, горизонтальная ось наряду со време-
нем также отображает и изменение частоты.
2S.3.1. Режим непрерывной
развертки генератора сигналов
Обычно мы устанавливаем вручную фикси-
рованную частоту генерируемого сигнала. Но
генератор сигналов можно также настроить
на плавное изменение (качание) частоты вы-
ходного сигнала от начальной частоты до ко-
нечной.
Аналоговый генератор сигналов
В наших аналоговых генераторах сигналов эта
функция называется непрерывной разверткой14.
В этом режиме работы генератор сигналов мо-
жет также выдавать пилообразный сигнал для
управления основной частотой. С помощью
этого сигнала (который на наших генераторах
сигналов снимается с разъема, обозначенно-
го RAMP) можно обеспечить синхронизацию
осциллографа.
Из рис. 2S.18 можно видеть, как частота созда-
ваемого генератором синусоидального сигнала
возрастает с повышением уровня пилообраз-
ного сигнала развертки.
Размах пилообразного сигнала постоянный,
но частоту его повторения (т. е. период) можно
регулировать. Частотный диапазон основного
сигнала, выдаваемого генератором сигналов
(на рис. 2S.18 это синусоидальный сигнал),
определяется выбором начальной (START) и
конечной (STOP) частот. В генераторах сиг-
налов, используемых в нашей лаборатории,
:hif 2.00 v
5.00 V M4.00ms Aj Ch1 \ 2.76 Vs
Рис. 2S.18. Пилообразный сигнал развертки {вверху) и*
основной синусоидальный сигнал (внизу), частота которого
управляется пилообразным сигналом (непрерывная раз-
вертка)
14 Англ. frequency sweep.
122
2S. Дополнительный материал: RC-цепи
Конечная частота.
Непрерывная развертка
Выбор частотного диапазона
Начальная частота —
Пилообразный сигал
развертки из генератора^
сигналов
сигнал с
генератора сигналов
подается на вход
схемы
"Подается на вход X
осциллографа
Осциллограф отображает
частотную характеристику
схемы, в которой >
горизонтальная ось /
представляет частоту
Рис. 2S.19. Подключение генератора сигналов к осциллографу для работы в режиме частотной развертки
Для горизонтальной
развертки задан
режим X-Y
эти настройки задаются двумя ползунковыми
потенциометрами (находятся на левой сто-
роне лицевой панели генератора сигналов;
рис. 2S.19) совместно с тремя кнопками выбора
обычного диапазона (справа вверху на лицевой
панели).
2S.3.2. Частотная развертка
с использованием аналоговых
осциллографа и генератора
сигналов
Основываясь на нашем опыте, выбор спосо-
ба развертки для аналогового и цифрового
осциллографа различается. Развертку на ана-
логовом осциллографе лучше всего выполнять
в режиме X-Y, а на цифровом — в обычном ре-
жиме временной развертки.
Режим X-Y
В этом режиме развертки осциллографа она
запускается не от встроенного генератора раз-
вертки, а от сигнала, подаваемого на вход его
первого канала («Канал 1»). При выборе ре-
жима X-Y этот канал называется входом X, по-
скольку подаваемый на него сигнал управляет
горизонтальным отклонением луча осцилло-
графа, а буква X традиционно обозначает гори-
зонтальную ось графика двух переменных.
Множитель частоты
сигнал
Частота
пилообразного
сигнала развертки
Пилообразный
сигнал
развертки
7ШШ)
Входной
устройство
сигнал
Рис. 2S.20. Подключение генератора сигналов к осциллографу для работы в режиме частотной развертки
Выходной
сигнал
2S.3. Частотная развертка
123
Подключение генератора сигналов к осцилло-
графу для работы в режиме частотной разверт-
ки иллюстрируется дважды: на рис. 2S.19 по-
казана экспериментальная установка в нашей
лаборатории, а на рис. 2S.20 — эскиз схемы
подключения приборов.
На вход X осциллографа подается пилообраз-
ный сигнал, который снимается с выхода гене-
ратора сигналов, обозначенного RAMP. С левой
стороны экрана осциллографа отображается
частотная характеристика исследуемой схемы
на начальной (START) частоте, а с правой — на
конечной (END) частоте; между этими двумя
пределами отображается график при промежу-
точных частотах.
Настройка осциллографа
Сначала настроим осциллограф:
♦ Установите режим X-Y горизонтальной раз-
вертки. На аналоговых осциллографах для
этого нужно провернуть ручку развертки
против часовой стрелки в самое крайнее по-
ложение (см. рис. 2S.21).
♦ Временно установите канал Y (второй канал
на двухканальных осциллографах) в поло-
жение GND («земля»).
♦ Подайте пилообразный сигнал на канал X и
настройте усиление канала X, чтобы линия
развертки немного не доходила до края экра-
на. Но будьте осторожны, чтобы не вывести
ее за пределы экрана: слишком большое
усиление выведет конец линии развертки за
правый край экрана, где он исчезнет из виду,
или даже может пройти по кругу и выйти с
левого края экрана. В таком случае уменьши-
те усиление, чтобы линия развертки доходи-
ла только до половины экрана, как показано
на рис. 2S.22, а.
♦ Затем снова увеличьте усиление, чтобы ко-
нец линии развертки почти касался правого
края экрана, как показано на рис. 2S.22, б.
♦ Теперь переключите канал Y из положения
GND в положение DC. Наш осциллограф го-
тов отображать график амплитуды сигнала
в зависимости от частоты.
Рис. 2S.21. Установка режима X-Y развертки на аналоговом
осциллографе
Рис. 2S.22. Настройка усиления по оси X: а — усиление по
оси X («Канал 1») слишком мало: линия развертки доходит
лишь до половины экрана; б — правильное значение усиле-
ния по оси X: линия развертки проходит через весь экран, но
не выходит за его пределы
124
2S. Дополнительный материал: RC-цепи
2S.3.3. Настройка генератора
сигналов
♦ Отрегулируйте начальную (START) и конеч-
ную (STOP) частоты, чтобы отображаемый
график выглядел приемлемо. Приведем част-
ные случаи.
• Начальная частота как для НЧ-, так и для
ВЧ-фильтра должна быть нулевой (или са-
мая низкая доступная частота); конечную
частоту можно настраивать, чтобы по-
лучить желаемый график. Но эта частота
должна быть, по крайне мере, значительно
выше частоты/3дВ.
• Например, для резонансного ДЬС-контура
из лабораторного занятия 3L начальная ча-
стота должна быть не нулевой, а близкой к
частоте резонанса, чтобы можно было по-
лучить подробный вид узкой полосы про-
пускания. А конечная частота должна быть,
конечно же, выше частоты резонанса.
♦ Частота следования.
• В режиме X-Y частоту повторения импуль-
сов развертки можно свободно варьиро-
вать, не нарушая размещения изображения
графика на экране осциллографа. Этим и
объясняется использование этого режима
вместо временной развертки.
• Тем не менее частота повторения важна.
При слишком высокой частоте изображе-
ние будет грубым, поскольку слишком ма-
лое количество периодов будут доходить до
исследуемой схемы. В случае RLC-фильтра
слишком высокая частота пилообразного
сигнала развертки будет иметь еще худ-
ший эффект, выражающийся в странных
артефактах на изображении. В частности,
изображение частотной характеристики
будет содержать всплески и провалы по-
сле частоты резонанса, как показано на
рис. 2S.23.
Эти искажения объясняются тем, что коле-
бания в резонансном контуре продолжают-
ся некоторое время после снятия входного
воздействия. Эта реверберация — незату-
хающие колебания на частоте резонанса —
затем взаимодействует с входным сигналом
с постепенно меняющейся частотой.
Эти две частоты начинают накладываться
друг на друга. Иногда их амплитуды скла-
дываются, в результате чего получается
усиленный сигнал, который отображается
в виде всплеска. А иногда — при противо-
положных фазах — амплитуды вычитают-
ся, ослабляя общий сигнал, который ото-
бражается на графике в виде провала.
• Поэтому следует задать самую низкую ча-
стоту развертки, при которой график удоб-
но наблюдать (рис. 2S.24): на аналоговых
осциллографах низкая частота следования
импульсов развертки вызывает заметное
мерцание изображения.
В случае цифровых осциллографов низкая ча-
стота развертки не вызывает мерцания изобра-
жения, поскольку эти устройства сохраняют
сигнал в памяти. Но это влечет за собой задерж-
ку с обновлением изображения, что тоже неу-
добно. Например, при частоте 1 с/деление об-
новление экрана занимает около 10 с. Поэтому
найдите компромиссную частоту развертки,
с которой вам будет удобно работать.
Иногда предпочтительно использовать
режим временной развертки. Если необхо-
димо сравнить частотные характеристики двух
Рис. 2S.23. Слишком высокая частота развертки искажает
изображение частотной характеристики
Рис. 2S.24. Низкая частота развертки позволяет получить
аккуратную картину
2S3. Частотная развертка
125
И.-"
При слишком быстрой развертке
цифровой осциллограф, подобно
аналоговому, создает артефакты
Медленная развертка обеспечивает
четкое изображение (без мерцания
Огибающая кривая подчеркивает
отчетливую форму частотной
характеристики
-Рис. 2S.25. Частота следования импульсов развертки должна быть низкой, чтобы изображение на цифровом осциллографе
было четким
схем на двухканальном осциллографе, тогда
режим X-Y окажется недоступен. В этом случае
придется использовать стандартную времен-
ную развертку осциллографа (управляемую,
как обычно, ручкой настройки горизонтальной
развертки). Мы столкнемся с такой ситуацией
на лабораторном занятии 9L, где нам нуж-
но будет сравнить частотные характеристики
двух фильтров: активного и пассивного. А для
цифровых осциллографов, как упоминается в
разделе 2S3.4, этот стандартный режим ото-
бражения рекомендуется использовать во всех
случаях.
2S.3.4. Частотная развертка
на цифровом осциллографе
Настроить частотную развертку на цифровом
осциллографе проще. Хотя эти осциллографы
имеют режим X-Y, здесь он не потребуется15.
Это возможно благодаря тому, что в цифровых
осциллографах можно задать очень низкую ча-
стоту развертки без каких-либо отрицательных
эффектов в виде мерцания изображения.
Таким образом, при работе с цифровым осцил-
лографом установите временную развертку. При
этом внешний пилообразный сигнал использу-
ется не для управления осью X, а для запуска
сигнала развертки. Запуск осуществляется отри-
цательным перепадом сигнала, который обла-
дает достаточной крутизной и непосредственно
предшествует плоской части сигнала, управляю-
щей выходной частотой основного сигнала.
15 Кроме того, мы обнаружили, что на наших осцилло-
графах Tektronix TDS3014 этот режим работает не совсем
должным образом.
Единственная проблема как и для аналогового
осциллографа (см. раздел 2S.3.2), которая так-
же присутствует и для цифрового, — это про-
блема артефактов, возникающих из-за слиш-
ком высокой частоты развертки.
На рис. 2S.25 приведен пример неудачного
изображения при слишком быстрой развертке
(левое изображение) и четкого изображения,
получаемого при более медленной развертке
(среднее и правое изображения). Правое изо-
бражение отличается тем, что осциллограф
выделяет контуры частотной характеристики
огибающей кривой, делая ее более отчетливой.
Для этого вместо обычной опции «Sample»
(выборка) нужно выбрать опцию «Envelope»
(огибающая).
2S.3.5. Частотная развертка
с использованием цифровых
осциллографа и генератора
сигналов
С цифровым генератором сигналов
режим X-Y осциллографа не
используется; устанавливается обычная
временная развертка
С одной стороны цифровой генератор сигна-
лов лучше аналогового: он обеспечивает более
высокую точность развертки. Но с другой сто-
роны он хуже, поскольку не выдает пилообраз-
ного сигнала, который можно использовать
для работы в режиме X-Y. Поэтому не остается
ничего другого, кроме как установить времен-
ную развертку. В результате любое изменение
126
2S. Дополнительный материал: RC-цепи
Маркер-
Начальная частота
Выход £/.£-срильтра; сигнал с качающейся частотой
от 15,5 до 16,5 кГц
Конечная частота
Частота, соответствующая маркеру
Рис. 2S.26. Цифровой генератор сигналов позволяет выполнять более точную развертку, но использовать режим X-Y осцил-
лографа при этом нельзя
тактирования генератора сигналов вызывает
необходимость подрегулировать настройки ос-
циллографа.
На рис. 2S.26 показаны настройки генерато-
ра сигналов Agilent 33210A и соответствую-
щее изображение частотной характеристики
1?1С-фильтра из лабораторного занятия 3L.
Резонансная частота данного фильтра состав-
ляет примерно 16 кГц, а генератор сигналов
был настроен на качание частоты в диапазоне
от 15,5 до 16,5 кГц.
Генератор сигналов предоставляет удобную воз-
можность под названием «маркер», суть кото-
рой состоит в создании отрицательного перепа-
да при заданной частоте. С помощью этого мы
визуально определили максимум частотной ха-
рактеристики JRLC-фильтра (рис. 2S.26). Когда
этот отрицательный перепад совпадает с пиком
частотной характеристики, который соответ-
ствует частоте резонанса, мы можем опреде-
лить эту частоту по частоте маркера. Эта частота
(приблизительно 16,09 кГц) видна на индикато-
ре прибора в правом нижнем углу рисунка.
Но таким способом мы получаем только при-
близительное значение частоты резонанса.
Чтобы определить точное значение, потребу-
ется метод, предлагаемый на лабораторном за-
нятии 3L: наблюдать за входным и выходным
сигналами. Сначала устанавливаем частоту
входного сигнала вблизи частоты резонанса,
а затем выполняем точную настройку частоты,
пока фазы входного и выходного сигналов не
будут совпадать. При совпадении фаз мы име-
ем точную частоту резонанса.
Медленная развертка
дает наилучшие результаты
Поскольку при использовании цифрового
осциллографа изображение не мерцает, разу-
мно выбрать медленную развертку. Это позво-
лит избежать уродливых искажений графика
частотной характеристики, пример которых
приводится справа на рис. 2S.27. Мы уже упо-
минали об этой проблеме в разделах 2S.3.3 и
2S.3A.
Развертка с периодом в 1 секунду обеспечивает
достаточно четкое изображение (хотя даже и в
этом случае можно, если присмотреться, уви-
деть признаки артефактов). А вот изображе-
ние при развертке с периодом 30 мс содержит
2S.3. Частотная развертка
127
s t
Маркер
Медленная развертка (время развертки: 1 с) Быстрая развертка (время развертки: 30 мс)
Рис. 2S.27. Медленная развертка позволяет получить качественное изображение частотной характеристики, тогда как бы-
страя развертка искажает его
очевидные признаки биения входной и резо-
нансной частот, подобные тем, что мы видели
на рис. 2S.23 в разделе 2S.33.
Кроме того, на изображении при быстрой раз-
вертке наблюдается еще более странное искаже-
ние: сдвиг кажущейся частоты резонанса. Это ил-
люзия, создаваемая в результате задержки, необ-
ходимой для того, чтобы довести Д1С-контур до
резонанса. Справа на осциллограмме рис. 2S.27
видна задержка почти в 1 мс между моментом
подачи частоты резонанса (обозначаемого от-
рицательным перепадом сигнала тактирования)
и моментом, когда выходное напряжение RLC-
контура достигает максимального значения.
Чтобы получить истинное изображение, нуж-
но запастись терпением и подождать секунду-
другую, пока не закончится цикл развертки.
2W. Примеры с решениями: /?С-цепи
2\Л/.1./?С-фильтры
2W.1.1. Фильтр для выделения
сигнала и ослабления помехи
Задача: создать фильтр
для устранения пульсаций
Предположим, что сигнал у вас выглядит так,
как показано на рис. 2W.1: частота не слишком
высокая, а амплитуда искажена помехой в виде
пульсаций с большей частотой.
Рис 2W.1. Сигнал с пульсациями огибающей
1. Сначала набросайте базовую принципиаль-
ную схему (без значений элементов), которая
будет пропускать большую часть полезного
сигнала, удаляя из него пульсации.
2. Затем определите значения компонентов:
♦ Если нагрузка превышает 100 кОм, опреде-
лите значение R для схемы.
♦ Определите частоту /3дЪ; вкратце объясните
свое решение.
♦ Определите значение емкости С, чтобы полу-
чить выбранную вами частоту^дБ.
♦ Оцените, насколько ваша схема будет ослаб-
лять помеху. Подумайте, какой входной им-
педанс будет у вашей схемы в различных
случаях:
• на очень низких частотах?
• на очень высоких частотах?
• на частотеУздБ?
3. Что будет с сигналом на выходе схемы в слу-
чае сопротивления нагрузки величиной не
100 кОм, а 10 кОм?
Решение
Выбор базовой принципиальной схемы.
Прежде всего нам нужно решить, какой тип
фильтра нам требуется: низкочастотный или
высокочастотный, поскольку полезный сигнал
и помеха имеют разные частоты (находящие-
ся на значительном расстоянии друг от друга,
что дает нам надежду удалить помеху, не за-
трагивая полезный сигнал, с помощью простых
фильтров, которые мы только что рассмотре-
ли). Поскольку в постановке задачи полезный
сигнал определен, как низкочастотный, нам
требуется низкочастотный фильтр. Базовая
принципиальная схема такого фильтра показа-
на на рис. 2W.2.
Рис. 2W.2. Базовая принципиальная схема НЧ-фильтра
Определяем значение резистора R для за-
данной нагрузки. Зависимость значения ре-
зистора R от величины сопротивления нагруз-
ки следует из того заключения, что номинал
резистора R ДС-фильтра определяет входной и
выходной импедансы фильтра для наихудшего
случая (см. главу 2N). Мы хотим, чтобы выход-
ной импеданс был низким относительно импе-
данса нагрузки. Наше эмпирическое правило
гласит, что «низкий» означает в 10 раз мень-
ший. Таким образом, сопротивление нашего
резистора должно быть jR < Д^^/ДО, т. е. со-
противление R должно быть <10 кОм. Давайте
выберем номинал 10 кОм.
2W.L ЙСфильтры
129
Выбираем частоту f3jjfi. Это единственная
часть нашей задачи, решение которой не со-
всем прямолинейно. Мы знаем, что нам нужно
пропускать низкие частоты и ослаблять высо-
кие, но означает ли это, что мы должны уста-
новить частотуУздБ посередине между частотой
полезного сигнала и помехи? Или ближе к ча-
стоте полезного сигнала? А может быть, ближе
к частоте помехи? Должны ли эти частоты на-
ходиться на крутом спаде частотной характе-
ристики фильтра?
ПОМЕХ
Рис. 2W.3. Возможные значения частоты fz
ЗдБ
Поскольку наша цель — получить большое от-
ношение между полезным и мешающим сигна-
лами, частоту/3дЪ не следует выбирать близко к
частоте помехи, поскольку в таком случае по-
меха не будет ослабляться должным образом.
Выбор частотыУздБ посередине между частотой
сигнала и помехи немногим лучше предыдуще-
го. Наилучшим значением/3дБ будет вблизи ча-
стоты сигнала: мы будем максимально ослаб-
лять помеху, при этом почти не затрагивая по-
лезный сигнал.
Наблюдательный студент может сказать, что
отношение сигнал/помеха будет наибольшим,
когда обе частоты находятся на наиболее кру-
той части кривой частотной характеристики,
иными словами, частоту /3дБ следует взять на-
столько низкой, чтобы ослаблялась как по-
лезная, так и помеховая частота. Это разумное
решение, но в большинстве обстоятельств не-
правильное.
Проблема здесь состоит в том, что полезный
сигнал предполагается состоящим лишь из
одной частоты. Но обычно сигнал содержит
диапазон частот, и выбор частотыУздБ где-либо
в пределах этого диапазона будет иметь пло-
хие последствия в виде искажения сигнала
фильтром.
Поэтому, выберем для частоты /3лБ значение
2 '/СИГНАЛАСМАКО' Т- е' W™ В РаЙ0Не 2 КГЧ* ЭТ0
оставит нам около 89% амплитуды исходного
сигнала (мы утверждали это в главе 2N; если
хотите, вы можете проверить это утверждение,
начертив векторную диаграмму или выполнив
расчет). Кстати, фазовый сдвиг на этой часто-
те также не слишком велик — около 25°. Опять
же, это можно проверить с помощью векторной
диаграммы или вычислений. При этом мы смо-
жем значительно ослабить помеху на частоте
16 кГц (насколько значительно мы увидим чуть
далее).
Определяем емкость С, чтобы получить вы-
бранную частотуУздб* Это можно сделать, про-
сто подставив значения в формулу для вычисле-
ния частоты^:
(2nRC)
1
=>С =
6(2.1О3)(НЫО3) (120 -106)
«0,008-10-6Ф.
Конденсатор емкостью 0,01 мкФ будет впол-
не приемлемым. При этой емкости частота /3дБ
окажется на 25% ниже — в районе 1,6 кГц,
но наш первоначальный выбор был в любом
случае первым приближением1.
Но насколько наш фильтр будет ослаблять по-
меху (пульсации)? Ответ на этот вопрос можно
получить двумя способами:
♦ Расчет отношения^^х,,/^^. Ослабление
будет приблизительно пропорционально это-
му отношению, поскольку амплитуда умень-
шается в пропорции 1/f (или -6 дБ/октаву).
В нашем случае/П0МЕХИ//3дБ = 16 кГц/2 кГц = 8:1.
Таким образом, на частоте /3дБ амплитуда
должна понизиться до приблизительно 1/8 ее
начального уровня. Таким образом, результат
будет приблизительно 0,125 • 0,7 = 0,08. Но в
действительности амплитуда окажется немно-
го большей, поскольку крутизна полностью
соответствует1//"только в пределах нескольких
октав выше частоты^дБ.
1 Мы можем получить точное значение частоты /3дБ, из-
меняя значение резистора R. Тогда как выбор номинала
конденсатора ограничен, мы можем выбрать любое значе-
ние резистора (хотя, при допуске значения конденсатора
в пределах ±10% не имеет смысла задавать значение рези-
стора более точно, чем с погрешностью ±10%).
130
2W. Примеры с решениями: RC-цепи
♦ Подсчет октав. Можно также сказать, что
частота удваивается трижды (= 23) между
частотой/3дБ и частотой помехи. Грубо гово-
ря, это означает, что амплитуда пульсаций
уменьшается наполовину такое же количе-
ство раз: до (1/2)3:1/8. Опять же, это верно
относительно амплитуды на частоте ^дБ, где
амплитуда уже снижена до 70%.
Что будет с сигналом на выходе схемы
при сопротивлении нагрузки не 100 кОм,
а 10 кОм?
На рис. 2W.4 приведена принципиальная схема
с такой нагрузкой.
10 кОм <*— ZBbEX: наихудший случай"
ЮкОм ---!-
__ 0,01 мкФ
= ЮкОм
Рис. 2W.4. Перегруженный фильтр
Если вы уже хорошо научились пользоваться
эквивалентными схемами Тевенина, то легко
сможете преобразовать исходную схему, изо-
браженную на рис. 2W.5, в более знакомую.
Эффективное сопротивление уменьшено вдвое
5кОм
: 0,01 мкФ
Рис. 2W.5. Нагруженная схем в преобразованном виде
Амплитуда упала, но что еще хуже, частота/3аЪ
удвоилась. Данный эффект показан на графике
на рис. 3N.2.
Каков входной импеданс вашей схемы:
1. На очень низких частотах?
Ответ: очень высокий. Импеданс конденсато-
ра высокий; источник сигнала «видит» только
нагрузку, которая имеет очень высокий импе-
данс (достаточно высокий, чтобы его можно
было игнорировать при оценке эффективности
фильтра).
2. На очень высоких частотах?
Ответ: равный сопротивлению R. Импеданс
конденсатора стремится к нулю и входной им-
педанс определяется номиналом резистора R.
3. На частоте^?
Ответить на этот вопрос легко, если исполь-
зовать не формулы, а векторную диаграмму.
Сначала вспомним, что на частоте/3дБ величи-
на реактивного сопротивления конденсатора
Zc = R. Затем, если учесть, что напряжения на
резисторе R и конденсаторе С сдвинуты по фазе
на 90° по отношению друг к другу, в результа-
те чего их можно отобразить в виде векторов
под прямым углом друг к другу, мы получим
векторную диаграмму как на рис. 2N.32. Теперь
можно воспользоваться геометрическим дока-
зательством, чтобы показать, что величина ги-
потенузы (которая пропорциональна входному
импедансу ZBX) будет составлять R\JY.
2W.1.2. Полоса пропускания
Задача: Полосовой фильтр
Разработайте полосовой фильтр для пропу-
скания сигналов в диапазоне от приблизитель-
но 1,5 кГц до 8 кГц. Для этого обе частоты /3лЪ
должны быть вдвое больше, чем ближайшая
граничная частота. (Таким образом, ослабле-
ние составляет около 10%, как мы узнали из
раздела 2W.1.1.) Предположим, что выходной
сигнал нашего полосового фильтра подается на
следующую схему, входной импеданс которой
составляет > 1 МОм.
Решение
На рис. 2W.6 показан примерный график ча-
стотной характеристики, который мы хотим
получить от этого фильтра.
Чтобы получить такую частотную характери-
стику, нам нужно последовательно соединить
'ЗдБ
Частота
Рис. 2W.6. Требуемая частотная характеристика разрабаты-
ваемого полосового фильтра
2W.I RC-фильтры
131
ВЧ- и НЧ-фильтр. Частота y^u для ВЧ-фильтра
должна быть около половины самой нижней тре-
буемой частоты, поэтому примем ее равной око-
ло 750 Гц. А частота/^ для НЧ-фильтра должна
быть вдвое выше самой высокой требуемой ча-
стоты, поэтому примем ее равной около 16 кГц.
На рис. 2W.7 показаны частотные характери-
стики для ВЧ (слева) и НЧ (справа) фильтров.
Частота отображается на горизонтальной оси в
диапазоне от почти нулевой до 30 кГц.
При каскадном (т. е. последовательном) соеди-
нении этих двух фильтров входной сигнал будет
подвергаться двойной нагрузке, в результате
чего на граничных частотах будет происходить
ослабление сигнала, а посередине диапазона
появится небольшой подъем (рис. 2W.8).
На линейном графике частотной характеристи-
ки можно убедиться, что полоса пропускания
далеко не идеальна, где под идеалом подразуме-
вается фильтр, задерживающий все ненужные
и пропускающий все нужные частоты. Вместо
«плато» с крутыми краями этот график боль-
ше похож на пологое «предгорье». На логариф-
мическом графике частотная характеристика
выглядит немного более привлекательной и
ВЧ-фильтр (^3дБ = 750 Гц)
Частота по оси Хот 0 до 30 кГц
НЧ-фильтр (f3uB = 16 кГц)
Частота по оси Хот 0 до 30 кГц
Рис. 2W.7. Частота f составляет 750 Гц и 16 кГц для ВЧ- и НЧ-фильтра соответственно
f3aB ВЧ-фильтра
Частотный диапазон сигнала
^здб НЧ-фильтра
-ЗдБ
«
'/^ШШтт®^
Полоса пропускания: линейный масштаб
(Частота по оси Хот 0 до 30 кГц)
» " ).- 'Si**'*
111
;^"^ *
V
Полоса пропускания: логарифмический масштаб
(Частота по оси Хот 0 до 30 кГц)
Рис. 2W.8. Требуемая частотная характеристика полосового фильтра: линейный (слева) и логарифмический (справа) графики
132
2W. Примеры с решениями: RC-цепи
ЮкОм
(Т) Выберите такие значения резисторов,
чтобы Z^ « ZBX4:nEfl.MCKAflA
0,002 ллкФ
Затем вычислите
номиналы
конденсаторов
= 0,001 мкФ
100 кОм
= 1 МОм
Рис. 2W.9. Принципиальная схема полосового фильтра
будто бы содержит плоский участок в пределах
полосы пропускания. Но, конечно же, видоиз-
мененный масштаб не меняет саму характери-
стику. Но если мы ограничены простыми RC-
фильтрами, то придется довольствоваться этой
неидеальной, пологой полосой пропускания.
Определяем значения резисторов
фильтров
Теперь нам нужно выбрать номиналы резисто-
ров, поскольку они будут определять импедан-
сы наихудших случаев для этих двух фильтров.
Выходной импеданс ZBbIX фильтра второго ка-
скада должен быть низким относительно на-
грузки, которая составляет 1 МОм; а выходной
импеданс ZBUX фильтра первого каскада дол-
жен быть низким относительно входного им-
педанса ZBX фильтра второго каскада.
Так что пусть номинал резистора фильтра
второго каскада будет 100 кОм, а первого —
10 кОм.
Затем вычисляем значения конденсаторов
Единственная тонкость состоит в том, чтобы
не перепутать фильтры: условие, что частота
/здб Д°лжна быть ниже для высокочастотно-
го фильтра, кажется неправильным, но это в
действительности так. Обратите внимание,
что при вычислениях мы стараемся использо-
вать экспоненциальное представление чисел,
например, 10 • ДО3, а не ДО4. Хотя такая запись
выглядит неуклюже, зато мы получаем ответы
в стандартных единицах. Польза здесь еще и
в том, что легко выявить нелогичности в поста-
новке задачи: увидеть, что 10 • ДО3 некорректно
представляет 10 кОм легче, чем ошибочную
запись ДО5.
Расчет номиналов обоих конденсаторов стан-
дартный.
Для НЧ-фильтра:
/здб-нч=16кГц=>С =
1
2я1610310103
«1/109 =0,001 мкФ.
Для ВЧ-фильтра:
1
2я - 0,75 -103-100 -103
« 1/(0,45-109)« 0,002 мкФ.
А теперь давайте изобразим принципиальную
схему двухкаскадного полосового фильтра
(рис. 2W.9).
2W.2. Переходная
характеристика /?С-цепи
Недавно на одном из занятий мы были непри-
ятно удивлены, насколько непривычной может
оказаться такая «старая» тема, как поведение
JRC-цепей, когда она даже слегка отличается
от стандартного случая. Несколько студентов
убедили нас в необходимости дополнительной
практики по данной теме. Далее приводится
несколько упражнений по ДС-цепям.
2W.2.1. Задача: переходная
характеристика /?С-цепи
(анализ во временной области)
На рис. 2W.10 показана подача прямоугольно-
го импульса через конденсатор на некоторую
2W.2. Переходная характеристика RC-цепи
133
(Нужен график напряжения в этой точке)
10В
0В
Вход
Входной импульс
10 мкс
кФ
yf Последующий каскад
Рис. 2W.10. Прямоугольный импульс, подающийся через емкостную связь на последующий каскад
схему. Для каждого из таких случаев нарисуйте
график сигнала в точке, где конденсатор под-
ключается к следующему каскаду в точке, обо-
значенной X. Укажите масштаб для времени и
напряжения, а также обозначьте важные точки
на графике сигнала. Как обычно, нам будет до-
статочно ответов с погрешностью около 10%.
Как #вх_х, так и Свхх описывают параметры
параллельно соединенных компонентов — ре-
зистора и конденсатора, у каждого из которых
один из выводов подключен к фиксированному
потенциалу. Предположим, что этим потенциа-
лом является «земля», просто чтобы все наши
схемы выглядели одинаково.
Примечание
Нужно нарисовать график выходного напряжения
1/вых, а не напряжения на конденсаторе Uc
Далее приводится перечень возможных по-
следующих каскадов (для подстановки вме-
сто X):
♦ идеальный каскад: JRBX.X = «>, Свх.х = 0;
♦ смешанный каскад: Двх_х = °°, но Свх.х =
= 0,001 мкФ;
♦ смешанный каскад: Двх_х = 100 кОм, Свх.х = 0;
♦ смешанный каскад: RBXX = 1 кОм, Свх.х = 0;
♦ неидеальный каскад: #вхх = 100 кОм, Свхх =
= 0,01 мкФ.
Решение
Идеальный последующий каскад:
ЛВХ X = °°' СВХ-Х = 0
В связи с отсутствием пути для прохождения
тока на другую пластину конденсатора или
с нее 1С = 0 и Uc остается нулевым. Поэтому
10В
ob
п
J L
JU
HI—
Рис. 2W.11. Нулевое сопротивление, нулевая емкость
Смешанный последующий каскад:
10 В
Это будет емкостной делитель С-С (редко
встречающийся или нереализуемый в действи-
тельности). Форма выходного напряжения
ILTY точно такая же, как и входного [7 но
'вых
ВХ'
амплитуда ослаблена в зависимости от импе-
дансов двух конденсаторов. [/вых = 0,9 UBX (рис.
2W.12). Чтобы эта схема была практически зна-
чимой, для постоянного тока требуется путь на
«землю».
ю В
ов
0,01 мкФ
0,001 мкФ
Рис. 2W.12. Емкостной делитель
Смешанный последующий каскад:
Явхх=100кОм,Свхх = 0
Постоянная времени RC = 1 мс, значительно
превышает длительность импульса. Поэтому в
течение импульса напряжение Uc не изменится
2 Это нереалистичный случай. При отсутствии пути для
постоянного тока с правого вывода на «землю», конден-
сатор постепенно зарядится токами утечки. Для практиче-
ской схемы на выходе требуется резистивный путь на «зем-
лю», чтобы создать разность потенциалов на этом выходе.
134
2W. Примеры с решениями: RC-цепи
значительно. Таким образом, выходное напря- +ю В
жение [7ВЫХ выглядит подобно входному [/,
ВЫ ВХ
(рис. 2W.13). Данный случай почти соответ-
ствует первому случаю, рассмотренному в этом
разделе. Опять же, [/вых = UBX.
в
ов
0,01 мк*
"Л
- +10 В
ов
100 кОм
Рис. 2W.13. Приблизительно то же самое, что и первый слу-
чай: сигнал проходит полностью
Смешанный последующий каскад:
Постоянная времени RC = 0,01 мкс, соизмери-
ма с длительностью импульса. Поэтому в тече-
ние импульса выходное напряжение ослабится
до UBX • (1/е) « 0,3717вх. Выходное напряжение
ишх резко возрастает до +10 В, снижается до
ов
0,01 мкФ
—\\-r-
-6,3 В
Л кОм
Рис. 2W.14. Малая постоянная времени RC приводит к по-
явлению экспоненциальных спадов
около +4 В, резко падает до -6 В, а затем экспо-
ненциально уменьшается до нуля (рис. 2W.14).
Неидеальный последующий каскад:
Д^.х = 100 кОм, Свхх = 0,01 мкФ
Перерисуем схему в виде емкостного делителя
с резистором на выходе (это наша знакомая
эквивалентная схема Тевенина — резистивный
делитель). Как и в модели Тевенина эквива-
лентная емкость равна двум параллельным ем-
костям: 0,02 мкФ. Таким образом, постоянная
времени RC = 2 мс. Опять длительность им-
пульса намного меньше постоянной времени
RC, в результате чего он проходит на выход, но
амплитуда снижается вдвое (рис. 2W.15).
ов
0,01 мкФ
100 кОм
.л
*"
:O,oi мкФ
0,02 мкФ
Рис 2W.15. Емкостной делитель с резистором на выходе: пропускает импульс, но ослабляет его вдвое
3N. Схемы с диодами
Содержание
3N.1. Сильно нагруженный фильтр: еще одна причина, по которой следует
придерживаться правила 1:10 135
3N.2. Щуп осциллографа 136
3N.2.1. Неправильный щуп 10Х 137
3N.3. Индуктивности 139
3N.4. Резонансный LC-контур 140
3N.4.1. Резонанс 140
3N.4.2. Значение добротности Q 142
3N.4.3. Проверяем, был ли прав Фурье 143
3N.4.4. Реакция на низкочастотный прямоугольный сигнал: «звон» 144
3N.5. Схемы с диодами 145
3N.6. Самое важное применение диода: выпрямление переменного тока 146
3N.6.1. Однополупериодный выпрямитель и ограничитель напряжения 146
3N.6.2. Двухполупериодный мостовой выпрямитель 146
3N.6.3. Стабилитроны (зенеровские диоды) 148
3N.7. Самое важное применение диода: источник питания
(нестабилизированный) 149
3N.7.1. Напряжение вторичной обмотки трансформатора 150
3N.7.2. Конденсатор 150
3N.7.3. Номинальный ток трансформатора
(нагрев, вызываемый действующим током) 151
3N.7.4. Номинал плавкого предохранителя 152
3N.8. Радиоприемник 152
3N.8.1. Шаг 1: LC-фильтр пропускает одну несущую частоту 153
3N.8.2. Шаг 2: Детектируем огибающую АМ-сигнала 154
3N.8.3. Результаты выпрямления несущего колебания 155
3N.8.4. Извлечение аудиоинформации 155
3N.9. Материал для чтения в АоЕ 157
Цель этой главы
Задача, которую мы намереваемся решить с помощью рассматриваемой далее очень важной схемы,
заключается в преобразовании синусоидального напряжения питания, получаемого из электросети
(часто называется напряжением сети или линейным напряжением), в постоянное напряжение.
3N.1. Сильно нагруженный
фильтр: еще одна причина,
по которой следует
придерживаться
правила 1:10
В разделе 1N.4.6 мы установили эмпирическое
правило для разработки схем, гласящее, что им-
педанс входного каскада должен быть в десять
раз больше импеданса выходного каскада схе-
мы. Давайте еще раз проверим его, выяснив,
что происходит с фильтром при нарушении
этого правила.
Предположим, что имеется низкочастотный
фильтр (рис. 3N.1), частота У^; которого чуть
выше 1 кГц (мы рассматривали такой фильтр
в прошлый раз).
Если сопротивление нагрузки RH составляет
150 кОм или больше, такая нагрузка не слиш-
ком сильно ослабляет сигнал, и частота /3дЪ
136
3N. Схемы с диодами
15кОм
15кОлл
7,5 кОм
——. 0,01 мкФ
0,01 мкФ ZZZ
15кОлл =
__ 0,01 мкФ
а б в
Рис. 3N.1. Низкочастотный ЯС-фильтр: без нагрузки (а), перегруженный (б) и его эквивалентная схема (в)
1.0'
07
Частота
первоначальная
при нагрузке
Рис. 3N.2. Сильно нагруженный фильтр: ослабление сигнала
меньше и, что гораздо хуже, частота /здб смещена
не меняется. Выясним теперь, что будет, если
уменьшить нагрузку до RH = 15 кОм. Ослабление
сигнала будет меньшим из-за двух эффектов.
Посмотрите на рис. 3N.2 и вы поймете, что про-
исходит с частотойУздБ.
Сдвиг частоты /3дЪ с ее заданной точки (в дан-
ном случае происходит ее удвоение) — намно-
го более серьезная проблема, чем чрезмер-
ное ослабление сигнала по постоянному току.
Ослабление по постоянному току можно ском-
пенсировать, повысив усиление последующего
каскада, но смещенную частоту/^ не так легко
исправить с помощью каких-либо мероприятий
в следующем каскаде. Будем надеяться, что этот
пример подтвердит целесообразность правила
десятикратного входного импеданса. Это пра-
вило позволяет нам разрабатывать схемы по
частям с уверенностью, что подключение ново-
го каскада не окажет отрицательного влияния
на уже существующую схему.
3N.2. Щуп осциллографа
Рассмотренная ранее проблема подводит нас
к задаче, как правильно разработать щуп (или
пробник) для осциллографа. В частности, из
нее следует, что такой щуп должен иметь как
можно более высокий входной импеданс1.
Возможно, что такое требование покажется вам
излишним, поскольку осциллограф с подклю-
ченным щупом и BNC-кабелем имеет входной
импеданс величиной 1 МОм, параллельно ко-
торому подключена емкость самого кабеля.
Но этот входной импеданс, представляемый
кабелем и осциллографом, в действительности
является довольно скромным и может быть
причиной неприятностей в основном из-за па-
разитной емкости.
На первый взгляд импеданс в 1 МОм выгля-
дит внушительным, но давайте посмотрим, как
влияет на него повышение частоты. Для кабеля
длиной около одного метра паразитная емкость
совместно с входной емкостью осциллографа
составляет около 100 пФ. Может показаться,
что 100 пФ это совсем малая емкость, но на ча-
стоте 1 МГц нагрузка будет большой:
(б-Ю'-ОД-КГ9)
(б-
«1,6кОм.
Полученное значение довольно невелико, но
при высоком импедансе источника оказывает-
ся вообще недопустимо малым. Мы поймем это
в процессе разработки хорошего щупа. Но сна-
чала мы создадим пробник с неправильными
характеристиками.
Большая паразитная емкость BNC-кабеля на-
гружает исследуемые схемы, и в результате не
только ослабляется сигнал, но и возникают дру-
гие нежелательные эффекты. Наиболее распро-
страненное аномальное поведение исследуемой
схемы — самовозбуждающиеся колебания2.
АоЕ Exercise 1.44.
2 Проблема нежелательных колебаний (так называемых
паразитных колебаний) будет представлять для нас боль-
шой интерес, но на последующих лабораторных заняти-
ях (это основная тема лабораторного занятия 9L). Такие
колебания не могут возникнуть, пока мы не добавим к
нашим схемам усилитель. Поэтому, рассматриваемые
на данном этапе схемы не будут создавать паразитных
колебаний даже при большой нагрузке BNC-кабелем.
3/V.2 Щуп осциллографа
137
Поэтому мы почти всегда применяем пробники-
делители с коэффициентом ослабления 10Х:
с таким щупом входной импеданс осциллографа
в 10 раз выше, чем со щупом IX. Со щупом IX
импеданс осциллографа составляет 1 МОм при
параллельной емкости (кабеля щупа) 100 пФ,
со щупом 10Х входной импеданс оказывается
в 10 раз лучше: 10 МОм при параллельной ем-
кости кабеля 10-12 пФ.
3N.2.1. Неправильный щуп 10Х
На рис. 3N.3 изображена ошибочная принци-
пиальная схема щупа 10Х.
9 МОм
/V
Осциллограф
1МОм-
_:100 пФ
I Паразитная
1 емкость
Рис. 3N.3. Ошибочная принципиальная схема щупа 10Х для
осциллографа
Понятно ли вам, что не так с этой схемой? С сиг-
налами постоянного тока она работает долж-
ным образом. Но попробуйте преобразовать
ее в эквивалентную схему Тевенина, в которой
сигнал проходит через конденсатор на землю,
как в примере на рис. 3N.1. Это должно сделать
ошибку очевидной. Подумайте, какая у этой
схемы будет частота /3дБ. Довольно низкая, по-
скольку эффективное сопротивление, через ко-
торое сигнал подается на паразитную емкость
(ДТЕВ), велико (почти 1 МОм):
2nRC (2.3-106-100-l(r12)'
Подставив значения, получим
/здб1
0,6 • 10"
■«1,6 кГц.
Но в лабораторном занятии 4L мы можем увидеть это
нежелательное явление, поскольку любая из рассматри-
ваемых в нем транзисторных схем обладает усилением,
необходимым для поддержки колебаний. Паразитные ко-
лебания - это хотя и интересное, но весьма нежедатель-
ное явление, с которым мы вскоре столкнемся.
Это недопустимо для осциллографа, предна-
значенного для работы с частотами в диапазоне
многих десятков мегагерц.
Решение проблемы
Наш щуп не должен быть низкочастотным
фильтром, т. е. осциллограф и щуп должны
одинаково реагировать на все представляющие
интерес частоты (верхний предел диапазона за-
дается максимальной рабочей частотой осцил-
лографа, которая для большинства осцилло-
графов в нашей лаборатории равна 60 или даже
100 МГц).
Решить проблему несложно: нужно всего лишь
создать два параллельных делителя напряже-
ния — один резистивный, а другой емкостной
(рис. 3N.4). Тот или иной делитель будет до-
минировать на соответствующей граничной
частоте (т. е. будет пропускать большую часть
тока), а между этими пределами они будут ра-
ботать совместно. Но если каждый из этих де-
лителей выдает напряжение величиной С/вх/Ю,
то в этом промежуточном диапазоне будет все
в порядке.
9 МОм
1
9Х,
кС-ПАРАЗИТНОЕ
^С-ПАРАЗИТНОЕ
Рис. 3N.4. Два делителя ослабляют входной сигнал, подавае-
мый на осциллограф, в 10 раз
Что произойдет, если мы просто соединим вы-
воды этих двух делителей? Нужно ли нам бу-
дет анализировать получившуюся составную
схему как единое целое, что достаточно слож-
но? Нет, этого не понадобится. Вдоль линии,
соединяющей оба делителя, не протекает ни-
какого тока, поэтому все остается предельно
простым.
Таким образом, хороший пробник — это всего
лишь два соединенных вместе делителя напря-
жения, как показано на рис. 3N.5 (где паразит-
ная емкость С соответствует общей паразитной
емкости осциллографа и кабеля щупа). В на-
стоящих щупах величину добавленной емкости
можно регулировать. В результате возникает
138
3N. Схемы с диодами
щ 1
if с \
о\ 1 (
^ИпФ
^ <
^ <
I 100 пФ
t =|= Паразит
L _Lемкость
Рис. 3N.5. Высококачественный щуп: один из конденсаторов
можно регулировать, чтобы щуп можно было подключать
к осциллографам с разными входными емкостями
вопрос, как узнать, правильно ли отрегулиро-
ван щуп, чтобы он реагировал на все частоты
одинаково?
Проверка щупа методом частотного
сканирования
Один из способов проверить эквивалентную
характеристику щупа и осциллографа — скани-
ровать частоту в диапазоне от нуля до верхнего
предела частотного диапазона осциллографа,
одновременно наблюдая амплитуду сигнала на
экране. На рис. 3N.6 изображены фрагменты
осциллограмм при неправильной регулировке
корректировочной емкости СК0РР в обоих на-
правлениях, и с правильной настройкой по-
середине.
На низких частотах доминирует резистив-
ный делитель, а на высоких (выше точки, на-
зывающейся частотой перехода) — емкостной.
Каждый из делителей должен ослаблять сигнал
точно в 10 раз. При неправильной настройке ем-
костного делителя он будет выдавать больший
или меньший сигнал, как показано на рис. 3N.6.
Переходная частота зависит от эффективной
постоянной времени RC эквивалентной схемы,
изображенной на рис. 3N.7.
Но описанный способ проверки правильности
корректировочной емкости слишком непрак-
тичен. Во-первых, для него требуется высоко-
качественный генератор сигналов, а во-вторых,
не особенно удобно собирать установку каждый
раз, когда нужно просто проверить щуп.
Практичный способ настройки щупа
Более практичный способ настройки щупа —
подать на него сигнал прямоугольной фор-
мы, а затем посмотреть, выглядит ли он дей-
ствительно прямоугольным на экране. Если да
(рис. 3N.8, в), то со щупом все в порядке: все
частоты обрабатываются одинаково. Если же
форма сигнала на экране отлична от прямо-
угольной (рис. 3N.8, а, б), просто отрегулируйте
подстроечный конденсатор щупа, пока сигнал
не будет выглядеть должным образом.
Очевидно, что данный способ намного удоб-
ней предыдущего. Он настолько хорош, что у
и,
ОД
Завышенный уровень
Заниженный уровень
1 10 100 Гц 1 10 100 кГц 1 10 100 МГц
Рис. 3N.6. Проверка щупа методом частотного сканирования
Правильный
уровень
logf
К осциллографу
«110 пФ
U/10, если Сподстр
настроена правильно
К осциллографу
►
0,9 МОм
hm =>
Рис. 3N.7. Схема щупа, изображенная в виде эквивалентной КС-цеп и
3N.3. Индуктивности
139
1
;
1
Рис. 3N.8. Проверка и настройка щупа осциллографа с помощью прямоугольного сигнала: а — завышает высокие частоты;
б—занижает высокие частоты; в — пропускает высокие и нижние частоты одинаково (ослабляет сигнал в десять раз)
каждого более-менее солидного осциллографа
есть выход с сигналом прямоугольной формы
именно для этой цели. Данный разъем обозна-
чается как Probe Comp или Probe Adjust. Сигнал
на этом разъеме обычно имеет частоту 1 кГц и
амплитуду 1 В.
3N.3. Индуктивности
В курсе по физике к катушкам индуктивности
относятся с таким же уважением, как и к кон-
денсаторам, поскольку свойства этих двух ком-
понентов дополняют друг друга. Рассмотрим
импеданс каждого из них.
Импеданс конденсатора:
Импеданс катушки:
Импедансы этих двух устройств комплемен-
тарны в двух отношениях:
♦ импеданс конденсатора Zc снижается с повы-
шением частоты, а импеданс катушки индук-
тивности ZCL_ повышается;
♦ фазовые сдвиги между током и напряжением
на катушке и конденсаторе противоположны
друг другу, что обозначается противополож-
ными знаками в -j и j. В конденсаторе ток
опережает напряжение, а в катушке отстает
от него.
Отсюда можно сделать вывод, что как конден-
сатор, так и катушку можно использовать для
создания фильтра. Например, на рис. 3N.9
Низкочастотный А£-<рильтр Низкочастотный £/.-<рильтр
Рис 3N.9. В принципе, фильтр можно создать, используя со-
вместно с резистором как конденсатор, так и катушку
приводятся принципиальные схемы двух вари-
антов НЧ-фильтра — один с емкостью, а другой
с индуктивностью.
Оба варианта НЧ-фильтра работоспособны.
Но лишь фильтр с конденсатором практичен
на любых частотах, за исключением очень вы-
соких3.
В нашем курсе (и в электронике вообще) кон-
денсаторы встречаются намного чаще, чем ка-
тушки индуктивности4. Это предпочтение объ-
ясняется тем, что катушки имеют сравнительно
большие габариты и массу (они часто содержат
железный сердечник, или сердечник из дру-
гого магнитопроводящего материала). Кроме
того, в связи со своей неидеальностью катушки
рассеивают мощность, т. е. расточают электро-
энергию.
На шуточном5 рис. 3N.10 самодовольный кон-
денсатор напоминает нам об этой разнице, и,
3 Высоких по стандартам этого курса: около 1 МГц и
выше.
4 АоЕ§ 1.7.10.
5 Шутка будет более понятной, если учесть, что англий-
ское слово dissipate кроме «рассеивать, расточать»' также
имеет значение «кутить, развлекаться; вести распутный
образ жизни».
140
3N. Схемы с диодами
подобно многим самодовольным лицам, он
несколько преувеличивает свое достоинство6.
Рис. 3N.10 Конденсаторы в отличие от катушек обычно не
рассеивают большую мощность
Поэтому разработчики электронных устройств
отдают предпочтение конденсатором и избе-
гают катушек практически во всех случаях, за
исключением высокочастотных схем (при ча-
стотах выше 1 МГц, где небольшая индуктив-
ность будет достаточна для решения задачи)
или в инверторов (где без индуктивностей не
обойтись).
Резонансный Д1С-контур, который мы исполь-
зуем для выбора частоты радиопередачи на
лабораторном занятии 3L, служит наглядным
примером задачи, с которой индуктивности
справляются на «отлично». При относительно
высокой частоте катушка может быть неболь-
ших габаритов и с малой индуктивностью.
В низкочастотных схемах (с рабочей частотой
менее единиц мегагерц), где хорошо работают
обычные операционные усилители, с помощью
хитроумных методов можно заставить конден-
сатор функционировать как индуктивность (раз-
умеется, без присущих катушке недостатков)7.
3N А Резонансный
LC-контур
На рис. 3N.11 приведена принципиальная схе-
ма резонансного #1С-контура, с которым мы
будем работать на лабораторном занятии 3IA
6 В некоторых схемах, например импульсных источниках
питания, эквивалентное последовательное сопротивление
конденсатора (ЭПС) может рассеивать мощность и ухуд-
шать рабочие характеристики этих устройств. См. раз-
делы 6.2.1А и 9.6.3А в книге АоЕ. На лабораторном заня-
тии 11L мы увидим, что для импульсного стабилизатора
нам потребуется конденсатор с низким ЭПС.
7 АоЕ § 6.2.4.
8 АоЕ § 1.7.14А.
Прежде чем мы обратим внимание на новое
свойство этой схемы, воспользуемся уже име-
ющимися у нас знаниями об импедансах кон-
денсаторов и катушек, чтобы сделать простой
вывод, что это в действительности полосовой
фильтр, т. е. фильтр, который пропускает опре-
деленный диапазон частот, ослабляя частоты
на краях диапазона.
100 кОм
Вход
0,01 мкФ
Пленочный
-о Выход
ЮмГн
Рис. 3N.11. Принципиальная схема fiLC-контура из лабора-
торного занятия 3L
Если пренебречь индуктивностью, как изобра-
жено слева на рис. 3N.12, мы видим знакомый
низкочастотный ЯС-фильтр. На высоких ча-
стотах можно со спокойной совестью игнори-
ровать подключенную параллельно катушку: ее
импеданс намного выше, чем импеданс конден-
сатора.
На другом конце частотного диапазона импе-
данс катушки намного ниже, чем конденсато-
ра (вспомним, что ZL =jcoL =j2nfL). Здесь RL-
контур функционирует, как высокочастотный
фильтр.
Следовательно, в целом в пределах частотно-
го диапазона flLC-контур функционирует, как
полосовой фильтр. Вот сколько выводов мож-
но сделать об этой схеме, не рассматривая LC-
резонанс.
3NA1. Резонанс
Но наш поверхностный анализ не учитывает
новое интересное свойство этой схемы:9 уже
упоминаемого ранее явления резонанса. На
некоторой частоте, на которой величины им-
педансов конденсатора и индуктора становятся
равными, происходит нечто удивительное: им-
педанс этих параллельно соединенных компо-
нентов становится очень высоким.
9 АоЕ § 1.7.14.
3NA. Резонансный LC-контур
141
100 кОм
Вход
0,01 мкФ
Пленочный
Вьгход
100 кОм
о—wv
Вход
Выход
ЮмГн
100 кОм
О WV
Вход
0,01 мкФ
Пленочный
НЧ-фильтр (££) ВЧ-срильтр (RL) Полосовой фильтр (RLC)
Рис. 3N.12. Первое приближение Я/.С-контура с параллельными компонентами: ВЧ- и НЧ-фильтры
макс.
(«Подобно ВЧ-фильтру: а/) -.
„*-* («Подобно НЧ-фильтру: а Vf)
Рис. 3N.13. Амплитудно-частотная характеристика fiLC-фильтра
Вы можете сами с легкостью в этом убедиться,
выписав формулу для общего импеданса LC-
пары:
Z — Z
^IC-паралелыю ~~ ^С
Zr+Zr
Но поскольку Zc = -j/coC, a ZL =7'соЬ, то противо-
положные знаки для^ означают, что на некото-
рой частоте, при которой импедансы одинако-
вы, их сумма должна быть равной нулю. Когда
это происходит, знаменатель сводится к нулю,
в результате чего эквивалентный импеданс ста-
новится очень большим10.
Резонанс происходит при |ZC|=|ZJ, т. е. когда
|-7/coC|=l/coL| и 1/юС = ш1, ^резонансная часто-
та определяется следующей формулой:
co2=l/LC=>co =
или
/рез=1/(2тс71с).
10 У вас может возникнуть желание сказать «бесконеч-
ным». Но несовершенства LC-контура, обусловленные
главным образом активным сопротивлением и потерями
в сердечнике катушки, не дают этому случиться. Но все же
импеданс становится очень большим и чрезвычайно чув-
ствительным к малейшим изменениям частоты.
На резонансной частоте, когда общий им-
педанс параллельно соединенных емкости и
индуктивности становится очень большим,
контур пропускает наибольшую доступную
часть входного сигнала. В идеале эта часть со-
ставляла бы 100%, но потери в катушке озна-
чают, что при больших значениях R сигнал
на выходе может оказаться намного меньше,
чем 100%. #!С-контур не только обеспечивает
другой способ создания полосового фильтра,
но позволяет создавать чрезвычайно узкую
полосу пропускания, по сравнению с поло-
сой, которую можно получить с помощью RC-
фильтров.
Параметр, обозначаемый буквой Q описыва-
ет ширину диапазона пропускаемых частот:
Q. = ./риз/4/- Здесь выражение Af соответствует
полосе частот, в пределах которой мощность
сигнала уменьшается наполовину, т. е. ампли-
туда оказывается на 3 дБ ниже своего максиму-
ма, как иллюстрирует рис. 3N.13.
Но на этом различия между RLC- и ДС-филь-
трами не заканчиваются. .RLC-фильтр не просто
представляет собой частотно-избирательный
делитель напряжения, хотя данное утвержде-
ние справедливо. Еще одна его особенность —
свойство накопления энергии — он более по-
добен маятнику, чем фильтру для кофе. Если
142
3W. Схемы с диодами
частота входного сигнала близка к резонанс-
ной частоте LC-контура, в нем возникают ко-
лебания. В каждом периоде колебаний энергия
передается вперед и назад между катушкой и
конденсатором.
При максимальном напряжении на параллель-
но соединенных I и С энергия сохраняется в
электростатическом поле между пластинами
конденсатора, а когда конденсатор начинает
разряжаться через индуктивность, ток посте-
пенно возрастает и при его максимуме напря-
жение на конденсаторе Uc становится нулевым.
При этом вся энергия контура хранится в маг-
нитном поле, окружающем катушку. Таким об-
разом, энергия переходит вперед и назад между
конденсатором и катушкой11.
3N .4.2. Значение добротности Q
Определение Q с помощью Af
На лабораторном занятии нам нужно будет при-
ближенно определить добротность фсхемы.
Примечание
Кстати, Q — это сокращение термина Quality
Factor — добротность, отражающий факт приме-
нения резонансных контуров в радиоприемниках,
для которых высокая избирательность особенно
важна.
.ЗдБ
.... ^
Полоса
пропускания
1кГц
30 кГц
Рис. 3N.14. Добротность О является мерой частотной изби-
рательности резонансного контура
Как уже упоминалось (см. рис. 3N.13), доброт-
ность Q можно определить по следующей фор-
муле:
п -/рез
Здесь величина bf соответствует ширине пика
резонанса между его точками -3 дБ и назы-
вается полосой пропускания на уровне 3 дБ
(рис. 3N.14).
Измерение Q через время спада
Добротность Q. можно также определить через
скорость утечки энергии из резонансного кон-
тура вследствие его рассеивания на паразитном
сопротивлении
12.
сохраненная энергия
средняя рассеиваемая мощность"
Иначе добротность фможно определить как
0.= 2я • {количество периодов колебаний,
необходимое, чтобы энергия уменьшилась
до 1/е}
Но последнее определение не слишком нам
поможет, когда нужно получить частотную ха-
рактеристику LC-контура, как в данном упраж-
нении. Оно окажется более полезным, когда
мы начнем изучать материал раздела 3N.4.4,
в котором характеристики LC-контура рас-
сматриваются во временной области. А при
параллельном соединении катушки и конден-
сатора полезно помнить еще одну формулу до-
бротности Q:
Изменение добротности Q
Добротность Q. описывает эффективность
i?LC-KOHTypa, и зависит в основном от характе-
ристик катушки индуктивности. Но значение
Q.можно изменить, варьируя активное сопро-
тивление. Большие значения сопротивления
увеличивают Q, но снижают амплитуду сигна-
ла. Это объясняется необходимостью восста-
новления рассеиваемой в LC-контуре энергии,
11 См. Пурсел и Морин, раздел 8.1, и особенно рис. 8.3,
отображающий затухающие колебания.
12 См. Пурсел и Морин, уравнение 8.12.
3NA. Резонансный LC-контур
143
/? = 10 кОм
Максимальное
значение амплитуды: 8,0 В
/?=100кОм
Максимальное
значение амплитуды: 2,9 В
Я=1МОм
Максимальное
значение амплитуды: 0,47 В
Рис. 3N.15. Увеличение сопротивления повышает добротность Q контура, но в то же самое время снижает амплитуду выход-
ного сигнала
поскольку, чем больше активное сопротивле-
ние контура, тем больше падение напряжения
на нем. Таким образом, нельзя одновременно
получить высокую добротность Qh большую
амплитуду.
Чтобы убедиться в этом, можете посмотреть
сами, какое влияние на добротность (Докажет
замена в схеме на рис. 3N.12 резистора номина-
лом 100 кОм на 10 кОм. Амплитуда выходного
сигнала возрастет, но добротность Q. ухудшит-
ся. Как обычно, нам приходится жертвовать
одной желаемой характеристикой, чтобы полу-
чить другую. Но обычно намного важнее иметь
хорошую добротность Q, поскольку проблему
малой амплитуды можно решить с помощью
усилителя.
На рис. 3N.15 проиллюстрировано влияние на
добротность и амплитуду выходного сигнала
Ш>контура трех разных значений резистора:
10 кОм, 100 кОм и 1 МОм.
Более высокие значения сопротивления дей-
ствительно улучшают добротность Q. контура,
но за счет снижения амплитуды выходного
сигнала. Чтобы получить осциллограммы на
рис. 3N.15 усиление осциллографа коррек-
тировалось так, чтобы пик амплитуды был
на одном уровне для всех трех графиков. Это
сделано для того, чтобы удобнее было видеть
изменения в форме графика частотной харак-
теристики (и, соответственно, добротности
Q). Но обратите внимание на то обстоятель-
ство, что чувствительность осциллографа по-
вышается от левого графика до правого (т. е.
отношение вольт/деление уменьшается), так
что амплитуда выходного сигнала снижает-
ся больше, чем в 16 раз. Кроме того, увели-
чение сопротивления вызывает еще один,
второстепенный эффект: небольшой сдвиг ре-
зонансной частоты13.
На лабораторном занятии 13L, в котором мы
используем Д1С-контур в составе демодуля-
тора ЧМ, мы воспользуемся этим свойством
сопротивления влиять на настройку частот-
ной характеристики Д!С-контура. В процессе
этого эксперимента вы сможете воочию на-
блюдать соревнование между двумя характе-
ристиками: высокой амплитудой и хорошей
добротностью Q.
3NA3, Проверяем, был ли прав
Фурье
С помощью ULC-контура можно проверить
правильность одного из утверждений Фурье,
если у вас были какие-либо сомнения на этот
счет. На рис. 3N.16 приведен график из лабо-
раторного занятия этого раздела: несколько
первых гармоник для сигнала прямоугольной
формы.
Ряд Фурье для прямоугольного сигнала с ам-
плитудой А можно представить также в виде
следующей формулы:
4
1
-
1
Наш LC-контур может выбирать эти гармони-
ки, и собранная на лабораторном занятии схема
выдает довольно красивую картину, несколько
напоминающую ряд телефонных столбов или
забор вдоль дороги.
13 Это «второй порядок» для «небольшого затухания...»,
см. Пурсел, раздел 8.1.
144
ЗЛ/. Схемы с диодами
-1-
4 sm Wot
4 s\r\ Wot*
-1
Рис. 3N.16. Ряд Фурье для сигнала прямоугольной формы
3N.4.4. Реакция на низкочастотный
прямоугольный сигнал «звон»
Низкочастотный сигнал прямоугольной фор-
мы (точное значение частоты здесь не важно,
в лабораторном занятии 3L рекомендуется ча-
стота 20 Гц) тоже будет возбуждать LC-контур,
хотя эта частота намного ниже, чем резонанс-
ная частота нашего LC-контура 16 кГц. Как же
так? Это объясняется тем, что, согласно Фурье,
спектр прямоугольного сигнала содержит вы-
сокочастотные гармоники, в том числе близ-
кие к резонансной частоте контура. Амплитуда
этих гармоник небольшая (поскольку ампли-
туда гармоник для прямоугольного сигнала
уменьшается обратно пропорционально ча-
стоте 1//).
На рис. 3N.17 приведена осциллограмма от-
клика резонансного контура из лабораторного
занятия 3L, на который подается сигнал прямо-
угольной формы с частотой намного ниже его
резонансной частоты (прямоугольный сигнал
частотой «50 Гц).
Лоб. занятие 3 ^ ю мГн^= 0,01 мкФ
= 30
V
Сигнал прямоугольной формы
Рис. 3N.17. Затухающие колебания flLC-контура могут харак-
теризовать его добротность Q
Обратите внимание на тот факт, что ослаб-
лению до 1/е должна подвергаться не ам-
плитуда, а энергия, со скоростью, связанной
таким образом с добротностью Q, Поскольку
величина энергии, накопленной в конденса-
торе, пропорциональна квадрату амплитуды
(ЭНЕРГИЯК0НД = 1/2CU2), до 37% уменьшится
квадрат напряжения U2, а не само напряже-
ние [7, которое должно понизиться примерно
до 60%.
На рис. 3N.17 эта точка помечена курсором
(вертикальной пунктирной линией), она на-
ходится после приблизительно пяти периодов
колебаний. Это указывает на величину доброт-
ности (^около 30.
Но почему колебания затухают? Еще лучший
вопрос (который недавно задал один из моих
студентов), почему они затухают экспоненци-
ально? Краткий ответ — потому что скорость
потери энергии сигналом пропорциональна его
амплитуде.
А вот более подробное объяснение.
♦ Энергия в LC-контуре пропорциональна ква-
драту напряжения IP. Например, в той части
периода, в течение которой вся энергия на-
ходится в конденсаторе, ее величина будет
составлять ЭНЕРГИЯК0 = 1/2CU2, где на-
пряжение U является действующим напря-
жением идЕЙСТВ: нас не интересует ни знак на-
пряжения, ни его мгновенное значение.
♦ На последовательном сопротивлении #источ
энергия рассеивается пропорционально
IP/RL (это мощность, рассеиваемая в сопро-
тивлении).
Таким образом, как сама энергия, так и ско-
рость ее затухания пропорциональны квадра-
3N.5. Схемы с диодами
145
\ к*
'fyyvv
: *
Ш1 t 21 V
А
t
1 4
f
*
■J i ,M '
ШГ 1-25 V
:' , <
i
1
i
\
: — i
IW 1.25 V
\—> '
обе
Рис. 3N.18. При плохом заземлении щупа осциллографа создается резонансный контур из паразитной индуктивности и ем-
кости: а — щуп не заземлен (кроме как через источник питания осциллографа); б — щуп заземлен на расстоянии около 25 см
от измеряемой точки; в — щуп заземлен на расстоянии около 1,25 см от измеряемой точки.
ту амплитуды. Но возведение в квадрат меняет
только постоянную времени, а не экспоненци-
альную форму затухания14.
Плохое заземление может вызывать
резонансный «звон» в LC-контуре
Пример такого случая показан слева на
рис. 3N.18. Такая реакция LC-контура наблю-
дается всегда при измерении прямоугольного
сигнала щупом, не заземленным должным об-
разом вблизи измеряемой точки, в результате
протекания блуждающего тока по длинному
(индуктивному) пути. Паразитная индуктив-
ность и емкость образуют резонансный контур,
который и создает этот неприятный звон. Если
вам не терпится, то можете проверить этот эф-
фект прямо сейчас; в противном случае вы все
равно столкнетесь с этим эффектом не по своей
воле в какой то момент (который почти гаран-
тировано настанет).
На рис. 3N.18 демонстрируется, как умень-
шение длины заземляющего провода щупа
осциллографа уменьшает звон. Более короткий
заземляющий проводник обладает меньшей
индуктивностью, вследствие чего повышается
резонансная частота и уменьшается накапли-
ваемая энергия.
3N.5. Схемы с диодами
Диоды дают возможность по-новому управлять
сигналами: ток через диод протекает только
в одном направлении (рис. 3N.19)15.
14 См. «Introductory Electronics», автор R.E. Simpson,
2-е изд., 1984, с. 98-100.
15 АоЕ § 1.6.1.
(Протекает)
(Не протекает)
Рис. 3N.19. Диод как однонаправленный вентиль управле-
ния током
Символ диода на принципиальных схемах вы-
глядит как дорожный знак одностороннего
движения, что удобно для понимания: он ука-
зывает условному току, в каком направлении
можно протекать. Для многих приложений до-
статочно рассматривать диод как однонаправ-
ленный вентиль, хотя следует иметь в виду, что
открытый диод ведет себя не совсем подобно
проводу. Разница состоит в том, что при про-
текании тока через диод на нем возникает ха-
рактерное падение напряжения величиной
около 0,6 В, называемое прямым напряжением
диода. Мы наблюдали это явление на лабора-
торном занятии 1L.4 и начертили соответству-
ющий график. На рис. 3N.20 приведен пример
такого графика (называемого вольт-амперной
характеристикой диода), чтобы напомнить вам
об этом эксперименте.
Примечание
Мы не экспериментировали с пиковым обратным
напряжением (или напряжением пробоя), что
было хорошо как для вашей безопасности, так
и для здоровья диода.
Обратное
напряжение пробоя
(разрушающее)
Приблизительно
-100 В! /
10 мА
1мА
I Прямое
смещение диода
0,6 В
Рис. 3N.20. Графики вольт-амперных характеристик диода:
величина тока при обратном напряжении лежит в наноам-
перном диапазоне
146
3N. Схемы с диодами
3N.6. Самое важное
применение диода:
выпрямление переменного
тока
Как мы уже упоминали, электроэнергия выра-
батывается и распределятся в виде переменного
напряжения, чтобы уменьшить потери в лини-
ях передачи. Это позволяет использовать для
передачи электроэнергии высокие напряжения
и, соответственно, малые токи. Переменное на-
пряжение легко понизить или повысить с по-
мощью трансформаторов, простых устройств,
состоящих из двух катушек на сердечниках,
расположенных рядом друг с другом, в резуль-
тате чего между ними создается электромаг-
нитная связь. Пример сретением 1 W.2 наглядно
демонстрирует преимущество в эффективности
за счет применения высокого напряжения при
передаче электроэнергии.
Поскольку электроэнергия передается в виде
переменного напряжения, тогда как для рабо-
ты электронных устройств требуется постоян-
ное напряжение, преобразование переменного
напряжения в постоянное является важной за-
дачей диодных схем.
3N.6.1. Однополупериодный
выпрямитель и ограничитель
напряжения
Подобно резисторам и конденсаторам, диоды
часто используются в делителях напряжения16.
На рис. 3N.21 показано несколько делителей
напряжения, содержащих диоды. Можете ли
вы предположить, как будет выглядеть выход-
ное напряжение каждого из этих делителей?
Ограничители
Выпрямитель напряжения
Рис. 3N.21. Три делителя напряжения на диодах: один вы-
прямитель (слева) и два ограничителя напряжения (посере-
дине и справа)
Выходные сигналы первых двух схем очень по-
хожи друг на друга. Но лишь выпрямитель спо-
собен создавать постоянное напряжение, тре-
буемое для источников питания. Почему так?
Какое важное отличие, невидимое на экране
осциллографа, существует между выпрямите-
лем и ограничителем напряжения17? Хотя вы-
ходной сигнал выпрямителя еще далеко не той
формы, которая нам требуется для создания ис-
точника питания, преобразующего переменное
напряжение электросети в постоянное, но сгла-
дить пульсации способен конденсатор. Однако
сначала давайте рассмотрим наилучший вари-
ант выпрямителя.
3N.6.2. Двухполупериодный
мостовой выпрямитель
Схема выпрямителя, изображенная на
рис. 3N.22, заполняет пустые промежутки меж-
ду полуволнами выходного сигнала однополу-
периодного выпрямителя за счет выпрямлен-
ного отрицательного полупериода18.
Входное ^
переменное j
напряжение <
Рис. 3N.22. Двухполупериодный мостовой выпрямитель
Хорошо придумано, не так ли? Увидев форму
выходного сигнала этого выпрямителя, сразу
можно понять, почему предыдущий более про-
стой выпрямитель называется однополупери-
одным.
16 АоЕ § 1.6.2.
17 Очевидная разница в сигналах (один сигнал сдвинут на
-0,6 В, а другой нет) не является правильным ответом, по-
скольку тогда выходной сигнал второй схемы (ограничи-
теля) окажется даже более предпочтительным. Но не это
главное. Важна разница между выходными импедансами
этих двух схем. (Помните? Мы ведь обещали вам, что им-
педанс будет лейтмотивом аналоговой части этого курса.)
В схеме слева (выпрямителе) между источником сигнала
(которым обычно является силовой трансформатор) и на-
грузкой находится только диод, тогда как в ограничителе
между источником и нагрузкой включен резистор. В ре-
зультате выпрямитель пригоден для создания источника
питания, а ограничитель — нет.
18 АоЕ § 1.6.2.
ЗЛ/.б. Самое важное применение диода: выпрямление переменного тока
147
На рис. 3N.23 приведен график выходного сиг-
нала двухполупериодного выпрямителя, содер-
жащий некоторые особенности, в том числе тот
не совсем очевидный факт, что в течение одной
половины периода входной сигнал опускается
ниже нуля.
Один вывод вторичной обмотки Выход
трансформатора ~~ -
Второй вывод вторичной обмотки трансформатора
Рис. 3N.23. График выходного сигнала двухполупериодного
мостового выпрямителя
Из-за этой особенности двухполупериодный
мостовой выпрямитель можно использовать
только с плавающим входным напряжением,
таким, которое присутствует на вторичной об-
мотке трансформатора. Если один из выходных
проводов двухполупериодного выпрямителя за-
землен, никакой из входов этого выпрямителя
подключать к земле нельзя.
В настоящее время использование в источнике
питания выпрямителя иного типа, чем двухпо-
лупериодный, может быть оправдано только
в очень редких случаях. На заре электрони-
ки диод представлял собой вакуумную лампу
стоимостью около 5 долларов, вследствие чего
разработчики прилагали все усилия, чтобы
ограничить количество таких элементов. Но
сейчас легко можно приобрести готовый ди-
одный мост: небольшое устройство в залитом
эпоксидной смолой корпусе, содержащее че-
тыре диода и четыре вывода. Такой компонент
даже большой мощности может стоить около
доллара.
Двухполупериодный мост
в двухполярном источнике питания
Двухполупериодный выпрямительный мост по-
дойдет и для сборки двухполярного источника
питания, т. е. выдающего как положительное,
так и отрицательное напряжение относительно
X/ П
земли. На рис. 3N.24 приведена принципиаль-
ная схема такого выпрямителя.
Входное —% §
переменное!!)
напряжение^ |
Рис. 3N.24. Двухполупериодный мостовой выпрямитель вы-
дает двухполярное, т. е. и положительное, и отрицательное
напряжение
Очевидно, что единственное отличие от одно-
полярного источника питания, изображенного
на рис. 3N.22, состоит в центральном отводе от
вторичной обмотки трансформатора, который
подключается к шине земли (общему проводу)
двухполярного источника питания.
Примечание
В схеме на рис. 3N.24 не показаны нагрузочные
сопротивления; нагрузка, конечно же, подразуме-
вается, зачем собирать источник питания, если не
для подключения нагрузки?
Можно поддаться искушению считать, что за-
землять среднюю точку вторичной обмотки
трансформатора не обязательно, и что двухпо-
лярный источник питания можно создать, просто
подключив к земле точку между конденсаторами
в схеме на рис. 3N.24. Но это будет ошибкой.
При отсутствии центрального отвода вторич-
ной обмотки распределение выходного напря-
жения между положительной и отрицательной
клеммами будет непредсказуемым, поскольку
оно будет зависеть от относительной нагрузки
каждого из этих двух выводов. При заземлен-
ном центральном отводе обмотки эти выходы
становятся независимыми и трансформатор
определяет не только общее напряжение, но и
U+ минус 17.. В результате на каждой выходной
клемме (U+ и U_) присутствует напряжение,
определяемое половиной вторичной обмотки
трансформатора.
Если приведенное утверждение кажется вам
неясным и сбивает вас с толку, можете попро-
бовать проследить путь тока при каждом полу-
периоде входного напряжения. На рис. 3N.25
приведена такая трассировка.
148
3N. Схемы с диодами
Двухполярный источник питания
г\
Входное
переменное [
напряжение [
Положительный вывод
Земля»
(общий)
О —
J* «Земля»
(общий)
переменное V -w
напряжение L. %
Г\
Входное
переменное
напряжение
Отрицательный вывод
+ «Земля»
(общий)
Входное,
переменное ^
напряжение [
Рис. 3N.25. Протекание тока в выпрямителе двухполярного источника питания: сигналы на положительном и отрицательном
выходах показаны отдельно
На рис. 3N.25 показаны четыре случая, но в
действительности, конечно же, рассматрива-
ются только два полупериода. Положительный
и отрицательный выводы изображены отдель-
но по той причине, что мы опасались, что одно-
временное рассмотрение обеих полярностей
может оказаться слишком непонятным. Кроме
того, обратите внимание, что оба символа зем-
ли соединены между собой пунктирной линией;
это сделано, чтобы наглядно показать путь тока
к центральному отводу обмотки.
Скоро мы познакомимся со схемой полноцен-
ного источника питания, собранного на двух-
полупериодном выпрямительном диодном мо-
сте. Но прежде чем приступать к этой теме, рас-
смотрим еще один тип диода: стабилитрон (или
зенеровский диод).
предпочтителен для сборки простого радио-
приемника, чем мы будем заниматься в конце
лабораторного занятия 3L.
Стабилитрон проводит ток при определенном
(не очень большом) обратном напряжении19.
Включив стабилитрон в делитель напряжения
в «обратном» направлении (т. е. с обратным
смещением, при котором ток будет протекать
в направлении, противоположном по сравне-
нию с обычными диодами), мы получим схему,
выходное напряжение которой будет довольно
постоянным, несмотря на возможные колеба-
ния входного напряжения и на изменения ве-
личины нагрузки.
Пример такого включения стабилитрона при-
веден на рис. 3N.26.
3N.6.3. Стабилитроны
(зенеровские диоды)
На наших лабораторных занятиях стабилитро-
ны нам не понадобятся (хотя на лабораторном
занятии 11L нам придется познакомиться с
более сложным устройством — стабилизато-
ром напряжения). Но мы бы хотели вкратце
упомянуть стабилитроны наряду с другими
диодами, с которыми нам придется работать на
сегодняшнем лабораторном занятии 3L: стан-
дартный кремниевый диод (наподобие диода
1N914, который мы постоянно используем) и
диод Шоттки, который имеет малое напряже-
ние прямого смещения. Последний тип диода
Нестабилизированное,
содержит небольшие
пульсации
Рис. 3N.26. Подключение стабилитрона
Вольтамперная характеристика стабилитрона
показана слева на рис. 3N.26. По этой характе-
ристике можно видеть, что проводимость при-
бора при обратном смещении неидеальна: кри-
вая не вертикальна. Этот график иллюстрирует,
почему необходимо следовать эмпирическому
АоЕ § 1.2.6А.
3N.Z Самое важное применение диода: источник питания (нестабилизированный)
149
Обычный
стабилитрон
Идеальный
стабилитрон
Прямое
смещение диода
Напряжение
на стабилитроне
График напряжения источника напряжения
должен выглядеть почти горизонтальным
(низкий выходной импеданс),
поэтому ток через стабилитрон должен быть
не меньше 10 /аА
В этой точке стабилитрон работает
в качестве источника напряжения лучше,
чем вот в этой точке
Обычный график вольтамперной характеристики
Вольтамперная характеристика повернута на 90°, чтобы
наглядно показать импеданс
Рис. 3N.27. Графики вольтамперной характеристики стабилитрона. В обычном ракурсе (слева) и повернутый на 90°, чтобы
показать импедансы
правилу, гласящему, что даже при подключении
нагрузки через стабилитрон должен протекать
ток не менее 10 мА.
Поворот вольтамперной характеристики на
рис. 3N.27 на 90° против часовой стрелки по-
зволит нам использовать крутизну графика
для определения значения импеданса в Омах.
В частности, крутизна графика представляет от-
ношение AU/AI, или дифференциальное сопро-
тивление устройства. Эта величина описывает
качество стабилитрона в роли источника опор-
ного напряжения: как будет изменяться выход-
ное напряжение в ответ на варьирование тока.
Примечание
В данном случае ток варьируется по двум причи-
нам: из-за колебаний входного напряжения и/или
изменения нагрузки.
Здесь мы можем видеть, насколько плохо будет
функционировать диод, если подняться вверх
по кривой в область, где ток 1СТАБ очень мал.
В настоящем источнике питания никогда (поч-
ти никогда) стабилитрон не используется само-
стоятельно, как в только что рассмотренных
схемах. Вместе с ним всегда будет последова-
тельно включаться схема на транзисторе или
операционном усилителе для уменьшения ко-
лебаний выходного тока (см. книгу АоЕ, раз-
дел 2.2.4). Такой подход реализован в стаби-
лизаторах напряжения, рассматриваемых в
главе 11 (и в главе 9 книги АоЕ), хотя вместо
стабилитронов здесь используются интеграль-
ные микросхемы — источники опорного на-
пряжения. Но, по крайней мере, вы должны
лучше понимать подобные схемы благодаря
этому краткому обзору стабилитронов. Теперь
самое время рассмотреть наиболее часто встре-
чающиеся варианты применения диодов.
3N.7. Самое важное
применение диода:
источник питания
(нестабилизированный)
На рис. 3N.28 приведена принципиальная схема
стандартного нестабилизированного источника
питания20. Мы узнаем позже значение выраже-
ния «нестабилизированный», поскольку вы не
сможете понять его смысл полностью, пока мы
не познакомимся со стабилизированными ис-
точниками питания, в которых предусмотрена
отрицательная обратная связь для поддержа-
ния постоянного уровня выходного напряже-
ния 1ГЁЫХ, несмотря на изменения как входного
напряжения [7ВХ, так и выходного тока.
Теперь давайте рассмотрим процесс выбора
значений компонентов. Здесь мы не будем по-
дробно рассматривать эту задачу, а выполним
грубую оценку номиналов элементов схемы. Но
в Примере сретением 3Wприведено детальное
20 АоЕ §9.5.
150
3N. Схемы с диодами
От сети
220 В 50 Гц
„Разрядный
"резистор
НАГРУЗКА
Рис. 3N.28. Принципиальная схема простого источника питания
решение подобной задачи. Предположим, что
мы хотим получить следующие характеристики:
♦ выходное напряжение Г7ВЫХ: приблизительно
12 В;
♦ пульсации: приблизительно 1 В;
♦ сопротивление нагрузки RH = 120 Ом.
Нам нужно оценить следующие значения:
♦ емкость конденсатора в мкФ;
♦ напряжение вторичной обмотки трансфор-
матора (1/ДЕЙСТВ);
♦ номинал предохранителя.
На данном этапе мы опустим два менее важных
параметра (поскольку часто их можно просто
прикинуть). Но их расчет подробно рассматри-
вается в Примере сретением 3W. Вот эти пара-
метры:
♦ требования по номинальному току транс-
форматора;
♦ значение сопротивления разрядного рези-
стора.
Работу будем выполнять поэтапно. Для начала
следует начертить принципиальную схему, не
указывая значения компонентов, как в приме-
ре на рис. 3N.28.
3N7.1. Напряжение вторичной
обмотки трансформатора
Это напряжение просто равно выходному на-
пряжению ивых плюс потеря напряжения на
мостовом выпрямителе21. На пути тока через
выпрямительный мост всегда присутствуют два
диода. Величина напряжения на обмотке транс-
форматора указывается для действующего на-
пряжения, что для синусоидального сигнала
означает UnilKA/'{2. В нашем случае напряжение
ишкА на трансформаторе величиной около
14 В соответствует действующему значению
около 10 В (рис. 3N.29).
Размах напряжения пульсаций Выходное напряжение
i/ под нагрузкой
л***** ^ .г Выходное напряжение
без конденсатора
Рис. 3N.29. Форма напряжения на вторичной обмотке транс-
форматора
Как видно из рис. 3N.30, пульсации напряже-
ния сопровождаются скачками тока. Сигнал
(помеченный как 1ТРШСФ на рисунке) измеряет-
ся в общей шине.
Примечание
Обратите внимание, что осциллограмма снята при
высокой чувствительности второго канала вер-
тикального отклонения (СН2:50 мВ/деление)
Чь
Д:5,28мс
Частота сигнала на
втором канале (Канал 2)
Рис. 3N.30. Пульсации выходного напряжения источника
питания: / = 1 А, С= 3300 мкФ
3N.7.2. Конденсатор
Теперь перейдем к самому интересному22. Во-
обще предстоящая задача довольно трудная,
но мы упростим ее, сделав два предположения.
На рис. 3N.31 изображен график пульсаций вы-
ходного сигнала.
21 АоЕ§ 9.5.2.
АоЕ § 1.6.3А, АоЕ § 9.5.3А.
3N.7. Самое важное применение диода: источник питания (нестабилизированный)
151
At
приблизительное точная крутизна
Д'ТОЧНое Кривая
экспоненциального
затухания
Приблизив
тельная
крутизна
Рис. 3N.31. Временные параметры сигнала пульсаций
Мы можем примерно определить величину
пульсаций (или рассчитать требуемую емкость
при пульсациях указанной величины, как в этой
задаче), используя следующую общую формулу:
Здесь dU или AU — пульсации, dt или AT — пе-
риод времени, в течение которого разряжается
конденсатор, a J — ток, потребляемый из ис-
точника питания. Чтобы определить точное
значение емкости конденсатора, при котором
пульсации не превысят указанной величины
при заданной максимальной нагрузке, требует-
ся ответить на некоторые вопросы:
♦ Какой у нас выходной ток 1ВЫХ? Если нагруз-
ка резистивная, выходной ток не будет по-
стоянным, а будет спадать экспоненциально
в каждом полупериоде.
♦ Какой у нас временной интервал AT ? To есть
в течение какого периода времени происхо-
дит разряд конденсатора (прежде чем напря-
жение с трансформатора снова повысится,
чтобы зарядить его)?
Как обычно, мы легко обойдем эти трудности,
если рассмотрим наихудшие случаи. В частно-
сти, мы будем предполагать, что:
♦ выходной ток /вых постоянный, а его значе-
ние максимально;
♦ конденсатор разряжается в течение всего пе-
риода между максимумами амплитуды.
Оба допущения увеличивают величину полу-
чаемых пульсаций. Но поскольку пульсации
желательно уменьшить, ничего плохого, если
в нашей схеме величина пульсаций будет мень-
шей, чем рассчитанная. Зададим следующие
приблизительные значения:
♦ выходной ток /вых будет просто 1ВЫХ МАКС, т. е.
100 мА;
♦ период времени AT равен половине перио-
да входного сигнала частотой 50 Гц, т. е.
1/100 Гц = Юме.
В результате получим следующее значение
емкости:
ЛТ
~3
На первый взгляд емкость выглядит внуши-
тельной, но для накопительного конденсатора
источника питания это типичное значение.
3N7.3. Номинальный ток
трансформатора
(нагрев, вызываемый
действующим током)
Поскольку ток, который заряжает конденса-
тор, поступает периодически, а не постоянно,
это сильнее нагревает трансформатор, чем при
равномерном протекании тока, как в нагрузке23.
Дополнительную информацию на эту тему см.
в Примере сретением 3Wпо источникам пита-
ния. Величину дополнительного нагрева мож-
но вычислить, используя действующее (средне-
квадратическое) значение тока трансформато-
ра. Это простая задача, если знать скважность
сигнала, т. е. интервал, в течение которого ток
течет через обмотку трансформатора. Это от-
ношение трудно вычислить математически, но
легко определить визуально.
На рис. 3N.30 показаны пульсации, которые
мы наблюдали на одной из наших, лаборатор-
ных макетных плат, оснащенных источником
питания, при постоянном потреблении тока ве-
личиной 1А (на момент отвлечемся от текущей
задачи, ток в которой значительно ниже: всего
лишь 100 мА).
В течение времени, когда трансформатор за-
ряжает накопительный конденсатор, он дол-
жен возместить весь заряд, израсходованный
нагрузкой в течение периода. Таким образом,
величина тока, протекающего в течение актив-
ной части периода (составляющей примерно
3/8 от всего периода на рис. 3N.30), должна
быть пропорционально большей, чем ток для
постоянной нагрузки. В данном случае этот ток
должен быть на 8/3 больше выходного тока по-
стоянной нагрузки величиной 1 А. Такой бро-
сок тока вызывает больший нагрев, чем ток
23 Supplement 3S, АоЕ § 9.5.2.
152
ЗЛ/. Схемы с диодами
неизменной амплитуды, который бы обеспечил
такой же самый заряд. Поэтому для определе-
ния характеристик требуемого нам трансфор-
матора необходимо ориентироваться на это
большее значение тока.
Если, как на графике на рис. 3N.30, ток проте-
кает в течение около 3/8 полного периода, его
действующее значение определяется следую-
щей формулой:
/(часть периода, в течение
действ у которой протекает ток) • (ток)2)
/2 «1,67.
(8//3)2) =
7,112 =
Таким образом, для тока нагрузки 100 мА нам
потребуется трансформатор с такими характе-
ристиками, которые позволят ему выдавать ми-
нимум 160 мА. А если мы хотим предусмотреть
запас, то полезно задать значение 200 мА.
3N.7A Номинал плавкого
предохранителя
Ток в первичной обмотке трансформатора
меньше, чем во вторичной приблизительно в
таком же отношении, как напряжение первич-
ной обмотки выше напряжения вторичной. Это
объясняется тем, что трансформатор рассеива-
ет очень небольшую мощность: Рвх « Рвых.
В нашем случае (рис. 3N.32), когда напряже-
ние на выходе почти в 22 раза меньше сетевого
напряжения, ток в первичной обмотке будет
меньшим, чем во вторичной обмотке, при-
близительно во столько же раз. Таким обра-
зом, при токе нагрузки 100 мА величина тока в
первичной обмотке трансформатора составит
около 4,5 мА.
гвход
220 В
' 0,09 А
10 В
$> 1А
При понижении напряжения ток увеличивается
Рис. 3N.32. Трансформатор рассеивает сравнительно не-
большую мощность. Поэтому понижающий трансформатор
потребляет меньший ток, чем выдает
В действительности броски тока, которые на-
гревают трансформатор, также воздействуют и
на плавкий предохранитель, в результате чего
ток несколько возрастает (см. раздел 3N.73).
Пусть это будет 10 мА. Мы не хотим, чтобы
наш плавкий предохранитель сгорел при мак-
симальном токе нагрузки. Поэтому, возьмем
плавкий предохранитель с номинальным то-
ком в четыре раза большим, чем максималь-
ный выходной ток с учетом возможного нагре-
ва: 40 мА. Вряд ли мы найдем предохранитель
с таким рабочим током, но предохранители на
100 мА, или ОД А, широко распространены, так
что нам придется согласиться на такой предо-
хранитель. Это значение не является критиче-
ским, поскольку плавкий предохранитель пред-
назначен для внештатных ситуаций, в которых
могут ожидаться очень большие токи.
Целесообразно выбрать плавкий предохрани-
тель инерционного типа, поскольку при вклю-
чении источника питания в сеть большой на-
чальный ток заряжает конденсатор фильтра,
и перегорание предохранителя при каждом
включении источника питания нежелательно.
Но обратите внимание на то, что для перего-
рания предохранителя требуется значительная
перегрузка: быстродействующий предохрани-
тель на 1 А не перегорит мгновенно при токе
1 А. Вот данные о длительности интервала вре-
мени, в течение которого быстродействующий
стеклянный предохранитель (типа AGX24) сго-
рает после нескольких перегрузок:
Процент от
номинального тока
110%
135%
200%
Время для
перегорания
4 ч (минимум)
60 мин (максимум)
5 с (максимум)
3N.8. Радиоприемник
В этом разделе мы познакомимся с двумя эле-
ментами, играющими важную роль в АМ-
радиоприемнике25:
1. Высокоизбирательный полосовой фильтр,
который может выделить одну частоту радио-
вещательного диапазона.
24 Справочный листок для быстродействующих стеклян-
ных предохранителей с рабочим током от 1/16 А до 2 А
серии AGX компании Cooper-Bussmann.
25 AM — амплитудная модуляция.
3N.8. Радиоприемник
153
помехи = 16 мс
, частота помехи 60 Гц
L
SOOmV
Mji 0.0ms Ц Line "V.~100mV
Сигнал с антенны, подаваемый непосредственно на щуп
осциллографа
infio.oms
Сигнал с антенны, подаваемый на /.^-контур
с резонансной частотой, равной частоте несущей:
помехи частотой 60 Гц больше нет, и сигнал
(варьирование амплитуды) намного больший
Рис. 3N.33. Радиосигнал: исходный, непосредственно с антенны (слева) и после обработки /.С-контуром (справа)
2. Детектор (демодулятор), который способен
извлечь информацию, зашифрованную в
АМ-сигнале (с помощью диода с ЯС-филь-
тром, чтобы избавиться от высокочастот-
ного сигнала несущей частоты).
3N.8.1. Шаг 1: /.С-фильтр пропускает
одну несущую частоту
Каждой радиопередающей станции выделя-
ется ее собственная определенная частота26.
Эта частота называется несущей и выбирается
на основе таких критериев, как способность
к хорошему распространению и передаче ин-
формации посредством ее изменения опреде-
ленным способом, называемым модуляцией.
Самый первый и наиболее простой способ мо-
дуляции — амплитудная модуляция — делает
это так, как и подразумевается в его названии:
меняя амплитуду несущей частоты. Этот метод
накладывает аудиосигнал частотой в диапазоне
нескольких килогерц (речь или музыка) на сиг-
нал несущей (частотой около 1 МГц), модули-
руя таким образом амплитуду несущей частоты
полезным сигналом.
LC-контур хорошо подходит для выделения
радиочастотной несущей: это самая чувстви-
Примечание
26 Строго говоря, выделяется не одна частота, а диапазон
разрешенных частот, шириной 10 кГц для АМ-передач
и шириной 200 кГц для ЧМ-передач (частотная моду-
ляция).
На лабораторном занятии 13L мы будем работать
с методом частотной модуляции, который надеж-
нее, чем амплитудная модуляция, но далеко не так
прост. Но чтобы облегчить наш эксперимент, мы не
будем подвергать частотной модуляции сигналы
радиочастот, а возьмем сигнал с намного меньшей
частотой.
тельная из известных нам схем, которую можно
с легкостью настроить для резонанса на стан-
дартных АМ-частотах, например 1 МГц. Для
подачи сигнала на параллельный LC-контур
не потребуется даже резистор, как в контуре
в первом эксперименте на лабораторном заня-
тии 3L (см. рис. 3L.1), поскольку его роль игра-
ет импеданс антенны.
LC-контур не пропускает не только нежелатель-
ные радиочастоты, но также и помеху частотой
60 Гц27, амплитуда которой намного больше,
чем у любого радиосигнала. Этот эффект мож-
но наблюдать на рис. 3N.33.
Слева на рисунке изображен синусоидальный
сигнал частотой 60 Гц, но подозрительно «тол-
стый». Это «утолщение» является несущей ча-
стотой 1 МГц. Изменение амплитуды сигнала
трудно увидеть на данной осциллограмме, но
именно это изменение содержит всю переда-
ваемую полезную информацию. А на осцилло-
грамме справа и помехи частотой 60 Гц больше
Частота сетевого напряжения в США. - Примеч. ред.
154
3N. Схемы с диодами
нет, поскольку она была отфильтрована резо-
нансным контуром.
На осциллограмме справа на рис. 3N.33 можно
заметить еще один эффект, более интересный и
неожиданный. Резонансный LC-контур делает
что-то загадочно новое: амплитуда выходно-
го сигнала LC-контура больше, чем входного.
Обратите внимание на то, что чувствительность
осциллографа одинакова для обоих изображений
на рис. 3N.33. Таким образом, LC-контур дей-
ствительно усиливает модулированный сигнал.
Никакой ЯС-фильтр не смог бы выполнить та-
кой трюк28. Это возможно только в том случае,
когда входной сигнал поступает от источника
тока, а не напряжения, как в случае с антенной.
Контур из L и С накапливает энергию и подоб-
но раскачиваемому маятнику или качелям ам-
плитуда выходного сигнала LC-контура может
нарастать выше амплитуды входного сигнала.
Подобным образом, раскачиваемые качели мо-
гут выходить далеко за пределы досягаемости
раскачивающего, если тот придает им понем-
ногу энергии в нужный момент при каждом их
прохождении мимо него.
Явление увеличения амплитуды выходного сиг-
нала по сравнению с входным можно объяснить
другим, более прозаичным, способом. Если LC-
контур обладает большой добротностью Q, что
имеет место в данном случае, то при равен-
стве амплитуд входного и выходного сигнала
в контур поступает намного больше энергии,
чем теряется в нем. Таким образом, амплитуда
выходного сигнала нарастает до тех пор, пока
скорость рассеивания энергии не сравняется
со скоростью ее поступления, что происходит,
когда амплитуда на выходе оказывается намно-
го больше, чем на входе. Отсюда и увеличение
выходного сигнала этой пассивной схемой.
Примечание
Слово «пассивная» здесь означает, что выходной
сигнал не подпитывается энергией от источника
питания, как происходит в случае с усилителем, а
всю энергию поставляет источник сигнала.
28 Д1С-контур из лабораторного занятия 3L также не смог
бы выполнить этот трюк. Это объясняется тем, что любая
схема, подающая сигнал от источника напряжения на LC-
контур через резистор, никогда не сможет выдать ампли-
туду больше, чем амплитуда входного сигнала. Причина
заключается в потерях на резистивной связи источника
сигнала с LC-контуром; тогда как емкостная связь антенны
с LC-контуром потерь не вызывает.
3N.8.2. Шаг 2: детектируем
огибающую АМ-сигнала
Если на осциллографе установить быструю
развертку, чтобы получить достаточное раз-
решение для детального отображения несущей
частоты, то мы сможем увидеть модуляцию ее
амплитуды, которая выражается в варьирова-
нии последней (рис. 3N.34).
На осциллограмме (рис. 3N.34, а) показано не-
сколько варьирующихся амплитуд, наложен-
ных друг на друга, а на рис. 3N.34, б — одно-
кратный захват сигнала. Теперь перед нами
стоит задача восстановить информацию, зако-
дированную в изменении амплитуды, игнори-
руя при этом высокочастотную несущую.
soomv i ми. oo jis
Осциллограмма АМ-радиосигнала при быстрой
развертке позволяет увидеть отдельные периоды
несущей
Тот же самый сигнал, но синхронизированный
на интервале периода огибающей
Рис. 3N.34. АМ-сигнал, исследуемый с разрешением, позво-
ляющим видеть изменение его амплитуды
3N.8. Радиоприемник
155
Удаляем несущую
Детектор должен игнорировать или удалять
частоту несущей (приблизительно 1 МГц).
Несущая выполнила свою задачу, заключав-
шуюся в доставке аудиоинформации, и теперь
ее можно удалить.
Примечание
ВЧ-несущая (частотой около 1,5 МГц на рис. 3N.34)
необходима по той причине, что высокочастотные
сигналы передаются с помощью радиоволн лучше,
чем низкочастотные.
Использование несущей частоты обусловлено
двумя причинами. Одна из веских причин —
размер антенны, который бы потребовался для
передачи сигнала с аудиочастотой. Для успеш-
ного приема АМ-сигнала частотой 1 МГц тре-
буется антенна длиной в половину длины вол-
ны, т. е. около 150 м. В нашей лаборатории мы
умудряемся принимать такой сигнал на менее
эффективную антенну, в пять раз короче. Но
длина оптимальной антенны (половина волны
сигнала) для приема сигнала частотой 1 кГц бу-
дет составлять около 150 км! Кстати, мобильные
телефоны умудряются работать с весьма миниа-
тюрными антеннами по той причине, что они ис-
пользуют несущую с очень малой длиной волны.
В частности, для большинства мобильных теле-
фонов стандарта GSM принята несущая с часто-
той около 2 ГГц, для работы с которой требуется
антенна длиной всего лишь около 7,5 см29.
Другая веская причина использования несу-
щей — необходимость обеспечить работу не-
скольких близкорасположенных радиостан-
ций, чтобы они взаимно не мешали друг другу.
Это невозможно, если передавать просто аудио-
частоты без несущей.
Удаление несущей частоты напоминает задачу
для низкочастотного фильтра. В действитель-
ности это так, но и не так. Простой низкочас-
тотный фильтр для выделения аудиосигнала
(частотой не выше 5 кГц согласно стандарту для
АМ-передач) и одновременного подавления
сигнала несущей отфильтрует, к сожалению,
все сигналы, так сказать, «выплеснет младенца
вместе с водой». Поэтому, до низкочастотного
фильтра, нам потребуется еще одна схема из ла-
бораторного занятия 3L.
29 На веб-сайте журнала EDN можно найти очень хоро-
шую статью по антеннам (не перегруженную математиче-
скими расчетами, опубликована в 2002 г.): http://in.eet.
com/media/1141963/21352-82250.pdf.
Детектирование огибающей
Как только что говорилось, непосредственная
подача на НЧ-фильтр модулированного сигна-
ла несущей, поступившего из LC-контура, вы-
полнит требуемую задачу избавления от несу-
щей. Но вместе с несущей исчезнут и колебания
ее амплитуды, поскольку они симметричны.
В результате на выходе низкочастотного филь-
тра окажется сигнал с нулевой амплитудой.
Чтобы не допустить такого крайне нежелатель-
ного результата, нам нужно нарушить симме-
трию выходного сигнала LC-контура. Если мы
выпрямим этот сигнал и далее подадим на НЧ-
фильтр, то сможем сохранить форму огибаю-
щей АМ-сигнала.
3N.8.3. Результаты выпрямления
несущего колебания
Выпрямление АМ-колебания, а затем удаление
несущей с помощью низкочастотного фильт-
ра выполняются последовательно. Собственно
огибающая, которая содержит аудиоинформа-
цию, — это нижняя осциллограмма справа на
рис. 3N.35. Обратите внимание, что эта огиба-
ющая соответствует несущей, изображенной на
осциллограмме сверху здесь же, а не из сигнала,
показанного на левом изображении рис. 3N.35,
который соответствует другому моменту ради-
опередачи.
3N.8A Извлечение
аудиоинформации
Выпрямление несущей:
однополупериодное
или двухполупериодное?
♦ Однополупериодного выпрямления не-
сущей волны будет достаточно. Зная, что
двухполупериодный выпрямитель лучше,
чем однополупериодный в источниках пи-
тания, можно предположить, что также бу-
дет лучше применить двухполупериодное
выпрямление несущей волны радиосигнала.
Более того, можно предположить, что такое
выпрямление не только лучше, а необхо-
димо, чтобы не потерять половину инфор-
мации, содержащейся в отрицательных по-
лупериодах АМ-сигнала. Но все эти страхи
оказываются напрасными. Симметричность
156
3N. Схемы с диодами
Демодуляция АМ-радиосигнала:
выпрямление
Отфильтрованный для удаления несущей
и выделения огибающей
Рис. 3N.35. Этапы демодуляции АМ-радиосигнала: выпрямление с последующей фильтрацией НЧ-фильтром
несущей означает, что ничего не теряем, ис-
пользуя только положительные полуперио-
ды, поскольку мы получим требуемую нам
информацию о ее амплитуде. Также не следу-
ет беспокоиться, что амплитуда несущего ко-
лебания может измениться между положи-
тельным и отрицательным полупериодами
(в действительности иногда такое изменение
является необходимым). Наш детектор вы-
даст среднее значение амплитуд сотен пе-
риодов несущей, поскольку в одном периоде
аудиосигнала самой высокой частоты (5 кГц)
будет содержаться около 200 периодов несу-
щего колебания частотой 1 МГц.
♦ Однополупериодное выпрямление даже
лучше, чем двухполупериодное. На самом
деле в данной ситуации есть веские причины,
чтобы отказаться от двухполупериодного
выпрямления несущей.
• Вход и выход двухполупериодного выпрями-
теля нельзя соединить с общей земляной
шиной. Если выход соединен с общей ши-
ной (обычный подход), то землю нельзя
будет подключить ни к одному из входных
контактов. Этот факт, упомянутый в раз-
деле 3N.6.2 и проиллюстрированный при-
мером на рис. 3N.22, указан также в виде
предупреждения в начале раздела 3L3.
В источнике питания, на который входное
питание подается из вторичной обмотки
трансформатора, это ограничение не яв-
ляется проблемой, поскольку для обмот-
ки трансформатора опорная «земля» не
требуется. И если внимательно рассмо-
треть входные и выходные сигналы (сле-
дуя предупреждению не заземлять вход),
можно увидеть, что напряжение на каж-
дом входе становится отрицательным на
величину падения напряжения на диоде в
той половине периода, когда с этого вхо-
да положительный заряд не поступает на
выход. Эти отрицательные отклонения
можно наблюдать на графике входного и
выходного сигналов двухполупериодного
выпрямителя на рис. 3N.23.
Эта особенность мостового выпрямителя
делает очень неудобным его применение
для выпрямления несущей радиосигнала:
или вход или выход необходимо гальва-
нически развязать с землей. Для антенны
очень важно подключение к физической
земле; хотя выход заземлять необязатель-
но, отсутствие заземления все же доставля-
ет большие неудобства. Если общую шину
не подключать к земле, а оставить «пла-
вающей», мы не сможем, как обычно, ис-
следовать выходной сигнал иъых на осцил-
лографе, поскольку клемма заземления
осциллографа подключена к физической
земле. Заземлив один из входов моста,
можно использовать осциллограф в диф-
ференциальном режиме для исследования
выходного сигнала 1/вых, подсоединив два
щупа: один щуп подключается к обычному
выходу сигнала, а второй — к его «плаваю-
щей» земле, и одни показания вычитаются
из других. Но это такая морока...
В результате уменьшения входного сигнала
на величину двойного падения напряжения
на диоде в двухполупериодном выпрямите-
ле может потеряться значительная часть
сигнала. Напряжение сигнала, поступаю-
щего с антенны, составляет около одного
3N.9. Материал для чтения в АоЕ
157
Один из вариантов АМ-демодулятора
10 Я
Лучший вариант демодулятора (проще)
актирование пика
Детектирование пика с утечкой
Рис. 3N.36. Пиковый детектор с резистором утечки проще, чем выпрямитель с низкочастотным фильтром
вольта, поэтому недопустима дополни-
тельная потеря, величиной 21/ДИ0ДА, даже
если применены диоды Шоттки с низким
падением напряжения30. В простом одно-
полупериодном выпрямителе теряется
только [7ДИ0ДА.
Особенность низкочастотного фильтра
в детекторе
Простым способом избавиться от сигнала несу-
щей и выделить его огибающую представляется
обычный выпрямитель (с диодом и выходом,
соединенным через резистор на «землю»), а
затем подать его выходной сигнал на низко-
частотный фильтр (с резистором с номиналом
в 10 раз большим, чем предыдущий резистор,
чтобы не перегрузить выпрямитель). Такая схе-
ма будет работать, но эту задачу можно решить
с помощью более простой схемы, содержащей
всего один резистор. В таком детекторе сигнал с
диода поступает на конденсатор, второй вывод
которого подключен к земле. Диод с конденса-
тором образует пиковый детектор, в котором
конденсатор заряжается до уровня максималь-
ного входного напряжения (минус падение на-
пряжения на диоде). Затем, чтобы осуществить
спад выходного сигнала детектора при умень-
шении амплитуды, мы подключаем выход через
резистор (параллельный конденсатору) на зем-
лю. Получившаяся схема (рис. 3N.36) называ-
ется пиковым детектором с резистором утечки.
30 Падение напряжения при прямом смещении на диоде
Шоттки 1N5711, который рекомендуется для лаборатор-
ного занятия по экспериментам с радиоприемником, со-
ставляет 0,4 В при токе 1 мА.
Данная схема с трудом поддается анализу в
частотной области, но очень легко во времен-
ной: скорость спада сигнала пикового детек-
тора должна быть небольшой относительно
быстрых изменений несущего колебания ча-
стотой 1 МГц, но значительной по сравнению
с изменением аудиосигнала. Эти две частоты —
несущая и аудио — находятся так далеко друг
от друга, что выбрать постоянную времени RC
где-то посередине несложно. Более того, зна-
чение этой постоянной времени не слишком
критично. На лабораторном занятии полезно
поэкспериментировать, непосредственно вос-
принимая на слух, насколько чувствительным
к значению постоянной времени окажется вы-
ходной аудиосигнал вашего радиоприемника.
3N.9. Материал для чтения
в АоЕ
Завершите главу 1, включая разделы 1.5-1.6.8 и
раздел 1.7.2 по катушкам индуктивности, транс-
форматорам и диодам, которые мы пропустили
в прошлый раз.
Приложение по составлению чертежей прин-
ципиальных схем (Приложение В).
Приложение I: Телевидение: Краткое учебное
пособие.
Задачи
Задачи в тексте и дополнительные упражнения
(Additional Exercises) 1.43 и 1.44.
3L Лабораторное занятие:
схемы с диодами
3L1. Резонансный LC-контур
3L1.1. Частотная характеристика
для синусоидального сигнала
Соберите параллельный резонансный LC-
контур, принципиальная схема которого изо-
бражена на рис. 3L.1.
100 кОм
Вход о WV
0,01 мкФ
Пленочный
О Выход
ЮмГн
Рис. 3L.1. Параллельный резонансный LC-контур
Подайте на его вход синусоидальный сигнал,
варьируя его частоту в пределах диапазона,
включающего резонансную частоту, рассчи-
танную при заданных номиналах элементов
контура. Сравните наблюдаемую резонансную
частоту с расчетной.
Примечание
Учтите, что схема значительно ослабляет сигнал
даже на резонансной частоте. Это объясняется
неидеальностью катуыки индуктивности, которая
обладает определенным последовательным ак-
тивным сопротивлением.
Чтобы определить резонансную частоту fPE3,
ищите не максимум амплитуды сигнала (этот
факт трудно точно установить), а второй основ-
ной признак резонанса: частоту, при которой
выходной сигнал совпадает по фазе с входным.
3L1.2. Добротность Q
Приближенно определите добротность Осхемы.
Примечание
Q — это сокращение термина Quality Factor —
добротность, который отражает использование
резонансных контуров в радиоприемниках, где
очень важна высокая избирательная способность.
Формула для расчета добротности Q. следую-
щая:
п _/рез
Здесь Lf — полоса пропускания, определяемая
как интервал частот между точками половин-
ной мощности на резонансной кривой (точка
-3 дБ). Чем меньше полоса пропускания, тем
выше добротность О.(рис. 3L.2).
Добротность Q можно определить с очень
высокой точностью, используя частотомер1,
позволяющий обнаружить небольшие из-
менения частоты между точками, находящи-
мися ниже и выше резонансной частоты/РЕЗ,
где амплитуда выходного сигнала меньше на
3 дБ. Обратите внимание, что снижение на 3 дБ
рассматривается не относительно амплитуды
входного сигнала, а относительно максималь-
ной амплитуды выходного сигнала, т. е. ам-
плитуды на резонансной частоте. Амплитуда
выходного сигнала никогда не будет равна ам-
плитуде входного сигнала (только, если ком-
поненты идеальны).
1 Ваш цифровой мультиметр может обладать функцией
частотомера. Частотомер вам может потребоваться, если
вы пользуетесь аналоговым осциллографом. Но если у вас
цифровой осциллограф, частоту можно измерять и с его
помощью.
3L1. Резонансный LC-контур
159
max
0,7
(«Подобно ВЧ-фильтру: af) * - -«.
m~~ — (^Подобно НЧ-фильтру: a • 1/f)
'РЕЗ
Рис. 3L.2. Добротность Q можно определить, точно замерив Af с помощью цифрового мультиметра
Интересно посмотреть, какое влияние на до-
бротность (Докажет замена в схеме резистора
номиналом 100 кОм на номинал 10 кОм. Вы
должны заметить, что при меньшем сопротив-
лении амплитуда выходного сигнала возрас-
тает. Коэффициент передачи, определяемый
как ишх/иъх, повышается. Но с повышением
амплитуды выходного сигнала добротность Q,
падает. Как обычно, нам приходится жертво-
вать одной желаемой характеристикой, что-
бы получить другую. Но чаще всего намного
важнее иметь хорошую добротность Q, чем
большую амплитуду, поскольку проблему низ-
кой амплитуды можно решить с помощью уси-
лителя.
3L1.3. Частотная развертка
Настройте генератор сигналов на работу в ре-
жиме качающейся частоты, чтобы наблюдать
на осциллографе амплитудно-частотную ха-
рактеристику.
Примечание
В разделе 2S.3 подробно описано, как организо-
вать этот эксперимент.
Получив требуемую картину на экране осцил-
лографа, попробуйте объяснить, почему при
увеличении скорости развертки с одной сторо-
ны резонансной кривой появляются непонят-
ные пульсации.
Подсказка
Эти странные пульсации появляются после того,
как в контуре уже возникли резонансные коле-
бания и дополнительная энергия в колебатель-
ный контур теперь поступает от генератора сиг-
налов.
3L1 А. Определение Фурье-
спектра последовательности
прямоугольных импульсов
Данный резонансный контур можно использо-
вать в качестве импровизированного анализа-
тора Фурье: характеристика контура приблизи-
тельно измеряет амплитуду сигнала на частоте
16 кГц.
Подайте на вход контура последовательность
прямоугольных импульсов с частотой, равной
резонансной частоте контура, и заметьте ам-
плитуду выходного (синусоидального) сиг-
нала. Теперь постепенно понижайте частоту
входного сигнала, пока не получите другой
пик выходного сигнала (который должен по-
явиться на 1/3 резонансной частоты) и за-
мерьте его амплитуду. Ее величина должна со-
ставлять 1/3 амплитуды резонанса на основ-
ной частоте. Если запастись терпением, то
таким образом можно проверить амплитуду и
частоту первых пяти или шести членов ряда
Фурье.
На рис. 3L.3 приводится пример первых не-
скольких частот ряда Фурье для прямоугольно-
го сигнала. Мы уже встречались с этим рядом
ранее в этой главе (см. рис. 3N.16).
3L1.5. График частотного спектра
Если перевести генератор в режим качания ча-
стоты и варьировать частоту прямоугольного
сигнала, подаваемого на колебательный кон-
тур, работающий как детектор частоты 16 кГц,
то мы получим что-то типа частотного спектра:
на резонансной частоте^ должен наблюдать-
ся большой пик, на частоте 1/3/РЕЗ — несколько
меньший пик, и т. д.
160
3L Лабораторное занятие: схемы с диодами
4 sin Wot
% sin Шо£+ -I"sin Зшо^+ 4 sin 5wot
/\
\7
-1
-1
Рис. 3L.3. Ряд Фурье для сигнала прямоугольной формы
3L1.6.3boh
Теперь подайте на вход контура прямоуголь-
ный сигнал достаточно низкой частоты, для на-
чала попробуйте 20 Гц.
Совет
Низкую частоту можно задать произвольно. Нам
важен только крутой перепад сигнала, содержа-
щий высокочастотные составляющие. Перепад
сигнала можно рассматривать как вливание в наш
резонансный контур определенного объема энер-
гии, которая затем перемещается туда и сюда меж-
ду катушкой и конденсатором, пока не рассеется.
При каждом перепаде входного прямоугольного
сигнала на выходе должен появляться кратко-
временный всплеск. Если внимательно присмо-
треться к этому сигналу, то можно увидеть, что
это затухающий сигнал синусоидальной формы.
Совет
Если изображение на осциллографе слишком
тусклое, увеличьте частоту входного прямоуголь-
ного сигнала приблизительно до 100 Гц.
Проверьте, какова частота этого синусоидаль-
ного сигнала. Ничего удивительного с часто-
той, не так ли?
Сможете ли вы установить, что этот сигнал за-
тухает экспоненциально? Если помните, мы
рассматривали такое поведение в разделе
3N.4.4.
Определение добротности Q
по огибающей затухающего сигнала
Как упоминалось в разделе 3L.1.2, добротность
Q. контура можно определить по скорости
(\ Сигнал прямоугольной формы
затухания огибающей колебаний, после одно-
кратного воздействия на ЯЬС-контур. В част-
ности, добротность О.можно рассчитать по сле-
дующей формуле:
где N3 означает число периодов, необходимых,
чтобы уровень энергии упал до величины 1/е9
при котором амплитуда понизится приблизи-
тельно до 60% от максимума, поскольку энер-
гия пропорциональна квадрату напряжения IP
(см. главу 3N).
Наблюдая за реакцией схемы на медленный пря-
моугольный сигнал, посчитайте, сколько перио-
дов проходит, пока амплитуда сигнала не умень-
шится приблизительно до 60% первоначальной
величины, и проверьте, совпадает ли полученная
таким образом величина добротности Q.co зна-
чением добротности, вычисленным с использо-
ванием метода, рассмотренного в разделе 3L.1.2.
Проверьте также правильность утверждения из
раздела 3NAA (см. рис. 3N.17), что некачествен-
ное заземление щупа осциллографа будет вызы-
вать звон. Для этого в процессе наблюдения за
прямоугольным сигналом на осциллографе от-
соедините зажим заземления щупа. Получается
не очень красивая картина, не так ли?
3L.2. Однополупериодный
выпрямитель
Соберите однополупериодный выпрямитель
на диоде 1N914 и трансформаторе с дей-
ствующим напряжением вторичной обмотки
6,3 В2. Принципиальная схема изображена на
рис. 3L.4.
2 У Вас может возникнуть вопрос, почему такое странное
напряжение на вторичной обмотке: 6,3 В? Ответ можно
3L.3. Двухполупериодный мостовой выпрямитель
161
Переменное
напряжение
220 В
1N914
<—«Переменное,
С напряжение
<—16,3 В
2,2 кОм
■м-
Рис. 3L.4. Принципиальная схема однололупериодного выпрямителя
lN914's
Переменное^
напряжение J
220 В 3
Переменное
напряжение
6,3 В
2,2 кОм
Рис. 3L.5. Принципиальная схема двухполупериодного мостового выпрямителя
Подключите к выпрямителю нагрузку величи-
ной 2,3 кОм и исследуйте выходной сигнал на
осциллографе. Соответствует ли осциллограм-
ма сигнала вашим ожиданиям? Как насчет по-
лярности? Почему пиковое напряжение [7ПИК
больше, чем 6,3 В?
Примечание
Не удивляйтесь, если пиковое напряжение Unm
окажется даже чуть больше, чем 6,3x^/2 В, так как
разработчики трансформатора хотят гарантиро-
вать, что выходное напряжение источника питания
будет номинальным даже при тяжелых нагрузках,
а в этом эксперименте мы даем ему очень легкую
нагрузку.
получить, зная историю радиооборудования на вакуумных
лампах. Нить накала радиолампы нужно было нагревать
до определенной температуры, чтобы катод мог излучать
электроны. На ранних этапах развития радиоэлектроники
для разогрева нитей накала часто применялись батареи из
трех соединенных последовательно свинцово-кислотных
элементов, каждый из которых выдавал напряжение ве-
личиной 2,1 В. Когда стали использовать питание от
электросети, выходное действующее напряжение вторич-
ной обмотки было установлено таким, чтобы нагрев нити
был таким же, как и от батареи. Обратите внимание, что
синусоидальный сигнал переменного тока с действую-
щим напряжением 6,3 В имеет пиковое значение, равное
V2 • £/ДЕЙСТВ, и его мощность такая же, как и у источника
питания постоянного тока с напряжением, равным 6,3 В.
3L.3. Двухполупериодный
мостовой выпрямитель
Теперь соберите двухполупериодный выпрями-
тель с диодным мостом, принципиальная схема
которого показана на рис. 3L.5.
Будьте внимательны, соблюдайте правильную
полярность диодов. Полоска на одном конце
корпуса диода (см. справа на рис. 3L.5) озна-
чает, что данный вьюод является катодом.
Исследуйте выходной сигнал выпрямителя на
осциллографе.
Внимание!
Не пытайтесь одновременно посмотреть входной
сигнал (напряжение на выводах вторичной обмот-
ки трансформатора) на втором канале, поскольку
для этого нужно подключить зажим земли второ-
го щупа к одному из выводов вторичной обмотки.
А это чревато большими неприятностями. Можете
сказать, какими3?
3 Неприятность произойдет вследствие закорачивания
одного из четырех диодов моста. (Внимательно изучите
рис. 3L.5, чтобы понять, почему это случится.) В резуль-
тате ничто не будет ограничивать ток второго диода, кото-
рый безусловно сразу же сгорит.
162
3L Лабораторное занятие: схемы с диодами
Что вы думаете о выходном сигнале, насколь-
ко он соответствует теории? Почему его пи-
ковая амплитуда меньше, чем в предыдущей
схеме выпрямителя? Какой она должна быть?
Подумайте, что бы случилось, если поменять
полярность любого из четырех диодов моста.
Ни в коем случае не делайте этого!
Не слишком переживайте, если в процессе это-
го эксперимента вы выведете диоды из строя.
Подумайте, замыкает или размыкает цепь не-
исправный диод? Понимаете ли вы, почему
диоды в этой схеме обычно выходят из строя
парами, как будто бы они заключили некую до-
говоренность о «совместном самоубийстве»4?
Исследуйте область выходного сигнала вбли*
зи нулевого напряжения. Что это за плоские
участки сигнала? Измерьте их длительность и
объясните результат.
3L3.1. Пульсации
Исследуем пульсации
при подключенном сглаживающем
конденсаторе и нагрузке
Теперь подключите к выходу фильтра кон-
денсатор номиналом 15 мкФ (Осторожно:
соблюдайте полярность!) и наблюдайте, ка-
кой эффект он окажет на выходной сигнал. Что
вы думаете о выходном сигнале, соответствует
ли он теории? Вычислите, какой должна быть
амплитуда пульсаций, а затем измерьте ее.
Совпали ли результаты ваших расчетов с изме-
рениями?
Подсказка
Если теоретические и экспериментальные значе-
ния не совпадают, проверьте, не предположили ли
вы неправильное время разряда, например, вдвое
большее?
4 Эта договоренность о «совместном самоубийстве» дио-
дов делает проверку двухполупериодного мостового вы-
прямителя интересной задачей, когда выходной сигнал
выглядит не так, как он должен. Отсоедините трансфор-
матор от выпрямителя и проверьте исправность диодов
моста. (Это можно сделать с помощью функции тестиро-
вания диодов вашего цифрового мультиметра.) Не пре-
кращайте поиск неисправности после обнаружения одно-
го перегоревшего диода. Если есть один неисправный
диод, его «напарник» также будет неисправным.
3L3.2. Упражнение по разработке:
подбор емкости для достижения
приемлемой величины пульсаций
Теперь предположим, что вы хотите, чтобы
ваш источник питания выдавал ток величи-
ной до 20 мА и чтобы максимальный размах
пульсаций выходного напряжения не превы-
шал 1 В.
Ваша задача разработчика состоит в следу-
ющем:
♦ определить значение сопротивления нагруз-
ки Дн, при которой пиковое значение тока
составит 20 мА;
♦ определить значение емкости сглаживаю-
щего конденсатора, при которой величина
пульсаций будет около 1 В.
Начертите принципиальную схему, соберите
ее, а затем испытайте в действии. Получились
ли пульсации приблизительно требуемой вели-
чины? Попытайтесь объяснить любые откло-
нения от ожидаемых результатов.
Если схема работоспособна, то теперь у вас есть
источник, пригодный для питания маломощ-
ных устройств. Для питания более мощных
устройств потребуются более мощные диоды
(например, 1N4002) и сглаживающий конден-
сатор большей емкости.
Примечание
На практике, прежде чем подавать напряжение
источника питания на выход, оно поступает на
активный стабилизатор (с которым мы позна-
комимся на лабораторном занятии 11L) и лишь
после этого подается на внешние питаемые
устройства.
3LA Упражнение
по разработке:
АМ-радиоприемник
Чтобы это упражнение было интересным, вам
потребуется мощный источник радиосигна-
лов, иначе говоря довольно хорошая приемная
антенна. Можно обойтись и плохой антенной,
но снимаемый с нее высокочастотный сигнал
3L4. Упражнение по разработке: АМ-радиоприемник
163
нужно будет усилить. Вы можете сделать это
сами или попросить кого-либо другого, кто
разбирается в высокочастотных усилителях.
Чтобы получить сильный сигнал в нашей лабо-
ратории, мы протянули антенну длиной около
9 м из окна лаборатории к пожарной лестнице
на соседнем здании. Эта антенна не представ-
ляет собой ничего особенного: просто отрезок
провода, привязанный к пожарной лестнице
куском пластмассовой бечевки, чтобы изо-
лировать антенну от лестницы. Такая антенна
дает нам выходной радиосигнал величиной
почти 1 В.
Если исследовать выходной сигнал с антенны
на осциллографе, то осциллограмма будет вы-
глядеть примерно так, как показано слева на
рис. 3N.33 на с. 153. После резонансного конту-
ра этот сигнал будет выглядеть наподобие по-
казанного справа на этом же рисунке. Сетевой
помехи частотой 60 Гц5 больше не будет. Но на
этих осциллограммах не видно другого эффек-
та: исходный сигнал с антенны состоял из ме-
шанины сигналов разных частот других радио-
станций, которые были отфильтрованы.
3L4.1. Небольшой, но важный
аспект
Как упоминалось в разделе 3N.8.1, резонанс-
ный контур не только выделяет одну несущую
частоту среди многих других, но он также зна-
чительно увеличивает амплитуду выходного
сигнала по сравнению с входным.
3L4.2. Детектирование
АМ-си гнала
Чтобы продетектировать АМ-радиосигнал,
нужно выполнить две задачи, которые мы уже
знаем, как делать:
1. Выпрямить сигнал. Используем для этого
диод Шоттки, 1N511 или подобный; его ма-
лое напряжение прямого смещения позволит
выпрямить сигнал величиной всего в не-
сколько десятых вольта.
2. Подать выпрямленный сигнал на низкоча-
стотный фильтр.
5 Частота сети электропитания США. В России и странах
СНГ частота сети составляет 50 Гц.
В результате на выходе нашей схемы будет сла-
бый звуковой сигнал (напряжением намного
меньше одного вольта). Без дополнительной
обработки этот сигнал можно прослушивать с
помощью старомодных наушников с высоким
входным импедансом. Но чтобы прослуши-
вать его на обычном динамике с импедансом
катушки 8 Ом, его нужно сначала пропустить
через аудиоусилитель с коэффициентом усиле-
ния около 20 (для этой цели хорошо подойдет
микросхема звукового усилителя LM386). Вы,
наверное, уже заметили, что была предложена
только общая стратегия решения задачи, без
номиналов компонентов. Мы сказали «вы-
делите несущую», но не конкретизировали,
как это сделать. Также мы сказали «выпрями-
те сигнал», но не задали номинал резистора,
подключенного на «землю». Еще мы сказали
«используем низкочастотный фильтр», но не
предложили частоту ^дБ. Таким образом, вам
осталась трудная, но интересная часть работы.
Далее приведем несколько рекомендаций по ее
выполнению.
♦ Для детектирования несущей используйте
LC-контур подобный тому, который мы со-
брали в начале этого лабораторного занятия,
но со следующими отличиями:
• резонансная частота контура должна быть
около 1 МГц;
• верхний резистор «делителя» не нужен:
сигнал на LC-контур будет подаваться не-
посредственно с антенны.
♦ Значение подключенного на землю резисто-
ра не критично, попробуйте 10 кОм.
♦ Задача низкочастотного фильтра состоит
в том, чтобы устранить несущую частоту,
оставив при этом частоту звукового сигнала
(огибающую). К счастью, эти две частоты
расположены на значительном расстоянии
друг от друга, что дает вам большой выбор
частоты^. Схема низкочастотного фильтра
может показаться вам странной (хотя это за-
висит от того, каким способом вы будете ре-
шать поставленную задачу: в этой необыч-
ной конфигурации, которая описывается в
разделе 3N.8.4 и показана на рис. 3N.36, под-
ключенный на землю резистор выпрямите-
ля служит резистором низкочастотного RC-
фильтра). Только обязательно рассматри-
вайте задачу в ракурсе временной области:
постоянная времени RC должна быть очень
164
3L Лабораторное занятие: схемы с диодами
велика относительно периода несущей ча- Подсказка
стоты 1 МГц, но мала относительно периода
аудиосигнала.
Мы надеемся, что в награду за все свои труды
вы сможете услышать, конечно же, радиопере-
дачу. Вам, скорее всего, придется поэкспери-
ментировать с LC-контуром, добавляя конден-
саторы параллельно основному конденсатору
контура, чтобы выбрать определенную радио-
станцию. Можно пойти и другим путем, кото-
рым идут практически все, кто когда-либо со-
бирал радиоприемник, а именно использовать
переменный конденсатор. Если у вас нет ни
высокоомных наушников, ни аудиоусилителя,
тогда, по крайней мере, посмотрите на резуль-
таты своего труда на осциллографе.
Вы должны увидеть на экране что-то более-
менее похожее на АМ-сигнал, который мы
рассматривали в главе 3N. Сначала исследуйте
осциллографом необработанный сигнал, по-
ступающий с антенны (перед тем как подклю-
чить ее к LC-контуру), затем посмотрите на
несущую частоту, выделенную LC-контуром,
затем на выпрямленный носитель с аудиоин-
формацией и, наконец, на отфильтрованный
ЗВукОВОЙ Сигнал. Вход
Вы должны увидеть кривые разряда ЯС-контура
как с резистором 2,2 кОм, так и без него. Но здесь
задача заключается в том, чтобы выяснить, что же
это за /?С-цепь, переходный процесс в которой мы
наблюдаем, и эта задача довольно-таки непростая6.
3L5.2. Диодные ограничители
Соберите простой диодный ограничитель,
принципиальная схема которого изображена
на рис. 3L.77. Подайте на вход собранной схе-
мы синусоидальный сигнал с максимальной
выходной амплитудой, обеспечиваемой гене-
ратором сигналов, и наблюдайте за выходным
сигналом. Если вы видите, что форма вершины
ограниченного напряжения не совсем плоская,
значит, вы наблюдаете влияние ненулевого
дифференциального импеданса диода.
Попытайтесь примерно определить значе-
ние этого дифференциального сопротивления
(см. раздел 3N.6.3), но используйте для этого
треугольный сигнал.
1 кОм
-о Выход
3L5. Сигнальные диоды
3L5.1. Выпрямляющий
дифференциатор
Соберите выпрямляющий дифференциатор,
принципиальная схема которого показана на
рис. 3L.6. Подайте на вход схемы прямоуголь-
ный сигнал частотой около 10 кГц с максималь-
ной выходной амплитудой, обеспечиваемой ге-
нератором сигналов. Пронаблюдайте входной и
выходной сигналы, используя оба канала осцил-
лографа. По результатам эксперимента сделайте
вывод, правильно ли функционирует устрой-
ство? Какова роль нагрузочного резистора но-
миналом 2,2 кОм? Попробуйте удалить его.
560 пФ
1N914
Вход
Выход
2,2 кОм
1N914
+5 вольт
Рис. 3L7. Диодный ограничитель
Теперь исследуйте схему (рис. 3L.8), в которой
уровень ограничения напряжения задается де-
лителем напряжения8.
Подсказка
Поразмышляйте, какой импеданс у «источника на-
пряжения», образуемого делителем напряжения?
Если вы все еще недоумеваете, нарисуйте эквива-
лентную схему Тевенина. Кстати, эту схему, навер-
ное, будет лучше всего исследовать во временной
области.
Рис. 3L6. Выпрямляющий дифференциатор
6 После удаления заземляющего резистора номиналом
2,2 кОм важную роль начинает играть сам щуп осцилло-
графа. Теперь разряд происходит чрезвычайно медленно,
поскольку емкость щупа (возможно, 12 пФ) разряжается на
землю через импеданс щупа величиной 10 МОм. При вы-
сокой частоте прямоугольного входного сигнала, сигнал на
выходе щупа может выглядеть как плоская прямая.
7 АоЕ§1.6.6С.
8 АоЕ § 1.6.6, Fig. 1.76.
3LS Сигнальные диоды
165
Подайте на вход схемы синусоидальный сигнал
большой амплитуды и исследуйте пик выход-
ного сигнала. Как вы думаете, почему он такой
закругленный?
Чтобы проверить свое объяснение, подайте на
вход схемы сигнал треугольной формы.
Попробуйте исправить ситуацию, добавив в
схему конденсатор емкостью 15 мкФ, как пока-
зано пунктирной линией на схеме. Не забывай-
те соблюдать полярность при этом. Исследуй-
те модифицированную таким образом схему.
Объясните сами себе, почему она работает.
(Для этого можно применить как анализ во
Вход
о Выход
АЛЛ +15 вольт
2 кОм
Рис. 3L.8. Ограничитель с уровнем ограничения, задавае-
мым делителем напряжения
временной, так и в частотной области.) В этом
эксперименте иллюстрируется понятие шунти-
рующего конденсатора. Подумайте, что именно
он шунтирует и почему.
3S. Дополнительный материал и глоссарий
3S.1. Почему звон
LC-контура затухает,
несмотря на теорию Фурье
Этот интересный и непростой вопрос мне не-
давно задал один студент. Вопрос поставил
меня в тупик, пока меня неожиданно не осе-
нило (как Ньютона после падения яблока на
голову), когда я крутил педали велосипеда по
дороге на работу.
3S.1.1. Постановка задачи
Низкочастотный (скажем, 50 Гц) прямоуголь-
ный сигнал вызывает кратковременные коле-
бания в LC-контуре с резонансной частотой
16 кГц (мы собрали схему этого контура на
лабораторном занятии 3L). Такая реакция кон-
тура объясняется тем, что наш прямоугольный
сигнал содержит гармонику на частоте 16 кГц,
хотя и небольшой амплитуды.
В связи с этим наш студент сформулировал та-
кой вопрос:
Согласно теории Фурье не только перепады
сигнала, но и весь сигнал содержит составляю-
щую на частоте 16 кГц. Почему же тогда резо-
нансный контур не возбуждается постоянно,
а колебания возникают только при перепадах
сигнала?
Замечательнейший вопрос.
3S.1.2. Решение
Ключевой момент здесь следующий: резонанс-
ный контур реагирует на диапазон частот, а не
только на частоту 16 кГц. Из этого можно сде-
лать первый (ошибочный) вывод, что в таком
случае между перепадами амплитуда должна
быть еще больше, поскольку она стимулирует-
ся несколькими гармониками. Но ошибочность
этого вывода заключается в том, что фазы всех
этих нескольких гармоник совпадают только
на перепадах, усиливая друг друга. Вдали от
перепадов гармоники взаимно уничтожают
друг друга, чем и объясняется равномерность
вершины прямоугольного сигнала между пере-
падами: после ступенчатого перепада эти не-
сколько гармоник «сговариваются», чтобы
аннулировать друг друга. Неужели это правда,
скажете вы? Ну, лично мне все это не кажется
таким очевидным.
Резонансный контур пропускает не только одну
гармонику, а набор гармоник, члены которо-
го аннулируют друг друга вдали от перепадов
сигнала. Это происходит потому, что кривая
амплитудно-частотной характеристики конту-
ра достаточно широкая, чтобы пропустить этот
набор частот.
Ситуация с ограниченной добротностью Q.
также подтверждается анализом во временной
области. Звон после перепада прямоугольного
сигнала затухает со скоростью, определяемой
добротностью Q: высокая добротность Q, под-
разумевает медленное затухание (в этом отно-
шении добротность Q, соответствует потерям
энергии за период колебаний).
И мы уже наблюдали ранее нечто подобное
в упражнении на лабораторном занятии 3L.
Когда частота прямоугольного сигнала доста-
точно близка к резонансной частоте/РЕЗ (ска-
жем, составляет 1/3 или 1/5 резонансной ча-
стоты), звон (гармоника 16 кГц) действительно
длится все время, когда прямоугольный сигнал
находится на высоком или низком уровне. На
рис. 3S.1 приведены изображения из экспери-
ментов лабораторного занятия 3L, на которых
показаны ожидаемые компоненты прямоуголь-
ного сигнала на частоте в 3, 7 и 9 раз выше ча-
стоты этого сигнала.
3S.1. Почему звон LC-контура затухает, несмотря на теорию Фурье
167
3 'прям, сигн )
Очень малое /
затухание
°'прям сигн
Малое, но заметное
затухание
Рис. 3S.1. Амплитуда гармоник Фурье не уменьшается, если частота прямоугольного сигнала не слишком далека от резонанс-
ной частоты контура
'*прям, сигн
Малое
затухание
Во всех этих случаях компонент Фурье не за-
тухает на протяжении плоской части прямо-
угольного сигнала. Но почему это происходит?
При анализе во временной области ответ ка-
жется очевидным: у него нет времени, чтобы
затухнуть. Но этот факт также (конечно же)
подтверждается анализом в частотной области:
другие ближайшие гармоники находятся доста-
точно далеко от резонансной частоты и поэто-
му ослабляются.
1 ПРЯМ СИГН
Намного ниже
рБЗ
Затухание
очевидно
Рис. 3S.2. Для низкочастотного прямоугольного сигнала за-
тухание звона хорошо заметно
Иными словами, случай, когда звон продолжа-
ется, и случай, когда он затухает, можно объяс-
нить ограниченной добротностью контура при
анализе как во временной, так и в частотной
области. В частности, в нашем случае доброт-
ность Q. достаточно высока, чтобы объяснить
малое затухание звона при анализе:
♦ во временной области: звон не сильно
ослабевает в течение времени между пере-
падами (половина периода прямоугольного
сигнала);
♦ в частотной области: контур обладает до-
статочной избирательностью, чтобы поддер-
живать колебания на частоте 16 кГц, в то же
самое время удаляя вдали от перепадов сиг-
нала любые смежные гармоники, которые
могли бы скомпенсировать эту гармонику.
На рис. 3S.2 приведена осциллограмма для
случая, породившего первоначальный вопрос.
Здесь частота прямоугольного сигнала намного
ниже резонансной частоты, в результате чего
звон затухает.
168
3S. Дополнительный материал и глоссарий
3S.2. Глоссарий
для пассивных устройств
Время нарастания (risetime) — время, за ко-
торое сигнал нарастает от 10% своего конечно-
го значения до 90%.
Вторичная обмотка (secondary) — выходная
обмотка трансформатора.
Действующее напряжение (rms) — также на-
зывается среднеквадратическим напряжением.
Описывает энергию изменяющегося во вре-
мени сигнала. Для синусоидального сигнала
^действ = ^пика/^. Соответствует напряжению
действ = ^пика
постоянного тока, имеющего такую же мощ-
ность, как и переменное напряжение.
Добротность <£ (quality factor) — величи-
на, характеризующая остроту пика частотно-
избирательного 1?1С-контура. Определяется
следующей формулой:
Д/здв
Здесь/рЕЗ — резонансная частота; А/3лЪ — полоса
пропускания контура по уровню 3 дБ.
С другой стороны, Q= количество радиан, не-
обходимых для затухания энергии до 1/е свое-
го пикового значения.
Дроссель — катушка индуктивности.
Мощный (stiff) — для источника напряжения
означает, что напряжение проседает под на-
грузкой незначительно.
Первичная обмотка (primary) — входная об-
мотка трансформатора.
Пиковое напряжение UmK — пиковое (мак-
симальное) напряжение или амплитуда. На-
пример, в формуле u(f) = A sin cof множитель А
означает пиковое напряжение.
Проседание (droop) — падение напряжения
в результате подключения нагрузки (нагрузка
подразумевает потребление тока). Также иска-
жение формы сигнала при прохождении низко-
частотного прямоугольного сигнала через ВЧ-
фильтр.
Пульсации (ripple) — колебания напряжения,
вызываемые частичным разрядом сглаживаю-
щего конденсатора источника питания в про-
межутках между его зарядом от трансфор-
матора.
Размах сигнала 1/п.п — размах сигнала от
пика до пика. Другой способ описания вели-
чины сигнала. Применяется значительно реже,
чем ишк.
3W. Примеры с решениями:
схемы с диодами
3W.1. Разработка источника
питания
3WJ .1. Еще один источник питания
Это более подробно проработанное решение
задачи, которую мы вкратце рассмотрели в раз-
деле 3N. Если у вас не возникает трудностей с
процессом разработки источника питания, мо-
жете пропустить этот материал и перейти к раз-
делам 3W.1.6 и 3W.1.7, в которых рассматрива-
ются новые темы.
Перед нами стоит задача — разработать схему
обычного нестабилизированного источника
питания. Здесь мы рассмотрим процесс выбора
значений компонентов более подробно, чем в
разделе 3N.7. Постановка задачи следующая.
Задача. Нестабилизированный источник пи-
тания
Разработайте источник питания для преобра-
зования 110 В переменного напряжения элек-
тросети в постоянное напряжение. Исходные
данные:
♦ выходное напряжение UBUX: не менее 20 В;
♦ пульсации: приблизительно 2 В;
♦ максимальный ток нагрузки /н: 1 А.
Определите требуемые значения следующих
компонентов:
♦ емкость конденсатора в мкФ;
♦ напряжение вторичной обмотки трансфор-
матора (1/ДЕЙСТВ);
♦ номинал плавкого предохранителя (ток сра-
батывания);
♦ значение сопротивления нагрузочного (раз-
рядного) резистора;
♦ требуемый ток вторичной обмотки транс-
форматора.
Вопросы
Как будет отличаться выходное напряжение
схемы, если:
♦ Включить ее в электросеть в одной из евро-
пейский стран, где напряжение сети состав-
ляет 220 В, 50 Гц?
♦ Сгорит один диод выпрямительного моста
(создавая разрыв в цепи, а не короткое за-
мыкание)?
3W.1.2. Принципиальная схема
Первым делом мы, как обычно, начертим
принципиальную схему без значений компо-
нентов (рис. 3N.28). Плавкий предохранитель
включен в цепь первичной обмотки транс-
форматора, чтобы предотвратить как можно
больше возможных неполадок, включая вы-
ход из строя трансформатора и выключателя.
Обязательно выбираем двухполупериодную
(мостовую) схему. Большинство однополупе-
риодных схем источников питания, которые
приведены в учебниках, являются пережитка-
ми тех времен, когда диод представлял собой
дорогостоящую вакуумную лампу. В настоя-
щее же время диод — это крошечный кристалл
кремния, и специально для создания выпря-
мителей четыре диода монтируются в общем
корпусе, образуя компонент, называющийся
диодным мостом. Поэтому использование в
выпрямителе чего-либо другого, кроме диод-
ного моста, может быть оправдано только в
исключительных случаях. Разрядный резистор
также полезен в лабораторном источнике пита-
ния, к которому не всегда подключена внешняя
нагрузка: мы хотим, чтобы после выключения
источника его выходное напряжение снизилось
практически до нуля в течение нескольких се-
кунд. Это и обеспечивает разрядный резистор.
170
3W. Примеры с решениями: схемы с диодами
Рис. 3W.1. Форма пульсаций
Lt Европа
Пульсации
Во многих источниках питания всегда подклю-
чена нагрузка, как минимум в виде стабилиза-
тора, и, возможно, в виде схемы, для питания
которой они и предназначены. Сглаживающие
конденсаторы таких источников питания га-
рантированно разряжаются очень быстро без
помощи разрядного резистора.
3W.1.3. Определение
напряжения вторичной обмотки
трансформатора
Это напряжение должно равняться сумме пи-
кового значения выходного напряжения [/вых
и удвоенной величины падения напряжения
на диоде выпрямительного моста. Чтобы по-
лучить выходное напряжение 20 В без пульса-
ций, пиковое напряжение должно быть на два
вольта выше, т. е. около 22 В. Таким образом,
выходное напряжение трансформатора должно
быть примерно 23 В.
При расчете характеристик трансформатора
нужно использовать действующие значения на-
пряжения ЦдЕЙСТВ, а не пиковое [7ПИК (вспомни-
те, что действующее напряжение соответствует
такому постоянному напряжению, которое дает
мощность, равную переменному напряжению).
Как мы знаем, для синусоидального напряже-
ния ^
действ
В нашем ^У4^
'пик
23 В
^ ДЕЙСТВ
V2 1,4
=16 В.
Это как раз стандартное трансформаторное на-
пряжение1.
Если бы расчетное напряжение оказалось не-
стандартным, то пришлось бы взять большее
стандартное значение, или же трансформатор с
отводами в первичной обмотке, чтобы настра-
ивать коэффициент трансформации.
3W.1 А. Выбор конденсатора
На рис. 3W.1 изображена форма выпрямленно-
го напряжения с пульсациями. В подписях на
рисунке указывается, что величина Д£ зависит
от обстоятельств — в данной условной задаче,
поскольку мы хотим использовать наш источ-
ник питания в европейских странах. Поэтому
Д£ меняется в разных ситуациях, рассмотрен-
ных далее.
Берем следующую формулу:
dt
подставляем в нее имеющиеся у нас значения и
вычисляем величину емкости конденсатора С.
Нам известно, что:
♦ величина пульсаций, dU или Д[7, равна
2ВП.П;
♦ dt или ДГ это время между пиками входно-
го напряжения (период синусоиды), которое
равно 1/2 • 60 Гц * 8 мс (в США);
♦ J — это пиковый выходной ток, который ра-
вен 1 А.
Указание тока, а не сопротивления нагрузки мо-
жет в данный момент показаться странным, но
это обычный подход. Типичной нагрузкой для
нестабилизированного источника питания слу-
жит стабилизатор — схема, выходное напряжение
которой поддерживается на постоянном уровне.
Учитывая все эти значения, получим требуе-
мую нам емкость:
ДГ 8-ИГ3-
Д[/~
С =
2B
= 4000 мкФ.
Для трансформаторов в США.
Получилась довольно большая емкость, но не
чрезмерная. У вас может возникнуть желание
записать значение емкости в более короткой
ЗИ/.7. Разработка источника питания
171
Действ =16 В
1А
инерционный
4000 мкФ
Рис. 3W.2. Принципиальная схема источника питания с указанием номиналов элементов
форме (в миллифарадах) — 4 мФ. Это можно
сделать, но такая единица измерения не являет-
ся общепринятой в электронике, и использова-
ние ее будет выдавать вас как непрофессионала.
3W.1.5. Выбор плавкого
предохранителя
Поскольку данный источник питания понижает
напряжение с 100 В до 16 В, то выходной ток по-
вышается пропорционально понижению напря-
жения, т. е. приблизительно в семь раз. Таким
образом, выходной ток (во вторичной обмот-
ке) величиной 1 А соответствует входному току
(в первичной обмотке) около 1/7 А « 140 мА.
Но в этом расчете среднего входного тока не учи-
тываются эффект нагрева первичной обмотки и
колебания токов в первичной и вторичной об-
мотках трансформатора. Токи в этих обмотках
протекают неравномерно, перезаряжая сглажи-
вающий конденсатор только в течение опреде-
ленной части периода, в результате чего величи-
на токов в некоторые моменты времени оказы-
вается большой. Эти всплески тока подвергают
плавкий предохранитель большему нагреву, чем
равномерный ток такой же величины, поэтому
номинал плавкого предохранителя необходи-
мо увеличить примерно вдвое, а затем еще раз
вдвое, чтобы предохранитель мог выдерживать
полную нагрузку. (Второе удвоение номинала
предохранителя предназначено для аварий-
ных ситуаций.) С учетом описанных эмпири-
ческих правил получим следующий результат:
Номинал плавкого предохранителя (ток сра-
батывания) = 140 мА • 2 (чтобы выдерживал
всплески тока) • 2 (чтобы выдерживал полную
нормальную нагрузку) » 560 мА.
Таким образом, можно взять инерционный
предохранитель номиналом примерно 600 мА.
Почему предпочтительнее инерционный предо-
хранитель? Потому что при включении источ-
ника питания его сглаживающий конденсатор
резко заряжается в течение нескольких перио-
дов, что приводит к увеличению тока. Поэтому
безынерционный предохранитель будет пере-
горать при каждом включении источника пи-
тания. Инерционный плавкий предохранитель
имеет большую тепловую массу, способную
выдерживать избыточный ток в течение боль-
шего времени, чем обычный предохранитель,
прежде чем срабатывать.
3W.1.6. Расчет номинала
разрядного резистора
Разработчики, беспокоящиеся о безопасности
своих изделий, добавляют в источник питания
такой резистор или какую-либо другую вну-
треннюю нагрузку, чтобы не допустить удара
током из-за остаточного заряда сглаживающего
конденсатора. Значение сопротивления такого
резистора в целом не критично. Самое главное,
чтобы он смог разрядить сглаживающий конден-
сатор не более, чем за несколько секунд. Также
не следует брать резистор слишком малого но-
минала, который будет значительно нагружать
источник питания. Итак, предполагая постоян-
ную времени RC величиной несколько секунд,
значение сопротивления разрядного резистора
можно вычислить по следующей формуле:
R = {несколько секунд}/С « 1 кОм.
Прежде чем двигаться далее, начертим прин-
ципиальную схему нашего источника питания,
указав значения компонентов (рис. 3W.2).
3W.1.7. Требования
по номинальному току
трансформатора
Эта задача будет посложнее. Ток от транс-
форматора поступает в конденсатор кратко-
временными импульсами, которые нагревают
172
3W. Примеры с решениями: схемы с диодами
трансформатор больше, чем равномерный ток
такой же самой величины. Этот аспект уже рас-
сматривался ранее в разделе 3N. На рис. 3W.3
приведена форма тока во вторичной обмотке
трансформатора для двух возможных уровней
пульсаций:
♦ умеренные пульсации:
♦ малые пульсации: 1тств = (1/20 [20А]2)1/2 =
= V20 А = 4,4А (трансформатор подвергается
вдвое большему нагреву).
Рис 3W.3. Ток трансформатора в зависимости от величины
пульсаций: малые пульсации означают кратковременные
импульсы большого тока и избыточный нагрев
Слева на рис. 3W.3 изображен график тока,
протекающего в течение около 1/5 периода
импульсами амплитудой 5 А, чтобы перезаря-
дить сглаживающий конденсатор, равномерно
разряжающийся током 1 А. А справа на том
же рисунке показан график тока перезарядки
сглаживающего конденсатора, протекающего
в течение около 1/20 периода импульсами ам-
плитудой 20 А.
Заключение
Можно сделать вывод, что умеренные пуль-
сации предпочтительнее. Мы увидим, что это
действительно так, когда начнем рассматри-
вать стабилизаторы напряжения, которые мо-
гут снизить амплитуду пульсаций напряжения
с 1В на входе до милливольта и меньше на вы-
ходе, т. е. на нагрузке.
Вопросы
Как будет отличаться выходное напряжение
схемы, если:
1. Мы используем этот источник питания в
одной из европейских стран, где напряжение
сети 220 В, 50 Гц?
2. Сгорит один диод выпрямительного моста
(создавая разрыв в цепи, а не короткое за-
мыкание)?
Ответы
1. Очевидным эффектом будет удвоение выход-
ного напряжения, в результате чего, скорее
всего, устройство, подключенное к источни-
ку питания, перегорит. (Этим объясняется,
почему направляющиеся в Европу амери-
канцы часто берут с собой небольшие транс-
форматоры с коэффициентом трансформа-
ции 2:1. Хотя на практике все современные
источники питания обычно импульсного
типа и достаточно «умные», чтобы выда-
вать одинаковое выходное напряжение при
удвоенном входном.) Кроме того, удвоенное
входное напряжение может повредить как
трансформатор, так и сглаживающий кон-
денсатор. Теоретически можно выбрать сгла-
живающий конденсатор с рабочим напряже-
нием вдвое большим, чем ожидаемое. Но это
очень неразумный подход, поскольку разме-
ры конденсаторов сильно увеличиваются с
увеличением их рабочего напряжения.
Поскольку источник сразу же сгорит, то ис-
следовать другие менее очевидные измене-
ния в его работе вам не удастся. Но давайте
рассмотрим вопрос хотя бы теоретически.
Во-первых, изменится характер пульсаций
выходного напряжения: ДГ будет 1/50 Гц =
= 10 мс, а не 8 мс. В результате амплитуда
пульсаций пропорционально повысится.
При постоянной нагрузке пульсации повы-
сятся до приблизительно 2,5 В. В случае ре-
зистивной нагрузки ток нагрузки удвоится
вместе с выходным напряжением, и величи-
на пульсаций увеличится вдвое относитель-
но только что рассчитанного значения: при-
близительно до 5 В.
2. При отсутствии в мосте сгоревшего диода
мост будет функционировать, как однополу-
периодный выпрямитель. Соответственно,
AT удвоится, в результате чего приблизи-
тельно удвоится и амплитуда пульсаций. Но
частота пульсаций уменьшится вдвое: с 120
до 60 Гц.
Эта информация может помочь вам опреде-
лить, в чем проблема с вашим старым радио-
приемником. Если он начинает «фонить» на
частоте 50 Гц, возможно, вышла из строя по-
ловина выпрямительного моста; а если фон
на частоте 100 Гц, тогда, вероятно, вышел из
строя сглаживающий конденсатор. Если вам
нравится такая детективная работа с элек-
тронными устройствами, то возможностей
заняться нею очень много.
3W.2. Входной импеданс Z
вх
173
3W.2. Входной импеданс ZBX
Задача. Разработать процедуру для определе-
ния Явх и Свх
Предложите процедуру для определения со-
противления RBX и емкости Свх для устройства,
принципиальная схема которого изображена
на рис. 3W.4. Обратите внимание на то, что
результаты должны оставаться правильными
даже в том случае, если нижний вывод рези-
стора, соответствующего сопротивлению RBX,
не подключен на «землю». Это требование не-
сколько усложняет поставленную задачу.
Рис. 3W.4. Задача по определению входного импеданса
Решение
Первым шагом подключим резистор известно-
го значения последовательно нашему «черно-
му ящику» (так и будем называть его в даль-
нейшем — черный ящик). Затем наблюдаем на
осциллографе исходный сигнал на одном кана-
ле, и сигнал в точке, нагружаемой нашим чер-
ным ящиком, — на другом (рис. 3W.5).
Измеряем Явх
Здесь трудность, по существу, такая же, как и в
упражнении в разделе 2L1.1, в котором нужно
было оценить значения сопротивления и емко-
сти (RC) после определения произведения этих
величин (т. е. постоянной времени цепи). Нам
нужно отделить влияние сопротивления R от
емкости С.
Наш подход к измерению входного сопротив-
ления R^ будет состоять в исследовании схемы
на достаточно низкой частоте, чтобы импеданс
конденсатора был ничтожным по сравнению с
сопротивлением резистора: Хс » R. Это условие
выполняется на низкой частоте. Но вопрос, тре-
бующий некоторого размышления, заключается
в том, как установить факт, что мы находимся
именно на такой частоте. Далее предлагаются три
альтернативных метода решения этой задачи.
Измеряем Явх с помощью постоянного
напряжения
Мы можем измерить входное напряжение
разомкнутой цепи, что позволяет узнать на-
пряжение внутри черного ящика. Затем с по-
мощью тестового резистора jR^^ как в схеме
на рис. 3W.5, создаем обычный делитель. Если
внутреннее напряжение равно нулю, то в каче-
стве входного нам требуется внешний источник
питания постоянного тока.
Измеряем /?вх с помощью синусоидального
напряжения
Если на вход схемы подать синусоидальное на-
пряжение и наблюдать за точками А и Б, то нам
нужно убедиться, что наблюдаемое ослабление
сигнала является эффектом сопротивления R
без влияния реактивного сопротивления ем-
кости Хс Резистивный делитель R:R не будет
создавать фазового сдвига; делитель с рези-
стором R в верхней ветви и резистором R, па-
раллельным конденсатору С, будет создавать
фазовый сдвиг, за исключением случая, когда
реактивное сопротивление конденсатора Хс
очень большое по сравнению с сопротивлени-
ем R черного ящика. Таким образом, подаем на
вход схемы низкочастотный синусоидальный
сигнал и смотрим, наблюдается ли фазовый
Первый способ:
подаем сигнал
синусоидальной
формы
Второй способ:
подаем ступенчатый
или прямоугольный
сигнал
Рис. 3W.5. Шаг 1: подключаем резистор с известным сопротивлением последовательно с черным ящиком
174
3W. Примеры с решениями: схемы с диодами
и
/
/
/Г
1
1
л
х \
*. «\. ♦».
\
V «.»
\
\
2 00V
: [
\ j
Л
\
\
"СИ4
\ *■
\ 1
\ |
\ 1
5 Гц, вход в АС-режиме: находимся 50 Гц, вход в АС-режилле: (разовый 1 кГц: делитель 10 кОм'ЛО кОм,
ниже точки /^дБ ВЧ-фильтра на входе сдвиг отсутствует. При этом входное измеряемый щупом с BNC-кабелем
осциллографа, поэтому создается сопротивление определяем правильно длиной около 1 м: снова появляется
(разовый сдвиг фазовый сдвиг, в этот раз вызываемый
эффектом НЧ-фильтра, создаваемого
емкостью кабеля щупа
Рис. 3W.6. Подавая на вход схемы синусоидальный сигнал, смотрим, когда отсутствует фазовый сдвиг, что является индикато-
ром измерения неискаженного входного сопротивления /?вх
сдвиг. Если нет, значит, наше измеренное зна-
чение входного сопротивления не искажается
из-за влияния Свх. На рис. 3W.6 приведены изо-
бражения результатов измерений, когда входы
осциллографа находятся в режиме АС.
Две возможные опасности
♦ На очень низкой частоте, если использовать
режим АС только для канала осциллографа,
подключенного к точке Б, возможно наблю-
дение фазового сдвига, который в действи-
тельности является всего лишь паразитным
эффектом осциллографа. АС-режим полезен
в том случае, если изображение отцентриро-
вано на отметке 0%: поскольку нижняя часть
синусоидального сигнала уходит с экрана,
смещение постоянной составляющей сигна-
ла может ввести вас в заблуждение. Но при
работе в АС-режиме на чрезвычайно низких
частотах (ниже 10 Гц) может наблюдать-
ся влияние блокировочного конденсатора2.
Этот эффект можно видеть на левом изобра-
жении на рис. 3W.6.
♦ На более высоких частотах возможно появле-
ние фазового сдвига (в этот раз отставания),
2 Как для аналоговых, так и для цифровых осциллогра-
фов частота /3лВ составляет около 7 Гц (ВЧ-фильтр) при
АС-режиме и работе со щупом с BNC-кабелем (тип IX).
Если взять щуп с ослаблением 10Х, то частота^дБ осцилло-
графа окажется настолько низкой (около 0,7 Гц), что она,
скорее всего, не будет создавать для вас никаких проблем.
Но в данном случае, когда нам необходимо работать с обо-
ими каналами в АС-режиме, фазовый сдвиг не доставля-
ет хлопот, поскольку он будет одинаково проявляться на
обоих каналах. В отличие от этого на рис. 3W.6 показаны
результаты работы канала 1 в DC-режиме, а канала 2 —
в АС-режиме.
вызываемого НЧ-фильтром, создаваемым
комбинацией тестового резистора и пара-
зитной емкостью BNC-кабеля щупа и канала
осциллографа, который подключен к точ-
ке Б. Этот эффект можно видеть на правом
изображении на рис. 3W.6.
Чтобы быть уверенным, что никакой из этих
эффектов не вводит вас в заблуждение, убеди-
тесь в отсутствии фазового сдвига между кана-
лами при наблюдении сигналов в точках А и Б,
как показано на рис. 3W.6. Ослабление сигнала,
которое можно видеть на этом изображении,
является результатом влияния только входного
сопротивления JRBX схемы и не подвержено эф-
фекту паразитной емкости.
Измеряем /?вх с помощью прямоугольного
сигнала
Определить входное сопротивление схемы RBX
можно также с помощью прямоугольного сиг-
нала. Справа на рис. 3W.7 видно влияние по-
стоянной составляющей на нижнем выводе
измеряемого сопротивления черного ящика.
Постоянное смещение является еще одним на-
поминанием, почему входное сопротивление
RBX не следует пытаться измерять, подавая по-
стоянное напряжение на тестируемое устрой-
ство. Если предположительно оценить входное
напряжение #вх для этого случая, постоянное
напряжение на нижнем выводе R могло бы
сбить нас с верного пути. Но, как и при сину-
соидальном сигнале, ступенчатый сигнал тоже
позволяет выполнять правильное измерение.
3W.2. Входной импеданс Zm
175
Измерение
уровней —■ ._
постоянного
напряжения даст . .
неправильное
значение/?вх ш iM^ Ch4| 1Ш,~ SM 00|W
Прямоугольный входной сигнал: напряжение
на нижнем выводе R падает до потенциала земли
Сравнение амплитуд
при входном
ступенчатом
сигнале дает
правильное значение
&вх, несмотря
на смещение
постоянной
составляющей
Напряжение на нижнем выводе R поднимается до
+1,5 В; это исказит результат измерения при подаче
постоянного напряжения, но не при прямоугольном или
ступенчатом сигнале
Рис. 3W.7. Входное сопротивление /?вх можно измерить с помощью прямоугольного сигнала
Чтобы оценить входное сопротивление
сравниваем амплитуду входного ступенчатого
сигнала с амплитудой выходного сигнала чер-
ного ящика.
Слева на рис. 3W.7 показано неправильное из-
мерение уровня постоянного напряжения в
точках А и Б (определенных на рис. 3W.5) из-за
смещения постоянной составляющей. При по-
даче ступенчатого или прямоугольного сигна-
ла, результаты будут верными, как можно ви-
деть справа на рис. 3W.7.
Определяем Свх
Получив значение входного сопротивления
Двх, следующим шагом следует определить по-
стоянную времени RC. Наличие этого значения
позволит нам вычислить емкость входа Свх.
Значение постоянной времени можно вычис-
лить одним из двух способов.
Используя синусоидальный сигнал: опре-
деляем АС, а затем С, измеряя ^3дБ
На вход схемы подается синусоидальный сиг-
нал, как было описано ранее, постепенно по-
вышают его частоту и наблюдают за понижени-
ем амплитуды сигнала, снимаемого в точке Б,
пока она не снизится на 30% своего уровня при
низкой частоте. Таким образом мы определим
частоту /3дЪ. Имея значение /3дЪ и зная значение
сопротивления R, мы можем легко вычислить
значение емкости Свх.
При расчете следует учесть, что эффективное
сопротивление R, нагружающее емкость Свх,
состоит из параллельно соединенных сопро-
тивлений ДВХ||ДТЕСГ
Используя прямоугольный сигнал:
определить постоянную времени RC
напрямую, а затем вычислить емкость С
Подавая на вход схемы прямоугольный сиг-
нал, можно определить постоянную времени
HBI 1 оо v м 2 oom*
см i оо v
Развертка слишком медленная для Скорость развертки выбрана верно: Развертка слишком быстрая
отображения постоянной времени кС отображаются как кС, так и конечные
уровни
Рис. 3W.8. Для определения постоянной времени нужно установить оптимальную скорость развертки
176
3W. Примеры с решениями: схемы с диодами
напрямую, по осциллограмме (во временной
области) сигнала на экране. Как обычно, для
этого нужно выбрать соответствующую ско-
рость развертки (см. рис. 3W.8). Но эта задача
вам уже известна, поскольку мы сталкивались с
ней в начале лабораторного занятия 2L.
Хотя по средней осциллограмме на рис. 3W.8
можно определить значение постоянной вре-
мени, выполнить эту задачу еще удобнее, если
увеличить область экрана осциллографа для
наблюдения за временем нарастания сигнала
от самого низкого уровня до 63% его макси-
мального уровня.
Получив значение постоянной времени, нуж-
но учесть, что, как и в случае с синусоидаль-
ным сигналом, эквивалентное сопротивление R
в действительности это параллельно соединен-
ные сопротивления #ТЕСТ и Двх.
Часть II
Аналоговые устройства:
транзисторы
4N. Транзисторы I
Содержание
4N.1. Краткий обзор рассматриваемого материала 179
4N.2. Предварительная информация 181
4N.2.1. Название транзистора 181
4N.2.2. Простейшая модель транзистора 181
4N.2.3. Символ транзистора 182
4N.2.4. Исходные упрощения 182
4N.2.5. Две простые модели транзистора 182
4N.3. Простое представление без j8 182
4N.3.1. Транзистор как источник тока 183
4N.3.2. Усилитель с общим эмиттером 184
4N.3.3. Эмиттерный повторитель... повторяет 184
4N.3.4. Двухтактный эмиттерный повторитель работает, но искажает сигнал 185
4N.4. Введем коэффициент «бета» 185
4N.4.1. Подробнее о «бета» 185
4N.4.2. Эмиттерный повторитель как преобразователь импедансов 186
4N.4.3. Первые сложности: смещение 188
4N.4.4. Еще одно усложнение: асимметрия схемы может вызывать отсечку 191
4N.4.5. Решение проблемы отсечки с помощью двухтактного каскада 193
4N.5. Переключатель: транзисторная схема особого типа 194
4N.6. Краткий обзор основных транзисторных схем для закрепления
пройденного материала 194
4N.6.1. Об импедансе на коллекторе 195
4N.6.2. Транзисторный переключатель как особая категория схем 195
4N.7. Материал для чтения в АоЕ 195
Цель этой главы
Для решения каких задач предназначены тран-
зисторы, которые мы начнем рассматривать
сегодня? Они могут воздействовать на сигналы
следующими способами:
♦ улучшить импеданс схемы: повысить вход-
ной или понизить выходной;
♦ поддерживать ток постоянным при варьиру-
ющемся уровне напряжения (т. е. создавать
«источник тока»);
♦ усиливать напряжение (AL/);
♦ включать и выключать ток в нагрузке под
действием входного управляющего сигнала.
4N.1. Краткий обзор
рассматриваемого
материала
В этой и следующей главе мы рассмотрим но-
вые эффективные электронные устройства,
которые способны усиливать подаваемые на
них сигналы. Одни из этих схем усиливают
напряжение, что обычно рассматривают как
собственно работу усилителя. А другие схемы
усиливают только ток. Такой тип усиления на-
зывается преобразованием импедансов. Как мы
знаем из наших предыдущих лабораторных за-
нятий, это тоже весьма полезная возможность.
180
4Л/. Транзисторы I
Транзисторы, которые мы будем в основном
рассматривать далее, называются биполярны-
ми. Данное название объясняется тем, что меха-
низм переноса заряда использует носители обе-
их полярностей, но это уже предмет для другого
курса. Только в конце раздела по аналоговым
устройствам мы познакомимся с транзисторами
другого типа — с полевым эффектом или просто
полевыми. Хотя в них перенос заряда осущест-
вляет носитель только одной полярности, они,
тем не менее, не называются однополярными
(хотя вначале они действительно так называ-
лись). Полевые транзисторы были открыты
после биполярных, хотя, как подробно рассма-
тривается далее, разработчики биполярного
транзистора обнаружили его случайно, пыта-
ясь создать полевой транзистор. Для цифровых
устройств вариант полевого транзистора (МОП-
транзистор1) оказался более важным, чем би-
полярные транзисторы. Далее в этом курсе мы
будем работать с большим количеством логиче-
ских схем, содержащих полевые транзисторы.
Биполярные транзисторы продолжают доми-
нировать в аналоговых схемах, но даже в этой
области полевые транзисторы завоевывают все
больше позиций.
Иногда мы будем рассматривать транзисторы
отдельно, как дискретные устройства. Но чаще
мы будем комбинировать транзисторы с опе-
рационными усилителями2, чтобы получить
большой ток или мощность, которые не по си-
лам обычному операционному усилителю. Но
изучение транзисторных схем играет важную
роль в курсе схемотехники главным образом
потому, что знакомство с разработкой схем на
дискретных транзисторах поможет вам понять
внутреннее устройство интегральных микро-
схем, без которых вам, наверняка, не обой-
тись ни в одном из более-менее практических
разрабатываемых устройств. После освоения
материала этого раздела вы сможете распозна-
вать в структуре интегральной микросхемы со-
вокупность уже знакомых вам транзисторных
схем. Для лучшего освоения операционных
1 Затвор такого полевого транзистора (в частности, со
структурой метал-оксид-полупроводник) изолирован от
канала оксидом кремния SiO2. МОП-транзисторы рассма-
триваются более подробно в главе 12N.
2 Операционные усилители представляют собой уси-
лители с высоким коэффициентом усиления, которые
используются для реализации схем, охваченных цепью
отрицательной обратной связи. Начиная с главы 6N, опе-
рационные усилители будут нашими основными элемен-
тами аналоговых схем.
усилителей в конце лабораторного занятия 5L
вам будет предложено собрать операционный
усилитель из нескольких транзисторов. Изучив
внутреннее строение операционного усилите-
ля, вы сможете понять его недостатки, посколь-
ку они обусловлены свойствами уже знакомых
вам транзисторных схемных элементов.
Материал по транзисторам будет непростым
для изучения. Вам предстоит освоить новый
элемент и в то же самое время воспользоваться
знаниями, которые вы приобрели ранее, изучая
пассивные компоненты. Вам снова нужно будет
учитывать взаимодействие импедансов: рас-
считывать номиналы и размещение элементов
схемы так, чтобы выходной сигнал фрагмента
схемы А можно было подавать на вход фрагмен-
та схемы Б без чрезмерного ослабления сигнала.
Вам придется разработать и собрать множество
схем с jRC-цепочками. Часто, чтобы определить
эффективное сопротивление, вам необходимо
будет создавать эквивалентную схему Тевенина.
Конечно же, мы надеемся, что предстоящая ра-
бота доставит вам удовольствие и вы сможете на
практике применить свои новые знания и навы-
ки; но одновременно вам придется приложить
много усилий в освоении достаточно сложного
материала данной главы.
Мы подчеркиваем это не для того, чтобы запу-
гать вас, а наоборот, чтобы вы знали, что если
у вас возникнут какие-либо трудности с изуче-
нием правил разработки схем на транзисторах,
то это не означает, что вы не способны их усво-
ить. Транзисторная схемотехника — это очень
обширный раздел курса и, возможно, самый
трудный.
Но на лабораторном занятии 6L мы начнем ра-
ботать с операционными усилителями и ваша
жизнь как разработчика схем станет гораздо
легче. При наличии цепи обратной связи опера-
ционные усилители сделают задачу разработки
высококачественных схем достаточно простой.
И тогда вы, наверное, начнете задаваться во-
просом, а зачем вы вообще мучились с трудны-
ми проектами с дискретными транзисторами.
Но мы не будем сейчас разглашать вам секрет,
что с операционными усилителями легко рабо-
тать, поскольку мы не хотим охладить ваш пыл
к работе с дискретными транзисторами. Ваше
усердие будет вознаграждено, и транзисторы
будут выполнять для вас очень важную работу.
Вместо того чтобы думать об операционных
усилителях, попытайтесь настроить себя на та-
кое состояние, какое было у трех изобретателей
4N.2. Предварительная информация
181
видите, конструкция выглядит очень шаткой,
хотя сделана не из скрепок, клейкой ленты и
жевательной резинки5.
Рис. 4N.1. Самый первый транзистор точечного типа (1947)
транзистора, которые к своему восхищению об-
наружили, что из куска германия они смогли
создать миниатюрный усилитель. Но в то время
они, наверное, еще не могли представить себе,
что настанет время, когда вакуумные лампы3
вместе с высоковольтными источниками пита-
ниями больше не потребуются, и что огромные
объемы энергии больше не будут тратиться на
нагрев нитей накала ламп. Но мир уже мог смо-
треть с надеждой в будущее с микрокомпьюте-
рами, iPod-ами, смартфонами и со всеми дру-
гими чудесными устройствами, существование
которых было обусловлено появлением микро-
схем4. На рис. 4N.1 приведено изображение би-
полярного транзистора, изобретатели которого
получили за него Нобелевскую премию. Как
3 Если уж совсем точно, то почти без вакуумных ламп.
Гитаристы-рокеры и некоторые сумасшедшие меломаны
до сих пор предпочитают звук, создаваемый вакуумными
лампами. Гитаристам нравится звучание лампового усили-
теля при перегрузке. А поклонникам музыки просто нра-
вится тратить деньги.
4 История изобретения биполярного транзистора заме-
чательно описана в книге «Crystal Fire» («Кристальный
огонь»), авторы Майкл Риордан (Michael Riordan) и Л ил-
лиан Ходдсон (Lillian Hoddeson), издательство Norton
(1997), на странице 138ff, а также в короткой статье, в чис-
ло авторов которой входит бывший руководитель лабора-
торий Белл Уильям Бринкман (William Brinkman): «A His-
tory of the Invention of the Transistor and Where It Will Lead
Us» («История изобретения транзистора и куда он при-
ведет нас»), опубликованной в журнале организации ШЕЕ
Journal of Solid-State Circuits (Журнал полупроводниковой
схемотехники), № 32, декабрь 1997 г.
4N.2. Предварительная
информация
4N.2.1. Название транзистора
Название транзистор происходит из комбина-
ции английских слов TRANS [fer]+[res] ISTOR:
нечто отдаленно похожее на резистор, но с воз-
можностью управления, и способное переме-
щать (transfer) сигнал с входа на выход. Обладая
тремя выводами, это устройство отличается от
пассивных компонентов, с которыми мы имели
дело до сих пор (за исключением трансформато-
ра с четырьмя или пятью выводами, чье назва-
ние также указывает на его поведение). Наличие
трех выводов сделает трудными ваши первые
несколько дней работы с транзисторами.
Но не следует отчаиваться, если вы столкне-
тесь с такими трудностями: очень скоро вы вы-
беретесь из этого мрака на светлые просторы
операционных усилителей, как мы обещали в
разделе 4W.1. Там мы особо подчеркнули, что
хотели, чтобы вы знали внутреннее устройство
операционных усилителей и не считали их ра-
боту каким-то волшебством.
4N.2.2. Простейшая модель
транзистора
Транзистор можно сравнить с вентилем, как
показано на рис. 4N.2. Но обратите внимание,
что в данной аналогии транзистор не является
Большой ток
Ток коллектора Гк
Слабый
управляющий
сигнал
Ток базы ГБ 17
4
41
Ток эмиттера 1Э
Рис. 4N.2. Транзистор — это вентиль (но не насос!)
5 Фотография публикуется с разрешения компании AT&T
Bell Labs.
182
4N. Транзисторы I
Коллектор
База
Эмиттер
Транзистор, созданный
в Лаборатории Белла
в 1947 г.
Повернутый на 90°
Выглядит очень похожим
на символ транзистора
Рис. 4N.3. Похоже, что символ транзистора является просто эскизом первого прототипа устройства
насосом: он не заставляет ток протекать по
цепи. Он лишь разрешает ему протекать, управ-
ляя силой тока, а вот «протолкнуть» ток через
транзистор пытается источник питания.
4N.2.3. Символ транзистора
Похоже, что символ транзистора (условное
графическое обозначение) является эскизом
его самого раннего прототипа6. На рис. 4N.3
справа показан фрагмент фотографии ориги-
нального транзистора, созданного в компании
Лаборатории Белла7.
Такая версия происхождения символа транзи-
стора, несомненно, выглядит правдоподобной.
База буквально является базой, т. е. основа-
нием, всей структуры. Томас Ли (Thomas Lee)
как-то заметил, что Шокли (Shockley), Бардин
(Bardeen) и Браттайн (Brattain) открыли би-
полярный транзистор, а не изобрели его, по-
скольку эти три исследователя натолкнулись
на структуру случайным образом. Они не пыта-
лись создать биполярный транзистор, а хотели
обнаружить причину неполадок с их нерабо-
тоспособным макетом устройства с полевым
эффектом, зондируя поверхность базы, чтобы
исследовать нарушения протекания тока.
2. Структура транзистора устроена так, что
разность напряжений UB-U3 составляет око-
ло 0,6 В (переход «база - эмиттер» являет-
ся диодом и должен находиться под прямым
смещением).
4N.2.5, Две простые модели
транзистора
Начнем наше рассмотрение транзистора с двух
его моделей: одной простой, а другой еще более
простой. Но далее мы усложним их.
♦ Простая модель: транзистор как усилитель
тока: 1К = /3- 1Б (рис. 4N.4).
Рис. 4N.4. Модель тран-
зистора, как управляе-
мого током вентиля или
усилителя
♦ Очень простая модель: коэффициент р
игнорируем (хотя предполагаем, что тран-
зистор выполняет свои функции). Формулы
упрощаются:
4N.2A Исходные упрощения
Для транзисторов типа п-р-п8:
1. UK > иэ (как минимум на пару десятых
вольта).
6 Книга «Planar Microwave Engineering» («Планерная мик-
роволновая инженерия») автор Томас X. Ли (Thomas
Н. Lee), издательство Cambridge University Press (2004 г.),
ст. 342.
7 Англ. - Bell Labs или Bell Laboratories.
8 АоЕ §2.1.1
4N.3. Простое
представление без
Многие схемы можно анализировать и даже
разрабатывать, не используя явно коэффици-
ент усиления «бета» (также обозначается AFE9),
который является отношением выходного тока
9 Или h21 — Примеч. ред.
4N3. Простое представление без /3
183
к входному: р = /К/1Б. Это самое простое опи-
сание транзистора позволит вам легче уяснить
понятия, рассматриваемые в следующих раз-
делах.
4N.3.1. Транзистор
как источник тока
Это понятие иллюстрируется на рис. 4N.510.
Абсолютно ничего сложного, не так ли? Это
всего лишь закон Ома, определяющий ве-
личину выходного тока, благодаря извест-
ному падению напряжения 17БЭ на переходе
«база - эмиттер».
и
|Нагрузка|
+5,6 В _
Входное
Когда напряжение
Ub не меняется,
напряжение Ц также
остается постоянным
и определяет
стабильный ток
эмиттера Гэ
Но ГК*ГЭ
Рис. 4N.5. Транзистор как источник тока
Теперь посмотрим на рис. 4N.6 и выясним, что
будет происходить при изменении сопротивле-
ния резистора в цепи коллектора — RH. Также
подключим резистор в цепь базы, что не прин-
ципиально, за исключением экстремального
случая, ковда источник тока выходит из строя
(мы рассмотрим этот случай немного позже).
Если мы будем изменять величину нагруз-
ки 2?н, как будет вести себя ток нагрузки 7НИ?
(/=20 В
+5,6 В
(входное)
Рис. 4N.6. Транзистор, как источник тока с переменной на-
грузкой
10 АоЕ § 2.2.5В.
11 АоЕ § 2.2.6D.
Предположим, что мы уменьшим сопротивле-
ние нагрузки RH с 10 кОм до 1 кОм. Возрастет
ли вследствие этого ток?
Если вы намереваетесь сказать, что да, ток
возрастет, значит, вы вспомнили материал по
пассивным компонентам, и по старым знако-
мым — резисторам. Вы ожидаете, что транзи-
стор будет действовать так же, как и эти ваши
давние друзья: как омическое устройство — чем
выше напряжение на нем, тем больше ток. Но
транзисторы не ведут себя таким образом.
Если при уменьшении значения RH напряжение
коллектора UK повышается, то из этого не сле-
дует, что также возрастает ток коллектора 7К.
Это объясняется тем, что 1К« 1Э, а 1Э ограничен,
поскольку он определяется напряжением на
базе UB. Такое поведение, может быть, незна-
комо вам, но оно может оказаться полезным.
Если уменьшить RH до самого нуля, будет ли ток
оставаться постоянным? Да, будет.
Но что будет с током в противном случае? Будет
ли он оставаться постоянным при повышении
значения #н? В данном случае ответ будет отри-
цательным, поскольку источник тока прекратит
функционировать. Причиной будет нарушение
одного из предположений, которые мы сделали
в разделе 4N.2.4.
При увеличении сопротивления резистора RH
в схеме на рис. 4N.6 свыше 15 кОм напряже-
ние коллектора UK падает до слишком низкого
уровня, при котором условие UK > U3 больше
не выдерживается, и схема не может поддер-
живать ток на постоянном уровне. Транзистор
больше не может выполнять свою задачу кор-
ректирования напряжения коллектора UK тре-
буемым образом, чтобы поддерживать ток
коллектора 7К постоянным. Ситуация, когда
напряжение 1/кэ падает ниже двух десятых
вольта, называется режимом насыщения тран-
зистора.
Когда это происходит, все обычные правила,
которые мы здесь излагали, больше не приме-
нимы. Схема становится омической, в которой
транзистор выглядит, как резистор с неболь-
шим сопротивлением, и дальнейшее повыше-
ние Дн просто уменьшает /н. Например, повы-
шение RH до 50 кОм снизит ток нагрузки 7Н до
0,4 мА (20 В на сопротивлении 55 кОм): пове-
дение чисто в рамках закона Ома.
184
4Л/. Транзисторы I
(Г) Небольшое изменение UBX : Л(УБ
Рис. 4N.7. Усилитель с общим эмиттером
Небольшое изменение Гк (АГК) =:
небольшое изменение (Увых
(большое /^ => большое ДЦЫХ)
(2) (ДЦ) небольшое изменение UBX =>
небольшое изменение Ц =>
небольшое изменение Гэ я Гк
(малое /?э => большое ДХК)
Это ограничение на диапазон источника тока —
называющееся соответствием выходному на-
пряжению — напоминает нам о том, что хотя
транзисторные схемы достаточно «интеллекту-
альные», с ними все равно нужно обходиться с
умом. Они не работают, если не следовать за-
данным правилам.
является резистор, который преобразует вы-
ходной ток и его колебания в напряжение; это
каскад «J в U». Вы можете возразить, что на-
зывать простой резистор «преобразователем
тока в напряжение» слишком экстравагантно.
Возможно, но такова на самом деле функция
этого резистора в данной схеме13.
4N.3.2. Усилитель с общим
эмиттером
Для того чтобы сделать из источника тока уси-
литель напряжения, нужно всего лишь подклю-
чить резистор к коллектору транзистора, как
показано на рис. 4N.712.
Усилитель с общим эмиттером можно рассма-
тривать в виде последовательного соединения
двух каскадов, как показано на рис. 4N.8.
Первый каскад является источником тока
(в котором ток управляется входным напряже-
нием [/вх); это каскад «[/в I». Вторым каскадом
и
Преобразователь Преобразователь
«напряжение — ток» «ток — напряжение»
Рис. 4N.8. Усилитель с общим эмиттером можно рассматри-
вать как каскад «U в /», подающий сигнал на каскад «/ в U»
4N3.3. Эмиттерный повторитель...
повторяет
На первый взгляд схема, изображенная на
рис. 4N.9, может показаться совершенно бес-
смысленной: мы подаем на вход небольшое
изменение напряжения и снимаем с выхода
точно такое же небольшое изменение напря-
жения14. Очевидно, что это не усилитель на-
пряжения.
12 АоЕ § 2.2.7.
13 И если вы считаете, что мы перегнули палку с нашим
вычурным названием обычного резистора, оцените еще
более впечатляющий пример экстравагантности. Не-
скольким инженерам стало скучно, а может они позави-
довали возможностям своих начальников посещать раз-
ные конференции и делать на них доклады. Как-то раз
они собрались вместе и решили представить на рассмо-
трение научной конференции свой доклад. В аннотации
они описали изобретенный ими новый схемный элемент:
очень полезное устройство, выполняющее двунаправ-
ленное преобразование тока и напряжения, и которое,
ко всему прочему, выполняет эти преобразования в ли-
нейной зависимости. Это новое устройство они назвали
линистором. К их радости, они получили приглашение
от спонсоров конференции: их приглашали прочитать
полный доклад с подробным описанием изобретения. К
нашему огорчению, на этом этапе они струсили, и всему
миру электроники никогда не пришлось узнать о лини-
сторе. Покойный Боб Пиз (Bob Pease) рассказывает об
этом случае (и многих других) в статье «What's All this
Hoax Stuff, Anyhow?» («В чем дело со всеми этими ро-
зыгрышами, каждый раз?»), опубликованной в журнале
Electronic Design, номер от 4-го апреля 1994 г. (https://
www.electronicdesign.com/lighting/whats-all-hoax-
stuff-anyhow).
14 АоЕ § 2.2.3.
4N.4. Введем коэффициент «бета»
185
и.
(выходное напряжение
лишь на 0,6 В меньше
входного)
Рис. 4N.9. Эмиттерный повторитель
Но, как оказывается, эта схема усиливает ток и
изменяет импеданс. Вы оцените работу такой
схемы, когда мы добавим еще один элемент к
нашему описанию поведения транзисторов:
коэффициент усиления по току р (см. раз-
дел 4NA). Но в рамках текущего очень простого
представления транзистора мы можем только
подтвердить, что эмиттерный повторитель по-
вторяет.
4N.3 А Двухтактный эмиттерный
повторитель работает, но искажает
сигнал
Опять же, схема на рис. 4N.10 понятна, но чем
она полезна — неясно15. Но очень скоро мы
увидим, в чем состоит чрезвычайная ценность
этой разновидности эмиттерного повторителя.
Повышающий
n-p-п транзисто
Просто «сиамские» повторители
Понижающий
р-п-р-транзистор
U.
Но оба транзистора закрыты до
тех пор, пока | (УБЭ| > 0,6 В.
Таким образом, при переходе
через ноль образуется
«мертвая» зона
Рис. 4N.10. Двухтактный эмиттерный повторитель
4NА. Введем коэффициент
«бета»
Чтобы понять, в чем заключается полезность
эмиттерного повторителя, в наше простейшее
описание транзистора нужно ввести количе-
ственный параметр, который мы проигнориро-
вали вначале. В частности, нам следует обратить
внимание на то обстоятельство, что выходной
ток 1К (или почти равнозначный ток /э) намного
больше, чем входной ток 1Б. Отношение между
выходным и входным током, показывающее,
насколько выходной ток больше входного, на-
зывается коэффициентом усиления по току
или коэффициентом «бета» и обозначается
символом р. Понятие усиления по току может
быть вам незнакомым и вызывать неприятные
чувства.
Но хотя это логичное описание свойств эмит-
терного повторителя, чаще поведение этой
схемы трактуется, как преобразование импе-
дансов. К этому понятию также нужно привык-
нуть. Но сама идея совсем несложная и осно-
вывается на законе Ома16. Заключается она в
следующем: колебания напряжения на входе
и выходе одинаковы по величине, но соответ-
ствующие токи сильно отличаются. Поскольку
отношения (Д LT/AI) сильно различаются, вход-
ной импеданс RBX оказывается высоким, а вы-
ходной Двых — низким.
4N.4.1. Подробнее о «бета»
К нашему обращению с этой характеристикой
транзисторов, коэффициентом усиления р, ко-
торое мы переняли из книги АоЕ, может быть
не так просто привыкнуть17.
С одной стороны, мы прилагаем большие уси-
лия, чтобы донести до вас полезный совет: ни-
когда не разрабатывайте схему, полагая, что вы
точно знаете значение р. Этого не стоит делать,
поскольку значение р на самом деле непредска-
зуемо. Оно будет разным для каждого экзем-
пляра транзистора данного типа; для выбран-
ного транзистора оно будет разным при разных
токах коллектора 7К; и, наконец, оно будет раз-
ным при различных температурах.
Но с другой стороны, мы обычно задаем р « 100
для маломощных транзисторов типа 2N3904.
Вот и получается: «мы не знаем р, но считаем,
что р = 100» — «король умер, да здравствует ко-
роль». Это только одно из правил авторов кни-
ги АоЕ «ошибаться, но ошибаться в правиль-
ном направлении»18. Нам не обязательно точно
15 АоЕ § 2.4.1.
16 Мы не отказываемся от нашего более раннего утвержде-
ния (см. раздел 4N.3.1), что поведение перехода «коллек-
тор - эмиттер» транзистора не является омическим. Импе-
дансы, о которых здесь идет речь, характеризуют вход (на
базе) и выход (на эмиттере).
17 АоЕ § 2.1.1.
18 См. раздел 4N.4.
186
4N. Транзисторы I
знать значение коэффициента р, при условии,
что мы занижаем его, поскольку в таком случае
действительное значение коэффициента бета
будет заведомо хорошим.
4NA2. Эмиттерный повторитель
как преобразователь импедансов
Эмиттерный повторитель усиливает ток. Этот
же факт делает данную схему преобразовате-
лем импедансов: схема, которая имеет высокий
входной импеданс 2?^ и низкий выходной Двых
(рис. 4N.11)19.
На рис. 4N.12 приведена шуточная сценка, ил-
люстрирующая эффект преобразования им-
педанса. Представьте себе плохо подходящую
друг другу пару в тускло освещенном баре.
После нескольких рюмок они смотрят друг
на друга. «Эффект рюмок» (представляющий
эмиттерный повторитель) играет роль «двуна-
правленных розовых очков», каждый видит в
другом то, что он/она желает увидеть20.
Оценка р по входному импедансу /?вх
На лабораторном занятии 4L вам нужно будет
определить значение коэффициента р по экспе-
риментальному значению входного импеданса
#вх. На этом занятии вам потребуется собрать
Одинаковые Дш
Но очень разные токи ЛГ
Большой ЛГЭ
Рис. 4N.11. Как эмиттерный повторитель преобразует импе-
дансы
делитель напряжения, используя резистор с из-
вестным номиналом (33 кОм, см. пример чуть
далее), напряжение с которого подается на базу
транзистора в схеме эмиттерного повторителя,
а затем сравнить амплитуды сигналов на обоих
выводах резистора. На рис. 4N.13 приведены
осциллограммы сигналов на входе и выходе,
полученные нами при выполнении описанного
эксперимента
21
На левой осциллограмме видно значительное
(около 1,5 В) смещение по постоянному напря-
жению между входом и эмиттером. Почему это
Боже правый! Что за изящная
малютка в 100 Ом!
Рис. 4N.12. Эмиттерный повторитель в роли «двунаправленных розовых очков»: через него каждый видит то, что желает
увидеть
19 АоЕ § 2.2.3. 21 Поскольку мы наблюдаем изменение амплитуд сигна-
20 Если рис. 4N.12 кажется вам не в ногу со временем, мо- лов (Д17), то можем брать измеряемые значения или на
жете поменять действующих лиц. базе, или на эмиттере.
4N.4. Введем коэффициент «бета»
187
Вход, Выход в
Канал 1, размах
сигнала 1,006 В
Канал 2, размах
сигнала 941,1 мВ
Режим входа DC (наблюдается падение на резисторе
базы, плюс иъъ)
Рис. 4N.13. Зная ослабление сигнала, вызываемое входным сопротивлением эмиттерного повторителя, можно оценить
коэффициент «бета» транзистора
\ СИ. 1, размах
s сигнала 1,001 В
iCh. 2, размах
| сигнала 926,5 мВ
Режим входа АС
Около 93%
1 ВХОДНОГО
: сигнала
сохраняется
происходит?22 Более четкую ситуацию с вход-
ным импедансом RBX можно получить, убрав это
смещение, переведя оба канала осциллографа
в АС-режим. Осциллограмма таких сигналов
показана справа на рис. 4N.13.
Замечание
Обычно настоятельно рекомендуется не исполь-
зовать АС-режим осциллографа, поскольку при
этом теряется информация, представляющая ин-
терес. Но в данном случае мы хотим избавиться
от ненужной разницы в постоянном напряжении.
АС-режим способствует визуальному сравне-
нию сигналов, хотя в данном случае разница
между ними настолько мала, что ее было бы
трудно оценить на глаз. Но осциллограф помо-
жет нам с этой задачей, измеряя размах обоих
сигналов. В результате мы узнаем, что на вы-
ходе амплитуда сигнала составляет 93-94% от
исходной. На основе этой информации опреде-
лим коэффициент «бета».
22 Возможно, вас Этот эффект совсем не удивляет. Тем не
менее следует вспомнить, что в данном эксперименте нас
интересует передача изменения напряжения, а не уровня
постоянного напряжения, поэтому разница в уровнях по-
стоянного напряжения не представляет для нас большого
интереса. Но давайте разберемся, все ли в порядке с вы-
числениями.
Падение постоянного напряжения величиной 1,5 В вклю-
чает в себя значительное напряжение 1/ю, а также падение
напряжения, вызываемое током /Б через резистор в цепи
базы. Номинал резистора в цепи базы составляет 33 кОм,
поэтому ток через резистор окажется равным 0,9 В/33 кОм »
« 27 мкА. Величина тока эмиттера составляет около
13 В/3,3 кОм « 4 мА. Соотношение токов 1Э/1Ъ будет, по
сути, коэффициентом усиления «бета». В данном случае
это соотношение равно 4 мА/27 мкА « 145. Это значение
не слишком отличается от нашей оценки методом опре-
деления амплитуды. Таким образом, значения вроде бы
более-менее совпадают.
Если взять 93% как более точное значение (по-
скольку для него используется большая область
экрана осциллографа, осциллограмма в АС-
режиме должна иметь лучшее разрешение), тог-
да мы теряем 7% сигнала и сохраняем 93%. Или,
иными словами, мы теряем одну часть сигнала
и получаем 13 частей. Это означает, что входной
импеданс RBX приблизительно в 13 раз больше
известного сопротивления величиной 33 кОм.
Теперь нетрудно вычислить входной импеданс
RBX, а затем по его значению определить величи-
ну коэффициента «бета». Но если вы не хотите
напрягаться, попробуйте просто предположить,
в качестве ориентира, что получится, если за-
дать коэффициент «бета» равным 100, а затем
сравните теоретическое и экспериментальное
значения.
Если значение коэффициента «бета» было 100,
тогда величина входного импеданса RBX была
бы 330 кОм, чуть больше чем в десять раз,
чем величина тестового резистора 330 кОм
(наблюдаемое ослабление сигнала было бы
■15 В
Рис. 4N.14. Прикидочный расчет: оцените, каким было бы
значение RBX, если р = 100
188
4N. Транзисторы I
Вход
2N3904
£ыход
3,3 кОм
Вход (на базе), положительное
смещение
На эмиттере (при положительном
\ смещении на базе)
- (Потенциал земли)
На эмиттере (без смещения)
Вход (на базе) без смещения
Рис. 4N.15. Для эмиттерного повторителя с однополярным источником питания на базу необходимо подать положительное
смещение
чуть меньше 10%). Но мы в эксперименте полу-
чили входной импеданс JRBX, который прибли-
зительно в 13 раз больше тестового сопротив-
ления R^^ Поэтому величина коэффициента
«бета» должна быть не 100, а 130, что вполне
правдоподобно. Вспомните, мы ведь не пред-
сказывали, что величина коэффициента «бета»
будет точно 100, а сказали: «Зададимся коэф-
фициентом «бета» равным 100, и это будет до-
пустимое уменьшение его значения»23.
4N A3. Первые сложности:
смещение
До сих пор (и в начале лабораторного заня-
тия 4L) мы предполагали использование двух-
полярных источников питания24. Это позволяет
нашим схемам реагировать на симметричные
относительно земли сигналы без отсечения ча-
сти сигнала (т. е. без ограничения сигнала при
превышении предельных значений).
Схема эмиттерного повторителя, который мы
соберем на лабораторном занятии к этой гла-
ве, питается только от положительного источ-
ника, и не может пропустить участки входного
сигнала, напряжение которых ниже «земли»
(т. е. нуля), и даже те положительные участ-
ки, амплитуда которых окажется меньше ве-
личины падения напряжения на диоде. В этом
случае при входном сигнале без постоянной
составляющей на выходе присутствует однопо-
лупериодный выпрямленный выходной сигнал
23 Вот еще одно подтверждение тезиса авторов книги
АоЕ на «ошибаться в правильном направлении». Вспом-
ните оценку входного импеданса ДС-фильтра Zbx = R> и
величину At = 8 мс при вычислении пульсаций источника
питания, как упоминается в разделе 4N.4.
24 АоЕ § 2.2.4.
(нижняя осциллограмма сигнала на эмиттере
на рис. 4N.15).
Этот результат напоминает нам о том, насколь-
ко эмиттерный повторитель может быть по-
хожим на простой диод с нагрузкой в виде ре-
зистора. Разве выходной сигнал комбинации
диода с резистором (первый выпрямитель, с
которым мы познакомились на лабораторном
занятии 3L) не будет точно таким же, как и сиг-
нал, показанный на рис. 4N.15?
Иными словами, не будут ли идентичными
сигналы на выходах двух схем, показанных
на рис. 4N.16? Действительно, сигналы будут
очень схожи.
>Д 1г
\ *?*ол Вход—-М-Т—В^ход
13,3 кОм
:з,з ком
Рис. 4N.16. В чем же разница между эмиттерным повторите-
лем и однополупериодным выпрямителем?
Маленькая хитрость
для привлечения внимания к вопросу
Признаемся, нам нравится подшучивать над
студентами, используя схожесть в работе этих
двух схем. Мы рассматриваем эмиттерный по-
вторитель, чертим его схему (рис. 4N.17), а за-
тем показываем на осциллографе сигналы на
входе и выходе схемы. В чем же заключается
шутка, спросите вы. А вот в чем, мы «забываем»
4N.4. Введем коэффициент «бета»
189
+и
f
Вход Ь/
I
^Ч Выход
< 3,3 кОм
< Рис. 4N.17. Принципиальная
JL, схема «мошеннического»
^ эмиттерного повторителя
Вход
(на базе)
«Земля»
Ch^Tl^^
\
Питание
включено
Питание
выключено
Рис. 4N.18. Выходные сигналы эмиттерного повторителя
с включенным и выключенным питанием трудно отличить
друг от друга
-о Выход
>3,3 кОм
Эмиттерный повторитель
Выпрямитель
Рис. 4N.19. Включение резистора в цепь базы делает видимым преобразование импеданса или усиление тока в эмиттерном
повторителе
включить источник питания. И кажется, будто
бы для схемы это безразлично25.
На рис. 4N.18 показаны осциллограммы выход-
ного сигнала как при включенном питании схе-
мы, так и при выключенном. Как можно видеть,
между ними нет большой разницы. Почему же
такое возможно? Может быть для эмиттер-
ного повторителя источник питания вообще
не требуется?
Нет, это не так. Описанный эксперимент де-
монстрирует лишь то обстоятельство, что наш
прибор для наблюдения сигналов в виде напря-
жения (осциллограф) не может показать на-
прямую, что делает схема повторителя.
Делаем работу эмиттерного
повторителя видимой
Как уже говорилось ранее, эмиттерный по-
вторитель не усиливает напряжение. Чем
он является, так это усилителем тока, или,
25 Следует отметить, что для удачи описанного фокуса нам
необходимо добавить в цепь коллектора последовательно
включенный диод. Это требуется для того, чтобы через
переход база-коллектор ток не мог поступать в источник
питания, что происходит даже при выключенном источни-
ке (см. рис. 4N.17).
равнозначно, преобразователем импеданса.
Поэтому нам нужно добавить в схему тесто-
вый резистор, чтобы на экране осциллографа
можно было видеть величину тока. На вход
наших двух сравниваемых схем (эмиттерного
повторителя и выпрямителя, причем выпря-
митель моделирует повторитель с выключен-
ным питанием) подключим резистор номи-
налом 33 кОм. Таким образом мы создадим
делитель напряжения, вторым резистором в
котором будет входной импеданс RBX каждой
из этих схем (рис. 4N.19).
Что же мы увидим в этом случае, наблюдая
входной и выходной сигналы эмиттерного по-
вторителя при включенном и выключенном
питании? Как оказывается, наличие или от-
сутствие питания сильно влияет на импеданс
эмиттерного повторителя, что можно видеть на
рис. 4N.20.
При включенном питании входной импеданс
эмиттерного повторителя составляет, как и
было сказано, р • Дэ, т. е. как минимум 330 кОм.
Таким образом, выходной сигнал на эмиттере
выглядит почти идентичным входному (и де-
монстрирует характерное падение напряжения
на переходе «база - эмиттер» 17БЭ).
190
4N. Транзисторы I
Входной сигнал
(на резисторе 33 кОм
в цепи базы)
Выходной сигнал на
эмиттере, питание
включено
Выходной сигнал на
эмиттере, питание
выключено
Выходной сигнал на
эмиттере, питание
выключено, при
увеличении 10х
(0,1 В/деление)
СИ1| 1.00 V СИ2| lOOrtlV
Входной сигнал
Канал 1, размах
сигнала 2,463 В
Выходной сигнал на
эмиттере, питание
выключено
Канал 2, размах сигнала
179,5 мВ
«Земля»
Рис. 4N.20. Включение резистора в цепь базы позволяет наблюдать разницу в выходном сигнале эмиттерного повторителя
при включенном и выключенном питании
И наоборот, при выключенном питании по-
вторитель становится просто диодным вы-
прямителем, где роль диода выполнят переход
«база - эмиттер» транзистора. Поскольку в
этом случае входное сопротивление составля-
ет всего лишь 3,3 кОм, наблюдается большое
ослабление входного сигнала: на выход дохо-
дит меньше 10%.
Этот незамысловатый эксперимент свидетель-
ствует о том, что выходной ток транзистора —
снимается ли он с эмиттера или с коллектора —
практически весь поставляется источником пи-
тания, а не базой транзистора (т. е. не входным
сигналом). Это и есть «волшебная палочка»
магии преобразования импеданса. Образно вы-
ражаясь, ток базы — всего лишь небольшой на-
чальный «платеж», необходимый, чтобы полу-
чить большой «заем» от источника питания26.
Между прочим этот эксперимент напоминает
нам, что термин «источник питания» в точно-
сти соответствует своему названию.
Смещение отделителя напряжения
На наших лабораторных занятиях мы поначалу
обеспечивали положительное напряжение сме-
щения самым легким способом: просто задавая
положительное смещение сигнала в настройках
26 Вообще-то, сравнение не совсем точное, поскольку мы
никогда не выплачиваем этот «заем» назад. Но, с другой
стороны, мы все же недалеки от истины. Разве наше совре-
менное общество не живет в долг, который оно никогда
не планирует отдавать?
генератора сигналов27. Но такой подход не всег-
да возможен на практике.
Более общим подходом к решению этой про-
блемы, позволяющим обойтись одним источ-
ником питания, будет задействование делителя
напряжения, который смещает напряжение на
базе в положительном направлении. Одна из
возможных принципиальных схем, реализую-
щих такой подход, приведена на рис. 4N.21.
Постоянное положительное смещение на базе
позволяет выходному сигналу на эмиттере уве-
личиваться и уменьшаться, оставаясь при этом
положительным, в ответ на положительные и
отрицательные колебания входного сигнала.
Разделительный конденсатор обеспечивает
«мирное сосуществование» разных уровней
постоянного напряжения в источнике сигнала
и на базе, в то же самое время пропуская без
проблем колебания входного сигнала на базу.
Делитель для напряжения смещения должен
обеспечивать достаточный ток, чтобы поддер-
живать потенциал базы транзистора на требуе-
мом уровне (с выходным напряжением посере-
дине между напряжением питания U+ и «зем-
лей»). В то же самое время делитель не должен
сильно нагружать ни источник питания, ни ис-
точник сигнала.
Задача с напряжением смещения уже зна-
кома нам: устройство А подает сигнал на
27 АоЕ § 2.2.4.
4NA. Введем коэффициент «бета»
191
Разделительный
конденсатор
15 В
0 В -
Разделяет потенциалы
источника сигнала
(с нулевым смещением)
и базы (со смещением +8 В).
В то же самое время он
пропускает колебания
входного сигнала от
источника на базу
Рис. 4N.21. В эмиттерном повторителе с однополярным ис-
/ Разделительный конденсатор
((«закорочен» на частоте сигнала)
«А» ^ «Б»
Источник
сигнала
Напряжение
сигнала I/ '
смещение <
"транзистора
Напряжение
смещения Ц.
Рис. 4N.22. Реализация подачи напряжения смещения на
точником питания смещение на базе создает резистивный базу транзистора
делитель напряжения
Импеданс «со стороны базы» (А
(это характеристика транзистора
I Rt (смещение) и его эмиттерНОй нагрузки)
(смещение) Импеданс на базе «со стороны
входа» (эта характеристика
зависит не от транзистора,
а от цепи смещения
и импеданса источника
на частоте сигнала)
Рис. 4N.23. Импедансы с одной и с другой стороны
устройство Б, а устройство Б — на устройство В
(рис. 4N.22). Как обычно последовательном со-
единении каскадов мы хотим, чтобы выходной
импеданс ZBHX каждого предыдущего каскада
был низким относительно входного импеданса
ZBX последующего каскада.
Вы заметите, что делитель смещения уменьшает
входной импеданс схемы в десять раз по срав-
нению со случаем двухполярного источника
питания. Это обстоятельство является «ложкой
дегтя» в, казалось бы, удачном решении задачи
обеспечения смещения базы транзистора. Если
у вас есть желание изучить вопрос подробнее,
то почитайте раздел 2.43 по цепям с компен-
сационной обратной связью в книге АоЕ. Вам
придется привыкнуть к необычному приему:
мы часто будем рассматривать импедансы не
только в точках схемы, но также в каком-либо
направлении. Например, мы будем рассматри-
вать импеданс на базе с двух сторон, как иллю-
стрирует рис. 4N.2328.
♦ Импеданс, «со стороны базы» (это характе-
ристика транзистора и его эмиттерной на-
грузки);
♦ Импеданс на базе «со стороны входа» (эта
характеристика не определяется транзисто-
ром; она зависит от цепи смещения и от им-
педанса источника на частоте сигнала).
4N.4.4. Еще одно усложнение:
асимметрия схемы может вызывать
отсечку
До сих пор мы хвалили низкий выходной им-
педанс #вых эмиттерного повторителя (а на
лабораторном занятии 4L и измеряем эту его
характеристику)29. Но мы должны быть откро-
венными и выложить всю правду об эмиттерном
повторителе. А правда заключается в том, что,
несмотря на низкий выходной импеданс, наш
повторитель может иногда и пошаливать. Для
иллюстрации подобных шалостей рассмотрим
28 АоЕ § 2.2.4.
29 АоЕ § 2.2.3D.
192
4N. Транзисторы I
15 В
Рис. 4N.24. Сможет ли этот эмиттерный повторитель по-
тянуть подключенную к нему нагрузку?
гипотетический эмиттерный повторитель с ре-
зистивной нагрузкой, принципиальная схема
которого приведена на рис. 4N.24.
Чтобы выяснить, будет ли эта схема работать
должным образом, вычислим ее входной и вы-
ходной импедансы.
♦ Входной импеданс RBX на базе. Полагая, что
величина коэффициента усиления «бета»
составляет как минимум 100, получим
Двх = р • (ДЭ||ДНАГР) * 75 кОм. Поскольку
2?вх> (10 • Дисточ), наше обычное правило для
каскадных импедансов удовлетворяется.
♦ Выходное сопротивление со стороны эмит-
тера равно (#Э||ДИ) / р « 50 Ом (как всегда,
влияние Яэ незначительно). Этот выходной
импеданс приблизительно в 20 раз меньше
сопротивления нагрузки 2?н, так что правило
десятикратного отношения входного и вы-
ходного импедансов снова удовлетворяется.
Все эти расчеты правильны, но только для сиг-
налов с умеренной амплитудой. Если амплитуда
сигнала окажется больше 4 В, то схема начнет
Входной
сигнал
Выходной
сигнал
2.00 V
2.00 V
Рис. 4N.25. Несмотря на низкий выходной импеданс, под
нагрузкой эмиттерный повторитель может отсекать отрица-
тельную часть сигнала
давать сбои, выражающиеся в частичном от-
сечении отрицательных полуволн сигнала, как
показано на рис. 4N.25.
Почему так происходит? И почему отсекает-
ся только отрицательная полуволна сигнала?
Ответ на этот вопрос прост и почти очевиден,
если признать, что эмиттерный повторитель
обладает существенной асимметрией. Ток в
нагрузку поступает с помощью транзистора,
но одновременно из нагрузки ток забирает
резистор 2?э. Но если транзистор со своей за-
дачей поставки тока справляется хорошо, ре-
зистор со своей задачей не очень справляется.
Поэтому в области предельных отрицательных
амплитуд транзистор запирается (переходит в
режим отсечки). Эту ситуацию иллюстрирует
рис. 4N.26.
Тотчас все транзисторное «волшебство», кото-
рое благодаря коэффициенту «бета» и «розо-
вым очкам» создавало хороший низкий выход-
ной импеданс, рассеивается прямо как в сказке
3,3 кОм<
-15 В
кОм<
-15 В
При больших отрицательных
амплитудах входного сигнала
UBX транзистор полностью
выключается
При выключенном
транзисторе схема
превращается в простой
пассивный делитель
напряжения
Рис. 4N.26. При больших отрицательных амплитудах входного сигнала транзистор нагруженного эмиттерного повторителя
полностью выключается и повторитель отсекает соответствующую часть выходного сигнала
Который выдает
приблизительно
1/4 часть напряжения
питания U
А из эквивалентной схемы
Тевенина предельное
отрицательное значение
выходного сигнала вполне
очевидно — это просто С^в
4N.4. Введем коэффициент «бета»
193
Повышающий
транзистор
Понижающий
транзистор
U
Но обо транзистора заперты,
noKa|C№|>0,6B.
Таким образом, при переходе
сигнала через ноль образуется
«мертвая» зона
Входной сигнал /\ /\
(набазе) ^^>Л /Л
Выходной сигнал , JJ ,\L 11 \L
(на эмиттере) -~*/Г \ /Г \
У V X
«Земля»
Рис. 4N.27. Двухтактный эмиттерный повторитель и сигналы на его входе и выходе
про Золушку. Схема превращается из «кареты»
обратно в «тыкву»: она становится простым
резистивным делителем, а выходное напряже-
ние фиксируется на уровне, составляющем чуть
меньше четверти отрицательного напряжения
питания, т. е. -3,5 В.
4NA5. Решение проблемы отсечки
с помощью двухтактного каскада
Как же решить проблему отсечки? Сделать это
можно двумя способами: глупым и умным30.
Глупый способ состоит в уменьшении сопро-
тивления резистора эмиттера, чтобы отсечка
происходила настолько близко к уровню отри-
цательного напряжения питания, как необхо-
димо. Например, для отсечки на уровне -10 В
нужно уменьшить номинал резистора эмиттера
до 500 Ом.
На первый взгляд это решение выглядит до-
статочно разумным. Но его недостаток стано-
вится очевидным, если мы поменяем нагрузку.
Допустим, мы хотим подключить к нашей схе-
ме нагрузку в виде динамика с сопротивлени-
ем 8 Ом. Для отсечки на уровне -10 В сопро-
тивление эмиттерного резистора R3 должно
быть 4 Ом. Это будет приемлемо при воспро-
изведении звука, но посмотрим, что проис-
ходит с рассеиванием мощности при нулевом
выходном напряжении, иными словами, когда
звук отсутствует. Величина тока покоя составит
15 В / 4 Ом « 4 А. Мощность, рассеиваемая при
таком токе и общем напряжении питания 30 В,
будет почти 120 Вт. И лишь для того, чтобы из
динамиков ничего не звучало!
Очевидно, нам требуется решение получше.
Правильный подход — двухтактная схема
эмиттерного повторителя, в которой резистор
заменяется комплементарным понижающим
транзистором. Такая принципиальная схема
изображена слева на рис. 4N.27, а справа по-
казаны входной и выходной сигналы на экране
осциллографа. Обратите внимание на характер-
ные искажения в выходном сигнале.
Двухтактный эмиттерный повторитель намно-
го эффективнее простого, причем при нулевом
значении напряжения выходного сигнала рас-
сеиваемая мощность мала или вообще отсут-
ствует31. Благодаря своей эффективности двух-
тактные схемы можно встретить в выходных
каскадах различных усилителей. В частности,
двухтактный каскад используется в вашем ге-
нераторе сигналов, возможно, в вашем аудио-
усилителе32, а также в операционных усилите-
лях, с которыми мы вскоре познакомимся.
Высококачественный двухтактный усилитель
должен быть свободен от переходных искаже-
ний типа «ступенька»33, которые есть в простой
схеме, рассмотренной в предыдущем примере.
Эту проблему можно решить, сместив потен-
циалы на базах выходных транзисторов с по-
мощью двух диодов или двух транзисторных
переходов «база - эмиттер». Другой вариант —
использовать операционный усилитель или об-
ратную связь. Эти решения демонстрируются
на лабораторном занятии 6L.
30 АоЕ § 2.4.1.
31 Можно утверждать, что в нашем случае для простого
двухтактного каскада рассеивание мощности полностью
отсутствует. Но в улучшенных вариантах такого усилителя
искажения стремятся устранить, обеспечивая протекание
небольшого тока через оба транзистора при нулевом на-
пряжении выходного сигнала, что вызывает соответству-
ющее небольшое рассеивание мощности. См. книгу АоЕ,
раздел 2.4.1Б.
32 Но не в цифровых проигрывателях. В них во многих
случаях используется мощный коммутатор для обеспече-
ния еще большей эффективности. См. раздел 2.4.1С в кни-
ге АоЕ и материал по интегральному усилителю LM4667
на лабораторном занятии 12L.
33 АоЕ § 2.4.1а.
194
4N. Транзисторы I
4N.5. Переключатель:
транзисторная схема
особого типа
В книге АоЕ34 этот тип транзисторных схем рас-
сматривается самым первым, поскольку ее дей-
ствие легко понять. Мы же рассматриваем ее
последней, так как она стоит особняком. В лю-
бом случае эту схему важно выделять среди всех
других вариантов применения транзисторов,
поскольку она намеренно нарушает основное
правило разработки обычных схем: переклю-
чатель (или ключевой каскад) имеет только
два режима работы, оба из которых являются
аномальными для обычных транзисторных
схем — или полностью включен (режим насы-
щения), или полностью выключен (режим от-
сечки). Поскольку при полностью включенном
состоянии оба перехода транзистора находятся
в режиме насыщения, входной импеданс оказы-
вается низким, хотя именно высокий импеданс
считается одним из достоинств транзисторной
схемы. Пример схемы транзисторного пере-
ключателя приведен на рис. 4N.28.
+5 В
1 кОм < \ рис 4N.28. Транзисторный переклю-
L чатель. Очень полезная схема, которая
J_ на первый взгляд может показаться
~ нелепой
Для транзисторов, работающих в качестве
переключателя, обычное правило /к = р • /Б не-
применимо. Базу такого транзистора требуется
преднамеренно перегружать током приблизи-
тельно в десять раз больше минимального, что-
бы он мог выдавать требуемый коллекторный
ток 7К. В результате транзистор сильно насы-
щается, а напряжение коллектор-эмиттер (U^)
поддерживается на низком уровне, чтобы све-
сти потери в транзисторе к минимуму. В идеа-
ле включенный транзисторный переключатель
полностью «исчезает» в электрическом отно-
шении, подавая всю мощность на нагрузку, без
внутренних затрат мощности.
Можно задаться вопросом, а зачем все это?
Мы подаем высокий или низкий входной уро-
вень, которой просто создает высокий или
низкий уровень на выходе. Какой в этом резон?
Хороший вопрос.
Примечание
Сомнение касательно целесообразности транзи-
сторного переключателя подобно недоумению
о целесообразности эмиттерного повторителя,
выходной уровень которого просто повторяет
входной.
Ответ заключается в том, что входной уровень
обычно подает не ручной переключатель, а
часть схемы, которая недостаточно мощная,
чтобы включить нагрузку. Поэтому транзи-
сторный переключатель можно рассматривать
подобно схеме усилителя тока. Транзисторный
ключ похож на эмиттерный повторитель, но
проще. Еще одно преимущество транзистор-
ного ключа — возможность собирать схемы
переключателей, управляющие другими пере-
ключателями, из которых можно составить
полезные двоичные цифровые схемы. Мы бу-
дем рассматривать цифровые схемы во второй
половине этой книги. Следует признать, что
почти ни в одной из цифровых схем не исполь-
зуются биполярные транзисторы, наподобие
рассматриваемым в данном разделе. Их заме-
нили МОП-транзисторы, с которыми мы бу-
дем работать на лабораторном занятии 12L. Но
МОП-транзисторы цифровых микросхем тоже
работают в ключевом режиме, который мы рас-
сматриваем здесь.
Таким образом, сделаем вывод, что переклю-
чатели являются важными схемами, но также
давайте будем рассматривать их отдельно от
остальных схем, потому что правила их приме-
нения радикально отличаются от схем эмиттер-
ных повторителей, источников тока и усилите-
лей. А именно такие устройства мы в основном
и будем разрабатывать в нашем курсе.
4N.6. Краткий обзор
основных транзисторных
схем для закрепления
пройденного материала
Для закрепления рассмотренного материала35,
в частности, для усвоения разницы в функцио-
нировании транзисторных схем, в зависимости
от того, с какого вывода снимается выходной
34 АоЕ § 2.2.1.
35 АоЕ § 2.2.9В.
4N.7. Материал для чтения в АоЕ
195
Фиксирован
Фиксирован
Выход
Вход
—(Б I
Фиксирован
Выход
Фиксирован
Эмиттерный повторитель Источник тока
Рис. 4N.29. Основные типы транзисторных схем
сигнал, на рис. 4N.29 приведены четыре основ-
ные транзисторные схемы36.
Обратите внимание, что во всех этих транзи-
сторных схемах только в эмиттерном повто-
рителе выходной сигнал снимается с эмиттера.
Импеданс здесь может быть низким.
4N.6.1. Об импедансе на коллекторе
А вот импеданс выхода на коллекторе, наоборот,
высокий, потому что на этом выводе задается ток,
а не напряжение. Поэтому отношение AUK3/AZK
очень большое (поскольку значение А1К очень ма-
ленькое, в идеале — нулевое). Это тот случай, ко-
торый мы предвидели в разделе 1N.2.1, когда мы
утверждали, что дифференциальное сопротивле-
ние (#дИФФ) будет очень важным для понимания
транзисторных схем. На коллекторе сопротивле-
ние #дИфф очень большое, в идеале — бесконеч-
ное, на практике — как минимум несколько со-
тен килоом. Этот факт очень важен не только для
схем источников тока, но также и для усилителей
с общим эмиттером, выходной импеданс Двых
для которых определяется только одним импе-
дансом коллектора RK, поскольку эффективный
выходной импеданс #вых состоит из параллель-
ных импедансов коллектора RK и его громадного
динамического сопротивления ЯтФФ>
4N.6.2. Транзисторный
переключатель как особая
категория схем
Транзисторный переключатель ведет себя со-
всем не так, как все остальные рассмотренные
36 Здесь сохранен авторский стиль; в схемотехнике
к основным обычно относят три транзисторные схемы:
каскад с общим эмиттером (ОЭ), общей базой (ОБ) и об-
щим коллектором (ОК) — Примеч. ред.
Выход
Выход
Вход
Фиксирован
Усилитель
Фиксирован
Переключатель
схемы. Он принадлежит к особому классу
устройств, поскольку два его рабочих состоя-
ния — полностью включен (режим насыщения)
и полностью выключен — не используются в
других схемах. Эта особенность транзисторно-
го переключателя означает, что базовая схема
ключа, изображенная на рис. 4N.29, соответ-
ствует идеализированному случаю.
В главе 5N мы начнем рассматривать более
сложную модель транзистора — модель Эберса-
Молла. Но описанная здесь простейшая модель
транзистора далее тоже обязательно пригодит-
ся. Мы всегда будем пытаться объяснить ра-
боту схем как можно проще, и довольно часто
такого объяснения будет достаточно.
4N.7. Материал для чтения
в АоЕ
Материал для изучения
Глава 2, разделы 2.1-2.2.8 и 2.4.1 (двухтактный
эмиттерный повторитель).
Ознакомьтесь с материалом раздела 2.2.9 (сверх-
проводимость). В следующей главе мы рас-
смотрим модель Эберса-Молла для транзисто-
ров. В разделе 4L4.1 будет описана схема уси-
лителя с высоким коэффициентом усиления,
требующая анализа с помощью этой модели.
Задачи
Задачи в тексте и дополнительные упражнения
(Additional Exercises) 225.
4L Лабораторное занятие: транзисторы
4L1. Предварительное
знакомство с транзисторами
4L1.1 • Транзисторные переходы
являются диодами
Транзистор можно быстро проверить, протести-
ровав по отдельности каждый из его переходов.
Исправный транзистор должен представлять
собой два диода (рис. 4L.1). Но не поддавайтесь
искушению рассматривать это представление
транзистора как описание его принципа дей-
ствия. В процессе работы транзистор не ведет
себя подобно двум соединенным вместе диодам.
Более того, на практике схемы из двух диодов,
соединенных, как показано на рис. 4L.1, были
бы совершенно неработоспособными.
Определение типа и назначения
выводов транзисторов
Предположим, что ваша яхта потерпела круше-
ние посередине океана, и вам пришлось пере-
сесть в спасательную лодку. К счастью, вблизи
оказался остров, но, к сожалению, он необита-
ем. Но к счастью, среди вещей, захваченных в
лодку с яхты, оказался ваш набор радиодеталей,
из которых можно собрать простенький радио-
передатчик и послать сигнал SOS. Но, к сожа-
лению, у вас нет таблицы цоколевки выводов
Коллектор
База
Корпус типа ТО-92
транзисторов (которая приведена в конце этой
книги), но, к счастью (везет же людям...), есть
цифровой мультиметр.
Переключив мультиметр в режим тестирова-
ния диодов, вы сможете определить назначение
выводов своих транзисторов. (В большинстве
цифровых мультиметров эта функция обозна-
чена символом диода.) Процесс тестирования
диодов состоит в подаче на диод небольшого
тока (несколько миллиампер, в направлении от
красного (положительный) к черному (земля)
щупу), а прибор измеряет напряжение на пере-
ходе диода. Меняя направление подключения
щупов к данной паре выводов, можно опреде-
лить, в каком направлении протекает ток меж-
ду ними. Таким образом можно выяснить тип
транзистора — п-р-п илир-п-р. А различить пе-
реходы «база - коллектор» и «база - эмиттер»
(т. е. назначение выводов транзисторов) мож-
но, используя то обстоятельство, что размер
перехода «база - коллектор» больше размера
перехода «база - эмиттер», и несколько мень-
шая плотность тока на этом переходе определя-
ется по меньшему падению напряжения на нем.
4L1.2. Борьба с пульсациями
посредством развязки источников
питания
Это первое лабораторное занятие, на котором
вам, возможно, придется увидеть высокоча-
стотные пульсации в выходном сигнале ваших
Эмиттер
База
Эмиттер
Коллектор
NPN
PNP
Рис. 4L1. Представление переходов транзистора в виде двух соединенных вместе диодов. Это представление подходит только
для проверки транзисторов, но не описывает их работу
4L2. Эмиттерный повторитель
197
схем. При умеренной скорости развертки эти
пульсации будут выглядеть как утолщение ли-
нии трассировки, но на высоких скоростях они
могут отображаться в виде более-менее сину-
соидального сигнала в диапазоне частот от не-
скольких сотен килогерц до ста мегагерц. При
наличии таких помех для их удаления потре-
буются развязывающие конденсаторы. Более
подробную информацию по этому вопросу
см. в разделе 4L6.
4L2. Эмиттерный
повторитель
Возьмите транзистор типа п-р-п и соберите
эмиттерный повторитель, принципиальная
схема которого приведена на рис. 4L.2.
Вход
Рис. 4L2. Эмиттерный повторитель. Резистор небольшого
номинала в цепи базы часто требуется для предотвращения
пульсаций
Подайте на схему синусоидальный сигнал без
постоянной составляющей (убедитесь в том, что
смещение постоянной составляющей генерато-
ра сигналов установлено на ноль) и посмотрите
с помощью осциллографа на выходной сигнал,
искаженный по сравнению с входным. Почему
так происходит1? А если повысить амплитуду
входного сигнала, то в выходном сигнале начи-
нают наблюдаться искажения в отрицательной
области. Чем можно объяснить этот эффект2?
1 Ответ на этот вопрос очень простой: когда напряжение
входного сигнала Um опускается ниже приблизительно
+0,6 В, в нашей схеме не выполняется одно из основных
правил транзисторов. Напряжение прямого смещения на
переходе «база - эмиттер» падает ниже допустимого, в ре-
зультате чего ток коллектора 1К и ток эмиттера /э убывают
до нуля.
2 Полезная подсказка: в справочном листке для транзисто-
ра 2N3904 указано, что при напряжении обратного смеще-
ния на переходе «база - эмиттер» пробой этого перехода
может происходить даже при таком низком напряжении,
как 6 В.
Теперь попробуйте подключить вывод резисто-
ра в цепи эмиттера (точку, обозначенную 1/э) не
к земле, а к источнику -15 В, и наблюдайте за
выходным сигналом. Попробуйте объяснить
улучшение выходного сигнала.
4L2.1. Входной и выходной
импедансы эмиттерного
повторителя
Измерьте входной (ZBX) и выходной (ZBbIX)
импедансы эмиттерного повторителя, прин-
ципиальная схема которого изображена на
рис. 4L.33.
+15 В
2N3904
3,3 кОм
«•• 1 кОм
-15 В
Рис. 4L.3. Принципиальная схема эмиттерного повторителя
для измерения входного ZBX и выходного ZBWX импедансов.
При измерении входного импеданса 2^х отключите резистор
нагрузки номиналом 1 кОм
Измеряем входной импеданс ZBX
В схеме, изображенной на рис. 4L.2, постепенно
увеличивайте сопротивление резистора в цепи
базы, чтобы смоделировать источник сигнала
с умеренно высоким импедансом, т. е. с неболь-
шим током.
Начните с резистора номиналом 33 кОм, как
показано на рис. 4L.3. В этом случае ослабле-
ние будет, вероятно, всего лишь около 5-10%.
Оценить коэффициент «бета» при таком ма-
лом затухании довольно сложно.
По мере увеличения номинала резистора за-
тухание возрастет до 50%, после чего вести
наблюдение и выполнять вычисления станет
легко. Мы знаем, что при ослаблении сигнала
3 Хотя мы называем эти характеристики импедансом Z,
в действительности мы здесь заинтересованы в чисто ак-
тивном сопротивлении R, поскольку хотим избежать эф-
фектов, зависящих от частоты. В особенности мы не хотим
оказаться в ситуации, когда исследуем ослабление, вызы-
ваемое паразитной емкостью.
198
4L Лабораторное занятие: транзисторы
на 50% сопротивление резистора в цепи базы
приблизительно равно входному сопротивле-
нию RBX. Используйте эти данные, чтобы оце-
нить значение коэффициента р.
Внимание!
Убедитесь, что вы наблюдаете именно входное со-
противление /?вх/ а не влияние входной емкости Свх
или емкости щупа СЩУПА. Для этого подстраивайте
частоту входного сигнала, пока не добьетесь лишь
незначительного смещения по фазе между вход-
ным сигналом и сигналом, снимаемым с базы тран-
зистора.
Отключите нагрузочный резистор номиналом
1 кОм и измерьте входной импеданс ZBX схемы.
В данном случае это будет импеданс со стороны
базы транзистора.
Примечание
Последовательный резистор номиналом 33 кОм
или большего номинала, который вы установили,
не является частью схемы эмиттерного повтори-
теля. Мы его подключили, чтобы увеличить (т. е.
ухудшить) выходное сопротивление /?вых источни-
ка сигнала.
Входной импеданс ZBX можно определить, ис-
следуя сигнал на обоих выводах резистора в
цепи базы с помощью двухканального осцил-
лографа. При этом измерении резистор номи-
налом 3,3 кОм в цепи эмиттера рассматривает-
ся, как «нагрузка» эмиттерного повторителя.
Амплитуда входного сигнала не должна превы-
шать одного вольта.
Наблюдаемое ослабление сигнала может быть
небольшим, по крайней мере, сначала, и поэто-
му его трудно измерить. Задачу можно облег-
чить, используя функцию измерения ампли-
туды цифрового осциллографа. Но при работе
с аналоговым осциллографом придется немно-
го потрудиться. Самый лучший способ изме-
рить небольшое затухание с помощью анало-
гового осциллографа — по процентным меткам
на его экране.
Советы по измерению входного
импеданса ZBX с помощью аналогового
осциллографа
♦ Отцентрируйте оба сигнала на отметке 0%.
Имеются в виду сигналы, снимаемые с двух
выводов резистора в цепи базы; будем на-
зывать эти сигналы входным и выходным.
♦ Сигналы подаются на вход осциллографа
в АС-режиме, чтобы обеспечить их вырав-
нивание по центру экрана.
♦ На генераторе сигналов настройте амплиту-
ду сигнала источника, чтобы его пик был на
отметке 100%.
♦ Теперь измерьте амплитуду входного сигна-
ла в процентах.
Выглядит ли правдоподобным наблюдаемый
вами результат? Преобразует ли эмиттерный
повторитель наблюдаемый «через него» импе-
данс так, как мы ранее утверждали? Получив
значение входного импеданса Z^, можно опре-
делить коэффициент «бета» (или h^4) транзи-
стора5. Запомните, а еще лучше, запишите, по-
лученное значение коэффициента «бета», что-
бы позднее сравнить его со значением этого же
коэффициента, рассчитанным по результатам
измерения выходного импеданса ZBMX.
Измеряем выходной импеданс ZBblx
Удалите установленный вами в цепь базы ре-
зистор, возвратив на место резистор номина-
лом 33 кОм, как показано в схеме на рис. 4L.36.
Теперь измерьте выходной импеданс ZBbIX
эмиттерного повторителя. Для этого подклю-
чите к его выходу нагрузку величиной 1 кОм
и наблюдайте падение амплитуды выходно-
го сигнала. Амплитуда входного сигнала, как
и раньше, должна быть небольшой, меньше
чем один вольт. Процедура для измерения вы-
ходного импеданса ZBHX слегка отличается от
предыдущего случая и состоит из следующих
этапов:
4 Сокращение от Hybrid parameter forward current gain,
common emitter — гибридный параметр усиления прямого
тока, общий эмиттер. Соответствует коэффициенту усиле-
ния по постоянному току плоскостного транзистора. См.
раздел 2.23 книги АоЕ.
5 Параметр р для схем с общим эмиттером, общей базой
и общим коллектором обозначают как h213, h21B, h21K соот-
ветственно — Примеч. ред.
6 Более высокое сопротивление резистора усложняет ра-
боту, не позволяя игнорировать эффект сопротивления
эмиттера Дэ, чье значение строго соответствует пути через
транзистор. Отношение Ди/р обычно намного меньше,
чем сопротивление эмиттера Дэ, так что последнее мож-
но игнорировать. Использование в цепи базы резистора
с большим сопротивлением делает невозможным такое
упрощение. Это упражнение и так достаточно трудное,
чтобы добавлять в него это усложнение.
4L.3. Источник тока
199
♦ не подключая нагрузку к выходу эмиттерного
повторителя, измерьте амплитуду выходного
сигнала [7ВЫХ;
♦ подключите к выходу схемы нагрузочный ре-
зистор номиналом 1 кОм, после чего опреде-
лите ослабление выходного сигнала;
♦ определите значение выходного импеданса
ZBbIX, считая, что вы собрали делитель на-
пряжения, в котором верхним «резистором»
является выходной импеданс ZBbIX схемы, а
нижним «резистором» — подключенная на-
грузка. Конечно же, значение резистора в
цепи базы является критическим для этих
вычислений, поскольку это «сопротивление
источника», которое эмиттерный повтори-
тель уменьшает в р раз. Поэтому обратите
внимание на величину сопротивления рези-
стора в цепи базы вашей схемы.
Снова рассчитайте значение коэффициента р.
В принципе, оно должно совпасть со значением
р, которое вы определили по измеренному зна-
чению входного импеданса ZBX.
Роль разделительного конденсатора
при измерении ZBblx
Почему при измерении выходного импеданса
ZBHX рекомендуется добавить разделительный
конденсатор? Ответ на этот вопрос не так оче-
виден, поскольку в данном случае можно было
бы обойтись и без него. Но во многих других
случаях этот конденсатор необходим.
Он требуется для того, чтобы избежать нару-
шения в схеме уровней постоянного напряже-
ния, когда мы наблюдаем, что происходит с
варьирующимися во времени (т. е. переменны-
ми) сигналами. В данном случае уровень по-
стоянного напряжения на эмиттере составляет
приблизительно -1В. Это достаточно близко
к потенциалу земли (т. е. нулю), так что отсут-
ствие разделительного конденсатора не при-
чинило бы никакого вреда. Без конденсатора
этот уровень изменился бы незначительно. Но
во многих других случаях, где постоянное на-
пряжение на эмиттере значительно отличается
от потенциала земли, подключение нагрузки
величиной 1 кОм сильно повлияет на уровень
(или смещение) постоянного напряжения. Но
такое развитие событий будет для нас неже-
лательным. Для нас важно выяснить, как эта
нагрузка влияет на амплитуду сигнала (пред-
полагая, что полезный сигнал является пере-
менным напряжением).
Жаль, конечно же, что эффект конденсатора
в данном эксперименте не особо впечатляю-
щий, чтобы понять его важность. Но мы хо-
тим выработать у вас хорошую привычку:
если вас интересует поведение сигналов пере-
менного тока, проводите исследование, не на-
рушая соотношения уровней постоянной со-
ставляющей.
4L3. Источник тока
Соберите источник тока, принципиальная схе-
ма которого изображена на рис. 4L.4.7
;820
(наблюдайте за UK)
Цифровой
мул ьт и метр
Рис. 4L.4. Источник тока на транзисторе
Медленно изменяйте сопротивление потен-
циометра нагрузки и наблюдайте за измене-
ниями тока, измеряемого цифровым мульти-
метром. Что происходит при максимальном
сопротивлении?
Можете ли вы объяснить наблюдаемый эффект
учитывая диапазон соответствия8 рабочего на-
пряжения источника тока9?
7 К сожалению, термин «источник тока» может быть не-
однозначным. Он описывает целый класс схем, которые,
несмотря на изменение напряжения, поддерживают силу
тока постоянной. Но этот термин также употребляется
для описания определенного подкласса схем, из которых
ток поступает в нагрузку, второй вывод которой имеет
более отрицательный потенциал. Такой источник тока
противопоставляется потребителю тока, подобному пока-
занному на рис. 4L.4, который поглощает ток из нагрузки.
Таким образом, существуют два типа источников тока, не
очень удачно называемые «источниками» (англ. - source)
и «поглотителями» (англ. - sink). Определить, имеется ли
в виду источник тока в смысле направления протекания
тока или в смысле стабильности тока, можно по контексту.
8 Англ. compliance voltage. Диапазон напряжений, в кото-
ром схема работает должным образом. — Примеч. пер.
9 При насыщении транзистора источник тока больше
не в состоянии функционировать должным образом.
Цифровой мультиметр поможет вам измерить напря-
жение между коллектором и эмиттером U^. Таким об-
разом, вы сможете попытаться определить связь между
насыщением транзистора и падением его выходного
тока Invtv.
200
4L Лабораторное занятие: транзисторы
Но даже в пределах рабочего диапазона при
варьировании нагрузки наблюдаются замет-
ные колебания выходного тока. Что вызывает
эти колебания?10
зистивную нагрузку, скажем, 7,5 кОм. Как уже
упоминалось ранее, разделительный конден-
сатор позволяет измерить импеданс на частоте
сигнала, не нарушая режим каскада по посто-
янному току.
4LA Усилитель с общим
эмиттером
Соберите усилитель с общим эмиттером, прин-
ципиальная схема которого изображена на
рис. 4L.5. Каким должно быть его усиление по
напряжению? Проверьте свое предположение
на практике. Наблюдается ли инвертирование
фазы сигнала?
+15 В
5,6 кОм
7,5 кОм
2N3904
750
Рис. 4L.5. Усилитель с общим эмиттером
Правильно ли выбрана статическая рабочая
точка коллектора (т. е. его напряжение покоя)11?
А что вы можете сказать о точке 3 дБ в области
низких частот усилителя12? Каким должен быть
его выходной импеданс13? Проверьте его, под-
ключив через разделительный конденсатор ре-
10 Основная причина - эффект Эрли (или эффект модуля-
ции базы): изменение напряжения между коллектором и
эмиттером U^ вызывает небольшое варьирование эффек-
тивной ширины базы. Более подробную информацию по
этому вопросу см. в разделе 5S.2.
11 Какой уровень напряжения покоя был бы «правиль-
ным»? Такой, который обеспечивает наибольший размах
сигнала без искажения при верхнем или нижнем пределе.
Грубо говоря, напряжение точки покоя должно быть рав-
ным половине напряжения питания. Идеалист мог бы ска-
зать: «Лучше, чтобы она была посередине между нижним
пределом равным 1 В ([/э), и напряжением питания». Но
при напряжении питания, равном 15 В, нас вполне устроит
более простой ответ — половина напряжения питания. Это
будет наш стандартный подход для схем с однополярным
источником питания.
12 Чтобы вычислить это значение, нужно выяснить, какое
эффективное сопротивление образует вместе с раздели-
тельным конденсатором низкочастотный фильтр.
13 Да, просто RK. Это обстоятельство объясняется в гла-
ве 4N.
4L А1. Максимизирование
усиления: предварительный взгляд
на работу модели Эберса-Молла
Теперь давайте рассмотрим несколько более
сложный случай работы усилителя с общим
эмиттером. Проверьте, что будет, если парал-
лельно резистору в цепи эмиттера 1^ подклю-
чить конденсатор большой емкости, чтобы он
закорачивал этот резистор на частоте сигнала.
Для этого добавьте в схему рис. 4L.5 конденса-
тор, как показано на рис. 4L.6.
+15 В
Единственное
изменение
предыдущей схемы
Рис. 4L.6. Усилитель с заземленным эмиттером
На. какие свойства схемы повлияет добавлен-
ный шунтирующий конденсатор? Изменится
усиление, поскольку сопротивление резистора
в цепи эмиттера Кэ удалено из уравнения уси-
ления. Подумайте, изменит ли добавленный
конденсатор смещение постоянной составляю-
щей на выходе (который был рассчитан таким
образом, чтобы потенциал $а выходе соот-
ветствовал половине напряжения питания)14?
Теперь подайте на вход модифицированного
таким образом усилителя сигнал треугольной
формы частотой 10 кГц с максимально воз-
можной (без отсечения выходного сигнала)
амплитудой. Для этого на генераторе сигналов
нужно будет внести в сигнал большое ослабле-
ние (порядка 40 дБ или больше). Похож ли вы-
ходной сигнал на изображенный на рис. 4L.7?
14 Нет, не изменит, поскольку на смещение влияет только
режим по постоянному току.
4L5. Транзисторный переключатель
201
и
+5 В
0 Время —►
Рис. 4L.7. Форма выходного сигнала большой амплитуды
на выходе усилителя с общим эмиттером при треугольном
входном сигнале
Сравните его с сигналом, приведенным на
рис. 5N.12, и объясните, по какой именно при-
чине происходит это своеобразное искажение.
К сожалению, наличие конденсатора, шунти-
рующего резистор в цепи эмиттера 1?э, не уве-
личивает усиление до бесконечности. В гла-
ве 5N мы узнаем, что можно прогнозировать
величину усиления, добавив в цепь эмиттера
нашей модели транзистора подобный резисто-
ру элемент с небольшим сопротивлением. Мы
назовем этот параметр моделирования «малое
гэ». В данной схеме, в которой ток покоя со-
ставляет около 1 мА, значение малого гэ со-
ставляет около 25 Ом. Проверьте, соответству-
ет ли усиление схемы с этим значением гэ ранее
полученному.
Выполнить это измерение будет непросто.
Первым делом нужно уменьшить амплитуду
выходного сигнала генератора до минимально
возможного уровня. При таком входном сигна-
ле уровень выходного сигнала будет слишком
мал, чтобы его можно было измерить с помо-
щью щупа 10х. Это тот редкий случай, когда для
измерения входного сигнала потребуется щуп
Iх, а не 10х.15
Обычно величина усиления окажется около
250, что меньше предсказанного значения. Это
обстоятельство можно объяснить малым током
коллектора 7К, отсюда следуют и искажения вы-
ходного сигнала: величина усиления будет ино-
гда больше, чем в статическом случае, иногда
меньше, но в целом все это объясняется сниже-
нием коэффициента усиления.
4L.5. Транзисторный
переключатель
Устройство, принципиальная схема которого
изображена на рис. 4L.8, отличается от всех
*\ Лампа накаливания
J мощностью 1 Вт
470
бкэ
Рис. 4L.8. Принципиальная схема транзисторного ключа.
Изогните все выводы транзистора под 90°, чтобы их было
легко вставить в отверстия макетной платы
других устройств, которые мы собирали до сих
пор: это транзисторный ключ, который может
находиться в режиме насыщения.
В этом режиме работы транзистора равенство
/к = Р • 1Б не выполняется. Можете пояснить,
почему так происходит16? Кроме того, коэффи-
циент «бета» для мощного транзистора намно-
го меньше, чем для маломощного (например,
2N3904), по крайней мере, при больших токах.
Минимальный коэффициент «бета» для транзи-
стора MJE3055T составлйет всего лишь 20 при
токе коллектора /к = 4 А (см. рис. 4L.9). Но и сам
транзистор имеет большие габариты и заключен
в корпус большого размера (ТО-220), который
предназначен для рассеивания значительного
объема тепла, особенно, если к нему прикре-
пить еще массивный металлический теплоотвод.
В результате плотность тока через переходы
транзистора и напряжение насыщения оказы-
ваются низкими. Мы рассмотрим, как измерить
напряжение насыщения и^ъш? ЧУТЬ R^uiee.
Включайте и выключайте подачу тока в базу тум-
блером (или, если у вас нет подходящего пере-
ключателя или неохота монтировать его, извле-
кая один вывод резистора из макетной платы и
касаясь им или шины питания +5 В и «земли»).
Какой приблизительно ток базы 7Б? Какой ми-
нимальный требуемый коэффициент «бета»17?
15 Если ваш щуп осциллографа оснащен переключателем
10х/1\ просто переведите его в положение Iх.
16 Следует обратить внимание на то обстоятельство, что
для получения большого тока потребовалось бы или со-
противление меньшей величины в цепи коллектора, или
более мощный источник питания. Когда транзистор нахо-
дится в режиме насыщения, величина тока ограничивается
не транзистором, а нагрузкой.
17 Обратите внимание на то, что в данном случае мы пере-
гружаем базу, что типично для транзисторного ключа. По-
скольку ток базы в данном случае меньше 10 мА, даже при
указанном минимальном значении коэффициента р, рав-
ном 20, транзистор мог бы пропускать больше тока, чем
может позволить нагрузка. Это хорошо, поскольку насы-
щение переключателя будет сильным, вследствие чего па-
дение напряжения на переходе «коллектор - эмиттер» U^
будет небольшим.
202
4L Лабораторное занятие: транзисторы
+5 в
470;
10
10 Ом
Мощный резистор:
2,5 Вт или больше
MJE3055
0,01
UL
ГКЭ(НАС)
од
1 10
TOK коллектора
100
Рис. 4L.9. Насыщение транзисторного ключа: для большего тока нагрузки требуется транзистор большего размера (данные
предоставлены компанией ON Semiconducor)
4L5.1. Напряжение включения
или насыщения UK3HAC
Теперь давайте заставим транзистор подна-
прячься еще больше. Замените лампочку мощ-
ным резистором номиналом 10 Ом. Здесь по-
надобится не обычный резистор мощностью
0,25 Вт, а компонент, который сможетрассеивать
требуемую мощность: U 2/R = 25/10 = 2,5 Вт.
Резистор мощностью 0,25 Вт сгорит в этой
схеме.
Измерьте напряжение насыщения 1ГКЭ НАС с по-
мощью цифрового мультиметра или осцилло-
графа. Затем подключите параллельно рези-
стору в цепи базы резистор номиналом 150 Ом
и обратите внимание на улучшенное напряже-
ние насыщения. Сравните полученные резуль-
таты с данными, приведенными на графике
справа на рис. 4L.9. Обратите внимание на то,
что здесь предполагается большой ток базы
!Б=1к/10,анеур.
Мы возвратимся к транзисторным переклю-
чателям позже, на лабораторном занятии
12L, на котором мы познакомимся с глав-
ным соперником биполярному транзистору
MJE3055 — мощным МОП-транзистором.
Там мы устроим «соревнование» между эти-
ми двумя транзисторами, чтобы посмотреть,
который из них лучше справляется с подачей
тока на нагрузку.
4L5.2. Включение индуктивной
нагрузки
Теперь замените резистор в цепи коллектора ка-
тушкой с индуктивностью 10 мГн, как показано
на рис. 4L.10.
Элемент АА
напряжением 1,5 В
1N914 (добавьте
диод только
при наличии
«cTTL»
Рис. 4L.10. Транзисторный переключатель, управляющий
индуктивной нагрузкой
Кроме этого, замените источник питания напря-
жением 5 В гальваническим элементом форм-
фактора АА напряжением 1,5 В. Это нужно для
того, чтобы не перегреть катушку. Кроме того,
импульс напряжения, который мы вскоре уви-
дим, будет выглядеть еще более впечатляющим
на фоне такого низкого напряжения питания.
Подайте на резистор номиналом 1 кОм в цепи
базы прямоугольный сигнал с выхода «TTL»
или «Sync» генератора сигналов. (Это будет
сигнал логических уровней: напряжение, пере-
ключающееся между нулем и уровнем 4-5 В.)
Вы должны обнаружить, что индуктивность
создает большой импульс напряжения на кол-
лекторе транзистора (мы лично наблюдали им-
пульс величиной 100 В). Это объясняется тем,
что когда транзистор пытается выключиться,
4L6. Проблема помех источников питания
203
катушка стремится поддерживать протекание
тока. В итоге напряжение на коллекторе увели-
чивается до тех пор, пока не наступит пробой
транзистора, и ток лавинообразно возрастет,
несмотря на попытку транзистора резко вы-
ключить его.
Диод, подключенный между коллектором и
положительным полюсом источника пита-
ния, гасит этот выброс напряжения. Такой
диодный ограничитель напряжения является
стандартной защитой в Схемах, переключаю-
щих индуктивные нагрузки. Для большинства
транзисторов пробои крайне опасны, но на сей
раз мы не возражали, поскольку нашей целью
было продемонстрировать большой всплеск
напряжения. Кстати, при рассмотрении им-
пульсных источников питания на лаборатор-
ном занятии 12L мы познакомимся со схемой,
которая извлекает пользу из подобного скачка
напряжения.
4L6. Проблема помех
источников питания
Проблема помех в источниках питания под-
робно рассматривается в разделе 9S.3, а здесь
мы только дадим несколько советов касательно
одного типа помех.
На рис. 4L.11 показана осциллограмма сигна-
ла одной из схем эмиттерного повторителя,
которые мы рассматривали в этой главе, из-
меряемая при довольно медленной разверт-
ке (20 мкс/деление). На вход схемы подает-
ся синусоидальный сигнал частотой около
15 кГц от генератора сигналов. Как можно ви-
деть, осциллограмма сигнала выглядит в виде
странной утолщенной линии.
ж
Рис. 4L.11. Утолщение осциллограммы сигнала указывает на
серьезные паразитные колебания
При более быстрой развертке в 10 не/деление
утолщение превращается в синусоиду с очень
высокой частотой, вплоть до частоты ЧМ-ра-
диодиапазона (рис. 4L.12). Эта проблема реша-
ется развязкой источника питания, реализация
которой описывается далее.
{Канал 2
1 Частота
j 77,48 МГц
Рис. 4L.12. Быстрая развертка позволяет увидеть утолщенную
осциллограмму сигнала при более высоком разрешении
Помехи и радиочастотные наводки
При наличии такой помехи в полезном сигнале
попробуйте определить его источник, выклю-
чив источник питания схемы. Если помеха ис-
чезнет, значит, причиной является сама ваша
схема, функционирующая как неумышленный
генератор колебаний. Мы рассмотрим более
подробно причины возникновения таких ко-
лебаний на лабораторном занятии 9L. Если же
помеха сохранится, следовательно, схема не ви-
новата, и источником, вероятно, являются ра-
диочастотные наводки на проводниках схемы.
Быстрого способа устранения этой проблемы
нет. Подобные наводки можно увидеть всегда,
когда усиление осциллографа очень большое и
когда на этих частотах импеданс исследуемой
точки высокий.
Решение проблемы
В случае, когда ваша схема сама создает пара-
зитные колебания, а не просто воспринимает
внешние наводки, проблему можно попытаться
решить, последовательно применяя следую-
щие меры:
1. Подавайте сигнал на осциллограф через щуп,
а не BNC-кабель. Емкостная нагрузка BNC-
кабеля в десять раз больше и часто вызывает
паразитные колебания.
2. Укоротите оба провода питания схемы.
Провод длиной около 20 см может иметь
значительное индуктивное реактивное со-
противление на частотах в мегагерцовом
диапазоне. Более короткие провода питания
обладают низким импедансом и амплитуда
наводок будет меньше.
3. Если после принятия этих двух мер пара-
зитные колебания продолжаются, добавьте
развязывающий или шунтирующий кон-
денсатор между каждой положительной
204
4L Лабораторное занятие: транзисторы
линией питания и землей. Возьмите керами-
ческие конденсаторы номиналом 0,01 или
ОД мкФ и установите их как можно ближе к
схеме; на высоких частотах даже несколько
сантиметров могут играть важную роль.
Кстати, последний совет приводится послед-
ним совсем не потому, что он может вызвать
какие-либо другие отрицательные эффекты в
работе схемы. Вовсе нет, вскоре мы увидим, что
применение развязывающих конденсаторов на
шинах питания является практически стандарт-
ной практикой. Этот способ мы оставили напо-
следок просто потому, что его эффективность
слишком очевидна, а мы хотели, чтобы вы сна-
чала убедились, что и первые два решения мо-
гут иногда дать положительный результат.
4W. Примеры с решениями: транзисторы I
4W.1. Эмиттерный
повторитель
Подобная задача подробно описана в разде-
ле 2.2АА книги АоЕ1. Наша задача отличает-
ся тем, что в ней рассматривается эмиттерный
повторитель для сигналов переменного тока.
Задачи отличаются только в этом аспекте, а в
остальном они очень схожи.
4WJ .1. Задача. Создать эмиттерный
повторитель со связью
по переменному току
Разработайте эмиттерный повторитель, рабо-
тающий от однополярного источника питания,
причем входной сигнал от источника при за-
данной нагрузке (рис. 4W.1) не должен ослаб-
ляться более чем на 10%. Предположим, что
напряжение питания U+ = 15 В, ток покоя кол-
лектора 1К = 0,5 мА, а частота^ = 100 Гц.
+15 В
Источник
Разделительный
конденсатор
большой
емкости легко
пропускает
сигналы:
V /
Рис. 4W.1. Ваш эмиттерный повторитель должен передать
сигнал от источника в нагрузку
4W.1.2. Решение
Прежде чем приступать к разработке схемы
эмиттерного повторителя, полезно вспомнить
свойства данного устройства. Как уже упоми-
налось, устройство не усиливает напряжение
входного сигнала. Более того, в техническом
задании указывается, что ожидается опреде-
ленное ослабление этого сигнала, которое не-
обходимо ограничить. Но такой транзистор-
ный каскад обладает и некоторыми полезными
свойствами: источник сигнала с выходным им-
педансом 10 кОм не мог бы передать сигнал с
небольшим ослаблением в нагрузку величиной
4,7 кОм без помощи транзистора. Каким бы
было ослабление в таком случае? По мере раз-
работки транзисторной схемы мы будем рас-
сматривать доступные нам решения подробно,
хотя это и трудоемкий путь.
Создаем базовую принципиальную схему
Начнем с базовой принципиальной схемы (т. е.
без указания номиналов компонентов), кото-
рая изображена на рис. 4W.2. Номиналы будем
определять постепенно в ходе разработки.
Источник
сигнала
АоЕ § 2.2.4А.
Рис. 4W.2. Базовая принципиальная схема эмиттерного по-
вторителя с нагрузкой, связанной по переменному току
Выбираем значение /?э,
чтобы отцентрировать (7ВЫХ
Проявим немного осторожности и допустим,
что мы стремимся отцентрировать выходное
статическое напряжение 1/вых при заданном
токе покоя коллектора /к.
Статическое в данном контексте означает пре-
обладающий потенциал на выходе при от-
сутствии входного сигнала. Таким образом,
на практике условия покоя означают условия
206
4W. Примеры с решениями: транзисторы I
,+15 В
Стремимся к средней точке, Ц = 7,5 В
Рис. 4W.3. Выбираем такое значение
оказалось посредине доступного диапазона напряжений
чтобы UBblx в покое
постоянного тока в усилителе со связью по
переменному току, подобному разрабатывае-
мому нами.
Предвидя некоторые возможные усложнения,
с которыми нам придется столкнуться в других
транзисторных схемах (например, в усилителе
с общим эмиттером и дифференциальном уси-
лителе), мы признаем, что, строго говоря, наша
цель — задать напряжение выходного сигнала
ишх посередине доступного для него диапа-
зона напряжений. В нашем случае этот диапа-
зон простирается от самого низкого потенциа-
ла («земля») до самого высокого (1Г+). Но эти
условия не всегда так просты.
Центрируем напряжение на базе UB
Напряжение на базе центрируется для того,
чтобы получить одинаковые значения резисто-
ров делителя напряжения, что в свою очередь
облегчает вычисление их эквивалентного со-
противления
Но, упрощая эту задачу, мы приносим в жертву
точность центрирования напряжения выход-
ного сигнала 17ВЫХ. Но это не слишком большая
жертва, поскольку величина смещения от цен-
тра будет всего лишь 0,6 В, что не играет роли
при достаточно большом напряжении питания.
Например, для напряжения питания величи-
ной 15 В ошибка будет составлять всего лишь
около 4%.
Выбираем величину сопротивления
делителя смещения /?и, чтобы обеспечить
достаточное смещение
Согласно нашему эмпирическому правилу
это означает, что сопротивление должно быть
меньше 1/10 сопротивления каскада, на кото-
рый подается снимаемый с него сигнал. А сиг-
нал подается на базу транзистора, поэтому нам
нужно знать значение входного сопротивления
на базе #ВХ_Б в статических условиях (т. е. не
принимая во внимание частоту сигнала). Если
мы будем придерживаться данного правила,
нагрузка цепи базы не нарушит напряжение
смещения больше чем на 10%.
Как обычно, входное сопротивление базы
будет просто р • Яэ. Эта задача довольно пря-
молинейна. Менее очевидно, что нам следует
игнорировать нагрузку, существующую по пе-
ременному току. Делитель смещения «не ви-
дит» эту нагрузку, поскольку он задает усло-
вия по постоянному току (статический режим
покоя), тогда как сигналы переменного тока
проходят на нагрузку через разделительный
+15 в
; зоо ком:
150 кОм
зоо ком:
+15 В
Рис. 4W.4. Задаем R^^
4W.I Эмиттерный повторитель
207
конденсатор. Этот процесс иллюстрируется
поэтапно на рис. 4W.4, но учтите, что ход про-
цесса справа налево, и начальным этапом яв-
ляется импеданс, на который подается сигнал
с делителя.
На этом задание условий по постоянному току
заканчивается. Теперь мы можем завершить
весь процесс, определив значение конденсато-
ра связи, который также является и раздели-
тельным конденсатором. Здесь нет никакого
противоречия — этот конденсатор пропускает
сигналы одного типа и блокирует сигналы дру-
гого типа.
Примечание
Последовательно и параллельно соединенные
сопротивления. Внимательно изучите схему и
постарайтесь убедиться в истинности только что
сделанного утверждения. Если у вас возникают с
этим проблемы, представьте себя носителем заря-
да —электроном, если это вам по душе—и отметь-
те каждую точку схемы, в которой у вас есть выбор
маршрута. В таких точках есть параллельные пути
для протекания тока. В тех же точках, в которых
такого выбора нет, эти пути последовательные. Не
сделайте ошибку, полагая, что делитель смещения
и транзистор подключены последовательно толь-
ко потому, что они следуют один за другим при ва-
шем перемещении слева направо.
Определяем значение разделительного
конденсатора
Нам нужно выбрать такое значение конденса-
тора Cv которое позволит создать ВЧ-фильтр,
пропускающий только требуемые нам частоты.
Согласно условиям задачи частота /3лБ должна
быть в районе 100 Гц. Единственная трудность
в этой задаче возникает при попытке опреде-
литься с подходящим значением сопротивле-
ния R нашего ВЧ-фильтра (рис. 4W.5).
R' = £вх схемы
= ^(смещения) 11 /?вх(на базе)
Рис. 4W.5. Каким должно быть значение сопротивления ре-
зистора £в ВЧ-фильтре?
Для решения задачи нам нужно рассмотреть
входной импеданс эмиттерного повторителя.
Делитель смещения и транзистор выглядят со-
единенными параллельно.
Таким образом, входной импеданс эмиттер-
ного повторителя ZBxnBTP равен сопротивле-
нию параллельно соединенных RrEB<M и ДВХБ.
Некоторая сложность возникает при попытке
определиться со значением входного сопротив-
ления на базе ДВХБ. Определенно, оно должно
быть р, умноженное на что-то. Но умноженное
на что именно? Просто на сопротивление цепи
эмиттера #э, как было в обычных случаях?
В частности, мы использовали это сопротив-
ление при выборе значения RTEB для делителя
смещения.
Но на этот раз обойтись просто R3 не получит-
ся, поскольку в отличие от постоянного тока
смещения сигнал проходит через разделитель-
ный конденсатор, связывающий эмиттерный
повторитель с нагрузкой. Поэтому в данном
случае нужно также учесть сопротивление на-
грузки Дн, параллельно подсоединенное к со-
противлению цепи эмиттера R3.
Тогда импеданс, который увеличивается в р раз,
будет не 15 кОм, а 15 кОм || 4,7 кОм, или около
15 кОм/4 или 3,75 кОм. Даже при увеличении
в р раз этот импеданс нельзя игнорировать при
желаемой погрешности в 10%:
« 150 кОм || 375 кОм * 100 кОм.
Далее, выбираем значение конденсатора Cv
чтобы получить частоту/3дБ, равную 100 Гц.
Используем для этого следующую формулу:
С,=
2тгЮ0 Гц • 100 кОм 6 • 102 • 100 • 103
=—10"6 «0,016 мкФ.
ои
Таким образом, конденсатора номиналом
0,02 мкФ будет более чем достаточно.
Подведем итоги
Для тех, кто предпочитает один раз увидеть,
чем тысячу раз услышать, на рис. 4W.6 приво-
дится наглядная иллюстрация предшествую-
щему объяснению.
208
4W. Примеры с решениями: транзисторы I
5. Выбираем
достаточно большую емкость Cv
чтобы обеспечить
* 100 Гц.
в (смещения) 11 /^ (базы)
1. Определяемся
с требуемой
0,02 мкФ >£
ЗООкО
2. Выбираем такое
значение £э, чтобы
отцентрировать Ц для
данного тока покоя 1^окоя
4. Задаем /?тев (смещения)« RBX
(базы); Л^ (базы) < 1/101> • 15 кОм
«100
3. Центрируем UB (покоя) посредине диапазона
напряжения питания (7,5 В), при этом
приблизительно центрируя ишх (Ц). Это определяет
соотношение R{-R2: здесь /^ = /?2
Рис. 4W.6. Наглядное представление этапов разработки эмиттерного повторителя
4W.2. Фазорасщепитель:
входной и выходной
импедансы транзисторной
схемы
4W.2.1. Задача
Разработайте схему, которая выдает два выход-
ных сигнала, инвертированных по отношению
друг к другу.
На рис. 4W.7 приведен эскиз схемы, которую
можно понять на основе знаний о транзисто-
ре, полученных в первый день занятий с ними,
используя простейшее представление о работе
транзистора.
Эта схема называется фазорасщепителем, по-
тому что она выдает на выходе два сигнала
одинаковой амплитуды, но сдвинутые по фазе
на 180°. Но в данный момент эта схема полез-
на для нас, поскольку она позволяет потрени-
роваться в вычислении импедансов, а такая
тренировка позволит нам повторить большую
[\^Г~^ Рис. 4W.7. Общая схема
r\f ВХ°Д 1 j^> фазорасщепителя с еди-
I ^«* r\j ничным коэффициентом
*^ У передачи
часть материала, с которым мы познакомились
на лабораторном занятии 4L.
♦ Исходные требования:
• источник питания: однополярный, +20 В;
• частотный диапазон сигнала: 100 Гц и
выше;
• выходное сопротивление источника сиг-
нала Явых_и ^ 5 кОм;
• ток покоя (/к).
♦ Нужно вычислить входной и выходной им-
педансы.
4W.2.1. Решение
Прежде всего разработаем принципиальную
схему (рис. 4W.8), а затем вычислим требуемые
значения ее компонентов.
+20 В
Выход
с коллектора
+10 В
Выход с
эмиттера
0В
Piic.4W.8. Базовая принципиальная схема фазорасщепителя
4W.2. Фазорасщепитель: входной и выходной импедансы транзисторной схемы
209
Выбираем значения компонентов
Нам потребуются два правила, изложенные на
первом занятии по транзисторам:
♦ простая модель: 1К = 7Б • р;
♦ простейшая модель: 1К «1Б; иъэ = 0,6 В.
Первое правило нам нужно для того, чтобы
вычислить большинство входных и выходных
импедансов, а второго правила будет достаточ-
но, чтобы рассчитать усиление по напряжению
схемы. Задачу будем решать поэтапно.
Определяем значение резистора
в цепи коллектора RK
Схема для определения номинала резистора
в цепи коллектора RK изображена на рис. 4W.9.
+20 В
Коллекторный выход
Рис. 4W.9. Рассчитываем значение резистора в цепи кол-
лектора
Чтобы решить, какое значение требуется, нам
нужно сначала определить исходную харак-
теристику схемы — ее ток покоя коллектора.
Не будем утруждать себя и возьмем типовое
значение — 1 мА. При этом допущении мы мо-
жем выбрать значение резистора, определив
требуемое значение напряжения покоя на кол-
лекторном выходе.
Но если задать напряжение покоя на коллек-
торе равным половине напряжения источника
питания, то результат будет неудовлетвори-
тельным. Ошибка в том, что напряжение по-
коя нужно установить для обеспечения макси-
мального размаха неискаженного выходного
сигнала, не допуская его отсечения. При этом
напряжение на эмиттере не находится в состоя-
нии покоя, как в обычном усилителе с общим
эмиттером. Оно колеблется с таким же разма-
хом, как и напряжение на коллекторе. Таким
образом, на коллекторном выходе доступен не
весь диапазон напряжения питания, а только
его половина.
Поэтому напряжение покоя коллектора UK_U0Km
следует установить посредине доступного ему
диапазона напряжения. Этот диапазон лежит
в пределах 10-20 В, вследствие чего напря-
жение покоя коллектора должно быть 15 В.
Чтобы получить такое напряжение покоя кол-
лектора, нам нужно понизить напряжение пи-
тания на 5 В (обеспечив падение напряжения
на резисторе). Таким образом, сопротивление
резистора RK = 5 кОм, наиболее близким к это-
му значению будет номинал резистора 4,7 кОм
(с погрешностью 10%).
Определяем значение резистора
в цепи эмиттера R3
Схема для определения номинала резистора
в цепи эмиттера Яэ изображена на рис. 4W.10.
Эмиттерный выход
4,7 кОм
X
Рис. 4W.10. Рассчитываем
значение резистора в цепи
эмиттера
Как и в случае с резистором в цепи коллектора,
здесь целью является обеспечение максималь-
ного размаха выходного сигнала на эмитте-
ре. Поэтому его выходное напряжение покоя
должно быть посредине доступного ему диапа-
зона (т. е. 5 В). При токе покоя 1 мА нам снова
потребуется резистор номиналом 4,7 кОм.
Делитель напряжения смещения
Схема для определения резисторов делителя
изображена на рис. 4W.11.
180 кОм
68кОм
Рис.4УУ.11.
Определяем значения
резисторов делителя
напряжения смещения
210
4W. Примеры с решениями: транзисторы I
Эта задача будет более трудоемкой.
♦ Напряжение на базе должно быть немного
больше, чем напряжение покоя эмиттера
Цэ-покоя. т- е- около 5,6 В. Но, имея в своем
распоряжении диапазон напряжения 0-20 В,
мы вместо 5,6 В зададим на базе напряжение
5 В. Это упростит наши вычисления: 5 В со-
ставляет 1/4 напряжения питания 20 В, по-
этому соотношение резисторов RX:R2 делите-
ля будет 3:1.
♦ Номиналы резисторов делителя должны
быть такими, чтобы обеспечить стабильное
напряжение смещения на базе транзистора.
• 1^_г Как мы уже знаем, величина это-
го сопротивления определяется, как
> 180 кОм
4,7 кОм
ОД мкФ
Разделительный
конденсатор
68 кОм«
20 В
:одА
Выход Б
,7 кОм
• JRj^ делителя должно быть малым относи-
тельно нагрузки делителя: < 50 кОм.
• Значения резисторов Rx и R2. Rj.EB_
делителя = *i II Rr Поскольку R2 = 3RV
•^тев = 3/4Д. Таким образом, сопротивле-
ние меньшего резистора должно быть око-
ло 3/4RTEB9 или 66 кОм, для чего прекрас-
но подойдет ближайшее значение 68 кОм.
Сопротивлениеверхнегорезисторадолжно
быть в три раза больше нижнего. Номинал
180 кОм несколько маловат, но нас это не
особенно беспокоит, поскольку, учитывая
падение напряжения [7БЭ величиной 0,6 В,
напряжение на базе иъ можно сделать чуть
выше 5 В.
Разделительный конденсатор2
Схема с разделительным конденсатором Ср
изображена на рис. 4W.12. На рисунке уже ука-
зано значение емкости этого конденсатора. Мы
объясним, каким образом это значение было
получено, далее в тексте.
Прежде всего нам необходимо определить тре-
буемую частоту УздБ. Предположим, что мы хо-
тим пропускать аудиосигнал низкого качества;
в таком случае мы можем выбрать частоту /3дВ
равной 50 Гц.
Определившись с требуемым значением часто-
ты/3дБ, остается только решить, какое эффек-
тивное сопротивление R нужно использовать
Рис. 4W.12. Определяем требуемое значение разделитель-
ного конденсатора
с данной емкостью С. Эффективное сопро-
тивление состоит из делителя напряжения
смещения, соединенного параллельно с базой
транзистора.3 Мы могли бы вычислить это со-
противление, но, как обычно, мы пойдем бо-
лее легким путем. Мы знаем, что входное со-
противление базы fl^g намного больше, чем
Ятев-делителя- Откуда это известно? Да ведь мы
сами задали эти параметры чуть ранее. Таким
образом, мы может пренебречь входным со-
противлением базы JR^.g и считать эффектив-
ным сопротивлением R только сопротивление
^ев-делителя- А поскольку мы знаем его значе-
ние, то нет необходимости вычислять его. Это
значение, которое мы задали в качестве тре-
буемого при разработке делителя напряжения
смещения, а именно 50 кОм.
Точное значение емкости С составляет около
0,06 мкФ, но номинал 0,1 мкФ будет вполне
приемлемым. В данном случае небольшое по-
нижение частоты УздБ не причинит никакого
вреда, поскольку конденсатор предназначен
только для блокировки сигналов постоянного
тока. Если он будет пропускать частоты чуть
меньшие, чем планировалось, тем лучше.
Теперь, когда мы определились со значениями
всех компонентов, можно вычислить входной
и выходной импедансы.
/?вых на коллекторе
Схема для определения выходного сопротивле-
ния #вых_к изображена на рис. 4W.13.
2 Как мы уже знаем, этот конденсатор можно называть
и конденсатором связи — он блокирует сигналы постоянно-
го тока и одновременно пропускает сигналы переменного.
3 Смотрите, не попадите в ловушку, считая эти импедансы
соединенными последовательно, просто потому, что один
из них нарисован слева от другого. Эти два пути соедине-
ны перемычкой. Мы подробно рассмотрели такую про-
блему ранее в тексте, в примечании «Последовательно и
параллельно соединенные сопротивления».
4W.2. Фазорасщепитель: входной и выходной импедансы транзисторной схемы
211
4,7 кОм
+20 В
Коллекторный
выход
Рис. 4W.13. Выходное сопротивление на коллекторе /?выхк
оказывается просто равным сопротивлению резистора в це-
пи коллектора
Определить этот импеданс легко. Как обычно,
размещаем оба пути параллельно.
Примечание
Как и при расчете ЯТЕВ описанный подход не огра-
ничивается только активными сопротивлениями
и полезен для определения импедансов в общем
случае.
Как нам следует рассматривать импеданс,
наблюдаемый со стороны коллектора?
Шаг 1. Не допустите ошибки, считая, что кол-
лектор аналогичен эмиттеру, в результате чего
на нем будет наблюдаться усиление в р раз. Это
совсем не так, и поведение коллектора и эмит-
тера радикально различается.
Шаг 2. Воспользуемся тем обстоятельством,
что эмиттер является источником напряжения,
а коллектор является источником тока: ток в
его цепи жестко задан. Этот факт отмечался и
ранее, но мы снова повторим его: при фикси-
рованном токе напряжение может меняться,
не оказывая заметного влияния на ток. Таким
образом, отношение Д1//Д7 очень большое
(в идеале бесконечное). Это отношение являет-
ся просто нашим определением эффективного
сопротивления (также называемым диффе-
ренциальным или динамическим сопротивле-
нием) в какой-либо точке.
Таким образом, этот очень большой импеданс
коллектора никак не влияет при параллель-
ном соединении с сопротивлением коллекто-
ра Дк: последнее доминирует и в этой схеме
определяет выходное сопротивление йвых на
коллекторе. А в случае усилителя с общим
эмиттером выходным сопротивлением на
коллекторе будет сопротивление резистора
в цепи коллектора.
Выходное сопротивление /?вых
на эмиттере
Схема для определения выходного сопротивле-
ния #вых_э изображена на рис. 4W.14.
; 4,7 кОм
Эмиттерный выход
Рис. 4W.14. Определить выходное сопротивление #вых.э до-
вольно сложно, но расчет можно упростить, если считать,
Задача определения этого импеданса сложнее,
чем расчет выходного импеданса на коллекто-
ре. В данном случае отсутствует эффект транзи-
сторной «линзы», и для определения выходно-
го сопротивления на эмиттере мы «смотрим»
через транзистор по направлению к источнику
сигнала. Мы уже прорабатывали такую пробле-
му на лабораторном занятии 4L, когда опреде-
ляли выходной импеданс эмиттерного повто-
рителя.
Выходное сопротивление Явых является сопро-
тивлением на эмиттере #э, соединенном парал-
лельно с другим путем (через эмиттер). Сначала
запишем всю соответствующую формулу со
всеми ее подробностями, а затем удалим те ее
части, которые не играют важной роли:
*вых-э=*эИ
Формула выглядит довольно сложной, поэтому
упростим ее.
♦ Без сопротивления эмиттера R3 обычно мож-
но обойтись, поскольку оно должно быть на-
много большим, чем параллельное ему со-
противление.
♦ Также можно пренебречь сопротивлением
смещения ЛгЕВ.ш, поскольку оно определяет
входной импеданс ZBX схемы, как мы видели
ранее, и этот импеданс должен быть боль-
шим относительно выходного сопротивле-
ния источника сигнала Двых_и.
212
4W. Примеры с решениями: транзисторы I
♦ А вот без малого гэ4 не обойтись, поскольку
его значение при JK = 1 мА составляет 25 Ом
и не является незначительным по сравнению
со значением #BHX_H/P: 5 кОм/100 = 50 Ом.
Таким образом, удаление из исходной формулы
некритических элементов сводит ее к следую-
щей упрощенной версии:
* 5кОм
Полученное таким способом значение Двых_э
равно 75 Ом, тогда как точное значение равно
69 Ом. Погрешность составляет около 8%, что
вполне терпимо по нашим меркам.
Входной импеданс ZBX
Схема для определения входного импеданса
показана на рис. 4W.15.
180 кОм
4,7 кОм
Коллекторный выход
ОД мкФ
68кОм
♦20 В
Эмиттерный выход
4,7 кОм
Рис. 4W.15. Во входном импедансе ZBX преобладает сопро-
тивление делителя напряжения смещения
Как обычно, мы упростим задачу, пренебрегая
элементами, которые не играют важной роли.
♦ Конденсатор. Здесь главное состоит в том,
чтобы увидеть, что интересующим нас аспек-
том является поведение схемы на частоте по-
лезного сигнала. Нам не важно, как выглядят
компоненты сигнала, которые мы считаем
помехой: частоты ниже частоты Д^ нашего
входного каскада. Соответственно, емкость
конденсатора С не играет абсолютно ника-
кой роли: как обычно, сигнал проходит через
него без проблем. (В противном случае ем-
кость конденсатора потребуется увеличить.)
♦ Делитель напряжения смещения. Мы зна-
ем, что значение этого импеданса мало по
4 Следует признать, что использование этого обозначения
до того, как мы дойдем до его объяснения в главе 5N, не со-
всем честно. Но здесь мы считаем необходимым оставить
его, чтобы получить как можно более общее решение. А в
главе 5N мы рассмотрим этот параметр более подробно.
сравнению с импедансом базы, потому что
так было задано в исходных технических ха-
рактеристиках. Таким образом,...
... мы можем пренебречь входным импедан-
сом на базе, который по техническим усло-
виям больше как минимум в десять раз, чем
Итак, кратким ответом будет, что входной им-
педанс ZbX « ВТВВ<М = 50 кОм. Эта величина ле-
жит в пределах 10% точного значения, т. е. зна-
чения, при вычислении которого принимается
во внимание нагрузка р • (гэ+#э). Но опять же,
это приблизительное значение удовлетворяет
нашим стандартам.
Возможно, следует отметить, что мы здесь не-
правомерно пренебрегли возможной нагруз-
кой, подключенной к эмиттеру по переменному
току (т. е. через конденсатор). На практике эту
нагрузку тоже нужно учитывать в вычислениях.
Тогда формулу для вычисления входного импе-
данса Zj^ следует скорректировать следующим
образом:5
VK хгН-ПО-ПЕР-ТОКУ/'
В отличие от сопротивления R3 (которое пред-
ставляет для делителя напряжения нагрузку по
постоянному току), величину нагрузки по пере-
менному току нельзя предполагать большой по
сравнению с сопротивлением #rEB_CM. И если та-
кая нагрузка подключена, то необходимо, что-
бы сопротивление RBblx.ll было меньшим, чем
используемое в этом примере, т. е. оно должно
быть меньше 5 кОм (с предельным значением
порядка 1 кОм; тогда RH > 400 Ом). В результате
подключения такой нагрузки входной импеданс
Z^ понизится до 22 кОм. Итоговая принципи-
альная схема фазорасщепителя изображена на
рис. 4W.16.
+20 В
180 кОм<
4<7кОм ОДмкФ
68 кОм<
-X
7
>4,7кОм
| Коллекторный
выход
10 В
Эмиттерный
, выход
0 В
Рис 4W.16. Законченная принципиальная схема фазорас-
щепителя со значениями всех элементов
5 Для еще большей точности, в этом расчете можно
принять во внимание сопротивление Дэ, параллельное
нагрузке.
4W.3. Транзисторный переключатель
213
Вход
Выкл Вкл
+5 | Нагрузка
~~ч50Ом
!
I
Рис. 4W.17. Две возможные принципиальные схемы транзисторного переключателя
Получение точных значений не было нашей
основной целью при проработке данного при-
мера. Вместо этого мы хотели напомнить вам о
нескольких основных понятиях и дать вам воз-
можность применить их:
♦ выходные импедансы на эмиттере и коллек-
торе сильно отличаются друг от друга.
♦ необходимо различать пути сигналов пере-
менного и постоянного тока, а частоты по-
лезного сигнала следует отличать от всех
других частот.
4W.3. Транзисторный
переключатель
Идеальный переключатель во включенном ре-
жиме должен выдавать в нагрузку максималь-
ную мощность, не рассеивая никакой мощно-
сти сам. На рис. 4W.17 приведены две возмож-
ные схемы транзисторного переключателя, на
основании которых далее сформулированы
задачи.
4W3.1. Задача
1. Ток в нагрузке. Каким приблизитель-
но будет ток нагрузки в обоих случаях?
Предположим, что р = 100.
2. Мощность, рассеиваемая переключате-
лем. Какая мощность рассеивается в тран-
зисторном переключателе в каждом из этих
двух случаев, если предположить, что напря-
жение насыщения икэ_НАС « 0,2 В? (В рассеи-
ваемую мощность также входит мощность,
рассеиваемая резистором в цепи базы.)
3. Почему одна из этих схем лучше другой?
Кратко поясните, почему одна из этих схем
предпочтительней другой.
4W.3.1. Решение
1. Ток в нагрузке.
Рассмотрим схему А на рис. 4W.17. Это ти-
пичная схема транзисторного ключа с общим
эмиттером:
/б = 4,4В/1к0м = 4,
Такого тока более чем достаточно, чтобы
вызвать насыщение транзистора. При насы-
щении падение напряжения на транзисторе
составляет приблизительно 0,2 В, вследствие
чего напряжение нагрузки UH * 4,8 В.
Таким образом, ток нагрузки JH =
= 4,8 В/50 Ом = 100 мА. Обратите внимание
на то обстоятельство, что ток здесь опреде-
ляется нагрузкой.
Теперь рассмотрим схему Б, которая в дей-
ствительности является схемой эмиттерного
повторителя (схема с общим коллектором),
а не переключателя. Перерисуем ее в виде
делителя напряжения, содержащего #э, иъэ
и RB. Обратите внимание на то, что сопро-
тивление RB преобразуется коэффициентом
«бета» транзистора следующим образом:
1 кОм/р = 10 Ом (рис. 4W.18). Тогда
1Н = 1Э « /к = 4,4 В/60 Ом « 70 мА.
10 Ом
50Ом
0,7 В^
,6 В
3,7 В-
Влияет на
рассеиваемую
мощность
Рис. 4W.18. Схема Б эмиттерного повторителя, перерисо-
ванная в виде делителя напряжения, чтобы показать, где
происходит рассеивание мощности
214
4W. Примеры с решениями: транзисторы I
2. Рассеиваемая мощность.
Схема А, транзисторный ключ:
Р = Д/=Ркэ + РБЭ + Рр_Б=(0,1А.0,2В) +
+ (4,4 мА • 0,6 В) + [(4,4 мА)2 • 1 кОм] =
= 0,02 Вт + 2,6 мВт + 20 мВт = 43 мВт.
Схема Б, эмиттерный повторитель:
Р = ГО = РЮ + РВВ + РМ= (70 НА-13 В) +
+ (0,7 мА • 0,6 В) + (0,7 мА • 0,7 В) =
= 91 мВт + 0,4 мВт + 0,5 мВт * 92 мВт.
Здесь РР_Б — мощность, рассеиваемая рези-
стором в цепи базы.
3. Почему одна из этих схем лучше другой?
Транзисторный ключ (схема А) обеспечива-
ет большую мощность в нагрузке и меньшую
рассеиваемую мощность (примерно наполо-
вину меньше, как мы только что увидели в
предыдущих вычислениях). Ключ подает на
нагрузку напряжение более близкое к пол*
ному напряжению питания, чем эмиттерный
повторитель: 4,8 В и 3,7 В соответственно.
Если сравнивать подаваемую в нагрузку
мощность в процентах, разница выглядит
следующим образом:
Транзисторный ключ (схема А):
Рн = 0,1 А-4,8 В = 0,48 Вт;
Р^ = 0,043 Вт; ==> РИ/Р0БЩ = 0,48/0,52 = 92%.
Повторитель (схема Б):
Рн = 0,07 А-3,7 В = 0,26 Вт;
Рпвт = 0,09 Вт; ==> РН/РОБЩ = 0,26/0,35 = 74%.
Короче говоря, как вы уже, наверное, поня-
ли, когда нам требуется, чтобы биполярный
транзистор работал в режиме ключа, мы
предпочитаем схему переключателя с общим
эмиттером из-за ее большей эффективности.
Эта схема также предпочтительнее, когда
нужно, чтобы выходной уровень мог при-
близиться к уровню напряжения питания,
независимо от диапазона напряжения сигна-
ла на базе.
5N. Транзисторы II
Содержание
5N.1. Новое не отменяет старого 215
5N.1.1. Возможные трудности понимания транзисторов 216
SN.2. Вкратце снова о фазорасщепителе 216
5N.2.1. Выходные импедансы 217
5N.2.2. Входной импеданс 217
SN.3. Модель Эберса-Молла транзистора 217
5N.3.1. Случай, требующий применения модели Эберса-Молла 217
5N.3.2. Уравнение Эберса-Молла описывает зависимость тока коллектора 1К
транзистора от напряжения иъэ 218
5N.3.3. Малое гэ 219
5N.3.4. Малое гэ решает проблемы импеданса 220
SNA. Искажения в усилителе с высоким коэффициентом усиления 221
5N.4.1. Решение проблемы искажений добавлением резистора в цепь эмиттера,
жертвуя при этом величиной усиления 222
SN.5. Искажения, вызываемые температурной неустойчивостью 222
5N.5.1. Термостабилизация посредством обратной связи через резистор
в цепи эмиттера 223
5N.5.2. Температурная стабильность и высокое усиление 224
5N.5.3. Термостабилизация посредством обратной связи по постоянному току 226
5N.5.4. Стабилизация схемы посредством компенсирующего транзистора 226
5N.6. Согласование модели Эберса-Молла с моделью /к = р х /Б 227
5N.7. Разностный или дифференциальный усилитель 227
5N.7.1. Зачем нужен дифференциальный усилитель? 227
5N.7.2. Схема дифференциального усилителя 230
5N.7.3. Эволюция дифференциального усилителя в операционный 232
5N.8. Послесловие 232
5N.9. Материал для чтения в АоЕ 233
Цель этой главы
В этой главе мы рассмотрим устройство, которое усиливает разницу между двумя сигналами, а не
разницу между сигналом и землей. Эта новая схема позволяет реализовать такой очень важный
компонент, как операционный усилитель, который, начиная со следующего занятия, будет нашим
основным аналоговым конструктивным блоком во всех дальнейших разработках.
5N.1. Новое не отменяет
старого
Сегодня мы рассмотрим некоторые уже знако-
мые нам схемы, которые выявляют недостатки
нашего первого упрощенного представления
о транзисторах. Особенно ярко это проявля-
ется при рассмотрении усилителей с большим
коэффициентом усиления. Тем не менее мы
и далее не откажемся от упрощенной модели
транзистора в тех случаях, где она применима.
Другая важная тема этой главы — новая, более
сложная и более важная, схема, не требующая
дополнительных знаний о транзисторах, ко-
торая создается на основе компонентов, изу-
ченных в главе 4N: усилитель с заземленным
216
5N. Транзисторы II
эмиттером и эмиттерный повторитель. Эта но-
вая схема называется дифференциальным усили-
телем, которая при подключении на ее выход
буфера в виде эмиттерного повторителя стано-
вится операционным усилителем. Мы соберем
такую схему на лабораторном занятии 5L, чтобы
продемонстрировать, что она не представляет
ничего нового, а является просто комбинацией
уже известных нам простых элементов. В итоге
вы сможете оценить удивительные характери-
стики операционного усилителя (с которыми вы
познакомитесь на следующем занятии) не про-
сто как результаты какого-то волшебства внутри
этого «черного ящика», а с пониманием, каким
образом эти результаты достигаются.
Функционирование схем с операционным уси-
лителем иногда действительно кажется вол-
шебством, но одновременно вы испытываете
чувство удовлетворения, зная, что само это
устройство является просто комбинацией уже
знакомых вам схем.
5N.1.1. Возможные трудности
понимания транзисторов
Основная трудность понимания транзистор-
ных схем1 (и их новизна) является результатом
наличия у этих устройств трех выводов вме-
сто двух, к которым мы привыкли в процессе
работы с пассивными устройствами: резисто-
рами, конденсаторами, диодами и катушками
индуктивности2. Эту особенность мы уже упо-
минали ранее.
Мы также обращали ваше внимание на слож-
ность разработки схем на дискретных тран-
зисторах из-за наличия у них трех выводов.
С другой стороны, вас может утешить то, что
подход к рассмотрению транзисторов, исполь-
зуемый в других учебниках и другими препода-
вателями, намного труднее и запутанней, чем в
нашем учебнике и в книге АоЕ. Также облегчит
понимание то обстоятельство, что мы вско-
ре приступим к рассмотрению операционных
усилителей, которые будут функционировать
должным образом, не требуя от вас детально-
го изучения подробностей разработки транзи-
сторных схем.
1 АоЕ § 2.1.
2 Вы можете возразить, что мы уже работали даже с четы-
рехвыводным устройством - трансформатором, так что
три вывода вас не пугают. В таком случае можете пропу-
стить эту часть материала.
5N.2. Вкратце снова
о фазорасщепителе
В примере 4W.2 мы всесторонне рассмотрели
устройство, принципиальная схема которого
приводится на рис. 5N.1, разработав сначала
его базовую схему, а затем определив значения
ее компонентов, а также входного и выходного
импедансов3. Здесь мы снова обратимся к этой
схеме, чтобы прояснить некоторые моменты,
с которыми мы познакомились на первом ла-
бораторном занятии по транзисторам 4L.
20 В
ю в
4,7 кОм
Выход
с коллектора
Рис. 5N.1. Принципиальная схема фазорасщепителя
Далее мы будем полагаться на два простых
представления работы транзистора из наших
прошлых занятий, которых будет почти до-
статочно для анализа работы этой схемы. Но
нам придется столкнуться с одним ограниче-
нием этих простых представлений, которое
заставит перейти (после предварительных ис-
следований) ко второму, более продвинутому,
представлению транзисторов. Это второе пред-
ставление и будет центральной частью данной
главы.
Почти все аспекты схемы фазорасщепителя,
изображенного на рис. 5N.1, можно объяснить
и понять на основе наших двух упрощенных
представлений транзисторов:
простое: 1К = 1Б • р;
еще проще: 1К «1Э;
= 0,6 В.
Ток эмиттера /э. Второе представление (то,
которое «проще») позволяет нам вычислить
ток эмиттера /э. Напряжение на базе тран-
зистора в схеме на рис. 5N.1 составляет чет-
верть от 20 В напряжения питания, т.. е. 5 В.
Напряжение на эмиттере иэ меньше напряже-
ния на коллекторе на величину падения напря-
жения на р-я-переходе, но это приблизительно
5 В (погрешность в 0,6 В по сравнению с 20 В
3 АоЕ § 2.2.8.
5N.3. Модель Эберса-Молла транзистора
217
пренебрежимо мала), а величина тока эмиттера
равна просто Ud/R3 « 1 мА (это наша любимая
величина тока, поскольку она очень упрощает
вычисления).
Ток коллектора 1К. Ток коллектора 1К просто
приблизительно равен току эмиттера /э.
Выходные напряжения покоя. Таким обра-
зом, мы можем вычислить напряжения покоя
на эмиттере и коллекторе: 5 В и 15 В (20 В ми-
нус падение 5 В на резисторе #к) соответствен-
но. Выглядят ли эти результаты корректными?
Да, выглядят, поскольку они обеспечивают
максимальный размах сигнала без отсечения в
его верхней или нижней части.
5N.2.1. Выходные импедансы
Импеданс на коллекторе4. Здесь выходной
импеданс 1?вых будет равен сопротивлению ре-
зистора в цепи коллектора JRK, т. е. 4,7 кОм (если
вам непонятно, почему так, еще раз взгляните
на пример фазорасщепителя в разделе 4W.2).
Импеданс на эмиттере5. В данном случае
присутствует эффект «розовых очков» (лин-
зы), который мы наблюдали с эмиттерным по-
вторителем на лабораторном занятии 4L: со-
противление источника Дисточ уменьшается на
коэффициент усиления по току транзистора р.
(Здесь нам потребовалось первое из двух пред-
ставлений — то, которое «простое».) Таким
образом, можно предположить, что выходной
импеданс будет Двых ^ 50 Ом.
Однако в данном случае наше предположение
ошибочно. Правильный ответ будет 75 Ом
вследствие влияния фактора, который мы на-
зываем малое гэ или собственное сопротивление
эмиттера. Это новое понятие, которое мы бу-
дем подробно рассматривать в разделе 5N.3.3,
но пару раз оно уже использовалось для прак-
тических целей, в частности, в разделе 4W.2.
5N.2.2. Входной импеданс
В этом импедансе доминирует цепь делителя
смещения, в результате чего задача его опреде-
ления легче, чем в случае эмиттерного повто-
рителя с двухполярным источником питания,
входной импеданс которого мы измеряли на
4 АоЕ § 2.1.3В.
5 АоЕ § 2.2.7А.
лабораторном занятии 4L. Сопротивление RnsB
для этого делителя напряжения смещения на-
много меньше, чем входной импеданс транзи-
стора, в результате чего в данном случае отсут-
ствует эффект «линзы».
Примечание
Конечно же, разработка схем на практике отличает-
ся от анализа, который мы здесь описываем, и тре-
бует пристального внимания к бета-превращению,
которое определяет входное сопротивление на
базе. Этот процесс был подробно описан в разделе
4W.2, в котором рассматривалась схема фазорас-
щепителя.
5N.3. Модель Эберса-Молла
транзистора
Для анализа некоторых схем, с которыми мы ра-
ботали в предыдущей главе, упрощенное пред-
ставление транзистора будет недостаточным;
для них требуется другая модель — Эберса-
Молла6. Мы только что столкнулись со схемой,
выходной импеданс 1?вых которой оказался не
таким низким, как мы предположили на основе
первых упрощений. Но нашим основным при-
мером использования этой модели будет схема
другого *ипа — усилитель с общим эмиттером.
5N.3.1. Случай, требующий
применения модели Эберса-Молла
Усилитель с заземленным эмиттером (рис. 5N.2),
с которым мы работали на лабораторном заня-
тии 4L, легко поддается анализу: это, по сути,
источник тока, к которому подключен резистор
(сила тока варьируется при изменении напря-
жения входного сигнала fJBX).
+5 в
7,5 кОм
2N3904
750
Рис. 5N.2. Усилитель с общим
эмиттером с коэффициентом
усиления равным 10
6 АоЕ § 2.3.
218
5N. Транзисторы II
Этот резистор преобразовывает подаваемый на
него ток обратно в напряжение, но повышенное
во столько раз, во сколько сопротивление кол-
лектора RK превышает сопротивление эмиттера
1?э. Величина усиления этой схемы определяет-
ся простым отношением RK/R3, с которым удоб-
но работать: оно не учитывает какие бы то ни
было характеристики транзистора, а зависит
только от подключенных к нему резисторов.
Пока что все хорошо.
Но что будет, если нам захочется увеличить
усиление? Могли бы мы установить отношение
Дк/Яэ равное, например, 100 или 1000? А что
будет, если сделать сопротивление резистора
£э равным нулю? Возможно, последнее пред-
положение неприемлемо с точки зрения мате-
матики, но не в этом его ошибочность. Предел
возможностей транзистора будет достигнут на-
много раньше, чем станет ясной нереальность
усилителя с бесконечным усилением.
Но давайте начнем анализ именно с этого, са-
мого трудного, случая, когда сопротивление
резистора 2?э равно нулю7. Соответствующая
принципиальная схема такого усилителя пока-
зана на рис. 5N.3.
графиками состоит в том, что крутизна графика
для транзистора более резкая, чем для диода,
как показано на рис. 5N.4.
"'ДИОДА]
1/крутизна:
60мВ/декоду
Ц>э транзистора
1/крутизна:
90-12° мВ/декаду
"ДИОДА
Рис. 5N.3. Усилитель с заземленным эмиттером. Неужели
бесконечное усиление?
Рис. 5N.4. Графики зависимости тока от напряжения для
транзистора и для диода схожи
Если удалить из схемы сопротивление в цепи
эмиттера, сигнал будет подаваться непосред-
ственно на переход «база-эмиттер». Поэтому
небольшое повышение напряжения будет вы-
зывать большое увеличение тока, что и следует
ожидать при экспоненциальной форме графика
(рис 5N.5). Соответственно, коэффициент уси-
ления схемы будет большим, но, конечно же, не
бесконечным.
Выход
(ток)
небольшое ДСС ^ -. \
(18 мВ) * ...вызывает большое АГВЬГХ
% (изменения тока вдвое
о / больше изменений
а* *: напряжения)
Рис. 5N.5. Небольшие изменения входного сигнала (напря-
жения 0БЭ) вызывают большие изменения тока коллектора /к
5-
/
Какой подход следует использовать в этом слу-
чае? На рисунке можно видеть входной сигнал
небольшой амплитуды, подаваемый на переход
«база-эмиттер», но ранее мы оговорили, что
напряжение на этом переходе зафиксирова-
но на уровне 0,6 В. Допустим, что не имелось
в виду точно 0,6 В. Это одна из тех схем, для
которых мы вынуждены признать, что напря-
жение ивэ слегка варьируется при изменении
тока коллектора 1К. Более того, график зави-
симости тока коллектора 1К от напряжения [7БЭ
выглядит точно так же, как и график этой за-
висимости для диода, с которым мы уже знако-
мы. Единственная разница между этими двумя
5N.3.2. Уравнение Эберса-Молла
описывает зависимость тока
коллектора /к транзистора
от напряжения 1/БЭ
Модель Эберса-Молла описывает транзистор
как устройство преобразования напряжения
в ток, тогда как наше первое представление
транзистора описывает его как устройство пре-
образования тока в ток (степень которого опре-
деляется коэффициентом р)8. Эти два представ-
ления транзистора вполне совместимы друг
АоЕ § 2.3.4.
8 АоЕ § 2.3.1.
5N.3. Модель Эберса-Молла транзистора
219
с другом, поскольку ток базы протекает в дио-
де, которым является переход «база-эмиттер»
(см. раздел 5N.6).
Сначала мы приведем подробное уравнение
Эберса-Молла, из которого затем удалим не-
критичные компоненты, чтобы с ним было про-
ще работать. После этого мы будем обращать-
ся к полной версии данного уравнения только
в очень редких случаях и будем учитывать его
последствия в более удобных формах. Полное
уравнение Эберса-Молла выглядит следую-
щим образом:
* К"~ *НАС
(5N.1)
Известно, что значение выражения kT/q при
комнатной температуре равно 25 мВ, а минус
единица не играет важной роли при функцио-
нировании транзистора9. Благодаря этому мы
можем несколько упростить наше уравнение:
(5N.2)
Поскольку мы обычно не знаем значения тока
насыщения /НАС, суть уравнения Эберса-Молла
сводится к интуитивному пониманию, что ток
коллектора является экспоненциальной функ-
цией напряжения ию.
Уравнение Эберса-Молла нам будет нужно
время от времени для вычисления относитель-
ных значений тока /к при изменениях напряже-
ния [/ю. Например, что будет, если повысить
напряжение U^ на 18 мВ? Обозначим первона-
чальный ток коллектора 1К1, а новый — 1К1:
_ tUm-Um)/25 _
где (Um - I/B3i)=^Al/|a измеряется в милливоль-
тах (мВ). Но это просто:
р18мВ/25мВ= о
Это число стоит запомнить: изменение напря-
жения база-эмитгер (АЦ^) на 18 мВ удваи-
вает ток коллектора /к. Иногда также может
9 Член 4-1», который приводит к -I^c важен ПРИ отрица-
тельном значении экспоненты, т. е. когда транзистор вы-
ключен. Тогда /к » -/„дс, что объясняет, почему ток -1^
называется током обратной утечки.
пригодиться и другая величина — 60 мВ
которая вызывает десятикратное увеличение
тока коллектора 1К.
Теперь мы можем отойти еще дальше от перво-
начальной формы уравнения Эберса-Молла,
и рассмотреть простое и наглядное его приме-
нение.
5N.3.3. Малое гэ
Теперь для упрощения уравнения Эберса-
Молла мы сделаем необычную первую опера-
цию, а именно положим график зависимости
тока коллектора 1К от напряжения U^ «на бок»,
как показано на рис. 5N.610.
г- 25Ом
Рис. 5N.6. График транзисторной характеристики, положен-
ный «на бок»: теперь крутизна измеряется в омах
Польза от такой модификации графика стано-
вится сразу очевидной: теперь усиление11 тран-
зистора можно представить в виде сопротивле-
ния. Это «сопротивление» просто описывает,
сколько дополнительного тока будет браться
из эмиттера, если понизить напряжение на нем
(полагая, что напряжение на базе фиксиро-
вано). Более подробное описание, как можно
представить себе свойство гэ, приводится ъ раз-
деле 5N.8. И, как можно видеть из рис. 5N.6, это
эффективное сопротивление очень легко под-
дается вычислению: нужно просто разделить
25 мВ на ток коллектора в миллиамперах.
Усилитель с заземленным эмиттером
Если понятие гэ кажется вам несколько аб-
страктным, взгляните на рис. 5N.7. Как можно
10 АоЕ§ 2.3.4.
11 Это «усиление» особого вида: оно не выражается в ве-
личине изменения выходного напряжения на величину
изменения входного напряжения, которое мы использова-
ли на лабораторном занятии 4L. Вместо этого оно пред-
ставляет «крутизну»: величину изменения выходного тока
на величину изменения входного напряжения.
220
5N. Транзисторы II
видеть, задача анализа усилителя с заземлен-
ным эмиттером существенно упрощается, ког-
да гэ отображается в схеме в виде небольшого
резистора.
(смещение не показано)
Загадка Упрощающая модель Загадка разгадана
Рис. 5N.7. Малое гэ делает понятным функционирование
усилителя с заземленным эмиттером
Укажем значения элементов схемы (рис. 5N.8).
(смещение
не показано) "=
Рис. 5N.8. Указаны значения элементов
Коэффициент усиления, RK/r3 можно вычис-
лить, если нам известна величина тока коллек-
тора /к. Известна ли она нам? Вообще-то, если
схема была должным образом разработана, то
да, известна. При правильно собранной схеме
напряжение покоя (£/покоя) должно находиться
посередине доступного для него диапазона, что
в данном случае будет 5 В. А чтобы получить
это напряжение, величина тока коллектора
должна составлять 1 мА.
Зная величину тока коллектора, мы мо-
жем вычислить малое гэ, которое будет все-
го лишь 25 Ом (НЕ 25 кОмг делим на ток
коллектора в миллиамперах, а не амперах).
Таким образом, коэффициент усиления бу-
дет -5 кОм/0,025 кОм = -200. (Знак минус
обозначает инверсию фазы сигнала, а не его
ослабление: когда UBX идет вверх, [7ВЫХ идет
вниз.) К сожалению, как мы вскоре увидим,
полученный ответ относится только к точке
покоя. Тем не менее в качестве начального
приближения это подходит.
5N.3 А Малое гэ решает проблемы
импеданса
Малое гэ не дает «провалиться» входному
импедансу /?вх
Наша новая модель также решает проблему,
которую мы еще не упоминали, а именно опре-
деление входного импеданса RBX для усилителя
с заземленным эмиттером12. Без учета гэ этот
импеданс был бы равен нулю. Но с введением
малого гэ RBX = р х гэ, что и является правиль-
ным ответом.
Малое гэ не дает «провалиться»
выходному импедансу /?вых
При нашем первом представлении эмиттерного
повторителя (с его эффектом «розовых очков/
линзы») выходной импеданс Двых получался
чрезвычайно низким, однако малое гъ вытаски-
вает его из этого «провала»
13
Например, для схемы на рис. 5N.9 при ранее
введенных упрощениях выходной импеданс
Диыу оказался бы меньше, чем 0,5 Ом.
«25 0м (гэ доминирует)
=7,5 кОм
Рис. 5N.9. Малое гэ дает реалистичное значение выходному
импедансу /?вых
Но из-за наличия гэ действительное значение
импеданса не будет таким. Повышение тока
коллектора 1К может понизить выходной им-
педанс 1?вых, но не до такого уровня, который
предполагается при использовании простой
модели транзистора, если только не продол-
жать повышать ток коллектора до очень боль-
ших значений. В этом случае малое гэ снова ре-
шает проблему.
На этом завершаются хорошие новости об уси-
лителе с заземленным эмиттером. Как мы скоро
12 АоЕ§ 2.3.4.
13 АоЕ § 2.3.3.
SNA, Искажения в усилителе с высоким коэффициентом усиления
221
узнаем, в том виде, в каком это устройство было
описано здесь, оно, по сути, непригодно для
практического применения. Причины, порож-
дающие эту непригодность и вынуждающие
нас усовершенствовать данную схему, рассма-
триваются в последующих разделах.
5N А Искажения в усилителе
с высоким коэффициентом
усиления
Коэффициент усиления 200 довольно боль-
шой14. Но очевидно, что усиление не постоянно,
поскольку ток коллектора 1К должен варьиро-
ваться при изменении выходного сигнала ишх
(на самом деле это варьирование /к, что вызы-
вает изменение ишх).
На рис. 5N.10-5N.12 иллюстрируется купо-
лообразное искажение выходного сигнала,
получаемое при небольшом изменении вход-
ного сигнала, которое мы впервые наблюдали
на лабораторном занятии 4L.4.1. Сначала на
рис. 5N.10 демонстрируется изменение величи-
ны усиления, которое можно предположить по
► Усиление
7,5 В 0,5 мА 50 Он
5 В 1 мА 25 Ом
0,2 В 2 мА 12,5 Ом
Малое усиление при мапом токе
Большое усиление при большом токе
Время
Рис. 5N.10. Величина усиления усилителя с заземленным эмиттером варьируется при изменении выходного сигнала, как
можно видеть по его оценке в трех точках
данному варьированию тока коллектора /к при
изменениях выходного напряжения Е/вых.
На графиках на рис. 5N.11 демонстрируется не-
прерывное варьирование величины усиления
400 * при изменении выходного сигнала. Как можно
2оо 1 видеть, выходной сигнал сильно искажен от
о | -50% до+100%.
А на рис. 5N.12 показана осциллограмма, под-
тверждающая предсказанное искажение сигна-
ла. Как же решить проблему искажений?
Малое
усиление
усиление
25
«а 5
4о
< 2
k
0
А
/
/
щ
•
N
Время
^"---^
Время
Время
Рис. 5N.11. При изменении выходного напряжения Ц,ых ва-
рьируется ток коллектора и, соответственно, гэ и величина
усиления
Выходной сигнал
(на коллекторе'
Входной сигнал
(на базе)
Меньшее усиление при меньшем токе
Уровень земли для U^
Большее усиление при большем токе
Уровень земли для ишх
Рис. 5N.12. Осциллограмма выходного сигнала с куполообразным искажением. Обратите внимание, что усиление осцилло-
графа для входного сигнала в 100 больше, чем для выходного
14 АоЕ § 2.3.4А.
222
5N. Транзисторы II
5NA1. Решение проблемы
искажений добавлением
резистора в цепь эмиттера,
жертвуя при этом величиной
усиления
Поскольку варьирование гэ нельзя устранить,
можно лишь сделать его влияние незначитель-
ным. Для этого нужно просто добавить в схему
сопротивление намного большего значения,
чем гэ, в результате чего знаменатель в формуле
усиления будет оставаться практически неиз-
менным15.
При добавлении такого резистора в цепь эмит-
тера нестабильность величины усиления резко
уменьшается, как можно видеть на рис. 5N.13.
♦юв
(смещение
не показано)
Коэффициент^
усиления ="
варьируется от
-9,75 ±4%
Рис. 5N.13. Хотя резистор в цепи эмиттера снижает усиле-
ние, он также уменьшает его варьирование
Малое гэ продолжает сильно варьироваться,
как и раньше, но это нивелируется большой
константой в знаменателе. Теперь величина
усиления схемы варьируется от самого низ-
кого значения -9,1 до самого высокого -9,75,
что составляет -4% и +3%, соответственно, от
среднего значения 9,5.
Вывод: резистор в цепи эмиттера значитель-
но уменьшает погрешность выходного сигнала
(варьирование величины усиления и вызывае-
мые этим искажения).
За это улучшение выходного сигнала нам при-
ходится расплачиваться некоторым снижением
усиления. Здесь наблюдается одно из многих
проявлений «электронной справедливости»:
алчущие большого усиления будут наказаны
уродливым выходным сигналом.
Чуть далее мы увидим, что резистор в цепи
эмиттера способствует решению и других
проблем, таких как проблемы температурной
неустойчивости (см. раздел 5N.5) и даже иска-
жений, вызываемых эффектом Эрли. Как может
скромный резистор решать такой большой круг
проблем? Это объясняется тем, что в последних
двух случаях этот резистор создает отрица-
тельную обратную связь — схемотехнический
прием, обладающий почти волшебными спо-
собностями. В дальнейшем, познакомившись с
операционными усилителями, мы увидим, как
отрицательная обратная связь превращается из
актера второстепенных ролей в главного кино-
героя. Смотреть «игру» отрицательной обрат-
ной связи в этой роли одно наслаждение. Но
впереди нас ждет еще много подобных прият-
ных сюрпризов.
5N.5. Искажения,
вызываемые температурной
неустойчивостью
Полупроводниковые переходы реагируют на-
столько сильно на температурные изменения,
что они часто используются в качестве темпе-
ратурных датчиков. Например, если поддер-
живать напряжение 17БЭ неизменным на одном
уровне, можно наблюдать, как ток коллектора
/к варьируется экспоненциально при измене-
нии температуры (рис. 5N.14).
Повышенная
температура
При 25 °С
.Пониженная
температура
15 АоЕ§2.3.4А.
Рис. 5N.14. Крутизна графика вольт-амперной характеристи-
ки транзистора резко меняется при изменении температуры
Но в любой схеме, не предназначенной для из-
мерения температуры, реакция транзистора
на температурные изменения нежелательна.
Однако большинство нежелательных темпе-
ратурных эффектов можно устранить про-
стым добавлением резистора в цепь эмиттера.
Далее мы рассмотрим механизм работы этого
решения.
5N.5. Искажения, вызываемые температурной неустойчивостью
223
Важное предупреждение
Не ищите описание этой температурной зави-
симости в уравнении Эберса-Молла. Это урав-
нение (неправильно истолкованное) направит
вас в диаметрально противоположном направ-
лении, наводя на мысль, что повышение темпе-
ратуры должно уменьшать знаменатель экспо-
ненты16:
■*к~" ■'нас
Остерегайтесь впасть в заблуждение, что из
уравнения Эберса-Молла вроде бы следует, что
ток коллектора 1К уменьшается при повышении
температуры. Это абсолютно не верно.
Реальные результаты совершенно противопо-
ложны тем, которые кажутся: в действительно-
сти при повышении температуры ток коллек-
тора 1К нарастает, и очень быстро. Разгадка со-
стоит в том, что при повышении температуры
происходит очень быстрое нарастание сомно-
жителя 1НАС, которое подавляет влияние умень-
шающейся экспоненты.
Далее приводятся две формулировки реагирова-
ния транзистора на повышение температуры
17.
♦ при постоянном напряжении U^ ток коллек-
тора 1К нарастает со скоростью приблизи-
тельно 9%/1 °С;
♦ при постоянном токе коллектора 1К напряже-
ние t^ падает со скоростью приблизительно
2мВ/1°С.
Первая из этих формулировок легче поддается
интуитивному пониманию: нагрев устройства
делает его более «энергичным», в результа-
те чего оно пропускает больше тока. А вторая
формулировка часто облегчает вычисления. Но
при использовании второй формулировки не
подумайте, что для «успокоения» схем неплохо
бы развести небольшой костер.
5N.5.1. Термостабилизация
посредством обратной связи через
резистор в цепи эмиттера
Это простое и широко распространенное ре-
шение, которое одновременно также довольно
хитроумное18. Схема слева на рис. 5N.15 на-
столько нестабильна, что является бесполез-
ной. При повышении температуры на 8 °С про-
исходит насыщение транзистора.
6,8 кОм
16 АоЕ§ 2.3.1.
17 АоЕ § 2.3.2с.
Схема «проворачивается» назад,
чтобы подрегулировать кран
Ловкая отрицательная обратная связь
Рис. 5N.15. Стабилизация схемы с помощью резистора в
цепи эмиттера. Обратите внимание, что напряжение базы Ц.
должно быть постоянным
А вот схема справа на рис. 5N.15 работает на-
много лучше. Почему? Каким образом резистор
в цепи эмиттера способствует стабилизации схе-
мы при нарастании тока коллектора /к? Он дела-
ет это, образуя отрицательную обратную связь.
Схема распознает зарождающуюся проблему:
♦ реагируя на возросшую температуру, ток кол-
лектора /к начинает нарастать;
♦ в результате повышения тока коллектора 1К
начинает увеличиваться напряжение эмитте-
ра 1ГЭ (здесь просто срабатывает закон Ома).
Но, поскольку напряжение базы UB зафикси-
ровано, повышение напряжения эмиттера иэ
уменьшает напряжение U^. Это уменьшение
напряжения U^ на переходе «база-эмиттер»
прикрывает вентиль транзистора. Таким об-
разом, схема стабилизирует сама себя (как
несколько своеобразно иллюстрируется на
рис. 5N.15),
Но это не означает, что ток коллектора /к не
меняется совсем. Некоторое изменение тока
коллектора Д/к при повышении температуры
необходимо для того, чтобы создать сигнал
корректировки. Но резистор в цепи эмиттера
предотвращает большое отклонение этого тока
от его значения точки покоя.
График на рис. 5N.16 демонстрирует, как по-
ведение резистора в цепи эмиттера (представ-
ляемое прямой «линией нагрузки», пресекаю-
щейся со смещающейся кривой транзистора)
ограничивает варьирование тока коллектора 1К
при меняющейся температуре.
18 АоЕ § 2.3.4В.
224
5Л/. Транзисторы II
Повышенная
температура
«Линии нагрузки»
резистора
(крутизна= 1/R)
При 25 °С
i Пониженная
/ температура
Варьирование тока Гк небольшое, поскольку его
изменение корректирует напряжение Цэ
2 кОм R3
Чэ
Рис 5N.16. Иллюстрация влияния резистора в цепи эмиттера в виде «линии нагрузки», пересекающей кривые транзисторных
характеристик
Чем больше значение резистора Дэ, тем сильнее
обратная связь и тем меньше ток коллектора /к
зависит от температуры.
5N.5.2. Температурная стабильность
и высокое усиление
Вопреки впечатлению, которое вы, возможно,
получили после прочтения материала раздела
5N.5.1, совсем не обязательно жертвовать уси-
лением, чтобы получить температурную ста-
бильность19. Можно обеспечить как стабиль-
ность, так и высокое усиление, организовав
схему таким образом, чтобы резистор Яэ вы-
полнял свою работу по стабилизации тока кол-
лектора, не уменьшая при этом усиление сиг-
нала. Решение состоит в том, чтобы добавить
в цепь эмиттера резистор R3, но затем сделать
его «невидимым» на частотах полезного сиг-
нала. А это делает шунтирующий конденсатор,
как показано на рис. 5N.17.
15 В
6,8 кОм
Большое усиление
Меньше, чем &э благодаря
шунтирующему конденсатору С
ЮмкФ
Рис 5N.17. Шунтирование резистора в цепи эмиттера кон-
денсатором обеспечивает как температурную стабильность,
так и большое усиление
19 АоЕ §2.3.5А
Осциллограмма усиления
усовершенствованной схемы
На рис. 5N.18 приведена осциллограмма вход-
ного и выходного сигналов усовершенствован-
ной схемы. Как можно видеть, усиление этой
схемы такое же высокое, как и у предыдущей
схемы усилителя с заземленным эмиттером.
А при малом изменении выходного сигнала ис-
кажения в нем будут практически незаметны.
Коэффициент усиления в точке покоя состав-
ляет около -280 (знак минус обозначает толь-
ко инверсию выходного сигнала). Согласно вы-
числениям коэффициент усиления будет -300:
К, = Д£/вых/Д1/вх = - V. = ~7'5 кОм/25 = -300-
Разница между вычисленным коэффициентом
усиления и усилением, наблюдаемым по осцил-
лограмме на рис. 5N.18, объяснятся тем, что
ток коллектора в данной схеме оказывается не-
сколько ниже, чем предполагаемый ток в 1 мА.
Наглядная иллюстрация температурной
стабильности усовершенствованной
схемы
На рис. 5N.19 показаны осциллограммы сигна-
лов обычной (рис. 5N8) и усовершенствован-
ной схем. На обе схемы подается входной сиг-
нал с небольшими колебаниями, а затем каждая
из них нагревается с помощью фена. Хорошо
заметны искажения выходного сигнала усили-
теля с заземленным эмиттером по схеме 5N.8.
При нагреве центрирование выходного сигнала
стабилизированной схемы не было нарушено,
5N.5. Искажения, вызываемые температурной неустойчивостью
225
Выходной сигнал
(на коллекторе) —
Входной сигнал —
(на базе)
Канал 1, размах
сигнала 2,116 мВ
Канал 2,
размах
сигнала 498,9 мВ
ч
/
Отношение UBbLX/UBX соответствует
коэффициенту усиления около 235
Рис. 5N.18. Усиление в точке покоя (при небольшом изменении выходного сигнала) остается постоянным и близко к вычис-
ленному значению. (Обратите внимание на стократную разницу в усилении каналов осциллографа.)
Выходной сигнал,
стабилизированный с помощью
резистора в цепи эмиттера.
Обратите внимание на
искажения нижних пиков
Входной сигнал (разрешение
50 мВ/деление). Обратите
внимание на небольшое"
сглаживание пиков сигнала
Выходной сигнал усилителя/®
с заземленным эмиттером '
Уровень земли для
"входного сигнала
Уровень земли для
"выходного сигнала
Рис. 5N.19. Сравнение стабилизированной и обычной схем: при нагреве происходит отсечение нижних пиков выходного
сигнала нестабилизированной схемы
а выходной сигнал нестабилизированной схе-
мы сместился вниз к земле, в результате чего
начали отсекаться его нижние пики.
Интересная особенность: входной
импеданс ухудшается при насыщении
Следует обратить ваше внимание на одну
особенность осциллограмм на рис. 5N.19:
влияние насыщения на входной импеданс.
Нестабильный выходной сигнал смещается
вниз и сплющивается (отсекается) на уровне
земли. При таком отсечении сигнала происхо-
дит насыщение транзистора, т. е. он полностью
включается. Когда это происходит, обычное
поведение транзистора нарушается. Обычные
правила применимы только в так называемой
линейной области функционирования тран-
зистора, в которой устройство ни полностью
включено (находится в режиме насыщения), ни
полностью выключено.
Когда транзистор находится в режиме насыще-
ния, его входное сопротивление (обычно рав-
ное р • Лэ) сильно уменьшается: умножение на р
больше не происходит. Доказательством этого
эффекта служат две особенности осциллограм-
мы на рис. 5N.19.
♦ Искажению подвергается сам входной сиг-
нал — его верхний пик сплющивается. Это
указывает на то, что даже генератор сигна-
лов, с его выходным сопротивлением 2?вых =
= 50 Ом, испытывает перегрузку из-за мало-
го входного сопротивления #вх транзистора.
♦ Выходной сигнал стабилизированной схемы,
на которую сигнал подается с того же самого
генератора сигналов, что и на нестабильную
схему, также содержит искажения, которые
являются результатом перегрузки источника
сигнала, общего для обеих схем.
Отсюда можно сделать вывод, что не следует
связываться с «плохой компанией»: разделяя
входной сигнал с «заблудшим» усилителем с за-
земленным эмиттером, даже приличная термо-
стабильная схема подвергается его «тлетвор-
ному» влиянию.
Резистор в цепи эмиттера не решает
проблему искажения сигнала
Хотя резистор в цепи эмиттера решает пробле-
му температурной стабильности, но проблема
искажения сигнала остается. Как можно видеть
на рис. 5N.12, это искажение присутствует в вы-
ходных сигналах обеих схем. Данную проблему
226
5Л/. Транзисторы II
решить невозможно, если вы хотите получить
такое большое усиление в одном каскаде.
5N.5.3. Термостабилизация
посредством обратной связи
по постоянному току
На рис. 5N.20 демонстрируется обратная связь
в более очевидной форме, чем через резистор
в цепи эмиттера Дэ, но дающая подобный эф-
фект20.
+ 15 В
8,2 кОм
Вход
Выход
Напряжение UK = 11 • UB3
Рис. 5N.20. Обратная связь по постоянному току предохра-
няет от влияния температуры
Этот тип обратной связи очень похож на об-
ратную связь, используемую в некоторых схе-
мах на операционных усилителях (с которыми
нам предстоит познакомиться в дальнейшем):
1/11 часть выходного напряжения подает-
ся обратно на вход21. Но в данном случае есть
определенная тонкость, которая обычно не
присуща схемам на операционных усилителях:
обратная связь влияет на уровни постоян-
ного напряжения, но не на усиление схемы.
Отсутствие влияния на усиление объясняется
тем, что генератор сигналов, у которого низ-
кий выходной импеданс, в силах преодолеть
сравнительно слабый сигнал обратной связи на
частотах сигнала (тех, которые пропускаются
разделительным конденсатором). В то же са-
мое время обратная связь по постоянному току
достаточно сильная, чтобы решить проблему
смещения сигнала к земле.
20 АоЕ § 2.3.5С.
21 Сигнал этой обратной связи подается не совсем на вход
схемы, но почти на него: на базу транзистора, а не на про-
тивоположный вывод разделительного конденсатора. Как
было только что отмечено, это обратная связь по постоян-
ному току.
5N.5А Стабилизация схемы
посредством компенсирующего
транзистора
Схема на рис. 5N.21 нейтрализует любые из-
менения сигнала в одном направлении с помо-
щью схемного элемента, который подвергает
сигнал эквивалентному изменению в обратном
направлении22.
+20 В
ЮкОм
Выходной
, сигнал
+10 В
сигнал
Повышающаяся температура
снижает напряжение Цэ
транзистора Qt
... что «прикручивает кран» — транзистор Qz
Рис. 5N.21. Обеспечение температурной стабильности схе-
мы посредством использования компенсирующего транзи-
стора
Схема на рис. 5N.21 будет работать должным
образом только в том случае, если оба транзи-
стора выполнены на одной и той же кремниевой
заготовке, чтобы при изменении температуры
их характеристики изменялись одинаково, как
показано на рис. 5N.22.
При повышении температуры схемы напряже-
ние иъэ транзистора Q понижается. Но это по-
ниженное напряжение «придавливает» тран-
зистор Qg, который нагревается в такой же са-
мой степени, как и транзистор Q, не позволяя
его выходному току нарастать с повышением
температуры. Резистор номиналом 10 кОм
в цепи базы транзистора Q^ предотвращает
слишком жесткий ток смещения, в результате
чего источник сигнала (выходной импеданс
которого предполагается «10 кОм) может,
как обычно, без проблем управлять базой. Эта
схема является близким родственником схе-
мы токового зеркала, которая рассматривает-
ся в разделе 5S.2 этой книги и в разделе 23.7
книги АоЕ.
АоЕ § 2.3.5В.
5N.7. Разностный или дифференциальный усилитель
227
Повышенная
температура
Горячий <?,
/Пониженная Л
' температура
1мА
Повышенная
температура
А
/Пониженная
/ температура
низкое иъэ но горячий Qz => 1 мА при низком
Рис. 5N.22. Два транзистора с согласованными параметрами могут компенсировать смещение выходного сигнала, вызывае-
мое температурными колебаниями
5N.6. Согласование модели
Эберса-Молла
с моделью /к = р • /Б
В начале этого курса мы ограничивались пред-
ставлением транзистора, выражаемым форму-
лой JK = p • 7Б, а затем познакомились с более
точной моделью, Эберса-Молла, выражаемой
формулой 1к = 1нясеи*>/ит.
Если вы обеспокоены, что эти две модели могут
противоречить друг другу, далее приводится
иллюстрированный аргумент, чтобы убедить
вас в обратном.
♦ Поскольку переход «база-эмиттер» явля-
ется диодом, подача в него тока (/Б) создает
на нем соответствующее падение напряже-
ния иъэ. Согласно модели Эберса-Молла
напряжение [7БЭ вызывает соответствующий
ток коллектора 1К. Если мы используем этот
аргумент в поддержку нашего первого, про-
стейшего, представления работы транзисто-
ра, в котором ток базы рассматривается как
входной сигнал, мы признаем и используем
модель Эберса-Молла.
Диод Б-Э создает
напряжение
4<А
это иъэ вызывает
Логарифмическая машина Экспоненциальная машина
♦ Этот аргумент иллюстрируется на рис. 5N.23.
Но если ни сам аргумент, ни иллюстрирую-
щий его рисунок не убеждают вас, забудьте
об этом вопросе; если вы не хотите, то вам и
не нужно согласовывать эти две модели.
5N.7. Разностный
или дифференциальный
усилитель
Последней из семейства стандартных транзи-
сторных схем мы рассмотрим схему дифферен-
циального усилителя23. Эта схема для нас очень
важна, поскольку она позволит нам понять ра-
боту операционных усилителей, с которыми
мы вскоре познакомимся. Эти замечательные
устройства представляют собой просто очень
качественные дифференциальные усилители,
применяемые хитроумным способом24.
5N.7.1. Зачем нужен
дифференциальный усилитель?
Дифференциальный усилитель обладает вну-
тренней симметрией, которая позволяет ему
скомпенсировать погрешности, общие для его
обеих плеч, независимо от происхождения
этих погрешностей. Иногда симметрия ис-
пользуется для аннулирования погрешностей,
Рис. 5N.23. Согласование двух моделей описания транзи-
сторного усиления
23 АоЕ§ 2.3.8.
24 Рискуя чрезмерно усложнить эту идею, следует отме-
тить, что хитроумное применение имеет фундаменталь-
ную важность. Хитрость заключается в использовании от-
рицательной обратной связи. Именно это обстоятельство,
а не просто старый добрый дифференциальный усилитель,
обусловливает по-настоящему впечатляющие характери-
стики схем на операционном усилителе, с которыми мы
вскоре познакомимся.
228
5N. Транзисторы II
возникающих внутри самого усилителя, напри-
мер, температурные эффекты, которые стано-
вятся безвредными, если влияют в одинаковой
степени на оба плеча усилителя. В других усло-
виях общей погрешностью, которую требуется
устранить, является помеха, наводимая на оба
входа усилителя. При таком использовании
усилитель принимает сигнал, смешанный с по-
мехой особого типа, называемой синфазной по-
мехой.
На лабораторном занятии 2L мы занимались
чем-то подобным: передавали сигнал и ослаб-
ляли помеху. Но рассмотренный там ЯС-фильтр
работает только при большой разнице в часто-
тах полезного сигнала и помехи. Для диффе-
ренциального усилителя такая разница частот
не является обязательной. Однако непремен-
но требуется наличие одинаковой помехи на
обоих входах усилителя, и наоборот, полез-
ный сигнал должен присутствовать в виде
разницы потенциалов на обоих входах. Такая
ситуация довольно распространена, и диффе-
ренциальный усилитель может ослабить син-
фазную помеху, при этом усиливая полезный
сигнал. Таким образом, дифференциальный
усилитель устраняет мешающее и сохраняет
полезное.
Приложение для дифференциального
усилителя: электроэнцефалограф
Приведем пример задачи, которую можно ре-
шить с помощью дифференциального усилите-
ля. Активность мозга проявляется в виде сла-
бых (в микровольтовом диапазоне) электриче-
ских сигналов, которые можно детектировать
посредством контакта с кожным покровом го-
ловы. Источники этих сигналов имеют высо-
кий выходной импеданс. На рис. 5N.24 приво-
дится набросок возможной организации схемы
для детектирования этих сигналов.
Синфазные колебания большой
' амплитуды (помеха)
Разностные колебания малой
амплитуды (сигнал)
Как только что упоминалось, полезные сиг-
налы здесь очень слабые, в результате чего их
трудно продетектировать. Проще всего собрать
усилитель с высоким коэффициентом усиле-
ния, который значительно усилил бы эти сиг-
налы. Но загвоздка состоит в том, что если не
проявить достаточную бдительность, он усилит
не только полезные сигналы, но и сопутствую-
щие помехи. Проблему можно отчасти решить,
экранировав схему. Но если основной источ-
ник помех воздействует на обе линии в равной
степени, вместо этого усилителя, или наряду
с ним, можно использовать дифференциаль-
ный усилитель. Аналогично можно создать
электрокардиограф — прибор для измерения
электрической активности сердца.
Помеха из линии электропередачи частотой
50 Гц будет попадать на оба входа, и будет, ско-
рей всего, намного больше, чем микровольтовые
уровни полезного сигнала. Качественный диф-
ференциальный усилитель способен ослабить
эту помеху возможно в тысячу раз, при этом
усиливая полезный сигнал, например, в 100 раз.
Дифференциальный усилитель с такими харак-
теристиками будет обладать коэффициентом
подавления синфазной составляющей (так назы-
вается предпочтение разностных сигналов син-
фазному) величиной в 105 или 100 дБ.
Очистка музыки от фоновой помехи
частотой 50 Гц
В одном из моих университетских классов мы
собрали простую имитацию подобного прибо-
ра. Источником дифференциального сигнала
в нем служил проигрыватель компакт-дисков,
подключенный к дифференциальному усилите-
лю парой неэкранированных проводов25. Эскиз
этого устройства приведен на рис. 5N.25.
На каждом из двух проводов длиной около
одного метра присутствуют сильные колебания
частотой 50 Гц, которые показаны на осцилло-
граммах на рис. 5N.26.
Намного меньший разностный сигнал (в дан-
ном случае аудио) выглядит как еле заметное
дрожание на фоне помехи с частотой 50 Гц.
Усиливается
только разность
Дифференциальный усилитель
Рис. 5N.24. Применение дифференциального усилителя:
электроэнцефалограф
25 Мы собрали это устройство на операционном усили-
теле, а не на дискретных транзисторах, поскольку так на-
много легче. Мы уверены, что вскоре вы будете разделять
наше предпочтение операционных усилителей схемам,
собранным на дискретных элементах.
5N.7. Разностный или дифференциальный усилитель
229
Источник
аудиосигнала
Синфазный сигнал (гудение частотой 60 Гц)
Дифференциальный
Разностный сигнал (музыка) усилитель Восстановленный полезный сигнал
Рис. 5N.25. Схема для извлечения аудиосигнала при наличии сильной синфазной помехи
Сигналы двух
входных линий,
едва различимы
На обеих входных линиях присутствуют
сильные наводки частотой 50 Гц и полезные
разностные сигналы малой амплитуды
Вверху, после удаления синфазной
помехи можно видеть малоамплитудные
разностные сигналы
(обратите внимание на более высокое
усиление на этой осциллограмме — 3)
Вверху, после удаления синфазной помехи можно
видеть малоамплитудные разностные сигналы
Рис. 5N.26. Дифференциальный усилитель может выделить небольшую разность между двумя сигналами в присутствии боль-
шой помехи, общей (синфазной) для обоих сигналов
Этот сигнал можно с трудом заметить на левом
изображении на рис. 5N.26 в виде более темных
участков помехи, создаваемых почти идентич-
ными сигналами, следующими один за другим.
Но после удаления общей помехи разницу меж-
ду этим двумя сигналами (показана на правом
изображении) можно легко различить. В дан-
ном случае разностный сигнал не усилен (ко-
эффициент передачи равен единице), т. е. все,
что сделал наш усилитель, это удалил общую
помеху.
Примечание
Сигнал на рис. 5N.26 выглядит так, будто бы он был
усилен, но это всего лишь видимость, создаваемая
большей чувствительностью осциллографа к вы-
ходному сигналу.
Для слушателя эффект этой операции очень за-
метен. Если исходный сигнал звучал как гром-
кое жужжание частотой 50 Гц без какого бы то
ни было намека на музыку, то разностный сиг-
нал звучит как чистая музыка, без следов фона
частотой 50 Гц.
Дифференциальная передача сигналов
полезна даже в цифровых схемах
При рассмотрении цифровых логических
элементов на лабораторном занятии 14L мы
встретимся с дифференциальными передат-
чиками и приемниками, обеспечивающими
помехозащищенность в присутствии сильной
синфазной помехи.
Этот метод, используемый в схемах LVDS26,
может дать хорошие результаты даже при на-
личии источников питания с очень низким
напряжением (которые начинают доминиро-
вать в цифровой схемотехнике) — 2,5 В, 1,8 В
и ниже. На рис. 5N.27 не показана синфазная
помеха, но когда мы попробовали работать с
этой схемой (см. главу 14N), она с легкостью
подавляла синфазный сигнал в пять-шесть раз
больше полезного. Осциллограмма подавления
сильной высокочастотной помехи схемой LVDS
приводится на рис. 12.126 в книге АоЕ.
Слабый сигнал (0,35 В)
Дисрференциальньхй
усилитель
Дифференциальный
усилитель
Рис. 5N.27. Дифференциальная передача сигналов, применя-
емая в цифровой электронике, обеспечивает хорошую поме-
хозащищенность, несмотря на низкое напряжение питания
26 Англ. Low Voltage Differential Signaling - низковольтная
дифференциальная передача сигнала.
230
5Л/. Транзисторы II
5N.7.2. Схема дифференциального
усилителя
На рис. 5N.28 приведена принципиальная схе-
ма дифференциального усилителя27. Мы собе-
рем эту схему на лабораторном занятии 5L. Оба
транзистора должны обладать согласованными
характеристиками, поэтому мы используем
для нее интегральную транзисторную сборку
(СА3096).
15 В
ВходА
Вход Б
Рис. 5N.28. Принципиальная схема дифференциального
усилителя
Схема может выглядеть сложной, но она с лег-
костью поддается анализу. После установки
условий покоя по постоянному току мы при-
бегнем к подходу, рекомендуемому в книге АоЕ:
рассматривать только идеальные случаи — сна-
чала чисто синфазные сигналы, а затем чисто
дифференциальные сигналы. Прежде чем вы-
яснять, что эта схема будет делать с входными
сигналами, определим параметры покоя по по-
стоянному току.
Точки покоя
Выходное напряжение [/вых. Прежде чем
предполагать напряжение 1ГВЫХ, нужно опреде-
лить токи.
Токи. Предположим для простоты, что базы
транзисторов подключены к земле. Тогда напря-
жения на эмиттерах будут близки к потенциалу
земли, откуда следует, что потенциал точки А
окажется недалеко от потенциала земли (око-
ло -1 В) что видно из рис. 5N.29. Отсюда мож-
но приблизительно вычислить, что ток /ХВОСТ28
(через нижний резистор номиналом 10 кОм)
равен приблизительно 14 В/10 кОм » 1,5 мА.
27 См. АоЕ, рис. 2.63.
28 Схему можно рассматривать, как «головастика», тело
которого составляют два транзистора и сопутствующие
резисторы, а хвост - нижний резистор.
Потенциал
близок ^
к потенциалу
земли
ВходА
|0,75мА
Потенциал на входах предполагается
близким к потенциалу земли
Рис. 5N.29. Принципиальная схема дифференциального
усилителя с указанными токами и напряжениями покоя
Поскольку потенциал на обоих входах одина-
ковый, симметричность29 схемы требует, чтобы
оба транзистора разделяли поровну ток «хво-
ста» величиной 1,5 мА. Таким образом, ток
коллектора каждого транзистора будет около
0,75 мА. Отсюда легко получаем выходное на-
пряжение покоя £/вых-покоя' как всегДа» отцен-
трированное по доступному ему диапазону на-
пряжений. (Но не между противоположными
напряжениями питания, поскольку в таком
случае центр приходился бы на 0 В.) А нам
нужно передать колебания выходного сигнала
при заданном напряжении питания. Это всег-
да является более дальней целью. Поскольку
нижний предел выходного сигнала определя-
ется не отрицательным напряжением источ-
ника питания, а напряжением на эмиттере, это
значение находится вблизи потенциала земли,
а[7вых-покоябУДетоколо7'5В-
Дифференциальное усиление
Предположим чисто дифференциальный сиг-
нал: положительное колебание на одном входе
и отрицательное точно такой же амплитуды на
другом. Отсюда следует, как вы вскоре смо-
жете сами убедиться после нескольких минут
размышлений, что напряжение в точке А на
рис. 5N.29 не меняется.
29 Какая симметричность? — можете спросить вы. Цепь
коллектора одного транзистора содержит резистор, а дру-
гого — нет. Все верно. Но попытайтесь сначала объяснить
сами себе, почему это не играет роли. Этот резистор дей-
ствительно влияет на напряжения на коллекторах транзи-
сторов. Но какое влияние это напряжение оказывает на
ток коллектора? Не очень сильное, а в идеале вовсе ни-
какое, поскольку согласно эффекту Эрли это напряжение
влияет очень слабо.
5N.7. Разностный или дифференциальный усилитель
231
Это наблюдение позволяет нам рассматри-
вать правую часть усилителя как уже извест-
ную нам схему: усилитель с общим эмиттером
(рис. 5N.30).
■тсвосг
В результате добавления значения Я
кхвост
V^3
м/2(133) =
= приблизительно 40
33 Ом
100 Ом<
В общем случае ] В данном случае
«А» «А»
Рис. 5N.30. Дифференциальное усиление такое же, как и
у обычного усилителя с общим эмиттером
Может показаться, что усиление можно опи-
сать следующей формулой:
_ *к
Это будет почти правильно. Но нам нужно
добавить в знаменатель множитель 2, чтобы
отобразить исходную постановку задачи: на-
пряжение Д[/, подаваемое на вход этого «уси-
лителя с общим эмиттером», составляет всего
лишь половину дифференциального сигнала,
который мы подаем на оба входа. Также следу-
ет избавиться от знака минус, поскольку мы не
определили, что может означать положитель-
ная или отрицательная разница между входны-
ми сигналами.
Таким образом, чтобы получить выражение
дифференциального усиления, в знаменатель
предыдущей формулы следует добавить мно-
житель 2 и удалить из нее знак минус:
тДИФФ"
Синфазное усиление
Теперь предполагаем чисто синфазный сигнал:
соединяем оба входа вместе и подаем на них ко-
лебания сигнала. Теперь напряжение в точке А
будет меняться. Следовательно, этот усилитель
с общим эмиттером имеет намного меньшее
усиление, поскольку знаменатель уравнения
усиления содержит величину сопротивления
знаменатель, который для чисто дифференци-
ального случая был просто 2(гэ + Лэ), теперь
будет намного большим.
Опять же, это почти все, но не совсем. Теперь
у нас появляется другой множитель 2, чтобы
отразить то обстоятельство, что второй усили-
тель с общим эмиттером (тот, который нахо-
дится в другом плече дифференциального уси-
лителя) поставляет в резистор #хвост порции
тока такой же самой величины. В результате
этого напряжение в точке А поднимается вдвое
выше, чем можно было ожидать в противном
случае: это можно выразить по-иному, сказав,
что эффективное сопротивление #хвост состав-
ляет 2R
хвост*
Откорректируем принципиальную схему уси-
лителя, чтобы показать, что происходит, когда
на оба входа подается одинаковый сигнал (син-
фазный режим). Откорректированная схема
изображена на рис. 5N.31.
+15 В
20 кО/tf
-15 В
Рис. 5N.31. Откорректированная принципиальная схема
дифференциального усилителя, отображающая его работу
в синфазном режиме
Чтобы вычислить усиление, мы можем рас-
смотреть только правый усилитель с общим
эмиттером (показанный отдельно справа на
рис. 5N.31). А усиление в синфазном режиме
будет определяться следующей формулой:
^СИНФАЗ
Очевидно, что чем больше сопротивление
тем лУчи1^°- Следовательно, наилучшее
30 АоЕ § 2.3.8.
232
5Л/. Транзисторы II
ослабление синфазного сигнала происходит,
когда в «хвосте» находится источник тока.
Любой приличный дифференциальный усили-
тель обычно содержит источник тока в «хво-
сте», подобно тому, как его содержит наша экс-
периментальная схема после удаления из нее
«хвостового» резистора. Этот резистор был
добавлен, чтобы измерить предсказуемое син-
фазное усиление, а также для контраста с улуч-
шением, вызываемым присутствием источника
тока.
Операционный усилитель на микросхеме, с ко-
торым мы познакомимся на лабораторном за-
нятии 6L, имеет усиление в пару сотен раз луч-
ше, при этом также лучше подавляет синфаз-
ный сигнал. Но только что рассмотренная схе-
ма служит хорошей отправной точкой, а также,
мы надеемся, упростит понимание условных
графических обозначений в виде треугольни-
ков, которые встретятся нам начиная со сле-
дующего занятия.
5N7.3. Эволюция
дифференциального усилителя
в операционный
После ознакомления с дифференциальным уси-
лителем на лабораторном занятии 5L мы доба-
вим к нему два дополнительных каскада, чтобы
преобразовать его в неплохой операционный
усилитель.
По сути, операционный усилитель — это про-
сто дифференциальный усилитель с высоким
коэффициентом усиления31. Но хороший опе-
рационный усилитель также содержит и буфер,
чтобы обеспечить достаточно низкий выходной
импеданс. На рис. 5N.32 приведена блок-схема
нашего лабораторного операционного усилите-
ля, коэффициент усиления которого составляет
приблизительно 1000, что довольно неплохо.
Дифференциальный Усилитель Эмиттерный
усилитель напряжения повторитель
Х25
Х40
XI =>
Рис. 5N.32. Блок-схема трехкаскадного операционного уси-
лителя из лабораторного занятия 5L
5N.8. Послесловие
Вывод формулы для малого гэ
Как вы уже знаете, собственное сопротивле-
ние эмиттера, или малое гэ, является инверсией
крутизны кривой характеристики усиления
транзистора: AIBVLX/AUBX (см. раздел 5N.3.3).
Формально малое гэ является производной
функции зависимости напряжения от тока, т. е.
<ШБЭ/ЛК. Давайте выполним это вычисление,
определив сначала крутизну кривой вольт-
амперной характеристики.
Если использовать упрощенную версию фор-
мулы Эберса-Молла:
тогда:
^=(1/25мВ)(1НАСе^/25мв)я
* (1/25 мВ) (1К) = 1к/25 мВ.
А формула для малого гэ, обратной величины
крутизны кривой усиления, будет:
25 мВ
1к(в амперах)'
которую мы предпочитаем записать в следую-
щем виде:
25 0м
31 Сравните эту схему со схемой на рис. 2.91 в книге АоЕ
(в которой, однако, обратная связь реализуется внутренне).
1к(вмА)
Альтернативный подход: «доярочка
из Биполярска»
Аналогичный результат можно получить,
задействовав альтернативный подход. Пред-
ставьте себе хорошенькую доярочку, сидящую
5N.9. Материал для чтения в АоЕ
233
перед транзистором с фиксированным напря-
жением базы и тянущую за его эмиттер. Она
слегка потянула за эмиттер, пока в подойник
не потекло около 1 мА тока. Сколько дополни-
тельного тока потечет в подойник, если она по-
тянет за эмиттер слегка посильнее?
(и
♦Цл
и%
ветное слово!
Он ведет себя, как J
f маленький резистор!/
Протекает определенный ток покоя (Гэ)
Дополнительные «потяжки» за эмиттер: ЛГЕ * ЛХК
Рис. 5N.33. Доярочка экспериментально открывает для себя
значение гэ
Если напряжение базы зафиксировано, «по-
тяжки» за эмиттер слегка изменяют напряже-
ние иъэ, но в ответ ток коллектора 1К меняется
довольно значительно. Струйки А1Э (которые
мы считаем эквивалентными Л7К) открывают
взаимосвязь между A U^ и А1К. Частное А иъэ/А1к
является малым гэ, которое ведет себе подобно
резистору, потенциал нижнего вывода которо-
го фиксирован.
Таким образом, хотя малое гэ является всего
лишь моделью, для всех практических целей
оно ведет себя подобно небольшому резистору.
Этим и объясняется, почему его изображают на
схемах в виде резистора.
5N.9. Материал для чтения
в АоЕ
В главе 2 книги АоЕ рассматриваются как би-
полярные транзисторы, так и элементарные
применения операционных усилителей, поэто-
му материал в ней подходит для текущей темы,
хотя, как обычно, он содержит намного больше
информации, чем нам требуется. Далее приво-
дится список подходящих разделов.
♦ Модель Эберса-Молла: раздел 2.3.
♦ Раздел 2.3 до конца главы, но...
• пропускаем раздел 2.3.7 (токовые зерка-
ла, которые нам нравятся, но мы не хотим
перегружать вас);
• пропускаем большинство подробностей
про отрицательную обратную связь: раз-
дел 2.5; мы вскоре будем уделять много
внимания отрицательной обратной свя-
зи—в контексте схем операционных уси-
лителей. Но в разделе 2.5 очень подходя-
щей для наших целей является схема В (не-
инвертирующий усилитель) на рис. 2.85.
♦ Наиболее важные разделы для чтения:
• модель Эберса-Молла: раздел 2.3;
• дифференциальные усилители: раздел
2.3.8;
• двухтактные выходные каскады: раздел
2.4.1;
• следящая обратная связь (общее пред-
ставление приложений более широкого
круга, чем рассмотренный здесь простой
эмиттерный повторитель, со схемой на
рис. 2.80): раздел 2.4.3.
♦ Задачи: Упражнения 2.28.
В этой книге. При желании можете взглянуть
в разделе 9S.4 на полную схему микросхемы
операционного усилителя LF411. Она подобна
схеме дифференциального усилителя, рассмо-
тренного в этой главе, но содержит множество
дополнительных каскадов. Не переживайте
сильно, если вы не поймете этих усовершен-
ствований; мы разберемся с ними позже.
5L Лабораторное занятие: транзисторы II
Обзор лабораторного занятия
Сегодняшнее лабораторное занятие станет
проверкой ваших знаний и умения их приме-
нять: в нем используется самая сложная схема
из всех, которые мы собирали до сих пор, и
у вас могут возникнуть затруднения с ее сбор-
кой на некоторых этапах. Но это не должно
вас беспокоить, поскольку сейчас наиболее
важен только сам дифференциальный усили-
тель (см. раздел 5L1), а не его преобразование
в операционный усилитель. Мы надеемся, что
вы сможете хотя бы частично выполнить сбор-
ку операционного усилителя, поскольку этот
опыт даст вам уверенность при изучении опе-
рационных усилителей в дальнейшем. Но воз-
можные проблемы с этой задачей не страшны,
поскольку она не является обязательной.
5L.1. Разностный или
дифференциальный
усилитель
Рассчитайте дифференциальный и синфаз-
ный коэффициенты усиления для усилителя,
принципиальная схема которого приведена на
рис. 5L.1 (не забудьте принять во внимание
малое гэ). Обратите внимание на то, что схема
♦15 В
ВходА
Вход 6
-15 В
Используйте транзисторную сборку
3096, а не отдельные транзисторы
Рис. 5L1. Первый каскад: дифференциальный усилитель,
реализованный на транзисторной сборке
реализована на основе интегральной транзи-
сторной сборки типа 3096, а не на обычных дис-
кретных биполярных транзисторах 2N3904.
5L1.1. Транзисторная сборка
Для реализации схемы дифференциально-
го усилителя желательно использовать инте-
гральную транзисторную сборку СА3096 или
HFA3096. Транзисторы этой сборки довольно
хорошо согласованы1 по параметрам и име-
ют одинаковую температуру, что способствует
поддержанию температурной стабильности
устройства.
На рис. 5L.2 приводится цоколевка, которая
применима к обоим типам корпуса микросхе-
мы: СА3096 (DIP2) и HFA3096 (SOIC3).
Цоколевка
СА3096 (16-DIP)
HFA3096 (16-SOIC)
><
Вывод 16:
СА3096: подложка
HFA3096: Не подключен
10 13
12 15
3 n-p-п транзистора 2 p-n-р транзистора
Рис. 5L2. Микросхема СА3096 сборки биполярных транзи-
сторов
Подложка микросхемы подключена к вы-
воду 16 и выполнена из материала, легиро-
ваннного донорной примесью, на котором
вытравлены транзисторы. Поскольку мы не
хотим, чтобы данный внутренний набор р-п-
переходов оказался в режиме проводимо-
сти ни при каких обстоятельствах, подложку
1 Транзисторы типа п-р-п сборки HFA3096 согласованы
по напряжению 1/БЭ в пределах 1,5 мВ, максимум 5 мВ (при
токе коллектора 1Э = 10 мА).
2 Англ. Dual Inline Package — корпус с двухрядным рас-
положением выводов.
3 Англ. Small Outline Integrated Circuit — микрокорпус ин-
тегральной микросхемы с двусторонним расположением
выводов.
5LL Разностный или дифференциальный усилитель
235
необходимо подключить к точке схемы с са-
мым отрицательным потенциалом. В данном
случае это будет -15 В.
Поскольку микросхема HFA3096 выполнена в
корпусе для поверхностного монтажа (SOIC),
то для подключения к макетной плате микро-
схему необходимо припаять к переходной
плате. Это можете сделать вы сами или кто-
либо другой, кто обладает необходимыми на-
выками. На рис. 5L.3 показаны оба варианта
корпуса микросхемы 3096: DIP (слева) и SOIC
(справа).
Рис. 5L.3. Два варианта микросхемы 3096: СА3096 в корпусе
DIP (слева) и HFA3096 в корпусе SOIC, впаянная на переход-
ную плату типа DIP (справа)
На рис. 5L.4 показаны нумерация выводов
микросхемы типа DIP и способ ее крепления
на беспаечной макетной плате. Микросхема
вставляется в гнезда по обе стороны вдоль цен-
тральной выемки макетной платы, чтобы все
ее 16 выводов были доступны индивидуально.
Аналогично крепится микросхема HFA3096,
смонтированная на адаптерной плате.
Микросхема вставляется выводами
каждой стороны в гнезда по разным
сторонам центральной выемки
макетной платы
Нумерация выводов
(Корпус DIP)
з о о тНВПГ It 1r W fir n О
3 I О S 3 О D 3 30S0C
00020 DGQGO00O
о о аза оапаиаао
Рис. 5L.4. Нумерация выводов микросхемы 3096 в корпусе
DIP и ее установка на макетной плате
5L1.2. Формирование тестовых
сигналов
Смесь синфазного и дифференциального сиг-
налов формируется с помощью двух генера-
торов.
5L1.3. Конфигурация I:
использование генератора
сигналов с «плавающим» общим
выводом
Данную конфигурацию легко реализовать
при наличии генератора сигналов с «плаваю-
щим» общим выходом. Этот вывод подклю-
чен к экрану BNC-кабеля и до сих пор всегда
подключался к земле. В данном случае термин
«плавающий» просто означает «не подключен-
ный к заземлению». Но не все генераторы сиг-
налов позволяют делать это, и для таких случа-
ев в разделе 5L1.4 предлагается альтернативная
конфигурация.
Предварительная информация
Сигнал с одного генератора сигналов будет по-
даваться на другой. При этом генератор сигна-
лов, на который подается сигнал, должен быть
переведен в «плавающий» режим. Обычно это
можно сделать одним из двух способов, как по-
казано на рис. 5L.5: отключив локальную зем-
лю генератора сигналов от физической земли,
сняв металлическую перемычку (слева) или
установив переключатель в положение FLOAT.
У большинства генераторов сигналов эти эле-
менты находятся на задней панели.
(Плавающий* (корпус)
Металлическая
перемычка
ТТолзунковый
переключатель
Рис. 5L.5. Переключение генератора сигналов в «плаваю-
щий» режим
При подключении двух генераторов сигналов
к нашему усилителю нужно быть вниматель-
ным, чтобы не аннулировать «плавающий»
режим работы внешнего генератора сигналов.
Вспомните, что BNC-кабели и разъемы могут
неявно быть подключенными к физической
земле. Поэтому следует принять меры, чтобы
случайно не подключить внешний генератор
сигналов к заземлению посредством такого
кабеля или разъема. Таким образом, следует
избегать использования BNC-разъемов на ма-
кетной плате; также нельзя подключать через
BNC-кабель генератор сигналов к осциллогра-
фу с целью внешнего запуска развертки. Для
236
5L Лабораторное занятие: транзисторы II
подключения генератора сигналов к схеме мо-
гут быть полезными переходники с BNC на ми-
ниатюрные крючковые зажимы (или зажимы
типа «крокодил»), применение которых позво-
лит избежать подключения экрана BNC-кабеля
к заземлению.
Подача составного сигнала
на дифференциальный усилитель
Теперь подключим положительный вывод ге-
нератора сигналов на макетной плате к обоим
выводам внешнего генератора сигналов и по-
дадим полученный комбинированный сигнал
на входы нашего дифференциального усили-
теля, как показано на рис. 5L.6. Таким образом
мы сможем подавать на вход усилителя чисто
синфазный сигнал, чисто дифференциальный
сигнал или же смесь этих двух сигналов. Мы
воспользуемся этим разнообразием сигналов в
разделе 51.1.5.
5L1.4. Конфигурация II:
использование генератора
сигналов без «плавающего» выхода
Если ваш генератор сигналов не оснащен
средством переключения его в «плавающий
режим», требуемое раздельное управление
дифференциальным и синфазным сигналами
можно организовать с помощью трансфор-
матора.
Такая конфигурация, с трансформатором с
вторичной обмоткой на 6,3 В (таким же, как
на лабораторном занятии 3L), изображена на
рис. 5L.7.
Обратите внимание на то, что первичная об-
мотка трансформатора не подключается к ро-
зетке электросети! Вместо этого на нее подает-
ся сигнал от внешнего генератора.
Генератор сигналов
«плавающий»
Вход
Тереходник с BNC
на крючковые зажимы
Генератор ^
на макетной плате \
Канал 1
Канал 2)
Выход
Наш дифф^енциальный
усилитель
Рис. 5L.6. Подача комбинации разностного и синфазного сигналов на дифференциальный усилитель
Дисрференциальный
сигнал: внешний
генератор сигналов
6,3 В действующее
Синфазный сигнал:
генератор сигналов
на макетной плате
Дифференциальный усилитель
Рис. 5L.7. Использование трансформатора для развязки источников дифференциального и синфазного сигналов
А
CTf
В
Дифференциальные сигналы
(синфазный сигнал отсутствует)
Синфазный сигнал
(дифференциальный сигнал отсутствует)
Рис. 5L8. Наличие трансформатора позволяет подавать на вход усилителя чисто дифференциальный и чисто синфазный
сигналы
5LI Разностный или дифференциальный усилитель
237
А сигнал из генератора на макетной плате по-
дается на средний отвод вторичной обмотки
трансформатора, в результате чего на два входа
дифференциального усилителя поступают два
одинаковых (синфазных) сигнала.
На рис. 5L.8 показаны осциллограммы сигна-
лов, которые можно создавать с помощью этой
конфигурации и подавать на входы дифферен-
циального усилителя. Это только чисто диффе-
ренциальный и чисто синфазный сигналы.
5L1.5. Посредственный
дифференциальный усилитель
с резистором в «хвосте»
Для практики попробуйте измерить синфаз-
ный и дифференциальный коэффициенты уси-
ления.
Синфазный коэффициент усиления
(первая попытка)
♦ Процедура измерения синфазного коэффи-
циента усиления.
• Отключите от усилителя дифференциаль-
ный сигнал (выключив внешний генера-
тор сигналов)4 и подавайте на его входы
только синфазный сигнал с амплитудой
в несколько вольт. Измерьте усиление
синфазного сигнала. Совпадает ли его
значение с тем, которое вы предполо-
жили? Если усиление слишком высокое,
возможной причиной может быть не-
большая разность между двумя вводами
усилителя, в результате чего усиление
выходного сигнала содержит кроме син-
фазного усиления, также и определен-
ную дифференциальную составляющую.
Проверить, действительно ли это так,
можно, просто закоротив входы диффе-
ренциального усилителя, запараллелив
резисторы номиналом 27 Ом проволоч-
ной перемычкой. Таким образом мы обес-
печим подачу на входы усилителя чисто
синфазного сигнала. Завершив измерение
синфазного коэффициента усиления, не
забудьте удалить проволочную перемыч-
ку. На следующем шаге, где мы измеряем
4 Вместо того, чтобы выключать генератор сигналов,
можно просто уменьшить амплитуду его выходного сигна-
ла к минимальной.
дифференциальный коэффициент уси-
ления, необходимо разрешить на входах
присутствие разных сигналов.
Дифференциальный коэффициент
усиления
♦ Процедура измерения дифференциального
коэффициента усиления.
• Включите внешний генератор сигналов
и уменьшите до минимума амплитуду вы-
ходного сигнала генератора на макетной
плате (этот генератор сигналов не оснащен
выключателем).
• Подайте на вход усилителя дифферен-
циальный сигнал небольшой амплитуды
и измерьте его усиление. Совпадает ли его
значение с тем, которое вы предположили?
Если дифференциальное усиление кажется
приблизительно вдвое большим, чем сле-
довало бы, вспомните, что при измерении
сигнала на одном входе мы в действитель-
ности наблюдаем приблизительно поло-
вину всего дифференциального сигнала,
подаваемого на усилитель. Вы можете
убедиться в этом, одновременно наблю-
дая сигналы на обоих входах усилителя на
двух каналах осциллографа. Они должны
быть приблизительно одинаковыми по
амплитуде и противоположными (сдвину-
тыми на 180°) по фазе.
• Теперь включите оба генератора и сравни-
те сигнал на выходе усилителя с составным
сигналом на его входе. Чтобы было легче
различать сигналы, их частоты можно раз-
нести достаточно далеко друг от друга. Но
не подумайте, что такое разнесение частот
сигналов необходимо для работы диф-
ференциального усилителя. Совсем нет.
Мы просто делаем это здесь для удобства.
А вот для метода, который мы использо-
вали в лабораторном занятии 2L2 для
пропускания одного сигнала и ослабления
другого, такой разнос между частотами
сигналов был необходим.
Этот эксперимент должен дать вам понимание
выражения «коэффициент подавления син-
фазной составляющей»: небольшое усиление
синфазного (одинакового на обоих входах)
сигнала и сравнительно большое усиление
дифференциального (разного на каждом вхо-
де) сигнала.
238
5L Лабораторное занятие: транзисторы II
Но эта схема все еще пропускает часть сильно-
го синфазного сигнала на выход. На следующем
шаге мы усовершенствуем ее, чтобы значитель-
но уменьшить этот эффект.
Синфазное усиление (вторая попытка)
Синфазное подавление можно улучшить, за-
менив «хвостовой» резистор номиналом
10 кОм источником тока величиной 1,5 мА.
Такой источник тока можно создать несколь-
кими способами. Самый легкий способ —
использовать пару полевых транзисторов
1N5294 (с управляющим р-л-переходом, ко-
торые мы не будем рассматривать в этом кур-
се) в качестве токоограничивающих диодов.
Номинальный ток каждого из этих транзи-
сторов составляет 0,75 мА ±10%, а два соеди-
ненных параллельно (рис. 5L.9) могут выдать
требуемые 1,5 мА.
0,75 мА
0,75 мА
-15 ВI
'Полевой транзистор с управляющим
р-Аьпереходом 1N5294 в роли
^токоограничивающего диода
Рис. 5L.9. Источник тока на основе полевых транзисторов
с р-л-переходом в роли токоограничивающих диодов
Если описанный подход вам не нравится, то
можно собрать источник тока на биполярных
транзисторах. На рис. 5L.10 показаны две воз-
можные принципиальные схемы такого ис-
точника.
! 1*1,4 мА
«2 В
10 кОм
-15 В
Простой источник
(потребитель) тока
Рис. 5L.10. Две альтернативные схемы источника тока на
основе биполярных транзисторов
Замена «хвостового» резистора источником
тока должна значительно понизить синфазное
усиление (т. е. улучшить подавление синфазной
составляющей сигнала).
Совет
Подумайте, каким будет синфазное усиление, если
выходной импеданс источника тока составляет
около 1 МОм5?
На низких частотах, скажем, в области 100 Гц,
у нас должен быть очень хороший коэффици-
ент подавления синфазной составляющей. Но
с ростом частоты также будет повышаться и
усиление синфазного сигнала. Причиной этого,
по-видимому, является емкостная связь между
входом и выходом, что рассматривается в раз-
деле 5LJ.il.
Комбинированный синфазный
и дифференциальный сигнал
Наблюдайте, как наша усовершенствованная
схема обрабатывает комбинированный синфаз-
ный и дифференциальный сигнал. Сохраните
собранную схему, поскольку мы будем расши-
рять ее в дальнейшем.
5L1.6. Самодельный операционный
усилитель
В этом разделе мы соединим последовательно
три каскада, составляющие стандартный опе-
рационный усилитель. Операционный усили-
тель — это всего лишь хороший дифференци-
альный усилитель с высоким коэффициентом
усиления, поэтому можно считать, что на дан-
ном этапе лабораторного занятия мы уже на
полпути к нашей цели.
Типичный операционный усилитель пред-
ставляет собой трехкаскадный усилитель:
дифференциальный усилитель, усилитель на-
пряжения и выходной двухтактный усилитель.
Добавим к уже имеющемуся у нас дифферен-
циальному усилителю следующие два каска-
да: усилитель с общим эмиттером и выход-
ной двухтактный усилитель. В результате наш
дифференциальный усилитель превратится
в простейший операционный усилитель. Как
уже неоднократно говорилось, это устройство
5 Синфазное усиление приблизительно равно
х R^^) « 10 кОм/2 МОм = 0,5 • 10"2.
5L7. Разностный или дифференциальный усилитель
239
является стандартным блоком, на который мы
будем полагаться для создания большинства
наших аналоговых устройств, начиная с лабо-
раторного занятия 6L и далее. Характеристики
операционного усилителя, который мы со-
берем здесь, не будут такими хорошими, как
у аналогичного устройства на микросхеме, с
которым мы будем работать на лабораторном
занятии 6L, но он должен помочь вам полу-
чить определенное понимание, что такое опе-
рационный усилитель и как он обеспечивает
результаты на грани волшебства.
На рис. 5L.11 приведена блок-схема, соответ-
ствующая нашему определению операционного
усилителя: это дифференциальный усилитель
с высоким коэффициентом усиления и низким
выходным импедансом.
Дифференциальный Основной Буфер
усилитель усилитель
Упрощенный
операционный
усилитель
(-) _^ L^(*
Вход I А В)
Рис. 5L11. Типичный трехкаскадный операционный уси-
литель
5L1.7. Этап 1: повышение усиления
биполярного дифференциального
усилителя
Первая модификация схемы:
максимизация усиления
Удалите из схемы резисторы номиналом 100 Ом
в цепях эмиттеров. Как вы полагаете, окажет
ли удаление этих резисторов отрицательный
эффект на температурную стабильность схе-
мы? А что будет с постоянством усиления6?
Проверьте свои предположения:
♦ чтобы протестировать температурную ста-
бильность, прижмите к транзисторной сбор-
ке палец, чтобы нагреть ее, и наблюдайте
(с помощью осциллографа или цифрового
мультиметра) за напряжением выходного
сигнала 1/вых;
♦ чтобы протестировать постоянство усиле-
ния, подайте на вход усилителя сигнал тре-
угольной формы с небольшой амплитудой,
и проверьте, наблюдается ли куполообраз-
ное искажение выходного сигнала, подобное
тому, которое мы наблюдали на лаборатор-
ном занятии 4L.
Вторая модификация схемы: поднимаем
выходную точку покоя
Чтобы подготовить схему к добавлению второго
каскада, замените резистор в цепи коллектора
RK номиналом 10 кОм на номинал 1,5 кОм. Это
не соответствует нашему обычному правилу,
согласно которому выходной сигнал покоя цен-
трируется в доступном диапазоне напряжений
Чтобы увеличить усиление нашего дифферен-
циального усилителя, а также, чтобы подгото-
вить его для лучшей передачи сигнала на второй
каскад, мы слегка изменим его. После этого мы
протестируем модифицированный таким обра-
зом дифференциальный усилитель, затем про-
верим совместную работу первых двух каска-
дов, а затем и всех трех. Наконец, в завершение
этого упражнения мы введем общую обратную
связь. Мы еще не рассматривали данную тему,
поэтому, возможно, она будет вам непонятна,
но попытайтесь разобраться самостоятельно,
насколько сможете, пока мы не рассмотрим ее
в деталях позже.
6 Удаление резисторов из цепей эмиттеров не повлия-
ет на температурную стабильность схемы, поскольку оба
транзистора будут продолжать работать при одинаковой
температуре. Хотя варьирование температуры будет изме-
нять их напряжения £/БЭ, это не окажет никакого эффекта
на долю потребления тока 1^^- Таким образом, напря-
жение покоя не будет меняться в ответ на температурные
колебания. Этот способ достижения температурной ста-
бильности рассматривался в разделе SN.S (см. рис. 5N.22).
А вот постоянство усиления, наоборот, пострадает: будут
наблюдаться искажения выходного сигнала. Варьирова-
ние амплитуды выходного сигнала будет сопровождаться
изменением усиления, в большой мере по тем же самым
причинам, которые вызывали куполообразное искажение
выходного сигнала в усилителе с общим эмиттером, как
рассматривалось в главе 5N. Но, в отличие от того случая,
искажения выходного сигнала дифференциального усили-
теля имеют другую форму (см. раздел 5S.1).
240
5L Лабораторное занятие: транзисторы II
(в данном случае 0-15 В). В результате также
снизится коэффициент усиления схемы. Но
скромное усиление нашей схемы не так уж и
плохо, как может показаться на первый взгляд.
Будем надеяться, что коэффициент подавления
синфазной составляющей останется прилич-
ным. Вычислите новые значения дифференци-
ального и синфазного коэффициентов усиления
модифицированной схемы или же измерьте их
экспериментально.
Внешний
генератор сигналов
Дифференциальный
сигнал
:100
чСинсразныйГ|)
^сигнал
IN5299
,(0,75мЛ)
-15 В
Рис. 5L.12. Первый этап модифицирования схемы диффе-
ренциального усилителя: подготовка ее к подаче сигнала на
последующие каскады
5L1.8. Этап 2: каскад усилителя
с общим эмиттером
Мы уменьшили номинал резистора в цепи кол-
лектора RK до 1,5 кОм, чтобы выходное напря-
жение покоя дифференциального усилителя
сместилось по направлению к положитель-
ному полюсу источника питания, поскольку
мы хотим подавать этот выходной сигнал на
+15 в
Выход
Рис. 5L.13. Первые два каскада операционного усилителя:
дифференциальный усилитель и усилитель с общим эмитте-
ром
усилитель с общим эмиттером, собранный на
р-я-р-транзисторе.
Второй каскад будет обеспечивать большую
часть усиления напряжения в нашей схеме.
На рис. 5L.13 приведена предлагаемая схема
усилителя. Это обычный усилитель с общим
эмиттером (с тем исключением, что для тех, кто
в основном работают с я-/?-я-транзисторами,
схема выглядит перевернутой). Как обычно,
выходной импеданс усилителя достаточно вы-
сокий, чтобы не нагружать значительно пред-
шествующий каскад.
Измеряем усиление
Наблюдайте за входным и выходным сигнала-
ми каскада усилителя с общим эмиттером, и из-
мерьте усиление этого каскада. Затем опреде-
лите общее дифференциальное усиление от
входа схемы до ее выхода (просто подключите
на землю вывод 1 и подавайте псевдо-диффе-
ренциальный сигнал на вывод 5),
Возможно придется немного повозиться со
смещением по постоянному току генератора
сигналов, чтобы не допустить отсечения сигна-
ла ни в первом, ни во втором каскаде.
5L1.9. Этап 3: двухтактный
выходной каскад
Чтобы обеспечить низкий выходной импеданс
нашего усилителя, оснастим его двухтактным
выходным каскадом. Поскольку мы не хотим
ЮкОм
-15 В
Рис. 5L.14. Двухтактный выходной каскад на биполярных
транзисторах
5U. Разностный или дифференциальный усилитель
241
♦15 В
Выход
ЮкОм
1кОм
Рис. 5L.15. Завершенный трехкаскадный самодельный операционный усилитель, но еще без обратной связи
слишком усложнять схему, не будем заботиться
0 переходных искажениях этого каскада. Чуть
далее мы попробуем исправить эти искаже-
ния с помощью обратной связи. На рис. 5L.14
приведена схема двухтактного повторителя на-
пряжения, собранного на двух транзисторах
микросхемы СА3096 транзисторной сборки.
Добавление выходного двухтактного каскада
завершает создание нашего самодельного опе-
рационного усилителя. Его принципиальная
схема изображена на рис. 5L.15. На его вход все
еще подается псевдодифференциальный сиг-
нал, а обратная связь еще не реализована.
Подайте на вход усилителя сигнал с частотой
1 кГц или ниже и небольшой амплитудой и на-
блюдайте сигнал на входе и выходе двухтактно-
го каскада. Выходной сигнал должен содержать
переходные искажения: мертвые зоны, когда
амплитуда сигнала настолько близка к нулю,
что любой из транзисторов каскада заперт. Для
отображения переходных искажений выходной
сигнал должен пересекать нулевой уровень.
Чтобы отцентрировать выходной сигнал, мо-
жет потребоваться отрегулировать смещение
по постоянному току входного сигнала.
5L1.10, Вводим обратную связь
В операционных усилителях почти всегда ис-
пользуется общая обратная связь. Ее мы и по-
пробуем применить в нашей схеме.
Усилитель с коэффициентом усиления 11
Теперь испытаем работу нашего операционно-
го усилителя в режиме, являющемся обычным
для этих устройств: возьмем часть сигнала с
выхода усилителя и подадим его обратно на
вход. Этот режим называется обратной связью,
и конфигурация для его реализации показана
на рис. 5L.16. Данная обратная связь является
отрицательной, поскольку подаваемый на вход
выходной сигнал ослабляет входной сигнал.
Вход
# Выход
10 кОм
1 кОм
Рис. 5L.16. Усилитель с коэффициентом усиления 11
Подайте на вход усилителя (вывод 1 схемы)
1/11 часть выходного сигнала (на выводах 7
и 13 схемы), снимая ее в точке, обозначенной
X на схеме на рис. 5L.15. Это подключение, по-
казанное на рис. 5L.16, будет заставлять усили-
тель пытаться поднять уровень сигнала на этом
входе (вывод 1 схемы) до уровня, подаваемо-
го на другой вход усилителя (вывод 5 схемы).
В результате мы вынудим нашу схему усили-
вать входной сигнал приблизительно в 11 раз
(это общее усиление, поскольку одну часть
242
5L Лабораторное занятие: транзисторы II
из этих 11 мы направляем обратно на вход).
Проверьте работу обратной связи на практике.
Коэффициент усиления, скорее всего, будет
меньше, чем ожидаемый 11, поскольку усиле-
ние нашей схемы такое скромное7. Но малое
усиление не является фактором, делающим
эту схему полезной и интересной. Как мистеру
Блэку8 и сказали в британском бюро патентов:
снижение усиления не является целью при раз-
работке усилителей9. Но усиление приносится
в жертву другим желаемым характеристикам.
Мы надеемся, что после реализации обратной
связи на своем усилителе вы сможете увидеть
два вида улучшения его характеристик.
♦ Самое интересное отличие от схемы без
обратной связи, которую мы испытали на
предыдущем этапе, состоит в исчезновении
переходных искажений из выходного сиг-
нала схемы, по крайней мере, на умеренных
частотах.
Подайте на вход усилителя низкоамплитуд-
ный синусоидальный сигнал и наблюдайте
сигнал на входе и выходе последнего каскада.
Будем надеяться, что выходной сигнал ваше-
го усилителя будет синусоидальным, тогда
как сигнал на входе двухтактного усилите-
ля (выводы 8 и 14 схемы) будет выглядеть
странным, потому что сигнал обратной свя-
зи заставляет эту точку делать что-то, что-
бы нейтрализовать переходные искажения.
Прямо волшебство какое-то, не так ли?
♦ Менее удивительным, но также положитель-
ным результатом реализации отрицательной
обратной связи должно быть исчезновение
варьирующегося усиления, вызывающего
куполообразное искажение треугольного
сигнала. Этот тип искажений был определен-
ной проблемой в области схемотехники до
изобретения обратной связи.
Если в вашей схеме начнут возникать авто-
колебания, нужно уменьшить ее усиление на
7 Если вы хотите сравнить усиление своей схемы с тео-
ретически вычисленным усилением, см. раздел 2.5.2 книги
АоЕ. Усиление схемы должно быть АД1+АВ), где А обо-
значает усиление схемы без обратной связи (дифференци-
альное усиление, которое мы только что измерили), а В —
часть выходного сигнала, подаваемого обратно на вход (в
данном случае 1/11).
8 Harold Stephen Black — изобретатель отрицательной
обратной связи.
9 См. раздел 2.5.1 в книге АоЕ и раздел 6N.1 в этой книге.
Конечно же, соль этой истории заключается в том, что ми-
стер Блэк смеялся последним.
высоких частотах. Чтобы сделать это, лучше
всего подключить конденсатор небольшой ем-
кости (для начала попробуйте 100 пФ) между
коллектором и базой усилителя напряжения с
общим эмиттером (выводы 11 и 12 схемы), как
показано на рис. 5L.17.
ззо
(12)
100 пФ
Рис 5L.17. Компенсирующий конденсатор небольшой ем-
кости может стабилизировать схему с обратной связью, сни-
жая усиление на высоких частотах
Здесь работает эффект Миллера (см. раз-
дел 2.4.5 книги АоЕ), т. е. образуется низкоча-
стотный фильтр, кажущаяся емкость которого
увеличивается усилением этого каскада. Такое
снижение высокочастотного усиления для обес-
печения стабильности схемы называется ком-
пенсированием и регулярно используется в опе-
рационных усилителях.
Повторитель напряжения (рискованный
вариант, применять с осторожностью)
Достаточно странно, но более простую схему
повторителя напряжения (рис. 5L.18) стабили-
зировать труднее, чем 11-кратный усилитель.
Иными словами, шанс возникновения пара-
зитных колебаний более высокий для повто-
рителя напряжения. Если схема собрана очень
аккуратно, повторитель напряжения может ра-
ботать стабильно. Но некоторые самодельные
операционные усилители нельзя стабилизиро-
вать при единичном усилении, даже применяя
описанный выше прием компенсирования.
Вход
Ф
@fNw
Выход
"10 кОм
Рис. 5L.18. Повторитель напряжения с общей обратной
связью
5L7. Разностный или дифференциальный усилитель
243
5L1.11. Снижение коэффициента
подавления синфазной
составляющей при повышении
частоты
В конце раздела 5L.1.5 мы затронули вопрос по-
вышения коэффициента усиления (т. е. умень-
шение коэффициента подавления) синфазной
составляющей при повышении частоты. Здесь
мы объясним причины данного явления. Фаза
и частотная характеристика сигнала предостав-
ляют нам доказательство того, что причиной
этого эффекта не является плохой источник
тока в «хвосте» дифференциального усилителя.
Далее приводится пара осциллограмм выход-
ного сигнала для синфазного входного сигнала.
На первой из них (рис. 5L.10) показаны вы-
ходные сигналы для входных синусоидальных
сигналов на двух частотах: 1 кГц и 10 кГц.
Амплитуда выходного сигнала намного выше
для входного сигнала более высокой частоты.
Это определенно выглядит как действие высо-
кочастотного фильтра. На рис. 5L.20 то же яв-
ление проиллюстрировано другим способом:
выходной сигнал выглядит подобно произво-
дной входного.
Наблюдается ли в вашей схеме подобное пове-
дение? Если да, то оно вызывается емкостным
проникновением сигнала со входа (база вход-
ного транзистора) на выход (резистор в цепи
коллектора). Этот эффект можно было бы ми-
нимизировать с помощью каскода (см. обсуж-
дение эффекта Миллера в разделе 2А.5 книги
АоЕ), но давайте не будем обсуждать здесь та-
кие нюансы.
Синфазный сигнал (подается на оба входа)
Выходной сигнал с частотой 1 кГц:
очень слабый (10 мВ/деление)
Выходной сигнал с частотой 10 кГц:
амплитуда приблизительно в 10 раз выше
сигнала с частотой 1 кГц
Рис. 5L.19. Сравнение выходов синфазных сигналов частотой 1 кГц и 10 кГц: подавление синфазной составляющей ухудшается
с повышением частоты (Обратите внимание на то, что усиление канала осциллографа для выходного сигнала в 20 раз больше,
чем для входного.)
Вход
Выходной сигнал первого
дифференциального усилителя
выглядит как производная
входного сигнала
Рис. 5L.20. Выходной синфазный сигнал выглядит как производная входного: соответствует крутизне входного треугольного
сигнала
5S. Дополнительный материал и глоссарий:
транзисторы II
5S.1. Два новых
эффекта в поведении
дифференциального
усилителя
До сих пор мы рассматривали дифференциаль-
ный усилитель как просто пару усилителей с
общим эмиттером и обещали вам, что для по-
нимания его работы не потребуется изучать
много нового, а можно использовать те знания,
которые вы получили в процессе разработки и
сборки усилителей с общим эмиттером на двух
предыдущих лабораторных занятиях. Но наши
студенты заметили некоторые новые эффекты,
присутствие которых не ожидалось в обычном
усилителе с общим эмиттером. Один из этих
эффектов, скорее всего, не вызовет затрудне-
ний, а вот второй эффект довольно мудреный.
5S.1.1. Отсечка сигнала
в операционном усилителе
из лабораторного занятия 5L
резистора в цепи коллектора RK до 1,5 кОм, вам
еще не знакома. На рис. 5S.1 приведена осцилло-
грамма двух выходных сигналов после того, как
мы добавили резистор в цепь коллектора тран-
зистора левого плеча усилителя. Это сделало
схему идеально симметричной, за исключением
подаваемого на нее входного сигнала, который
мы называем псевдодифференциальным1.
С искажением верхней части выходного сигна-
ла мы уже сталкивались ранее. Необычны сле-
дующие два явления.
♦ Первое. Сигнал также сплющивается снизу
вместо того, чтобы становится более крутым,
как было в случаях с куполообразным иска-
жением сигнала.
♦ Второе. Сплющивание происходит не в об-
ласти напряжения насыщения транзистора
(близким к потенциалу земли), но прибли-
зительно на уровне 12,5 В выше потенциала
земли, что очень далеко от напряжения на-
сыщения транзистора.
С описанным явлением мы еще не встречались,
но его природу можно понять, если вспомнить,
\
Дополнительный
выходной сигнал
(коллектор транзистора
левого плеча) 5 В/деление
Основной выходной сигнал
(коллектор транзистора
правого плеча)
-шшт
\ Входной сигнал
(0,2 В/деление)
Рис. 5S.1. Осциллограмма входного и вы-
ходных сигналов дифференциального уси-
лителя из лабораторного занятия 5L с ре-
зисторами номиналом 1,5 кОм в цепи кол-
лекторов обоих транзисторов. Искажения
симметричны у обоих показанных выход-
ных сигналов. (Обратите внимание на то,
что усиление канала осциллографа для
входного сигнала в 50 раз больше усиле-
ния для каналов выходных сигналов.)
В усилителе с общим эмиттером мы привыкли
видеть отсечку выходного сигнала на уровне
положительного напряжения питания, а так-
же вблизи потенциала земли, где происходит
насыщение транзистора. Таким образом, от-
сечка сигнала, происходящая в дифференци-
альном усилителе после уменьшения значения
1 Такой сигнал представляет собой смесь разностного
и синфазного сигналов. Амплитуда дифференциального
сигнала равна полной амплитуде подаваемого сигнала,
а амплитуда синфазного сигнала составляет половину
амплитуды полного сигнала. При условии, что диффе-
ренциальное усиление намного больше синфазного, этот
входной сигнал является очень близким эквивалентом на-
стоящего дифференциального сигнала, с которым мы ра-
ботали на лабораторном занятии 5L.
55.1 Два новых эффекта в поведении дифференциального усилителя
245
что ток через каждый транзистор ограничен ис-
точником тока в «хвосте». Таким образом, са-
мое низкое напряжение на коллекторе наблю-
дается не при насыщении транзистора, а когда
он забирает весь ток из хвоста, не оставляя ни-
чего для транзистора другого плеча. Это явле-
ние может поначалу выглядеть непривычным,
но оно вполне объяснимо.
5S.12. Более детальное
рассмотрение искажения
На осциллограмме на рис. 5S.1 мы видели, что
искажения выходного сигнала дифференциаль-
ного усилителя симметричные, в отличие от ку-
полообразного искажения усилителя с общим
эмиттером. Но если посмотреть более внима-
тельно на это искажение (рис. 5S.2) при более
слабом входном сигнале, чем на рис. 5S.1, мож-
но обнаружить подобие смещенного в сторону
и отраженного куполообразного искажения2.
Hi!
^Erjip'^i I
, . > ,, ...... г.., .«у
Рис. 5S.2. Искажения выходного сигнала усилителя с об-
щим эмиттером и дифференциального усилителя различны:
во втором случае искажается как положительная, так и отри-
цательная части выходного сигнала (Обратите внимание на
то, что усиление канала осциллографа для входного сигнала
в 10 раз больше усиления для канала выходного сигнала.)
Если вам требуется математическое объясне-
ние (чего мы стараемся избегать в этом курсе)
явлению симметричности искажений, далее
приводится попытка такого доказательства.
Мы хотим дать ответ на вопрос, почему усиле-
ние уменьшается по обеим сторонам точки по-
коя, создавая симметричное искажение в виде
купола и его отражения. Аргументация будет
следующей.
♦ Коэффициент усиления дифференциального
усилителя с одним из его входов, подклю-
2 Выходной сигнал на рис. 5S.2 выглядит отцентрирован-
ным по нулевому уровню. Это иллюзия из-за АС-режима
входа осциллографа.
ченным к земле, определяется следующей
формулой:
Гэ1+ Гэ2
(5S.1)
♦ В точке покоя это уравнение сводится к до-
статочно простой форме: Ку = -RK/2r3.
♦ Но вспомним из нашего опыта с усилителем
с общим эмиттером, что коэффициент усиле-
ния варьируется при изменении уровня вы-
ходного сигнала, поскольку ток коллектора
/к должен меняться, чтобы вызывать коле-
бания выходного сигнала. Кроме того, при
колебании выходного сигнала дифференци-
ального усилителя сумма гэ1+гэ2 не остается
постоянной, хотя одно малое гэ увеличивает-
ся, тогда как другое уменьшается.
♦ Более конкретно, если обозначить ток вы-
ходного транзистора как Iv а общий ток хво-
ста как /хвостд (полагая, что оба тока измеря-
ются в миллиамперах), то:
К,-
Г31+
ХХВОСТА
п\-'хвоста
•WxBOCTA "" J
(5S.2)
ХВОСТА
Если весь ток хвоста создает ток Iv то усиле-
ние равно нулю. Если ток 1г составляет поло-
вину тока хвоста, коэффициент усиления будет
максимальным — около 22, для jRk = 1,5 кОм и
^хвоста = 1»5 мА, как в схеме дифференциально-
го усилителя из предыдущего лабораторного
занятия.
Зависимость коэффициента усиления от соот-
ношения токов в плечах будет выглядеть, как
показано на рис. 5S.3. Из этого графика очевид-
но, что максимальное усиление происходит при
разделении тока хвоста в отношении 50:50.
Производная уравнения
дит следующим образом:
усиления выгля-
1 - (21г/
^хвоста
) и приводит к аналогичному результату:
246
55. Дополнительный материал и глоссарий: транзисторы II
Зависимость усиления дифференциального усилителя от соотношения тока между транзисторами (?, и Q2
20
15
| 10
> 5
при
в отношении 50:50
(одинаковый ток в
1ьное уси. 1ение наблюдается4
разделении то са хвоста
саждом плече)
Нулевое усиление — и отсечение
О 0,2 0,4 0,6
Ток выходного транзистора, как доля тока хвоста
Рис. 5S.3. Зависимость усиления дифференциального усилителя от соотношения токов в плечах
максимальное усиление происходит тогда, ког-
да ток 71 составляет половину тока хвоста.
А сплющивание сигнала, которое мы видели
на рис. 5S.1, происходит, когда усиление схемы
снижается до нуля. Это соответствует ситуации,
когда любой из транзисторов «пожирает» весь
ток.
5S.2. Токовые зеркала
и эффект Эрли
5S.2.1. Токовые зеркала
В принципе этот раздел можно пропустить,
хотя эта рекомендация выглядит несколько
странно. Такое отношение к токовым зерка-
лам объясняется нашей неопределенностью
относительно этих схем. Мы решили убрать
эту тему из лабораторных занятий, считая их
менее важными для разработчика, чем другие
транзисторные схемы, сборкой которых мы за-
нимались. Но с токовыми зеркалами довольно
часто приходится сталкиваться при изучении
схем с операционными усилителями. Поэтому
будет полезным разобраться, как они работа-
ют, даже если токовое зеркало не понадобится
в ваших разработках.
Токовые зеркала полезны в плане обучения, в
частности, для демонстрации эффекта Эрли.
Мы удалили эту тему из лабораторных заня-
тий, но хотим предоставить возможность для
любопытных ознакомиться с ней. Эффект Эрли
интересен тем, что он позволяет количественно
оценить выходной импеданс источника тока.
До сих пор нам приходилось довольствоваться
утверждением, что источники тока имеют вы-
сокий выходной импеданс.
Мы начнем разбираться с изучения токового
зеркала, а затем используем его для наблюде-
ния за эффектом Эрли в действии.
Применение модели Эберса-Молла
к схемам токовых зеркал
Для объяснения функционирования токового
зеркала потребуется модель Эберса-Молла,
как показано на рис. 5S.43.
= о#б в 4г
Напряжение (/Ю2 варьируется
от 0,9 В до 14 В
Рис. 5S.4. Объяснение работы токового зеркала требует
применения модели Эберса-Молла. УПР — управляющий
Чем полезно токовое зеркало, если мы распо-
лагаем другими способами создания источни-
ков тока? Тем, что с его помощью можно легко
связать токи в схеме, согласуя их один с другим.
Такая связь особенно полезна в интегральных
микросхемах. Токовое зеркало также допускает
наиболее широкий диапазон рабочих напря-
жений источника тока. В схеме операционного
усилителя LF411 (см. раздел 9S.4), который мы
применяем во многих из наших лабораторных
занятий, можно увидеть разнообразнейший
набор токовых зеркал, используемых с обеими
этими целями.
АоЕ § 2.3.7.
55.2. Токовые зеркала и эффект Эрли
247
Управляющий ток /УПР легко сделать равным
выходному току /вых, и лишь немного труднее
масштабировать выходной ток согласно задан-
ному.
Как эффект Эрли, так и влияние температуры
могут испортить четкое равенство между тока-
ми /УПР и /вых. Мы рассмотрим далее (в разде-
ле 5S.2.7) как решить эти проблемы. До тех же
пор оставим токовое зеркало в его простейшей
форме, как показано на схеме выше, и разбе-
ремся с его работой.
5S.2.2. Управляющий ток зеркала
задается обратной связью
Посмотрите на схему на рис. 5S.5. Плечо управ-
ления токового зеркала выглядит довольно
простым,.хотя и несколько необычным (база
и эмиттер соединены вместе?!). Но это весьма
удачный прием применения отрицательной об-
ратной связи.
+15 В U
15к0м
ток коллектора...
определяет ]
напряжение иъъ, I
которое в свою /
очередь определяет
Рис. 5S.5. Ловкий прием применения отрицательной обрат-
ной связи: управляющее плечо токового зеркала
При изучении работы этого фрагмента схемы
(который выдает нашу любимую величину
тока 1 мА) полезно обратить внимание на то,
что почти весь ток течет не в цепи базы, а от
коллектора к эмиттеру4.
5S.23. Одинаковые напряжения UB3
обеспечивают равные,
или зеркальные, токи /к
Таким образом, благодаря одинаковым зна-
чениям напряжений 1ГБЭ транзисторов
и
4 Имеет ли это смысл? Напряжение на базе (как и напря-
жение на коллекторе) определяется падением напряжения
на управляющем резисторе R^. Но значение напряжения
L/ J R Б й
L/бэ задается произведением JK
Более высокий ток
бэ K ^
коллектора 1К понижает напряжение U^, так что это цепь
отрицательной обратной связи. Ток /к стабилизируется,
когда установится такое его значение, которое будет соз-
давать напряжение U^, согласующееся с этим током.
токи 1ВЫХ и /упр также оказываются одинаковы-
ми. Пока что все выглядит хорошо.
Основное достоинство этой схемы — ее спо-
собность работать в диапазоне напряжений от
положительного напряжения питания до отри-
цательного. Схема будет функционировать до
тех пор, пока не произойдет насыщение тран-
зистора Qg, демонстрируя, таким образом, ши-
рокий диапазон рабочих напряжений источни-
ка тока. При варьировании сопротивления на-
грузки Дддрр в схеме на рис. 5S.4 величина тока
остается практически постоянной на уровне
1 мА. При этом напряжение варьируется от [7+
(в данном случае 15 В) вплоть до 0,2 В (чуть
выше напряжения насыщения транзистора Q^).
Такой обширный диапазон рабочих напряже-
ний обусловливает широкое использование то-
ковых зеркал в операционных усилителях, как
отмечалось ранее. (Другой причиной является
предпочтение транзисторов резисторам при из-
готовлении интегральных схем.)
5S.2A Возможные проблемы
с токовыми зеркалами
Легко решаемая проблема:
влияние температуры
При разных температурах транзисторов Q и
Q2 соотношение зеркалирования 1:1 больше
не выдерживается. В главе 5N мы видели, на-
сколько сильно ток коллектора 7К зависит от
температуры транзистора.
Но задача поддержания равной температу-
ры обоих транзисторов решается очень легко:
транзисторы просто размещаются близко друг
к другу на интегральной схеме. Любой другой
способ реализации токового зеркала будет ^не-
целесообразным. Таким образом, проблема
согласования температур решается сама со-
бой. (В главе 5N мы видели, как этот способ
температурной стабилизации используется
также в схеме усилителя с общим эмиттером
(рис. 5N.21) — компенсирующий транзистор
в этой похожей на токовое зеркало схему обес-
печивает температурную стабильность усили-
теля.) Это правда, что при данном токе крллек-
тора 1К напряжение иъэ варьируется в зависи-
мости от температуры, например, понижается
при повышении температуры. Но это понижен-
ное напряжение 17БЭ транзистора Q подается на
248
55. Дополнительный материал и глоссарий: транзисторы II
транзистор Qg, чей ток коллектора 1К величиной
1 мА обусловлен именно таким пониженным
напряжением [7БЭ.
5S.2.5. Более сложная проблема,
хорошо иллюстрируемая токовыми
зеркалами: эффект Эрли5
Другое отклонение от идеального зеркалирова-
ния токов заключается в небольшом изменении
тока коллектора при варьировании напряже-
ния на транзисторе. Данную проблему решить
не так просто.
В идеале источник тока имеет бесконечно
большой выходной импеданс (поскольку со-
противление ДдИфф, эквивалентное AUK/AIK,
будет бесконечно большим, если ток 7К поддер-
живается совершенно постоянным). Но в дей-
ствительности при повышении напряжения UK3
ток JK слегка возрастает: реальный источник
тока функционирует подобно большому со-
противлению. Это несовершенство иллюстри-
рует рис. 5S.6.
U С \ ^ Большое сопротивление к
Р \!У Смоделирует эффект Эрли
Возможно, вам эта модель уже знакома как эк-
вивалентная схема источника тока (или эквива-
лентная схема Нортона)6. Подобно модели Те-
венина для напряжений она позволяет количе-
ственно оценить степень несовершенства схемы.
На рис. 5S.7 этот эффект представлен иначе:
в виде ненулевой крутизны графика зависимо-
сти тока коллектора 1К от напряжения 17^,
Напряжение Эрли
Рис. 5S.6. Неидеальный источник тока можно смоделиро-
вать, добавив большое сопротивление
Рис. 5S.7. Напряжение Эрли в точке схождения всех кривых
показывает меру отклонения тока от постоянного значения
Строго говоря, напряжение UA измеряется не
относительно нуля на оси U^, а относитель-
но точки, в которой берется касательная. Но
обычно разница между этими двумя точками
не особо велика. Напряжение U^ обычно на-
много меньше, чем значение UA.
На рис. 5S.8 показаны экспериментальные гра-
фики реакции трех транзисторов на повышение
напряжения U^7.
Как можно видеть, наилучшее поведение источ-
ника тока отображено на левом графике кривых
15
5
0
ЦЭ=О,53ОВ
(УБЭ=0,513 В
(4= 0,495 В
<Л,= 0,477 В
i
t
20
15
Iю
5
О
10 20 30 40
UK3 (вольт)
По крутизне,
показанной на графиках УА = 6,8 кВ
MPSA42
hFE = 76 1мА
10
(4 = 0,522 В
(4= 0,505 В
20 30
3 (вольт)
40
2N3904
/?FE = 370 4мА
UA = 150 В
10 20 30
UK3 (вольт)
40
2N5963
/7FE = 4700 5мА
UA = 45 В
Рис. 5S.8. Эффект Эрли: напряжение UA определяется по крутизне зависимости Гк от ию. (Взято из раздела 2х.8 книги The Art
of Electronics — the X-Chapters.)
AoE § 2.3.7A.
6 Сравните с рис. 2.59 в книге AoE.
7 Данные взяты из рис. 2.59 книги АоЕ. Средний график
обсуждается в разделе 2х.8 книги The Art of Electronics - the
x-Chapters. (На момент перевода данной книги эта книга
еще не была в продаже. — Примеч. пер.).
5S.2 Токовые зеркала и эффект Эрли
249
транзисторных характеристик. Но в других от-
ношениях (например, с точки зрения преоб-
разования импеданса в качестве эмиттерного
повторителя) этот транзистор, с его малым р,
можно считать самым худшим из трех.
Механизм эффекта Эр/ти
Реакция транзистора на напряжение U^, ко-
торая подобна реакции резистора, вызывается
модуляцией ширины базы транзистора: повы-
шение напряжения U^ увеличивает ширину
обедненной носителями области между коллек-
тором и базой, уменьшая эффективную ширину
базы и таким образом повышая ток коллектора.
В зависимости от естественной ширины базы
эффект Эрли может быть умеренным или боль-
шим: более узкая база реагирует на сужение
сильнее, поскольку в процентном соотношении
изменение эффективной ширины базы оказы-
вается больше.
Таким образом, транзисторы с узкой областью
базы, т. е. с высоким коэффициентом р, особен-
но чувствительны к варьированию напряжения
икэ. Эта зависимость демонстрируется в табли-
це 5.1 в виде пар значений UA и р для транзи-
сторов, кривые вольт-амперных характеристик
которых изображены на рис. 5S.8.
Таблица 5.1. Эффект Эрли для транзисторов
разных типов
Транзистор
MPSA42
2N3904
2N5963
Р (типич-
ный)
25
130
1200 (мин)
Напряжение Эрли 1/А
(из кривых графика)
6,8 кВ
150 В
45В
Параметр UA полезен, но обычно не приво-
дится в справочных листках транзисторов8.
Измерение кривых, подобных показанным на
рис. 5S.8, может быть сопряжено с трудностя-
ми, поскольку температурные эффекты могут
исказить их и затруднить попытку различить
8 Такое упущение характеристики UA из справочных
листков транзисторов выглядит странным. Мы в свое вре-
мя спросили у покойного Роберта Пиза, корифея в обла-
сти аналоговой схемотехники, почему так. Он ответил (по
электронной почте), что это значение редко кто спраши-
вает. А те, кому требуется эта информация, знают, как ее
получить, т. е. они могут измерить значение Al/^ для соот-
ветствующего значения АС/^. Все равно, мы продолжаем
недоумевать по поводу этого упущения.
эффект Эрли. При отсутствии значения UA или
соответствующих кривых нужно ориентиро-
ваться на оценку напряжения UA исходя из диа-
пазона коэффициента р транзистора. Хотя это
значение будет по определению приблизитель-
ным, им можно пользоваться. Для маломощно-
го транзистора типа 2N3904 значение UA мож-
но прикидочно оценить где-то в районе 100 В.
5S.2.6. Использование результатов
эффекта Эрли
Параметр UA позволяет быстро оценить воз-
можность транзистора работать в качестве
источника тока. Но это довольно абстрактное
представление. Гораздо важнее соотнести на-
пряжение UA (или какую-либо другую оценку
эффекта Эрли) с поведением определенной схе-
мы. Особенно полезными были бы следующие
два результата эффекта Эрли:
♦ оценка выходного импеданса источника тока;
♦ вычисление верхнего предела коэффициента
усиления транзисторного усилителя, когда
его нагрузка (импеданс на коллекторе) явля-
ется источником тока.
Собственно говоря, мы можем вычислить оба
эти результата.
Вычисление /?вых для источника тока
Первый способ: по крутизне кривых зави-
симости /к от 1/де
Если у вас в распоряжении есть кривые зави-
симости 1К от икэ (наподобие показанных на
рис. 5S.8), то величину выходного импеданса
Двых можно определить напрямую из графика.
Например, для транзистора 2N3904 простое
токовое зеркало (без резистора в цепи эмитте-
ра) дает следующий результат, соответствую-
щий конкретной кривой, которая начинается
приблизительно в точке 17 мкА:
А1К/А1ГКЭ = 4 (хА/40 В = 0,1 • 10"6 Ом1.
Единицы измерения — обратные Омы (Ом1
или сименсы). Обратной величиной является
выходное сопротивление на коллекторе #вых,
измеряемое в Омах: 10 МОм. Это не общее ре-
шение, но импеданс при определенном выход-
ном токе (в данном случае около 17 мкА).
250
5S. Дополнительный материал и глоссарий: транзисторы II
Тем не менее начало положено. Описанный
подход можно расширить для вычисления вы-
ходного сопротивления Двых при других значе-
ниях тока. Давайте переопределим крутизну в
виде относительного изменения тока на вольт,
выраженного в процентах. На рис. 5S.9 показан
гипотетический график эффекта Эрли, наподо-
бие кривых для транзистора 2N3904, но с пред-
полагаемым напряжением Эрли UA величиной
100 В. Такое значение UA было выбрано для
того, чтобы как можно больше упростить вы-
числения.
ДГ=Г/оОтГК0
А(У=1 В = 1% от (Л
(-100 В)
Рис. 5S.9. Эффект Эрли представлен в виде относительного
изменения тока на вольт (в процентах)
При напряжении UA = 100 В повышение напря-
жения 17КЭ на 1 В от его первоначального близ-
кого к нулю значения соответствует увеличе-
нию на 1%. Прямая наклонная линия графика
тока коллектора 1К, возрастающего от нулевого
значения при напряжении 1/А, обеспечивает ре-
зультирующее повышение тока коллектора ве-
личиной 1%.
Это удобный способ для описания эффекта
Эрли, поскольку он позволяет вычислить вы-
ходной импеданс ЯБЫХ при любом начальном
токе коллектора 7К0. Например, при началь-
ном токе коллектора 1К0=1 мА, 1% от А7К =
= 0,01 мА = 10 мкА. Таким образом, выходной
импеданс #вых при токе 1 мА является обратной
величиной крутизны: 0,1 МОм = 10 кОм.
Второй способ. Вместо крутизны графика за-
висимости напряжения UA или тока коллектора
7К от напряжения [7КЭ можно задать полезное
отношение — AU^/AU^9. Это отношение (ре-
зультат которого обозначается символом ц)
полезно при оценке выходного импеданса Двых
для источников тока:
ЛГ7
БЭ
кэ
при фиксированном значении тока коллек-
тора^.
Параметр г| трудно поддается интуитивному
пониманию: это изменение (понижение) на-
пряжения [/БЭ, необходимое для поддержания
тока коллектора 1К постоянным при повыше-
нии напряжения С/кэ на один вольт.
Значение т| можно вычислить, используя гипо-
тетические кривые зависимости тока коллекто-
ра 1К от напряжения икэ из рис. 5S.8. Здесь на
каждый 1В повышения напряжения U^ наблю-
дается рост тока коллектора 7К на 1%. Кстати,
далее следует один из редких случаев явного
использования уравнения Эберса-Молла.
Согласно уравнению Эберса-Молла ток кол-
лектора 1К «1тс(еи™/25 мВ).
Примечание
Как обычно, мы игнорируем несущественную «-1»,
. присутствующую в полном выражении. См. раз-
дел 23.1 книги АоЕ. Величина 25 мВ соответствует
значению kT/q при комнатной температуре.
Таким образом, отношение этих двух коллек-
торных токов будет следующим:
Если ток коллектора 1^ на 1% больше тока 1К2,
как на графике на рис. 5S.8, то соответствующее
изменение напряжения 1/БЭ можно вычислить
с помощью уравнения Эберса-Молла.
Таким образом, для изменения в 1% е^*/25 мВ=
=1,01. Следует признать неудобный факт, что
полученный результат описывает не тот ре-
зультат, который мы намеревались вычислить.
В частности, он соответствует случаю, когда
напряжение U^ поддерживается постоянным,
а повышение напряжения ивэ вызывает рост
тока коллектора 1К. У вас может создаться впе-
чатление, что начинать с иного случая несколь-
ко странно, и мы разделяем ваше мнение. Но
не спешите с выводами, эта процедура действи-
тельно работает:
9 АоЕ § 2.3.2D.
БЭ ^
= 0,01 • 25 мВ = 0,25 мВ.
Теперь мы можем завершить наш мысленный
эксперимент и признаться, что нам в действи-
тельности нужно — это величина уменьшения
напряжения [/БЭ, которое нам требовалось бы,
55.2 Токовые зеркала и эффект Эрли
251
чтобы поддерживать ток коллектора постоян-
ным при возрастании напряжения икэ. Это то
же самое значение, что и для Лиъэ, но только
с противоположным знаком:
= 0,25 мВ/1 В = 0,25 • 103.
Пока просто отметим для себя, что мы откры-
ли способ вычисления значения т). Но вскоре,
в разделе 5S.2.7, мы начнем использовать это
значение.
5S.2.7. Улучшение Явых источника
тока
Каскодная схема или токовое зеркало
Уилсона
Один из способов устранить эффект изменения
напряжения UK3 состоит в добавлении в схему
дополнительного транзистора10. Этот прием
(который был предложен еще во времена ва-
куумных ламп11 в 1939 г.) называется каскод-
ной схемой, или просто каскодом. Через допол-
нительный транзистор просто протекает ток,
подаваемый на него транзистором, который
подлежит защите от эффекта Эрли. Такой про-
ходной транзистор вполне «ощущает» широкое
варьирование напряжения [/кэ, но он не задает
выходной ток, а просто пропускает ток, опреде-
ляемый защищаемым транзистором. Данная
схема, пример которой приведен на рис. 5S.10,
легко реализуется в интегральном исполнении
и является стандартом для токовых зеркал в
операционных усилителях, включая микросхе-
му операционного усилителя LF411, которую
мы используем в большинстве наших лабора-
торных занятий по операционным усилителям.
Фрагмент схемы слева на рис. 5S.11, который
взят из справочного листка для микросхемы
операционного усилителя LF411 и на первый
взгляд выглядит непривычно, как какая-то не-
известная схема. Но его перерисованный вари-
ант справа изображен так же, как и на рис. 5S.10
(хотя с транзисторами типа р-я-р, а на п-р-п,
чтобы служить источником, а не приемником
тока). Вы, наверное, заметили, что в исход-
ной схеме транзистор Q^ выглядит довольно
10 АоЕ§ 2.3.7В.
11 Откуда происходит и его название — соединение частей
слов из словосочетания «КАСКад через катОД» (англ.
CASCade to cathODE).
Рис. 5S.10. Токовое зеркало Уилсона или каскодная схема
нивелирует изменения напряжения 1/НАГР
Рис. 5S.11. Каскодная схема или токовое зеркало Уилсона
в операционном усилителе LF411
необычно. На схеме справа он перерисован в
более привычном виде — как два отдельных
транзистора с соединенными эмиттерами и ба-
зами.
Усовершенствование источника тока
с помощью резисторов в цели эмиттера
Параметр т], с которым мы познакомились
в разделе 5S.2.6, поможет нам вычислить улуч-
шение выходного импеданса 2?вых, достигаемое
с помощью резисторов в цепи эмиттера. На
рис. 5S.12 приведена принципиальная схема
простого токового зеркала, содержащая рези-
сторы в цепи эмиттера.
I***
п
1кОм
Рис. 5S.12. Простое токовое зеркало, улучшенное добавле-
нием резисторов в цепь эмиттера
252
5S. Дополнительный материал и глоссарий: транзисторы II
Если вы соглашаетесь с аргументацией (изло-
женной в главе 5N), что установка резистора в
цепь эмиттера усилителя с общим эмиттером
стабилизирует ток коллектора 1К, то вы также
найдете убедительным предположение, что до-
бавление резисторов в цепь эмиттера должно
способствовать стабилизации тока коллектора
/к в токовом зеркале. В обоих случаях ключе-
вым фактором улучшения является отрица-
тельная обратная связь.
В дальнейшем мы попытаемся обосновать это
предположение, а не просто утверждать, что
такой эффект возможен. В частности, мы ис-
пользуем параметр т|, чтобы вычислить коли-
чественный эффект от введения таких рези-
сторов.
Использование п для вычисления Йшх
в токовом зеркале с резисторами в цепи
эмиттера
Повышение напряжения на коллекторе на 1В
вызывает понижение напряжения U^ нат! • 1 В,
что в свою очередь вызывает рост напряжения
на эмиттере на такую же величину: 0,25 В (для
значения у\ равного 0,25 • 10~3, которое мы вы-
числили в разделе 5S.2.6). Согласно закону Ома
это изменение напряжения иэ вызовет увели-
чение токов 1Э и JK на:
AUJRs = 0,25 • 10"3B/103 Ом = 0,25 • 106А.
Выходной импеданс RBhsx на коллекторе будет
инверсией этого результата: 4 МОм. Обобщая
этот результат, можно видеть, что рост напря-
жения на коллекторе на 1 В вызывает в г\ раз
меньшее повышение напряжения на эмиттере.
Таким образом, если рассматривать транзистор
со стороны коллектора, то его поведение по-
добно линзе, как иллюстрируется на рйс. 5S.13.
,4
1 кОм
Рис. 5S.13. Если рассматривать транзистор со стороны кол-
лектора, то транзисторный источник тока ведет себя подоб-
но линзе, увеличивающей Яэ и гэ
Это сравнение с линзой напоминает эмиттер-
ный повторитель, который мы сравнивали с
«розовыми очками/линзой», но здесь резуль-
тат совершенно иной: линза повышает выход-
ной импеданс #вых, увеличивая сопротивление
эмиттера в 1/rj раз. В рассмотренном примере
множитель равен 4000, что преобразовывает
сопротивление Дэ величиной 1 кОм в выходной
импеданс величиной 4 МОм.
Подтверждаем полезность г|/
вычисляя /?вых для первоначального
токового зеркала
Ранее мы вычислили выходной импеданс для
простого токового зеркала, используя для этого
крутизну кривых зависимости тока коллекто-
ра 7К от напряжения U^. Давайте укрепим нашу
веру в параметр г|, снова вычислив это значение,
но на этот раз через ц и малое гэ (наш обычный
обход Эберса-Молла). Посмотрим, получим ли
мы такой же самый результат: 100 кОм12.
Проводя расчеты для случая, когда в цепь эмит-
тера добавлены резисторы, отметим, что мы
получим изменение напряжения AU^ 0,25 мВ
на 1 В изменения напряжения Аикэ и (с верой
в нашу модель малого гэ); мы рассматриваем
это как повышение напряжения на гэ на такую
же величину.
Для источника тока величиной 1 мА значение гэ
при комнатной температуре составляет 25 Ом,
поэтому ток коллектора /к возрастает:
Для предполагаемого изменения напряжения
икэ на 1В частное равно:
[(т1-41/кэ)=0,25В]/25Ом.
Выходной импеданс 1?вых является обратной
величиной, т. е. 1/АГк:
*вых = 25 Ом/0,25 мВ = 100 кОм.
Как видим, наши надежды оправдались.
Этот результат можно объяснить более про-
стым (и более образным) способом, подобно
и Было бы странно, если не получили — ведь мы просто
выполняем в обратном направлении вычисление, посред-
ством которого мы определили значение х\.
5S.2. Токовые зеркала и эффект Эрли
253
тому, как мы это сделали на рис. 5S.13, сказав,
что «линза» эффекта Эрли снова увеличи-
вает величину сопротивления на эмиттере»в
1/т| раз. Ранее мы определили, что для данного
случая значение этого множителя равно 4000.
Поскольку схема в этом примере не содержит
резистора в цепи эмиттера 1^, приходится ори-
ентироваться на гэ, значение которого при токе
1 мА составляет 25 Ом. Таким образом, #вых =
= 4000 • 25 Ом = 100 кОм. Такой метод линзы
представляется нам наиболее прямолинейным.
Токовое зеркало можно улучшить,
с помощью как каскода, так и эмиттерных
резисторов
Схемы токового зеркала Уилсона выпускают-
ся в виде микросхем. Одна из таких микро-
схем — REF200, предлагаемая компанией
Texas Instruments — содержит два токоограни-
чивающих элемента и одно токовое зеркало
Уилсона13, в котором применены оба описан-
ные ранее усовершенствования: каскод и рези-
сторы в цепи эмиттера. На рис. 5S.14 изобра-
жена принципиальная схема токового зеркала
этой микросхемы.
также добавлены резисторы в цепи эмиттера14.
Обладая такой двойной защитой, токовое зер-
кало микросхемы REF200 обеспечивает огром-
ные значения выходного импеданса Яшх (ти-
пичная величина равна 100 МОм).
5S.2.8. Другое следствие эффекта
Эрли: ограничение коэффициента
усиления
При рассмотрении операционных усилителей
мы увидим, что резисторы15 в цепи коллектора
регулярно заменяются транзисторными источ-
никами тока для получения максимального ко-
эффициента усиления как дифференциального
каскада, так и каскада с общим эмиттером. При
такой модификации важен не только импеданс
источника тока, но и выходной импеданс тран-
зистора усилителя. Упрощая ситуацию, мож-
но предположить, что при нагрузке источника
тока будет обеспечено бесконечное усиление.
Как обычно, такие чрезмерные ожидания мож-
но свести к реалистичным, учитывая эффект
Эрли, чтобы установить количественный пре-
дел усиления схемы.
1 кОм
1 кОм
Рис. 5S.14 Токовое зеркало микросхемы REF200 содержит
как каскод, так и резисторы в цепи эмиттера
На этой схеме зеркало Уилсона распознать
намного легче, чем на схеме из справочного
листка микросхемы LF411. Кроме того, здесь
13 Данная микросхема рассматривается в главе UN. В при-
мечаниях компании Texas Instruments по применению этой
микросхемы приводится много схем источников тока,
в том числе с каскодными схемами, позволяющими полу-
чит очень большие выходные импедансы (свыше 10 ГОм).
См. публикацию «Implementation and Applications of Current
Sources and Current Receivers» («Реализация и применения ис-
точников и приемников тока»), доступную по URL-адресу
http://www.ti.com/lit/an/sboa046/sboa046.pdf.
Усиление обычных усилителей с общим
эмиттером определяется резистором /?к
и сопротивлением эмиттера
В случаях, с которыми мы ознакомились в на-
шем курсе, транзисторный усилитель преоб-
разовывает меняющийся коллекторный ток
в варьирующееся коллекторное напряжение
посредством резистора в цепи коллектора16.
Как упоминалось, коэффициент усиления уси-
лителя с общим эмиттером определяется со-
отношением сопротивления резистора RK к
сопротивлению резистора #э или к подобной
резистору модели транзистора, которую мы на-
зывали малым г.
14 Схема также содержит четвертый транзистор, играю-
щий роль проходного элемента для плеча управления, что
дополнительно повышает и так впечатляющий уровень за-
щиты зеркала Уилсона. Этот четвертый транзистор уравно-
вешивает напряжения икэ двух нижних транзисторов при
падении напряжения U^ на одном транзисторе, в отличие
от напряжения U^ одного транзистора и напряжения U^
двух транзисторов, как в стандартном зеркале Уилсона.
15 Эквиваленты коллекторных резисторов являются «по-
глощающими» резисторами для подобных усилителей на
полевых транзисторах, как, например, в операционном
усилителе микросхемы LF411.
16 АоЕ § 2.3.4А.
254
55. Дополнительный материал и глоссарий: транзисторы II
Таким же образом, максимальный коэффици-
ент усиления обычного усилителя можно опи-
сать выражением £Утах = ^ • Дк, где ^ = 1/гэ17.
Член gm представляет крутизну кривой усиле-
ния, или величину изменения выходного тока
на величину изменения входного напряжения:
Здесь эффект Эрли не учитывается, и до сих
пор такое игнорирование сходило нам с рук.
Чтобы принять в расчет эффект Эрли, необхо-
димо признать, что сопротивление, в которое
подается сигнал с коллектора, строго опреде-
лятся как ЯкЦгвых а (назовем его просто гвых),
где гвых учитывает эффект Эрли. В предыдущих
случаях сопротивление резистора RK было го-
раздо меньше, чем сопротивление гвых, поэтому
не было необходимости принимать в расчет
что-либо другое, кроме сопротивления рези-
стора RK.
Усиление в усилителе с общим
эмиттером с источником тока в цепи
коллектора
Теперь, если рассматривать наш случай мак-
симизации усиления заменой резистора RK на
очень хороший источник тока, то эффект Эрли
необходимо принимать во внимание, т. е. в рас-
четы надо включать эффект собственного г
■*• * выл
транзистора. Чтобы держать все под контро-
лем, предположим в качестве нагрузки идеаль-
ный источник тока (если «идеальный» вам не
по душе, возьмите источник тока наподобие
зеркала Уилсона REF200, сопротивление гвых
которого составляет около 100 МОм)18.
В этом случае коэффициент усиления напряже-
ния схемы будет определять не знакомое нам
сопротивление резистора 1^, а сопротивление
резистора гвых. Коэффициент усиления будет вы-
ражаться формулой gm • гвых или (равнозначно)
гвых/гэ- ПРИ токе 1м^ Для транзистора, который
мы предложили для рассмотрения, с его напря-
жением [7А, составляющим 100 В, коэффициент
усиления будет равным 100 кОм/25 = 4000.
Это, конечно же, очень большое усиление, но
далеко не бесконечное.
17 Это определение, намекающее на то, что член gm получа-
ется из малого гэ, важно в нашем курсе вследствие нашего
постоянного использования последнего. Но в мире схемо-
техники за пределами учебного курса это определение не-
сколько необычно, поскольку использование понятия gm
намного более обширно.
18 АоЕ x-Chapters, § 2х.8.
5S.3. Резюме
по транзисторам
Мы предполагаем, что, приближаясь к концу
раздела по дискретным транзисторам, вы чув-
ствуете себя перегруженными информацией.
Мы рассмотрели важные моменты и подроб-
ности, но существует определенная опасность,
что мелочи могут заслонить более фундамен-
тальную информацию. Во избежание этого
далее кратко обобщен весь материал, который
мы рассмотрели в предыдущих главах.
5S.3.1. Зачем нужно изучать
дискретные транзисторы?
Начиная с главы 6N мы будем разрабатывать
электронные устройства на микросхемах опе-
рационных усилителей, и простые схемы на
транзисторах (например, усилитель с общим
эмиттером), которые мы рассматривали до сих
пор, будут выглядеть неуклюжими, громоздки-
ми и очень сложными. Действительно ли необ-
ходимо понимать функционирование усилите-
ля с общим эмиттером?
Может быть и нет, но основной аргумент в
пользу изучения базовых схем на транзисторах
заключается в том, что такие усилители всег-
да присутствуют в операционных усилителях,
например, во втором каскаде операционного
усилителя на микросхеме 411. Кроме того, диф-
ференциальный усилитель, составляющий пер-
вый каскад каждого операционного усилителя,
является, по сути, парой соединенных вместе
усилителей с общим эмиттером. Как уже упо-
миналось ранее, понимание работы операци-
онного усилителя полезно, но не обязательно
при изучении схемотехники, поскольку позво-
ляет увидеть, что волшебные результаты ра-
боты операционных усилителей основаны на
твердых законах физики.
Но схемы на дискретных транзисторах все же
находят применение в определенных областях,
например, на высоких частотах, где невозмож-
ны обычные операционные усилители. Но еще
чаще дискретные транзисторы применяются
в силовой схемотехнике для регулирования
больших токов, при этом сами будучи управ-
ляемыми операционными усилителями. В ка-
честве примера можно привести двухтактный
каскад в контуре обратной связи операционно-
го усилителя (см. раздел 6L.8).
5S3. Резюме по транзисторам
255
5S.3.2. Основные аспекты и факты
о биполярных транзисторах
♦ Простая модель (глава 4N). Простого пред-
ставления транзисторов вполне достаточно
во многих случаях.
• Напряжение [/БЭ » 0,6 В. Этот факт (ко-
торый не отрицается моделью Эберса-
Молла) часто позволяет выполнять бы-
стрый анализ или разработку.
• /к « 7Э. Это следует из концепции высокого
коэффициента р (т. е. 1К »1Б).
• Ток коллектора /к в пять раз больше тока
базы /Б. Это понятие нам требуется для
того, чтобы оценить входной импеданс
эмиттерного повторителя или усилителя
с общим эмиттером, а также способность
эмиттерного повторителя преобразовы-
вать импеданс (эффект «розовых очков/
линзы»): эмиттерный повторитель повы-
шает входной импеданс Двх и понижает
выходной Двых.
♦ Более сложная модель Эберса-Молла (гла-
ва 5N).
• Ток коллектора /к определяется напряже-
нием перехода «база-эмиттер» иъэ, а не
током базы /Б. Более конкретно, ток кол-
лектора 7К является экспоненциальной
функцией напряжения U^19.
• Эта информация часто применяется со-
вместно с полезным приемом введения
малого гэ, которое представляет собой мо-
дель собственного сопротивления эмит-
тера транзистора (и отображается в виде
резистора в выводе эмиттера). Этот прием
моделирования позволяет проще пред-
ставить транзистор (см. лабораторное за-
нятие 4L) при вычислении коэффициента
усиления и входного импеданса транзи-
сторных схем, в которых резистор в цепи
эмиттера Яэ имеет очень малое сопротив-
ление или вообще отсутствует.
Несколько полезных формул.
Входной и выходной импедансы эмиттер-
ного повторителя (эффект «розовых очков/
линзы»):
19 этот тезис можно согласовать с понятием из главы 4 (что
ток коллектора /к определяется током базы 7Б), вспомнив,
что, в конце концов, переход «база-эмиттер» является
диодом, вследствие чего напряжение ию и ток 1Б связаны
между собой. Более конкретно, ток базы /Б выглядит напо-
добие экспоненциальной функции напряжения U^. Таким
образом, заявляя (как это делается в главе 4N), что ток
коллектора /к является значением тока базы /Б, умножен-
ным на постоянную величину, мы неявно утверждаем, что
ток коллектора 1К представляет собой экспоненциальную
функцию напряжения иъэ, как это утверждается в модели
Эберса-Молла.
♦ Обычно эти формулы можно упростить, иг-
норируя член Дэ, поскольку это значение
обычно намного больше, чем сопротивление
Дисточ/|3, наблюдаемое через «линзу» тран-
зистора.
♦ Если на схему подается напряжение смеще-
ния, тогда сопротивление RrBB<M параллель-
но сопротивлению Дисгоч: [Д^очН Ятев-oJ/P-
Опять же, Дисточ обычно задается намно-
го меньшим, чем I^cm, так что результат
обычно снова сводится к Дисточ/р.
♦ Выходной импеданс (на коллекторе) Двых
усилителя с общим эмиттером: « RK, по-
скольку Двых = RK || Z^ а значение ZK очень
велико21.
♦ Коэффициент усиления для усилителя с об-
щим эмиттером составляет -RK/(r3 + Дэ).
♦ Коэффициент усиления для дифференциаль-
ного усилителя:
Дифференциальное усиление: RK/2(r3 + Яэ)22.
Синфазное усиление: КуСИНФ = -RK/(r3 + Дэ +
+ 2*xboct)' или приблизительно -Дк/2*хвосг
Большое значение R^ocr Дает низкое значе-
ние КуСИНФ. Наилучшее, т. е. самое низкое
20 Обычно мы не вычисляем выражения типа «1 +...», по-
скольку нет никакой пользы в знании значения коэффи-
циента р с такой точностью. В этих формулах мы пишем
просто р, а не правильное, но нелепое выражение (1+р).
Кстати, обратите внимание на то, что R3 соответствует
полному импедансу на эмиттере (например, иногда па-
раллельно резистору в цепи эмиттера подключается на-
грузка).
21 Этот импеданс очень велик, поскольку вывод коллекто-
ра ведет себя подобно источнику (или поглотителю) тока,
а для любого более-менее хорошего источника тока отно-
шение AL7/AI имеет очень большое значение. При варьи-
рующемся напряжении коллектора UK транзистор поддер-
живает ток коллектора 1К почти постоянным. Отклонение
от этого идеала описывается эффектом Эрли. Но эффект
Эрли дает небольшую корректировку общей истины, за-
ключающейся в том, что транзистор поддерживает ток
коллектора постоянным.
22 Множитель «2» в знаменателе отображает способ орга-
низации предполагаемого входа: чисто дифференциаль-
ный входной сигнал выглядит как ALT на одном входе и как
-ALTна другом. Таким образом, величина всего дифферен-
циального сигнала не одно ALT, а два ALT, отсюда и выраже-
ние дифференциального усиления: Дк/2(гэ + IQ.
256
55. Дополнительный материал и глоссарий: транзисторы II
значение ЯуСИНФ обеспечивается источником
тока вместо
♦ Транзисторные переключатели стоят особ-
няком от всех других рассмотренных нами
схем:
• в рабочем состоянии они или полностью
включены (в режиме насыщения), или
полностью выключены, тогда как во всех
других типах транзисторных схем этих со-
стояний стремятся избегать;
• ни одно из правил для обычных транзи-
сторов, работающих в линейной области,
неприменимо к переключателям:
- выражение 1К = р • 1В неприменимо к
переключателям. Вместо этого мы хо-
тим перегрузить базу приблизительно в
10 раз;
- ток нагрузки определяется самой на-
грузкой, а не выражением р • 7Б;
- входной импеданс на базе не равен
р • Дэ или р • гэ. Поскольку транзистор
в роли переключателя насыщен, его
входной импеданс намного ниже, чем
этот. Величина тока базы не ограничи-
вается коэффициентом р.
5S.4. Важные схемы
Большинство из нас запоминают схемы в виде
рисунков, а не текстовых описаний. Мы ис-
пользуем их подобно идиоматическим выра-
жениям, а не выводим их каждый раз из основ-
ных принципов или формул. Далее для справки
приводятся несколько наиболее важных тран-
зисторных схем.
♦ Источник тока
• На одном транзисторе:
♦ Эмиттерный повторитель
• С двухполярным источником питания (са-
мая простая схема, но требует второго ис-
точника напряжения)
Повторитель напряжения 0L
(«эмиттерный повторитель»)
с двухполярным источником
питания
С однополярным источником питания (ме-
нее элегантная, но более дешевая версия):
и
Напряжение смещения
повторителя напряжения
напряжение смещения
на базе...
Входной и выходной импедансы
Источник
сигнала
Импедансы эмиттерного / более точно:
повторителя I Двх = Ятев-см 11 (Ь
Двухтактный эмиттерный повторитель. Ре-
шает проблему однотранзисторного эмит-
терного повторителя, состоящую в том,
что вследствие асимметричности своей
схемы он плохо поглощает ток из нагрузки
(в случае я-р-я-транзистора).
Двухтактный эмиттерный
повторитель
5S.4. Важные схемы
257
♦ Усилители напряжения
• Усилители с общим эмиттером:
Посредственное
усиление
Большое усиление
на частотах сигнала,
где Дк« Дэ
Импедансы усилителя с обпцш эмиттером
Входной и выходной
импедансы усилителя
с общим эмиттером
Дифференциальный усилитель
Резистор в цепи коллектора
обычно отсутствует *
Вход А
Входной и выходной импе-
дансы дифференциального
усилителя
'Для получения максимального усиления
можно исключить из схемы резистор в цепи
эмиттера /?э. Это не скажется отрицательно
на температурной стабильности схемы при
условии, что оба транзистора находятся на
одной подложке
♦ Транзисторный переключатель (абсолют-
но иная схема, чем все предыдущие!)
Устраняет выброс напряжения,
возникающий при выключении
индуктивной нагрузки /
10 В
(Поскольку транзистор
находится в режиме
насыщения, ток коллектора Гк
определяется нагрузкой, а не
током базы)
ГБ»ГК/(У. чтобы ввести транзистор в режим
насыщения и минимизировать напряжение ию
и, соответственно, потери мощности в транзисторе,
необходим значительно увеличенный ток базы.
(Желаемый результат — передача всей мощности
на нагрузку)
5SA1. Некоторые тонкости
Далее вкратце излагаются некоторые тонко-
сти, которые желательно иметь в виду, хотя на
практике при вычислении соответствующих
значений это может и не понадобиться.
♦ Следующие три понятия очень важны, но в
нашем курсе вам, скорее всего, не придет-
ся работать с их количественными значе-
ниями.
• Температурные эффекты — высокая
температурная чувствительность тран-
зисторов является фундаментальным
аспектом, при этом формулы для коли-
чественной оценки влияния температу-
ры не столь важны. Устройства должны
содержать защиту против температурной
чувствительности..В большинстве случа-
ев такая защита может быть достигнута
с помощью обратной связи, которая реа-
лизуется добавлением резистора в цепь
эмиттера.
258
5S. Дополнительный материал и глоссарий: транзисторы II
• Эффект Эрли — учитывает несовершен-
ство транзисторного источника тока.
Иными словами, описывает изменение
тока коллектора при изменении напряже-
ния [7КЭ. Этот эффект часто незначителен,
обычно вследствие использования рези-
стора в цепи эмиттера для создания об-
ратной связи. Но при отсутствии такого
резистора в токовом зеркале могут наблю-
даться значительные искажения.
• Эффект Миллера — представляет серьез-
ную трудность при разработке высоко-
частотных усилителей. Эффект Миллера
вызывается емкостной обратной свя-
зью в любом инвертирующем усилителе.
Поскольку в наших лабораторных заняти-
ях мы не предполагаем собирать высоко-
частотные усилители, у вас не будет воз-
можности почувствовать важность этого
эффекта. Но такая возможность предста-
вится при первой же попытке разработ-
ки усилителя, рабочие частоты которого
выше, скажем, 1 МГц.
♦ Следующие аспекты представляют опреде-
ленный интерес, но менее важны.
• Следящая связь — довольно изящная
идея: заставить схемный элемент «исчез-
нуть» в электрическом смысле, когда оба
его вывода ведут себя одинаково.
• Пара Дарлингтона — составной транзи-
сторный каскад.
5S.5. Глоссарий
по биполярным
транзисторам
Двухполярный источник питания (см. раз-
дел 2.2.5В книги АоЕ) — источник питания, вы-
дающий как положительное, так и отрицатель-
ное напряжение23. Обычный источник питания
с положительным потенциалом и потенциалом
земли, называется однополярным24.
Задание смещения (см., например,раздел 2.2.5
книги АоЕ) — задание таких условий режи-
ма покоя, чтобы схемные элементы работали
должным образом. Смещение в данном кон-
тексте означает перемещение от центральной
23 Англоязычный эквивалент — split supply.
24 Англоязычный эквивалент - single supply.
точки. Смещение используется в транзистор-
ных схемах, работающих с однополярным ис-
точником питания. Этот термин также имеет
и другие значения (см., например, раздел 1.6.6k
книги АоЕ, где смещение служит для ввода вы-
прямительного диода в режим проводимости).
Импеданс в определенном направлении —
импеданс в определенной точке схемы с уче-
том только элементов, находящихся в том или
ином направлении. Например, импеданс на
базе транзистора, если смотреть назад, состо-
ит из делителя напряжения смещения и Дисточ,
а если смотреть в направлении базы — только
изр-Дэ.
Каскод (применяется в токовом зеркале Уил-
сона, см. раздел 2.3.7 книги АоЕ) — схема, в ко-
торой один транзистор служит буфером для
другого, чтобы изолировать его от варьирова-
ния напряжения и, соответственно, улучшить
его рабочие характеристики. Используется
в каскадных усилителях для подавления эф-
фекта Миллера и в источниках тока для устра-
нения эффекта Эрли.
Крутизна (передаточная проводимость)
(см. раздел 2.2.9 книги АоЕ) — вкратце,
gm = А1шх/Аивх (хорошее определение дается
в книге АоЕ).
Отрицательная обратная связь в цепи эмит-
тера (см. раздел 2.3.4 книги АоЕ) — резистор,
установленный между эмиттером транзистора
и землей (или иным отрицательным источни-
ком напряжения), в усилителе с общим эмит-
тером с целью температурной стабилизации
схемы. (Английский эквивалент emitter degen-
eration отражает факт ослабления или «вырож-
дение» усиления; но общие характеристики
схемы улучшаются.)
Отсечка (иллюстрируется в разделе 2.2.3D кни-
ге АоЕ) — «сплющивание» выходного сигнала,
вызываемого достижением им предельно до-
ступного напряжения. Например, все напряже-
ния выходного сигнала, превышающие потен-
циал земли и/или потенциал положительного
источника питания, будут отсекаться и пред-
ставляться напряжениями одинакового уровня.
Рабочий диапазон (источника тока) (см. раз-
дел 2.2.6D книги АоЕ) — диапазон выходного
напряжения, при котором источник тока со-
храняет работоспособность.
5S.5. Глоссарий по биполярным транзисторам
259
Следящая связь (см., например, раздел 23.5
книги АоЕ) — в данной главе обозначает прием,
с помощью которого импеданс делителя напря-
жения смещения можно заставить выглядеть
очень большим, чтобы улучшить входной им-
педанс схемы. Также следящая связь в коллек-
торной нагрузке. См. раздел 2.43А книги АоЕ.
Токовое зеркало Уилсона (см. раздел 23.7
книги АоЕ) — улучшенный вариант токового
зеркала, в котором дополнительный транзи-
стор (подключенный по каскодной схеме) за-
щищает выходной транзистор от варьирования
напряжения на нагрузке.
Характеристики режима покоя (напряже-
ния, тока) (см. например, раздел 2.2,5 книги
АоЕ) — условия схемы по току или напряжению,
преобладающие при отсутствии входного сиг-
нала. В том числе режим по постоянному току
в усилителе, предназначенном для усиления
сигналов переменного тока. Например, чтобы
обеспечить максимальный размах выходного
сигнала без отсечки для эмиттерного повтори-
теля с однополярным источником питания, его
выходное напряжение покоя ишх_покоя должно
быть посередине между положительным на-
пряжением питания и потенциалом земли.
Шунтирование (резистора в цепи эмиттера)
(см., например, раздел 23.5А книги АоЕ) —
в усилителе с общим эмиттером конденсатор,
подключенный параллельно резистору в цепи
эмиттера, шунтирует этот резистор, обеспе-
чивая протекание переменного тока в обход
более высокого импеданса данного резистора.
Применяется для повышения усиления, при
этом сопротивление резистора R3 выбирают
достаточно большим для обеспечения хорошей
стабильности.
Эффект Миллера (см. раздел 2.4.5 книги
АоЕ) — эквивалентное увеличение емкости
между выходом и входом инвертирующего уси-
лителя, когда небольшая емкость ведет себя
подобно емкости намного большей величины
[в (1+Ку) раз больше, чем реальная емкость],
подключенной между входом и «землей».
Эффект Эрли (см., например, раздел 23.7к
книги АоЕ) — изменение тока коллектора JK,
вызываемое варьированием напряжения UK3
при заданном значении напряжения ивэ или
тока коллектора /к. Иными словами, описывает
отклонение характеристик транзистора от ха-
рактеристик идеального источника тока.
5W. Примеры с решениями: транзисторы II
5W.1. Усилители с высоким
коэффициентом усиления
Задача № 1
Сравните усилители с большим коэффициен-
том усиления, принципиальные схемы которых
приведены на рис. 5W.1, по линейности или по-
стоянству усиления во всем динамическом диа-
пазоне выходного сигнала. Кратко обоснуйте
свои выводы. Предполагается, что входной сиг-
нал, подаваемый на усилители, имеет должное
смещение.
Pvic. Ж\ «Усилители с высоким коэффициентом усиления
Схема на рис, 5W.1, б очень похожа на токовое
зеркало, которое мы разрешили вам не изучать,
поэтому мы дадим для нее несколько подсказок.
Транзистор Qj в этой схеме может пропустить
ток величиной около Um/2R. Такой же ток бу-
дет также поступать и в транзистор Qg, если не
нарушать равновесие схемы. Таким образом,
транзистор (^ зеркалирует (т. е. дублирует) ток,
проходящий через транзистор Q, так как на-
пряжение [7БЭ на обоих транзисторах одинако-
вое. Смещение схемы выполнено обычным об-
разом: выходное напряжение покоя иъых_покоя
выставлено на уровне +0,5 В. Предполагается,
что оба транзистора согласованы по параме-
трам и находятся рядом друг с другом на под-
ложке интегральной схемы.
Решение № 1
За исключением рис. 5W.1, в, все остальные
схемы имеют одинаковую линейность усиле-
ния по всему диапазону выходного сигнала.
В частности, их усиление будет варьировать-
ся с изменением выходного напряжения, по-
скольку меняется ток коллектора JK, а зна-
менатель уравнения усиления для схем а, б, г
содержит только собственное сопротивление
эмиттера гэ, значение которого варьируется
при изменении тока коллектора 1К. Схема на
рис. 5W.1, в отличается от остальных тем, что
в ней к варьирующемуся значению малого тъ
добавляется постоянное значение резистора
R3. В результате ее усиление будет меньше, но
оно более стабильно.
Другой способ решения этой задачи — исполь-
зовать не малое гэ, но его инверсию gm — кру-
тизну кривой зависимости тока коллектора 1К
от напряжения на переходе «база-эмиттер»
1/БЭ. Эта крутизна (или передаточная проводи-
мость транзистора) пропорциональна току кол-
лектора JK, каковым является и усиление схемы
при отсутствии резистора в цепи эмиттера Кэ.
В частности, коэффициент усиления схемы вы-
ражается формулой gm-RK. Данный подход не
добавляет ничего нового к нашему обычному
приему с использованием малого гэ, но делает
более очевидной зависимость усиления от тока
коллектора.
5W.2. Дифференциальный усилитель
261
Задача № 2
Какая (или какие) из схем на рис. 5W.1 обла-
дают температурной стабильностью и каким
образом она достигается? Объясните меха-
низм^) защиты.
Решение № 2
Температурной стабильностью обладают схе-
мы, изображенные на рис. 5W.1, в и г, за счет
резистора в цепи эмиттера Дэ, посредством ко-
торого реализуется отрицательная обратная
связь (см. главу 5N). Схема на рис. 5W.1, г кро-
ме температурной стабильности, также имеет
высокий коэффициент усиления (но, как отме-
чалось ранее, плохое постоянство усиления).
Характеристики смещения схемы, показанной
на рис. 5W.1, а, нестабильны, в результате чего
это плохая схема.
Как уже упоминалось в постановке задачи, схему
рис. 5W.1, б мы подробно не рассматривали. Эта
схема обладает температурной стабильностью,
но она достигается не за счет обратной связи,
а благодаря симметрии. Но такой подход эф-
фективен только в том случае, когда параметры
обоих транзисторов хорошо согласованы, чего
можно достичь, только поместив оба транзи-
стора рядом друг с другом в одной интегральной
схеме, что и оговаривается в постановке задачи.
Поскольку токи коллекторов обоих тран-
зисторов схемы одинаковы, их напряжения
перехода «база-эмиттер» иъэ также равны.
Предположим, что температура окружающей
среды схемы поднялась на 9 °С. В результате
напряжение иъэ транзистора Q понизится при-
близительно на 18 мВ (см. главу 5N: при посто-
янном токе коллектора 1К, отношение А//ДГ =
= - 2,1 мВ/1 °С). Если бы эта схема была подоб-
но схеме на рис. 5W.1, а не защищена от влия-
ния температуры, то такое изменение умень-
шило бы выходное напряжение транзистора Qx
до половины его исходного значения, иными
словами, выходное напряжение покоя было бы
существенно нарушено.
Но поскольку транзистор Q^ подвергается точ-
но такому же нагреву, как и транзистор Qj, то
этот нагрев не влияет на его ток. Повышение
температуры понижает напряжение [7БЭ тран-
зистора Qj, но это уменьшенное напряжение
вызывает первоначальный ток в нагретом
транзисторе Qg. Эту схему температурной
стабилизации можно назвать стабилизацией
посредством компенсирования, а не посред-
ством обратной связи: изменение характери-
стики одного компонента, которое нарушало
бы равновесие схемы при других обстоятель-
ствах, компенсируется точно таким же измене-
нием этой же характеристики другого компо-
нента. Мы встретимся с использованием этого
эффекта в следующем разделе.
5W.2. Дифференциальный
усилитель
Задача №3
На рис. 5W.2 приведена принципиальная схема
дифференциального усилителя с небольшим
коэффициентом усиления (номинал резистора
в цепи коллектора составляет 10 кОм, а номи-
налы резисторов в цепи эмиттера — 100 Ом).
Усовершенствуйте схему так, чтобы максими-
зировать ее усиление (использование источни-
ков тока для этой цели не разрешается). Какое
дифференциальное усиление будет у модифи-
цированной схемы? А синфазное усиление?
+15 В
ВходА
Вход Б
Рис. 5W.2. Принципиальная схема дифференциального уси-
лителя (из лабораторного занятия 5L)
Решение № 3
Усиление схемы можно максимизировать (не
прибегая к хитроумным приемам, используе-
мым в настоящих операционных усилителях,
например, нагрузке в виде токового зеркала),
просто убрав из нее резисторы в цепях эмитте-
ров. После этого усиление будет зависеть толь-
ко от собственного сопротивления эмиттера гэ,
статическое значение которого при токе кол-
лектора 0,75 мА составляет около 33 Ом:
гэ) = ЮкОм/(2-ЗЗОм)«150;
= 10кОм/20кОм = -
262
5W. Примеры с решениями: транзисторы II
Задача № 4
После максимизации усиления в Задаче № 3 со-
хранит ли схема температурную стабильность?
Обоснуйте свой ответ.
Решение № 4
Да, сохранит, но при условии, что оба транзи-
стора будут работать при одинаковой темпера-
туре. Это условие выполняется, когда транзи-
сторы находятся в одной интегральной схеме:
при температурных изменениях их кривые
зависимости тока от напряжения изменяют-
ся одинаковым образом. Но если бы эта схема
была собрана на дискретных транзисторах, то
она бы не обладала температурной стабиль-
ностью.
Задача № 5 (Хвост дифференциального усилителя)
На лабораторном занятии 5L предлагалось за-
менить резистор номиналом 10 кОм в хвосте
дифференциального усилителя источником
(поглотителем) тока. Зачем нужна такая заме-
на? Как можно аргументировать, что источник
тока в хвосте улучшит коэффициент подавле-
ния синфазной составляющей?
Решение № 5
Коэффициент подавления синфазной составля-
ющей (КПСС) представляет собой отношение
дифференциального усиления к синфазному:
ЯудиФф/^усинФ- Резистор хвоста Яхвост диффе-
ренциального усилителя влияет на синфазное
усиление, но не на дифференциальное. Таким
образом, повышение сопротивления этого ре-
зистора выглядит целесообразным: выраже-
ние для синфазного усиления КуСИНФ содержит
в знаменателе член 2#хвост, тогда как выраже-
ние для дифференциального усиления Ку фф
вообще не содержит члена R^ocr- Таким обра-
зом, источник тока, который обладает боль-
шим динамическим сопротивлением, AU/AJ,
повышает эффективное сопротивление рези-
стора #хвост, снижая синфазное усиление КуСИНФ
и не затрагивая при этом дифференциальное
усиление £удифф.
Задача № б
Улучшится ли подавление синфазной составля-
ющей при увеличении сопротивления хвосто-
вого резистора Яхвост до, скажем, 100 кОм, по
сравнению со схемой на рис. 5W.2? Обоснуйте
свой ответ.
Решение № б
Нет, не улучшит. В отличие от источника тока,
увеличенное сопротивление резистора хво-
ста снизит ток коллектора в 10 раз. Чтобы вы-
ходное напряжение покоя £/вых_покоя осталось
прежним, значение резистора RK необходимо
повысить в 10 раз. Тем временем, из-за умень-
шения тока коллектора 1К, малое гэ повысится
во столько же раз.
Таким образом, результатом этой модифика-
ции будет прежнее значение как синфазного
усиления — Ку синф = 1/2, так и дифференци-
ального - Кудифф = 100 кОм/(2 • 33 Ом) = 150.
Естественно, что тогда и коэффициент подавле-
ния синфазной составляющей останется преж-
ним. Таким образом, КПСС можно улучшить,
только используя источник тока в хвосте.
5W.3. Дифференциальный
усилитель в микросхеме
операционного усилителя
Слева на рис. 5W.3 изображена сильно упро-
щенная принципиальная схема операцион-
ного усилителя на микросхеме 411 с входом
на полевом транзисторе с управляющим р-п-
переходом. Соответствующая исходная схе-
ма показана справа на рисунке, но вы должны
решить следующую задачу, пользуясь только
упрощенным вариантом схемы. Далее в тек-
сте мы рассмотрим все элементы, обведенные
кружками на рис. 5W.3.
Справочная информация
В первом каскаде (вход на дифференциальный
усилитель) усилителя использованы полевые
транзисторы с управляющим р-л-переходом,
чтобы получить очень малый ток смещения
(типичное значение для микросхемы 411 —
50 пА). Во втором каскаде — усилителе с об-
щим эмиттером — применены биполярные
транзисторы, поскольку их экспоненциальная
кривая зависимости тока от напряжения более
крутая, чем параболическая кривая полевых
транзисторов, что обеспечивает более высо-
кое усиление1.
1 Точнее, биполярные транзисторы имеют более высокую
передаточную проводимость - Д/вх/Д1/вых.
5W.3. Дифференциальный усилитель в микросхеме операционного усилителя
263
%
Ограничивающий
транзистор Осп,
Упрощенная схема
Рис. 5W.3. Внутреннее устройство операционного усилителя
Задача №7
Объясните, зачем нужны все эти источники
тока. В частности, поясните, почему не рези-
сторы, а источники тока используются в хвосте
и в выходе первого каскада, а также в цепи кол-
лектора второго каскада?
Примечание
В этой схеме все источники тока являются токовы-
ми зеркалами — любимыми устройствами разра-
ботчиков микросхем).
Решение № 7
Зачем нужны все эти источники тока? Источник
тока в хвосте входного каскада дифференци-
ального усилителя (в данном случае «хвост»
находится вверху) служит, как обычно, для
обеспечения низкого синфазного усиления
(создавая большой КПСС: Ку тФФ/Ку синф).
Как мы знаем, при использовании биполяр-
ных транзисторов усиление синфазного сигна-
ла определяется формулой Кусинф = -#к/(гэ +
+ R3 + 2ДХВ0СТ). Но для полевых транзисто-
ров эту формулу нужно подкорректировать
с учетом специфических названий их выво-
ДОВ: 2Сусинф = -Дсток/(1/£т + «исток + 2ДХВ0Ст)-
Таким образом, большое значение резистора
^хвост будет целесообразным.
А источник тока делает значение #хвост очень
большим, поскольку, как мы хорошо знаем,
хороший источник тока обеспечивает близ-
кие к нулю колебания тока А/, вызываемые
Подробная схема
варьированиями напряжения. Иными словами,
источник тока имеет очень большое диффе-
ренциальное сопротивление: #дифф = AU/AI =
= Л [//(малая величина). Это громадное эффек-
тивное сопротивление #хвост делает синфазное
усиление очень низким, а КПСС очень большим
(типичное значение для микросхемы LF411 со-
ставляет 100 дБ).
Токовые зеркала на стоках
транзисторов дифференциального
усилителя
Краткий ответ. Рассматриваем токовое зер-
кало просто как источник (в данном случае по-
требитель) тока. Тогда очень большое ДДИФФ
этого источника тока обеспечивает данному
каскаду большое усиление (это большое #дифф
заменяет обычный RK, вернее, поскольку в дан-
ном случае используются полевые транзисто-
ры, J?CT0K).
Подробный ответ. Если вы немного разобра-
лись с токовыми зеркалами, то должны знать,
что их цель — поддержание обоих токов одина-
ковыми. Строго говоря, следует поддерживать
один ток — выходной 1ВЫХ — равным другому —
току управления 1УПР.
И наоборот, задача двух полевых транзисто-
ров с управляющим переходом заключается
в том, чтобы сделать эти два тока неравными
при наличии разницы между двумя входными
264
5W. Примеры с решениями: транзисторы II
напряжениями. В результате комбинации этих
двух каскадов с противоположными свойства-
ми достигается очень высокое усиление по на-
пряжению.
Предположим, что ток покоя каждого из двух
транзисторов равен 1 мА (в данном случае
это условная величина, поскольку она намно-
го больше, чем в реальной микросхеме 411).
Теперь предположим, что разность входных
напряжений делает эти токи неравными, ска-
жем, входной, или управляющий, ток стано-
вится 0,9 мА, тогда как ток другого транзистора
повышается до 1,1 мА, поскольку общий ток,
задаваемый током хвоста /хвост, поддержива-
ется постоянным. Зеркало примет только эти
0,9 мА, а разница в 0,2 мА должна поступить
из этого каскада на следующий (усилитель
с общим эмиттером). Таким образом, зеркало
удвоило выходной ток первого каскада по срав-
нению с током, который бы поступил на второй
каскад, если на первый каскад был подан обыч-
ный ток.
Используя термины, типичные для усилителей
напряжения, можно сказать, что импеданс то-
кового зеркала не просто большой (каковым
является динамическое сопротивление любого
источника тока), а сверхбольшой, поскольку,
как только ток, подаваемый на резистор #сток,
повышается (до 1,1 мА в данном случае), так-
же возрастает и кажущийся импеданс данного
плеча зеркала. Зеркало не только пытается под-
держивать ток на постоянном уровне (как это
делает любой источник тока), но в данном слу-
чае также старается понизить ток, еще больше
усиливая реакцию на изменение напряжения
AU. Возможно, объяснение в терминах тока
лучше поддается пониманию, чем объяснение
в терминах усиления напряжения.
Источник тока в цепи коллектора
в каскаде усилителя с общим
эмиттером (точка В)
Этот источник тока, который заменяет привыч-
ный для нас резистор в цепи коллектора усили-
теля с общим эмиттером, также обеспечивает
очень большое усиление2. Но модифицирован-
ный таким образом обычный усилитель (в ко-
тором отсутствует общая обратная связь) был
АоЕ § 2.2.7.
бы «неудачной схемой». Без обратной связи
такая модификация была бы бесполезной, по-
скольку выходной сигнал усилителя ограничи-
вался бы уровнями напряжения питания (т. е.
отсекался бы на этих.уровнях). Но в опера-
ционных усилителях, в которых, как обычно,
предусмотрена отрицательная обратная связь,
такое поведение является не недостатком, а до-
стоинством.
Задача № 8
Для чего нужны элементы, обозначенные сим-
волом «А» в обоих вариантах схем на рис. 5W.3?
Обратите внимание на то, что оба варианта
равнозначны. Если подробная схема выглядит
слишком сложно, работайте с упрощенным ва-
риантом.
Решение № 8
Эти два транзистора образуют так называе-
мый каскад сдвига уровня, формирующий два
напряжения 1ГБЭ. Их можно рассматривать как
два последовательных диода, как показано
на упрощенном варианте схемы на рис. 5W.3.
Поскольку верхний уровень этого напряжения
иъэ подается на базу верхнего выходного тран-
зистора, а нижний — на базу нижнего, на базах
этих транзисторов устанавливается разное на-
пряжение смещения, в результате чего устраня-
ется «мертвая» зона, которая в противном слу-
чае возникает в двухтактном усилителе вблизи
нулевого потенциала и создает переходные ис-
кажения типа «ступенька».
Переходные искажения можно довольно эффек-
тивно устранить с помощью обратной связи (как
мы увидим в главе 6N), поэтому может возник-
нуть вопрос, почему этот метод не реализован
здесь. Потому что обратная связь недостаточно
быстрая, чтобы справиться с этой задачей на
высоких частотах. Чтобы устранить переходные
искажения, входной сигнал двухтактного усили-
теля должен подняться или опуститься на 1,2 В,
на что требуется время. Пока выполняется это
повышение или понижение, на выходе появит-
ся искажение. На рис. 5W.4 приведена осцилло-
грамма этого эффекта в самодельном операци-
онном усилителе из лабораторного занятия 5L.
Схема действительно устраняет большую часть
переходного искажения, но при более близ-
ком рассмотрении (на более высокой скорости
развертки) можно видеть, что искажение со-
храняется, как показано на правом изображе-
нии. Изменение двух напряжений С/БЭ занимает
5W.3. Дифференциальный усилитель в микросхеме операционного усилителя
265
Выход схема
(выход каскада
двухтактного
усилителя)
Выход каскада
усилителя
с общим
эмиттером г "
(вход на каскад ^^"""
двухтактного *^^
усилителя) т
Обратная связь устраняет переходное искажение
достаточно хорошо...
Переходные искажения
сохраняются в течение перехода
входного сигнала каскада
* двухтактного усилителя до
требуемого уровня
...но не идеально, поскольку переход занимает некоторое время
Рис. 5W.4. Смещение выходного сигнала каскада усилителя с общим эмиттером для устранения переходных искажений вы-
ходного сигнала каскада двухтактного усилителя не является идеальным решением этой проблемы
некоторое время, в течение которого эффектив-
ность обратной связи теряется.
Временной масштаб на рис. 5W.4 не подходит
для операционного усилителя на микросхеме
411, который выполняет переход через мерт-
вую зону намного быстрее, чем наш самодель-
ный операционный усилитель из лаборатор-
ного занятия 5L. Но если бы операционный
усилитель микросхемы 411 не был оснащен
пассивной защитой против переходных иска-
жений, при определенном временном масшта-
бе он также столкнулся бы с этой проблемой3.
Необходимость в таких средствах пассивной
защиты напоминает нам об ограниченных воз-
можностях обратной связи: она не работает до-
статочно хорошо на высоких частотах в обыч-
ных операционных усилителях.
Задача № 9
Обязательно ли наличие резисторов, помечен-
ных буквой С на рис. 5W.3? Обоснуйте свой
ответ.
Решение № 9
Да, эти резисторы необходимы. Их задача за-
ключается в предотвращении теплового про-
боя, который в противном случае с большой
вероятностью вывел бы из строя транзисторы
каскада двухтактного усилителя. Вследствие
разнесенного напряжения смещения на базах
этих транзисторов, о чем упоминалось чуть ра-
нее, когда входной и выходной сигналы этого
каскада находятся на уровне потенциала земли,
транзисторы работают в режиме минимальной
3 Не все операционные усилители оснащаются средствами
пассивной защиты против переходных искажений. Напри-
мер, в операционном усилителе на микросхеме LM385 с
однополярным питанием, который мы используем на ла-
бораторных занятиях 7L и 10L, такая защита отсутствует.
проводимости. Это предотвращает помеховый
выброс, когда схема реагирует на отклонение
уровня входного сигнала от потенциала земли.
Но без резисторов в цепях эмиттеров транзи-
сторов могут возникнуть серьезные проблемы.
Когда через транзисторы начинает протекать
небольшой ток, они слегка нагреваются. Но этот
нагрев повышает ток, протекающий при данном
напряжении [7БЭ, которое задается рассмотрен-
ной ранее цепью смещения. Дополнительный
ток нагревает транзисторы еще больше, и так
далее в том же духе. Здесь мы имеем дело с по-
ложительной обратной связью, вызывающей
эффект, заканчивающийся в итоге тепловым
пробоем. Резисторы в цепи эмиттера обеспечи-
вают отрицательную обратную связь, предот-
вращающую пробой: при нарастании тока на-
пряжения на эмиттерах становятся несколько
отличными друг от друга, понижая напряжение
иъэ. Мы уже встречались с этим механизмом
чуть ранее, когда аргументировали необходи-
мость наличия резистора в цепи эмиттера для
повышения коэффициента усиления усилителя
с общим эмиттером.
В этой же схеме эмиттерные резисторы име-
ют другое назначение. Они реализуют простой
прием для ограничения выходного тока опера-
ционного усилителя, чтобы не допустить его
повреждения вследствие перегрузки. Данная
схема настолько эффективна, что выход опера-
ционного усилителя на микросхеме 411 можно
закоротить на плюс или «землю» источника
питания без каких бы то ни было отрицатель-
ных последствий.
Любой входной или выходной ток на выходе
операционного усилителя проходит через один
из этих резисторов, вызывая на нем падение
266
5W. Примеры с решениями: транзисторы II
напряжения. Это напряжение подается как иъэ
на один или другой из ограничивающих тран-
зисторов Q^p. Когда выходной ток достаточ-
но велик, чтобы создать на резисторе падение
напряжения величиной 0,5-0,6 В, транзистор
Qqpp начинает отбирать ток из базы транзи-
стора двухтактного каскада. Совмещение этого
приема с ограничением тока, доступного из кас-
када усилителя с общим эмиттером, позволяет
установить безопасный верхний предел на вы-
ходной ток операционного усилителя. Мы сно-
ва встретимся с таким приемом в стабилизато-
рах напряжения в главе ПЫи на лабораторном
занятии 11L.
Часть
АНАЛОГОВЫЕ УСТРОЙСТВА.
ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ
И ИХ ПРИМЕНЕНИЕ
6N. Операционные усилители I
Содержание
6N.1. Общие сведения об обратной связи 269
Два совета, как получить наибольшее удовольствие от работы со схемами
с обратной связью 271
6N.2. Сущность отрицательной обратной связи 272
6N.3. Обратная связь в электронике 273
Схемы с обратной связью и без таковой 274
Примеры обратной связи без операционного усилителя 274
Обратная связь с операционными усилителями 275
6N.4. «Золотые правила* для работы с операционными усилителями 275
6N.5. Применение операционных усилителей 276
6N.5.1. Повторитель 276
6N.5.2. Влияние обратной связи на выходное сопротивление повторителя 276
6N.6. Усилители двух типов 277
6N.6.1. Неинвертирующий усилитель 277
6N.6.2. Сомнения в справедливости золотых правил 277
6N.6.3. Некоторые характеристики неинвертирующего операционного усилителя 278
6N.7. Инвертирующий усилитель 278
6N.7.1. Что такое «виртуальная земля» 279
6N.8. Когда применимы «золотые правила»? 280
6N.8.L Улучшенные варианты старых схем 281
6N.9. Необычные элементы, которые можно поместить в цепь обратной связи 282
6N.9.1. Общие понятия 282
6N.10. Материал для чтения в АоЕ 285
Цель этой главы
В этой главе мы рассмотрим схемотехнические методы, которые предназначены для решения та-
кой общей задачи, как улучшение рабочих характеристик многих электронных схем, с которыми
мы уже познакомились посредством использования отрицательной обратной связи.
6N.1. Общие сведения
об обратной связи
На рис. 6N.1 показана газетная страница, на
которой Гарольд Блэк (Harold Black) изобра-
зил свои наброски касательно обратной связи.
На данной странице приведена не основная
мысль, которую он сформулировал на странице
из газеты «Нью-Йорк Тайме» четырьмя дня-
ми раньше, а идея применения обратной связи
для согласования импедансов. Он сделал этот
набросок на пароме, когда однажды летним
утром в 1927 г. отправлялся с острова Стейтен-
Айленд (Staten Island) на работу. Что побудило
его сделать эту зарисовку на странице с датой,
просто случай или предусмотрительность1?
1 Авторское право от 1977 г. принадлежит организации
ШЕЕ. Перепечатано с разрешением из статьи Гарольда С.
Блэка Изобретение усилителя с отрицательной обратной
связью в издании журнала IEEE Spectrum за декабрь 1977 г.
Можно возразить, что газетная страница с датой вряд
ли может считаться неопровержимым доказательством
даты его изобретения. Он мог просто найти старую газету,
270
6/V. Операционные усилители I
Рис. 6N.1. Наброски Гарольда Блэка по применению усили-
теля с обратной связью
В предыдущих разделах мы постоянно расхва-
ливали возможности обратной связи. Скорее
всего вам знакомо это понятие, даже если
вы не использовали его в своих разработках.
Наконец мы начнем подробно рассматривать
этот эффект.
Обратная связь будет намного большим, чем
просто схемотехнический метод из вашего
арсенала. Этот важный прием вы будете по-
стоянно применять в различных обстоятель-
ствах, причем они могут не иметь никакого
отношения к операционным усилителям. Мы
уже встречались с разными способами приме-
нения обратной связи в схемах на дискретных
транзисторах. Теперь же мы будем постоянно
использовать ее в оставшихся лабораторных
занятиях по аналоговой электронике. Мы так-
же задействуем ее и в лабораторных занятиях
по цифровым схемам при изучении аналогово-
цифрового преобразователя, а затем схемы фа-
зовой синхронизации на лабораторном заня-
тии 18L. Это очень важная тема.
Мы начнем рассматривать схемы с отрицатель-
ной обратной связью так же, как и биполяр-
ные транзисторы: с простых, идеализирован-
ных представлений. В конце лабораторного
чтобы датировать свое изобретение задним числом. Нет,
поскольку он был достаточно предусмотрительным и сра-
зу же по прибытии на работу предпринял меры, чтобы за-
свидетельствовать и скрепить подписью каждый свой на-
бросок на газетной странице.
занятия 5L мы собрали простой операцион-
ный усилитель на дискретных компонентах.
Начиная с этого момента, мы будем полагаться
на интегральные версии дифференциальных
усилителей с высоким коэффициентом усиле-
ния. Они облегчают задачу разработки высоко-
качественных схем с обратной связью.
Но далее нам скоро придется снова разочаро-
вать вас — рассказать о некоторых несовер-
шенствах операционных усилителей. Но это
мелочи по сравнению с их замечательными
достоинствами. В своей работе мы постоянно
пытаемся найти новые варианты применения
для обратной связи, и мы никогда не разочаро-
вываемся в этих схемах. Они работают так хо-
рошо, как будто бы по волшебству.
На лабораторном занятии 8L мы познакомим-
ся с другим вариантом обратной связи: поло-
жительной. Этот тип обратной связи делает
работу схем нестабильной или вызывает огра-
ничение выходного сигнала на том и другом
уровне напряжения питания (т. е. выходной
сигнал отсекается на этих уровнях). Иногда это
полезная возможность, а иногда нет. На лабо-
раторном занятии 8L мы рассмотрим полезные
аспекты положительной обратной связи, вклю-
чая ее использование в генераторах колебаний.
Лабораторное занятие 9L начинается с одного
из более эффективных способов применения
этого типа обратной связи: в активном фильтре.
А остальная часть этого лабораторного занятия
посвящена более сложным аспектам положи-
тельной обратной связи: паразитным колеба-
ниям, вызываемым нежелательной обратной
связью и дестабилизирующим схему. Мы рас-
смотрим несколько способов защиты от этих
проблем. Информация о том, как применять
такую защиту, может высоко поднять ваш статус
в глазах однокурсников, тщетно пытающихся
избавиться от загадочных шумовых пульсаций
на осциллограммах разрабатываемого проекта.
После этого мы посвятим еще три лаборатор-
ных занятия трем конкретным вариантам при-
менения отрицательной обратной связи.
♦ Схема управления электродвигателем, ис-
пользующая ПИД-регулирование (в котором
в цепи обратной связи имеются три сигнала
рассогласования: пропорциональный, инте-
гральный и дифференциальный). Этим мы
будем заниматься на лабораторном заня-
тии 10L. Это будет не только самая сложная
6N.1. Общие сведения об обратной связи
271
схема из рассмотренных до сих пор, но и
очень полезная, поскольку позволит нам по-
казать применение многих схем, изученных
ранее в виде фрагментов. В ПИД-регуляторе
присутствуют не только дифференциатор и
интегратор, но также сумматор, дифферен-
циальный каскад с операционным усилите-
лем и мощный драйвер электродвигателя.
♦ Стабилизаторы напряжения представляют
собой специализированные схемы, предна-
значенные для частного, но важного при-
менения: создания стабилизированных ис-
точников питания. На лабораторном заня-
тии 11L мы рассмотрим как линейные, так и
импульсные разработки.
♦ Комплексный проект по сборке в одно целое
нескольких подсхем, некоторые из которых
пассивные, а в большинстве есть обратная
связь. В этом проекте вы разработаете и со-
берете вместе несколько схем, чтобы соз-
дать систему для передачи звука, с помощью
частотно-модулированного инфракрасного
излучения. Это будет лабораторное заня-
тие 13L, перескакивая через занятие 12L,
которое является последним лабораторным
занятием по дискретным транзисторам, в
частности, МОП-транзисторам, где обратная
связь не играет важной роли.
Лабораторное занятие 13L завершает анало-
говую часть этого курса, а уже со следующего
лабораторного занятия мы будем иметь дело со
схемами совершенно иного типа — цифровы-
ми. Но это уже совсем другая история.
Два совета, как получить наиболь-
шее удовольствие от работы
со схемами с обратной связью
Первый совет
В процессе работы с какой-либо схемой на
операционном усилителе вспомните аналогич-
ную схему, выполненную без обратной связи,
и связанные с нею трудности. Например, эмит-
терный повторитель или источник тока на дис-
кретных транзисторах. В общем и целом схемы
на операционном усилителе будут работать
настолько лучше, что наверняка приведут вас
в изумление.
Вы хорошо потрудились над схемами на дис-
кретных транзисторах, и теперь имеете полное
право наслаждаться легкостью работы с опера-
ционными усилителями и обратной связью.
На рис. 6N.2 мы в шутку изобразили ваше вос-
хождение из темных ущелий, через которые
вы пробирались до этого момента, на залитые
солнцем заоблачные вершины, где рабочие ха-
рактеристики схем приближаются к идеальным.
Небесная четверка2
^_^^- Темный, сатанический
^"""эффект Миллера ^ -;
} П Трясина
Л -л t f1 "\ Эберса-Молла
Температурные
эффекты ~с* /
4 * Клоака Эрли /
Рис. 6N.2. Добродетельный и трудолюбивый студент на по-
роге получения вознаграждения за свои мучения с дискрет-
ными транзисторами
2 Намек на микросхемы операционных усилителей, обыч-
но содержащие четыре таких усилителя.
272
6Л/. Операционные усилители I
Наконец-то вы на солнечных высокогорных лу-
гах, где процветает обратная связь. Похлопайте
сами себя по спине и развлекайтесь с операци-
онными усилителями.
Второй совет
Вспомните, что в электронике отрицательная
обратная связь использовалась не всегда, по-
скольку причины для этого не были очевидны,
пока Гарольд Блэк не смог убедить патентное
бюро в ее полезности. Он может считаться наи-
более вероятным изобретателем отрицатель-
ной обратной связи в электронике изо всех
претендентов на эту роль.
Выцветшая газетная страница с набросками на
ней, которая изображена в начале этой главы,
должна помочь вам почувствовать всю полно-
ту удивления и удовольствия, которые должен
ощущать изобретатель, когда он набрасывал
эскизы и формулы на своей газете. Факсимиле
этой страницы, содержащей второе основное
изобретение Гарольда Блэка в этой области,
сопровождало статью, которую он написал
спустя много лет, чтобы описать, как у него за-
родилось изобретение. В следующий раз, когда
вы изобретаете что-либо, имеющее подобную
ценность, не забудьте набросать свои заметки
на газетной странице (и попросите кого-либо
засвидетельствовать дату своих заметок), и со-
храните ее, пока у вас не появится возможность
написать свои мемуары.
6N.2. Сущность отрица-
тельной обратной связи
Идея отрицательной обратной связи является
самой глубокой и важной в нашем курсе схемо-
техники. Ее полезность настолько велика, что
эта фраза мигрировала в повседневную жизнь,
где она потеряла четкое значение (см. рис. 6N.3).
Начнем наше рассмотрение обратной связи с не-
скольких примеров такого общего использова-
ния этого понятия — одного настоящего комикса
(в том смысле, что он не был выдуман для иллю-
страции этого вопроса) и трех придуманных ко-
миксов.
Применяется ли здесь обратная связь в смыс-
ле, относящемся к электронике? Какого типа
эта обратная связь, положительная или отри-
цательная? Далее приводится пример неверно
понятого смысла обратной связи.
В обычной жизни слово «отрицательный» име-
ет негативный подтекст, поэтому выражение
«отрицательная обратная связь» звучит плохо,
На дальнем Западе
Ну, я полагаю, что ты была
достаточно хорошей лошадкой.
Работящая. Не самое расторопное
животное, с которым мне когда-
либо приходилось иметь дело,
но...
Да нет, идиот.
Я сказала не оценить
меня, а покормить3
Рис. 6N.3. Обратная связь за пределами электроники. Авторские права принадлежат Марку Стайверсу (Mark Stivers) с 1985 г.,
впервые опубликовано в Suttertown News, воспроизведено с разрешения
Игра слов: оценить — покормить. В оригинале: feedback —feedbag.
6Л/.3. Обратная связь в электронике
273
а «положительная обратная связь» — хорошо.
Одна из статей в газете New York Times (выпуск
за 8 октября 2008 г.) о замедлении темпа эконо-
мической активности начиналась следующим
образом.
Технари называют это «цепочкой отрица-
тельной обратной связи», а все остальные
именуют происходящее просто паникой.
Как еще можно объяснить новое резкое па-
дение цен на бирже во вторник, в результате
которого фондовый индекс Standard & Poor's
500 упал до самого низкого уровня за пять
лет, особенно при отсутствии каких-либо
других плохих новостей.
Конечно же, описанный здесь эффект является
положительной обратной связью. Но посколь-
ку новость плохая — паника — репортер авто-
матически рассматривает ее как «отрицатель-
ную».
Иногда сигнал, который обычно являлся бы от-
рицательной обратной связью, оказывается по-
ложительным.
Примечание
Мы еще вернемся к теме положительной обратной
связи, которая вызывает нестабильность схем, на
лабораторном занятии 9L
Как по вашему, персонаж справа на рис. 6N.4
применяет положительную или отрицательную
обратную связь по отношению к двум парням
слева? Чтобы определить вид этой обратной
связи, необходимо выяснить, какое влияние
она оказывает на поведение изображенных
слева.
терминах операционного усилителя (но не
Голливуда).
Рис. 6N.4. Ненормальные? Обидит ли их его высказывание?
Пример, изображенный на рис. 6N.5, ближе
всего соответствует смыслу отрицательной об-
ратной связи в электронике. Поразмышляйте,
какую роль играет каждый из участников в
- Крановщик
не может видеть
результатов
манипуляций
рычагами
управления.
Ему нужны ..-•*'"
корректирующие
сигналы...
от наблюдателя;
который видит
эти результаты
и сообщает
крановщику, как
откорректировать
их
/
Стукач
Марлон Молден
Брандо
Рис. 6N.5. Пример отрицательной обратной связи из жизни
во многом подобен обратной связи в операционном усили-
теле4
6N.3. Обратная связь
в электронике
В обычной беседе положительная обратная
связь употребляется в положительном (в обыч-
ном значении этого слова) смысле, а отрица-
тельная — в отрицательном (также в обыч-
ном значении этого слова)5. Но в электронике
смысл обратной связи обычно противополож-
ный. В сущности, в электронике отрицательная
обратная связь является замечательнейшей
вещью, а положительная — мерзкой и отврати-
тельной. Но если хорошенько подумать, то ви-
ды обратной связи в электронике имеют то же
значение, как и в обычной жизни.
Гарольд Блэк был первым, кто формализовал
влияние отрицательной обратной связи в элек-
тронных схемах. Далее приводится отрывок из
патента6, объясняющий его идею.
Заявитель открыл, как использовать эффек-
тивную отрицательную обратную связь, ко-
торая рассматривалась на предшествующем
уровне техники, для новых и важных усовер-
шенствований работы вакуумных ламп. Одно
4 Похоже, что это рисунок по мотивам фильма «On the Wa-
terfront» («В порту») с Марлоном Брандо (Marlon Brando)
и Карлом Малденом (Karl Maiden) в главных ролях -
Примеч. пер.
5 АоЕ § 2.5.1.
6 Гарольд С. Блэк (Harold S. Black), «Система преобразо-
вания сигналов» («Wave Translation System»), патент США
2102671 (1937 г.).
274
6N. Операционные усилители I
из усовершенствований состоит в уменьше-
нии искажений, возникающих в усилителе.
Другим усовершенствованием является более
стабильная работа, в частности, большее по-
стоянство усиления, несмотря на варьирую-
щиеся факторы, которые обычно влияли бы
на усиление. Другие рабочие характеристики
схемы также становятся более стабильными.
Заявитель открыл, что эти усовершенство-
вания сопровождаются пропорциональным
снижением коэффициента усиления усили-
теля, и что посредством создания схемы с из-
быточным усилением, которое затем умень-
шается отрицательной обратной связью,
можно реализовать любой требуемый уро-
вень линейности между входным и выходным
сигналами, и любой требуемый уровень по-
стоянства или стабильности рабочих харак-
теристик, при этом ограничивающим фак-
тором является величина усиления, которую
можно получить, а не какие бы то ни было
ограничения в способе усовершенствования,
обеспечиваемого данным Изобретением.
Много лет позже он обобщил свою идею в
статье:
...создав усилитель с коэффициентом усиле-
ния преднамеренно завышенным, скажем, на
40 децибел, чем требуемый уровень (избыток
в 10 000 раз в терминах мощности), а затем,
подавая выход обратно на вход таким обра-
зом, чтобы уменьшить избыточное усиление,
можно получить замечательное улучшение
усиления и избавиться от нелинейности7.
Одним из доказательств оригинальности идеи
Гарольда Блэка является то, что Британское
Патентное бюро отклонило его заявку, считая
его тупицей, не способным понять, что усили-
тель должен усиливать, так что фраза «умень-
шить усиление» демонстрировала отсутствие
у изобретателя понимания предмета8. Но, как
уже упоминалось ранее, Гарольд Блэк посмеял-
ся последним.
Чтобы не перехвалить изобретение Гарольда
Блэка, следует признать, что он не изобрел или
открыл обратную связь. Обратная связь при-
сутствует во многих природных процессах.
Например, наши тела изобилуют гомеостатиче-
скими системами, наподобие системы для под-
держания температуры тела в районе 37,22 °С;
независимо от того, дрожим ли мы от холода или
потеем от жары. (Кстати, дрожание и потение
являются частью регулировочного механизма.)
Также обратная связь применялась в различ-
ных механизмах задолго до ее формализации
Гарольдом Блэком. Например, Томас Ньюкомен
(Thomas Newcomen) использовал в своих паро-
вых насосах регулятор скорости. В зависимости
от скорости вращения вала специальные грузи-
ки поднимались или опускались, пропорцио-
нально призакрывая или приоткрывая паровой
клапан. В результате скорость вращения поддер-
живалась практически постоянной, независимо
от изменения нагрузки.
Схемы с обратной связью
и без таковой
До сих пор почти во всех рассмотренных нами
схемах (за исключением упомянутых чуть да-
лее) обратная связь отсутствовала. Поэтому вы,
возможно, привыкли разрабатывать усилители
без обратной связи. Мы избавим вас от этой
привычки. Ведь вы же не вздумали бы управ-
лять автомобилем без обратной связи. Также
вы, наверное, знаете, что без обратной связи
практически невозможно осмысленно обсуж-
дать что-либо.
Примеры обратной связи без
операционного усилителя
Понятие обратной связи не должно быть абсо-
лютно чем-то новым для вас9. Вы, скорее всего,
имеете довольно хорошее представление о нем
из своей повседневной деятельности. Кроме
того, мы применяли обратную связь в некото-
рых наших транзисторных схемах. На рис. 6N.6
приводится краткое напоминание о такой об-
ратной связи.
Обратная связь с операционными
усилителями
10Операционные усилители делают обратную
связь очевидной, а также используют ее для по-
лучения лучших рабочих характеристик, чем в
схемах с импровизированной обратной связью.
Название операционный усилитель связано с его
7 Журнал IEEE Spectrum, выпуск за декабрь 1977 г.
8 АоЕ § 2.5.1.
9 АоЕ § 2.3.4В.
10 АоЕ § 4.1.1.
6N.4. «Золотые правила» для работы с операционными усилителями
275
"♦I
Без обратной связи
Стабилизированная схема
Повышение тока коллектора увеличивает
напряжение эмиттера Ц, что в свою
очередь снижает напряжение ивэ
Рис. 6N.6. Несколько примеров обратной связи без операционного усилителя
Обратная связь по постоянному току
корректирует напряжение U53, при этом
не препятствуя колебаниям входного
сигнала в окрестности рабочей точки
предполагаемым первоначальным назначени-
ем — выполнением математических операций
в аналоговых компьютерах11.
Операционные усилители обладают очень
большим усилением.. Их коэффициент уси-
ления при разомкнутой цепи обратной связи
огромен. Например, микросхема LF411, кото-
рую мы будем использовать в большинстве на-
ших лабораторных занятий, в таком режиме
имеет коэффициент усиления по постоянному
току равный около 200 000.
Но, как и предлагал Гарольд Блэк, в схемах на
операционных усилителях преднамеренно сбра-
сывают большую часть этого усиления, чтобы
улучшить другие рабочие характеристики.
6N.4. «Золотые правила» для
работы с операционными
усилителями
Подобно тому, как мы начали изучать биполяр-
ные транзисторы с простой модели, которая
11 Похоже, что это название было впервые упомянуто в
1947 г. в докладе, в котором сведения об операционном
усилителе операционных усилителей сформулированы сле-
дующим образом: Термин «операционный усилитель» яв-
ляется общим названием усилителей, обладающих такими
функциями усиления, которые позволяют им выполнять
определенные полезные операции, такие как суммирова-
ние, интегрирование, дифференцирование или комбинация
таких операций. // Рагаззини (Ragazzini), Рэндалл (Randall)
и Рассел (Russell), статья «Анализ проблем в динамике с по-
мощью электронных схем» («Analysis of Problems in Dynamics
by Electronic Circuits»), Доклад Института радиоинженеров
США, 35, май 1947 г., с. 444-452, цитируется в книге «Спра-
вочник по операционным усилителям» («Op Amp Applications
Handbook»), Уолт Джунг (Walt Jung), почетный редактор,
(серия Analog Devices Series, 2007 г.), с. 779.
была достаточной для анализа и разработки
многих схем, так и изучение операционных
усилителей начнем с их простого, идеализиро-
ванного представления, и будем пользоваться
этим представлением даже после знакомства
с более подробной моделью.
Приводимые далее золотые правила (ЗП) яв-
ляются аппроксимациями поведения операци-
онных усилителей12.
ЗП № 1. Выход операционного усилителя
стремится сделать все возможное, чтобы
разность напряжений между двумя входами
оказалась нулевой.
ЗП № 2. Входной ток операционного усили-
теля практически равен нулю.
Прежде чем применять эти правила, сделаем
три замечания.
♦ Слово «стремится» является ключевым. Оно
напоминает нам, разработчикам схем, что
наша обязанность — обеспечить операци-
онному усилителю условия для поддержа-
ния равных напряжений на входах. Если мы
просчитаемся, например, перегрузив схему,
то операционный усилитель перестанет пра-
вильно функционировать.
♦ Мы уверены в том, что вы понимаете, что
входы, которые не потребляют никакого
тока, являются входами сигнала, которые
помечены «+» и «-», а не выводами питания
микросхемы усилителя13.
12 AdE § 4.1.3.
13 Время от времени некоторые студенты, под впечатле-
нием наших похвал операционным усилителям и их вол-
шебным возможностям, не подключают к микросхеме
питание. Затем они ждут с надеждой сверхъестественной
работы схемы и жестоко разочаровываются.
276
б/V. Операционные усилители I
♦ В более общих чертах: эти правила примени-
мы только к схемам на операционных усили-
телях, в которых присутствует отрицатель-
ная обратная связь.
Эти простые правила позволят вам анализиро-
вать множество разных мудреных схем.
6N.5. Применение
операционного усилителя
6N.5.1, Повторитель
На рис. 6N.7 показана, наверное, самая простая
схема, которую можно собрать на операцион-
ном усилителе14. Она может выглядеть баналь-
но, но это самый лучший повторитель, с кото-
рым мы имели дело.
Используя наши «Золотые правила», можно
оценить следующие параметры схемы:
♦ входной импеданс #вх (ЗП №2);
♦ напряжение смещения UCM (ЗП №1). Срав-
ните это напряжение со смещением по по-
стоянному току, которое мы привыкли ви-
деть в повторителе на биполярном транзи-
сторе;
♦ возможно, выходной импеданс Двых?
Вход
Выход
Рис. 6N7. Повторитель на операционном усилителе
6N.5.2. Влияние обратной связи
на выходное сопротивление
повторителя
Вопрос выходного сопротивления Двых являет-
ся более сложным15. «Золотые правила» не за-
трагивают его, но можно предвидеть, что #вых
будет очень низким. Элементом новизны здесь
будет то обстоятельство, что выходное сопро-
тивление определяется не малым выходным
сопротивлением самой микросхемы (которое
в действительности не слишком мало и состав-
ляет примерно 100 Ом). Нет, эта схема (и почти
все другие схемы на операционных усилителях)
имеет очень низкое выходное сопротивление
благодаря обратной связи16.
Перерисуем схему операционного усилителя,
чтобы она была похожа на модель Тевенина:
идеальный источник напряжения, к которому
подключено последовательное сопротивление,
обозначенное, скажем, гвых. Наша модифици-
рованная схема также содержит операционный
усилитель с высоким коэффициентом усиления
без обратной связи. Далее мы проведем мыс-
ленный эксперимент: слегка изменим выходное
напряжение (AU) и понаблюдаем за реакцией
выходного сигнала (рис. 6N.8).
«Выход
ИВ
Общий случай
Частный случай
Рис. 6N.8. Обратная связь снижает выходной импеданс схе-
мы на операционном усилителе
Если попытаться изменить выходное напря-
жение 1/вых, схема «узнает» об этом через об-
ратную связь и чрезвычайно «возмутится».
Усилитель с большим коэффициентом усиления
отреагирует броском тока, пытаясь противо-
действовать смещению выходного сигнала от-
носительно уровня, на котором операционный
усилитель «хочет его видеть». Пока мы оставим
этот спор на этом качественном уровне и будем
считать выходной импеданс «очень низким».
Позже (в основном в главе 9N) мы сможем ко-
личественно оценить влияние обратной связи,
чтобы получить значения выходного импеданса
14 АоЕ§ 4.2.3.
15 АоЕ § 2.5.3С.
16 Единственным исключением из этого правила являет-
ся источник тока на операционном усилителе, выходной
импеданс которого должен быть высоким. (Как мы знаем,
идеальный источник тока должен иметь бесконечно боль-
шой выходной импеданс Двых.)
бЛ/.б. Усилители двух типов
277
6N.6. Усилители двух типов
6N.6.1. Неинвертирующий усилитель
Эта схема более интересна, чем повторитель17,
поскольку она обеспечивает усиление напря-
и,
гди«*
Выход
Усиление = ?
ИВ
Общий случай
Частный случай
Рис. 6N.9. Обратная связь снижает выходной импеданс схе-
мы на операционном усилителе
Очевидно, что при подаче на вход сигнала
уровнем 1 В, чтобы удовлетворять «золотым
правилам», операционный усилитель должен
повысить уровень выходного сигнала до 11 В.
Обобщая, можно заметить, что усиление об-
ратно пропорционально доле выходного сиг-
нала, подаваемой обратно на вход. Поскольку
обратно на вход подается 1/11 выходного сиг-
нала, то коэффициент усиления равен 11. Но
обычно коэффициент усиления записывают
в более простом виде:
Некоторые студенты склонны забывать это на-
доедливое слагаемое «1 +», но мы надеемся, что
вы не из их числа. Но, конечно же, иногда це-
лесообразно забыть о нем, т. е. забыть в смыс-
ле игнорировать: когда отношение Щ/^ очень
17 АоЕ § 4.2.2.
18 Кстати, именно этот тип схемы интересовал Гарольда
Блэка. Он занимался вопросом создания ретрансляцион-
ного усилителя для телефонной компании, чтобы передать
речевые сигналы на большие расстояния. Именно необхо-
димость передачи сигнала через множество каскадов (не-
сколько сотен для передачи сигнала, другой конец страны)
заставила телефонную компанию заинтересоваться про-
блемой искажений в усилителях. Небольшое искажение
в одном или двух каскадах может оказаться катастрофиче-
ским при сотнях каскадов.
Интересный исторический факт - телефонная компания,
которую часто рассматривают как обычное предприятие
по предоставлению коммунальных услуг, постоянно была
на переднем крае инноваций: не только изобретение Га-
рольда Блэка, но также биполярный и полевой транзисто-
ры, передача сигналов по волоконно-оптической линии
были разработаны, по большому счету, в той же телефон-
ной компании в составе знаменитой Лаборатории Белла.
большое. Но так можно делать только тогда,
когда ясно, что влияние этого слагаемого на
конечный результат ничтожно.
6N.6.2. Сомнения в справедливости
«золотых правил»
Предположим, что какой-либо особо скептиче-
ски настроенный студент хочет воспользоваться
своей осведомленностью о том, что операцион-
ный усилитель представляет собой просто диф-
ференциальный усилитель с подключенной к
нему другой схемой, знакомой ему из второго
лабораторного занятия. Такой студент может
выразить сомнение в справедливости «золотых
правил». В частности, он не верит, что опера-
ционный усилитель представляет собой всего
лишь небольшой треугольник, работа которого
основана на чистом волшебстве.
Поэтому он может возразить, что наш ана-
лиз на основе «золотых правил» должен быть
ошибочным, поскольку он не согласуется с
пониманием дифференциального усилите-
ля, который является основной схемой любо-
го операционного усилителя. Наши «золотые
правила» (ЗП) предсказывают, что ишх = 11 В.
Но если ЗП № 1 утверждает, что выход опера-
ционного усилителя устанавливает на его вхо-
дах сигналы одинакового уровня, тогда — ага!
Оказывается, что наш анализ содержит проти-
воречие! Напряжения одинакового уровня на
входах дифференциального усилителя не могут
создать 11 В на его выходе, поэтому ЗП № 1 не
соответствует истине.
Однако это неверный аргумент; не попадитесь
на него. Кажущееся противоречие можно разре-
шить, просто признав, что наши «золотые пра-
вила» являются лишь приближениями. Уровни
на входах операционного усилителя не абсолют-
но одинаковые, а почти одинаковые. До какой
степени почти одинаковые? Лишь настолько
одинаковые, чтобы наша модель дифференци-
ального усилителя могла работать. Чтобы вы-
ходной сигнал был 11 В, разница между вход-
ными сигналами (£/дифф на рис. 6N.9) должна
быть не О В, а ивых/КУЪ0С, где £УБ0С обозначает
коэффициент усиления операционного усили-
теля без обратной связи. Для операционного
усилителя на микросхеме 411 в режиме покоя
это означает [7ДИФФ » 11 В/200000 = 50 мкВ. Не
совсем нулевое, но достаточно близкое к нему.
278
6N. Операционные усилители I
Этот численный расчет поможет вам оценить
полезность наличия избыточного усиления,
которое можно уменьшить: чем выше усиле-
ние без обратной связи, тем ближе к истине
приближения «золотых правил». Например,
при Ку Б0С = 1 000 000 (которым обладают мно-
гие операционные усилители высшего класса)
[7ДИФФ в только что рассмотренном примере
уменьшится до 10 мкВ.
Вход
ЮкОм
Усиление = ? 0 В -
(Виртуальная «земля»)
-10 В
Инвертирующий усилитель Частный случай
общий случай
Рис. 6N.10. Инвертирующий усилитель
6N.63. Некоторые характеристики
неинвертирующего операционного
усилителя
Рекомендуем обратить внимание на две харак-
теристики операционного усилителя, хотя, воз-
можно, они кажутся вам очевидными.
♦ Входной импеданс RBX — огромный, как и
у повторителя.
♦ Выходной импеданс 2?вых — очень низкий,
как и у повторителя19.
Кстати, можно заметить, что повторитель мож-
но рассматривать, как особый случай неинвер-
тирующего усилителя. Каким будет номинал
его ft20?
6N.7. Инвертирующий
усилитель
Схема на рис. 6N.13 также является усилите-
лем21. Она отличается от неинвертирующего
усилителя в одном очевидном отношении —
она инвертирует сигнал. Есть еще несколько не
столь очевидных отличий.
Согласно ЗП № 1 напряжение на инвертирую-
щем входе должно быть равным нулю. На осно-
вании этого мы можем разобраться со свой-
ствами схемы.
19 Мы увидим далее, когда будем рассматривать эффекты
обратной связи количественно, что в обмен на усиление
схема отдает очень малую толику своих достоинств по им-
педансу. Но все равно, эта лишь незначительная корректи-
ровка утверждения, что как усилитель, так и повторитель
обладают хорошими входными и выходными импеданса-
ми. Зависимость импедансов схемы на В (часть выходного
сигнала, который подается обратно на вход) рассматрива-
ется в разделах 2.5.3В и 2.5.3С книги АоЕ. Мы вернемся
к этой теме в главе 9.
20 Повторитель имеет бесконечно большое значение Rv по-
этому его коэффициент усиления приближается к единице.
21 АоЕ § 4.2.1.
Усиление
Рассмотрим частный случай: сигнал напряже-
нием 1 В вызывает протекание тока величиной
1 мА по направлению к инвертирующему входу.
Куда идет этот ток? ЗП № 2 запрещает его вход
в операционный усилитель, поэтому он должен
идти в обход — через резистор обратной связи
номиналом 10 кОм, и по пути вызывает паде-
ние напряжения величиной 10 В. Таким обра-
зом, выходное напряжение [7ВЫХ = 10 В.
Обобщенное выражение коэффициента усиле-
ния для этой схемы не содержит члена «1 +», это
просто Ку = - #2/Дг Подобно усилителю с общим
эмиттером знак минус означает инвертирование
входного сигнала: выходной сигнал сдвинут по
фазе относительно входного на 180°.
Если вы не возражаете против примитивной
модели этой схемы, основанной на ее внешнем
виде и фиксированном потенциале виртуаль-
ной земли на инвертирующем входе, попро-
буйте представить себе детские качели. Схема
«вращается» на оси виртуальной земли. Если
обе стороны качелей одинаковой длины, то
схема сбалансирована с одинаковыми напря-
жениями: ее коэффициент усиления равен -1.
Но если одна из сторон длиннее другой в 10 раз,
как на рис. 6N.10, размах этой длинной сторо-
ны в 10 раз больше, чем короткой. И так далее
в том же духе.
Входной и выходной импедансы
Теперь давайте рассмотрим входной импеданс
инвертирующих усилителей на рис. 6N.10. Если
допустить, что напряжение на инвертирующем
входе зафиксировано на уровне 0 В, то можно
сформулировать некоторые особенности этой
схемы.
♦ Входной импеданс RBX. He дайте ввести вас
в заблуждение неправильными ответами:
б/V.Z Инвертирующий усилитель
279
• первый неправильный ответ. Входной им-
педанс громадный, поскольку сигнал по-
дается на вход операционного усилителя,
а согласно ЗП № 2 входы операционного
усилителя не потребляют никакого тока;
• второй неправильный ответ. А нет, что я за-
был, так это то, что низкий импеданс имеет
выход схемы (мы видели это ранее в разде-
ле 6N.6.1). Таким образом, Двх = Rx+ Rr
Почему эти ответы неверные? Мы предоста-
вим вам шанс самим разобраться с этим и да-
дим объяснение в сноске22.
♦ Инвертирующий вход операционного уси-
лителя (обозначенный знаком «-») часто
называют виртуальной «землей». Почему
«виртуальной»23? Эта точка, которую часто
называют «суммирующим соединением»,
оказывается полезной и помогает характе-
ризировать схему.
6N.7.1. Что такое «виртуальная
земля»
Входной импеданс /?вх
Прежде всего виртуальная земля — точка, на-
пряжение в которой зафиксировано на уровне
О В. В результате вопрос входного импеданса
схемы очень упрощается: это просто сопротив-
ление резистора Rr Таким образом, по сравне-
нию с неинвертирующим усилителем инверти-
рующий усилитель обладает не слишком хоро-
шим входным импедансом.
— Не слишком хорошим? — можете возразить
вы. — Но ведь его можно сделать каким угодно
22 В первом ответе перепутаны два разных понятия: вход-
ной импеданс схемы и входной импеданс операционного
усилителя. В данном случае это две разные характери-
стики. Да, ЗП № 2 утверждает, что инвертирующий вход
операционного усилителя не потребляет ток, но никакое
правило не говорит, что вся схема не потребляет тока,
в данном случае через резистор Rv Ток может протекать
в обход операционного усилителя: через резистор R2 на
выход операционного усилителя. Это, конечно же, дей-
ствительный путь протекания входного тока. А во втором
ответе игнорируется тот факт, что напряжение на инверти-
рующем входе зафиксировано обратной связью на уровне
нуля, поэтому резистор R2 в большой степени невидим со
стороны входа схемы.
23 Потому, что он ведет себя как обычная (настоящая) зем-
ля. В частности, ток, втекающий в виртуальную землю, не
исчезает, а течет куда-то дальше (в обход операционного
усилителя по пути обратной связи), где он остается до-
ступным для измерения.
большим, просто задав желаемое значение ре-
зистора Rv Например, 10 МОм или, при жела-
нии, все 100 МОм. — К сожалению, нет. Такое
предположение имеет смысл только на на-
чальном этапе рассмотрения операционных
усилителей, когда мы делаем вид, что они об-
ладают идеальными характеристиками. Но как
только мы спустимся с небес на землю (в сле-
дующей главе), нам придется признать, что
с очень большими значениями этого резистора
ситуация начинает выходить из-под контроля.
Таким образом, если считать значение при-
близительно 10 МОм практическим пределам
сопротивления резистора Rv следует признать,
что по величине входного импеданса, инверти-
рующий усилитель не может сравниться с не-
инвертирующим.
А что случится с входным импедансом схемы,
если резистор Rt просто заменить проволочной
перемычкой? Несмотря на то что результирую-
щий входной импеданс #вх~ 0 может вызывать
беспокойство, такое его значение как раз хо-
рошо подойдет для одного класса источников
сигнала — источнику тока. На лабораторном
занятии 6L мы воспользуемся этим обстоятель-
ством, когда будем преобразовывать ток фото-
диода в напряжение.
Суммирующая схема
Тот факт, что напряжение на виртуальной «зем-
ле» зафиксировано, позволят вводить в эту
точку несколько разных токов, не создавая
никакого взаимодействия между сигналами,
в результате чего они суммируются24. Слева на
рис. 6N.11 изображена схема пассивного сум-
матора. Эта схема хуже, чем схема на операци-
онном усилителе справа, поскольку сигнал на
любом из входов слегка влияет на любой дру-
гой входа.
1кОм
1кОм
Выход
Пассивный сумматор Активный сумматор
Рис. 6N.11. Схемы сумматоров двух разных типов
24 AoE§4.3.1D.
280
6N. Операционные усилители I
На лабораторном занятии мы соберем раз-
новидность этой схемы на операционном уси-
лителе. В частности, в ней мы с помощью по-
тенциометра будем регулировать смещение
постоянной составляющей выходного сигнала
операционного усилителя. Схемы на рис. 6N.13
формируют на выходе двоично-взвешенную
сумму входных сигналов25. В принципе это
один из способов создания цифроаналогово-
го преобразователя (ЦАП), но он очень редко
встречается на практике.
Еще один сумматор
Обязательно ли использовать в сумматоре опе-
рационный усилитель в инвертирующем вклю-
чении? Нет, но схемы с неинвертирующим уси-
лителем сложнее и трудно масштабируются к
более чем двум входам. Является ли выходной
сигнал схемы на рис. 6N.12 суммой напряже-
ний UA и UB?
Рис. 6N.12. Суммирующая схема или нет?
Это почти суммирующая схема. Ее выходной
сигнал будет средним, а не суммой входных
сигналов. Но схема на операционном усилителе
может с легкостью преобразовать его в сумму.
Подумайте, каким коэффициентом усиления
должна обладать такая схема26. Но в отличие
от инвертирующего сумматора, данную схему
нельзя с легкостью расширить до трех, четырех
и больше входов. Поэтому обычно суммирую-
щие схемы собираются на инвертирующей кон-
фигурации.
Интегрирующие, дифференцирующие
и прочие схемы
Как мы увидим далее, виртуальная «земля»
позволяет создать почти идеальный инте-
гратор. Опять же, ключевым моментом здесь
25 Термин «двоично-взвешенный» означает, что каж-
дый из трех входов схемы можно рассматривать как
двоичную цифру, вес которой вдвое больше веса со-
седней младшей цифры. Таким образом, выходное на-
пряжение схемы справа на рис. 6N.11 будет следующим:
является требование, что точка соединения
резистора R с конденсатором С, потенциал
которой в пассивном варианте схемы должен
быть близким к потенциалу земли, в схеме на
операционном усилителе должен жестко под-
держивается на уровне потенциала земли27
(pnc.6N.13).
Рис. 6N.13. Интегратор на операционном усилителе почти
идеально решает задачу, а пассивная схема — лишь прибли-
женно
Дифференциатор на операционном усилителе
тоже обладает лучшими свойствами, хотя в дан-
ном случае улучшение не такое впечатляющее,
и есть одна тонкость, рассмотрение которой
мы с удовольствием отложим на будущее: бес-
покойство о стабильной работе схемы. Схемы
дифференциатора и интегратора подробно рас-
сматриваются в главе 7.
6N.8. Когда применимы
«золотые правила»?
Теперь, применив «золотые правила» несколь-
ко раз, мы готовы признать, что в некоторых
случаях они неприменимы
28
Несколько простых примеров
На рис. 6N.14 изображены три схемы на опе-
рационных усилителях. Можете ли вы сказать,
применимы ли вообще наши «золотые прави-
ла» для данных схем? Этот вопрос может пока-
заться вам глупым: вполне очевидно, что схема
слева не попадает под действие «золотых пра-
вил», поскольку это просто усилитель с боль-
шим коэффициентом усиления без обратной
связи. К схеме посередине правила применимы,
а к схеме справа — нет, потому что у нее обрат-
ная связь не того типа: положительная.
Правильный ответ — 2.
27 Ну, хорошо, очень близко к потенциалу земли. В сле-
дующий раз мы увидим, что отклонения от идеала не из-
бежать.
28 АоЕ § 4.2.7.
6N.8. Когда применимы «золотые правила»?
281
Bxo5
Вход
Правила
применимы?
а
Правила
применимы?
б
Правила
применимы?
в
Рис. 6N.14. Применимы ли «золотые правила» к этим схемам?
Обобщая эти примеры, можно видеть, что «зо-
лотые правила» неприменимы автоматически
ко всем типам схем на операционных усилите-
лях. Они применимы к схемам, которые одно-
временно удовлетворяют трем перечисленным
далее условиям:
♦ используют обратную связь;
♦ вид этой обратной связи отрицательный;
♦ выход схемы поддерживается в активном
диапазоне напряжений (не позволяйте вы-
ходу операционного усилителя подняться до
граничного уровня, что введет его в режим
насыщения).
Более хитрые случаи
Будет ли успешной попытка операционного
усилителя поддерживать одинаковые напряже-
ния на входах в схемах на рис. 6N.15? Нет. Но
если изменить полярность сигнала, подаваемо-
го на каждую схему, тогда да. В следующей гла-
ве мы возвратимся к рассмотрению таких схем
с условной обратной связью.
+1В
Выход
Вход
Источник тока
Схема слева на рис. 6N.16 прямолинейна, но
обычно не обладает удовлетворительными
рабочими характеристиками29. Прежде всего
ее нагрузка находится в неопределенном со-
стоянии, поскольку ни один из ее выводов не
подключен ни к «земле», ни к источнику пита-
ния. Кроме того, весь ток нагрузки должен по-
ступать от самого операционного усилителя,
а в обычном случае предельное значение тока
составляет ± 25 мА.
Рис. 6N.15. Применимы ли «золотые правила» к этим схемам?
Рис. 6N.16. Схемы источника тока на операционном усили-
теле
Схема справа на рис. 5N.15 лучше левой. Она
хорошо иллюстрирует способность опера-
ционного усилителя сделать помещенное в
цепь обратной связи устройство таким, будто
бы оно идеальное. В данном случае опера-
ционный усилитель скрывает варьирование
напряжения [7БЭ, вызываемые изменением
температуры и/или тока, а также крутизну
кривой зависимости тока коллектора JK от
напряжения [/кэ.
Примечание
Эта крутизна разоблачает тот факт, что транзистор
не является идеальным источником тока. Данное
несовершенство описывается эффектом Эрли, ко-
торый мы рассматривали в разделе 5S.2.
6N.8.1. Улучшенные варианты
старых схем
Почти все схемы на операционных усилителях,
которые мы будем рассматривать дальше, де-
лают то же самое, что и ранее рассмотренные
схемы (без обратной связи), но они функцио-
нируют лучше. Это относится ко всем схемам
на операционных усилителях, с которыми мы
будем работать на лабораторном занятии для
этой главы. Рассмотрим вкратце несколько по-
добных схем: источник тока, сумматор, повто-
ритель и преобразователь «ток-напряжение».
Начинаете ли вы понимать, как операционный
усилитель может осуществлять все свое вол-
шебство? Поначалу даже не верится в его воз-
можности, и требуется некоторое время, чтобы
привыкнуть ко всем этим чудесам.
Повторители
На рис. 6N.17 изображены одна схема эмиттер-
ного повторителя на биполярном транзисторе
29 АоЕ § 4.2.5.
282
6N. Операционные усилители I
Пр
иход
Активная схема
Схема без обратной связи
(смещение не показано)
Активная
сильноточная
схема
Активная схема
с двухтактным
выходным каскадом
Рис. 6N.17. Повторители на биполярном транзисторе и операционных усилителях
Фотометр
Идеальный амперметр
(ал. вопрос в тексте)
Гальванометр
Пассивная
схема Активная схема
Рис. 6N.18. Два способа применения преобразователя «ток-напряжение»: фотометр (слева) и идеальный амперметр (справа)
и три схемы повторителей на операционных
усилителях
-30
В каких отношениях схемы повторителей на
операционных усилителях лучше варианта на
биполярном транзисторе? Очевидно, что в схе-
мах на операционных усилителях компенсиру-
ется досадное падение напряжения величиной
0,6 В на диоде (переходе «база-эмиттер» бипо-
лярного транзистора). Более тонкой разницей,
не столь очевидной, является то, что схемы на
операционных усилителях обладают намного
лучшим выходным импедансом. А что вы мо-
жете сказать о входном импедансе31?
Преобразователь «ток-напряжение»
На рис. 6N.18 показаны две схемы усилителя с
выходным напряжением, пропорциональным
входному току, выполненные на операционном
усилителе.
Попробуйте разгадать следующую загадку.
Если мы можем так легко создать «идеальный»
амперметр, почему те мультиметры, которы-
ми мы пользуемся, не работают по такому же
принципу? Или мы настолько умнее всех дру-
гих разработчиков32?
30 АоЕ§4.3.1Е.
31 Здесь схемы на операционных усилителях также выиг-
рывают. Вспомните «золотое правило» № 2.
32 Немного размышлений касательно данного вопроса.
Как и в источнике тока на рис. 6N.16 почти весь входной
6N.9. Необычные элементы,
которые можно поместить
в цепь обратной связи
Повторитель с двухтактным выходным кас-
кадом, примеры которого изображены на
рис. 6N.16 и 6N.20, показывает, как операцион-
ный усилитель может справиться со странно-
стями схемных элементов наподобие биполяр-
ных транзисторов или диодов, и скомпенсиро-
вать эти особенности.
6N.9.1. Общие понятия
На рис. 6N.19 приведена занимательная схема,
иллюстрирующая два отдельных типа схем на
операционных усилителях, с которыми мы бу-
дем иметь дело.
Прячем «собаку»
Иногда вместо того, чтобы рассматривать вы-
ход операционного усилителя как выход схемы
(создавая, таким образом, инверсию подавае-
мого обратно на вход сигнала, как это делает-
ся, например, в наших усилителях напряжения
на операционных усилителях), мы используем
ток проходит через операционный усилитель, поэтому
максимальный ток будет невелик, и батареи питания схе-
мы надолго не хватит.
6N.9. Необычные элементы, которые можно поместить в цепь обратной связи
283
Странные вещи
Входной
сигнал (обычный)
Выходной сигнал (странный)
Входной
сигнал (обычный)
А иногда выходной сигнал бывает таким.
Мы пытаемся спрятать «собаку».
Иногда выходной сигнал бывает таким.
Нам нравится его необычность,
(представлена на рисунке в виде собаки1)
Рис. 6N.19. Операционные усилители могут «окультурить» странные вещи в цепи обратной связи
операционный усилитель, чтобы, образно го-
воря, спрятать «собаку». Один из таких слу-
чаев — повторитель с двухтактным выходным
каскадом. Необычность функции преобразова-
ния неизолированного двухтактного каскада не
представляет ни интереса, ни пользы, а являет-
ся дефектом, который мы с радостью устраним.
Подобный прием используется в активных вы-
прямителях, чтобы скомпенсировать падение
напряжения на диодах.
Можно прийти в изумление, наблюдая впервые,
как операционный усилитель покорно создает
на входе двухтактного каскада сигнал любой
причудливой формы, необходимый для того,
чтобы уменьшить искажения. Посмотрите, вы-
зовут ли такой эффект его действия у вас. На
рис. 6N.21 и 6N.22 приведены несколько осцил-
лограмм этого процесса.
Две формы переходных искажений
На рис. 6N.20 изображена схема, которую мы
специально подобрали, чтобы продемонстри-
ровать «смышленость» операционного усили-
теля, переключая цепь обратной связи между
двумя разными точками. Точка-«глупышка»
на выходе операционного усилителя создает
чистый синусоидальный сигнал не в том месте,
одновременно создавая на выходе схемы ужас-
ные переходные искажения. А точка-«умница»
формирует чистый синусоидальный сигнал
там, где он нам требуется.
Выбор пути
обратной связи
Рис. 6N.20. Схема для демонстрации способности операци-
онного усилителя устранить переходные искажения
Рассмотрим, как эта схема справляется с дву-
мя типами переходных искажений. Слева на
рис. 6N.21 приведена осциллограмма переход-
ных искажений «ступенька» при резистивной
нагрузке. Эту ситуацию можно называть клас-
сическим переходным искажением. А справа на
рис. 6N.21 изображена осциллограмма, когда
нагрузкой является динамик с сопротивлением
Входной сигнал
(изображение уменьшено:
2 В/деление)
Сигнал на выходе
операционного усилителя
Сигнал на выходе схемы
Резистивная нагрузка Нагрузка в виде динамика
(классические переходные искажения) (причудливые переходные искажения)
Рис. 6N.21. Две формы переходных искажений: при резистивной нагрузке (классические) и при нагрузке в виде динамика
(необычные)
284
6N. Операционные усилители I
Входной сигнал
Выход
операционного усилителя f
Выход схемы
Резистивная нагрузка (классические
переходные искажения)
Нагрузка в виде динамика
(причудливые переходные искажения)
Рис. 6N.22. Операционный усилитель устраняет переходные искажения, создавая инверсию функции преобразования пере-
ходных искажений
катушки 8 Ом, индуктивность которой создает
более причудливые искажения.
Устранение переходных искажений
с помощью операционного усилителя
Способен ли наш хваленый операционный
усилитель устранить искажения, вносимые в
выходной сигнал двухтактным каскадом при
резистивной нагрузке, которые выглядят еще
причудливей при индуктивной нагрузке в виде
динамика? Вряд ли он «интеллектуален» до та-
кой степени.
А вот и да, смышленый (по крайней мере, на
умеренных частотах): он создает точно такой
сигнал, который требуется, чтобы получить чи-
стый выходной сигнал. На рис. 6N.22 показан
результат «очистки» выходного сигнала опера-
ционным усилителем.
Внимание!
Обратите внимание на то, что входной сигнал по-
казан при четырехкратном понижении усиления
осциллографа по сравнению с выходным сигналом.
Любуемся «собакой»
Как упоминается в комментарии к рис. 6N.19,
мы хотим использовать выходной сигнал опе-
рационного усилителя, а также рассматривать
его как выходной сигнал схемы33. В таких слу-
чаях в цепь обратной связи помещают элемен-
ты с необычными свойствами для того, чтобы
заставить операционный усилитель создать их
инверсию.
Но элементы в цепи обратной связи не обя-
зательно должны быть в действительности
странными. Например, мы можем вставить
простой делитель напряжения, отправляющий
назад 1/11 выходного сигнала, тогда уровень
выходного сигнала 1/вых будет 10 • [/вх.
Но рассмотрим два более экзотических случая,
в которых необычный сигнал, вызываемый
«странными элементами» в цепи обратной свя-
зи, оказывается полезным (рис. 6N.23). Схема
слева с диодом в цепи обратной связи может
выглядеть как выпрямитель. Но рассмотрим,
что она делает с входным напряжением, кото-
рое всегда отрицательное.
Виход
33 АоЕ§4.3.1Е.
Схема возведения
в квадрат
Рис. 6N.23. Два примера, в которых в цепь обратной связи
вставляется необычный элемент, чтобы получить интерес-
ный выходной сигнал операционного усилителя
В схеме, изображенной слева, при отрицатель-
ном уровне входного сигнала выходное напря-
жение 1/вых будет пропорционально логарифму
входного напряжения 1ГВХ. А в схеме справа при
положительном уровне входного сигнала вы-
ходное напряжение будет квадратом входного.
При обратной полярности входного напряже-
ния обе эти схемы теряют работоспособность,
на что мы и намекали, когда показали эти схе-
мы первый раз на рис. 6N.15.
На лабораторном занятии 6L мы немного по-
экспериментируем и вставим в цепь обрат-
ной связи сам осциллограф, как показано на
рис. 6N.24. Это немного нестандартная опера-
ция, но зато весьма увлекательная.
6N.10. Материал для чтения в АоЕ
285
отранзистор
Осциллограф
Усилитель
Напряжение, зависящее
от координаты (от яркости)
Преобразование яркости
в напряжение
Рис. 6N.24. Осциллограф в цепи обратной связи сам корректирует положение луча развертки
В этой главе мы увидели и далее еще увидим
много хитроумных схем, а вскоре вы и сами
будете изобретать такие схемы. Операционные
усилители обеспечивают нам широкие возмож-
ности для этого. В справочных листках на свои
компоненты производители микросхем приво-
дят примеры их использования. Например, в
приложении по применению справочного лист-
ка компании Texas Instruments приводится око-
ло 30 страниц схем (перепечатанных с прило-
жения по применению № 31 компании National
Semiconductor). Данный справочный материал
можно загрузить по адресу http://www.ti.com/
ww/en/bobpease/assets/AN-31.pdf. А в при-
ложении по применению № 6 компании Linear
Technology собраны рекомендации по примене-
нию операционных усилителей покойного мэ-
тра аналоговой электроники Джима Уильямса
0im Williams). Данный справочный материал
можно загрузить по адресу http://cds.linear.
com/docs/en/application-note/an6.pdf.
6N.10. Материал для чтения
в АоЕ
♦ Глава 2. Введение в отрицательную обратную
связь: раздел 2.5.
♦ Глава 4. Разделы 4.1-4.2.
6L Лабораторное занятие:
операционные усилители I
6L1. Предварительные
сведения
Корпус Mini-DIP
На предыдущем лабораторном занятии мы по-
знакомились с корпусом DIP1. На рис. 6L.1
изображен уменьшенный вариант такого кор-
пуса: Mini-DIP с восемью выводами. Данный
корпус используется в микросхемах операци-
онных усилителей, с которыми мы будем ра-
ботать на этом и последующих лабораторных
занятиях.
Цоколевка, изображенная справа на рис. 6L.1,
была принята для операционных усилителей
даже до появления классической микросхемы
LM7412 и является стандартной для микросхем
с одним операционным усилителем в корпусе
этого типа. Микросхема операционного усили-
теля 741 и более новая LT1150, с которыми мы
будем работать на лабораторном занятии 7L,
также имеют аналогичную цоколевку. Такая
стандартизация очень удобна для всех пользо-
вателей. К сожалению, с уменьшением разме-
ров электронных деталей компоненты в корпу-
се DIP встречаются все реже, и многие новые
разработки выпускаются только в корпусах для
поверхностного монтажа.
Питание
Необходимость питания может показаться
само собой разумеющейся, но иногда это нуж-
но оговаривать: для операционного усилителя
всегда требуется напряжение питания, кото-
рое подается на два его вывода. В нашем кур-
се почти всегда используется питание ±15 В.
Необходимость в этом напоминании вызвана
тем обстоятельством, что на принципиальных
схемах подключение питания микросхем обыч-
но не указывают. С другой стороны, во многих
схемах операционных усилителей отсутству-
ет непосредственное соединение микросхемы
с «землей». Но пусть это вас не смущает: под-
ключение к «земле» в смысле общего опорного
нулевого потенциала всегда присутствует.
Микросхема вставляется в гнезда,
. расположенные с разных сторон
а и п а относительно центральной
D п о а
opddDodq выемки макетной платы
опааааоо
а а л л д л а а
О О ТППГТГ о D
0OOQOQQO
D 0 0 0 00 О О
О QQDQQO О
Нумерация выводов
(корпус Mini-DIP)
а р о о а п
а д д и л а
О
D
о о о а о а
Рис. 6L.1. Внешний вид и нумерация выводов микросхемы LF411 в корпусе Mini-DIP (посередине), ее цоколевка (справа) и
установка на макетную плату (слева)
1 Англ.: Dual In-line Package — корпус с двухрядным рас-
положением выводов.
2 Эта цоколевка появилась впервые еще в 1965 г. у микро-
схемы [х709 компании Fairchild.
Развязка питания
Всегда следует выполнять развязку источников
питания, используя керамический конденсатор
613. Вводим обратную связь, получаем повторитель
287
небольшой емкости (0,01-0,1 мкФ), как упо-
миналось на лабораторном занятии 4L и как
демонстрируется на рис. 6L.2. Если выходной
сигнал содержит пульсации, проверьте, не за-
были ли вы выполнить развязку источника
питания. Большинство студентов рассматри-
вают развязку как что-то необязательное,
пока не встретятся с пульсациями. Схемы
операционных усилителей, которые всег-
да содержат цепь обратной связи, особенно
уязвимы к таким паразитным колебаниям.
Их чувствительность к этому типу искаже-
ний еще ббльшая, чем у транзисторных схем
(см. предупреждение по этому вопросу в гла-
ве Щ.
LF411
+15
Керамический конденсатор
емкостью 0,01-0,1 мкФ
=■ устанавливается как можно ближе
к операционному усилителю
Рис. 6L.2. Всегда осуществляйте развязку источников пита-
ния. В противном случае сигналы вашей схемы могут содер-
жать пульсации (паразитные колебания)
6L2. Экспериментальная
схема с операционным
усилителем без обратной
связи
Поразвлекайтесь немного, наблюдая за уров-
нем выходного сигнала схемы, изображенной
на рис. 6L.3. Медленно проворачивая ручку
потенциометра, постарайтесь подать на вход
усилителя нулевое напряжение. Соответствует
ли наблюдаемое вами поведение заявленной
производителем характеристике микросхемы
LF411 «Усиление (типичное) = 200 В/мВ»3?
Но не экспериментируйте слишком долго, по-
скольку это ненормальный способ включения
операционного усилителя. Лучше будем дви-
гаться далее, к более полезным схемам.
Выход
г
-15
Рис 6L.3. Включение операционного усилителя без обрат-
ной связи
6L.3. Вводим обратную
связь, получаем
повторитель
Соберите повторитель на микросхеме LF411,
принципиальная схема которого приведена на
рис. 6L.4. Исследуйте его свойства. В частно-
сти, измерьте (если это удастся) его входной и
выходной импедансы (ZBX и ZBWX), как писано
далее.
Вход
Выход
Рис. 6L4. Повторитель на операционном усилителе
6L3.1. Входной импеданс
Попробуйте измерить входной импеданс схемы
на частоте 1 кГц, подключив на вход последова-
тельный резистор номиналом 1 МОм. Будьте на-
чеку относительно следующих двух трудностей:
♦ не доверяйте результату 10 МОм4;
♦ входной импеданс RBX настолько велик, что в
нем преобладает влияние Свх. Значение Свх
можно вычислить, определив частоту /3яБ.
Опять же, смотрите, чтобы результат не был
искажен влиянием импеданса щупа осцил-
лографа (сбить вас с толку на этот раз может
емкость щупа).
6L3.2. Выходной импеданс
Можно сразу же сказать, что выходной импе-
данс повторителя будет «низким». Настолько
Англ. Gain (typical) = 200 V/mV. - Примеч. пер.
4 Обмануться таким образом очень легко, поскольку это
первая встретившаяся нам схема, входной импеданс кото-
рой намного больше, чем входной импеданс осциллографа
со щупом, который составляет 10 МОм.
288
6L Лабораторное занятие: операционные усилители I
низкий, что измерить его довольно трудно.
Поэтому вместо непосредственного измерения
попытайтесь убедиться, что такой низкий вы-
ходной импеданс создается благодаря обрат-
ной связи.
Сделать это можно следующим образом: под-
ключите на выход повторителя последователь-
ный резистор номиналом 1 кОм. Предположите,
что этот резистор является частью повторителя,
и снимите показания выходного напряжения
ишх как с подключенной нагрузкой, так и без
нее. Это наш обычный способ определения вы-
ходного импеданса. Никаких сюрпризов здесь
не предвидится: выходной импеданс #вых дол-
жен быть равен 1 кОм.
Теперь переместите точку снятия сигнала об-
ратной связи с вывода резистора, подключен-
ного к выходу операционного усилителя, на
его противоположный вывод, как показано на
рис. 6L.5. Каким будет новый выходной импе-
данс 1?вых? Объясните полученный результат.
(Объяснение этого результата дано в главе
6N.)
Обратная связь № 1
Обратная связь № 2
Рис. 6L.5. Измерение выходного импеданса /?ВЬ|Х и влияние
обратной связи на его значение
Если вы действительно не боитесь трудностей,
то можете попробовать измерить выходной
импеданс повторителя без подключения на его
выход последовательного резистора. Обратите
внимание на то, что разделительный конденса-
тор не потребуется. Можете объяснить, поче-
му нет5? Скорее всего опыт у вас не получится:
самое большее, что вам удастся сделать, — это
подтвердить, что значение выходного импедан-
са действительно очень низкое.
Не впадите в заблуждение, приняв влияние
ограниченного выходного тока операционно-
го усилителя за низкий выходной импеданс.
Чтобы не превысить предельный ток, амплиту-
ду сигнала нужно будет поддерживать довольно
малой. Это демонстрируется графически кри-
выми зависимости тока от напряжения на
рис. 6L.6.
+10 +20 +30
Выходной ток —
Рис. 6L.6. Влияние ограниченного выходного тока операци-
онного усилителя (LF411)
Из рис. 6L.6 можно четко увидеть, что в диа-
пазоне выходного напряжения ±10 В ток огра-
ничен величиной ±25 мА, а когда выходное на-
пряжение приближается к одному или другому
напряжению питания, ток уменьшается. Это
ограничение тока является полезным механиз-
мом самозащиты, встроенным в операционный
усилитель, о наличии которого следует знать.
6L.4. Неинвертирующий
усилитель
Соберите неинвертирующий усилитель, прин-
ципиальная схема которого приведена на
рис. 6L.7. Схема очень похожа на повторитель,
но теперь мы заставляем операционный уси-
литель выдавать выходной сигнал большей
амплитуды, чем входной. Можете сказать, на-
сколько большей6?
Вход
Выход
1 кОм
Рис. 6L.7. Неинвертирующий усилитель
Каков максимальный размах выходного сиг-
нала? А что можно сказать о его линейности
5 Поскольку нет постоянного напряжения, которое нуж-
но блокировать.
6 Амплитуда выходного сигнала будет равна 1ГВЫХ = 11 х иъх,
1/11 отбирается на обратную связь. Вы уже встречались с
этим в схеме из лабораторного занятия 5L, не так ли?
6L6. Суммирующий усилитель
289
(попробуйте подать на вход треугольный сиг-
нал)? Также подайте синусоидальный входной
сигнал с разными частотами. Обратите внимание
на то, что на определенной довольно высокой
частоте усилитель перестает .правильно функ-
ционировать: входной синусоидальный сигнал
не дает соответствующего выходного сигнала.
Сегодня мы не будем ставить вам задание дать
количественную оценку этим эффектам, а про-
сто хотим, чтобы вы имели в виду, что на высо-
ких частотах операционный усилитель начина-
ет терять свои достоинства. На лабораторном
занятии 7L мы посвятим некоторое время из-
мерению скорости нарастания выходного на-
пряжения, которая накладывает ограничение
на величину размаха выходного сигнала на
определенной частоте.
Снова измерять входной и выходной импе-
дансы нет надобности. Позже мы узнаем, что
пожертвовали некоторыми другими достоин-
ствами в обмен на повышенное усиление по на-
пряжению; тем не менее характеристики этого
усилителя остаются довольно впечатляющими.
Подайте на вход усилителя синусоидальный
сигнал с частотой 1 кГц. Какое получается уси-
ление? Сравните с неинвертирующим усилите-
лем из предыдущего раздела.
Снова подайте на вход усилителя синусо-
идальный сигнал с частотой 1 кГц. Добавьте
в схему резистор номиналом 1 кОм, вклю-
ченный последовательно с входом усилите-
ля (моделируя источник сигнала с плохим
выходным импедансом), и измерьте вход-
ной импеданс усилителя. На этот раз у вас не
должно возникнуть никаких проблем с этим
измерением. Если предположить, что сопро-
тивление величиной 1 кОм, включенное по-
следовательно с источником сигнала, опреде-
ляет выходной импеданс этого источника, то
каким же будет усиление инвертирующего
усилителя для такого источника7? Чтобы ре-
шить проблему плохого выходного импеданса
источника сигнала, воспользуйтесь собран-
ной ранее схемой повторителя. С ее помо-
щью общее усиление нашего инвертирующего
усилителя должно принять первоначальное
значение (-10).
6L5. Инвертирующий
усилитель
Соберите инвертирующий усилитель, прин-
ципиальная схема которого приведена на
рис. 6L.8. Проявив немного смекалки, можно
догадаться, что схему не нужно собирать за-
ново, а можно воспользоваться предыдущей
схемой неинвертирующего усилителя, просто
изменив подключение выводов: на отрицатель-
ный (инвертирующий) вывод будет подаваться
сигнал, а положительный будет заземленным.
6L6. Суммирующий
усилитель
Слегка модифицируйте инвертирующий уси-
литель, чтобы получить схему, изображенную
на рис. 6L.9. Эта схема суммирует определен-
ный уровень постоянного напряжения с на-
пряжением входного сигнала. В результате в
сигнал можно добавлять смещение постоянной
составляющей. Подумайте, можно ли создать
другие схемы на операционном усилителе для
выполнения аналогичной задачи8?
Источник сигнала с большим £ВЬ1Х
ЮкОм
1 кОм
\
Вход
Выход
Рис. 6L.8. Инвертирующий усилитель
Примечание
После завершения работы с этой схемой не раз-
бирайте ее, поскольку она понадобится нам далее
в разделах 6L6 и 6L7.
7 Все правильно: усиление уменьшается до половины сво-
его первоначального значения, поскольку эффективное Яг
в уравнении усиления Ку = - Я/^ удваивается.
8 Можно, но сомнительно, что они будут такими же простыми.
290
6L Лабораторное занятие: операционные усилители I
ЮкОм
ЮкОм
Входной сигнал —Лдд,
-15 В—АМл-+15В
ЮкОм
Смещение
годной сигнал
(Диапазон смещения = ± 10 В
Рис. 6L9. Суммирующий усилитель добавляет в сигнал постоянное напряжение смещения
6L7. Разработка
фазовращателя
с единичным усилением
6L7.1. Фазовращатель I:
использование 1/вх и его инверсии
В схеме на рис. 6L.10 сигнал и его инверсия по-
даются на соединенные последовательно по-
тенциометр Rи конденсатор С9. Варьируя вели-
чину сопротивления потенциометра, выходной
сигнал ILIY можно делать более похожим на
входной сигнал UBX или на его инверсию Е/инв.
Таким образом, фазу выходного сигнала мож-
но регулировать в диапазоне 180°. Пока что все
выглядит просто.
Входной сигнал
Инвертирующий
усилитель
с единичным
усилением
Рис. 6L10. Простой фазовращатель
Выходной
R ^«h сигнал
\ инвертированное
Тонкость и хитроумность этой схемы состоит
в том, что независимо от величины фазового
сдвига, амплитуда выходного сигнала всегда
равна амплитуде входного.
Замечание
Это поведение радикально отличается от поведе-
ния, например, низкочастотного фильтра, величи-
на фазового сдвига которого также может варьи-
роваться в довольно широком диапазоне: от 0°
до почти -90°. Но при изменении фазового сдвига
выходного сигнала фильтра, вызываемого измене-
нием частоты входного сигнала, также меняется и
его амплитуда.
Такой полезный и приятный результат можно
объяснить с помощью векторной диаграммы,
изображенной на рис. 6L.11.
АоЕ § 2.2.8.
и
Рис. 6L.11. Векторная диаграмма для фазовращателя на
рис. 6L10 (взята из книги АоЕ)
Амплитуда сигнала, подаваемого на последова-
тельную цепочку ВС, равна 2 • [7, что отражает-
ся на горизонтальной (действительной) оси на
рис. 6L.11. Напряжения UR и Uc сдвинуты на 90°
по отношению друг к другу; мы знакомы с этим
поведением по опыту с ДС-фильтрами. Сумма
напряжений UR и Uc составляет 2 • U. Это отно-
шение изображено на рисунке в виде треуголь-
ника, гипотенузой которого (суммой) является
горизонтальная ось 2 • U.
По-настоящему важным является тот факт, что
выходное напряжение Увых, представленное в
виде расстояния от земли до точки пресечения
векторов UR и Uc всегда равно входному на-
пряжению или 17. Точка, которую мы называем
«землей», это просто средняя точка горизон-
тальной оси посередине между входным сигна-
лом UBX и его инверсией.
Иными словами, пересечение UR и Uc всегда на-
ходится на полукруге радиусом U. На рис. 6L.11
этот радиус изображен в виде вектора [7ВЫХ, со-
единяющего начало координат с пересечением
Теперь рассчитайте номиналы элементов, со-
берите свой фазовращатель на операционном
61.7. Разработка фазовращателя с единичным усилением
291
усилителе и испытайте его. При выборе рези-
стора и конденсатора обратите внимание на
то, что, максимальное значение установлен-
ного сопротивления (не номинал потенцио-
метра) должно быть намного больше, чем мо-
дуль реактивного сопротивления конденсатора
на частоте подаваемого на схему сигнала. Не
разочаровывайтесь, если обнаружится, что при
определенном положении движка потенциоме-
тра величина фазового сдвига будет зависеть от
частоты входного сигнала. Просто такова осо-
бенность данной схемы.
6L7.2. Фазовращатель II:
управление сдвигом фазы
посредством варьирования
напряжения
На рис. 6L.12 тоже приведена схема для сдвига
фазы выходного сигнала, но функционирую-
щая по-другому.
Преимущество этой схемы перед предыдущей
из раздела 6L.7.1 состоит в том, что величину
фазового сдвига можно регулировать, варьи-
руя сопротивление, соединенное с общей ши-
ной. В результате появляется возможность
управлять величиной фазового сдвига элек-
тронным сигналом, а не ручкой потенциоме-
тра. Например, можно использовать полевой
транзистор, работающий в качестве регули-
руемого резистора10, а затем подать на него
периодический сигнал для регулировки фазо-
вого сдвига во всем рабочем диапазоне. А если
сдвинутый по фазе выходной сигнал смешать
с исходным и подать эту смесь на динамики,
то можно получить эффект фланжера11. Если у
вас есть свободное время, то попробуйте реа-
лизовать такое устройство.
Механизм работы схемы
Это более сложный вариант фазовращателя,
чем тот, который мы собрали в разделе 6L.7.112.
Чтобы разобраться с механизмом его работы,
представьте себе результат задания предель-
ных значений сопротивления R потенцио-
метра:
♦ при R = 0 это будет просто инвертирующий
усилитель с единичным усилением;
♦ а при R » Хс получим [/вых = UBX.
Различие между предельными значениями
фазы выходного сигнала составляет 180°13.
Фазу неинвертирующего входа можно на-
страивать в пределах всего этого диапазона.
Данное свойство постоянной объясняется так
же, как и для более простого фазовращателя
(см. раздел 2.2.8 книги АоЕ). Здесь мы ограни-
чимся этим кратким объяснением, предоста-
вив выяснять остальные подробности чита-
телю, поскольку мы не хотим отрывать вас от
лабораторного занятия длинным отступлени-
ем на эту тему.
ЮкОм
Л -н • ОД мкФ
Вход
Выход
100 кОм
Модуляция: меняет сопротивление полевого транзистора
Рис. 6L.12. Другой способ реализации фазовращателя
Управляемое напряжением
сопротивление полевого транзистора...
... может заменить потенциометр
номиналом 100 кОм
| Регулировка
о У напряжения
J смещения
1а В нашем курсе схемотехники мы не изучаем полевые
транзисторы с управляющим р-л-переходом, но такие
управляемые напряжением схемы рассматриваются в раз-
деле 33.7 книги АоЕ.
11 Фланжер (англ. ftanger, flange - фланжировать, фла-
нец, фланцевать) — звуковой эффект или соответствую-
щее устройство. Напоминает «летящее» звучание.
12 Сравните с разделам 63.5 книги АоЕ.
13 Эта схема подобна схеме «от повторителя к инвертеру»,
изображенной на рис. 4.20 в разделе 4.3 книги АоЕ.
292
6L Лабораторное занятие: операционные усилители I
6L8. Двухтактный буфер
искажения должны исчезнуть. Если это дей-
ствительно произошло, то подумайте, как дол-
Соберите схему, изображенную на рис. 6L.1314. жен выглядеть сигнал на выходе операционно-
100 кОм
Изогните все выводы под углом 90°
1кОм
3055,2955 |К
Рис. 6L13. Усилитель с двухтактным буфером
Подайте на вход схемы синусоидальный сигнал
частотой 100-500 Гц. Исследуйте с помощью
осциллографа сигнал на выходе операционно-
го усилителя, а затем на выходе двухтактного
каскада. При этом амплитуда выходного сигна-
ла должна быть хотя бы несколько вольт, а ге-
нератор сигналов нужно установить в режим
работы без смещения по постоянному току.
Должны наблюдаться классические переход-
ные искажения «ступенька».
Подайте выходной сигнал на динамик с сопро-
тивлением катушки 8 Ом. Выходную мощность
можете контролировать на слух. Но предва-
рительно следует определить максимальную
безопасную амплитуду, которую сможет вы-
держать динамик с его скромной номинальной
мощностью. Хотя используемые транзисторы
довольно мощные, все же желательно посмо-
треть, не лучше ли снизить напряжение пита-
ния, чтобы не перегреть их, и вообще, чтобы
уложиться в следующие значения номиналь-
ной мощности:
♦ транзисторы способны выдержать 75 Вт с
хорошим радиатором, чтобы температу-
ра корпуса не превышала 25°С. Допустимая
мощность без радиатора намного меньше
(0,6 Вт), что более вероятно в вашей реали-
зации схемы;
♦ мощность динамика 25 мВт.
Теперь отключите резистор обратной связи
от выхода операционного усилителя и под-
ключите его к выходу двухтактного каскада
(см. рис. 6N.20), и снова исследуйте выход-
ной сигнал двухтактного каскада. Переходные
го усилителя. Проверьте свое предположение.
Разве операционный усилитель не кажется вам
волшебником?
Подайте улучшенный выходной сигнал на
динамик. Звучит ли он более мягко (напо-
добие флейты), чем в предыдущем случае?
Поразмышляйте, почему переходные искаже-
ния вызывают жесткий и металлический звук
(более похожий на звучание кларнета, чем
флейты), как будто в синусоидальный сигнал
подмешан сигнал более высокой частоты15?
Если повысить частоту сигнала, то обнару-
жится ограничение описанного приема, ха-
рактерное для всех операционных усилите-
лей: в выходном сигнале снова появятся ис-
кажения16.
14 См. рис. 4.26 в разделе 4.3.1Е книги АоЕ.
15 Потому что добавляются компоненты с более высокой
частотой - резкие изломы, заметные при переходе сигна-
ла от отрицательного уровня к положительному, содержат
высокочастотные составляющие. Ваш слух сразу чувству-
ет их, даже если вы в данный момент и не задумываетесь
о теории Фурье.
16 В этой схеме при переходе входного сигнала через ну-
левой уровень операционный усилитель должен резко
поднять уровень выходного сигнала с уровня, находяще-
гося ниже нуля на величину падения напряжения на диоде,
до уровня, находящегося выше нуля на эту же величину.
Этот переход величиной около вольта занимает некоторое
время. Скорость нарастания выходного сигнала операци-
онного усилителя не беспредельна, и в данном случае она
намного ниже необходимой (которую мы измерим в сле-
дующий раз), поскольку в течение краткого перехода вход
операционного усилителя не сильно перегружен. Поэтому
в процессе перехода на выходе операционного усилителя
сигнал остается постоянным. Это искажение становится
заметным на осциллографе при крутом выходном сигнале
и быстрой развертке.
6L9. Преобразователь «ток-напряжение»
293
6L9. Преобразователь
«ток-напряжение»
В предыдущих упражнениях мы столкнулись
(и решили) «проблему» сравнительно низкого
входного импеданса инвертирующего усили-
теля. Но иногда этот недостаток инвертирую-
щего усилителя становится его достоинством.
Это происходит, когда источник сигнала явля-
ется источником тока, а не напряжения, к ко-
торому мы привыкли. Один из таких источни-
ков сигнала — фотодиод, для которого низкий
входной импеданс R^ инвертирующего входа
операционного усилителя очень даже кстати.
Заодно попробуйте оценить, какова величина
этого входного импеданса17.
Фотодиод
Соберите схему фотометра, изображенную
на рис. 6L.14, используя фототранзистор
BPV11 или LPT100 в качестве фотодиода.
Чувствительность этих устройств наибольшая
в ближней инфракрасной части спектра (дли-
на волны около 850 нм), но около 80% макси-
мальной чувствительности сохраняется и к ви-
димому красному цвету. Исследуйте выходной
сигнал с помощью осциллографа. Если уровень
постоянного напряжения превышает 10 В,
уменьшите сопротивление резистора обратной
связи до 4,7 МОм или даже до 1 МОм.
ЮМОм
Свет
BPV11
Эмиттер не подключен
Рис. 6L14. Схема фотометра на фотодиоде
Если выходной сигнал содержит пульсации,
подключите параллельно резистору обрат-
ной связи конденсатор небольшой емкости.
Сопротивление резистора настолько велико,
что будет достаточно небольшой емкости, по-
скольку даже 22 пФ вызывает падение усиле-
ния схемы при частоте /3дБ (l/2nRC) меньшей,
чем 1 кГц. Сопротивление резистора обратной
связи в схеме с фототранзистором на рис. 6L16
17 Да, в идеале 2?ю равно нулю, но в действительности
просто очень мало. Далее, в главе 9N, мы научимся вычис-
лять его как Дос/А, где А — усиление с разомкнутой цепью
обратной связи.
намного меньше, поэтому для нее емкость
должна быть пропорционально в 100 раз боль-
ше. Почему этот конденсатор устраняет пара-
зитные помехи? Потому что колебания не мо-
гут быть устойчивыми при отсутствии усиле-
ния схемы на (высокой) частоте, при которой
схема «хочет» создавать колебания. Колебания
возникают на вполне определенной частоте,
поскольку при этом в схеме существуют неком-
пенсированные фазовые сдвиги. Эта проблема
рассматривается более подробно на лаборатор-
ном занятии 9L.
Каков средний уровень постоянной составляю-
щей выходного сигнала, и каково процентное
содержание сигнала «модуляции»?
Замечание
Если помещение освещается устаревшими лампами
дневного света, которые мерцают с частотой 120 Гц,
то модуляция сигнала будет сравнительно заметна,
и она намного меньше при использовании совре-
менных ламп дневного света, работающих на часто-
те 40 кГц, или простых лампочек накаливания.
Какому входному фототоку соответствует вы-
ходной уровень сигнала? Попробуйте закры-
вать фототранзистор рукой и исследуйте на
осциллографе сигнал в точке X при варьиро-
вании выходного напряжения. Каким оказался
результат18?
Надеемся, вам ясно, почему эта схема луч-
ше, чем более простой преобразователь
«ток-напряжение» в виде резистора, изобра-
женный на рис. 6L.1519.
Свет
Фототранзистор "i
ЮМОм
Рис. 6L.15. Менее качественная схема преобразователя
«ток-на п ряжен ие»
18 Точка X является «виртуальной землей» и должна иметь
нулевой потенциал. Если это не так, значит, вы где-то
ошиблись. Скорее всего выходной сигнал достиг предель-
ного значения (усилитель вошел в режим насыщения),
в результате чего обратная связь не может сделать уровень
сигнала в данной точке равным уровню сигнала на неин-
вертирующем выводе операционного усилителя.
19 Потому что фотодиоду «не нравятся» большие колеба-
ния напряжения. В пассивной схеме падение напряжения
на резисторе влияет на фотодиод, ток которого слегка ме-
няется. В результате взаимосвязь между интенсивностью
света и током диода искажается.
294
6L Лабораторное занятие: операционные усилители I
Фототранзистор
Теперь подключите фототранзистор BPV11 по
стандартной схеме, как показано на рис. 6L.16.
Из рисунка видно, что база фототранзистора не
подключена. Снова проверьте на осциллографе
сигнал в точке X. Сохраните эту схему в сборе
для следующего этапа.
Свет
100 кОлл (или больше)
LPT-100
(база не подключена)
Рис. 6L.16. Схема фотометра на фототранзисторе
бумаги и разместив его перед экраном осцил-
лографа так, чтобы луч осциллографа едва
проглядывал через кромку маски. Таким об-
разом можно создавать сигналы произволь-
ной формы. Если вы попробуете реализовать
этот трюк, размер осциллограммы не должен
превышать 5 см. В результате можно создать
сигналы по-настоящему причудливой формы,
например, в виде горы Даймонд-Хэд, автомо-
биля Фольксваген или горы Маттерхорн. Это
простая альтернатива способу формирования
сигналов с помощью компьютера, который
способен сохранять в памяти оцифрованные
произвольные сигналы. Компьютерный вари-
ант используется в реальных генераторах сиг-
налов произвольной формы.
Применение фотометра
Подключив фототранзистор к схеме с помощью
отрезка кабеля, можно немного поразвлечься,
наблюдая за «изображением» фототранзистора
на экране осциллографа (в действительности за
выходным сигналом фототранзистора).
Замечание
Для данного эксперимента хорошо подойдет
BNC-кабель с крючковыми зажимами на обоих
концах. Но при этом обратите внимание на то, что
ни один из выводов этой схемы нельзя подклю-
чить к физической земле, поэтому не используй-
те BNC-разъемы, встроенные в макетную плату.
Подключение устройств показано на рис. 6L17.
6L10. Источник тока
Соберите схему источника тока, изображенную
на рис. 6L.18. Каким должен быть ее выходной
ток? Регулируйте сопротивление нагрузочного
потенциометра и наблюдайте за током, под-
ключив для этого цифровой мультиметр. Этот
источник тока должен быть настолько хорош,
что исследовать его будет даже скучно. Теперь
замените потенциометр с номиналом 10 кОм
на потенциометр 1 кОм, изменяйте его сопро-
тивление и наблюдайте за выходным напря-
жением с помощью другого мультиметра или
осциллографа. В результате вы должны понять
причину выхода источника тока из строя, когда
это произойдет.
Рис. 6L17. Фотометр «наблюдает» за своим выходным сиг-
налом
Осциллограмма на экране кажется «застенчи-
вой»: ей не «нравится», что фототранзистор
«наблюдает» за ней. Обратите внимание на
то, что в этой схеме сам осциллограф является
компонентом цепи обратной связи.
Развлечение можно разнообразить, оснастив
фототранзистор теневой маской из плотной
Определите пределы
работоспособности этого
источника тока
10 кОм Нагрузка
Цифровой мультиметр
Рис. 6L.18. Источник тока
Обратите внимание на то, что, хотя этот ис-
точник тока намного точнее и стабильнее, чем
рассмотренный ранее простой транзисторный
источник тока, у него есть недостаток — его
нагрузка должна быть «плавающей», т. е. не
подключена к земле. Кроме того, у него суще-
ственные ограничения по быстродействию,
6LW. Источник тока
295
вызывающие проблемы в ситуации, когда или
выходной ток, или импеданс нагрузки изменяет-
ся со скоростью в микросекундном диапазоне.
Схема, изображенная на рис. 6L.19, решает пер-
вую из этих проблем — здесь нагрузка подклю-
чена к земле.
+15 В
2N39O6
К
470
> 10 мА Э Б
(цифровой мультиллетр)
Рис. 6L19. Источник тока, нагрузку которого можно под-
ключать к земле
Регулируйте потенциометр нагрузки RH и на-
блюдайте за соответствующим изменением
выходного тока 1ВЫХ. Опять же, рабочие харак-
теристики этого источника тока должны быть
настолько хороши, что исследовать его будет
неинтересно. Но если выставить сопротивле-
ние потенциометра приблизительно на 2 кОм,
произойдет отказ источника тока. Причину от-
каза можно выяснить, измеряя напряжение икэ
с помощью другого вольтметра.
Возможно, что в схеме на биполярном тран-
зисторе 2N3906 вам не удастся обнаружить
никаких изменений тока. Если же вам удаст-
ся обнаружить небольшую нестабильность,
попробуйте заменить этот транзистор МОП-
транзистором BS250P. Цоколевка у этих тран-
зисторов одинаковая, так что его можно вста-
вить точно так же вместо биполярного транзи-
стора 2N3906.
С каким транзистором схема должна работать
лучше, с полевым или биполярным20? Удалось
ли вам обнаружить разницу, подтверждаю-
щую это предположение? (Эта разница должна
быть чрезвычайно маленькой.) Независимо от
типа транзистора, описанный источник тока
настолько хорош, что вам придется очень по-
трудиться, чтобы увидеть разницу между его
вариантами на полевом и биполярном тран-
зисторах. Обратите внимание на то, что вы не
сможете заметить эту разницу с помощью ана-
логового вольтметра, поэтому нужно исполь-
зовать цифровой прибор.
20 Схема на полевом транзисторе работает чуточку лучше.
Цепь обратной связи следит за током эмиттера /э, а ток
коллектора /к - выходной; разница между этими тока-
ми (ток базы 1Б) очень мала. Поэтому в схеме на полевом
транзисторе выходной ток будет практически идентичен
отслеживаемому току.
6W. Примеры с решениями: операционные
усилители I
На этот раз задачи будут посвящены только ана-
лизу схем. Это редкое отступление от нашего
обычного правила, когда мы даем задачи на раз-
работку, а не на анализ. Изобретение разност-
ного усилителя1 было трудной задачей, и его
функционирование тоже далеко не очевидно.
Поэтому далее приводится небольшое упражне-
ние по прояснению работы этой схемы.
6W.1. Простой разностный
усилитель на операционном
усилителе
На рис. 6W.1 изображены две схемы разност-
ного усилителя, собранные на операционном
усилителе2: стандартная схема (вверху) и про-
стой усилитель с единичным усилением (вни-
зу). Последнюю схему мы рассмотрим здесь
в первую очередь.
В общем, как известно, для усилителя необхо-
димо, чтобы номиналы резисторов на входах
иг и U2 были как можно ближе друг к другу.
От этой подгонки зависит качество подавле-
ния синфазной составляющей3. Дифференци-
ц—лл^-ч.
1 Эту схему чаще называют «дифференциальным усилите-
лем». Но здесь мы предпочитаем термин «разностный уси-
литель» (англ. difference amplifier, т. е. усилитель разницы),
который также употребляется в разделе 4.2.4 книги АоЕ.
Термин «дифференциальный усилитель» может создать
впечатление, что эта схема осуществляет какие-то вычис-
ления по высшей математике, тогда как слово «разност-
ный» лучше описывает выполняемое схемой действие.
Тем не менее следует признать, что мы часто возвращаем-
ся к более традиционному термину, называя схему диффе-
ренциальным усилителем. (В английском языке эти разно-
гласия в терминологии в некоторой степени сглаживаются
благодаря термину diff-amp.)
2 АоЕ § 4.2.4.
3 Поскольку обеспечить равенство номиналов дискретных
резисторов очень трудно, наилучшим подходом будет ис-
пользовать микросхемы наборов резисторов, сопротивле-
ния которых подогнаны в пределах 0,001% (см. раздел 4.2.4
Разностный усилитель: стандартная схема
Разностный усилитель с единичный усилением
Рис. 6W.1. Два типа разностных усилителей на операцион-
ном усилителе
альное усиление усилителя определяется как
Несколько примеров определения
коэффициента усиления
Коэффициент усиления схемы можно опреде-
лить, выполнив алгебраические вычисления
(см. раздел 6W.1.5). Но теоретические расчеты
часто недостаточно убедительны. Поэтому да-
вайте сначала пойдем другим путем: рассмо-
трим несколько частных случаев с известны-
ми напряжениями входных сигналов, чтобы
убедиться, что схема работает как положено.
Этот подход является одной из разновидностей
в книге АоЕ). Другой вариант — применить готовую ми-
кросхему разностного усилителя, например, INA105 ком-
пании TI/Burr-Brown, усиление которой равно единице с
погрешностью в пределах 0,05%. Можно рекомендовать
также микросхему разностного усилителя INA149 (рас-
сматривается чуть далее в разделе 6W.2) с коэффициентом
подавления синфазной составляющей равным 100 дБ.
6W. l Простой разностный усилитель на операционном усилителе
297
распространенного метода, который мы ис-
пользуем, когда сталкиваемся с новой схемой:
попытаться перерисовать ее, чтобы она вы-
глядела как уже знакомая нам схема, функ-
ционирование которой мы хорошо понимаем.
Например, в разделе 6W.1.1 дифференциаль-
ный усилитель становится уже знакомым нам
инвертирующим усилителем.
Вспомните, что для упрощения анализа схемы мы
сделали все резисторы одинаковыми, в результа-
те чего коэффициент усиления нашего диффе-
ренциального усилителя стал равным единице.
6W.1.1. Первый пример:
инвертирующий усилитель
Подключаем вход U2 на землю, а на вход их
подаем сигнал (рис. 6W.2). Таким образом мы
задаем нулевой уровень на неинвертирующем
входе, в результате чего на инвертирующем
входе устанавливается уровень виртуальной
земли, а сама схема становится обычным ин-
вертирующим усилителем с коэффициентом
усиления равным минус единице.
R
Рис. 6W.2. Дифференциальный усилитель с коэффициентом
усиления -1
В табл. 6N.1 приведены параметры для данной
схемы.
Таблица 6N.1. Параметры инвертирующего
усилителя
При-
мер
А
Входы
и,
1
0
Внутренние
точки
X
0
Y
0
Выход
-1
Примечание
Инвертирую-
щий усилитель
6W.1.2. Второй пример:
неинвертирующий усилитель
Подключаем вход U2 к земле, а на вход Ul пода-
ем сигнал (рис. 6W.3). Теперь у нас получилась
схема неинвертирующего усилителя с коэф-
фициентом усиления равным двум для сиг-
нала, подаваемого в точке Y (вспомните, что
Рис. 6W.3. Дифференциальный усилитель с коэффициентом
усиления +1
В табл. 6N.2 приведены параметры для данной
схемы.
Таблица 6N.2. Параметры неинвертирующего
усилителя
При-
мер
В
Входы
0
1
Внут-
ренние
точки
X
0,5
У
0,5
Выход
1
Примечание
Неинвертирую-
щий усилитель
с коэффициентом
усиления равным
2 х (1/2)1/,
На первый взгляд коэффициент усиления рав-
ный двум выглядит ошибкой, но учтите, что
неинвертированный сигнал ослабляется в два
раза перед точкой Y. Таким образом, усиление
неинвертированного сигнала равно +1, как и
следовало ожидать.
6W.13. Третий пример: одинаковые
сигналы на обоих входах
Одинаковые сигналы на обоих входах должны
дать нулевой выходной сигнал. Подадим на оба
входа схемы на рис. 6W.4 сигналы напряжени-
ем +1 В.
R
-ЛЛЛг-
1В
Рис. 6W.4. Схема дифференциального усилителя, в которой
входные сигналы одинакового уровня дают нулевой выход-
ной сигнал
298
6W. Примеры с решениями: операционные усилители I
В табл. 6N.3 приведены параметры для данной
схемы.
Таблица 6N.3. Параметры дифференциального
усилителя
При-
мер
С
Входы
Л
1
1
Внут-
ренние
точки
X
0,5
У
0,5
Выход
^вых
0
Примечание
Напряжения на
выходах делителей
напряжения оди-
наковые на уровне
земли
Одинаковые входные сигналы создают одина-
ковые напряжения на входах операционного
усилителя, что вызывает одинаковые напря-
жения на концах обоих делителей напряжения.
Таким образом, выходной сигнал 17ВЫХ должен
быть на уровне потенциала земли. Иными
словами, имеем нулевое синфазное усиление.
(При условии, что номиналы всех четырех ре-
зисторов очень хорошо подогнаны.)
Таблица 6N.4. Параметры инвертирующего
усилителя
При-
мер
D
Входы
JL
1
2
Внут-
ренние
точки
X
1
Y
1
Выход
1
Примечание
Инвертирующий
усилитель, но сиг-
нал усиливается
относительно l/Y и
добавляется к UY
Этот пример точно такой же, как и второй при-
мер неинвертирующего усилителя (см. раз-
дел 6W.1.2), с той разницей, что уровни обоих
входных сигналов выше на 1 В. Усилитель иг-
норирует это общее различие.
С другой стороны, эту схему можно рассмат-
ривать как инвертирующий усилитель, кото-
рый усиливает сигнал иг по отношению к на-
пряжениям в точках Ux и Ur В этом случае нет
разницы сигналов для усиления и на выходе
просто базовое напряжение Ur
6W.1 А Четвертый пример: входные
сигналы ненулевого уровня
с разницей между уровнями
в 1 вольт
Соответствующая схема усилителя изображена
на рис. 6W.5. Усилитель должен игнорировать
одинаковые уровни обоих сигналов, но усилить
разницу между ними (1 В) в 1 раз.
Да, в данном случае можно сказать, что при-
сутствует синфазный (общий) сигнал напряже-
нием 1 В и разностный сигнал величиной 1 В.
Усилитель игнорирует общую часть сигнала и
усиливает разницу в 1 раз.
6W.1.5. Формальное определение
усиления
Если разбор конкретных примеров и сравнение
их с уже знакомыми конфигурациями усилите-
лей покажется слишком трудоемкой задачей, то
возможно, вам больше по душе придется более
традиционный анализ схем. Для начала пере-
рисуем нашу схему и добавим к ней пару новых
обозначений (рис. 6W.6).
2 В (У
Рис. 6W.6. Обобщенная схема разностного усилителя
Рис. 6W.5. Дифференциальный усилитель с двумя положи-
тельными входными сигналам с разницей в 1 В между ними
В табл. 6N.4 приведены параметры для данной
схемы.
схему для тою, чтойы по-
лучить усиление, отличное от единичного,
продолжим работать с единичным усилением,
чтобы предельно упростить математические
вычисления. Таким образом, предположим, что
все резисторы R снова имеют одинаковое зна-
чение. Это не обязательное условие, чтобы по-
лучить хорошее дифференциальное усиление;
6W.2. Более интересый разностный усилитель—микросхема INA149...
299
как было сказано в самом начале, необходимо
только, чтобы значения соотношений рези-
сторный пар были одинаковыми: RJ^ = RJRy
Входной ток /х = (L/j - Ux)/R, aUx=UY= VJ2.
Таким образом:
I, =
Ui-(U2/2).
R
Члены R взаимно сокращаются, в результате
Хотя мы опять рассмотрели пример с единич-
ным усилением, данный алгебраический под-
ход будет справедлив для любого согласован-
ного набора соотношений сопротивлений ре-
зисторов, где Л/!?! = RJRy Но если соотноше-
ние номиналов резисторов не равно единице,
то, конечно же, выходное напряжение не будет
равно разнице между напряжениями на входах,
а станет кратно этой разнице.
Какой из этих подходов использовать, алге-
браическое решение или конкретные примеры,
которые мы рассмотрели вначале, полностью
зависит только от ваших предпочтений.
6W.2. Более интересный
разностный усилитель —
микросхема INA149
с широким диапазоном
входных напряжений
синфазного сигнала
Компания Texas Instruments (TI) выпускает
несколько микросхем стандартного разност-
ного усилителя, содержащих подогнанные по
значениям резисторы, которые обеспечивают
хорошее подавление синфазной составляю-
щей сигнала (100 дБ для микросхемы INA149).
Одна из этих микросхем — INA149 — содер-
жит дополнительный пятый резистор, кото-
рый предохраняет операционный усилитель от
перегрузки даже при величине входного сигна-
ла до ±275 В. Этот резистор является частью
делителя, который уменьшает высокое на-
пряжение до 13,5 В на входах операционного
усилителя. Если вы задаетесь вопросом, зачем
кому-либо может понадобиться такой диапа-
зон напряжений синфазного сигнала, компа-
ния TI рекомендует, например, что он может
быть полезным для мониторинга тока на высо-
ковольтной линии: дифференциальный усили-
тель может обнаружить падение напряжения на
резисторе с небольшим сопротивлением, через
который протекает ток.
Такая схема показана сверху на рис. 6W.74, а
снизу на этом рисунке изображена та же схема,
но с добавленными обозначениями, чтобы об-
легчить ее рассмотрение.
20 кОм 380 кОм
20 кОм 380 кОлл
Рис. 6W.7. Микросхема разностного усилителя INA149
Если исходить из общего выражения для уси-
ления дифференциального усилителя (см. раз-
дел 6W.1), то можно подумать, что выходной
сигнал этого усилителя должен быть ослаблен
вследствие его дифференциального усиления
равного 1/20, которое задается отношением
сопротивления резистора величиной 19 кОм
к сопротивлению входного резистора величи-
ной 380 кОм в плече Ur Но оказывается, что
дифференциальное усиление этой схемы равно
единице. Когда мы будем разбираться с при-
чинами, вызывающими такой результат, то об-
наружим, что поведение этой схемы далеко не
очевидно.
4 В схеме на рис. 6W.7 резисторы номиналом 20 кОм и
19 кОм соединены с общей шиной, но их можно подклю-
чить к другим опорным напряжениям, если требуется сме-
щение выходного сигнала.
300
6W. Примеры с решениями: операционные усилители I
Опять же, мы предлагаем два разных подхода к
рассмотрению этой схемы. Сначала мы рассмо-
трим пару особых случаев, легко поддающихся
анализу, а затем выполним определенный объ-
ем алгебраических вычислений, чтобы полу-
чить общий результат.
6W.2.1. Частные случаи
Как мы убедились при рассмотрении общего
случая разностного усилителя в разделе 6W.1,
некоторые типы входных сигналов более легко
поддаются анализу. Мы используем пару таких
сигналов далее, чтобы доказать, что вопреки
кажущемуся ослаблению сигнала эта схема в
действительности дает единичное усиление.
Вход Uy подключен на землю
При подключении на землю входа Ux на землю
также подключаются параллельно соединен-
ные резисторы номиналом 380 кОм и 20 кОм,
общее сопротивление которых будет 19 кОм.
Таким образом, у нас получается интересная
симметрия: сигнал на входе U2 делится на 21
(= 19 кОм/(380 кОм + 19 кОм)), а инвертирую-
щий путь делит выходное напряжение на такую
же самую величину. Таким образом, Е/вых= UBX.
При желании можно изложить по-другому.
Скажем, что сигнал на входе U2 делится на 21,
а коэффициент усиления неинвертирующего
усилителя, на который подается полученный
таким образом сигнал, составляет 1 + 380 кОм/
/(20 кОм || 380 кОм) = 1 + 380 кОм/19 кОм = 21.
Отсюда получается, что коэффициент усиления
равен единице.
Вход U2 подключен на землю
Этот случай более легкий. Подключение входа
U2 на землю заземляет оба входа операционно-
го усилителя (обозначены Ux на схеме справа).
Таким образом, наш усилитель выглядит как
простой инвертирующий усилитель. (Резистор
номиналом 20 кОм не оказывает на схему ни-
какого влияния, так как в результате нулевого
напряжения на нем ток через него отсутствует.)
Коэффициент усиления равен минус единице.
6W.2.2, Общее решение
Алгебраические вычисления, которые обобща-
ют эти результаты, более трудоемкие. Но их не
избежать, поэтому приступим. В вычислениях
будем использовать сигналы, обозначенные на
правой схеме на рис. 6W.7: напряжения Uv Uv
Ux и токи Iv Ic и Ioc Мы хотим узнать ток обрат-
ной связи 10С. Зная это значение и величину Ur
мы сможем вычислить напряжение выходного
сигнала [7ВЫХ. Значение Ux вычисляется таким
образом: Ux = UJ21.
Вычисляем токи:
*ос = п ~*с =
Цг-Цх _ Ux _Ul-U2/21 UJ21
380 кОм 20кОм 380 кОм 20кОм'
Теперь мы можем использовать этот ток, чтобы
вычислить I
вых*
= Ux "
[//21 - (U, -U2/21 -
/( 1 + 19) -
= и2- Uv
После рассмотрения двух частных случаев, ког-
да мы поочередно подключали входы схемы
на землю, этот результат не должен оказаться
неожиданным. Но, тем не менее, он добавляет
уверенности в то, что мы на правильном пути.
6W.3. Необычная
суммирующая схема
Предположим, что нам нужно суммировать
сигналы от двух датчиков (А и В), при этом сиг-
налам обоих датчиков присваиваются одинако-
вые полномасштабные веса. Полученный таким
образом выходной сигнал подается на аналого-
цифровой преобразователь (АЦП)5, входной
диапазон напряжений которого определяет
допустимый диапазон напряжений выходного
сигнала нашего сумматора. Предположим, что
датчики выдают сигналы постоянного напря-
жения одной полярности. Далее приводятся со-
ответствующие характеристики.
♦ Диапазон входных напряжений АЦП: 0 до
+2,5 В.
5 Для решения поставленной задачи понимание работы
этого устройства не требуется.
6И/.3. Необычная суммирующая схема
301
♦ Источник сигнала А:
• диапазон постоянных напряжений: 0 до
0,5 В;
• выходной импеданс: < 10 МОм.
♦ Источник сигнала В:
• диапазон амплитуд: 0 до 1 мА (потреби-
тель тока);
• выходной импеданс: > 10 МОм;
• диапазон запаса по напряжению: < ОД В.
6W.3.1. Решение
Предварительная подготовка
На первый взгляд со списком только что пере-
численных характеристик может быть трудно
разобраться, но все становится ясным, когда
мы заметим, что источник А выдает напряже-
ние, а источник В — ток. Уяснив это важное раз-
личие, мы сможем разобраться с остальными
подробностями.
Суммирующая схема, которую нам предсто-
ит собрать, будет использовать, как обычно,
операционный усилитель в инвертирующем
режиме. Такая схема, по сути, суммирует токи,
поэтому для подачи на нее напряжений мы
вставляем входные резисторы между источни-
ком сигналов и точкой суммирования, вирту-
альной «землей». Эти резисторы преобразо-
вывают входные напряжения во входные токи.
Такая модификация потребуется для сигнала от
датчика А, а датчик В, будучи источником тока,
такого входного резистора не требует: он идет
напрямую к точке суммирования токов — вир-
туальной «земле».
Создаем базовую принципиальную схему
На рис. 6W.8 изображена базовая схема без
указания значений компонентов.
Над базовой схемой придется немного по-
думать.
■ЛЛЛ/ 1
Далее укажем пару моментов, которые для нас
выглядели не совсем очевидными.
♦ Узкий диапазон устойчивости по напряже-
нию для источника сигнала В означает, что
сигнал В должен подаваться на суммирую-
щее соединение. В этом нет ничего неожи-
данного или обременительного, поскольку
вы, вероятно, и так намеревались выбрать
эту стандартную суммирующую конфигура-
цию. При этом вы должны не поддаться ис-
кушению вставить резистор между точкой В
и виртуальной землей.
— Почему? — можете спросить вы. — Что
будет не так, если вставить резистор номи-
налом, скажем, 1 кОм между точкой В и вир-
туальной землей? — Это сопротивление не
будет мешать суммированию токов в точке
виртуальной земли. Но оно сдвинет напряже-
ние максимального тока в точке В слишком
далеко от потенциала земли — на 1 В, далеко
за рамки нашего диапазона устойчивости по
напряжению величиной 0,1 В.
♦ Для входа А потребуется буфер с высоким
импедансом — входной повторитель, пока-
занный на рис. 6W.8, поскольку без такого
буфера высокий выходной импеданс ис-
точника А будет противоречить скромному
входному импедансу суммирующей схемы.
— Скромному? — можете удивиться вы.—
Но. почему он должен быть скромным? Мы
можем сделать его громадным, вставив ре-
зистор с большим сопротивлением в инвер-
тирующий каскад, который принимает сиг-
нал А. — (Инвертирующий каскад требуется
для того, чтобы скомпенсировать инверсию,
присущую суммирующей схеме.)
На самом деле этот импеданс должен быть
средним потому, что даже при сопротивле-
нии 100 МОм резисторы могут вносить по-
грешность до 10%, в результате чего их зна-
чение следует ограничить величиной около
10 МОм, чтобы избежать всяких неприятных
побочных явлений.
на АЦП
Рис. 6W.8. Базовая принципиальная схема устройства
302
6W. Примеры с решениями: операционные усилители I
ЮкОм
Потребляет от 0 до 1 м/
Roc1,25kOm
Потребляет от 0 до
оТГ\
- 0,5 BJ
силение выбирается
таким, чтобы установить
максимальное значение
~ 2,5 В (при токе 2 мА)
Рис. 6W.9. Полная принципиальная схема сумматора с указанием номиналов компонентов
В число побочных явлений входят большие
ошибки, вызываемые током смещения /см,
протекающим в несогласованных резистив-
ных путях, а также, возможно более про-
блематично, внесение непреднамеренного
эффекта низкочастотного фильтра в цепь об-
ратной связи. Это вызывает фазовые сдвиги,
которые могут сделать схему нестабильной6.
Теперь убедимся в очевидной несостоятель-
ности следующего аргумента. Воспользуемся
Двых источника А, чтобы создать инверти-
рующий каскад: возьмем резистор обратной
связи номиналом 10 МОм. Этот подход не бу-
дет работать потому, что Явых источника А не
задано точно равным 10 МОм, а, как обычно,
указана только максимальная величина. Мы
уже встречались с этим параметром много
раз.
6W.3.2. Определяем значения
компонентов
Значения двух компонентов особенно важны:
♦ резистор обратной связи Roc определяет мак-
симальное значение выходного напряжения
Ц
ВЫХ'
6 Таким проблемам стабильности посвящена ббльшая
часть лабораторного занятия 9L.
♦ резистор, подключенный к виртуальной зем-
ле, задает усиление сигнала А относительно
сигнала В.
На рис. 6W.9 изображена законченная принци-
пиальная схема. Для ее создания не требуется
больших интеллектуальных усилий, а нужно
лишь немного арифметических операций.
Далее приводятся подробности арифметиче-
ских вычислений значений компонентов.
Резистор обратной связи /?ос
При максимальном значении обоих сигналов
А и £ мы хотим иметь выходное напряжение
ивых = 2,5 В. Поскольку вес обоих сигналов оди-
наков, ток величиной 1 мА источника А должен
создавать выходное напряжение 1/вых = 1,25 В.
Для этого значение резистора обратной связи
Roc должно быть 1,25 кОм.
Резистор, подающий сигнал
на виртуальную «землю»
Чтобы оба сигнала имели одинаковый вес при
наибольшем значении диапазона, этот рези-
стор должен преобразовывать максимальное
входное напряжение 17ВХ= 0,5 В в ток 1 мА. Для
этого номинал этого резистора должен быть
0,5 кОм.
7N. Операционные усилители II:
отклонения от идеальности
Содержание
7N.1.
7N.2.
Анализ некоторых схем
7N.1.1. Когда применимы «золотые правила»?
7N.1.2. Улучшение схемы активного выпрямителя
Неидеальность операционных усилителей
7N.2.1. Насколько важны эти несовершенства?
7N.2.2. Входное напряжение смещения нуля иш
7N.2.3. Входной ток смещения 1Ш
7N.2.4. Ток сдвига
7N.2.5. Скорость нарастания выходного сигнала и спад усиления
7N.2.6. Ограничение выходного тока
7N.2.7. Шум
7N.2.8. Диапазон входных и выходных напряжений
7N.2.9. Избранные характеристики операционных усилителей:
обычных и высшего класса
7N.3. Еще несколько вариантов применения: интегратор, дифференциатор,
выпрямитель, разностный усилитель, усилитель по переменному току
7N.3.1. Интегратор
7N.3.2. Предотвращение насыщения интегратора на операционном усилителе
7N.3.3. Т-образная резистивная цепь
7N.3.4. Интегратор может предъявлять повышенные требования
к качеству операционного усилителя
7N.3.5. Иногда достаточно ручного сброса интегратора
Дифференциатор
Разностный усилитель на операционном усилителе
7N.5.1. Интересное достоинство: широкий диапазон входного сигнала
7N.6. Усилитель переменного тока: хороший способ минимизировать
влияние погрешности по постоянному току операционного усилителя
7N.7. Материал для чтения в АоЕ
7N.4.
7N.5.
304
304
306
307
308
309
312
313
314
315
316
317
319
320
320
321
323
324
324
325
326
326
327
328
Цель этой главы
Нам предстоит решить задачу оптимизации ра-
бочих характеристик схем путем выбора наибо-
лее подходящих операционных усилителей из
большого числа доступных на рынке. Мы по-
пытаемся разобраться с тем фактом (который
трудно объяснить исходя из нашего первого
представления об операционных усилителях,
как, по сути, идеальных устройствах), что на
рынке предлагается не один или два операци-
онных усилителя, а приблизительно 37 тысяч
таких устройств1.
1 Согласно перечню на веб-сайте компании Digikey -
одного из многих дистрибьюторов электронных компо-
нентов, на момент подготовки этого материала.
Признание несовершенства операционных уси-
лителей положит конец нашему «медовому ме-
сяцу» с ними. Но мы будем и дальше восхищать-
ся ими: мы рассмотрим другие способы приме-
нения операционных усилителей, и при этом
будем полагаться на нашу первую, простейшую
модель этих устройств, суть которой была изло-
жена в «золотых правилах» в разделе 6N.4.
Чтобы получить более реалистичное представ-
ление об операционных усилителях, мы уточ-
ним «золотые правила», признавая, например,
что сигнальные входы операционного усилите-
ля все-таки потребляют небольшой ток. Начнем
с рассмотрения трех новых важных примеров,
а затем перейдем непосредственно к теме несо-
вершенства операционных усилителей.
304
7N. Операционные усилители II: отклонения от идеальности
Основные моменты ранее
рассмотренного материала
♦ Обратная связь и высокий коэффициент уси-
ления операционных усилителей облегчают
разработку и анализ схем с помощью «золо-
тых правил».
♦ В число важных вариантов применения опе-
рационных усилителей входят схемы усили-
телей и источников тока.
♦ В общем случае характеристики схем на опе-
рационных усилителях зависят главным об-
разом от свойств элементов в цепи обратной
связи.
7N.1. Анализ некоторых
схем
В предыдущих разделах мы только слегка
коснулись вопроса возможности применения
«Золотых правил» как в частных, так и в общих
случаях схемотехники на операционном усили-
теле. Теперь мы изучим этот вопрос более под-
робно.
7N.1.1. Когда применимы «золотые
правила»?
Прежде чем использовать наши чрезвычайно
полезные «золотые правила», следует прове-
рить, применимы ли они в конкретном случае.
Например, справедливы ли эти правила для
схемы, изображенной на рис. 7N.1? Ответ бу-
дет неоднозначным: и да и нет. Более точным
ответом будет, что они применимы только для
положительных сигналов.
Входной
сигнал
Входной /\
сигнал
Выходной,
сигнал
V7
Г\
Обстоятельства, когда правила
применимы
Входной сигнал положительной полярности
создает положительный выходной сигнал (бу-
дет полезно вспомнить внутреннее устройство
операционного усилителя, в частности, то об-
стоятельство, что он является дифференциаль-
ным усилителем). При положительном выход-
ном сигнале ток может поступать обратно на
инвертирующий вход усилителя, поддерживая
напряжение на этом входе на уровне, равном
17ВХ, как следовало бы ожидать от схемы в со-
ответствии с «золотыми правилами». Эта схема
похожа на повторитель, к которому добавлен
диод и резистор с заземленным выводом, кото-
рый не влияет на работу схемы, а просто явля-
ется нагрузкой для выходного сигнала. В целом
Обстоятельства, когда правила
неприменимы
Но при входном сигнале отрицательной поляр-
ности обратная связь не работает: диод блоки-
рует выходной сигнал, который теперь имеет
потенциал ниже уровня земли. А без обратной
связи операционный усилитель просто резко
входит в.режим отрицательного насыщения
(уровень которого для обычного операционно-
го усилителя типа 411 на один вольт выше от-
рицательного напряжения питания) и остается
на этом уровне.
На первый взгляд ситуация выглядит некор-
ректной, но это не так. Поскольку диод блоки-
рует ток, теперь цепь, связывающая выход опе-
рационного усилителя с входом, оказывается
разомкнутой. Выход теперь просто привязан
к земле через резистор. Если рассмотреть эти
операционного усилителя
Выходной
сигнал
у*
Приближение к насыщению,
ограничиваемое скоростью
| изменения сигнала
уменьшается на 0.6 В Приближение к насыщению,
ограничиваемое скоростью
изменения сигнала
Рис. 7N.1. Более трудный случай для анализа с помощью «золотых правил»
7Л/. /. Анализ некоторых схем
305
два случая совместно, то можно прийти к вы-
воду, что сигнал на выходе устройства просто
представляет собой выпрямленный входной
сигнал.
Пассивный выпрямитель, изображенный слева
на рис. 7N.1, напоминает вам о падении напря-
жения на диоде, которое отсутствует в актив-
ной схеме. Активный выпрямитель, устраняя
падение напряжения на диоде (благодаря на-
личию операционного усилителя с цепью об-
ратной связи), способен выпрямлять даже сиг-
налы, амплитуда которых намного меньше, чем
0,6 В. Это большое достоинство данной схемы.
А ее недостаток состоит в том, что она работа-
ет только на сравнительно невысоких частотах,
иначе в выходном сигнале все сильнее появля-
ются искажения.
Осциллограммы входного и выходного
сигналов схемы
Упомянутое искажение сигнала показано на
рис. 7R2. Оно выглядит несколько хуже, чем
можно было бы ожидать. Длительность иска-
жения оказывается в пять раз больше, чем мож-
но было бы ожидать исходя из заявленной ско-
рости нарастания для данного операционного
усилителя (15 В/мкс). Но здесь сигнал нарас-
тает намного медленнее, чем согласно заявлен-
ной скорости, которая предполагает перегрузку
входа операционного усилителя.
В разделе 7N.2.5 мы увидим, что сигнал нараста-
ет максимально быстро лишь тогда, когда весь
ток хвоста поступает только в одно плечо диф-
ференциального каскада операционного уси-
лителя. А это происходит, когда на входы пода-
ется большое дифференциальное напряжение.
Сигнал на выходе
ционного усилителя
Выходной сигнал выпрямлен,
но содержит искажение...
гы TWy ЦЩ s.'oov"" *мййС6'|иГ"Ц"chi""7~
... поскольку операционному усилителю
требуется некоторое время,
чтобы выйти из режима насыщения
Рис. 7N.2. Выходной сигнал простого активного выпрямителя содержит искажение, создаваемое задержкой при выходе опе-
рационного усилителя из режима насыщения (усиление осциллографа — 500 мВ/деление)
Длительность искажения
' составляет приблизительно 6 мке
Сигнал на выходе
операционного усилителя
Сигнал на выходе
схемы выпрямителя
Входной сигнал
Входной
Длительность искажения
Выходной сигнал искажается, пока операционный
усилитель выходит из режима насыщения
Сигнал на выходе
схемы выпрямителя
Сигнал на выходе операционного
усилителя в процессе выхода из
режима насыщения (усиление
осциллографа — 5 В/деление)
Рис. 7N.3. Операционный усилитель медленно выходит из режима насыщения (усиление осциллографа: 500 мВ/деление; для
выходного сигнала операционного усилителя на нижней правой осциллограмме — 5 В/деление)
306
7N. Операционные усилители II: отклонения от идеальности
Но в нашем случае при кратковременном иска-
жении начальная разность напряжений очень
маленькая и она постепенно увеличивается до
0,25 В. Было бы целесообразно изменить схему
так, чтобы избежать насыщения операционно-
го усилителя. В действительности это вполне
можно сделать.
7N.1.2. Улучшение схемы активного
выпрямителя
Рабочие характеристики активного выпрями-
теля можно улучшить (сократить длительность
искажения как минимум в 10 раз), создав усло-
вия для постоянного наличия обратной связи,
в результате чего операционный усилитель ни-
когда не будет входить в режим насыщения2.
На рис. 7N.4 приведена усовершенствованная
таким образом схема активного выпрямителя.
В этой схеме один из диодов всегда открыт.
ЮкОм
Выход
ЮкОм
Вход
Обратная связь всегда присутствует,
поэтому операционный усилитель
никогда не переходит в режим
насыщения
Рис. 7N.4. Дополнительный диод улучшает активный усили-
тель, предотвращая переход в режим насыщения
Для сигнала положительной полярности это
просто инвертирующий усилитель. А в другом
случае, который вызывал переход в режим на-
сыщения3 простого активного выпрямителя по
схеме на рис. 7N.1, в данной схеме обратная
связь не исчезает, поскольку здесь есть второй
диод.
Рекомендуем подробно исследовать эту схему,
чтобы укрепить свою веру в операционные уси-
лители. В частности, попробуйте выяснить, не
оказывает ли отрицательного воздействия на
выходной сигнал диод между выходом опера-
ционного усилителя и выходом схемы.
Описанный выпрямитель инвертирует вход-
ной сигнал. Осциллограмма слева на рис. 7N.5
демонстрирует обычное достоинство актив-
ного выпрямителя: способность выпрямлять
небольшие напряжения, не внося в выход-
ной сигнал падения напряжения на диоде. На
осциллограмме справа на рис. 7N.5 изображен
выходной сигнал операционного усилителя.
Искажения здесь меньше, поскольку теперь
при смене полярности динамический диапазон
выходного сигнала существенно сужен.
На осциллограммах на рис. 7N.6 показана об-
ласть входного и выходных сигналов в момент
смены полярности на более высокой частоте
развертки, откуда видно значительное умень-
шение искажения. Даже при скорости разверт-
ки 400 не/деление для осциллограммы слева
на рис. 7N.6, что в 25 раз быстрее, чем для
осциллограммы на рис. 7N.3, искажение едва
заметно.
Входной
сигнал "
Выходной/
сигнал
Выход операционного
усилителя
t (падение напряжения
| на диоде)
Выходной сигнал
выпрямителя
Входной и выходной сигналы
инвертирующего выпрямителя
L?gy J
При смене полярности входного сигнала
разность между входным и выходным сигналами
не превышает одного вольта
WlT№^t^^vyw
2 АоЕ, рис. 4.38.
ъ Полярность сипшоъ ъ этой
сравнению с предыдущей.
теюертротанъ но
7N.2. Неидеальность операционных усилителей
307
Улучшенная схема выпрямителя:
искажения меньше
Выходной
сигнал
Сигнал
на выходе
схемы
Сигнал
на выходе
операционного
усилителя
Более высокое разрешение осциллограммы
(более быстрая развертка)
Рис. 7N.6. Подробный вид выходного сигнала в момент смены полярности входного сигнала: искажение почти отсутствует
Выходной импеданс
усовершенствованного выпрямителя
Представляет интерес вопрос о выходном им-
педансе 1?вых схемы выпрямителя. Хотя в этой
схеме обратная связь функционирует посто-
янно (и таким образом уменьшает искажение,
присутствующее в более простой схеме вы-
прямителя), импеданс на выходе устройства не
всегда низкий, как можно было бы ожидать от
схемы на операционном усилителе. Если вы-
ходной импеданс оказывается слишком боль-
шим, то в схему добавляют дополнительный
каскад, который решает эту проблему4.
7N.2. Неидеальность
операционных усилителей
Мы вынуждены признать, что операционные
усилители не настолько идеальны, как мы вам
рассказывали5. Это плохая новость. Но есть и
хорошая новость: на рынке доступен обшир-
ный ассортимент операционных усилителей,
буквально тысячи разных типов, для самых
разных областей применения, та или иная ха-
рактеристика которых близка к идеалу. Можно
с легкостью найти операционный усилитель с
низким входным током, с малой погрешностью
напряжения (напряжение Ucw которое мы рас-
смотрим вскоре в этой главе), с небольшими
искажениями. Существуют операционные уси-
лители как с очень высокими рабочими напря-
жениями (сотни вольт), так и с очень низкими
(около 0,9 В), с выходным током, как в десятки
4 Если этот вопрос непонятен вам, можно посмотреть объ-
яснение в книге АоЕ. Но если у вас нет этой книги, дадим
ценную подсказку: наиболее сложна ситуация, когда сигнал
обратной связи проходит через нижний диод. В этом случае
верхний диод не проводит ток, в результате чего значение
выходного импеданса составляет всего лишь 10 кОм. Этот
недостаток можно исправить с помощью повторителя.
5 АоЕ §4.4.1
ампер, так и в наноамперы. Если вам требуется
быстродействующий операционный усилитель,
то такие также доступны на рынке. Но будет
трудно или, скорее всего, невозможно, найти
операционный усилитель, совмещающий все
оптимизированные характеристики.
Несовершенства операционных усилителей
условно делятся на две категории: статические
(по постоянному току) и динамические.
Динамические погрешности
Динамические погрешности проявляются в
виде ухудшения рабочих характеристик при
работе с сигналами высокой частоты.
♦ Спад усиления. Высокий коэффициент уси-
ления, который необходим для реализации
всех возможностей обратной связи, снижа-
ется с повышением частоты. На частоте/х
усиление становится единичным. Эту харак-
теристику часто указывают в виде произве-
дения коэффициента усиления на ширину
полосы пропускания (GBW)6.
♦ Ограниченная скорость нарастания опе-
рационного усилителя приводит к тому, что
сигналы малой амплитуды могут обрабаты-
ваться на более высоких частотах, чем сигна-
лы большой амплитуды.
♦ Снижение помехоустойчивости. Это такая
тонкость, которая не будет иметь значения в
наших экспериментальных схемах.
Далее в этой главе мы подробнее рассмотрим
погрешности операционных усилителей.
Погрешности по постоянному току
Для нас наибольшую важность представляют
два эффекта, которые свидетельствуют о не-
идеальности операционных усилителей.
6 Англ. gain-bandwidth product (GBW). - Примеч. пер.
308
7Л/. Операционные усилители II: отклонения от идеальности
♦ Входы в действительности потребляют (или
выдают) небольшой ток. Этот ток называет-
ся током смещения JCM и он является средней
величиной токов, протекающих через оба
входа операционного усилителя.
♦ Напряжения на входах не абсолютно оди-
наковые. Основной причиной разности на-
пряжений на входах является напряжение
смещения UCM, образно говоря это мера от-
клонения от равнозначности входов опера-
ционного усилителя7.
Скорее всего вас это не очень удивляет. На
рис. 7N.7 изображены три схемы, выход кото-
рых довольно быстро переходит в режим насы-
щения. Если бы операционные усилители были
идеальными, ни в одной из этих схем такого бы
не наблюдалось.
г
Г
Рис. 7N.7. Эти три схемы непременно переходят в режим на-
сыщения. Можете сказать, почему?
Несомненно, вы сможете сами разобраться, по-
чему эти схемы переходят в режим насыщения.
Но поскольку причины различны, будет полез-
но рассмотреть их подробнее.
♦ Схема А. Выходной сигнал этой схемы будет
равен нулю только при нулевом напряже-
ния смещения 1ГСМ, а этого никогда не может
быть.
♦ Схема Б. Выходной сигнал этой схемы бу-
дет равен нулю только при нулевом токе
смещения 1СМ, каковым он не может быть.
Если входной каскад собран на биполярных
транзисторах, ток смещения 1СМ является то-
ком базы транзистора, и этот ток постепен-
но заряжает конденсатор. А если входной
каскад операционного усилителя выполнен
на полевых транзисторах, ток смещения 1СМ
является током утечки транзистора. В лю-
бом случае, этот ток заряжает конденсатор,
в результате потенциал неинвертирующего
7 Другой причиной, но обычно менее значимой, является
ограниченное усиление операционного усилителя. Напри-
мер, в разделе 6N.6.2 мы вычислили разницу между двумя
входными сигналами, требуемую для создания выходного
сигнала напряжением 11 В.
входа приближается к напряжению питания
той или другой полярности.
Примечание
Выходной сигнал операционного усилителя на ми-
кросхеме 411 в такой схеме будет приближаться к
отрицательному напряжению питания (см. обсуж-
дение схемы выборки и хранения на этой микро-
схеме в разделе 12N.7.1).
♦ Схема В. Если бы напряжение смещения Ucu
и ток смещения JCM были нулевыми, напря-
жение на инвертирующем входе также было
бы нулевым, и этот случай был бы таким же,
как и случай Б. Как упоминалось при рассмо-
трении интегратора* конденсатор не образует
обратной связи в условиях постоянного тока.
Поэтому наличие конденсатора не предохра-
няет операционный усилитель от перехода
в режим насыщения.
7N.2.1. Насколько важны
эти несовершенства?
Если посмотреть на численные значения ре-
альных характеристик операционного усили-
теля, которые отличны от идеальных, то откло-
нения выглядят довольно незначительными.
Рассмотрим, например, типичные значения па-
раметров операционного усилителя на микро-
схеме 411: Е/см = 0,8 мВ, 1СМ = 50 пА, скорость
нарастания выходного напряжения равна
15 В/мкс, усиление по постоянному току (без
обратной связи) не бесконечное, но составля-
ет 200 000. Вы только посмотрите на единицы
измерения: пА (пикоамперы), мВ (милливоль-
ты)! Они же совсем крошечные! Неужели эти
отклонения от идеальных характеристик име-
ют значение? Ответом на данный вопрос будет
неопределенное «иногда».
Уже само по себе большое количество самых
разнообразных операционных усилителей,
предлагаемых на рынке, должно навести на
мысль, что эти небольшие отклонения могут
быть важны. Если бы это было не так, то рынок
бы обошелся одним или несколькими разными
операционными усилителями. Но вместо этого
мы имеем дело с поразительным разнообразием
операционных усилителей, и каждые несколько
месяцев нам предлагают новые. Ибо улучшение
одной характеристики влечет за собой ухудше-
ние какой-либо другой. Поэтому советуем вни-
мательно изучать технические характеристики
7N.2. Неидеальность операционных усилителей
309
конкретных компонентов, даже признавая, что
для многих вариантов применения большин-
ство операционных усилителей можно считать
идеальными, даже такие недорогие и широко
распространенные устройства, как, например,
микросхема 411.
Далее приведены несколько примеров наиме-
нований операционных усилителей, предлага-
емых тремя ведущими фирмами-производи-
телями.
Компания Texas Instruments. Свыше 1800 ма-
рок микросхем, включая пару сотен разновид-
ностей устройств дочерней компании National
Semiconductor.
Компания Linear Technology. Около 350 наи-
менований.
Компания Analog Devices. Около 320 типов
микросхем.
Даже отдельный производитель операционных
усилителей может предлагать такое большое
количество наименований, поэтому для удоб-
ства разработчиков выделяют несколько ка-
тегорий компонентов. Далее приведен список
категорий операционных усилителей, предла-
гаемых компанией Texas Instruments.
♦ Низкое напряжение смещения (Low Offset
Voltage);
♦ Маломощные (Low Power);
♦ Малошумящие (Low Noise);
♦ Низкий входной ток смещения (Low Input
Bias Current);
♦ Широкая полоса пропускания (Wide Band-
width);
♦ Широкий диапазон напряжений питания
(Wide Supply Voltage);
♦ Однополярное напряжение питания (Single
Supply Voltage).
И этот список еще не содержит более специали-
зированных операционных усилителей, таких
как, например, усилители мощности и буферы
(Power Amplifiers and Buffers). Даже с этой раз-
бивкой на категории, разнообразие операцион-
ных усилителей впечатляет.
В разделе 7N.2.9 дана таблица из книги АоЕ,
в которой дан образец обычно указываемых
рабочих характеристик операционных усили-
телей. Беглого ознакомления с этой таблицей
достаточно, чтобы напомнить нам, что невоз-
можно иметь все и сразу. Например, микросхе-
мы на биполярных транзисторах имеют лучшее
(примерно в 50 раз) напряжение смещения £/см,
чем на МОП-транзисторах, но расплачиваются
за это смещением входного тока JCM в несколько
тысяч раз бблыпим, чем для КМОП-устройств.
Этого, конечно же, следовало ожидать — про-
сто еще один случай справедливости в элект-
ронике.
Еще одна таблица, из раздела 4.7 книги АоЕ,
содержит 34 типа операционных усилителей,
включая два, на которые мы ориентируемся
больше всего на наших лабораторных заняти-
ях, — LF411 и LM358. Номенклатура параме-
тров для компонентов в этой таблице несколько
шире, чем в таблице в разделе 7N.2.9, включая
размах входного и выходного сигналов и ток
источника питания. Не правда ли удивительное
разнообразие?
Две схемы, в которых неидеальность
нужно учитывать
Далее мы рассмотрим два случая, в которых
небольшие погрешности по постоянному току
могут оказаться важными:
♦ чувствительный усилитель постоянного тока
(рассматривается в разделе 7W.1);
♦ интегратор (он рассматривается в разде-
ле 7W.1).
А пока мы подробнее изучим самые важные от-
клонения операционных усилителей от идеаль-
ных рабочих характеристик.
7N.2.2. Входное напряжение
смещения нуля (Усм
Входное напряжение смещения нуля (или про-
сто напряжение смещения) — это разница на-
пряжений на входах, необходимая для получе-
ния нулевого выходного напряжения8.
Этот параметр характеризует наличие разни-
цы напряжений на входах операционного уси-
лителя, когда в действительности этой разни-
цы не должно быть. Эту погрешность можно
8 АоЕ §4.4.1А
310
7N. Операционные усилители II: отклонения от идеальности
представить в виде постоянного напряжения,
подаваемого на один из входов идеального
внутреннего дифференциального усилителя
с нулевым смещением, как показано слева на
рис. 7N.89.
Нулевое
Напряжение
Выход
\ режиме
"Ф" ~U"^ насыщения
Рис. 7N.8. Слева: напряжение смещения UCM соответствует
напряжению, подаваемому на один из входов идеального
операционного усилителя. Справа: результаты, вызываемые
напряжением смещения
Это разделение идеальных и действительных
характеристик напоминает модель Тевенина из
главы IN. На рис. 7N.8 представлены два воз-
можных результата, вызываемые наличием
напряжения смещения. Но идея, что уровень
выходного сигнала можно свести к нулю, подав
на вход операционного усилителя напряжение,
равное по величине напряжению смещения,
только обратной полярности, не вполне соот-
ветствует действительности.
Погрешность напряжения смещения возникает
вследствие неидеальной подгонки параметров
элементов двух плеч входного дифференциаль-
ного каскада. Чтобы получить недостижимое
UCM = 0, не только параметры всех транзисто-
ров дифференциального каскада операционно-
го усилителя должны идеально совпадать, но
также и параметры транзисторов токового зер-
кала, которое служит нагрузкой первого каска-
да. Эти схемные элементы показаны на упро-
щенной принципиальной схеме операционного
усилителя на рис. 7N.11. Полная принципиаль-
ная схема микросхемы операционного усили-
теля 411 приведена на рис. 9S.31. В табл. 7N.1
приведены характеристики напряжения сме-
щения UCM для нашего основного операцион-
ного усилителя, используемого на лаборатор-
ных занятиях.
Несовпадение характеристик можно компен-
сировать, увеличив ток одного плеча входного
каскада по сравнению с другим, чтобы снова
сбалансировать их. Это может выглядеть не-
разумным, ведь, в конце концов, производитель
сделал все возможное, чтобы согласовать пара-
метры схемных элементов. Почему вы думаете,
что можете своими грязными руками залезть в
«мозг» операционному усилителю и улучшить
его работу?!
Вообще-то можете, если в процессе корректи-
ровки наблюдать за выходным сигналом с по-
мощью чувствительного вольтметра. Таким
образом можно определить момент, когда
напряжение смещения будет оптимизирова-
но11. Эта операция называется подстройкой
смещения (англ. offset trimming), и мы рассмо-
трим, как ее выполнять на лабораторном за-
нятии 7L. Но осуществлять такую подстройку
на практике неудобно, а ее результаты не-
стабильны: с течением времени и при изме-
нении температуры напряжение смещения
снова отклоняется от заданного (см. раздел
4.4.1В книги АоЕ). Это приемлемый способ
улучшить рабочие характеристики единич-
ного экземпляра лабораторного прибора, но
не устройства, массово выпускаемого в боль-
ших количествах. Представьте себе, насколь-
ко возрастет стоимость устройства, если его
придется вручную настраивать в конце сбо-
рочной линии. Даже если автоматизировать
эту операцию, все равно стоимость устрой-
ства увеличится довольно ощутимо.
Автоматическая установка нуля
в операционных усилителях
с самокоррекцией
В некоторых операционных усилителях на-
пряжение смещения подстраивается автома-
тически благодаря наличию в них встроенного
вспомогательного операционного усилителя.
Таблица 7N.1. Характеристики напряжения смещения операционного усилителя 411
Обозначение
(Ucu)
Характеристика
Входное напряже-
ние смещения нуля
Условия
Rs = 10Q,
ГА = = 25°С
LF411A
Мин.
Типичное
0,3
Макс.
0,5
LF411
Мин.
Типичное
0,8
Макс.
2,0
Единицы
мВ
9 Спасибо Давиду Абрамсу (David Abrams) за совет, как
откорректировать эту схему.
10 Так указано в оригинале справочного листка. OS — offset, являетесь частью цепи обратной связи.
11 Вероятно, вам понятно, что, вращая ручку потенциоме-
тра, вы можете выполнить эту деликатную операцию толь-
ко потому, что, наблюдая за показаниями вольтметра, вы
7N.2. Неидеальность операционных усилителей
311
«Заблуждающийся» операционный усилитель: до и после.
Осанка исправляется с помощью ортопедического ботинка = настройка
Но ведь я же стою прямо!
После
Одна нога короче на UCH
возможно теперь я все-таки^
твую себя лучше
Подобран ортопедический
ботинок: высота подошвы = Ц.м
Рис. 7N.10. Корректировка напряжения смещения в сравнении с ортопедическим ботинком
Такой встроенный усилитель работает ци-
клически на частоте в несколько десятков
или сотен герц и посредством прерывания
между двумя состояниями стабилизирует вы-
ход12. Такой периодический процесс обнуле-
ния, т. е. коррекция нуля прерыванием13, не
идентичен схеме операционного усилителя с
преобразованием сигнала. В последней схеме
прерыватель периодически отключает входы
основного усилителя, создавая, таким обра-
зом, эффект выборки, который значитель-
но ограничивает полосу пропускания. При
стабилизации напряжения смещения нуля с
помощью встроенного дополнительного уси-
лителя основной усилитель всегда включен и
поэтому не частотные характеристики схемы
не ухудшаются14.
Основная польза, получаемая в результате кор-
рекции нуля, состоит, конечно же, в чрезвычай-
но низком напряжении смещения, типичное
значение которого может быть порядка 1 мкВ,
12 АоЕ § 4.7.
13 кит. chopper stabilizing.
14 В случае если вам интересно, этот способ обнуления ра-
ботает таким образом. Самокорректирующийся операци-
онный усилитель сначала обнуляет свое собственное сме-
щение. Для этого входы усилителя соединяются вместе, и
сигнал подается с выхода на вход обнуления. (Эта опера-
ция реализует ту же самую задачу, которую мы выполняем
вручную, вращая ручку потенциометра, подключенного
между двумя выводами.) После этого сигнальные входы
подключаются к сигнальным входам основного усилителя,
и выходной сигнал поступает на вход обнуления смещения
основного усилителя. Эти два напряжения обнуления со-
храняются в конденсаторах в течение периодических пре-
рываний. Таким образом, отрицательная обратная связь
сведет значения сигналов на входах основного усилителя
почти к идеальному равенству.
а максимальное — 5 мкВ15. А дополнительные
преимущества — очень большой коэффициент
усиления при разорванной цепи обратной свя-
зи и очень хорошая устойчивость ко всем типам
помех при работе по постоянному току и при
низкой частоте, включая помехи по питанию
и дрейф напряжения смещения со временем и
температурой.
Мы познакомимся с одним из таких усилителей
со стабилизацией нуля прерыванием, LTC1150,
на лабораторном занятии 7L. И мы надеемся,
что упражнение по ручному обнулению напря-
жения смещения для операционного усилителя
411 на этом же лабораторном занятии не засло-
нит общеизвестную истину, что обычно будет
предпочтительней:
♦ выбирать качественный операционный уси-
литель с низким напряжением смещения
♦ разрабатывать схемы так, чтобы они хорошо
работали с напряжением смещения исполь-
зуемого вами операционного усилителя. На
рис. 7N.10 приводится шуточная иллюстра-
ция в напоминание о том, что при подстрой-
ке напряжения смещения мы пытаемся вруч-
ную исправить встроенную в операционный
усилитель асимметрию.
На рис. 7N.11 изображена более точная схе-
ма корректировки напряжения смещения:
15 Хорошее объяснение принципов работы самообнуляю-
щихся усилителей приводится в статье «Demystifying Auto-
Zero Amplifiers Part 1» («Прояснение самообнуляющихся
усилителей, часть 1») журнала Analog Dialog, издание 34,
№ 2, март 2000 г., которая доступна по адресу http:/^ww.
analog.com/en/analog-dialogue/articles/demystifying-
auto-zero-amplifiers-part- l.html.
312
7N. Операционные усилители II: отклонения от идеальности
Подстройка напряжения смещения, путем отбора разных по
величине токов из двух плеч дифференциального усилителя
и токового зеркала. Из-за разницы токов исходный дисбаланс
оказывается скорректированным.
Рис. 7N.11. Внутренний механизм корректировки напряжения смещения операционного усилителя на микросхеме 411.
Слева: упрощенная принципиальная схема. Справа: подробная схема
подстроенная цепь встроена во входной каскад
операционного усилителя и забирает больше
тока из одного его плеча, чем из другого, в объ-
еме, достаточном для того, чтобы скорректиро-
вать исходный дисбаланс токов.
7N.2.3, Входной ток смещения /см
Ток смещения /см представляет собой постоян-
ный ток, протекающий через входные выводы
операционного усилителя16. Этот ток опреде-
ляется как среднее значение величин тока двух
входов (см. табл. 7N.2).
Для операционных усилителей с биполярными
транзисторами во входном каскаде ток смеще-
ния JCM является током базы. А в случае поле-
вых транзисторов во входном каскаде, как в
микросхеме 411, это ток утечки, незначитель-
ный, но резко возрастающий с повышением
температуры (рис. 7N.13).
10
1
од
0,01
0,001
LF411
-50° 0°С +50 °С +100 °С
Температура
Рис. 7N.13. Входной ток смещения операционного усилите-
ля на микросхеме 411; он небольшой, но резко возрастает
с повышением температуры
Таблица 7N.2. Рабочие характеристики операционного усилителя 411: ток смещения и ток сдвига
Обозна-
чение
'оз('сд)
''BIAS
(U
Характе-
ристика
Входной
ток сдвига
Входной
ток сме-
щения
Условия
17ИП = ±15В
Цт = ±15В
Г; = 25°С
2} = 70°С
2} = 125 "С
7} = 25°С
7} = 70 "С
1}=125°С
LF411A
Мин.
Типичное
25
50
Макс
100
2
25
200
4
50
LF411
Мин.
Типичное
25
50
Макс.
100
2
25
200
4
50
Еди-
ницы
пА
нА
нА
пА
нА
нА
16 АоЕ § 4.4.1С.
7Ы.2. Неидеальность операционных усилителей
313
Подбор резисторов
для минимизации влияния
входного тока смещения
Входной ток смещения протекает через рези-
сторы, поступая на каждый вход операцион-
ного усилителя17. Поэтому он может создавать
входное напряжение рассогласования, кото-
рое после усиления вызывает значительную
ошибку в выходном сигнале. На рис. 7N.14
показана схема усилителя постоянного тока с
высоким коэффициентом усиления, в которой
входные резистивные пути преднамеренно
рассогласованы.
Вход
ЮкОм
Выход
Рис. 7N.14. Демонстрационная схема на операционном уси-
лителе с высоким коэффициентом усиления по постоянному
току, позволяющая измерять погрешности
Эту схему можно использовать для демонстра-
ции влияния тока и напряжения смещения JCM
Ток смещения величиной 80 нА (типичное зна-
чение) протекает через резистор сопротивле-
нием 10 кОм по одному пути и через резистор
сопротивлением 100 Ом по другому18, в резуль-
тате чего на неинвертирующем входе создается
разностный сигнал величиной около -0,8 мВ19.
Полагая напряжение смещения UCM равным
нулю (нереалистичное предположение, но бу-
дем решать проблемы последовательно), по-
лучим, что этот псевдосигнал создаст ложный
выходной сигнал величиной около -0,8 В.
При очень малом токе смещения можно
обойтись без балансировки
Но для того, чтобы в схеме на рис. 7N.14 про-
демонстрировать влияние тока смещения,
17 См. рис. 4.55 в книге АоЕ.
18 Это просто 2?ТЕВ для делителя, с которого сигнал посту-
пает на инвертирующий вход.
19 Напряжение будет отрицательным, поскольку ток сме-
щения /см микросхемы 741 представляет собой ток базы
л-р-л-транзисторов входного каскада.
в ней необходимо заменить микросхему 411
на какой-либо более старый компонент, типа
микросхемы 741 (что и сделано в этой схеме).
В микросхеме 411 ток смещения не вызывает
никаких поддающихся измерению эффектов.
То обстоятельство, что для демонстрации та-
ких эффектов потребовалась микросхема 741,
наводит на мысль, что нам зачастую не нужно
беспокоиться о балансировке, так как в на-
стоящее время можно найти операционный
усилитель стоимостью меньше одного долла-
ра с током смещения в 103 раз меньшим, чем
в микросхеме 411. Предположение, что ба-
лансировка может быть ненужной, является
обоснованным, но при этом следует знать, как
выяснить, нужно ли беспокоиться о влиянии
тока смещения или нет.
Если входной ток смещения вызывают про-
блемы, то следует предпринять меры для их
минимизации, тщательно согласовывая сопро-
тивления во входных цепях операционного
усилителя. На рис. 7N.15 приведено несколько
примеров схем с сбалансированными и несба-
лансированными путями.
После правильной балансировки резисторов
ток смещения больше не будет вызывать по-
грешность выходного сигнала. Но останется
погрешность, обусловленная разностью между
токами входов. Эта разность токов называется
током сдвига 1СД.
7N.2A Ток сдвига
Ток сдвига /сд представляет собой разность
токов смещения, протекающих через два вхо-
да20. Для операционного усилителя на микро-
схеме 411 ток сдвига /сд приблизительно равен
току смещения /см. Для операционных усилите-
лей с биполярными транзисторами во входном
каскаде ток сдвига меньше, чем ток смещения.
Но вспомните, насколько мал ток смещения
операционного усилителя на микросхеме 411 и
других усилителей с входным каскадом на по-
левых транзисторах.
Наличие тока сдвига означает существование
погрешности выходного сигнала даже при сба-
лансированных сопротивлениях на обоих вхо-
дах. Как решить эту проблему? Использовать
резисторы не слишком большого номинала
20 АоЕ § 4.4.1D.
314
7А/. Операционные усилители II: отклонения от идеальности
10 кОм
10 кОм
Плохая схема
Плохая схема
ЮкОм
Некачественное решение
Хорошая схема
Сбалансированная схема
Хотим получить нулевой
выходной сигнал при
нулевом входном сигнале
Модель для балансировки
инвертирующего усилителя
Рис. 7N.15. Балансировка резисторов минимизирует погрешность выходного сигнала, вызываемую током смещения
(меньше, чем несколько десятков мегаомов; см.
описание хитроумного приема с Т-образной
резистивной цепочкой в разделе 7N.3.2).
7N.2.5. Скорость нарастания
выходного сигнала и спад усиления
Оказывается, что ограниченные значения
скорости нарастания выходного сигнала и ко-
эффициента усиления объясняются компенси-
рующим конденсатором, встроенным в опера-
ционный усилитель21. Этот компонент присут-
ствует в схеме на рис. 7N.11, но его назначение
не объяснено. Мы рассмотрим подробно ком-
пенсирующий конденсатор в главе 9N при об-
суждении темы стабильности операционных
усилителей.
Спад усиления
Здесь мы просто отметим, что результатом на-
личия компенсирующего конденсатора (на-
зывающегося таким образом потому, что он
компенсирует склонность схемы к самовозбуж-
дению) является спад усиления операционно-
го усилителя величиной -6 дБ/октаву. Иными
словами, операционный усилитель ведет себя
так, будто его выходной сигнал проходит через
простой низкочастотный ЛС-фильтр. В дей-
ствительности это и происходит, но только во
внутреннем втором каскаде. Таким образом,
очень высокое усиление устройства, необходи-
мое для действия обратной связи, неуклонно
уменьшается при повышении частоты, и сходит
на нет при частоте в несколько мегагерц (ти-
пичное значение для микросхемы 411 состав-
ляет 4 МГц; см. табл. 7N.3 и рис. 7N.16).
Таблица 7N.3. Параметры микросхемы LF4U
Обозначение
GBW
Характеристика
Усиление по напряжению
большого сигнала
Произведение «усиление-
полоса пропускания»22
Условия
1/вых= ±10 В
Ян = 2 кОм, ГА = 25 °С
с температурой
[/ип=±15В
ГА = 25°С
LF411
Мин.
25
15
2,7
Типичное
200
200
4
Макс.
Единицы
В/мВ
В/мВ
МГц
21 АоЕ § 4.4.1К.
22 Англ. — Gain-Bandwidth Product
7/V.2 Неидеальность операционных усилителей
315
100
80
3
20
1 10 102 103 104 105 106 107
Частота, Гц
Рис. 7N.16. Спад усиления операционного усилителя на
микросхеме 411
Эта частота23, обозначаемая fv при которой
коэффициент усиления падает до единичного,
определяет частотный предел работоспособно-
сти любой схемы на операционном усилителе24.
Зная это ограничение, можно понять, почему не
все схемы следует собирать на операционных
усилителях, какими бы чудесными не были эф-
фекты отрицательной обратной связи.
Скорость нарастания выходного
напряжения
Компенсирующий конденсатор также влияет
на скорость нарастания выходного напряжения
операционного усилителя25. Скорость нараста-
ния, максимальное значение отношения dU/dt
выходного сигнала операционного усилителя,
достигается, когда максимальный ток входного
каскада — весь ток хвоста, исходящий из раз-
балансированного дифференциального каска-
да, - заряжает этот компенсирующий конден-
сатор. Для операционного усилителя 411 ток
хвоста первого каскада можно оценить, зная
скорость нарастания и емкость компенсирую-
щего конденсатора:
I = CdU/dt = 10 • 1012 • (15 В/мкс) = 150 мкА.
23 АоЕ § 4.4.1j.
24 Частота/j тесно связана с произведением «усиление —
полоса пропускания» GBW (англ. Gain-BandWidth [prod-
uct]). Эти две величины отличаются только у неском-
пенсированных (декомпенсированных) операционных
усилителей, которые не могут стабильно работать при
единичном усилении. См. книгу «1С Op-Amp Cookbook»
(«Справочник по микросхемам операционных усилите-
лей»), автор Вальтер Г. Юнг (Walter G.Jung), издательство
SAMS, 3-е изд., 1997 г., ее. 67-70.
25 Англ. slew rate.
На рис. 7N.11 показан компенсирующий кон-
денсатор, подключенный между базой и кол-
лектором второго каскада операционного уси-
лителя, который является усилителем с общим
эмиттером
26
Но мы не хотим завершить этот раздел, оставив
вас под впечатлением, что произведение «уси-
ление — полоса пропускания» микросхемы 411
величиной в 4 МГц является пределом, который
можно ожидать от всех операционных усили-
телей. Вовсе нет. На рынке доступны операци-
онные усилители с любой оптимизированной
характеристикой (но, как уже упоминалось, в
ущерб другим возможностям). Если вам нужен
операционный усилитель с характеристикой
GBW = 1 ГГц, то вы легко найдете его27.
7N.2.6. Ограничение выходного тока
Наличие ограничения выходного тока предо-
храняет маломощные транзисторы выходно-
го каскада28. Таким образом предотвращается
перегрев, который в противном случае мог бы
произойти в результате перегрузки усили-
теля по неосторожности или небрежности.
Большинство операционных усилителей, вклю-
чая микросхему 411, могут выдерживать даже
такое издевательство, как закорачивание выхо-
да не только на землю, но и на шину питания
любой полярности. Мы отложим рассмотрение
механизма работы этой схемы, пока не начнем
изучать материал по стабилизаторам напряже-
ния в главе 11N.
Мы видели влияние этого ограничения тока на
лабораторном занятии 6L. Этот эффект еще раз
иллюстрируется на рис. 7N.17.
Как и следовало ожидать, на рынке доступны
сильноточные и высоковольтные операцион-
ные усилители. Но требуемый большой ток ча-
сто можно получить, используя операционный
усилитель для управления усилителем тока, на-
подобие эмиттерного повторителя с двухтакт-
ным выходным каскадом, который мы собрали
на лабораторном занятии 6L.8. Но если вам
26 На самом деле схема слегка усложнена наличием в ней
повторителя, сигнал с которого подается на базу усилителя
с общим эмиттером.
27 Например, заявленная частота/х микросхемы ОРА640
компании TI/Burr-Brown составляет 1,3 ГГц. Устройства
с обратной связью по току могут работать на еще более
высоких частотах.
28 АоЕ § 4.4.1Н.
316
7W. Операционные усилители II: отклонения от идеальности
LF411
100 0м 1КОм 10 КОм
Сопротивление нагрузки
(логарифмический масштаб)
вых
ограниченный (25 мА)
LF411
1К0м
Сопротивление нагрузки, Омы,
линейный масштаб)
Рис. 7N.17. Ограничение выходного тока: несмотря на низкое выходное сопротивление Явых при наличии нагрузки проис-
ходит отсечка выходного сигнала
неохота собирать схему самостоятельно, чтобы
получить десятки ампер тока при напряжении
в сотни вольт, на рынке присутствуют операци-
онные усилители с такими характеристиками.
Например, компания Apex/Cirrus Logic выпу-
скает операционный усилитель МР38, выдаю-
щий ток 10 А при напряжении 200 В, обеспечи-
вая мощность 125 Вт.
7N.2.7. Шум
В процессе работы любой операционный усили-
тель добавляет к выходному сигналу определен-
ное количество шума29. Этот эффект слишком
слабый, чтобы его можно было наблюдать на
наших лабораторных занятиях, но, тем не менее,
достаточно серьезный, чтобы изготовители ука-
зывали его величину для каждого операционно-
го усилителя. В частности, указывается два типа
шума: шум напряжения (ел) и токовый шум (in).
Эффекты от этих обоих типов шума складыва-
ются, но тот или другой тип может быть более
важным в зависимости от конкретного диапа-
зона сопротивления источник? сигнала. В слу-
чае высокого сопротивления источника сигнала
более важным является токовый шум (при про-
текании через сопротивление источника Ди то-
ковый шум создает шумовой сигнал). В справоч-
ном листке для микросхемы 411 среди прочего
приведена величина токового шума всего лишь
0,01 пАДГц. На рис. 7N.18 приводится начало
этого справочного листка. Данные из справоч-
ного листка приведены в табл. 7N.4.
National
Semiconductor
LF411A/LF411 Low Offset, Low Drift
JFET Input Operational Amplifier
July 108?
General Description
These devices are low cost, high speed, JFET Input opera-
tional amplifier» with very low Input offset voltage and guar-
anteed input offset voltage drift. They require low supply
current yet maintain a large gain bandwidth product and fast
slew rate. In addition, well matched Ngh voltage JFET input
devices provide very low Input bias and offset currents. The
LF411 kt pin compatible with the standard Ш741 allowing
designers to immediately upgrade the overall performance
of existing designs.
These amplifiers may be used In applications such as ЩЬ
speed integrators» fast D/A converters» sample and hold
circuits and many other circuits requiring low input offset
voltage and drift, low input bias current» high Input Imped-
ance» high slew rate and wide bandwidth.
Features
ft Internally trimmed offset voltage
« Input offset voltage drift
ft Low input bias current
ft low input noise current
■ Wtde gain bandwidtn
« High slew rate
ft Low supply cutrent
ft High Input impedance
ft tow total harmonic distortion Ay» Ю,
R^IOk, Уо**20 Vp~p, 8W^20 Hz~20 kHz
» Low 1/f noise comer
я Fast settling time to 0.01%
50 pA
3 MNzCmtn)
1.8 mA
<O»02%
50 M*
Рис. 7N.18. В справочном листке для микросхемы операционного усилителя LF411 отмечается, среди прочих его достоинств,
низкий токовый шум (с разрешения компании National Semiconductor)
29 АоЕ,глава8.
7N.2. Неидеальность операционных усилителей
317
Таблица 7N.4. Данные из справочного листка микросхемы LF411
National Semiconductor
Операционный усилитель LF411A/LF411 с входным каскадом на полевом транзисторе,
низким напряжением смещения и малым дрейфом
Общее описание
Отличительные особенности
Эти недорогие, высокоскоростные устрой-
ства являются операционными усилителями
с входным полевым транзистором и очень
низким входным напряжением смещения
и гарантированным дрейфом этого напря-
жения. Они могут работать от слаботочно-
го источника питания, но при этом имеют
большое произведение «усиление - полоса
пропускания» и высокую скорость нарас-
тания выходного сигнала. Кроме того, хоро-
шо подобранные высоковольтные полевые
транзисторы с управляющим р-я-переходом
во входном каскаде обеспечивают очень
низкие входные токи смещения и сдвига.
Цоколевка микросхемы LF411 совместима
со стандартной микросхемой операцион-
ного усилителя LM741, что позволяет раз-
работчикам без труда улучшить рабочие ха-
рактеристики существующих устройств.
Эти усилители можно использовать в та-
ких приложениях, как высокоскоростные
интеграторы, быстродействующие цифро-
аналоговые преобразователи, схемы выбор-
ки и хранения и во многих других схемах,
требующих низкого входного напряжения
смещения с малым дрейфом, низкого вход-
ного тока смещения, высокого выходного
импеданса, высокой скорости нарастания
сигнала и широкой полосы пропускания
Напряжение смещения с внутренней
подстройкой (Internally trimmed
offset voltage)
Дрейф входного напряжения смеще-
ния нуля (Input offset voltage drift)
Низкий входной ток смещения (Low
input bias current);
Низкий входной токовый шум (Low
input noise current);
Широкая полоса пропускания усиле-
ния (Wide gain bandwidth)
Высокая скорость нарастания вы-
ходного сигнала (High slew rate)
Низкий потребляемый ток от источ-
ника питания (Low supply current)
Высокий входной импеданс (High
input impedance)
Низкий коэффициент нелинейных
искажений (Low total harmonic
distortion) \ «10, Дн = 10 кОм,
11ШХ = 20 В, при полосе пропускания
20 Гц...2О кГц
Низкая частота среза 50 Гц
Малое время установления до 0,01%
(Fast settling time) 2 мкс
0,5 мВ (макс.)
10 мкВ/ГС (макс.)
50 nF
0,01 пАДГц
не менее 3 МГц
не менее 10 В/мкс
1...8мА
1012Ом
<0,02%
7N.2.8. Диапазон входных
и выходных напряжений
Обычные операционные усилители
(наподобие микросхемы 411)
Большинство операционных усилителей не мо-
гут работать с входными сигналами, напряже-
ние которых приближается к максимальному
напряжению источника питания любой поляр-
ности, а также не способны выдавать выходной
сигнал с уровнем, близким к максимальному
напряжению источника питания любой по-
лярности30. Эти ограниченности иллюстриру-
ются в операционном усилителе на микросхе-
ме 411 (предполагаются напряжения питания:
для 411А - ±20 В, для 411 - ±15 В), соответ-
ствующие характеристики которого (1/вых
и исшф) приведены в табл. 7N.531.
Последствия превышения диапазона напряже-
ний входных синфазных сигналов могут быть
весьма необычными. Операционный усили-
тель на микросхеме 411 (подобно некоторым
другим похожим операционным усилителям32)
30 АоЕ §§ 4.4.1f, 4.4.1G, 4.4.1Н.
31 Приведенные в табл. 7N.5 характеристики усложняются
тем, что в рекомендациях по применению в данном спра-
вочном листке заявлено» что микросхема операционного
усилителя 411 будет работать с входными сигналами, уро-
вень которых может достигать уровня положительного на-
пряжения источника питания, но при этом произведение
«усиление — полоса пропускания» и максимальная скорость
нарастания выходного сигнала могут быть уменьшены.
32 Джим Уильяме составил список нескольких операци-
онных усилителей, имеющих такие особенности: LF147,
LF351, LF156. Подобно микросхеме 411, все они содержат
входной каскад на полевых транзисторах с управляющим
р-я-переходом.
318
7N. Операционные усилители II: отклонения от идеальности
Таблица 7N.5. Напряжения входного и выходного сигналов
операционного усилителя на микросхеме LF411
Электрические характеристики по постоянному напряжению (Примечание 5)
Обозначение
"вых
^СИНФ
Характеристика
Размах выходно-
го напряжения
(Output voltage
swing)
Диапазон на-
пряжений вход-
ных синфазных
сигналов (Input
Common-Mode
Voltage Range)
Условия
иип=±15В,
(К„ = 10кОм)
LF411A
Мин.
±12
±16
Типичное
±13,5
+19,5
-16,5
Макс.
LF411
Мин.
±12
±11
Типичное
±13,5
+14,5
-11,5
Макс.
Еди-
ницы
В
В
В
ведет себя необычно, если уровень напряжения
на одном или обоих его входах окажется мень-
ше заявленного нижнего предела диапазона
входных напряжений. Эта особенность указа-
на не на первой странице справочного листка,
а на его восьмой странице среди рекомендаций
по применению, соответствующий отрывок из
которых приведен далее.
Рекомендации по применению
Линейка операционных усилителей LF411 с вход-
ным каскадом на полевых транзисторах с управ-
ляющим р-п-переходом и с внутренним механиз-
мом подстройки напряжения смещения (BI-FETII™)
обеспечивают очень низкое входное напряжение
смещения с гарантированным дрейфом...
Превышение предельного отрицательного напря-
жения на любом из двух входов вызовет переход
выходного сигнала на высокий уровень и возмож-
ную инверсию фазы выходного сигнала...
Это необычное свойство (которое может пре-
вратить отрицательную обратную связь в по-
ложительную) поставило нас в тупик, когда мы
на лабораторном занятии 10L собирали на ма-
кетной плате ПИД-схему для управления элек-
тродвигателем. В конечном итоге мы разобра-
лись, в чем заключалась проблема, и заменили
микросхему 411 на LM358, которая не обладает
этой странностью.
Разработчики знают об этом странном пове-
дении, и в одной компании решили, что могут
немного подзаработать, модифицировав по-
пулярный операционный усилитель, чтобы
устранить это обращение фазы. Покойный
Джим Уильяме, работавший в течение долгого
времени инженером по прикладным решениям
и первым специалистом по аналоговой схемо-
технике в компании Linear Technology Co., рас-
сказал нам поразительную историю об этом.
Его компания создала такой улучшенный опе-
рационный усилитель и отослала его образцы
и имитационные модели компании General
Motors, которая использовала операционный
усилитель наподобие микросхемы 411 для
управления трансмиссией своих дизельных ло-
комотивов.
Некоторое время спустя компания General
Motors прислала отчет о результатах исследо-
вания «улучшенного» операционного усилите-
ля, которые оказались далеко не улучшенными.
Наоборот, на тестируемых локомотивах время
от времени неожиданно включалась задняя
передача. В результате все решили отказать-
ся от планов заменить старые операционные
усилители новыми «улучшенными». По всей
видимости, компания General Motors адапти-
ровала свое программное обеспечение для ра-
боты со старым усилителем, чтобы учитывать
инверсию фазы, и когда этого не происходило
с новым усилителем, возникала проблема. Этот
случай напоминает анекдотическую, но весьма
правдоподобную историю о человеке, который
просыпается, потому что не зазвонил будиль-
ник. Подобным образом локомотивы компа-
нии General Motors «просыпались», т. е. вклю-
чали заднюю передачу, когда операционные
усилители не инвертировали фазу.
Эта история также объясняет, почему никто
особенно не спешит заменять старые микро-
схемы в работающей должным образом схеме
на новые, «улучшенные». В свою очередь, это
7N.2. Неидеальность операционных усилителей
319
нежелание объясняет тот любопытный факт,
что современные версии старых микросхем,
наподобие операционного усилителя LM741,
намного лучше исходных компонентов, но про-
изводители не пишут об этом в справочных
листках. Если бы они решили похвастаться
этими возможностями, изменив справочный
листок, то это оказалась бы уже не микросхема
741, и любому разработчику, предлагающему
использовать новый улучшенный компонент,
пришлось бы сначала убедить свое начальство,
что все требуемое тестирование, чтобы при-
нять новое устройство в эксплуатацию, будет
того стоить.
Операционные усилители
с увеличенным размахом входного
и/или выходного сигнала
Некоторые операционные усилители облада-
ют лучшим диапазоном напряжения входных
синфазных сигналов, чем усилитель на микро-
схеме 41133. Усилители с однополярным ис-
точником питания (наподобие усилителя на
микросхеме 358, с которым мы познакомим-
ся на лабораторном занятии 7L) обладают
диапазоном напряжений входных синфазных
сигналов, включающим отрицательное на-
пряжение, что в данном контексте обычно
означает потенциал земли. Операционные
усилители другого класса обладают еще луч-
шим входным диапазоном напряжений — это
усилители с размахом сигнала в полном диа-
пазоне напряжений питания, так называемые
R/R-усилители34.
Одни усилители способны принимать вход-
ные R/R-сигналы, другие — выдавать выход-
ные R/R-сигналы, а некоторые могут делать и
то и другое. Это хорошие возможности, но за
них приходится расплачиваться другими ха-
рактеристиками, такими как, например, напря-
жение смещения. Поэтому обычно усилители
R/R-типа следует использовать только в тех
случаях, когда такая возможность действи-
тельно необходима. Но нужно признать, что с
понижением напряжения типичных источни-
ков питания надобность в такой возможности
возникает все чаще. При напряжении источни-
ка питания ±15 В пожертвовать одним вольтом
от напряжения каждой полярности не такая уж
и большая потеря. Но при питании, например,
от батарейки напряжением 3 В такое расточи-
тельство неприемлемо.
Схема с расширенным диапазоном
напряжений входных синфазных
сигналов
В разностном или дифференциальном уси-
лителе на операционном усилителе диапазон
напряжений входных синфазных сигналов
может быть существенно шире, чем диапазон
напряжений питания. Может показаться, что
это утверждение противоречит строгим огра-
ничениям, упомянутым в разделе 7N.2.8, но
в действительности это не так: оно относится
к размаху напряжения на входах схемы, а не
операционного усилителя. Если это покажется
непонятным, вспомните, что в обычной инвер-
тирующей схеме на операционном усилителе
может возникать аналогичная ситуация, по-
скольку входное напряжение UBX подается не
на сам операционный усилитель.
Для микросхемы INA149 компании Texas
Instruments35 в конфигурации дифференциаль-
ного усилителя заявлены потрясающие напря-
жения входных синфазных сигналов в диапа-
зоне ±275 В. Такой результат вполне возможен
в дифференциальной схеме, которая рассма-
тривается в разделе 7N.5.
7N.2.9. Избранные характеристики
операционных усилителей:
обычных и высшего класса
В табл. 7N.5, взятой из книги АоЕ, приведены
некоторые характеристики операционных уси-
лителей36. Значения «высшего класса» — это
наилучшие возможные значения и, как сказано
в книге АоЕ, получить комбинацию нескольких
наилучших характеристик нельзя — операци-
онный усилитель нужно выбирать с наилучши-
ми значениями тех характеристик, которые для
вас важнее всего.
33 AoE§4.4.1F.
34 Англ. R/R (иногда R-t-R) — rail-to-rail Rail в данном слу-
чае означает напряжение (шину) питания, положительное
и отрицательное. В дальнейшем для краткости будем упо-
треблять обозначение - R/R-усилитель, R/R-сигнал и т.п.
35 Эта микросхема была изначально разработана компа-
нией Burr-Brown, которую впоследствии приобрела ком-
пания Texas Instruments.
36 АоЕ § 4.4.1.
320
7N. Операционные усилители II: отклонения от идеальности
Таблица 7N.5. Избранные характеристики операционных усилителей
Характеристика
Vos (%ых)
(макс.)
/в (Типичное)
fr (типичное)
SR (скорость
нарастания)
(типичное)
Биполярные
микросхемы
Обычная
3
50 нА
2
2
Высшего
класса
0,025
25 пА
2000
4000
Входной каскад на полевых
транзисторах с управляющим
р-я-переходом
Обычная
2
50 п А
5
15
Высшего класса
ОД
40 фА
400
300
КМОП-микросхемы
Обычная
2
1пА
2
5
Высшего
класса
ОД
2fA
10
10
Единицы
мВ
25 °С
МГц
В/мкс
Можно видеть, что типовые характеристи-
ки устройств с входным каскадом на полевых
транзисторах с управляющим р-л-переходом
практически такие же, как и для операционного
усилителя на микросхеме 411, который мы ис-
пользуем в большинстве наших лабораторных
занятий по операционным усилителям.
7N.3. Еще несколько
вариантов применения:
интегратор, дифференциатор,
выпрямитель, разностный
усилитель, усилитель
по переменному току
7N.3.1. Интегратор
Чтобы оценить, насколько хорошим может
быть схема интегратора на операционном уси-
лителе, следует вспомнить простой пассивный
ЯС-интегратор, с которым мы познакомились в
главе IN.
Пассивный /?С-интегратор
Чтобы заставить ЯС-цепочку вести себя подоб-
но интегратору, нужно обеспечить выполнение
следующего условия
Г37.
Таким образом при подаче на вход прямоуголь-
ного сигнала выходной сигнал поддерживается
на почти прямом участке экспоненциально из-
меняющейся кривой. Эта схема теряла работо-
способность, когда уровень выходного сигна-
ла [7ВЫХ значительно повышался над уровнем
земли. Но чтобы получить выходной сигнал,
его уровень должен хоть немного превышать
уровень земли; кроме того, имеет значение и
частота входного сигнала (рис. 7N.21).
Входной
сигнал
лги
Выходной
сигнал
Входной
сигнал
Выходной
сигнал
Рис. 7N.21. Пассивный ЯС-интегратор работает, если на его
вход подавать сигнал требуемой частоты
Интегратор на операционном усилителе
Интегратор на операционном усилителе легко
решает указанную проблему, используя вирту-
альную землю, что позволяет нам обеспечить в
точке заряда конденсатора нулевой потенциал
и в то же самое время сформировать выходной
сигнал (рис. 7N.22)38.
Рис. 7N.22. Интегратор на операционном усилителе: вирту-
альная «земля» как раз то, что нам требовалось
Как можно видеть по осциллограмме, изо-
браженной на рис. 7N.23, уровень выходного
37 АоЕ § 14.4.
38 АоЕ §§ 4.2.6,4.5.5.
7N.3. Еще несколько вариантов применения: интегратор, дифференциатор, выпрямитель...
321
сигнала схемы выше, чем входного, а процесс
интегрирования не искажается.
Рис. 7N.23. Для интегратора на операционном усилителе не
требуется (Увых«(Увх
Интегратор на операционном усилителе на-
столько хорош, что нужно следить за тем,
чтобы его выход не перешел в режим насы-
щения (т. е. выходной сигнал не поднялся до
уровня одного из напряжений питания) по
мере интегрирования сигнала рассогласова-
ния: небольшая асимметрия входного сигнала
будет накапливаться со временем, так же, как
и погрешности операционного усилителя. На
осциллограмме, изображенной на рис. 7N.24,
приведен участок выходного сигнала интегра-
тора: сначала уровень сигнала находится вбли-
зи точки отрицательного насыщения, затем
смещается по направлению к положительному
напряжению, пока не достигнет положитель-
ного предела рабочего диапазона операцион-
ного усилителя.
Рис. 7N.24. При отсутствии обратной связи по постоянному
току выходной сигнал интегратора переходит в состояние
насыщения
Таким образом, следует признать, что схема
интегратора на рис. 7N.22 неработоспособна.
Чтобы схема оставалась простой, в ее цепи об-
ратной связи достаточно только конденсатора.
Чтобы схема была работоспособной, нужно ор-
ганизовать обратную связь лучше.
Недостаток схем интегратора, изображенных
на рис. 7N.22 и 7N.7, можно понять, просто
обратив внимание на тот факт, что эта схема
вовсе не содержит обратной связи по постоян-
ному току (мы уже упоминали об этом ранее в
разделе 7N.2). При такой организации схемы
со временем выходной сигнал гарантированно
достигнет состояния насыщения.
Таким образом, в реальных интеграторах на
операционном усилителе должен быть какой-
либо механизм для предотвращения заряда
конденсатора до насыщения.
7N.3.2. Предотвращение
насыщения интегратора
на операционном усилителе
Одно из возможных решений: резистор с
большим сопротивлением39
Переход выходного сигнала в состояние на-
сыщения можно предотвратить, подключив
параллельно конденсатору резистор с боль-
шим сопротивлением, как показано слева на
рис. 7N.25. Через этот резистор будет проте-
кать небольшой ток, компенсируя влияние не-
большого входного тока смещения.
В схеме, изображенной справа на рис. 7N.25,
присутствует так называемая Т-образная ре-
зистивная цепочка, с использованием которой
исчезает необходимость в резисторах очень
больших номиналов. Подробнее эта цепочка
рассматривается в разделе 7N.3.3.
100кОм100кОм
10 МОм
100 кОм
I
100 кОм
1 мкФ
Рис. 7N.25. Устранение насыщения интегратора с помощью
резистора, включенного параллельно конденсатору обрат-
ной связи
Если сопротивление резистора обратной свя-
зи Roc = 100 • Rlt как показано на рис. 7N.25,
то ток утечки через данный резистор состав-
ляет всего лишь 1% от тока сигнала, когда
ишх сравнимо с J7BX. Во многих случаях этот
небольшой недостаток интегратора является
приемлемым.
39 См. АоЕ, рис. 4.66.
322
7N. Операционные усилители II: отклонения от идеальности
Влияние резистора
в цепи обратной связи
Очевидно, что резистор в цепи обратной связи
отрицательно влияет на рабочие характеристи-
ки интегратора. Количественный эффект этого
воздействия можно вычислить. Влияние рези-
стора можно описать несколькими альтерна-
тивными способами.
♦ Резистор ограничивает усиление по по-
стоянному току. В схеме на рис. 7N.25
входное сопротивление RBX = 100 кОм, а со-
противление обратной связи Roc = 10 МОм,
поэтому коэффициент усиления по постоян-
ному току составляет -100. Таким образом,
изменение входного сигнала по постоянному
току величиной ±1 мВ ведет к погрешности
выходного сигнала величиной ±100 мВ. За
исключением этой погрешности, во всех дру-
гих отношениях наш интегратор работает
должным образом.
♦ Резистор в цепи обратной связи спо-
собствует утечке по постоянному току.
Предположим, что в течение некоторого
времени мы подаем на вход схемы постоян-
ный сигнал напряжением 1 В. Когда уровень
выходного сигнала достигает -1В, погреш-
ность по току составляет 1/100 входного
или сигнального тока. Это объясняется тем,
что, как было только что отмечено, значение
сопротивления резистора обратной связи
Дос = 100 • Двх. Эта погрешность увеличивает-
ся, если ишх повышается относительно 17ВХ.
♦ При частоте сигнала выше определенной
резистор в цепи обратной связи не ока-
зывает ощутимого отрицательного воз-
действия. При повышении частоты до не-
которого (достаточно небольшого) значения
реактивное сопротивление конденсатора Хс
становится меньше, чем сопротивление рези-
стора, и по мере дальнейшего роста частоты
резистор вскоре перестает играть роль. Как
вам известно, Хс = R при частоте/= 1/2tijRC.
При указанных на рис. 7N.25 значениях ком-
понентов схемы (2?ос = 10 МОм, а С = 1 мкФ)
эта частота составляет около 0,02 Гц!
Резистор может привести к проблемам
Сначала появляется искажение в виде неболь-
шой кривизны... Резистор в цепи обратной связи
может привести к проблеме, когда 1ГВЫХ намно-
го превышает [/вх, как показано на рис. 7N.26.
Здесь искривление выходного сигнала означа-
ет, что мы наблюдаем не идеальное интегри-
рование, которое выглядит как линейно нарас-
тающий сигнал.
Рис. 7N.26. Искажение интегрирования становится оче-
видным, когда UBblx » UBr (Усиление осциллографа: вход-
ной сигнал (прямоугольный сигнал небольшой амплиту-
ды) — 10 мВ/деление; выходной сигнал (пилообразный) —
ЮОмВ/деление.)
В пределе ограниченное усиление по постоянно-
му току полностью нарушает работу интегра-
тора. Если двигаться дальше и допустить еще
большее превышение [7ВЫХ над Uw например,
подавая совсем слабый сигнал очень низкой
частоты, то интегратор с резистором в цепи об-
ратной связи вообще перестает работать. На
рис. 7N.27 приведена осциллограмма выходно-
го сигнала такого интегратора, из которой ясно,
что данная схема действует всего лишь как уси-
литель по постоянному тому с коэффициентом
усиления равным 100.
Рис. 7N.27. При работе интегратора с входными сигналами
на пределе динамического диапазона его работоспособ-
ность полностью утрачивается. (Усиление осциллографа:
входной сигнал (прямоугольный сигнал небольшой ампли-
туды) — 100 мВ/деление; выходной сигнал (экспоненциаль-
ный) — 5 мВ/деление.)
Но пусть сказанное не отпугнет вас от исполь-
зования резистора в интеграторе: чтобы про-
демонстрировать эти искажения нам пришлось
хорошо потрудиться, подавая входной сигнал
очень малой амплитуды и весьма низкой ча-
стоты.
7N.3. Еще несколько применений: интегратор, дифференциатор, выпрямитель, разностный..
323
Виртуальная «земля»
Несмотря на то что в цепи обратной связи
присутствует только Rv I^ * 1/100,
"поскольку эквивалентное R^ * 100 * Rx
100 кОм 1 кОм
Рис. 7N.28. Повышение эквивалентного сопротивления с помощью Т-образной резистивной цепи
7N.33. Т-образная резистивная цепь
Когда для схемы требуются резисторы боль-
шого номинала (как, например, в случае с ре-
зистором обратной связи для интегратора),
применение так называемой Т-образной рези-
стивной цепи (Т-моста) позволяет уменьшить
номиналы резисторов и избежать некоторых
отрицательных эффектов, которые присущи
большим сопротивлениям40.
На рис. 7N.28 изображена схема, которая долж-
на убедить вас, что хитроумная комбинация
резисторов в схеме справа на рис. 7N.25 дей-
ствительно может увеличить эквивалентное
сопротивление резистора номиналом 100 кОм
в 100 раз.
Хитроумно, не так ли? Эта схема полезна по
той причине, что более низкое JR^ Т-образной
цепи обратной связи дает два преимущества:
♦ снижается погрешность из-за тока смещения
1СМ, по сравнению с использованием резисто-
ров большого номинала (см. раздел 7N.2.3);
♦ уменьшается влияние паразитной емкости
на входе операционного усилителя, в резуль-
тате чего исчезают непредсказуемые эффек-
ты обратной связи. Это не особенно важно
в данном случае, но существенно для схемы,
в которой нет конденсатора, подключенного
параллельно резистору обратной связи.
Однако схема с Т-образной резистивной це-
почкой все же имеет один недостаток: увели-
чивается погрешность из-за входного напря-
жения смещения UCM (см. раздел 7N.2.2), даже
когда источником сигнала служит источник
тока. Если это обстоятельство вам непонятно,
обратитесь к разделу 7W.1, в котором рассма-
триваются два случая дрейфа в интеграторах:
один с источниками напряжения, а другой с ис-
точниками тока.
Другое решение: ключ
Ключ, подключенный параллельно конденса-
тору, может предотвратить насыщение инте-
гратора (см. раздел 7N.29)41. Однако данный
ключ необходимо периодически замыкать, и
это может оказаться неудобным.
+5 в |—* Сброс
о—I I—
1 кОм
Выходной сигнал
~ может иметь только
положительную
полярность
Рис. 7N.29. Предотвращение насыщения интегратора с по-
мощью ключа
Использование ключа позволяет создать бо-
лее совершенный интегратор благодаря тому,
что операция интегрирования не нарушает-
ся из-за тока утечки через резистор обратной
связи. Решение, окупается ли это преимуще-
ство затратами на организацию схемы подачи
сигнала сброса, будет зависеть от конкретного
приложения. Обратите внимание, что при от-
рицательном выходном сигнале интегратора
транзисторный каскад в схеме на рис. 7N.29
40 См. АоЕ, рис. 4.66.
41 См. АоЕ, рис. 4.18.
324
7N. Операционные усилители II: отклонения от идеальности
неработоспособен. Транзисторный ключ, со-
храняющий работоспособность при любой по-
лярности выходного сигнала, можно реализо-
вать на МОП-транзисторах. Мы познакомим-
ся с аналоговыми переключателями на этих
устройствах в главе 12N.
7N.3A Интегратор может
предъявлять повышенные
требования к качеству
операционного усилителя
В усилителе с высоким коэффициентом усиле-
ния (например, в разделе 7N.2.3) влияние не-
больших погрешностей входных сигналов (UCM
и 1СМ) может оказаться значительным. То же
самое присуще и интегратору, поскольку он на-
капливает эффекты таких погрешностей.
Схема интегратора, демонстрирующая
влияние погрешностей операционного
усилителя
Для наглядной демонстрации мы сравним ста-
рый биполярный операционный усилитель
(LM741) и обычный операционный усилитель
с входным каскадом на полевых транзисторах
(LF411). Схему, изображенную на рис. 7N.30,
мы собрали на обеих микросхемах.
Сначала мы заземлили входы обоих инте-
граторов и наблюдали за дрейфом на выходе.
Результат демонстрирует осциллограмма слева
на рис. 7N.31.
Так что в этом соревновании побеждает микро-
схема операционного усилителя 411, хотя и
Дрейф микросхемы
; 741 заметен "^Т
Дрейфует ли 4
микросхема 411? I
Сброс интегратора
(Вход заземлен,
а не «плавающий»)
- также на 741
(Собираются две схемы,
по одной на каждом операционном усилителе)
Рис. 7N.30. Схема интегратора для изучения влияния напря-
жения смещения Ц^ и тока смещения /см
с небольшим перевесом, возможно, 15:1. Затем
мы разомкнули оба входа, имитируя источ-
ник тока, подключенный к интегратору. Здесь
убедительную победу одержал операционный
усилитель на микросхеме 411 с его входным
каскадом на полевых транзисторах (что озна-
чает малый ток смещения 7СМ). Чтобы увидеть
дрейф в интеграторе на микросхеме 411, нам
пришлось значительно повысить чувствитель-
ность осциллографа (до 50 мВ/деление), а так-
же набраться терпения.
В разделе 7W.1 различия между этими двумя
операционными усилителями рассматривают-
ся более подробно.
7N3.5. Иногда достаточно ручного
сброса интегратора
Один из наших бывших студентов представил
нам случай, когда вполне достаточно сбра-
сывать интегратор вручную. Этот студент со-
бирал данные о реакции мышцы лягушки на
Яде; <*"••
Входы интегратора заземлены
"grasp™'""
Микросхема 411 тоже дрейфует, но это можно увидеть лишь
при чувствительности осциллограсра в 100 выше, чем для
741 (50 мВ/деление)
Рис. 7N.31. Скорость дрейфа сравниваемых интеграторов: микросхема 411 с входным каскадом на полевых транзисторах
выигрывает. Выигрыш еще заметнее при подаче сигнала от источника тока. (Усиление каналов осциллографа: 5 В/деление для
всех осциллограмм, за исключением осциллограммы дрейфа для 411 на правом крайнем изображении, для которой задано
50 мВ/деление.)
7N.4. Дифференциатор
325
Цифровой
мул ьти метр
Ручной \
переключатель сброосг)
Стимулирующее воздействие
Стимулирующее^
чвоздействие
Реакция ~—~^л^~
ов ^
Интеграл -1 4<v*~
СбросЛ
(несколько секунд)
Рис. 7N.32. При медленном процессе интегрирования возможен ручной сброс
стимулирующий импульс электрического тока.
На рис. 7N.32 приведен эскиз его эксперимен-
тальной установки.
Процесс интегрирования был длительным, а
продолжительность эксперимента достаточ-
но велика, так что имело смысл обнулять ин-
тегратор вручную, после чего подавать сигнал
стимула и записывать интегрированное значе-
ние, и все это делать в течение многих секунд.
Конечно же, для этого требовался точный ин-
тегратор, т. е. с малым дрейфом. И поиск такого
интегратора как раз и был причиной, по кото-
рой этот студент обратился к нам.
7N .4. Дифференциатор
Оценить возможности дифференциатора на
операционном усилителе позволяет сравнение
с пассивным дифференциатором. На рис. 7N.33
изображена схема пассивного дифференциато-
ра, с которой мы познакомились на лаборатор-
ном занятии 2L.
Чтобы заставить ДС-цепочку вести себя подобно
дифференциатору, нужно выполнить условие:
dUBUX/dt«dUBX/dt
Подобно интегратору, дифференциатор на опе-
рационном усилителе снимает это ограничение
благодаря наличию виртуальной «земли».
Но дифференциатор на операционном усили-
теле не так впечатляет, как интегратор. Чтобы
схема дифференциатора на операционном уси-
лителе могла вообще работать, ее параметры
приходится ухудшать. В частности, чтобы обес-
печить стабильную работу схемы, необходимо
уменьшить ее усиление на высоких частотах.
На рис. 7N.34 изображена схема дифференциа-
тора, который на высокой частоте превращает-
ся, как это ни странно, в интегратор.
Такая модификация необходима для предотвра-
щения нежелательных паразитных колебаний.
(Эта тема рассматривается более подробно на
лабораторных занятиях 9L и 10L.) На рис. 7N.35
приведен наглядный пример, иллюстрирующий
проблему стабильности, с которой мы будем
подробно разбираться дальше42. Простой, иде-
альный дифференциатор обладает минималь-
ной стабильностью и начинает возбуждаться в
ответ на сигнал с крутыми перепадами. (На схе-
му подается входной прямоугольный сигнал.)
Это самовозбуждение недопустимо, поэтому
приходится жертвовать возможностью работы
на высоких частотах, обеспечивая нормальную
работу в ограниченном частотном диапазоне.
Входной сигнал
Выходной сигнал
Г
Соответствует постоянной
времени ££-цепи
Рис. 7N.33. Пассивный ЯС-дифференциатор работает только при небольшой постоянной времени ЯС-цепи
42 этот рИСуНок взят из главы 10N.
326
7N. Операционные усилители II: отклонения от идеальности
R
-л/w»
Простой (идеализированный)
дифференциатор
превращается в
Дифференциатор^
(+6,дБ/октаву)
интегратор
(-6 дБ/октаву)
Частота (логарифмический масштаб)
превращается
Дифференциатор
(стабильный)
2В
0,2 мс
Практически реализуемый дифференциатор
Рис. 7N.34. Идеализированный и практически реализуемый дифференциаторы. Дифференциатор на высоких частотах пре-
вращается в интегратор
интегральных наборов резисторов. Например,
в микросхеме дифференциального усилителя
INA194 компании Texas Instruments резисто-
ры интегрированы вместе с операционным
усилителем и их значения подгоняют, удаляя
излишки проводящего материала с помощью
лазера. Подавление синфазной составляющей43
для микросхемы INA194 составляет 90 дБ.
В разделе 6W.1 приведен анализ схемы этого
стандартного разностного усилителя, чтобы
облегчить ее понимание. Здесь мы, конечно,
не будем излагать полностью тот материал. Но
прежде всего отметим то обстоятельство, что
при одинаковых напряжениях на входах на-
пряжения на правых концах делителей также
должны быть одинаковыми. Один из них под-
ключен к «земле», поэтому уровень выходного
сигнала операционного усилителя также дол-
жен быть нулевым. Иными словами, при оди-
наковых входных сигналах выходной сигнал
будет равен нулю. Можете попробовать некото-
рые другие комбинации входных воздействий,
например, подключить к «земле» один вход, за-
тем другой, и т. п.
Рис. 7N.35. Для стабильной работы дифференциатора на
операционном усилителе необходимо ограничить частоту
входного сигнала
7N.5. Разностный усилитель
на операционном усилителе
На рис. 7N.36 изображена стандартная схе-
ма разностного усилителя на операционном
усилителе. Усиление схемы составляет RJRV
Это, конечно же, дифференциальное усиле-
ние. Синфазное усиление в идеале равно нулю.
Подавление синфазной составляющей схемой
может быть очень хорошим при тщательном
согласовании соотношений двух делителей на-
пряжения, чего можно добиться с помощью
♦-с-..
7N.5.1. Интересное достоинство:
широкий диапазон входного
сигнала
Разностный усилитель может работать с весь-
ма широким диапазоном напряжений синфаз-
ных сигналов. Как мы помним, напряжение
Рис. 7N.36. Простой разностный усилитель
43 В данном случае «подавление синфазной составляющей»
означает то же самое, что и более знакомое выражение «ко-
эффициент подавления синфазной составляющей» — от-
ношение «полезного» усиления к «вредному» — поскольку
полезное усиление, дифференциальное, равно единице.
7N.6. Усилитель переменного тока: хороший способ минимизировать влияние погрешности...
327
входного синфазного сигнала означает отсут-
ствие напряжения выходного сигнала 1ГВЫХ; не-
большая разница между входами, на которые
подается общий синфазный сигнал, дает не-
большой выходной сигнал [/вых. В разделе 6W.2
и на рис. 6W.7 рассматривается разностный
усилитель на микросхеме INA149, который
обладает огромным диапазоном напряжений
входного синфазного сигнала ±275 В.
7N.6. Усилитель
переменного тока: хороший
способ минимизировать
влияние погрешности
по постоянному току
операционного усилителя
Если требуется усиливать только сигналы пе-
ременного тока44, то существует практичный
способ свести к минимуму погрешности, вы-
зываемые напряжением смещения 1/см, током
смещения /см и током сдвига 1СД, заключаю-
щийся в снижении усиления по постоянному
току до единичного, как иллюстрируется на
рис. 7N.3745.
который мы привыкли видеть в схемах на опе-
рационных усилителях. Наличие однополяр-
ного источника питания вынуждает создать
положительное смещение на входе схемы, в
результате чего получается ситуация, изобра-
женная справа на рис. 7N.37, где переменный
сигнал небольшого размаха имеет большую
постоянную составляющую. Нам нужно уси-
лить этот полезный сигнал, но не постоянное
напряжение смещения.
Какая частота^^ для схемы на рис. 7N.37? Если
игнорировать «1» в выражении усиления, то
амплитуда выходного сигнала уменьшается на
3 дБ, когда знаменатель этого выражения равен
V2 • Rv Это справедливо, когда Хс = | Zc\ = Rv что
происходит, как вы хорошо знаете, при частоте
Замечание
Не дайте ввести себя в заблуждение тем обстоя-
тельством, что на схеме конденсатор подключен
к «земле», что делает /?С-цепь похожей на низкоча-
стотный фильтр. Будьте начеку и помните, что это
высокочастотный фильтр в «овечьей шкуре».
Требуемый здесь анализ ДС-цепочки такой же,
как был описан при выборе конденсатора для
шунтирования эмиттера в схеме усилителя
в главе 5N. На рис. 7N.38 изображена схема,
Значительный уровень
постоянной составляющей
у Сигнал —^
(^небольшой амплитуды
Усиление снижается на 3 дБ,
когда А^
Усиление постоянной)
составляющей: 1
_ Усиление сигнала: 1+
Пример микрофонного усилителя с однополярным
Усилитель переменного тока: общий случай источником питания
Рис. 7N.37. Усилитель переменного тока увеличивает полезный сигнал и избавляет его от постоянной составляющей
Схема на рис. 7N.37 используется на лабора-
торном занятии 7L для усиления сигнала от
микрофона. Она питается от однополярного
источника, а не от обычного двухполярного,
44 АоЕ§4.2.2А.
45 Обозначение U подстрочным шрифтом в выражении
усиления на рис. 7N.37 обозначает усиление по напряже-
нию в противоположность, например, усилению по току.
Обычно мы опускаем это обозначение.
которая должна напомнить вам об усилителе с
общим эмиттером с высоким коэффициентом
усиления. Схема операционного усилителя с
однополярным источником питания, требую-
щая подачи напряжения смещения, является
исключением при использовании операцион-
ных усилителей, но она должна быть вам хоро-
шо знакома по работе со схемами на дискрет-
ных транзисторах.
328
7Л/. Операционные усилители II: отклонения от идеальности
Усиление уменьшается на 3 дБ,
когда Хс = гэ
Рис. 7N.38. Для усилителя переменного тока коэффициент усиления снижается на 3 дБ, когда знаменатель выражения усиле-
ния (последовательный импеданс R и Q увеличивается до Ry/2
7N.7. Материал для чтения
вАоЕ
Чтение
♦ Раздел 4.4: подробное рассмотрение опера-
ционных усилителей.
♦ Раздел 4.5: подробное рассмотрение избран-
ных схем на операционных усилителях.
♦ Раздел 4.6: работа операционных усилителей
с однополярным источником питания.
♦ Раздел 4.7: другие типы усилителей и опера-
ционных усилителей.
Задачи
Дополнительные упражнения (Additional Exer-
cises) 4.31-4.33.
7L Лабораторное занятие:
операционные усилители II
Это лабораторное занятие открывает вам не-
приглядную правду об операционных усилите-
лях: они не такие замечательные, как мы их вам
раньше представляли! Увы... Но после изуче-
ния погрешностей операционных усилителей
в упражнении 7L.1 мы снова займемся более
приятной задачей — исследованием новых ва-
риантов применения операционных усилите-
лей. Здесь мы снова будем рассматривать эти
устройства как идеальные.
Следуя принципу, что аперитив должен идти
перед основным блюдом, начнем с рассмотре-
ния погрешностей операционных усилителей.
Упражнение с интегратором как нельзя более
подходит для данной цели. Скучное исследо-
вание напряжения и тока смещения станет
увлекательней при реализации трудной задачи
интегрирования, которую вообще невозможно
решить, не преодолев влияние этих двух несо-
вершенств операционных усилителей.
Мы хотим, чтобы вы считали интегратор одним
из весьма важных схемотехнических устройств.
Но эта схема способна также хорошо проде-
монстрировать влияние возможных погрешно-
стей операционных усилителей, которые могут
выглядеть пренебрежительно малыми: токов
смещения величиной в пикоамперы и напря-
жений смещения меньших, чем милливольт.
Интегратор не «прощает» ошибок: он, конечно
же, накапливает такие погрешности, «затаив
обиду» за пикокулоны заряда, доставленные в
далеком прошлом, многие миллисекунды тому
назад. В нашей новой экспериментальной схеме
вам представится возможность интегрировать
сигнал, создаваемый для разнообразия настоя-
щим устройством (приводом дисков или элек-
тродвигателем постоянного тока), а не надоев-
шим генератором сигналов. В результате схема
интегратора перемещения двигателя привода
диска окажется действительно полезной.
7L.1. Интегратор
Исследуем интегратор
Соберите интегратор на микросхеме операци-
онного усилителя 411, принципиальная схема
которого приведена на рис. 7L.1. Вначале кно-
почный переключатель будет излишним, по-
скольку в схеме есть резистор обратной связи
номиналом 10 МОм. Но позже мы удалим этот
резистор и будем пользоваться кнопкой руч-
ного сброса. После завершения работы с инте-
гратором сохраните схему в сборе, так как она
понадобится нам при исследовании дифферен-
циатора в разделе 7L2.
JL
10 МОм
Входнойг 22 кОм
сигнал
ОД мкФ
Выходной
сигнал
Рис. 7L1. Принципиальная схема интегратора
Подайте на вход интегратора сигнал с часто-
той в диапазоне от 50 Гц до 1 кГц. Исследуйте
сигналы всех трех видов, перечисленные в
конце этого раздела. Не забывайте, что схема
очень чувствительна к небольшому смещению
постоянной составляющей входного сигнала
(ее усиление по постоянному току составля-
ет около 500); при уровне выходного сигнала
приближающемся к ±15 В, высока вероятность
перехода в режим насыщения. Чтобы избежать
такого развития событий, нужно откорректи-
ровать смещение постоянной составляющей
на генераторе сигналов. Такую корректировку
330
7L Лабораторное занятие: операционные усилители II
будет проще выполнить, если установить на
генераторе ослабление сигнала в 20 дБ.
Попробуйте подавать на вход схемы сигналы
прямоугольной, синусоидальной и треугольной
формы. Зная номиналы компонентов, рассчи-
тайте размах выходного сигнала треугольной
формы, который получится при входном сиг-
нале прямоугольной формы с частотой 50 Гц и
размахом 2 В. Затем проверьте свой расчет на
практике.
«Укрощение» интегратора с помощью
резистора обратной связи
Резистор обратной связи номиналом 10 МОм
«укрощает» этот интегратор, и в то же самое
время нарушает его функционирование. Если
аккуратно настроить генератор сигналов, то
при наличии резистора можно предотвратить
переход выходного сигнала в режим насыще-
ния. Но в результате интегрирование стано-
вится не совсем точным и недостаточно хо-
рошим для длительного процесса, подобного
тому, который мы попытаемся вскоре реали-
зовать. Резистор обратной свйзи обусловли-
вает утечку тока с конденсатора. В некоторых
случаях это не важно. Поскольку отношение
сопротивления обратной связи Roc к сопро-
тивлению резистора на входе составляет почти
500:1, то при сравнимых значениях 17ВЫХ и иж
погрешность, создаваемая резистором RQC, со-
ставит лишь 0,2% сигнала. Исследуя реакцию
интегратора на сигналы различной формы, вы
будете даже рады этому резистору обратной
связи.
Без резистора обратной связи
интегратор менее управляемый,
но более точный
Если удалить резистор обратной связи номи-
налом 10 МОм, то схема даст вам шанс полу-
чить настоящее понимание значения интегра-
ла. К тому же, постоянная подстройка генера-
тора сигналов, чтобы предотвратить режим
насыщения, может показаться чрезвычайно
неудобной. Но такое развитие событий можно
легко предотвратить, нажав кнопку сброса, в
результате чего выходной сигнал возвратится
к нулевому уровню, и вы сможете начать все
сначала.
7L1.1. Использование интегратора
для оценки /см и UCN[
Дрейф по неизвестным причинам
Заземлите вход интегратора, нажмите кнопку
сброса, чтобы обнулить выход, затем отпустите
кнопку и наблюдайте дрейф выходного сигна-
ла. Для этого может понадобиться установить
очень низкую частоту развертки осциллографа.
Для начала попробуйте значение 1 сек/деление.
Примечание
В этом эксперименте лучше использовать цифро-
вой осциллограф, если таковой имеется.
Оцените величину скорости дрейфа. Также об-
ратите внимание, что как JCM, так и 17Ш вносит
свой вклад в этот эффект. Значительно хуже,
что два эффекта могут усиливать друг друга,
или же один может компенсироваться другим.
Давайте-ка разделим их.
Определяем /см на основе скорости
дрейфа при отсутствии UCM
Устранить влияние напряжения смещения Ucu
очень просто: нужно просто перевести вход в
плавающий режим. Теперь Е/смне вызывает про-
текание тока через входной резистор, следова-
тельно оно не вносит свою долю в ток, заряжаю-
щий конденсатор. С учетом этого упрощения
измерьте скорость дрейфа и оцените значение
тока смещения 7Ш. Проверьте, соответствует ли
полученная экспериментальная оценка паспорт-
ному значению для микросхемы 411, а именно,
50 пА (типичное) и 200 пА (максимальное). Вам
придется набраться терпения, чтобы измерить
скорость дрейфа. Как только вы определите зна-
чение скорости, используйте его, чтобы вычис-
лить величину тока смещения 7СМ.
Определяем UCM на основе скорости
дрейфа
Теперь вам предстоит оценить напряжение сме-
щения Ucu на основе скорости дрейфа, которую
вы определили в начале этого лабораторного
занятия.
Внимание!
Не забывайте обращать внимание на знак каждой
из этих скоростей дрейфа.
7LI Интегратор
331
Сравните вашу полученную величину с значени-
ем, заявленным для микросхемы 411:0,9 мВ (ти-
пичное), 2,0 мВ (максимальное). Совпадает ли
это с вашим экспериментально измеренным UCM?
7L1.2. Два способа реализации
интегратора с малой скоростью
дрейфа
Первый способ: настройка
минимального значения Um (для 411)
Будем надеяться, что вам удалось установить,
что напряжение смещения Ucu в наибольшей
степени способствует дрейфу выходного сиг-
нала интегратора. Давайте теперь устраним
эту проблему. Добавьте цепь коррекции на-
пряжения смещения, как показано на рис. 7L.2.
Заземлите вход интегратора, нажмите кнопку
сброса, чтобы обнулить выход, затем попытай-
тесь минимизировать скорость дрейфа выход-
ного сигнала.
22 кОм < <22 кОм
|10 кОм1
Рис. 7L.2. Цепь коррекции напряжения смещения для опе-
рационного усилителя на микросхеме 411
Коррекция напряжения смещения — непростая
задача. Начните с чувствительности осцилло-
графа, скажем, 1 В/деление, и по мере подгонки
напряжения смещения к нулевому уровню по-
степенно повышайте чувствительность. Время
от времени нажимайте кнопку сброса, чтобы об-
нулить интегратор. Попробуйте уменьшить ско-
рость дрейфа до нескольких милливольт в се-
кунду. Добившись самой низкой скорости дрей-
фа, выясните, какому остаточному напряжению
смещения UCM соответствует эта скорость.
Теперь, чтобы вы не подумали, что коррекция
действительно окончательно решает пробле-
му напряжения смещения, нагрейте или охла-
дите микросхему 411 (с помощью фена или
охлаждающего спрея) и посмотрите, что про-
исходит с дрейфом теперь. Чтобы быть спра-
ведливым к микросхеме 411, следует отметить,
что даже для хорошей микросхемы с внутрен-
ней коррекцией нуля, которую мы рассмотрим
следующей, не очень желательны большие
температурные изменения. Вы сможете удо-
стовериться в этом сами, когда будете работать
с данной схемой.
Второй способ: операционный усилитель
с внутренней коррекцией на микросхеме
LTC1150
Операционный усилитель с внутренней кор-
рекцией нуля, каковым является микросхема
LTC1150, содержит встроенный операционный
усилитель, автоматически выполняющий зада-
чу корректировки напряжения смещения, ко-
торую мы выполняли вручную в предыдущем
разделе. Для этого он стремится свести к нулю
разницу между двумя входными сигналами
основного усилителя. Попробуйте этот усили-
тель вместо микросхемы 411.
Цоколевка микросхем LTC1150 и 411 одина-
кова, поэтому одну микросхему можно просто
вставить на место другой. Но при этом из схе-
мы предыдущего эксперимента нужно удалить
подстроечный потенциометр, чтобы выводы 1
и 5 микросхемы не были подключены.
Заземлите неинвертирующий вход усилителя1
и наблюдайте скорость дрейфа.
Что касается микросхемы LTC1150, в данный
момент точная причина ее дрейфа пока не
ясна. Разделите влияние тока смещения 1СМ и
напряжения смещения Ucu, устранив послед-
ний эффект так же, как мы это сделали в случае
микросхемы 411. Определите напряжение сме-
щения UCM операционного усилителя на основе
скорости дрейфа, которую вы наблюдали при
закороченном на «землю» входе, и запомните,
а еще лучше запишите его. Согласно паспорт-
ным характеристикам микросхемы LTC115 ее
напряжение смещения UCM составляет ±0,5 мкВ
1 Мы обнаружили, что в зависимости от точки заземления
входа на макетной плате скорость дрейфа варьировалась
больше, чем в два раза. Эти микровольтовые изменения
входного сигнала, по-видимому, создаются небольшими
токами, протекающими по общей шине. Подключение не-
посредственно к точке неинвертирующего входа на макет-
ной плате обеспечивает наилучшее заземление: операци-
онный усилитель четко фиксирует нулевой уровень.
332
7L Лабораторное занятие: операционные усилители II
. Вывод катушки
__ Головка
записи/чтения
Постоянный
магнит
1 ^ Катушка на шпинделе
(катушку не видно под магнитом)
Электродвигатель в качестве Высококачественный источник постоянного напряжения:
источника постоянного напряжения катушка привода жесткого диска
Рис. 7L.3. Различные источники сигнала: электродвигатели постоянного тока (слева) и катушка привода жесткого диска (справа)
(типичное), 10 мкВ (максимальное). В нашем
случае мы были разочарованы, получив значе-
ния выше заявленного максимального. Будем
надеяться, что ваши результаты будут лучше2.
7L1.3. Интегратор в схеме датчика
положения двигателя привода
После всех рассуждений об интеграторе вы, на-
верное, задаетесь врпросом, а зачем, собствен-
но говоря, нужна эта схема? Чтобы ответить
на этот законный вопрос, мы для начала при-
думали пример сигнала, который, кажется, сам
«хочет», чтобы его проинтегрировали. Следует
признать, что мы создали этот пример главным
образом потому, что он занимательный, а не
потому, что практичный. Но в результате это
возможно наведет вас на мысль о других спосо-
бах применениях интегратора.
В поисках сигнала, интеграл которого мог бы
быть интересным, мы3 вспомнили о сигналах,
создаваемых обмотками, перемещающимися в
меняющемся магнитном поле. Амплитуда та-
кого сигнала должна быть пропорциональна
скорости изменения магнитного потока через
катушку. Сначала мы попробовали перемещать
диффузор большого динамика, но затем вспом-
нили про обмотку привода жесткого диска. Эта
катушка (основная идея которой была позаим-
ствована из акустических динамиков) представ-
ляет собой простой электродвигатель, который
перемещает магнитную головку привода по ра-
диусу диска, чтобы найти требуемую дорожку.
Если вскрытие привода жесткого диска, чтобы
достать из него катушку, выглядит слишком
трудоемким, то ее можно заменить обычным
электродвигателем постоянного тока, пара при-
меров которого показаны слева на рис. 7L.3.
Это два дешевых небольших электродвигате-
ля постоянного тока, на вал которых мы при-
клеили рычаг, отрезанный от пластмассовой
крыльчатки сервомашинки. (Мы познакомим-
ся с этим устройством на лабораторном заня-
тии 24L.) Электродвигатель меньшего разме-
ра работает от напряжения 9 В, а большего —
3,3-5 В4. Для наших целей подойдет практиче-
ски любой электродвигатель постоянного тока,
поскольку чувствительность интегратора мож-
но настроить по желанию. (Можете сказать,
как это делается5?)
Мы будем использовать наш электродвигатель
в качестве генератора. Вместо того чтобы по-
давать напряжение для перемещения головки
привода диска, мы будем вручную перемещать
головку катушки, генерируя на ее выводах на-
пряжение, прямо пропорциональное скорости
перемещения. В случае с электродвигателем
мы будем вращать его вал, получая на выводах
напряжение, прямо пропорциональное скоро-
сти вращения. Интегрируя сигнал, снимаемый
с выводов катушки привода диска или с обмот-
ки электродвигателя, мы должны получить на-
пряжение, пропорциональное положению го-
ловки или вала электродвигателя.
Вопрос. Быстрое перемещение головки катуш-
ки привода диска или вращение вала электро-
двигателя создает большее входное напряжение
2 Когда мы установим причину повышенной скорости
дрейфа в нашем случае, мы дадим вам знать.
3 Здесь «мы» означает просто его Величество Поль (Поль
Хоровиц).
4 Если хотите купить один из электродвигателей, с кото-
рым мы работали, то двигатель большего размера (Mabu-
chi FF-130RH) предлагается многими поставщиками. Мы
приобрели электродвигатели в магазине All Electronics по
цене чуть больше доллара за штуку.
5 Мы уверены, что вы знаете ответ: регулируя значение
входного резистора интегратора.
7L2. Дифференциатор
333
на интеграторе, а медленное — меньшее. Как
вы думаете, зависит ли выходной сигнал инте-
гратора от скорости перемещения головки ка-
тушки привода, или поворота вала двигателя,
из положения А в положение Б6?
Цель нашего упражнения заключается в том,
чтобы отобразить положение головки (или
вала) на экране осциллографа. Но мы не хотим,
чтобы в течение нескольких секунд изображе-
ние заметно смещалось. Поэтому нам потребу-
ется интегратор с малым дрейфом, наподобие
тех двух устройств, которые мы только что со-
брали.
Подадим на наш интегратор (схема на LTC1150
будет удобнее, так как она все еще собрана)
выходной сигнал катушки привода жесткого
диска. Наблюдайте за сигналом на входе ин-
тегратора (подаваемым на него с двух про-
водов, выходящих из катушки или обмотки
электродвигателя) и сигналом на его выхо-
де. Для наблюдения за выходным сигналом
интегратора установите чувствительность
осциллографа 2 В/деление. Обнулите инте-
гратор, после чего переместите головку ка-
тушки привода по направлению к шпинделю
диска, а затем обратно. Будем надеяться, что
вам понравится сигнал, выдаваемый интегра-
тором. Полагаем также, что вы убедитесь, что
на экране осциллографа действительно ото-
бражается радиальное положение головки
жесткого диска (или угловое положение вала
электродвигателя).
Если вам еще не наскучил этот эксперимент,
замените микросхему LTC1150 интегратора на
микросхему 411, вставив обратно подстроеч-
ный потенциометр.
Примечание
Вам повезет, если настройка потенциометра не
собьется. В противном случае снова подстрой-
те потенциометр, пока не получите приемлемый
медленный дрейф интегратора, а затем подайте на
него сигнал с катушки привода.
6 Не зависит. Быстрое перемещение/вращение действи-
тельно создает на входе интегратора больший сигнал, но
в течение более короткого времени, чем медленное. Таким
образом, выходной сигнал интегратора честно измеряет
положение головки катушки или вала электродвигате-
ля. Ему все равно, с какой скоростью головка/вал пере-
местилась в это положение. Он интегрирует входное на-
пряжение, которое является производной по времени от
положения, если вам нравится излагать простые вещи в
математических терминах.
Оцените, насколько хорошо микросхема 411 с
откорректированной скоростью дрейфа справ-
ляется с отображением положения головки
жесткого диска.
7L2. Дифференциатор
На рис. 7L.4 изображена схема дифференциа-
тора на операционном усилителе. Попробуйте
подать на его вход сигнал треугольной формы
с частотой 1 кГц.
100 пФ
Рис. 7L.4. Схема дифференциатора с дополнительным рези-
стором и конденсатором для улучшения стабильности
Интереснее всего исследовать дифференциа-
тор, если он работает не так, как ожидалось.
Такое поведение он может проявить при подаче
на него синусоидального сигнала от генерато-
ра. В ответ на этот сигнал вы можете ожидать
на выходе также чистый синусоидальный сиг-
нал, если только не обнаружили совсем другой
результат на лабораторном занятии 3L. Дело
в том, что при дифференцировании синусои-
дальных сигналов некоторых генераторов сиг-
налов (особенно генераторов компании Krohn-
Hite, которые мы предпочитаем использовать
в нашей лаборатории), обнаруживается, что в
действительности эти сигналы представляют
собой комбинацию, составленную из отрезков
прямых. Эта странная форма якобы синусои-
дального сигнала получается в результате спо-
соба его формирования: исходный сигнал име-
ет треугольную форму, затем его вершины по-
степенно срезаются четырех- или пятизвенной
цепью диодов. Каждое последующее диодное
звено подключается при все большем напря-
жении, «округляя» треугольник все сильнее по
мере приближения к его вершине (рис. 7L.5).
По выходному сигналу дифференциатора вам,
может быть, даже удастся определить число ди-
одных звеньев, хотя нам никогда не удавалось
обнаружить признаки всех звеньев.
334
71. Лабораторное занятие: операционные усилители II
Входной треугольный сигнал
Выходной «синусоидальный» сигнал
A/Y
+2,4 В
-2,4 В
Рис. 7L.5 Схема формирования синусоидального сигнала из треугольного
Замечание насчет стабильности
Здесь нам придется упомянуть непростой во-
прос о стабильности, который рассматривается
более подробно в главе 9N7. Для этого рассмо-
трим простой дифференциатор с одним рези-
стором и одним конденсатором (рис. 7L.6).
Рис. 7L.6. Простой дифференциатор (нестабильный)
Он неизбежно балансирует на краю стабиль-
ности, поскольку коэффициент усиления тако-
го дифференциатора возрастает со скоростью
6 дБ/октаву («>Д в дифференциаторе, собран-
ном точно по схеме на рис. 7L.6, нарушается
критерий стабильности для усилителей с об-
ратной связью (см. раздел 4.9.3 книги АоЕ).
Чтобы обойти эту проблему, в схему обычно
добавляют как последовательный входной ре-
зистор, так и конденсатор, шунтирующий рези-
стор обратной связи, как показано на рис. 7L.4.
Но выше определенной предельной частоты
дифференциатор превращается в интегратор.
Мы уже видели такую частотную характери-
стику на рис. 7N.34.
Такая компрометация рабочих характеристик
дифференциатора разочаровывает. Влияние
этой резистивно-емкостной цепочки можно
увидеть, наблюдая за фазовым сдвигом между
входным и выходным сигналами по мере посте-
пенного повышения частоты входного сигнала
до частоты перехода и далее. На частоте пере-
хода фазовый сдвиг должен быть нулевым. На
более высоких частотах фазовый сдвиг будет
соответствовать характеристике интегратора.
Между прочим, операционный усилитель с бо-
лее высокой частотой единичного усиления fx
будет работать лучше: переход в режим инте-
гратора будет происходить, но на более высо-
кой частоте.
Интегрирование производной. Более за-
нимательный способ выявить несовершен-
ство дифференциатора — подать его выход-
ной сигнал на интегратор, который мы собра-
ли ранее, а затем сравнить исходный и конеч-
ный сигналы.
В идеале они должны быть идентичными, по
крайней мере, по фазе (не считая усиления).
Являются они таковыми? Зависит ли ответ от
частоты входного сигнала8?
Качание частоты. Вам также может доставить
удовольствие наблюдать за частотной характе-
ристикой дифференциатора на операционном
усилителе, чтобы подтвердить закономерность,
указанную ранее: возрастает ли сначала усиле-
ние схемы с повышением частоты (поведение
дифференциатора), а затем снижается ли оно
при дальнейшем повышении частоты (поведе-
ние интегратора)?
7L3. Скорость нарастания
выходного напряжения
Начните с измерения скорости нарастания на-
пряжения выходного сигнала, используя схему,
изображенную на рис. 7L.7. Эту задачу следует
выполнять в два этапа: сначала с прямоуголь-
ным, а затем с синусоидальным сигналом.
АоЕ §4.5.7.
8 Должен зависеть. Интегратор является «честной» схе-
мой, но дифференциатор работает должным образом
только до частоты перехода, которую можно вычислить по
значениям его резисторов и конденсаторов.
7L4. Микрофонный усилитель переменного тока
335
Примечание
Подключенный последовательно к входу резистор
предотвращает повреждение микросхемы при по-
даче сигнала, превышающего напряжение питания.
Входной *9 к?м
сигнал
Рис 7L7. Схема для измерения скорости нарастания напря-
жения выходного сигнала
7L3.1. Прямоугольный входной
сигнал
Подайте на вход схемы прямоугольный сигнал
с частотой около 1 кГц и наблюдайте на осцилло-
графе выходной сигнал. Измерьте скорость на-
растания выходного сигнала по крутизне пере-
ходов. Обратите внимание на то, что наивысшая
скорость нарастания наблюдается только при
сильно разбалансированном входном каскаде
операционного усилителя. Таким образом, если
скорость нарастания кажется низкой, проверьте,
достаточна ли амплитуда входного сигнала.
7L3.2. Синусоидальный сигнал
Далее подайте на вход схемы синусоидальный
сигнал с амплитудой около одного вольта и из-
мерьте частоту, на которой выходной сигнал
начинает искажаться. (Это будет частота, на
которой также начнет уменьшаться амплиту-
да.) Согласуется ли этот результат со скоростью
нарастания, измеренной для прямоугольного
сигнала? Здесь нужно иметь в виду одну тон-
кость: наивысшая скорость нарастания опера-
ционного усилителя не достигается до тех пор,
пока не будут сильно разбалансированы его
входы. При прямоугольном сигнале большой
амплитуды это требование легко выполняется,
тогда как при синусоидальном сигнале может
не выполняться, и может потребоваться сигнал
большой амплитуды и в то же самое время вы-
сокой частоты.
Теперь вернитесь назад и замерьте те же самые
параметры (скорость нарастания и характери-
стики синусоидального сигнала, при которых
она максимальна) для более старого операци-
онного усилителя на микросхеме 741. Для этой
микросхемы заявлена типичная скорость нарас-
тания 0,5 В/мкс, а для микросхемы 411 — 15 В/
мкс. Как эти значения сопоставляются с вашими
экспериментальными результатами?
7L4. Микрофонный
усилитель переменного тока
7L4.1. Операционный усилитель
с однополярным напряжением
питания
В этом упражнении мы познакомимся с опера-
ционным усилителем с однополярным источни-
ком питания, который в данном случае исполь-
зуется для того, чтобы можно было работать
с напряжением питания +5 В, которое позже
понадобится для питания вашего компьютера.
Этот операционный усилитель, сдвоенный ва-
риант на микросхеме 358 (выпускается также
микросхема 324, содержащая четыре усилителя
в одном корпусе), может работать, как и любой
другой операционный усилитель с двухполяр-
ным напряжением питания ±15 В. Но в отличие
от, например, операционного усилителя на ми-
кросхеме 411, он также может работать с отри-
цательным напряжением на уровне потенциала
земли (17. = GND). Это достигается за счет того,
что диапазон его входных напряжений синфаз-
ного сигнала включает [7, а отрицательный раз-
мах выходного сигнала может доходить до Щ.
В рассматриваемой схеме эта отличительная
особенность операционного усилителя с одно-
полярным питанием, его возможность работать
с напряжениями, достигающими уровня отри-
цательного напряжения питания, не имеет зна-
чения. На практике такая возможность часто
является основной причиной выбора операци-
онного усилителя с однополярным напряжени-
ем питания. Например, в отличие от описанно-
го здесь микрофонного усилителя эта особен-
ность микросхемы 358 используется в схеме
милливольтметра на операционном усилителе,
который рассматривается в разделе 7W.
Примечание
Рекомендуем вам собрать микрофонный усили-
тель на отдельной макетной плате, чтобы сохра-
нить его для будущего проекта, в котором он будет
источником сигнала для вашего компьютера.
336
7L Лабораторное занятие: операционные усилители II
+5 В
в
Х от 0,01 мкФ до ОД мкФ
X (керамический)
от 10 кОм
до 100 кОм
з~ 4,7 мкФ
гаг
4С
358
Рис. 7L.8. Микрофонный усилитель с однополярным источником питания
На рис. 7L.8 изображена схема усилителя на
микросхеме 358 для работы с микрофоном, вы-
дающим напряжение не более 20 мВ. Амплиту-
да выходного сигнала усилителя составляет не-
сколько вольт. В данном случае это усилитель
переменного тока: входное напряжение смеще-
ния не усиливается (коэффициент усиления по
постоянному току равен единице).
В устройстве используется микрофон электрет-
ного типа. В таком микрофоне датчиком звука
служит конденсатор: звуковое давление меня-
ет расстояние между пластинами конденсато-
ра, из-за чего его емкость изменяется. Заряд
конденсатора поддерживается практически на
одном и том же уровне, в результате чего вы-
ходное напряжение U изменяется в ответ на
звуковое давление согласно формуле Q = CU.
В состав микрофона входит полевой транзистор
+5 В
1
" О'1 мкф
1,2кОм| J ф или больше
Микрофон
Рис. 7L.9. Развязка источника питания микрофона
1/120 с « 8 мс
Рис. 7L.10. Помеха в микрофонном усилителе, собранном на
макетной плате РВ503, вызываемая пульсациями на конден-
саторе фильтра
с высоким входным импедансом, который слу-
жит буфером.
Изменяющийся выходной ток полевого транзи-
стора преобразуется повышающим резистором
номиналом 2,2 кОм в выходное напряжение.
Таким образом, выходной импеданс микрофо-
на равен значению повышающего резистора:
2,2 кОм.
Добавьте развязывающие конденсаторы к ис-
точнику питания микрофона, как показано на
рис. 7L.9.
Может оказаться, что, несмотря на ваши ста-
рания, в усилитель продолжают проникать се-
тевые помехи величиной в несколько десятков
милливольт на частоте 120 Гц9. На рис. 7L.10
показано, как выглядят эти импульсы.
Вероятно, вам придется смириться с этими по-
мехами, если только вы не против использо-
вания отдельного источника питания. В таком
случае хорошо подойдет регулируемый источ-
ник питания, который был у нас на лаборатор-
ном занятии 1L. Импульсы помех возникают
из-за наводок на общей шине, когда конденса-
тор фильтра источника питания перезаряжается
на пиках выходного напряжения выпрямителя.
Их не должно здесь быть, но полностью изба-
виться от них трудно. Они возникают вслед-
ствие некачественной разводки проводников и
заземления на макетных платах со встроенным
источником питания наподобие платы РВ503,
и этот дефект нельзя исправить, не переделав
внутреннюю проводку макетной платы.
9 При частоте сети 60 Гц. - Примеч. ред.
7S. Дополнительный материал:
глоссарий по операционным усилителям
Виртуальная земля (virtual ground) — инвер-
тирующий вход (-) операционного усилите-
ля при заземленном неинвертирующем входе.
Обратная связь старается поддерживать на-
пряжение на инвертирующем входе на нулевом
уровне, и протекающий через этот вход ток не
замыкается на землю, а протекает по цепи об-
ратной связи (поэтому «земля» называется
«виртуальной»).
Входной ток смещения — ICM (bias current —
IBIAS) — среднее значение входных токов, про-
текающих через два входа (инвертирующий и
неинвертирующий) операционного усилителя.
Гистерезис (hysteresis) — применительно к
схемам компаратора на триггере Шмидта раз-
ница напряжений между верхним и нижним
пороговыми значениями.
Напряжение смещения — UCM (offset voltage —
^offset или ^os) ~" напряжение рассогласования
входного каскада операционного усилителя:
напряжение, которое нужно приложить между
входами, чтобы получить нулевое выходное
напряжение.
Операционный усилитель с однополяр-
ным напряжением питания (single-supply op-
amp) — устройство, уровни входных сигналов
которого близки (а иногда и меньше) уровня
отрицательного напряжения питания, которым
обычно служит «земля». Такое устройство так-
же может выдавать выходные сигналы с уровнем
близким к отрицательному питанию («земле»).
Произведение «усиление — полоса пропу-
скания» — (gain-bandwidth product) — постоян-
ная, описывающая усиление и частотную харак-
теристику операционного усилителя. Равняется
экстраполированной частоте, при которой уси-
ление операционного усилителя с разомкнутой
цепью обратной связи снижается до единич-
ного.
Режим насыщения (saturation) — состояние,
при котором выходное напряжение операци-
онного усилителя достигает одного из двух
(±) пределов выходного напряжения, который
обычно меньше на 1,5 В напряжения пита-
ния обоих полярностей, но намного меньше в
устройствах с выходным RR-сигналом.
С размахом в полном диапазоне напряже-
ния питания (rail-to-rail) — применительно к
входным и выходным сигналам операционно-
го усилителя. (Английское rail здесь означает
шину или напряжение питания.) В данной кни-
ге для краткости используется обозначение RR.
Одни микросхемы работают с входными RR-
сигналами, другие — с выходными сигналами
практически во всем этом диапазоне, существу-
ют также микросхемы, которые поддерживают
обе возможности.
С разомкнутой цепью обратной связи (open
loop) — схема, в которой отсутствует обратная
связь.
Скорость нарастания выходного напряже-
ния (slewrate) — максимальная скорость (dU/dt)
изменения напряжения выходного сигнала
операционного усилителя (при значительной
разности напряжений между входами операци-
онного усилителя).
Суммирующее соединение (summing junc-
tion) — суммирующий токи инвертирующий
вход операционного усилителя при инверти-
рующем включении. При этом ток обратной
связи 70С является алгебраической суммой
всех токов, входящих в суммирующее соеди-
нение.
Ток сдвига — 7СД (offset current — 70S) — раз-
ница между входными токами, протекающими
чрез два входа (инвертирующий и неинверти-
рующий) операционного усилителя.
338 75. Дополнительный материал: глоссарий по операционным усилителям
Триггер Шмидта (Schmitt trigger) - схе- Частотная коррекция (frequency compensa-
ма компаратора с положительной обратной tion) — преднамеренное снижение усиления
связью. операционного усилителя при повышении ча-
стоты входного сигнала. Применяется для обес-
Усилитель, преобразующий сопротивле- печения стабильности цепей обратной связи
ние (transresistance amplifier) - преобразова- при чрезмерных фазовых сдвигах на высоких
тель «ток-напряжение». частотах.
7W. Примеры с решениями:
операционные усилители II
7W.1. Задача
Далее приведено описание задачи разработки
схемы и некоторые сопутствующие вопросы.
Разработка схемы
Создайте схему интегратора на операционных
усилителях со следующими рабочими характе-
ристиками:
♦ при подаче на вход схемы сигнала напряже-
нием +1 В ее выходной сигнал должен ли-
нейно нарастать со скоростью +1 В/с;
♦ выходной импеданс #вых источника сигнала
неизвестен;
♦ схема должна содержать защиту от перехода
в режим насыщения, вызываемого длитель-
ным интегрированием небольших погреш-
ностей по постоянному току.
Вопросы
Частотная характеристика. Предположим,
что интегратор содержит резистор, шунтирую-
щий конденсатор обратной связи. Какова при-
близительно будет низкочастотная граница ча-
стотной характеристики вашей схемы, если эта
граница определяется как частота, на которой
выходной сигнал ослабляется приблизительно
на 3 дБ?
Погрешности интегратора. Предположим,
что интегратор содержит вместо резистора,
шунтирующего конденсатор обратной связи,
переключатель сброса. С какой скоростью ме-
няется выходной сигнал такого интегратора
(в В/с) при одном из двух состояний входа: за-
земленном или разомкнутом?
Предположим, что используется операционный
усилитель на микросхеме LF411 с типичными
параметрами.
Случай 1. Вход заземлен (как будто бы сигнал
на него подается от датчика, являющегося ис-
точником напряжения).
Случай 2. Вход разомкнут (как будто бы сиг-
нал на него подается от датчика, являющего-
ся источником тока). Обратите внимание, что
в этом случае нужно удалить из схемы входной
буфер, находящийся перед интегратором.
Используйте лучший операционный уси-
литель: теперь выберите из перечня операци-
онных усилителей, приведенных в табл. 7W.1,
микросхему, которая улучшит характеристи-
ки интегратора приблизительно в 5 раз. Под
улучшением имеется в виду снижение погреш-
ности интегратора до меньшего значения, чем
1/5 величины, полученной для интегратора на
микросхеме 411 при заземленном входе.
Назовите выбранный операционный усилитель
и вычислите погрешность dU/dt (при подклю-
ченном на «землю» входе).
7 W. 1.1. Решение
Разрабатываем базовую
принципиальную схему
Для решения этой задачи нам потребуется стан-
дартный интегратор на операционном усилите-
ле с защитой от перехода в режим насыщения.
Как обычно, в схеме будем использовать рези-
стор обратной связи сопротивлением 100 • Динт.
340
7W. Примеры с решениями: операционные усилители II
Нам также потребуется две дополнительные
схемы на операционных усилителях:
♦ инвертер, чтобы придать выходному сигналу
требуемую полярность (положительный вы-
ход для положительного входного сигнала);
♦ входной буфер (повторитель), поскольку, как
указано в постановке задачи, «выходной им-
педанс jRbmx источника сигнала неизвестен».
Готовая базовая (без значений компонентов)
принципиальная схема интегратора показана
на рис. 7W.1.
Рис. 7W.1. Базовая (без указания значений компонентов)
принципиальная схема интегратора
Определяем значения компонентов
Наше решение взять резистор обратной связи
с сопротивлением, равным 100 #инт, склоняет к
выбору не слишком большого сопротивления
для резистора интегратора (это резистор, через
который сигнал подается на вход интегратора).
Если мы, как обычно, ограничимся номиналом
10 МОм, то сопротивление резистора обратной
связи Roc будет 10 МОм, а резистора интеграто-
ра #инт — 100 кОм. Теперь мы знаем, какой ток
будет протекать при заданном входном сигнале
величиной 1 В: /МАКС = 1 В/100 кОм = 0,01 мА.
Исходя из этого выбираем значение емкости
конденсатора:
=
dt IB/mc
Полная принципиальная схема интеграто-
ра со значениями компонентов приведена на
рис. 7W.2.
10 МОм
Частотная характеристика
Резистор обратной связи уменьшит выходной
сигнал иъых на 3 дБ, когда |ZC| = JR1. Это равен-
ство выполняется на частоте, которую обычно
называют частотой /3дВ: 1/(2%RC). Как вы хо-
рошо знаете, такое название обусловлено тем
фактом, что на этой частоте выходной сигнал
ДС-фильтра (в котором R и С соединены после-
довательно) снижается на 3 дБ.
Но в данном случае частота будет иметь также
иной смысл. В этой схеме, в которой резистор R
и конденсатор С соединены параллельно, луч-
ше называть эту частоту частотой перехода^ЕР.
Это частота, на которой токи, протекающие че-
рез 1? и С, уравниваются. Ниже пороговой ча-
стоты больше тока протекает через резистор, а
выше — через конденсатор. Но на этой частоте
интегратор ослабит уровень выходного сигна-
ла UBUX на 3 дБ по сравнению с тем, каким бы
этот уровень был без резистора обратной свя-
зи. Таким образом, упоминание величины 3 дБ
тоже будет правильным.
Если это отступление касательно вычисления
частоты f3 Б было длительным, то само вы-
числение будет прямолинейным и быстрым.
Резистор обратной связи снизит уровень вы-
ходного сигнала ишх на 3 дБ при частоте/ =
= l/(2nRC) « 1/(6 • 10 • 106 Ом • 0,01 • 10"6 Ф) =
= 1/(6 • ОД) = 1,6 Гц. Это очень низкая частота,
как нам бы и хотелось надеяться. Таким обра-
зом, на большинстве частот резистор обратной
связи не должен оказывать значительного от-
рицательного воздействия на качество инте-
грирования.
Погрешности интегратора
Предскажите скорость дрейфа выходного
сигнала (при отсутствии резистора обратной
связи). Типичные параметры операционно-
го усилителя LF411: напряжение смещения
[/ш = 0,8 мВ, ток смещения 1ГМ = 50 пА.
Вход интегратора подключен на «землю»
Напряжение смещения Ucu создает погреш-
ность как в повторителе, так и в интеграторе
в схеме на рис. 7W.2. Эти обе погрешности усу-
губляют дрейф выходного сигнала интегратора.
Рис. 7W.2. Полная принципиальная схема интегратора со
значениями компонентов
1 Можете или поверить нам на слово, или же вычислить
сами значение Zc||£, когда |ZC|=#.
7W.I Задача
341
При этом погрешность в выходном инверторе
на дрейф не влияет. В наихудшем случае оба
значения UCM могут быть одинаковой полярно-
сти и, таким образом, будут суммироваться.
Вызываемый ими ток погрешности 7П0ГР, за-
ряжающий конденсатор интегратора, является
результатом этого двойного напряжения сме-
щения (в наихудшем случае), создаваемом на
резисторе интегратора #инт:
'погр= 2 • Усм/Динт = 1,6 мВ/100 кОм = 16 нА.
Этот ток создает дрейф со скоростью:
dU/dt = I/C = 16 нА/0,01 мкФ = 1,6 В/с. (7W.1)
Таким образом, влияние тока смещения 7СМ
(равного 50 пА) является ничтожным по срав-
нению с током величиной 16 нА, создаваемым
напряжением смещения UCM.
Вход интегратора разомкнут
В этом случае мы моделируем поведение вход-
ного преобразователя, являющегося источни-
ком тока. Чтобы смоделировать такой источ-
ник, удалим повторитель, служащий буфером
для входного каскада, поскольку, образно го-
воря, источник тока очень рад видеть низкий
входной импеданс, который встречает его на
инвертирующем входе.
Также удалим со схемы резистор интегратора,
в котором нет надобности при входном сигнале
в виде тока и который, более того, может созда-
вать проблемы. При протекании тока этот ре-
зистор просто повышает входное напряжение
схемы по отношению к потенциалу «земли».
Такое смещение может нарушить работу источ-
ника тока (особенно источника с узким диапа-
зоном рабочих напряжений).
Теперь напряжение смещения UCM не влияет
на токи (так как это напряжение, которое по-
вышает уровень на инвертирующем входе по
отношению к потенциалу «земли», не изменя-
ет величину тока, поступающего из источника
тока, служащего источником сигнала для инте-
гратора). Дрейф выходного сигнала интеграто-
ра вызывается только током смещения 7СМ:
dU/dt = I/C=50 пА/(0,01 мкФ = 10 нФ) = 5 мВ/с.
Удаляем этот каскад для источника сигнала
в виде источника тока
(«вход разомкнут» в терминах постановки задачи)
ЮМОм
Рис. 7W.3. Использование источника сигнала в виде источ-
ника тока упрощает входную часть интегратора
Это радикально лучший (приблизительно в
300 раз) результат, чем тот, который мы по-
лучили при использовании источника сигнала
в виде источника напряжения. Таким образом,
если у вас есть выбор, в качестве источника сиг-
нала для интегратора следует использовать ис-
точник тока.
Улучшаем рабочие характеристики
схемы, используя лучший операционный
усилитель
В случае поступления сигнала с источника на-
пряжения рабочие характеристики интеграто-
ра можно улучшить, используя операционный
усилитель с лучшими параметрами, чем у ми-
кросхемы 411. Чтобы получить требуемое в по-
становке задачи пятикратное улучшение ско-
рости дрейфа по сравнению с данным параме-
тром для микросхемы 411, нам нужно снизить
скорость дрейфа с 1,6 В/с (см. формулу (7W.1))
до приблизительно 0,3 В/с.
Так как мы ранее выяснили, что дрейф в опе-
рационном усилителе на микросхеме 411 вы-
зывается только напряжением смещения Ucu
(влияние тока смещения 1СМ было ничтожным),
все, что нам нужно сделать, это найти операци-
онный усилитель с напряжением смещения не
большим, чем 1/5 напряжения смещения ми-
кросхемы 411. Этот операционный усилитель
также должен иметь низкий ток смещения /см,
сравнимый с этим параметром для микросхе-
мы 411. Таким образом, нам требуется опера-
ционный усилитель с напряжением смещения
UCM < 0,8 мВ/5 = 0,16 мВ и низким током сме-
щения 1СМ.
Скорость дрейфа этого операционного усили-
теля (предполагая, опять же, что интегратор
342
7W. Примеры с решениями: операционные усилители II
«видит» 2 • UCM вследствие присутствия повто-
рителя перед интегратором) должна быть сле-
дующей:
dt
(2
= ОДмВ/ОДМОм =
" 0,01 мкФ
= 1нА/10нФ = 0ДВ/с.
Смотрим табл. 7W.1 и видим, что первым
устройством, отвечающим этому требованию,
является операционный усилитель на микро-
схеме ОРАШВ.
В этой же таблице можно видеть, что при не-
обходимости операционного усилителя с на-
много меньшим напряжением смещения такие
устройства доступны на рынке. Мы познако-
мимся с одним из таких устройств в следующем
разделе. Но нет смысла использовать лучший
операционный усилитель, чем необходимо,
поэтому для нашей текущей работы мы будем
довольствоваться микросхемой LF411.
7W.2. Милливольтметр
на операционном усилителе
Задача
Дано:
♦ гальванометр с током отклонения на полную
шкалу, равным 1 мА, и сопротивлением ка-
тушки 100 Ом;
♦ операционный усилитель (и) по вашему вы-
бору;
♦ другие требуемые компоненты.
Требуется разработать схему вольтметра со сле-
дующими рабочими характеристиками:
♦ если возможно, используйте однополярный
источник питания; если это вам не по плечу,
тогда используйте двухполярный источник
питания напряжением ±15 В;
♦ напряжение отклонения полной шкалы:
10 мВ;
♦ погрешность: 1% полной шкалы;
♦ входное сопротивление: 1 МОм;
♦ показания при заземленном или разомкну-
том входе: 0 В (к обычному 1% отклонения
полной шкалы);
Справившись с основным заданием или одно-
временно с ним, если у вас есть желание, можно
добавить пару желательный возможностей:
♦ защиту для гальванометра от последствий
превышения допустимого напряжения вхо-
дящего сигнала;
♦ возможность показаний при любой поляр-
ности входного сигнал, при этом полярность
указывается с помощью светодиода.
7W.2.1. Решение задачи разработки
схемы милливольтметра на
операционном усилителе
Начинаем с усиления
Определить требуемое усиление можно, срав-
нивая диапазон входных напряжений с диа-
пазоном выходных, которые требуются для
работы гальванометра2. При этом нужно рас-
смотреть вопрос, какой тип усилителя будет
подходящим для данной задачи.
Требуемое усиление
Вспомним спецификации задачи, касающиеся
усиления:
♦ диапазон входных напряжений: 0-10 мВ;
♦ требуемый диапазон выходных напряже-
ний: 0-100 мВ, поскольку на гальванометре
происходит падение напряжения; 100 мВ
для отклонения полной шкалы. Согласно
описанию сопротивление катушки состав-
ляет 100 Ом, а ток отклонения полной шка-
лы — 1 мА.
Таким образом, коэффициент усиления 10 бу-
дет достаточным.
Определяемся с типом усилителя
Какой тип усилителя следует использовать, ин-
вертирующий или неинвертирующий? Любой
из них будет удовлетворять требование вход-
ного сопротивления (1 МОм). Рассмотрим как
может выглядеть каждая из этих схем.
2 См. АоЕ, рис. 4.56
7W.2. Милливольтметр на операционном усилителе
343
Неинвертирующий усилитель
Усилитель этого типа будет очевидным выбо-
ром, поскольку это устройство с однополярным
источником питания, а нам требуется довольно
высокий входной импеданс. Схема такого уси-
лителя показана на рис. 7W.4.
от 0 до 10 мВ
от 0 до 10 мВ
J Гальванометр
7
Рис 7W.4. Неинвертирующий усилитель для приведения в
действие гальванометра
Усилитель должен быть с однополярным ис-
точником питания: его вход должен быть в си-
лах работать с входными сигналами вплоть до
нулевого уровня, а уровень выходного сигна-
ла должен быть в силах приближаться близко
к нулевому уровню. Этим условиям удовлетво-
ряет операционный усилитель на микросхеме
LM358, который мы использовали для сборки
микрофонного усилителя на лабораторном за-
нятии 7L.4.
Неинвертирующий усилитель с входным
сигналом в виде источника тока
Для приведения в действие гальванометра на
его катушку вместо напряжения можно пода-
вать ток. На рис. 7W.5 изображена принципи-
альная схема такого варианта усилителя.
Ограничивает протекающий^
через гальванометр ток при
.любом значении UBX
Рис. 7W.5. Схема для подачи на гальванометр сигнала в виде
тока вместо напряжения
Схема, изображенная на рис. 7W.5, содержит
токоограничивающий резистор номиналом
10 кОм для защиты усилителя от чрезмерного
напряжения. Эта защита удовлетворяет соот-
ветствующему требованию, изложенному в по-
становке задачи в разделе 7W.2.2.
Инвертирующий усилитель
Можно ли решить эту задачу с помощью инвер-
тирующего усилителя? Можно, но при исполь-
зовании однополярного источника питания
схема будет неуклюжей, А при наличии двупо-
лярного источника питания решение достаточ-
но простое, как показано на рис. 7W.6.
ЮМОм
1М0м
VW
(от 0 до -100 мЕР
Рис. 7W.6. Инвертирующая схема усилителя прямолинейна
при литании от двухполярного источника
Использование однополярного питания услож-
няет решение данной задачи. Это объясняется
тем, что схема должна работать с напряже-
ниями, приближающимися к ее «положитель-
ному» напряжению питания (т. е. к ее более
положительному напряжению питания, кото-
рым в данном случае является потенциал зем-
ли). Соответствующая схема изображена на
рис. 7W.7.
ЮМОм
-100м|)
Рис. 7W.7. Инвертирующий усилитель для приведения в
действие гальванометра
Термин инвертирующий означает, что выход-
ной сигнал операционного усилителя всегда
будет отрицательной полярности, поэтому пи-
тание операционного усилителя должно осу-
ществляться таким странным способом, как
показано на схеме. Теперь вход операционного
усилителя находится на уровне положитель-
ного напряжения питания, а выходной сигнал
может быть в диапазоне от этого уровня до
100 мВ ниже его. Это обстоятельство исклю-
чает использование обычного операционно-
го усилителя с однополярным питанием типа
микросхемы 358. Нам нужен операционный
усилитель с двухполярным питанием, способ-
ный понимать входные сигналы в диапазоне
вплоть до уровня положительного напряжения
питания. Найти такой операционный усили-
тель не составит особого труда. Можно взять,
344
7W. Примеры с решениями: операционные усилители II
например, микросхему ОР282 или AD8531 ком-
пании ADI. Но напряжение питания последней
микросхемы ограничено до 6 В, что является
распространенным ограничением для КМОП-
устройств. Поэтому для нее пришлось бы ис-
пользовать напряжение питания меньшее, чем
15 В, скажем, 5 В.
Наш операционный усилитель должен быть в
состоянии выдавать выходной сигнал уровнем
вплоть до уровня положительного питания.
В этом отношении мы задали для себя такую
странную конфигурацию, что требуемая для
нее характеристика даже не указывается для
этих двух устройств. Но возможно, что они мо-
гут поглощать ток при напряжении, близком к
положительному напряжению питания. (Что
указано для этих устройств, так это сдвиг от по-
ложительного напряжения питания при работе
в качестве источника тока.)
Таким образом, найти устройство, отвечающее
требованиям данной конфигурации, возмож-
но. Но мы вскоре узнаем, что эта конфигурация
исключается характеристиками операционных
усилителей, которые могут обеспечить то, что
нам требуется для этой конфигурации: входной
и выходной ##-сигналы положительного на-
пряжения.
Характеристики операционного
усилителя, требуемые для схемы
До сих пор мы разобрались только с вопросом
получения коэффициента усиления равным 10.
Теперь нам предстоит решить более трудную
часть задачи: как получить точные результаты.
Постановка задачи требует удерживать погреш-
ности в пределах ±1%. Кроме этого, при разом-
кнутом входе прибор должен показывать нуле-
вое напряжение (в пределах 1% полного откло-
нения). Мы не хотим раздражать пользователей
блуждающими показаниями милливольтметра,
когда к нему ничего не подключено.
Устранение блужданий при разомкнутом
входе
Выходной сигнал неинвертирующего усили-
теля, схема которого показана на рис. 7W.4,
будет «блуждать» по причине очень большого
значения входного сопротивления RBX. После
определенного времени уровень входного сиг-
нала, а следовательно, и выходного, сместится
до предела, зашкалив стрелку гальванометра.
Чтобы не допустить такого развития событий
вход нужно подключить на «землю» через ре-
зистор, как показано на рис. 7W.8.
от 0 до 10 мВ
Рис. 7W.8. Подключение входа на «землю» через резистор
предотвращает дрейф сигнала в не инвертирующей схеме
усилителя
Номинал этого резистора выбирается таким,
чтобы удовлетворять исходное требование по-
становки задачи: #вх > 1 МОм. Инвертирующая
версия усилителя уже содержит такой резистор
и не нуждается ни в каких дополнениях для
предотвращения блуждания сигнала.
Допустимая величина погрешности
на входе
Согласно постановке задачи погрешность по-
казаний должна быть меньше 1%. Это озна-
чает, что допустимый уровень погрешно-
сти входного сигнала должен быть f/BX.norp =
= 0,01 • t/
полн-откл
= ОД
= 100 мкВ. Это
значение можно называть нашим «бюджетом
на погрешности».
Допустимое напряжение смещения
Эта общая погрешность по постоянному току
является суммой двух эффектов: напряжения
смещения Ucu и тока смещения 7СМ. Поскольку
эти два эффекта могут быть одинаковой поляр-
ности, мы позволим каждому из них использо-
вать только половину нашего бюджета на по-
грешности, т. е. по 50 мкВ3.
Напряжение смещения UCM
Таким образом, нам нужно найти операцион-
ный усилитель с напряжением смещения UCM
около 50 мкВ. Это очень малое значение, мень-
шее приблизительно в 15 раз, чем эта характе-
ристика для микросхемы операционного уси-
лителя 411. Тем не менее такие операционные
усилители доступны на рынке. Но при этом не
следует ожидать это значение напряжения сме-
щения в операционном усилителе, с оптимизи-
рованной какой-либо другой характеристикой.
3 Обычно части бюджета распределяются после выясне-
ния, какой эффект преобладает, вместо того, чтобы с са-
мого начала предполагать, что они оба одинаковые.
7И/12. Милливольтметр на операционном усилителе
345
В поисках удовлетворяющего наше требование
по 17СМ операционного усилителя обнаружива-
ется, что в результате из списка возможных
кандидатов следует исключить операционные
усилители с однополярным питанием и RR-
способностями, которые необходимы для ин-
вертирующей версии схемы. Два устройства,
которые могли работать с уровнями входного
сигнал вплоть до положительного напряже-
ния питания, имели значения Ucu величиной
3 мВ и 25 мВ. Поэтому от инвертирующей вер-
сии придется отказаться (но она выглядела не-
сколько извращенной с самого начала в любом
случае).
Напряжение смещения l/CM ^ 50 мкВ?
Этому требованию отвечают лишь несколько
устройств изо всех, перечисленйых в табл. 7W.1.
А именно:
♦ 1Л1012А(25мкВ,макс);
♦ МАХ420Е (5 мкВ, макс). — это операцион-
ный усилитель со стабилизацией нуля пре-
рываниями, постоянно корректирующий
свое смещение выходного напряжения к ну-
левому;
♦ LMP2014MT (5 мкВ). Еще один операцион-
ный усилитель со стабилизацией нуля пре-
рываниями, но с напряжением питания не
+15 В, а всего лишь +5В.
Два других устройства — ОРА627Ь и ОРА336
с напряжением смещения 100 и 125 мкВ со-
ответственно — почти проходят конкурс, но
слегка не вписываются в наш бюджет на по-
грешности. Но типичное значение 60 мкВ ми-
кросхемы ОРА336 было бы приемлемым. Мы
не будем здесь вдаваться в трудный вопрос,
когда может быть приемлемым использовать
устройства с характеристиками иными, чем для
наихудшего случая4. На всякий случай будем
держать эти два устройства на примете. Но если
будем реализовывать версию с однополярным
питанием, тогда подойдет только микросхема
LMP2015.
Ток смещения L
см
4 Один из наших компетентных друзей, который зани-
мался разработкой цифровых схем для крупного произво-
дителя компьютерного оборудования, рассказал нам, что
его компания не смогла бы конкурировать на рынке, если
бы они не допускали, что используемые в их разработках
устройства могут работать немного лучше, чем указано в
их технических характеристиках для наихудшего случая в
полном температурном диапазоне.
Ток смещения протекает через входной рези-
стор номиналом 1 МОм, создавая напряже-
ние, вызывающее погрешности. Опять же, мы
предположим, что для этой погрешности мы
можем использовать всего лишь половину на-
шего бюджета на погрешности: 50 мкВ. Тогда
ток смещения, с которым мы можем жить, бу-
дет таким:
1СМ ^ 50 мкВ/1 МОм = 50 пА,
Это малое значение для этой характеристики,
но, тем не менее, отвечающие этому требова-
нию устройства доступны на рынке. (Даже наш
скромный операционный усилитель LF411 поч-
ти подходит, заявляя типичное значение тока
смещения величиной 50 пА.) Трудность заклю-
чается в том, чтобы найти компонент, который
обладает такой хорошей характеристикой по
току смещения и одновременно приемлемым
значением для напряжения смещения. Если
же реализовывать версию с однополярным
питанием, тогда нам также потребуются осо-
бые способности операционного усилителя,
который может работать с уровнями входных
и выходных сигналов, близкими к потенциалу
«земли».
Только операционные усилители со стабили-
зацией нуля прерываниями способны удер-
живать общую погрешность ниже 100 мкВ.
Если реализовывать версию схемы с двухпо-
лярным питанием, приемлемым будет опера-
ционный усилитель на микросхеме ОРА627Ь
с его максимальными UCM = 100 мкВ и /см =
= 5 пА. Операционный усилитель на микросхе-
ме LMP2015 единственный изо всех, перечис-
ленных в табл. 7W.1, который может справиться
со всеми поставленными задачами: удерживать
погрешность входного сигнала ниже 100 мкВ
и использовать однополярное питание.
7W.2.2. Усовершенствования
Защита гальванометра
от перенапряжения
Схемы на рис. 7W.4 и 7W.6 могут пода-
вать на гальванометр сигнал напряжением
вплоть до напряжения 15 В источника пита-
ния. Поскольку выходной ток операционно-
го усилителя обычно ограничен несколькими
346
7W. Примеры с решениями: операционные усилители II
десятками миллиампер, то такой сигнал может
и не повредить гальванометр. Но схему можно
с легкостью модифицировать, чтобы устранить
любою возможность повреждения гальвано-
метра. Для этого нужно просто вставить после-
довательный резистор между выходом схемы и
входом гальванометра и повысить коэффици-
ент усиления схемы, как показано на рис. 7W.9.
Таким образом будет гарантировано, что уро-
вень подаваемого на гальванометр сигнала ни-
когда не превысит 150% уровня сигнала полно-
го отклонения шкалы.
от 0 до 10 мВ ^ ц.
1+
от 0 до 10 В
(или (Л для операционного усилителя
с двухполярным питанием)
Рис. 7W.9. Небольшое усовершенствование предотвращает
перенапряжение гальванометра
через гальванометр только в прямом направ-
лении, независимо от полярности входящего в
мост сигнала. На рис. 7W.10 показана модифи-
цированная таким образом схема, работающая
по принципу источника тока (подобно рассма-
триваемому в разделе 4N.3.1). Когда схема за-
дает ток, а не напряжение, падение напряжения
на диодах моста не играет роли. Полярность
входного сигнала указывается с помощью све-
тодиодов соответствующего цвета.
7W.23. Цель этого упражнения
Это упражнение было довольно требователь-
ным. Что мы хотели продемонстрировать в
нем, так это то, что очень простая задача ста-
новится сложной, если проектируемая схема
может допускать только небольшие погрешно-
сти. Мы надеемся, что это упражнение поможет
вам получить интуитивное понимание необхо-
димости такого поразительного разнообразия
предлагаемых на рынке операционных уси-
лителей, постоянно обновляющегося новыми
предложениями.
Разрешаем входной сигнал любой
полярности
Для этой возможности необходимо использо-
вать операционный усилитель с двухполярным
питанием. В случае однополярного5 гальвано-
метра мост из четырех диодов (знакомый нам
по источникам питания) заставит ток протекать
Кандидатуры операционных усилителей
Все, за исключением одного, перечисленные
в табл. 7W.1 операционные усилители не под-
ходят для работы с однополярным питанием.
Все они подойдут для схемы милливольтметра
с двухполярным питанием. При этом напряже-
ние питания для экземпляра, способного рабо-
тать с однополярным питанием, ограничено до
+5 В общего напряжения.
ПОЛОЖ. ^ ZX ОТРИЦ. <10 Ом
(зеленый) I [ (красный)
(Диодный мост подает ток
на гальванометр в требуемом
направлении, независимо от
полярности входного сигнала.
Падение напряжения на диодах
моста и катушке гальванометра
не имеет большого значения:
оно скрывается цепью обратной
связи)
Полярность входного сигнала
отображается светодиодом
соответствующего цвета,
который зажигается, когда
уровень входного сигнала
превышает 15% величины
отклонения полной шкалы
Рис. 7W.10. Схема, позволяющая работать с входными сигналами любой полярности
5 Существуют двухполярные гальванометры с исходным
положением стрелки посередине шкалы.
7W.2. Милливольтметр на операционном усилителе
347
Таблица 7W.1. Операционные усилители, которые можно потенциально использовать в схеме
милливольтметра
LM741C
LF411
ОРАШВ
ОРА627В
LT102A
ОРА336
МАХ420Е
иш, мкВ
Типичное
2000
800
50
40
8
60
1
Макс.
6000
2000
250
100
25
125
5
ГКисм,мкВ/°С
Типичное
-
7
0,5
0,4
0,2
1,5
0,02
Макс.
15*
20
1
0,8
0,6
-
0,05
'см'ПА
Типичное
80 000
50
0,5
1
25
1
10
Макс.
500 000
200
1
5
100
10
30
Примечания
На биполярных транзисторах,
устарелый, низкопробный
На полевых транзисторах
с управляющим р-я-переходом,
обычные характеристики
На полевых транзисторах, вы-
сокой точности
На полевых транзисторах с
управляющим р-л-переходом,
высокой точности, малошум-
ный
На полевых транзисторах с
низким смещением, высокой
точности
КМОП,[/пит = 5,5Вмакс.
КМОП, со стабилизацией нуля
прерываниями, иШТ до ±15 В
С однополярным напряжением питания
LMP2015
0,8
5
0,015
0,05
3
КМОП, со стабилизацией нуля
прерываниями, Unm = 5 В
макс.
* Только для высшего качества, в противном случае не указывается.
8N. Операционные усилители
положительная обратная связь
Содержание
8N.1. Полезная положительная обратная связь 348
8N.2. Компараторы 349
8N.2.1. Что такое компаратор? 349
8N.2.2. Проблемы с помехами 350
8N.2.3. Стабилизация компаратора с помощью положительной обратной связи 353
8N.2.4. Для хорошей схемы компаратора всегда нужна положительная
обратная связь 353
8N.2.5. Альтернативный способ реализации гистерезиса с помощью
обратной связи только по переменному току . 355
8N.3. Релаксационный ЯС-генератор колебаний 357
8N.3.1. Релаксационный генератор колебаний на операционном усилителе 357
8N.3.2. Каковы параметры? 357
8N.3.3. Более простой способ создания ЯС-генератора колебаний 357
8N.3.4. Микросхема 555 ДС-генератора колебаний/таймера 358
8N.3.5. Более современные микросхемы генератора колебаний 360
8N.4. Генератор синусоидальных колебаний на мосте Вина 360
8N.4.1. Цепь положительной обратной связи на мосте Вина 361
8N.4.2. Цепь отрицательной обратной связи генератора на мосте Вина 361
8N.5. Материал для чтения в АоЕ 364
Цель этой главы
В этой главе мы хотим научиться разрабаты-
вать следующие устройства:
♦ компараторы;
♦ генераторы колебаний.
Для функционирования этих схем необходима
положительная обратная связь.
8N.1. Полезная
положительная обратная
связь
До сих пор мы рассматривали положитель-
ную обратную связь как нежелательное яв-
ление, в одном ряду с, например, результатом
опечатки, меняющей смысл текста на противо-
положный.
Но оказывается, что, хотя отрицательная об-
ратная связь преобладает в большинстве об-
ластей применения, положительная обратная
связь может быть полезной для многих прило-
жений (рис. 8N.1).
неправильно...
...такая обратная связь
может быть полезной
Рис. 8N.1. Положительная обратная связь может быть по-
лезной
В этой главе мы рассмотрим несколько случа-
ев, в которых положительная обратная связь
8N.2. Компараторы
349
нужна для принятия решения, а затем случаи,
в которых она позволяет создавать генерато-
ры колебаний. В главе 9N мы продолжим рас-
смотрение положительной обратной связи,
но уже совсем с другой стороны. Мы встре-
тимся со многими случаями, когда положи-
тельная обратная связь заставляет сходить с
ума схему, которая до этого вела себя вполне
прилично. Но в этой главе мы увидим только
хорошую сторону положительной обратной
связи.
8N.2. Компараторы
8N.2.1. Что такое компаратор?
Компаратор представляет собой просто диффе-
ренциальный усилитель с высоким коэффици-
ентом усиления1. Такой усилитель сравнивает
сигналы, поступающие на два его входа, хотя до
сих пор мы и не описывали его функциониро-
вание таким образом. Но отличительная черта
компаратора — не столько само устройство, как
его применение. Операционный усилитель так-
же может работать в качестве компаратора, но,
как мы увидим на лабораторном занятии, это
будет некачественный компаратор из-за его
малого быстродействия. Микросхема, разрабо-
танная специально для выполнения операций
сравнения2, наподобие микросхемы компара-
тора 311, работает почти в 100 раз быстрее. А на
рынке доступны и другие более современные
компараторы, скорость работы которых еще в
100 раз выше, чем у микросхемы 311.
Сравнение компаратора
и операционного усилителя
Хотя операционный усилитель может иногда
функционировать, как компаратор, смена ро-
лей невозможна: компаратор не способен рабо-
тать в схеме с отрицательной обратной связью
вместо операционного усилителя. Компаратор
в такой схеме окажется нестабильным, и его
выходной сигнал на высоких частотах может
переходить в автоколебания. Операционный
усилитель работает стабильно потому, что есть
цепь отрицательной обратной связи. А в схеме
компаратора обратной связи нет. Компаратор
должен работать быстро, поэтому при его раз-
работке цепь отрицательной обратной связи не
предусматривается.
Многие компараторы также отличаются от опе-
рационного усилителя тем, что они оснащены
универсальным выходным каскадом3, который
состоит из переключателя, а не двухтактного
усилителя4. В компараторе на микросхеме 311
нагрузку можно подключить как к эмиттеру,
так и к коллектору, как показано на рис. 8N.2.
Поначалу необходимость позаботиться о под-
ключении и эмиттера, и коллектора может вы-
зывать раздражение, заставляя думать еще об
одной, а то и двух задачах. Но компараторы
устроены таким образом не случайно, а имен-
но, чтобы пользователь мог сам установить
верхний и нижний пределы размаха выходно-
го сигнала. Таким образом, с помощью компа-
ратора, например, на микросхеме 311 можно
с легкостью организовать стандартный диа-
пазон логических уровней от 0 В до 5 В вместо
размаха выходного сигнала, как у операцион-
ного усилителя в пределах ±15 В. Между про-
чим, в схеме на рис. 8N.2 база транзистора не
подключена к чему-либо. Конечно же, это не
так; разработчики микросхемы позаботились
о том, чтобы каскад работал должным образом
с широким диапазоном выходных напряжений,
при этом независимо от напряжений питания
дифференциального усилителя, который явля-
ется сердцем компаратора.
Испытываем компаратор
и сравниваем с операционным
усилителем
Если задача сравнения не слишком сложна,
то и операционный усилитель, и компаратор
справляются с ней с сопоставимыми результа-
тами. Например, на рис. 8N.3 показана осцил-
лограмма выходных сигналов операционного
1 АоЕ § 4.3.2А.
2 Англ. compare — сравнивать, comparator — устройство
сравнения. - Примеч. пер.
3 Некоторые компараторы содержат двухтактный пере-
ключатель в выходном каскаде, чтобы получить более вы-
сокую скорость за счет его низкого выходного импеданса.
Одно из таких устройств — микросхема LT1717 компании
Linear Technology с быстродействием в 4 не.
4 Строго говоря, этот каскад не обязательно использовать
как переключатель. Его можно подключить как повтори-
тель, соединив резистор не с коллектором, а с эмиттером.
Достоинство этого варианта — его более низкий выход-
ной импеданс. Но мы не будем работать с ним на наших
занятиях.
350
8N. Операционные усилители III: положительная обратная связь
Транзисторный переключатель. Источник
подающий управляющий сигнал на его
базу, не показан, но, несмотря на большие
колебания выходного напряжения
Чых'на базу тоже должен подаваться
соответствующий сигнал.
3
Определяет верхний максимум выходного
сигнала (УВЬ1Х (который не обязательно
'должен быть +15 В, а может быть даже ниже
потенциала «земли»).
Наличие повышающего резистора
^ обязательно. В противном случае при
выключенном транзисторе выходной
сигнал будет плавающим.
Определяет нижний предел выходного
сигнала ишх (который не обязательно
"должен быть на уровне потенциала
«земли», а может быть даже ниже его).
Питание компаратора (как положительное,
так и отрицательное) независимо от
напряжения выходного сигнала UBbLX
Рис. 8N.2. Отличия компаратора 311 от простого операционного усилителя
Выходной сигнал операционного усилителя
I 264mVj
Входной сигнал
Выходной сигнал компаратора
"Переход в режим насыщения операционного
усилителя: на один вольт меньше,
чем отрицательное напряжение питания
Рис. 8N.3. Как операционный усилитель, так и компаратор без проблем справляются с легкой задачей: обработкой низко-
частотного сигнала большой амплитуды. (Усиление осциллографа: входной сигнал — 1 В/деление; выходные сигналы —
5 В/деление.)
Выходной сигнал
компаратора
Выходной сигнал
операционного
усилителя
Входной сигнал
Рис. 8N.4. Операционный усилитель не поспевает за вход-
ным сигналом более высокой частоты. (Усиление осцилло-
графа: входной сигнал — 100 мВ/деление; выходные сигна-
лы — 5 В/деление.)
усилителя 411 и компаратора 3115, на вход
которых подается высокочастотный синусои-
дальный сигнал большой амплитуды. У компа-
ратора лучше крутизна выходного сигнала, но и
операционный усилитель не слишком отстает.
Но ситуация меняется при входном сигна-
ле высокой частоты: тогда как компаратор
5 Конкретный тип микросхемы не важен.
продолжает справляться с поставленной зада-
чей, операционный усилитель начинает барах-
лить, как показано на соответствующих осцил-
лограммах на рис. 8N.4.
При входном синусоидальном сигнале более
высокой частоты форма выходного сигнала
операционного усилителя уже не прямоуголь-
ная. Уровень выходного сигнала не успевает
снижаться даже до потенциала «земли». А вот
выходной сигнал компаратора прямоугольный,
но признаки возможной проблемы тоже замет-
ны. И фронт, и спад выходного сигнала компа-
ратора содержат множество переходов, хотя на
самом деле такого не должно быть. Вскоре мы
встретимся со многими другими примерами та-
кого некорректного поведения.
8N.2.2. Проблемы с помехами
На рис. 8N.5 приведено несколько нарисован-
ных вручную осциллограмм, чтобы показать
вам, как может выглядеть выходной сигнал этих
двух простых компараторов (реализованных
8N.2. Компараторы
351
Входной
аналоговый сигнал
411
(выходной сигнал
операционного
усилителя)
311
(выходной сигнал
компаратора)
Размах сигнала
[приблизительно ±13 В
Полный размах сигнале
" В до потенциала
1мкс
перехода ОД мкс
Рис BHS. Влияние помех на выходной сигнал компаратора и операционного усилителя
Входной
сигнал
Выходной сигнал
компаратора 311
Входной
сигнал
Уровень
«земли» (!)
Напряжение
питания +15 В
Выходной сигнал
компаратора 311
Рис. 8N.6. Без обратной связи компаратор плохо обрабатывает пологий сигнал небольшой амплитуды. (Усиление осцилло-
графа: входной сигнал, «земля» и питание —100 мВ/деление; выходные сигналы —10 В/деление.)
на микросхемах 411 и 311) при входном сиг-
нале, содержащем помехи. Предположим, что
мы хотим, чтобы компаратор переключался на
пресечении нулевого уровня низкочастотным
сигналом большой амплитуды, игнорируя при
этом небольшие колебания.
Замечание
Чтобы этот пример выглядел более реалистично,
можно предположить, что частота входного сигна-
ла 60 Гц, и что мы пытаемся сделать схему часов,
подсчитывая количество переходов через нуле-
вой уровень.
Практикум
Если попытаться создать таким способом
опорный сигнал для часов (например, при-
способив для входного сигнала выходное на-
пряжение сетевого трансформатора6), то наши
6 Под сетевое напряжение США, частота которого 60 Гц.
В России и большинстве стран СНГ, как известно, частота
сетевого электричества составляет 50 Гц.
часы получатся не очень точными. Для осцил-
лограмм, показанных на рис. 8N.6, в качестве
источника входного сигнала для компаратора
использовался не трансформатор, а генератор
сигналов. Как можно видеть на обеих осцил-
лограммах, выходной сигнал компаратора
(внизу) содержит искажения. Очевидно, что
при использовании этого выходного сигнала в
качестве опорного для наших часов часы будут
спешить.
При взгляде на рис. 8N.5 и 8N.6 у вас может
создаться впечатление, что проблемой являет-
ся искаженный входной сигнал. Ведь, в конце
концов, совершенно ясно, что входной сигнал
не чистый, а содержит небольшие колебания.
Так, может быть, все, что нам требуется, это
лучший источник сигнала? Или, может быть,
прежде чем подавать входной сигнал на ком-
паратор, его следует пропустить через низкоча-
стотный фильтр, чтобы избавиться от всех этих
пульсаций? Все это вполне правдоподобно, но,
тем не мене, неверно.
352
8N. Операционные усилители III: положительная обратная связь
Кажущаяся пляска снижающегося бейсбольного мяча
[относительно скачущего обозревателя)
f <f *X/' \J (Некомпетентный аутфилдер^
W * * ^~^^ Внутреннее поле
(Скачущая система координат)
Рис. 8N.7. При скачущей системе координат аутфилдера падающий бейсбольный мяч прыгает подобно входному сигналу
компаратора при нестабильном потенциале земли
Входной сигнал начинает дрожать в самое
неподходящее время: когда он пересекает пороговый
уровень переключения. Просто невезение?
Дрожание входного сигнала выглядит подобно
траектории бейсбольного мяча, которая кажется
бегущему ловцу скачущей в небе
Рис. 8N.8. Дрожание входного сигнала наблюдается как раз при переходе порогового уровня
На самом деле здесь перепутаны причина и
следствие: в действительности помеха не про-
никает на вход компаратора с его выхода. На
правой осциллограмме на рис. 8N.6 видны два
дополнительных уровня: потенциала «земли»
и напряжения положительного питания +15 В.
Когда потенциал «земли» нестабилен, даже
гладкий как стекло входной сигнал на выходе
компаратора будет содержать колебания. Если
помехи присутствуют и на шине «земли» и на
положительной шине питания (отрицательное
напряжение не показано, но оно выглядит по-
добным образом), то не удивительно, что ком-
паратор постоянно меняет свое решение.
Этот случай напоминает мне о моих бесслав-
ных днях аутфилдера7 в начальной школе.
Высоко забитый мяч взлетал в голубую высь
достаточно плавно, но когда он начинал па-
дать, а я бежал ему навстречу, чтобы поймать
7 В бейсболе [baseball] игроки, располагающиеся на внеш-
ней части поля [outfield], называются левым, центральным
и правым аутфилдерами.
его, мяч начинал вести себя очень неправиль-
но. Он прыгал вверх и вниз, затрудняя мою за-
дачу, подобно тому, как прыгающий входной
сигнал создает проблему для компаратора 311.
На рис. 8N.7 изображена соответствующая шу-
точная интерпретация этой истории.
Если хорошо присмотреться к входному сигна-
лу схемы компаратора с дрожащим выходным
сигналом, можно увидеть сходство с прыгаю-
щим бейсбольным мячом. Кажется, что сину-
соидальный сигнал генератора сигналов начи-
нает искажаться пульсациями в самый худший
момент, как раз, когда он пересекает пороговый
уровень компаратора (которым в данном слу-
чае является потенциал «земли»). На рис. 8N.8
изображены осциллограммы этих помеховых
пульсаций при двух разных скоростях разверт-
ки осциллографа.
Но это не случай постоянного невезения
или дефективного генератора сигналов. Это
кажущееся дрожание вызывается помехами,
8N.2. Компараторы
353
присутствующими на земляной шине. Генератор
сигналов ни в чем не виноват. (Как и бейсболь-
ный мяч не прыгал вверх-вниз при падении.)
Помехи на шинах «земли» и питания микросхе-
мы 311 являются результатом периодических
всплесков тока, происходящих каждый раз,
когда уровень выходного сигнала начинает ме-
няться. Выход компаратора переключается, со-
ответственно потребляя или выдавая ток через
линии питания и «земли». Всплески (в индук-
тивности линий, которая играет более важную
роль, чем сопротивление) и вызывают колеба-
ния потенциалов положительного напряжения
питания и «земли». Это колебание определя-
ется дифференциальным усилителем входного
каскада с большим коэффициентом усиления и
вынуждает компаратор изменить свое решение
и не переключаться. Но соответствующее от-
ключение тока снова вызывает искажение на
линиях питания и «земли», заставляя возобно-
вить процесс переключения, и т. д.
Если в процессе колебаний уровень входного
сигнала находится вблизи порогового уровня
переключения, схема будет постоянно переклю-
чаться, доставляя нам соответствующую голов-
ную боль. Но эта проблема легко устраняется
введением положительной обратной связи.
8N.2.3. Стабилизация компаратора
с помощью положительной
обратной связи
Разновидности обратной связи
Как упоминалось в разделе 8N.1, нам нужно
расширить наше представление о положитель-
ной обратной связи. Здесь возможно несколько
вариантов. На рис. 8N.9 изображены три схе-
мы, которые помогут вам получить более раз-
ностороннее представление о положительной
Входной
сигнал
Входной
сигнал
Входной
сигнал
Рис. 8N.9. Только один из трех способов включения компа-
ратора эффективен
обратной связи. Одна из этих схем просто не-
лепа и полностью бесполезна, вторая — схема
невысокого качества, но работоспособная, а
последняя схема довольно эффективна.
Схема на рис. 8N.9, а обречена постоянно на-
ходиться в режиме насыщения. Хотя реши-
тельность изначально присуща хорошему
компаратору, эта схема слишком упорна, про-
сто фанатична. Что делает ее совершенно бес-
полезной — заставить эту схему изменить свое
решение почти невозможно.
В схеме на рис. 8.N9, б вообще нет никакой
обратной связи: ни положительной, ни отри-
цательной. Эта схема работоспособна, но, как
мы уже видели, неэффективна. Она может вы-
полнять операцию сравнения, когда входной
сигнал быстро пересекает пороговый уровень.
Но при входном сигнале с пологими перепада-
ми эта схема очень склонна к переходу в режим
автоколебаний.
Схема на рис. 8N.9, в — это обычная, стан-
дартная схема включения компаратора. В ней
есть положительная обратная связь, обеспе-
чивающая правильность принятия решений.
(В данной схеме, конечно же, вопрос глуби-
ны используемой положительной обратной
связи не освещен.) Этот подход реализован
во всех наших практических схемах компа-
раторов.
8N.2 А Для хорошей схемы
компаратора всегда нужна
положительная обратная связь
Оказывается, что заставить схему компаратора
игнорировать небольшие колебания входного
сигнала, наподобие изображенных на рис. 8N.5
и 8N.6, непросто. Для этого прежде всего не-
обходимо подавать на вход небольшую часть
выходного сигнала. Но делать это нужно в по-
ложительном смысле, т. е. так, чтобы эта часть
подтверждала предварительное решение ком-
паратора.
Такая положительная обратная связь делает
компаратор решительным: она, образно гово-
ря, как бы хлопает компаратор по плечу, говоря
ему: «Что бы ты ни решил делать, это должно
быть правильное решение». Таким образом,
действие подкрепляет решение.
354
8Л/. Операционные усилители III: положительная обратная связь
Входной
аналоговый
сигнал
Пороговый уровень
(нижний график)
-15
<н~—АЛЛ f
300 кОм
Г+15В-
свое \^
Г состояние/пока не будет пересечен
верхний пороговый уровень
^
311
(компаратор) 4 0
Выходной сигнал!
1-15В
311
(компаратор) *
Пороговый уровень
♦0,1В
0
1-0,1 В
Рис. 8N.10. Поведение хорошего компаратора предсказуемо
Входной сигнал
Входной |
сигнал
Выходной сигнал
компаратора 311
—Т Гистерезис
^Пороговые
уровни
Выходной сигнал
компаратора 311
Без гистерезиса: сильно искажен Введение гистерезиса улучшает сигнал
Рис. 8N.11 • Введение гистерезиса может успокоить выходной сигнал компаратора. (Усиление каналов осциллографа: входной
сигнал и гистерезис —100 мВ/деление; выходные сигналы —10 В/деление.)
Схема компаратора с положительной обратной
связью называется триггером Шмитта8.
На рис. 8N.10 представлен графический аргу-
мент, что небольшой гистерезис должен по-
зволить компаратору игнорировать колебания
входного сигнала9.
На рис. 8N.11 изображены несколько осцил-
лограмм, иллюстрирующих наши попытки
подать пологий синусоидальный сигнал, ко-
торый создавал такие большие искажения
в осциллограммах на рис. 8N.6, и применить
гистерезис.
Мы взяли небольшую часть выходного сигала
и подали ее обратно на неинвертирующий вход
компаратора (так что обратная связь в дей-
ствительности положительная). Слева пока-
зана осциллограмма нестабилизированного
компаратора, а справа — стабилизированного.
8 Названа в честь Отто X. Шмитта (Otto H. Schmitt), аме-
риканского аспиранта, который описал такую схему на
вакуумных лампах в 1934 г. Заслуживает ли эта скромная
схема такой чести?
9 Сравните с рис. 4.33 книги АоЕ.
Очевидно, что справиться с задачей стабили-
зации позволяет очень небольшой гистерезис,
около 20 мВ.
Гистерезис распространен
не только в электронике
Возможно, что понятия гистерезиса10 и поло-
жительной обратной связи являются новыми
для вас в области электроники, но гистерезис
встречается повсеместно и в обычной жизни.
Это форма мошенничества: корректировка
вопроса после того, как вы приняли решение.
Например, вы колеблетесь, куда поступать,
в Гарвардский университет или Стэнфордский.
Решив поступать в Гарвардский, вы говорите
сами себе: «Конечно же. Вся эта солнечная по-
года со временем так приедается»11.
Сильный гистерезис наблюдается на вступи-
тельных экзаменах с точки зрения колледжа,
10 От греческого отставание, запаздывание. Ничего обще-
го с истерикой.
11 Стэнфордский университет находится в Калифорнии.
8N.2. Компараторы
355
когда приемная комиссия рассматривает ваше
заявление и задает себе вопрос: «Он действи-
тельно так виртуозно играет на гобое или же
это просто еще один золотой медалист с иде-
альным БАТ12-баллом?»
А после того как вы поступили, вопрос каса-
тельно вашего отчисления может быть сфор-
мулирован так: «Этот арест за хранение нарко-
тиков тяжкое уголовное преступление или же
еще одно мелкое правонарушение?» Стандарты
меняются, потому что приемным комиссиям
нравится считать, что любое принятое ими ре-
шение должно быть правильным, точно так же,
как это делают стабильные компараторы.
С избранием в Конгресс и удалением из него
наблюдается такая же закономерность: если
вы туда попали, то убрать вас оттуда не так-то
легко. Положительная обратная связь приятна
человеку, она делает его решительным и само-
довольным. А отрицательная обратная связь —
склонность считать принятое решение ошибоч-
ным, потому что это было его решение — делает
человека нерешительным и, в крайнем случае,
неврастеником. Положительная обратная связь
может сделать вас удовлетворенным диктато-
ром, а отсутствие таковой — Вуди Алленом13.
Сколько нужно гистерезиса?
Если гистерезис делает компаратор решитель-
ным, то какую величину гистерезиса нужно
заложить в проект схемы? Столько, сколь-
ко можно? Что мы потеряем при увеличении
гистерезиса? Гистерезис является очень эф-
фективным лекарством, но прописывать его
нужно не больше, чем требуется, из-за его
побочных эффектов, как демонстрируется на
рис. 8N.12.
==> Гистерезис = сколько давать?
Ответ: обязательно больше,
чем полный размах помехи (Упом
«Помеха»
Рис. 8N.12. Взаимосвязь между величиной помехи и гисте-
резиса
Гистерезис придает схемам иммунитет к
12 Англ. Scholastic Assessment Test— отборочный тест типа ЕГЭ.
13 Англ. Woody Allen, американский режиссер и артист
кино. Наверное, намек на то, что довольно многие из его
фильмов, особенно ранних, в том числе комедии, перегру-
жены унылыми и философскими мотивами.
помехам, можно сказать, делает их слепыми к
патологиям входного сигнала, вплоть до опре-
деленной величины. Но этот же иммунитет
делает схему невосприимчивой также и к по-
лезному сигналу. Таким образом, схема опреде-
ления пересечения сигналом нулевого уровня
с симметричным гистерезисом величиной 200
мВ совсем не будет переключаться при входном
сигнале с амплитудой меньшей, чем 200 мВ.
Часто величину гистерезиса приходится зада-
вать приблизительно. Для схем, которые мы
собираем на наших лабораторных занятиях,
обычно достаточно 100-200 мВ. При разра-
ботке единичной специализированной схемы
величину гистерезиса можно сделать регули-
руемой и экспериментальным путем настроить
гистерезис, обеспечивающий необходимую
стабильность схемы.
Еще одним побочным эффектом гистерезиса,
который иногда имеет значение, является за-
держка. Таким образом, даже при входном сиг-
нале достаточно большом, чтобы переключить
компаратор, это переключение будет выпол-
нено слишком поздно, и момент пересечения
нулевого уровня окажется ошибочным. Далее
рассматривается прием, который может испра-
вить этот дефект, но за счет некоторого повы-
шения чувствительности схемы к частоте вход-
ного сигнала.
8N.2.5. Альтернативный способ
реализации гистерезиса
с помощью обратной связи только
по переменному току
Устранить задержку, которая обычно вносится
гистерезисом, можно с помощью гистерезиса,
который действует только в течение короткого
времени после перехода. Это осуществляется
с помощью обратной связи по переменному
току, как показано на схемах и осциллограммах
на рис. 8N.13.
Схемы определения пересечения нулевого
уровня, изображенные на рис. 8N.13, обладают
одинаковым гистерезисом, но в схеме справа,
с обратной связью по переменному току, по-
роговый уровень сдвигается только в течение
короткого времени после переключения вы-
ходного сигнала. В результате эта схема точно и
без задержки определяет пересечение нулевого
356
8N. Операционные усилители III: положительная обратная связь
Задержка переключения
Выходной сигнал
компаратора 311
Выходной сигнал
Пороговые уровни"
Выходной сигнал
компаратора 311
Выходной сигнал
Пороговые
уровни
Обратная связь по постоянному току Обратная связь по переменному току
100 кОм
=390
0,001 мФ
100 кОм
=390
Рис. 8N.13. Обратная связь по переменному току может устранить задержку, вносимую гистерезисом. (Усиление каналов
осциллографа: входной сигнал и пороговый уровни — 100 мВ/деление; выходные сигналы — 20 В/деление.)
уровня сигналом.
Но при низкочастотном входном сигнале с по-
логими перепадами уровней в данной схеме
возникнут автоколебания, поскольку сигнал
будет долго находиться вблизи порогового
уровня после разряда ЛС-цепочки, и сдвиг по-
рогового уровня не произойдет.
Генераторы колебаний
В процессе обсуждения способов стабилиза-
ции схем мы рассматривали различные вари-
анты их защиты от нежелательных случайных
повторяющихся колебаний. Так мы и позна-
комились с явлением возникновения колеба-
ний, даже не пытаясь собрать сам генератор
колебаний. Многочисленные перепады уровня
сигнала или пульсации, создаваемые схемой
компаратора без гистерезиса (например, пока-
занные на осциллограммах на рис. 8N.6), в дей-
ствительности являются колебаниями. Теперь
мы хотим научиться создавать такие сигналы
преднамеренно, так, чтобы они были управляе-
мыми и предсказуемыми.
Довольно очевидно, что схема, создающая
управляемые колебания, может быть полезной.
Человечество знакомо с этим с тех пор, как на-
учились измерять время с помощью маятника,
а не солнечных или водяных часов. Образно
выражаясь, генератор колебаний является су-
тью, которая «разговаривает» сама с собой, при
этом противореча себе. Но это противоречие
должно также содержать задержку. Схема слева
на рис. 8N.14 не удовлетворяет данному усло-
вию, задержка здесь недостаточна, в резуль-
тате чего выходной сигнал все время находит-
ся вблизи порогового уровня переключения.
(Следует признать, что этот сигнал все равно
является колебаниями, но нам хотелось бы,
чтобы они были большей амплитуды.) А вот в
схеме справа обеспечена достаточная задержка
за счет пары последовательных инверторов, в
результате чего амплитуда колебаний достига-
ет полного размаха.
Рис 8N.14. Внутреннее противоречие вместе с достаточной
задержкой создают колебания
Показанные на рис. 8N.14 инвертирующие уси-
лители являются логическими вентилями, по
сути, компараторами с однополярным источ-
ником питания, пороги переключения которых
расположены на уровне половины напряжения
питания.
8N3. Релаксационный RC-генератор колебаний
357
8N.3. Релаксационный
ЯС-генератор колебаний
8N.3.1. Релаксационный генератор
колебаний на операционном
усилителе
На рис. 8N.15 изображена схема, похожая на
триггер Шмитта, показанный на рис. 8N.10, но
с необычно большим гистерезисом. В данном
случае триггер Шмитта включен новым спосо-
бом: он сам создает свой входной сигнал.
100 кОм
0,01 мкФ ±
4,7 кОм
Рис. 8N.15. Принципиальная схема релаксационного RC-
генератора колебаний
8N.32. Каковы параметры?
Но каковы значения пороговых уровней?
И сколько требуется времени на заряд и разряд
конденсатора, чтобы перейти от одного поро-
гового уровня к другому?
Дать ответ на этот вопрос можно, используя
значение et/RC, чтобы вычислить время перехо-
да от одного порогового уровня до другого для
ДС-цепочки, состоящей из резистора номина-
лом 100 кОм и конденсатора емкостью 0,1 мкФ
и определить уровень напряжения. Расчеты
дают приблизительный ответ:
1/11 • |t/± 15 В| « ±1,4 В.
Но такой путь слишком трудоемок.
Размах приблизительно в 2,8 В является доста-
точно небольшой частью полного диапазона
величиной около 16 В, в результате чего ток бу-
дет почти постоянным14. Это делает пригодной
14 Значение 16 В - это максимальная разность напряже-
ний между начальным значением напряжения на конден-
саторе (около ±1,4 В) и напряжением на другом выводе
простую формулу I = CdU/dt, где I представля-
ет собой значение средней точки 15 В/100 кОм.
Как упоминается на лабораторном занятии 8L,
погрешность полученного таким образом ре-
зультата будет в пределах 1% по сравнению
с более точным ответом, полученным в итоге
трудоемких вычислений с использованием экс-
поненциального времени заряда. Проблему
можно упростить еще больше, игнорируя по-
вышающий резистор, влияющий на заряд, но
не разряд контура. Мы можем позволить себе
погрешность амплитуды величиной 5%.
8N.3.3. Более простой способ
создания /?С-генератора колебаний
Быстро создать схему генератора колебаний
можно, заменив схему компаратора, показан-
ную на рис. 8N.2, интегральным триггером
Шмитта с инверсией. Этот логический эле-
мент (микросхема 74НС14) оснащен встроен-
ным гистерезисом, а значения его пороговых
уровней равны приблизительно половине ве-
личины напряжения питания, как и в более
простых генераторах колебаний, изображен-
ных на рис. 8N.13. На рис. 8N.16 показано два
варианта такого генератора колебаний. В схе-
ме слева используется резистор, как и в релак-
сационном генераторе колебаний на компара-
торе на рис. 8N.15. В схеме справа этот рези-
стор заменен на токоограничивающий диод,
чтобы получить сигнал пилообразной формы.
Обратите внимание на то, что выходной сиг-
нал второй схемы снимается с конденсатора, а
не с выхода логического элемента, как в пер-
вой схеме.
Недостаток описанного простого генератора
колебаний — непредсказуемость частоты его
выходного сигнала. Далее приведены соответ-
ствующие характеристики, взятые из результа-
тов лабораторного занятия 8L:
♦ пороговые напряжения:
• отрицательный уровень: 1,8 В (типичное),
0,9 В (мин.), 2,2 В (макс);
• положительный уровень: 2,7 В (типичное),
2,0 В (мин.), 3,15 В (макс);
♦ гистерезис: 0,9 В (типичное), 0,4V (мин.),
1,4 В (макс).
резистора обратной связи (около ±15 В), а не размах вы-
ходного напряжения компаратора.
358
8N. Операционные усилители III: положительная обратная связь
Выходной сигнал
компаратора
НС14 (5 В/деление)
Uc(l В/деление)
Uc{\ В/деление)
(сглажен усреднением)
Aj Ch2 Jt 2 80 V
1000 пФ 4=
0,1мкФ~£ 075 мА
Рис. 8N.16. Релаксационный /?С-генератор колебаний на микросхеме триггера Шмитта вместо операционного усилителя
Какое из этих значений играет роль в определе-
нии частоты колебаний ^ых15? Генератор коле-
баний на микросхеме НС14 не очень стабилен,
но он, безусловно, прост!
Схема релаксационного генератора колебаний
на операционном усилителе, изображенная на
рис. 8N.15, является классической, и иногда
это наилучший источник прямоугольного сиг-
нала умеренной частоты16. А релаксационный
генератор на логическом элементе, показанный
на рис. 8N.16, дает более легкий и простой
способ получить тот же результат. Но проще
всего использовать микросхему, специально
предназначенную для реализации генераторов
колебаний.
8N.3A Микросхема 555
/?С-генератора колебаний/таймера
Микросхема 555 представляет собой своеоб-
разный, не особенно элегантный генератор
15 Величина гистерезиса играет роль. Но его местонахож-
дение в диапазоне напряжений — нет. Иными словами, нет
разницы, занимает ли диапазон гистерезиса интервал от
0,9 В до 1,8 В или от 1,8 В до 2,7 В.
16 Один из наиболее почитаемых нами людей, покойный
Боб Пиз (Bob Pease), некогда работавший в компании Na-
tional Semiconductor, использовал эту схему для создания
генератора колебаний частотой 1 Гц сверхмалой мощности.
Его схема представляла собой релаксационный генератор
колебаний с однополярным питанием, рассматриваемый
в разделах 8N.3.1 и 8N.3.3, на маломощном компараторе,
которая потребляла 1,4 мкА при напряжении 6 В.
http://electronicdesign.com/analog/whats-all-oscilla-
tor-stuff-anyhow.
колебаний прямоугольной формы17. Эта ми-
кросхема появилась еще раньше, чем микро-
схема 741 (555 выпущена в 1971 г.), но это, на-
верное, наиболее популярный компонент из
всех микросхем, когда-либо выпускавшихся18.
В настоящее время ее доминирование идет на
убыль, но до сих пор она выпускается широким
кругом поставщиков; на рынке также можно
свободно найти множество небольших букле-
тов с рекомендуемыми устройствами на этой
микросхеме. На лабораторном занятии мы бу-
дем использовать одну из улучшенных версий
этой микросхемы: микросхему 7555 или С555.
А для приложений с низким энергопотребле-
нием выберем микросхему 55С. Это устрой-
ство на полевых МОП-транзисторах19 с более
высокой рабочей частотой, чем оригинальная
микросхема на биполярных транзисторах.
Микросхема 55520 содержит схему триггера,
с которой мы еще не знакомы, поэтому объ-
яснить ее работу будет непросто. Но мы по-
пробуем, как сможем. На рис. 8N.17 показаны
17 АоЕ § 7.1.3.
18 Согласно данным ее разработчика эта микросхема был
лидером продаж около 30 лет, и к 2004 г. было продано
более миллиарда ее экземпляров. См.
http://semiconductormuseum.com/Transistors/
LectureHall/Camenzind/Camenzindlndex.htm.
19 Полевой транзистор со структурой металл-оксид-полу-
проводник.
20 Мы будем называть эту микросхему 555, хотя вы-
бранная нами версия микросхемы содержит КМ0П-
транзисторы и называется 7555. Но для объяснения рабо-
ты микросхемы 555 ее точная марка не имеет абсолютно
никакой важности.
8N.3. Релаксационный RC-генератор колебаний
359
I
Высокий
уровень^
Сброс Q
Запу<
Установка
'555 (сброс не показан)
Транзистор
цепи
разряда
Выход
Выход
Релаксационный генератор на микросхеме 555
Стандартная схема включения
Рис. 8N.17. Внутреннее устройство и включение микросхемы генератора колебаний 555
Бедняга Uc\
Отфутболивают его :
от одной границы к другой.
Рис. 8N.18. Шуточное объяснение работы микросхемы 555
Верхняя граница
— Нижняя граница
внутреннее устройство этой микросхемы и два
способа ее включения.
Слева на рисунке изображен вариант подклю-
чения, в котором выходной сигнал подается на
времязадающий конденсатор, точно таким же
образом, как и в релаксационном генераторе
колебаний на операционном усилителе, пока-
занном на рис. 8N.15 (и в версии на логическом
элементе справа на рис. 8N.16). Надеемся, что
вы уже начинаете узнавать эту схему.
А справа на рис. 8N.17 показано стандартное
подключение микросхемы 555, которое вы-
глядит несколько странно. Здесь ЯС-цепочка
задержки не подключается к выходу, а требуе-
мый разряд конденсатора обеспечивается с по-
мощью специально предназначенного для этой
цели транзистора. Такая организация дополни-
тельно усложняет и так уже непростую схему,
но она обладает тем достоинством, что изоли-
рует схему тактирования от нагрузки, таким
образом исключая влияние нагрузки на часто-
ту сигнала. А вот ослабление нагрузкой выход-
ного сигнала [7ВЫХ схемы слева на рис. 8N.17
'вых
вызовет изменение его частоты
Г21
Как и в релаксационном генераторе колебаний
на операционном усилителе в этой схеме на-
пряжение на конденсаторе изменяется в диа-
пазоне между двумя пороговыми уровнями.
В релаксационных генераторах колебаний из
разделов 8N.3.1 и 8N.3.1 два пороговых уровня
создаются с помощью гистерезиса. В микросхе-
ме 555 для этой цели используется более про-
стой подход: два компаратора, с фиксирован-
ным пороговым уровнем каждый (и, кстати,
никакого гистерезиса).
Эти два компаратора ведут себя подобно двум
пограничникам на границах 1/317+ и 2/317+:
когда напряжение на конденсаторе пересекает
одну границу, его отправляют назад к другой
подобно несчастному беженцу без граждан-
ства. Эту ситуацию наглядно иллюстрирует
рис. 8N.18.
21 Сравните рис. 7.8 в книге АоЕ с рис. 7.9.
360
8N. Операционные усилители III: положительная обратная связь
В стандартной схеме справа на рис. 8N.17 на-
пряжение на конденсаторе управляется транзи-
стором цепи заряда: когда транзистор открыт,
он разряжает конденсатор, а когда закрыт —
позволяет конденсатору зарядиться до уровня
напряжения положительного питания.
Форму сигнала на конденсаторе можно варьи-
ровать, заменив резисторы RA и RB другими
элементами, например источниками тока, или
даже отрезком проволоки (но только резистор
JRB, а не RA). Можете ли вы представить форму
сигнала (на конденсаторе, а не на выходе ми-
кросхемы 555) для нескольких разных вариан-
тов замены этих резисторов22?
Микросхема 555 имеет и другие области при-
менения, в частности, на ней можно собрать
генератор колебаний, управляемый напря-
жением. Мы попытаемся сделать это на лабо-
раторном занятии 8L, а также применим этот
метод в заключительном проекте аналоговой
части книги. Кроме того, микросхему 555 мож-
но включить таким образом, чтобы она выда-
вала одиночный импульс по импульсу запуска
(функционируя подобно так называемому жду-
щему, или одноходовому, мультивибратору).
А на самом деле, проявив некоторую смекалку,
эту микросхему можно заставить делать много
разных других трюков.
8N.3.5. Более современные
микросхемы генератора колебаний
Вряд ли вы удивитесь, узнав, что спустя 40 лет
после появления на свет микросхемы 555 в на-
стоящее время на рынке предлагается большой
выбор других микросхем генераторов коле-
баний23. Некоторые из них легче подключать
22 Использование отрезка проволоки в цепи разряда вы-
зывает быстрый и резкий разряд, при этом заряд остается
медленным, по ДС-кривой. Один раздраженный студент по-
жаловался, что не увидел ничего полезного в этом сигнале
в форме плавника акулы. Здесь он был прав.
Но, заменив в этой же схеме резистор заряда конденсатора
на источник тока и оставив отрезок провода в цепи разряда,
можно получить сигнал вполне приличной формы, называ-
ющейся пилообразной. А эти сигналы полезны для многих
областей применения, например, в широтно-импульсном
модуляторе (ШИМ), который мы рассмотрим в разде-
ле 8L4, используется сигнал такой формы. Цифровой эк-
вивалент генератора такого сигнала демонстрируется на
лабораторном занятии 22L.2.7. А если поместить источник
тока как в цепь заряда, так и разряда, то форма сигнала на
конденсаторе станет треугольной. См. АоЕ § 7.1.3Е.
23 АоЕ § 7.1.4А.
Например, микросхема LTC6906 содержит
встроенный конденсатор, что позволяет зада-
вать частоту выходного сигнала^ых (в диапазо-
не от 10 кГц до 1 МГц) с помощью только одно-
го резистора. К сожалению, мы не сможем ис-
пользовать эту микросхему в наших проектах,
поскольку она не выпускается в корпусе DIP
для монтажа в отверстия на плате (или гнезда
макетной платы). Многие новые микросхемы
имеют более низкие напряжения питания, чем
минимальное напряжение 4,5 В для микросхе-
мы 555. Некоторые микросхемы можно про-
граммировать с помощью микроконтроллера.
Особый компонент такого типа — микросхема
DS1065 в трехвыводном корпусе ТО-92 компа-
нии Dallas/Maxim. Выходной сигнал этой ми-
кросхемы лежит в диапазоне частот от 30 кГц
до 100 МГц. Но, несмотря на столь обширный
выбор, микросхема 555 остается полезной ра-
бочей лошадкой.
8N А Генератор
синусоидальных колебаний
на мосте Вина
Схема этого генератора24 колебаний (един-
ственного генератора синусоидальных ко-
лебаний, который мы соберем в этом курсе)
довольно хитроумная, и ее анализ доставляет
одно удовольствие. Каким образом она уму-
дряется формировать сигнал синусоидальной
формы, а не обычной прямоугольной или тре-
угольной формы (которые легко создавать)?
Она делает это, предотвращая отсечение сиг-
нала, которое создает обычный прямоуголь-
ный выходной сигнал, с помощью искусного
регулирования усиления. Ее цепь положитель-
ной обратной связи отдает предпочтение сиг-
налу одной частоты среди всех прочих. Только
сигнал этой сильнейшей частоты выживает,
а если выживает сигнал только одной часто-
ты, то этот единственный сигнал по опреде-
лению будет чисто синусоидальным. Подобно
многим другим генераторам колебаний в этой
схеме используется как положительная, так
и отрицательная обратная связь. Для целей
анализа мы разделили эти две обратные свя-
зи, чтобы рассмотреть каждую из них индиви-
дуально.
24 АоЕ § 7.1.5В.
8N.4. Генератор синусоидальных колебаний на мосте Вина
361
Лампочка накаливания
мощностью 0,14 Вт
560
—VVV 1
Выходной сигнал
1 мкФ
Рис. 8N.19. Генератор синусоидальных сигналов на мосте
Вина
8NA1. Цепь положительной
обратной связи на мосте Вина
Эта цепь положительной обратной связи яв-
ляется частотно-избирательной и, работая на
наиболее предпочитаемой частоте, передает
обратно на неинвертирующий вход не более
чем 1/3 часть выходного сигнала. Со всеми
прочими частотами, выше и ниже ее предпочи-
таемой частоты, она поступает не так хорошо.
На рис. 8N.20 показаны схема моста Вина (сле-
ва) и ее амплитудно-частотная характеристика
(справа).
Предпочитаемая частота
Рис. 8N.20. За счет положительной обратной связи через
мост Вина часть выходного сигнала поступает обратно на
неинвертирующий вход
На этой предпочитаемой частоте фазовый
сдвиг равен нулю. Предпочитаемой частотой,
на которой генератор колебаний будет рабо-
тать, оказывается частота l/(2nRC)25.
25 Да, это кажется слишком хорошим, чтобы быть прав-
дой. Но мы не будем пытаться доказать вам это, поскольку
для доказательства, что на этой частоте амплитуда сигнала
обратной связи максимальна, требуется выполнить кучу
сложных вычислений высшей математики. Но вы можете
с легкостью подтвердить, по крайней мере, что на этой ча-
стоте импеданс последовательной ЯС-цепочки равен V2R,
а импеданс параллельной ЯС-цепочки составляет поло-
вину последовательного. Таким образом, назад подается
1/3 часть выходного сигнала.
8NА2. Цепь отрицательной
обратной связи генератора
на мосте Вина
Отрицательная обратная связь (рис. 8N.21)
корректирует усиление, используя для это-
го токозависимое сопротивление лампочки.
Номинальный ток лампочки 14 мА при 10 В,
на основе чего можно приблизительно оценить
значение ее сопротивления. Но ключевым мо-
ментом является то, что это сопротивление не
остается постоянным.
почка (ее сопротивление
повышается при увеличении тока)
Figure 8N.21. Самокорректирующееся усиление: отрица-
тельная обратная связь
Использование лампочки было ключевой
идеей Уильяма Хьюлетта (William Hewlett) в ге-
нераторе синусоидальных колебаний с низким
уровнем искажений. Его заявка на патент, по-
данная в 1942 г., описывает элегантно простую
схему26. Формулировка была предельно проста
(небольшая лампочка накаливания, или подоб-
ное устройство...). Но простота оказалась чрез-
вычайно эффективной — на этом изобретении
он и его друг Дэвид Паккард (David Packard)
основали свою компанию. Приведем отрывок
из патента У. Хьюлетта.
Отрывок из патента
Управление амплитудой для предотвращения на-
растания колебаний до такого большого значения,
при котором возникают искажения, достигается
соответственно моему изобретению нелинейным
процессом в схеме усилителя. Чтобы создать это
нелинейное изменение, в качестве резистора R3
используется небольшая лампочка накаливания
или другое подобное устройство, в котором со-
противление быстро возрастает при увеличении
протекающего тока, при этом лампочка нагрева-
ется анодным током ламп 10 и 11 или каким-либо
вспомогательным источником до такой темпера-
туры, при которой ее сопротивление будет быстро
26 Патент США 2 268 872 (1942). Но Л.А. Мичам (L.A. Меа-
cham) опередил его приблизительно на год в использова-
нии лампочки для управления усилением. См. «Bell System
Technicaljournal 17», цитируется в английской Википедии в
статье «Wien Bridge Oscillator».
362
8N. Операционные усилители III: положительная обратная связь
меняться в ответ на небольшие изменения величи-
ны тока. Таким образом, при увеличении амплиту-
ды колебаний повышается температура лампочки
R3, в результате чего возрастает ее сопротивле-
ние, тем самым создавая большую отрицательную
обратную связь и таким образом снижая усиление.
Подобным образом, при уменьшении амплиту-
ды колебаний уменьшается протекающий через
лампочку ток, позволяя ей охладиться, что со-
провождается уменьшением ее сопротивления и
величины отрицательной обратной связи, таким
образом увеличивая амплитуду генерируемых
колебаний. В результате система поддерживает
амплитуду в значительной степени постоянной,
причем заранее задается значение ниже значения,
при котором протекает анодный ток. В результате
форма сигнала не искажается.
Странная вольтамперная характеристика
лампочки
Возможно, вы помните наш эксперимент на
первом лабораторном занятии, в котором вам
нужно было начертить графики вольтампер-
ных характеристик двух черных ящиков. Один
из этих графиков, для резистора, должен был
быть в виде прямой линии. А в другом должен
содержаться изгиб: этот график был для не-
большой лампочки накаливания.
На лабораторном занятии для этой главы (8L.7)
используется лампочка № 344 (мощностью
0,14 Вт), а не №47 (мощностью 1 Вт), как на
том лабораторном занятии, но график ее воль-
тамперной характеристики содержит такой же
изгиб. Этот изгиб в графиках отображает эф-
фект нагрева нити накалывания, поскольку со-
противление металла возрастает с повышением
температуры. На рис. 8N.23 в виде двух прямых
линий изображен график эффективного со-
противления лампочки в двух произвольных
средних точках зависимости тока от напряже-
ния. Сопротивление лампочки из нашей лабо-
раторной схемы находится между этими двумя
линиями27.
27 Выходной сигнал нашего генератора колебаний на мо-
сте Вина имел амплитуду около 9 В. Действующее (средне-
квадратическое) значение будет около 6,4 В, а для графика
реагирования лампочки на температуру как раз и важно
действующее значение напряжения.
Чтобы поддерживать на выходе генератора колебаний на
мосте Вина колебания величиной 6,6 В, входной сигнал
генератора (т. е. величина напряжения, которое чувствует
лампочка) должен быть 1/3 выходного, т. е. около 2,1 В.
При этом действующем значении по графику на рис. 8N.23
можно определить сопротивление лампочки равным око-
Обратите внимание на то, что кривые на графике
отображают не реакцию лампочки на быстрые
изменения тока или напряжения, но комбина-
ции тока и напряжения, которые устанавлива-
ются после нескольких секунд работы лампочки
при данном среднем — достаточно длительном,
чтобы ее температура стабилизировалась28.
Температура создается за счет нагрева этого
конкретного произведения тока и напряжения.
Это довольно тонкая идея, от которой у вас мо-
жет кратковременно затуманиться в голове при
первой попытке разобраться, что именно пред-
ставляют собой эти графики.
Убедитесь в том, что изменение сопротивления
лампочки действительно стабилизирует усиле-
ние на требуемом уровне. Не забывайте, что на
графике на рис. 8N.23 ток I отображается как
обычно на вертикальной оси. Для графика со-
противления оси поменялись бы местами, и
крутизна кривой возрастала бы с повышением
тока и напряжения (и температуры).
Какое усиление требуется, чтобы поддержи-
вать колебания неискаженными? Вам может
График зависимости тока Гот напряжения U
для лампочки № 344 (0,14 Вт)
10]
Крутизна при бол"\е£
9f~ низкой темп
Крутизна при более
высокой температуре
0,5 1 1,5 2 2,5 3 3,5 4 4,5
Рис. 8N.23. Графики вольтамперной характеристики для
лампочки № 344 (0,14 Вт)
ло 330 Ом. Тогда при сопротивлении такой величины, что-
бы обеспечить требуемый коэффициент усиления равный
3, потребуется резистор обратной связи сопротивлением
около 660 Ом. На лабораторном занятии мы используем
не 660 Ом, а 560 Ом, поэтому график для лампочки в ге-
нераторе колебаний с амплитудой выходного сигнала 9 В
должен немного отличаться от кривой, показанной на
рис. 8N.23.
28 Строго говоря, значения тока и напряжения на графике
соответствуют средним действующим значениям, посколь-
ку то, что нас интересует, так это их тепловое действие. Как
раз в этом и заключается важность действующих значений.
Например, действующее значение синусоидального сигна-
ла равно 1/V2-UMAKC, и соответствует постоянному напря-
жению, обеспечивающему такую же самую мощность, как
и действующее значение синусоидального сигнала.
8NA. Генератор синусоидальных колебаний на мосте Вина
363
потребоваться несколько секунд, чтобы отве-
тить на этот вопрос, но операционному усили-
телю требуется намного меньше времени29.
Резиноподобное поведение
Самым трудным для объяснения аспектом
работы этого генератора является его так на-
зываемое резиноподобное поведение, возни-
кающее при касании неинвертирующего входа
в процессе работы схемы. На рис. 8N.24 приве-
ден эскиз сигнала, иллюстрирующий влияние
этого эффекта, а на рис. 8N.25 — собственно
осциллограмма.
«Огибающая»
Рис. 8N.24. Эскизы осциллограмм (на разных частотах раз-
вертки) выходного сигнала генератора колебаний на мосте
Вина при касании пальцем неинвертирующего входа
Выходной сигнал при
касании входа пальцем
(при медленной
развертке)
Этот же сигнал
при более быстрой
развертке. Можно
видеть разные амплитуды,
накладывающиеся друг на друга
МЛ
'езиноподобное
поведение
Рис. 8N.25. Генератор колебаний на мосте Вина работает на-
столько близко к границе нестабильности, что прикоснове-
ние пальцем вызывает дрожание выходного сигнала
Касание пальцем приводит схему в расстрой-
ство, наверное, потому, что емкость пальца
нарушает деликатное равновесие схемы регу-
лировки усиления30. Вспомним, что, хотя цепь
отрицательной обратной связи проявляет ста-
бильность, это минимальная стабильность,
так как лампочка (обладающая большой по-
стоянной времени реагирования) выглядит в
этой цепи как фильтр чрезвычайно низких ча-
стот. Эта ситуация похожа на ситуацию с не-
стабильностью дифференциатора, которую
мы видели в главе 7. Эта схема, с ее автомати-
ческой регулировкой усиления, не подойдет
29 Теперь, когда прошли эти несколько секунд, объявим
результат: да, для поддержания колебаний нам нужен ко-
эффициент усиления равный трем.
30 На лабораторном занятии вместо касания пальцем мо-
жете попробовать подключить неинвертирующий вход на
«землю» через конденсатор емкостью 10 пФ. Мы обнару-
жили, что эффект от этого будет подобен касанию пальцем.
в качестве усилителя общего назначения. Она
слишком инерционна, перекорректирует уси-
ление, после чего ей нужно длительное время,
чтобы возвратиться в стабильный режим ра-
боты. Но оказывается, что чем инерционнее
схема, т. е. чем больше времени ей требуется,
чтобы стабилизироваться после воздействия,
вследствие ее слабого успокоения, тем луч-
ше она поддерживает единственную частоту
при отсутствии других отрицательных воз-
действий. Да, этот генератор колебаний впол-
не подходит для нас, поскольку обычно мы
не нарушаем его спокойствие, тыкая в него
пальцем.
Схема также чувствительна к механическим
вибрациям, что объясняет, почему лампочку
часто заменяют электронным аналогом31.
Насколько хорош генератор колебаний
на мосте Вина?
Ответ краток — весьма хорош. Мы сравнили
частотные спектры нашей лабораторной схемы
и генератора сигналов макетных плат со встро-
енным источником питания. Соответствующие
осциллограммы приведены на рис. 8N.26.
Синусоидальный сигнал лабораторной схемы
выглядел намного лучше, чем сигнал генерато-
ра сигналов макетной платы.
Следует признать, что мы сравнили нашего
силача — лабораторную схему — с довольной
слабым соперником — микросхемой ICL8038,
недорогим устройством, которое создает си-
нусоидальный сигнал, скругляя вершины тре-
угольного сигнала. Аналогичный подход ис-
пользуется в наших лабораторных генераторах
сигналов, хотя они выполняют такую операцию
не так грубо, что при их стоимости в 100 раз
большей, чем микросхема 8038, не должно
быть удивительным.
Но несмотря на хорошее качество синусоидаль-
ного сигнала генератора колебаний на мосте
Вина, это устройство не покорило мир. Метод
31 См., например, рис. 7.20В в разделе 7.1.5В книги АоЕ,
или генератор сигналов на мосте Вина Джима Уильямса
0im Williams) в его заметке по применению «High Speed
Amplifier Techniques» («Методы работы с высокоскорост-
ными усилителями») в журнале «Linear Technology AN47»,
август 1991 г., стр. 49, рис. 114. В каждом из этих случа-
ев вместо лампочки используется полевой транзистор
с управляющим р-я-переходом в качестве управляемого
напряжением сопротивления.
364
8N. Операционные усилители III: положительная обратная связь
скругления вершин треугольного сигнала про-
должает преобладать среди аналоговых гене-
раторов сигналов. Это объясняется тем, что с
помощью данного метода можно легко созда-
вать сигналы в широком частотном диапазоне.
Например, в наших лабораторных генераторах
колебаний это диапазон от 0,3 Гц до 3 МГц.
Кроме того, теперь составляет конкуренцию
более новый метод цифрового синтеза, состоя-
щий в подаче на цифроаналоговый преобразо-
ватель (ЦАП) таблицы значений синусоидаль-
ного сигнала. Мы познакомимся с ЦАП далее в
этой книге.
Синусоидальный сигнал
из прямоугольного
В цифровой части нашего курса мы познако-
мимся с гибридным аналогово-цифровым ме-
тодом формирования чистого синусоидального
сигнала, состоящим в подаче прямоугольного
сигнала на аналоговый фильтр с крутой ча-
стотной характеристикой при одновременной
регулировке частоты срезами фильтра, чтобы
оставить только сигнал основной гармоники
прямоугольного сигнала, который является чи-
стым синусоидальным сигналом.
Выходной сигнал
генератора
колебаний ^^
на мосте Вина
Спектр
синусоидального- 1
сигнала встроенного
генератора колебаний
макетной платы
УСЛАЛА
Спектр
синусоидального
сигнала нашего
генератора колебаний
на мосте Вина
Рис. 8Ы.26.Частотные спектры собранной в лабораторном
занятии схемы генератора колебаний на мосте Вина (внизу)
и генератора колебаний макетной платы (вверху)
Но на данном этапе единственным источником
самого чистого синусоидального сигнала явля-
ется генератор колебаний на мосте Вина.
8N.5. Материал для чтения
вАоЕ
Чтение
♦ Глава 4 (операционные усилители):
• раздел 4.3.2А: компараторы;
• раздел 4.3.2В: триггер Шмитта (обычная
схема компаратора);
• раздел 4.3.3: генератор колебаний сигнала
треугольной формы;
• раздел 4.6.4: управляемый напряжением
генератор колебаний.
♦ Глава 7 (генераторы колебаний):
• от начала главы по раздел 7.1.5В, Генератор
синусоидальных сигналов на мосте Вина;
• для лабораторного занятия, наверное,
наиболее важна микросхема 555, а гене-
ратор колебаний на мосте Вина наиболее
интересен;
• раздел 7.2.1Е: генерирование длительных
импульсов с помощью микросхемы 555;
• раздел 7.1.7А, табл. 7.2 с обширным спи-
ском разнообразных генераторов коле-
баний.
♦ Глава 12: (сопряжение логических схем):
• раздел 12.1.7А: компараторы (более по-
дробный материал, чем в главе 4).
Задачи
♦ Дополнительное упражнение (Additional
Exercises) 4.34 (компаратор с использованием
медленного операционного усилителя).
8L Лабораторное занятие:
операционные усилители
Хорошая и плохая обратная связь
Как упоминалось в главе 8N, до сих пор мы рас-
сматривали положительную обратную связь
как некое зло или недоразумение, нечто похо-
жее на то, что получается, если перепутать вхо-
ды операционного усилителя. Но сегодня мы
смягчим это представление, дополнив его ин-
формацией, что положительная обратная связь
в определенных случаях может быть полезной.
В частности, она может, например, улучшить
рабочие характеристики компаратора, или ее
можно использовать совместно с отрицатель-
ной обратной связью, чтобы создать генератор
колебаний (релаксационного типа, в котором
преобладает положительная обратная связь)
или преобразователь отрицательных импедан-
сов. В этой схеме доминирует отрицательная
обратная связь. Мы не будем собирать эту схему
здесь, но рекомендуем обратиться к рис. 4.104
в разделе 4.107 книги АоЕ. Также, комбинируя
положительную и отрицательную обратную
связь, можно создать генератор синусоидаль-
ных колебаний, так называемый генератор ко-
лебаний на мосте Вина.
Но несмотря на все достоинства положитель-
ной обратной связи, в главе 9N мы увидим, ка-
кие неудобства она может создавать, когда за-
является незваной.
8L1. Две схемы
компаратора
Компараторы лучше всего работают при нали-
чии положительной обратной связи. Но пре-
жде чем мы начнем рассматривать высокока-
чественные схемы компараторов, взглянем на
две плохие: одна на операционном усилителе,
а другая на специальной микросхеме компара-
тора. Обе схемы обладают плохими рабочими
характеристиками, а более быстродействующая
из них поможет вам уяснить хорошие аспекты
компаратора, усовершенствованного за счет
положительной обратной связи.
8L1.1. Операционный усилитель
в качестве компаратора
На рис. 8L.1 приведена схема «компаратора»,
которая в действительности является нашей
первой собранной схемой операционного уси-
лителя, задачей которой было просто проде-
монстрировать «поразительно» высокий ко-
эффициент усиления устройства. При первом
рассмотрении операционного усилителя высо-
кий коэффициент усиления, вероятно, казался
бесполезным. Но, обращаясь вновь к данной
схеме, работающей как компаратор, можно от-
метить, что ее высокое усиление и фиксирован-
ный выходной сигнал являются как раз тем, что
нам теперь требуется.
ЮкОм
Рис. 8L1. Операционный усилитель в качестве простого
компаратора
Подайте на вход схемы синусоидальный сигнал
частотой около 100 кГц и обратите внимание
на то, что форма выходного сигнала, которая
должна быть строго прямоугольной, в действи-
тельности не такая хорошая, как нам бы хоте-
лось. Можете пояснить, почему это так1?
1 Вследствие медленного нарастания/спада амплитуды
сигнала, определяемого скоростью нарастания нашего опе-
рационного усилителя. Это ограничение рассматривалось
на лабораторном занятии 7L и составляло 15 В/мкс для
366
8L Лабораторное занятие: операционные усилители III
8L1.2. Компаратор
на специализированной
микросхеме
Теперь уберите из схемы микросхему 411 и
вставьте вместо нее микросхему компаратора
311(рис.8Ь.2).
Внимание!
Обратите внимание на то, что эти две микросхемы
имеют разную цоколевку.
4,7 кОм
Рис. 8L2. Схема компаратора без обратной связи на микро-
схеме 311
Наверное, вы заметили, что выходной каскад
схемы на рис. 8N.2 выгладит несколько стран-
но. В частности, он совсем не похож на обычный
двухтактный выходной каскад операционного
усилителя. Вместо этого и коллектор, и эмит-
тер выходного транзистора непосредственно
подключены к выводам микросхемы. С помо-
щью этих выводов можно задавать верхнюю и
нижнюю границы размаха выходного сигнала.
Например, если на один вывод подать напря-
жение +5 В (через внешний повышающий ре-
зистор), а другой подключить на «землю», то
размах выходного сигнала будет в диапазоне
логических уровней, т. е. от 0 до +5 В, что де-
лает его совместимым со стандартными циф-
ровыми устройствами. В наших последующих
схемах размах выходного сигнала будет в диа-
пазоне ±15 В. Таким образом, выходной сигнал
микросхемы компаратора 311 будет напоми-
нать о поведении операционного усилителя.
Подумайте, работает ли компаратор на микро-
схеме 311 лучше, чем на микросхеме 4112.
операционного усилителя на микросхеме 411. Таким обра-
зом, переход от одного края диапазона до другого занимает
пару микросекунд плюс еще немного, поскольку операци-
онному усилителю требуется время на восстановление по-
сле режима насыщения, в котором эта схема без обратной
связи вынуждает его проводить большую часть времени.
2 Эта мысль напомнила нам о вопросе, который один из
наших студентов задал нам несколько лет тому назад:
Паразитные колебания
Побочным эффектом более высокого быстро-
действия микросхемы 311 является ее готов-
ность переходить в режим автоколебаний, ког-
да от нее требуется ответить на тонкий вопрос,
т. е. распознать небольшую разницу напряже-
ний на входах. Попробуйте вынудить свою ми-
кросхему 311 перейти в режим автоколебаний,
подав на вход схемы пологий синусоидальный
сигнал. Немного экспериментируя, можно до-
биться появления на выходе сигналов стран-
ных и причудливых форм, напоминающих од-
ним освещенный лунным светом Тадж-Махал,
а другим цистерны для хранения газа. Судите
сами по рис. 8L.33.
Рис. 8L.3. Выходной сигнал микросхемы 311 при наличии
автоколебаний
Способы минимизации автоколебаний
Компаратор иногда можно стабилизировать
с помощью гистерезиса, что мы далее и рас-
смотрим. Посмотрим, насколько эффектив-
ным будет этот подход. Но сначала разберем-
ся, почему микросхема 311 приходит в «заме-
шательство». Для этого подключите один щуп
осциллографа к выходу сигнала, а другой —
в режиме АС к линии питания +15 В вблизи
микросхемы 311. Посмотрите, присутствует
ли на осциллограмме линии питания тот же
«Я не могу найти микросхему 411. Будет ли микросхема
311 достаточно подходящей заменой?» Несомненно, зада-
вая этот вопрос, он руководствовался нашими многократ-
ными наставлениями: «Отложите в сторону этот калькуля-
тор! Ответ с погрешностью в 10% будет для нас достаточно
хорошим» и т.п.
3 Сигнал этой причудливой формы получили два студента
Елена Кригер (Elena Krieger) и Белл Ковен (Belle Koven) в
октябре 2004 г.
8L2. Релаксационный RC-генератор колебаний на операционном усилителе
367
самый «мусор», что и на осциллограмме вы-
ходного сигнала. Скорее всего вы убедитесь,
что помеха присутствует.
Не отключая щупов осциллографа, попробуйте
сделать следующее.
♦ Подключите керамические развязывающие
конденсаторы к положительной и отрица-
тельной шинам питания. Если автоколебания
исчезнут, восстановите их, уменьшив крутиз-
ну входного синусоидального сигнала.
♦ Закоротите выводы 5 и 6 микросхемы между
собой. На эти вспомогательные выводы часто
наводятся шумы, усложняя работу микросхе-
мы. Если после этого автоколебания прекра-
тятся, верните все в исходное состояние.
8L1.3. Комбинация положительной
обратной связи с триггером
Шмитта
Положительная обратная связь, организован-
ная, как показано в схеме на рис. 8L.4, устра-
нит эти красивые, но вредные автоколебания.
Посмотрим, каким минимальным гистерези-
сом мы сможем обойтись.
Примечание
Сначала эти выводы ни
к чему не подключаем.
Затем соедините их
между собой
4,7 кОм
Рис. 8L.4. Триггер Шмитта: компаратор с положительной об-
ратной связью (и гистерезисом)
Подайте на вход схемы синусоидальный сигнал
небольшой амплитуды (<200 мВ) и частотой
около 1 кГц, и с помощью потенциометра на-
стройки гистерезиса определите границу меж-
ду стабильной и нестабильной работой схемы.
Затем исследуйте с помощью осциллографа
сигнал на неинвертирующем входе компара-
тора. Здесь должен присутствовать небольшой
прямоугольный сигнал.
Этот сигнал, возможно, будет зашумлен высоко-
частотными искажениями, создаваемыми источ-
ником, находящимся вне вашей схемы. Например,
это могут быть наводки радиоволн, заметные бла-
годаря столь высокому усилению.
Этот небольшой прямоугольный сигнал обо-
значает два пороговых уровня микросхемы 311
и, соответственно (по определению), величину
гистерезиса. Наконец, установите значение ги-
стерезиса примерно в три раза больше опреде-
ленной вами границы (это нужно в целях без-
опасности).
Если описать нашу схему как «определитель
пересечения нулевого уровня», с какой задерж-
кой она определяет это событие? Можете ли вы
предложить способ уменьшить эту задержку4?
Не разбирайте эту схему, поскольку она нам по^
надобится для следующего эксперимента.
8L.2. Релаксационный
/?С-генератор колебаний
на операционном усилителе
В схеме на рис. 8L.4 зафиксируйте максималь-
но возможную величину гистерезиса, заменив
потенциометр резистором номиналом 10 кОм.
Затем подключите между выходом компарато-
ра и его инвертирующим входом ЯС-цепочку,
как показано на рис. 8L.5. Этот сигнал обрат-
ной связи заменяет любой внешний источник
сигнала, таким образом, на схему не подается
никаких внешних воздействий. Кстати, это
100 кОм
0,01 мкФ
4,7 кОм
100 кОм
<10 кОм Можно использовать
] потенциометр, выставленный
на максимальное значение
Рис. 8L.5. Принципиальная схема релаксационного /?С-гене-
ратора колебаний
4 Такой метод уже изобретен. В частности, см. раздел
8N.2.5n особенно рис. 8N.13, где показана положительная
обратная связь по переменному току.
368
8L Лабораторное занятие: операционные усилители III
первый случай, когда используется как отрица-
тельная, так и положительная обратная связь.
Попробуйте определить частоту выходных ко-
лебаний, а затем сравните свою оценку с наблю-
даемым значением. Можете сэкономить время
на расчеты, предполагая, что сигнал заряда/
разряда конденсатора имеет пилообразную
форму, как будто бы на конденсатор поступал
постоянный ток величиной 15 B/Roc (см. раз-
дел 8N.3.2).
8L3. Самая простая схема
/?С-генератора колебаний
на триггере Шмитта
Рассмотрим еще один способ получения пря-
моугольного выходного сигнала, в котором пе-
риод задается посредством ЯС-цепочки. Этот
метод очень похож на релаксационный RC-
генератор колебаний из предыдущего раздела,
но здесь применена микросхема со встроенным
гистерезисом. Размах ее выходного сигнала на-
ходится в диапазоне логических уровней, от О
до 5 В. А недостатком схемы является плохая
предсказуемость ее гистерезиса; эта неопреде-
ленность делает, в свою очередь, нестабильной
частоту выходных колебаний. Но схема пред-
ставляет несомненный интерес из-за ее просто-
ты и выходного сигнала с размахом логических
уровней.
8L3.1. Обратная связь через
/?С-цепь
На рис. 8L.6 показано все, что нужно знать об
этой микросхеме и ее подключении. Возьмите
конденсатор емкостью 1000 пФ5 и подберите
такое сопротивление резистора обратной свя-
зи, чтобы получить выходные колебания ча-
стотойУвЫХ »1 МГц.
При выборе значения резистора обратите вни-
мание на следующие характеристики микро-
схемы:
5 Емкость конденсатора была выбрана большой относи-
тельно собственной емкости щупа осциллографа (величи-
ной около 10 пФ), чтобы при выполнении измерений на
конденсаторе с помощью осциллографа частота выходных
колебанийУвЫХ оставалась постоянной.
♦ пороговые напряжения:
• отрицательное: 1,8 В (типичное), 0,9 В
(мин.), 2,2 В (макс);
• положительное: 2,7 В (типичное), 2,0 В
(мин.), 3,15 В (макс);
♦ гистерезис: 0,9 В (типичное), 0,4 В (мин.), 1,4
В (макс).
+5
[14 19 12 И 10 9 8
'НС14
74НС14
1 2 3 45 6J7
Сф
Рис. 8L.6. Принципиальная схема релаксационного /?С-гене-
ратора колебаний
Такой диапазон возможных значений услож-
няет задачу расчета частоты /шх, но волно-
ваться не нужно. Просто задайте типичные
значения для определения требуемого сопро-
тивления резистора обратной связи, а затем
посмотрите, насколько близок полученный
результат к желаемой частоте 1 МГц. (Или к
периоду в 1 мкс, если выражаться в терминах,
более соответствующих нашему использова-
нию осциллографа, где мы наблюдаем период,
а не частоту.)
8L3.2. Пилообразный сигнал
Один из наших студентов однажды пожаловал-
ся, что форма сигнала, создаваемого схемой из
раздела 8.3.1, выглядит некрасиво и напомина-
ет плавник акулы. Как и этому парню, вам мо-
жет быть больше по душе генератор колебаний,
создающий пилообразные колебания. Такой
сигнал можно с легкостью получить, заменив
резистор обратной связи токоограничиваю-
щим диодом 1N5294, с которым мы познако-
мились в процессе создания дифференциаль-
ного усилителя на лабораторном занятии 5L.
Номинальный рабочий ток этого диода со-
ставляет 0,75 мА. А конденсатор большей ем-
кости, например, 0,1 мкФ, поможет вам полу-
чить более аккуратный пилообразный сигнал.
Обратите внимание на размах этого пилооб-
разного сигнала, поскольку мы вскоре найдем
ему применение.
8L4. Использование пилообразного сигнала для ШИМ-питания электродвигателя
369
8LA Использование
пилообразного сигнала
для ШИМ-питания
электродвигателя
На данный момент нам знакомы обе составляю-
щие широтно-импульсной модуляции (ШИМ):
пилообразный сигнал генератора колебаний и
компаратор. Совместив эти два элемента, мож-
но создать ШИМ-драйвер для электродвигате-
ля постоянного тока. На рис. 8L.7 приведена
принципиальная схема такого драйвера (без
некоторых подробностей).
+5 в
1/6 74НС14
тора в широком диапазоне, например, от 10%
до 90%?
Примечание
Термин «коэффициент заполнения» означает дли-
тельность периода в процентах, в течение которо-
го выходной сигнал находится на высоком уровне.
Если этот диапазон не такой широкий, как вам
бы хотелось, поиграйте со значениями рези-
сторов по обеим сторонам потенциометра на-
стройки порогового уровня. Также проверьте,
что транзистор функционирует должным об-
разом.
+10 В
0,01 мкфф
Рис. 8L.7. Схема ШИМ-драйвера электродвигателя постоянного тока. Проставьте номиналы компонентов в качестве упражнения
Схему компаратора снабдим небольшим гисте-
резисом: 50-100 мВ должно быть достаточно.
Обратите внимание на то, что транзистор в не-
которой степени нагружает схему, в результате
чего размах выходных колебаний получается
не 5 В, а около 4 В.
В процессе настройки схемы, а также, возмож-
но, при корректировке значений элементов ре-
комендуем заменить электродвигатель резисто-
ром сопротивлением 100 Ом или больше. При
регулировке порогового уровня с помощью по-
тенциометра наблюдайте за выходными сигна-
лами генератора колебаний и компаратора.
Получается ли у вас регулировать коэффици-
ент заполнения6 выходного сигнала компара-
Удостоверившись, что все работает как следует,
замените резистор, который служил тестовой
нагрузкой, небольшим электродвигателем по-
стоянного тока. Можно взять тот же электро-
двигатель, что был в лабораторном занятии 7L
в качестве источника сигнала для интегратора7.
Напряжение источника питания указано рав-
ным 10 В, чтобы не перегреть электродвигатель
с номинальным рабочим напряжением 12 В. Но
если у вас под рукой нет источника питания на-
пряжением 10 В, то подойдет и источник на-
пряжением 15 В.
Неплохо прикрепить на вал двигателя хорошо
заметный указатель, а в случае использования
электродвигателя из лабораторного занятия 7L
можно просто оставить установленный на валу
6 Употребляется также термин «скважность сигнала» как
отношение периода сигнала к длительности импульса. —
Примеч. ред.
7 Мы сами использовали электродвигатель Mabuchi FF-
130SH-11340. Но подойдет любой электродвигатель, спо-
собный выдержать 10 В.
370
8L Лабораторное занятие: операционные усилители III
рычаг. Это поможет нам судить о скорости
вращения электродвигателя при регулировке
коэффициента заполнения. Попробуйте нагру-
зить электродвигатель, слегка притормаживая
его вал пальцами. Вы должны обнаружить, что
даже при низком коэффициенте заполнения
вращающий момент электродвигателя остается
довольно хорошим, тогда как просто снижение
напряжения питания, чтобы уменьшить оборо-
ты, подобно тому, как это делалось с помощью
реостата для электродвигателя швейной ма-
шинки вашей бабушки, дает слабый вращаю-
щий момент.
8L5. Релаксационный
ЯС-генератор колебаний
на микросхеме 555
Микросхема 555 и ее различные варианты зна-
чительно упростили задачу проектирования
генераторов колебаний не слишком высокой
частоты. Теперь редко возникает необходи-
мость проектировать генератор колебаний
на операционном усилителе с чистого ли-
ста, подобно тому, как мы это делали ранее.
Микросхемы ICM7555, LMC7555 и TLC555
являются усовершенствованными КМОП-
версиями микросхемы 555. (Для краткости мы
будем называть все эти КМОП-микросхемы
просто 555.) Микросхема ICM7555 может ге-
нерировать колебания частотой до 1 МГц,
а микросхема LMC7555 — до 3 МГц по срав-
нению с частотой 100 кГц оригинальной ми-
кросхемы 555 на биполярных транзисторах.
Кроме того, такие особенности этих компо-
нентов, как очень высокий входной импеданс
и 2У?-размах выходного сигнала, могут упро-
стить задачу проектирования.
8L5.1. Генератор прямоугольного
сигнала на микросхеме 555
Подключите микросхему 7555 по стандартной
конфигурации релаксационного генератора ко-
лебаний на микросхеме 555, как показано на
рис. 8L.8.
Исследуйте выходной сигнал схемы с помощью
осциллографа. Соответствует ли его частота
10 кОм S
10 к&м <
С Z
ОД мкФ
7
>
2
1 С 6
•а»
•а»
<
4
•
D 7555 ИП
== Выходной
1К сигнал
TU
1 И
&
1
3
+15 В
Рис. 8L.8. Релаксационный генератор колебаний на микро-
схеме 7555
значению, рассчитанному по следующей фор-
муле:
-I
/вых =
0,7[ЯА+2Яв]С'
Теперь исследуйте сигнал на конденсаторе. Ка-
ковы пиковые напряжения? Правдоподобен ли
наблюдаемый вами результат?
И снова генератор сигналов
в виде плавника акулы
Теперь закоротите резистор RB проволочной
перемычкой. Как вы полагаете, какой формы
сигнал должен быть теперь на конденсаторе?
А на выходе схемы?
Примечание
Небольшое уточнение: теперь напряжение на кон-
денсаторе должно упасть намного ниже нижнего
порогового уровня величиной +^ип/3. Это объяс-
няется тем, что для микросхемы 7555 требуется не-
которое время для реагирования на пересечение
этого порогового уровня, и теперь напряжение
падает быстрее.
Сигнал с заполнением в 50%
Микросхема 7555 способна выдавать правиль-
ный прямоугольный сигнал с заполнением
в 50%, но при условии наличия схемы, позво-
ляющей ей заряжать и разряжать конденсатор
через один резистор. Попытайтесь собрать та-
кую схему, а затем испытайте ее.
8L5. Релаксационный RC-генератор колебаний на микросхеме 555
371
Подсказка
Старая микросхема 555 не смогла бы выполнить
этот трюк, но микросхема 7555 может благодаря
fifi-размаху ее выходного сигнала.
Настроив схему, рассмотрите следующие во-
просы.
♦ В чем разница между формой выходного сиг-
нала данной схемы и сигналом мультивибра-
тора (так иногда называется генератор коле-
баний) на стандартной микросхеме 555?
♦ Влияет ли нагрузка на период колебаний это-
го генератора? Например, посмотрите, какой
эффект будет от подключения резистивной
нагрузки сопротивлением 10 кОм.
Если вы собрали такую же схему, как и мы, то
частота выходных колебаний должна быть:
л
/вых =
1ARC
Это такая же частота, как и для классической
конфигурации, с тем исключением, что в схе-
ме генератора колебаний на микросхеме 7555
устранено усложнение в виде разных путей за-
ряда и разряда конденсатора. Уравнение для
классической схемы такое же с очень хорошим
приближением при условии, что сопротивле-
ние резистора RA намного меньше, чем резисто-
ра RB. Совпадает ли измеренная частота коле-
баний/вых вашей схемы со значением частоты,
которое вы рассчитали для нее?
Наконец, попробуйте подать напряжение пи-
тания 17+ величиной +5 В на любую из ваших
схем, чтобы узнать, насколько выходная ча-
стота зависит от величины напряжения пи-
тания.
8L5.2. Генератор сигнала
треугольной формы
Добавив в схему два диода 1N5294, можно
получить сигнал треугольной формы. Анало-
гичный результат можно получить с помощью
двухполупериодного моста и одного диода
1N5294. Если у вас есть желание, попробуй-
те собрать и испытать схему генератора тре-
угольных сигналов.
8L6. Частотная модуляция
с помощью микросхемы 555 '
Здесь мы несколько забежим вперед и вкратце
рассмотрим метод (который мы будем исполь-
зовать на лабораторном занятии 13L) для пере-
дачи аудиосигналов из одного конца комнаты
в другой по оптическому каналу. Информация
будет кодироваться скоростью, т. е. частотой
мигания светодиода. Кодирование можно осу-
ществлять посредством микросхемы 555, пре-
образуя меняющееся во времени напряжение
(музыкальный сигнал) в варьирующуюся ча-
стоту. Простой параллельный #1С-контур, как
мы собрали на лабораторном занятии 3L, мо-
жет декодировать частотно-модулированный
Используйте восходящую или нисходящую
часть кривой (разница только в фазе
(у+ выходного сигнала)
555 1,0
CL
Диапазон изменения f (входной сигнал)
Диапазон изменения (У (выходной
сигнал) (это будет выглядеть как
амплитудная модуляция — ДМ)
Форму Q можно настраивать,
Т подбирая сопротивление й
...такой ЧМ-сигнал можно демодулировать простым
параллельным /&£-контуром как на лабораторном
занятии 3L
Варьируя напряжение на выводе 5
микросхемы 555, можно управлять частотой ее
выходных колебаний. Если это осуществляется
сигналом, несущим инсрормацию, то данный
процесс называется частотной модуляцией (ЧМ8)...
Рис. 8L9. С помощью микросхемы 555 можно реализовать частотную модуляцию сигнала, а его демодуляцию можно выпол-
нить с помощью параллельного RLC-контура
8 Англ. frequency modulation (FM.)
372
8L Лабораторное занятие: операционные усилители III
сигнал, преобразуя его обратно в изменяющее-
ся во времени напряжение, т. е. восстанавливая
музыкальный сигнал.
Микросхема 555 может выполнять такую мо-
дуляцию благодаря подключенной к выводу 5
точке внутреннего трехрезисторного делителя
напряжения, которая определяет верхний по-
роговый уровень компаратора. Если амплитуда
модулирующего сигнала повышается на этом
выводе выше его нормального напряжения по-
коя величиной 2/Зх[/+, то частота выходных
колебаний снижается, а при уменьшении на-
пряжения на этом выводе частота повышается.
Если у вас мало времени, то можно просто
ограничиться легкой задачей проверки рабо*
тоспособности этой схемы частотной модуля-
ции. Для этого подайте на вывод 5 микросхе-
мы низкочастотный синусоидальный сигнал
(например, частотой 100 Гц и амплитудой
0,5 В), и наблюдайте выходной сигнал микро-
схемы 555 на осциллографе. Не забудьте, что
подавать сигнал с выхода генератора сигналов
на вывод 5 микросхемы 555 необходимо через
разделительный конденсатор. Это объясняется
тем, что напряжение покоя на выводе 5 обыч-
но 10 В, тогда как напряжение питания микро-
схемы 555 составляет +15 В. Выходной сигнал
будет содержать нечто, похожее на прыгающие
искажения. Если у вас возникнут трудности
с их интерпретацией, попробуйте сделать ча-
стоту модулирующего сигнала намного ниже
100 Гц.
8L7. Генератор
синусоидальных сигналов
на мосте Вина
Достаточно любопытный факт: синусоидаль-
ный сигнал синтезировать труднее всего. Как
упоминалось ранее, большинство генерато-
ров сигналов создают синусоидальный сиг-
нал, скругляя вершины треугольного сигнала.
Генератор синусоидальных сигналов на мосте
Вина справляется с этой задачей, корректируя
уровень усиления, чтобы предотвратить отсе-
чение выходного сигнала (которое происходи-
ло бы при слишком большом усилении), одно-
временно не позволяя колебаниям затухнуть
(что случилось при слишком малом усилении).
Лампочка накаливания
\ мощностью 0Д4 Вт
560
^Выходной
сигнал
ZtiRC
R
ЮкОм
Рис. 8L.10. Генератор синусоидальных сигналов на мосте
Вина
Частота, задаваемая цепью положительной об-
ратной связи, определяется формулой:
55с- (8L1>
Проверьте, соответствует ли расчетное значе-
ние измеренной частоте выходного сигнала ва-
шего генератора колебаний.
На этой частоте сигнал обратной связи дол-
жен совпадать по фазе с выходным сигналом и
иметь 1/3 его амплитуды9. Отрицательная об-
ратная связь через лампочку накаливания регу-
лирует уровень усиления за счет нелинейного
сопротивления лампочки. Убедитесь в том, что
изменение сопротивления лампочки действи-
тельно стабилизирует усиление на требуемом
уровне. Какое усиление требуется, чтобы под-
держивать колебания без искажений10?
Амплитуду выходного сигнала можно умень-
шить, заменив резистор номиналом 560 Ом
в цепи отрицательной обратной связи рези-
стором меньшего номинала11. Попробуйте при-
коснуться пальцем к неинвертирующему входу
микросхемы и обратите внимание на резинопо-
добное поведение выходного сигнала. При этом
наблюдайте за выходным сигналом на медлен-
ной развертке осциллографа: это позволит вам
9 На этой частоте, где (величина Хс = Д), импеданс после-
довательно включенных резистора и конденсатора (верх-
нее плечо делителя напряжения) составляет V2-R, тогда как
импеданс параллельно включенных резистора и конденса-
тора (нижнее плечо делителя) равен R. Отсюда вытекает
величина 1/3 выходного напряжения, которая подается
обратно на вход в виде обратной связи на этой предпочи-
таемой частоте. Но, наверное, более удивительным явля-
ется тот факт, что этот делитель выдает сигнал, совпадаю-
щий по фазе с входным сигналом.
10 Да, вы правы: усиление точно равно трем.
11 Довольно смышленая схемка, не так ли? Она сама под-
страивает сопротивление лампочки, чтобы оно подходило
новому значению резистора обратной связи!
8L.7. Генератор синусоидальных сигналов на мосте Вина
373
отследить медленное затухание огибающей си-
нусоидального сигнала.
Если у вас есть желание, можете подтвердить,
что полученный синусоидальный сигнал на-
много чище синусоидального сигнала, созда-
ваемого генератором сигналов, пропустив его
через дифференциатор на операционном уси-
лителе. При подаче на дифференциатор выход-
ного сигнала генератора колебаний на мосте
Вина его выходной сигнал будет выглядеть, как
вполне хороший синусоидальный сигнал, а не
как зиккуратоподобный12 ступенчатый сигнал,
12 Будем надеяться, что вы понимаете, какая форма сигна-
который получается при дифференцировании
псевдосинусоидального сигнала генератора
сигналов, как мы наблюдали на лабораторных
занятиях 2L и 7L. Или же, если у вас цифровой
осциллограф со встроенной функцией БПФ13,
то вместо дифференциатора можно просто
сравнить спектры этих двух синусоидальных
сигналов — генератора сигналов и вашего ге-
нератора колебаний на мосте Вина, как мы это
делали в главе 8N.
ла здесь имеется в виду, и не потратите оставшееся время
на поиски этой формы сигнала в справочниках по электро-
нике.
13 Быстрое преобразование Фурье.
8W. Примеры с решениями:
операционные усилители
8W.1. Советы по разработке
схем с триггером Шмитта
8W.1.1. Установка пороговых
уровней
Задача установки определенных значений по-
роговых уровней может быть довольно слож-
ной, требующей трудоемких алгебраических
вычислений. Но имеется и пара легких частных
случаев.
Первый случай: пороги симметричны
относительно нулевого уровня
Предположим, например, что требуются поро-
говые уровни величиной ± 1В и размах выходно-
го сигнала ±15 В. Напряжение на делителе цепи
обратной связи распределяется одинаково отно-
сительно потенциала «земли», поскольку ниж-
ний резистор делителя подключен к «земле».
Напряжение на выходе делителя должно со-
ставлять 1 В из 15, следовательно R2 » 15 • J?x
(или 14х, если быть более точным). Ключевая
идея состоит в том, что напряжение на ниж-
нем резисторе делителя составляет половину
размаха выходного сигнала. Такой же резуль-
тат можно получить с пороговыми уровнями,
симметричными относительно приблизитель-
но +2,5 В, скажем, равными +2,4 В и +2,5 В, и
при размахе выходного сигнала между 0 и +5 В
(рис. 8W.1).
Второй случай: пороговые уровни
несимметричны
Пусть требуются пороговые уровни, например,
величиной О В и +0,1 В при размахе выходно-
го сигнала от 0 до +5 В. В этом случае делитель
цепи обратной связи повышает напряжение,
а не понижает (рис. 8W.2). Так что просто про-
ектируем делитель, который повышает порого-
вый уровень до 0,1 В:
Отсюда следует, что 17П0Р составляет около
одной части из 50, a R2 равно примерно 50 • Rv
Я2<150кОлл
| +1В
-IB
1+15 В
$4,7 кОм
А(УВЫХ = 30 В
+15 В <
Ш
-15 В
-(почти: %0 кОм 15 В)
v 165 кОм '
(очень близко: не доходит
-до -15 В всего лишь
на величину UHAC)
Рис. 8W.1. Первый легкий случай: пороговые уровни симметричны относительно нулевого потенциала
8W.L Советы по разработке схем с триггером Шмитта
375
Я2|150кОлл
кОм
+1В
ОВ
♦15 В
i размах выходного сигнала
ОВ ■*
> пороговые уровни
Рис. 8W.2. Второй легкий случай: пороговые уровни задаются только в одном направлении (очень далеко от симметрии)
8W.12. Более легкая задача:
определение гистерезиса
Предположим, что стоящая перед нами задача
заключается не в установке пороговых значений
величиной 1Ви1,1В,ав формировании гистере-
зиса величиной 0,1 В и фиксации пороговых уров-
ней вблизи 1 В.
Эти две формулировки выглядят почти экви-
валентным, но вторая задача оказывается на-
много легче, чем первая. Попробуем решить ее.
Предположим, что размах выходного сигнала
находится в диапазоне от 0 до +5 В (рис. 8W.3).
Ход решения задачи следующий.
♦ Гистерезис. Определяется исключительно
соотношением сопротивлений делителя. Мы
снова хотим ОД В / 5 В: одну часть из 50; и
опять R2» 50xRv
♦ Пороговые уровни вблизи 1 В. Этот пара-
метр определяется напряжением, к которому
подключен нижний резистор делителя.
Замечание
Временно предположим, что у нас имеется под
рукой напряжение 1 В от идеального источника
напряжения. В действительности мы будем ис-
пользовать делитель напряжения, а затем будем
рассматривать 1/та как напряжение, к которому
подключен нижний резистор. Если этот вопрос
вас пока не беспокоит, отложите вникание в смысл
данного замечания на потом.
Это напряжение величиной 1 В мы обеспе-
чим посредством делителя напряжения, но
он обладает определенным Д^. Будет ли это
5 в
В => коэффициент деления = ngp =
= 0,8 кОм
Модель, эквивалент настоящего делителя
Рис. 8W.3. Установка конкретного значения гиаерезиса вблизи заданного напряжения: пороговые уровни и гистерезис
рассматриваются отдельно друг от друга
376
8W. Примеры с решениями: операционные усилители III
обстоятельство иметь отрицательный эффект?
Нет. Пусть R^g будет иметь значение, которое
мы хотим для резистора Rv
Такая приблизительная оценка пороговых
уровней может выглядеть слишком поверх-
ностной. Но во многих случаях это не так, по-
скольку часто нам требуются пороговые уровни
не с точными значениями напряжения, а при-
близительными, а также соответствующий ги-
стерезис. И грубая оценка в этом случае вполне
оправдана.
Нюанс: регулируемый пороговый
уровень
Можете ли вы предложить какой-либо способ,
чтобы можно было регулировать пороговый
уровень, при этом сохраняя гистерезис посто-
янным? (Возможное решение: вспомните, что
операционные усилители стоят дешево.)
15кОм
+5 В
50 кОм
напряжением вторичной обмотки 12,6 В, пер-
вичная обмотка которого питается от электро-
сети (частотой 60 Гц14)15.
Решение
Решение представлено на рис. 8W.5.
Задача
Триггер Шмитта, пороговые уровни
заданы
Спроектируйте схему триггера Шмитта на ми-
кросхеме 311 с питанием ±5 В и следующими
характеристиками:
♦ размах выходного сигнала: 0 до +5 В;
♦ пороговые уровни: ±0,1 В (приблизительно).
Решение
Решение представлено на рис. 8W.6.
Точно решить эту задачу трудно, поэтому не
стесняйтесь заниматься приближениями. Бу-
1кОм
Уг /^в =7 (2,5 кОм 11 2,5 кОм) — значение в средней точке
< 1,25 кОм
Рис. 8W.4. Два способа сохранить величину гистерезиса при изменениях пороговых уровней
Задача решается с помощью потенциометра,
выходное сопротивление которого #вых « Rv
как показано слева на рис. 8W.4. Если вам лень
разбираться с R^^ то задачу также можно ре-
шить с помощью буфера на операционном уси-
лителе, как показано справа на этом рисунке.
Задача
Разработать схему определителя перехода
сигнала через ноль
Мы хотим знать момент, когда сигнал пере-
менного напряжения электросети пересекает
нулевой уровень (в пределах нескольких сотен
микросекунд). В нашем распоряжении име-.
ется компаратор с однополярным питанием
напряжением +5 В, а также трансформатор с
дет полезным рассмотреть два случая по от-
дельности: что будет при низком выходном
уровне (0 В), и что будет при высоком (5 В).
8W.2. Задача
проектирования схемы
управления нагревателем
Цель — разработать схему компаратора не на
микросхеме 311, как обычно, а на микросхеме
с однополярным питанием (TLCD372), которая
14 Частота электросети в США.
15 См. АоЕ, рис. 4.85.
8W.2. Задача проектирования схемы управления нагревателем
377
12.6ВУ^~**18В
ЦХТ _+5i
10 кОм|
-6 в
Ограничитель напряжения
/вместо делителя
^^ гфгЮО лФ «ускоряющий
конденсатор» — дает
быстрый «толчок»
гистерезиса
1 кОм<
Более крутой сигнал,
выше точность, меньше задержка
Какова длительность задержки?
Пороговый уровень
(приблизительный):
«ОД мс
Рис. 8W.5. Схема определения перехода через ноль
Обеспечьте, чтобы нижний пороговый уровень
был меньше нуля; в противном случае компаратор
с однополярным питанием может не сработать.
c/v/df = 2-nAf
= 6,18 В • 60 Гц
Входной
сигнал
>1кОм
Выходной JC У
"^сигнал ~ >&г
6_П. f—0Д0
|50Л,
Рассмотрим два случая:
1. Выходной сигнал низкого уровня
Микросхема 311 незначительно
влияет на Unof>. Соответственно, пусть
делитель на \ и R2 выдает -0,1 В=>
-ОД В/-5 В = 1/50 или R2 = 50/?,.
2. Выходной сигнал высокого уровня
! Теперь нам нужно поднять
напряжение с -0,1 В вдвое выше
(на 0,2 В) до +0,1 В. Таким образом,
пусть /?3 * 25/S^g делителя:
но &ТЗД делителя « Rt - 10 кОм =>
£3* 250 кОм
Рис. 8W.6. Решение: нацеливаемся на конкретные пороговые уровни, но ничего, если попадем не в яблочко, а где-то рядом
будет поддерживать температуру вашего кофе
такой, какая вам нравится. Мы разместим дат-
чик температуры на нагревателе и будем под-
держивать температуру нагревателя на регули-
руемом уровне, всегда чуть ниже температуры
кипения.
8W.2.1 • Датчик температуры
и компаратор
Датчик температуры на микросхеме LM50 вы-
дает напряжение, величина которого прямо
пропорциональна окружающей его температу-
ре, плюс дополнительная константа величиной
полвольта. Этот датчик будет осуществлять
мониторинг температуры нагревателя, как по-
казано на рис. 8W.7.
В отличие от компаратора на микросхеме 311,
в котором мы можем задавать напряжение на
эмиттере его выходного транзистора, нижний
вывод выходного ключа используемого нами
компаратора TLCD372 с однополярным пита-
нием заземлен внутри микросхемы.
378
8W. Примеры с решениями: операционные усилители III
(от 4,5 В до 10 В)
LM50
4 кОм
— Выходной сигнал
Чих Темп- °с
Чых = +2<750 в ПРИ +125 °
Чых= +750 мВ ПРИ +25 °с
1/вьгх=+100мВпри-40°С
Рис. 8W.7. Датчик температуры и компаратор
Микросхема TLC372 — компаратор
с однополярным питанием
+5 В
50° мВ
/Транзисторный ключ Л
^полевой МОП-транзистор))
8W.2.2- Схема компаратора
(вашей разработки)
Покажите, как использовать этот датчик темпе-
ратуры и управляемый вручную потенциометр
для включения и выключения нагревательно-
го элемента в соответствии с понижением или
повышением его температуры относительно
заданного значения. Исходные данные для раз-
работки следующие:
диапазон температуры: 50-100 °С;
гистерезис: 5 °С;
погружаемый нагреватель является рези-
стивным и в некоторой степени индуктив-
ным компонентом. Рабочее напряжение на-
гревателя постоянное и составляет 20 В.
Типичные характеристики
10 000
12 3 4 5
напряжение «коллектор-эмиттер»
а
0,1 1
Хк [А], ток коллектора
б
10
10 000
1000
100
о Ю
(Ую (насищ.)
-—.—--
U^ (насищ.)
^ = 500*.
0#01 ОД 1
-^ [А] Ток коллектора
в
Эквивалентная схема К
ТО-220
1. База 2. Коллектор 3. Эмиттер
? 10 кОм
2sr 0,6 кОм
Рис. 8W^. Несколько типичных характеристик пары Дарлингтона TIP110 (а —- статические характеристики; б—кривая усиле-
ния по постоянному току; в — напряжение насыщения «база-эмиттер» и «коллектор-эмиттер»; г — корпус и цоколевка
8И/.2. Задача проектирования схемы управления нагревателем
379
8W.2.3. Пара Дарлингтона
Если вам понадобится такой электронный ком-
понент16, то далее приводятся его типичные ха-
рактеристики, которые могут вам пригодиться
при разработке вашей схемы.
Компания Digikey предлагает такой компо-
нент TIP 110 производства компании Texas
Instruments с большим коэффициентом р. Это
значение является произведением коэффици-
ентов передачи двух составных транзисторов,
поскольку ток эмиттера первого транзистора
поступает в базу выходного транзистора. На
рис. 8W.8 показаны графики нескольких ти-
пичных характеристик для этого устройства.
Воспользуемся этими типовыми зависимостя-
ми просто ради новизны получения данных из
графика, а не из таблицы параметров.
Дополнительные резисторы ускоряют вы-
ключение компонента (что в нашем случае
не важно). Подключенный параллельно паре
Дарлингтона диод обычно закрыт.
Хотя мы предлагаем использовать типичные
характеристики устройства, давайте попробу-
ем обеспечить двойной запас надежности для
нашей схемы. Подумайте, какая приблизитель-
но часть напряжения источника питания будет
падать на вашей нагрузке?
8W.2A Решение задачи
проектирования схемы управления
нагревателем
Сопоставление температурного диапазона диа-
пазону напряжений.
К показаниям датчика величиной 10 мВ/1 °С
добавляется смещение в 500 мВ. Таким обра-
зом, температурный диапазон 50-100 °С сопо-
ставляется следующему диапазону напряжений:
♦ нижняя граница = смещение + минимальное
показание = 500 мВ + (50 °С • 10 мВ/1 °С) =
= 1,0 В;
♦ верхняя граница = смещение + максималь-
ное показание = 500 мВ + (100 °С • 10 мВ/
/1 °С) = = 1,5 В.
Таким образом, для покрытия этого диапазона
в схему необходимо добавить потенциометр
для ручной регулировки. На рис. 8W.9 приведе-
ны некоторые произвольные значения сопро-
тивления потенциометра (выбранные таким
образом, чтобы облегчить вычисления).
+5 в
3,5 В
0,5 В
1В
3,5кОм<
0,5 кОла *
1кОм:
-1,5 В
-1,0 В
16 Можете считать это подсказкой.
Рис. 8W.9. Потенциометр в схеме сопоставления диапазона
напряжений 1-1,5 В температурному диапазону 50-100 °С
Схема компаратора
Чтобы получить требуемый гистерезис, нам
потребуется положительная обратная связь
определенной величины. Базовая схема (без
значений компонентов) для реализации такой
обратной связи изображена на рис. 8W.10.
+5 В
Выход на
нагреватель
Рис. 8W.10. Базовая принципиальная схема компаратора
Значения номиналов компонентов
Далее определяем значения компонентов.
♦ Повышающий резистор Япов. Отложим
определение значения этого компонента,
пока не будет разработана переключающая
схема. А пока достаточно просто отметить,
что значение этого резистора будет намного
меньше, чем резистора R2 на рис. 8W.10, и мы
сможем игнорировать его при расчете гисте-
резиса.
♦ Резисторы Rt и R2. Эти резисторы нужны
для установки величины гистерезиса. И сно-
ва нам нужно отложить определение их зна-
чений, пока мы не вычислим значение ДТЕВ
для потенциометра ручной регулировки.
♦ Вычисляем величину R^:
• как обычно, нам нужно рассмотреть наи-
худший случай, а затем обеспечить, что-
бы изменение #ТЕВ в процессе настройки
380
8W. Примеры с решениями: операционные усилители III
порогового уровня не меняло значительно
величину гистерезиса17.
• наихудшим случаем будет максималь-
ное значение JR^. Это событие наступит,
когда между значениями обоих путей (от
ползунка потенциометра до +5 В и пол-
зунка до «земли») будет минимальная
разница. Это случится при крайнем верх-
нем положении ползунка. В этой точке
сопротивление двух ветвей будет равно
3,5 кОм || 1,5 кОм « 1 кОм.
♦ Определяем значение Rv Зная, что зна-
чение ДТЕВ « 1 кОм, мы теперь можем вы-
брать номинал резистора Rr Как обычно,
мы хотим, чтобы его значение было намного
большим, чем сопротивление источника по-
даваемого на него сигнала. Поэтому примем
Rx = 10 кОм.
♦ Определяем значение R2. Нам нужен ги-
стерезис величиной в 5 °С, что соответству-
ет напряжению 50 мВ. Поэтому мы хотим
подавать обратно на вход небольшую часть
от пяти вольт выходного сигнала, а именно:
50 мВ/5 В = 50/5000 = 1/1000. Таким обра-
зом, сопротивление резистора R2 « 100 • Rv
Итак, пусть R2 = 1 МОм.
8W.2.5, Питание нагревателя
Может ли выходной сигнал микросхемы 372
напрямую питать нагреватель, через который
мы хотим пропускать ток величиной 1 А? Нет,
компаратор не способен сам обеспечить такой
большой ток, но он может управлять транзи-
сторным ключом, которому такой ток по пле-
чу. Наше эмпирическое правило для сигнала
управления ключом гласит, что 1Б « /к/10, а не
1к/р, поскольку мы хотим надежно перевести
транзистор в режим насыщения.
Согласно этому правилу наш компаратор дол-
жен выдавать 100 мА, что намного больше,
чем может выдержать выходной транзистор
компаратора TLC372 (максимальный выход-
ной ток составляет 20 мА). Поэтому нам при-
дется использовать или переключать на МОП-
транзисторе (что будет нечестно, поскольку
мы еще ничего не знаем об этом устройстве,
с которым мы познакомимся лишь в главе 121),
или на паре Дарлингтона18. Мы уже упоминали
этот компонент ранее при постановке задачи,
поэтому выберем пару Дарлингтона TIP110.
8W.2.6. Переключатель на паре
Дарлингтона
Вторая кривая на рис. 8W.8 отображает доста-
точное усиление вблизи максимального тока
в 1 А: коэффициент усиления по току (р), пре-
вышающий 2000. Поэтому зададим коэффи-
циент р равным 1000. Согласно нашему эмпи-
рическому правилу сигнал управления должен
быть в 10 раз больше, как будто коэффициент
р равен 100. Но это правило не совсем приме-
нимо к паре Дарлингтона, поскольку только
первый транзистор может переходить в режим
насыщения, а основной (выходной) транзистор
не может. Кроме того, нам не нужно полагаться
на это эмпирическое правило, поскольку гра-
фик статической характеристики на рис. 8W.8
отображает зависимость выходного тока кол-
лектора 1К от входного тока базы 7Б. Из этих
графиков можно определить, каким должен
быть управляющий сигнал на базе (величину
которого мы еще и удвоим для надежности).
Похоже, что выходной ток в 1 А можно полу-
чить при входном токе величиной 300 мкА (это
означает коэффициент усиления около 3000).
Как уже упоминалось, мы удвоим входной ток
до 600 мкА. Скорее всего запас по току следо-
вало бы увеличить, поскольку удвоение тока
базы, как правило, не удваивает выходной ток
коллектора пары Дарлингтона. Поэтому пусть
ток базы будет 1 мА (хорошее, круглое число
для тока в нашем курсе).
Теперь мы можем, наконец, вычислить требуе-
мое значение для повышающего резистора Дпов.
Входное напряжение для пары Дарлингтона
составит около 1,5 В19. Так что мы будем по-
давать около 3,5 В на 1?пов компаратора, когда
17 Мы не будем стремиться к вычислению дробных долей
изменения гистерезиса, которое может происходить в ре-
зультате варьирования значения потенциометра. Для нас
будет достаточно обычного правила десятикратного зна-
18 В принципе можно было бы использовать и подобную
пару Шиклаи, но эти компоненты не предлагаются в мага-
зине Digikey в виде микросхемы. Поэтому будем работать
с парой Дарлингтона.
19 При беглом взгляде на схему можно предположить, что
входное напряжение будет «два напряжения 17^ » 1,2 В».
Но более тщательное изучение графиков на рис. 8W.8 дает
основание полагать, что входное напряжение несколько
выше. Это, конечно же, расширяет диапазон требуемого
значения, но если у нас есть подробная инфоршция, то,
разумеется, ее нужно использовать.
8W.2. Задача проектирования схемы управления нагревателем
381
необходимо включить переключатель. Таким
образом, чтобы получить требуемый нам ток
величиной 1 мА, мы можем выбрать резистор
RU0B = 470 Ом, а резистор в цепи базы должен
быть величиной приблизительно 3,5 В/1 мА =
= 3,5 кОм, ближайший номинал будет 3,3 кОм.
Наконец, нам необходимо подключить парал-
лельно нагрузке демпфирующий диод, чтобы
защитить пару Дарлингтона от всплесков на-
пряжения при коммутации ключа. Без такой
защиты индуктивная нагрузка может повре-
дить пару Дарлингтона.
8W.2.7. Законченная схема
На рис. 8W.11 показан результат наших тру-
дов: полная принципиальная схема устройства.
Поскольку резисторов номиналом 3,5 кОм не
существует, в скобках показан номинал рези-
стора с допуском 1%, доступного на рынке.
Какая часть напряжения питания +20 В
будет падать на нагрузке?
Можно сформулировать вопрос иначе: какое
будет напряжение на замкнутом транзистор-
ном ключе?
+20 В
JIP210
кОм
1МОм
Рис. 8W.11. Законченная схема управления нагревателем
Мы можем узнать из двух источников, что на-
пряжение на замкнутом ключе при токе 1 А
должно быть примерно 1 В:
♦ на третьем графике на рис, 8W.8 показано,
что напряжение насыщения «коллектор-
эмиттер» составляет около 0,8 В;
♦ это же напряжение при большом сигнале
на базе и токе 1К=1 А показано на первом
графике.
Таким образом, на нагрузку будет расходо-
ваться около 19 В из 20 В источника питания,
что соответствует довольно высокому КПД
устройства.
9N. Операционные усилители IV:
паразитные колебания и активный фильтр
Содержание
9N.1. Введение 382
9N.2. Активные фильтры 383
9N.3. Общий взгляд на проблему паразитных колебаний 385
9N.4. Паразитные колебания в схемах на операционных усилителях 385
9N.4.1. Иногда неправильный объект в цепи обратной связи
обращает фазу сигнала на всех частотах 386
9N.4.2. Но намного чаще тип обратной связи меняется только
на высоких частотах 387
9N.4.3. Почему операционные усилители добавляют в сигнал задержку в 90° 389
9N.4.4. Ввиду вносимого операционным усилителем фазового сдвига
как можно достичь его стабильной работы? 389
9N.5. Решения для стабилизации работы операционных усилителей 390
9N.5.1. Искусственный спад усиления на высоких частотах 390
9N.5.2. Схема с фотодиодом 390
9N.5.3. Передача сигнала по длинному коаксиальному кабелю 391
9N.6. Общий критерий стабильности: петлевое усиление,
когда фазовый сдвиг приближается к 180° 395
9N.7. Паразитные автоколебания в схемах без операционного усилителя 397
9N.8. Решения для проблемы паразитных автоколебаний 399
9N.8.1. Первое решение: зашунтировать источник питания
(уменьшить обратную связь) 399
9N.8.2. Другое решение: подавить усиление на высоких частотах 399
9N.9. Подведение итогов по вопросу стабилизации схем 401
9N.10. Материал для чтения в АоЕ 401
Цель этой главы
Сегодня мы хотим попробовать решить две за-
дачи, вторая из которых более сложная и более
фундаментальная:
♦ создать улучшенный фильтр на операцион-
ных усилителях;
♦ избавиться от нежелательных, или паразит-
ных, колебаний.
9N.1. Введение
В этой главе мы вкратце рассмотрим актив-
ные фильтры, чтобы вы знали о наличии та-
ких устройств на случай, когда вам потребу-
ется фильтр с лучшими частотными харак-
теристиками, чем у обычных 1?С-фильтров.
А бблыпую часть этой главы мы посвятим
вредным паразитным колебаниям.
Из предыдущей главы мы узнали, что положи-
тельная обратная связь может быть полезной,
в частности при создании схем компараторов
и генераторов колебаний. Но в целом из двух
видов обратной связи отрицательная обратная
связь гораздо полезнее. Теперь мы приступим
к рассмотрению негативных свойств поло-
жительной обратной связи: те случаи, когда
она подкрадывается незаметно, когда ее со-
всем не ожидаешь, и вызывает нежелательные
(и обычно нежданные) колебания. Закон под-
лости при этом гласит, что паразитные коле-
бания возникают не в генераторах колебаний,
а в усилителях.
9N.2. Активные фильтры
383
Чтобы хорошо изучить эту проблему, мы рас-
смотрим несколько случаев паразитных ко-
лебаний, а затем опишем средства защиты от
них, в частности, необходимые модификации
схем для предотвращения такого поведения.
Конечно же, наш главный интерес состоит в по-
иске средств предотвращения паразитных коле-
баний. Если помехи засоряют выходной сигнал
схемы, над которой вы и ваши однокурсники
работаете на лабораторном занятии, и вы смо-
жете избавиться от них, внеся несколько изме-
нений в схему, то вы будете выглядеть героем
в глазах остальных. Это похоже на черную ма-
гию, когда схема оживает буквально благода-
ря движению рук1 и объяснениям, состоящим
в основном из жестов руками, так и интуиции,
непосредственно полученной из нашего курса.
9N.2. Активные фильтры
Как указывается в разделе 9S.2, мотивом для
использования таких фильтров вместо простых
ДС-фильтров является желание получить ча-
стотные характеристики, более близкие к иде-
альным: плоскую вершину в пределах полосы
пропускания и резкий спад с большим ослабле-
нием сигнала в полосе ослабления2. Как видно
на рис. 9N.1, эти две характеристики можно
улучшить, применяя операционный усилитель
с двухкаскадным ДС-фильтром.
Активный фильтр
Два RC-срильтра,
соединенные последовательно
Рис. 9N.1. Сопоставление частотных характеристик пассив-
ного и активного фильтров
В схеме на рис. 9N.2 обе эти характеристи-
ки удается улучшить за счет положительной
обратной связи. Она выравнивает полосу
1 Да, жесты действительно иногда влияют на работу элек-
тронных устройств. Помахав рукой вблизи схемы с пара-
зитными колебаниями, одновременно наблюдая за эффек-
том, вызываемым близостью вашей руки (важный фактор
вследствие ее паразитной емкости), иногда можно полу-
чить подсказку о местонахождении источника колебаний.
2 АоЕ § 6.2.4.
пропускания, усиливая сигнал на частоте чуть
ниже частоты^ дБ, где выходной сигнал пассив-
ного ЯС-фильтра начинает проседать. Также
она обеспечивает предельную крутизну вели-
чиной 1/f2, но этого можно достичь и с помо-
щью обычного двухкаскадного ЯС-фильтра.
Что больше впечатляет, так это более крутой
переход между полосой пропускания и полосой
ослабления, чем у двухкаскадного пассивного
фильтра3.
Выходной
сигнал
Положительная обратная связь
усиливает входной сигнал
на частоте чуть ниже частоты f3/l6,
выравнивая полосу пропускания
Рис. 9N.2. Активный \/О/54-фильтр (двухкаскадный или
двухполюсный)
Более того, просто регулируя коэффициент
усиления5, можно оптимизировать ту или иную
характеристику фильтра: равномерность поло-
сы пропускания (наилучшая в так называемом
фильтре Баттерворта6), крутизну спада сигна-
ла (наилучшая в фильтре Чебышева) или со-
хранность формы сигнала (наилучшая в филь-
тре Бесселя7)5. Фильтр, изображенный на
рис. 9N.2, называется двухполюсным; с филь-
тром этого типа мы будем работать на лабо-
раторном занятии для этой главы. Частотные
характеристики фильтра можно улучшить еще
больше, подключив дополнительные каскады.
В этой книге мы продвигали метод, состоящий
в составлении сложных схем путем последо-
вательного соединения независимых модулей.
К сожалению, этот метод плохо работает при-
менительно к фильтрам. В частности, четы-
рехполюсный фильтр нельзя создать, соеди-
няя каскадом два идентичных двухполюсных
фильтра. Вместо этого необходимо выполнять
более трудную работу, которой мы обычно
3 АоЕ § 6.3.1.
4 Англ.: voltage-controlled voltage source — источник напря-
жения, управляемый напряжением. — Примеч. пер.
5 АоЕ § 6.2.5.
6 Butterworth filter.
7 Bessel filter.
8 Фильтр Бесселя сохраняет форму сигнала, создавая фа-
зовый сдвиг, линейно изменяющийся с частотой, обеспе-
чивая постоянное время запаздывания. См. раздел 6.2.6В
книги АоЕ.
384
9N. Операционные усилители IV: паразитные колебания и активный фильтр
избегаем: выполнять детальный расчет схе-
мы как четырехполюсника. На практике это
может означать необходимость обращения к
таблице с информацией о частотных характе-
ристиках нескольких каскадов фильтров раз-
ных типов, наподобие табл. 6.2 в разделе 6.3.2
книги АоЕ.
Данный расчет можно автоматизировать, ис-
пользуя специальную компьютерную програм-
му для проектирования фильтров. Такие про-
граммы предоставляются многими производи-
телями микросхем, включая компании Analog
Devices, Microchip, LTC и Texas Instruments9.
На рис. 9N.3 приведены скриншоты из одной
такой программы: FiiterPro компании Texas
Instruments. Вы просто вводите требуемые ха-
рактеристики фильтра в специальную форму,
как показано слева на рисунке.
Используя заданные вами требуемые характе-
ристики, программа FiiterPro составляет соот-
ветствующую принципиальную схему фильтра,
указывая значения всех компонентов, как по-
казано справа на рис. 9N.3. В данном случае
были заданы достаточно жесткие характери-
стики фильтра, для удовлетворения которых
требуется четырехполюсный фильтр. Для это-
го программа FiiterPro соединила последова-
тельно два каскада, похожих на VCVS-фильтр
на рис. 9N.2, с тем исключением, что исполь-
зуется единичное усиление. Этот тип фильтра
называется фильтром Саллена-Ки10. Программа
FiiterPro держит разработчика за руку, как за-
ботливая мать ребенка: она не только создает
схему фильтра, указывая номиналы всех эле-
ментов, которые в противном случае разработ-
чику пришлось бы искать по таблице, но также
вежливо спрашивает, какие допуски задать при
указании номиналов, а затем предоставляет
перечень всех требуемых деталей.
Спрашиваете, с какой это стати компания Texas
Instruments так заботится о нас? Ну, возможно,
они надеются, что, поскольку мы пользуемся их
инструментом, то купим требуемые операцион-
ные усилители их производства. Но, возможно,
они больше всего желают, чтобы мы купили
их специализированную микросхему активно-
го фильтра UAF42 (рис. 9N.4)11. Это хитроум-
ная микросхема, содержащая конденсаторы со
значениями, подогнанными до 0,5%. Но это
довольно дорогостоящая микросхема, цена на
которую на момент подготовки этой книги со-
ставляла $16 за один экземпляр. Так что может
быть целесообразнее использовать программ-
ное обеспечение компании Texas Instruments,
но покупать операционные усилители, которые
соответствуют вашим техническим требовани-
ям и финансовым возможностям.
■мшшшшнш
\ \, """ ■ ■ "
N ,.. .. X ; :
Рис. 9N.3. Программа проектирования фильтров FiiterPro компании Texas Instruments выполнит за вас всю тяжелую работу.
Пример частотной характеристики и принципиальная схема соответствующего фильтра приводятся только в общих ознако-
мительных целях, поскольку подробная информация на рисунке может быть нечитаемой
9 Analog Devices: http://www.analog.com/designtools/
en/filterwizardA^/type; Microchip: www.microchip.com,
выполните поиск по выражению «FilterLab;» TI: http://
www.ti.com/tool/filterpro.
10 Фильтры типа Саллена-Ки подробно рассматриваются в
разделе 6.2.4Е книги АоЕ.
11 Унаследованная от компании Burr-Brown, приобретен-
ной компанией Texas Instruments.
9N.4. Паразитные колебания в схемах на операционных усилителях
385
Выход Выход Выход
высокочастотного полосового низкочастотного
фильтра фильтра фильтра
ВЫХОД 9 9 ВЫХОД о о ВЫХОД
/?=50кОм =
«земля»
Рис. 9N.4. Микросхема активного фильтра UAF42 выпускае-
мая компанией Texas Instruments
9N.3. Общий взгляд
на проблему паразитных
колебаний
Условия, ведущие к возникновению как неже-
лательных, так и полезных колебаний, конечно
же, схожи. Для генерации незатухающих коле-
баний таких условий всего два.
♦ Усиление12. Без усиления помеха просто за-
тухнет, как это происходит, например, при
кратковременной подаче прямоугольного
импульса на резонансный LC-контур. Более
конкретно, в процессе возникновения поме-
хи на выходе, подачи ее назад на вход и пе-
редачи снова на выход, величина помехи не
должна уменьшаться, т. е. общее усиление
в данном контуре должно быть как минимум
единичным.
12 Требуется усиление по напряжению. Строго говоря, луч-
ше сказать «усиление по мощности», поскольку усиление
по напряжению может обеспечить и трансформатор (но
трансформатор не может поддерживать незатухающие ко-
лебания). Изобретатели транзистора прекрасно понима-
ли разницу между усилением по напряжению и усилением
по мощности. Вальтер Браттейн (Walter Brattain), один из
трех изобретателей транзистора, 15 декабря 1947 г. запи-
сал в своем лабораторном журнале: «получил приблизи-
тельно двойное усиление по напряжению, но не усиление
по мощности». А днем позже он отметил: «...усиление по
мощности — 1,3; усиление по напряжению — 15». Важный
шаг вперед. Выдержка из архивов Лаборатории Белла, ци-
тируемая в статье в Википедии по истории транзистора.
В этом материале мы употребляем выражении «усиле-
ние по напряжению», надеясь, что это более знакомый
и понятный термин. При условии, что выходной ток не
уменьшается пропорционально повышению напряже-
ния, как это происходит в трансформаторе, усиление по
напряжению сопровождается необходимым усилением
по мощности.
♦ Положительная обратная связь. Схема
должна «разговаривать» сама с собой, похло-
пывая себя по плечу и говоря: «Прекрасно.
Продолжаем дальше в том же духе». (При
описании первого условия в виде усиления
подразумевалась положительная обратная
связь, но это два отдельных условия.)
Иновда наличие какой-либо обратной связи
очевидно, как это было во всех наших схемах
на операционном усилителе. Тогда тонкость
проблемы заключается в том, чтобы понять,
почему тип обратной связи изменился с полез-
ной отрицательной на вредную положитель-
ную. Но иногда (как в случае с эмиттерным по-
вторителем, рассматриваемым в разделе 9N.7)
наличие обратной связи любого типа далеко не
очевидно. Но если, тем не менее, схема выра-
батывает автоколебания, потребуется экспери-
ментировать и, возможно, даже поразмыслить,
чтобы определить причину возникновения
этой обратной связи. Но наша конечная цель
всегда будет состоять в нахождении средств для
предотвращения таких автоколебаний.
9N А Паразитные колебания
в схемах на операционных
усилителях
Схемы на операционных усилителях обычно
содержат цепь отрицательной обратной связи,
и поэтому они, очевидно, представляют благо-
приятную среду для возникновения автоколе-
баний. Если в схеме произойдет что-либо, из-
меняющее тип обратной связи с отрицательной
на положительную, «спокойный» усилитель
может превратиться в «мятежный» генератор
колебаний.
Любая рассмотренная нами схема на операци-
онном усилителе выглядит наподобие показан-
ной на рис. 9N.5.
Отрицательная обратная связь
Рис. 9N.5. Стабильность этой схемы зависти от содержимого
мешка
386
9Л/. Операционные усилители IV: паразитные колебания и активный фильтр
Мы знаем, что операционный усилитель можно
заставить делать то, что нам требуется, поме-
стив соответствующее содержимое в «мешок»
в цепи обратной связи. Но сегодня мы узнаем,
что операционный усилитель может взбунто-
ваться и начать буянить, если в «мешок» поло-
жить содержимое определенного типа.
9NA1. Иногда неправильный объект
в цепи обратной связи обращает
фазу сигнала на всех частотах
Применяется ли отрицательная обратная связь
в схеме на рис. 9N.6? — Конечно же, применя-
ется. — можете поддаться искушению вы. —
Сигнал обратной связи подается на инвертиру-
ющий вход. — Но что, если «мешок» содержит
инвертор? — Да, ну. — говорите вы. — Это про-
сто глупо, такое никогда не может быть. А если
бы это произошло, то мы бы просто поменяли
входы.
Входной
сигнал
Выходной
сигнал
Опорное
напряжение
Рис. 9N.6. Возможно, что эта схема выглядит правильно, но,
тем не менее, она неправильная: обратная связь в ней по-
ложительная
По большому счету вы будете правы: такие
случаи встречаются чрезвычайно редко. Но
схема, изображенная на рис. 9N.6, как раз и яв-
ляется таким исключением. Это стабилизатор
напряжения с малым падением напряжения,
с которым мы познакомимся на лабораторном
занятии 11L. Вы также правы, что переключе-
ние входов решит проблему. Мы сделали это в
схеме на рис. 9N.7, которая выглядит странно,
но, тем не менее, является вполне правильной.
А правильная эта схема потому, что ее цепь
обратной связи содержит инвертирующий ка-
скад — усилитель с общим эмиттером нар-п-р-
транзисторе.
Чтобы попытаться убедить вас в полезности
этой схемы, и что мы не просто придумали ее
для демонстрационных целей, рассмотрим
подробно ее полезное качество. В отличие от
обычного стабилизатора напряжения, содержа-
щего эмиттерный повторитель в цепи обратной
связи, данный стабилизатор не добавляет паде-
ние напряжения на переходе «база-эмиттер»
UB3 между входным и выходным сигналами.
В результате разница между входным и выход-
ным сигналами может быть всего лишь 100 мВ.
Отсюда и название схемы: стабилизатор с ма-
лым падением напряжения.
Справа на рис. 9N.7 изображена схема с допол-
нительными стабилизирующими элементами,
которые обычно нужно добавить к основной
схеме стабилизатора. Но в любом случае стран-
ная обратная связь в обеих схемах является
правильной, а не бредовой.
В курсах по схемам управления часто приво-
дится такой пример инвертированной обрат-
ной связи.
В этой связи можно привести такую шуточную
сценку. Пара пользуется электрическим одея-
лом, и каждый из них имеет пульт управления
для части одеяла на его/ее стороне. Допустим,
случайно пользователи одеяла поменялись
пультами управления. Теперь, когда одному
из них становится холодно и он/она начина-
ет повышать температуру своей части одеяла,
Входной
сигнал
Опорное
т напряжение
Эта обратная связь, возможно,
выглядит неправильно,
но она правильна...
Входной
сигнал
Опорное
напряжение
...потому что ее цепь содержит инвертор
Выходной
(сигнал
Эта же схема с добавленной
стабилизирующей обратной связью
Рис. 9N.7. Эта схема может выглядеть неправильной, но она правильная. Это очень редкая схема, цепь обратной связи кото-
рой содержит инвертор
9N.4. Паразитные колебания в схемах на операционных усилителях
387
постарайтесь представить себе реакцию друго-
го пользователя одеяла и последующее разви-
тие событий.
9N.4.2. Но намного чаще тип
обратной связи меняется только
на высоких частотах
На рис. 9N.8 показан намного более распро-
страненный случай: пес (т. е. обратная связь)
не инвертирован, а просто ленив (низкая ча-
стота сигнала). Таким образом, подаваемый
обратно на вход сигнал поступает с некоторой
задержкой.
во внимание дополнительную задержку в 90°,
накладываемую самим операционным усили-
телем. (Эта задержка в операционном усили-
теле рассматривается более подробно в раз-
деле 9N.43.) Таким образом, если на простой
дифференциатор (как на рис. 9N.9) подать пря-
моугольный сигнал, он начинает «дрожать».
Прямоугольный сигнал особенно проблемати-
чен из-за содержащихся в его фронтах высоко-
частотных составляющих (рис. 9N.10)13.
Рис. 9N.8. Инерционный элемент в цепи обратной связи мо-
жет быть причиной проблемы
На рис. 9N.9 показан более конкретный пример
«ленивого пса» в цепи обратной связи: низко-
частотный фильтр.
Дифференциатор
(нестабильный)
Рис. 9N.10. При отсутствии дополнительного резистора
и конденсатора реакция дифференциатора на прямоуголь-
ный сигнал нестабильна. Проблема возникает из-за низко-
частотного фильтра в цепи обратной связи
Эти паразитные колебания являются неприем-
лемыми и обычно устраняются введением до-
полнительного резистора и конденсатора, как
показано на рис. 9N.11. Дополнительная RC-
цепочка подавляет усиление схемы на высоких
частотах. Иными словами, она останавливает
фазовую задержку, которая становится опасно
большой при повышении частоты, а затем ре-
версирует фазовый сдвиг.
Низкочастотный фильтр
в цепи обратной связи?
Входной
сигнал
Такая ситуация
может выглядеть
неправдоподобной
Да, это схема дифференциатора
(и очень нестабильного к тому же)
100 пФ
\
2 В 0,2 мс /
Дифферен циатор
(нестабильный)
Рис. 9N.9. Низкочастотный фильтр в цепи обратной связи
может вызывать проблемы
При низких частотах сигнала НЧ-фильтр не
причиняет никакого вреда. Поскольку входной
сигнал меняется медленно, сигнал, подаваемый
с выхода обратно на вход, может быть несколь-
ко запоздалым, но все равно довольно похож
на текущий. Поэтому обратная связь работает
должным образом.
Но если входной и выходной сигналы изменя-
ются с большой скоростью, то запаздывающий
сигнал обратной связи может быть полностью
устарелым: до 90° на входе в операционный
усилитель и вплоть до 180°, если принимать
Рис. 9N.11. При наличии дополнительного резистора и кон-
денсатора дифференциатор стабильно работает с прямо-
угольным сигналом
Схема дифференциатора, которую мы собрали
на лабораторном занятии 7L.2, содержала та-
кую дополнительную стабилизирующую RC-
цепочку, как и в схеме на рис. 9N.11. Поэтому на
том лабораторном занятии мы и не наблюдали
паразитных колебаний.
Обратите внимание на тот факт, что мы не смог-
ли бы решить проблему с дифференциатором
таким же образом, как и в схеме с простым ин-
вертором в цепи обратной связи (см. рис. 9N.6).
13 См. книгу АоЕ, раздел 4.5.6 и рис. 4.69.
388
9/V. Операционные усилители IV: паразитные колебания и активный фильтр
В схеме дифференциатора мы не можем поме-
нять входы местами, как мы это сделали в слу-
чае со стабилизатором с малым падением на-
пряжения. Это объясняется тем, что при смене
входов местами дифференциатор будет созда-
вать положительную обратную связь на низких
частотах и для входного сигнала постоянного
тока14. При входном сигнале постоянного тока
эта положительная обратная связь заблокирует
схему, при этом выходной сигнал «застрянет»
на уровне вблизи напряжения питания той или
иной полярности.
Для иллюстрации этой проблемы, где инфор-
мация о результатах предпринимаемого дей-
ствия доходит до лица, выполняющего это дей-
ствие, с большой задержкой, трудно придумать
простую аналогию.
Но мы попытаемся. Представьте себе, что вы ре-
шили проверить, сможете ли вести автомобиль
вслепую по указкам поводыря. Вы закрываете
себе глаза повязкой, а ваш пассажир указывает
вам, в какую сторону поворачивать руль, чтобы
оставаться в своей полосе движения. Если ваша
скорость не очень высока и если ваш поводырь
быстро дает вам непрерывные указания, то вы
сможете справиться с этой задачей. Но у вас
возникнут проблемы, если другой автомобиль
резко свернет в вашу полосу прямо перед вами.
Вряд ли ваш поводырь успеет вовремя дать вам
требуемое указание, а вы мгновенно среагиро-
вать на него. Но при медленной езде где-то на
проселочной дороге описанный процесс может
работать15.
Но предположим, что вашим поводырем явля-
ется тянущий слова, до противности хладно-
кровный ковбой, который не спеша дает вам
указания наподобие:
— Так, парень, я полагаю, что тебе нужно слег-
ка провернуть руль, слегка, я тебе говорю, не
много, на запад, то есть налево...
В таком случае вряд ли вы сможете удержать
машину на дороге, если только вы не едете
14 Вы можете вполне законно возразить, что вам не нужна
производная уровня напряжения постоянного тока. Со-
вершенно верно, но мы приводим случай с уровнем напря-
жения постоянного тока в качестве примера чрезвычайно
низкой частоты, просто выбрав случай, который легко
поддается анализу.
15 Ни в коем случае не вздумайте проводить такой опыт
на практике! Это всего лишь мысленный эксперимент.
со скоростью пешехода. Указания поступают
вам с большой задержкой, и на момент при-
бытия не соответствуют текущей дорожной
обстановке. Вскоре вам нужно будет выпол-
нить радикальную корректировку в противо-
положном направлении; в результате таких
запоздалых указаний вы будете делать зигза-
ги, т. е. колебаться, от одной стороны дороги
к другой.
Мы привели способ описания проблемы во
временной области, но описание ее в частот-
ной области может быть более понятным.
Рассматривая низкочастотный фильтр в цепи
обратной связи на рис. 9N.90, можно увидеть,
что на низких частотах сигнал обратной связи
будет, по большому счету, совпадать по фазе
с выходным сигналом операционного усили-
теля, и что конденсатор не будет оказывать
почти никакого влияния: обратная связь отри-
цательная и полезная. Но на высоких частотах
(значение «высоких частот», конечно же, за-
висит от номиналов резистора и конденсатора
цепочки) между сигналом на выходе операци-
онного усилителя и сигналом, поступающим
на его инвертирующий вход, может возникать
значительный фазовый сдвиг, приближаю-
щийся к -90°.
Но можно возразить, что 90° не обращает сиг-
нал, и что нужен сдвиг на 180°, чтобы у нас воз-
никли проблемы. Да, все это так. Но дело в том,
что причина, по которой проблемы наступают
при задержке в 90°, обычно незаметны при на-
блюдении работы операционных усилителей.
А состоит эта причина в том, что операцион-
ные усилители содержат внутреннюю задерж-
ку, равную 90°. Как бы странно это не звучало,
операционный усилитель ведет себя подобно
интегратору, начиная с очень низких частот.
Например, операционный усилитель на микро-
схеме LF411 начинает вести себя как интегра-
тор на частоте приблизительно 20 Гц. Да, да —
не килогерц, а именно герц.
Частотная коррекция для стабилизации
операционного усилителя
На рис. 9N.12 приведен график спада усиления
скорректированного по частоте операционного
усилителя и соответствующего фазового сдвига
между входным и выходным сигналами16.
16 АоЕ§§ 4.9,2.5.4В.
9N.4. Паразитные колебания в схемах на операционных усилителях
389
Частотная характеристика
без обратной связи
мммимм
"V,
\
V
V
ч
100
Усиление (дБ)
0 &
Усиление (дБ)
Усиление
-45° в точке 3 дБ
1 10
102 103 104 105 106
Частота (Гц)
107
Точка -3 дБ
Операционный усилитель
обеспечивает (разовый сдвиг в 90°
-6 дБ/октаву на большей части своего частотного
'диапазона, а вблизи частоты
единичного усиления фазовый
сдвиг возрастает ▲
-135° ^
V g
Фаза
Частота —►
(логарифмическая шкала)
График усиления из справочного
листка микросхемы 411
20 Гц для микросхемы 411
(Начало спада усиления)
4 МГц для микросхемы 411
(Единичное усиление)
Рис. 9N.12. Операционный усилитель с частотной коррекцией, типа 411, проявляет спад усиления величиной 1/f и фазовый
сдвиг величиной -90°
Мы указали на графике данные, подходящие
для операционного усилителя LF411, кото-
рый мы используем на наших лабораторных
занятиях. На графике видно, как усиление
операционного усилителя 411 уменьшается с
повышением частоты сигнала; также можно
видеть результирующий фазовый сдвиг меж-
ду сигналом на неинвертирующем входе и на
выводе.
Замечание
Обратите внимание на то, что здесь предполагает-
ся работа усилителя без обратной связи, что почти
никогда не применяется. Но поведение усилителя
без обратной связи критично для его склонностей
в обычных схемах с обратной связью.
В разделе 9S.1 мы подробно исследуем методы
реализации частотной коррекции операцион-
ного усилителя17.
9N A3. Почему операционные
усилители добавляют в сигнал
задержку в 90°
Еще более странным является тот факт, что
функция внесения операционными усилителя-
ми в сигнал задержки в 90°, а также этот при-
скорбный спад усиления величиной 1/f, пред-
намеренно встроен в них разработчиками18.
Но зачем нужно было делать это? Если объяс-
нять вкратце, то без этой коррекции ситуация
была бы еще хуже: несколько последователь-
ных схем операционного усилителя образуют
каскад низкочастотных фильтров, которые в
конечном итоге создавали бы убийственную
задержку в 180°, выводя операционный усили-
тель из строя. Поэтому специальная задержка
в 90° может казаться странной, но это намного
лучше, чем вообще без такой коррекции.
Эффект вносимой операционным усилите-
лем задержки в 90° (и обычно даже несколько
большей19) состоит в том, что для случайного
создания положительной обратной связи нуж-
но добавить только еще 90°, а не 180°. А эту
задержку в 90° может создать любой низкоча-
стотный фильтр.
9N.4A Ввиду вносимого
операционным усилителем
фазового сдвига как можно достичь
его стабильной работы?
Если цепь обратной связи чисто резистивная,
то нет никакой проблемы: такая цепь не соз-
дает фазового сдвига, так что схема окажет-
ся стабильной при любых условиях. Но если
в схему закладывается какое-либо свойство
низкочастотного фильтра, то нужно быть на-
стороже.
17 АоЕ§ 4.9.1.
18 АоЕ § 4.9.2А.
19 На частоте^ целых 45° больше. См. рис. 9S.8.
390
9/V. Операционные усилители IV: паразитные колебания и активный фильтр
Неприемлемое решение: я не буду
работать с высокими частотами
Первым наивным решением проблемы неста-
бильности операционного усилителя на высо-
ких частотах может быть попытка воспользо-
ваться тем обстоятельством, что эта проблема
возникает на сравнительно высоких частотах.
Если так, то почему бы не работать только
с низкочастотными сигналами?
Потому что так у вас не получится. Вполне мо-
жет быть, что ваш конкретный операционный
усилитель становится нестабильным только на
частотах выше, например, 50 кГц, а вы плани-
руете использовать этот усилитель только для
обработки сигналов ниже 10 кГц. Но этот план
ничего вам не даст.
Проблема здесь состоит в том, что схема реа-
гирует не только на сигналы (довольно низкой
частоты), которые мы подаем на нее, но так-
же и на помехи, наличие которых необходимо
предполагать на всех частотах.
Это одна из горьких истин, на основе которых
базируется удручающее наблюдение, сформу-
лированное в начале этой главы, что паразит-
ные колебания создаются не генераторами ко-
лебаний, а усилителями.
Несколько действенных решений
Встроенная в операционные усилители частот-
ная коррекция предназначена для обеспечения
стабильности с резистивной обратной связью,
но не при наличии элементов низкочастотно-
го фильтра в цепи обратной связи. Если такие
элементы присутствуют в цепи обратной связи,
то необходимо предпринимать меры по пред-
отвращению возникновения автоколебаний.
Далее приводим несколько примеров решения
данной проблемы.
♦ Вдобавок к спаду усиления, встроенному в
каждый операционный усилитель с частот-
ной коррекцией, обеспечьте принудитель-
ный спад усиления на высоких частотах. Этот
метод иллюстрируется в схеме с фотодиодом
на рис. 9N.14.
♦ Организуйте обход «мешка с котом» (см.
рис. 9N.5) на высоких частотах, где он мог бы
вносить опасную задержку фазы. Этот метод
называется «разделенной обратной связью»;
мы рассмотрим этот метод более подробно
чуть далее в этой главе в подразделе «реше-
ние 3. Усовершенствованное решение длинно-
го кабеля: разделенная обратная связь».
♦ Примените экстремальное решение, моди-
фицировав сам операционный усилитель.
Для этого нужно разработать конкретный
операционный усилитель, который сможет
аннулировать вредные фазовые задержки.
Эта стратегия используется в цепи ПИД20,
которую мы соберем на лабораторном заня-
тии 10L.
Далее рассматриваются первые два из этих ре-
шений. Анализ решения, вовлекающего моди-
фикацию операционного усилителя, отложим
до тех пор, пока не познакомимся с ПИД-петлей
на лабораторном занятии 10L.
9N.5. Решения
для стабилизации работы
операционных усилителей
9N.5.1. Искусственный спад
усиления на высоких частотах
Изображенные на рис. 9N.13 схемы в той или
иной степени восприимчивы к паразитным
колебаниям из-за наличия фазовой задержки
(влияние элементов низкочастотного фильтра)
в цепи обратной связи.
Длинный BNC-кабель
(около 3 метров)
Фотодиод 10МОм
Рис. 9N.13. Две схемы, склонные к паразитным колебаниям
9N.5.2. Схема с фотодиодом
В схеме с фотодиодом наличие подразумевае-
мых или случайных элементов низкочастотно-
го фильтра далеко не очевидно. В данной схеме
20 Сокращение от выражения «пропорционально-инте-
грально-дифференциальная», описывающее три функции
коррекции погрешности обратной связи, применяемые
в этой цепи управления. Рассмотрению этого метода по-
священо лабораторное занятие 10L.
9N.5. Решения для стабилизации работы операционных усилителей
391
этот элемент создается посредством резистора
обратной связи большого номинала, сигнал
с которого попадает на паразитную емкость на
виртуальной «земле» (величиной в несколько
пикофарад). Сопротивление этого резистора ве-
личиной 10 МОм не уменьшается из-за наличия
параллельно включенного фотодиода, посколь-
ку фотодиод является источником тока с боль-
шим динамическим сопротивлением AU/AL
Предположим, что величина паразитной емко-
сти на инвертирующем входе составляет, ска-
жем, 3 пФ. В этом случае большое сопротивле-
ние резистора обратной связи создает низкоча-
стотный фильтр с частотой/3дБ величиной око-
ло 5 кГц. На этой частоте фазовый сдвиг в цепи
обратной связи будет задерживаться на 45°, что
недостаточно для возбуждения автоколебаний.
Но на более высоких частотах задержка фазы
нарастает, приближаясь к роковым 90°.
Для схемы с фотодиодом (которую мы собрали
на лабораторном занятии 6L) наилучшим ре-
шением будет подключить параллельно рези-
стору обратной связи конденсатор небольшой
емкости, скажем, 10 пФ, или даже меньшей,
как показано на рис. 9N.14. Этот конденсатор
устранит возможность схемы реагировать на
высокочастотные оптические сигналы.
100 пФ
Рис. 9N.14. Стабилизированная схема с фотодиодом
Теперь на частоте чуть выше 1 кГц (там, где
Хс « 10 МОм) усиление схемы уменьшено на
3 дБ. Иными словами, выше этой частоты
в цепи обратной связи больше нет низкоча-
стотного фильтра с его отстающим фазовым
сдвигом. Вместо этого в ней создается емкост-
ной делитель напряжения, который при даль-
нейшем повышении частоты сдвигает фазу об-
ратно к нулю.
9N.5.3. Передача сигнала
по длинному коаксиальному кабелю
В случае длинного коаксиального кабеля низ-
кочастотный фильтр создается значительной
паразитной емкостью BNC-кабеля (около
30 пФ/30 см) и небольшим, но ненулевым вы-
ходным импедансом операционного усилите-
ля21. Величина последнего составляет порядка
50-100 Ом22, но критически меняется под воз-
действием обратной связи. По сути, обратная
связь преобразует этот выходной импеданс
в кажущуюся выходную индуктивность, созда-
вая низкочастотный фильтр, резонансная ча-
стота которого намного ниже, чем частота^ дБ,
которую бы обеспечивал простой ЯС-фильтр.
Вот эта виртуальная индуктивность и объясня-
ет частоту колебаний, создаваемых емкостной
нагрузкой. Простой резистивный выходной
импеданс выглядит как правдоподобное объ-
яснение колебаний, но не подтверждается вы-
числениями23.
Если предположить, что этот выходной импе-
данс #вых совместно с емкостью кабеля созда-
ет эффект низкочастотного фильтра, который
вызывает паразитные колебания, то можно
предсказать, что частота возникновения па-
разитных колебаний будет намного большей,
чем частота /г усилителя. На этой частоте уси-
ления операционного усилителя уже давно нет
и возникновение автоколебаний невозможно.
Подставляя данные для настоящего случая —
2?вых « 40 Ом, Сн = 450 пФ (предполагая кабель
длиной около 4,5 м), можно вычислить частоту
УздБ нашего случайного фильтра, которая будет
около 8 МГц. На этой частоте усиление у опе-
рационного усилителя 411 напрочь отсутствует,
поэтому автоколебания никогда не возникнут.
Но представление выходного импеданса опе-
рационного усилителя как индуктивного
импеданса не соответствует наблюдаемым
колебаниям. Выход операционного усили-
теля ведет себя индуктивно не потому, что
микросхема в действительности обладает ин-
дуктивностью, а потому, что импеданс схемы
21 АоЕ § 4.6.2.
22 В справочных листках операционных усилителей обыч-
но не указывается выходной аппаратный импеданс (т. е.
его значение только для самой микросхемы, без учета об-
ратной связи). Но в справочном листке для микросхемы
операционного усилителя 411 подразумевается значение
величиной около 40 Ом. Это предположение основано на
графике выходного импеданса (см. рис. 9N.15), который
на высоких частотах выравнивается приблизительно на
40 Ом, если назад подается лишь небольшая часть выход-
ного сигнала В (ОД или 0,01). На этих частотах величина
произведения АВ небольшая, поэтому эффективный вы-
ходной импеданс Явш (т. е. улучшенный обратной связью)
достигает предела Явых без обратной связи.
23 См. АоЕ, рис. 4.53.
392
9N. Операционные усилители IV: паразитные колебания и активный фильтр
Виртуальная «индуктивность»
(потому что £ВЬ1Х повышается
с ростом частоты)
Предельное значение £вьгх указано
для работы без обратной связи
Выходной импеданс
Длинный BNC-кабель
"""А^__Емкость кабеля
Эквивалентный выходной импеданс возрастает
с повышением частоты аналогично индуктивному
импедансу (хотя это возрастание вызвано спадом
усиления без обратной связи А) *""
102 103 104 105 106
Частота (Гц)
Рис. 9N.15. Выходной импеданс операционного усилителя ведет себя подобно индуктивному импедансу, понижая частоту,
при которой создается опасная фазовая задержка
с задействованной обратной связью повыша-
ется линейно с повышением частоты, подобно
тому, как это свойственно катушке24. Эта ин-
дуктивность совместно с емкостью нагрузки
Сн образует колебательный контур, резонанс-
ная частота которого совпадает с наблюдае-
мыми колебаниями.
В схеме на рис. 9N.16 автоколебания возни-
кают на частоте около 3,4 МГц. Эта частота
находится вблизи максимальной рабочей ча-
стоты операционного усилителя, где его запас
по фазе (разница между фазовым сдвигом воз-
никновения автоколебаний (180°) и фазовым
сдвигом, который он сам вносит в сигнал) со-
ставляет около 50°. Если резонансная частота
находится вблизи этой частоты, то колеба-
тельный контур может внести необходимую
недостающую задержку фазы. (Как уже упо-
миналось, вблизи к частоте /г операционного
усилителя достаточно задержки чуть меньше,
чем 90°.) На рис. 9N.16 показаны осцилло-
граммы прямоугольного сигнала, подаваемо-
го с выходного каскада микросхемы LF411 в
отрезок коаксиального кабеля длиной около
4,5 м.
24 Как мы увидим в разделе 9S.5, это происходит потому,
что эквивалентный выходной импеданс схемы является
выходным импедансом самой микросхемы, разделенным
на величину 1 + АВ, а величина А (коэффициент усиления)
уменьшается с повышением частоты со скоростью 1/£
В готовящейся к выпуску книге «АоЕ - the x-Chapters» этот
аспект подвергается всестороннему рассмотрению, с при-
влечением осциллограмм для демонстрации, что выходной
импеданс операционного усилителя в действительности
является индуктивным, вплоть до разницы фаз между то-
ком и напряжением. В своей книге «Troubleshooting Analog
Circuits» («Поиск неисправностей в аналоговых схемах»),
Боб Пиз (Bob Pease) советует не полагать, что выход опе-
рационного усилителя является просто резистивным.
Рис. 9N.16. Подключение длинного коаксиального кабеля
к выходу операционного усилителя может вызвать автоко-
лебания
По этим осциллограммам можно видеть, ка-
кими странными и причудливыми могут быть
такие колебания: прямоугольный сигнал не
вводит схему в постоянный режим автоколе-
баний, а вызывает их только иногда. В этом
аспекте прямоугольный сигнал является са-
мым проблематичным, поскольку его фронты
содержат стимулирующую составляющую в
широком частотном диапазоне. Но на осцил-
лограммах на рис. 9N.16 прямоугольный
сигнал вызывает автоколебания только для
сигналов, уровень которых ниже потенциа-
ла «земли». По-видимому, выходной импе-
данс схемы различен для участков сигнала
выше и ниже потенциала «земли», которые
создаются разными транзисторами выходно-
го двухтактного каскада. Из правой осцилло-
граммы на рис. 9N.16 можно видеть, что даже
Рис. 9N.17. Сначала синусоидальный сигнал не вызывает ав-
токолебаний, а потом они могут возникнуть
9N.5. Решения для стабилизации работы операционных усилителей
393
отрицательные перепады не всегда вызывают
автоколебания.
Синусоидальный сигнал менее проблематич-
ный, и с ним автоколебания могут и не возни-
кать. Слева на осциллограмме на рис. 9N.17 он
вроде бы обрабатывается без проблем.
Но на полпути развертки мы смогли создать ав-
токолебания, просто нажав кнопку диапазонов
генератора сигналов: этого кратковременного
прерывания сигнала было достаточно, чтобы
схема «сошла с рельсов». Из всего этого можно
сделать вывод, что емкостная нагрузка схем на
операционных усилителях чревата опасностью
появления автоколебаний. Нам нужны реше-
ния для устранения этой проблемы.
выходного сигнала колебания в нем поддержи-
ваются вплоть до тех пор, пока обратно на вход
подается не менее 1/3 части выходного сигна-
ла. Ослабление подаваемого в цепь обратной
связи сигнала при данном усилении выходного
сигнала подавит автоколебания.
В результате повышения усиления сигнала, по-
даваемого в кабель, назад непременно посту-
пит меньше, поскольку усиление определяется
как 1/В, где В соответствует подаваемой назад
части сигнала. На рис. 9N.18 показаны осцил-
лограммы эффекта подачи обратно все умень-
шающейся доли выходного сигнала. К тому
времени, когда назад на вход подается лишь
1/5 часть (при общем усилении, равном 5), схе-
ма полностью стабильна26.
Рис. 9N.18. Операционный усилитель с емкостной нагрузкой можно стабилизировать, подавая обратно на вход меньшую
часть выходного сигнала, увеличив для этого усиление
Решение 1. Уменьшение величины
обратной связи
Одно из таких решений на первый взгляд не-
логично: подавать сигнал на кабель не из по-
вторителя, а через усилитель25. Усилим сигнал,
скажем, раз в пять, и, может быть, схема успо-
коится.
Изначально такое решение может вызвать про-
тест, что усиление как раз и является причи-
ной автоколебаний. Да, это верно. Но только
в случае усиления сигнала, подаваемого назад
через контур обратной связи. Эта ситуация
хорошо иллюстрируется генератором колеба-
ний на мосте Вина: при трехкратном усилении
25 См. АоЕ, рис. 4.102.
26 В случае если вас интересует факт «индуктивного» по-
ведения выхода операционных усилителей, то вам может
понравиться другое описание эффекта подачи назад мень-
шей доли, т. е. переход от повторителя к усилителю. Пода-
ча назад меньшей доли выходного сигнала (т. е. уменьше-
ние В) повышает выходной импеданс схемы с включенной
обратной связью, увеличивая значение мнимой «индук-
тивности». Это изменение вызывает снижение резонанс-
ной частоты в (V2 х отношение значений мнимых L) раз.
Само по себе это изменение было бы дестабилизирующим.
Но в то же самое время противоположный, стабилизирую-
щий, эффект перевешивает. Подача обратно на вход мень-
шей части сигнала понижает частоту единичного усиления
пропорционально величине уменьшения подаваемой назад
части - перевешивая, или опережая, скорость падения ре-
зонансной частоты. Все это хорошо объясняется (включая
полезные графики) в готовящейся к изданию книге АоЕ,
the x-Chapters в материалах по операционным усилите-
лям, которая планируется к изданию в 2019 г. (На момент
перевода данная книга еще отсутствовала в продаже. -
Примеч. пер.)
394
9N. Операционные усилители IV: паразитные колебания и активный фильтр
Эти осциллограммы показывают, что суще-
ствуют разные уровни стабильности, а не про-
сто резкая граница между нестабильностью
и стабильностью. На второй осциллограм-
ме на рис. 9N.18, где коэффициент усиления
чуть-чуть больше единицы, колебания воз-
никают, но не удерживаются. Но и эти зату-
хающие колебания скорее всего были бы до-
статочно проблематичными и от них нужно
избавиться.
Мы встретимся с этой идеей уровней стабиль-
ности еще при других обстоятельствах. Во-
первых, в задаче коррекции операционного
усилителя (рассматриваемой в разделе 9S.1),
где запас по фазе описывает, насколько близ-
ко операционный усилитель приближается к
предельной точке — сдвигу фазы на 180°. А во-
вторых, в ПИД-петле (рассматривается на ла-
бораторном занятии 10L), где мы снова сможем
подкорректировать усиление нашего самодель-
ного операционного усилителя, чтобы поиграть
с такой нестабильностью.
Решение 2. Вынос сдвигаемой
по фазе точки за пределы контура
обратной связи
Проблему длинного кабеля можно очень просто
решить с помощью последовательного резисто-
ра сопротивлением около 100 Ом (рис. 9N.19).
100 0м
Кабель
не сдвигает по
сразе сигнал в точке
обратной
Рис. 9N.19. Простое решение проблемы длинного кабеля:
подключение последовательного резистора
Емкость кабеля продолжает создавать фазо-
вый сдвиг, который, более того, становится
еще больше. Но точка в схеме, где создается
бблыная часть этого нежелательного фазово-
го сдвига, теперь находится вне контура об-
ратной связи. Но за все приходится платить,
и мы расплачиваемся за повышение стабиль-
ности схемы ухудшением ее выходного им-
педанса из-за добавления последовательного
резистора.
Решение 3. Усовершенствованное
решение проблемы длинного кабеля:
разделенная обратная связь
Добавив в схему несколько дополнительных
элементов, можно получить стабильность од-
новременно с хорошим выходным импедансом
на низких частотах, как и у исходной схемы с
повторителем. Это модифицированное реше-
ние проблемы длинного кабеля, разделяющее
путь обратной связи (рис. 9N.20)27.
100 Ом
Установите значительно
ниже частоты паразитных
колебаний (скажем, на 50 кГц)]
«разделение» на «50 кГц
Рис. 9N.20. Усовершенствованное решение проблемы длин-
ного кабеля: разделенная обратная связь
Установите частоту перехода — частоту, на ко-
торой большая часть сигнала проходит через
конденсатор, обходя фазосдвигающий кон-
тур — на безопасном расстоянии ниже частоты
возникновения автоколебаний в схеме.
Такая частота может показаться слишком вы-
сокой для, например, аудиосигнала. Но обра-
тите внимание на то, что частоту перехода не
следует делать более низкой, чем необходимо.
Положительные свойства обратной связи на-
рушаются на этой частоте. Например, слишком
низкая частота перехода отрицательно скажет-
ся на коррекции искажения сигнала двухтакт-
ным каскадом. Низкая частота перехода также
ухудшит сигнал операционного усилителя, не-
обходимый для компенсации эффектов двух-
тактного каскада. Вспомним, как в разделе 6N.9
операционный усилитель исправлял переход-
ные искажения, поддерживая уровень выход-
ного сигнала выше или ниже |0,6 В|.
Понятие разделенной обратной связи очень
важное28. Мы воспользуемся им в схеме двух-
тактного драйвера в конце лабораторного за-
нятия 9L и в схеме ПИД-драйвера электродви-
гателя на лабораторном занятии 10L29.
27 См. АоЕ, рис. 4.76.
28 Опять же, см. АоЕ, раздел 4.6.2.
29 Существуют также и другие, более тонкие решения. Неко-
торые из них подробно рассматриваются Бобом Пизом (Bob
Pease) в примечании по применению Linear Brief, опублико-
ванном в журнале «National Semiconductor LB-42», а также
более кратко в его книге «Troubleshooting Analog Circuits».
9N.6. Общий критерий стабильности: петлевое усиление, когда фазовый сдвиг приближается к 180° 395
Еще одно решение проблемы длинного
кабеля: использование специальной
микросхемы-драйвера
Некоторые повторители разрабатываются
специально для работы с тяжелыми емкост-
ными нагрузками, например микросхема
AD817 компании Analog Devices или микро-
схема LM8271/2 компании Texas Instruments/
National. Устройства такого типа просто за-
медляют работу при подключении тяжелой ем-
костной нагрузки: величина «компенсирующе-
го» конденсатора, который снижает усиление
на высоких частотах, фактически повышается
емкостью нагрузки30. Таким образом, схема яв-
ляется самостабилизирующейся.
Это решение может выглядеть привлекатель-
ным, но когда вам срочно требуется стабили-
зировать схему, добавление последовательного
резистора может быть предпочтительней ожи-
данию от одного дня до нескольких недель, ко-
торые может занять доставка такой специали-
зированной микросхемы.
9INL6. Общий критерий
стабильности: петлевое
усиление, когда фазовый
сдвиг приближается к 180°
Термин «петлевое усиление» описывает общее
усиление сигнала при прохождении через пет-
лю обратной связи: через микросхему усили-
теля (это усиление обозначается А), а затем
через цепь обратной связи (усиление которой
в действительности часто является ослаблени-
ем и обозначается В)31. Таким образом, общее
усиление сигнала после полного прохождения
петли равно АВ. В большинстве случаев мы
хотим добиться высокого петлевого усиления.
Именно высокое петлевое усиление является
тем фактором, который обусловливает досто-
инства схем с обратной связью: постоянство
усиления, низкий выходной импеданс и т. п. Но
оно также является и фактором, делающим схе-
мы на операционных усилителях уязвимыми к
паразитным автоколебаниям (рис. 9N.21).
Чтобы схема оставалась стабильной, необходи-
мо, чтобы петлевое усиление АВ было меньше
единицы на частоте, при которой значение фа-
зового сдвига достигает предельных 180°.
Предположим, что шум присутствует на всех
частотах и вносит искажения Д[/вх на входе
схемы. Эти искажения усиливаются, создавая
искажение ДС/ВЫХ на выходе, которое в А раз
больше входного. Затем определенная часть
Д[/вых подается обратно на вход. Поскольку на
вход поступает часть В сигнала, то на выходе
цепи обратной связи получается АВД[/ВХ. Если
на частоте, при которой фазовый сдвиг состав-
ляет 180°, величина этого подаваемого обратно
сигнала такая же или больше, чем исходного
сигнала, то в схеме возникают паразитные ав-
токолебания. Иными словами, АВ ^ 1 при сдви-
ге -180° вызывает паразитные автоколебания.
Исходя из этого, можно предложить следую-
щие пути решения данной проблемы:
♦ ограничить величину А;
♦ ограничить величину В;
♦ ограничить величину как А, так и В.
Усиление А без обратной связи
Проблема:
На определенной (высокой) частоте
фазовые сдвиги складываются,
в результате чего ДUmx начинает
СОВПАДАТЬ ПО ФАЗЕ с сигналом,
подаваемым на инвертирующий (-) вход.
Рис. 9N.21. Обобщенные условия стабильности
ЛА^ должно быть <1 на частоте,
создающей фазовый сдвиг величиной 180°
делитель обратной связи:
подает обратно на вход часть В
30 Это понятие рассматривается более подробно в разде-
ле 9S.1.
31 АоЕ § 4.9.1А.
396
9Л/. Операционные усилители IV: паразитные колебания и активный фильтр
Нескорректированный Все еи*е слишком
большое усиление на
частоте, создающей
опасный фазовый сдвиг
...усиление меньше единичного,
при котором фазовый сдвиг
представляет опасность
Частота
(логарифмическая шкала)
Рис. 9N.22. Кривые усиления скорректированного и нескорректированного по частоте операционных усилителей
В любом случае нам нужно ограничить произ-
ведение АВ. Рассмотрим по отдельности спосо-
бы ограничения величины А, а затем В.
Ограничение величины А: частотная
коррекция
На рис. 9N.22 изображены кривые усиления
для скорректированного и нескорректирован-
ного усилителей. Как можно видеть, на частоте
фазового сдвига величиной 180° усиление не-
скорректированного усилителя слишком боль-
шое. Таким образом, нескорректированный
операционный усилитель, включенный по схе-
ме повторителя (В = 1), будет создавать пара-
зитные автоколебания32.
Стабильность скорректированного усилите-
ля достигается посредством создания упре-
ждающего преднамеренного спада усиления
с повышением частоты сигнала. Его усиление
скорректировано таким образом, чтобы оно
становилось меньше единичного, прежде чем
частота сигнала повысится до значения, при
котором возникает предельный фазовый сдвиг.
Вопрос коррекции операционных усилите-
лей рассматривается более подробно в раз-
деле 9S.1. На лабораторном занятии 10L мы
узнаем, что можно настраивать и другие па-
раметры, а не только спад усиления А; в част-
ности, можно даже изменять его смещение
фазы.
Ограничение величины В
Этот подход мы рассмотрели довольно подроб-
но в подразделе «Решение 1. Уменьшить величи-
ну обратной связи» раздела 9N.5.2.
32 АоЕ§4.9.
Вывод: ограничить величину петлевого
усиления АВ
Для стабильной работы схемы необходимо под-
держивать петлевое усиление ниже единичного
на частотах, на которых создается проблема-
тичный фазовый сдвиг. На рис. 9N.23 показан
график кривой усиления операционного уси-
лителя, напоминающий нам отличие петлевого
усиления от усиления схемы.
График на рис. 9N.23 повторяет концепцию,
графически иллюстрируемую на рис. 9N.21, на
котором перечисляются необходимые условия
для возникновения паразитных автоколеба-
ний. Решающим фактором стабильности или
нестабильности схемы является значение АВ на
частоте, создающей проблематичный фазовый
сдвиг. Большое значение АВ может служить по-
водом для беспокойства.
Но величина АВ также определяет действен-
ность обратной связи; в частности, она опре-
деляет способность операционного усилите-
ля улучшить рабочие характеристики схемы.
В разделе 9S.5 мы рассмотрим более подробно
зависимость петлевого усиления как от конфи-
гурации схемы, так и от характеристик микро-
схемы. Иными словами, его зависимость как от
В, так и от А.
Скорее всего вам приходилось быть в такой
ситуации, когда нужно пожертвовать одним
(в нашем случае стабильностью схемы), чтобы
получить что-то другое (в нашем случае улуч-
шенные рабочие характеристики посредством
применения обратной связи). Например, в уси-
лителях с общим эмиттером на дискретных
компонентах мы могли обменять величину
усиления на его линейность. В данном случае
из двух интересующих нас свойств стабиль-
ность является более важной. Имея эту самую
важную цель в уме, мы должны поддерживать
9N.7. Паразитные автоколебания в схемах без операционного усилителя
397
§
о
I
100 дБ
80 дБ
3 60 дБ
.| 40 дБ
f 20 дБ
ОдБ
«Петлевое
-. усиление», А В
Усиление с замкнутой А
_ цепью обратной связи
(усиление схемы):
. 1000 / (= 1/В)
(В = 1/1000)
А»
Нескорректированный
Л £ уменьшается до единицы
Частота
(логарифмическая шкала)
.-270° -
до возникновения
проблематичного фазового сдвига
Рис. 9N.23. Петлевое усиление АВ определяет стабильность обратной связи, а также ее достоинства. (Показан график для не-
скорректированного усилителя, который едва сохраняет стабильность при усилении величиной 1000.)
усиление АВ на безопасно низком уровне, удо-
влетворяясь остальными рабочими характери-
стиками, какие получатся в результате решения
главной задачи.
9N.7. Паразитные
автоколебания в схемах
без операционного
усилителя
Несомненно, в этой схеме
возникновение автоколебаний
невозможно
Нежелательная обратная связь не обязательно
должна быть явной, как в схемах на операци-
онных усилителях. Для примера на рис. 9N.24
изображена схема, в которой паразитные коле-
бания обусловлены неявными причинами. На
первый взгляд эту схему можно было бы при-
числить к разряду схем с самой низкой веро-
ятностью возникновения паразитных автоко-
лебаний. Она выглядит полностью лишенной
всех необходимых условий для этого: ни усиле-
ния по напряжению, ни какой бы то ни было
обратной связи. Вроде бы никаких сомнений в
том, что эта схема не в силах создавать автоко-
лебания33.
Ш)1 мкФ до ОД мкФ)
Рис. 9N.24. Эмиттерный повторитель как генератор коле-
баний
Тем не менее они возникают
В схеме все же возникают автоколебания,
причем на достаточно высокой частоте, по-
этому мы используем ее для глушения пере-
дач (рис. 9N.25). ЧМ-радиостанций в нашей
лаборатории, просто чтобы убедить всех в том,
что паразитные автоколебания действительно
могут создавать проблемы. В частности, этот
vwwwwi
*94,5 МГц
5В
33 Лабораторное занятие 9L.
94,5 МГц
Рис. 9N.25. Помеха на частоте 94,5 МГц (установка осцилло-
графа 5В/деление, 10 не/деление)
398
9Л/. Операционные усилители IV: паразитные колебания и активный фильтр
паразитный сигнал полностью глушит в нашей
лаборатории ЧМ-радиостанцию, ведущую пе-
редачу на частоте 94,5 МГц. (Мы надеемся, что
глушение не выходит за пределы нашего лабо-
раторного помещения.)
Признаки паразитных автоколебаний
Вполне возможно, что некоторые ваши схе-
мы могут генерировать колебания, когда вы
не наблюдаете за ней с помощью осцилло-
графа. Какие признаки могут указывать на
присутствие паразитных колебаний? Без дол-
гих размышлений на ум приходят два возмож-
ных признака.
♦ Первый признак. Если вам повезет, вы мо-
жете слушать в это время ЧМ-радиостанцию
и заметите помехи с приемом. Но вряд ли
вам так повезет.
♦ Второй признак. В данном случае прояв-
ляется при проверке напряжения на выходе
схемы в виде неправдоподобных значений,
как демонстрируется на рис. 9N.26.
+15 В
Рис. 9N.26. Неправдоподобные значения постоянного на-
пряжения могут свидетельствовать о наличии паразитных
автоколебаний
Напряжение на эмиттере более положительное,
чем на базе? Похоже, что да. Но это неправ-
доподобные значения: автоколебания ввели
мультиметр в заблуждение, когда он случайно
выпрямил часть высокочастотного синусои-
дального сигнала.
Однако в реальных условиях обнаружение
любого из этих признаков маловероятно.
Подтверждением тому может служить расска-
зываемая Бобом Пизом (Bob Pease) история о
паразитных автоколебаниях, создаваемых точ-
но такой же схемой, которые не были обнаруже-
ны до тех пор, пока содержащий эту схему ком-
пьютер не прошел проверку по радиочастотным
помехам, проводимую Федеральной комиссией
по связи (США). См. примечание 37 в конце
этого раздела.
Но как может эта схема генерировать колеба-
ния? Чтобы ответить на этот вопрос, необхо-
димо дать ответ на два вспомогательных во-
проса:
♦ Каким образом схема обеспечивает усиление
по напряжению (чтобы не дать колебаниям
затухнуть)?
♦ Каким образом в схеме возникает положи-
тельная обратная связь?
Ответы на эти вопросы выявляются, если при-
нять во внимание несовершенства схемы. В то
время как идеальный эмиттерный повторитель
не может создавать паразитные автоколебания,
реальный вполне способен на это.
♦ Усиление выявляется, если на схеме явно
отобразить индуктивность34, которая всегда
неявно присутствует в источнике питания, а
также паразитную емкость (рис. 9N.27).
+15
Неидеальный J
источник питания!
Положительная
обратная связь
Рис. 9N.27. Перерисованная схема эмиттерного повторите-
ля, отображающая индуктивность и обратную связь, кото-
рые могут обеспечивать усиление по напряжению
Когда вы будете собирать эту схему на ла-
бораторном занятии 9L.2, мы настоятельно
рекомендуем использовать чрезвычайно
длинный провод для подачи питания, чтобы
преувеличить паразитную индуктивность,
которая присутствует даже в собранных по
всем правилам схемах. Вы можете подтвер-
дить, что шина питания выглядит подоб-
но резонансному контуру (состоящему из
34 Какова приблизительная величина этой индуктивно-
сти? Возможно, 500 нГн/м, хотя значение зависит от рас-
стояния до других проводников.
9N.8. Решения для проблемы паразитных автоколебаний
399
параллельно соединенных индуктивности
и емкости) и похожа на LC-контур, кото-
рый вы собрали на лабораторном занятии
3L. Для этого поднесите руку близко к про-
воду питания или даже возьмите его в руку.
Частота паразитных автоколебаний поме-
няется вследствие изменения паразитной
емкости, которая теперь увеличена вашей
рукой.
♦ Обратную связь можно выявить, если заме-
тить35, что изменение сигнала в линии пи-
тания, которое здесь подается на коллектор,
может вызвать изменение в сигнале на эмит-
тере (через емкость «коллектор-эмиттер»),
которое увеличит изменение тока коллекто-
ра. Иными словами, здесь мы имеем поло-
жительную обратную связь36.
Перерисованная схема почти идентична схеме
источника тока, автоколебания в котором объ-
ясняются в книге АоЕ. Там эта схема уподобля-
ется схеме настоящего генератора колебаний,
называющегося LC-генератором Хартли.
Для большинства из нас будет достаточно из-
учить несколько эмпирических правил для
прекращения возникающих паразитных авто-
колебаний. Создать подробную модель схемы,
включая паразитные индуктивность и емкость
нелегко. Но еще одна версия электронного за-
кона подлости гласит, что если схема может
найти частоту, на которой она способна генери-
ровать паразитные автоколебания, она найдет
эту частоту и будет генерировать паразитные
автоколебания, вызывая чрезвычайное раздра-
жение у своего разработчика37.
35 В данном случае имеется в виду заметить концептуаль-
но, поскольку эти подробности нельзя будет наблюдать на
осциллографе. Подключение щупа осциллографа к кол-
лектору почти наверняка остановит автоколебания, как
отмечается далее в разделе 9N.8.1.
36 Сравните с АоЕ § 7.1.5D, особенно рис. 7.30.
37 Эта схема не просто придумана для демонстрационных
целей. Она в действительности причинила много неприят-
ностей инженерам, которые использовали ее для подачи
сигнала сброса на выпускаемые одним предприятием ком-
пьютеры. Компьютеры затем не смогли пройти проверку
Федеральной комиссии связи (США) на соответствие тре-
бованиям по радиочастотным помехам, поскольку каж-
дый из этих компьютеров содержал небольшой непред-
намеренный радиопередатчик. См. книгу «Troubleshooting
Analog Circuits» («Поиск неисправностей в аналоговых
схемах»), автор Robert Pease (Роберт Пиз), ст. 109, изда-
тельство Newness (1991).
9N.8. Решения
для проблемы паразитных
автоколебаний
9IM8.1. Первое решение:
зашунтировать источник питания
(уменьшить обратную связь)
Иногда предотвратить возникновение паразит-
ных автоколебаний можно, зашунтировав цепь
коллектора; это уменьшит величину наводок
на нем. На ум приходят два очевидных способа
сделать это:
♦ укоротите шину питания (+15 В). Это умень-
шит индуктивность шины и задаст такую
высокую резонансную частоту, при которой
у транзистора не будет достаточного усиле-
ния;
♦ подключите к коллектору шунтирующий
керамический конденсатор небольшой ем-
кости.
В действительности паразитные колебания
имеют свойство быть на удивление нестойки-
ми, но это свойство может сделать их более
проблематичными. Вы можете подозревать ко-
лебания на коллекторе и подключаете к нему
щуп осциллографа, чтобы проверить, дей-
ствительно ли они там есть. Нет, никаких ко-
лебаний на коллекторе не обнаруживается. Но
сама проверка (т. е. подключение на «землю»
емкости щупа величиной 10 пФ) могла сорвать
автоколебания, но конечно же, только на вре-
мя проверки. Более надежный способ — под-
соединить к щупу короткий отрезок провода,
а затем поводить им над схемой на расстоянии
около одного или двух сантиметров, чтобы об-
наружить автоколебания, не останавливая их.
Действительно, черная магия, да и только.
9N.8.2. Другое решение: подавить
усиление на высоких частотах
Даже если вам не удастся избавить свою схему
от некоторых подаваемых обратно на вход па-
разитных сигналов, которые могли бы вызвать
автоколебания, такие колебания не возникнут
при недостаточном усилении схемы. Таким об-
разом, сигнал может содержать немного крат-
ковременных выбросов, но не устойчивые
400
9Л/. Операционные усилители IV: паразитные колебания и активный фильтр
автоколебания. В схеме эмиттерного повтори-
теля этот эффект создается с помощью резисто-
ра, подключенного к базе, который уменьшает
усиление схемы на высоких частотах, где в про-
тивном случае могли бы возникать автоколе-
бания.
Объяснение решения подключением^-
резистора в цепь базы
Для этого объяснения перерисуем схему в виде
усилителя с общей базой. На рис. 9N.28 изо-
бражена такая схема, в которой транзистор
рассматривается как усилитель с общей базой с
подачей управляющего сигнала на эмиттер.
£Б: очень малое сопротивление,
пока не подключим R = 270 Ом
Рис. 9N.28. Схема эмиттерного повторителя, перерисован-
ная в виде усилителя с общей базой
Скорее всего вам раньше не приходилось ви-
деть усилитель, на который сигнал управления
подается таким образом.
Замечание
Разве что мимоходом в книге АоЕ, где приводит-
ся схема для устранения эффекта Миллера в виде
усилителя с общей базой, подключенной на «зем-
лю». См. книгу АоЕ, рис. 2.84С.
В данном случае, как можно судить по схеме,
изображенной на рис. 9N.28, мы хотим полу-
чить эффект, противоположный тому, который
создается той схемой: мы хотим подавить уси-
ление на высоких частотах. Усиление схемы с
общей базой определяется по следующей фор-
муле:
Дс[или Zc]
Усиление = .
гэ+[ (сопротивление, подающее
сигнал на базу)/(1+|3)]
Для нашего случая, где база управляется (или
поддерживается на постоянном уровне) мощ-
ным источником напряжения, знаменатель
дроби равен просто малому г. Но мы можем
ослабить усиление таким же способом, как и
для усилителя с общим эмиттером: подключив
резистор, который увеличивает значение зна-
менателя в формуле усиления. В данном слу-
чае мы подключим резистор последовательно
в цепь базы. В случае с усилителем с общим
эмиттером такое же снижение усиления дости-
гается включением резистора последовательно
в цепь эмиттера
38
Эффект Миллера как еще одно
объяснение решения подключением
резистора на базу
Результат, обеспечиваемый резистором, под-
ключаемым к базе, можно объяснить еще од-
ним способом: эффектом Миллера. Несмотря
на то что мы едва упомянули эффект Миллера
в этой книге, вы можете найти это объяснение
более доходчивым. На рис. 9N.29 изображена
схема нашего эмиттерного повторителя, в кото-
рую были добавлены два соревнующихся меж-
ду собой пути обратной связи: СКБ и С^. Как мы
знаем, путь Скэ образует цепь положительной
обратной связи; а путь СКБ — отрицательной об-
ратной связи, смещая напряжение на базе. Эта
вторая обратная связь, которая уменьшает уси-
ление инвертирующего усилителя на высоких
частотах, и называется эффектом Миллера.
Какова должна быть величина отрицательной
обратной связи? Величину части колебаний
на коллекторе, которая подается обратно, за-
дает делитель напряжения, состоящий из СКБ и
#ТЕВ, подающего управляющий сигнал на базу.
Повысив значение этого сопротивления от нуля
до 270 Ом, мы значительно увеличим величину
отрицательной обратной связи. Таким обра-
зом, в соревновании между двумя типами об-
ратной связи мы создадим лучшие условия для
полезной, т. е. отрицательной, обратной связи,
что должно остановить автоколебания.
Решения
Таким образом, решения, по большому счету,
такие же, как и для предотвращения автоколе-
баний в операционных усилителях:
♦ уменьшить величину подаваемого назад па-
разитного сигнала;
♦ уменьшить усиление схемы на высоких ча-
стотах.
38 АоЕ § 2.4.4В.
9N.9. Подведение итогов по вопросу стабилизации схем
401
Отрицательная обратная связь
'Вспомните эффект Миллера'
15 В
f —
^J [Полезная обратная связь]
270 Ом
-vw—
Паразитные L и С шиньГ4
В источника питания
^Положительная обратная
...благодаря резистору номиналом 270 Ом
отрицательная обратная связь (с коллектора)
теперь может воздействовать на базуJ
[Вредная обратная связь]
/Примечание. Не подключайте этот конденсате
к базе при добавлении резистора номиналом
270 Ом, так как он нивелирует эффект от
^подключения этого резистора
Рис. 9N.29. Соревнующиеся пути обратной связи: стабилизация против дестабилизации
9N.9. Подведение итогов
по вопросу стабилизации
схем
Некоторые методы, которые могут предотвра-
тить возникновение паразитных автоколеба-
ний, очевидны, тогда как другие нет. К очевид-
ным методам можно отнести следующие:
♦ делайте провода/дорожки питания коротки-
ми и толстыми/широкими, чтобы свести их
паразитную индуктивность к минимуму;
♦ выполняйте развязку источников питания
(обычная практика).
А к менее очевидным методам можно отнести
следующие:
♦ в любом эмиттерном повторителе на дис-
кретных компонентах подавайте сигнал на
базу через резистор;
♦ в схемах с проблематичной нагрузкой (т. е.
с нагрузкой, которая может вызвать значи-
тельную фазовую задержку) разделяйте пути
обратной связи (см. Решение 3 на стр. 394).
На лабораторном занятии 10L мы возвра-
тимся к вопросам стабильности и попробуем
применить еще одно решение: мы попытаемся
разработать что-то типа специализированно-
го операционного усилителя, который сможет
устранить некоторые проблематичные фазо-
вые задержки.
Не забывайте, что паразитные автоколебания
всегда будут таиться «на задворках», создавая
угрозу для ваших схем. Будучи хорошо подго-
товленными, вы сможете лучше предотвратить
или устранить их.
9N.10. Материал для чтения
вАоЕ
Чтение
♦ Глава 7:
• раздел 7.1.5Е: паразитные автоколебания.
♦ Глава 4:
• раздел 4.9: частотная коррекция операци-
онных усилителей;
• раздел 4.5.7: дифференциаторы;
• раздел 4.6.2: емкостные нагрузки.
9L Лабораторное занятие:
операционные усилители IV
На этом лабораторном занятии мы сначала рас-
смотрим одно полезное применение положи-
тельной обратной связи — активный фильтр, а
затем посвятим оставшуюся большую часть за-
нятия схемам, которые создают автоколебания
тогда, когда это нежелательно. На этом лабора-
торном занятии мы хотим, чтобы вы увидели
паразитные колебания и убедились в актуаль-
ности данной проблемы. В обычной ситуации
автоколебания, которые могут возникать в
таких схемах, будут представлять проблему,
которую потребуется устранить. Некоторые
из вас, возможно, уже встречались с этими так
называемыми паразитными колебаниями на
предыдущих лабораторных занятиях, так что
вы уже знаете об их нежелательных эффектах.
В рассматриваемых далее упражнениях мы сна-
чала будем пытаться вызвать автоколебания, а
затем найти решения, чтобы предотвратить их
возникновение.
Если какая-либо область электроники заслужи-
вает определения «искусство», то укрощение
нежелательных автоколебаний как раз и есть
эта область. Испытывая некоторую тревогу, мы
приглашаем вас попытаться вызвать эти вред-
ные колебания. В главе 9N мы приводили закон
подлости применительно к электронике, суть
которого сводится к тому, что паразитные ав-
токолебания возникают не в генераторах коле-
баний, а в усилителях. Поскольку исследуемые
на этом лабораторном занятии схемы являются
усилителями, а не генераторами колебаний, то,
вероятно, в них будут возникать паразитные
автоколебания.
9L1. Активный VCVS-фильтр
Соберите два варианта двухполюсного филь-
тра: простой каскад из двух пассивных RC-
фильтров (рис. 9L.1, а) и активный НЧ-фильтр
(рис. 9L.1, б). Оба фильтра имеют одинаковую
частоту/^1.
Сопротивление резистора Rv активного филь-
тра лучше подбирать с помощью магазина со-
противлений, если он у вас есть. В отличие от
потенциометра, магазин сопротивлений позво-
ляет узнать величину установленного сопро-
тивления.
8,2 кОм 82 кОм Выходной сигнал
(пассивный срильтр)
>ДмкФ[0,(Ю1мкФ
15 кОм15 кОм
Входной
сигнал
~Р,01мкф|
0,01 мкФ
Выходной
сигнал
Рис. 9L.1. Схемы двухкаскадного пассивного и активного
VCVS-фильтра для сравнения
Установите для резистора Ry сопротивление
2,2 кОм, чтобы получить частотную характе-
ристику с наиболее равномерной вершиной
(фильтр Баттерворта). Удостоверьтесь в том,
что обе схемы ведут себя как НЧ-фильтр, из-
мерьте частоту y^i; для каждого из них, а так-
же приблизительное ослабление на частотах
2/здз и 4/здБ. Будем надеяться, что ваши филь-
тры будут иметь крутизну спада величиной
-12 дБ/октаву, которая характерна для двухпо-
люсного фильтра, хотя такая крутизна не будет
1 На первый взгляд может показаться, что частота f3aE
этих фильтров должна быть разной, поскольку они име-
ют различные параметры ЯС-цепей: 2 кГц — пассивный и
1 кГц — активный. Это действительно так — значения RC
этих фильтров разные. Но только для активного фильтра
частота ^= l/(2itRC), а два элемента пассивного филь-
тра имеют одинаковое значение RC. Но частота/^ всего
пассивного фильтра равна половине частоты/3дБ каждого
каскада, поскольку каждый каскад пассивного фильтра
вносит затухание величиной 3 дБ, а весь фильтр обеспечи-
вает затухание 6 дБ.
9U. Активный VCVS-фильтр
403
полностью наблюдаться в первой октаве выше
частоты £ к.
Также будем надеяться, что вы обнаружите, что
простой пассивный двухкаскадный ДС-фильтр
уступает активному фильтру. Но оба фильтра
должны иметь одинаковую частоту^дБ.
9L1.1. Подайте на оба фильтра
качающуюся частоту
Предположительно, вы подавали общий сигнал
на оба фильтра, изменяли частоту сигнала вруч-
ную и наблюдали выходные сигналы фильтров
на осциллографе. Для наглядной демонстра-
ции частотных характеристик обоих фильтров
следует изменять частоту входного сигнала ав-
томатически. Функцию качающейся частоты
генератора сигналов мы уже использовали и
раньше, но теперь это нужно будет делать не-
сколько иначе, чем ранее.
На этот раз мы не можем применить X-Y-
режим отображения осциллографа. Вместо
этого нужно установить обычную развертку
(что позволяет наблюдать на осциллографе не
один сигнал, а два), а сигнал запуска развертки
подавать на осциллограф с выхода RAMP гене-
ратора сигналов (используя при этом задний
фронт сигнала развертки).
9L1.2. Регулировка величины
положительной обратной
связи для изменения частотных
характеристик фильтра
В эксперименте с подачей на активный фильтр
сигнала качающейся частоты попробуйте из-
менить его частотные характеристики, регу-
лируя величину сопротивления резистора Rv.
Поскольку в результате изменения величины
Ry будет меняться не только частотная харак-
теристика схемы, но и амплитуда выходного
сигнала, при каждом изменении Ry нужно бу-
дет также откорректировать величину усиле-
ния осциллографа. Желательно, чтобы раз-
меры осциллограмм для активного и пассив-
ного фильтров были сравнимыми, поскольку
осциллограмма пассивного фильтра представ-
ляет собой удобный эталон, по сравнению с
которым можно судить о реакции активного
фильтра. Значения резисторов вашего мага-
зина сопротивлений могут отличаться от зна-
чений, указанных в табл. 9N.1 (которые были
выбраны с помощью табл. 6.2 раздела 6.3.2 из
книги АоЕ). В таком случае установите наибо-
лее близкие значения. Для справки в скобках
указаны еще более точные желаемые значения
резисторов.
Таблица 9N.1. Параметры активного фильтра
Тип фильтра
Наилучшее время задержки
(фильтр Бесселя)
Самая равномерная харак-
теристика в пределах по-
лосы пропускания (фильтр
Баттерворта)
Самая лучшая крутизна
(фильтр Чебышева)
Плохая характеристика
Генератор колебаний!
1кОм
2,2 кОм
(2,3 кОм)
4,7 кОм
(4,3 кОм)
6,8 кОм
ЮкОм
Усиление
1,3
1,6
2,1
Почти 3
3,5
Последние два случая, в которых величина по-
ложительной обратной связи преднамеренно
завышена, не имеют смысла для разработки на-
стоящих фильтров, но могут быть полезными
для целей сегодняшнего лабораторного заня-
тия. Они служат напоминанием о той границе,
к рассмотрению которой мы приступаем далее
на этом лабораторном занятии, за которой по-
ложительная обратная связь превращается из
полезной во вредную.
9L1.3. Реакция на ступенчатый
сигнал; искажение формы сигнала
Наблюдайте реакцию схемы на прямоуголь-
ный сигнал частотой 200 Гц, и особенно об-
ратите внимание на искажение отклика на сту-
пенчатое воздействие, которое увеличивается
с повышением коэффициента усиления схемы.
Если у вас есть желание, можете также прове-
рить утверждение, что фильтр Бесселя (с J?y =
= 1 кОм), который демонстрирует самую луч-
шую реакцию на ступенчатый сигнал, также
меньше всего искажает выходной сигнал. А вот
фильтр с R = 4,6 кОм должен продемонстриро-
вать наибольшее искажение. Попробуйте в ка-
честве теста подать на фильтры треугольный
сигнал. Контраст не будет особенно большим;
в нашем случае наблюдалось лишь небольшое
искажение для самого худшего фильтра.
404
9L Лабораторное занятие: операционные усилители IV
9L.2. Эмиттерный
повторитель на дискретных
элементах
Как такое может случиться, что в такой прове-
ренной и надежной схеме (рис. 9L.2) могут воз-
никать автоколебания?
+5 в
питания (т. е. при достаточно большой ее ин-
дуктивности) автоколебания должны непре-
менно возникнуть.
Рис. 9L.2. Эмиттерный повторитель как генератор коле-
баний
Чтобы ответить на этот вопрос, необходимо
дать ответ на два вспомогательных вопроса
(как мы это делали в разделе 9N.7).
♦ Каким образом схема создает усиление по
напряжению (чтобы не дать колебаниям за-
тухнуть)?
♦ Каким образом схема создает положитель-
ную обратную связь?
Ответы на эти вопросы основаны на том факте,
что источники питания не являются идеальны-
ми и обладают паразитной емкостью, которая
может создать условия для транзистора начать
вести «беседу» с самим собой (т. е. создать по-
ложительную обратную связь).
Соберите схему, подайте на нее питание через
отрезок провода длиной 7-45 см и исследуйте с
помощью осциллографа сигнал на эмиттере.
Примечание
Если попытаться наблюдать за сигналом на кол-
лекторе, емкость щупа, вероятно, сорвет автоко-
лебания.
Также проверьте, что происходит в точке под-
ключения резистора эмиттера к земле. (Для
этого потребуется заземлить щуп осциллогра-
фа на некотором расстоянии от этой точки.)
Если автоколебания в схеме отсутствуют, то по-
пробуйте ухудшить качество источника пита-
ния, удлинив положительную шину питания до
60 см. При достаточно плохом качестве шины
Решение проблемы
Будем надеяться, что вы смогли создать высо-
кочастотные колебания в собранной вами схе-
ме эмиттерного повторителя.
Примечание
В нашем случае мы наблюдали синусоидальные
колебания амплитудой около 2 В на частоте около
60 МГц. Укоротив провод положительного питания,
мы смогли повысить частоту до 100 МГц.
Теперь попробуйте устранить эти автоколеба-
ния, применяя рассмотренные в главе 9N ме-
тоды, краткое описание которых приводится
далее.
Зашунтируйте источник питания
Предотвратить возникновение паразитных ав-
токолебаний можно, стабилизировав коллек-
тор; это уменьшит паразитные наводки на нем
в смысле, изложенном в главе 9N. Это можно
сделать двумя следующими способами.
Укоротите провода питания
Этот подход достаточно тривиальный, и вы,
возможно, примете его действенность на веру,
даже перед тем, как применить его. Но умень-
шение длины проводов питания скорее всего
остановит автоколебания. В таком случае воз-
вратите на место длинный провод, чтобы вос-
становить их и испробовать другой подход.
Выполните развязку источника питания
Коллектор можно стабилизировать, зашун-
тировав его конденсатором на «землю». Этот
конденсатор как бы изолирует шину питания
от транзисторной схемы. Или, иными словами,
он представляет собой локальный источник
заряда. Когда через транзистор начинает течь
большой ток, этот бросок тока не подается че-
рез линии питания и, таким образом, не будет
вносить в них никаких помех. Требуемый до-
полнительный ток берется из конденсатора.
Попробуйте добавить в схему керамический
конденсатор емкостью около 0,01-0,1 мкФ.
Если это не поможет, обратитесь за справкой
к разделу 9S.3. В любом случае по завершении
9L3. Нестабильность операционных усилителей: фазовый сдвиг может вызывать автоколебания... 405
экспериментирования с конденсатором удалите
его. Нам нужно наличие автоколебаний, чтобы
попробовать более интересные решения для их
устранения, которые рассматриваются далее.
9L2.1. Уменьшите усиление
на высоких частотах
Убедившись в наличии паразитных автоколе-
баний, посмотрим, сможем ли мы остановить
их, снизив усиление эмиттерного повторите-
ля (который, в конце концов, не предназначен
быть усилителем) на высоких частотах.
Решение 1. Резистор в цепи базы
Вставьте между источником напряжения +5 В
и базш резистор сопротивлением в несколько
сотен ом. Но обязательно удалите развязываю-
щий конденсатор, который поддерживал на-
пряжение на базе на высоких частотах. Будем
надеяться, что это сорвет автоколебания. Если
же не остановит, попробуйте увеличить сопро-
тивление.
Эквивалентная схема
Частотная характеристика
полного сопротивления
(На высоких частотах
преобладает резистивная
составляющая)
1
X
ас
N
800
600
400
200
Я
/f \\
Ж %
10 100 1
1000
Частота (МГц)
Рис. 9L.3. Частотная характеристика ферритовой шайбы
BLMP21P компании Murata
Обычный монтажный провод 22-го калибра3
будет слишком толстым и не пройдет в от-
верстие в шайбе, поэтому следует выбрать бо-
лее тонкий провод, например 30-го калибра4.
Если через шайбу продеть две петли провода,
это увеличит эффективный импеданс в четыре
раза5. На рис. 9L.4 показана ферритовая шайба
с продетой через нее проволочной петлей.
Решение 2. Ферритовая шайба
Еще один способ укрощения паразитных авто-
колебаний (вполне возможно, что самый прак-
тичный, поскольку он останавливает высоко-
частотные колебания, не ухудшая при этом вы-
ходной импеданс на низких частотах) состоит
в установке ферритовой шайбы на вывод базы
транзистора (или последовательно с выводом,
если шайба для поверхностного монтажа, ка-
кими являются большинство современных эле-
ментов). Это повышает индуктивность вывода
базы, а также делает его импеданс резистив-
ным, а не индуктивным на высоких частотах.
(Последнее представляет опасность на высо-
ких частотах, поскольку индуктивность может
резонировать с паразитной емкостью, снова
вызывая колебания.) На рис. 9L.3 показана ти-
пичная частотная характеристика ферритовой
шайбы2.
Мы, конечно же, не будем использовать элемент
для поверхностного монтажа, а возьмем обыч-
ный миниатюрный ферритовый цилиндрик.
Рис. 9L4. Ферритовая шайба с продетой через нее прово-
лочной петлей
9L3. Нестабильность
операционных усилителей:
фазовый сдвиг может
вызывать автоколебания
в операционном усилителе
9L3.1. Простой операционный
усилитель с разными нагрузками
Низкочастотный фильтр
в петле обратной связи
Схема на рис. 9L.5 представляет собой хорошо
знакомый нам неинвертирующий усилитель,
2 Это типичные графики, представленные в справочном
материале по техническим вопросам компанией Vishay
Intertechnology. Материал доступен по адресу: http://
www.vishay.com/docs/ilbilbbenote.pdf.
3 По американской системе сортамента проводов AWG со-
ответствует диаметру провода 0,644 мм. — Примеч. ред.
4 Соответствует диаметру 0,255 мм. — Примеч. ред.
5 Вторая петля удваивает магнитное поле при данном токе,
а также удваивает реакцию на магнитное поле.
406
9L Лабораторное занятие: операционные усилители IV
к выходу которого подключена нагрузка с боль-
шой емкостью, в результате чего его стабиль-
ность находится на пределе. В качестве такой
нагрузки используется отрезок BNC-кабеля
длиной около 3 м (емкость около 100 пФ/м).
Если нет цельного отрезка кабеля, соедините
вместе несколько отрезков с помощью прямых
или Т-образных BNC-разъемов6.
BNC-кабель (около 3 м)
1100 кОм>(Чтобы максимизировать
(проблему, установите
10 кОм )с помощью
потенциометра
единичное усиление)
Рис. 9L5. Емкостная нагрузка может сделать нестабильной
схему с обратной связью
Наша первая задача — заставить схему генери-
ровать автоколебания. Для этого установите
минимальное усиление, выставив потенцио-
метр для подачи обратно всего выходного сиг-
нала.
Поначалу автоколебания могут не возникать.
В таком случае подайте на вход схемы прямо-
угольный сигнал. Это должно запустить авто-
колебания, которые скорее всего не затухнут
даже после снятия сигнала с входа или замены
его на синусоидальный.
Решение 1. Уменьшить подаваемый
обратно сигнал
Теперь, когда ваша схема генерирует автоколе-
бания, медленно проворачивайте ручку потен-
циометра, чтобы уменьшить часть подаваемого
назад выходного сигнала. (Кстати, какой эффект
это оказывает на усиление?) Когда автоколеба-
ния прекратятся, проверьте реакцию схемы на
прямоугольный сигнал небольшой амплитуды
(небольшой, чтобы не допустить перехода в ре-
жим насыщения). Если наблюдается что-то на-
подобие звона (или затухающие колебания ре-
зонансного контура), продолжайте уменьшать
долю подаваемого назад выходного сигнала до
тех пор, пока не прекратится звон.
Будем надеяться, что теперь вы удостовери-
лись, что стабильность схемы может зависеть
от усиления в петле обратной связи. Этим
объясняется факт наличия на рынке так назы-
ваемых нескорректированных операционных
усилителей: если вы знаете, как включить свой
операционный усилитель, чтобы получить зна-
чительное усиление, то будете лишь понапрас-
ну тратить полосу пропускания при использо-
вании операционного усилителя, скорректиро-
ванного для стабильной работы при единичном
усилении.
Другие решения
Но, предположим, что вы хотите обеспечить
единичное усиление, и вам нужно передавать
сигнал по длинному коаксиальному кабелю.
Здесь можно попробовать любое из несколь-
ких решений. Решение для самых ленивых —
найти на рынке операционный усилитель или
буфер, который будет сохранять стабильность
при нагрузке с большой емкостью (большой
емкостью будем считать емкость больше, чем,
скажем, 100 пФ).
А более трудолюбивые могут испробовать рас-
сматриваемые далее два способа. Реализуйте их
по отдельности и посмотрите, является ли каж-
дый из них достаточным. Если нет, тогда можно
попробовать применить их одновременно.
Последовательный резистор на выходе. Вы-
несите нагрузку из петли обратной связи, до-
бавив последовательно с BNC-кабелем рези-
стор номиналом 100-220 Ом, как показано на
рис. 9L.6. Проверьте, стабилизирует ли это ра-
боту операционного усилителя.
100 Ом
- К нагрузке
6 Использование Т-образных разъемов может быть не-
приемлемым на высоких частотах, но вполне подойдет для
частот, используемых в нашем операционном усилителе.
Рис. 9L.6. Подключение резистора последовательно нагруз-
ке может вынести точку сдвига фазы за пределы петли об-
ратной связи.
Демпфер. Подключите к выходу операцион-
ного усилителя цепочку из последовательно
соединенных резистора небольшого номинала
и конденсатора (для заземления по переменно-
му току) как показано на рис. 9L.7.
Принцип работы демпфера весьма поучите-
лен. Все выглядит так, будто бы он подавляет
высокие частоты необычно грубым способом:
создавая большую нагрузку на выходе на высо-
ких частотах: в диапазоне частот, где выходной
9L.4. Операционный усилитель с буфером в петле обратной связи
407
К нагрузке
Рис. 9L.7. Демпфер
импеданс повышается, когда импеданс демпфе-
ра стремится к минимальному — лишь к сопро-
тивлению резистора.
Примечание
Импеданс демпфера, изображенного на рис. 9L.7,
снижается до V2R « 14 Ом на частоте около
160 кГц.
9LA Операционный
усилитель с буфером
в петле обратной связи
Схема на рис. 9L.8 похожа на другие схемы, ко-
торые мы собирали раньше. Но она отличается
от них тем, что является источником потенци-
альных проблем.
Для двухтактного буфера возьмите мощные
транзисторы типа MJE3055 или MJE2955. Эти
транзисторы использовались в упражнении по
двухтактному каскаду в разделе 6L8. Цоколевка
выводов — Б-К-Э при взгляде спереди (на сто-
рону с маркировкой).
Основное отличие этой схемы от остальных,
которое существенно повышает возможность
чем у микросхемы 411. В данной схеме уста-
новлен операционный усилитель на микро-
схеме LT1215, у которого начальное значение
коэффициента усиления намного выше, чем
у 411 (106 по постоянному току по сравнению
с 200 000 для 411), а частота единичного усиле-
ния составляет 23 МГц по сравнению с 4 МГц
для 411. Таким образом, этот усилитель облада-
ет не только существенным преимуществом, но
также и большим потенциальным недостатком
на частотах, где фазовые сдвиги внутри пет-
ли обратной связи приближаются угрожающе
близко к точке, в которой отрицательная обрат-
ная связь превращается в положительную. Мы
надеемся, что схема, собранная вами на этом
усилителе, начнет создавать автоколебания,
чтобы вы могли испробовать новый способ их
устранения.
Внимание!
Обратите внимание на то, что цоколевка у этой
микросхемы стандартная для сдвоенных опера-
ционных усилителей, такая же, как и, например, у
микросхемы LM358, но она отличается от цоколев-
ки для более знакомой нам микросхемы операци-
онного усилителя LF411.
Начните работать со схемой без подключенного
динамика: подайте на нее синусоидальный сиг-
нал амплитудой около вольта и частотой около
1 кГц, и убедитесь, что схема пропускает этот
сигнал, не создавая переходных искажений7.
Теперь подключите на выход схемы нагрузку
в виде динамика с сопротивлением катушки
8 Ом. (Если вам не нравится издаваемый им
звук, уменьшите громкость.) Будем надеяться,
1/2 LT1215
10 Ом Нагрузка
Локальная
обратная связь
\ 8-омный
•динамик
;одмкф
} Демпфер
i (индуктивная
/ и емкостная
' нагрузка)
LT1215
Поначалу не добавляйте в схему компоненты, обведенные пунктиром
Рис. 9L8. Двухтактный буфер в петле обратной связи
возникновения проблем, состоит в применении
здесь операционного усилителя со значительно
более высоким коэффициентом усиления,
7 Если вам повезет, даже при этом предварительном
тестировании схема может начать генерировать авто-
колебания.
408
9L Лабораторное занятие: операционные усилители IV
что теперь на выходе вашего усилителя появят-
ся автоколебания (но они могут не оказывать
никакого влияния на качество звука).
Чтобы заставить схему создавать паразитные
автоколебания, подайте на ее вход синусои-
дальный сигнал низкой частоты. Определите
приблизительную частоту паразитных помех,
чтобы выяснить, кто в этом виноват — опе-
рационный усилитель или транзисторы. Если
частота помех находится в диапазоне, в кото-
ром операционный усилитель сохраняет зна-
чительное усиление с разомкнутой цепью об-
ратной связи, то можно с полной уверенностью
возлагать вину на операционный усилитель.
Автоколебания, создаваемые транзисторами,
будут иметь намного более высокую частоту.
В нашем случае мы получили красивые автоко-
лебания, осциллограммы которых приведены
на рис. 9L.9.
ЗЯ 5о
Source»
ш
I .41/10
txi frotx*
M2.O0ms A txl I 2*4 б mW -more-
: 2 Ml
Source ■• Ctrnplimj ' Slop*
Рис. 9L.9. Паразитные колебания, создаваемые транзисто-
рами двухтактного каскада при отсутствии разделенной об-
ратной связи и подключенном динамике
Если необходимо, схитрите,
чтобы получить автоколебания
Если вам не удается заставить схему генериро-
вать автоколебания с динамиком в качестве на-
грузки, то попробуйте подключить емкостную
нагрузку: конденсатор емкостью, допустим,
0,001 мкФ. Экспериментируйте, чтобы подо-
брать такое значение нагрузочного конден-
сатора, которое вызовет автоколебания. Но
имейте в виду, что слишком большая емкость
конденсатора будет предотвращать их возник-
новение, просто перегружая операционный
усилитель подобно схеме демпфера.
Возможные решения
Попробуйте по отдельности следующие реше-
ния, чтобы остановить автоколебания.
♦ Выполните развязку линий питания (если вы
еще этого не сделали).
♦ Если вы подозреваете, что причина автоко-
лебаний кроется в транзисторах, подключи-
те на их базы последовательные резисторы
сопротивлением в несколько сотен ом.
♦ Создайте локальную (или разделенную)
обратную связь, подключив выход опера-
ционного усилителя к инвертирующему
входу через конденсатор емкостью 100 пФ.
Сопротивление резистора в исходной петле
обратной связи нужно будет откорректиро-
вать под эту емкость. В частности, мы хотим,
чтобы резистор обеспечивал обратную связь
на умеренных частотах, а конденсатор на бо-
лее высоких, на которых возможны фазовые
сдвиги, нарушающие стабильность схемы.
Выберите такое значение этого резистора,
чтобы оно равнялось эффективному сопро-
тивлению конденсатора на частоте, находя-
щейся ниже частоты, на которой вы наблю-
дали автоколебания.
♦ Добавьте демпфирующую ДС-цепочку (сно-
ва 10 Ом и ОД мкФ). Посмотрите, сможет ли
демпфер самостоятельно остановить автоко-
лебания (для этого удалите элементы разде-
ленной обратной связи).
♦ Стабилизировав схему (с помощью разде-
ленной обратной связи или демпфера) про-
верьте, не нарушит ли эту стабильность уда-
ление резистора из цепи базы.
♦ Попробуйте подключить вне петли обрат-
ной связи резистор с небольшим номиналом
(начните со значения ниже 10 Ом) последо-
вательно динамику или нагрузочному кон-
денсатору (это решение должно быть вам
знакомо по рис. 9L.6).
Будем надеяться, что вы сможете «успокоить»
свой усилитель. Если же нет, обратитесь за по-
мощью к нам.
9S. Дополнительный материал:
операционные усилители IV
9S.1. Частотная коррекция
операционных усилителей
Ранее уже отмечалось, что все операционные
усилители, с которыми нам придется работать
в этом курсе, оснащены возможностью частот-
ной коррекции, чтобы придать им стабиль-
ность, по крайней мере, в тех случаях, когда мы
не помещаем необычные элементы в их петлю
обратной связи1. Но достаточно парадоксально,
что реализация частотной коррекции означает
преднамеренное снижение коэффициента уси-
ления операционного усилителя. Это может ка-
заться неправильным, особенно ввиду фунда-
ментального озарения Гарольда Блэка (Harold
Black), что избыточное усиление является как
раз необходимым условием для получения
пользы от отрицательной обратной связи2. Но
требование стабильной работы является таким
фундаментальным, что любые другие аспекты
должны отходить на задний план.
Операционный усилитель на микросхеме 741
пользуется огромной популярностью благо-
даря тому, что это был первый операционный
усилитель со встроенной частотной коррек-
цией, и работать с ним было восхитительно
легко3. Спустя 45 лет после его выпуска ком-
1 АоЕ § 4.9; АоЕ § 2.54В.
2 В случае, если вы забыли, напомним еще раз соответ-
ствующую выдержку из его патента (№2102671 [19370]):
«...посредством создания схемы с избыточным усилени-
ем, которое затем понижается отрицательной обратной
связью, можно реализовать любой требуемый уровень
линейности между входным и выходным сигналами, при
этом ограничивающим фактором является величина уси-
ления, которую можно получить».
3 См. раздел 8-4:1С Op Amps (стр. 808) книги Юр Amp
Applications Handbook» («Справочник по применению
операционных усилителей»), https://www.analog.com/
панией Fairchild (которая также разработала
первую полностью интегрированную микро-
схему) операционный усилитель 741 все еще
иногда встречается в новых разработках. По
крайней мере, в разработках из развивающих-
ся стран, где его широкая доступность и низ-
кая стоимость могут быть особенно привлека-
тельными. Операционный усилитель 411, ко-
торый мы используем на большинстве наших
лабораторных занятий, имеет по существу та-
кую же структуру, как и усилитель 741, а также
содержит встроенную частотную коррекцию,
которая в настоящее время является стандарт-
ной для операционных усилителей. Главное
различие между операционными усилителями
411 и 741 состоит в использовании в первом
полевых транзисторов во входном каскаде.
На принципиальной схеме операционного уси-
лителя 411 (рис. 9S.1) можно заметить кон-
денсатор небольшой емкости, подключенный
между выходом и входом каскада с высоким
коэффициентом усиления. Этот конденсатор
функционирует точно так же, как и конденса-
тор, подключенный между выходом и инверти-
рующим входом операционного усилителя —
он образует интегратор.
Поведение интегратора — спад усиления и фа-
зовый сдвиг — вносится по той причине, что оно
лучше, чем альтернатива: чрезмерный фазовый
сдвиг, который нарушал бы стабильность рабо-
ты усилителя.
en/education/education-library/op-amp-applications-
handbook.html. Так что инженеры ухватились обеими
руками за это устройство, для которого не нужно было
добавлять еще один маленький конденсатор. Меня всегда
утешает любое доказательство того факта, что весь осталь-
ной мир такой же ленивый, как и я!
410
9S. Дополнительный материал: операционные усилители IV
Усиление при разомкнутой
цепи обратной связи
Усиление «200 000 по постоянному току,
120 дБ rjT^i-^ Н9 начинает падать при f » 20 Гц
100 дБ
80 дБ
60 дБ
40 дБ
20 дБ
ОдБ
LF411
Вход
... и снижается до единичного
г"* 4 МГц
1 10 102 103 104 105106107
Частота (Гц)
-И
Входной дифференциальный каскад
егратор - 'Д*У*™™*Й
*■ к" "V' повторитель
...этот спад усиления создается
корректирующим конденсатором СК0РР
Интегратор, создаваемый подключением конденсатора
между выходом и входом инвертирующего усилителя
Рис. 9S.1. Спад усиления для скорректированного операционного усилителя LF411 и его причина
9S.1.1. Осциллограммы в качестве
доказательства интегрирования
операционным усилителем
Скептически настроенный читатель может
вполне отвергнуть только что сказанное: разве
мы не видели множество раз на лабораторных
занятиях, что операционный усилитель не про-
являет фазового сдвига? Мы ведь наблюдали
на осциллографе входной и выходной сигналы
повторителей и усилителей. Повторитель на
выходе точно воспроизводит входной сигнал,
разве не так?
У вас есть полное право на такой скептицизм.
Но мы можем возразить, вспомнив, что каж-
дый операционный усилитель, с которым нам
приходилось иметь дело (за исключением пары
схем компараторов), содержит отрицательную
обратную связь. Эта отрицательная обратная
связь скрывает внутреннюю функцию инте-
грирования в операционном усилителе, точно
так же, как она прячет любую другую функцию
преобразования, помещаемую в петлю обрат-
ной связи. В частности, она устраняет пере-
ходные искажения двухтактного выходного
каскада; а в общем случае она скрывает любую
На частоте f = 4 Гц очень
небольшой (разовый сдвиг
На частоте г*= 100 Гц
величина фазового сдвига около -90°
г •■ i ?
На частоте f"= 100 Гц прямоугольный сигнал
оказывается проинтегрированным
Канал 2.
Частота 99,73 Гц
Рис. 9S.2. Операция интегрирования операционного усилителя становится видимой, когда он работает с разомкнутой целью
обратной связи
9S.1. Частотная коррекция операционных усилителей
411
«собаку» в цепи обратной связи, как показано
на рис. 6N.19 в разделе 6N.9.
Только если операционный усилитель работает
с разомкнутой цепью обратной связи, его опе-
рация интегрирования становится видимой.
(Выполнение этого эксперимента связано с не-
которыми трудностями, поэтому не рекоменду-
ем вам самостоятельно собирать эту схему.)
Нужно аккуратно выставить смещение посто-
янной составляющей, чтобы не допустить вы-
хода операционного усилителя из линейного
режима, а затем подать на вход сигнал неболь-
шой амплитуды. Выполнив эти операции, мы
получили выходные сигналы, осциллограммы
которых изображены на рис. 9S.2 и которые
делают видимой операцию интегрирования,
выполняемую операционным усилителем. На
самых низких частотах (4 Гц вверху слева) про-
является только небольшой фазовый сдвиг,
а вот на частоте 100 Гц (вверху справа) очеви-
ден полный фазовый сдвиг величиной -90°,
свойственный интегратору.
9S.1.2. Зачем нужна частотная
коррекция? Опасности
нескорректированного
операционного усилителя
Нескорректированный операционный усили-
тель требует дополнительной заботы4. Спад уси-
ления при коррекции должен происходить для
того, чтобы поддерживать схему в стабильном
состоянии, будь то при встроенной внутренней
коррекции или внешней посредством подклю-
чения корректирующего конденсатора. Чтобы
понять, почему это необходимо, нужно при-
нять во внимание тот факт, что операционный
усилитель — многокаскадная схема (рис. 9S.3),
которая ведет себя подобно нескольким сое-
диненным последовательно низкочастотным
фильтрам.
А ведет он себя так потому, что несколько ка-
скадов как источники сигнала имеют ненуле-
вые паразитные сопротивления (причем два
каскада являются источниками тока5).
Если не вмешаться в это поведение, общий фа-
зовый сдвиг опасно повышается, как демон-
стрируется на рис. 9S.46.
Рис. 9S.4. Нескорректированный операционный усилитель
будет давать нежелательный фазовый сдвиг
При единичном петлевом усилении (подавае-
мый обратно на вход усиленный сигнал) фазо-
вый сдвиг, достигающий величины 180°, явля-
ется неприемлемым. Вспомните, что петлевое
усиление обычно выражается в виде произве-
дения АВ, где А соответствует усилению опе-
рационного усилителя с разомкнутой цепью
Вход
—VvV | АДА,—ф~~А№»—•—Вых<
III
Рис. 9S.3. Нескорректированный операционный усилитель ведет себя подобно двум-трем низкочастотным фильтрам, соеди-
ненным последовательно
5 Конечно же, источники тока здесь действительно соот-
ветствуют описанию «источники с ненулевым сопротивле-
нием».
АоЕ § 4.9.
6 АоЕ § 4.9.1.
412
95- Дополнительный материал: операционные усилители IV
Усиление А без обратной связи
Если схему рассчитать так, чтобы ее усиление без
обратной связи было очень высоким (скажем, 1000),
'обратно на вход будет подаваться небольшая часть
выходного сигнала ишу,,..
... вследствие чего
петлевое усиление сойдет на нет...
. -
... прежде чем мы дойдем до
опасной частоты фазового сдвига
Рис. 9S.5. Нестандартное решение: даже нескорректированный операционный усилитель может работать стабильно при
условии, что обратно подается лишь малая часть выходного сигнала
обратной связи (график характеристики кото-
рого показан на рис. 9S.4), а В — это часть вы-
ходного сигнала, подаваемая обратно на вход.
Два возможных решения
Стабилизировать такой операционный усили-
тель можно, в принципе, двумя способами (как
упоминалось в главе 9N):
♦ уменьшить часть В, подавая обратно меньше,
чем весь выходной сигнал 1ГВЫХ;
♦ уменьшить усиление А, преднамеренно сни-
жая усиление операционного усилителя при
повышении частоты7.
Ограничиваем часть В
Даже нескорректированный операционный
усилитель может работать стабильно,
если обратно подается очень малая доля
выходного сигнала. Первое из этих решений
графически представлено на рис. 9S.5: умень-
шаем долю подаваемого обратно на вход вы-
ходного сигнала, установив в петле обратной
связи делитель (коэффициент усиления данно-
го операционного усилителя составляет 1000).
Но нескорректированныйусилитель, вклю-
ченный как повторитель, «сходит с ума».
Нескорректированный классический операци-
онный усилитель 741 имеет слишком большое
усиление на частоте, где фазовый сдвиг дости-
гает -180°, и если его включить, как повтори-
тель, он теряет контроль над сигналом, как по-
казано на рис. 9S.6.
Рис. 9S.6. Нескорректированный операционный усилитель,
включенный по схеме повторителя, будет создавать пара-
зитные автоколебания
Ограничиваем А
Но стандартным способом является
ограничение усиления на высоких часто-
тах. Можете себе представить, разработчи-
ки предпочитают иметь дело со стабильным
операционным усилителем, даже если он не
обладает очень большим коэффициентом
усиления. Самым лучшим будет операцион-
ный усилитель (подобный всем в нашей лабо-
ратории), который сохраняет стабильность,
даже когда обратно подается весь выходной
сигнал (иными словами, когда он включен
как повторитель). Чтобы стабильно работать
со 100%-ной обратной связью (В = 1), к тому
времени, когда величина фазового сдвига
достигнет -180°, усиление такого операци-
онного усилителя должно отсутствовать. На
рис. 9S.7 слева изображена схема операци-
онного усилителя, включенного как повтори-
тель, а справа — график требуемого снижения
усиления8.
АоЕ § 4.9.1А.
8 АоЕ § 4.9.1.
9S.1. Частотная коррекция операционных усилителей
413
Усиление А без обратной связи
8100дБ
80 дБ
60 дБ
40 дБ
20 дБ
ОдБ
Все еще слишком большое усиление на частоте,
создающей опасный фазовый сдвиг
Частота (логарифмическая шкала) Г»
... усиление меньше единичного, поскольку
фазовый сдвиг представляет опасность^
Проблема!
-270°
-90° a
Простой повторитель является наиболее
проблемной схемой: поскольку в нем подается ,§
обратно 100% выходного сигнала, то для него
требуется плавное снижение усиления
Рис. 9S.7. Стандартное решение состоит в снижении усиления при разомкнутой петле обратной связи (А) для обеспечения
стабильности даже при В= 1
30
^ 20
ID
3 10
§-10
>-20
-30
График Боде
>
s
1
ycnj
I
jflrv
|\
пение!
Vs =±15
С= 100 pF
mi
Ш<
\W
150
100
50
о
-150 "^
Это не «фаза», как обозначено, а «запас по
фазе» — разница между фазовым сдвигом
операционного усилителя и -180°
...запас по фазе составляет около 50°
ОД 1 10 100
Частота (МГц)
На частоте единичного усиления...
Рис. 9S.8. Фазовый сдвиг операционного усилителя смещается по направлению к -180°, но останавливается на безопасном
расстоянии
Запас по фазе
По мере того как частота входного сигнала в
скорректированном усилителе приближается
к его предельной частоте, а его усиление стре-
мится к единичному, фаза выходного сигнала
входит в проблемную зону: сдвигается больше
-90°, но не достигает предельного значения
-180°.
Оставшееся расстояние до точки катастрофы
-180° называется запасом по фазе операцион-
ного усилителя. Запас по фазе для большинства
операционных усилителей составляет от 45° до
60°. На рис. 9S.8 приведен график из справоч-
ного листка для операционного усилителя 411,
на котором можно видеть, что запас по фазе для
данного усилителя составляет около 50°. Этот
параметр здесь ошибочно обозначен как про-
сто phase (фаза), тогда как должно быть phase
margin (запас по фазе).
Это обстоятельство объясняет, почему даже фа-
зовый сдвиг меньше -90°, создаваемый какой-
либо «собакой» в петле обратной связи, может
привести к нестабильности схемы.
9S.13. Операционные усилители
с частичной и полной частотной
коррекцией
Нескорректированные операционные
усилители9
На рынке предлагаются операционные усили-
тели без встроенного корректирующего кон-
денсатора для снижения усиления; задача
установки такого конденсатора (вне микро-
схемы конечно же) оставлена на усмотрение
АоЕ § 4.9.2В.
414
9S. Дополнительный материал: операционные усилители IV
LTC6230-10 (стабильные при усилении 10 или больше)
Зависимость фазы и усиления от частоты при разомкнутой
цепи обратной связи
Если задано усиление 10
90
...запаса по сразе вполне
достаточно^
(должно быть не просто (фаза),
а (запас по фазе))
исвгзо/
Зависимость усиления при разомкнутой цепи
обратной связи от частоты
120
100
-80
...запаса по сразе вполне
достаточно (50°)
Когда усиление при разомкнутой цепи обратной связи
снижается до единичного (0 дБ) хм w
Когда усиление при разомкнутой цепи обратной связи
снижается до единичного (0 дБ)
О4 105
Частота (Гц)
106
...запаса по сразе вполне
достаточно (55 до 60°)
Две модификации операционного усилителя: с частичной
коррецией (нестабильный при единичном усилении)...
...по сравнению с скорректированным (стабильный при
единичном усилении)
Рис. 9S.9. Операционный усилитель LT6230 предлагается в двух вариантах: с полной и частичной коррекцией. Последний
обеспечивает большее усиление, но нестабилен в конфигурации повторителя
пользователя. Поначалу все операционные
усилители были нескорректированными, но
после появления микросхемы 741 такой подход
стал исключением. Но нескорректированные
операционные усилители по-прежнему присут-
ствуют на рынке, поскольку в операционных
усилителях со встроенной коррекцией усиле-
ние снижают, чтобы обеспечить стабильность
устройства в самом трудном случае — при его
включении, как повторитель. На графике на
рис. 9S.7 сопоставляется спад усиления для
обычного скорректированного и нескоррек-
тированного операционных усилителей. При
единичном усилении нескорректированный
операционный усилитель будет нестабильным,
но его можно откорректировать, чтобы он смог
работать при усилении разомкнутой цепи об-
ратной связи в конкретном приложении.
Операционные усилители
с частичной коррекцией
Компромиссным решением является опера-
ционный усилитель с частичной коррекцией10,
10 В книге АоЕ отмечается, что лучшим термином было бы
недокорректированный (under-compensated).
т. е. усилитель, нестабильный при единичном
усилении (когда назад подается 100% выходно-
го сигнала), но стабильный при определенном
значении (например, 10) усиления при разом-
кнутой цепи обратной связи (когда обратно по-
дается только 1/10 выходного сигнала). Если
известно, что усиление схемы не уменьшится
ниже 10, тогда можно позволить более высокое
усиление разомкнутой цепи обратной связи на
данной частоте. Например, компания Linear
Technology предлагает два варианта своего опе-
рационного усилителя LT6230 с рабочей часто-
той 215 МГц: один с полной, а другой с частич-
ной коррекцией, приспособленный для ста-
бильной работы с усилением 10 или выше. На
рис. 9S.9 показаны характеристики этих двух
модификаций операционного усилителя для их
сопоставления. К сожалению, на графике при-
ведено много информации, что затрудняет вос-
приятие11.
Поскольку схема с усилением 10 работает с
меньшей частью обратного сигнала В, она
может также сохранять стабильность при по-
вышенном усилении разомкнутой цепи А.
11 Из справочного листка компании Linear Technology на
операционные усилители LT6230/LT6230-10.
9S.2. Активные фильтры: как улучшить простой RC-фильтр
415
Обратите внимание на то, что усилитель с ча-
стичной коррекцией обеспечивает более вы-
сокое усиление на всех частотах. Он «может
позволить» себе это, поскольку важно именно
петлевое усиление — произведение АВ, а усиле-
ние величиной 10 поддерживает это произведе-
ние на безопасном уровне для данного опера-
ционного усилителя.
9S.2. Активные фильтры:
как улучшить простой
/?С-фильтр
На рис. 9S.10 изображен линейный график
амплитудно-частотной характеристики (АЧХ)
обычного низкочастотного JRC-фильтра.
Рис. 9S.10. Линейный график амплитудно-частотной харак-
теристики низкочастотного ЯС-фильтра
проблем. Крутизна спада при этом удваивается
(до -12 дБ/октаву), но на равномерность это
влияет незначительно.
На первый взгляд каскадное соединение даже
ухудшает АЧХ, делая ее менее прямоугольной.
Это иллюстрируется и подтверждается осцил-
лограммой на рис. 9S.1112, на котором сравни-
ваются простой одиночный ДС-фильтр с часто-
той/здБ = 1 кГц и схема из двух соединенных по-
следовательно низкочастотных ДС-фильтров, с
частотой/3дБ каждого равной 1 кГц.
Частота, которая ранее была частотой f3^%
теперь является частотой ^дБ, поскольку вы-
ходной сигнал ослаблен на 6 дБ. Но для объ-
ективного сопоставления АЧХ сравниваемые
фильтры должны иметь одинаковую часто-
ту УздБ. На нормированном таким образом
графике характеристики каскадного фильтра
выглядят лучше, как показано на рис. 9S.12.
Фактически АЧХ каскадного ДС-фильтра «про-
висает» меньше, чем одиночного JRC-фильтра,
что может противоречить вашей интуиции.
При отсутствии чего-либо лучшего нам бы
пришлось удовлетвориться этими неравномер-
Одиночный ££-срильтр
Два ££-<рильтра,
"соединенные последовательно
s Частота (Гц)
| Спад для
< многокаскадных фильтров
Рис. 9S.11. АЧХ RC-фильтров, соединенных последовательно «провисает»
Эта характеристика разочаровывает нас в двух
отношениях.
♦ Характеристика не так равномерна в преде-
лах полосы пропускания, как нам бы хоте-
лось. Это ясно видно из графика, который
вовсе не похож на плоский график АЧХ, ко-
торый обычно рисуют в учебниках.
♦ Спад АЧХ не такой крутой, как нам бы хо-
телось. Мы привыкли к спаду величиной
-6 дБ/октаву, который характерен для про-
стых низкочастотных ДС-фильтров, но ино-
гда нам требуется больше.
Простое последовательное соединение ВС-
фильтров не решает ни одну из этих двух
ными АЧХ, чтобы получить крутой конечный
спад. Но лучшие характеристики можно полу-
чить с помощью LC-фильтров, а также (как мы
увидим на лабораторном занятии 9L) исполь-
зуя схемы активных фильтров, которые могут
имитировать характеристики LC-фильтров без
применения катушек.
Чтобы получить лучшую форму выходного сиг-
нала, т. е. лучшую частотную характеристику,
12 Левое изображение взято из рис. 6.2 книги АоЕ. Два
изображения на рис. 9S.11 нельзя сравнивать напря-
мую, поскольку осциллограмма справа представлена в
логарифмическо-линейном масштабе (частота в логариф-
мическом, а амплитуда в линейном), тогда как обе оси гра-
фиков слева в линейном масштабе.
416
9S. Дополнительный материал: операционные усилители IV
Однокаскадный
Нормированная частота
Нормированный спад для пассивных
ЗДГ-срильтров с разным числом каскадов
Детализированный вид спада дляоднокаскадного
и двухкаскадного фильтров
Рис. 9S.12. Нормированный график частотных характеристик одно- и двухкаскадных низкочастотных /?С-фильтров: двух-
каскадный выглядит лучше. Левое изображение скопировано из рис. 6.2В книги АоЕ
нам нужен какой-то прием, который позволит
выровнять АЧХ в пределах полосы пропуска-
ния, одновременно обеспечивая хорошую кру-
тизну спада.
Чтобы выровнять АЧХ простого двухкаскад-
ного низкочастотного ЯС-фильтра, нам нужно
усилить выходной сигнал фильтра (дать ему
«пинок под зад») в его самой слабой точке:
чуть ниже частоты Уз дБ (ниже для низкочастот-
ного фильтра). С другой стороны, чтобы улуч-
шить крутизну спада на краях АЧХ, нам нужно
всего лишь объединить эффект двух подобных
соединенных последовательно ЯС-фильтров.
В скором времени ваши требования повысятся,
и захочется еще лучших характеристик, напри-
мер улучшенной крутизны АЧХ при приближе-
нии к частоте f3 дБ. Но для начала посмотрим,
сможете ли вы понять на интуитивном уровне,
каким образом определенный активный фильтр
способен выровнять АЧХ низкочастотного
JRC-фильтра, достигая при этом, спада величи-
ной -12 дБ/октаву, присущего двухкаскадно-
му фильтру (спад, получаемый на выходе двух
соединенных последовательно низкочастотных
ДС-фильтров).
9S.2.1. Простой активный
VCVS-фильтр
Изображенный на рис. 9S.12 фильтр охаракте-
ризован в книге АоЕ следующей фразой: «и даже
частично поддается пониманию на интуитив-
ном уровне»13. Тем самым признается тот факт,
что большинство активных фильтров удручаю-
ще «неинтуитивные»: их структура получается
в результате сложных математических расче-
тов, а это вынуждает заниматься разработкой
с применением решений из справочников, что
не очень поучительно. Показанный на рисунке
фильтр называется УСУБ14-фильтром Саллена-
Ки и реализует оба улучшения, которые нам
нужны.
Низкочастотный
Входной^ \ \ЪЛ ! (>ч^
гигилп ' » » 111 ^*
сигнал
Высокочастотный фильтр
(для сигнала обратной связи)
Рис. 9S.13. Один из вариантов фильтра Саллена-Ки: двух-
каскадный активный низкочастотный VCVS-фильтр
Активный фильтр выравнивает АЧХ
в полосе пропускания
Положительная обратная связь улучшает фор-
му АЧХ, подавая обратно на вход то, что можно
рассматривать как «пинок под зад» для АЧХ.
Почему для АЧХ? Цепь обратной связи высо-
кочастотная, но источником сигнала обратной
связи является выход низкочастотного фильтра
(базовая схема, которую мы собираем); их про-
изведение будет низкочастотным, что и объяс-
няет хороший стимул, приложенный в нужное
место.
То что мы охарактеризовали как «пинок
под зад» можно также описать как подобие
13 АоЕ § 6.3.1.
14 Англ. Voltage Controlled Voltage Source — источник на-
пряжения, управляемый напряжением. Расшифровка со-
кращения названия схемы, конечно же, не дает ясного по-
нимания ее работы.
9S.2. Активные фильтры: как улучшить простой RC-фильтр
417
ВЧ-<рильтр {Сх, [^ 11 /у, Сг) ...активный
НЧ-филътр (£2, Сг) ^n У пассивный..:—) \ «Пинок под зад» в правильное место
рбпосоъом фильтр (сое
последовательно НЧ- и
Результирующая частота f3i
Рис. 9S.14. Активный фильтр как полосовой фильтр
постановки Сх на самообеспечение и даже с
отбором у него излишка: Сх не только не на-
гружает подаваемый на Rx сигнал на частотах
ниже частоты f3 дБ, но даже усиливает сигнал,
подаваемый на пассивный НЧ-фильтр, состоя-
щий из R2C2. Это объясняется тем, что в данном
частотном диапазоне сигнал, поступающий на
нижний вывод Сг совпадает по фазе с входным
сигналом и имеет большую амплитуду.
В полосе ослабления первый конденсатор Сг
нагружает резистор Rv вместо того чтобы уси-
ливать сигнал на нем, поскольку выходной сиг-
нал схемы, который подается на нижний вывод
этого конденсатора, имеет небольшую вели-
чину вследствие подавления низкочастотным
фильтром R2Cr В глубине полосы задержания
фильтр ведет себя подобно каскаду из двух про-
стых низкочастотных ЯС-фильтров. Отсюда и
крутой конечный спад: -12 дБ/октаву.
-Двухкаскадный VCVS-фильтр
-Простой /&Г-фильтр
Активный фильтр может
обеспечить очень крутой спад
Но наша аналогия в виде «пинка под зад»
не объясняет очень крутой спад, получае-
мый вблизи частоты среза (или частоты/3дБ).
Предположительно его можно объяснить слу-
чайной совокупностью фазовых сдвигов. Не
очень удовлетворительное объяснение, но поч-
ти все, что можно предложить на интуитивном
уровне без математических выкладок.
На рис. 9S.15 приведены осциллограммы харак-
теристик VCVS-фильтра, простого ЯС-фильтра
и двухкаскадного ЯС-фильтра, которые имеют
одинаковую частоту^ ^ Двухкаскадный актив-
ный фильтр выравнивает АЧХ в полосе про-
пускания, одновременно увеличивая крутизну
спада
15
Двухкаскадный VCVS-фильтр
Два простых /&Г-фильтра,
соединенные последовательно
Рис. 9S.15. Сравнительные осциллограммы характеристик двухкаскадного VCVS-фильтра, простого ЯС-фильтра и двухкаскад-
ного ЯС-фильтра
Замечание
Вообще-то на самом деле не все так просто, по-
скольку соотношение импедансов этих двух филь-
тров не равно 1:10, поэтому возможно их взаимо-
действие.
Характеристики активного фильтра
можно оптимизировать
Корректируя усиление активного филь-
тра, можно оптимизировать ту или иную
15 См. сравнение характеристик фильтров этих трех типов
на рис. 6.30 в книге АоЕ.
418
9S. Дополнительный материал: операционные усилители IV
Самая равномерная АЧХ
(фильтр Баттерворта) где-то здесь
Усиление слишком велико
Рис. 9S.16. Частотная характеристика фильтра зависит от величины положительной обратной связи. Различные значения
этой величины приводят к разным характеристикам
характеристику фильтра, но за счет ухудше-
ния каких-либо других его характеристик.
Например, усиление одного уровня обеспечи-
вает самую плоскую вершину в полосе пропу-
скания (фильтр Баттерворта), другого, более
высокого, уровня — дает самый крутой спад
(фильтр Чебышева), а более низкого, чем пер-
вый, уровня — обеспечивает наилучшее со-
хранение формы сигнала (фильтр Бесселя). На
рис. 9S.16 показано влияние этих трех разных
уровней усиления.
Поскольку положительная обратная связь уве-
личивает амплитуду АЧХ, ее нужно использо-
вать с осторожностью: при слишком сильной
обратной связи мы сначала вместо спада созда-
дим чрезмерный подъем в полосе пропускания,
а затем, если по-настоящему переборщить, схе-
ма перейдет в режим паразитных автоколеба-
ний. Осциллограммы на рис. 9S.16 иллюстри-
руют возможный диапазон характеристик для
различных значений обратной связи. Эти изо-
бражения были получены для различных зна-
чений обратной связи.
Замечание
При изменении величины обратной связи также
меняется и усиление. Графики на рисунке не были
нормированы для отображения постоянной ам-
плитуды в полосе пропускания.
Фильтры с большим числом каскадов
Если вам требуется трех- или четырехполюс-
ный фильтр, или фильтр с еще большим числом
каскадов, его можно создать, соединив после-
довательно необходимое количество активных
двухполюсных секций. Но интуитивно понять
работу таких фильтров совершенно невозмож-
но: несколько секций отличаются друг от друга,
а для объяснения непонятных коэффициентов
(усилений в VCVS-форме и значений частот
Лдб требуется применение сложнейших мате-
матических формул.
В этом отношении несколько утешает то обсто-
ятельство, что сложное, замысловатое уравне-
ние, описывающее желаемую характеристику,
скажем, 4-полюсного фильтра (которое содер-
жит выражения частот вплоть до четвертой
степени), можно разложить на несколько более
удобную квадратичную форму, которую мы уже
собирали, — скромный 2-полюсный фильтр.
Но в целом эти фантастические фильтры яв-
ляются удручающе загадочными. Разумеется,
если вы не имеете ничего против загадочности,
то можете разрабатывать качественные ак-
тивные фильтры, используя таблицы из книги
АоЕ (таблица в разделе 6.3.2: низкочастотный
фильтр, четыре альтернативные формы выход-
ного сигнала)16.
А последним словом в разработке фильтров бу-
дет применение программы для синтеза филь-
тров FilterPro от компании Texas Instruments/
Burr-Brown. В этом случае вы сможете почув-
ствовать себя недостаточно умным, но про-
грамма выдаст хороший результат. Независимо
от избранного вами подхода, будем надеяться,
что беглое знакомство с активным фильтром на
лабораторном занятии 9L подвигнет вас на ис-
пользование этих схем17.
Реакция на ступенчатый сигнал
и сохранение формы сигнала
На рис. 9S.17 изображены переходные ха-
рактеристики 2-полюсного низкочастотного
VCVS-фильтра для трех разных установленных
16 А если у вас есть желание узнать больше об активных
фильтрах, то в этом вам может помочь полезная книга
«Active Filter Cookbook» («Рецептурный справочник по ак-
тивным фильтрам»), автор Дон Ланкастер (Don Lancaster),
издательство Sams, 1975 г.
17 АоЕ §6.3.3.
9S.3. Диагностирование помех
419
Реакция на ступенчатый
сигнал
Фильтр Бесселя
^ 13
Низкому усилению сопутствует
спокойная реакция на ступенчатый сигнал
Фильтр Баттерворта
К, = 1,6
\ > >
Фильтр Чебышева
Л 2Д
feftftM ...более высокое усиление сопровождается
i^wv^ большими искажениями формы выходного сигнала
у
Фильтр Чебышева ^
Фильтр Баттерворта ~
Фильтр Бесселя ^г .
наибольшее искажение соответствует
максимальному усилению (и самый крутой спад)
Самое низкое усиление обеспечивает наименьшие
искажения (наилучшее качество задержки)
и самый пологий спад
Рис. 9S.17. Переходная характеристика иллюстрирует компромисс между сохранением формы сигнала и крутизной спада
значений усиления: самого низкого (наилуч-
шие запаздывание и сохранение формы сигна-
ла), среднее (самая плоская вершина АЧХ в по-
лосе пропускания) и самое высокое (наиболее
крутой спад)18.
Замечание
Вы поэкспериментируете с этими разными уров-
нями усиления на лабораторном занятии.
Из графиков можно понять, что с повышени-
ем усиления возрастает последействие, а также
увеличивается крутизна спада. Как обычно, за
улучшение одной характеристики приходится
расплачиваться ухудшением какой-либо другой.
На нижнем изображении на рис. 9S.17 показа-
но, как треугольный сигнал проходит через три
разных типа фильтров. Здесь можно видеть,
что фильтр Бесселя справляется несколько луч-
ше с задачей сохранения формы сигнала, как и
ожидается от фильтра данного типа.
18 Сравните АоЕ рис. 6.27.
9S.3. Диагностирование
помех
Что может быть причиной, что выходной
(а иногда и входной тоже) сигнал вашего филь-
тра зашумлен помехами? Причиной могут быть
паразитные автоколебания, хотя и не обяза-
тельно они. Но если возникают автоколебания,
то что тогда создает их? Обычно определить
причину автоколебаний можно достаточно лег-
ко, хотя иногда придется и потрудиться.
9S.3.1. Предварительный
вопрос: что такое паразитные
автоколебания?
Действительно ли эти автоколебания «пара-
зитные»? Не обязательно. Что-то создает их,
но виновником помех может быть и не ваша
схема. Рассмотрите несколько других вероят-
ных причин. Иногда полезно измерить частоту
420
9S. Дополнительный материал: операционные усилители IV
пульсаций, но сразу определить ее трудно, осо-
бенно, если частота вредных колебаний оказы-
вается намного выше или ниже частоты вашего
полезного сигнала. Все что можно увидеть —
это просто наличие помех. Эту проблему мож-
но решить, настроив частоту развертки осцил-
лографа.
Если частота пульсаций намного ниже частоты
сигнала, обычно их причиной будет наводка
сети частотой 60 Гц. Если же частота пульса-
ций намного выше частоты сигнала, возможной
причиной может быть наводка радио- или теле-
передачи. Частоты между этими двумя предела-
ми могут указывать на возможные паразитные
автоколебания.
9S3.2. Наводки электросети
Пример
На рис. 9S.18 видно, что нижняя осциллограм-
ма синусоидального сигнала частотой около
1 кГц неприятно утолщенная или расплывча-
тая, и это нельзя исправить настройкой фокуса
луча. В чем здесь дело?
1/ДТ 60,24 Гц
ЕХТ
50 мВ 5 мс
Рис. 9S.18. Постоянно присутствующие низкочастотные по-
мехи на сигнале более высокой частоты указывают на навод-
ки электросети (частота развертки: вверху — 5 мс/деление,
внизу — 0,2 мс/деление)
Это могут быть или высокочастотные, или низ-
кочастотные шумовые помехи. Помехи, вызы-
ваемые наводками электросети частотой 60 Гц,
легко заметить: попробуйте установить запуск
развертки от сигнала частотой 60 Гц (синхро-
низация от сети), а скорость развертки умень-
шите до нескольких микросекунд на деление.
Именно таким образом мы получили верхнюю
осцилограмму на рис. 9S.18, синхронизировав
помеховые выбросы. Когда это произойдет, эф-
фект будет очевиден с первого взгляда. Кроме
того, сигнал на рисунке повторяется с часто-
той 60 Гц, как показано двумя вертикальными
линиями (а также вычислением 1/АГ, отобра-
женным над верхней осциллограммой). Это не
удивительно, но сообщает нам немножко боль-
ше, чем мы можем узнать, исходя из факта ста-
билизации картинки синхронизацией от сети.
Но иногда частота помехи составляет не 60 Гц,
а 120 Гц, как мы вскоре увидим.
Кстати, на рис. 9S.19 изображена схема, которая
генерировала эти сигналы. Мы подключили по-
следовательный резистор номиналом 10 МОм,
а затем наблюдали сигнал на входе операцион-
ного усилителя (как будто бы пытаясь изме-
рить, скажем, его входной импеданс). Сигнал в
точке измерения очень слабый, вследствие чего
он особенно восприимчив к помехам.
К осциллографу
Рис. 9S.19. Высокий импеданс входа операционного усили-
теля делает его восприимчивым к наводкам
Процедура поиска причины помех
Если при синхронизации от сети на экране
осциллографа стабильно наблюдаются помехи,
значит, эти выбросы синхронизованы с часто-
той источника питания (60 Гц) и почти навер-
няка вызваны источником питания.
♦ Но даже если частота помех равна 60 Гц (или
120 Гц, частота двухполупериодного выпрям-
ленного напряжения, выдаваемого источни-
ком питания), все еще возможны другие при-
чины помех.
• Возможно, что на каком-то высокоимпе-
дансном входе схемы создаются наводки
электросети частотой 60 Гц. Мы только
что видели такую ситуацию в схеме на
рис. 9S.19, и это более распространенная
причина.
• Эти выбросы могут быть помехами по
шине заземления, создаваемыми разно-
стью напряжений между шинами «земли»
нескольких ваших приборов, которые в
свою очередь вызываются токами, проте-
кающими в длинных цепях возврата через
9S.3. Диагностирование помех
421
«землю». Позаботьтесь, чтобы все ваши
приборы были подключены к одному мно-
горозеточному блоку или, в любом случае,
к одной розетке. Эта проблема контура за-
земления рассматривается чуть более по-
дробно в следующем подразделе.
• Если выбросы с частотой 120 Гц имеют
одинаковую полярность, то они, вероят-
но, являются результатом бросков тока на
шинах питания (положительной и отри-
цательной), которые возникают при пере-
зарядке конденсаторов фильтра вашего
источника питания каждый полупериод
входного напряжения. Эти помехи устра-
нению не поддаются, за исключением ра-
дикального решения — замены источника
питания на более стабильный, как реко-
мендуется в разделе 9S.3.3.
9S.3.3. Помехи контура заземления
На рис. 9S.20 иллюстрируется вторая причина
помех в сигнале схемы: не наводки электросе-
ти, но помехи по шине заземления, возникаю-
щие в результате подключения измерительных
приборов в разные розетки. Верхняя осцилло-
грамма на рисунке отображает синусоидаль-
ный сигнал, подаваемый генератором сигналов
на макетную плату. Хотя сигнал имеет пра-
вильную синусоидальную форму, он доволь-
но расплывчатый. Применив синхронизацию
осциллографа от сети и замедлив скорость раз-
вертки, мы видим то, что показано на нижней
осциллограмме. Выбросы стабилизировались,
так что это похоже на наводки электросети.
%Т 60,06 Гц
.--'.Ч ><" ч -'v
20 мВ
v 5 мс
1) Входной сигнал при первом подходе: утолщенная
трассировка
2) ...при медленной развертке обнаруживается помеха
с частотой 60 Гц
Рис 9S.20. Помехи по «земле» зашумляют обе осциллограммы
Но посмотрите на схему, изображенную на
рис. 9S.21. Помехи здесь — не вина генератора
сигналов, это также не наводки электросети.
В данном случае входной импеданс схемы низ-
кий: не 10 МОм, как в предыдущем случае, но
всего лишь 50 Ом генератора сигналов. Поэтому
наводки электросети маловероятны.
К осциллографу
Рис. 9S.21. Схема, в которой наблюдается помеха с частотой
60 Гц на входе, неуязвима к наводкам электросети
Проблема решилась переключением вилки
питания осциллографа из розетки, располо-
женной на расстоянии около полметра дальше
на столе, в розетку, к которой подключены ге-
нератор сигналов и источник питания. Теперь
входной сигнал выглядит как показано в трас-
сировке 3 на рис. 9S.22. (На осциллограммах на
рис. 9S.20 и 9S.22 скорости развертки разные.)
Здесь помеховые выбросы едва заметны.
3) Хорошее заземление очищает
синусоидальный сигнал...
4) ...и при медленной развертке помеха
с частотой 60 Гц не наблюдается
Рис. 9S.22. Улучшение заземления очищает сигнал от сете-
вых помех
Причиной помех на осциллограммах на
рис. 9S.20 было то обстоятельство, что осцил-
лограф и генератор сигналов были включены
в разные розетки электросети. Линии зазем-
ления этих розеток соединялись скорее всего
на значительном расстоянии от них, создавая
протяженный контур заземления. Когда этот
контур пересекается магнитным полем часто-
той 60 Гц (создаваемым током, протекающим
в других линиях электросети здания), в нем
наводятся токи. Если эти токи проходят через
ненулевой импеданс земляной шины, то созда-
ется падение напряжения, которое проявляется
в виде помех на сигнале.
Другой пример помех
по цепи заземления
Осциллограмма на рис. 9S.23 тоже иллюстри-
рует помеху, создаваемую контуром заземле-
ния, но выглядит более эффектно.
422
9S. Дополнительный материал: операционные усилители IV
— Что за чертовщина?! — можете воскликнуть
вы, если собранная вами со всеми мерами пред-
осторожности схема создает такую картину.
Рис. 9S.23. Помеха из контура заземления может возникать,
когда устройства не имеют общей земли. Такая помеха мо-
жет полностью нарушить наблюдение полезного сигнала
Осциллограмма на рис. 9S.23 отображает по-
пытку получить 4-канальную осциллограм-
му на осциллографе с мультиплексирован-
ным входом (возможно, вы предпримете ее на
одном из лабораторных занятий далее в нашем
курсе). На рис. 9S.24 показано, как эти осцил-
лограммы должны выглядеть в действительно-
сти. На самом деле это осциллограмма работы
4-разрядного счетчика с четкими переходами
между уровнями. А уродливая картина, изо-
браженная на рис. 9S.23, является результатом,
опять же, подключения осциллографа не в ту
розетку, к которой были подключены источник
питания макетной платы и генератор сигналов.
Рис. 9S.24. Правильная осциллограмма 4-канальной трасси-
ровки
Еще пример: некачественное заземление
Еще один пример помех из контура «земли», где
выбросы имеют одинаковую полярность и сле-
дуют с частотой 120 Гц. Используемая нами ма-
кетная плата со встроенным источником пита-
ния РВ503 имеет некачественную линию «зем-
ли», на которой происходят скачки потенциала,
вызываемые бросками тока источника питания
при перезарядке конденсаторов фильтра источ-
ника каждый полупериод напряжения питания
электросети. Для этой проблемы нет никакого
практического решения, кроме замены источ-
ника питания на более качественный. Наши ма-
кетные платы со встроенным источником пита-
ния дают много таких помех по шине «земли».
Выскокачественные лабораторные источники
питания, например производства компании
Agilent Technologies, такого дефекта не имеют.
На лабораторном занятии 7L.4 (микрофонный
усилитель) обсуждается именно такая про-
блема шумящего источника питания и реко-
мендуется решение заменой его качественным
устройством.
Помеху от такого источника питания иллю-
стрирует рис. 9S.25.
Это осциллограмма при первоначальном обна-
ружении проблемы — слегка утолщенная линия
сигнала.
Если подозревается, что это помеха электросе-
ти или источника питания, то установите син-
хронизацию запуска развертки от сети и замед-
лите скорость развертки. Если бугорки стаби-
лизируются, то их причиной является источник
питания.
При более подробном исследовании самой ли-
нии земли обнаруживаем на ней помеху, вызы-
ваемую бросками тока, причиной которых яв-
ляется заряд конденсатора фильтра источника
питания на каждом полупериоде напряжения
электросети частотой 60 Гц.
Рис. 9S.25 Помехи из контура «земли» зашумляют все сиг-
налы, наблюдаемые в схеме (скорость развертки на верхней
осциллограмме намного выше, чем на двух нижних)
9S.3. Диагностирование помех
423
На верхней осциллограмме видно то, что ско-
рее всего будет замечено сразу же: утолщение
или расплывчатость выходного сигнала, (На
этот раз это небольшое утолщение.) Установите
режим синхронизации от сети, замедлите ско-
рость развертки, и бугорки стабилизируются.
Поскольку их частота повторения 120 Гц, зна-
чит, это не наводка электросети частотой 60 Гц,
а проблема источника питания. Наиболее по-
казательной является нижняя осциллограмма:
сама шина «земли» зашумлена этими помеха-
ми! Пора обзаводиться более качественным ис-
точником питания.
9S.3А. Еще одни источник помех:
радиочастотные наводки
Иногда на сигнале можно заметить помехи
(обычно малой амплитуды), проявляющие-
ся на другом конце частотного диапазона, ко-
торые можно различить на высокой скоро-
сти развертки. На нижней осциллограмме на
рис. 9S.26 показан пример таких наводок. Если
установить режим синхронизации по этим
пульсациям и высокую скорость развертки, то
можно убедиться, что эти помехи лежат в диа-
пазоне нескольких мегагерц. Верхняя осцилло-
грамма была снята именно с такими настройка-
ми. Окончательно подтвердить, что это радио-
частотные наводки, можно, выключив питание
минимально возможной длину проводов, под-
ключенных в точках схемы с высоким импе-
дансом. Кроме того, низкий импеданс снижает
уязвимость схем к помехам данного типа. В лю-
бом случае полезно убедиться, что источником
помех не является ваша схема: теперь вам не
придется тратить время, исследуя разные части
схемы в поисках причины.
9S.3.5. Настоящие паразитные
автоколебания
Но если помеха является настоящими паразит-
ными автоколебаниями, то возникает вопрос,
что является ее источником. Часто ответ на
этот вопрос можно получить, определив часто-
ту автоколебаний19. Рассмотрим два примера.
Пример 1. Эмиттерный повторитель
на дискретных элементах
Возвратимся обратно к рис. 9L.2, на котором
показан случай только с одним потенциальным
источником помех20. Если выходной сигнал
расплывчатый, виной тому является транзи-
стор. Чтобы определить это, не требуется ни-
каких чрезмерных усилий. Но этот легкий слу-
чай поможет нам решить другую, более слож-
ную, проблему, рассматриваемую в примере 2
Быстрая развертка может повысить
разрешение и сделать наглядным
отображение радиочастотной помехи
Тогда как при медленной
развертке можно увидеть только
расплывчатость или утолщение луча
Рис 9S.26. Высокая скорость развертки иногда помогает превратить неясные помехи в различимый высокочастотный си-
нусоидальный сигнал. Верхняя осциллограмма выполнена при быстрой развертке, а нижняя — при медленной. Обратите
внимание на разные величины усиления осциллографа для этих двух осциллограмм
схемы и наблюдая сигнал на ее входе. Если по-
мехи продолжаются, то ваша схема не является
их причиной.
У этой проблемы нет легкого решения. В прин-
ципе, что следует сделать, так это заэкраниро-
вать схему или, по крайней мере, укоротить до
19 За эту и много другой полезной информации по вопросу
стабильности операционных усилителей мы признатель-
ны Томасу Фредериксену (Thomas Frederiksen) и его кни-
ге «Intuitive 1С OP Amps*, ст. 154ff, издательство National
Semiconductor Corporation» 1984 г.
20 Могут ли причиной этой расплывчатости сигнала быть
радиочастотные наводки? Маловероятно, поскольку точка
наблюдения (эмиттер транзистора) должна иметь очень
низкий импеданс.
424
9S. Дополнительный материал: операционные усилители IV
(рис. 9S.28). На рис. 9S.27 показано, как дол-
жен выглядеть выходной сигнал эмиттерного
повторителя при разных скоростях развертки.
Медленная развертка:
10 мкс/деление
Быстрая развертка:
10 не/деление
А при более быстрой развертке можно изме-
рить частоту этих автоколебаний (рис. 9S.30).
Она составляет несколько сотен килогерц (точ-
нее 500 кГц) — слишком низкая для паразит-
ных автоколебаний, генерируемых транзисто-
ром, как в эмиттерном повторителе, который
мы исследовали в разделе 9L2.
2 мке
Рис. 9S.27. При более высоком разрешении можно видеть,
что расплывчатость выходного сигнала является колебания-
ми радиочастотного диапазона. Но на этот раз это не радио-
частотные наводки!
Пример 2. Операционный усилитель
с выходным двухтактным каскадом
Как мы и обещали, определить виновника рас-
плывчатости выходного сигнала схемы, изо-
браженной на рис. 9S.28, гораздо труднее. На
первый взгляд все выглядит так, будто при-
чиной является операционный усилитель или
транзисторы. Но давайте внимательно исследу-
ем выходной сигнал с помощью осциллографа.
(помехи присутствуют
при закороченном резисторе базы)
* Ц-ч1 динамик)
Рис. 9S.28. Схема, виновниками автоколебаний в которой
можно было бы считать или операционный усилитель, или
транзисторы
Сначала при довольно малой скорости разверт-
ки (подходящей для исследования только вы-
ходного аудио сигнала) наблюдаются весьма
эффектные выбросы (рис. 9S.29).
Рис. 9S.29. Паразитные выбросы в выходном сигнале двух-
тактного выходного каскада, подаваемом на динамик
Рис. 9S.30. Быстрая развертка позволяет определить часто-
ту паразитных автоколебаний
Соответственно, мы возлагаем вину за эти авто-
колебания на операционный усилитель и пред-
принимаем соответствующие меры по реше-
нию проблемы — более короткий путь, в обход
двухтактного каскада на высоких частотах (см.
рис. 9L.8). По-видимому, автоколебания гене-
рирует операционный усилитель. Частота дан-
ного сигнала находится в диапазоне, в котором
паразитные элементы низкочастотного филь-
тра в петле обратной связи могут вызывать фа-
зовые сдвиги, близкие к их максимально допу-
стимому значению, когда величины усиления
операционного усилителя еще достаточного
для того, чтобы отрицательная обратная связь
превратилась в положительную.
Почему шунтирование конденсатором
иногда не работает
Иногда стандартное решение остановить авто-
колебания добавлением шунтирующего кера-
мического конденсатора небольшой емкости
на шины питания вызывает противоположный
эффект: автоколебания усиливаются. Причиной
может быть простое невезение: вставленная
емкость «скооперировалась» с паразитной ин-
дуктивностью шины питания, и они образовали
резонансный контур. Попытайтесь решить эту
проблему, заменив конденсатор другим с номи-
налом в 10 раз больше; также попробуйте заме-
нить керамический конденсатор танталовым.
Если ни одно из этих решений не даст положи-
тельного результата, попробуйте подключить
конденсатор к шине питания через последова-
тельный резистор небольшого номинала. Но это
приведет к некоторому повышению импеданса
9S.4. Схема операционного усилителя LF411
425
.Токовое
зеркало
Уилсона
,: Компенсация эффекта
:ра транзистора
--ТИсточник тока для создания
^усмещения на стабилитроне.
D
ГВычисляется по скорости нарастанияХ \
увыходного напряжения и значению <^K0Pj \
Дифференциальная^ ^ 150 мкА
пара (перевернутая - \ Вход ,*~
«хвост» вверху) ) (^\ *,А\
(Усилитель с общим эмитт
(Ист
повторитель с понижающим источни
Двухтактный
повторитель;
резисторы
небольших номиналов^
в цепяхз
предотвращают
тепловой пробой, 1
а также защищают \
от короткого
замыкания выхода)
Ограничение
выходного
тока Qu отбирает '
токбазыуЛ,когда\
1^22 O 06F'
(Токовое зеркало «активной нагрузкю*Х
для дифференциального усилителя Q )
уменьшает влияние тока базы Q2 _/
то же самое
идля(?ю, i
который отбирает/
j^. Зтокбазы
(iQ через
гПадение напряжения 2хС^
для обеспечения смещения
для <5Jj, Q9 и предотвращения
искажений
токового зеркала:
[транзисторов Qia и Q19
Рис. 9S.31. Схема с операционного усилителя LF411 с комментариями
(получение низкого импеданса и было целью
добавления конденсатора). Резистор уменьшит
добротность Q создаваемого конденсатором и
паразитной индуктивностью нежелательного
резонансного LC-контура, предотвращая коле-
бания.
9S.4. Схема операционного
усилителя LF411
Знать внутреннее устройство и работу микро-
схемы операционного усилителя необходимо
только в очень редких случаях. Но будет весь-
ма познавательно исследовать какую-либо
«страшную» схему, наподобие показанной на
рис. 9S.32, и осознать, что вам знакомы многие
из ее составляющих.
Если с первого взгляда сам размер схемы вас не
отпугнул, то возможно, вы сможете самостоя-
тельно узнать в ней, по крайней мере, следую-
щие элементы:
♦ дифференциальный усилитель во входном
каскаде;
♦ усилитель с общим эмиттером в следующем
каскаде;
♦ двухтактный усилитель в выходном каскаде;
♦ целый набор зеркал (если вы не поленились
изучить раздел 5S.2).
Функция ограничения тока реализуется прие-
мом, используемым в стабилизаторах напряже-
ния, которые мы рассмотрим в главе UN.
Однако назначение некоторых отдельных эле-
ментов схемы довольно тонкое, и в коммента-
риях мы постарались объяснить цель этих эле-
ментов. Данная схема приводится не только для
повторения пройденного материала, но и для
вознаграждения за усилия, вложенные вами в
изучение дискретных транзисторов и схем на
их основе. Мы надеемся, что исследование этой
схемы позволит вам почувствовать себя более
знающим, осознать тот факт, что вы начинаете
понимать, как читать схемы, которые ничего не
значили для вас всего лишь несколько недель
тому назад.
426
9S. Дополнительный материал: операционные усилители IV
9S.5. Количественное
описание обратной связи
Подробные расчеты усиления схемы при из-
менении усиления разомкнутой цепи обрат-
ной связи
г21
мы рассмотрим в примере 9W.1. лителя).
Здесь же мы удовлетворимся кратким описани-
ем, объясняющим работу обратной связи. На
рис. 9S.32 изображена общая модель обратной
связи22.
А
В
Обычная структура перерисованная так, чтобы
выглядеть более похожей на схему
с операционным усилителем
Рис. 9S.32. Блок-схема обратной связи
Схему на рис. 9S.32 еще легче понять, если еще
перерисовать и блок В, чтобы показать часть
выходного сигнала 17ВЫХ, подаваемого обратно
на вход, как это делается в обычных случаях.
Модифицированная таким образом схема изо-
бражена на рис. 9S.33.
Часть В, снимаемая
с делителя
и подаваемая обратно
на вход:
♦ В = часть выходного сигнала, подаваемая об-
ратно на вход (характеристика самой схемы,
а не микросхемы операционного усилителя);
♦ А = усиление разомкнутой цепи (характе-
ристика микросхемы операционного уси-
Обратите внимание на произведение АВ9 назы-
вающееся усилением петли. Поскольку боль-
шие значения А и В увеличивают полезные
свойства обратной связи, будет неудивитель-
ным обнаружить (вразделе 9S.5.1 и далее), что
при оценке влияния обратной связи мы будем
пользоваться этим произведением АВ.
Этих понятий будет достаточно, чтобы дать ко-
личественную оценку характеристикам схемы,
которые до сих пор мы могли описать только,
употребляя прилагательные: большое, малое,
очень хорошее и т.п., применительно, напри-
мер, к входному и выходному импедансу и по-
стоянству усиления.
Мы выведем выражение для усиления схемы
и попытаемся показать посредством только
качественного подхода, каким образом обрат-
ная связь улучшает входной и выходной импе-
дансы. Для начала попробуйте самостоятель-
но применить этот метод для оценки влияния
обратной связи на входной или выходной им-
педанс неинвертирующего усилителя, прин-
ципиальная схема которого изображена на
рис. 9S.34.
Примечание
Пример влияния обратной связи на выходной им-
педанс был рассмотрен в разделе 6N.5.2.
Рис. 9S33. Перерисованная блок-схема, на которой видно,
что часть В снимается с делителя
Эффект
самообеспечения1
Д(Л почти равно Д(/+
=> напряжение Д(/на Л^ очень мало
=> входной ток J^ чрезвычайно мал
=> входное сопротивление г^ очень велико
Рис 9S34. Пример улучшения Я^ и Явых в неинвертирующем усилителе с обратной связью
вьхх'
Подаем изменение
напряжения LU
Операционный усилитель
реагирует большим Д(/
=> большой ток (&I) на выходе
=> малое /v-v
21 АоЕ§2.53.
22 АоЕ§ 2.5.2.
9S.5. Количественное описание обратной связи
427
9S.5J. Входной импеданс /?вх
Входной импеданс RBX дополняется следящей
обратной связью: при небольших изменениях
входного сигнала Г7ВХ на инвертирующем вхо-
де создается приблизительно такое же изме-
нение23. Как оказывается, входной импеданс
#вх дифференциального каскада улучшается в
(1 + АВ) раз. Это так называемый эффект са-
мообеспечения, упоминаемый в разделе 9S.2.1
при рассмотрении VCVS-фильтра. Принцип
здесь состоит в том, что параметр на выходе
какого-либо компонента меняется при измене-
нии параметра на входе (самообеспечивается),
после чего компонент «исчезает» в электриче-
ском смысле. Но этот аргумент не действует,
когда входной импеданс составляет 1012 Ом, как
в операционном усилителе 411: тогда входная
емкость Свх преобладает над входным импе-
дансом RBX. К сожалению, большая часть этой
входной емкости не самообеспечивается.
ив
вых
95.5.2. Выходной импеданс /?,
Подобная аргументация применяется и для вы-
ходного импеданса24: на небольшое изменение
выходного сигнала (подачей небольшого AU)
операционный усилитель реагирует большим
перемещением точки X, создавая большое на-
пряжение на своем выходном импедансе #вых.
В результате поставляется или поглощается
большой выходной ток 1ВЫХ. Несомненно, что
вы можете понять вытекающий из этого полез-
ный результат — как будто бы по волшебству
низкое эффективное выходное сопротивление
#вых. Используя А и В, мы можем подтвердить
этот аргумент количественным, что мы и сдела-
ем в разделе 9S.5.4.
95.5.3. Усиление
Как уже упоминалось ранее, усиление схемы на
операционном усилителе составляет 1/В, где В
соответствует подаваемой обратно на вход части
выходного сигнала. Например, в неинвертирую-
щем усилителе подача обратно на вход 1/10 ча-
сти выходного сигнала дает усиление, равное
1025. Давайте обоснуем этот результат, используя
для этого наши определения для А и В.
23 АоЕ § 2.5.3В, АоЕ § 2.4.3.
24 АоЕ § 2.5.3С.
25 Возможно, вы припомните, что в главе 6N мы называ-
ли это поведение способностью операционного усилителя
создавать так называемую инверсию «собаки». А «соба-
кой» в данном случае являлась функция преобразования
любого сигнала, подаваемого в петлю обратной связи.
Рис. 9S.35. Получение общего выражения для усиления схемы
Под «усилением» имеется в виду ивых/ивх26.
Мы знаем, что операционный усилитель пред-
ставляет собой дифференциальный усилитель,
который усиливает иДИФФ в соответствии с ко-
эффициентом усиления при разомкнутой цепи
обратной связи А. Давайте взглянем, как он
усиливает эту разницу, а также, что делает об-
ратная связь с его усилением:
«вых =
("вх -
- АВи
ъых>
вых
При большом значении А и когда АВ »1, тогда
Усиление « 1/В. Это обычный, привычный для
всех нас случай, и именно это постоянство уси-
ления представляло наибольший интерес для
Гарольда Блэка, когда он начал размышлять об
использовании обратной связи для стабилиза-
ции усилителей телефонных ретрансляторов.
Конечно же, при повышении частоты усиление
А падает и вместе с ним уменьшаются замеча-
тельные эффекты обратной связи.
9S.5A Количественный пример
Попробуйте определить коэффициент улуч-
шения входного или выходного импеданса для
неинвертирующего усилителя со следующими
характеристиками.
26 Прописная буква U при описании характеристики реа-
гирования усилителя на малые сигналы эквивалентна
более обычному выражению Ку = Дивых/Аивх. В данной
ситуации не стоит придавать большое значение различи-
ям между обозначениями Via и или Аи, поскольку мы рас-
сматриваем усилитель по постоянному току. Он не похож
на рассматриваемые ранее усилители на дискретных тран-
зисторах, в которых связь осуществляется по переменному
току. Поэтому при работе с ними важность для нас пред-
ставляла только величина АС/.
428
9S. Дополнительный материал: операционные усилители IV
Предполагаемые характеристики
операционного усилителя
♦ Входной импеданс RBX операционного уси-
лителя с разомкнутой цепью обратной свя-
зи (дифференциального каскада, между его
двумя входами) составляет 1 МОм.
♦ Входной импеданс #вых операционного уси-
лителя с разомкнутой цепью обратной связи
составляет 100 Ом.
♦ Усиление схемы на операционном усилителе
при замкнутой цепи обратной связи состав-
ляет 10.
♦ Коэффициент усиления микросхемы опера-
ционного усилителя при разомкнутой цепи
обратной связи составляется 1000 при часто-
те 4 кГц27.
Оба импеданса, входной и выходной, улучша-
ются в (1+АВ) раз28.
Примечание
Этот аргумент очень похож на аргумент, что бипо-
лярный транзистор улучшает параметры на выхо-
де в (1 + ($) раз посредством так называемого эф-
фекта «розовых очков».
Какова величина (1 + АВ)? В постановке за-
дачи для усиления А указана величина 1000;
а В представляет часть выходного сигнала, ко-
торый подается обратно на вход. В данном слу-
чае А делится на 10, т. е. В = 0,1. Вот почему ко-
эффициент усиления равен 10. Таким образом,
произведение АВ = 100. Поэтому аппаратные
характеристики микросхемы улучшаются во
столько же раз:
♦ входной импеданс RBX (каскада дифференци-
ального усилителя) повышается от 1 МОм до
100 МОм;
♦ выходной импеданс #вых уменьшается от
100 Ом до 1 Ом.
Обратите внимание на то, что эти эффекты не
совсем такие, как влияние коэффициента уси-
ления р биполярного транзистора, который
воздействовал на импеданс на выходе транзи-
стора. Коэффициент (1 + АВ) операционного
усилителя воздействует на величину внутри
петли обратной связи: мы не можем «посмо-
треть через операционный усилитель»29.
Важные замечания
Полезные свойства схемы с обратной связью
зависят как от усиления А, так и от подаваемой
обратно части выходного сигнала В: схема ра-
ботает лучше всего при большом произведении
АВ, или петлевом усилении. Величина А умень-
шается с повышением частоты, а величина В
наибольшая в повторителе и наименьшая, если
нам требуется большое усиление. Еще один
пример «электронной» справедливости: за вы-
сокое усиление схемы нужно расплачиваться
некоторыми полезными свойствами обратной
связи.
Полезное усовершенствование
Спад усиления в скорректированных опера-
ционных усилителях заставляет их вести себя
А (логарифмическая
шкала)
Усиление схемы = )
= 100 (усилитель^
Усиление схемы =
=1(повторитель)
Меньшее петлевое
усиление АВ
Спад усиления 6 дБ
на октаву при разомкнутой
цепи обратной связи
Большое петлевое
усиление^* Повторитель^
£=1
Хорошие
характеристики
5=0,01
Менее хорошие
характеристики
Частота (логарифмическая шкала)
Рис. 9S.36. Усиление при разомкнутой петле снижается с повышением частоты; часть В самая большая для повторителя
27 Действительные параметры для микросхемы операци-
онного усилителя LF411.
28 АоЕ§4А2А.
29 Частичное исключение из этого правила справедливо в
случае инвертирующей конфигурации, в которой Ди игра-
ет роль в вычислении части В выходного сигнала, подавае-
мой обратно.
9S.5. Количественное описание обратной связи
429
на частотах выше нескольких десятков герц
подобно интеграторам с разомкнутой цепью
обратной связи. Это вы уже знаете. Фазовый
сдвиг величиной -90° поначалу выглядит как
будто бы он нарушает все наши расчеты по уси-
лению. Ранее мы огласили правило, что уси-
ление для операционного усилителя с ограни-
ченным усилением определяется по формуле
А/(1 + АВ), и в разделе 9S.5.4 использовали эту
формулу для вычисления эффективного усиле-
ния схемы. Но что будет с этим расчетом, если
мы усложним его, признав правду, что почти на
всех частотах усиление А при разомкнутой цепи
обратной связи отстает от входного сигнала на
90°? В комплексной, или векторной, записи это
означает, что усиление при разомкнутой цепи
описывается как -j\A\.
На первый взгляд это, несомненно, выглядит
как очень неприятное усложнение и разочаро-
вание для нашего курса, в котором мы всегда
заверяли вас, что обычно не нужно беспоко-
иться о фазовых сдвигах. Ранее мы уже встре-
тились с исключением из этого правила: нам
нужно беспокоиться о фазовых сдвигах, когда
мы рассматриваем стабильность схем с обрат-
ной связью. До сих пор это представляло для
нас проблему. Теперь же, на удивление, фазо-
вый сдвиг выплатит нам неожиданный диви-
денд в виде улучшения усиления операцион-
ного усилителя.
В книге АоЕ этот момент рассматривается на
гипотетическом случае, который мы повторим
здесь, расписывая подробно шаги вычислений,
выполняемые в книге АоЕ.
Гипотетический случай: схема
с усилением 10 и ограниченным А
Усиление Аи подаваемая обратно часть В по-
добны параметрам, которые приводятся в по-
становке задачи в разделе 9S.5.430. Но в этот раз
усиление А меньше: А = 100, В = ОД.
Усиление схемы без учета фазового сдвига
Усиление схемы:
А 100
Это значение с погрешностью в 9%. С учетом
наших «золотых правил» мы надеялись на луч-
ший результат. Как оказывается, наши надеж-
ды вполне обоснованы.
Усиление схемы с учетом фазового сдвига
Теперь смиримся с непривлекательностью ком-
плексной записи в надежде получить лучшее
усиление, нечто более близкое к идеальному
представлению поведения операционного уси-
лителя, выраженного «золотыми правилами».
Представим усиление при разомкнутой цепи
обратной связи не как 100, а как -100/, и по-
смотрим, что из этого выйдет.
Усиление схемы:
А _ -100; _ -100;
1 + АВ (1+(-НЮ/) • ОД) 1-Ю./'
Пока что все выглядит как расчет с игнориро-
ванием фазового сдвига. Но теперь позволим,
чтобы -j сделало свое дело. Вычислим величи-
ну усиления в два этапа:
1. Упростим знаменатель, избавившись от/, для
чего умножаем числитель и знаменатель на
комплексно-сопряженное значение знамена-
теля 1+10/:
-100; 1+10; _-ЮР;* 1000 _
1-107 1+10./
-1007+1000
101
1+100
= -0,997+9,9.
2. Получив комплексный результат а + bj, опре-
деляем его модуль:
Здесь,
У = V9,92+0,992 = V98,01+0,98 =
= 9,95.
Погрешность этого результата составляет всего
лишь 0,5%, что значительно лучше, чем резуль-
тат вычислений без учета фазового сдвига.
1+АВ 1 + 10
= 9,1.
АОЕ § 2.5.4В.
9W. Примеры с решениями:
операционные усилители IV
9W.1. Польза, получаемая
от усиления операционных
усилителей
Подавая обратно на вход, скажем, одну со-
тую часть выходного сигнала, для вычисле-
ния соответствующего усиления мы прибе-
гаем к помощи «золотых правил». При этом
выдвигается предположение, что усиление
операционного усилителя очень высокое
(поскольку, говоря словами Гарольда Блэка,
«...усовершенствования получаются пропор-
ционально потере коэффициента усиления
операционного усилителя...»). Предполагая
громадное усиление собственно операци-
онного усилителя, что мы и подразумеваем,
пользуясь «золотыми правилами», можно
сказать, что усиление схемы на рис. 9W.1
равно 100.
Рис. 9W.1. Доля сигнала обратной связи равна 1%
Давайте посмотрим, что будет в схеме на
рис. 9W.1, если предположить усиление опера-
ционного усилителя при разомкнутой цепи об-
ратной связи (обозначается буквой А) несколь-
ко меньше, чем в идеальном случае.
Задачи: Усиление схемы на разных
частотах
9W.1 Л. Предполагаем отсутствие
фазового сдвига для А
Прежде всего предположим, что усиление опе-
рационного усилителя при разомкнутой цепи
обратной связи не сопровождается фазовым
сдвигом.
Задача
Определить, каким будет коэффициент усиле-
ния схемы, изображенной на рис. 9W.1, при:
♦ А =100;
♦ А =1000;
♦ А =100 000.
Решение
Как мы знаем, в общем случае коэффициент
усиления Ку = А/(1 + АВ). По условию задачи
В = 0,01, поэтому для наших значений А соот-
ветствующие значения произведения АВ бу-
дут равны 1,10 и 1000. При наивысшем значе-
нии усиления А, равном 100 000, мы получим
Ку = 100 000/(1 +1000) = 100 (с погрешностью
в 0,1%). При А = 1000 Ку = 1000/(1 + 10) = 91.
А при А = 100 Ку = 100/(1 +1) = 50.
Приведенные результаты выглядят довольно
неутешительно. Однако далее мы убедимся, что
не все так плохо.
9W.2. Вопросы стабильности
431
9W,12. Сопоставление двух случаев:
без фазового сдвига и с фазовым
сдвигом величиной -90°
Теперь мы сравним два случая и рассчитаем
коэффициент усиления при разомкнутой цепи
обратной связи. Сначала, как и в предыдущей
задаче 9W.1.1, мы будем считать, что фазово-
го сдвига нет. А затем мы предположим, более
точно, что А содержит фазовый сдвиг вели-
чиной 90°, как это в действительности проис-
ходит на частотах выше нескольких десятков
герц. На первый взгляд данный фазовый сдвиг
выглядит проблематично, но в действительно-
сти он улучшает коэффициент усиления схемы.
Оказывается, что наши вычисленные в разделе
9W.1.1 результаты несколько более мрачные,
чем они в действительности есть.
Задача № 1
Разработайте неинвертирующий усилитель с
коэффициентом усиления величиной 20 (руко-
водствуясь при этом «золотыми правилами»).
Как обычно, считайте операционный усилитель
идеальным. Вычислите коэффициент усиления
для заданного А.
Решение
В данной схеме обратно на вход поступает одна
часть из 20 выходного сигнала, т. е. В = 0,05.
В этот раз допустим, что А = 100.
Это предполагаемое усиление ниже, чем мы
обычно наблюдали в наших лабораторных схе-
мах. Операционный усилитель 411 имеет такое
усиление при разомкнутой цепи обратной свя-
зи на частоте 40 кГц. В этом примере мы задаем
небольшое занчение А для того, чтобы подчер-
кнуть полезный эффект фазового сдвига опера-
ционного усилителя. Произведение АВ = 5.
Задача №2
Вычислите коэффициент усиления, предпола-
гая отсутствие фазового сдвига. Каким будет
усиление схемы, если А операционного усили-
теля равно 100?
Решение
Предполагая отсутствие фазового сдвига:
А 100
Это на 20% ниже усиления по «золотым прави-
лам», которое мы надеялись получить.
Задача № 3
Вычислите коэффициент усиления, предпола-
гая фазовый сдвиг равным -90°. Каким будет
усиление, если признать присутствие фазового
сдвига и предположить усиление при разом-
кнутой цепи обратной связи А = -100/?
Решение
Предполагая фазовый сдвиг величиной -9(Г
Теперь мы запишем усиление при разомкнутой
цепи обратной связи в комплексном виде, учи-
тывающем отставание по фазе: А = -100/.
v _ А -100/
1+5
= 16.
у 1+АВ (1-5;)
Мы выполняли подобный расчет в разделе 9S.3.
Здесь мы можем ускорить определение величи-
ны этого комплексного выражения, воспользо-
вавшись тем фактом, что коэффициент усиле-
ния есть отношение величин иъых/иъг Тогда:
Ку = 100/V(l+25) = 19,6.
Этот результат намного лучше предыдущего:
всего лишь на 2% меньше, чем усиление по «зо-
лотым правилам». Учет фазового сдвига восста-
навливает веру в «золотые правила», не так ли?
9W.2. Вопросы стабильности
Задача
На рис. 9W.2 изображены три схемы, в кото-
рых могут возникать помехи или на перепадах,
или постоянно вследствие паразитных авто-
колебаний.
Для каждой схемы дайте краткое объяснение,
какие ее элементы могут быть причиной воз-
никновения паразитных колебаний, а также
укажите наиболее важные решения по обеспе-
чению стабильности.
Для третьей схемы (двухтактного повторителя
с обратной связью) предположите использова-
ние операционного усилителя LF411 и рассмо-
трите две гипотетические частоты паразитных
автоколебаний: эти частоты могут подсказать
432
9W. Примеры с решениями: операционные усилители IV
BNC-кабель длиной
около 6 м
ЮМОм
1Ш J
А. Сигнал с операционного усилителя В. Сигнал в схему преобразователя С. Двухтактный усилитель
подается в длинный коаксиальный кабель «ток-напряжение» поступает от фотодиода и емкостная нагрузка
Рис. 9W.2. Три схемы, обладающие минимальным запасом по стабильности
альтернативные объяснения причин пробле-
мы. Допустим, что существуют две такие ча-
стоты паразитных колебаний: 100 кГц в одном
случае и 20 МГц — в другом.
Решение
Возможная причина автоколебаний. Кста-
ти, как упоминается в главе 9N, такой длинный
кабель необходимо рассматривать как линию
передачи для хорошей работы на высоких ча-
стотах (выше нескольких мегагерц), или с вы-
сокой скоростью перепадов уровня сигнала.
В данном случае предполагается, что использу-
ются достаточно низкие частоты, чтобы такие
эффекты можно было игнорировать.
BNC-кабель длиной
около 6 м
('Компьютерный4!
Рис. 9W.3. Сигнал от операционного усилителя поступает
в длинный коаксиальный кабель
Емкость нашего коаксиального кабеля, со-
ставляющая около 98 пФ/м, образует низко-
частотный фильтр, поскольку она заряжает-
ся от ненулевого выходного импеданса Двых
операционного усилителя. На самом деле этот
импеданс еще более проблематичен, чем он вы-
глядит, когда мы обозначаем его просто #вых,
поскольку имеет еще и индуктивную составля-
ющую. Данный низкочастотный фильтр может
вызвать отставание по фазе, приближающееся
к 90° (см. главу 9N). Вместе с фазовым сдвигом
величиной 90°, создаваемым самим операци-
онным усилителем, дополнительный сдвиг мо-
жет превратить отрицательную обратную связь
в положительную.
Выходной импеданс операционного усилителя
в действительности выглядит индуктивным,
поскольку значение Явых возрастает с повыше-
нием частоты, тогда как усиление операционно-
го усилителя при разомкнутой цепи обратной
связи снижается, в результате чего уменьшается
положительное действие обратной связи1. Это
индуктивное поведение выходного импеданса
вносит опасные фазовые задержки величиной
90° в частотном диапазоне, в котором опера-
ционный усилитель еще обладает достаточно
большим усилением.
Решения для проблемы длинного кабеля
Простейшее решение
Эту схему можно стабилизировать, вынеся
точку фазового сдвига за пределы петли об-
ратной связи, подключив кабель к опера-
ционному усилителю через последователь-
ный резистор небольшого номинала, скажем
100 Ом. Соответствующая схема изображена
на рис. 9W.4, Но за это решение приходится
расплачиваться существенным повышением
выходного импеданса схемы (в данном случае
на 100 Ом или около того), тогда как одним из
важных требований к повторителю является
его низкий выходной импеданс ZBbIx.
BNC-кабель длиной
=100 Ом около 6 м
['Компьютерный^
Ш )
Рис. 9W.4. Простое решение проблемы длинного кабеля:
подключение через резистор
Решение посредством разделенной обрат-
ной связи
Разделенная цепь обратной связи может стаби-
лизировать схему, не ухудшая ее выходной им-
педанс. На рис. 9W.5 показана принципиальная
схема, реализующая такое решение. Частота,
на которой сигнал обратной связи переходит из
резистивного пути на емкостной, определяется
значениями резистора Roc и конденсатора Сос.
Например, если паразитные колебания на-
блюдаются на частоте 1 МГц, то частоту пе-
рехода нужно установить в районе 100 кГц.
1 См. раздел 9S.1.
9W.2. Вопросы стабильности
433
BNC-кабель длиной
100 около 6 м (Компьютерный)
'"1 J
10 МОм
«о.
Рис. 9W.5. Лучшее решение проблемы длинного кабеля:
разделение обратной связи на высокочастотную и низкоча-
стотную цепи
Следовательно
ЯСПЕР = 1/(2* ./ПЕР) « 1/(6 • ОД • 106) = 1,6 • Ю-6.
Этому условию удовлетворяют различные ком-
бинации RC, например С = 100 пФ, R = 15 кОм.
На высоких частотах контур обратной связи
сводится к показанному на рис. 9W.4. А на низ-
ких частотах обратная связь компенсирует со-
противление величиной 100 Ом, создавая низ-
кий выходной импеданс, который мы и хотим
иметь в повторителе.
Повышение усиления схемы (тривиаль-
ный прием)
В результате повышения коэффициента усиле-
ния схемы можно уменьшить часть выходного
сигнала, подаваемого в цепь обратной связи.
Этого может быть достаточно, чтобы стаби-
лизировать схему. Такой способ иллюстрирует
рис. 9N.18.
Выбор специализированного операцион-
ного усилителя
Этот прием еще проще, хотя может оказаться
более дорогостоящим. С проблемной емкост-
ной нагрузкой можно справиться, просто вы-
брав операционный усилитель, специально
предназначенный для такой ситуации. Более
подробно можно ознакомиться в разделе 9.5
этой книги и в разделе 4.6.2 книги АоЕ.
Преобразователь «ток-напряжение»
на операционном усилителе,
управляемый фотодиодом
Паразитная емкость, обозначенная пунктиром
в правой схеме на рис. 9W.6, напоминает нам о
том, что низкочастотный фильтр в петле обрат-
ной связи образуется, когда в ней присутствует
ЮМОм
VSA/
емкость
Рис. 9W.6. Паразитная емкость делает эту схему с фотодио-
дом склонной к автоколебаниям
резистор с большим сопротивлением, а сигнал
поступает от источника тока (которым в дан-
ном случае является фотодиод).
Эффективное сопротивление резистора 2?, заря-
жающего эту небольшую паразитную емкость
(величиной порядка 10 пФ: сумма емкости опе-
рационного усилителя, фотодиода и разводки
схемы), составляет 10 МОм. На входе нет ис-
точника напряжения, как например, в инверти-
рующем усилителе с коэффициентом усиления
равным 100. В таком усилителе, в противопо-
ложность рассматриваемой схеме, эффективное
значение сопротивления, которое заряжает па-
разитную емкость существенно меньше. Также
в таком усилителе номинал входного резистора
был бы порядка 10 кОм и паразитная емкость
заряжалась бы через это небольшое сопротив-
ление. Но в нашей схеме с фотодиодом емкость
в 5 пФ заряжается через резистор с номиналом
10 МОм, в результате чего частота^дБ этого не-
преднамеренного низкочастотного фильтра
окажется равной 300 кГц, что достаточно для
возникновения паразитный автоколебаний.
Решение проблемы схемы
с фотодиодом: используем
конденсатор обратной связи
Схему можно стабилизировать, подключив па-
раллельно резистору обратной связи конденса-
тор небольшой емкости ССТАБ, как показано на
рис. 9W.7.
Паразитная емкость
Рис. 9W.7. Конденсатор в петле обратной связи может ста-
билизировать усилитель с фотодиодом
434
9W. Примеры с решениями: операционные усилители IV
Эффективным будет конденсатор даже малой
емкости. Например, емкость величиной 1 пФ
будет доминировать в цепи обратной связи
(с эффектами, рассматриваемыми чуть ниже) на
частотах выше приблизительно 16 кГц. Стаби-
лизирующее действие конденсатора в цепи об-
ратной связи можно описать двумя способами.
♦ Первый способ — анализ влияния дополни-
тельного конденсатора на сигнал, поступаю-
щий через цепь обратной связи. Конденсатор
ССТАБ создает емкостной делитель на часто-
тах, где его эффективное сопротивление
ХССТАБ намного меньше, чем сопротивление
10 МОм резистора обратной связи. Этот ем-
костной делитель не дает фазового сдвига,
не вызывая, таким образом, проблем со ста-
бильностью.
♦ Другой способ — анализ усиления схемы.
Без стабилизирующего конденсатора в цепи
обратной связи усиление схемы повышает-
ся с ростом частоты, пока это повышение не
столкнется с уменьшающимся усилением са-
мого операционного усилителя. Это состоя-
ние вызывает нестабильность, точно так же,
как это делал простейший дифференциатор
на операционном усилителе (см. главу 9N
в этой книге и раздел 4.5.7 в книге АоЕ).
Конденсатор в цепи обратной связи ограничи-
вает усиление схемы выше частот, где начина-
ет преобладать его эффективное сопротивле-
ние Хс. А это состояние является стабильным.
Операционный усилитель
с подключенным двухтактным
каскадом и емкостной нагрузкой
Опять же, здесь основную проблему создает
емкостная нагрузка, но наличие двухтактного
каскада также уменьшает стабильность этой
схемы, как мы видели в случае с повторителем
на одном транзисторе в разделе 9L.2.
В постановке задачи описываются два гипоте-
тических случая с паразитными автоколебани-
ями на разных частотах: 100 кГц и 20 МГц.
Значение частоты паразитных
автоколебаний
Частота паразитных автоколебаний может
дать хорошую, и даже решающую, подсказку
относительно их источника: операционный ли
это усилитель или дискретные транзисторы.
Операционный усилитель 411 не может быть
источником паразитных колебаний частотой
20 МГц, поскольку его усиление при разомкну-
той цепи обратной связи снижается до единич-
ного уже на частоте 4 МГц.
И совсем маловероятно, что источником па-
разитных колебаний частотой 100 кГц может
быть каскад на дискретных транзисторах,
поскольку усиление по напряжению в этой
схеме зависит от импеданса паразитной ин-
дуктивности (см. главу 9N). На столь низкой
частоте импеданс такой индуктивности при-
мерно в 1000 раз меньше, чем на частотах, с
которыми мы имели дело в упражнении по
эмиттерному повторителю на лабораторном
занятии 9L.2. Таким образом, намного более
вероятной причиной паразитных колебаний
частотой 100 кГц будет операционный уси-
литель.
Решение проблемы зависит от ее причины.
При частоте 100 кГц стабилизируем
операционный усилитель
Наиболее эффективным решением для опера-
ционного усилителя (после выполнения раз-
вязки шин питания, поскольку было бы очень
неловко обнаружить, что вы забыли эту стан-
дартную предосторожность), наверное, бу-
дет подход с разделенной обратной связью,
как и для случая с длинным коаксиальным
кабелем.
Как мы знаем из рассмотренного ранее ре-
шения для этой проблемы, частоту перехода
такого контура разделенной обратной связи
определяют значения сопротивления резисто-
ра и емкости конденсатора. Частоту перехода
можно задать величиной 50 кГц, используя
следующие значения компонентов: R = 27 кОм,
С = 100 пФ. Соответствующая схема изображе-
на на рис. 9W.8.
Значения элементов демпфера являются до-
вольно стандартными и не критичными, их вы-
бирают так, чтобы надежно предотвратить ав-
токолебания. Как обычно, мы задаем значения
10 Ом и 0,1 мкФ. Этот аспект не представляет
интереса, но на практике действует безотказно.
9W.2. Вопросы стабильности
435
Рис. 9W.8. Стабилизация схемы с двухтактным повторите-
лем, в которой истосчником автоколебаний является опера-
ционный усилитель
При частоте 20 МГц стабилизируем
каскад на транзисторах
В данном случае наша стратегия состоит в том,
чтобы погасить усиление на высоких частотах,
и для этой цели будет эффективным подавать
выходной сигнал на базы транзисторов че-
рез резистор сопротивлением в несколько со-
тен ом. Соответствующая схема изображена
на рис. 9W.9. Если вы подошли к выполнению
лабораторных занятий с должной ответствен-
ностью, то должны были убедиться в действен-
ности этого решения на лабораторном заня-
тии 9L.4.
Рис. 9W.9. Стабилизация схемы с двухтактным повторите-
лем, в которой источником автоколебаний являются тран-
зисторы
Конечно же, не будет никакого вреда, если
применить оба решения одновременно. Опре-
деленно следует всегда выполнять развязку
шин питания и следить за тем, чтобы они были
короткими и имели низкий импеданс. Также
следует всегда подавать сигнал на базы двух-
тактного повторителя через последовательный
резистор. В этом упражнении для наглядности
мы разделили решения на два типа: одно для
автоколебаний, вызываемых операционным
усилителем, и другое для паразитных колеба-
ний, вызываемых транзисторами. Но на прак-
тике так не поступают. Можно не скупиться и
предпринять все предохранительные меры.
ION. Операционные усилители IV:
ПИД-регулятор для электродвигателя
Содержание
1ON.1. Примеры реальных задач, требующих такого решения 437
10N.1.1. Области применения ПИД-регуляторов 437
10N.2. ПИД-цепь управления электродвигателем 437
10N.2.1. Петля потенциометр-на-двигатель выглядит очень простой 437
10N.2.2. Интегрирование в петле обратной связи 438
10N.3. Проектирование контроллера
(специализированного операционного усилителя) 439
10N.4. Схема только для пропорциональной составляющей П: расчет усиления 441
10N.4.L Частотная характеристика объекта управления (усиление системы Ас) 441
10N.4.2. Усиление контроллера 442
10N.4.3. Уровни стабильности: запас по фазе 442
10N.5. Дифференциальная составляющая Д 444
10N.5.1. Интуитивное объяснение воздействия дифференциальной
составляющей на схему 445
10N.5.2. Как вычислить необходимое усиление дифференциального звена 447
10N.5.3. Но мы не хотим слишком большой дифференциальной составляющей 448
10N.5.4. Интегральная составляющая 449
10N.6. Материал для чтения в АоЕ 450
Проблема, решаемая с помощью
ПИД-регулятора
Данная проблема уже знакома нам: как под-
держивать стабильность петли обратной связи,
несмотря на отставание по фазе внутри нее. На
лабораторном занятии 9L мы исследовали не-
сколько проблематичных схем и обнаружили,
что фазовый сдвиг, вносимый даже простым
низкочастотным фильтром, может нарушить
стабильность петли обратной связи. Мы рас-
смотрели несколько способов для стабилиза-
ции таких схем:
♦ подавление усиления на высоких частотах,
например, включением конденсатора не-
большой емкости параллельно пути обрат-
ной связи;
♦ разделение пути обратной связи таким обра-
зом, чтобы на высоких частотах сигнал об-
ратной связи не проходил через элемент, вы-
зывающий отрицательный фазовый сдвиг;
♦ повышение доли отрицательной обратной
связи относительно положительной, как в
эмиттерном повторителе на дискретных эле-
ментах.
Сегодняшняя задача содержит два новых мо-
мента:
♦ на этот раз петля обратной связи содержит
не просто низкочастотный фильтр, а инте-
гратор;
♦ в связи с этим усложнением, которое не под-
дается решению ни одним из рассмотренных
ранее способов, требуется больше, чем про-
сто менять содержимое петли обратной свя-
зи: нам нужно модифицировать сам управ-
ляющий операционный усилитель.
Это звучит довольно радикально, и так оно и
есть. Конечно же, мы не планируем вскрывать
интегральную схему усилителя. Вместо этого
мы соберем схему, имитирующую операцион-
ный усилитель, характеристиками которой мы
можем управлять.
ION. 7. Примеры реальных задач, требующих такого решения
437
10N.1. Примеры реальных
задач, требующих такого
решения
Схема, которую мы соберем на лабораторном
занятии 10L, называется ПИД-регулятором,
где ПИД означает «пропорционально-инте-
грально-дифференциальный». Это выражение
описывает три функции погрешности контура
управления (разницы между входным напряже-
нием и подаваемым обратно на вход сигналом),
которые реализуются нашим самодельным опе-
рационным ПИД-усилителем. Если вам пока
непонятно, о чем идет речь, не переживайте.
Все станет понятным, когда далее мы подробно
рассмотрим все эти три составляющие.
10N.1.1. Области применения
ПИД-регуляторов
ПИД-регуляторы используются во многих
случаях, когда нужно управлять каким-либо
сравнительно инерционным устройством. На-
пример, автоматический лифт спроектирован
таким образом, чтобы при остановке его пол
был на уровне с полом этажа, не допуская при
этом значительного расхождения. Другой при-
мер система круиз-контроля удерживает ско-
рость автомобиля почти постоянной, не до-
пуская больших отклонений от заданной ско-
рости. ПИД-управление также применяется
в таких производственных процессах, как на-
грев или химическое смешивание материалов1.
Наконец, в современных самолетах управление
рулевыми механизмами осуществляется не по-
средством тросов, как это делалось раньше, а
с помощью электронных систем управления,
на сигналы которых управляемые элементы
должны реагировать быстро и надежно.
На лабораторном занятии 10L мы сымитируем
нечто, что можно считать системой электрон-
ного управления (самолетом или автомоби-
лем). А именно, мы попытаемся заставить вал
электродвигателя постоянного тока принимать
положение, соответствующее положению руко-
ятки потенциометра.
Генератор колебаний с мостом Вина
как эталон
Как вы хорошо знаете, поработав на лабо-
раторном занятии 9L со схемами, которые
норовили срываться в режим автоколебаний,
что отрицательный фазовый сдвиг в петле об-
ратной связи создает проблемы. Но вместо того,
чтобы снова повторять сделанные на том лабо-
раторном занятии выводы, подойдем к вопро-
су критериев стабильности через черный ход,
вспомнив, как мы должны были спроектировать
генератор колебаний с мостом Вина, чтобы он
выдавал стабильный синусоидальный сигнал.
В частности, этот генератор колебаний создавал
стабильные колебания, если петлевое усиление
было единичным. Если усиление было меньше
единичного, то колебания затухали. А при уси-
лении больше единичного колебания сохраня-
лись, но при этом выходной сигнал искажался.
Подобным образом, в любой схеме с обратной
связью колебания будут затухать, если на ча-
стоте, соответствующей фазовому сдвигу ве-
личиной 180°, усиление окажется меньше еди-
ничного2. При рассмотрении темы коррекции
операционных усилителей мы познакомились
с одним из способов обеспечения стабильности,
состоящим в подавлении усиления при разом-
кнутой цепи обратной связи с повышением ча-
стоты. Мы начнем с этого примитивного спосо-
ба, поскольку уменьшение усиления является
наиболее знакомым среди наших стандартных
решений. Опишем этот подход как ограничение
П-усиления (пропорционального). Позже мы
перейдем к остальным составляющим ПИД3.
10N.2. ПИД-цепь управления
электродвигателем
г
10N.2.1. Петля потенциометр-на-дви-
гатель выглядит очень простой
Рассматриваемая здесь задача выглядит легче,
чем на самом деле. Определенно, мы ставим
перед собой скромную цель, суть которой ил-
люстрируется на рис. 10N.1.
1 Использование ПИД-управления на производстве объ-
ясняет некоторые необычные термины из этой области.
Например, управляемое устройство часто называется
«оборудованием» (в оригинале plant: в данном контек-
сте - оборудование, установка, агрегат. —Примеч. пер.).
2 Во всех случаях опасность представляет отрицательный
фазовый сдвиг величиной 180°, а не положительный. Но
инверсия направления обратной связи является основным
моментом, поэтому подчеркнем здесь именно это обстоя-
тельство, говоря о фатальных 180°, вместо того, чтобы де-
лать акцент на знаке.
3 В этом обсуждении, как и на лабораторном занятии, мы
будем добавлять эти элементы не в том порядке, в котором
они следуют в сокращении ПИД, а сначала рассмотрим П
(пропорциональный), затем Д (дифференциальный), нако-
нец, И (интегральный).
438
10N. Операционные усилители IV: ПИД-регулятор для электродвигателя
Целевой
уровень
U.
■
Электродвигател
" Потенциометр
Рис. 10N.1. Петля управления для позиционирования вала
электродвигателя. Выглядит очень просто!
Что может быть проще этой схемы? На бумаге
все гладко. Но оказывается, что проблема за-
ключается в поддержании схемы в стабильном
состоянии. По сути, это та же проблема, как и на
лабораторном занятии 9L, когда мы заметили,
что наличие простого низкочастотного фильтра
в цепи обратной связи может преобразовать
отрицательную обратную связь в положитель-
ную. В том случае проблема возникала из-за
фазового сдвига величиной -90°, создаваемого
самим операционным усилителем (и даже еще
большим фазовым сдвигом вблизи его частоты
единичного усиления). Эти -90° означали, что
мы не могли позволить, чтобы в цепи обратной
связи создавался сколь-нибудь большой фазо-
вый сдвиг.
Рассматриваемая схема более сложная. Кроме
обычного фазового сдвига, создаваемого самим
операционным усилителем, она вносит допол-
нительный фазовый сдвиг, или интегрирова-
ние, величиной -90°, от которого невозможно
избавиться. Это дополнительное интегрирова-
ние заставляет нас применять другие подходы к
решению данной проблемы.
На этот раз причиной интегрирования является
природа элементов внутри петли обратной свя-
зи: электродвигателя, положение вала которого
мы пытаемся определить. Поскольку фазовый
сдвиг обычного операционного усилителя в
данном случае неприемлем, нам нужно самим
собрать специализированный операционный
усилитель, который будет иметь средний коэф-
фициент усиления и не будет создавать фазово-
го сдвига.
10N.2.2. Интегрирование
в петле обратной связи
Интегрирование, или задержка, в цепи обрат-
ной связи возникает вследствие фазового сдви-
га, присущего конструкции нашей конкретной
нагрузки. В частности, задержка возникает
вследствие того, что мы хотим регулировать
положение вала электродвигателя, в то время
как управление этим электродвигателем осу-
ществляется сигналом рассогласования, кото-
рый является напряжением4. В результате воз-
никает неявное интегрирование.
Это объясняется тем, что скорость вращения
электродвигателя постоянного тока пропор-
циональна подаваемому на него напряжению5;
поддерживаемая в течение некоторого времени
скорость вращения вызывает изменение поло-
жения вала. Отсюда и неизбежное интегриро-
вание в цепи обратной связи.
Чтобы проиллюстрировать сказанное, на
рис. 10N.2 приведен график сигнала на потен-
циометре при подаче на электродвигатель пря-
моугольного сигнала.
Входной сигнал ч^^
(на электродвигатель]
Выходной сигнал
(с потенциометра,
вращаемого
электродвигателем)
Рис. 10N.2. Привод электродвигателя, связанный с потен-
циометром, образует интегратор
За исключением инверсии, треугольный вы-
ходной сигнал очень похож на сигнал, созда-
ваемый интегратором на лабораторном заня-
тии 7L, не так ли?
L
X
\
ВС
ш
г
i
1
1
/
i
т
V
(Р
т
1
W
f
т
/
■1
к
1
—!*~~
I /
у,
и
4 Это напряжение представляет собой усиленный сигнал
рассогласования: меру отклонения значения выходного
сигнала от заданного целевого значения. В схеме управ-
ления электродвигателем как целевой, так и измеряемый
сигнал являются постоянным напряжением.
5 Если приведенного объяснения вам недостаточно, то
вы можете легко убедиться в этом, вспомнив, что при
вращении, например вручную, вала электродвигателя по-
стоянного тока он ведет себя как генератор постоянного
напряжения. В частности, он генерирует напряжение, ве-
личина которого прямо пропорциональна скорости вра-
щения вала.
Таким образом, когда вал электродвигателя вращается при
подаче напряжения, он реагирует на это вращение, гене-
рируя напряжение — так называемая противо-ЭДС (про-
тивоэлектродвижущая сила).
Величина противо-ЭДС почти равна подаваемому на
электродвигатель напряжению. Скорость вращения ста-
билизируется, когда разница между этими двумя напряже-
ниями обеспечивает протекание тока достаточного, чтобы
восполнить энергию, теряемую электродвигателем на тре-
ние, механическую нагрузку и нагрев.
WN.3. Проектирование контроллера (специализированного операционного усилителя)
439
10N.3. Проектирование
контроллера
(специализированного
операционного усилителя)
Для проектирования этого контура управления
нам нужно возвратиться к базовым первона-
чальным принципам. Мы знаем, что для реали-
зации преимуществ отрицательной обратной
связи нам требуется усиление. Но мы подозре-
ваем, что у нас не получится воспользоваться
обычным высоким усилением стандартного
операционного усилителя. (Может потребо-
ваться подавлять усиление или всегда поддер-
живать его низким.) Также мы знаем, что не
можем допустить фазовый сдвиг величиной
как минимум 90°, как у обычного усилителя.
Сможем ли мы самостоятельно спроектировать
такой усилитель?
Да, сможем. Как мы выяснили в процессе сбор-
ки операционного усилителя из отдельных
транзисторов, это устройство представляет со-
бой, по сути, дифференциальный усилитель.
Все остальное является незначительными ме-
лочами. Так что давайте начнем со сборки диф-
ференциального усилителя, который не дает
фазового сдвига величиной -90°, присущего
обычному операционному усилителю.
На рис. 10N.2 изображена схема стандартного
дифференциального усилителя, который мы
будем использовать на лабораторном занятии
по теме ПИД. Его коэффициент усиления равен
единице, поэтому потребуется дополнительный
усилительный каскад.
100 кОм 100 кОм
«Рассогласование»
Рис. 10N.3. Дифференциальный усилитель с единичным
усилением
Фазовый сдвиг отсутствует
Возможно, что вы подвергаете сомнению наше
утверждение, что в дифференциальном усили-
теле фазовый сдвиг может отсутствовать. Как
такое может быть, если он был собран на обыч-
ном операционном усилителе, который, как мы
опять же утверждаем, вносит фазовый сдвиг
величиной 90°? Отсутствие фазового сдвига в
дифференциальном усилителе является доста-
точно удивительным, хотя, возможно, и не для
вас, с учетом того, что вы собирали повторители
и другие схемы на операционном усилителе, ко-
торые не проявляли интегрирования, скрытого
в операционном усилителе. Но наше утвержде-
ние верно: фазовый сдвиг операционного уси-
лителя — всего лишь еще одна дополнительная
«собака», которую обратная связь «скрывает»
от нас. Наш ПИД-регулятор не будет «видеть»
внутренний фазовый сдвиг операционного уси-
лителя, поскольку обратная связь обезвредила
этот сдвиг.
А усиление умеренное
Даже после устранения фазового сдвига в на-
шем самодельном операционном усилителе
петля обратной связи будет уязвимой к не-
стабильности вследствие задержек, которые
могут возникать в дополнение к задержке, вы-
зываемой процессом интегрирования в связке
электродвигателя и потенциометра. Поэтому
мы сделаем усиление нашего самодельного
операционного усилителя намного меньше,
чем у обычной микросхемы (у 411 усиление по
постоянному току составляет 200 000). Кроме
того, будет удобно, если обеспечить регули-
ровку уровня усиления нашего самодельного
устройства. На рис. 10N.4 приведена принци-
пиальная схема устройства, обладающего этой
возможностью.
Целевой
уровень
Потенциометр
Регулировка Электродвигатель
усиления
Рис. 10N.4. Привод только с пропорциональной составляю-
щей. Теперь мы можем проверить, какой уровень усиления
сможет выдержать петля обратной связи нашего устройства
Теперь у нас есть базовая схема, которая долж-
на позволить нам создать стабильную петлю
обратной связи. Но как определить, сколько
требуется усиления? В нашей лаборатории от-
вет на данный вопрос определяется полностью
экспериментальным путем: мы постепенно по-
вышаем усиление, пока не увидим признаки
440
ION. Операционные усилители IV: ПИД-регулятор для электродвигателя
нестабильности, после чего отрабатываем на-
зад. В этом и следующем разделах мы попыта-
емся описать, что происходит при приближе-
нии к границе нестабильности.
Блок-схема петли обратной связи
Немного отклонимся от главной темы, что-
бы описать петлю обратной связи более фор-
мальным способом, чем обычно в нашем кур-
се (рис. 10N.5). Тем не менее вам может быть
интересно познакомиться с терминологией,
которую любят использовать профессионалы
в области теории управления. Здесь вы можете
заметить любопытное слово «оборудование»6,
обозначающее управляемое устройство.
Примечание
В нашем случае управляемым устройством (обору-
дованием) является связка «электродвигатель-по-
тенциометр». Как упоминалось ранее, этот термин
свидетельствует о промышленных истоках теории
управления.
Контроллером служит наш самодельный управ-
ляющий усилитель. Если блок-схема на рис. 10N.5
вам не совсем понятна, не переживайте: вскоре
мы ее перерисуем, чтобы она выглядела более
похожей на петлю обратной связи, которая нам
знакома.
На рис. 10N.6 эта же блок-схема перерисована
в более знакомом виде: управляемое устрой-
ство в виде связки «электродвигатель-потен-
циометр» является обычной «собакой» в петле
обратной связи.
Эти две блок-схемы не содержат ничего нового
по сравнению с исходной постановкой задачи.
Но блок-схема на рис. 10N.5 может помочь вам
увидеть, что сигнал в контуре управления прохо-
дит через управляемое устройство и контроллер,
и что стабильность будет зависеть от того, что
случится с сигналом в процессе его прохождения
через контур или как это повлияет на помеху.
Дополнительным аспектом в данном случае
является учет «помехи». По-новому также
-(«усиление системы»)
Внешнее
воздействие
€>
Управляемая
система
(оборудование]
Корректирующая переменная
(усиленный сигнал
рассогласования)
(рассогласование)
Контроллер
Выходной
X сигнал Управляемая переменная
(«А») (в нашем случае это угловое положение)
( Л^
щ—^_/ Лщ—W Опорный сигнал
(W-A)
-(«усиление контроллера»)
Рис. 10N.5. Классический вариант блок-схемы контура управления положением вала электродвигателя
Входной сигнал
(«с
(опорный сигнал)
Новое обстоятельство: ранее мы не указывали такие помехи,
\ а рассчитывали на обратную связь для их устранения
Внешнее воздействие
Управляемое
устройство
Выходной сигнал
(Усиленное рассогласование)
Рис. 10N.6. Блок-схема контура управления положением вала электродвигателя в форме, обычной для схемотехники опера-
ционных усилителей
6 В оригинале plant — оборудование, установка, агрегат. —
Примеч. пер.
10N.4. Схема только для пропорциональной составляющей П: расчет усиления
441
обозначены функции преобразования, или уси-
ления, для каждого из двух блоков: усиление
объекта управления, или системы, обозначено
Ас, а усиление контроллера — Ак. В результа-
те мы можем записать общее выражение для
усиления, которое справедливо для любого
элемента, который проходит через петлю, будь
то сигнал, шум или помеха. Это выражение на-
зывается петлевым усилением и имеет следую-
щий вид (усиление контроллера умножается на
усиление системы):
Связка «электродвигатель-потенциометр» (интегрирует)
\. дополнительный низкочастотный фильтр
V . ./ . ,
В этой петле мы ничего не можем поделать с
сомножителем Ас, который определяется по-
ведением объекта управления. Проблемой при
установке и подстройке ПИД-регулятора будет
правильный подбор другого сомножителя —
усиления контроллера Ак.
Сначала, чтобы обеспечить стабильность, под-
бирается величина Ак. Затем, после добавления
дифференциальной составляющей Д, также ре-
гулируется фаза усиления Ак. Как мы увидим,
фаза и усиление взаимодействуют друг с дру-
гом: правильное поведение фазы позволяет по-
лучить более высокое усиление.
10N А Схема только
для пропорциональной
составляющей П:
расчет усиления
10N.4.1. Частотная характеристика
объекта управления
(усиление системы Ас)
На рис. 10N.7 показан график частотной харак-
теристики гипотетического элемента преоб-
разования «двигатель в позицию» (это только
усиление Ас; мы еще не рассматриваем контур
целиком). Хотя это условный график, он до-
вольно близок к тому, который вы вероятнее
всего увидите на лабораторном занятии по
ПИД-регулятору.
Если этот график кажется вам слишком аб-
страктным, далее приводится его словесное
описание применительно к связке «электро-
двигатель-потенциометр». Таким образом мы
-180
10 Гц
и еще одинуяизкочастотныи фильтр
Рис. 10N.7. Характеристики усиления и фазы связки «дви-
гатель-потенциометр»: фазовый сдвиг величиной -90°, на-
чиная с самых низких частот
попытаемся дать неформальное объяснение в
терминах спада усиления в частотной области.
Нисходящая кривая указывает, что на низких
частотах при данной амплитуде входного (си-
нусоидального) сигнала вполне хватит време-
ни, чтобы вал электродвигателя повернулся
на достаточно большое расстояние, прежде
чем полярность входного сигнала изменится
на противоположную. На высоких же частотах
в течение доступного времени (около одного
полупериода) вал провернется только на не-
большое расстояние. Если у вас складывается
впечатление, что это выглядит как описание
поведения напряжения на конденсаторе в RC-
цепочке при рассмотрении его во временной
области, то это правильно. Эти два процесса
очень похожи друг на друга.
Вы должны заметить, что данный график отли-
чается от обычной частотной характеристики
операционного усилителя в том отношении, что
на самых низких частотах спад начинается при
фазовой задержке в 90°. Это просто следствие
механизма связки вольтажный привод/позици-
онное определение, описанного ранее. В данном
случае отсутствует область без фазового сдви-
га, которая есть в частотной характеристике
операционного усилителя. Но более важным
является не отличие, а сходство с графиком ча-
стотной характеристики операционного усили-
теля: оба графика позволяют предвидеть, когда
могут начать возникать проблемы.
В данном случае можно ожидать потенциаль-
ных проблем, когда фазовый сдвиг объекта
управления приближается к значению .180°.
Это происходит на изгибе кривой усиления на
442
ION. Операционные усилители IV: ПИД-регулятор для электродвигателя
едва стабильный
нестабильный
Ак': нестабильный
10 дБ/деление
Усиление
10 дБ
ОдБ
ОД
-90
Фазовый сдвиг -135
-180
Рис 10N.8. Частотная характеристика для пропорциональной составляющей: система стабильна при умеренном усилении
и теряет стабильность при росте усиления
рис. 10N.7, где второй фазовый сдвиг добавля-
ется к постоянному фазовому сдвигу интегра-
тора величиной -90°. Когда наступает второй
фазовый сдвиг величиной 90°, отрицательная
обратная связь может превратиться в положи-
тельную.
Но по отдельности сам факт возможности соз-
дания объектом управления проблематичного
фазового сдвига еще не решает вопрос, будет
ли схема генерировать автоколебания или нет.
Возможность возникновения автоколебаний
из-за фазового сдвига зависит от величины уси-
ления контроллера. Вспомните конструкцию
генератора колебаний на основе моста Вина:
для поддержания колебаний усиление должно
быть достаточным, чтобы компенсировать по-
тери в цепи положительной обратной связи.
При разработке нашего ПИД-регулятора мы не
будем приближаться к границе нестабильно-
сти, но нам необходимо знать, где она находит-
ся. Мы хотим внимательно следить за частотой
перехода, являющейся границей проблемы.
1 ON A2. Усиление контроллера
На рис. 10N.8 изображен видоизмененный гра-
фик частотной характеристики усиления систе-
мы Ас из рис. 10N.7, в который добавлены два
гипотетических значения усиления контрол-
лера Ак. Сомножитель усиления контроллера
Ак, на который умножается усиление системы
Ас, поднимает кривую Ас вверх, создавая на
графике на рис. 10N.8 усиление петли Ак • Ас.
В обоих случаях линия усиления контролле-
ра Ак идет параллельно частотной оси.
В одном случае усиление контроллера Ак доста-
точно низкое, чтобы общее усиление понизи-
лось до значения меньше единичного, прежде
чем будет достигнута опасная частота излома.
В другом же случае при большем усилении кон-
троллера (обозначено на графике как AKf) об-
щее усиление превышает единичное на частоте
излома. При этом более высоком усилении Ак
схема будет генерировать автоколебания.
Далее на лабораторном занятии нужно будет
определить частоту собственных колебаний.
По терминологии ПИД это частота возник-
новения автоколебаний, когда усиление чуть
выше граничного. Для ее определения нужно
постепенно повышать усиление Ак (в данном
случае это просто усиление пропорционально-
го звена «П»), пока не возникнут автоколеба-
ния. Для нашей лабораторной схемы это всего
лишь несколько герц (возможно 3 Гц). Для вос-
становления стабильности (т. е. для прекраще-
ния автоколебаний) нужно уменьшить усиле-
ние контроллера Ак.
10N A3. Уровни стабильности:
запас по фазе
Вы также узнаете, что стабильность определяет-
ся коэффициентом усиления: по мере повыше-
ния усиления и приближения к возникновению
ION А. Схема только для пропорциональной составляющей П: расчет усиления
443
автоколебаний контур управления будет стано-
виться все более неуравновешенным. Эту неу-
равновешенность легче всего обнаружить по
реакции схемы на преднамеренно внесенную
помеху.
В лабораторных условиях помеху в схему мож-
но внести одним из двух способов. Можно
резко изменить целевое входное напряжение.
Это можно сделать с помощью ступенчатого
воздействия, или резко провернув рукоятку
потенциометра, или подав низкочастотный
прямоугольный сигнал от генератора сигналов.
Можно внести ступенчатую помеху, вручную
провернув вал электродвигателя из его поло-
жения покоя и наблюдая за переходным про-
цессом в схеме. Когда устройство находится
вблизи границы автоколебаний, в выходном
сигнале будет возникать повторяющийся из-
быточный отклик, прежде чем произойдет воз-
врат в стабильное конечное состояние.
С помощью кривой Ас (частотной характе-
ристики системы или объекта управления с
учетом фазового сдвига) можно определить,
насколько далек фазовый сдвиг петли от гра-
ничного значения -180° при заданном значе-
нии усиления контроллера Ак. Эту величину,
выраженную в градусах, называют запасом по
фазе. Мы уже встречались с этим понятием
ранее при рассмотрении частотной коррекции
операционных усилителей. Напомним, что за-
пас по фазе скорректированных операционных
усилителей составляет около 45-60°.
На рис. 10N.9 показана реакция контура управ-
ления на прямоугольный сигнал при разных
значениях запаса по фазе. В реальной ситуа-
ции более вероятно, что вы будете выполнять
эту процедуру в обратном порядке: наблюдать
В схеме ПИД-регулятора из лабораторного за-
нятия вы сможете увидеть, что при более низ-
ком усилении Ак схема действительно ведет себя
спокойно, с меньшей склонностью к перерегу-
лированию. Но низкое усиление Ак также со-
провождается и некоторыми отрицательными
эффектами: реакция схемы довольно медлен-
ная, а остаточная погрешность значительна.
На рис. 10N.10 показан график реагирования
схемы на низкое усиление пропорционально-
го звена. Этот график выглядит как график для
ДС-цепи, что логично, поскольку перемещение
ротора электродвигателя уменьшается с умень-
шением рассогласования (в то время как поло-
жение его вала приближается все ближе к це-
левому).
Уровень обратной связи
(выходной потенциометр)
Figure 10N.10. Низкий уровень (четыре) усиления пропор-
ционального звена П обеспечивает стабильность, но за это
приходится расплачиваться
Усиление пропорционального звена можно
немного повысить и улучшить некоторые ха-
рактеристики (уменьшить остаточную погреш-
ность и время отклика). Но в таком случае воз-
никает определенное перерегулирование, как
показано на рис. 10N.11.
А еще большее усиление звена П подводит нас к
границе нестабильности. На рис. 10N.12 задний
фронт входного сигнала вызывает несколько
периодов паразитных колебаний (звона) вы-
ходного сигнала, а передний фронт создает
Реакция на прямоугольный
входной сигнал
\
Запое по фазе (градусы):
/ 90 (медленная)
Г 60 (небольшое перерегулирование,
J НО бкТГТПО ВКТУОЛМТ ЫЛ ТПр/л/Р AAhTW V!
J
но быстро выходит на требуемый уровень)
45 (быстро выходит на требуемый
уровень, но требует больше времени
для стабилизации)
Рис. 10N.9. Реакция на прямоугольный сигнал показывает влияние запаса по фазе разной величины на стабильность7
реакцию и по результатам наблюдений опреде-
лять запас по фазе.
7 По кн.: Tietze U., Schenk С. Electronic Circuits: Handbook
for Design. 2nd ed. Springer, 2008.1005 p.
444
/ON. Операционные усилители IV: ПИД-регулятор для электродвигателя
Уровень обратной связи
выходной потенциометр)
Входной
импульс
Рис. 10N.11. Промежуточное усиление звена П (60) вызыва-
ет некоторое перерегулирование
l Уровень обратной связи
(выходной потенциометр)
Входной
импульс
Рис. 10N.12. Высокое (80) усиление звена П создает некото-
рое перерегулирование и звон: схема едва стабильна
постоянный звон. При высоком значении уси-
ления звена П схема нестабильна. Но ее можно
сделать стабильной даже при этом более высо-
ком усилении, добавив дифференциальную со-
ставляющую Д, т. е. производную сигнала рас-
согласования.
10N.5. Дифференциальная
составляющая Д
Поскольку проблемы создаются отрицатель-
ными фазовыми сдвигами, можно ли улучшить
реакцию схемы, добавив фазовый сдвиг друго-
го типа, положительного? Да, можно, но толь-
ко соблюдая определенную осторожность. Для
начала рассмотрим, какой эффект от внедрения
такой дифференциальной составляющей (звена
Д) мы бы хотели получить, а затем, как можно
определить ее величину.
На рис. 10N.13 показан еще раз измененный
исходный график петлевого усиления Ак • Ас.
Теперь мы добавили в него пунктирную линию,
показывающую, как бы мы хотели выровнять
излом отклика Ак.
Чтобы получить желаемый результат (в про-
изведении Ак • Ас), нам необходимо направить
наклон кривой усиления контроллера Ак вверх.
Иными словами, нам нужно, чтобы кривая ре-
акции контроллера выглядела как производная
на той частоте, на которой в противном случае
начинались бы проблемы.
/L: нестабильный, если только мы
\L' * не "сможем скомпенсировать излом
и добавочный (разовый сдвиг
: стабильный
4 n^s * Можно ли устранить этот
^ . \<^х излом, чтобы скомпенси-
\ ровать проблематичный
\ * ЯМЗОВЫЙ СДВИГ?
Рис. 10N.13. Желаемый результат: устранить фазовую за-
держку
Как можно получить этот результат? Диффе-
ренцируя сомножитель рассогласования, полу-
чив его производную Д и добавив ее к рассогла-
сованию П, а затем усилив обе эти величины,
чтобы получить изогнутую кривую усиления
Ак, а не горизонтальную, как на рис. 10N.8. Мы
используем сумму этих двух функций рассогла-
сования8 для формирования корректирующего
сигнала в нашей петле отрицательной обратной
связи.
Чтобы в кривую добавить восходящий излом
на требуемой частоте (на которой происходит
системный переход), необходимо настроить
контур управления таким образом, чтобы на
этой частоте величины составляющих Д и П
были одинаковыми. На графике на рис. 10N.14
величина дифференциальной составляющей Д
постоянно повышается с ростом частоты, а ког-
да эта составляющая складывается с составля-
ющей П, она начинает доминировать на часто-
те излома. Таким образом, она вступает в дей-
ствие как раз вовремя, чтобы спасти ситуацию
и аннулировать вторую фазовую задержку ве-
личиной 90°. Добавление дифференциальной
составляющей Д позволило нам задать более
высокое усиление, чем при наличии только
одной пропорциональной составляющей П.
8 Если в последнее время вам не приходилось сталкивать-
ся с графиками в логарифмическом масштабе, то кривая
на рис. 10N.14 может показаться вам необычной. Здесь
производная составляющей Д выглядит, как будто бы про-
сто заменяет составляющую П, а не суммируется с ней. На
более низких частотах усиление контроллера Лк выглядит
просто как составляющая П, без Д; а на более высоких ча-
стотах — как составляющая Д.
Да. Но все это вполне объяснимо, если вспомнить, что на
графике в логарифмическом масштабе, как только диффе-
ренциальная составляющая Д поднимается заметно выше
пропорциональной составляющей П, ее значение настоль-
ко больше другого, что сумма этих двух значений является
практически значением одной Д. Таким образом, на низ-
ких частотах полностью доминирует составляющая П, а на
высоких — преобладает составляющая Д.
IONS Дифференциальная составляющая Д
445
Лк: изогнута вверх за счет
дифференциальной составляющей
. Ак * Ас,
выровнена за счет
дифференциальной
составляющей, \
сразовый сдвиг
v отсрочен
Гц 1Гц Д \ ю Гц
юльной
Figure 10N.14. Добавление дифференциальной состав-
ляющей Д к пропорциональной составляющей П делает
стабильным контур управления и предотвращает автоко-
лебания
10N.5.1. Интуитивное объяснение
воздействия дифференциальной
составляющей на схему
Если предыдущее описание преимуществ, пре-
доставляемых дифференциальной составляю-
щей Д, кажется вам несколько абстрактным, то
возможно аргументация, которую мы приведем
далее, будет более доходчивой.
Проблему легче всего понять, если рассма-
тривать контур управления в состоянии спо-
койствия и стабильности, в который затем
поступает воздействие, вызванное внезапным
ступенчатым изменением входного сигнала.
Это внезапное изменение входного сигнала
заставляет значение функции рассогласова-
ния П резко подняться от нуля до величины
«усиление х входной ступенчатый сигнал».
А что делает дифференциальная составляю-
щая? Она добавляет сильный дополнитель-
ный сигнал в том же самом направлении, по-
скольку рассогласование не только возникло,
но возникло быстро, резко повысившись от
нулевого значения до своего нового значения.
Соответствующие осциллограммы сигналов
изображены на рис. 10N.15.
Поначалу кажется, что схема вовсе не реагиру-
ет, но затем отклик постепенно согласовывает-
ся с входным сигналом, и рассогласование сно-
ва сводится к нулю. На правой осциллограмме
на рис. 10N.15 показан сильный выброс, соз-
даваемый дифференциальной составляющей
на перепаде сигнала рассогласования. Этот вы-
брос ускоряет отклик схемы.
Если повысить частоту развертки, чтобы
увеличить разрешение осциллограммы от-
клика (см. рис. 10N.16), то можно увидеть,
что в данном случае дифференциальная со-
ставляющая дает толчок, который в несколь-
ко раз сильнее, чем предоставляемый одной
Входной сигнал (целевой)
Сигнал обратной связи
(отклик)
Сигнал рассогласования
(разность между целевым сигналом и откликом)
Входной ступенчатый сигнал отклик и сигнал
рассогласования
Производная рассогласования
Сигнал рассогласования
Сигнал рассогласования и его дифференциальная
составляющая
Рис. 10N.15. Реакция контура управления на ступенчатый входной сигнал: рассогласование и производная рассогласования.
(Усиление каналов осциллографа: 500 мВ/деление на левом изображении; 1 В/деление для осциллофаммы дифференциаль-
ной составляющей; 5 В/деление для сигнала рассогласования на изображении справа.)
446
10N. Операционные усилители IV: ПИД-регулятор для электродвигателя
Входной сигнал
Отклик
L
Сигнал рассогласование i
ТВходной сигнал
Отклик 1
Сигнал рассогласования
Н ■
Дифференциальная составляющая
рассогласования
Входной сигнал, отклик, сигнал
рассогласования и его дифференциальная
составляющая (шкала дифференциальной
составляющей сжата)
Дифференциальная составляющая
рассогласования
Те же сигналы, но шкала дифференциальной
составляющей такая же, как для остальных
Рис. 10N.16. Более быстрая развертка позволяет увидеть, что корректирующий дифференциальный сигнал более сильный,
чем пропорциональный. (Усиление осциллографа: 1 В/деление, за исключением осциллограммы дифференциального сигна-
ла на изображении слева.)
пропорциональной составляющей (обратите
внимание на разное усиление каналов осцилло-
графа для этих двух составляющих). На осцил-
лограмме слева, чтобы вместить большой сиг-
нал дифференциальной составляющей в преде-
лы экрана, нужно было уменьшить усиление
для соответствующего входного канала осцил-
лографа в пять раз. А на осциллограмме спра-
ва для обоих каналов установлено разрешение
1 В/деление, что позволяет показать, насколь-
ко больше дифференциальная составляющая
по сравнению с пропорциональной.
Простое объяснение влияния
дифференциальной составляющей
Дифференциальная составляющая (произ-
водная сигнала рассогласования) несколько
трудно поддается интуитивному пониманию.
Но мы попробуем облегчить эту задачу сле-
дующим толкованием. Предположим, что нам
требуется поставить автомобиль на стоянку,
передняя сторона которой ограничена бетон-
ной стеной. В решении этой задачи роль кон-
троллера играют служащие стоянки. Один из
них — контроллер только с П-составляющей —
осторожный старичок, давно вышедший на
пенсию. Его стратегия для парковки автомо-
биля, чтобы избежать столкновения с пре-
градой, очень простая: ехать чрезвычайно
медленно и осторожно. В конечном итоге
он припаркует автомобиль, но только затра-
тив изрядное время: по мере того, как стена
становится все ближе, он начинает ехать все
медленнее, и на последних этапах автомобиль
еле двигается.
А другой «контроллер» — П-плюс-Д типа. Это
бесшабашный юнец, который запрыгивает на
водительское сиденье, жмет по газам, стрелой
влетает на парковочное место и сразу же на-
чинает постепенно тормозить, останавливая
автомобиль перед самой стеной. Вы еще трех
шагов не отошли, а он уже запарковал ваш ав-
томобиль.
Все это может показаться вам лишь метафори-
ческой ерундой, но на рис. 10N.17 изображены
графики сигналов из рис. 10N.15, которые опи-
сывают точно такое же поведение, как и служа-
щие парковки.
Основным эффектом здесь является сильный
«рывок» на старте — нажатие педали газа при
первых признаках рассогласования. А второ-
степенный эффект — это постепенное тормо-
жение в конце процесса. Возможно, что вы не
понимаете, откуда берется большое усиление
составляющей Д, поскольку мы спроектиро-
вали схему таким образом, чтобы на частоте
излома усиления звеньев Д и П были одина-
ковыми. Большое усиление звена Д при рез-
ком перепаде сигнала рассогласования объяс-
няется наличием высоких частот в этом кру-
том фронте, как мы должны знать из теории
Фурье.
10N.5. Дифференциальная составляющая Д
447
В самом начале выброса
сигнала рассогласования
дифференциальная
составляющая командует:
«По газам! Утопил педаль!»
Дифференциальная
составляющая рассогласования
По мере уменьшения
рассогласования
дифференциальная составляющая
меняет знак и говорит:
«Тормозим, но очень нежно».
Сигнал рассогласования и его дифференциальная составляющая
Рис. 10N.17. Действие дифференциальной составляющей можно сравнить с парковочным служащим, который сначала дает
газу, а затем тормозит. (Усиление каналов осциллографа: сигнал рассогласования — 5 В/деление, дифференциальная состав-
ляющая — 1 В/деление)
10N.5.2. Как вычислить
необходимое усиление
дифференциального звена
Во избежание усложнений предположим еди-
ничное усиление пропорционального звена П.
Тогда нам нужно упорядочить все таким обра-
зом, чтобы дифференциальная составляющая Д
равнялась пропорциональной составляющей П
на частоте, на которой в противном случае воз-
никла бы проблема. Составляющая Д должна
поддерживать стабильность схемы до тех пор,
пока в действие не вступит другой низкоча-
стотный фильтр. В этой точке у нас все должно
быть готово для того, чтобы сделать петлевое
усиление безопасно низким: меньше единично-
го, чтобы помеха затухла.
Для начала повторим, что имеется в виду под
усилением дифференциатора, а затем вычис-
лим постоянную времени RC, необходимую
для стабильности. Усиление дифференциатора
определяется следующей формулой:
'вых
dUJdt
Мы знаем, что для дифференциатора на опера-
ционном усилителе
= * "
А ток I просто равен:
'вх
Отсюда (не учитывая инвертирующее включе-
ние операционного усилителя):
Усиление
(Дифф)"
£/вых _R-C-dUBX/dt_
dujdt
Таким образом, усиление дифференциатора
определяется постоянной времени RC
Если иж=Asin(Grf), тогда ивых_щфф=coJRCAcos(Grf).
Мы хотим найти такое значение RC, т. е. усиле-
ние дифференциатора, при котором £/вых_дифф
будет равным ивых.ПрОп- Будем считать усиле-
ние пропорционального звена единичным; тог-
да мы хотим, чтобы и сигналы на выходе зве-
ньев П и Д были оба равными UBX.
Если задать усиление дифференциального зве-
на Д равным единице, то
^ВЫХ-ДИФФ ^ВЫХ-ПРОП
следовательно,
(oRRCAcos(f) = Asin(arf).
Рассмотрим только максимальные значения
17Ю и dUBX/dt (когда члены sin и cos равны еди-
нице). Мы хотим, чтобы эти амплитуды были
одинаковыми, и при этом обе равны входной
амплитуде А. Тогда:
<uRCA = А =>соДС = 1, или RC = 1/со.
dt
9 Возможно, что вам это кажется повторением очевидного.
Всего лишь взглянув на единицы измерения, можно быть
достаточно уверенным, что усилением дифференциатора
должна быть постоянная времени RC: входные единицы —
вольты/секунды, выходные — вольты, а единицами для
переводного коэффициента, являются секунды.
448
10N. Операционные усилители IV: ПИД-регулятор для электродвигателя
Иными словами:
RC =
2nf
Иначе говоря, это выражение означает, что ве-
личина RC должна быть равной около 1/6 пе-
риода собственных колебаний.
На рис. 10N.18 изображена осциллограмма,
демонстрирующая полезные эффекты добавле-
ния определенной величины составляющей Д.
Здесь усиление пропорциональной составляю-
щей П достаточно высокое, и если бы она была
единственным звеном в цепи обратной связи,
то схема работала бы в режиме незатухающих
колебаний. Но при добавлении составляющей
Д схема быстро и без перерегулирования до-
стигает заданной точки.
Уровень обратной связи
(выходной потенциометр)
Входной
импульЬ *
г~
Рис. 10N.18. Дифференциальная составляющая помогает
быстрее стабилизировать схему (общее усиление — 120, ре-
зистор звена Д — 220 кОм)
10N.5.3. Но мы не хотим слишком
большой дифференциальной
составляющей
Слишком большая дифференциальная
составляющая делает схему «робкой»
Как можно было ожидать и как можно видеть
на осциллограмме на рис. 10N.19, слишком
большая дифференциальная составляющая
создает новые проблемы. Сначала схема ста-
новится «робкой»: когда сигнал начинает при-
ближаться к заданному значению, схема теряет
«мужество» и «тормозит» слишком рано.
Уровень обратной связи
(выходной потенциометр)
Входной
импульс"
Рис. 10N.19. Слишком большая дифференциальная состав-
ляющая делает схему «робкой», замедляя ее переход к за-
данному значению (общее усиление — 120, резистор звена
Д — 680 кОм)
А дальнейшее увеличение
дифференциальной составляющей
вызывает автоколебания
Еще более удивительно, что при дальнейшем
увеличении дифференциальной составляю-
щей схема снова становится нестабильной. На
рис. 10N.20 приводится графическое объясне-
ние этому феномену.
Примечание
На графике фазового сдвига смена фазы изобра-
жена преувеличенно резко, что может ввести в за-
блуждение, если воспринимать эту картину слиш-
ком буквально.
Дифференцированный сигнал рассогласования
звена Д используется в качестве стабилизирую-
щего средства. Как показано на рис. 10N.14, эта
дифференциальная составляющая Д аннулиру-
ет отрицательный фазовый сдвиг, что позволяет
повысить общее усиление до уровня, который в
противном случае вызывал бы нестабильную
работу схемы. Действенность данного подхода
объясняется тем, что усиление контроллера Ак
было достаточно низким, чтобы при его умно-
жении на усиление управляемого устройства
Ас петлевое усиление становилось меньше еди-
ничного, прежде чем фазовый сдвиг достигал
проблематичной величины.
Но при слишком большом усилении звена
Д, как иллюстрируется на рис. 10N.20, со-
ставляющая Д задействуется слишком рано10.
(Кстати, для наглядности на этом рисунке фа-
зовый сдвиг показан нереалистично резким.)
В результате общее усиление контроллера ста-
новится избыточным, что в свою очередь вы-
зывает чрезмерное петлевое усиление. В итоге
возникают автоколебания, как было ранее при
использовании только одной пропорциональ-
ной составляющей, когда большое усиление П
вызывало избыточное усиление контролле-
ра Ак. Чрезмерное петлевое усиление создает
проблемы на частоте, при которой величина
фазового сдвига достигает -180°, независимо
от причины этого избыточного усиления.
10 Выражение «задействуется слишком рано» просто озна-
чает, что усиление составляющей Д избыточно, поскольку
эта составляющая задействуется в точке графика, где уси-
ление Д превышает усиление П.
10N.5. Дифференциальная составляющая Д
449
Слишком много Д: здесь усиление звена Д больше
усиления звена П (Д задействуете* слишком рано)
3
Ак\ ТТ и избыток Д (нестабильная)
^~^*"~>1К: П и Д (стабильная)
Частота
(логарифмическая шкала)
-ТТ и избыток Д
\ ТТ и Д (стабильная или нестабильная)
Избыток Д аннулирует отрицательный (разовый сдвиг
Но возникает проблема: когда величина фазового
сдвига достигает -180й, Д дает слишком большое
усиление (петлевое усиление больше единицы)
(якобы стабилизирующая Д теперь дестабилизирует)
зависимости от петлевого усиления (АК*АС)
на этой частоте и при данном (разовом
сдвиге схема может быть или стабильной,
или нестабильной:
1) схема нестабильна, если на этой частоте
петлевое усиление > 1, каким оно будет при
избыточной дифференциальной составляющей;
2) схема стабильна, если на этой частоте
петлевое усиление < 1
Рис. 10N.20. Избыток дифференциальной составляющей (Д) может снова вызвать автоколебания, делая слишком большим
общее усиление >АК« Ас
Входной сигнал (целевой) Отклик
Ч^Сигнал рассогласования /
Входной сигнал Отклик Отклик = входной сигнал
Рассогласование
сводится к нулю
посредством
добавления интеграла
сигнала рассогласования И
к пропорциональной
составляющей ТТ
Без интегральной составляющей
при низком усилении сохраняется
значительное рассогласование
ш
SOOmV M 2 00 s
Интеграл сигнала рассогласования И добавляется к
пропорциональной корректирующей составляющей П:
рассогласование сводится к нулю
Рис. 10N.21. Интегральная составляющая корректирующего сигнала позволяет уменьшить накопленные ошибки даже при низ-
ком усилении (усиление каналов осциллографа: 1 В/деление изображении слева; 500 мВ/делении на изображении справа)
10N.5A Интегральная
составляющая
Полезное воздействие последней из коррек-
тировочных функций, интеграла сигнала рас-
согласования И, обычно менее важно, чем диф-
ференциала сигнала рассогласования. Инте-
гратор не помогает в стабилизации схемы, но
уменьшает накопленные погрешности, сводя
их к нулю.
Эффект интегральной составляющей звена И
очевиден, если посмотреть, как она воздей-
ствует на отклик схемы с очень низким усиле-
нием звена П, осциллограмма которого пока-
зана на рис. 10N.10. Эта осциллограмма снова
приведена слева на рис. 10N.21, а справа на ри-
сунке изображена осциллограмма отклика той
же схемы, но только с добавленной интеграль-
ной корректирующей составляющей.
Интеграл сигнала рассогласования приводит
уровень регулируемого сигнала к заданному
значению, но только после задержки длитель-
ностью почти в 5 с в данном примере (как вид-
но на осциллограмме справа на рис. 10N.21)11.
11 Эта задержка вызвана «статическим трением» или «при-
липанием» (англ. stiction, от ST-aticfr-ICTION), как отме-
чается на лабораторном занятии 10L. Электродвигатель не
начинает вращаться до тех пор, пока его напряжение пита-
ния не достигнет необходимого минимального уровня.
450
ЮЛ/. Операционные усилители IV: ПИД-регулятор для электродвигателя
Как может ПИД-регулятор сохранять
стабильность при наличии
интегрирующего звена?
В обсуждении мы не раз обращали внимание
на то, что интегратор вызывает отрицательный
фазовый сдвиг величиной 90°. Поэтому будет
логично сделать вывод, что добавление в контур
управления еще одного отрицательного сдви-
га величиной 90° нарушит его стабильность.
Действительно, интегральная составляющая
добавляет в сигнал контура еще один фазовый
сдвиг величиной -90°. Но эта задержка по фазе
не нарушает стабильность схемы, поскольку
в критической точке, где усиление становится
единичным, ее эффект уже давно исчез.
В качестве упражнения попытайтесь отве-
тить на вопрос, почему можно допустить про-
блематичный фазовый сдвиг при условии его
устранения перед достижением частоты еди-
ничного усиления12. Сообщите нам, как только
придумаете хорошее интуитивное объяснение
этому «чуду»
13
10N.6. Материал для чтения
вАоЕ
♦ Раздел 15.6.2 аналоговый ПИД-регулятор.
12 Конечно же мы это делаем по той причине, что не знаем
правильного ответа.
13 Сведущие люди говорят нам, что, действительно, отри-
цательный фазовый сдвиг величиной 180° и даже больше
является допустимым при условии его отката до значения
меньшего чем 180° на частоте единичного усиления. Эта
истина снова демонстрируется при рассмотрении схем
фазовой синхронизации в цифровой части этой книги.
Но пока интуиция нас подводит: мы не можем дать объ-
яснение данному феномену, потому что не совсем пони-
маем его.
10L Лабораторное занятие:
операционные усилители V
10L1. Какая польза
от ПИД-регулятора?
Рассматриваемая петля
обратной связи
Последовательность действий на данном ла-
бораторном занятии выглядит прямолинейно:
с помощью потенциометра задаем требуемое
положение для вала электродвигателя посто-
янного тока, электродвигатель пытается выста-
вить вал в это положение, текущее положение
вала электродвигателя измеряется связанным с
ним другим потенциометром, сигнал с которо-
го подается на контроллер двигателя, который
на основе этого сигнала принимает решение о
дальнейшем действии — продолжать вращение,
остановить, вращать в обратном направлении
и т.п. Но в этой на первый взгляд простой схеме
основная проблема связана с задержкой: кор-
ректировочной сигнал скорее всего будет по-
ступать на контроллер слишком поздно, чтобы
вызвать соответствующее действие. В результа-
те этого корректировка может лишь усугубить
проблему.
Описанная схема управления положением вала
электродвигателя является классической це-
пью обратной связи, называемой ПИД-регу-
лятором. Ее реагирование определяется тремя
функциями сигнала рассогласования схемы:
пропорциональной (П), интегральной (И) и
дифференциальной (Д). Главной задачей, кото-
рую требуется решить в такой схеме, является
ее стабильность.
Чем эта схема интересна нам
Эта задача из области обратной связи интерес-
на нам двумя аспектами.
♦ Обучающим. Она дает возможность изу-
чить всю совокупность схем, которые до сих
пор мы видели только в виде фрагментов или
только на бумаге:
• дифференциальный усилитель, состоящий
из операционных усилителей (с этой схе-
мой мы знакомы только в теории);
• дифференциатор;
• интегратор;
• сумматор;
• сильноточный драйвер (с электродвигате-
лем в качестве нагрузки).
♦ Практическим. ПИД-регулятор решает
классическую задачу управления; эта схема
имеет множество вариантов практического
применения.
Схема, которую можно потрогать
руками
Студенты часто говорят нам, что им нравится
собирать устройства, которые что-то делают, в
отличие от схем, которые просто выводят сиг-
нал на экран осциллографа. Это лабораторное
занятие им понравится: собранная схема га-
рантированно приведет в движение маленький
электромоторчик. При нестабильной работе
схемы он будет лишь дрожать, а при стабиль-
ной — послушно проворачивать свой вал, оста-
навливая его в заданном положении.
Схема ПИД-контроллера, разумеется, самая
сложная изо всех схем, с которыми нам при-
ходилось иметь дело на сегодняшний день.
Поэтому она будет хорошей площадкой для усо-
вершенствования ваших навыков поиска при-
чин неполадок. (Скорее всего вам не избежать
ошибок при ее сборке.) В нашем курсе мы часто
подчеркиваем, что самым важным результатом
452
10L Лабораторное занятие: операционные усилители V
обучения являются ошибки. Этот тезис стано-
вится наиболее убедительным в конце курса,
когда вы, возможно, решите собрать компьютер
из отдельных микросхем. Но даже сегодняшняя
схема достаточно сложна, чтобы бросить вызов
вашим способностям схемотехника.
Примечание
Процесс наладки устройства может быть особен-
но трудным, если ваш напарник не следует прави-
лу использовать провода согласно определенной
цветовой маркировке и делать их короткими, или
забудет поставить развязывающие конденсаторы
на шинах питания. Вы сами, мы уверены, никогда
бы не допустили таких ошибок.
Наконец, на этом лабораторном занятии сно-
ва возникает вопрос, впервые рассмотренный
на лабораторном занятии 9L: стабильность.
Сегодняшняя схема содержит только один
проблемный элемент — интегратор в цепи
обратной связи, разработка которого по-
требует более тонкого подхода, чем обычно.
Но общая проблема стабильности предстает
перед нами почти в каждой схеме, в которой
есть усиление.
10L2. ПИД-контроллер
электродвигателя
Задача, решением которой мы займемся здесь,
подробно описана в главе 10N. Здесь мы повто-
рим некоторые моменты из материала той гла-
вы, чтобы не отрывать вас от работы ссылками
к разъяснительной информации. Но материал
в главе 10N более подробный, чем предостав-
ляемый в данном разделе.
Кратко говоря, наша цель состоит в том, чтобы
уравнять два постоянных напряжения с помо-
щью контура обратной связи. А поскольку оба
эти напряжения снимаются с потенциометров,
нашу цель можно описать так: обеспечить,
чтобы положение движка одного потенцио-
метра повторяло положение движка другого.
Мы хотим вращать рукоятку одного потенцио-
метра вручную и видеть, как движок другого
потенциометра, вращаемый соединенным с
ним валом электродвигателя, повторяет наше
действие. Такие элементы управления иногда
встречаются в аудиооборудовании высше-
го класса, чтобы им можно было управлять,
вращая ручку или локально, или дистанци-
онно с пульта дистанционного управления.
Еще более впечатляющий пример применения
ПИД-контроллера — дистанционное выполне-
ние хирургических операций.
10L2.1. Сборка «электродвигатель-
потенциометр»
На рынке представлены два типа готовой сбор-
ки «электродвигатель-потенциометр». Боль-
шинство осциллограмм и графиков частотных
характеристик в главе 10N и на лабораторном
занятии 10L были получены нами с помощью
сборки с поворотным потенциометром, ко-
торая изображена слева на рис. 10L.1. В дру-
гом варианте сборки, показанном справа на
рис. 10L.1, поворотный потенциометр заменен
на ползунковый. Отклик этой конструкции на-
много быстрей, чем первой. Используйте лю-
бое из устройств, доступное вам1.
Муфта в сборке с поворотным потенциометром
имеет двойное назначение: во-первых, она по-
зволяет проворачивать вал потенциометра
вручную при остановленном электродвигате-
ле. Во-вторых, она предохраняет электродви-
гатель от торможения и перегрева при выходе
вала потенциометра за пределы его диапазона
положений. В сборке с ползунковым потен-
циометром такой возможности нет, и затор-
моженный электродвигатель будет потреблять
ток около 800 мА, но без каких-либо катастро-
фических последствий. Поскольку в сборке с
ползунковым потенциометром нет скользящей
муфты, рекомендуем выбрать поворотную кон-
струкцию.
10L2.2. Контур управления
электродвигателем
На рис. 10N.1 была представлена упрощенная
схема сегодняшней лабораторной установ-
ки. Особую трудность для нас представляет
1 Например, можно использовать сборку с поворотным
потенциометром RK16812MG099 компании Alps Elec-
tric Со. А сборка с ползунковым потенциометром пред-
лагается компанией SparkFun Electronics, артикул номер
СОМ-10734. Тип функциональной характеристики по-
тенциометра не играет роли. Если линейная характери-
стика — хорошо, если обратная логарифмическая — тоже
подойдет (упомянутое устройство компании Alps имеет
обратную логарифмическую зависимость ВЗ).
10L2. ПИД-контроллер электродвигателя
453
Скользящая муфта: нейлоновый диск,
/прижатый к другому диску спиральной пружт
Потенциометр (слева — поворотный, справа — ползунковый)
Электродвигатель постоянного тока-
Двойной червячный привод;
низкая скорость, большой крутящий момент
Рис. 10L1. Два варианта сборки «электродвигатель-потенциометр»: слева — с поворотным потенциометром, справа —
с ползунковым
то, что сборка заключается в том, что сборка
«двигатель-потенциометр», которая являет-
ся нагрузкой схемы, интегрирует напряже-
ние. Поэтому обычный операционный усили-
тель в этой схеме оказывается непригодным.
Дополнительный отрицательный фазовый
сдвиг величиной 90°, создаваемый интегриро-
ванием, заставляет нас искать другие подходы
к реализации этой схемы. Поскольку фазовый
сдвиг обычного операционного усилителя в
данной ситуации не подходит, нам нужно са-
мим собрать специализированный операцион-
ный усилитель, который будет иметь умеренное
усиление и не будет создавать фазового сдвига.
Таким образом, мы прибегнем к радикально-
му решению: изменим не нагрузку в цепи об-
ратной связи операционного усилителя, а сам
операционный усилитель. На рис. 10L.2 изо-
бражена такая же принципиальная схема, как
и на рис. 10N.4, которая является практически
копией схемы на рис. 10N.1, но с одним добав-
ленным элементом, позволяющим управлять
уровнем усиления операционного усилителя.
Эта схема обеспечивает лишь самую простую
корректирующую составляющую — пропор-
циональную (П). Далее мы добавим модифика-
ции для управления фазой.
Рис. 10L.2. Управление только посредством пропорцио-
нальной составляющей будет вызывать определенное пере-
регулирование, величина которого определяется уровнем
усиления
Сначала мы испытаем эту схему в работе при
небольшом усилении, при котором мы ожида-
ем, что схема будет довольно стабильна. Затем,
по мере повышения усиления возникнет пере-
регулирование и звон, а при еще большем по-
вышении усиления схема перейдет в режим
незатухающих автоколебаний. В конце этого
раздела приведено несколько осциллограмм,
иллюстрирующих такие отклики на простое
пропорциональное усиление.
10L2.3. Драйвер электродвигателя
Начнем с уже знакомой нам схемы сильноточ-
ного драйвера, способного выдавать значи-
тельный ток (до пары сотен миллиампер). При
сборке этого блока будем использовать уже
знакомые нам транзисторы: MJE3055 (n-p-ri)
и MJE2955 (p-n-р). Электродвигатель является
проблематичной нагрузкой и может вызывать
паразитные автоколебания, как было показано
в последнем упражнении на лабораторном за-
нятии 9L. Поэтому нам требуется предпринять
такие же меры предосторожности, как и на
том лабораторном занятии: не только выпол-
нить развязку шин питания, но также добавить
демпфер и разделенную обратную связь, кото-
рая обходит проблематичные элементы, вызы-
вающие фазовый сдвиг.
Здесь мы обеспечиваем тщательную развязку
одной части схемы от другой: конденсаторы ем-
костью 15 мкФ предотвращают проникновение
помех от источника питания. Такие же конден-
саторы, подключенные к выводам потенциоме-
тра, соединенного с электродвигателем служат
для стабилизации сигнала обратной связи.
Если у вас есть лишний подходящий источник
питания, то полезно запитать электродвигатель
от отдельного источника напряжением ±15 В.
Это рекомендуется не просто для развязки шин
электропитания, но также и потому, что мак-
симальный потребляемый электродвигателем
454
10L Лабораторное занятие: операционные усилители V
ток превышает номинальный выходной ток ис-
точника питания макетной величиной 100 мА,
и может создавать помехи в линиях питания
даже при наличии достаточного количества
развязывающих конденсаторов. В отличие от
источника питания макетной платы, внешний
источник способен обеспечить ток, необходи-
мый для устойчивой работы электродвигателя.
Но даже если у вас нет дополнительного источ-
ника питания, это не должно быть проблемой,
поскольку мы собрали данную схему без такого
отдельного источника питания.
Примечание
Сопротивление потенциометра вашей сборки мо-
жет отличаться от номинала 10 кОм как в схеме на
рис. 10L3. В таком случае нужно будет подкоррек-
тировать значения других резисторов в его цепи
в соответствующем соотношении. Например, если
номинал вашего потенциометра равен 100 кОм,
то сопротивления резисторов номиналом 4,7 кОм
также нужно повысить в десять раз.
опустится ниже указанного напряжения входного
синфазного сигнала2. В результате, если входной
сигнал на мгновение приблизится к отрицательно-
му напряжению питания, то положительная обрат-
ная связь скорее всего вызовет зависание петли3.
Подключите к схеме оба потенциометра, а так-
же сам электродвигатель. Резисторы на концах
обоих потенциометров (номиналом 6,8 кОм на
входном потенциометре и 4,7 кОм на потен-
циометре сборки) ограничивают напряжения
входного и выходного диапазоном приблизи-
тельно +7 В, чтобы все сигналы находились в
пределах рабочего диапазона операционного
усилителя. Разница в значениях резисторов га-
рантирует, что диапазон напряжений входного
сигнала не превысит границ диапазона напря-
жений выходного сигнала.
Собранный драйвер электродвигателя можно
протестировать, меняя входное напряжение и
измеряя напряжение на выходе потенциометра
/ —ч ^Операционный усилитель N
(Потенциометр но макетной плате] ((не такой, как микросхема 411))
+15 В
Внешний источник питания
Электро-
двигатель
ЮкОм
0,33 мк* 1
>4 7 мкФ
Внешний источник литания
miniDIP: 358
Рис. 1OL3. Драйвер электродвигателя
Примечание
Ни в коем случае не используйте в схеме опера-
ционный усилитель 411. Этот усилитель облада-
ет мерзким свойством, присущим микросхемам
с комбинацией биполярных и полевых транзи-
сторов. А именно, он может реверсировать фазу
своего выходного сигнала, если уровень на входе
2 В таком случае выходной сигнал операционного уси-
лителя принудительно переводится на высокий уровень.
Если напряжение на неинвертирующем входе становится
слишком отрицательным, то тип обратной связи меняется
с отрицательного на положительный.
3 Это не гипотетическая опасность. Мы сначала собрали
эту схему на макетной плате с операционным усилителем
411, и эта неприятная особенность данной микросхемы
тотчас же проявилась, периодически блокируя контур об-
ратной связи.
70L2 ПИД-контроллер электродвигателя
455
связки. Не отчаивайтесь, если на экране осцил-
лографа присутствует много помех. Эти помехи
могут выглядеть очень похожими на паразит-
ные автоколебания, знакомые вам по лабора-
торному занятию 9L. На рис. 10L.4 приведена
осциллограмма сигнала, который мы получи-
ли, наблюдая выходной сигнал потенциометра
связки при работающем электродвигателе.
Рис. 10L.4. Помехи в выходном сигнале потенциометра связ-
ки выглядят похожими на паразитные автоколебания
Но если взглянуть на помехи при более высоком
разрешении, как показано на осциллограмме на
рис. 10L.5, то можно убедиться, что это совсем
не обычные паразитные автоколебания.
i Ь о V
Рис. 10L.5. Помехи в выходном сигнале потенциометра
связки при более высоком разрешении оказываются вовсе
не паразитными автоколебаниями
Всплески помех создаются в результате перио-
дического разрыва между щетками электро-
двигателя и его коммутатором. Одним из при-
знаков является тот факт, что помехи не посто-
янные, а представляют собой узкие выбросы,
повторяющиеся с низкой скоростью. Другой
довольно убедительный признак — тот факт,
что амплитуда импульсов превышает напряже-
ние источника питания. Этот эффект выглядит
очень похожим на поведение индуктивности
(обмотки электродвигателя), вырабатывающей
ЭДС при каждом отключении тока коммутато-
ром. Поэтому не стоит слишком волноваться по
поводу данных помех. Они выглядят противно,
но с ними можно жить.
Подача входного сигнала величиной больше,
чем несколько десятых вольта, должна вызы-
вать изменение выходного сигнала. Вы услы-
шите жужжание электродвигателя ц увидите,
что движок потенциометра медленно враща-
ется (другой конец оси потенциометра под-
ключен к валу электродвигателя через пони-
жающий двухступенчатый редуктор с червяч-
ной или обычной шестереночной передачей)4.
Приблизительно через 20 с движок потенцио-
метра достигнет предела своего хода и вра-
щение прекратится. Но никаких проблем не
возникнет, поскольку механизм предохрани-
тельной муфты, упомянутый в разделе 10L2.1,
позволяет электродвигателю вращаться, даже
когда потенциометр достигает предела своего
хода в любом направлении. Если полярность
входного сигнала 1/вх не совпадает с изменени-
ем выходного сигнала 1ГВЫХ, поменяйте местами
провода на крайних выводах одного из потен-
циометров. Мы не хотим, чтобы у нас происхо-
дила скрытая инверсия, поскольку это расстро-
ит нашу схему, когда мы позже замкнем контур
обратной связи.
10L2.4. Псевдооперационный
усилитель
Теперь мы соберем не совсем обычное устрой-
ство — схему (рис. 10L.6), функционирующую
как низкокачественный операционный усили-
тель из трех микросхем операционных усили-
телей. Это именно та схема, которую мы ранее
называли управляющим усилителем.
Первый каскад представляет собой стандарт-
ный дифференциальный усилитель с единич-
ным усилением. Второй каскад просто инвер-
тирует сигнал5, а третий каскад аннулирует
инвертирование предыдущего каскада, а также
позволяет регулировать усиление. Но вско-
ре мы будем использовать данную схему в
4 Внутреннее устройство связок «электродвигатель-по-
тенциометр» посмотрите на рис. 10L.1.
5 Инвертирование добавлено здесь для того, чтобы по-
лярность сигнала совпадала с дифференциальным и ин-
тегральным сигналами, которые мы вскоре создадим. Эти
сигналы формируются схемами, которые непременно ин-
вертируют исходный сигнал.
456
70L Лабораторное занятие: операционные усилители V
/Потенциометр
(намакетной плате]
Наш самодельный псевдооперационный усилитель
г
1. Заземлить для тестирования псевдо-
дифференциального режима.
2. Соединить с другим входом для
тестирования синфазного режима.
«Сумма»
Все микросхемы — LM358
Рис. 10L6, Дифференциальный усилитель, за которым следует каскад усиления и инвертор
качестве сумматора с двумя дополнительными
входами. При таком использовании она будет
суммировать три составляющих ПИД-сигна-
ла: пропорциональную (П), интегральную (И)
и дифференциальную (Д). В данной версии
схемы, содержащей только П-составляющую6,
третий каскад служит также для регулировки
общего усиления нашего самодельного опера-
ционного усилителя.
Таким образом, вся наша схема на данном этапе
является простым дифференциальным усили-
телем с регулируемым усилением. И это усиле-
ние всегда мало по сравнению с очень больши-
ми значениями, которые мы привыкли видеть
у операционных усилителей. Сейчас нам тре-
буется скромное усиление и отсутствие фазо-
вого сдвига в выходном сигнале относительно
входного. Как вы знаете, оба эти свойства не
характерны для обычных операционных уси-
лителей. Постоянное высокое усиление обыч-
ного операционного усилителя в комбинации с
его поведением интегратора, проявляющимся
уже при частоте 10-20 Гц, создавало бы для нас
проблему в данном случае, превращая отрица-
тельную обратную связь в положительную.
6 Мы обозначаем этот сигнал П, подобно тому, как мы
обозначаем другие сигналы, которые вскоре будут добав-
лены, Д и И, хотя два последних сигнала инвертированы
относительно исходного. Таким образом, строго говоря,
это сигнал -П. Но мы опускаем знак «минус» в обозначе-
ниях для удобства: мы полагаем, что легче сказать просто
«П», чем «минус П».
Проверяем синфазное
и дифференциальное усиления
Синфазное усиление
Для подбора усиления суммирующей схемы
рекомендуется использовать магазин сопро-
тивлений. Установите усиление равным десяти,
подайте на оба входа сигнал с амплитудой око-
ло одного вольта и посмотрите, каков будет вы-
ходной сигнал. Ожидаете ли вы, что выходной
сигнал будет нулевым?
Псевдодифференциальное усиление
Затем заземлите один вход (резистор номина-
лом 100 кОм, через который подается сигнал на
инвертирующий вход операционного усилите-
ля), а на другой вход подайте сигнал с потенци-
ометра. Наблюдайте за входным и выходным
сигналами, установив с помощью магазина
сопротивлений значение Ry равным 100 кОм.
Посмотрите, сможете ли вы получить ожидае-
мое десятикратное усиление.
Два обстоятельства данного эксперимента нуж-
но объяснить более подробно.
♦ Когда на вход подается сигнал с потенцио-
метра, усиление будет положительным, по-
скольку за дифференциальным усилителем
следуют два инвертирующих каскада.
10L2. ПИД-контроллер электродвигателя
457
♦ На усилитель подается псевдодифференци-
альный входной сигнал, для чего один вход
заземляется, а сигнал подается на другой
вход. (Мы так уже делали на лабораторном
занятии 5L, когда подавали сигнал на наш
самодельный операционный усилитель.)
Поскольку дифференциальное усиление на-
много больше синфазного, псевдодиффе-
ренциальный сигнал по своему действию
похож на настоящий дифференциальный
сигнал. Подаваемый сигнал и представляет
собой дифференциальный сигнал с амплиту-
дой и, совмещенный с синфазным сигналом
с амплитудой и/2. Даже при небольшом ко-
эффициенте подавления синфазной состав-
ляющей этот синфазный сигнал, смешанный
с дифференциальным, не окажет вредного
воздействия.
В данном случае удобней пользоваться не
осциллографом, а цифровым мультиметром,
чтобы удостовериться, что сигнал на выхо-
де этой цепочки операционных усилителей
в 10 раз больше, чем напряжение с потенцио-
метра, подаваемое на вход. Завершив экспери-
мент, установите уровень выходного напряже-
ния близкий к нулю.
10L2.5. Управление
электродвигателем
Мы уже протестировали схему драйвера элек-
тродвигателя. Теперь давайте проверим три
новых каскада, составляющих наш псевдоопе-
рационный усилитель, подав его выходной сиг-
нал на вход драйвера электродвигателя. Для
этого эксперимента заземлите инвертирующий
вход нашего самодельного операционного уси-
лителя, как показано пунктирной линией на
рис. 10L.7. Второе подключение (к контакту
ползунка выходного потенциометра) кото-
рое изображено другой, длинной, пунктирной
линией на этом рисунке, на данном этапе осу-
ществлять не нужно.
Проверьте, что вы можете заставить электро-
двигатель вращаться сначала в одном направ-
лении, а затем в другом, варьируя с помощью
входного потенциометра уровень входно-
го сигнала слегка выше, а затем слегка ниже
нуля.
Замечание
Как уже упоминалось ранее, благодаря встроенной
в сборку скользящей муфте достижение движком
выходного потенциометра пределов вращения не
представляет опасности ни для потенциометра, ни
для вращающего его электродвигателя.
10L2.6. Замыкаем петлю
обратной связи
Теперь замкнем петлю обратной связи. Умень-
шите усиление примерно до 1,5. Для этого уста-
новите значение Ry равным 15 кОм. Отключите
от «земли» инвертирующий вход нашего псев-
дооперационного усилителя и подайте на этот
вход сигнал с выходного потенциометра. Это но-
вое подключение показано на рис. 10L.7 длин-
ной пунктирной линией. Еще раз напомним,
что нужно обязательно отключить инвертиру-
ющий вход от «земли», прежде чем подавать на
него сигнал с выходного потенциометра.
Псевдооперационный усилитель
6,8 кОм
ЮкОм
6,8 кОм
.
Драйвер электродвигателя
ЮкОм
.а затем отключите этот вход от «земли»
подключите его к ползунковому контакту ^,7 кОм
выходного потенциометра, замкнув таким
образом петлю обратной связи.
4Сначала заземлите этот вход, чтобы протестировать операционный усилитель и драйвер
электродвигателя с разомкнутой цепью обратной связи...
Рис. 10L.7. Операционный усилитель и драйвер электродвигателя: сначала испытайте дифференциальный усилитель, каскад
усиления, сумматор и драйвер электродвигателя с разомкнутой петлей обратной связи. Затем замкните петлю обратной связи
458
10L Лабораторное занятие: операционные усилители V
На одном канале осциллографа наблюдайте за
входным сигналом f/BX, а на другом канале — за
выходным сигналом U
вых-пог
Замечание
Если в вашем распоряжении имеется цифровой
осциллограф, то целесообразнее использовать
именно его, поскольку наблюдение желатель-
но выполнять при очень медленной развертке:
0,5 с/деление или даже 1 с/деление.
Несколько способов тестирования петли
обратной связи
Схему с замкнутой петлей обратной связи мож-
но протестировать двумя или тремя спосо-
бами.
Два способа подачи входного сигнала
♦ Прямоугольный сигнал от генератора
сигналов. Генератор сигналов может выда-
вать прямоугольный сигнал небольшой ам-
плитуды (скажем, ±0,5 В) на самой низкой
возможной частоте. Этот источник входного
сигнала может временно заменить управляе-
мый вручную входной потенциометр. Такой
способ будет, наверное, самым лучшим, по-
скольку он позволяет получить единообраз-
ный входной сигнал, что невозможно сделать
вручную.
♦ Подача входного ступенчатого сигнала
вручную. Но вы можете отдать предпочте-
ние более простому способу: вручную пода-
вать ступенчатый сигнал величиной около
1В с входного потенциометра.
Сигнал выходного потенциометра должен по-
вторять входной сигнал с несколькими циклами
перерегулирования и затухающих колебаний.
Альтернативный тест: нарушаем
выходной сигнал и наблюдаем его
восстановление.
♦ Протестировать работоспособность схемы
можно и другим способом. Для этого при по-
стоянном входном напряжении вручную про-
верните ось выходного потенциометра из ее
установившегося положения в ту или другую
сторону. Затем отпустите ось и наблюдайте,
как она возвращается в исходное положение,
опять же, как и в случае с изменением сиг-
нала входного потенциометра, демонстрируя
несколько циклов перерегулирования и зату-
хающих колебаний.
Для начала установите очень низкое усиле-
ние (1,5), при котором схема должна быть
стабильной даже в такой ситуации, когда кор-
ректирующий сигнал имеет только пропор-
циональную составляющую. Теперь увеличьте
усиление, выбрав в магазине сопротивлений
резистор соответствующего номинала. В на-
шем случае при значении Ry = 220 кОм (т. е.
при коэффициенте усиления, равном 22) на-
блюдалось некоторое перерегулирование и
несколько колебаний, проявляющихся во
вращении вала электродвигателя и движка
потенциометра. Если бы эта схема управля-
ла, скажем, рулем направления самолета, то
полученный эффект был бы довольно трево-
жащим. В целом схема работает, но желатель-
но уменьшить перерегулирование и ускорить
установление равновесия.
Повысив усиление до 68, установив для этого
значение RY = 680 кОм, мы смогли получить не-
сколько периодов автоколебаний. На рис. 10L.8
изображена осциллограмма напряжения на вы-
ходе драйвера электродвигателя (при сигнале
бблыней амплитуды), в которой эти автоколе-
бания более очевидны.
О •• ЕаЗЖЭ б v ШХШШ
Напряжение Т|ИД: ТТ, И и Д П, R = 680кОм;трлько П
сигнал
у Обратная связь (положение)
.:i: г"" "t""
вер электродвигателя
Драй
—Ш « 3$8,63« м$ 133 ЛП «V
>--И) - «tt.8Jtt ю 411.385 «V
318.181? т -18.8934 «V
Д • 318.181? т
/AX ■ 3,14285$ Нг
Рис. 10L8. Корректирующий сигнал содержит только
П-составляющую: достаточно высокое усиление подводит
схему к границе режима автоколебаний
А повысив усиление еще немного (до 100), уста-
новив для этого значение Ry = 1 МОм, и подавая
на вход схемы или прямоугольный сигнал от
генератора, или создавая на входе ступенчатый
перепад вручную с помощью входного потен-
циометра, мы получим незатухающие автоко-
лебания на выходе. Выясните, какая величина
10L.3. Добавляем дифференциальную составляющую
459
усиления вызывает незатухающие автоколе-
бания в вашей схеме, а затем измерьте период
незатухающих автоколебаний, получаемых
при наименьшем уровне усиления. Назовем это
значение периодом собственных колебаний;
вскоре данная величина нам понадобится при
выборе решений для устранения незатухаю-
щих автоколебаний.
10L3. Добавляем
дифференциальную
составляющую
Если получится ускорить достижение выход-
ным сигналом состояния равновесия, то мы
сможем улучшить характеристики нашей
схемы. Добавив дифференциальную состав-
ляющую, мы сможем существенно ускорить
достижение схемой состояния равновесия,
и даже значительно повысить усиление П.
Рассматривая вопрос стабильности как про-
блему фазовых сдвигов синусоидальных сиг-
налов (общий подход, который мы применя-
ли к операционным усилителям), становится
ясно, что добавление в контур обратной свя-
зи дифференциальной составляющей создаст
условия для устранения интегрирования.
Интегрирование в данной ситуации представ-
ляет опасность, и одна из неприятностей за-
ведомо присуща схеме — преобразование ско-
рости вращения электродвигателя в положение
его вала. Дополнительное интегрирование обу-
словлено отрицательными фазовыми сдвига-
ми, достигающими проблематичной величины
-180°, при которой полезная обратная связь
превращается во вредную и возникают пара-
зитные незатухающие автоколебания, которые
мы только что наблюдали.
10L3.1. Схема для получения
дифференциальной составляющей
Выходной сигнал стандартного дифференциа-
тора операционного усилителя, принципиаль-
ная схема которого изображена на рис. 10L.9,
может подаваться на суммирующую схему.
Схема на рис. 10L.9 отличается от изображен-
ной на рис. 10L.7 только наличием каскада
дифференциатора для получения дифферен-
циальной составляющей. Спад усиления диф-
ференциатора начинается приблизительно на
частоте 1,5 кГц. Опять же, для установки усиле-
ния сигнала дифференциальной составляющей
Д рекомендуется использовать магазин сопро-
тивлений при условии, если он есть в наличии.
ТТсевдооперационный усилитель
Драйвер электродвигателя
Магазин сопротивлений R
(& = 220 кОм => умеренное усиление)
IkOm
L-vw
Рис. 10L.9. Добавление в контур обратной связи дифференциальной составляющей
460
10L Лабораторное занятие: операционные усилители V
На рис. 10L.9 также показан тумблер в цепи
обратной связи для отключения дифференци-
альной составляющей в случае такой необхо-
димости.
Величина дифференциальной
составляющей
Цель добавления дифференциальной состав-
ляющей — устранение дополнительного фа-
зового сдвига, который создается эффектом
низкочастотного фильтра и ведет к нестабиль-
ности. Как узнать, на какой частоте возникает
эта проблема и, таким образом, как нам опре-
делить частотную характеристику (или, иными
словами, усиление) дифференциатора?
Оказывается, у нас уже есть вся необходимая
для этого информация, которую мы получили
при измерении частоты (или периода) соб-
ственных колебаний ранее в разделе 10L.2.6.
Там мы постепенно повышали уровень усиле-
ния составляющей П до тех пор, пока не увели-
чивалось время установления равновесия вы-
ходного сигнала или схема вообще переходила
в режим незатухающих автоколебаний.
Примечание
Например, когда мы проводили этот эксперимент
в нашей лаборатории, применяя сборку с пово-
ротным потенциометром, то получили период
собственных колебаний величиной около 0,6 с, а
при ползунковом потенциометре величина это-
го периода была около 40 мс. Если у вас сборка
«электродвигатель-потенциометр» с ползунковым
потенциометром, то усиление дифференциальной
составляющей Д следует измерить соответствую-
щим образом (не используйте значения, указывае-
мые далее, которые относятся к сборке с поворот-
ным потенциометром).
Наша цель — уравнять вклад дифференциаль-
ной составляющей Д и пропорциональной со-
ставляющей П на частоте излома, на которой
могут возникать незатухающие автоколеба-
ния. Свойства дифференциатора определяют-
ся постоянной времени RC. Подробное объяс-
нение и обоснование этого утверждения при-
водится в главе 10N. Чтобы уравнять усиление
составляющих Д и П на частоте собственных
колебаний, нужно обеспечить выполнение
условия RC = 1/(2я/), где/— частота автоко-
лебаний.
Эмпирическое правило: частота
собственных автоколебаний определяет
параметры звена Д
Если, как следует из формулы, величина посто-
янной времени RC должна быть равной около
1/6 периода собственных автоколебаний, тогда
для нашего периода Гкол = 0,6 с величина по-
стоянной времени RC должна быть около 0,1 с
или чуть меньше7. Если взять конденсатор С
стандартной емкости 0,1 мкФ, то величина тре-
буемого сопротивления R будет около 1 МОм.
Но сделаем это значение регулируемым, по-
скольку мы хотим исследовать влияние боль-
шей или меньшей чем обычно доли дифферен-
циальной составляющей. Устанавливать уро-
вень усиления дифференцирующего звена (т. е.
постоянной времени RC) также предпочти-
тельнее с помощью магазина сопротивлений,
если у вас имеется еще одно такое устройство.
В противном случае используйте потенциометр
номиналом 1 МОм. Величину сопротивления R
можно, приблизительно задать в пределах 20%
по положению движка потенциометра. В сред-
нем положении это значение будет определенно
500 кОм, а при повороте на около 3/4 полного
хода значение будет 750 кОм. Сигнал с выхода
дифференциатора подается на собранную ранее
схему суммирования через резистор, значение
которого подобрано так, чтобы доля этой со-
ставляющей была равна доле пропорциональ-
ной составляющей.
Мы надеемся, что вы убедитесь, что диффе-
ренциальная составляющая корректирующе-
го сигнала является мощным и эффективным
«лекарством» против автоколебаний. После
7 См. например, книгу Tietze U., Schenk <C. Electronic Cir-
cuits: Handbook for Design. 2nd ed. Springer, 2008. 1005 p.
Менее формальный подход описывается в книге «Control-
ler Tuning and Control Loop Performance» («Настройка кон-
троллера и характеристики контура управления»), автор
Дэвид Сент-Клер (David St. Clair), издательство Straight-
Line Controls, Inc. А на сайте автора (members.aol.com/
pidcontrol/) можно загрузить эмулятор, с помощью ко-
торого попробовать применить описываемые им прави-
ла. (Загрузить демоверсию можно здесь: https://www.
straightUnecontrol.com/DemoTune.zip.) Самый легкий
в использовании эмулятор настройки ПИД, совместно
с хорошим руководством, можно найти по этому адресу:
http://newton.ex.ac.uk/teaching/CDHW/Feedback/.)
Этот эмулятор позволяет проверить влияние изменения
усиления пропорциональной составляющей и добавления
в корректирующей дифференциальной и интегральной со-
ставляющих, точно так, как мы это делаем здесь.
10L.4. Добавляем интегральную составляющую
461
того как вы усовершенствуете характеристики Тумблер
схемы, устранив перерегулирование и звон, по-
высьте уровень усиления пропорциональной
составляющей П до 20 (#сум_усл= 220 кОм) или
больше. Остается ли выходной сигнал вашей
схемы стабильным? Попробуйте повысить уро-
вень усиления дифференциальной составляю-
щей Д. Вызывает ли это какие-либо проблемы?
Судить о величине доли дифференциальной
составляющей можно с помощью осциллогра-
фа. Если доля недостаточна, то на экране будут
видны следы перерегулирования, которые на-
блюдались, когда использовалась только про-
порциональная составляющая. А если доля из-
быточна, то выходной сигнал будет похож на
график изменения постоянной времени RC: по
мере приближения выходного напряжения к
целевому сигнал как бы «пугается» и начина-
ет «осторожничать». А дальнейшее повышение
усиления дифференциальной составляющей Д
(как отмечалось в главе 10N и особенно в раз-
деле 10NS2) вызывает нестабильность схемы с
переходом в режим автоколебаний.
Псевдооперационный усилитель
Драйвер электродвигателя
Тумблер, подключенный параллельно рези-
стору обратной связи, позволяет включать и
выключать дифференциальную составляю-
щую корректирующего сигнала по желанию.
Тумблер здесь предпочтительней, чем, напри-
мер, потенциометр с очень большим сопротив-
лением для подачи сигнала в схему суммирова-
ния. Наличие нескольких потенциометров за-
трудняет запоминание положений их движков
и ответ на вопрос, добавляем ли мы дифферен-
циальную составляющую или нет. А тумблер
легко решает эту проблему.
10LA Добавляем интеграль-
ную составляющую
Добавление третьей, интегральной, составля-
ющей корректировочного сигнала содействует
сведению остаточной погрешности (разницы
между напряжениями входного и выходного
потенциометров) к нулю. На
рис. 10L.10 приведена полная
схема ПИД-регулятора с добав-
ленным интегратором.
Магазин сопротивлений R
(R- 220 кОм => умеренное усиление)
(Емкость всех
конденсаторов
ЮкОм
ЛАД/
15 мкФ)
Рис. 10L.10. Добавление интегратора делает завершенной схему ПИД-регулятора
462
10L Лабораторное занятие: операционные усилители V
Пару аспектов интегратора нужно рассмотреть
более подробно.
♦ Два полярных конденсатора, соединен-
ных положительными обкладками. Этот
необычный прием позволяет использовать
полярные конденсаторы в условиях, в кото-
рых на конденсатор может быть подано на-
пряжение любой полярности. Конечно же,
эквивалентная емкость равна лишь полови-
не емкости каждого конденсатора. Полярные
конденсаторы выбраны, поскольку неполяр-
ные конденсаторы такой большой емкости
трудно найти.
♦ Кажущееся отсутствие обратной связи
по постоянному току. На первый взгляд
кажется, что этот интегратор обречен на пе-
реход в режим насыщения, поскольку в нем
отсутствуют обычные средства защиты — ре-
зистор обратной связи или быстродействую-
щий разрядник. Но ни одно из этих средств
здесь не требуется, поскольку общая обрат-
ная связь — по всей большой петле, от вход-
ного потенциометра до выходного — делает
такой нежелательный дрейф невозможным.
Таким образом, несмотря на кажущееся от-
сутствие, обратная связь по постоянному
току здесь присутствует.
Наблюдаем влияние интегральной
составляющей И
В собранной нами схеме остаточную погрешность
трудно увидеть на осциллографе, поэтому добав-
ление интегральной составляющей не принесет
такого быстрого вознаграждения, как в случае с
добавлением дифференциальной составляющей.
Наилучшее условие для наблюдения влияния
этой составляющей будет в случае чрезмерного
снижения уровня усиления пропорциональной
составляющей. Попробуйте для начала уста-
новить значение Ду = 100 кОм, чтобы обратная
связь схемы вносила заметную остаточную по-
грешность при отсутствии интегральной состав-
ляющей. Если вы подаЕали ступенчатый входной
сигнал от генератора, то замените этот источник
сигнала потенциометром с ручной регулировкой.
Уменьшите скорость развертки осциллографа до
такой, которая позволит видеть эффект интегри-
рования длительностью в несколько секунд.
На цифровом осциллографе вы легко сможете
наблюдать входной сигнал (целевой), выход-
ной сигнал (с потенциометра электродвигате-
ля) и сигналы интегратора, реагирующего на
ступенчатый сигнал, подаваемый с входного
потенциометра. При достаточном терпении вы
сможете даже различить эффекты статическо-
го трения, когда электродвигатель и потенцио-
метр не реагируют сразу же при подаче медлен-
но изменяющегося входного сигнала (которым
в данном случае является интегральная состав-
ляющая И). Вместо этого электродвигатель не
вращается до тех пор, пока напряжение инте-
гральной составляющей не достигнет некото-
рого минимального уровня, после чего выход-
ное напряжение скачком возрастает до нового
уровня и останавливается здесь до следующего
перепада входного напряжения. Эти эффекты
можно видеть на некоторых осциллограммах в
разделе 10L.5.
Увеличение интегральной
составляющей снова вызывает
нестабильность
Звучит угрожающе, не так ли? Добавление
интегральной составляющей критично в си-
туации, когда интегрирование и другие отри-
цательные фазовые сдвиги как раз и являются
факторами, опасными для стабильности схе-
мы. Эта составляющая действительно опас-
на, в чем можно удостовериться, повысив ее
до слишком большого уровня. В таком случае
возможно возникновение незатухающих авто-
колебаний. Тем более удивляет тот факт, что
строго дозированная величина интегральной
составляющей действительно улучшает харак-
теристики контура обратной связи, сводя на-
копленную погрешность к нулю, и не вызыва-
ет нестабильности.
10L.5. Осциллограммы
На рис. 10L.11 приведены осциллограммы, ил-
люстрирующие влияние повышения усиления
пропорциональной составляющей на выход-
ной сигнал схемы ПИД-регулятора.
10L5. Осциллограммы
463
Производная сигнала рассогласования
, ,. f
•ходной сигнал Л • •-. 1 - J
.Обратная связь ^7; ;
'{полЬжение с выходного потенциометра)
Ж.
Обратная связь
Tipomзводная сигнала
^согласования
( I /
#Г-'1
СУММ
(незначительное усиление)
Пример 1 из трех значений усиления
RamK = 220 кОм
Пример 2 из трех значений усиления
кратная сштъ
"(8й>1ходной"пот'еици6метр)
Входной сигна'л
ТТройзводнсш сигнала i
^СУММ = 330 К°М
(наибольшее усиление, но схема все
еще стабильна, заметно лишь небольшое
перерегулирование)
Пример 3 из трех значений усиления
Рис. 10L.11. Повышение усиления только пропорциональной составляющей вызывает возрастающее перерегулирование
11N. Стабилизаторы напряжения
Содержание
11N.1. Эволюция стабилизированного источника питания 465
11N.1.1. Нестабилизированный источник питания 465
11N.1.2. Выходное напряжение задается стабилитроном 465
11N.1.3. Стабилитрон плюс повторитель на транзисторе 466
11N.1.4. Стабилитрон или опорное напряжение плюс повторитель
на операционном усилителе 466
11N.1.5. Опорное напряжение плюс повторитель на операционном усилителе
плюс регулирующий транзистор 466
11N.1.6. Стабилизированная схема 467
11N.1.7. Полная схема стабилизатора с ограничением тока 467
11N.1.8. Напряжение отключения 468
11N.2. Более простые интегральные стабилизаторы 469
11N.2.1. Микросхемы стабилизатора напряжения 78хх
с фиксированным выходным напряжением 469
11N.2.2. Интегральные стабилизаторы напряжения серии 318
с регулируемым выходным напряжением 470
11N.3. Проектирование с учетом тепловой защиты 471
11N.3.1. Общие сведения о теплопередаче 471
11N.4. Источники тока 472
11N.4.1. Микросхема для токов средней величины 472
11N.4.2. Биполярная микросхема для малых токов 473
11N.4.3. Полевой транзистор с управляющим р-я-переходом как источник тока 473
11N.5. Защита от перенапряжения посредством автоматического шунтирования
на «землю» 474
11N.6. Импульсные стабилизаторы напряжения 474
11N.6.1. О специфических свойствах катушек 475
11N.6.2. Три схемы импульсных стабилизаторов: повышающая,
понижающая и инвертирующая 476
11N.6.3. Эффективность 477
11N.6.4. Реализация обратной связи 478
11N.6.5. Импульсные стабилизаторы не всегда то, что вы хотите 479
11N.7. Материал для чтения в АоЕ 480
Цель этой главы
Какую задачу нам предстоит сегодня решить? Мы попытаемся спроектировать схему источника
питания, уровень напряжения на выходе которого остается постоянным, несмотря на колебания,
которые могут возникать как во входном напряжении, так и в выходной нагрузке.
Стабилизаторы напряжения можно было бы найти подходящее место в
главе по операционным усилителям. Но раз-
Можно довольно убедительно аргументиро- ве стабилизатор не является повторителем,
вать, что предмет данной главы не самостоя- на который подается опорное напряжение?
тельная тема, а всего лишь еще одно приме- Да, это так, хотя мы вскоре усовершенствуем
нение отрицательной обратной связи, и ему такой повторитель. Но эта функция требуется
11Ш. Эволюция стабилизированного источника питания
465
так часто, что для ее реализации постепенно
были разработаны разнообразные МИКрОСХе- Пульсации
мы, в результате чего для решения данной за- 1/5 В *
дачи операционные усилители почти никогда
не применяются. А источники питания и ста-
билизаторы применяются настолько широко
в разных областях, что в книге АоЕ им посвя-
щена отдельная глава. Мы также последуем
этому примеру и выделим на них отдельное
лабораторное занятие.
Рис. 11N.1. Стабилизатор напряжения является лишь еще
одним из многих вариантов применения обратной связи
11N.1. Эволюция
стабилизированного
источника питания
11 N.1.1. Нестабилизированный
источник питания
В начале нашего курса (по крайней мере, в главе
ЗЫи на лабораторном занятии 3L) был нестаби-
лизированный источник питания1. Посмотрите
на схему, изображенную на рис. 3N.28, входное
переменное сетевое напряжение она преобразу-
ет в выходное постоянное напряжение. Почему
эта схема недостаточно хороша? В чем состоят
ее недостатки? Перечислим их.
♦ Из рис. 11N.2 можно увидеть, что, хотя вы-
ходное напряжение постоянное, его уро-
вень не постоянный, а содержит пульса-
ции. Полностью решить эту проблему до-
бавлением конденсатора большей емкости
не удается. Хотя величина пульсаций дей-
ствительно уменьшится, за это пришлось
бы расплачиваться повышенным нагревом
трансформатора, поэтому пришлось бы ис-
пользовать трансформатор большего раз-
мера и веса.
Уровень»
«земли»
'10 1
ззд
Рис. 11N.2. Выходное напряжение нестабилизированного
источника питания содержит значительные пульсации (уси-
ление канала осциллографа — 2 В/деление)
При нагрузке выходное напряжение ишх
сколько меняется.
не-
• Выходной импеданс трансформатора не
слишком хороший. Например, на лабора-
торном занятии 3L при переходе от легкой
до полной нагрузки наших лабораторных
трансформаторов с номинальным выход-
ным напряжением 6,3 В мы наблюдали па-
дение напряжения величиной 20%.
• Даже не считая падения выходного на-
пряжения трансформатора под нагрузкой,
нагрузка уменьшает среднее выходное на-
пряжение ишх из-за повышения величи-
ны пульсаций.
Выходное напряжение 17ВЫХ может изменять-
ся в широком диапазоне вследствие большо-
го варьирования сетевого напряжения (но-
минально его величина равна 120 В, но диа-
пазон изменений достигает ±10 В, а иногда
при тяжелой нагрузке даже больше2).
11 N.1.2. Выходное напряжение
задается стабилитроном
Стабилизировать выходное напряжение мож-
но с помощью стабилитрона (диода Зенера),
как показано в схеме на рис. 11N.3. Но и этот
подход имеет свои недостатки. Можете сказать,
какие?
АоЕ § 9.5.
2 Нормативные документы штата Иллинойс (США) раз-
решают варьирование напряжения, предназначенного
для «силовых» целей, в пределах 10%, а для освещения -
в пределах 6%, т. е. в диапазоне 113-127 В, при номиналь-
ном напряжении электросети 120 В.
http://answers.google.com/answers/threadview/
id/525096.htm
466
ИЛ/. Стабилизаторы напряжения
(нестабилизированное,
содержит пульсации)
Рис. 11N.3. Стабилизация напряжения с помощью стабили-
трона
♦ Малая эффективность. Например, чтобы
обеспечить выходной ток в 100 мА при пол-
ной нагрузке, при работе в холостом режиме
через стабилитрон должен протекать ток ве-
личиной 110 мА. Значение 110 мА объясняет-
ся тем, что мы хотим, чтобы даже при полной
нагрузке через стабилитрон протекал ток не
меньше 10 мА.
♦ Колебание уровня выходного напряже-
ния. Выходное напряжение стабилитрона
несколько изменяется при варьировании
тока, причем последнее обязательно проис-
ходит при изменении нагрузки.
♦ Большие погрешности. Даже для номи-
нального напряжения стабилитрона разброс
достаточно велик.
11 N.1.3. Стабилитрон плюс
повторитель на транзисторе
Подача выходного напряжения стабилитрона
на эмиттерный повторитель (рис. 11N.4) улуч-
шает параметры стабилизатора: теперь при
большом токе нагрузки 1Н и его больших коле-
баниях нет необходимости пропускать значи-
тельный ток через стабилитрон3. Это уже луч-
ше, но все равно недостаточно хорошо.
Рис. 11N.4. Стабилитрон плюс повторитель на транзисторе.
Это уже стабилизатор?
Напряжение [7БЭ несколько варьируется, что
вызывает изменение выходного напряжения
[7ВЫХ даже при постоянном напряжении
3 АоЕ § 2.2.3.
11 N.1 А Стабилитрон или опорное
напряжение плюс повторитель
на операционном усилителе
Операционный усилитель может компенсиро-
вать падение напряжения на переходе «база-
эмиттер» Ugg и его нестабильность, а также
может обеспечить гораздо более низкий вы-
ходной импеданс (рис. 11N.5).
LM285
(2,5 В) *
Рабочее напряжение Опорное напряжение 4~
стабилитрона равно 5 В составляет 2,5 В
Рис. 11N.5. Стабилитрон плюс повторитель на операцион-
ном усилителе. Это уже хороший стабилизатор?
Схема справа на рис. 11N.5 содержит неболь-
шое улучшение: в ней на микросхему подано
опорное напряжение (величиной 2,5 В, такое
же, как и в главе 111), которое обеспечивает
более точное начальное напряжение (с погреш-
ностью в пределах ±3% в устройствах лабора-
торного класса), а также хорошее постоянство
в широком диапазоне значений тока (от 20 мкА
до 20 мА). Но в этой схеме отсутствуют неко-
торые другие усовершенствования, которые
мы бы хотели иметь. К тому же она обладает
существенным недостатком — небольшим вы-
ходным током (25 мА), ограниченным возмож-
ностями самого операционного усилителя. Это
типичное значение для микросхемы 411; все
обычные операционные усилители имеют та-
кое ограничение выходного тока.
11 N.1.5. Опорное напряжение плюс
повторитель на операционном
усилителе плюс регулирующий
транзистор
Этот вариант почти то, что нам требуется,
поскольку он может выдать большой ток.
Выходной ток можно увеличить еще боль-
ше, используя пару Дарлингтона проходного
типа (которая имеет квадратичное усиление)
или силовой МОП-транзистор (полевой тран-
зистор, для которого требуется практически
нулевой входной ток). Операционный усили-
тель, благодаря его обратной связи, в контур
11 N.I Эволюция стабилизированного источника питания
467
LM285-2,5
(2,5 В)
Рис. 11N.6. Стабилитрон, операционный усилитель и регу-
лирующий транзистор. Это уже настоящий стабилизатор?
которой входит регулирующий транзистор,
обеспечивает очень низкий выходной импе-
данс (рис. 11N.6).
Но эта схема также имеет один недостаток, ко-
торый делает ее непредсказуемой, и, возможно,
непригодной для практического применения.
Выходное напряжение с нее подается на шину
питания, на которой много развязывающих
конденсаторов. Эти конденсаторы с большой
вероятностью будут создавать отрицательный
фазовый сдвиг, который может вызвать пере-
ход операционного усилителя в режим автоко-
лебаний, как мы знаем из нашего опыта, полу-
ченного на лабораторном занятии 9L4.
11 N.1.6. Стабилизированная схема
Чтобы, несмотря на емкостную нагрузку, схема
оставалась стабильной, мы используем метод,
LM285-2,5
(2,5 В)
1
Рис. 11 N.7. Стабилизированная схема
с которым познакомились на лабораторном за-
нятии 9L — разделение пути обратной связи.
Стабилизированная таким образом схема изо-
бражена на рис. 11N.7.
Эффективное сопротивление R, которое со-
вместно с емкостью обратной связи С опреде-
ляет частоту перехода fnEp9 является сопротив-
лением #ТЕВ для делителя обратной связи. Эта
схема уже работоспособная. Добавив в нее еще
одну возможность — ограничение тока — мы,
наконец, получим готовую схему.
11N.1.7. Полная схема
стабилизатора с ограничением тока
Чтобы обезопасить нашу схему «от дураков», в
ней нужно предусмотреть защиту от неправиль-
ного включения, например от закорачивания
выхода на «землю»5. Все более-менее солидные
<?РЕг %) «Регулирующий» транзистор
л
= 0,6В//?о
I то С?0ГР начинает отбирать ток базы у (?РЕГ
} (<?огр «пересиливает» маломощный
I операционный усилитель)
Корректирующий
конденсатор
■A 4r\^_^ Предотвращает переходные процессы
Рис. 11N.8. Полноценный стабилизатор напряжения с защитой по току
4 Вы можете подумать, что такая емкостная нагрузка опре-
деленно будет вызывать автоколебания. Но в действитель-
ности чрезмерная емкостная нагрузка может даже остано-
вить автоколебания. Поэтому правильнее будет сказать,
что эта схема уязвима к паразитным автоколебаниям и ее
необходимо стабилизировать.
источники питания содержат такую защиту, ко-
торая реализуется путем добавления в схему
еще одного транзистора. Видоизмененная та-
ким образом схема изображена на рис. 11N.8.
Дураками, конечно же, являемся все мы — пользователи.
468
//Л/. Стабилизаторы напряжения
Схема ограничения тока
Если выходной ток становится слишком боль-
шим, транзистор Qqpp начинает забирать ток от
регулирующего транзистора6. Обратите вни-
мание на то, что эта схема работоспособна, по-
скольку выходной ток операционного усилителя
ограничен. Если этого ограничения не было, то
ограничивающий транзистор на самом деле уве-
личивал бы выходной ток, усугубляя ситуацию.
Все операционные усилители
используют одинаковую схему
ограничения тока
В выходных каскадах всех операционных уси-
лителей реализован одинаковый принцип
ограничения тока. Например, каскад ограни-
чения тока можно распознать на схеме опера-
ционного усилителя LF411, изображенной на
рис. 11N.97.
Выходные каскады
микросхемы LF 411
Практически
идентична схеме
J стабилизатора
Похожая схема,
но механизм
ограничения вступает
в действие,
когда транзистор Q10
начинает открываться
Рис. 11 N.9. Схемы ограничения тока в операционных усили-
телях (в данном случае это усилитель 411) и в стабилизаторе
напряжения схожи
11 N.1.8. Напряжение отключения
Для любого стабилизатора этого типа (линей-
ного, а не импульсного, с которым мы позна-
комимся в разделе UN.6) требуется некоторая
6 АоЕ, рис. 9.2.
7 Полная принципиальная схема операционного усилите-
ля 411 приведена в разделе 9S.4.
минимальная разница между входным и вы-
ходным напряжениями. Эта разница называет-
ся напряжением отключения, поскольку стаби-
лизация выходного напряжения прекращается,
если это условие нарушено.
Для большинства стабилизаторов напряже-
ние отключения составляет 2-3 В. Такое ми-
нимальное напряжение обусловлено падением
напряжения [7БЭ в эмиттерном повторителе,
разницей в один вольт между напряжением вы-
ходного сигнала и положительным напряже-
нием питания для большинства операционных
усилителей, а также схемотехникой каскада
ограничения тока.
Специализированные стабилизаторы с низким
напряжением отключения могут работать с
разницей между выходным и входным напря-
жениями величиной всего лишь в несколько
десятых вольта. Эта характеристика важна в
устройствах с питанием от батарей, в которых
питающее напряжение постепенно снижается.
В таких схемах стабилизатор с низким напряже-
нием отключения будет продолжать функцио-
нировать даже тогда, когда обычный линей-
ный стабилизатор уже давно бы отключился.
Но обратите внимание на то, что для устройств
с питанием от батарей может быть предпочти-
тельней использовать импульсные стабилиза-
торы. Более подробную информацию по этому
вопросу см. в разделе 11N.6 далее в этой книге.
Стабилизатор с малым напряжением
отключения
Стратегия, используемая для уменьшения на-
пряжения отключения, состоит в изменении
схемы включения регулирующего транзистора8.
В обычном стабилизаторе, наподобие показан-
ного на рис. 11N.8, в котором регулирующий
транзистор включен как повторитель, величи-
на падения напряжения 17БЭ лежит в пределах
между входным и выходным напряжением.
Кроме того, в самом операционном усилителе
должно теряться некоторое напряжение между
положительным напряжением питания и на-
пряжением выходного сигнала.
В стабилизаторах с малым напряжением от-
ключения регулирующий транзистор вклю-
чен не как повторитель, а как инвертирующий
8 АоЕ § 9.3.7.
11N.2. Более простые интегральные стабилизаторы
469
Малое напряжение отключения ~~L -J=-
Рис. 11 N.10. Стабилизатор с малым напряжением отключе-
ния с регулирующим транзистором, включенным как инвер-
тор. Обратите внимание на необычную обратную связь!
усилитель. Соответствующая схема изображе-
на на рис. 11N.10.
Эту схему мы уже упоминали в главе 9N как
редкий случай инверсии внутри цепи обратной
связи. Конденсатор здесь требуется для раз-
деления пути обратной связи. Резистор между
опорным напряжением и инвертирующим вхо-
дом позволяет подавать сигнал обратной связи
на этот вход, несмотря на наличие источника
опорного напряжения.
Конденсатор большой емкости на выходе так-
же способствует большей стабильности схемы9.
Если малое напряжение отключения не требу-
ется, то лучше предпочесть обычную схему, ко-
торая более стабильна.
111NL2. Более простые
интегральные стабилизаторы
Теперь, когда мы отдали должное теории, «изо-
бретя» заново стабилизатор напряжения, мож-
но познакомиться с некоторыми готовыми ре-
шениями, которые гораздо практичнее.
11 N.2.1. Микросхемы
стабилизатора напряжения 78хх
с фиксированным выходным
напряжением
Интегральные стабилизаторы напряжения, схе-
ма которых (см. рис. 11N.8) содержит источник
9 Сравните с разделом 9.3.2 книги АоЕ, в котором обра-
щается внимание на роль конденсатора большой емкости
в обеспечении стабильной работы стабилизатора отрица-
тельного напряжения LM7905, с подобным включением
регулирующего транзистора.
опорного напряжения, операционный усили-
тель, регулирующий транзистор и еще некото-
рые дополнительные элементы, выпускаются
в виде разных микросхем10. Самый простой из
них — стабилизатор с фиксированным выход-
ным напряжением на трехвыводной микросхе-
ме 78L05, схема включения которой показана
на рис. 11N.11.
Защищает
от паразитных
автоколебаний
+5 В
ОД мкФ
=j= керамический
Обеспечивает кратковременное сглаживание
выходного напряжения (быстрее, чем обратная связь
может реагировать на резкое изменение нагрузки).
Рис. 11 N.11. Схема включения трехвыводной микросхемы
стабилизатора с фиксированным выходным напряжением
Глядя на рис. 11N.12 вы обнаружите, что раз-
работчики микросхем стабилизатора 78хх как
будто бы подсматривали через плечо на нашу
работу по совершенствованию линейного ста-
билизатора.
3,9 В
Общий
Рис. 11N.12. Упрощенная схема классического стабилизато-
ра напряжения на микросхеме LM7805 выглядит очень похо-
жей на недавно разработанную нами схему стабилизатора
За исключением регулирующего транзистора в
виде пары Дарлингтона и необычного повыше-
ния напряжения базы транзистора схемы огра-
ничения тока, эта схема совершенно такая же,
как и разработанная нами. Здесь также не пока-
заны необходимые элементы для стабилизации
работы схемы.
10 АоЕ § 9.3.2.
470
ИЛ/. Стабилизаторы напряжения
Это устройство, подобно другим интегральным
стабилизаторам напряжения, ограничивает не
только выходной ток, но также и рабочую тем-
пературу. Такая тепловая защита предохраняет
стабилизатор в случаях, когда чрезмерным яв-
ляется не только ток, но мощность.
Замечание
Вы сами продемонстрируете действие этой защиты
на лабораторном занятии, создавая большое паде-
ние напряжения на стабилизаторе: 1/вх» 1/вых.
Тепловая защита также предохраняет устрой-
ство от потенциально опасных эффектов недо-
статочного теплоотвода (см. раздел 11N.3).
11 N.2.2. Интегральные
стабилизаторы напряжения
серии 318 с регулируемым
выходным напряжением
Использовать стабилизатор на микросхеме 317
так же легко, как и более простой стабилиза-
тор на микросхеме 78L05, но он более универ-
сальный, поскольку обеспечивает регулировку
величины выходного напряжения. Таким обра-
зом нет необходимости иметь в запасе стабили-
затор для каждого напряжения, которое может
вам потребоваться. Этот стабилизатор также
пригоден для сборки источника тока, превы-
шающего 5 мА.
Слева на рис. 11N.13 изображена упрощенная
схема микросхемы 31711. Справа на том же ри-
сунке показано включение стабилизатора в ка-
честве источника тока величиной 100 мА с воз-
вратом через «землю» (или отрицательную
шину питания).
Падение напряжения на микросхеме 317 состав-
ляет 1,25 В. Как можно видеть из рис. 11N.13,
в ней не используется вывод земли.
Включение стабилизатора 317 в конфигурации
источника тока показано не потому, что это рас-
пространенное использование данной микро-
схемы. Это не так. Настоящая причина в дру-
гом — это самый простой способ понять процесс
стабилизации, выполняемый микросхемой 317.
Фиксированный ток здесь поступает через ре-
зистор на землю. Напряжение на выходе ADJ
определяется этим сопротивлением, умножен-
ным на фиксированный ток. Тогда !УВЫХ = U?ET +
+ 1,25. Таким образом, схема на рис. 11N.14
позволяет регулировать выходное напряже-
ние иъых в диапазоне напряжений от 5 до 10 В.
Объяснение, что устройство обеспечивает ток
постоянной величины через резистор Rv яв-
ляется только одним из способов понять его
работу. С другой стороны, справедлива следую-
щая формула:
где Rx — резистор установки величины тока, а
R2 — резистор, подключенный к земле. Но изящ-
ные формулы всегда опасны тем, что они могут
скрыть процесс функционирования схемы.
Пример схемы с регулируемым
выходным напряжением
На рис. 11N.14 изображена более конкретная
схема. Падение напряжения на двух последова-
тельно соединенных резисторах (ниже вывода
ADJ микросхемы) при токе величиной 10 мА
составляет от 3,75 до 8,75 В. Тем самым обес-
печивается заявленный диапазон выходных
напряжений.
Входное
напряженив|
Регулировка
Минимум
на 3,5В > ии
Выходное
напряжение
LM317
25 В
Рис. 11 N.13. Микросхема LM317 регулируемого стабилизатора напряжения. Слева: упрощенная схема, справа: включение
в конфигурации источника тока
11 Более подробная схема с каскадом ограничения тока
и регулирующей парой Дарлингтона приведена на рис. 9.9
в книге АоЕ.
11 N3. Проектирование с учетом тепловой защиты
471
LM317
Вход Выход
Регулировка
Г "0,124 k
= 10мА
500
374
от 0,375 кОм
до
0,875 кОм
„25 В
от 3,75 кОм
до
8,75 кОм
Рис. 11 N.14. Пример стабилизатора на микросхеме 317
с выходным напряжением, регулируемым в диапазоне от 5 В
до 10 В
Не слишком увлекайтесь регулировкой
Ц*ых' поскольку она имеет ограниченный
диапазон
Познакомившись с возможностью регулиров-
ки выходного напряжения стабилизатора на
микросхеме 317, вы можете подумать, что с по-
мощью резистора номиналом 100 кОм можно
получить выходное напряжение величиной
1000 В. Ничего такого не получится. Выходное
напряжение ограничено пределом в 37 В по
причине 40-вольтового ограничения на разни-
цу между входным и выходным напряжениями.
Если при очень большом выходном напряже-
нии (значительно большем, чем 40 В) закоро-
тить выход на «землю», устройство будет без-
возвратно повреждено.
Особенность микросхемы 317:
необходимость поддержания
минимального выходного тока
Как уже упоминалось ранее, у микросхемы 317
отсутствует вывод «земли»12. Но побочным
эффектом этого является тот факт, что дан-
ная микросхема питается током, проходящим
через нее, — от вывода IN (вход) до вывода
OUT (выход). Если задать слишком малую ве-
личину тока, то стабилизатор не будет рабо-
тать. Минимальная величина выходного тока
для микросхемы иногда указывается как 5 мА,
а иногда как 10 мА13. На всякий случай следует
12 - Что в этом особенного? - можете спросить вы. Ну,
это позволяет микросхеме функционировать в качестве
«плавающего» источника тока, что дает возможность ре-
гулировать выходное напряжение просто изменением зна-
чения одного резистора.
13 В справочном листке изделия компании National Semi-
conductor (в настоящее время является частью компании
задавать выходной ток величиной 10 мА. Для
этого номинал резистора R2 должен быть около
120 Ом (124 Ом, если резистор с допуском 1%).
11 N3. Проектирование
с учетом тепловой защиты
До сих пор мы еще не рассматривали проблему
перегрева (за исключением мощных транзисто-
ров для двухтактных драйверов на нескольких
лабораторных занятиях по операционным уси-
лителям). Но при проектировании источников
питания этот вопрос необходимо рассмотреть
подробно, поскольку токи здесь намного боль-
ше, чем те, с которыми мы работали до сих пор.
Чтобы не допустить перегрева элемента, необ-
ходимо отводить от него тепло с такой же ско-
ростью, с какой оно создается протекающим по
нему током.
Пока что все это очевидно. Но скорость отвода
тепла невозможно вычислить с помощью ме-
тодов, которые полностью аналогичны закону
Ома. Здесь нам нужно привыкнуть к другим
единицам измерения.
11 N3.1. Общие сведения
о теплопередаче
Взглянув на единицы измерения, мы обнару-
жим некоторую аналогию между протеканием
тепла и тока и сопротивлениями14. Вместо на-
пряжения (которое всегда обозначает разность
потенциалов) здесь присутствует разность тем-
ператур. Разность температур приводит к пере-
носу тепла, точно так же, как и разность потен-
циалов приводит к протеканию тока. Скорость
теплового потока, т. е. скорость передачи энер-
гии или тепла, измеряется в виде мощности:
в ваттах (сокращенно — Вт).
Сопротивление теплопередаче аналогично эле-
ктрическому сопротивлению, и измеряется
в единицах °С/Вт: разность температур на ско-
рость теплопередачи15. В более знакомой нам
Texas Instruments) этот аспект освещается неоднозначно.
В таблице Electrical Characteristics, в которой приводят-
ся свойства устройства, выходной ток указывается как
1оит > 10 тА. Но в примерах схем далее в том же справоч-
ном листке указывается вдвое меньшее значение.
14 АоЕ § 9.4.
15 АоЕ § 9.4.1А.
472
11N. Стабилизаторы напряжения
электротехнике эквивалентом будет сопротив-
ление в омах: разность потенциалов, деленная
на величину тока (которая является скоростью
передачи заряда).
Электротехника:
I=U/R.
Теплопередача:
Скорость теплопередачи =
= (Разность температур/Тепловое сопротивление.
Вт = (Разность температур/О^д)
На рис. 11N.15 эта аналогия изображена графи-
чески, а для большей наглядности на рис. 11N.16
показаны микросхема и ее теплоотвод с указа-
нием точек возникновения тепловых сопротив-
лений. Обозначения на этих рисунках требуют
объяснения. Например, 2?епк обозначает тепло-
вое сопротивление между переходом (сердцем
микросхемы) и корпусом.
Скорость переноса заряда
Разность потенциалов UPA
^РАЗИ
Разность температур ТРАЗИ
тг-
I ^ТЕТТЛ
Скорость переноса тепла
Рис. 11 N.15. Расчеты теплового сопротивления во многом
похожи на расчеты с использованием закона Ома
(уОкружающий воздух)
Корпус типа Т0220
ь микросхемы)
Единицы
°С/Вт
Рис. 11 N.I б. Тепловые сопротивления в различных точках
Если известно, какую мощность должна рас-
сеивать ваша деталь, то определить общее тепло-
вое сопротивление, которое сможет выдержать
ваша схема, можно по следующей формуле:
Г - Г
D _ Перехода Воздуха
ТЕПЛ Мощность
Некоторые тепловые сопротивления не зави-
сят от разработчика, например, сопротивление
«переход-корпус», значение которого опреде-
ляется конструкцией микросхемы. Но, будучи
свободными в выборе теплоотвода (который
также называется радиатором), вы можете
подобрать достаточно эффективный, чтобы
общее тепловое сопротивление #ТЕПЛ было при-
емлемым. Упражнение по выбору теплоотвода
приводится в главе 11W.
11 N.4. Источники тока
Как уже упоминалось ранее, микросхема 317
может работать в качестве источника тока, но
только при токах величиной 5 мА и больше16.
Давайте рассмотрим несколько более универ-
сальных микросхем источников тока.
11N.4.1. Микросхема для токов
средней величины
Изображенная на рис. 11N.17 микросхема
LT3092 может выдавать или потреблять ток
в диапазоне 0,5-200 мА17. Способность ТЕПЛ
как поставлять, так и поглощать ток обеспечи-
вается благодаря тому, что это двухвыводное
устройство. Тип источника тока определяет-
ся подключением нагрузки. Подобная уни-
версальность отличает схему от источников
тока на биполярных транзисторах, с которы-
ми мы имели дело ранее, где схемы на п-р-п-
транзисторах могут только потреблять ток, а на
р-я-р-транзисторах — только поставлять.
Примечание
С другой стороны, ранее мы уже познакомились
с двухвыводным устройством ограничения тока,
а именно с полевым транзистором с управляющим
р-л-переходом. Этот элемент описывается в раз-
деле 11N.4.3, а на лабораторном занятии 5L мы ис-
пользовали его для установки тока «хвоста» диф-
ференциального усилителя.
16 АоЕ § 9.3.14А.
17 АоЕ § 9.3.14В.
UNA. Источники тока
473
1,3 В до 40 В
(но минимальное отношение /^ст'^вых Равно 50:1)
Рис. 11 N.17. Двухвыводная микросхема ограничителя тока
LT3092
Микросхема LT3092 имеет огромный динами-
ческий импеданс (#вых) по постоянному току
(100 МОм) и достаточно большой на низких
частотах — около 3 МОм на частоте 1 кГц.
11N A3. Полевой транзистор
с управляющим р-л-переходом
как источник тока
Мы познакомились с этим двухвыводным
электронным компонентом, изображенным
на рис. 11N.19, на лабораторном занятии 5L.
Такой полевой транзистор с управляющим р-л-
переходом часто изготавливают в стеклянном
корпусе наподобие диода, и работать с ним не-
сложно. С транзисторами данного типа в на-
шем курсе мы будем встречаться не так часто
(вспомните мимолетное упоминание, что опе-
рационный усилитель 411 обязан своим высо-
ким входным импедансом транзисторам этого
типа). Управляющие выводы транзистора за-
корочены внутри корпуса, в результате чего он
работает в режиме фиксированного тока.
1 мА (от 1 В до 50 В)
11NА2. Биполярная микросхема
для малых токов
Для меньших токов (50-400 мА) хорошо под-
ходит микросхема REF200 (рис. 11N.18), кото-
рая, подобно микросхеме LT3092, имеет очень
большой выходной импеданс по постоянному
току.
Токовое зеркало обеспечивает
равенство токов правого и левого плеча
100 мкА каждый
(от 2,5 В до 40 В) 1:1
REF200
Токовое зеркало
Рис. 11N.18. Микросхема источника тока REF200
В разделе 11W.2 приведено несколько задач,
требующих решить, как применять три эле-
мента этого устройства для выдачи или потреб-
ления токов разных величин: 50,100, 200, 300
и 400 мкА. Как показано на рисунке, токовое
зеркало обеспечивает равенство токов правого
и левого плеча18.
I SST505
Jl или
Г*4"! 1N5297
Рис. 11 N.19. Источник тока в виде полевого транзистора
с управляющим р-п-переходом
Как уже упоминалось, простота в использова-
нии является сильной стороной этого компо-
нента. Но он имеет и свои слабости. В частно-
сти, хотя он имеет хороший динамический им-
педанс (#вых) величиной около 1 МОм при токе
1 мА, по сравнению с микросхемами LT3092
и REF200 это не особенно впечатляет. Но глав-
ные его недостатки — сравнительно высокая
цена (несколько долларов, в зависимости от
величины тока19) и большая погрешность (око-
ло ±20% для транзистора SST-505, а также для
компонентов марки 1N5294 производства ком-
пании Central Semiconductor).
18 На рисунке токовое зеркало выглядит как обычно, хотя
в действительности это зеркало Вильсона или каскодное
зеркало, как отмечается в главе 5S.
19 Мы были беспредельно рады обнаружить в странной
ценовой структуре этих устройств первое, когда-либо
приведенное объективное доказательство утверждения,
что большинство практикующих инженеров такие же ле-
нивые, как и мы. Когда на рынке впервые появился такой
компонент с рабочим током в 1 мА, его стоимость оказа-
лась значительно выше, чем устройств с рабочим током
в 0,75 мА, которые мы используем. Почему так? Потому
что все предпочитают выполнять расчеты по закону Ома,
подставляя значение равное единице, и своим спросом на
это устройство мы, ленивые люди, значительно подняли
цену на него.
474
UN. Стабилизаторы напряжения
11 N.5. Защита
от перенапряжения
посредством
автоматического
шунтирования на «землю»
В случае выхода из строя стабилизатора напря-
жения на его выходе может оказаться слиш-
ком высокое напряжение и это повредит боль-
шое количество дорогостоящих электронных
устройств. Наиболее серьезная опасность —
возможность подачи чрезмерного напряжения
(или всплеска) на компьютер20. На рис. 11N.20
изображена схема, которая шунтирует шину
положительного питания на «землю» (огра-
ничивает напряжение на ней приблизительно
до 1 В), когда выходное напряжение оказыва-
ется слишком высоким.
Замечание
На рынке также доступны микросхемы, которые
могут определять величину напряжения21.
Регулируемый
источник питания
Управляющий
электрод
Рис. 11 N.20. Защита от перенапряжения посредством авто-
матического шунтирования на «землю» (см. также схему на
рис.1И.8)
20 На лабораторных занятиях в завершающей части это-
го курса два студента собрали компьютер на дискретных
микросхемах и случайно продемонстрировали эту уязви-
мость жутким способом. Свой самодельный компьютер
они подключили к регулируемому источнику питания,
выставив выходное напряжение равным 5 В. В один пре-
красный день, когда они забыли проверить величину вы-
ходного напряжения источника питания, они пережгли
много микросхем в своем компьютере. Обнаружение и за-
мена выведенных из строя деталей стали для них горьким
опытом на тему опасности перенапряжения. Предлагаемая
на том лабораторном занятии схема микрокомпьютера со-
держит средство автоматического шунтирования на «зем-
лю», подобное описанному в данном разделе. Таким обра-
зом, теперь шансы подобных катастроф намного меньше.
21 АоЕ § 9.1.1С.
Поскольку тиристор (похожий на диод эле-
мент справа на схеме на рис. 11N.20) включа-
ется, когда напряжение на его управляющем
электроде достигает значения около 0,6 В, во
многом подобно тому, как это делает тран-
зистор, схема срабатывает и автоматически
шунтирует выход на «землю», когда напряже-
ние достигает значения около 6,2 В. Но чтобы
эта схема могла успешно защитить питаемые
устройства, шунтирующий элемент должен
быть мощнее, чем предшествующие ему эле-
менты. Для этого перед регулятором устанав-
ливается плавкий предохранитель, который
сгорает при срабатывании шунта.
Особой чертой тиристора, в отличие от силовых
транзисторов, которые в некоторой степени по-
хожи на него, является то, что, включившись,
он остается включенным даже после снятия
сигнала с управляющего электрода. Таким об-
разом, схема автоматического шунтирования
на «землю» работает подобно размыкателю,
блокируя источник питания в выключенном
состоянии. Выключить тиристор можно, толь-
ко уменьшив протекающий через него ток, вы-
ключив неисправный источник питания или
вручную или вследствие перегорания плавкого
предохранителя.
11 N.6. Импульсные
стабилизаторы напряжения
Линейный стабилизатор имеет малый КПД,
поскольку его метод поддержания выходно-
го напряжения на постоянном уровне при ва-
рьирующемся входном напряжении состоит
в простом поглощении разности напряжений22.
Линейный стабилизатор, на который подается
пульсирующее входное напряжение величи-
ной 10 В, может выдавать напряжение, фикси-
рованное на уровне 5 В. Но в этом случае те-
ряемая в стабилизаторе мощность будет равна
мощности, выдаваемой в нагрузку. Таким обра-
зом, его КПД будет 50%. Эту величину нельзя
значительно повысить из-за нестабильности
сетевого напряжения. Поскольку нельзя до-
пускать снижения уровня пульсаций меньше
напряжения отключения стабилизатора, вход-
ное напряжение всегда должно быть на 4-4,5 В
выше выходного. Как же можно решить эту
проблему?
22 АоЕ § 9.6.1.
11N.6. Импульсные стабилизаторы напряжения
475
Решение состоит в использовании совершенно
другого метода. Его суть заключается в том, что
при поддержании выходного напряжения на
заданном уровне разница между этим напряже-
нием и входным напряжением не поглощается
стабилизатором. Вместо этого переключатель
по мере необходимости подает импульсы тока
в накопительный элемент. Когда ток не требу-
ется, переключатель остается в выключенном
положении.
11 N,6.1.0 специфических свойствах
катушек
Поскольку в этом курсе мы не уделяли осо-
бо много внимания катушкам индуктивности,
стоит напомнить о такой особенности этих
устройств, как свойство сопротивляться пре-
кращению протекания тока в них. Импульсные
источники питания всех конфигураций (кото-
рые рассматриваются далее в разделе 11N.6.2)
используют эту особенность.
Мы надеемся, что вы сами убедились в таком
поведении катушки, проделав эксперимент с
транзисторным переключателем на лабора-
торном занятии 4L.5.2. На наших занятиях мы
повторяем это упражнение для демонстрации,
провоцируя катушку на проявление своего по-
добного маховику поведения. Используемая
нами схема содержит просто ключ, замы-
кающий шину положительного питания на
«землю» (роль которого выполняет МОП-
транзистор, с которым мы познакомимся чуть
далее), при этом напряжение подается на ключ
через катушку индуктивности. Источником пи-
тания служит батарейка АА напряжением око-
ло 1,6 В. Соответствующая схема приведена на
рис. 11N.21.
На первом этапе соберем основную демон-
страционную схему. Когда управляющий пря-
моугольный сигнал замыкает ключ на полевом
транзисторе, в катушке начинает протекать на-
растающий ток. А когда ключ размыкается, ка-
тушка препятствует уменьшению тока. Реакция
катушки на включение и выключение транзи-
сторного ключа показана на рис. 11N.22.
При размыкании ключа «возмущенная» катуш-
ка «настаивает» на дальнейшем протекании
тока, повышая напряжение на переключателе
(в точке X на рис. 11N.21) все больше и больше
до тех пор, пока, приблизительно при напря-
жении 76 В, в транзисторном ключе не проис-
ходит пробой и он снова замыкается.
Пробой вреден для транзисторного ключа.
Большая индуктивность может вывести тран-
зистор из строя за один период, хотя силовые
МОП-транзисторы (но не биполярные транзи-
сторы) содержат встроенный диод, допустимое
значение обратного тока для которого указано
в справочном листке на компонент. Обычно
для защиты ключа параллельно катушке
Ограничительный диод
Демонстрационная схема (первый этап) Накопительная схема (второй этап) Схема защиты
Рис. 11 N.21. Демонстрация переключателя с катушкой в цепи: всплески напряжения можно накапливать для генерирования
большого выходного напряжения
Входной прямоугольный сигнал
(управляет МОП-ключом)
Напряжение на верхнем выводе ключа
(сток полевого АЛОТТ-транзистора)
Примечание: 20 В/деление
Катушка поднимает напряжение
транзисторного ключа приблизительно
до 80 В, при котором происходит
пробой транзистора
Рис. 11 N.22. При размыкании ключа катушка создает всплеск напряжения (усиление каналов осциллографа: прямоугольный
сигнал — 5 В/деление; всплеск — 20 В/деление)
476
7 IN. Стабилизаторы напряжения
подключается ограничивающий диод, как по-
казано справа на рис. 11N.21. Но цель данной
демонстрационной схемы — показать вам боль-
шие всплески напряжения, которые мы вскоре
начнем использовать. Обратите внимание на
скромную величину напряжения источника пи-
тания — всего лишь 1,6 В.
«Упрямство» катушки можно применить в по-
лезных целях, а именно всплески напряжения
можно использовать для заряда конденсатора.
Таким образом, конденсатор можно зарядить
до напряжения намного большего уровня, чем
исходное напряжение питания
23
На рис. 11N.23 показано полезное применение
вредных всплесков напряжения. Напряжение
конденсатора оказывается очень близким к
амплитуде повторяющихся всплесков напря-
жения, которые на рисунке показаны для трех
входных импульсов различной длительности.
Как видно из рис. 11N.23, варьирование дли-
тельности входного импульса меняет вели-
чину выходного напряжения от 5 до 25 В.
Длительность замкнутого состояния ключа,
которое задается продолжительностью вход-
ного импульса, определяет, насколько ток ка-
тушки приближается к своему максимальному
значению. При данной частоте повторения им-
пульсов мы обнаружили, что дальнейшее уве-
личение длительности входного импульса не
повышало выходное напряжение ишх.
11 N.6.2. Три схемы импульсных
стабилизаторов: повышающая,
понижающая и инвертирующая
На рис. 11N.24 изображены три основные схе-
мы импульсных стабилизаторов напряжения24.
В эксперименте по демонстрации полезного
использования всплесков напряжения, в кото-
ром напряжение на конденсаторе было подня-
то с 1,6 В до 20 В или около того, применялась
одна из трех основных разновидностей им-
пульсных стабилизаторов, а именно повышаю-
щая конфигурация (рис. 11N.24, б).
Входной* сигнал на*клк?чр ~
(варьируемой длительности)
СК0Нд,после диода схемь| накопления
Всплеск на стоке транзисторного ключа
ВШ,,§£о„ вшшюуении_ _ j
Продолжительный
входной импульс: UBbLX = 25 В
Входной импульс средней
длительности: UBbDC = 10 В
Входной импульс малой
длительности: LL.X = 5 В
Рис. 11 N.23. Диод и конденсатор можно использовать для накопления всплесков напряжения на катушке (показаны всплески
для входных импульсов трех разных длительностей) (усиление осциллографа — 5 В/деление)
^
♦t*r/
-Й-
—о
-г -Ч
Понижающая Повышающая Инвертирующая
а б в
Рис. 11 N.24. Три схемы импульсных стабилизаторов напряжения
23 Скорее всего этот метод используется для зарядки
вспышки вашего фотоаппарата: ее начальное напряжение
равно напряжению батареи фотоаппарата, а при вклю-
чении вспышки может слышаться звук, похожий на писк
комаров, издаваемый схемой управления вспышки. Это
переключается катушка, которая заряжает накопительный
конденсатор до напряжения величиной 300-400 В, необ-
ходимого для срабатывания вспышки.
Примечание
Все три схемы содержат диоды Шоттки из-за их низ-
кого падения напряжения при прямом включении,
чтобы обеспечить еще большую эффективность.
Но этот диод можно заменить МОП-ключом.
24 АоЕ § 9.6.4.
11N.6. Импульсные стабилизаторы напряжения
477
Напряжение на управляющем электроде 0—у—|П"П [—
ON ON ON
Диод открыт, когда ключ разомкнут Входной ток 0—^—-Л А
тгтг
1
ТочкаХ О*
Выходное напряжение О
Холостой ход
I «г
J
Заряд
М
hi
Рис. 11 N.25. Форма сигналов тока и напряжения в стабилизаторе напряжения понижающей конфигурации
Первая конфигурация — понижающая. Для
того чтобы лучше понять поведение катушки,
на рис. 11N.25 приводится набросок сигналов
напряжения и тока для этой конфигурации.
Обратите внимание на то, что транзисторный
ключ включается при замыкании управляю-
щего электрода на «землю» (это р-канальный
МОП-транзистор аналогичный биполярному
р-л-р-транзистору).
Пульсации в выходном напряжении на
рис. 11N.25 выглядят похожими на пульсации
с частотой 120 Гц в выходном напряжении не-
стабилизированного источника питания. И да,
и нет. Обратите внимание на другую частоту
пульсаций в данном случае: частота переключе-
ний обычно находится в диапазоне от 100 кГц
до 1 МГц, чтобы уменьшить индуктивность ка-
тушки и емкость конденсатора. В данном слу-
чае длительность спада пульсации составляет
около микросекунды, а не 8 мс, как в двухполу-
периодном выпрямителе сетевого напряжения.
11 N,6.3. Эффективность
Подумав несколько секунд, вы можете доказать
себе, что полностью включенный или полно-
стью выключенный ключ в идеале не рассеи-
вает никакой мощности25. Рассмотрим эти два
случая, показанные на рис. 11N.26.
В реальной жизни, конечно же, не все так хо-
рошо. В действительности в импульсном ста-
билизаторе рассеивается некоторая мощность:
в катушке; в ключе, сопротивление и емкость
которого во включенном состоянии не равны
нулю; в диоде, который проводит ток, когда
ключ разомкнут (отбирая его из шины «зем-
ли», что выглядит дико для тех, кто незнаком
со странными свойствами катушки). Тем не
менее эффективность может приближаться
к идеальной; в любом случае, намного ближе,
чем это может обеспечить линейный стабили-
затор. Вполне возможно достичь КПД от 80 до
95%. На рис. 11N.27 показана часть таблицы с
параметрами повышающих стабилизаторов (у
которых UBWi > UBX) производства компании
National Semiconductors26. Обратите внимание
на впечатляющие значения КПД. Их скорее
всего трудно прочитать на этом рисунке, но все
они 85% или больше.
Высокий КПД является только одним большим
достоинством импульсных стабилизаторов.
Кроме того, они имеют и другие преимущества:
они могут создавать выходное напряжение, ко-
торое больше входного. Они также могут изме-
нять полярность входного напряжения или же
выполнять оба преобразования одновременно.
Все это позволяет выдавать напряжения раз-
ной величины (например, 3,3 В, 2,5 В и 1,8 В)
от одного источника.
'W—t
! Г
I
Ключ разомкнут
U на переключателе: большое4)
I : нулевой J'
Ключ замкнут
(Уна переключателе: нулевое ")
I : большой]
Рис. 11 N.26. Идеальный импульсный стабилизатор рассеивает нулевую мощность
25 АоЕ § 9.6.1А.
26 Компания National Semiconductors была поглощена ком-
панией Texas Instruments.
478
11N. Стабилизаторы напряжения
к :#;я Шй&т С 0ftv*rters {11 / 38)
Рис. 11N.27. Часть таблицы параметров импульсных стабилизаторов производства компании National Semiconductor
Для устройств, питаемых от батарей, напо-
добие мобильных телефонов, важность КПД
очевидна: обеспечивается длительное время
работы от батареи. Для устройств, питаемых от
сети, важность КПД менее очевидна. В данном
случае можно уменьшить габариты и вес ис-
точника питания по сравнению с линейными
источниками, которые к тому же и греются на-
много больше.
11 N.6.4. Реализация обратной связи
До сих пор мы не упоминали, как осуществля-
ется управление ключом импульсного стаби-
лизатора напряжения. Отрицательная обрат-
ная связь сравнивает выходное напряжение
с опорным напряжением. В этом отношении
импульсный стабилизатор ведет себя подобно
линейному. Но цепь обратной связи не просто
поддерживает ключ в замкнутом состоянии,
когда выходное напряжение ниже опорного,
и в разомкнутом, когда оно выше. При таком
подходе выходное напряжение содержало бы
пульсации большой величины, для выравни-
вания которых потребовались бы большие ка-
тушки и конденсаторы значительной емкости.
Вместо этого переключение происходит посто-
янно, или почти постоянно, с варьирующимся
коэффициентом заполнения переключения,
т. е. временем во включенном состоянии в каж-
дом периоде.
Замечание
Аналогичный результат можно получить, варьируя
частоту, но изменение коэффициента заполнения
(скважности) является более распространенным
подходом.
В импульсном стабилизаторе напряжения,
с которым мы познакомимся на лабораторном
занятии по источникам питания, реализован
гибридный подход, когда варьируется не ко-
эффициент заполнения или частота, а дли-
тельность пачки высокочастотных импульсов
управления.
Замечание
Такой импульсный стабилизатор называется им-
пульсным стабилизатором с управляемым гене-
ратором, другие называют этот метод пакетно-
импульсной модуляцией или гистерезисным пре-
образованием.
Когда выходное напряжение понижается не-
много ниже опорного напряжения (на величи-
ну, заданную встроенной схемой гистерезиса),
стабилизатор генерирует пачку импульсов ча-
стотой 20 кГц, повышая тем самым выходное
напряжение. Когда выходное напряжение под-
нимется на достаточно высокий уровень, пере-
ключение прекращается, и энергопотребление
стабилизатора уменьшается до нуля.
В результате частота пульсаций оказывается
намного меньше, чем частота переключения
20 кГц: в случаях, показанных на рис. 11N.28,
частота составляет всего лишь 2 кГц. К сожале-
нию, эта частота находится в пределах диапазо-
на частот, воспринимаемых человеком, и звук
переключения может быть очень раздражаю-
щим27. Поэтому данный выбор разработчиков
устройства кажется очень странным.
27 — Раздражающим? — можете удивиться вы. Но кто бу-
дет слышать эту частоту переключений? Ну, в идеале ни-
кто. Мы не слышали нашу лабораторную схему. Но катуш-
ки могут пищать при подаче сигнала на этой частоте, также
могут это делать и конденсаторы, а это может вызывать
писк ЭЛТ-мониторов. Поэтому лучше, чтобы шум пере-
ключений был вне диапазона звуковых частот.
11N.6. Импульсные стабилизаторы напряжения
479
Импульсный
стабилизатор LT1073
Рис. 11 N.28. Пульсации в выходном напряжении пакетно-
импульсного стабилизатора LT1073
Причин применению этого подхода две. Одна
из них — минимизация мощности, рассеивае-
мой стабилизатором: когда переключение пре-
кращается, потребление тока падает с сотен
миллиампер до приблизительно 100 мкА, и при
очень легких нагрузках, согласно справочным
данным, схема может работать в режиме холо-
стого хода в течение нескольких секунд. Другая
причина двухпозиционного гистерезиса пет-
ли обратной связи заключается в том, что она
нечувствительна к нестабильностям, которые
могут создавать проблемы в схемах с постоян-
ной обратной связью. Как вы должны знать по
своему опыту работы с вредными автоколеба-
ниями и лабораторными занятиями по ПИД-
управлению, стабильность работы обычных
контуров обратной связи можно нарушить,
особенно емкостной нагрузкой.
11N.6.5. Импульсные
стабилизаторы не всегда то,
что вы хотите
Они создают помехи
Для цифровых устройств, которым безразлич-
ны маломощные помехи, импульсные стаби-
лизаторы будут правильным выбором. Но им-
пульсные помехи, которые всегда присутствуют
в выходном напряжении, могут исключить ис-
пользование таких стабилизаторов в чувстви-
тельных аналоговых схемах28.
С ними может быть трудно работать
Следует упомянуть еще одну причину, поче-
му многие отдают предпочтение линейным
стабилизаторам: проектирование импульсного
источника питания может оказаться трудной
задачей. В частности, могут возникать сложно-
сти со стабильностью их работы. И не только
студенты начальных курсов стараются избе-
гать применения импульсных стабилизаторов.
Производители микросхем знают, что импульс-
ные источники питания имеют репутацию, от-
пугивающую даже опытных инженеров.
Поэтому производители предлагают
помощь
Компания National Semiconductor/Texas Instru-
ments предлагает серию устройств под названи-
ем Simple Switchers (простые импульсные ста-
билизаторы). Но поскольку одного названия
может быть недостаточно, чтобы убедить сво-
их клиентов использовать эти устройства, они
также предоставляют браузерную программу
проектирования Webench Power Designer, ко-
торая склоняет пользователей к выбору пред-
лагаемых компанией микросхем29, подходящих
для целей проекта, и создает проект для вас
(во многом подобно тому, как их программа
FilterPro делает это для активных фильтров).
На рис. 11N.29 показана часть интерфейса этой
программы.
Эта программа даже создает перечень необхо-
димых деталей, как показано на рис. 11N.3030.
Работая с подобной программой, поневоле на-
чинаешь чувствовать себя несколько тупым.
Но никто не требует от вас признаваться, как
вы «разработали» свой импульсный источник
питания.
Да, импульсные устройства могут создать труд-
ности даже для опытных инженеров. Компания
Linear Technology, также чувствуя страдания
разработчиков, предлагает объемное руковод-
ство по применению авторства их покойного
кудесника, Джима Уильямса, под названием
«Switching Regulators for Poets. A Gentle Guide
for the Trepidatious» («Импульсные стабили-
заторы для поэтов. Легкое руководство для
боязливых»31). В нем Уильяме, который был
28 АоЕ § 9.5.5, особенно рис. 9.51.
29 http://www.ti.com/tools-software/design-center/we-
bench-power-designer.html. Почему-то эта программа не
знает о деталях, предлагаемых конкурентами компании.
30 АоЕ § 9.6.5.
31 Это примечание было написано свыше тридцати лет
тому назад, но с тех пор основные трудности импульс-
ных стабилизаторов не претерпели больших изменений,
480
UN. Стабилизаторы напряжения
Рис. 11 N.29. Программа Webench Designer от компании Texas instruments для проектирования импульсных источников
питания
Рис. 11 N30. Программа Webench делает задачу проектирования импульсных стабилизаторов очень легкой
далеко не новичком в электронике, пишет: «До
этой работы уровень моего энтузиазма отно-
сительно импульсных устройств находился
где-то между волнением и ужасом. Теперь эта
точка зрения изменилась на осторожный опти-
мизм».
Если Джим Уильяме мог испытывать оптимизм,
то вы сможете тоже.
за исключением появления очень удобных инструментов
наподобие программы Wenbench Designer компании Na-
tional Semiconductor. The note is AN25fa (1987). https://
www.analog.com/media/en/technical-documentation/
application-notes/an25fa.pdf
11 N.7. Материал для чтения
вАоЕ
Чтение
♦ Глава 9:
• раздел 9.5: нестабилизированный источ-
ник питания;
• раздел 9.1: эволюция линейного стабили-
затора;
• раздел 9.3: микросхемы стабилизаторов
напряжения;
• раздел 9.6.1ff: импульсные стабилизаторы
напряжения.
11L Лабораторное занятие:
стабилизаторы напряжения
Это лабораторное занятие начинается с иссле-
дования вашего самодельного стабилизатора
напряжения. Здесь для вас не должно быть ни-
чего нового. Единственное, с чем вам не прихо-
дилось иметь дело на предыдущих лаборатор-
ных занятиях:
1) источник опорного напряжения, который,
по сути, является прецизионным стабили-
троном;
2) ограничитель тока в стабилизаторе на би-
полярном транзисторе.
Альтернативная конструкция стабилизатора на
МОП-транзисторе позволит вам испытать этот
новый тип транзистора в процессе работы со
стабилизатором. Оба самодельных стабилиза-
тора имеют проблемы с обеспечением стабиль-
ности, которые вам уже знакомые по опыту ра-
боты с «вредными» генераторами колебаний на
лабораторном занятии 9L. Это упражнение чи-
сто учебное, поскольку вам вряд ли когда-либо
понадобится разрабатывать стабилизатор на
дискретных компонентах. Но мы надеемся, что
в процессе разработки такого стабилизатора вы
уясните работу линейных стабилизаторов.
Далее на лабораторном занятии мы сначала
испытаем микросхемы линейных стабилизато-
ров, а затем микросхему импульсного стабили-
затора. В последнем типе стабилизатора стаби-
лизация выходного напряжения осуществляет-
ся с помощью обратной связи, подобно тому,
как и в линейном стабилизаторе. Но применяе-
мый способ для регулирования выходного на-
пряжения еще не встречался нам в этом курсе:
за счет свойства катушки поддерживать проте-
кание тока при размыкании цепи. Результаты,
которые можно получить с помощью импульс-
ного стабилизатора, на первый взгляд могут
казаться каким-то волшебством: выходное
напряжение может быть больше входного или
выходное напряжение имеет противополож-
ную полярность по сравнению с входным. Мы
надеемся, что эта маленькая микросхема по-
разит вас своими возможностями.
11L1. Линейные
стабилизаторы напряжения
11L1.1. Источник опорного
напряжения
Стабилизатор напряжения, который вам нуж-
но будет собрать в упражнении 11L.1.2, должен
выдавать напряжение, уровень которого дол-
жен быть постоянным, несмотря на варьиро-
вание нагрузки. Это поведение знакомо нам по
опыту сборки и работы с устройствами с низ-
ким выходным импедансом RBUX, включая по-
вторители напряжения. Но перед стабилиза-
тором, собираемым вами в этом упражнении,
будет стоять задача, решение которой ранее не
требовалось: поддерживать уровень выходного
напряжения постоянным, несмотря на варьи-
рование его входного напряжения.
Как вы знаете, такое постоянство можно обес-
печить с помощью стабилитрона, что мы и сде-
лаем в упражнении 11L.1.6. Но для лучшего по-
стоянства выходного напряжения, которое мы
хотим получить от наших самодельных стаби-
лизаторов, мы возьмем микросхему опорного
источника напряжения LM385-2.5.
По своим свойствам она похожа на стабили-
трон, но только намного лучше. Она обеспечи-
вает очень хорошую устойчивость выходного
напряжения при изменении тока в весьма ши-
роком диапазоне. Этот эффект хорошо иллю-
стрирует левый график на рис. 11L.L
482
11L Лабораторное занятие: стабилизаторы напряжения
зв
iz 2B
1В
1N746
источника
опорного напряжения 2,5 В
(шкала справа)
Стабилитрон с рабочим
напряжением 3,3 В
-^ (шкала
слева)
Точка пробоя
оо /стабилитрона
-5мВ
Прямая проводимость диода
J
U
__. 10 мВ
ЮмкА 100 мкА 1мА 10 мА
ток стабилитрона (или микросхемы LM385-2.5)
Рис. 11L.1. Сравнение вольт-амперных характеристик стабилитрона и микросхемы опорного напряжения
При изучении этого графика обратите внима-
ние на разницу в почти 200 раз между шкалами
напряжения для этих двух компонентов (шкала
стабилитрона слева, а микросхемы — справа).
11L1.2. Проектируем стабилизатор
напряжения
Разработайте, а затем испытайте на практике
стабилизатор напряжения, отвечающий при-
веденным далее исходным данным. Кроме тех-
нических характеристик, каждая задача проек-
тирования содержит перечень требуемых дета-
лей. После формулировки задачи дается более
подробное объяснение, что имеется в виду под
испытанием собранной схемы.
• источник опорного напряжения: LM385-
2.5, прецизионный стабилитрон с рабочим
напряжением 2,5 В (см. рис. 11L.2);
• частотная коррекция: изначально отсут-
ствует; добавляется при обнаружении про-
блемы.
N.C
ТО-92:
Рис. 11L.2. Цоколевка микросхемы LM385 источника опор-
ного напряжения
Задание на проектирование
Вариант А: биполярный стабилизатор с вы-
ходным напряжением 5 В и ограничением
тока
♦ Выходное напряжение [/вых: 5 В (±5%).
♦ Входное напряжение 1/вх: 8-25 В.
♦ Ограничение выходного тока: приблизитель-
но 100 мА.
♦ Перечень деталей:
• операционный усилитель: 1/2 LM358
(сдвоенная микросхема операционно-
го усилителя с однополярным питанием;
см. лабораторное занятие 9L);
• регулирующий транзистор: 2N3055 (цоко-
левка: Б К Э при виде спереди);
• транзистор ограничения выходного тока:
2N3904;
Подсказки
♦ Изучите принципиальную схему микросхемы
723, которая приводится в разделе 9.2 книги
АоЕ и разделе 9.2.1 этой книги. По сути мы
собираем здесь самодельную версию этой
микросхемы.
♦ При расчете значения резистора для обес-
печения предельного значения тока 100 мА
обратите внимания на два усложняющих эту
задачу обстоятельства:
• максимальный выходной ток операцион-
ного усилителя LM358 довольно большой
(типично 40 мА). Большая часть этого тока
будет добавлена к выходному току вашей
схемы при ограничении тока1;
1 Величину тока, которую токоограничивающий тран-
зистор может добавлять к выходному току, можно огра-
ничить, подключив резистор в цепь базы регулирующего
транзистора. Например, сопротивление величиной 300 Ом
ограничит ток до 25 мА при входном напряжении 8-10 В.
1 /L /. Линейные стабилизаторы напряжения
483
• когда это происходит, ток через ограни-
чивающий транзистор станет настолько
велик, что обычное правило [7БЭ = 0,6 В
больше не будет действовать. Обратите
внимание на то, что для транзистора 3904
напряжение 1/БЭ » 0,6 при токе 1 мА. Это
напряжение возрастает приблизительно
на 60 мВ на каждую декаду тока, поэтому,
например, при токе 35 мА оно может быть
около 0,7 В, а в вашей конкретной схеме
даже целых 0,75 В.
Как вариант, спроектируйте еще одно устрой-
ство (немного более сложное в налаживании
из-за склонности к автоколебаниям).
Вариант Б: стабилизатор с малым напря-
жением отключения с выходным напряже-
нием величиной 5 В
Эта схема отличается тем, что в ней отсутству-
ет функция ограничения тока (которая обычно
очень желательна), чтобы можно было мини-
мизировать напряжение отключения — мини-
мальную разность между входным и выходным
напряжениями стабилизатора. Эта разница на-
пряжений определят минимальную мощность,
теряемую в линейном регуляторе, и, что наибо-
лее важно в питаемых от батарей устройствах,
определяет минимальное входное напряжение,
ниже которого отключается выходное напря-
жение.
♦ Выходное напряжение Е/вых: 5 В (±5%).
♦ Входное напряжение 1/вх: от 5,2 до 25 В.
♦ Перечень деталей:
• операционный усилитель: 1/2 LMC6482
(сдвоенная микросхема операционного
усилителя с однополярным питанием и RR-
размахом сигнала; цоколевка такая же, как
и у LM358, см. лабораторное занятие 7L);
• регулирующий транзистор: биполярный:
2Т3906 (такая же цоколевка, как и у тран-
зистора 2N3904: Э Б К) или МОП-тран-
зистор (Явкл = 14 Ом; цоколевка: И 3 С при
виде спереди), или VP01 (RBKJl = 8 Ом), или
IR-LIB9343PBF (Явкл = 0,12 Ом; цоколевка:
ЗСИ);
• источник опорного напряжения: LM385-
2.5, прецизионный стабилитрон с рабочим
напряжением 2,5 В;
• частотная коррекция: вначале отсутствует;
добавляется при обнаружении проблемы.
Совет
Остерегайтесь инверсии в транзисторной схеме,
которая является не повторителем, а инвертирую-
щим усилителем. Сигнал обратной связи нужно
будет снимать с вывода стока транзистора (сток
полевого транзистора равнозначен коллектору
биполярного): ток стока /с повышается при сниже-
нии напряжения на затворе. Если вы осведомлены
об этой особенности, то никаких трудностей не
возникнет, поскольку вы знаете, как обеспечить
отрицательный тип обратной связи (хотя на бумаге
обратная связь может выглядеть непривычно).
11L1.3. Тестирование собранной
схемы
Автоколебания
Скорее всего собранная вами схема будет ра-
ботать не очень хорошо, если вы следовали
инструкциям в постановке задачи. В частно-
сти, там указывалось не применять частотную
коррекцию, и поэтому очень вероятно, что на
выходе вашей схемы будут присутствовать ав-
токолебания, по крайней мере, при подключе-
нии емкостной нагрузки. Зашунтируйте выход
схемы на «землю» керамическим конденса-
тором емкостью 0,01-0,1 мкФ. Обычно такой
конденсатор стабилизирует источник пита-
ния, но биполярный стабилизатор он может
и дестабилизировать, функционируя подобно
емкостной нагрузке. Обязательно наблюдай-
те выходной сигнал на осциллографе. Если вы
совершите ошибку, полагая, что, поскольку это
схема выдает постоянное напряжение, которое
можно измерять с помощью вольтметра, уста-
новленного в режим измерения напряжения
постоянного тока, то обнаружите, что автоко-
лебания в выходном сигнале могут привести
к неверным показаниям.
Обнаружив автоколебания, попытайтесь устра-.
нить их. В обоих стабилизаторах эту проблему
можно решить с помощью конденсатора об-
ратной связи, подключенного между выходом
и инвертирующим входом2 операционного
2 Обратите внимание на то, что даже для схемы с низким
напряжением отключения (где вследствие инвертирова-
ния, вызываемого схемой на р-МОП-транзисторе, сигнал
обратной связи подается с выхода схемы на неинверти-
рующий вход) высокочастотный сигнал обратной связи
должен подаваться с конденсатора обратной связи на ин-
вертирующий вход для того, что получить требуемый тип
обратной связи.
484
/ JL Лабораторное занятие: стабилизаторы напряжения
усилителя (подавляя, таким образом, высоко-
частотное усиление3). Если вы помните, это
решение называется разделением пути обрат-
ной связи. Какой должна быть емкость этого
конденсатора? Это будет зависеть от величины
соответствующего сопротивления: сопротивле-
ния низкочастотной ветви пути обратной свя-
зи (здесь ЯТЕВ для делителя обратной связи).
Выберите такое значение RC, которое позволит
обойти проблему на частоте, намного меньшей,
чем частота наблюдаемых автоколебаний.
Кроме того, следует зашунтировать выход на
«землю» парой конденсаторов: керамическим
небольшой емкости (скажем, 0,01-0,1 мкФ, для
высоких частот) и танталовым большой емко-
сти (менее эффективен на высоких частотах,
попробуйте емкость 4,7 мкФ или больше).
Варьируйте входное напряжение 1/вх
Стабилизатор напряжения должен выдавать
постоянное выходное напряжение, невзирая на
варьирование входного, включая пульсации ча-
стотой 120 Гц в нестабилизированном входном
напряжении. Чтобы сэкономить время и не до-
бавлять пульсации во входное напряжение,
просто варьируйте его вручную (предполагая,
что используется лабораторный регулируемый
источник питания). Если ваша схема работает
должным образом, то скорее всего это не вызо-
вет никаких колебаний выходного напряжения,
пока входное напряжение не будет снижено до
такого уровня, что схема стабилизатора просто
отключится.
Измерьте напряжение отключения
Напряжение отключения стабилизатора — это
просто минимальная разница между входным
и выходным напряжениями, необходимая для
того, чтобы стабилизатор мог поддерживать
выходное напряжение на требуемом уровне.
Измерьте напряжение отключения [70ТКЛ ваше-
го самодельного стабилизатора. Какой пара-
метр и какого элемента (или элементов) вашей
схемы ограничивает эту минимальную разницу
входного напряжения4?
3 С другой стороны, можно считать, как мы это делали
на лабораторном занятии 9L, что этот конденсатор предо-
ставляет отдельный путь, обходя цепь обратной связи,
которая создает проблематичные фазовые сдвиги на вы-
соких частотах.
4 Это риторический вопрос.
Как и следует ожидать, ответы на эти вопросы
будут разными для каждого варианта схемы.
Вариант А: схема с проходным я-р-л-тран-
зистором
Напряжение отключения U0TKJl является сум-
мой следующих величин:
♦ минимальной разницы между положитель-
ным напряжением питания операционного
усилителя и напряжением его выходного
сигнала (около 1,5 В);
♦ напряжения 17Ю для регулирующего транзи-
стора («0,6 В);
♦ падения напряжения на резисторе 2?огр в схе-
ме ограничения тока (до 0,6 В).
Вариант Б: схема с низким напряжением
отключения
♦ Предполагая, что используется полевой тран-
зистор типа р-МОП5 (для которого разница
напряжений между его входом (истоком)
и управляющим электродом (затвором), на
который подается сигнал с операционно-
го усилителя, должна составлять несколько
вольт), нам не нужно беспокоиться об упо-
мянутом ранее параметре, называемом «ми-
нимальной разницей между положитель-
ным напряжением питания операционного
усилителя и напряжением его выходного
сигнала». Напряжение выходного сигнала
операционного усилителя будет намного
ниже положительного напряжения питания.
♦ Вместо напряжения 17БЭ для регулирующего
транзистора нам нужно учесть только ми-
нимальное напряжение между его входом
(истоком) и выходом (стоком). При низких
значениях напряжения UCV[ МОП-транзистор
ведет себя подобно небольшому сопротивле-
нию, поэтому минимум зависит от выходно-
го тока и сопротивления включения транзи-
стора*^.
Можно заметить, что в данной схеме со-
противление Двкл играет важную роль. При
токе величиной 100 мА маломощный МОП-
транзистор вызовет падение напряжения
величиной почти 1,5 В, а мощный — всего
лишь 4 мВ.
♦ Поскольку в схеме с низким напряжением от-
ключения стабилизатора отсутствует каскад
5 р-канальный МОП-транзистор. — Пер.
1 /L 7. Линейные стабилизаторы напряжения
485
для ограничения выходного тока, больше
нет ничего, что нужно учитывать при оценке
напряжения отключения для нее.
Нагрузка
Теперь посмотрим, насколько постоянным
будет оставаться выходное напряжение, неза-
висимо от нагрузки. В качестве нагрузки возь-
мите резисторы номиналом 100 Ом, соединен-
ные параллельно. (Можете сказать, почему не
меньшего номинала?)
Совет
Измерить ток нагрузки можно, подключив ампер-
метр последовательно между выходом схемы и
нагрузкой.
Не слишком усердствуйте с нагрузкой схемы с ма-
лым напряжением отключения, поскольку она не
оснащена функцией ограничения тока. Но убедив-
шись, что функция ограничения тока нормально
работает, можете спокойно экспериментировать,
даже закорачивая выход на «землю».
Вы должны обнаружить (если у вас будет такое
желание), что величина напряжения отключе-
ния в схеме стабилизатора с низким напряже-
нием отключения варьируется в зависимости
от нагрузки. Определив, что ограничивает ми-
нимальное напряжение отключения, вы пойме-
те, почему это отношение между отключением
и нагрузкой является необходимым.
ограничения тока, но также и с помощью те-
плодатчика, который предотвращает повреж-
дение в результате избыточного рассеивания
мощности (1ВЫХ х [17ВХ - ивш\). Такая тепловая
перегрузка может произойти, даже если вели-
чина тока будет ниже предельного значения.
Мы будем наблюдать теплозащиту в работе
и попутно также исследуем влияние теплоот-
вода на стабилизатор.
BxoA
Общий
Рис. 11L.3 Трехвыводной стабилизатор напряжения 78L05
с выходным напряжением 5 В
Наблюдать эту теплозащиту можно, подклю-
чив на выход стабилизатора нагрузку, которая
потребляет меньший ток, чем максимальный
ток микросхемы величиной 100 мА. В качестве
такой нагрузки можно использовать два парал-
лельных резистора номиналом 120 Ом, как по-
казано на рис. 11L.4.
Совет
Выполнив быстрый расчет, убедитесь, что эти ре-
зисторы мощностью 0,25 Вт не подвергаются пере-
грузке.
11L1 А. Трехвыводной
стабилизатор с фиксированным
выходным напряжением
Эту микросхему, изображенную на рис. 11L.3,
очень легко использовать. Она настолько
удобна, что знакомство с ней здесь будет сто-
ить потраченного времени. Это устройство
снабжено защитой не только посредством
Примечание
Рекомендуется подключить регулируемый источ-
ник питания последовательно источнику питания
с фиксированным напряжением +15 В на макетной
плате. При этом отрицательный вывод регулируе-
мого источника питания подключается к положи-
тельному выводу источника питания на макетной
плате. Ни в коем случае не соединяйте отрицатель-
ный вывод регулируемого источника питания с об-
щей шиной или заземлением.
Регулируемый
источник питания
Источник питания
с фиксированным
напряжением 15 В
(на макетной плате)
78L05
15
+5 В
J Hi
Рис. 11 L.4. Демонстрация теплозащиты микросхемы стабилизатора 78L05
486
11L Лабораторное занятие: стабилизаторы напряжения
Вычисления для энтузиастов
Этот эксперимент должен доставить вам удо-
вольствие, даже если вы не сможете предска-
зать, при какой величине входного напряже-
ния будет задействована функция ограничения
тока. Но еще приятнее попытаться предвари-
тельно рассчитать величину напряжения на
стабилизаторе, которая приведет к срабатыва-
нию теплозащиты. Сделать это несложно, хотя
для того, чтобы найти все необходимые спра-
вочные сведения может потребоваться некото-
рое время. В справочном листке указана мак-
симальная допустимая температура перехода
величиной 125 °С. Здесь же приводятся данные
по тепловому сопротивлению между перехо-
дом и окружающей средой, что в данном случае
означает как окружающий устройство воздух,
так и монтажную плату, к которой прикрепле-
ны выводы стабилизатора. У нас микросхема
в пластмассовом корпусе типа ТО92, поэтому
значительный объем тепла рассеивается че-
рез выводы. Следовательно, даже длина этих
выводов играет роль, как демонстрируется на
рис. 11L.6.
Таблица 11L.1. Тепловые параметры
микросхемы 78L05
ы
Рис. 11 L.5. Теплоотвод для компонентов в корпусе ТО92
Типичные рабочие характеристики
Максимальная средняя рассеиваемая
мощность (Корпус типа Z)
10
5,0
1,0
0,5
ОД
Длина выводов до печатной платы
.0,125 дюйма с jenjiooTBOflOM 72 °С/Вт
до печатной платы
теплоотвода
15 30/45 60 75
Длина выводов до печатной платы
ОД25 дюйма, без теплоотвода
Температура окружающей среды (°С)
Рис. 11L6. Максимальная рассеиваемая мощность стабили-
затора 78L05 в корпусе типа ТО92 зависит от длины выводов
между корпусом микросхемы и печатной платой
Максимальную мощность, которую устройство
может рассеивать, не допуская перегрева пере-
хода, можно вычислить, подставив значения из
табл. 11L.1.
Тип
корпуса
ТО39
ТО92
Тепловое сопро-
тивление между
переходом и кор-
пусом, Яепк, °С/Вт
(среднее/макси-
мальное)
20/40
180
Тепловое сопротив-
ление между пере-
ходом и окружаю-
щей средой, Rmoc,
°С/Вт (среднее/
максимальное)
140/190
190
Примечание
/?впк — тепловое сопротивление между переходом
и корпусом. /?впос — тепловое Сопротивление меж-
ду переходом и окружающей средой: состоит из
последовательных сопротивлений П-К (переход/
корпус) и К-ОС (корпус/окружающая среда)
Можете предположить, что устройство начина-
ет задействовать тепловое ограничение, когда
температура его перехода поднимается прибли-
зительно до 150 °С. Но пусть вас не пугает, если
расчеты укажут, что устройство выдерживает
более высокую температуру, вплоть до 200 °С.
Обратите внимание на единицы измерения те-
плового сопротивления RQ: °С/Вт.
Эксперимент: напряжение отключения
и тепловая самозащита
Начиная с нуля, постепенно повышайте вход-
ное напряжение [7ВХ, обращая внимание на сле-
дующие характеристики:
♦ напряжение отключения;
♦ входное напряжение, при котором срабаты-
вает тепловая самозащита микросхемы.
Между прочим подумайте, каким образом
микросхема ограничивает свою рассеиваемую
мощность? Как вы узнаете, когда микросхема
начнет задействовать защитную функцию6?
Когда микросхема начинает ограничивать свою
рассеиваемую мощность, температура корпуса
начнет снижаться и работоспособность стаби-
лизатора восстановится. Охладить микросхему
можно, приложив кусочек влажной салфетки
к корпусу микросхемы, в результате чего ее
нормальное тепловое состояние сразу же вос-
становится. Салфетку можно также заменить
6 Для ограничения рассеиваемой мощности (7 • U) микро-
схема ограничивает свой выходной ток. Признаком этого
будет падение входного напряжения ниже его начального
уровня 5 В.
1 1LI Линейные стабилизаторы напряжения
487
на теплоотвод, предназначенный специально
для корпусов типа ТО92 (рис. 11L.5).
После охлаждения микросхемы любым из этих
способов, чтобы заставить ее снова задейство-
вать функцию теплозащиты, нужно будет по-
высить входное напряжение. Теперь попро-
буйте охладить микросхему, направив на нее
поток воздуха от вентилятора или просто подув
на нее. Оказался ли этот метод охлаждения ми-
кросхемы эффективным в восстановлении ее
нормального температурного режима?
4,7 мкф[
Рис. 11 L.7. Стабилизатор напряжения на микросхеме 317
317 в режиме регулируемого выходного напря-
жения. Какое минимальное выходное напря-
жение вам удалось получить (при 5 = 0)?
11L1.5. Трехвыводная микросхема
317 стабилизатора с регулируемым
выходным напряжением
Этот стабилизатор позволяет задать желаемое
выходное напряжение с помощью двух резисто-
ров. А заменив один из резисторов потенцио-
метром, выходное напряжение можно регули-
ровать в процессе работы с источником пита-
ния. Таким образом, микросхема 317 позволяет
держать в запасе только одно устройство для
всех требуемых положительных напряжений
питания (по крайней мере, с величиной выход-
ного тока до 1 А). Она также позволяет полу-
чить точное выходное напряжение, например,
5 В, тогда как выходное напряжение микро-
схемы стабилизатора 78L05 находится в преде-
лах погрешности величиной 5%. Кроме того,
микросхему 317 легко подключить в качестве
источника тока. Во всех других отношениях эта
микросхема стабилизатора во многом подоб-
на микросхеме 78L05. Она содержит функции
определения предельного тока и температуры
для защиты от перегрузок.
Соберите схему, изображенную на рис. 11L.7.
Подключите резистор R сопротивлением
750 Ом. Каким должно быть при этом выход-
ное напряжение? Измерьте его.
Но следует иметь в виду одну особенность ми-
кросхемы 317 (которая недавно подвела Тома):
чтобы она работала должным образом, выход-
ной ток должен быть не менее 10 мА. Поэтому
следует избегать использования в цепи обрат-
ной связи резисторов с большим сопротивле-
нием, если только вы не уверены, что нагрузка
будет всегда потреблять значительный ток.
Замените резистор 1? потенциометром номина-
лом 1 кОм, и протестируйте работу микросхемы
11L1.6. Защита от перенапряжения
посредством автоматического
шунтирования на «землю»
Здесь мы рассмотрим небольшую схему, кото-
рая сможет защитить ваше питаемое устрой-
ство от неприятных последствий выхода из
строя источника питания, фиксируя напряже-
ние на уровне, близком к потенциалу «земли»,
когда оно превысит определенное пороговое
значение. В данном случае для порогового на-
пряжения установлено значение около 6 В, что
приемлемо при напряжении 5 В. Мы выбрали
значение 5 В, поскольку это стандартное на-
пряжение питания в компьютерах. Но посколь-
ку напряжение пробоя стабилитрона имеет
большой разброс, порог срабатывания защи-
ты можно установить только приблизительно.
На практике может быть предпочтительней ис-
пользовать микросхему датчика перенапряже-
ния7, которая обеспечивает точное опорное на-
пряжение. Некоторые из этих микросхем также
содержат тиристор.
На лабораторных занятиях, выполненных
ранее, нам еще не приходилось встречаться
с управляемым кремниевым тиристором, ко-
торый показан на рис. 11N.8. Это устройство
Регулируемый
источник
питания
IN
752
100 Ом <
УЭ
Тиристор
Рис. 11L.8 Схема автоматического шунтирования на «зем-
лю» (слева) и цоколевка тиристора: УЭ — управляющий
электрод; К — катод; А — анод
7 Например, микросхему МС3423 компании ON Semi-
conductor. См. раздел 9.13D книги АоЕ.
488
7 7L Лабораторное занятие: стабилизаторы напряжения
ведет себя наподобие силового транзистора:
чтобы включить его на управляющий электрод
нужно подать ток определенной величины.
А чтобы ток мог протекать через управляющий
электрод, напряжение на нем должно быть при-
близительно на 0,6 В выше, чем на катоде.
Но тиристор отличается от транзистора тем, что,
включившись, он фиксируется в этом состоянии.
Чтобы выключить тиристор, необходимо пре-
кратить протекание тока через него каким-либо
внешним способом. В данной схеме это делает-
ся выключением источника питания. Очевидно,
что тиристор хорошо подходит для решения
нашей задачи защиты от перенапряжения: он
включается, отключая тем самым питание, ког-
да напряжение становится опасным, и выклю-
чить его можно только внешним воздействием.
Обратите внимание на то, что шунтирование на
«землю» не прекращается, когда напряжение
источника питания просто возвращается к без-
опасному уровню, в данном случае — 5 В.
В настоящей схеме управляющий электрод
тиристора был бы зашунтирован на «землю»
конденсатором для предотвращения его сра-
батывания из-за кратковременных помех. Но
поскольку у нас источник питания не нагружен
ничем, кроме этой защитной схемы, то такие
помехи отсутствуют. Поэтому в шунтирующем
конденсаторе нет надобности.
Протестируйте собранную схему, постепенно
повышая напряжение источника питания, ис-
пользуя или отдельный регулируемый источ-
ник питания, или источник питания, встроен-
ный в макетную плату, выходное напряжение
которого (на макетной плате РВ503) можно
регулировать с помощью встроенного потен-
циометра. Завершив эксперимент, установите
выходное напряжение источника питания ма-
кетной платы снова на 15 В, поскольку такое
напряжение скорее всего понадобится в следу-
ющий раз для питания других устройств.
11L.2. Импульсный
стабилизатор напряжения
Принцип действия импульсного стабилизатора
прост: вместо того, чтобы поглощать разницу
между входным (нестабилизированным) и вы-
ходным (стабилизированным) напряжениями,
он попеременно то соединяет, то размыкает
входное и выходное напряжения (используя
подходящий фильтр для сглаживания пульса-
ций выходного напряжения). В принципе, та-
кой стабилизатор, который сводится просто к
интеллектуальному переключателю, не должен
рассеивать никакой мощности. В любое вре-
мя то или другое напряжение или ток выклю-
чателя равны нулю. Это идеальная ситуация.
Настоящие импульсные стабилизаторы обыч-
но имеют КПД 80%, а некоторые устройства —
95%.
11 L2.1. Микросхема импульсного
стабилизатора LT1073
На рис. 11L.9 изображена блок-схема микро-
схемы импульсного стабилизатора LT1073.
Это слаботочное устройство, которое в высшей
степени легко использовать. Первый довод в
пользу приобретения этой микросхемы — ука-
зание в его справочном листке «не требуется
никакого проектирования». С одной стороны,
это умаляет наши способности как инженеров,
пусть и начинающих. На, с другой стороны, это
также служит доказательством того, что проек-
тирование импульсных стабилизаторов напря-
жения пугает многих инженеров.
Установка
6
JCL.
Опорное
напряже-
ние
212 мВ
UJ
«Земля»
JT
Генератор
колебаний
SW1
Драйвер
LT1073
SW2
Обратная связь
LJ
8
Рис. 11 L.9. Блок-схема микросхемы импульсного стабилиза-
тора напряжения LT1073
11 L.2.2. Повышающий импульсный
стабилизатор
На рис. 11L.10 изображена схема, которая мо-
жет делать трюк, на который линейный стаби-
лизатор неспособен: получить выходное на-
пряжение величиной +5 В из входного напря-
жения величиной +1,5 В. Основную роль в ней,
как обычно, играет обратная связь. Необычно
здесь то, что теперь обратная связь управляет
генератором колебаний, который возбужда-
ет катушку индуктивности (на частоте около
11L2. Импульсный стабилизатор напряжения
489
(*15В)
Опорное
напряжение
212 мВ
DVM
ЮОмкГн IN5817 (Л„
\l
становка
А0
«Зс;мля»
енератор
(колебаний
SW13
йвер s^2
Драйвер
LT1073
Обратная связь
8
Рис. 11L.10. Повышающий стабилизатор напряжения на
микросхеме LT1073
20 кГц), когда выходное напряжение начинает
падать ниже заданного.
Расчет делителя обратной связи
Для опорного напряжения величиной 212 мВ
выберите такие номиналы резисторов Rx и Rr
чтобы получить выходное напряжение величи-
ной около 5 В. Если взять резисторы номина-
лом меньше 100 кОм, то можно получить чи-
стое выходное напряжение. Но можно выбрать
и намного большие номиналы.
Выходной конденсатор. На выходе установи-
те танталовый конденсатор емкостью 100 мкФ
или конденсатор типа OS-CON производства
компании Sanyo, если сможете найти такой.
Этот конденсатор имеет более низкое последо-
вательное сопротивление (и в некоторой степе-
ни более низкую индуктивность), в результате
чего он создает меньшие всплески напряжения
в схеме, когда в него поступает порция тока при
размыкании ключа. Проверьте реакцию вашей
схемы на варьирующуюся нагрузку, используя
схему, изображенную на рис. 11L.11, подклю-
чив цифровой амперметр для измерения тока
нагрузки 1Н. Обратите внимание на то, что наши
обычные потенциометры с номинальной мощ-
ностью 0,5 Вт здесь не подойдут. Для данной
схемы номинальная мощность потенциометра
должна быть 1 Вт8.
8 Задача вычисления требуемой номинальной мощности
потенциометра одновременно и простая и тонкая. На пер-
вый взгляд можно предположить, что если для потенцио-
метра на рис. 11L.11 установить сопротивление величиной,
скажем, 10 Ом, то на этом сопротивлении будет рассеивать-
ся очень малая мощность (около 20 мВт при токе 50 мА).
Но ошибка здесь состоит в том, что часть потенциометра,
которая должна рассеивать эту мощность, настолько мала,
что она не сможет отводить все это тепло. Поэтому не-
ГШ1
Цифровой мультиметр|
в режиме амперметра
Варьируемая нагрузка
(при выходном напряжении 5 В — IH < 50 мА)
Рис. 11L.11. Варьируемая нагрузка (номинальная мощность
потенциометра должна быть 1 Вт или больше)
Наблюдайте на осциллографе выходное на-
пряжение и сигнал на ключе микросхемы SW1
(вывод 3). Пульсации величиной около 150 мВ в
выходном напряжении (которые в свою очередь
содержат остроконечные ступенчатые всплески)
отражают гистерезис компаратора на микросхе-
ме 1073: выходное напряжение стабилизатора
немного понижается, а затем снова повышается.
Вопрос. Если величина гистерезиса компара-
тора равна 5 мВ (типично), почему в данном
случае кажущийся гистерезис намного больше?9
На рис. 11L.12 приведены осциллограммы, ко-
торые мы получили для токов нагрузки трех
разных величин.
Импульсный
стабилизатор LT1073
|50 мВ/деление
00 мВ/^еление
Рис. 11L12. Пульсации в выходном напряжении импульс-
ного стабилизатора и ступенчатое повышение уровня при
переключении ключа с частотой 40 кГц (усиление осцил-
лографа — 50 мВ/деление, скорость развертки — 500 мкс/
деление)
обходимо рассчитывать мощность, которую нужно было
бы рассеивать при полном токе нагрузки 50 мА через весь
потенциометр, хотя это и не будет происходить в данной
схеме (при сопротивлении 500 Ом ток через потенциометр
будет намного меньше, чем 50 мА). Величиной, которая не
должна превышать технические условия, является количе-
ство тепла на единицу длины резистивного элемента.
Отсюда и вытекает наше значение 1 Вт номинальной мощ-
ности потенциометра: мы рассчитываем мощность I2R
(около 1,25 Вт), когда ток величиной 50 мА протекает
через сопротивление потенциометра величиной 0,5 кОм.
8 остальных случаях мощность будет меньше.
9 Потому что обратно на вход подается только часть вы-
ходного напряжения, где мы наблюдаем пульсации, кото-
рые отображают влияние гистерезиса компаратора.
490
17L Лабораторное занятие: стабилизаторы напряжения
Уменьшение пульсаций (по желанию)
Микросхема 1073 содержит усилитель с ко-
эффициентом усиления 1000, который можно
использовать для уменьшения выходного ги-
стерезиса схемы. Все что нужно сделать — вста-
вить этот усилитель в цепь обратной связи, как
показано на рис. 11L.13.
Примечание
Резистор номиналом 470 кОм в этой схеме явля-
ется просто повышающим резистором, поскольку
здесь выходной каскад усилителя однотактный.
Обратная связь |470 кОм
16
А0
Установка 7
(внутренне подключен
к опорному напряжению)
Рис. 11L.13. Операционный усилитель в контуре обратной
связи уменьшает пульсации выходного напряжения
Вопрос. Как именно это усовершенствование
понижает уровень пульсаций?10
11 L2.3. Понижающий импульсный
стабилизатор
Схема понижающего стабилизатора напряже-
ния на рис. 11L.15 похожа на схему повышаю-
щего стабилизатора, но здесь транзисторный
ключ расположен между входным напряжени-
ем и катушкой, а не между катушкой и общей
шиной как в первой схеме11.
При размыкании ключа в данной схеме ток те-
чет через диод и катушку. Для этого напряже-
ние на диоде делается слегка отрицательным,
что может показаться довольно необычным,
если у вас нет опыта работы с катушками.
10 Здесь нет ничего особенного. Благодаря коэффици-
енту усиления внутреннего усилителя величиной 1000
схема реагирует на изменения на входе SET (Установ-
ка) в 1000 раз меньшие, чем изменения на входе SENSE
(Обратная связь). Таким образом наблюдаемые пульса-
ции в выходном напряжении уменьшаются приблизитель-
но с 120 мВ до значительно меньше одного милливольта.
Но справочный листок обещает более скромные результа-
ты: «несколько милливольт», и это вызывает недоумение.
См. справочный листок на микросхему импульсного ста-
билизатора 1073, особенно первые 10 страниц: http://cds.
linear.com/docs/en/datasheet/1073fa.pdf.
11 Типичная форма сигнала выходного напряжения тако-
го импульсного понижающего стабилизатора напряжения
приводится в книге АоЕ на рис. 9.60.
Рис. 11L.14. Понижающий импульсный стабилизатор
напряжения
Подайте на эту схему питание из внешнего ре-
гулируемого источника питания. Она должна
работать с входным напряжением, величина
которого варьируется от нескольких вольт до
максимальных 30 В (положительной поляр-
ности). Конденсатор на выходе способствует
выравниванию выходного напряжения в мо-
менты времени, когда ключ замкнут. Опять же,
выходное напряжение величиной +5 В устанав-
ливается подбором соответствующих номина-
лов резисторов Rx и Rr
Можете ли вы предположить по поведению вы-
ходного сигнала, что именно делает стабилиза-
тор для поддержания постоянного выходного
напряжения при варьирующемся входном на-
пряжении12?
11L2А Инвертирующий
стабилизатор напряжения
Понижающий стабилизатор можно заставить
инвертировать входное положительное напря-
жение в выходное отрицательное. Все, что для
этого нужно сделать, — переопределить «зем-
лю» в схеме на рис. 11L.14, как выход, а выход-
ной сигнал ишх как «землю». Довольно про-
сто, не так ли?
Попробуйте выполнить эту модернизацию. Но
при этом имейте в виду, что все ваши приборы,
которые подключены к «земле» (источник пи-
тания, осциллограф) тоже нужно согласовать
с этим переопределением «земли».
12 Возможно, вы увидите изменение скважности срабаты-
вания ключа.
11W. Примеры с решениями:
стабилизаторы напряжения
11 W.1. Выбор теплоотвода
Задача
Для стабилизатора напряжения на микросхеме
317 рассчитайте теплоотвод, достаточный для
рассеивания тепла, при падении напряжения
на этом устройстве величиной 5 В и токе 1 А.
Например, можно предположить, что входное
напряжение иж = 10 В, а выходное напряжение
ишх = 5 В. Заодно подберите и наилучший тип
корпуса для микросхемы 317.
Эта задача такая же, как и в разделе 9АЛА кни-
ги АоЕ, только со слегка иными числами.
Решение
Определите характеристики теплового со-
противления для используемых устройств.
Нам требуется рассеять мощность 5 Вт (5 В при
токе 1 А). Сначала нужно определить некото-
рые значения:
♦ максимальную допустимую температуру пе-
рехода;
♦ разницу температур между переходом и
окружающей средой;
♦ общее допустимое тепловое сопротивление
этого пути при известных двух предыдущих
значениях.
Получив эти данные, можно вычислить требуе-
мый размер теплоотвода, достаточный для от-
вода генерируемого тепла.
♦ Температура перехода. Микросхема 317
может выдерживать температуру перехода
до 125 °С. Мы не будем нацеливаться на этот
предел, а зададим максимум в 100 °С.
♦ Окружающая среда. Можно взять сред-
нюю температуру 25 °С, но не забудьте, что
наше устройство будет, вероятно, размещено
в закрытом корпусе, содержащем и другие
электронные компоненты. Поэтому будем
консервативны и примем температуру окру-
жающей среды равной 50 °С.
Допустимое тепловое сопротивление. Имея
данные для разницы температур (50 °С) и рас-
сеиваемой мощности (5 Вт), мы можем вычис-
лить допустимое тепловое сопротивление:
Г - Г
р _ Перехода Среды
Мощность
Тепловое
50 °С _ 10 °С
5 Вт 1 Вт '
Это общее тепловое сопротивление, допусти-
мое между нагретым переходом и окружающей
средой.
Без теплоотвода? Данные, приведенные в
табл. 11W.1, содержат информацию о тепло-
вом сопротивлении между переходом и окру-
жающей средой самой детали при отсутствии
теплоотвода1.
Тепловое сопротивление между переходом
и окружающей средой для компонента в кор-
пусе типа ТО-220 составляет 80 °С/Вт. Нам
это не подойдет. Что еще хуже, температура
окружающей среды здесь всего 25 °С, что не-
реалистично низко. Так что без теплоотвода
не обойтись.
1 Данные взяты из справочного листка компании Fair-
child Semiconductor для микросхемы LM317 в корпусе
ТО-220.
492
11W. Примеры с решениями: стабилизаторы напряжения
Таблица 11W.1. Тепловые сопротивления микросхемы 317
из ее справочного листка (тепловые характеристики)
Обозначение
•^епос
^епк
Характеристика
Рассеиваемая мощность
Тепловое сопротивление между переходом
и окружающей средой
Тепловое сопротивление между переходом и корпусом
Значение
Ограничена внутрен-
ней температурой
80
5
Единицы
Вт
°С/Вт
°С/Вт
Примечание. Значения для температуры окружающей среды ТОС = 25 °С, если не указано иное.
Требуется теплоотвод. Использование те-
плоотвода означает наличие нескольких тепло-
вых сопротивлений между переходом и окру-
жающей средой: «переход-корпус», «корпус-
теплоотвод» и «теплоотвод — окружающий
воздух». Поскольку корпус микросхемы нахо-
дится под напряжением, то для изоляции тепло-
отвода от корпуса необходима теплопроводная
прокладка (с тепловым сопротивлением 1?^),
а поверх нее устанавливаем теплоотвод (с те-
пловым сопротивлением Rj^). Тогда общее те-
пловое сопротивление:
Общее тепловое сопротивление должно быть
меньше 10 единиц (каких именно, пока не бу-
дем уточнять). Мы знаем, что тепловое сопро-
тивление «переход — корпус #епк» составляет
5 единиц, следовательно, остается еще 5 еди-
ниц. Теперь настало время обратиться к ката-
Там мы нашли прокладку с тепловым сопро-
тивлением 0,07 единиц. Таким образом, что-
бы общее тепловое сопротивление вложилось
в 10 единиц, нам нужен теплоотвод с тепловым
сопротивлением чуть меньше 5 единиц. Ищем
его в столбце "Тепловое сопротивление при
естественном охлаждении", т. е. естественное
охлаждение без вентилятора. Находим пару
радиаторов с сопротивлением 4,4 единиц. На
рис. 11W.1 показан фрагмент экрана поиска
требуемых деталей. Можно выбрать любой из
этих двух теплоотводов. Теперь наше общее
тепловое сопротивление равно 9,5 единиц, так
что мы не превысили предел в 10 единиц.
В нашем случае требования оказались доволь-
но жесткими, но при проектировании реаль-
ных устройств такие расчеты всегда окупятся.
Они помогут вам избежать стыда за возгорание
или иные тепловые повреждения спроектиро-
ванных вами устройств2.
Рис. 11 W.I. Поиск подходящего теплоотвода
логу доступных деталей. Подходящие проклад-
ки и теплоотводы можно поискать на веб-сайте
компании Digikey.
2 Один из наших студентов прислал нам сообщение, пред-
лагая добавить в курс материал по расчету теплового ре-
жима. Он закончил наш курс и никогда не слышал об этой
проблеме. А первая схема, которую он спроектировал на
своей новой работе, поставила его (и, следует сказать, нас
тоже) в неловкое положение из-за ее перегрева.
11W.2. Применение микросхемы-источника тока
493
потребитель) J^
Токовое
зеркало
"J400
Токовое
зеркало
Токовое
зеркало
300
||400
50
(только
источник)
Рис. 11 W.2. Варианты применения микросхемы сдвоенного источника тока REF200: источники тока от 50 до 400 мкА
11 W.2. Применение
микросхемы-источника тока
Задача
На базе микросхемы REF200 разработайте не-
сколько источников тока с различными выход-
ными токами.
Мы познакомились с этой микросхемой в гла-
ве 11N (см. рис. 11N.18). Производитель данно-
го компонента обещает, что его два встроенных
источника тока величиной 100 мкА каждый и
токовое зеркало могут поставлять (подавать
или потреблять) токи разной величины: 50,
100,200,300 и 400 мкА.
Некоторые подробности
Токовое зеркало. Токовые зеркала подробно
не изучаются в нашей книге, но поведение токо-
вого зеркала можно описать довольно просто,
как это сделано на рис. 11N.18: зеркало поддер-
живает равными токи, поступающие в два его
верхних выхода. Ток левого плеча играет роль
задающего тока, а ток правого плеча уравнива-
ется с этим током. Токовые зеркала рассматри-
ваются более подробно в разделе 5S.2.
Поставщик и потребитель Каскады, обес-
печивающие ток величиной 100 мкА, имеют по
два вывода и могут одинаково эффективно слу-
жить как источником, так и потребителем тока.
Кстати, схемы с током 50 мкА не будут такими
универсальными, поскольку они будут разли-
чаться в зависимости от того, выдают они ток
или потребляют. Остальные схемы будут рабо-
тоспособны в любой конфигурации.
Разработка некоторых из этих решений будет
непростой.
Решение
Варианты включения микросхемы REF200
при разных требуемых токах изображены на
рис. 11W.2. Не находите ли вы некоторые из
этих решений довольно тонкими? Особенно
источник тока величиной 50 мкА и источники
тока величиной 300 мкА и 400 мкА3.
Показалась ли вам эта задача легкой или труд-
ной? Я полагаю, что без подсказки из справоч-
ного листка для микросхемы REF200 я не смог
бы самостоятельно придумать решение с ис-
точником тока 50 мкА.
3 Эти примеры взяты из справочного листка микросхемы
REF200 компании Texas Instruments.
12N. Ключи на полевых МОП-транзисторах
Содержание
12N.1. Почему мы отводим полевым транзисторам всего лишь одно занятие 494
12N.1.1. Некоторые понятия для полевых и биполярных транзисторов сходны 495
12N.1.2. Просто еще один трехвыводной вентиль 495
12N.1.3. Различные обозначения МОП-транзисторов 496
12N.1.4. Преимущества полевых транзисторов 497
12N.2. Включение и выключение устройств большой мощности 498
12N.2.1. Теряемая мощность 498
12N.2.2. Насколько легко управлять ключом? 499
12N.2.3. Влияние емкости полевого транзистора на процесс переключения 499
12N.3. Применение силового ключа: усилитель звуковой частоты 500
12N.3.1. Сигналы 501
12N.4. Логические вентили 502
12N.4.1. Простой логический инвертор 502
12N.4.2. Усовершенствованный КМОП-инвертор 502
12N.5. Аналоговые коммутаторы 503
12N.5.1. Аналоговый коммутатор на одном МОП-транзисторе 503
12N.5.2. Усовершенствованный аналоговый КМОП-коммутатор 503
12N.5.3. Несовершенства 504
12N.6. Применение аналоговых коммутаторов 504
12N.6.1. Сброс интегратора 504
12N.6.2. Множество других приложений 505
12N.6.3. Особенно интересное применение мультиплексора в фильтре
с коммутируемым конденсатором 506
12N.6.4. Выборка и хранение 507
12N.6.5. Выбор компонентов 507
12N.6.6. Стандартные вопросы разработки 508
12N.6.7. Кратко о погрешностях схемы выборки и хранения 508
12N.7. Исследуем схему выборки и хранения 509
12N.7.1. Поведение схемы и ее несовершенства 509
12N.7.2. Инжекция заряда 510
12N.7.3. Большая емкость может устранить эффект инжекции заряда 511
12N.7.4. Ограничение скорости в процессе выборки 512
12N.8. Материал для чтения в АоЕ 513
12N.1. Почему мы отводим
полевым транзисторам
всего лишь одно занятие
Возможно, вас может смутить то обстоятель-
ство, что мы предлагаем разобраться с полевы-
ми транзисторами всего лишь за одно занятие,
тогда как биполярным транзисторам и опера-
ционным усилителям посвятили намного боль-
ше времени1.
1 АоЕ § 3.1.5.
Но мы полагаем, что одного занятия будет до-
статочно, поскольку самое важное применение
полевых транзисторов состоит в использова-
нии их в качестве переключателей, а это пред-
мет, который, как мы полагаем, будет сравни-
тельно легким для освоения. А линейные тран-
зисторные схемы, наподобие тех, которыми мы
занимались ранее, намного сложнее, что вы,
несомненно, заметили.
Полевые транзисторы, с которыми мы будем ра-
ботать на лабораторном занятии 12L, относятся
12N.I Почему мы отводим полевым транзисторам всего лишь одно занятие
495
к типу, называемому МОП-транзисторами2.
Эти транзисторы полностью преобладают в
цифровой электронике, и цифровые устрой-
ства в большинстве собраны именно на таких
транзисторах.
Начиная с главы 14N мы тоже будем изучать
цифровые логические элементы на МОП-
транзисторах.
Но пока что мы будем применять МОП-
транзисторы по-другому: сначала как силовые
ключи (где они составляют конкуренцию клю-
чам на биполярных транзисторах), а затем как
аналоговые коммутаторы, также называемые
интегральными прерывателями.
12N.1.1. Некоторые понятия
для полевых и биполярных
транзисторов сходны
Некоторые основные понятия биполярных и
полевых транзисторов сходны, что будет боль-
шим подспорьем в изучении последних. В этой
главе мы почти не обсуждаем большой класс
полевых транзисторов: с управляющим р-п~
переходом3. Эти устройства упомянуты в гла-
ве 12S. Здесь же мы познакомимся с полевыми
транзисторами с изолированным затвором.
Разница между этими двумя типами полевых
транзисторов отражена в их условных обо-
значениях: в первом случае вход обозначается
как р-л-переход, а во втором вход изолирован
(в МОП-структуре оксидом).
12N.1.2. Просто еще один
трехвыводной вентиль
Подобно биполярному транзистору, полевой
транзистор является трехвыводным вентилем,
управляемым напряжением между двумя выво-
дами4. Если обратиться к наиболее распростра-
ненному типу полевых транзисторов, анало-
гичному биполярным я-р-я-транзисторам, так
называемому канальному МОП-транзистору, то
полярность его напряжения управления и на-
правление тока будут такие же, как у биполяр-
ных транзисторов. На рис. 12N.1 показан вен-
тиль как аналогия транзистора (слева), символ
биполярного транзистора (посередине) и обо-
значение МОП-транзистора (справа).
На обозначении МОП-транзистора есть проме-
жуток между управляющим выводом и прово-
дящим каналом, что делает видимым большое
достоинство МОП-транзисторов — их чрезвы-
чайно высокое входное сопротивление. При
рассмотрении эмиттерного повторителя на
биполярном транзисторе мы расхваливали до
небес его способность повышать входной им-
педанс пропорционально коэффициенту усиле-
ния р. В этом отношении возможности МОП-
транзисторов значительно лучше. Упомянутый
промежуток представляет собой изолирующий
слой диоксида кремния (SiO2). На рис. 12N.2
иллюстрируется забавный опыт, который мы
иногда проводим для демонстрации высокого
входного импеданса МОП-транзисторов. Один
из студентов здесь служит в качестве «провода»
для передачи небольшого заряда от преподава-
[Нагрузка |
+5
О—)Z--w* К
Вентиль или (более простой) Биполярный транзистор МОТТ-транзистор
выключатель
Рис. 12N.1. МОП-транзисторы похожи на биполярные транзисторы
2 МОП - метал-оксид-полупроводник; иногда МДП —
метал-диэлектрик-полупроводник. Англ. MOSFET —
Metal-Oxide-FET. Также называются полевыми транзисто-
рами с изолированным затвором. Англ. IGFET — Insulated
Gate FET.
3 Мы мимоходом встретились с этими устройствами в ка-
честве токоограничивающих элементов в главе SL и UN.
теля к МОП-транзистору, управляющему схе-
мой включения лампочки.
Одной рукой преподаватель дотрагивается до
источника напряжения величиной +5 В или
4 АоЕ § 3.1.1А.
496
UN. Ключи на полевых МОП-транзисторах
Лампочка
Ключ на МОП-транзисторе
Преподаватель может передавать заряд через студента
Рис. 12N.2. Демонстрация высокого входного импеданса
МОП-транзисторов
до общей шины, а другой — до руки студента,
который другой рукой касается управляющего
вывода (затвора) МОП-транзистора в схеме
включения лампочки. В результате лампочка
загорается. Хотя это чисто демонстрационная
схема, действует она очень убедительно, иллю-
стрируя основное свойство МОП-транзисторов.
Если после загорания лампочки разорвать цепь
от источника напряжения до управляющего
вывода МОП-транзистора, то лампочка все
равно будет продолжать гореть. Можете пояс-
нить, почему?5
На самом деле полевой транзистор больше на-
поминает электронно-вакуумную лампу, чем
биполярный транзистор. (Знаком ли вам тер-
мин «электронно-вакуумная лампа»?6) Наличие
изолятора на входе МОП-транзистора озна-
чает, что только полевой эффект здесь может
воздействовать на проводящий канал и управ-
лять им.
5 Этот эффект еще раз подчеркивает наличие огромного
входного сопротивления МОП-транзистора. Лампочка
продолжает гореть потому, что паразитная емкость на за-
творе МОП-транзистора сохраняет заряд, поскольку вход-
ной ток транзистора практически равен нулю. Это свойство
используется во многих полупроводниковых устройствах
памяти, таких как, например, динамическая память, флэш-
память, СППЗУ (англ. EPROM — erasable programmable
read-only memory.) и ЭСППЗУ (англ. EEPROM - electrical
EPROM). Некоторые из этих устройств памяти могут хра-
нить заряд на затворе МОП-транзистора в течение многих
лет. Устройства памяти на основе полевых транзисторов
рассматриваются более подробно в главе 17N.
6 Скорее всего не знаком по причине вашей молодости. Но
мой первый преподаватель электроники учился по ваку-
умным лампам и презирал биполярные транзисторы из-за
их зависимости от входного (базового) тока. Когда появи-
лись первые полевые транзисторы, он вздохнул с облег-
чением и признался: наконец-то вернулся «правильный»
электронный вентиль! Ведь исследователи в Лаборатории
Белла тоже пытались создать полевой транзистор, когда
они случайно натолкнулись на биполярный. Поведение
полевого транзистора больше похоже на поведение ваку-
умных ламп, хотя следует отметить, что механизм здесь
абсолютно разный.
12N.1.3. Различные обозначения
МОП-транзисторов
К сожалению, МОП-транзисторы обозначают-
ся разнообразными символами, одни из кото-
рых более распространены, чем другие. Неко-
торые из них изображены на рис. 12N.3. Мы
будем употреблять самый левый из них7.
Затвор
рок
I Исток
Упрощенный символ; но не подумайте,
что здесь /?-А7-переход
С обозначением паразитного
р-л-перехода в виде вывода подложки
6
(подложка) I
С обозначением паразитного р-п-
перехода, соединенного с истоком
в
Рис. 12N.3. Несколько условных графических обозначений
Все приведенные обозначения (в отличие от
некоторых других, не показанных) помогают
читателю понять работу обозначаемого устрой-
ства, указывая, какой из его выводов является
истоком (тот, который ближе к выводу затво-
ра), а какой — стоком. Символ на рис. 12N.3,
а привлекательно простой, но пусть подобный
диоду символ на выводе истока не вводит вас
в заблуждение — в действительности транзи-
стор не содержит такого диода. (Внутреннее
строение МОП-транзистора было изображено
на рис. 12N.5.)
На условном обозначении на рис. 12N.3, в по-
казан паразитный р-л-переход (или диод под-
ложки8) — подразумеваемый переход между
подложкой и каналом9.
7 В отечественной литературе данное обозначение МОП-
транзистора практически не встречается. — Примеч. ред.
8 Англ. body diode. — Примеч. пер.
9 АоЕ § 3.5.4С.
12N.L Почему мы отводим полевым транзисторам всего лишь одно занятие
497
На рис. 12N.3, б подложка обозначена в виде
четвертого вывода, это может быть удобным
для схем внутреннего устройства некоторых
микросхем. Но у силовых МОП-транзисторов
подложка всегда соединена внутри с истоком,
как показано рис. 12N.3, в. Это внутреннее сое-
динение создает неявный диод между истоком
и стоком, как показано на рис. 12N.410.
Из-за наличия диода силовой МОП-транзистор
нельзя использовать в качестве двунаправлен-
ного выключателя, поскольку недопустимо,
чтобы напряжение на стоке было ниже напря-
жения на истоке, больше, чем на величину па-
дения напряжения на диоде.
Рис. 12N.4. Подложка образует диод, соединяющий исток со
стоком
Внутреннее устройство
МОП-транзистора
На рис. 12N.5 показан эскиз структуры
я-канального МОП-транзистора. Теперь ста-
новится понятным этот странный паразитный
диод, который иногда присутствует в символе
МОП-транзистора. МОП-транзистор всегда со-
держит этотр-л-переход, который является не-
явным результатом строения транзистора, а не
добавлен в него как отдельный диод.
s.o2
(изолятор)
Исток
Рис. 12N.5. Внутреннее строение полевого МОП-транзис-
тора. Паразитный диод является неявным р-п-переходом
«подложка-канал» (канал на рисунке не показан)
Паразитный диод создается между подложкой
р-типа и каналом, и никогда не должен нахо-
диться в режиме прямого смещения. Поэтому
потенциал подложки л-канального полевого
транзистора должен быть таким же отрица-
тельным, как потенциал истока, потенциал ко-
торого в свою очередь более отрицательный,
чем потенциал стока11. Будем надеяться, что
этого поверхностного знакомства с полевым
транзистором будет достаточно, чтобы присту-
пить к рассмотрению других его свойств.
12N.1 А Преимущества полевых
транзисторов
После того как мы так долго изучали все аспек-
ты биполярных транзисторов, возможно, вы
задаетесь вопросом, а зачем вообще нужно изу-
чать еще один тип электронных компонентов12.
Ответ на этот вопрос очень прост: потому что
полевые транзисторы могут выполнять неко-
торые задачи лучше, чем биполярные. В част-
ности, МОП-транзисторы предпочтительнее
в случаях, когда требуется:
♦ очень высокий входной импеданс;
♦ двунаправленный аналоговый переключа-
тель;
♦ силовой ключ.
Первое из этих достоинств полевых транзи-
сторов — огромный входной импеданс — яв-
ляется также и самым важным. Вообще то,
строго говоря, громадным является входное
сопротивление. Значительная входная ем-
кость мощных МОП-транзисторов, наподобие
силовых ключей, с которыми мы будем рабо-
тать на лабораторном занятии 12L, на высоких
частотах может ухудшить входное реактивное
сопротивление.
10 АоЕ § 3.1.3.
11 Если потенциал стока окажется более отрицательным,
чем потенциал истока, то более отрицательный вывод
станет эффективным истоком. См. раздел 3.1.3 книги АоЕ.
Такое развитие событий возможно вследствие почти сим-
метричного строения полевого транзистора, сток и исток
которого отличаются только емкостью. Но обратите вни-
мание на то обстоятельство, что у силового л-канального
МОП-транзистора неявный паразитный диод не допуска-
ет, чтобы потенциал на стоке становился ниже потенциа-
ла истока более чем на величину падения напряжения на
диоде. Более подробно см. в разделе 12N.1.3 зтой книги и
разделе 3.5АС книги АоЕ.
12 АоЕ § 3.L
498
UN. Ключи на полевых МОП-транзисторах
12N.2. Включение
и выключение устройств
большой мощности
Ранее на лабораторном занятии 4L мы собра-
ли переключатель на биполярном транзисто-
ре. Сегодня мы соберем эквивалентную схе-
му на силовом МОП-транзисторе, т. е. МОП-
транзисторе, способном работать с большими
токами. На рис. 12N.6 изображены варианты
схемы на обоих типах транзистора. Какие кри-
терии нужно рассматривать, решая, какую из
этих схем предпочесть?
+5
Нагрузка
1к0м J
0
+5
Нагрузка
И
Рис. 12N.6. Два силовых ключа: на биполярном транзисторе
(слева) и МОП-транзисторе (справа)
Наиболее важные вопросы при выборе схемы:
♦ какую мощность ключ рассеивает во вклю-
ченном состоянии;
♦ насколько легко управлять ключом.
12N.2.1. Теряемая мощность
Идеальный переключатель во включенном ре-
жиме должен выдавать в нагрузку всю мощ-
ность, при этом не рассеивая никакой мощно-
сти сам. Таким образом, вопрос выбора сводит-
ся к тому, какой из этих двух переключателей
будет иметь более низкий выходной уровень
в открытом состоянии. Соответствующими ха-
рактеристиками будет напряжение насыщения
^кэ-нас для биполярного транзистора и сопро-
тивление открытого канала R0K для полевого
транзистора.
Замечание
Но имейте в виду, что режим насыщения означает
нечто совершенно иное в случае с полевыми тран-
зисторами. См. раздел 3. /. 1А книги АоЕ.
Биполярный транзистор рассеивает определен-
ную мощность на переходе «база-эмиттер»,
тогда как полевой транзистор совершенно не
теряет мощности на затворе, через который не
протекает никакого тока13.
МОП-транзисторы легко соединять
параллельно
Уникальные свойства полевых транзисторов
позволяют с легкостью соединять параллель-
но несколько МОП-транзисторов для работы
с большими токами (и для снижения #ок). При
большом токе и высоком напряжении Ьш ра-
бочий ток МОП-транзисторов снижается, тог-
да как у биполярных транзисторов происходит
все наоборот. Благодаря этому свойству не-
сколько МОП-транзисторов можно соединить
параллельно друг другу даже без нагрузочных
резисторов, которые требуются для биполяр-
ных транзисторов при таком подключении.
Эти резисторы подключаются к эмиттеру би-
полярного транзистора и создают обратную
связь, как показано на рис. 12N.7. При парал-
лельном включении биполярных транзисторов
без нагрузочных резисторов транзистор с более
высокой температурой будет брать на себя все
большую и бблыпую часть общего тока, нагре-
ваясь все больше и больше, и т. д. Скоро через
него будет проходить весь или почти весь ток и
транзистор сгорит.
При параллельном соединении
нескольких биполярных транзисторов
для каждого из них требуется резистор £э,
чтобы обеспечить равномерное
распределение общего тока между ними
Вкл
I Нагрузка
1 Нагрузка |
Выкл
Для полевых транзисторов
в такой конфигурации
резисторы не требуются
Рис. 12N.7. В отличие от биполярных транзисторов, МОП-
транзисторы можно соединять параллельно без нагрузоч-
ных резисторов
Биполярный транзистор реагирует на темпе-
ратуру самоубийственным образом: чем выше
его температура, тем больший ток через него
проходит. Это вызывает неравномерное рас-
пределение тока не только в случае нескольких
13 АоЕ § 3.5.6А.
12N.2. Включение и выключение устройств большой мощности
499
параллельных транзисторов, но также и на ми-
кроскопическом уровне в отдельном приборе.
В частности, если определенная область бипо-
лярного перехода имеет более высокую темпе-
ратуру, чем сопредельные области, то через нее
протекает больший ток, в результате чего она
нагревается еще больше.14
Вследствие локального перераспределения то-
ка при значительном напряжении на устройст-
ве номинальная мощность биполярного тран-
зистора снижается. (В книге АоЕ этот эффект
на рис. 3.94 начинается уже при напряжении
10 В.)
Образно говоря, биполярные транзисторы
являются «трудоголиками», тогда как МОП-
транзисторы ведут себя подобно большинству
из нас: они предпочитают «отлынивать» от ра-
боты вместо того, чтобы быть «стахановцами».
Но все это не означает, что биполярные тран-
зисторы непригодны для выполнения опреде-
ленных задач, просто придется использовать
более мощный транзистор, чем можно было бы
ожидать. Но чтобы вы не очень восхищались
преимуществами МОП-транзисторов, имейте
в виду, что возможность параллельного соеди-
нения этих транзисторов не применима в ли-
нейных схемах с их использованием. В таких
ситуациях они обычно работают с более сла-
быми токами и проявляют такую же скверную
реакцию на повышение температуры, как и би-
полярные транзисторы — чем выше температу-
ра, тем больше протекающий ток.
12N.2.2. Насколько легко управлять
ключом?
Ранее мы придавали особое значение гигантско-
му входному импедансу МОП-транзисторов в
режиме постоянного тока15. Мы продемонстри-
руем это свойство на лабораторном занятии,
включая и выключая МОП-переключатель, до-
трагиваясь до его затвора пальцем одной руки,
а другой рукой прикасаясь к напряжению +5 В,
а затем к шине «земли». Но в режиме перемен-
ного тока характеристики полевых транзисто-
ров начинают ухудшаться вследствие их более
высоких емкостей16.
Большие емкости мощных МОП-транзисторов
даже привели к необходимости создания специ-
ализированных микросхем-драйверов для них.
Примечание
Эти микросхемы можно сравнить со странными
и узкоспециализированными формами животного
и растительного мира, с которыми Дарвин сталки-
вался на Галапагосских островах.
Эти драйверы могут выдавать очень большой
ток на протяжении весьма короткого времени,
чтобы быстро зарядить входную емкость поле-
вого транзистора.
12N.2.3. Влияние емкости
полевого транзистора на процесс
переключения
Полевые транзисторы имеют большие вход-
ные емкости — Сзи и Сзс, достигающие значе-
ний в сотни пикофарад для МОП-транзистора,
который может работать с током в несколько
ампер при низком сопротивлении открытого
канала17. А обратная связь ухудшает ситуацию
еще больше. Влияние емкости Сзс увеличива-
ется в результате быстрой смены напряжения
на затворе при переключении транзистора:
большое значение производной dU/dt вызы-
вает протекание большого тока через емкость
Сзс. Вы сможете сами наблюдать этот эффект
на лабораторном занятии. Внешне все выгля-
дит как странный излом или колебания на кри-
вой нарастания напряжения затвора при пере-
ключении МОП-транзистора. Но этот эффект
наблюдаются только при подаче небольшого
управляющего сигнала на затвор, как показано
на рис. 12N.8.
+50 В
'1кОм
ЮкОм
14 АоЕ § 3.5.7с.
15 АоЕ § 3.5.2.
16 АоЕ, раздел 3.5.3: драйвер для МОП-транзисторов.
Рис. 12N.8 Слабый сигнал управления на затворе МОП-
транзистора делает заметным эффект его емкостей
17 АоЕ § 3.5.4А.
500
UN. Ключи на полевых МОП-транзисторах
Кажется, будто бы напряжение
на затворе колеблется " ^
при нарастании...
«Земля»
(Ц. ис)
... в то время как напряжение
на стоке падает (увеличение
емкости «затвор-сток»
вследствие эффекта Миллера)
«Земля»
(вход)
Подробный вид:
Кривая повышения напряжения
затвора Ц выглядит подобно
изломанной ££-кривой, но не
совсем такая плавная, потому
что емкость «сток-затвор»
Ссз возрастает по мере снижения
напряжения стока Uc
Рис. 12N.9. Емкости МОП-транзистора могут замедлить процесс его переключения
Здесь резистор номиналом 10 кОм замедляет
заряд паразитных емкостей на затворе, в ре-
зультате чего замедляется и переключение по-
левого транзистора. Процесс иллюстрируют
соответствующие графики, приведенные на
рис. 12N.918.
Повышение емкости «затвор - сток» Сзс вслед-
ствие снижения напряжения стока Uc при росте
напряжения на затворе U3 является примером
эффекта Миллера. Эта проблема хорошо зна-
кома каждому, кто пытается собрать высокоча-
стотный инвертирующий усилитель.
Примечание
Эта тема не обсуждается в нашей книге, хотя мы
и рассмотрели вкратце в разделе 9N.8.2 эффект
Миллера для лучшего объяснения процесса ста-
билизации эмиттерного повторителя на дискрет-
ных элементах с помощью резистора в цепи его
базы19.
Биполярные транзисторы
с изолированным затвором
Вкратце отметим гибрид МОП-транзистора и
биполярного транзистора, называемый бипо-
лярным транзистором с изолированным затво-
ром. Эти транзисторы имеют высокий входной
импеданс, присущий МОП-транзисторам, но
обладают лучшим напряжением открытого ка-
нала для высоковольтной нагрузки, чем МОП-
транзисторы. Поскольку в нашем курсе мы не
18 АоЕ§ 3.5.4В и рис. 3.102.
19 АоЕ § 3.5.8А.
будем иметь дело с такими нагрузками, нам не
понадобятся и эти транзисторы. Если вы хотите
узнать больше об этих устройствах, то они рас-
сматриваются подробно в книге АоЕ.
12N3. Применение силового
ключа: усилитель звуковой
частоты
На лабораторном занятии 11L мы имели воз-
можность убедиться, насколько высокий КПД
может иметь импульсный стабилизатор напря-
жения. В идеале ключ не рассеивает никакой
мощности, тогда как линейный стабилизатор
должен поглощать разность между входящим и
выходящим напряжением. КПД линейного ста-
билизатора вряд ли может превысить 50%, тог-
да как КПД импульсного стабилизатора может
приближаться к 90%.
Подобное повышение эффективности усили-
теля звуковой частоты можно получить, заме-
нив двухтактный усилитель на переключатель
с двумя состояниями — «включен» и «выклю-
чен». Такой усилитель относится к классу D,
в отличие от класса АВ двухтактного усилите-
ля. Но при этом возникает сложность в виде
помех, появляющихся при коммутации, как мы
увидим на лабораторном занятии 12L, когда
попробуем собрать такой усилитель.
Но такие помехи не обязательно должны соз-
давать звуковой шум. Частота коммутации на-
ходится намного выше звукового диапазона
12N.3. Применение силового ключа: усилитель звуковой частоты
501
(как минимум в области сотен килогерц). Тем
не менее, глядя на осциллограммы сигналов на
рис. 12N.12 и 12N.12, вы можете испытать чув-
ство тревоги. Помехи на синусоидальном сиг-
нале вверху на каждой осциллограмме относят-
ся к входному сигналу схемы. Резкие импульсы
управления переключателем нарушают потен-
циал «земли» и излучают высокочастотные
электрические помехи. Эти помехи возникают,
несмотря на предпринятые обычные меры по
развязке источника питания: установка раз-
вязывающего конденсатора емкостью 1 мкФ и
еще нескольких емкостью 0,1 мкФ. В примеча-
нии по применению для МОП-ключей указаны
опасности, создаваемые узкими и крутыми вы-
ходными пульсациями: электромагнитные на-
водки — это агрессивный сигнал, который мо-
жет распространяться через излучение или по
проводникам на другие компоненты системы и
создавать помехи.
Если ваша схема чувствительна к таким поме-
хам, то следует предпочесть менее эффектив-
ный (и менее агрессивный) двухтактный вы-
ходной каскад.
Импульсный усилитель выдает очень короткие
импульсы величиной напряжения питания (5 В
на соответствующем лабораторном занятии
12L.3).
Эти пульсации эффективно отфильтровыва-
ются индуктивностью динамика, формируя
кратковременный пилообразный ток в дина-
мике. Такое свойство индуктивности динамика
позволяет получить конструкцию без фильтра
(уменьшив габариты и стоимость) и с высоким
КПД: от 70% до 90% в наилучшем случае. Такой
КПД особенно востребован для устройств, пи-
таемых от батарей — мобильных телефонов
или портативных проигрывателей.
12N.3.1. Сигналы
Синусоидальный
На рис. 12N.10 показаны входной синусоидаль-
ный сигнал частотой около 1 кГц и выходные
серии импульсов, которые поступают на дина-
мик от микросхемы LM4667.
Визуально шум коммутации во входном сигнале
может вызывать беспокойство, но он не создает
никаких проблем при прослушивании. Кроме
Рис 12N.10. Входной синусоидальный сигнал
(зашумленный помехами переключения) и два выходных
сигнала импульсного усилителя звуковой частоты
того, при размещении схемы на должным об-
разом спроектированной печатной плате соз-
даваемые переключениями помехи окажутся
намного меньше, чем при сборе схемы на ма-
кетной плате. Доказательством могут служить
осциллограммы чистого сигнала, показанные
на рис. 2.73 в книге АоЕ. При переходе входно-
го сигнала через среднюю точку наблюдается
попеременное доминирование выходных сиг-
налов (обозначены цифрами 2 и 3 на рисунке),
которые заставляют звуковую катушку динами-
ка перемещаться сначала в одном направлении,
а затем в противоположном. Эти два нижних
сигнала немного похожи на ШИМ-сигналы,
которые вы имели возможность наблюдать на
лабораторном занятии 7L, но более правильно
назвать такой сигнал импульсно-плотностной
модуляцией.
Подробности и шум потока импульсов
На рис. 12N.11 серии импульсов, рассмотрен-
ные в предыдущем разделе, показаны более
подробно; здесь также видны помехи, создавае-
мые ими во всей схеме, включая входной сину-
соидальный сигнал.
Рис. 12N.11. Подробное представление выходных серий им-
пульсов и зашумленного входного синусоидального сигнала
Неравномерный интервал следования импуль-
сов разоблачает довольно хитроумное устрой-
ство усилителя, в котором применен метод под
502
UN. Ключи на полевых МОП-транзисторах
названием дельта-сигма-модуляция для созда-
ния выходных серий импульсов. Эти импульсы
служат для получения требуемого среднего зна-
чения тока через динамик в течение нескольких
пачек импульсов. Обратите внимание на то, что
интервал между импульсами намного меньше
периода звукового сигнала, который нужно
воспроизвести.
Музыкальный сигнал
Наконец, на рис. 12N.12 изображены осцилло-
граммы музыкального сигнала, обработанного
описанным усилителем. Здесь помехи пере-
ключений хорошо заметны, но мы надеемся,
что когда вы попробуете повторить этот экспе-
римент на лабораторном занятии, то сможете
убедиться в том, что эти помехи создают очень
незначительный звуковой эффект.
Рис. 12N.12. Входной музыкальный сигнал (вверху) и два
выходных потока импульсов, полученных после обработки
входного сигнала
12N.4. Логические вентили
Силовой ключ, подобный изображенному на
рис. 12N.6, является, по сути, такой же схемой,
что и простой логический инвертор, схема ко-
торого показана слева на рис. 12N.13. Но ин-
вертор отличается от мощного переключателя
тем, что задачей этого логического устройства
является не подача мощности в нагрузку, а со-
всем наоборот.
Простой Усовершенствованный КМОП
логический инвертор логический инвертор
Рис. 12N.13. Два логических инвертора
Логический элемент служит только для форми-
рования выходного уровня напряжения (вы-
сокого или низкого), который определяется
высоким или низким входным уровнем, при
этом мощность, рассеиваемая в схеме, долж-
на быть минимальной. Очевидно, что вход
МОП-транзистора хорошо подходит для эко-
номии мощности, поскольку затвор почти не
потребляет тока. Но чтобы гарантировать ра-
боту остальной части схемы без рассеивания
мощности, необходимо проявить некоторую
хитрость. Улучшенный логический вентиль,
изображенный справа на рис. 12N.13 является
примером такой схемы.
12N.4.1. Простой логический
инвертор
Простой логический инвертер, изображенный
справа на рис. 12N.13, работает не слишком хо-
рошо. Далее на лабораторном занятии 14L мы
убедимся, что уровень его выходного сигнала не
может нарастать достаточно быстро вследствие
необходимости заряжать через повышающий
резистор паразитную емкость на выходе схе-
мы. Это делает скорость переключений низкой.
Кроме того, данная схема также неэффективна
в энергетическом плане, поскольку при низком
уровне выходного сигнала [/вых на резисторе
рассеивается мощность. Мало того, при высо-
ком уровне выходного сигнала выходной импе-
данс этого вентиля слишком высок, вследствие
чего его помехозащищенность очень низкая.
Таким образом, подобные логические инверто-
ры используются очень редко.
12N .4.2. Усовершенствованный
КМОП-инвертор
Элегантная схема инвертора, изображенная
справа на рис. 12N.13, является простейшим
примером логических устройств на МОП-
транзисторе, которые завоевали мир цифровой
электроники. Комбинация п- и р-канального
МОП-транзисторов в этой схеме называет-
ся КМОП-структурой, где буква «К» означает
комплементарная. Мы продемонстрируем пре-
восходство этого логического инвертора на ла-
бораторном занятии 14L. Но даже не применяя
эту схему на практике, по ее симметрии мож-
но предвидеть, что она не имеет недостатков,
свойственных однотранзисторному инвертору.
12N.5. Аналоговые коммутаторы
503
12N.5. Аналоговые
коммутаторы
В этом разделе мы познакомимся с еще одним
полезным применением КМОП-устройств в
аналоговых переключателях.
В качестве силовых ключей МОП-транзисторы
конкурируют с биполярными. Но в области
аналоговых коммутаторов — устройств, кото-
рые пропускают или блокируют прохождение
сигнала, а не просто электрического тока на на-
грузку, — МОП-транзисторы не имеют никаких
конкурентов.
12N.5.1 • Аналоговый коммутатор
на одном МОП-транзисторе
Оценить аналоговый коммутатор на КМОП-
транзисторе можно подобно тому, как мы это
делали с логическим КМОП-инвертором —
сравнив его с менее совершенным устрой-
ством20. На рис. 12N.14 изображен такой про-
стой вентиль: один МОП-транзистор, про-
пускающий или блокирующий сигнал. Чтобы
подробно разобраться со схемой справа на
рисунке, нам нужно признать наличие паразит-
ного диода в МОП-транзисторе. Этот элемент
полевого транзистора мы еще не учитывали.
Вкл
Выкл
+15 В: Вкл П
-15 В: Выкл
необходимо принимать меры предосторожно-
сти и подключить подложку к такому напря-
жению, полярность которого никогда не будет
неправильной относительно входного или вы-
ходного сигнала. Если подложку подключить
к истоку, как это сделано в силовых МОП-
транзисторах, то при закрытом транзисторе от-
рицательный входной сигнал вызовет переход
паразитного диода в режим проводимости.
Аналоговый коммутатор на МОП-транзисторе
работает должным образом только при усло-
вии, что уровень входного сигнала находится
ниже положительного напряжения управления,
подаваемого на затвор. В противном случае,
когда уровень входного сигнала приблизится
вплотную к уровню положительного питания,
напряжение Um МОП-транзистора снизится и
в конечном итоге он закроется.
12N.5.2. Усовершенствованный
аналоговый КМОП-коммутатор
Изящное усовершенствование коммутатора
на одном МОП-транзисторе — добавка па-
раллельно ему другого МОП-транзистора, но
с каналом противоположного, или комплемен-
тарного, типа, в данном случае р-канально-
го21. Соответствующая схема изображена на
рис. 12N.15. Второй транзистор управляется
—iirrE
П г 10 ком
пропускает <Г
Аналоговый коммутатор,
концептуальное представление
-15 В /
блокирует
Реализация на МОП-транзисторе Более подробное представление
(я-канальном) с подключением подложки
Рис. 12N.14. Аналоговый коммутатор на одном МОП-транзисторе
На рисунке паразитный диод подключен к от-
рицательной шине питания -15 В. Поскольку
это самая отрицательная точка в схеме, то такое
подключение гарантирует, что этот диод никог-
да не окажется под прямым смещением.
В случае аналогового коммутатора напряже-
ние на истоке и затворе колеблется с таким же
размахом, как входной и выходной сигналы,
и обычно может принимать, как положитель-
ное, так и отрицательное значения. Поэтому
сигналом обратной полярности, по сравнению
с подаваемым на затвор л-канального МОП-
транзистора, в результате чего эти два транзи-
стора или оба выключены (закрыты), или оба
включены (открыты).
Эта небольшая схемка обладает широкими воз-
можностями, в чем вы можете убедиться, мыс-
ленно представив подачу на ее вход сигнала
с RR-размахом. При входном сигнале, скажем,
вблизи отрицательного напряжения питания
20 АоЕ § 3.5.4С.
АоЕ § 3.4.1А.
504
UN. Ключи на полевых МОП-транзисторах
Входной
сигнал
U+ (открыт)
U. (закрыт)
(Л = +15 В
Транзистор Qz
полностью открыт
дЗдесь напряженней^
сигнал
,, на транзисторе^
<3» недостаточно
Транзистор Q1
i полностью открыт
уЗдесь нехватка
напряжения U^
на транзисторе Qz,
а с транзистором Q
|все в порядке
(Л = -15 В
Транзисторы Qx и Q2 помогают
друг другу поддерживать коммутатор открытым
Рис. 12N.15. Аналоговый КМОП-коммутатор, в котором п-канальный и р-канальный МОП-транзисторы помогают друг другу
Открыт?
Ослаблен?
Открыт * ~ Закрыт
Рис. 12N.16. Отклонения аналогового коммутатора от идеала: открытое и закрытое состояния
влияние ^-канального МОП-транзистора осла-
бевает, но р-канальный полностью открыт,
а в противоположной ситуации роли транзи-
сторов меняются. Посередине размаха вход-
ного сигнала оба транзистора работают доста-
точно удовлетворительно. Хорошие КМОП-
коммутаторы, наподобие тех, с которыми мы
будем работать на лабораторном занятии, без
труда справляются с таким широким размахом
входного сигнала, имея почти постоянное со-
противление открытого канала R0K.
12N.5.3. Несовершенства
Идеальный транзисторный аналоговый ком-
мутатор будет вести себя как механический
переключатель: или полностью открыт, или
полностью закрыт22. В реальности, конечно же,
и аналоговые коммутаторы, и силовые ключи
не соответствуют этому идеалу.
В открытом режиме переключатель выглядит
наподобие резистора с малым сопротивлением
(например, сопротивление транзистора DG403,
который мы будем использовать на лаборатор-
ном занятии, составляет 30 Ом или меньше).
А в закрытом состоянии переключатель выгля-
дит наподобие небольшой емкости, связываю-
щей вход с выходом (емкость того же DG403
будет около 0,5 пФ). Также в переключателе
22 АоЕ § 3.4.2.
присутствует небольшой ток утечки (для DG403
^ 0,5 нА). Важны или нет такие несовершен-
ства — зависит от конкретной схемы.
Чтобы получить представление, почему такие
несовершенства могут быть проблематичны-
ми, мы рассмотрим конкретный случай. В раз-
деле 12N.6.4 мы сможем увидеть влияние не-
которых характеристик транзистора DG403
на особенно требовательную схему выборки
и хранения. Но прежде чем приступить к этой
тяжелой работе, немного поразвлечемся, рас-
смотрев некоторые варианты применения опи-
санных устройств.
12N.6. Применение
аналоговых коммутаторов
С помощью аналоговых коммутаторов можно
решить много задач, справиться с которыми
трудно без этих устройств. Далее рассматрива-
ются несколько таких вариантов применения,
чтобы дать вам общее представление о полез-
ности этих устройств.
12N.6.1. Сброс интегратора
Рассмотрим задачу, которая на первый взгляд
кажется полностью тривиальной — сброс инте-
гратора.
UN.6. Применение аналоговых коммутаторов
505
Ручной сброс
Сброс легко осуществить с помощью механи-
ческой кнопки. Но подключить эту кнопку в
схему нужно правильным образом, не допустив
распространенной ошибки, обозначенной сло-
вом «НЕТ!» на рис. 12N.17. Такое подключение
кажется вполне правильным: просто принуди-
тельно установить нулевой выходной уровень
интегратора. В чем же заключается ошибка?23
НЕТ!
Рис. 12N.17. При правильной реализации задача ручного
сброса интегратора очень проста
Сброс с помощью транзистора
Задача сброса интегратора с помощью сигна-
ла управления оказывается не такой простой.
Будут ли работать схемы, изображенные на
рис. 12N.18? Да, будут. Но только в половине
случаев — при положительном уровне выход-
ного сигнала интегратора. При отрицательном
же уровне схема сброса будет терять работоспо-
собность: более отрицательный вывод станет
эффективным источником опорного напряже-
ния, и транзисторы обоих типов начнут откры-
ваться, даже если сигнал управления останется
на нулевом уровне, который предназначен для
закрытия транзистора-переключателя.
Простая работоспособная схема сброса
Задача сброса с помощью сигнала управления
решается с помощью аналогового коммутато-
ра. Схема, изображенная на рис. 12N.19, может
работать с выходным сигналом интегратора с
уровнем, равным максимальному уровню лю-
бого напряжения питания, при условии, что на
коммутатор подаются такие же напряжения пи-
тания, как и на операционный усилитель.
+5
о
Сброс
Рис. 12N.19. Аналоговый коммутатор с легкостью решает
задачу сброса, работая с выходным сигналом любой поляр-
ности
12N.6.2, Множество других
приложений
Мультиплексоры и их применение
Аналоговый коммутатор может пропускать
сигнал в том или ином направлении. Такая
операция, выполняемая с целью общего ис-
пользования ресурса, называется мульти-
плексированием. Примеров мультиплексиро-
вания для решения реальных задач большое
множество. Например, одна телефонная ли-
ния может использоваться несколькими або-
+5
О-
5 |—">рос г
I wv—(^
+5
0-
- Сброс
Неправильный сброс
посредством биполярного транзистора
Рис. 12N.18. Два примера неправильной схемы сброса интегратора
Неправильный сброс посредством МОП-транзистора
23 Разумеется, такое подключение не разряжает конден-
сатор. Вместо этого потенциал на противоположной об-
кладке конденсатора удаляется от виртуальной земли. В
конечном итоге конденсатор может разрядиться или не
разрядиться, в зависимости от текущего входного сигна-
ла интегратора. В любом случае, эта схема непригодна для
выполнения сброса.
нентами, подключаемыми к ней поперемен-
но коммутационной телефонной станцией.
На лабораторном занятии 12L мы соберем
более скромную схему для мультиплексиро-
вания ресурсов: мультиплексор канала ос-
циллографа, который позволит подавать на
506
12N. Ключи на полевых МОП-транзисторах
один канал осциллографа два входных сиг-
нала. А в компьютере такое устройство, как
аналого-цифровой преобразовать (АЦП), мо-
жет подключаться к нескольким источникам,
поскольку обычно одновременно его задей-
ствует только один процесс. Для этого про-
сто осуществляется маршрутизация всех этих
сигналов через аналоговый мультиплексор,
который подает сигнал на АЦП. Сначала вы-
полняется преобразование сигнала от одного
источника, после чего выполняется переход
на другой источник. Это устройство функцио-
нирует в режиме разделения времени
24
Освоив аналоговый коммутатор, вы сможете
придумать для него множество вариантов при-
менения. Это будет полезное добавление в ваш
набор приемов, позволяющее решать такие за-
дачи, как сброс интегратора, которые было бы
трудно или невозможно решить иначе.
12N.6.3. Особенно интересное
применение мультиплексора
в фильтре с коммутируемым
конденсатором
Ближе к концу лабораторного занятия 12L у
вас будет возможность испытать новый тип
низкочастотного фильтра, знаменующий сме-
ну аналоговых функций цифровыми, которая
произойдет вскоре в нашем курсе25. В данном
фильтре аналоговые переключатели дозиру-
ют заряд дискретными пакетами, эмулируя
поведение резистора. Этот метод позволяет
управлять эффективным сопротивлением
с помощью двоичного цифрового сигнала
(сигнал с двумя состояниями — включенное
и выключенное), варьируя частоту достав-
ки доз сигнала26. Скорее всего все это звучит
пока очень абстрактно. Схема на рис. 12N.20
поможет вам понять, насколько проста эта
идея.
24 АоЕ § 3.4.3.
25 АоЕ § 6.3.6.
26 Метод доставки заряда в дискретных пакетах имеет
сходство с цифровыми методами, но мы не хотим сказать,
что такой фильтр с коммутируемым конденсатором пред-
ставляет собой цифровое устройство. Нет, он не является
таковым, поскольку он управляется сигналом с непре-
рывно изменяющейся частотой. А, несмотря на дискрет-
ность доставляемых порций заряда, их величина может
непрерывно варьироваться. Более очевидно то, что вы-
ходной сигнал схемы является аналоговой величиной —
напряжением.
«30 кГц
лгих
ТТЛ
+5 В
1 кОм
Входной^
сигнал
330 пфТ 0,01 мкфТ
Выход
Рис. 12N.20. Фильтр с коммутируемым конденсатором (схе-
ма из лабораторного занятия)
В каждом периоде прямоугольного сигнала,
обозначенного как ТТЛ, небольшая порция
заряда перемещается между конденсатором
меньшей емкости и конденсатором большей
емкости. Таким образом, уровень выходного
напряжения постепенно повышается до уровня
входного.
На рис. 12N.21 приводится аналогия комму-
тации конденсатора, на которой напряжения
представлены (как обычно) уровнями воды.
Здесь пользователь пытается поддерживать
уровень воды в ведре одинаковым с уровнем
воды в проточном бассейне, набирая столовой
ложкой воду из бассейна и выливая ее в ведро.
Столовая ложка: перемещает порции
воды, стараясь
уравновесить
уровень воды
А ведре с уровнем
воды в бассейне
Бассейн с водой _
(уровень воды варьируетсяj4
={=10,000 п*
Рис. 12N.2T. Аналогия схемы коммутируемого конденсато-
ра в виде проточного бассейна, ложки и ведра
Если вы полагаете, что это слишком неуклю-
жий способ имитировать поведение резистора,
подумайте, насколько легко компьютеру варьи-
ровать частоту прямоугольного сигнала. А ведь
это все, что требуется для управления частотой
/3дБ данного фильтра.
Если после лабораторного занятия у вас оста-
нется время, то вы можете поэкспериментиро-
вать с микросхемной версией фильтра этого
типа. Это активный фильтр27 с чрезвычайно
крутым фронтом, но вместо резисторов в нем
установлен коммутируемый конденсатор, что
позволяет управлять частотой f3 дБ фильтра
27 Это 8-полюсный активный «эллиптический» фильтр
(на микросхеме МАХ294). Резкий спад его АЧХ показан
на рис. 12L.14.
12N.6. Применение аналоговых коммутаторов
507
простым поворотом рукоятки частоты на ге-
нераторе сигналов. Такая возможность легкого
управления частотой /3 также будет полез-
ной на дальнейших лабораторных занятиях,
когда этот фильтр понадобится для удаления
паразитных эффектов, вносимых в процессе
аналого-цифрового преобразования.
12N.6.4. Выборка и хранение
Эта важная схема позволяет лучше изучить
влияние несовершенства переключателя:
28
Схема выборки и хранения полезна в тех слу-
чаях, когда аналоговое значение необходимо
поддерживать постоянным в течение некото-
рого времени. Эта функция наиболее часто
востребована при подаче сигнала на аналого-
цифровой преобразователь — устройство, для
которого (в большинстве случаев) требуется
значительное время для выполнения соответ-
ствующего преобразования. В процессе преоб-
разования необходимо, чтобы напряжение на
входе АЦП не менялось.
Обычно на входе добавляется буфер, как пока-
зано на рис. 12N.22, для того, чтобы сразу же
поднять напряжение конденсатора до уровня
напряжения выборки. Для простоты в схеме из
лабораторного занятия мы опустим этот буфер,
поскольку сопротивление генератора сигналов
достаточно мало. Выходной буфер всегда тре-
буется для того, чтобы не допустить утечки за-
ряда из конденсатора.
Буфер
Вход
ВЫ6°РК1П_ хранение
Выход
Рис. 12N.22. Простая схема выборки и хранения
12N.6.5. Выбор компонентов
Прежде чем приступить к рассмотрению опре-
деленной схемы со значениями компонентов,
28 АоЕ § 3.4.3С, рис. 3.84, § 4.5.2.
рассмотрим вкратце факторы, которыми мы
будем руководствоваться при выборе емкости
конденсатора хранения.
Выбор емкости конденсатора
Чем важен правильный выбор емкости конден-
сатора хранения? Какие будут положительные
и отрицательные последствия использова-
ния конденсатора большой емкости? А малой
емкости?
Большая емкость помогает легко поддерживать
напряжение, но при этом трудно делать выбор-
ку, т. е. сложно быстро получить значение на-
пряжения.
Выборка. В процессе выборки мы хотим бы-
стро поднять напряжение на конденсаторе
[/конд до уровня входного напряжения UBX.
Конденсатор хранения заряжается через со-
противление, значение которого определяется
как сумма всех сопротивлений в цепи заряда.
Обычно среди этих сопротивлений преоблада-
ет сопротивление открытого канала аналого-
вого переключателя. Оно намного больше, чем
выходное сопротивление схемы на операцион-
ном усилителе, который буферизирует источ-
ник сигнала.
Определив значение постоянной времени RC,
можно получить первое приближение времени
захвата: подсчитываем количество постоянных
RC, чтобы определить, сколько должен длиться
импульс, чтобы свести погрешность до опреде-
ленного уровня. Например, 5 постоянных вре-
мени RC обеспечат погрешность меньше 1%.
Но могут иметь место и более тонкие эффекты.
Например, для конденсатора хранения боль-
шой емкости может потребоваться значитель-
ный ток, возможно больший, чем может обе-
спечить обычный операционный усилитель.
Кроме того, может потребоваться операцион-
ный усилитель, способный работать с емкост-
ной нагрузкой. Как вы знаете, этот тип нагруз-
ки может вызывать нестабильность (см. АоЕ,
раздел 4.5.2).
Хранение. В течение времени хранения важно
учитывать уменьшение заряда конденсатора,
которое будет иметь место в результате сумми-
рования всех токов, входящих в конденсатор и
выходящих из него. В число этих токов входят
ток утечки конденсатора, ток закрытого канала,
ток смещения операционного усилителя и ток
508
UN. Ключи на полевых МОП-транзисторах
саморазряда конденсатора. Последний скорее
всего будет ничтожным по сравнению с двумя
другими токами.
Инжекция заряда29. Это очень неприятное
осложнение, которое может вынудить исполь-
зовать конденсатор намного большей емкости,
чем необходимо при учете снижения заряда.
Явление инжекции заряда состоит в броске заря-
да, выдаваемом переключателем при его закры-
тии. Причина заключается в несимметричности
переключателя: чтобы выключить оба парал-
лельных МОП-транзистора, уровни внутренних
напряжений, управляющих их затворами, на-
растают в разных направлениях. Эти сигналы
через емкость связаны с выходом. Если бы связи
были одинаковыми, то оба эффекта аннулиро-
вали бы друг друга. Но поскольку связи не оди-
наковые, результирующий заряд на конденсатор
хранения подается в самое неудачное время —
когда он отключен от источника сигнала. Таким
образом, инжектируемый заряд добавляет ска-
чок напряжения к сохраненному значению. Чем
меньше емкость конденсатора хранения, тем
больше всплеск напряжения за счет инжекции
заряда. Далее, в разделе 12N.7.2, мы рассмотрим
некоторые ошибки, наблюдаемые в демонстра-
ционной схеме выборки и хранения.
12N.6.6. Стандартные вопросы
разработки
Далее приведен перечень вопросов, которые с
большой вероятностью могут возникнуть в про-
цессе разработки схемы выборки и хранения.
♦ Какой должна быть емкость конденсатора
хранения? (Мы знаем, что, выбирая любое
предельное значение, мы ухудшаем какие-
либо характеристики.) Достаточно большим,
чтобы ослабление заряда было приемлемым.
Рассчитаем подходящее значение по форму-
ле I=CdU/dt
♦ Здесь I обозначает сумму всех токов утечки
(аналогового переключателя, саморазрядка
конденсатора и тока смещения буфера опе-
рационного усилителя).
♦ Величина dt или At обозначает время хра-
нения, которое должно быть достаточным,
чтобы АЦП мог завершить выполняемое
преобразование.
29 АоЕ § 3.4.2Е.
♦ А величина dU или A U соответствует при-
емлемому изменению напряжения в про-
цессе преобразования. Оценка, что явля-
ется приемлемым, несколько произвольна.
Предположим, что мы допускаем общую
погрешность величиной в 1/2 разрешения
преобразователя. Но мы уже использовали
около половины общей погрешности на эта-
пе выборки: если вы вспомните, напряже-
ние конденсатора хранения 1/конд не совсем
достигло уровня входного напряжения [/вх.
Поэтому мы можем позволить ослаблению
заряда израсходовать остаток «бюджета»:
1/4 разрешения преобразователя.
Этот результат определяет нижний предел ем-
кости конденсатора хранения. Аспекты выбор-
ки задают верхний предел для данного времени
выборки. Как обычно, нам нужно сделать выбор
с учетом двух противоположных требований.
Влияние инжекции заряда
в аналоговом коммутаторе DG403
Величина инжектируемого заряда для микро-
схемы DG403 составляет 60 пКл. На первый
взгляд такая величина заряда не выглядит
большой, но только до тех пор, пока мы не уви-
дим, какой скачок напряжения A U он вызывает
при вбросе в конденсатор небольшой емкости.
Для конденсатора емкостью 100 пФ заряд ве-
личиной 60 пКл дает напряжение:
Q.= CU; LU = AQ/C = 60 пКл/100 пФ = 0,6 В.
Таким образом, опасность инжекции заряда за-
ставляет нас увеличить емкость конденсатора.
В этом же направлении нас вынуждает двигать-
ся и проблема паразитного проникновения сиг-
нала, состоящая в передаче высокочастотного
сигнала при выключении переключателя.
Короче говоря, нам требуется конденсатор с ем-
костью намного большей, чем при учете только
уменьшения заряда в нем.
12N.6.7. Кратко о погрешностях
схемы выборки и хранения
На рис. 12N.23 дано графическое представление
погрешностей схемы выборки и хранения с до-
бавленной задержкой переключения. Влияние
инжекции заряда, который также называется
12NJ. Исследуем схему выборки и хранения
509
иы
конд
г Заряд в течение RC, чтобы достигнуть уровня * UBX
-Уменьшение заряда
(ХРАНЕНИЕ)! ^"""Эффект инжекции заряда (скачок напряжения хранения)
Время захвата
I
Время
переключения
Рис. 12N.23. Графическое представление погрешностей в схеме выборки и хранения
скачком напряжения хранения30, в данном случае
является погрешностью с отрицательным на-
правлением. В примере далее в этой главе (см.
рис. 12N.26) направление эффекта противопо-
ложное. Задержки при переключении являются
еще одной причиной необходимости довольно
длительного времени для выборки или захва-
та. Аналоговому коммутатору на микросхе-
ме DG403 для переключения требуется около
100 не. Очевидно, что, рассчитав уменьшение
хранимого заряда и переменную времени RC
для захвата и решив, что выборку данных можно
осуществить в течение 10 не, мы бы серьезно за-
блуждались.
Наконец, чтобы у вас было некоторое представ-
ление, какие значения следует ожидать, далее
приводятся некоторые параметры более каче-
ственного аналогового коммутатора и хорошей
микросхемы устройства выборки и хранения.
Для аналогового переключателя ADG1211 ве-
личина инжектируемого заряда составляет
1 пКл. Это в 60 раз лучше, чем для микросхе-
мы DG403, которую мы используем на нашем
лабораторном занятии (см. раздел 12N.7.2).
А для специализированной микросхемы LF198
выборки и хранения максимальная величина
скачка напряжения хранения указывается рав-
ной 1 мВ. Это приблизительно в 100 раз лучше,
чем значение этого параметра, которое мы по-
лучили в нашей самодельной схеме выборки и
хранения, рассматриваемой в разделе 12N.7.2.
12N.7. Исследуем схему
выборки и хранения
На рис. 12N.24 изображена схема выбор-
ки и хранения, собранная на операционном
30 Англ. hold step или pedestal (пьедестал) или sample-to-
hold offset (смещение между напряжениями выборки и хра-
нения.) - Примеч. пер.
усилителе 411 и микросхеме аналогового ком-
мутатора DG403, с которой мы также будем
работать на лабораторном занятии 12L. Мы
исследуем некоторые сигналы, описывающие
эффективность работы этой схемы.
DG403
Сначала 100 пФ,
затем 0,33 мкФ
Рис. 12N.24. Упрощенное представление схемы выборки
и хранения
12N.7.1 • Поведение схемы
и ее несовершенства
Уменьшение заряда при хранении
Конденсатор небольшой емкости заряжается
быстро, но также быстро и разряжается. На
рис. 12N.25 приведена осциллограмма умень-
шения заряда (разряд) конденсатора хранения
выборки. По скорости разряда можно рассчи-
тать ток разряда:
ХРАЗР
= CdU/dt = 100 пФ • 130 мВ/600 мс ••
«100пФ-215мВ/с =
= 100 • 1012 Ф • 0,215 В « 22 пА.
Этот ток создается током утечки переключате-
ля, током смещения операционного усилите-
ля или же обоими токами? Равномерный спад
напряжения на конденсаторе 1/конд дает ответ:
очевидно, что преобладает ток смещения опе-
рационного усилителя.
Ток утечки не может быть причиной спада,
поскольку напряжение £/конд уменьшается в
510
UN. Ключи на полевых МОП-транзисторах
Время хранения: 600 ллс
Ослабление:
130 мВ
Рис. 12N.25. Скорость уменьшения заряда позволяет найти
ток утечки (С= 100 пф) (усиление осциллографа —100 мВ/де-
ление, за исключением импульса выборки на 2 канале —
5 В/деление)
интервале между первым и вторым импульсами
выборки на рис. 12N.25. Оно понижается здесь,
даже несмотря на то, что уровень входного на-
пряжения [7ВХ находится выше уровня напря-
жения UvnuTJ в течение большей части этого пе-
риода хранения. Таким образом, конденсатор
не разряжается через переключатель до уровня
входного напряжения UBX31.
Постоянный спад также соответствует поляр-
ности тока смещения операционного усилите-
ля 41132.
31 Возможно, но маловероятно, что конденсатор разряжа-
ется через переключатель к уровню отрицательного пита-
ния переключателя. Справочный листок для микросхемы
DG403 не содержит информации о знаке или пути тока
утечки разомкнутого коммутатора, но говорят, что утечка
через канал может быть намного большей, чем утечка че-
рез оксид на затвор или на подложку. Справочный листок
неявно указывает на это предположение, поскольку в нем
задается ток утечки выключенного переключателя (Switch
OFF Leakage Current). Указывается два условия входа
с уровнями входного и выходного сигналов переключате-
ля, находящимися на противоположных пределах диапа-
зона ±15 В, и в каждом из двух направлений. Токи утечки
показаны достигающими предельных значений обеих по-
лярностей. По-видимому, направление токов утечки соот-
ветствует полярности напряжения на ключе. В противном
случае не было бы смысла указывать эти предельные на-
пряжения.
32 Управляющий р-л-переход полевых р-канальных тран-
зисторов микросхемы 41 и всегда обратносмещенный,
и ток утечки направлен к двум другим выводам тран-
зистора — истоку и стоку, которые имеют более отрица-
тельный потенциал, чем затвор. Общий ток утечки также
может дополняться утечкой на подложку или корпус. Но
поскольку ток смещения возрастает экспоненциально
при повышении температуры (см. справочный листок),
можно сделать вывод, что доминирующим является ток
утечки перехода. См. кривую зависимости тока смещения
1СМЩН от температуры в разделе DC Electrical Characteristics
(Электрические характеристики по постоянному току) и
примечание (Note) 7 в справочном листке на 411. Загру-
Хотя приведенная аргументация должна быть
достаточно убедительной сама по себе, подтвер-
дим ее, используя КМОП операционный уси-
литель с чрезвычайно низким током смещения,
снова наблюдая уменьшение заряда конденсато-
ра. Для этого заменим операционный усилитель
411 (с входным каскадом на полевом транзи-
сторе с управляющим р-л-переходом и типич-
ным током смещения 1СМ = 50 пА (максималь-
ный — 200 пА) КМОП операционным усилите-
лем LMC662CN (типичный ток смещения 7СМ =
2 мкА, максимальный — 2 пА). На рис. 12N.26
показаны сравнительные осциллограммы для
схемы с этим операционным усилителем и уси-
лителем 411. Снижение величины заряда проис-
ходит приблизительно в течение 0,6 с.
Скорость разряда конденсатора хранения в
схеме с КМОП-буфером очень низкая. Разряд
можно едва различить, даже при наблюдении
в течение 20 с, как показано на осциллограмме
на рис. 12N.27.
Такая скорость разряда подразумевает чрез-
вычайно малый ток. С помощью двух горизон-
тальных курсоров мы оценили падение напря-
жение величиной около 12 мВ в течение 18 с.
Отсюда можно вычислить ток разряда:
1РАЗ = С • dU/dt = 100 • 1012 пФ • 0,66 х
х 10"3 В/с = 66 • 1015 А = 66 фА.
Это значение тока утечки находится в пределах
возможного диапазона тока смещения 7СМ для
операционного усилителя КМОП-типа. В итоге
можно сделать вывод, что данный аналоговый
коммутатор почти не имеет тока утечки:
33
12N.7.2. Инжекция заряда
Хороший буфер операционного усилителя мо-
жет свести разряд к минимуму даже при малой
емкости конденсатора. Но, как упоминалось
ранее в разделе 12N.6.5, небольшая емкость
конденсатора хранения делает схему уязвимой
к другой проблеме, решить которую труднее:
зить справочный листок на изделие компании National
Semiconductor можно здесь: http://www.ti.com/general/
docs/lit/getliterature.tsp?genericPartNumber=lf411-
n&fileType=pdf
33 Хотя ток утечки в 66 фА намного больше типичного
тока смещения 1СМ, он составляет всего лишь несколько
процентов от указанного максимального значения. Воз-
можно, что причиной утечки была наша беспаечная ма-
кетная плата.
12NJ. Исследуем схему выборки и хранения
511
Выборка
(захват)
Хранение
Хранение
Напряжение
на конденсаторе
хранения
Входной сигнал
Импульс выборки
Chi {OOmV
СЩ
Выборка и хранение с выходным бусрером микросхемы LF411
Выборка и хранение с выходным бусрером КМОТТ
операционного усилителя
Рис. 12N.26. Буфер операционного усилителя КМОП-типа уменьшает скорость уменьшения заряда в схеме выборки и хра-
нения (усиление осциллографа —100 мВ/деление, за исключением импульса выборки на канале 2 — 5 В/деление)
1
: 12,0 мВ
сигнал т
Импульс
выборки"
*L X: 1
Разряд едва
различим
(около 12 мВ
за 18 с)
Chi; 5.00 V W2.00*
Рис. 12N.27. Разряд конденсатора хранения в схеме вы-
борки и хранения с КМОП-буфером едва различим даже
при хранении в течение 20 с (усиление осциллографа —
200 мВ/деление, за исключением импульса выборки на кана-
ле 2 — 5 В/деление. Обратите внимание на другую шкалу вре-
мени, чем в рис. 12N.26: в этом рисунке шкала 2 с/деление)
влиянию инжекции заряда. При закрытии
транзисторного ключа на его выходе появляет-
ся порция заряда (типичной величины 60 пКл
для микросхемы DG403).
Поступление этого заряда на конденсатор не-
большой емкости (в данном случае 100 пФ) вы-
зывает большой скачок напряжения.
Замечание
Предсказуемая величина этого скачка составляет
0,6 В. На наших осциллограммах этот скачок мень-
шей величины, но все равно заметный. Скачок на-
пряжения хранения можно наблюдать на осцилло-
граммах на рис. 12N.26 и 12N.28.
Скачок напряжения происходит как раз в тот
момент, когда схема должна запомнить ве-
личину входного уровня, и, разумеется, не
s.oo
Рис. 12N.28. Инжекция заряда создает значительную по-
грешность при использовании конденсатора небольшой ем-
кости (100 пФ) (усиление осциллографа: 200 мВ/деление, за
исключением импульса выборки на канале 2 — 5 В/деление)
представляет ничего хорошего. Что еще хуже,
величина этого скачка непостоянна и зави-
сит от значения входного напряжения. Скачок
больше в верхней части входного сигнала, и
намного меньше в нижней части синусоиды.
Поэтому его нельзя скомпенсировать, напри-
мер, откорректировав цифровое значение, счи-
тываемое АЦП, на который подается сигнал со
схемы выборки и хранения. Разная величина
скачка напряжения хорошо заметна на осцил-
лограмме на рис. 12N.28.
12N.7.3. Большая емкость может
устранить эффект инжекции заряда
Таким образом, чтобы улучшить точность на-
шей схемы выборки и хранения, нам требуется
512
UN. Ключи на полевых МОП-транзисторах
cbiiSDomy ch2 s.oov w.ooms
Ch3 SOOmV 1Ш 500mV
Эффект инжекции заряда: С - 100 пФ
fjh
Chi «JGOmV
сиз sodmv
""сиз? s.oo'v"
ЯШ soomv
Эффект инжекции больше не наблюдается: С = 0,33 мкФ
Рис. 12N.29. Большая емкость конденсатора хранения замедляет скорость разряда, а также значительно уменьшает эффект
инжекции заряда (усиление осциллографа — 500 мВ/деление, за исключением импульса выборки на канале 2 — 5 В/деление)
конденсатор хранения намного большей емко-
сти. Это действительно так: большая емкость
уменьшит эффект от инжекции заряда, а так-
же замедлит скорость разряда конденсатора
хранения. На рис. 12N.29 показаны осцилло-
граммы, демонстрирующие, что скачок напря-
жения хранения вследствие инжекции заряда
исчезает при замене конденсатора емкостью
100 пФ конденсатором намного большей ем-
кости — 0,33 мкФ. Хотя это решение и явля-
ется эффективным, за него тоже приходится
расплачиваться, как мы увидим в следующем
разделе.
12N.7А Ограничение скорости
в процессе выборки
Увеличение емкости конденсатора хранения
решает проблему инжекции заряда, но за счет
ухудшения других характеристик схемы —
она замедляет скорость захвата выборки. На
рис. 12N.30 изображены две осциллограм-
мы сигналов схемы выборки и хранения, в
которой исходный конденсатор хранения ем-
костью 100 пФ заменен конденсатором емко-
стью 0,33 мкФ. На них можно видеть, что в те-
чение короткого периода захвата, пока длится
импульс выборки, уровень напряжения на кон-
денсаторе хранения Е/конд никогда полностью
не достигает уровня входного напряжения [7ВХ.
Можно выделить две причины задержки при
захвате входного напряжения UBX.
Линейно нарастающий заряд
На первый взгляд линейно нарастающий сиг-
нал заряда конденсатора выглядит подобно
максимальной скорости нарастания сигнала
операционного усилителя. Однако его кру-
тизна (0,04 В/мкс на левой осциллограмме на
рис. 12N.30) слишком мала для данного опера-
ционного усилителя.
Таким образом, причиной должно быть что-
то другое. Так оно и есть — это ограниченный
ток операционного усилителя, который должен
Входной
сигнал ^
^конд -
Импульс
. кС~кривая заряда
линейно нарастающий сигнал:
выгладит больше подобным
на ограничение тока, чем на
/&Г-кривую заряда
SOOmV ~ CH2 S 00 V
CM SOOmV
заряда приближается
целевому уровню...
ц
„.но затем кончается
'время выборки,.
Рис. 12N.30. Большая емкость конденсатора хранения замедляет захват: короткий импульс выборки не позволяет напряже-
нию конденсатора 1/конд достигнуть уровня напряжения входного сигнала 1/вх (усиление осциллографа — 500 мВ/деление, за
исключением импульса выборки на канале 2 — 5 В/деление)
12N.8. Материал для чтения в АоЕ
513
заряжать или разряжать конденсатор хранения.
Максимальный выходной ток JBbIX_MAKC можно
рассчитать по крутизне этой кривой:
hblX-UAKC=CdU/dt =
= 0,33 мкФ • 0,04 В/мкс « 0,013 А = 13 мА.
Это лежит в пределах паспортных значений для
микросхемы LMC66234.
Закругленный конечный участок кривой
Закругленный участок в конце линейно нарас-
тающей кривой заряда похож на 1?С-кривую
заряда: здесь ключ на полевом транзисторе
работает как резистор, и конденсатор хране-
ния заряжается через сопротивление открыто-
го канала. Если считать постоянную времени
RC равной 10 мкс (очень грубое приближение,
поскольку по этой части ЯОкривой трудно су-
дить), тогда:
R = ДС/0,33 мкФ = 10 мкс/0,33 мкФ * 30 Ом.
Это значение также находится в пределах заяв-
ленных характеристик устройства
,35
Импульс выборки должен быть коротким, по-
скольку желательно побыстрее выполнить пре-
образование аналогового значения в цифровое.
Поэтому замедляющий эффект, из-за большой
емкости конденсатора хранения, создает про-
блему. Таким образом, нам снова напомни-
ли общеизвестную истину: ресурсы проекта
обычно ограничены, и за оптимизацию одной
характеристики (в рассматриваемом случае
подавление эффекта инжекции заряда) прихо-
дится расплачиваться ухудшением какой-либо
другой характеристики (в данном случае вре-
менем захвата). Увеличение емкости конденса-
тора хранения при этом нежелательно.
Отсюда можно сделать вывод, что разработка
хорошей схемы выборки и хранения являет-
ся нелегкой задачей. Нам в действительности
нужен высококачественный переключатель с
малой инжекцией заряда, а не обычный ключ,
для которого затем потребуется конденсатор
хранения большой емкости для подавления
инжекции.
34 Для микросхемы LMC662C указывается предельный
выходной ток /вых величиной 13 мА при напряжении пита-
ния 5 В. Наша схема питается от двухполярного источника
напряжением ±5 В.
35 Для микросхемы DG403 типичное значение сопротив-
ления открытого канала равно 20 Ом, а максимальное -
45 0м.
А в реальной жизни, чтобы получить хоро-
шую схему выборки и хранения, мы почти
всегда пойдем самым легким путем — при-
обретем это устройство у тех, кто зарабаты-
вает себе на жизнь разработкой таких схем.
Следующая схема выборки и хранения, с ко-
торой нам придется иметь дело, будет скрыта
внутри аналого-цифрового преобразовате-
ля, с которым мы будем работать на лабора-
торном занятии по микрокомпьютерам. Это
будет микросхема AD7569 компании Analog
Devices или АЦП, встроенный в контроллер
компании SiLabs. Разработчики АЦП позабо-
тились о том, чтобы влияние скачка напряже-
ния хранения не превышало значимый уро-
вень, и используют конденсаторы хранения
достаточно малой емкости, чтобы обеспечить
быстрый захват (достаточно быстрый, чтобы
удовлетворить требованиям заданного време-
ни преобразования)36.
12N.8. Материал для чтения
в АоЕ
Чтение
♦ Глава 3:
• вводный обзор: раздел 3.1 (введение, ха-
рактеристики полевых транзисторов) по
раздел 3.14 (линейная область и область
насыщения);
• раздел 3.2.8С: ток затвора, в особенности
динамический ток затвора;
• более важным является очень длинный
раздел 3.4 по полевым транзисторам.
Игнорируйте в нем материал по переклю-
чателям на полевых транзисторах с управ-
ляющим р-я-переходом;
• раздел 6.3.6: краткое обсуждение разра-
ботки фильтра с коммутируемым конден-
сатором.
36 Микросхема АЦП AD7569 выполняет преобразование
в 8-разнядное число в течение 2 мкс, причем около 200 не
(один такт) приходится на захват аналогового уровня
встроенной схемой выборки и хранения. А для АЦП ком-
пании SiLabs требуется 5 мкс, но разрешение сигнала здесь
в 16 раз выше, поэтому характеристики схемы выборки
и хранения еще более впечатляющие.
12L Лабораторное занятие: ключи
на полевых МОП-транзисторах
Это лабораторное занятие начинается с крат-
кого обзора способов применения мощных по-
левых МОП-транзисторов в качестве силовых
ключей. Полевые МОП-транзисторы составля-
ют альтернативу мощным биполярным тран-
зисторам, с которыми мы познакомились на
лабораторном занятии 4L. Сначала мы выпол-
ним небольшое упражнение по использованию
мощных полевых МОП-транзисторов. В этом
упражнении мы хотим продемонстрировать
громадное входное сопротивление по постоян-
ному току этих устройства, но также и большую
входную емкость, в результате которой возни-
кают трудности с быстрым переключением.
Оставшаяся часть лабораторного занятия от-
водится на работу с приложениями для анало-
гового коммутатора или интегрального преры-
вателя. Этот переключатель может пропускать
сигнал в любом направлении и является хоро-
шим приближением механического (или более
точно, электромеханического) переключателя,
который называется реле.
В самой важной из рассмотренных схем анало-
говый ключ сочетается с операционным уси-
лителем. Последнее обстоятельство является
одной из причин, по которым мы решили от-
ложить данное лабораторное занятие по по-
левым транзисторам до настоящего времени.
(Логически было бы естественным, если поле-
вые МОП-транзисторы рассматривались вслед
за биполярными транзисторов.) Эта комби-
нация является схемой выборки и хранения,
которая часто используется в устройстве для
преобразования аналоговых сигналов в соот-
ветствующую цифровую форму. Схема выбор-
ки и хранения захватывает значение входного
сигнала и в течение процесса преобразования
поддерживает его постоянным. Кроме того,
в нашем случае схема выборки и хранения слу-
жит для нас хорошей тестовой площадкой для
демонстрации возможностей аналогового пе-
реключателя, позволяя раскрыть несовершен-
ства этого компонента.
12L1. Мощный полевой
МОП-транзистор
В этом эксперименте мы повторим задание, ко-
торое выполняли в упражнении 4L.5, используя
биполярный транзистор. Но в данном случае
биполярный транзистор мы заменим на поле-
вой МОП-транзистор (рис. 12L.1). В табл. 12L.1
приведены основные параметры двух полевых
транзисторов, которые мы будем использовать.
Оба транзистора открываются при подаче на их
затвор только высокого уровня напряжения иж
В некоторых отношениях МОП-транзисторы
намного лучше, чем их биполярные эквивален-
ты. Их громадным достоинством, которое мы
вскоре подтвердим, является очень большой
входной импеданс, по крайней мере, по посто-
янному току.
Таблица 12L.1. Параметры мощных
МОП-транзисторов
Транзистор
BUK9509-40B
IRLZ34
^си-вкл
(макс),
мОм
10
70
1/зи (порого-
вое макс), В
4,5
4,0*
Произво-
дитель
NXP
IR
Примечание
Для порогового напряжения 1/зи в справочнике
указана величина 2,0 В, но это значение не очень
полезно, потому что оно дано для малого тока
(0,25 мА для транзистора IRLZ34). Очень маловеро-
ятно, что данный мощный МОП-транзистор будет
использоваться при таком малом токе. При оценке
необходимого управляющего напряжения (Узи луч-
ше учесть то обстоятельство, что сопротивление
открытого канала /?вкл указано для напряжения 1/зи
величиной 4 и 5 В. Поэтому для порогового значе-
ния напряжения (Узи мы приняли значение 4 В.
J2L7. Мощный полевой МОП-транзистор
515
| Нагрузка]
IRLZ34
BUK9509-40B
(NXP)
тепловое сопротивление «переход
щая среда» будет:
окружаю-
*Пороговое напряжение
логического уровня (низкого)
Рис. 12L.1. Ключ на мощном МОП-транзисторе
12L1.1. Рассеиваемая мощность
Оба прибора являются сильноточными: рабо-
чий ток транзистора BUK9509-40B составляет
75 A, a IRLZ34 — 30 А. Но эти большие зна-
чения могут быть обманчивыми. Указанные
характеристики даны при условии, что тем-
пература корпуса устройств составляет 25 °С,
что практически невозможно при больших
токах. Более важна номинальная мощность.
Хотя и эти параметры могут вводить в за-
блуждение. Для устройств заявлена высокая
предельная рассеиваемая мощность: 175 Вт для
BUK9509-40B и 68 Вт для IRLZ34. Но опять
же, при температуре корпуса 25 °С. А при тем-
пературе, например, 75 °С, что более вероятно
при сильном токе, транзистор BUK9509-40B
может рассеивать всего лишь около 100 Вт,
a IRLZ34 - 45 Вт, а при температуре 100 °С -
80 и 44 Вт соответственно1.
Поэтому мы обязаны учитывать повышение
температуры этих транзисторов, вызываемое
выделяющейся в них мощностью. В справоч-
ных данных для транзисторов указывается их
тепловое сопротивление, что позволяет нам
вычислить мощность, которую они могут рас-
сеивать как с теплоотводом, так и без него.
Так,длявертикальноустановленноготранзисто-
ра BUK9509-40B без теплоотвода приводится
типичное тепловое сопротивление «переход —
окружающая среда» #епос = бОК/Вт = 60 °С/Вт2.
Добавление теплоотвода, конечно же, значи-
тельно улучшает тепловые характеристики.
Теплоотвод больших размеров 7022BG компа-
нии Aavid для корпуса типа 220 обеспечивает
6,5 °С/Вт. А теплопроводная прокладка до-
бавляет еще 0,6 °С/Вт, в результате чего общее
1 АоЕ§§9.12.1С и 9.4.2В.
2 В наших примечаниях по тепловому сопротивлению ис-
пользуются единицы °С/Вт, а не К/Вт. Эти единицы равно-
значны. Обратите внимание на то, что в единицах с граду-
сами Кельвина знак градусов (°) не указывается.
*епос =
*екос = <0'95
Если переход транзистора нагрет до темпера-
туры 150 °С (что 25 °С меньше предельного
значения) и температура окружающей среды
составляет 50 °С, то разница между этим двумя
параметрами будет 100 °С. Посмотрим, какую
мощность транзистор сможет рассеивать в этих
условиях как с теплоотводом, так и без него.
♦ Рассеиваемая мощность вертикально установ-
ленного транзистора без теплоотвода (пас-
сивного или активного) будет следующей:
Р = (скорость теплопередачи) х
х (перепад температур) = (1/Де) • АГ =
= (1/Rmoc)-AT = (1/60). 100 =
= 0,016 • 100 * 1,6 Вт.
♦ С теплоотводом:
Р= (1/8,1). 100 «12 Вт.
Таким образом, полученные реальные величи-
ны очень далеки от впечатляющего значения
175 Вт, заявляемого для устройства, работаю-
щего при температуре корпуса, равной 25 °С.
12L1.2. Входной импеданс
Соберите схему, изображенную на рис. 12L.2.
В качестве нагрузки возьмите лампочку № 47
(6 В, 0,15 А) и убедитесь, что полевой транзи-
стор будет включать и выключать лампочку при
подаче на его затвор через резистор номиналом
10 кОм управляющего сигнала низкой частоты.
(Подача сигнала на резистор выполняется вруч-
ную, переключением провода между шиной
«земли» и шиной питания +5 В.) Как мы знаем,
высокий входной импеданс является сильной
стороной полевых МОП-транзисторов.
5В
О Ю кОм I
1
#Лампочка № 47 (6 В, 0,15 А)
Замените двумя параллельными
резисторами номиналом 100 Ом
для следующего эксперимента
Рис. 12L.2. Схема для демонстрации высокого входного им-
педанса (Изогните выводы транзистора в корпусе ТО-220 на
90°, чтобы облегчить вставку транзистора в макетную плату.)
516
12L Лабораторное занятие: ключи на полевых МОП-транзисторах
Чтобы получить более наглядное представ-
ление, что именно означает высокий входной
импеданс, не подключайте ни к чему вывод ре-
зистора, на который подается сигнал, а затем
одной рукой прикоснитесь к этому вывода, а
другой рукой попеременно дотрагивайтесь то
до шины «земли», то до шины питания +5 В.
Впечатляет? Теперь, после открытия или за-
крытия полевого транзистора, отпустите вы-
вод входного резистора. Подумайте, почему
полевой транзистор как будто бы помнит по-
следнее «указание», которое вы ему дали3. Это
упражнение, каким бы легкомысленным оно
ни казалось, напоминает об удивительных ре-
зультатах, которые вы будете получать, если
забудете подключить вход МОП-устройства
к положительному или отрицательному по-
тенциалу. При этом результаты могут быть со-
вершенно непредсказуемыми.
12L1.3. Переключение
на высоких частотах
Влияние входной емкости
Заменив лампочку резисторами (рис. 12L.3),
подайте на вход МОП-транзистора однопо-
лярный прямоугольный сигнал амплитудой
+5 В от генератора сигналов. Пусть входной
резистор номиналом 10 кОм пока остается
в схеме. Наблюдайте за напряжением на за-
творе U3 и выходным напряжением по мере
повышения частоты входного сигнала начиная
+5.В
100 Ом
£Г
ЮкОм
100 0м
Рис. 12L.3. Схема для демонстрации ограниченной скоро-
сти переключения полевого транзистора
приблизительно с 10 кГц. В чем здесь пробле-
ма4? Сигнал на затворе должен выглядеть до-
вольно странно.
Эта проблема решается заменой резистора
10 кОм на меньший, который работает лучше
на высоких частотах. Теперь посмотрите, как
функционирует переключатель на частоте в не-
сколько сотен килогерц.
12L1А Сравнение биполярного
и полевого транзисторов
по мощности рассеивания
Теперь мы проведем более интересный экспе-
римент, устроив «соревнование» по рассеива-
нию мощности между биполярным и полевым
транзисторами. Схема для такого опыта изо-
бражена на рис. 12N.4.
(Большие мощные резисторы!)
+5 В
Подсоедините к шине +5 В,
чтобы включить (открыть)
транзисторы.
82 0м
.,5. _!?_ JL)" Биполярный
«•?- ir. К} МОП-транзистор
Рис. 12L.4. Соревнование по рассеиванию мощности между биполярным и полевым МОП-транзисторами. (Изогните выводы
транзистора на 90°, чтобы облегчить его вставку в макетную плату.)
3 Ваш конкретный полевой МОП-транзистор может или
«помнить» или нет, в зависимости от максимальной ско-
рости утечки, которая может быть довольно высокой (см.
соответствующий справочный листок).
4 Да, резистор номиналом 10 кОм создает трудности с за-
рядом емкости затвора, особенно емкости Сзс, которая по-
вышается (удваивается) вследствие того, что полярность
выходного сигнала (на стоке) противоположна полярно-
сти входного сигнала (на затворе). Этот эффект подробно
рассматривается в разделе 12N.2.3.
12L2. Аналоговые коммутаторы
517
В некоторых отношениях эти транзисторы по-
хожи друг на друга: у них одинаковый корпус
(типа ТО-220), и некоторые их рабочие харак-
теристики находятся приблизительно в оди-
наковом диапазоне. Для биполярного транзи-
стора заявлен непрерывный рабочий ток вели-
чиной 10 А. (Но, опять же, без учета тепловых
ограничений, которые рассматривались для
МОП-транзисторов в разделе 12L.1.1.)
По максимальному рабочему току и рассеи-
ваемой мощности пока трудно сказать, какой
из транзисторов станет победителем. Победа
будет зависеть в основном от падения напря-
жения на транзисторе, которое указывается
по-разному для биполярных и полевых тран-
зисторов. Но МОП-транзистор должен иметь
довольно хорошие шансы на победу в соревно-
вании, целью которого является передать пода-
ваемую мощность в нагрузку, а не рассеивать ее
в виде тепла.
Запустите процесс соревнования, пропуская
одинаковый ток (приблизительно 0,5 А) через
оба транзистора, и измерьте падение напряже-
ния на каждом из них. Нагрузочные резисторы
должны иметь номинальную мощность 5 Вт
или больше. Если вы забудете этот совет и возь-
мете резисторы с номинальной мощностью,
например, 0,25 Вт, то сожженный резистор или
даже обожженные пальцы сразу напомнят вам
об ошибке.
Сравнение по падению напряжения
По значению падения напряжения иси можно
рассчитать сопротивление открытого канала
1?вкл полевого транзистора, а по значению на-
пряжения икэ — эквивалентное значение для
биполярного (хотя для биполярных транзи-
сторов этот термин не применяется). Затем
можно вычислить рассеиваемую каждым
транзистором мощность (что выставит поле-
вой транзистор в еще лучшем свете), не забы-
вая при этом включить в расчет значительную
мощность, рассеиваемую в результате наличия
тока базы.
Тот факт, что большая часть мощности в этих
схемах передается в нагрузку, а не рассеивается
в транзисторах, можно практически подтвер-
дить, прикоснувшись пальцем к нагрузочному
резистору, а затем к транзистору. Резистор дол-
жен быть намного теплее, чем транзистор.
12L2. Аналоговые
коммутаторы
Аналоговые коммутаторы на КМОП-устройст-
вах часто являются наиболее подходящими для
задач, которые трудно решить иным способом.
Цель данного лабораторного занятия — позна-
комить вас с этим полезным устройством. Как
можно увидеть по схеме на рис. 12L.5, аналого-
вый коммутатор работает предельно просто: он
или пропускает сигнал, или нет.
Исток
А,
Сток
Вход _
о-
Рис. 12L5. Общее представление аналогового коммутатора
Используемый нами коммутатор обладает осо-
бенно хорошими характеристиками: он управ-
ляется стандартными логическими уровнями
0 В (выключен) и +5 В (включен). Но он может
передавать аналоговый сигнал с величинами в
диапазоне его напряжений питания, для кото-
рых мы будем использовать ±15 В. Это двухпо-
зиционный переключатель, который прекрасно
подходит для выбора одного из двух источни-
ков или нагрузок.
На рис. 12L.6 показаны внутреннее устройство
прибора и его цоколевка.
Входной сигнал подавайте от генератора, а
в качестве источника логических уровней для
включения и выключения коммутатора ис-
пользуйте один из ползунковых переключате-
лей на макетной плате. Наиболее удобным бу-
дет 8-позиционный переключатель. Установите
один из его ползунков во включенное положе-
ние. Теперь уровень этой точки будет высоким
или низким, в зависимости от положения пол-
зунка переключателя.
Внимание!
Микросхема DG403 содержит два аналоговых ком-
мутатора. Подсоедините неиспользуемые выводы
микросхемы к общей шине или к шине +5 В. Таким
образом входной логический сигнал не окажется
где-то посередине между этими двумя уровнями,
что может вызвать чрезмерный нагрев или даже
выход микросхемы из строя.
518
12L Лабораторное занятие: ключи на полевых МОП-транзисторах
(Логическое устройство) (Цоколевка)
Микросхема аналогового коммутатора DG403. Ключи показаны с высоким уровнем на входе (логическая «1»)
Рис. 12L.6. Блок-схема и цоколевка микросхемы DG403 производства компании Maxim
Еще одно напоминание: для этой микросхе-
мы требуется три напряжения питания: +15 В,
-15 В, +5 В и «земля». Непременно подключи-
те микросхему ко всем четырем шинам.
12L2.1. Несовершенства
аналогового коммутатора
К сожалению, как все в нашей жизни, так и
в электронике, аналоговый коммутатор не яв-
ляется идеальным устройством. Вы можете
убедиться в этом, измерив его сопротивление
во включенном состоянии и проходную ем-
кость в выключенном состоянии. Но основным
и более интересным предметом оставшейся ча-
сти этого лабораторного занятия является при-
менение аналоговых коммутаторов. Поэтому
не медлите и быстренько выполните эти пред-
варительные измерения.
измерьте сопротивление открытого канала
^вкл-
вольт
1к0м
1кГц
■ К осциллографу
■2-0-
+5
Рис. 12L7. Измерение сопротивления открытого канала /?вкл
«Просачивание» сигнала
В схеме на рис. 12L.8 наш коммутатор выглядит
лучше: по сравнению с резистором номиналом
100 кОм его сопротивление открытого канала
незначительное. Убедитесь в этом на опыте.
Измерение сопротивления
открытого канала
В идеале во включенном состоянии коммутатор
должен быть просто закорочен. Но в действи-
тельности он обладает небольшим сопротивле-
нием, называемым сопротивлением открытого
канала Двкл. Соберите схему, изображенную на
рис. 12L.7, и используйте ее, чтобы измерить
это сопротивление. Подайте на вход коммута-
тора синусоидальный сигнал частотой 1 кГц
и амплитудой в несколько вольт. Убедитесь,
что ключ включается и выключается, а затем
Входной
сигнал
>ААЛ<1» Х-**
«Земля»
К осциллографу
: 100 кОм
Рис. 12L.8. Более типичная прикладная схема (/?вкл сделано
незначительным)
Проходит ли сигнал через выключенный ком-
мутатор? Попробуйте выяснить это сначала с
синусоидальным сигналом высокой частоты
UL2. Аналоговые коммутаторы
519
(^ 100 кГц), а затем с прямоугольным сигна-
лом. Если сигнал проходит через выключенный
коммутатор, то как это объяснить?5
Примечание
При проведении опыта не забудьте, что вы наблю-
даете выходной сигнал, используя щуп осцилло-
графа, чья емкость (с «землей») может быть более
важной, чем его большое входное сопротивление:
т. е. вы в действительности наблюдаете за работой
емкостного делителя. При условии, что вы не забу-
дете об этой емкости щупа, у вас не должно воз-
никнуть никаких проблем с вычислением проход-
К осциллографу
ной емкости С
си*
12L2.2. Применения аналогового
коммутатора
Работа с вариантами применения аналогового
переключателя на этом лабораторном занятии
будет занимательной. Может оказаться, вам не
хватит времени, чтобы испробовать все пред-
лагаемые схемы. Но в любом случае мы наде-
емся, что вы сможете поэкспериментировать
с применением схемы выборки и хранения.
Схема коммутатора каналов
для осциллографа
Схему на рис. 12L.9 можно использовать в качест-
ве простого способа превратить одноканальный
Основной сигнал
(с постоянной
составляющей)
ТТЛ/Тактирование1.
MSWX.
«ТТЛ» макетной плати
Рис. 12L.9. Схема коммутатора позволяет отображать два
сигнала на одноканальном осциллографе
Вопрос. Какие ограничения у этого метода?6
Чтобы изображение на экране было стабиль-
ным, используйте для запуска развертки один
из входных сигналов (предпочтительней пря-
моугольный TTL-сигнал*), а не сигнал с выхода
коммутатора, который содержит переходные
помехи, которые могут нарушить синхрони-
зацию осциллографа. Если ваш осциллограф
имеет опцию отображения только в виде точек,
используйте ее: в этом режиме не отображается
линия, соединяющая верхний и нижний сигна-
лы. На рис. 12L.10 показан обычный режим и
режим отображения только точек.
Справа на рис. 12L.10 показана осциллограм-
ма сигнала в режиме отображения только то-
чек при остановленном осциллографе. Можно
ясно видеть отдельные точки переключае-
мых изображений сигнала: сначала точка на
\.
Обычный режим отображения: Режим отображения только точек Режим отображения только точек,
луч соединяет точки на верхнем зафиксированный сигнал.
и нижнем сигнале Можно наблюдать эффект коммутации
Рис. 12L10. Цифровой осциллограф может скрывать луч в промежутке между двумя отображаемыми сигналами
осциллограф в двухканальный (и даже с
большим числом каналов, если хотите).
5 В выключенном состоянии вход и выход связывает па-
разитная емкость.
6 Основным ограничением является скорость. Кратковре-
менный импульс, возникший на одном входе, не появится
на экране осциллографа, если в этот момент схема пере-
ключена на другой вход. Кроме того, сопротивление от-
крытого канала в комбинации с емкостью осциллографа
ограничивает время нарастания и спада сигнала.
7 Сокращение термина транзисторно-транзисторная ло-
гика: семейство логических микросхем на биполярных
транзисторах. Мы познакомимся с этим типом логики на
лабораторном занятии 14L.
520
12L Лабораторное занятие: ключи на полевых МОП-транзисторах
синусоидальном сигнале, затем на прямоуголь-
ном, потом снова на синусоидальном.
Схема выборки и хранения
Эта схема очень важна. Оно используется для
захвата (выборки) напряжения сигнала и хра-
нения захваченного значения выборки, пока
выполняется какой-либо процесс (обычно
преобразование из аналоговой в цифровую
форму).
Соберите схему, изображенную на рис. 12L.11,
и поэкспериментируйте с ней. Можете ли вы
предположить по уменьшению уровня сигнала
в режиме хранения какие пути утечки являются
преобладающими?
Совет
Это будет трудной задачей даже после присталь-
ного рассматривания экрана осциллографа в тече-
ние нескольких минут, поэтому не стоит уделять ей
все оставшееся время.
(ручной переключатель)
Рис. 12L.11. Схема выборки и хранения
Вопрос. Какие факторы принимаются к рас-
смотрению при выборе значения емкости кон-
денсатора хранения? Какие хорошие эффекты
и какие плохие будут результатом выбора ем-
кости этого конденсатора, которая: а) очень
велика и б) очень мала8?
Можете ли вы заметить эффект инжекции за-
ряда сразу же после смены полярности вход-
ного управляющего сигнала? Сравните сте-
пень влияния инжекции заряда и скачка на-
пряжения, который вы бы предсказали для
заряда, указанного в справочном листке на
устройство (типичное значение < 60 пКл для
микросхемы DG403), и емкости конденсато-
ра хранения.
Динамическое представление инжекции
заряда (факультативное задание). Если пе-
риодически выполнять инжекцию заряда,
включая и выключая ключ, подавая на него
прямоугольный сигнал, то можно четко увидеть
вызываемый этой инжекцией скачок напряже-
ния9. Когда мы выполняли данное упражнение,
уровень напряжения хранения значительно
превышал уровень входного напряжения. При
этом разница между двумя уровнями зависит
от напряжения сигнала, как вы сами сможете
убедиться. Можете ли вы объяснить причину
этого эффекта?10
Несомненно, что высококачественные спе-
циализированные схемы выборки и хранения
должны работать лучше, что в действительно-
сти так и есть. Например, величина заряда ин-
жекции микросхемы AD582 составляет < 2 пКл.
Также см. раздел 3.4.2Е книги АоЕ.
Отрицательное питание
из положительного
(«плавающий» конденсатор)
Мы знаем, что с помощью катушки индуктив-
ности в импульсном стабилизаторе напряже-
ния можно создать отрицательное выходное
напряжение из положительного входного.
Возможно, что вы даже собрали такую схе-
му на лабораторном занятии 11L. Но иногда
для слаботочных устройств предпочтительней
схема, изображенная на рис. 12L.12, которая
не требует катушки. Секрет этой схемы состо-
ит в перемещении «земли» хитрым способом.
«Плавающий» конденсатор также можно ис-
пользовать подобным образом для получения
выходного напряжения, превышающего вход-
ное. Но эта схема обеспечивает небольшой вы-
ходной ток, в чем можно удостовериться, под-
ключив к ней нагрузку.
Подобные схемы часто встраиваются в ми-
кросхемы, для которых в противном слу-
чае потребовался бы или источник отрица-
тельного напряжения, или другой источник
8 Конденсатор очень большой емкости будет разряжаться
весьма медленно и не даст больших скачков напряжения
выборки вследствие инжекции заряда. Но он очень мед-
ленно заряжается до уровня напряжения входного сигнала,
требуя длительного импульса выборки. Такой длительный
импульс выборки замедляет процесс выборки и хранения.
9 Мы благодарим наших студентов, Вольфа Баума (Wolf
Baum) и Тома Киллиана (Tom Killian), за то, что они по-
казали нам этот метод в 1988 г.
10 По-видимому, изменение напряжения на переключа-
теле вызывает варьирование емкостей между двумя вну-
тренними сигналами переключения микросхемы и ее вы-
ходом. В идеале эти емкости были бы одинаковыми, и их
эффекты аннулировали бы друг друга.
12L2. Аналоговые коммутаторы
521
I СЬ
Входное постоянное
напряжение (положительное)
ОД мкф£
Сигнал ТТЛ
от макетной платы •
10-100 кГц
Выходное постоянное напряжение * -UBX
+J1 мкФ
к ll i
(вывод 14) '
1!_ Схема инвертора напряжения,
^ которая питает сама себя!
Рис. 12L.12. Схема инвертора напряжения с «плавающим» конденсатором
положительного напряжения более высокого, заряда), а также от скорости перемещения за-
чем первое1
ряда (fTAKT):
Упражнение 1. Фильтр с коммутируемым
конденсатором из дискретных деталей
Соберите схему фильтра12, изображенную на
рис. 12L.13. Подайте на ее вход синусоидаль-
ный сигнал от генератора сигналов, при этом
тактируя схему прямоугольным ТТЛ-сигналом
от макетной платы. Частота^ дБ этого фильтра
задается частотой сигнала тактирования, что
делает фильтр удобным для управления с по-
мощью компьютера.
+5 В
1
1 кОм
Выход
/ТАКТ*
(12L.1)
«30 кГц
«ТТЛ» ~~Й>
Входной сигнал
330пФ|0,01мкФ I
Рис. 12L.13. Низкочастотный фильтр с коммутируемыми
конденсаторами
Эквивалентная #С-цепочка, эмулируемая этой
схемой заряда порциями, зависит от соотноше-
ния емкости двух конденсаторов (т. е. от раз-
мера отдельной порции относительно общего
11 Например, такой источник напряжения иногда требу-
ется для полупроводниковых устройств хранения (памя-
ти). Когда-то в прошлом некоторым микросхемам памяти
требовалось питание как напряжением +12 В, так и напря-
жением +5 В. Прием с «плавающим» конденсатором по-
ложил конец этому, обеспечив дополнительный источник
питания, встроенный в саму микросхему. Микросхемы,
которые не обладали такой возможностью, были вытесне-
ны с рынка.
12 АоЕ § 6.3.6А.
Для данной схемы формула преобразуется так:
/3дБ=(0,03/2я)-/т
ТАКТ*
(12L.2)
Поэкспериментируйте с этой схемой и сравни-
те получаемое вами значение^ дБ для нее с зна-
чением, рассчитанным по формуле. Похожи ли
в общем характеристики данного фильтра на
характеристики обычного ЯС-фильтра? В част-
ности, дает ли он такой же фазовый сдвиг на
частоте /3дЪ, который бы наблюдался в низко-
частотном ЯС-фильтре? Варьируется ли его ча-
стота^ дБ при изменении частоты сигнала так-
тирования? Поскольку это фильтр дискретного
сигнала, можно ожидать, что быстрое измене-
ние входного сигнала относительно скорости
передачи выборок прямоугольным сигналом
(частота выборки) нарушит работу фильтра.
Этот эффект называется наложением спектров.
Вопросы частоты выборки, включая проблему
наложения спектров, подробно рассматрива-
ются на лабораторном занятии 18L по аналого-
цифровым преобразованиям. Однако имейте
в виду, что проблемы возникнут, когда частота
входного синусоидального сигнала приближа-
ется к половине частоты сигнала выборки, по-
даваемого на входы управления аналогового
переключателя.
Можете ли вы наблюдать просачивание сиг-
нала тактирования в основной сигнал? Иногда
для того, чтобы ослабить эти помехи, на выход
фильтра с коммутируемыми конденсаторами
устанавливается пассивный низкочастотный
фильтр.
522
12L Лабораторное занятие: ключи на полевых МОП-транзисторах
Упражнение 2. Фильтр
с коммутируемыми конденсаторами
на микросхеме
Этот фильтр на микросхеме более сложный, чем
тот, который мы собрали в предыдущем упраж-
нении из дискретных деталей. Предлагается
несколько разных видов микросхем фильтров
с коммутируемыми конденсаторами. Главным
образом это активные фильтры на операцион-
ных усилителях, подобные тому, с которым мы
вкратце имели дело на лабораторном занятии
9L, с тем исключением, что в них используются
коммутируемые конденсаторы для эмулирова-
ния работы резистора. Такой принцип позво-
ляет с легкостью управлять параметрами эк-
вивалентной ЛС-цепочки, как мы убедились в
предыдущем упражнении. Некоторые фильтры
на микросхемах позволяют пользователю зада-
вать тип фильтра.
Фильтр, с которым мы будем работать, такими
возможностями не обладает и жестко сконфи-
гурирован как низкочастотный, что облегчает
его подключение в схему. Это 8-полюсный эл-
липтический фильтр. Такой фильтр жертвует
другими характеристиками, чтобы получить
невероятно крутой спад. Мы будем изучать ра-
боту этого фильтра далее на лабораторном за-
нятии 23L по аналого-цифровому сопряжению.
Здесь мы просто хотим, чтобы вы увидели его
резкий спад и как легко с ним работать.
Примечание
Если вы решите собрать эту схему сейчас, сделайте
это на отдельной макетной плате, чтобы потом ис-
пользовать данный фильтр на лабораторном заня-
тии 23L В противном случае фильтр можно будет
собрать, когда в нем возникнет надобность.
+5 В
Подобно простому фильтру с коммутируемы-
ми конденсаторами частота/3дБ этого фильтра
пропорциональна его частоте тактирования.
Эта свойство будет особенно полезно далее,
когда нам нужно будет варьировать эту часто-
ту в широких пределах, не переделывая полно-
стью схему фильтра.
Соберите схему, изображенную на рис. 12L.13,
используя в качестве сигнала тактирования
ТТЛ-источник прямоугольного сигнала на
макетной плате. Сигнал на аналоговый вход
фильтра подавайте от внешнего генератора
сигналов. Входной сигнал необходимо сме-
стить по постоянному току, чтобы его размах
был в диапазоне приблизительно от 1 до 4 В.
Необходимость смещения по постоянному
току объясняется тем, что фильтр питается
не от двухполярного источника, как в нашем
самодельном фильтре с коммутируемыми
конденсаторами (см. рис. 12N.13), а от одно-
полярного.
Для тестирования этого фильтра установите
частоту ТТЛ-сигнала на макетной плате около
100 кГц, что обеспечит частоту /3дБ фильтра в
районе 1 кГц. (Частота/3дБ=/ТАКГ/100.) Подайте
на вход фильтра синусоидальный сигнал ам-
плитудой около 1 В, отцентрированный на
уровне 2,5 В; варьируйте частоту сигнала, начи-
ная со значения, намного меньшего до намно-
го большего, чем частота ^дБ. Опять же, этот
фильтр не сможет работать должным образом,
когда частота входного сигнала превысит при-
близительно половину частоты ТТЛ-сигнала
тактирования (который задает частоту выбор-
ки фильтра). В таком случае снова имеет место
наложение спектров.
ОД мкФ
— (Л
(логические уровни: 0-5 В)
ОД мкФ
»10кОм
20
Частотная характеристика
фильтра МАХ294
Тактирование
Выход Выход фильтра
юерационного усилителя)
Вход Земля
операционного усилителя)
Вход фильтра
Выход £-20
фильтра
5-40
<1
1
ЮкОм
-80
-100
0 12 3 4 5
Частота входного сигнала (кГц)
Рис. 12L14. Низкочастотный фильтр с коммутируемыми конденсаторами на микросхеме МАХ294. (Частотная
характеристика показана относительно частоты т*3д6 которую можно настраивать.)
12L3. Импульсный усилитель звуковой частоты
523
Фильтр должен обеспечивать резкий спад ча-
стотной характеристики. Также должна быть
видна дискретная природа выходного сигнала
фильтра: он будет ступенчатым, а не плавным.
Еще два эксперимента с фильтром
(факультативно)
Отделяем частотные составляющие пря-
моугольного сигнала. Как вы должны знать
по своему опыту коррекции щупов осциллогра-
фа, частотную характеристику схемы можно
определить с помощью прямоугольного сиг-
нала. Попробуйте сделать следующее: подайте
на фильтр прямоугольный сигнал частотой
приблизительно 100 кГц, а затем постепенно
уменьшайте частоту тактирования, начиная с ее
максимального значения. Можете ли вы разли-
чить частотные составляющие 5 -/ПРШ и 3 -/ирш
непосредственно перед тем, как прямоуголь-
ный сигнал преобразуется в синусоидальный?
Демонстрация управления частотой f3 дБ
(для особо энергичных). Самое привлека-
тельное представление характеристик фильтра
можно получить, качая входной сигнал по ча-
стоте и наблюдая реакцию фильтра на измене-
ние частоты тактирования. Частота^ дБ должна
поддаваться варьированию в широких преде-
лах: до 1 кГц при подаче в качестве сигнала так-
тирования ТТЛ-сигнала с макетной платы и до
приблизительно 25 кГц при подаче сигнала бо-
лее высокой частоты от ТТЛ-выхода внешнего
генератора сигналов.
Наблюдается ли просачивание сигнала такти-
рования в выходной сигнал фильтра? Можете
ли вы подтвердить заявленный для устрой-
ства крутой спад частотной характеристики:
48 дБ/октаву чуть выше частоты^ дБ? Пусть вас
не удивляет, если в полосе задержания обна-
ружится несколько «отскоков». На графике на
рис. 12L.14 можно заметить, что частотная ха-
рактеристика фильтра на микросхеме МАХ294
резко падает, но затем делает несколько коле-
баний, подобно уроненному мячу.
12L3. Импульсный
усилитель звуковой частоты
Обычный усилитель звуковой частоты, наподо-
бие знакомого нам двухтактного повторителя,
в процессе передачи мощности на нагрузку дол-
жен и сам потреблять определенную мощность.
Например, в двухтактном усилителе с напряже-
нием питания ±2,5 В и выходным синусоидаль-
ным сигналом размахом 2,5 В на нагрузку будет
приходиться самое большее половина напряже-
ния питания (±1,25 В), а остальное напряжение
будет падать на транзисторах двухтактного ка-
скада. Таким образом, КПД такого усилителя
окажется меньше 50%13. При столь малой ампли-
туде выходного сигнала повышение напряжения
источника питания уменьшит КПД еще больше.
С помощью импульсного усилителя можно
решить эту проблему, используя стратегию,
с которой вы познакомились по импульсному
стабилизатору напряжения на лабораторном
занятии 11L. Переключатель, который нахо-
дится или во включенном или выключенном
состоянии, и никогда в промежуточном, в идеа-
ле не рассеивает никакой мощности, передавая
ее всю на нагрузку.
Попробуйте поэкспериментировать с импульс-
ным усилителем звуковой частоты на микросхе-
ме LM4667 компании National Semiconductor/
Texas Instruments. С двух выходов усилителя
сигнал поступает на оба контакта динамика.
В результате максимальное напряжение, пода-
ваемое на динамик, удваивается по сравнению
с напряжением, которое было бы доступно при
подаче сигнала только на один контакт динами-
ка, со вторым, подключенным на «землю».
В главе 12N были приведены осциллограммы,
которые должны дать вам представление об
электрических помехах этого усилителя.
12L3.1. Схема усилителя
В схеме на рис. 12L.15 используется микросхе-
ма для поверхностного монтажа (в отличие от
микросхемы для монтажа в отверстия на пе-
чатной плате14). Для возможности монтажа
данной микросхемы на макетную плату компо-
нент установлен на переходную плату, которая
вставляется в гнезда на макетной плате15.
13 КПД определяется по формуле (тс/4) • (ишх.шк/ит),
и в данном случае будет около 40%. Вы можете вычис-
лить это сами, если вам нравится решать интегральные
уравнения.
14 Мы уже использовали подобную микросхему транзи-
сторной сборки СА3096 на лабораторном занятии 5L.
15 Внимательного читателя могут обеспокоить конденсаторы
на входе, поскольку мы предостерегали о недостатках таких
524
12L Лабораторное занятие: ключи на полевых МОП-транзисторах
+5 В
о,зз
Вход,
Вывод 1
Рис. 12L.15. Микросхема импульсного усилителя звуковой
частоты LM4667, подключенная в конфигурации с одним
входом и усилением 6 дБ
Соберите схему, изображенную на рис. 12L.15,
на отдельной макетной плате, которая вам не
будет нужна для других проектов. Этот усили-
тель звуковой частоты пригодится нам впослед-
ствии, когда мы будем экспериментировать с
генерированием звуковых сигналов с помощью
компьютера.
схем. По схеме кажется, будто бы между входом усилителя
и «землей» нет требуемого пути по постоянному току. Но это
заблуждение, поскольку такой путь на «землю» обеспечива-
ется внутри самого усилителя. Однако это не означает, что
вход привязан к нулевому потенциалу. В этой схеме с однопо-
лярным питанием вход, как обычно, смещен по постоянному
току, в данном случае приблизительно на 1,2 В.
Установите развязывающие конденсаторы как
можно ближе к микросхеме, чтобы минимизи-
ровать паразитные индуктивности шин пита-
ния. Установите один конденсатор емкостью
1 мкФ и несколько керамических емкостью по
ОД мкФ.
Подайте на вход схемы синусоидальный сигнал
амплитудой около половины вольта и частотой
в несколько сотен герц16, и на слух определяйте
изменения в выходном сигнале, сопутствую-
щие установке развязывающих конденсаторов.
Экспериментируйте с количеством и местом
установки этих конденсаторов. Скорее всего вы
еще раз убедитесь, что установка развязываю-
щих конденсаторов стоит того.
Осциллограммы сигналов для этой схемы пока-
заны на рис. 12N.10, и, как говорилось там, соз-
даваемые переключателем помехи чрезвычай-
но велики. Но будем надеяться, что с помощью
разумной развязки шин питания вы сможете
сделать эти помехи едва слышимыми.
16 Выбраны такие значения, чтобы не мешать коллегам,
работающим рядом с вами.
12S. Дополнительный материал:
ключи на полевых МОП-транзисторах
В главе 12N мы рассмотрели ключи на полевых
МОП-транзисторах и некоторые варианты их
применения. Здесь мы немного дополним ин-
формацию по полевым МОП-транзисторам,
а также по полевым транзисторам с управляю-
щим переходом. Если вас интересует только
применение МОП-транзисторов, с которыми
мы работаем на наших лабораторных заняти-
ях, то этот материал можно игнорировать со
спокойной совестью.
12S.1. Физическое
представление
Работу полевого транзистора легче описать,
чем работу биполярного1. Как вы помните, мы
даже и не пытались объяснять работу биполяр-
ного транзистора.
И наоборот, полевой транзистор сам «напра-
шивается», чтобы объяснить его функциониро-
вание наглядно на рисунке. Такая иллюстрация
приведена на рис. 12S.1, и одного взгляда на
нее будет достаточно, чтобы вспомнить самою
сильную сторону полевых транзисторов — их
высокий входной импеданс.
Затвор (<0 В)
Исток | Сток
Г-»--1
Полевой транзистор с
управляющим р-n-переходом
Полевой
МОП-транзистор
Рис. 12S.1. Структура полевых МОП-транзистора и транзи-
стора с управляющим переходом
АоЕ, рис. 3.5.
Входной вывод МОП-транзистора изолиро-
ван от остального устройства, а у транзистора
с управляющим переходом есть /?-я-переход,
который, в отличие от перехода «база-эмиттер»
биполярного транзистора, никогда не находит-
ся при прямом смещении.
Таким образом, ток через управляющий вывод
не протекает. На этот вывод, называющийся за-
твором, просто подается напряжение, а управ-
ление транзистором осуществляется создавае-
мым этим напряжением электрическим полем.
Отсюда, конечно же, происходит и название
транзисторов этого типа — полевые.
Судя по структуре МОП-транзистора на
рис. 12S.1 можно подумать, что ток не будет
протекать из стока в исток, поскольку вслед-
ствие положительного напряжения на стоке
правый л-р-переход окажется обратносмещен-
ным. В действительности так оно есть, и чтобы
ток смог протекать через канал, транзистору
нужно немного помочь с этим.
Полевой МОП-транзистор начинает проводить
ток (становится открытым), если на затвор по-
дать положительное напряжение. В результате
этого создается слой полупроводника л-типа
(обогащенного электронами), который свя-
зывает между собой области я-типа на стоке
и истоке. Обогащенный таким образом МОП-
транзистор похож на транзистор с управляю-
щим переходом: проводящий канал соединяет
исток со стоком. Полевой МОП-транзистор,
изображенный на рис. 12S.2, находится в за-
крытом (выключенном) состоянии (подобно
большинству, но не всем, МОП-транзисторам)
до тех пор, пока на его затвор не будет подано
положительное напряжение, которое и вклю-
чит транзистор. Такое устройство называется
транзистором, работающим в режиме обогаще-
ния (или просто обогащенным транзистором)
526
US. Дополнительный материал: ключи на полевых МОП-транзисторах
-1
*с(вкл) v^h = +5 &) МОП-транзистор (обогащенный)
(л-канал)
п-МОП-транзистор,
обогащенный
И
«Канал»
Ци = 0; положительное Ци:
закрыт индуцирует канал, обеспечивая
протекание тока от истока к стоку
+1 +2 +3 +4 +5
Рис. 12S.2. Полевой МОП-транзистор закрыт при нулевом напряжении на затворе. Он открывается (проводит ток), когда
положительное напряжение на затворе U3 индуцирует канал, связывающий n-области стока и истока
Полевой транзистор с управляющим переходом (обедненный)
(п- канальный)
n-канальныи полевой транзистору
с управляющим переходом
Ц<0
-4 -3 -2 -1 О
Ци = ^: ^зи обратного смещения:
При отсутствии напряжения Отрицательное напряжение
смещения на затворе на затворе уменьшает
транзистора открыт проводимость канала
Рис. 12S.3. Вольт-амперные характеристики полевого транзистора с управляющим переходом и МОП-транзистора схожи, но
первая смещена на квадрант влево от напряжения (Узи= 0: транзистор с управляющим переходом открыт до тех пор, пока на
затвор не подан запирающий потенциал
поскольку оно работает (т. е. проводит ток)
только тогда, когда его проводящий канал обо-
гащается электронами.
Как МОП-транзистор, так и транзистор с управ-
ляющим /?-я-переходом содержат кристалл ле-
гированного полупроводникового материала,
к которому подсоединены выводы стока и ис-
тока2. Таким образом, можно ожидать, что при
подаче разности напряжений на эти выводы
между ними будет протекать ток. При низком
2 Возможно, что водопроводная аналогия, которая напра-
шивается наименованиями выводов, смущает вас, как так
получается, что ток протекает от стока (англ. drain — слив)
по направлению к истоку (англ. source — источник). Разве
такое направление не случается только при забитом кол-
лекторе? Объяснить эти странные названия поможет то
обстоятельство, что разработчиками МОП-транзистора
были те же самые люди, которые назвали выводы би-
полярного транзистора «коллектор» и «эмиттер» (хотя
в этом случае вопрос усложняется конфигурацией р-п-р,
в которой доминирует поток дырок). И эти исследователи
размышляли как физики, а не как инженеры. Похоже, что
они рассматривали направление потока электронов, а не
условного тока. Видимо так и было, хотя этот тип тран-
зистора называется биполярным, поскольку ток частично
зависит от движения как дырок, так и электронов.
напряжении3 Ucll на этих выводах транзистор
с управляющим переходом и МОП-транзистор
имеют омические характеристики, т. е. ток 1СИ
пропорционален прикладываемому напряже-
нию иСИ.
Таким образом, пока что поведение транзисто-
ра в некоторой мере понятно на интуитивном
уровне. Вскоре (в разделе 12S.1.1) мы попыта-
емся дать ответ на более трудный вопрос, по-
чему при более высоком напряжении пСИ оми-
ческое поведение транзистора меняется на по-
ведение источника тока.
Для сравнения с вольт-амперной характери-
стикой МОП-транзистора на рис. 12S.3 при-
ведена зависимость тока стока /с от напряже-
ния на затворе Um для полевого транзистора
3 В данном случае низкое напряжение означает напряже-
ние меньшее, чем С/зи - Unor Разница напряжений опреде-
ляет уровень сигнала на затворе, открывающего транзи-
стор, или, образно говоря, насколько приоткрыт затвор.
Пороговое напряжение Uuop — это напряжение, при ко-
тором ток стока 1С увеличивается от нуля до небольшого,
но измеримого значения, обычно в несколько наноампер.
См. раздел 3.2.7 книги АоЕ.
12S.I Физическое представление
527
с управляющим р-я-переходом. Пока не подан
запирающий сигнал, этот транзистор обычно
включен (открыт). Подача на затвор отрица-
тельного напряжения сужает проводящий ка-
нал и закрывает транзистор.
Такие устройства называются работающими в
режиме обеднения, или просто обедненными
транзисторами. В этом режиме работают все
полевые транзисторы с управляющим перехо-
дом и некоторые МОП-транзисторы.
Обедненные при отрицательном напряжении
транзисторы функционируют как переключа-
тели общего назначения. Обогащенные МОП-
транзисторы, наоборот, могут работать с одно-
полярным положительным питанием и способ-
ны переключать другой транзистор такого же
типа (рис. 12S.4).
Меняется с О до7£)
Рис. 12S.4. Обогащенный МОП-транзистор может управлять
другим подобным транзистором, работая при положитель-
ном напряжении питания
Таким образом, в принципе можно собрать
разветвленную систему переключателей на
обогащенных МОП-транзисторах с однопо-
лярным источником питания. Но такой способ
не применяется в логических устройствах. Мы
упоминали в главе 12N, что КМОП-устройства
обладают намного большей эффективностью в
этом отношении (см. также раздел ЗАЛА книги
АоЕ). С обедненными транзисторами достичь
такой эффективности невозможно.
12S.1.1. Попытка объяснить
свойство стабильного тока
МОП-транзисторов
Хотя в этом курсе мы игнорируем подроб-
ности из области физики, которые могли бы
объяснить внутренние процессы в транзисто-
ре, полевые транзисторы вызывают желание
остановиться более подробно на их поведе-
нии. Мы попытаемся предпринять такое уси-
лие, хотя и не ожидая, что оно будет особенно
успешным.
Линейная область и режим источника
тока: омическое поведение при малом 1/си
В разделе 12S.1 мы утверждали, что легирован-
ная полупроводниковая пластина может прово-
дить ток4. Также возможно, что протекающий
по ней ток будет пропорционален подаваемому
на пластину напряжению (на ее сток и исток).
Такое поведение наблюдается при низком на-
пряжении [7СИ, как показано в левой, линейной,
области вольт-амперной характеристики на
рис. 12S.5.
Область
насыщения
Линейная область
Крутизна Линейная область
пропорциональна простирается
(ЧЧ) (
Рис. 12S.5. При малом напряжении 1/си полевой транзистор
имеет омические характеристики, но при более высоком ве-
дет себя подобно источнику тока
Это семейство кривых во многом похоже на на-
бор кривых зависимости тока коллектора JK от
напряжения U^ для биполярного транзистора,
где каждая кривая определяется не напряже-
нием 17ЗИ, а или напряжением UB3 или током 1Б.
На рис. 12S.6 для сравнения приведены вольт-
амперные характеристики для биполярного и
полевого транзисторов.
Замечание
Сравнение крутизны в области токов может быть
не совсем справедливым для биполярного транзи-
стора, но обратите внимание на меньший масштаб
шкалы тока для него.
Напряжение, подаваемое на транзистор, ото-
бражается на горизонтальной оси. Каждая
кривая соответствует определенному входному
управляющему уровню: U3ll или [7БЭ.
4 АоЕ § 3.2.7.
528
US. Дополнительный материал: ключи на полевых МОП-транзисторах
3, 0,5
0,67 В
10
■ 0,65
1 5
10
20
.0,63
■0,61
0,59
1,95 В
10
20
1,85
■1,80
1,75
il,70
0
Биполярный Полевой
Рис. 12S.6. Семейства вольт-амперных характеристик для биполярного и полевого транзисторов (см. рис. 3.2 из книги АоЕ)
100
со/ оэ/
* <?
100
50
0,1
0,2
Биполярный
0,2
Полевой
Рис. 12S.7. При низких напряжениях вольт-амперная характеристика полевого транзистора более линейная, чем
биполярного (см. рис. 3.2 из книги АоЕ)
Вы можете задать вопрос, не обладает ли би-
полярный транзистор омическим поведением,
подобным полевому. В некоторой степени об-
ладает, но при низких напряжениях его вольт-
амперная характеристика менее линейна, чем у
полевого транзистора (рис. 12S.7).
А с помощью простого приема вольт-амперную
характеристику полевого транзистора можно
выровнять еще больше, превращая его в полез-
ный варистор5.
Пока что все выглядит просто: омическое по-
ведение при низком напряжении вполне объ-
яснимо. Труднее понять режим источника по-
стоянного тока, который более типичен для по-
левых транзисторов.
5 Прием состоит в использовании резистивного делите-
ля R:R для подачи на затвор половины напряжения Ucu.
Более подробно этот вопрос освещается в разделе 3.2.7А
книги АоЕ.
Область насыщения: режим источника
тока при более высоких напряжениях (7СИ
Омическое поведение, которое интуитивно
удобно для нас, почитателей резисторов, являет-
ся необычным режимом работы полевого тран-
зистора. Обычно полевой транзистор, подобно
биполярному, пропускает ток, определяемый
сигналом управления, которым для него явля-
ется напряжение на затворе Um. Этот режим
источника тока отображен практически по все-
му графику вольт-амперной характеристики на
рис. 12S.5, за исключением самого нижнего диа-
пазона значений напряжения Ucvl: А остальная
горизонтальная ветвь похожа на график, кото-
рый можно было бы ожидать для биполярного
транзистора. Чем же объясняется этот эффект?
Мы попробуем дать неформальное объяснение.
По мере постепенного роста напряжения иси
повышающееся напряжение возле стока сужает
725.7. Физическое представление
529
Подложка r^
Подложка^
Подложка^
Чи > Цтор' Чи малое
(линейная область)
Чи
Канал перекрыт
1Р, (Л, более высокое
(транзистор закрыт) (линейная область) (область насыщения: постоянный выходной ток)
Рис. 12S.8.Tpn режима в области проводимости полевого МОП-транзистора
проводящий канал в этой области, и в конеч-
ном итоге канал перекрывается. На рис. 12S.8
слева показан полевой транзистор с закрытым
каналом при напряжении Um = 0. Другие два
изображения соответствуют транзистору в ре-
жиме проводимости, сначала в линейной обла-
сти, а затем в области с перекрытым каналом.
Как раз на самом правом рисунке и предпри-
нимается попытка представить графически об-
ласть постоянного тока или режим насыщения
полевого транзистора6.
На первый взгляд логично предположить, что
при напряжении [7СИ, достаточно высоком для
того, чтобы перекрыть проводящий канал, ток
стока Jc упал бы до нуля. Но этого не проис-
ходит, а наоборот, при повышении напряже-
ния Ucll ток стока 1С выравнивается. Область
подложки между точкой перекрытия и стоком
менее насыщена носителями, чем индуциро-
ванный канал, но электрическое поле в этой
точке достаточно сильное для того, чтобы пе-
ремещать дрейфующие через канал электроны
к стоку.
Вот такова наша попытка объяснить этот эф-
фект на интуитивном уровне. В случае, если
она оказалась не очень успешной, возможно,
приведенные далее рассуждения будут более
доходчивы.
Перекрытая область создает «бутылочное гор-
лышко», т. е. узкий проход, в котором переме-
щающиеся носители заряда попадают в свое-
образную трафиковую пробку, как показано на
рис. 12S.9.
По мере повышения напряжения UCVL большая
часть такого падения подвижности носителей
происходит на коротком перекрытом участке,
6 Слово «насыщение» не совсем удачно описывает нор-
мальный режим работы полевого транзистора, поскольку
применительно к биполярным транзисторам и операци-
онным усилителям оно означает нечто радикально иное.
Но это стандартный термин в случае с полевыми транзи-
сторами.
Область насыщения: И
постоянный
выходной ток
Подложка
Миниатюрная «трасриковая пробка»
(подвижность зарядов падает)
Рис. 12S.9. Миниатюрная «трафиковая пробка» как причина
насыщения полевого транзистора: увеличение поля вызыва-
ет снижение подвижности носителей
в результате чего плотность тока в этом «бу-
тылочном горлышке» повышается. Затем, при
дальнейшем росте напряжения 1/си, усиливаю-
щем электрическое поле еще больше, «буты-
лочное горлышко» удлиняется, и «трафик», т. е.
ток 1С, выравнивается на уровне насыщения.
В общем, дальнейшее повышение напряжения
Um создает два противоположных эффекта,
которые почти аннулируют друг друга: более
сильное электрическое поле, но уменьшенную
подвижность носителей заряда. В результате
величина тока остается более-менее постоян-
ной7.
12S.1.2. Насыщение не совсем
постоянное: модуляция длины
канала похожа на эффект Эрли
Возможно, вы заметили, что вольт-амперные
характеристики для полевых транзисторов по-
хожи на соответствующие кривые для бипо-
лярных транзисторов не только по форме, как
указывается в разделе 12S.1.1 и на рис. 12S.6, но
7 Более подробное объяснение, сопровождаемое боль-
шим количеством диаграмм, можно найти в разделе 5.2
книги «Principles of Electronic Circuits» («Основы электрон-
ных схем»), авторы Burns, S. и Bond P., издательство West
(1987). Также будет информативным раздел 4.24 книги
«Microelectronic Circuit Design» («Проектирование микро-
электронных схем»), авторы Jaeger, R. и Blalock, Т., изда-
тельство McGraw-Hill (2011).
530
US. Дополнительный материал: ключи на полевых МОП-транзисторах
также и по наклону8. Этот наклон, описываемый
эффектом Эрли для биполярных транзисторов,
возникает в результате модуляции длины ка-
нала полевого транзистора. Данный механизм
похож на механизм эффекта Эрли. По мере по-
вышения напряжения [7СИ длина проводящего
канала транзистора уменьшается из-за увели-
чения перекрытой области. В результате сила
тока слегка увеличивается.
Примечание
На самом деле ток возрастает незначительно:
например, токоограничивающий диод полево-
го транзистора с управляющим р-п-переходом
1N5294, который мы используем на нескольких
лабораторных занятиях, имеет высокий динами-
ческий импеданс — выше 1 МОм при напряжении
12S.1.3, Применение режима
постоянного тока
Благодаря своему свойству поддерживать ток
постоянным даже при напряжении Um = 0
полевой транзистор с управляющим перехо-
дом прекрасно подходит для работы в качестве
двухполюсного токоограничивающего устрой-
ства9. Если вы помните, мы использовали та-
кое устройство на лабораторном занятии 5L
в «хвосте» дифференциального усилителя. Но
вольт-амперные характеристики на рис. 12S.5
напоминают нам, что режим постоянного тока
можно ожидать только тогда, когда напряже-
ние Ucvl превышает некий минимальный уро-
вень, выше которого прекращается омический
режим. Для транзистора 1N5294 такое мини-
мальное напряжение равно 1,2 В (рис. 12S.10).
/Работает при максимальном
Двухполюсный
токоограничивающий диод
Рис. 12S.10. Полевой транзистор с управляющим перехо-
дом можно использовать как простой токоограничивающий
диод
8 АоЕ§3.1.1А.
9 АоЕ§ 3.2.2 и рис. 3.20.
13N. Совместный аудиопроект
Содержание
13N.1. День совместных усилий
13N.1.1. Схемы, выполняющие конкретные операции
13N.1.2. Схемы вашей собственной разработки
13N.1.3. Техническое задание
13N.1.4. Звенья цепи аудиопередачи
13N.2. Общая проблема обеспечения стабильности
13N.3. Параметры светодиода и фототранзистора
531
531
531
532
532
535
535
Цель этой главы
Отчасти сегодняшней нашей целью является
закрепление пройденного материала, посколь-
ку схема, которую мы соберем, содержит самые
разнообразные элементы. А само разрабаты-
ваемое устройство предназначено для беспро-
водной передачи закодированного звукового
сигнала с помощью оптического канала.
13N.1. День совместных
усилий
Это занятие радикально отличается от других
занятий нашего курса. На теоретическом за-
нятии мы хотим увидеть вас в роли учителя,
рассказывающего своим однокурсникам о той
части устройства, которую вы создали в рамках
всего проекта. Также мы хотим, чтобы ваши
слушатели указали вам (вежливо), что можно
улучшить в вашей разработке. Отличительная
черта этого лабораторного занятия — совмест-
ная работа. Ваш блок не сможет функциони-
ровать до тех пор, пока он не будет объединен
с разработкой ваших однокурсников.
13N.1.1. Схемы, выполняющие
конкретные операции
Мы придумали такой формат нынешнего лек-
ционного и соответствующего лабораторно-
го занятия в ответ на пожелания студентов,
чтобы им предоставили возможность соби-
рать схемы, результаты работы которых мож-
но наблюдать без измерительных приборов.
Похоже, что им надоело видеть только осцил-
лограммы. Мы уже пытались учесть эти по-
желания на предшествующих лабораторных
занятиях по сборке самодельного операцион-
ного усилителя и ПИД-регулятора. Нынешнее
лабораторное занятие также предоставляет
подобную возможность. Но оно отличается от
предыдущих тем, что на нем вам нужно само-
стоятельно проделать всю работу по проекти-
рованию схемы.
13N.1.2. Схемы вашей собственной
разработки
Обычно мы не решались организовывать ла-
бораторные занятия подобным образом. Мы
опасались, что такой процесс был бы слишком
медленным: сначала нужно начертить схему,
найти ее недостатки, исправить, испытать усо-
вершенствованную схему и т.д. Такой объем ра-
боты трудно выполнить за полдня. Применение
такого метода каждый день сделало бы наш
курс совершенно другим — хорошим, но в то же
самое время таким, в котором мы бы не смогли
охватывать большой объем материала, как мы
стараемся это сделать сейчас. Но мы осмели-
лись испробовать этот метод на сегодняшнем
занятии, поскольку мы уверены, что вы сможе-
те придумать требуемые рабочие схемы: каж-
дый отдельный фрагмент схемы вполне в пре-
делах ваших знаний и навыков.
532
13N. Совместный аудиопроект
+5 в +15 в
/вых * 30 кГц
Источник
аудио-
сигнала
Генератор,
управляемый
напряжением
Драйвер
светодиода
\i
3 метра
Z=8
©
Детектор
(преобразователь
«ток-напряжение»)
Усилитель-
' ограничитель
Преобразователь
«частота-напряжение»
(демодуляция)
Усилитель динамика
(у) (v
Приблизительно 25 мкА
Гвых «100 мА
(номинальный)
Рис. 13N.1. Блок-схема группового аудио проекта
Мы надеемся, что этим упражнением мы одно-
временно достигнем нескольких целей. Работа
над ним должна доставить вам удовольствие,
а также приятное подтверждение, что в тече-
ние прошедших нескольких недель вы чему-то
научились.
13N.1.3. Техническое задание
На рис. 13N.1 изображена блок-схема устрой-
ства, которое вам нужно собрать. Далее описа-
на функциональность каждого блока.
Мы будем передавать музыку по беспроводной
связи с одной стороны комнаты в другую или,
самое малое, на расстояние нескольких метров.
Во времена Маркони, а и еще сравнительно не-
давно, беспроводная связь означала использо-
вание радиоволн. Но не в данном случае. В на-
шем проекте мы задействуем инфракрасный
свет1. Более конкретно мы запишем звуковую
информацию на носитель, частота которого
выше диапазона частот человеческого слуха,
но намного ниже радиочастотного диапазона.
В частности, частота нашей несущей будет око-
ло 30 кГц. В эту несущую будет кодироваться
в виде разных частот исходная информация —
варьирующиеся во времени напряжения. Как
мы знаем, такой метод называется частотной
модуляцией (ЧМ).
В данном случае применение частотной модуля-
ции привлекательно благодаря ее хорошей по-
мехозащищенности, а также способности вклю-
чать светодиод на полную яркость, позволяя по-
лучить максимальную дальность передачи2.
1 Свет ли это, если он невидим человеческому глазу? Хо-
роший вопрос, которым мы будем постоянно задаваться.
2 Вы можете убедиться, что помехозащищенность и
дальность передачи это, в принципе, одно и то же.
Варьирование частоты не обязательно должно
быть большим. В частности, чтобы передать
аудиосигнал частотой вплоть до 3 кГц, вполне
хватит изменения частоты значительно ниже
ЗкГц.
13N.1 А Звенья цепи
аудиопередачи
Далее приведены перечень и краткое описание
компонентов собираемой схемы. В некоторых
случаях описание будет преднамеренно рас-
плывчатым, поскольку мы не хотим ограничи-
вать процесс разработки, который, мы надеем-
ся, вы предпримете.
Сторона передачи
Модулятор — эту роль играет генератор ко-
лебаний, управляемый напряжением (ГУН).
Мы будем использовать микросхему генера-
тора колебаний 555 для преобразования из-
меняющегося напряжения звукового сигнала
в прямоугольный сигнал переменной частоты.
Функция этой схемы для преобразования на-
пряжения в частоту не будет линейной, но ока-
жется достаточно приемлемой для целей на-
стоящего лабораторного занятия. Можно было
бы взять более качественный ГУН, например,
ГУН, встроенный в микросхему 74НС4046,
с которой мы познакомимся на лабораторном
занятии 18L. Но это дополнительное усилие не
даст никакого заметного улучшения качества
передаваемого звука по сравнению с предлагае-
мым более простым решением.
Поскольку требуется лишь небольшое из-
менение частоты, мы можем допустить не-
которую нелинейность зависимости частоты
13N. I День совместных усилий
533
от напряжения. Это объясняется не особенно
высокими требованиями для этой задачи, а
также тем, что мы ожидаем нелинейную ха-
рактеристику демодулятора.
Изменять частоту выходного сигнала гене-
ратора колебаний на микросхеме 555 можно
как простым, так и сложным способом. В по-
следнем случае мы, наверное, использовали
бы управляемый напряжением источник тока
для варьирования частоты пилообразного
сигнала. А при простом способе звуковой
сигнал подается на вход управления (вывод 5
для микросхемы в DIP-корпусе) и варьирует
пороговые напряжения.
Не забудьте учесть коэффициент заполнения
(т. е. долю высокого уровня в течение перио-
да, в процентах). Поразмышляйте, позволяет
ли ваша спроектированная схема получить
50%-ный коэффициент заполнения? Важен
ли коэффициент заполнения вообще?
Обеспечьте возможность регулирования сред-
ней частоты несущей, манипулируя потен-
циометром, сконфигурированным как пере-
менный резистор. Не забудьте подключить
постоянный резистор последовательно регу-
лируемому, чтобы не допустить сбоя в работе
схемы при случайной установке предельного
значения потенциометра.
Несущая частота. Частоту несущей мы вы-
брали в районе 30 кГц, посередине предель-
ных значений, которые могли бы создавать
трудности.
• Частота несущей не должна быть слиш-
ком низкой. А именно, она не должна быть
в диапазоне, воспринимаемом человече-
ским ухом, поскольку скорее всего неко-
торая часть несущей будет просачиваться
в демодулированный сигнал в виде помех,
смешанных с полезным аудиосигналом.
• Частота несущей не должна быть слишком
высокой. Она не должна оказаться в таком
диапазоне частот, где наши операционные
усилители и компараторы начнут давать
сбой.
Драйвер светодиода — эта часть схемы вос-
принимает сравнительно слабый прямоуголь-
ный сигнал, выдаваемый ГУН (генератором
сигналов на микросхеме 555) и преобразует
его в достаточно сильный сигнал для управ-
ления сильноточным инфракрасным свето-
диодом. Такой светодиод может потреблять
номинальный ток величиной 100 мА, и в режи-
ме проводимости на нем создается падение на-
пряжения величиной около 2 В.
Подробности для разработки драйвера
светодиода
Номинальный ток (максимальный длитель-
ный ток) светодиода указан в табл. 13N.1
в разделе 13N.3. Должен ли ваш драйвер све-
тодиода быть источником или потребителем
тока?
Примите к рассмотрению электрические па-
раметры выходного сигнала генератора сиг-
налов на микросхеме 555, а также параметры
нагрузки (падение напряжения на светодио-
де величиной около 2 В).
Стремитесь минимизировать рассеиваемую
мощность. Мы имеем дело с большим током,
и не хотим, чтобы напряжение было более
высоким, чем требуется. Если будете исполь-
зовать резистор, убедитесь, что он не нагре-
вается до такой степени, чтобы обжечь вам
пальцы3.
Сторона приема
Фотодатчик — это устройство преобразует
создаваемый инфракрасным фототранзисто-
ром ток в напряжение. Размах напряжения дол-
жен быть максимально возможным, при этом
без искажения сигнала.
Некоторые дополнительные подробности
Обратите внимание на то обстоятельство,
что окружающий свет будет содержать неко-
торую инфракрасную составляющую, в ре-
зультате чего ток фототранзистора никогда
не будет нулевым, несмотря на его темный
корпус, непроницаемый для видимого све-
та. Также обратите внимание на то, что ток
фототранзистора протекает только в одном
направлении.
Скорее всего ток нужно будет снимать с
эмиттера фототранзистора (сравните со схе-
мами с фототранзистором из лабораторного
занятия 6L.9). Но не подумайте, что характе-
ристики схемы будут подобны характеристи-
кам эмиттерного повторителя (лабораторное
занятие 4L), в котором выходной сигнал сни-
мался с эмиттера.
3 Для этого не нужны толстые перчатки, следует просто
сравнить рассеиваемую мощность с номинальной мощно-
стью резистора.
534
13N. Совместный аудиопроект
Усилитель-ограничитель — эта схема при-
нимает выходной сигнал схемы фотодатчика,
который может быть небольшой амплитуды,
и преобразует его в прямоугольный сигнал с
размахом ±15 В. Большая амплитуда сигнала
будет полезной для последующих каскадов.
Постоянная амплитуда, формируемая этой
схемой важна, поскольку при колебаниях ам-
плитуды, присутствующих в выходном сигна-
ле фотодатчика, конечный демодулированный
выходной звуковой сигнал был бы искажен.
Некоторые подробности
Обратите внимание на то, что выходной сиг-
нал фотодатчика будет содержать постоян-
ную составляющую (если только разработ-
чики схемы фотодатчика не устранят ее для
вас). Этот уровень постоянного напряжения
не содержит никакой информации; полезная
информация содержится только в частоте
варьируемого напряжения.
Чтобы обеспечить чистоту выходного сигна-
ла вам потребуется гистерезис. А гистерезис
должен быть регулируемым вплоть до нуле-
вого значения, поскольку мы хотим, чтобы
наша подсхема обладала максимально воз-
можной чувствительностью, т. е. обеспечи-
вала максимальный рабочий диапазон для
всей схемы.
Демодулятор — на вход этой схемы подается
выходной прямоугольный сигнал варьирую-
щейся частоты от усилителя-ограничителя, ко-
торый она подвергает двухэтапному преобра-
зованию в амплитуду, меняющуюся со време-
нем, т. е. аудиосигнал, подобный тому, который
использовался для управления ГУН на стороне
передачи.
• Первый этап. С помощью фильтра с кру-
тыми скатами изменение частоты преоб-
разуется в колебание амплитуды.
• Второй этап. С помощью обычного ампли-
тудного демодулятора формируется аудио-
сигнал.
Некоторые подробности
Подойдет любой фильтр с крутой частот-
ной характеристикой, но самым легким для
реализации скорее всего будет резонансный
Д1С-контур. Вспомним, по нашему лабора-
торному занятию 3L, особенно по упраж-
нению 3L.1.2, что скат кривой отношения
изменения амплитуды к изменению часто-
ты (АА/ДЧ) можно сделать очень крутым.
Для наилучшего преобразования АА в Ач нам
бы хотелось, чтобы эта кривая была близка
к линейно нарастающей прямой. Мы реко-
мендуем вам не напрягаться, пытаясь вы-
числить наилучшую форму данной кривой.
Вместо этого, в утилитарном стиле нашего
курса, сделайте регулируемой форму кривой
частотной характеристики этой схемы.
Вспомните, какие схемные элементы ре-
зонансного контура из главы 3L влияли на
форму частотной характеристики. А имен-
но высокое сопротивление R обеспечивало
большие значения добротности Q (крутая
кривая). Но при этом амплитуда выходного
сигнала оказывается малой, т. е. вся кривая
становится узкой, но крутой. В общем, боль-
шое сопротивление R создает узкую, но кру-
тую кривую наподобие Эльбруса, а малое —
широкую и растянутую кривую наподобие
Уральских гор.
Обратите внимание на фазу. А именно уве-
личивается или уменьшается напряжение
выходного сигнала демодулятора при повы-
шении частоты? Важен ли ответ на этот во-
прос?
Усилитель усиливает выходной сигнал демо-
дулятора для подачи на динамик с сопротивле-
нием звуковой катушки 8 Ом.
Некоторые подробности
Мы уже собирали эту схему на предыдущих
занятиях. Сделайте уровень ее усиления ре-
гулируемым. (Поскольку громкий выходной
сигнал может быть очень раздражающим,
когда группа работает над испытанием и ре-
гулировкой всей схемы.) Скорее всего мини-
мальный уровень усиления не нужно будет
устанавливать ниже единичного (и эта на-
стройка позволит использовать вариант уси-
лителя с высоким импедансом).
Обратите внимание на крайнюю нежела-
тельность протекания через динамик посто-
янного тока. Только колебания напряжения
создают звук, а постоянное напряжение при-
водит только к нагреву.
Основная трудность — обеспечить стабиль-
ность этой схемы.
13N.3. Параметры светодиода и фототранзистора
535
Шина питания,
снятая со старой макетной платы
Отдельная макетная плата, содержащая один
каскад передатчика или приемника проекта
Рис. 13N.2. Удачный выбор и размещение шин питания по-
могает бороться с паразитными автоколебаниями
13N.2. Общая проблема
обеспечения стабильности
Каждый блок этого устройства собирается на
своей отдельной макетной плате. Затем все эти
макетные платы соединяются в общую схему,
на которую подается питание. Собранная таким
образом схема особенно уязвима к паразитным
автоколебаниям. Во избежание этой опасности
предпримите следующие меры:
♦ выполните развязку всех линий питания на
каждой отдельной макетной плате, исполь-
зуя для этого керамические конденсаторы
емкостью 0,01-0,1 мкФ;
предпримите все возможные усилия, чтобы
укоротить провода питания.
Замечание
В нашем курсе мы подаем питание через шины,
снятые со старых макетных плат, как показано на
рис. 13N.2. Достоинством такого подхода являет-
ся низкая индуктивность и значительная емкость
этих шин питания.
13N.3. Параметры
светодиода
и фототранзистора
Светодиод и фототранзистор работают в ближ-
ней инфракрасной области спектра, близко со-
поставляя предельную чувствительность длине
волны максимума излучения. Оба устройства
являются узконаправленными, выбранными,
чтобы максимизировать дальность действия.
Но это несет с собой недостаток в виде не-
обходимости аккуратно совмещать поле дей-
ствия передатчика с приемником. В табл. 13N.1
приведены релевантные характеристики этих
устройств.
Цоколевка этих компонентов показана на
рис. 13N.3.
Таблица 13N.1. Параметры светодиода и фототранзистора
Компонент
Светодиод:
TSTS7100
Фототранзистор:
QSD124
Центральная
длина волны, нм
950
880
Угол излучения/
приема, град
±5
±12 (угол половинной
мощности)
Ток, мА
250 мА (максимальный
длительный)*
6 (минимальный
открытия)
Время нараста-
ния и спада, мкс
0,8
7
* Но ток величиной 100 мА более типичен для этого компонента.
Схема
Анод
(соединен
с корпусом)^
Катод
Анод
(соединен с корпусом)
Плоская
Эмиттер
Схема
? Коллектор
J Эмиттер
Диаграмма направленности
Рис. 13N.3. Цоколевка инфракрасных светодиода TSTS7100 (а) и фототранзистора QSD124 (б) и его диаграмма
направленности (в)
13L Лабораторное занятие:
совместный аудиопроект
13L1. Типичные сигналы
На рис. 13L.1 приведены примеры сигналов, ко-
торые следует ожидать в разных точках разраба-
тываемой схемы. Без наличия соответствующих
схем эти сигналы могут быть не очень информа-
тивными, но, изучив их, вы лучше поймете функ-
ционирование всего проекта целиком. В конце
лабораторного занятия мы дадим несколько ре-
комендаций по тестированию ваших схем.
для всей группы будет полезнее, если пробле-
мы разработки будут совместно рассмотрены
всей группой, а не решены за кулисами отдель-
ными разработчиками. Мы надеемся, что раз-
работанная вами схема не окажется идеальной,
поскольку в этом случае вы не получите новых
знаний и опыта. Кроме того, не тестируйте свою
разработку загодя, собрав ее. Заявления типа
«Я не знаю, почему номинал этого резистора
10 кОм, но я его использовал, и оно работает»
гсг
Выходной сигнал фотодатчика
преобразован в прямоугольный сигнал
каскадом усилителя-ограничителя
Сигнал после LC-срильтра
Частота на СИ4 — 2,044 кГц
Малая амплитуда сигнала
Частота на ChZ — 34,99 кГц
Выходной аудиосигнал (сигнал после LC-срильтра,
выпрямленный и отфильтрованный)
Рис. 13L.1. Сигналы на нескольких этапах приема
13L.1.1. Что нужно знать о других
узлах схемы?
Мы считаем, что вам не потребуется много ин-
формации о других узлах устройства, смежных
с вашим. Если какой-либо из узлов преподнесет
вам «сюрприз», то от вас ожидается достаточная
гибкость, чтобы совладать с ним в день работы
над проектом. Определенно, будет вполне за-
конным расспросить разработчиков смежных
схем о возможных проблематичных аспектах их
узлов, но скорее всего это тоже не потребуется.
13L1.2. Предварительные советы
Мы не считаем целесообразным давать вам по-
дробные предварительные советы, поскольку
не способствуют продуктивному обсуждению.
Для целей обзора и оценки работы намного луч-
ше обсуждать причины того или иного действия.
13L.2. Стратегии поиска
и устранения причин
неполадок
Далее приведены несколько советов по диагно-
стированию неполадок, которые могут упро-
стить эту задачу: сначала мы соединяем по-
парно модули, которые «общаются» друг с дру-
гом, а затем, когда эта пара работает должным
образом, мы соединяем все элементы схемы.
Блок-схема всего устройства была показана на
рис. 13N.1.
13L2. Стратегии поиска и устранения причин неполадок
537
13L2.1. Диагностика ГУН
и демодулятора
Настроить эти узлы особенно сложно. Разра-
ботчики узла генератора, управляемого напря-
жением (ГУН), могут настроить его централь-
ную частоту. Измерьте эту частоту, используя
цифровой мультиметр в качестве частотомера.
Отметьте частоту, на которой схема работает
наилучшим образом (т. е. выдает наиболее чи-
стый синусоидальный сигнал из узла демодуля-
тора), на случай, если вы собьете настройку, и
нужно будет восстановить центральную часто-
ту. По нашему опыту, подключение резистора
номиналом 1 кОм последовательно выводу 5
КМОП-микросхемы 555 помогает предохра-
нить ее от повреждений. Этот резистор не влия-
ет на рабочие характеристики схемы, поскольку
резисторы внутреннего делителя микросхемы
дают эквивалентное сопротивление величиной
33 кОм.
Генератор сигналов
Синусоидальный сигнал, 0,5 В?
Рис. 13L.2. Тестирование узла ГУН и демодулятора
+5 В +15 В
Тем временем разработчики узла демодулятора
могут откорректировать форму этой кривой,
регулируя величину добротности Q своей схе-
мы в поисках достаточно линейной области.
Но не позволяйте разработчикам узла ГУН и
демодулятора выполнять свои настройки одно-
временно! Они должны делать это поочередно.
Когда выходной сигнал демодулятора является
достаточно хорошим приближением исходно-
го синусоидального сигнала, оставьте текущие
настройки, как они есть. На более позднем эта-
пе, когда вы будете работать со всей цепочкой
узлов схемы, оптимизировать частотную ха-
рактеристику будет труднее.
13L2.2. Диагностика оптического
канала
Разработчикам фотодатчика нужно будет на-
строить, по крайней мере, уровень усиления,
и, возможно, смещение постоянной составляю-
щей. Если вы не уверены, работает светодиод
или нет, проверьте это с помощью детектора
инфракрасного излучения.
Совет
Только что извлеченный из темного места хране-
ния детектор ИК-излучения нужно выдержать в
течение нескольких минут в условиях комнатного
освещения, чтобы он активировался1.
Фотодатчик
(преобразователь 1ъ U)
Приблизительно 25 мкА
Рис. 13L.3. Проверка работоспособности оптического канала
Прежде чем соединять демодулятор вместе
с узлом ГУН, его разработчикам нужно будет
тщательно протестировать узел демодулятора
отдельно, подавая на него прямоугольный сиг-
нал качающейся частоты. Выдаваемый схемой
демодулятора выходной сигнал должен быть
достаточно хорошим линейно нарастающим
сигналом, который вызывает прямоугольный
сигнал качающейся частоты.
При совместном тестировании ГУН и демоду-
лятора разработчики узла ГУН должны попы-
таться найти подходящую точку на скате кри-
вой частотной характеристики демодулятора.
13L2.3. Диагностика фотодатчика
и усилителя-ограничителя
Иногда подключение компаратора к фотодат-
чику в виде нагрузки может дестабилизиро-
вать этот последний узел. При таком разви-
тии событий в выходном сигнале фотодатчика
появятся импульсные помехи. В таком случае
1 Лабораторные устройства детектирования инфракрас-
ного излучения стоят дорого, но на eBay можно найти не-
дорогие варианты. В зависимости от используемого в ней
фильтра даже камера вашего мобильного телефона может
реагировать на инфракрасное излучение.
538
13L Лабораторное занятие: совместный аудиопроект
/йЬту*30кГц +5 В +15 В
х
"'Д
Драйвер
светодиода
Фотодатчик
(преобразователь I в U)
Усилитель-
ограничитель
Приблизительно 25 мкА
Рис. 13L4. Тестирование усилителя-ограничителя
'вых
Генератор сигналов:
ГУН
Преобразователь fsU
Синусоидальный сигнал, 0,5 В
Усилитель динамика
Рис. 13L5. Восстановление звукового сигнала, тестирование усилителя динамика
в обязательном порядке выполните развяз-
ку всех шин питания, а также минимизируйте
длину проводов питания.
Разработчикам усилителя-ограничителя нужно
будет настроить величину гистерезиса. Им необ-
ходимо получить минимальный гистерезис (для
обеспечения максимальной чувствительности),
при котором схема работает стабильно.
Внимание!
Ни в коем случае не используйте в усилителе мало-
мощные транзисторы типа 2N3904 или 2N3906.
Для тестирования усилителя лучше подклю-
чить его к узлу демодулятора, а не подавать
входной сигнал от генератора сигналов.
13L2.4. Диагностика звукового
усилителя
Опять же, здесь самой трудной проблемой яв-
ляется стабильность, а сам процесс настройки
усиления прямолинеен.
Часть IV
ЦИФРОВЫЕ УСТРОЙСТВА: ЛОГИЧЕСКИЕ
ЭЛЕМЕНТЫ, ТРИГГЕРЫ, СЧЕТЧИКИ, ПЛМ,
ПАМЯТЬ
14N. Логические устройства
Содержание
14N.1. Аналоговые и цифровые системы 542
14N.1.1. Разница между этими системами 542
14N.1.2. Зачем вообще нужны цифровые системы? 542
14N.1.3. Альтернативы двоичной системе 544
14N.1.4. Особые случаи применения цифровой обработки 545
14N.2. Двоичная система счисления 545
14N.2.1. Представление отрицательных чисел с помощью дополнительного
двоичного кода 546
14N.2.2. Шестнадцатеричная система счисления 547
14N.3. Комбинационная логика 547
14N.3.1. Краткая история цифровой логики 548
14N.3.2. Теорема де Моргана 549
14N.3.3. Сигналы с высоким и низким активным уровнем 550
14N.3.4. Логика для запуска ядерных ракет 551
14N.4. Реализация цифровой логики с помощью программируемых матриц 553
14N.4.1. Использование логического компилятора для работы
с низкими активными уровнями в ПЛУ 554
14N.5. Логические элементы типа ТТЛ и КМОП 555
14N.5.1. Сравнение внутреннего устройства логических элементов
ТТЛ и КМОП 555
14N.5.2. Пороговые уровни и помехоустойчивость 556
14N.6. Помехоустойчивость 557
14N.6.1. Помехоустойчивость по постоянному току микросхем КМОП и ТТЛ 557
14N.6.2. Обеспечение хорошей помехоустойчивости
с помощью дифференциальной передачи 559
14N.7. Дополнительные сведения о типах логических вентилей 560
14N.7.1. Конфигурации выхода 560
14N.7.2. Реализация логики на микросхемах ТТЛ и КМОП 561
14N.7.3. Скорость и энергопотребление 562
14N.8. Материал для чтения в АоЕ 563
Цель этой главы
В данной главе мы хотим использовать биполярные и полевые МОП-транзисторы для создания
устройств, способных реализовать логические булевы функции, а также намереваемся исследовать
некоторые из этих логических операций.
542
UN. Логические устройства
14N.1. Аналоговые
и цифровые системы
14N.1.1. Разница между этими
системами
Сначала мы рассмотрим, в чем заключается
разница между аналоговыми и цифровыми си-
стемами, а затем выясним разницу между дво-
ичными системами и более общим и интерес-
ным понятием цифровых систем.
♦ Разница между аналоговыми и цифровыми
системами.
В аналоговых системах информация представ-
ляется в виде непрерывной функции. Например,
напряжение может быть пропорциональным
температуре или звуковому давлению1.
В противоположность в цифровых системах
информация представляется в виде дискретных
кодов. Например, значения повышающейся
температуры можно было бы представить уве-
личивающимися цифровыми числами (0001,
0010, ООН и т. д.), но их также можно было бы
выразить в виде другого удобного цифрового
кода. Цифровое представление не обязательно
должно быть двоичным. Далее мы рассмотрим
это более узкое понятие.
Двоичная система представляет собой частный
случай цифровых систем, в которых возможны
только два значения, часто обозначаемые как
Истина и Ложь. При необходимости закодиро-
вать в двоичной системе более чем два значе-
ния, потребуется несколько двоичных цифр.
Двоичные цифры называются битами2.
Двоичный логический элемент сортирует вход-
ные значения в одну из двух категорий, т. е. это
устройство по существу является компаратором,
простым и быстродействующим (рис. 14N.1).
Цифровой элемент похож на обычный компа-
ратор. Но чем отличается цифровой логиче-
ский элемент от обычного компаратора, ска-
жем микросхемы LM311?
+5 В
Вход
1 В общем случае напряжение не обязательно должно быть
прямо пропорциональным представляемой величине, по-
скольку, например, результат логарифмического преобра-
зователя, может выглядеть более необычным.
2 Англ. bit — Binary digiT (двоичная цифра).
Выход
Вход
+2,5 В
Выход
Рис. 14N.1. Две приблизительно эквивалентные схемы
компаратора: цифровой инвертер и типичный компаратор
Примечание
Далее мы не будем делать различия между общи-
ми цифровыми системами и особым случаем дво-
ичной системы, полагая, что все наши цифровые
устройства относятся к двоичному типу.
Перечислим основные различия.
♦ Схемотехника входа и выхода — компара-
тор более гибкий, позволяет задавать порого-
вое значение и гистерезис, а также выбирать
выходной диапазон. Большинство цифровых
устройств не поддерживают возможность ги-
стерезиса. Те из них, которые поддерживают
гистерезис, обычно предназначены для рабо-
ты на линиях компьютерных шин (которые
содержат особо высокие уровни помех) или
с входами некоторых больших интегральных
схем, типа ПЛМ3. На наших лабораторных
занятиях мы познакомимся с одной из таких
микросхем, XC9572XL, в которой предусмо-
трен гистерезис величиной 50 мВ на всех
входах.
♦ Скорость — логический элемент принима-
ет решение (и выдает сигнал на выходе) как
минимум в 20 раз быстрее, чем компаратор
типа 311.
♦ Простота — логический элемент не требует
внешних компонентов, а подключается толь-
ко к шинам питания (положительной и об-
щей), получает сигнал на входе и выдает на
выходе. Он может работать без гистерезиса,
поскольку уровни подаваемых на его вхо-
ды логических сигналов меняются быстро
и резко.
14N.1.2. Зачем вообще нужны
цифровые системы?
Разве разумно заставлять аналоговый сигнал,
который может передавать богатую палитру
Программируемая матричная логика.
UN. I Аналоговые и цифровые системы
543
информации по одному проводу, в грубое циф-
ровое представление низких и высоких уров-
ней? Рассмотрим все преимущества и недо-
статки такого подхода. На рис. 14N.2 показа-
на карикатура на цифровое аудио, на которой
звучание скрипки Страдивари преобразовано в
звук с качеством компьютерной игры. Мы со-
мневаемся, что, глядя на рисунок, вы поймете
принцип цифрового аудио.
ЛА
♦5 В
К к
Звук дешевой
компьютерной игры
Звук скрипки I ^>~^~ '—' ^
Страдивари +2,5Т£'о11
(логический элемент)
Рис. 14N.2. Упрощенная версия цифрового аудио звучит до-
вольно непривлекательно
Недостатки цифровых систем
♦ Сложность — для передачи такого же объ-
ема информации требуется большее количе-
ство линий4.
♦ Скорость — обработка чисел, в которых за-
кодирована информация, иногда может за-
нимать больше времени, чем обработка со-
ответствующего аналогового сигнала.
Преимущества цифровых систем
♦ Помехоустойчивость — в цифровых си-
стемах сигнал заново восстанавливается на
каждом элементе, что способствует следую-
щим важным их применениям:
• компьютеры с хранимой программой. На
данном этапе это применение может ка-
заться несущественным, но, конечно же,
оно оказывается очень важным на прак-
тике;
• передача и многократная обработка ин-
формации без ошибок, за исключением
округления и дискретизации;
• обработка информации не в реальном
времени, а когда удобно, также является
следствием уже упомянутой помехозащи-
щенности.
4 Большее количество линий часто не относится к пере-
даче сигналов, поскольку для этого часто используется по-
следовательная передача по одному проводу. Но, по край-
ней мере, в своей «внутренней кухне» цифровые системы
кодируют значения в виде множественных параллельных
битов.
Возможны ли преимущества цифровых
систем без потери качества?
Аналоговый сигнал может быть представлен в
цифровой форме, хотя и с некоторой потерей
качества, но все же с достаточно большими
подробностями, чтобы быть практически неот-
личимым от оригинала. Пример такого преоб-
разования с использованием множественных
линий (битов) показан на рис. 14N.3.
ЛА
Звук скрипки
Страдивари
Аналоговый
в цифровой
Аналоговый
в цифровой
■ЛА
Звук скрипки
Страдивари
Рис. 14N.3. Качественное цифровое аудио
Один бит позволяет представлять только два
уровня. Соответственно, в случае с музыкаль-
ным сигналом он может представлять только
верхнюю или нижнюю половину звукового
диапазона. Два бита обеспечивают более под-
робную разрешающую способность из четырех
уровней: верхний, третий, второй и нижний
квадрант диапазона. Каждая дополнительная
линия или бит удваивает количество делений
всего диапазона.
Компьютеры в нашей лаборатории исполь-
зуют 8 битов, которые называются байтом5,
что дает 28 = 256 делений6. В коммерческих
компакт-дисках (CD) и большинстве совре-
менных цифровых аудиоформатах использу-
ется 16 битов, что обеспечивает 216« 65 000 де-
лений. Иными словами, в 16-битовом форма-
те, каждое из делений наших лабораторных
компьютеров разбивается еще на 28 делений.
Таким образом, звуковой сигнал делится на
очень мелкие части.
5 Некоторые консерваторы настаивают на необходимости
называть 8-битовое число октетом, вспоминая давно про-
шедшие времена, когда длина байта составляла не 8 битов,
а зависела от количества битов в слове конкретного ком-
пьютера. Но в настоящее время байтом общепринято на-
зывать 8-битовое число.
Будет интересно и познавательно знать названия других
двоичных значений. Так, четырехбитовое значение назы-
вается полубайтом или ниблом (англ. nibble), а двухбито-
вое — дибитом (англ. crumb),
6 Контроллер производства компании SiLabs, который
некоторые студенты предпочитают использовать на лабо-
раторных занятиях по микроконтроллерам, может кван-
товать в 16 раз мельче: на 2й делений. Но с нашими макет-
ными платами мы не можем воспользоваться на практике
таким разрешением.
544
14N. Логические устройства
Входной
аналоговый
сигнал
Выходной
сигнал
ЦАП:
1-битовый
V -V
3-битовый
5-битовый
2-биТОВЫЙ сКГТво
4-битовый
8-битовый
Рис. 14N.4. Увеличение количества битов (разрядов) улучшает цифровое представление аналоговой величины
На рис. 14N.4 демонстрируется влияние исполь-
зования 1, 2, 3, 4, 5 и, наконец, 8 битов в пре-
образованиях аналогового сигнала в цифровой
и обратно — из цифровой формы в аналоговую.
14N.1.3, Альтернативы двоичной
системе7
Почти во всех устройствах цифровой электро-
ники используется двоичная система, посколь-
ку двоичное кодирование простое и надежное.
Но в некоторых микросхемах применяется
больше чем два логических уровня. В частно-
сти, в нескольких микросхемах для внутренней
обработки используются три или четыре уров-
ня напряжения, чтобы повысить плотность дан-
ных. Например, в микросхемах флеш-памяти
на логических элементах И-НЕ предусмотрены
четыре или даже восемь уровней напряжения,
что дает пропорциональное повышение плот-
ности данных. Но за эту плотность приходится
расплачиваться уменьшением простоты и по-
мехозащищенности. Лучшая помехозащищен-
ность более старых двухуровневых устройств
иногда рекламируется как одно из их досто-
инств, но в настоящее время многоуровневые
устройства на логике И-НЕ преобладают в об-
ласти флеш-памяти.
Более важные случаи недвоичной кодиров-
ки встречаются в протоколах передачи дан-
ных. Например, телефонные модемы в борьбе
с жесткими ограничениями, накладываемы-
ми предельной частотой в 3,4 кГц телефонной
линии, умудрились втиснуть дополнитель-
ный объем цифровой информации в эту по-
лосу пропускания, используя как кодирование
множественными (больше чем двумя) уров-
нями, так и фазовое кодирование. Одна из та-
ких комбинаций этих двух типов кодирования,
называющаяся 16QAM, «втискивает» 4 бита
информации в один символ передачи, в резуль-
тате чего скорость передачи повышается до
9600 бит/с. Это выглядит удивительно для ли-
нии с полосой пропускания в 3,4 кГц? Конечно
же, это возможно. Процесс усложнения мето-
дов кодирования продолжается, еще больше
повышая скорость передачи данных.
На графике, напоминающем векторную диа-
грамму, содержащем действительную и мнимую
оси, можно отобразить несколько фаз, а также
амплитуду однобитовых кодировок. Например,
на рис. 14N.5 показан график одноуровневой,
четырехфазной угловой кодировки 4-QAM8,
позволяющей передавать четыре однозначных
«символа» (или «два бита на символ»), суммируя
два сигнала со смещением по фазе относительно
друг друга на 90° (обозначается термином ква-
дратурная модуляция, сокращенно КАМ)9.
^Белая точка представляет
битовое значение...
„.а его ориентация
по отношению к началу
координат (ориентация
«стрелки») представляет
фазу
Рис. 14N.5. Диаграмма цифровой информации, закодиро-
ванной в фазе и амплитуде двух квадратурных сигналов
С помощью этого же метода можно осущест-
влять еще более плотную кодировку данных.
АоЕ § 14.5.5В.
8 Quadrature Amplitude Modulation — квадратурная ам-
плитудная модуляция.
9 Источник: руководство «Quadrature Amplitude Modula-
tion» («Квадратурная амплитудная модуляция») компании
National Instruments (http://zone.ni.com/devzone/cda/
tut/p/id/3896). Здесь можно просматривать в замедлен-
ном режиме соотношение между сигналом во временной
области и фазово-амплитудной диаграммой, что способ-
ствует пониманию происходящего процесса.
14N.2. Двоичная система счисления
545
Расстояние от начала координат
представляет амплитуду
1КИ»
представляет сразу
< Граница принятия решений
16QAM
Рис. 14N.6. Диаграмма кодировки 16QAM
1011 1001 0010 ООН
1010 1000 0000 0001
1101 1100 0100 0110
1111 1110 0101 0111
16QAM
• Г и Q или совпадают по фазе, или сдвинуты на 180 градусов
> Г и Q являются четырьмя дискретными независимыми уровнями
Элементы кодировки КЛАЛ: два сигнала,
сдвинутые по фазе и отображающие четыре'
амплитудных уровня.
И сумма этих двух элементов — передаваемый^^ q
сигнал весьма необычной формы
Рис. 14N.7. Сигналы кодировки КАМ
Символ 1 Символ 2 Символ 3 Символ 4
На рис. 14N.6 изображена диаграмма кодиров-
ки 16QAM, которая позволяет передавать че-
тыре бита в одном символе передачи. На диа-
грамме символы представлены точками
10
Форма сигнала КАМ во временной области
чрезвычайно необычна (рис. 14N.7)11.
Сложные схемы кодировки наподобие КАМ хо-
рошо подходят для передачи информации, но,
к счастью для нас, для хранения и обработки
цифровых данных преимущественно использу-
ется двоичная система, которую намного легче
понять.
10 Источник: Учебное пособие компании Acterna (http://
www.viavisolutions.com/sites/default/files/technical-
ИЬгагу-items/digital-qam-signals-overview-and-basics-
testing-white-paper-en.pdf). В 2005 г. компания Acterna
была приобретена компанией JSDU, расположенной
в г. Милпитас (Milpitas), штат Калифорния, США.
11 Источник: Учебное пособие компании Acterna (http://
www.viavisolutions.com/sites/default/files/technical-
library-items/digital-qam-signals-overview-and-basics-
testing-white-paper-en.pdf).
14N.1 А Особые случаи
применения цифровой обработки
В некоторых случаях информация создается
уже в цифровой форме, вследствие чего ни-
какого преобразования не требуется. Такой
информацией могут быть числа (например, в
карманном калькуляторе) или слова (напри-
мер, в текстовом редакторе). Поскольку в этих
случаях информация никогда не существует в
аналоговой форме (только в голове человека),
имеет смысл обрабатывать эту информацию
сразу же цифровым способом в виде наборов
кодов. Применение иного способа было бы по
крайне мере странным. Можете ли вы предста-
вить себе хранение вашей контрольной работы
в виде напряжения на конденсаторах?
14N.2. Двоичная система
счисления
Возможно, что вы уже знакомы с двоичной
системой счисления, в которой вес каждого
546
74Л/. Логические устройства
следующего бита (разряда) равен двойному
весу предыдущего разряда. Эта система анало-
гична повседневно используемой нами десятич-
ной системе, в которой вес каждого следующего
разряда в десять раз больше веса предыдущего
разряда. Представленное в двоичной системе
число равно просто сумме значений его разря-
дов. Например: 10012 = 23+ 2°= 8 + 1 = 910 (под-
строчные цифры обозначают систему счисле-
ния: 2 — двоичная, 10 — десятичная).
Еще один пример показан на рис. 14N.8.
Десятичная Двоичная
102 101 10°
2 1 3
200 + 10+3 = 213
22 21 2°
1 0 1
4 + 0 + 1 = 5„
Рис. 14N.8. Сравнение десятичной и двоичной систем счис-
ления
14N.2.1. Представление
отрицательных чисел с помощью
дополнительного двоичного кода
Но двоичное число121001 не обязательно может
представлять десятичное число 9. Что означает
конкретное число в определенной ситуации,
зависит от того, как мы решили представлять
данную последовательность битов. Это утверж-
дение может показаться вам тривиальным,
но оно не совсем из категории высказываний
Шалтая-Болтая13. Разумеется, мы не хотим ска-
зать, что двоичное число, например 1001, мо-
жет представлять любое значение, а всего лишь
отмечаем тот факт, что иногда полезно, чтобы
оно могло представлять нечто иное, нежели 910.
В частности, довольно часто полезнее, чтобы
двоичное число 1001 представляло не 910, а от-
рицательное число.
Наиболее распространенным способом пред-
ставления отрицательных чисел в двоичной
системе счисления является разновидность
двоичного представления, называющаяся до-
полнительным двоичным кодом. Определить
значение числа в дополнительном двоичном
коде предельно просто: самый старший разряд
12 АоЕ § 10.1.3С.
13 Кроме всем известного факта, что вся королевская рать
не может Шалтая-Болтая собрать, он еще известен тем,
что его слова означают именно то, что он хочет, чтобы они
значили. Ни больше ни меньше.
(бит) имеет то же самое значение, что и в обыч-
ном двоичном представлении, но только отри-
цательное. Остальные разряды представляют
то же самое значение, что и в обычном двоич-
ном представлении, включая знак.
Таким образом, в обычном представлении дво-
ичное 1000 будет +810, но в дополнительном
двоичном представлении — -810. Подобным
образом дополнительное двоичное число 1001
будет -710 (-8 +1). На рис. 14N.9 показано еще
два примера чисел в дополнительном двоич-
ном коде. Число 1011 в обычном двоичном коде
представляет 1110, а в дополнительном 510.
Но двоичное число 0101 представляет 510 как
в обычном двоичном коде, так и в дополни-
тельном.
Обычный Дополнительный
двоичный код двоичный код
1011 8 + 2 + 1 = 1110 -8 + 2 + 1 =-5I0
0101 4 + 1 = 510 ...= 5Ю
Рис. 14N.9. Интерпретирование двух двоичных чисел как
беззнаковое (обычный двоичный код) и со знаком (дополни-
тельный двоичный код)
Приведенная ранее формулировка не является
стандартной. Чаще нас учат иному правилу соз-
дания дополнительного двоичного представле-
ния отрицательного числа и обратного преоб-
разования. Например, в книге АоЕ это правило
излагается следующим образом14.
Чтобы сделать число отрицательным, снача-
ла меняем на противоположный каждый его
бит (т. е. меняем 1 на 0 и наоборот, в резуль-
тате чего получаем число в обратном двоичном
коде), а затем к этому числу прибавляем 1, в ре-
зультате чего и получим число в дополнитель-
ном двоичном коде.
Но наш способ формирования и чтения чисел
в дополнительном двоичном коде проще, по-
скольку мы просто берем отрицательное чис-
ло, представляемое самим старшим битом (раз-
рядом), а затем суммируем с ним положитель-
ное число, представляемое остальными битами
(разрядами)15.
На данном этапе дополнительный двоичный
код может показаться вам довольно странным и
абстрактным. Но когда вы немного поработаете
14 АоЕ § 10.1.3С.
15 АоЕ § 10.1.3D.
14N.3. Комбинационная логика
547
с ним на практике, то убедитесь, что он очень
простой и рациональный. Например, при раз-
работке программы для микрокомпьютера
иногда следует указать машине, куда перейти,
вперед или назад, в коде программы. (Такое
действие называется ветвлением или перехо-
дом.) Далее в тексте приводится пример такого
указания посредством положительного или от-
рицательного значения в дополнительном дво-
ичном коде. Но сначала несколько слов о шест-
надцатеричном числовом формате.
14N.2.2. Шестнадцатеричная
система счисления
Шестнадцатеричная система счисления позво-
ляет удобно представлять многоразрядные дво-
ичные числа. Согласно ее названию в системе
используется 16 цифр, первые десять из кото-
рых такие же, как и в десятеричной системе, т. е.
с 0 по 9, и представляют те же самые значения.
А остальные шесть цифр записываются пер-
выми шестью буквами английского алфавита:
А, В, С, D, Е и F. Эти цифры представляют деся-
тичные значения с 10 по 15 соответственно.
Из табл. 14N.1 видно, что записывать много-
разрядные двоичные числа в шестнадцатерич-
ном представлении гораздо удобнее.
Таблица 14N.1. Запись чисел в разных
форматах
Двоичный
формат
0111
1001
1100
1111
10011100
Шестнадца-
теричный
формат
7
9
С
F
9С
Десятичный
формат
7
9
12
15
156
Теперь вы не будете сбивать с толку своих на-
парников по проекту, сообщая им данные
в форме типа:
— На моем счетчике значение один, ноль, ноль,
один, ноль, один, один, один, ноль.
— Сколько? — спрашивает ваш озадаченный
собеседник. Но если сказать:
— Мой счетчик показывает значение 96h, то
такой реакции, скорее всего, не последует.
В данном случае суффикс h означает, что чис-
ло записано в шестнадцатеричном формате.
Шестнадцатеричные числа можно также запи-
сывать как 0х9616.
Теперь вернемся к вопросу, как использовать
числа в дополнительном двоичном формате,
чтобы дать указание программе перейти впе-
ред или назад. Для этого не нужны две разные
команды: одна — для перехода вперед, а дру-
гая — для перехода назад. Вместо этого ис-
пользуется общая команда перехода, которой
передается числовой параметр, указывающий,
к какой следующей инструкции нужно перейти.
Если число отрицательное (в дополнительном
двоичном формате), то программа переходит
к инструкции, находящейся перед текущей ин-
струкцией, т. е. назад. А если число положи-
тельное, то переход выполняется вперед.
Возможно, пример на рис. 14N.10 убедит вас в
том, что существует различие между операци-
ей «вычесть А из В» и операцией «сложить от-
рицательное А с В». Для выполнения операции
вычитания, если рассматривать вычитание в
прямом смысле, требуется специальное аппа-
ратное обеспечение. В противоположность,
для сложения отрицательных чисел подойдет
то же самое аппаратное обеспечение, что и для
сложения обычных чисел. Вот почему допол-
нительный двоичный код так удобен в опера-
циях ветвления и перехода в компьютерных
программах.
Ш Текущее значение
(местоположение)
+ смещение
,. 0 10 0 Следующее значение
3
а
О ... О 1 0 4
+ 0 ... О 00 4 * ■
О ... 0 10 8 Следующее значение
Рис. 14N.10. Пример использования дополнительного дво-
ичного кода: операции сложения и вычитания могут выпол-
няться тем же самым аппаратным обеспечением. В зависи-
мости от знака слагаемого переход выполняется вперед или
назад
14N3. Комбинационная
логика
Объяснить, почему может потребоваться пре-
образование информации в цифровую форму,
16 Компилятор/ассемблер RIDE, с которым мы вскоре по-
знакомимся, распознает оба формата.
548
14N. Логические устройства
труднее, чем объяснить, как манипулировать
цифровыми сигналами. Но в действительно-
сти, по сравнению с проектированием аналого-
вых схем, цифровая схемотехника существенно
проще.
14N.3.1. Краткая история цифровой
логики
Если вы разделяете мнение Генри Форда, что
«всякая история — в той или иной степени
вздор», то можете пропустить этот подраздел.
Буль и де Морган
Довольно странно, почти сверхъестественно,
что правила компьютерной логики были доста-
точно всесторонне изложены английскими ма-
тематиками в середине XIX столетия, за 100 лет
до появления оборудования, которое могло ис-
пользовать эти правила. Джордж Буль (George
Boole) разработал большинство логических
правил в попытке применить математиче-
скую строгость к рассуждениям, выражаемым
обычным языком. Были и другие мыслители,
которые пытались решить эту задачу, в част-
ности Аристотель и Лейбниц, но им не удалось
продвинуться в данном направлении. Джордж
Буль не мог позволить себе платить за обуче-
ние в университете, поэтому он преподавал
в школе, одновременно проводя научные ис-
следования как любитель, задолго до того, как
благодаря одному из своих выдающихся докла-
дов получил должность в университете.
Он рассматривал утверждения на обычном
языке как суждение о членстве в классах.
Например, о годе, в котором большая часть
Европы была охвачена революциями, Буль пи-
сал следующим образом: «...в течение текущего
года 1848... аспекты политического изменения
[являются событиями, на которые] ...нереши-
тельные люди смотрят с ужасом, а активные —
с надеждой».
Затем он объясняет, что это замечание можно
описать, как утверждение о классах: «...слова-
ми "нерешительные" и "активные" мы отмеча-
ем из общего класса... тех, кто обладает этими
конкретными свойствами...»17
17 «The Nature of Logic» («Сущность логики») (1848) в кни-
ге «George Boole: Selected Manuscripts on Logic and its Philoso-
phy» («Джордж Буль. Избранные рукописи по логике и ее
Наконец, он предложил нотацию для ком-
пактного описания утверждений о членстве
в классах: «...если х представляет "люди", у -
"разумные существа", a z — "животные", тогда
уравнение
x = yz
будет выражать утверждение: «люди и разум-
ные животные идентичны».
Так утверждал господин Буль, человек — самое
разумное из животных! А затем он изложил
утверждение, которое намекает на его большие
надежды на эту логическую систему: «С по-
мощью вышеприведенной нотации можно вы-
разить любое категорическое суждение в виде
уравнения. Потому что для этого лишь необхо-
димо представить члены утверждения... симво-
лами... а затем соединить выражения... знаком
равенства»18.
Таблица для отображения отношения между
входными и выходными значениями получи-
ла претенциозное название «таблица истин-
ности». Никакой инженер не дал бы этому
небольшому списку операций такое название.
По-видимому, назвал таблицу так не сам Буль, а
философ Людвиг Виттгенштейн 70 лет спустя19.
Но поскольку Буль ставил перед собой цель си-
стематизировать анализ мышления, название
выглядит довольно уместным, несмотря на то,
что оно может звучать странно для инженера.
Прежде чем возвратиться к нашим скромным
электронным схемам, которые мы будем опи-
сывать с помощью булевой системы обозначе-
ний, давайте еще раз взглянем на тип утвержде-
ний, с которыми Булю так нравилось работать.
Этот пример должен вызвать у вас чувство глу-
бокого облегчения, что мы будем всего лишь
включать и выключать светодиоды в ответ на
переключение одного или двух тумблеров.
Итак, Буль предлагает изложить в виде матема-
тических символов отрывок из работы римско-
го философа Цицерона, обрабатывая условные
суждения.
философии»), ред. I. Grattan-Guinness и G. Bornet, изда-
тельство Birkhouser (1997), с. 5.
18 «On the Foundations of the Mathematical Theory of Logic»
(«Об основах математической теории логики») (1856),
с. 89.
19 По-видимому, источником этого названия является
единственная книга Витттенштейна, изданная при его
жизни. И если «таблица истинности» звучит несколько
устрашающе, как вам название этой книги Виттгенштейна:
«Tractates Logico-Philosophicus» (1921)?!
14N3. Комбинационная логика
549
В частности, он представляет логическое урав-
нение
20
и объясняет: «которое интерпретируется сле-
дующим образом: или Фабий родился при вос-
ходе Сириуса, и не погибнет в море; или он не
родился при восходе Сириуса, и погибнет в
море; или он не родился при восходе Сириуса,
и не погибнет в море».
После чтения этой фразы можно быть благо-
дарным Булю за компактность его системы
обозначений. (Обратите внимание на то, если
вы не поленитесь разобрать это уравнение),
что используемое Булем обозначение (J - х)
в современном виде пишется как х или х* (т. е.
не х)21.
Таким образом, если обозначить одно из буле-
вых утверждений (время рождения Фабия) как
Р, а другое (его гибель в море) — как Г, то функ-
цию f в современной нотации можно записать
следующим образом:
Эту довольно неудобную форму можно выра-
зить более компактно в виде функции, которая
может быть «ложью» только при условии, что Р
и Г имеют значение «истина»:
Соответствующая таблица истинности будет
выглядеть так:
р
0
0
1
1
г
0
1
0
1
/
1
1
1
0
Возможно, вы уже знаете, что это логическая
функция И-НЕ.
Хорошая новость № 1
Любое цифровое устройство22, вплоть до наи-
сложнейшего компьютера, можно собрать всего
20 Употребляются также термины булева функция и функ-
ция алгебры логики (ФАЛ). — Примеч. ред.
21 God Created the Integers (Бог создал целые числа), редак-
тор Стивен Хокинг (Stephen Howking), издательство Run-
ning Press (2005), с. 808.
22 АоЕ § 10.1.4Е.
лишь на трех функциональных логических эле-
ментах (или логических вентилях), которые
изображены на рис. 14N.11. Все логические
схемы являются комбинациями этих и только
этих трех функций.
и
и или не
о о -о
Рис. 14N.11.Три фундаментальные функции цифровой элек-
троники
Хорошая и замечательная новость № 2
Что еще более удивительно, оказывается, что
собрать любое цифровое устройство можно
всего лишь на логическом элементе одного типа
(а не трех). Им может быть элемент И-НЕ или
ИЛИ-НЕ (рис. 14N.12); эти два типа элементов
называются универсальными.
Рис. 14N.12. Универсальные логические элементы: И-НЕ
и ИЛИ-НЕ
Друг Буля по переписке, де Морган, доказал,
что с помощью инверторов функцию И мож-
но преобразовать в функцию ИЛИ и наоборот.
Это и есть тот мощный прием, позволяющий на
основе логического элемента одного типа реа-
лизовать любые другие логические функции.
14N.3.2. Теорема де Моргана
Это единственное важное правило булевой ал-
гебры, которое вам нужно будет запомнить.
(Другие правила довольно очевидны, типа
утверждений наподобие А + А* = 1.)
Формулировка теоремы де Моргана
Логические элементы можно поменять места-
ми, если одновременно инвертировать все их
входы и выходы. На рис. 14N.13 эта теорема
иллюстрируется графически.
и т.п.
Рис. 14N.13. Теорема де Моргана в графическом виде
550
UN. Логические устройства
При этом меняются только символы, обозна-
чающие логические элементы, но не выполняе-
мая ими логика и аппаратные средства.
Замечание
Последнее утверждение легко сформулировать,
но к нему трудно привыкнуть. Так что, не смущай-
тесь, если вам понадобится некоторое время, что-
бы свыкнуться с этим понятием.
Таким образом, любой логический вентиль, ко-
торый может выполнять инвертирование, мо-
жет выполнять это преобразование. Поэтому
в прошлом, когда еще использовались дискрет-
ные логические элементы, некоторые разра-
ботчики проектировали и собирали свои схемы
исключительно на элементах И-НЕ. Это было
возможным благодаря тому, что одна микро-
схема содержала несколько вентилей, поэтому
желательно было уменьшить число микросхем.
В настоящее время проектирование обычно
осуществляется с большими массивами логи-
ческих вентилей, и необходимость минимизи-
ровать количество микросхем больше не акту-
альна. Но теорема де Моргана остается важной
при работе с сигналами с активными низкими
уровнями, которые рассматриваются в следую-
щем разделе.
Теорема де Моргана, а также концепция низ-
кого активного уровня и логики высказываний
могут пока быть трудными, если вам никогда
раньше не приходилось иметь с ними дело. Но
вы будете вознаграждены за свои усилия (к кон-
цу этого курса) в овладении этими понятиями,
когда вам придется работать с множеством сиг-
налов с активным низким уровнем. Такие сиг-
налы большую часть времени имеют уровень,
близкий к 5 В (или к какому-либо другому по-
тенциалу, который соответствует высокому
логическому уровню), и переходят на низкий
уровень (близкий к 0 В) только в тех случаях,
когда нужно выполнить какое-либо действие.
14N.3.3. Сигналы с высоким
и низким активным уровнем
Активный логический уровень сигналов мо-
жет быть как высоким, так и низким23. На
рис. 14N.14 показаны эти два типа активных
логических уровней.
сто
23 АоЕ § 10.1.2А.
Рис. 14N.14. Сигналы с высоким и низким активным уровнем
Верхний сигнал на рис. 14N.15 обычно обозна-
чается «Готов», а нижний — «Готов», где чер-
та сверху обозначает, что активным является
низкий уровень, или «истина, когда низкий».
Низкие активные уровни нужны не для того,
чтобы сбить вас с толку, а по причинам, связан-
ным с аппаратным обеспечением. Мы рассмо-
трим эти причины после того, как познакомим-
ся с технологией изготовления логических эле-
ментов. А пока попробуем поработать с логи-
ческими вентилями, наблюдая, какой уровень
является активным.
Влияние на логику высокого
и низкого активного уровня
Когда в разделе 14N.2.1 мы рассматривали зна-
чение набора битов 1001 в виде номера, то стол-
кнулись с интересным фактом, что мы можем
задать любое удобное условное соглашение
о значении этой последовательности. В одних
случаях мы может рассматривать ее как +910, а
в других — как -710. Мы сами решаем, что она
представляет.
То же самое происходит при определении, ка-
кую операцию некоторый логический вентиль
выполняет в схеме. Выполняемая вентилем
операция жестко прошита в аппаратном обес-
печении, но значение этой операции открыто
для нашей интерпретации.
Чтобы пояснить этот вопрос, рассмотрим соот-
ветствующий пример. В большинстве случаев
предполагается, что высокий уровень пред-
ставляет логическое значение ИСТИНА. Таким
образом, операция, например, логического
элемента И обычно описывается следующим
образом: на выходе ИСТИНА, если ИСТИНА
на обоих входах.
То же самое говорится в и таблице истинно-
сти для логического вентиля И, только симво-
лами.
14N.3. Комбинационная логика
551
Таблица истинности для логического вентиля И
с использованием высоких активных уровней.
А
0
0
1
1
Б
0
1
0
1
А-В
0
0
0
1
Та же таблица в более абстрактной форме без
указания уровней.
А
Л
Л
И
И
В
Л
И
л
и
А-В
Л
Л
Л
И
Вторая таблица, в которой используются обо-
значения И (Истина) и Л (Ложь), более общая.
В первой же таблице указаны числа 1 и 0, кото-
рые могут намекать на использование высоких
и низких уровней напряжения. Пока что все
понятия нам знакомы24.
Но, как обещал де Морган, если мы заявим,
что, как на входе, так и на выходе, нас больше
интересует «О», а не «1», то таблицы истинно-
сти примут другой вид, а вентиль, поведение
которого описывается в таблице, очевидно, бу-
дет делать что-то другое.
Иллюстрация влияния сигналов с низким ак-
тивным уровнем: вентиль И (якобы) выполня-
ет операцию ИЛИ на низких уровнях.
А
0
0
1
1
В
0
1
0
1
А-В
0
0
0
1
или
А
И
И
F
F
В
И
Л
и
F
А-В
И
И
И
F
24 В книге АоЕ (в § 10.1.2А) заявлено о намерении авто-
ров различать обозначение «1» и «высокий уровень» в
логических утверждениях. Мы же не такие консерваторы.
Обычно у нас «1» означает высокий уровень, поскольку
это компактное обозначение, и совпадает с его значением
в двоичном представлении.
Если на обоих входах, А и В, присутствует логи-
ческий «О», мы также получим «О» и на выходе.
Иными словами, если мы перевернем значения
сигналов с «ног на голову», то получим функ-
цию ИЛИ. Тогда мы получим вентиль, который
выполняет операции ИЛИ с низкими уровня-
ми, как показано на рис. 14N.15. Это правиль-
ный способ представлять вентиль И, когда он
работает с низкими уровнями, представляю-
щими логическое ИСТИНА.
Рис. 14N.15. Обозначение вентиля И для указания, что он
выполняет операцию ИЛИ с низкими уровнями
Оказывается, что необходимость работать с
уровнями, «перевернутыми с ног на голову»,
т. е. когда активный уровень низкий, возника-
ет довольно часто. Но обратите внимание, что,
независимо от логической функции, выпол-
няемой элементом аппаратного обеспечения
в конкретной схеме, он все равно называется
вентилем И. То есть даже при обозначении, как
показано на рис. 14N.16, он все равно называет-
ся И. Называть один элемент аппаратного обе-
спечения двумя разными способами было бы
слишком запутанным.
Чтобы не усложнять вопрос, мы будем назы-
вать этот вентиль И, но уточнять, что он вы-
полняет функцию ИЛИ (в данном случае вы-
полняет операцию ИЛИ с низкими уровнями).
Но иногда проще всего ссылаться на вентиль по
его номеру. Например, это номер 08. Полагаю,
что все согласятся с таким утверждением.
14N.3A Логика для запуска
ядерных ракет
Далее приводится несколько драматичный
пример сигналов с активным низким уровнем.
Предположим, вам нужно спроектировать ло-
гический блок для схемы, управляемой двумя
сумасшедшими, желающими начать третью
мировую войну (рис. 14N.16).
Какой элемент нам нужно вставить в логиче-
ское устройство, чтобы выполнить требуемую
задачу?25
25 Для решения этой задачи требуется логический элемент,
который при низких уровнях на обоих входах выдает так-
же низкий уровень на выходе. Это вентиль, выполняющий
552
UN. Логические устройства
Логическое устройство
Сумасшедший А
ЧкОм
{Резистор нагревается
и поджигает бикфордов шнур
mm mm *m mm J
Сумасшедший Б ^
Рис. 14N.16. Чтобы логическое устройство подожгло бикфордов шнур, оба оператора должны одновременно нажать кнопку
запуска
Как он называется?26 Сейчас эти вопросы мо-
гут показаться излишними. Но в конце нашего
курса, когда вам придется работать с микро-
компьютерной схемой, в которой практически
все управляющие сигналы имеют низкий ак-
тивный уровень, вы будете благодарны за воз-
можность разобраться с понятиями активного
низкого уровня и соответствующими условны-
ми обозначениями.
Зачем вообще нужны активные низкие
уровни?
На рис. 14N.17 показана комбинация логиче-
ских элементов, которую нужно будет реализо-
вать при сборке микрокомпьютера из дискрет-
ных микросхем на лабораторном занятии 20L.
(Эту логику нужно будет запрограммировать
в микросхему ПМЛ27.)
Не подумайте, что мы специально придумали
эту схему таким образом, чтобы заставить вас
поупражнять свои мыслительные способности.
Это совсем не так. Наши логические венти-
ли выглядят необычно (полагаем, что вы раз-
операцию И с низкими уровнями, и его следует отобра-
жать таким: символ вентиля И с кружками инверсии на
обоих входах и на выходе.
26 Это логический элемент ИЛИ, несмотря на то, что
в описанных условиях он выполняет операцию И с сиг-
налами с низкими активными уровнями.
27 Это сокращение для термина «программируемая ма-
тричная логика», который является вариантом термина
«программируемая логическая матрица» (ПЛМ). Но сле-
дует отметить, что ПМЛ — это не просто переименован-
ная ПЛМ. Термин ПМЛ описывает подмножество ПЛМ,
в частности конкретную конфигурацию: операцию ИЛИ
над операндами И (т. е. операцию суммы логических про-
изведений). Дополнительная информация на эту тему при-
водится в Приложении А.
ЗАГРУЗЧИК I г-*
Рис. 14N.17. Пример практического применения сигналов
с активными низкими уровнями
деляете мнение большинства людей, что все
эти кружочки только добавляют ненужные
усложнения) потому, что мы были вынуждены
работать с сигналами с низким активным уров-
нем, а не потому, что нам так хотелось.
Все становится понятным из названий входных
и выходных сигналов вентилей на рис. 14N.18.
В частности, все эти сигналы имеют активный
низкий уровень. Единственное исключение со-
ставляют сигналы на линиях А и D, по которым
передаются сигналы адресов и данных. Эти сиг-
налы не имеют активного состояния, поскольку
оба уровня, как высокий, так и низкий, равно-
значны, оба представляют значение ИСТИНА.
Сигнал записи в оперативную память (RAM28)
обозначен WR*. На входах разрешения микро-
схемы справа также присутствуют кружочки,
которые означают, что сигналы разрешения
схемы также имеют низкий активный уровень.
На рис. 14N.18 показан фрагмент процессо-
ра, который, образно выражаясь, является
28 Англ. random access memory - память с произвольным
доступом (оперативное запоминающее устройство, ОЗУ).
UNA. Реализация цифровой логики с помощью программируемых матриц
553
«мозгом» компьютера. Сигналы его выводов
управления (WR*, RD* и PSEN*29) также имеют
низкий активный уровень. Так что, хотите вы
того или нет, лучше набраться опыта работы с
сигналами с низким активным уровнем.
Vss
PS6W
ЗАГРУЗЧИК
Рис. 14N.18. Сигналы управления, выдаваемые процессо-
ром, также имеют низкий активный уровень
Почему сигналы управления обычно имеют
низкий активный уровень, мы объясним чуть
далее. Но сначала вкратце рассмотрим програм-
мируемые логические схемы, которые в настоя-
щее время являются стандартным подходом к
реализации цифровой логики. ПЛМ заменили
стандартную логику в виде цифровых микро-
схем, подобных рассматриваемым в разде-
ле 14N.5.1 далее. Вам будет приятно узнать, что
логический компилятор может помочь легко
решить досадную проблему низких активных
уровней.
14NA Реализация цифровой
логики с помощью
программируемых матриц
Небольшие наборы логических вентилей, на-
подобие микросхемы 74НС00, содержащей
четыре элемента И-НЕ, с которой мы познако-
мимся на лабораторном занятии 14L, не дают
29 Если вам интересно знать, название сигнала PSEN озна-
чает Program Store Enable (разрешить программный нако-
питель). Это особый тип операции специально для чтения
программного кода, а не обычных данных. У вас будет воз-
можность близко познакомиться с этими сигналами на ла-
бораторных занятиях по микропроцессорам.
эффективного способа реализации цифровой
логики. Лучшим подходом к разработке цифро-
вых схем будет использование программируе-
мых микросхем, содержащих большое количе-
ство вентилей. В этом курсе мы будем приме-
нять небольшие (по современным стандартам)
модификации таких микросхем, содержащие
около 1600 вентилей. Возможно, что вам при-
дется познакомиться с более сложными микро-
схемами после окончания этого курса.
Программируемые логические микросхемы об-
ладают двумя преимуществами. Во-первых,
они более гибкие в использовании, чем жестко
прошитые микросхемы вентилей. Логику таких
схем можно изменить, даже когда устройство
уже собрано. (Для этого предусмотрено спе-
циальное внутрисхемное программирование.)
Во-вторых, эти микросхемы намного дешевле,
чем обычные логические микросхемы венти-
лей, просто благодаря большей степени инте-
грации. (Используемая нами программируемая
микросхема с 1600 вентилями стоит всего лишь
несколько долларов.) Далее приводится крат-
кое описание двух типов этих микросхем.
♦ Вентильные матрицы (микросхемы FPGA).
Существуют две категории этих устройств:
• специализированные микросхемы30. Про-
ектирование таких микросхем стоит очень
дорого (реализация проекта может стоить
около 100 000 долларов). Применение та-
ких микросхем имеет смысл только в том
случае, если планируется изготовление
очень большого их количества;.
• программируемые вентильные матрицы31.
Цена этих устройств более высокая за еди-
ницу, но их использование в проектируе-
мой схеме ничего не стоит, кроме времени
на создание качественного кода для их
программирования. Эти устройства могут
сохранять конфигурацию связей между
вентилями или в энергозависимой памяти,
содержимое которой теряется при выклю-
чении питания, или в энергонезависимой
памяти, обычно флеш-памяти.
♦ Программируемые логические устрой-
ства (ПЛУ, их часто называют также
ПМЛ). Эти устройства менее сложные, чем
30 Англ. ASIC — Application Specific 1С. Далее для краткости
будем использовать это название.
31 Англ. FPGA — Field-Programmable Gate Array. Далее для
краткости будем использовать это название.
554
UN, Логические устройства
микросхемы FPGA, и представляют собой
набор логических элементов ИЛИ или И
с несколькими входами. Вскоре мы будем ра-
ботать с этими микросхемами.
14N.4.1. Использование
логического компилятора для
работы с низкими активными
уровнями в ПЛУ
Для программирования программируемых ло-
гических устройств существует компьютерная
программа, называемая логическим компиля-
тором. Эта программа преобразует команды,
написанные на языке, удобном для понима-
ния человеком, в схемы логических связей.
Логический компилятор может упростить ра-
боту с сигналами с низким активным уровнем.
Логический компилятор также называется
языком описания аппаратных средств?2. В этом
курсе мы будем использовать язык HDL, назы-
ваемый Verilog. Конкуренцию ему составляет
другой язык HDL, называемый VHDL33.
Метод для облегчения работы с низкими ак-
тивными уровнями заключается в создании эк-
вивалентного высокого активного уровня для
каждого сигнала с низким активным уровнем.
Иными словами, мы определяем дополнитель-
ный сигнал для каждого сигнала с низким ак-
тивным уровнем34. С помощью этих сигналов,
можно создавать логические уравнения для ло-
гики с чисто высокими активными уровнями,
не беспокоясь об активном уровне конкретных
сигналов. Такой подход не только облегчает со-
ставление логических функций, но и позволяет
создавать намного более понятный код.
На рис. 14N.19 показан простой пример реали-
зации данного подхода: логический вентиль,
выполняющий операцию И с двумя сигнала-
ми, один из которых имеет высокий активный
уровень, а другой — низкий. Выходной сиг-
нал вентиля имеет низкий активный уровень.
Такую логику достаточно легко отображать
в виде программного кода35. На языке Verilog
эту логику можно описать любым из двух спо-
собов.
Неудачный вариант логики
Можно просто записать каждый сигнал в его
текущем виде — с высоким активным уров-
нем или низким. Но получившаяся логическая
функция будет выглядеть довольно странно.
Далее приводится листинг на языке Verilog.
Листинг 14N.1. Первый вариант записи логиче-
ской функции на языке Verilog
module actlow_ugly_oct11 (
input a_bar,
input b,
output out_bar
// Смотрите, как отвратительно выглядит логическая
формула, если использовать смесь высоких и низких ак-
тивных уровней:
assign out_bar = !(!a_bar & b);
endmodule
Листинг начинается с перечня всех сигналов,
входных и выходных. К названиям сигналов
с активным низким уровнем добавлен суффикс
d>
Рис. 14N.19. Схема простой логики со смешанными сигналами с высоким и низким активными уровнями
32 Англ. Hardware Description Language — HDL. В дальней-
шем для краткости будем использовать это сокращение.
Например, язык HDL.
33 Англ. Very [High Speed Integrated Circuit] Hardware De-
scription Language. Этот язык был разработан по запросу
Министерства обороны США, тогда как язык Verilog был
разработан в частном секторе промышленности.
34 Эти новые, определенные нами сигналы существуют
только на бумаге для удобства программистов и не тре-
буют никакой дополнительной реализации в аппаратных
средствах.
_bar36, чтобы отличить их от сигналов с высоким
активным уровнем. Символ восклицательного
35 Эта схема была создана логическим компилятором,
который и добавил инвертор на выходе. Человек бы этого
не сделал, а просто бы добавил кружок инвертирования на
выходе логического вентиля И.
36 Английское bar в данном случае означает символ над-
черкивания, которым обозначаются низкие активные
уровни. — Примеч. пер.
14N.5. Логические элементы типа ТТЛ и КМОП
555
знака (!)37 обозначает логическую инверсию,
а символ & — логическую операцию И.
Логическая формула, реализующая функцию И,
содержит восклицательные знаки, что делает ее
трудной для восприятия. Эти восклицательные
знаки не означают, что сигнал имеет значение
ЛОЖЬ или снят, а лишь то, что они имеют низ-
кий активный уровень.
Правильный вариант логики
Если вы не возражаете против создания экви-
валента с высоким активным уровнем для каж-
дого сигнала с низким активным уровнем (что
потребует дополнительной работы), то вашей
наградой будет понятное логическое выраже-
ние.
В листинге 14N.2 после перечня действитель-
ных сигналов определяются два эквивален-
та с высоким активным уровнем для одного
входного сигнала с активным низким уровнем
и выходного сигнала тоже с активным низким
уровнем. Строка кода с инструкцией wire out-
указывает компилятору тип нашего «самодель-
ного» выходного сигнала.
Листинг 14N.2. Второй вариант записи логиче-
module actlow_pretty_oct11 (
input a__bar,
input b,
output outjDar
);
wire out;
// Теперь инвертируем все сигналы с активным низким
уровнем, чтобы при создании логической формулы мож-
но было работать со ВСЕМИ сигналами как с активным
высоким уровнем.
assign a = !a_bar; // Создает временный внутренний сиг-
нал (а), который не подается ни на какой вывод.
Данная логическая формула выражает то, что
должно означать, независимо от типа активно-
го уровня: если оба входные условия удовлет-
воряются, выполняется какая-либо операция.
Другими словами, логический компилятор по-
зволяет нам разделить два вопроса, с которым
мы хотим иметь дело по отдельности:
1. Какие активные уровни используются — вы-
сокие или низкие? Этот вопрос решается в
начале листинга.
2. Какие логические операции мы хотим выпол-
нить с входными данными? Это часть задачи,
которая представляет основной интерес.
Не переживайте, если на данном этапе у вас воз-
никают проблемы с пониманием листинга про-
граммы на языке Verilog. Мы будем рассматри-
вать этот язык и то, как он обрабатывает сиг-
налы с низким активным уровнем, далее в этой
книге. Как и все прочие более-менее сложные
темы, для его изучения нужно некоторое вре-
мя, чтобы накопить достаточный опыт.
14N.5. Логические элементы
типа ТТЛ и КМОП
14N.5.1. Сравнение внутреннего
устройства логических элементов
ТТЛ и КМОП
Некоторые особенности этих двух типов логи-
ческих элементов показаны на рис. 14N.2038.
Выход ~~н I— Выход
Lfi
ТТЛШ-элемент И-НБ
КМОП-элемент НЕ
Рис. 14N.20. Элементы И-НЕ и НЕ, реализованные по техно-
логии TTL и КМОП
Перечислим основные отличия.
♦ Входы — у ТТЛ-элемента на входе присут-
ствует высокий уровень, а у КМОП — нет.
♦ Пороговый уровень — пороговый уровень
элемента на ТТЛ смещен к уровню логиче-
ского нуля, а на КМОП расположен прибли-
зительно по центру.
37 На английском жаргоне этот символ называется bang.
АоЕ § 12.1.1,10.2.2,10.2.3.
556
14N. Логические устройства
♦ Выход — выходной сигнал ТТЛ-элемента от-
личен от напряжения питания 5 В, тогда как
у элемента на КМОП этот сигнал примерно
равен 5 В.
♦ Энергопотребление — при любом состоя-
нии выхода (высокий или низкий) логиче-
ского элемента на КМОП ток с шины +5 В на
«землю» через него не проходит. И наоборот,
при любом состоянии выхода ТТЛ-элемента
через него проходит ток или через повышаю-
щий транзистор на базе (если на входе низ-
кий уровень), или через первый транзистор
(который открыт, если на обоих входах при-
сутствует высокий уровень).
14N.5.2. Пороговые уровни
и помехоустойчивость
Все цифровые устройства обладают определен-
ной помехоустойчивостью. Сравнивая поро-
говые уровни для ТТЛ-устройств и для 5-воль-
товых КМОП-устройств, можно сделать вывод,
что КМОП-микросхемы обладают лучшей по-
мехоустойчивостью (рис. 14N.21).
Выход
Высокий
уровень
Входу,
ттлш
Низкий
уровень
КМОП (Высокоскоростная)
Рис. 14N.21. Сравнение пороговых уровней и помехоустой-
чивости устройств на ТТЛ и КМОП
Интересное примечание
Микросхемы на ТТЛ и n-канальные МОП-микро-
схемы получили такое широкое применение, что
некоторым семействам КМОП-устройств (обозна-
чаемым 74ххСТхх) целенаправленно привили
«плохие привычки» ТТЛ-устройств. А именно для
их пороговых уровней заданы значения низких
уровней ТТЛ-устройств. Символы «СТ» в обозна-
чении таких микросхем означают «КМОП с поро-
говыми уровнями ТТЛ»39. Мы будем использовать
много таких микросхем семейств 74НСТхх на на-
ших лабораторных занятиях по микрокомпьюте-
рам, поскольку нам нужно будет приспосабливать-
ся к микропроцессору, выходные высокие уровни
которого такие же, как и уровни ТТЛ-микросхем
(несмотря на то, что он изготовлен по КМОП-тех-
нологии). Но при наличии выбора мы предпочи-
таем использовать обычные КМОП-микросхемы,
хотя весь мир проголосовал за семейство НСТ40.
Семейства НСТ предоставляют больше функций,
чем семейства НС.
Причина, по которой типичный сигнал
управления имеет активный низкий
уровень
Ранее мы обещали, что рассмотрение внутренне-
го устройства микросхемы логического вентиля
даст ответ на этот вопрос, что и было сделано в
описании пороговых уровней в разделе 14N.5.1.
В частности, предпочтение низких активных
уровней объясняется асимметрией пороговых
уровней ТТЛ-устройств. Если у нас есть несколь-
ко шин управления, которые неактивны боль-
шую часть времени, то будет лучше, чтобы неак-
тивные сигналы имели высокий уровень, а низ-
кий уровень устанавливать только для активных
сигналов. Но можно возразить, что это объясне-
ние применимо только к ТТЛ-микросхемам, а не
к КМОП. Дело в том, что эти соглашения были
установлены в те времена, когда царили ТТЛ-
устройства, и продолжают действовать даже по-
сле того, как исходные причины для них давно
неактуальны.
Далее вкратце рассматриваются две характе-
ристики ТТЛ-устройств, благодаря которым
предпочтение отдается использованию сигна-
лов с низкими активными уровнями.
♦ Входные сигналы высокого уровня ТТЛ-
устройств менее восприимчивы к по-
мехам, чем входные сигналы низкого
уровня. Хотя гарантированный запас поме-
хоустойчивости для этих двух уровней раз-
личается всего лишь несколькими десятыми
вольта, типичный запас отличается больше.
Поэтому надежнее оставить контрольные
шины большую часть времени на высоком
уровне, с которого они будут опускаться на
более «опасный» низкий уровень лишь вре-
мя от времени.
♦ На входах ТТЛ-устройств легко устано-
вить высокий уровень. Более того, по-
скольку входы ТТЛ-устройств изначально
имеют высокий уровень, этот уровень уста-
навливается по сути «бесплатно», не требуя
39 Англ. CMOS with TTL levels.
40 Англ. High Speed with TTL levels — высокоскоростные
с уровнями ТТЛ.
14N.6. Помехоустойчивость
557
никакого тока. Поэтому, если вы проекти-
руете микропроцессор для управления ТТЛ-
устройствами, то облегчите ему жизнь, по-
зволив его линиям управления большую
часть «отдыхать» на высоком уровне с низ-
ким потреблением тока.
Оба свойства подталкивают нас в одном и том
же направлении полезности сигналов с низ-
ким активным уровнем. Вы сможете убедить-
ся в этом самостоятельно, когда соберете свой
микрокомпьютер, в котором все шины управ-
ления будут иметь активный низкий уровень.
Примечание
Фраза «шины управления» может несколько озада-
чить вас. Да, мы не говорим, что все сигналы имеют
низкий активный уровень, поскольку это неотносит-
ся к шинам адресов и данных. Но для каждой шины,
которая имеет активный и неактивный уровни, ак-
тивный уровень будет низким. Но некоторые шины
не имеют активных и неактивных уровней. К таким
шинам относятся, например, шины данных, которые
активны как при высоком, так и при низком уровне.
То же самое относится и к шинам адреса. Поэтому
для этих шин разработчики используют соглашение
о высоком активном уровне. Что очень даже кстати
для нас, так как мы можем интерпретировать значе-
ние, например, 1001 на шинах данных как 9 без не-
обходимости инвертировать каждый бит. Поэтому
вместо того, чтобы ворчать о необходимости раз-
бираться с низкими активными уровнями, считайте,
что вам повезло, ибо могло быть и хуже.
14N.6. Помехоустойчивость
Все логические элементы могут игнорировать
некоторый уровень помех на своих входах. В
разделе 14N.6.1 приведены результаты тести-
рования, которые показывают, что помехо-
устойчивость устройств одного семейства
лучше, чем другого. Сначала мы рассмотрим
самый простой тип помехоустойчивости — по
постоянному току. Затем опишем стратегию
помехоподавления, называющуюся дифферен-
циальной передачей.
14N.6.1. Помехоустойчивость
по постоянному току микросхем
КМОП и ТТЛ
На рис. 14N.22 показана тестовая установка
для добавления помех в логические сигналы,
которые затем подавались на логические вен-
тили микросхем разных семейств, одна — ТТЛ,
а три остальные — КМОП.
Сигнал
374LS04
(ТТЛ)
.J4HCT04
о—
(КМОП, входные ТТЛ-уровни)
Z4HC04
(КМОП)
74НС14
(КМОП с гистерезисом)
Рис. 14N.22. Установка для тестирования помехоустойчиво-
сти логических вентилей
Постепенно повышаем уровень помех
Сначала в сигнал добавляется умеренный уро-
вень помех, и микросхемы всех типов справ-
ляются с этим. На левой осциллограмме на
рис. 14N.24 можно видеть, что логические вен-
тили микросхем всех семейств игнорируют по-
меховый сигнал треугольной формы. Иными
словами, эти вентили демонстрируют сильную
сторону цифровых устройств.
На правой осциллограмме на рис. 14N.23 ми-
кросхемы ТТЛ и КМОП с уровнями ТТЛ (НСТ)
не справляются с помехами в сигнале с низким
уровнем. Микросхемы КМОП с уровнями ТТЛ
не справляются с такими же помехами, как и
микросхемы ТТЛ. Это логично, поскольку ми-
кросхемы обоих типов работают с одинаковы-
ми уровнями.
Примечание
Возможно, вас интересует, какая выгода произ-
водителям предлагать высокоскоростные микро-
схемы КМОП с ТТЛ-уровнями (НСТ), уровень по-
мехоустойчивости которых хуже, чем у обычных
высокоскоростных КМОП-микросхем (НС). Этот
тип микросхем предназначен для того, чтобы
можно было усовершенствовать устройства с ТТЛ-
микросхемами, просто заменив старые компонен-
ты на новые (НСТ), а также для того, чтобы обеспе-
чить совместимость между схемами с уровнями
ТТЛ и технологией КМОП. Мы используем микро-
схемы КМОП НСТ таким образом в одной из вер-
сий лабораторных занятий по микрокомпьютерам,
завершающим этот курс {разделы 20L1 и 211.7):
для того чтобы принимать сигнал от несколь-
ких микросхем с ТТЛ-уровнями. Одна из таких
558
UN. Логические устройства
Лаб. занятие 13. Помехоустойчивость: вентили типа
НС (высокоскоростная КМОП) показывают лучшие
результаты помехоустойчивости по постоянному току,
чггА типа ТТЛ
LAB 13: NOISE IMMUNITY НС beats TU (DC immunity)
Входной
сигнал
Лаб. занятие 13. Помехоустойчивость: вентили типа
НС (высокоскоростная КМОП) показывают лучшие
результаты помехоустойчивости по постоянному току,
чем типа ТТЛ
Входной
сигнал
immunity)!
V\ fWWWVWi !
•VVVVWVW t/WvW
Умеренные помехи: все цифровые вентили игнорируют их Более сильные помехи: вентили на ТТЛ и КМОП с ТТЛ-
уровнями не проходят тест
Рис. 14N.23. Вентили микросхем всех семейств игнорируют умеренный уровень помех, но с более сильными помехами
микросхемы ТТЛ не справляются. (Усиление осциллографа: 5 В/дел.)
микросхем — 74НСТ139 — для декодирования
двух двоичных ТТЛ-сигналов микроконтроллера
в четыре шины, которая используется на лабора-
торном занятии 21L (Полная схема этого микро-
контроллера изображена на рис. 20L1.)
Микросхемы КМОП показали лучшие резуль-
таты благодаря их большему запасу помехо-
устойчивости.
Испытание сильными помехами
выдерживают только микросхемы
на триггере Шмитта
Дальнейшего повышения уровня помех не
выдерживают даже микросхемы КМОП. Но
микросхемы одного семейства показали даже
лучшие результаты (рис. 14N.24, самая нижняя
осциллограмма), чем КМОП-инвертор. Это ми-
кросхема 74НС14 со встроенным гистерезисом,
для которой помехи даже большой амплитуды
оказались нипочем.
Поскольку эта микросхема прошла тест, можно
подумать, что все микросхемы логических вен-
тилей должны со временем снабдить встроен-
ным гистерезисом. Но этого не произошло, по-
скольку гистерезис слегка замедляет переклю-
чение, а вопрос скорости зачастую более важен,
чем необходимость в наилучшей помехоустой-
чивости. Это правило действует для всех микро-
схем логических вентилей, за исключением тех,
13: NOISE IMMUNITY: НС beats TTL (DC immunity)
ММ! 1ААМ/
j 74C14 (КМОП с гистерезисом)]
Лаб. занятие 13. Помехоустойчивость: вентили типа
НС (высокоскоростная КМОП) показывают лучшие
результаты помехоустойчивости по постоянному току,
чем типа ТТЛ
Рис. 14N.24. Испытание сильными помехами проходит толь-
ко микросхема с гистерезисом (74С14). (Усиление осцилло-
графа: 5 В/дел.)
которые предназначены для работы в особенно
шумном окружении. Например, микросхемы
вентилей для получения входных сигналов из
длинных линий шин (буферы) часто обладают
гистерезисом.
Далее, в разделе 14N.6.2, мы познакомимся с
типом вентилей, в которых реализован другой
подход, называемый LVDS41. На рис. 14N.25
41 Англ. Low Voltage Differential Signaling — низковольтная
дифференциальная передача сигнала.
14N.6. Помехоустойчивость
559
приводится сравнительный график напряже-
ний сигналов для логических вентилей разных
типов, включая сигналы типа LVDS42.
N5B
•
3B
fSS
КАЛОП
ТТЛ
LVDS
Рис. 14N.25. Небольшой размах сигнала может быть вполне
пригодным, но при этом требуется дифференциальный ме-
тод передачи
Небольшой размах сигнала вентилей LVDS дает
два дополнительных преимущества: низкие
электромагнитные помехи и меньшее влияние
на стабильность источника питания. Мы на-
зываем эти преимущества дополнительными
потому, что основной сильной стороной мало-
го размаха сигнала является хорошая помехо-
устойчивость при низких напряжениях пита-
ния, как рассматривается в разделе 14N.6.243.
14N.6.2. Обеспечение хорошей
помехоустойчивости с помощью
дифференциальной передачи
Современные логические устройства проек-
тируются для работы с источниками питания
с более низким напряжением, чем традицион-
ные +5 В: 3,3, 2,5 и 1,8 В. Тенденция снижения
напряжения питания, скорее всего, будет про-
должаться. Такие низкие напряжения питания
затрудняют защиту логических вентилей от
ошибок, вызываемых помехами. Запас помехо-
устойчивости по постоянному току величиной
U+ например, 1,8 В
0,4 В, которым обладают устройства ТТЛ и вы-
сокоскоростные КМОП-устройства, возможен
лишь благодаря относительно высокому напря-
жению питания. Например, пропорционально
сжав все характеристики, мы бы получили на
50% меньший запас помехоустойчивости при
напряжении питания 2,5 В. При еще меньшем
напряжении питания этот запас уменьшится
еще больше. Хуже всего эта проблема прояв-
ляется с длинными шинами питаниями, как на
задней панели компьютера.
Указанная проблема решается с помощью диф-
ференциальной передачи сигнала. При этом
передается и принимается не один сигнал, а
сигнал и его логическое дополнение (инвер-
тированный сигнал) по двум проводам, как
показано на рис. 14N.26. (Мы впервые встре-
тились с этим типом передачи в разделе 5N.7,
рис. 5N.27.)
Обычно помехи воздействуют на оба сигнала
одинаково, в результате чего вычитание одно-
го сигнала из другого очистит общий сигнал от
большинства посторонних помех. Мы уже на-
блюдали этот процесс на лабораторном занятии
по аналоговому дифференциальному усилите-
лю в разделе 51.1, так что он не представляет
для нас ничего нового, с тем лишь исключени-
ем, что данный метод применяется к цифровым
сигналам. Дифференциальные драйверы LVDS
передают токи, а не напряжения. Эти токи пре-
образуются в разницу напряжений резистором,
подключенным к линиям передачи на прием-
ном конце.
Примечание
Такое подключение также полезно тем, что этот ре-
зистор создает согласующую нагрузку, предотвра-
щающую отражения сигнала. Более подробную
информацию по этому вопросу см. в Приложении В.
Небольшой размах (0,35 В)
(/+ например, 1,8 В
JL
Рис. 14N.26. Несмотря на низкое напряжение питания, дифференциальная передача сигнала может обеспечить хорошую
помехоустойч и вость
42 National Semiconductor: http://www.ti.com/lit/ml/
snlal87/snlal87.pdf, §5=-4.
43 Рис. 14N.26 создан на основе рисунка из руководства
по LVDS компании National Semiconductor: http://www.
ti.com/lit/ml/snlal87/snlal87.pdf.
На рис. 14N.27 мы вставили стандартный логи-
ческий сигнал с уровнями 0/5 В (ТТЛ) в диффе-
ренциальный драйвер, а затем добавили в него
560
UN. Логические устройства
помеху величиной около вольта (треугольный
сигнал)44.
Входной сигнал
Выходной Помеха с размахом окопо 1 В
дифференциальный сигнал*
Выходной
Дифференциальный сигнал:
'""около 0,35 В
дифференциальный сигнал-
МП... . , И П Н *
■ 't V ^ f! У ' i if I ? ^! V * st! "*' 11 ?
Выходной сигнал
(дифф. сигнал + дифф. сигнал)
аи s.oov, }СИ2; i.opy !'М;4ОЛо&$; ai cm £ 2.60 V;
an '"_'"i"?oo"y"l!'""r!"JSKDB:'"""5'Гоо_уГ1'.1'1 ' '
Рис. 14N.27. Дифференциальные сигналы LVDS могут вы-
держивать шум большей величины, чем размах самого сиг-
нала.
Две средние осциллограммы на рис. 14N.28 ото-
бражают выходной сигнал микросхемы драй-
вера: дифференциальную пару сигналов, один
из элементов которой совпадает по фазе с вход-
ным ТТЛ-сигналом, а другой сдвинут на 180°.
Драйвер преобразует напряжения входного
ТТЛ-сигнала в токи дифф+ и дифф-, которые на
приемном конце преобразуются нагрузочным
резистором (номиналом 100 Ом) обратно в на-
пряжения45. Размах этого дифференциального
сигнала небольшой (около 0,35 В), и по срав-
нению с треугольным помеховым сигналом
на рис. 14N.28 выглядит карликовым. Но по-
скольку приемник дифференциального сигнала
работает с разницей между его составляющими
(дифф+ и дифф-), он восстанавливает чистый
исходный сигнал ТТЛ, отбрасывая помеховую
составляющую.
Такая успешная передача дифференциального
сигнала с небольшим размахом иллюстрирует,
44 Для этого мы применили довольно необычный способ:
подавая этот треугольный сигнал с размахом 1В на вывод
«земли» микросхемы передатчика.
45 Резистор для преобразования тока в напряжение на
приемном конце также служит и другой полезной цели: со-
гласовывая характеристические импедансы линий переда-
чи, он не допускает возникновения всплесков напряжения,
вызываемых отражением сигнала, которые в противном
случае могли бы появляться при поступлении сигнала на
высокоимпедансный вход принимающего вентиля. Более
подробную информацию по этому вопросу см. в Приложе-
нии В.
каким образом дифференциальная передача
может обеспечить хорошую помехоустойчи-
вость в логических системах с чрезвычайно
низкими напряжениями питания. Согласно
спецификации LVDS размах напряжения
на приемном конце может быть всего лишь
100 мВ.
Дифференциальные вентили обладают двумя
другими преимуществами:
♦ высокой скоростью передачи данных. За-
держка распространения для передатчика и
приемника составляет меньше 3 не;
♦ меньшей интенсивностью излучаемых по-
мех, чем обычные вентили, работающие с
напряжениями (как отмечалось ранее).
Эти свойства возможны благодаря небольшому
размаху напряжения, а также благодаря симме-
тричным токовым сигналам, распространяю-
щимся по информационным шинам. Эти сиг-
налы противоположной полярности протекают
по шинам параллельно друг другу, что способ-
ствует взаимному подавлению их магнитных
полей46.
14N.7. Дополнительные
сведения о типах логических
вентилей
14N.7.1. Конфигурации выхода
Активное повышение напряжения
Во всех солидных логических вентилях на вы-
ходах применяется активное повышение на-
пряжения для обеспечения четких высоких
и низких уровней. На лабораторном занятии
14L у вас будет возможность убедиться в том,
что пассивное повышение напряжения (пред-
ставленное на рис. 14N.28, а) не только уве-
личивает энергопотребление, но и снижает
быстродействие. Можете сказать, почему это
происходит?47
46 См. руководство по LVDS компании National Semicon-
ductor, доступное по адресу: http://www.ti.com/lit/inl/
snlal87/snlal87.pdf
47 Потому что неизбежная паразитная емкость должна
заряжаться через повышающий резистор, а не через тран-
зисторный ключ.
14N.7. Дополнительные сведения о типах логических вентилей
561
Повышающий резистор
(внешний)
120Ом
Рис. 14N.28. Пассивный и активные повышающие выходные
каскады
Логические вентили с открытым
коллектором и открытым стоком48
Иногда бывают полезны вентили с выходами
с открытым стоком или открытым коллекто-
ром (рис. 14N.29)49. Мы уже встречались с та-
кой конфигурацией в схеме компаратора на
микросхеме 311.
Выход <
Рис. 14N.29. Мало распространенные вентили с выходами
с открытым стоком и открытым коллектором
Такие вентили легко выполняют операцию
ИЛИ для нескольких сигналов. Например, если
для сигналов А, В и С с активным низким уров-
нем используются выходы с открытым сто-
ком, то для всех этих трех выходов достаточно
одного повышающего резистора. Тогда любой
из трех сигналов может установить на этой об-
щей линии низкий уровень. Такая конфигура-
ция часто называется схемой монтажного ИЛИ.
Возможные применения такой конфигурации
рассматриваются в разделе по прерываниям в
главе 22N.
Выходы с тремя состояниями
Очень часто удобно использовать вентили с
выходами с тремя состояниями50, поскольку
таким образом несколько вентилей могут по-
давать выходной сигнал на общую выходную
шину. Такие вентили широко распространены
в компьютерном оборудовании.
Не подумайте, что третье состояние таких вен-
тилей является третьим выходным уровнем
напряжения. В действительности в третьем
состоянии на выводе вентиля нет никакого
напряжения, этот вывод просто отключен. На
рис. 14N.30 показана схема для реализации
такого выходного каскада, слева вверху блок-
схема, а слева внизу и справа в том виде, в ка-
ком мы предлагаем вам собрать ее на лабора-
торном занятии 14L.
14N.7.2. Реализация логики
на микросхемах ТТЛ и КМОП
В базовом ТТЛ-элементе И-НЕ, который мы
рассмотрели в разделе 14N.5.1, для выполнения
логических операций предусмотрены диоды.
Логические операции в КМОП-элементе вы-
полняются по-другому: два или более транзи-
сторов соединены последовательно или парал-
лельно. Справа на рис. 14N.31 показано строе-
ние КМОП-вентиля И-НЕ, который мы соберем
на лабораторном занятии 14L. Слева на том же
рисунке изображена упрощенная схема его ра-
боты, из которой видно, что такой вентиль яв-
ляется всего лишь набором последовательных
и параллельных транзисторных ключей.
В данном случае логика работы вентиля до-
статочно проста, и для ее понимания таблица
истинности не требуется. Можно видеть, что
низкий уровень выходного сигнала устанав-
ливается только в том случае, если на обоих
входах вентиля присутствуют высокие уров-
ни, которые включают оба последовательных
транзистора, подключая их на «землю». Таким
образом реализуется функция И-НЕ.
48 АоЕ § 10.2.4С.
49 Открытый коллектор для вентилей на биполярных
транзисторах, открытый сток — для МОП-вентилей.
50 На английском языке такие вентили часто называются
Tri-State, в отличие от three-state. Термин Tri-State являет-
ся торговой маркой, принадлежащей компании National
Semiconductor (в настоящее время поглощенная компа-
нией Texas Instruments), а термин three-state является пра-
вильным обобщающим термином. На русский язык оба
термина переводятся одинаково - с тремя состояниями
(третье - высокоимпедансное или z-состояние).
562
UN. Логические устройства
Выход-
-Выход
Разрешение-
X
+5
Вход
Разрешение
Разрешение А
В
Разрешение В
С
Разрешение С
D
лев 1
Разрешение
—Выход
Общая линия для
выходного сигнала (шина)
Рис. 14N.3O. Выход с тремя состояниями: блок-схема (слева вверху), принципиальная схема для сборки на лабораторном
занятии (слева внизу), несколько выводов, выдающих сигнал в общую шину (справа)
А
Рис. 14N.31. Вентиль И-НЕ, собранный на КМОП
14N.7.3. Скорость
и энергопотребление
На рис. 14N.32 изображен график, демон-
стрирующий взаимоотношение между скоро-
стью и энергопотреблением для некоторых
семейств стандартной цифровой логики51. Как
видно из этого графика, все стремятся занять
место в левом нижнем углу, где можно полу-
чить быстрые результаты практически за так.
В настоящее время наиболее обещающими
выглядят микросхемы, использующие техно-
логию LVDS и более быстрые типы КМОП-
вентилей (например, микросхемы LVC и еще
более быстрые устройства AUC компании
Texas Instruments).
74С
;4000В
Обозначения:
ОКМОП
• ТТЛ
ОТТрочие
74LS
74НС •
О
74ХХ
OLVC
OAUC
LVDC
О •
74AS
GqAs
51 АоЕ рис. 10.26.
1 \ I"
| ОД 1 10 100
™ Энергопотребление (мВт/вентиль при 1 МГц)
Рис. 14N.32. Скорость и энергопотребление некоторых
современных и устаревших семейств логических
микросхем
74Л/.8. Материал для чтения в АоЕ
563
А вентильные матрицы, ПМЛ и FPGA, могут
продемонстрировать еще лучшие скорости, чем
показанные на рис. 14N.33. Это объясняется
тем, что уменьшить паразитные емкости легче
в единой микросхеме, чем при использовании
дискретных компонентов.
14N.8. Материал для чтения
в АоЕ
♦ Глава 10. (Цифровая логика 1):
• Раздел 10.1. Базовые логические понятия;
• Раздел 10.2. Цифровые микросхемы,
КМОП и биполярные (ТТЛ);
• Общая картина конкуренции среди се-
мейств логических микросхем см. на
рис. 10.22;
• Раздел 10.3;
• Раздел 10.3.1. Здесь полезный материал по
логическим тождествам; особенно важна
теорема де Моргана;
• Раздел 10.3.2. Материал о картах Карно
можно пропустить;
• Раздел 10.3.3. Не тратьте время на изуче-
ние длинного перечня доступных комби-
национных функций;
• Раздел 10.6. Беглый взгляд на некоторые
типичные цифровые схемы.
♦ Глава 11. (Цифровая логика 1):
• Раздел 11.1. История семейств логических
микросхем;
• Раздел 11.2.1. Программируемая матрич-
ная логика;
• Разделы 11.3.3А и 11.3.4. Просмотрите
сравнительные методы проектирования;
• Разделы 11.4.1 и 11.4.1. Сводные советы.
14L Лабораторное занятие:
логические устройства
В первой части этого лабораторного занятия
предлагается поработать с логическими микро-
схемами (довольно интересными «черными
ящиками») для выполнения некоторых буле-
вых логических операций.
А в последующих разделах вам нужно будет по-
смотреть, что находится внутри этих «черных
ящиков», собрав для этого логическое устрой-
ство на дискретных транзисторах. Цель этих
упражнений — понять причины, по которым
логические элементы проектируются именно
таким, а не иным способом, а также обратить
внимание на некоторые свойства входных и
выходных каскадов КМОП-вентилей. На этом
лабораторном занятии, как и во всем нашем
курсе, мы будем концентрироваться на КМОП-
устройствах. Слегка преувеличивая, можно
сказать, что мы будем рассматривать обычные
ТТЛ-устройства, как древний почитаемый «ан-
тиквариат».
Но все, что мы будем делать на этом лабора-
торном занятии, является до некоторой сте-
пени «антиквариатом», поскольку в настоя-
щее время цифровая логика редко реализу-
ется на микросхемах, содержащих несколько
вентилей. Логические устройства обычно со-
бирают из больших массивов вентилей, за-
программированных для выполнения опре-
деленной функции. Вскоре мы будем иметь
возможность работать с такой микросхемой,
содержащей 1600 логических вентилей. Но
сегодня мы будем работать всего лишь с од-
ним или несколькими логическими элемен-
тами одновременно, поскольку это хороший
способ начать разбираться с работой логиче-
ских устройств.
14L1. Предварительная
информация
При работе с логическими схемами необходи-
мо следовать некоторым основным правилам:
1. Напряжение подаваемого сигнала никогда
не должно превышать напряжение питания
любой микросхемы.
2. Для логических микросхем это означает, что
напряжение сигналов должно быть 0 и +5 В.
Примечание
Это правило в общем виде — напряжение сигнала
должно быть в пределах размаха напряжения пи-
тания — также относится и к аналоговым схемам.
Новым в случае с цифровыми схемами является
практически повсеместное использование в них
однополярного напряжения питания.
3. Все свои схемы подключайте только к шине
+5 В и «земле». По крайней мере до тех пор,
пока мы не дойдем до устройств СПЛИС1 и
ПМЛ2, для питания которых может исполь-
зоваться напряжение величиной +3,3 В.
Это правило в равной мере относится как к
устройствам КМОП (в их стандартном ва-
рианте с питанием 5 В3), так и к устройствам
1 Сложная программируемая логическая интегральная
схема. Англ. термин Complex Programmable Logic Device
(CPLD).
2 Программируемая матричная логика, если вы забыли,
что это значит.
3 Напряжение питания 5 В в настоящее время повсемест-
но заменяется более низкими напряжениями. На момент
подготовки этой книги общепринятыми были напряжения
питания 3,3,2,5 и 1,8 В. Но мы в большинстве случаев бу-
дем работать с логическими микросхемами с напряжени-
ем питания 5 В.
14L1. Предварительная информация
565
ТТЛ. В обычных цифровых микросхемах (но
не в сложных микросхемах наподобие ПМЛ
и микроконтроллеров) выводы питания рас-
положены в диаметрально противополож-
ных углах корпуса микросхемы, как показа-
но на рис. 14L.1.
Установите тип выходного сигнала генератора
сигналов макетной платы в режим ТТЛ и ис-
следуйте этот сигнал с помощью логического
пробника. Повысьте частоту сигнала на не-
сколько килогерц. Мигает ли светодиод проб-
ника на частоте сигнала? Можете пояснить, по-
чему нет?5
Обычном цифровая микросхема
Рис. 14L.1. В большинстве обычных цифровых микросхем
выводы питания (плюс и «земля») расположены в диаме-
трально противоположных углах корпуса
14L1.1. Логический пробник
Логический пробник представляет собой гад-
жет размером с тонкую сосиску с кабелем на
одном конце и острым наконечником на дру-
гом. Кабель предназначен для подачи питания
(+5 В и «земля») на пробник, а острие нако-
нечника прикладывается к точке в схеме, в ко-
торой нужно узнать состояние логического
сигнала. Таким образом, логический пробник
сам является измерительным устройством, а не
средством для подачи измеряемого сигнала на
осциллограф.
Если кабель питания вашего логического проб-
ника оснащен разъемом BNC, положительное
питание (+5 В) подключается к его централь-
ному проводнику. Если же у кабеля зажимы
типа «крокодил» или крючкообразные зажи-
мы, подключите их к соответствующим напря-
жениям.
Работа с логическим пробником
В большинстве логических пробников высо-
кий и низкий уровни, а также «плавающее»
состояние (т. е. без сигнала) указываются све-
тодиодами разного цвета. Последняя возмож-
ность логического пробника особенно полезна.
Подумайте, можно ли определить это состояние
с помощью вольтметра или осциллографа?4
4 Нет, нельзя. Особым достоинством логического проб-
ника является его способность отличить низкий логиче-
ский уровень от простого нулевого напряжения, которое
можно измерить с помощью цифрового мультиметра. Но
цифровой мультиметр не может отличить «плавающее»
состояние, т. е. отсутствие подключения к чему-либо, от
14L1.2. Светодиодные индикаторы
макетной платы
Восемь светодиодов на макетной плате осна-
щены буферами из логических вентилей.
Светодиод можно включить высоким логиче-
ским уровнем, при этом вентиль обеспечивает
высокий импеданс (100 кОм).
Чтобы оценить возможности логического
пробника, попробуйте подать на один из этих
светодиодов сигнал прямоугольной формы
ТТЛ-типа от генератора сигналов макетной
платы частотой около 1 кГц. Выглядит ли пра-
вильным наблюдаемый вами результат? Теперь
вы можете видеть, что логический пробник
удлиняет короткие импульсы, делая их види-
мыми для наших глаз. В частности, он может
преобразовать импульс длительностью 30 не
в импульс длительностью около одной деся-
той секунды. А более качественные пробники
могут проделывать этот трюк даже с еще более
короткими импульсами.
14L1.3. Переключатели
на макетной плате
Макетные платы со встроенным источником пи-
тания оснащены несколькими переключателя-
ми. В частности, на передней панели макетной
платы РВ503 есть три типа переключателей:
♦ Две кнопки с противодребезговой защитой
(в левом нижнем углу макетной платы, обо-
значенные РВ1 и РВ2). При замыкании эти
кнопки выдают сигнал с открытого коллек-
тора, что означает, что они пригодны только
для создания сигнала низкого уровня, но не
подключения на «землю», которое логический пробник
определяет как низкий уровень.
5 Почему не мигает? Потому что наши глаза недостаточ-
но быстрые, чтобы видеть это мигание на частоте 1 кГц
и выше. Более того, мы не в силах различить мигание на
частоте выше приблизительно 25 Гц. Поэтому логический
пробник замедляет быстрое мигание до частоты в несколь-
ко герц, которое мы можем различать.
566
14L Лабораторное занятие: логические устройства
сигнала положительного уровня. Чтобы по-
лучить с этих кнопок логический сигнал вы-
сокого уровня напряжением 5 В, нужно до-
бавить повышающий резистор, как показано
на рис. 14L.2.
«HP»
(нормально
разомкнуты)
+5
Нормально низкий
Схема
устранения
дребезга
i
I
I «HP»
i (нормально
1 замкнуты)
Рис. 14L2. Чтобы получить высокий уровень на кнопках на
макетной плате РВ503, нужны повышающие резисторы
Обратите внимание на то, что все обведенные
пунктиром компоненты, включая транзисто-
ры, являются частью схематики макетной
платы и что только повышающие резисторы
добавляются пользователем.
♦ Набор из 8 логических ключей (без противо-
дребезговой защиты), на общие контакты
которых подается напряжение 0/+5 В через
ползунковый переключатель. Схема показа-
на на рис. 14L.3. На макетной плате эта груп-
па обозначена как Logic Switches. На первый
взгляд может показаться, что это дает нам
восемь отдельных сигналов, но это не совсем
так. В действительности на выходные кон-
такты всех этих ключей подается только или
высокий, или низкий логический уровень,
в зависимости от положения ползункового
переключателя, подающего сигнал на соеди-
ненные вместе входные контакты этих клю-
чей. Это при условии, что ключи замкнуты.
При разомкнутых ключах на их выходной
контакт не подается никакого сигнала, в ре-
зультате чего он находится в «плавающем»
состоянии: ни низкий уровень, ни высокий.
Ползунковый переключатель
(устанавливает напряжение,подаваемое
на все 8 логических ключей)
Рис. 14L.3. Общий ползунковый переключатель задает уро-
вень напряжения на выходах логических ключей
Чтобы эти ключи могли выдавать незави-
симые логические уровни, на их выходные
контакты нужно подключить повышающие
резисторы, а общий ползунковый переклю-
чатель установить на подачу низкого напря-
жения. Это, конечно же, дополнительная ра-
бота, поэтому в большинстве случаев, скорее
всего, удобнее использовать эти ключи для
подачи только одного логического уровня.
Во избежание возможных ошибок при ра-
боте с этими ключами рекомендуем просто
оставить их все замкнутыми, а требуемый
уровень задавать общим ползунковым пере-
ключателем.
В более новых версиях макетной платы РВ-
503 все эти восемь ключей независимы и вы-
дают высокий или низкий уровень. Эти усо-
вершенствования делают логические ключи
более полезными. Но для всех ключей можно
задавать одну из двух величин положитель-
ного напряжения для высокого логического
уровня, что создает источник опасности для
цифровых схем. Эти напряжения задаются
с помощью отдельного ползункового пере-
ключателя, установив его или в положение
+5 (+5 В), или в положение +V.
Вот это напряжение +V и таит в себе опас-
ность: его величина определяется величиной
положительного напряжения на шине регу-
лируемого положительного напряжения и
может быть в диапазоне от 1,3 до 15 В. Как
вы должны знать, любое напряжение выше
+5 В выведет из строя обычную цифровую
микросхему. Мы узнали об этой особенности
логических ключей, когда собранная схема
вдруг задымилась.
♦ Два незадействованных ползунковых пере-
ключателя (однополюсные двухпозици-
онные). Эти переключатели не оснащены
противодребезговой защитой и расположе-
ны в правом нижнем углу макетной платы.
Чтобы задействовать эти переключатели,
подключите один из их контактов к напря-
жению +5 В, другой — к «земле», а общий
контакт используйте как выход. Не отклады-
вайте это, а выполните подключения сейчас,
поработайте с переключателями на этом ла-
бораторном занятии, при этом оставьте их
подключенными таким образом для следую-
щих лабораторных занятий.
14L2. Входные и выходные характеристики микросхем ТТЛ и КМОП
567
Хороший способ создания входных
цифровых сигналов
Логические уровни можно легко подать туда,
где они требуются, подключив контакты на
одной стороне переключателя DIP непосред-
ственно к шине «земли». На макетную плату
DIP-переключатель нужно установить таким
образом, чтобы при нижнем положении его
ползунков на выход переключателя подавался
низкий логический уровень. На рис. 14L.4 по-
казано подключение такого переключателя,
выдающего значение 00.
+5В-
«Земля»
Повышающие
"резисторы
. Два выхода
■ логических уровней
Переключатель установлен так, чтобы при нижнем
положении ползунков на его выходы подавался низкий
логический уровень
Рис. 14L.4. Установленный на макетную плату DIP-пере-
ключатель может служить источником логических уровней
Если выходы переключателя подключены на-
прямую к входам микросхемы, то повышающие
резисторы может потребоваться установить на
макетную плату горизонтально, как показано на
рис. 14L.5. На этом рисунке DIP-переключатель
опять выдает значение 00, которое на этот раз
подается на два входа логического вентиля
И-НЕ микросхемы 74НС00.
ТТовышающив
резисторы
* * # * vi№#.;«r V
* * • * $11$рщщр# ♦ • iff « « » »
Рис. 14L.5. С помощью DIP-переключателя логические уров-
ни можно подать в любую требуемую точку
14L2. Входные и выходные
характеристики микросхем
ТТЛ и КМОП
14L2.1. Уровни выходных
напряжений
Положительное питание и «земля»
Как упоминалось в разделе 14L.1, в микросхемах
в корпусе DIP с 14 выводами, с которыми мы
будем работать на этом лабораторном занятии,
выводы питания (положительного и «земли»)
расположены диагонально противоположно
друг другу. Иными словами, при горизонталь-
ном расположении микросхемы с первым вы-
водом в левом нижнем углу положительное пи-
тание подается на вывод 14, который находится
в левом верхнем углу, а отрицательное («зем-
ля») — на вывод 7, который находится в правом
нижнем углу.
Входные сигналы
Подайте на два входа логического элемента
И-НЕ низкий (0 В) или высокий (+5 В) уро-
вень, используя в качестве источника сигналов
DIP-переключатель или какой-либо другой
источник. При желании состояние входных
и выходных сигналов можно отображать на
светодиодах макетной платы со встроенным
источником питания. Таким образом можно
одновременно наблюдать за состоянием как
входов, так и выхода, как будто бы светодиоды
обозначают строку в таблице истинности.
На рис. 14L.6 показана цоколевка микросхем
И-НЕ 74LS006 (ТТЛ) и 74НС007 (КМОП).
6 Обозначение LS означает Low power Shottky (маломощ-
ная микросхема с диодами Шотки). Это технология, уско-
ряющая переключение. Когда префикс LS был принят
в 1976 г., технология ТТЛ подразумевалась как сама собой
разумеющаяся. Этим объясняется отсутствие в обозначе-
нии английской буквы «Т» в противоположность более
поздней технологии КМОП, которая всегда обозначается
английской буквой «С» где-либо в префиксе: НС, НСТ, АС,
ACT и т.п. См. микросхему 74НС00 чуть далее.
7 Число 74 означает, что для микросхемы применяется
схема обозначения детали и распиновка, установленные
доминирующим семейством логических микросхем: ли-
нейкой 74хх ТТЛ-микросхем компании Texas Instruments.
Буква «С» означает технологию КМОП (англ. CMOS), a
буква «Н» — высокую скорость переключений (англ. High
speed), равную скорости доминирующего в то время семей-
ства 74LS микросхем ТТЛ.
568
14L Лабораторное занятие: логические устройства
LJJ |2J 13J Ц] [5J 16! [71
Рис. 14L.6. Микросхемы ТТЛ и КМОП элементов И-НЕ
Примечание
Для микросхемы КМОП (но не для ТТЛ) соедини-
те все неиспользуемые входы вместе и временно
подключите их на «землю». Не поленитесь снача-
ла соединить все выводы вместе, а не подключать
их на «землю» по отдельности, поскольку вскоре
(в разделе 14L.3.1) мы будем подавать на все эти
контакты общий сигнал. Теперь посмотрите, каки-
ми будут выходные логические уровни и напряже-
ния при подаче входных комбинаций, и запишите
их в таблицу 14L.1. (Таблица содержит только один
столбец для логических выходных уровней, по-
скольку выходные уровни вентилей ТТЛ и КМОП
должны быть одинаковыми.) В качестве нагрузки
используйте резистор номиналом 10 кОм, подклю-
. ченный на «землю».
Таблица 11L.1. Состояния входов и выходов
логических микросхем
ВХОД
0
0
1
1
0
1
0
1
выход
Логические
уровни
Напряжение
(вольты):
ТТЛ
Напряжение
(вольты):
КМОП
14L3. Аномалии
14L3.1. «Плавающие» входы
Логические элементы ТТЛ
Отключите оба входа элемента И-НЕ и наблю-
дайте выходной логический уровень. (Впредь
мы не будем беспокоиться о выходных напря-
жениях, а только о логических уровнях.) Как
вы полагаете, что «думает» ТТЛ-вентиль, когда
его входы «плавают»?8
8 Он «думает», что «видит» высокий уровень, хотя этот
высокий уровень чувствителен к помехам. На схеме вну-
Логические элементы КМОП
Эти устройства представляют более сложный
случай, поэтому будем проводить эксперимент
в два этапа9.
1. Эквивалентный входной логический уро-
вень при «плавающем» входе. Подайте на
один вход вентиля И-НЕ высокий логиче-
ский уровень, а ко второму входу подключите
отрезок провода длиной около 15 см, оставив
другой конец этого провода неподключен-
ным (т. е. «плавающим»). Приблизьте свою
руку к свободному концу этого провода, или
даже возьмитесь за него рукой (за оголенный
участок), и наблюдайте состояние выхода
вентиля с помощью логического пробника
или осциллографа.
Примечание
Здесь мы повторяем эксперимент, который про-
водили с силовым полевым МОП-транзистором
в разделе 12L1.2.
Другой рукой прикоснитесь к напряжению
+5 В, потенциалу «земли», выходу ТТЛ ге-
нератора сигналов макетной платы, или под-
несите ее к трансформатору внутреннего ис-
точника питания макетной платы. Цель это-
го эксперимента — продемонстрировать вам,
что «плавающие» входы микросхем КМОП
менее предсказуемы, чем ТТЛ. Но при всей
предсказуемости входов последних, мы на-
стоятельно рекомендуем не оставлять не-
подключенными входы никаких логических
микросхем.
2. Влияние «плавающих» входов на энер-
гопотребление логических микросхем
КМОП. Надеемся, что вы вняли рекомен-
дации не оставлять неподключенными вхо-
ды логических вентилей КМОП. Теперь мы
продемонстрируем вам, почему это правило
разумно (хотя, как большинство правил, мо-
жет время от времени нарушаться10).
треннего устройства вентиля на рис. 14N.21 можно видеть
внутренний повышающий резистор на базе первого тран-
зистора. Вследствие этого при отключенных входах этот
транзистор находится во включенном состоянии, как буд-
то бы на него подавался настоящий высокий логический
уровень.
9 АоЕ § 10.8.3В.
10 В частности, при сборке схем на макетной плате на на-
ших лабораторных занятиях не обязательно подавать
сигнал на все неиспользуемые входы. Это необходимо де-
лать для законченных, постоянных вариантов устройств,
но ваше время на лабораторных занятиях ценнее, чем
14L3. Аномалии
569
Подключите два входа вентиля И-НЕ, с кото-
рыми вы работали, к другим шести входам, ко-
торые вы ранее подключили на «землю», а за-
тем отключите все эти входы от «земли» и под-
ключите их к потенциометру, который может
выдавать напряжение в диапазоне от 0 до +5 В.
Соответствующая схема подключения входов
вентилей показана на рис. 14L.7. Далее про-
верните рукоятку потенциометра до предела в
любую сторону, подавая таким образом какой-
либо логический уровень на входы всех четы-
рех вентилей И-НЕ микросхемы.
+5 В
+5 В
10
1С ПАЛ ^£^*^* *" "»""■•'"»«<
1
о
проворачивайте рукоятку потенциометра, что-
бы приблизить напряжение входных уровней
к пороговой области, при которой выходной
сигнал не зафиксирован ни на низком, ни на
высоком уровне. Таким образом мы сбива-
ем микросхему КМОП с толку, поскольку она
«предполагает», что в выходном каскаде вклю-
чен один и только один транзистор. А когда
напряжение входных логических уровней на-
ходится близко к половине значения напряже-
ния питания [/+, что является типичным поро-
говым уровнем переключения, оба транзисто-
ра могут быть частично включены. Цену этому
«заблуждению» микросхемы можно наблюдать
на амперметре: энергопотребление окажется
в тысячи раз выше нормального.
Таким образом, при «плавающих» входах су-
ществует вероятность, что устройство КМОП
будет расходовать понапрасну значительный
объем электроэнергии. Производители КМОП-
микросхем предупреждают, что такое энерго-
потребление может также вызвать перегрев
и повреждение компонента. Как уже упоми-
налось, чтобы сэкономить время, в этом курсе
при сборке схем на макетной плате мы иногда
будем допускать «плавающие» входы КМОП-
микросхем. Но теперь вы должны знать, что
в законченных устройствах никогда нельзя до-
пускать неподключенных входов.
Рис. 14L.7. Схема для демонстрации повышенного энерго-
потребления при подаче промежуточных логических уров-
ней на входы вентилей КМОП
Отключите питание схемы, установите муль-
тиметр на измерение тока в наиболее чув-
ствительном диапазоне и подключите его
щупы между шиной положительного (+5 В)
питания и выводом U+ (номер 14) на микро-
схеме КМОП. Снова подключите питание и
наблюдайте потребляемый микросхемой ток.
Энергопотребление должно быть очень малым,
ведь, в конце концов, малое энергопотребле-
ние является одним из достоинств технологии
КМОП.
Теперь переключите мультиметр на изме-
рение тока с предельным значением 150 мА
(или в подобный диапазон) и постепенно
дополнительная мощность, которую может потребить
ваша схема, если оставить «плавающими» несколько ее
входов. Также ваше время дороже, даже чем сама микро-
схема, которая предположительно может быть поврежде-
на из-за неподключения всех ее неиспользуемых входов.
14L3.2. Последствия
неподключения положительного
или отрицательного («земли»)
питания для логической КМОП-
микросхемы
Здесь мы хотим, чтобы вы специально сделали
то, что студенты часто делают непреднамерен-
но11 при сборке схем на макетной плате: не под-
ключать к микросхеме КМОП положительное
или отрицательное («землю») питание. Эффект
будет не тот, который можно было бы ожидать.
Возможно, вы предполагали, что микросхе-
ма без питания будет выдавать постоянный
11 Вы можете быть уверены, что сами никогда не допусти-
те такой ошибки, но многие другие допускают ее. Однажды
эту ошибку стали допускать так часто, что ассистент пре-
подавателя начал раздавать конфеты в качестве возна-
граждения тем студентам, которые не допускали ошибки:
тем, которые первым делом подключали питание, вместо
того, чтобы откладывать эту задачу после того, как они
выполнили монтаж более интересных компонентов.
570
14L Лабораторное занятие: логические устройства
низкий выходной уровень или же «плаваю-
щий» уровень.
Но защитные диоды на входах и выходе каж-
дого вентиля усложняют это поведение. На
рис. 14L.8 показано, как выглядят эти ограни-
чительные диоды для микросхем серии 74НС12.
увидим, что логический вентиль И-НЕ реали-
зует функцию Исключающее-ИЛИ. Можете
ли вы объяснить этот эффект?13 Но следует
признать, что поведение Исключающего-ИЛИ
не может быть гарантировано, поскольку ва-
риации в защитной схемотехнике микросхем
разных производителей делают результат не-
предсказуемым.
Вход
200 0м
Вентиль
КМОП
Выход
О
о
и.
Рис. 14L.8. Защитная схемотехника логического вентиля
микросхемы серии 74НС
Ограничивающие диоды позволяют входам
(а иногда и выходам) предоставлять ток, кото-
рый может питать микросхему. Таким образом,
высокий входной логический уровень может
подавать положительное {+5 В) напряжение на
соответствующую линию через верхние огра-
ничивающие диоды (хотя они и не выглядят
подключенными). А низкий входной логиче-
ский уровень может подавать отрицательное
(«землю») питание через нижний ограничи-
тельный диод. Но при этом полученное таким
образом как положительное, так и отрицатель-
ное питание имеет аномальные уровни. Так что
при подаче на микросхему как высокого, так
и низкого входного логического уровня на нее
подается напряжение для ее питания! Как мож-
но себе представить, результатом такого пита-
ния будет очень странное функционирование
микросхемы: все вроде бы работает, но только
до тех пор, пока не наступит неудачная комби-
нация входных уровней.
Если выходной логический сигнал вентиля
И-НЕ микросхемы 74НС00 подать на нагрузку
в виде резистора номиналом 10 кОм (второй
вывод которого подключен к «земле»), а так-
же подать этот же сигнал на один из буфе-
ризированных светодиодов макетной платы
(чтобы можно было легко наблюдать его), мы
14LA Использование
вентилей микросхем для
создания определенных
логических функций
Прежде чем мы начнем разбираться во всех
подробностях с внутренним содержимым логи-
ческих вентилей, давайте немного позабавим-
ся с этими логическими элементами. Сначала
мы выполним три упражнения с элементами
И-НЕ, чтобы свыкнуться с поразительным фак-
том, что на вентилях И-НЕ можно реализовать
любую логическую функцию. Затем использу-
ем любую из стандартных логических функ-
ций, включая функцию Исключающее-ИЛИ,
для того, чтобы создать два типа цифрового
компаратора.
Большинству студентов эти эксперименты нра-
вятся больше, чем конспектирование на протя-
жении всего урока. Но не допустите, чтобы эти
развлекательные задачи оторвали вас от основ-
ного лабораторного занятия! Уделите каждой
из этих задач не больше десяти минут своего
ценного лабораторного времени. А завершить
эксперименты всегда можно самостоятельно
у себя дома.
12 Примечание по применению (Application Note) AN248
компании Fairchild.
13 Результат функции Исключающее-ИЛИ можно объ-
яснить тем, что только эта комбинация входных сигна-
лов предоставляет как +5 В, так и «землю», в результате
чего вентиль выдает выходной высокий уровень, который
вентиль И-НЕ должен был бы выдать в ответ на комби-
нации входных уровней 01 или 10. Комбинация входных
уровней 00 не обеспечивает питание +5 В, поэтому вен-
тиль не сможет выдавать высокий выходной уровень (как
это должен делать вентиль И-НЕ при такой комбинации
входных уровней). Комбинация входных уровней 11 более
проблематична: хотя при такой комбинации микросхема
не запитана, вентили И-НЕ некоторых микросхем 74НС00
(например, производства компании Motorola) выдают вы-
сокий выходной уровень при такой комбинации входов,
тогда как микросхемы производства других компаний (на-
пример, компании National Instruments) выдают низкий
выходной уровень. Но вентиль не работает должным об-
разом ни в одном из этих случаев.
14L5. Исследуем внутреннее устройство логических элементов КМОП
571
14LA1. Логические элементы И-НЕ
Высокий уровень на обоих входах
Используйте элементы И-НЕ (на микросхемах
КМОП или ТТЛ), чтобы зажечь один из буфе-
ризированных светодиодов макетной платы,
когда на оба входа вентиля подается высокий
уровень.
Высокий уровень на любом из входов
Используйте элементы И-НЕ (на микросхемах
КМОП или ТТЛ), чтобы зажечь один из буфе-
ризированных светодиодов макетной платы,
когда на любой из входов вентиля подается
низкий уровень.
Примечание
Это задача с подвохом! Не слишком усердствуйте.
14L4.2, Цифровые компараторы
на любых вентилях
Двухразрядный детектор
равнозначности
На любых логических элементах соберите ком-
паратор, который определяет равнозначность
двух двоичных двухразрядных чисел.
Примечание
Эта схема в увеличенном масштабе используется
во многих компьютерах, когда устройству нужно
определить присутствие его особого адреса на об-
щей адресной шине.
Подсказка:
Большую помощь в решении этой задачи может
оказать использование функции Исключающее-
ИЛИ. Микросхема 74НС86 содержит элементы
Исключающее-ИЛИ. Цоколевка этой микросхемы
такая же, как и микросхемы 74НС00. Более того,
все микросхемы логических вентилей линейки
74ХХ имеют одинаковую цоколевку. Исключением
из этого семейства является микросхема 74НС02,
имеющая обратную цоколевку. Более подробную
информацию по этому вопросу см. в Приложении К.
Вентиль Исключающее-ИЛИ можно рассматривать
как одноразрядный детектор равнозначность*/
неравнозначность™.
Двухразрядный детектор А > В
Используя любые вентили, соберите компара-
тор, который определяет, когда одно из двух
двоичных двухразрядных чисел (назовем его
А) больше другого такого же числа (назовем
его В). Эта схема не обязательно должна быть
симметричной, поскольку от нее не требуется
определять, когда В > А, а только когда А > В,
в отличие от А < В.
Внимание
Эта схема может оказаться довольно сложной.
Поэтому мы настоятельно рекомендуем не уде-
лять этой проблеме слишком много своего лабо-
раторного времени.
14L5. Исследуем
внутреннее устройство
логических элементов КМОП
В следующих экспериментах нам понадобятся
две микросхемы CD4007 (или СА3600); эта ми-
кросхема содержит набор КМОП-транзисторов.
Принципиальная схема внутреннего устройства
этой микросхемы изображена на рис. 14L.9.
п
ul
3-н» 10-
-12
14 Возможно, что это ваша первая встреча с соглашением,
в котором звездочка (как в равнозначность*) служит для
Рис. 14L9. Принципиальная схема внутреннего устройства
микросхемы набора инверторов CD4007 (или САЗбОО)
14L5.1. Два логических инвертора
Пассивное повышение напряжения
Соберите схему, изображенную на рис. 14L.10,
используя один из одинарных полевых МОП-
транзисторов микросхемы CD4007. Обязатель-
указания активного низкого уровня сигнала. Это альтерна-
тивное обозначение вместо горизонтальной черты сверху:
равнозначность/неравнозначность.
572
14L Лабораторное занятие: логические устройства
но убедитесь в правильности подключения
напряжения питания микросхемы: вывод 14
подключается к +5 В, а вывод 7 — к «земле».
Эта процедура должна быть вам знакомой, по-
скольку мы уже описывали соглашение по вы-
водам питания микросхем этого типа ранее
в разделе 14L1: питание подается на угловые
выводы. По сути, это стандартные выводы пи-
тания для микросхемы, изображенной на ри-
сунке, но следует иметь это в виду при исполь-
зовании других микросхем с полевыми МОП-
транзисторами.
Рис. 14L.10. Простейший инвертор: пассивное повышение
напряжения
Проверьте, что эта знакомая нам схема в дей-
ствительности инвертирует входной сигнал.
Для этого подайте на ее вход уровень ТТЛ от
внешнего генератора сигналов. (Генератор сиг-
налов на макетной плате слишком медленный,
чтобы выставить эту схему в плохом свете, как
мы вскоре захотим сделать.) Высокий уровень
выходного сигнала ТТЛ генератора сигналов
недостаточно высок, чтобы удовлетворить
требование вентилей КМОП к высокому уров-
ню, близкому к +5 В (хотя ТТЛ-сигнал обыч-
но вызовет переключение вентилей КМОП)15.
Стандартное решение этой проблемы — по-
вышение напряжения высокого уровня вы-
ходного ТТЛ-сигнала до +5 В с помощью по-
вышающего резистора номиналом в несколько
килоом16. Наблюдайте выходной сигнал схемы
15 Если вы забыли значение напряжения высокого уровня
выходного сигнала ТТЛ-вентилей, можете освежить свою
память по этому вопросу по таблице полученных вами
значений в разделе 14L.2,
16 Такой способ повышения напряжения высокого уров-
ня может работать на вашем генераторе сигналов, но он
не сработал на наших генераторах Krohn-Hite. Это объяс-
няется тем, что их якобы ТТЛ-сигналы в действительно-
сти не являются настоящими ТТЛ-сигналами: их высокий
уровень нельзя поднять выше 4 В. Настоящий выходной
сигнал вентиля ТТЛ легко поднимается до +5 В таким спо-
собом. Но уровень в 4 В достаточен для управления венти-
лями КМОП.
на осциллографе (здесь и далее вольтметр или
логический пробник будет недостаточным).
Теперь повысьте частоту входного сигнала до
максимально возможного значения. Видите
ли вы результаты данного действия? Можете
ли вы объяснить, почему это происходит?17
Нарисуйте, как выглядит выходной сигнал.
Активное повышение напряжения
Теперь замените резистор номиналом 10 кОм
полевым р-канальным МОП-транзистором,
собрав схему, изображенную на рис. 14L.11.
Подавайте на вход схемы сигнал высокой и
низкой частоты и наблюдайте за соответствую-
щим выходным сигналом.
+5
6
14
13
8
7
Рис. 14L.11. Активное повышение напряжения: КМОП-
инвертор
Наблюдая на выходе результат обработки вход-
ного сигнала высокой частоты, вы поймете, по-
чему во всех настоящих логических элементах
реализовано активное повышение выходного
напряжения.
Примечание
Пассивное повышение напряжения, называющее-
ся открытым коллектором для ТТЛ-микросхем и
открытым стоком для микросхем МОП, иногда
встречается в специальных приложениях, таких
как питание нагрузки с напряжением, отличным от
+5 В, или когда нужно, чтобы несколько устройств
управляли одной линией. Но в последнем случае
лучше применять третье состояние. Более подроб-
но см. далее в тексте.
17 Нарастание происходит медленно по той причине, что
паразитные емкости обычно заряжаются через повышаю-
щий резистор номиналом 10 кОм, образующий инерцион-
ную ДС-цепочку.
14L5. Исследуем внутреннее устройство логических элементов КМОП
573
14L5.2. Логические функции
из КМОП-устройств
Функция И-НЕ
Соберите схему, изображенную на рис. 14L.12,
и проверьте, что она действительно реализует
функцию И-НЕ,
Рис. 14L.12. Функция И-НЕ на КМОП-устройствах
Третье состояние КМОП-вентилей
Выходной каскад логических вентилей с тремя
состояниями кроме высокого и низкого уров-
ней может иметь третье состояние: выключен-
ное. Эта возможность чрезвычайно полезна в
компьютерах, поскольку позволяет подключать
несколько выходов вентилей к одной общей
линии, называющейся шиной. В этом упраж-
нении вам нужно собрать буфер (устройство,
которое ничего не делает, а лишь транслирует
сигнал) и перевести его выходной сигнал в вы-
ключенное состояние. Это будет буфер с тремя
состояниями.
Вход
8
Разрешение -
^ПОВЫШАЮЩИЙ
Выход
^ПОНИЖАЮЩИЙ
1
Рис. 14L.13. Блок-схема буфера с тремя выходными состоя-
ниями
Как вы должны увидеть, для решения этой
задачи нужно просто добавить схему логики,
которая может выключить как повышающий,
так и понижающий транзистор. Когда это про-
исходит, выход отключается как от питания
+5 В, так и от потенциала «земли», в результате
чего он переходит в «плавающее» состояние.
О таком вентиле говорят, что он находится в
третьем состоянии, или в состоянии высокого
импеданса.
Если у вас есть настроение заниматься проек-
тированием логических схем, попробуйте раз-
работать схему, которая будет выполнять дан-
ную задачу, используя вентили И-НЕ вместе с
полевыми МОП-транзисторами на микросхеме
4007. Схема должна функционировать следую-
щим образом:
♦ Когда на линии Разрешение присутствует
низкий уровень, оба транзистора, как повы-
шающий, так и понижающий, должны пере-
йти в выключенное состояние. Это означает
следующее:
• на затвор верхнего транзистора должен
подаваться сигнал высокого уровня;
• на затвор нижнего транзистора должен по-
даваться сигнал низкого уровня.
♦ Когда на линии Разрешение присутствует
высокий уровень, входной сигнал должен
включить или верхний, или нижний транзи-
стор. Это означает следующее:
• на затворы этих транзисторов должен по-
даваться одинаковый сигнал — или вы-
сокого, или низкого уровня, который и
включит один из этих транзисторов и вы-
ключит другой. (Потому что один из этих
транзисторов р-канальный, а другой —
л-канальный.)
Возможно, что словесное описание схемы зву-
чит запутанно, но сама схема полностью пря-
молинейна. Если вы не желаете тратить вре-
мя на разработку своей версии схемы, може-
те воспользоваться нашей, изображенной на
рис. 14L.14. Таким образом вы сможете сразу
приступить к ее сборке.
Сигнал Разрешение для управления третьим
состоянием выхода схемы подается с помощью
ползункового переключателя, как показано на
рис. 14L.15.
574
14L Лабораторное занятие: логические устройства
Вход
Разрешение
Рис. 14L.14. Схема с выходом с тремя состояниями подает
входные сигналы на затворы повышающего и понижающего
транзисторов через вентили И-НЕ микросхемы 74НС00
JLR
На осциллограф
Рис. 14L.15. Схема для демонстрации работы буфера с тре-
мя состояниями
Второй ползунковый переключатель подает
сигнал на резистор номиналом 100 кОм, под-
ключенный к выходу схемы. Сигнал 0 или +5 В
с этого переключателя ослабляется резистором
номиналом 100 кОм и подается на общую вы-
ходную линию. Необходимость дополнитель-
ных компонентов объясняется тем, что таким
образом мы можем определить, находится ли
выход в третьем состоянии или нет. Как упоми-
налось ранее, это состояние не поддается опре-
делению с помощью одного только вольтметра
или осциллографа.
Протестируйте собранную вами схему, подав на
ее вход сигнал с генератора сигналов макетной
платы и наблюдая эффект сигнала Разрешение.
Когда третье состояние не разрешено, даже ре-
зистор в 100 кОм должен зафиксировать вы-
ходной уровень. А при разрешенном третьем
состоянии на общую выходную линию должен
уверенно подаваться прямоугольный сигнал.
Эта общая выходная линия служит прообразом
шины данных.
Сейчас, когда вы еще не видели применений
третьему состоянию, его возможность «исче-
зать» электрически может показаться вам не
особенно впечатляющей. Но позже, когда вы
соберете свой компьютер, то обнаружите, что
хотя третье состояние и не является впечатля-
ющим, оно очень полезно.
На рис. 14L.16 показано одно из возможных
применений. Правда, здесь иллюстрируется
всего одна линия общей шины, тогда как на-
стоящая параллельная компьютерная шина
содержит как минимум восемь линий, а часто
даже больше18.
Jp линия для
выходного сигнала (шина)
Разрешение D
Рис. 14L.16. Устройства с тремя состояниями, подающие
сигналы в общую шину. (Схема предназначена только для
иллюстрации, а не для сборки.)
18 В современных разработках начинают использоваться
высокоскоростные шины с одной линией, по которым дан-
ные передаются последовательно.
14S. Дополнительный материал:
глоссарий по цифровой электронике
Высокий/низкий активный уровень (active
high/low) — определяет уровень (высокий или
низкий), при котором сигнал принимает значе-
ние ИСТИНА, или является Активным. Мы из-
бегаем употреблять первый термин, поскольку
для многих значение ИСТИНА ассоциируется
с высоким уровнем, и вот эту связь мы должны
разорвать.
Активировать (Assert) — применительно
к сигналу этот термин предпочитается тер-
мину ИСТИНА вследствие своей нейтраль-
ности, которая отсутствовала бы во фразе
«Установить значение ИСТИНА», поскольку
многие предрасположены связывать значе-
ние ИСТИНА с высоким уровнем. Таким об-
разом, мы можем с равной уместностью ска-
зать как «Активировать WR*» (или WR ), так
и «Активировать СБРОС51». В первом случае
это будет означать сделать уровень сигнала
низким, а во втором — высоким (поскольку на-
звания сигналов указывают, что первый сигнал
активный при низком уровне, а второй — при
высоком).
Символ уровня активации (Assertion-level
symbol) — это логический символ, один из
двух символов, которые согласно теореме де
Моргана всегда эквивалентны, выбранных для
указания активных уровней. Таким образом,
вентиль, выполняющий операцию И над дву-
мя низкими входными сигналами и выход
которого управляет входом, обозначенным
РАЗРЕШЕНИЕ*, следует отображать в виде
символа И с кружочками на входах и выходе,
хотя его общепринятое название может быть
ИЛИ. Обратите внимание на то, что общепри-
нятое название предполагает, что сигналы име-
ют активный высокий уровень.
Асинхронный (Asynchronous) — понятие,
противоположное синхронному. Асинхронные
устройства не имеют общего сигнала тактиро-
вания, и могут не иметь его вообще. В боль-
шинстве триггеров реализована асинхронная
функция обнуления, которая также называ-
ется функцией JAM-типа. Ситуация усложня-
ется тем, что асинхронная функция, такая как
СБРОС*, может быть элементом синхронной
схемы, например, счетчика. Такая комбина-
ция присутствует в счетчике на микросхеме
74НС161.
Обнуление (Clear) — принудительная уста-
новка нулевых выходных уровней. Применимо
только к последовательным устройствам. То же
самое, что и Сброс (Reset).
Комбинационная логика (Combinational lo-
gic) — то же самое, что и «комбинаторная»,
применительно к логике. Выходной сигнал
является функцией текущих входных сигна-
лов, а не предыдущих (за исключением неко-
торой небольшой задержки распространения).
Противопоставляется последовательной логике.
Декодер (Decoder) — схема комбинационной
логики, принимающая на входах двоичное
число и активирующая один из своих выходов,
соответствующий данному числу. (Также суще-
ствуют и другие типы декодеров. С данным ти-
пом декодера мы будем работать на наших ла-
бораторных занятиях.) Например, микросхема
139 содержит два декодера типа два-на-четыре,
которые принимают на двух входах двухраз-
рядное двоичное число и активируют одну из
четырех выходных линий, в зависимости от
значения числа.
Демультиплексор (Demultiplexer1) — схема
комбинационной логики, которая направляет
одну входную линию с разделением времени
Также используется сокращенный вариант - demux.
576
US. Дополнительный материал: глоссарий по цифровой электронике
доступа на ту или иную линию назначения.
Входная линия может быть шиной, напри-
мер мультиплексированной шиной адреса и
данных, как в микроконтроллере DS89C430
компании Dallas Semicounductor (приобретена
компанией Maxim Integrated Products в 2001 г.)
Запускаемый фронтом/перепадом (сиг-
нала) (Edge-triggered) — описание поведения
триггеров или счетчиков: схема реагирует на
перепад сигнала тактирования, а не на его уро-
вень. Это, безусловно, наиболее распростра-
ненный метод тактирования.
Разрешение (Enable) — точное значение ва-
рьируется в зависимости от контекста, но в
общем означает «включить устройство»: за-
пустить схему счетчика, активировать один из
выходов декодера, включить буфер с тремя со-
стояниями и т. п.
Плавающее состояние (Float) — примени-
тельно к входам или выходам с тремя состоя-
ниями: без присутствия сигнала ни высокого,
ни низкого уровня.
Триггер (Flip-flop, также flop) — все названия
означают одно: бистабильный мультивибра-
тор. Из-за громоздкости последнего термина
неудивительно, что первые получили более
широкое применение. (Кстати, английское flop
в данном контексте не следует путать с сокра-
щением FLOP, которое означает Floating Point
Operation — операция с плавающей запятой/
точкой.)
Время удержания (Hold time) — временной
интервал после активного перепада сигнала
тактирования, в течение которого сигнал на
определенном входе цифровой схемы должен
удерживаться стабильным (сохранять свой
уровень). В современных схемах время удер-
жания обычно равно нулю.
Асинхронное обнуление/загрузка (Asyn-
chronous clear/load, также jam clear/load) — тип
обнуления/загрузки цифровой схемы, не тре-
бующий сигнала тактирования.
Триггер-защелка (Latch) - строго говоря, это
«прозрачная» защелка (transparent latch), но
часто этот термин применяется также для обо-
значения регистра (запускаемого перепадом
сигнала).
Задержка (Latency) — задержка между сти-
мулом и реакцией. Часто употребляется в кон-
тексте реагирования на прерывание, где важен
быстрый отклик.
Загрузка (Load) — функция счетчика, по-
средством которой триггеры счетчика загру-
жаются, как элементы простого регистра на
D-триггерах.
Мультиплексор (Multiplexer2) — схема ком-
бинационной логики, которая пропускает один
из нескольких входов на единственный вы-
ход. Пропускаемый вход определяется пода-
чей на линии выборки двоичного кода входа.
Например, в мультиплексоре четыре-на-один
для передачи одного из его входов на выход
используются две линии выборки. Обратная
операция осуществляется с помощью демуль-
типлексора.
Одновибратор (One-shot circuit) — схема, ко-
торая выдает один импульс в ответ на входной
сигнал (обычно называемый сигналом запу-
ска), которым может быть уровень или пере-
пад. Большинство одновибраторов снабжены
ЯС-цепочкой, но для тактирования некоторых
из них необходим сигнал тактирования.
Предустановка (Preset) — принудительная
установка высокого уровня/уровней на выхо-
де последовательной схемы. То же самое, что и
Установка (Set).
Задержка распространения (Propagation
delay) — время, необходимое для того, чтобы
сигнал прошел через схему. Отсчитывается от
момента пересечения входным сигналом ло-
гического порогового уровня для пересечения
логического порогового уровня выходным сиг-
налом.
Регистр (Register) — набор D-триггеров; все-
гда активируется перепадом сигнала тактиро-
вания.
Сброс (Reset) — то же самое, что и Обнуление
(Clear): принудительная установка нулевого
значения на выходе.
Счётчик со сквозным переносом (Ripple
counter) — простой, но некачественный тип
2 Также используется сокращенный вариант — тих.
14S. Дополнительный материал: глоссарий по цифровой электронике
577
асинхронного счетчика. Вход Q, одного триг-
гера подает сигнал тактирования на другой.
Выходное состояние устанавливается медлен-
но, что способствует появлению большого ко-
личества ложных переходных состояний.
Последовательная логика (Sequential lo-
gic) — логическая схема, состояние выхода
которой зависит от прошлых и (в некото-
рых случаях) текущих состояний на входах.
Примером такой логической схемы может слу-
жить Т-триггер, следующее состояние которо-
го зависит как от истории прошлых состояний,
так и от уровня, подаваемого перед тактирова-
нием на вход Т. Противопоставляется комби-
национной логике.
Установка (Set) — то же самое, что и Пре-
дустановка (Preset). Принудительная установ-
ка высокого уровня/уровней на выходе (при-
менительно только триггерам и другим после-
довательным устройствам).
Время вхождения в режим (Setup time) -
временной интервал перед сигналом тактиро-
вания, в течение которого сигнал на определен-
ном входе цифровой схемы должен оставаться
стабильным (сохранять свой уровень). Никогда
не бывает меньше нуля. Самое худшее время
у микросхем серии 74НС: около 20 не.
Сдвиговый регистр (Shift register) — набор
триггеров, у которых выход Q, предыдущего
триггера подключен к входу D следующего.
Часто применяется для преобразования между
параллельным и последовательным формата-
ми данных.
Состояние (State) — состояние схемы последо-
вательной логики, определяемое уровнями вы-
ходов Q его триггеров. Например, состоянием
счетчика будет просто комбинация значений на
его выходах Q.
Конечный автомат (Finite state machine) — об-
щее описание схемы последовательной логики,
поскольку любая такая схема проходит пошаго-
во через определенную последовательность со-
стояний. Обычно зарезервировано для автома-
тов, которые исполняют нестандартные после-
довательности. Например, Т-триггер и декад-
ный счетчик являются конечными автоматами,
но никогда так не называются. Микропроцессор,
исполняющий микропрограмму, является ко-
нечным автоматом, как и весь компьютер.
Синхронный (Synchronous) — с общим сигна-
лом тактирования (греческое син-кронос озна-
чает одинаковое время). Синхронные функции
ожидают сигнала тактирования. (Например, в
счетчике на лабораторном занятии 16L таким
образом ведет себя функция SYNCJLD*. А дру-
гая функция загрузки, LD*, в этом же счетчике
является асинхронной и срабатывает сразу же
после ее активирования.)
С тремя состояниями (three-state) — описы-
вает выход логической схемы, который можно
отключить, вместо подачи на него высокого или
низкого уровня. То же самое, что и tri-state.
Tri-state — термин, аналогичный three-state
(с тремя состояниями), и зарегистрированная
торговая марка компании National Semicon-
ductor, в настоящее время являющейся частью
компании Texas Instruments.
14W. Примеры с решениями:
логические устройства
14W.1. Общие сведения
о мультиплексировании
В этом разделе мы рассмотрим три способа раз-
работки небольшого мультиплексора1:
♦ на обычных логических элементах;
♦ на логических элементах с тремя состояния-
ми;
♦ на аналоговых коммутаторах.
Понятие мультиплексирования, или разделе-
ния времени, является более общим и более
важным, чем аппаратное устройство, назы-
ваемое мультиплексором. Сам мультиплексор
встречается не так часто, а мультиплексирова-
ние используется постоянно в любом компью-
тере и во многих схемах по сбору данных.
На рис. 14W.1 иллюстрируется метод мульти-
плексирования в его простейшем виде: выбор
одного из нескольких источников с помощью
механического переключателя. Источниками
могут быть, например, микрофоны, установ-
ленные в квартирах политически неблагона-
дежных лиц. Раз в месяц (или каждый час, если
необходимо) полицейский агент переводит пе-
реключатель на другую линию, таким образом
подключаясь к другому из четырех микрофонов.
Микрофоны
D
D
а
D
О
а
□
D »
Q*
а*
В данном случае причиной для использования
мультиплексирования, как всегда, является же-
лание уменьшить количество линий для пере-
дачи информации.
Только что приведенный пример является, ко-
нечно же, чрезвычайно надуманным. Более
типичный пример дефицитного ресурса —
аналогово-цифровой преобразователь (АЦП),
а самый знакомый для всех нас — телефонная
система. Если бы телефонные линии не исполь-
зовались по принципу разделения во времени,
они бы выглядели как паутина какого-то ги-
гантского арахнида. Представьте себе, как весь
город был бы опутан проводами, если все воз-
можные пары абонентов соединялись друг с
другом по отдельным телефонным линиям! На
рис. 14W.2 иллюстрируется, как будет выгля-
деть сеть телефонных линий для соединения
всех возможных пар всего лишь восьми або-
нентов.
Подобный метод применяется для эффектив-
ного общего использования линий в компью-
терных системах, где они называются шинами.
Но в последнее время для подключения цен-
трального процессора компьютера к памяти
и периферийным устройствам наблюдается
тенденция к применению быстрых последова-
тельных каналов вместо параллельных шин.
1 Министерство
правды
Выбор линии прослушки
Рис. 14W.1. Четыре источника поочередно подключаются к одной линии с помощью механического мультиплексирования
АоЕ § 10.3.3С.
14W.1. Общие сведения о мультиплексировании
579
Коммутатор
Восемь телефонов. Мамочки! Восемь телефонов + коммутатор: намного лучше
Рис. 14W.2. Аргумент в пользу мультиплексирования: существенное уменьшение количества соединительных линий
Периферийные устройства и память
Пароля* л ьные
пины
Периферийные устройства и память
Высокоскоростные последовательные шины
Компьютер с традиционными параллельными шинами\// /Компьютер с высокоскоростными последовательными шинами
Преобразователи последовательный м-** параллельный (Сер./Дес.) (сериализатор/десериализатор)
Рис. 14W.3. Организация связи в компьютерах с параллельными (слева) и с высокоскоростными последовательными (справа)
шинами
Более того, в настоящее время последователь-
ные каналы доминируют. Такая прямая связь
между двумя узлами менее уязвима к отраже-
ниям сигнала в линиях передачи, чем много-
абонентская схема с параллельной шиной.
Вследствие этого последовательные каналы
обеспечивают более высокие скорости пере-
дачи данных2.
Но даже в тех случаях, где внешние каналы со-
стоят всего лишь из нескольких проводов (на-
пример, по дифференциальной паре в каждом
направлении для последовательной шины PCI
Express), параллельные шины продолжают ис-
пользоваться внутри микросхем. Пример при-
веден справа на рис. 14W.3.
14W.1.1. Аппаратное обеспечение
для мультиплексирования
С задачей мультиплексирования линий может
справиться простой механический многопози-
ционный переключатель или его транзистор-
ный эквивалент, состоящий из набора анало-
говых ключей3. Эта задача под силу и логиче-
ским вентилям, но, в отличие от предыдущих
двух устройств, они передают данные только
в одном направлении. Если у вас нет опыта в
этой области, то цифровая реализация потре-
бует больше предварительной работы. И даже
схема на основе аналоговых коммутаторов по-
требует использования декодера, как только
мультиплексировать нужно будет больше двух
сигналов.
Нам требуются два элемента:
1. Схема для пропуска/блокировки, аналогич-
ная замкнутому/разомкнутому переклю-
чателю.
2. Схема для декодирования, которая будет од-
новременно закрывать только один из эле-
ментов пропуска/блокировки.
Рассмотрим каждый их этих элементов, снача-
ла для реализации на обычных вентилях.
2 АоЕ § 14.6.1.
АоЕ § 14.6.2С.
580
14W. Примеры с решениями: логические устройства
А в
Блокировка / О О
Пропускание /} °
А*В
Выход = 0
Сигнал
В-
Выход
\ Пропускание/Блокировка
Выходной сигнал = Входному сигналу
Рис. 14W.4. Операцию Пропуск/Блокировка* можно реализовать с помощью логического элемента И
Элемент пропуска/блокировки
С этой задачей более-менее справится логиче-
ский вентиль И, как показано на рис. 14W.4.
Чтобы пропустить подаваемый на один из вхо-
дов сигнал, на другой вход подается высокий
уровень. В результате сигнал на первом входе
отображается на выходе. А чтобы заблоки-
ровать сигнал, на вход управления подается
сигнал низкого уровня. Блокировка выглядит
необычно, поскольку в этом случае на выходе
принудительно устанавливается сигнал низ-
кого уровня, что неэквивалентно размыканию
механического переключателя.
Соединение выходов
Выходы логических вентилей И ни в коем слу-
чае нельзя соединять вместе (рис. 14W.5).
Рис. 14W.5. Никогда не соединяйте вместе выходы обычных
логических вентилей
Вместо этого нам нужно подать выходные сиг-
налы на входы вентиля, который игнорирует
низкие уровни и пропускает высокие (посколь-
ку логический вентиль И в режиме блокировки
будет выдавать низкий уровень). Требуемым
поведением обладает логический вентиль ИЛИ.
Выходу Одновременно
| ^активируется
J только один выход
выход, Выхо/ц
Входной сигнал, закодированный в виде
двухразрядного двоичного числа
Итоговая схема мультиплексора на обычных
вентилях изображена на рис. 14W.6.
Выход
х/7= Выборка—1
Рис. 14W.6. Мультиплексор двух линий в одну
Декодер
Если число входов мультиплексора больше, чем
два, то нам нужна более сложная схема, чтобы
обеспечить передачу сигнала одному и только
одному вентилю. Схема, которая решает эту
задачу выборки одного объекта из набора, на-
зывается декодером. На входы схемы подается
двоичное число (компактное в закодирован-
ной форме: как мы знаем, посредством п линий
можно закодировать 2я комбинаций), которое
схема преобразует в форму 1-из-л.
Примечание
Декодированная форма числа уже не такая ком-
пактная и плохо подходит для передачи информа-
ции, но эта форма часто требуется для иницииро-
вания какого-либо аппаратного действия.
Задача декодера состоит в определении каждой
возможной входной комбинации. Например,
на рис. 14W.7 показана частичная реализация
декодера двух линий в четыре.
Г""**)—
«01»
Рис. 14W.7. Декодер двух линий в четыре: а — блок<хема, б — частичная реализация
14W.1. Общие сведения о мультиплексировании
581
Декодеры полезны сами по себе. Например, вам
понадобится микросхема декодера 74НСТ139
при сборке из дискретных деталей своего ми-
крокомпьютера. Декодер содержится в каждом
мультиплексоре и в каждой схеме мультиплек-
сирования с количеством шин больше двух.
14W.1.2. Рабочий пример
мультиплексора
Задача (три варианта схемы мультиплексора
Покажите, как собрать мультиплексор с че-
тырьмя входами, используя:
♦ обычные логические вентили;
♦ аналоговые коммутаторы;
♦ логические вентили с выходами с тремя со-
стояниями.
Решение
Декодер. Для всех трех решений требуется де-
кодер, так что с него и начнем.
Нам нужно определить все четыре возможные
комбинации. Решение этой задачи начнем, как
и в предыдущем примере, с создания дополне-
ния каждого входа выборки.
Примечание
Нужно ли объяснять, что для определения четырех
комбинаций требуются две линии выборки? Если
да, то мы только что разъяснили этот момент. Если
же это все равно непонятно, то вскоре все станет
ясно.
0,0
Q
О!
Q
00
Рис. 14W.8. Декодер 1-из-4
Модуль Пропуск/Блокировка на обычных
логических вентилях. Мы уже знаем, как ре-
шить эту задачу с помощью логических элемен-
тов И. На рис. 14W.9 изображена схема, которая
формирует все четыре входные комбинации и
подает их на модуль Пропуск/Блокировка*, со-
бранный на логических вентилях И, подобно
схеме на рис. 14W.4.
Декодер 1-из-4
(как на рис. 14W.8)
Рис. 14W.9 Реализация мультиплексора 4-в-1 на обычных
логических вентилях
Модуль Пропуск/Блокировка на аналого-
вых коммутаторах. Эта задача более легкая.
Конечно же, вы должны помнить, что представ-
ляют собой аналоговые коммутаторы. Если же
вы забыли, то возвратитесь к лабораторному
занятию 12L и освежите свою память.
Здесь снова необходим декодер. На этот раз мы
можем просто соединять выходы коммутатора,
поскольку, в отличие от обычных логических
вентилей, которые при блокировке выдают
низкий уровень на свой выход, аналоговые
коммутаторы, блокирующие источник сигнала,
переводят выход в «плавающее» (третье) со-
стояние. Соответствующая схема изображена
на рис. 14W.10.
Модуль Пропуск/Блокировка на логических
вентилях с тремя состояниями
После реализации предыдущей схемы эта вер-
сия не представляет никаких проблем. В ней
опять присутствует декодер и снова можно со-
единять выходы вентилей. Логический вентиль
с выходом в третьем состоянии, т. е. блокирую-
щий вход, не «вступает в пререкания» ни с ка-
кими другими вентилями. В этом, конечно же,
и заключается удобство третьего состояния.
Задача
При каких обстоятельствах предпочтитель-
нее второе решение (на аналоговых коммута-
торах)?
Решение
По большому счету это решение целесообраз-
но только для работы с аналоговыми сигнала-
ми. Более того, для этой цели оно не просто
582
14W. Примеры с решениями: логические устройства
—F
f\
U2
[\
С
V-
/
/ I
i
Декодер
-Выход
-Выход
Рис. 14W.10. Реализация мультиплексора 4-в-1: на аналоговых коммутаторах (слева) и на логических вентилях с тремя
состояниями (справа)
предпочтительно, а просто необходимо. Но для
цифровых сигналов этот вариант будет цаихуд-
шим, поскольку не обладает крайне важным
достоинством цифровых устройств: помехо-
устойчивостью, или способностью очищать об-
рабатываемый сигнал. Цифровые устройства
игнорируют помехи (до некоторого приемле-
мого уровня), а также выдают на выход сигнал,
из которого удалены помехи, присутствующие
во входном сигнале, и делают это при хорошем
низком выходном импедансе. Подобно любой
аналоговой схеме, аналоговый мультиплексор
не сможет проделать этот трюк; даже наоборот,
он слегка ухудшает качество сигнала. Кроме
того, выходной импеданс источника сигнала
тоже будет хуже из-за дополнительного после-
довательного сопротивления открытого кана-
ла R0K величиной около 100 Ом.
Не следует воспринимать эти сведения как
категорическое утверждение нежелательности
использования аналогового мультиплексора,
или одиночного аналогового переключате-
ля, для маршрутизации цифровых сигналов.
В действительности аналоговые переключатели
с низким сопротивлением открытого канала R0K
могут обеспечить самый быстрый способ для
подключения или отключения шины, выполняя
эту задачу быстрее, чем обыкновенные венти-
ли с тремя состояниями, расплачиваясь за это
потерей возможности регенерации сигнала. На
рынке такие устройства предлагаются под мар-
кетинговым лозунгом Zero Delay Logic (Логика с
нулевой задержкой). Примером такого устрой-
ства может служить компонент Quickswitch ком-
пании Integrated Device Technology4. К тому же
4 Для этого устройства заявлена очень низкая задержка
распространения (названная нулевой — Zero Delay) благо-
даря его предельной простоте. В действительности задерж-
ка возникает, но она в основном вызывается постоянной
времени ДС-цепи, состоящей из сопротивления открытого
аналоговые коммутаторы входят в состав спе-
циализированных микросхем. Но обычной об-
ластью применения для аналоговых переклю-
чателей (как можно предположить по их назва-
нию) является обработка аналоговых сигналов.
Между прочим, аналоговый мультиплексор
может передавать сигнал в любом направле-
нии, в результате чего он может работать и как
демультиплексор. И все же, если вам нужно де-
мультиплексировать цифровые сигналы, лучше
используйте цифровой демультиплексор.
14W.2. Двоичная
арифметика
В этом примере рассматриваются пять тем дво-
ичной арифметики:
♦ Двоичный дополнительный код — по
сравнению с беззнаковым кодом, а также
проблема переполнения.
♦ Сложение — задача проектирования аппа-
ратного устройства, иллюстрирующая сум-
матор с переносом.
♦ Компараторы величин — сначала реализу-
ются с большими усилиями вручную, а затем
с помощью языка Verilog.
♦ Умножение — правильный и неправильный
способы выполнения этой операции.
♦ АЛУ и флаги — предзнаменование работы
с микропроцессором, цель этого упражне-
ния — дать вам понять, что внутренность
ЦПУ не представляет собой ничего сложно-
го, а состоит из набора знакомых элементов.
канала R0K ключа и паразитной емкости линии, на которую
подается сигнал.
UW.2. Двоичная арифметика
583
14W.2.1. Дополнительный
двоичный код
Это упражнение даст вам шанс привыкнуть
к нотации дополнительного двоичного кода.
В описанных примерах мы хотим подчеркнуть
два момента:
♦ данный набор битов не обладает внутренним
значением; он обладает тем значением, кото-
рым мы позволим ему обладать согласно на-
шим соглашениям. (Этот момент подробно
рассмотрен в главе 14N);
♦ правильно вычисленная сумма (или произ-
ведение, или результат другой арифмети-
ческой операции) может тем не менее быть
неправильной при переполнении доступного
диапазона.
Оба эти момента довольно очевидны. Тем не
менее большинству людей необходимо уви-
деть определенное количество соответствую-
щих примеров, чтобы почувствовать себя
полностью уверенными в них. Особенно мо-
жет удивить вас переполнение, поскольку оно
отличается от переноса. Перенос может да-
вать правильный результат. Но результат мо-
жет быть и неправильным (в дополнительном
двоичном коде), даже при отсутствии переноса
из самого старшего бита. Попытка понять это
на словах может привести вас в замешатель-
ство. Поэтому полезно рассмотреть несколько
примеров.
Предположим, что на входы сумматора пода-
ется пара четырехразрядных двоичных чисел.
Запишем полученный результат суммирования,
а затем решим, правильный ли это результат
согласно двум противоположным предположе-
ниям: что эти четырехразрядные значения яв-
ляются беззнаковыми и что они представлены
в дополнительном двоичном коде.
Задача (дополнительный двоичный код)
Предположим, что вы ввели в четырехразряд-
ный сумматор два четырехразрядных значения
А и Б, указанных далее. Запишите следующее:
1. Максимальное значение, которое можно вы-
разить в этом четырехразрядном результате:
• беззнаковое;
• в дополнительном двоичном коде.
2. Полученную сумму.
3. Затем значения входов и выходов в десятич-
ном представлении согласно двум противо-
положным предположениям:
• значения (четырехразрядные) беззнаковые;
• значения (четырехразрядные) в дополни-
тельном двоичном коде.
4. Наконец, запишите, действителен ли полу-
ченный результат согласно каждому предпо-
ложению.
В качестве примера приведем решение для пер-
вого случая (табл. 14WJ).
Таблица 14W.1. Сложение двоичных чисел
ВХОД
Двоичный
Десятичный
Беззнаковый
Дополнительный двоичный код
Двоичный
Десятичный
Беззнаковый
Дополнительный двоичный код
Двоичный
Десятичный
Беззнаковый
Дополнительный двоичный код
Двоичный
Десятичный
Беззнаковый
Дополнительный двоичный код
Двоичный
Десятичный
Беззнаковый
Дополнительный двоичный код
А
0111
7
7
0111
0111
0111
1001
В
1000
8
-8
0111
1010
0100
1000
А плюс В
1111
15
-1
Правилен ли результат?
Да
Да
584
14W. Примеры с решениями: логические устройства
Попробуйте сначала сами решить эти примеры,
а затем проверьте, совпадают ли ваши решения
с нашими, изложенными чуть далее.
Решение (дополнительный двоичный код)
Максимальное значение, которое можно выра-
зить четырьмя двоичными разрядами (битами):
♦ беззнаковое: 15
10'
♦ в дополнительном двоичном коде: +710, -810.
В табл. 14W.2 приведены варианты решений.
Таблица 14W.2. Варианты решений
вход
Двоичный
Десятичный
Беззнаковый
Дополнительный
двоичный код
Двоичный
Десятичный
Беззнаковый
Дополнительный
двоичный код
Двоичный
Десятичный
Беззнаковый
Дополнительный
двоичный код
Двоичный
Десятичный
Беззнаковый
Дополнительный
двоичный код
А
0111
7
7
0111
7
7
0111
7
7
1001
9
-7
В
0111
7
7
1010
10
-6
0100
4
4
1000
8
-8
А плюс
В
1110
14
_2
0001
1
+1
1011
11
-5
001
1
+1
Действи-
тельный?
Да
Нет
Нет
Нет
Да
Нет
Нет
Нет
Задача
Как определить, правилен ли результат или
нет?
Решение
Для беззнаковых значений просто смотрим,
формируется ли бит переноса из самого стар-
шего разряда. Если да, то четырехразрядное
значение недействительно.
Для значений в дополнительном двоичном коде
правило более сложное: если разряд знака мо-
дифицируется переносом в него, то результат
недействителен. Перенос в разряд знака может
быть проблемой, но только в том случае, если
нет одновременного переноса из этого разряда,
и наоборот.
Иными словами, переполнение значения в до-
полнительном двоичном формате определя-
ется операцией Исключающее-ИЛИ над пере-
носами в самый старший разряд и из него. Эта
логика используется в микропроцессоре, с ко-
торым мы начнем работать на лабораторном
занятии 20L, для определения именного тако-
го переполнения (которое указывается флагом
OV, если вам интересно это знать на данном эта-
пе). Если у вас есть желание, можете проверить
это правило Исключающее-ИЛИ на примерах,
приведенных ранее.
14W.2.2. Сложение
Вам, вероятно, доставит удовольствие заново
изобрести сумматор. В таблице 14W.3 приве-
дена таблица истинности для одноразрядного
полного сумматора. Определение «полный»
означает, что такой сумматор может принимать
на входной сигнал переноса, что позволяет ка-
скадирование таких множественных полных
сумматоров.
Таблица 14W.3. Таблица истинности
для одноразрядного полного сумматора
ВХОД
Входной
перенос
0
0
0
0
1
1
1
1
А
0
0
1
1
0
0
1
1
в
0
1
0
1
0
1
0
1
выход
Выходной
перенос
0
0
0
1
0
1
1
1
Сумма
0
1
1
0
1
0
0
1
Обратите внимание на то, что при желании вы-
ход можно рассматривать как одно двухразряд-
ное двоичное число, а не как отдельные сумму
и перенос. Преимущество последнего представ-
ления состоит в том, что оно допускает увели-
чение разрядности слов: при переполнении че-
тырехразрядного двоичного числа также гене-
рируется бит переноса.
/41/1/12 Двоичная арифметика
585
Задача проектирования одноразрядного
полного сумматора
Спроектируйте полный сумматор. При не-
обходимости обращайтесь к табл. 14W.3. На
рис. 14W.11 приведена блок-схема такого сум-
матора.
Выход
переноса
Сумма
Вход
переноса
Рис. 14W.11. Блок-схема полного сумматора одноразряд-
ных двоичных чисел
Решение
При отсутствии входного переноса (ПРНСВХ =
= НИЗКИЙ) сумма будет А ИСКЛ-ИЛИ В; а при на-
личии входного переноса (ПРНСВХ = ВЫСОКИЙ)
сумма будет дополнением результата этой опе-
рации. Можно ли из этого предположить, что
сумма является функцией трех входных пере-
менных, одной из которых является входной
перенос? Да, можно — сумма будет резуль-
татом операции ИСКЛ-ИЛИ над всеми тремя
входными переменными. Как можно видеть на
рис. 14W.12, результат будет «1», если значение
«1» (высокий уровень) подается на нечетное
количество входов.
ПРНСВХ
Рис. 14W.12. Сумма будет равна ПРНСВХ ИСКЛ-ИЛИ А
ИСКЛ-ИЛИ В
А как насчет выходного переноса? Возможно,
что, изучая таблицу истинности некоторое
время, вы сможете увидеть закономерность.
Можно получить требуемую функцию мето-
дом логических рассуждений: выходной пере-
нос должен активироваться, когда активиро-
ваны два или больше входных бита, включая
входной перенос. Возможно, вам захочется на-
учиться применять старинный метод с исполь-
зованием карт Карно. Пример на рис. 14W.13
поможет вам понять закономерности, которые
показывают возможности проигнорировать
одну-другую переменную.
ГТРНС,
вых
Рис. 14W.13. Карта Карно для выходного переноса
Независимо от используемого способа, вы
должны получить схему полного сумматора од-
норазрядных двоичных чисел, подобную изо-
браженной на рис. 14W.14.
ТТРНС
ТТРНСВЬГХ
Сумма
Рис. 14W.14. Принципиальная схема полного сумматора
одноразрядных двоичных чисел
Альтернативное решение с использовани-
ем Verilog
Но больших усилий по овладению булевыми
манипуляциями можно избежать благодаря
наличию логических компиляторов. Такие
компиляторы берут в качестве входных данных
ваше описание схемы на очень высоком уров-
не абстракции и на его основании создают со-
ответствующую принципиальную логическую
схему. Листинг 14W.1 содержит описание на
языке Verilog сумматора одноразрядных дво-
ичных чисел.
Листинг 14W.1. Описание сумматора одно-
разрядных двоичных чисел на языке Verilog
module adder_assign(
input a,
input b,
input c_in,
output sum,
output c_out
assign {c_out,sum} = a + b + c_in;
endmodule
586
14W. Примеры с решениями: логические устройства
Действительно ли задача разработки может
быть такой легкой? По-видимому, да, как мож-
но судить по следующему результату моделиро-
вания этого решения (листинг 14W.2).
Листинг 14W.2. Результат моделирования
сумматора
Finished circuit initialization process.
(Процесс инициализации созданной схемы.)
{a,b,c_in} = 000, {c_out, sum} = 00
{a,b,c_in} = 100, {c_out, sum} = 01
{a,b,c_in} = 010, {c_outr sum} = 01
{a,b,cjn} = 001, {c__put, sum} = 01
{a,b,cjn} =101, {c_out, sum} = 10
{a,b,cjn} = 111, {c_out, sum} = 11
{a,b,cJn} = 011, {c_out, sum} = 10
{a,b,cjn} = 001, {c_out, sum} = 01
{a,b,cjn} = 000, {c_out, sum} = 00
Здесь c_in — входной перенос; c_out — выход-
ной перенос.
В листинге все выглядит правильно. А на
рис, 14W.15 изображена причудливая схема,
посредством которой Verilog получил такой хо-
роший результат.
Ни один человек не разработал бы такую схе-
му; сумма выглядит нормально, но перенос вы-
глядит более чем странно:
с out = ((axorb)c in)xor(ab)
Но, несмотря на всю странность, результат пра-
вильный, и это то, что для нас действительно
важно. Всю тяжелую работу выполнила про-
грамма Verilog.
Определив одноразрядную функцию с входным
и выходным переносами, мы можем «нанизы-
вать» эти функции до бесконечности, создавая
сумматор требуемой разрядности (хотя обра-
ботка длинных строк может быть медленной).
Позже мы также порекомендуем вам поискать
одинаковую повторяющуюся закономерность
при разработке схемы умножителя.
Но, опять же, если использовать для разработ-
ки язык Verilog, то расширение сумматора от
одного разряда до нескольких является пол-
ностью прямолинейной задачей. Все, что для
этого нужно сделать, так это определить вход а
(который ранее состоял из одного бита) в виде
набора битов. То же самое нужно сделать для
входа b и суммы, и на этом наша работа закан-
чивается, а программа Verilog выполняет всю
дальнейшую работу. Листинг 14W.3 содержит
программу на Verilog с определением четырех-
разрядного сумматора.
Листинг 14W.3. Описание четырехразрядного
сумматора на языке Verilog
module adder_assign_4bit(
input [ЗЮ] a,
input [3:0] b,
input c_jn,
output [3:0] sum,
output c_put
assign {c_out, sum} = a + b + cjn;
endmodule
»ock*addef .assign
ANOF
Рис. 14W.15. Логическая схема, созданная программой на языке Verilog для реализации полного сумматора одноразрядных
двоичных чисел
14W.2. Двоичная арифметика
587
14W.2.3. Цифровые компараторы
Определение равнозначности5
Периферийным компьютерным устройствам
часто приходится выполнять задачу определе-
ния, когда значение на шине адреса равно зна-
чению адреса данного периферийного устрой-
ства. (Иными словами, когда компьютер хочет
работать с данным устройством.) Такую равно-
значность можно определить поразрядно с по-
мощью набора функций Исключающее-ИЛИ.
Соответствующая принципиальная схема изо-
бражена на рис. 14W.16.
А=В
Побитовое сравнение
Рис. 14W.16. Равнозначность двух двоичных значений мож-
но определить поразрядно с помощью функций Исключаю-
щее-ИЛИ
На лабораторном занятии 14L вам нужно
было разработать детектор равнозначности,
и вы, несомненно, уяснили, что для решения
этой задачи требуется поразрядное опреде-
ление равнозначности посредством вентилей
Исключающее-ИЛИ, на которые нужно пода-
вать соответствующие биты многоразрядных
слов: А1 ИСКЛ-ИЛИ Вг Ао ИСКЛ-ИЛИ Во. Затем
над низкими выходными уровнями несколь-
ких вентилей Исключающее-ИЛИ выполняет-
ся операция И. Логический вентиль, который
выполняет операцию И над низкими уровня-
ми, называется ИЛИ-НЕ, хотя это название,
конечно же, не описывает функцию вентиля в
данном случае.
Определение неравнозначности А > В
(компаратор величин)
Задача разработки схемы для определения
больше ли одно двухразрядное двоичное
число, чем другое
Используя логические вентили любого типа
(вентили Исключающее-ИЛИ удобны, но не
обязательны), разработайте схему, на выходе
которой присутствует высокий уровень, когда
двухразрядное двоичное число А больше, чем
такое же число В. На рис. 14W.17 изображена
блок-схема устройства, которое вам нужно раз-
работать.
АоЕ § 10.3.3Е.
В
Рис. 14W.17. Блок-схема для определения неравнозначно-
сти двухразрядных двоичных чисел
Обратите внимание на то, что эту задачу мож-
но решить двумя способами. В одном из них
используется систематический подход посред-
ством карт Карно. Другой способ привлекает к
работе ваши мыслительные способности: сна-
чала решите, как можно определить равнознач-
ность двух одноразрядных двоичных чисел, за-
тем, как можно определить, что одно из одно-
разрядных чисел больше, чем другое, затем, ка-
кая связь между старшими и младшими битами
и т. д. Мы рассмотрим оба эти способа.
Решение с помощью карт Карно
Этот метод иллюстрируется на рис. 14W.18. Но
мы не думаем, что кому-либо хотелось бы изу-
чать, как работать с картами Карно (что вкрат-
це рассматривается в § 10.3.3 книги АоЕ), лишь
для того, чтобы решать такие задачи.
Решение посредством логических умоза-
ключений
Более интересный способ решения этой задачи
показан на рис. 14W.19.
Как видим, решение, полученное посредством
умственного труда, ничем не лучше результата,
полученного систематическим методом. Оба ре-
шения используют примерно одинаковое коли-
чество логических элементов. Выберите любой
из этих двух подходов, который вам больше по
душе. У некоторых людей карты Карно вызыва-
ют аллергию, тогда как другим они нравятся.
Решение с помощью программы Verilog
Как обычно, использование языка Verilog пор-
тит все удовольствие, поскольку программа
выполняет всю умственную работу. (Конечно
же, сначала вам нужно научиться работать с
языком Verilog.) Листинг 14N.4 содержит про-
грамму на языке Verilog, которая решает нашу
задачу.
588
14W. Примеры с решениями: логические устройства
f = А1(Й + АО 60) ♦ АО BI ВО
V .Общий член: АО ВО
Рис. 14W.18. Решение задачи определения неравнозначности одноразрядных чисел посредством карт Карно и соответствую-
щая принципиальная схема
Старший бит ы У
ААладший бит
во
...и А = 1...
Это решает задачу: поскольку А1>В1, то А>В
^/ ^Старшие
биты одинаковые, а младший А > младшего В
^Проверим, если младший бит А > младшего бита В
А1 = В1, поэтому нужно рассматривать младшие биты
Рис. 14W.19. Решение задачи определения неравнозначности одноразрядных чисел посредством логических умозаключений
Рис. 14W.20. Реализация схемы посредством программы на языке Verilog
Листинг 14W.4. Программа логической
операции неравнозначности
module comparator_2bit(
input [1:0] а,
input [1:0] b,
output reg a__beats_b
always @(a, b)
begin
if(a>b)
a_beats_b=1 Ts-
etse
a_beats_b = VbO;
end
endmodule
14W.2. Двоичная арифметика
589
Рис. 14W.21. Моделирование схемы, созданной программой Verilog, доказывает ее работоспособность
Рис. 14W.22. Реализация схемы восьмиразрядного компаратора посредством программы на языке Verilog
Опять же, результатом работы программы
Verilog является очень странная схема6, изобра-
женная на рис. 14W.20.
Но, несмотря на всю свою странность, схема
работает должным образом. На рис. 14W.21 по-
казаны результаты ее моделирования.
Посредством Verilog схему можно
с легкостью масштабировать
Разработка вручную компаратора величин с
разрядностью больше чем два была бы чрез-
вычайно сложной задачей. Применение язы-
ка Verilog делает решение этой задачи таким
легким, что даже неловко. Например, чтобы
получить восьмиразрядный компаратор, про-
сто корректируем определения значений а и b
соответствующим образом: указываем восемь
бит вместо двух. Листинг 14N.5 содержит соот-
ветствующую программу.
Листинг 14W.5. Программа логического
8-разрядного компаратора
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIUI
module comparator_8bit(
input [7:0] а,
input [7Ю] b,
output reg a_beats_b
always @(a, b)
begin
if(a>b)
a_beats_b = 1'b1;
else
a_beats_b = 1'bO;
end
endmodule
6 Данная компиляция и моделирование были выполнены
с помощью программного пакета Xilinx ISE 10, тогда как
другие в этой главе были реализованы посредством Xilinx
ISE 11. Схемы различаются в этих двух версиях, но резуль-
таты моделирования одинаковы (какими они, естествен-
но, и должны быть).
Как можно видеть на рис. 14W.22, созданная
программой схема выгладит кошмарно. Но,
опять же, поскольку всю тяжелую работу вы-
полняет Verilog, то нам все равно.
Модификация программы для создания схе-
мы для других операций сравнения — простая
590
14W. Примеры с решениями: логические устройства
задача. Для этого просто добавляем другие вы-
ходы, например А = В,А<ВиА>В. Заниматься
этим мы сейчас не будем. Но вам уже, наверное,
понятно, что программа на языке Verilog с лег-
костью справится и с этой задачей.
14W.2.4. Умножение
Умножители менее важны, чем сумматоры,
поэтому не нужно особенно разбираться, как
они работают. Умножители важны в цифровой
обработке сигналов, но не в той области, в ко-
торой мы будем работать в этой книге. Но если
данный вопрос вас интересует, можете прора-
ботать соответствующий материал.
Один из способов для определения логики, не-
обходимой для выполнения операции умноже-
ния, — использовать карты Карно или какой-
либо другой метод, чтобы сформировать функ-
цию, необходимую для каждого бита произве-
дения.
Но следующий пример по умножению неболь-
ших значений должен убедить вас, что должен
быть лучший способ для решения этой зада-
чи. В случае умножителя двух трехразрядных
двоичных чисел с его шестью входными пере-
менными вы погрязнете в дебрях карт Карно,
а ведь умножение еще больших значений явля-
ется совсем заурядным событием. К счастью,
существует лучший способ.
Эта задача оказывается одной из тех, которую
не следует решать с помощью карт Карно или
любого другого утомительного метода мини-
мизации. Вместо этого следует воспользоваться
упорядоченностью функции произведения, ко-
торая позволяет реализовать по сути один по-
вторяющийся способ для умножения большого
Десятичные Двоичные Двоичные, общий подход
количества битов. Эта закономерность почти
такая же простая, как и для сумматора.
Умножение двоичных чисел вручную можно
выполнять таким же способом, как и десятич-
ных чисел. Более того, как можно видеть из
рис. 14W.23, ручное умножение двоичных чи-
сел намного легче, чем десятичных.
Когда вы увидите эту аккуратную закономер-
ность, то осознаете, что все, что требуется для
реализации умножителя, — это двухвходовые
логические вентили И и несколько сумматоров.
Этот метод упрощает задачу умножения двух
четырехразрядных чисел, решить которую с
помощью карт Карно было чрезвычайно труд-
но. Давайте попробуем решить эту задачу.
Примечание
Кстати, для реализации умножителя нужны только
полусумматоры, а не полные сумматоры. Но вместо
того, чтобы собирать все на логических элементах,
можно воспользоваться микросхемой сумматора,
например микросхемой 74LS83 или 74НС83.
Задача
Спроектируйте умножитель двух трехразряд-
ных двоичных чисел, но на этот раз используя
два четырехразрядных полных сумматора (на
микросхеме 74НС83) и необходимое количе-
ство двухвходовых логических элементов.
Решение
Схема для решения этой задачи изображена на
рис. 14W.24. Но такую схему легче купить, а не
«А
а2Ь0
Льо
Рис. 14W.23. Ручное умножение десятичных (слева) и дво-
ичных (посередине) чисел, а также общий метод для ручного
умножения двоичных чисел (справа). Умножение двоичных
чисел намного легче, чем десятичных!
! ц
р=
-Д.
rw 4».
a2b2
■k Т
J-L
р4
XI
_г!_
Ц
р3
-U-
ц
рг
0 0
р.
Р 1
.- ~ - j
Ро
Рис. 14W.24. Умножитель двух трехразрядных двоичных чи-
сел с использованием сумматоров на микросхеме
14W.2. Двоичная арифметика
591
собирать самому! Тем не менее она демонстри-
рует общий принцип, который можно легко
масштабировать для умножения четырехраз-
рядных или даже шестнадцатиразрядных дво-
ичных чисел.
14W.2.5. Арифметико-логическое
устройство
В завершение этого обсуждения цифровой
арифметики рассмотрим устройство, без кото-
рого не может обойтись ни один компьютер.
Это арифметико-логическое устройство (АЛУ),
которое, как видно из его названия, выполняет
разные арифметические и логические операции.
Для проектирования этого устройства не требу-
ется изобретать ничего нового, а просто соеди-
нить вместе уже знакомые нам компоненты.
Задача проектирования одноразрядного
АЛУ
На рис. 14W.25 изображена таблица истинно-
сти и блок-схема упрощенного АЛУ. Она осна-
щена входом и выходом переноса, а на выходе
устанавливается низкий уровень во всех слу-
чаях, когда не формируется выходной перенос
(например, при операции А ИЛИ В).
Решение посредством программы языка
Verilog
Как обычно, эта задача достаточно легко подда-
ется решению с помощью программы на язьже
Verilog. Мультиплексор можно реализовать, ис-
пользуя стандартный оператор CASE (подобно
тому, как мы это делаем при проектировании
счетчика в Приложении А). Листинг 14N.6 содер-
жит программу на Verilog для реализации АЛУ.
Листинг 14W.6 Программа на Verilog для реали-
зации АЛУ
module ALU(
input [1:0] S, // Это двухразрядный код для выборки
// операции АЛУ
input A,
input В,
input CIN,
output reg OUT,
output reg COUT
parameter AND = ЪОО, OR = Ъ01, XOR = 'Ы 0, SUM= 'Ы1 ;
// Определения, которые позволяют нам использовать
описательные названия для сигналов выборки опе-
рации
Входной
перенос
0
0
0
0
1
1
1
1
А
0
0
1
1
0
0
1
1
В
0
1
0
1
0
1
0
1
и
0
0
0
1
или
0
1
1
1
искл-
или
0
1
1
0
СЛОЖЕНИЕ
Выходной
перенос
0
0
0
1
0
1
1
1
Сумма
0
1
1
0
1
о
0
1
А—
в —
Входной
перенос
АЛУ
si s'o
Выходной
перенос
—Выход
Рис. 14W.25. Блок-схема одноразрядного АЛУ
Операция, которую должно выполнять АЛУ в
схеме на рис. 14W.25, задается двумя линиями
выборки: S1 и SO.
Решение с использованием вентилей и
мультиплексора
Все, что нам нужно сделать, чтобы собрать тре-
буемое устройство, так это соединить вместе
стандартные логические вентили и сумматор
с мультиплексором. Соответствующая схема
изображена на рис. 14W.26.
Входной
перенос
Выход
Выходной
перенос
Рис. 14W.26. Принципиальная схема простого одноразряд-
ного АЛУ
592
14W. Примеры с решениями: логические устройства
always@(S,A,B,CIN)
begin
case(S)
AND:
begin
OUT<=A&B;
COUT<=0;
end
OR:
begin
OUT<=A|B;
COUT<=0;
end
XOR:
begin
OUT<=AAB;
COUT<=0;
end
SUM:
begin
OUT<=AABACIN;
COUT<=CIN&(A|B);
end
endcase
end
endmoduie
14W.2.6. Усовершенствование
АЛУ — добавление флагов
Компьютерное АЛУ всегда содержит триг-
геры, которые ведут учет важных фактов о
результатах самой последней выполненной
операции, т. е. выдают не сам результат, а крат-
кие описания его разных аспектов. В число та-
ких аспектов могут входить следующие:
♦ был ли сформирован выходной перенос;
♦ не оказался ли результат нулевым;
♦ результат положительный или отрицатель-
ный (в дополнительном двоичном коде);
♦ было ли переполнение значения в дополни-
тельном двоичном коде,
♦ а также, некоторые другие аспекты (на-
пример, полуперенос для микроконтролле-
ров 8051, используемый для преобразования
двоичных значений в двоично-десятичные).
Примечание
Прежде чем пытаться решить эту задачу, вы долж-
ны обладать знаниями хотя бы о D-триггере.
Задача оснащения АЛУ флагами
К разработанному в предыдущем разделе АЛУ
добавьте флаги для записи следующих сведе-
ний о результатах выполненной операции:
♦ Перенос — был ли сформирован выходной
перенос?
♦ Ноль — был ли результат нулевым?
♦ Знак — результат положительный или от-
рицательный (в дополнительном двоичном
коде)? (Можно предположить, что однораз-
рядный выход данного каскада содержит-
ся в самом старшем бите более длинного
слова.)
А-
в-
Входной
перенос
Выход
— D Q
Выходной перенос
D Q
>
Из переноса следующего каскада
Обновляем некоторые или все флаги: (
(сигналы тактирования для триггеров) t
D Q
-Ноль
-Знак
(предполагается, что это самый
старший бит более длинного слова)
D Q
-Перенос
-Переполнение
Рис. 14W.27. Решение задачи добавления флагов к АЛУ
14W.2. Двоичная арифметика 593
♦ Переполнение — было ли переполнение Предположим, что триггеры тактируются сиг-
значения в дополнительном двоичном коде? налом тактирования спустя небольшое время
(Так сами делаем предположение, что этот после стабилизации результата на выходе,
выход содержится в самом старшем бите бо-
лее длинного слова и, таким образом, пред-
ставляет собой бит знака, когда это слово Решение
рассматривается, как значение в дополни- Схема, изображенная на рис. 14W.27, иллю-
тельном двоичном коде.) стрирует решение этой задачи.
15N. Триггеры
Содержание
15N.1. Реализация комбинационной функции 595
15N.1.1. Упрощение или минимизация логических схем 596
15N.2. Снова о сигналах с низким активным уровнем 596
15N.2.1. Начертите схему с логическими вентилями 596
15N.2.2. Использование логического компилятора Verilog 598
15N.3. Вентили как функции «Делай это/делай то» 600
15N.3.1. Вентиль И в качестве функции ЕСЛИ 601
15N.4. Функция Исключающее-ИЛИ в качестве функции Инверсия/Пропуск* 601
15N.5. Функция ИЛИ в качестве функции Установка/Пропуск* 601
15N.6. Последовательные схемы в общем и триггеры в частности 601
15N.6.1. Простейший триггер-защелка на двух транзисторах 602
15N.6.2. Снова простейший триггер-защелка, но на двух логических элементах 603
15N.6.3. Схемы устранения дребезга контактов переключателя 603
15N.6.4. Простого RS-триггера обычно недостаточно 604
15N.6.5. Запуск по фронту сигнала тактирования 605
15N.7. Применение триггеров в схемах устранения дребезга контактов 608
15N.7.1. D-триггер и низкочастотный сигнал тактирования 608
15N.7.2. Схема устранения дребезга с положительной обратной связью 609
15N.8. Счетчики 609
15N.8.1. Счетчики со сквозным переносом 609
15N.9. Синхронные счетчики 610
15N.9.1. Понятие синхронности 610
15N.9.2. Для синхронных счетчиков требуются более «умные» триггеры 610
15N.9.3. Требуемое поведение счетчика 611
15N.10. Сдвиговый регистр на триггерах 612
15N.1L Материал для чтения в АоЕ 613
Цель этой главы
В этой главе мы познакомимся с логическими устройствами, которые запоминают состояния дво-
ичных сигналов. Такие схемы могут иметь более разнообразное применение, чем простые ком-
бинационные устройства, которые мы рассмотрели в главе 14N. Но сначала повторим, к каким
выводам мы пришли ранее.
♦ Цифровые схемы обладают хорошей помехо-
устойчивостью.
Помехоустойчивость цифровых схем обеспе-
чивает их замечательные возможности:
• двоичное кодирование информации по-
зволяет использовать очень простые
электронные схемы, вследствие чего мож-
но получить малогабаритные и дешевые
устройства;
• помехоустойчивость важна при хранении
данных и их передаче в неблагоприятных
условиях;
• кодирование информации позволяет в
процессе ее обработки выявлять и исправ-
лять ошибки (например, при воспроизве-
дении музыки в цифровом формате).
Чем выше помехоустойчивость, тем качествен-
нее происходит обработка данных. Отсюда
15N.I Реализация комбинационной функции
595
следует, что 5-вольтовая технология КМОП
превосходит устаревшую технологию ТТЛ. Для
передачи сигналов лучше всего подходит диф-
ференциальный способ, который в настоящее
время широко применяется в устройствах с
низкими напряжениями.
♦ Массивы логических вентилей (ПМЛ, ПЛУ и
FPGA) широко используются вместо микро-
схем с несколькими логическими вентилями
заданного типа.
♦ Задача минимизации схем обычно решается
логическим компилятором, который выпол-
няет программирование таких устройств.
♦ Большинство цифровых сигналов управле-
ния имеют низкий активный уровень (по
историческим причинам).
♦ Возможные проблемы с путаницей высоких
и низких активных уровней решаются с по-
мощью того же логического компилятора,
который скрывает этот аспект от разработ-
чика.
♦ В двоичной системе счисления для пред-
ставления отрицательных чисел использу-
ется дополнительный двоичный код. В этом
коде для указания знака числа служит самый
старший разряд; единица в этом разряде
означает отрицательное число, а ноль — по-
ложительное. Но двоичное представление
само по себе не содержит никаких призна-
ков какого-либо определенного формата,
и его интерпретация полностью зависит от
соглашения, применяемого в каждом кон-
кретном случае.
15N.1. Реализация
комбинационной функции
В большинстве случаев разрабатываемая ком-
бинационная логика настолько проста, что для
выбора наилучшего варианта ее реализации не
требуется ничего большего, чем умение рисо-
вать. Поэтому основная трудность заключается
в том, чтобы привыкнуть к широкому исполь-
зованию сигналов с активным низким уровнем.
Пример сигналов с активным низким уровнем
показан в схеме на рис. 15N.1. Здесь сигнал так-
тирования подается на триггер в том случае,
когда активирована линия RD* или WR* и при
этом также активирована линия Now*.
Поскольку это вход сигнала :
разрешения по положительному
фронту J [_
Активный уровень этого сигнала
должен быть высоким
Рис. 15N.1. Пример схемы комбинационной логики, в кото-
рой некоторые сигналы имеют активный низкий уровень
Но даже задачу разработки комбинационной
логики можно сделать трудной, если думать
над ее решением слишком усердно. Например,
размышляя следующим образом: «Так, имеем
низкий входной сигнал, и если другой входной
сигнал также низкий, я хочу, чтобы выходной
сигнал был высоким. Это будет логический
вентиль Исключающее-ИЛИ», вы сразу же соз-
дадите себе проблему. Вместо этого применяй-
те легкий способ разработки.
Далее мы опишем легкий процесс для создания
правильных и понятных логических схем, в ко-
торых используются сигналы с низким актив-
ным уровнем.
1. Нарисуйте символы логических вентилей,
соответствующие описанию: например, сим-
вол И для слова «и», независимо от активно-
го уровня.
2. Где необходимо, к входам и выходам нарисо-
ванных символов вентилей пририсуйте кру-
жочки инверсии, чтобы согласовать с актив-
ными уровнями.
3. Определите, какие типы вентилей вам нуж-
ны. (Обратите внимание на то, что этот шаг
выполняется последним, и не нужен, если ис-
пользуется ПЛУ и логический компилятор.)
В общем, в правильно нарисованной принци-
пиальной схеме кружочки на выходах совпада-
ют с кружочками на входах, в результате чего
они аннулируют друг друга. Но это общее пра-
вило неприменимо в исключительных случаях,
когда нужно деактивировать сигнал. Мы встре-
тимся с такими ситуациями в разделе 15N.2.1.
Также оно часто неприменимо к случаям с
тактированием по фронту сигнала, где выбор
фронта (передний или задний) зависит от мо-
мента времени.
596
15N. Триггеры
15N.1.1. Упрощение или
минимизация логических схем
Если логическая схема содержит много элемен-
тов, то может возникнуть вопрос является ли
ваша реализация минимальной, т. е. самой про-
стой? В былые времена создание таких простей-
ших схем составляло серьезную часть работы
проектировщика. Для упрощения логических
формул можно использовать булеву алгебру,
например разложение на множители. Допустим,
что в те старые времена вам дали таблицу ис-
тинности, изображенную на рис. 15N.21, и по-
ручили разработать для нее схему. Как бы вы
подошли к решению такого задания?
* Выход
Рис. 15N.2. Таблица истинности, для которой нужно разра-
ботать логическую схему
о
0
1
1
0
1
0
1
1
0
1
А ■■ т. ■■
л
D „„., . ,,„1ЛЛ11 „.
Но навыки работы с булевой алгеброй так же
устарели, как и привычка работать, например,
со счетами или логарифмической линейкой.
То же самое относится и графическим сред-
ствам упрощения в виде карт Карно. Теперь
любой разработчик с доступом к компьютеру
может воспользоваться автоматическим ло-
гическим компилятором. Логический компи-
лятор реализует язык HDL (язык описания
аппаратных средств), обычно это язык VHDL
или Verilog. В нашем курсе мы используем язык
Verilog.
Логический компилятор быстро упрощает вво-
димые в него уравнения в письменном или гра-
фическом виде (некоторые компиляторы могут
воспринимать графический ввод). Поэтому мы
больше не будем уделять внимание проблеме,
которая милосердно была убрана из жизни раз-
работчиков логических схем. Таким образом
мы сохраним нашу мыслительную энергию для
более интересных задач.
1. Вы можете просто внимательно изучить та-
блицу истинности и обнаружить закономер-
ность. Некоторым людям нравится такой
подход.
2. Можно также написать булево выражение
для каждой комбинации входов, которая
дает единицу на выходе:
f=A*B*+A*B + AB.
Затем с помощью булевой же алгебры упроща-
ем это выражение посредством разложения на
множители:
f=A*(B* +В)+АВ = А * +АВ.
Таким образом мы обнаруживаем, что из двух
членов можно убрать переменную А. Затем,
проявив достаточную наблюдательность, мож-
но увидеть возможность применить другое бу-
лево правило и в результате получить весьма
простое выражение2:
f=A*+B.
1 Может возникнуть уместный вопрос, насколько велика
вероятность такой ситуации в реальной жизни. Таблицы
истинности создаются только в тех случаях, если они удоб-
ны для проектирования. Если же начать описание схемы с
рисования символов вентилей, то задача разработки схе-
мы по таблице не возникнет.
2 Логическое выражение для случая низкого выходного
сигнала создать еще проще:/* = АВ*.
15N.2. Снова о сигналах
с низким активным уровнем
В одном из предыдущих примеров мы исполь-
зовали сигналы с активным низким уровнем в
вымышленной схеме запуска ядерных ракет.
Теперь давайте рассмотрим более реалистич-
ный пример. Теперь в нашей задаче некоторые
из сигналов имеют высокий активный уровень,
но активный уровень большинства сигналов
низкий, как у сигналов управления3.
15N.2.1. Начертите схему
с логическими вентилями
Нарисуйте логическое устройство, которое бу-
дет активировать сигнал DOIT, если:
♦ активированы все сигналы WRITE, VALID и
TIMED, но при этом не активирован ни сиг-
нал PROTECTED, ни сигнал BLOCK;
♦ или активирован или сигнал WILLY, или сиг-
нал NILLY.
3 Причины преобладания сигналов с низким активным
уровнем просто исторические. Такие сигналы были удоб-
ны во времена биполярной логики, как упоминалось
в главе 14N.
15N.2. Снова о сигналах с низким активным уровнем
597
Трудный выбор обозначения
Как это ни странно, это упражнение содержит
единственный аспект в нашем курсе, вызываю-
щий недовольство студентов. Будто мы вне-
запно пренебрежительно высказались об их
религии.
Почему они вдруг так возбуждаются? Потому
что им кажется, что фраза «сигнал х toWRITE
активирован» звучит сомнительно. Мы не на-
стаиваем на том, что наше понимание фразы
единственно верное. Мы всего лишь хотим по-
просить вас присоединиться к общепринятому
пониманию этой фразы, которое является всего
лишь соглашением. Мы хотим, чтобы вы пони-
мали ее так же, как и мы, и у нас не возникало
разногласий насчет ее значения.
Мы полагаем, что фраза «сигнал х toWRITE ак-
тивирован» означает, что сигнал, называющий-
ся х toWRITE , имеет низкий уровень. В данном
случае черта над названием сигнала означает,
что он имеет активный низкий уровень4.
Негодующие студенты иногда протестуют, что
сказать «сигнал х toWRITE активирован» то же
самое, что сказать, что WRITE имеет значение
ЛОЖЬ. А если WRITE имеет значение ЛОЖЬ,
тогда он имеет низкий уровень, а его дополне-
ние х toWRITE имеет высокий уровень.
Такой протест оправдан, но просто в рамках
налагаемого нами повсеместно используемого
соглашения многие сигналы (в действительно-
сти, подавляющее большинство сигналов) име-
ют активный низкий уровень, что обозначается
чертой над названием сигнала или добавлением
к нему звездочки. Такой сигнал обычно имеет
активный низкий уровень с самого начала, а не
является инверсией сигнала с таким же назва-
нием, но с высоким активным уровнем.
Мы действительно написали слово WRITE без
надчеркивания слева от разграничивающей
черты и кружочка на ней на рис. 15N.3. Но мы
не имели в виду, что такой сигнал в действи-
тельности существует. Скорее всего, он не су-
ществует, и на этом рисунке не указана точка,
в которой можно было бы проверить наличие
сигнала WRITE с активным высоким уровнем.
Такую проверку можно выполнить только для
сигнала WRITE с низким активным уровнем.
В случае сигнала DOIT* мы использовали мар-
кировку низкого активного уровня по той при-
чине, что метка находится слева от кружочка,
в среде, в которой можно выполнять провер-
ку сигналов. В противоположность, в крайней
левой части рисунка мы указали символы без
надчеркиваний (например, просто WRITE), по-
скольку фиктивная точка и внешняя среда,
в которой распространяется сигнал WRITE, раз-
делены кружочком.
Мы потратили много слов, чтобы изложить
вроде бы незначительный вопрос. Но в дей-
ствительности этот вопрос довольно значи-
тельный, поскольку от нашего общего понима-
ния его зависит наша способность обсуждать
работу логических схем с активными низкими
сигналами.
В завершение на рис. 15N.3 изображена логи-
ческая схема, описанная словами в начале этого
раздела.
Protected
Block
Willy
Nilly
Или используйте этот символ
Рис. 15N.3. Блок-схема на логических вентилях для реализации устройства, описанного в начале раздела
4 АоЕ § 10.1.2А.
598
75W. Триггеры
Реализовать такую логику не так просто, как
следовать правилу, что «кружочки встречают-
ся с кружочками». Для большинства сигналов
в схеме на рис. 15N.3 это правило выдержива-
ется, так что инверсии аннулируют друг друга.
Но такое правило не следует применять меха-
нически.
Это простое правило работает в тех случаях,
когда вентили используются для выявления
активации сигналов. Но, как отмечалось в раз-
деле 15N.1, оно не работает, если вентиль дол-
жен выявить снятие активации сигнала. Самый
левый двухвходовый вентиль И на рис. 15N.3
служит для определения такого снятия акти^
вации сигналов х toPROTECTED и х toBLOCK .
В этом случае кружочки не встречаются с кру-
жочками. Такое явно заметное несовпадение
позволяет сразу же заметить, что задачей дан-
ного вентиля И является выявление состояния
ЛОЖЬ или снятия активации сигнала.
Теорема де Моргана иногда позволяет
использовать два равнозначных символа
Согласно теореме де Моргана, любую логиче-
скую функцию можно представить двумя аль-
тернативными символами. Мы показали эти
альтернативные варианты в схеме на рис. 15N.3
для определения снятия активации сигнала или
его состояния ЛОЖЬ. Но обычно один из этих
эквивалентных по де Моргану символов ото-
бражает происходящее в схеме лучше, чем дру-
гой. Поэтому следует выбрать тот из них, кото-
рый, по вашему мнению, представляет проис-
ходящее в схеме наилучшим образом.
Но время от времени, как и в случае с сигналами
х toPROTECTED и х toBLOCK, оба альтернатив-
ных символа справляются с задачей представ-
ления необходимой логики одинаково хорошо.
Первый из них определяет, что оба сигнала
имеют значение ЛОЖЬ, т. е. деактивированы.
А альтернативный символ ниже определяет
активацию любого из сигналов и по этому со-
бытию снимает активацию со входа следующе-
го вентиля. Конечно же, логически эти резуль-
таты идентичны, поэтому допустим любой из
этих символов, который вам нравится боль-
ше. Символ ИЛИ лучше отображает изложе-
ние технического задания: «ни тот ни другой».
А символ И, определяя, что оба сигнала имеют
значение ЛОЖЬ, отображает логику, с которой
может быть легче работать в уме.
15N.2.2. Использование
логического компилятора Verilog
Verilog можно заставить подавлять
активные низкие уровни5
Это можно сделать, используя дополнительные
названия сигналов с чисто высокими активны-
ми уровнями, т. е. дополнения неудобных сиг-
налов с низкими активными уровнями. Пример
такого решения показан в листинге 15N.1 про-
граммы Verilog далее. В результате, создавая
логические выражения, которые реализуют
требуемую логику, мы можем не думать о том,
какие уровни являются активными. В этом за-
щищенном мире цифровой логики, который
мы создали для себя, не существует такого яв-
ления, как активные низкие сигналы. В этом
мире символ знака восклицания означает то,
что он должен означать: что сигнал деактиви-
рован или имеет значение ЛОЖЬ. Примерами
такого сигнала являются сигналы prot и block в
выражении для действия doit в следующем ли-
стинге 15N.1.
Листинг 15N.1. Первый пример программы на
языке Verilog
module act_lo_verilog(write_bar, valid, timed_bar, prot_bar,
block_bar, willy_bar, nilly, doit_bar);
input write_bar;
input valid;
input timed_bar;
input prot_bar;
input block_bar;
input willy_bar;
input nllly;
output doit_bar;
wire doit;
// все входные и выходные сигналы являются обычными
//сигналами (wire), а не сигналами, которые
// по умолчанию удерживают значение (reg);
//Сигнал doit, который никогда не выводится на выход,
// а используется в качестве входа в функцию, явно
// объявляется типом wire.
//Теперь инвертируем все сигналы с активным низким
//уровнем, чтобы при создании логических
// выражений можно было работать со ВСЕМИ
// сигналами как с активным высоким уровнем.
АоЕ § 11.3.4В.
15N.2. Снова о сигналах с низким активным уровнем
599
assign write = !write_bar; // Создает временный
// внутренний сигнал (write), который не подается
// ни на какой вывод.
assign timed = !timed_bar;
assign prot = !prot_bar;
assign block = !block_bar;
assign willy = !willy_bar;
assign doit_bar = Idoit; // Эта выходная логика
// инвертируются потому, что в нее будет подаваться
// сигнал с высоким активным уровнем doit,
// используемый для генерирования сигнала OUTPUT.
assign doit = write & valid & timed & (Iprot &! block) |
(willy | nilly); // (& означает И, |означает ИЛИ)
endmodule
Неудобные сигналы с низким активным уров-
нем с названиями типа willy_bar в наших ло-
гических выражениях не показываются. Наше
выражение выглядит просто и аккуратно.
Некоторые пользователи Verilog относятся
пренебрежительно к такому подспорью. Но мы
лично считаем удобным при создании логиче-
ских выражений не беспокоится о том, какие
уровни являются активными. В мире активных
высоких уровней при виде знака восклицания
(или ~) его можно принять за обозначение де-
активации сигнала.
Если сигналы не преобразовывать принуди-
тельно в тип с высоким активным уровнем, то
лучше всего присваивать соответствующим пе-
ременным такие названия, которые позволяют
определить, какой уровень является активным.
Логические выражения, полученные с исполь-
зованием такого подхода, не такие аккурат-
ные, поскольку содержат знаки восклицания
для обозначения активации сигналов с низким
активным уровнем. Пример такой программы
Verilog иллюстрирует листинг 15N.2.
Листинг 15N.2. Второй пример программы
на языке Verilog
module actjo_verilog(write_bar, valid, timed_bar,
prot_barf block_bar, willy_bar, nilly, doit_bar);
input write_bar;
input valid;
input timed_bar;
input prot_bar;
input block_bar;
input willy_bar;
input nilly;
output doit_bar;
wire write_barf valid, timed_bar, prot_bar,
block_bar, willy_bar,nilly, doit_bar;
// указываем все входные и выходные сигналы, а также
// промежуточный сигнал doit как обычные сигналы
// (wire), а не сигналы, которые удерживают значение (reg);
assign doit.bar = !( (!write_bar & valid & !timedj>ar) &
!(!prot_bar | !block_bar) |(!willy_bar | nilly) );
// В этот раз выполняем операцию ИЛИ-НЕ над
//активированными сигналами ргоЦэаг* и ЫосЫэаг*
endmodule
Судите сами, какой из этих двух подходов более
понятен.
Логический компилятор создает одинаковые
схемы по обеим этим программам, а также вы-
черчивает принципиальную логическую схему,
реализующую полученное выражение6. В про-
стых случаях полезно просмотреть эту схему,
поскольку графическое представление может
сделать явными некоторые ошибки, которые
можно проглядеть в исходном коде. Если же схе-
ма выглядит правильно, то это лишний раз под-
твердит правильность логического выражения.
На рис. 15N.4 изображена созданная компиля-
тором Verilog принципиальная схема логиче-
ской функции doit_bar: никаких сюрпризов, но
приятно убедиться, что все правильно.
В схеме, созданной Verilog, присутствует один
многовходовый логический элемент И, тогда
как в схеме, созданной вручную, используют-
ся два уровня вентилей. Поэтому созданная
6 Программа Verilog предоставляет в разделе Synthesize
две версии реализации схемы. Версия RTL (Register Trans-
fer Logic — логика межрегистровой пересылки. Очевидно,
имеется в виду не очень интересное обстоятельство, что
типичная схема содержит регистры (триггеры), соединен-
ные с другими регистрами) описывает общий дизайн и
обычно проще и понятнее. А версия Technology Schematic
показывает, как дизайн будет реализован на конкретных
аппаратных устройствах, выбранных для схемы. Ино-
гда версия схемы RTL оказывается бесполезной. Напри-
мер, версия Verilog компании Xilinx иногда использует
сумматор для создания счетчика по инструкции count <=
count+1. В противоположность, в версии Technology Sche-
matic Verilog проявляет «благоразумие» и создает более
простую схему с традиционным счетчиком. Чтобы не ри-
сковать, если версия RTL схемы окажется не тем, что вы
ожидали, обратитесь к версии Technology Schematic.
600
15N. Триггеры
•ctfevtfloe
Рис. 15N.4. Принципиальная схема, созданная компилятором Verilog (версия RTL)
Verilog схема лучше, поскольку обеспечива-
ет меньшую задержку, чем схема, созданная
вручную. Версия ISE11 и более поздние вер-
сии Verilog компании Xilinx позволяют раз-
работчику самому решать, какие сигналы по-
казывать в схеме. Это очень полезная возмож-
ность в разработках с большим количеством
сигналов.
15N3. Вентили как функции
«Делай это/делай то»
Поскольку таблица истинности полностью
описывает логическую функцию, вы можете
решить, что можно ограничиться понимани-
ем работы вентилей на этом уровне: просто
расписываем (или запоминаем) таблицы ис-
тинности для основных функций: И, ИЛИ и
Исключающее-ИЛИ. Но иногда полезно рас-
смотреть возможность управления одного из
входов двухвходового логического элемента
сигналом, подаваемым на другой вход. Если
вам не совсем понятно, что имеется в виду,
возможно, несколько примеров прояснят
вопрос.
Логический вентиль И как функция
Пропуск/Блокировка*
Рассматриваем вход А как вход управления.
Тогда вентиль И будет пропускать сигнал на
входе В при высоком уровне на входе А и бло-
кировать — при низком. На рис. 15N.5 показана
соответствующая таблица истинности (слева) и
схема использования вентиля (справа).
Мы увидим использование вентиля И таким
способом для реализации синхронного clear*
(обнуление) счетчика в главе 16N, а затем при
А
0
0
1
1
В
0
1
0
1
АВ
0
0
0
1
? Блокировка В
| Пропуск В А:
Пропуск/Блокировка
Сигнал А определяет, пропускает ли
вентиль сигнал В или блокирует его
Рис. 15N.5. Вентиль И в качестве функции Пропуск/Блоки-
ровка*
рассмотрении маскирования программным
способом в главе 22N.
Обратите внимание на то, что при выполнении
такой операции, которую мы описываем, как
блокировка, на выходе логического вентиля
присутствует сигнал низкого уровня, а не просто
какое-то «ничего», как на выходе буфера с тре-
мя состояниями. Поэтому такой заблокирован-
ный сигнал комбинируется с пропущенным сиг-
налом, его нужно подать на вход вентиля ИЛИ,
как в мультиплексоре 2:1. Соответствующая
схема изображена на рис. 15N.6.
х/у = Выборка
Рис. 15N.6. Выходы вентилей И, используемых для блоки-
ровки, нужно подать на входы вентиля ИЛИ, который игно-
рирует низкие уровни
Как мы знаем, вентиль ИЛИ игнорирует низкие
уровни. Конечно же, простое соединение вме-
сте выходов двух вентилей И ничего бы не дало,
поскольку в этом случае эти два вентиля «сра-
жались» бы друг с другом7.
Мы обратили внимание на этот аспект в разделе 14W.1.
15N.4. Функция Исключающее-ИЛИ в качестве функции Инверсия/Пропуск*
601
15N.3.1. Вентиль И в качестве
функции ЕСЛИ
Описать полезность функции И иногда мож-
но еще одним способом: рассматривайте ее
как механизм для пропускания или разреше-
ния сигнала, ЕСЛИ выполняется определенное
условие. Например, пропускать сигнал на входе
В, если активирован вход А.
В обычном (английском) языке слово «и»
(and) иногда означает «если». В любом случае
так было во времена Шекспира. Несомненно,
вы помните эти строки из трагедии «Ромео и
Джульетта»8:
And you be mine, I'll give you to my friend
And you be not, hang, beg, starve, die in the
streets
(И ты моя, отдам тебя я другу.
И не моя ты, тогда виси, подаянья проси,
голодная ходи, на улице умри.)
Конечно же, в современном языке вместо на-
чальных "и" в этом отрывке были бы "если".
15N .4. Функция
Исключающее-ИЛИ
в качестве функции
Инверсия/Пропуск*
Логический вентиль Исключающее-ИЛИ мо-
жет выполнять полезную работу в качестве
управляемого инвертора. Этот вентиль будет
инвертировать сигнал на входе В при высоком
уровне на входе А и пропускать его — при низ-
ком. На рис. 15N.7 показана соответствующая
^Пропуск В
Инверсия В
таблица истинности (слева) и логическая схема
(справа). Пример такого использования вен-
тиля Исключающее-ИЛИ приводится далее, в
конце раздела 15N.9.2.
15N.5. Функция ИЛИ
в качестве функции
Установка/Пропуск*
Вентиль ИЛИ будет устанавливать значение ло-
гической «1» (высокий уровень) на своем выхо-
де при высоком уровне на входе А и пропускать
сигнал на входе В при низком уровне на входе
А. На рис. 15N.7 показана соответствующая
таблица истинности (слева) и схема использо-
вания вентиля (справа). Такое применение ло-
гического вентиля ИЛИ рассматривается при
обсуждении темы маскирования программным
способом в главе 23N.
А
0
0
1
1
В
0
1
0
1
А+В
0
1
1
1
жропуск В
(Установка выхода
А:
Установка/Т
А
0
0
1
1
В
0
1
0
1
A0B
0
1
1
1
Инверсия/Пропуск
Сигнал А определяет, пропускает ли
вентиль сигнал В или инвертирует его
Рис. 15N.7. Вентиль Исключающее-ИЛИ, рассматриваемый
как управляемый инвертор
8 Шутка. Если вы помните эти строки (Ромео и Джульетта,
акт III, сцена 5), то, наверное, ошиблись классной комна-
той или читаете не ту книгу.
Сигнал А определяет, пропускает ли вентиль
сигнал В или устанавливает «1» на выходе
Рис. 15N.8. Вентиль ИЛИ, рассматриваемый как функция
Установка/Пропуск*
15N.6. Последовательные
схемы в общем и триггеры
в частности
Комбинационные схемы, которые мы рассматри-
вали в разделе 14N.3, «живут» текущим момен-
том, подобно резистивным схемам, которые мы
обсуждали в главе IN. Последовательностные
схемы проявляют противоположное поведе-
ние, которое можно сравнить с поведением
схем в главе 2N. В частности, текущее поведе-
ние jRC-цепей зависит от событий в прошлом,
в результате чего их характеристики более
сложные и более интересные, чем для чисто
резистивных схем (см. раздел 2S.2, рис. 2S.11).
Последовательностные цифровые схемы таким
образом контрастируют с комбинационными
схемами (рис. 15N.9).
602
J5W. Триггеры
а—
В—
Комбинационная логика
—«АД...
, and past)
ТТоследовательностная логика
Рис. 15N.9. Сравнение блок-схем комбинационной и после-
довательностей логики
Если бы в электронике существовала только
комбинационная логика, то цифровая часть
этой книги была бы практически завершена.
Вам можно было бы закрыть книгу и поздра-
вить себе с успешным овладением новой обла-
стью знаний.
Но все не так просто: интересную часть циф-
ровой электроники составляют последователь-
ностные схемы. Благодаря этим схемам мы мо-
жем собирать счетчики, устройства хранения
данных (память), процессоры и на вершине
всего этого компьютеры.
Принцип работы триггеров легко понять. Но
при более подробном взгляде на них возника-
ет более трудный вопрос: в чем состоит полез-
ность тактируемых схем? Чтобы ответить на
этот вопрос, мы начнем с примитивных схем
и будем совершенствовать их, чтобы получить
качественный тактируемый триггер. В процессе
работы мы будем стараться понять, что делает
это устройство предпочтительней более про-
стым устройствам.
15N.6.1. Простейший триггер-
защелка на двух транзисторах
Показанная в блок-схеме на рис. 15N.9 об-
ратная связь присутствует в схеме справа на
рис. 15N.10 в качестве связи между выходом
каждого транзисторного ключа и затвором,
управляющим другим ключом. Эта схема за-
пирает (защелкивает) сама себя в одном или
другом состоянии: один из транзисторов будет
включен, а другой — выключен9.
Рис. 15N.10. Простейший триггер из инверторов с пере-
крестной связью
На первый взгляд эта схема может показать-
ся полностью бесполезной: зафиксированная
в одном состоянии, и что еще хуже, непред-
сказуемая. Но в действительности состояние
схемы не зависшее, поскольку ее легко пере-
вести в другое требуемое состояние. Для этого
нужно выключить транзистор, который вклю-
чен в данный момент, закоротив его затвор на
«землю». Когда этот транзистор выключится,
включится другой транзистор, который перед
этим был выключен. Таким образом, кратко-
временное закорачивание затвора полевого
транзистора на «землю» может «перевернуть»
(англ. flip) схему из одного состояния в дру-
гое. А это же действие с другим транзистором
«перебросит» (англ. flop) ее в прежнее состоя-
ние. Откуда и английское название этого типа
схем —flip-flop™.
Англоязычное название устройства flip-
flop прелестно просто описывает поведение
схемы.
Примечание
Инженеры знают, как говорить по-простому. Более
претенциозная братия любит скрывать поведение
этой схемы, называя ее бистабильным мультиви-
братором.
Эта транзисторная защелка может сохранять
один бит информации. В микросхемном ис-
полнении повышающие резисторы реализу-
ются в виде транзисторов, как показано на
рис. 15N.11.
Два дополнительных транзистора позволяют
выполнять операцию записи и чтения состоя-
ния защелки. Запись осуществляется принуди-
тельной установкой транзисторов с перекрест-
АоЕ § 14.5.3; сравните рис. 14.20.
10 Русскоязычное название триггер, скорее всего, происхо-
дит из действия инициирования смены состояний, которое,
опять же на английском, будет triggering. — Примеч. пер.
75Л/.6. Последовательные схемы в общем и триггеры в частности
603
Два дополнительных транзистора позволят
выполнять запись и чтение состояния защелки
Одиночная линия: служит как для чтения,
так и для записи
Рис. 15N.11. Применение простейшего триггера для хранения одного бита в статической памяти (RAM)
ными обратными связями в требуемое со-
стояние, а чтение выполняется подключением
транзисторов к внешним цепям.
15N.6.2. Снова простейший
триггер-защелка, но на двух
логических элементах
На рис. 15N.12 изображена принципиальная
схема триггера-защелки с перекрестными об-
ратными связями, но на этот раз реализован-
ная на логических вентилях, а не на простых
транзисторах. Эту схему мы соберем далее на
лабораторном занятии11.
Кнопка
или ползунковый
переключатель
Рис. 15N.12. Элементы И-НЕ с перекрестными обратными
связями образуют простой RS-триггер-защелку
Кружочки на входах вентилей И-НЕ означают,
что эти вентили реагируют на низкие уровни.
Иными словами, триггер устанавливается (т. е.
на выходе Q. выдается высокий уровень) низ-
ким уровнем на входе Sn(S = Set - Установка).
11 АоЕ § ю.4.1.
12 Строго говоря, входы 5 и R должны бы обозначаться
х toS и R, поскольку они активируются низкими уровня-
ми. Но мы не осмелились обозначить эти выводы таким
образом, опасаясь, что студенты могут подумать, что это
А низкий уровень на входе R(R = Reset — Сброс)
выполнит сброс (или обнуление) триггера, т. е.
установит на выходе Q,низкий уровень.
Как и в случае с защелкой, собранной на тран-
зисторах, полезность данного триггера состоит
в его способности фиксировать установленное
состояние после снятия сигнала установки.
Теперь подумайте, при каких входных уровнях
устройство будет выполнять эту фиксацию?13
(Можно сказать, что эти входные уровни опре-
деляют состояние покоя схемы.)
Это устройство работает, как и предназнача-
лось, но его трудно использовать для проек-
тирования схем. Оно полезно для устранения
дребезга контактов переключателя, но в этой
простейшей форме практически бесполезно
для каких-либо других целей.
15N.6.3. Схемы устранения дребезга
контактов переключателя14
Существует несколько способов устранения
дребезга контактов переключателя. Один из
них — использование RS-триггера, но только
для двухпозиционных (перекидных) переклю-
чателей. Для более простых переключателей,
замыкающих или размыкающих два контакта,
он не подходит. На рис. 15N.13 слева показано
подключение RS-триггера для устранения дре-
безга контактов, а справа — осциллограммы
инверсии каких-то других сигналов. Но этот триггер обыч-
но называется ДЯ-триггер, а не 1?*5*-триггер, так что, мо-
жет быть, эта маркировка является приемлемой.
13 Для фиксации или запоминания последнего установлен-
ного состояния на обоих входах должны присутствовать
высокие уровни (двоичное 11), деактивируя как вход S, так
и вход R.
14 АоЕ § 10.4.1А.
604
15N. Триггеры
Небольшой дребезг есть
даже при размыкании
Сильный дребезг,
когда контакт замыкается
на вход Л*
Выходной сигнал без
дребезга
Рис. 15N.13. Дребезг контактов: первое замыкание устанавливает или сбрасывает триггер; дребезг на выход не проходит
входных сигналов S* и R* и выходного сигнала,
свободного от дребезга.
Эта схема демонстрирует способность RS-
триггера помнить последнее состояние, кото-
рое на нем было установлено. Когда уровень
на входе S* поднимается до +5 В и несколько
раз скачет вниз и вверх, это не вызывает со-
ответствующих скачков уровня на выходе Q.
Эти скачки входного уровня на входе S* просто
переключают триггер между режимом уста-
новки (SET) и хранения (REMEMBER). А когда
на вход R* подается низкий уровень, это при-
водит к появлению на выходе фнизкого уров-
ня. Последующие скачки входного уровня на
этом входе не вызывают никаких изменений
выходного сигнала, поскольку триггер про-
сто запоминает низкий уровень, который был
установлен первой подачей низкого уровня на
вход R*. Как и в случае со скачками входного
уровня на входе S*, триггер просто переключа-
ется между режимом установки (SET) и хране-
ния (REMEMBER).
(Изменение
уровня)
Рис. 15N.14. Пример схемы для демонстрации трудностей
анализа и разработки асинхронных схем
время ломать голову над тем, что происходит
в схеме. Они хотели, чтобы сигналы могли ме-
няться в любой последовательности в течение
некоторого времени. На рис. 15N.15 показан
пример подобных сигналов. При этом поведе-
ние схемы не так жестко определено и нет от-
рицательных последствий15.
Активация Состояние покоя Активация
Рис. 15N.15. Цель разработчиков — небольшое ослабление
требований схемы
15N.6A Простого RS-тригтера
обычно недостаточно
При других обстоятельствах данный триггер
может доставить разработчику много непри-
ятностей. Чтобы получить некоторое представ-
ление о таких неприятностях, рассмотрим ги-
потетическую схему на рис. 15N.14, собранную
на таких простых триггерах и содержащую не-
сколько перекрестных связей. Представьте, что
будет, если попытаться предсказать поведение
этой схемы для всех возможных комбинаций
входных сигналов и предыдущих состояний.
Будет очень непросто справиться с такой зада-
чей, если вообще возможно.
Поэтому разработчики хотели получить уст-
ройство, с которым им не нужно было бы все
Шагом в этом направлении будет тактируе-
мая RS-защелка или прозрачная защелка. Это
устройство представляет собой просто защелку
на вентилях И-НЕ и дополнительный входной
каскад, который может изолировать защелку от
сигналов на входах S и R, т. е. работает подобно
затвору фотокамеры.
На рис. 15N.16 слева изображен двухвходовый
вариант такого RS-триггера, который обычно
упрощается до формы D-триггера, показанной
15 Не напоминает ли вам форма этого сигнала дни неде-
ли среднего студента, с тем исключением, что коэффици-
ент заполнения для студента будет меньшим, возможно,
появится короткий импульс в воскресенье вечером? Если
напоминает, то неделя студента будет больше похожа на
тактирование запускаемого фронтом триггера, который
мы рассматриваем чуть далее, в разделе 15N.6.5.
75Л/.6. Последовательные схемы в общем и триггеры в частности
605
справа. Один вход делает работу с триггером
более удобной, поскольку это устраняет про-
блематичный случай для RS-триггера, когда
активированы оба входа.
Разрешение
Разрешение
Рис. 15N.16. Тактируемая RS-защелка (слева) и ее более удобная
форма в виде прозрачной D-защелки (справа)
Осциллограмма на рис. 15N.17 показывает, что
в результате мы получили почти то, что хотели,
но не совсем.
Входные сигналы
оказывают влияние
Разрешение
Состояние на входе t
не имеет значения !
Состояние на входе снова
не имеет значения
Рис. 15N.17. С прозрачной защелкой мы продолжаем дви-
гаться в правильном направлении: теперь мы можем неко-
торое время не беспокоиться о проблемных уровнях
Тем не менее это устройство все равно трудно
использовать при разработке схем. Например,
рассмотрим, какой тип сигнала тактирования
мы бы хотели иметь, чтобы избежать про-
блем с обратной связью. Нам нужен импульс
РАЗРЕШЕНИЕ определенной длительности: до-
статочной, чтобы обновить состояние всех
триггеров, но не слишком продолжительный,
чтобы у изменения на выходе было время
«проскочить» обратно на вход и потребовать
другое изменение состояния. Довольно жест-
кие требования.
Поскольку с простой защелкой на логических
вентилях И-НЕ так трудно работать, на прак-
тике почти всегда используются более сложные
триггеры, которые запускаются по фронту сиг-
нала тактирования.
15N.6.5. Запуск по фронту сигнала
тактирования
Запускаемые по фронту триггеры16 реагируют
на уровни на своих входах только в течение
короткого времени непосредственно до (а в не-
которых редких случаях после) перепада, или
фронта, сигнала тактирования. Это понятие
запуска по фронту сигнала иллюстрируется на
рис. 15N.18.
Входные сигналы принимаются во внимание
Время установки
Входные сигналы не учитываются
Рис. 15N.18. Запуск по фронту позволяет ослабить аппарат-
ные требования
Таким образом, устаревший тип триггера, на-
зываемый двухступенчатым или MS-тригге-
ром17, часто вел себя не по правилам18 и был
заменен триггером, запускаемым по фронту.
Единственное достоинство MS-триггера —
его простота, но мы не будем рассматривать
его здесь. (Если вас интересует эта схема,
см. § 10А.2 в книге АоЕ.)
Понятие запуска по фронту (перепаду) может
звучать просто, но для людей обычно требует-
ся порядочное время, чтобы осознать его. По-
видимому, это понятие плохо поддается интуи-
тивному пониманию: триггер реагирует на про-
исшедшее событие до тактирования, а не после.
Как это возможно?
Подсказка
Вы могли видеть нечто подобное этому явлению на
своем осциллографе, который может показывать
состояние сигнала, каким оно было короткое вре-
мя до события запуска. Можете ли вы объяснить,
как совершается это волшебство?19
Вход данных
+51^ ^Установка* и Сброс*
—&-—- (нормально деактивированы)
Вход
тактирования
(реагирует на
фронт сигнала
тактирования)
Рис. 15N.19. Микросхема 74НС74 запускаемого по фронту
D-триггера
16 АоЕ § 10.4.2А.
17 Англ. MS = master-slave — главный-подчиненный.
18 Некоторые MS-триггеры типа JK обладали недостатком,
называемым захватом единиц. В частности, эти устрой-
ства были чувствительны к событиям, происшедшим при
высоком уровне сигнала тактирования, а не реагировали
только на перепад этого сигнала.
19 Ответ можно найти в разделе 16N.1.1, особенно на
PHC.16N.7h16N.8.
606
75Л/. Триггеры
Сигнал тактирования
Задержка распространения
В течение времени установки уровень \
на входе Ь должен быть стабильным. \
Качественный триггер реагирует на Ч, Время установки
входной сигнал только здесь (иными /
словами, время удержания равно нулю/
Время удержания (часто равно нулю)
Рис. 15N.20. Временные характеристики D-триггера: время установки и задержка распространения. Время удержания
должно быть нулевым
D-триггер
На рисунке 15N.20 показаны временные ха-
рактеристики D-триггера. Этот триггер толь-
ко хранит информацию, но не преобразует ее.
Такая простая возможность на практике весьма
полезна20.
Замечание относительно сигнала
тактирования
Употребление слова «тактирование» (англ.
clock) в названии сигнала для обновления дан-
ных может ввести в заблуждение. Для вдум-
чивых читателей оно может предполагать не-
сколько понятий, которые в данном случае не-
применимы:
♦ данный термин намекает на нечто, что ведет
учет времени, измеряет его или накапливает21;
♦ может возникнуть мысль о чем-то таком, что
тикает регулярно: типа метронома или бие-
ния пульса.
Но ни одно из этих понятий неприменимо к
сигналу тактирования триггера. (Сигнал так-
тирования может быть, и довольно часто яв-
ляется, постоянным сигналом прямоугольной
формы, но не обязательно должен быть та-
ким22.) Сигнал тактирования применительно к
триггерам представляет собой всего лишь сиг-
нал запуска, который определяет, когда триггер
обновляет свою память.
20 АоЕ § 10.4.2С.
21 По крайней мере, это можно сказать об английском
clock. — Примеч. пер.
22 Например, этот сигнал может подаваться кнопкой,
как в схемах одношаговой логики лабораторного микро-
компьютера. В этой схеме кнопку нажимает пользователь.
Такой сигнал нажатия кнопки (без дребезга) подает перед-
ний фронт на D-триггер, на входе данных которого при-
сутствует постоянный высокий уровень. Такие схемы при-
меняются довольно часто.
Лучшим названием этого сигнала было бы
«сигнал обновления». Но употребление обще-
принятого термина сложилось исторически, и
нам от этого никуда не деться. Просто выра-
ботайте привычку не воспринимать название
буквально. Инженеры, которые назвали этот
сигнал таким образом, были не очень хороши-
ми поэтами.
Сравнение запуска по положительному
и отрицательному фронту сигнала
тактирования
На рис. 15N.21 слева изображен триггер, кото-
рый реагирует на положительный фронт (на-
растание) сигнала тактирования. Некоторые
триггеры срабатывают по отрицательному
фронту (спаду) сигнала тактирования. Но ни
один триггер не реагирует на оба фронта одно-
временно23. Как и в случае с логическими венти-
лями, по умолчанию предполагается нарастаю-
щий фронт. А при отрицательном фронте это
указывается кружочком инвертирования перед
входом сигнала тактирования (рис. 15N.21
справа).
Триггеры, активируемые по фронту
и по уровню
Некоторые триггеры реагируют не на фронт,
а на уровень сигнала тактирования. Иными
словами, устройство не блокирует последую-
щие изменения входного сигнала, происходя-
щие, пока на входе управления присутствует
активный уровень. Одно из таких устройств —
прозрачный триггер-защелка, изображенный
на рис. 15N.16.
23 Триггеры, использующие оба фронта, по всей видимо-
сти, есть только среди программируемых логических схем
типа Coolrunner II компании Xilinx.
15N.6. Последовательные схемы в общем и триггеры в частности
607
-Треугольник обозначает запуск
по фронту
\ Кружочек означает активный
^■^ отрицательный фронт (спад)
Активный положительный фронт
(нарастание по умолчанию)
Рис. 15N.21. Положительный и отрицательный фронт сигнала тактирования
Далее приводится несколько примеров уст-
ройств, реагирующих на уровень активирую-
щего сигнала.
Прозрачный триггер-защелка, наподобие за-
щелок на плате ЖК-дисплея, описываемого
на лабораторном занятии 16L. На рис. 15N.22
показан принцип работы буквенно-цифровых
дисплеев, которые мы иногда используем на
наших лабораторных занятиях.
Хранение/-
AD558
Прозрачность
Разрешение
У
Рис. 15N.22. Прозрачный триггер-защелка реагирует на
уровень сигнала тактирования: пока на входе Разрешение*
удерживается низкий уровень, выходной сигнал соответ-
ствует входному
Защелки, входящие в состав цифроаналогово-
го преобразователя AD558, с которым мы по-
знакомимся на лабораторном занятии 18L.1.1.
Принцип работы этих защелок показан на
рис. 15N.23. Прозрачное поведение устройства
позволяет ему игнорировать входной регистр
и выдавать «живое» отображение цифрового
входа, просто зафиксировав низкий уровень
сигнала на входе Разрешение*.
Разрешение*.
Подключите на «землю» для
непрерывного преобразования
Рис. 15N.23. Прозрачная защелка на входе ЦАП позволяет
использовать его в непрерывном режиме
♦ Вход сброса триггера. Сигналы Сброс* и
Установка*, которые подаются на выходную
защелку D-триггера и превалируют над схе-
мой запуска по фронту, предшествующей
выходной защелке. Принцип действия этих
сигналов показан на рис. 15N.24. Эти асин-
хронные сигналы вызывают немедленную
реакцию24.
Это схема «установка или сброс» общепринята
для триггеров, но в счетчиках она используется
не так часто. Но сигнал сброса никогда не рас-
сматривается, как собственно сигнал тактиро-
вания. Это также относится и к тем случаям,
когда сброс выполняется по сигналу тактиро-
вания. Такой сброс называется синхронным.
Активирование фронтом зарезервировано для
Сброс
Установка
D Q
>
Установка
То же самое относится и к сигналу установки, который,
кстати, превалирует над сигналом сброса при их
одновременном (что недопустимо) активировании
Сброс
Рис. 15N.24. Сигналы Сброс* и Установка* D-триггера на микросхеме 74хх74
АоЕ § 10.4.2А.
608
15N. Триггеры
сигналов тактирования, с чрезвычайно редки-
ми исключениями (наподобие линий запроса
прерывания микроконтроллера 8051)25.
Запуск по фронту обычно работает лучше, чем
запуск по уровню, т. е. облегчает разработку
схем. Поэтому запуск по фронту встречается
намного чаще.
15N.7. Применение
триггеров в схемах
устранения дребезга
контактов
15N.7.1.D-Tpi/irrep
и низкочастотный сигнал
тактирования
При наличии сигнала тактирования с большим
периодом D-триггер позволяет устранить дре-
безг контактов переключателя. Данный подход
состоит в том, чтобы не допустить повторной
подачи сигнала тактирования, пока дребезг не
прекратится. Таким образом, при достаточно
медленном сигнале тактирования выходной
сигнал не может попасть с выхода (^обратно на
вход.
В отличие от схемы устранения дребезга контак-
тов на RS-триггере, этот метод вносит задержку
между замыканием переключателя и появлени-
ем выходного сигнала. Иногда эта особенность
Сигнал с переключателя)
члюбого типа /
О Q
Сигнал тактирования
Период > времени дребезга
Рис. 15N.25. Еще одна схема устранения дребезга контак-
тов с использованием D-триггера и сигнала тактирования
с большим периодом
имеет значение, как, например, в измерителе
скорости реакции, рассматриваемом в раз-
деле 19L.1.2. Но в большинстве случаев это не
важно. Достоинство метода — его способность
работать с более простыми, недорогими пере-
ключателями — однополюсными однопозици-
онными. На рис. 15N.25 изображена подобная
схема устранения дребезга контактов.
На рис. 15N.26 и 15N.27 показаны осцилло-
граммы сигналов, подчеркивающие важность
условия, что период сигнала тактирования дол-
жен быть больше продолжительности времени
дребезга. Если частота сигнала тактирования
слишком высокая, то триггер пропускает дре-
безг на выход, что плохо (рис. 15N.26).
При более низкой частоте сигнала тактирова-
ния, как показано на рис. 15N.27, схема работа-
ет должным образом. Кроме неопределенного
времени задержки единственным недостатком
этого метода является необходимость генери-
рования низкочастотного сигнала тактирова-
ния. Если нужно устранить дребезг всего для
одного переключателя, то это не самый лучший
Устранение дребезга с помощью D-триггера
Слишком быстрое тактирование
пропускает дребезг {
BL
Сигнал тактирования
Сигнал с дребезжащего контакта
Q: выходной сигнал, у которого
устраняется дребезг
(дребезг не устранен)
Рис. 15N.26. В схеме устранения дребезга контактов на D-триггере необходимо использовать сигнал тактирования с большим
периодом. В данном случае сигнал тактирования имеет слишком высокую частоту
25 Эти входные линии INT* для запроса прерывания реаги-
руют не совсем на фронт сигнала, а на псевдофронт, т. е. на
переход, который определяется как разница между уров-
нями до и после цикла сигнала тактирования процессора.
Но это очень близко к реагированию на фронт.
способ. Но если дребезг нужно устранить на не-
скольких линиях, как в наших макетных платах
со встроенным источником питания, в которых
дребезг устраняется с двух переключателей,
15N.8. Счетчики
609
ГТЖ73___Г
*» чпяпг шгег
Сигнал
тактирования
Сигнал
с дребезжащего
контакта
Q: выходной
сигнал, у кото-
рого устраняется
дребезг
Рис. 15N.27. В схеме устранения дребезга контактов на
D-триггере необходимо использовать сигнал тактирования
с большим периодом. В данном случае период сигнала так-
тирования имеет достаточную длительность
р. СМожно, но не обязательно^
\^\использовать резистор
(КМОТТ-вентиль)
(Только однополюсный двухпозиционный
переключатель)
Рис 15N.28. Еще одна схема устранения дребезга
контактов с использованием КМОП-вентиля
положить, что форма бегущей волны выходных
сигналов этого счетчика лежит в основе его на-
звания27.
или в клавишной панели микрокомпьютера
с ее пятью линиями, с которой мы вскоре по-
знакомимся, тогда использование этого метода
будет иметь смысл.
15N.7.2, Схема устранения дребезга
с положительной обратной связью
Самой простой схемой устранения дребезга для
однополюсного двухпозиционного переключа-
теля будет просто неинвертирующий КМОП-
вентиль с обратной связью. Такая схема изо-
бражена на рис. 15N.28.
На первый взгляд эта схема может показаться
слишком простой, но она действительно ра-
ботает. Здесь основная идея состоит в том, что
вход вентиля никогда не находится в третьем
состоянии, поскольку на него всегда подается
сигнал с выхода схемы даже при переходе кон-
такта переключателя, когда он не касается ни
+5 В, ни «земли».
15N.8. Счетчики
15N.8.1 • Счетчики со сквозным
переносом
Достоинством счетчиков со сквозным пере-
носом является их простое устройство, а не-
достатком то, что их выходы Q. не могут все
изменяться одновременно26. На рис. 15N.29
показана осциллограмма выходных сигналов
счетчика со сквозным переносом. Можно пред-
Сигнол тактирования
2 ойiv'""м4 oohs
Осциллограмма сигналов счетчика со сквозным
переносом на триггерах микросхемы 74НС74
Рис. 15N.29. Двухразрядный счетчик со сквозным перено-
сом имеет задержку между выходными сигналами, что вы-
зывает ложные переходные состояния (усиление осцилло-
графа: 2 В/дел., 4 нс/дел.)
Поскольку состояние нескольких триггеров из-
меняется последовательно, а не одновременно,
не только установка стабильного состояния за-
нимает длительное время, но также возника-
ют переходные состояния, которых не должно
быть.
На рис. 15N.30 изображена схема двухразряд-
ного вычитающего счетчика. Вычитающий он
по той причине, что выход второго триггера
меняется только тогда, когда выход первого
имеет низкий уровень до появления активи-
рующего фронта сигнала тактирования. Этот
счетчик легко преобразовать в суммирующий
счетчик28.
26 АоЕ § 10.4.2D.
27 Англоязычное название счетчика ripple counter. A ripple
обычно переводится как волна, зыбь. — Примеч. пер.
28 Как это делается? Просто снимаем выходные сигналы
с выходов Q*. Можно снимать сигналы с выходов Q, но для
тактирования использовать сигналы с выходов Q*.
610
15N. Триггеры
1>о Qo
Qo
A
Qo
0, Q,
A
Q,
Сигнал тактирования Сигнал тактирования
Рис. 15N.30. Простые счетчики со сквозным переносом: делитель на 2 (слева) и делитель на 4 (справа)
Счетчики со сквозным переносом на микро-
схемах, наподобие 74НС393, используют от-
рицательный фронт сигнала тактирования.
Задержка в цепи сквозного переноса таких
счетчиков меньше, чем в счетчике на микро-
схеме D-триггеров 74НС74 (см. рис. 15N.29).
Задержка между триггерами микросхемы 393
составляет около 4 не (рис. 15N.31).
Задержка
(4 нс)
Осциллограмма сигналов счетчика со сквозным
переносом микросхемы 74НС393
Рис. 15N.31. Счетчик со сквозным переносом на микросхе-
ме имеет меньшую задержку распространения сигнала меж-
ду составляющими триггерами, но все равно демонстрирует
эффект бегущей волны (усиление осциллографа: 2 В/дел.,
4 нс/дел.)
15N.9. Синхронные счетчики
15N.9.1. Понятие синхронности
В синхронной схеме общий сигнал тактирова-
ния подается одновременно на все триггеры,
в результате чего они все меняют свое состоя-
ние одновременно29. Это тот тип устройства,
который обычно стремятся получить. ,
На принципиальных схемах синхронные счетчи-
ки обозначаются просто общей линией сигнала
тактирования для всех триггеров. Синхронные
счетчики подобно синхронным схемам в общем
предпочтительнее счетчиков со сквозным пере-
носом или асинхронных счетчиков. Счетчики
последнего типа существуют только по той при-
чине, что простота их внутреннего устройства
позволяет соединить последовательно большое
количество триггеров в одной микросхеме. В ка-
честве примеров таких счетчиков можно назвать
счетчик-делитель на 16 на микросхеме 4020, ко-
торый мы используем в нашей лаборатории, или
еще более впечатляющий счетчик-делитель на
16 М на микросхеме 4536.
На рис. 15N.32 изображена общая синхронная
схема. Хотя она не содержит никаких индика-
торов касательно ее функции, ее синхронность
вполне очевидна.
Вход
Вход
й Q
0 СЭ—lZ[_J— О Q
Сигнал тактирования
Рис. 15N.32. Общий сигнал тактирования для всех компо-
нентов является отличительным признаком синхронной
схемы
15N.9.2. Для синхронных счетчиков
требуются более «умные» триггеры30
Для счетчиков, работающих в синхронном ре-
жиме, требуются более «интеллектуальные»
триггеры, чем для асинхронных счетчиков
29 Без учета разницы между задержками распространения
в разных триггерах.
30 АоЕ § 10.4.3F.
15N.9. Синхронные счетчики
611
со сквозным переносом. Тогда как триггеры
счетчика со сквозным переносом меняют свое
состояние только по сигналу тактирования,
синхронные счетчики тактируются постоян-
но и должны изменять свое состояние только
иногда. Более конкретно: выходной сигнал Qj
второго триггера в схеме на рис. 15N.35 и на
временной диаграмме на рис. 15N.34 должен
меняться по каждому второму периоду сигна-
ла тактирования. Если бы в схеме присутство-
вал третий триггер, то его выходной сигнал
Qg должен был бы меняться по каждому чет-
вертому периоду сигнала тактирования, и т. д.
Чтобы триггеры, которые тактируются посто-
янным сигналом тактирования, могли вести
себя подобным образом, необходимо, чтобы
триггер (в данном случае будем рассматривать
второй триггер на схеме на рис. 15N.35) под
внешним управлением или удерживал свое те-
кущее состояние или переключался в другое.
Английское слово, обозначающее переключе-
ние, — toggle, откуда и название такого типа
триггеров — Т-триггер.
Преобразование D-триггера в Т-триггер
с помощью элемента Исключающее-ИЛИ
Оказывается, что преобразовать простой
D-триггер в более интеллектуальный Т-триггер
можно с помощью простого вентиля ИСКЛ-
ИЛИ. В разделе 15NA упоминалось, что функ-
цию ИСКЛ-ИЛИ можно рассматривать как
функцию, которая позволяет сигналу на одном
из ее входов определять, проходит ли сигнал
на ее втором входе без изменений или инвер-
тируется. Вот благодаря этому обстоятельству
вентиль ИСКЛ-ИЛИ и может преобразовать
D-триггер в Т-триггер, выходной сигнал кото-
рого изменяется по следующему периоду сиг-
нала тактирования только в том случае, если
на его входе Г присутствует сигнал высокого
уровня. Соответствующая схема изображена на
рис. 15N.33.
^j j )
Clock
й
л
Q
15N.9.3. Требуемое поведение
счетчика
На рис. 15N.34 показана временная диаграмма
для синхронного счетчика-делителя на четыре с
обозначенными местами, в которых мы хотим,
чтобы сигнал на выходе Q второго счетчика
менялся или оставался в текущем состоянии.
Чтобы получить это требуемое нам поведение,
нужно соединить D-триггеры и Т-триггеры
должным образом.
Сигнал
тактирования
Не меняется у Меняется
Частота
f/г
(«делитель на два»)
/74
(«делитель
на четыре»)
Рис. 15N.33. Преобразование D-триггера в Т-триггер с помо-
щью вентиля ИСКЛ-ИЛИ
Рис. 15N.34. Временная диаграмма желаемого поведения
синхронного счетчика-делителя на четыре
Поскольку сигнал на выходе (^ первого тригге-
ра меняется по каждому периоду сигнала такти-
рования, этому триггеру нет надобности быть
особенно «умным»: просто подключаем выход
Qo* обратно на вход Do, подобно тому, как это
делается в счетчике со сквозным переносом.
Но второй триггер должен быть несколько
«умнее».
В двух случаях, показанных на рис. 15N.34, сиг-
нал на выходе Q второго триггера после перио-
да сигнала тактирования остается в прежнем
состоянии (на рисунке эти случаи обозначены
«Не меняется»), а в двух других случаях состо-
яние этого сигнала меняется. Тогда нам нужно
организовать все так, чтобы, когда необходимо,
на следующем периоде сигнала тактирования
состояние выходного сигнала второго тригге-
ра изменилось, а на Т-вход этого триггера по-
давался бы сигнал высокого уровня. А когда
нужно, чтобы по следующему сигналу тактиро-
вания состояние его выходного сигнала не ме-
нялось, на этом входе должен присутствовать
сигнал низкого уровня.
Важная тонкость — время установки
При разработке синхронных схем важно, чтобы
перед подачей сигнала тактирования (в нашем
случае это положительный фронт) все входные
612
15N. Триггеры
сигналы были должным образом установле-
ны. Поэтому недостаточно просто посмотреть
на рис. 15N.34 и сказать: «О, я вижу». Сигнал
на выходе Q должен меняться, когда на выхо-
де Qq установлен сигнал низкого уровня. Эта
информация «на выходе Q низкий уровень»
приходит слишком поздно. Сигнал на входе Гх
должен быть установлен должным образом до
прихода следующего фронта сигнала тактиро-
вания. Более точно: сигнал на входе Тг должен
быть установлен с запасом по времени, чтобы
сигнал на входе Dx был в должном состоянии
к моменту установки и до времени появления
фронта сигнала тактирования.
Примечание
Для триггеров микросхемы 74НС74 максимальное
время установки fsetup составляет 16 не, а типичное
значение всего лишь несколько наносекунд.
Таким образом, сигнал на выходе Q будет ве-
сти себя требуемым образом, если мы дадим
ему «инструкцию» изменять свое состояние
по следующему фронту сигнала тактирования,
когда на выходе Qq присутствует сигнал высо-
кого уровня. Реализация этих требований по-
казана на рис. 15N.35.
л
л
Сигнал тактирования
Рис. 15N.35. Синхронный счетчик
15N.10. Сдвиговый регистр
на триггерах31
На рис. 15N.36 приведена самая простая схема
с использованием триггеров: просто цепочка
триггеров, соединенных последовательно.
Вход
Сигнал
тактиро-
вания^
Рис 15N.36. Схема сдвигового регистра
Сдвиговый регистр формирует упорядочен-
ную и предсказуемую задержку; он сдвигает
сигнал во времени и может преобразовывать
поток последовательных данных в параллель-
ную форму или наоборот. На рис. 15N.37 изо-
бражена блок-схема устройства для преобра-
зования последовательных данных в парал-
лельные.
Параллельный выход U
Последовательный вход
Сигнал тактирования
Рис. 15N.37. Сдвиговый регистр можно использовать
для преобразования последовательных данных в парал-
лельные
Эта схема полезна тем, что она позволяет ис-
пользовать малое число линий для передачи
большого числа битов информации.
Замечание
Для простого сдвигового регистра требуются как
минимум две линии: одна для данных, а другая —
для сигнала тактирования. Другие, более сложные
схемы, могут обходиться без линии для сигнала
тактирования32.
Преобразование параллельных данных в по-
следовательные — более сложная задача. Для
этого нужно, чтобы сначала сигнал на каждый
вход D (за исключением первого) подавался
посредством мультиплексной логики, чтобы
направлять параллельные данные в каждый
вход Д загружающий сдвиговый регистр. Затем
возвращаемся обратно к обычной компоновке
последовательно соединенных триггеров, что-
бы выполнить сдвиг последовательных данных
в выходную линию.
На лабораторном занятии мы будем исполь-
зовать сдвиговый регистр с другой целью: для
генерирования импульса наподобие однови-
братора. Для этой цели к сдвиговому регистру
добавляется логический элемент И-НЕ. (Далее
31 АоЕ § 10.5.3.
32 Мы вкратце упомянем такие последовательные прото-
колы далее в курсе. Это, в частности, традиционный по-
следовательный протокол RS232 (рассматривается в раз-
деле 24N.4.1) и более современный USB-протокол. Но
в последнем протоколе используются две линии передачи
данных, поскольку в нем применяется дифференциальная
передача сигнала, чтобы обеспечить хорошую помехо-
устойчивость при низких напряжениях.
/5Л/.77. Материал для чтения в АоЕ
613
на лабораторном занятии мы будем использо-
вать два таких элемента, поскольку нам потре-
буется сдвоенный одновибратор.) Попробуйте
нарисовать соответствующую временную диа-
грамму, а затем посмотрите, что будет, если
подключить логический вентиль И-НЕ, чтобы
наблюдать за выходами
15N.11. Материал
для чтения в АоЕ
♦ Глава 10. (Цифровая логика I):
• Раздел 10.4. Последовательностная логика;
• Раздел 10.5. Последовательные функции,
доступные на микросхемах. В частности:
* Раздел 10.5.1. Защелки и регистры;
* Раздел 10.5.4. Программируемые логи-
ческие устройства (ПЛУ);
• Раздел 10.8. Проблемы логических схем.
В частности:
* Раздел 10.8.2. Проблемы с переключе-
нием;
* Раздел 10.8.3. Слабые стороны ТТЛ и
КМОП.
Глава 11. (Цифровая логика II):
• Раздел 11.1. История программируемых
логических устройств;
* Раздел 11.2.1. Структура программируе-
мой матричной логики (ПМЛ);
* Раздел 11.2.3. Вкратце взгляните на
FPGA.
Особый совет
Не беспокойтесь о картах Карно. Это был полез-
ный метод до эры компьютерных логических ком-
пиляторов, которые отправили карты Карно на
пенсию. Фокусируйтесь на триггерах и счетчиках
в разделе 10А.
15L Лабораторное занятие: триггеры
15L.1. Самый простой
триггер: RS-защелка
На рис. 15L.1 показана самая фундаменталь-
ная из схем триггеров или памяти, собрать
которую можно как на логических элементах
И-НЕ, так и на элементах ИЛИ-НЕ. Мы собе-
рем ее, используя логические вентили И-НЕ.
Триггер называется SR по первым буквам ан-
глийских слов, описывающих ее действие — Set
(Установка) и Reset (Сброс)1. Вариант тригге-
ра на логических элементах И-НЕ называется
«триггер-защелка с перекрестными связями на
элементах И-НЕ»2. Соберите этот триггер, про-
тестируйте его в работе и запишите полученные
результаты. Обратите особое внимание на то,
какие комбинации входных уровней опреде-
ляют режим хранения3, и обязательно разбери-
тесь, почему это состояние так называется.
Оставьте эту схему собранной, поскольку она
нам вскоре понадобится.
15L2. D-тригтеры
Практичные триггеры
Оказывается, что только что рассмотренная
простая защелка очень редко используется для
разработки практических схем. На практике
легче работать с более сложной схемой — так-
тируемым D-триггером. Простейший из такти-
руемых триггеров, D-триггер просто сохраняет
на своем выходе Q. состояние, которое присут-
ствовало на его входе D непосредственно перед
подачей последнего фронта сигнала тактиро-
вания. На рис. 15L.2 слева изображена логиче-
ская схема D-триггера на микросхеме 74НС74,
Таблица состоянии
S
0
0
1
1
R Q
0
1
0
1
+5 Повышающий резистор от 1 до 10 кОм
Вывод 7 = «Земля»
" Вывод 14 = +Um/+U
Рис. 15L.1. Простейший триггер, собранный на логических элементах И-НЕ с перекрестной связью
От ползункового
переключателя
От переключателя [
без дребезга контактов ]
74НС74
1
14
|
I*
|Т
13
А
2
12 11
1 1
0 v
10
Л
74НС74
Л * *
9
8
|
Y
1
1 Г
у
4
т
I
7
2 3 4 5 6
+Э Микросхема с двумя D-триггерами 74ХХ754
Рис. 15L.2. D-триггер: логическая схема (слева) и цоколевка микросхемы (справа)
1 Употребляется также термин RS-триггер. - Примеч. ред.
2 Англ. cross-coupledNfAND latch.
3 Англ. memory state.
а справа — цоколевка этой микросхемы. Дан-
ный триггер реагирует на положительный
фронт (нарастание) сигнала тактирования.
J5L.2 D-триггеры
615
D-триггер является «рабочей лошадкой» в ав-
топарке триггеров. На каждый более сложный
JK-триггер приходится около ста D-триггеров.
Вы, возможно, слышали о JK-триггере, из-за
его устарелости мы не используем его на наших
лабораторных занятиях. Возможно, что вам
вообще не понадобится этот триггер.
15L2.1. Основные операции
сохранения уровня и сброса
Работа D-триггера ничем не блещет, и понача-
лу может быть трудно по достоинству оценить
это устройство. Но все равно протестируйте его
в работе. Соберите схему, изображенную на
рис. 15N.2.
Для начала подайте на вход D сигнал от ползун-
кового переключателя макетной платы, а затем
сигнал тактирования от кнопки с устраненным
дребезгом контактов. В качестве такой кнопки
можно использовать одну из кнопок с левой
стороны макетной платы. Обратите внимание
на то, что для этих кнопок требуются повышаю-
щие резисторы, поскольку они являются выхо-
дами схем с открытым коллектором.
Внимание!
Неожиданная опасность. Значение сопротивления
повышающего резистора на кнопке подачи сигна-
ла тактирования тоже имеет значение. Большое
значение, скажем, больше 10 кОм, может привести
к проблемам. Этот вопрос рассматривается чуть
далее в разделе Ищете приключений?
Деактивируйте входы установки (S) и сбро-
са (Д), которые иногда также называются
Предустановка (Preset) и Обнуление (Clear),
подав на них высокий уровень.
Обратите внимание на то, что микросхема
74ХХ74 содержит два D-триггера. Выводы не-
используемого триггера пока можно не под-
ключать к высокому или низкому уровню. Это
настоятельно рекомендуется делать при сборке
законченных схем, поскольку таким образом
предупреждается возможное промежуточное
логическое состояние, в котором значительно
возрастает энергопотребление, как рассматри-
валось ранее. Но при сборке схемы на макетной
плате это только займет лишнее время, которое
дороже, чем доли копейки лишнего израсходо-
ванного электричества.
♦ Убедитесь, что D-триггер игнорирует инфор-
мацию на своем входе до тех пор, пока не
придет сигнал тактирования.
♦ Попробуйте активировать вход сброса (R).
Это можно сделать, просто отключив про-
вод от шины питания; в данном случае о дре-
безге можно не беспокоиться. Можете пояс-
нить, почему?4 Что будет, если подать сигнал
тактирования, чтобы попытаться записать в
триггер высокий уровень на входе D при ак-
тивированном входе сброса (R)?
♦ Попробуйте сделать нечто, что никогда не
делается преднамеренно в практической
схеме — одновременно активировать входы
установки (S) и сброса (К). Что будет в этом
случае? (Исследуйте сигналы на обоих вы-
ходах.) Что определяет конечное состояние
триггера после деактивирования обоих этих
входов?5 Понятно ли вам, почему в схеме не
следует одновременно активировать входы
установки и сброса?
15L2.2. Переключение. Вариант I:
выходной сигнал постоянно
меняется (делитель на два)
На первый взгляд обратная связь6 в схеме на
рис. 15L.3 может показаться проблематичной.
Не будет ли она вызывать в схеме автоколеба-
ния? Но благодаря сигналу тактирования эта
схема легко поддается анализу. По сути, сигнал
тактирования разрывает путь обратной связи.
Соберите эту схему и протестируйте ее работу.
т
+5
Рис. 15L.3. Подобно скорпиону, D-триггер «жалит» свой соб-
ственный «хвост»
4 Сброс осуществляется первым низким уровнем. Дре-
безг — деактивирование и любое последующее активиро-
вание входа сброса — не вызывает никаких дальнейших
изменений сигнала на выходе Q.
5 Результат будет непредсказуем, поскольку он зависит
от того, который из входов (5* или Д*) деактивируется по-
следним.
6 Проблемы, создаваемые обратной связью в нетакти-
руемых последовательных схемах, рассматриваются в гла-
ве 15N.
616
15L Лабораторное занятие: триггеры
этого будет задействована одна из кнопок ма-
кетной платы РВ503 с устраненным дребезгом
контактов. Скорее всего это будет кнопка с нор-
мально замкнутыми контактами, чтобы полу-
чить сигнал при ее нажатии (рис. 15L.4).
Этот повышающий резистор должен быть впол-
не определенного номинала. На первый взгляд
может казаться, что номинал данного резисто-
ра не имеет значения при условии, что он не так
мал, чтобы перегружать транзистор. Но в дей-
ствительности значение повышающего резисто-
ра важно. Чтобы увидеть, как ведет себя триггер,
подключите его выход Qk одному из светодио-
дов макетной платы. Теперь попробуйте ис-
пользовать повышающий резистор номиналом
1 кОм. При этом все должно работать нормально
и триггер должен переключаться при каждом на-
жатии кнопки. Теперь попробуйте взять повы-
шающий резистор номиналом 1 МОм. При этом
все окажется уже не так хорошо: иногда выход-
ной сигнал будет переключаться, а иногда не бу-
дет реагировать на сигнал тактирования вообще.
Это объясняется тем, что слишком большое со-
противление повышающего резистора замед-
ляет нарастание фронта сигнала тактирования.
Большое сопротивление, через которое заря-
жается паразитная емкость, создает медленно
нарастающий фронт, который вызывает труд-
ности у запускаемого по фронту устройства.
Это точно такая же проблема, как и та, которая
вызывала странную нестабильность компара-
тора LM311 в разделе 8L.1.2 (помните, «Тадж-
Махал при лунном свете»?).
На рис. 16N.11 в разделе 16N.2.1 показана
осциллограмма с подробностями эффекта та-
«НР»
(нормально разомкнуты)
«НЗ»
(нормально замкнуты)
Схетх устранения дребезга
Рис. 15L.4. Кнопки макетной платы с противодребезговой защитой требуют использования повышающего резистора
♦ Сначала подавайте сигнал тактирования
вручную. (Но загляните в раздел Ищем при-
ключений? относительно значения повышаю-
щего резистора.)
♦ Затем подайте прямоугольный сигнал так-
тирования генератора сигналов. (Для этого
лучше подойдет внешний генератор сигна-
лов, поскольку он имеет более высокую мак-
симальную частоту, чем генератор, встроен-
ный в макетную плату.) Наблюдайте с по-
мощью осциллографа сигнал тактирования
и сигнал на выходе Q. Какая связь между
частотой сигнала тактирования и частотой
выходного сигнала? Теперь вы знаете, по-
чему эту скромную схему иногда называют
счетчиком-делителем на два.
♦ Установите максимальное значение частоты
генератора сигналов (т. е. частоты сигнала
тактирования) и замерьте задержку распро-
странения триггера. Для этого вам нужно
будет решить, какие входные и выходные
напряжения использовать при измерении
истекшего времени. Этот вопрос можно ре-
шить, задав себе вопрос, что именно «рас-
пространится». Если ответом на него будет
что распространяется изменение логическо-
го уровня, тогда каким должно быть подхо-
дящее напряжение, при котором следует из-
мерять задержку распространения?7
Ищем приключений?
Для любителей поэкспериментировать немно-
го отвлечемся от нашей главной темы.
Когда мы рекомендуем подавать сигнал так-
тирования вручную, предполагается, что для
Нормально низкий уровень
7 Поскольку распространяется изменение логического
уровня, то нам нужно измерить время, требуемое для из-
менения напряжение, которое обычно определяет логиче-
ский уровень. Для микросхем КМОП с питанием +5 В это
будет 2,5 В.
кого медленно нарастающего фронта. С по-
мощью осциллографа наблюдайте сигнал
тактирования и сигнал на выходе Q, запуская
развертку осциллографа сигналом с выхода Q,
75L3. Счетчики со сквозным переносом и синхронные счетчики
617
и постарайтесь разобраться, что не так, когда
значение повышающего резистора слишком
большое.
Затем возвратите обратно повышающий рези-
стор номиналом 1 кОм, чтобы должным обра-
зом тактировать схемы, с которыми мы будем
работать далее.
15L2.3. Переключение. Версия II:
состояние выхода меняется, когда
указано (Т-триггер)
В более полезной схеме переключения реше-
ние, должен ли триггер поменять свое выход-
ное состояние на следующем периоде сигнала
тактирования, принимается в зависимости от
входного сигнала. Триггер, функционирующий
таким образом, называется Т-триггером, от ан-
глийского toggle — переключать. Схема из пре-
дыдущего раздела, в которой состояние выход-
ного сигнала переключается всегда, не является
Т-триггером. Самое лучшее название для нее
будет, наверное, счетчик-делитель на два.
На рис. 15L.5 показано, как должна вести себя
такая схема триггера. Покажите, как собрать
такой Т-триггер, используя логический вентиль
ИСКЛ-ИЛИ и D-триггер. Обратите внимание
на то, что вентиль ИСКЛ-ИЛИ может работать
в качестве управляемого инвертора при подаче
на один из его входов сигнала управления, а на
другой — сигнала, подлежащего управлению.
Такая схема рассматривалась в главе 15N.
Вся схема представляет
собой Т-триггер
tiq (режим
^хранени
'—й (режим
переключения)
DQ
(логическое
устройство)
Сигнал тактирования :
Рис. 15L.5. Блок-схема поведения Т-триггера
Протестируйте свою схему Т-триггера, подавая
на нее тактовый сигнал от генератора сигналов
и управляя с помощью ручной кнопки, наблю-
дая на осциллографе сигнал тактирования и
сигнал на выходе Q.
После завершения работы с этой схемой не раз-
бирайте ее, поскольку мы будем использовать
ее далее.
15L.3. Счетчики со сквозным
переносом и синхронные
счетчики
15L3.1. Счетчик со сквозным
переносом
Если триггер подключить так, чтобы состояние
его выхода переключалось по каждому периоду
сигнала тактирования (проще всего это сделать
с D-триггером8), и соединить последователь-
но два таких триггера, чтобы сигнал на выхо-
де d первого подавал сигнал тактирования на
D-вход второго, то мы получим схему счетчика-
делителя на четыре. Состояние выходного сиг-
нала первого триггера будет меняться на каж-
дом периоде сигнала тактирования, а второго —
на каждом последующем периоде. Очевидно,
что эту схему можно масштабировать, чтобы
создать счетчик-делитель на любое требуемое
число. Но сегодня мы не пойдем дальше деле-
ния на четыре.
Подключите выход Q* второго D-триггера на
его вход, затем соедините эти два триггера по-
следовательно, и мы получим такой счетчик-
делитель на четыре со сквозным переносом.
Нарисуйте собранную вами схему.
♦ Наблюдайте выходные сигналы триггеров на
светодиодах, подавая на нее сигнал тактиро-
вания с частотой в несколько герц. Делит ли
схема частоту тактирования на четыре? Если
нет, тогда или ваша схема работает непра-
вильно, или вы неверно понимаете эту фразу.
Исправьте требуемое.
Поведение этого счетчика необычно в одном
отношении: он считает в обратном направле-
нии, т. е. вычитает. Но изменить направление
счета (или, возможно, всего лишь создать
видимость этого?) не составляет никакого
труда: нужно всего лишь снимать выходной
сигнал с выходов Q*, а не Q. (Счетчики со
сквозным переносом обычно тактируются
отрицательным фронтом; тогда сигналы на
выходах (^считают в прямом направлении.)
♦ Теперь подайте на счетчик сигнал тактиро-
вания с максимально возможной частотой
8 Для сборки счетчика со сквозным переносом не требу-
ется более сложный Т-триггер. А вот для сборки синхрон-
ного счетчика Т-триггер будет востребован.
618
15L Лабораторное занятие: триггеры
и наблюдайте на осциллографе как сигнал
тактирования, так и сначала сигнал на выхо-
де Qq, а затем на выходе Q. Запуск развертки
осциллографа осуществляйте сигналом с вы-
хода Q.
♦ Теперь наблюдайте оба выходных сигнала
вместе и попробуйте различить эффект бегу-
щей волны (англ. ripple), который дал этому
счетчику его название (англ. ripple counter),
а именно задержку между изменением со-
стояний выходов Qq и Qj.
Примечание
Если у вас аналоговый осциллограф, то нужно уста-
новить максимально возможную частоту разверт-
ки, в то же самое время подавая на схему сигнал
тактирования максимально допустимой частоты,
чтобы изображение на дисплее было достаточно
ярким.
15L3.2, Синхронный счетчик
На временной диаграмме на рис. 15L.6 показа-
но, как должен функционировать синхронный
счетчик-делитель на четыре.
Не меняется
Сигнал
тактирования
-Время установки
Рис. 15L.6. Временная диаграмма синхронного счетчика-
делителя на четыре
Как вы знаете, временная диаграмма для син-
хронного счетчика такая же, как и для асин-
хронного счетчика (со сквозным переносом), за
исключением одного важного обстоятельства:
в синхронном счетчике состояние всех выходов
Q. меняется одновременно (по крайней мере, в
пределах погрешности величиной в несколько
наносекунд). Чтобы получить такое небольшое
изменение в поведении счетчика, его необхо-
димо капитально переработать.
Для сборки синхронного счетчика нам потре-
буются Т-триггеры. Затем нужно будет най-
ти на временной диаграмме закономерность
условий, существующих до сигнала тактирова-
ния, определяющую, должно ли меняться (пе-
реключаться) состояние сигнала на выходе Qj.
Чтобы разрешить синхронную работу, нам не-
обходимо исследовать условия, существующие
до прихода фронта сигнала тактирования (т. е.
в течение времени установки). Просто предпо-
ложить, что можно разрешить переключение
сигнала на выходе Q, если на выходе Q^ уста-
навливается низкий уровень, недостаточно, по-
скольку таким образом мы снова получим не-
приятный эффект бегущей волны. .
Определив необходимую закономерность, по-
давайте на вход Го соответствующий сигнал и
протестируйте свою схему. Опять же, после за-
вершения работы с этим счетчиком не разби-
райте его.
Попробуйте с помощью осциллографа убедить-
ся, что эффекта бегущей волны больше нет; для
этого снова одновременно наблюдайте сигналы
на выходах Qq и Q. Синхронные счетчики при-
меняются повсеместно, в то время как счетчики
со сквозным переносом встречаются очень ред-
ко. Медленная установка состояния в счетчиках
со сквозным переносом и наличие в них ложных
переходных состояний делают этот тип счетчика
неприемлемым для многих приложений.
15LА Дребезг контактов
переключателей и три
схемы устранения дребезга
На рис. 15L7 приведена фотография экрана за-
поминающего осциллографа9 с осциллограммой
сигнала дребезга контактов кнопки между высо-
ким и низким уровнями. Напряжение на кнопку
подается с повышающего резистора номиналом
100 кОм, Обратите внимание на то/что это зна-
чение повышающего резистора слишком боль-
шое, чтобы обеспечить качественный быстро
нарастающий фронт сигнала тактирования.
9 Между прочим, этим запоминающим осциллографом
был обычный аналоговый осциллограф, входной сигнал на
который подавался от микрокомпьютера, наподобие того,
который вы соберете сами далее в этом курсе. Компьютер
делал выборки в течение процесса дребезга, сохранял их
в памяти, а затем непрерывно воспроизводил их, чтобы
получить стабильное изображение. У вас будет возмож-
ность при желании выполнить этот эксперимент самому,
когда будете работать на лабораторном занятии 24L.1.1
или 25L.2.3.
15L4. Дребезг контактов переключателей и три схемы устранения дребезга
619
2ms
Рис. 15L.7. Из-за дребезга контактов микропереключателя
уровень его выходного сигнала скачет вверх и вниз
Чтобы увидеть вредное воздействие дребезга
контактов, подавайте сигнал тактирования на
свою схему счетчика-делителя на четыре, ис-
пользуя обычный переключатель (т. е. без ан-
тидребезговой защиты), например такой, как
на рйс. 15L.8. Наблюдайте выходные сигналы
счетчика на двух светодиодах. Вызываемые
дребезгом контактов скачки выходного сигна-
ла переключателя трудно увидеть на аналого-
вом осциллографе (но легко на цифровом), но
эффект дребезга должен быть очевиден по по-
ведению выходных сигналов счетчика.
Кнопочный микропереключатель
Н.З. Н.Р. Общий контак?
«Нормально)
замкнут» /.
' «Нормально
разомкнут»
Рис. 15L.8. Установка для демонстрации дребезга контактов
переключателя
15L4.1. Наблюдение дребезга
контактов (факультативно
для энтузиастов работы
с осциллографом)
Дребезг контактов трудно наблюдать на ана-
логовом осциллографе, поскольку он не воз-
никает с регулярной периодичностью, а также
потому, что после нажатия кнопки дребезг не
происходит в точно повторяемых точках. А на
цифровом осциллографе исключительно лег-
ко сначала сохранить скачущий сигнал, а затем
воспроизводить его сколько угодно.
Но трудно не означает невозможно: дребезг
можно наблюдать, хотя и не очень хорошо, если
в нормальном режиме установить развертку с
периодом около ОД мс/см. Для этого вам потре-
буется запастись терпением, а также нужно бу-
дет аккуратно настроить уровень запуска. Кроме
того, у разных переключателей дребезг происхо-
дит по-разному, и у некоторых он очень слабый.
Поэтому для этого эксперимента рекомендуется
взять кнопочный микропереключатель.
15L4.2. Три способа устранения
дребезга контактов
Использование логического элемента
И-НЕ с перекрестными связями
Вернемся к нашей схеме первого и простейше-
го триггера10 (которую, будем надеяться, вы со-
хранили) — защелке на вентилях И-НЕ с пере-
крестными связями, которая также называется
SR-триггером (см. рис. 15L.1 в разделе 15L.1).
В качестве источника входного сигнала ис-
пользуйте кнопку-переключатель без антидре-
безговой защиты. Заземлите общий контакт
переключателя и обязательно подключите к
обоим входам триггера по повышающему ре-
зистору. В принципе, если вы используете схе-
му, собранную вами в разделе 15L1, то они уже
должны быть подключенными, но очередной
раз напомнить об этом будет не лишним. На
рис. 15L.9 показано, как должна выглядеть со-
бранная схема для этого эксперимента.
Можете ли вы объяснить, почему триггер-
защелка, который является устройством хра-
нения, может устранять последствия дребезга
контактов в выходном сигнале кнопки?11
(ваша схема счетчика)
Рис. 15L.9. Использование защелки из вентилей И-НЕ в каче-
стве схемы устранения дребезга контактов
10 АоЕ § 10.4.1А.
11 Эта возможность данного триггера объясняется тем,
что скачки уровней (эффект дребезга контактов или про-
сто дребезг) вызывают возврат входов триггера в режим
хранения, в котором они просто сохраняют то состояние,
в которое были установлены, когда на соответствующий
вход был подан первоначальный низкий уровень.
620
15L Лабораторное занятие: триггеры
Буфер из КМОП-устройств
с положительной обратной связью
На рис. 15L.10 показан намного более про-
стой способ устранения последствий дребезга
контактов двухпозиционного переключателя.
В данном случае просто используем неинвер-
тирующий КМОП-вентиль12 И с обратной
связью.
+5
JL /HC08 или НСТ08 /
® (дребезг незаметен) \
(D (сигнал, свободный от дребезга)
Рис. 15L.10. Использование КМОП-вентиля И в качестве
средства устранения дребезга
Эта схема довольно интересна тем, что по-
следствия дребезга в ней отсутствуют даже на
входе. Когда вы разберетесь, чем объясняется
эта особенность, вы также поймете, почему
эта схема удаляет дребезг из выходного сиг-
нала. В частности, попробуйте ответить на во-
прос: что происходит в течение времени, когда
переключатель, подающий входной сигнал на
вентиль И, не подключен ни к шине +5 В, ни
к «земле»?
Использование D-триггера; определение
длительности дребезга
При наличии соответствующего сигнала так-
тирования D-триггер может устранять дребезг.
На рис. 15L.11 изображена схема включения
D-триггера для выполнения этой функции.
Соберите эту схему и протестируйте ее работу.
Используйте один из четырех триггеров микро-
схемы 175, поскольку вскоре нам понадобятся
остальные для другой схемы.
Сигнал с переключателя .-1
с дребезгом
Для начала подайте на D-триггер прямоуголь-
ный сигнал тактирования высокой частоты
(скажем, 100 кГц или выше). Дребезг должен
привести к неправильной работе счетчика.
Теперь уменьшите частоту сигнала тактирова-
ния до 100 Гц. Отрицательное влияние дребезга
на счетчик должно прекратиться. Далее посте-
пенно повышайте частоту сигнала тактирова-
ния, пока дребезг снова не начнет влиять на ра-
боту счетчика. Измерьте период сигнала такти-
рования, при котором это произойдет. Конечно
же, наиболее точное значение можно получить,
наблюдая сигнал тактирования на осциллогра-
фе. Информация со шкалы установки частоты
генератора колебаний будет довольно прибли-
зительной. Величина полученного таким об-
разом периода сигнала тактирования поможет
оценить длительность дребезга контактов ва-
шего переключателя.
15L5. Сдвиговый регистр
Это очень важное устройство, но иногда слу-
чается, что некоторые студенты уже истратили
все время, отведенное на данное лабораторное
занятие. Не переживайте, если такое случилось
и с вами. Работу этой схемы легко понять, даже
если у вас не будет возможности собрать ее.
Основанный на сдвиговом регистре цифровой
одновибратор из раздела 15L.5.2 используется
в одной из следующих схем: измерителе емко-
сти. Эта схема изучается на лабораторном за-
нятии 16L, а также входит в число цифровых
устройств, рекомендуемых для сборки. Но
если у вас нет времени сейчас, эту схему мож-
но будет собрать позже, если вам понадобится
одновибратор. Некоторые студенты не собира-
ют схему измерителя емкости, вследствие чего
одновибратор им не нужен.
16 15 14 13 12 И10
~^ I I I I I I I i
(ваша схема счетчика)Г "3 удилтд
р «Земля»
Сигнал тактирования
Рис. 15L.11. Устранение дребезга с помощью D-триггера
YI ГТ III!
12 3 4 5 6 7 8
Микросхема 74ХХ175 с четырьмя D-триггерами
12 Эта схема надежно работает только с КМОП-устройст-
вами, но не с ТТЛ.
С учетом изложенного, соберите изображен-
ную на рис. 15L.12 схему одновибратора с
15L5. Сдвиговый регистр
621
Входной сигнал
Сигнал тактирования^,
1
74НС175
«Земля» = 8
[2 5lZ~
Рис. 15L.12. Сдвиговый регистр
цифровым тактированием, которая родствен-
на сдвиговому регистру. Сборку схемы выпол-
няйте на отдельной плате и не разбирайте ее,
поскольку это устройство может понадобиться
вам в дальнейшем.
В этой схеме мы применяем удобную структу-
ру, в состав которой входят четыре триггера
с общим сигналом тактирования. Такая кон-
фигурация называется регистром и в данном
случае применяется как сдвиговый регистр.
Эта схема задерживает входной сигнал и син-
хронизирует его с сигналом тактирования.
Оба эти действия могут быть полезными. Мы
используем эту схему в течение нескольких
минут в виде одновибратора — схемы, которая
генерирует один импульс в ответ (продолжая
использовать метафоры13) на входной сигнал
запуска.
Подайте на вход тактирования схемы логи-
ческий сигнал от внешнего генератора сигна-
лов, а входной сигнал подавайте от генерато-
ра колебаний, встроенного в макетную плату.
Частота сигнала тактирования должна быть
как минимум в десять раз выше частоты вход-
ного сигнала.
13 Как вы, возможно, уже поняли, инженеры обладают, по
крайней мере, некоторыми характеристиками поэтов в том
смысле, что могут создавать простые и яркие образы. На-
пример, если для педанта это «моностабильный мультиви-
братор», (англ. monostable multivibrator), то для инженеров
это «одновибратор» (англ. one-shot), а то, что у педантов
«бистабильный мультивибратор» (англ. bistable multivi-
brator), у них «триггер» (англ. flop-flop или просто flop). A
выходной каскад ТТЛ-вентиля с активным повышением
выходного напряжения (active pullup) они называют «то-
темным столбом» (двухтактный выходной каскад; англ. to-
tem pole), поскольку схема похожа на него. Импульс цвето-
вой сигнализации телевизионного сигнала у них сидит на
«заднем крыльце сигнала» (back porch - задняя площадка
импульса). Инженерная терминология содержит много
других красочных определений, подобных приведенным
примерам. Может ли терминология общественных наук
предложить какие-либо похожие перлы?
15L5.1. Один триггер:
синхронизатор
♦ С помощью осциллографа наблюдайте вход-
ной сигнал и сигнал на выходе Qq (выход Q
самого первого триггера). Развертку осцил-
лографа запускайте от входного сигнала.
♦ Что является причиной дрожания сигнала на
выходе Qo?
♦ Теперь запускайте развертку осциллографа
по сигналу тактирования. Какой сигнал не-
стабилен теперь?
♦ Какой сигнал будет более обоснованно на-
зывать дрожащим или нестабильным?
Предполагается, что для тактирования триг-
геров используется системный сигнал так-
тирования, т. е. сигнал, который выполняет
синхронизацию многих других устройств,
14
кроме этих четырех триггеров
15L5.2. Несколько триггеров:
задержка
♦ Теперь наблюдайте на осциллографе входной
сигнал и сигналы на выходах Q, Q, и Q^. (На
этот раз вы может сами решить, как органи-
зовать запуск развертки осциллографа.)
♦ Обратите внимание на изменение частоты
сигнала тактирования.
15L5.3. Двойной одновибратор
из нескольких триггеров и вентилей
Предыдущая логическая схема для изучения
состояний сдвигового регистра может выдавать
14 Поскольку мы рассматриваем сигнал тактирования как
начало отсчета при запуске развертки осциллографа по
сигналу тактирования, в синхронизации входных сигна-
лов наблюдается неопределенность. Поэтому будет логич-
но сказать, что входной сигнал «дрожит».
622
15L Лабораторное занятие: триггеры
импульсы фиксированной длительности в ответ
на входной импульс произвольной длительно-
сти. Но при условии, что этот импульс должен
длиться достаточно долго, чтобы он мог быть
обнаружен по фронту сигнала тактирования.
Иными словами, длительность импульса долж-
на быть больше, чем период сигнала тактиро-
вания. Этот одиночный импульс входного сиг-
нала называется импульсом запуска схемы.
На рис. 15L.13 показана пара выходных им-
пульсов, которые мы хотим, чтобы вы создали.
Заполнив на этом рисунке графики сигналов на
выходах с (^ по Qg сдвигового регистра, вы смо-
жете понять логику, требуемую для выработки
этих импульсов.
Сигнал
тактирования
г+5
Рис. 15L.13. Временная диаграмма для одновибратора с
цифровым тактированием
Между прочим, эта полностью цифровая схема,
выходной импульс которой задается посред-
ством сигнала тактирования, не является тем,
что обычно называют одновибратором, в наи-
более распространенной схеме которого дли-
тельность импульса задается с помощью RC-
цепочки. Такой вариант одновибратора иногда
более удобен, но не обладает большим досто-
инством согласованности с остальной частью
цифровой схемы.
Нарисуйте свою схему и проверьте следующие
моменты:
♦ Медленный режим работы. Сначала по-
давайте сигнал запуска с помощью ручного
переключателя, а для сигнала тактирова-
ния установите частоту в несколько герц.
Наблюдайте выходные сигналы одновибра-
тора на буферизированных светодиодах ма-
кетной платы. Сначала удерживайте сигнал
запуска на низком уровне в течение около се-
кунды, а затем переключите его на высокий
уровень. Реакцией на переход уровня сигна-
ла запуска с низкого уровня на высокий бу-
дет мигание при выключении сначала одного
светодиода, а затем другого.
♦ Режим полной скорости. Удостоверив-
шись, что схема работает должным образом,
подайте на нее прямоугольный сигнал за-
пуска от генератора сигналов, встроенного
в макетную плату, одновременно подавая
сигнал тактирования более высокой частоты
от внешнего генератора сигналов.
Как бы вы сформулировали сильные и слабые
стороны этого одновибратора по сравнению
с более традиционным одновибратором с RC-
цепочкой?15
15 Если вам интересно, то наше мнение по этому вопросу
такое. Большим достоинством одновибратора с цифровым
управлением является синхронность его выходного сигна-
ла с системным сигналом тактирования, в результате чего
его выходной импульс начинается и заканчивается в пред-
сказуемое время, вскоре после фронта сигнала тактирова-
ния, на безопасном расстоянии от времени установки. Не-
достатки - повышенная сложность схемы по сравнению
с традиционным RC-одновибратором, а также более дли-
тельное время задержки: выходной сигнал может задер-
живаться на полный период сигнала тактирования после
перехода сигнала запуска на высокий уровень. Цифровой
одновибратор также вовсе не будет реагировать на слиш-
ком короткий сигнал запуска.
15S. Дополнительный материал:
триггеры
15S.1 Программируемые
логические устройства
Услышав слово «программируемые», мож-
но подумать, что речь идет об устройствах
хранения (памяти), которые действительно
являются программируемыми логическими
устройствами. Но термин «программируемое
логическое устройство» (ПЛУ) зарезервиро-
ван для устройств со структурой иной, чем
устройства памяти, которые, говоря в общих
чертах, предназначены для замены дискрет-
ных логических вентилей, а не для хранения
данных и кода программы, как в обычной
памяти1. Программируемые устройства заме-
нили микросхемы вентилей, наподобие тех,
с представителями которых мы познакоми-
лись на лабораторном занятии 14L: четыре-
хэлементные микросхемы логических эле-
ментов И-НЕ, например микросхема 74НС00.
Устройства ПЛУ намного более универсаль-
ные, чем «шкафчик», забитый микросхемами
вентилей, а также имеют намного более высо-
кую степень интеграции, что делает реализа-
цию разработок дешевле, а их модификацию
намного легче. Привлекательность програм-
мируемых логических устройств неотразима.
1 Микросхемы памяти можно использовать в качестве
логических устройств: адреса могут играть роль входов,
а хранимые данные — выходов. Но такой подход встреча-
ется нечасто из-за излишней сложности устройств памяти.
Но один класс программируемых логических устройств
является исключением. Это программируемые пользова-
телем вентильные матрицы FPGA (Field Programmable Gate
Array), в которых действительно используются блоки па-
мяти небольшого размера, называющиеся таблицами пре-
образований (lookup tables), которые создают логические
функции. Устройства FPGA рассматриваются чуть более
подробно далее в этой главе.
15S.1.1. Разновидности
программируемых устройств2
Программируемые логические устройства в
виде микросхем программируемой матричной
логики (ПМЛ3) и типовой матричной логики
(ТМЛ) начали появляться в середине 1970-х гг.
После некоторого экспериментирования с фор-
мой внутренней логики, выкристаллизовалась
одна преобладающая схема, названная про-
граммируемой матричной логикой (ПМЛ). Это
набор вентилей И, выходы которых подаются
на входы вентиля ИЛИ (форма сумма произве-
дений). Соответствующая схема изображена на
рис. 15S.1.
Структура ТТМЛ
Рис. 15S.1. Ячейка ПМЛ
Простота этой структуры обеспечила высо-
кую скорость работы устройств на ее основе,
которая несколько выще, чем скорость рабо-
ты микросхем вентилей технологии SSI4, по-
скольку их внутренние емкости были мень-
шими, чем емкости печатных плат. Благодаря
уменьшенным емкостям не только логические
уровни могут меняться быстрее, но и вентили
могут обходиться без драйверных каскадов.
Результатом всех этих факторов и была более
высокая скорость работы.
2 АоЕ § 11.1,11.2.1.
3 Англ. PAL — Programmable Array Logic.
4 Англ. Small Scale Integration — малая степень интег-
рации.
624
15S. Дополнительный материал: триггеры
Появились разные типы устройств ПМЛ: неко-
торые с активным низким уровнем выходных
сигналов, другие — с высоким; некоторые со-
держали триггеры, другие — нет; еще некото-
рые содержали несколько вентилей И с множе-
ственными входами, а другие были с большим
количеством вентилей И с меньшим количе-
ством входов, выходы которых подавались на
входы вентиля ИЛИ. Такое разнообразие было,
с одной стороны, хорошо, но с другой — плохо,
поскольку пользователям нужно было иметь
в запасе большое количество компонентов.
Устройства ПМЛ раннего выпуска программи-
ровались подобно памяти ROM, путем пере-
жигания перемычек на требуемых сигналь-
ных линиях. Отсюда и происходит выражение
«прожигать» в значении программировать.
Более поздние версии ПМЛ можно было пере-
программировать.
Чтобы решить проблему чрезмерного разно-
образия типов устройств ПМЛ, одна компания
разработала более универсальную стандартную
схему, которую можно было конфигурировать
требуемым образом: с высокими или низкими
активными уровнями, с триггером или без него.
Этот тип устройств получил название GAL5; на
рис. 15S.2 изображена его блок-схема.
Выбор: комбинация/триггер
с тремя состояниями
Ти повоя макроячей ка
(использовать триггер или нет)
Рис. 15S.2. Ячейка ТМЛ
Первые микросхемы ПМЛ содержали несколь-
ко сотен вентилей. Такие устройства ПМЛ в
настоящее время называются программируе-
мыми логическими устройствами (ПЛУ). ПМЛ
следующих поколений могут содержать тысячи
вентилей. Эти устройства называются сложны-
ми ПЛУ6. Элементы, составляющие СПЛУ, на-
зываются макроячейками (macrocells).
15S.1.2. Устройства FPGA7
Тем временем были реализованы хитроумные
схемы на больших массивах транзисторов, ко-
торые в некоторой степени можно программи-
ровать, но не реконфигурировать. Подобные
схемы предназначались для выполнения одной
конкретной задачи и изготавливались в боль-
ших количествах, чтобы окупить высокую
стоимость их проектирования8. Поскольку
они предназначались для выполнения кон-
кретных задач, то соответственно назывались
специализированными интегральными микро-
схемами (ASIS9). Разница между стоимостью
ПЛУ (и даже СПЛУ) и устройств ASIC была
огромной. Стоимость проектирования послед-
них могла составлять 100 000 долл.; а первые
можно было разработать и запрограммировать
в течение нескольких часов с соответствую-
щими затратами в пару долларов. Стоимость
устройств ASIC за единицу могла быть меньшей
только при условии их изготовления в больших
количествах.
Затем, в конце 1980-х гг. появилась проме-
жуточная версия устройств ASIC, которые
можно было программировать. Но структу-
ра, лежащая в основе этих устройств, была
более гибкая, чем у ПМЛ: массив вентилей,
подобно устройствам ASIC, но с возможно-
стью программирования пользователем на
месте, а не на фабрике. Это были устройства
FPGA10. Самые сложные представители этих
микросхем содержат миллионы вентилей, для
работы с которыми могут быть предусмотре-
ны встроенные микропроцессоры с перифе-
рийными устройствами. Работать с FPGA не-
сколько труднее, чем с ПЛУ, величина задер-
жек в которых довольно предсказуема по при-
чине жесткости их структуры. Хронирование в
FPGA-устройствах зависит от компоновки их
элементов, и поскольку теперь задержки в вен-
тилях столь малы, роль играют даже задержки
в путях распространения сигналов. Поэтому
задача проектирования устройств FPGA имеет
множество тонкостей11.
5 Англ. General Array Logic — типовая матричная логика.
6 Используемое в нашем курсе ПЛУ содержит 1600 вен-
тилей. Через несколько лет сокращение СПЛУ будет, не-
сомненно, означать «Симпатичное (маленькое) ПЛУ».
Сложность этих устройств постоянно возрастает.
7 АоЕ § 11.2.3.
8 Так называемые неповторяющиеся (разовые) расходы
на проектирование и внедрение в производство.
9 Application Specific Integrated Circuits.
10 Англ. Field Programmable Gate Arrays — матрица логиче-
ских элементов с эксплуатационным программировани-
ем. — Примеч. пер.
11 Увлекательное и одновременно полезное введение в об-
ласть FPGA содержится в книге Clive Maxfield «The Design
Warrior's Guide to FPGAs: Devices, Tools and Flows» («Руковод-
15S.2. Приемы работы с триггерами
625
Но для менее сложных задач знать подробно-
сти устройств FPGA и СПЛУ нет надобности:
необходимое проектирование можно выпол-
нить, используя высокоуровневый язык опи-
сания аппаратных средств наподобие Verilog
или VHDL, а затем реализовать полученную
разработку или в СПЛУ, или в FPGA. Для
простых разработок обычно предпочтитель-
нее использовать менее сложное и дорогосто-
ящее устройство, которое к тому же обладает
более предсказуемыми временными характе-
ристиками. Таким устройством будет СПЛУ.
В этом курсе мы будем использовать СПЛУ,
поскольку наши разработки не того масшта-
ба, для которого требовалась бы микросхема
FPGA.
15S.1.3. Внутреннее устройство ПЛУ
На рис. 15S.2 изображена блок-схема вну-
треннего устройства макроячейки одного из
72 логических субблоков небольшого ПЛУ:
XL/CX9572 компании Xilinx12. Как уже упо-
миналось, это универсальное устройство
ТМЛ, поскольку его можно запрограммиро-
вать на активацию или дезактивацию встро-
енного триггера, а также выбрать несколько
других характеристик, например активный
уровень.
Также уже упоминалось, что это универсаль-
ное аппаратное устройство. Но для работы
с этой микросхемой необходимо быть зна-
комым с языком логического компилятора13.
В качестве такого языка мы выбрали язык
Verilog. В Приложении А дается введение
в язык Verilog, и мы надеемся, что вы буде-
те обращаться к нему в процессе вашего зна-
комства с программируемыми логическими
устройствами.
ство для воителя проектирования по FPGA. Устройства,
инструменты и потоки»), издательство Newnes, 2004 г.
12 Данный материал основан или адаптирован из ри-
сунков и текста справочного листка XC9500XL High-Per-
formance CPLD Family Data Sheet (Справочный листок на
семейство XC9500XL высокопроизводительных СПЛУ) ©
Xilinx, 2009 г. Приводится с разрешения компании Xilinx,
Inc.
13 В данном случае имеется в виду именно быть знакомым,
а не знать все тонкости или быть экспертом. В этом крат-
ком курсе у нас нет времени на большее, чем поверхност-
ное знакомство с выбранным языком логического компи-
лятора.
15S.2. Приемы работы
с триггерами
Далее приводятся краткие описания наиболее
важных конфигураций триггеров, которые мы
рассматривали в этом курсе. Иногда удобно
иметь под рукой такой перечень чрезвычайно
полезных схем. Каждая из этих схем сопрово-
ждается кодом Verilog для ее реализации.
Простейший RS-триггер с асинхронной
установкой и сбросом
На рис. 15S.3 изображена схема RS-триггера,
реализованная на основе стандартного D-триг-
гера. Обычно это легче, чем собирать такую
схему на вентилях. Но на всякий случай на
рисунке также показана реализация схемы на
вентилях.
+5
+5
I
Рис. 15S.3. Схема RS-триггера на вентилях (слева) и на осно-
ве D-триггера (справа)
Эту простую схему можно спроектировать на
языке Verilog одним из двух способов, которые
более-менее повторяют две схемы, изображен-
ные на рис. 15S.3:
♦ одна разработка реализует буквально логику
вентилей И-НЕ с перекрестными обратными
связями в виде комбинаторной схемы;
♦ в другой схеме используется прозрачная за-
щелка с асинхронным сбросом.
Реализация схемы на вентилях И-НЕ
с перекрестными связями
На рис. 15S.4 показано, как выглядит первая
разработка. Эта разработка буквально повто-
ряет исходную и самую простую разработку
RS-защелки. Но она заставляет Verilog «по-
нервничать», поскольку содержит петлю, или
внутреннее противоречие. Поэтому Verilog вы-
дает предупреждение о том, что «the following
626
15S. Дополнительный материал: триггеры
sjjatch:1
module s_r_latch(
input s,
input r,
output q,
output cjbar
assign q « ~s j ~qbar;
assign qbar « ~r j ~q;
or2b2
ог2Ь2
endmodule
$_rjatch
Рис. 15S.4. Реализация RS-защелки на логических вентилях И-НЕ с перекрестными обратными связями
signal(s) from a combinatorial loop: qbar, q» (сле-
дующие сигналы создают комбинаторную пет-
лю: qbar, q). Но, несмотря на это предупрежде-
ние, схема работает должным образом.
Реализация версии прозрачной защелки
Здесь можно сразу указать триггер вместо вен-
тилей. Программа Verilog использует прозрач-
ную защелку. Полученная схема, изображенная
на рис. 15S.5, не совсем такая, как справа на
рис. 15S.3.
module s_r_using_f1op(
input s,
input r,
output reg q = 0 // initialize, to start simulation
// in known state
)
a1ways©(s or r)
begin
if Os)
?<¥ 1;
se
if (Ir)
end Я<-°; k-..- - ~-
endnoduie s_r_usingjlop
Рис. 15S.5. Реализация RS-триггера в Verilog на основе прозрачной защелки
Вместо асинхронного входа Сброс*, как это
делали мы, программа Verilog использует про-
зрачную защелку, на которую подается входной
сигнал низкого уровня. Программа Verilog до-
статочно «умная», чтобы «увидеть», что это
полностью эквивалентно подаче сигнала низ-
кого уровня на вход Сброс* (Reset*). Если у вас
возникают какие-либо сомнения насчет этого,
посмотрите на внутреннее устройство прозрач-
ной защелки.
На рис. 15S.6 показано, как выглядит прозрач-
ная защелка с сигналом низкого уровня на вхо-
XSTJ3ND
1
1
i
* j „
IPMJLATCHJ
М* ;„„ 1 9
„О <„ „
<тц.^,
к. „„ „„ „. А
Я
Сигнал низкого уровня на входе £...
Разрешение
...создает сигнал низкого уровня здесь,
если активирован вход Разрешение. Сигнал
низкого уровня выполняет сброс RS-триггера.
(Это вход /2* (Сброс*) RS-триггера)
Рис. 15S.6. При низком уровне на входе D прозрачная за-
щелка активирует Сброс* (/?*), если активирован вход раз-
решения
де D. Сигнал низкого уровня на входе D акти-
вирует Сброс* (R*) выходной RS-защелки, как
и должно быть.
Версия на триггере лучше
Хотя обе схемы работают должным образом,
версия на триггере лучше, поскольку, несмо-
тря на свою крайнюю простоту, схема на вен-
тилях И-НЕ с перекрестными обратными свя-
зями задействует две макроячейки устройства
ПМЛ. Каждый вентиль И-НЕ использует всю
макроячейку. Это не причинит никакого вреда,
если есть лишние макроячейки, но потратить
две ячейки, когда можно обойтись одной, не-
разумно.
15S.2. Приемы работы с триггерами
627
Установка
module flagL.sync_set(
input slfe,
input sync_set,
input reset_bar,
output reg q
if (~reset_bar)
q<=0;
else
q <sx (q I syncjset);
endmoduld
Рис. 15S.7. Для триггера с запуском по фронту можно сбросить, даже если продолжает присутствовать сигнал, который уста-
новил высокий уровень на выходе О
Достоинства и недостатки
этой простой RS-защелки
Достоинство — простота. Хорошо подходит
для устранения дребезга контактов для одно-
полюсного двухпозиционного переключателя.
Недостаток — при активированном входе уста-
новки (S) попытка сброса не будет выполнена.
Поэтому обычно предпочтительнее триггер-
защелка с запуском по фронту. Схема такой за-
щелки изображена на рис. 15S.7.
Тактируемый фронтом флаг:
асинхронная установки
и сброс по фронту
Сигнал на выходе Q. этого триггера часто игра-
ет роль флага — сигнала, который продолжает
присутствовать до тех пор, пока не будет пред-
намеренно сброшен.
Достоинство — триггер можно сбросить, не-
смотря на присутствие сигнала, который уста-
новил высокий уровень на выходе Q.
Схема с закрепленным флагом:
синхронная установка,
асинхронный сброс
Если схема с асинхронным тактированием,
изображенная на рис. 15S.7, не отвечает требо-
ваниям, например, поскольку линия установки
может содержать помехи, то нужна схема с син-
хронно тактируемым флагом, наподобие пока-
занной на рис. 15S.8.
Достоинство — синхронное тактирование
обеспечивает защиту от помех на линии сброса
схемы на рис. 15S.7 (предполагая, что помехи
возникают после тактирования триггера на
рис. 15S.8, как обычно делается).
Достоинство — как и для асинхронно такти-
руемой схемы, показанной на рис. 15S.7, сброс
этой схемы можно выполнить, несмотря на
присутствие сигнала, который установил высо-
кий уровень на выходе Q.
Другая схема с закрепленным флагом:
синхронная установка,
синхронный сброс
Добавление еще одного вентиля в схему на
рис. 15S.8 делает эту схему полностью синхрон-
ной, поскольку теперь сброс также выполняется
по сигналу тактирования. Модифицированная
таким образом схема изображена на рис. 15S.9.
Установка 1 \—i
Сигнал
тактирования
R
Щос
module flagL.sync_set(
input elk,
input syncjset,
input reseLbar,
output reg q
);
always@(negedge reset_bar or posedge №)
if(HreseLbar)
q<=0;
else
q <m (q i sync_set);
endmoduld
Рис. 15S.8. Схема с закрепленным флагом: синхронная уста-
новка
Достоинство — полностью синхронный ре-
жим работы.
628
755. Дополнительный материал: триггеры
Установка
Сброс
Сигнал тактирования
module flag_sync_»et_reset(
input sync_set/
input syncjslear,
output reg q,
input elk
always* (posedge elk)
if (sync clear)
q <• 1'bO;
else
q <• (syncjset I q);
Универсальная синхронная схема
триггера
Переопределив логику, которая подает сигнал
на вход D-триггера, в виде мультиплексора 2:1,
получим схему, изображенную на рис. 15S.10.
Эта схема более универсальная, чем предыду-
щие, единственной целью которых была уста-
новка или сброс триггера. Эту же схему можно
использовать для различения, например, меж-
ду параллельной и последовательной загрузкой
сдвигового регистра.
Достоинство — полностью синхронный ре-
жим работы.
Рис. 15S.9. Другая схема с закрепленным флагом: синхрон-
ная установка, синхронный сброс
(мультиплексор 2:1)
Делай_А
Делай_Б
Сигнал тактирования
module f lop_do__a__do_b(
input; elk,
input do_a,
input do_b,
input aJbJMur,
output ceg q
always8(posedge elk)
it (aJijMK)
q <» do_a;
else ~
q <• do^to;
endnoodule
Рис. 15S.10. Обобщенная схема триггера: мультиплексор реализует синхронную схему «Делай.Одно, Делай_Другое»
16N. Счетчики
Содержание
16N.1. Краткое повторение пройденного материала 629
16N.1.1. Суммирование характеристик триггера 629
16N.1.2. Повторение: синхронные и асинхронные счетчики из триггеров 632
16N.2. Аномалии и опасности схем на триггерах 633
16N.2.1. Пологий фронт сигнала тактирования 633
16N.2.2. Временная диаграмма может помочь с проблемной схемой 634
16N.3. Более универсальный счетчик 636
16N.3.1. Для счетчика потребуются четыре Т-тригтера 636
16N.3.2. Указываем сигналам на нескольких входах Г, когда изменяться,
а также добавляем входной и выходной переносы 637
16N.3.3. Более точный, синхронный, выходной перенос 638
16N.4. Выводы относительно функций счетчиков 640
16N.5. Счетчик-делитель на N из лабораторного занятия 16L 641
16N.6. Счет как стратегия проектирования цифровых схем 642
Цель этой главы
Сегодня мы хотим разобраться, как определить количество цифровых событий (т. е. мы хотим,
чтобы наша схема вела счет) и сохранить эту информацию.
16N.1. Краткое повторение
пройденного материала
16N.1.1. Суммирование
характеристик триггера
Зачем вообще нужен сигнал тактирования1?
Потому что разрыв цепи обратной связи облег-
чает задачу разработки и анализа последова-
тельностных логических схем. Это обстоятель-
ство иллюстрируется графически примером на
рис. 16N.1.
Выходной сигнал схемы, собранной с исполь-
зованием прозрачного триггера-защелки, со-
держал автоколебания с частотой чуть выше
60МГц (рис. 16N.2).
Этот триггер-защелка неработоспособен
«О»
А этот запускаемый по фронту
триггер работает как положено
elk-
Разрешение
Прозрачный триггер-защелка
Запускаемый по фронту триггер
Рис. 16N.1. Прозрачная защелка может быть нестабильной. Тактируемое устройство (запускаемое по фронту) делает обрат-
ную связь безвредной, в результате чего нестабильность становится невозможной
1 АоЕ § 10.4.2С.
630
16N. Счетчики
СО
1 мс/дел 20 нс/дел.
Рис. 16N.2. Если сигнал с выхода Q* подается обратно на вход D прозрачной защелки, на ее выходе Q возникают автоколебания
Запускаемая по фронту схема, изображенная
справа на рис. 16N.1, вполне работоспособна,
как вы имели возможность убедиться на лабо-
раторном занятии 15L.
Достоинства синхронных запускаемых
по фронту схем
Подобно лезвию ножа фронт сигнала тактиро-
вания аккуратно «разделяет» причины изме-
нений, которые находятся слева от него, и ре-
зультаты этих изменений, которые находятся
справа от фронта. Эта идея графически иллю-
стрируется на рис. 16N.3.
Сигнал
^
Все спокойно /
Все снова спокойно
Новые изменения...
/
Теперь множество тактируемых устройств
реагируют на новые входные сигналы
Рис. 16N.3. Тактирование синхронных схем, запускаемых по
фронту
Все вышесказанное предполагает нулевое вре-
мя удержания, хотя этот параметр не является
универсальным. Разные производители одно-
го и того же устройства, например микро-
схемы 74НС74, подходят к вопросу времени
удержания по-разному. Некоторые действи-
тельно предоставляют устройства с нулевым
временем удержания (например, компании
STMicrosystems и Texas Instruments), тогда как
компоненты других компаний (например, ком-
пании National Semiconductor и NXP/Philips)
имеют ненулевое время удержания (3 не). На
рис. 16N.4 изображены временные диаграммы
с временем удержания для некоторых микро-
схем. Для логической матрицы (СПЛУ), кото-
рую мы используем в этом курсе, микросхемы
XC9572XL производства компании Xilinx, за-
явлено нулевое время удержания.
74НС74:
15
it i+
|>СТ/ИЯ*1| 'УДЕРЖАНИЯ
уш.—
Ъ
нс
Fairchild
NXP/Philips
Рис. 16N.4. Две микросхемы 74НС74, иллюстрирующие, как
разработчики микросхем могут уменьшать время удержа-
ния за счет увеличения времени установки, и наоборот
Но в нулевом времени удержания нет никакого
волшебства. Просто разработчики микросхем
корректируют относительные пути внутрен-
них задержек на линиях данных и тактиро-
вания, чтобы сдвинуть окно времени (назы-
ваемое апертурой в других обстоятельствах,
таких как аналогово-цифровые преобразова-
ния), в течение которого уровни данных важ-
но учитывать. При прочих равных условиях
смещение окна вправо для увеличения вре-
мени удержания сокращает время установки.
Но нулевое время удержания является жела-
тельной характеристикой, поскольку это по-
зволяет просто и беспроблемно тактировать
микросхему, тогда как при ненулевом времени
удержания требуется учитывать такой экзоти-
ческий параметр, как минимальное время рас-
пространения, которое обычно не указывается
в справочных листках.
Частный пример
Как упоминалось в разделе 16N.1.1 и было про-
демонстрировано на лабораторном занятии
15L, схема на рис. 16N.5 работает как следует,
но только до тех пор, пока частота сигнала так-
тирования не окажется слишком высокой. В та-
ком случае начинают возникать проблемы, как
иллюстрируется на рис. 16N.6
При слишком быстром тактировании эта схе-
ма не успевает за ним, поскольку сигнал на
входе D меняется в течение времени установ-
ки. В результате состояние выходного сигнала
76Л/.7. Краткое повторение пройденного материала
631
Сигнал
тактирования
Рис. 16N.5. Обратная связь в D-триггере безвредна
Сигнал
тактирования
1 РАСПРОСТРАНЕНИЯ
Рис. 16N.6. При слишком высокой частоте тактирования
даже чудесная синхронная схема ломается, поскольку нару-
шается время установки
оказывается непредсказуемым. Схема может да-
же «зависнуть», отказываясь принимать реше-
ния в течение необычно длительного времени.
Примечание
Зависшие таким образом устройства называются
метастабильными; см. осциллограммы в § W.4.2C
книги АоЕ.
Время установки
Термин «время установки» на первый взгляд
кажется не слишком важным, но нужно хоро-
шо понимать этот параметр, чтобы успешно ре-
шать проблемы тактирования.
Время установки для D-триггера микро-
схемы 74НС74
Время установки — это время, необходи-
мое для того, чтобы изменение уровня на
входе D дошло до требуемого места внутри
триггера — точки, помеченной звездочкой на
рис. 16N.7. Между прочим, пока вы изучаете
внутреннее устройство триггера микросхемы
74, по этой схеме вы можете разобраться, как
работает запуск по фронту.
♦ Запуск по фронту (положительному или на-
растающему в данном случае и в большинстве
триггеров) означает, что информация входит
в триггер во время нарастания сигнала так-
тирования. На рисунке видно, что только в
процессе нарастания сигнала тактирования
до положительного логического уровня со-
стояние сигнала на выходе RS-защелки мож-
но изменить — установить (Set) или сбросить
(Reset), в зависимости от того, на какой из ее
входов, С2 или С2, подается сигнал низкого
уровня.
♦ Запуск по фронту также означает, что инфор-
мация не проходит в триггер после заверше-
ния нарастания сигнала тактирования. Это
запирание происходит потому, что сигна-
лы с выходов Сх и С2 поступают обратно на
входы, в результате чего на том или другом
входе RS-защелки будет присутствовать сиг-
нал низкого уровня. Этот пришедший на-
зад сигнал сохраняет сигнал низкого уровня
(предотвращая установку сигнала низкого
уровня на другом входе С), независимо от
последующих изменений уровня сигнала на
входе D.
Чтобы установить (т. е. подготовить) триггер
для действия должным образом по сигналу так-
тирования, новая информация должна пройти
через «конвейер» длиной в два вентиля. Можно
догадаться, что этот процесс может занимать
вплоть до двух задержек прохождения сигна-
ла через вентиль, около 20-25 не, и это время
Процесс блокировки изменений, происходящих
на входе й после нарастания сигнала тактирования
(это и есть запуск по фронту):
74хх74
Триггер установлен, когда ,
изменение уровня на входе й \
дойдет до точки * в схеме *
1) Если на входе О присутствует сигнал высокого
уровня, по нарастанию сигнала тактирования
уровень сигнала на выходе Сх меняется на низкий,
сохраняется на этом уровне и поддерживает высокий
уровень на выходе С2, независимо от последующих
изменений уровня сигнала на входе й
2) Если на входе й присутствует сигнал низкого уровня,
то по нарастанию сигнала тактирования уровень сигнала
на выходе С2 меняется на низкий, закрывая «наружную дверь»
■+- *- - - от последующих изменений уровня сигнала на входе Ь
Рис. 16N.7. Конвейер данных D-триггера поясняет время установки триггера. (Показан D-триггер микросхемы 74хх74)
2 АоЕ, § 10.4.2А.
632
16N. Счетчики
приблизительно равно значению, указанному
как время установки триггера.
Замечание
В действительности время задержки внутренних
вентилей микросхемы меньше, чем время задерж-
ки обычных дискретных вентилей, но порядок ве-
личины задержки приблизительно такой же.
Близкий аналог времени установки
триггера: «конвейер» сигнала
аналогового осциллографа
Возможно, вы заметили странный (и удиви-
тельный) факт, что ваш старый аналоговый
осциллограф может отображать информацию,
вводимую в него до события запуска развертки.
Каким образом он умудряется путешествовать
назад во времени? Аналогично тому, как соз-
дается время установки триггера: подлежащий
отображению сигнал проходит через «конвей-
ер», который задерживает его появление на
экране осциллографа, тогда как сигнал запуска
действует быстро. Просто ради интереса мы
вскрыли старый аналоговый осциллограф, что-
бы посмотреть на его «конвейер» сигнала. Как
можно понять из рис. 16N.8, метод настолько
прост, что в него почти невозможно поверить.
Секрет способности осциллографа заглядывать
назад во времени: «конвейер» сигнала в виде v-
коаксиального кабеля, который задерживает
входной сигнал, относительно сигнала запуска,
который не задерживается
Осциллограф Tektronix 2213
Мы ожидали, что длина кабеля будет око-
ло 30 метров, чтобы объяснить способность
осциллографа отображать данные, поступив-
шие за 100 не до события запуска. В действи-
тельности же благодаря хитроумной конструк-
ции, замедляющей скорость сигнала, кабель
намного короче — около 2,5 метров3.
16N.12. Повторение: синхронные
и асинхронные счетчики из
триггеров
Оба типа счетчиков изображены на рис. 16N9.
Счетчик со сквозным переносом (асинхрон-
ный) легче разрабатывать и собирать, но во
всех других отношениях синхронный счетчик
предпочтительнее.
На рис. 16N.10 приведена осциллограмма сиг-
налов на двух выходах асинхронного и син-
хронного счетчиков в действии.
На левой осциллограмме показаны сигналы на
двух выходах Онижнего разряда асинхронного
счетчика (мы уже видели подобную осцилло-
грамму на рис. 15N.30), а на правой осцилло-
грамме — сигналы двух выходов (^синхронного
счетчика. Вы сами можете легко понять, какой
Событие запуска
Верти кальнаяр- —
развертка
Горизонтальная
развертка
Входной
Быстрый
отклик
сигнал
Осциллограф
Рис. 16N.8. Линия задержки сигнала в осциллографе: простой и эффективный способ (старый осциллограф Tektronix 2213)
Сигнал —J
тактирования
Сигнал
тактирования
Синхронный счетчик
Рис. 16N.9. Счетчик со сквозным переносом (слева) и синхронный счетчик (справа)
Счетчик со сквозным переносом
(асинхронный) (делитель на 4)
АоЕ § Н .4.3, рис. Н.19.
16N.2. Аномалии и опасности схем на триггерах
633
V4
•Сигнал
тактирования
^ А:10,2 HC3
Счетчик со сквозным переносом,
^Усигнал тактирования и сигналы
на выходах Qn и
Сигнал
<?,\
Счетчик со сквозным переносом, сигнал тактирования
и сигналы на выходах Qo и Qt
Синхронный счетчик, сигнал тактирования
и сигналы на выходах Qo и Qt
Рис. 16N.10. Сигналы асинхронного счетчика (микросхема 74НС93) в сравнении с синхронным (микросхема 74НС163).
Скорость развертки = 10 нс/дел.
сигнал служит в качестве сигнала тактирования
для каждого триггера, как и легко сделать вы-
вод, почему предпочтение отдается синхрон-
ным счетчикам4.
медленные счетчики. Например, использу-
емые для управления дисплеем, поскольку
для человеческого глаза ложные состоя-
ния незаметны.
ДостЬинства синхронных счетчиков
♦ После сигнала тактирования эти счетчики
быстрее достигают стабильного состояния
(длительность ожидания составляет всего
лишь одну задержку триггера).
♦ Нет ложных промежуточных состояний5.
Достоинства счетчиков со сквозным
переносом (асинхронных)
♦ Простота. Вследствие этого счетчик может
содержать больше каскадов, чем синхрон-
ный. (Но обратите внимание на то, что эта
разница исчезает в случае счетчика, реали-
зованного на ПЛУ, поскольку эти устройства
обладают большим запасом вентилей.)
♦ В некоторых применениях недостатки асин-
хронных счетчиков не важны. Например:
• в делителях частоты. Здесь относитель-
ное тактирование входных и выходных
сигналов не важно и нет необходимости
снимать сигналы с нескольких параллель-
ных выходов Q. Все, что нас интересует,
так это отношение частот, т. е. частота вы-
ходного сигнала по сравнению с частотой
входного;
4 АоЕ § 10.4.3R
5 Даже синхронные счетчики могут давать ложные про-
межуточные состояния при значительном рассогласова-
нии задержек распространения триггеров счетчика. Этот
эффект может вызываться неравномерной емкостной на-
грузкой. См. § 10.4.3F книги АоЕ.
16INL2. Аномалии и опас-
ности схем на триггерах
16N.2.1. Пологий фронт сигнала
тактирования
То обстоятельство, что вход сигнала тактиро-
вания запускаемой по фронту схемы реагирует
на каждый фронт (или положительный, или от-
рицательный, но не оба сразу в случае одного
устройства), делает этот вход уязвимым к дре-
безгу контактов. (Если сигнал не используется
в качестве тактового, то он редко подвергает-
ся очистке от дребезга.) Но реагирующие на
фронт входы также уязвимы к более неочевид-
ной опасности: недостаточно крутому (иными
словами, слишком затянутому) фронту сигнала
тактирования.
На рис. 16N.11 изображены осциллограммы
выходного сигнала счетчика-делителя на два
на фронт сигнала тактирования, поступивше-
го с переключателя, значение повышающего
резистора которого было слишком большим
(100 кОм). Из-за.такого большого сопротивле-
ния повышающего резистора, объединенного
с паразитной емкостью, фронт тактирования
получился слишком пологим.
Эта проблема очень похожа на ту, которую мы
наблюдали в схеме компаратора на лаборатор-
ном занятии 8L, когда на схему без гистерезиса
634
76Л/. Счетчики
Сигнал
тактирования
Фронт сигнала
тактирования
2-oov ш 2-oov *2.oom*h2/ '-:«v
Подозрительно: это не похоже на При более быстрой развертке ... и одновременное дрожание
выходной сигнал счетчика-делителя можно заметить дрожание в сигнале напряжения питания
на 2 тактирования...
Рис 16N.11. Пологий фронт сигнала тактирования может создавать проблемы для входа, реагирующего на фронт
подавался сигнал с очень малой крутизной.
Как упоминалось в главе 14N, некоторые ло-
гические устройства содержат гистерезис. Все
входы устройств ПМЛ, которые мы будем рас-
сматривать в этой главе, имеют гистерезис ве-
личиной 5 мВ. Но мы обнаружили, что этого
гистерезиса недостаточно для предотвращения
«нерешительности» схемы, подобной пока-
занной на рис. 16N.11, когда мы использовали
пологий фронт сигнала тактирования со счет-
чиком, собранным на такой микросхеме ПМЛ
(XC9572XL).
если применить академический подход) го-
ворит нам, что уровень выходного сигнала
всегда должен быть высоким: задача мульти-
плексора состоит в том, чтобы выбрать вход
А или вход В, на которых присутствует сигнал
высокого уровня. Поскольку, подключив вы-
ход к шине +[/, мы бы получили на нем такой
же сигнал, схему на рис. 16N.12 следует рас-
сматривать только как иллюстрацию специ-
фичной комбинации входных сигналов, кото-
рые могут присутствовать на входе в опреде-
ленное время.
16N.2.2. Временная диаграмма
может помочь с проблемной
схемой6
На рис. 16N.12 изображена простая, но полез-
ная комбинационная схема, мультиплексор 2:1,
спроектированная на обычных логических вен-
тилях и реализованная на микросхеме ПМЛ7.
Чтобы проиллюстрировать потенциальную
проблему, мы собрали схему для простейшей
операции. Здравый смысл (или булев анализ,
По временной диаграмме, включающей за-
держки на вентилях, которая показана на
рис. 16N.13, можно предсказать, что схема бу-
дет вести себя не так хорошо.
Искажение в выходном сигнале может остаться
незамеченным при исследовании этого сигна-
ла и сигнала выборки (S — Select) с помощью
осциллографа, если только преднамеренно не
искать его. Левая осциллограмма на рис. 16N.14
была сделана с медленной разверткой, в резуль-
тате чего кратковременный низкоуровневый
импульс очень трудно увидеть.
Для этого упражнения
предположим, что как на А, так и
на В присутствуют высокие уровни^
(А/В)
Выборка
Выход
Булев анализ:
Выход =BxS+A*5
если А = В = 1, выход = 5 + S = 1
Рис. 16N.12. В проблемном случае с мультиплексором 2:1 предполагается, что на обоих входах присутствуют высокие уровни
6 АоЕ § 10.4.4В.
7 См. раздел 14W.1.
Но на средней осциллограмме, сделанной с бо-
лее быстрой разверткой, искажение в выход-
16N.2. Аномалии и опасности схем на триггерах
635
Задержка на одном вентиле
Сигнал выборки
Сигнал выборки
Выходной сигнал
Рис. 16N.13. Временная диаграмма мультиплексора пред-
сказывает искажение выходного сигнала
дополнительного вентиля, чтобы не допустить
искажений подобного типа. Соответствующая
схема изображена на рис. 16N.168. Этот вен-
тиль (который, в действительности не совсем
избыточный, поскольку устранение искажения
является необходимой операцией) принуди-
тельно устанавливает сигнал высокого уровня
на выходе, когда на обоих входах присутствуют
сигналы высокого уровня, независимо от уров-
ня сигнала выборки.
Сигнал выборки
Выходной сигнал
400 мкс/дел.
400 нс/дел.
10 нс/дел.
Рис. 16N.14. Возможность различить искажение выходного сигнала в схеме с мультиплексором зависит от скорости разверт-
ки осциллографа
ном сигнале уже можно различить. А на правой
осциллограмме, сделанной с еще более быстрой
разверткой, величину искажения можно даже
измерить, хотя она и очень мала. (Эта схема
мультиплексора реализована на устройстве
ПМЛ, задержки внутренних вентилей которо-
го, вызывающие искажение, очень небольшие,
меньшие, чем у дискретных логических венти-
лей.) Но при всей кратковременности длитель-
ность этого искажения скорее всего достаточна,
чтобы другое устройство, реализованное по та-
кой же технологии, могло его обнаружить.
Каковы же возможные решения описанной про-
блемы? Мультиплексоры, реализованные в виде
микросхем, не дают такого искажения, хотя их
принципиальная схема выглядит точно так же,
как и нашего устройства. Чем это объясняется?
У нас нет однозначного ответа на этот вопрос.
Возможно тем, что разработчики микросхем
могут согласовать задержки именно там, где
это требуется. Например, микросхемный муль-
типлексор может содержать задержку в пути
неинвертированного сигнала выборки, совпа-
дающую с задержкой, налагаемой инвертором в
пути инвертированного сигнала выборки.
Но разработчикам доступна и другая возмож-
ность для предотвращения искажения, которая
является единственным вариантом, если вы со-
бираете мультиплексор сами. Данная возмож-
ность состоит в добавлении так называемого
Дополнительный вентиль поддерживает
на выходе сигнал высокого уровня,
независимо от уровня сигнала выборки
OUT
Рис. 16N.15. Дополнительный вентиль может помочь устра-
нить ожидаемое искажение
Какой урок можно извлечь из сказанного?
Прежде всего целью этого примера не являет-
ся выработать у вас «нервную боязнь» иска-
жений. Искажения не выскакивают в схемах
просто так, когда им захочется. Мы надеемся,
что вышеприведенный пример иллюстрирует
несколько аспектов. В частности:
1. Если существует возможность создания
проблем из-за переходных процессов на
выходах схемы, то такую схему необходи-
мо рассматривать динамически, а не только
в булевых, статических терминах. Конечно
же, существует множество схем, для кото-
рых выходные переходные процессы будут
безвредными.
8 Ветераны цифровой логики, которые помнят использо-
вание в картах Карно фигур или накладок для группиро-
вания логических единиц, могут назвать это решение из-
быточной накладкой.
636
/6Л/. Счетчики
2. В обнаружении возможности возникновения
таких искажений может быть полезна вре-
менная диаграмма.
3. Искажение выходного сигнала, подобное
показанному на рис. 16N.14, является след-
ствием так называемой опасности (англ.
hazard)9. Причиной возникновения такой
проблемы является необходимость одновре-
менного изменения своего состояния двумя
внутренними сигналами. Логический компи-
лятор, используемый для создания кода для
микросхемы ПМЛ, удалит любой логически
избыточный вентиль, наподобие вентиля
для предотвращения искажения, если только
минимизатору компилятора не были даны
предварительные указания не делать этого
и разрешить неминимизированную реализа-
цию схемы.
Очевидно, что труднее всего обнаружить воз-
можность возникновения искажения, прежде
чем оно «объявит» о себе и вызовет проблемы
в работе схемы. Если вы знаете, что существует
возможность возникновения искажения, тогда
его можно предотвратить без большого труда.
16N.3. Более универсальный
счетчик
В разделе 15N.9 мы спроектировали двухраз-
рядный синхронный счетчик, который, мы на-
деемся, вы собрали на лабораторном занятии.
Давайте продолжим работу в этом направле-
нии, предприняв попытку спроектировать бо-
лее универсальный счетчик, который будет
похож на микросхемы счетчиков, предлагае-
мые на рынке. (В том случае, если вы пред-
почтете купить готовый счетчик, а не собрать
его на микросхеме ПЛУ.) Далее рассматрива-
ются несколько возможностей, которые будут
желательными в таком улучшенном счетчике,
размер которого мы предлагаем ограничить
скромными четырьмя разрядами. Таким обра-
зом, это будет счетчик-делитель на 16, если не
изменить каким-либо образом его естествен-
ный предел счета.
♦ Счетчик должен легко поддаваться каскади-
рованию, т. е. нужно, чтобы его можно было
легко соединять с другими подобными счет-
чиками для создания счетчиков большей
разрядности.
♦ Счетчик должен иметь синхронную функ-
цию сброса.
♦ Счетчик должен быть оснащен функцией за-
грузки, т. е. пользователь должен иметь воз-
можность выполнить параллельную загрузку
триггеров, чтобы установить любое началь-
ное значение счета.
Для получения требуемого результата будем
работать поэтапно.
16N.3.1. Для счетчика потребуются
четыре Т-триггера
На рис. 16N.16 изображены четыре соединен-
ных последовательно Т-триггера, полученные
из D-триггеров.
Общая линия тактирования обеспечивает син-
хронное тактирование триггеров. В данном слу-
чае, в отличие от двухразрядного синхронного
счетчика из раздела 16N.1.1, даже для самого
старшего разряда мы используем Т-триггер.
В этом более простом счетчике самый млад-
ший разряд переключался по каждому сигна-
лу тактирования при любых обстоятельствах.
'о
А
А
Сигнал тактирования
А
А
Рис. 16N.16. Четыре Т-триггера без логической схемы управления
9 Если вам это интересно, такая опасность, создающая
ложное переходное состояние, называется статической
опасностью. Разница между одним состоянием с техниче-
ским названием «опасность» (hazard) и другим состояни-
ем, называемым «гонками» (race), не представляет для нас
большого интереса. Нас интересует получаемое в резуль-
тате этого искажение.
Данная разработка не так проста: для функции
входного переноса требуется управляемый вход
Т-триггера самого младшего разряда.
Требуемое поведение счетчика показано на
временной диаграмме на рис. 16N.17. Чтобы
fa/V.3. Более универсальный счетчик
637
Сигнал тактирования <
Q,
Q3
Выходной перенос
J—I
J L
г
Счет 12 13 14 15 0 1 2 3
Рис. 16N.17. Временная диаграмма четырехразрядного суммирующего счетчика
сэкономить время и силы, мы начали эту диа-
грамму не с нуля, а со счета 1210.
16N.3.2. Указываем сигналам
на нескольких входах 7", когда
изменяться, а также добавляем
входной и выходной переносы
Как и в случае с двухразрядным счетчиком, ко-
торый мы разработали в прошлый раз, правила
работы этого счетчика и автомобильного одо-
метра схожи: значение следующего старшего
разряда меняется только тогда, когда все пре-
дыдущие младшие разряды обнуляются. Таким
образом, чтобы обеспечить синхронное пове-
дение, нам нужно дать указание триггеру из-
менить свое значение по следующему сигналу
тактирования, когда предстоит переход в нуле-
вое состояние триггеров всех предшествующих
разрядов. Такой переход предстоит в том слу-
чае, когда на выходе всех триггеров младших
разрядов присутствует сигнал высокого уровня.
Для этого мы просто выполняем операцию И
с выходами триггеров младших разрядов, по-
давая выходной сигнал после этой операции
на вход Т любого соответствующего тригге-
ра. Пока мы занимаемся этим, также добавим
в нашу схему входной (ПРНСВХ) и выходной
(ПРНСВЫХ) переносы, что позволит нам после-
довательно соединять этот счетчик с другими
подобными ему счетчиками.
Одно обстоятельство в формировании выход-
ного переноса ПРНСВЫХ может показаться вам
необычным. В частности, вентиль И-НЕ этой
функции содержит не только входы для сигна-
лов четырех выходов Q, но также вход для сиг-
нала входного переноса ПРНСВХ* для данного
каскада счетчика. Данный вентиль содержит
этот вход потому, что на него будет подаваться
сигнал выходного переноса ПРНСВЫХ* предше-
ствующего младшего каскада, если счетчик яв-
ляется частью большего каскадного счетчика.
Таким образом, выходной перенос ПРНСВЫХ,
в состав которого входит входной перенос
ПРНСВХ, обозначает заполненность не только
данного каскада, но также и всех младших ка-
скадов. Эта простая и изящная схема обеспе-
чивает каскадирование нескольких счетчиков,
просто подавая выходной перенос ПРНСВЫХ
каждого предыдущего каскада на входной пе-
ренос ПРНСВХ следующего каскада.
ПРНС,
выходной
перенос
Рис. 16N.18. Четыре Т-триггера, управляемые таким образом, чтобы получить суммирующий счетчик. Чтобы обеспечить ка-
скадное соединение нескольких подобных счетчиков, добавлены функции входного и выходного переноса (ПРНСвх и ПРНСвых)
638
16N. Счетчики
Каскадирование
Любой приличный счетчик допускает возмож-
ность каскадирования нескольких экземпля-
ров, чтобы создать счетчик большей разряд-
ности. Переносы (входной и выходной), реа-
лизованные в разделе 16N.3.2, позволяют нам
при желании создать, например, 12-разрядный
счетчик, соединив последовательно три четы-
рехразрядных счетчика, подобных счетчику,
показанному на рис. 16N.18.
Входной перенос
Это разрешающий сигнал, который при активи-
ровании дает указание счетчику реагировать на
свой сигнал тактирования. Обратите внимание
на то, что в схеме на рис. 16N.19 все устройства
подключены к общей линии сигнала тактиро-
вания.
Но не подавайте сигнал выходного переноса на
вход тактирования счетчика самого младшего
разряда, поскольку в таком случае это будет
возврат к схеме счетчика со сквозным перено-
сом, а не полностью синхронный счетчик.
Выходной перенос
Этот сигнал предупреждает, что счетчик нахо-
дится на грани обнуления или переполнения.
В случае обычного двоичного суммирующего
счетчика он определяет наличие логической
единицы на выходах всех триггеров. В случае
вычитающего счетчика этот сигнал определяет
наличие логического нуля на всех выходах.
Обратите внимание на то, что этот сигнал дол-
жен появиться до обнуления, а не после него,
поскольку должен дать знать следующему (бо-
лее старшего разряда) счетчику, что тому де-
лать по очередному сигналу тактирования.
На рис. 16N.19 показана блок-схема каскадно-
го соединения трех счетчиков, демонстрирую-
щая, насколько легко можно выполнять такое
соединение счетчиков с правильно сформи-
рованными сигналами выходного и входного
переносов. Но хотя счетчики легко каскадиро-
вать, скорость счетчика со слишком большим
количеством каскадов будет ограничена из-за
задержки переносов в цепи сквозного пере-
носа. Большую частоту тактирования можно
обеспечить, выполняя внешнюю операцию И
с выходными переносами нескольких счет-
чиков.
Входной Выходной Входной Выходной Входной
перенос перенос перенос перенос перенос
ТТРНС ПРНС ТТРНС ПРНС ТТРНС
TTPHCBX ПРНС
вих ТТРНСВХ
1 1 J
Самый w
старший
Сигнал
ПРНСВЬГХ
f (
Л
Самый w
младший
рдзряд
тактирования
Рис. 16N.19. Каскадирование трех счетчиков — очень лег-
кая задача
Особенность выходного переноса
Входной перенос необходимо включать в стро-
бирование для выходного переноса только при
каскадировании больше чем двух счетчиков,
как показано на рис. 16N.19. Мы хотим, чтобы
значение третьего счетчика — самого старшего
разряда — инкрементировалось только в том
случае, когда предельного значения достигли
оба счетчика меньших разрядов, а не только
счетчик, сопредельный ему. Это такая же ситуа-
ция, как и в случае с обнулением автомобиль-
ного одометра. На рис. 16N.20 показан пример
такого одометра, который в данном случае яв-
ляется просто механическим счетчиком кассет-
ного магнитофона. Этот пример напоминает
нам, что третья цифра переходит на следующее
значение только после того, как предыдущие
две цифры достигнут своего предельного зна-
чения, т. е. 99.
090 переходит на 091:
третья цифра не меняется
099 переходит на 100:
третья цифра меняется
Рис. 16N.20. Одометр или механический счетчик: третья
цифра переходит на следующее значение только после того,
когда обе предыдущие цифры достигнут своего максималь-
ного значения (99), а затем перейдут на нули
16N.3.3. Более точный, синхронный,
выходной перенос
Рассмотренная ранее функция выходного пе-
реноса обычно работает должным образом,
поскольку он подается на синхронный вход
входного переноса. Но при использовании это-
го сигнала в асинхронном режиме может воз-
никнуть проблема, заключающаяся в том, что
скомбинированный сигнал выходного переноса
16N.3. Более универсальный счетчик
639
Искажения
2Г
Сигнал тактирования
Выходной перенос ТТРНСВИХ*
(скомбинированный) ;4
Сигнал на выходе Q триггера-
делителя на два, тактируемого
сигналом ТТРНСВЬГХ.
(триггер реагирует на искажения
входного сигнала тактирования)
т
Y
ч.
Ж
Счетчик-делитель на 17 (вычитающий счетчик, Подробности искажения в сигнале ПРНСВЬГХ*
загружаемый значением 16 по сигналу ПРНСВЬГХ«)
Рис. 16N.21. Скомбинированный сигнал выходного переноса ПРНСВЫХ, в асинхронной схеме может содержать достаточно
значительные искажения, чтобы вызывать тактирование триггера
ПРНСВЫХ* может содержать искажения. Такая
проблема может возникнуть в том случае, если
между сигналами нескольких выходов Q, от ко-
торых он зависит, наблюдается достаточный
сдвиг, т. е. состояние этих сигналов изменяется
в разное время, несмотря на общий сигнал так-
тирования. Скомбинированный сигнал выход-
ного переноса ПРНСВЫХ* для счетчика, реали-
зованного на микросхеме ПМЛ, как на лабора-
торном занятии 16L, содержал такие искажения
(рис. 16N.21). На подробной осциллограмме
справа на этом рисунке можно ясно видеть, что
время возникновения этого искажения — по-
сле фронта сигнала тактирования — делает его
безвредным в синхронной схеме, которая сни-
мает значения со своих входов только в тече-
ние времени установки непосредственно перед
активным фронтом сигнала тактирования10.
Указанный «иммунитет» является большим
достоинством синхронных схем.
Но когда сигнал выходного переноса ПРНСВЫХ*
служит для управления схемой, реагирующей
на фронт этого сигнала (наподобие сигнала
тактирования триггера, показанного на ниж-
ней осциллограмме на рис. 16N.21, или наподо-
бие сигнала тактирования триггера для опреде-
ления переполнения), тогда искажения могут
создавать проблемы, для которых нужно найти
решение11.
10 Если вы помните, некоторые устройства имеют нену-
левое время удержания. Но время удержания даже этих
устройств очень редко настолько велико, чтобы захватить
искажение на рис. 16N.21.
11 Мы были удивлены, когда в счетчике из лабораторно-
го занятия 16L эти искажения были очень серьезными в
режиме вычитания и едва заметными в режиме суммиро-
вания. По-видимому, эта разница объясняется некоторым
Чтобы очисть сигнал переноса от искажений,
его нужно сделать синхронным, прежде чем
использовать его. Вместо определения состоя-
ния максимального значения счета (которое
служит признаком обнуления по следующему
сигналу тактирования) синхронный сигнал пе-
реноса подается на комбинационную схему для
определения состояния счетчика (на единицу
меньшего, чем максимальное для суммирую-
щего счетчика; и на единицу большего, чем ми-
нимальное состояние для вычитающего счет-
чика) и далее на вход тактируемого D-триггера.
Этот метод иллюстрируется на рис. 16N.22.
, (Для суммирующего счета)
► макс-ll
• мин+lj
ЧДля вычитающего счета)
Сигнал тактирования
D Q
Синхронный сигнал
выходного переноса
TTPHCOUTV
Рис. 16N.22. Формирование синхронного переноса с помо-
щью D-триггера
Это метод синхронизации слишком прост, что-
бы создать удовлетворительный синхронный
выходной перенос для счетчика, будь то сумми-
рующий или вычитающий. В нашем счетчике
из лабораторного занятия 16L мы не пытались
решить создаваемые им тонкие проблемы12.
несоответствием между характеристиками времени нарас-
тания и времени спада, поскольку сигнал выходного пере-
носа зависит от низких уровней для вычитающего счета
и высоких — для суммирующего.
12 Представленный на рис. 16N.22 метод работает поч-
ти всегда. Но он может не сработать, если изменить на-
правление счета или на максимальном или минималь-
ном значении счета, поскольку схема определяет только
640
16N. Счетчики
Сигнал ПРНСВЬГХ* содержит искажения, но они безвредные
' ж * i« a i» т ш w ^ий Ь * */» I» и» I» m I» * I *• * * •* •** -• ** *» ** *• «* »*
Сигнал тактирования j / I ' i '
Сигнал выходного переноса
ТТРНСВЬГХ* (скомбинированный),41
Выход Q триггера-делителя на два, f
тактируемый сигналом ПРНСВЬ1Х„ ^
Счетчик-делитель на 17: синхронный Дополнительная очистка посредством
сигнал выходного переноса ПРНСВЬ1Х* развязки линий питания вблизи от ТТЛУ
Рис. 16N.23. В отличие от асинхронного комбинированного сигнала переноса, синхронный сигнал не содержит искажений
Поскольку это синхронный сигнал выходного
переноса, он не содержит искажений: не пере-
дает искажения, возникающие в неупорядочен-
ное время вскоре после фронта сигнала такти-
рования. На рис. 16N.23 приведена осцилло-
грамма сигнала такого синхронного переноса.
(Это разработка, которую мы применили для
счетчика на микросхеме ПМЛ из лабораторно-
го занятия 16L.)
Сигнал выходного переноса продолжает со-
держать искажения, но они малы и не пред-
ставляют проблем. Как можно видеть на
рис. 16N.23, триггер игнорирует эти всплески
помех, реагируя только на настоящий сигнал
выходного переноса ПРНСВЫХ* (осциллограм-
ма для счетчика-делителя на два, тактируемо-
го сигналом ПРНСВЫХ*). Сравните эту работу
счетчика-делителя на два с ужасными искаже-
ниями в сигнале переноса на осциллограмме на
рис. 16N.21.
Справа на рис. 16N.23 приведена осциллограм-
ма сигнала переноса, дополнительно очищен-
ного от искажений посредством добавления
развязывающего конденсатора, на шинах пи-
тания вблизи ПЛУ13. Эта развязка питания не
влияет на поведение схем, поскольку такие по-
мехи были безвредны, но делает осциллограм-
му сигнала более приятной на вид. (Кроме того,
мы надеемся, что использование развязочных
конденсаторов на шинах питания уже вошло у
вас в привычку.)
состояние, непосредственно предшествующее максималь-
ному или минимальному.
13 Развязывающий керамический конденсатор емкостью
ОД мкФ вставляется в гнездо ПЛУ.
Добавляем синхронное обнуление
Счетчики обычно снабжаются функцией об-
нуления, и синхронный вариант часто пред-
почтительнее асинхронного. Такую функцию
легко реализовать, как иллюстрируется на
рис. 16N.24.
(Схгма обычной
логики счетчика)
г
>|
й Q
Обнуление
Сигнал тактирования \
Рис. 16N.24. Для реализации синхронного обнуления требу-
ется всего лишь один вентиль И
16NA Выводы относительно
функций счетчиков
На рынке доступны микросхемные счетчики
с разнообразными возможностями; любые из
этих функций можно реализовать самостоя-
тельно с помощью ПМЛ.
Каскадирование счетчиков
для увеличения разрядности
Как упоминалось в разделе 16N.3.1, подобно
триггерам счетчики можно соединять после-
довательно, чтобы создать устройство боль-
шей разрядности. Такая операция всегда воз-
можна с синхронными счетчиками: для этого
мы просто подаем сигнал выходного переноса
предыдущего каскада на вход сигнала входно-
го переноса последующего каскада. Правильно
спроектированная логика выходного переноса
16N.5. Счетчик-делитель на N из лабораторного занятия 16L
641
будет активироваться только тогда, когда все
предыдущие каскады достигли своего макси-
мального значения. Этот момент иллюстриру-
ется на примере с механическим счетчиком на
рис. 16N.20.
Загрузка счетчика
Во многих счетчиках допускается параллель-
ная загрузка значений в триггеры.
Процесс загрузки
Активирование входа загрузки LD* счет-
чика преобразует его в простой регистр из
D-триггеров, которые по следующему фронту
сигнала тактирования просто принимают зна-
чения, присутствующие на их входах данных.
Данный тип загрузки называется синхронным.
Возможна также асинхронная загрузка, кото-
рая работает подобно асинхронному обнуле-
нию, рассматриваемому далее. Счетчик из ла-
бораторного занятия 16L, реализованный на
микросхеме ПМЛ, допускает оба типа загрузки.
Асинхронная загрузка удобна при иницииро-
вании загрузки вручную, например, нажатием
кнопки. А синхронная лучше подходит, когда
загрузка инициируется схемным сигналом, как,
например, в схеме создания музыки на лабора-
торном занятии 16L.
После деактивации сигнала загрузки LD* счет-
чик возвращается к функционированию в ре-
жиме счетчика. Понять процесс загрузки по
словесному описанию может быть трудно. Мы
рассмотрим пример загрузки на лаборатор-
ном занятии 16L, используя счетчик-делитель
Обнуление счетчика14
Обнуление можно назвать особым случаем за-
грузки, но эта функция настолько полезна, что
предлагается почти во всех счетчиках (более
часто, чем функция загрузки). Кроме того, до-
ступны два типа функции обнуления.
Асинхронное обнуление
Асинхронное обнуление происходит в течение
короткого времени, около 5-10 не, после ак-
тивирования сигнала обнуления (Clear*) или
сброса (Reset*). При этом процесс обнуления
не зависит от сигнала тактирования. Такой тип
обнуления знаком нам по работе с триггерами,
в которых всегда реализовано асинхронное об-
нуление.
Синхронное обнуление
Синхронное обнуление выполняется при ак-
тивированном сигнале обнуления (Clear*) или
сброса (Reset*) по сигналу тактирования. До
сигнала тактирования ничего не происходит.
Реализация синхронного обнуления рассма-
тривалась в разделе Добавляем синхронное об-
нуление ранее в этой главе.
Вопрос
Какой тип обнуления вы бы хотели иметь в про-
граммируемом счетчике-делителе на N, наподо-
бие того, с которым мы будем работать на лабора-
торном занятии 16L для этой главы?
На рис. 16N.25 изображено несколько стан-
дартных устаревших счетчиков на микросхе-
мах средней степени интеграции, оснащенных
тем или иным типом функции обнуления.
Отличаются только в этом отношении
\
'163
'90
■161
14 Счетчики с функциями синхронной и асинхронной за-
грузки рассматриваются в § 10.5.2 книги АоЕ.
Синхронное Асинхронное Асинхронное
Рис. 16N.25. Три микросхемных счетчика с синхронным и
асинхронным обнулением
Некоторые задачи применения счетчиков под-
робно рассматриваются в главе 16W. Здесь же
мы сконцентрируем наше внимание на приме-
нениях счетчиков, с которыми будем работать
на лабораторном занятии.
16N.5. Счетчик-делитель
на N из лабораторного
занятия 16L
Как вы знаете, счетчик, который устанавли-
вается на макетную плату, оснащен функцией
загрузки. Восемь из его 16 линий управляются
посредством цифровой клавиатуры, шесть дру-
гих линий подключены к шине «земли» внутри
микросхемы, а две оставшиеся линии управ-
ляются с помощью двухпозиционного DIP-
переключателя. На рис. 16N.26 изображена
642
16N. Счетчики
Синхронная загрузка
DIP- переключатель
Выходной перенос
ПРНС
Шесть линий заземлены
внутри микросхемы
Шина данных цифровой клавиатуры
Рис. 16N.26. Линии ввода данных счетчика: восемь линий управляются с цифровой клавиатуры
часть схемы компьютера из рис. F.1, содержа-
щая сам счетчик и его вспомогательные эле-
менты.
Если позволить счетчику перезагружаться са-
мостоятельно по достижении максимального
значения (нуля при вычитающем счете), то на
цифровой клавиатуре можно задать число со-
стояний, через которые устройство будет счи-
тать в каждом цикле. Соответствующая схема
изображена на рис. 16N.27.
L—С
ТТРНСО|
Синхронная загрузка
Суммированием/Вычитание
Сигнал
тактирования
+5 В
Цифровая
клавиатура
Рис. 16N.27. Подключение счетчика для самостоятельной
перезагрузки при достижении нулевого значения
Вычитающий счет позволяет нам воспользо-
ваться линиями данных, подключенными на
«землю», чтобы установить с цифровой кла-
виатуры не слишком длинный счет циклов.
Примечание
Для самого меньшего значения цифровой кла-
виатуры (единицы) получается 17 состояний15. Это
число состояний объясняется тем, что внутренние
нули создают единицу из загруженного с клавиа-
туры значения 1610, а нулевое состояние соответ-
ствует 17-му шагу. Ввод с клавиатуры значения 2
задает 33 состояния и т. д.
15 Загрузка с клавиатуры нуля не будет работать, посколь-
ку это значение устанавливает счетчик в конечное значе-
ние счета в начале счета.
16N.6. Счет как стратегия
проектирования цифровых
схем
Из предшествующего материала можно ви-
деть, что создать цифровой счетчик довольно
просто. Этим обстоятельством можно вос-
пользоваться, когда необходимо разработать
цифровое устройство для измерения опреде-
ленной величины. В частности, можно просто
создать, по сути, секундомер для измерения
длительности генерируемого особым образом
импульса. Более конкретно идея состоит в сле-
дующем:
1. Создаем счетчик, который ведет счет фрон-
тов сигнала тактирования. Это своего рода
хронометр.
2. Добавляем логические вентили управления
для запуска и остановки хронометра, т. е.
превращая его в секундомер.
3. Создаем схему для создания сигнала с пе-
риодом, пропорциональным длительности
интересующей нас величины. Назовем эту
величину входным сигналом.
4. С помощью нашего секундомера определя-
ем период, измеряя таким образом входной
сигнал.
Далее приводится пример, иллюстрирующий
этот метод.
Цифровой вольтметр
Схема, изображенная на рис. 16N.28, измеряет
время, в течение которого пропорционально
нарастающее напряжение достигает значения
напряжения, обозначенного «Вход». Чем выше
16N.6. Счет как стратегия проектирования цифровых схем
643
♦«Л
Вход-
\
Остается на высоком уровне...
пока компаратор не обнаружит, что иконд > UBX
II I МЛ Ш
Цифровой ,, ^
выход Напряжение на конден-
саторе равно нулю
В течение этого времени
выполняется разрешение счетчика
Рис. 16N.28. Пример Измерения напряжения посредством определения периода с помощью счетчика
значение напряжения «Вход», тем больше тре-
буется времени для получения результата и тем
больше сам результат. Это АЦП с однократ-
ным интегрированием. Предпочтительнее не-
сколько более сложная схема преобразования,
так называемое преобразование с двукратным
интегрированием (см. раздел 18N.4.3). Но этот
подход, по сути, такой же, как и с однократным
интегрированием, схема для которого показана
на рис. 16N.28.
16L Лабораторное занятие: счетчики
16L1. Два пути
к микроконтроллерам
Начиная с этого момента, в нашем курсе пред-
лагаются два альтернативных пути к изучению
микроконтроллеров, из которых вы можете
выбрать тот или иной (хотя фанатики, у кото-
рых есть лишнее время, могут пойти по обоим).
Далее кратко описан каждый из этих путей,
с перечислением их достоинств (с нашей точки
зрения). Если вы прорабатываете эти лабора-
торные занятия самостоятельно, то, конечно
же, вы можете сами выбрать тот путь, который
вам больше по душе. Но если лабораторные за-
нятия являются частью курса, то возможно, что
решение, по какому из этих двух путей следо-
вать, примет ваш преподаватель.
16L1.1. Первый путь:
Сборка микрокомпьютера
из дискретных деталей
Этим путем мы следовали в нашем курсе в те-
чение последних 25 лет или около того. В част-
ности, на нескольких лабораторных занятиях
мы собирали небольшой компьютер из 9 ми-
кросхем, постепенно добавляя их в исходную
схему. В этом подходе используется счетчик и
память RAM, которые мы соберем на лабора-
торных занятиях 16L и 17L. Память RAM будет
хранить данные и программный код для боль-
шинства наших приложений.
♦ Лаб. занятие 20L. Добавляем процессор/
контроллер (совместимый с микроконтрол-
лером 8051), а также его сопутствующее
устройство ПМЛ, связывающее микрокон-
троллер с периферийными устройствами и
памятью, которое также обеспечивает поша-
говое исполнение программ.
♦ На следующих лабораторных занятиях до-
бавляем различные периферийные устрой-
ства и тестируем их, исполняя небольшие
программы:
• Лаб. занятие 21L. Цифровая клавиатура
и дисплей для ввода и вывода байтов; под-
программы.
• Лаб. занятие 22L. Ввод и вывод битов;
методом опроса и используя прерывания.
• Лаб. занятие 23L. Добавляем АЦП и
ЦАП.
• Лаб. занятие 24L. Средства хранения и
воспроизведения аналоговых данных; по-
следовательные периферийные устрой-
ства; таймеры.
• Лаб. занятие 25L. Тестирование авто-
номного контроллера (в данном случае со-
бранная на большой макетной плате схема
имитирует схему SiLabs).
16L1.2. Второй путь: Начинаем
с автономного микроконтроллера
При этом используется микроконтроллер 8051,
которым можно управлять и опрашивать с по-
мощью обычного персонального компьютера
(ПК). Такая рабочая площадка делает ненужной
большую часть сборки, требуемой на первом
пути, но для нее необходим ПК для каждой кон-
фигурации. Лабораторные занятия здесь орга-
низованы иным образом. Последовательность
лабораторных занятий может быть короче
или длиннее на два дня, если не выдерживать
ритм одного лабораторного занятия в день.
(Большинство студентов не соблюдают распи-
сание, по крайней мере, на полдня при сборке
первой схемы на лабораторном занятии 20L.)
♦ Лаб. занятие SiLabs 20L.3. Настройка от-
ладчика; вывод битов; задержка.
♦ Лаб. занятие SiLabs 21L.2. Цифровая па-
нель и дисплей для ввода и вывода байтов;
подпрограммы.
16LI Два пути к микроконтроллерам
645
♦ Лаб. занятие SiLabs 22L.2. ШИМ; компа-
ратор.
♦ Лаб. занятие SiLabs 23L.2. Прерывания,
АЦП и ЦАП.
♦ Лаб. занятие SiLabs 24L.2. Последователь-
ные шины: УАПП и SPI16.
♦ Лаб. занятие SiLabs 25L.2. Таблица дан-
ных; память RAM для интерфейса SPI.
16L.1.3. Пути сходятся
Эти два пути сходятся в главе 26N, в которой
студенты должны использовать микроконтрол-
лер 8051 в автономном режиме для реализации
какой-либо схемы собственной разработки.
16L.1 А Достоинства каждого пути
Что нам нравится в первом пути
Этот метод сводит к минимуму кажущееся вол-
шебство во взаимодействии с компьютером.
Микроконтроллер 8051 не знает ничего, чему
вы его не научите, включая отсутствие встро-
енной загадочной программы монитора. Вы
управляете устройством напрямую, и даже по-
шаговое выполнение программ выполняется
посредством простого аппаратного обеспече-
ния. Это аппаратное обеспечение ставит ком-
пьютер на паузу, чтобы дать вам время иссле-
довать шину данных и адресную шину, а также
интересующие вас сигналы управления. Для
этого оно просто отключает сигнал тактиро-
вания. В большой мере функционирование
такого компьютера делается прозрачным, но
его «мозг» в виде процессора 8051, который
пошагово исполняет инструкции, остается не-
прозрачным.
Например, на рис. 16L.1 показано взятие пока-
заний из шины данных при пошаговом испол-
нении программы ввода/вывода из лаборатор-
ного занятия 21L.
Значения, снятые с шины данных и адресной
шины, отображаются на дисплее. Тестирование
Тестирование вывода RD* (чтение) процессора посредством логического пробника
показывает, что на нем присутствует низкий уровень, что подтверждает прием
значения с цифровой клавиатуры процессором 8051 (через шину данных)
Рис. 16L.1. Функционирование микрокомпьютера, собранного на макетной плате, очень удобно изучать
16 Англ. Serial Peripheral Interface — последовательный ин-
терфейс (периферийных устройств).
646
16L Лабораторное занятие: счетчики
состояния вывода RD* с помощью логического
пробника (см. рис. 16L.1) показывает наличие
на нем активированного сигнала, это означает,
что процессор считывает данные из шины дан-
ных. Источником данных является цифровая
клавиатура, и отображение на дисплее значе-
ния, введенного с нее, успокаивает, что схема
работает должным образом. Такой тип низко-
уровневой информации о сигналах снимает
«покров таинства» с функционирования ком-
пьютера, делая его чем-то простым.
Нам нравится эта простота. Также нам нравит-
ся предоставлять вам возможность допускать
ошибки при монтаже схемы, а затем искать их.
В главе 20W мы подробно излагаем некоторые
диагностические процедуры, которые могут по-
требоваться, чтобы разобраться с какой-либо
неисправностью. Сборка этого небольшого
компьютера даст вам возможность поупраж-
няться в применении ваших навыков поиска
причин неполадок.
Что нам нравится во втором пути
Это путь, которым следуют все другие, ра-
ботающие с микроконтроллерами. Этот ме-
тод позволяет получить быстрые результаты.
Кажется, что любой набор разработчика (или
оценочная плата, как это оборудование ино-
гда называется) готов мигать светодиодом
в течение пяти минут после извлечения его из
коробки. Всем нравится видеть подтвержде-
ние работоспособности устройства и то, что
мы можем заставить его выполнять наши ко-
манды с первой же встречи с ним. Мы также
восприимчивы к очарованию символическим
признанием наших возможностей в этой об-
ласти, как и в любой другой. Поэтому нет ни-
какой загадки в том, почему людям нравится
работать таким способом.
И поскольку, несомненно, что после заверше-
ния этого курса вы будете работать с микро-
контроллерами таким способом, существует
очевидная привлекательность в том, чтобы
сразу же начать работать так, как вы будете ра-
ботать впоследствии.
На рис. 16L.2 показано, как выглядит кон-
троллер, который мы будем использовать на
этом пути. Это небольшая микросхема по-
верхностного монтажа с 32 выводами, впаян-
ная в адаптерную плату, чтобы ее можно было
вставлять в гнезда макетной платы. Это кро-
шечное устройство вмещает в себе эквивалент
почти всех дискретных компонентов схемы
микроконтроллера из первого пути (за ис-
ключением памяти RAM объемом 32 Кб) плюс
другие компоненты, отсутствующие в первом
варианте.
Рис. 16L2. Микроконтроллер C8051F410, впаянный в адап-
тер для удобства установки на макетную плату
Мы не знаем, какой из двух описанных путей
вам придется больше по душе. Нам нравятся
оба. Если у вас достаточно времени, то наилуч-
шим подходом будет сначала собрать компью-
тер из дискретных компонентов, а затем экспе-
риментировать с интегрированным микрокон-
троллером.
16L1.5. Слияние обоих путей в
реализации собственного проекта
Как уже упоминалось ранее, мы надеемся, что
когда вы познакомитесь с контроллером, то ис-
пользуете его в автономном режиме для реали-
зации какого-либо своего проекта. Эта задача
рассматривается в главе 26N.
Для этого, возможно, подойдет или микросхе-
ма компании Dallas Semiconductor, или микро-
процессор C8051F410 компании Silicon Labs.
Те из вас, кто собирает компьютер из дискрет-
ных компонентов, может запрограммировать
интегрированную память ROM микрокон-
троллера 8051 с помощью ПК; альтернативно,
когда настанет время установить контроллер
автономно на макетную плату, можно ис-
пользовать микросхему 410 компании Silicon
Labs (SiLabs). Благодаря наличию в микросхе-
ме 410 возможности интерактивной отладки
с этим устройством легче работать, чем с ми-
кроконтроллером 8051, в который программы
можно только загружать, но не выполнять их
отладку.
16L2. Лабораторное занятие по счетчикам
647
16L2. Лабораторное занятие
по счетчикам
На этом лабораторном занятии мы переходим
от скромного счетчика-делителя на четыре из
главы 15 к 16-разрядному полностью синхрон-
ному счетчику. Мы рассмотрим некоторые из
его полезных возможностей, в особенности
его синхронную загрузку, а затем используем
его в двух схемах. Первой из этих схем будет
счетчик-делитель на N, а второй — схема из-
мерения периода, которую можно использо-
вать для измерения емкостей, оснастив ее для
этого минимальным дополнительным обору-
дованием. Сначала для оценки работы счет-
чика нам понадобится только осциллограф и
логический пробник, а затем добавим шест-
надцатеричный дисплей, который сделает на-
блюдение за работой счетчика более легкой и
удобной. А управлять счетчиком, в частности
загружать в него данные, будем с цифровой
клавиатуры.
Примечание
Данная цифровая клавиатура не является стан-
дартной предлагаемой на рынке деталью. Инфор-
мацию для приобретения этой клавиатуры см. в
Приложении Д. Плата дисплея также является схе-
мой специального изготовления, в которой исполь-
зуется ЖКД для отображения 16 линий адреса и 8
или 16 линий данных.
В главе 17 те из вас, кто избрал путь сборки
компьютера из дискретных компонентов, будут
использовать этот счетчик и дисплей для по-
лучения адреса памяти. Цифровая клавиатура
позволит вам записывать восьмибитовые зна-
чения в любую ячейку памяти. На последую-
щих лабораторных занятиях счетчик и память
составят основу, на которой вы будете собирать
свой микрокомпьютер. Так что сегодня те из
вас, кто решил собирать компьютер из дис-
кретных компонентов, уже приступили к его
сборке.
Те же из вас, кто избрал второй путь с исполь-
зованием платы микрокомпьютера, может
собрать этот счетчик на отдельной макетной
плате. Такой подход рассматривается в разде-
ле 16L3.2.
Примечание
Если вы решили собирать компьютер из дискрет-
ных компонентов, то будете собирать схемы се-
годняшнего занятия на своей отдельной макетной
плате. В материалах лабораторного занятия по
сборке компьютера из дискретных компонентов
предполагается печатная плата, на которой раз-
мещено несколько макетных плат. Эта макетная
плата будет основой микрокомпьютера, который
вы вскоре будете собирать.
Если у вас нет этой общей печатной платы, то,
конечно же, можно собрать свой компьютер на
нескольких макетных платах. Общая печатная
плата только несколько облегчает соединение
схем на отдельных макетных платах в одну об-
щую схему.
Чтобы облегчить сборку компьютера из дис-
кретных компонентов, мы создали печатную
плату с шинами для компьютера, но оставили
вам задачу соединения этих шин между собой и
с другими компонентами схемы. Наличие гото-
вых шин дает два преимущества:
1. Во-первых, мы надеемся, что они помогут
сделать понятие шины менее абстрактным
для вас. Эти шины обозначены соответст-
вующим образом и определяются дорожка-
ми, расположенными вдоль всей платы.
2. Во-вторых, эти шины позволяют (как в лю-
бом компьютере) упорядочить монтаж эле-
ментов схемы. Благодаря им у вас не должна
возникать частая необходимость соединять
компоненты вашей схемы длинными прово-
дами. Линии шин расположены вблизи слоя
«земли» платы, что делаем их менее уязви-
мыми к перекрестным наводкам, чем длин-
ные, запутанные провода. Кроме того, шины
выглядят намного аккуратнее, чем мешанина
проводов17.
На рис. 16L.3 показано, как выглядят шины
верхнего и нижнего слоя печатной платы.
17 Вы можете возразить, что вероятность перекрестных
наводок будет большей для дорожек, расположенных
близко друг с другом на протяжении почти полметра, чем
для пучков проводов, извивающихся над платой. Вы правы
в этом отношении. Но мы предвидели эту проблему и рас-
положили дорожку «земли» между смежными сигнальны-
ми дорожками шин. В результате перекрестные наводки
значительно уменьшаются.
648
16L Лабораторное занятие: счетчики
Нижний слой
Верхний слой
Цифровая
лавиатура
одключена
своей
!ине
^Свободные Дисплей подключен
шины внутренне к шине данных
Выделенные шины и адресной
(шины адреса, данных,
цифровой клавиатуры)
Рис. 16L.3. Шины печатной платы, на которой расположены
обычные макетные платы
На правом изображении можно видеть, что не-
которые внешние устройства уже подключены
к выделенным шинам. В частности:
♦ плата дисплея подключена к 16-разрядной
адресной шине и к 8-разрядной шине данных;
♦ цифровая панель подключена к 8-разрядной
шине данных цифровой клавиатуры. Эта
шина данных отличается от общей шины
данных. Разница между этими двумя шина-
ми данных станет скоро понятной, когда мы
запустим в работу общую шину данных на
лабораторном занятии 17L.
Обзор конфигурации
На рис. 16L.4 показан общий вид подключения
дисплея и цифровой панели к большой макет-
ной плате.
16L3.16-разрядный счетчик
Сегодня мы установим на общую макетную
плату универсальное 16-разрядное устройство,
предназначенное для ручного определения
адреса в нашем микрокомпьютере. Это устрой-
ство реализовано на микросхеме ПМЛ, во мно-
гом подобной ПМЛ, которую вы разработаете
и, возможно, запрограммируете для реализа-
ции логики, связывающей процессор с другими
компонентами компьютера18. Это устройство
обладает следующими возможностями:
♦ Режим счета может быть как суммирующий,
так и вычитающий, что удобно для наших
целей: вскоре (на лабораторном занятии
17L) мы будем использовать этот счетчик
для того, чтобы переходить на определенную
ячейку памяти, т. е. для указания определен-
ного адреса.
♦ Счетчик имеет выходы с тремя состояниями,
что позволит нам подключить их непосред-
ственно к адресной шине компьютера.
♦ В счетчик можно загружать начальное зна-
чение. Сегодня мы используем сигнал за-
грузки LOAD* для того, что создать счетчик-
делитель на произвольное число. Позже, на
лабораторных занятиях по микропроцессо-
ру, мы используем этот сигнал для перехода
по конкретному адресу памяти.
Функция загрузки реализована двумя аль-
тернативными способами с помощью двух
выводов управления:
• Асинхронная загрузка. Загрузка в этом
режиме осуществляется сразу же по активи-
рованию сигнала загрузки. В данном случае
. это происходит при нажатии кнопки. Такой
режим загрузки удобен в тех случаях, когда
нужно заставить счетчик перейти на опре-
деленный начальный адрес при обращении
к выбранной области памяти. Асинхронная
загрузка управляется подачей соответству-
ющего сигнала на вывод LOAD*.
• Синхронная загрузка. Загрузка в этом
режиме выполняется только по следующе-
му сигналу тактирования после активиро-
вания этого сигнала. Этот тип загрузки ра-
ботает лучше, чем асинхронная, когда она
реализует автоматическую перезагрузку в
Рис. 16L.4. Подключение дисплея и цифровой панели к ма-
кетной плате.
18 Более конкретно: наш счетчик реализован на устройстве
ПМЛ XC9572XL с питанием 3,3 В производства компании
Xilinx.
16L.3.16-разрядный счетчик
649
счетном цикле. Мы используем этот тип
загрузки на лабораторном занятии 16L.4
для создания программируемого счетчика-
делителя на JV, где значение N вводится с
цифровой клавиатуры. Синхронная за-
грузка управляется подачей соответствую-
щего сигнала на вывод SYNC_LD*.
♦ Устройство содержит выход входного пере-
носа CarryIN* и выходного переноса Саггуоит*,
которые обычно предназначены для каска-
дирования нескольких устройств для созда-
ния счетчика с большим количеством раз-
рядов. Вход CarryIN можно использовать для
управления счетчиков, в частности или вести
счет, или сохранять текущее значение, игно-
рируя сигнал тактирования. Вход входного
переноса CarryIN можно рассматривать как
эквивалент входа Г, который управляет од-
ним Т-триггером. Мы собрали такой триггер
из D-триггера и вентиля ИСКЛ-ИЛИ на лабо-
раторном занятии 15L.
Мы воспользуемся функцией CarryIN, кото-
рую также можно рассматривать как функ-
цию разрешения при создании секундомера
на лабораторном занятии 16L.5.1, а затем
измерителя периода на лабораторном заня-
тии 16L.5.2. А функция выходного переноса
Саггуоит* будет полезной для тех, кто будет
использовать этот счетчик для реализации
измерителя скорости реакции на лаборатор-
ном занятии 19L.
♦ Счетчик также оснащен функцией синхрон-
ного сброса RESET*.
16L3.1. Предварительное
знакомство со счетчиком
и его сигналами
На рис. 16L.5 приведен фрагмент схемы ком-
пьютера, собираемого из дискретных компо-
нентов на большой макетной плате, содержа-
щий рассматриваемый счетчик. Независимо от
того, используется ли счетчик в схеме компью-
тера на большой макетной плате или автоном-
но на отдельной макетной плате, сигналы будут
одинаковыми.
Микросхема ПМЛ, на которой реализован наш
счетчик, предназначена для поверхностного
монтажа и для того, чтобы ее можно было
установить на макетной плате, она смонтиро-
вана на соответствующей переходной плате.
(Возможно, вы уже встречались с подобной
переходной платой на лабораторных заняти-
ях 5L и 12L.) На рис. 16L.6 изображена такая
Дисплей отображения адресов (светодиодный)
Загрузка f
адреса*^
Внешняя цифровая
клавиатура
(сигналы и питание
подаются через
DIP-шлейаэ) щ$ t Д
т
Шина данных цифровой панели
Рис. 16L5.16-разрядный счетчик на микросхеме ПМЛ и его сигналы управления
650
16L Лабораторное занятие: счетчики
подключены к восьми выходным линиям циф-
ровой панели, а 16 выходных линий (выходы
счетчика Q^...^, обозначенные на рис. 16L.7
как А15...А0) будут подключены к 16 адресным
линиям на плате жидкокристаллического дис-
плея.
Рис. 16L.6. Микросхема ПМЛ (в корпусе TQFP), установлен-
ная на переходную плату, чтобы использовать ее в макетной
плате
Примечание
Цоколевка микросхемы ПМЛ на рис. 16L7 несколь-
ко иная, чем микросхемы ПМЛ, используемой на
этом лабораторном занятии (рис. 16L8).
переходная плата с установленной на ней ми-
кросхемой ПМЛ. Мы рекомендуем добавить
на эту плату метки с обозначениями выводов
микросхемы.
16L3.2. Сборка счетчика
на отдельной макетной плате
На рис. 16L.7 показан пример сборки счетчика
на отдельной макетной плате, а не на большой
16L3.3. Сборка счетчика на
большой общей макетной плате
На рис. 16L.8 показана цоколевка микросхемы
ПМЛ, на которой реализуется наш счетчик.
Названия сигналов в левом и правом столбцах
таблицы справа на рис. 16L.8, которые разме-
щены в столбце ближе к центру, обозначают
выводы питания (положительное напряжение
Рис. 16L.7. Сборка счетчика на отдельной макетной плате
общей макетной плате для сборки компьютера
из дискретных компонентов. Правда, на этом
рисунке изображена микросхема ПМЛ в корпу-
се PLCC19, тогда как наша микросхема выпол-
нена в корпусе TQFP20.
На рисунке изображены подключения толь-
ко линии управления входом, а также линии
параллельного ввода Р9 и Р8, которые пока-
заны подключенными на «землю» через DIP-
переключатель. Позже (на лабораторном за-
нятии 16L.4) линии ввода данных Р7...Р0 будут
19 Англ. plastic leadless chip carrier — безвыводной пласти-
ковый кристаллодержатель.
20 Англ. thin quad flat package — тонкий плоский микро-
корпус с четырехсторонним расположением выводов.
и «земля»), а также выводы для программиро-
вания устройства. Выводы для программиро-
вания устройства TMS, TDI, TDO и ТСК можно
игнорировать.
16L3A Подключение микросхемы
ПМЛ
Первым делом подключаем
положительное питание и «землю»
Для питания нашей микросхемы ПМЛ исполь-
зуется шесть линий: три для положительного на-
пряжения и три для «земли». Мы рекомендуем
первым делом подключить эти шины питания.
16L3.16-разрядный счетчик
651
Название входа/выхода Функциональный блок
С Направление Вывод
ррррррррррр
44444333333
43210987654
Р1
Р2
РЗ
Р32
£* Микросхема Р30
м ПМЛ счетчика ^
Р7 в корпусе QFP р
Р26
Р24
Р23
РРРРРРРРРРР
111111112 2 2
2345678Э012
Счетчик
reset bar
syndoadjjar
a!5
G
a!3
all
a9
a7
TDI
TMS
TCK
a5
a3
Al
3 3V
d9
G
d6
d4
d2
d8
dO
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
cout bar
elk
loacLbar
upbar__down
cinjaar
oe_bar
al4
al2
alO
3 3V
a8
a6
a4
a2
aO
d7
d5
d3
3.3V
G
TDO
dl
Рис. 16L.8. Цоколевка микросхемы ПМЛ, на которой реализован наш счетчик
Обычно все считают, что подключение питания
является нудным занятием, которым должен
заниматься напарник по лабораторному заня-
тию. Тем не менее попытайтесь выработать у
себя привычку подключать шины питания пер-
вым делом21. Если ваша микросхема ПМЛ тре-
бует питания +3,3 В, как, например, XC9572XL,
то обязательно убедитесь, что подается именно
это напряжение питания, а не +5 В.
Питание («земля» и, возможно, положитель-
ное напряжение) на ваше устройство в корпу-
се PLCC будет подаваться с белых макетных
плат. Поэтому не упустите или не отклады-
вайте на потом подключение питания к вер-
тикальным шинам «земли» и положительного
напряжения макетных плат, которое берется
из точек G («земля») и Vcc (+U)> расположен-
ных на обоих концах каждой белой макетной
платы. Положительное напряжение питания
составляет +5 В, даже если вы используете для
своего счетчика ПМЛ с напряжением питания
+3,3 В, поскольку с макетных плат будет по-
ступать питание на 5-вольтовую логику. Мы
рекомендуем вам потратить пять минут на
то, чтобы подключить питание на эти макет-
ные платы, а также соединить перемычками
обе половины всех 10 шин питания. Если вы
отложите эту небольшую работу на потом, то
21 Может показаться, что было бы маловероятным не
подключить линии питания, но, как уже отмечалось ранее,
это распространенная ошибка.
сэкономите несколько минут сейчас, но, воз-
можно, испытаете досаду и раздражение поз-
же, когда какая-либо часть вашей схемы не
будет работать так, как ожидается, потому что
на нее не подается питание.
Линии управления
Далее мы рекомендуем, чтобы те из вас, кто со-
бирает компьютер на большой макетной плате
из дискретных компонентов, подключили ли-
нии управления счетчика на кристаллодержа-
теле типа PLCC устройства ПМЛ к свободным
линиям шины на макетной плате. Эти свобод-
ные шины, так и обозначенные на рис. 16L.3,
находятся у верхнего и нижнего краев печатной
платы. Количество линий свободных шин до-
статочно большое, поэтому полезно промарки-
ровать те из них, которые будут использовать-
ся. Для этого можно прикрепить наклейки или
к идущим к ним проводам, или на саму плату.
Далее приводится список и краткое описание
этих сигналов управления:
♦ CLK — сигнал тактирования (активный по-
ложительный фронт, как обычно).
♦ CIN* — входной перенос или разрешение.
♦ COUT* — выходной перенос; активируется
значением FFFFh для суммирующего счета
и значением 0000h для вычитающего).
♦ ОЕ* — управление третьим состоянием.
652
16L Лабораторное занятие: счетчики
♦ LD* — асинхронная загрузка. По активиро-
ванию этого сигнала загружается значение
00 в самые старшие два бита счетчика, значе-
ния с DIP-переключателя — в следующие два
бита, значение с цифровой клавиатуры — в
следующие восемь битов, и значение 0000 —
в самые младшие четыре бита.
♦ SYNCLD* — синхронная загрузка. Счетчик
загружается, как и при асинхронной загруз-
ке, но по следующему сигналу тактирования.
♦ RESET* — сброс. Счетчик обнуляется.
♦ U*/D — задание суммирующего или вычита-
ющего счета. При низком уровне (U*) значе-
ние счетчика инкрементируется по следую-
щему сигналу тактирования, при высоком —
декрементируется.
Эти же сигналы, а также выводы Q счетчика по-
казаны графически на рис. 16L.9.
(5 или 3,3 В,
в зависимости
от устройства)
> (3 вывода)
Счетчик на
микросхеме ТТМЛ
DIP-переключатель—*?-
Цифровая ~4-~
клавиатура
(3 вывода)"*
Рис. 16L.9. Сигналы управления счетчика на микросхеме
ПМЛ
DIP-переключатель управляет четырьмя
линиями
Мы выбрали четырехэлементный DIP-пере-
ключатель для управления двумя линиями:
синхронной загрузки SYNC_LOAD* и сброса
RESET*, а для управления асинхронной загруз-
кой LOAD* — быстродействующую кнопку. (Два
других элемента DIP-переключателя служат
для управления двумя линиями данных счет-
чика: Р9 и Р8.) На рис. 16L.10 слева изображе-
на принципиальная схема подключения DIP-
переключателя к управляемым им линиям, а
справа — монтажная.
DIP-переключатель такого же типа использу-
ется для управления этими четырьмя линиями
также и в варианте схемы на отдельной макет-
ной плате, как показано на рис. 16L.7.
Функция загрузки управляется кнопкой
Управление асинхронной функцией загрузки
счетчика, которая передает в счетчик значение
в параллельном режиме, осуществляется с по-
мощью кнопки. При выполнении этой функ-
ции счетчик ведет себя подобно регистру из
триггеров, а не как обычный счетчик. Восемь
битов загружаемого значения поступают с
цифровой клавиатуры, а два бита — от DIP-
переключателя, описанного на рис. 16L.10.
Кстати, мы редко изменяем положения DIP-
переключателя для этих битов на линиях Р9
и Р8. В большинстве случаев мы оставляем их
на низком уровне.
Используемая нами кнопка имеет два контакта,
которые подключены к четырем выводам. Это
обстоятельство может сбивать с толку, поэтому
на рис. 16L.11 иллюстрируется, как все работа-
ет. На нем также показано, как обработать вы-
воды кнопки, чтобы их можно было вставить
в макетную плату. В их исходном состоянии эти
выводы слишком широкие для гнезд в макет-
ной плате.
ЮкОм
-+5В
Р9-
Р8-
~SYNC_LD
-reset*
II IF W W
Рис. 16L.10. DIP-переключатель управляет четырьмя сигналами счетчика как на большой макетной плате, так и на отдельной
макетной плате
16L3.16-разрядный счетчик
653
Выводы кнопки нужно провернуть, чтобы
они входили в гнезда макетной платы
J* исходном состоянии выводы слишком
"широкие для гнезд в макетной плате
Рис. 16L.11. Конструкция кнопочного переключателя
На рис. 16L.12 кнопка показана установленной
в макетную плату и подключенная для управ-
ления входом асинхронной загрузки LD* счет-
чика.
подключаются; их подключение будет выпол-
нено на следующем этапе, когда в схему будет
добавлена память.
В версии счетчика на отдельной макетной пла-
те эти восемь линий данных цифровой панели
подключаются к линиям Р0...Р7, как уже отме-
чалось в разделе 16L3.2.
Входы управления
Далее подключаем входы управления счетчика.
В частности:
LOAD- (asMic) : : Ж
Рис. 16L.12. Кнопочный переключатель, вставленный в макетную плату и подключенный для управления асинхронной за-
грузкой счетчика
Линии выходов счетчика
Линии 16 выходов счетчика (А0...А15) под-
ключаются к 16 линиям адресной шины. В вер-
сии счетчика на отдельной макетной плате эти
16 линий идут напрямую на плату жидкокри-
сталлического дисплея (см. рис. 16L.15).
Выходные сигналы цифровой
клавиатуры подаются на параллельные
входы счетчика
Другие восемь входных линий подключаются
к счетчику от цифровой клавиатуры. Обратите
внимание на то, что эти линии, исходящие из
DIP-разъема цифровой клавиатуры, внутрен-
не подключены на макетной плате микропро-
цессора к линиям шины, обозначенным KD0...
KD7. Также обратите внимание на то, что эти
линии данных цифровой клавиатуры, обозна-
ченные KD0...KD7, не имеют ничего общего с
линиями основной шины данных, помеченных
D0...D7. Линии основной шины данных пока не
♦ К входу тактирования счетчика CLK подклю-
чаем линию тактирования с цифровой кла-
виатуры ADR CLK.
♦ К входу U*/D микросхемы ПМЛ счетчика
подключаем сигнальную линию цифровой
клавиатуры с таким же названием.
♦ Установите элементы DIP-переключателя,
управляющие входами сброса RESET* и син-
хронной загрузки SYNC-LD*, чтобы деакти-
вировать эти входы, а элементы для входов
Р9 и Р8 таким образом, чтобы на эти входы
подавался сигнал низкого уровня.
♦ Подключите вход разрешения CIN* и вход
управления третьим состоянием ОЕ* к «зем-
ле», чтобы они были постоянно активиро-
ванными.
♦ На данном этапе оставьте вход выходного
переноса COUT* неподключенным.
Список сигнальных входов довольно длинный,
поэтому полезно при их подключении сверять-
ся с рис. 16L.9.
654
16L Лабораторное занятие: счетчики
Выходы Q счетчика
(подают сигналы на
адресную шину, А19...АО)"
Параллельный
с цифровой клавиЯгурьх
Рис. 16L.13. Все необходимые линии подключены к микросхеме ПМЛ счетчика
Счетчик, собранный на общей макетной
плате
На рис. 16L.13 показано, как может выглядеть
монтаж микросхемы счетчика в корпусе PLCC
после подключения адресных линий, линий
данных цифровой клавиатуры и нескольких
линий управления. Мы старались расположить
монтажные провода низко, чтобы в процессе
дальнейшего монтажа какой-либо из них слу-
чайно не выпал. Мы будет постоянно отклады-
вать эту плату в сторону на время, а затем снова
возвращать ее на рабочее место. Нам нравится
монтаж, который может выдержать эти пере-
мещения. Вам он также понравится.
♦ Питание. Переведите ползунковый пере-
ключатель в правом верхнем углу платы
ЖКД в положение «external», чтобы брать
питание +5 В с большой зеленой платы.
♦ Линии адресной шины. Разъем DIN свя-
зывает 16 линий входа дисплея с 16 линиями
адресной шины на печатной плате. Сигналы
на эти линии подаются с выходов Q16 триг-
геров счетчика.
♦ Линии шины данных. Отображаться могут
8 или 16 линий данных. На данном этапе у
нас нет никаких данных для отображения,
но тем не менее сигналы этих «плавающих»
16L.3.5. Добавляем плату дисплея
Вскоре мы будем наблюдать сигналы счетчи-
ка на осциллографе, но прежде чем двигаться
дальше, реализуем другой способ для наблюде-
ния этих сигналов.
Дисплей в версии счетчика, собранного
на общей макетной плате
Плата жидкокристаллического дисплея встав-
ляется в разъем DIN22 на общей печатной пла-
те. Этот разъем обеспечивает следующее:
22 Deutsches Institutfar Normung — Немецкий институт по
стандартизации. Этот институт разработал тысячи европей-
ских технологических стандартов. Данный 48-контактный
разъем — всего лишь один из этих стандартов.
Рис. 16L14. Отображение выходных данных счетчика на
жидкокристаллическом дисплее
16L3.16-разрядный счетчик
655
Питание +3,3 В
■ Сигнал
*""' тактирования"
Питание +5 В
Отображение данных в двоичном формате Отображение данных в шестнадцатиричном формате
Рис. 16L.15. Отображение данных выходов версии счетчика на отдельной макетной плате на подключенном к нему жидко-
кристаллическом дисплее
входов будут отображаться на дисплее. На
последующих этапах они будут отображать
данные, хранящиеся в памяти RAM.
Выходные сигналы счетчика могут отображать-
ся или в шестнадцатеричном или в двоичном
формате. На рис. 16L.14 показан пример отобра-
жения данных в шестнадцатеричном формате,
а на рис. 16L.15 данные отображаются в обоих
форматах. Значение числа намного легче опре-
делить с первого взгляда в шестнадцатеричном
формате. Но когда вы начнете экспериментиро-
вать со счетчиком, мы рекомендуем двоичное
представление, особенно при медленном сигна-
ле тактирования счетчика. Двоичный формат
позволяет понять закономерности счета.
16L3.6. Подключаем цифровую
клавиатуру
К версии счетчика на большой общей
макетной плате
Цифровая клавиатура подключается, вставив
DIP-разъемы 16-жильного кабеля в соответ-
ствующие DIP-разъемы на цифровой панели и
на общей макетной плате. После подключения
цифровой клавиатуры сигнал с линий данных
KD0...KD7 будет поступать на линии входа
счетчика Р0...Р7, которые мы раньше подклю-
чили к линиям данных KD0...KD7 макетной
платы микрокомпьютера.
Дисплей в версии счетчика, собранного
на отдельной макетной плате
Подключите все 16 выходов Q счетчика к двум
8-контактным разъемам шины адреса на пла-
те ЖКД. На рис. 16L.15 плата ЖКД показа-
на подключенной к макетной плате счетчика,
при этом плата счетчика перевернута верхним
краем вниз. Такая ориентация макетной платы
счетчика необязательна. Мы это сделали, по-
скольку так нам не пришлось перекручивать
сигнальные шлейфы, чтобы правильно под-
ключить их.
На рис. 16L.15 заметно искажение младших
разрядов в обоих форматах отображения. Это
объясняется просто высокой частотой счета и
медленной скоростью затвора камеры, которой
делался снимок.
К версии счетчика на отдельной
макетной плате
Вставьте цифровую панель в макетную плату и
подключите ее восемь линий данных к входам
Р0...Р7 счетчика. Сигнал с этих линий данных
будет поступать на средние восемь из 16 линий
входных данных счетчика23. Эти восемь линий
23 Такое подключение может показаться несколько стран-
ным. Но цифровая клавиатура имеет только восемь из 16
линий счетчика, и подключение этих восьми линий по-
середине всех 16 линий, в частности, для подачи сигналов
на выходы Q4...Q11, выглядит как компромиссное реше-
ние. Таким образом, счетчик может загрузить значение,
кратное 16 (что вскоре будет означать адрес, кратный 16).
Добираться от этого значения до требуемого нужно будет
вручную. Но при этом мы никогда не можем быть дальше,
чем за восемь значений от требуемого.
В то же самое время с цифровой клавиатуры нельзя за-
дать очень большие адреса, поскольку она не управляет
четырьмя самыми верхними разрядами счетчика. (В этом
656
16L Лабораторное занятие: счетчики
важны только в том случае, когда счетчик пере-
ходит в режим загрузки.
режим выполнения сброса: синхронный или
асинхронный25.
Работает ли ваш счетчик должным
образом?
Будем надеяться, что ваш счетчик работает
должным образом. Удостовериться в этом мож-
но, нажав кнопку инкрементации INC на циф-
ровой клавиатуре. Значение счетчика должно
увеличиться на единицу. А при нажатии кнопки
декрементации DN значение счетчика должно
уменьшиться на единицу. Нажатие кнопки RPT
тактирует счетчик сигналом частотой около
20 Гц, по умолчанию в суммирующем режиме;
вычитающий режим включается одновремен-
ным нажатием кнопок DN и RPT.
Попробуйте выполнить загрузку и сброс
счетчика
Нажмите кнопку загрузки LD*. В результате
в средних двух разрядах числа в шестнадца-
теричном формате на дисплее должно ото-
бразиться значение, введенное на цифровой
клавиатуре24. Далее попробуйте выполнить
синхронную загрузку. Для этого переместите
соответствующий ползунок DIP-переключате-
ля, чтобы подать на линию синхронной загруз-
ки SYNC_LOAD* сигнал низкого уровня (что не
окажет немедленного эффекта), а затем подайте
на счетчик сигнал тактирования с линии ADCLK*
цифровой панели. Протестировав синхронную
загрузку, деактивируйте сигнал SYNC_LOAD*.
Далее попробуйте выполнить сброс счетчика,
подав соответствующий сигнал на линию RESET*
с помощью DIP-переключателя. Установите
16L3.7. Испытываем счетчик
на высокой скорости
Теперь вместо сигнала ADRCLK* цифровой кла-
виатуры, которая подавала сигнал тактирова-
ния на счетчик, подключите сигнал логическо-
го уровня от генератора сигналов. Попробуйте
подать сигнал тактирования с частотой в не-
сколько килогерц.
Наблюдайте на осциллографе сигнал такти-
рования и выход счетчика Qq, а затем сигнал
тактирования и выход Q^ (В обоих случаях
запускайте развертку сигналом с наблюдаемо-
го выхода Q, при этом если наблюдается более
чем один выход Q, то для запуска развертки ис-
пользуйте самый медленный из них.)
В маловероятном случае неустойчивого пове-
дения счетчика может потребоваться очистить
сигнал тактирования. Для этого сигнал ТТЛ с
генератора сигналов, используемый в качестве
сигнала тактирования, пропустите через от-
дельный логический вентиль с гистерезисом.
Принцип иллюстрируется на рис. 16L.16.
Затем исследуйте сигналы на выходах (^ и Q^.
Наблюдаете ли вы какую-либо задержку сиг-
нала выхода Q высшего разряда относительно
сигнала выхода меньшего разряда, подобную
той, которая наблюдалась в счетчике со сквоз-
ным переносом даже небольшой разрядности,
который вы собрали на лабораторном заня-
тии 15L?26 Теперь исследуйте сигнал выходно-
го переноса COUT*27. Развертку нужно будет
Сигнал ТТЛ 74НС14
от генератора сигналов
Рис. 16L.16. Зашумленный сигнал тактирования можно очистить, пропустив его через отдельный логический вентиль
локальный сигнал тактирования подается
на вход тактирования счетчика
отношении некоторую помощь могут оказать линии Р9 и
Р8, подключенные в DIP-переключателю.) Но мы не дума-
ем, что эти ограничения функции загрузки LOAD счетчика
будут слишком проблематичными.
24 Как упоминалось ранее в разделе 16L.3.5, значения на
дисплее могут отображать число как в шестнадцатерич-
ном, так и в двоичном формате. Требуемый формат уста-
навливается с помощью ползункового переключателя,
расположенного слева внизу на плате дисплея.
25 Подобно всем функциям счетчика, за исключением
асинхронной загрузки, сброс выполняется в синхронном
режиме, т. е. по приходу сигнала тактирования.
26 Будем надеяться, что нет.
27 В суммирующем/вычитающем счетчике, подобном дан-
ному, этот перенос иногда еще называется «заниманием»
при работе в режиме вычитания, по аналогии с арифмети-
ческой операцией вычитания. Мы же будем называть его
просто переносом.
16LA. Создаем ужасную музыку
657
запускать по этому сигналу переноса. Обратите
внимание, что длительность этого сигнала со-
ставляет всего один период сигнала тактирова-
ния, поэтому он может выглядеть очень узким,
если развертка экрана охватывает несколько
сигналов тактирования.
Если наблюдать сигналы выходов (^ и Q на до-
полнительной паре каналов осциллографа, то
можно увидеть разницу между сигналом пере-
носа при суммирующем и вычитающем счете.
Если у вас есть настроение снова поэкспери-
ментировать с жидкокристаллическим диспле-
ем, уменьшите частоту сигнала тактирования,
чтобы можно было наблюдать отдельные со-
стояния. Удостоверьтесь, что эта разница в сиг-
нале переноса действительно присутствует при
разных режимах счета.
16L4. Создаем ужасную
музыку
Если сигнал выходного переноса COUT* счет-
чика подать на его вход синхронной загруз-
ки SYNC_LOAD*, то при каждом переполнении
счетчик будет перезагружать сам себя. В част-
ности, он будет загружать в себя 16-битовое
значение, которое создается из двух битов ли-
ний DIP-переключателя (Р9 и Р8, на которых
установлен низкий уровень), восьми битов
цифровой панели и четырех самых младших
битов, которые постоянно установлены в нуле-
вое значение внутри счетчика. Таким образом,
вводимое с цифровой клавиатуры число может,
определить начальное значение счета.
Процесс счета в вычитающем режиме доволь-
но прямолинеен, поэтому мы рекомендуем
временно подать постоянный высокий уро-
вень (+5 В) на вход управления направлением
счета UPVDN, пока мы будем работать на дан-
ном этапе.
На вход синхронной загрузки SYNC_LOAD*
подается сигнал выходного переноса COUT*,
поэтому эти два сигнала активируются толь-
ко тогда, когда счетчик находится на грани
обнуления, поскольку вычитающий счетчик
перезагружается каждый раз, когда значение
счета достигает нуля. Следовательно, с цифро-
вой клавиатуры можно задавать значение сче-
та, который выполняется между загрузками.
Таким образом, цифровая клавиатура задает
период и частоту сигнала выходного переноса
COUT*.
Наблюдайте сигнал выходного переноса COUT*
и сигнал на выходе Q^ счетчика, варьируя при
этом значение, вводимое с цифровой клавиату-
ры. Соответствует ли реакция счетчика вашим
ожиданиям? Вводимое с цифровой клавиату-
ры значение содержит восемь битов, а нажатие
одной кнопки обновляет только самые млад-
шие четыре бита. В процессе этого эксперимен-
та желательно сохранять значение старшего
полубайта нулевым. Для этого соответствую-
щие линии можно временно подключить к зем-
ле, чтобы с цифровой клавиатуры на счетчик
подавались только значения битов P0...P3. Это
сделает ваше устройство подобным клавишно-
му музыкальному инструменту, как мы вскоре
и будем использовать его.
Звуковой эффект загрузки:
счетчик с необычным модулем
Для более впечатляющей демонстрации спо-
собности этого загружаемого счетчика варьи-
ровать модуль, т. е. количество устойчивых
состояний, прослушаем частоту его выходного
сигнала. Для этого подадим сигнал выходного
переноса COUT на транзисторный ключ (лучше
всего взять силовой МОП-транзистор), выход-
ной сигнал которого, в свою очередь, подается
на динамик макетной платы. Соответствующая
схема изображена на рис. 16L.17.
Сигнал тактирования-
COU
Счетчик SYNC_
U*/D p7...pO LD
♦5 В
Ж
Цифровая
панель
+5 В
100 Ом
Счетчик-
делитель на 2
100 мкФ
Рис. 16L.17. Счетчик, как музыкальный инструмент: увеличивает громкость, независимо от частоты
658
16L Лабораторное занятие: счетчики
Если вы хотите пощекотать нервы своим со-
седям по лаборатории более громким звуком,
пропустите сигнал выходного переноса COUT*
на Т-триггер, прежде чем подавать его на ди-
намик. Выходной сигнал Т-триггера со скваж-
ностью в 50% будет громче, чем короткий им-
пульс сигнала выходного переноса. Без такой
модификации из-за низкой скважности сигнал
выходного переноса может быть едва слышим
при некоторых периодах счета.
Исправляем интересный изъян
в этой схеме
Проблема искажений в сигнале выходного
переноса COUT*
Когда мы попробовали выполнить этот экс-
перимент, то с удивлением обнаружили, что
сигнал выходного переноса COUT*, который
соответствует нулевому состоянию счетчика
в вычитающем режиме, содержал жуткие иска-
жения. Эти искажения были настолько значи-
тельными, что тактировали триггер-делитель
на два, используемый для создания выходного
сигнала со скважностью величиной 50%. В ре-
зультате работа нашей «музыкальной маши-
ны» была полностью нарушена, как показано
на рис. 16L.18.
Проблема решается синхронизацией сиг-
нала COUT* посредством триггера
На осциллограммах на рис. 16L.18 можно заме-
тить, что искажения происходят после фронта
сигнала тактирования. Это обычное развитие
событий, поскольку искажения создаются из-
менениями сигналов, вызываемых тактирова-
нием. Такие искажения полностью безвредны
Сигнал тактирования
Выходной перенос ПРНСВЬГХ*
(скомбинированный)
Выход Q триггера-делителя на два,
тактируемый сигналом ТТРНСВЬГХ*
Триггер реагирует на искажения
входного сигнала тактирования
для триггера, тактируемого сигналом, вызы-
вающим их, которым в данном случае является
сигнал тактирования основного счетчика.
Проблема искажений в сигнале переноса реша-
ется с помощью схемы синхронизации, которая
блокирует искажения (рис. 16L.19). Теперь ис-
кажения не проходят через триггер, поскольку
они происходят после фронта тактирования,
который обновляет состояние этого синхрони-
зирующего триггера.
Если искажения в сигнале выходного перено-
са нарушают нормальную работу вашей музы-
кальной машины, добавьте в ее схему такой
синхронизирующий триггер перед триггером-
делителем на два, который повышает скваж-
ность выходного сигнала и подает его на ди-
намик. Зарисуйте чистый выходной сигнал
триггера-делителя на два. (Чтобы, посмотрев
на этот рисунок спустя месяц-другой, вы снова
вспомнили, какой вы умный.)
Когда все работает должным образом, цифро-
вая клавиатура должна функционировать, как
клавиатура грубого музыкального инструмента.
Замечаете ли вы снижение тона сигнала на окта-
ву при изменении значения кнопки с X на 2Х?
Фальшь вследствие нулевого состояния
При очень низких значениях, вводимых с циф-
ровой клавиатуры, наш музыкальный инстру-
мент начинает «фальшивить», потому что в
каждый цикл вычитаемого счета включается
дополнительное нулевое состояние.
Например, при загрузке в счетчик значения 1
с цифровой клавиатуры, счетчик в действи-
тельности получает значение 1610, потому что
Искажения
гш:
Счетчик-делитель на 17 (вычитающий счетчик,
загружаемый значением 16 по сигналу TTPHCg^)
Подробности искажения
в сигнале ТТРНСВШХ*
Рис. 16L.18. Искажения в сигнале выходного переноса COUT* (ПРНСВЫХ.) могут нарушать работу устройства, тактируемого
этим сигналом
16L5. Применение счетчика: секундомер
659
с
Сигнал ТТРНСВЬЕХ*
с искажениями
Очищенный от
искажений сигнал
TTPHCDkTV.
Сигнал
тактирования счетчика
Рис. 16L.19. Синхронизирующий триггер может удалить
искажения из сигнала выходного переноса
четыре младших бита имеют постоянное нуле-
вое значение. Счетчик ведет вычитающий счет
от 16 до 0, а затем перезагружает значение 16.
Таким образом, он проходит через 17 состоя-
ний, а не через 16. При загрузке с цифровой
клавиатуры значения 2 можно ожидать удвое-
ния периода, но значение 2 создает 33 состоя-
ния, тон которых отличается от тона 17 состоя-
ний не совсем на октаву. В действительности
это небольшое различие в числе состояний вы-
зывает разницу звучания почти на полтона, в
чем можно убедиться на слух28.
16L5. Применение счетчика:
секундомер
Мы признаем, что это длинное лабораторное
занятие. Но мы задаем эти упражнения пото-
му, что думаем, что вы найдете их как развле-
кательными, так и познавательными. Так что
делайте столько, сколько вам под силу, и не ис-
пытывайте чувства вины, если вы не соберете
схему секундомера. У вас будет еще одна воз-
можность собрать эту схему на лабораторном
занятии 19L, а также использовать ее на прак-
тике как измеритель емкости.
Очень незначительная переделка нашего 16-
битового счетчика позволит запускать и оста-
навливать его по желанию. Все, что для этого
нужно, так это добавить в схему переключатель
для управления уровнем сигнала входного пе-
реноса CIN*. С такой модификацией наш счет-
чик станет примитивным секундомером. Его
можно сделать более продвинутым и удобным,
добавив несколько триггеров и два логических
вентиля И-НЕ. Это позволит нам фиксировать
выходное значение счетчика на дисплее (в ре-
зультате чего процесс суммирующего счета
больше не будет отображаться на дисплее), а
после фиксации результата автоматически вы-
полнять сброс счетчика.
На рис. 16L.20 изображена схема, которая спо-
собна измерять (в ее текущей конфигурации)
длительность периода, в течение которого сиг-
нал находится на низком уровне.
Схеме измерения периода можно найти не-
сколько разных применений. Например, на
лабораторном занятии 19L мы предлагаем ис-
пользовать ее для измерения периода (или,
более точно, полупериода) выходного сигнала
RC-генератора на микросхеме 555. Затем, не
меняя значения резистора R, можно подклю-
чать конденсаторы С различной емкости и из-
мерять период полученного сигнала. Иными
словами, мы получим устройство измерения
емкости конденсаторов. Это может быть до-
стойной наградой за полчаса, потраченные на
монтаж схемы.
Наигравшись вдоволь со схемой, верните ее в
исходное состояние. Поэтому обозначайте вно-
симые в нее изменения, например, вставляя
какие-либо хорошо заметные провода в точ-
ках, из которых вы удалили рабочие провода
схемы. (Схема содержит всего лишь несколько
таких точек.)
пауза/счет
Сигнал тактирования"
(от генератора^ 1
сигналов) » >
CIN (входной
перенос)
Сброс
г1 L
Рис. 16L.20. Блок-схема секундомера
SyncLd %
(Синхронная
загрузка)
28 Возможно, вы узнали в интервале от 2 до 1 большую
септиму.
16
Дисплей
660
16L Лабораторное занятие: счетчики
16L5.1. Первый этап: создаем
простой секундомер . rr^Z^rTZTZZTTI
Удалите провода, которые подают соответству- щ ><*^^*~"****-w^*,*^,- апуск
ющие сигналы на вход тактирования CLK и вход [^
синхронной загрузки SYNC_LD*; также удали- * Импульс1*
те ПрОВОД, ПОДКЛЮЧаЮЩИЙ КОНТаКТ ВХОДНОГО 3 (сохранение*)
переноса CIN* на «землю». Далее подайте на *«~~^^ <- ^
вход тактирования CLK ТТЛ-сигнал от генера- Щ (обнуление*)
тора сигналов. Используйте для этого внешний
генератор сигналов, а не встроенный в макет- ; ш >
НуЮ плату, ПОСКОЛЬКУ нам ВСКОре потребуется Рмс 16L22. Требуемое тактирование сигналов сохранения
частота выше, чего его максимальные 100 кГц. save и обнуления clear
Подайте на вход SYNC_LD* сигнал высокого
уровня. __
Jr Импульс сохранения выхода приходит рань-
Сначала удостоверьтесь в том, что счетчик
можно запустить и остановить, подав с помо-
щью кнопки на вход входного переноса CIN*
сначала сигнал низкого уровня, а затем — вы-
сокого. Как уже рассматривалось ранее, обну-
лить (сбросить) счетчик можно, нажав кнопку
сброса, подающую соответствующий сигнал на
вход сброса RESET*. Теперь у нас есть простей-
ший секундомер.
16L5.2. Второй этап: создаем
автоматический измеритель
периода
Собранный в предыдущем разделе секундомер
можно преобразовать в измеритель периода,
добавив в него функцию автоматической фик-
сации выходных сигналов и функцию сброса
счетчика, упомянутые ранее. На рис. 16L.21
изображена блок-схема счетчика с этими изме-
нениями.
Для сохранения результатов и последующего
сброса счетчика нам нужна схема, которая бу-
дет вырабатывать импульсы, тактируемые, как
показано на рис. 16L.22.
ше, чем импульс сброса, чтобы не допустить
затирания процессом сброса данных, которые
мы хотим сохранить. Возможно, что вы узнае-
те в этой паре импульсов, вызываемых нарас-
танием сигнала счета Count* (обозначенного
на рис. 16L.22 как «Запуск» по выводу одно-
вибратора), точный выходной сигнал однови-
братора с цифровым тактированием, который
вы собрали на лабораторном занятии 15L. Мы
надеемся, что вы сохранили ту схему. Если нет,
то она снова показана на рис. 16L.23, и вы ее
опять можете собрать приблизительно за пять
минут.
Первый импульс, обозначенный Latch_En* (Раз-
решение защелки) на рис. 16L.21 и Сохранение*
на рис. 16L.22, обновляет состояние дисплея.
Этот импульс подается на два вывода платы
жидкокристаллического дисплея, обозначен-
ные Latch_En*, каждый из которых управляет
одной 8-битовой защелкой. Чтобы обновить
16 битов, эти выводы нужно соединить вме-
сте. Также нужно задать следующие параметры
дисплея:
♦ no labels (не использовать метки);
♦ 16-битовый дисплей;
♦ двухлинейный дисплей;
-Счет-
Двойной
►одновибратор
A Reset* (Сброс)
Сигнал
тактирования
Счетчик
Рис 16L.21. Блок-схема измерителя периода
Latch_En*
(Разрешение
защелки)
Дисплей
16L5. Применение счетчика: секундомер
661
♦ 8-элементный DIP-переключатель у правого
верхнего края платы ЖКД нужно установить
в положение 16 (а не в положение Мих).
Прозрачная защелка будет принимать новую
информацию, пока на входе разрешения при-
сутствует сигнал низкого уровня, и будет сохра-
нять полученную информацию без изменений,
когда уровень сигнала разрешения сменится на
высокий.
Обратите внимание на то обстоятельство,
что, поскольку в дисплее используются про-
зрачные защелки, а незапускаемые по фронту
триггеры, нам нужно генерировать разрешаю-
щий импульс, а не обычный фронт. Этот при-
мер иллюстрирует неудобство такого псевдо-
тактирования. Тактирование по фронту на-
много лучше. (Возможно, вы спросите, поче-
му же тогда мы не спроектировали запуск по
фронту29.)
Второй импульс обнуляет счетчик после того,
как результат счета был надежно сохранен в за-
щелках.
Формируем требуемые импульсы
посредством двойного одновибратора
На рис. 16L.23 показана схема одновибратора,
который вы собрали на лабораторном заня-
тии 15L.
Сигнал Latch_En* (разрешение защелки) с этой
схемы подается на вход Latch_En* дисплея.
Введите на цифровой клавиатуре значение О,
чтобы загрузить нули, а затем подайте сигнал
Clear* (обнуление) на вход LD*, который, если
Запуск—^
J
Сигнал
тактирования
«Земля» = 8
Clear*
(Обнуление)
(Разрешение
защелки)
29 И возможно, вы вспомните ответ на этот вопрос: про-
зрачная защелка используется потому, что когда мы хотим
вживую отображать входные уровни, нам нужно всего
лишь заземлить вход разрешения, что является нашим
предпочитаемым подходом. А чтобы получить почти жи-
вое отображение, используя запуск по фронту, нам при-
шлось бы подать прямоугольный сигнал тактирования
высокой частоты, а это создавало бы неудобства.
Рис. 16L.23. Схема двойного одновибратора, которую вы со-
брали на лабораторном занятии 15L
вы помните, управляет асинхронной загрузкой.
Мы используем его в качестве асинхронного об-
нуления, поскольку это удобнее» чем синхрон-
ный сброс RESET*, так как для LD* не требуется
сигнала тактирования, чтобы реализовать этот
тип обнуления.
В качестве сигнала тактирования как для одно-
вибратора, так и для счетчика подайте пря-
моугольный сигнал от внешнего генератора
сигналов. Теперь можно установить любую же-
лаемую частоту тактирования. Для начала по-
пробуйте частоту 1 МГц.
С помощью кнопки подайте сигнал на вход за-
пуска одновибратора (обозначенный Запуск
на рис. 16L.23) и на вход входного переноса
счетчика CIN*. Вы должны увидеть, что схема
измеряет время, в течение которого вы удер-
живаете низкий уровень сигнала на входе пере-
носа CIN*. (При частоте сигнала тактирования
1 МГц длительность этого интервала, конечно
же, измеряется в микросекундах.) Обратите
внимание, что счет ведется в шестнадцате-
ричном формате, что несколько неудобно для
большинства из нас.
Наигравшись вдоволь со своим измерителем
периода, восстановите исходный монтаж счет-
чика и дисплея, чтобы в следующий раз счет-
чик можно было задействовать по обычному
назначению: формировать адреса памяти, ко-
торую мы установим на лабораторном заня-
тии 17L.
16W. Примеры с решениями:
применения счетчиков
16W.1. Счетчики
с необычными модулями
Когда-то задача проектирования схем, в кото-
рых используются счетчики, требовала разра-
ботки самого счетчика. Необходимость в этом
отпала с появлением счетчиков на микросхе-
мах, в результате чего проектирование основ-
ной схемы стало довольно простой задачей.
А программируемые устройства счетчиков, до-
ступные в настоящее время, делают эту задачу
по-настоящему легкой.
Метод применения микросхемного счетчика,
описанный в этой главе, не самый современ-
ный, поскольку такие счетчики дают возмож-
ность рассмотреть некоторые полезные во-
просы тактирования. В частности, мы сможем
рассмотреть разницу между синхронными и
асинхронными функциями. На рынке предла-
гаются микросхемные счетчики с обоими типа-
ми сброса. Например, 4-разрядный двоичный
счетчик на микросхеме 74НС161 оснащен функ-
цией асинхронного сброса, а такой же счетчик
на микросхеме 74НС163 имеет синхронный
сброс. Затем мы рассмотрим несколько более
интересных проблем, которые возникают при
создании инструмента для измерения какой-то
величины на основе счетчика.
Мы соберем счетчик-делитель на 13. Полностью
синхронный загружаемый счетчик позволяет со-
брать один из таких счетчиков почти с такой
же легкостью, как просто вытащить счетчик-
делитель на 16 из ящика.
Первым делом сравним синхронные и асин-
хронные функции загрузки или обнуления.
Указать разницу будет нетрудно: синхронная за-
грузка данных, присутствующих на входах, осу-
ществляется строго по сигналу тактирования.
При асинхронной же загрузке присутствующие
на входах данные загружаются сразу же (конеч-
но же, после задержки распространения), т. е.
асинхронные функции не ожидают сигнала так-
тирования. Как синхронная, так и асинхронная
загрузка или сброс имеют больший приоритет,
чем обычная операция счета.
Но понять важность этой разницы будет труд-
но, не рассмотрев несколько соответствующих
примеров.
Задача: счетчик-делитель на 13
Имея в наличии счетчик-делитель на 16 (кото-
рый ведет счет в обычном двоичном формате
от 0 до 15), создайте из него счетчик-делитель
на 13, т. е. счетчик, который ведет счет от 0 до
12 или через другой набор из 13 состояний.
Определитесь, хотите ли вы использовать функ-
ции сброса и/или загрузки, а также с типом этих
функций — синхронный или асинхронный.
Неудачное решение:
асинхронное обнуление
На рис. 16W.1 изображена схема возможного,
но плохого решения. В частности, схема обна-
руживает излишнее 13-е состояние и по этому
событию обнуляет счетчик.
Почему этот подход плохой? Кратко можно
сказать, что эта схема счетчика принимает не-
нужное или ложное состояние. В частности,
он содержит изъян в виде кратковременного
ошибочного состояния выходного сигнала.
Чтобы увидеть наличие такого недействитель-
ного состояния, не обязательно прибегать к
временной диаграмме, но она приведена на
рис. 16W.2, где можно увидеть длительность
ложного состояния.
16W.1. Счетчики с необычными модулями
663
Обнаруживаем значение 1101
1
Q3
-13
I
Q2 Qi G
ASYN
ч
lo
С CLR
Рис. 16W.1. Плохой способ преобразования счетчика с обыч-
ным двоичным счетом в счетчик-делитель на 13
Сбойное состояние
Сигнал
тактирования
Оо
«11»
Рис. 16W.2. Плохой дизайн счетчика-делителя на 13: ложное
13-е состояние между значениями 12 и О
В некоторых применениях наличие такого лож-
ного состояния неважно. В конце концов, асин-
хронные счетчики проходят через подобные
ложные промежуточные состояния, но ведь
они все еще востребованы и предлагаются на
рынке. Но проблема может оказаться серьез-
нее. В частности, сигнал обнуления CLR* сни-
мается сразу же после того, как наступает со-
стояние 13. Триггер, который обнулится самым
первым, прекращает этот сигнал. Но это может
произойти до того, как более медленные триг-
геры успеют отреагировать на него, в резуль-
тате чего счетчик может не обнулиться, а при-
нять какое либо произвольное нежелательное
состояние - 12, 9, 8, 5, 4 или 1. Это будет уже
не просто переходное состояние, а серьезная
ошибка. (Очень похожий пример рассматрива-
ется в § 10S2D книги АоЕ.)
Правильное решение:
синхронный счетчик
Счетчик, оснащенный синхронной функцией
обнуления или загрузки, как на микросхеме
74НС163, позволяет легко изменить период
счета, не вызывая ложных переходных со-
стояний и без риска установки неправильной
комбинации. Его также чрезвычайно легко
p< '-
SD!
Q3 Q2 Qi Qo
-13 SYNC
^ OEAR
использовать. На рис. 16W.3 приведена схема
такого счетчика.
Обнаружение
состояния
12ю(И002)
Рис. 16W.3. Синхронный счетчик-делитель на 13, созданный
из счетчика-делителя на 16
Чтобы прервать процесс счета, ограничив пе-
риод 13 состояниями, нам снова нужно опреде-
лить конечное состояние и активировать сигнал
обнуления CLR*. Но на этот раз нам необходимо
определить не значение 13, как раньше, а зна-
чение 12. При наступлении этого состояния
логическая схема дает инструкцию счетчику
выполнить обнуление по следующему сигналу
тактирования.
В случае если этот аргумент вас не убедил, то
на рис. 16W.4 показана временная диаграмма,
отображающая примерное поведение данной
схемы.
Рис 16W.4. Правильный способ модификации счетчика
с синхронной функцией обнуления
Сигнал обнуления CLR* остается активирован-
ным в течение целого периода тактирования,
прежде чем происходит реагирование на него.
Теперь у нас есть правильно работающая схема
счетчика-делителя на 13 с синхронной функ-
цией обнуления. Но слишком плохо, что для
ее реализации потребовался дополнительный
вентиль И-НЕ1. Можно ли каким-либо образом
обойтись без лишнего вентиля?
Используя вместо функции обнуления функ-
цию загрузки, можно получить почти такой
же результат, добавив один инвертор вместо
вентиля И-НЕ. Эта разница несущественна, но
1 Признаемся, что при наличии ПЛУ это сожаление об
одном дополнительном вентиле выглядит нелепо. Но да-
вайте предположим, что мы действительно хотим создать
такую схему на основе микросхемного счетчика.
664
16W. Примеры с решениями: применения счетчиков
давайте воспользуемся нашими универсальны-
ми способностями, создав счетчик-делитель
на 13 таким образом. Замена функции обнуле-
ния на функцию загрузки дает некоторые по-
бочные эффекты. В частности:
♦ применение функции загрузки может выну-
дить использовать необычный набор состоя-
ний (например, начиная счет со значения 3
и заканчивая значением 15, а затем снова
загружая значение 3, чтобы задать 13 со-
стояний). Это неважно, если нас интересует
только конечная частота, но проблематично,
если мы хотим видеть значения счета от О
до 12.
Если же нам нужны состояния 0...12, то исполь-
зование функции загрузки требует, чтобы счет-
чик работал в вычитающем режиме. Мы при-
менили этот подход на лабораторном занятии
16L для создания счетчика с варьируемым мо-
дулем: загружаем начальное значение, считаем
до нуля, а затем используем сигнал займа, что-
бы снова выполнить загрузку. (Сигнал займа —
это просто сигнал переноса для вычитающего
счетчика.)
После переполнения
загружаем 3
Загружаем 3 (13 в дополнительном двоичном коде)
как начальное значение счета
Рис. 16W.5. Счетчик-делитель на 13 с использованием син-
хронной функции загрузки
Не следует слишком беспокоиться об этих эф-
фектах, поскольку количество состояний, через
которые проходит счетчик, всегда по-разному
интерпретируется. Например, при загрузке и
вычитающем счете — кол-во состояний = (счет +
+ 1); при загрузке и суммирующем счете — кол-
во состояний = (дополнительный двоичный
код загруженного значения); а при определе-
нии и обнулении — кол-во состояний = (счет -
- определенное значение + 1). Так что ситуация
сложная во всех случаях, поэтому не имеет зна-
чения, какой подход задействовать.
Синхронные функции загрузки и обнуления хо-
роши тем, что они поддерживают идеал полно-
стью синхронной разработки. Но синхронные
функции не вытеснили полностью асинхрон-
ные просто потому, что иногда первые совер-
шенно неудобны. Например, в схеме счетчика
на лабораторном занятии 16L мы обеспечили
асинхронную загрузку, чтобы пользователь
мог загрузить счетчик, просто нажав кнопку2.
Но в большинстве случаев предпочтение все же
отдается синхронным функциям.
16W.2. При измерении
периода с помощью
счетчика возможны
различные входные
величины
Счет как стратегия проектирования
цифровых схем
Как уже упоминалось ранее в главе 16N, можно
создать разнообразные инструменты, исполь-
зуя следующий общий двухэтапный шаблон:
♦ специализированный под данное приложе-
ние интерфейс генерирует импульс, длитель-
ность которого пропорциональна какой-
либо интересующей нас величине;
♦ схема «секундомера» измеряет длительность
этого импульса.
Сначала рассмотрим несколько неудачных
примеров реализации этого шаблона, а затем
приведем упражнение, в котором попытаемся
решить задачу правильным способом.
16\Л/.2.1.Три неудачные попытки
Первая попытка: датчик силы нажатия
клавиши цифрового пианино
На рис. 16W.6 показана реализация непра-
вильного подхода: часть устройства, которое,
2 По своему горькому опыту мы знаем, что наши студенты
никогда не бывают достаточно сообразительными, что-
бы выполнить двухшаговую процедуру, необходимую для
синхронной функции загрузки. Для некоторых из них за-
дача нажатия кнопки загрузки одной рукой, а затем кноп-
ки тактирования счетчика - другой оказалась слишком
трудной. Иногда нам приходилось наблюдать, как студент
раз за разом нажимает кнопку загрузки, бормоча себе под
нос: «Ну почему же он не загружается?»
16W.2. При измерении периода с помощью счетчика возможны различные входные величины
665
Светодиод
*< «-Фотодатчик
ф* «-Фотодатчик
Выходные сигналы
фотодатчика
Клавиша пианино
Частота клавиши
™aTon Как использовать Тз?
усилия Что делать с этой п
усиления взаимосвязью?
Рис. 16W.6. Первая неудачная попытка: определение силы нажатия клавиши посредством измерения периода
по идее, должно определять громкость звука,
создаваемого нажатием клавиши электронно-
го инструмента, по усилию нажатия клавиши.
Взаимосвязь между цифровым счетом и гром-
костью оказывается обратной.
Мы рассмотрели этот пример в качестве пре-
достережения: скорее всего эту схему для
определения силы нажатия клавиши стоит за-
браковать. Схему можно было бы сделать ра-
ботоспособной, подвергнув сигнал некоторой
постобработке, но необходимость в этом на-
водит на мысль, что должен быль лучший
способ.
Вторая попытка: фиксирование
конечного значения счета
Вся схема на рис. 16W.7 оказывается беспо-
лезной, поскольку содержит одну маленькую
ошибку. Операции обнуления и фиксирования
выполняются по общему импульсу, в результа-
те чего сохраняется обнуленное значение: бес-
конечные нули.
Третья попытка: снова пропускается
последнее состояние счета
Схема, изображенная на рис. 16W.8, тоже не
идеальна.
Хранение: высокий уровень на Б*
Вход/выход: низкий уровень на Е*
Входная частота
Показывает нули после сброса
(таким образом, защелка прозрачная)
Рис. 16W.7. Вторая неудачная попытка: прозрачная защелка фиксирует нули
Решение: исполь
1Гц
по фронту регистр
Остается незначительная проблема: триггер
тактируется в то время, как счетчик продолжает
считать -> время от времени на дисплее появляется
неправильное значение, но лишь в течение секунды,
и редко, если входная частота fBX мала
, 7ici 2ns
:одящая частота
v Период входного сигнала
Рис. 16W.8. Третья неудачная попытка: неправильное время установки регистра
666
16W. Примеры с решениями: применения счётчиков
Эта схема намного лучше, чем предыдущая
(рис. 16W.7), но время от времени она может ге-
нерировать ложное значение счета. Выходной
регистр данной схемы тактируется в то время,
когда счетчик продолжает считать, в результате
чего значение счета может измениться в течение
времени установки счетчика. Но последствия
этого изъяна схемы не особенно серьезные,
просто периодически в течение одной секунды
будет отображаться неправильное значение.
16W.2.2. Успешная схема
ультразвукового дальномера
Теперь, когда у вас есть хороший опыт разра-
ботки схем этого типа (или по крайней мере
опыт выявления недостатков в схемах дру-
гих разработчиков), исследуем одну из таких
схем — ультразвукового дальномера — более
основательно.
Ультразвуковойдальномер3генерируетимпульс
высокого уровня в течение периода, начинаю-
щегося с момента передачи пачки импульсов
ультразвуковой частоты и заканчивающегося
моментом получения отражения этого пере-
данного сигнала. Это показано на временной
диаграмме на рис. 16W.9.
Приход Приход
Посылка отраженного Посылка отраженного
импульса сигнала импульса сигнала
ill i
l
-tocdl
-tocd2
Рис 16W.9. Временная диаграмма работы ультразвукового
дальномера
Таким образом, длительность ультразвукового
импульса пропорциональна расстоянию между
датчиком и поверхностью, от которой этот им-
пульс отразился. В секунду посылается всего
лишь два ультразвуковых импульса.
Задача
Разработайте схему, которая будет генериро-
вать отсчет, измеряющий длительность импуль-
са и, таким образом, расстояние. Схема должна
работать в постоянном цикле, выполняя новые
измерения с наибольшей возможной частотой.
Предполагается, что длительность импульса
может варьироваться от 100 мкс до 100 мс. Вам
доступен генератор колебаний логического
уровня частотой 1 МГц. В частности:
♦ убедитесь в сохранении выходного значения
счетчика, после чего счетчик обнуляется для
начала нового цикла;
♦ выберите соответствующую частоту сигнала
тактирования, чтобы счетчик не перепол-
нялся и чтобы разрешение было не слишком
высоким.
Решение
Решение будет поэтапным. Сначала начер-
тим общую блок-схему, которая показана на
рис. 16W.10. Это решение выглядит почти
точно таким же, как и предыдущие примеры.
Отличается только устройство, которое гене-
рирует период, подлежащий измерению нашим
секундомером.
Датчик отраженного
сигнала
(передача/прием)
Разрешение
Счетчик
Сброс Q
Хп
Дисплей
3 Первоначально схема была разработана для фотокамер
Polaroid, а теперь она часто применяется в роботехнике.
Рис. 16W.10. Блок-схема вывода данных в ультразвуковом
дальномере
Все, что нам осталось сделать, — позаботить-
ся о надлежащем тактировании. Как обычно,
именно этот аспект по-настоящему труден.
В конце каждого цикла нам нужно сохранить
конечное значение счета, а затем обнулить
счетчик. Точно такое же задание стояло перед
нами на лабораторном занятии 16L, но в том
случае наша задача усложнялась тем обстоя-
тельством, что регистр, используемый нами,
был проблематичной прозрачной защелкой на
плате дисплея. Мы решили эту проблему, до-
бавив в схему двойной одновибратор. В данном
же случае мы будем применять триггеры, за-
пускаемые по фронту. Запускаемые по фронту
устройства упрощают задачу проектирования
почти во всех случаях.
16W.2. При измерении периода с помощью счетчика возможны различные входные величины
667
Сигнал тактирования
Счет
Счет* = сигнал тактирования триггера
Счет** = Загрузка'
Дольно/
*лер
Счет** = Зпг
1
Счет
Чо
Счетчик >
Л_ Q
J /■
'8
^ х8
-Сигнал тактирования
8
18 Выходной сигнал
Рис. 16W.11. Пытаемся обеспечить сохранение значения счета до его обнуления
Предположим, что мы взяли счетчик на ми-
кросхеме ПМЛ из лабораторного занятия 16L.
Этот счетчик поддерживает синхронное об-
нуление и асинхронную загрузку, и нам нуж-
но будет решить, какую из этих двух функций
использовать для выполнения операции обну-
ления. Счетчик также имеет входной перенос,
с помощью которого счетчик можно запустить
и остановить с помощью логического сигна-
ла. Как вам нравится временная диаграмма
синхронного сброса счетчика, изображенная
на рис. 16W.11? Тактирование не выглядит
слишком запутанным? Будет ли сохраняться
значение счета, или возможно сохранение зна-
чения обнуления? По временной диаграмме
на рис. 16W.11 можно видеть, что D-триггеры
определенно получат свои данные перед вы-
полнением операции обнуления по следующе-
му сигналу тактирования.
Чтобы немного попрактиковаться в обдумы-
вании этой задачи, рассмотрим другой, не-
много отличающийся пример, показанный на
рис. 16W.12: гипотетический счетчик с асин-
хронной функцией обнуления. Проблема за-
ключается в том, что на регистр подается сиг-
нал тактирования в то время, когда счетчик еще
продолжает считать. Это такой же недостаток,
как и в схеме на рис. 16W.8.
Возможно, что эта сложная схема окажется все-
го лишь эквивалентом более простой схемы,
изображенной на рис. 16W.13.
Поэтому нам следует продолжать работать
с исходной схемой, которая подает сигнал так-
тирования на D-триггеры чуть раньше до об-
нуления счетчика и использует синхронную
Рис. 16W.12. Другой пример: неудачное решение той же са-
мой задачи
Выходной сигнал
Рис. 16W.13. Печальный эквивалент плохой схемы счетчика
с функциями сохранения и обнуления
функцию обнуления. Но и при этом остается
еще одна проблема, которую нужно учиты-
вать, если мы хотим предотвратить случайную
ошибку счетчика.
Такая ошибка возникает по той причине, что
иногда состояния на выходах Q счетчика бу-
дут находиться в процессе изменения в течение
времени установки регистра D. Это опасная си-
туация. Самая сложная проблема заключается
в том, что некоторые D-триггеры регистра по-
лучали бы старые данные (со счета N), тогда
как другие получали бы новые (со счета N+1).
Это хуже, чем может показаться на первый
взгляд, поскольку такая ситуация подразуме-
вает не ошибку в одно значение счета, но воз-
можную громадную ошибку. Представьте себе,
что такая ситуация возникнет между счетом
7Fh (суффикс h означает шестнадцатеричный
формат) и счетом 80h. В таком случае, если нам
сильно не повезет, содержимое регистра может
оказаться равным 8Fh. Это ошибка величиной
почти в два порядка.
668
16W. Примеры с решениями: применения счетчиков
Но такая ситуация будет возникать очень ред-
ко. Прикинем, насколько часто будут состоя-
ния выходов Q. изменяться в течение времени
установки. Период времени, в течение которо-
го уровень на входах триггера важен (на тех-
ническом жаргоне этот интервал называется
апертурой), составляет 1-2 не (сравните с 20 не
для наихудшего случая времени установки).
При частоте сигнала тактирования 1 МГц это
опасное время составляет очень малую долю
периода сигнала тактирования: одну или две
тысячных. Таким образом, шансы получения
ложного счета составляют один к тысяче. Если
мы просто наблюдаем результат на дисплее, та-
кая ошибка не имеет абсолютно никакого зна-
чения. Но если же выходной сигнал управля-
ет устройством, в котором недопустимы даже
очень редкие неправильные значения счета, то
необходимо принять меры для их устранения.
Очень осторожное решение
Далее приводится один способ решения этой
проблемы. В частности, синхронизируется сиг-
нал, который останавливает счет (используя
один триггер), и тактирование триггера задер-
живается на один полный период сигнала так-
тирования, чтобы обеспечить полную установ-
ку значения счета. На рис. 16W.14 приведены
соответствующие временные диаграммы и схе-
ма. Возможно, вы сможете разработать более
простую схему.
Задача. Оснастить схему дальномера
флагом переполнения
Можете ли вы разработать схему, которая бу-
дет записывать факт переполнения счетчика
ультразвукового дальномера? То есть будет
предупреждать нас, когда последним показани-
ям нельзя доверять.
Подсказка
Триггеры имеют свойство запоминания. Качест-
венная схема будет обнулять флаг предупреж-
дения сразу же после прекращения события, вы-
звавшего его установку, т. е. по получению дей-
ствительного значения.
Решение
Далее рассматривается один из способов реше-
ния этой задачи.
♦ Пусть конечная часть импульса переноса так-
тирует триггер, на вход D которого подается
постоянный сигнал высокого уровня. Выход
(^триггера будем называть переполнением.
♦ По завершении периода счетчика сигнал вы-
хода переполнения Q, сохраним в триггере
Предупреждение, который будет сохранять
это значение до завершения следующего из-
мерения.
♦ Тем временем, чтобы все подготовить долж-
ным образом для следующего измерения,
Управляющий
сигнал тактирования
Счет
Qo
Q* = Входной перенос*
Qj = Загрузка
Сигнал тактирования регистра
\
\.
ч
х
Последнее изменение
выходного значения счетчика
i
Обновляем триггеры
(регистр)
Обнуляем
счетчик
Счетчик ■
О, Q,
/
¥■
Входной перенос'
Загрузка*
Счетчик
Сигнал тактирования-
й
х8
Рис. 16W.14. Задержка тактирования триггеров, чтобы не допустить нарушения времени установки
16W3. Измеритель скорости пули
669
Счет1
Предупреждение
Счет
Счет*
TTPHCft,
Счет
•переполнение
предупреждение
Счет
Рис. 16W.15. Один триггер фиксирует факт переполнения, а другой извещает нас об этом
пусть в конце периода триггер переполнения
обнуляется, чтобы он был свободным в тече-
ние следующего периода.
Соответствующая схема изображена на рис.
16W.15 и выглядит довольно изощренной. По-
смотрите, сможете ли вы разработать более
простую схему.
Внимательный разработчик может заметить,
что в этой схеме мы допускаем возможность
кратковременного импульса на сигнале перено-
са. Поскольку сигнал переноса счетчика пред-
ставляет собой просто результат операции И
над значениями нескольких выходов Q, он мо-
жет содержать импульс помехи в переходном
состоянии счетчика. Мы рассмотрели эту воз-
можность в разделе 16N.3.3, где на рис. 16N.21
приведены осциллограммы, показывающие не-
которые из этих событий. Такой импульс поме-
хи может привести к ложной индикации пере-
полнения.
В наиболее грамотной разработке использо-
вался бы синхронный перенос с определением
состояния на единицу меньше состояния пере-
полнения (максимальное значение счета минус
один) и подачей соответствующего сигнала на
синхронизирующий D-триггер. Но мы не хотим
слишком утруждать вас, а только предупредить
о проблемах тактирования, по причине кото-
рых разработка цифровых схем не так проста,
как было описано в главе 14N, где все схемы
были комбинационными и не возникало ника-
ких проблем тактирования.
Как видим, эта схема довольно замысловатая,
но один из используемых в ней методов понадо-
бится нам еще несколько раз: подача постоян-
ного сигнала на вход Д чтобы воспользоваться
хорошим поведением входа, запускаемого по
фронту. Мы снова применим этот метод для ре-
ализации кнопки ввода на лабораторном заня-
тии 22L и реализации аппаратного прерывания
на лабораторном занятии 23L.
16W.2.3, Подведение итогов: полная
схема ультразвукового дальномера
На рис. 16W.16 показана схема с краткими объ-
яснениями простого решения задачи ультра-
звукового дальномера. На рисунке не показа-
на логика предупреждения о переполнении и
логика из раздела Очень осторожное решение.
В схеме изображены четырехразрядные деко-
деры и дисплеи, которые в настоящее время
встречаются очень редко благодаря широкой
доступности жидкокристаллических и даже ор-
ганических светодиодных дисплеев.
16W3. Измеритель скорости
пули
Здесь мы рассмотрим применение триггеров
и счетчиков: схему для измерения начальной
скорости пули. После выстрела пуля пролетает
через два провода, расположенные на расстоя-
нии 10 см друг от друга, перебивая их. Обрыв
первого провода запускает счетчик, а обрыв
второго — останавливает его. Начальная ско-
рость пули винтовки для соревнований состав-
ляет около 900 м/с. С помощью данного ин-
струмента можно сравнивать характеристики
других винтовок с этой скоростью. Эта задача
похожа на разработку измерителя скорости ре-
акции, рассматриваемую на лабораторном за-
нятии 19L, но немного попроще.
На рис. 16W.17 изображена возможная схема
такого устройства.
Далее приводятся желаемые характеристики
схемы:
♦ для определения прохождения пули исполь-
зуется тонкий провод, один конец которого
заземлен, а другой подключен к повышаю-
щему резистору, другой вывод которого
670
16W. Примеры с решениями: применения счетчиков
Период ^Дробности формирования тактовых сигналов:
—-£—- ^регистры тактирования
-Перед обнулением счетчика
(асинхронное обнуление)
Еп| \Со Еп| [Со Еп| [Со En| [Со En| [Co En
Генератор колебании
частотой 1 МГц
Декодер с BCD,
в 7-сегментныи
Декодер с BCDw
в 7-сегментныи
Декодер с BCD
в 7-сегментный
Декодер с BCD
в 7-сегментный
формат
En (разрешение)
Со (выходной перенос ПРНСВЬЕХ)
Рис. 16W.16. Полная схема ультразвукового дальномера, работающего по принципу измерения периода
start...
ARM
Рис. 16W.17. Одно событие запускает счет, другое останав-
ливает
соединен с шиной +5 В. Когда пуля перебива-
ет провод, напряжение повышается до +5 В.
Полагая паразитную емкость величиной
50 пФ, нужно выбрать такое значение сопро-
тивления повышающего резистора, которое
не будет вносить в результат значительной
погрешности;
♦ определитесь, следует ли вам учитывать дре-
безг, состоящий в прерывистом соединении
на «землю» в процессе столкновения с пу-
лей, которая может скрести по перебитому
проводу;
♦ мы хотим обеспечить разрешение величи-
ной 0,1 мкс. Определитесь, сколько разрядов
(двоичных) потребуется вашему счетчику.
Вам нужно будет примерно определить вре-
мя, за которое пуля из винтовки для соревно-
ваний проходит 10 см;
♦ соберите счетчик, соединив последователь-
но несколько микросхем 4-разрядных счет-
чиков. Используйте микросхему 74НС162
синхронного двоично-десятичного счетчика
(с периодом от 0 до 9 и синхронными функ-
циями обнуления и загрузки). Возьмите до-
статочное количество этих микросхем, что-
бы измерить варьирование скорости пули
величиной, скажем, 30%. Сделайте свой
счетчик синхронным;
♦ источником сигнала тактирования служит
кварцевый генератор с частотой 30 МГц.
Разделите эту частоту, чтобы получить тре-
буемое разрешение;
♦ оснастите схему кнопкой для генерирования
сигнала ARM* (готовность). Нажатие этой
кнопки обнуляет триггер, на выходе которо-
го появляется сигнал высокого уровня при
разрыве пулей первого провода;
16W.3. Измеритель скорости пули
671
♦ используйте этот триггер для запуска
счетчика, когда пуля перебивает первый
провод;
♦ разрыв пулей второго провода обнуляет
триггер и останавливает счетчик;
♦ результат отображается на дисплеях, подоб-
ных используемым в вашем компьютере;
♦ оснастите схему функцией определения пе-
реполнения многоразрядного счетчика. Со-
стояние переполнения отображается вклю-
чением красного светодиода. Активирование
сигнала ARM* (готовность) обнуляет сигнал
переполнения. Предполагается возможность
выдачи асинхронного сигнала выходного
переноса.
функция обнуления, чтобы избежать возникно-
вения нежелательных помеховых всплесков4.
Чтобы получить разрешение величиной ОД мкс, частота
сигнала тактирования должна быть 10 МГц => нужно
разделить сигнал генератора с частотой 30 МГц на 3.
Можно использовать схему, разработанную в разделе 16W1
10 МГц
30 МГц
Обнуляем при 210
+5V
Разрешение
Рис. 16W.18. Схема счетчика-делителя на 3 для получения
сигнала тактирования нужной частоты
16W.3.1. Разработка измерителя
скорости пули
Сначала мы рассмотрим возможные варианты
нескольких фрагментов схемы, функциони-
рующие требуемым образом, а затем начертим
полностью всю схему. Если объяснения фраг-
ментов схемы покажутся вам избыточными,
то можете смело пропустить их и перейти пря-
мо к конечному решению, которое содержит
краткие объяснения большинства принятых
решений.
Запуск и остановка счетчика
Счетчик запускается, когда пуля перебивает
один провод, и останавливается, при разрыве
пулей другого провода. Чтобы счетчик работал
между этими двумя событиями, нам потребует-
ся элемент, который будет хранить состояние
счета, т. е. триггер.
Пуля должна дважды переключать уровень
сигнала. Пусть пуля перебивает провод, кото-
рый подключен к одному уровню, тогда как ре-
зистор повышает его к другому.
Генерируем сигнал тактирования
Поскольку частота нашего генератора колеба-
ний составляет 30 МГц и нам нужно получить
разрешение величиной 0,1 мкс, что подразуме-
вает частоту сигнала тактирования величиной
10 МГц, нам требуется счетчик-делитель на
три. На рис. 16W.18 изображена схема такого
счетчика, в которой реализована синхронная
Подробности тактирования
Мы пытаемся измерить довольно короткий
промежуток времени с разрешением величи1
ной ОД мкс, поэтому нам необходимо принять
меры, чтобы задержки в нашей схеме не ухуд-
шили ее характеристики.
Задержка RC-цепи при разрыве провода
Резистор повышения/понижения совместно
с паразитной емкостью, величину которой мы
примерно определили в 50 пФ, создают RC-
цепочку. Насколько малым должны мы взять
сопротивление резистора 1?? Таким, чтобы
сделать постоянную времени RC значительно
меньше величины разрешения в ОД мкс. Пусть
эта постоянная времени составляет полови-
ну или четверть величины разрешения, т. е.
50 или 25 не (см. соответствующую схему на
рис. 16W.19). Для этого подойдет резистор но-
миналом 1 кОм или, лучше, 470 Ом.
Значение £? Нужна постоянная времени
RC« ОД мкс = 100 не; скажем, 50 не =>
R< ^|= 103 = 1кОм; или 470 Ом
R-1 кОм или 470 Ом
Рис. 16W.19. Задержка, вызываемая цепочкой из повы-
шающего резистора и паразитной емкости, должна быть
небольшой
4 В схеме показано использование микросхемы 74НС162.
Это счетчик двоично-десятичного кода или счетчик-
делитель на 10. Для этой цели подойдет также микросхе-
ма 74НС162 обычного двоичного счетчика. Оба счетчика
оснащены функцией синхронного обнуления (Clear*).
672
16W. Примеры с решениями: применения счетчиков
Дребезг при прохождении пули
через провод
Безопасный ли этот эффект? Да, безопасный.
Длина пули соизмерима с расстоянием в 10 см
между проводами запуска и остановки счет-
чика. Если предположить, что пуля скребет по
обоим концам разорванного провода в течение
этого времени, то, возможно, возникнет ситуа-
ция, подобная дребезгу контактов. Но в дей-
ствительности никакой проблемы нет. Триггер,
как он подключен в схеме, реагирует только на
первый перепад (на входе тактирования), а за-
тем на первое появление низкого уровня (на
входе сброса). Таким образом, триггер сам по
себе играет роль средства устранения дребезга.
Этого аргумента достаточно. Но, скорее всего,
разрыв провода обеспечит чистое размыкание
контакта, в результате чего электрический сиг-
нал изначально не будет содержать последствий
дребезга.
Определяем необходимое количество
счетчиков
За сколько времени пуля пройдет расстояние
10 см между проводами запуска и остановки
счетчика? Как упоминалось ранее, эталонная
скорость пули из винтовки для соревнований
составляет около 900 м/с, отсюда следует, что
расстояние в 10 см такая пуля преодолеет при-
близительно за 110 мкс. Если мы хотим обе-
спечить результат измерений с точностью до
0,1 мкс, то потребуются четыре десятичных
разряда (хотя один из них будет отображать
только значение «1»; в цифровом мульти-
метре такое количество разрядов называется
Г1
/ /
Еп
Со
О
En
R
Co
En
R
Co
En
R
Со
Сигнал тактирования
с частотой 10 МГц
Еп (разрешение)
Со (вых. перенос)
Рис 16W.20. Время будем измерять с помощью четырех
счетчиков-делителей на десять
3-1/2). Соответственно понадобятся четыре
4-разрядных счетчика-делителя на 10.
Определив временной диапазон, в пределах
которого нам нужно выполнять измерения
(пределы которого составляют ±30% эталон-
ной скорости), и требуемое нам разрешение,
задача проектирования счетчика становится
довольно прозаичной. На рис. 16W.20 показана
схема подключения четырех 4-разрядных ин-
дикаторов. Возможно, что их лучше заменить
16-разрядными жидкокристаллическими дис-
плеями.
Определение переполнения
Задача определения переполнения представля-
ет больший интерес. Для определения состоя-
ния переполнения нам нужно использовать
сигнал выходного переноса счетчика самого
высшего разряда. Переполнение предупрежда-
ет нас, что сохраненному значению счета нель-
зя доверять.
Примечание
Со всей откровенностью можно заявить, что пе-
реполнение в этой схеме будет маловероятным
событием. Но уметь определять это состояние
полезно, поэтому мы оснастим нашу схему такой
возможностью, хотя, опять же, вы можете и воз-
разить, что мы уже рассматривали этот вопрос, по
крайней мере, дважды.
Но прежде всего нам нужно определиться, что
именно означает сигнал переноса: собственно
переполнение или же предстоящее переполне-
ние. В должным образом разработанных син-
хронных счетчиках сигнал выходного перено-
са означает последнее: что переполнение про-
изойдет по следующему сигналу тактирования.
Таким образом, собственно переполнение будет
указываться завершением сигнала выходного
переноса. Также мы хотим, чтобы триггер со-
хранял включенным светодиодный индикатор
переполнения до тех пор, пока пользователь не
выключит его.
Простейший способ определения перепол-
нения с помощью асинхронного выходного
переноса
На рис. 16W.21 показан прямолинейный способ
определения переполнения. Появление сигна-
ла выходного переноса указывает на состояние
16W3. Измеритель скорости пули
673
переполнения счетчика. Этот сигнал активиру-
ется при максимальном значении счета, кото-
рое на единицу меньше значения переполнения.
+5 в
Красный светодиод
кОм<* СТТереполнени^>
Завершение сигнала максимального
счета (отрицательный фронт сигнала)
указывает состояние переполнения
Рис. 16W.21. Датчик переполнения поддерживает инди-
каторный светодиод включенным даже после завершения
этого состояния
Такой подход возможен, но в главе 16N отме-
чалось, что помехи на линии выходного пере-
носа могут сбить с толку простой определитель
переполнения, изображенный на рис. 16W.21.
В частности, он может дать сбой в том случае,
если между сигналами на выходах Q. счетчика
наблюдается такой сдвиг, что эти сигналы, хотя
по идее и должны быть синхронными, тем не
менее изменяются не совсем одновременно.
Такое рассогласование тактирования может со-
здавать ложный сигнал выходного переноса.
Эту проблему можно решить, используя для
указания переполнения синхронный сигнал вы-
ходного переноса. Если разрабатывать счетчик
с нуля, в него можно также встроить и перенос
такого типа. Мы могли бы реализовать такой
перенос в счетчике на микросхеме ПМЛ, с ко-
торой мы работали на лабораторном занятии
16L. В листинге 16W1 приведена программа на
Verilog для реализации такого переноса (кото-
рый мы решили не включать в счетчик на лабо-
раторном занятии).
Листинг 16W1. Программа на Verilog для реали-
зации переноса
if (upbar_down) // сигнал высокого уровня на этой
// линии устанавливает режим вычитающего счета
begin
count <= count -1;
if (count == 16'b 0000000000000001) // минимальное
// значение счета плюс один
cout_sync_bar <= 0; // активируем сигнал переноса
// по следующему сигналу тактирования,
// значение счета нулевое
else
cout_sync_bar <= 1;
end
else
begin
count <= count+1;
if (count == 16'b 1111111111111110) // максимальное
// значение счета минус один
cout_sync_bar <= 0; // активируем сигнал переноса
// по следующему сигналу тактирования, значение
// счета максимальное
else
cout_sync_bar <= 1;
end
Код программы не очень изящный и пере-
стает работать должным образом, если изме-
нить направление счета (определяемое сиг-
налом upbar__down) при крайнем значении
счета. Поэтому мы ранее и не включили в схе-
му эту замысловатую функцию синхронного
переноса.
При использовании микросхемых счетчиков
возможность создания собственной функции
синхронного переноса недоступна, но мы мо-
жем реализовать ее почти эквивалентный ва-
риант, добавив в схему счетчика синхронизи-
рующий триггер, который не будет пропускать
помеховых импульсов. Возможный вариант та-
кой схемы изображен на рис. 16W.22.
Выходной перенос
тактирования
(синхронизатор)
сброс -
Рис. 16W.22. Добавление синхронизирующего триггера
в линию выходного переноса может обезопасить триггер
определения состояния переполнения от помех
Импульсы помех на линии асинхронного вы-
ходного переноса возникают вскоре после
завершения фронта сигнала тактирования,
поэтому они не пройдут через синхронизирую-
щий триггер. Это графически иллюстрируется
на рис. 16W.23: синхронизированный сигнал
переноса ПРНСВЫХ не содержит помеховых им-
пульсов, которые присутствуют в несинхрони-
зированном сигнале.
674
16W. Примеры с решениями: применения счетчиков
Сигнал тактирования \ г ?
(ОТКРЫТЫЙ СТОК, гк т *
с повышающим j
резистором) Г"*
Q3*
Сигнал TTPHCDUTV
Синхронизированный
сигнал ТТРНСВЫХ
Cm 5 0BV ШШК 5 00 V
Ch3' 5,00 V Ch4 5,00 V
Рис. 16W.23. Импульсы помех из сигнала выходного пере-
носа ПРНСВЫХ можно убрать с помощью синхронизирующего
триггера
полезным запомнить этот метод синхрониза-
ции. Асинхронные схемы, т. е. схемы, готовые
реагировать в любое время, уязвимы к поме-
хам в сигналах тактирования, тогда как син-
хронные схемы обладают «иммунитетом», но
только при условии, что помехи не возникают
во время установки, что обычно и имеет место.
Принципиальная схема всего устройства
На рис. 16W.24 изображена полная принци-
пиальная схема устройства для измерения
'Значение R? Нужна постоянная времени
, RC « ОД мкс = 100 не; скажем, 50 нс^
\=> R <50 не = 103 = 10 кОм \
v 50 пФ— -у-
Пуля перебивает
первый провод,
дребезг не опасен? (UtT~) Вероятно, что да. ТТервая^Ч
транзакция должна запустить триггер. Хотя длина \
пули соизмерима с расстоянием 10 см, триггер должен]
(Сработать по первому разрыву^-
RED
En (разрешение)
Со (ТТРНСВИХ)
Сигнал тактирования
с частотой 10 МГц
а затем второй +5
сигнала максимального счет
(отрицательный фронт сигнала) указывает^
состояние переполнения
. Тотовнс
4
Рис. 16W.24. Принципиальная схема измерителя начальной скорости пули
Но это средство безопасности может быть со-
вершенно излишним. Чтобы создать импульсы
помех, показанные на рис. 16W.23, нам при-
шлось хорошенько потрудиться5. Но будет
5 Нам пришлось «подразнить» схему, замедлив фронт
тактирования. По-видимому, из-за такого пологого фрон-
та разные триггеры запускались по нему в слегка разное
время. Емкостная нагрузка некоторых выходов ((^...Qj) не
дала никакого эффекта, возможно, потому, что выходные
сигналы триггеров буферизируются перед подачей на вы-
воды микросхемы. Но внедрение помеховых импульсов
посредством замедления нарастания фронта тактирова-
ния — это не вполне профессиональный подход, поскольку
такой пологий фронт становится ненадежным синхрони-
начальной скорости пули, содержащая боль-
шинство объяснений разных функциональных
компонентов.
зирующим сигналом. Точно так же, как он может тактиро-
вать разные триггеры синхронного счетчика в слегка раз-
ное время, он может тактировать синхронизатор в другое
время, чем счетчик. Такое несогласование моментов так-
тирования может аннулировать очистку сигнала переноса
от помех, в результате чего они будут передаваться на вы-
ход синхронизирующего триггера, если его тактирование
происходит чуть позже.
17N. Память
Содержание
17N.1. Шины
17N.1.1. Когда нужны выходы с третьим состоянием?
17N.1.2. Пример использования выходов с тремя состояниями с шиной данных
17N.2. Память
17N.2.1. Память описывает способ организации хранения данных
17N.2.2. Типы памяти и используемая терминология
17N.2.3. Обозначение характеристик памяти
17N.3. Конечный автомат: новое название старого устройства
17N.3.1. Разработка последовательностной схемы
17N.3.2. Проектирование счетчика-делителя на три вручную
17N.3.3. Проектирование счетчика-делителя на три с помощью Verilog
17N.3.4. Использование памяти вместо вентилей в схемах
со сложной комбинационной логикой
17N.3.5. Подведение итогов: возможны несколько вариантов
последовательных конечных автоматов
675
675
676
678
679
680
682
683
684
684
686
687
688
171У1.1.Шины
Шины представляют собой что-то типа «об-
щественного транспорта», который останав-
ливается, чтобы подобрать кого-то или дать
сойти любому, кому нужно куда-то добраться.
Английское название шины bus имеет такое же
происхождение, как и пассажирский автобус1.
Шины питания «подвозят» положительное
и отрицательное («земля») питание к каждо-
му компоненту, а шины данных и адреса пере-
дают соответствующие данные на микросхемы
и другие устройства компьютера. Некоторые
линии управления также могут подключаться
более чем к одному компоненту, например ли-
ния записи/чтения R/W*.
17N.1.1. Когда нужны выходы
с третьим состоянием?
Выходы с третьим (высокоимпедансным) со-
стоянием требуются в каждом случае, когда к
1 Если обратиться к латыни, то слово bus является просто
сокращением латинского слова omnibus, которое означает
«для всех». Такое название было присвоено в начале XIX
столетия городскому автобусу в Англии, чтобы противо-
поставить его коляске, которая нанималась для поездки из
одной точки в другую.
одной линии подключен больше чем один ис-
точник сигнала. Можете ли вы определить,
в каких местах на рис. 17N.1 требуется третье
состояние?
Примечание
Если вы забыли, то напоминаем, что выход с тремя
состояниями представляет собой выход, который
можно полностью отключить, а не выдавать на
нем низкий или высокий уровень, как на выходах
обычных логических вентилей.
В случае нескольких устройств, подключенных
к общей шине и только принимающих сигналы,
ни одно из таких устройств не требует выводов
с тремя состояниями. Если у вас возникают
какие-либо трудности с уяснением данного по-
нятия, попробуйте сравнить его со спаренной
телефонной линией. Если второй абонент будет
иногда подслушивать ваши разговоры, то это
может влиять на ваше душевное спокойствие,
но если он при этом молчит, то качество связи в
результате не ухудшается. Попробуйте приме-
нить данный пример к схеме на рис. 17N.1.
Детальное рассмотрение начнем с шины дан-
ных. Выходы памяти ОЗУ (RAM) и ПЗУ (ROM)
(2, 4, 7), а также центрального процессора
(ЦП), подключенные к шине данных, должны
обладать третьим состоянием, поскольку все
676
17N. Память
Адресная шина
Более трудный случай: это источник
сигналов, но есть ли другой источник?
В этой схеме нет, но обычно есть.
Не требуется: эти устройства только
принимают сигналы
Требуется: все эти устройства
выдают сигналы в общую шину
Рис. 17N.1. Где требуются выходы с тремя состояниями?
эти устройства являются поставщиками сигна-
лов в шину. Обратите внимание на то обстоя-
тельство, что для выводов памяти ПЗУ третье
состояние требуется в такой же мере, как и для
памяти ОЗУ и для центрального процессора,
независимо от направления, будь оно двухсто-
роннее или одностороннее. Третье состояние
нужно и для клавиатуры (9), а вот для цифро-
аналогового преобразователя (ЦАП) оно не
требуется, поскольку это устройство только
принимает сигналы с шины данных.
Что касается адресной шины, то память ОЗУ
(3), ПЗУ (6) и дешифратор (5) только при-
нимают сигналы с нее, поэтому здесь третье
состояние для этих устройств не требуется.
А как насчет центрального процессора (1)? Это
устройство является поставщиком сигналов.
Более того, судя по схеме, это единственный
поставщик сигналов на адресную шину. Если
это действительно так, то для его подключения
к адресной шине третье состояние не требуется.
Именно такой была философия разработчиков
ранних процессоров, включая процессор 8051,
с которым мы вскоре познакомимся. Но после
запуска в производство первых устройств раз-
работчики начали замечать, что иногда полез-
но, чтобы доступ к адресной шине могли иметь
и другие устройства.
Частный случай такой необходимости — со-
вместная работа более чем одного процессора,
но в обыденном случае это требовалось для
того, чтобы процессор мог иногда уступать
управление шиной, чтобы обеспечить бы-
стрый обмен данными между памятью и дру-
гим устройством, минуя процессор. Этот про-
цесс называется прямым доступом к памяти
(ПДП2). Например, данные с жесткого диска
можно передавать в ОЗУ напрямую, используя
для этого выделенный счетчик адресов памяти.
Передача данных таким способом осуществля-
ется намного быстрее, чем при передаче каждо-
го слова через центральный процессор.
Нужна ли возможность прямого доступа к па-
мяти нашему скромному компьютеру из лабо-
раторного занятия? Конечно же, нет, скажете
вы, поскольку это такое простое устройство.
И будете неправы. Хотя это и несложный ком-
пьютер, в нем реализован прямой доступ к па-
мяти. В частности, когда мы загружаем данные
в память вручную, мы осуществляем прямой
доступ к памяти, хотя и делаем это со скоро-
стью улитки. Как мы можем делать это, если
разработчики процессора 8051 не оснасти-
ли его возможностью общего использования
адресной шины? Симулируя третье состояние,
для чего адресные выводы процессора перево-
дятся в состояние их наивысшего импеданса.
В этом режиме они не полностью отключены,
как в настоящем третьем состоянии, а находят-
ся под небольшим положительным потенциа-
лом, в результате чего любое внешнее устрой-
ство может управлять адресными линиями.
Небольшой положительный потенциал созда-
ется, активируя вход сброса процессора 8051.
17N.1.2. Пример использования
выходов с тремя состояниями
с шиной данных
На рис. 17N.2 изображена часть схемы, кото-
рую мы будем собирать на лабораторном заня-
2 Англ. DMA — Direct Memory Access.
ПЫЛ. Шины
677
Внешняя
цифровая клавиатура
Сигналы и питание /
подаются через
DIP-шлейф
Выходы памяти включаются,
активируя сигнал выбора
микросхемы CS* (chip select)
и сигнал разрешения вывода ОЕ*
(output enable). А активирование .—££
сигнала записи WE* (write enable) •*■ А
отключает выходные буферы памяти/
при выполнении операции записи
«
Микросхема 541 содержит набор из восьми буферов
с тремя состояниями, которые служат для того, чтобы
предотвратить монополизирование шины данных
цифровой клавиатурой. Выводы этих буферов включаются
только тогда, когда выполняется ручной ввод данных
с цифровой клавиатуры
Микросхема 74НС541 -
восемь буферов
с выходами
\
Статическая память ОЗУ,
32Кх8
Шина данных
УИ Ли*
7F
с тремя состояниями \
5>Bf -
-•07
00
Т Дисплей данных
(ЖКД)
[Конечно же, в микросхеме памяти RAM
предусмотрено отключение выходных буферов
при выполнении операции записи
Микросхема памяти содержит встроенные буферы с выходами с тремя
состояниями. Разработчики микросхемы знают, что устройство будет
подключаться к общей шине данных (т. е. к шине будет подключаться другой
поставщик сигналов, чтобы загружать данные в память при операции записи)
Рис. 17N.2. Использование буферов с выходами с тремя состояниями на примере подключения цифровой панели клавиату-
ры к памяти
тии 17L. На этом рисунке один случай выходов
с третьим состоянием показан явно — это во-
семь буферов микросхемы 541; а во втором слу-
чае — внутри памяти RAM — выходы с тремя
состояниями подразумеваются.
Монополизирование шины данных цифровой
клавиатурой предотвращает микросхема 541,
вернее, ее буферы с тремя состояниями. А ка-
ким образом предотвращается захват шины
данных памятью ОЗУ? (Обратите внимание на
то, что вход ОЕ* явного управления выходны-
ми буферами ОЗУ всегда активирован, т. е. на
нем зафиксирован сигнал низкого уровня.)
Выходные буферы памяти ОЗУ отключаются
активированием сигнала разрешения записи
WE*.
Память ОЗУ также содержит буферы
с выходами с тремя состояниями
На рис. 17N.3 изображена блок-схема вну-
треннего устройства ОЗУ3, с которым мы бу-
3 Микросхема памяти CY7C1399BN компании Cypress
Semiconductor.
дем работать на лабораторном занятии для
этой главы.
Это обычная асинхронная память ОЗУ. Син-
хронная статическая память ОЗУ может иметь
более высокую скорость, но с ней сложнее ра-
ботать, и в этой книге мы не будем рассматри-
вать такой тип памяти. Те, кого интересует эта
область, могут обратиться к § 14.53С книги
АоЕ. На рис. 17N.3 показаны роли сигналов
СЕ* (разрешение микросхемы), ОЕ* (разреше-
ние выхода) и WE* (разрешение записи). То
обстоятельство, что активирование сигнала
разрешения записи WE* переводит выходные
буферы в состояние высокого импеданса (тре-
тье состояние), т. е. отключает выходные бу-
феры от шины, позволяет нам поддерживать
постоянно активированными сигналы разре-
шения микросхемы СЕ* и разрешения выхода
ОЕ*, как мы это делаем на лабораторном заня-
тии 17L (см. рис. 17N.2). На последующих ла-
бораторных занятиях, когда сложность нашей
схемы повысится за счет включения в нее цен-
трального процессора, мы будем использовать
эти сигналы обычным способом.
678
17N. Память
Логическая блок-схема
СЕ* управляет
прохождением WE*
i/o0
I/O,
Усилители считывания
Активирование WE* отключает буферы \ Отключение
с выходами с тремя состояниями \ питвния
ОЕ* управляет буферами
с выходами с тремя состояниями
Рис. 17N.3. Внутреннее устройство ОЗУ (32Кх8) и роль трех сигналов разрешения: СЕ*, ОЕ* и WE*
На рис 17N.3 показаны следующие взаимоот-
ношения между тремя сигналами разрешения:
♦ Разрешение записи — WE*. Активирова-
ние этого сигнала для выполнения операции
записи в память переводит выходные бу-
феры памяти в третье состояние, отключая
их от шины данных. Иными словами, ОЗУ
прекращает поставлять сигналы на шину,
чтобы иметь возможность принимать их
с шины.
♦ Разрешение микросхемы — СЕ*. Сигнал
СЕ* управляет прохождением сигнала разре-
шения записи WE*. Таким образом, пока не
выполнено разрешение микросхемы, сигнал
разрешения записи WE* не оказывает ника-
кого влияния. Мы воспользуемся этим свой-
ством в компьютере, который будем собирать
из дискретных компонентов на большой ма-
кетной плате. В частности, этот сигнал дает
возможность не усложнять механизм управ-
ления сигналами компьютера, поскольку
он позволяет сигналу разрешения записи
WE* поступать на память ОЗУ при записи
в устройства ввода-вывода. Но это не влечет
за собой никаких отрицательных послед-
ствий, поскольку в адресном пространстве
ввода-вывода сигнал СЕ* деактивирован.
На рис. 17N.3 ошибочно предполагается,
что сигнал СЕ* не обусловливает операции
чтения данных. В справочном листке, из
которого взят этот рисунок, ясно говорит-
ся, что для того, чтобы разрешить операции
любого типа с памятью, будь то чтение или
запись, сигнал разрешения микросхемы СЕ*
должен быть активирован.
Разрешение выхода — ОЕ*. Этот сигнал не-
посредственно управляет выходными буфе-
рами с тремя состояниями. Реагирование на
этот сигнал происходит быстрее, чем отклик
на сигнал разрешения микросхемы СЕ*, кото-
рый управляет более сложными функциями
ОЗУ.
17N.2. Память4
Все это время мы постоянно используем термин
«память», не объясняя, что именно это такое.
Исправим это упущение. Память представляет
собой массив триггеров (или других устройств,
которые могут хранить один бит информации),
организованных таким образом, чтобы свести
к минимуму число линий, необходимых для
доступа к хранимой в ней информации. Как
вы, возможно, знаете, наиболее часто память
служит для хранения данных и программы для
компьютеров. Но ее также можно использовать
и для генерирования функций комбинацион-
ной логики. Мы увидим такое применение на
лабораторном занятии 17L.
4 АоЕ § 14.5.
J7/V.2. Память
679
D7-
DO-
D Q
--Q7
Вход
данных
WE*-
Демультиплексор
DATA
_Выход
донных
Адресная.шина
А2, А1, АО
Демул ьти пл ексор
А2, А1, АО
Организация
регистра
Организация памяти
с отдельными линиями для
ввода и вывода данных
Организация памяти
с одной двунаправленной
линией данных
Рис. 17N.4. Память представляет собой способ организации хранения данных с минимальным количеством внешних под-
ключений
17N.2.1. Память описывает способ
организации хранения данных
В регистре можно сохранить 8 битов. Регистр
представляет собой просто набор триггеров с
общим входом сигнала тактирования, все вхо-
ды D и выходы Q. которого имеют параллель-
ный доступ. Если же эти 8 битов сохранить в па-
мяти, тогда все входы и выходы данных можно
мультиплексировать в одну линию для каждого
направления, а еще одна модификация позво-
ляет даже убрать разницу между направления-
ми и использовать одну двунаправленную ли-
нию как для ввода, так и для вывода данных.
На первый взгляд такая организация памяти
выглядит не очень практичной, поскольку тре-
бует дополнительных внутренних аппаратных
элементов лишь для того, чтобы сократить ко-
личество внешних выводов. Подсчитаем коли-
чество выводов, требуемых для регистра и для
памяти (табл. 17N.1).
Таблица 17N.1. Требуемое число выводов при
различной организации памяти
Функция
Вход данных
Выход данных
Тактирование/
запись
Положительное
питание и «земля»
Адресная шина
Всего
Число выводов
для регистра
8
8
1
9
0
19
Число вьюодов
для памяти
1
1 или 1 общий
для ввода и вы-
вода данных
1
9
3
7 или 8
Сравнение числа выводов регистра
и памяти
Экономия выводов в случае памяти не выгля-
дит слишком внушительной, но только до тех
пор, пока мы не увеличим число сохраняемых
битов до определенного уровня. Тогда оказы-
вается, что единственно возможным способом
сохранить эту информацию будет применение
памяти. Например, подсчитайте количество
выводов, необходимых для хранения 1 Мб ин-
формации в устройстве типа регистра.
Обычно при организации хранения в виде па-
мяти число выводов можно сократить еще на
один, используя один вывод как для ввода, так
и для вывода данных (см. рис. 17N.4 справа).
Сигнал разрешения записи WE* переводит
выходные буферы, которые обычно отобра-
жают содержимое памяти, в третье состояние,
отключая их таким образом от шины данных
(см. рис. 17N.3).
Память обеспечивает доступ только к одному
значению за раз, тогда как регистр предостав-
ляет параллельный доступ ко всем своим битам.
Но организация памяти хорошо соответствует
последовательной природе компьютерной об-
работки данных. Обратите внимание, что по от-
ношению к параллельным и последовательным
данным разрядность памяти на рис. 17N.4 со-
ставляет всего лишь один бит. Но память RAM,
с которой мы будем работать на лаборатор-
ном занятии, содержит восемь параллельных
структур этого типа, т. е. хранит в одной ячейке
(или по одному значению адреса) 8 битов. Это
стандартная организация памяти. Мы исполь-
зовали однобитовую память в примере только
из-за ее простоты. Вот и все, что следует знать
680
Ш. Память
о понятии памяти. Далее рассмотрим термино-
логию, применяемую относительно памяти.
17N.2.2. Типы памяти
и используемая терминология
Память делится на несколько типов5.
ОЗУ (RAM) и ПЗУ (ROM)
ROM6 — этот тип памяти позволяет пользовате-
лю только считывать записанные в нее данные.
Данные в память ROM записываются произво-
дителем при ее изготовлении. Таким образом,
название памяти не совсем точно отображает
ее природу, а только применительно к поль-
зователю.
PROM7 — подобно памяти ROM, память это-
го типа позволяет пользователю выполнять
в основном только чтение. Но, в отличие от
памяти ROM, пользователь также может и за-
писывать данные в память PROM, хотя и не так
легко, как в память RAM.
Существует несколько типов памяти PROM:
EPROM8 — стираемая память PROM. Самый
старый тип памяти PROM. Для того чтобы сте-
реть содержимое памяти, микросхему нужно
было извлечь из гнезда в схеме и через спе-
циальное отверстие в корпусе подвергнуть ее
ультрафиолетовому облучению на протяже-
нии около 15 минут9. Эта была сложная про-
5 АоЕ § 14.4.
6 Англ. Read Only Memory — память только для чтения.
В русскоязычной литературе также используется термин
ПЗУ — постоянное запоминающее устройство.
7 Англ. Programmable Read Only Memory - программируе-
мая память только для чтения. В русскоязычной литерату-
ре также употребляется термин ППЗУ — программируемое
постоянное запоминающее устройство.
8 Англ. Erasable Programmable Read Only Memory - сти-
раемая программируемая память только для чтения.
8 русскоязычной литературе также используется термин
СППЗУ — стираемое программируемое постоянное запо-
минающее устройство.
9 Если вам кажется, что все эти сокращения слишком
громоздкие, то приведем еще один характерный пример
сокращения названия типа EPROM для микросхемы, ко-
торая предлагалась в более дешевом корпусе, чем микро-
схема с кварцевым окошком для стирания ее содержимого
ультрафиолетовым светом. Цена микросхемы в таком кор-
пусе была в десять раз меньше, чем в корпусе с кварцевым
окошком. Но отсутствие окошка означало, что содержимое
такой памяти нельзя было стереть. Подоплека предложе-
ния такого корпуса состояла в том, что, по идее, пользова-
цедура, и такая память была заменена памятью
EEPROM10 разных типов. Информация в памя-
ти этого типа хранится в виде небольшого за-
ряда на плавающем затворе МОП-транзистора.
Это такой же подход, который используется в
динамической памяти RAM, но, в отличие от
RAM, в которой заряд сохраняется в течение
нескольких миллисекунд, заряд в EEPROM мо-
жет храниться на протяжении 10-15 лет11.
EEPROM — электрически стираемая PROM.
Содержимое этого типа памяти можно стирать
по отдельному байту, не извлекая ее из схемы.
Очевидно, что такой подход намного удобнее,
чем в случае с памятью EPROM. Эта техноло-
гия реализована в устройствах ПМЛ.
Флеш-память12 — память большой емкости,
но без возможности стирания любого отдель-
ного байта. Стирание выполняется большими
блоками байтов. В микропроцессоре 8051 ис-
пользуется этот тип памяти. Также этот тип па-
мяти реализован во всех флешках, включая SD
и MHKpoSD-карточки.
RAM13 — память с произвольным доступом,
данные в которую можно записывать, не тре-
буя никакого специального аппаратного или
программного обеспечения, а обычными про-
граммными средствами. По сути, это не совсем
правильное название такого типа памяти, по-
скольку доступ к содержимому всех типов па-
мяти можно осуществлять произвольной вы-
боркой14. Но такое название прижилось.
тель мог разработать проект, используя обычную (с окош-
ком) микросхему памяти EPROM, а после того, как он был
удовлетворен запрограммированным содержимым, он
мог заказать требуемое количество микросхем памяти в
более дешевом корпусе. Так вот, такие микросхемы памя-
ти назывались one-time-programmable erasable programmable
read-only memory (однократно программируемая стирае-
мая программируемая память только для чтения). А соот-
ветствующее сокращение, естественно, было ОТР EPROM.
К счастью для мира цифровой электроники, такая память
устарела и в настоящее время не применяется.
10 Англ. Electrically Erasable Programmable Read Only Me-
mory — электрически стираемая программируемая память
только для чтения. В русскоязычной литературе также ис-
пользуется термин ЭСППЗУ — электрически стираемое
программируемое постоянное запоминающее устройство.
11 АоЕ § 14.4.5В, С.
12 Англ. Flash memory. В основе названия, по-видимому,
лежит то обстоятельство, что такую память можно стереть
in a flash, т. е. очень быстро.
13 Англ. Random Access Memory — память с произвольным
доступом. В русскоязычной литературе также распростра-
нен термин оперативное запоминающее устройство — ОЗУ.
14 На первый взгляд такое название может привести в за-
мешательство. Но оно, конечно же, не означает, что память
17N.2. Память
681
Существуют две главные разновидности памя-
ти RAM:
Технология хранения — в статической памя-
ти SRAM для хранения данных применяются
триггеры, а в динамической DRAM — кон-
денсаторы. Можно видеть, что эти названия,
должно быть, были придуманы изготовителя-
ми динамической памяти, т. е. памяти, в кото-
рой используются конденсаторы. Память на
конденсаторах было бы более подходящим
называть «забывакой», поскольку помнить
такая память может лишь в течение пары мил-
лисекунд. Поэтому, чтобы сохранять инфор-
мацию в такой памяти, конденсаторы нужно
постоянно подзаряжать, выполняя для этого
операцию псевдочтения. Но, несмотря на та-
кой, казалось бы, большой недостаток, дина-
мическая память доминирует на рынке памяти
RAM. Это объясняется очень малым размером
ее единицы хранения бита, а также малым
энергопотреблением. Но в нашем лаборатор-
ном компьютере мы отдаем предпочтение ста-
тической памяти RAM, поскольку ее содержи-
мое не нужно постоянно обновлять. По сути,
эта память настолько проста и обладает столь
малым энергопотреблением, что мы остав-
ляем ее постоянно включенной, с питанием
от таблеточной батарейки напряжением 3 В.
В таком состоянии данные в памяти могут со-
храняться в течение приблизительно года.
Псевдостатическая память RAM — псевдо-
статическая память RAM сочетает легкость
использования статической памяти и почти
такую же плотность, как и динамическая. Это
возможно благодаря тому, что процесс обнов-
ления содержимого выполняется внутренним
механизмом самой памяти и прозрачен для
пользователя. Этот тип памяти SRAM почти
полностью вытеснил обычную память SRAM,
за исключением тех случаев, когда требуется
чрезвычайно низкое энергопотребление (как,
например, в памяти нашего компьютера из дис-
кретных компонентов с подпиткой от батарей-
ки) или когда нужна очень высокая скорость
работы (как, например, в кэш-памяти).
выдает содержимое произвольно выбранной ячейки. Оно
означает, что запись или чтение содержимого ячеек такой
памяти можно осуществлять в любом порядке, а время до-
ступа ко всем ячейкам в значительной мере одинаковое.
Такой тип выборки и время доступа радикально контра-
стируют с аналогичными параметрами для таких носите-
лей, как, например, магнитная лента и в меньшей степени
все типы дисковых устройств хранения.
Синхронная RAM — как статическая, так и
динамическая память RAM доступна в более
сложной версии, содержащей тактируемый ко-
нечный автомат, управляющий асинхронным
содержимым. В нашей книге мы не рассматри-
ваем этот тип памяти, но те, кому это интерес-
но, могут найти информацию о ней в § 14.5.3С
и 14.5АВ книги АоЕ.
Энергозависимость — память также делит-
ся на энергозависимую и энергонезависимую.
Содержимое энергозависимой памяти теря-
ется после выключения питания, а энерго-
независимой — нет. В общем, память ROM
и все типы памяти PROM энергонезависимые,
а память RAM всех типов энергозависима.
Но некоторые типы памяти, будучи сами энер-
гозависимыми, оснащаются встроенными ис-
точниками питания, которые делают их псевдо-
энергонезависимыми. В частности15:
• Память BBSRAM16 — или как ее называ-
ют на жаргоне, «пухлая» (chubby) RAM. На
рис. 17N.5 показаны две микросхемы такой
памяти: в DIP-корпусе (слева) и в корпу-
се для поверхностного монтажа (справа).
Причина больших, чем обычно, размеров
корпуса микросхемы памяти должна быть
понятной из названия памяти17. Вариация
этой схемы — гнездо микросхемы с бата-
рейкой и электроникой для включения
и выключения питания.
SNAPHAf (SH)
Battory/crysta
Рис. 17N.5. Благодаря встроенной батарейке псевдо-стати-
ческая память RAM может хранить данные в течение 10 лет.
(Воспроизведение с разрешения компании Dallas Semicon-
ductor/Maxim)
Такую память так же легко использовать, как
и обычную память RAM, но она более доро-
гостоящая. Например, микросхема памяти
М48Т35 компании STM стоит 10 долларов,
a DS1244Y компании Dallas Semiconductor —
свыше 30 долларов.
15 АоЕ § 14.4.1.
16 Англ. Battery Backup SRAM — статическая память RAM
с подпиткой от (встроенной) батарейки.
17 Если вам лень немного пошевелить мозгами, то увели-
чение размера корпуса микросхемы объясняется тем, что
кроме самой памяти он также содержит и литиевую бата-
рейку для ее питания.
682
77Л/. Память
Также используются и другие схемы резервного
питания памяти. Например, теневая RAM пред-
ставляет собой комбинацию обычной RAM
и энергонезависимой памяти. Содержимое
RAM копируется в энергонезависимую память
перед выключением питания. В качестве при-
мера можно назвать микросхему CY14B101KA
компании CY14B101KA. Корпуса микросхем
памяти этого типа имеют меньший размер, чем
памяти со встроенной батарейкой. Они обе-
спечивают неограниченное количество циклов
хранения RAM и автоматическое копирование
содержимого в энергонезависимую память при
отключении питания. Резервным источником
питания служит конденсатор, заряда которого
достаточно для выполнения копирования со-
держимого RAM в энергонезависимую память.
17N.2.3. Обозначение
характеристик памяти
Организация
Емкость памяти указывается в формате «коли-
чество слов х длина слова». Например, на на-
ших лабораторных занятиях мы будем исполь-
зовать RAM емкостью 32 Кх8 (или 32 Кбх8),
что равно 32 768 словам (или ячейкам) длиной
8 битов каждое18.
Единицы емкости памяти
Префикс «кило-» в термине «килобайт» мо-
жет быть неоднозначным. Сколько, по-вашему,
байтов в одном килобайте? Это может выгля-
деть глупым вопросом, но, действительно,
сколько? Будет ли это 210 (1024) байтов или 103
(1000) байтов?
Один из вариантов ответа на данный вопрос:
«это не важно, поскольку разница между эти-
ми двумя значениями составляет всего лишь
2,4%». В качестве контраргумента на такой от-
вет можно довести до сведения читателя, что
для некоторых адвокатов важность есть. В част-
ности, было подано как минимум два иска ка-
сательно определения килобайта, обозначен-
ного как 103, и оба иска были удовлетворены19.
Даже в самой электронной промышленности
производители имеют разные мнения по это-
му вопросу. В частности, у некоторых произ-
водителей жестких дисков килобайт равен ДО3
(1000) байтам. Благодаря этому емкость таких
жестких дисков выглядит несколько большей
(но не намного), чем при традиционном обо-
значении килобайта, как 210 (1024) байта. Это
и было причиной одного из исков. У произво-
дителей памяти «килобайт» обычно означает
210. В частности, емкость полупроводниковых
дисков (флешёк) обычно указывают, используя
степень двойки, например, 230 байтов20.
Но было бы намного удобнее отказаться от та-
кой двусмысленности. С этой целью в одном со-
глашении, чтобы отличить значение килобайта
в степенях двойки (т. е. 210) от общепринятого
значения термина «кило», как 103, указывает-
ся заглавная буква К. А в другом соглашении,
принятом в 1998 г., но все еще не очень широ-
ко распространенном, для этой цели использу-
ется обозначение КиБи (KiBi), которое часто
сокращается до КиБ (KiB). Обозначение КиБи
легко отличить от обычного обозначения кило.
Подобным образом для обозначения мегабай-
та, гигабайта и так далее употребляются тер-
мины МиБи, ГиБи и т. д. В этой книге килобайт
в степенях двойки (210) мы будем обозначать
заглавной буквой 1С.
При маркировке микросхем памяти наблюда-
ется тенденция к указанию в них количества
битов, возможно, по той причине, что это более
впечатляющее число. Тем не менее это честное
описание общего размера памяти. Например,
компания Cypress называет свою микросхему
памяти размером 32Кх8 как CY62256N (т. е.
256 Кб).
Тактирование памяти
Самой важной характеристикой памяти, неза-
висимо от ее типа и размера, является время
доступа, т. е. задержка между указанием дей-
ствительного адреса (что является обязанно-
стью пользователя) и выдачей содержимого
по этому адресу (что обеспечивает микросхема
памяти).
18 Если вы не знаете, что значит обозначение КиБ, см.
объяснение в следующем разделе.
19 См.: http://en.wikipedia.org/wiki/Binary_prefix#Orin
Safier_v._Western__Digital_Corporation.
20 Один из редких производителей флеш-памяти, который
использовал степени десятки для указания объема своих
устройств, должен был выплатить компенсацию за то, что
преувеличил их размер на 7%.
17N.3. Конечный автомат: новое название старого устройства
683
От указания действительного адреса... до получения действительных данных = время доступа
Указание адреса... !<
Адрес
выборка микросхемы
ОЕ
...и данные поступают
5 мин.
Рис. 17N.6. Временная диаграмма операции чтения для статической RAM с временем доступа 70 не
Тактирование памяти RAM
На рис. 17N.6 показана временная диаграм-
ма для памяти RAM объемом 32 Кх8, исполь-
зуемой на наших лабораторных занятиях по
микрокомпьютеру, предполагая для нее время
доступа в 70 не (не слишком малое по сравне-
нию с другими подобными устройствами)21.
Не стоит пугаться всех этих подробностей так-
тирования. Для нас самое большое значение
имеет только период времени между заданием
адреса и получением стабильных данных. Этот
интервал времени называется временем досту-
па в его обычном значении. Другой, менее важ-
ный параметр — время между активированием
сигнала выборки или разрешения микросхемы
и получением стабильных данных. Для ука-
занной RAM оба параметра имеют одинаковое
значение. Поскольку сигнал выборки микро-
схемы CS* обычно генерируется в виде функции
адреса, период времени между активировани-
ем этого сигнала и получением данных и будет
временем доступа.
Когда вы соберете микрокомпьютер, у вас бу-
дет возможность исследовать время доступа
памяти.
Примечание
Но только в том случае, если вы собираете свой
микрокомпьютер из дискретных компонентов, по-
скольку в микрокомпьютере на одной микросхеме
производства компании Silicon Laboratories внеш-
няя RAM не требуется.
В компьютере нашей разработки релевантным
временем доступа является более быстрое реа-
гирование на сигнал разрешения выхода ОЕ*.
Если к тому времени, когда вы дойдете до этого
эксперимента на лабораторном занятии, у вас
останутся силы, попробуйте взглянуть на пе-
риод времени между моментом активирования
сигнала разрешения выхода ОЕ* и появлением
стабильных данных.
17N.3. Конечный автомат:
новое название старого
устройства
На данном этапе мы познакомились с разно-
образными счетчиками: асинхронным и син-
хронным, счетчиками на микросхемах средней
степени интеграции и счетчиками, реализован-
ными на ПМЛ. Счетчик является особым слу-
чаем (наверное, самым простым) более общего
устройства: конечного автомата22, или, более
формально, автомата с конечным количеством
состояний23.
Конечный автомат — последовательностное
устройство, которое проходит через предска-
зуемые состояния. Если вы не забыли, состоя-
ние определяется как комбинация сигналов на
выходах триггеров устройства. Это может зву-
чать таинственно абстрактно, но если это по-
нятие применить к простому счетчику, то мож-
но увидеть, что это простая и, более того, уже
знакомая идея. Чтобы освежить вашу память,
на рис. 17N.7 изображена диаграмма состояний
АоЕ § 14.5.3А.
22 Англ. final state machine (FSM).
23 Такой автомат не идентичен машине Тьюринга, которая
представляет собой теоретическую модель компьютера
общего назначения. Предполагается, что машина Тью-
ринга имеет бесконечное количество состояний (и беско-
нечный объем памяти), тогда как конечный автомат этими
свойствами не обладает.
684
UN. Память
(или блок-схема) и таблица состояний для
двухразрядного суммирующего счетчика, пока-
зывающие (признаемся, довольно абстрактно)
поведение счетчика.
Наименование
состояния
А
В
С
D
QiQo
00
01
10
И
Рис. 17N.7. Блок-схема и таблица состояний для двухразряд-
ного суммирующего счетчика
17N.3.1. Разработка
последовательностной схемы24
На рис. 17N.8 показана очень обобщенная схе-
ма любого тактируемого последовательностно-
го устройства25.
Вход-
Текущее
состояние
Комбинационная Выход
логика
Следующее
состояние
Сигнал тактирования '
Рис. 17N.8. Общая схема последовательностного устройства
Как можно видеть, сигналы поступают на вхо-
ды D-триггеров и преобразуются в сигналы на
выходах Qnocne появления очередного сигнала
тактирования. Таким образом, текущее состоя-
ние на выходах фсхемы изменится на значения
на входах D по следующему сигналу тактиро-
вания, а значения на входах D соответствуют
следующему состоянию схемы. В книге АоЕ
показано, как использовать это обстоятельство
для разработки счетчика-делителя на три. Мы
решим почти такую же задачу, но с другими
комбинациями состояний.
В счетчиках (единственные конечные автома-
ты, с которыми мы работали на данном этапе)
24 АоЕ § 10.4.3.
25 Конечный автомат не обязательно нуждается в тактиро-
вании. В еще более обобщенной модели вместо блока, по-
казанного на рисунке в виде набора D-триггеров, был бы
просто блок задержки. Проектирование нетактируемых
конечных автоматов — более сложная задача по сравне-
нию с рассматриваемыми в этой книге, и потребность в та-
ких конечных автоматах возникает очень редко.
выходами являются просто выходы Q. тригге-
ров, не считая выходного переноса в некото-
рых редких случаях. Значения выходов могут
определяться только состоянием автомата или
же могут зависеть как от состояния, так и от
значений входов. Первый тип устройства назы-
вается автоматом Мура, а другой — автоматом
Мили.
Таким образом, счетчик, в котором выходной
перенос зависит только от уровней выходов Q
счетчика, будет автоматом Мура. А счетчик, в
котором выходной перенос зависит также и от
входного переноса (обычно так и есть), будет
автоматом Мили26. Мы признаем, что привели
эти названия не для запоминания. И все же вам
может пригодиться знание этих определений.
17N3.2. Проектирование счетчика-
делителя на три вручную
На первый взгляд, на рис. 17N.9 приведено
описание обычного счетчика, но мы преднаме-
ренно сделали его характеристики несколько
необычными. Во-первых, данный счетчик име-
ет всего три состояния, а не 2п состояний, как в
большинстве счетчиков, с которыми мы имели
дело. Во-вторых, последовательность его со-
стояний отличается от обычного двухразряд-
ного счетчика с укороченным циклом счета.
Текущее Последующее
состояние состояние
©
00
01
10
11
01
11
хх
00
Рис. 17N.9. Счетчик-делитель на три со слегка необычной
последовательностью счета
Последовательность состояний этого счетчи-
ка имеет вид 0,1, 3, 0,... В блок-схеме показа-
но четвертое состояние (D), находящееся вне
основной последовательности. Таблица теку-
щих и последующих состояний также содержит
это неиспользуемое состояние 10, и указывает-
ся (в виде значения XX), что нам безразлично,
какое состояние будет следующим. Впрочем,
это не совсем так, поскольку данное состояние
все же нужно учитывать: вскоре мы признаем,
26 Инженеры Мили и Мур написали в середине 1950-х гг.
важные доклады, которые определили эти идеи. Мур был
профессором в области компьютерных наук, а Мили рабо-
тал в Лаборатории Белла.
17N3. Конечный автомат: новое название старого устройства
685
что для нас важно, чтобы счетчик не застрял
на этом неиспользуемом состоянии 10. Но во
времена, когда такие схемы разрабатывались
вручную, было привычным делом использо-
вать безразличные состояния, в частности ука-
зывать безразличное состояние как следующее
состояние для любого неиспользуемого состоя-
ния. Причиной тому было стремление накла-
дывать на схему минимальные ограничения
и свести логику к минимальному объему.
Но самой схеме, конечно же, последующее со-
стояние не будет безразлично: после завер-
шения разработки это состояние будет так же
полностью определено, как и любое другое.
Более того, через несколько минут мы увидим,
что представляет собой это последующее со-
стояние.
В настоящее время, когда разработчикам до-
ступно большое количество вентилей в логи-
ческом массиве (ПЛУ или FPGA), такое ми-
нимизирование не стоит затраченных на него
усилий, и в таблице текущих и последующих
состояний можно указать все следующие со-
стояния. Но на данном этапе мы не будем де-
лать этого, поскольку хотим продемонстри-
ровать, какую опасность могут представлять
такие безразличные состояния.
В таблице текущих и последующих состоя-
ний показаны состояния триггеров до и после
какого-либо определенного сигнала тактиро-
вания. Поскольку мы планируем использовать
D-триггеры в разработке этой схемы, после-
дующее состояние также определяет пару зна-
чений, которые мы должны подавать на D вхо-
ды двух триггеров, и мы так и назвали столбец
«Последующее состояние».
Таблица 17N.2. Состояния счетчика
Текущее состояние
Q1QP
00
01
10
11
Последующее состояние
D1D0
01
11
XX
00
Эта схема достаточно проста, и принцип ее
работы, скорее всего, можно понять, просто
изучив табл. 17N.2. Вспомните, что XX озна-
чает, что мы можем по желанию присваивать
этому состоянию или высокий уровень, или
низкий, чтобы облегчить сборку схемы.
Если в каком-либо случае сразу увидеть требуе-
мые для входов D логические функции не уда-
ется, то их несложно определить. Можно про-
сто перечислить все входные комбинации, ко-
торые могут генерировать значение 1, а затем
выполнить над этими входными комбинация-
ми операцию ИЛИ. Например, в данном случае
для D1 можно создать логическое выражение
D1=(Q1*QP)+(Q1QO*). Это логическая функ-
ция Исключающее-ИЛИ, но ее можно реализо-
вать, выполняя операцию ИЛИ над результата-
ми двух функций И.
В данном случае эти две функции, скорее всего,
просто бросаются вам в глаза. Действуя анало-
гичным методом, вы сможете получить все не-
обходимые логические выражения:
♦ значение для D1 может быть результатом
операции Исключающее-ИЛИ над значения-
ми выходов Q1Q0;
♦ а определить значение для D1 еще проще: это
высокий уровень, когда на выходе Q1 при-
сутствует низкий уровень; таким образом,
это просто инверсия значения Q1, т. е. Q1*.
Мы получили эти функции, предполагая удоб-
ные уровни для значений X. Теперь посмотрим,
какое последующее состояние мы обеспечили
для неиспользуемого состояния D. На D1 при-
сутствует высокий уровень, а на D0 — низкий.
Оба-на! Это означает, что состояние D перехо-
дит в D.
Но почему это вдруг стало важным? Ведь мы
же с самого начала сказали, что нам все равно.
В действительности для нас важно избежать
одного результата: автомат не должен «за-
стрять» в одном из своих неиспользуемых со-
стояний, каким является и состояние D.
И если вы собираетесь возразить, что автомат
никогда не примет состояние Д то вы слишком
оптимистичны, поскольку он может принять
это состояние сразу же при включении пита-
ния. Даже если вы оснастите свою схему воз-
можностью автоматического сброса при вклю-
чении питания для перевода ее в разрешенное
состояние (например, состояние А), помеха в
процессе работы может перевести ее в состоя-
ние D. Поэтому не будет излишней предосто-
рожностью выполнить разработку так, чтобы
автомат не оказался в каком-либо неиспользуе-
мом состоянии.
686
77N. Память
Эта проблема легко решается заменой XX
каким-либо другим состоянием и соответству-
ющим изменением логики схемы. Если сделать
состояние А (закодированное как 00) следую-
щим после состояния D (закодированное как
10), то функция для Ш будет отличаться от
Исключающее-ИЛИ. Это последующее состоя-
ние означает, что в таблице состояний высо-
кий уровень для Ш создает только одна ком-
бинация — Q1*QQ. А эту функцию реализовать
даже легче, чем функцию Исключающее-ИЛИ,
поскольку это просто операция И над значе-
ниями Q1* и Q0. Триггеры обычно имеют ин-
вертированные выходы, в результате чего для
реализации логики D1 потребуется всего лишь
один логический элемент И. На рис. 17N.10
изображена принципиальная схема счетчика-
делителя на три, спроектированного в виде ко-
нечного автомата.
I—о.
ъ
Сигнал щ
тактирования
Рис. 17N.10. Счетчик-делитель на три в виде автомата со-
стояний
Это упражнение (или подобный проект на ла-
бораторном занятии 17L) будет, наверное, по-
следней возможностью для вас решать подоб-
ные задачи вручную. В дальнейшем все рутин-
ные операции за вас будет выполнять логиче-
ский компилятор, например, Verilog.
17N.3.3. Проектирование счетчика-
делителя на три с помощью Verilog
Вместо того, чтобы самому разрабатывать ло-
гику конечного автомата, всю эту работу за
вас может выполнить программа Verilog. В ли-
стинге 17N.1 приведена программа на Verilog
для создания практически такого же счетчика-
делителя на три, какой мы спроектировали
вручную в предыдущем разделе. Единственное
отличие — наличие одного дополнительно-
го сигнала startup, который задает начальные
значения для эмуляции. Начальная часть про-
граммы состоит из некоторых обычных под-
готовительных операций, а следующая за ней
основная часть представляет собой, по сути,
просто таблицу состояний, отображающую
последующее состояние для каждого из четы-
рех текущих состояний.
Листинг 17N.1. Программа на Verilog для созда-
ния счетчика-делителя на три
module div3_state(
input elk,
output reg [1:0] Q = 0
);
parameter zero = ЪОО, one = 'b01, two = 'Ы 0, three = 'Ы1;
always@(posedge cik)
begin
case (Q)
zero:
Q <= one;
one:
Q <= three;
two: // неиспользуемое состояние D
Q <= zero;
three:
Q <= zero;
endcase
end
endmodule
С этого времени благодаря языку Verilog мы
сможем работать на таком высшем уровне. На
рис. 17N.11 изображена принципиальная схе-
ма логики счетчика, созданная программой
Verilog. Схема получилась такой же, как и при
разработке вручную, в этом нет ничего удиви-
тельного, но придает уверенности в наших спо-
собностях разработчиков.
При эмуляции схемы, разработанной програм-
мой Verilog, была получена осциллограмма сиг-
налов (рис. 17N.12), которые выглядели, как и
следовало ожидать.
Для разработки следующего конечного автома-
та после завершения этого лабораторного заня-
тия вы, скорее всего, воспользуетесь для этого
логическим компилятором наподобие Verilog,
который позволяет работать на более высоком
уровне абстракции. Рассмотренный конечный
автомат счетчика-делителя на три был нети-
пичным, выбранным единственно из-за его
простоты. В Приложении А.11 мы разработали
проект более практически важного конечного
автомата — арбитра шины.
17N3. Конечный автомат: новое название старого устройства
687
Dl = Qi* A Q0
Рис. 17N.11. Принципиальная схема счетчика-делителя на три, созданная программой Verilog
с
139
Ш
SBB
;:f и-
3
r'i'i:i i a,
[
jams
1__J—
140 и-;
""I
!
|
1 _
"*1
|60ns ,
tZDCZ
~+~ ■— ™~
:
I
liGOriS
I
Рис. 17N.12. Осциллограмма эмуляции работы счетчика, созданного программой Verilog
17N.3A Использование памяти
вместо вентилей в схемах со
сложной комбинационной логикой
Логический компилятор и микросхемы ПЛУ
или FPGA значительно облегчают задачу раз-
работки конечных автоматов. Но для решения
подобных задач можно также использовать па-
мять, хотя это будет исключением из обычно
применяемых подходов. Для его реализации
предлагалось несколько специализированных
микросхем, наподобие микросхемы RPOM
CY7C258/9 объемом 2Кх16 компании Cypress
Semiconductor. Похоже, что эти устройства
в настоящее время вышли из употребления. Но
мы рассмотрим это решение на лабораторном
занятии 17L, поскольку там для него почти иде-
ально подходит аппаратное обеспечение.
Адресные линии памяти могут передавать
входные переменные и биты текущего состоя-
ния, тогда как линии данных могут выдавать
выходные функции, при этом также генерируя
информацию о следующем состоянии. Память
позволяет легко создать большое количество
выходных сигналов, для чего нужно просто
выбрать микросхему с большей разрядностью
слова. А более длинные последовательности
операций можно получить, просто увеличив
число триггеров. Создать конечный автомат,
который сможет выполнять большое количе-
ство разных задач, можно, увеличив количе-
ство входных сигналов, для чего нужно просто
увеличить число линий адреса, иными словами,
взять память большего объема (в словах).
На рис. 17N.13 приведена схема, которая при
восьми входах будет функционировать по-
добно микроконтроллеру, который мы начнем
вскоре рассматривать. Наличие восьми линий
адресов позволяет ей выдавать приблизитель-
но 256 разных комбинаций27. Этот конечный
автомат выполняет функции дешифратора
команд процессора. Командами являются
восьмибитовые значения, которые подаются
на входы дешифратора и каждое из которых
вызывает определенную последовательность
операций.
Данные
-Выход
Следующее
состояние
Адрес
Текущее
состояние
Сигнал тактирования
Рис. 17N.13. Конечный автомат, реализованный посред-
ством памяти вместо обычной комбинационной логики
27 Вы можете спросить, почему приблизительно, ведь 28
равно точно 256. Количество состояний было бы точно
256, если бы реализовывались все коды и никакой код не
использовался для добавления второго байта, который
может расширить набор команд.
688
17N. Память
Выходы дешифратора инструкций реализуют
ответы на команды. Ответ представляет собой
последовательность многоходовых операций,
необходимых, например, для копирования со-
держимого из одного встроенного регистра
процессора в другой. Иными словами, если
команда означает «копировать содержимое ре-
гистра 0 в регистр 1», тогда конечный автомат
может выполнить эту операцию за три шага:
♦ буфер регистра 0 подключается к внутренней
шине данных и содержимое этого регистра
выдается на шину данных;
♦ выполняется тактирование регистра 1, за-
хватывая значения с внутренней шины
данных;
♦ буфер регистра 0 отключается от шины
данных.
Это очень простая операция. Для сложных
операций, таких как арифметическое деление,
требуется большое количество последователь-
ных действий. Например, команда деления DIV
процессора, который мы будем использовать
на наших лабораторных занятиях по микро-
процессору, требует 40 циклов сигнала такти-
рования по сравнению с четырьмя циклами
для простейших операций наподобие рассмо-
тренной операции копирования данных между
регистрами28.
28 Это подходящее сравнение, но задача'подсчета количе-
ства циклов для микропроцессора 8051 усложняется тем
обстоятельством, что разные модификации этого процес-
сора выполняют одно и то же действие за разное количе-
ство циклов тактирования. Более того, микропроцессор
DS89C430 производства компании Dallas Semiconductor,
на основе которого мы собираем компьютер из дискрет-
ных компонентов, использует разное число циклов для вы-
17N.3.5. Подведение итогов:
возможны несколько вариантов
последовательных конечных
автоматов
♦ Внешние входы отсутствуют — схема на-
строена на выполнение только одной опера-
ции. Такой схемой может быть, например,
счетчик, двоичный, десятичный или с какой-
либо необычной последовательностью сче-
та. Независимо от типа последовательности,
счетчик может выполнять только ее, и ника-
кую другую. Его последующее состояние за-
висит только от его текущего состояния.
♦ Один внешний вход — такой конечный ав-
томат может выполнять любую из двух опе-
раций. Примером может служить счетчик
с возможностью суммирующего или вычи-
тающего счета.
Восемь внешних входов (как, например,
у процессора 8051) — такой конечный авто-
мат способен выполнять большое количество
альтернативных последовательностей, вплоть
до 256. Восемь входных линий позволяют вы-
брать одно действие из большого набора дей-
ствий. Эти восемь входных линий передают
процессору команды. А последовательность
команд составляет программу.
полнения одной и той же команды в зависимости от того,
где хранится код этой команды. Команды, хранящиеся во
встроенной памяти микропроцессора, могут выполнять-
ся за один сигнал тактирования на цикл доступа к шине,
тогда как для команд, хранящихся во внешней памяти,
требуется четыре сигнала тактирования. Оригинальный
микропроцессор 8051 требовал 12 циклов тактирования
для каждого цикла доступа к шине.
17L Лабораторное занятие: память
Подобно лабораторному занятию 16L это заня-
тие также состоит из двух альтернативных ча-
стей, каждая из которых предлагает несколько
иной путь для тех, кто планирует собирать ком-
пьютер из дискретных компонентов на боль-
шой макетной плате, и тех, кто предпочитает
компьютер на микросхеме.
♦ Первая часть необходима для тех, кто пла-
нирует собирать свой компьютер из дис-
кретных компонентов. Вам нужно будет до-
бавить память к собранному ранее счетчи-
ку. Эта память, которую можно адресовать
вручную, и аппаратное обеспечение для за-
грузки в нее данных послужат основой для
компьютера, собираемого вами из дискрет-
ных компонентов.
♦ А во второй части занятия мы будем экспе-
риментировать с конечными автоматами.
• Один из таких автоматов мы создадим на
основе уже собранной вами схемы, ис-
пользуя память RAM и загружаемый счет-
чик, который предоставляет адреса в этой
памяти.
• Второй конечный автомат представляет
собой схему последовательной логики для
управления замком, реализованную на
ПЛУ, запрограммированном посредством
языка Verilog. У тех, кто не занимается до-
бавлением памяти RAM к схеме счетчика
(т. е. собирает компьютер на микропро-
цессоре), будет свободное время зани-'
маться этой задачей. Для реализации схе-
мы последовательной логики для управ-
ления замком потребуется разработать
соответствующую программу на языке
Verilog. Описание же самой схемы приво-
дится в главе 17W. Затем нужно будет за-
программировать разработанную схему
в устройство ПМЛ, чтобы иметь возмож-
ность выполнить эту часть сегодняшнего
лабораторного занятия. Так что это лабо-
раторное занятие необычно тем, что для
него нужно выполнить некоторые подго-
товительные работы.
Конечные автоматы являются предваритель-
ным шагом к работе с микропроцессором,
с которым мы познакомимся на лабораторном
занятии 20L. Выполнение первой части сегод-
няшнего лабораторного занятия необходимо
для тех, кто планирует собирать свой компью-
тер из дискретных компонентов на большой
макетной плате, а не на основе микроконтрол-
лера. Решение, какую из этих версий компью-
тера собирать, вы сможете принять на лабо-
раторном занятии 20L. Вы не сможете присту-
пить к выполнению следующих этапов сборки
компьютера из дискретных компонентов до тех
пор, пока не установите память RAM.
Вторая часть этого лабораторного занятия не
является необходимой предварительной ра-
ботой. В ней просто демонстрируется фунда-
ментальный для компьютеров концепт, но вы
сможете выполнить всю дальнейшую работу,
не собирая этих схем. Если у вас очень мало
времени и вы решили собирать компьютер из
дискретных компонентов, тогда очевидно, что
вам нужно выполнить первую часть этого лабо-
раторного занятия, а затем то, что сможете из
его второй части.
Тем, кто планирует собирать компьютер на ми-
кропроцессоре, следует собрать схему конечно-
го автомата из раздела 17L.2.1. После выполне-
ния этой работы у вас должно остаться время,
чтобы реализовать задачу из лабораторного
занятия 16L, которую большинство студентов
не успевают сделать во время, отведенное на
это занятие, а именно добавить к счетчику эле-
менты, которые превращают его в измеритель
периода.
690
17L Лабораторное занятие: память
17L1. Память RAM
Память, адреса которой будет вырабатывать
ваш 16-разрядный счетчик, представляет со-
бой массив КМОП-триггеров. Ее объем со-
ставляет 32 КБ, или 32 КиБ, для обеспечения
которого потребуется 256К триггеров1. Эти
триггеры организованы в виде 32К слов, или
адресуемых ячеек, каждое из которых содер-
жит 8 битов. Благодаря использованию триг-
геров, а не конденсаторов данная память явля-
ется статической, т. е. не требует постоянного
обновления. Но эта память энергозависимая,
т. е. при отключении питания ее содержимое
теряется. Но для ее питания требуется на-
столько малая мощность, что с этой задачей
может с легкостью справиться таблеточная
батарейка напряжением 3 В, в чем у вас бу-
дет возможность убедиться, когда вы начнете
использовать RAM для хранения своих про-
грамм. Таким образом, эту RAM можно сде-
лать псевдоэнергонезависимой, просто под-
ключив к ней миниатюрную батарейку, чтобы
постоянно подавать питание2. На сегодняшнем
лабораторном занятии мы не будем питать па-
мять от батарейки, поскольку сейчас мы не
станем создавать никаких важных программ,
требующих сохранения для дальнейшего при-
менения.
Поскольку выходы микросхемы памяти осна-
щены внутренними буферами с тремя состоя-
ниями, для нее не требуются отдельные вход-
ные и выходные линии данных. Пока не ак-
тивирован сигнал разрешения записи WE*,
эти общие линии данных служат в качестве
выходных. При активировании этого сигнала
выходы буферов переходят в третье состоя-
ние, отключая таким образом выходы памяти
от шины данных. После этого к шине данных
подключены только входы памяти, в которую
теперь можно записывать данные. Этот момент
подробно рассматривается в главе 17N.
Описанный хитрый метод реализован в схеме
шины данных: третье состояние 8-разрядных
1 Если это кому-либо интересно (а обычным людям это
обычно неинтересно), 32 КиБ равно 32 768 байтам, для хра-
нения которых требуется 32 768 • 8 = 262144 триггеров.
2 На лабораторном занятии 21L мы увидим, что описание
«подключив батарейку» несколько упрощает требуемую
компоновку. Мы используем микросхему с резервным пи-
танием от батарейки, которая осуществляет переключение
между основным источником питания и питанием от ба-
тарейки.
буферов микросхемы 541 включается той же
самой линией, которая также активирует раз-
решение записи WE*. Таким образом, выход-
ные буферы RAM отключаются от шины дан-
ных как раз тогда, когда мы подключаем свои,
и наоборот3.
17L1.1. Подключение RAM и буфера
данных для цифровой клавиатуры
к счетчику
Теперь подключите к схеме счетчика микросхе-
му памяти RAM и микросхему буферов с вы-
водами с тремя состояниями, которая служит
интерфейсом между цифровой клавиатурой и
шиной данных.
Буфер с выходами с тремя состояниями не до-
пускает конфликтов между цифровой клавиа-
турой и другими подключенными к шине дан-
ных устройствами, которые выдают данные.
Хотя на данном этапе таким другим устрой-
ством является только RAM, в скором времени
к ним присоединится центральный процессор
и периферийные устройства. Память RAM и
буфер цифровой клавиатуры подключены к не-
скольким шинам на макетной плате: адресной
шине, шине данных и шине данных цифровой
клавиатуры.
Примечание
Мы рекомендуем вам сделать фотокопию (или
скопировать каким-либо другим образом) цоко-
левки, которая показана на рис. 17L11 в конце
этой главы, и наклеить ее на микросхему RAM. Эта
наклейка поможет вам сэкономить много усилий,
которые в противном случае вам придется тратить
на пересчет выводов4.
3 Это приблизительное описание происходящего, но не
с точностью до наносекунды. В частности, поскольку RAM
реализована по технологии КМОП, ее буферы отключают-
ся медленнее, чем наши включаются. Таким образом, эти
два набора буферов могут быть одновременно подключе-
ны к шине данных в течение от 10 до 20 не. Но это «со-
ревнование за шину» длится достаточно короткое время
и потому безвредно.
4 Обратите внимание на то обстоятельство, что мы пере-
определили некоторые выводы шины данных и адресной
шины по сравнению со стандартной цоколевкой. Это было
сделано для того, чтобы эти выводы были расположены
в последовательном порядке (хотя среди них и вставлено
несколько выводов управления и питания). Выводы для
сигналов старшей разрядности размещены выше (ближе
к верхнему краю микросхемы памяти, где находятся выво-
ды 1 и 28). Это должно немного облегчить монтаж схемы,
предполагая, что микросхема RAM устанавливается таким
17L2. Конечные автоматы
691
Внешняя
цифровая клавиатура
Сигналы и питание
подаются через
DIP-шлейф «.
(обратите внимание, это не та же
шина, что и общая шина данных)
(от счетчиков, установленных на
предыдущем лабораторном занятии)
Буфер шины данных
цифровой клавиатуры
QtfCt tg X& f* bt 8* W
oei Микросхема 8-разрядных
J5 ««буферов 74НСТ541
Статическая RAM
объемом 32К*8
ЧТУ
8 Шина данных
г
Данные ЖКД
Рис. 17L.1. Добавление к счетчикам памяти RAM и буфера с выходами с тремя состояниями
Как мы уже несколько раз упоминали ранее,
сигналы на линии адресов RAM будут пода-
ваться счетчиком на устройстве ПМЛ, которое
вы должны были подключить в схему на про-
шлом лабораторном занятии.
17L1.2. Проверка работы
собранной схемы
Удостовериться в том, что память сохраняет
данные должным образом, не составляет ни-
какого труда. Для этого просто выполняем сле-
дующую процедуру:
♦ вводим с цифровой клавиатуры два числа,
например А и В. Эти значения отображаются
на дисплее;
♦ нажимаем кнопку разрешения записи WR*,
в результате чего введенное значение АВ
должно отобразиться на жидкокристалличе-
ском дисплее. Если все так и происходит, зна-
чит, вы правильно подключили микросхему
541 буферов с выходами с тремя состояния-
ми: значение АВ передается с цифровой кла-
виатуры на шину данных;
♦ после прекращения нажатия кнопки раз-
решения записи WR* на дисплее должно
образом, что ее край с выводом 1 будет дальним от вас
(дальним от дисплея и цифровой клавиатуры).
Поразмыслив несколько минут, вы сможете убедиться в
том, что при работе с памятью RAM линии адреса можно
перемешивать между собой любым образом, и то же самое
можно делать с линиями данных. Но в случае с памятью
ROM, программируемой вне схемы, так делать нельзя.
продолжать отображаться значение АВ. Но
теперь эти данные поставляет память, ко-
торая после отпускания кнопки разрешения
записи WR* возобновляет подачу данных на
шину данных;
♦ введите на цифровой клавиатуре какое-либо
другое число, но не нажимайте кнопку WR*.
Отображаемое на дисплее значение не долж-
но измениться;
♦ инкрементируйте адрес. Отображаемое зна-
чение должно измениться, поскольку теперь
мы обращаемся к другой ячейке памяти RAM.
Теперь декрементируйте адрес. На дисплее
должно опять отображаться значение АВ.
Все работает, как описано? Если да, то поздрав-
ляем вас.
17L.2. Конечные автоматы
17L2.1. Простой конечный автомат:
счетчик-делитель на 3
В следующем упражнении мы не будем исполь-
зовать только что установленную RAM, а воз-
вратимся к ней позже на этом лабораторном
занятии.
Сейчас попытаемся обобщить наше пред-
ставление о типе последовательностных схем,
которые мы можем проектировать. До на-
стоящего времени почти все собранные нами
692
17L Лабораторное занятие: память
Входы
Текущее
состояние
—Выходы
Следующее
состояние
^~-—
Текущее
состояние
ОДо
00
01
10
11
Следующее
состояние
ЯтиЧапи
гч |ч
DlD0
XX
11
01
10
Рис. 17L.2. Блок-схема обобщенного конечного автомата и таблица состояний для вычитающего счетчика-делителя на 3
последовательностные схемы были счетчика-
ми5. Как уже упоминалось ранее, счетчик яв-
ляется особым случаем более общего устрой-
ства — конечного автомата.
Обобщенный конечный автомат
На рис. 17L.2 снова приведена блок-схема обоб-
щенного конечного автомата, которую мы впер-
вые показали на рис. 17N.8. Если бы эта блок-
схема представляла, например, суммирующий
и вычитающий счетчик, то входом была бы
одна линия выбора направления счета, а выхо-
дами — просто выходы (^триггеров.
Конкретный конечный автомат в
виде простого счетчика на триггерах
и логических элементах
Первым конечным автоматом, который мы
предлагаем на ваше рассмотрение, является
простой счетчик: хорошо знакомое вам устрой-
ство, которое сравнительно легко поддается
разработке. Вам нужно разработать и собрать
счетчик-делитель на три, используя для этого
D-триггеры и любые необходимые логические
вентили. Чтобы вы случайно не уснули в про-
цессе разработки этого простого устройства,
ваш счетчик должен реализовать необычную
счетную последовательность, которую нельзя
с легкостью обеспечить, применяя методы раз-
работки счетчиков, которые мы рассматривали
до настоящего времени.
Чтобы сделать задачу более увлекательной,
создадим счетчик-делитель на три, отличаю-
щийся от тех счетчиков, с которыми вы уже
имели дело.
Примечание
Мы не хотим, чтобы вы просто открыли кни-
гу АоЕ и взяли решение из нее или вспомнили
5 Другими, не так часто используемыми схемами были
триггер, сдвиговый регистр и цифровой одновибратор.
демонстрационную версию счетчика-делителя на
три, которую мы создали на основе счетчика с син-
хронным обнулением.
Ваш счетчик должен считать от 3 до 1, т. е. быть
счетчиком вычитающего типа.
На рис. 17L.2 кроме блок-схемы счетчика так-
же показана таблица состояний, содержащая
требуемую счетную последовательность.
Вспомните, что значения XX (безразлично) для
последующего состояния означают, что нам все
равно, что будет делать схема после неисполь-
зуемого состояния. Но все равно будет только
для нас, когда мы приступаем к разработке схе-
мы. А вот для спроектированной схемы будет
не все равно, в том смысле, что она перейдет от
текущего состояния 00 только к одному полно-
стью определенному последующему состоянию,
а не к какому-либо произвольному состоянию.
В главе 17N мы видели, как счетчик мог «за-
стрять» в неиспользуемом состоянии.
Мы надеемся, что внимательно изучив эту таб-
лицу состояний в течение некоторого времени,
вы сможете понять, каким образом можно соз-
дать требуемые две функции Dx и Dr Для этого
не нужно применять каких-либо хитроумных
операций, а требуется просто перечислить все
входные комбинации, которые могут генериро-
вать значение логической единицы, а затем вы-
полнить над этими входными комбинациями
операцию ИЛИ.
Между прочим, мы слегка испортили ваше удо-
вольствие, которое вы намеревались получить
от проектирования этой схемы полностью са-
мостоятельно, подсказав, что вам потребуются
два триггера и что одно состояние (безразлич-
. но) не используется. Но ведь вы и сами знали
это в любом случае. Готовый проект схемы сле-
дует проверить на бумаге, чтобы удостоверить-
ся в том, что для неиспользуемого состояния
случайно не будет присвоено значение XX = 00.
17L2. Конечные автоматы
693
Зачем это нужно? Мы уже упоминали ранее,
что беспокоимся о том, чтобы наша схема не
застряла в неиспользуемом состоянии.
Это был достаточно простой пример, хотя, воз-
можно, и не самый легкий. Ни одна задача не
бывает легкой в первый раз, когда вы пытае-
тесь решить ее. В разделе 17L.2.3 описывается
конечный автомат на основе памяти RAM, ко-
торый уже не такой простой, но намного лег-
че поддается проектированию, поскольку для
него не требуется вообще никаких логических
вентилей, а вся соответствующая работа вы-
полняется памятью RAM.
17L2.2. Проектирование
счетчика-делителя на три
посредством Verilog
В этом подразделе вам не нужно будет ничего
делать. Вам будет интересно узнать, что всю
грязную работу по проектированию конечно-
го автомата за вас может выполнить програм-
ма Verilog. Листинг 17L1 содержит программу
на Verilog для создания практически такого
же счетчика-делителя на три, какой мы спро-
ектировали вручную в предыдущем разделе.
Единственное отличие — наличие одного до-
полнительного сигнала startup, который задает
начальные значения для эмуляции.
Листинг 17L1. Программа на Verilog для проек-
тирования счетчика-делителя на три
module ctr_down_3(dk, startup, Q);
input clk,startup;
output [1:0] Q;
wire elk, startup;
reg Q;
parameter zero = Ъ00, one = 'b01, two = 'Ы0, three = 'Ы1 ;
always@(posedge elk, posedge startup)
begin
if (startup)
Q <= three;
else
case(Q)
three:
Q <= two;
two:
Q <= one;
one:
Q <= three;
zero:
Q <= three; // Неиспользуемое состояние
// инициализируется произвольным значением
endcase
end
endmodule
Как можно видеть, язык Verilog выполняет за
вас практически всю работу. Но мы надеемся,
что вам доставит удовольствие определить, ка-
кие функции следует подавать на каждый триг-
гер (по крайней мере, один раз в вашей жизни).
На рис. 17L.3 изображена принципиальная схе-
ма счетчика, созданная программой Verilog.
Интересно, насколько похожа эта схема на раз-
работанную вами? Ваша схема, скорее всего,
будет более простой, поскольку в ней не преду-
смотрена возможность установки в известное
начальное состояние (которое в программе
Verilog реализовано посредством асинхронного
сброса обоих триггеров) и она может восполь-
зоваться состояниями «безразлично»6. При
эмуляции схемы, разработанной программой
Verilog, была получена осциллограмма сигна-
лов (рис. 17L.4), которые выглядели так, как
и следовало ожидать.
01. Oil
Рис. 17L.3. Принципиальная схема счетчика-делителя на три, созданная программой Verilog
6 В компании Zilinx операцию установки (set) называют
предустановкой (preset).
694
17L Лабораторное занятие: память
Time: 1000 m
200
800
ll
startup
0(10]
QfOj
2Ь2
Рис. 17L.4. Осциллограмма эмуляции работы счетчика, созданного программой Veriiog
Завершив это лабораторное занятие, вы, скорее
всего, решите описанную задачу легким спосо-
бом, используя логический компилятор типа
Veriiog.
17L2.3. Добавление регистра
в конечный автомат на основе
RAM, чтобы определять следующее
состояние
Это упражнение (выполнить которое смогут
только те, кто установил память RAM) пред-
лагается вам с двоякой целью. Первая — про-
демонстрировать один из способов создания
сложного конечного автомата (хотя этот метод
встречается намного реже, чем язык HDL типа
Veriiog), а вторая заключается в том, чтобы по-
ближе познакомить вас с микропроцессором.
Мы надеемся донести до вас истину, что про-
цессор является всего лишь более сложной
версией устройств, с которыми вы уже имеете
опыт работы. Это всего лишь интеллектуаль-
ный конечный автомат, близкий родственник
обычных счетчиков. Его отличие состоит толь-
ко в том, что он более универсален, чем любой
счетчик.
Мы предполагаем, что, приступая к этому раз-
делу лабораторного занятия, вы собрали схему,
которая позволяет адресовать любую ячейку
RAM и записывать в эту ячейку число, вводи-
мое с цифровой клавиатуры. Как вы уже начали
понимать (собрав схему простого счетчика на
лабораторном занятии 17L.2.1), можно создать
произвольный конечный автомат, сначала пода-
вая значения последующего состояния на входы
D нескольких триггеров, а затем подав на эти
триггеры сигнал тактирования. В этом упраж-
нении у вас будет возможность испытать про-
стейший способ генерирования этих значений
следующего состояния, используя память RAM.
Память RAM хорошо подходит для выполнения
описанной задачи, поскольку подача адреса на
адресные линии приводит к появлению данных
на линиях данных; в этом и заключается суть
памяти. Применительно к конечному автомату
процесс выглядит так:
.АДРЕС (=текущее состояние) ~> (вызывает) -->
-> ДАННЫЕ (=следующее состояние)
Сегодня мы будем работать с памятью RAM,
поскольку она уже есть в нашем распоряже-
нии. Но обычно в конечном автомате на основе
памяти использовалась бы память ROM (т. е.
энергонезависимая память). Идея заключает-
ся в следующем. Слева на рис. 17L.5 показан
нестабильный вариант конечного автомата на
основе памяти, а справа — вариант, в котором
дефект исправлен посредством добавления ре-
гистра из триггеров, чтобы разомкнуть петлю
обратной связи и стабилизировать схему.
Регистр триггеров решает проблему, с ко-
торой мы уже сталкивались. Переключение
Текущее
состояние
Последующее
состояние
Текущее
состояние
п линий
Нестабильная
D
Последующее
состояние
Сигнал тактирования -
Регистр
D Q-
п линий
Стабильная
Рис. 17L5. Память RAM хорошо подходит для выполнения задач типа «текущее — последующее состояние». Для придания
схеме стабильности используется регистр из триггеров
17L2. Конечные автоматы
695
запуском по фронту D-триггера (в схеме справа
на рис. 17L.6) размыкает цепь обратной связи,
что обеспечивает стабильность работы схемы.
Состояние выходов триггера меняется по каж-
дому сигналу тактирования. Такая схема долж-
на быть вам уже знакома, поскольку мы соби-
рали ее на лабораторном занятии 15L.
Разрешение
Нестабильная
Стабильная
Рис. 17L6. Прозрачная защелка может быть нестабильной.
Тактируемое устройство (запускаемое по фронту) делает об-
ратную связь безвредной, в результате чего схема стабили-
зируется
Прозрачная защелка, изображенная слева на
рис. 17L.6, нестабильна, как вы имели возмож-
ность убедиться в главе 16N. В разрешенном
состоянии схема переходит в режим автоколе-
баний.
Счетчик, используемый как регистр
Для хранения текущего состояния обычно ис-
пользуется регистр из D-триггеров. Как отме-
чалось в главе 17N, некоторые микросхемы,
которые в настоящее время вышли из употре-
бления, содержали как память, так и регистр.
Чтобы сэкономить немного времени и уси-
лий на монтаже, мы выберем в качестве реги-
стра уже установленную микросхему ХС9572
16-битового триггера.
Вспомните, что до тех пор, пока на вход син-
хронной загрузки счетчика SYNCLD* подается
сигнал активирования, счетчик не считает, а
загружает по сигналу тактирования данные,
присутствующие на его 10 входах данных. (На
остальные шесть линий данных подается сиг-
нал низкого уровня, т. е. на них установлен ло-
гический ноль.) Таким образом, чтобы счетчик
работал как регистр, нужно просто подать на
вход синхронной загрузки SYNCLD* постоян-
ный сигнал низкого уровня.
Подачей сигнала на вход синхронной загруз-
ки SYNCLD* управляет ползунковый пере-
ключатель D3 DIP-переключателя, который
мы установили на лабораторном занятии 16L.
Соответствующая часть схемы изображена на
рис. 17.L.7.
(Элемент D3 DIP-переключателя,
установленного на лабораторном занятии 16L.3.4.)
Sync LD
(синхронная загрузка)
Микросхема
счетчика ХС9572
Разомкнут при программировании,
замкнут на «землю» при работе
Рис. 17L.7. DIP-переключатель, установленный на лабора-
торном занятии 16L, теперь может служить для переключе-
ния между режимами программирования и работы
Теперь с помощью переключателя можно пере-
ходить от режима программирования к рабоче-
му режиму. Посредством этого переключателя
мы будем подавать на вход синхронной загруз-
ки SYNCLD* сигнал активирования только тог-
да, когда хотим запустить конечный автомат на
исполнение.
Данные из RAM подаются
на регистр из счетчика
На рис. 17L.8 изображена блок-схема нашего
конечного автомата: мы создаем классический
автомат состояний, контур, в котором данные
из RAM подаются на счетчик (который зафик-
сирован в режиме регистра заземлением входа
синхронной загрузки SYNCLD*), а счетчик вы-
дает значения на адресные линии RAM.
(Не используется в нашей разработке,
поскольку мы формируем только
одну последовательность)
Вход
+А—Выход
(к дисплею)
Сигнал тактирования
Переводит устройство
ТТААЛ на микросхеме
9572 в режим работы
регистра, а не счетчика
Рис. 17L8. С помощью RAM и загружаемого счетчика можно
создать классический конечный автомат
696
17L Лабораторное занятие: память
Загружаем последовательность
программы в RAM
Загрузку выполняем, пока выходные сигна-
лы с цифровой клавиатуры подаются на
все восемь входов Рп счетчика. Все линии KD
цифровой клавиатуры пока должны оставать-
ся подключенными к входам Р счетчика. Как
обычно, на вход синхронной загрузки SYNCLD*
счетчика (см. рис. 17L.8) должен подаваться
сигнал высокого уровня. В дальнейшем мы по-
меняем схему для исполнения программы, как
будет показано на рис. 17L.9.
Программа-пример. Загрузите данные из
табл. 17L.1 в восемь указанных ячеек RAM. Эти
ячейки не являются самыми первыми, посколь-
ку цифровая клавиатура управляет только ли-
ниями D4...D11, а самые младшие разряды за-
гружаемого адреса имеют постоянное нулевое
значение. Кроме того, двум старшим разрядам
адреса также следует присвоить нулевые значе-
ния, используя для этого цифровую клавиатуру
и DIP-переключатель, который управляет ли-
ниями двух старших разрядов адреса.
Самостоятельно разобраться с содержимым
табл. 17L.1 может быть нелегко, поэтому попы-
таемся облегчить задачу, рассмотрев два шага
из последовательности состояний.
вая строка в таблице содержит адрес (для линий
А15...А0), равный нулю, и 8-битовое значение
ячейки по этому адресу, равное 03h. Поскольку
линии младших трех разрядов подключены
к линиям адреса А6...А48 (см. рис. 17L.8), сохра-
ненное значение «3» переводит автомат в по-
следующее состояние, которое соответствует
не 3, a 30h. Подобным образом, значение «2»,
хранящееся в ячейке по адресу 30h, переводит
автомат по адресу 20h.
Обратите внимание на один нюанс, который
довольно трудно понять из таблицы: восемь за-
писей в таблице не указывают на восемь после-
довательных адресов 0...7. Вместо этого каж-
дый последующий адрес больше предыдущего
на 10h: 0,10h, 20h,..., 60h, 70h.
В результате получим следующее:
♦ в ячейке по адресу 0 хранится значение 03h;
♦ в ячейке по адресу 10h хранится значение D5;
♦ в ячейке по адресу 20h хранится значение А1;
♦ в ячейке по адресу 30h хранится значение В2;
♦ в ячейке по адресу 40h хранится значение 07;
♦ в ячейке по адресу 50h хранится значение F4;
♦ в ячейке по адресу 60h хранится значение D3;
♦ в ячейке по адресу 70h хранится значение 06.
Адрес
(в шестнадцате-
ричном формате)
А15-А14
(Постоянные)
0
А13-А12
(DIP-пере-
ключатель)
0
Таблица
17L.1. Данные и
следующие адреса, загружаемые в RAM
Вводится с цифровой клавиатуры
KD7
(Р7
А11-А7
(С цифровой
клавиатуры)
0
...KD0
...РО)
А6-А4
(С цифровой
клавиатуры)
0
1
2
3
4
5
6
7
АЗ-АО
Данные
(произ-
вольные)
D7-D4
(Постоянные) (RAM)
0
0
0
0
0
0
0
0
0
D
А
В
0
F
D
0
Следующий
адрес
D3-D0
(RAM)
3
5
1
2
7
4
3
6
Предположим, что автомат начинает работу
случайным образом7 по нулевому адресу. Пер-
7 Или используя сигнал сброса RESET*.
8 Сигналы на линии А6...А4 подаются с выводов Р2...Р0,
поскольку линии четырех младших разрядов адреса, ко-
торые недоступны извне ПМЛ, закорочены на «землю»
внутри микросхемы. Таким образом, первой доступной
линией адреса является линия А4.
17L2. Конечные автоматы
697
Чтобы сохранить эту таблицу с «разбросанны-
ми» данными, используем сигнал асинхронной
загрузки LOAD* для доступа к ячейке с требуе-
мым адресом. Например:
♦ чтобы получить доступ к ячейке с адресом
10h, введите на цифровой клавиатуре значе-
ние 01, нажмите кнопку загрузки Load, а за-
тем запишите в ячейку указанные для нее
данные (D5h);
♦ чтобы получить доступ к ячейке с адресом
20h, введите на цифровой клавиатуре зна-
чение 02, нажмите кнопку загрузки Load, a
затем запишите в ячейку указанные для нее
данные (Alh);
♦ и так далее таким же образом.
Описанный процесс весьма трудоемкий, а ре-
зультаты, полученные после всех усилий, до-
вольно скромные. Но мы надеемся, что это не-
большое упражнение поможет снять вуаль за-
гадочности с конечных автоматов.
Модифицируем схему
и исполняем программу
Загрузив значения программы в RAM, измени-
те монтаж схемы, как показано на рис. 17L.9.
В частности, отсоедините линии трех младших
разрядов KD шины цифровой клавиатуры от
входов Р0...Р2 счетчика, в результате чего
данные на эти входы будут подаваться с линий
трех самых младших разрядов основной шины
данных.
На рис. 17L.9 изображены три линии данных
памяти RAM, подающих сигнал на три линии
Р2...Р0 загрузки данных счетчика (сама RAM
на рисунке не показана). В этой схеме, когда
на вход синхронной загрузки счетчика SYNC_
LD* подается сигнал низкого уровня (потен-
циала «земли»), счетчик работает в режиме
16-разрядного регистра. Три линии данных,
на которые подается сигнал с шины данных,
в данном случае получают сигнал с линий дан-
ных D2...D0 памяти RAM. Доступ к этим ли-
ниям данных можно получить через разъем
шины данных макетной платы, на которой со-
бирается микрокомпьютер.
Испытываем схему в работе
Испытайте работоспособность собранной вами
схемы и загруженной в нее программы, следуя
нижеизложенной процедуре:
Полагаем, что вы уже загрузили данные в RAM,
отсоединили линии данных трех нижних раз-
рядов D0...D2 счетчика от шины данных циф-
ровой клавиатуры (которая является стан-
дартным источником данных для этих линий)
и подключили их к линиям трех младших раз-
рядов основной шины данных:
Адресная шина
Микросхема ТТЛЛЛ
счетчика адресов
Обратите внимание на то,
что это две разные шины
Загрузка адреса
Теперь переключатель
синхронной загрузки (SYNCLD*)
управляет режимами
программирования и исполнения
Для этого упражнения введите нулевое
значение с цифровой ют
Шина данных цифровой клавиатуры^
Шина донцу, , , , ff
На микросхеме ТТМЛ эти линии обозначены 92,
PI, P0. В процессе загрузки программы сигналы на
них будут как обычно подаваться с линий KD2...KD0
шины данных цифровой клавиатуры. В процессе
исполнения программы сигналы на них будут
подаваться с линий D2...DO основной шины данных
(а не шины данных цифровой клавиатуры).
Рис. 17L.9. Регистр из восьми D-триггеров (счетчик с заземленным входом LD*), на которые подаются три бита данных из RAM;
теперь цепь обратной связи замкнута
698
17L Лабораторное занятие: память
1. С помощью соответствующего DIP-пере-
ключателя подайте сигнал низкого уровня
(потенциала «земли») на вход синхронной
загрузки SYNCJLD* регистра. Таким обра-
зом мы переводим схему в режим исполне-
ния программы.
2. Подайте сигнал тактирования на регистр, на-
жав кнопку INC на цифровой клавиатуре.
На дисплее должен отобразиться следующий
адрес в младшем полубайте данных с шины
данных и последовательность букв в старшем
полубайте. В действительности эта последо-
вательность букв в старшем полубайте содер-
жит зашифрованное сообщение. Попробуйте
расшифровать его. (Это довольно нелепое со-
общение, но, с другой стороны, у нас были
только буквы от А до F, чтобы создать его.)
Информацию о следующем адресе, отвлекаю-
щую внимание, можно устранить, закрыв соот-
ветствующую часть дисплея листом бумаги или
чем-либо другим, подходящим для этой цели.
На этом мы завершим эксперимент с конечным
автоматом. Будем надеяться, что вы в резуль-
тате поняли, как можно расширить описанную
схему. Например, добавление одного входа в
виде линии адреса позволит нам выбирать две
альтернативные последовательности; два входа
увеличат число последовательностей (или по-
ведений) до четырех, а восемь входных линий
(как в микропроцессоре 8051, с которым мы
начнем работать на лабораторном занятии 21L)
обеспечат 256 разных последовательностей.
Таким образом, микропроцессор 8051 являет-
ся большим конечным автоматом. В принципе,
при наличии достаточного времени, вы бы и
сами смогли разработать такой микропроцес-
сор. Но не переживайте, такую задачу мы перед
вами на лабораторном занятии не поставим.
17L3. Создание конечного
автомата с помощью
программирования микро-
схемы ПМЛ логическим
компилятором Verilog
Как упоминалось ранее в разделе 17L.2.2, логи-
ческий компилятор Verilog превращает разра-
ботку конечного автомата в довольно простую
задачу, позволяя описать его так, как мы его
представляем: просто перечислив все состоя-
ния и указав для каждого из них как выходное
значение, так и последующее состояние. Теперь
мы предлагаем вам продемонстрировать такой
конечный автомат, который не является про-
стым счетчиком, каким была схема в примере
из раздела 17L2.2.
Для этого вы должны были спроектировать
схему последовательной логики для управле-
ния замком, описанную в главе 17W, а также
реализовать этот проект, запрограммировав
устройство ПМЛ соответствующим образом.
Если же вы этого не сделали, то мы предоста-
вим вам такое устройство. Но тогда вы не по-
лучите удовольствия, как если бы вы сделали
его сами. Тем не менее это лучше, чем упустить
возможность наблюдать конечный автомат в
действии.
Если в собранном вами устройстве цоколевка
такая же, как и у нас (входы находятся в левом
нижнем углу адаптерной платы микросхемы, а
выходы — в левом верхнем углу), то ваша ма-
кетная плата может выглядеть подобно нашей,
показанной на рис. 17L.10.
Рис. 17L.10. Схема последовательностной логики для управ-
ления замком, собранная на макетной плате
Как и на лабораторном занятии 16L, мы ис-
пользуем микросхему для поверхностного мон-
тажа, установленную на адаптерную плату, что-
бы вставить ее в макетную плату9. Мы устрани-
ли дребезг контактов в сигнале тактирования
CLK, используя для этого простой прием подачи
обратно на вход выходного сигнала неинвер-
тирующего вентиля (микросхема НС08). Для
генерирования сигнала тактирования таким
способом потребуется однополюсный двухпо-
зиционный переключатель. Можно обойтись
без схемы для устранения дребезга, подав для
9 На рис. 17L.10 изображена микросхема в корпусе дру-
гого типа, установленного в гнездо. У вас будет микросхе-
ма в корпусе TQFP, а не в корпусе PLCC, как на рисунке.
17L.3. Создание конечного автомата с помощью программирования микросхемы ПМЛ...
699
тактирования схемы низкочастотный ТТЛ-сиг-
нал от генератора сигналов.
Мы оснастили нашу схему тремя светодиодами
для индикации состояния конечного автомата.
В рабочей версии схемы управления замком
эти светодиоды будут скрыты, но они очень
полезны для отладки схемы или для опреде-
ления, что делает автомат в данный момент.
Наблюдение за сигналом на выходе UNLOCK
предоставляет намного меньший объем ин-
формации.
Несомненно, что вам нужно будет попробовать
ввести несколько неправильных кодов, чтобы
увидеть реакцию схемы на них. Когда активиру-
ется сигнал открытия замка UNLOCK, он должен
оставаться активированным до тех пор, пока
остается активированным сигнал TRY, независи-
мо от сигнала тактирования. Снятие сигнала TRY
с последующим фронтом сигнала тактирования
должно снять сигнал UNLOCK. Соответствует ли
поведение собранной вами схемы этому сцена-
рию? Будем надеяться, что да.
На рис. 17L.11 изображена цоколевка микро-
схемы RAM, копию которой рекомендуется на-
клеить на корпус микросхемы. Если необходи-
мо, измените размер вашей копии таким обра-
зом, чтобы расстояние между выводами было
2,54 мм.
1
2
3
4
5
6
7
*
9
19
11
12
13
14
Рис. 17L.11. Цоколевка микросхемы RAM
А9
А8
А7
А6
А5
А4
A3
А2
А1
АО
D2
Ot
00
GND
R
A
M
3
2
к
Vcc
WE*
A14
A13
A12
A11
or
A10
CS#
07
06
06
04
03
28
27
26
25
24
23
22
21
20
19
18
17
Ы
15
AS
A8
A7
AS
AS
A4
A3
A2
A1
АО
02
01
00
R
A
M
3
2
4w
l\
GND
Vcc
WE*
A14
A13
A12
A11
OE*
A10
CS*
07
06
06
04
03
17S. Дополнительный материал: диагностика
цифровых схем и декодирование адресов
17S.1. Советы
по диагностированию
цифровых схем
Далее приводятся некоторые размышления на
тему диагностирования цифровых схем.
Используйте логический пробник,
а не мультиметр
Это должно быть само собой разумеющимся,
но мы не уверены, что вы вполне осознаете
важность данного принципа. Пристальное рас-
сматривание проводов монтажа при попытках
понять, подключены ли они туда, куда долж-
ны, — слишком утомительное занятие. Гораздо
удобнее исследовать сомнительный провод
с помощью логического пробника, чтобы убе-
диться, все ли правильно в монтаже.
Подключайте пробник к выводам
микросхем, а не в гнезда макетной платы
Обычно выводы микросхем имеют надежный
контакт с гнездами макетной платы. Но иногда
Рис. 17S.1. Изогнутый вывод микросхемы не позволит убе-
диться в ее работоспособности при подключении пробника
к соответствующему ряду гнезд макетной платы
бывают и исключения. В частности, при встав-
ке микросхемы в макетную плату какой-либо
из ее выводов может подогнуться и не войти в
гнездо (рис. 17S.1). Также возможна ситуация,
когда из-за вставки выводов слишком большо-
го диаметра с чрезмерным усилием контактные
лепестки гнезда расходятся, что влечет за собой
нарушение контакта в этом гнезде. Поэтому
сначала всегда проверяйте первоисточник.
Отключите нагрузку от проблемного
выхода
Предположим, что сигнал на выходе одного
из буферов с тремя состояниями микросхемы
541 не соответствует входному. В частности,
при разрешении буфера на этом выходе отсут-
ствует как высокий, так и низкий уровень. Это
состояние легче всего определить с помощью
логического пробника, поскольку осцилло-
граф будет показывать напряжение посередине
между двумя логическими уровнями. Кто вино-
ват в этом проблематичном выходном уровне?
Микросхема буфера или какой-либо компонент
дальше на этой линии данных? Нисходящее
устройство может подавать сигнал на данную
линию, в результате чего возникает конфликт
на шине — соревнование между высоким и низ-
ким уровнями, результатом которого является
средний уровень.
Этот вопрос можно легко решить, отключив
от данного вывода буфера микросхемы 541 все
подключенные к нему устройства. После это-
го снова включаем микросхему и наблюдаем
сигнал на ее проблемном выходе. Если теперь
выход функционирует должным образом, про-
веряем ряд гнезд макетной платы, в который,
по идее, вставлен вывод микросхемы. Тем са-
мым мы проверяем, действительно ли этот
вывод вставлен, а не подогнут, как показано
на рис. 17S.1. Далее проверяем все провода,
17S.I Советы по диагностированию цифровых схем
701
которые подключаются к данному выходу.
Часто будет так, что микросхема и контактные
гнезда макетной платы окажутся в порядке, но
на один из проводов все равно будет подавать-
ся активный сигнал, тогда как на этом проводе
должен присутствовать сигнал только с выхода
буфера, к которому он подключается. В таком
случае продолжаем искать «виновника», про-
веряя проблемный провод.
Проверьте источники питания
Это правило может показаться вам тривиаль-
ным, но оно очень полезное: прежде чем искать
другие причины проблемы, проверьте, что на
тестируемое устройство подается питание.
Разумеется, вы можете возразить: «если бы на
устройство не подавалось питание, то оно было
просто полностью нерабочим, а мое устройство
все же работает, но только странным образом».
Такое логическое мышление основано на оши-
бочном предположении, что устройства КМОП
не смогут работать, если они не подключены
к источнику питания. Но в действительности,
если вы вспомните свой опыт из лабораторно-
го занятия 14L, то убедитесь, что микросхемы
КМОП могут работать даже в такой ситуации.
Такая аномальная возможность объясняется
тем, что защитные диоды на входах позволяют
за счет входных сигналов (или выходных, но ве-
роятность того, что эти сигналы могут постав-
лять питание на микросхему, намного меньше)
обеспечивать питание, как положительное, так
и отрицательное, хотя напряжение окажется
слегка пониженным. На рис. 17S.2 показана ти-
пичная схема защиты входов и выходов микро-
схем КМОП с помощью диодов.
Входной
сигнал
• ЛЛЛг
Выходной
сигнал
Рис. 17S.2. Защитные диоды микросхем КМОП могут по*
ставлять напряжение с входных сигнальных линий на линии
питания
Неподключенные линии питания могут вы-
зывать непонятные проблемы, которые то
появляются, то исчезают. В случае подобных
непостоянных проблем рекомендуем прове-
рить наличие питания, как положительного,
так и отрицательного («земли»). При отсут-
ствии таких подключений питание на микро-
схему может подаваться входными сигналь-
ными линиями. Рассмотрим для примера про-
стой случай использования одного вентиля И
микросхемы, как показано на рис. 17S.3.
[ (Разомкнуто в некоторых случаях)
(Разомкнуто
в некоторых случаях)
Выход
(к подобному вентилю)
Рис. 17S.3. Гипотетическое использование одного вентиля
И многоэлементной микросхемы
При неподключенных линиях питания (как по-
ложительного, так и отрицательного) этот вен-
тиль будет работать непонятным образом, как
мы впервые убедились на лабораторном заня-
тии 14LA В табл. 17S.1 приводятся подробности
этого поведения.
Таблица 17S.1. Состояния логического вентиля
без питания
Вход
А
0
0
1
1
В
0
1
0
1
Будет ли вентиль работать
Разомкнуты
цепи +Um
и «земля»
Нет
Да
Да
Нет
Разомкнута
только цепь
Нет
Да
Да
Да
Разомкнута
только
«земля»
Да
Да
Да
Нет
Таким образом, даже если на микросхему не
подавать питание, ее вентили иногда могут
работать, но не обязательно правильно. В та-
ких случаях микросхема получает питание
из сигнальных линий при условии одновре-
менного наличия как высокого, так и низко-
го уровня на ее входах (иногда выходах). Но
1 Как упоминалось на том лабораторном занятии, мы об-
наружили, что подобным образом вела себя микросхема
74НС00 производства компании Texas Instruments/Natio-
nal Semiconductor. Эта же микросхема производства ком-
пании Motorola при высоких логических уровнях на обоих
входах вентиля выдавала на выходе высокий уровень.
702
77S. Дополнительный материал: диагностика цифровых схем и декодирование адресов
при наличии одинаковых уровней на входах
и выходе микросхема с таким «питанием» ра-
ботать не будет.
Таким образом, если какой-либо вентиль ведет
себя странным образом, вы можете сэкономить
себе кучу времени и нервов, сразу же проверив
наличие питания на микросхеме.
Три распространенные причины
«плавающих» уровней
Иногда логический пробник покажет наличие
«плавающего» уровня там, где его не должно
быть.
Примечание
Слово «плавающий» касательно уровня исполь-
зуется как сокращение термина «промежуточный
логический уровень», как рассматривалось чуть
ранее в этом разделе: ни высокий, ни низкий.
Часто такой уровень не является следствием пе-
ревода выхода в действительно «плавающее» со-
стояние, которое возможно только в выключен-
ном, третьем (высокоимпедансном), состоянии
выхода.
Такой «плавающий» уровень является при-
знаком специфической проблемы. Иногда он
выглядит еще более странно — не просто пла-
вающим, но и осциллирующим с высокой ча-
стотой. Обнаружить плавающие уровни помо-
жет логический пробник. Если ваш пробник
оснащен переключателем технологий (КМОП
или ТТЛ), его нужно установить в правильное
положение. (Недавно я попал впросак, забыв
об этом переключателе.) Пробник сможет
обнаружить и высокочастотные колебания,
если установить его соответствующий пере-
ключатель в положение Pulse (Импульс), а не
Memory (Память).
При обнаружении колебаний для продолжения
диагностирования потребуется осциллограф.
Этот аспект рассматривается более подробно
далее, в разделе 17S.1.1. Возможные причины
странного «плавающего» уровня:
1. Отключен источник сигнала (некачествен-
ный контакт, возможно оголенный конец
проволочной перемычки слишком короткий
и не достает до контактов гнезда макетной
платы).
2. Отсутствие положительного или отрица-
тельного питания на микросхеме — источ-
нике логических сигналов. Не забывайте про
изложенный ранее факт, что даже при от-
сутствии питания (как положительного, так
и отрицательного, так и обоих) микросхемы
КМОП иногда могут создавать видимость
рабочих, получая питание со своих входных
сигнальных линий.
3. Конфликт между двумя выходными сигнала-
ми. Чтобы проверить эту возможность, про-
сто отключите все кроме одного источника
сигналов, как описывалось ранее.
Определив, какой именно бит является про-
блемным, исследуйте сигнал с помощью логи-
ческого пробника. Часто высокий логический
уровень оказывается не настоящим высоким
уровнем, а «плавающим». Логические анали-
заторы могут интерпретировать «плавающие»
уровни как логические высокие уровни, напо-
добие уровней ТТЛ, или же могут просто ото-
бражать полученное ранее значение, сохранен-
ное за счет паразитной емкости.
Но наиболее распространенная причина «пла-
вающего» уровня самая банальная — просто
некачественное (разомкнутое) соединение на
пути сигнала.
Необычные значения данных или
адресов предоставляют ценные
сведения о проблеме
Рассмотрим такую возможную последователь-
ность: после 0 идет 2, после 4 — 6, после 8 — А,
и т. д. Для диагностирования этой проблемы
переключите режим работы дисплея с обыч-
ного шестнадцатеричного на двоичный и по-
шагово медленно пройдитесь по последова-
тельности. Запишите полученные значения.
Как правило, в двоичном формате необычная
битовая комбинация сразу же бросается в гла-
за. Но если аномалию таким образом обнару-
жить не удастся, то попробуйте выписать в до-
полнительной колонке таблицы истинности
ожидаемую битовую комбинацию и сравните
ее с получаемой. В табл. 17S.2 приводится пара
примеров неправильных последовательностей
шестнадцатеричных значений, выяснить при-
чину проблемы в которых помогла их запись
в двоичном формате.
775.7. Советы по диагностированию цифровых схем
703
Таблица 17S.2. Проблемные последовательности шестнадцатеричных значений
и соответствующие двоичные значения
Последовательность
Шестнадцатеричный
3
2
3
6
7
6
7
А
0
1
8
9
4
5
С
D
Двоичный
ООН
0010
ООН
оно
0111
оно
0111
1010
0000
0001
1000
1001
0100
0101
1100
1101
==> Диагностика
Уровень разряда D1 всегда высокий.
Возможно, «плавающий» уровень.
Проверяем частоту переключения каждого разряда:
Разряд DO переключается по каждому импульсу тактирования.
Это хорошо.
Один разряд переключается по каждому второму импульсу тактиро-
вания; иными словами, он ведет себя, как разряд D1. Но этот разряд
не в том месте: это самый левый разряд.
В то же самое время медленнее всех переключается разряд D1,
тогда как это должен быть разряд D3.
По-видимому, линии разрядов D1 и D3 поменялись местами или,
иными словами, произошел «поворот» старших трех разрядов вокруг
разряда D2.
(Эту ошибку легко допустить с шестнадцатеричным дисплеем про-
изводства компании Hewlett-Packard, который имеет непривычную
цоколевку.)
Необычная последовательность
шестнадцатеричных значений вместо
ожидаемой инкрементации
Рассмотрим еще одну возможную последова-
тельность: после 0 идет 0, после 1 — 8, после
8 — 1, после 3 — С. Иными словами, вместо
ожидаемой простой инкрементации получена
странная последовательность без видимой за-
кономерности. Как и ранее, выписываем зна-
чения получаемой последовательности в дво-
ичном представлении. Обычно в таких случаях
причиной проблемы оказывается обмен места-
ми каких-либо двух разрядов. Для только что
описанной последовательности местами поме-
нялись разряды D3 и D0, а также разряды D2
и D1. Иными словами, шлейф подачи сигналов
на эти четыре разряда был развернут на 180°.
17S.1.1. Более сложный случай:
автоколебания
Загадочные паразитные автоколебания явля-
ются, возможно, второй самой трудной про-
блемой для диагностирования. (Труднее всего
выявить неполадку, которая спонтанно появ-
ляется и исчезает время от времени.) Причины
возникновения автоколебаний в цифровых
и аналоговых схемах различны. Поскольку
цифровые схемы обычно невосприимчивы к
шумовым сигналам малой амплитуды, они не
усиливают и не передают эти сигналы, подобно
тому, как это могут делать аналоговые схемы.
Но даже в цифровых схемах можно не-
умышленно получить генератор колебаний,
создав по ошибке петлю обратной связи,
704
775. Дополнительный материал: диагностика цифровых схем и декодирование адресов
инвертирующую выходной сигнал. Это выгля-
дит как отрицательная обратная связь, которая
в аналоговых схемах содействует стабилизации
выходного сигнала. Но в цифровых схемах, с их
быстрыми перепадами уровней, отрицательная
обратная связь совместно с неизбежными за-
держками срабатывания логических вентилей
часто вызывает автоколебания. Это явление
можно рассматривать как выходной сигнал,
противоречащий входному. В свете такого об-
стоятельства возникновение паразитных ав-
токолебаний выглядит возможным развитием
событий. Период (или частота) колебаний ча-
сто дают подсказку о наиболее вероятном пути
обратной связи. Далее рассмотрим два случая,
иллюстрирующих этот момент.
Случай 1. Высокая частота
автоколебаний указывает на короткий
путь обратной связи
На рис. 17S.4 показана осциллограмма авто-
колебаний очень высокой частоты — с перио-
дом величиной всего лишь в пару вентильных
[Выход логического вентиля Диагностика I
микросхемы НС14 Частота неожидаемых j
[подключен к его входу автоколебаний может i
{,■ ■ ■••'\ , ч. ^"\{ дарь-.под сказку "•-, ' j
F i > касательно их. причины!
J
Период приблизительно 12 не
Рис. 17S.4. Случай 1. Цепь обратной связи, вызывающей ав-
токолебания, содержит лишь один логический вентиль
Диагностика
Частота неожиданных автоколебаний может дать подсказку
[касательно их причины Случай 2
DO
[7
задержек. Можно предположить, что в данном
случае цепь обратной связи содержит только
один логический вентиль.
Вспомните, что один период соответствует двум
проходам сигнала через вентиль, т. е. двум вен-
тильным задержкам. Данная осциллограмма
сигнала вентиля микросхемы НС14 воспроиз-
водит случай, который мы недавно наблюдали
в нашей лаборатории: кто-то подключил выход
логического вентиля (инвертирующего тригге-
ра Шмитта) к одному из его входов. Согласно
справочному листку типичная вентильная за-
держка микросхемы НС14 составляет прибли-
зительно 11 не при напряжении питания 5 В.
Частота автоколебаний в данном случае будет
более высокая, чем это значение, но все равно
находится в подходящем диапазоне.
Случай 2. Автоколебания с более низкой
частотой указывают, что путь обратной
связи проходит через инерционное
устройство
Наверное, единственным легким аспектом в
данном случае является заключение, что ко-
личество вентилей в петле обратной связи на-
много больше, чем один. Исходя из величины
периода автоколебания, нам следует ожидать,
что задержка в цепи обратной связи будет со-
ответствовать половине периода, или прибли-
зительно 60-65 не. Такая задержка слишком
велика для одного вентиля и слишком мала для
процессорного цикла (период цикла тактирова-
ния ЦП составляет около 90 не, а выполнение
самой короткой процессорной опера-
ции занимает несколько циклов сигнала
тактирования). А вот для памяти такая
задержка выглядит как раз впору.
до
Противоречие создано в памяти
Период: приблизительно 120 не
получает сигнал с СЮ, буферизованный микросхемой ЯС14
tnt
^^J
п
W.
Рис. 17S.5. Случай 2. В данном случае частота автоколебаний слишком
низкая, чтобы подозревать одну или две вентильные задержки
Действительно, мы создали сигнал, ос-
циллограмма которого показана на
рис. 17S.5, пропустив противоречивую
комбинацию через память. В частности,
мы подключили линию АО к линии DO,
затем записали данные, которые заста-
вили DO противоречить АО: по адресу 0
мы записали значение 1, а по адресу 1 —
значение 0.
Распространение сигнала в цепи обрат-
ной связи должно занять время *Д0СГУПА.
Мы должны отметить, что в данном слу-
чае прямое подключение выхода на вход
J7S.2 Декодирование адресов
705
не вызвало автоколебаний, поскольку сигнал
адреса (от ЦП) сильнее, чем сигнал данных (от
RAM на КМОП-микросхемах). Поэтому мы не-
много смухлевали, пропустив сигнал с DO через
буфер микросхемы 74НСТ08. Это уравновешива-
ет сигналы с двух линий, в результате чего возни-
кают автоколебания. (Кроме того, возможно, что
буферная микросхема также добавляет дополни-
тельные 6-9 не задержки2.) В общем, не трать-
те слишком много своего времени (больше чем
5 минут), пытаясь решить назойливую проблему.
Если не получается устранить ее в течение этого
времени, то обратитесь за помощью.
17S.2. Декодирование
адресов
двоичному числу, предоставляемому централь-
ным процессором, из многих устройств опреде-
ляется именно то, к которому процессор хочет
обратиться для выполнения с ним определен-
ного действия. Задача логики декодирования и
состоит в том, чтобы осуществить это опреде-
ление.
Эта идея иллюстрируется графически на
рис. 17S.6. В одних случаях декодеру нужно
работать с устройством, определяемым одним
адресом. На рис. 17S.6 такими устройствами
будет буфер клавиатуры (устройство ввода) и
регистр ЦАП (устройство вывода). А в других
случаях декодер должен разрешить устройство,
содержащее диапазон адресов. Таким устрой-
ством на рисунке будет микросхема памяти
RAM объемом 32 К.
175.2.1. Что такое декодирование
адресов?
Декодирование адресов — это логическая опе-
рация, в результате выполнения которой то или
иное устройство реагирует на предоставленный
компьютером определенный адрес. Обычно в
процессе декодирования адресов кроме сигна-
лов адреса также задействуются контрольные
сигналы, т. е. сигналы, которые несут информа-
цию о том, какую операцию нужно выполнить.
Операция называется декодированием по той
причине, что в результате ее исполнения по
175.2.2. Частичное или «ленивое»
декодирование
Полное декодирование
На рис. 17S.6 показано 16 адресных линий, вхо-
дящих в декодер. (Для простоты, на рисунке
не показаны линии управления.) Полагая, что
адресные линии компьютера доступны (верное
предположение для процессора 8051, с кото-
рым мы будем работать на наших лаборатор-
ных занятиях по компьютеру3), использование
всех этих линий позволяет однозначно указать
[Клавиатура] g
Буфер с выходом с третьим состоянием
Шина данных
А15-
А14-
А1 -
А0-
Ad
de
dc
г о
ed
se
Устройства
с одним адресом
Память RAM
объемом 32 К
Адрес _^_
(А14...А0)
•15
Устройство с большим
блоком адресов (32 К)
Рис. 17S.6. Пример декодера адресов
8
DQ
х8
DAC
2 Частота автоколебаний здесь намного выше, чем можно
было бы предположить по 100 не времени доступа 2д0СТУПА
памяти RAM; но такие устройства обычно работают бы-
стрее, чем указано в характеристике для наихудшего слу-
чая. Поэтому полученное значение опять достаточно близ-
ко к ожидаемому, и определив период колебаний, можно
понять их причину.
3 Как вы знаете, современные процессоры, а также ваш
персональный компьютер используют намного большее
количество адресных линий. Некоторые последние вер-
сии процессора 8051 имеют 24 адресные линии, а старый
добрый процессор 68000 — целых 32 адресные линии.
Причина наличия большего количества адресных линий
должна быть очевидной — чтобы обеспечить легкий до-
ступ к памяти большого объема. Шестнадцать адресных
линий дают доступ к 216 ячейкам памяти, но только с по-
мощью неудобного приема страничной организации па-
мяти, который применялся в старых ПК компании IBM,
а также реализован в процессоре DS89C430, с которым
вам, возможно, придется работать на лабораторных за-
нятиях по компьютеру. Но мы не будем использовать эту
возможность.
706
US. Дополнительный материал: диагностика цифровых схем и декодирование адресов
адрес любой ячейки памяти или устройства
ввода-вывода. Но при сборке компьютера на
лабораторном занятии мы сэкономим значи-
тельное время и силы, применяя так называе-
мое ленивое декодирование адресов.
Ленивое декодирование
В компьютере, который мы соберем на лабо-
раторном занятии, мы будем использовать
адресную линию А15 для указания типа адре-
са, подаваемого на остальные адресные линии:
ячейки памяти от устройства ввода-вывода.
К устройствам ввода-вывода относится все
кроме памяти: клавиатура, дисплей, ЦАП,
АЦП, электродвигатели, кнопки, в общем, лю-
бое устройство, которое можно подключить к
компьютеру. Это означает, что одна полови-
на всего доступного адресного пространства*
будет служить для адресации ячеек памяти,
а другая — для адресации устройств ввода-
вывода. Эта идея графически демонстрируется
на рис. 17S.7.
Адрес
(шестнадцатеричный формат) Адресное
А15
Д
0
(16 битов)
8000И
0000И
«пространство»
Устройства
ввода-вывода
Память
Рис. 17S.7. Упрощенная схема декодирования адресов:
адресное пространство делится поровну между памятью и
устройствами ввода-вывода
В случае с памятью такой подход выглядит
целесообразным: 32 К адресов для 32 К ячеек
памяти. Но ситуация с остальными устройства-
ми выглядит не такой разумной. Неужели мы
планируем установить 32 К устройств ввода-
вывода на компьютер, который соберем на ла-
бораторном занятии? Конечно же, нет. Мы пла-
нируем установить всего лишь четыре устрой-
ства ввода-вывода. Поскольку мы используем
линию адреса А15, чтобы определять, когда
происходит обращение к устройствам ввода-
вывода, то можем обойтись всего лишь двумя
дополнительными адресными линиями (АО
и А1) для указания конкретного требуемого
устройства ввода-вывода из наших планируе-
мых четырех устройств5. В результате каждое
из наших четырех устройств ввода-вывода бу-
дет иметь 8 К адресов. Этот прием иногда на-
зывают совмещением адресов.
17S.2.3. Пример: RAM и ROM
используют общее адресное
пространство
Предположим, что мы решили оснастить наш
компьютер памятью RAM и ROM, а также не-
сколькими устройствами ввода-вывода. В дан-
ном случае мы не будем применять схему лени-
вого декодирования адресов, которую только
что рассмотрели. Вместо этого мы выделим для
устройств ввода-вывода только верхние 1 К
адресного пространства. Даже при таком рас-
пределении адресов мы сможем обращаться к
большому числу устройств ввода-вывода. Для
обращения к ROM выделим нижние 32 К адре-
сов, а к RAM — верхние 32 К, за исключением
1 К, предназначенного для работы с устрой-
ствами ввода-вывода.
♦ Организация адресации ROM — это легкая
задача, такая же как и разделение адресного
пространства поровну между RAM и устрой-
ствами ввода-вывода, рассмотренное ранее.
В частности, адресация ROM указывается
низким уровнем на адресной линии А15.
♦ Организация адресации RAM — адреса
RAM занимают верхнюю половину адрес-
ного пространства и указываются высоким
уровнем на адресной линии А15, за исключе-
нием адресного пространства, выделенного
для устройств ввода-вывода.
♦ Организация адресации устройств вво-
да-вывода — эта задача несколько слож-
нее. Обычно мы подходим к решению задач
такого типа в обратном порядке: определяя
число адресных линий, которые смогут обе-
спечить необходимое количество адресов.
В данном случае нам нужно 1К адресов,
4 Термин «адресное пространство» обозначает диапазон
всех отдельных адресов, соответствующих ячейке памяти
или устройству ввода-вывода, которые можно получить
через доступные линии адреса.
5 В принципе, для обращения к нашим четырем устрой-
ствам ввода-вывода можно было бы выбрать любые две
адресные линии и любую адресную линию, чтобы отли-
чать адреса памяти от адресов устройств ввода-вывода. Но
комбинация адресных линий, отличная от ранее описан-
ной, создавала бы сложное переплетение адресов памяти
и устройств ввода-вывода.
/7S.2 Декодирование адресов
707
или 210, следовательно, нам потребуется де-
сять адресных линий. Эти десять адресных
линий нижних разрядов (А0-А96) позволят
создать любое возможное значение адреса.
На остальных шести линиях верхних разря-
дов (А10-А15) должен поддерживаться по-
стоянный высокий уровень.
Таблица адресов
На рис. 17S.8 показано, как выглядит получен-
ная таблица адресов.
А15А14А13А12А11А10
Устройства ввода-вывода:
нужно десять линий, чтобы
получить 2ю адресов
Блоки адресов
ROM:Al5
RAM: A15*AIO
I/O: А15хА14*А13*А12*А11хА10
Рис. 17S.8. Таблица адресов для обращения к ROM, RAM
и устройствам ввода-вывода
Для декодирования адресов ROM потребуется
одна адресная линия (А15 с низким уровнем),
а для декодирования адресов устройств ввода-
вывода нужно использовать логическую функ-
цию И с шестью входными переменными7. Для
6 Не забывайте, что в цифровой электронике счисление
начинается с нуля.
7 В данном случае мы избегаем использования слова «вен-
тиль», поскольку возможное использование активных
низких уровней (особенно для разрешения ROM и RAM)
означает, что функция И будет реализовываться вентилем
И-НЕ, а не И. Здесь мы не хотим загромождать рассмотре-
ние вопроса такими подробностями.
декодирования адресов RAM нужна функция И
с двумя переменными, одной из которых слу-
жит результат функции И для декодирования
адресов устройств ввода-вывода.
Схема реализации декодирования
на логических элементах
На рис. 17S.9 изображена схема для реализации
описанного декодирования адресов, выполнен-
ная на логических элементах.
Самая верхняя часть верхней
половины адресного пространства
Верхняя половина
адресного пространства
А15
Устройства
ввода-вывода
RAM
ROM
Рис. 17S.9. Схема для реализации декодирования адресов
ROM, RAM и устройств ввода-вывода
Предположительно, сигналы декодирования
адресов могут быть дополнены такими сигна-
лами управления, как разрешение чтения дан-
ных RD*, записи кода PSEN* и, возможно, записи
данных WR*. Поэтому в данной схеме показаны
выходы с активными высокими уровнями, а не
с низкими, как в случае подачи этих сигналов
непосредственно на входы разрешения соот-
ветствующих микросхем.
17W. Примеры с решениями: память
17W.1. Цифровая
последовательностная
схема управления замком
Мы хотим, чтобы вы решили эту задачу тремя
разными способами. Это любимый прием со-
ставителей экзаменационных заданий. С точки
зрения преподавателя, это позволяет добить-
ся некой связности в изучении материала. Но
у студентов подобный подход может вызывать
другие чувства.
Поскольку разрабатываемая схема будет необ-
ходима некоторым студентам на лабораторном
занятии L17, сначала мы создадим обычную
схему на логических элементах без примене-
ния микроконтроллера. А когда вы будете чув-
ствовать себя уверенно с контроллерами, то
сможете вернуться заново к соответствующим
разделам.
Сначала мы попытаемся описать, как должна
вести себя наша схема. Возможно, что блок-
схема поможет вам увидеть, чего мы хотим
в итоге достичь.
Постановка задачи следующая.
Пользовательский интерфейс схемы управле-
ния замком содержит следующие три переклю-
чателя:
• тумблер, посредством которого пользова-
тель может установить высокий или низ-
кий входной уровень;
• кнопочный переключатель CLOCKIT, по-
средством которого пользователь может
включать сигнал для тактирования вход-
ного уровня;
• другой кнопочный переключатель TRY, на-
жатием которого пользователь подтверж-
дает введенный код.
♦ Схема должна реагировать на действия поль-
зователя таким образом:
• при каждом нажатии кнопки тактирова-
ния CLOCKIT схема воспринимает теку-
щий установленный уровень;
• после нажатия кнопки TRY с последующим
нажатием кнопки CLOCKIT схема решает,
совпадает ли введенная комбинация уров-
ней (битов) с кодом для открытия замка:
• если совпадает схема выдает выходной
сигнал UNLOCK для управления механиз-
мом открытия замка;
• если не совпадает, выполняется сброс схе-
мы в ее исходное состояние (конечно же,
в этом случае сигнал для открытия замка
не выдается).
17W.1.1. Задача I. Рисуем
обобщенную схему
На рис. 17W.1 изображена блок-схема устрой-
ства управления замком. Задача — разработать
все схемы, включая схему для генерирования
сигнала тактирования CLOCKIT и сигнала вво-
да комбинации TRY. Код для открытия замка
определяется трехэлементным DIP-переклю-
чателем, выходные сигналы которого подают-
ся на схему сравнения COMPARE. Так сделано
для того, чтобы можно было менять код от-
крытия замка.
17W.1.2. Задача II. Решение
HaVerilog
Листинг 17W.1 содержит программу на язы-
ке Verilog, которая выполнит всю требуемую
работу (за исключением схемы сравнения).
Программа реализует конечный автомат (а не
сдвиговый регистр), который принимает трех-
битовую последовательность и функционирует
аналогично схеме, изображенной на рис. 17W.1.
17W.1. Цифровая последовательностная схема управления замком
709
(Неверный код)
Высокий
Низкий
Сдвиговый
регистр
CLOCKLT
(Вы выбираете, какой
переключатель использовать)
|Код открытия замка}-
TRY _Л
Q's
(Правильный
код)
COMPARE
D Q
А
CLOCKIT-
Рис. 17W.1. Обобщенная схема ввода и проверки кода открытия замка
UNLOCK
Для решения этой задачи хорошо подходит кон-
струкция CASE. Возможно, что это самый легкий
способ. Пример программы на Verilog с исполь-
зованием операторов case для реализации ко-
нечного автомата приведен в Приложении А.11.
Листинг 17W.1. Тестовая программа на Verilog
для управления замком
'timescale 1 ns /1 ps
Illlllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll
II Компания:
// Разработчик:
//
// Дата создания: 11:36:07 04/23/2008
// Название проекта:
// Имя модуля: sequence_detect
// Имя проекта:
// Целевые устройства
// Версии инструментов:
//Описание:
//
// Зависимости:
//
// Версия:
// Версия: 0.01 - Файл создан
//Дополнительные комментарии:
module sequence_detect(dk,reset_bar,in,try, unlock,state);
// правильная последовательность вводимых значений
// равна 011 (постоянный сигнал try формирует
// выходной сигнал открытия)
input dk,reset_bar,in, try;
output unlock;
output [2:0] state;
wire dlcreset-baoi^unlock;
reg [2:0] state;
parameter A = ЗЪООО, В = 3'bOOI, С = 3'bOW,
JACKPOT = ЗЪ011, OPEN = З'Ы 00;
// четыре правильных нажатия кнопки генерируют
// сигнал открытия
assign unlock = (state == OPEN); // выходное значение
// автомата Мура, поскольку оно зависит только
// от состояния
end
endmodule
На рис. 17W.2 показаны результаты эмуляции
схемы, созданной этой программой. Эти сигна-
лы помогут описать поведение, которое мы на-
деемся получить.
17W.1.3. Задача III.
Использование процессора 8051
Возможно ли решение на языке
ассемблера?
Эта задача также хорошо подходит для реше-
ния с помощью микроконтроллера, поскольку
особого быстродействия здесь не требуется.
Листинг 17W.2 содержит соответствующую
программу. Программа начинается с присвое-
ния переменных определенным выводам. Для
этого мы использовали сдвиговый регистр, но
вы можете применить любой метод, который
вам по душе.
Напомним, что в бит переноса (С — CARRY)
можно поместить один бит, откуда его можно
переместить в аккумулятор с помощью опера-
ции сдвига или циклического сдвига.
710
77И/. Примеры с решениями: память
*<lilJllli
равильное входное значение^
1" . , """' ™ , \ -ч Сигна^теу сформирован^
входное значение / Сигнал TRY после правильного\ слишком рано
| входного значения
Возвращаем автомат
в исходное состояние Генерируе*Гсигнал отпирания
(по сигналу тактирования) замка по сигналу тактирования
в состояние
А (асинхронный)
Возвращаем автомат в исходное состояние
(по сигналу тактирования)
Рис. 17W.2. Результаты эмуляции схемы управления замком, созданной тестовой программой
Листинг 17W.2. Программа для процессора 8051
; sequence_detect_408.a51 детектирование определенной последовательности; входных битов для управления замком
SNOSYMBOLS
SINCLUDE (Z:\MICRO\8051\RAISON\INaREG320JNC); Файл Рейсона (Raison) определения регистров процессора DS310
SINCLUDE (Z:\MICRO\8051\RAISON\INaVECTORS320.INC); Файл Тома определения векторов
STACKBOT EQU 07Fh ; размещаем стек в начале рабочей области памяти блок косвенной адресации (80h и выше)
SOFTFLAG EQU 0 ; флаг (признак), который будет устанавливать
; процедура обработки прерывания
; вводимый пользователем уровень (бит кода)
; вводимый пользователем бит команды проверки кода
; бит управления замком
INBITEQUP1.0
TRYEQUP1.1
UNLOCK EQU PI.2
KEY EQU 011b ; устанавливаем код ключа
ORG 0 ; указываем ассемблеру начальный адрес для размещения этого кода
UMP START ; код начинается здесь - с перехода на начало
; собственно программы. ВСЕ наши профаммы будут начинаться таким образом
ORG 280h
START: MOV SP, #STACKBOT
END
; ...вот здесь начинается собственно программа
17W.2. Решения
17W.2.1. Решение I. Рисуем схему
В схеме на рис. 17W.3 отсутствует кнопка
сброса. Сброс осуществляется выполнением
довольно неудобной процедуры подачи двух
сигналов тактирования при нажатой кнопке
проверки введенного значения (TRY), что рас-
сматривается автоматом как ввод неверного
значения, в результате чего выполняется сброс.
Возможно, было бы лучше добавить отдельную
кнопку сброса.
17W.2. Решения
711
Сдвиговый регистр
Правильный код
Первый в последовательности
Сигнал
отпирания замка
К входам сброса триггеров
сдвигового регистра
Рис. 17W3. Схема для управления замком, собранная на сдвиговом регистре и логических вентилях
17W.2.2. Решение II. Программа
на языке Verilog
Листинг 17W.3 содержит код программы, в ре-
зультате исполнения которого была получе-
на эмуляция, показанная на рис. 17W.2. Здесь
нет сдвигового регистра, а сама схема является
классическим автоматом конечных состояний.
Листинг 17W3. Программа на Verilog
для создания cxei
// Код Verilog для логической схемы управления замком
'timescale1ns/1ps
II Компания:
// Разработчик:
//
// Дата создания: 11:36:07 04/23/2008
// Название проекта:
// Имя модуля: sequence.detect
// Имя проекта:
// Целевые устройства:
// Версии инструментов:
// Описание:
// Зависимости:
// Версия:
// Версия 0.01 - Файл создан
//Дополнительные комментарии:
//
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII1IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIHII
module sequence_detect(dk,reset_bar,in,try, unlock,state);
// правильная последовательность входных значений
// равна 011 (постоянный сигнал try формирует
// выходной сигнал открытия)
input dk,reset_bar,in, try;
output unlock;
output [2:0] state;
wire clk,reset_bar,in,unlock;
reg [2:0] state;
parameter A = ЗЪООО, В = 3'bOOl, С = 3'bOW,
JACKPOT = 3'b011, OPEN = 3fb100;
// четыре правильных нажатия кнопки генерируют
// сигнал открытия
assign unlock = (state == OPEN); // выходное значение
// автомата Мура, поскольку оно зависит только
// от состояния
always @(posedge elk, negedge reset_bar)
begin
if(~resetj>ar)
712
17W. Примеры с решениями: память
state <= А ;
else
case (state)
А:
if (try)
state <= A; // преждевременное нажатие
// кнопки TRY возвращает автомат
// в исходное состояние
else
Iffln)
state <= В;
else
state <= A; // в случае ошибки начинаем сначала
В:
if (try)
state <= А; // преждевременное нажатие
// кнопки TRY возвращает автомат
// в исходное состояние
else
if (in)
state <= С;
else
state <= A; // в случае ошибки начинаем
// сначала
С:
if (try)
state <= А; // преждевременное нажатие
// кнопки TRY возвращает автомат
// в исходное состояние
else
if (in)
state <= JACKPOT;
else
state <= A; // в случае ошибки начинаем
// сначала
JACKPOT:
if (try)
state <= OPEN; // если нажата кнопка TRY
// и кнопка тактирования,
// выдаем сигнал отпирания
else
state <= A; // если не была нажата кнопка TRY,
// начинаем сначала
OPEN:
if (try)
state <= OPEN; // если продолжаем нажимать
// кнопку TRY и кнопку
//тактирования, продолжает
// выдаваться сигнал отпирания
else
state <= A; // начинаем сначала
// (и снимаем сигнал отпирания)
endcase
end
endmodule
В результате выполнения этой программы по-
лучается довольно сложная схема, изображен-
ная на рис. 17W.4. Но поскольку вся работа по
ее созданию выполняется программой Verilog,
то нам все равно.
Рис. 17W.4. Схема устройства управления замком, созданная программой Verilog
17W.2. Решения
713
17W.2.3, Решение III. Использование
процессора 8051 и программы
на ассемблере
Аппаратное обеспечение
Аппаратное обеспечение для этого подхода до-
вольно очевидное, тем не менее на рис. 17W.5
изображена соответствующая схема, которая
должна помочь разобраться с кодом программы.
Ввод битов
+5V -С
8051
UNLOCK
CLOCKLTj-J*
Рис. 17W.5. Схема для управления замком на процессоре 8051
Код на ассемблере
Код программы на ассемблере (листинг 17W.4)
выглядит не таким сложным, как на Verilog.
Подобно первой схеме на рис. 17W.3, создан-
ной нами вручную, в создаваемой этим кодом
схеме присутствует сдвиговый регистр. После
ввода трех битов программа выполняет опера-
цию сравнения ONE над текущим содержимым
сдвигового регистра и сохраненным контроль-
ным значением. Данное решение содержит код
маски (закомментированный) для вводимого
значения, которая позволяет вводить более
трех значений, но использовать для сравнения
только три последние бита. Если этих строк
кода не будет, то после запуска автомата в рабо-
ту (т. е. после сброса контроллера) допускается
ввести только ровно три бита.
Листинг 17W.4. Программа на ассемблере для процессора 8051
; sequence_detect_511 .а51 детектирование определенной последовательности входных битов для управления замком
SNOSYMBOLS
$INCLUDE (C:\MICRO\8051\RAISON\INC\REG320.INC); Файл Рейсона (Raison) определения регистров процессора
DS320
SINCLUDE (C:\MICRO\8051\RAISON\INCWECTORS320.INC); Файл Тома определения векторов
STACKBOT EQU 07Fh ; размещаем стек в начале рабочего косвенно адресуемого блока памяти (80h и выше)
SOFTFLAG EQU 0 ; флаг (признак), который будет устанавливать процедура обработки прерывания
UNLOCK EQU P1.2 ; бит управления замком
INBIT EQU P1.0 ; вводимый пользователем уровень (бит кода)
TRY EQU PI .1 ; вводимый пользователем бит команды проверки кода
; Кнопка CLOCKIT подает сигнал INTO*
KEY EQU 011b
; устанавливаем код ключа
ORG 0 ; указываем ассемблеру начальный адрес для размещения этого кода
UMP START ; Код начинается здесь - с перехода на начало собственно программы.
; ВСЕ наши программы будут начинаться таким образом
ORG280h
; Вот здесь начинается собственно программа
START: MOVSR#STACKBOT
ACALLINITS
714
17W. Примеры сретениями: память
ACALLINTSETUP
REINIT: ACALL IN ITS ; Начинаем заново
TEST: JNB SOFTFLAG, TEST ; Ожидаем здесь, пока пользователь не нажмет кнопку тактирования CLOCKIT
CLR SOFTFLAG ; Устанавливаем новый проход
NOW: JNB TRY, TAKEIN ; Проверяем, готов ли пользователь вводить свой код
; Следующая строка кода позволяет пользователю вводить больше чем три значения, поскольку система будет
принимать только последние три бита
; ANL А, #07п ; Удаляем все биты, кроме последних трех
ONE A, #KEY, FLUNK ; Проверяем, совпадает ли введенное значение с образцом
SETB UNLOCK ;Оно!
HERE: JB TRY, HERE ; Пока нажата кнопка TRY, удерживаем сигнал отпирания замка
SJMP REINIT
TAKEIN: MOV С, INBIT ; Принимаем текущий вводимый бит
RLC А ; Принимаем текущий вводимый бит в младший разряд
SJMP TEST ; ...и идем ожидать следующий ввод.
FLUNK:CLRA
SJMP REINIT
; Переходим сюда после ошибки ввода и начинаем сначала
; ISR: Просто устанавливаем программный флаг
ORGINT0VECTOR ; Это определяется в файле VECTORS3210.1NC, который был включен выше.
; Это адрес ОЗп, по которому переходит программа в ответ на нулевое прерывание.
ISR: SETB SOFTFLAG
RETI
INITS: CLR A
CLR UNLOCK
CLR TRY
RET
; Обнуляем регистр ввода для начала работы
; Запираем замок (Активный разряд с высоким логическим уровнем)
; —Теперь разрешаем прерывания—
INTSETUP: SETB ГГО ; Делаем INTO чувствительным к переладу (р. 22)
SETB EXO ; ...и разрешаем прерывание INTO
SETB EA ; Разрешаем глобальные прерывания (р. 31-32)
RET
END
Код программы на языке С
Код на языке С (листинг 17W.5), наверное, вы-
глядит более сложным, чем на ассемблере. Его
самая интересная особенность — громоздкая
процедура для выполнения операции цикли-
ческого сдвига содержимого регистра, которая
отсутствует в языке С. Код этой процедуры сле-
дующий:
SEQUENCE = (SEQUENCE « 1) | (SEQUENCE »(8-1));
// Циклический сдвиг влево, старший бит переходит
//в младший бит.
Эта процедура довольно необычна и требует
объяснения. Операция сдвига влево проста:
SEQUENCE = (SEQUENCE « 1).
17W.2. Решения
715
А вот следующий шаг хитроумный (авторство
не наше; мы взяли его из Википедии):
| (SEQUENCE»(8-1)).
Эта операция выполняет сдвиг вправо на семь
позиций, в результате чего значение самого
старшего разряда оказывается в позиции са-
мого младшего разряда. Затем над сдвинутым
таким образом значением и результатом пре-
дыдущего левого сдвига выполняется операция
ИЛИ. Таким образом, после сдвига самый стар-
ший бит становится самым младшим. Иными
словами, все выглядит так, будто с 8-разрядным
регистром был выполнен циклический сдвиг
влево. Возможно, что вы сможете создать более
простое решение задачи определения правиль-
ности вводимого значения.
Листинг 17W.5. программа на языке С
/* sequence_detect_412.c revisited 4/12 */
// Выполняет ввод бита, сдвигая его с вывода порта
#include // Используется для определения "Р1"
#include // Возможно, требуется для булевых операций?
// Р1.1 принимает последовательность битов: "LEVEL"
// INTO играет роль сигнала тактирования
// Р1.2 является входом для сигнала TRY
//91.0 является выходом сигнала UNLOCK
sbit volatile LEVEL = P1Л1; // Вводимый пользователем побитно код
sbit volatile TRY = Р1Л2; // При активировании пытается создать сигнал отпирания; если попытка неудачна —
// выполняет сброс автомата
sbit volatile UNLOCK = Р1 ДО;
bit INTFLAG = 0; // Обнуляем флаг для первого прохода
char n; // Индекс к хранимым битам
bdata char SEQUENCE = 0; // Вводимое сдвигом значение bdata указывает поместить значения в ячейку, адресуемую
// побитно (не критично)
sbit INBIT = SEQUENCEA7; // Вводимый бит помещается в самый старший разряд
#defineKEY0x3
void intsetup (void);
void miscjnits (void);
void it_extO (void);
void main (void)
miscJnitsO;
intsetupO;
while (1)
while (INTFLAG)
// Сообщаем, что будет несколько функций
UNLOCK = 0;
INTFLAG = 0;
if (TRY)
// Подготавливаемся к работе
// Ожидаем здесь, пока на будет нажата кнопка тактирования
// Если выдается сигнал отпирания, снимаем его по следующему сигналу тактирования
// Проверяем введенное значение
// Удерживаем сигнал отпирания до тех пор, пока нажата кнопка TRY
716 17W. Примеры с решениями: память
if (SEQUENCE == KEY)
{
UNLOCK =1;
SEQUENCE = 0;
}
else
UNLOCK = 0;
SEQUENCE = 0;
// Если кнопка тактирования TRY не нажата, переходим сюда
else
{
INTFLAG = 0;
INBIT = LEVEL; // Помещаем введенный бит в самый младший разряд
SEQUENCE = (SEQUENCE « 1) | (SEQUENCE » (8-1));
// Циклический сдвиг влево, старший бит переходит в младший бит.
// Внешнее прерывание 0
void it_extO (void) interrupt 0 using 0 // Используем блок регистров 0; контекстный переключатель отсутствует
{
INTFLAG = 1; // Устанавливаем программный флаг для главной программы
void intsetup (void)
{
ЕХ0=1;
1Т0 = 1; // Прерывание по фронту
ЕА=1;
void misc_inits (void)
{
TRY = 0;
LEVEL = 0;
INTFLAG = 0;
SEQUENCE = 0;
UNLOCK = 0;
Часть V
ЦИФРОВЫЕ УСТРОЙСТВА:
АЦП, ЦАП, ФАПЧ
18N. Аналоговые и цифровые
преобразования; ФАПЧ
Содержание
18N.1. Сопряжение устройств разных логических семейств 719
18N.1.1. Пятивольтовые микросхемы: проблемы с подачей сигналов
на микросхемы КМОП 720
18N.1.2. Устройства с более низкими напряжениями питания 722
18N.2. Общие сведения о цифроаналоговых и обратных преобразованиях 723
18N.2.1. Квантование по вертикальной оси: разрешение по амплитуде
или по напряжению 724
18N.2.2. «Нарезка» по горизонтали: частота дискретизации 725
18N.2.3. Влияние недостаточной частоты дискретизации 727
18N.3. Методы цифроаналоговых преобразований 728
18N.3.1. ЦАП, управляемый унарным кодом 728
18N.3.2. Схема суммирования токов на операционном усилителе 728
18N.3.3. Матрица резисторов R-2R 729
18N.3.4. ЦАП с коммутируемыми конденсаторами 730
18N.3.5. Одноразрядный ЦАП; широтно-импульсная модуляция (ШИМ) 731
18N.4. Аналого-цифровое преобразование 732
18N.4.1. Методы без обратной связи 732
18N.4.2. АЦП с двойным интегрированием 734
18N.4.3. АЦП с обратной связью 735
18N.4.4. Пример двоичного поиска 738
18N.4.5. Дельта-сигма АЦП 738
18N.5. Ложные сигналы в процессе выборки 745
18N.5.1. Предсказание ложных сигналов в частотной области
в процессе выборки 745
18N.5.2. Побочные сигналы предсказуемы 747
18N.6. Добавление случайного шума 747
18N.7. Система фазовой автоподстройки частоты 749
18N.7.1. Простейший фазовый детектор: ИСКЛ-ИЛИ 749
18N.7.2. Фазовые детекторы, чувствительные к фронту 750
18N.7.3. Применения 752
18N.7.4. Проблемы стабильности во многом такие же, как и для системы ПИД 754
N17N.8. Материал для чтения в АоЕ 756
Цель этой главы
В этой главе мы рассмотрим решение задачи преобразования диапазона напряжений в цифровой
код. Обратный процесс преобразования цифровых значений в напряжение проще и встречается не
так часто, но тем не менее тоже полезен на практике.
18N.1. Сопряжение устройств
разных логических семейств
Это скучная, но иногда необходимая тема. То,
что выходной сигнал логического элемента
микросхемы 74НСхх может служить в качестве
входного сигнала другой микросхемы 74НСхх,
не вызывает никаких вопросов. Разумеет-
ся, устаревшие ТТЛ-микросхемы (например,
74LSxx на 74LSxx) также совместимы друг
с другом. Но иногда возникает необходимость
использовать в одной схеме микросхемы раз-
ных логических семейств; обычно это вызвано
требованием наличия функции, которая недо-
ступна в микросхемах основного логического
720
18N. Аналоговые и цифровые преобразования; ФАПЧ
семейства, применяемых в проекте. В таком
случае нужно знать, смогут ли микросхемы
разных логических семейств взаимодейство-
вать друг с другом на уровне сигналов, и если
нет, то как решить эту проблему.
18N.1.1 • Пятивольтовые
микросхемы: проблемы с подачей
сигналов на микросхемы КМОП
В большинстве случаев вам, скорее всего, при-
дется использовать логические микросхемы
технологии КМОП. Как мы узнали из лабора-
торного занятия 14L, устройства КМОП обла-
дают хорошими свойствами входных и выход-
ных уровней. В частности, высокий и низкий
уровни выходных сигналов находятся в преде-
лах нескольких десятых вольта от напряже-
ния положительного питания и потенциала
«земли» соответственно; а пороговые значения
входных уровней расположены достаточно да-
леко от допустимых значений выходных уров-
ней. Входы микросхем КМОП не потребляют
значительного тока (максимум один микроам-
пер по всему температурному диапазону, а ти-
пичное потребление намного меньше макси-
мального). Кроме того, их входы представляют
собой нагрузку со скромной емкостью, макси-
мум 10 пФ1. Выходы могут выдерживать значи-
тельную нагрузку, обеспечивая входящий или
исходящий ток величиной 4 мА (микросхемы
74НСхх). Короче, работать с этими устройства-
ми — одно удовольствие.
Но если на вход микросхемы 74НСхх подать вы-
ходной уровень от микросхемы ТТЛ, то могут
возникнуть неприятности. Проблема состоит в
недостаточности напряжения высокого уровня
выходного сигнала (V0_H — ^Вых-выс) микросхем
ТТЛ, которое ниже, чем необходимое напряже-
ние высокого уровня входного (Vj.H — UBX_BUC)
сигнала КМОП-микросхем. Напряжение вы-
сокого уровня выходного сигнала иъых_шс
микросхем ТТЛ составляет всего лишь 2,4 В.
А напряжение высокого уровня входного сиг-
нала Е/вых_выс микросхем семейства 74НСхх
составляет чуть больше 2/3 уровня напряже-
ния питания, или 3,15 В при величине напря-
жения питания 4,5 В. Эту проблему образно
иллюстрирует рис. 18N.1.
(О, ТТЛ, ТТЛ, почему ты
Высокий уровень
для ТТЛ
(минимальный
гарантированный)
Выход
5 В Вход
0В
Высокий уровень
для КМОП
(минимальный
необходимый)
Рис. 18N.1. Напряжения высокого выходного уровня ми-
кросхем ТТЛ недостаточно для подачи на вход микросхем
КМОП
Как же решить данную проблему? Очевидно,
что необходимо или усилить выходной сигнал
высокого уровня ТТЛ, или понизить требо-
вания ко входному сигналу высокого уровня
КМОП. Возможна комбинация обоих этих ре-
шений. Некоторые микросхемы КМОП спо-
собны работать с более низкими входными
уровнями, в частности микросхемы семейства
74НСТхх. В таком случае проблема решается
использованием пороговых значений ТТЛ за
счет отказа от симметричности уровней КМОП
и превосходных характеристик помехоустой-
чивости. Альтернативно выходной сигнал ТТЛ
можно повысить до 5 В с помощью повышаю-
щего резистора. Данный подход иллюстрирует-
ся на рис. 18N.2.
Повышающий резистор
74LS
ТТЛ получает помощь
74НСТ
КМОП снисходит
1 Это характеристики для микросхемы 74НС00 компании
ON Semiconductor.
Рис. 18N.2. С помощью повышающего резистора микросхе-
мы ТТЛ и КМОП могут работать совместно
Чтобы понять эффективность такого просто-
го решения, как повышающий резистор, нуж-
но знать, что недостаточно высокое выходное
напряжение ТТЛ-устройств (около 3-3,5 В
типичное, 2,5 В в наихудшем случае) не за-
фиксировано на этом уровне. Это не источник
с низким импедансом, которым является низ-
кий логический уровень ТТЛ. Его можно рас-
сматривать как источник, который «теряет
18N. I Сопряжение устройств разных логических семейств
721
силы» при таком высоком напряжении ТТЛ,
но не возражает, если какой-либо «любезный»
повышающий резистор подключится в трудной
ситуации и завершит работу. В случае с устрой-
ствами ТТЛ потеря сил является результатом
использования внутреннего повышающего
транзистора типа п-р-п (в отличие от повы-
шающего транзистора типа р-МОП на выходе
микросхем КМОП).
Но при выборе номинала повышающего рези-
стора следует избегать крайностей: очень боль-
шое значение замедлит нарастание высокого
уровня, поскольку этот резистор должен заря-
дить паразитную емкость. А слишком низкое
значение перегрузит выходной вентиль микро-
схемы, требуя, чтобы она поглощала ток, пре-
вышающий ее способности (максимальный
ток указывается как параметр I0L — /вых_низ).
Для маломощных микросхем ТТЛШ (LSTTL)
достаточно резистора номиналом в несколь-
ко килоом. Следует быть осторожным, что-
бы не перегрузить устройства, выдающие
более слабые сигналы, например некоторые
микропроцессоры: нужно внимательно сле-
дить за тем, чтобы не превысить предель-
ный выходной ток *вых_низ. Для стандартного
микропроцессора 8051 производства компа-
нии Dallas Semiconductor допустим ток 1,6 мА;
для процессора производства компании Silicon
Laboratories — 8,5 мА.
Многие не ТТЛ-устройства ведут себя
подобно им
Можно возразить, что в современных схемах
нет места ТТЛ-микросхемам (которые дей-
ствительно почти вышли из употребления,
включая маломощную версию LS с диодами
Шотки — ТТЛШ)2. Возможно, что это и так,
или, по крайней мере, с устройствами соб-
ственно ТТЛ вам придется встречаться в очень
редких случаях. Но одно обстоятельство де-
лает проблему ТТЛ уровней более обширной,
чем кажется. В частности, многие устройства,
в которых отсутствуют биполярные транзисто-
ры (как в устройствах ТТЛ), тем не менее ис-
пользуют входные и выходные уровни с ТТЛ
характеристиками. Понятно, что микросхемы
л-МОП, в которых есть только транзисторы с
я-каналом, не могут обеспечить хорошие на-
пряжения высокого выходного уровня 1/вых.выс
2 АоЕ § 12.1.2А.
(именно благодаря транзисторам с р-каналом
устройства КМОП так хорошо справляются
с задачей предоставления высокого выходного
уровня). Но самой плохой новостью являет-
ся то обстоятельство, что многие собственно
КМОП-устройства обеспечивают более низкие
ТТЛ-уровни! Вероятной причиной является то
обстоятельство, что таким образом несколько
упрощается работа разработчиков и произво-
дителей за счет использования повышающих
транзисторов я-МОП, а нер-МОП.
Пятивольтовые устройства, использующие
уровни ТТЛ
Далее приводится несколько важных случаев
устройств КМОП с такими ухудшенными ха-
рактеристиками:
♦ Устройства ПМЛ и СПЛУ с напряже-
нием питания 5 В, например микросхема
ХС9572ХС компании Xilinx. С последним
устройством мы будем иметь дело на лабора-
торном занятии. Если вы попытаетесь заме-
нить эту микросхему на устройство с напря-
жением питания 3,3 В, например микросхе-
му XC9572XL, то опять возникнет проблема
совместимости логических уровней, когда
нужно будет работать совместно с логиче-
скими устройствами с напряжением питания
5 В. См. раздел 18N.1.2 далее в этой главе.
♦ Некоторые процессоры с напряжением
питания 5 В, наподобие микроконтроллера
DS89C430, совместимого с микроконтрол-
лером 8051, с которым вы будете работать,
если избрали путь сборки компьютера из
дискретных компонентов на большой макет-
ной плате.
В схеме компьютера, собираемого из дис-
кретных компонентов, вы увидите как микро-
схемы 74НСТхх, так и микросхемы 74НСхх.
Микросхемы 74НСТхх присутствуют в тех ме-
стах, где сигналы с уровнями ТТЛ подаются на
входы КМОП-логики. В частности, такие сиг-
налы выдает процессор, совместимый с микро-
контроллером 8051, а также устройство СПЛУ,
хотя обе эти микросхемы с уровнями ТТЛ из-
готовлены по КМОП-технологии.
На рис. 18N.3 приводится один такой случай:
для декодера ввода-вывода выбрана микро-
схема 139 типа НСТ, а не просто НС, для того,
чтобы можно было работать со слабыми вы-
сокими уровнями трех устройств КМОП: двух
устройств ПМЛ и процессора 8051.
722
18N. Аналоговые и цифровые преобразования; ФАПЧ
Микросхема типа ИСТ, необходимая для работы
со слабыми высокими уровнями типа ТТЛ
Микросхема ТТМП
типа КМОГТ
Устройство ТТМЛ
связывающей логики.
Адресная шина
р
Адрес от процессора ^
типа КМОГТ Микросхема ПМЛ счетчика адресов
Рис. 18N.3. Пример использования КМОП-микросхемы типа
НСТ для того, чтобы можно было работать с сигналами уров-
ня ТТЛ, выдаваемыми микросхемами КМОП с напряжением
питания 5 В (часть схемы компьютера из дискретных компо-
нентов)
Для сопряжения сигналов этих устройств мож-
но было бы использовать повышающие рези-
сторы. Но вы, несомненно, согласитесь, что
применение микросхемы типа НСТ — более
простое решение. Этим и объясняется присут-
ствие устройств типа НСТ в схемах с простыми
устройствами типа НС. Возможность устройств
НСТ работать со слабыми ТТЛ-уровнями мо-
жет быть очень полезной.
18N.12. Устройства с более
низкими напряжениями питания
В некоторых низковольтных
микросхемах используются уровни ТТЛ
По мере понижения напряжения питания ниже
5 В вялые высокие логические уровни (уровни
намного ниже напряжения питания) исчезают.
В схеме с напряжением питания 3,3 В никто не
будет выбрасывать 1,5 В, как это делает логика
ТТЛ. Но логические ТТЛ-уровни продолжают
играть важную роль в областях, очень далеких
от области биполярной схемотехники, в ко-
торой они берут свое начало. Не только неко-
торые микросхемы КМОП с напряжением пи-
тания 5 В используют входные или выходные
уровни ТТЛ-типа, как было только что изложе-
но, но и устройства КМОП с напряжением пи-
тания 3,3 В могут работать как с входными, так
и выходными ТТЛ-уровнями.
В процессе разработки схемы с напряжением
питания, меньшим чем 5 В, например 3,3 В,
возможно возникновение ситуации, когда тре-
буется функция, доступная только в микросхе-
ме с напряжением питания 5 В. Мы встретим-
ся с таким случаем при сборке компьютера из
дискретных компонентов, где одним из таких
компонентов является контролер с напряже-
нием питания 5 В. Иногда выполнить сопря-
жение не представляет никаких трудностей, но
в других случаях, при большей разности на-
пряжений, необходим специальный вентиль-
преобразователь напряжения.
Некоторые устройства совместно рабо-
тают с напряжением питания 5 и 3,3 В
Устройства ПМЛ, которые мы используем на
наших лабораторных занятиях, могут совмест-
но работать с устройствами с напряжением пи-
тания 5 и 3,3 В без проблем.
Устройства ПМЛ с напряжением питания
3,3 В могут принимать логические уров-
ни устройств с напряжением питания 5 В,
а также подавать логические уровни на та-
кие устройства
Некоторые устройства с напряжением пита-
ния 3 В, такие как микросхемы ПМЛ компании
Xilinx, допускают совместную работу с устрой-
ствами с напряжением питания 5 и 3,3 В.
Они могут как принимать логические уровни
устройств с напряжением питания 5 В (такие
входы называются толерантными к напряже-
нию 5 В — 5 V tolerant), а также могут подавать
логические уровни ТТЛ-типа на устройства с
напряжением питания 5 В. Напряжение выход-
ных уровней таких устройств с напряжением
питания 3,3 В достаточно высокое, чтобы их
можно было без проблем подавать на входы
устройств 74НСТхх с напряжением питания
5 В, хотя не на входы устройств 74НСхх. На
рис. 18N.4 показана блок-схема взаимодей-
ствия таких устройств.
Мы учитываем эту приспособляемость на на-
ших лабораторных занятиях следующим об-
разом:
♦ Входные уровни - микросхема ПМЛ с на-
пряжением питания 3 В может принимать
входные уровни от двух типов устройств
с напряжением питания 5 В:
18N. I Сопряжение устройств разных логических семейств
723
Микросхема КМОТТ
с питанием 5 В
5В -у-
ов -Л.
Микросхема ТТЛ
с питанием 5 В
о в !Х_
Микросхема КМОТТ
с питанием 3.3 В
3,3 В-w-
ов _Л_
Микросхема ТТЛ
с питанием 2,5 В
2,5 В -^г
ОВ _Х.
3,3 В
1
t I
VCCINT VCCIO
XC9500XL
CPLD
Вход Выход
«Земля»
Микрс
с питс
)схема КМОТТ
мнием 3,3 В
0 В _Х_
1
Рис. 18N.4. Низковольтная логика позволяет с легкостью со-
прягать устройства с напряжением питания 5 и 3,3 В3
• Микросхем КМОП семейства 74НСТхх
(напряжение низкого выходного уровня
^вых-низ< О»4 В' напряжение высокого вы-
ходного уровня ишх_ъыс > 3,7 В — при на-
пряжении питания 4,5 В). Примером та-
кого уровня может служить сигнал сброса
цифровой клавиатуры KRESET, инвертируе-
мый микросхемой 74НСТ14 на его пути
к устройству ПМЛ связывающей логики.
• Уровни ТТЛ (напряжение низкого вы-
ходного уровня и
шх_нт
< 0,4 В, на-
пряжение высокого выходного уровня
1/вых-выс > 2,4 В). Примером таких сигна-
лов может служить сигнал RD*, создавае-
мый микросхемой контроллера DS89C430
с напряжением питания 5 В.
♦ Выходные уровни — устройство ПМЛ с на-
пряжением питания 3 В может поставлять
сигнал на устройства с напряжением пита-
ния 5 В, которые используют входные ТТЛ-
уровни. В качестве примеров можно назвать
несколько сигналов, подающихся на конт-
роллер DS89C430 (сигнал тактирования,
сигнал сброса и сигнал PSENDRV*) и на ми-
кросхему RAM с напряжением питания 5 В.
♦ Устройство ПМЛ с напряжением пи-
тания 5 В допускает напряжение 3,3 В
для ввода-вывода — микросхема ПМЛ
ХС95ххХС компании Xilinx с напряжени-
ем питания 5 В, которую мы использовали
3 Рисунок на основе заметки DS054 к справочному листку
на семейство высокопроизводительных устройств СПЛУ
семейства XC9500XL - XC9500XL High-Рефгтапсе CPLD
Family Data Sheet
на наших лабораторных занятиях, облада-
ет этой способностью. Хотя для питания ее
внутренней схематики требуется напряже-
ние 5 В, если на ее вывод VCCI0 подать напря-
жение 3,3 В, то микросхема сможет прини-
мать и поставлять сигналы с ТТЛ-уровнями
устройствам с напряжением питания как
3,3 В, так и 5 В.
Но при большей разнице между напряже-
ниями питания потребуется микросхема-
преобразователь логических уровней, чтобы
сигналы от устройства с более низким на-
пряжением питания могли восприниматься
устройством с более высоким напряжением
питания. Например, компания Maxim выпуска-
ет универсальный двунаправленный преобра-
зователь МАХ3370 для сопряжения устройств
с такими разными напряжениями питания, как
1,2 и 5,5 В. Данная микросхема позволяет пре-
образовывать уровни только для одной линии.
А компания NXP (ранее Philips Electronics)
разработала более простой двунаправленный
преобразователь логических уровней на одном
МОП-транзисторе. Эта оригинальная схема
рассматривается в разделе 18W.2.
18ISL2. Общие сведения
о цифроаналоговых
и обратных преобразованиях
Аналоговые и цифровые
преобразования
Задача преобразования из любой формы дан-
ных в другую может потребовать выполнения
сложных аналоговых операций. Чтобы преоб-
разовать данные из аналоговой формы в циф-
ровую (т. е. выполнить аналогово-цифровое
преобразование — АЦП), схема должна выпол-
нить классификацию входных данных (кото-
рыми обычно является напряжение), поместив
их в соответствующую цифровую категорию.
Часто такие преобразования требуется выпол-
нить очень быстро.
Обратное преобразование — цифроаналоговое,
ЦАП — более легкое на понятийном уровне. Но
выполнить такое преобразование с требуемой
точностью (с разрешением с требуемым чис-
лом разрядов) достаточно трудно. Кроме того,
724
18N. Аналоговые и цифровые преобразования; ФАПЧ
цифровая обработка вносит в полученный ре-
зультат искажения в виде ступенчатости в дис-
кретизированном и восстановленном сигнале,
которые требуется удалить.
Работа по удалению этого «мусора» может пре-
вратиться в непростую задачу, но ее можно
решить с помощью простого низкочастотного
фильтра, используемого для очистки выход-
ного сигнала в каждом цифровом аудиоплеере.
Фильтрацию также можно частично выполнить
в цифровой области. Определенный объем этой
обработки, которая называется передискре-
тизацией, выполняется, интерполируя псев-
довыборки между фактическими выборками4.
Цифровая фильтрация, включая передискре-
тизацию, которая повышает кажущуюся часто-
ту дискретизации, облегчает задачу последнего
аналогового этапа, выполняемую посредством
сглаживающего НЧ-фильтра.
осуществлялась бы мгновенно, но в действи-
тельности дискретизирующий импульс может
длиться несколько десятков наносекунд.
АЦП: разрешение по напряжению
(по вертикали) и по времени
(по горизонтали)
Если мы хотим преобразовать аналоговый си-
нусоидальный сигнал в цифровую форму, а
затем обратно в аналоговую, то сразу же стол-
кнемся с необходимостью решить, сколько
информации нужно перенести в цифровую об-
ласть. Нам придется удовлетвориться ограни-
ченным количеством «нарезок» (квантов) как
в вертикальном (разрешение по амплитуде),
так и в горизонтальном направлении, где число
«нарезок» определяется частотой выборки.
Чем дискретизация не является
Мы еще возвратимся к вопросу, как нужно
дискретизировать аналоговый сигнал, что-
бы преобразовать его в цифровую форму. Но
на данном этапе рассмотрения устраним одно
из возможных ошибочных представлений о
дискретизации. В частности, если, как пока-
зано на рис. 18N.5, в течение одного периода
берутся три выборки синусоидального сигна-
ла, выборочное значение не является средним
значением сигнала в течение этого временного
интервала. Это будет значение сигнала, при-
сутствующее в течение длительности очень ко-
роткого импульса выборки. В идеале выборка
18N.2.1. Квантование
по вертикальной оси: разрешение
по амплитуде или по напряжению
Это довольно прямолинейная задача. Как
обычно, принимается решение о допустимой
величине погрешности. В данном курсе почти
все преобразователи, которые мы будем со-
бирать или использовать на лабораторных
занятиях, будут 8-разрядными устройства-
ми. Следовательно, нам придется удовлетво-
риться 256 уровнями квантования, каждый из
которых величиной от 10 до 16 мВ. Величина
кванта зависит от максимального напряжения
Насколько велика неопределенность
/напряжения при взятии выборки?
Цифровое значение: насколько
близко к действительному?
(Какое разрешение?)
Восстановленный ступенчатый
аналоговый сигнал
^Посторонние высокочастотные
Время выборки: насколько Л \ компоненты. Подлежат устранению
близко к мгновенному?
Частота выборки: достаточная ли?
(>2/период)
Рис. 18N.5. Аналоговый сигнал подается на вход АЦП, цифровой выходной сигнал с которого затем поступает на вход ЦАП
для восстановления исходного аналогового сигнала
4 Интерполяция — один из способов описания процесса
цифровой фильтрации.
78Л/.2 Общие сведения о цифроаналоговых и обратных преобразованиях
725
сигнала, поскольку величина кванта равна
Напряжения,
сохраненные АЦП
В коммерческом цифровом аудио, в котором
задействовано 16 битов, каждый из наших
8-битовых квантов разбивается дополни-
тельно на 256 подквантов (16-битовое раз-
решение ==> 1 доля из 64 К)5. Наши собран-
ные на макетных платах схемы завалили бы
любое такое мнимое разрешение лавинами
шума. Вспомните, какие большие шумовые
пульсации можно видеть на осциллогра-
фе, если выставить максимальное усиление.
В упражнении 23L.2.2 мы предлагаем студен-
там, использующим контроллер компании
Silicon Laboratories, попробовать задать пол-
ное 12-битовое разрешение, поддерживаемое
ЦАП этого контроллера. Но основной целью
того упражнения является продемонстриро-
вать, что для наших схем на макетных платах
такое разрешение бесполезно. И вообще, вели-
чина полезного разрешения преобразования
определяется уровнем шума в преобразовы-
ваемом аналоговом сигнале. Кроме того, при
преобразовании аудиосигнала следует иметь
в виду тот факт, что нет смысла преобразовы-
вать аудиосигнал с разрешением ниже предела
человеческого слуха.
Погрешность квантования
Поскольку преобразование из аналоговой фор-
мы сигнала в цифровую заключается в разбие-
нии непрерывного входного сигнала на конеч-
ное количество частей, этот процесс неизбежно
вносит погрешности в получаемый результат.
На рис. 18N.6 иллюстрируется процесс пре-
образования входного аналогового сигнала
в цифровую форму, в котором он сопоставля-
ется ближайшим доступным уровням, вместе
с соответствующими отклонениями (погреш-
ностями) каждой выборки от действительного
значения6.
5 Величина наименьшего кванта (самого младшего бита),
например, в портативном плеере, полное напряжение сиг-
нала которого может быть меньше 2 В, чрезвычайно мала.
При таком напряжении 16-разрядное разрешение озна-
чает, что величина младшего бита составит всего лишь
30 мкВ.
6 Этот рисунок основан на рис. 2.7 на с. 31 книги К. Pohl-
mann «Principles of Digital Audio» («Основы цифрового
аудио»), 6-е изд., издательство McGraw Hill, 2011 г. Черные
точки представляют выборки, что может сбивать с толку,
поскольку каждая точка показывает в аналоговой форме
предполагаемое цифровое представление исходного вход-
ного сигнала. Тем не менее мы полагаем, что этот рисунок
\
\
Вход
Погрешность |
ч /^
У
\
\
X
ч 1 ■ 1
♦ч
Время
Рис. 18N.6. Максимальная погрешность квантования со-
ставляет 1/2 величины наименьшего кванта напряжения
Данный рисунок приводится, чтобы убедить
вас, что максимальная погрешность в процессе
преобразования будет составлять 1/2 величи-
ны наименьшего кванта. Такие погрешности
являются неизбежным результатом присвое-
ния постоянно варьирующемуся аналоговому
напряжению дискретных цифровых значений.
Таким образом, квантование неизбежно добав-
ляет этот шум на уровне половины значения
самого младшего бита.
18N.2.2. «Нарезка» по горизонтали:
частота дискретизации
Те, кто не знаком с этим процессом, будут удив-
лены одним из его результатов. В частности,
в теореме Найквиста — Шеннона утверждается,
что чуть больше чем две выборки за один пери-
од синусоидального сигнала будут содержать
полную информацию об этом сигнале7. Таким
образом, исходный сигнал можно восстановить
всего лишь по паре выборок. (Но это действи-
тельно только при наличии многих периодов
этих двух выборок.) Эта теорема в изложении
Клода Шеннона (Claude Shannon) выглядит та-
ким образом8:
делает менее абстрактным понятие «погрешность меньше,
чем 1/2 величины младшего бита».
7 Эта теорема была предложена, но без четкой формули-
ровки, Гарри Найквистом (Harry Nyquist) в 1928 г. и до-
казана Клодом Шенноном (Claude Shannon) в 1949 г., ино-
гда называется теоремой отсчетов Найквиста — Шеннона
(в русскоязычной литературе — теоремой отсчетов Шен-
нона — Котельникова).
8 Claude Shannon (Клод Шеннон) в «Proceedings of the Insti-
tution of Radio Engineers» («Записки института радиоинже-
неров»), 1949, № 37 (1), p. 10-21, как цитирует Nika Aldrich
(Ника Олдрич) на с. 111 своей превосходной книги «Digital
Audio Explained for the Audio Engineer» («Объяснение циф-
рового аудио для радиоинженера»), 2-е изд., издательство
Sweetwater, 2005 г.
726
18N. Аналоговые и цифровые преобразования; ФАПЧ
Теорема Найквиста
Любую функцию F(t), состоящую из частот от 0 до
fv можно непрерывно передавать с любой точно-
стью при помощи чисел, следующих друг за дру-
гом через 1/(2^) секунд. Это общеизвестный факт
в технике связи.
О чем не говорится в теореме Найквиста
Мы хотим предупредить вас не попасть в ло-
вушку возможного неправильного понимания
теоремы Найквиста. В частности, мы хотим
подчеркнуть тот факт, что в точности двух вы-
борок за период будет недостаточно. В своей
книге Ника Олдрич приводит один достаточ-
ный аргумент в поддержку этого факта: имея
всего лишь две точки, можно начертить сину-
соиду для данной частоты и любой амплитуды.
Таким образом, этой информации недостаточ-
но, чтобы удовлетворить основному требова-
нию: чтобы через точки выборки можно было
начертить только одну форму волны сигнала9.
Если задача воспроизведения синусоидального
сигнала одной частоты кажется вам чисто ака-
демическим упражнением, вспомните мудрость
учения Фурье, в котором отмечается, что сиг-
нал любой формы можно выразить в виде сум-
мы синусоидальных сигналов. Также обратите
внимание на то, что если мы можем выпол-
нить адекватную выборку компонента сигнала
с наивысшей частотой, то неизбежно получим
обильную информацию о составляющих с бо-
лее низкими частотами10.
9 Олдрич на с. 123 ранее цитируемой работы. Также следу-
ет иметь в виду важное уточнение, которое подчеркивает
Олдрич, что теорема применима только к синусоидальным
сигналам. Создание других необычных форм сигналов, ко-
торые могли мы проходить через выбранные точки, будет
нарушением правил. Сигналы таких необычных форм бу-
дут содержать более высокие частоты, чем частота предпо-
лагаемого синусоидального сигнала. Если этот аспект вам
незнаком, обратитесь к работам М. Фурье (см., например,
главы 3N и 31).
10 Обычно теорема Найквиста цитируется применительно
к составляющей входного сигнала с наивысшей частотой
(см. например, § 13S10C книги АоЕ). В редких случаях
необходима иная формулировка теоремы как требующей
более частой выборки, чем чуть больше удвоенной ча-
стоты диапазона сигнала. Когда частотный диапазон сиг-
нала начинается в районе нуля, что имеет место в случае
с аудиосигналом, его наивысшая частота и диапазон частот
будут одинаковыми. Но в необычном случае возможно,
например, делать выборку в узкой полосе частот сигнала
высокой частоты, используя умеренную частоту выборки.
Такая ситуация может возникнуть, например, при оциф-
ровке радиосигнала.
Эту идею иллюстрирует на рис. 18N.7 с исполь-
зованием 8-разрядного АЦП/ЦАП (AD7569), с
которым мы будем работать на лабораторном
занятии 23L.1. В данном случае мы не пытаемся
быть чрезвычайно жадными с частотой выбор-
ки, а делаем приблизительно четыре выборки
за период. На осциллограмме показан полный
процесс преобразования аналогового сигнала в
цифровую форму и восстановление из нее ис-
ходного сигнала.
Аналоговый сигнал
на входе АЦП
Выходной сигнал из ЦАП
(восстановленный
из цифровой формы
исходного сигнала)
Рис. 18N.7. Осциллограмма аналогового сигнала на входе
АЦП и восстановленного сигнала на выходе ЦАП
Возможно, вам будет трудно поверить, что это-
му ступенчатому восстановленному сигналу
можно придать его естественную синусоидаль-
ную форму, однако это действительно возмож-
но. Правда, потребуется хороший низкочастот-
ный фильтр, намного лучший, чем простой низ-
кочастотный RC-фильтр. На рис. 18N.8 показа-
на осциллограмма восстановленного сигнала,
сглаженного таким фильтром практически к
виду исходного входного аналогового сигнала,
разве что только смещенного по фазе.
Входной
аналоговый сигнал
Выходной сигнал из ЦАП
(восстановленный из его
цифровой формы)
Отфильтрованный
выходной сигнал из ЦАП
Рис. 18N.8. Осциллограмма аналогового сигнала на входе
АЦП, восстановленного сигнала на выходе ЦАП и конечного
выходного сигнала, полученного посредством фильтрации
восстановленного сигнала с помощью НЧ-фильтра
Мы еще вернемся к вопросу выбора необходи-
мой частоты дискретизации, а также требова-
ний к качеству низкочастотного фильтра далее
в этой главе и более подробно рассмотрим эти
аспекты в главе 18S.
У вас будет возможность воспроизвести опи-
санный эффект на лабораторном занятии 23L,
в котором вам нужно будет использовать свой
18N.2. Общие сведения о цифроаналоговых и обратных преобразованиях
727
микрокомпьютер для управления частотой вы-
борки. Очевидно, что требуемая частота дис-
кретизации зависит от частоты входного ана-
логового сигнала: если этот сигнал содержит
много составляющих с другими частотами,
тогда нас интересует составляющая с самой
высокой частотой, поскольку более низкие ча-
стоты легче поддаются выборке. Коммерческое
цифровое аудио снова предоставляет нам при-
мер соответствующего случая. В этих системах
ставится целью сохранять и восстанавливать
аудиосигналы с частотой вплоть до 20 кГц, для
чего дискретизация осуществляется с частотой
44,1 кГц. Это можно назвать передискретиза-
цией на 10%, т. е. частота выборки превышает
теоретический минимум по теореме Наиквита
чуть больше чем на 10%.
18N.2.3. Влияние недостаточной
частоты дискретизации
Пренебрежение требованиями теоремы Найк-
виста приведет к проблемам. В частности, вы
не только не достигнете правильного резуль-
тата, а получите бессмысленный набор дан-
ных. Слишком низкая частота выборки создает
паразитный эффект в виде ложного сигнала,
смешанного с настоящим сигналом без воз-
можности его отделения. Такой ложный сигнал
называется побочным11, поскольку он создается
из сигнала правильной частоты. Сам же эффект
возникновения побочной составляющей назы-
вается наложением спектров. Это может пока-
заться странным, но настоящий сигнал также
захватывается, однако присутствие паразитной
побочной составляющей обычно безвозвратно
искажает сигнал12.
На рис. 18N.9 приведена осциллограмма ана-
логового сигнала частотой 1 кГц, дискрети-
зированного с частотой выборки 1,2 кГц, что
намного ниже теоретической частоты выбор-
ки Найквиста, составляющей свыше 2 кГц для
11 Англ. alias signal
12 В некоторых исключительных случаях побочные сигна-
лы могут быть безвредными или даже полезными. Если ис-
ходный сигнал состоит только из одной частоты, тогда его
побочный сигнал можно удалить с помощью узкополос-
ного заграждающего фильтра. Кроме того, предсказуемое
поведение наложения спектров позволяет преднамеренно
переместить высокие частоты в более низкий диапазон ча-
стот. Этот метод пригоден для преобразования высокоча-
стотного радиосигнала в сигнал промежуточной частоты,
который далее подвергается демодуляции. См. с. 35 ранее
цитируемой книги Олдрич.
данного сигнала. На осциллограмме показан
исходный аналоговый сигнал с точками выбор-
ки в нем, обозначенными кружочками, а так-
же восстановленный сигнал (выходной сигнал
ЦАП) до и после применения низкочастотно-
го фильтра. Ложный синусоидальный сигнал
в самом низу выглядит убедительным, но это
обманчивое впечатление. (Точки выборки, вы-
ходной сигнал ЦАП и конечный отфильтрован-
ный сигналы не совпадают по фазе, что являет-
ся результатом задержек, вносимых процесса-
ми создания этих сигналов.)
Последовательность.
импульсов выборки
(1,2 кГц)
Входной
синусоидальный
сигнал (1 кГц)
Восстановленный
сигнал (на выходе
ЦАП): захвачено
несколько точек
(задержки вызывают
сдвиг по фазе
относительно ^ „
входного сигнала) Восстановленный синусоидальный
сигнал после низкочастотной
фильтрации: выглядит
правдоподобным, но не является
исходным входным сигналом
Рис. 18N.9. Результат пренебрежения требованиями тео-
ремы Найквиста при осуществлении выборки. (Разрешение
осциллографа: верхний сигнал — 5 В/дел., остальные —
2 В/дел.; 400 мкс/дел.)
Восстановленный сигнал может иметь стран-
ную, даже несинусоидальную, форму. Но по-
сле обработки этого сигнала низкочастотным
фильтром получается синусоидальный сигнал,
как можно видеть на рис. 18N.9. Этот синусои-
дальный сигнал не является восстановленной
версией исходного сигнала, но неотличим от
входного сигнала частотой 200 Гц. (Побочный
сигнал создается на частоте^ЫБ ~/ж = 1,2 кГц -
- 1 кГц = 200 Гц.) Такие ложные сигналы при
дискретизации рассматриваются более подроб-
но в главе 18S.
Чтобы защититься от побочных сигналов, кро-
ме выходного низкочастотного фильтра нуж-
но использовать еще один хороший низкоча-
стотный фильтр на входе АЦП. Этот входной
фильтр не пропускает посторонние частоты
в преобразователь. Такой подход стандартно
применяется в системах АЦП, но мы предна-
меренно не будем использовать его на лабо-
раторном занятии 23L, где вам нужно будет
экспериментировать с частотами выборки.
728
18N. Аналоговые и цифровые преобразования; ФАПЧ
Это объясняется тем, что наложение спектров
является необычным и интересным эффектом,
с которым вам следует встретиться, по крайней
мере, один раз в лабораторных условиях, где он
не причинит никакого вреда. Познакомившись
с этим эффектом, вы будете убеждены, что его
нельзя допускать.
Но достаточно рассмотрения общих понятий.
Возвратимся обратно к аппаратному обеспече-
нию, в частности рассмотрим некоторые спо-
собы осуществления преобразований в обоих
направлениях.
18N.3. Методы
цифроаналоговых
преобразований
Процесс ЦАП концептуально простой
Все, что нам требуется, — это способ для сум-
мирования набора двоичных значений на-
пряжения или тока. В частности, если самый
старший бит входного значения соответствует
выходному напряжению величиной 1 В, сле-
дующий бит соответствует напряжению 0,5 В,
а оба бита вместе соответствуют напряжению
1,5 В. Соответствие следующих битов напряже-
нию устанавливается аналогично. Некоторые
методы реализации такого суммирования оче-
видны, а другие требуют объяснения.
18N.3.1. ЦАП, управляемый
унарным кодом
С этой задачей может справиться делитель на-
пряжения13 с переключателями на отводах, ко-
торые управляются цифровым входом14. Этот
подход обладает достойной родослбвной: он был
разработан самим лордом Кельвином15, хотя и
не такой древний, как можно предположить из
13 АоЕ § 13.2.1.
14 См. с. 148-152 книги Олдрич «Analog Devices Tutorial»
(«Учебное пособие по аналоговым устройствам»): http://
www.analog.com/media/en/training-seminars/tutori-
als/MT-014.pdf.
15 Удивительное происхождение этого метода мы взяли
из работы, предоставляемой онлайн компанией Analog
Devices: https://www.analog.com/media/en/training-
seminars/design-handbooks/Data-Conversion-Hand-
book/Chapter3.pdf.
этого факта. В настоящее время данный подход
используется для цифровых потенциометров
и некоторых малоразрядных устройств ЦАП.
Для его реализации требуется всего лишь рези-
стивный делитель, несколько переключателей
и логическая схема для декодирования.
3-битовый
цифровой
вход
К переключателям
Аналоговый
выход
Рис. 18N.10. ЦАП, управляемый унарным кодом (на основе
онлайнового учебного пособия компании Analog Devices)
При наличии качественных аналоговых пе-
реключателей 16-битовый делитель может
справиться с этой задачей — требуя для этого
65 тысяч высокоточных резисторов. Примером
устройства, реализующего такой подход, можно
назвать микросхему ЦАП DAC8564 производ-
ства компании Texas Instruments. Как указано
в справочном листке на это устройство, такой
дизайн минимизирует нежелательные между-
кодовые переходные напряжения (импульсные
помехи) по сравнению с устройствами ЦАП,
линейность которых зависит от точного согла-
сования соотношений значений резисторов.
18N.3.2. Схема суммирования токов
на операционном усилителе
Для создания двоичной взвешенной суммы
устройства ЦАП можно применить схему сум-
мирования токов на операционном усилителе
совместно с резисторами со значениями R, 2R,
4R и т. д.16 Хотя этот метод выглядит весьма
привлекательно для тех из нас, кто привык к ра-
боте с операционными усилителями, он редко
встречается на практике. Причина заключает-
ся в том, что для него требуются высокоточные
резисторы множества различных номиналов.
16 Сравните с рис. 13.3 в АоЕ.
18N.3. Методы цифроаналоговых преобразований
729
18N.3.3. Матрица резисторов R-2R17
Такой же результат — двоичное взвешивание
токов — можно получить с помощью ориги-
нальной схемы, называющейся матрицей рези-
сторов R-2R, для которой требуются резисторы
всего лишь двух значений. Очевидно, что из-
готовить резисторы всего лишь двух номина-
лов намного легче, чем резисторы п значений,
которые потребовались бы для ^-разрядного
преобразователя, схема которого показана на
рис. 18N.11. Эти п значений должны были бы
покрывать широкий диапазон, а сами резисто-
ры должны быть высокоточными, чтобы обе-
спечить многобитовое разрешение.
Старший
бит
Рис. 18N.11. Концептуально простая, но сложная в реализа-
ции схема ЦАП
Как матрица резисторов R-2R делит
напряжение
Матрица R-2R состоит из каскадов, изобра-
женных слева на рис. 18N.12. Поскольку при
рассмотрении слева (т. е. с входа) этот каскад
выглядит как 2R, то вместо его правого рези-
стора 2R мы можем подключить другой, точно
такой же каскад. Этот процесс можно повто-
рять столько раз, сколько требуется. На правом
выводе каждого резистора R такой комбинации
каскадов напряжение будет составлять полови-
ну от напряжения на его левом выводе.
На рис. 18N.13 «умная» схема R-2R (спра-
ва) сравнивается с обычным делителем (сле-
ва), который представляет собой двоично-
взвешенный делитель по нашим обычным пра-
вилам нагрузки.
В простом делителе входное сопротивление
RBX каждого последующего каскада составляет
100хДвых непосредственно предшествующего
ему каскада, что позволяет получить значения
RBX = 2R
Базовый модуль
v—ww—t
2R$ \2R
Поскольку RBX одного каскада равно 2R, правый резистор
можно заменить точно таким же каскадом
Рис. 18N.12. Матрица резисторов R-2R
Заменяет правый резистор 2R
... и так далее
Рис. 18N.13. Сравнение обычного делителя с «умным» двоичным делителем R-2R
17 АоЕ § 13.2.2.
730
18N. Аналоговые и цифровые преобразования; ФАПЧ
делимых напряжений с точностью до 1%. Это
довольно посредственная рабочая характери-
стика (эквивалентная меньше чем 7 битам точ-
ности). Кроме того, значения резисторов очень
быстро становятся громадными, а вместе с ними
таким же становится входной импеданс после-
дующих точек делителя. Тем временем, «умная»
матрица резисторов R-2R справляется с той же
задачей, используя только два значения резисто-
ров, а также обеспечивает постоянное выходное
сопротивление #вых. К тому же в обычном дели-
теле погрешности вызывает еще и нагрузка, а в
делителе R-2R такой эффект отсутствует.
Применение матрицы резисторов R-2R
На рис. 18N.14 изображены две схемы на осно-
ве матрицы резисторов R-2R18. В схеме слева
матрица резисторов служит в качестве источ-
ника тока для суммирующего включения опе-
рационного усилителя. В правой схеме (кото-
рая является схемой внутреннего устройства
микросхемы ЦАП) операционный усилитель
обходится, в результате чего на выход подается
ток. В обеих схемах ЦАП требуются резисторы
только двух номиналов.
На первый взгляд одна подробность на
рис. 18N.14 может показаться вам неправиль-
ной, в частности обратная связь на операцион-
ный усилитель в правой схеме. Но, немного по-
размыслив, вы должны вспомнить, что мы уже
встречались с этим ранее — в стабилизаторе с
низким напряжением отключения в главе UN.
18N.3A ЦАП с коммутируемыми
конденсаторами
Для формирования двоично-взвешенного вы-
ходного сигнала ЦАП резисторы можно заме-
нить конденсаторами. Производители микро-
схем предпочитают использовать конденсато-
ры вместо резисторов, особенно для микросхем
КМОП. Схема 3-разрядного ЦАП на рис. 18N.15
похожа на суммирующую схему на операцион-
ном усилителе, но более простая19.
Сброс
Рис. 18N.15. Схема 3-разрядного ЦАП с коммутируемыми
конденсаторами
Схема с конденсаторами суммирует заряды на-
прямую, тогда как для суммирующей схемы на
операционном усилителе, которая суммирует
токи, требуются или взвешенные источники
тока или же источник опорного напряжения и
взвешенные резисторы. (Сравните с рис. 13.4
в книге АоЕ.) Хотя схема с конденсаторами
может давать утечку, она хорошо подходит
для микросхем ЦАП, выходной сигнал кото-
рых используется в течение только короткого
5Y 2.SV MSV
Входное (или опорное)
напряжение; не обязательно -gr-
должно быть постоянным i
Цифровой вход
СБ;2
i, IS, I i, I |, I i.
! и, 2 1
MSB А«
Аналоговый
ВЬГХ выход
(добавляем
"дополнительные
биты, если
Y* ' необходимо)
Двоично-взвешенные перепады напряжения;
"Источник опорного напряжения создают двоично-взвешенные токи.
Рис. 18N.14. Две схемы ЦАП с матрицей резисторов R-2R: с выходным напряжением (слева) и с выходным током (справа)
В обоих случаях присутствует инверсия сигна-
ла в цепи обратной связи.
АоЕ § 13.2.3.
19 На основе рисунка на с. 806 книги R.Jacob Baker «CMOS
Circuit Design, Layout, and Simulation» («Проектирование,
разводка и эмуляция КМОП-схем»), издательство IEEE
Press, Wiley, 1998 г.
18N3. Методы цифроаналоговых преобразований
731
001-► J_
*t
4= с
т 7С
- 1/8 (Л,
100-
.u^
и„
Lie U
101-^|— = <— =!
T*Te Jx
Рис. 18N.16. Емкостные делители, создаваемые тремя разными входными цифровыми значениями в ЦАП с коммутируемыми
конденсаторами
времени, как, например, в АЦП с регистром по-
следовательных приближений (РПП)20.
После обнуления каждого из двоично-взве-
шенных конденсаторов они подключаются
или к «земле», или к опорному напряжению
£70П, в зависимости от логического значения
входного бита. Когда все биты установлены,
т. е. имеют логическое значение «1», выход-
ное напряжение С/вых равно Uon х 7/8. Иными
словами, при Uon = 8 В значение 111 на входе
создаст выходное напряжение величиной 7 В.
На рис. 18N.16 изображены схемы емкостных
делителей, создаваемых входным значением
111 и парой других входных значений.
18N.3.5. Одноразрядный ЦАП;
широтно-импульсная модуляция
(ШИМ)
Создать высококачественный ЦАП
непросто
Хотя схематически ЦАП выглядит просто, со-
брать настоящее устройство ЦАП, работающее
с хорошим разрешением (т. е. ЦАП, который
реагирует должным образом на большое коли-
чество битов) нелегко21. В этом курсе мы будем
использовать ЦАП со скромным разрешением
в 8 битов, что в терминах выходного напря-
жения подразумевает разрешение величиной
10 мВ в диапазоне напряжений от 0 до 2,5 В.
Такое разрешение мы можем обеспечить даже в
наших схемах, собранных на макетных платах.
20 См.: http://www.analog.com/media/en/training-sem>
inars/tutorials/MT-015.pdf.
21 АоЕ § 13.2.8.
Но высокое разрешение выходного аналого-
вого сигнала можно получить даже при вход-
ном цифровом сигнале с низким разрешением,
даже таким простым, как однобитовый сигнал
включения-выключения. Для этого использует-
ся метод усреднения. Если это звучит не совсем
понятно, вспомните, что мы уже встречались на
практике с этим эффектом, когда собрали схему
ШИМ на лабораторном занятии 8L.4. Сигнал
включения-выключения с варьирующимся за-
полнением может создавать очень высокое раз-
решение, если сгладить пульсирующий сигнал
с помощью усредняющей схемы.
Этот метод был реализован в первых компью-
терах для создания аудиосигнала. Он также
используется в усилителях звуковой частоты
класса D (Class D), выходные каскады которых
представляют собой простые переключатели,
обычно на положительное или отрицательное
напряжение. Мы уже имели возможность по-
знакомиться с таким усилителем, микросхе-
мой LM4667, на лабораторном занятии 12L.
Усилители класса D могут работать с очень
высокой эффективностью, в результате чего
им отдается предпочтение в аудиоустройствах
с питанием от батарей. Они также хорошо под-
ходят для управления электродвигателями (как
было продемонстрировано на лабораторном
занятии 8L), поскольку ШИМ обеспечивает бо-
лее плавную регулировку мощности и лучшее
крутящее усилие, чем при обычном изменении
напряжения питания электродвигателя.
На рис. 18N.17 показана осциллограмма сигна-
лов ШИМ, получаемых в процессе работы схе-
мы из лабораторного занятия 8L.4. Справа воз-
ле каждого сигнала ШИМ находится изображе-
ние светодиода, на который подается этот сиг-
нал. Светодиод включается низким логическим
732
/8Л/. Аналоговые и цифровые преобразования; ФАПЧ
Пилообразный сигнал, j
пороговое значение U
(показано 75%) ]
Сигналы ШИМ ё(
Обратите внимание j
на то, что светодиоды Rtj
включаются низким
Коэффициент заполнения
(% включения)
уровнем
cm tloov
сьзГС
' 1 00 V M|40.0jiS
Рис. 18N.17. Статические сигналы ШИМ (слева) и светодиоды соответствующей яркости (справа). (Разрешение осциллографа:
пилообразный сигнал — 1 В/дел., сигналы ШИМ — 10 В/дел.)
уровнем, поэтому в сигналах ШИМ на рисунке
обычное значение активного логического уров-
ня инвертировано.
В данном случае сигналы ШИМ имеют посто-
янный коэффициент заполнения с целью де-
монстрации метода, хорошо подходящего для
управления с помощью микроконтроллера
не только яркостью одноцветного светодиода
(с одним катодом), но также цветом двух- или
трехцветного светодиода за счет изменения
интенсивности каждого из двух или трех со-
ставляющих цветов. У вас будет возможность
поэкспериментировать с этим методом на ла-
бораторном занятии 22L.2.9.
Варьируя во времени коэффициент заполне-
ния сигнала ШИМ, можно создать аналоговый
сигнал. На рис. 18N.18 показан гипотетический
сигнал ШИМ (вверху) и синусоидальный сиг-
нал, который можно получить из этого сигнала
ШИМ, усреднив его с помощью НЧ-фильтра.
Сигнал ШИМ
Усредненный
сигнал ШИМ
Время
Рис. 18N.18. Из сигнала ШИМ с варьирующимся коэффици-
ентом заполнения можно получить аналоговый сигнал
Тот факт, что однобитовый поток данных мо-
жет описать аналоговый сигнал, закладыва-
ет основу для более тонких методов цифро-
аналоговых преобразований с использованием
однобитового входного сигнала, или входного
сигнала с малым количеством битов. В разде-
ле 18N.4.5 далее в этой главе мы рассмотрим
идущий вразрез с интуицией метод цифро-
аналогового преобразования дельта-сигма,
в котором однобитовый выходной поток мо-
жет обеспечить высокое разрешение.
18N А Аналого-цифровое
преобразование
Задача преобразования аналоговых сигналов
в цифровую форму труднее, чем преобразова-
ние в обратном направлении, и для ее решения
было предложено множество разнообразных
методов. В табл. 18N.1 приведено несколько ос-
новных методов и их краткие характеристики.
Еще одно представление альтернативных ме-
тодов АЦП приводится на хорошем, четком
графике на рис. 18.68 раздела 18.12 книги Ulrich
Tietze и Christoph Schenk «Electronic Circuits:
Handbook for Design and Applications» («Полу-
проводниковая схемотехника. Справочник для
разработки и применений»), 2-е изд., издатель-
ство Springer, 2008 г.
18N.4.1. Методы без обратной связи
Параллельный метод22
Начнем наше рассмотрение с самого простого
концептуально, на наиболее трудного в реали-
зации метода параллельного преобразования.
Этот подход может напомнить вам ЦАП с управ-
лением унарным кодом из раздела 18N.3.1,
АоЕ § 13.6.
18N.4. Аналого-цифровое преобразование
733
Таблица 18N.1. Основные методы аналого-цифровых преобразований
Метод
Параллельное
Двоичный поиск
Дельта-сигма
Двойное
интегрирование
Скорость
быстрое
>5 не с 10 битами
> 1 не с 8 битами
Средняя
>1 мкс с 20 битами*
Низкая — средняя
>4 К выборок/с с 31 битом**
Медленная
Несколько выборок
с 24 битами
Разрешение
низкое
< 10 битов
Довольное высокое
< 20 битов
Высокое — очень высокое
< 32 бита
Высокое
< 24 бита
Применения
Запоминающий осцилло-
граф, радиосигналы
Общего назначения.
Широкий круг применений
Общего назначения.
Применяется все шире
Цифровые вольтметры.
Должен конкурировать
с методом дельта-сигма
* Микросхема LTC378-20.
** Микросхема LTC344x: 24 бита, без задержек; с задержкой в 1 цикл — 8 К выборок/с. Микросхема ADS1282 ком-
пании Texas Instruments позволяет захватывающую скорость в 4 К выборки/с с 31 битом.
в котором процесс преобразования протекает в
обратном направлении. На рис. 18N.19 изобра-
жен пример схемы такого преобразователя.
Результат на выходах компаратора похож на
унарный код. Этот избыточный код нужно
сжать с помощью кодирующей схемы.
Для этого метода требуется много аналоговых
электронных компонентов, чтобы получить
скромное количество битов. В частности, для
9-разрядного преобразователя необходимо
511 компараторов. Если вы привыкли к тому,
что в технической литературе постоянно упо-
минаются цифровые устройства, содержащие
миллионы транзисторов, и многогигабайтные
микросхемы памяти, то несколько сотен ком-
параторов не впечатляют. Но тот факт, что со-
временные параллельные преобразователи
ограничиваются 9-10 битами, подчеркивает
тот момент, что создание точных и быстрых
аналоговых схем является трудной задачей,
тогда как задача построения быстродействую-
щих цифровых схем сравнительно легкая.
В частности, на каждом из выходов памяти
со временем доступа, скажем, в 10 не должно
быть принято решение, ближе ли сохраненное
значение к логической единице или логиче-
скому нулю. В противоположность каждому
компаратору 9-разрядного АЦП с диапазоном
напряжений 0-2,5 В для принятия решения
предоставлено около 5 мВ; кроме того, чтобы
обеспечить такую же скорость, как у памяти,
это решение нужно принять быстро — чуть
меньше чем за 10 не. Очевидно, что из двух
этих устройств компаратору приходится тру-
диться более усердно.
Хотя в небольшом примере на рис. 18N.19 труд-
но увидеть необходимость устройства кодиро-
вания, его наличие обязательно. Устройство
Гипотетическое U,
вх
Выходы
компаратора
г Ж*_Эффективный код
2,8 В
2,0 В
1,0 В
0,25 В
1
0
0
0
1
1
0
0
1
1
1
0
1
1
0
0
ЗГ1
if
1
0
Qo
или заменить
'кодом Грея
малая эерфектив
Задействовано три бита,
определить всего четыре
комбинации, поэтому кодируем
IBHOefV^v
i, чтобы/
Рис. 18N.19. Параллельный АЦП
734
18N. Аналоговые и цифровые преобразования; ФАПЧ
кодирования сжимает семь линий в три, что
является полезным, хотя и не впечатляющим,
улучшением эффективности. Но при восьми
разрядах необходимость в устройстве коди-
рования становится очень очевидной: вместо
255 линий (выходы всех компараторов), кото-
рые нужно взять с АЦП, мы берем закодиро-
ванную информацию на восьми линиях.
На первый взгляд АЦП может работать не-
прерывно, но обычно он не функционирует
таким образом. Захват сигнала, когда компа-
раторы находятся в процессе изменения значе-
ния, имел бы пагубные результаты. Например,
в процессе перехода от значения 01 до значе-
ния 10 мы могли бы получить выходное значе-
ние 00 или 11. Поэтому, подобно АЦП других
типов, устройство этого типа управляется сиг-
налом тактирования выборок. Схема выборки
и хранения поддерживает постоянные значе-
ния на входах компараторов до тех пор, пока
компараторы не стабилизируются и цифровой
выходной сигнал не будет передан в регистр23.
Параллельные АЦП — это, скорее, специализи-
рованные устройства. У них высокое энергопо-
требление и низкое разрешение. Как автоном-
ные устройства параллельные АЦП зарезерви-
рованы для очень нетерпеливых. Но они часто
входят в состав поддиапазонных АЦП, которые
обеспечивают более высокое разрешение при
несколько меньшей скорости, применяя парал-
лельные преобразователи к частям всего пре-
образуемого диапазона.
Конвейерные преобразователи
Для выполнения преобразования поддиапа-
зонному устройству требуется несколько цик-
лов тактирования. Но такой преобразователь
может работать быстрее, чем можно было бы
судить по его необходимости использовать
несколько циклов. Для этого ему нужно по-
ставлять поток новых данных, пока он вы-
полняет преобразование ранее поступивших
данных.
Входной сигнал сначала подвергается грубо-
му преобразованию в трехразрядное значе-
ние трехбитовым параллельным АЦП. Затем
23 См., например, примечание по применению компании
Linear Technology, доступное по адресу: http://www.max-
im4c.com/appnotes.cfm/appnotenumber/810/CMP/
WP-17.
это выходное значение АЦП подается на ЦАП
и преобразуется в значение, представляющее
старшие три бита, после чего этот грубый уро-
вень вычитается из входного уровня. Результат
вычитания, остаток, передается второму трех-
битовому параллельному АЦП. Выходные зна-
чения этих двух параллельных АЦП образуют
шестибитовый результат, и эти два преобразо-
вания выполняются последовательно друг за
другом. Таким образом, если сохранить самые
старшие биты из выборки N для дальнейшего
их комбинирования с самыми младшими бита-
ми, когда те будут готовы, преобразование по-
следующих самых старших битов выборки N+1
можно начать, пока завершается обработка би-
тов выборки N.
АЦП на микросхеме LTC2207 компании Linear
Technology обеспечивает ошеломляющую ча-
стоту дискретизации — 105 мегавыборок в се-
кунду, преобразуя входной сигнал в 16-битовое
значение приблизительно за 10 не. Такая ско-
рость достигается благодаря конвейерной об-
работке выборок пятью параллельным АЦП,
каждый раз преобразовывая часть общего диа-
пазона. С учетом некоторого времени на вспо-
могательные операции ему требуется семь ци-
клов для выполнения одного преобразования.
Но это все равно чрезвычайно быстрое преоб-
разование — 16 битов приблизительно за 65 не,
даже если бы устройство выполняло одно пре-
образование без конвейеризации. Задержка
в конвейере величиной в семь циклов сигнала
тактирования называется временем ожидания
(latency).
18NA2. АЦП с двойным
интегрированием
При рассмотрении применений счетчиков в
разделе 16N.6 мы также познакомились и с
однотактным интегрирующим преобразовате-
лем24 (см. рис. 16N.28)25. Этот АЦП позволял
измерить время, за которое линейно нарас-
тающий сигнал достигал напряжения UBX.
Преобразователь с двойным интегрированием
работает подобным образом: он исходя из ве-
личины напряжения UBX задает ток, заряжаю-
щий конденсатор в течение установленного
времени, по истечении которого конденсатор
24 АоЕ § 13.5.7.
25 Эта схема также рассматривается в § 13.5.5 книги АоЕ.
18N.4. Аналого-цифровое преобразование
735
Заряжаем в течение установленного времени
со скоростью, определяемой UBX
\ ...затем разряжаем с установленной
скоростью и замеряем время разряда
Преобразователь
UI
ъ
Высокое UBX —
Сумма помех
может быть нулевой
Более низкое U,
Выход измеряет
время разряда
Фиксированное к
время
Рис. 18N.20. Конвертер с двойным интегрированием: конденсатор заряжается в течение установленного времени со скоро-
стью, определяемой входным напряжением, а затем разряжается с различным временем разряда
переключается на разряд током установленной
величины. Время, требуемое для разряда кон-
денсатора до нулевого напряжения, измеряется
счетчиком.
Преобразователь с двойным интегрировани-
ем отличается от других описанных ца данное
время преобразователей в одном важном отно-
шении: это интегрирующий преобразователь, а
не дискретизирующий. Из-за этой особенности
колебания напряжения выше и ниже среднего
входного напряжения обычно компенсиру-
ются, а не фиксируются в качестве истинного
уровня. Компенсация происходит полностью,
если преобразователь принимает целое число
периодов посторонних помех (в таком случае
интеграл равен нулю).
В итоге можно получить правильный резуль-
тат при наличии периодических помех. В част-
ности, если ожидаются периодические помехи
на частоте 60 Гц и их гармоники (что обычно
для линий электроснабжения в США), можно
допустить включение в преобразование целого
числа периодов этого сигнала, в результате чего
выбросы выше и ниже среднего значения будут
аннулироваться. Такой метод мы используем в
цифровых мультиметрах на наших лаборатор-
ных занятиях26.
Другим достоинством АЦП с двойным инте-
грированием является то, что он устраняет по-
грешности своих компонентов по постоянному
току: для того, чтобы знать, когда конденсатор
26 В АЦП этого типа, предназначенных для европейского
рынка, где частота электросети составляет 50 Гц, использу-
ется более длительное время интегрирования. В принципе
время интегрирования можно задать как кратное целое пе-
риодов как для 50 Гц, так и для 60 Гц. Но такие параметры
вызывали бы неприемлемую задержку. Длительность ин-
тервала интегрирования часто задается величиной в ОД с.
Это будет 6 периодов помех линий электропитания в США
и 5 периодов в Европе.
разрядился до потенциала «земли», в схеме
требуется точный компаратор. Чтобы измерять
входное напряжение с точностью, скажем, до
ОД мВ, может казаться, что для компаратора
потребуется напряжение меньшей величины.
Но подход двойного интегрирования устраня-
ет это требование. Компаратору нужно только
разрядить конденсатор до его начального на-
пряжения, а не до нулевого. Если, например, на-
чальное напряжение было 1,5 мВ (предполагая,
что это напряжение смещения UCM компарато-
ра), то разряд конденсатора до начального зна-
чения 1,5 мВ не вносит никаких погрешностей.
Влияние напряжения смещения подавляется.
В настоящее время преобразователям с двой-
ным интегрированием составляют конкурен-
цию так называемые АЦП типа дельта-сигма
(см.раздел 18N.4.5далее в этой главе). Подобно
АЦП с двойным интегрированием эти преоб-
разователи также относятся к интегрирующему
типу и способны выполнять преобразования с
высокой точностью, и их также можно настро-
ить на подавление частоты 60 Гц. Такие инте-
граторы хорошо подходят для цифровых муль-
тиметров.
18NA3. АЦП с обратной связью
Для задач общего назначения АЦП с обрат-
ной связью27, в особенности те, которые ис-
пользуют двоичный поиск, превосходят как
параллельные преобразователи, так и пре-
образователи с двойным интегрированием.
Параллельные АЦП слишком дороги, при
этом их точность невысока, а преобразовате-
ли с двойным интегрированием имеют низкое
быстродействие.
27 Это не стандартный термин для таких АЦП, а только
наш способ противопоставить их преобразователям па-
раллельного типа и АЦП с двойным интегрированием.
736
18N. Аналоговые и цифровые преобразования; ФАПЧ
Входной сигнал
ЦАП
Цифровой
компаратор
Входной
ступенчатый сигнал
L
подается на следящее устройство
и на преобразователь
последовательных приближений
\
Это напряжение показано на обеих осциллограммах:
отклик обоих преобразователей
Рис. 18N.21. Сравнение сигналов следящего АЦП и преобразователя двоичного поиска (или последовательных приближе-
ний) при подаче ступенчатого входного сигнала
Преобразователь с обратной связью работает
подобно повторителю на операционном усили-
теле с дискретным шагом. В частности, он соз-
дает оценочное цифровое значение входного
сигнала, преобразует это значение в его анало-
говый эквивалент и подает это напряжение об-
ратно. Затем компаратор решает, высокое или
низкое это оценочное значение (относительно
аналогового входа, конечно же). Выходной сиг-
нал компаратора затем указывает цифровому
компаратору («оценщику»), в каком направле-
нии ему следует идти при формировании сле-
дующего, улучшенного оценочного значения.
Таким образом, отрицательная обратная связь
приближает оценочное цифровое значение к
входному значению.
На рис. 18N.21 показаны сигналы на выходах
ЦАП для двух типов АЦП с обратной связью.
Видно, что оценочные аналоговые значения,
созданные этими двумя преобразователями,
постепенно приближаются к входному значе-
нию напряжения.
Примечание
Входной
аналог
сигнал
Суммирующий/
UP/DN вычитающий
счетчик
ЦАП
'8
Выходной
Эти сигналы представляют аналоговые напряже-
ния, отображающие оценочные цифровые значе-
ния; но не будем забывать, что в конечном итоге
нам требуются цифровые значения, а не их анало-
говые эквиваленты. Ведь это же, в конце концов,
аналого-цифровые преобразователи.
АЦП методом последовательных
приближений и слежения
На рис. 18N.22 демонстрируется реализация
АЦП с обратной связью, используя два типа
цифрового компаратора, результаты работы
которых показаны справа на рис. 18N.21. Один
из этих компараторов «умный», а другой —
нет.
Обратите внимание на схему выборки и хране-
ния в блок-схеме АЦП последовательных при-
ближений (правая схема на рис. 18N.22). Мы
рассмотрели (и собрали) схему выборки и хра-
нения на лабораторном занятии 12L на МОП-
транзисторах. А для следящего АЦП, который
работает постоянно, обновляя состояние по
каждому сигналу тактирования, схема выборки
и хранения не требуется.
Следящий АЦП
цифровой сигнал
Входной
аналоп
сигнал
(Схема выборки и хранения)
_L
Регистр
последовательных
приближений (РПП)
Сигнал
тактирования
ЦАП
АЦП последовательных приближений
Выходной
регистр
_АЦП
последовательных
приближений
Рис. 18N.22. Два АЦП с обратной связью: следящий и последовательных приближений (двоичного поиска)
18NA. Аналого-цифровое преобразование
737
Следящий АЦП
Следящий АЦП, схема которого изображе-
на слева на рис. 18N.22, обладает необычны-
ми свойствами. В частности, он формирует и
улучшает свою цифровую оценку аналогового
сигнала, просто считая в режиме суммирова-
ния или вычитания. Хотя этот тип преобра-
зователя не очень распространен, он продол-
жает использоваться благодаря своим двум
достоинствам. Во-первых, в отличие от АЦП
последовательных приближений, которому
для создания результата требуется несколь-
ко циклов сигнала тактирования, он всегда
предоставляет наилучший текущий результат.
Во-вторых, он почти нечувствителен к им-
пульсным помехам, которые могут вызывать
большие погрешности в АЦП последователь-
ных приближений: ложный фронт сигнала
тактирования вызывает ошибку величиной
только в один младший бит. Таким образом,
непритязательный следящий АЦП может ока-
заться наилучшим решением для монотонных
задач, наподобие преобразования выходного
сигнала медленно вращающегося вала (в дат-
чике кругового положения28). Сформировав
наилучшее приближение постоянного вход-
ного сигнала, следящий преобразователь дол-
жен постоянно менять лишь значение самого
младшего бита.
АЦП последовательных приближений
(двоичного поиска)
По сравнению с предыдущим АЦП преобра-
зователь последовательных приближений об-
ладает «смекалкой»: он выполняет двоичный
поиск наилучшего приближения, начиная с се-
редины диапазона и «спрашивая» у компарато-
ра, в каком направлении ему идти в следующий
раз29. В процессе поиска наилучшего приближе-
ния он всегда начинает следующий поиск с се-
редины оставшегося диапазона. Это может вы-
глядеть сложно, но в действительности очень
легко для устройства, которое по своей приро-
де уже является двоичным. Компаратор побит-
но информирует устройство двоичного поиска,
была ли его последняя оценка завышенной или
заниженной относительно входного аналого-
вого значения.
В результате этого постепенного процесса в вы-
ходной регистр передается значение для хра-
нения последнего, наилучшего приближения.
Промежуточные цифровые приближения мо-
гут выглядеть странными до тех пор, пока про-
цесс не будет завершен, поэтому их не следует
представлять на обозрение внешнему миру.
Кроме того, входной аналоговый сигнал дол-
жен пройти через схему выборки и хранения,
которая фиксирует значения в течение процес-
са преобразования. Чтобы не усложнять АЦП,
мы не используем схему выборки и хранения в
нашем лабораторном устройстве. В результате
мы теряем определенность во времени выбор-
ки, и это влечет значительные погрешности на-
пряжения в наших преобразованиях30.
Выборку нужно брать через одинаковые
интервалы
Любое преобразование сигнала, включая са-
мое простейшее — воспроизведение через ЦАП
и низкочастотный фильтр, подразумевает пе-
риодическую выборку. При отсутствии схемы
выборки и хранения преобразованное значе-
ние будет равно входному значению в какой-
либо точке интервала выборки, но нельзя
сказать с точностью, в какой именно. Таким
образом, в последующих выборках частота вы-
борки становится неопределенной, меняющей-
ся. В разделе 18N.5 мы увидим, что выборку
обычно требуется выполнять с контролируе-
мой и регулярной частотой31.
Мы рассмотрели схему следящего АЦП с един-
ственной целью — чтобы на его фоне преобра-
зователь двоичного поиска выглядел хорошо.
На практике существует очень ограниченное
число задач, для решения которых целесообра-
зен следящий АЦП.
28 См.: приложение по применению компании Analog
Devices (https://www.analog.com/media/cn/training-
seminars/tutorials/MT-030.pdf).
29 AoE § 13.7.
30 В какой-либо точке процесса преобразования преоб-
разованное значение будет соответствовать значению
входного напряжения. Но до тех пор, пока это не случится,
уровень входного сигнала может значительно измениться,
часто намного больше, чем желаемое разрешение АЦП ве-
личиной в половину значения самого младшего бита.
31 Используя слово «обычно», мы перестраховались вви-
ду наблюдения Шеннона, что «выборки могут браться
неравномерно», хотя в таком случае «значения выборок
должны быть известными с большой точностью» и «про-
цесс восстановления также будет более сложным» (Клод
Шеннон, с. 12 ранее цитируемой работы). В таком слу-
чае нужно было бы знать с большой точностью не только
входные уровни, но также время точек выборок. Мы будем
обходить далеко стороной такие тонкости.
738
18N. Аналоговые и цифровые преобразования; ФАПЧ
Л-ГЪ
«100 кГц—I
запуску развертки
"циллограсра
К осциллографу
Сигнал
тактирования
\\\\ \
Задержка
распространения
РТТП
40 не макс.
Время
стабилизации
ЦАП
1000 не макс.
Задержка
компаратора
700 не макс.
Время
установки РТТП
16 не макс.
Рис. 18N.23. АЦП с обратной связью: период сигнала тактирования должен быть достаточно большим, чтобы дать время
на все задержки в цепи обратной связи
Как уже упоминалось ранее, изготовление точ-
ных аналоговых устройств, например ЦАП с вы-
соким разрешением, является трудной задачей.
И наоборот, изготовление цифровых устройств
не представляет больших трудностей, и такие
устройства также можно с легкостью соединять
последовательно для обработки большого объ-
ема информации. Например, можно с легкостью
собрать суммирующе-вычитающий счетчик
или регистр последовательных приближений
на 100 битов. Таким образом, точность преоб-
разователя с обратной связью ограничивается
его аналоговыми компонентами: ЦАП и компа-
ратором. Они также ограничивают быстродей-
ствие АЦП, как иллюстрируется на рис. 18N.23
(сравните с рис. 18L.7).
18N.4A Пример двоичного поиска
Для тех, кто все еще сомневается в эффективно-
сти стратегии двоичного поиска, реализован-
ной в регистре последовательных приближений
АЦП (с которым мы будем работать на лабора-
торном занятии 18L), далее приводится демон-
страционный пример такого поиска. Пусть кто-
то выберет число от 0 до 255 и сообщает вам,
если каждое из ваших последовательных при-
ближений в стиле РПП слишком мало. В итоге
вам потребуется всего лишь восемь попыток,
чтобы угадать ответ. Если записать ваши пред-
положения в двоичной форме (подобно тому,
как это сделано в таблице «Двоичное значение»
на рис. 18N.24), то можно увидеть, как РПП по-
разрядно формирует ответ.
Процесс формирования ответа начинается с са-
мого старшего бита и выполняется по направ-
лению к самому младшему, всегда присваивая
последующему биту значение «О». После каж-
дого приближения компаратор сообщает РПП,
меньше ли это приближение, чем искомое зна-
чение, или нет. Если меньше, то РПП присваи-
вает значение «1» биту, которому только что
было присвоено значение «О», одновременно
присваивая следующему биту значение «О».
Прибытие этой «перемещающейся проверки»
к самому младшему биту регистра с присвоени-
ем этому биту значения «1» или «О» завершает
поиск. В случае, рассмотренном на рис. 18N.24,
мы выбрали произвольное исходное значение
156.
На рис. 18N.25 показана осциллограмма тако-
го поиска: РПП подгоняет выходное значение
ЦАП по направлению к величине входного ана-
логового сигнала. Хотя составляющие D3 и D1
преобразуемого значения на осциллограмме
отличаются от этих значений на рис. 18N.24,
очевидно, что закономерности в обоих случаях
довольно схожи.
18NА5. Дельта-сигма АЦП
В настоящее время преобразователям двоично-
го поиска (последовательных приближений)32,
которые в течение долгого времени были наи-
более универсальным и широко распростра-
ненным типом АЦП, начинают составлять
конкуренцию преобразователи другого типа,
использующие стратегию преобразования, на-
зывающуюся дельта-сигма33.
32 АоЕ § 13.9, особенно 13.9.4А.
33 Этот тип преобразования иногда называют «сигма-
дельта», даже когда последовательность операций, по
сути, не меняется на обратную. Конкретное название зави-
сит от производителя. С исторической точки зрения назва-
ние «сигма-дельта» может быть более точным, совпадая
с названием, применяемым изобретателями этого метода.
См.: http://www.beis.de/Elektronik/DeltaSigma/Delta-
Sigma.html. (В русскоязычной литературе в основном ис-
пользуется название сигма-дельта.)
18NA. Аналого-цифровое преобразование
739
Дерево
двоичного поиска
Номер сигнала
тактирования
J1L
JSL
Результат из
компаратора
Слишком низкое
Не слишком низков
J-ie .слишком низкое
Слишком низкое.
слишком низкое
^ Слишком низкое
Слишком низкое
Не слишком низкое
Для значения,
которое мы
видим как
битможет'Р0»**»'
^парат
иметь
любое
вмяаст
из двух произвольный
значений ответ
Наилучшее, последнее приближение. Это приближение
захватывается и сохраняется в выходном регистре из
восьми D-триггеров: 10011100 (в данном случае, где наш
выбор ограничен целыми числами, значение самого
младшего бита неопределенное)
Единственный путь поиска
Рис. 18N.24. Единственный двоичный поиск: восемь предположений, чтобы получить 8-битовое значение
СС* (преобразование
завершено)
Выход ЦАЛ, отображающий
последовательные приближения \
Входной аналоговый сигнал I
^Наилучшее, последнее приближение
Г 'soomv"~ *c
Приближения (побитовые) после коррекции, 1 0 0 101 10 = 96h
указанной компаратором:
Рис. 18N.25. Регистр последовательных приближений сужает поле возможных значений к значению входного аналогового
сигнала. (Разрешение осциллографа: сигнал СС* — 5 В/дел., 200 мкс/дел.; остальные сигналы — 500 мВ/дел.)
На рис. 18N.26 изображена схема модулятора
дельта-сигма, реализующего этот подход. Мы
обвели всю схему треугольником, чтобы под-
черкнуть тот факт, что это петля обратной связи,
знакомая нам по работе с операционными уси-
лителями. Сигнал обратной связи, подаваемый
на разностный блок, является на удивление не-
точным, колеблясь от одного предела полного
диапазона уровней входного сигнала к друго-
му: от +1 до -1В в этом гипотетическом случае.
Это значение никогда не может совпадать со
значением входного аналогового сигнала (если
740
18N. Аналоговые и цифровые преобразования; ФАПЧ
Входной аналоговый сигнал
Грубое приближение входного |
аналогового сигнала
Выходной поток битов
Сигнал-^
^l В тактирования
передискретизации
Рис. 18N.26. Модулятор дельта-сигма
...и заимствуем ^
информацию из потока
до и после этой выборки
только уровень входного сигнала действитель-
но не является одним из максимальных). Но
долговременное среднее значение выходного
потока битов может совпасть с уровнем вход-
ного аналогового сигнала.
На рис. 18N.26 дается подробное (возможно,
больше, чем необходимо) объяснение принци-
па работы этого модулятора.
1. Схема определяет знак разницы между зна-
чением входного аналогового сигнала и его
текущего приближения. На рис. 18N.26 ве-
личина приближения равна просто верхнему
или нижнему пределу (+1 или -1В), опреде-
ляемому однобитовым цифровым выходом.
Эта разница, выдаваемая дифференциаль-
ным усилителем, является дельтой. Затем...
2. В ответ модулятор передает в аналоговую
суммирующую схему порцию заряда с со-
ответствующим знаком и амплитудой (это
будет сигмой), пытаясь привести подавае-
мое обратно приближение близко к уровню
исходного аналогового сигнала. Обратная
связь поддерживает выходной сигнал инте-
гратора на близком к нулю уровне. В ходе
этого преобразователь генерирует выходной
поток битов, среднее значение которого за
много циклов совпадает с значением входно-
го аналогового сигнала.
Модулятор
дельта-сигма
(из рис. 18N.26)
Битовый поток
(1-битовый)
Цифровой
НЧ-срильтр
Пока что в этой схеме нет ничего необычного.
Выходной поток битов похож на сигнал ШИМ
(см. раздел 18N.3.5). А контур обратной связи
представляет собой просто еще одну схему отри-
цательной обратной связи, несколько похожую
на грубый следящий АЦП из раздела 18N.4.3,
который «впрыскивает» положительный или
отрицательный инкремент в цифровой сумма-
тор (счетчик), содержащий текущее наилучшее
приближение. Выходной сигнал того следящего
АЦП формировался очень простым способом:
это было просто текущее многобитовое значение,
которое было сформировано на суммирующе-
вычитающем счетчике. Следящий АЦП также
был очень медленным, поскольку для получения
^-битового цифрового эквивалента значения
входного аналогового сигнала, изменившегося от
одного предела диапазона к другому, требовалось
2п сигналов тактирования.
А вот преобразователь дельта-сигма намно-
го «умнее» и намного более интересен. На
рис. 18N.25 изображена блок-схема АЦП
дельта-сигма. Ее составляющие элементы пред-
ставлены в самом общем виде, и мы не ожида-
ем, что она вас чем-то удивит, по крайней мере,
не на данном этапе.
Обратите внимание на то, что низкочастотный
фильтр здесь является цифровым. Его выход-
ной сигнал — последовательность ^-битовых
Многобитовые выборки,
, с обычной частотой Найквиста
Щ (>2 на каждый период входящего
аналогового сигнала)
стота битов = 64 х частоту Найквиста^
лш около того
Рис. 18N.27. Очень общая (пока) блок-схема АЦП дельта-сигма
18NA. Аналого-цифровое преобразование
741
выборок, собранных из высокоскоростного по-
тока однобитовых данных, создаваемого пере-
дискретизирующим модулятором дельта-сиг-
ма, подробная схема которого изображена на
рис. 18N.26. Как говорится в книге АоЕ, именно
он творит чудеса.
Если бы для получения результата с разрядно-
стью в п битов преобразователю дельта-сигма,
подобно следящему АЦП, требовалось 2п им-
пульсов сигнала тактирования (в наихудшем
случае), то в его работе не было бы ничего
удивительного. Следящий преобразователь
обеспечивает такие же результаты, и их также
можно получить с помощью простого ШИМ-
потока битов. Но в практических схемах преоб-
разователей дельта-сигма этого не происходит.
В действительности они умудряются получить
высокое разрешение при довольно скромной
частоте передискретизации, например 64 (что
подразумевает довольно реалистичную частоту
сигнала тактирования). Тем не менее даже при
такой ограниченной передискретизации АЦП
этого типа могут достигать разрешения вели-
чиной 16 или 24 бита.
Волшебство преобразователей дельта-сигма
очень трудно поддается интуитивному понима-
нию. В книге АоЕ дано много ссылок на лите-
ратуру, признавая, что этот метод преобразо-
вания не поддается интуитивному пониманию.
Как отмечается в этой книге, обычные «объ-
яснения» данного метода изобилуют ловкими
увиливаниями и уходом в абстрактную частот-
ную область34.
Например, объяснение, предоставляемое ком-
панией Analog Devices (ADI), начинается (по-
добно тому, как это часто делают подобные
просветители принципа дельта-сигма) с при-
знания, что предоставляемые всеми другими
источниками объяснения трудно поддаются
пониманию: «...большинство из них начинают-
ся с лабиринта интегралов и дальше становятся
только хуже. Некоторые инженеры... убежде-
ны, что понять (принцип работы дельта-сигма)
очень трудно, изучая типичную опубликован-
ную статью»35. Но нужно отдать должное ком-
пании ADI за то, что она также предоставляет
интерактивную анимацию во временной обла-
сти поведения модулятора дельта-сигма, кото-
рую можно тактировать вручную, чтобы полу-
чить представление о способе, реализованном
в схеме кодирования сигнала напряжения по-
стоянного тока36. Эта анимация действительно
способствует пониманию данного предмета.
А в учебном пособии компании Maxim Integ-
rated, объясняющем преобразователи дельта-
сигма, отмечается, что «Разработчики часто из-
бирают классическую схему АЦП с регистром
последовательных приближений, поскольку
они не понимают принципов работы преобра-
зователей дельта-сигма». И ничего удивитель-
ного в этом нет! — была наша реакция, когда
в этом в общем ясном пособии мы дошли до
места, в котором без каких бы то ни было объ-
яснений заявляется, что «...интегратор играет
роль низкочастотного фильтра для входного
сигнала и высокочастотного фильтра для шума
квантования»37. Это ключевое замечание по-
вторяется во всех обсуждениях метода преоб-
разования, но его объяснение наконец приво-
дится в книге АоЕ и в оставшемся материале
этого раздела данной книги38.
Прежде чем приступать к рассмотрению во-
проса о низкочастотном и высокочастотном
фильтрах, отметим один предварительный
аспект в пользу однобитового преобразовате-
ля39. В частности, в нем шум квантования рас-
пределен по широкому диапазону частот, и его
можно снизить в определенном, более узком,
диапазоне, представляющем интерес. Эта ис-
ходная идея почти банальна.
Размен разрядности на частоту выборки:
передискретизация
Выбор отсчетов с меньшим интервалом, чем
требуется по критерию Найквиста (с частотой
чуть больше двойной максимальной частоты
34 Которая является, перефразируя известное высказыва-
ние, последним убежищем негодяев (с точки зрения неко-
торых из нас, не любителей абстракций).
35 Примечание по применению от компании ADI: https://
www.analog.com/media/en/training-seminars/tutori-
als/MT-022.pdf.
36 https://www.analog.com/en/design-center/interac-
tive-design-tools/sigma-delta-adc-tutorial.html.
37 Учебное пособие (tutorial) 1870 компании Maxim Integ-
rated: https://www.maximintegrated.com/en/app-notes/
index.mvp/id/1870.
38 Мы также хотим отметить чрезвычайно подробные объ-
яснения, которые Ника Олдрич приводит в своей книге,
сопровождая их множеством осциллограмм сигналов, что
весьма способствует пониманию этого трудного предмета.
39 В некоторых преобразователях используется больше чем
один бит. Такие преобразователи правильно называть ма-
лоразрядными преобразователями. Но принцип их работы
в основном подобен однобитовым преобразователям.
742
18N. Аналоговые и цифровые преобразования; ФАПЧ
входного сигнала), называется передискрети-
зацией. Но данный объем информации можно
передать в более коротких словах (выборках с
меньшим количеством битов), передавая эти
слова с более высокой скоростью40. Безусловно,
данное утверждение справедливо, в этом нет
никакого волшебства. Например, на рис. 18N.28
демонстрируется, как поддиапазонный преоб-
разователь может преобразовать многоразряд-
ное слово по частям за несколько циклов.
Отношение
сигнал-шум
или количество
битов в выборке:
длина слова
i
f
2Х
4Х
IX
(обычная частота выборки)
Рис. 18N.28. Длину слова можно разменять на частоту вы-
борки, при этом скорость передачи информации останется
прежней
Но если попытаться применить описанный
подход к однобитовым АЦП, чтобы получить
выходной сигнал высокого разрешения, напри-
мер в 16 битов, то результат получится неле-
пым. Для разрешения в 16 битов потребовалась
бы частота выборки в 65 000 раз больше, чем
частота Найквиста. Текущий уровень развития
технологии этого не позволяет.
Но для эффективного хранения данных
лучше всего подходят длинные слова
Хотя стратегия уменьшения числа битов может
окупиться для процесса преобразования, для
хранения данных это невозможно. Как отме-
чает Джон Уоткинсон41, один бит может пере-
давать намного больше информации в более
длинном слове. В частности, согласно ему, в
4-битовом слове с его 16 возможными состоя-
ниями, каждый бит несет в себе четыре бита
информации. А в 16-битовом слове, с его 65 000
возможными состояниями, каждый бит несет
4096 фрагментов информации. Таким образом,
например, никто не поддерживает хранение
цифрового аудио в 4-битовых словах42.
40 См. с. 253 книги John Watkinson «The Art of Digital Audio
(«Искусство цифрового аудио»), 3-е изд., издательство Fo-
cal Press, 2001 г.
41 Страница 254 ранее цитируемой работы Джона Уоткинсона.
42 Но следует признать, что формат Super CD компании
Sony, который сохраняет аудио в однобитовом потоке би-
Метод дельта-сигма позволяет получить высо-
кое разрешение, используя довольно скромную
частоту передискретизации, например 64 (что
подразумевает довольно реалистичную часто-
ту сигнала тактирования — ниже 3 МГц для
16-битового аудиосигнала). Это достигается
посредством распределения шума квантова-
ния по более широкому передискретизирован1
ному частотному диапазону, перераспределяя
бблыную часть этого шума в область более вы-
соких частот, где его можно отфильтровать43.
Как видно из самого нижнего изображения на
рис. 18N.29, уровень шума можно уменьшить
еще больше, если в процессе преобразования
выполнить формирование шума квантования
посредством высокочастотной фильтрации,
а затем удалить большую часть этого шума на
выходе с помощью НЧ-фильтра. Как демон-
стрируется далее, такое формирование шума
свойственно работе модулятора.
Это очень успешный метод, который в настоя-
щее время дает самый недорогой способ выпол-
нения преобразований с высоким разрешени-
ем на низких частотах. Например, микросхема
AD7748 такого АЦП производства компании
Analog Devices выдает выходное 24-битовое
значение за 20 мс. Этот метод также доминиру-
ет в области преобразования аудиосигналов.
Как дельта-сигма помещает шум
квантования туда, где он будет менее
проблематичным
Как мы упоминали ранее, метод дельта-сигма
полагается на прием формирования шума, ко-
торый частично присущ функционированию
модулятора, часто повторяется в рассмотрении
работы этого метода. Этот процесс показан на
рис. 18N.29 и подробно объясняется в книге
АоЕ. Также рекомендуем вам ознакомиться с
превосходным объяснением на веб-сайте Уве
Байса (Uwe Beis)44.
тов типа дельта-сигма, является поразительным исключе-
нием из этого обобщения о предпочтении длинных слов
для хранения данных. Формат Super CD не получил ши-
рокого распространения, но продолжает использоваться
аудиофилами.
43 Боже правый! Неужели мы только что произнесли фор-
мулировку, которую так критиковали чуть раньше? Но мы
не остановимся на этом замечании, а постараемся обосно-
вать сделанное утверждение.
44 https://www.beis.de/Elektronik/DeltaSigma/Delta-
Sigma.html.
18N.4. Аналого-цифровое преобразование
743
Обычная дискретизация
Весь шум квантования находится
в частотной полосе сигнала
Повышение частоты выборки в К раз
перераспределяет шум квантования
по частотной полосе, в К раз более
широкой, в результате чего в частотной
полосе сигнала шума станет меньше
Формирование шума квантования
(применением высокочастотного
фильтра) может еще больше уменьшить
его влияние в частотной полосе сигнала
, Шум квантования = q/ Л?
q = 1 МБ — младший бит
fs/2
kfs/2
Рис. 18N.29. Передискретизация распределяет шум квантования по более широкому частотному диапазону
Здесь мы пытаемся отобразить графически эф-
фекты, описанные з книге АоЕ45. На рис. 18N.30
показана полностью аналоговая версия дельта-
модулятора, в которой выполняется инжекция
шума квантования (UKB) там, где в цифровом
модуляторе был бы компаратор и триггер.
Контраст между обработкой в контуре обрат-
ной связи шума (в области высоких частот) и
полезного сигнала (в области низких частот)
становится более очевидным, если перерисо-
вать этот контур для обоих случаев, что и дела-
ется в следующих двух разделах.
Как шум пропускается (удаляется)
на высоких частотах
Шум квантования возникает после дифферен-
цирования и интегрирования. Мы нарисовали
эти два элемента, отобразив их в одном тре-
угольнике наподобие операционного усили-
теля. Такая перерисованная схема не должна
вызывать у вас беспокойства, поскольку обыч-
ный операционный усилитель с частотной кор-
рекцией является именно дифференциальным
усилителем, усиление которого снижается вме-
сте с уменьшением усиления интегратора.
Если рассматривать шум квантования про-
сто, как еще одну «собаку» в контуре обратной
связи (см. раздел 6N.9.1), тогда операционный
усилитель подавляет шум, но только до тех пор,
пока усиление операционного усилителя оста-
ется достаточно высоким, чтобы быть в силах
творить свое «волшебство» с обратной связью.
Когда же усиление начинает падать, все большая
часть шума квантования остается без измене-
Совмещенные дифференциатор и интегратор
я операционный усилитель
Здесь усиление интегратора =1
j
(Предполагается
отсутствующим)
При высоком усилении шум UKB на низких частотах незаметен;
когда усиление становится недостаточным, шум UKB проходит на выход.
Таким образом, шум проходит на высоких частотах.
OdB ---
ВЧ-фильтр для шума квантования UKB
Рис. 18N.30. Схема модулятора дельта-сигма, перерисованная для объяснения удаления шума квантования ВЧ-фильтром
ний. В конечном итоге этот шум проходит пря-
мо на выход, не подвергаясь какому бы то ни
45 АоЕ § 13.5.10Е.
744
/8Л/. Аналоговые и цифровые преобразования; ФАПЧ
было подавлению. Иными словами, шум уда-
ляется на высоких частотах. Обычно большая
часть шума находится выше диапазона частот,
считающихся полезным сигналом для АЦП.
Как сигнал пропускается
с низкими частотами
Одновременно с переносом шума в область вы-
соких частот модулятор пропускает сигнал в
низкочастотном диапазоне. Таким образом, он
оставляет то, что нам требуется, при этом «вы-
талкивая» ненужное нам за пределы интересую-
щего нас частотного диапазона. На рис. 18N.31
приводится объяснение, как модулятор дельта-
сигма пропускает сигнал на низких частотах.
вания, остается более глубокая тайна (как от-
мечается в книге АоЕ). Подход дельта-сигма
позволяет получить более высокое разрешение
(например, 16 битов), используя передискре-
тизацию только в 64х. То есть в 64 раза боль-
ше минимальной частоты Найквиста, равной
двум выборкам на период входного сигнала.
Но это подразумевало бы, что всего лишь 128
последовательных битов могли бы закодиро-
вать значение одной части в 64 К. Но как это
возможно, если для такого процесса нужно
64 К последовательных битов? Примечание,
взятое из учебного пособия компании Analog
Devices, признает, что такой результат вызы-
вает недоумение.
Предполагается отсутствующим, поскольку здесь
мы рассматриваем только влияние на сигнал
OdB
Спад усиления
интегратора
Интегрирование пропускает исигн на низких частотах
НЧ-фильтр для fo logf
сигнала Uruiru ^Ч
^Здесь усиление интегратора =1
*
Рис. 18N.31. Схема модулятора дельта-сигма, перерисованная для объяснения передачи сигнала на низких частотах
Опять же, мы нарисовали дифференциатор
и интегратор в виде одного треугольника на-
подобие операционного усилителя. Обратите
внимание на то, что мы не говорим, что вся
эта похожая на повторитель схема на рисунке
является фильтром. Мы лишь утверждаем, что
наш треугольник — фрагмент схемы модуля-
тора, который мы приравняли к операцион-
ному усилителю, — реализует функцию НЧ-
фильтра. Обычно, операционные усилители
не рассматривают таким образом, но мы-то
знаем, что обычный (с частотной коррекцией)
операционный усилитель в действительности
подавляет высокие частоты. Таким образом,
он является НЧ-фильтром, или интегратором,
хотя общая обратная связь скрывает это об-
стоятельство от нас.
Примечание
Для любого заданного входного значения в одном
выборочном интервале выходные данные одно-
битового АЦП, по сути, не имеют смысла. Только в
результате усреднения большого числа выборок
получается содержательное значение. Вследствие
этой кажущейся случайности выходного однобито-
вого сигнала работу модулятора сигма-дельта очень
трудно анализировать во временной области46.
Таким образом, любая 16-битовая выборка,
созданная АЦП дельта-сигма, использует циф-
ровой низкочастотный фильтр, показанный
на рис. 18N.27, чтобы собрать информацию из
значительно большего количества битов, чем
ближайшие 128 битов. Этот цифровой фильтр
исследует выборки, не только предшествующие
текущей, но также следующие за ней47. Иными
Поразительный результат: при скромном
числе битов разрешение оказывается
высоким
Но даже после понимания (или принятия на
веру) этого аспекта о смещении шума кванто-
46 Учебное пособие «Tutorial MT-022» компании Analog
Devices, а также книга W. Kester «ADC Architecture III: Sig-
ma-Delta ADC Basics» («Архитектура АЦП III. Основы АЦП
сигма-дельта»), с. 6 (https://www.analog.com/media/
en/training-seminars/tutorials/MT-022.pdf).
47 Это особенность цифровых фильтров: они могут «загля-
дывать наперед», располагая выборками по обеим сторонам
текущей выборки за счет задержки выходного значения.
18N.5. Ложные сигналы в процессе выборки
745
словами, битовый поток, по сути, намного
длиннее, чем те 128 битов, как мы заявили чуть
ранее. В действительности, цифровой фильтр
может брать информацию из нескольких со-
тен и даже тысяч последовательных битов (или
отводов48) в потоке49. Кроме того, в книге АоЕ
утверждается, что положение битов имеет зна-
чение, так что 128-битовый поток содержит
намного больше информации, чем просто его
среднее значение (которое обеспечило бы раз-
решение всего лишь в 7 битов)50.
Отсюда следует, что для работы АЦП дельта-
сигма одной отдельной выборки недостаточно,
а требуется поток выборок.
где п — любое целое число. Ложные сигналы
выборки рассматриваются подробно в гла-
ве 18S, где мы пытаемся объяснить, почему они
создаются на указанных частотах. На данном
этапе мы не будем предпринимать попыток до-
казать правильность уравнения (18N.1).
На рис. 18N.32 показаны два ложных сигнала
для гипотетического диапазона частот входно-
го сигнала. Частота этих ложных сигналов та-
кова, что в центре их полосы находится частота
выборки /ШБ для первого сигнала и 2 -/ВЫБ для
второго сигнала. Иными словами, полоса этих
сигналов как будто бы отображается по обе сто-
роны от частоты выборки и кратных ей частот.
18N.5. Ложные сигналы
в процессе выборки
18N.5.1 • Предсказание ложных
сигналов в частотной области
в процессе выборки
Согласно правилу Найквиста, которое мы рас-
смотрели в разделе 18N.2.2, чтобы получить пол-
ное представление входного синусоидального
сигнала, требуется брать чуть больше чем две
выборки за каждый период этого сигнала (по-
лагая дискретизацию многих циклов). Теперь
мы можем представить правило Найквиста в
таком виде, который упрощает разработку си-
стемы выборки, а именно позволяет предска-
зать ложные сигналы (которые также называ-
ются «духами»), которые будут создаваться в
процессе выборки.
В общем, если дискретизация аналогового сиг-
нала частотой/вх (для простоты, предположим
один входной синусоидальный сигнал) осу-
ществляется с частотой выборки /шъ, то в ре-
зультате будут формироваться ложные сигналы
предсказуемой частоты:
I
48 Англ. tap. — Примеч. пер.
49 Учебное пособие компании Analog Devices (https://
www.analog.com/media/en/training-seminars/tutori-
als/MT-022.pdf).
50 Касательно 64-битового потока, в разделе 13.9АС кни-
ги АоЕ говорится следующее: «Поскольку отдельные биты
имеют разные веса, можно получить намного больше, чем
64 бита результата».
f
/ДО U/
ВЫБ "'
ч
\
1
'ВХ(МАКС)
JX(MAKC) 'ВЬГБ + 'ВХ(МАКС) ~f
| ' ВЫБ ' ВХ(МАКС)
[
1
i
^'ВЫБ
i
f
Рис. 18N.32. Ложные сигналы выборки центрируются по ча-
стоте выборки и ее кратных частот
На рис. 18N.33 показана осциллограмма ча-
стотного спектра для определенного случая
входного сигнала одной частоты (а не более
реалистичного входного сигнала с полосой
частот, показанного на рис. 18N.32). Частота
этого входного сигнала равна 500 Гц. Частота
выборки осциллограмм, изображенных на
рисунке, постепенно уменьшается от верхней
трассировки к нижней, а ложные сигналы вы-
борки находятся в этих частотных спектрах.
На рис. 18N.33 мы обозначили ложный сигнал
выборки с самой низкой частотой, поскольку,
как оказалось, это единственный из ложных
сигналов, представляющий для нас интерес.
Конечно же, при восстановлении сигнала нуж-
но устранить и все другие ложные сигналы, но
фильтр, который устраняет компонент с самой
низкой частотой, заодно устраняет и все другие
ложные сигналы с более высокой частотой.
Таким образом, уравнение (18N.1), которое
предсказывает бесконечное повторение лож-
ных сигналов выборки, является правиль-
ным, но предоставляет избыточную инфор-
мацию. Все, что нас интересует, так это толь-
ко ложный сигнал с самой низкой частотой:
/ложн = (/выб -/вх)- Не бУДем стесняться заявить
746
18N. Аналоговые и цифровые преобразования; ФАПЧ
fBX=500 Гц
20 кГц
Ложный сигнал для самой низкой частоты выборки
///
Частота ложного сигнала для fBbLB = 20 кГц
настолько высока, что выходит
далеко за пределы экрана
Стрелки (<->) показывают частоты
i "49.0 38 S00 Иг j
Рис. 18N33. Ложные сигналы для четырех разных частот выборки. (Разрешение осциллографа: БПФ частотного спектра
500 Гц/дел.)
об этом во всеуслышание, поскольку это прав-
да, которая полезнее, чем общее уравнение
(18N.1). Таким образом, частота ложного сиг-
нала, о котором мы должны беспокоиться и для
которого должны создать фильтр для его устра-
нения, следующая:
/ложн-мин
VBbffi
(18N.2)
По мере снижения частоты выборки задача
фильтрации ложного сигнала становится все
сложнее, поскольку частота самого первого
компонента подходит все ближе к частоте на-
стоящего сигнала/^.
Например, самый нижний случай на рис. 18N.33,
где частота первого ложного сигнала состав-
ляет 600 Гц при частоте настоящего сигнала
500 Гц, довольно труден для фильтра. В дру-
гих случаях, с более высокой частотой выбор-
ки, устранение первого побочного сигнала не
представляет больших проблем. Разработчики
исходного стандарта для аудиокомпакт-дисков
столкнулись с подобной проблемой (которая
была даже еще труднее): при частоте выбор-
ки 44,1 кГц и аудиочастотах вплоть до 20 кГц
первый ложный сигнал создавался на частоте
24,1 кГц. Обнаружилось, что создание фильтра
с такими крутыми характеристиками, который
не вносил бы в сигнал слышимые искажения,
было невыполнимой задачей51. Этот провал
51 По крайней мере, для некоторых аудиофилов с чрез-
вычайно тонким слухом. См., например, комментарий
на одном веб-сайте любителей звукотехники: «Все эти
14-битовые плееры проявляли склонность к удалению
тонких пространственно-временных эффектов... Звук
был скорее пространственно плоским, затухание ревер-
берации происходило в плоскости всех динамиков, а не
послужил поводом для введения стратегии
передискретизации, которая после начального
разочарования завоевала область цифрового
аудио. Кроме того, вскоре стоимость цифровой
фильтрации стала меньше, чем стоимость
создания высококачественных аналоговых
фильтров.
Трудность задачи отфильтровывания самого
первого ложного сигнала выборки иллюстри-
руется на осциллограмме на рис. 18N.34, в ко-
торой самая низкая трассировка имитирует
низкую частоту выборки, используемую в пер-
вых реализациях компакт-дисков.
Во втором поколении плееров компакт-дисков
была принята двукратная передискретиза-
ция (см. раздел 18N.2), что позволило полу-
чить кажущуюся частоту передискретизации
величиной 88 кГц. В последующих плеерах
компакт-дисков применялась еще большая
передискретизация. В результате этих из-
менений задача создания рабочего фильтра
восстановления аналогового сигнала стала
осуществимой52.
спереди назад. ...последующие плееры Sony... продемон-
стрировали, по крайней мере для меня лично, значитель-
ное улучшение в воспроизведении акустических характе-
ристик» (https://www.harbeth.co.uk/usergroup/forum/
subjective-soundings-your-views-on-audio/electronics-
sources-stands-cables-accessories/cd-players-and-digi-
tal-source-discussion/1998-first-generation-cd-players-
how-good). Безусловно, мы вправе сомневаться, есть ли
для таких жалоб веские основания.
52 См. с. 94 ранее цитируемой книги Pohlmann «Principles
of Digital Audio».
/8Л/.6. Добавление случайного шума
747
Фиксированная fBX: 500 Гц Частота выборки fm5:
20 кГц
Высокая частота выборки
(4 выборки/период) 2 кГц
1,5 кГц
Низкая частота выборки j j крц
(2,2 выборки/период)
Рис. 18N.34. Низкая частота выборки может сделать трудной или даже невозможной фильтрацию ложных сигналов при вос-
становлении сигнала (Разрешение осциллографа: БПФ частотного спектра 500 Гц/дел.)
Задача фильтрации сравнительно легкая
Задача фильтрации трудная
18N.5.2. Побочные сигналы
предсказуемы
Рассмотренное в разделе 18N.5.1 представление
в частотной области также позволяет предска-
зать частоту побочных сигналов. Оказывается,
что частоты, которые слишком высоки для
правильного преобразования, сворачиваются в
более низкую частоту. Эту идею иллюстрирует
рис. 18N.35.
Амплитуда
fBBP - fux : Побочный сигнал!
' вх х •
ГВЫБ
Рис. 18N.35. Побочный сигнал при слишком низкой частоте
выборки (здесь равной 1,5 х fBX).
Понять, как это происходит, можно, вспом-
нив, что частота создаваемого ложного сигна-
ла составляет /ШБ -fBX. Если частота выборки
меньше, чем удвоенная частота входного сиг-
нала, то частота первого побочного сигнала
должна быть ниже частоты входного сигнала.
Последствие такого развития нельзя испра-
вить. Низкочастотный фильтр не сможет уда-
лить побочный сигнал, не удалив вместе с ним
и настоящий входной сигнал. Мы видели ра-
нее этот эффект на осциллограмме наложения
спектров на рис. 18N.9.
18N.6. Добавление
случайного шума
Рассмотрим еще одну идущую вразрез с интуи-
цией особенность аналого-цифровых преобра-
зований. В частности, добавление некоторого
случайного шума (аналогового или цифрово-
го) может улучшить эффективность АЦП или
ЦАП.
Примечание
В англоязычной литературе используется термин
dither. Значение этого слова в обычном смысле
означает дрожать, трястись, колебаться, ви-
брировать. В переносном смысле оно означает
колебаться (действовать, принимать решение),
быть нерешительным, колебаться между раз-
ными мнениями или образами действия. В любом
из этих смыслов оно хорошо описывает действие
в данном случае: принуждение входного сиг-
нала колебаться туда и назад через пороговое
значение.
Ника Олдрич на с. 250 своей книги (см. ранее) рас-
сказывает удивительную историю происхождения
этого термина, которая, мы надеемся, является
правдивой. Во время Второй мировой войны за-
метили, что механические навигационные ком-
пьютеры на британских самолетах работали в по-
лете с большей точностью, чем когда находились
на земле. Кто-то высказал гипотезу, что вибрации
двигателей в полете высвобождали элементы этих
устройств, в результате чего храповики, шестерен-
ки и рычаги перемещались, легче преодолевая
механические пределы. Удостоверившись в этом
поведении, англичане установили в этих механи-
ческих навигаторах вибрационные устройства, ко-
торые имитировали двигатели самолета, добавляя
случайный шум, который назвали dither. Другие
также рассказывают подобные истории. Например,
устройства, которые работали на винтовых само-
летах В29, не работали, когда были установлены
на реактивные самолеты. Или механические ком-
пьютеры управления корабельными орудиями ра-
ботали при боевых действиях во Вьетнаме, но не
работали при испытаниях в порту Бостона. Все эти
истории очень правдоподобны, но в то же самое
время их трудно подтвердить.
748
18N. Аналоговые и цифровые преобразования; ФАПЧ
Добавление случайного шума
повышает пороговое значение шума...
Входной
аналоговый сигнал I
г"
МБ
(аналоговый сигнал,
восстановленный из цифровой
формы исходного сигнала)
Частотный спектр |«|;l||ili!ili!:l;i!
он soomv wch? soomv
.но также уменьшает импульсные
гармоники прямоугольного сигнала
Рис. 18N.36. Добавление в сигнал случайного шума может повысить чувствительность АЦП. (Разрешение осциллографа:
500 мВ/дел.; БПФ частотного спектра — 500 Гц/дел.)
Необходимость такого добавления возникает
только для входных сигналов АЦП (или вы-
ходных сигналов ЦАП) низкого уровня. По
мере уменьшения уровня сигнала отношение
сигнал/шум для АЦП (которое для сигнала
полного уровня составляет почти 100 дБ при
разрешении в 16 битов) начинает сходить
на нет. Если в синусоидальный сигнал с ам-
плитудой, близкой к значению одного лишь
младшего бита, не добавить случайный шум,
то его восстановление в ЦАП создаст на вы-
ходе прямоугольный сигнал небольшой ам-
плитуды. Этот прямоугольный сигнал также
будет содержать высокочастотные гармони-
ки, побочные сигналы, внедренные дискре-
тизацией.
Достаточно удивительно, что добавление в сиг-
нал случайного шума позволяет получить точ-
ность намного ниже уровня значения одного
младшего бита53. Мы рассмотрим этот эффект
более подробно в главе 18S, а пока покажем (на
рис. 18N.36) осциллограмму, иллюстрирую-
щую полезные результаты добавления шума во
входные сигналы низкой амплитуды.
Прямоугольный сигнал на средней осцилло-
грамме левого изображения на рис. 18N.36
представляет собой восстановленный сигнал,
полученный из цифрового значения низкоуров-
невого входного сигнала, который находится
53 См. с. 42 цитируемой ранее книги Pohlmann «Principles
of Digital Audio», где воспроизводится работа Вандеркоой
(Vanderkooy) и Липшица (Lipshitz). Этот метод предпола-
гает преобразователь, который может работать с частота-
ми намного выше, чем частота сигнала, в который добав-
ляется случайный шум. Частота сигнала случайного шума
может находиться между максимальной частотой сигнала
и частотой Найквиста (fBm/2).
между двумя уровнями54. А на нижней осцил-
лограмме видно множество отчетливых звуко-
вых гармоник в частотном спектре этого пря-
моугольного сигнала, добавленных в исходный
сигнал в процессе его дискретизации.
Если не обратить внимания на частоту прямо-
угольного сигнала, то можно ошибочно предпо-
ложить, что эти гармоники способен устранить
низкочастотный фильтр на выходе ЦАП. Это
предположение будет ошибочным, поскольку
гармоники находятся в самой гуще диапазона
аудиочастот. Фильтр их не удалит, и они будут
звучать очень неприятно.
На правой осциллограмме на рис. 18N.36 мож-
но видеть побочный эффект добавления слу-
чайного шума в сигнал: утолщение огибающей
входного аналогового сигнала. В частотном
спектре восстановленного сигнала это отобра-
жается в виде повышенного шумового порога.
Значение младшего бита (выход ЦАП) на сред-
ней осциллограмме теперь колеблется вверх и
вниз вокруг среднего уровня. Усреднение этого
54 Чтобы получить эти осциллограммы, мы использовали
низкоуровневый перепад довольно большой величины,
чтобы смоделировать младший бит. Можно видеть, что
его величина составляет около 250 мВ. Но для целей де-
монстрации эффекта добавления случайного шума его ве-
личина не играет роли.
На осциллограмме сигнала после добавления случайно-
го шума, которая показана справа на рис. 18N.36, можно
заметить дополнительные перепады, величина которых
меньше, чем величина большого перепада, обозначенного
МБ (младший бит). Этих дополнительных перепадов не
было бы в обычном процессе добавления шума; они яв-
ляются побочным эффектом отображения не настоящего
значения младшего бита, а прямоугольного сигнала боль-
шей амплитуды, чем величина значения младшего бита
нашего ЦАП, используемого для демонстрации.
78Л/.7. Система фазовой автоподстройки частоты
749
«рваного» сигнала создало бы синусоидальный
сигнал, близкий к исходному.
Повышение шумового порога может вызывать
у вас беспокойство. Но, скорее всего, вам не
стоит беспокоиться об этом. Его уровень до-
статочно низкий и, например, в аудиосигнале
вообще несущественный. Но даже если этот
белый шум будет слышимым, он окажется на-
много менее неприятным, чем резкие звуки,
вызываемые гармониками сигнала без добав-
ленного случайного шума. За счет добавления
случайного шума можно придать случайный
характер низкоуровневому шуму и уменьшить
побочные сигналы выборки, маскируя таким
образом эффекты, которые в ином случае были
бы слышимы55. Прекрасное описание метода
добавления постороннего шума дается в книге
Ники Олдрич56.
18N.7. Система фазовой
автоподстройки частоты
В системе фазовой автоподстройки частоты
(ФАПЧ) используется обратная связь, чтобы
создать реализацию входного сигнала или сиг-
нал с частотой, кратной входному57. Система во
многом подобна операционному усилителю,
с той лишь разницей, что она усиливает не раз-
ность напряжений между входами, а разность
между частотами или фазами. Принцип ФАПЧ
иллюстрируется на рис. 18N.37.
>з: а.
2 §
А0
Низкочастотный
фильтр
ГО
ГУН
1 кОм
В ЛАБОРАТОРНОЙ
СХЕМЕ
Делитель частоты
'ОПОР 'ВХ
Рис. 18N.37. Система фазовой автоподстройки частоты
55 См. с. 94 ранее цитируемой книги Pohlmann «Principles
of Digital Audio».
56 См. главу 15 ранее цитируемой книги Ники Олдрич. До-
бавление случайного шума обычным способом повыша-
ет шумовой порог на 3 дБ, тогда как в нашем примере на
рис. 18N.36 повышение больше. Но будем надеяться, что
этот упрощенный пример будет полезен для иллюстрации
описанного принципа.
57 АоЕ § 13.8.1.
При достижении совпадения частот, что про-
исходит при «блокировке» схемы, оставшейся
погрешностью является только разность фаз.
Сигнал фазовой ошибки подается на ГУН58, ко-
торый уменьшает эту погрешность, стремясь
свести ее к нулю59.
Это выглядит знакомо, подобно принципу ра-
боты операционного усилителя, не так ли?
Сама схема достаточно проста, единственная
трудность состоит в создании фильтра. Но мы
отложим этот вопрос на некоторое время.
18N.7.1. Простейший фазовый
детектор: ИСКЛ-ИЛИ
В качестве простейшего фазового детектора
можно использовать просто вентиль Исклю-
чающее-ИЛИ, который определяет неравен-
ство сигналов на своих входах'
Примечание
60
В данном случае предполагаются цифровые вход-
ные сигналы. Для синусоидальных аналоговых
сигналов требуются другие фазовые детекторы, но
принцип тот же самый.
Разность фаз вызывает импульсы на выходе
вентиля ИСКЛ-ИЛИ, усреднение которых соз-
дает уровень постоянного напряжения, которое
подается на ГУН. После захвата частоты должна
присутствовать некоторая разность фаз, чтобы
сигнал обратной связи был ненулевым.
Аналогия с операционным усилителем
1000
100
58 Мы рассматривали ГУН (генератор колебаний, управляе-
мый напряжением) на лабораторном занятии 13L, где ис-
пользовали микросхему 555 в качестве такого генератора.
59 Некоторые фазовые детекторы, наподобие простого с
элементом Исключающее-ИЛИ, рассматриваемым в раз-
деле 18N.7.1, не могут свести разность фаз полностью к
нулю. Другие же, наподобие чувствительного к фронту
детектора, рассматриваемого в разделе 18N.7.2, могут это
делать.
60 АоЕ § 13.8.2А.
750
18N. Аналоговые и цифровые преобразования; ФАПЧ
Отфильтрованный
Входной сигнал сигнлЛ< ??™™?**
»г-~-чфункцией ИСКЛ-ИЛИ
—)} J) ***Г~Т Отфильтрованный
Сигнал ГУН у сигнал, обработанный
▼ функцией ИСКЛ-ИЛИ
Входной сигнал
Сигнал ГУН
__ __ Отфильтрованный сигнал,
_ _~ .. _" _ _ ^ОБРАБОТАННЫЙ ФУНКЦИЕЙ ИСКЛ-ИЛИ
Рис. 18N.38. Простейшим фазовым детектором является логический элемент Исключающее-ИЛИ
Входной сигнал
Сигнал ГУН
ИСКЛ-ИЛИ
Большая разность фаз,
Входной и ГУН сигналы
Небольшая разность фаз
^ Большая разность фаз,
ш* Входной и ГУН сигналы i
• Несовпадение результата -
ИСКЛ-ИЛИ почти на 100%...
...ДОВОДИТ СРЕДНЕЕ ЗНАЧЕНИЕ
ПОЧТИ ДО ПРЕДЕЛА
(ВСКОРЕ ПРОИЗОЙДЕТ
НАСЫЩЕНИЕ И ПОТЕРЯ ЗАХВАТА)
Чрезвычайно большая разность фаз
Рис. 18N.39. Фазовый детектор из вентиля ИСКЛ-ИЛИ. Требует наличия некоторой разности фаз, чтобы сформировать сигнал
обратной связи для ГУН. Чрезмерно большая разность фаз может вызвать потерю захвата частоты. (Разрешение осциллогра-
фа: 2 В/дел, для сигнала усреднения; 5 В/дел, для всех остальных сигналов.)
Если фазовый сдвиг приближается к нулю или
к 180° (как показано на правой осциллограмме
на рис. 18N.39), то сигнал ГУН приближается
к предельному значению. Если фаза сдвинется
еще немного, то ФАПЧ потеряет захват, точно
так же, как и операционный усилитель теряет
обратную связь при насыщении выходного сиг-
нала. Второй недостаток фазового детектора на
логическом вентиле ИСКЛ-ИЛИ состоит в том,
что он может осуществить захват частоты в том
случае, если частота опорного сигнала кратна
частоте входного сигнала. Эта особенность рас-
сматривается далее в разделе 18N.7.2.
18N.7.2. Фазовые детекторы,
чувствительные к фронту
Микросхема КМОП 4046, с которой мы позна-
комимся на лабораторном занятии, содержит
более сложный фазовый детектор (так называе-
мого типа II). Этот фазовый детектор обладает
двумя основными достоинствами: 1) он не за-
хватывает частоты, кратные входной частоте;
2) он может выполнять захват при нулевом
сдвиге фаз между двумя сигналами. Кроме
того, он более энергоэффективен, поскольку
после захвата частоты вход фильтра отключа-
ется. Он уступает фазовому детектору на вен-
тиле ИСКЛ-ИЛИ только в одном отношении:
ложный импульс нарушает его работу намного
более серьезно, чем в случае применения вен-
тиля ИСКЛ-ИЛИ. Последний просто поглотил
бы этот импульс в свой процесс усреднения.
Превосходная помехоустойчивость этого фа-
зового детектора, которая важна в некоторых
приложениях, является причиной, по которой
в микросхеме ФАПЧ 4046 кроме фазового де-
тектора типа II (чувствительного к фронту)
также содержится и простой фазовой детектор
на логическом вентиле ИСКЛ-ИЛИ (который
принадлежит к типу I).
Чувствительный к фронту фазовый
детектор обладает лучшими
характеристиками
На рис. 18N.40 показаны осциллограммы, срав-
нивающие характеристики двух рассмотрен-
ных фазовых детекторов. С характеристиками
фазового детектора на вентиле ИСКЛ-ИЛИ вы
уже знакомы.
На правой осциллограмме изображены сигна-
лы фазового детектора на вентиле ИСКЛ-ИЛИ,
выполнившего захват частоты. Как и следова-
ло ожидать, наблюдается некоторый фазовый
сдвиг, но в остальном контур работает долж-
ным образом.
18N.7. Система фазовой автоподстройки частоты
751
Входной сигнал
Сигнал ГУН*
ИСКЛ-ИЛИ к"
(выходной сигнал
ИСКЛ-ИЛИ) и-
Чувствительный
к фронту
(разовый детектор
Усредненный
результат
операции™ so°
ИСКЛ-ИЛИ
Locked, with phace-dif f erence
После поступления входного сигнала
выход чувствительного к фронту (розового
детектора отключается (но только на момент)
Чувствительный к уровню / \
фазовый детектор
' (простой вентиль ИСКЛ-
ИЛИ) может работать при ,rr~ "Z"X"
' наличии фазового сдвига / \
X (более того, требует
•*■">■ такого сдвига)
Чувствительный к фронту ч
._ \^<разовый детектор v
определяет, что сигнал ГУН
запаздывает, и начинает
«подгонять* ГУН ,
Сильный, почти постоянный
на ГУН, чтобы тот замедлил темп
Тем временем «самодовольный» усреднитель схемы
на ИСКЛ-ИЛИ «думает», что все в порядке
Захват по нескольким входным сигналам:
чувствительный к фронту фазовый детектор «недоволен»
Рис. 18N.40. Сравнение характеристик двух фазовых детекторов: детектору на вентиле ИСКЛ-ИЛИ нужен сдвиг по фазе; он
также может выполнять захват по нескольким входным сигналам. (Разрешение осциллографа: 2 В/дел. — для сигнала усред-
нения; 5 В/дел. — для всех остальных сигналов.)
Но в случае с чувствительным к фронту фазо-
вым детектором эта разность фаз побуждает
его генерировать импульсы, пытаясь свести ее
к нулю. (В данной демонстрации эти сигналы
не используются, но если бы они были, то до-
стигли бы требуемого результата.) Эти импуль-
сы начинают создаваться в виде высоких логи-
ческих уровней в течение короткого времени,
когда входной сигнал опережает по фазе сиг-
нал ГУН. При подаче на вход ГУН эти сигналы
указывали бы ему повысить частоту, чтобы на-
чать сводить разницу фаз к нулю. Таким обра-
зом была бы достигнута фазовая стабильность
опорного сигнала и сигнала ГУН61.
На правой осциллограмме на рис. 18N.40 пока-
зана реакция чувствительного к фронту фазо-
61 Когда чувствительный к фронту фазовый детектор удо-
влетворен состоянием фаз и не пытается изменить частоту
ГУН, на его выходе нет ни высокого, ни низкого уровня,
он находится в третьем состоянии, т. е. выключен. В книге
АоЕ указывается, что такое отсутствие корректирующего
сигнала может вызывать так называемое рыскание. Этот
дефект был исправлен в улучшенных модификациях фа-
зового детектора данного типа. См. § 13.8.2А книги АоЕ,
особенно рис. 13.89.
На осциллограмме на рис. 18N.40 выходной сигнал чув-
ствительного к фронту фазового детектора выглядит не-
сколько странно: понижается ступеньками, тогда как дол-
жен находиться на постоянном уровне. Это паразитный
эффект, вызванный нагрузкой в виде тестовой схемы, и он
не имеет значения.
вого детектора на опорный сигнал, частота ко-
торого кратна частоте входного сигнала. В этом
случае фазовый детектор на вентиле ИСКЛ-
ИЛИ никак не реагирует и продолжает удер-
живать захват частоты. Но чувствительный к
фронту фазовый детектор обнаруживает это и
выдает почти постоянный сигнал на пониже-
ние частоты (низкий логический уровень), за
исключением короткого времени после перед-
него фронта входного сигнала (когда детектор
еще считает, что все может быть в порядке).
Принцип работы фазового детектора,
чувствительного к фронту
На рис. 18N.41 показана блок-схема чувстви-
тельного к фронту фазового детектора, а также
его сигналы. Данная схема реализует конечный
автомат, который генерирует корректирующие
сигналы в течение времени, когда положитель-
ный фронт одного прямоугольного сигнала
опережает по фазе фронт другого.
При нулевой разнице фаз выход фазового де-
тектора отключается, т. е. переходит в третье
состояние. В это время конденсатор фильтра
просто сохраняет свой заряд, и фильтр, по сути,
работает как устройство выборки и хранения.
На рис. 18N.42 показана последовательность
операций для этого конечного автомата.
752
78Л/. Аналоговые и цифровые преобразования; ФАПЧ
Опорный сигнал^
(входной)
Сигнал ГУН
(ГУН)
Фазовый компаратор
Л
Отставание
Опережение
(входной)-
(ГУН) J
Выходной сигнал
(разового детектора
ючен
(в третьем состоянии)
ii ir
Захват почти выполнен
■■-ft
\ При большом сигнале рассогласования
) ГУН должен снизить темп
Сигналы с кратными
частотами игнорируются
Рис. 18N.41. Чувствительный к фронту фазовый детектор йа микросхеме 4046. Он более интеллектуальный, чем фазовый
детектор на вентиле ИСКЛ-ИЛИ, и может распознавать сигналы ГУН с частотами, кратными входной
Ага! Сигнал ГУН
пришел первым:,
снижаем частоту ГУН!
Оба-на! Входной
t сигнал опередил
I сигнал ГУН:
| повышаем частоту
1ГУН
jАга! Оба
•сигнала
Выходной Низкий j"?!?™.
сигнал уровень,^
детектора
Высокий уровень
они совпадают
по фазе
Отключен
(в третьем состоянии)
Рис. 18N.42. Диаграмма состояний чувствительного к фрон-
ту фазового детектора на микросхеме 4046 (по данным ком-
пании National Semiconductor)
Фазовый детектор начинает действовать, ког-
да фронт одного из сигналов приходит раньше
фронта другого. В таком случае конечный авто-
мат выясняет, какой из двух сигналов прибыл
первым. Если, например, сигнал А (входной
сигнал) опередил сигнал В (сигнал с ГУН), то
фазовый детектор говорит: «Ага, сигнал В что-
то замешкался. Нужно немного ускорить ГУН».
В результате включается верхний (по схеме на
рис. 18N.41) транзистор, инжектируя немного
заряда в конденсатор фильтра (это состояние
соответствует правому блоку диаграммы на
рис. 18N.42).
В результате сигнал В ускоряется, и теперь оба
сигнала, А и В, прибывают одновременно. Де-
тектор (подобно детектору на вентиле ИСКЛ-
ИЛИ) видит это и говорит: «Пока что все в
порядке. Сигналы А и В ведут себя одинако-
во». Происходит отключение выхода (посред-
ством перевода его в третье состояние); теперь
конденсатор фильтра просто сохраняет по-
следний уровень напряжения (это состояние
соответствует среднему блоку диаграммы на
рис. 18N.42).
Такая последовательность имеет тенденцию
повышать частоту ГУН, в результате чего его
сигнал В поступает на компаратор чуть раньше.
Но это уменьшает время, в течение которого
фазовый компаратор работает в правом бло-
ке диаграммы. Теперь он проводит все больше
времени в среднем блоке («Все в порядке»).
В этом блоке он проводит время, когда выпол-
нен захват частоты. Вы сможете увидеть это
в фазовом детекторе на микросхеме 4046, на-
блюдая светодиод, управляемый сигналом с вы-
вода микросхемы 4046, что означает «Выход
находится в третьем состоянии». Это эквива-
лентно «Я не вижу большой разности фаз» или
просто «Захват частоты выполнен».
На рис. 18N.43 изображена схема, которая ра-
ботает только что описанным образом.
18N.7.3. Применения
Система ФАПЧ позволяет генерировать сиг-
нал с частотой, точно кратной частоте вход-
ного сигнала. Например, схема на рис. 18N.37
формирует выходной сигнал с частотой
/шх = 210 -fBX. Все, что для этого необходимо, —
18N.7. Система фазовой автоподстройки частоты
753
Захват
Опорный сигнал
(входной)
Сигнал ГУН
(<- ГУН)
Высокий уровень
на обоих выходах:
"отключаем выход ГУН,
поскольку оба сигнала
совпадают по (разе
Сигнал, фронт которого появляется первым,
включает соответствующий выходной транзистор.
Входной сигнал первый -> включается <?ВЕРХ.
Сигнал ГУН первый -> включается <?нижн.
Рис. 18N.43. Фазовый детектор микросхемы 4046 реализован просто на двух триггерах. Победитель гонки включает свой вы-
ходной транзистор до тех пор, пока на обоих выходах не будет высокий уровень
v
(Подавление помех
дискретизации)
Фильтр
(коммутируемый
конденсатор:
МАХ 294)
8
Ми кроком п ьютер
Выборка
f Г™
L
D Q
—1
1
J
V
(Восстановление)
Фильтр
(коммутируемый
конденсатор:
МАХ 294)
ФАПЧ
Оделит* 64
\ Устанавливает /^равной ^выб/З,
j или = 2/3 частоты Найквиста
| Система ФАПЧ корректирует
Г ^здб °боих фильтров, чтобы она
) соответствовала частоте выборки
Рис. 18N.44. Система ФАПЧ из лабораторного занятия 23L автоматически корректирует частоту тактирования фильтра при
варьировании частоты выборки
-V
поместить схему-делитель на 1 К в контур об-
ратной связи62.
Этот прием часто используется в микросхемах
для тактирования внутренних компонентов бо-
лее высокими частотами, чем частота внешнего
тактового сигнала.
Например, система ФАПЧ микросхемы АЦП
ADuC848 производства компании Analog De-
vices умножает скромную стандартную «часо-
вую» частоту 32,768 кГц63 на 384, создавая сиг-
нал тактирования для внутренних компонентов
частотой свыше 12 МГц (цитируется в § 15.10
книги АоЕ).
62 В образных терминах главы 6N эта схема-делитель на
1К является «собакой» в цепи обратной связи, которая
побуждает схему обратной связи генерировать «инверс-
ную собаку», т. е. умножение на 1 К.
63 Спрашиваете, почему такая странная частота? Отвечаем,
это частота 215 Гц, так что часы могут получить такт в 1 Гц,
просто пропустив эту частоту через двоичный 15-битовый
счетчик со сквозным переносом.
Этот прием может понадобиться на лабора-
торном занятии 23L по сборке компьютера из
дискретных компонентов, в котором требует-
ся сигнал тактирования с частотой, в 64 раза
большей частоты выборки для управления вы-
ходным фильтром на коммутируемых конден-
саторах. Цель здесь состоит в том, чтобы систе-
ма ФАПЧ автоматически корректировала спад
фильтра для соответствия регулируемой нами
частоты выборки. Частота /3ц!Б фильтра про-
порциональна частоте сигнала тактирования
(/здб =fTAKT/100). Таким образом, применение
системы ФАПЧ для того, чтобы сопоставлять
частоту тактирования фильтра частоте дискре-
тизации позволяет нам свободно варьировать
частоту выборки, поскольку фильтр автомати-
чески корректирует свою частоту тактирования
требуемым образом.
На рис. 18N.44 изображена блок-схема этого
метода.
Рассмотрим некоторые аспекты схемы на
рис. 18N.44 (более подробная версия которой
754
/8Л/. Аналоговые и цифровые преобразования; ФАПЧ
Источник: возможно, радиосигнал
Аудио-
сигнал
ГУН
Радиотрансляция ЧМ
Фазовый
детектор
Частота варьируется, модулируемая
аудиосигналом источника
Аудиосигнал извлечен
(продетектирован)
ГУН
Рис. 18N.45. Использование системы ФАПЧ для детектирования частотно-модулированного радиосигнала
приводится на лабораторном занятии 18L).
Сигнал, обозначенный «Выборка», является
коротким импульсом, поэтому он пропуска-
ется через триггер-делитель на два, чтобы
подавать на систему ФАПЧ прямоуголь-
ный сигнал с величиной скважности в 50%.
(Система ФАПЧ плохо работает с кратков-
ременными входными импульсами.) Система
ФАПЧ умножает частоту этого сигнала на 64,
подавая на фильтр из коммутируемого кон-
денсатора сигнал частотой 32-/ВЫБ. Частота/3дБ
этого фильтра составляет l/100-fTAKV поэтому
такая конфигурация устанавливает частоту
/3дБ фильтра равной приблизительно 1/3 ча-
стоты выборки. Это позволяет обрабатывать
входные сигналы с частотой приблизительно
2/3 от теоретического максимума, допускае-
мого правилом Найквиста — 1/2 частоты вы-
борки64.
Система ФАПЧ также способна выполнить
демодуляцию ЧМ-сигналов: просто наблюда-
ем входной сигнал ГУНа (который представ-
ляет собой отфильтрованный сигнал рассо-
гласования, несущий информацию о колеба-
ниях частоты входного сигнала). Блок-схема
такого устройства изображена на рис. 18N.45.
Это упражнение предлагается выполнить на
лабораторном занятии 18L.2. Систему ФАПЧ
можно было бы использовать для демодуля-
ции частотно-модулированного сигнала низ-
кой частоты в аудиопроекте лабораторного
занятия 13L, но тогда мы еще не знали об
этом.
64 Возможно, нам следует признать, что на лабораторном
занятии 23L большинство студентов не находят времени
для работы с системой ФАПЧ, поскольку они слишком
заняты другими задачами. Тем не менее это довольно
изящное применение системы ФАПЧ, поэтому мы наде-
емся, что некоторые из вас смогут поэкспериментировать
с ней.
18N7A Проблемы стабильности
во многом такие же,
как и для системы ПИД
Вследствие неявного фазового сдвига величи-
ной 90° в цепи обратной связи из-за интегри-
рования, вызываемого фазовым детектором,
система ФАПЧ подвержена паразитным авто-
колебаниям65. На определенной частоте допол-
нительный простой НЧ-фильтр может увели-
чить этот сдвиг до общих 180°. Такое развитие
событий вызовет паразитные автоколебания —
бесконечное «рыскание» в попытках выпол-
нить захват частоты.
Это, по сути, то же самое, что и ситуация, кото-
рую мы обсуждали ранее касательно стабиль-
ности и частотной коррекции операционных
усилителей. Также это во многом похоже на
проблему системы ПИД для управления элек-
тродвигателем, с которой мы разбирались на
лабораторном занятии 10L, где в петлю обрат-
ной связи помещался интегратор.
Для устранения этой опасности в низкочастот-
ном фильтре используется резистор, который
по мере повышения частоты смещает фазовый
сдвиг в фильтре к нулю. Этот подход иллюстри-
руется на рис. 18N.46.
Слева на рис. 18N.47 изображен график спада
такого стабилизирующего фильтра: сначала
спад происходит подобно 1/f, как и в обычном
НЧ-фильтре, но затем кривая спада выравнива-
ется. Влияние этого выравнивания на систему
ФАПЧ показано на графике справа на рисунке.
В течение некоторого времени спад продолжа-
ется с большой скоростью -12 дБ/октаву (по-
добно 1/f2), что является следствием неявно-
го интегрирования системы ФАПЧ совместно
65 АоЕ § 13.8.3А.
18N.Z Система фазовой автоподстройки частоты
755
На высоких частотах схема слева
выглядит, как эта (ZC ничтожно мал)4
=> На высоких частотах схема слева выглядит,
как эта (ZC ничтожно мал)
Рис. 18N.46. Стабилизирующий RC-фильтр ограничивает фазовый сдвиг, который на высоких частотах смещается к нулю
dB
^ = 1/(2тт/?2С)
O-VW-£ О
-6 дБ/октаву
\ogf
НЧ-аэильтр
(стабилизирующий)
dB
-6 дБ/октаву
-12 дБ/октаву
-6 дБ/октаву
Петлевое усиление
(фильтр, ГУН и фазовый детектор)
Рис. 18N.47. Стабилизирующий НЧ-фильтр предотвращает возникновение автоколебаний в системе ФАПЧ, ограничивая фа-
зовый сдвиг
Фазовый сдвиг
только в фильтре
Этот изгиб определяется
'цепочкой R(RR)
Фазовый сдвиг во
всей системе ФАТТЧ,
включая фильтр
Запас по фазе
... цепочкой R2C
Рис. 18N.48. Фазовый сдвиг в стабилизирующем фильтре и во всей системе ФАПЧ сначала быстро увеличивается, но затем
возвращается к обычному
с фазовым сдвигом фильтра в -90°. Но затем
усиление контура обратной связи возвращает-
ся обратно к безопасной величине -6 дБ/окта-
ву (подобно 1/J).
На рис. 18N.48 приводится описание такого же
фильтра, но здесь изображены только фазовые
сдвиги: сначала (слева) только в фильтре, а за-
тем (справа) в петле ФАПЧ, содержащей этот
фильтр.
Обратите внимание на то, что петлевое усиле-
ние системы ФАПЧ подходит к опасному фазо-
вому сдвигу величиной -180°, но затем вовре-
мя возвращается обратно к -90°, что (на удив-
ление) достаточно хорошо для нас66.
Интегрирование в фазовом детекторе
В фазовом детекторе происходит неявное инте-
грирование, поскольку фаза (величина, изме-
ряемая и применяемая в петле обратной связи)
66 Вспомните, что на лабораторном занятии 10L мы удив-
лялись допустимости такой фазовой задержки. Применяя
научное определение, можно утверждать, что фильтр дан-
ного типа является фильтром с полюсами и нулями.
является интегралом частоты. Это легко вы-
сказать, но трудно понять. Возможно, что рас-
смотрение соответствующих единиц измере-
ния поможет в понимании фазы как интеграла
частоты. В частности, если измерять частоту в
радианах/секунду, то, интегрировав ее по вре-
мени, получим радианы, которые являются ве-
личиной измерения фазы67.
А на рис. 18N.49 изображена осциллограмма
сигналов, которая может помочь сделать эту
идею менее абстрактной68. В частности, осцил-
67 Также может быть полезным рассмотреть утверждение,
что разница фаз является интегралом разницы частот.
Представьте себе, что между частотами входного сигнала
и сигнала ГУН существует небольшая разница, которая
не меняется в течение некоторого времени. На осцилло-
грамме этих двух сигналов, которая отображает их во вре-
менной области, один из этих сигналов будет медленно
опережать другой. Детектор разности фаз измерял бы это
опережение как линейно нарастающую разницу фаз (до
тех пор, пока разница не достигла бы максимального зна-
чения, стала нулевой, а затем снова стала линейно нарас-
тать и т. д.). Этот эффект иллюстрируется на рис. 18N.49.
68 Один наш внимательный студент возразил на это до-
казательство тем, что интегрирование вызывалось RC-
цепочкой, а не фазовым детектором. Хотя это возраже-
ние выглядит состоятельным, оно неверно. Это правда,
756
18N. Аналоговые и цифровые преобразования; ФАПЧ
Входной сигнал
Сигнал ГУН
/11: 5,230 кГц
fJL\ 5,296 кГц
Разница частот = 70 Гц
Фазовый детектор на
вентиле ИСКЛ-ИЛИ
Разность сраз
Усредненный выходной
сигнал с вентиля ИСКЛ-ИЛИ
w~"*"
cm 5.00 V
5.00 V Щ 400MS
Рис. 18N.49. Доказательство того, что фазовый детектор интегрирует разность частот: линейно нарастающий сигнал разности
фаз при постоянной разности частот
лограмма отображает выходной сигнал фа-
зового детектора69, входной сигнал и сигнал
ГУН, которые имеют немного разные частоты.
Один из сигналов медленно опережает другой,
и сигнал разности фаз отображает это в виде
линейного нарастания, которое мы бы ожидали
от интегратора при подаче на него постоянной
величины. Эта осциллограмма может убедить
вас в том, что в контуре обратной связи фазо-
вого детектора в действительности происходит
интегрирование, в результате чего перед нами
возникает опасность потери стабильности, по-
добная той, с которой мы встретились на лабо-
раторном занятии 10L по системе ПИД.
18N.8. Материал для чтения
вАоЕ
♦ Глава 12. Сопряжение логических микросхем.
* Раздел 12.1.1. Хронология логических
семейств — краткая история.
* Раздел 12.1.2. Входные и выходные ха-
рактеристики.
что линейное нарастание можно видеть на рис. 18N.49
в виде аналогового сигнала только благодаря RC-цепи,
которая преобразует в напряжение коэффициент запол-
нения выходного сигнала фазового детектора на вентиле
ИСКЛ-ИЛИ. Но выполняемое фазовым детектором ин-
тегрирование завершается до того, как выполняется это
преобразование. Выходной сигнал вентиля ИСКЛ-ИЛИ
выражает разность фаз сигналов на своих входах в виде
коэффициента заполнения. Эта разность фаз является ин-
тегралом разности частот сигналов, подаваемых на фазо-
вый детектор.
69 Это выходной сигнал, усредненный RC-фильтром, про-
стого фазового детектора на вентиле Исключающее-ИЛИ.
* Раздел 12.1.3. Сопряжение микросхем
разных логических семейств.
Глава 13. Цифровые и аналоговые системы.
• ЦАПиАЦП.
• Раздел 13.2. Цифроаналоговые преобразо-
ватели (ЦАП).
• Раздел 13.5. Аналого-цифровые преобра-
зователи (АЦП).
* Раздел 13.5.2. Метод последовательных
приближений (важно для нас — это ме-
тод, используемый на лабораторном за-
нятии 18L).
* Раздел 13.5.10. Преобразователи дельта-
сигма (трудная тема, которая здесь под-
робно объясняется).
• Обзор главы 13. Хорошее, краткое обозре-
ние многих методов АЦП и ЦАП.
• Системы фазовой автоподстройки частоты.
• Раздел 13.13. Системы фазовой автопод-
стройки частоты.
* Раздел 13.13.2А. Фазовый детектор.
* Раздел 13.13.4А. Стабильность и фазо-
вые сдвиги.
* Раздел 13.13.6С. Демодуляция частотно-
модулированных сигналов.
• Раздел 13.14. Быстро просмотрите раз-
дел 13.14.2 по последовательностям сдви-
говых регистров обратной связи. (Мы ис-
пользовали этот метод для генерирования
случайного шума, добавляемого в сигналы
малой амплитуды при аналого-цифровых
преобразованиях.)
18L Лабораторное занятие: аналоговые
и цифровые преобразования; ФАПЧ
На этом лабораторном занятии мы рассмотрим
два устройства, оба частично цифровые, об-
щей чертой которых является использование
обратной связи для генерирования выходного
сигнала, который зависит от входного сигнала.
В первой схеме, аналого-цифровом преобразо-
вателе, обратная связь служит для формирова-
ния цифрового эквивалента входного аналого-
вого напряжения. А во второй схеме, системе
фазовой автоматической подстройки частоты
(ФАПЧ), обратная связь предназначена для ге-
нерирования сигнала с такой же частотой, что и
частота входного сигнала, или с частотой, крат-
ной этой частоте.
18L1. Аналого-цифровой
преобразователь
На лабораторном занятии для реализации
аналого-цифрового преобразования мы будем
применять метод последовательных прибли-
жений или двоичного поиска. Этот метод, на-
верное, является все еще наиболее широко рас-
пространенным, хотя в настоящее время ему
приходится конкурировать с методом дельта-
сигма. Это решение обеспечивает хороший
компромисс между скоростью и стоимостью.
Вход тактового сигнала
-ППЛ-
Аналоговый вход
самом быстром методе параллельного преоб-
разования, здесь реализован более интеллекту-
альный подход1.
На рис. 18L.1 изображена блок-схема такого
АЦП.
Обратите внимание на то обстоятельство, что
АЦП, который мы будем собирать на этом за-
нятии из четырех микросхем, можно было бы
реализовать в виде одной микросхемы. Мы
собираем этот преобразователь, используя по
сути вышедший из употребления регистр по-
следовательных приближений (РПП), чтобы
предоставить вам возможность наблюдать про-
цесс преобразования. В АЦП на интегральной
микросхеме наблюдение процесса приближе-
ния сопряжено с трудностями, поскольку по-
следовательные аналоговые приближения не
выводятся ни на какой вывод микросхемы, хотя
поток битов, формирующих это приближение,
может выводиться. Кроме того, для упрощения
нашего преобразователя мы не будем исполь-
зовать в нем схему выборки и хранения.
18L1.1. Цифроаналоговый
преобразователь
Процесс преобразования цифрового сигнала в
его аналоговый эквивалент более легкий и не
Регистр последовательных
приближений (РТТТТ) q
Схема выборки
и хранения (С/Х
ом паратор
Приближение \ ЦАТТ
8-битовый ;
Преобразование завершено
'8
аналогового сигнала
Цифровой выход
О Q
8-битовый
регистр
3 Цифровой
выход
Рис. 18L.1. Блок-схема АЦП последовательных приближений
Вместо «грубой силы» (т. е. большого объема
аналогового оборудования), что имеет место в
1 Мы признаем, что для реализации параллельного АЦП
нужно задействовать много аналоговых компонентов.
758
18L Лабораторное занятие: аналоговые и цифровые преобразования; ФАПЧ
Цифровой
вход
^(Выход
напряжения
DS400 мВ на
полную
К шкалу)
Выходной аналоговый сигнал
(О до +3,5 В)
Не подключен (НТТ)
СБ
Рис. 18L2. Подключение микросхемы ЦАП AD558
J0,01 до ОД мкФ
(керамический)
такой интересный, чем преобразование в про-
тивоположном направлении. Подобно любому
методу АЦП с контуром обратной связи, АЦП
методом последовательных приближений ис-
пользует ЦАП для замыкания цепи обратной
связи. В частности, ЦАП выдает аналоговое
представление цифрового приближения исход-
ного аналогового сигнала, позволяя корректи-
ровать и улучшать это цифровое приближение.
Поэтому первым делом в сборке нашего АЦП
мы подключим ЦАП, для которого мы выбра-
ли микросхему AD558 от компании Analog
Devices. Схема подключения этого устройства
изображена на рис. 18L.2.
Микросхема AD558 содержит не только мо-
дуль ЦАП, но также и выходной усилитель и
входную защелку. Это простая прозрачная за-
щелка, а не активируемая фронтом; на лабо-
раторном занятии мы будем игнорировать ее,
поддерживая ее все время в прозрачном режи-
ме, подключив на «землю» выводы 9 (CS* —
выбор микросхемы) и 10 (СЕ* — разрешение
микросхемы).
Проверка работы ЦАП
Выполните проверку, показанную на рис. 18L.3
и описанную более подробно далее в тексте.
Проверьте, что подключенная вами микросхе-
ма ЦАП AD558 работает должным образом.
Для этого подайте на входы двух самих стар-
ших битов и на вход самого младшего бита на-
пряжение +5 или 0 В («земля»). На все осталь-
ные пять входных линий подавайте низкий
уровень.
Примечание
Для этой цели может оказаться удобным ленточ-
ный кабель, хотя пока можно соединить все от-
дельными проводами. В любом случае через не-
сколько минут вам нужно будет подавать сигнал
на все 8 линий.
Обратите внимание на взаимоотношение меж-
ду положениями переключателя и выходным
напряжением 17ВЫХ. Выходное напряжение пол-
ной шкалы должно быть в диапазоне прибли-
зительно 0-3,8 В. Подумайте, какой вес (в раз-
махе выходного напряжения) должен иметь
разряд D7. А разряд D6?2
Обратите внимание на вес самого младшего
разряда. Если наблюдать выход этого разряда
на осциллографе, на нем, скорее всего, будет
присутствовать шум величиной, сравнимой
с самим сигналом. Но если частота этого шума
очень высокая, то он может быть довольно без-
вредным. Как этот шум отображается на циф-
ровом мультиметре? Подумайте, как будет реа:
гировать на этот шум компаратор после того,
как ЦАП будет вставлен в петлю обратной свя-
зи АЦП3.
2 Вес разряда D7 должен быть равен половине напряже-
ния полной шкалы, а разряда D6 — одной четверти этого
напряжения.
3 Мы хотим сказать, что данная схема АЦП может не
обнаруживать шум очень высокой частоты (т. е. шум на
радиочастоте, который часто можно видеть, когда выстав-
лено высокое разрешение осциллографа), подобно тому,
как такой шум может не обнаруживаться цифровым муль-
тиметром. Но цифровой мультиметр может случайно вы-
прямлять мощные высокочастотные сигналы, что может
привести к ложным показаниям. Возможно, вам пришлось
наблюдать этот эффект на лабораторном занятии 9L,
18LI Аналого-цифровой преобразователь
759
Цифровой вход
0
0
1
0
1
0
0
0
0
оо и ц.
0 -1
1
0
0
/Вес младшего бита
v —КвесбитаОб
^Вес старшего бита
Рис. 18L.3. Тестирование ЦАП путем проверки весов конкретных входных битов
(Светодиод) сс
LS 503 (РПП) en
I
I I I
470-820 Ом
Светодиод)
I Вывод подключается
на^зедллю»
аналоговый сигнал
Рис. 18L.4. Схема для проверки АЦП последовательных преобразований с ручным тактированием
Подключение микросхемы
РПП 74LS502
Подключение микросхемы
РПП 74LS503
18L1.2. Наблюдение процесса
преобразования в АЦП
Убедившись, что подключенный ЦАП работа-
ет должным образом, добавьте в схему преоб-
разователя методом последовательных при-
ближений остальные его составляющие: ком-
паратор и регистр последовательных прибли-
жений с ЦАП. Если вместо микросхемы РПП
74LS502 взята микросхема 74LS503, то необ-
ходимо заземлить ее вывод 1, на который по-
дается сигнал разрешения ENABLE*. В микро-
схеме 74LS5024 этот вывод можно оставить не
подключенным.
Если же вместо одной из этих микросхем вы
используете специально запрограммирован-
ное устройство ПМЛ, которое эмулирует ми-
кросхему 74LS502, то обратите внимание, 4to
цоколевка этого устройства будет отличаться
от цоколевки двух упомянутых микросхем.
За подробной информацией касательно цо-
колевки своего устройства обратитесь к его
справочному листку. Подключите к восьми
выводам ЦАП 8 светодиодов макетной платы,
чтобы можно было наблюдать процесс при-
ближения.
когда повторитель из дискретных компонентов иногда мог
заставлять цифровой мультиметр выдавать ложные по-
казания, превышающие величину напряжения источника
питания.
4 В микросхеме 74LS502 этот вывод является синхронной
версией входа D, который для наших целей без надоб-
ности.
Проверка с ручным тактированием
Выполните проверку собранной схемы, такти-
руя ее вручную. Сигнал тактирования Clk по-
давайте с помощью кнопочного переключате-
ля с противодребезговой защитой; для подачи
сигнала запуска Start* (S*) подойдет кнопка без
противодребезговой защиты. Наблюдайте сиг-
нал завершения преобразования (СС* — Con-
version Complete), подключив соответствую-
щий вывод к светодиоду. Схема организации
этой проверки изображена на рис. 18L.4.
Для девятого светодиода нужно будет ограни-
чить ток, используя резистор. При выборе зна-
чения резистора мы руководствовались тем, что
вывод ТТЛШ может поглощать ток величиной
8 мА, что вполне достаточно для энергоэффек-
тивного светодиода. Падение напряжения на
включенном светодиоде составляет около 2 В.
Имейте в виду, что работа сигнала запуска S* мо-
жет показаться вам необычной. В частности:
♦ во-первых, РПП работает в полностью син-
хронном режиме: активирование самого сиг-
нала запуска S* не дает никакого эффекта.
Регистр приближений игнорирует сигнал S*,
если только одновременно с его активирова-
нием не подать сигнал тактирования;
♦ во-вторых, называть этот сигнал сигналом
запуска (англ. Start) не совсем правильно.
Для него больше бы подошло название типа
«сигнал инициализации», поскольку для
760
18L Лабораторное занятие: аналоговые и цифровые преобразования; ФАПЧ
того, чтобы процесс преобразования про-
должился после начального приближения,
этот сигнал необходимо снять.
Подключите на «землю» вывод для подачи
входного аналогового сигнала5 и пошагово вы-
полните цикл преобразования. Наблюдайте
цифровые приближения на восьми светодио-
дах, а их аналоговые эквиваленты, т. е. анало-
говые приближения, наблюдайте с помощью
цифрового мультиметра или осциллографа.
По мере прохождения цикла преобразования
с каждым сигналом тактирования выходной
сигнал ЦАП (отображающий аналоговый эк-
вивалент цифровых приближений РПП) дол-
жен подходить все ближе к правильному зна-
чению входного аналогового сигнала в 0 В.
Можете ли вы видеть схему двоичного поиска
в этих последовательных приближениях? Если
конечным цифровым значением вашего пре-
образования будет 1, а не 0 (т. е. если уровень
младшего разряда окажется высоким, а не
низким), проверьте, что точка подключения
входа на «землю» находится на близком рас-
стоянии от преобразователя. Затем с помощью
осциллографа проверьте линии питания (+5 В
и «землю») на отсутствие на них помех. Но
из-за того, что вес младшего бита всего лишь
около 15 мВ при максимальном значении на-
пряжения смещения компаратора, указанном
как 5 мВ, конечный цифровой результат ве-
личиной ...01 не должен шокировать вас. Даже
небольшое уменьшение потенциала «земли»,
добавленное к напряжению смещения, может
оказаться достаточным, чтобы изменить зна-
чение младшего бита.
Проверка с обычным тактированием
Теперь внесите в схему следующие изменения:
1. Подключите вывод завершения преобразова-
ния (СС* — Conversion Complete) к выводу за-
пуска (S* — Start) как показано на рис. 18L.5.
Это позволит начать новый цикл преобразо-
вания сразу же по завершении предыдущего.
(Само собой разумеется, что кнопку для по-
дачи сигнала на вывод S* нужно отключить.)
Clk (тактирование) •
5 Обратите внимание на то, что аналоговый сигнал пода-
ется НЕ на неинвертирующий вход компаратора, а на ре-
зистор сопротивлением 10 кОм. Этот резистор требуется
для того, чтобы обеспечить гистерезис.
10 6
Start (запуск)
СС (преобразование
завершено)
'502/3
Рис. 18L.5. Подключение сигнала СС* на вход запуска S*
обеспечивает автоматический запуск РПП
кОм<
'372
Рис. 18L6. Организация подачи на преобразователь
варьируемого аналогового напряжения
2. Подключите вход АЦП не напрямую на «зем-
лю», а через потенциометр сопротивлением
2,5 кОм или меньше. (Можете сказать, поче-
му меньше?6) См. рис. 18L.6.
3. В качестве источника сигнала тактирования
для преобразователя используйте генератор
сигналов с ТТЛ-выходом, а не кнопку. Для
этой цели удобен генератор сигналов, встро-
енный в макетную плату. Задайте частоту
сигнала тактирования равной 100 кГц.
Наблюдайте входной сигнал АЦП и выходной
сигнал ЦАП на осциллографе. Если хотите по-
лучить стабильную осциллограмму, то раз-
вертку осциллографа запускайте сигналом за-
вершения обработки СС*. Варьируйте входное
напряжение, вращая ручку потенциометра, и
убедитесь, что преобразователь постепенно
сводит выходное значение к входному.
Отображение всего дерева поиска
Итак, мы убедились, что АЦП последовательно
создает наилучшие приближения, постепенно
сводя выходное значение к входному. Если на
преобразователь подавать все возможные вход-
ные значения, то на осциллографе можно будет
наблюдать интересный эффект, когда преобра-
зователь проверяет каждую ветку своего дерева
приближений (двоичного поиска). Схема для
проведения такого эксперимента изображена
6 Это необходимо, чтобы сопротивление источника не
нарушило правильную работу преобразователя. В данном
случае слишком большое сопротивление потенциометра
могло создать такое нарушение в работе, вызвав значи-
тельное увеличение гистерезиса.
/8L7. Аналого-цифровой преобразователь
761
-TLTL
* 100 кГц
К запуску развертки
осциллографа
► К каналу вертикального отклонения осциллограсра
Рис. 18L.7. Схема для отображения полного дерева двоичного поиска
на рис. 18L.7. Подайте на вход АЦП треуголь-
ный сигнал с частотой приблизительно 100 Гц и
с размахом в полный входной диапазон преоб-
разователя. В качестве источника входного сиг-
нала используйте внешний генератор сигналов.
Развертку осциллографа запускайте сигналом
завершения преобразования СС*.
Если потребуется, откорректируйте частоту и
амплитуду входного сигнала, пока не получите
отображение всего дерева двоичного поиска.
Осциллограмма выходного сигнала для такого
входного сигнала окажется очень интересной.
Возможно, что вы даже сможете увидеть эф-
фект «дрожащей осины». Вам повезло увидеть
двоичный поиск в таком «живом» виде, тогда
как для большинства других он остается всего
лишь сухой абстракцией теории вычислитель-
ных систем. (Осциллограмма дерева двоично-
го поиска, полученная с помощью этой схемы,
изображена на рис. 13.31 книги АоЕ.)
18L1.3. Ограничение скорости
Наш АЦП выполняет 8-битовое преобразова-
ние за девять циклов сигнала тактирования.
Очевидно, что чем выше частота сигнала такти-
рования, тем быстрее будут выполняться пре-
образования. Соответственно чем быстрее вы-
полняются преобразования, тем выше частота
входного сигнала, с которым преобразователь
может работать.
Какой может быть наивысшая частота сигна-
ла тактирования нашего преобразователя? На
Сигнал
тактирования
\ч\\ \
рис. 18L.8 показано, что должно произойти
в период времени между фронтами сигнала
тактирования. Таким образом максимальная
частота сигнала тактирования в нашем случае
окажется чуть ниже 600 кГц.
Подайте на вход АЦП постоянное напряжение
и постепенно повышайте частоту сигнала так-
тирования, наблюдая при этом на осциллогра-
фе аналоговые приближения входного сигнала.
Но на этот раз сигнал тактирования подавайте
от внешнего генератора сигналов (максималь-
ная частота генератора сигналов, встроенного
в макетную плату, слишком мала для наших
целей). При некой частоте сигнала тактирова-
ния вы увидите нарушение нормальной работы
АЦП. Это будет выражаться меняющимся по-
следним приближением, поскольку слишком
короткий период сигнала тактирования не бу-
дет оставлять времени для стабилизации всех
сигналов. По всей вероятности, это произойдет
на частоте намного более высокой, чем частота
наихудшего случая в 570 кГц. В большинстве
случаев, которые мы наблюдали, это была ча-
стота выше 1 МГц.
18L1А Завершение схемы АЦП:
фиксация выходного цифрового
сигнала
До сих пор мы наблюдали выходной сигнал
ЦАП петли обратной связи АЦП. Но внима-
ние к этому аналоговому сигналу не должно
Задержка
распространения
РТТТТ
40 не макс.
Время
стабилизации
ЦАП
1000 не макс.
Задержка
компаратора
700 не макс.
Время
установки РПП
16 не макс.
Рис. 18L.8. Определение максимальной частоты сигнала тактирования ЦАП по операциям, которые нужно выполнить за один
период сигнала тактирования
762
18L Лабораторное занятие: аналоговые и цифровые преобразования; ФАПЧ
заслонить вам тот очевидный факт, что вы-
ходной сигнал ЦАП петли обратной связи
не является выходным сигналом АЦП. Мы
используем АЦП для того, чтобы получить
цифровой выходной сигнал, и, как отмеча-
лось в начале этой главы, у реальных АЦП на
микросхемах аналоговое приближение даже
не выводится на какой бы то ни было вывод
микросхемы.
Но теперь мы снова направим наше внимание
на основной интересующий нас объект: цифро-
вой выход АЦП.
Выходной регистр
Микросхема АЦП обычно также содержит ре-
гистр для сохранения его выходного значения.
Замечание
Поскольку мы живем в компьютерную эпоху, этот
регистр оснащен выходами с тремя состояниями,
чтобы облегчить его подключение к шине данных
компьютера.
Теперь мы завершим схему АЦП, добавив в нее
8-битовый регистр из D-триггеров. Нам так-
же нужно обеспечить импульс тактирования
с должным тактированием, который будет за-
хватывать наилучшее приближение АЦП, и
сохранять его до тех пор, пока не будет готово
следующее. Вопросы тактирования делают эту
задачу более деликатной, чем она может пока-
заться на первый взгляд.
Сигнал завершения преобразования СС* вроде
бы выглядит хорошо подходящим для исполь-
зования его в качестве сигнала тактирования.
Но оказывается, что это не совсем так. Его зад-
ний фронт (нарастание) появляется слишком
поздно, а другой фронт, инвертировав который
можно было бы получить положительный пе-
репад, приходит слишком рано. Это наглядно
иллюстрируется на рис. 18L.9.
В начале (отрицательный перепад) сигнала
СС* регистр последовательных приближений
выдает начальное приближение значения са-
мого младшего разряда; если это значение
TZ "X.
Слишком рано
нуждается в корректировке (установке значе-
ния «1»), такая корректировка еще не была
выполнена. Таким образом, если фиксировать
выходное значение по моменту начала сигнала
СС*, то мы будем терять данные самого млад-
шего бита, значение которого будет всегда
равно нулю.
А в конце (положительный перепад) сигнала
СС* регистр последовательных приближений
уже предоставляет первое приближение своего
следующего цикла (0111 111)7.
Следовательно, нам нужен импульс, который
начинается намного раньше обоих перепадов
сигнала СС*, как показано на рис. 18L.10. С за-
Сигнал тактирования
7Z—О
Требуемый импульс
Рис. 18L.10. Импульс, необходимый для тактирования
регистра фиксации результата преобразования
дачей формирования такого импульса может
справиться один логический вентиль.
Добавьте этот вентиль в свою схему и подайте
его выходной сигнал на вход тактирования ре-
гистра (микросхема 74НС574). Подключите
к выходам регистра 8 светодиодов макетной
платы. Не забудьте подключить питание, как
положительное, так и «землю», которые не по-
казаны на рис. 18L.11. Как обычно, для цифро-
вых микросхем питание подается на угловые
выводы.
Наблюдайте выходной цифровой сигнал АЦП
и убедитесь в том, что он соответствует входно-
му аналоговому сигналу, подаваемому с потен-
циометра. Выходной сигнал может колебаться в
пределах значения младшего бита. Подумайте,
можно ли избежать такого эффекта8.
7 Почему так? Потому что как положительный перепад
сигнала СС*, так и первоначальное приближение иниции-
руются сигналом тактирования РПП, а сигнал СС* проис-
ходит чуть позже (см. справочный листок на микросхе-
му 74LS502): время ^(низ-выс) (W больше, чем время
'рспрсвыс-низ) &> Как вам это нравитс
8 М
^(низвыс) W
Как вам это нравится?
Слишком поздно
Рис. 18L9. Временная диаграмма сигнала завершения
преобразования СС*
рс)
8 Мы не имеем в виду ничего мудреного, а просто указы-
ваем (как в разделе 18L1.1) на вероятность того, что шум
вашей схемы, собранной на макетной плате, может быть
соизмерим со значением младшего бита.
18L2. Система фазовой автоподстройки частоты: умножитель частоты
763
—-j Ваша логическая ]
-Iсхема тактирования!"
Ком парат*
РПП
ЦАП
i
£2
£4
£6
07
ОБ
QP
НСТ Q1
576 Q2
8-битовый Q3
регистр из <?4
D-триггеров Q5
Q6
ЯГ
Ж.
XL.
13_
На светодиоды
Рис. 18L.11. Добавление выходного регистра к РПП АЦП (схему для тактирования этого регистра вы разрабатываете само-
стоятельно)
18L2. Система фазовой
автоподстройки частоты:
умножитель частоты
Схему системы фазовой автоподстройки ча-
стоты следует собрать на отдельной макетной
плате9. Мы рекомендуем использовать плату
с микрофонным усилителем, который вы со-
брали на лабораторном занятии 7L.
Если у вас будет желание, то можете применить
эту схему ФАПЧ на лабораторном занятии 23L.
На том лабораторном занятии вам нужно бу-
дет сгенерировать сигнал с частотой, кратной
частоте, с которой компьютер выполняет вы-
борку сигнала. В частности, необходимо бу-
дет создать прямоугольный сигнал с частотой
в 32 раза больше частоты выборки. Мы будем
использовать этот умножитель для регулиров-
ки частоты/3дБ НЧ-фильтра с коммутируемым
конденсатором, наподобие фильтра, который
мы собрали на лабораторном занятии 12L.
Таким способом мы сможем заставить фильтр
следовать частоте нашей выборке. (Чтобы
избавиться от ложных высокочастотных со-
ставляющих в ступенчатом выходном сигнале
ЦАП.) Это будущее применение схемы ФАПЧ
объясняет некоторые ее элементы, в особенно-
сти ее частотный диапазон, установленный та-
ким образом, чтобы покрывать большую часть
диапазона частот выборки, которые вы будете
использовать.
Но первым применением этой схемы будет
генерирование сигнала с частотой, кратной
частоте тока электросети, 60 Гц. Этот пример
подробно рассматривается в § 13.8.4 книги АоЕ,
а схема, изображенная на рис. 18L.12, разрабо-
тана в процессе этого рассмотрения, с тем лишь
исключением, что мы изменили в ней значения
компонентов ГУН, чтобы обеспечить более
широкий диапазон работы.
Соберите схему, изображенную на рис. 18L.12.
На схеме фазовый детектор и ГУН показаны от-
дельными блоками, но оба элемента содержат-
ся в одной микросхеме 4046. Микросхема 4040
является 12-каскадным счетчиком со сквозным
переносом
10
18L2.1. Генерирование сигнала
с частотой, кратной частоте
входного сигнала: детектор типа II
Снимаем сигнал ГУН с выхода Q? микросхе-
мы 4040 (вывод 14). (На этом выходе исходная
частота тактирования делится на 210. Если вам
это кажется странным, вспомните, что на вы-
ходе QP этого счетчика частота входного сигна-
ла делится на 2, а не на 1.) Установите частоту
сигнала генератора сигналов, используемого в
качестве источника входного сигнала, прибли-
зительно на 10 кГц. С помощью осциллографа
сравните входной сигнал с синтезированным
9 АоЕ § 13.8.4.
10 Здесь выводы микросхем обозначены как обычно, ко-
гда вывод Q. самого младшего разряда обозначается на
устройстве как Q0, но не показывается на рисунке. Этот
метод маркировки используется компанией NXP/Philips.
Компании National Semiconductor и Fairchild нумеруют
выходы Q. своих устройств странным образом, начиная с
Q1 (см., например, микросхему CD74HC4040 на веб-сайте
компании Texas Instruments). Это различие можно встре-
тить в справочном листке на устройства кампании National
Semiconductor. А вот компания Texas Instrument обходит
этот вопрос нумерации стороной, используя буквы вместо
цифр: QA, 0В...(микросхема SN74HC4O4O).
764
18L Лабораторное занятие: аналоговые и цифровые преобразования; ФАПЧ
100к
fi
J8
Демодулированный сигнал
- (к каналу вертикального
отклонения осциллограсра)
Захват
(Примечание. Микросхема 4046 содержит
как фазовый детектор, так и ГУН)
Светодиод
1
Демодулированный сигнал
ходной сигнал Тип *'
Фазовый
Сигнал с ГУН Детектор Тип II
1/2НС4046
Счетчик-делитель на 1024-
220k* +г.
61 17 111 114 Выходной
"a vTI сигнал
ГУН
UrfCvhrftv (Для моделирования /
-__„£ частотной демодуляции 230k
И Щ\Щ
^io аз Об а4
аи м а7 os
74НС4040
Счетчик со сквозным
переносом
уменьшите емкость
конденсатора до ОД мкФ)
10
(Замените на 22 кОм
для последнего случая)
Демодулированный сигнал
(к каналу вертикального
отклонения осциллограсра)
Рис. 18L.12. Схема умножителя частоты с фазовой автоподстройкой частоты (микросхема ФАПЧ 74НС4046)
сигналом ГУН, подаваемым на вывод 3 микро-
схемы 4046. Убедитесь, что система ФАПЧ осу-
ществляет захват входной частоты в течение
нескольких секунд. Совпадают ли по фазе эти
два сигнала? Захват определяется по свечению
светодиода индикации захвата.
Примечание
Высокий логический уровень на выводе 1 означа-
ет, что вывод фазового детектора находится в тре-
тьем состоянии, т. е. что детектор «удовлетворен»
данной частотой, и корректировать частоту ГУН
нет необходимости.
Проверьте, следует ли частота сигнала ГУН ча-
стоте входного сигнала при медленном варьи-
ровании последней. Затем подвергните систему
ФАПЧ испытанию, резко меняя частоту вход-
ного сигнала. Должен наблюдаться короткий
процесс рыскания, после чего снова осущест-
вляется захват частоты.
Пределы диапазонов частот захвата и отсле-
живания входного сигнала (которые для дан-
ной схемы ФАПЧ одинаковые) определяются
частотным диапазоном ГУН: приблизитель-
но от 40 до 250 кГц для указанных значений
R. = 220 кОм и С, = 220 пФ. Поскольку счетчик
в контуре обратной связи делит частоту ГУН
на 210, входной сигнал может быть в диапазоне
частот от 40 до 250 Гц.
Фильтр контура обратной связи
Трудная часть проектирования системы ФАПЧ
состоит в разработке НЧ-фильтра для обеспе-
чения стабильности. Цепь обратной связи в
системе ФАПЧ поразительно похожа на цепь
обратной связи, с которой мы работали на ла-
бораторном занятии 10L по системе ПИД для
управления электродвигателем. В том упраж-
нении преобразователь «двигатель в позицию»
добавлял в петлю ОС эффект интегрирования.
Наличие этого отрицательного фазового сдвига
величиной 90° требовало от нас осторожности,
чтобы не внедрить еще одну фазовую задержку
величиной 90° на частотах, при которых петле-
вое усиление было больше единичного.
Подобным образом контур обратной связи си-
стемы ФАПЧ вносит эффект интегрирования,
что также угрожает стабильности работы схе-
мы. В данном случае интегрирование возника-
ет в результате того, что мы детектируем фазу,
которая является интегралом частоты, которой
должен управлять наш контур обратной связи.
В данном случае задача определения местона-
хождения интегрирования труднее, чем в слу-
чае с ПИД-контуром, в котором этот эффект
явно возникал в связке «двигатель — потен-
циометр». В системе ФАПЧ интегрирование —
эквивалент связки «электродвигатель — потен-
циометр» — создается парой «ГУН — фазовый
детектор». Фазовая погрешность измеряется
18L2. Система фазовой автоподстройки частоты: умножитель частоты
765
выходным сигналом фазового детектора11.
Чтобы обеспечить постоянную разность ча-
стот, фазовая погрешность (рассогласование
по фазе между входным сигналом и сигналом
ГУН) меняется линейно нарастающим образом
(см. рис. 18N.49). Иными словами, она инте-
грирует ошибку по частоте. Осциллограмму,
демонстрирующую этот эффект линейного на-
растания, можно найти в главе 18N. Это поведе-
ние очень похоже на то, которое мы наблюдали
в связке «электродвигатель — потенциометр»:
постоянный сигнал рассогласования, подавае-
мый на связку, создавал выходное линейно на-
растающее напряжение, т. е. опять имеем дело
с интегрированием
12
Нам требуется НЧ-фильтр в контуре обратной
связи, чтобы сгладить сигнал, поступающий на
ГУН, но мы не можем позволить создать еще
одну фазовую задержку в 90°. Как же решить
эту проблему? Решение состоит в простой моди-
фикации схемы: использовании НЧ-фильтра, у
которого на высоких частотах фаза сдвигается
к нулю, а не к 90°. В частности, как обсуждается
в разделе 18N.7.4, таким решением будет НЧ-
фильтр с дополнительным резистором между
конденсатором и «землей».
Если заменить в этом фильтре резистор номи-
налом 330 кОм резистором номиналом 22 кОм,
то мы должны увидеть, как процесс захвата ча-
стоты занимает намного больше времени, ко-
гда петля обратной связи то перерегулирует, то
недорегулирует. Этот процесс рыскания можно
графически наблюдать на осциллографе, подав
на его вход канала вертикального отклонения
демодулированный сигнал с вывода 10, с кото-
рого снимается входное напряжение для ГУН.
11 Можно задаться вопросом: «А зачем делать это таким
образом? Почему бы не пойти более прямым путем и из-
мерить рассогласование частот непосредственно?» Потому
что у нас нет способа быстро выполнить такое измерение.
Чтобы измерить частоту даже не напрямую, а неявно по ее
периоду, нужно, чтобы прошел целый период двух сигна-
лов. А информация о рассогласовании фаз доступна бы-
стро: после каждого соответствующего положительного
перепада в фазовом детекторе второго типа.
12 Если вы еще не устали от этого обсуждения, рекомен-
дуем рассмотреть дополнительное усложнение: еще одно
интегрирование, создаваемое RC-цепочкой. По крайней
мере, выяснить, как эта цепь используется в чувствитель-
ном к перепаду фазовом детекторе типа II: постоянная раз-
ность фаз вызывает в данном фазовом детекторе линейно
нарастающий выходной сигнал. Это второе интегриро-
вание аналогично составляющей И в схеме ПИД. Данная
составляющая И сводит погрешность ПИД к нулю. Подоб-
ным образом интегрирование в фазовом детекторе типа П
сводит разность фаз к нулю.
Уменьшив сопротивление резистора, мы ри-
скованно уменьшили запас по фазе, т. е. безо-
пасное расстояние между фазовым сдвигом в
контуре обратной связи (на частоте, при кото-
рой петлевое усиление становится единичным)
и его предельным значением -180°. Вспомните,
что мы рассматривали этот момент на лабора-
торном занятии 9L и в упражнении по ПИД-
контроллеру в разделе 10N.4.3 (см. рис. 10N.9).
Уровень риска можно повысить еще больше,
закоротив нижний резистор. В результате за-
пас по фазе будет сведен к нулю, а схема мо-
жет рыскать вечно в поисках частоты захвата.
Ознакомившись с этим эффектом, поставьте
обратно резистор номиналом 330 кОм, чтобы
восстановить стабильность схемы.
Как вы полагаете, какой частоты должен быть
сигнал на выходе ГУН при выполненном захва-
те частоты? Проверьте свое предположение, ис-
следовав эту точку (вывод 4 микросхемы 4046)
с помощью осциллографа. Почему этот сигнал
так дрожит? (В мире без помех он не дрожал
бы13.)
Теперь исследуйте выходной сигнал фазово-
го детектора (снимается на выводе 13 микро-
схемы 4046). Это фазовый детектор типа II,
чувствительный к перепаду. Здесь вы должны
увидеть поток коротких положительных им-
пульсов, затухающих экспоненциально, когда
выход детектора возвращается в третье состоя-
ние. Также могут наблюдаться отрицательные
импульсы меньшей амплитуды, в зависимости
от степени зашумления схемы.
. Согласно теории в состоянии захвата корректи-
ровочные импульсы должны исчезнуть. Но на-
грузка в 10 МОм щупа осциллографа разряжает
конденсатор фильтра достаточно быстро, что-
бы вызывать такие импульсы. Потребляемый
13 Дрожание сигнала возникает вследствие того, что часто-
та ГУН корректируется только один раз за 1024 периода
выходного сигнала. Поэтому небольшие блуждания ча-
стоты между этими проверками не корректируются. Как
обычно, для нас, преподавателей колледжа, это напоми-
нает нам о том обстоятельстве (возможно, полезном для
человечества, но вызывающем беспокойство в аналогии
с ФАПЧ), что способность студентов усваивать учебный
материал проверяется только время от времени: в лучшем
случае — только раз в неделю, а большая проверка выпол-
няется вообще только раз в семестр. И кто знает, чем зани-
маются студенты в течение времени между этими провер-
ками? Несомненно, жизнь была бы полна тряски, если бы
кто-то, достаточно бесцеремонный, проверял бы ее между
контрольными точками.
766
18L Лабораторное занятие: аналоговые и цифровые преобразования; ФАПЧ
осциллографом ток также слегка ослабляет
входной сигнал ГУН, в результате чего послед-
ний немного отстает и устанавливается посто-
янная задержка по фазе. Это объясняется тем,
что контуру обратной связи теперь требуется
разность фаз для того, чтобы обеспечить по-
ложительные импульсы, разряжаемые через
сопротивление осциллографа на «землю».
Если у вас есть время и желание, подключите
щуп осциллографа к конденсатору через повто-
ритель на операционном усилителе на микро-
схеме 358. Положительные импульсы должны
стать уже, а разность фаз инвертироваться: те-
перь выходной сигнал ГУН немного забегает
вперед14.
18L2.2. Частотная демодуляция
(в замедленном режиме)
Если наблюдать на осциллографе входной сиг-
нал ГУН (который можно снимать с буфера на
выводе 10 микросхемы), то можно определить
частоту сигнала ГУН. При постоянной частоте
входного сигнала это не представляет большого
интереса, но ситуация меняется, когда варьиро-
вание частоты входного сигнала нагружает его
информацией, подобно тому, как это происхо-
дит при передаче программ ЧМ-радиовещания.
(Или как это происходило в нашем аналоговом
проекте, в котором мы посредством миганий
светодиода передавали музыку на другую сто-
рону комнаты.) Мы не будем долго задержи-
ваться, чтобы выполнить здесь такое упражне-
ние, но рекомендуем вам взглянуть на способ,
как это может работать, попробовав выполнить
демонстрацию, которая займет пару минут ва-
шего времени.
Замените конденсатор номиналом 1 мкФ кон-
денсатором номиналом 0,1 мкФ (чтобы уско-
рить осуществление захвата частоты конту-
ром обратной связи). Медленно варьируйте
частоту синусоидального сигнала генератора
сигналов^ подаваемого на вход схемы, и наблю-
дайте демодулированьый сигнал (на выводе 10
микросхемы 4046). При этом развертка осцил-
лографа должна быть очень медленной. Если
у вас есть цифровой осциллограф, включите
режим сканирования (возможно, 1 с/дел.).
Мы надеемся, что наблюдаемый демодулиро-
ванный сигнал будет выглядеть подобно сину-
соидальному сигналу, который варьирует, или
«модулирует», частоту входного сигнала схемы
ФАПЧ. Как плохо, что мы не знали о ФАПЧ,
когда работали над совместным проектом пе-
редачи аудио посредством мигания светодиода.
Наигравшись достаточно, поставьте обратно на
место конденсатор емкостью 1 мкФ.
Фазовый детектор типа I
Микросхема 74НС4046 содержит три типа фа-
зовых детекторов. Детекторы первых двух ти-
пов (I и II) рассматриваются в § 13.13.2А книги
АоЕ15. Третий детектор микросхемы 74НС4046,
типа III, является просто разновидностью SR-
защелки, на входы 5 и 1? которой подаются по-
ложительные уровни входного сигнала и сиг-
нала с ГУН соответственно. Мы не будем рас-
сматривать этот тип детектора16: для первого
знакомства с системой ФАПЧ более чем доста-
точно детекторов первых двух типов. Но если
у вас есть желание, то можете исследовать его
выходной сигнал (который снимается с вывода
15 микросхемы) самостоятельно.
Выходной сигнал детектора типа I снимается
с вывода 2 микросхемы, а входные сигналы по-
даются на те же выводы, что и для детектора типа
П. Таким образом, чтобы задействовать детек-
тор типа I, просто переместите провод с вывода
13 микросхемы на вывод 2. (Выходной сигнал
детектора типа III подается на вывод 15.) В слу-
чае детектора как типа I, так и типа III должно
наблюдаться колебание частоты сигнала ГУН
в течение периода входного сигнала, которую
можно увеличить, уменьшив емкость конден-
сатора фильтра контура обратной связи (теку-
щий номинал которого составляет 1 мкФ).
А если резко и на большую величину изме-
нить частоту входного сигнала, детектор типа I
можно «обмануть», чтобы он выполнил захват
гармоники входной частоты (частота, крат-
ная частоте входного сигнала). Такая ошиб-
ка сделала бы схему бесполезной для целей,
14 Чем это объясняется? Это довольно педантичная под-
робность, но теперь вместо разряда конденсатора, как это
делал щуп осциллографа, происходит его заряд, когда с
базы входного р-я-р-транзистора операционного усилите-
ля инжектируется некоторая часть тока смещения /см.
15 В книге АоЕ рассматривается версия детектора на ми-
кросхеме CD4046, а не 74НС4046.
16 Похоже, что детектор типа III был добавлен как будто
бы после запоздалых размышлений, поскольку в ранних
модификациях микросхемы 4046 его не было. Подобно
простому детектору на ИСКЛ-ИЛИ (тип I) для этого де-
тектора требуется наличие разности фаз между входным
сигналом и сигналом с ГУН.
18L2. Система фазовой автоподстройки частоты: умножитель частоты
767
рассматриваемых в разделе 23N.5.2, поэтому
мы будем использовать детектор типа П.
Вероятнее всего такой выбор также будет бо-
лее подходящим и для большинства других
приложений.
Также обратите внимание на фазовый сдвиг,
который остается между входным сигналом
и сигналом с ГУН после того, как был. выпол-
нен захват частоты. Этот простой фазовый де-
тектор (подобно детектору типа III) требует на-
личия такой разности фаз для генерирования
сигнала управления ГУН. Приближение раз-
ницы фаз к нулю (или я) вызывает потерю об-
ратной связи, в результате чего корректировка
частоты требуемым образом в любом направ-
лении становится невозможной. Эта ситуация
подобна ситуации с контуром обратной связи
операционного усилителя, которая теряет ра-
ботоспособность вследствие перехода выход-
ного сигнала усилителя в режим насыщения
и не может больше осуществлять необходимые
корректировки. Качество фазового детектора
типа II намного лучше: для него не требуется
расхождение фаз, чтобы удерживать захват ча-
стоты; кроме того, в состоянии захвата в нем
можно использовать конденсатор в качестве
средства выборки и хранения, а не как обыч-
ный фильтр.
Завершив исследование работы фазового де-
тектора типа I, восстановите схему для работы
с детектором типа II (сигнал на ГУН подается с
вывода 13 микросхемы).
18L2.3. Расширенный диапазон
удержания
Теперь изменим схему ФАПЧ для ее после-
дующего использования на лабораторном
Фильтр kohtvdq обратной связи
Цифровой делитель
Первый случай
(<c*1024»)
4,7 МОм
«1/15
1/1024
330 кОМ
Второй случай S 4,7 М
(«*64») }
47 МОад
* 1/215
1/64
22 кОМ
занятии 23L. В частности, сигнал ГУН для по-
дачи на фазовый детектор будем снимать не с
выхода Q? счетчика со сквозным переносом, а с
выхода Q5 (вывод 2 микросхемы 4040). Теперь
частота выходного сигнала ГУН будет всего
лишь 64 -fBX. Поскольку теперь мы подаем об-
ратно большую часть входного сигнала, осла-
бление фильтром сигнала в контуре обратной
связи должно быть большим. Мы заботимся о
петлевом усилении, как и при работе с опера-
ционными усилителями.
Подача обратно одной части из 64, а не одной
из 1024, т. е. приблизительно в 16 раз больше,
требует пропорционального уменьшения доли,
пропускаемой фильтром контура. Для этого мы
уменьшим сопротивление резистора, подклю-
ченного последовательно конденсатору фильт-
ра, тоже в 16 раз, приблизительно до 22 кОм.
На рис. 18L.13 показаны два делителя для двух
случаев: первый случай, когда в петле частота
умножается на 1024, а второй — когда частота
умножается на 64. В обоих случаях задержива-
ется примерно одинаковая доля сигнала (при-
близительно до 12%).
Возможно, вы заметили, что мы нарисовали
фильтр контура обратной связи, как будто бы
он был просто резистивным делителем. Это
объясняется тем, что на высоких частотах, где
мы ожидаем проблемы со стабильностью, по
сравнению со значениями R величина Хс незна-
чительна.
Каков же теперь диапазон частот входного сиг-
нала, в котором выполняется захват частоты?
Нам нужен широкий диапазон, чтобы обеспе-
чить гибкость схемы выборки на лаборатор-
ном занятии 23L. Система ФАПЧ на микро-
схеме 4046 способна выполнять захват и удер-
жание в диапазоне частот с приблизительным
Деление
* 1/16,000 * 60 • Ю-6
* 1/14,000 * 70 • 10-6
(разница в 12%)
Рис. 18L13. Делитель фильтра схемы ФАПЧ изменяется, чтобы задерживаемая часть подаваемого обратно сигнала в обоих
случаях была приблизительно одинаковой
768
18L Лабораторное занятие: аналоговые и цифровые преобразования; ФАПЧ
отношением 6:117. Нас удовлетворит диапазон
частот входного сигнала между 600 Гц и 4 кГц.
Для фазового детектора типа II полоса захва-
та и полоса удержания одинаковы. Для менее
17 Это приблизительный диапазон при подаче на ГУН сиг-
нала в области разрешенных напряжений от 1,1 до 3,4 В.
(В справочном листке диапазон рабочих напряжений ука-
зывается для напряжения питания 4,5 В. При напряжении
питания 5 В предельные рабочие напряжения будут при-
близительно на 10% больше.)
«умных» фазовых детекторов область захвата
(диапазон частот, в котором контур обратной
связи может осуществить захват) более узкая,
чем область удержания (диапазон частот, в ко-
тором контур будет удерживать выполненный
захват). Эта способность фазового детектора
типа II выполнять захват любой частоты, кото-
рую он может удерживать, следует из его невос-
приимчивости к гармоникам. Детектор этого
типа не так легко «обмануть».
18S. Дополнительный материал: правила
осуществления выборки; ложные сигналы
при выборке
18S.1. Содержимое этой
главы
В этой главе мы повторим правило Найквиста
для осуществления выборки, а также рассмо-
трим некоторые побочные эффекты, возни-
кающие в процессе дискретизации. Также на-
помним о ложных сигналах, которые могут
возникать в процессе дискретизации, предо-
ставив соответствующие осциллограммы в раз-
деле 18S3.
Эти осциллограммы, в особенности на рис.
18S.3, отображают влияние выборки на четы-
рех разных частотах применительно к синусои-
дальному сигналу частотой 1 кГц. Эти четыре
частоты дискретизации можно грубо описать
как избыточную, достаточную, низкую и недо-
статочную. Но прежде чем изучать эти осцил-
лограммы, вспомним общие понятия, кото-
рые важны при дискретизации. Это поможет
уяснить, почему частотные спектры выглядят
именно так, а не иначе. Наконец, в разделе 18SA
мы попытаемся дать интуитивное объяснение
побочных эффектов дискретизации, в частно-
сти возникновения ложных сигналов.
18S.2. Дискретизация
создает предсказуемые
ложные сигналы
Для начала вспомним очень кратко некоторые
аксиомы дискретизации:
♦ дискретизация создает ложные образы вход-
ного сигнала при частоте/ВЫБ±/ВХ, которые
повторяются попарно выше и ниже каждой
частоты, кратной частоте выборки^^. В об-
щем случае/ложн = (лх/ШБ) ±/вх;
♦ одна из причин этих ложных сигналов выра-
жается в виде правила Найквиста для выбор-
ки: частота выборки должна быть немного
выше, чем удвоенная максимальная частота
входного сигнала1.
Аналоговый
сигнал
Ложные сигналы, вносимые
в процессе дискретизации
Дискретизированный
сигнал
Рис. 18S.1. Дискретизация создает множественные образы
настоящего сигнала с более высокими частотами
Причина возникновения этих ложных сигна-
лов не совсем очевидна. В конце этой главы
мы дадим объяснение этому явлению, которое,
мы надеемся, будет понятным на интуитивном
уровне. С другой стороны, вы можете просто
принять его на веру.
Изо всех этих ложных сигналов только один
создает проблему: сигнал с самой низкой ча-
стотой: /шъ-/ъх. В принципе, этот сигнал, как
и все прочие ложные сигналы, можно удалить
с помощью НЧ-фильтра при условии, что ча-
стота этих побочных сигналов выше частоты
настоящего сигнала. (Опять же, при условии,
что применялась достаточная частота выбор-
ки. Этот аспект рассматривается далее более
детально.) Но иногда требуемую фильтрацию
трудно осуществить. В частности, в тех случаях,
1 Это следует из предыдущего замечания об образах, по-
скольку первый образ (ложный сигнал) возникает на ча-
стоте /шъ - fBX. Поэтому, чтобы не допустить наложения
этого ложного сигнала на истинный сигнал частотой^,
частота выборки должна быть больше чем 2JBX. Этот мо-
мент рассматривается более подробно чуть далее.
770
18S. Дополнительный материал: правила осуществления выборки; ложные сигналы при выборке
когда частота ложного сигнала близка к часто-
те настоящего сигнала, как рассматривается в
примере далее в этой главе.
18S.2.1. Наложение спектров
Нарушение правила Найквиста для выборки,
т. е. использование слишком низкой частоты
дискретизации, вызывает катастрофическую
ошибку, называемую наложением спектров:
формирование ложных сигналов, которые нель-
зя отделить от настоящего сигнала.
В частности, проблема существует тогда, когда
частота ложного сигнала ^ЫБ -fBX находится в
диапазоне частот входного аналогового сигна-
ла. Такую проблему нельзя решить с помощью
фильтра. Слева на рис. 18S.2 изображен график
дискретизации входного сигнала, выполненной
при едва достаточной частоте выборке. В ре-
зультате самая нижняя частота самого первого
ложного сигнала находится чуть выше предель-
ной частоты входного сигнала. Таким образом,
хороший низкочастотный фильтр должен уда-
лить этот ложный сигнал.
Справа на рис. 18S.2 показана проблемная си-
туация при дискретизации, называющаяся на-
ложением спектров. Такая проблема возникает,
когда частота выборки не удовлетворяет пра-
вилу Найквиста, т. е. когда/ВЫБ не превышает
максимальную частоту дискретизируемого сиг-
нала чуть больше, чем вдвое. Таким образом,
частота выборки должна быть >2х^х(МАКС), ибо
в противном случае у нас возникнут неприят-
ности. Суть проблемы состоит в том, что мы
получим бессмысленный выходной сигнал,
состоящий из смеси ложного сигнала с настоя-
щим. Ложный сигнал пересекается с настоящим
сигналом в точке^ЫБ -/^ создавая наложение
спектров этих двух сигналов. Ложный сигнал,
наложенный на настоящий сигнал, нельзя уда-
лить с помощью фильтра, поскольку часть его
диапазона частот совпадает с частью диапазона
частот настоящего сигнала.
18S.2.2. Фильтрация
Плееры компакт-дисков воспроизводят аудио
с частотой 20 кГц, при дискретизации которо-
го использовалась частота выборки величиной
приблизительно 44 кГц, что всего лишь на 10%
больше, чем теоретическая минимальная часто-
та выборки. В результате нужно решить слож-
ную проблему фильтрации, поскольку нижний
предел частотного диапазона первого ложного
сигнала расположен очень близко к верхнему
пределу частотного диапазона настоящего сиг-
нала. В индустрии плееров компакт-дисков су-
мели решить эту проблему, имитируя более вы-
сокую частоту выборки — интерполируя между
настоящими выборками псевдовыборки, полу-
ченной методом цифровых вычислений. Как вы
знаете, этот прием называется передискрети-
зацией. Впервые услышав, что плеер компакт-
дисков может передискретизировать музыку,
в это утверждение трудно поверить. Разве часто-
та дискретизации не была зафиксирована при
изготовлении компакт-диска? Да, была. Но когда
вы поймете, что имеется в виду, то увидите, что
выражение «передискретизация» — всего лишь
безобидная фигура речи. Эта операция иногда
также называется цифровой фильтрацией2 или
даже цифровым интерполированием, что больше
соответствует рассматриваемому предмету.
18S.3. Примеры побочных
сигналов во временной
и частотной областях
Осциллограммы сигналов в этом разделе были
получены с помощью тестовой схемы, исполь-
зованной в наших учебных демонстрациях,
Самый первый ложный сигнал (fmB - fBX) Самый первый ложный сигнал (fBtiLB - fBX)
Достаточная частота
выборки
Недостаточная частота
выборки создает
наложенный компонент
/ТУ)
Наложение
Рис. 18S.2. Графическое представление проблемы наложения спектров
2 Операция цифровой фильтрации может быть более
сложной, чем простое интерполирование.
18S.3. Примеры побочных сигналов во временной и частотной областях
771
в которых аналоговый синусоидальный сигнал
подавался на 8-битовый АЦП, выходной сиг-
нал которого поступал для обработки на ЦАП.
Затем восстановленный аналоговый сигнал
пропускался через НЧ-фильтр.
На осциллограммах изображены следующие
сигналы:
1. Вверху показан входной сигнал.
2. Следующий сигнал — это неотфильтрован-
ный выходной сигнал 8-битового ЦАП, ко-
торый был восстановлен из цифровых зна-
чений входного аналогового сигнала.
Четыре разные частоты выборки иллюстриру-
ют четыре разных случая:
♦ Избыточная частота выборки — 100 кГц,
что в действительности слишком много.
♦ Достаточная частота выборки — 4 кГц
или 4 выборки/период. Это достаточно хо-
рошая частота, если использовать хороший
выходной фильтр.
♦ Низкая частота выборки — 2,2 кГц, что
всего лишь на 10% больше, чем теорети-
ческий минимум двух выборок за период.
Потребуется фильтр с крутой характеристи-
кой (например, восьмиполюсный эллипти-
ческий фильтр на микросхеме МАХ294).
♦ Недостаточная частота выборки —1,5 кГц,
а затем 1,2 кГц, что едва больше, чем одна вы-
борка за период. При такой частоте дискрети-
зации возникает наложение спектров.
Избыточная частота выборки
Этот случай иллюстрируется на рис. 18S.3.
Частота выборки настолько высока, что самый
Входной
аналоговый сигнал
Восстановленный
аналоговый сигнал
(выходной сигнал ЦАП)
Частотный спектр
1кГц
Рис. 18S.3. Избыточная частота выборки: 100 выборок/пе-
риод. (Разрешение осциллографа: 1 В/дел.; БПФ частотного
спектра —1,25 кГц/дел.)
первый побочный сигнал, на частоте 99 кГц,
находится далеко за правым краем осцилло-
граммы.
Как можно видеть по восстановленному сиг-
налу, данная частота выборки хороша только
в одном смысле: она позволяет точно восста-
новить аналоговый сигнал. Но это абсурдно
затратный способ достижения такого результа-
та, создающий объем цифровых данных почти
в 50 раз больший, чем необходимо. Для того
чтобы сохранить все эти данные на компакт-
диске, нам бы потребовался диск размером
с большую пиццу.
Достаточная частота выборки
На рис. 18S.4 иллюстрируется более разумная
частота выборки, чем в предыдущем примере.
Частота побочных сигналов намного выше ча-
стоты настоящего сигнала, так что задача по их
фильтрации не выглядит трудной, да в действи-
тельности и не является таковой.
Входной
аналоговый сигнал
Восстановленный аналоговый
сигнал (выходной сигнал ЦАП)
Частотный спектр
восстановленного сигнала
Входной сигнал (1
Первый побочный сигнал на
частоте fBaB - fBX = 3 кГц
в 4 кГц
Рис. 18S.4. Достаточная частота выборки: побочные сигналы видимы на осциллограмме. (Разрешение осциллографа: 2 В/дел.;
БПФ частотного спектра —1,25 кГц/дел.)
772
18S. Дополнительный материал: правила осуществления выборки; ложные сигналы при выборке
Входной
аналоговый сигнал
я
Восстановленный
аналоговый сигнал
(выходной сигнал ЦАТТ)2
Частотный спектр
восстановленного сигнала
1 Отфильтрованный
восстановленный
аналоговый сигнал
Частотный спектр
отфильтрованного
восстановленного
w сигнала
Рис. 18S.5. Низкочастотный фильтр может удалить побочные сигналы, вносимые дискретизацией. (Разрешение
осциллографа: 2 В/дел.; БПФ частотного спектра — 1,25 кГц/дел.)
Осциллограмма на рис. 18S.5 иллюстрирует
эффект пропускания восстановленного сигна-
ла через фильтр: из частотного спектра сигна-
ла удаляются все побочные сигналы; фильтр
также удаляет ступенчатость из восстановлен-
ного сигнала. Сглаживание восстановленного
сигнала фильтром очевидно на третьем сигна-
ле правой осциллограммы на рис. 18S.5. Как
можно видеть, это, по сути, восстановленный
исходный синусоидальный сигнал.
Низкая частота выборки
В общем случае на практике стремятся исполь-
зовать наиболее низкую возможную частоту
выборки, чтобы избежать получения избыточ-
ных цифровых данных. Полученные отсчеты
необходимо хранить и, возможно, передавать.
Поэтому мы хотим свести к минимуму слож-
ность и стоимость этих операций. Согласно
правилу Найквиста, нам требуется делать чуть
больше двух выборок за период входного сиг-
нала. Но насколько больше? Это зависит от
качества низкочастотного фильтра, предна-
значенного для удаления побочных сигналов,
вносимых дискретизацией. Хороший фильтр,
наподобие активного восьмиполюсного эллип-
тического фильтра на микросхеме МАХ294,
который мы будем использовать на лаборатор-
ных занятиях, позволяет приблизиться доволь-
но близко к минимальной частоте выборки по
Найквисту величиной в две выборки за каждый
период входного аналогового сигнала3.
3 Для упрощения в этом рассмотрении мы обычно пред-
полагаем простой чистый синусоидальный входной сиг-
нал. Но если входной аналоговый сигнал содержит много
частот, то нужно беспокоиться только о самой высокой
из них. Например, для музыки это будет частота 20 кГц.
Если частота выборки будет достаточной для этой часто-
ты входного сигнала, то она будет достаточной и для всего
спектра частот.
На рис. 18S.6 изображена осциллограмма дис-
кретизации входного сигнала частотой 1 кГц с
частотой выборки 2,2 кГц, что всего лишь на
10% выше теоретического минимума в 2 кГц.
Замечание
В данном случае мы так прижимисты с частотой вы-
борки, как и в случае с компакт-дисками, когда для
дискретизации сигнала частотой вплоть до 20 кГц
используется частота дискретизации 44,4 кГц, что
тоже составляет лишь около 10% больше теоре-
тического минимума по Найквисту. фильтр едва
справляется с удалением самого первого ложного
сигнала и в действительности даже слегка осла-
бляет настоящий сигнал в процессе удаления по-
бочного сигнала.
На левой осциллограмме на рис. 18S.6 можно
видеть, насколько близко к настоящему сигна-
лу находится первый ложный сигнал: на частоте
1,2 кГц, что всего лишь на 200 Гц выше настоя-
щего сигнала. Но хотя данная задача фильтра-
ции побочного сигнала и является трудной, она
не такая трудная, как в случае с аудиостандар-
том для компакт-дисков. Разрешение преоб-
разования для компакт-дисков в 256 раз выше,
чем то, которое мы демонстрируем с нашим
8-битовым преобразованием, и поэтому тре-
бует большего ослабления сигнала фильтром4.
Вскоре после создания стандарта5 для компакт-
дисков разработчики компакт-дисков фактиче-
ски признали, что они поставили перед собой
4 Но можно обоснованно возразить, что в музыке невоз-
можен сигнал полного размаха частотой 20 кГц, поэтому
в действительности ослабление в фильтре не должно быть
таким большим, как разница в разрешении между нашим
8-битовым преобразованием и 16-битовым преобразова-
нием для компакт-дисков.
5 Стандарт для компакт-дисков был разработан компани-
ей Philips, которая создала «лазерный диск» большого раз-
мера в качестве носителя для фильмов, и компанией Sony,
которая разработала портативное аудиоустройство Walk-
man — кассетный магнитофон с наушниками.
18S.3. Примеры побочных сигналов во временной и частотной областях
773
Входной аналоговый д д д Л Л д л Л Л. Л
сигнал (1 кГц) /VWVVVVVV\
Восстановленный
аналоговый сигнал
(выходной сигнал ЦАТТ)
Частотный спектр
восстановленного
сигнала
^Самый первый ложный
сигнал (1,2 кГц)
Самый первый ложный
сигнал (1,2 кГц)
fVVVVVVWW.
Остается только исходный
(восстановленный) сигнал
'"-"(фильтр удаляет все побочные
сигналы)
Рис. 18S.6. Дискретизация с частотой выборки всего лишь на 10% выше минимума по Найквисту выполняется успешно, но
лишь едва. (Разрешение осциллографа: 2 В/дел.; БПФ частотного спектра — 1,25 кГц/дел.)
слишком трудную задачу, чтобы ее можно было
бы решить с помощью аналоговых фильтров.
Поэтому в плеерах компакт-дисков второго по-
коления промышленность начала использовать
передискретизацию, или интерполирование вы-
борок, полученных с помощью цифровых пре-
образований (см. раздел 18S.2.2).
Недостаточная частота выборки
Недостаточная частота выборки, т. е. часто-
та, нарушающая требование Найквиста чуть
больше двух выборок за период самой высокой
интересующей нас частоты сигнала6, вызывает
проблему, называющуюся наложением спект-
ров, как упоминалось в разделе 18S.2.1. Когда
6 Выражение «самая высокая интересующая нас часто-
та» не помешает объяснить более подробно.
Прежде всего рассмотрим элементарный аспект: тогда как
в этой главе мы иллюстрируем примеры дискретизации,
используя в качестве входного сигнала простой синусои-
дальный сигнал одной частоты, в настоящих приложени-
ях на вход АЦП обычно подается сигнал в определенном
диапазоне частот. Если частота выборки достаточна для
самой высокой частотной составляющей сигнала, то она
неизбежно окажется достаточной для всех его более низ-
ких частотных составляющих, как упоминалось в разде-
ле 18NS1.
Второй аспект более тонкий. В частности, частота выбор-
ки не обязательно должна быть всегда больше чем вдвое
выше, чем самая высокая частотная составляющая вход-
ного сигнала. Вместо этого, строго говоря, частота вы-
борки должна быть больше чем вдвое выше, чем полоса
частот подаваемого на АЦП сигнала. Когда диапазон вход-
ных частот простирается от практически нуля до/шкс, как
это имеет место в аудиоприложениях, эти два определения
дают одинаковый результат. Тем не менее бывают случаи,
когда разница между этими двумя определениями имеет
значение. В частности, иногда целью является дискрети-
зация узкой полосы на высоких частотах. В таком случае
различие между этими двумя определениями играет роль.
Например, чтобы дискретизировать полосу частот от 1 до
1,1 МГц, частота выборки должна быть чуть выше, чем
200 кГц, а не 2,2 МГц. См. § 13.6.3 книги АоЕ.
это происходит, высокая частота входящего
сигнала «перегибается», создавая ложный сиг-
нал низкой частоты.
Примеры побочных сигналов
Согласно правилу Найквиста, частота выбор-
ки для дискретизации сигнала частотой 1 кГц
должна быть выше 2 кГц. Игнорирование это-
го правила порождает проблемы. На рис. 18S.7
показана осциллограмма дискретизации сиг-
нала частотой /вх= 1 кГц с частотой выборки
/ШБ = 1,2 кГц. Данная частота выборки намного
ниже минимальной необходимой и создает по-
бочный сигнал частотой 200 Гц, или^ЫБ -fBX.
Частота данного побочного сигнала ниже ча-
стоты настоящего сигнала, что делает его вред-
ным.
На третьем месте на осциллограмме на
рис. 18S.7 показан синусоидальный сигнал ча-
стотой 200 Гц, но очевидно, что это ложный
сигнал. Настоящим сигналом является верхний
синусоидальный сигнал частотой 1 кГц, кото-
рый также можно видеть в частотном спектре
выходного сигнала. То обстоятельство, что
входной сигнал захватывается даже при ис-
пользовании выборки недостаточно высокой
частоты, идет вразрез с интуицией. Ведь, ка-
залось бы, что в этом случае мы не получаем
достаточно информации, чтобы полностью
описать входной сигнал. Но точки выборки,
которые определяют побочный сигнал, долж-
ны также входить и в исходный сигнал часто-
той 1 кГц, ведь оттуда они были взяты. Таким
образом, сигнал частотой 1 кГц является дру-
гим компонентом восстановленного выходно-
го сигнала7. Дискретизация создала ложный
Мы благодарим Давида Абрамса (David Abrams) за то,
774
18S. Дополнительный материал: правила осуществления выборки; ложные сигналы при выборке
А а а д д а А А А А А д> Л А А - ^ А Л Л
^ -V v v V V V v V V к/ V V У V V V У у' V*
1 Chi Freq
Ч 1004kHz
//южный сигнал 200 Гц; f8bI5 - fBX\
-входной сигнал (1 кГц)!
Входной сигнал (1 кГц)
Восстановленный сигнал, дискретизированный
с частотой выборки 1,2 кГц
|
Отфильтрованный восстановленный аналоговый
сигнал (ложный сигнал частотой 0,2 кГ)
Частотный спектр восстановленного сигнала
(неотфи л ьтрованного)
Рис. 18S.7. Недостаточно высокая частота выборки создает побочный сигнал, частота которого слишком низкая, чтобы его мож-
но было бы удалить с помощью фильтра. (Разрешение осциллографа: 2 В/дел., 2 мс/дел.; БПФ частотного спектра — 500 Гц/дел.)
сигнал частотой 200 Гц, который, конечно же,
также отображается в частотном спектре. Этот
ложный сигнал создает большую проблему:
НЧ-фильтр не может устранить его, не удалив
при этом и настоящий сигнал8.
18S.3.1. Подробности относительно
побочных сигналов
Отфильтрованный сигнал содержит
побочную составляющую, которую
можно услышать
Если этот восстановленный сигнал пропустить
через низкочастотный фильтр так, чтобы он со-
держал настоящий сигнал, как это обычно было
бы после выхода сигнала из ЦАП, то отфильтро-
ванный сигнал также будет содержать побочную
составляющую. На рис. 18S.8 можно видеть, что
в данном случае амплитуда побочного сигнала
частотой 200 Гц больше, чем настоящего сигнала
частотой 1 кГц. Вместе эти два сигнала создают
звук низкого тона жесткого, металлического от-
тенка (вносимого частотой 1 кГц), который вряд
ли кто-либо хотел услышать.
что он подробно объяснил нам этот момент, который
вопреки своей поразительности очень редко упоминается
в литературе по дискретизации.
8 Наверное, эту плохую новость следует уточнить для
определенных специальных случаев. В частности, если по-
бочный сигнал полностью предсказуем (каким он являет-
ся при нахождении высокочастотного сигнала в известной
и узкой частотной полосе), тогда, возможно, можно ис-
пользовать узкополосный задерживающий фильтр. Также
существуют редкие случаи, когда побочные сигналы могут
оказаться полезными. В частности, несущую радиочастоту
можно специально сместить в побочный сигнал, выполняя
этим функцию, которая обычно выполняется радиочастот-
ным смесителем. См. § 13.6.3 книги АоЕ.
Обычно появление побочных составляющих
можно предотвратить, добавив НЧ-фильтр
перед входом АЦП. Этот фильтр защиты от на-
ложения спектров блокирует любую частоту,
выборку которой нельзя выполнить с достаточ-
ной частотой. В наших примерах мы не исполь-
зуем такой фильтр, потому что сейчас заинте-
ресованы в наличии эффекта побочных частот.
Но обычно на практике такой эффект создает
только проблемы.
18SA Объяснение ложных
сигналов на интуитивном
уровне
Далее мы попытаемся дать интуитивное объ-
яснение явления создания в процессе дис-
кретизации побочных сигналов с частотой
п '/выв ±/вх-
18S.4.1. Дискретизация похожа
на амплитудную модуляцию
Задачу объяснения возникновения ложных
сигналов можно облегчить, применив анало-
гию с амплитудной модуляцией9. При ампли-
тудной модуляции информационный сигнал
модулирует передающий сигнал, или сигнал
несущей частоты. Далее мы намереваемся про-
демонстрировать сходство между амплитудной
модуляцией и дискретизацией аналогового сиг-
нала. Амплитудная модуляция является самым
9 R. E. Simpson «Introductory Electronics for Scientists and
Engineers» («Введение в электронику для ученых и инже-
неров»), 2-е изд., 1987 г., с. 720-721.
78S.4. Объяснение ложных сигналов на интуитивном уровне
775
Входной сигнал
частотой 1 кГц
Восстановленный сигнал, дискретизированныйЧ
с частотой выборки 1,2 кГц Л**** ^Г^
Отфильтрованный
восстановленный аналоговый сигнал
3:
Частотный спектр
отфильтрованного ;
восстановленного сигнала
CM! 2;00V
СЬЩ 2.00 V
<
Ложный сигнал
Входной сигнал
частотой 200 Гц (fna - fBX) частотой 1 кГц
Рис. 18S.8. Влияние побочного сигнала: в данном случае второй тон создает аккорд с настоящим сигналом. В обычном случае
частотный спектр диапазона частот побочных сигналов был бы инвертирован. (Разрешение осциллографа: 2 В/дел.; БПФ ча-
стотного спектра —1,25 кГц/дел.)
старым и самым простым способом наложе-
ния информационного сигнала на сигнал несу-
щей радиочастоты. Суть этого способа состоит
в умножении несущего сигнала на информаци-
онный, или модулирующий, сигнал, как иллю-
стрируется на рис. 18S.9.
Сигнал AM = (1 + mcosu)Mt)coswct
^ ч Несущая частота
Этот член сохраняет саму несущую"^
Модулирующая частота
Рис. 18S.9. Амплитудная модуляция умножает модулирую-
щую частоту на несущую частоту
Выполнив немного тригонометрических вы-
числений, можно увидеть, что умножение в
процессе амплитудной модуляции создает сум-
му и разницу двух частот:
coso^ • cosco2= 0,5 cos(co1+co2)+ 0,5 cos(co1-co2),
или более компактно:
/боковых-полос ""/несущего ""/модулирующего*
Член «1+» в уравнении на рис. 18S.9 включен
в него по той причине, что в обычных АМ-
радиопередачах преднамеренно сохраняет-
ся несущий сигнал, чтобы облегчить работу
приемника. Это удобно, но не обязательно.
Опустив этот член уравнения, мы получим на
выходе только боковые полосы10, а несущего сиг-
нала не будет.
10 В некоторых методах амплитудной модуляции несущая
удаляется, а в других подавляется одна из боковых полос.
Оба эти подхода более энергоэффективные, но получен-
ный таким образом сигнал труднее демодулировать.
Этот результат очень похож на эффект в циф-
ровой дискретизации, который создает ложные
сигналы, частота которых является суммой и
разностью частоты входного сигнала и частоты
выборки. Здесь входной сигнал соответствует
модулирующему сигналу в амплитудной моду-
ляции, а импульсы выборки соответствуют не-
сущему сигналу. В общем, мы утверждаем, что
получаемые при дискретизации побочные сиг-
налы частотой/рЫБ ±/ж эквивалентны боковым
полосам, получаемым при амплитудной моду-
ляции, ЧаСТОТОЙ/НЕСущЕЙ ±/МоДулИРУЮ1ЦЕЙ-
Мы вскоре узнаем, что дискретизация так-
же содержит член смещения наподобие «1+»
в амплитудной модуляции, чтобы сохранить
исходный входной сигнал, восстановленный
из цифрового значения. Но будем подходить
к этому моменту постепенно.
На рис. 18S.10 показаны некоторые подробно-
сти амплитудной модуляции несущего сигнала
модулирующим. В частотном спектре резуль-
тата сумма и разность частот отображены как
боковые полосы11.
Но осциллограммы будут более убедитель-
ными, чем рисунки. Слева на рис. 18S.11 изо-
бражена осциллограмма немодулированного
несущего сигнала (что не представляет ниче-
го интересного), а справа — осциллограмма
модулированного сигнала и восстановленно-
го модулирующего сигнала (что должно быть
знакомо вам по лабораторному занятию 3L).
11 См. с. 120 ранее цитируемой книги Simpson «Introductory
Electronics for Scientists and Engineers».
776
785. Дополнительный материал: правила осуществления выборки; ложные сигналы при выборке
Период несущего
сигнала
-Ц
НЕСУЩЕГО
НЕСУЩЕГО/2
Несущий сигнал со 100%-ной
амплитудной модуляцией
Составляющие Фурье 100%-ного
модулированного несущего сигнала
Рис. 18S.10. Амплитудная модуляция создает боковые полосы с частотами по обе стороны частоты несущего сигнала. Из
книги ARRL «Handbook for Radio Amateurs» («Справочник радиолюбителя ARRL»), 17-е изд., 1993 г., с. 9-5. Авторское право на
изображения принадлежит ARRL; воспроизведено с разрешения
Немодулированный
несущий сигнал
Модулированный
несущий сигнал
Восстановленный аудиосигнал
(«огибающая несущего сигнала»)
Частотный спектр Частотный спектр модулированного несущего
несущего сигнала ; сигнала, содержащий боковые сигналы
7^ (частота которых равна частоте несущего
| сигнала плюс/минус частота модулирующего
I сигнала)
Рис. 18S.11. В амплитудной модуляции боковые сигналы по сторонам несущего сигнала похожи на образы аналого-цифрового
преобразования с частотами по сторонам частоты выборки (г*ВЬ|Б ± fBX)
Под осциллограммами сигналов показаны их
частотные спектры: слева одного несущего
сигнала, а справа — модулированного и боко-
вых сигналов. Частота боковых сигналов со-
ставляет/НЕСУЩЕГ0 ±/СИГНАЛА' где в данном случае
«СИГНАЛ» означает модулирующий аудио-
сигнал.
Модуляция на рис. 18S.11 отличается от моду-
ляции на рис. 18S.10 тем, что в ней модулирую-
щий сигнал содержит не одну частоту, а (что
более типично) является набором частот, со-
ставляющих речевой сигнал.
Далее мы покажем несколько примеров умно-
жения сигналов наподобие амплитудной мо-
дуляции, выполненных в лаборатории с по-
мощью микросхемы аналогового умножителя.
Цель этого исследования состоит в том, чтобы
попытаться убедить вас, что дискретизация
очень похожа на процесс умножения и поэтому
не более загадочна, чем амплитудная модуля-
ция радиосигналов. Последний процесс должен
быть вам уже хорошо знаком.
18S.4.2. Частотный спектр синусо-
идального сигнала по сравнению
с последовательностью импульсов
В более конкретных терминах дискретизация
представляет собой умножение входного сигна-
ла на последовательность коротких импульсов,
следующих с частотой выборки12. Поэтому будет
полезным вспомнить, как выглядит частотный
спектр такой последовательности импульсов.
Синусоидальный сигнал по сравнению
с последовательностью импульсов
Частотный спектр синусоидального сигнала
(одной частоты) должен быть вам хорошо зна-
ком: одиночный всплеск. Слева на рис. 18S.12
12 Для более близкой аналогии с амплитудной модуляцией
этот момент, наверное, следовало бы изложить в обратном
порядке: дискретизация подобна умножению последова-
тельности коротких импульсов (роль которых подобна
несущему сигналу AM) модулирующим входным анало-
говым сигналом. Мы изложили это в другом виде потому,
что обычно рассматриваем дискретизацию как процесс
обработки входного сигнала, а не последовательности им-
пульсов выборки. Но, конечно же, оба эти понятия экви-
валентны.
785.4. Объяснение ложных сигналов на интуитивном уровне
777
1кИг Е
Последовательность
импульсов, 1 кГЦ
Частотный
спектр
Частотный спектр
последовательности
импульсов
Частотные спектры:
синусоидального сигнала...
1k 2k 3k
..и последовательности импульсов
Рис. 18S.12. Сравнение частотных спектров: синусоидального сигнала частотой 1 кГц и последовательности коротких им-
пульсов частотой 1 кГц. (Разрешение осциллографа: 5 В/дел.; БПФ частотного спектра — 1,25 кГц/дел.; скорость развертки:
левая осциллограмма — 1 мс/дел., правая — 4 мс/дел.)
показаны осциллограммы синусоидального
сигнала частотой 1 кГц (вверху) и его частотно-
го спектра (внизу).
А справа на рис. 18S.12 изображены осцилло-
граммы последовательности коротких (дли-
тельностью 20 мкс) импульсов с частотой 1 кГц
(вверху) и его частотного спектра (внизу).
(Скорость развертки осциллограммы последо-
вательности импульсов в четыре раза меньше,
чем для осциллограммы синусоидального сиг-
нала.) В частотном спектре последовательности
мы опять видим всплеск на частоте 1 кГц, как и
в случае с синусоидальным сигналом. Но кроме
этого всплеска спектр содержит дополнитель-
ные компоненты на частоте 2,3 кГц и так далее
до бесконечности. Иными словами, всплески
повторяются по частотам, кратным частоте по-
следовательности импульсов.
Эффект умножения двух сигналов
Синусоидальный на синусоидальный (как в
AM). Вспомним, что при умножении двух сину-
соидальных сигналов получаем два новых сиг-
нала, частоты которых равны сумме и разности
частот исходных сигналов. Это иллюстрирует
осциллограмма на рис. 18S.13. В данном простом
случае имеем /г = 1 кГц и/2 = 4 кГц. Разность и
сумма этих частот будет 3 и 5 кГц соответствен-
но. При этом ни один из исходных сигналов в
конечный сигнал не попадает.
Синусоидальный на синусоидальный со
смещением. Если, подобно предыдущему
примеру, умножить синусоидальный сигнал с
частотой 1 кГц на другой синусоидальный сиг-
нал с частотой 4 кГц, но, в отличие от преды-
дущего примера, добавить ко второму сигналу
постоянную составляющую, мы также получим
сумму и разность частот этих двух сигналов.
Но кроме этих двух новых сигналов мы также
получим и исходный сигнал с частотой 1 кГц.
Соответствующая осциллограмма показа-
на на рис. 18S.14. Учитывая, что нашей целью
ft: 1кГц я
Произведение
Частотный *
спектр
произведения
аш iv.uv
СМ 10 0 V
Разность (3 кГц)
Сумма (5 кГц)
Рис. 18S.13. Произведение двух синусоидальных сигналов:
сумма и разность. (Разрешение осциллографа: 10 В/дел.;
БПФ частотного спектра —1,25 кГц/дел.)
£4 кГц
•0 В
Произведение
Частотный
спектр
произведения
| Разность (3 кГц) 8S;
fj Сумма (5 кГц)
(1 кОм)
остается
Рис. 18S.14 Умножение двух синусоидальных сигналов,
в один из которых добавлено постоянное смещение, дает
сумму и разность, а также и исходный сигнал. (Разрешение
осциллографа: 10 В/дел., 1 мс/дел.; БПФ частотного спек-
тра —1,25 кГц/дел.)
778
785. Дополнительный материал: правила осуществления выборки; ложные сигналы при выборке
является восстановление исходного дискрети-
зированного аналогового сигнала, похоже, что
это обстоятельство может быть полезным, не
так ли?
Показанный на рис. 18S.14 результат действи-
тельно напоминает то, что мы получаем, или
хотим получить, при дискретизации. Что нам
требуется, так это исходный сигнал; сигналы с
частотами, равными сумме и разности частот
исходных сигналов, являются побочными сиг-
налами, которые мы планируем удалить
13
Синусоидальный сигнал, умноженный
на последовательность импульсов
(более похоже на дискретизацию)
Мы уже показали, что в частотной области по-
следовательность импульсов выглядит подоб-
но синусоидальным сигналам на частотах у^,
2/gx, 3/нх и т. д. Поэтому вас не должно удивлять
то, что спектр произведения синусоидального
сигнала на последовательность импульсов вы-
глядит подобно бесконечно повторяющемуся
произведению синусоидального сигнала на
синусоидальный сигнал, т. е. повторяющиеся
разности и суммы. А смещение, прилагаемое к
последовательности импульсов, обеспечивает
добавление в спектр исходного синусоидально-
го сигнала с частотой 1 кГц.
То, что произведение содержит исходный сину-
соидальный сигнал, является для нас хорошей
новостью. Ведь при дискретизации аналогово-
го сигнала восстановление этого сигнала вы-
бором его среди всех побочных сигналов явля-
ется нашей единственной целью. А побочные
сигналы можно убрать с помощью хорошего
НЧ-фильтра.
Подведем итоги: в аналого-цифровой дискрети-
зации последовательность импульсов выборки
играет роль несущего сигнала в амплитудной
модуляции. Эти импульсы (которые имеют по-
стоянную амплитуду) модулируются входным
аналоговым сигналом, который играет роль
модулирующего сигнала в процессе амплитуд-
ной модуляции.
Повторение образов на частотах, кратных ча-
стоте выборки (явление, которое отсутствует
при амплитудной модуляции), происходит по
той причине, что импульсы выборки являются
не синусоидальным сигналом, а узкими вспле-
сками, содержащими множество составляющих
Входной ;;
сигнал pjj
частотой 1 кГц |; V
Последовательность <
импульсов
частотой 4 кГц
Произведение ш
Частотный
спектр
произведения
'СУМ/VLl
4 kOm
20.0 dli
10 0 V
'BX 'РАЗИ1
1 кГц 4 кОм
-1 kOm ♦ 1 kOm fPA3u г fPA3» г
ЗкОм 5кОм 8kOm 8 kOm
- 1 kOm + 1 kOm
7kOm 9kOm
Рис. 18S.15. Произведение синусоидального сигнала и последовательности импульсов, содержащей постоянную состав-
ляющую, состоит из бесконечного числа сумм и разностей частот, а также содержит исходный синусоидальный сигнал.
(Разрешение осциллографа: 2 В/дел., 1 мс/дел.; БПФ частотного спектра —1,25 кГц/дел.)
ряда Фурье, которые и повторяются на часто-
13 Мы надеемся, что вас не смущает это отличие от ампли-
тудной модуляции. Там смещение модулирующего сигнала тах^ЫБ, 2/ШБ, 3/ШБ И Т. Д.
сохраняет несущий сигнал, а здесь модулирующий сигнал
сохраняется благодаря смещению последовательности им-
пульсов, подобной несущему сигналу. Мы утверждаем, что
дискретизация похожа на амплитудную модуляцию, а не
то, что эти два процесса идентичны.
Те из вас, кто обладает математическими по-
знаниями, могут узнать в этом явлении про-
сто свертку спектров (в частотной области)
18S.4. Объяснение ложных сигналов на интуитивном уровне
779
произведения дискретизированного сигнала с
периодической дельта-функцией (во времен-
ной области), что является следствием теоремы
о свертке.
18SA3. Ключевой момент:
дискретизированные данные
выглядят во многом подобно
перемноженным данным
На рис. 18S.16 изображены две осциллограм-
мы, подтверждающие наше высказывание, что
дискретизация сигнала похожа на его умноже-
ние на последовательность импульсов. Здесь
дискретизированный сигнал был восстановлен
посредством ЦАП.
Умножение на
последовательность импульсов
Входной сигнал
с частотой 1 кГц а]
Последовательность \
импульсов ri
с частотой 4 кГц
Произведение п
Частотный
спектр
произведения
'вх 'рл
1кГц4i
- 1кОм+1кОм
3 кОм 5 кОм fD.
'сумм_1
4кОм
8 кОм
+1 кОм
9к0м
8к0м
-1 кОм
7к0м
ла, отличается от умноженных сигналов, которые
мы только рассматривали, в одном отношении.
В частности, тогда как восстановленный сигнал
сохраняет непрерывность между точками вы-
борки, умноженный сигнал (как на рис. 18S.16)
такой непрерывности не имеет, а возвращается
к нулю между умножающими импульсами.
Сохранение непрерывности восстановленного
сигнала, как это происходит при обычном вос-
становлении аналогового сигнала из дискрети-
зированного представления, вызывает эффект
низкочастотной фильтрации восстановленного
сигнала. Этот эффект можно наблюдать в ча-
стотном спектре восстановленного аналогового
сигнала: амплитуды побочных сигналов умень-
шаются с ростом частоты, тогда как в частот-
ном спектре умноженного сигнала такого спада
не наблюдается.
Дискретизация
sar^e 2f sar-pie
Входной сигнал
с частотой
Восстановленный
сигнал с ЦАП
Частотный спектр
восстановленного
сигнала
mm I 20 о 4е
Входной | | | |
СИГНаЛ Льгв^вьгв-2^ 2fmB
с частотой^ fBx -fBx -fBx
1 кГц з кОмб к0м7 кОм 9 кОм
Рис. 18S.1 б. Дискретизированный синусоидальный сигнал (частота 1 кГц, частота выборки 4 кГц) в сравнении с синусоидаль-
ным сигналом с частотой 1 кГц, умноженным на последовательность импульсов с частотой 4 кГц. (Разрешение осциллографа:
2 В/дел., 1 мс/дел.; БПФ частотного спектра — 1,25 кГц/дел.)
Видно, что частотные спектры этих двух про-
цессов совпадают. В частности, частотный
спектр аналогового сигнала, восстановленного
из дискретизированного исходного сигнала, со-
впадает с частотным спектром произведения
синусоидального сигнала и последовательности
импульсов. Это именно тот результат, которого
мы добивались в данной главе.
18SA4. Уточнение или коррекция
утверждения
Аналоговый сигнал, восстановленный из диск-
ретизированного исходного аналогового сигна-
На рис. 18S.17 иллюстрируется аргумент в под-
держку этого различия. Здесь сравниваются ча-
стотные спектры последовательности импуль-
сов и прямоугольного сигнала. Безусловно,
прямоугольный сигнал не то же самое, что и не-
прерывный ступенчатый сигнал, выдаваемый
ЦАП, но он похож на этот сигнал больше, чем
на выходную последовательность импульсов.
Это всего лишь попытка придать правдоподоб-
ность наблюдаемому спаду амплитуды частот-
ных компонентов выходного сигнала ЦАП14.
14 Мы благодарим нашего коллегу Джейсона Галличчио
(Jason Gallicchio) за то, что он предложил этот эвристи-
ческий аргумент, хотя мы не можем винить его, если этот
аргумент покажется вам притянутым за уши.
780
18S. Дополнительный материал: правила осуществления выборки; ложные сигналы при выборке
Частотный спектр
последовательности импульсов
Последовательность u
импульсов
Частотный спектр
последовательности о
импульсов
i^-L
Частотный спектр
последовательности импульсов
Прямоугольный сигнал
(похожий на непрерывный
выходной сигнал ЦАП,
хотя не аналогичный)
Частотный спектр
прямоугольного сигнала
Рис. 18S.17. Иллюстрация эвристической аргументации в поддержку спада амплитуды побочных сигналов в восстановлен-
ном дискретизированном сигнале. (Разрешение осциллографа: левая осциллограмма — 2 В/дел., 1 мс/дел.; БПФ частотного
спектра —1,25 кГц/дел.; правая осциллограмма — то же самое, за исключением 2 В/дел.)
Чтобы внести поправку на этот спад (который
воздействует как на сигналы в интересующей
нас частотной полосе, так и на подлежащие
удалению побочные сигналы), подключенный
на выход ЦАП фильтр должен обеспечивать
небольшое высокочастотное усиление в ча-
стотном диапазоне, в котором нужно внести та-
кую поправку. Выходные фильтры цифровых
аудиоустройств в действительности обеспечи-
вают такое усиление.
18W. Примеры с решениями: аналоговые
и цифровые преобразования
18W.1. Аналого-цифровые
преобразования
18W.1.1. Погрешность и величина
кванта
Если диапазон напряжений разделить на п
квантов, обозначив каждый из них цифровым
значением, то это значение будет иметь точ-
ность до 1/2 размера кванта, или на цифровом
жаргоне, до 1/2 младшего бита. Возможно, что
это вам и так очевидно. Но если нет, то следую-
щий пример поможет вам разобраться с дан-
ным понятием.
Пример
Сколько битов требуется для выражения числа
с точностью до 0,01%?
4,412
можем допустить кванты шириной в две части
из 10 000, или 1/5000. Используя 12 разрядов,
мы получим 4 К кванта (4096), что даст нам по-
грешность в 1/8 К, или 0,012%. Такая погреш-
ность не удовлетворяет нашим требованиям.
Добавив еще один разряд, мы сократим эту по-
грешность вдвое до 0,006%, что более чем удо-
влетворяет нашему минимуму. Таким образом,
выбираем преобразователь с 13 разрядами.
18W.1.2. Применение АЦП
для цифрового аудио
Разработчики первых компакт-дисков создали
стандарт дискретизации, который до сих пор
позволяет получить звук достаточно хорошего
качества: 16-разрядное квантование с частотой
выборки 44 кГц (что приблизительно на 10%
выше теоретического минимума для дискре-
тизации составляющей аудиосигнала частотой
4,4115-
У/У У
4,4105-
Это самое близкое к настоящему значение Величина погрешности равна 1/2
В» >- с точностью до 4 разрядов I {величины кванта} => величина кванта
) или с погрешностью менее ±0,5 мВ [ ртп 2/10,0О0 « 1/5,000 * 1.4Ком « 1/2«
4,410
]■
Рис. 18W.1. Что означает погрешность в 0,01 %: погрешность полученного значения величиной 4,411 В может составлять ±0,5 В
Решение
В числовом представлении процентное значе-
ние 0,01% означает одну часть из 10 000. Если
преобразователь может работать с диапазоном
напряжений, например, от 0 до 5 В, это озна-
чает, что ожидаемая погрешность получен-
ного числового значения, например, 4,411 В,
будет не больше чем 0,5 мВ (т. е. 1 часть из
10 000 частей полного диапазона измерений:
0,5 мВ/5 В = 0,0001, или 0,01%).
Какую разрядность должен иметь преобразо-
ватель, чтобы обеспечить такую точность? Мы
20 кГц). Подсчитаем, какой объем данных мож-
но сохранить на стандартном компакт-диске1.
Пример
Сколько байтов нужно сохранить на аудио-
компакт-диске длительностью в 74 минуты?
1 Согласно легенде длительность звучания компакт-
диска — 74 минуты была выбрана компанией Sony, чтобы
осуществить запись Девятой симфонии Бетховена. Это до-
вольно необычно, учитывая наиболее вероятный состав
слушателей большинства компакт-дисков. Более подроб-
ную информацию относительно этого аспекта см. на с. 265
книги Ken С. Pohlman «Principles of Digital Audio» («Прин-
ципы цифрового аудио»), 3-е изд., 1995 г.
782
18W. Примеры с решениями: аналоговые и цифровые преобразования
Решение
Для каждой выборки требуются 2 байта на ка-
нал; для стерео — 4 байта. Следовательно,
Число байтов = 2 байта/канал • 2 канала/вы-
борку • 44 К выборок/с • 74 мин • 60 с/мин »
* 780 млн байт « 745 М, или 745 Мб.
Это громадный объем данных. В действитель-
ности же компакт-диск содержит приблизи-
тельно втрое больше байтов, причем дополни-
тельные байты используются для коррекции
ошибок и для других служебных целей2.
18W.1.3. Более интересное
приложение с учетом шума
и с применением фильтра
Преобразование зашумленного сигнала
Предположим, что вам поставлена задача опре-
делить характеристики АЦП для передачи циф-
рового аудиосигнала. Колебания амплитуды
аудиосигнала необходимо различать прибли-
зительно до уровня 50 дБ (-50 дБ относительно
полной шкалы, или -50 дБпш, что является на-
много более низким разрешением, чем разре-
шение по стандарту компакт-дисков), но нужно
полностью воспроизводить стандартный диа-
пазон аудиочастот от 10 Гц до 20 кГц.
Пример
Какая разрядность требуется, чтобы преобра-
зовать аудиосигнал с разницей в 50 дБ между
самым громким (наивысшая амплитуда) и са-
мым низким (наименьшая амплитуда) звуча-
нием?
Решение
Мы хотим, чтобы самый тихий звук (и величи-
на самого младшего бита) был на 50 дБ ниже
полной шкалы звука. Мы можем подставить
это число в определение децибела:
МБ/полная шкала = -50 дБ;
= 20loglOA2/A1;
Таким образом, нам требуется достаточное ко-
личество разрядов, чтобы получить прибли-
зительно 315 квантов. Восемь разрядов позво-
ляют получить 256 квантов, что недостаточно.
Поэтому будем использовать девять разрядов,
что позволит нам получить 512 квантов.
Такой же результат можно получить, обойдя
определение децибела. В частности, можно
учесть то обстоятельство, что каждый дополни-
тельный разряд уменьшает размер кванта напо-
ловину, или на 6 дБ. Таким образом, при таком
подходе для 50 дБ нужно будет чуть больше
восьми разрядов, а девяти будет вполне доста-
точно.
Простой случай без шума
Предположим, что сигнал достаточно чистый:
ничего значительного выше частоты 20 кГц.
Задача
Какую частоту выборки следует задать?
Решение
Частота выборки должна быть достаточной
для захвата самой высокой интересующей нас
частоты, которой в данном случае является
частота 20 кГц. Пользователь, не особо ис-
кушенный в правиле Найквиста, может ска-
зать, что для того, чтобы брать две выборки
за период входного сигнала, частота выборки
должна быть 40 кГц. Но это будет неправиль-
ный ответ.
При выборе частоты выборки необходимо учи-
тывать ограниченную крутизну любого филь-
тра, перед которым будет стоять задача про-
пустить самую высокую частоту, ослабляя при
этом частоту первого образа. На рис. 18W.2
изображен график такой фильтрации.
Самый первый ложный сигнал
'выв" 'вх
Амплитуда
., = -50/20; kjkx = 10-(5/2) = 1/316. Mqkc.
f***+
-*.f
24 кОм: Макс. /L20 кГц
2 См. с. 265 ранее цитируемой книги «Principles of Digital
Audio».
Рис. 18W.2. Крутизна спада частотной характеристики филь-
тра определяет, насколько близким к наивысшей входной
частоте может быть самый первый ложный сигнал
18W.1. Аналого-цифровые преобразования
783
Для этой задачи мы возьмем фильтр, который
будем использовать на лабораторном занятии
(если у вас не было возможности работать с
ним на лабораторном занятии 12L). Как видно
из графика на рис. 18W.3, у него действительно
крутой спад частотной характеристики.
Частотная характеристика
фильтра МАХ294
20-
МАКС. Подставляя в эту формулу наши данные,
получим:/ВЫБ -/№МАКС = 24 кГц, а/ВЫБ = 24 кГц +
+ /вх-макс = 44 кГЧ- То' что наши Расчеты ока"
зались в районе частоты выборки для компакт-
дисков, не должно быть удивительным, но ока-
зались они там с такой точностью случайно.
Обратите внимание на то, что на графике ча-
стотной характеристики фильтра МАХ294 по-
казана частота^ = 1 кГц, но ее можно регули-
ровать в диапазоне от 1 Гц до 25 кГц. График
можно масштабировать до любого значения
-во-:
-80.
-100
0 12 3 4 5
Частота входного сигнала (кГц)
Рис. 18W.3. Частотная характеристика фильтра МАХ294
Фильтр должен ослаблять самый первый лож-
ный сигнал до величины, меньшей чем один
младший бит. На графике частотной характе-
ристики фильтра на рис. 18W.3 можно видеть
ослабление сигнала величиной -60 дБ на ча-
стоте приблизительно на 20% выше частоты,
на которой начинается спад характеристики
(частота перегиба, грубо /3дЪ). Этого будет до-
статочно (и мы, наверное, не сможем получить
более точный ответ по графику спада). Поэтому
необходимо, чтобы частота самого первого
ложного сигнала была на 20% выше самой вы-
сокой интересующей нас частоты. При этом
условии частота самого первого побочного сиг-
нала будет 24 кГц.
Какая частота выборки позволит нам получить
такую частоту самого первого ложного сиг-
нала? Вспомним правило, что частота самого
первого побочного сигнала составляет/^ -fBX_
Более сложный случай с зашумлением
Теперь предположим, что на вход вашего пре-
образователя подается не чистый аудиосиг-
нал, а чрезвычайно зашумленный, как показа-
но в осциллограмме на рис. 18W.4.
Возможно, вы вспомните, что такая же осцил-
лограмма во временной и частотной областях
аудиосигнала была, когда мы передавали и при-
нимали сигнал в проекте по инфракрасной свя-
зи на лабораторном занятии 13L. Данный сиг-
нал зашумлен остатками несущей с частотой
30 кГц.
Предположим, что, как и прежде, нашей целью
является преобразование этого сигнала и других
подобных ему сигналов в цифровую форму для
передачи по проводам на дальнее расстояние.
Задача
Что будет, если не использовать фильтр для за-
щиты от наложения спектров?
Если взять частоту выборки такую же, как в
предыдущем случае для незашумленного сигна-
ла, то как будет выглядеть или звучать помеха
О Гц
50 кГц
Временная область ,
(развертка осциллографа)!
График
частотного спектра
Колебание амплитуды составляет
приблизительно 50 дБ
20 кГц (максимальная
требуемая нам частота)
Рис. 18W.4. Частотный спектр зашумленного аудиосигнала
j 1 мс/дел.
5 кГц/дел.
Несущий сигнал
частотой 30 кГц
784
18W. Примеры с решениями: аналоговые и цифровые преобразования
от несущего сигнала с частотой 30 кГц после
преобразования цифрового сигнала обратно
в аналоговый? Что будет с другим большим
всплеском шума, находящимся в частотном
спектре выше частоты несущего сигнала?
Решение
Мы знаем, что вы бы не забыли установить
фильтр защиты от наложения спектров на вхо-
де в АЦП, но мы забыли. Мы решили в пре-
дыдущем примере, что для незашумленного
сигнала (или при наличии фильтра защиты от
наложения спектров) частота выборки должна
быть 44 кГц. На осциллограмме на рис. 18W.4
несущий сигнал частотой 30 кГц выглядит, как
большой пик чуть справа от центра графика ча-
стотного спектра. В результате частота самого
первого ложного сигнала будет/шв -fBX_MAKC =
= 44 кГц - 30 кГц = 14 кГц. Этот сигнал будет
воспроизводиться, как ноющий звук высокой
частоты. А пик меньшей амплитуды на часто-
те приблизительно 40 кГц будет создавать еще
более проблемный побочный сигнал с частотой
4 кГц.
Вывод: используйте фильтр для защиты от на-
ложения спектров.
18W.2. Преобразователь
логических уровней
Это, по сути, не пример с ответом, поскольку
задача преобразования уровней напряжения
настолько трудна, что здесь нельзя ожидать
такого элегантного решения. Скорее это воз-
можность восхищаться искусным простым ди-
зайном.
Может случиться, что устройствам с разными
напряжениями питания нужно взаимодейство-
вать друг с другом. В главе 18N мы уже рассмо-
трели проблему сопряжения выходных сигна-
лов микросхем одного типа с входами микро-
схем другого. Например, мы узнали, что микро-
схемы 74НСТхх с напряжением питания 5 В
могут успешно принимать сигналы микросхем
74НСхх с напряжением питания 3,3 В. А вот
3V
5V
Вход:
Высокий (3 I
5
8SS138
QOFF,
3V
5V
т
Выход:
Высокий (3 В)
3V
5V
ни
Вход:
Низкий (О В)
BSS138
QON
3V
Выход:
Низкий (О В) Е£>
Выход:
Высокий (5 В)
Вход:
Высокий (5 В)
Выход:
Низкий (0 В)
Вход:
<2£] Низкий (О В)
Два простых случая: наличие высокого уровня на любой
из сторон создает высокий уровень на другой
Низкий уровень на стороне устройства с питанием 3 В
включает транзистор <?, в результате чего на стороне
устройства с питанием 5 В устанавливается низкий уровень
Низкий уровень на стороне устройства с питанием 5 В
дает такой же результат, но реализация более интересная.
В частности, транзистор Q включается не подачей сигнала
высокого уровня на его затвор, но с помощью неявного диода
подложки стока, устанавливая низкий уровень на его стоке
и истоке
Рис. 18W.5. Двунаправленный преобразователь логических уровней компании Philips (источник: примечание по примене-
нию AN97055 компании Philips/NXP)
18W.2. Преобразователь логических уровней
785
микросхемы с напряжением питания 3,3 В
могут принимать сигналы микросхем с напря-
жением питания 5 В только в том случае, если
такая возможность была предусмотрена при их
разработке, что было сделано в случае многих
устройств. Но настоящая задача слегка иного
рода.
Задача
Разработайте двунаправленный преобразова-
тель уровней напряжения, который позволит
обмениваться сигналами по одной линии в лю-
бом направлении между устройствами с разны-
ми напряжениями питания. Требование двуна-
правленное™ является тем моментом, который
делает эту задачу нестандартной.
Такие двунаправленные линии не особо рас-
пространены, но они используются как мини-
мум в интерфейсе 12С, который вкратце рассма-
тривается в главе 24N. Но даже если в настоя-
щее время вам не требуется такая возможность,
то вы получите удовольствие, оценив находчи-
вость реализации этого интерфейса.
Решение
Решение состоит в сопряжении цифровых
устройств с разными напряжениями питания
с помощью одного МОП-транзистора и пары
резисторов. Подробно это решение рассматри-
вается в примечании по применению AN97055
компании Philips3, а на рис. 18W.5 приводятся
его схемы с кратким описанием работы.
3 Данное примечание по применению можно загрузить с
веб-сайта компании Adafruit: http://www.adafruit.com/
datasheets/an97055.pdf. Компании Adafruit и Sparkfun
были одними из первых, которые реализовали на практи-
ке идею этого интерфейса.
19L Лабораторное занятие по цифровым
схемам
Содержание
19L.L Цифровой проект
19L.1.1. Измеритель емкости
19L.1.2. Измеритель скорости реакции
19L.1.3. Генератор синусоидальных колебаний
19L.1.4. Четырехканальный мультиплексор для осциллографа
786
786
787
788
789
19L1. Цифровой проект
Это лабораторное занятие отличается от других
тем, что мы хотим, чтобы на нем вы, подобно
лабораторному занятию 13, получили удоволь-
ствие от возможности собрать какую-либо схе-
му, разработанную самостоятельно. Но, в отли-
чие от лабораторного занятия 13, для данного
лабораторного занятия не требуется никакой
новой информации, а используется информа-
ция, которую мы рассмотрели в части IV. Далее
приводится описание нескольких задач, реше-
ние которых должно быть вам под силу. Мы
хотим, чтобы вы изложили в письменном виде
решение и собрали разработанную вами схему.
В двух рассмотренных схемах используются
дисплеи из лабораторного занятия 17L, что
должно сэкономить вам некоторое время.
19L1.1. Измеритель емкости
Данная схема является небольшим изменением
схемы измерителя периода, которую мы рас-
смотрели в качестве упражнения в конце лабо-
раторного занятия 16L. Как вам должно быть
известно, период выходного сигнала генера-
тора колебаний 555 пропорционален произве-
дению RC. Если поддерживать значение R по-
стоянным, то любое значение С можно неявно
вычислить по периоду выходного сигнала ге-
нератора колебаний (или по полупериоду, если
вам так легче).
Схема должна работать постоянно, отображая
полученный результат на ЖКД, который был в
схеме счетчика на лабораторном занятии 16L.
Если вместо адресных линий задействовать
линии данных, то можно воспользоваться про-
зрачной защелкой, встроенной в этот дисплей
данных. Значение емкости можно отображать
в каких-либо удобных единицах, например со-
тых микрофарады. Вы можете сами выбрать
единицы измерения, но при этом не исполь-
зуйте какие-либо странные единицы, которые
могут сбивать с толку пользователя вашего
прибора. Сделав частоту выходного сигнала
генератора колебаний 555 настраиваемой в
широком диапазоне значений, вы сможете от-
калибровать схему измерителя емкости таким
образом, что, например, он будет отображать
емкость 0,1 мкФ как 0100.
В разделе 15L5.3 приводится схема цифрового
сдвоенного (т. е. с двумя выходами) одновибра-
тора, которая может пригодиться вам для фик-
сации результата измерений на дисплее.
Если задействовать линии адресов (что позво-
лит отображать четыре разряда, а не два), то вам
нужно будет добавить регистры, в которых бу-
дет сохраняться значение счетчика для вывода
на дисплей. Таким образом, регистры-защелки
позволят вам уменьшить объем работы.
Мы рекомендуем монтировать схему на от-
дельной макетной плате, а не загромождать
плату, на которой вы будете собирать свой
19LL Цифровой проект
787
компьютер. Мы также рекомендуем не исполь-
зовать счетчик из собираемого вами компью-
тера, поскольку он работает в шестнадцатерич-
ном формате. Вместо него будет лучше взять
два счетчика ДДК (двоично-десятичный код:
от 0 до 9). Например, синхронный 4-разрядный
счетчик 74НС160, который во многом такой же,
как и счетчик 74НС163, с которым мы позна-
комились в разделе 16W.1, с тем исключением,
что его конечное состояние равно 9, а не Fh.
Двухэлементный счетчик 74НС390 тоже типа
ДДК, но со сквозным переносом. Поскольку ре-
зультат у нас двухразрядный, то одного счетчи-
ка 74НС390 будет достаточно для наших целей.
(Цоколевки для этих счетчиков приводятся в
Приложении К.)
Задачи и тактирование
Несомненно, вы можете видеть, что для требуе-
мой нам постоянной работы измерителя, схема
должна правильно синхронизировать события
всех компонентов. В частности:
♦ Запускать и останавливать счетчик по выход-
ному сигналу генератора колебаний 555. Для
этой цели можно использовать сигнал вход-
ного переноса для генератора 74НС160; а для
счетчика со сквозным переносом (74НС390)
нужно будет пропускать сигнал тактирова-
ния через логический вентиль.
♦ После остановки счетчика, его содержимое
фиксируется в триггере-защелке линий дан-
ных порта дисплея. Этот порт, в отличие от 16
линий адреса, содержит прозрачную триггер-
защелку, о которой вы можете не знать, по-
скольку до сих пор он работал в прозрачном
режиме. По умолчанию на вывод сигнала раз-
решения защелки LATCH_EN* подается низ-
кий уровень (через резистор номиналом 100
кОм). Сигналы вашей логики могут с легко-
стью пересилить этот уровень по умолчанию.
♦ Наконец, счетчик нужно обнулить, чтобы
подготовить его для следующего цикла. Как
синхронный счетчик 74НС160, так и асин-
хронный счетчик 74НС390 оснащен функци-
ей асинхронного сброса.
♦ Мы рекомендуем в качестве источника сиг-
нала тактирования для счетчиков использо-
вать кварцевый генератор частотой (такой
генератор с частотой 11 МГц1 содержится
1 Строго говоря, частота этого кварцевого генератора
равна 11,059 МГц.
в комплекте деталей). Но если у вас мало
времени, то кварцевый генератор можно за-
менить ТТЛ-генератором сигналов.
19L1.2. Измеритель скорости
реакции
Эту схему можно реализовать двумя способа-
ми: или на счетчиках, логических вентилях и
триггерах, или же на счетчиках и микросхеме
ПМЛ. Далее приводятся требуемые характери-
стики схемы:
♦ Кнопка А запускает процесс тактирования, а
кнопка Б останавливает его. Нажатие кноп-
ки А одним участником также включает зе-
леный светодиод (для которого нужно обе-
спечить ток в 3 мА при напряжении питании
2 В), на что другой участник должен отреаги-
ровать нажатием кнопки Б.
• Если требуется защита от дребезга, кнопоч-
ные переключатели должны быть однопо-
люсными двухпозиционными; в противном
случае достаточно однополюсных однопо-
зиционных кнопочных переключателей.
♦ Вам дается генератор колебаний с уровнями
ТТЛ и частотой 11 МГц, что нужно принять
во внимание в процессе проектирования схе-
мы на бумаге. Но при сборке схемы можно
сэкономить время, просто взяв сигнал такти-
рования с уровнями ТТЛ от генератора коле-
баний и используя его для создания требуе-
мого сигнала с частотой 1 кГц.
♦ Разрешение в 1 мс будет достаточным для ва-
шего таймера.
♦ Применяйте защиту от дребезга контактов
только в тех случаях, когда это необходимо.
♦ Для инициализации устройства используй-
те третью кнопку В. При нажатии кнопки В
устройство очищает все дисплеи и ожидает
следующего цикла измерений.
♦ Скорость реакции можно измерить одним из
следующих двух способов:
• использовать 16-разрядный счетчик, кото-
рый вы собрали на лабораторном занятии
16L. Это будет более быстрый способ;
• если вы хотите выбрать не шестнадцатерич-
ный, а десятичный дисплей, то потребуется
12-разрядный счетчик, составленный из
ДДК-счетчиков 74НС160 с синхронной за-
грузкой, входным и выходным переносами,
а также с асинхронным сбросом.
788
19L Лабораторное занятие по цифровым схемам
♦ Время реакции можно отображать на вашем
ЖКД, или, если вы предпочитаете автоном-
ную схему, то можно установить шестнад-
цатеричные светодиодные индикаторы TIL-
311. (В этом приложении индикаторы будут
отображать только десятичные значения.)
♦ Если участник Б нажмет свою кнопку до того,
как участник А нажмет свою (преднамеренно
или непреднамеренно), включаем красный
светодиод ошибки.
♦ При переполнении счетчика включаем жел-
тый светодиод для индикации этого события.
Решение I
Собираем схему измерителя реакции на тригге-
рах и логических вентилях.
Сборку рекомендуется выполнять на отдель-
ной макетной плате, чтобы при необходимости
ею можно было пользоваться в будущем.
Решение II
Реализуем логику управления на микросхеме
ПМЛ.
В качестве альтернативы вам может быть
больше по душе реализовать логику управле-
ния (триггеры и вентили, но не счетчики) на
микросхеме ПМЛ. Это позволило бы вам по-
лучить немного опыта работы в Verilog в об-
ласти, в которой вы еще не работали, а именно
использовать отдельные триггеры.
Далее приводится список рекомендуемых де-
талей:
♦ Микросхема ПМЛ с комбинационной и пос-
ледовательностной логикой. Возьмите мик-
росхему ХС9572 (или микросхему XC9572XL
с напряжением питания 3 В), которую вы ис-
пользовали для реализации связывающей
логики. Данная микросхема ПМЛ содержит
72 триггера, каждый из которых оснащен
своим программируемым сигналом такти-
рования, а также функциями установки и
сброса.
♦ Реализованная на микросхеме ПМЛ логика
управляет счетчиком. Файл Verilog для циф-
ровых лабораторных занятий с цоколевкой и
тестовыми наборами можно загрузить с веб-
сайта этой книги. Вам нужно будет создать
только два логических уравнения.
♦ Эта схема в одном отношении более про-
стая, чем измеритель емкости: она работает
циклами, и в конце каждого цикла счетчик
останавливается, позволяя увидеть конеч-
ное значение счета, без необходимости при-
лагать усилия для того, чтобы захватить и
удерживать содержимое счетчика в другом
регистре.
19L1.3. Генератор синусоидальных
колебаний
Чтобы создать синусоидальный сигнал на осно-
ве прямоугольного сигнала, можно использо-
вать стратегию, изложенную в конце лабора-
торного занятия 12L. В частности, пропустить
прямоугольный сигнал через низкочастотный
фильтр с очень крутым спадом, чтобы полу-
чить на выходе только основную составляю-
щую. Чтобы проектирование вашей схемы не
было слишком легким, включите в нее систему
фазовой автоподстройки частоты для генери-
рования сигнала тактирования для фильтра
МАХ294. Частота сигнала тактирования долж-
на быть кратна частоте входного прямоуголь-
ного сигнала.
Далее приводится список рекомендуемых де-
талей:
♦ Фильтр с коммутируемым конденсато-
ром. Микросхема МАХ294 (8-полюсный,
эллиптический). Частота /3дЪ этого фильтра
составляет 1/100 частоты сигнала тактиро-
вания, подаваемого на микросхему филь-
тра. Справочный листок на фильтр МАХ294,
также содержащий типичные схемы, можно
найти в Интернете.
♦ Счетчик. Простое решение — взять пря-
моугольный сигнал с частотой сигнала так-
тирования фильтра, а затем разделить эту
частоту, чтобы получить входной сигнал для
фильтра.
♦ Мы хотим, чтобы частота /3лБ фильтра была
выше частоты входного прямоугольного сиг-
нала, но ниже частоты его первой гармони-
ки. (Вспомните, что гармоника возникает на
частоте в три раза выше частоты входного
прямоугольного сигнала.) Частоту сигнала
тактирования фильтра может потребовать-
ся разделить на 128. Эту задачу можно вы-
полнить с помощью счетчика на микросхеме
ПМЛ, который вы собрали на лабораторном
занятии 16L.
19L1. Цифровой проект
789
Режим чередования (ALT): отображается один Режим разделения времени (CHOP): каждый
источник за один проход развертки проход развертки разделяется между
четырьмя источниками
Рис. 19L.1. Осциллограммы двух альтернативных режимов мультиплексирования входа осциллографа между четырьмя ис-
точниками сигнала
♦ Система ФАПЧ. Продемонстрировав ра-
ботоспособность схемы с только что рас-
смотренной более простой конфигураций,
можно попробовать более сложный подход:
взять прямоугольный сигнал с частотой си-
нусоидального сигнала, который мы хотим
сгенерировать, а затем использовать систе-
му ФАПЧ для генерирования сигнала такти-
рования фильтра МАХ294. Частоту сигнала
тактирования фильтра можно задать равной
частоте синусоидального сигнала, умножен-
ной на 128. Вследствие этого частота /3дВ бу-
дет равна половине частоты первой гармо-
ники прямоугольного сигнала. Схемы ФАПЧ
на лабораторном занятии 18L обладают до-
статочно близкими характеристиками для
решения этой задачи.
♦ Частота синусоидального сигнала должна
быть регулируемой в как можно больших
пределах: как минимум от 50 Гц до 5 кГц.
♦ Однополярное напряжение питания.
Скорее всего, эту схему лучше запитать от
однополярного источника напряжением 5 В.
19L1А Четырехканальный
мультиплексор для осциллографа
Данная схема мультиплексора для осциллогра-
фа поможет вам познакомиться с несколькими
полезными понятиями:
♦ Последовательности двоичного счета и их
временные диаграммы (возможно, что вы
уже знакомы с этими понятиями).
♦ Использование выходов с тремя состояниями.
♦ Мультиплексирование (разделение во вре-
мени одной сигнальной линии).
Собранная схема должна отображать выходной
сигнал счетчика (с четырех цифровых линий)
на одном канале обычного осциллографа, как
показано на рис. 19L.1.
Попутно, мы хотим, чтобы вы также решили
следующие задачи:
♦ Соберите двойной 4-разрядный счетчик со
сквозным переносом (микросхема 393).
Соберите мультиплексор 4:1 на основе декоде-
ра 2:4 74НС139 (или декодера 3:8 74НС138) и
микросхемы буферов с выходами с тремя со-
стояниями (74НС125).
♦ Соберите простой двухразрядный ЦАП, ко-
торый будет добавлять смещение в ваши
цифровые сигналы, чтобы можно было ото-
бражать все четыре сигнала на экране осцил-
лографа.
♦ Настройте свою схему таким образом, чтобы
мультиплексор переходил к отображению
следующего сигнала в должное время.
Опишем поэтапно элементы этого мультиплек-
сора входных сигналов осциллографа, чтобы
сделать задачу выполнимой. Но это не означа-
ет, что вам нужно рисовать отдельные схемы
всех этих составляющих компонентов. Будет
достаточно нарисовать только полную схему,
(Также не нужно рисовать блок-cfetoy устрой-
ства с указанием номеров выводов микросхем.)
Далее приводится краткое описание только что
перечисленных компонентов схемы мульти-
плексора, которые вам нужно спроектировать.
790
19L Лабораторное занятие по цифровым схемам
Два четырехразрядных счетчика
В Приложении К приводится информация
по цоколевке двухэлементной микросхемы
4-разрядных счетчиков 74НС393. Руководст-
вуясь этой информацией, выполните монтаж
обоих счетчиков микросхемы. Один из этих
счетчиков входит в состав схемы мульти-
плексора для осциллографа; для целей дан-
ного обсуждения будем называть его MUX
COUNTER. А второй счетчик просто предо-
ставляет четыре линии данных для подачи
на осциллограф через мультиплексор. Этот
счетчик будем называть DATA COUNTER.
(Нет надобности рисовать отдельную схему
монтажа этого компонента; просто покажите
ее на общей схеме мультиплексора.)
Мультиплексор 4:1 из дискретных
компонентов
Нарисуйте схему мультиплексора 4:1, исполь-
зуя декодер 2:4 74НС139 (или декодер 3:8
74НС138) и микросхему буферов с выходами
с тремя состояниями 74НС125. Это можно сде-
лать как в виде отдельной схемы, так и в со-
ставе полной схемы мультиплексора. Сигналы
двух разрядов счетчика MUX COUNTER пода-
дим на два вывода SELECT декодера 74НС139.
(Информация о микросхеме декодера 74НС139
приводится на лабораторном занятии 21L, а
также в Приложении Е. А цоколевку микросхе-
мы 74НС125 можно найти в Приложении К.)
Выбор сигнала тактирования для счетчика
MUX COUNTER будет зависеть от выбранного
вами режима работы мультиплексора — раз-
деления времени CHOP или чередования ALT.
Этот аспект рассматривается более подроб-
но чуть далее. В одном случае частота сигнала
тактирования должна быть как можно более
высокой, и здесь будет прямой входной сиг-
нал тактирования. А в другом случае в качестве
источника сигнала тактирования следует ис-
пользовать один из выходов Q. счетчика DATA
COUNTER.
Примечание
Несомненно, что, прочитав этот абзац в первый
раз, вы не все в нем поймете. Но пусть вас это не
смущает. Просто нарисуйте свои схемы, а затем
снова прочитайте этот абзац и посмотрите, стало
ли его содержимое более понятным.
Использование простой схемы ЦАП
На рис. 19L.2 изображена схема простого двух-
разрядного цифроаналогового преобразова-
теля.
1 кОм : (См. выше)
Q-.,-Wv 1
(Со счетчика)
^ 2 кОм
^100
Рис. 19L2. Простой цифроаналоговый преобразователь
Сигналы 0^ и Q^+1 поступают со счетчика и соз-
дают на выходе бесконечный цикл линейно
нарастающего четырехступенчатого сигнала.
Изображенная здесь схема обеспечивает ци-
клически повторяющийся сигнал смещения,
или базовый уровень. Через резистор номи-
налом 3,3 кОм к этому сигналу смещения до-
бавляется выходной сигнал мультиплексора
(рис. 19L.3).
Собираем все вместе
Нарисуйте схему всех компонентов, чтобы
отображать на осциллографе результат на
4-разрядном выходе одного из двух счетчиков.
На рис. 19L.3 приводится общая блок-схема,
на основе которой должна базироваться ваша
схема.
Мультиплексор
('139, '125)
1/2 '393
Счетчик
Оо
4:1
Счетчик
Сигнал '—9—' ~ТТ £3,3 кОм
тактирования
1/2 '393
ЦАП
Сигнал
тактирования
Рис. 19L.3. Блок-схема мультиплексора для входа осцилло-
графа
Компоненты
Двухэлементная микросхема 4-разрядного счет-
чика 74НС393 (или 74НСТ393).
Двухэлементная микросхема декодера 2:4
74НС139 (или 74НСТ139).
Четырехэлементная микросхема 74НС125 бу-
фера с выходами с тремя состояниями.
Часть VI
МИКРОКОНТРОЛЛЕРЫ
20N. Микропроцессоры I
Содержание
20N.1. Основные сведения о микрокомпьютерах
20N.1.1. Немного истории
20N.2. Минимальные необходимые компоненты компьютера
20N.3. Выбор микроконтроллера
20N.3.1. Разница между микропроцессором и микроконтроллером
20N.4. Возможные основания для выбора более трудного пути
сборки компьютера из дискретных компонентов
20N.4.1. Зачем использовать микроконтроллер 5081?
20N.5. Сигналы управления микроконтроллера
20N.5.1. Применение сигналов управления
20N.6. Некоторые подробности о компьютере,
собираемом из дискретных компонентов
20N.6.1. Фон-неймановская и гарвардская компьютерные архитектуры
20N.6.2. Мультиплексирование адресов
20N.6.3. Логика пошагового исполнения программы
20N.7. Первое занятие с компьютером на одной микросхеме
20N.7.1. Тестовая программа для автономного микроконтроллера:
мигаем светодиодом
20N.7.2. Полная версия программы
20N.7.3. Первая программа: мигаем светодиодом
20N.7.4. Разрешаем ввод-вывод
20N.7.5. Сторожевой таймер
20N.8. Материал для чтения из АоЕ
793
793
797
799
799
801
802
802
805
809
809
809
810
812
813
813
813
814
815
816
Цель этой главы
В этой главе мы хотим решить следующую задачу: создать конечный автомат, который будет пол-
ностью универсальным и программируемым, или, иными словами, преобразовать память и свя-
зывающую логическую схему в компьютер. В настоящее время компьютеры настолько привычны,
что, казалось бы, эта задача не является ничем особенным. Но когда-то она была весьма непростой.
20N.1. Основные сведения
о микрокомпьютерах
20N.1.1. Немного истории
Времена до микропроцессора
Компьютеры были в обиходе, хотя и не очень
широком, задолго до того времени, которое
принято считать появлением компьютеров. В
частности, в 1930-х гг. создавались цифровые
электромеханические компьютеры на реле;
некоторые из этих компьютеров были настоя-
щими машинами Тьюринга, т. е. полностью
программируемыми. В то же самое время, не
подозревая, что их эра подходила к концу, про-
должали развиваться последние гигантские
аналоговые компьютеры, в частности, диф-
ференциальный анализатор, разработанный
Ванневаром Бушем (Vannever Bush) и постро-
енный в конце 1920-х гг. в Массачусетском тех-
нологическом институте. Но первым полно-
стью электронным компьютером был Colossus
(«Колосс»), введенный в действие в 1943 г. в
794
20N. Микропроцессоры I
рамках британской программы криптогра-
фического анализа в Блетчли-парке (Bletchley
Park)1. Но поскольку этот компьютер исполь-
зовался для секретных работ, широкая публика
не знала о нем до 1970-х гг. В 1946 г. был вве-
ден в действие первый полностью электрон-
ный американский компьютер. Поскольку
это устройство не было секретным, оно часто
считается первым электронным компьюте-
ром в мире. Этим компьютером был ENIAC2.
Он имел громадные размеры (рис. 20N.1) и на
первых порах мог работать лишь несколько ча-
сов до выхода из строя какой-либо вакуумной
лампы. Благодаря усовершенствованным лам-
пам и бесперебойной подаче питания время
непрерывной работы до сбоя увеличилось при-
близительно до двух дней. Но этот компьютер
обладал высоким быстродействием — он был
приблизительно в 1000 раз быстрее, чем его
электромеханические предшественники.
зисторами. А микросхемы позволили уплот-
нить и удешевить цифровые схемы на порядки.
На рис. 20N.2 изображена плата процессора
компьютера Data General Nova, выпущенная
приблизительно в 1973 г.
Регистры
Разъемы для подключения
к системной плате
Рис. 20N.2. Плата процессора компьютера Data General
Nova, выпущенная приблизительно в 1973 г.
Рис. 20N.1. Первый американский полностью электронный
компьютер ENIAC (фотография из архивов армии США)
Но ни Colossus, ни ENIAC не были компьюте-
рами общего назначения, какими мы считаем
компьютеры в настоящее время. Оба устройства
были мощными калькуляторами, программи-
рование которых осуществлялось посредством
переключателей и проволочных перемычек.
Они не поддерживали идею Тьюринга о ком-
пьютере с хранимой программой3.
Процессор на печатной плате
Проблема ненадежности и короткого времени
работы компьютеров, связанная с вакуумны-
ми лампами, была решена заменой их тран-
1 Хорошее краткое изложение истории компьютеров (на
английском языке) приведено на веб-странице http://pla-
to^tanfordedu/entries/computing-Mstory/#Col.
2 Electronic Numerical Integrator and Calculator — электрон-
ный цифровой интегратор и калькулятор.
3 http://plato^tanford.edu/entries/computing-history.
Размеры платы процессора составляют прибли-
зительно 40x40 см, и она собрана на микросхе-
мах ТТЛ малой и средней степени интеграции.
Обратите внимание на модификации, реали-
зованные впаянными вручную проволочными
перемычками. Хотя это была плата серийного
выпуска, а не просто прототип.
Первые микропроцессоры
В 1970 г. компания Intel представила 4-би-
товый процессор 4004. Но этот процессор не
предназначался для использования в качестве
устройства общего назначения, а был создан
для калькулятора. Но хотя процессор обла-
дал более обширными вычислительными воз-
можностями, он никого особо не заинтересо-
вал. Спустя два года та же компания создала
первый 8-битовый микропроцессор — 8008.
Микросхема этого микропроцессора имела
18 выводов, рассеивала один ватт мощности,
стоила 400 долл. и не получила широкого рас-
пространения.
Наконец, в 1974 г. компания Intel выпустила
микропроцессор 8080, который пользовался
определенным успехом. Но это не был настоя-
щий однокристальный процессор, посколь-
ку для его связи с остальной частью компью-
тера требовалось 20 других микросхем. Эти
первые процессоры получили применение
20N.I Основные сведения о микрокомпьютерах
795
в играх, в частности в таких играх, как Pong4
и Space Invaders (космические захватчики).
Микропроцессор 8080 также был основой ран-
них любительских домашних компьютеров.
Говорят, что Билл Гейтс и его друг Поль Аллен,
увидев в одном из изданий журнала «Popular
Electronics» за 1975 г. описание домашнего ком-
пьютера Altair, поняли, что назревало что-то
большое, чего им не следовало пропустить. Они
быстро написали интерпретатор языка BASIC
для компьютеров на основе 8080, а Билл Гейтс
бросил колледж и основал компанию для раз-
работки этого продукта. Тем временем набира-
ла обороты конкуренция среди разработчиков
микропроцессоров, центрального компонен-
та полноценных персональных компьютеров.
В частности, в 1976 г. несколько работников
компании Intel ушли из нее и основали компа-
нию Zilog, которая выпустила микропроцессор
Z80. (Названный так, поскольку подразумева-
лось, что он будет последним словом в микро-
процессорах типа 80805.) Но, как часто бывает,
этот процессор не смог вытеснить процессор с
худшими характеристиками.
В следующем году компания Apple запустила
в продажу свой первый компьютер массового
производства — Apple II, в котором использо-
вался микропроцессор 6052 производства не-
большой компании MOS Technology. А в 1979 г.
микропроцессор 8086 компании Intel занял
лидирующую позицию в индустрии благодаря
тому, что на его основе был создан персональ-
ный компьютер компании IBM, который стал
своеобразным стандартом в этой области. При
этом новый микропроцессор 68000 компании
Motorola (используемый в намного менее по-
пулярном компьютере Macintosh) обладал на-
много лучшими характеристиками.
На рис. 20N.3 показана материнская (или си-
стемная) плата ПК версии 3866.
Разъемы для
плат расширения
4 Игра Pong пользовалась громадным успехом, хотя ее
разработчик презирал ее. Он говорил, что после того, как
его более сложная игра не получила должного признания,
он решил «...создать игру настолько глупую и простую,
что даже обезьяна, или ее эквивалент (пьяница в баре),
могла мгновенно научиться играть в нее», (см. с. 137 кни-
ги М. Malone «The Microprocessor: A Biography» («Микро-
процессор. Биография»), издательство Springer-Verlag,
1995 г.)
5 Буква Z - последняя буква английского алфавита.
6 Материнская плата представляет собой основную печат-
ную плату компьютера, в разъемы которой вставляются
платы расширения и память. Сама по себе материнская
СТТТТЗУ
с,
'азъемы для микросхем памяти
Рис. 20N.3. Материнская плата ПК IBM (процессоры 386/87)
приблизительно 1990 г. выпуска
Микроконтроллеры
Еще задолго до того, когда кто-либо мог пред-
ставить массовый рынок для персональных
компьютеров, нетрудно было предвидеть воз-
можные применения универсального одно-
кристального устройства для реализации, на-
пример, калькулятора высшего класса или, воз-
можно, какой-либо игры. Ранее мы уже отмети-
ли решение компании Intel предоставить в виде
своего процессора 4004 устройство с бблыними
возможностями, чем необходимо для простого
калькулятора. А игровые компьютеры можно
было бы сделать дешевле, если реализовать их
с меньшим числом микросхем.
Поэтому неудивительно, что первый микрокон-
троллер — самодостаточный однокристальный
компьютер — увидел свет в 1976 г., всего лишь
несколько лет спустя после первого микропро-
цессора. Это опять была разработка компании
Intel: микроконтроллер 8048. В действитель-
ности как компания Intel, так и весь мир были
удивлены быстрым распространением персо-
нального компьютера. В то время мало кто мог
предвидеть какую-либо необходимость в таком
устройстве для широкой публики. Поначалу
только заядлые любители считали, что им нуж-
но обладать домашним компьютером.
В 1980 г. компания Intel выпустила свой второй
микроконтроллер — 8051, продажи которого
достигли громадных объемов: в первый год
плата является компьютером, но не очень полезным, по-
скольку может не обладать основными функциональными
' возможностями, например драйвером видеодисплея или
запоминающим устройством большой емкости типа жест-
кого диска.
796
20N. Микропроцессоры I
Микроконтроллер 8051 компании Silicon Laboratories
невероятно малых размеров (корпус QFN)
Микроконтроллер 8051, используемый на лабораторных
занятиях по микроконтроллерам (корпус LQFP) ^vl
;
Микроконтроллер 8051, используемый для сборки
компьютера из дискретных компонентов (корпус DIP)
С
Тот же микроконтроллер 8051 (корпус PLCC)
Микроконтроллер 8051 компании
Silicon Laboratories (корпус QFN)
(^ Микроконтроллер 8051, установленный
на плате ЖКД (корпус QFP)
Рис. 20N.4. Микроконтроллер 8051 в корпусах разных типов
было продано 22 млн этих устройств7. Два года
спустя компания Motorola представила самый
продаваемый микроконтроллер своего време-
ни — 6805, продажи которого достигли 5 млрд
единиц к 2001 г. В течение многих лет компания
Motorola занимала лидерскую позицию на рын-
ке контроллеров, но не процессоров. Основной
причиной было ее доминирование на растущем
автомобильном рынке. Но в настоящее время
оба этих гиганта на рынке микроконтролле-
ров уступили свои позиции новоприбывшим
компаниям. Например, на момент подготовки
этой книги компании Renesas (дочернее пред-
приятие компании Hitachi) и Microchip прода-
ют больше устройств, чем компания Motorola.
Конечно же, микроконтроллеры становятся
все более и более «микро». Эта тенденция ил-
люстрируется на рис. 20N.4. Самую большую
из показанных на рисунке микросхем 8051
(в широком корпусе DIP, производства компа-
нии Dallas Semiconductor) мы будем использо-
вать на лабораторном занятии 20L при сбор-
ке компьютера из дискретных компонентов.
Следующая по размеру микросхема — это такое
же устройство, но только в меньшем корпусе
PLCC.
Все показанные на рис. 20N.4 устройства явля-
ются одним и тем же контроллером — почтен-
ным 8051, с которым мы вскоре познакомимся
на лабораторном занятии. Размеры самого ма-
ленького из них всего лишь 2x2 мм8.
7 См. книгу «The Microprocessor: A Biography» («Микропро-
цессор. Биография»), цитируемую ранее.
8 Устройства, слева направо: микросхема DS89C430 про-
изводства компании Dallas Semiconductor в корпусе DIP и
PLCC; микросхема 8051F700 производства компании Sili-
con Laboratories в корпусе QFP; микросхема 8051F410 про-
изводства компании Silicon Laboratories в корпусе LQFP
(мы будем использовать эту микросхему на лабораторном
занятии по сборке компьютера на микроконтроллере);
микросхема C8051F990 производства компании Silicon
С уменьшением размеров микроконтроллеров
снижается и их цена. В настоящее время неко-
торые небольшие контроллеры можно купить
по оптовой цене 25-30 центов при покупке
партии в 1000 штук. А стоимость некоторых
^протестированных контроллеров даже на-
много меньше этой цены (недавно мы слышали
о цене в 7 центов). Несомненно, что к тому вре-
мени, когда вы будете читать эту книгу, цены на
микроконтроллеры снизятся еще больше.
Вспомним, что мы называем
компьютером
Компьютеры, с которыми мы привыкли ра-
ботать дома и на работе, являются машинами
Тьюринга, т. е. конечными автоматами, кото-
рые пошагово переходят из одного состояния в
следующее, выполняя определенные действия
в каждом состоянии. Входные данные, которые
требуют выполнения определенного действия
и которые направляют автомат к определен-
ному набору следующих состояний, представ-
ляют собой то, что мы считаем инструкциями,
или командами, для автомата.
Целью абстрактной модели, предложенной
Аланом Тьюрингом в 1936 г., было опреде-
лить границы вычислительной обработки
данных, а не служить проектом для вычисли-
тельного устройства9. Большинство современ-
ных компьютеров имеют фон-неймановскую
архитектуру в том смысле, что в них данные и
инструкции хранятся вместе. Но существуют
также и компьютеры с другой архитектурой,
Laboratories в корпусе QFN и микросхема C8051T606-ZM
производства компании Silicon Laboratories в корпусе QFN
размером 2x2 мм.
9 Разве это странным образом не напоминает разработку
Булем своей алгебры с целью сделать процесс философ-
ского анализа более строгим?
20N.2. Минимальные необходимые компоненты компьютера
797
Команда 8
входов обеспечивают 28 по-
следовательностей (операций)
екущее
состояние процес
Сигнал тактирования
5 '
/Управляют всем, чем
микроконтроллеру нужно
управлять: например, включить
внутренний выход с третьим
состоянием, подать сигнал
тактирования на определенный
внутренний регистр,
активировать внешний сигнал
управления и т. п. j
1едующее
ояние процес
сора)
/Мо
Ч^иг
жет быть быстрее, чем\
^игнал тактирования ЦПУ/
/п триггеров обеспечивают
Упоследовательиость длиной в 2п шаго^
Рис. 20N.5. Процессор представляет собой конечный автомат; это «мозг» более масштабного конечного автомата, которым
является компьютер
гарвардской, когда инструкции и данные хра-
нятся отдельно. По замыслам разработчиков,
эта схема должна применяться и в процессоре
8051, который мы будем использовать на на-
ших лабораторных занятиях по микроконтрол-
лерам. Но, как мы вскоре увидим, при сборке
нашего компьютера на большой макетной пла-
те из дискретных компонентов, несмотря на на-
мерения разработчиков, мы будем применять в
нем более общепринятую фон-неймановскую
архитектуру. Этот момент рассматривается бо-
лее подробно чуть далее.
Автомат с хранимой программой
Процессор представляет собой конечный авто-
мат (сокращения для «автомат с конечным чис-
лом состояний») внутри конечного автомата,
каковым является сам компьютер. Процессор
считывает из памяти одну инструкцию, испол-
няет ее, а затем считывает следующую инструк-
цию10. Такая последовательность инструкций КОМПЬЮТбрд
возможное количество определенных опера-
ций составляет 28 или 256). При исполнении
одной команды процессор проходит через не-
сколько состояний, или шагов, требуемых для
ее выполнения. На рис. 20N.5 изображена
блок-схема дешифратора команд в виде, обыч-
но принятом для конечных автоматов. В про-
цессе исполнения каждой операции (который,
как уже упоминалось, заключается в прохож-
дении через несколько состояний) этот компо-
нент компьютера может включать свои выходы
с тремя состояниями, чтобы подавать сигналы
на ту или иную линию, может тактировать ре-
гистры, чтобы получать сигналы, и выполнять
другие подобные действия.
20N.2. Минимальные
необходимые компоненты
составляет программу, которая хранится в па-
мяти.
В конечный автомат меньшего масштаба, ко-
торым является микропроцессор, подаются
команды (в нашем случае это 8-битовые коды),
которые указывают ему, какую операцию из его
репертуара ему нужно выполнить. (В принципе,
10 Большинство процессоров работают в режиме предва-
рительной выборки команд, при котором они считывают
из памяти следующую инструкцию, находясь в процессе
декодирования текущей. В частности, несмотря на свою
древность, процессор 8051 использует этот режим выбор-
ки команд.
Чтобы обычный микропроцессор мог выпол-
нять что-либо полезное, т. е. чтобы сделать из
него микрокомпьютер, его необходимо обеспе-
чить многими вспомогательными компонента-
ми. Самое меньшее, ему нужна память. Также
его нужно снабдить какими-либо средствами
ввода-вывода, чтобы он мог взаимодейство-
вать с внешним миром. На рис. 20N.6 изобра-
жена блок-схема типичного компьютера.
Какие из показанных на рис. 20N.6 компонен-
тов являются обязательными, а без каких мож-
но обойтись? Можно ли обойтись без RAM?
798
20N. Микропроцессоры I
2.
Адресная шина
ROM
RAM
Шина
данных
Г/ /~/
О О
Клавиатура
АЦП
[Дисплей данных "1
[(обычно ЭЛТ или ЖКД-монитор)]
ЦАТТ
! Жесткий
{диск
Обычно!
Рис. 20N.6. Общая блок-схема компьютера
Без ROM? Без жесткого диска? Клавиатуры?
Дисплея? (Несомненно, можно обойтись без
АЦП и ЦАП.) Некоторые из этих компонентов
являются обязательными, тогда как без других
можно обойтись.
♦ RAM — память RAM важна для компьюте-
ров общего назначения, но не является обя-
зательной для выделенного контроллера.
В полноценном компьютере память RAM
служит для хранения кода программы и дан-
ных, которые оба можно загрузить с внешнего
жесткого диска. (В настоящее время Жесткие
диски продолжают широко использоваться,
но все чаще заменяются полупроводниковы-
ми устройствами хранения большого объ-
ема.) Но для контроллера, предназначенного,
например, для управления торговым автома-
том, код будет храниться не в RAM, а в ROM.
В данном случае контроллеру нужно будет
запоминать временные переменные, но тре-
буемый для этого объем памяти настолько
ничтожен, что более подходящим названием
для нее будет «регистры».
♦ ROM — память ROM позволяет компьютеру
работать при включении питания, прежде
чем в память RAM будет загружен какой либо
код из внешнего хранилища. Когда-то, когда
еще не было ROM, при выключении питания
компьютера терялся весь код программы,
в результате чего при каждом включении пи-
тания нужно было вручную вводить началь-
ную программу. В качестве примера такого
компьютера можно привести старую модель
компьютера Nova, который мы когда-то еже-
дневно использовали в нашем офисе. На
рис. 20N.7 показана передняя панель этого
компьютера11. Спрашивается, зачем на ней
так много тумблеров? Они предназначались
для ввода начальной программы, по одно-
му слову за раз. Введенная с помощью этих
тумблеров программа затем запускалась на
исполнение и загружала более сложную про-
грамму с бумажной ленты.
Самозагрузка. Наверное, трудно представить
себе работу с устройством (которое к тому же
обошлось вам в почти 8000 долл.), запуск ко-
торого столь трудоемок. Поэтому, когда появи-
лись компьютеры, которые после включения
питания запускались самостоятельно, это каза-
лось почти что каким-то чудом. Компьютер вы-
полнял, казалось бы, невозможное, наподобие
поднятия самого себя за петли на внутренней
стороне сапог12 (рис. 20N.8). Отсюда и пошло
выражение bootstrap loading (самозагрузка), или
просто booting компьютера, в значении началь-
ная загрузка или, более точно, загрузка опера-
ционной системы.
♦ Устройства ввода-вывода — чтобы компь-
ютер мог как-то взаимодействовать с внеш-
ним миром, необходимо наличие какого-
либо типа оборудования ввода-вывода, хотя
Рис. 20N.7. Передняя панель компьютера Nova компании
Data General (выпущен в 1969 г.)
11 Источник изображения: http://upload.wikimedia.
org/wikipedia/commons/5/58/Noval200.agr.jpg. Изо-
бражение используется по лицензии Gnu GPL.
12 Англ. lift (pull) oneself up by bootstraps. Русский эквива-
лент — вытащить самого себя за волосы, после знаменито-
го барона Мюнхгаузена, который вытащил самого себя из
болота за косичку. — Примеч. пер.
20N.3. Выбор микроконтроллера
799
Рис. 20N.8. Чудо 1960-х: ковбой, наподобие компьютера, под-
нимает самого себя за петли на внутренней стороне сапог
не обязательно какого-либо конкретного
типа. Для компьютеров общего назначения
необходимы клавиатуры и дисплеи, но для
контроллера для управления процессом мо-
жет оказаться достаточно АЦП и ЦАП и, воз-
можно, нескольких потенциометров (управ-
ляемых вручную и считываемых АЦП). А для
еще более простого приложения, например
управления электрической зубочисткой, не
требуется ничего кроме светодиода, транзи-
сторного переключателя и кнопки.
20N.3. Выбор
микроконтроллера13
В настоящее время на рынке предлагается
огромное количество микроконтроллеров раз-
ных типов. Поначалу может показаться, что для
выбора подходящего контроллера понадобит-
ся потратить около месяца на изучение их. Но
обычно все в этом отношении намного проще,
в основном по той причине, что люди по своей
природе не настолько рациональные существа,
чтобы самостоятельно проверять и оценивать
все альтернативные устройства. Вместо этого
большинство из нас просто обращаются за со-
ветом к сотрудникам и следуют полученной ре-
комендации14.
Такой подход имеет смысл, поскольку очень
желательно получить совет именно от тех, кто
работал с устройством того типа, который вы
сами намереваетесь использовать. Данный кон-
серватизм, даже среди людей, которые гордятся
тем, что работают с прогрессивными техноло-
гиями, объясняет тот поразительный факт, что
микроконтроллер 8051 (с которым мы будем
13 АоЕ,§15.3.
14 АоЕ, § 15.10.4.
работать на наших лабораторных занятиях)
остается предлагаемым самым большим коли-
чеством производителей почти 40 лет после его
выпуска компанией Intel в 1980 г.
На более ранних этапах основной причиной
этого консерватизма было, возможно, желание
воспользоваться большим объемом сущест-
вующего программного кода для определен-
ного процессора или контроллера. Это было
важно, когда программы создавались на ассем-
блере, поскольку в случае перехода на другой
процессор нужно было бы полностью перепи-
сывать все существующие программы.
Но в настоящее время, когда программы соз-
даются на языках высокого уровня (больше
всего на языке С для микроконтроллеров), этот
фактор больше не имеет такой важности. За ис-
ключением выбора расширения языка С для
каждого конкретного процессора, программы
на языке высокого уровня можно переносить
на другой процессор без необходимости полно-
стью переписывать их. Но продолжать приме-
нять контроллер того же самого типа в после-
дующих проектах просто удобно. Небольшие
различия в котроллерах требуют изучения
определенных подробностей, что может быть
интересно один раз, но не постоянно.
20N3.1. Разница между
микропроцессором
и микроконтроллером
Для тех из вас, кто планирует собирать ком-
пьютер из дискретных компонентов на боль-
шой макетной плате, слева на рис. 20N.9 изо-
бражена блок-схема вашего компьютера.
А на рис. 20N.10 показано, как такой компью-
тер может выглядеть: большая макетная плата
с установленным на ней процессором, микро-
схемами памяти, устройств ввода-вывода и
связывающей логики.
Но «мозгами» вашего компьютера, его цен-
тральным процессором, даже если вы со-
бираетесь собирать свой компьютер из дис-
кретных компонентов, в действительности
является микроконтроллер. Как для ком-
пьютера из дискретных компонентов, так и
для компьютера на одной микросхеме, этими
800
20N. Микропроцессоры I
Устройства
ввода
Устройства
выво,
ЦП
Шина данных
погическая
хема
ROM
RAM
[По^едоватёльный:
[порт, таймер и_т. п.]
Адресная шина
ЦП
Устройства
ввода
Устройства
вывода
Шина данных | f
. '—n
\Связывак
Злогическ
ссхема
эщая)
ая \+*
Адресная шина
ROM
[►RAM
|Поа
!порт
педовательный; !
, таймер и т. п.! |
Все на одной микросхеме => микроконтроллер
Рис. 20N.9. Микропроцессор плюс отдельные дополнительные компоненты ==> компьютер (слева); все на одной микро-
схеме ==> микроконтроллер (справа)
Компьютер из дискретных компонентов
на большой макетной плате
Компьютер на одной микросхеме
Рис. 20N.10. Компьютер из дискретных компонентов и компьютер на одной микросхеме
«мозгами» является микроконтроллер 805115.
Элементы, показанные внутри пунктирной
рамки справа на рис. 20N.9, составляют пол-
ноценный компьютер и являются составны-
ми частями микроконтроллера 8051, который
мы вначале используем просто как процессор,
а не самодостаточный контроллер. Эта блок-
схема также описывает компьютер на одной
микросхеме, который будут собирать некото-
рые из вас.
Но даже еще лучше, чем на блок-схеме, упо-
рядоченность и плотность схемы контролле-
ра можно видеть на фотографиях этих двух
15 Мы употребляем название «8051» как общее обозначе-
ние контроллера, хотя будем работать с двумя из многих
вариантов базовой конструкции этого микроконтроллера.
В компьютере из дискретных компонентов мы будем ис-
пользовать микросхему этого контроллера производства
компании Maxim/Dallas Semiconductor, а в компьютере
на одной микросхеме - микросхему производства Silicon
Laboratories.
альтернативных сборок (на рис. 20N.10) — ком-
пьютера из дискретных элементов на большой
макетной плате и компьютера на одной микро-
схеме (т. е. микроконтроллера).
Микросхема контроллера производства ком-
пании Silicon Laboratories не выпускается в
DIP-корпусе, а существует только в корпу-
се для поверхностного монтажа. Для удоб-
ства работы с этой микросхемой мы впаяли
ее на переходную плату с DIP-разъемом. На
рис. 20N.11 изображена еще более подробная
блок-схема внутренней организации микро-
контроллера 8051.
Примечание
Половина линий 16-разрядной адресной шины
подключена к мультиплексируемым выводам ми-
кросхемы. Те из вас, кто собирает компьютер из
дискретных компонентов, смогут увидеть это на
лабораторном занятии 20L
20N.4. Возможные основания для выбора более трудного пути сборки компьютера из дискретных... 801
/ " => Микропроцессор с интегрированной памятьк$\
Микроконтроллер ^аппаратным обеспечением ввода-вывода^У
Сигналы [«*—
управления}*—
(УПРАВЛЕНИЕ)
ЦП
Внутренняя память J 1
Указатель
данных
ROM
RAM
RAM
стека
Счетчик
команд
Адресная
логика
16
Внутренняя адресная шина
Внутренняя шина данных
Регистр
команд
I
Дешифратор
команд
Регистры
(включая
регистры
специального
назначения)
Последовательный
ввод-вывод
Таймеры
Порты
ввода-вывода
х16
х8
16
Внешняя
адресная
шина
8
Внутренняя
адресная
шина
Рис. 20N.11. Подробная блок-схема внутреннего устройства микроконтроллера 8051
20N.4. Возможные
основания для выбора
более трудного пути сборки
компьютера из дискретных
компонентов
Прежде чем отправлять вас начинать работу
по сборке компьютера из набора микросхем,
мы должны признаться, что микроконтроллер
можно использовать более легкими способами.
В начале лабораторного занятия 16L мы предо-
ставили вам возможность следования более
быстрым путем. Как упоминалось ранее, обыч-
но экспериментирование с микроконтроллером
состоит в приобретении платы разработчика
или демонстрационной платы приблизительно
за 50 долл., подключении ее к порту USB обыч-
ного компьютера, установки программных
средств разработки, и 5 минут спустя уже можно
наблюдать за мигающим светодиодом на плате
разработчика. Производители демонстрацион-
ных плат прекрасно знают, что мы все хотим
получить результаты как можно быстрее, а так-
же убедиться в том, что наша схема работает
должным образом. Несколько таких наборов
описываются в § 15.9 книги АоЕ, а на рис. 15.24
этой книги показано, как выглядят некоторые
из этих плат. Вы, несомненно, горите желанием
получить подтверждение работоспособности
своих схем, но тем не менее в варианте сборки
компьютера из дискретных компонентов мы
отказываем вам в удовольствии получить такие
быстрые результаты. Почему мы делаем это?
Мы можем предложить несколько объяснений.
Во-первых, мы полагаем, что вы получите мно-
го удовольствия от процесса сборки устройства,
внутренняя структура которого содержит ми-
нимум загадочных процессов. Ваш небольшой
компьютер не будет иметь умной операционной
системы или даже программы монитора; всему,
что он сможет делать, вам придется научить его
самостоятельно.
Примечание
При этом сам процессор останется черным ящи-
ком. У нас не хватило смелости поставить перед
вами задачу сборки процессора из логических
вентилей и триггеров. Сборка процессора таким
образом могла бы занять большую часть этого
курса.
Вторая причина, которая несколько отличается
от нашей цели (свести к минимуму загадочность
содержимого компьютера), состоит в том, что
мы хотим сделать обычно непрозрачную работу
компьютера прозрачной. Собранная вами схе-
ма будет отображать свою работу на двух ши-
нах — адреса и данных. При работе на полной
скорости отображаемые таким образом данные
были бы бессмысленными, но при пошаговом
исполнении программы16 вы сможете не спеша
исследовать все формируемые машиной сигна-
лы. Аппаратное обеспечение будет сдерживать
дальнейшее исполнение программы до тех пор,
пока вы не будете готовы продолжить его. Мы
16 Для собираемого вами компьютера «пошаговое» ис-
полнение означает исполнение по одному циклу доступа к
шине за раз. Это немного более высокая степень пошаго-
вого исполнения, чем его обычное значение: исполнение
по одной команде за раз.
802
20N. Микропроцессоры I
полагаем, что после такого пристального рас-
смотрения работы схемы такие понятия, как
адресация памяти и упреждающая выборка ко-
манд, больше не будут для вас просто абстрак-
циями.
А третьей причиной, связанной с первыми
двумя, является то, что мы предоставляем
вам обилие возможностей совершать ошибки.
Возможно, это обстоятельство вам не особо
по душе, но когда мы в главе 20W шутливо го-
ворим, что ошибки являются нашим наиболее
важным продуктом, мы утверждаем это с неко-
торой гордостью. Несомненно, что вам прихо-
дилось и ранее диагностировать схемы, кото-
рые вы создавали на протяжении нашего курса.
Но схема микрокомпьютера, с ее 400-500 точ-
ками соединения, предоставит более сложные
головоломки, чем предыдущие схемы меньше-
го размера.
20N.4.1. Зачем использовать
микроконтроллер 5081 ?
Первоначальному проекту микроконтролле-
ра 8051 больше лет17, чем практически любо-
му из наших студентов18. В настоящее время на
рынке предлагаются более быстродействую-
щие микроконтроллеры с большим числом воз-
можностей и периферийных устройств. Хотя
версия 8051 производства компании Silicon
Laboratories содержит довольно богатый на-
бор периферийных устройств, включая АЦП
и ЦАП (см. рис. 15.7 в книге АоЕ), мы решили
выбрать микропроцессор 8051 по той причине,
что это наиболее широко распространенное
устройство, т. е. его изготавливает очень многие
производители. Он также выпускается в виде
процессорного модуля, который можно загру-
зить в микросхему FPGA. Например, ядра 8051
компаний Cast и Hitech Global можно загрузить
в устройство FPGA компании Zilinx, а также в
другие микросхемы FPGA. Также этот микро-
контроллер входит в состав программируемой
микросхемы внешнего аналогового интерфейса
ADuC842 компании Analog Devices. Это один из
двух альтернативных процессоров, предлагае-
мых в последних программируемых системах
на кристалле компанией Cypress Semiconductor,
которые содержат программируемые аналого-
вые модули совместно с контроллером.
Микросхема 8051 является классикой микро-
контроллеров и иллюстрирует бблыную часть
возможностей любого другого микроконтрол-
лера, с которым вам, возможно, придется рабо-
тать. Но его возраст отражается на некоторых
его особенностях. Например, в ограничениях
на режимы внешней адресации, а также в том
обстоятельстве, что все внешние данные долж-
ны проходить через регистр аккумулятора.
Но количество странностей намного меньше
при работе с внутренними регистрами, что яв-
ляется обычным способом использования ми-
кроконтроллера. В частности, на лабораторном
занятии по микрокомпьютеру на одной мик-
росхеме микроконтроллер компании Silicon
Laboratories функционирует именно таким об-
разом19. Контроллер 8051 активно применяет-
ся для разных разработок, включая некоторые
инновации, которые еще не доступны для дру-
гих процессоров, например микроконтроллера
производства компании Silicon Laboratories,
работающего от поразительно низкого напря-
жения питания величиной 0,9 В. Мы надеемся,
что даже если вы в будущем и будете использо-
вать более новые контроллеры, их архитектура
покажется вам знакомой, поскольку она проис-
ходит из проекта этого первого, оригинального
микроконтроллера.
20N.5. Сигналы управления
микроконтроллера
Все правильно функционирующие процессо-
ры более-менее одинаковы: их сигналы управ-
ления похожи друг на друга. Но каждый не
работающий должным образом компьютер
делает это своим собственным способом. Вы
вскоре сможете в этом убедиться, тестируя
17 АоЕ, § 15.3 и 15.10.4.
18 В действительности, старым является первоначальный
дизайн микроконтроллера 8051. А используемые нами
версии этого микроконтроллера производства компаний
Maxim/Dallas Semiconductor и Silicon Laboratories намного
более современные.
19 Единственным исключением, когда программа микро-
контроллера 8051 компании Silicon Laboratories исполня-
ется вне микроконтроллера, является случай, когда данные
хранятся в памяти MOVX RAM. Но в действительности
даже эта операция исполняется внутри микроконтролле-
ра, только с тем же самым способом адресации, как для
доступа к настоящей внешней памяти, в результате чего и
возникает особенность этого способа. В частности, адрес
должен предоставляться выделенным регистром указате-
ля данных.
20N.5. Сигналы управления микроконтроллера
803
свой компьютер, собранный из дискретных
компонентов. А диагностирование составля-
ет большую часть того удовольствия, которое
можно получить, собирая эту схему и преодо-
левая вызовы, возникающие в процессе. В раз-
деле 22W.2 приводится несколько стандартных
методов диагностирования, а также несколь-
ко распространенных проблем, с которыми
нам пришлось иметь дело в этом компьютере.
В этом разделе мы хотим рассмотреть сигналы
управления, которые были бы нужны любому
процессору для того, чтобы взаимодействовать
с подключенными к нему устройствами.
Процессор компьютера можно сравнить с ди-
ректором завода или дирижером оркестра. Он
решает, когда должно происходить каждое со-
бытие, и посылает сигналы, чтобы эти события
происходили. Процессор должен указать тип
выполняемой операции, ее участников и точ-
ное время ее выполнения. В приводимой далее
табл. 20N.1 перечисляются необходимые виды
информации, а рядом с этими общими описа-
ниями указываются соответствующие сигналы
шины ISA и процессоров.
♦ Сигналы управления микроконтроллера
8051 — используется в нашем лабораторном
компьютере для управления внешней ши-
ной20.
♦ Классический процессор 68000 компании
Motorola21 — чтобы проиллюстрировать
другой способ работы с сигналами тактиро-
вания22.
Мы не ожидаем, что вы сразу усвоите всю ин-
формацию из этой таблицы. Но обратите вни-
мание на некоторые аспекты. В частности, все
эти процессоры и шины едины в том, что нужно
сказать.
♦ Направление обмена обозначает направле-
ние передачи информации: к ЦП или от него.
В этом отношении существует жесткое согла-
шение, согласно которому центром обмена
является ЦП (рис. 20N.12):
• RD* (чтение) означает операцию по на-
правлению к ЦП;
• WR* (запись) означает операцию по на-
правлению от ЦП.
Таблица 20N.1. Виды информации и сигналы процессоров
Тип информации
Направление об-
мена
Тактирование
Категория: память
или ввод-вывод
Какой адрес в кате-
гории
Шина ISA
MEMR*, MEMW*,
I0RM0W*
Включено в сиг-
нал управления
Включено в сиг-
нал управления
Адрес: 20 линий
(10 линий для
ввода-вывода)
8051
RD*,WR*
Включено
Безразлично.
Но нам важно выделить линию
адреса, чтобы отличить память
от устройства ввода-вывода.
Мы используем линию А15
Адрес: 16 линий
(15, если использовать одну
линию для разделения памяти и
устройств ввода-вывода)
68000
R/W*
Стробирующий импульс
для данных. Стробирующий
импульс для адреса
Безразлично
Адрес: 32 линии
В частности, мы будем рассматривать сигналы
на следующих шинах:
♦ Старая 16-разрядная шина ISA/EISA для
IBM PC — в настоящее время больше не ис-
пользуется в настольных компьютерах, но
продолжает применяться в промышленных
компьютерах в стандарте РС104.
20 Вывод шин наружу не является стандартным поведени-
ем для микроконтроллера. В частности, в микроконтрол-
лере C8051F410 компании Silicon Laboratories шины нель-
зя вывести наружу.
21 Этот 16-разрядный процессор когда-то был «мозгами»
компьютеров Macintosh и пр. В настоящее время выпуска-
ется только одна версия процессора 68000, но компанией
Freescale, а не Motorola.
22 АоЕ, § 14.3,14.4.1, табл. 14.2.
804
20N. Микропроцессоры I
КБ
Рис. 20N.12. Центрирование операций по ЦП определяет
направление в случае неоднозначных операций чтения и
записи
В шине ISA и микроконтроллере 8051 сигна-
лы схожи, названия типа RD* или WR*, что не
должно быть удивительным, вспомните, что
процессоры для обоих случаев были разра-
ботаны компанией Intel. Компания Motorola
применила другой подход, введя сигнал на-
правления R/W*23, который не содержит ни-
какой информации о тактировании.
♦ Тактирование. Вместе с другой информаци-
ей сигналы шины ISA и микроконтроллера
8051 содержат информацию о тактирова-
нии: начало или конец сигнала (иногда, но
не всегда, оба) указывает, когда происходит
действие. Например, когда на линии RD*
устанавливается низкий уровень, это озна-
чает, что процессор хочет, чтобы память или
периферийное устройство включило драй-
вер своего выхода с тремя состояниями (т. е.
выложило данные на линии шины данных).
А когда на линии RD* снова устанавливается
высокий уровень, это обозначает время, ког-
да процессор'будетсчитывать предоставлен-
ные данные. Этот подход иллюстрируется на
рис. 20N.13.
, когда память или перисрерийноеЧ
устройство предоставляет данные J
(бремя, когда ЦА считывает данные)
Рис. 20N.13. Сигнал RD* указывает не только, какое дей-
ствие должен выполнять процессор, но и когда он должен
его выполнять
В процессоре 68000 реализован другой подход.
В нем вырабатывается отдельный импульс так-
тирования, называющийся стробирующим им-
пульсом, какими часто являются тактовые сиг-
налы. Таким образом, для того, чтобы передать
23 Наверное, вы уже догадались, что название этого сиг-
нала содержит информацию о том, какой уровень какую
операцию указывает. Например, низкий уровень на линии
R/W* обозначает запись.
информацию, эквивалентную сигналу RD* в
микроконтроллере 8051, для процессора 68000
требуются два сигнала: сигнал R/W* высокого
уровня и сигнал DS* низкого уровня. Подход,
используемый в процессоре 68000, имеет своих
сторонников (для него не требуется дополни-
тельных линий, поскольку стробирующие сиг-
налы могут быть общими); оба подхода рабо-
тают одинаково хорошо.
♦ Память или ввод-вывод. Это различие полез-
но для нас, пользователей. Память она и есть
память, но ввод-вывод это нечто иное: все,
что не относится к памяти. Даже устройства,
которые вы можете считать необходимыми
для компьютера, типа клавиатуры или дис-
плея, являются устройствами ввода-вывода.
Но для процессора (или шины) различие меж-
ду устройствами памяти и устройствами ввода-
вывода важно лишь в том случае, если он хочет
работать с ними разными способами. Шина ISA
делает различие между этими двумя типами
устройств, что позволяет обходиться меньшим
количеством адресных линий для устройств
ввода-вывода (10 линий), чем для памяти. Это
несколько облегчает работу разработчиков ап-
паратного оборудования. А для микроконтрол-
лера 8051 не играет роли, какой тип устройства
адресовать: все, что он может делать с содер-
жимым памяти, он может делать и с содержи-
мым устройства ввода-вывода. Этот способ
обращения к устройствам ввода-вывода на-
зывается отображением портов ввода-вывода
в память24.
Но на наших лабораторных занятиях по ком-
пьютерам мы различаем обращения к памя-
ти и обращения к устройствам ввода-вывода,
поскольку это позволяет нам чрезвычайно
легко декодировать адреса устройств ввода-
вывода. Это возможно благодаря тому, что
у нас очень малое число устройств ввода-
вывода. По сути, мы делаем в меньшем мас-
штабе то, что шина ISA делает в своей рабо-
те с устройствами ввода-вывода. В частно-
сти, для адресации устройств ввода-вывода
в шине ISA предусмотрено 10 адресных ли-
ний, тогда как в нашем компьютере для этих
целей всего лишь две линии.
Наоборот, в присвоенной памяти категории
(нижняя половина всего адресного про-
странства) мы сохраняем обычный способ
24 Англ. memory-mappedI/O. — Примеч. пер.
20N.5. Сигналы управления микроконтроллера
805
адресации: используем 15 адресных линий
для обращения к 32 К словам памяти RAM.
Не переживайте особенно, если эти обсужде-
ния схем декодирования пока вам не очень
понятны. Мы рассмотрим декодирование
адресов устройств ввода-вывода более под-
робно чуть далее. Также полезно повторить
материал по декодированию адресов из раз-
дела 17S.2.
♦ Какой адрес в категории. Для выполнения
этой задачи все процессоры используют
адресные линии. Шина ISA давно устарела,
поскольку содержала слишком малое чис-
ло адресных линий для полноценного ком-
пьютера — 20 линий в общем, 16 из которых
были от самого процессора 8086. В резуль-
тате Intel и IBM были вынуждены изобрести
неуклюжий способ для расширения адресно-
го пространства, называющийся страничной
организацией памяти25. Возможности адре-
сации микроконтроллера 8051 ограничены
подобным образом, и в его новых версиях
предлагается возможность страничной ор-
ганизации памяти для расширения адресно-
го пространства. А вот компания Motorola
в своем процессоре 68000 с самого начала по-
дошла к этому вопросу с большим размахом,
беря пример с мини-компьютеров: этот ми-
кропроцессор имеет 32 адресные линии, что
почти адекватно даже в настоящее время.
20N.5.1. Применение сигналов
управления
Попробуем применить сигналы управления
шины ISA и микроконтроллера 8051 для под-
ключения простого периферийного устройства.
Этим устройством будет пара 8-разрядных
шестнадцатеричных индикаторов, содержащих
встроенные регистры-защелки, которые будут
служить для захвата данных, выкладываемых
на шину.
Шина ISA
Сначала выберем сигналы шины ISA, кото-
рые могут приблизительно служить нашей це-
ли26. Для записи данных в устройства ввода-
вывода предназначена команда OUT (версия
команды WRITE для ввода-вывода), поскольку
25 Англ. paging. — Примеч. пер.
26 АоЕ, § 14.2.6.
информация передается в направлении от
ЦП. Таким образом, нам нужна одна из двух
операций WRITE. Поскольку это не операция с
памятью, нам нужен сигнал работы с вводом-
выводом IOW*. Этим решается большая часть
задачи: этот сигнал определяет направление об-
мена и тактирование, а также указывает на тип
обмена — с памятью или устройством ввода-
вывода. Все, что осталось сделать, — присво-
ить индикатору однозначный адрес (чтобы
он не мешал другим устройствам в компьюте-
ре) после чего процессор может посылать ему
данные.
При работе с полноценным компьютером, по-
добным старому компьютеру с шиной ISA, на
котором мы испытали эту схему для демон-
страции, необходимо учитывать устройства,
которые уже установлены в компьютере, и
присвоить новому периферийному устройству
адрес ввода-вывода, не используемый никаким
другим устройством. В нашем IBM ПК есть сво-
бодное адресное пространство, начиная с шест-
надцатеричного адреса 300h; туда мы и поста-
вим наш индикатор.
Но как именно мы его «поставим туда»? Все,
что мы хотим сказать этим, — это то, что дан-
ное периферийное устройство должно опреде-
лять, когда компьютер выкладывает этот адрес
на адресную шину. Если одновременно с на-
хождением этого адреса на адресной шине ак-
тивирован сигнал записи порта ввода-вывода
IOW*, то логика декодирования адресов должна
создать сигнал OUT300h*, который выполнит
захват данных.
Шестнадцатеричное число 300h представляет
12-разрядное двоичное число, но в шине ISA
для определения адресов устройств ввода-
вывода есть только 10 линий. Поэтому мы де-
кодируем только первые десять битов адреса:
А9...А0. Таким образом, с учетом этого шест-
надцатеричный адрес 300h в двоичном форма-
те будет выглядеть так:
А9..А0:
110000 0000.
Наша логика декодирования должна детекти-
ровать эту последовательность битов. Кроме
того, нам потребуется многовходовый логиче-
ский вентиль И, который будет комбинировать
это сочетание битов с активированным сиг-
налом записи устройства ввода-вывода IOW*.
Дополнительно нам нужно будет обеспечить
806
20N. Микропроцессоры I
отсутствие активации сигнала прямого доступа
к памяти AEN. На рис. 20N.15 приводится вре-
менная диаграмма требуемого нам поведения
шины.
А15...А0 у
IOW*
Данные еще не готовы
Данные -
-Л^рИспользуем
этот перепад
Действительные
Рис. 20N.14. Временная диаграмма для операции записи
для шины ISA
Как видно из диаграммы, нужно использовать
задний фронт сигнала IOW*, а не передний.
Сводим все сигналы вместе во многовходовый
вентиль И (реализованный, вероятно, на ми-
кросхеме ПМЛ), и все готово (рис. 20N.15).
IOW*
AEN
Шина данных
Рис. 20N.15. Декодирование адреса индикатора для шины ISA
Декодирование адреса
Мы реализовали эту простую схему декоди-
рования адреса на микросхеме ПМЛ с выво-
дом одной дополнительной сигнальной ли-
нии Address_Match для индикации неполного
декодирования (т. е. игнорируя сигналы AEN
и IOW*). Затем мы запустили на компьютере
небольшую программу на BASIC, отправляю-
щую нарастающую последовательность байтов
в порт 300h, а потом наблюдали все задей-
ствованные сигналы на осциллографе, запус-
кая развертку от трех разных сигналов. Со-
ответствующие осциллограммы приведены на
рис. 20N.16.
Полученные результаты применимы не только
для этого старого ПК, но и для компьютеров в
целом. Рассмотрим по отдельности каждый из
трех случаев.
Случай А. Запуск развертки по сигналу
IOW* (левая осциллограмма)
На осциллограмме этого случая можно видеть
наложение широких и узких импульсов сиг-
нала IOW*, а также слабые импульсы сигналов
AddressJVIatch (300h) и OUT300h. Эти слабые
импульсы означают, что последние два сигна-
ла совпадают с сигналом IOW* только в неко-
торых случаях, когда этот сигнал активирован
(хотя вследствие слабости сигналов в этом не-
возможно быть уверенным). Почему возможно
присутствие импульсов сигнала IOW*, которые
не совпадают с другими сигналами? Потому
что на ПК, исполняющем программу для ис-
пытания индикатора, кроме нашей программы
исполняются еще другие программы. Какая-то
другая фоновая программа также выполняет
операции записи на устройство ввода-вывода.
Так что, только один из импульсов сигнала IOW*
является нашим.
Случай Б. Запуск развертки по сигналу
Address Match (средняя осциллограмма)
Мы приняли меры, чтобы адрес 300h не был
присвоен никакому другому устройству ввода-
вывода. Но на осциллограмме можно видеть
raw*
ADDRESS
match
(300h)
Г
OUT 300h*
D5
(линия
данных 5)
h
у .j
§■•'
„ ,_ , , i_
i,aim л
%.WX? СИ4, *> 8
MMMi
Отображение нарастающей
последовательности байтов
а) Запуск развертки по сигналу IOW*
b) Запуск развертки по сигналу
Address_Match. Запуск
развертки по сигналу IOW*
с) Запуск развертки по сигналу
OUT300h*. Запуск развертки по
сигналу Address_Match. Запуск
развертки по сигналу IOW*
Рис. 20N.16. Сигналы шины ISA, генерируемые программой вывода на индикатор нарастающей последовательности байтов.
(Настройки осциллографа: 5 В/дел., 1 мкс/дел.)
20N.5. Сигналы управления микроконтроллера
807
импульсы сигнала 300h, для которых нет совпа-
дающих импульсов сигнала IOW*, даже самых
слабых. Это обстоятельство дает основание
полагать, что большинство импульсов сигнала
300h не являются нашими. Как это возможно?
Этому есть простое объяснение: адрес 300h
может принадлежать не только адресному про-
странству ввода-ввода, но также и памяти, и в
таких случаях сигнал IOW* активироваться не
будет.
Случай В. Запуск развертки по сигналу
OUT300h* (правая осциллограмма)
Наконец все просто. В этом случае все три
сигнала аккуратно совпадают: сигнал IOW* со-
впадает с сигналом адреса 300h и генерирует
сигнал OUT300h*, как это и должно быть. На
протяжении импульса OUT300h самый нижний
сигнал на осциллограмме, отображающий ли-
нию 5 шины данных, имеет как низкий, так и
высокий уровень. Это тоже логично, если пред-
положить, что мы снова наблюдаем несколько
накладывающихся друг на друга осциллограмм
сигнала: программа передачи возрастающей
последовательности байтов вызывает пере-
ключение любого отдельного бита инкремен-
тированного значения. Поэтому сигнал линии
D5 иногда имеет высокий уровень, а иногда
низкий.
А что еще происходит на этой линии данных?
Ее сигнал имеет сложную форму, но выглядит
постоянным, по крайней мере, в последнем
случае. А в первых двух случаях этот сигнал
выглядит довольно хаотично и иногда имеет
пилообразную форму, а не аккуратные логиче-
ские уровни.
Подробности этого сигнала не важны для нас,
но можно понять, что странные уровни возни-
кают на линии в то время, когда на нее не пода-
ется сигнал каким-либо устройством. В частно-
сти, пилообразные сигналы соответствуют тем
периодам времени, когда на линию не подается
ни низкий, ни высокий уровень и она находит-
ся в третьем состоянии. Поэтому ее потенциал
дрейфует к уровню посередине диапазона на-
пряжений логических уровней, подтягивае-
мый, вероятно, входом индикатора27.
27 Вход светодиодного индикатора компании Hewlett-
Packard имеет характеристики ТТЛ; в наших заказных
платах ЖКД на входе присутствует слабый положитель-
ный потенциал.
Главный момент, который мы хотим подчер-
кнуть здесь, заключается в том, что бблыпая
часть сигналов, передаваемых по шине дан-
ных, не являются данными, по крайней мере
не данными в строгом смысле этого слова.
Большинство трафика в традиционных маши-
нах с фон-неймановской архитектурой, к како-
вым относится наш ПК с шиной ISA, составляют
команды. В компьютерах с такой архитектурой
команды и данные (в узком смысле этого сло-
ва) хранятся совместно в общей памяти и пере-
даются по общей шине данных. Постоянные
уровни, наблюдаемые на линии данных D5 на
рис. 20N.16, соответствуют битам команд. Они
постоянны по той причине, что наша програм-
ма исполняется в коротком цикле, и поэтому
биты повторяются, когда мы наблюдаем на
осциллографе сигнал этой линии. Вскоре мы
увидим, что собираемый нами компьютер так-
же имеет традиционную фон-неймановскую
архитектуру.
Используем контрольные сигналы
с микроконтроллером 8051
В некоторых отношениях задачу, которую мы
только что поставили перед шиной ISA, легче
выполнить, используя микроконтроллер 8051.
Легче по той причине, что нам не нужно смо-
треть в таблице, как распределены доступные
адреса между другими аппаратными и про-
граммными устройствами, а мы сами можем
присваивать их по своему усмотрению.
Для данного примера, используя внешние ши-
ны, расположим наш дисплей данных на порту,
который будем называть Порт 0; также при-
мем условие, что нам нужно отличать Порт 0
от другого порта, называемого Порт 1. Далее,
применим подход, который мы реализуем в
собираемом нами компьютере: отдадим ниж-
нюю половину адресного пространства памя-
ти, а верхнюю — устройствам ввода-вывода.
Соответствующая диаграмма показана на
рис. 20N.17. При таком подходе тип адреса —
памяти или ввода-вывода — указывается с по-
мощью адресной линии А15, а Порт 0 будет
просто первым адресом адресного простран-
ства ввода-вывода.
Чтобы декодировать адрес Порта 0, нам нуж-
но определиться с необходимыми сигналами
управления микроконтроллера 8051 и выбрать
несколько адресных линий. На рис. 20N.18
808
20N. Микропроцессоры I
Адрес
(шестнадцатеричный формат) Адресное
А15
1
0
(16 битов; пространство
8000Н
0000И
Ввод-вывод
Память
Рис. 20N.17. Для простоты мы разделили адресное про-
странство пополам между памятью и устройствами ввода-
вывода
Сигнал тактирования для фиксирования
половины адресов, чтобы 8 выводов
можно было использовать по двойному
назначению: сначала для передачи адреса,
а затем для передачи данных
Сигналы управления
обмена данными
(вспомним, что
они предполагают
точку зрения
микроконтроллера;
WR* => запись данных
микроконтроллером)
Сигналы управления передачи команд
(эквивалентны сигналу RD* для данных)
Внешний доступ: указывает микроконтроллеру, что
команды и данные находятся вне микроконтроллера
Рис. 20N.18. Сигналы управления микроконтроллера 8051
показаны кандидаты для требуемых сигналов
управления микроконтроллера 8051.
Мы решили, что наличие высокого уровня на
старшей линии адресной шины (А15) будет
означать обращение к адресному простран-
ству устройств ввода-вывода. Поскольку это
операция вывода, в которой информация пере-
дается от ЦП в наружный мир, то подходящим
сигналом для нее будет сигнал WR*. Теперь
осталось только отличить Порт 0 от Порта 1.
Очевидный способ для этого — использовать
линию самого младшего разряда (АО), как по-
казано на рис. 20N.19.
Замечание
Какой-либо другой способ, кроме этого очевидно-
го, только сбивал бы с толку других пользователей
нашего компьютера.
Сколько разных портов можно адресовать
с помощью данного метода декодирования?
Ну, можно адресовать Порт 1, устанавливая вы-
сокий уровень на линии АО. Также можно ис-
пользовать два порта ввода с такими же адре-
сами, как и порты вывода: IN0* и IN1*. Таким
образом, наш метод декодирования позволяет
адресовать четыре порта: два порта ввода и два
порта вывода (или, иными словами, два двуна-
правленных порта). С этой схемой декодиро-
вания возможности компьютера будут сильно
ограничены. Даже собираемому нами компью-
теру будет нужно вдвое больше портов ввода-
вывода.
Но этот простой пример позволяет увидеть,
насколько простой может быть наша схема
декодирования. Этот подход называется «ле-
нивым», поскольку мы преднамеренно не ис-
пользуем большое число адресов, чтобы не
усложнять аппаратное обеспечение. Но при
необходимости мы можем адресовать вдвое
больше портов, добавив вторую адресную ли-
нию (А1) и т. д. В следующем примере мы так
и сделаем.
/Направление передачи (от ЦП^Ч
\и тактирование (~и~) J
:сокий уровень => адресное
пространство ввода-вывода
П,
WE-
А15-
А0"
D
OUT 0
и
kEN*
1 1
и
-4
Шина данных
(Низкий уровень => Порт 0, в отличие от Порта j)
Рис. 20N.19. Декодирование порта для выполнения команды OUTO* микроконтроллером 8051
20Л/.6. Некоторые подробности о компьютере, собираемом из дискретных компонентов
809
20N.6. Некоторые
подробности о компьютере,
собираемом из дискретных
компонентов
Собираемый нами компьютер представляет
для нас интерес как устройство, с помощью ко-
торого можно ознакомиться с некоторыми об-
щими аспектами работы компьютеров и микро-
контроллеров. Но вместе с общими понятиями,
которые отображают сходные черты всех со-
временных компьютеров, необходимо также
ознакомиться с некоторыми особенностями,
специфичными для процессора. Эти аспекты не
нужно будет реализовывать в компьютере, со-
бираемом из дискретных компонентов, и они
неприменимы к компьютеру на одной микро-
схеме C8051F410. Они необходимы лишь для
того, чтобы те из вас, кто собирает компьютер из
дискретных компонентов, понимали принципы
его работы. А те из вас, кто избрал путь работы
с компьютером на микросхеме C8051F410, мо-
жет пропустить этот материал и сразу перейти
к разделу 20N.7.
20N.6.1. Фон-неймановская
и гарвардская компьютерные
архитектуры
Можно было бы ожидать, чта компьютер, раз-
работанный в Гарвардском университете, будет
иметь и гарвардскую архитектуру, но это не так
в случае с нашим компьютером, собираемым
из дискретных компонентов. Более того, мы
приложили немного лишних усилий, чтобы из-
бежать использования этой архитектуры. Но,
прежде чем продолжать, наверное, лучше объ-
яснить эти термины. В некоторых компьютерах
команды и данные хранятся в отдельной па-
мяти. Но в большинстве компьютеров коман-
ды хранятся в той же самой области памяти,
что и данные. Компьютеры, в которых коман-
ды и данные хранятся раздельно, называются
компьютерами с гарвардской архитектурой28.
Такое хранение команд и данных было исклю-
чением до недавних пор, когда этот подход стал
применяться более часто в микроконтролле-
рах (в частности, в микроконтроллерах PIC).
Хотя разработчики микроконтроллера 8051
также оснастили его возможностью такого раз-
деления, но мы не будем этим пользоваться,
поскольку не хотим, чтобы вы устанавливали
в своем собираемом компьютере две отдельные
памяти. К тому же мы хотим предоставить вам
возможность работать с компьютером обще-
принятой архитектуры.
В микроконтроллере 8051 операция выбор-
ки команды отличается от операции чтения
данных. Для разрешения памяти программы
предназначена команда PSEN* (Program Store
Enable — разрешение памяти программы), а
команда RD* предназначена для разрешения
чтения памяти данных. Эти два типа памяти
объединяются микросхемой ПМЛ связываю-
щей логики, которая просто выполняет опера-
цию ИЛИ над сигналами PSEN* и RD*, создавая
на выходе сигнал, который подается на вывод
ОЕ* микросхемы памяти RAM, управляющей
выводами ее буферов с тремя состояниями
(рис. 20N.20)29.
RD
Рис. 20N.20. Выполнение операции ИЛИ над сигналами RD*
и PSEN* устраняет различие между памятью для кода и па-
мятью для данных
20N.6.2. Мультиплексирование
адресов
Подобно большинству микроконтроллеров,
в микроконтроллере 8051 некоторые выво-
ды имеют двойное назначение, что позволяет
уменьшить физические размеры микросхе-
мы. Корпус DIP30 имеет 40 выводов, а более
компактный и соответственно менее дорогой
корпус PLCC31 имеет 44 вывода. В частности,
28 Это название происходит из структуры, которая исполь-
зовалась в компьютере Гарвард Марк I (Harvard Mark I),
одном из первых в мире автоматическом цифровом ком-
пьютере/калькуляторе (созданном в 1944 г.).
29 Третий входной сигнал операции ИЛИ BR* предназна-
чен для предоставления пользователю возможности ра-
боты с шиной; а сигнал ALE необходим в исключительном
случае последовательной загрузки программы.
30 Напомним, что DIP означает Dual Mine Package - кор-
пус с двухрядным расположением выводов. Это обычный
корпус микросхем для установки на макетной плате.
31 Сокращение PLCC означает Plastic Leaded Chip Car-
rier — пластмассовый кристаллоноситель с четырехсто-
ронним расположением J-образных выводов. Это корпус
810
20N. Микропроцессоры I
в микроконтроллере 8051 восемь выводов
предназначены для работы как с адресами, так
и с данными, что позволяет сэкономить семь
выводов. Семь, а не восемь потому, что один
вывод используется для указания типа обмена.
В начале каждого цикла шины32 по этим общим
восьми линиям передаются 8 битов младших
разрядов адреса. Короткое время спустя (око-
ло 80 не при сигнале тактирования частотой
11 МГц) эти линии переключаются на передачу
8 битов данных. Прежде чем адресная инфор-
мация заменяется данными, она фиксируется
в регистре-защелке с помощью сигнала ALE
(Address Latch Enable — разрешение защелки
адреса). На рис. 20N.21 приводится временная
диаграмма соответствующего тактирования
(для тактовой частоты 11 МГц)33.
XTAL1
операции
'Адрес фиксируется в регистре демультиплексора
Рис. 20N.21. При активировании сигнала ALE адресная ин-
формация фиксируется в регистре. Позже на эти выводы бу-
дут поданы данные (тактовая частота равна 11 МГц)
Адресная шина
Ajdpec (младшие 8 битов)
захватывается по сигналу ALE
Подключены к шине данных
(большую часть времени)
Шина данных
Рис. 20N.22. Общие линии AD7...AD0 кратковременно со-
держат младшую половину адреса, а затем данные
На первый взгляд эта схема может выглядеть
очень сложной. Но эта сложность является це-
ной, уплачиваемой за уменьшение количества
выводов в микросхеме. Несколько других вы-
водов микроконтроллера 8051 также имеют
двойное назначение. Например, вывод RST
обычно функционирует в режиме входа, но в
случае проблем, вынуждающих сброс системы,
переключается в режим выхода. А вывод PSEN*
обычно работает в режиме выхода, но при не-
обходимости включить внутреннюю схему за-
грузчика переключается в режим входа. Но эти
другие общие выводы мультиплексируются не
очень часто, тогда как выводы AD нам прихо-
дится мультиплексировать постоянно.
Эти общие, или мультиплексированные, линии
называются AD7...AD0. На первый взгляд мож-
но подумать, что эти названия означают Адрес
(ADdress), но в действительности AD означа-
ет Address/Data (Адрес/данные). В схеме на
рис. 20N.22 можно видеть, что эти линии под-
ключены как регистру-защелке, так и к шине
данных.
сравнительно больших размеров по современным стан-
дартам. Его можно использовать как для поверхностного
монтажа, так и вставлять в гнездо.
32 Обратите внимание на то, что такое мультиплексиро-
вание применяется только при работе микроконтроллера
8051 с внешними шинами.
33 Изображенная временная диаграмма фиксирования
адреса является стандартной для микроконтроллера 8051.
В некоторых версиях этого микроконтроллера, например
в контроллерах DS89C4xO компании Dallas Semiconduc-
tor, предлагается опция фиксирования старшей половины
адреса, а не младшей. В большинстве случаев (в пределах
страницы памяти размером 256 байт) это обеспечивает
более быстрый доступ к памяти.
20N.6.3. Логика пошагового
исполнения программы
Как объясняется на лабораторном занятии 20L,
собираемый нами компьютер реализует полно-
стью аппаратную функцию пошагового испол-
нения программы. Эта функция очень проста:
она просто посылает несколько импульсов
сигнала тактирования, а затем отключает ис-
точник этого сигнала. Синхронизацию схемы
обеспечивает сигнал ALE, вследствие чего она
всегда останавливается на полпути операции
доступа к шине, в момент времени, когда все
сигналы управления, данных и адресов явля-
ются действительными.
Такое поведение делает возможность пошаго-
вого исполнения очень полезной для диагно-
стирования проблем аппаратного обеспече-
ния. С ее помощью можно также тестировать
небольшие программы, исполняя их по одной
20N.6. Некоторые подробности о компьютере, собираемом из дискретных компонентов
811
строчке кода за раз34. Или же с цифровой кла-
виатуры вместо команды RUN можно ввести ко-
манду STEP, а затем нажимать клавишу INC. При
каждом нажатии этой клавиши процессору по-
ставляется достаточно циклов сигнала тактиро-
вания, чтобы он мог выполнить приблизитель-
но половину операции (например, операции
выборки данных или операции ввода-вывода).
Схема пошагового исполнения на микросхеме
ПМЛ осуществляет это, отключая сигнал так-
тирования процессора вскоре после импульса
разрешения регистра-защелки адресов ALE, ко-
торый обозначает начало каждой операции.
На рис. 20N.23 показана осциллограмма одного
такого пакета из четырех импульсов тактиро-
вания, заканчивающегося вскоре после сигнала
ALE. К этому времени захват адреса был выпол-
нен защелкой на микросхеме 573, и общие ли-
нии используются для передачи данных.
Сигналы
Большинство команд исполняются за четы-
ре импульса сигнала тактирования частотой
11 МГц, подаваемого на вывод XTAL1 микро-
контроллера35. Но для команды, исполнение
t Тактирование пошагового исполнения
^ с ЦП 8051 компании Dallas Semiconductor.
|* Пакет из четырех импульсов тактирования
f (предназначенный для процессора компании
^ODll Semiconductor)
Рис. 20N.23. Схема пошагового исполнения на устройстве ПМЛ реализует пошаговое исполнение, отключая сигнал тактиро-
вания вскоре после сигнала разрешения защелки адреса ALE
Примечание
Существуют и другие способы реализации поша-
гового исполнения. Например, можно разрешить
прерывания, а затем прерывать исполнение про-
граммы после каждой команды. Подробности
этого метода изложены на с. 326 Руководства
пользователя микроконтроллера MCS51 (MCS52
Microcontroller's User's Manual) компании Intel. В
более современных микроконтроллерах поша-
говым исполнением можно управлять с внешне-
го компьютера. Подобный метод применяется в
нашем компьютере на микросхеме C8051F410.
Подключив этот микроконтроллер к компьютеру
через последовательный порт можно включить
режим пошагового исполнения программы и ис-
следовать его регистры. Такая возможность отсут-
ствует в компьютере, собираемом из дискретных
компонентов.
которой занимает значительное время, потре-
буется намного больше циклов сигнала такти-
рования. Аппаратная схема для пошагового
исполнения всегда дает возможность пройти
двум циклам сигнала тактирования после спада
сигнала разрешения защелки адреса ALE, чем
34 «По одной строчке...» не совсем верно: строго говоря,
исполняется один цикл доступа к шине.
35 Это утверждение справедливо для циклов шины при
использовании внешних шин. При исполнении команд из
внутренней памяти ROM процессор исполняет многие из
них за один цикл сигнала тактирования. Дополнительным
усложнением (но таким, о котором вам не нужно беспоко-
иться) является то обстоятельство, что частота сигнала
тактирования, подаваемого на вход XTAL1, не обязатель-
но такая же, как частота внутреннего сигнала тактирова-
ния в микроконтроллере. Частота внутреннего сигнала
тактирования может быть вдвое или вчетверо выше ча-
стоты сигнала тактирования XTAL1 вследствие ее повы-
шения внутренним множителем частоты (см. с. 64-65 ру-
ководства пользователя «High-Speed Microcontroller User's
Guide» компании Maxim/Dallas Semiconductor, доступного
по адресу: http://pdfserv.maximintegrated.com/en/an/
AN4827.pdf).
812
20N. Микропроцессоры I
1. Процесс запускается нажатием кнопки
на цифровой клавиатуре, в результате чего
устанавливается высокий уровень сигнала
TRIG-SYNC, что обеспечивает прохождение
сигнала тактирования
2. Низкий уровень сигнала ALE отключает
сигнал тактирования, но не сразу. Для
подачи сигнала на выходе DELAY требуется
спад сигнала тактирования, а затем нужен
еще один цикл сигнала тактирования,
чтобы установить низкий уровень сигнала
TRI6_SYNC для прекращения сигнала /
тактирования. Таким образом, после спада
сигнала ALE проходят еще два цикла
сигнала тактирования
STEP_RUN* (пошагово/непрерывно)
BUSRQST* (запрос доступа к шине)
LOADER* (загрузчик):
pRESET* (сброс микроконтроллера)
3. Непрерывное исполнение. Реализуется
одним из двух способов: 1) выбор опции
RUN* или 2) любого из трех условий,
требующих сигнал тактирования для своих
собственных целей
Рис. 20N.24. Подробности реализации пошагового исполнения программы
FULL_SPEED
(непрерывное исполнение)
[!DELAY
i6ATED_a.OCK
(Управляемый
_ сигнал тактирования)
Х CLOCKout
(выход
сигнала
Ьг— — тактирования)
!(Выход HDX)
обеспечивает пошаговое исполнение, незави-
симо от количества циклов сигнала тактирова-
ния, используемых определенной командой.
Схема
Тогда как общая идея довольно проста, ее реа-
лизация весьма сложна. Чтобы сохранять це-
лостность сигналов тактирования, не допуская
их урезания или (еще хуже) всплесков на них,
синхронизирующие триггеры используют от-
рицательный перепад сигнала тактирования.
На рис. 20N.24 показана попытка объяснить
происходящее. Но если у вас нет желания, мо-
жете не рассматривать все эти непривлекатель-
ные подробности36.
20N.7. Первое занятие
с компьютером на одной
микросхеме
На лабораторных занятиях по компьютерам,
в которых используется автономный микро-
контроллер C8051F410 производства компании
Silicon Laboratories, вам не нужно собирать
практически никаких схем, чтобы начать экс-
периментировать с исполнением некоторых
программ. Вам потребуется лишь подключить
контроллер к ПК с помощью метода общего
использования выводов микроконтроллера,
позволяющего выполнять отладку программ
без необходимости постоянного выделения
каких-либо выводов контроллера. Это впол-
не разумный метод при ограниченном ко-
личестве выводов микроконтроллера (всего
лишь 32) и более предпочтительный по срав-
нению с выделением четырех выводов, как это
делается в стандартном протоколе JTAG37. Это
специальное последовательное соединение
(которое разработавшая его компания Silicon
Laboratories называет С2) описывается в раз-
деле 20L3.2.
Поскольку на наших лабораторных занятиях
вам практически не придется работать с ап-
паратным обеспечением, то у вас будет доста-
точно свободного времени, чтобы ознакомить-
ся с ассемблером и интерфейсом отладчика.
Вы увидите, что при пошаговом исполнении
36 Мы знаем, что разобраться с особенностями чужой схе-
мы или кода программы - задача не из легких.
37 Сокращение JTAG означает Joint Test Action Group —
Объединенная рабочая группа по автоматизации тести-
рования. Это название промышленной группы, которая
разработала стандартный способ для тестирования ми-
кросхем посредством подключения их внутренних узлов
к выводам микросхемы, где их можно последовательно
считывать.
20N.7. Первое занятие с компьютером на одной микросхеме
813
программы на микроконтроллере можно ис-
следовать содержимое его регистров. Первая
программа (рассматриваемая подробно в раз-
деле 20L3.5) всего лишь мигает светодиодом,
предоставляя то, что большинство из нас хотят
при работе с микроконтроллером: удоволь-
ствие немедленного наблюдения результатов
своих трудов.
20N.7.1. Тестовая программа
для автономного микроконтрол-
лера: мигаем светодиодом
Ядро программы: две строки кода
Эта программа так же проста, как и первая
программа для компьютера из дискретных
компонентов. Программа, листинг которой
приводится в конце лабораторного занятия
20L, представляет собой просто бесконечный
цикл и рассматривается более подробно в гла-
ве 21N. Отличие заключается лишь в некото-
рых фоновых командах для микроконтроллера
C8Q51F410, используемого в этом варианте ла-
бораторных занятий по компьютерам.
Как отмечается на лабораторном занятии 20L,
главная часть программы содержит всего лишь
две строчки кода:
FLIPIT: CPL P0.0; Включаем светодиод, затем выключаем.
Повторяем в бесконечном цикле
SJMP FLIPIT
Команда CPL выполняет операцию дополне-
ния над одним битом. Параметр этой коман-
ды — РО.О — указывает бит 0 Порта 0, т. е. вывод
микроконтроллера, к которому подключен наш
светодиод.
20N.7.2. Полная версия программы
Инициализация регистров
Универсальность микроконтроллеров может
быть как благом, так и напастью. В частности,
прежде чем выполнить простейшую операцию,
может потребоваться выполнить подготови-
тельную работу по определению роли реги-
стров и установке их начальных значений.
Некоторые из этих подготовительных опера-
ций можно будет увидеть и в нашей простой
программе. Задача предварительной настройки
усложняется при подготовке к работе со слож-
ными периферийными устройствами, такими
как таймер, широтно-импульсный модулятор
или последовательный порт. Например, чтобы
программа seriaLmessage_silabs.a51, рассма-
триваемая в разделе 20L.3.7, могла отправить
короткое сообщение на ПК, необходимо вы-
полнить предварительную настройку десяти
регистров управления. Наша программа для
мигания светодиодом достаточно проста и по-
требует выполнения всего лишь двух предвари-
тельных настроек:
♦ разрешить выходной порт (включить ма-
тричный переключатель, на жаргоне компа-
нии Silicon Labs);
♦ выключить сторожевой таймер.
Может показаться странным, что эти необхо-
димые подготовительные операции не выпол-
няются микроконтроллером по умолчанию, но
это действительно так.
20N.7.3. Первая программа:
мигаем светодиодом
Рассмотрим более подробно эту небольшую
программу. Несмотря не ее крохотный размер,
поначалу некоторые ее аспекты непременно
будут вызывать вопросы. На рис. 20N.25 пока-
зан листинг программы на ассемблере (справа)
с соответствующим машинным кодом (слева),
который эта программа генерирует на ПК.
Машинный код и есть та программа, которая
загружается в микроконтроллер 8051 и которая
исполняется им, выбирая команды по одному
байту. То обстоятельство, что код для одно-
битового параметра РО.О одинаков в командах
SETB РО.О и CPL РО.О, обнадеживает. Очевидно,
что адрес этого бита — 80h.
Ассемблер нашел этот адрес, обратившись к
файлу C8051F410.INC, указанному в операторе
SINCLUDE в начале программы. Файл С8051F410.
INC содержит, наряду со многими другими эк-
вивалентностями, адрес порта Р0 — 80h. В ли-
стинге 20N.1 приводится отрывок этого файла
с этой информацией.
814
20N. Микропроцессоры I
0000
0000
0003
0006
0008
000 А
53D9BF
"5Е240
D?S0
В/80
8OFC
гьь
2 о '
268
270
27:
27 i
214
275
2~fc
27"?
278
LUC OBJ LINE SOURCE
1 ; bit flip.351 trsi<* blinics LED—but at a i*t& too fast to see unless run *n s.ngle-step
3 snosymbols , kc^pa i.atinq .hott.. ИнТврвСНИИ СПОСОб ОбнуЛвНИЯ ОДНОГО
4 $ include (C:\Mrc40\80^i\eA2SON\ittc\c805iF4i^o.5HC) ^^*~>—"* ' бита. ИСПОЛЬЗувТСЯ ПО ТОЙ ПрИЧИНв,
2(55 ^^^^^^^ что данную ячейку памяти нельзя
ORfi 0 ; U4» a»s«nbSei rheart^pMr^^T^ch to pfac* th»a code ОДрвСОваТЬ ПОбИТНО
,4^1ёЙ^^;040Н) ; Ci.ar Watchdoq «nablo bit ТТОДОбНЫМ ОбрОЗОМ ДОННОЯ КОМйНДО
MOV присваивает значение 1 одному
интересующему нас биту (обнуляя
при этом остальные 7 битов)
ТВ РО.О ; starr with LEtt off (it's active Isw^, ^u«t ro make- it pr«*<lict««i>i<»
27"? ГЛ»1*: CPL PD.O^"
278 &JMP I
2Ь0 "ш Эти операции с битами выглядят более аккуратно,
поскольку они могут обращаться к ячейке памяти побитно
Рис. 20N.25. Первая программа для компьютера на автономном микроконтроллере С8051F410: инициализирует 2 бита управ-
ления, после чего мигает светодиодом
Листинг 20N.1. Фрагмент файла С8051F410.INC
i ~~ "" ~ ~" " "~" "~~~ ~~ • ——«
;C8051F410.INC
/ ————————— - ——.-——————
; Copyright 2005 Silicon Laboratories, Inc.
; http://www.silabs.com
; Program Description:
; (Описание программы:)
; Register/bit definitions for the C8051 F41x family.
; (Определение регистров и битов для семейства микро-
контроллеров С8051 F41x.
; Byte Registers
; (Байтовые регистры)
Р0 DATA 080H; Port 0 latch (Защелка порта 0)
SP DATA 081Н; Stack pointer (Указатель стека)
Адрес 80h для порта Р0 является байтовым адре-
сом. Разница между побайтовой и побитовой
адресацией может сбивать с толку. Поскольку
РО.О является нулевым битом в байте по адресу
80h, его адрес также будет 80h. (Адрес бита РОЛ
будет 81 h и т. д.)
Функционирование параметра 80h как адрес
байта или бита определяется в зависимости от
контекста. Например, в битовой операции типа
SETB адрес 80h может быть только адресом бита.
А число 80 в машинном коде 855090 байтовой
операции типа MOV Р1, Р0 (указывающее целе-
вой адрес операции MOV) может означать толь-
ко байт38. Напротив, РЗ будет всегда ссылаться
на байт, а не на бит. Но, увидев несколько раз
использование этих параметров, разница меж-
ду ними должна стать более понятной.
Последняя строка кода в цикле программы
SJMP FLIPIT выполняет переход к метке FLIPIT,
поставленной в левом поле. Ассемблер вычис-
ляет расстояние до этой метки, которое в дан-
ном случае составляет четыре адреса (от ОСЬ
назад до 08h)39, и подставляет значение FCh, ко-
торое равно минус четырем в дополнительном
двоичном коде. В результате получается беско-
нечный цикл (если только он вам не надоест до
скончания века и вы не выполните сброс своего
компьютера или не выключите его).
20N.7A Разрешаем ввод-вывод
Необходимость включить матричный пере-
ключатель для того, чтобы иметь возможность
выполнять операции ввода-вывода, выглядит
так странно, что напоминает ситуацию, отобра-
женную на комиксе о Дилберте на рис 20N.26.
Выход микроконтроллера не будет работать до
тех пор, пока не отключить опцию «хряп, вжик,
38 Оператор MOV всегда выполняет перемещение байта, за
исключением одного случая — перемещение в флаг пере-
носа. Например, MOVC, P0.0. Это единственная возможная
операция перемещения бита.
39 Вы можете быть озадаченным нашим утверждением,
что это четыре адреса назад. В таком случае обратитесь
к главе 21N за подробным объяснением переходов вперед
и назад при исполнении программы на ассемблере.
20N.7. Первое занятие с компьютером на одной микросхеме
815
Количество копий...
Двухсторонние копии...
Уменьшить до 98%...
Сортировать...Скрепить
скобами...ТТортретная
ориентация...Двухцветные
копии...ТТритемнить...
Бумага АА
Если тебе нужно сделать
фотокопию, установи
«Нет» для опции «Хряп,
вжик, боинк»
/ Она еще и фотокопии
I делает? ?
Рис. 20N.26. Ксерокс Дилберта похож на микроконтроллер C8051F410 компании SiLabs, который отказывается выполнять
ввод-вывод, пока не будет разрешен порт (воспроизведено с разрешения компании United Features Syndicate, inc.)
боинк», присвоив биту bit6 в регистре XBR1 зна-
чение 1 (см. раздел 20N.7.3).
Разрешение и конфигурирование выходного
порта посредством матричного переключателя
позволяет воспользоваться усовершенствова-
ниями микроконтроллера C8051F410, которые
компания SiLabs внесла в стандартную схему
ввода-вывода микроконтроллера типа 8051.
Эти улучшения в виде матричного переключа-
теля позволяют коммутировать определенные
сигналы на определенные выводы микрокон-
троллера. Эта возможность обеспечивает гиб-
кость, доступную в схемах на ПМЛ, где любой
сигнал можно подключить к любому выводу
микросхемы. (За исключением некоторых вы-
водов, жестко выделенных под JTAG и питание,
и некоторых выводов, избранно подключенных
к глобальным сигналам тактирования.)
Необходимость разрешения матричного пере-
ключателя доставляет некоторые хлопоты, но
настолько стандартна, что вы быстро привы-
кнете всегда выполнять его. Мы выделим эти
стандартные настройки в подпрограмму с на-
званием USUAL SETUP.
20N7.5. Сторожевой таймер
Сторожевой таймер, который мы в данном слу-
чае отключаем, предоставляет полезную услу-
гу в конечной версии любого кода для микро-
контроллера, но здесь мы уклоняемся от этого
усложнения. Сторожевой таймер действитель-
но похож на сторожа, которому постоянно по-
ступают сообщения о состоянии охраняемых
объектов.
Если сообщения перестают поступать, сто-
рож предполагает самое худшее. В частности,
отсутствие сообщения сторожевому таймеру
подразумевает какой-то серьезный сбой про-
граммы. В таком случае контроллер выполняет
сброс самого себя. Мы не хотим без надобности
усложнять наши тестовые программы, поэтому
просто отключили сторожевой таймер.
Код для отключения сторожевого таймера (ли-
стинг 20N.2) использует специальный прием
программирования, называемый маской, кото-
рый мы рассмотрим в главе 22N40.
Листинг 20N.2. Код для отключения сторожевого таймера
ADDRESS CODE line # ASSEMBLY CODE COMMENTS
268 ; Отключаем сторожевой таймер
0000 53D9BF 269 ANL PCAOMD, #NOT(040H) ; Обнуляем бит разрешения сторожевого таймера
Директивы ассемблера $INCLUDE,
$NOSYMBOLS\aORG
Не все содержимое программы направлено
на исполнение в микроконтроллере 8051; не-
которые ее команды дают указания програм-
ме ассемблера, которая исполняется на вашем
ПК. Такие команды называются директивами
ассемблера.
40 Но если вам не терпится узнать, что это такое, то вкратце
команда ANL выполняет операцию И над содержимым ре-
гистра PCAOMD и значением BFh, которое является допол-
нением указанного в коде значения 040Н. В результате этой
операции биту 6-го регистра присваивается значение 0.
816
20N. Микропроцессоры I
Директива $INCLUDE
Следующая строка кода в листинге на
рис. 20N.25
INCLUDE (C:\MICRO\8051\RAISON\INC\C8051 F410.INC)
дает указание программе ассемблера, где на-
ходится длинная таблица эквивалентов. Эта
таблица позволяет программистам задать для
микроконтроллера 8051 более-менее описа-
тельные названия для регистров, портов и даже
битов. Обратите внимание на то, что на ком-
пьютере, на котором у вас исполняется инте-
грированная среда разработки (IDE) компании
SiLabs, путь к этому файлу С8051 F410.INC будет
другой, чем тот, который указан в листинге.
Поэтому обязательно узнайте, где на вашем
компьютере хранятся файлы .INC, и откоррек-
тируйте должным образом команду SINCLUDE
в своей программе.
Благодаря файлу C8051F410.INC мы можем об-
ращаться к порту 0 как Р0, а не по его шестнад-
цатеричному адресу 80h. Подобным образом,
мы можем обращаться к регистру PCA0MD по
его названию (которое тоже не из самых легких
для запоминания), а не искать его адрес (D9h).
Директива $NOSYMBOLS
При всей полезности файла C8051F410.INC мы
не хотим выводить на экран всю его длинную
таблицу эквивалентов и поэтому используем
еще одну директиву ассемблера: $NOSYMBOLS.
В листинге на рис. 20N.25 эта директива выгля-
дит так:
$NOSYMBOLS; keeps listing short (не выводить всю
таблицу эквивалентов)
Комментарий к этой директиве напоминает
нам о ее назначении: подавлять стремление ас-
семблера выводить листинг всех эквивалентно-
стей, содержащихся в файле С8051 F410.INC
Директива ORG
Директива ORG 0 означает «Origin 0» и дает
указание ассемблеру присвоить адрес 0 первой
исполняемой строки кода. В действительности
у нас не было большого выбора в использова-
нии этой директивы, поскольку после сброса
(выполняемого подачей низкого уровня на вы-
вод RESET*) микроконтроллер 8051 всегда на-
чинает исполнение команды, расположенной
по адресу 0. Таким образом, этот адрес был бы
и так назначен ассемблером по умолчанию, но
в данном случае мы еще и принудительно на-
значаем его посредством директивы ORG.
Для простоты в нашей первой программе мы
размещаем программу после начального адре-
са 0. Но в дальнейших программах, по крайней
мере в программах для компьютера из дискрет-
ных компонентов, мы не будем этого делать.
Вместо этого нашей первой командой будет
переход к более высокому адресу, по которому
будет начинаться наша основная программа.
Такой подход объясняется тем, что определен-
ные низкие адреса памяти выделены для спе-
циальных целей.
Например, адрес 03h предназначен для вектора
прерывания, т. е. адреса, по которому переда-
ется управление программы после прерывания
ее исполнения каким-либо источником преры-
вания (внешнее нулевое прерывание). Поэтому
использовать этот адрес и другие подобные ему
выделенные адреса для хранения нашего кода
или данных нельзя. В сегодняшней программе
мы не будем беспокоиться об этом вопросе, по-
скольку в ней нет прерываний.
Мы можем получать удовольствие от тех при-
вилегий, которыми обладаем, будучи «дикта-
тором» нашего скромного компьютера: нам
нет надобности считаться с другими возмож-
но исполняющимися на нем программами,
которым может потребоваться нулевое пре-
рывание. Мы единолично управляем нашим
компьютером и поэтому знаем, что без нашего
ведома на нем не может исполняться никакая
другая программа.
20N.8. Материал для чтения
изАоЕ
♦ Глава 14. (Компьютеры, контроллеры и ка-
налы передачи данных):
• Раздел 14.1. Терминология: микропроцес-
соры, микроконтроллеры. Архитектура:
ЦП и шина данных, в особенности раз-
дел 14.1.6. Шина данных;
• Раздел 14.2.2В. Адресация;
• Раздел 14.3.1. Основные сигналы шины:
данные, адрес, стробирование.
20N.8. Материал для чтения из АоЕ
817
Глава 15. (Микроконтроллеры):
• Раздел 15.1. Введение;
• Раздел 15.3. Обзор семейств микрокон-
троллеров;
• Раздел 15.9.1. Программное обеспечение;
• Раздел 15.10.3. Как выбрать микроконт-
роллер.
Интернет-ресурсы по 8051.
Пара источников общих ресурсов по 8051/2:
• Учебное пособие по общему микрокон-
троллеру 8051 (http://www.8052.com/
tut8051, разделы 1,2,4,6);
• Учебное пособие по версии 8051 компа-
нии Dallas Semiconductor, 80C320 (http://
www.8052.com/320tut);
• Руководство пользователя компании
Dallas Semiconductor/Maxim «Ultra-High-
Speed Flash Microcontroller User Guide»
(http://pdfserv.maximintegrated.com/
en/an/AN4833.pdf);
• возможности, с 3;
• типичное подключение: только RAM, толь-
ко ROM, с. 63, 57;
• модель программирования, с. 4-6 (карта
распределения памяти);
• DS89C430/50 «Ultra-High-Speed Flash Micro-
controller» (https://www.maximintegrated.
com/en/products/digital/microcontrollers/
DS89C430.html#popuppd);
• описание сигналов, с. 12-13;
• функциональная диаграмма блока управ-
ления, с. 14;
• карта распределения памяти, с. 19-21.
♦ Справочный листок компании Silicon
Laboratories:
• Справочный листок на микроконтрол-
лер C8051F410 (http://www.silabs.com/
Support Documents/TechnicalDocs/
C8051F41x.pdf);
• Интерфейс программирования С2 (https://
www.silabs.com/Support).
20L Лабораторное занятие:
микропроцессоры I
20L.1. Микрокомпьютер
из дискретных компонентов
Это первое из лабораторных занятий по ми-
крокомпьютеру/микроконтроллеру, на кото-
ром вы можете сделать выбор в пользу сборки
компьютера из дискретных компонентов (око-
ло 10 разных микросхем), а не использовать
автономный микроконтроллер C8051F410 ком-
пании Silicon Laboratories (SiLabs). Мы будем
называть этот первый вариант «путь Dallas»
по названию фирмы, разработавшей данную
конкретную версию микроконтроллера 8051 —
Dallas Semiconductor, также иногда мы будем
называть этот подход «сборка компьютера на
большой макетной плате» по очевидной причи-
не — большому размеру макетной платы, необ-
ходимой для монтажа схемы такого типа. В ка-
честве альтернативы вы можете избрать работу
с автономным микроконтроллером C8051F410
компании Silicon Laboratories (SiLabs). Данный
подход мы будем называть «путь SiLabs», опять
же, по названию фирмы, разработавшей эту
конкретную версию микроконтроллера 8051.
В первой части лабораторного занятия мы бу-
дем работать с версией Dallas микрокомпьюте-
ра (собираемой из дискретных компонентов на
большой макетной плате); с версией SiLabs (ав-
тономный микроконтроллер C8051F410) мы
будет работать в последнем разделе 20L3.
20L1.1. Что мы будем собирать
Мы предполагаем, что вы выполнили все зада-
ния лабораторного занятия 17L и имеете в сво-
ем распоряжении рабочие счетчик и память и
подключенные к ним дисплеи. На сегодняшнем
лабораторном занятии мы добавим к этим
компонентам микроконтроллер, который яв-
ляется «мозгами» нашего компьютера. Также
для сопряжения микроконтроллера с осталь-
ными компонентами компьютера установим
микросхему ПМЛ, запрограммированную
для реализации соответствующей связываю-
щей логики. В частности, ПМЛ (которую для
краткости будем называть просто GLUEPAL)
содержит чисто комбинационную логику, ко-
торую вы разработали в примере с решением
в разделе 17W. Кроме этого, GLUEPAL также
содержит схему наподобие сдвигового реги-
стра, которая реализует функцию пошагового
исполнения программы микрокомпьютером.
Схема пошагового исполнения программы по-
дает на процессор пакет импульсов тактиро-
вания при нажатии на цифровой клавиатуре
кнопки INC. После завершения этой после-
довательности импульсов тактирования про-
цессор останавливает исполнение программы,
что позволяет отображать на дисплее текущие
значения данных и адреса. Такой перевод ап-
паратного обеспечения в статическое состоя-
ние позволяет диагностировать проблемы, ко-
торые потенциально могут возникнуть.
Добавляемые компоненты
На рис. 20L.1 изображена принципиальная схе-
ма практически всего компьютера, из которой
можно понять, что ранее уже была выполнена
большая часть работы по его монтажу. После
сегодняшнего лабораторного занятия к этой
схеме нужно будет добавить только второсте-
пенные аппаратные компоненты, выделенные
на рисунке серой заливкой.
20L.2. Устанавливаем GLUEPAL и выполняем частичный монтаж
819
\
л&с амг
Новые компоненты, добавляемые на лабораторном занятии I по микрокомпьютерам
Рис. 20L.1. Компоненты, добавляемые к схеме компьютера на сегодняшнем лабораторном занятии
20L.2. Устанавливаем
GLUEPAL и выполняем
частичный монтаж
20L2.1. Частичный монтаж GLUEPAL
На данном этапе мы не будем подключать не-
которые выводы микросхемы ПМЛ: выводы
для подключения к микроконтроллеру 8051
и к компонентам, которые будут установле-
ны на последующих лабораторных занятиях.
Подключаемые и неподключаемые выводы
описываются далее в тексте.
На данном этапе мы подключим лишь некото-
рые входные и выходные линии GLUEPAL.
Входы
Одни входы на данном этапе необходимо под-
ключить к соответствующему источнику сиг-
нала (например, на вход BR* подается сигнал
с цифровой клавиатуры). Другие входы не-
обходимо деактивировать (например, вход
LOADER*). А некоторые входы нужно оставить
неподключенными (например, вход CLKIN).
Выходы
Одни выходы подключаются к их соответствую-
щим нагрузкам (например, выход RAMWE*
подключается к соответствующему выводу ми-
кросхемы RAM). Другие выходы на данном эта-
пе оставляются неподключенными, поскольку
их нужно подключить к процессору или иному,
пока не установленному аппаратному устрой-
ству (например, выход RESET51). А некото-
рые выходы вообще никогда не подключаются.
Например, выводы TRIG_LATCH, TRIGJ5YNC,
ALE_LATCH, DELAY, PAL предназначены толь-
ко для тестирования.
Полная информация о подключении микросхе-
мы GLUEPAL показана на рис. 20L.2.
На рис. 20L.3 подробно показаны два момента
подключения устройства GLUEPAL. Во-первых,
820
201. Лабораторное занятие: микропроцессоры /
(
GLUEPAL
Подключаем <
if
Деактивируем
(подключаем
к положительной Y с
шине питания) \
A13
A12
All
RD
psIn
LOADER
INO
STEP/RUN*
ALE
CLKIN
PAMWE
CTROE
KBUFEN
IOR
IQW
RESET51
PSENDRV
CLOCKJDUT
ROM
Счетчик на
микросхеме ТТМЛ
э—с|ОВ,ОЕ2 Микросхема
8-битовых буферов 541
На данном этапе
не подключаем
На данном этапе )
не подключаем \
Рис. 20L.2. Подключение выводов микросхемы GLUEPAL до установки процессора и логики пошагового исполнения
Сброс
(на цифровой клавиатуре)
fW\ HC14
KRESET
GLUE PAL
CTROE
DMA
£? (зеленый)
(указывает, что шинами
управляет пользователь)
Рис. 20L.3. Подробности двух моментов подключения микросхемы GLUEPAL
3.3V
Я™*
III
Микросхема ТТМЛ
в корпусе QFP
3.3V
3.3V
mm
demuxoe*
ckin
ctroe*
G
trigjatch
triRjsync
iOW*
TO!
TMS
TCK
kbufen*
Mr*
3.3V
delay
ramwe*
ramoe*
ramce*
alejateh
br*
I
2
$
4
5
6
7
8
9
10
11
12
IS
14
15
16
17
IS
1$
20
21
22
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
alS
trig
alS
a!3
al2
all
ale
psen*
psendrv*
3 3V
ckjMit
resets*
kres^t*
wr*
rd*
kwr*
3.3V
6
TOO
step
Рис. 20L.4. Разводка сигналов GLUEPAL на выводы (корпус QFP)
необходимо обеспечить защиту от дребезга для
сигнала сброса. При отсутствии такой защиты
возможно непредсказуемое поведение про-
цессора. Во-вторых, подключаем светодиод,
указывающий ситуацию, когда мы управляем
шинами.
На рис. 20L.4 показаны все входные и выход-
ные сигналы устройства GLUEPAL. Игнори-
руйте выходы для программирования микро-
схемы ПМЛ, которые обозначены JTAG. Также
игнорируйте выходы сигналов, которые не по-
требуются нам. Эти сигналы были выведены
для того, чтобы облегчить тестирование в
процессе разработки пошагово исполняемого
кода на ПМЛ. Это сигналы, которые находятся
в левом столбце таблицы справа на рис. 20L.4:
TRIG_LATCH, TRIG_SYNC, ALE_LATCH и
DELAY.
При подключении этих сигналов управления к
линиям шин на макетной плате (16 свободных
линий находятся в верхней и нижней части ма-
кетной платы) или к установленным на ней ми-
кросхемам рекомендуется обозначить метками
некоторые из них.
2012. Устанавливаем GLUEPAL и выполняем частичный монтаж
821
20L2.2. Замена предыдущих
подключений
Одна из специфичных сложностей монтажа
этого компьютера связана с тем обстоятель-
ством, что данная схема эволюционирует
в ходе нескольких лабораторных занятий,
вследствие чего некоторые подключения не-
обходимо заменить другими, более сложными.
Эти обязательные модификации очень легко
упустить из виду. Чтобы помочь вам избежать
этого, мы рассмотрим их здесь, сопровождая
соответствующими иллюстрациями.
Отключаем «землю» от входов CIN* и ОЕ*
и подключаем к ним выход CTR_OE*
микросхемы GLUEPAL
Сигнал запроса шины BUSRQST* (который здесь
сокращен до BR*) поступает на устройство
GLUEPAL, где он слегка улучшается1, после чего
выходит как сигнал CTR_OE*, который подается
на входы ОЕ* и CIN* 16-разрядного счетчика на
ПМЛ, установленного в схему на лабораторном
занятии 16L. Этот сигнал теперь заменит под-
ключение данных выводов на «землю», выпол-
ненное на том же лабораторном занятии. Эта
модификация показана на рис. 20L.5.
Многие поколения студентов совершали по-
добную ошибку — забывали выполнить эти
изменения. Мы настоятельно рекомендуем не
составить им компанию.
Отключаем «землю» от двух входов разреше-
ния RAM и подключаем к ним выходы RAMCE*
и RAMOE* микросхемы GLUEPAL.
На лабораторном занятии 17L мы заземлили
вывод CS* (или СЕ*) и вывод ОЕ* (управление
выходами с тремя состояниями) микросхемы
RAM, чтобы она была постоянно в разрешен-
ном состоянии. (Конфликты между RAM и бу-
фером цифровой клавиатуры предотвращались
за счет сигнала WE* RAM.) Теперь ко входу СЕ*
(или CS*) микросхемы RAM (вывод 20) нам
нужно подключить выход RAMCE* устрой-
ства GLUEPAL, а ко входу ОЕ* микросхемы
RAM (вывод 22) — выход RAMOE* устройства
GLUEPAL. Данная модификация необходима по
той причине, что теперь RAM нельзя позволить
монополизировать шину данных, поскольку
она должна разделять ее с установленным про-
цессором. Разрешение RAM на доступ к шине
данных для записи будет выдавать процессор
(т. е. микроконтроллер 8051) через GLUEPAL.
Соответствующий фрагмент схемы показан на
рис. 20L.6. Этот рисунок также содержит под-
цифровая
клавиатура
(сигналы
и питание
подаются ^L
через I/
DIP-шлеиш)и/р
ft€SCT bt
ЗМР
DIP-
переключатель \V У
Микросхема ГТМЛ
счетчика адресов
На лабораторном занятии 16L эти два вывода
были подключены на «землю». Теперь же на них
подается сигнал CTROP>
^r
шина данных цифровой клавиатуры
DMA
(зеленый)
Загрузка адреса
Рис. 20L.5. Новый источник сигнала для входов ОЕ* и CIN* счетчика: счетчик запускается только тогда, когда шиной управляет
пользователь
1 Как можно видеть на рис. 20L.5, это улучшение со-
стоит в деактивации сигнала LOADER*, активный уровень
которого низкий. На данном этапе не беспокойтесь о под-
робностях работы сигнала LOADER*. Нам он потребуется
только в разделе 24L1, когда мы начнем загружать код из
персонального компьютера непосредственно в память.
робности подключения микросхемы MXD1210
для резервного питания RAM. Но эта часть схе-
мы изображена серым цветом, поскольку на
данном этапе эта микросхема не устанавлива-
ется. Мы добавим ее позже.
822
201. Лабораторное занятие: микропроцессоры I
Микросхеме ТМП
связывающей логики
Эта микросхема батарейки резервного питания для RAM
(MXD1210) будет установлена на лабораторном занятии 21L
вместо выполненных сегодня подключений
ж|Ы
Статическая память йА1й, 32 К • 8
Щ ЩЩ Ч Щ fli н И
(Цифровая клавиатура) u \j////j •////,
Рис. 20L.6. Модификация подключений входов CS* и ОЕ* памяти RAM
Подключаем ко входу WE* микросхемы
RAM (вывод 27) выход RAMWE*
устройства GLUEPAL
Это соединение заменяет прямое подключение
линии KWR* цифровой клавиатуры, которое
было сделано на лабораторном занятии 17L.
Теперь сигнал KWR* является лишь одним из
нескольких входных сигналов, которые могут
вырабатывать сигнал RAMWE*.
память KWR*, поступающим с цифровой клавиа-
туры (который мы на лабораторном занятии
17L подключили напрямую ко входу WE* ми-
кросхемы RAM), и сигналом записи в память,
подаваемым процессором. Теперь сигнал циф-
ровой клавиатуры KWR* предоставляет только
одно из двух условий для включения буфера
цифровой клавиатуры. Устройство GLUEPAL
обеспечивает альтернативу этому сигналу: те-
перь и процессор может управлять буфером.
Подключаем на входы ОЕ* микросхемы
541 (выводы 1 и 19) выход KBUFEN*
устройства GLUEPAL
Данное подключение показано на рис. 20L.7.
Таким образом, теперь микросхема GLUEPAL
посредничает между сигналом ручной записи в
Ш^
Рис. 20L.7. Новый сигнал управления входом WE* памяти
RAM
Эмуляция сигнала запроса-разрешения
шины busrequest/busgrant посредством
сигнала RESET
Далее мы объясним способ эмулирования за-
проса шины с помощью сигнала сброса 8051.
Микроконтроллер 8051 не предоставляет воз-
можности общего доступа к шине, которая реа-
лизована в обычных микропроцессорах. Более
конкретно, мы не можем запросить управление
шиной для прямого доступа к памяти (DMA),
поскольку разработчики компании Intel не
видели необходимости в такой возможности,
когда создавали микроконтроллер несколько
десятилетий тому назад.
Но эту функцию можно эмулировать, подавая
на процессор сигнал сброса, когда мы хотим
взять управление шинами.
Примечание
На схемах для этого лабораторного занятия данный
сигнал обозначен как RESET51. Это один из немно-
гих сигналов с высоким активным уровнем. Данный
сигнал сброса вызывает отключение всех драйве-
ров портов процессора (на их выводы поступает
небольшое положительное напряжение).
20L2. Устанавливаем GLUEPAL и выполняем частичный монтаж
823
На этом этапе мы подключаемся к процессу,
чтобы воспользоваться этим обстоятельством:
используем сигнал BR*, чтобы включить буфе-
ры с выходами с тремя состояниями нашего
счетчика адреса в то же самое время, когда этот
сигнал заставляет процессор отключить свои
драйверы портов. Наши драйверы с легкостью
пересиливают слабое положительное напряже-
ние, создаваемое драйверами процессора. За-
тем 16-разрядный счетчик управляет адресной
шиной, а буферу с выходами с тремя состояния-
ми 541 теперь можно выложить значение циф-
ровой панели на шину данных (но только после
того, как мы нажмем кнопку WR*). В общем,
активирование сигнала BR* вызывает возвра-
щение схемы к состоянию, в котором она нахо-
дилась на лабораторном занятии 17L, когда вы
могли вручную записывать данные в RAM.
Далее приводится обобщение эффекта, вызы-
ваемого активированием сигнала BR*:
♦ включаются буферы счетчика с выходами
с тремя состояниями;
♦ создаются условия для ручной записи в
память;
♦ активированный сигнал BR* разрешает рабо-
ту счетчика и фиксирует состояние счетчика
при деактивировании (посредством управле-
ния входом CIN* счетчика).
Третий из перечисленных эффектов позво-
ляет нам использовать кнопку INC цифровой
клавиатуры для разных целей в процессе ис-
полнения программы, не нарушая при этом
состояния счетчика адреса. Если при функцио-
нировании компьютера сигнал BR* находится
в деактированном состоянии, то счетчик будет
игнорировать импульс сигнала тактирования,
создаваемый нажатием кнопку INC цифровой
клавиатуры.
20L2.3, Тестирование
Подключив частично микросхему GLUEPAL,
как показано на рис. 20L.2, можно выпол-
нить некоторые тесты, несмотря на отсутствие
управляющих сигналов микроконтроллера.
Все ли еще возможно ручное управление
памятью?
При запросе шины (активировании сигнала BR*
на цифровой клавиатуре) загорается зеленый
светодиод, означающий получение управления
шинами. В результате должна быть разрешена
запись в RAM и счетчик адреса и память долж-
ны функционировать таким же образом, как
они работали на лабораторном занятии 17L.
Наоборот, при деактивировании сигнала BR*
линии шины адреса и данных должны перейти
в «плавающее» состояние: на них не подается
никаких сигналов, а снимаемые с них сигна-
лы, скорее всего, будут иметь значение FFh,
поскольку на эти линии подается слабое поло-
жительное напряжение от платы ЖКД. После
установки в схему микроконтроллера 8051
(что мы сделаем далее на этом лабораторном
занятии) он будет брать управление шинами
на себя сразу же после деактивирования сиг-
нала BR*.
Работает ли возможность защиты
от записи микросхемы GLUEPAL?
Работоспособность защиты от записи можно
проверить, указав адрес на границе между за-
щищенной и незащищенной RAM и эмулируя
операцию записи ЦП. Для этого применяется
следующая процедура:
♦ берем на себя управление шиной (активируя
сигнал BR*);
♦ указываем в RAM самый последний защи-
щенный адрес: 7FFh. Для этого загружаем
адрес 800h, а затем декрементируем счетчик
адреса;
♦ вручную подключите на «землю» вывод WR*
микросхемы GLUEPAL. Этот вывод обычно
подключен к шине положительного питания.
Поэтому перед подключением на «землю»
его, конечно же, нужно отключить от шины
положительного питания. Данная манипуля-
ция с подключением на «землю» этого выво-
да эмулирует запись центральным процес-
сором. Но обратите внимание на то, что это
совсем иная операция, чем ручная операция
записи, инициируемая сигналом KWR*;
♦ исследуйте состояние вывода WE* микро-
схемы RAM с помощью логического пробни-
ка. На нем должен присутствовать высокий
уровень;
♦ теперь инкрементируйте адрес, чтобы обра-
титься к первой ячейке незащищенной памя-
ти по адресу 800h;
824
20L Лабораторное занятие: микропроцессоры I
♦ проверьте, что сигнал на выводе WE* ми-
кросхемы RAM имеет соответствующий
уровень2.
Удовлетворившись, что все сигналы обраба-
тываются логическими вентилями должным
образом, непременно отключите вывод WR*
микросхемы GLUEPAL от «земли». В следую-
щем подразделе мы подключим к этому выводу
линию сигнала WR* процессора.
20L2А Устанавливаем процессор
Теперь можно установить микроконтроллер
8051, или, более точно, его совместимую вер-
сию производства компании Dallas Semicon-
ductors — DS89C430. При установке микро-
контроллера на макетную плату позаботьтесь
о том, чтобы он был достаточно близко к гнез-
дам шины макетной платы, поскольку нам
нужно будет подключить много выводов ми-
кроконтроллера к этой шине. Может оказаться
удобным установить микроконтроллер, напра-
вив его вывод 1 вниз, чтобы ориентация шин
микроконтроллера совпадала с ориентацией
шин макетной платы (самый старший разряд
направлен вверх).
Примечание
Теперь нужно отключить выводы RD*, WR* и PSEN*
микросхемы GLUEPAL от шины положительного
напряжения, к которой мы подключили их в раз-
деле 20L2, чтобы подать на них сигнал деактивиро-
вания. Теперь сигналы управления на эти выводы
будут подаваться от микроконтроллера 8051.
Сигнал PSENDRV*
Также обратите внимание на такое интересное
обстоятельство, что вывод PSEN* микрокон-
троллера 8051 (рис. 20L.8) играет двойную роль
входа и выхода. В частности, выходной сигнал
с него подается на вход PSEN* микросхемы
GLUEPAL, а входной сигнал на него подается
с другого вывода GLUEPAL - PSENDRV*3.
Р$£Н
2 Активный сигнал на входе WR* микросхемы GLUEPAL
теперь должен вызвать активирование его выходного сиг-
нала RAMWE*, который подается на вывод WE* микросхе-
мы RAM, в результате чего на последнем должен устано-
виться низкий уровень.
3 Такая система может несколько озадачить вас. Разве
соединение двух выводов не вызовет конфликт их логиче-
ских сигналов? Нет, не вызовет, поскольку любой возмож-
ный конфликт предотвращается выходами с тремя состоя-
8051
На данном этапе деактивирован
(подключен к высокому уровню)
Рис. 20L.8. Вывод PSEN* работает как выход (обычно) и как
вход (время от времени)
На данном этапе мы не будем подключать все
44 вывода микроконтроллера 8051 (а некото-
рые выводы не будем подключать вообще). На
рис. 20L.9 показана цоколевка микроконтрол-
лера. Рекомендуется скопировать ее и наклеить
на ваш микроконтроллер.
Р1.СЛ2
Р1.1Л2ЕХ
Р1.2
Р1.3
Pimm
Р15ШЗ*
P16/INT4
P1J/INT5*
RST
P3.0/RXD0
P3.1/TXD0
P3.2/1NT0*
РЗ.ЗЛМТ1*
Р3.4Л0
Р3.5Я1
WR*
RD*
XTAL2
XTAL1
GND
VCC
ADO
AD1
AD2
AD3
AD4
AD5
AD6
AD7
EA*
ALE
PSEN*
A15
A14
A13
A12
A11
A10
A9
A8
Рис. 20L.9. Цоколевка микроконтроллера 8051
На рис. 20L.10 изображен фрагмент схемы
рис. 20L.1, содержащий детальную инфор-
мацию о подключении микроконтроллера.
Здесь также показана микросхема регистров
74НСТ573, которая описана далее. Выполните
монтаж, как показано на рисунке. Некоторые
выводы вы уже должны были подключить
раньше: KRESET*, BR* и LOADER*.
Подключение сброса для 8051
Заземлите вывод ЕА*. Сокращение ЕА означает
external access, т. е. внешний доступ, и активиро-
вание этого сигнала дает указание процессору
ниями микросхемы GLUEPAL. Сигнал выхода PSENDRV*
активируется только в тех случаях, когда выход PSEN*
деактивирован. Разумеется, вы понимаете, что сигналы
PSEN* и PSENDRV* устройства GLUEPAL являются двумя
разными сигналами, а не одним.
2012. Устанавливаем GLUEPAL и выполняем частичный монтаж
825
Дисплей отображения адресов
Сброс
(на цифровой клавиатуре) z
Заземлите вывод ЕА*, чтобы
использовать внешние шины
Рис. 20L10. Подключение микроконтроллера (за исключением выводов для микросхемы ПМЛ для пошагового исполнения,
которая будет установлена позже)
обращаться к внешней памяти для получения
кода программы. На лабораторном занятии
25L мы подадим на этот вывод сигнал высо-
кого уровня, что позволит микроконтроллеру
исполнять код, находящийся в его внутренней
памяти ROM. Но до тех пор вывод ЕА* будет
оставаться заземленным.
Управляющий сигнал на линию сброса про-
цессора (обозначенную на наших принципи-
альных схемах, включая схему на рис. 20L.10,
как RST или RESET51) подается от микросхемы
GLUEPAL через резистор номиналом 4,7 кОм.
Наличие этого последовательного резисто-
ра может выглядеть странным, но в действи-
тельности является полезным. Дело в том, что
вывод RST микроконтроллера 8051 иногда
работает в режиме выхода, и такой резистор
позволяет нам определять независимо друг
от друга сигнал RST микроконтроллера 8051,
с одной стороны, а с другой — сигнал RESET51
микросхемы GLUEPAL, который подается на
вывод RST.
Иногда сам процессор активирует вывод RST
(подавая на него высокий уровень), чтобы
указать, что он столкнулся с проблемой, ко-
торую не может решить. В отчаянии, он де-
лает то, что делали поколения компьютерных
пользователей, когда все перепробованные
ими способы решить проблему не имели успе-
ха: нажимает кнопку сброса. Это делается для
инициализации всех подключенных к нему
устройств; иными словами, таким образом
микроконтроллер 8051 предпринимает попыт-
ку выполнить перезагрузку. В схеме, которую
мы собираем сегодня, активирование процес-
сором вывода RST не даст никакого полезного
результата. Но последовательный резистор в
цепи вывода RST будет полезен нам для вы-
полнения диагностики: он позволяет опреде-
лить, кто активирует вывод RST: пользователь
(обычная ситуация) или процессор (аномаль-
ная ситуация, возникающая вследствие какой-
либо проблемы). Последний случай, т. е. ак-
тивирование вывода RST микроконтроллером
8051, вызывает его зависание, для выхода
из которого необходимо выключить и снова
включить питание компьютера.
Подключаем шины адреса и данных
Подключите мультиплексированные линии
адреса-данных AD (выводы 32 по 39) к микро-
схеме триггера-защелки 74НСТ573. Обратите
внимание на то, что обозначение AD не означа-
ет адрес (address); линии адреса обозначаются
одной буквой А (английского алфавита).
Сокращение AD означает адрес-данные (ad-
dress-data), т. е. иногда по этим линиям пере-
даются адреса, а иногда — данные.
Пусть вас не смущает то обстоятельство, что
восемь входных линий микросхемы 74НСТ573
(AD0...AD7) нужно также подключить и к
шине данных. Это работает как демультиплек-
сирование: один источник, два приемника.
826
20L Лабораторное занятие: микропроцессоры I
Цикл записи данных в память
Выходящие значения линий
А8-А15 адреса
AD0...AD7 Входящая^
команда //
Линии AD0...AD7 передают Линии AD0...AD7
младший байт адреса передают данные
Рис. 20L.11. Мультиплексирование восьми линий адреса-данных AD0...AD7
Также обратите внимание на то, что в схеме на
рис. 20L.10 на выходной стороне микросхемы
74НСТ573 для этих восьми линий меньшие но-
мера присвоены более высоким номерам линий
адреса. Но при желании этот порядок присвое-
ния можно изменить на обратный — присвоив
высокие номера линий адреса высоким номе-
рам выводов. Это может облегчить монтаж
схемы. Но в таком случае порядок присвоения
нужно менять на обратный по обоим сторонам
микросхемы 74НСТ573: как на входной, так
и на выходной. Опять же, если вы хотите ис-
пользовать назначения сигналов, показанные в
схемах для этого лабораторного занятия, вклю-
чая схему на рис. 20L.10, то может оказаться
полезным установить микросхему триггеров-
защелок 74НСТ573 на макетной плате верхней
стороной вниз.
Микросхема защелок 74НСТ573 тактируется
сигналом разрешения ALE и демультиплекси-
рует линии AD0...AD7: пока в начале цикла
доступа к шине сигнал ALE поддерживается
на высоком уровне, прозрачная защелка про-
пускает сигналы с восьми линий AD0...AD7 на
линии А0...А7 шины адреса (младшие восемь
разрядов адреса). А когда уровень сигнала
разрешения ALE меняется на низкий, защелка
фиксирует и удерживает эти восемь значений.
Когда значение этих восьми адресных линий
зафиксированы в защелке 74НСТ573, микро-
контроллер 8051 может использовать эти ли-
нии адреса-данных в их альтернативной роли:
для передачи восьми разрядов данных.
На рис. 20L.11 показана временная диаграмма
демультиплексирования микросхемой защелки
74НСТ573 восьми линий адреса-данных ADO...
AD7 для операции записи, выполняемой ми-
кроконтроллером. На диаграмме можно ви-
деть, что линии адреса-данных AD0...AD7 сна-
чала передают адрес (младший байт), а затем
данные. Значение адреса в прозрачной защел-
ке 74НСТ573 захватывается высоким уровнем
сигнала разрешения защелки ALE и фиксиру-
ется, когда уровень этого сигнала меняется на
низкий.
20L2.5. Функция пошагового
исполнения в GLUEPAL
Другая часть нашего устройства GLUEPAL вы-
полняет задачу выдачи пакета импульсов так-
тирования (число которых обычно равно че-
тырем), синхронизированного по сигналу ALE
микроконтроллера, который подается в начале
каждого цикла доступа к шине. Мы будем обра-
щаться к этой функции пошагового исполнения
всякий раз, когда нам нужно наблюдать испол-
нение процессором команд по одной за раз. Это
ПЛУ пошагового исполнения, которое являет-
ся частью устройства GLUEPAL, задействует
входные и выходные сигналы, показанные на
рис. 20L.12. Некоторые из этих входных сигна-
лов должны быть вам знакомы по их использо-
ванию для других целей.
20L2.6. Входные и выходные
сигналы части STEP
На данном этапе просто деактивируйте вход
LOADER* (подав на него высокий логический
2012. Устанавливаем GLUEPAL и выполняем частичный монтаж
827
RESET (сброс)
(на цифровой клавиатуре)
Логическая схема
пошагового исполнения
Эти выводы вы
подключили ранее
С цифровой '
клавиатуры {лШ€Як --
(От центрального процесс
Генератор колебаний!
частотой 11,059 МГц
Рис. 20L.12. Входные и выходные сигналы части STEP пошагового исполнения устройства GLUEPAL
уровень). Сигнал на вход TRIG подается с вы-
хода ADCLK цифровой клавиатуры, а сигнал
ALE поступает от микроконтроллера.
Сигналам цифровой клавиатуры пошагового
и непрерывного исполнения STEPVRUN, а так-
же защищенному от дребезга сигналу сброса
RESET необходимо придать прямоугольную
форму с помощью триггера Шмитта 74НС14
(рис. 20L.12). Триггер Шмитта также инверти-
рует эти сигналы, и эта инверсия отражается в
измененных активных уровнях соответствую-
щих входов микросхемы GLUEPAL. Инверсия
активных уровней отображается в названи-
ях входов GLUEPAL: STEP/RUN* и KRESET*.
Необычная нумерация выводов генератора
колебаний объясняется далее в разделе 20L2.7.
Сигнал CLOCKJDUT подается на вход XTAL1
микроконтроллера (вывод 19).
20L2.7. Кварцевый генератор
сигналов тактирования с частотой
11МГц
Схема генератора колебаний сигналов тактиро-
вания4 изображена на рис. 20L.13. Сам генера-
тор размещен в квадратном корпусе, похожем
на корпус DIP с восемью выводами. Выводы ге-
нератора пронумерованы так, будто их восемь,
хотя в действительности их только четыре.
Значение частоты генератора выглядит доволь-
но странным — почему бы не использовать
+5 в
ОД мкФ,
керамический
Прямоугольный сигнал
с логическими уровнями
ВиходП_Го5
J4
Не подключен ~
Рис. 20L.13. Принципиальная схема кварцевого генератора
тактового сигнала с частотой 11 МГц
какое-либо целое число? Но такое значение
было выбрано с целью облегчить последова-
тельную связь микроконтроллера 8051 с персо-
нальным компьютером. Далее вам понадобится
такая связь5. Исследуйте выходной сигнал гене-
ратора колебаний на осциллографе. Если края
сигнала искажены, то это, скорее всего, вызва-
но слишком длинным соединением на «землю»
щупа осциллографа. Если укоротить заземляю-
щий проводник, как показано на рис. 20L.14, то
вы сможете увидеть более четкое отображение
сигнала тактирования.
Заземляющий провод с намоткой в виде спи-
рали на верхнем изображении щупа являет-
ся специальным адаптером, поставляемым
4 АоЕ§ 12.2 и рис. 12.32.
5 Данная частота обеспечивает удобную временную шкалу
для микроконтроллера 8051, который исполняет встроен-
ную программу, которая пытается подобрать скорость об-
мена, совпадающую с наиболее вероятными стандартны-
ми скоростями обмена в ПК. Объяснение выбора частоты
11,059 МГц и ее применения для генерирования опреде-
ленной скорости передачи в бодах предлагается на веб-
сайте http://www.8052mcu.com/tutser.phtml.
828
20L Лабораторное занятие: микропроцессоры I
подключенные ранее сигналы связывающей
логики (см. рис. 20L.2), и только что добав-
ленные сигналы логики пошагового исполне-
ния. Теперь мы будем называть это устройство
STEPGLUEPAL.
Рис. 20L14. Заземляющий провод минимальной длины сво-
дит к минимуму искажение сигнала тактирования
компанией Tektronix. На нижнем изображении
показан более легкий способ минимизировать
длину провода заземления: просто короткий
отрезок провода, намотанный на конец щупа.
Не у всех и не всегда будет специальный адап-
тер компании Tektronix, но у всех всегда най-
дется короткий отрезок провода. Это, в конце
концов, цифровой сигнал, и при отсутствии ис-
кажений на перепадах искажения на высоких и
низких уровнях не должны создавать проблем
для вашего компьютера.
20L2.8. Полностью подключенное
устройство STEPGLUEPAL
На рис. 20L.15 показаны все сигналы полно-
стью подключенной микросхемы ПМЛ, т. е.
Выходной сигнал STEPPAL
Как вы знаете, логическая схема STEPPAL
была добавлена к устройству GLUEPAL, что-
бы обеспечить пошаговое исполнение про-
грамм на нашем компьютере. Как упоми-
налось в разделе 20L.1.1, если вместо RUN
выбрать опцию STEP (с помощью ползунко-
вого переключателя ST*/RUN на цифровой
клавиатуре), то при каждом нажатии кнопки
INC на цифровой клавиатуре процессору по-
ставляется достаточное число циклов сигна-
ла тактирования, чтобы он мог выполнить
приблизительно половину операции. Такой
операцией может быть, например, выборка
команды или операция ввода или вывода.
Логика пошагового исполнения STEPPAL на
микросхеме ПМЛ осуществляет это, отключая
сигнал тактирования процессора вскоре по-
сле прихода импульса разрешения регистра-
защелки адресов ALE, который обозначает на-
чало каждой операции.
Сброс
(на цифровой клавиатуре)
GLUE PAL
Q
(на цифровой
От 8051
(С цифровой клавиатуры)-
(Подключите все
адресные линии, А12...
А15, к шине адреса и,
таким образом,
к микроконтроллеру 8051)
Добавлены к ТТМЛ, чтобы J
обеспечить пошаговое исполнение!
44
41
3£
41
23
(Выводы 4,17,25) г—
KRESET VCC
KBUFEN
BUSRQST CTROE
RD RAMWE
LOADER RAM0E
WR RAMCE
KWR
A15
A14
A13
10W
All
A12
ALE PSENDRV*
ак_шак_оит
IG RESET51
STEP/RUN*
£ND
+5
(Выводы 15, 26, 35)
) (На данном этапе,
\ не подключаем)
-19
20
(зеленый)
(Указывает, что шинами
управляет пользователь)
\ (На данном этапе
j" не подключаем)
39
-40
-36
-34
-33
\ Добавлены к ТТМЛ, чтобы
Г обеспечить пошаговое исполнение
Рис. 20L.15. Полное подключение устройства STEPGLUEPAL
20L2. Устанавливаем GLUEPAL и выполняем частичный монтаж
829
...устанавливает высокий уровень
на выходе Q триггера, который пропускает
сигнал тактирования, начиная со ...в результате чего следующий импульс
следующего отрицательного перепада сигнала тактирования проходит на выход
сигнала тактирования... /
'.в результате чего следующий импульс
сигнала тактирования проходит на выход
Сигнал TRIG,
создаваемый кнопкой...
... на выход пропускается всего лишь еще
два импульса сигнала тактирования
В этот момент микроконтроллер
8051 выдает адрес...
Ъ адресная шина (младшие 8 разрядов) показывает этот
адрес здесь, даже до спада сигнала ALE, поскольку
защелка прозрачная. После спада сигнала ALE защелка
фиксирует это значение адреса
Рис. 20L.16. Схема пошагового исполнения на микросхеме ПМЛ (STEPPAL) реализует пошаговое исполнение, отключая
сигнал тактирования вскоре после сигнала разрешения защелки адреса ALE
На рис. 20L.16 приведена осциллограмма одного
такого пакета четырех циклов сигнала тактиро-
вания. В это время адрес зафиксирован в защел-
ке 74НСТ573, а по мультиплексированным ли-
ниям адреса-данных передаются данные. После
того как мы проверим возможность пошагового
исполнения нашего компьютера, сможем на-
блюдать этот процесс. Для этой цели желатель-
но использовать цифровой осциллограф.
Подписи внизу рис. 20L.16 объясняют процесс
пошагового перехода от одной инструкции к
другой в тестовой программе, рассматриваемой
в разделе 20L.2.9. Как можно видеть по линиям
адреса (обозначенным ADDR_lo8) и данных, в
этой линии кода выбирается инструкция 80 по
адресу llh. Далее приводится краткое описание
логики пошагового исполнения:
♦ Сигнал ALE обеспечивает надежный отсчет
времени, поскольку он происходит:
• один раз в каждом цикле шины;
• близко к началу каждого цикла.
♦ Спад (задний фронт) сигнала ALE обознача-
ет время, когда.присутствуют все 16 разря-
дов адреса (младший байт зафиксирован в
регистре).
♦ Вскоре после этого события становятся ак-
тивированными линиями данных.
В этот момент наша логическая схема пошаго-
вого исполнения перекрывает процессору сиг-
нал тактирования и мы можем не спеша иссле-
довать действительные значения линий адре-
сов и данных.
20L2.9. Тестовая программа
Вводим программу
Введите эту крошечную тестовую программу
(листинг 20L.1), обращая внимание на адреса
при вводе значений. Столбец, обозначенный
LOC, содержит адрес, а столбец OBJ содержит
код инструкции (называемый объектным ко-
дом), который нужно исполнить. Четыре шест-
надцатеричных символа по адресу ноль не
означают, что нужно попробовать втиснуть
16 битов в одну ячейку памяти. Это значит, что
нужно поместить данную пару байтов в две
ячейки памяти: первый байт в ячейку по адре-
су 0, а второй байт — в следующую ячейку (т. е.
по адресу!).
830
20L Лабораторное занятие: микропроцессоры I
Листинг 20L.1. Тестовая программа
MACRO ASSEMBLER FIRSTJTEST
LOC OBJ LINE SOURCE
1 ; FIRST__TEST.A51 Lab 18L: Проверяем, что схема является компьютером
2
0000 3 ORG 0; Указываем ассемблеру начальный адрес для размещения этого кода
4
0000800Е 5SJMP DO_ZIP; код начинается здесь - с перехода на начало
6 ; собственно программы. ВСЕ наши программы будут начинаться таким образом
7
0010 8 ORG 10Н; Здесь начинается собственно программа, по шестнадцатеричному
адресу 10h.
9
001000 10DO_ZIP: NOP; Самая скучная операция: ничего не делать.
001180FD11SJMP DO_ZIP; И делать (или не делать?) это снова.
12
13 END
Код команды 80h означает переход исполне-
ния программы (JMP — jump) по указанному
адресу. А адрес перехода указывается значени-
ем, следующим после кода инструкции, — OEh.
В частности, это значение указывает, на сколь-
ко ячеек памяти относительно текущей ячейки
(ячейка с адресом 2 сразу же после ячейки, со-
держащей инструкцию перехода) следует пере-
йти. Или, иными словами, значение OEh пред-
ставляет собой сдвиг или смещение, выражен-
ное в дополнительном двоичном коде: 0Е16 =
= 1410. Таким образом, исполнение программы
переходит с текущего адреса 2 по адресу 1016 =
= 1610. Последняя инструкция в цикле очень по-
хожа на эту: 80FDh. В данном случае значение
FDh опять представляет смещение в дополни-
тельном двоичном коде, десятичное значение
которого будет -3. Таким образом, исполнение
программы переходит с текущего адреса 1316
назад по адресу 1016.
Мы рассмотрим эту программу более подроб-
но в главе 21N, где снова повторим некоторые
только что изложенные моменты. Поэтому не
особенно волнуйтесь, если вы не понимаете
программу полностью, и не тратьте много вре-
мени и усилий, пытаясь понять ее на данном
этапе.
Исполняем программу
После того как программа загружена в RAM,
процедура ее исполнения очень проста.
1. Установите пошаговый режим исполнения,
переместив ползунковый переключатель
ST*/RUN на цифровой клавиатуре в положе-
ние ST*.
2. Активируйте сигнал сброса RESET, переме-
стив одноименный переключатель на циф-
ровой клавиатуре вправо.
3. Деактивируйте сигнал запроса шины
BUSREQUEST*, переместив переключатель BR
на цифровой клавиатуре вправо. На дисплее
должны отобразиться значения Fh для всех
данных и адреса, поскольку все линии этих
шин находятся в «плавающем» состоянии6.
Эти состояния линий отображаются на дис-
плее в виде значений Fh по той причине, что
на входы платы ЖКД подается небольшое
положительное напряжение7.
4. Деактивируйте сигнал сброса RESET, пере-
местив соответствующий ползунковый пере-
ключатель влево.
5. Дважды нажмите кнопку INC.
6 Эти линии не находятся в идеальном «плавающем»
состоянии в обычном значении этого термина, а под не-
большим положительным напряжением, что позволяет
внешним устройствам выкладывать данные на линии. Это
что-то типа эрзаца третьего состояния, как упоминалось
ранее в рассмотрении эмуляции запроса шины в разделе
Эмуляция, сигнала запроса-разрешения шины busrequest/bus-
grant посредством сигнала RESET.
7 Входные линии платы ЖКД идут на другой микрокон-
троллер 8051, который принимает байты параллельного
входа и отправляет их на жидкокристаллический дисплей.
20L.3. Начальный этап пути SiLabs
831
На дисплее адреса должно отобразиться значе-
ние 0000, а на дисплее данных — значение 808.
Если все работает должным образом, то вы
сможете наблюдать, как процессор пошагово
исполняет введенную вами крохотную про-
грамму. Первая команда процессора, которую
он берет по адресу 0, указывает ему перейти
по адресу 10h. Эта ячейка памяти содержит ко-
манду ничего не делать NOP. После исполнения
этой команды процессор исполняет команду в
следующей ячейке по адресу 0011 h, которая от-
правляет его обратно по адресу 001 Oh. Таким
образом, процессор исполняет бесконечный
цикл команд в диапазоне адресов от 001 Oh до
0012h.
Кстати, вы увидите, что процессор выбира-
ет одну команду за пределами своего цикла.
В частности, в двух случаях в этой маленькой
программе он берет один байт из ячейки, на-
ходящейся сразу же после ячейки с командой
перехода SJMP: из ячеек по адресам 2h и 13h.
Процессор будет крутиться между адресами 10
и 13 до бесконечности или до тех пор, пока вам
не надоест наблюдать за этим. В таком случае
попробуйте переключиться из пошагового ре-
жима исполнения в непрерывный, переведя
ползунковый переключатель ST*/RUN в поло-
жение RUN.
Если ваш компьютер исполняет этот цикл, вы
имеете полное право поздравить себя и взять
небольшую передышку. На данном этапе вы
выполнили трудную часть монтажа компьюте-
ра. На последующих лабораторных занятиях
мы будем добавлять к нему только второсте-
пенные аппаратные компоненты.
20L3. Начальным этап пути
SiLabs
Начиная с данного лабораторного занятия, мы
пойдем по быстрому пути знакомства с ком-
пьютерами, используя для этого автономный
микроконтроллер. Как упоминалось ранее, по-
сле лабораторного занятия 25L.2 эти два пути
сходятся. Мы надеемся, что к тому времени вы
сможете разработать собственное приложение
для своего компьютера, независимо от выбран-
ного вами пути, приведшего вас в эту точку.
20L3.1. Микроконтроллер
C8051F410 компании Silicon
Laboratories
Мы решили выбрать совместимый с 8051 ми-
кроконтроллер, чтобы сделать согласующимися
два пути части нашего курса по микрокомпью-
терам. В частности, рассмотрение внутренней
архитектуры и языка ассемблера применимо
как к версии C8051F410 (производства компа-
нии Silicon Laboratories) этого микроконтрол-
лера, так и к версии производства компании
Dallas Semiconductors, используемой в другом
пути. Конечно же, существует много других
модификаций микроконтроллеров, совмести-
мых с 8051, и многие из них подошли бы впол-
не удовлетворительно для наших целей. Далее
приводится краткое описание соображений, по
которым мы решили остановить свой выбор на
микросхеме C8051F410:
♦ корпус небольшого размера (32 вывода),
который довольно легко припаять к пере-
ходной DIP-плате. Хотя и не такой удобный,
как собственно DIP-корпус, подобно микро-
схемам AVR9;
♦ содержит хороший набор встроенных пери-
ферийный устройств;
♦ содержит как АЦП, так и ЦАП10;
♦ содержит аналоговые компараторы;
8 Если эти значения не будут отображаться, кратковре-
менно переместите ползунковый переключатель ST*/RUN
в положение RUN после деактивирования сигнала сброса
RESET. Затем переместите переключатель обратно в поло-
жение ST* и снова выполните процедуру сброса: активи-
руйте сброс, деактивируйте его, а затем дважды нажмите
кнопку INC. Теперь все должно работать как следует.
9 Микросхемы в корпусе DIP встречаются все реже, так
что знакомство с навыками работы с компонентами для
поверхностного монтажа может быть вам на пользу. По-
скольку компоненты для поверхностного монтажа вытес-
няют DIP-компоненты, некоторые находчивые произво-
дители выпускают переходные платы DIP-форм-фактора,
позволяющие использовать такие компоненты для разра-
ботки прототипов на макетной плате. Но для работы с та-
кими переходными платами требуется наличие некоторых
навыков работы с паяльником или как минимум немного
терпения. Но сравнительно большое расстояние в 0,8 мм
между выводами микросхемы C8051F410, что почти вдвое
больше, чем у некоторых других микросхем, делает задачу
пайки ее на переходную плату не особо трудной.
10 Наличие АЦП более распространено, чем наличие
ЦАП.
832
20L Лабораторное занятие: микропроцессоры I
♦ предоставляет выход ШИМ;
♦ поддерживает несколько протоколов после-
довательной связи:
• UART11 — стандартный последовательный
обмен через RS232, полезный для обеспе-
чения взаимодействия микроконтроллера
с ПК. (Практически все микроконтролле-
ры оснащены этой возможностью.)
Интерфейс SPI12 — самый простой из после-
довательных протоколов для взаимодействия
с периферийными устройствами. Этот интер-
фейс настолько прост, что в пути Dallas лабо-
раторных занятий по микрокомпьютеру мы
смогли реализовать его программно, посколь-
ку микроконтроллер 8051 не оснащен такой
аппаратной возможностью. (См. лабораторное
занятие 24L.) Но работать с протоколом SPI
еще легче, когда он реализован аппаратно, как
в случае с микроконтроллером C8051F410;
Интерфейс 12С — более сложный последова-
тельный протокол.
♦ Встроенный генератор колебаний, достаточ-
но точный, чтобы обеспечить связь по UART
и другую работу, не требуя дополнительного
кварцевого генератора колебаний;
♦ Разнообразные интерфейсы для сигналов и
напряжения питания:
• микроконтроллер оснащен встроенным
стабилизатором напряжения, что позво-
лять использовать общее напряжение пи-
тания +5 В, а напряжение для питания ло-
гики ядра составляет +2,5 В13;
• размах входных и выходных логических
уровней можно регулировать с помощью
вывода Vj0. Обычно заданы уровни вели-
чиной +5 В, но в одном упражнении нам
нужно будет выполнить сопряжение с на-
шим компьютером последовательной RAM
11 Англ. Universal Asynchronous Receiver-Transmitter—универ-
сальный асинхронный приемопередатчик. — Примеч пер.
12 Англ. Serial Peripheral Interface — последовательный ин-
терфейс (периферийных устройств). - Примеч. пер.
13 Низкое напряжение питания ядра микроконтроллера
характерно для современных микросхем. Компания Silicon
Laboratories предлагает несколько микроконтроллеров для
применения в схемах с низким напряжением, включая ми-
кроконтроллеры с напряжением питания 0,9 В. Но это не
такое волшебство, как может поначалу показаться: вход-
ное напряжение питания повышается внутри микросхемы
генератором подкачки заряда на «плавающем» конденса-
торе. Но в любом случае напряжение питания величиной
всего 0,9 В весьма впечатляет.
с напряжением питания +3,3 В. Чтобы
обеспечить такое напряжение питания, на
вывод Vl0 нужно будет подать напряжение
+3,3 В;
• довольно приличная скорость: частота
сигнала тактирования 24,5 МГц, а мно-
гие команды исполняются (как и на ми-
кроконтроллере 8051 компании Dallas
Semiconductor) за один цикл сигнала так-
тирования. В оригинальном 8051 для ис-
полнения большинства команд требова-
лось 12 циклов сигнала тактирования.
Это основные характеристики микроконтрол-
лера C8051F410, которые демонстрируют его
возможности. Но более важным, чем любая
из этих возможностей, является средство от-
ладки, предоставляемое компанией Silicon La-
boratories. Подобно любому другому микро-
контроллеру, в микросхему C8051F410 мож-
но загружать код из ПК (микроконтроллер
8051 также позволяет делать это). Но микро-
контроллер C8051F410 также поддерживает
важные возможности отладки, без которых
контроллер может стать загадочным черным
ящиком, сводящим с ума. В частности, кроме
стандартной возможности загрузки програм-
мы отладочный интерфейс позволяет осущест-
влять следующие операции:
♦ пошаговое исполнение программы. В ком-
пьютере на микроконтроллере 8051 мы реа-
лизовали эту возможность с помощью допол-
нительного аппаратного устройства ПМЛ, за-
программированного должным образом;
♦ отображение содержимого большинства ре-
гистров и портов микроконтроллера, а также
внутренней RAM. Это не такое продвинутое
средство, как предоставляемое эмулятором
RIDE, которое позволяет протестировать
код, не загружая его в микроконтроллер. Но
оно предоставляет удобные возможности
отображения адресов, данных и кода, что по-
зволяет получить хорошее представление о
состоянии микроконтроллера в процессе ис-
полнения программы.
20L.3.2. Выводы интерфейса
программирования С2
Компания Silicon Laboratories разработала
фирменный двухпроводный интерфейс С2 для
программирования и опроса изготавливаемых
20L3. Начальный этап пути SiLabs
833
микроконтроллеров. Он хорошо подходит для
работы с микроконтроллерами с небольшим
числом выводов, поскольку для него не требу-
ются выделенные выводы, как в случае с ин-
терфейсом JTAG. Плата ЖКД, которую вы ис-
пользовали в качестве дисплея на последних
лабораторных занятиях, оснащена линиями
сигналов C2D (данные) и С2СК интерфейса
С2. Эти линии обеспечивают сопряжение ми-
кроконтроллера с ПК через порт USB. Линии
C2D и С2СК подключаются к выводам 32 и 2
микроконтроллера C8051F410 соответственно.
На плате ЖКД линии сигналов интерфейса С2
подключены к разъему в левом верхнем углу
платы.
Направляем сигналы USB на линии
интерфейса С2
Важный момент
Чтобы использовать плату ЖКД для програм-
мирования через интерфейс С2, переключатель
в нижнем левом углу платы (рис. 20L.17) необ-
ходимо установить в положение С2.
Чтобы программировать
микроконтроллер через интерсрейс
CZ, переместите ползунковый ^
переключатель вверх, в положение
С1 (из положения 5ER)
Рис. 20L.17. Включение интерфейса С2 микроконтроллера
Подключение линий интерфейса С2
на макетной плате
Можно просто подключить два вывода ин-
терфейса С2 (сигнал тактирования и данные)
модуля программирования напрямую к со-
ответствующим выводам микроконтроллера
C8051F410, как показано на рис. 20L.18.
С2СК-
C2D-
Рис. 20L.18. Самый простой способ работы с интерфейсом
С2. Но поскольку такой метод требует выделения двух ли-
ний, для нас он не подходит
Но с учетом и так небольшого количества выво-
дов на нашем микроконтроллере, мы не хотим
выделять два вывода исключительно для це-
лей отладки. В некоторых микроконтроллерах
компании Silicon Laboratories, изготавливае-
мых в корпусах большего размера, реализован
стандартный интерфейс JTAG, требующий вы-
деленных выводов. Для этого интерфейса не-
обходимо четыре вывода исключительно для
его нужд. Но для микроконтроллера C8051F410
с его 32 выводами выделение даже двух выво-
дов будет непозволительной роскошью. Кроме
того, нам в любом случае требуется функция
сброса.
Поэтому вместо простого метода задейство-
вания интерфейса С2, изображенного на
рис. 20L.18, мы применим более сложный ме-
тод, показанный на рис. 20L.20. При таком под-
ходе мы сохраняем стандартные функции вы-
водов, когда они не используются интерфейсом
С2. В частности, вывод 2 служит у нас для ввода
ручного сигнала сброса, а вывод 32 — для ин-
терфейса ввода-вывода общего назначения.
Подключение, обеспечивающее такое общее
использование выводов, довольно сложное;
также для реализации подключения интерфей-
са С2 мы разработали оригинальную собствен-
ную схему. Мы избрали такой подход, посколь-
ку хотим, чтобы микроконтроллер C8051F410
был для вас просто одним из многих аппарат-
ных устройств, схемы с которыми вы собирали
на макетной плате в этом курсе. Иными слова-
ми, мы хотим свести к минимуму впечатление
какого-то «волшебного черного ящика», кото-
рое он может производить на вас.
Возможно, что нам следовало бы признаться
в существовании более легкого способа зна-
комства с микроконтроллерами, хотя на се-
годняшнем занятии мы и не будем применять
его. Данный способ состоит в использовании
так называемой дочерней платы производства
компании Silicon Laboratories. Это небольшая
печатная плата с установленным на ней микро-
контроллером C8051F410 и несколькими други-
ми компонентами, включая точки для припаи-
вания линий к контактам ввода-вывода. Эту
дочернюю плату можно установить в базовую
адаптерную плату, также производства компа-
нии Silicon Laboratories, которая подключается
к персональному компьютеру через порт USB.
При таком подходе вам не придется самостоя-
тельно собирать схемы.
Мы ожидаем, что когда по завершении этого
курса вы снова будете работать с микрокон-
троллерами, то предпочтете данный подход.
834
20L Лабораторное занятие: микропроцессоры I
Лично нам очень понравилась универсальность
дочерних плат SiLabs. Например, когда нам тре-
бовалось большое число линий ввода-вывода,
как было при наличии платы ЖКД, то мы про-
сто взяли дочернюю плату микроконтролле-
ра SiLabs с 60 выводами и вставили ее в ту же
самую базовую адаптерную плату, которую ис-
пользовали для работы с микроконтроллером
C8051F410, а также с микроконтроллерами с
еще меньшим количеством выводов. Данная
система разработки с базовой адаптерной
платой прекрасно работает с широким кругом
компонентов производства компании Silicon
Laboratories. Но на сегодняшнем занятии вы не
сможете воспользоваться ею, и вам придется
немного потрудиться.
Чтобы вставить разъем программатора SiLabs
в макетную плату, используя его 10-жильный
шлейф, нужно согнуть штыревые контакты
разъема, как показано на рис. 20L.1914.
Рис. 20L.19. 10-контактный разъем программатора SiLabs:
выводы нужно изогнуть для монтажа на макетной плате
На рис. 20L.24 этот разъем показан с друго-
го ракурса, вставленный в макетную плату.
Соединительный кабель и цоколевка разъема
приведены на рис. 20L.20.
Жила
о цвета на шлейфе
CZCK
READBACK
+5 В
Рис. 20L.20. Кабель и цоколевка разъема: две сигнальные
линии интерфейса С2, еще одна линия эхосчитывания,
а также линии питания (положительное и «земля»)
14 Изображенный на рис. 20L.19 низкопрофильный разъ-
ем с выводами, изогнутыми под прямым углом, выпуска-
ется компанией ТЕ Connectivity, номер артикула 5103310.
Такой же разъем также поставляется и компанией Digikey,
номер артикула А33179.
Два из десяти выводов разъема не задействова-
ны. Также мы не будем подключать вывод пи-
тания 3,3 В, поскольку питание + 5 В на микро-
контроллер будет подаваться с ПК через порт
USB. Таким образом, вам не понадобятся ни-
какие дополнительные источники питания для
работы своих схем. Мы оставим неподключен-
ным вывод питания 3,3 В до раздела 25L.2, где
нам потребуется более низкое напряжение для
питания последовательной RAM.
На рис. 20L.21 изображена схема подключения
выводов 2 и 32 микроконтроллера C8051F410,
позволяющая использовать их как для связи с
ПК, так и для других целей.
410
Эхо-считивание' '
(h6)
Выход Р2.7 доступен
для периферийного
устройства сгь
1 кОм 100 Ом
(К4)
v
32
RSTVC2CK
P2/7VC2D
Рис 20L.21. Подробная схема подключения выводов 2 и
32 микроконтроллера C8051F410 для работы с интерфей-
сом С2
Как и было упомянуто, это подключение обла-
дает некоторыми особенностями, при этом ряд
его аспектов не совсем очевиден.
♦ Понять назначение двух резисторов номина-
лом 1 кОм, подключенных между выходом
C2D (данные) и периферийным устройством,
обозначенным Р2.7 GPIO, нетрудно. Эти ре-
зисторы создают развязку: сигнал C2D может
поступать на соответствующий вход микро-
контроллера C8051F410 без сопротивления
со стороны периферийного устройства.
♦ Резисторы номиналом 100 Ом между ли-
ниями С2 и входами микроконтроллера
C8051F410 просто обеспечивают защиту.
Они ограничивают ток, протекающий в дио-
дах защиты выводов микроконтроллера
C8051F410 если при отключенном питании
на него подаются сигналы С2.
Наличие двух резисторов номиналом 1 кОм
в точке подключения к линии C2D служит для
поддержания постоянного напряжения пери-
ферийного устройства, несмотря на активность
на линии С2. Это средство работает даже в
том случае, когда периферийным устройством
20L.3. Начальный этап пути SiLabs
835
Два случая использования вывода совместно
с линией интерфейса отладки С2
а) Выход Р2.7
подключен
к линии С2Ьата
б) То же самое, после
резисторов развязки
номиналом 1 кОм
без эхосчитывания точки (б);
CZ искажает выходные данные
С эхосчитыванием точки (б):
влияние С2 устраняется
Ь) Опять —
но в этот раз
с подключением
к выходу
эхосчитывания
разъема &
Рис. 20L22. Подробности передачи сигналов интерфейса С2: модуль программирования может предотвратить влияние ак-
тивности интерфейса С2 на общих контактах ввода-вывода
является выход микроконтроллера C8051F410
(как иллюстрируют осциллограммы на
рис. 20L.22). Данная возможность требуется
не всегда, но становится полезной при поша-
говом исполнении программы, использующей
устройство Р2.7. В таком случае на линиях С2
присутствует периодическая активность даже
тогда, когда микроконтроллер C8051F410 по-
дает сигнал на линию Р2.7, функционирующую
в качестве выхода.
Эффект дополнительного подключения, обо-
значенного «эхосчитывание», можно видеть на
осциллограмме на рис. 20L.22. В данном случае
это осциллограмма сигналов программы, кото-
рая мигает светодиодом (с которой мы вскоре
познакомимся в разделе 20L3.4). Программа
исполняется в пошаговом режиме, управляе-
мом по интерфейсу С2.
В процессе исполнения программы через ин-
терфейс С2 идет обмен сигналами с микрокон-
троллером C8051F410, которые отображаются
на обеих верхних осциллограммах в виде крат-
ковременных импульсов вперемежку с длин-
ными прямоугольными сигналами. Сигналы
интерфейса С2 присутствуют на периферийном
устройстве на линии (б) на левой осциллограм-
ме на рис. 20L.22, но пропадают после коррек-
тировки дополнительным подключением эхо-
считывания. На нижней правой осциллограмме
на рис. 20L.22 можно видеть, что на светодиод
подается чистый сигнал.
Очистка сигнала не особо важна, а при работе
в непрерывном режиме и вовсе не играет ни-
какой роли. Но ее легко реализовать, поэтому
воспользуемся этой возможностью.
Подключение линий питания
к микроконтроллеру С8051F410
Число выводов питания микроконтроллера
C8051F410 невелико (рис. 20L.23).
'410
VRES
4,7 mF
Рис. 20L.23. Выводы питания микроконтроллера С8051F410
Выводы питания требуют некоторого объяснения:
♦ Вывод 1/стаб ( Vreg): + 5 В — это вход встроен-
ного стабилизатора, который обеспечивает
питание ядра напряжением 2,1 или 2,5 В.
♦ Вывод 1/вх.вых (VIO): + 5 В — определяет верх-
ний предел размаха выходных сигналов. При
подаче на этот контакт напряжения величи-
ной +5 В входные и выходные сигналы будут
иметь характеристики, подобные сигналам
микросхем семейства 74НСхх: £/Вх-выс(мин)=
= 3,5 В; [/вых-выс(мин)= 4,5 В при выдаче тока
величиной 3 мА в двухтактном режиме. (Это
улучшенный режим, который позволяет
выдавать намного более сильный ток, чем
обычный выходной ток 8051, который, по-
добно токам ТТЛ, очень асимметричный).
♦ «Земля» — соедините этот вывод напрямую
с общей шиной.
♦ Вывод U+ (Vdd) — просто подключите на
«землю» через танталовый конденсатор
емкостью как минимум 1 мкФ. Это выход
встроенного стабилизатора питания. На дан-
ном этапе мы его не используем.
836
20L Лабораторное занятие: микропроцессоры I
Напряжение питания величиной -«-5 В
подается на плату микроконтроллера
C8051F410 с модуля программирования Выход Р2.7 доступен для
V периферийного устройства *
+59—
Выход Р2.7
на микроконтроллере
C8051F410
1ИЯ)
+5 В на (УВХ.ВЬЕХ (VIO): ground +5 В на U^
Рис. 20L.24. Подключение выводов питания (положительного и «земли») и совместно используемых выводов сигналов
интерфейса С2
На рис. 20L.24 показано, как мы подключили
разъем интерфейса С2 и кнопку на макетной
плате. Слева на рисунке изображена макетная
плата, подготовленная для вставки микрокон-
троллера C8051F410. На ней также показаны
подключения линий питания вместе с развя-
зывающими конденсаторами. Напряжение пи-
тания +5 В подается с платы ЖКД (на которую
оно, в свою очередь, поступает через порт USB).
Справа на рисунке изображена макетная плата
с установленным на ней микроконтроллером
(на переходной плате) и подключенным кабе-
лем модуля программирования.
Непременно предусмотрите доступ, по крайней
мере, к одному ряду точек подключения в каж-
дом из трех портов: РО, Р1 и Р2. А еще лучше,
обеспечьте себе доступ к двум рядам вверху
(у портов Р2 и РО), поскольку некоторые выво-
ды порта РО имеют двойное назначение и будет
удобно не вынимать и снова вставлять провода,
а оставить их на месте. Также полезно устано-
вить на переходную плату микроконтроллера
C8051F410 наклейку с его цоколевкой.
Резисторы размещены на плате не идеально,
чтобы обеспечить как можно более компакт-
ный монтаж. Возможно, вы сможете выпол-
нить более аккуратный монтаж.
20L33. Цоколевка
микроконтроллера С8051F410
для целей лабораторных занятий
В случае с микроконтроллером C8051F410
пользователь обладает определенной свободой
в назначении сигналов выводам, поэтому его
цоколевка не похожа на цоколевку обычной
микросхемы. В этом отношении микроконт-
роллер C8051F410 похож на микросхемы ПМЛ,
с которыми мы работали, но с меньшей свобо-
дой в назначении сигналов выводам. Данная
возможность назначать сигналы выводам обес-
печивается матричным переключателем. Мат-
ричный переключатель (который не является
собственной возможностью микроконтролле-
ра 8051) необходимо включать в любой про-
грамме, в которой он необходим.
На рис. 20L.25 показано назначение выводов
микроконтроллера C8051F410 для работы на
лабораторных занятиях 20-25.
Мы понимаем, что рис. 20L.25 содержит на-
много больше информации, чем вам нужно
знать сегодня, а также то, что некоторые на-
звания сигналов могут быть непонятными. Вам
необязательно на этом этапе знать назначение
всех сигналов, но мы приводим их все здесь на
тот случай, если в будущем они вам потребуют-
ся. Номера в скобках рядом с названиями сиг-
налов (LI, L2 и т. п.) обозначают конкретное
лабораторное занятие, в котором потребуется
данный вывод.
Для некоторых из выводов указывается альтер-
нативное применение. Например, первое на-
значение вывода РО.О обозначено как LED (что
означает управление светодиодом), а альтер-
нативное назначение этого вывода обозначено
как ADC0. Это альтернативное назначение по-
требуется нам в разделе 23L2; для этого нужно
будет отключить устройство, управляемое пер-
вым назначением (в данном случае светодиод).
20L.3. Начальный этап пути SiLabs
837
<U)
Цифровая
клавиатура
410
Р2
Р1
Р0,7
Р0,6
Р0,5
Р0,4
Р0,3
Р0,2
РОД
Р0,0
8
Дисплей (младший байт)(Ь2)
СОАДР- (с компаратором) (L3) / INT1* (L4, L5) / NSS* (с интерфейсом SPI) (L5, L6)
СОМР- (с компаратором)
INTO* (L4, L6)
PUSHBUTTON (L2,L4)
MOSFET_DRIVE (L3)
PWM (L3)
DAC1 (L4, L5, L6)
LED (LI, L2)
/ RXO (L5)
/ TXO (L5)
/ MOSI* (с интерфейсом SPI) (L5, L6)
8/
/ MI50 (с интерфейсом SPI) (L5, L6)
/ SCK (с интерфейсом SPI) (L5, L6)
DISPUY
(старший байт)
/ АЪСО (L4, L5, L6)
Рис. 20L.25. Цоколевка микроконтроллера С8051F410 для работы на лабораторных занятиях 20-25
Некоторые функции можно назначать любым
выводам, как, например, в случае функции
управления светодиодом. Но некоторые функ-
ции, как, например, RX0 или TX0, можно на-
значить только определенным выводам.
Поскольку цоколевка микроконтроллера
C8051F410 не фиксирована, в начале каждого
лабораторного занятия по этому микрокон-
троллеру мы будем указывать, какие функции
какому выводу назначены. Например, для се-
годняшнего лабораторного занятия нам будет
нужна только функция управления светодио-
дом, которая назначена выводу Р0.0, как пока-
зано на рис. 20L.26.
22222222
Рис. 20L.26. Использование вывода порта РО.О на сегодняш-
нем лабораторном занятии
20L3.4 Очень простая программа
для мигания светодиодом
Как мы говорили ранее, все получают удоволь-
ствие от мигания светодиода, когда этот эффект
свидетельствует, что собранная вами схема ра-
ботает должным образом15.
15 В действительности, нам нравятся всякие светодиоды,
а не только мигающие. Чтобы мы были довольны, све-
тодиод даже не обязательно должен мигать. Например,
постоянно светящийся светодиод включенного в сеть за-
рядного устройства успокаивает нас, информируя о том,
что он действительно заряжает наш мобильный. Зарядные
устройства, разработчики которых сэкономили 50 цен-
тов, не оснастив их таким индикаторным светодиодом, не
пользуются популярностью на рынке. Пользователям нра-
вится спокойствие души.
Некоторые аппаратные тонкости:
С8051F410 является потребителем тока
Подключите светодиод к выводу РО.О (правый
верхний вывод) таким образом, чтобы вклю-
чать его, потребляя этим выводом ток от источ-
ника питания напряжением +5 В, как показано
на соответствующей схеме на рис. 20L.2716.
РО.О
Рис 20L.27 Подключение светодиода: вывод РО.О работает в
режиме потребителя, а не источника тока
По умолчанию микроконтроллер C8051F410
работает в обычном ассиметричном режиме,
но его можно сконфигурировать для работы в
симметричном режиме.
16 Это стандартный способ управления нагрузкой выво-
дом, проявляющим ассиметричный ток наподобие ТТЛ-
устройств. В частности, в режиме потребления тока старые
логические ТТЛ-микросхемы могут работать с намного
большим током, чем в режиме источника тока. Если бы эта
особенность была присуща только микросхемам ТТЛ, то
ее можно было бы игнорировать как исторический факт.
Но мы не можем сделать это по той причине, что многие
КМОП-микросхемы подражают ТТЛ-технологии. В част-
ности, подобным образом ведет себя микросхема ПМЛ
компании Xilinx, с которой мы недавно познакомились.
Так же функционирует и микроконтроллер 8051 произ-
водства компании Dallas Semiconductors, с которым мы
работаем на других лабораторных занятиях по микроком-
пьютерам. Такие устройства могут потреблять ток значи-
тельной величины (например, 1,6 мА в случае микрокон-
троллера 8051 компании Dallas), но выдавать способны
лишь очень слабый ток (50 мкА для того же микрокон-
троллера 8051 компании Dallas). В противоположность
обычные КМОП-устройства, имеют почти симметричные
токи (т. е. одинаковые как в режиме потребления, так и в
режиме источника тока).
838
20L Лабораторное занятие: микропроцессоры I
Примечание
В компании Silicon Laboratories эту возможность
называют двухтактным режимом17, чтобы подчер-
кнуть симметричную выходную КМОП-структуру.
в одном байте. Поскольку значение байта с
адресом перехода выражено в дополнительном
двоичном коде, доступный диапазон будет от
-128 до+127.
Возможности двухтактной схемы почти симме-
тричны: она может как подавать ток в светодиод
(3 мА/4,5 В), так и потреблять его через свето-
диод (8,5 мА/0,4 В)18. Но мы оставили данный
вывод в обычной конфигурации открытого
стока и поэтому вынуждены использовать его
в качестве потребителя для тока светодиода19.
Сделали мы это по той причине, что вам будет
полезно выработать привычку, чтобы ваши
схемы служили потребителем для тока на-
грузки, поскольку вам часто придется рабо-
тать с устройствами, обладающими выводами
с ассиметричными характеристиками по току:
хорошо потребляют ток, но плохо поставляют
его. Такими устройствами являются КМОП-
устройства ПМЛ, а также микроконтроллер
8051 в его оригинальном выходном режиме.
Вывод РО.О служит потребителем для тока све-
тодиода, поступающего на его анод через рези-
стор номиналом 1 кОм от положительного ис-
точника питания напряжением +5 В.
20L3.5. Код программы для
мигания светодиодом
Главный цикл
Основная часть программы очень проста —
всего две строчки кода:
FLIPIT: CPL РО.О ; Переключает светодиод: включаем,
; затем выключаем...
SJMP FLIPIT
Команда ассемблера CPL соответствует опе-
рации дополнения; а команда SJMP означает
короткий переход (short jump), где «короткий»
означает, что пределы перехода можно указать
17 Англ. push-pull — Примеч. пер.
18 См. табл. 18.1 в справочном листке на микроконтроллер
C8051F410.
19 Особенность порта PORT0 микроконтроллера 8051 со-
стоит в том, что его конфигурацией по умолчанию явля-
ется открытый сток. И наоборот, другие порты оснащены
повышающим резистором, создающим небольшое поло-
жительное напряжение и более сильный кратковремен-
ный сигнал высокого уровня, который ускоряет зарядку
паразитной емкости нагрузки.
Исходный код программы на ассемблере
В листинге 20L.2 приводится полный исходный
код программы, включая предварительные
настройки, требуемые для микроконтролле-
ра C8051F410 (которые обсуждались в гла-
ве 20N).
Листинг 20L.2. Исходный код программы
мигания светодиодом
; bitf)ip.a51. Эта программа мигает светодиодом, но слиш-
ком быстро, и чтобы процесс можно было наблюдать, ее
нужно исполнять в пошаговом режиме.
SNOSYMBOLS; Сокращаем объем кода...
SINCLUDE (C:\MICRO\8051\RAISON\INC\c8051f410.inc)
ORG 0 ; Указываем ассемблеру начальный адрес
; для размещения этого кода
; Отключаем сторожевой таймер
ANL PCAOMD, #NOT(040h) ; Обнуляем бит разрешения
; сторожевого таймера
; Разрешаем матричный переключатель
; порта входа-выхода
MOV XBR1, #40h ; Разрешаем матричный
; переключатель
SETB РО.О ; Начинаем с выключенным светодиодом
; (активируется низким уровнем),
; просто, чтобы исполнение было
; предсказуемым
FLIPIT: CPL РО.О;flip LED
SJMP FLIPIT
END
Машинный код, полученный
из исходного кода ассемблера
Программа ассемблера для микроконтроллера
C8051F410 (или программа RIDE) преобразует
исходный код в вид кода, который микрокон-
троллер может исполнять. Этот исполняемый,
или машинный, код приведен в листинге 20L.3,
рядом с соответствующими командами исход-
ного кода на ассемблере.
20L3. Начальный этап пути SiLabs
839
Листинг 20L.3. Машинный код программы
мигания светодиодом
АДРЕС КОД № строки
КОД НА АССЕМБЛЕРЕ
0000 266
267
268
0000 53D9BF 269
270
271
0003 75Е240 272
273
274
0006 D280 275
276
0008 В280 277
000А 80FC 278
ORG 0 ; Указываем ассемблеру начальный адрес для размещения этого кода
; Отключаем сторожевой таймер
ANL PCA0MD, #NOT(040H) ; Обнуляем бит разрешения сторожевого таймера
; Разрешаем матричный переключатель порта входа-выхода
MOV XBR1, #40Н ; Разрешаем матричный переключатель
SETB P0.0 ; Начинаем с выключенным светодиодом (активируется низким уровнем)
FLIPIT: CPL P0.0 ; Переключаем светодиод — включаем, выключаем...
SJMP FLIPIT
Таблица 20L.1. Инициализация регистров микроконтроллера
Регистр
PCA0MD
XBARE
XBR1
Значение бита/байта
d6 (= WDTE)
d6(=XBARE)
40h
Функция
0 ==> Отключение сторожевого таймера
1 ==> Разрешение матричного переключателя (позволяет пода-
вать выходные сигналы на выводы)
Это байтовое значение регистра, которое содержит бит XBARE
Мы упомянули в разделе 20N.7, что для испол-
нения любой программы на микроконтроллере
C8051F410 необходимо выполнить инициали-
зацию его регистров. Такую инициализацию
необходимо выполнить даже для нашей кро-
хотной программы мигания светодиодом.
В табл. 20L.1 приводится информация по
инициализации регистров, которая на этот
раз достаточно простая, что ее, возможно,
и не требовалось бы предоставлять. Но мы
хотим, чтобы выполнение такой инициали-
зации вошло у вас в привычку. Мы считаем,
что это подчеркивает тот аспект микрокон-
троллеров, что инициализация может быть
более сложной, чем сама программа. Часто
это относится даже к простым программам, с
которыми мы будем работать на лаборатор-
ных занятиях. Но для более сложных задач,
сложность инициализации становится мень-
ше сложности собственно программы. Но мы
надеемся, что это поможет вам увидеть выде-
ление инициализации регистров в отдельную
задачу.
Не прилагайте слишком больших умственных
усилий, пытаясь разобраться в подробностях
инициализации. В будущем вам придется стол-
кнуться с большим количеством таких ини-
циализаций, включая показанные две, и вам
пойдет на пользу привыкнуть к ним. Но сэко-
номьте свои умственные силы для более ин-
тересных задач. В следующий раз мы начнем
использовать мастер конфигурации компании
Silicon Laboratories, благодаря которому за-
дача начальной настройки микроконтроллера
C8051F410 становится довольно легкой. В част-
ности, вам не нужно будет вникать в побитовые
подробности, показанные в предыдущей табли-
це. Вместо этого вам необходимо будет просто
установить флажки для выбора требуемого по-
ведения, что намного легче.
20L.3.6. Исполняем код
на микроконтроллере С8051F410
Наконец мы можем приступить к наиболее
интересной части разработки программы: ее
840
20L Лабораторное занятие: микропроцессоры I
fV r,;f -,.,.; (;).Mv.? C-vl',-,? Jr.;'', ';,;.■:■? ';•.,' ;<j • H-;
■: '■: i'c. 11 4 I Q
Рис. 20L.28. Среда разработки Silicon Laboratories позволяет выводить на экран содержимое портов, а также значения других
внутренних состояний микроконтроллера
Щ I" :>
Содержимое порта
, PORTO можно наблюдать
в процессе пошагового
исполнения программы
Рис. 20L.29. Отображение значения порта PORTO в окне отладчика при пошаговом исполнении программы
загрузке и исполнению. Следуя инструкциям
из раздела 20S.2, выполните ассемблирование
и сборку и программы bitflip.aSl и загрузите
ее в микроконтроллер C8051F410. Вам может
быть интересно наблюдать состояние порта Р0
при пошаговом исполнении программы. Для
этого можно воспользоваться опцией Ports
среды разработки Silicon Laboratories, выпол-
нив последовательность команд меню View/
Debug Windows/SFRs/Ports. Процесс исполне-
ния этой последовательности команд показан
на рис. 20L.28.
Вы должны увидеть, как содержимое порта
Р0 переключается между значениями FEh и
FFh (в процессе исполнения программы на
семи старших линиях сохраняется высокий
уровень, а уровни семи младших линий пере-
ключаются). Этот процесс иллюстрируется на
рис. 20L.29.
Но основной способ определить успех нашей
тестовой программы — проверить ее способ-
ность переключать светодиод несколько раз
в секунду, исполняясь в непрерывном режиме.
Если она будет делать это, то вы будете знать,
что, в принципе, можете управлять своим
скромным микроконтроллером C8051F410.
20L3.7. Добавляем в программу
задержку, чтобы обеспечить
непрерывное исполнение
Если исполнять нашу программу мигания све-
тодиодом в непрерывном режиме, то мы не
увидим никаких интересных результатов. Об
этом обстоятельстве предупреждают в ком-
ментарии в начале программы. Светодиод бу-
дет лишь светиться вполсилы (поскольку будет
включен только половину времени); отладчик
также не будет ничего отображать в своем
окне, поскольку не способен выполнять мо-
ниторинг исполнения программы в непрерыв-
ном режиме.
20L3. Начальный этап пути SiLabs
841
Но если в исходный код программы добавить
код, который создает задержку между пере-
ключениями светодиода, то мы сможем ис-
полнять программу в непрерывном режиме и
наблюдать результаты ее функционирования.
Программа для переключения светодиода, со-
держащая такую задержку, приведена в листин-
ге 20L4. Но модифицированная таким образом
программа не совсем готова, поскольку мы не
указали, сколько раз должен исполняться двух-
байтовый цикл задержки. Это значение будет
определяться числом, загружаемым в регистр
R4 в строке кода, начинающейся с MOV R4,
# . Символ # означает, что значение, ко-
торое заполнит следующий за ним пробел, нуж-
но рассматривать как константу, а не как адрес
ячейки, в которой будет храниться какое-либо
другое число. Такой способ называется непо-
средственной адресацией.
Заполните это значение, стараясь получить
задержку длительностью приблизительно в
одну секунду при каждом исполнении цикла.
Предположим, что двухбайтовое значение за-
держки (время, которое будет умножать содер-
жимое регистра R4) составляет приблизитель-
но 10 мс. Содержимое регистра R4 необходимо
ввести в шестнадцатеричном формате, указы-
вая его буквой h после вводимого значения:
MOV xbri, #4 Oh ; Разрешаем матричный
; переключатель
Листинг 20L4. Программа для переключения светодиода с задержкой
bitflip_delay_inline.a51
; Программа переключения светодиода bitflip с задержкой для постоянного исполнения
SNOSYMBOLS; Сокращаем объем кода...
SINCLUDE (C:\MICRO\8051\RAISON\INC\c8051f410Jnc)
ORG 0; Указываем ассемблеру начальный адрес для размещения этого кода
; Отключаем сторожевой таймер
ANL PCAOMD, #NOT(040h) ; Обнуляем бит разрешения сторожевого таймера
; Разрешаем матричный переключатель порта входа-выхода
MOV XBR1, #40h ; Разрешаем матричный переключатель
; ...на этот раз мы позволяем процессору работать непрерывно
; (пропускаем обычную строку кода деления на восемь)
MOVOSCICN,#87h
MOV А,#0 ; Максимизируем два значения задержки (0 максимальное значение, ;потому что декрементируем
; перед тестом)
MOV В,#0 ; ...и второе значение задержки в цикле
SETB P0.0
; Начинаем с выключенным светодиодом (активируется низким ;уровнем)
DELAY: MOV R4, #; Задержка длительностью в 1 секунду: произведение ;64 К других циклов
INNERLOOP:DJNZ В, INNERLOOP; Декрементируем счетчик внутреннего цикла, ;пока не станет нулевым
DJNZ ACCJNNERLOOP;... затем декрементируем счетчик второго ;цикла и снова запускаем внутренний цикл
DJNZ R4, INNERLOOP; Когда счетчик второго цикла становится нулевым, ;декрементируем счетчик внешнего цикла
CPL P0.0; Переключаем светодиод
SJMP DELAY
END
842
201. Лабораторное занятие: микропроцессоры I
С этими модификациями для реализации за-
держки наша крохотная программа уже не так и
мала, к тому же она начинает выглядеть доволь-
но неуклюже. В частности, теперь в ней трудно
различить самый важный центральный цикл,
поскольку ход его исполнения прерывается до-
бавленным кодом, реализующим задержку. Но
мы исправим эту ситуацию на следующем за-
нятии, когда будем рассматривать применение
подпрограмм. На данном этапе вкратце скажем,
что подпрограммы позволят нам разбить эту
неаккуратную программу на модули меньшего
размера, что даст возможность выделить инте-
ресующую нас часть программы, которой в дан-
ном случае является цикл bitflip для переключе-
ния светодиода.
А и В. Это упрощение нам сходит с рук по
той причине, что в конце каждого цикла
DJNZ значение декрементированного реги-
стра равно нулю.
♦ Наконец, аспект настолько привередливый,
что его даже как-то стыдно упоминать: ино-
гда к регистру А необходимо обращаться по
его полному имени АСС20. Он хочет, чтобы
к нему так обращались в операции DJNZ,
а также, как мы увидим в следующий раз,
в операции стека PUSH. Нам не понять, поче-
му разработчики ассемблеров не могут сде-
лать так, чтобы они считали команду PUSH A
эквивалентной команде PUSH АСС.
20L3.8. Некоторые особенности
цикла задержки DELAY
Некоторые аспекты цикла задержки DELAY
не совсем очевидны и требуют дополнитель-
ного объяснения. В цикле используются три
8-разрядных регистра для формирования
длительной задержки. При правильной ини-
циализации регистра R4 длительность за-
держки для указанных значений составит
приблизительно одну секунду. Максимальная
длительность задержки будет чуть меньше
трех секунд при частоте сигнала тактирова-
ния, равной 24,5 МГц, как мы делаем в дан-
ном случае.
Инициализации здесь выглядят необычно:
♦ Во-первых, на первый взгляд выглядит
странным инициализировать два регистра
нулевым значением в цикле с обратным от-
счетом. Кажется, что такое значение даст ми-
нимальную задержку. Но в действительности
оказывается, что нулевое начальное значение
даст максимальную задержку, так как снача-
ла выполняет проверку на ноль операция
обратного счета DJNZ (Decrement Jump if Not
Zero — Декрементировать, выполнить пере-
ход, если не ноль) — декрементирует прове-
ряемое значение.
♦ Во-вторых, может показаться непонятным,
что мы не выполняем повторную инициа-
лизацию этих двух регистров внутри цик-
ла. Ведь мы же выполняем повторную ини-
циализацию регистра R4 (DELAY: MOV R4,
#iOh), но почему-то не этих двух регистров
Исполняем программу в непрерывном
режиме с контрольной точкой
Загрузив программу в микроконтроллер, запу-
стите ее на исполнение в непрерывном режиме,
выполнив последовательность команд Debug/
Go или щелкнув зеленый значок Go на панели
инструментов среды разработки.
Эта программа также предоставляет нам воз-
можность продемонстрировать полезность
контрольных точек. Создайте контрольную
точку где-нибудь в цикле bitflip. Для этого вы-
делите строку кода, в которой нужно вставить
контрольную точку, затем щелкните правой
кнопкой и в открывшемся контекстном меню
выберите опцию Insert/Remove Breakpoint
(рис. 20L.30).
После установки контрольной точки програм-
ма будет работать непрерывно, но только до
этой контрольной точки, в которой исполне-
ние приостанавливается. Повторный щелчок
по кнопке Go возобновит ее исполнение после
контрольной точки. Если постоянно щелкать по
кнопке Go, светодиод будет переключаться при
каждом щелчке с задержкой длительностью
приблизительно в одну секунду: программа ис-
полняет код задержки DELAY, останавливается
на контрольной точке, возобновляет исполне-
ние и т. д.
20 Оба названия обозначают один и тот же регистр. От-
личие состоит в разных режимах адресации: прямой (ис-
пользуется АСС) по сравнению с неявной (используется А
как MOV A, P0). Спасибо Г. Колю (G. Cole) за это объяс-
нение, которое можно найти по адресу: http://www.keil.
com/forum/3761/definition-of-terminologies/.
20L.3. Начальный этап пути SiLabs
843
DELAY' Ш? 14, #*8Ь
ШЯГОХХЯР: ШН2 i, XMEBIOQF
ШЕЕ ёССЛШЮЕКШЖ
Ш82 INL ХШШЖООР
1 ткхшй diun? tt&is imltiplii&s thm 64K otb&r loops
ODumi йотш гяашста*Ь loop, till жшикг hitm
thais 4ac шюапй loop, aiid start ximar
I£D
END
1).
Рис. 20L.30. Вставка контрольной точки в программу
Лучший способ создания задержки
Но разве это не извращение — взять быстрый
процессор (в данном случае работающий на
своей максимальной частоте тактирования
24,5 МГц21), а затем стреножить его, чтобы он
еле полз? Действительно, это неудачное реше-
ние, и существует лучший способ замедлить
исполнение программы, чем удерживание про-
цессора в цикле длительностью в несколько
21 Скорость можно увеличить вдвое, если удвоить дей-
ствительную частоту сигнала тактирования, используя ре-
гистр CLKMUL
сотен тысяч итераций. Данный способ, кото-
рый мы рассмотрим на лабораторном занятии
22L, состоит в использовании аппаратных тай-
меров. Такой таймер загружается значением за-
держки, после чего ему дается указание по ис-
течении времени задержки уведомить програм-
му об этом. Такой подход оставляет процессор
свободным на протяжении задержки, в тече-
ние которой он может выполнять какие-либо
другие задачи. Это намного лучший способ
реализации задержки мигания светодиода, чем
тот, который мы продемонстрировали в разде-
ле 20L.3.7.
20S. Дополнительный материал:
микропроцессоры I
20S.1. Устройство ПМЛ
для микрокомпьютеров
Используемое нами устройство ПМЛ реа-
лизует как связывающую (GLUEPAL) логи-
ку (чисто комбинационную, для сопряжения
процессора с RAM и периферийными устрой-
ствами), так и логику пошагового исполнения
программ (STEPPAL) (последовательностную,
чтобы обеспечить пошаговую работу компью-
тера). Мы рассмотрим каждый из этих элемен-
тов отдельно, хотя они оба совмещены в одной
микросхеме ПМЛ — XC9572XL (с напряжени-
ем питания 3 В) или ХС9572 (с напряжением
питания 5 В).
20S.1.1. Элемент GLUEPAL
Цоколевка для GLUEPAL показана на рис.
20L.4.
№Щ1
^
29
Файл программы на Verilog
Программа на Verilog, которая реализует свя-
зывающую логику (часть GLUE) и логику по-
шагового исполнения (часть STEP), находится
в файле stepglue_3v.v, который можно загру-
зить с веб-сайта этой книги.
20S.1.2. Элемент STEPPAL
Краткое описание логики пошагового
исполнения STEP
♦ Сигнал ALE обеспечивает надежный отсчет
времени, поскольку он происходит:
• один раз за каждый цикл шины;
• близко к началу каждого цикла.
♦ Спад (задний фронт) сигнала ALE обозна-
чает время, когда присутствуют все 16 раз-
рядов адреса (младший байт зафиксирован
в регистре).
I/ / / У
1
А\9
'//л
5ЯГ
IOR*, IOW*
RAMWE* KBUFEN*
Н&Е^Я
От ЦП
(Цифровая
клавиатура, 6)
DEUMUXOE
TSENDBX*
loads* :
oawxoe- й^»
***** *1 RESET51
LOADER*
It* 1
LOAO€^75"
3
PSENDRV
CTR.OE*
RAMOE*
Рис. 20S.1. Логические блок-схемы элемента GLUEPAL
20S.2 Примечания о среде разработки Silicon Labs IDE
845
38
43
ALE
TRIG
D Q
21
ALE_LATCH
TRI6J.ATC6
J±
TRI6 SYNC
23
22
14
30
STEP/RIN*
BUSRQST*
LOADER*
KRESET*
J16
DELAY
Управляемый
сигнал тактирования
---- ^
Непрерывное исполнение
CLOCKout
i (Выход сигнала
У тактирования)
(Выход
мул ьти плексора)
Рис. 20S.2. Цоколевка и логическая блок-схема пошагового исполнения STEPPAL
♦ Вскоре после этого события становятся дей-
ствительными линии данных.
На рис. 20S.2 изображена логическая схема по-
шагового исполнения STEPPAL.
Программа на Verilog для реализации
STEPPAL
Листинг 20S.1 содержит программу на Verilog
для реализации логической схемы STEPPAL.
begin
TRIG.SYNC <=TRIG_LATCH;
end
always @(negedge CLKJN)
DELAY <= (TRIG.SYNC & ALEJ.ATCH);
assign full.speed = (!STEP_RUNBAR |! BR_bar | !LOADER_bar
| !KRESET_bar);
assign CLKJDUT = (CLKJN & fulLspeed) | ((TRIG_
Листинг 20S.1. Программа на Verilog
для реализации STEPPAL
//Логика пошагового исполнения программы
initial
DELAY = 1ЪО; // Инициализация для разрешения
//эмуляции
always @(negedge ALE, posedge DELAY)
if (DELAY)
ALE_LATCH <= VbO;
else
ALE_LATCH<=1'b1;
always @(posedgeTRIG, posedge DELAY)
if (DELAY)
TRIG_LATCH<=VbO;
else
TRIG_LATCH<=1'b1;
always @(negedge CLKJN)
20S.2. Примечания
о среде разработки
Silicon Labs IDE
205.2Л. Подключение отладчика
на ПК к микроконтроллеру
C8051F410
Подключив модуль программирования к ми-
кроконтроллеру C8051F410 через линии ин-
терфейса С2 и к ПК через порт USB, на микро-
контроллер можно подать питание и запустить
среду разработки Silicon Laboratories IDE1.
1 Сокращение IDE означает Integrated Development Envi-
ronment — интегрированная среда разработки. Ассемблер/
компилятор/симулятор RIDE является другой средой раз-
работки для микроконтроллеров 8051 (среди прочих).
846
20S. Дополнительный материал: микропроцессоры I
Подключение ПК к микроконтроллеру
C8051F410
Запустите среду разработки Silicon Laboratories
(SiLabs) и создайте новый проект. Можно от-
крыть наш проект bitflip.wsp, содержащий
первую программу, которая мигает светодио-
дом. Для созданного вами проекта нужно будет
загрузить в него файл bitflip.a51. Для этого
выполните последовательность команд меню
Project/Add Files to Project, в открывшемся
средстве навигации по файловой системе пе-
рейдите в папку, содержащую требуемый файл,
и выполните по нему двойной щелчок мышью.
После этого файл отобразится в панели ресур-
сов проекта, расположенной в левой стороне
экрана.
Опции подключения
Прежде чем пытаться подключиться к микро-
контроллеру, проверьте, что среда разработки
SiLabs обнаруживает USB-подключение и что
эта опция установлена. Если для подключения
задана опция последовательного подключе-
ния RS232, то подключиться к микропроцес-
сору не получится. Чтобы установить опцию
USB-подключения, выполните последователь-
ность команд Options/Connection Options и
в открывшемся диалоговом окне Connection
Options установите переключатель USB Debug
Adapter (рис. 20S.3).
выключите и снова включите питание микро-
контроллера C8051F4102. Убедившись в том,
что установлена правильная опция подклю-
чения, подключитесь к микроконтроллеру,
выполнив последовательность команд меню
Debug/Connect.
Ассемблируем программу
Выполнив подключение к микроконтроллеру,
можно приступать к ассемблированию про-
граммы. Для этого выполните последователь-
ность команд меню Project/Assemble или на-
жмите соответствующую кнопку (самая левая
кнопка в группе кнопок Build справа от группы
стандартных кнопок File). После завершения
ассемблирования при желании можно просмо-
треть содержимое файла полученного листин-
га, который будет иметь расширение .LST. Мы
уже просматривали такой файл в главе 20N,
поэтому не стоит тратить время на это сейчас.
Вместо этого перейдем к загрузке полученного
кода в микроконтроллер C8051F410.
Загрузка кода в микроконтроллер
C8051F410
Чтобы загрузить код программы в микро-
контроллер, щелкните самую правую кнопку
в группе кнопок Build. Эта кнопка обозначе-
на направленной вниз стрелкой и буквами DL.
В течение нескольких секунд код должен за-
грузиться в микроконтроллер. После успеш-
ной загрузки кода рядом с первой исполняемой
строчкой кода программы должен появиться
курсор синего цвета, а значки разных режимов
исполнения программы справа от значка непре-
рывного исполнения (в группу значков Debug)
должны стать доступными для использования.
Это можно понять, поскольку с них снимается
окраска серого цвета (см. рис. 20S.5).
Рис. 20S.3. Установки опции USB-подключения в диалого-
вом окне Connection Options
Если по какой-либо причине не удается уста-
новить переключатель для USB-подключения,
закройте программу среды разработки, а затем
Разные режимы мониторинга
в отладчике
Теперь мы можем воспользоваться интерак-
тивной связью среды разработки SiLabs с
микроконтроллером C8051F410 (т. е. подклю-
чением по интерфейсу С2). Подключение С2
2 При работе в среде разработки, используя Parallels на
Макинтош, мы обнаружили, что также необходимо вы-
полнить Parallels Reset, чтобы восстановить контроль над
опцией подключения.
20S.2. Примечания о среде разработки Silicon Labs IDE
847
позволяет не только загружать код программы
в микроконтроллер, но также делает возмож-
ным управлять с ПК исполнением этого кода
на микроконтроллере, а также выполнять мо-
ниторинг регистров и внутренней памяти ми-
кроконтроллера. Эта возможность избавляет
нас от необходимости применять старый метод
отладки, называемый «прожигание и сбой»3.
Этот метод состоит в загрузке кода в микрокон-
троллер и попытке исполнить его. Если код не
работает должным образом, называем это сбо-
ем и повторяем процедуру. Интерфейс С2 по-
зволяет нам видеть, что делает микроконтрол-
лер в процессе исполнения кода.
Пошаговое исполнение, контрольные
точки и исследование регистров
Среда разработки Silicon Laboratories предо-
ставляет три важных средства отладки.
Пошаговое исполнение
Назначение этого средства понятно по его на-
званию — возможность исполнять по одной
инструкции за раз. Эта возможность необхо-
дима для того, чтобы можно было реализовать
другую возможность — выполнять мониторинг
регистров микроконтроллера.
Установка контрольных точек
При установке контрольной точки в определен-
ной строке кода программа исполняется в не-
прерывном режиме до этой точки и останавли-
вается в ней. Это позволяет нам исследовать со-
держимое регистров микроконтроллера и при
желании продолжить исполнение программы
или в непрерывном, или в пошаговом режиме.
Контрольные точки удобны при отладке про-
грамм больших размеров, исполнение которых
пошагово может быть слишком утомитель-
ным.
Мониторинг регистров
Как уже упоминалось ранее, среда разработки
SiLabs позволяет исследовать содержимое ре-
гистров микроконтроллера, а также его вну-
тренней памяти обоих типов: как ROM, так и
RAM.
Изменение содержимого регистров
Среда разработки SiLabs позволяет модифици-
ровать некоторые регистры микроконтроллера,
например регистр РО, как это делается в нашей
программе мигания светодиодом.
Многошаговое исполнение программы
Кроме непрерывного и пошагового режимов
исполнения среда разработки SiLabs поддер-
живает еще один режим исполнения — много-
шаговый, который может быть полезным в не-
которых случаях. Например, мы задействуем
этот режим в нашей первой программе — ми-
гания светодиодом. Как вы уже знаете, данная
программа переключает состояния светодиода,
подключенного к линии Р0.0. В режиме посто-
янного исполнения результаты работы про-
граммы непонятны, поскольку визуально све-
тодиод просто светится вполсилы. Но в много-
шаговом режиме исполнения светодиод пере-
ключается с частотой в несколько герц.
Выбор ресурсов для мониторинга
Ресурсы для мониторинга выбирают, выполнив
последовательность команд меню View/Debug
Windows, как показано на рис. 20S.4. Ресурсы,
наиболее часто необходимые для мониторинга,
например основные регистры микроконтрол-
лера, также можно выбрать с помощью соот-
ветствующих кнопок в группе кнопок View на
панели инструментов.
3 Англ. burn and crash. Выражение «прожигать» в значении
«программировать» берет начало из истоков микрокон-
троллеров, когда код в память ROM записывался (про-
граммировался), расплавляя или пережигая плавкие ме-
таллические перемычки.
Рис. 20S.4. Среда разработки SiLabs позволяет выбрать ре-
сурсы для мониторинга в процессе пошагового исполнения
программы
На рис. 20S.5 мы выбрали некоторые наиболее
очевидные для мониторинга ресурсы: набор
регистров (которые в среде разработки назы-
ваются 8051 Controller/Misc) и порты Ports,
включая единственный порт РО, используемый
в программе мигания светодиодом.
848
20S. Дополнительный материал: микропроцессоры I
шштвш
Рис. 20S.5. Мониторинг значений регистров и внутренних портов микроконтроллера в среде разработки SiLabs
пли:., ш-
\ и^Ь'й! SET17F
.•. BLUE.„LED
;:^>;'-V$;'^."v:iY§*VV
bit
Рис. 20S.6. Добавление регистра для наблюдения в окно Watch
20S.2. Примечания о среде разработки Silicon Labs IDE
849
Наша программа мигания светодиодом на-
столько проста, что в ней нет ничего, стоящего
мониторинга. Все, что в ней изменяется, — са-
мый младший разряд порта РО. Но мы, по край-
ней мере, можем видеть это как изменение зна-
чения порта РО между FEh и FFh.
Окно мониторинга регистров Watch
Наш микроконтроллер содержит такое боль-
шое число регистров, что среда разработки
SiLabs благоразумно не пытается отображать
содержимое их всех. Вместо этого в ней мож-
но выбрать определенный регистр в листинге
программы, а затем добавить его в специаль-
ное окно для мониторинга регистров Watch.
На рис. 20S.6 показано это окно с выбранным
регистром, который содержит бит разрешения
сторожевого таймера (не потому, что он особо
важен для наблюдения, а потому, что это до-
вольно второстепенный регистр, не включен-
ный ни в один из стандартных наборов реги-
стров).
Выбор регистров для помещения в окно Watch
сопряжен с определенной сложностью, кото-
рая может создать проблему. В частности, при
выборе регистра также необходимо указать
правильный подробный тип Detailed Type
этого регистра (рис. 20S.6). При указании не-
правильного типа, например char вместо sfr для
регистра PCA0MD (что является вполне логич-
ным выбором, поскольку, как регистр PCA0MD,
так и значение типа char занимают один байт),
мы будем жестоко наказаны. Среда разработ-
ки SiLabs не выводит никаких сообщений об
ошибке. Она просто «беззаботно» отображает
в окне Watch полнейшую ерунду: не содержи-
мое регистра PCA0MD, а что-то абсолютно дру-
гое (и мы не имеем ни малейшего понятия, что
именно).
Полезная возможность окна мониторинга —
выбор формата отображаемых значений: шест-
надцатеричный или десятичный. На рис. 20S.6
мы, как обычно, выбрали шестнадцатеричный.
Но формат по умолчанию — десятеричный.
20W. Примеры с решениями:
«Инсектарий»
Недавно на нас снизошло озарение, что больше
всего обучаемся на трудностях, испытываемых
студентами на лабораторных занятиях, мы —
учителя: студенты постоянно предоставляют
нам трудные, но интересные проблемы с непо-
слушными микроконтроллерами. Мы решили,
что будет логично поделиться некоторыми из
интересных проблем с вами.
Процесс изложения будет следующий: сначала
разрабатывается теория, согласно которой на-
блюдаемой проблеме может быть поставлен
диагноз, а затем излагается процедура тестиро-
вания (в случаях, для которых одного теорети-
ческого диагноза недостаточно, чтобы опреде-
лить проблему).
На рис. 20W.1 изображена схема, собранная на
макетной плате, для которой, на первый взгляд,
диагностирование какой-либо проблемы было
бы трудной задачей. Но, как показывает бе-
лая стрелка, в один конкретный день задача не
оказалась трудной. Как эта моль умудрилась за-
браться в такое место и отойти в мир иной, яв-
ляется загадкой, которую мы так и не решили.
Возможно, что некий проказничающий студент
сыграл в этом какую-то роль, но мы надеемся,
что это не так. Мы предпочитаем верить в слу-
чайные события.
Мы должны признаться, что время от времени
мы даже восхищаемся обнаруженными багами
(т. е. ошибками). Мы иногда заявляем, и только
частично шутя, как в случае, когда мы излагали
достоинства сборки компьютера из дискретных
компонентов, что ошибки — наш самый глав-
ный «продукт». Мы, конечно же, говорим это
не совсем серьезно, но очень близко к этому.
Мы даем указание студентам собрать эту слож-
ную схему, выполняя монтаж проволочными
перемычками, тогда как мы могли бы дать им
соответствующую печатную плату, используя
которую у них был бы рабочий компьютер в
первый же день. Но мы избрали первый подход,
Рис. 20W.1. Иногда диагностировать проблему несложно, но обычно все наоборот
Баг № 7. Микроконтроллер отказывается выполнять команды
851
поскольку полагаем, что сборка компьютера в
таких подробностях доставит вам чувство глу-
бокого удовлетворения. Но другой причиной
является то, что схема такого размера предо-
ставляет так много возможностей совершить
какую-либо ошибку при ее сборке, что даже при
внимательном отношении к этому процессу из-
бежать ошибок вряд ли удастся. Мы надеемся,
что вы получите удовольствие от выискивания
причин своих ошибок, допущенных при сборке
данной схемы. Далее приводится краткое опи-
сание некоторых ошибок, удовольствие от по-
иска причин которых получили мы.
Баг № 1. Микроконтроллер
отказывается выполнять
команды
Наша программа, скажем, тестовая программа
из лабораторного занятия 20L, содержит по
адресам 0 и I команду начального перехода по
адресу lOh1 к собственно программе. Когда про-
цессор доходит до адреса 1 (после чего он со-
вершает предвыборку команды по адресу 2), он
выполняет данный переход, но только вместо
того, чтобы идти по адресу 10h, он идет куда-то
в другое место, возможно, по адресу llh. Там он
снова отображает правильный код, но на сле-
дующем шаге «убегает» по какому-то странно-
му дальнему адресу.
Объяснение бага № 1
Мы видим на шине данных не такие данные, как
те, которые поступают на центральный процес-
сор. Иными словами, где-то на пути к централь-
ному процессору в шине данных происходит
искажение данных. Это может быть следствием
перестановки линий или же следствием нека-
чественного контакта какой-либо линии шины
с выводом центрального процессора, в резуль-
тате чего данная линия находится в «плаваю-
щем» состоянии. Этот случай рассматривается
подробно в следующем абзаце.
Наше предположение легко проверить, поша-
гово исполняя программу до точки, в которой
процессор должен получать векторную кон-
станту или команду, которую, как мы заметили,
он неправильно интерпретирует. Например,
предположим, что вместо перехода по адре-
су 10h процессор выполняет переход по адре-
су llh. В таком случае остановите исполнение
программы по адресу 1, в котором, похоже,
процессор получает из RAM байт со значением
OEh, а затем проверьте пробником все восемь
линий шины данных, где они подключаются
к центральному процессору. Скорее всего, на
них будет значение 0000 1111, т. е. шестнадца-
теричное OFh, а не OEh, которое должно быть.
Мы получили этот результат, в качестве приме-
ра вытащив из гнезда одну из линий, которая
должна была подключать к шине самый млад-
ший разряд данных центрального процессора
(ADO). В результате центральный процессор
интерпретировал «плавающий» уровень на
своем выходе ADO как высокий, вследствие
чего он перешел по адресу, на единицу больше-
му, чем требовалось. Сама по себе эта ошибка
не сбила бы программу с правильного пути,
поскольку по адресу 10h пропускалась толь-
ко команда NOP. Но по адресу llh, в котором
центральный процессор должен был бы полу-
чить команду 80h (относительный переход), он
получил код команды 81h. А это код команды
перехода AJMP, конечный адрес которого фор-
мируется неправильно и который далеко не тот,
который нам требовался2.
Баг № 2. У нас разногласия
с микроконтроллером
относительно содержимого
RAM
Пользователь загружает программу в RAM и
удостоверяется, что код загружен: проходит по
ячейкам памяти после загрузки, проверяя их
содержимое, все это время имея шину в своем
распоряжении.
1 Более точно, код дает процессу следующее указание:
«Перейти вперед на ячейку памяти, расположенную от
ячейки, на которую нужно было бы перейти при обычном
исполнении (в данном случае это 02h), на расстоянии ука-
занного смещения OEh».
2 Подробности формирования адреса перехода доволь-
но скучные, но если вам интересно, мы изложим их. Это
11-разрядное смещение от адреса, в котором была бы по-
лучена следующая инструкция, если бы программа про-
должала прямолинейное исполнение. В данном случае это
адрес 13h. Величина смещения создается из старших трех
разрядов кода операции (в данном случае это 4) и следую-
щего байта (в данном случае это FDh). В результате по-
лучается переход по адресу FDlOh, если я не ошибаюсь
в моих шестнадцатеричных вычислениях.
852
20W. Примеры с решениями: «Инсектарий»
Попытка исполнить загруженную программу
завершается неудачей: при исполнении в не-
прерывном режиме программа завершается
сбоем. При пошаговом исполнении компью-
тер показывает значения в RAM, отличающие-
ся от загруженных и проверенных несколько
минут тому назад. Пользователь снова берет
управление шиной, проверяет память и обна-
руживает, что ее содержимое точно такое, как
он ввел изначально.
Вариант бага: иногда программа функциони-
рует правильно и код совпадает с тем, который
видит пользователь, а иногда код не совпадает
и программа не исполняется.
Объяснение бага № 2
Данные, которые пользователь видит на шине
данных, не совпадают с теми, которые выклады-
вает на нее центральный процессор. Иными сло-
вами, где-то на пути от центрального процессора
к памяти линии шины адреса перепутались.
Выполните проверку каждой линии адреса на
микросхеме RAM. Именно на микросхеме, а не
в гнездах рядов макетной платы, в которые она
вставлена, поскольку один из выводов микро-
схемы может быть согнут и не вставлен в гнез-
до. Поэтому проверьте логическим пробником
каждый вывод адреса RAM на наличие «плаваю-
щего» уровня. Данную проверку лучше всего
выполнять, когда шиной адреса управляет цен-
тральный процессор, поскольку таким образом
вы сможете обнаружить обрыв не только меж-
ду шиной адреса и микросхемой RAM, но также
в любом месте цепочки — между центральным
процессором и защелкой демультиплексора
74НСТ573 или между этой защелкой и шиной.
Что касается варианта этого бага, то он объяс-
няется подобным образом, но вследствие свое-
го непостоянства труднее поддается диагно-
стированию: некоторые линии адреса (обычно
только одна) находятся в «плавающем» со-
стоянии. Обычно это будет одна из старших
линий адреса. Когда пользователь загружает
программу, на ней присутствует один уровень,
а когда контроль над шиной берет централь-
ный процессор, уровень меняется. Возможной
причиной может быть переключение соседней
линии при смене задатчика шины. В результа-
те мы обращаемся к разным блокам RAM, хотя
отображаемые значения шины адреса не ме-
няются. Линии адреса дисплея не «плавают»,
а получают четко определенные уровни, сна-
чала от управляемого вручную счетчика адреса
(16-разрядный счетчик на микросхеме ПМЛ),
а затем от центрального процессора.
Баг № 3. При попытке
использовать кнопку Ready
происходит фатальный сбой
компьютера
Программа исполняется без проблем, но толь-
ко до тех пор, пока пользователь не пытается
воспользоваться новой возможностью — кноп-
кой Ready (см. раздел 22W.1). По-видимому,
компьютер обнаруживает нажатие кнопки за-
писи Write на цифровой клавиатуре, но реаги-
рует на это действие не принятием вводимого
значения, а фатальным сбоем.
Объяснение бага № 3
Кнопка записи Write и создаваемый ею сигнал
KWR* остаются подключенными напрямую или
к выводу WE* микросхемы RAM, или к выво-
дам ENABLE* микросхемы 541.
Таким образом, нажатие кнопки Write вызыва-
ет или искажение данных на шине данных, или
изменение содержимого RAM на случайных
этапах исполнения программы. Это неправиль-
ное подключение объясняется тем, что ранее,
на лабораторном занятии 17L, мы подключили
кнопку Write напрямую как к выводу WE*, так
и к выводам ENABLE* и забыли удалить эти
подключения, когда изменяли схему.
При правильно выполненном монтаже схемы
нажатие кнопки Write при исполнении про-
граммы не вызывает никаких отрицательных
последствий поскольку во всех случаях, ког-
да контроль шиной находится у центрального
процессора, ее сигнал KWR* заблокирован как
от вывода WE*, так и от выводов ENABLE* ми-
кросхемы 541. Активированные сигналы KWR*
и BR* обрабатываются логическим вентилем И;
пока центральный процессор исполняет про-
грамму, сигнал BR* никогда не активируется.
Таким образом, пока центральный процессор
исполняет программу, сигнал KWR* не оказыва-
ет никакого эффекта, за исключением триггера
Ready, как и было запланировано.
Баг № 4. При попытке АЦП выложить данные на шину данных возникает конфликт
853
Баг № 4. При попытке АЦП
выложить данные на шину
данных возникает конфликт
Компьютер работает без каких бы то ни было
проблем, исполняя все программы вплоть до
лабораторного занятия 23L, на котором выпол-
няется проверка работоспособности аналого-
цифрового преобразователя. При такой про-
верке при чтении с порта 3 (порт данных АЦП)
АЦП выдает выходной сигнал постоянного
уровня на вход компьютера (значение которого
случайно оказывается равным FFh).
При тестировании АЦП мы подали на него
входной сигнал уровня потенциала «земли» и
выполнили один цикл. Мы обнаружили, что в
течение цикла чтения некоторые выходные ли-
нии данных АЦП находились в «плавающем»
состоянии. Отключив АЦП от шины, мы выяс-
нили, что он пытался выдавать на шину сигнал
низкого уровня, который конфликтовал с сиг-
налом высокого уровня, поступающим на шину
от какого-то другого устройства. В результате
этого конфликта на шине устанавливался сиг-
нал промежуточного уровня, похожий на «пла-
вающее» состояние.
Объяснение бага № 4
В течение всего этого времени память RAM
была постоянно разрешена и ее выходные сиг-
налы конфликтовали с входными сигналами
устройств ввода-вывода, адресное простран-
ство которых не должно было быть доступным
для RAM.
Это довольно тонкая проблема, поскольку
она возникает на таком позднем этапе ра-
боты с нашим компьютером. В частности,
к этому времени мы уже успешно выполня-
ли ввод данных с другого устройства ввода-
вывода — цифровой клавиатуры. Каким же
образом ввод с того устройства не приводил
ни к каким проблемам, а ввод с АЦП потер-
пел неудачу? Очень просто — выходной сигнал
микросхемы 541 цифровой клавиатуры на-
много мощнее, чем выходной сигнал микро-
схемы АЦП AD7569. Соответствующие дан-
ные приводятся в табл. 20W.1. Обратите вни-
мание на контраст в значениях токов 1ВЫХ_НИЗ
и вых-выс*
Таблица 20W.1. Выходные токи микросхем,
соответствующие логическим уровням
Компонент
74НС541
AD7569
RAM
'ВЫХ-НИЗ
6мА
1,6 мА
2,1 мА
-'вых-выс
6мА
200 мкА
1мА
Таким образом, сигналы от мощной микросхе-
мы 541 буферов цифровой клавиатуры с легко-
стью пересиливали сигналы микросхемы RAM
в их конфликте за управление шиной данных.
А вот сигналам микросхемы AD7569 аналого-
цифрового преобразователя в этом конфлик-
те пришлось намного труднее. Выходной ток
сигналов этой микросхемы немного ниже, чем
микросхемы RAM, в результате чего уровень
конечного сигнала получается ни действитель-
ный низкий, ни действительный высокий. По
крайней мере, в некоторых случаях, поскольку
ток сигнала низкого уровня АЦП сравним с то-
ком сигнала высокого уровня памяти RAM.
Данная проблема решается исправлением
ошибки разрешения памяти RAM. В частности,
сигнал CS* для RAM должен активироваться
только для адресного пространства памяти, ко-
торое определяется низким уровнем на линии
адреса А15. (Подробности см. на лабораторном
занятии 20L и на рис. 20L.1.)
Баг № 5. АЦП работает
при пошаговом исполнении
программы, но не при
непрерывном
Программа тестирования работы АЦП запуска-
ет это устройство, возвращается назад, считы-
вает его выходное значение и выводит резуль-
тат (на ЦАП или на дисплей). Выдаваемое АЦП
значение или постоянное, или беспорядочно
меняется. А в пошаговом режиме исполнения
программы АЦП работает идеально (что было
проверено подачей на него входного сигнала от
потенциометра).
Объяснение бага № 5
Частота генератора колебаний для АЦП слиш-
ком низкая. Конечно же, важным ключом к
решению данной проблемы является разница
854
201V. Примеры с решениями: «Инсектарий»
в скорости преобразования, которую цент-
ральный процессор требует от АЦП в каждом
из этих двух случаев. В частности, при пошаго-
вом исполнении программы центральный про-
цессор дает преобразователю целую вечность
для выполнения преобразования; а при рабо-
те в непрерывном режиме он может выделить
АЦП очень небольшое время.
Если к тому времени, когда центральный про-
цессор пытается считать значение преобразо-
вания, оно еще не готово (а программа не ждет
вежливо, пока ей не скажут, что значение гото-
во; она считывает его тогда, когда мы предпо-
лагаем, что оно готово), АЦП «мстит» ей за ее
поспешность, выдавая недействительные дан-
ные. Наиболее вероятная причина медленного
преобразования — просто неправильная по-
стоянная времени RC генератора сигнала так-
тирования АЦП.
Слишком большую постоянную времени RC
можно получить, если использовать компо-
ненты RC-цепочки со стандартными номи-
налами вместо указанных. Например, вместо
резистора сопротивлением 6,2 кОм взять ре-
зистор сопротивлением 6,8 кОм, а конденсатор
емкостью 68 пФ заменить на конденсатор емко-
стью 100 пФ. Получившаяся в результате такой
замены постоянная времени RC будет на 60%
больше требуемой. Кроме того, постоянную
времени радикально большего значения можно
получить, неправильно прочитав значение но-
минала конденсатора. Распространенной ошиб-
кой является предположение, что 0,068 мкФ
означает 68 пФ. В результате такого заблуж-
дения некоторые могут использовать значение
0,1 мкФ, полагая его достаточно близким.
Данная проблема решается довольно скучным
образом: внимательно проверьте номиналы
конденсатора и резистора в цепочке. Если они
неправильны, замените их правильными. Если
вам захочется поэкспериментировать с провер-
кой скорости преобразования вашего АЦП, то
можно подать сигнал тактирования на АЦП от
внешнего генератора. Преобразования в посто-
янном режиме исполнения должны выполнять-
ся должным образом при частоте тактирования
величиной 4 МГц. При понижении частоты так-
тирования АЦП его выходные данные должны
стать недействительными, когда время преоб-
разования превысит время между командами
START и READ программного цикла.
21 N. Микропроцессоры II. Ввод-вывод и первая
программа на ассемблере
Содержание
21 N.1. Язык ассемблера и причины для его использования 855
21N.1.1. Тестовая программа для компьютера из дискретных компонентов 856
21N.1.2. Директивы ассемблера 859
21N.1.3. Исполнение тестовой программы для дискретного компьютера
в пошаговом режиме 861
21N.2. Снова о декодировании 861
21N.3. Код ввода-вывода для дискретного компьютера 863
21N.3.1. Адрес порта 0 на языке процессора 863
21N.3.2. Формат команд ассемблера 864
21N.3.3. Завершаем создание тестовой программы 865
21N.3.4. Программа тестирования в действии 865
21N.3.5. Компьютер на автономном микроконтроллере C8051F410
не отображает такие подробности 866
21N.4. Сравнение версий на ассемблере и на языке С программы вывода
на дисплей значений, вводимых с цифровой клавиатуры 866
21N.5. Вызов подпрограмм 867
21N.5.1. Стек как кратковременное хранилище общего назначения 868
21N.5.2. Вызов подпрограмм и функций в языке С 870
21N.6. Расширение операций до 16 разрядов 871
21N.7. Материал для чтения из АоЕ 872
Цель этой главы
Сегодняшняя задача состоит в том, чтобы осна-
стить наш компьютер возможностью прини-
мать и выдавать информацию по одному байту
за раз. Но прежде чем продолжать, освежим в
нашей памяти некоторые основные понятия из
главы 20.
♦ Чтобы подключенные к шинам память и пе-
риферийные устройства работали должным
образом, необходимо декодировать сигналы
управления и адреса, выдаваемые процес-
сором.
♦ Хотя контрольные сигналы разных микро-
процессоров отличаются в деталях, в общем
они передают довольно стандартную ин-
формацию: направление обмена данны-
ми, синхронизацию обмена, устройство
назначения, а часто также информацию о
типе участника обмена — устройство ввода-
вывода или память.
21N Л. Язык ассемблера
и причины для его
использования
Язык ассемблера представляет собой язык на
основе английского (или любого другого чело-
веческого) языка, с помощью которого люди
определяют операции для выполнения микро-
процессором. Например, выражение MOV R0,
#38h на языке ассемблера представляет два бай-
та машинного кода 78h и 38h. Данная команда
дает процессору указание загрузить в рабочий
регистр под номером ноль шестнадцатеричное
значение 38. Язык ассемблера отличается от
языков более высокого уровня, таких как С, тем,
что в нем одна строчка кода соответствует одной
команде на машинном языке. Напротив, в том
же языке С одна строка кода часто выражает бо-
лее сложную операцию, для выполнения кото-
рой требуется несколько команд на машинном
языке (и на языке ассемблера).
856
21 N. Микропроцессоры II. Ввод-вывод и первая программа на ассемблере
Но программирование на языке ассемблера
становится все менее популярным по той при-
чине, что оно слишком дорого в единицах за-
траченного времени. Программисты иногда го-
ворят, что за один день разработчик может соз-
дать приблизительно десять строк полностью
отлаженного кода. Если это действительно так,
то, несомненно, будет более выгодно создавать
строки кода, которые выполняют больший
объем работы. Но в этом курсе мы програм-
мируем на языке ассемблера по той причине,
что нам нравится соотношение один к одному
между кодом и соответствующим действием
компьютера. (Хотя иногда это действие неви-
димо для нас, как в ранее приведенном приме-
ре загрузки константы во внутренний регистр
микропроцессора 8051.) Для программ на язы-
ке ассемблера не требуется никаких накладных
расходов в виде библиотек или специальных
вспомогательных процедур (подпрограмм).
Но в процессе работы с языком ассемблера для
вас вскоре станет очевидной цена, которую
приходится платить за его эффективность:
необходимость вдаваться во многие подроб-
ности и зависимость языка от конкретного ис-
пользуемого процессора. В особенности шоки-
руют странности и недостатки набора команд
микроконтроллера 8051, которые отражают
глубокую древность его проекта, который
появился на свет в 1976 г. Язык более высоко-
го уровня скрывал бы эти непривлекательные
аспекты процессора, но язык ассемблера при-
нуждает программиста иметь дело с такими
поразительными особенностями процессора
8051, как, например, то обстоятельство, что
он может только инкрементировать свой 16-
разрядный указатель, но не декрементировать
его. Невероятно, но факт. Ближе к концу лабо-
раторных занятий по микрокомпьютеру, когда
мы будет загружать код программы в собран-
ный нами компьютер с настоящего компьюте-
ра, вы сможете создавать для него программы
на языке С, если захотите. Но до тех пор мы
будем работать исключительно с языком ас-
семблера.
Теперь мы разберемся более подробно с нашими
двумя небольшими тестовыми программами,
служащими в качестве первой программы для
каждого пути нашей работы с микрокомпьюте-
рами. Описание каждой из этих программ под-
ходит для любой работы с микроконтроллером
8051, поэтому мы настоятельно рекомендуем
вам рассмотреть подробности обеих программ.
Несомненно, что вы будете больше заинтересо-
ваны в изучении программы для тестирования
вашего конкретного компьютера, чем програм-
мы для компьютера из другого пути. Но некото-
рые понятия будут рассматриваться в описании
только одной из этих программ. Например, в
первой тестовой программе мы рассматриваем
смещение для команд перехода, которое в дру-
гой тестовой программе объясняться не будет.
Будет предполагаться, что вы прочитали объ-
яснение первой тестовой программы, хотя вы
и не будете использовать ее для своей версии
микрокомпьютера.
21 N.1.1. Тестовая программа
для компьютера из дискретных
компонентов
Чтобы удостовериться в правильности под-
ключения всех монтажных проводов вашего
компьютера, в конце лабораторного занятия
20L мы исполнили на нем небольшую тестовую
программу, настолько простую и небольшую,
насколько мы смогли сделать. Здесь мы пре-
парируем этот небольшой объем кода, рассма-
тривая, что должен делать процессор в ходе его
исполнения. Результаты этого рассмотрения
даются в виде аннотаций к соответствующим
элементам программы на рис. 21N.1.
Эта крошечная программа ничего не делает
снова и снова, до бесконечности (или пока вам
не надоест). Она просто передает управление по
кругу или петле, которая называется циклом3.
Смещения для команды перехода SJMP
Работа по вычислению смещения для перехо-
да к определенному адресу выполняется про-
граммой ассемблера. Как иллюстрируется на
рис. 21N.1, программисту нужно только по-
ставить метку перехода в необходимом месте,
3 На английском цикл так и называется — петля (loop).
В настоящее время программная «петля» является теоре-
тическим понятием, но в первых компьютерах, в частно-
сти в компьютере Mark I Гарвардского университета, петля
в программе была физической. Последовательность ин-
струкций программы для исполнения на этом компьютере
записывалась в виде перфораций на бумажной ленте. Что-
бы компьютер мог повторять последовательность опера-
ций, программист склеивал эту бумажную ленту в кольцо
или петлю. См.: http://en.wikipedia.org/wiki/Harvard_
MarkJ и https://ru.wikipedia.org/wiki/MapK I (ком-
пьютер).
21Ш. Язык ассемблера и причины для его использования
857
Адрес памяти,
по которому хранится код
(адрес первого байта кода,
если больше чем один)
Команды на ассемблере
(этот столбец содержит исходный код программы,
Код введенный пользователем на языке ассемблера,
(это исполняемый машинный код который более-менее понятен для людей
t шестнадцатеричном формате) и используется программой ассемблера
для создания исполняемого машинного кода)
Это команда не для исполнения
микроконтроллером 8051,
а для программы ассемблера.
Команда OkG указывает
ассемблеру начальный адрес
для размещения этого кода
Адрес первой ячейки памяти
с кодом программы
ОБЯЗАТЕЛЬНО должен быть
0, поскольку микропроцессор
жестко прошит, начинать
исполнение с этого адреса после
включения питания или сброса
Начало главного цикла,
к которому переходит управление
программы после запуска
и который затем исполняется
бесконечно
;onfxrrr that the circuit xz & computer*
tells asseatblei the acidresc at which to place thxs cod©
here cock* begins- with just a Juxtp to 3t,art of
ALL our programs wil^ start thus
...and here the program starts, at hex 10 {"...h")
least exeifcina of operAcions, do
.n& do it a$am!
Текст DO_ZIP называется меткой перехода. При исполнении
команды перехода ассемблер вычисляет, как далеко от
текущего адреса находится данная метка, и задает это
смещение в машинном коде. Для первой команды перехода
вперед смещение равно ОБИ или 14, а для второго перехода
назад — FDh (в обратном двоичном коде) или 3, относительно
адреса, по которому продолжилось бы исполнение программы,
если бы она исполнялась в прямолинейном режиме (13И)
Данная метка ставится в поле слева от основного кода,
а затем служит для указания адреса перехода. Программа
ассемблера запоминает адрес, по которому расположена
метка (в данном случае это 10h), и использует этот адрес
при вычислении, куда нужно переходить при исполнении
команд перехода типа SJMP DO_ZIP
Рис. 21 N.1. Тестовая программа для компьютера из дискретных компонентов с объяснениями некоторых ее элементов
а затем указывать эту метку как адрес, по кото-
рому нужно переходить. Но, наверное, следует
рассмотреть более подробно работу, выполняе-
мую процессором при подстановке смещений
для выполнения этих инструкций относитель-
ного перехода. Команде относительного пере-
хода необходимо предоставить информацию,
как далеко ей нужно перейти от адреса, по ко-
торому продолжалось бы исполнение програм-
мы в обычном последовательном режиме, ког-
да выборка кода следующей команды осущест-
влялась бы из следующего адреса.
Таким образом, переход из вектора сброса
RESET (как называется принудительное начало
исполнения по адресу OOOOh) осуществляется
из адреса, в котором процессор осуществлял
бы выборку следующей команды, если бы он не
выполнял текущую команду перехода. В част-
ности, это будет адрес 0002h. Почему 0002h?
Потому что сама команда перехода SJMP зани-
мает два адреса — OOOOh и OOOlh. Если бы вме-
сто команды перехода исполнялась обычная
последовательная команда, следующая коман-
да для исполнения была бы взята из ячейки по
адресу 0002h.
Эта разница и определяется смещением перехо-
да: адрес, по которому переходить, минус адрес,
по которому продолжалось бы исполнение без
перехода. Данная разница вычисляется таким
образом:
Нужно перейти по адресу: 10h = 0001 0000
Исполнение продолжалось бы по адресу:
02h = 0000 0010
Разница:
OEh = OOOO 1110
В случае, если вы забыли правила двоично-
го вычитания, вспомните, что занимаемая из
левого разряда величина равна 210. Этим объ-
ясняется, например, разница величиной в 1 в
первом разряде (втором справа). Число OEh
(1410) является положительным. Не стоит пере-
живать, если у вас не особо получается с вычис-
лениями смещений: эта задача обычно выпол-
няется программой ассемблера.
При исполнении команды перехода SJMP про-
цессор добавляет величину смещения OEh к
текущему значению счетчика команд. Счетчик
команд представляет собой 16-разрядный
858
21 N. Микропроцессоры //. Ввод-вывод и первая программа на ассемблере
регистр, содержащий адрес следующей вы-
бираемой команды либо следующего байта
(слова) программы.
Текущее значение счетчика команд: 02h = 0000 0010
Смещение: 0Eh = 00001110
Сумма — адрес перехода: 10h = 0001 0000
Поскольку сумма равна OOlOh, программа пере-
ходит по этому адресу, из которого выполняет-
ся выборка следующей команды.
Переход в конце цикла выполняется в направ-
лении, противоположном нормальному ходу
исполнения программы. Но команда перехода
для такого перехода такая же, как и для пере-
хода в прямом направлении — SJMP. При таком
переходе программа переходит назад, к более
раннему адресу, поскольку в данном случае зна-
чение смещения отрицательное (выраженное в
дополнительном двоичном коде). Аппаратное
устройство, которое исполняет переход, пред-
ставляет собой простой 16-разрядный сумма-
тор, выполняющий операции с содержимым
счетчика команд.
Переход назад выполняется по большему счету
так же, как и переход вперед:
♦ от адреса, в котором процессор взял бы свою
следующую команду, если бы вместо коман-
ды перехода исполнялась обычная последо-
вательная команда — 0013h;
♦ по адресу 0010h.
Разница следующая:
Нужно перейти по адресу: 10h = 0001 0000
Исполнение продолжалось бы по адресу:
13h = 0001 0011
Разница:
FDh = 1111 1101
Число FDh — отрицательное, десятичное -3.
Отрицательным в дополнительном двоичном
коде его делает единица в самом старшем разря-
де. Опять, добавляя значение смещения к значе-
нию счетчика команд, получаем адрес перехода:
FDh + 0013h = 0010h.
Текущее значение счетчика команд: 13h = 0001 0011
Смещение: FDh = 1111 1101
Решение загадки 8-разрядного смещения
и 16-разрядного адреса
Но как может сложение 8-разрядного значения
смещения с 16-разрядным значением счетчика
команд дать требуемое значение 16-разрядного
адреса? Хороший вопрос. Ответом на него бу-
дет объяснение, что микроконтроллер 8051 «за
кулисами» расширяет 8-разрядное значение.
Мы предоставляем 8-разрядное значение сме-
щения — FDh или OEh. А у процессора, который
формирует адрес перехода в своем 16-разрядном
сумматоре, хватает ума, чтобы расширить эти
8-разрядные значения до 16-разрядных. Все, что
ему нужно для этого сделать, так это повторить
то, что он обнаруживает в самом старшем раз-
ряде, называемом знаковым разрядом. Таким
образом процессор расширяет оба предостав-
ляемые нами значения смещений:
OEh = 0000 1110 расширяется до 16 разрядов,
повторяя 0 в самом старшем разряде смещения:
0000 0000 0000 1110 = OOOEh
FDh = 1111 1101 расширяется до 16 разрядов,
повторяя 1 в самом старшем разряде смещения:
1111 1111 1111 1101 =FFFDh
Быстрый способ вычисления небольших
значений в дополнительном двоичном коде
Может быть эта небольшая экскурсия в вы-
числения в дополнительном двоичном коде от-
била у вас охоту когда-либо снова заниматься
такими вычислениями, но в случае, если это не
так, вам может пригодиться следующий про-
стой способ работы с ними. Предположим, что
вам нужно преобразовать небольшое (меньше
чем 16) отрицательное значение в его дополни-
тельный двоичный эквивалент с последующим
представлением в шестнадцатеричном форма-
те. Трюк состоит в том, чтобы вычесть наше
исходное число из гибридного значения F16,
цифра F которого дана в шестнадцатеричном
формате, а «цифра» 16 — в десятеричном. Если
такая числовая «химера» вас не смущает, по-
пробуем выполнить преобразование.
Например, каким будет дополнительный дво-
ичный эквивалент десятичного числа -3?
F16
-03h
Сумма — адрес перехода: 10h = 0001 0000
F13 = FDh
Получилось?
21Ш. Язык ассемблера и причины для его использования
859
21 N.1.2. Директивы ассемблера
Мы уже обратили внимание на эти аспекты
в главе 20N, поэтому здесь только вкратце на-
помним о них.
Несколько байтов в одной строке кода
Как мы видели в главе 20N, иногда кажется,
будто два байта находятся по одному адресу,
как в следующем примере:
0000 800Е SJMP DO_ZIP; Код начинается здесь - просто
; с перехода
В действительности же это не так, а 16-разряд-
ное значение сохраняется в двух последова-
тельных адресах: 0 и 1. Некоторые команды,
с которыми вам придется работать в будущем,
состоят даже из большего количества байтов,
чем два.
Директивы для ассемблера
Примерами таких элементов программы явля-
ются директивы ассемблера ORG и $INCLUDE.
Директива ORG
0000 ORG 0; Указывает ассемблеру начальный адрес
для размещения этого кода
Инструкция ORG 0 предназначена для ассембле-
ра, а не для исполнения микроконтроллером.
Директива $INCLUDE
4 $INCLUDE (C:\MICRO\8051\RAISON\INC\REG320.INC)
Директива $ INCLUDE дает ассемблеру указание
включить в текст программы код из внешнего
файла. Результатом исполнения ассемблером
этой директивы код из внешнего файла стано-
вится частью программы, как будто бы он был
введен в нее изначально.
Пример полезности директивы $INCLUDE
Далее приводится подробное рассмотрение
способа использования ассемблером названий
портов, например, Р1 или Р2. Предположим,
что для реализации операции передачи данных
с цифровой клавиатуры на дисплей, рассма-
триваемой в разделе 21N.4, мы задействуем не
внешние шины, а внутренние порты4.
С этой задачей справится следующая строка
кода, в которой предполагается, что цифровая
клавиатура и дисплей подключены к портам Р2
и Р1 соответственно.
COPY: MOV PI, P2; Копирование байта с цифровой
клавиатуры на дисплей в одну операцию
Чтобы этот код работал должным образом,
в программу необходимо подключить файл
REG320.INC, который позволяет ассемблеру
вычислить, что означают обозначения Р1 и Р2.
Как вы знаете, ассемблер находит адреса этих
символических идентификаторов в подключен-
ном файле и подставляет их в создаваемый им
исполняемый код. Далее приводится строка кода,
в которой показано значение, подставленное
ассемблером вместо идентификаторов Р1 и Р2,
и соответствующий машинный код. Для порта
назначения Р1 ассемблер подставляет значение
144, а для Р2 — 160 (оба значения десятичные).
85А090
. COPY: MOV 144,160
4 Если вас беспокоит то обстоятельство, что порт Р2 недо-
ступен в компьютере из дискретных компонентов, возмож-
Эти значения отображаются в шестнадцатерич-
ном формате в машинном коде в левом столбце
ассемблера после кода операции: А016 для 14410,
9016для16010.
Директива EQU для описательных
идентификаторов
Директива ассемблера EQU позволяет присваи-
вать значения описательным идентификато-
рам. Например, вместо идентификаторов Р1
и Р2 можно указать понятные P0RT1 и P0RT2.
Такие описательные идентификаторы позво-
лят нам сделать код для операции копирования
данных TRANSFER почти не требующим разъяс-
нений. Ее можно было представить следующим
образом:
TRANSFER: MOV DISPLAY, KEYPAD
Два случая идентификаторов, определенных с
помощью директивы EQU, в коде листинга 21N.1
но, нам следует признать один не особо важный момент.
В частности, порты Р1 и Р2 можно было бы использовать
таким образом как с микроконтроллером C8051F410, так
и с микроконтроллером 8051, применяемым для сборки
компьютера на большой макетной плате, работающим в
автономном режиме, а не как центральный процессор ком-
пьютера из дискретных компонентов. В компьютере из дис-
кретных компонентов порт Р2 обычно служит для других
целей, в частности для определения 8 битов адресной шины.
860
27Л/. Микропроцессоры II. Ввод-вывод и первая программа на ассемблере
реализуют первый этап двухэтапной замены.
После этих определений ассемблер заменяет их
соответствующим кратким идентификатором,
например Р1 для DISPLAY.
Листинг 21N1. Пример использования
директивы EQU
; byte_in_out_ports.a51
SNOSYMBOLS; Сокращаем объем кода в листинге..
SINCLUDE (C:\MICR0\8051\RAIS0N\INC\REG320.inc)
KEYPAD EQU P2
DISPLAY EQU P1
ORGOh
SJMP TRANSFER
ORG 020h
TRANSFER: MOV DISPLAY, KEYPAD
SJMP TRANSFER
После этого, на втором этапе замены, трансля-
тор сверяется с подключенным файлом .INC и
заменяет идентификатор Р1 адресом AOh, как
мы только что видели. Такая же двухэтапная
замена выполняется ассемблером и для иденти-
фикатора KEYPAD, в результате чего получается
такая же строка кода, как и в первом случае:
8 5А090 178 TRANSFER: MOV 144,160
После сброса микроконтроллер переходит по
адресу OOOOh и берет находящуюся в нем команду
Регистр
команд
80~
ТТредвыборка
Адрес
Данные
00
80
-не—
Память
Выбрана команда 80h, но микроконтроллер все
еще декодирует ее, тем временем выбирая из
памяти следующий байт
Регистр „ ^ АдРеС
команд Предвыборка
г " 1 i—rrp-j Данные
01
>
ОЕ
<
Память
На данном этапе процессор уже декодировал
значение команды 80h: 5JMP (выполнить переход).
Значение команды также содержит инсрормацию,
означающую сложить значение OEh следующего
байта с текущим значением счетчика команд.
Значение хх, полученное в предвыборке, пропадает
даром, но это не наносит никакого вреда
Результатом сложения значения ОЕЬ и текущего
значения счетчика команд 02h является новое
значение счетчика команд — 10h. По адресу 10И
исполнения начинается с начала....
Микроконтроллеру снова требуется некоторое
время, чтобы декодировать команду 00, в течение
которого он также выполняет предвыборку
следующей команды 80h
Регистр АдРес
команд Предвыборка
f 3p"'j i——-j Данные
02
> ■ ■
XX
.....п. <
Память
Регистр АдРес
команд Предвыборка
rwy-\—М°^
10
00
; ш, «- .^ ,
Память
Регистр ААРес
команд Предвыборка
. ^ , .—. Данные
] 00 }—[ВО]
и
80
Память
Команда 00 означает «Ничего не делать». Поэтому
процессор переходит к предвыбранной команде
80h и в процессе декодирования этой команды
опять выполняет предвыборку следующего байта
Регистр АдРес
команд Предвыборка
12
FD
1 ,£
Память
Декодированная команда означает сложить
предвыбранное значение (FDh) с текущим
значением счетчика команд. Сушла равна
13h + FDh = 10h. Так что, эта программа в действи-
тельности является бесконечным циклом
Рис. 21 N.2. Этапы пошагового исполнения тестовой программы
Регистр „ ^ АР
команд Предвыборка
{ 1 1 1
13
XX
Память
2/Л/.2 Снова о декодировании
861
Те, кто привык к программированию на языках
высокого уровня, скорее всего, не будут особо
удивлены такими возможностями. Но, согла-
ситесь, что такие замены могут сделать код на
языке ассемблера более понятным.
21 N.1.3. Исполнение тестовой
программы для дискретного
компьютера в пошаговом режиме
На рис. 21N.2 изображена блок-схема испол-
нения тестовой программы для компьютера из
дискретных компонентов в пошаговом режиме
с кратким объяснением каждого шага.
Основные моменты, которые мы надеемся сде-
лать ясными с помощью этой блок-схемы:
1. Циклическое поведение процессора — он
похож на поршневой двигатель, постоянно
движется вперед и назад: выдавая адрес при
движении вперед и снимая данные при дви-
жении назад.
2. Временная задержка, создаваемая операци-
ей предвыборки, которую вы увидите при
пошаговом исполнении программ на своем
собранном компьютере.
21 N.2. Снова
о декодировании
Декодирование сигналов адресов и сигналов
управления необходимо выполнять как в пол-
номасштабном компьютере, так и в компью-
тере, собираемом нами на макетной плате, в
котором адреса и данные передаются по соот-
ветствующим шинам. Но при использовании
микроконтроллера в автономном режиме, как
мы это делаем во второй ветви наших лабора-
торных занятий по микрокомпьютерам, такое
декодирование не требуется. Это одно из не-
скольких различий между двумя ветвями ла-
бораторных занятий по микрокомпьютерам.
В версии микрокомпьютера на автономном
микроконтроллере декодирование реализуется
внутренне самим микроконтроллером, поэто-
му пользователю не требуется знать что-либо
об этом. С образовательной точки зрения не-
обходимость выполнять декодирование в ком-
пьютере из дискретных компонентов делает
его более познавательным, но ее отсутствие в
компьютере на автономном микроконтроллере
упрощает его применение. Здесь мы рассмо-
трим декодирование, которое необходимо вы-
полнять в компьютере, в котором используют-
ся шины, т. е. собираемом из дискретных ком-
понентов. Если вы не следуете этим путем, то
можете пропустить это рассмотрение без каких
бы то ни было отрицательных последствий. Но
вам может пойти на пользу все же задержать-
ся на этом материале, чтобы понять принципы
декодирования, поскольку оно необходимо для
компьютеров, которые используют традицион-
ную общую (многоабонентскую) шину.
Последний раз мы выполняли простое декоди-
рование с помощью вентиля И. На этот раз мы
воспользуемся микросхемой декодера (хотя в
реальной ситуации для этого, скорее всего, по-
дошла бы микросхема ПМЛ). Вспомним сигна-
лы микроконтроллера 8051:
♦ PSEN*;
♦ RD*;
♦ WR*;
♦ 16 адресных линий.
Возвращаясь к задаче декодирования, кото-
рую мы решали последний раз, начертим схе-
му декодирования (выбора) одного из четырех
портов ввода, полагая, что мы также хотим раз-
решить четыре порта вывода. Такая схема изо-
бражена на рис. 21N.3.
ысокии у ровен
=> пространство
вода-вывода
Рис. 21N.3. Декодирование (выбор) одного из четырех пор-
тов ввода
В этот раз выполним похожее декодирование,
заменив логический вентиль И двухэлемент-
ной микросхемой 74НС139 декодера двух ли-
ний на четыре, чтобы определить четыре порта
ввода и четыре порта вывода, как показано на
рис. 21N.4. Данная микросхема представля-
ет собой просто сборку восьми функций И, во
многом похожих на только что нарисованную
нами на рис. 21N.35.
5 Для простоты, на рис. 21N.4 мы не показываем сигнал
PSEN*, который в компьютере из дискретных компонентов
862
21N. Микропроцессоры II. Ввод-вывод и первая программа на ассемблере
/MS.
SI
50
3 ">
Шф
*ф
Рис. 21N.4. Использование микросхемы декодирования для
определения четырех портов ввода и четырех портов вывода
Обратите внимание на общее использование
адресных линий А1 и АО обоими декодерами
микросхемы 74НС139. Некоторые студенты
ошибочно полагали, что для каждого из этих
двух декодеров требовался отдельный набор
адресных линий, чтобы избежать конфликта с
другим. Это не так.
Вывод разрешения EN* микросхемы выполня-
ет свою функцию: разрешает микросхему при
активировании, обеспечивая активирование
(установку низкого уровня) на одном из четы-
рех выходов. А деактивирование вывода EN*
(подача на него высокого уровня) деактивирует
все четыре выхода (устанавливает на них вы-
сокий уровень). Обратите внимание на то, что
при деактивированном декодере эти выводы не
находятся в третьем состоянии. Можете объяс-
нить, почему это происходит?6
Применяем декодер
с устройствами ввода-вывода
Теперь давайте применим два из декодиро-
ванных сигналов выбора порта. Один из этих
сигналов предназначен для получения байта с
цифровой клавиатуры, а другой будет фикси-
ровать выходной байт в шестнадцатеричном
дисплее. Для контраста мы также показали (на
рис. 21N.6), как легко работать с входными и
выходными устройствами, когда используют-
ся встроенные порты микроконтроллера, а не
шина данных.
При работе с шиной управление третьим состоя-
нием линий осуществляется с помощью вывода
разрешения выхода ОЕ*, на который подается
сигнал IN0* (рис. 21N.5). А вывод разрешения
защелки latchen* управляет прозрачной защел-
кой, в которой можно захватывать значение
с шины данных, подав на него импульс низкого
уровня сигнала OUT0*. До сего времени мы ра-
ботали с дисплеями таким образом, как будто
бы в них не было регистра-защелки: они про-
сто постоянно отображали все, что подавалось
на них. Такое поведение возможно благодаря
подключению понижающего резистора (номи-
налом 100 кОм) к линии latchen*, в результате
чего защелка становится прозрачной по умол-
чанию.
Цифровая
клавиатура
Буфер с ьяхою™* с
Третьим состоянием
Шина данных
VI
latchen*
Цифровая
клавиатура
Микроконтроллер
C8051F410
Ъ7
Ь0
OUTO*-
Дисплей данных (ЖКД)
latchen*X Дисплей данных (ЖКД)
Рис. 21N.5. Аппаратные устройства ввода (цифровая клавиатура) и вывода (дисплей) с использованием шины данных (слева)
и встроенных портов микроконтроллера (справа)
обрабатывается функцией ИЛИ вместе с сигналом RD*.
(См. полную схему данного компьютера на рис. 20L.1.)
Показывать сигнал PSEN* не важно для целей настоящего
рассмотрения. Данный сигнал разрешает некоторые режи-
мы адресации, которые встречаются только в редких слу-
чаях. В коде для этих лабораторных занятий мы не будем
использовать эти режимы адресации.
6 Оставлять неактивные линии декодера в «плавающем»
состоянии не следует по той причине, что в них наводи-
лись бы помехи, в результате чего периферийные устрой-
ства включались бы произвольным образом.
Справа на рис. 21N.5 показано прямое подклю-
чение линии latchen* на «землю».
Ввод-вывод на автономном
микроконтроллере
Рассмотрим достоинства и недостатки простого
ввода-вывода автономного микроконтроллера.
21N3. Код ввода-вывода для дискретного компьютера
863
Хорошо то, что аппаратное обеспечение для пе-
редачи данных с цифровой панели на дисплей
очень простое, как показано на рис. 21N.6.
Цифровая
клавиатура
Микроконтроллер
Р2 Р1
II-
Рис. 21N.6. Организация аппаратного обеспечения ввода-
вывода микроконтроллера, не использующего шины, очень
простая
Что не так хорошо, так это то, что за эту просто-
ту нужно платить: для простого ввода и вывода
одного байта потребуется 16 выводов микро-
схемы микроконтроллера. В схеме с исполь-
зованием шины эти выводы могут совместно
взаимодействовать с почти неограниченным
числом других устройств ввода-вывода.
21 N3. Код ввода-вывода для
дискретного компьютера
Теперь, когда у нас есть необходимое аппарат-
ное оборудование для декодирования и устрой-
ства ввода и вывода, можно приступить к на-
писанию кода программы для испытания этого
оборудования. Сделаем этот код таким про-
стым, насколько это возможно: цикл, который
считывает значение с цифровой клавиатуры и
отправляет его на дисплей, повторяющийся до
бесконечности. На псевдокоде такая програм-
ма будет выглядеть следующим образом:
; Берем байт с цифровой клавиатуры
; ...отправляем этот байт на дисплей
; повторяем эти две операции до бесконечности
Прежде чем приступать к изучению команд для
микроконтроллера 8051, которые нам могут
понадобиться для создания такой программы,
взглянем на некоторые внутренние подробно-
сти этого микроконтроллера, показанные на
рис. 21N.7.
8051
Шина адреса
Шина данных
Рис. 21N.7. Регистры, используемые микроконтроллером
8051 для операций ввода-вывода при работе с шинами
На этом рисунке иллюстрируется обычная про-
цедура микроконтроллера 8051 для операций
ввода-вывода при использовании внешних
шин:
Адрес обычно предоставляется специальным
16-разрядным регистром Data Pointer (DPTR)7,
единственное назначение которого — выдача
таких адресов.
Обмен данными по внешним шинам всегда про-
исходит через специальный привилегирован-
ный регистр А (полное название Accumulator).
Регистр А также служит привилегированным
источником и назначением для многих других
процессов, включая все арифметические и бу-
левы операции.
Из-за этих ограничений нам нужно будет до-
бавить один предварительный шаг в начале на-
шей программы. В частности, нам потребуется
инициализировать регистр указателя данных
DPTR, загрузив в него начальный адрес перифе-
рийных устройств:
; Инициализируем регистр DPTR указателем на перифе-
рийные устройства
И только после инициализации регистра DPTR
мы можем приступать к выполнению операции
ввода-вывода:
; Берем байт с цифровой клавиатуры...
21 N3.1. Адрес порта 0 на языке
процессора
В ситуации с компьютером из дискретных ком-
понентов, где используются внешние шины8,
термин «Порт 0» понятен для людей, но не для
7 Мы вскоре увидим другой способ для выполнения этой
задачи, который иногда предпочтительнее, но обычно не
такой полезный: применение команды MOVX@Rn. Более
подробную информацию по этому моменту см. в разде-
ле 21S.1.4 далее в этой книге.
8 Остерегайтесь одного возможного заблуждения: тер-
мин «Порт 0» в ситуации с использованием внешних шин
не то же самое, что и встроенный порт микроконтроллера
PORT 0 (Р0). Более того, при работе с внешними шинами
этот порт Р0 нам вообще недоступен, поскольку он уже за-
действован микроконтроллером для передачи некоторой
информации с шины (в частности, сигналов линий ADO...
AD7). Зная о существования возможности путаницы, мы
стараемся уточнять, какой именно тип порта имеется в
виду, обычно фразой наподобие «при работе с внешними
шинами».
864
21 N. Микропроцессоры II. Ввод-вывод и первая программа на ассемблере
микроконтроллера 8051. Прежде всего, при
работе с шинами микроконтроллер не отлича-
ет память от устройств ввода-вывода, поэтому
для него понятие порта неизвестно. Далее, ему
абсолютно ничего не известно о нашем произ-
вольном выборе средней точки общего адрес-
ного пространства в качестве начала адресного
пространства для устройств ввода-вывода.
Таким образом, нам нужно преобразовать по-
нятный нам термин «Порт 0» в понятный про-
цессору адрес. Но в какой адрес? Это опреде-
ляется подключением декодера адресов ввода-
вывода. Данный декодер обращает внимание
только на три адресные линии: А15 (на которой
должен присутствовать высокий уровень) и А1
и АО (которые используются со всеми комби-
нациями уровней, но обе должны иметь низ-
кий уровень, чтобы означать число «0»). Таким
образом, Порт 0 определяется линиями адреса
следующим образом:
А15...А11.А7..АЗА2А1 АО
1 ххх хххх хххх х х 0 0
Данное выражение содержит много безразлич-
ных состояний (уровней), обозначенных как х,
поскольку мы применяем здесь частичное или
«ленивое» декодирование. Но поскольку через
х обозначают безразличные уровни, заменим
их нулями, что даст нам понятное число:
А15...А11.А7..АЗА2А1 АО
1 000 0000 0000 0 0 0 0
Которое в шестнадцатеричном формате выгля-
дит как:
8 0 0 0
Число 8000h и будет нашим способом обраще-
ния к Порту 0 при написании кода (символ h
информирует ассемблер о том, что значение
в шестнадцатеричном формате — hexadecimal).
Шестнадцатеричный формат удобен, посколь-
ку наши дисплеи и цифровая клавиатура под-
держивают этот формат.
21 N3.2. Формат команд ассемблера
Теперь, когда мы знаем, как дать указание
ассемблеру, какой адрес использовать для
Порта 0, мы можем приступить к написанию
небольшой программы, задействующей ап-
паратные устройства ввода-вывода. Первым
делом загрузим адрес цифровой клавиатуры и
дисплея (Порт 0) в регистр указателя данных
DPTR. На рис. 21N.8 показана эта команда и
объясняются ее элементы.
# означает
непосредственную адресацию
код операции MOV DPTfc, #8000h
(почти на — """ / ^\
английском) / адрес источника
адрес назначения
указываем,
как на
дисплей (OUTO),
так и на
цифровую
клавиатуру (IN0)
Рис. 21N.8. Загрузка константы в регистр DPTR
Пример на рис. 21N.8 иллюстрирует обычный
формат команд ассемблера.
Команда начинается с кода операции MOV, ко-
торый является более-менее понятным словом
на английском языке, хотя и не совсем пра-
вильно написанным. Кроме того, название опе-
рации не совсем верное, поскольку выполняет-
ся операция копирования (исходное значение
остается на своем месте), а не перемещения
(move — переместить).
Далее указывается адрес назначения — регистр
указателя данных DPTR.
♦ И затем идет адрес источника данных —
8000h.
Порядок адресов может показаться стран-
ным, но к нему можно быстро привыкнуть.
Символ # перед адресом источника данных
означает очень простой режим адресации,
называющийся непосредственным. Иными
словами, это означает, что значение, следую-
щее за этим символом, является числом, ко-
торое нужно загрузить в адрес назначения,
а не адресом, из которого нужно взять значе-
ние для загрузки. Таким образом, данная ко-
манда загружает в регистр DPTR число 8000И.
(Понятие непосредственной адресации мож-
но попробовать объяснить, рассмотрев его
с другой стороны — спросив, что означала бы
команда MOV DPTR, 8000h, если бы она была
возможна?9) Данная операция копирования в
регистр DPTR 16-разрядного числа относится
9 Такая команда, если бы она была возможной, но каковой
она не является, означала бы копирование в регистр DPTR
значения, хранящегося в ячейке памяти с адресом 8000h,
что совсем нам не нужно.
21N3. Код ввода-вывода для дискретного компьютера
865
к редкой операции микроконтроллера 8051,
способной работать с такими значениями.
Загрузив требуемое значение в регистр DPTR,
мы теперь можем выполнять ввод и вывод дан-
ных в микроконтроллер 8051, используя это
значение. Очень удобно то обстоятельство,
что цифровая клавиатура и дисплей по счаст-
ливой случайности имеют одинаковый адрес,
поскольку благодаря этому значение в регистре
DPTR не нужно менять между операциями чте-
ния данных с цифровой клавиатуры и записи
их на дисплей.
Листинг 21N.2. Машинный код тестовой
программы
[Адрес Код Команды на ассемблере]
0028 908000 STARTUP: MOV DPTR, #8000H
; Указатель как на дисплей (OUT0),
; так и на цифровую клавиатуру (IN0)
002В Е0 GETIT: MOVX A, @DPTR
; Считываем значение с цифровой клавиатуры
002С F0 MOVX @DPTR, A; Отображаем его на дисплее
002D 80FC SJMPGETIT
Косвенная адресация с использованием
указателя @DPTR
Чтение данных с клавиатуры осуществляется
с помощью команды MOV и регистра DPTR, но
другим способом, как показано на рис. 21N.9.
Операция MOVX, как почти все другие опера-
ции микроконтроллера 8051, работает с байта-
ми (т. е. 8-разрядными значениями), а не с 16-
разрядными, как операция MOV, посредством
которой мы инициализировали регистр DPTR.
Адрес назначения Адрес источника
MOVXA, @DPRT ;Plck U.P
> \ key value
Буква X означает внешнюю
операцию обмена данными
(в отличие от операции
внутри микроконтроллера, как
операция MOV DPRT, #8000h)
Символ @ означает, что следующее за ним значение
является указателем, т. е. адресом ячейки памяти,
содержимое которой нужно загрузить
(в отличие от того, что означала бы команда MOVX A,
DPTR, если бы такая команда существовала:
загрузить содержимое регистра DPTR,
а не содержимое ячейки памяти, на которую указывает
значение в регистре DPTR)
Рис. 21N.9. Команда MOVX использует инициализирован-
ный ранее регистр DPTR
21 N.3.3. Завершаем создание
тестовой программы
Считав значение с клавиатуры, отправим его на
дисплей для отображения. Для этой операции
мы приведем в листинге 21N.2 ее машинный
код, который нас обычно не интересует.
В этих двух применениях регистра DPTR можно
заметить симметричность: сначала берем то, на
что он указывает, и сохраняем его в регистре А;
затем берем значение из регистра А и помеща-
ем его туда, куда указывает регистр DPTR. Мы
решили показать машинный код для того, что-
бы вы могли видеть отдачу от неуклюжей кос-
венной адресации.
Прежде чем мы смогли выполнять какие-либо
операции за пределами микросхемы микро-
контроллера, нам пришлось выполнить трудо-
емкую операцию загрузки регистра DPTR. Но
после этой загрузки код становится в высшей
степени компактным: для выполнения каждой
операции ввода и вывода достаточно всего лишь
одного байта (и не нужно указывать адрес при
их выполнении). Таким образом, наш код полу-
чился компактным и быстрым. Также приятно
видеть, что разница между этими симметрич-
ными операциями определяется одним битом
в коде операции: для операции ввода использу-
ется код EOh, а для операции вывода — FOh.
21 N.3A Программа тестирования
в действии
На рис. 21N.10 изображены осциллограммы
разных сигналов, задействованных при выпол-
нении операций ввода и вывода в ходе испол-
нения нашей тестовой программы. Тот факт,
что сигналы А15 и PSEN* ведут себя должным
образом, определенно придает нам уверенно-
сти в наших способностях программирования.
Мы также надеемся, что присутствие импуль-
са сигнала RD* при операции ввода значения
с цифровой клавиатуры и импульса сигнала
WR* при операции вывода значения на дисплей
866
2/Л/. Микропроцессоры IL Ввод-вывод и первая программа на ассемблере
При исполнении операций ввода
и вывода уровень А15 высокий
Сигнал ALE отмечает каждый
доступ к шине
Сигнал PSEN* отмечает каждую
выборку инструкции
Значение, снимаемое с цифровой клавиатуры,
а затем отправляемое на дисплей
00 — младший байт адреса порта 8000И
Рис. 21 N.10. Осциллограмма разных сигналов, задействованных при исполнении программы чтения значения с цифровой
клавиатуры с последующей его отправкой на дисплей
убедит всех скептиков в том, что идея исполь-
зования одного адреса 8000h для получения и
доставки значения не так и глупа, как может
поначалу показаться. В частности, при этих
двух обращениях к одному адресу машина ни-
чего не делает, в противоположность тому, если
бы адрес 8000h указывал на ячейку памяти. Эти
два периферийных устройства имеют общий
адрес (как два жильца в одной общей кварти-
ре), но они никоим образом не являются одним
и тем же устройством: цифровая клавиатура не
является дисплеем (как один из двух жильцов
общей квартиры не может быть своим же со-
седом в ней)10.
21 N3.5. Компьютер на автономном
микроконтроллере С8051F410 не
отображает такие подробности
Что касается сигналов компьютера на автоном-
ном микроконтроллере C8051F410, исполняю-
щего свою версию программы тестирования,
то для них мы не можем предоставить эквива-
лентную осциллограмму. Достоинством микро-
контроллера на одной микросхеме является его
способность работать, скрывая все подробности
10 Эта аргументация несколько ошибочна в том, что если
бы по одному адресу мог проживать только один человек,
тогда один из жильцов общей квартиры должен быть и
своим соседом. Но мы надеемся, что вы не заметите этого
логического изъяна.
внутри корпуса. Но это достоинство также де-
лает его загадочным и плохой платформой для
обучения: он или работает, или не работает, и
понять, что происходит в его внутренностях
можно только с помощью средства отладки
среды разработки Silicon Laboratories.
21N А Сравнение версий
на ассемблере и на языке С
программы вывода
на дисплей значений,
вводимых с цифровой
клавиатуры
Листинг 21N.3 содержит программу на ассемб-
лере, а листинг 21N.4 — на языке С.
Листинг 21N.3. Программа вывода значений
с клавиатуры на дисплей на ассемблере
ORG0
UMP STARTUP
ORG 90h
STARTUP: MOV DPTR, #8000h; Указываем адрес цифровой
клавиатуры и дисплея
COPY: MOVXA,@DPTR
; Считываем значение с цифровой клавиатуры
21N.5. Вызов подпрограмм 867
movx @dptr, А элементы такие же, как и в предыдущем коде
; Отображаем это значение на дисплее на ассемблере. Но компилятор С добавил не-
SJ.^PCOPY ;Повторяем.до^бесконечности нужную повторную инициализацию регистра
DPTR, а также лишнюю операцию сохранения
_ ""1"1711 „ и извлечения значения, вводимого с цифровой
Листинг 21N.4. Программа вывода значении _ _ /г
склавиатурынадисплейнаязыкеС клавиатуры. Но если вам не нужна большая
скорость исполнения программы, то вы не бу-
// keypad_to_diplay_408.c дете особо переживать по поводу этих лишних
#include<C:\MICRO\8051\RAISON\INC\REG320.H> строк кода.
void main()
{
xdata char volatile *KEY_DISP;
KEY_DISP = 0x8000; // Показываем определенный адрес
для использовании в указателе
while (1) // Повторяем до бесконечности
*KEY_DISP = *KEY_DISP;
В программе на языке С можно увидеть эле-
менты программы на языке ассемблера. В част-
ности:
♦ Инициализация указателя:
• оператор xdata char volatile *KEY_DISP; опре-
деляет 16-разрядный указатель xdata типа
char на внешнюю память;
• модификатор volatile дает указание компи-
лятору не оптимизировать данное опреде-
ление указателя;
• оператор KEYJDISP = 0x8000; присваивает
указателю значение.
♦ Цикл, который в программе на языке ассем-
блера реализуется посредством двух команд
MOVX, в программе на языке С выглядит в
виде одной строки кода:
• *KEY_DISP = *KEY_DISP;
♦ А оператор while (1) обеспечивает бесконеч-
ное исполнение цикла.
Машинный код, генерируемый
компилятором языка С
Генерируемый компилятором код ассемблера
(листинг 21N.5) выглядит так, как будто он на-
писан разработчиком, который чувствовал себя
не вполне удобно с этим заданием. Основные
Листинг 21N.5. Машинный код, сформирован-
ный компиляторами языков ассемблер и С
; FUNCTION main (BEGIN)
0000 7WHILE1:
0000 908000
0003 Е0
0004 FA
0005 908000
0008 ЕА
0009 F0
000A80F4
; SOURCE LINE #13
MOVDPTR,#0 8 000H
MOVXA,@DPTR
MOV R2,A
MOVDPTR,#0 8 000H
MOVA,R2
MOVX @DPTR,A
SJMP 7WHILE1
21 N.5. Вызов подпрограмм
Предположим, что вы создали блок кода, кото-
рый хотите использовать в другом месте своей
программы. Например, на лабораторном заня-
тии 21L нам нужно было вставить в программу
определенный код, чтобы замедлить ее испол-
нение. Данная программа постоянно инкремен-
тирует отображаемое на дисплее значение, но
чтобы эти изменения мог различать пользова-
тель, скорость этого инкрементирования долж-
на быть намного ниже, чем при работе процес-
сора при максимальном быстродействии.
Конечно же, можно вставлять код задержки
в каждое место программы, где он требуется.
Такой неуклюжий линейный подход иллюстри-
руется слева на рис. 21N.11, где одинаковый код
задержки вставляется в двух разных местах
программы. А справа на рис. 21N.11 показано
улучшенное решение задачи создания одинако-
вой задержки в двух разных местах программы.
Но здесь возникает вопрос, как продолжить ис-
полнение основной программы после вызова
подпрограммы задержки?
Компьютеру нужно знать, куда в основной про-
грамме выполнять возврат после завершения
868
21N. Микропроцессоры II. Ввод-вывод и первая программа на ассемблере
Основная
программа
Основная
программа
Основная
программа
Код задержки
Код задержки
Код задержки
I
:
Вызов
подпрограммы
задержки
Вызов
подпрограммы
задержки
«Линейный подход» Лучше, но как возвратиться назад
к основной программе?
Рис. 21 N.11. Линейный подход обычно неуклюжий. Лучше
вызывать код из одного места много раз
выполнения побочной программы, которая
называется подпрограммой. Каждый раз, когда
компьютер отклоняется от основной програм-
мы на исполнение подпрограммы задержки, он
должен создать для себя временную заметку об
адресе возврата — адресе следующей коман-
ды основной программы, которая бы испол-
нилась, если бы не произошло отклонение на
выполнение подпрограммы. При отклонении
на исполнение подпрограммы компьютер авто-
матически сохраняет адрес возврата в области
памяти RAM, называемой стеком, по адресу,
указываемому указателем стека. В микрокон-
троллерах 8051 указатель стека представляет
собой 8-разрядный регистр, а сам стек должен
находиться во внутренней памяти RAM микро-
контроллера, а не во внешней, которая может
быть подключена к нему.
Таким образом, чтобы использовать стек для
перехода по адресу подпрограммы с последую-
щим возвратом в точку основной программы,
из которой был выполнен этот переход, все,
что нам нужно сделать, так это вместо команды
прямого перехода JMP указать команду вызова
подпрограммы CALL. Для микроконтроллеров
8051 существуют три варианта команды CALL
(три — команды JMP)11.
На рис. 21N.12 иллюстрируется процедура со-
хранения адреса возврата в стеке при вызове
подпрограммы.
11 Команда вызова подпрограммы ACALL выполняет отно-
сительный переход, используя 11-разрядное значение сме-
щения, что позволяет ей выполнять переход в диапазоне
адресов размером 2 К (грубо, +1 К). Команда LCALL вы-
полняет прямой переход по 16-разрядному адресу, указан-
ному в ней; таким образом, эта команда может выполнять
переход по любому адресу адресного пространства микро-
контроллеров 8051. Команды переходов AJMP и LJMP рабо-
тают так же, как и команды вызова подпрограммы ACALL
и LCALL, но только без автоматического возврата. А третья
команда перехода SJMP (short jump — короткий переход)
использует 8-разрядное смещение (диапазон +127, -128).
400h
500h
•AC
100k
'ACALL1
Подпрограмма задержки
Сохраняет
Команда «адрес возврата»
возврата RET
80h
«Стек» находится в RAM
на микросхеме 8051
(стек расположен по
адресу внутренней RAM,
на который указывает
указатель стека)
«Указатель стека»
(8-разрядный
регистр на 8051)
Рис. 21 N.12. Механизм возврата к основной программе по-
сле завершения исполнения подпрограммы
Процесс сохранения адреса возврата полно-
стью автоматический. Последняя команда в
подпрограмме — команда RET — служит для
возврата из подпрограммы обратно в основную
программу. Обратите внимание, что адресом
возврата является адрес команды в основной
программе, следующей сразу же после команды
вызова подпрограммы. В случае первого вызо-
ва подпрограммы в примере на рис. 21N.12 это
адрес 402h.
21 N.5.1. Стек как кратковременное
хранилище общего назначения
При вызове подпрограмм стек используется
автоматически и прозрачно для разработчи-
ка. Но в стеке также можно явно хранить со-
держимое регистров. Более того, часто при
вызове подпрограммы необходимо сохранить
содержимое регистров, поскольку они будут
использоваться подпрограммой, что может
нарушить целостность из значений, которые
могут впоследствии потребоваться основной
программе. Это особенно касается специаль-
ного регистра А, называемого аккумулято-
ром, который всегда необходим в операциях
ввода и вывода с внешними шинами. Этот
регистр также используется для выполнения
большинства арифметических и логических
операций.
Таким образом, чтобы не потерять содержимое
регистра А, значение которого модифицирует-
ся при исполнении подпрограммы задержки
DELAY, данная подпрограмма первым делом
21N.5. Вызов подпрограмм
869
сохраняет содержимое этого регистра в стеке12,
как показано в листинге 21N.6.
Листинг 21N.6. Пример подпрограммы сохране-
DELAY: PUSH ACC ; Для некоторых операций регистр А
; необходимо называть АСС, что довольно неудобно.
MOV A, #80h ; Инициализируем регистр А новым
; значением задержки.
KILLTIME: DJNZ A,KILLTIME ; Декрементируем значение
; регистра А, пока не станет нулевым
POP ACC ; Восстанавливаем значение регистра А,
;снимая его со стека.
RET
Кстати, этот код задержки проще, чем его дру-
гие варианты, используемые в упражнениях
на лабораторных занятиях. Данная подпро-
грамма декрементирует значение всего лишь
8-разрядного регистра, что позволяет получить
скромную задержку длительностью в несколько
сотен микросекунд. В тестовой программе для
микрокомпьютера из дискретных компонентов
код задержки содержит два вложенных цикла
декрементирования 8-разрядных регистров,
что позволяет получить намного большую
задержку — не в два раза, а в 28 раз. Но при
рабочей частоте 11 МГц, даже эта растянутая
задержка не очень велика — максимум 120 мс.
А вот код задержки в тестовой программе для
компьютера на автономном микроконтроллере
C8051F410 использует три вложенных цикла,
что позволяет получить задержку величиной в
одну секунду.
Если вас расстраивает то обстоятельство, что
вашего трудягу-процессора заставляют выпол-
нять бессмысленную работу просто для того,
чтобы убить время, то это хорошо. Это обстоя-
тельство должно расстраивать вас, поскольку
вы сможете оценить альтернативный способ
внедрения длительных задержек в программу,
с помощью встроенных аппаратных таймеров
микроконтроллера. Мы воспользуемся этими
таймерами на лабораторных занятиях 24L.1
и 24.2.
Эмулирование операции вызова
подпрограммы в RIDE
На рис. 21N.13 показан снимок экрана эмули-
рования в RIDE13 исполнения программы, вы-
зывающей нашу подпрограмму задержки.
Адрес возврата: адрес следующей
команды после команды вызова
подпрограммы
(Снимок экрана программы
эмулирования берется в этой
точке исполнения: выполнена
одна строка подпрограммы)
01СВ
01СВ
01СЕ
01СГ
0100
0100
0102
3100
FO
04
SOFA
COEO
£A
186
187
188
189
X90
191
192
193
194
СОШГГОР
DELAY:
: ACALL DELAY
KOVX ®>ГП>., А
INC A
SJBP С0Ш1ТОР
QRG 100H
PUSH ACCк
KOV А^Д
\
; Sow
; add
; awe
,* «et
s«xv& it to the display
1 to the accumulator, £o
and do it again (forever:1
registers tbat*ll get me
outer-loop delay value
В этой точке адрес возврата сохраняется
в стеке (по адресам 80, 81h)
Это значение регистра А (АСС), сохраненное в стеке операцией PUSH
Рис. 21 N.13. Вызов подпрограммы: показаны сохраненные в стеке значения адреса возврата и аккумулятора (регистра А)
12 В некоторых случаях регистр А хочет, чтобы его назы-
вали АСС. В частности, это более длинное название АСС
регистра А необходимо при указании его в операциях
PUSH и POP. Это обстоятельство, в действительности яв-
ляющееся свойством программы ассемблера, довольно
раздражительно, и с нашей точки зрения ему нет извине-
ний. Но так сложилось исторически, и нам с этим ничего
не поделать.
13 Сокращение RIDE означает Raisonance Integrated Design
Environment - интегрированная среда разработки Raiso-
nance. Это бесплатная программа с функциями ассемблера,
компилятора и эмулятора, которую мы рекомендуем вам
загрузить и попробовать поработать с ней. Мы использу-
ем функции ассемблера и компилятора этой программы
в среде разработки Silicon Laboratories. Более подробно эта
среда разработки рассматривается в разделе 23S.1.
870
21N. Микропроцессоры II. Ввод-вывод и первая программа на ассемблере
Мы настоятельно рекомендуем вам начать раз-
рабатывать свои программы в среде RIDE. Она
будет полезна тем, что ее ассемблер будет со-
общать вам каждый раз, когда вы допустите
какую-либо глупую ошибку, например написав
MOV A, @DPTR вместо MOVX A, @DPTR. Такие
подсказки позволят вам ускорить изучение
языка ассемблера. Кроме того, возможность
эмулирования исполнения разрабатываемой
программы доставит вам удовольствие от на-
блюдения работы своего кода. При повышении
сложности разрабатываемых программ воз-
можность эмулирования их исполнения позво-
лит вам проверить правильность работы реа-
лизованных в них алгоритмов.
Вызов подпрограмм в программе для
компьютера на автономном контроллере
Код программы для мигания светодиодом для
компьютера на автономном микроконтроллере
C8051F410 (листинг 21N.7), которую мы моди-
фицировали в разделе 21L1, добавив в нее код
задержки, почти такой же, как для соответст-
вующей программы для компьютера на дис-
кретных компонентах.
Листинг 21N.7. Программа мигания свето-
; bitflip_delay_subroutine.a51 Программа переключения
светодиода bitflip с задержкой для постоянного
исполнения
SNOSYMBOLS; Сокращаем объем кода в листинге...
SINCLUDE (C:\MICRO\8051\RAISON\INC\c8051f410.inc)
ORG 0; Указывает ассемблеру начальный адрес
для размещения этого кода
ACALL USUAL.SETUP
SETB P0.0; Начинаем с выключенным светодиодом
(активируется низким уровнем)
FLIPIT: CPL P0.0 ; Переключаем светодиод
ACALL DELAY ; Выжидаем некоторое время
Основная программа для малого компьютера
еще проще, чем программа для большого ком-
пьютера. В этот раз она не содержит полный
код задержки. Код задержки программы для
малого компьютера использует три вложенных
цикла декрементирования 8-разрядных реги-
стров, чтобы создать значительную задержку
(длительностью в 1 секунду), даже при часто-
те тактирования микропроцессора величиной
24,5 МГц.
Прерывание как разновидность вызова
подпрограммы
В следующий раз мы рассмотрим вызовы под-
программы, инициируемые аппаратными ком-
понентами. Такие операции называются аппа-
ратными прерываниями. Если вы разобрались
с механизмом вызова подпрограмм из пользо-
вательских программ, то увидите, что преры-
вания являются просто разновидностью таких
вызовов.
21 N.5.2. Вызов подпрограмм
и функций в языке С
Возможно, что из описания работы подпро-
грамм, вы поняли, что эти подпрограммы, явля-
ются элементами программирования, которые
в языке С называются функциями. Программа
на языке С, эквивалентная основной программе
на ассемблере, которая вызывает подпрограм-
му задержки DELAY, может выглядеть наподо-
бие показанной в листинге 21N.8 (за исключе-
нием отсутствующих в ней некоторых предва-
рительных определений)14. Функция задержки
приведена в листинге 21N.9.
Листинг 21N.8. Программа мигания
светодиодом и функция задержки на языке С
// Основная программа, соответственно называющаяся
MAIN (основная)
void main (void) // Ключевое слово void означает,
// что программа не принимает
// и не выдает никаких данных
SJMP FLIPIT; Повторяем до бесконечности
; —ПОДПРОГРАММЫ —
DELAY: PUSH ACC ; Сохраняем в стеке регистры,
которые эта подпрограмма модифицирует
whileO) // Мудреный способ указания
// "выполнять до бесконечности"
14 Здесь отсутствуют определения типов переменных и по-
стоянных, используемых в программе (чтобы компиля-
тор С знал, сколько памяти выделить каждой из них).
27Л/.6. Расширение операций до 16 разрядов
871
delayO; // Здесь вызываем функцию
OUT_BIT = ~OUT_BIT; // А здесь основное действие —
// переключение значения бита
// Код функции (подпрограммы)
void delay (void)
for(n= 0; n< 0x8600; n++)0 // Значение задержки 2 Гц
(задержка в 250 мс)
Функция задержки (листинг 21N.9) просто ве-
дет счет до тех пор, пока значение п не достиг-
нет целевого значения, после чего управление
возвращается обратно в основную программу.
Код на ассемблере для этой функции задержки,
генерируемый компилятором С, выглядит до-
вольно странно и не похож на код, который бы
написал человек.
Листинг 21N.9. Подпрограмма-функция
формирования задержки
JUNCTION delay (BEGIN)
; SOURCE LINE #26 (Строка 26 исходного кода)
0000 750000 R MOV n,#000H
0003 ?F0R1:
0003 7480 MOVA,#080H
0005 B48105 ONE A,#081 H,?LAB5
0008 E500 R MOVA,n
000A B42800 ONE A,#02 8НЛАВ5
000D ?LAB5:
000D 5006 JNC ?NXT4
OOOFAAOO R MOVR2,n
00110500 R INCn
0013 80EE SJMP7F0R1
0015 7NXT4:
; SOURCE LINE # 28 (Строка 28 исходного кода)
0015 22 RET
; FUNCTION delay (END)
Но для нас абсолютно не важно, что этот код
странный или неуклюжий. Главное для нас —
что цикл for в программе на С позволил легко
выполнять стоящую перед нами задачу.
Основная программа на языке С
Основная программа вызывает функцию за-
держки, код которой на ассемблере точно такой
же, как в листинге 21N.5. В листинге 21N.10
приводится код на ассемблере для реализации
основной программы, генерируемый компиля-
тором С.
Листинг 21N.10. Код на ассемблере,
сгенерированный компилятором С
; FUNCTION main (BEGIN)
7WHILE1:
LCALL delay
CPLOUT_BIT
SJMP 7WHILE1
;^FUNCTION main (END)
Между прочим, одна особенность языка С под-
черкивает эквивалентность функций в языке С
и подпрограмм на ассемблере: в языке С можно
выполнить принудительное завершение испол-
нения функции с помощью ключевого слова
RETURN. Но здесь мы не иллюстрировали эту
особенность.
21 N.6. Расширение
операций до 16 разрядов
Обе программы вычисления текущей суммы на
лабораторном занятии 21L (как для большого,
так и для малого компьютера) демонстрируют,
что микроконтроллеры 8051 могут выполнять
арифметические операции с числами, превы-
шающими байтовый размер их регистров.
Суммирование 16-разрядных значений выпол-
няется с помощью интересного приема про-
граммирования, который приводится в листин-
ге 21N.11 (версия для малого компьютера).
Листинг 21N.11. Программа суммирования
16-разрядных значений
Transfer: mov A, RUN_SUM_LO ; Восстанавливаем
; значение текущей суммы (младший байт)
add A, KEYPAD ; Формируем новое значение
; текущей суммы (low byte)
872
21N. Микропроцессоры IL Ввод-вывод и первая программа на ассемблере
mov RUN_SUM_LO, A; Сохраняем его,
mov DISPLAY_LO, A ; и выводим на дисплей
mov A, RUN_SUM_HI ; Получаем старший байт суммы
addc A, #0 ; Если есть выходной перенос
; с младшего байта, включаем его в старший
В этой программе могут быть неясными такие
подробности, как использование бита выход-
ного переноса. Это однобитовый флаг (вну-
тренний триггер), который регистрирует пере-
полнение или выходной перенос в результате
выполнения некоторой операции, например
сложения ADD.
♦ Первая операция сложения ADD A, KEYPAD
при сложении игнорирует какие бы то ни
было входные переносы, поскольку она не
предназначена учитывать их. В то же самое
время эта операция обновляет значение фла-
га переноса по результатам сложения: в слу-
чае переполнения выполняется установка
флага выходного переноса.
♦ В отличие от ADD, операция ADDC учитывает
входные переносы. Поэтому, хотя на первый
взгляд может показаться, что операция ADDC
А, #0 суммирует значение регистра А со зна-
чением 0, в действительности она также до-
бавляет к нему и значение выходного пере-
носа, сгенерированное предыдущей опера-
цией сложения.
Таким образом, команда ADDC A, #0 обновляет
старший байт, инкрементируя его всякий раз,
когда суммирование младшего байта создает
выходной перенос. Это как раз то, что нам и
требуется.
21 N.7. Материал для чтения
изАоЕ
♦ Глава 14 (Компьютеры):
• Раздел 14.2.1. Язык ассемблера и машин-
ный язык;
• Раздел 14.3.2. Программируемый ввод-вы-
вод — вывод данных.
21L Лабораторное занятие: микропроцессоры II
Данное лабораторное занятие также можно проходить двумя разными путями: путь с компьюте-
ром из дискретных компонентов на большой макетной плате (большой компьютер) и путь с ком-
пьютером с автономным микроконтроллером C8051F410 (малый компьютер).
21L1. Ввод-вывод
на большом компьютере
На последнем лабораторном занятии мы «вдох-
нули жизнь» в схему из нескольких микросхем
счетчиков и памяти, которую собрали на ла-
бораторных занятиях 16L и 17L, подключив к
ней «мозги»: микроконтроллер 8051. Это пре-
вратило схему в компьютер, что мы доказали,
исполнив на нем крошечную программу.
На сегодняшнем лабораторном занятии мы не
будем подвергать наш компьютер подобным
фундаментальным модификациям, а просто
научим его «говорить» (посредством вывода
данных на дисплей) и «слушать» (посредством
считывания данных с цифровой клавиатуры).
Но прежде чем начнем заниматься разработ-
кой соответствующего кода, мы оснастим энер-
гозависимую память RAM нашего компьютера
батарейкой резервного питания, чтобы введен-
ные в нее программы сохранялись даже после
выключения основного питания. Конечно же,
ту крошечную программу, которую мы разра-
ботали на данном этапе, не представляло бы
большого труда вводить повторно (хотя даже
это достаточно неудобно). Но наши последую-
щие программы будут гораздо большего разме-
ра, и, очевидно, данная опция резервного пита-
ния позволит нам сэкономить большой объем
времени и усилий, не говоря уже о нервах.
21L1.1. Резервное питание для
энергозависимой памяти RAM
Память RAM нашего большого компьютера реа-
лизована на микросхемах КМОП-технологии,
поэтому для хранения данных она потребля-
ет очень малую мощность, равную приблизи-
тельно 0,8 мкА. Следовательно, таблеточной
литиевой батарейки будет достаточно, чтобы
обеспечить сохранность данных в RAM в тече-
ние нескольких лет (приблизительно три года).
Но чтобы эта схема была работоспособной, она
должна обеспечивать следующие две возмож-
ности:
1. Переключение питания, подаваемого на вы-
вод питания микросхемы RAM, между ре-
зервной батарейкой и основным источником
питания. Более того, такое переключение
должно выполняться в соответствующий
момент времени в процессе включения и вы-
ключения основного питания.
2. Память RAM необходимо отключать при
слишком низком напряжении питания, что-
бы предотвратить случайную запись в память
и нарушение целостности хранящихся в ней
данных в процессе включения и выключения
питания.
С обеими задачами отлично справится контрол-
лер энергонезависимой памяти RAM на микро-
схеме MXD1210. Данная микросхема содержит
источник опорного напряжения, два компара-
тора и переключатели. Обратите внимание на
то обстоятельство, что при добавлении этой ми-
кросхемы в схему нашего большого компьютера
необходимо удалить прямое соединение между
выводом RAMCE* микросхемы GLUEPAL и вы-
водом CS* микросхемы RAM (вывод 20). Это
подключение теперь будет реализовано посред-
ством контроллера MXD1210. Также необходи-
мо убрать существующее прямое подключение
напряжения питания +5 В к выводу 28 подачи
питания микросхемы RAM. Опять же, теперь
положительное питание на микросхему RAM
будет подаваться через контроллер MXD1210.
874
21L Лабораторное занятие: микропроцессоры II
Схема подключения микросхемы MXD1210
контроллера энергонезависимой памяти RAM
изображена на рис. 21L.1.
Оригинальный контроллер энергонезависимой
памяти RAM обеспечивает резервное питание
от батарейки и деактивирует выход CS* при
отсутствии питания +5 В, чтобы не допустить
случайную запись в RAM
Рис. 21L1. Схема реализации резервного питания для памя-
ти RAM
Но, обеспечив резервное питание для памяти
RAM нашего компьютера, следует иметь в виду
следующие две особенности:
1. При первом использовании схемы резервно-
го питания необходимо включить основной
источник питания (+5 В), а затем выключить
его.
2. Убедитесь в том, что ваш источник питания
действительно выдает +5 В. Если вы пользуе-
тесь источником питания старой макетной
платы РВ503, то он, скорее всего, перегру-
жен, и выдаваемое им положительное на-
пряжение может быть несколько меньшим,
чем минимальное напряжение +4,5 В, необ-
ходимое для стабилизатора MXD1210. В та-
ком случае при включении и выключении
основного источника питания контроллер
MXD1210 не будет обнаруживать факт вклю-
чения, а будет всегда считать основной ис-
точник питания выключенным.
21L1.2. Дисплей с регистром-
защелкой как единственный порт
вывода
До сих пор данные с шины данных выводились
на дисплей в непрерывном режиме, поскольку
мы заземлили вывод EN*, который управля-
ет прозрачной защелкой на дисплеях. Если же
вместо постоянного заземления выхода EN*
мы подадим на него управляющий сигнал WR*
с процессора, то дисплей будет захватывать и
отображать только те данные шины данных,
которые присутствуют на ней в течение опе-
рации OUT (т. е. вывода на устройства ввода-
вывода). Программа для проверки этого ме-
ханизма захвата данных для отображения на
дисплее приводится чуть далее. Она содержит
всего лишь одну операцию записи центрально-
го процессора. Эта операция активирует сигнал
WR*, с помощью которого мы будем обновлять
содержимое дисплеев. Это очень грубая схема.
Обратите внимание на то, что мы даже не пы-
таемся делать различие между устройствами
ввода-вывода и памятью. Вместо этого в про-
грамме тестирования мы просто выполняем
операции записи на устройство ввода-вывода.
21L13. Простейшая защелка
только с одним разрешенным
портом
Аппаратная реализация регистра-защелки по-
казана на рис. 21L.2.
WR* (потом сигнал OUT0*)
«Постоянный»
I
^ Разрешение
защелки
Рис. 21L.2. Простейшая схема для отображения выходных
данных. Годится только при наличии одного устройства
ввода-вывода и при отсутствии попыток записи в память
RAM
В данном случае тумблерный переключатель
выглядит избыточным, и так оно и есть; но
вскоре он будет полезным. Но даже здесь он
служит определенной цели. В частности, он
позволяет устанавливать режим постоянного
включения дисплея, в котором мы работали до
сих пор. Такой режим может потребоваться для
наблюдения происходящего на шине данных
при диагностировании программ при поша-
говом исполнении, В другом положении (раз-
решения защелки) он позволяет использовать
дисплей в качестве устройства вывода, что мы
и собираемся вскоре делать.
На рис. 21L.3 показана временная диаграмма,
иллюстрирующая способ, посредством ко-
торого сигнал WR* можно использовать для
21 LI Ввод-вывод на большом компьютере
875
Подробности мультиплекси-
рования адреса и данных
на линиях AD0...AD7
С1\С2\ C3I C4I Cl I C21 C3IC4
а\сг\сз\
rlJTJTTn
Данные, посылаемые контроллером...
...фиксируются в дисплее высоким уровнем
сигнала WR* (и сигнала LATCHEN*)
D0-D7 )-\А0-А7 \
t t t t
Выборка Адрес Данные Адрес
следующей данных команды следующей
команды команды fiAOVX команды
MOVX
Рис. 21L.3. Временная диаграмма операции ввода-вывода на регистр-защелку дисплея
фиксации значения, выкладываемого процес-
сором на шину данных при выполнении опера-
ции вывода1.
Сигнал WR* подается на вывод разрешения за-
щелки LATCHEN*, захватывая и фиксируя от-
правленные данные в течение низкого уровня.
Самый нижний элемент временной диаграммы,
обозначенный как Port 0, иллюстрирует под-
робности определенной части процесса муль-
типлексирования адреса и данных, который
происходит на восьми общий линиях ADO...
AD7. Активирование сигнала PSEN* обозначает
выборку команды, что на рисунке обозначается
как «Выборка следующей команды».
Программа для тестирования работы
защелки
Чтобы испытать нашу простую схему защелки
дисплея, потребуется программа, которая будет
выполнять операцию вывода данных на перифе-
рийное устройство (листинг 21L.1). Программа
записывает значения в ячейку памяти, опреде-
ляемую указателем данных, который представ-
ляет собой 16-разрядный регистр процессора,
выделенный специально для этой цели.
Листинг 21L.1. Программа тестирования
работы защелки дисплея
LOC OBJ LINE SOURCE
1; IOJ.OOP.A51 Лаб. занятие 20L
; Программа для тестирования схемы защелки дисплея
1 Данный рисунок является модифицированным фраг-
ментом рис. 6-4 из руководства пользователя по высо-
коскоростному микроконтроллеру «High Speed Microcon-
troller User's Guide» компании Dallas Semiconductor/Maxim
Integrated Products.
0000
адрес
3 ORG 0; Указывает ассемблеру начальный
; для размещения этого кода
0000 8016 5 SJMP STARTUP; Код начинается здесь -
; с перехода на начало
6 ; собственно программы. ВСЕ наши
; программы будут начинаться таким образом
7
0018 8 ORG 18Н ; Вот здесь начинается
; собственно программа
9 ; Начинается по адресу 18h
0018 908000 10 STARTUP: MOV DPTR, #8000H; Указываем
; на адрес: загружает
11 ; в регистр адрес Порта 0 для дисплеев
; и цифровой клавиатуры
001В Е4 12 CLR А ; Это просто дает нам понятное
; и предсказуемое значение
13 ; для вывода на дисплей (т. е. 0)
001С F0 14 COUNTUP: MOVX @DPTR, A ; Теперь
; отправляем его на дисплей
001D 04 15 INC A; Для небольшого разнообразия,
; добавляем к значению аккумулятора значение 1
001E80FC 16 SJMP COUNTUP ; И снова выводим его
; на дисплей.
; Повторяем до бесконечности.
17 END
Добавляем декодер адресов
ввода-вывода
Только что испытанная схема была бы до-
статочной, если бы нам никогда не пришлось
бы работать больше чем с одним устройством
ввода-вывода. В действительности, микрокон-
троллер 8051 может самостоятельно выполнять
876
21L Лабораторное занятие: микропроцессоры II
декодирование адресов ввода-вывода, но лишь
в автономном режиме. Мы познакомимся с
этим режимом позже, на лабораторном заня-
тии 25L. При работе без внешних шин он мо-
жет записывать один байт и даже один бит по
адресу одного из своих портов и хранить эти
данные в своих внутренних триггерах. Но в на-
стоящее время мы работаем с микроконтрол-
лером, используя внешние шины, поэтому нам
нужно обеспечить свой собственный механизм
декодирования адресов портов.
Для этого нам нужно собрать явный декодер
адресов ввода-вывода, отдельный от микро-
контроллера 8051. Этот декодер позволит нам
подключить четыре устройства вывода и че-
тыре устройства ввода. Схема такого декодера
изображена на рис. 21L.4.
Замечание
Скорее всего, после этого занятия вам никогда сно-
ва не придется подключать к микроконтроллеру
8051 такой внешний декодер, поскольку в следую-
щий раз вы вряд ли будете использовать внешние
шины с микроконтроллером. Способность микро-
контроллера обходиться без внешних шин являет-
ся одним из его больших достоинств.
Адресная шина
'f Л
Декодер адресов
ввода-вывода
Рис. 21L.4. Декодер адресов ввода-вывода на микросхеме
74НС139, управляемый сигналами микроконтроллера
Данный декодер декодирует двухразрядное
значение, подаваемое на его входы, и активиру-
ет одну из четырех возможных линий выхода.
Активируемая линия соответствует значению,
представляемому входным двухразрядным ко-
дом. Например, входное двоичное значение
10 = 210 вызывает активирование выходной ли-
нии 2. Конечно же, решить такую задачу деко-
дирования можно с помощью ПМЛ, и в настоя-
щее время это более вероятный подход. В дан-
ном случае мы выбрали декодер на микросхеме
по той причине, что с его работой легче разо-
браться, чем с работой ПМЛ. При использо-
вании устройства ПМЛ существует большая
вероятность необходимости обращаться к его
коду, чтобы понять, что от него ожидать в том
или ином случае.
Чтобы было легче отличить операции записи
процессора от операций чтения, подключите
к линии WR* светодиод красного, синего или
желтого цвета. В любом случае цвет не дол-
жен быть зеленым, поскольку светодиод такого
цвета обозначает сигнал BR*. Соответствующая
схема показана на рис. 21L.5.
89С430
(8051)
(Р3.6) WR
Рис. 21L.5 Светодиод на линии WR* облегчит задачу разли-
чения операций чтения от операций записи
Без такого светодиода, указывающего тип опе-
рации, общее использование адресов портов
может сбивать с толку при пошаговом исполне-
нии программы. Сравнительно большое значе-
ние резистора величиной 3,3 кОм выбрано для
того, чтобы не слишком нагружать линию WR*,
которая в режиме потребления тока может вы-
держивать всего лишь 1,6 мА.
Программа тестирования декодера
Листинг 21L.2 содержит текст небольшой про-
граммы, которая проверяет все четыре вход-
ных и выходных порта декодера. В програм-
ме используется команда условного перехода
DJNZ, которая совмещает в себе две операции.
В частности, команда сначала декрементирует
значение указанного регистра, и если получен-
ное значение не равно нулю, выполняет пере-
ход по указанному адресу. Когда же значение
регистра достигает нуля, исполнение переходит
к следующей команде.
Команда условного перехода DJNZ может ра-
ботать только с 8-разрядными регистрами, т. е.
с небольшими значениями. Но из этих опе-
раций можно создавать вложенные циклы,
чтобы получить большие значения счета или
задержки (см. раздел 21L.1.6). Данная коман-
да формируется добавлением к ней названия
регистра, который будет декрементироваться,
с последующим указанием адреса перехода, как
можно видеть из листинга программы.
21 LI Ввод-вывод на большом компьютере
877
MACRO ASSEMBLER TRYDCDR.01 08/01/101 17:27:00
LOC OBJ LINE SOURCE
1 ;TRYDCDR_01.A51 Лаб. занятие 20L Проверяем декодер ввода-вывода, подсчитывая циклы 4/13/01
2 ; Удалена команда INC А, 8/01/01
3
0000
0000 801Е
0020
0020 Е4
4
5
6
7
8
9
10
11
12
13
ORG 0 ; Указывает ассемблеру начальный адрес для размещения этого кода
SJMP STARTUP ; Код начинается здесь - с перехода на начало собственно программы.
; ВСЕ наши программы будут начинаться таким образом
ORG 2 ОН ; Вот здесь начинается собственно программа, по адресу 20h
STARTUP: CLR A ; Это просто дает нам понятное и предсказуемое значение
; для вывода на дисплей (т.е. 0)
0021 908000 14 STARTOVER: MOV DPTR, #8000Н ; Указатель на ячейку памяти: загружаем в регистр
15 ; указателя адрес Порта 0 для дисплеев и цифровой клавиатуры
0024 7804
0026 F0
0027 Е0
0028 A3
0029 D8FB
002В 80F4
16
17
18
19
20
21
22
23 END
MOV R0, #4Н ; Инициализируем счетчик цикла
COUNTUP: MOVX @DPTR, A ; Теперь отправляем его на декодер
MOVX A, @DPTR ; а также проверяем порты ввода.
INC DPTR ; Инкрементируем адрес ввода-вывода
DJNZ R0,COUNTUP ; Продолжаем до тех пор, пока не будут проверены все четыре адреса
SJMP STARTOVER ; Затем начинаем все сначала
При исполнении этой программы в пошаговом
режиме, для каждого из четырех адресов ввода-
вывода сначала должна выполняться операция
вывода, а затем операция ввода. Результат вы-
полнения этих операций можно будет наблю-
дать в виде отображаемых на дисплее адресов
ввода-вывода 8000-8003h. Подтвердить, что
декодер также видит эти операции, можно
также, исследуя линии выхода микросхемы
74НС139 (выводы 4-7) и входные линии (вы-
воды 12-9 для портов IN0-IN3 соответствен-
но) с помощью логического пробника.
При пошаговом исполнении программы опе-
рации ввода будут выглядеть несколько стран-
но. В частности, поскольку линии декодера для
разрешения ввода INx* еще ничего не разреша-
ют, то при выполнении компьютером операций
ввода шина данных будет находиться в «пла-
вающем» состоянии. На дисплее это состояние
будет, наверное, выглядеть, как значение FFh,
поскольку уровень «плавающих» входов дис-
плея будет, скорее всего, высоким, наподобие
устройств ТТЛ. Первая операция вывода вы-
ведет на дисплей содержимое аккумулятора,
т. е. значение 0, а последующие операции будут
выводить довольно странные значения, пред-
ставляющие результаты интерпретирования
процессором состояния своих «плавающих»
входов при пустой операции ввода. Светодиод
на линии WR* должен облегчить различение
операций ввода и вывода.
21L1А Добавляем входной буфер
для цифровой клавиатуры
Чтобы нашему декодеру не было скучно от од-
нообразия своих действий, нагрузим его еще
одной задачей. В частности, мы поручим ему
включать, когда необходимо, буфер цифро-
вой клавиатуры с трехстабильными выходами,
чтобы программно считывать с нее значения.
Затем мы объединим эту операцию ввода с опе-
рацией вывода на дисплеи.
878
21L Лабораторное занятие: микропроцессоры II
Сигнал /Л/0* включает буфер цифровой
клавиатуры
Осуществить такой ввод можно, выполнив
очень простую модификацию схемы, посколь-
ку необходимая логика уже заложена в наше
устройство GLUEPAL. Функция KBUFEN* вы-
полняет операцию ИЛИ над двумя входами:
♦ Результатом операции И сигнала KWR* с сиг-
налом BUSRQST* (или BR*). Эта операция И
определяет единственную легитимную, безо-
пасную ручную запись с цифровой клавиатуры
в память. Безопасной она является по той при-
чине, что сигнал запроса шины BUSRQST* обо-
значает, что шинами управляет пользователь.
♦ Сигналом IN0* с декодера 74НС139. Этот
сигнал активируется, когда микроконтрол-
лер выполняет операцию чтения из Порта О
(адрес 8000h).
На лабораторном занятии 16L память RAM
и цифровая клавиатура просто обращались
к шине данных поочередно, как показано на
рис. 21L.6.
Чтобы обеспечить подключение процессора,
наше устройство GLUEPAL необходимо осна-
стить соответствующей логикой, реализующей
функцию KBUFEN*, как показано на рис. 21L.7.
Сигнал KWR*, подаваемый
на вход WE* памяти RAM,
отключает трехстабильныеу
буферы памяти RAM...
...одновременно включая
буфер 541 цифровой
клавиатуры
S RAM
WE
1
и?
Ъ
'8
ОЕ
ое'541Л
Шина
данных
KWR
Цифровая
клавиатура
Рис. 21 L.6. Простая схема из лабораторного занятия 16L для
разрешения доступа к шине данных, или памяти RAM, или
буферу цифровой клавиатуры
На шину данных
От цифр
клавиатуры
(KD0...KD7)
Сигнал KBUFEN* заменяет сигнал^
\ KWR, который подавался на вывод)
\ EN микросхемы буфера 541 на
мтабораторных занятиях 16 и 18
Рис. 21 L.7. Входной буфер, управляемый сигналом KBUFEN*
устройства GLUEPAL
До сих пор линия IN0* устройства GLUEPAL
была деактивирована (на лабораторном за-
нятии 20L мы подключили ее к линии поло-
жительного питания). Теперь удалите это под-
ключение и подайте на вывод IN0* устройства
GLUEPAL сигнал с таким же названием с деко-
дера 74НС139.
Сигнал OUT0* управляет регистром-
защелкой дисплея
Вместо сигнала WR*, который был у нас на ла-
бораторном занятии 21L.1.3, теперь для разре-
шения младшего байта мы будем подавать на
вывод LATCHEN* выходной сигнал декодера
OUT0*.
Программа для опроса цифровой
клавиатуры и вывода на дисплей
Следующая программа позволит протестиро-
вать нашу модифицированную схему. Она про-
сто считывает значение с цифровой клавиатуры
и выводит его на дисплей. Цифровая клавиату-
ра и дисплей имеют один и тот же адрес, но они
различаются типом операции: ввода или выво-
да, или, иными словами, уровнями на линиях
RD* и WR* микроконтроллера 8051. Чтобы
напомнить вам, как работает этот подход, на
рис. 21L.8 изображена осциллограмма разных
сигналов, задействованных при выполнении
операций ввода и вывода в ходе исполнения
нашей тестовой программы. В частности, акти-
вирование сигнала RD* означает операцию вво-
да, а активирование сигнала WR* — операцию
вывода. Сигнал ALE и сигнал PSEN* (разрешает
память в течение выборки инструкции) показа-
ны, чтобы помочь вам сориентироваться в сиг-
налах ввода-вывода.
ALE
PSEN*
IN \
(movx a, @dptr)
RD*
OUT
(movx@dptr,a)
WR*
Рис 21L.8. Осциллограмма сигналов, задействованных при
непрерывном исполнении программы ввода-вывода
В листинге 21L.3 приведен код программы для
тестирования ввода-вывода.
21 LI Ввод-вывод на большом компьютере
879
Листинг 21L.3. Программа для тестирования ввода-вывода
MACRO ASSEMBLER INOUT 03/08/101 18:24:05 PAGE 1
LOC OBJ LINE SOURCE
1; INOUT.a51 Лаб. занятие 20L Считываем значение с цифровой клавиатуры и выводим его на дисплей
2
SNOSYMBOLS ; Сокращаем объем кода в листинге...
SINCLUDE (C:\MICRO\8051\RAISON\INaREG320.INC) ; а не то эта строка кода выдаст
; громаднейший список определений идентификаторов (все они для регистров 8051)
0000
0000 8026
0028
0028 908000
002В Е0
002С F0
002D80FC
3
4
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186 END
ORG0
; Указывает ассемблеру начальный адрес для размещения этого кода
SJMP STARTUP ; Код начинается здесь - с перехода на начало
; собственно программы. ВСЕ наши программы будут начинаться таким образом
ORG 28H ; Вот здесь начинается собственно программа
STARTUP: MOV DPTR, #8000H ; Указатель как на дисплей (OUT0),
; так и на цифровую клавиатуру (IN0)
GETIT: MOVX A, @DPTR ; Считываем значение с цифровой клавиатуры
MOVX @DPTR, A ; Отображаем его на дисплее
SJMPGET1T
Проверить, работает ли должным образом
операция ввода, можно, наблюдая значение на
шине данных в процессе операции ввода, ис-
полняя программу в пошаговом режиме. При
этом необходимо настроить дисплей для по-
стоянного отображения подаваемых на него
данных, а не с использованием защелки. Когда
в процессе операции IN0* на дисплее отобра-
жается адрес 8000h, вводите на цифровой кла-
виатуре разные числа. В момент, когда про-
грамма остановлена в середине исполнения
операции ввода, на дисплее должно сразу же
отображаться точно такое же значение шины
данных, которое вы ввели с цифровой клавиа-
туры.
Если теперь переключиться на режим дисплея
с использованием защелки и нажать кнопку
REPEAT, то вводимое на цифровой клавиатуре
значение также должно отображаться на дис-
плее, но обновляться только один раз в каждой
итерации цикла. Вы не сможете увидеть ника-
ких кодов промежуточных команд. Все также
должно работать и при непрерывном исполне-
нии программы.
21L1.5. Программа добавления
значения с цифровой клавиатуры
к текущей сумме
Восьмиразрядное суммирование
Сначала потренируемся на 8-разрядных числах.
Возможно, вы полагаете, что 8-разрядный ком-
пьютер не может работать с числами более вы-
соких разрядов. Здесь вы ошибаетесь. Как отме-
чалось в главе 21N, высокоразрядные значения
очень легко получить, соединяя 8-разрядные ре-
зультаты, что мы вскоре и продемонстрируем.
Версия программы 8-разрядного суммиро-
вания для пошагового исполнения
В листинге 21L.4 приведена программа, кото-
рая считывает значение с цифровой клавиату-
ры и добавляет его к текущей сумме, отображая
полученный результат на дисплее. Поскольку
программа еще не содержит задержек, то при
непрерывном исполнении она не может обе-
спечить нормальное отображение результата,
поэтому ее нужно исполнять пошагово. Но мы
вскоре исправим этот недостаток.
880
21L Лабораторное занятие: микропроцессоры II
Листинг 21L.4. Программа 8-разрядного суммирования
MACRO ASSEMBLER KEYSUM.402 07/31/102 18:03:55 PAGE 1
LOC OBJ
0000
0000 802E
0030
0030 908000
0033 75817F
0036 7A02
0038 7B04
003A 7800
003C F0
003D E0
003E 28
003F00
0040 F8
0041 F0
0042 80F9
LINE
1
2
3
4
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
SOURCE
; KEYSUM_402.a51 Лаб. занятие 20L Считываем значение с цифровой клавиатуры
; и добавляем его к текущей сумме
; Первая версия: без задержки 4/0
$NOSYMBOLS ; Сокращаем объем кода в листинге...
SINCLUDE (C:\MICRO\8051\RAISON\INC\REG320.INC); а не то эта строка кода
; выдаст громаднейший список определений идентификаторов (все они для регистров 8051)
ORG0
; Указывает ассемблеру начальный адрес для размещения этого кода
SJMP STARTUP ; Код начинается здесь - с перехода на начало
; собственно программы. ВСЕ наши программы будут начинаться таким образом
ORG ЗОН; Вот здесь начинается собственно программа
STARTUP: MOV DPTR, #8000H ; Указатель как на дисплей (OUT0), так и на цифровую
; клавиатуру (IN0)
MOV SP, #07FH ; Инициализируем указатель стека адресом, на единицу меньшим,
; чем начало черновой RAM
; Эта внутренняя память в настоящее время пустая, но мы вскоре будем использовать ее
MOV R2,#02 ; Инициализируем небольшую константу задержки. Не используется в данной
; программе, а только в следующей
MOV R3,#04 ; Но мы определяем ее здесь, чтобы все определения были вместе
MOV R0, #0 ; Обнуляем текущую сумму, чтобы всегда начинать с чистого листа
MOVX @DPTR, A ; Отображаем текущую (нулевую) сумму на дисплее:
; аккуратная первая итерация
188
189
190
191
192
193
194
195
196
197 END
COUNTUP: MOVX A, @DPTR ; Считываем значение с цифровой клавиатуры
ADD A, R0 ; Формируем новое значение текущей суммы новое + старое, результат в А
NOP ; На данном этапе просто пустышка-заполнитель
MOV R0, А ; сохраняем результат (обновляем значение текущей суммы)
MOVX @DPTR, A ; Отображаем текущую сумму на дисплее
SJMP COUNTUP Повторяем
Считывание с цифровой клавиатуры шестнад-
цатеричного значения вызывает особенно ин-
тересный эффект. Можете сказать, почему те-
кущая сумма меняется таким образом при вво-
де с цифровой клавиатуры значения FFh?2
2 Вспомните, что в дополнительном двоичном формате
значение FFh равно -1.
Десятичное сложение
При желании программу можно очень легко пе-
ределать для работы с десятичными значения-
ми. Для этого нужно просто заменить команду
NOP командой десятичной коррекции акку-
мулятора DA A (Decimal Adjust Accumulator).
(Операционный код команды DA A — D4h.)
21 LI Ввод-вывод на большом компьютере
881
Команда DA А преобразует шестнадцатеричные
значения в десятичные, например OAh в 1010.
Но не переоценивайте «умственные способ-
ности» этой команды: она работает только
сразу же после операции сложения, когда еще
доступен флаг полупереноса, описывающий
значение в аккумуляторе. Кроме того, она так-
же не работает должным образом, если с циф-
ровой клавиатуры ввести не десятичное зна-
чение. А так это довольно изящная команда.
Поэкспериментируйте с ней.
Касательно команды DAA: какое значение вы-
зывает такой же интересный эффект при рабо-
те с ней, как и значение FFh при работе в шест-
надцатеричном режиме?3
Версия программы 16-разрядного
суммирования для пошагового
исполнения
Шина данных нашего большого компьютера
имеет восемь разрядов (линий), но плата ЖКД
содержит два 8-разрядных регистра-защелки.
Эти две защелки могут захватывать два после-
довательных 8-разрядных значения, отправ-
ляемых микроконтроллером, и отображать их
как 16-разрядный результат.
Подключаем две защелки
Плата ЖКД содержит две 8-разрядные про-
зрачные защелки, которые могут захваты-
вать 16-разрядное значение с шины данных в
двух последовательных операциях вывода. На
рис. 21L.9 изображена схема подключения двух
регистров-защелок платы ЖКД для вывода на
дисплей 16-разрядных значений за две после-
довательные операции вывода.
Шина
Рис. 21L9. Две защелки могут демультиплексировать 16-
разрядное значение с 8-разрядной шины
Чтобы использовать эти две защелки таким об-
разом, нам нужно подавать на каждую из них
сигнал разрешения в точках, показанных на
рис. 21L10. Сигнал OUT0* продолжает управ-
лять выводом LATCH EN* разрешения защел-
ки младшего байта, а сигнал OUT1*, подавае-
мый декодером 74НС139, управляет выводом
LATCH
байта.
EN* разрешения защелки старшего
OUTO*
1
3 Возможно, что это 99?
Рис. 21L10. Сигналы OUTO* и OUT1* управляют выводами
разрешения двух защелок для отображения 16-разрядных
значений
Устанавливаем DIP-переключатель
в положение MUX
Чтобы наши две защелки могли сообща ис-
пользовать шину данных, DIP-переключатель,
расположенный справа на плате, фрагмент ко-
торой показан на рис. 21L.10, необходимо уста-
новить в положение MUX.
Примечание
Другое положение DIP-переключателя обеспечи-
вает параллельный ввод 16-разрядных значений в
эти две 8-разрядные защелки. Этот режим может
применяться, когда плата ЖКД функционирует са-
мостоятельно, а не с платой микрокомпьютера.
Код программы 16-разрядного
суммирования
В листинге 21L.5 приведен код программы, ко-
торая позволяет выполнять сложение 16-раз-
рядных значений.
Один аспект программы может потребовать до-
полнительного объяснения: две последователь-
ные операции сложения, выполняемые двумя
разными командами сложения. Мы уже обра-
щали внимание на этот момент в главе 21N, и
здесь дадим подобное объяснение:
♦ первая операция сложения выполняется ко-
мандой ADD, которая не принимает во вни-
мание значение флага переноса CY, но обнов-
ляет его по результатам сложения;
♦ а вторая операция сложения выполняется
командой ADDC, которая принимает во вни-
мание значение флага переноса CY.
882 21L Лабораторное занятие: микропроцессоры II
Листинг 21L.5. Программа 16-разрядного суммирования
LOC OBJ LINE SOURCE
1 ; 16_Sl)M_02.a51 Лаб. занятие 21. Вычисление и вывод на дисплей текущей суммы
; 16-разрядных значений
SNOSYMBOLS ; Сокращаем объем кода в листинге...
$INCLUDE (C:\MICRO\8051\RAISON\INC\REG320.INC) ; а не то эта строка кода
; выдаст громаднейший список определений идентификаторов
; (все они для регистров 8051)
ORG 0 ; Указывает ассемблеру начальный адрес для размещения этого кода
SJMP STARTUP ; Код начинается здесь - с перехода на начало
; собственно программы. ВСЕ наши программы будут начинаться таким образом
ORG 60H ; Вот здесь начинается собственно программа
STARTUP: MOV DPTR, #8000H ; Указатель на младший байт дисплея
; и цифровой клавиатуры
CLRA
MOV R0, А ; Обнуляем регистры хранения
MOVR1,A
GETIT: MOVX A, @DPTR ; Считываем значение с цифровой клавиатуры
ADD A,R0 ; Формируем младший байт текущей суммы,
MOVX @DPTR, A ; отправляем его на дисплей (порт 0)
MOV R0,A ; и сохраняем копию в регистре
CLRA
ADDC A,R1 ; Инкрементируем старший байт текущей суммы
; (Добавляется перенос, если было переполнение младшего байта.)
MOV R1 ,А ; Сохраняем результат
INC DPTR ; Указываем на старший байт дисплея (порт 1)
MOVX @DPTR, A ; Отправляем старший байт на дисплей (порт 1)
DEC DPL ; Восстанавливаем указатель на младший байт (операции декрементирования
; 16-разрядного указателя не существует,
199 ; но это небольшое декрементирование не представляет опасности)
; одноразовая декрементация из порта 8001
200 ; не может вызвать отрицательного переноса
0071 80F3 201 SJMPGETIT
202
203 END
На первый взгляд код сложения с помощью ко- Данная операция может выглядеть, как замыс-
мандыАОРС ловатый способ не выполнять никаких дей-
CLRA ствий, поскольку она означает добавить ноль
(значение регистра А) к значению регистра R1
addc a,ri (содержащего старший байт 16-разрядной сум-
выглядит бессмысленно, не так ли? мы). Но критическим отличием от простого
0000
0000
0060
0060
0063
0064
0065
0066
0067
0068
0069
006А
006В
006С
006D
006Е
006F
805Е
908000
Е4
F8
F9
Е0
28
F0
F8
Е4
39
F9
A3
F0
1582
2
3
4
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
21 LI Ввод-вывод на большом компьютере
883
добавления нуля (означающего ничего не де-
лать со значением регистра R1) является то, что
операция сложения команды ADDC имеет тре-
тье слагаемое — значение флага переноса CY по
результатам сложения младшего байта. Таким
образом, вторая операция сложения, выпол-
няемая командой ADDC, действительно расши-
ряет 8-разрядный результат должным образом.
Выходной перенос по результатам сложения
младшего байта можно рассматривать как сиг-
нал переполнения; а старший байт можно рас-
сматривать как счетчик переполнений от опе-
раций сложений младшего байта.
Отображение результата 16-разрядного
сложения
Чтобы отображать на дисплее результаты
16-разрядных сложений, переключатель DATA
необходимо перевести из положения 8 в поло-
жение 16, как показано на рис. 21L.11. Чтобы
сделать процесс сложения более интересным,
введите с цифровой клавиатуры достаточ-
но большое число для добавления к текущей
сумме, например 21h. В процессе пошагово-
го исполнения программы вскоре вы долж-
ны увидеть активность в старшем байте при
переполнении результата сложения младшего
байта.
Переключатель выбора
разрядности данных
Рис. 21 L.11. Плата ЖКД поддерживает возможность отобра-
жений 16 битов данных, а не только восьми
Дополнительный двоичный код
без загадок
Будет полезным ввести значение FFh. Когда
мы пробовали выводить это значение на
8-разрядный дисплей, компьютер выглядел
довольно смышленым, как будто бы он мог
видеть, что FFh означает -1 в дополнительном
двоичном коде.
Но отображение этого числа на 16-разрядном
дисплее позволяет увидеть, что в действи-
тельности происходит «за кулисами»: ничего
необычного, простое сложение. Компьютер
не такой уж и умный и не понимает дополни-
тельного двоичного кода. Значение FFh, кото-
рое мы рассматриваем как -1, действительно
декрементирует младший байт. Но этот резуль-
тат отображается только как побочный эффект
сложения, когда можно видеть 16-разрядный
результат. При каждом декрементировании
младшего байта сложение также инкременти-
рует старший байт.
21 L.1.6. Две версии программы
текущей суммы с задержкой
Код задержки в теле программы
Программа, приведенная в листинге 21L.6,
практически такая же, как и программа 8-раз-
рядного суммирования для пошагового испол-
нения (листинг 21L.4), с той лишь разницей,
что в нее добавлено несколько строк кода для
реализации задержки. Таким образом, вам не
нужно вводить всю программу заново, а мож-
но просто добавить в старую программу новый
код, начиная с адреса 42h. Этот код задержки
позволит вам наблюдать отображаемую на дис-
плее сумму, исполняя программу в непрерыв-
ном режиме.
Задержка снова реализована с помощью ко-
манды условного перехода DJNZ. Но микрокон-
троллер 8051 может исполнять эту операцию
только со своими 8-разрядными регистрами,
а обратный счет от значения 256 не обеспечи-
вает достаточно большую задержку. Поэтому,
чтобы получить более длительную задержку,
мы использовали две такие команды, одна,
вложенная в другую. Данное вложение позво-
лит нам умножить задержку внутреннего цик-
ла на 8-разрядную внешнюю постоянную. Мы
инициализировали регистры задержки неболь-
шими значениями, чтобы при исполнении про-
граммы в пошаговом режиме вы не умерли со
скуки. Но, поэкспериментировав с ней в свое
удовольствие в пошаговом режиме, измените
постоянные задержки для создания максималь-
ной задержки. Какими должны быть значения
постоянных для этого?
Подсказка
Команда DJNZ сначала декрементирует значение
регистра, а затем выполняет проверку его значе-
ния на ноль4.
4 Самую большую задержку даст начальное значение, рав-
ное нулю.
884
21L Лабораторное занятие: микропроцессоры II
Листинг 21L.6. Программа суммирования с введенной задержкой
MACRO ASSEMBLER KEYSUM_DELAY_INLINE_402 07/21/04 11:43:27 PAGE 1
LOC OBJ LINE SOURCE
1 ; KEYSUM_DELAY_INLINE_402.a51 Лаб. занятие 21L. Считываем значение с цифровой клавиатуры
2 ; и добавляем его к текущей сумме. Задержка в теле программы 4/02
3
4
170
171
0000 172
173
0000 802Е 174
175
176
0030 177
178
0030 908000 179
0033 75817F 180
0036
0038
003А
ООЗС
003D
ООЗЕ
003F
0040
0041
0042
0043
7А02
7В04
7800
F0
Е0
28
00
F8
F0
ЕА
8BF0
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
0045 D5F0FD 197
0048 D5E0F8 198
004В
199
80F0 200
END
SNOSYMBOLS ; Сокращаем объем кода в листинге...
SINCLUDE (C:\MICRO\8051\RAISON\INC\REG320.INC); а не то эта строка кода
; выдаст громаднейший список определений идентификаторов (все они для регистров 8051)
ORG0
; Указывает ассемблеру начальный адрес для размещения этого кода
SJMP STARTUP ; Код начинается здесь - с перехода на начало
; собственно программы. ВСЕ наши программы будут начинаться таким образом
ORG ЗОН ; Вот здесь начинается собственно программа
STARTUP: MOV DPTR, #8000H; Указатель как на дисплей (OUT0), так и на цифровую клавиатуру (IN0)
MOV SP, #07FH ; Инициализируем указатель стека адресом, на единицу меньшим,
; чем начало черновой RAM
; Эта внутренняя память в настоящее время пустая, но мы вскоре будем использовать ее
MOV R2,#02 ; Инициализируем небольшую константу задержки
MOVR3,#04
MOV R0, #0 ; Обнуляем текущую сумму, чтобы всегда начинать с чистого листа
MOVX @DPTR, A ; Отображаем текущую (нулевую) сумму на дисплее: аккуратная первая итерация
COUNTUP: MOVX A, @DPTR ; Считываем значение с цифровой клавиатуры
ADD A, R0 ; Формируем новое значение текущей суммы: новое + старое, результат в А
NOP
MOV R0, А ; сохраняем результат (обновляем значение текущей суммы)
MOVX @DPTR, A ; Отображаем текущую сумму на дисплее. Далее вставляем задержку.
MOV A,R2 ; Получаем значение задержки внешнего цикла
INITINNER: MOV B,R3 ; Инициализируем счетчик внутреннего цикла
INLOOP: DJNZ В, INLOOP ; Декрементируем счетчик внутреннего цикла,
; пока не станет нулевым
DJNZ ACCJNITINNER ;... затем декрементируем счетчик внешнего цикла и снова запускаем
; внутренний цикл
SJMP COUNTUP
; Повторяем
Вычислить задержку, создаваемую этой про-
граммой, довольно трудно; удобнее изме-
рить ее с помощью осциллографа, наблюдая
сигнал, происходящий раз за цикл задерж-
ки. Этому критерию отвечает сигнал OUT0*,
которым и воспользуемся. (В нашем случае
период цикла составлял около 120 мс при мак-
симальном значении задержки, а не с крошеч-
ными значениями, используемыми в листинге
программы.)
21 LI Ввод-вывод на большом компьютере
885
Цель маленьких значений задержки, как для
внешнего, так и для внутреннего цикла, — обе-
спечить наблюдение исполнения вложенного
цикла при исполнении программы в пошаго-
вом режиме. (При максимальных значениях
задержки исполнение программы в пошаговом
режиме будет очень скучным процессом.) Но
используемые в листинге значения задержки
слишком малы для исполнения программы
в непрерывном режиме. Поэтому, чтобы полу-
чить максимальную задержку в непрерывном
режиме, измените обе постоянные задержки
на ноль.
Но размещение кода задержки в теле основ-
ной программы делает ее не очень аккуратной.
Кроме того, этот код не очень тактичный по
отношению к другим элементам программы:
в процессе своего исполнения он изменяет зна-
чение регистра А. Хотя это обстоятельство не
имеет важности в случае данной программы,
в других программах это может быть неприем-
лемым. Мы исправим оба эти изъяна в нашей
следующей программе. В частности, во-первых,
мы уберем код задержки из основной програм-
мы и поместим его в отдельную подпрограмму;
во-вторых, мы обеспечим сохранность содер-
жимого регистров, изменяемых при выполне-
нии нашей подпрограммы.
21L1.7. Код задержки в виде
подпрограммы
Теперь мы реализуем задержку более аккурат-
но. В частности, мы выделим ее код в отдель-
ный автономный фрагмент кода, называемый
подпрограммой. Эту подпрограмму можно бу-
дет вызывать из нашей программы вычисления
текущей суммы. Но ее также можно вызывать из
любой другой программы, исполнение которой
вам может потребоваться. При создании нашей
подпрограммы задержки мы примем меры для
того, чтобы, в отличие от кода задержки в теле
основной программы, по завершении ее ис-
полнения восстанавливалось исходное содер-
жимое задействованных в ней регистров. Это
разумная предосторожность, поскольку данное
содержимое может требоваться в операциях
программы, следующих после вызова подпро-
граммы задержки.
Опять же, вам не нужно вводить всю програм-
му, а следует только изменить самую первую
программу вычисления текущей 8-разрядной
суммы, листинг которой приводится в начале
раздела 21L.1.5. Просто поменяйте две строки
кода в этой программе, начиная с адреса 42h.
Затем введите код подпрограммы задержки,
начиная с адреса 100h. Данное значение адреса
было выбрано по той причине, что, как мы по-
лагаем, его будет легко запомнить на тот слу-
чай, если нам снова потребуется подпрограмма
задержки.
Опять же, мы начнем с очень маленького зна-
чения задержки для пошагового варианта ис-
полнения программы. При достижении коман-
ды ACALL компьютер может немного призаду-
маться или игнорировать несколько нажатий
кнопки пошагового исполнения, после чего
перейдет к началу подпрограммы задержки.
Данная пауза объясняется тем, что процессор
занят сохранением на стек адреса возврата
(т. е. адреса команды, которую ему нужно бу-
дет выполнить после завершения выполнения
подпрограммы). Операции со стеком про-
зрачны для пользователя, поскольку они вы-
полняются полностью внутри микроконтрол-
лера, а не на внешних шинах, доступных для
пользователя.
Стек — это просто область внутренней памяти
RAM микроконтроллера для временного хра-
нения адресов возврата, а также других дан-
ных. В подпрограмме задержки DELAY, листинг
которой приводится далее, стек служит для
сохранения в нем не только адреса возврата
(что делается автоматически при исполнении
команды AC ALL), но также и для временного
хранения содержимого регистров, которое бу-
дет модифицировано этой подпрограммой. Это
регистр флагов PSW, а также регистры А и В.
Примечание
Как уже упоминалось ранее, по каким-то извест-
ным только разработчикам причинам при рабо-
те с командами PUSH (сохранение в стеке) и POP
(извлечение из стека) регистр А нужно называть
АСС.
Сохранение этих данных является типичным
использованием стека. Код для этих операций
не представляет никакой сложности, поскольку
вся необходимая работа выполняется стеком
при условии, что каждая команда PUSH имеет
соответствующую команду POP. Обратите вни-
мание на последовательность этих команд в ли-
стинге 21L.7.
886
21L Лабораторное занятие: микропроцессоры II
Листинг 21L.7. Программа суммирования с введенной задержкой
MACRO ASSEMBLER DELAYROUTINE_402
LOC OBJ LINE SOURCE
1
; KEYSUM_DELAYROUTINE_407.a51 Лаб. занятие 21L Опрашиваем клавиатуру и добавляем число
; к текущей сумме. С ПОДПРОГРАММОЙ ЗАДЕРЖКИ 4/02,9/02
; Начальный адрес изменен, чтобы позволить использовать для замены прежнего
; кода задержки в теле программы 4/07
4 $NOSYMBOLS ; Сокращаем объем кода...
5 SINCLUDE (C:\TOM\MICRO\8051\RAISON\INQREG320.INC)
172
0000 173
174
0000 802Е 175
' 176
177
0030 178
179
180
181
182
0030 908000 183
0033 75817F 184
0036
0038
003А
ООЗС
7А02
7В04
7800
F0
0 03D Е0
ООЗЕ 28
003F 00
0040 F8
0041 F0
185
186
187
188
189
190
191
192
193
194
195
196
ORG 0 ; Указывает ассемблеру начальный адрес для размещения этого кода
SJMP STARTUP; Код начинается здесь - с перехода на начало
; собственно программы. ВСЕ наши программы будут начинаться таким образом
ORG ЗОН ; Вот здесь начинается собственно программа
; Обратите внимание на то, что этот листинг такой же, как и предыдущая программа
; Это сделано преднамеренно, чтобы не нужно было вводить заново код
; до вызова подпрограммы по адресу 42h
STARTUP: MOV DPTR, #8000H; Указатель как на дисплей (OUT0),
; так и на цифровую клавиатуру (IN0)
MOVSP,#07FH
; Инициализируем указатель стека адресом, на единицу меньшим, чем начало черновой RAM
MOV R2,#02; Инициализируем небольшую константу задержки
MOV R3,#04
MOV R0, #0 ; Обнуляем текущую сумму, чтобы всегда начинать с чистого листа
MOVX @DPTR, A ; Отображаем текущую (нулевую) сумму на дисплее:
; аккуратная первая итерация
COUNTUP: MOVX A, @DPTR ; Считываем значение с цифровой клавиатуры
ADD A, R0; Формируем новое значение текущей суммы: новое + старое, результат в А
NOP
MOV R0, А ; сохраняем результат (обновляем значение текущей суммы)
MOVX @DPTR, A ; Отображаем текущую сумму на дисплее. Далее делаем задержку
; ЗДЕСЬ НАЧИНАЮТСЯ ИЗМЕНЕНИЯ В КОДЕ ПРОГРАММЫ С ЗАДЕРЖКОЙ В ТЕЛЕ
0042 3100 197
0044 80F7 198
199
200
201
0100 202
0100 C0D0 203
ACALL DELAY
SJMP COUNTUP
; - ПОДПРОГРАММА ЗАДЕРЖКИ 'DELAY' -
ORG 10ОН
DELAY: PUSH PSW ; Сохраняем содержимое регистров, которое будет изменено
21L2. Байтовые операции ввода в малом компьютере
887
0102 C0E0 204
0104 COFO 205
206
207
0106 ЕА 208
0107 8BF0 209
0109 D5F0FD 210
01 ОС D5E0F8 211
01 OF DOFO 212
0111 DOEO 213
0115 DODO 214
0115 22 215
216
217
PUSH ACC ; В данном случае это не является необходимым но при следующем вызове этой
PUSH В ; подпрограммы эти регистры могут использоваться
; основной программой, поэтому не помешает сохранить их.
MOV A,R2 ; Получаем значение задержки внешнего цикла
INITINNER: MOV B,R3 ; Инициализируем счетчик внутреннего цикла
INLOOP: DJNZ В, INLOOP ; Декрементируем счетчик внутреннего цикла, пока не станет нулевым
DJNZ ACCJNITINNER ;... затем декрементируем счетчик внешнего цикла и снова запускаем
; внутренний цикл
POP В ; Восстанавливаем содержимое сохраненных регистров.
POP ACC
POP PSW
RET ; Возвращаемся в основную программу.
END
21L2. Байтовые операции
ввода в малом компьютере
21 L2.1. Использование
выводов порта в сегодняшнем
лабораторном занятии
В этой ветви лабораторных занятий по микро-
компьютерам кроме вывода для управления
светодиодом, как на лабораторном занятии
20L.3, мы задействуем еще один дополнитель-
ный вывод порта PORTO: для подачи входного
сигнала с кнопки.
Позже, на лабораторном занятии 21L.2.8, мы
также добавим устройства ввода-вывода к двум
другим портам: P0RT1 (дисплей) и P0RT2 (циф-
ровая клавиатура). Также мы возложим на порт
PORTO задачу управления другим 8-разрядным
ЖКД. Последнее применение порта PORTO не
будет конфликтовать с его применениями, по-
казанными на рис. 21L.12.
|ч. >р 1П ^, со <\1 «-« О
122222222
Рис. 21 L.12. Использование дополнительного вывода порта
PORTO для подачи на него входного сигнал с кнопки
21 L2.2. Программа мигания
светодиодом с использованием
подпрограммы
В нашей предыдущей программе мигания све-
тодиодом мы вставили код задержки в тело
основной программы. Такой подход работает,
но его неудобно программировать, а код полу-
чается неуклюжим. Конечно же, для крошеч-
ной программы, как наша программа мигания
светодиодом, эти аспекты не слишком важны.
Но для программ большего размера полезно
разбить код на функциональные модули, на-
зываемые подпрограммами, которые сводятся
вместе основной, вызывающей их программой.
На этом занятии мы применим модульный под-
ход для реализации программы мигания свето-
диодом с кодом задержки, переделав должным
образом соответствующую программу из заня-
тия 20L.3. Полученная программа будет мигать
светодиодом точно так же, как и предыдущая,
но ее текст будет более удобочитаемым.
Листинг 21L.8 содержит код предыдущей про-
граммы мигания светодиодом, к которому был
просто добавлен новый код для вызова двух
подпрограмм. Одна из этих подпрограмм вы-
полняет предварительную инициализацию
процессора, специфическую для микроконт-
роллера C8051F410. Эта подпрограмма называ-
ется USUAL_SETUP и присутствует почти во всех
программах для этой ветви лабораторных за-
нятий по микрокомпьютеру. А вторая подпрог-
рамма, DELAY, просто создает паузу в исполне-
нии программы длительностью около одной
секунды, чтобы мигание светодиода было
888
21L Лабораторное занятие: микропроцессоры II
различимо человеческим глазом при непрерыв-
ном исполнении программы. Подробности этой
задержки рассматриваются в разделе 20L.3.7.
Но мы внесли одно небольшое изменение
в код подпрограммы USUAL_SETUP по срав-
нению с кодом задержки в программе из раз-
дела 20L3. В частности, воспользовавшись
соответствующей возможностью микрокон-
троллера C8051F410, мы замедлили системный
тактовый генератор в восемь раз, чтобы умень-
шить энергопотребление микроконтроллера.
В данном приложении это замедление, конеч-
но же, не окажет заметного эффекта. Поэтому
задавать его здесь нет необходимости, но мы
решили, что будет полезным показать вам на-
личие такой возможности. В принципе, такая
частота системного тактирования устанавли-
вается по умолчанию средой разработки, но
здесь мы ее установили принудительно явной
командой:
ORL OSCICN, \#04h; sysclk =24,5 МГц/8.
Некоторые аспекты листинга 21L.8 потребуют
более подробных разъяснений.
Листинг 21L.8. Программа мигания светодиодом с подпрограммой
; bitflip_delay_subroutine.a51 Программа переключения светодиода bitflip с задержкой для непрерывного исполнения
SNOSYMBOLS; Сокращаем объем кода в листинге
$INCLUDE (C:\MICRO\8051\RAISON\INC\c8051f410.inc)
ORG 0; Указываем ассемблеру начальный адрес для размещения этого кода
ACALL USUAL_SETUP
SETB P0.0 ; Начинаем с выключенным светодиодом (активируется низким уровнем)
FLIPIT: CPL P0.0 ; Переключаем светодиод
ACALL DELAY ; Выжидаем некоторое время
SJMP FLIPIT ; Повторяем до бесконечности
; -ПОДПРОГРАММЫ---
DELAY: PUSH ACC; Сохраняем в стеке регистры, которые эта подпрограмма модифицирует
PUSH В
PUSH 4; Сохраняем содержимое регистра R4 (находится в нулевом наборе регистров)
MOV А,#0; Максимизируем два значения задержки (0 максимальное значение, потому что декрементируем
; перед проверкой)
MOV В,#0; ...и второе значение задержки в цикле
MOV R4, #1 Oh; Задержка длительностью в 1 секунду: Это объединяет 64 К циклов
INNERLOOP: DJNZ В, INNERLOOP ; Декрементируем счетчик внутреннего цикла, пока не станет нулевым
DJNZ ACCINNERLOOP;... затем декрементируем счетчик второго цикла и снова запускаем внутренний цикл
DJNZ R4, INNERLOOP ; Когда счетчик второго цикла становится нулевым, декрементируем
; счетчик внешнего цикла
POP 4
POP В
POP ACC
RET; Возвращаемся в основную программу.
USUAL.SETUP: ANL PCAOMD, #NOT(040h) ; Отключаем сторожевой таймер
; Обнуляем бит разрешеният сторожевого таймера
; Конфигурируем генератор тактовых колебаний
ORL OSCICN, #04h ; sysclk = 24.5 МГц/8
; Разрешаем матричный переключатель порта входа-выхода
MOV XBR1, #40h ; Разрешаем матричный переключатель
RET
END
21L2. Байтовые операции ввода в малом компьютере
889
Данная подпрограмма вызывается командой
вызова ACALL. (Подпрограммы и стек рассма-
триваются подробно в главе 21N.) Правила
вызова подпрограмм требуют, чтобы вызы-
ваемая подпрограмма сохраняла все значе-
ния, которые она может изменить, чтобы по-
сле возвращения из подпрограммы основная
программа могла работать должным образом.
Для сохранения этих значений предусмотре-
ны команды PUSH, а для их восстановления
перед завершением подпрограммы и возвра-
щения в основную программу — команды POP.
Команда RET снимает адрес возврата со стека,
чтобы после возвращения из подпрограммы
исполнение основной программы могло про-
должиться командой, следующей за командой
вызова подпрограммы ACALL
21 L2.3. Некоторые особенности
команд PUSH и POP
Возможная неопределенность названия
регистров Rn
Одна из команд сохранения регистров выгля-
дит необычно — PUSH 4. Почему PUSH 4, а не
PUSH R4? Потому что название R4 неопреде-
ленное: микроконтроллер 8051 оснащен че-
тырьмя банками из восьми регистров обще-
го назначения, которые называются R0—R7.
Микроконтроллер решает эту проблему не-
определенности, проверяя состояние битов RSO
и RS1 в своем регистре (слове) состояния про-
граммы PSW (Program Status Word). Значение
этих двух битов определяет, какой из четырех
банков регистров общего назначения задей-
ствовать. После сброса эти биты обнуляются,
поэтому микроконтроллер по умолчанию ис-
пользует нулевой банк регистров общего на-
значения.
Но при указании названия регистра общего на-
значения программа на ассемблере не «осмели-
вается» предполагать, какой из четырех банков
регистров имеется в виду. Поэтому она требует,
чтобы для обращения к регистру R4 нулевого
банка был указан его внутренний адрес. Для
регистра R4 нулевого банка таким однознач-
ным адресом будет просто число 45.
Наконец, как уже упоминалось в главе 21N, при
работе с командами PUSH и POP регистр А ио-
обходимо называть АСС.
не-
Полученный в результате код более
понятный
Наличие подпрограмм делает даже эту простую
программу более понятной для пользователя.
Код основной части программы расположен
недалеко от ее начала:
FLIPIT: CPL P0.0
ACALL DELAY
SJMP FLIPIT
; Переключаем светодиод
; Выжидаем некоторое время
; Повторяем до бесконечности
5 Нам бы очень хотелось, чтобы у ассемблера было до-
статочно смелости предполагать, что конкретным реги-
стром R4 является тот, который используется в момент об-
ращения. Но ассемблер для 8051 работает иначе.
Так как этот код находится в начале програм-
мы и весь сосредоточен в одном месте, нам
легче понять, что он делает, чем код програм-
мы переключения светодиода с задержкой из
лабораторного занятия 20L.2, в которой коды
инициализации и задержки находились в теле
основной программы.
Начиная с этого момента, мы будем исполь-
зовать подпрограммы на регулярной основе,
стремясь к тому, чтобы сделать наши програм-
мы удобочитаемыми, а также для того, чтобы
их можно было бы создавать поэтапно. Этот
подход похож на наши методы, применяемые в
аналоговой части курса, где мы прилагали уси-
лия к тому, чтобы разрабатывать и тестировать
устройства помодульно. Такой метод облегчал
как разработку, так и анализ, и наш мотив для
предпочтения подпрограмм такой же.
21 L2.4. Ввод бита условия
На лабораторном занятии мы создали про-
грамму для непрерывного мигания светодио-
дом. Это не очень впечатляющее приложение
для интеллектуального контроллера. С таким
же успехом мы могли заставить светодиод мор-
гать с помощью схемы на генераторе колебаний
555. Но теперь мы немного усложним задачу,
чтобы программа прекращала мигание свето-
диода при нажатии кнопки пользователем. Вы
можете возразить, что это тоже не особо впе-
чатляет, поскольку такой же результат можно
было бы получить, установив кнопку на линию
сброса генератора колебаний 555.
С таким аргументом трудно спорить. Но мы бы
хотели возразить, что способность процессора
890
21L Лабораторное занятие: микропроцессоры II
выполнять одну задачу при одном условии и
другую — при другом равнозначна «пробле-
скам интеллекта». Данная способность являет-
ся фундаментальной для того, чтобы компью-
тер выглядел умным. Так что, давайте оснастим
нашу программу мигания светодиодом этой
возможностью.
21 L2.5. Ввод битов
Аппаратное обеспечение
При работе с микроконтроллером с исполь-
зованием внешних шин (как мы это делали в
главе 21N) реагирование на ввод битов требует
наличия определенного аппаратного обеспече-
ния (в частности, буфера с выводами с тремя
состояниями, чтобы выложить информацию
на шину данных), а также последующего вы-
полнения операции тестирования регистра ак-
кумулятора.
С другой стороны, при наличии встроенного
порта контроллера, как в микроконтроллере
C8051F410 (внутренние шины которого недо-
ступны для пользователя), ввод данных намно-
го проще. Входной сигнал {бит, как в следую-
щей далее программе bitflipjf.a51, или байт,
как в разделе 21L.2.8) подается напрямую на
вывод или выводы порта микроконтроллера.
Буфер с выводами с тремя состояниями не ну-
жен, поскольку данный вывод (выводы) микро-
контроллера подключается не к общей шине, а
к выделенной линии (линиям).
Таким образом, для реализации взаимодей-
ствия микроконтроллера C8051F410 требует-
ся крайне простое аппаратное обеспечение:
кнопка для подключения вывода микрокон-
троллера на «землю», и резистор для подачи
на него напряжения +5 В в противном слу-
чае6. Соответствующая схема показана на
рис. 21L.13.
Если присутствует дребезг контактов, то для
увеличения длительности фронта сигнала нуж-
но добавить, хотя бы конденсатор7. Но ради
' 10 кОм
to PO.4
6 Для некоторых портов микроконтроллера 8051/
C8051F410 внешний повышающий резистор может даже и
не требоваться, поскольку они оснащены внутренним по-
вышающим резистором. Но порт PORTO, который мы ис-
пользуем в данном случае, такого внутреннего резистора
не имеет.
7 Как вы должны знать, чтобы по-настоящему устранить
дребезг контактов однополюсного однопозиционного пе-
Рис. 21 L.13. Схема для подачи сигнала управления на вывод
порта Р0.4
максимальной простоты мы откажемся от него
в данном случае, поскольку для нашей про-
граммы дребезг контактов не важен.
21 L2.6. Код программы
с использованием подпрограмм
Применение подпрограмм делает код
понятным
Используя наши новые знания, приобретенные
в разделе 21L.2.2, мы снова удаляем подроб-
ности инициализации и реализации задержки
из тела основной программы и переносим их
в подпрограммы.
Использование идентификаторов
для облегчения понимания кода
Кроме добавления подпрограмм мы слегка мо-
дифицировали исходную программу мигания
светодиодом, чтобы сделать код более понят-
ным8. В частности, в этой программе мы исполь-
зовали идентификаторы, или описательные на-
звания, вместо номеров выводов портов.
В исходной версии программы мигания свето-
диодом bitflip.a51 мы обращались к выводу пор-
та как Р0.0, теперь мы заменим это обозначение
описательным названием BLUEJJED (синий
светодиод). Подобным образом мы заменим
обозначение линии ввода Р0.4 описательным
реключателя, требуется больше чем простой RC-контур.
В частности, для того, чтобы сделать прямоугольным пе-
реход медленного RC-контура, требуется также и триггер
Шмитта. Но, в отличие от, например, сигнала входа такти-
рования триггера, активируемого фронтом сигнала, вход-
ной сигнал для процессора не обязательно должен иметь
правильную прямоугольную форму. Мы сможем убедить-
ся в этом в лабораторном занятии 22L.2.
8 Достоинства идентификаторов и меток иногда преуве-
личивают, называя такой текст программы самодокумен-
тирующимся. Но мы не будем утверждать, что метки на-
столько замечательны.
2М2. Байтовые операции ввода в малом компьютере
891
названием РВ (pushbutton — кнопка). Таким
образом, если бесконечный цикл в исходной
программе мигания светодиодом выглядел так:
FLIPIT: CPL P0.0 ; Переключаем светодиод: включаем,
; затем выключаем...
SJMP FLIPIT
код этого цикла в модифицированной таким
способом программе flipjjм51 дает пользова-
телю дополнительную информацию о своем
назначении.
В начале программы мы определяем два иден-
тификатора — BLUEJ.ED и РВ, чтобы вместо
обозначений выводов портов в программе
можно было указать эти описательные имена.
Для определения этих идентификаторов слу-
жит директива ассемблера EQU:
BLUE_LED EQU PO.O
РВ EQU P0.4
Директива ассемблера — это команда не для
исполнения микроконтроллером 8051, а для
программы ассемблера9. Теперь, в процес-
се преобразования исходного кода на языке
ассемблера в исполняемый код, каждый раз,
когда ассемблеру встречается идентификатор
BLUE_LED, он будет заменять его обозначением
Р0.0. Подобная замена будет выполняться и для
идентификатора вывода кнопки РВ.
Определив эти идентификаторы, мы можем сде-
лать код нашей новой программы достаточно
удобопонятным. Но выполнить эту задачу по
написанию программы нужно будет вам самим.
Реализация программы на языке
ассемблера
На данном этапе мы определили идентифика-
тор РВ для обозначения линии входа порта ми-
кроконтроллера, состояние которой мы хотим
проверять. Обозначим меткой FLIPIT адрес, по
которому должна перейти наша программа по-
сле нажатия кнопки.
FLIPIT: РВ, FLIPIT ; Остаемся здесь до тех пор,
; пока нажата кнопка
CPLBLUE LED
Мы хотим, чтобы вы сами заполнили пробел
(обозначенный подчеркиванием) командой ас-
семблера для 8051, которая реализует эту опе-
рацию. Для выполнения этой задачи полезно
обратиться к списку команд ассемблера для
микроконтроллера 8051, который приведен в
главе 20S. Эту же информацию, в более расши-
ренном формате, можно найти на с. 13-16 руко-
водства программиста для микроконтроллера
8051, предлагаемого компанией Philips/NXP10.
После заполнения пробела кодом команды
метка и идентификатор должны предоставить
хорошую подсказку относительно логики этого
цикла. Возможно, что команды FLIPIT: РВ,
FLIPIT и CPL BLUEJ.ED все еще не очень вам по-
нятны. Но, согласитесь, что идентификаторы
все же полезны, не так ли?
Определение хода исполнения
программы состоянием кнопки
Кроме нового подхода к структурированию
кода программы, другим новым аспектом про-
граммы bitflipjf.a51 является проверка состоя-
ния входа программой. Команда условного
перехода, которую мы поручили вам ввести
в пробел в коде, реализует условие если (if)
в операторе «Мигать... если». Данное условие
(если) удерживает программу на этой строке кода
в течение всего времени, пока нажата кнопка,
т. е. пока на входе РОЛ присутствует логический
сигнал низкого уровня. Только при отпускании
кнопки, т. е. когда на входе РОЛ устанавливается
сигнал высокого уровня, программа переходит
к следующей строке кода, в которой выполняет-
ся переключение светодиода.
Листинг 21L.9 содержит полный код про-
граммы.
При исполнении этой программы мы обнару-
жили, что мигание было слишком медленным.
Попробуйте ускорить его, скажем, в четыре
раза.
21 L2.7, Версия программы
на языке С
Программа на языке С, которая дала бы такой
же результат, т. е. мигала бы светодиодом при
9 Эта тема обсуждается в главе 21N.
10 http://www.keil.com/dd/docs/datashts/philips/p51_
pg.pdf.
892 21L Лабораторное занятие: микропроцессоры II
Листинг 21L.9. Программа мигания светодиодом с управлением от кнопки
; bitflip_if.a51 Медленно мигает светодиодом, если не нажата кнопка
SNOSYMBOLS ; Сокращаем объем кода в листинге
SINCLUDE (C:\MICRO\8051\RAISON\INQc8051f410.inc)
BLUEJlED EQU РО.О
РВ EQU P0.4 ; Кнопка определяет, мигать светодиодом или нет
ORG 0 ; Указываем ассемблеру начальный адрес для размещения этого кода
SJMP STARTUP ; Код начинается здесь — с перехода на начало собственно программы. ВСЕ наши программы будут
; начинаться таким образом
ORG 80h ; Вот здесь начинается собственно программа
STARTUP: ACALL USUAL_SETUP
CLR BLUE_LED ; Начинаем с выключенным светодиодом, просто чтобы исполнение было предсказуемым
FLIPIT: РВ, FLIPIT ; Остаемся здесь до тех пор, пока нажата кнопка
CPL BLUEJ.ED ; Но мигаем светодиодом, если кнопка не нажата
ACALL DELAY
SJMP FLIPIT
;- -ПОДПРОГРАММЫ----
USUAL_SETUP: ; Отключаем сторожевой таймер
ANL PCAOMD, #NOT(040h) ; Обнуляем бит разрешения сторожевого таймера
; Конфигурируем генератор тактовых колебаний
ORL OSCICN, #04h ; sysclk = 24,5 МГц / 8, чтобы понизить энергопотребление
; Разрешаем матричный переключатель порта входа-выхода
MOV XBR1, #40h ; Разрешаем матричный переключатель
RET
DELAY: PUSH ACC ; Сохраняем в стеке регистры, которые эта подпрограмма модифицирует
PUSH В
PUSH 4 ; Сохраняем содержимое регистра R4 (находится в нулевом наборе регистров)
MOV А,#0 ; Максимизируем два значения задержки (0 максимальное значение,
; потому что декрементируем перед проверкой)
MOV В,#0 ; ...и второе значение задержки в цикле
MOV R4, #1 Oh ; Задержка длительностью в 1 секунду: это объединяет 64 К циклов
INNERLOOP: DJNZ В, INNERLOOP ; Декрементируем счетчик внутреннего цикла, пока не станет нулевым
DJNZ ACCJNNERLOOP ;... затем декрементируем счетчик второго цикла и снова запускаем внутренний цикл
DJNZ R4, INNERLOOP ; Когда счетчик второго цикла становится нулевым, декрементируем счетчик внешнего цикла
POP 4
POP В
POP ACC
RET; Возвращаемся в основную программу
END
21L2. Байтовые операции ввода в малом компьютере
893
условии, что нажатая кнопка не подключает на
«землю» вход inbit, во многом похожа на цикл
на языке ассемблера в разделе 21L2.6. В языке
С условие if является явным, тогда как в ассем-
блере оно встроено в команду условного пере-
хода, которую вы должны были вставить в про-
бел.
if(!inbit) outbit = outbit;
else outbit = ioutbit;
Но для такого простого кода программа на
языке С не дает никаких преимуществ над про-
граммой на языке ассемблера.
21 L.2.8. Байтовые операции ввода
и вывода
До сих пор мы использовали битовые опера-
ции, поскольку они позволяли получить бы-
стрый результат при минимальном монтаже в
схеме. Байтовые операции, с которыми мы на-
чали работать при сборке большого компьюте-
ра, так же легко реализовать в коде, но для них
требуется выполнить немного больший объем
монтажных работ. Давайте выполним эту ра-
боту по монтажу сейчас и реализуем несколько
байтовых операций.
Аппаратное обеспечение для байтового
ввода-вывода
Ввод байта с цифровой клавиатуры
В качестве устройства ввода байтов будем
использовать цифровую клавиатуру, кото-
рая оснащена DIP-разъемом с 16 контакта-
ми. Восемь линий данных DIP-разъема, к
DIP-разъем шлейфа
цифровой клавиатуры
\
Шлейф
(в данном случае никуда не подключен)
Рис. 21 L.14. Переходник на макетной плате с DIP-разъема на
шлейф
сожалению, расположены по обеим сторонам
разъема, но их можно расположить в ряд на
макетной плате, как показано на рис. 21L.14.
Такое расположение сделает более удобным
подключение цифровой клавиатуры к микро-
контроллеру C8051F410.
К этим выровненным в одну линию контактам
линий данных подключите один конец шлейфа,
другой конец которого подключается к порту
PORT2 микроконтроллера C8051F410, как по-
казано на рис. 21L.15.
Обратите внимание на то, что жила шлейфа для
линии D7 подключается не напрямую к выво-
ду порта Р2.7 микроконтроллера C8051F410,
а к выходу резисторной схемы, изолирующей
интерфейс С2. Эта схема описывается в разде-
ле 20L.3 и показана на рис. 20L.21.
Ввод байта с цифровой клавиатуры
и отображение его на дисплее
Сначала мы выполним операцию ввода байта
с цифровой клавиатуры и отображения его на
дисплее. Чтобы иметь возможность наблюдать
байтовоевыходноезначениемикроконтроллера
Вывод порта Р2.7, доступный для периферийного устройства через одну
жилу, отведенную от шлейфа. Периферийное устройство подключается
к выводу порта Р2.7 микроконтроллера через резисторную схему,
изолирующую от интерфейса С2
Рис. 21L.15. Подключение кабеля цифровой клавиатуры к микроконтроллеру С8051F410: жила к выводу порта Р2.7 отделена
от общего шлейфа
894
21L Лабораторное занятие: микропроцессоры II
C8051F410, используем нашу плату ЖКД. Она
предоставляет восемь линий для данных, и 16
линий для адреса (для большого компьютера).
Для отображения байтового значения выбе-
рем младший байт (D7...D0) дисплея данных —
один из правых 8-разрядных разъемов на плате
ЖКД.
Рис. 21 L.16. Подключение дисплея к микроконтроллеру для
байтовых операций ввода-вывода
Хотя в данном случае порт PORTO задействован
для управления дисплеем, отключать светоди-
од от линии РО.О и кнопку от линии Р0.4 этого
порта нет надобности. Эти устройства не долж-
ны оказывать никакого влияния на возмож-
ность микроконтроллера C8051F410 управлять
дисплеем. Это объясняется тем, что каждое из
них подключено к соответствующему выводу
микроконтроллера через повышающий ре-
зистор. Но при этом следует соблюдать осто-
рожность и не нажимать кнопку в процессе
использования порта PORTO для управления
дисплеем.
21 L2.9. Код для байтового ввода-
вывода
Код для передачи байта с цифровой клавиату-
ры на дисплей очень прост:
TRANSFER: MOV DISPLAY, KEYPAD
SJMP TRANSFER
Задача определения идентификаторов
Мы снова оставили в строках программы про-
белы с директивами ассемблера EQU, которые
вам нужно будет заполнить, чтобы определить
два идентификатора в программе: DISPLAY и
KEYPAD. Код с пробелами для заполнения вы-
глядит следующим образом:
; Завершите эти две директивы ассемблера EQU?
EQU
EQU
Листинг исходного кода программы на
языке ассемблера
Исходный код программы на языке ассемблера
приведен в листинге 21L.10.
Листинг 21L.10. Исходный код программы на ассемблере
;byte_in_out.a51
$NOSYMBOLS ; Сокращаем объем кода в листинге
$INCLUDE (C:\MICRO\8051\RAISON\INC\c8051f410jnc)
SINCLUDE (C:\MICRO\8051\RAISON\INCWECTORS320.INC); Файл тома определения векторов
STACKBOT EQU 80h ; Размещаем стек в начале рабочего косвенно адресуемого блока памяти (80h и дальше)
; Завершите эти две директивы ассемблера EQU
EQU
EQU
ORGOh
UMP STARTUP
ORG 080h
STARTUP: MOV SP, #STACKBOT-1; "-1" потому, что указатель стека
2/L2. Байтовые операции ввода в малом компьютере
895
; инкрементируется перед первым сохранением
ACALL USUAL_SETUP
TRANSFER: MOV DISPLAY, KEYPAD
SJMP TRANSFER
;-ПОДПРОГРАММЫ--
USUAL_SETUP: ANL PCAOMD, #NOT(040h) ; Отключаем сторожевой таймер
; Обнуляем бит разрешения сторожевого таймера
; Конфигурируем генератор тактовых колебаний
ORL OSCICN, #04h; sysclk = 24,5 МГц / 8
; Разрешаем матричный переключатель порта входа-выхода
MOV XBR1, #40h; Разрешаем матричный переключатель
RET
END
Запустите программу на исполнение и поэк- Основной цикл программы приведен в листин-
спериментируйте с ней. Удостоверившись в re21L.ll.
том, что программа действительно может пе-
редавать байтовые значения с клавиатуры на __ ««"«"л
г о Листинг 21L.11. Основной цикл программы
дисплеи, мы можем «попросить» микрокон- гуммиоования
троллер C8051F410 выполнить немного более
интересные задачи. Transfer: MOV A, RUN_SUM ; Восстанавливаем значение
; текущей суммы
ADD A, KEYPAD ; Формируем новое
21 L2.10. СлОЖеНИе ЧИСЛа ; значение текущей суммы
С ЦИфрОВОЙ Клавиатуры С Текущей результат сохраняется в регистре А
w MOVRUN_SUM,A Сохраняем его,
СуММОИ M0V D|SpLAY^ A . и выводим на дисплей
Возможно, что простая передача данных с по- acall delay
МОЩЬЮ вашего умного микроконтроллера SJMPTransfer Повторяем до бесконечности
C8051F410 не особо впечатляет. Ну что ж. Тогда
давайте позволим ему продемонстрировать
свои более продвинутые способности, как, на- Чтобы Разобраться в этом коде, нужно вспом-
пример, сложение. нить> что РезУльтат операции сложения ADD
сохраняется в регистре А, который также на-
зывается аккумулятором. Таким образом, при
Программа для вычисления текущей каждой итерации цикла выполняется обновле-
суммы 8-разрядных значений ние как "W* сУшал (RUN-SUM)' ™* и с°-
7 r r держимого дисплея.
Эта программа складывает вводимое с цифро-
вой клавиатуры число с текущей суммой и выво- Сначала попробуйте исполнить эту программу,
дит полученную сумму на дисплей. Сначала мы введя с цифровой клавиатуры значение Olh.
будем выполнять сложение 8-разрядных значе- В таком случае суммирование будет, конечно
ний, а затем 16-разрядных (просто для того, что- же, просто инкрементированием. Когда вы бу-
бы показать, что 8-разрядные микроконтролле- дете готовы к более увлекательным приключе-
ры не обязательно ограничены 8-разрядными ниям, попробуйте ввести с цифровой клавиату-
операциями). Когда происходит переполнение ры значение FFh.
текущей суммы, 8-разрядное значение остается
действительным по модулю 8. При этом инфор-
мация в переполнении теряется.
896
21L Лабораторное занятие: микропроцессоры II
Слегка откорректированная
подпрограмма задержки
В листинге 21L.12. мы слегка откорректиро-
вали подпрограмму задержки по сравнению с
предыдущими версиями. В частности, вместо
того, чтобы задать фиксированное значение за-
держки в соответствующей подпрограмме, как
мы делали ранее (например, в программе в раз-
деле 21L2.2), мы задали значение множителя
задержки в заголовке программы. Множитель
в этой подпрограмме определяет количество
повторений 16-разрядного вычитающего цикла
(при этом длительность одного повторения
равна около 80 мс).
Данная модификация делает подпрограмму за-
держки более универсальной. Кроме того, она
также иллюстрирует один аспект разработки
программ: рекомендуется выполнять инициа-
лизацию констант в начале программы, где их
можно легко видеть и изменять. Иными слова-
ми, если вы захотите увеличить длительность
задержки с одной секунды до двух, вам не нуж-
но будет искать в листинге программы место,
где устанавливается эта задержка.
Листинг 21L.12. Программа суммирования с десятичной коррекцией
; keysum_8bit.a51 Отображает значение сложения значения с цифровой клавиатуры и текущей суммы
; с вариантом десятичной коррекции
SNOSYMBOLS; Сокращаем объем кода в листинге
SINCLUDE (C:\MICRO\8051 \RAISON\INC\c8051 f410.inc)
STACKBOT EQU 80h; размещаем стек в начале рабочего косвенно адресуемого блока памяти (80h и выше)
DISPLAY EQU P0; Так называемый байт данных на плате ЖКД
KEYPAD EQU P2
RUN_SUM EQU R7; Эта опция по желанию
DELAY_MULTIPLIER EQU 08h ; Задержка длительностью около полсекунды, при рабочей частоте,
; равной 1/8 частоты тактирования
ORGOh
UMP STARTUP
ORG080h
STARTUP: MOV SP, #STACKBOT-1
ACALL USUAL_SETUP
; Инициализируем значение текущей суммы
CLRA
MOV RUN_SUM, A ; Обнуляем значение текущей суммы
Transfer: MOV A, RUN_SUM ; Восстанавливаем значение текущей суммы
ADD A, KEYPAD
DA A
MOV RUN_SUM, A
MOV DISPLAY, A
ACALL DELAY
SJMP Transfer
; Формируем новое значение текущей суммы
; Сумма в десятичном формате.
; Попробуйте после двоичного формата.
; Сохраняем его,
; и выводим на дисплей
; Повторяем до бесконечности
---ПОДПРОГРАММЫ---
DELAY: PUSH ACC ; Сохраняем в стеке регистры, которые эта подпрограмма модифицирует
21L2. Байтовые операции ввода в малом компьютере
897
PUSH В
PUSH 4; Сохраняем содержимое регистра R4 (находится в нулевом наборе регистров)
MOV А,#0 ; Максимизируем два значения задержки (0 максимальное значение,
; потому что декрементируем перед проверкой)
MOV В,#0 ; ...и второе значение задержки в цикле
MOV R4, #DELAY_MULTIPLIER ; Более общий способ задания значения задержки: Это объединяет 64 К циклов
INNERLOOP: DJNZ В, INNERLOOP ; Декрементируем счетчик внутреннего цикла, пока не станет нулевым
DJNZ ACQINNERLOOP ;... затем декрементируем счетчик второго цикла и снова запускаем внутренний цикл
DJNZ R4, INNERLOOP ; Когда счетчик второго цикла становится нулевым, декрементируем счетчик внешнего цикла
POP 4; Восстанавливаем содержимое сохраненных регистров.
POP В
РОРАСС
RET; Возвращаемся в основную программу.
USUAL_SETUP: ; Отключаем сторожевой таймер
ANL PCAOMD, #NOT(040h) ; Обнуляем бит разрешения сторожевого таймера
; Конфигурируем генератор тактовых колебаний
ORL OSCICN, #04h ; sysclk = 24,5 МГц / 8, чтобы понизить энергопотребление
; Разрешаем матричный переключатель порта входа-выхода
MOV XBR1, #40h ; Разрешаем матричный переключатель
RET
END
Десятичная коррекция 8-разрядного
выходного значения
Двоичное сложение эффективно использует
байты текущей суммы и вводимого с цифровой
клавиатуры значения, позволяя задействовать
все 256 комбинаций. Но когда отображаемые
значения предназначены для просмотра людь-
ми, часто предпочтительнее выводить их в
десятичном формате. Микроконтроллер 8051
знает, как ограничивать выходные значения
десятичными при условии, что с цифровой
клавиатуры также вводятся только десятич-
ные значения.
Чтобы увидеть это в действии, нужно просто
убрать признак комментария (символ точки
с запятой) в начале команды DA в листинге
программы. Команда десятичной коррекции
DA обрабатывает содержимое аккумулятора
(регистра А), наблюдая, когда происходит по-
луперенос из младшего полубайта. Например,
если регистр А содержит значение 09h и к нему
добавить значение 1, то следующее двоичное
значение будет OAh. Но команда DA прини-
мает во внимание полуперенос и выполняет
соответствующую коррекцию значения в акку-
муляторе. В частности, полуперенос указывает
процессору выполнить обнуление младшего
полубайта, при этом инкрементируя старший
полубайт. Таким образом, значение результата
становится 10h, которое является десятичным
значением, следующим за значением 09h.
Следует иметь в виду, что операция DA не пре-
образует шестнадцатеричное значение в деся-
тичное. Она работает должным образом только
сразу же после предшествующей ей операции,
например ADD, которая оказывает соответ-
ствующее воздействие на флаги, в особенности
на флаг полупереноса. Подробная информация
о флагах дается в описании каждой операции
процессора в справочнике по перечню команд
для микроконтроллера 8051.
При первом использовании операции, которая
зависит от поведения флагов, будет разумным
подробно изучить это поведение в справочнике
по перечню команд. Например, команды ин-
крементации INC и декрементации DEC не воз-
действуют на флаги. Это довольно неожидан-
ное поведение.
898
21L Лабораторное занятие: микропроцессоры II
Конечно же, обобщенное преобразование дво-
ичного значения в десятичное тоже возможно.
Но этот процесс требует многошагового алго-
ритма и не является ни простым, ни быстрым.
А команда десятичной коррекции DA предо-
ставляет подходящее средство для решения на-
шей насущной задачи.
21 L2.11. Вычисление 16-разрядной
текущей суммы
Теперь предоставим микроконтроллеру 8051
возможность показать, что он способен ра-
ботать не только с однобайтовыми значения-
ми. Мы не часто требуем от него выполнять
такую задачу; более того, предпочитаем, как
можно меньше нагружать его подобными вы-
числениями. Но за счет уменьшения скорости
8-разрядный процессор может конкатениро-
вать операции, чтобы обрабатывать значения,
большие чем один байт.
В этой программе мы будем вычислять 16-раз-
рядную текущую сумму и отображать ее на
ЖКД с четырьмя цифрами.
Аппаратное обеспечение для 16-разряд-
ного дисплея
Наша плата ЖКД содержит два 8-разрядных
разъема данных, обозначенных D15...D8 и D7...
DO. На эти разъемы мы будем подавать вы-
ходные данные нашего микроконтроллера. Но
прежде чем приступить к реализации дисплея,
установите правый DIP-переключатель в поло-
жение 16 (другое положение обозначено 8тих).
Это сделает два 8-разрядных порта независи-
мыми друг от друга.
Примечание
Установка DIP-переключателя в положение 8тих
объединяет входные сигналы, и разделить их мож-
но, только активируя по отдельности сигнал раз-
решения триггеров-защелок каждого из этих двух
портов. Но в данном случае мы не будем использо-
вать эту опцию.
Мы будем одновременно использовать три
8-разрядных порта. Слева на рис. 21L.17 пока-
зано подключение шлейфов к этим портам ми-
кроконтроллера C8051F410, а справа — к циф-
ровой клавиатуре и ЖКД.
Цифровая клавиатура уже подключена к порту
Р2, поэтому оставляем ее как есть. Младший
байт ЖКД также уже подключен, как показа-
но на рис. 21L.16. Все, что нам осталось сде-
лать, — подключить еще один шлейф одним
концом к порту Р1 микроконтроллера, а дру-
гим — к разъему старшего байта ЖКД (линии
D0...D15).
Установка переключателей ЖКД:
♦ Рекомендуется убрать отображение меток,
используя для этого ползунковый переклю-
чатель LABELS у правого нижнего края пла-
ты ЖКД.
♦ Также рекомендуется подавить верхнюю ли-
нию дисплея, в которой отображаются сиг-
налы 16 входов ЖКД платы, обозначенные
«address». Для этого нужно установить пере-
ключатель LINES в положение 1.
♦ Чтобы отображать 16-разрядные данные,
установите переключатель DATA в поло-
жение 16.
8-разряд*
по одному дл
портов:
Р0, PI, P2
Рис. 21L.17. Подключение ко всем трем портам можно реализовать с помощью 8-разрядных шлейфов
21L2. Байтовые операции ввода в малом компьютере
899
Программа для вычисления и отобра-
жения текущей суммы 16-разрядных
значений
Данная версия программы (листинг 21L.13),
которая суммирует вводимое с цифровой кла-
виатуры значение с текущей суммой и отобра-
жает полученный результат на дисплее, форми-
рует 16-разрядную текущую сумму, пользуясь
флагом переноса (CY), который устанавливает-
ся при переполнении 8-разрядной суммы.
Данный подход к формированию 16-разрядной
суммы объясняется в разделе 21N.6, но мы
вкратце повторим это объяснение здесь:
MOV A, RUN_SUM_HI ; Получаем старший байт суммы
ADDC А, #0; Если есть выходной перенос с младшего
; байта, включаем его в старший
На первый взгляд, сложение нуля с текущей
суммой выглядит бессмысленным. Но это
имеет смысл в случае использования команды
сложения ADDC, одним из слагаемых которой
является флаг переноса. Если предыдущая ко-
манда ADD (создающая младший байт суммы)
сгенерировала перенос, то команда ADDC вы-
полнит инкрементацию старшего байта. В про-
тивном случае старший байт не подвергается
изменению. Это как раз то поведение, которое
нам требуется.
Листинг 21L.13. Программа 16-разрядного суммирования
; keysum_16bita51 Отображает 16-разрядный результат сложения значения,
; введенного с цифровой клавиатуры и текущей суммы
SNOSYMBOLS ; Сокращаем объем кода в листинге...
SINCLUDE (C:\MICRO\8051\RAISON\INC\c8051f410.inc) ;... а не то эта строка может создать громадный список
; определений идентификаторов (все они для регистров 8051)
$INCLUDE (C:\MICRO\8051\RAISON\INCWECTORS320.INC) ; Файл тома определения векторов
STACKBOT EQU 80h ; Размещаем стек в начале рабочего косвенно адресуемого блока памяти (80h и выше)
; Старший байт адреса ЖКД
; Младший байт адреса ЖКД
DISPLAY.HI EQU P1 .
DISPLAY_LO EQU P0
KEYPAD EQU P2
RUN_SUM_HI EQU R7
RUN_SUMJLO EQU R6
RUN_SUM_HI EQU R7
RUN_SUM_LO EQU R6
DELAY_MULTIPLIER EQU 06h ; Задержка длительностью в полсекунды. Значение множителя сохраняется в R4
ORGOh
UMP STARTUP
ORG 080h
STARTUP: MOV SP, #STACKB0T-1
ACALL USUAL.SETUP
; Инициализируем значение текущей суммы (просто обнуляем ее)
MOV RUN_SUM_HI, #o ; Обнуляем значение текущей суммы
MOVRUN_SUM_LOf#0
Transfer: MOV A, RUN_SUM_LO ; Восстанавливаем значение текущей суммы (младший байт)
ADD A, KEYPAD ; Формируем новое значение текущей суммы (младший байт)
DAA
MOV RUN_SUM_LO, A ; Сохраняем его,
MOV DISPLAYJ.O, А ; и выводим на дисплей
MOV A, RUN_SUM_HI ; Получаем старший байт суммы
ADDC A, #0 ; Если есть выходной перенос с младшего байта, включаем его в старший
DAA
900
21L Лабораторное занятие: микропроцессоры II
MOVDISPLAY_HI,A
MOV RUN_SUM_H I, A
ACALL DELAY
SJMP Transfer
; и отображаем старший байт 16-разрядной суммы
; Сохраняем его
; Повторяем до бесконечности
;- -ПОДПРОГРАММЫ---
DELAY: PUSH ACC ; Сохраняем в стеке регистры, которые эта подпрограмма модифицирует
PUSH В
PUSH 4 ; Сохраняем содержимое регистра R4 (находится в нулевом наборе регистров)
MOV А,#0 ; Максимизируем два значения задержки (0 максимальное значение,
; потому что декрементируем перед проверкой)
MOV В,#0 ; ...и второе значение задержки в цикле
MOV R4, #DELAY_MULTIPLIER ; Более общий способ задания значения задержки:
; Это объединяет 64 К других циклов
INNERLOOP: DJNZ В, INNERLOOP ; Декрементируем счетчик внутреннего цикла, пока не станет нулевым
DJNZ ACCJNNERLOOP ;... затем декрементируем счетчик второго цикла и снова запускаем внутренний цикл
DJNZ R4, INNERLOOP ; Когда счетчик второго цикла становится нулевым, декрементируем
; счетчик внешнего цикла
POP 4 ; Восстанавливаем содержимое сохраненных регистров.
POP В
РОРАСС
RET ; Возвращаемся в основную программу.
USUAL_SETUP: ; Отключаем сторожевой таймер
ANL PCAOMD, #NOT(040h) ; Обнуляем бит разрешения сторожевого таймера
; Конфигурируем генератор тактовых колебаний
ORL OSCICN, #04h ; sysclk = 24,5 МГц / 8, чтобы понизить энергопотребление
; Разрешаем матричный переключатель порта входа-выхода
MOV XBR1, #40h ; Разрешаем матричный переключатель
RET
END
Попробуйте ввести на цифровой клавиатуре
значение FFh, как вы это делали с программой
для вычисления 8-разрядной текущей сум-
мы. В случае с 8-разрядной суммой сложение
значения FFh с текущей суммой декременти-
ровало ее значение. Но 16-разрядная версия
программы не рассматривает значение FFh
как -1, поскольку теперь учитываются пере-
носы в старший байт. Младший байт действи-
тельно декрементируется, но одновременно
инкрементируется старший байт. Теперь мы
вскрыли «черный ящик» для сложения бай-
тов и можем видеть все выполняемые в нем
операции.
Опять же, мы включили в программу команды
DA А для десятичной коррекции, которые при
желании можно использовать, удалив символы
комментария. Снова напоминаем, что коман-
да DA А работает должным образом лишь при
условии ввода с цифровой клавиатуры только
десятичных значений, т. е. никаких А, В и т. п.
Отключаем ненужное оборудование
Для следующего лабораторного занятия циф-
ровая клавиатура и дисплеи нам не понадобят-
ся. Поэтому можно отключить их.
Но оставьте на месте кнопку для прекращения
мигания светодиода (см. раздел 21L.2.5). Хотя
она нам больше не потребуется для этой цели,
мы будем использовать ее на лабораторном
занятии 23L.2 по прерываниям. Но не следу-
ет нажимать ее, когда захочется. Некоторые
студенты были неприятно удивлены тем, что
такое действие нарушало работу некоторых
последующих программ. А мы были просто
удивлены их удивлением.
21S. Дополнительный материал:
режимы адресации микроконтроллера 8051
21 S.I. Знакомство
с режимами адресации
микроконтроллера 8051
Вам не потребуется много знать о режимах
адресации микроконтроллера 8051. Набор
его режимов адресации небольшой, и мы бу-
дем использовать не все из них. Изучая язык
ассемблера, вас, наверное, обрадует то, что
микроконтроллер 8051 не обладает многосто-
ронними возможностями, в отличие от, на-
пример, микропроцессора 68000 компании
Motorola, который поддерживает четырнад-
цать режимов адресации. Таким образом, вам
нужно будет освоить меньший объем матери-
ала, чем для более сложного микроконтрол-
лера. Но, с другой стороны, если вы попы-
таетесь разработать программу для решения
более-менее сложной задачи, то ограничения
микроконтроллера 8051 уже не обрадуют вас.
В частности, ему недоступны многие режи-
мы адресации, которые, казалось бы, должен
поддерживать любой более-менее серьезный
микроконтроллер. Например, такие как MOVX
@DPTR, #012h, CLR R5 или MOV R3, R4. Такие
странности могут служить еще одним поводом
для выбора языка С.
21 S.1.1. Внутренняя и внешняя
память
Микроконтроллер содержит некий объем
встроенной памяти; большинство контролле-
ров используют исключительно эту память.
Таким образом работает микроконтроллер
C8051F410 в пути малого компьютера на лабо-
раторных занятиях. Но в нашем большом ком-
пьютере на начальных занятиях мы храним
как код программы, так и данные во внешней
памяти RAM объемом 32 К. Микроконтроллер
8051 также содержит встроенную память ROM,
которую мы задействуем позже, но пока мы
держим ее скрытой от вас. Микроконтроллер
C8051F410 снабжен встроенной памятью ROM
объемом 16 К для хранения данных и кода про-
граммы. Обе эти версии микроконтроллера
8051 содержат лишь небольшой объем встроен-
ной памяти RAM: микроконтроллер C8051F410
компании Silicon Laboratories содержит 2 К
этой памяти, а микроконтроллер 8051 компа-
нии Dallas Semiconductor — 256 байтов плюс
несколько 8-разрядных регистров.
21 S.1.2. Обмен данными внутри
микросхемы
При работе со встроенными регистрами или
рабочей памятью микроконтроллера задача
разработки программ является легкой: мы про-
сто задаем команду MOV назначение, источник.
Например, если цифровая клавиатура подклю-
чена к порту Р0, а дисплей — к порту Р1, то ввод
данных с клавиатуры и отображение их на дис-
плее выполняются командой MOV Р1, Р0. А вот
обмен данными с устройствами вне.микросхе-
мы будет уже посложнее. Мы рассмотрим этот
вопрос более подробно в последующем мате-
риале.
Доступ микроконтроллера 8051
к внешней памяти и устройствам ввода-
вывода
Метод обмена данными микроконтроллера
8051 с внешним миром посредством внешних
шин в нашем компьютере из дискретных ком-
понентов не отличается особой гибкостью.
Такое отсутствие гибкости обычно являет-
ся недостатком, но для студента, увидевшего
902
21S. Дополнительный материал: режимы адресации микроконтроллера 8051
микроконтроллер 8051 в первый раз, это даже
хорошо (как мы утверждали в более общих
словах в самом начале этой главы). В частно-
сти, ему нужно будет освоить всего один режим
внешней адресации. Ну хорошо, один с поло-
виной1.
21 S.1.3. Стандартный метод
адресации с использованием
регистра DPTR
Когда микроконтроллер 8051 обращается к
данным (в отличие от команд), хранящим-
ся во внешней памяти или предоставляемым
устройствам ввода-вывода, подключенным к
внешним шинам, он почти всегда использует
для этого адрес, находящийся во внутреннем
16-разрядном регистре указателя данных DPTR.
А внутренним источником или назначением
этих данных всегда является регистр А, или ак-
кумулятор. Это процесс демонстрируется гра-
фически на рис. 21S.1.
JQ&
8051
Вывод на внешнюю
шину (или запись во
внешнюю память)
Вывод на внешнюю
шину (или запись во
внешнюю память)
Рис. 21 S.1. Для обращения к внешней памяти и устройствам
на внешней шине микроконтроллер использует регистр
DPTR и аккумулятор (регистр А)
Таким образом, почти любую операцию ввода
с внешнего устройства можно выполнить с по-
мощью команды
MOVXA,@DPTR;
А любую операцию вывода на внешнее устрой-
ство можно выполнить с помощью команды
MOVX@DPTR,A;
Странный формат команды:
код операции, назначение, источник
Символ @ в команде MOVX обозначает, что мы
хотим скопировать содержимое регистра А
(8-разрядный регистр микроконтроллера 8051)
в ячейку памяти или устройство ввода-вывода,
чей адрес содержится в регистре DPTR (или из
ячейки памяти или устройства ввода-вывода
при противоположном обмене), а не в сам ре-
гистр DPTR2. В таком случае регистр DPTR име-
нуется указателем, а данный режим адресации
называется неявным.
С учетом такой зависимости микроконтролле-
ра от регистра DPTR успешный обмен данными
зависит не только от строки кода, выполняю-
щей этот обмен (как мы уже видели, формат
источника и назначения данных жестко зафик-
сирован), но также и от правильной предвари-
тельной подготовки регистра DPTR.
Подготовка регистра DPTR
Таким образом, практически любая програм-
ма, которая осуществляет обмен данным с
внешними устройствами, должна перед таким
обменом инициализировать регистр DPTR.
Инициализация всегда выполняется следую-
щей командой:
MOV DPTR,#AflPEC_nOPTA;
Здесь выражение АДРЕС_ПОРТА обозначает
16-разрядный адрес. Символ # перед адресом
порта обозначает непосредственную адреса-
цию. В данном режиме адресации значение
АДРЕС_ПОРТА (пусть это будет 8000h для кон-
кретики) помещается в 16-разрядный регистр
указателя DPTR.
Обратите внимание на отсутствие символа @
в этот раз, поскольку мы хотим поместить зна-
чение в регистр DPTR, а не по адресу, на кото-
рый он указывает. Команда MOV DPTR не опе-
рирует с внешней памятью или устройством
ввода-вывода; она выполняет операцию во
внутреннем регистре микроконтроллера 8051.
Этим объясняется то, почему для этой версии
команды применяется мнемоника MOV, а не
MOVX, которая предназначена для команд,
1 Этой «половиной» является режим MOVX @Rn, кото-
рый рассматривается в разделе 21S.1.4.
2 Такая операция не имела бы смысла в любом случае, по-
скольку регистр А 8-разрядный, а регистр DPTR — 16-раз-
рядный.
21S.L Знакомство с режимами адресации микроконтроллера 8051
903
осуществляющих внешний обмен3, и которые
мы рассмотрим далее.
Внешний обмен (MOVX) по сравнению
с внутренними операциями
В предыдущем разделе мы отметили, что даже
если микроконтроллер 8051 настроен для рабо-
ты с внешними шинами, как в нашем компью-
тере из дискретных компонентов, то он все еще
может, и даже должен, выполнять операции со
своими внутренними регистрами. Как уже было
сказано, одной из таких операций является опе-
рация MOV DPTR, #АДРЕС_ПОРТА. Кроме таких
внутренних команд обмена данными (MOV, а не
MOVX) все другие операции процессора рабо-
тают с его внутренними регистрами: операции
сложения ADDx, логические операции, операции
тестирования битов и т. п.
Внешние операции ограничиваются операци-
ей MOVX, которая выполняет простой обмен
данными. Для обработки значения, получае-
мого из устройства ввода, например цифровой
клавиатуры, это значение всегда необходимо
сначала поместить в один из внутренних ре-
гистров микроконтроллера 8051. Только по-
сле этого микроконтроллер сможет выполнять
какие-либо операции с этим значением.
регистра DPTR, а содержимым двух других ре-
гистров. Старшим байтом этого адреса является
значение, содержащееся во внутреннем порту Р2
микроконтроллера 8051, который представляет
собой просто внутренний регистр микрокон-
троллера, подключенный к старшей половине
линий внешней шины адреса. А младший байт
адреса определяется значением, содержащимся
в одном из восьми внутренних рабочих реги-
стров — R0 или R1. Эта идея иллюстрируется на
рис. 21S.2, где 16-разрядный адрес устройства
ввода-вывода определяется портом Р2 и реги-
стром R1.
Иллюстрация команды MOV @R1, A
R0
R1
8051
«Рабочие»
регистры
]~о
Порт 2
А7Аа
| Внешний
V 16-разрядный
адрес
Рис. 21S.2. Определение внешнего адреса с помощью реги-
стров Р2 и Rn.
Далее приводится пример считывания вывода
АЦП (порт 2) и подачи полученного значения
на вход ЦАП (порт 3). Сначала эта операция
выполняется с помощью регистра DPTR, а затем
посредством другого метода.
21S.1 А Комбинация базового
и индексного регистров
Для операций, обращающихся к небольшому
числу адресов, расположенных не слишком да-
леко друг от друга (в пределах 256), можно при-
менить метод адресации с использованием двух
8-разрядных регистров. Один из этих регистров
содержит фиксированный старший байт 16-
разрядного адреса, который играет роль базово-
го адреса, а другой регистр служит для форми-
рования младшего байта адреса. Данный режим
адресации хорошо подходит для обращения к
устройствам ввода-вывода, поскольку очень
вероятно, что адреса таких устройств будут рас-
положены близко друг к другу, как в нашем ком-
пьютере из дискретных компонентов.
При реализации описанного режима 16-раз-
рядный адрес внешней памяти или устройства
ввода-вывода определяется не содержимым
3 Буква X в мнемонике команды означает external —
внешняя (операция).
Адрес определяется посредством
регистра DPTR
Данный способ иллюстрирует листинг 21S.1.
Листинг 21S.1. Работа с АЦП и ЦАП через
регистр DPTR
STARTUP: MOV DPTR, #8003h ; Указатель на АЦП
PICKUP: MOVX A, @DPTR ; Считываем АЦП (первый
; проход, полученные данные недействительны)
MOVX @DPTR, A ; Запускаем АЦП для следующего
; прохода (АЦП будет выполнять преобразование, пока
; программа занята выполнением следующих пяти
; линий кода)
DEC DPL ; Указатель на ЦАП (просто
; декрементируем младший байт указателя данных
; декрементирование всего 16-разрядного значения
регистра DPTR не разрешается)
MOVX @DPTR, A; Отправляем выборку на ЦАП
INC DPTR; Восстанавливаем значение регистра DPTR
SJMP PICKUP
904
21S. Дополнительный материал: режимы адресации микроконтроллера 8051
Адрес определяется посредством
базового (старший байт) и индексного
(младший байт) регистров
Данный способ иллюстрирует листинг 21S.2.
Листинг 21S.2. Работа с АЦП и ЦАП через два
регистра
STARTUP: MOV P2,#80h ; Определяем старший байт
; адреса в качестве базового адреса ввода-вывода
MOV R0, #3h ; Определяем 8-разрядный индексный
; регистр как указатель на АЦП
MOV R1 ,#2п ; Определяем второй индексный
; регистр как указатель на ЦАП
TFR: MOVX A, @R0 ; Считываем АЦП (данные первого
; прохода недействительные, всех остальных
; проходов — действительные)
MOVX @R0,A ; Запускаем АЦП для следующего прохода
MOVX @R1, A ; Отправляем выборку на ЦАП
SJMP TFR ; Повторяем весь процесс
Код с использованием регистра DPTR выглядит
более компактным, но он исполняется медлен-
нее, чем второй вариант кода. Это объясняется
необходимостью выполнять дополнительные
операции INC и DEC. Но эта небольшая разни-
ца в скорости может не играть большой роли.
Более важным моментом в пользу применения
метода с двумя регистрами является то, что он
не занимает регистр DPTR, который можно за-
действовать для других операций.
Аппаратные особенности, позволяющие
использовать порт Р2 для определения
старшего байта адреса
На первый взгляд может показаться невозмож-
ным управлять портом Р2, определяя старший
байт, не влияя при этом на работу регистра
DPTR при обмене данными. Но данная схема
возможна благодаря переключателю (мульти-
плексору 2:1), который выбирает источник для
восьми старших адресных линий. Ббльшую
часть времени данный переключатель находит-
ся в положении для работы с регистром DPTR.
Но при реализации метода с двумя регистрами
мультиплексор конфигурируется для использо-
вания выхода защелки порта Р2.
На рис. 21S.2 изображена принципиальная схе-
ма данного переключателя.
Примечание
Можно было бы сказать, что наличие такого пере-
ключателя является просто обязательным, чтобы
такая операция была возможной; но, увидев его
собственными глазами на рисунке, вы убеждаетесь
в работоспособности данного подхода. Не так ли?
21S.1.5. Прямая и косвенная
адресация
Вполне может быть, что вы уже хорошо пони-
маете разницу между двумя рассмотренными
Линии
адреса
А8-А15
Управление
адресом
Задержка
= 2Т сигнала
тактирования
U
Внутренняя
шина данных
Переключатель
Отключение
питания
Разрешение
чтения
Чтение защелки/входного
порта
Рис. 21 S3. Схема, позволяющая порту Р2 использовать или регистр DPTR, или свои триггеры для определения старшего бай-
та адреса. Данный рисунок является разрешенной адаптацией рис. 10-2 из руководства пользователя по высокоскоростному
микроконтроллеру «High Speed Microcontroller User's Guide» компании Dallas Semiconductor/Maxim Integrated Products
21S.L Знакомство с режимами адресации микроконтроллера 8051
905
режимами адресации. Но на всякий случай, на-
помним, в чем она заключается:
При прямой адресации в регистр загружается
значение, указанное в команде. Например, ко-
манда MOV DPTR, #8000h загружает значение
8000h в регистр DPTR.
♦ А при косвенной адресации содержимое ре-
гистра DPTR указывает на ячейку (содержит
ее адрес), в которую нужно загрузить значе-
ние. Например, команда MOVX @DPTR, А за-
гружает содержимое аккумулятора в ячейку
памяти, адрес которой содержится в регистре
DPTR.
Косвенная адресация с использованием
выражения @DPTR
На рис. 21S.4 приводится графическая иллю-
страция принципа прямой и косвенной адре-
сации.
байт 16-разрядного адреса внешней памяти
или. устройства; при этом старший байт этого
адреса определяется содержимым порта (ре-
гистра) Р2. Но регистры R0 и R1 могут также
служить в качестве указателей на 8-разрядные
адреса внутренней RAM. В таком случае надоб-
ности в регистре Р2 не возникает. Такой менее
распространенный случай будет полезным для
освещения разницы между прямой и косвенной
адресацией.
Разница в данном случае такая же, как и при ис-
пользовании выражения @DPTR, пример кото-
рого был рассмотрен ранее. А именно:
♦ При прямой адресации в регистр загружает-
ся значение, указанное в команде. Например,
команда MOV RO, #34h4 загружает значение
34h в регистр R0.
♦ А при косвенной адресации содержимое ре-
гистра R0 указывает на ячейку (содержит ее
:DPTR,#8000h
8051
тот адрес также
называется нулевым
адресом внутренней
памяти данных RAM
MOVX ©DPTR, A
8051
з декодера адрес
да-вывода
Прямая адресация
Косвенная адресация
Рис. 21S.4. Пример прямой и косвенной адресации: загрузка командой MOVX @DPTR значения во внешнюю память или
устройство
MOV RO, #034h
RO, #0F9h
(Внутренняя память)
Косвенная адресация
от адрес также
называется нулевым
адресом внутренней
памяти данных RAM
8051
Непосредственная)
дня/"
Регистр R0 указь5ает)у
(содержит) на адр
34Н внутренней^
[Ж]
33
32
31
30
RAM
F9h
Прямая адресация Косвенная адресация
Рис. 21S.5. Косвенная адресация: 8-разрядный регистр указывает на адрес внутренней памяти RAM
Косвенная адресация с использованием
внутренней RAM
Мы знаем, что регистры R0 и R1 можно ис-
пользовать в качестве указателей на младший
4 Для значения 034h ведущий ноль не требуется. Но для
значений, первой цифрой которых является буква, он не-
обходим. Например, 0F9h. Это объясняется необходимо-
стью не допустить, чтобы ассемблер принял начинающее-
ся с буквы значение за строку, а не за цифровое значение.
906
275. Дополнительный материал: режимы адресации микроконтроллера 8051
адрес), в которую нужно загрузить значение.
Например, команда MOV @R0, #0F9h загру-
жает значение #0F9h в ячейку памяти, адрес
которой содержится в регистре R0.
В первом случае в регистр R0 загружается зна-
чение 34h, а во втором — значение F9h загру-
жается в ячейку памяти, адрес которой (34h)
содержится в регистре R0. Этот принцип иллю-
стрируется на рис. 21S.5.
Косвенная индексная адресация
Вместо того чтобы перемещать указатель, ин-
крементируя или декрементируя его, иногда
бывает удобнее использовать значение реги-
стра для определения элемента таблицы, кото-
рый нужно считать. Такая адресация называ-
ется индексной. Суть ее заключается в добавле-
нии значения индекса к базовому адресу, чтобы
получить исполнительный адрес, по которому
выполнять чтение. Некоторые процессоры
поддерживают большие наборы таких опера-
ций. Например, старая 8-разрядная «рабочая
лошадка» НС11 компании Motorola, который
когда-то конкурировал с микроконтроллером
8051. Сам же микроконтроллер 8051 знает
только два способа такой адресации: MOVC А,
@А+РС или MOVC A, @A+DPTR.
Эти команды:
♦ хранят значения индекса в регистре А (акку-
муляторе);
♦ используют в качестве базового адреса:
• регистр DPTR или
• значение программного счетчика (просто
адрес программы после исполнения дан-
ной индексной операции).
В листинге 21S.3 приводится пример исполь-
зования программного счетчика в качестве
базового адреса. (Достоинством данного под-
хода является то, что он не занимает регистр
DPTR, оставляя его свободным для других за-
дач.) В приведенном фрагменте кода введенное
с цифровой клавиатуры 4-разрядное5 значение
служит в качестве индекса для небольшой та-
блицы, в которой определяется маска для нало-
жения на значение, предоставляемое АЦП6.
5 Старшие 4 бита маскируются, чтобы учитывалось толь-
ко последнее введенное значение.
6 Данный код является фрагментом демонстрационной
Листинг 21S.3. Пример использования про-
граммного счетчика в качестве базового адреса
MOVX A, @DPTR ; Считываем значение с цифровой
;клавиатуры
ANL A, #OFh ; Оставляем из него только младший
;полубайт
MOVC А, @А+РС ; Который используем в качестве
; индекса к таблице значений масок
RET
TABLE: DB 80H; Таблица значений масок:
; Введенное с клавиатуры значение 1
; выбирает этот элемент
; (DB означает define byte — определить байт)
DB OCOh ; Введенное с клавиатуры значение 2
; выбирает этот элемент (и т. д.)
; (Ввод с клавиатуры значения 0
; не разрешается)
DBOEOh
DB OFOh
DB0F8h
DBOFCh
DBOFEh
DBOFFh
Обратите внимание на тот момент, что данная
таблица должна находиться в программе сразу
же после команды, не допуская никаких про-
межуточных команд (за исключением команды
возврата RET).
21 S.I .6. Примеры операций
ввода-вывода через внешние шины
и внутренние порты
Примеры с использованием внешних шин
Большинство операций ввода-вывода, которые
мы будем осуществлять на нашем компьюте-
ре из дискретных компонентов, используют
внешние шины. Далее приводится пример, в
котором код считывает байт из порта Р0 и за-
писывает его в этот же порт:
GETIT: MOVX A, @DPTR ; Считываем значение
; с цифровой клавиатуры
MOVX @DPTR, A ; Отображаем его на дисплее
SJMP GETIT ; Повторяем до бесконечности
программы, которую мы рассматривали в разделе 14N.1.2
при наблюдении влияния варьирования количества битов
в цифровой выборке.
21S.I Знакомство с режимами адресации микроконтроллера 8051
907
Конечно же, чтобы этот код работал должным
образом, необходимо выполнить предвари-
тельную подготовку, загрузив в регистр DPTR
адрес цифровой клавиатуры, который также
является и адресом дисплея. Но вы уже знаете,
как это делать.
Примеры с использованием внутренних
портов
Эту же задачу можно выполнить, используя
внутренние порты микроконтроллера 8051.
Для этого цифровая клавиатура подключает-
ся к порту Р1 (для ввода), а дисплей — к порту
РЗ (для вывода). Код при такой конфигурации
будет более компактный, чем код для работы
с внешними шинами, потому что значение не
нужно пропускать через аккумулятор, а также
не нужен регистр DPTR. Далее приводится со-
ответствующий пример, который повторяет
пример из раздела 21S.1.2, с тем исключением,
что в нем используются порты, доступные для
микроконтроллера 8051 производства компа-
нии Dallas Semiconductor, а не для совместимо-
го микроконтроллера C8051F410 производства
компании Silicon Laboratories.
GETIT: MOV РЗ, Р1 ; Считываем значение с цифровой
; клавиатуры и отображаем его на дисплее
SJMP GETIT; Повторяем до бесконечности
Но это может быть не самый лучший подход
к выполнению этой задачи, потому что он за-
нимает половину из 32 линий ввода-вывода
микроконтроллера 8051. Внутренние порты
более эффективны для операций с битами, а не
с байтами.
21S.17. Примеры битовых операций
Примеры битовых операций
с использованием внешних шин
Подход с внешней шиной более трудоемок, но
он позволяет видеть, какое аппаратное обеспе-
чение задействуется для выполнения операции;
а подход с внутренними портами микрокон-
троллера проще, но он скрывает от разработ-
чика, какие триггеры и драйверы выполняют
операцию. Поэтому начнем с более явного ме-
тода с использованием внешней шины. Наша
задача — управлять светодиодом одной вы-
ходной линией порта 1 (на внешней шине) и
определять входной сигнал на линии этого же
порта. При наличии сигнала высокого уровня
выполняется переключение состояния свето-
диода; при низком уровне входного сигнала со-
стояние светодиода не меняется.
Чтобы управлять светодиодом, нам нужно
оснастить триггером выходную линию порта.
Без наличия такого триггера компьютер сможет
сохранять выходной уровень только в течение
очень короткого времени, пока длится выход-
ной импульс OUT1*. А триггер поддерживает
постоянным уровень сигнала управления све-
тодиодом. Чтобы получить и протестировать
входной сигнал, компьютеру требуется буфер
с трехстабильным выходом между источником
сигнала и линией шины данных, на которую он
подается. На рис. 21S.6 изображена схема, тре-
буемая для решения этой задачи.
Переключение
Без изменений J_ у
Возможно, следует )
оснастить защитой
от дребезга
Рис. 21S.6. Принципиальная схема для решения задачи про-
верки состояния линии внешней шины данных и управления
светодиодом
Может быть, вы задаетесь вопросом, если мы
хотим управлять светодиодом посредством
переключателя, то почему бы не делать это на-
прямую, подключив переключатель к свето-
диоду. Что ж, вопрос справедливый. На это мы
можем ответить, что наш пример — самый про-
стой способ демонстрации ввода-вывода. В ре-
альной ситуации компьютер бы реагировал на
сигнал с переключателя некоторым более инте-
ресным способом, чем простой передачей его
уровня на светодиод.
По внешней шине требуется пересылать
весь байт
По внешней шине микроконтроллер 8051 мо-
жет пересылать данные только разрядностью
в один байт. Это, конечно же, разочаровываю-
щее обстоятельство. Похоже, что нам придется
впустую передавать остальные 7 битов.
Но в действительности необходимость пере-
давать целые байты не означает, что лишние
для данной задачи биты тратятся впустую. Все
908
21S. Дополнительный материал: режимы адресации микроконтроллера 8051
можно так организовать, что не пропадет ни
один бит. Хотя мы берем целый байт, но мо-
жем сделать наш ответ зависимым от значения
лишь одного бита в этом байте. Подобным об-
разом, хотя мы отправляем целый байт, можем
позаботиться о том, чтобы не изменять семь
неиспользуемых битов, в этом случае они мо-
гут потребоваться для других целей. В листин-
ге 21S.4 приводится код, способный делать это
на схеме, показанной на рис. 21S.6.
Листинг 21S.4. Пример управления
светодиодом через передачу бита
DOBITS: MOV DPTR, #8001 h ; Указатель на светодиод
; и входящий бит
CLR АСС.0 ; Для начала задаем выключенное
; состояние светодиода
SEND: MOVX @DPTR, A ; Отправляем уровень
; бита на драйвер светодиода
TEST: MOVX A,@DPTR ; Принимаем вводимый бит
; (плюс семь неиспользуемых битов)
JNB ACC.2JEST ; Тестируем интересующий нас бит.
; Если низкий уровень, не меняем состояние светодиода
CPL АСС.0 ; но если высокий, переключаем бит
; состояния светодиода:
; задаем уровень бита для подачи
; на драйвер светодиода
SJMP SEND
Неплохо, не так ли? Но мы вскоре увидим, что
эту же задачу еще легче выполнить, используя
выводы встроенных портов микроконтроллера
8051.
21 S.1.8. Битовые операции через
выводы встроенных портов
микроконтроллера 8051
Аппаратное обеспечение практически не
требуется
Для использования выводов встроенных пор-
тов микроконтроллера 8051 не требуется ни-
какого дополнительного оборудования: просто
подключаем переключатель входного сигнала и
светодиод к двум выводам порта, как показано
на рис. 12S.7.
Следует обратить внимание на одну особен-
ность в новом методе управления светодиодом.
В частности, порт 3 микроконтроллера 8051
Особый способ
подключения светодиода
РЗ.О
I+O
Переключение
JL Без изменений
Рис. 21S.7. Схема для проверки состояния входного бита и
управления светодиодом через выводы портов микрокон-
троллера 8051
может поставлять (в режиме источника) очень
малый ток (50 мкА), но может потреблять
(в режиме потребителя) намного больший ток:
1,6 мА, что тоже не очень-то и много. Порты
0 и 2 могут потреблять вдвое больший ток, но
они нам недоступны, поскольку задействованы
для работы с внешними шинами. Поэтому для
управления светодиодом нам пришлось скон-
фигурировать вывод порта для работы в ре-
жиме потребителя тока. Кроме того, нам также
пришлось увеличить сопротивление резистора,
поскольку ток /вых_низ микроконтроллера 8051
намного меньше, чем ток, доступный на венти-
ле микросхемы НС (или высокого уровня в ре-
жиме источника или низкого уровня в режиме
потребителя).
Замечание
Такой асимметричный ток сигнала управления —
сильный в режиме потребления и слабый в ре-
жиме источника — характерен для более старых
устройств ТТЛ и n-МОП. Хотя в микроконтроллере
8051 компании Dallas Semiconductor применяется
МОП-структура, ей присуща асимметрия токов.
Чтобы эмулировать оригинальный микрокон-
троллер 8051, микроконтроллер C8051F410
компании Silicon Laboratories поддерживает
такой асимметричный режим тока выводов, но
при необходимости может также предоставлять
почти симметричный режим тока выводов. Эта
опция называется двухтактным режимом, и
ее можно задать для любого требуемого бита
управления выходным устройством.
Использование выводов встроенных
портов упрощает код
Как и в разделе 21S.1.7, при работе с внутренни-
ми портами код для проверки состояния одного
бита и переключения состояния другого бита
проще (листинг 21S.5), чем код при использо-
вании внешних шин.
275.1. Знакомство с режимами адресации микроконтроллера 8051
909
Рабочая полаять RAM, используемая как стек
(в данном случае содержит адрес 0064И)
Регистр АСС или А
также имеет адрес БОН
Внутренний порт Р0
воьШ
Специальные
регистры Fn
. (Регистры АСС, В,
' РО-РЗ, DPTR, SP, Serial,
таймеры, флаги,
прерывания и прочие
регистры управления)
FFh
128 байтов I
(некоторые \
можно )
адресовать/
побито) /
Ч
80h
128 байтов
Прямо адресуемая память RAM Косвенно адресуемая память RAM
Рис. 21S.8. Порт Р0 и первая ячейка стека имеют одинаковый адрес
Листинг 21S.5. Пример управления
светодиодом с помощью внутренних портов
SETB P3.0 ; Начинаем с высокого уровня:
; светодиод выключен
TEST: JNB P3.1 JEST ; Пока входной бит низкого уровня,
; ждем здесь
; Когда входной бит переключается на высокий,
; идем дальше:
FLIPIT: CPLP3.0 ; Переключаем состояние только
; младшего бита (бит 0) порта
SJMPTEST
Этот код также исполняется быстрее, чем вер-
сия кода для внешних шин, поскольку ему тре-
буется намного меньшее число доступов к шине
как при выборке команд, так и при их исполне-
нии. Хотя в данном случае эта разница не игра-
ет большой роли.
21 S.1.9. Вроде бы неопределенные
случаи определяются контекстом
Бит или байт?
При компилировании следующего кода:
SOFTFLAG EQU 0 ; Директива ассемблера, а не команда
микроконтроллера 8051
CLR SOFTFLAG
ассемблер заменит идентификатор SOFTFLAG
значением 0. Но как может микроконтроллер
8051 знать, что означает этот ноль: то ли ну-
левой байт внутренней RAM (который так-
же является регистром R0), то ли нулевой бит
(который является первой побитово-адресуе-
мой ячейкой и находится в байте 20h)?
Ответ на этот вопрос до скучного простой: по-
скольку общей команды CLR для обнуления
байтов не существует (есть только команда CLR
А), для микроконтроллера этот случай не пред-
ставляет никакой неопределенности — это опе-
рация обнуления бита, поэтому она обнуляет
нулевой бит.
21 S.1.10. Указание одного имени
(или адреса) для нескольких ячеек
памяти или устройств
Внутренний порт Р0 имеет адрес 80h. Но это
также первый байт обычного стека, т. е. рабо-
чей области памяти RAM на микроконтроллере
8051/27. Возможен ли здесь конфликт? Собьем
ли мы микроконтроллер 8051 с толку, если раз-
местим стек по адресу 80h?
Нет, не собьем. Эти две ячейки, несмотря на
одинаковый адрес 80h, являются двумя разны-
ми ячейками, которые отличаются друг от дру-
га по методу доступа к ним. Если используется
косвенный режим адресации (как при работе
со стеком), то доступ осуществляется к рабо-
чей памяти RAM; в случае же прямого режима
адресации доступ происходит к порту Р0.
Мы добавили на рис. 21S.8 одну подроб-
ность, которую ранее упомянули мимоходом.
7 В данном случае называть микроконтроллер как 8051
не совсем правильно, поскольку только микроконтроллер
8052 (а также имитирующие его версии микроконтроллера
производства компании Dallas Semiconductor) предостав-
ляет память RAM по этому адресу. А внутренняя память
микроконтроллера 8051 составляла только половину это-
го объема и поэтому заканчивалась точно по адресу 80h.
910
21S. Дополнительный материал: режимы адресации микроконтроллера 8051
В частности, регистр А (который также называ-
ется АСС или аккумулятор) находится по опре-
деленному адресу, по которому к нему можно
обращаться (если вам нравится такой стиль
программирования).
Код листинга 21S.6 должен напомнить вам о
разнице между режимами прямой и косвенной
адресации. Каждая из этих двух строчек кода
обращается к ячейке памяти по адресу 80h. Но,
несмотря на то, что две ячейки памяти имеют
один адрес, это две отдельные ячейки.
Листинг 21S.6. Различие прямой и косвенной
адресации
MOV P0, #12h ; (Прямая адресация): записываем байт
; во внутренний порт Р0 (по адресу 0080h)
ACALL DELAY ; (Косвенная адресация): автоматически
; сохраняем адреса возврата на стеке, который
; начинался по адресу 80h (в нашей программе
; на лабораторном занятии 21L).
; (адрес возврата был 064h, как можно видеть
;на рис. 21S.8)
Таким образом, адрес 80h внутренней памяти
RAM обозначает две разные ячейки памяти,
разница между которыми определяется режи-
мом доступа к ней. В частности, доступ к порту
Р2 осуществляется в режиме прямой адресации,
а к ячейке рабочей памяти RAM (используемой
в качестве стека в наших приложениях) — в ре-
жиме косвенной адресации.
8051 в режиме гарвардской архитектуры, где
адрес 80h определяет две разные ячейки внеш-
ней памяти: одну в памяти для кода програм-
мы, а другую в памяти для данных. Теперь, ког-
да мы разложили по полочкам все о нескольких
ячейках памяти с одним адресом, этот вопрос
не должен сбивать вас с толку.
21S.1.11. Одна ячейка,
два идентификатора
Иногда вместо двух или нескольких разных
ячеек памяти, идентифицируемых одним адре-
сом (как, например, адрес 80h, рассматривае-
мый в разделе 21S.1.10), микроконтроллер 8051
может разрешить обращаться к одной ячейке
памяти, используя разные идентификаторы
или разные способы.
Обращение одним из двух способов
К области RAM, называемой рабочей памятью,
можно обращаться с помощью как прямой, так
и косвенной адресации. Таким образом, гипо-
тетически значение ABh, находящееся в ячей-
ке с адресом 34h, можно получить, используя
любой из этих режимов адресации. Возможно,
что это не настолько полезное знание, хотя
оно может уберечь вас от ошибочной идеи,
что данный блок памяти можно одновременно
задействовать двумя разными способами9.
Еще два возможных значения адреса 80h
Кроме рассмотренных ранее ячеек памяти с
адресом 80h существует еще одна, третья, ячей-
ка памяти с этим адресом. Это ячейка внеш-
ней8 памяти RAM в нашем микрокомпьютере
из дискретных компонентов. Если вы еще не
сбиты с толку, тогда мы предпримем еще одну
попытку в этом направлении. В частности, об-
радуем вас новостью о возможности существо-
вания еще одной ячейки памяти с адресом 80h.
Такая ячейка возможна в микроконтроллере
8 Эта память, которую мы называем «внешней», иногда
еще называется памятью MOVX RAM, что, возможно, яв-
ляется лучшим названием, поскольку некоторые версии
микроконтроллера 8051 содержат внутреннюю память
MOVX RAM, доступ к которой осуществляется с помощью
команд MOVX. Например, микроконтроллер C8051F410
компании Silicon Laboratories применяет такие операции.
Более подробную информацию по этому вопросу см. в раз-
деле 24L.2.2 далее в этой книге.
Два способа описания местонахождения
бит
К нулевому биту (первый бит в блоке 128 ин-
дивидуально адресуемых битов (рис. 21S.9))
можно так и обращаться, т. е. как к нулевому
биту. Например, команда JNB 0 выполняет про-
верку нулевого бита.
Нулевой бит находится в байте с адресом 20h.
Таким образом, к этому биту можно обращать-
ся как к нулевому биту байта 20h: JNB 20h.0.
Такой способ обращения к нему не дает ника-
ких преимуществ, но будет приятно знать, что
ассемблер понимает ситуацию, отображенную
в карте распределения памяти — что нулевой
9 Вспомните, что это различие частично объясняет су-
ществование двух идентификаторов для регистра аккуму-
лятора: А и АСС. Более подробную информацию по этому
вопросу см. в разделе 20L.3.8.
2/5.7. Знакомство с режимами адресации микроконтроллера 8051
911
Рабочая память
Адрес 34h
07h
80 байтов
адресуемая побитно? 16 байтов:
(0...7F) Ь 128 бит
Банк регистров 3
Банк регистров 2
Банк регистров 1
Банк регистров 0
4-8 байта
Копия
(дубликат)
Прямая адресация
mov A, R2
INCA
setb P0.3
Рис. 21S.9. Область памяти RAM с двумя разными идентификаторами
Косвенная адресация
mov A, @R0
бит байта 20h действительно также является и
нулевым битом сам по себе.
Два способа описания местонахождения
байтов
На рис. 21S.8 можно видеть, что регистр, ко-
торый мы обычно называем Р0 (внутренний
порт 0) имеет адрес 80h. К этому порту мож-
но было бы обращаться по данному адресу, но
обычно удобнее делать это через его функцио-
нальный идентификатор — Р0. Но далее мы
увидим, что иногда, чтобы избежать неопреде-
ленности, к этому порту необходимо обращать-
ся, указывая не его идентификатор, а его адрес.
21 S,1.12. Некоторые вещи,
которые запрещены, возможны,
если вежливо попросить
Обращение по внутреннему адресу
вместо идентификатора регистра
Казалось бы, операция обмена данными между
двумя внутренними регистрами должна быть
прямолинейной, например MOV R1, R2. Но такая
команда недопустима. Чтобы реализовать эту
операцию, нужно сначала выполнить команду
MOV A, R2, а затем команду MOV R1, А. Довольно
неуклюжий метод. Но обмен между двумя ре-
гистрами напрямую, минуя аккумулятор, воз-
можен, если к регистру-источнику обращаться
по его адресу, а не по идентификатору:
MOV R1,2; Такая команда допустима, хотя по адресу 2
находится регистр R2. Очень странно.
Это необычная ситуация, но не совсем из ряда
вон выходящая (и ассемблеру не под силу ис-
править ее10): хотя они и дают одинаковый
результат, эти две команды кодируются по-
разному в машинном коде. Иными словами, это
две разные операции. Пониманию ситуации
может способствовать сравнение двух разных
разрешенных команд, дающих одинаковых ре-
зультат, но с различными машинными кодами.
Хотя команды MOV R1, А и MOV R1, OEOh выпол-
няют одинаковую операцию копирования со-
держимого аккумулятора в регистр R1, это две
разные команды. Далее приводится выходной
фрагмент кода ассемблера, иллюстрирующий
этот момент:
F9 MOV R1, А ; Одинаковый результат в обоих случаях
А9Е0 MOV R1, ОЕОН; Но разные машинные коды
Похоже на то, что более компактный машин-
ный код для команды MOV R1, А отражает при-
вилегированную сущность регистра А.
Команду PUSHRO применить нельзя,
но команду PUSH 0 можно
Команда PUSH R0 не проходит по хорошей при-
чине: микроконтроллер 8051 имеет четыре
банка регистров общего назначения, каждый
из которых содержит семь регистров — с R0
по R7. Идентификатор регистра не содержит
никаких уточнений, какой именно из четырех
регистров R0 имеется в виду, а просто означает
10 Ассемблер может «решить», что реализовать запрещен-
ную команду MOV R1, R2 можно как разрешенную команду
MOV R1,2. Но это слишком по-панибратски для большин-
ства разработчиков: когда мы пишем код на ассемблере, то
ожидаем получить точно то, что указали, а не хитроумное
интерпретирование ассемблером нашего кода.
912
21S. Дополнительный материал: режимы адресации микроконтроллера 8051
текущий регистр R0. Какой текущий? Тот, кото-
рый определяется битами RSO и RS1 в регистре
(слове) состояния программы PSW (Program
Status Word). Для команд PUSH и POP не разре-
шается предположение, которое обычно дела-
ется, что подразумевается текущий банк реги-
стров. Таким образом,
PUSH R0 ; Не проходит, поскольку ассемблер
; считает ее неопределенной
PUSH 0 ; Проходит, поскольку 0 — это однознач-
; ный адрес самого первого из четырех регистров R0
Всю эту информацию может быть трудно запом-
нить, особенно с учетом того, что идентифика-
тор R0 считается однозначным, как, например,
в команде MOV A, R0. Правила, применяемые
ассемблером, были определены контекстом.
Очевидно, что команды PUSH и POP были отне-
сены к тем ситуациям, в которых программи-
сты вполне могут переключаться между банка-
ми регистров, как может ожидаться при реаги-
ровании на прерывание. А обычные команды
MOV не были отнесены к таким случаям11.
В завершение этой главы мы перечисляем не-
которые наиболее распространенные режимы
адресации, графически иллюстрируя их работу.
Если у вас не возникает никаких трудностей с
пониманием этих диаграмм, значит, вы начи-
наете осваиваться с несколько странной адре-
сацией, реализованной в микроконтроллере
8051.
8051
Прямая Прямая
адресация адресация
MOV PI, P2
Рис. 21S.10. Из одного регистра в другой (прямая-прямая)
Прямая Непосредственная
адресация адресация
MOV А, #012Н
8051
Шина
/Значение берется из\
\кода программы )
Рис. 21S.11. Непосредственная адресация: константа загру-
жается из самого кода программы
11 Возможно, что вам вдруг снова захотелось как-то обой-
тись без языка ассемблера. Не следует так переживать, по-
скольку в большинстве случаев он не такой заумный.
21S.2. Некоторые режимы
адресации с иллюстрацией
Прямую адресацию иллюстрирует рис. 21S.10.
Непосредственную адресацию иллюстрирует
рис. 21S.11.
Непосредственную 16-разрядную адресацию
иллюстрирует рис. 21S.12.
Внешнюю косвенную, прямую адресацию ил-
люстрирует рис. 21S.13. В данном случае в ка-
честве указателя используется 16-разрядый
регистр, чтобы иметь возможность доступа ко
всему адресному пространству.
Внешнюю косвенную адресацию с использова-
нием Rn (прямую) иллюстрирует рис. 21S.14.
В данном случае 16-разрядный указатель фор-
мируется из содержимого порта Р2 для старше-
го байта и содержимого регистра R0 или R1 для
младшего байта. Регистр DPTR не требуется.
Косвенную адресацию внутренней памяти ил-
люстрирует рис. 21S.15. В данном случае в ка-
честве указателя используется 8-разрядный
Прямая Непосредственная
адресация адресация
8051
Шина
MOV DPTR, #8000Н
(Значение берется из
\кода программы
Рис. 21S.12. Непосредственная адресация при загрузке 16-
разрядного регистра
Прямая Непосредственная
адресация адресация
MOVX ©DPTR, А
8051
Адресная
шина
Шина
данных
Рис. 21S.13. Косвенная адресация для обращения к
внешней памяти
Прямая Непосредственная
адресация адресация
MOVX @R1, A
Рис. 21S.14. Косвенная адресация внешней памяти; порт Р2
содержит старший байта адреса, а регистр Rn — младший
8051
Р2 R1
ЩЩ
1 12h I
Адресная
шина
Шина
данных
21S.2. Некоторые режимы адресации с иллюстрацией
913
/ь качестве указателя используется\
содержимое регистра Ro (должно
узагружаться заранее) )
Прямая Непосредственная
адресация адресация
MOV @R0, R2
Рис. 21S.15. Косвенная адресация внутренней памяти
Ro
1 h>>
Прямая Непосредственная
адресация адресация
MOVC А, @А + PC
Адресная
шина
Индекс.
Базовый адрес
к базовому адресу
Значение берется из
кода программы
Рис. 21S.16. Индексная адресация относительно базового
адреса, содержащегося в аккумуляторе (в других случаях ба-
зовый адрес берется из регистра DPTR)
регистр. Поскольку размер адресного про-
странства небольшой (256 байтов), то этого
достаточно.
Индексную адресацию иллюстрирует рис. 21S.16.
Сводная диаграмма адресного
пространства микроконтроллера 8051
На рис. 21S.17 наглядно показано распределе-
ние адресного пространства микроконтролле-
ра 8051.
80h
Специальные
регистры Fn
(Регистры АСС, В,
РО-РЗ, DPTR, SP, Serial,
таймеры, флаги,
прерывания и прочие
регистры управления)
FFh
До пол нр
1 о о ^ w 1/раоочая
lto сайтов ^
(некоторые
можно
адресовать
побитно)
80h
цельная
память
FFh
128 байтов
J
Рабочая память
ЗОИ
20h
18h
10h
08h
OOh
R7
7?
► 80 байтов
2F ?адресуемая побитно? 16 байтов:
M0...7F) S 128 бит
lFh
OFh TS:Zll^SZ^ M x 8 байта
07h
Банк регистров 1
Банк регистров 0
Копия
(дубликат)
24,4 кОм
Внутренняя
ROM
Внешняя
Если БА*
= земля
|ТТрямая адресация |
mov A, R2
INCA
setb P0.3
| Косвенная адресация!
mov A, @R0
«Код» (Строб чтения = PSEN*)
read-only «Данные»
(PSEN деактивирован)
read/write
Стробирует RD*, WR*
Рис. 21S.17. Адресное пространство микроконтроллера 8051
22N. Микропроцессоры III: операции с битами
Содержание
22N.1. Операции с битами 914
22N.1.1. Операции с битами с использованием внешних шин 914
22N.1.2. Битовые операции через встроенные порты микроконтроллера 8051 915
22N.1.3. Использование выводов встроенных портов упрощает код 918
22N.1.4. Эквивалентные битовые операции на языке С 919
22N.1.5. Аппаратный флаг: устройство ввода для одноразовой операции 919
22N.2. Условные переходы 919
22N.2.1. Команды условного перехода 920
22N.2.2. Применение масок для обработки больше одного бита 921
22N.2.3. Сравнение байтов с помощью команды CJNEE 924
22N.2.4. Аппаратное обеспечение реализации флага 925
Цель этой главы
В данной главе мы ставим перед собой цель — научить вас разбивать код программы на модули
(подпрограммы или функции). Также мы поэкспериментируем на нашем компьютере с операция-
ми ввода-вывода одного бита.
22N.1. Операции с битами
Микроконтроллер 8051 выглядит слабовато
при выполнении любых операций, требующих
высокой точности, т. е. при работе со значе-
ниями, определяемыми большим количеством
битов. Он ограничен байтовым размером сво-
их регистров и слов памяти. Этот маленький
контроллер намного лучше подходит для рабо-
ты с битами. В данной области он преуспевает.
Поэтому давайте полюбуемся на его работу
с задачами, которые ему больше под силу. Мы
начнем наши эксперименты по операциям с би-
тами с использования внешних шин, а затем
перейдем к работе со встроенными портами.
В последнем случае аппаратное оборудование
и код программы будут намного проще.
22N.1.1. Операции с битами
с использованием внешних шин
Подход с применением внешней шины бо-
лее трудоемок, но он позволяет видеть, какое
аппаратное обеспечение задействуется для
выполнения операции; а работа с внутренни-
ми портами микроконтроллера легче, но при
этом от разработчика скрыто, какие триггеры
и драйверы выполняют операцию. Поэтому
начнем с внешних шин. Нашей задачей будет
управлять светодиодом одной выходной ли-
нией порта 1 (на внешней шине) и определять
входной сигнал на линии этого же порта. При
наличии сигнала (бита) высокого уровня вы-
полняется переключение состояния светодио-
да; при низком уровне входного сигнала (бита)
состояние светодиода не меняется.
Чтобы управлять светодиодом, нам нужно
оснастить триггером выходную линию порта.
Без наличия такого триггера компьютер смо-
жет сохранять выходной уровень неизменным
только в течение очень короткого времени,
пока длится выходной импульс OUT1 * (что чуть
меньше, чем 100 не при сигнале тактирования
с частотой 11 МГц). А триггер поддерживает
постоянным уровень сигнала управления све-
тодиодом. Чтобы получить и протестировать
входной сигнал, компьютеру требуется буфер
с трехстабильным выходом между источником
22N.1. Операции с битами
915
сигнала и линией шины данных, на которую он
подается. На рис. 22N.1 изображена схема для
решения этой задачи.
Шина данных
+5
Переключение
Без изменений о
INI
8
60
D Q
OUT1
(возможно, следует оснастить
защитой от дребезга)
Рис. 22N.1. Принципиальная схема для проверки состояния
линии внешней шины данных и управления светодиодом
Листинг 22N.1 содержит код для работы с этой
схемой. Это не очень сложный код, но мы вско-
ре увидим, что аналогичную задачу легче ре-
шить, используя встроенный порт микрокон-
троллера 8051.
Листинг 22N.1. Проверка состояния линии
внешней шины данных и управление
светодиодом
DOBITS: MOV DPTR, #8001 h; Указатель на бит
; управления светодиодом и входящий бит
CLR АСС.О ; Для начала, задаем выключенное
; состояние светодиода
SEND: MOVX @DPTR, A ; Отправляем уровень бита
; на драйвер светодиода
PUSH ACC ; Сохраняем состояние бита,
; чтобы можно было переключить его позже
TEST: MOVX A,@DPTR ; Принимаем вводимый бит
; (плюс семь неиспользуемых битов)
JNB ACC.2JEST ; Тестируем интересующий нас бит
; Если низкий уровень, не меняем
; состояние светодиода
; (Обратите внимание на то, что для данной
; битовой операции
; регистр А нужно называть АСС)
POP ACC ; Снимаем со стека значение аккумулятора,
; которое содержит интересующий нас бит
CPL АСС.О ; Поскольку имеем высокий входной
; уровень, переключаем бит состояния
; светодиода: задаем уровень бита для подачи
; на драйвер светодиода
SJMPSEND
Задействуют ли эти битовые операции весь
байт порта? Ответ на этот вопрос не так прост.
Было бы неприятно, если бы ответом было
однозначное «да», означая, что для обработки
одного бита нужны все 8 битов значения пор-
та (или в данном случае 16 битов входного и
выходного портов для обработки двух битов,
одного входящего и одного выходящего). Но
все не так плохо.
Да, нам нужно вводить и отправлять целый
байт, поскольку процессор не может выполнять
обмен значениями, меньшими чем байт1. Но
это не означает, что незадействованные 7 битов
каждого порта (входного и выходного) пропа-
дают даром. Эти биты можно использовать для
других целей. Команда JNB проверяет только
один указанный бит, а команда дополнения CPL
оперирует только с одним битом.
22N.1.2. Битовые операции
через встроенные порты
микроконтроллера 8051
Внешняя шина в сравнении
со встроенными портами
На лабораторных занятиях с компьютером из
дискретных компонентов нам часто приходит-
ся выполнять операции ввода-вывода через
внешние шины микроконтроллера 8051. Такой
подход вынуждает нас учитывать аспекты, ко-
торые скрыты от нас при работе со встроенны-
ми портами микроконтроллера. В частности,
для операций ввода всегда необходим буфер
с трехстабильными выводами между любым
источником сигнала и шиной; а для операций
вывода обычно требуется триггер или регистр
между шиной и периферийным устройством,
которым нужно управлять. Конечно же, эти
правила относятся и к встроенным портам, но
разработчики микросхемы микроконтроллера
выполнили эту работу за нас. Таким образом,
мы рекомендуем вам использовать внешние
порты в некотором смысле потому, что с ними
интереснее работать.
Внешние шины обладают лишь одним потен-
циальным преимуществом над встроенными
портами: они позволяют подключить к
1 Единственным и частичным исключением из этого
утверждения являются внутренние операции копирова-
ния бита во флаг переноса или из него. Более подробно см.
раздел 22N.1.3.
916
22N. Микропроцессоры III: операции с битами
контроллеру почти неограниченное число
устройств. Но во всех других отношениях
встроенные порты предпочтительнее и являют-
ся обычным способом для сопряжения микро-
контроллера с внешним миром.
Аппаратное обеспечение практически
не требуется
Традиционный 8051 обеспечивает намного
больший ток в режиме потребления. При
битовых операциях через встроенные порты
микроконтроллера 8051 не требуется практиче-
ски никакого дополнительного оборудования:
просто подключаем переключатель входного
сигнала к одному выводу порта, а светодиод —
к другому. Соответствующая схема показана на
рис. 22N.2.
Примечание
Особым способ
управления
светодиодом
Переключение
Без изменений
Рис. 22N.2. Схема для проверки состояния входного бита
и управления светодиодом через выводы портов микро-
контроллера 8051
В этой схеме стоит обратить внимание на одну
особенность в новом методе управления свето-
диодом.
В частности, порт 3 микроконтроллера 8051
может поставлять (в режиме источника) очень
малый ток (50 мкА), но может потреблять
(в режиме потребления) намного больший ток:
1,6 мА, хотя это тоже не очень-то и много.
Поэтому для управления светодиодом нам
пришлось сконфигурировать вывод порта
для работы в режиме потребления. Кроме
того, нам также пришлось немного увеличить
сопротивление резистора, поскольку ток 1ВЫХ_
низ микроконтроллера 8051 намного меньше,
чем ток, доступный на вентиле микросхемы
серии НС (или высокого уровня в режиме ис-
точника, или низкого уровня в режиме потре-
бителя).
Такой асимметричный ток сигнала управления —
сильный в режиме потребления и слабый в ре-
жиме источника — характерен для более старых
устройств ТТЛ и п-МОП. Хотя в микроконтроллере
8051 компании Dallas Semiconductor применяется
МОП-структура, его разработчики решили сле-
довать данной традиции. Вопрос использования
ТТЛ-уровней МОП-структурами рассматривается
более подробно в главе 16N.
Опция двухтактного вывода в микрокон-
троллере C80S1F410. Разработчики модер-
низированных версий микроконтроллера 8051
не могут устоять перед искушением исправить
раздражающие недостатки исходного проек-
та. В частности, разработчики микроконтрол-
лера C8051F410 компании Silicon Laboratories
сочли одним из таких недостатков выходные
ТТЛ-уровни. Они устранили этот недостаток,
добавив опцию выбора симметричных выход-
ных уровней КМОП-структуры для каждого
отдельного вывода2. Для обеспечения такой
симметричности токов применяется метод
двухтактного выхода. (Мы употребили термин
«двухтактный выход» в основном для эмит-
терных повторителей, но этот термин также
применим и к выходному КМОП-ключу.) На
рис. 22N.3 изображена схема обеспечения тра-
диционных токов вывода микроконтроллера
8051, двухтактного выхода микроконтроллера
C8051F410, а также аналогового канала ввода-
вывода (аналогового ключа).
Данный рисунок поможет вам понять некото-
рые подробности настроек портов микрокон-
троллера C8051F410. В частности:
Небольшая подтяжка по питанию (weak
pull-up) — это МОП-транзистор в качестве по-
вышающего (подтягивающего) резистора, соз-
дающий импеданс величиной приблизительно
120 кОм.
Предварительные условия для исполь-
зования порта для цифрового ввода или
2 Токовые возможности двухтактного выхода остаются
несколько асимметричными: лучше в режиме потребле-
ния, чем в режиме источника, но без такой радикальной
разницы, как традиционные токи ТТЛ или стандартно-
го микроконтроллера 8051. Выдаваемый ток составляет
3 мА, а потребляемый — 8,5 мА при сравнимых падениях
напряжения (около 0,5 В между выходом и источником —
или «землей» или ^.вых^.) См. табл. 18.1 на с. 163 спра-
вочного листка 1.01 для микроконтроллера C8051F410.
22N.1. Операции с битами
917
Небольшая подтяжка
по питанию
Двухтактный режим
Разрешение выходного порт*
Разрешение порта с
матричного переключателя;
требуется для ЛЮБОГО типа
ввода-вывода
Двухтактный режим (КМОП)
(подтяжка по питанию через р-МОТТ)
Выходной порт]
Выбор аналогового режима
Аналоговый вход ~1 ~~
Входной порт
(Небольшая подтяжка)
Вывод
порта
Обычная небольшая
подтяжка по питанию
микроконтроллера 8051
Аналоговый интегральный прерыватель (для работы
с аналоговыми сигналами уровень выходного
сигнала на выводе должен быть высоким; разрешение
аналогового режима отключает даже небольшую
подтяжку по питанию)
Рис. 22N.3. Подробности устройства порта микроконтроллера C8051F410: традиционный ввод-вывод микроконтроллера
8051, двухтактный режим, аналоговый ввод-вывод
аналогового ввода-вывода. Для того чтобы
настроить вывод порта для цифрового ввода
или аналогового ввода-вывода, необходимо
отключить понижающий транзистор с низким
импедансом.
По этой причине на всех выводах (контак-
тах) ввода-вывода по умолчанию после сброса
микроконтроллера устанавливается высокий
уровень (с обычной небольшой подтяжкой по
питанию).
Кроме того, прежде чем использовать вывод
для подачи входного цифрового сигнала или
в аналоговом режиме, мы принимаем меры
предосторожности, записывая в него высокий
уровень. Небольшая подтяжка по питанию,
присутствующая на выводе одновременно с по-
даваемым на него высоким уровнем, достаточ-
но слабая, чтобы не влиять на цифровой ввод,
и полностью отключается для аналоговых опе-
раций3.
Код для разрешения аналогового режима при-
веден в листинге 22N.2 (в данном случае раз-
решает использование АЦП на выводе РО.О и
ЦАП на выводе Р0.1)4.
3 При записи высокого уровня слабая подтяжка по пита-
нию на короткое время делается сильной, чтобы ускорить
заряд паразитной емкости. Это стандартная характеристи-
ка микроконтроллера 8051. Но после этого короткого пе-
реходного заряда подтяжка по питанию возвращается об-
ратно к небольшому значению. А когда вывод переводится
в аналоговый режим, отключается даже эта подтяжка по
питанию. См. с. 151 справочного листка по микроконтрол-
леру C8051F410.
4 Мы не даем здесь другую инициализацию, которую вам
нужно будет выполнить на лабораторном занятии: для
опорного напряжения для АЦП на выводе Р1.2.
Листинг 22N.2. Пример кода для разрешения
аналогового режима
PORT_SETUP: setb РО.О ; Обеспечиваем высокий
; выходной уровень защелки (здесь для АЦП)
setb РОЛ ; а здесь для ЦАП
mov pomdin, #OFCh ; Устанавливаем низкий
; уровень битов управления DAC0 и АЦП (dO и d1),
; для работы в аналоговом режиме
; (это не уровень вывода)
mov poskip, #03h ; Даем указание матричному
; переключателю пропустить бит АЦП
; (младший бит) и бит DAC0 (бит 1)
ret
Комментарий к команде загрузки регистра
POSKIP ссылается на матричный переключатель,
который используется микроконтроллером
C8051F410 для присвоения выводам определен-
ных функций. Данный матричный переключа-
тель необходим во всех лабораторных занятиях
по микрокомпьютеру на автономном микрокон-
троллере C8051F410 по той причине, что микро-
контроллер C8051F410 предоставляет большее
количество сигналов, чем число доступных вы-
водов микросхемы. Поэтому выводы можно
присваивать тем функциям, которые вызывают-
ся конкретной программой. Некоторые из этих
функций присваиваются выводам по умолча-
нию, и в данном случае нужно заменить эти при-
своения теми, которые требуются нам5.
5 Функции, присваиваемые выводам по умолчанию,
определены на рис. 18.4 справочного листка для микро-
контроллера C8051F410. Но пользователям иногда тре-
буется отклонить автоматическое присвоение функций
некоторым выводам, используя регистр SKIP (пропустить).
Запись в этот регистр значения «1» для определенного вы-
вода дает указание микроконтроллеру C8051F410 пропу-
стить этот вывод при выполнении стандартной процедуры
присвоения функций выводам.
918
22N. Микропроцессоры III: операции с битами
Разрешение матричного переключателя
(crossbar enable). Как мы видели во всех про-
граммах для малого компьютера, матричный
переключатель должен быть включен: он на-
правляет сигналы на выводы, но по странной
причине выключен по умолчанию, как отмеча-
ется в главе 21N.
Запись значения «1» в бит 6 регистра XBR1 (сиг-
нал, называющийся XBARE) включает матрич-
ный переключатель:
; Разрешаем матричный переключатель портов
; входа-выхода
MOV XBR1, #40h ; Разрешаем матричный
; переключатель
22N.13. Использование выводов
встроенных портов упрощает код
Программа для проверки входного
бита и управления выходом через
встроенные порты
При использовании встроенных портов код
для проверки состояния одного бита и пере-
ключения состояния другого бита проще (ли-
стинг 22N.3), чем код при работе с внешними
шинами. Задействованные в данном коде порты
применимы с версией микроконтроллера 8051
производства компании Dallas Semiconductor.
Микроконтроллер C8051F410 производства
компании Silicon Laboratories не имеет порта 3.
Но код для микроконтроллера C8051F410 бу-
дет таким же, только с указанием другого порта
вместо порта 3.
Листинг 22N.3. Код для проверки входного бита
SETB P3.0 ; Начинаем с высокого уровня:
; светодиод выключен
TEST: JNB P3.2JEST ; Пока входной бит низкого уровня,
; ждем здесь
; Когда входной бит переключается на высокий,
; идем дальше:
FLIPIT: CPL P3.0 ; Переключаем состояние только
; младшего бита (бит 0) порта
SJMPTEST
Этот код также исполняется быстрее, чем вер-
сия кода для внешних шин, поскольку ему
требуется намного меньшее число доступов
к шине как при выборке команд, так и при их
исполнении.
Но еще более важно, что один 8-разрядный
порт можно одновременно использовать по-
битно частично для ввода, а частично для вы-
вода. И наоборот, аппаратное обеспечение для
операций ввода-вывода посредством внешних
шин (см. раздел 22N.1.1) заставляло нас выде-
лять все 8 битов одного порта для ввода, а дру-
гого для вывода (хотя мы могли задействовать
эти 16 битов для различных задач).
Код для передачи битов через
встроенный порт
Привилегированный бит. Бит переноса
позволяет выполнять перемещение битов
и некоторые другие операции. Обычно ми-
кроконтроллер 8051 выполняет перемещение
данных по целому байту за раз. Но флаг пере-
носа является исключением из этого правила:
существует довольно большой набор команд,
которые могут записывать или считывать
значение флага переноса. Кроме того, некото-
рые команды могут выполнять булевы опера-
ции с этим флагом, сохраняя результат в нем.
Далее приводится несколько примеров таких
команд:
♦ ORL С, бит — выполняет операцию ИЛИ над
указанным битом и флагом переноса, сохра-
няя результат в флаге переноса. Например,
ORLQA.0;
♦ ANL С, бит — выполняет операцию И над ука-
занным битом и флагом переноса, сохраняя
результат в флаге переноса. Например, ANL
СР2.2;
♦ ANL С, бит — выполняет операцию И над до-
полнением указанного бита и флагом пере-
носа, сохраняя результат в флаге переноса.
Например, ANL С, /Р1.2;
♦ MOV С, бит — копирует состояние указанного
бита в флаг переноса. Например, MOV С, Р3.7;
♦ MOV бит, С — копирует состояние флага пере-
носа в указанный бит. Например, MOV P1.1, С.
Для операций ввода-вывода через внешние
шины эквивалентных команд нет, поскольку в
таком режиме разрешено перемещение только
целых байтов.
22Л/.2 Условные переходы
919
22N.1 А Эквивалентные битовые
операции на языке С
Перемещение битов на языке С
Код на языке С для перемещения битов через
встроенные порты во многом похож на соот-
ветствующий код на языке ассемблера, но не-
сколько больше по объему (листинг 22N.4).
Листинг 22N.4. Код для перемещения битов
через встроенные порты на языке С
// bit_transfer_port.c
#include<Z:\MICR0\8051\RAIS0N\INQREG32 0.H>
sbit outbit = Р1Л0; // Объявляем битовые переменные
(Буква s означает special, что, в свою очередь, означает,
что бит находится в special function register (регистр спе-
циальных функций) SFR)
sbit inbit = P3A2;
void main()
{
while (1) // Повторяем до бесконечности
outbit = inbit; // Копируем состояние KWR* в LED,
// используя два встроенных порта
В данном случае компилятор генерирует точно
такой же код на ассемблере, как и созданный
нами (листинг 22N.5).
Листинг 22N.5. Код на ассемблере для переме-
щения битов через встроенные порты
КОД НА АССЕМБЛЕРЕ ДЛЯ МАШИННОГО КОДА,
СГЕНЕРИРОВАННЫЙ КОМПИЛЯТОРОМ С
; FUNCTION main (BEGIN)
0000 7WHILE1:
0000 А2В2 MOVCinbit
0002 9290 MOVoutbitfC
0004 80FA SJMP 7WHILE1
22N.1.5. Аппаратный флаг:
устройство ввода для одноразовой
операции
При работе с внешними шинами аппаратное
обеспечение для реализации ввода с кнопки
несложное, а при использовании встроенных
портов — совсем простое.
Но заставить с помощью кнопки процессор вы-
полнить какую-либо операцию только один
раз — более трудная задача. Мы отвели этому
вопросу главу 22W, главным образом, чтобы
дать вам возможность попрактиковаться в рас-
познавании недейственных решений, но также
и с целью представить понятие активируемого
по фронту флага, состояние которого проверя-
ется процессором. На рис. 22N.4 изображена
сравнительно сложная схема, с помощью кото-
рой можно решить эту задачу при использова-
нии внешних шин. Чтобы понять, каким путем
мы пришли к конечному варианту этой схемы,
обратитесь к примеру с решением в главе 22W.
Цель данной схемы — объяснить использова-
ние аппаратного флага.
Устранение дребезга
ШТ?
Рис. 22N.4. Схема для одноразового исполнения процессо-
ром какой-либо операции
Между прочим, функции, выполняемые триг-
гером и модулем устранения дребезга, можно
реализовать программным способом, но по-
скольку мы стремимся к тому, чтобы наш код
был как можно проще, мы предпочитаем нагру-
зить этой задачей оборудование. (Данная схема
используется в разделе 22L.1.)
22N.2. Условные переходы
Первой командой условного перехода, с ко-
торой мы познакомились, была команда JNB
из раздела 22N.1.1. Такие команды позволяют
выполнять одну операцию, если удовлетворя-
ется какое-либо условие, и другую — в про-
тивном случае. Благодаря таким командам
920
22N. Микропроцессоры III: операции с битами
компьютеры выглядят, как будто обладают
интеллектом. (Простое суммирование чисел
не впечатляет: любой механический настоль-
ный калькулятор может справиться с такой за-
дачей.) Набор команд условного перехода ми-
кроконтроллера 8051 довольно ограничен, но
подмножество этих команд для проверки со-
стояния одного бита обладает превосходным
быстродействием.
KWR
- На светодиод
Рис. 22N.5. Управление битом выходного порта в зависимо-
сти от состояния бита входного порта
22N.2.1. Команды условного
перехода
♦ JNB, JB ... — переход, если указанный бит не
установлен или установлен соответственно.
Команда JBC является необычной версией
предыдущих: выполняет переход при удо-
влетворении условий и обнуляет флаг, если
был установлен.
♦ JNC, JC ... — переход, если флаг переноса не
установлен или установлен соответственно.
♦ ONE A... — переход, если значение аккумуля-
тора не равно указанному значению. Может
также использоваться с регистром, напри-
мер: ONE R2, ДЕЛАЕМ.ЧТО-ЛИБО.
• Команда CJNE модифицирует флаг перено-
са/займа, поэтому ее можно использовать
с последующей проверкой флага переноса,
чтобы выполнить проверку, если одно зна-
чение меньше, чем другое.
♦ DJNZ Rn ... — декрементирует регистр Rn и
выполняет переход при ненулевом результа-
те декрементации.
♦ JNZ, JZ... — выполняет переход при ненуле-
вом/нулевом значении аккумулятора. (Эта
команда предназначена только для проверки
аккумулятора, но не регистра общего назна-
чения.)
Оборудование для проверки битов через
встроенный порт
На лабораторном занятии 22L выполняется
проверка бита входного порта РЗ, чтобы ре-
шить, переключать ли состояние бита выход-
ного порта Р1. Для этой задачи не требуется
практически никакого дополнительного обо-
рудования (рис. 22N.5).
Условный переход по результатам
проверки входного бита
Проверка состояния бита на языке ассем-
блера
Листинг 22N.6 содержит модифицированную
программу из лабораторного занятия 22L, ко-
торая мигает светодиодом, при условии, что на
цифровой клавиатуре не нажата кнопка WR.
Нажатие этой кнопки активирует сигнал KWR*,
в результате чего программа начинает испол-
нять цикл, который пропускает код переклю-
чения состояния бита, управляющего свето-
диодом.
Листинг 22N.6. Программа мигания светодио-
эы
1; PORTBRANCH_402.a51 Условный переход
; в зависимости от состояния бита входного
; порта контроллера,
0082 30B2FD 181 CHECKIT: JNB P3.2,CHECKIT
; Ждем в этом цикле, пока не будет установлен
; бит 2 (исполняем цикл, пока нажата кнопка WR)
0085 639001 182 XRLP1,#01H ; Другой способ
; переключения младшего бита (бита 0) порта РЗ,
; пока кнопка WR НЕ нажата
0088 8290 183 CPLP1.0 ; Более
; прямолинейный способ переключения бита
; управления светодиодом
008А 80F6 184 SJMP CHECKIT
Данный листинг отличается от листинга из ла-
бораторного занятия 22L тем, что мы добавили
в него прямолинейный способ переключения
состояния бита, используя команду CPL, как
это делается в коде, созданном компилятором
языка С.
Проверка состояния бита на языке С
Следующий код на языке С, приведенный в
листинге 22N.7, выполняет такое же условное
переключение состояния бита.
22N.2. Условные переходы
921
Листинг 22N.7. Программа условного переклю-
чения бита на языке С
sbit inbit = РЗА2;
sbit outbit = РГ0;
void test_blt_io (void)
while(1)
if(!inbit) outbit = outbit;
else outbit = loutbit;
Из этого исходного текста программы компи-
лятор генерирует код на языке ассемблера, ко-
торый приведен в листинге 22N.7. Этот код не
совсем такой, как написанный нами. В частно-
сти, вместо того, чтобы исполнять цикл, пока
нажата кнопка, код компилятора всегда считы-
вает состояние бита управления светодиодом
и записывает его обратно, переключая или не
переключая его между операциями чтения и
записи.
Листинг 22N.7. Код, сгенерированный компиля-
тором программы из листинга 22N.6
0000 7WHILE1:
; SOURCE LINE #14
0000 20В206 JB inbit,?ELSE1
0003 A2B3 MOVCoutbit
0005 92B3 MOVoutbit,C
0007 80F7 SJMP 7WHILE1
0009 7ELSE1:
; SOURCE LINE #15
0009 B2B3 CPL outbit
000B 80F3 SJMP WHILE 1
rtftb
Alff,
fttiV
1 Ef}U
t'OV ■, ', "'
!
ACC
■■••■\v;;PSV/
0004 j
RC
R1
22ISL2.2. Применение масок
для обработки больше одного бита
Программа на ассемблере
Для выполнения условного перехода в зависи-
мости от состояния бита лучше всего подходят
готовые команды проверки состояния битов
JB и JNB. Но иногда возникает необходимость
проверить состояние больше чем одного бита,
хотя и меньше чем всего байта. В таком случае
подойдет способ, называемый маскированием,
для того, чтобы отделить интересующие нас
биты от не интересующих.
Например, цифровые клавиатуры, имеющиеся
в нашей лаборатории, сохраняют байт, сфор-
мированный из значений двух последних нажа-
тий кнопок. Если мы хотим выполнить переход
по состоянию последней нажатой кнопки, то
нам нужно наложить на этот байт маску, чтобы
скрыть биты предыдущей кнопки (старший по-
лубайт) от операции проверки. Эти биты мож-
но обнулить, выполнив над каждым из них и
значением 0 операцию И. А значения младших
4 битов можно сохранить, выполнив над каж-
дым из них и значением 1 операцию И.
На рис. 22N.6 показан фрагмент программы,
который обнуляет старшие 4 бита, но не затра-
гивает младшие 4. Сначала программа коман-
дой MOV A, INPUT загружает в аккумулятор байт
АВ из регистра R0. Затем она обнуляет старший
полубайт, оставляя только В в младшем. В пра-
вой части рисунка показана эмуляция данного
эффекта: значение А, содержащееся в старших
4 битах, было удалено из аккумулятора.
Такая маска используется в листинге 22N.8 для
реализации проверки последней нажатой кноп-
ки. В частности, если последней была нажата
кнопка А, то программа выполняет переход
к метке DO_A, а если В —
к метке DO_B. В противном
случае программа выходит
из данного фрагмента кода
и идет дальше к командам,
которые здесь не указаны.
Рис. 22N.6 Фрагмент программы
для обнуления старшего полубайта
922
22N. Микропроцессоры III: операции с битами
Листинг 22N.8. Пример использования маски
MASK EQU OFh ; Объявляем идентификатор, который позволит менять значение маски в начале программы
TARGET1 EQU OBh ; To же самое для первого целевого значения
TARGET2 EQU OAh ; и для второго
MOV DPTR, #8000h ; Указатель на порт цифровой клавиатуры
MOVX A, @DPTR ; Считываем значение с цифровой клавиатуры
ANL A, #MASK ; Маскируем старшие 4 бита (старший полубайт). (Значение 1 во всех битах младшего
; полубайта маски позволяет пропустить значение кнопки)
CJNE A, #TARGET1, TRY_A ; Если кнопка не В, то проверяем, какая именно. В противном случае идем дальше к DO_B
SJMP DO_B ; Переходим к подпрограмме реагирования на нажатие кнопки В
TRY_A: CJNE A, #TARGET2, EXIT ; Проверяем, если нажата кнопка А; если нет, завершаем все проверки.
SJMP DO_A ; Если да, переходим к подпрограмме реагирования на нажатие кнопки А
EXIT:...
Операция маскирования графически иллю-
стрируется на рис. 22N.7: над значением маски
и считанным с цифровой клавиатуры числом
выполняется операция И, в результате кото-
рой биты старшего полубайта обнуляются, а
младшего — не меняются. Предполагается, что
с цифровой клавиатуры введено значение С,
которое было сохранено в младшем полубайте,
а в старшем полубайте может быть любое зна-
чение.
(Шестнадцатеричный формат)
Значения с цифровой
клавиатуры
Последняя кнопка
Байт до наложения маски
Побитовая операция И
Содержимое регистра А
после наложения маски
(в шестнадцатеричном
формате)
Рис 22N.7. Графическая иллюстрация маскирования стар-
шего полубайта аккумулятора (регистра А)
/* moskino.c V
?
х S
Предшествующая
кнопка
А
Маска
А
X
0000
0000
с
1100
1100
1111
1100
Программа на языке С
Операции маскирования на языке С и на ассемб-
лере схожи: побитовая операция И (символ &,
а не &&, если вы знакомы с языком С) над зна-
чениями маски и байта с целевыми значениями.
Код ассемблера, создаваемый компилятором
языка С, практически идентичен коду, который
мы создали ранее вручную. На рис. 22N.8 пока-
зан фрагмент программы на языке С, который
накладывает маску на переменную INPUT, в ре-
зультате чего получается значение result.
Далее приводится код на языке С для выполне-
ния операций, которые были реализованы на
языке ассемблера чуть ранее: наложение ма-
ски и проверка на наличие символов А или В.
Фрагмент программы на языке С можно соз-
дать одним из следующих двух способов.
Первый способ: имитируем код
ассемблера с использованием условных
операторов IF... ELSE
Этот код может быть очень похож на код на
языке ассемблера, который мы видели ранее.
char INPUT;
char RESULT;
*<fef if* MASK 0x0F
void «oinO
while (1)
ASSEMBLY LISTING OF GENERATED OBJECT COOE
// MASK with LSB's high, high nybblft zero'4
//forever...
0000
0000
0002
0004
0006
E500
S40F
F500
30F8
; FUNCTION main (BEGIN)
?*HILE1:
R MOV
ANL
R MOV
SJMP
A,INPUT
A,#00FH
RESULT,A
?WHILE1
{
RESULT - INPUT & MASK; // ...copy keypad to display,
> // but MASKed to kill top half
Рис. 22N.8. Код для наложения маски на языке С и код на языке ассемблера, полученный в результате его компиляции
22N.2. Условные переходы
923
Примечание
Обратите внимание на то, насколько близок он к
некоторым фрагментам кода на языке Verilog, ко-
торый также содержит условный оператор IL.EIse.
См., например, в приложении А код для всех счет-
чиков, который включает сброс.
В листинге 22N.9 приводится код на языке С,
который реализует описанный метод. Данная
программа исполняет бесконечный цикл, уста-
навливая один или другой бит при нажатии со-
ответствующей кнопки.
Листинг 22N.9. Программа маскирования
на языке С
/* masking jf.c */
// Накладываем постоянную маску на входной порт РО
//Указываем результат, устанавливая один или другой
//бит порта Р1
#include<C:\MICRO\8051\RAISON\INC\REG320.H>/*
Присваиваем идентификаторы регистрам*/
sbit ABIT = Р1А0; // Объявляем одиночные выходные биты
sbit BBIT = РП;
xdata char *KEYPAD; // Байтовая переменная,
// на которую указывает регистр DPTR
void maskingjf()
{
int MASK = OxOF; // Маска с установленными
// битами младшего полубайта и обнуленными
// битами старшего
KEYPAD = 0x8000; // Инициализируем указатель
while (1)
// Повторяем до бесконечности
if((*KEYPAD & MASK) == OxOA) // Выполняем
// проверку на наличие кнопки А; & обозначает
// побитовую операцию И
{ABIT = 1; // Если кнопка А, устанавливаем
// соответствующий бит выходного порта
BBIT = 0;}
else if ((*KEYPAD & MASK) == ОхОВ) // Выполняем
// проверку на наличие кнопки А
{АВ1Т = 0;
ВВ1Т=1;
Ключевое слово *KEYPAD обозначает значение,
на которое указывает переменная KEYPAD, в ре-
зультате чего код *KEYPAD & MASK считывает
8-битовое значение с цифровой клавиатуры
и накладывает маску6.
Второй способ:
используем операторы CASE
Альтернативная программа — похожа на не-
которые рассмотренные нами примеры реали-
зации конечного автомата на языке Verilog —
может выполнять проверку состояния входных
битов с помощью последовательных операто-
ров CASE. В листинге 22N.10 приводится при-
мер такой программы.
Листинг 22N.10. Программа маскирования
с операторами CASE
sbit ABIT = Р1А0; // Объявляем одиночные выходные биты
sbit BBIT =РП;
xdata char *KEYPAD; // Байтовая переменная, на которую
//указывает регистр DPTR
char MASK;
char MASKEDJNPUT; // Входное значение после
// наложения маски
#define KEYAD 0x8000 // Адрес цифровой клавиатуры
#define MASKVAL OxOF // Маска с установленными
// битами младшего полубайта и обнуленными
// битами старшего
void masking_case ()
{
MASK = MASKVAL; // Инициализируем маску
KEYPAD = KEYAD; // Инициализируем указатель
while (1) // Повторяем до бесконечности
{
MASKEDJNPUT = ("KEYPAD & MASK); // Считываем
// значение с цифровой клавиатуры
// и накладываем на него маску
switch (MASKEDJNPUT) //Теперь выполняем
// проверку замаскированного значения кнопки
case OxOA: // Выполняем проверку
// на наличие кнопки А
else
{ABIT = 0;
BBIT = 0;}
6 Данный код на языке С, возможно, несущественно отли-
чается от рассмотренного ранее кода на языке ассемблера.
Код на языке ассемблера выполняет ввод одного байта,
над которым затем выполняются последовательные про-
верки; а код на языке С выполняет ввод значения с каждой
операцией "KEYPAD & MASK.
924
22N. Микропроцессоры III: операции с битами
ABIT = 1 ;
BBIT = 0;
break; // Если есть совпадение, не исполняем
// альтернативные ветви
case OxOB: // Выполняем проверку на наличие
// кнопки В
АВ1Т = 0;
BBIT = 1 ;
break;
default:
АВ1Т = 0;
ВВ1Т = 0;
22N.2.3. Сравнение байтов
с помощью команды CJNEE
Проверка на равенство
В рассмотренных примерах маскирования на
языке ассемблера используется единственная
команда, доступная в микроконтроллере 8051
для сравнения 8-разрядных значений:
ONE A, #TARGET1,TRY.A ; Если кнопка не В,
; проверяем, какая именно
Команда CJNE является одной из команд ми-
кроконтроллера 8051, которая выполняет не-
сколько операций за одну команду. (Другой та-
кой командой является команда DJNZ, которую
мы использовали в качестве счетчика цикла.)
В частности, она сравнивает два операнда, и
если они не равны, выполняет переход.
Код на ассемблере для проверки больше
(меньше) ли одно значение другого
Несмотря на способность команды CJNE к мно-
гозадачности, в некоторых ситуациях она не-
достаточно многосторонняя, поскольку может
определять только равенство (или неравен-
ство) двух значений. Чтобы посредством этой
команды определить больше ли одно значе-
ние другого, после ее исполнения необходимо
проверить состояние флага переноса (которо-
му, наверное, лучше подходит название флага
займа). Называя этот бит флагов, мы просто
говорим, что это сигнал определенного уров-
ня на выходе выделенного триггера. Значение
флага сохраняется постоянным до тех пор, пока
не будет перезаписано.
В листинге 22N.11 приводится фрагмент кода
для определения, равно ли значение в регистре
А эталонному значению REF, или же оно мень-
ше (LESS_THAN) или больше (GREATERJHAN)
этого значения. Код начинается с обычной ко-
манды CJNE, а затем проверяет флаг переноса.
Листинг 22N.11. Программа сравнения
на ассемблере
CJNE A, #REF, NOT_EQUAL ; Начинаем
; последовательность сравнений
EQUAL: SJMP DO.EQUAL ; Переходим сюда,
; если А равно REF
NOT.EQUAL: JC LESSJTHAN ; А не равно REF;
; Если установлен флаг переноса/займа,
; тогда А < REF
GREATER_THAN: SJMP DO_GT ; Переходим сюда,
; если нет переноса/займа:
; ==>А > REF
LESSJTHAN: SJMP DO_LT; Переходим сюда, если А < REF
Код на языке С для проверки больше
(меньше) ли одно значение другого
Код на языке С для решения этой задачи не-
много более удобочитаемый (листинг 22N.12),
но не проще. Данная программа отображает
три возможных результата тремя выходны-
ми комбинациями, которые могут, например,
включать светодиоды.
Листинг 22N.12. Программа сравнения
на языке С
while (1) // Повторяем до бесконечности
{
if ("KEYPAD ==REF)
RESULT_OUT = EQUAL;
else
if(*KEYPAD>REF)
RESULT_OUT = GT;
else
RESULT_OUT = LT;
22N.2. Условные переходы
925
Как и в случае с кодом для маскирования, бай-
товое значение *KEYPAD вводится с цифровой
клавиатуры. Символ звездочки означает, что
это указатель, а значение KEYPAD — адрес, кото-
рый этот указатель использует. Как вы должны
знать, для микроконтроллера 8051 этим указа-
телем является регистр DPTR.
Маскирование для установки больше
одного бита
Стандартная команда устанавливает один
бит
Стандартная команда, например SETB P1.1,
устанавливает бит 1 встроенного порта. Но
чтобы установить больше одного бита, по-
лезно снова воспользоваться маской. Для ре-
шения данной задачи маска накладывается,
используя операцию ИЛИ, а не И. Например,
чтобы установить биты 1 по 3 порта Р1 (оста-
вив при этом остальные биты без изменений),
сначала нужно загрузить в аккумулятор значе-
ние из порта Р1, а затем выполнить операцию
над аккумулятором или необходимым значе-
нием маски. Вот необходимый для этого код
на языке ассемблера:
MOV A, P1 ; Загружаем в аккумулятор байт из порта,
; чтобы наложить маску
ORLA,#00Eh ; Устанавливаем биты 1-3,
; не меняя значение остальных битов
MOV P1, А ; Отправляем результат обратно в порт
Подобный эффект можно получить, выполнив
операцию Исключающее-ИЛИ над значением
и маской. В частности, установив биты маски
в требуемой позиции, выполнение этой опера-
ции поменяет значение соответствующих битов
в целевом байте на обратное.
22N.2 А Аппаратное обеспечение
реализации флага
Флаг представляет собой индикаторный бит,
который активируется (устанавливается) для
обозначения определенного состояния. Флаг
остается установленным до тех пор, пока не бу-
дет преднамеренно обнулен устройством, для
которого он предназначался.
В аппаратных терминах флаг является выход-
ным сигналом триггера. Установка флага вы-
полняется подачей сигнала установки на вход
триггера или фронтом сигнала тактирования
при одновременной подаче сигнала высокого
уровня на вход D. Обнуление (мы предполага-
ем, что активным состоянием флага является
высокий уровень) флага выполнятся сигналом
сброса. На лабораторном занятии 22L мы рас-
смотрим несколько неправильных способов
установки флага, а затем последний — пра-
вильный.
Независимо от того, реализуется ли аппарат-
ный флаг с внешними шинами или со встро-
енными портами, для него требуется внешний
триггер, чтобы состояние флага сохранялось до
тех пор, пока не будет выполнен преднамерен-
ный сброс. Соответствующая схема показана
на рис. 22N.9.
(Возможно, необходимо устранить дребезг)
+5
U
ЮкОм
Этот сигнал не является флагом
А этот сигнал является
Рис. 22N.9. Для аппаратного флага необходим триггер. Флаг
устанавливается по фронту сигнала тактирования
Код для проверки состояния
аппаратного флага
Код для проверки состояния аппаратного фла-
га точно такой же, как и код для проверки
состояния бита, рассматриваемый в разде-
ле 22N.2.1, с тем лишь исключением, что он
должен содержать дополнительную операцию,
которая может обнулять флаг. Для этой цели
подойдет команда записи в порт, чтобы акти-
вировать сигнал сброса RESET* триггера.
Мы вернемся к этой теме, когда будем рассма-
тривать прерывания в главе 23. Там мы узнаем,
что микроконтроллер 8051 позволяет реализо-
вать флаг, активируемый фронтом сигнала, без
внешнего триггера или буфера с выходом с тре-
мя состояниями в случае флага, реализуемого с
внешними шинами.
Предварительная информация
о прерываниях
Лабораторное занятие 22L с большим ком-
пьютером завершается задачей — попытаться
926
22N. Микропроцессоры III: операции с битами
реализовать прерывание. Чтобы исполнить
эту тестовую программу, вам нужно по-
нять, что лишь при реагировании на преры-
вание микроконтроллер 8051 переходит по
предопределенному фиксированному адре-
су и исполняет находящийся там код, кото-
рый называется подпрограммой обработки
прерывания. Это несколько особая форма
подпрограммы. При более подробном рассмо-
трении прерывания мы увидим, что это просто
вызов подпрограммы, инициализируемый ап-
паратным обеспечением. Если вы разобрались
с механизмом вызова подпрограмм из пользо-
вательских программ, то увидите, что преры-
вания являются просто разновидностью таких
вызовов.
22L Лабораторное занятие: микроконтроллеры
Операции с битами; таймеры
22L1. Компьютер
из дискретных компонентов.
Операции с битами;
прерывание
Введение
На этом лабораторном занятии мы будем ис-
пользовать собранный нами микрокомпьютер
для реализации задач, для которых он хорошо
подходит: работать с одиночными битами, а не
с целыми байтами. Результативность микро-
компьютера в этой области иногда позволя-
ет ему выглядеть довольно способным, даже
по сравнению с полноценным компьютером.
Обычный компьютер предназначен для переме-
щения больших объемов данных по сравнитель-
но многоразрядной шине данных. А маленький
микроконтроллер не очень хорошо справляется
с задачей такого масштаба, но быстро выполня-
ет битовые операции. Его можно сравнить с тем
мышонком, который смог вытащить занозу у
льва из лапы, которую тот был не в состоянии
вытащить сам. Несомненно, что и наш микро-
контроллер когда-то получит должное возна-
граждение за свою работу.
22L.1.1. Операции ввода-вывода
одиночных битов через
встроенный порт
Как правило, микроконтроллер воздейству-
ет на окружающий мир через выводы своих
портов, а не посредством выведенной из ми-
кросхемы шины. В обычных условиях шина
микроконтроллера невидима внешнему миру.
Хотя мы оснастили собранный нами компью-
тер внешними шинами (которыми мы вос-
пользуемся для работы с байтами), сначала мы
поэкспериментируем с выполнением задач, с
которыми микроконтроллер справляется осо-
бенно хорошо: изменим, а затем проверим со-
стояние одного бита.
Вывод одного бита
Аппаратное обеспечение для управления
светодиодом посредством бита порта
Для наблюдения вывода одного бита через
встроенный порт подключите светодиод к вы-
воду одного из портов, например младшему
биту порта Р1. Как уже упоминалось ранее, в ре-
жиме источника тока порты микроконтроллера
могут выдать очень слабый ток (всего лишь
около 50 мкА при напряжении 2,4 В), но могут
потреблять достаточно большой ток (1,6 мА
при напряжении 0,45 В). Поэтому светодиод
подключается таким образом, чтобы ток с него
поступал в микроконтроллер, а не наоборот, с
микроконтроллера в светодиод1. Кроме того,
светодиод подключается к выводу микрокон-
троллера не напрямую, а через последователь-
ный резистор номиналом 3,3 кОм, который
ограничивает протекающий через светодиод
ток приблизительно до 1 мА (падение напря-
жения на светодиоде составляет около 2 В).
8051
Р1.0
Рис. 22L.1. Подключение светодиода к порту микроконт-
роллера
1 Прежде чем КМОП-технология захватила цифровой
мир, это был стандартный способ подключения светодио-
дов. Микросхемы ТТЛ подобно нашему микроконтролле-
ру, в отличие от КМОП-устройств, имели хорошие токовые
характеристики в режиме потребления тока и плохие -
в режиме источника. А вентиль КМОП может обеспечить
те несколько миллиампер, достаточных для эффективной
работы светодиода как в режиме потребления, так и в ре-
жиме источника тока.
928
22L Лабораторное занятие: микроконтроллеры III. Операции с битами; таймеры
Программа для переключения состояния
бита порта
Следующая далее программа (листинг 22L.1)
тестирует работу этой схемы, переключая со-
стояние бита 0 порта Р1, или бита РОЛ. Для вы-
полнения этой операции мы использовали ко-
манду дополнения CPL. Поскольку к биту порта
можно обращаться напрямую, код получился
очень компактным2.
Листинг 22L.1. Код программы для проверки
состояния бита порта
MACRO ASSEMBLER PORTPIN_408
LOC OBJ LINE SOURCE
1 ; PORTPIN_408.a51 Лаб. занятие 21.
; Используем вывод порта контроллера
; для работы с битами
2
3 SNOSYMBOLS ; Сокращаем объем
; кода в листинге
4 $INCLUDE (C:\MICRO\8051\RAISON\
INC\REG320.INC)170
171
0000 172 ORGO ; Указываем ассемблеру
; начальный адрес для размещения
; этого кода
173
0000 8076 174 SJMP STARTUP; Код начинается здесь ~
; с перехода на начало
175 ; собственно программы. ВСЕ наши
; программы будут начинаться таким
; образом
0078 176 ORG 78H; Вот здесь начинается
; собственно программа
177
0078 С290 178 STARTUP: CLR PI .0 ; Начинаем
; с нулевого значения бита (светодиод
; включен), просто чтобы исполнение
; было предсказуемым
179
007АВ290 180 ; FLIPIT: CPL P1.0 ; Переключаем
; состояние только младшего бита
; (бит 0) порта 3
007C80FC 181 SJMP FLIPIT
182 END
2 Более трудоемким, но более общим подходом к решению
этой задачи была бы загрузка значения байта в аккумуля-
тор, а затем операция ИСКЛ-ИЛИ над аккумулятором и
маской со значением 1 в разряде, который нужно пере-
ключить. Нулевые значения всех других разрядов этой
8-разрядной маски (значение которой в данном случае
было бы 01h) оставили бы остальные соответствующие
7 битов аккумулятора без изменений. Операция ИСКЛ-
ИЛИ позволяет одновременно обрабатывать больше
одного бита.
Ввод одного бита
Аппаратное обеспечение для ввода одного
бита с клавиатуры
Микроконтроллер 8051 может с легкостью не
только выводить, но и вводить биты по одному.
Продемонстрировать эту возможность можно
следующим образом. Подайте очищенный от
дребезга сигнал KWR* с цифровой клавиатуры
на вывод 2 порта 3, или Р3.2. Произвольность
такого выбора вывода и порта может выгля-
деть странной, но это удобная комбинация,
в чем вы сможете убедиться позже, когда в раз-
деле 22L1.3 мы будем рассматривать работу
с прерываниями (см. также рис. 22N.5).
Условный переход по результатам провер-
ки входного бита
Листинг 22L.2 содержит программу, которая
мигает светодиодом при условии, что на циф-
ровой клавиатуре не нажата кнопка WR.
Листинг 22L.2. Программа условного перехода
по результатам проверки бита
MACRO ASSEMBLER PRTBRANCH_402 09/04/102 15:54:33
PAGE1
LOC OBJ LINE SOURCE
1 ; PORTBRANCH_402.a51 Условный
; переход в зависимости от состояния
; бита входного порта контроллера
2
3 $NOSYMBOLS; Сокращаем объем кода
; в листинге...
4 SINCLUDE (C:\MICRO\8051\RAISON\
INOREG320.INC)
170
171
0000 172 ORG 0; Указываем ассемблеру
; начальный адрес для размещения
; этого кода
173
0000 807Е 174 SJMP STARTUP; Код начинается здесь -
; с перехода на начало
175 ; собственно программы. ВСЕ наши
; программы будут начинаться таким
;образом
176
0080 177 ORG080H ; Вот здесь начинается
; собственно программа
178
0080 С290 179 STARTUP: CLR P1.0; Начинаем с низкого
; уровня, просто чтобы исполнение
; было предсказуемым
22U. Компьютер из дискретных компонентов. Операции с битами; прерывание
929
180
0082 30B2FD 181 CHECKITrJNB Р3.2/СНЕСКГГ;Ждем
; в этом цикле, пока не будет
; установлен бит 2 (исполняем цикл,
; пока нажата кнопка WR)
0085 639001 182 ; XRL P1 ,#01Н; Другой способ
; переключения младшего бита (бита 0)
; порта Р1, пока кнопка WR НЕ нажата
0088 80F8 183 ; SJMP CHECKIT
END
22L1.2. Кнопка Ready: аппаратный
флаг
Разница в скорости работы компьютера и поль-
зователя настолько огромна, что это может соз-
дать проблему, когда пользователь хочет дать
указание компьютеру выполнить какое-либо
действие один раз. Например, в только что
рассмотренной программе было достаточно
легко подать сигнал KWR*, чтобы дать указа-
ние микроконтроллеру мигать или не мигать
светодиодом. Но как использовать этот сигнал,
чтобы переключить состояние светодиода все-
го лишь один раз? Когда компьютер исполняет
программу в непрерывном режиме, это сделать
невозможно. Для этого в схему нужно добавить
триггер, который будет регистрировать факт
запроса действия, например, нажатием кноп-
ки WR. Кроме того, компьютеру нужно дать
инструкцию обнулить триггер после того, как
он принял запрос и начал его обработку. Это и
есть цель добавления кнопки Ready, которая
рассматривается далее.
Аппаратное обеспечение для
реализации триггера флага Ready
На рис. 22L.2 изображен фрагмент схемы, по-
казанной на рис. 20L.1, содержащей триггер,
который служит для этой цели и выполняет две
задачи:
1. Регистрирует факт запроса, в данном слу-
чае — нажатие кнопки. Это полезно в том слу-
чае, если в данный момент компьютер занят
каким-либо трудоемким процессом, чтобы
пользователь мог отпустить кнопку, а не дер-
жал ее нажатой до тех пор, пока компьютер не
освободится, чтобы проверить ее состояние.
2. Позволяет компьютеру обнулить флаг за-
проса (выход Q), даже если пользователь
продолжает удерживать кнопку нажатой.
Шина данных
+5
IN2
НС74
Рис. 22L.2. Триггер для реализации флага Ready
Вторая из этих задач важнее, чем первая, по-
скольку даже наш слабенький микроконтрол-
лер 8051, работающий на частоте 11 МГц, может
выполнить большой объем работы в процессе
обычного нажатия кнопки пользователем. Даже
при нажатии кнопки только на момент, длитель-
ность этого события будет по крайней мере 0,1 с,
в течение которой процессор может исполнить
сотню тысяч команд. Таким образом, обнару-
жив нажатую кнопку, компьютер выполнил бы
требуемые действия, проверил состояние кноп-
ки снова, обнаружил ее снова нажатой и снова
выполнил требуемые действия. Этот процесс
продолжался бы множество раз для каждого
нажатия кнопки, и чтобы сделать его однократ-
ным, внешний триггер должен устанавливаться
по фронту сигнала. Конечно же, после того, как
компьютер обнаружит высокий уровень на вы-
ходе Q, триггера, он должен сбросить его. Для
реализации этой задачи в схеме на рис. 21L.2 ис-
пользуется сигнал IN2*.
Сигнал KWR* обязательно должен быть очи-
щен от дребезга, ибо в противном случае сброс
флага будет выполняться, пока продолжается
дребезг, в результате чего будет устанавливать-
ся новый сигнал Ready, вызывая повторную
реакцию компьютера. Эти вопросы рассматри-
ваются более подробно в примерах с решением
в главе 22W.
Код для тестирования схемы флага Ready
Листинг 22L.3 содержит текст программы
GETREADY_1208.a51 для тестирования схемы
флага Ready. Это измененная версия програм-
мы для ввода данных с цифровой клавиатуры
и вывода их на дисплей из лабораторного за-
нятия 21L, которая вместо постоянного считы-
вания цифровой клавиатуры выполняет лишь
одну операцию считывания после нажатия
кнопки WR и загружает полученное значение в
аккумулятор. Микроконтроллер постоянно от-
правляет содержащееся в аккумуляторе значе-
ние на дисплей.
930
22L Лабораторное занятие: микроконтроллеры III. Операции с битами; таймеры
Листинг 22L.3. Программа для тестирования схемы флага Ready
SOURCE
;GETREADY_1208.a51
; Лаб. занятие 22. Условный переход по флагу Ready
; Выводит на дисплей постоянное значение,
; меняющееся нажатием кнопки WR, вызывающим новое считывание цифровой клавиатуры
$NOSYMBOLS; Сокращаем объем кода в листинге
$INCLUDE (C:\MICRO\8051\RAISON\INQREG320.INC)
STACKSTART EQU 080H ; Начальный адрес стека сразу же после регистров специальных
; функций (SFR)
SOFTFLAG EQU ОН; Побитно адресуемая ячейка
ORG 0; Начальный адрес для размещения этого кода
UMP STARTUP; Код начинается здесь - с перехода на начало
; собственно программы. Все наши программы начинаются так
ORG 090H ; Вот здесь начинается собственно программа
STARTUP: MOV SP, #127; Исходный код — «STARTUP: MOV SR
; #STACKBOT-1.» Ассемблер вставляет «127»
ACALL PTRINITS
CLR A; Обнуляем выводимое на дисплей значение, чтобы начало исполнения было
; предсказуемым
CLR 0; Обнуляем флаг для первого прохода
GETKEY: ACALL READYCHECK; Проверяем, считывать ли новое значение
; Обновляется подпрограммой и указывает программе, считывать ли снова значение
; с цифровой панели или нет
NB 0, USEOLD; Если флаг обнулен, не обновлять значение кнопки.
CLR 0; Но если выполнен переход сюда, флаг был установлен. Обнуляем его.
MOVX A, @DPTR; Считываем значение с цифровой клавиатуры (флаг был установлен)
USEOLD: MOVX @DPTR,A; и выводим его на дисплей
SJMP GETKEY; Ожидаем другое значение кнопки... бесконечно
LOC
OBJ
0080
0000
0000
0000
020090
0090
0090
0093
0095
0096
0098
009А
009D
009F
00А0
00А1
00A3
00А6
00А9
ООАВ
00AD
ООАЕ
OOAF
00В1
00В2
00В5
00В7
00В8
ООВА
758180
11 A3
Е4
С200
11AF
300003
С200
Е0
F0
80F5
LINE
1
2
3
4
5
6
174
175
176
177
178
179
180
181
184
185
186
187
188
189
190
191
192
193
194
195
908000 200
75А080201
7801
7902
ЕЗ
22
СОЕО
Е2
30Е703
D200
ЕЗ
DOEO
22
202
203
204
205
206
208
209
211
212
213
215
216
218
219
; ПОДПРОГРАММЫ-
PTRINITS: MOV DPTR, #8000Н; Указатель на дисплей и на цифровую клавиатуру
MOV P2, #80Н; Для команды MOVX @Rn это устанавливает
; старший байт адреса в качества базового адреса ввода-вывода
MOV R0, #01Н; Младший байт адреса порта READY
MOV R1, #02Н; Младший байт адреса порта READY-CLEAR
MOVX A, @R1; Импульс для обнуления триггера
RET
; Подпрограмма READYCHECK: при наличии условия Ready устанавливает нулевой бит
; в качестве флага
READYCHECK: PUSH ACC; Сохраняем рабочий регистр
MOVX A, @R0; Извлекаем флаг Ready
JNB ACC.7,NOCHANGE; Если флаг обнулен, не выполняем его сброс
CHANGE: SETBO
MOVX A,@R1; Посылаем импульс для обнуления триггера
NOCHANGE: POP ACC; Восстанавливаем содержимое сохраненного рабочего регистра
RET
221 END
22L/. Компьютер из дискретных компонентов. Операции с битами; прерывание
931
22L1.3. Прерывания
Программа из предыдущего раздела заставляет
процессор постоянно проверять состояние бита
порта, чтобы определить, считывать ли снова
цифровую клавиатуру или нет. Такой подход
может быть не самим лучшим, если мы хотим
оптимально использовать процессорное время.
При альтернативном подходе процессору мож-
но дать возможность заниматься другими де-
лами без необходимости постоянно проверять,
нужно ли считывать цифровую клавиатуру или
нет.
Вместо этого периферийное устройство, ко-
торое хочет, чтобы процессор обратил на него
внимание, устанавливает высокий уровень на
одном из выводов процессора. Только при на-
личии такого сигнала процессор перейдет к ис-
полнению запрошенной задачи, что в данном
случае является инкрементированием внутрен-
него регистра. В следующей программе мы по-
пробуем реализовать этот подход. Поведение
программы с использованием прерывания со-
держит два новых элемента:
♦ Процессору нужно дать знать, что он должен
обратить внимание на прерывание. Это не-
обходимо как:
• в общем: включением глобального распо-
знавания прерываний. Такая задача выпол-
няется установкой одного бита (выходного
уровня триггера), выделенного для данной
цели. В листинге 22L.4 это сигнал ЕА3;
• в частности: включением конкретного пре-
рывания, которое мы планируем задей-
ствовать, например внешнего нулевого
прерывания. Внешнее означает, что пре-
рывание создается подачей сигнала на вы-
вод процессора, а не генерируется в ответ
на какое-либо внутреннее событие, типа
переполнения счетчика.
♦ Код, который требуется выполнить в ответ
на прерывание (в данном случае код для ин-
крементирования значения, выводимого на
дисплей), должен находиться по определен-
ному адресу, выделенному для реакции на
прерывание 0. В данном случае это адрес 03h,
который также обозначен меткой INT0VECTOR
в листинге 22L.4.
Не требуется никакого аппаратного
обеспечения
Для реализации прерывания в схему не нужно
добавлять никакого дополнительного оборудо-
вания. Мы уже подключили линию KWR* к вы-
воду 12 микроконтроллера 8051 (т. е. к выводу
порта Р3.2) в разделе 22L.1.1. По счастливому
совпадению4 этот вывод присвоен запросам
прерывания INTERRUPTO*. Аппаратная часть
реализации нашего прерывания показана на
рис. 22L.3.
(Наш старый знакомый, вывод порта Р3^\
Мы несколько переделали схему, чтобы ^
отобразить его функционирование в качестве^
запроса прерыванийУ
3 К сожалению, название ЕА также имеет сигнал, кото-
рый сообщает микроконтроллеру 8051, что для выборки
команды ему нужно обратиться к внешним шинам. Эти
два сигнала ЕА никоим образом не связаны друг с другом.
Рис. 22L.3. Подключение сигнала KWR* к выводу порта Р3.2,
используемому в качестве линии запроса прерывания
Программа, использующая прерывание
для инкрементации отображаемого
значения
Данная программа приведена в листинге 22L.4.
Вызов подпрограммы обработки аппаратно-
го прерывания осуществляется аппаратными
средствами. Поскольку подача активного сиг-
нала на вывод запроса прерывания сама по
себе не указывает адрес подпрограммы обра-
ботки прерывания, при получении прерывания
компьютер должен применить определенную
стратегию, чтобы определить, где находится
эта подпрограмма. В микроконтроллере 8051
для этого реализована самая простая возмож-
ная схема: в ответ на определенный тип пре-
рывания микроконтроллер всегда переходит
по определенному адресу. Подобно обычному
программному вызову подпрограммы, прежде
чем переходить по адресу подпрограммы обра-
ботки прерывания, процессор сохраняет в сте-
ке адрес следующей инструкции.
Большая часть этой программы не представ-
ляет трудностей для понимания. Как и все
программы с прерываниями, если исполнять
эту программу в пошаговом режиме, можно
будет увидеть, что микропроцессор как бы
4 Признаемся: мы специально так подстроили.
932
221. Лабораторное занятие: микроконтроллеры III. Операции с битами; таймеры
Листинг 22L.4. Программа, увеличивающая значение по прерыванию
MACRO ASSEMBLER INTDSPLYJ 204 12/08/04 16:36:00 PAGE 1
LOC OBJ LINE SOURCE
; INTDSPLY_12O4.a51 Инкрементирует отображаемое на дисплее значение по прерыванию
1
2
3
4
5
6
172
007F 196
197
198
0000 199
0000 0200D0 200
201
00D0 202
203
00D0 75817F 204
00D3 908000 205
206
00D6 D288
00D8 D2A8
00DA D2AF
00DC Е4
00DD F0
OODE 80FD
0003
0003
0004
04
32
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
; Должна инкрементировать отображаемое значение по каждому прерыванию
$NOSYMBOLS
SINCLUDE (C:\MICRO\8051\RAISON\INC\REG320.INC)
SINCLUDE (C:\MICRO\8051\RAISON\INCWECTORS320.INC)
; Файл тома определения векторов
STACKBOT EQU 07FH; Размещаем стек в начале рабочей области памяти
; Косвенно адресуемая память (80h и выше)
ORG0H
UMP STARTUP
ORG 0D0H
STARTUP: MOV SP,# 127
MOVDPTR,#8000H
; —ТЕПЕРЬ РАЗРЕШАЕМ ПРЕРЫВАНИЯ—
SETBIT0; Делаем INTO чувствительным к перепаду уровней
SETB ЕХО; И разрешаем прерывание INTO
SETB EA; Разрешаем глобальные прерывания (р. 31-32)
CLR А; (Как обычно, для предсказуемого запуска)
STUCK: MOVX @DPTR, A; Отображаем постоянное значение, пока не будет инкрементировано
;прерыванием
SJMP STUCK; (Реагирует на отрицательный перепад — чувствительность к псевдоперепаду,
; поэтому необходимо подать несколько сигналов тактирования на высоком уровне,
; а затем на низком)
; ISR: ПРОСТО ИНКРЕМЕНТИРУЕМ АККУМУЛЯТОР
ORG INT0VECTOR; Это определяется в файле VECTORS3210.INC, который был включен выше.
; Это адрес 03h, по которому переходит программа
; в ответ на нулевое прерывание
ISR: INCA
RETI
226 END
2212. Ветвь малого компьютера: таймеры, ШИМ, компаратор
933
призадумывается после вызова прерывания,
как он делает после программного вызова
подпрограммы. Такая же небольшая задержка
наблюдается и при выполнении команд RET
(возврат из подпрограммы) и RETI (возврат из
подпрограммы обработки прерывания). Было
бы хорошо, если бы можно было наблюдать
процесс сохранения данных в стеке, но про-
цессор не обладает такой возможностью. Он
и так старается, позволяя нам наблюдать за
состоянием шин адреса и данных для большей
части своих операций.
Данная подпрограмма ISR (interrupt service rou-
tine — подпрограмма обработки прерывания)
настолько мала, что она помещается в 2 байта,
начиная с вектора (адреса) прерывания 03h. По
этому адресу для подпрограммы ISfl отводится
всего лишь 8 байтов, поэтому часто здесь раз-
мещается не сам код подпрограммы ISR, а ко-
манда перехода по адресу, где есть больший до-
ступный объем памяти для более длинной под-
программы ISR. Мы увидим, как это делается на
последующих лабораторных занятиях. Кроме
того, подпрограмма ISR обычно переходит на
новый банк рабочих регистров, R0 по R7 (один
из четырех доступных). В данном примере мы
этого не делаем, поскольку наша подпрограмма
ISR не использует никаких рабочих регистров.
22L2. Ветвь малого
компьютера: таймеры, ШИМ,
компаратор
22L2.1. Использование выводов
порта РО
Мы снова используем вывод порта PORTO для
управления светодиодом; кроме этого, мы
подключим другие периферийные устрой-
ства к другим четырем выводам этого порта
(рис. 22L.4).
22L2.2, Таймер: снова мигаем
светодиодом
Как мы признались на лабораторном занятии
20L, гонять микроконтроллер через цикл в не-
сколько сотен итераций лишь для замедления
мигания светодиода, чтобы оно было различимо
для человеческого глаза, — не совсем разумное
использование его и так ограниченных вы-
числительных ресурсов. Но эту задачу можно
решить более рациональным образом, с помо-
щью встроенного аппаратного таймера.
Подобно практически любому другому микро-
контроллеру, микроконтроллер 8051 содержит
набор таких таймеров. Сначала мы испробу-
ем довольно стандартный таймер (хотя он
улучшен по сравнению с самой первой верси-
ей таймера микроконтроллера 8051). Данный
таймер называется Timer2. Микроконтроллер
C8051F410 содержит три или четыре других
таймера (точное количество зависит от того,
считать ли часы реального времени тайме-
ром или нет). Как обычно, нам нужно будет
инициализировать набор регистров. Но, вы-
полнив эту задачу, программа не будет требо-
вать почти никакого внимания процессора.
Микроконтроллер C8051F410 также оснащен
16-разрядным счетчиком, на котором основан
его массив программируемых счетчиков РСА
(Programmable Counter Array), способный реа-
лизовывать определенные операции, включая
широтно-импульсную модуляцию. Мы поэк-
спериментируем с этой технологией в разде-
ле 22L.2.7.
Таймер микроконтроллера обычно функцио-
нирует подобно таймеру, например, электро-
духовки: устанавливается время задержки,
по истечении которого таймер дает нам знать
об этом. В случае таймера микроконтроллера
по истечении времени задержки инициирует-
ся прерывание, поскольку цель использования
таймера состоит в высвобождении процессора
для других операций, более важных, нежели
исполнять роль часов или измерять время за-
держки. Таким образом действует программа
в разделе 22L.2.4. Она вызывает подпрограм-
му ISR для переключения состояния светодиода
при каждом переполнении задействованного
h* чО Ю ^# ГО (VI тн О I
1222222221
Рис. 22L.4. Использование выводов порта PORTO на сегод-
няшнем лабораторном занятии
934
22L Лабораторное занятие: микроконтроллеры ///. Операции с битами; таймеры
в ней счетчика. Затем она автоматически пере-
загружает в счетчик значение задержки, и цикл
повторяется.
Таймер также может подавать сигнал на вы-
ходную линию напрямую; счетчик/таймер
РСА может делать это в высокоскоростном вы-
ходном режиме. Но здесь мы этого не делаем.
Наша подпрограмма ISR настолько проста, что
она практически эквивалентна прямому воз-
действию счетчика РСА. Она лишь переключа-
ет состояние светодиода на противоположное,
но, конечно же, могла бы выполнять какое-то
другое, более сложное действие.
Как обычно, наша программа до крайности
проста, вследствие чего большая часть наших
усилий по программированию идет на исследо-
вание справочного листка, чтобы определить,
какие регистры и как нужно инициализиро-
вать. На этот раз мы дадим вам задание выпол-
нить эту инициализацию самостоятельно.
22L2.3. Инициализируем управление
таймером Т1тег2 TMR2CN
Плохие и хорошие новости касательно
конфигурирования микроконтроллера
Плохой новостью является то, что микрокон-
троллер предоставляет такое большое количе-
ство опций для работы с его встроенными пе-
риферийными устройствами, что пользователю
приходится принимать большое количество
решений, прежде чем приступать к разработ-
ке кода. Мы иллюстрируем это непристойное
обилие возможностей на скромном примере:
побитовой настройке 16-разрядного таймера
с подробным описанием конфигурационного
регистра. Данная настройка описывается в раз-
деле 22L.2.4. Хорошей же новостью является то
обстоятельство, что конфигурацию не обяза-
тельно выполнять побитно, а можно воспользо-
ваться программным средством, называющимся
Мастером настройки (Configuration Wizard).
Для этой конкретной программы кроме обыч-
ной настройки, выполняемой подпрограммой
USUAL_SETUP, почти вся задача состоит в ини-
циализации только одного регистра, называе-
мого TMR2CN (Timer2 Control — Управление
Timer2). Но, как обычно, подробная инфор-
мация даже для этого одного регистра может
выглядеть чрезмерной, настолько велик ее
объем. Для данного регистра нам нужно будет
выполнить следующие настройки:
♦ настроить 16-разрядный таймер;
♦ разрешить таймер/счетчик;
♦ задать сигнал тактирования: частота систем-
ного тактового генератора /12;
♦ указать начальное значение таймера (необ-
ходимо только в первом проходе, который
мы рекомендуем наблюдать в пошаговом ре-
жиме исполнения): FF FOh;
♦ задать значение для перезагрузки таймера
(это значение, которое загружается после пе-
реполнения таймера и используется на всех
последующих проходах): 00 00h;
♦ установить прерывание при переполнении
(называется Time2 Interrupt).
Выполнить эту задачу вы можете одним из двух
следующих способов.
Первый способ, трудоемкий: побитовые
настройки
Слово «трудоемкий», наверное, заставило вас
поволноваться. Но в действительности этот
процесс, скорее всего, займет две-три минуты.
Далее приводится описание всех битов реги-
стра TMR2CN. Изучив назначение каждого из
этих битов, вы сможете решить, какое значение
присвоить этому регистру.
На первый взгляд, побитовое рассмотрение это-
го регистра может показаться своего рода са-
мобичеванием, и мы сомневаемся, что, испро-
бовав Мастер настройки, вы когда-либо снова
будете применять этот метод. Но мы полагаем,
что ознакомление с функциями нескольких
битов данного регистра поможет сделать ра-
боту микроконтроллера не столь похожей на
волшебство. Ведь не зря же Мастер настроек
называется волшебником (англ. Configuration
Wizard — дословно «волшебник настроек»):
преобразование решений в битовые значения
выглядит довольно магически.
Второй способ, более легкий:
Мастер настройки
Запустите Мастер настройки на своем компью-
тере. (Текущая версия приложения называется
2212. Ветвь малого компьютера: таймеры, ШИМ, компаратор
935
Wizard2 и является самостоятельным модулем,
который устанавливается отдельно от среды
разработки Silicon Laboratories.) Далее следуй-
те инструкциям в разделе 22L2.5 по работе с
Мастером настройки.
22L2.4. Побитовая настройка
регистра
Наша цель — настроить Timer2 (один из четы-
рех таймеров общего назначения) для рабо-
ты в режиме 16-разрядного таймера, который
генерирует прерывание при переполнении.
Большинство функций таймера управляются
одним регистром — TMR2CN. Далее приводится
страница из справочного листка для микрокон-
троллера C8051F410, описывающая функцию
каждого бита этого регистра.
Расшифруем обозначения на рис. 22L.5.
Определение регистров SFR 24.8 Регистр
TMR2CN: управление таймером Timer2:
♦ Бит 7. TF2H — флаг переполнения старшего
байта таймера Timer2.
Устанавливается аппаратно, когда старший
байт таймера Timer2 переполняется, т. е. пе-
реходит со значения OxFF в значение 0x00. В
16-разрядном режиме это событие проис-
ходит, когда таймер Timer2 переполняется
и переходит со значения OxFFFF в значение
0x0000. При разрешенном прерывании тай-
мера Timer2, установка этого бита вызывает
переход процессора к подпрограмме ISR тай-
мера Timer2. Бит TF2H не обнуляется автома-
тически аппаратными средствами, и его не-
обходимо обнулять программно.
♦ Bit6. TF2L — флаг переполнения младшего
байта таймера Timer2.
Устанавливается аппаратно, когда младший
байт таймера Timer2 переполняется, т. е.
переходит со значения OxFF в значение 0x00.
Если этот бит установлен, то при установке
бита TF2LEN и разрешенных прерываниях бу-
дет генерироваться прерывание. Независимо
от режима работы таймера Timer2, бит TF2L
устанавливается при переполнении младше-
го байта. Данный бит аппаратными средства-
ми автоматически не обнуляется.
BitS. TF2LEN — разрешение прерываний
младшего байта таймера Timer2.
Данный бит включает/выключает прерыва-
ния младшего байта таймера Timer2. Если
бит TF2LEN установлен и разрешены преры-
вания таймера Timer2, при переполнении
младшего байта таймера Timer2 будет гене-
рироваться прерывание. При использовании
таймера Timer2 в 16-разрядном режиме этот
бит должен быть обнулен.
0: Прерывания младшего байта таймера
Timer2 выключены.
1: Прерывания младшего байта таймера
Timer2 включены.
Bit4. TF2CEN — разрешение режима захвата
таймера Timer2.
0: Режим захвата таймера Timer2 выключен.
1: Режим захвата таймера Timer2 включен.
Bit3. T2SPLIT — разрешение режима разделе-
ния таймера Timer2.
При установленном бите таймер Timer2 ра-
ботает в режиме двух 8-разрядных таймеров
с автоматической перезагрузкой.
0: Таймер Timer2 работает в режиме одно-
го 16-разрядного таймера с автоматической
перезагрузкой.
1: Таймер Timer2 работает в режиме двух
8-разрядных таймеров с автоматической пе-
резагрузкой.
Bit2. TR2 — управление работой таймера
Timer2.
Данный бит включает/выключает таймер
Timer2. В 8-разрядном режиме этот бит
включает/выключает только старший тай-
мер TMR2H; младший таймер в этом режиме
всегда включен.
0: Таймер Timer2 выключен.
1: Таймер Timer2 включен.
R/W
R/W
R/W
R/W
TF2H
TF2L I TF2LEN I TF2CEN T2SPLIT TR2 I T2RCLK I T2XCLK
Значение после сброса
100000000
Brt6
BctS
8Й2
Bit
Bit® Адресуемый
побитно
Адрес регистров SFR: 0хС8
Рис. 22L.5. Побитовое описание регистра управления таймером Timer2, который нам нужно инициализировать
936
22L Лабораторное занятие: микроконтроллеры ///. Операции с битами; таймеры
♦ Bitl. T2RCLK — режим захвата таймера Timer2.
Этот бит управляет источником захвата тай-
мера Timer2, когда TF2CEN=1. Если T2XCLK =
= 1 и T2ML (CKCON.4) = 0, этот бит также
управляет источником сигнала тактирова-
ния таймера Timer2.
0: Захват на каждом импульсе сигнала ча-
стотой 1/8 частоты сигнала тактирования
таймера smaRTCIock. Если T2XCLK = 1 и T2ML
(CKC0N.4) = 0, счет на частоте, равной 1/8 ча-
стоты внешнего генератора колебаний.
1: Захват на каждом импульсе 1/8 частоты
сигнала внешнего генератора колебаний.
Если T2XCLK = 1 и T2ML (CKCON.4) = 0, счет на
частоте, равной 1/8 частоты сигнала такти-
рования таймера smaRTCIock.
♦ BitO. T2XCLK — выбор внешнего сигнала так-
тирования для таймера Timer2.
Управляет выбором источника сигнала так-
тирования для таймера Timer2. Если таймер
Timer2 работает в 8-разрядном режиме, дан-
ный бит задает внешний генератор тактовых
сигналов для обоих байтовых таймеров. Но
биты выбора сигнала тактирования таймера
Timer2 (биты Т2МН и T2ML в регистре CKCON)
также могут использоваться для выбора или
внешнего сигнала тактирования, или систем-
ного сигнала тактирования для любого из
этих таймеров.
0: В качестве внешнего сигнала тактирова-
ния таймера Timer2 выбран системный сиг-
нал тактирования, разделенный на 12.
1: Внешний сигнал тактирования таймера
Timer2 определяется битом T2RCLK.
Инициализация регистра управления
таймером
Мы полностью приводим эту страницу здесь
не потому, что вам нужна данная информация,
но для того, чтобы дать вам представление о
чувстве страха, которое может вызвать первый
взгляд на справочный листок микроконтролле-
ра. (В данном случае этот «листок» состоит из
270 страниц!) Если такая подробная информа-
ция по одному регистру вызывает у вас страх,
не унывайте, вы такой же, как и все мы. Но мы
надеемся, что несколько минут изучения дан-
ной информации покажут (по крайней мере,
на этот раз), что нам нужно знать лишь малую
часть приведенных несметных подробностей.
Затем мы исследуем каждый бит регистра
TMR2CN, чтобы понять, какое значение нужно
установить для него. Описание битов регистра:
♦ d7: TF2H — данный бит служит указателем
переполнения таймера, и ему следует уде-
лять должное внимание. Но нам не нужно
инициализировать этот бит, за исключением
инициализации в том смысле, что когда он
устанавливается при переполнении таймера,
обнуление его является обязанностью поль-
зователя (как явно и говорится в последнем
предложении описания этого бита в справоч-
ном листке). Этот флаговый бит пригоден
также для генерирования прерываний. Мы
будем использовать его таким образом в на-
шей программе.
Обязательно ли обнулять этот бит при за-
пуске программы? Нет, не обязательно. По
значению параметра Reset Value (значение
после сброса), показанного справа вверху на
рис. 22L.5, можно видеть, что этот бит, как
и все остальные биты этого регистра, после
сброса имеет нулевое значение.
♦ d6: TF2L — данный бит служит индикатором
переполнения младшего байта 16-разрядного
таймера Timer2. Нам он не понадобится.
♦ dS: TF2LEN — может генерировать прерыва-
ние на переполнении младшего байта. Мы
оставим этот бит деактивированным. Его
состояние после сброса — значение 0 — даст
нам требуемый результат.
♦ d4: TF2CEN — нам не потребуется режим за-
хвата (capture mode). Мы также не будем
вдаваться в подробности значения этого
термина. Если вам интересно, то можете по-
смотреть, как он используется в одной из
двух программ для измерения длительности
импульса в разделе 25L.1.5. Поэтому мы оста-
вим данному биту его значение после сброса,
т. е. 0.
♦ d3: T2SPLIT — служит для настройки рабо-
ты таймера в режиме одного 16-разрядного
таймера (значение 0) или в режиме двух
8-разрядных таймеров (значение 1). Мы
будем использовать данный таймер в режи-
ме одного 16-разрядного таймера, поэтому
оставим его в значении 0.
Продолжаем рассмотрение остальных битов:
♦ d2: TR2 — очень важный бит, так как он
управляет разрешением таймера Timer2.
22L2. Ветвь малого компьютера: таймеры, ШИМ, компаратор
937
Поскольку нам нужно разрешить этот тай-
мер, то значение бита должно быть 1.
♦ dl: T2RCLK — этот бит влияет только при
установленном бите режима захвата (бит
TF2CEN имеет значение 1), чего мы не сдела-
ли. Поэтому в данном случае он для нас не
играет никакой роли.
♦ dO: T2XCLK — это тоже важный бит. Он выби-
рает источник сигнала тактирования для тай-
мера. Но поскольку мы не применяем режим
захвата, то оставим его в состоянии сброса,
что даст нам частоту сигнала тактирования
равной 1/12 частоты системного тактового
генератора (System Clock /12).
Полезно записать на бумаге биты, которые по-
требуют вашего внимания. (Лично мне требу-
ется такое подспорье.) Имея точное представ-
ление о таких битах, вам нужно решить, каким
образом присвоить им требуемые значения.
В частности, использовать ли для этого коман-
ду загрузки значений в регистры MOV (которая
определяет уровни всех битов) или же коман-
ды работы с битами? В этом отношении нуж-
но знать, разрешены ли битовые операции для
данного регистра. Да, разрешены, как можно
видеть по пометке Bit Addressable (Адресуе-
мый побитно) справа вверху в описании реги-
стра на рис. 22L.5.
Часто будет предпочтительнее побитовая адре-
сация, поскольку это позволяет модифици-
ровать только интересующие нас биты, не за-
трагивая состояние остальных битов регистра.
Но в данном случае команда MOV будет лучше
по двум причинам. Во-первых, мы знаем на-
чальное состояние всех битов регистра (Reset
Value — значение после сброса), так что мож-
но не беспокоиться о возможном искажении
какой-либо полезной информации этой коман-
дой. Во-вторых, некоторые биты нужно обну-
лить (присвоить значение 0), а некоторые —
установить (присвоить значение 1). Команда
MOV может одновременно выполнить обе эти
задачи.
Поэтому вам необходимо вычислить значе-
ние байта, который нужно загрузить в регистр
TMR2CN (в шестнадцатеричном формате, чтобы
поддерживать единообразие со всеми другими
указанными значениями), а затем загрузить
этот байт в регистр, используя команду MOV.
Косвенно затрагиваемый регистр CKCON
Будет правильно сказать, что для инициали-
зации таймера Timer2 достаточно должным
образом настроить только один регистр —
TMR2CN, что приятно отличает данный случай
от других. Но при этом следует отметить, что в
процессе инициализации косвенно принимает
участие еще один регистр: CKCON. В частности,
бит Т2МН (d5) этого регистра может опреде-
лять (если он установлен) частоту сигнала так-
тирования таймера Timer2. Но мы оставляем
этот бит в состоянии сброса, т. е. обнуленным,
что позволяет задавать частоту сигнала так-
тирования регистром TMR2CN. Настройки по
умолчанию повторно задаются (без надобно-
сти, но и без вреда) строкой кода в настоящей
программе:
ANL CKCON, #DIV12; allowTMR2CN to set timer clock rate
(частота сигнала тактирования таймера задается реги-
стром TMR2CN)
Регистр CKCON упоминается здесь для того,
чтобы напомнить вам, что инициализация ре-
гистров обычно затрагивает больше чем один
регистр. Кроме того, значение бита одного ре-
гистра может зависеть от настройки другого
регистра, как в данном случае значение бита
Т2МН регистра CKCON зависит от значения
бита T2XCLK регистра TMR2CN. Но, как уже
отмечалось ранее, все эти хлопоты с инициа-
лизацией регистров являются ценой, которую
нам приходится платить за универсальность
контроллера.
22L2.5. Настройка регистра
TMR2CN с помощью Мастера
настроек
Как упоминалось ранее, настройку регистра
управления таймером Timer2 можно вы-
полнить более легким способом: с помощью
Мастера настроек. Далее приводится пример
его использования.
Запускаем процесс настройки
Первым делом нужно указать семейство на-
шего микроконтроллера и конкретный ми-
кроконтроллер данного семейства, а затем
выбрать опцию программы на ассемблере
(рис. 22L.6).
938
22L Лабораторное занятие: микроконтроллеры III. Операции с битами; таймеры
Рис. 22L.6. Выбираем наш микроконтроллер и указываем, что программируем на ассемблере
Рис. 22L7. Выбираем тип периферийного устройства (таймер), а затем конкретное устройство (Timer2)
Задаем периферийное устройство
Далее выбираем требуемый нам таймер: Timer2
(рис. 22L.7).
Выполняем настройку таймера
Окно настройки таймера (рис. 22L.8, справа)
содержит большинство параметров, которые
нужно принять во внимание. Многие из этих
параметров соответствуют одиночным битам
регистра TMR2CN (см. раздел 221.23). Но со-
путствующие описания этих битов в окне на-
стройки облегчают понимание их назначения.
Кроме того, в этом окне можно задать параме-
тры и для других регистров.
Чтобы завершить настройку таймера, нужно
задать параметры для его прерываний в соот-
ветствующем окне, которое открывается нажа-
тием кнопки Configure Timer Interrupts в раз-
деле Timer Interrupt текущего окна. В открыв-
шемся окне настройки прерываний (рис. 22L.9)
можно задать требуемые параметры прерыва-
ний таймера.
Результат этого процесса настройки сконцен-
трирован в несколько строчек кода на ассем-
блере (листинг 22L.5).
Листинг 22L.5. Результат настройки таймера
; Peripheral specific initialization functions,
; Функции инициализации для конкретного
; периферийного устройства
; Called from the lnit_Device label
; Вызывается с метки lnit_Device
Timerjnit:
movTMR2CN,#004h
ret
Interruptsjnit:
mov!Ef#020h
ret
Эти несколько строк кода на ассемблере реали-
зуют настройку параметров нескольких затра-
гиваемых регистров. Согласитесь, что этот спо-
соб настройки лучше, чем побитовый вариант,
рассмотренный в разделе 22L.2.4. Кроме того,
221.2. Ветвь малого компьютера: таймеры, ШИМ, компаратор
939
Рис. 22L.8. Настройку регистра можно выполнить, установив флажки для требуемых битов, для которых даются описания. По
завершении настроек в окне проекта отображается код ассемблера для реализации этих настроек
Рис. 22L.9. Диалоговое окно Interrupts для настройки пара-
метров прерывания таймера
что мастером настроек легче пользоваться, на
него можно положиться, поскольку он задаст
каждому биту правильное значение.
Возможность для диагностирования,
наблюдаем, как переполнение вызывает
прерывание
В следующем далее листинге 22L.6 программы
timer2_bitflip.a51 для мигания светодиодом мы
присвоили переменным HITIME и LOTIME зна-
чения FF FAh, что находится в предельной бли-
зости к конечному значению счета FF FFh. Это
было сделано, чтобы облегчить диагностиро-
вание программы. В частности, мы хотели, что-
бы у вас была возможность наблюдать таймер в
действии: после сброса микроконтроллера про-
грамму можно будет исполнять в пошаговом
режиме и наблюдать, как она приближается к
переполнению счетчика таймера.
Листинг 22L.6. Программа таймера
для переключения состояния бита
;timer2_bittlip.a51 Использует таймер Timer2
; для мигания светодиодом по прерыванию
; переполнения таймера
SNOSYMBOLS ; Сокращаем объем кода в листинге
SINCLUDE (C:\MICRO\8051\RAISON\INC\c8051f410.inc)
$INCLUDE (C:\MICRO\8051\RAISON\INCWECTORS320.INC)
; Файл тома определения векторов
STACKBOT EQU 80h ; Размещаем стек в начале
; рабочей области памяти
940
22L Лабораторное занятие: микроконтроллеры ///. Операции с битами; таймеры
DIV12 EQU ODFh ; Маска для регистра CKCON
; для установки частоты сигнала тактирования
; таймера равной 1/2 частоты системного
; генератора тактирования
TIM2INTEN EQU IE.5
TIM2_ENABLE EQU TMR2CN.2
SOFTFLAG EQU 0 ; Программный флаг, используемый
; подпрограммой ISR для взаимодействия с главной
; программой
BLUEJ.ED EQU P0.0 ; Бит управления светодиодом
GLOBALJNTEN EQU EA ; Более ясная мнемоника
; для общего разрешения прерываний
HITIME SET OFFh ; Задаем начало счета близким
; к значению переполнения — старший байт
LOTIME SET OFAh ; То же самое — младший байт
RELOAD SET Oh ; Значения для перезагрузки
; для максимальной задержки
; Использование порта:
; Светодиод подключен к порту РО.О
ORG0
SJMP STARTUP
ORG 80h
STARTUP: MOV SP, STACKBOT-1 ; Инициализируем
; указатель стека
ACALLUSUAL_SETUP
ACALLTIMERJNITS
SETBTIM2_ENABLE
STUCK: SJMP STUCK ; Ждем прерываний.
; Все действие происходит здесь
Добавляем возможность наблюдения ре-
гистра
В отладчике среды разработки Silicon Labora-
tories можно наблюдать за состоянием реги-
стра при исполнении программы в пошаговом
режиме. Для этого нужно выделить требуемый
регистр, затем щелкнуть по нему правой кноп-
кой мыши и в открывшемся контекстном меню
выбрать опцию Add to Watch. Для примера на
рис. 22L.10 показано наблюдение за состояни-
ем регистров TMR2RLH и TMR2RLL при исполне-
нии нашей программы мигания светодиодом.
Пошаговое выполнение еще нескольких циклов
вызовет переполнение таймера, т. е. переход
его значения от FF FFh до 00 00h, вследствие
чего будет сгенерирован запрос на прерывание,
в результате которого программа перейдет по
Нажатие кнопки исполнения нескольких команд за раз
инкрементировало счет от начального значения FF FAh до FF FEh
/ \
Рис. 22L.10. Исполняя программу в пошаговом режиме, можно наблюдать, как счетчик приближается к переполнению
Только что произошло переполнение
таймера, т. е. переход от значения FF FF
до значения 00 00
^^^ В результате чего генерируется прерывание,
-^^^ которое передает управление подпрограмме
I5R, которая выполняет переключение
состояния бита управления светодиодом
Рис. 22L11. Переполнение таймера вызывает передачу управления подпрограмме ISR
2212. Ветвь малого компьютера: таймеры, ШИМ, компаратор
941
адресу своей подпрограммы ISR. Эта ситуация
иллюстрируется на рис. 22L.11.
Первое переполнение (которое мы специально
настроили так, чтобы оно происходило быстро,
инициализировав таймер значением, близким к
его предельному счету) произошло всего лишь
после нескольких инкрементов таймера. При
безостановочном исполнении программы этот
процесс не создает никакой полезной задерж-
ки. Он необходим лишь для наблюдения за
работой таймера при пошаговом исполнении
программы.
Обычный режим работы: таймер отсчиты-
вает максимальное значение между пере-
полнениями
Но во всех последующих итерациях цикла (по-
сле первого переполнения таймера и переза-
грузки в него нулевых инициирующих значе-
ний из регистров TMR2RLH и TMR2RLL) таймер
создает максимальную задержку с начальным
значением ШИМ, равным 00 00h.
Но даже эта задержка меньше одной секунды,
хотя достаточна для того, чтобы уверенно раз-
личать мигание светодиода.
22L2.6. Программа таймера
для переключения состояния бита
Программу timer2_bitflip.a51 для мигания све-
тодиодом с помощью таймера можно загрузить
на сайте этой книги. Листинг 22L.7 содержит
код программы без инициализаций.
Листинг 22L.7. Программа мигания
светодиодом с помощью таймера
ORG80h
STARTUP: M0VSRSTACKB0T-1 Инициализируем
; указатель стека
ACALLUSUAL.SETUP
ACALL TIMERJNITS
SETBTIM2.ENABLE
STUCK: SJMP STUCK ; Ждем прерываний. Все действие
; происходит здесь
При данной конфигурации таймера он дает
задержку длительностью всего лишь прибли-
зительно полсекунды. Эту задержку можно
растянуть, если включить в подпрограмму ISR
программный счетчик. Использование одного
регистра в этой подпрограмме может растянуть
задержку до пары минут. А для более длитель-
ных задержек хорошо подходят часы реально-
го времени. На лабораторных занятиях мы не
будем работать с этим периферийным устрой-
ством, но вы можете поэкспериментировать
с ним самостоятельно.
Фокусы с таймерами
Таймер можно использовать в других режимах,
а также для реализации схемы сигнализации по
истечении заданного периода времени, которая
рассматривается в разделе 22L.2.2. Например, в
режиме External... Capture Mode, таймер Timer2
или Timer3 может измерять частоту внешнего
сигнала относительно частоты системного так-
тового генератора5. Таймеры 0,1 и 3 могут так-
же считать перепады входного сигнала6. Но мы
не располагаем достаточным временем, чтобы
исследовать эти разнообразные возможности.
22L2.7, Широтно-импульсная
модуляция: уменьшаем яркость
светодиода
Аналоговая и цифровая версии ШИМ
Метод изменения мощности подаваемого на
нагрузку сигнала посредством варьирования
коэффициента заполнения выходного сигнала
довольно легко реализовать с помощью микро-
контроллера. Для этого практически не требу-
ется никакого дополнительного оборудования,
что приятно контрастирует с методом непре-
рывного варьирования напряжения или тока,
для которого необходим ЦАП. Метод ШИМ
можно реализовать полностью программными
средствами. Но микроконтроллер C8051F410
предоставляет еще более легкий способ реализа-
ции ШИМ. В частности, этот микроконтроллер
содержит набор программируемых счетчиков
; Подпрограмма ISR: ПРОСТО ПЕРЕКЛЮЧАЕМ СВЕТОДИОД
0RGTIMER2VECT0R
ISR: CPLBLUEJ.ED
CLRTF2H; Обнуляем флаг переполнения таймера Timer2
; (Обнуляется ли при этом флаг прерывания?)
RETI
5 См. разделы 24.2.3, 24.3.3 справочного листка по
C8051F410 компании Silicon Laboratories.
6 Набор счетчиков РСА принимает входной сигнал ECI
(см. с. 249 справочного листка), который можно присво-
ить одному из выводов микроконтроллера посредством
матричного переключателя, как показано на с. 149 спра-
вочного листка.
942
22L Лабораторное занятие: микроконтроллеры III. Операции с битами; таймеры
Разрешение
8-разрядный
компаратор
Сигнал тактирования
для РСА >
КОНТРОЛЬНОЕ ЗНАЧЕНИЕ: для постоянного уровня
яркости это константа, с которой сравнивается линейно
нарастающее значение СЧЕТ в регистре PCAOL
Контрольное значение передается в регистр PCAOCPLn)
Совпадение
CEXnj Матричный , ю
^переключатель! ■&»
j
^переключатель!
ввода-вывода
СЧЕТ (инкрементируется по каждому импульсу сигнала
Переполнение тактирования). Когда значение СЧЕТ > КОНТРОЛЬНОЕ
ЗНАЧЕНИЕ, на выходе устанавливается высокий уровень
Рис. 22L.12. Микроконтроллер С8051F410 реализует ШИМ в цифровой форме. Рисунок скопирован с разрешением из рис. 25.8
справочного листка по микроконтроллеру C8051F410
РСА, который можно использовать как два
8-разрядных или как один 16-разрядный тай-
мер, который устанавливает бит при достиже-
нии счетом заданного контрольного значения.
Таким образом, в чисто цифровой форме кон-
троллер может имитировать аналоговый метод
ШИМ, в котором линейно нарастающий тре-
угольный или пилообразный сигнал активиру-
ет компаратор, когда его значение превышает
аналоговое контрольное значение. Если вам
нужно освежить свою память об этой схеме,
рис. 8L.7 в разделе 8L.4 поможет вам в этом.
На рис. 22L.12 изображена блок-схема эквива-
лентного цифрового способа, используемого
микроконтроллером C8051F410 для реализа-
ции 8-разрядной ШИМ. Когда значение Счет =
= Контрольное значение, выходной бит уста-
навливается, а когда значение Count перепол-
няется — выходной бит обнуляется.
Чтобы получить постоянный коэффициент за-
полнения, КОНТРОЛЬНОЕ ЗНАЧЕНИЕ в регистре
РСАОСРНп на рис. 22L.12 и в регистре РСАОСРНО
в программе pwmj)y_wizard_nov10.a51 должно
быть константой. (Данную программу можно
загрузить на веб-сайте этой книги.) Значение
регистра СЧЕТ инкрементируется с частотой,
задаваемой сигналом тактирования РСА.
Когда значение СЧЕТ становится большим, чем
КОНТРОЛЬНОЕ ЗНАЧЕНИЕ, на выходе ШИМ
устанавливается высокий уровень, а когда зна-
чение COUNT переполняется, на выходе ШИМ
устанавливается низкий уровень. Таким обра-
зом, КОНТРОЛЬНОЕ ЗНАЧЕНИЕ определяет ко-
эффициент заполнения сигнала ШИМ (в диа-
пазоне от 0,4 до 100%)7.
22L2.8. Программа управления
ШИМ-сигналом для медленного
повышения яркости светодиода
Программа pwm_by_wizard_nov10.a51 реали-
зует постепенное повышение яркости свето-
диода. Для этого она медленно повышает кон-
трольное значение (в течение приблизительно
трех секунд), после чего сбрасывает его обрат-
но к исходному, в результате чего контрольное
значение создает выходной сигнал ШИМ, эк-
вивалентный медленному аналоговому пило-
образному сигналу, повышая в цикле яркость
светодиода от минимальной до максимальной.
В листинге 22L.8 приводится основная часть
этой программы (без инициализаций).
7 Коэффициент заполнения можно сделать равным 0%, про-
граммно выполняя запись в отдельный регистр управления.
Листинг 22L.8. Программа формирования
ШИМ-сигнала для управления светодиодом
STARTUP: MOV SP, #STACKBOT
acall USUAL_SETUP
acall lnit_Device
mov РСАОСРНО, #0; Обнуляем выходной сигнал
; для предсказуемого запуска
UP: acall DELAY
inc РСАОСРНО
sjmpUP
Настройка параметров ШИМ с помощью
мастера настроек
Запустив мастер настроек, в меню Peripherals
выбираем опцию РСА. Затем в открывшем-
ся диалоговом окне Programmable Counter
22L2. Ветвь малого компьютера: таймеры, ШИМ, компаратор
943
Разрешение
таймера РСАО
Задаем коэффициент
заполнения
/
Рис. 22L.13. Включаем набор счетчиков РСА (слева) и 8-разрядную ШИМ (справа)
KJKX3», *О40»
к*осмю, *изь
КЛОСШ». *9«ОЛ
>>
* V
;
mart
- Х»л
::S Hi
агГк "'"й
::
It
Рис. 22L.14. Подключение функции ШИМ к выводу микроконтроллера
Array (рис. 22L.13, слева) выбираем вкладку
массива РСАО (который в действительности
является единственный массивом счетчиков,
доступным на микроконтроллере C8051F410)
и включаем его, установив флажок Enable
РСАО. Далее переходим на вкладку Module О
(рис. 22L.13, справа) и устанавливаем пере-
ключатель 8-Bit Pulse Width Modulator, зада-
вая таким образом 8-разрядный ШИМ режим
работы таймера. На этой же вкладке задаем
коэффициент заполнения (Duty Cycle) вели-
чиной 50%. Можете сказать, как это делается?8
Далее нажимаем кнопку Configure Port I/O
и в открывшемся окне Port I/O (рис. 22L.14)
подключаем сигнал ШИМ на требуемый вывод
микроконтроллера.
Конфигурируем двухтактный выход ШИМ и
подключаем эту функцию к свободному выводу
8 Для данного 8-разрядного ШИМ мы установили КОНТ-
РОЛЬНОЕ ЗНАЧЕНИЕ посередине доступного диапазона:
80h.
порта Р0.2, пропуская первые для вывода этого
порта, которые будут использоваться на сле-
дующем лабораторном занятии (рис. 22L.14)9.
Программа для работы с ШИМ
Программу pwmjby_wizard_novl0.a51 для ра-
боты с ШИМ можно загрузить на сайте этой
книги.
22L2.9. Улучшение 1: меняем цвет
светодиода
Линейное изменение яркости светодиода может
быть интересным занятием, но только на пер-
вых порах, и в скором времени интерес к нему
9 Вывод Р0.0, который на прошлом лабораторном заня-
тии мы задействовали для управления светодиодом, будет
использоваться на лабораторном занятии 24L в качестве
входа для АЦП, а вывод РОЛ — для выхода ЦАП.
944
22L Лабораторное занятие: микроконтроллеры III. Операции с битами; таймеры
пропадает. Когда это случится, можно слегка
разнообразить схему, чтобы варьировать не
яркость, а цвет светодиода. Для этого замените
простой светодиод двухцветным светодиодом
с тремя выводами, при этом установив между
его двумя катодами инвертор (для инвертора
используйте микросхему 74НС14 или 74НС04).
Схема для такого подключения светодиода по-
казана на рис. 22L.15.
Двухцветный
светодиод
Рис. 22L.15 Цвет двухцветного светодиода изменяется, ког-
да ШИМ повышает яркость составного зеленого светодиода,
уменьшая при этом яркость красного, и наоборот
Когда один из составных светодиодов становит-
ся тусклее, другой становится ярче, в результате
чего общий цвет светодиода плавно изменяется
от одного из этих цветов к другому.
22L2.10. Улучшение 2: плавное
повышение и снижение яркости
Если вместо пилообразного сигнала для мо-
дулирования яркости светодиода подать
треугольный сигнал, то можно получить бо-
лее привлекательный эстетический эффект.
Иными словами, постепенно не только увели-
чивать яркость светодиода, но и уменьшать ее.
Поэкспериментируйте с этим эффектом, мо-
дифицировав должным образом код програм-
мы из раздела 22L.2.7. Плавно повышающееся
значение аккумулятора можно отслеживать
с помощью команды CJNE, изменяя направле-
ние изменения на обратное при достижении
им одного из двух предельных значений — О
или FFh.
22L2.11. Компаратор: генератор
колебаний как начало чего-то
более интересного
В число аналоговых периферийных устройств
микроконтроллера C8051F410 входят два
компаратора. Их можно сконфигурировать как
простые аналоговые устройства: два аналого-
вых входа и один выход с логическими уровня-
ми на линию порта. Характеристики гистерези-
са можно задавать программно.
Более интересно, что выход компаратора мож-
но наблюдать методом опроса или же исполь-
зовать его для генерирования прерываний.
В программе в разделе 22L2.12 компаратор
просто обнуляет времязадающий конденсатор.
Но, как упоминается в разделе 22L2.13, он мо-
жет выполнять более интересные задания.
Мы же начнем со скромных деяний, поставив
вместо фототранзистора, который предлагает-
ся использовать в разделе 22L2.13, обычный
резистор, в результате чего схема будет копи-
ровать генератор колебаний на операционном
усилителе из главы 8L, с тем исключением, что
она работает от однополярного источника пи-
тания.
Аппаратная часть генератора колебаний
Аппаратная реализация генератора колебаний
изображена на рис. 22L.16.
+5 В
ОДмкФф
Рис. 22L.16. Генератор колебаний со встроенным компара-
тором микроконтроллера С8051F410
Настройка компаратора
Настройка компаратора с помощью масте-
ра настроек
На рис. 22L.17 показаны опции настройки ком-
паратора с помощью мастера настроек.
Чтобы присвоить входы компаратора линиям
порта Р0.6 и Р0.7, в окне настройки матричного
22L.2. Ветвь малого компьютера: таймеры, ШИМ, компаратор
945
Рис. 22L.17. Реализация простого RC-генератора колебаний посредством настройки компаратора с помощью Мастера
настроек
Таблица 22L.1. Описание битов регистра
Регистр
CPT0CN
СРТОМХ
CPT0MD
P0MDOUT
P0MDIN
РО
POSKIP
Значение бита/байта
D7 (= CP0EN)
D6 (= CP0OUT)
D3,D2 (= CPOHYPx)
D1,DO (= CPOHYNx)
D7..D4 (CMXONx)
D3..D0 (CMXOPx)
Dl, DO (=CPT0MDx)
D3 (байт 08h)
D7, D6 (байт 3Fh)
D7, D6 (байт OCOh)
D0...D5
Функция
1 ==> разрешение компаратора 0
1 ==> высокий выходной уровень, если {вход +} > {входа -}
01 ==> положительный гистерезис 5 мВ
01 ==> отрицательный гистерезис 5 мВ
ООН ==> отрицательный вход присвоен Р0.7
ООН ==> положительный вход присвоен Р0.6
11 ==> задание компаратору самых медленных настроек
при самом малом энергопотреблении
1 ==> установка РО.З в двухтактный режим для управления
полевым МОП-транзистором разряда
0 ==> установка режима аналогового входа для бита (Р0.7, Р0.6)
1 ==> установка высокого уровня защелки, чтобы позволить
использовать линию в режиме входа
1 ==> пропускаются, чтобы присвоить вводы компаратора битам
D6, D7 в матричном переключателе
переключателя необходимо пропустить преды-
дущие пять линий (матричный переключатель
присваивает входы линиям портов как можно
младшего разряда). Как можно видеть на ри-
сунке, бит РО.З для подачи входного сигнала
на МОП-транзистор установлен для работы в
двухтактном режиме, поэтому нет надобности
добавлять повышающий резистор на драйвер
затвора МОП-транзистора.
Конфигурационные параметры побитно
Если у вас возникнет желание исследовать кон-
фигурационные параметры побитно10, они из-
ложены в табл. 22L.1.
10 В чем мы серьезно сомневаемся. Изучение описаний
этих регистров доставляет такое же удовольствие, как и
изучение Налогового кодекса Соединенных Штатов.
946 22L Лабораторное занятие: микроконтроллеры ///. Операции с битами; таймеры
22L2.12. КОД/?С-Генератора содержит только основные функциональные
^ « компоненты этой программы. Мы пропусти-
КОлеоанИИ ли код ^я инициали3ации, чтобы не отвле-
Полный код программы comparator_oscillator_ кать ваше внимание от того, что действитель-
jan11.a51, которая реализует генератор коле- но важно. Обратите внимание, что вам нужно
баний по схеме на рис. 22L.16, можно загру- самостоятельно завершить код подпрограммы
зить на веб-сайте данной книги. Листинг 22L.9 CHECK_END.
Листинг 22L.9. Программа генератора колебаний
STARTUP: MOV SP, #STACKBOT-1
ACALL USUAL_SETUP
ACALL InitJDevice
ACALL MISCJNITS
OSC_LOOP: MOV A, CPTOCN ; Загружаем регистр управления компаратора
; в аккумулятор, где можно тестировать нужный нам бит
JNB АСС6, OSCJ.OOP ; Выполняем условный переход по состоянию выхода компаратора (не флага): до тех пор,
<'покаиконд>иэтлн
SETB P0.3 ; Разряд конденсатора (включаем полевой МОП-транзистор)
ACALL delay ; Задаем достаточное время для полного разряда конденсатора
CLR РО.З ; Выключаем полевой МОП-транзистор
MOV PI, R7 ; Отображаем старший байт счетчика итераций
SJMP OSCJ.OOP ; Продолжаем (вам нужно заменить это кодом, который подает сигнал завершения DONE,
; когда старший байт счетчика COOUNTJiigh равен значению KEYPAD, введенному с цифровой клавиатуры
;-- ПОДПРОГРАММЫ, КОТОРЫЕ ВАМ НУЖНО НАПИСАТЬ САМИМ:
CHECK__END: ; Получаем текущее значение счета для сравнения. Если еще не закончили, продолжаем счет
DONE: ; Включаем светодиод или зуммер для индикации завершения воздействия
HALT: SJMP $ ; Когда COUNTJiigh равен KEYPAD, остаемся здесь, пока не будет выполнен сброс
; Подпрограмма ISR для прерывания компаратора
ORGCOMP0JNT
ANL CPTOCN, #ODFh; Обнуляем флаг прерывания компаратора
UMP COMPARATORJNT.RESPONSE
ORG150h
COMPARATORJNTJtESPONSE: PUSH ACC; Сохраняем рабочий регистр
16_BIT_INC: MOV A, #1; Устанавливаем инкремент, влияющий на флаг переноса
ADD A, R6 ; Инкрементируем младший байт счета
MOVR6,A
MOV A, R7 ; Получаем старший байт
ADDC А, #0; Инкрементируем старший байт, если был перенос с младшего байта
MOVR7,A
POP ACC
RETI
2212. Ветвь малого компьютера: таймеры, ШИМ, компаратор
947
22L2.13. Применяем генератор
колебаний для мониторинга
уровня загара
Только что рассмотренная схема и программа
для нее сами по себе не делают ничего особен-
ного. Тот же эффект можно было бы получить,
используя компаратор или операционный уси-
литель с однополярным питанием или генера-
тор колебаний на микросхеме 555. За исклю-
чением того, что эта схема питается от одно-
полярного источника, она практически такая
же, как и схема нашего первого RC-генератора
колебаний, который мы собрали на лаборатор-
ном занятии 8L. Но эта программа могла бы
служить основанием для какого-либо полез-
ного приложения, например монитора уровня
загара, рассматриваемого в разделе 15.2 книги
АоЕ11. Приспособить данную схему для выпол-
нения этой задачи можно, проделав следующие
две модификации:
♦ В схеме на рис. 22L.16 замените постоянный
и переменный резисторы, подключенные к
шине положительного питания фототранзи-
стором (рис. 22L.18), чтобы обеспечить про-
порциональность частоты колебаний интен-
сивности освещения;
многоразрядный счетчик. При частоте вы-
ходного сигнала генератора колебаний такой
16-разрядный счетчик позволит измерять
периоды времени длительностью до одной
минуты; а 24-разрядный счетчик обеспечит
измерение намного больших периодов вре-
мени.
При достижении целевого значения (задавае-
мого, например, с цифровой клавиатуры или
выходным сигналом потенциометра, подавае-
мым на АЦП), программа может выполнять
любые действия, которые вы считаете нужны-
ми: подавать звуковой сигнал или, например,
наносить пользователю слабый удар током12.
Но, наверное, лучше, чем удар током, будет
звуковой сигнал, который мы предлагаем вам
установить. На рис. 22L.19 показан пример не-
большого зуммера с питанием 5 В, который мо-
жет включаться сигналом завершения сеанса
загорания13.
CUI CEM-1205C
Рис 22L.19. Для сигнализации об окончании сеанса загора-
ния подойдет такой зуммер
Фототранзистор
BPV11
В
Подключите коллектор к +U;
базу оставьте неподключенной
Рис. 22L.18. Фототранзистор для замены резисторов в схе-
ме генератора колебаний
♦ Кроме обнуления конденсатора задайте вы-
ходному сигналу компаратора дополнитель-
ную задачу: при каждом разряде конденса-
тора программа может инкрементировать
11 Монитор уровня загара в книге АоЕ был создан как шу-
точный экзаменационный вопрос. Можете представить
наше удивление и удовольствие, когда мы обнаружили,
что кто-то запатентовал как раз такой монитор уровня за-
гара. Мы не шутим. Это патент США №4428050, Ассистент
для загорания (Tanning Aid), заявку на который подал не-
кий Пеллегрино (Pellegrino) в 1984 г. Описание устройства
изобретателем содержит следующие моменты: «...Наконец
устройство содержит схему для подачи соответствующего
сигнала предупреждения при достижении предустанов-
ленной дозы для каждого сеанса и общей дозы, а также
предустановленную функцию "переворота", которую мож-
но использовать для разделения сеанса... с целью обеспе-
чения равномерного загара как передней, так и задней ча-
сти тела». Мы с грустью сообщаем, что не похоже, что это
изобретение обогатило г-на Пеллегрино.
22L2.14. Код программы
мониторинга уровня загара
Перечисленные в разделе 22L.2.13 возможно-
сти реализуются программой comparator_osc_
displayJan 11.a51, которую можно загрузить на
веб-сайте этой книги.
♦ Программа предполагает использование в
схеме фототранзистора (устройство, ток ко-
торого пропорционален уровню освещения,
с которым мы познакомились на лаборатор-
ном занятии 6L).
♦ Она инкрементирует 16-разрядный счетчик
по каждому циклу генератора колебаний.
♦ Вам нужно будет завершить код программы,
написав подпрограмму, которая сравнивает
старший байт 16-разрядного счетчика со зна-
чением, введенным с цифровой клавиатуры.
12 Шутка. Мы настоятельно не рекомендуем использовать
этот подход к оповещению пользователя.
13 Показанный на рисунке зуммер CUI CEM-1205C по-
требляет ток величиной 35 мА. Поставляется компанией
Digikey.
948
221. Лабораторное занятие: микроконтроллеры III. Операции с битами; таймеры
Когда эти значения одинаковые, программа
включает сигнал завершения DONE. Как уже
упоминалось ранее, этот сигнал может быть
«вежливым», в виде включения светодиода,
или не очень — в виде звукового сигнала.
♦ После этого программа приостанавливает
исполнение, ожидая, чтобы пользователь
выполнил сброс.
Испытайте монитор уровня загара
При исполнении программы монитора уровня
загара на ЖКД (подключенному к порту РО)
должно выводиться медленно увеличивающее-
ся значение накопленного загара; при этом ско-
рость инкрементации должна быть пропорцио-
нальна уровню освещенности, измеряемому
фототранзистором. Попробуйте затенить дат-
чик освещенности, чтобы имитировать тучу,
портящую удовольствие любителю позагорать.
22L2.15. Улучшение 3: добавляем
сигнал завершения DONE
Теперь попробуйте написать подпрограмму
CHECK_END для программы comparator__osc_
displayjan11.a51. Эта подпрограмма сравнива-
ет старший байт 16-разрядного значения счет-
чика COUNTER (назовем этот байт COUNTJHI) с
введенным с цифровой клавиатуры значением
KEYPAD. При совпадении этих двух значений
программа должна подать какой-либо сигнал
о завершении сеанса загорания (включив све-
тодиод или зуммер), а затем начать исполнять
бесконечный цикл, из которого ее можно вы-
вести, только выполнив сброс (сигнал RESET*).
До тех пор, пока эти два значения, COUNTJHI и
KEYPAD, не совпадут, программа должна позво-
лить генератору колебаний продолжать рабо-
тать. Для решения этой задачи может подойти
команда CJNE.
22W. Примеры с решениями.
Битовые операции: раздолье ошибок
Пусть расцветают сто сорняков! — бросил
когда-то клич председатель Мао, и сегодня мы
последуем его призыву. Цель этого мероприя-
тия состоит в том, чтобы показать вам, как
много может быть возможностей пойти непра-
вильным путем. Но наша главная задача — от-
точить ваши навыки по выявлению и исправле-
нию неправильных решений.
Далее приводится набор ошибочных проектов,
каждый из которых сопровождается логиче-
ским обоснованием, которое оказывается лож-
ным. Каждое последующее логическое обосно-
вание обычно содержит указание, что было не
так с предыдущим решением. Таким образом,
в финале мы получим правильный проект.
22W.1. Задача
Мы хотим добавить к нашему микрокомпью-
теру кнопку, при нажатии которой компьютер
будет выполнять какое-либо одноразовое дей-
ствие. Назовем эту кнопку Ready (Готово).
22W.2. Множество плохих
и одно хорошее решение
Решение № 1
Мы хотим отправить информацию на про-
цессор, поэтому нам требуется порт ввода.
Используем для этого обозначенный долж-
ным образом вывод декодера ввода-вывода
74НС139 - IN1*.
1/2 '139
Решение № 2
О, так контакт декодера 74НС139, обозначен-
ный IN1*, в действительности служит для вы-
вода данных? (Что это все пытаются сбить нас
с толку?)
Да, мы видим, что этот контакт используется
для разрешения другого устройства, так что он
сам не действует как вход.
Хорошо, мы задействуем шину данных вместо
этого вывода. В частности, используем одну из
доступных восьми линий данных. Ведь линии
данных предназначены для данных, а у нас есть
данные для ввода. Таким образом, у нас будет
простой прямой способ дать ЦП (или компью-
теру) знать, когда мы хотим, чтобы он выпол-
нил для нас какую-либо задачу.
+5 В
Шина данных
сЮ
Рис. 22W.1. Подаем наш входной сигнал на вход IN1 * декодера
ь 10 кОм
Рис. 22W.2. Прямое подключение к шине данных
Решение № 3
О, нет... Мы забыли, что для подачи сигнала на
шину нам требуется буфер с выходом с тремя
состояниями. Почти все данные, передаваемые
по шине данных, являются не данными как та-
ковыми, а командами.
Таким образом, принудительно удерживая в
течение некоторого времени линию данных на
каком-либо определенном уровне, как это де-
лается в решении № 2, мы гарантированно ис-
казим команды на шине, что вызовет сбой на-
шего компьютера.
Ну хорошо, тогда добавим в предыдущую схе-
му буфер с выходом с тремя состояниями.
950
22W. Примеры с решениями. Битовые операции: раздолье ошибок
Несомненно, это позволит нам не вмешиваться
в деятельность шины до тех пор, пока нам не
потребуется обратиться к компьютеру.
Рис. 22W.3. Подключение входного сигнала к шине данных
посредством буфера с выводом с тремя состояниями
Решение № 4
Ладно, решение № 3 было нисколько не лучше
решения № 2. Но теперь-то мы видим, что ре-
шение, когда и кому подавать данные на шину
данных, должно приниматься центральным
процессором, а не нами.
Следовательно, мы предоставим возможность
ЦП включать буфер с выводом с тремя состоя-
ниями, чтобы подать наш входной сигнал на
шину данных, когда он готов к этому. В каче-
стве сигнала управления возьмем выходной
сигнал IN 1* декодера 74НС139.
Рис. 22W.4. Подача нашего сигнала на шину данных через бу-
фер с трехстабильным выходом, управляемым компьютером
Решение № 5
Наверное, будет лучше добавить в нашу схему
триггер-защелку, чтобы:
♦ центральный процессор не пропустил нажа-
тие кнопки в случае, если он занят другими
делами, когда пользователь нажмет ее, и
"Пи
Шина данных
dO
INI
♦ центральный процессор не будет выполнять
наш запрос 1000 раз подряд, если наш палец
задержится на кнопке на некоторое время.
Шина данных
+5 В
10 кОм
TlNl
11 МГц или сигнал ALE
разрешения защелки адреса
Рис. 22W.5. Добавляем в схему триггер-защелку
Решение № б
Да, вы правы, сигнал тактирования подается на
этот триггер-защелку в решении № 5 слишком
часто. Добавление этого триггера в схему не по-
могло решить нашу проблему.
Но вот эта схема будет лучше, поскольку она
позволяет нам установить выходной сигнал
триггера (чтобы центральный процессор не
пропустил нажатие кнопки), при этом разре-
шая процессору самому выполнять сброс триг-
гера (чтобы он не выполнял задачу, задаваемую
нажатием кнопки, тысячи раз).
+5 В
_я_ £10 кОм
Шина данных
Q
—1>
INT
Рис. 22W.6. Используем RS-триггер
Решение № 7
Нет, решение № 6 тоже не годится. Сигнал IN1 *,
который выполняет сброс триггера в решении
№ 6, возникает слишком рано, до того, как цен-
тральный процессор считывает шину данных,
что происходит в конце сигнала RD* и, вслед-
ствие этого, в конце сигнала IN1*.
/~ ЦП считывает данные с шины данных
/ в конце импульса IN1*
Рис. 22W.7. Используем RS-триггер, подавая сигнал сброса по-другому
22И/.2. Множество плохих и одно хорошее решение
951
Решение № 8
Хорошее решение, но не совсем. Инвертор, до-
бавленный в решении № 7, создает постоянный
сигнал сброса, за исключением периодов, когда
активирован сигнал IN1*. Что ж, придется сми-
риться с тем, что сигнал IN1* не пригоден для
выполнения сброса триггера.
Тогда выберем для этого какой-либо другой
сигнал. Нажатие кнопки выполнит установку
триггера, а затем, когда ЦП готов, он может об-
нулить его.
♦5 В
:ю ком
Q
Шина данных
dO
ГОТ
-оитз
Рис. 22W.8. Используем RS-триггер, но с отдельным сигна-
лом сброса
Решение №>9
Однако решение № 8 тоже не годится. Сброс
посредством центрального процессора, как
предлагается в решении № 8, не будет выпол-
няться, когда кнопка все еще находится в нажа-
том состоянии.
Ну тогда мы немного перегруппируемся, что-
бы ЦП посылал не сигнал сброса, а установки,
поскольку, насколько нам известно, вход уста-
новки триггера преобладает над входом сброса
(в контексте определения уровня выхода Q),
когда оба входа активированы.
Решение №10
Опять не то. Никакие манипуляции с входом
установки и сброса не могут дать требуемого
результата. Поскольку после того, как ЦП пред-
принял попытку обнулить флаг, кнопка все еще
может находиться в нажатом состоянии, вслед-
ствие чего эта попытка обнуления будет неу-
спешной. Это касается как решения № 8, так
и решения № 9. Единственная разница между
этими двумя решениями состоит в том, что в
решении № 9 сигнал IN1* действительно обну-
ляет флаг, но от этого мало пользы, поскольку
обнуление не является постоянным.
Эту проблему можно решить с помощью акти-
вирования по фронту. В частности, обнуление
будет сохраняться даже при нажатой кнопке.
Кстати, в случае если вас волнует вопрос дре-
безга, обратите внимание на то, что положи-
тельный перепад устанавливает высокий уро-
вень на выходе Q, так что очищать от дребезга
сигнал тактирования нет надобности.
+5 в
Шина данных
-OUT3
Рис 22W.10. Используем запускаемый по фронту D-триггер
Решение № 11
Да, вы правы. Все же лучше добавить защиту от
дребезга, поскольку дребезг длится достаточно
долго (> 1 мс) по сравнению со скоростью реа-
гирования центрального процессора (< 10 мкс).
+5 В
^Ага! Для определения состояния
) выхода Q, вход установки преобладает
над входом сброса, поэтому мы <
преобладающим сигнал OUT3*
'Г
Ж
/переопределяем активную нагрузку как сигнал низкого уровня
^чтобы вход установки преобладал над входом сброса
Шина данных
-8
INT
-OUT3
Рис. 22W.9. Снова используем RS-триггер, но учитываем приоритет входа установки над входом сброса
952
221V. Примеры с решениями. Битовые операции: раздолье ошибок
В результате будет выполняться сброс, после
чего будет приходить множество фронтов, соз-
даваемых дребезгом, вызывая новые запросы
«делай, если». Кроме того, дребезг также будет
происходить и при отпускании кнопки, созда-
вая новые перепады.
+5 В
Рис. 22W.11. Устраняем дребезг с помощью запускаемого
по фронту D-триггера и RC-цепочки
Решение №12
Метод защиты от дребезга в решении № 11 не
совсем эффективен. Он просто создает мед-
ленные перепады, но на тактируемом входе
медленные перепады могут формировать не-
сколько перепадов. Таким образом, медленные
перепады сигнала тактирования имеют такие
же отрицательные последствия, как и дребезг.
Но эта проблема решается добавлением в схе-
му триггера Шмитта 74НС14 с гистерезисом ве-
личиной приблизительно 0,4 В (рис. 22W.12).
Данный триггер преобразует входной медлен-
ный перепад в выходной быстрый и чистый
перепад, который будет должным образом вос-
приниматься входом сигнала тактирования.
Вот это и будет конечный, рабочий проект!
Рис. 22W.12. Запускаемый по фронту D-триггер и триггер
Шмитта качественно удаляют дребезг, формируя прямо-
угольный сигнал тактирования
22W.3. Другой способ
реализации функции кнопки
Ready
Если рассмотрение всех этих решений изнури-
ло вас, можете радоваться, что вскоре можно
будет обойтись без всей такой тяжелой работы
(как в плане мышления, так и в плане реализа-
ции), воспользовавшись запускаемым по фрон-
ту прерыванием микроконтроллера 8051. Хотя
и здесь также придется обеспечить защиту от
дребезга для кнопки, больше ничего не нужно
будет делать. А при желании немного потру-
диться с кодом можно будет обойтись даже без
аппаратной защиты от дребезга, реализовав ее
программно. Но мы не будет рассматривать эту
опцию на лабораторных занятиях, поскольку
хотим минимизировать объем нашего кода.
Но вы можете попробовать описанный метод
в какой-либо другой ситуации. Программный
код намного дешевле, чем аппаратура.
23N. Микропроцессоры IV:
прерывания; АЦП и ЦАП
Содержание
23N.1. Основные моменты ранее рассмотренного материала 953
23N.2. Прерывания 953
23N.2.1. Когда нужны прерывания? 954
23N.2.2. Как реализовать прерывания? 955
23N.2.3. Разрешение прерываний; реагирование на перепад или уровень 957
23N.2.4. Приоритеты прерываний 957
23N.2.5. Разница между командами RET и RETI 958
23N.2.6. Демонстрационная программа по прерываниям 959
23N.3. Обработка прерываний в языке С 960
23N.4. Сопряжение АЦП и ЦАП с микроконтроллером 961
23N.4.1. Микросхема АЦП и ЦАП AD7569 962
23N.4.2. АЦП и ЦАП на микроконтроллере C8051F410 964
23N.4.3. Программа 965
23N.5. Некоторые подробности о лабораторных занятиях по АЦП/ЦАП 967
23N.5.1. Использование ФАПЧ для настройки частоты тактирования фильтра 968
23N.5.2. Усилитель звуковой частоты 968
23N.5.3. Используем импульсный усилитель из лабораторного занятия 12L 969
23N.5.4. Преобразование сигналов разных типов 970
23N.6. Предлагаемые лабораторные задания при экспериментах с АЦП и ЦАП 970
Цель этой главы
Мы хотим узнать, как выполнять ввод аналоговых значений в компьютер и вывод из него, а также
как использовать прерывания для модификации процесса исполнения программы.
23N.1 • Основные моменты
ранее рассмотренного
материала
Вызов подпрограмм
♦ Позволяет использовать блок кода несколь-
кими программами.
♦ Позволяет создавать модульный код: основ-
ная программа вызывает несколько вспомо-
гательных подпрограмм, каждая из которых
выполняет свою задачу.
Операции с битами
♦ Установка и обнуление одиночных битов
(позволяет управлять восемью устройства-
ми на одном 8-разрядном порту).
♦ Возможность тестирования одиночных би-
тов.
♦ Особенно легко эти операции выполняются
при работе со встроенными портами, а не
внешними шинами.
23N.2. Прерывания
Как ясно из названия, прерывание прерывает
ход выполнения одной программы, чтобы по-
зволить исполняться другой программе. Это
особый тип вызова подпрограммы, который
инициируется аппаратно, а не программно1.
1 Многие процессоры поддерживают программные пре-
рывания, которые работают подобно аппаратным, но ини-
циируются программой, а не аппаратным событием. Но у
микроконтроллера 8051 нет такой возможности.
954
23N. Микропроцессоры IV: прерывания; АЦП и ЦАП
Вспомним, в каких ситуациях нам может по-
требоваться вызывать прерывание, а затем
рассмотрим, как это делать.
23N.2.1. Когда нужны прерывания?
Ответ на этот вопрос можно предположить по
названию данного механизма управления хо-
дом исполнения программы: мы прерываем
что-либо или кого-либо, когда мы в спешке2.
С одной стороны, это верно, но с другой — нет.
Альтернативой прерываниям будет опрос. На-
пример, мы можем периодически опрашивать
кнопку Ready из лабораторного занятия 23L:
«Ты готова?». Но не лучше ли позволить кноп-
ке Ready просто дать компьютеру знать, когда
у нее есть для него задание, не мешая ему зани-
маться своими делами до тех пор? В некоторых
случаях так будет лучше.
Когда требуется быстрый ответ
Вызов прерывания, чтобы привлечь внимание
компьютера, когда у нас есть готовая для него
задача, может быть хорошей идеей. Можно
также представить и другие случаи, когда не-
медленный отклик компьютера может быть
еще больше необходим. Например, когда источ-
ник питания компьютера начинает выходить
из строя. В таком случае реакция компьютера
типа «Что, небо падает? Не приставай ко мне с
такими пустяками, пока я не закончу эту важ-
ную задачу по вычислению числа п с точностью
до 20 десятичных значений» будет далеко не та-
кой, какая требуется в данных обстоятельствах.
Обнаружив признаки наступающего прекраще-
ния питания, компьютер может сохранить важ-
ную информацию в энергонезависимом хра-
нилище данных. Версия DS89C4xx микрокон-
троллера 8051 производства компании Dallas
Semiconductor, которую мы используем, под-
держивает такое прерывание по перебою в пи-
тании, как и микроконтроллер C8051F410 про-
изводства компании Silicon Laboratories. В по-
следнем устройстве это прерывание называется
Voltage regulator dropout (Провал напряжения
стабилизатора). Но в обоих модификациях
микроконтроллера эти прерывания необходи-
мо разрешить программно. Микроконтроллер
8051 не поддерживает немаскируемые преры-
вания.
Можно также применить прерывание в другом
случае, с которым мы имели дело. В частности,
когда компьютер «зависнет» при исполнении
какой-либо программы, а мы хотим снова по-
лучить контроль над ним3. В этом случае можно
выполнить сброс процессора посредством сто-
рожевого таймера. Сторожевой таймер пред-
ставляет собой таймер, который необходимо
периодически программно обнулять. Если про-
грамма не выполняет такое обнуление, значит,
с ней что-то не в порядке. В таком случае про-
исходит переполнение счетчика, и он генериру-
ет сброс микроконтроллера.
На лабораторном занятии 23L, где наш компью-
тер принимает данные от АЦП, мы будем ис-
пользовать прерывание, чтобы обеспечить си-
стематическую выборку. Прерывание позволя-
ет нам задать скорость выборки, не беспокоясь
о возможной скорости исполнения определен-
ных блоков кода. В случае программы из этого
лабораторного занятия, выборки осуществля-
ются намного быстрее, чем любая другая вы-
полняемая программой операция, поэтому мы с
таким же результатом могли бы применить ме-
тод опроса. Мы выбрали прерывание в основ-
ном по той причине, что при прерывании у нас
есть возможность тактирования по фронту. Это
позволяет с легкостью реализовать требуемый
результат: делать одну выборку для каждого пе-
риода входного прямоугольного сигнала.
Типичное применение прерывания:
Очередь FIFO4 для входящих данных
Входной буфер способен удовлетворить две по-
требности, которые могут служить причиной
для вызова прерывания:
♦ быстро отреагировать на запрос внешнего
устройства;
♦ позволить основной программе выполнять
другие действия, пока ожидается преры-
вание.
2 АоЕ § 14.4.8.
3 Чтобы прервать программу, при любых обстоятельствах
требуется так называемое немаскируемое прерывание,
которые микроконтроллер 8051 не поддерживает. При
отсутствии такого типа прерывания мы можем прервать
«подвисшую» программу, используя аппаратный сброс.
Аппаратный сброс похож на прерывание в том отношении,
что он вынуждает компьютер начать исполнять код по вы-
деленному адресу, но он отличается от прерывания тем,
что не пытается сохранить никакую информацию о про-
грамме, которая исполнялась, когда был выполнен сброс.
4 Англ. First In First Out — первым пришел — первым вы-
шел. — Примеч. пер.
23N.2. Прерывания
955
Аналого-цифровому преобразователю обыч-
но необходимо получать данные с равномер-
ной скоростью. Это можно обеспечить с помо-
щью подпрограммы ISR, которая обслуживает
прерывание. Подпрограмма ISR может выпол-
нять выборку по прерыванию, а затем сохра-
нять данные в кольцевом буфере. Кольцевой
буфер представляет собой блок памяти RAM,
запись и чтение которого можно выполнять
на разных скоростях5. Такой буфер также яв-
ляется буфером типа FIFO, поскольку дан-
ные из него считываются в порядке поступле-
ния — первые записанные данные первыми
и считываются.
Подпрограмма АЦП, которая вызывается пре-
рыванием, может поспевать за жестко задан-
ной скоростью выборки, не накладывая на
основную программу необходимости следо-
вать такому строгому тактированию. Таким
образом, основной программе не требуется
реагировать немедленно при появлении каж-
дого отсчета, ей нужно лишь следовать сред-
ней скорости поступления отсчетов. Короче
говоря, основная программа может вести
себя как обычный студент: запустить немно-
го учебный материал, занимаясь чем-либо
более интересным, чем учеба, а затем прило-
жить дополнительное усилие, чтобы нагнать
пропущенное6.
Данные, поступающие в компьютер через по-
следовательный порт, могут представлять по-
добную проблему, которую также можно ре-
шить аналогичным способом. Мы не хотим,
чтобыкомпьютерпропустилсимвол,поступаю-
щий через порт RS232. (Подобно почти всем
микроконтроллерам, обе используемые нами
версии микроконтроллера, как 8051 произ-
водства Dallas Semiconductor, так и C8051F410
производства компании Silicon Laboratories,
оснащены таким портом.) Но мы также не
хотим, чтобы наша основная программа бро-
сила все, чем она занимается, чтобы немед-
ленно обработать поступивший символ. Эта
проблема легко решается с помощью буфера
FIFO.
Задержка
Хотя с помощью прерывания ответ можно по-
лучить быстрее, чем посредством опроса, меж-
ду событием запроса действия и реакцией на
этот запрос проходит определенное время, или
задержка. Данная задержка обработки преры-
вания может быть проблематичной, посколь-
ку она может варьироваться в зависимости от
уровня занятости процессора в момент возник-
новения прерывания.
Типичное применение прерывания:
часы реального времени
В данном случае возможность применения
прерывания не так очевидна. Но если задей-
ствовать для этой цели метод опроса, то резуль-
таты будут плачевными. Представьте себе, что
компьютер (подобно ребенку, спрашивающему
в длительной поездке на автомобиле: «Мы еще
не приехали?»), постоянно спрашивает у часов
реального времени7: «Десятая доля секунды
прошла? А сейчас? А сейчас»? Для этого будет
лучше, чтобы таймер прерывал компьютер по
истечении определенного интервала времени;
по такому прерыванию компьютер обновляет
свою информацию о времени и продолжает вы-
полнять задачу, которой он занимался в момент
прерывания. Такое прерывание также иллю-
стрирует другую причину для использования
прерываний: мы не хотим, чтобы обновление
времени было слишком длительным, посколь-
ку в таком случае тактирование компьютера
будет неточным.
23N.2.2. Как реализовать
прерывания?
Как уже упоминалось ранее, прерывание по-
хоже на вызов подпрограммы. Это означает,
что в ответ на прерывание, подобно ответу на
вызов подпрограммы, прежде чем переходить
к исполнению вызванной программы (или под-
программы обычного вызова, или подпрограм-
мы обработки прерывания), микропроцессор
5 Если вам интересны другие подробности кольцевого бу-
фера, то подпрограмма ISR сохраняет в нем текущую вы-
борку и обновляет указатели на буфер. Она также должна
создавать флаг, который может быть проверен основной
программой, указывающий, есть ли еще место в буфере,
или же он уже заполнен до предела.
6 Кстати, подобно большинству студентов, очередь FIFO
никогда не может забежать вперед.
7 Часы реального времени (или RTC — real time clock)
обычно представляют собой аппаратный счетчик, на-
строенный для ведения учета времени. Это стандартное
периферийное устройство, которое может считываться
компьютером и которое можно настроить на прерывание
процессора. Но предлагаемый нами вариант часов RTC
реализован программно. Микроконтроллер C8051F410
оснащен встроенными аппаратными RTC.
956
23N. Микропроцессоры IV: прерывания; АЦП и ЦАП
сохраняет в стеке адрес следующей инструкции.
Таким образом, исполнение прерванной про-
граммы может возобновляться автоматически,
как и возврат из обычной подпрограммы.
Но вызовов подпрограммы и прерывание от-
личаются друг от друга в двух важных аспек-
тах. В частности, вызов подпрограммы содер-
жит информацию об адресе вызываемой под-
программы, которую нужно исполнить. А вот
прерывание, которое запрашивается, подавая
сигнал на вывод микроконтроллера, явно не
указывает, по какому адресу находится подпро-
грамма ISR. Как можно ожидать, разные процес-
соры и микроконтроллеры применяют простые
и сложные способы, чтобы указать программе,
по какому адресу переходить, когда происходит
прерывание. В микроконтроллере 8051 реали-
зован простой подход, и мы рады сообщить,
что, похоже, что этот простой способ является
стандартным для микроконтроллеров.
Кроме того, обычный вызов подпрограммы и
прерывание отличаются еще тем, что разработ-
чик программы знает, чем занимается компью-
тер, когда происходит обычный вызов подпро-
граммы. В случае с прерыванием такого знания
нет. Поэтому при ответе на прерывание обычно
необходимо сохранить, по крайней мере, неко-
торую информацию, которая может понадо-
биться основной программе после возврата из
прерывания. В частности, микроконтроллер
8051 сохраняет слово состояния процессора
(ССП), которое состоит из флагов, отображаю-
щих результаты последних операций. Кроме
этого, подпрограмма обработки прерывания
может использовать несколько выделенных ра-
бочих регистров, переключаясь с набора реги-
стров, занятых основной программой, на один
из других четырех наборов.
Простейший отклик на прерывание:
автовекторизация8
Когда микроконтроллер 8051 реагирует на пре-
рывание (вопрос, будет ли он вообще отвечать
на него, рассматривается чуть далее), он сохра-
няет в стеке адрес возврата, а затем начинает ис-
полнять код, расположенный по выделенному
адресу, который связан с конкретным преры-
ванием. Такой адрес называется вектором пре-
рывания. Например, аппаратное прерывание
INTO* вызывает переход по адресу 03h, a INT1 * —
по адресу 13h. Для каждого прерывания по его
вектору выделяется 8 байтов для хранения его
подпрограммы ISR. Но если эта подпрограмма
не помещается в выделенные для нее 8 байтов
по вектору прерывания, тогда начальная под-
программа ISR в этих 8 байтах состоит просто
из команды перехода по адресу, где достаточно
места для размещения всего кода подпрограм-
мы обработки прерывания. Конечно же, такой
переход замедляет процесс обработки преры-
вания9.
Оригинальные версии микроконтроллера 8051
поддерживали два внешних прерывания. Мик-
роконтроллер производства компании Dallas
Semiconductor, которую мы используем в нашем
микрокомпьютере из дискретных компонен-
тов, поддерживает еще три. А вот разработчики
компании Silicon Laboratories расширили коли-
чество прерываний в своем микроконтроллере
C8051F410, добавив большое количество вну-
тренних источников прерываний.
Возможность выделения каждому прерываю-
щему устройству своего собственного выво-
да прерывания, существенно облегчает задачу
реагирования на них. Ответ на прерывание
INTO* помещается по адресу 03h, на прерывание
INT1* — по адресу 13h и т. д. В случае, если не-
скольким источникам необходима одна линия
запроса прерывания, то чтобы определить, ка-
кое из них создало его, требуется дополнитель-
ное аппаратное оборудование и немного про-
граммного кода
10
Эти два разных случая иллюстрируются на
рис. 23N.1.
Код для обработки совместного прерыва-
ния обязательно основан на методе опроса.
Поэтому реакция на такие прерывания не мо-
жет быть такой же оперативной, как в случае
с выделенными линиями. Между прочим, если
8 Compare PC104 vectoring, AoE §14.4.7.
9 Микроконтроллеры с архитектурой ARM реализуют
искусный вариант этой схемы перехода. Осознавая, что
такой переход занимает время, ARM-архитектура обеспе-
чивает одну беспереходную подпрограмму ISR для случая,
требующего самого быстрого реагирования. Этот вектор
FIQ (Fast Interrupt Response — быстрый отклик на преры-
вание) является последним в наборе векторов; все другие
векторы содержат команду перехода по адресу собственно
подпрограммы ISR. А подпрограмма обработки прерыва-
ния по вектору FIQ просто использует свободную память в
конце таблицы векторов прерываний.
10 АоЕ §14.4.8А.
23N.2. Прерывания
957
Просто реализовать, если каждое устройство
имеет свою линию запроса прерывания
ъ
8051
INT0
INT1
Не так просто в случае
общей линии запроса прерывания
+5 В
10 кОм<
8051
INT0
Р1.0
Адрес Адрес
03h [Код для обработки прерывания INTO*] 03h JNB P1.0. ЬОА; AA
13h ACALL DOB ACALL DOB ; если нет, тогда должно быть Б
RETT ^ DO/ ACALL ЬОА ; переходим к подпрограмме ISR для А
RETT
пи же переходим по адресу,
где достаточно памяти для
Рис. 23N.1. Обслуживание прерываний не представляет никаких трудностей, когда каждое устройство имеет свою собствен-
ную линию запроса прерывания, но более сложно, когда одна линия используется больше чем одним устройством
требуется наиболее быстрое реагирование, то
для перехода с вектора прерывания к собствен-
но подпрограмме ISR следует использовать ко-
манду JUMP, а не CALL. В таком случае команда
возврата с прерывания RETI завершит подпро-
грамму, к которой был выполнен переход по-
средством команды JUMP.
23N.2.3. Разрешение прерываний;
реагирование на перепад или
уровень
Разрешаем, когда готовы
По умолчанию после сброса все прерывания
отключены. Это логично, потому что обычно
для того, чтобы прерывания можно было обра-
батывать должным образом, необходимо вы-
полнить инициализацию компьютера. Только
когда все готово для того, чтобы процессор мог
принимать прерывания, их можно разрешать.
Это двухшаговая процедура:
1. Разрешаем определенное прерывание (на-
пример, внешнее прерывание INTO*).
2. После того как были разрешены все требуе-
мые конкретные прерывания, выполняем
глобальное разрешение прерываний11.
11 В микроконтроллере 8051 производства компании
Dallas Semiconductors прерывание по сбою питания, хотя
и требует явного разрешения, не зависит от глобального
разрешения прерываний ЕА.
Определяем тип прерывания: по перепаду сиг-
нала или по уровню. Первый вариант обладает
несколькими преимуществами по сравнению
со вторым.
♦ Прерывание по перепаду упрощает реагиро-
вание на одно событие ввода (например, на-
жатие кнопки или перепад прямоугольного
сигнала).
♦ В случае прерывания по перепаду компью-
тер запоминает запрос прерывания, который
он не смог обслужить. Например, компью-
тер может быть не в состоянии немедленно
отреагировать на прерывание, когда он на-
ходится в процессе обработки другого пре-
рывания. Но прерывание по перепаду будет
сохранено на триггере и будет доступно по
завершении этой обработки.
♦ Реагирование на прерывание по перепаду
автоматически обнуляет внутренний флаг
прерывания, который был установлен этим
прерыванием. Конечно же, такое обнуление
выполняется по завершении обработки пре-
рывания. А в случае прерывания по уровню
обнуление флага прерывания выполняется
специальной строкой кода. Ничего трудного,
но излишние хлопоты.
23N.2A Приоритеты прерываний
Если в компьютерной системе использует-
ся больше одного прерывания, то процессору
иногда будут одновременно поступать два или
958
23N. Микропроцессоры IV: прерывания; АЦП и ЦАП
больше запросов на прерывание. Какой из этих
запросов ему следует обрабатывать первым?
А если процессор уже обрабатывает один за-
прос на прерывание и получит другой запрос,
то должен ли он реагировать на второй? Если да,
то когда? Немедленно, бросив первый? После
завершения обработки первого? Каждый про-
цессор имеет свой подход к разрешению таких
конфликтов запросов на прерывание.
Процессор проверяет наличие запросов на пре-
рывание на позднем этапе каждого командного
цикла. Если он обнаруживает больше одного
запроса, то отвечает на тот из них, который
имеет более высокий приоритет. Но нам нужно
дать более точное определение термину «при-
оритет». Применительно к рассматриваемому
предмету приоритет может быть естественным
и запрограммированным.
Естественный приоритет прерываний
Уровни естественного приоритета присваи-
ваются произвольно нескольким источникам
прерываний. Микроконтроллер 8051 про-
изводства компании Dallas Semiconductor
(DS89C420/30) реализует 13 источников пре-
рываний, шесть из которых являются внеш-
ними. А микроконтроллер 8051 производства
компании Silicon Laboratories (C8051F410)
предоставляет 18 источников прерываний, два
из которых являются внешними.
По очевидным причинам в микроконтролле-
ре DS89C420 самый высший приоритет имеет
прерывание по сбою питания. Данное преры-
вание генерируется встроенной схемой мо-
ниторинга напряжения источника питания,
когда напряжение [7+ падает ниже +4,4 В.
Достаточно интересно, что в микроконтрол-
лере C8051F410 прерывание по сбою питания
имеет предпоследний приоритет. Каждому
прерыванию присваивается уровень приори-
тета. Например, прерывание INTO* имеет более
высокий приоритет, чем прерывания с боль-
шими номерами.
Каким образом учитывается приоритет пре-
рываний? Когда в процессе проверки наличия
прерываний процессор обнаруживает прерыва-
ния INTO* и INT1 *, первым он обрабатывает пре-
рывание INTO*. Пока что все это прямолиней-
но. Но что он делает по завершении обработки
прерывания INTO*, зависит от типа прерывания
INT1*: по перепаду или уровню.
Если это прерывание было по перепаду, тогда
(как отмечалось в разделе 23N.2.3) этот запрос
был сохранен внутренним триггером и будет
обработан сразу же после завершения обработ-
ки прерывания INTO*12. Если же запрос преры-
вания INT1* был по уровню, тогда после завер-
шения обработки прерывания INTO* он будет
проигнорирован, если только он не был снова
активирован (возможное, но не на 100% веро-
ятное развитие событий).
При использовании системы естественных
прерываний (которая задана по умолчанию),
никакое прерывание не может прервать обра-
ботку другого прерывания, даже если оно име-
ет более высокий приоритет, чем то, которое
обрабатывается.
Запрограммированные приоритеты
прерываний
Приоритеты запросов прерываний, присвоен-
ные по умолчанию, можно изменить. Например,
прерыванию INT1* можно назначить более вы-
сокий приоритет, чем прерыванию INTO*. Такое
присвоенное прерывание позволяет прерывать
обработку прерывания с более низким приори-
тетом, обработка которого продолжается после
завершения обработки прерывания с более вы-
соким приоритетом. Таким образом, подпро-
грамма ISR прерывания с более низким прио-
ритетом рассматривается так, как будто бы она
была основной программой.
23N.2.5. Разница между командами
RET v\ RETI
Для возврата из подпрограммы обработки пре-
рывания требуется не обычная команда воз-
врата из подпрограммы, а специальная команда
RETI. Это отличие объясняется необходимостью
отслеживать уровень текущего обслуживаемо-
го прерывания, что критически важно для реа-
лизации системы приоритетов прерываний.
Кроме выполнения таких же операций, что и ко-
манда возврата из обычной подпрограммы RET,
команда RETI обновляет информацию о теку-
щей исполняющейся подпрограмме обработки
12 Если вам интересны подробности, то по завершении
исполнения подпрограммы ISR управление возвращается
основной программе, где процессор исполняет одну ко-
манду, а затем переходит к подпрограмме обработки пре-
рывания INT1*.
23N.2. Прерывания
959
прерывания. Например, в конце исполнения
подпрограммы обработки прерывания INTO ко-
манда RETI создает возможность для обработки
прерывания INT1, тогда как при системе есте-
ственного приоритета прерываний при испол-
нении подпрограммы ISR для прерывания INTO
обслуживание было бы заблокировано.
Такую информацию можно назвать маской
прерываний, поскольку она определяет, отреа-
гирует ли процессор на другой запрос преры-
вания. Обеспечение обработки другого преры-
вания важно, например, в случаях, подобных
программе, рассматриваемой в разделе 23N.2.6,
где возможно одновременное возникновение
больше одного запроса на прерывание.
23N.2.6, Демонстрационная
программа по прерываниям
Чтобы придать этим теоретическим идеям не-
которую практическую направленность, рас-
смотрим следующую программу (листинг
23N.1), в которой прерыванию INT1* присвоен
приоритет более высокий, чем для прерывания
INTO*. (Программа бесполезна для какого-либо
применения, за исключением демонстрации
сложных подробностей запрограммированных
приоритетов прерываний.) В данной програм-
ме происходит конфликт двух прерываний:
одно увеличивает отображаемое значение, а
другое уменьшает его.
по
; INTPRIOR_D03.a51 Демонстрация запрограммированного приоритета прерывания
; Инкрементируем отображаемое значение по прерыванию INTO, декрементируем по прерыванию INT1
; Прерывание INT1 может прерывать подпрограмму ISR прерывания INTO
STACKBOT EQU 07Fh ; Размещаем стек в начале рабочего косвенно адресуемого блока памяти (80h и дальше)
ORGOh
UMP STARTUP
ORG ODOh
STARTUP: MOV SPr #STACKBOT
MOVDPTR,#8000h
; —ТЕПЕРЬ РАЗРЕШАЕМ ПРЕРЫВАНИЯ—
SETBITO ; Делаем INTO чувствительным к перепаду уровней
SETBIT1 ; То же самое и для INT1
SETB PX1 ; Присваиваем более высокий приоритет прерыванию INT1. (Регистр IP0 регистров SFR,
; см. руководство пользователя). Название взято из списка RIDE, "IP"..
SETB EXO ; И разрешаем прерывание INTO
SETB EX1 ; а также прерывание INT1
SETB EA ; Разрешаем глобальные прерывания
CLRA
; (Как обычно, для предсказуемого запуска)
STUCK: MOVX @DPTR, A; Отображаем постоянное значение, пока не будет инкрементировано прерыванием
SJMP STUCK ; (Реагирует на отрицательный перепад — псевдочувствительность к перепаду,
; поэтому необходимо подать несколько сигналов тактирования на высоком уровне, а затем на низком
; ISRO: Реагирование на INTO: Инкрементируем аккумулятор
ORG INT0VECTOR ; Это определяется в файле VECTORS3210.INC, который был включен выше.
; Это адрес 03h, по которому переходит программа в ответ на нулевое прерывание.
ISRO: NOP ; Бессмысленная операция — но предоставляет возможность для прерывания с более высоким
; приоритетом.
INCA
RETI
; ISR1: Реагирование на INT1: Декрементируем аккумулятор
ORG INT1 VECTOR ; Это определяется в файле VECTORS3210.INC, который был включен выше.
; Это адрес 13h, по которому переходит программа в ответ на прерывание INT1.
ISR1: NOP
DEC A
RETI
END
960
23N. Микропроцессоры IV: прерывания; АЦП и ЦАП
Поскольку эта программа меняет естественный
приоритет прерываний, прерывание INT1 будет
не только обрабатываться первым в случае од-
новременных запросов, но также сможет пре-
рывать подпрограмму обработки прерывания
INTO. Такая система отличается от естественной,
в которой текущей исполняющейся подпро-
грамме ISR всегда позволяется завершить свое
исполнение. Версия этой демонстрационной
программы для микроконтроллера C8051F410
дается на лабораторном занятии 23L.2. Ее
единственное отличие от данной состоит в том,
что в ней операции с дисплеем выполняются
без использования внешних шин.
23N.3. Обработка
прерываний в языке С
В листинге 23N.2 приведена программа на язы-
ке С, которая немного проще, чем программа
из раздела 23N.2.6. В ней используется только
одно прерывание INTO*, для инкрементирова-
ния значения, отображаемого на дисплее.
Программа на языке С выглядит сложнее,
чем на ассемблере. Но ее инициализации вы-
глядят во многом подобно инициализациям
в программе на ассемблере. Инициализации
Листинг 23N.2. Демонстрационная программа по прерываниям на языке С
// interrupt.testx Инкрементирует отображаемое на дисплее значение даже проще, чем программа из раздела 23N.2.6
#indude<C:\MICRO\8051\RAISON\INC\REG320.H>
data volatile char counter; // Данная 8-разрядная переменная будет храниться во встроенной памяти
// микроконтроллера
// Другой байт, на который указывает указатель display
// Инициализация: данная строка дает предупреждение компилятору о наличии данной
// функции — поскольку она определяется только после основной программы main
xdata char ^display;
void setupExO (void);
void main (void)
{
setupExOO;
while (1)
"display = counter; // Отображаем на дисплее текущее значение, инкрементируем его только по прерыванию
/* Внешнее прерывание 0 */
void it_extO (void) interrupt 0 using 1 // Используем блок регистров 1 для переключения контекста
// В данном случае в этом нет надобности, просто для выработки хороших навыков
{
counter++; // Подпрограмма ISR просто инкрементирует переменную counter, значение которой
// выводится на дисплей (она не отображает его)
void setupExO (void)
display = 0x8000; // Указатель на дисплей
"display = 0; // Начальное обнуление дисплея
counter = 0; // Также начальное обнуление регистра счетчика
ЕХО = 1; // Разрешаем внешнее прерывание INTO
1Т0 = 1; // Делаем его чувствительным к перепаду уровней
ЕА = 1; // Разрешаем глобальные прерывания
23NA. Сопряжение АЦП и ЦАП с микроконтроллером
961
прерываний, например ЕА = 1, очень похожи на
соответствующие инициализации на языке ас-
семблера, где используется команда SETB ЕА.
Но строка кода в начале подпрограммы ISR
выглядит непонятно: void it_extO (void) inter-
rupt 0 using 1. Она означает, что данная функ-
ция расположена по вектору interrupt 0; а фраза
using 1 означает, что нужно переключиться на
другой банк рабочих регистров: выбрать банк
№ 1 вместо банка № 0. В данном случае этот
код не является обязательным; мы включили
его лишь для того, чтобы напомнить о такой
возможности. Такая же возможность доступна
и в ассемблере, но мы ею не воспользовались.
Причиной для такого частичного переключения
контекста было желание сэкономить немного
времени. Вместо того, чтобы сохранять в стеке
несколько регистров, содержимое которых мо-
жет быть искажено подпрограммой обработки
прерывания, используя для этого несколько
команд PUSH, мы просто переключаемся одной
командой на новый банк регистров. Но в дан-
ном случае не было надобности сохранять реги-
стры. Все, что данная подпрограмма ISR делает,
так это инкрементирует одну переменную. Но
обратите внимание, что переключение банков
регистров переключает контекст лишь частич-
но, поскольку многие регистры нельзя пере-
ключить на другие. Например, для регистров
А (аккумулятор) и DPTR нет альтернативных
версий, подобно восьми рабочим регистрам.
Поэтому, если эти регистры задействованы в
подпрограмме ISR, их содержимое необходимо
сохранить в стеке командой PUSH.
Хотя подпрограмма ISR и не использует ре-
гистр А, компилятор С сохраняет его автома-
тически. Листинг 23N.3 содержит код подпро-
граммы ISR на языке ассемблера, созданной
компилятором.
Листинг 23N.3. Код программы на ассемблере,
созданный компилятором
; FUNCTION it.extO (BEGIN)
; SOURCE LINE # 23
0000 COEO PUSHACC
0002 CODO PUSHPSW
0004 75D008 MOV PSW,#008H
; SOURCE LINE #27
0007 0500 R INC counter
0009 DODO POPPSW
OOOBDOEO POPACC
; SOURCE LINE #28
000D 32 RETI
Переключение на банк регистров №1 реали-
зуется операцией PUSH, загрузкой и операцией
POP над регистром PSW (Program Status Word —
слово состояния программы). Очевидно, что
в данном случае переключение банков реги-
стров только расходует время понапрасну.
23N.4. Сопряжение АЦП
и ЦАП с микроконтроллером
Мы знаем, что для компьютера, который ис-
пользует внешние шины (как это делает наш
компьютер из дискретных компонентов), для
ввода данных в процессор требуется посредни-
чество буфера с трехстабильными выходами,
а для подачи входного сигнала на ЦАП необхо-
дим промежуточный регистр. Даже если вы на
лабораторных занятиях по микрокомпьютеру
экспериментируете с компьютером на автоном-
ном микроконтроллере C8051F410, который
содержит встроенные АЦП и ЦАП, рассмотри-
те случай с использованием внешних шин, по-
скольку в нем рассматриваются моменты, ко-
торые вследствие высокой степени интеграции
микроконтроллера C8051F410 скрыты от поль-
зователя.
Кроме входных и выходных буферов (первый с
выводами с тремя состояниями, а второй про-
стой регистр) добавим к интерфейсу АЦП две
довольно стандартные возможности:
♦ функцию START, позволяющую микроконт-
роллеру определять, когда начинать аналого-
цифровое преобразование. Для этой цели
АЦП требуется лишь короткий импульс;
♦ генерируемый АЦП сигнал завершения
DONE*, который нам нужно будет преобразо-
вать во флаг. Назовем этот флаг NEW_DATA.
Используя внешние шины, импульс START мож-
но легко сформировать: для этого подойдет
любая линия декодера ввода-вывода. В нашем
лабораторном компьютере для реализации
этого подхода можно выбрать линию OUT3*13.
Поскольку нам требуется только импульс, а не
постоянный уровень, это тот редкий случай,
когда нам не нужен триггер или регистр, кото-
рый обычно необходим для захвата входного
сигнала. В нашем случае выход, который нужно
13 На лабораторном занятии мы инвертируем сигнал
OUT3*, чтобы удовлетворить специфическое требование
аналого-цифрового преобразователя AD7569: в состоянии
покоя сигнал START* должен быть низкого уровня, хотя
АЦП реагирует на отрицательный перепад уровней.
962
23N. Микропроцессоры IV: прерывания; АЦП и ЦАП
захватить, отсутствует. Хотя при исполнении
операции вывода OUT данные подаются на шину
данных, в описанном случае они никуда не идут
и пропадают.
При использовании внешних шин импульс
можно отправить простой командой MOVX @
DPTR, А. Но при работе со встроенным портом
-оитз
Шина данных
(скажем, портом Р3.1) для этого потребуются
две команды: CLR P3.1 и SETB P3.1.
Аппаратное обеспечение для реализации флага
вам уже знакомо — такое же, как и для кнопки
Ready из лабораторного занятия 22L. В дан-
ном случае импульс DONE* мог бы создаваться
сигналом установки SET* триггера, поскольку
длительность этого импульса очень мала и к
тому времени, когда процессор будет пытаться
выполнить сброс триггера, он уже закончится
(тогда как палец будет, вероятно, оставаться на
кнопке долгое время после попытки сброса).
23NA1. Микросхема АЦП и ЦАП
AD7569
Микросхема, которую мы добавим к нашему
компьютеру на большой макетной плате на ла-
бораторном занятии 23L, реализует все, что мы
Источник опорного
напряжения, определяемого
шириной запрещенной зоны
Контур
диапазона
П диапазонам
Рис. 23N.2. Подключение АЦП и ЦАП при работе с внешни-
ми шинами
21 только что спроектировали,
~~и " ч как будто бы ее разработ-
чики подсматривали, когда
мы рисовали рис. 23N.2, на
котором изображена блок-
схема внутреннего устрой-
ства этой микросхемы.
На рис. 23N.4 показано
подключение микросхемы
ADC7569 к нашему ком-
пьютеру из дискретных
компонентов.
Диапазон Управляющая
Прерывание логическая
Занято схема
ffl-f--'
1811"Я 16T15r
Рис. 23N.3. Блок-схема внутреннего устройства микросхемы AD7569 во многом похожа на нашу самодельную схему АЦП и ЦАП
Сигнал RD* включает
внутренний буфер ^^
с трехстабильными выходами
подавая данные выборки
Шина данных ЦП
Диапазон
Сброс
Цифровая «земля»
t—
Аналоговый вход
От 0 до +2,5 В
Аналоговый вход
От 0 до +2,5 В
a Начало
^ преобразования
^Комбинированный ]
,АЦП/ЦАП
Не используется
Д Занят
Л Прерывание
тактирования АЦП
INT* — флаг, который
устанавливается по
завершении преобразования.,
т
Фиксирует данные на шине
данных в регистре ЦАП по
положительному перепаду
сигнала WR*
Данная RC-цепь задает частоту внутреннего
генератора тактовых сигналов (эти значения
обеспечивают максимальную частоту)
Рис. 23N.4. Подключение микросхемы AD7569 к нашему компьютеру из дискретных компонентов
23N.4. Сопряжение АЦП и ЦАП с микроконтроллером
963
Мы не используем флаг INT* микросхемы
AD7569 по той причине, что этот АЦП работа-
ет достаточно быстро (1,6 мкс), и поэтому нет
большого смысла прерывать его, спрашивая,
готов ли он. Данный процесс занимает некото-
рое время, поэтому ответ всегда будет положи-
тельным14.
Название INT* для данного сигнала определен-
но намекает на то, что он служит для преры-
вания процессора. Но мы не использовали его
таким образом по той же самой причине, по
которой мы не реализовали опрос вывода INT.
Из-за задержки отклика на запрос прерывания,
которая упоминалась ранее в разделе 23N.2.1,
операция прерывания намного медленнее, не-
жели код, который пользуется задержками при
исполнении программы, чтобы вовремя выпол-
нить преобразование15. Если бы между нача-
лом работы и чтением эта программа не делала
ничего особенного, то при рабочей частоте в
11 МГц процессор мог бы опередить АЦП. Но
программу можно легко написать так, чтобы
на протяжении интервала времени, в течение
которого осуществляется аналого-цифровое
преобразование, она выполняла какие-либо
другие полезные операции.
Программа должна обеспечить
достаточное время для преобразования
Например, на лабораторном занятии 23L, что-
бы предоставить достаточное время для выпол-
нения преобразования, на каждом прерывании
мы считываем АЦП, прежде чем запускать его,
а затем запускаем преобразователь для следую-
щего прохода. Таким образом, между запуском
и чтением выполняются не только вспомога-
тельные операции по обработке прерывания
(такие как сохранение в стеке адреса возвра-
та и чтение его из стека), но также все другие
операции, которые должна выполнять основ-
ная программа. В листинге 23N.4 приведена
14 Переназначение регистра DPTR на порт флага INT*, ввод
значения и проверка его занимают около 3 мкс, а восста-
новление указателя увеличивает время до около 4 мкс, что
не идет ни в какое сравнение с 1,6 мкс, в которые уклады-
вается АЦП. (Эти значения предполагают частоту такти-
рования 11,059 МГц, как в нашем лабораторном компью-
тере.)
15 В зависимости от операции, которую выполняет про-
цессор в момент поступления запроса на прерывание, от-
клик на него занимает от 1 до 2 мкс (при рабочей частоте
процессора 11 МГц). Если же, как обычно требуется, со-
хранять регистры, которые будут использоваться подпро-
граммой ISR, то время отклика будет еще больше.
подпрограмма обработки прерывания, которая
считывает АЦП, записывает данные в ЦАП и
запускает преобразователь для следующего
прохода. Данная подпрограмма ISR сначала
используется для простой программы ввода-
вывода, которая позволяет исследовать эффек-
ты выборки.
Данная программа использует компактные
команды MOVX @Rn, а не обычные команды
ввода-вывода с применением регистра DPTR.
Если это выглядит для вас незнакомо, допол-
нительную информацию можно найти в гла-
ве 21S. Подобное использование команд MOVX
@Rn предполагает предварительную инициа-
лизацию указателей, как показано в листин-
ге 23N.5.
Листинг 23N.4. Подпрограмма обработки
прерывания для АЦП
; ВЕКТОР ДЛЯ ПРЕРЫВАНИЯ
ORG INT0VECTOR
ISR: MOVX A, @R1 ; Считываем АЦП (данные первого
; прохода недействительные, всех
; остальных проходов — действительные)
MOVX @R1 ,A ; Запускаем АЦП для следующего прохода
MOVX @R0, A ; Отправляем выборку на ЦАП
RETI
Сигналы управления АЦП в действии
Следующая далее демонстрационная програм-
ма практически такая же, хотя в ней не ис-
пользуется прерывание. Она запускает АЦП и
считывает его данные. Как можно видеть по
осциллограммам данного цикла на рис. 23N.5,
он обеспечивает как раз достаточно времени
для выполнения преобразования.
Листинг 23N.5. Программа для управления
АЦП и ЦАП
MOV P2, #80h ; Инициализируем старший байт
; адреса порта (базовый адрес ввода-вывода)
MOV R1, #03п ; Младший байт: АЦП (как для запуска,
; так и для данных: вывод и ввод)
TRANSFER: MOVX Af@R1; Считываем АЦП (первый проход,
; недействительные данные)
MOVX @R1, A; Запускаем АЦП для следующего прохода
MOVX @R0, A; Отправляем выборку на ЦАП
SJMP TRANSFER
964
23N. Микропроцессоры IV: прерывания; АЦП и ЦАП
Значение достаточно бесполезного сигнала
BUSY* содержится в его названии (busy — за-
нят). A INT* представляет собой флаг, который
почти идентичен флагу, созданному нами в
нашей самодельной схеме АЦП на рис. 23N.2.
Отличается он только тем, что обнуляется не
активированием сигнала чтения данных (сиг-
нал RD*, но не такой, как сигнал RD* процессо-
ра), а положительным перепадом при заверше-
нии этого сигнала.
START
BUSY*
2.901*5
ft
RD*
Период времени между
курсорами (START по RD*) как
раз достаточен для того, чтобы
выполнить преобразование
Рис. 23N.5. Циклические сигналы управления преобразова-
теля AD7569. (Разрешение осциллографа: 2 В/дел., 1 мкс/дел.)
23МА2.АЦПиЦАПна
микроконтроллере С8051F410
Подобно другим периферийным устройствам,
устройства АЦП и ЦАП интегрированы в ми-
кроконтроллер C8051F410. Подробная инфор-
мация об этих устройствах излагается в разде-
ле 23L.2. Возможность выравнивания значений
преобразователей по левой границе двухбай-
тового слова позволяет использовать их как
8-разрядные или 12-разрядные устройства.
Этот аспект рассматривается чуть далее.
Запуск и завершение преобразования в
АЦП/ЦАП микроконтроллера С8051F410
Подобно микросхеме AD7569, аналого-циф-
ровой преобразователь микроконтроллера
C8051F410 необходимо запускать (положи-
тельным перепадом на линии внутреннего
регистра: бит 4 регистра AD0CN). Также наши
программы из лабораторных занятий тестиру-
ют бит флага, чтобы определить завершение
преобразования. Для этого используется экви-
валентный флагу INT* преобразователя AD7569
бит 5 регистра AD0CN. Как и в нашем самодель-
ном преобразователе, и в микросхеме преобра-
зователя AD7569 состояние ЦАП обновляется
по положительному перепаду.
Диапазоны напряжений АЦП и ЦАП
микроконтроллера С8051F410
Диапазоны напряжений АЦП и ЦАП слегка от-
личаются от соответствующих характеристик
для преобразователей на микросхеме AD7569.
В частности:
Диапазон напряжений для АЦП: для АЦП
микроконтроллера C8051F410 — с 0 до 2,2 В,
по сравнению с 0 до 2,55 В для АЦП на микро-
схеме AD7569.
Диапазон напряжения для ЦАП: для ЦАП
микроконтроллера C8051F410 — с 0 до 1,3 В
(на лабораторном занятии мы ограничим мак-
симальное напряжение до 1,2 В), по сравнению
с 0 до 2,55 В для ЦАП на микросхеме AD7569.
Разрешение преобразователей
микроконтроллера C8051F410
Преобразователи этого микроконтроллера под-
держивают 12-разрядное разрешение, но на на-
ших лабораторных занятиях мы почти всегда
используем их как 8-разрядные устройства16,
поскольку создаваемые нашими макетными
платами помехи обычно забивают младшие че-
тыре разряда.
Получение 8-разрядного разрешения
от 12-разрядного устройства
В разделе 23L.2 мы увидим, как при желании
младшие четыре бита устройства можно легко
16 Но мы предлагаем вам убедиться в возможности каче-
ственного 12-разрядного разрешения, считывая выход
ЦАП с помощью цифрового вольтметра, остановив испол-
нение программы посредством контрольной точки непо-
средственно после операции записи ЦАП. Этот не слиш-
ком изящный способ применения ЦАП дает цифровому
вольтметру время устранить помехи из выходного сигнала
ЦАП методом усреднения. Когда мы реализовали такое
преобразование, то обнаружили, что разрешение млад-
шего разряда составляло 0,5 мВ. Без такого интенсивного
усреднения ни ЦАП, ни АЦП микроконтроллера не могут
обеспечить 12-разрядное разрешение просто вследствие
помех, создаваемых самим микроконтроллером, даже не
учитывая помех, создаваемых собранными на макетной
плате схемами.
23N.4. Сопряжение АЦП и ЦАП с микроконтроллером
965
игнорировать. Эта легкость объясняется тем,
что, как показано на рис. 23L.9, у нас есть воз-
можность выбрать способ выравнивания 12-
разрядного значения в 16-разрядном байте.
В частности, выбрав выравнивание по левому
краю слова, мы можем использовать восемь
старших битов, игнорируя младшие четы-
ре. Таким образом, мы можем работать с 12-
разрядными преобразователями, как будто они
8-разрядные устройства17.
23N A3. Программа
Код собственно программы
преобразования прост
Код для взятия выборки из АЦП микроконтрол-
лера C8051F410 очень простой: начинаем пре-
образование, ждем, пока не будем проинформи-
рованы, что выборка готова, берем отсчеты.
Листинг 23N.6. Программа взятия выборки
из АЦП микроконтроллера C8051F410
GET.SAMPLE: CLR CNVRT_START ; Низкий уровень
; на AD0BUSY (чтобы разрешить положительный
;перепад)
SETB CNVRT_START ; Положительный перепад
; на ADOBUSY начинает процесс
; преобразования
JNB CNVRSN_DONE, $ ; Ждем здесь, пока не будет
; установлен флаг завершения преобразования
MOV SAMPLEJHI, ADC0H ; Теперь берем старший
; байт из АЦП и сохраняем его
RET
Команда JNB CNVRSN_DONE, $ содержит услов-
ное обозначение, которое вам, возможно, не-
знакомо. В частности, символ доллара $ озна-
чает «данная строка кода». Таким образом,
до тех пор, пока тестируемый бит содержит
нулевое значение, данная команда выполняет
переход сама на себя. Программа GET_SAMPLE
также содержит пару команд, которые обе-
спечивают положительный перепад на бите,
который запускает процесс преобразования,
а также тестовый цикл, реализующий задержку
до тех пор, пока не будет готова выборка. Биты
CNVRT_START и CNVRT_DONE определяются, как
обычно, в начале программы (эти определения
в листинге не показаны).
Инициализация сложнее самой
программы
Как обычно, у нас есть множество опций для
инициализации регистров. Подробности изло-
жены в табл. 23N.1. Чем сложнее периферий-
ное устройство, тем более трудоемка инициа-
лизация.
Таблица 23N.1. Инициализация регистров
17 Перфекционисты могут возразить, что значение следу-
ет округлять до восьми старших разрядов, в зависимости
от значения четырех младших разрядов — больше или
меньше их среднего значения. Но мы не перфекционисты
и делать это на лабораторном занятии 23L.2 не будем.
Регистр
ADC0CN
ADC0MX
ADC0TK
ADC0CF
РО
P0MDIN
POSKIP
REFOCN
Значение
бита/
байта
d7
d5
d4
d2
dl,dO
00b
02h
d3...dO
FBh
d2,dl
00b
d2,dl
0F9h
46h
13h
Функция
Разрешение ADCO: ==> раз-
решение
ADOINT: 1 ==> выборка го-
това (это флаг, который мы
проверяем)
ADOBUSY: положительный
перепад начинает процесс
преобразования
ADOLJST: 1 ==> выравни-
вание значения по левому
краю слова
Выборка события, запускаю-
щего преобразование
Выборка положительного
перепада на ADOBUSY
как события, начинающего
процесс преобразования
Назначение мультиплексора
ADC0 ==> биту Р0.2
Режим отслеживания
Двойной режим3
Количество преобразований
за цикл «запуск - преобра-
зование»
==> одна выборка/цикл
«запуск — преобразование»
Оба бита установлены, что-
бы задать для защелки сла-
бую подтяжку по питанию
Для выводов АЦП и ЦАП
задан аналоговый режим
(Р0.2,Р0.1)
пропускаем ЦАП и АЦП,
d2, dl
Разрешение U3V установка
полной шкалы на 2,2 В
а Значение взято из примера программы для АЦП микро-
контроллера C8051F410.
966
23N. Микропроцессоры IV: прерывания; АЦП и ЦАП
Использование Мастера настроек
значительно облегчает инициализацию
Задачу настройки параметров регистров для
АЦП и ЦАП можно немного упростить, за-
I Разрешаем
§ матричный
| переключатель
Задаем аналоговый режим
для выводов ДЦТТ и УЭТ
Рис. 23N.6. В Мастере настроек задаем аналоговый режим для выводов АЦП и U3J
давая их с помощью Мастера настроек. На ри-
сунках 23N.6-23N.8 показано использование
этого мастера для выполнения более простой
задачи настройки АЦП (но даже это не так
просто).
Порт ввода-вывода
Прежде всего мы задаем для
входа АЦП (РОЛ) аналоговый
режим и делаем то же самое для
вывода иэт (Р1.2). Как обычно,
также включаем матричный пе-
реключатель, что является обя-
зательным для любых опера-
ций ввода-вывода.
Дополнительные настройки
АЦП
Затем задаем дополнительные
настройки: выравнивание зна-
чения по левому краю слова,
способ запуска АЦП, а также
его эталонное напряжение иэт
(рис. 23N.7). Все еще довольно
трудоемкий процесс, но проще,
чем работать с отдельными би-
тами, постоянно заглядывая в
справочный листок.
у порта
Разрешаем запуск АЦГК'
Задаем метод запуска А ЦП
ю левому краю слова
Рис. 23N.7. Дополнительные настройки АЦП, задаваемые посредством Мастера настроек
23N.5. Некоторые подробности о лабораторных занятиях по АЦП/ЦАП
967
Наконец, задаем эталонное напряжение, опре-
деляющее диапазон полной шкалы значений
АЦП(рис.23Ы.8).
из ветвей лабораторных занятий по микроком-
пьютерам: как с компьютером из дискретных
компонентов, так и с компьютером на основе
автономного микроконтроллера C8051F410.
Рис. 23N.8. Определение диапазона значений АЦП через
меню эталонных напряжений в Мастере настроек
23N.5. Некоторые
подробности о лаборатор-
ных занятиях по АЦП/ЦАП
Почему эта информация
рассматривается здесь?
Здесь мы излагаем такие подробности, которые
обычно оставляем в разделах по лабораторным
занятиям. Это объясняется тем, что мы хотим,
чтобы эту информацию можно было приме-
нить в экспериментах с АЦП и ЦАП в любой
+5 В
Частота f
OUT
выо
Микросхема МАХ294 с коммутируемым
конденсатором в качестве
низкочастотного фильтра для ЦАП
Как мы имели возможность убедиться по де-
монстрационным осциллограммам в главе 18N,
качественный НЧ-фильтр на выходе ЦАП
может сгладить восстановленный ступенча-
тый сигнал. А на лабораторном занятии 12L
мы имели возможность познакомиться с НЧ-
фильтром на микросхеме МАХ294, обладаю-
щим крутой характеристикой.
Этот фильтр хорошо подходит для нашей теку-
щей задачи, поскольку мы можем легко настро-
ить его частоту^. Определяется ли частота/3дБ
данного фильтра его частотой тактирования?
Да, это фильтр с коммутируемым конденсато-
ром, с принципом действия которого мы озна-
комились на лабораторном занятии 12L.
Подключение микросхемы фильтра МАХ294
показано на рис. 23N.9. Делитель напряжения
формирует псевдопотенциал «земли» посере-
дине диапазона 0-5 В напряжения питания.
Это позволяет подавать на фильтр входной
униполярный сигнал (в диапазоне 0-2,3 В для
микроконтроллера C8051F410 и в диапазоне
0-2,55 В для микроконтроллера DS89C420).
Входной сигнал подается на фильтр через раз-
делительный конденсатор и со смещением по
постоянному току. Это объясняется тем, что
потенциал «земли» находится вне диапазона
входных напряжений фильтра: пределы вход-
ного сигнала должны находиться на расстоянии
Амплитудно-частотная
характеристика фильтра МАХ294
; 10 кОм
our
> 10 кОм
1
и
.1*
to
0 1 2 3 4 5
Частота входного сигнала (кГц)
Рис. 23N.9. Низкочастотный 8-полюсный эллиптический фильтр с коммутируемым конденсатором на микросхеме МАХ294
968
23N. Микропроцессоры IV: прерывания; АЦП и ЦАП
около 1В от отрицательного и положительного
напряжений питания (в данном случае отри-
цательным напряжением является потенциал
«земли»)18. В данном случае смещенный вход-
ной сигнал, отцентрированный по напряжению
2,5 В, отвечает этому требованию.
На графике амплитудно-частотной характе-
ристики фильтра на рис. 23N.9 его частота^
показана равной 1 кГц, но, если вы вспомните
материал из лабораторного занятия 12L, эту
частоту можно установить любой в широком
диапазоне (от 100 Гц до 25 кГц для микросхемы
МАХ294).
Этот качественный фильтр, обладающий кру-
той характеристикой, позволяет осуществлять
выборку с довольно низкой частотой. На
рис. 23N.10 изображен график восстановления
исходного синусоидального сигнала из выход-
ного сигнала ЦАП, который выглядит доволь-
но урезанным.
Входной
аналоговый
сигнал
Выходной
нал ЦАП (вос-
становленный
АЦП ~> ЦАП)
Выходной
сигнал ЦАП
после низко-
частотного^
фильтра ;;;; ;;;:;;__ ш tttlI, ;'*"*">
Рис 23N.10. Качественный восстанавливающий НЧ-фильтр
удаляет побочные сигналы даже при низкой частоте вы-
борки
Дополнительным преимуществом фильтра
МАХ294 для нашего применения является то
обстоятельство, что мы можем легко управлять
его частотой/3дБ (которая обычно называется
частотой среза). Подача сигнала тактирования
от генератора сигналов позволит с легкостью
управлять его амплитудно-частотной характе-
ристикой фильтра.
18 Требование, чтобы входной сигнал не приближал-
ся слишком близко к напряжениям питания, излагается
в справочном листке на микросхему МАХ294 косвенно.
В частности, информация по применению для динамиче-
ского диапазона входного сигнала отсылает пользователя
к графику типичного искажения в зависимости от ампли-
туды сигнала.
23N.5.L Использование ФАПЧ
для настройки частоты
тактирования фильтра
Вспомните (по разделам 18L.23 и 19L.1.3), что
система фазовой автоподстройки частоты мо-
жет вырабатывать сигнал тактирования филь-
тра, частота которого соответствует частоте
выборки вашего компьютера. Если частота вы-
борки задается сигналом от внешнего генера-
тора, подаваемым на вход прерывания, этот же
сигнал можно также подавать и на вход ФАПЧ.
Система ФАПЧ может генерировать сигнал
тактирования для фильтра МАХ294 с часто-
той, кратной частоте выборки.
23ISL5.2. Усилитель звуковой
частоты
Микросхема УЗЧ LM386
Создаваемые в процессе выборки эффекты,
т. е. вносимые побочные сигналы, можно про-
слушивать, что может быть в некоторой степе-
ни развлекательно. Волею случая у вас посто-
янно при себе очень эффективный анализатор
частотного спектра — ваши уши. Было бы грех
не воспользоваться такой врожденной возмож-
ностью. Для этого подайте выходной сигнал
сглаживающего фильтра ЦАП на вход усили-
теля звуковой частоты с подключенным к нему
динамиком с сопротивлением катушки 8 Ом.
(Выходной сигнал фильтра МАХ294 слишком
слаб для прослушивания на динамике напря-
мую.) В качестве такого УЗЧ хорошо подойдет
микросхема LM386.
Предварительные условия
Для обоих устройств с однополярным пита-
нием необходимо заблокировать смещение по
постоянному току. Это объясняется тем, что
наш источник сигнала (с восстанавливающего
фильтра МАХ294) является униполярным (от-
центрированным по 2,5 В) и таким же являет-
ся выход микросхемы LM386 со встроенным
смещением. Чтобы устранить это смещение по
постоянному току, необходимо добавить два
разделительных конденсатора. На рис. 23N.11
показана цоколевка микросхемы УЗЧ LM389 и
ее типичное подключение.
23N.5. Некоторые подробности о лабораторных занятиях по АЦП/ЦАП
969
г Усилитель звуковой частоты
с минимальным количеством
деталей и коэффициентом
усиления, равным 20
Рис. 23N.11. Микросхема усилителя звуковой частоты
LM386
На усилитель LM386 следует подавать мало-
мощный входной сигнал, симметричный от-
носительно потенциала «земли», что ввиду его
однополярного питания необычно19. Поэтому
выходной сигнал фильтра МАХ294 подаем на
потенциометр регулировки громкости номина-
лом 10 кОм через разделительный конденсатор.
Разделительный конденсатор между выходом
усилителя LM386 и динамиком должен быть
очень большой емкости, поскольку совместно с
очень низким сопротивлением динамика вели-
чиной 8 Ом он также играет роль высокочастот-
ного RC-фильтра. Также не забудьте выполнить
развязку источника питания усилителя LM386,
используя для этого как керамический кон-
денсатор емкостью ОД мкФ, так и танталовый
конденсатор емкостью как минимум 1 мкФ,
установив их как можно ближе к выводу пита-
ния микросхемы. Микросхема LM386 предрас-
положена к паразитным автоколебаниям.
23N.53. Используем импульсный
усилитель из лабораторного
занятия 12L
Для прослушивания эффектов дискретизации
вместо усилителя LM386 можно взять импульс-
ный усилитель LM4667, с которым мы познако-
мились на лабораторном занятии 12L. Но этот
усилитель более мощный, чем LM386, поэтому
целесообразно ослабить подаваемый на него
сигнал с восстанавливающего фильтра ЦАП,
используя для этого потенциометр, показан-
ный в схеме на рис. 23N.11. Также, возможно,
нужно будет установить два последовательных
разделительных конденсатора. Первый из них
(как в схеме на рис. 23N.11) нужен для того,
чтобы понизить смещение сигнала и отцентри-
ровать его относительно потенциала «земли»,
а другой — для передачи его на ненулевое на-
пряжение смещения на выводе 2 микросхемы.
Входное сопротивление этого усилителя со-
ставляет 90 кОм20. Схема подключения микро-
схемы импульсного усилителя LM4667 изобра-
жена на рис. 12L.15.
Скорее всего, эта схема будет создавать им-
пульсные шумовые помехи, но они будут едва
слышимы21.
Множество генераторов сигналов
за работой
Теперь нам нужны три генератора сигналов.
Самый легкий способ выполнить это требо-
вание — использовать три генератора сигна-
лов, если у вас есть такое количество этих
устройств. Но если вы не располагаете такой
роскошью, тогда можно собрать схему генера-
тора колебаний на таймере 555, чтобы исполь-
зовать ее в качестве источника прямоугольного
сигнала тактирования для фильтра. Примеры
типичных схем на таймере 555 можно найти в
главе 8L. Частоту выходного сигнала генерато-
ра сигналов на таймере 555 следует сделать на-
страиваемой в диапазоне 10-500 кГц. На схему
нужно подавать питание величиной 5 В.
Далее приводится краткое описание сигналов,
которые нужно генерировать.
Аналоговый вход
В качестве источника входного синусоидально-
го сигнала используйте имеющийся генератор
сигналов. Опять же, удостоверьтесь в том, что
уровни этого сигнала находятся в пределах до-
пустимого диапазона уровней входного сигна-
ла АЦП: 0-2,55 В для АЦП компьютера из дис-
кретных компонентов или 0-2,3 В для компью-
тера на основе автономного микроконтроллера
C8051F410. Повредить АЦП можно, только
если уровень его входного сигнала превышает
19 Данный усилитель может работать с входными сигна-
лами напряжением до 0,4 В ниже его напряжения отрица-
тельного питания, которым обычно является потенциал
«земли».
20 В справочном листке микросхемы это сопротивление
называется дифференциальным входным сопротивлением
(differential input resistance).
21 В схеме, реализованной на качественно разведенной
печатной плате, эти помехи вообще не будут заметны. Но
в нашем случае, когда схема собрана на макетной плате,
эти помехи могут быть слышны.
970
23N. Микропроцессоры IV: прерывания; АЦП и ЦАП
напряжение его источника питания — от 0 до
+5 В. Также не забудьте включить смещение по
постоянному току на генераторе сигналов.
Сигнал тактирования выборки
Источником этого сигнала, подаваемого на вход
запроса прерывания INTO* микроконтроллера
8051, может служить генератор сигналов ма-
кетной платы. При желании этот сигнал можно
наблюдать на цифровом вольтметре, оснащен-
ном частотомером.
Сигнал тактирования фильтра
Для подачи сигнала тактирования на фильтр
МАХ294 требуется еще один, третий, генера-
тор сигналов. Как уже упоминалось чуть ранее,
в качестве такого источника подойдет само-
дельный генератор сигналов на таймере 555.
Частота генератора сигналов на макетной плате
слишком низкая для этих целей. Максимальная
частота этого генератора сигналов составляет
100 кГц, что подразумевает максимальную ча-
стоту отсечки фильтра величиной всего лишь
1кГц.
23N.5A Преобразование сигналов
разных типов
Очевидным первым кандидатом для пропуска-
ния через наше АЦП-ЦАП устройство будет
синусоидальный сигнал (источником которого,
как упоминалось ранее, служит автономный ге-
нератор сигналов). Такой сигнал одной частоты
облегчает понимание процесса дискретизации.
(Если вы забыли, какие эффекты можно ожи-
дать, то можете освежить свои знания в этой
области, обратившись к главе 18S.)
Наэкспериментировавшись с синусоидальным
сигналом, вы можете захотеть узнать, какие
будут эффекты дискретизации в случае более
сложного сигнала, например музыкального.
В частности, наложение спектров ложных сиг-
налов при дискретизации такого исходного
сигнала создает причудливые эффекты благо-
даря инверсии частотного спектра всех ложных
сигналов.
Некоторые также получают удовольствие от
прослушивания эффектов дискретизации свое-
го собственного голоса. Вы можете удивиться,
насколько низкую частоту выборки можно ис-
пользовать для дискретизации голоса и при
этом получить понятную восстановленную
речь. Например, при наличии восстанавливаю-
щего фильтра МАХ294 мужскую речь можно
дискретизировать с частотой выборки намно-
го ниже 1 кГц. (Для дискретизации женского
голоса требуется несколько большая частота
выборки.) Для дискретизации своего голоса
используйте микрофонный усилитель, собран-
ный вами на лабораторном занятии 7L. Его вы-
ходной сигнал, отцентрированный по уровню
1,25 В, можно подавать напрямую на АЦП как
компьютера из дискретных компонентов, так и
компьютера на автономном микроконтроллере
C8051F410.
23N.6. Предлагаемые
лабораторные задания при
экспериментах с АЦП и ЦАП
Верна ли теорема Найквиста?
Ответ на этот вопрос должны дать ваши уши.
Если вы хотите выполнять дискретизацию на
частоте выборки, близкой к минимальной,
то может быть полезным наблюдать (напри-
мер, на цифровом мультиметре, оснащенным
функцией частотомера) частоту как входного
синусоидального сигнала, так и сигнала так-
тирования выборки (прямоугольный сигнал,
подаваемый на линию прерывания микрокон-
троллера 8051). Если вас не пугают приключе-
ния, попробуйте создать наложение спектров.
Позабавьтесь от души, дискретизируя эти сиг-
налы. Ведь не каждый день выдается возмож-
ность подтвердить эти понятия дискретизации,
которые часто выглядят скорее абстрактными
и загадочными.
Модифицирование формы сигналов
Здесь вам предоставляется возможность на-
писать свою программу для изменения формы
сигнала, захватываемого АЦП, который мы до-
бавим к нашему компьютеру на сегодняшнем
лабораторном занятии. Измененный этой про-
граммой сигнал затем отправляется на ЦАП
для восстановления. Технически вы будете
осуществлять цифровую обработку сигнала,
но при этом узнаете, почему микроконтроллер
8051 не называется обработчиком сигналов.
Потому что он справляется с этой задачей очень
23N.6. Предлагаемые лабораторные задания при экспериментах с АЦП и ЦАП
971
медленно и создание необходимого программ-
ного обеспечения сопряжено с большими труд-
ностями. Тем не менее это упражнение позволит
вам приобрести немного опыта в создании не-
больших программ подобного типа и получить
приятное вознаграждение. Наблюдать за изме-
ненными сигналами на экране осциллографа
еще интереснее, чем за мигающим светодиодом
из лабораторного занятия 20L.3.
Двухполупериодное выпрямление
В этом эксперименте преобразуем входной
синусоидальный сигнал (амплитуда которо-
го должна быть в пределах входного диапа-
зона АЦП - 0-2,55 В для версии DS89C420
микроконтроллера 8051 и 0-2,2 В для версии
C8051F410 этого микроконтроллера), выпол-
няя для него двухполупериодное выпрямление.
Выпрямление осуществляется относительно
среднего уровня диапазона напряжений АЦП и
ЦАП, как показано на рис. 23N.12.
2,55 В
1,28
ОВ
Рис. 23N.12. Двухполупериодное выпрямление посред-
ством АЦП-ЦАП
Код программы двухполупериодного
выпрямления для версии DS89C420
микроконтроллера
Загруженное в аккумулятор (который в дан-
ном случае называется АСС) значение выбор-
ки тестируется путем проверки его старшего
разряда (этот разряд имеет нулевое значение
в нижней половине диапазона). Код програм-
мы приведен в листинге 23N.7.
Листинг 23N.7. Программа двухполупериодного
выпрямления для DS89C420
MACRO ASSEMBLER FULLWAVE_401 В
FULLWAVE: JB ACC7,AS_IS ; Проверяем старший разряд,
; чтобы узнать, из какой половины диапазона
; это значение — верхней или нижней
CPL А ; Если из нижней, меняем значение каждого
; бита на обратное
NOP ; Заполнитель, чтобы облегчить создание
; следующей программы полупериодного выпрямителя
ASJS: DEC DPL ; Указатель на ЦАП
MOVX @DPTR,A
; В любом случае отправляем
; выборку на ЦАП
Обратите внимание на то, что среднее значение
диапазонов АЦП и ЦАП равно шестнадцате-
ричному 80h. Когда входной сигнал пересекает
это среднее значение, значение старшего байта
меняется на обратное.
Код двухполупериодного выпрямления
для версии C8051F410 микроконтроллера
Здесь в листинге 23N.8 применяется аналогич-
ная стратегия.
Листинг 23N.8. Программа двухполупериодного
выпрямления для C8051F410
;full_wave_silabs.a51: Восьмиразрядное
двухполупериодное выпрямление
; Теперь двухполупериодное выпрямление
MOV A, SAMPLE_HI ; Получаем значение выборки
JB АСС.7, ASJS ; Если из верхней половины
; диапазона, ничего с ним не делаем
CPL A ; Но если из нижней, меняем значение
; каждого бита на обратное
ASJS: MOV IDAOH, SAMPLEJHI ; Отправляем выборку
; на ЦАП
Как обычно, версия программы для микро-
контроллера C8051F410 проще, чем для микро-
схемы DS89C420, поскольку в ней не исполь-
зуется регистр DPTR. Но инициализации более
сложные.
Форматы данных АЦП: смещенный
двоичный код и дополнительный
двоичный код
В только что рассмотренных программах опе-
рация выпрямления выполняется в смещенном
двоичном формате22. Этот формат используется
микроконтроллером C8051F410 и преобразо-
вателем AD7569 при работе с однополярным
источником питания, как в случае с нашим ком-
пьютером из дискретных компонентов. Ради
интереса можете попробовать альтернативный
формат: дополнительный двоичный код. Он от-
личается от смещенного двоичного кода всего
лишь обратным значением самого старшего
разряда.
22 АоЕ § 10.1.3С.
972
23N. Микропроцессоры IV: прерывания; АЦП и ЦАП
АЦП AD7569 использует тот или другой фор-
мат в зависимости от выбранного источника
питания. В частности, при двуполярном источ-
нике питания (когда на вывод 3 микросхемы
подается напряжение -5 В), устройства АЦП и
ЦАП микросхемы будут работать в обратном
двоичном коде. Довольно изобретательно, не
так ли?
Но при желании обратный двоичный код мож-
но использовать и без двуполярного питания,
просто изменив формат данных программно.
В случае схемы выпрямителя польза от работы
с обратным двоичным кодом не сразу очевидна.
Этот эффект нельзя увидеть на осциллограмме,
но тем не менее такой эксперимент может пред-
ставлять определенный интерес.
Программа, которая использует смещенный
двоичный код, преобразует значение 07Fh в
80h, но ничего не делает со значением 80h; та-
ким образом, два исходных значения отобража-
ются на одно выходное значение (два «нуля»).
Обратный двоичный код этого не делает: ноль
не подвергается никаким изменениям (как зна-
чение 80h в программе выше); а минус один
(OFFh) преобразуется не в ноль, а в плюс один
(Olh). Этот подход выглядит более аккурат-
ным. При программном переходе на обратный
двоичный код не забудьте переключиться об-
ратно в смещенный двоичный код, прежде чем
отправлять данные на ЦАП.
Но если рассматривать более аккуратные под-
ходы, то, несомненно, нужно отдать предпо-
чтение чисто аналоговому методу с четырьмя
диодами?23 Но мы никогда не утверждали, что
наша обработка сигналов посредством микро-
контроллера 8051 является чем-либо большим,
чем просто упражнением.
Однополупериодное выпрямление
В этом упражнении вам нужно написать про-
грамму, которая заменяла бы резистор и один
диод.
Опять же, как показано на рис. 23N.13, мы хо-
тим выпрямить сигнал относительно среднего
уровня напряжения, что соответствует значе-
нию 80h.
2,55 В
1,28 В
OB
Рис. 23N.13. Однополупериодное выпрямление относи-
тельно среднего уровня входного сигнала
Для преобразователя AD7569 такой средний
уровень будет 1,27-1,28 В при разрешении
10 мВ на разряд, а для АЦП микроконтроллера
C8051F410 средний уровень составляет 1,10 В.
Замечание
Выходные значения АЦП можно преобразовать
в обратный двоичный формат и рассматривать
сигналы ниже средней точки как отрицательные
значения.
Несомненно, что код для этого упражнения
может быть очень похожим на код программы
двухполупериодного выпрямления.
Низкочастотный фильтр
Оказывается, что программа моделирования
низкочастотного фильтра достаточно прямо-
линейна24 , хотя, опять же, характеристики этой
примитивной версии не идут ни в какое срав-
нение с характеристиками фильтра, который
можно соорудить из деталей общей стоимостью
около 50 центов. Но, используя настоящую
цифровую обработку сигналов, реализуемую,
с помощью специализированных процессоров
или больших логических матриц, наподобие
суперПМЛ, можно получить чрезвычайно ка-
чественные фильтры. Такие устройства дела-
ют то же самое, что и мы проделали со своим
микроконтроллером, но реализуют это более
сложным способом. Более подробную инфор-
мацию по этой теме можно найти в главе 23S.
Предоставим процессору задачу — вычислить
среднее значение текущей выборки и предыду-
щего среднего значения и подать результат на
выход. (Присвойте самой последней выборке
вес, равный предыдущему среднему значению.)
Протестируйте свою программу на низкоча-
стотном (100 Гц или ниже) прямоугольном
23 Чтобы получить качественный выходной сигнал по-
средством аналогового выпрямителя потребуется один
или два операционных усилителя, чтобы скомпенсировать
падение напряжения на диодах.
24 Ладно, идея прямолинейна. Но вам может не понра-
виться вся работа по написанию кода, которую придется
выполнить, учитывая ограниченный набор команд микро-
контроллера 8051. Но ведь вам нравится преодолевать
трудности, иначе зачем вы выбрали наш курс?
23Л/.6. Предлагаемые лабораторные задания при экспериментах с АЦП и ЦАП
973
сигнале. Имеет ли выходной сигнал форму, ко-
торую можно приблизительно выразить фор-
мулой
UBUX=UBX(l-exV(-t/RC))?
Если вы не уверены, то посмотрите, нарастает
ли сигнал сначала быстро, а затем медленно?
Доходит ли сигнал в каждом перепаде лишь до
половины целевого значения (подобно зайцу
Зенона) ? Ответ на все эти вопросы должен быть
положительным.
Теперь испытайте работу схемы с входным си-
нусоидальным сигналом. Наблюдаются ли в
этом случае обычный для НЧ-фильтра сдвиг по
фазе?
Замечание
Должна наблюдаться постоянная задержка, кото-
рая является следствием цифровой обработки и
создается в основном временем преобразования
АЦП. Это совсем другой эффект, чем сдвиг по фазе,
который присущ аналоговому НЧ-фильтру.
Если вам известна частота выборки, вы так-
же знаете частоту усреднения старых и новых
значений, а также временной интервал между
«перепадами». Мы знаем, что на каждом пере-
паде выходной сигнал должен нарастать на по-
ловину оставшегося пути до целевого значения
(от начального значения до f/BX); также мы
узнали на лабораторном занятии 8L, что сигнал
таймера 555 проходит полпути за время 0,7 от
постоянной времени RC-цепи. На основе этих
знаний, можете ли вы предположить, эффек-
тивную «постоянную времени RC-цепи» этого
фильтра при данной частоте выборки? Чтобы
испробовать эту идею, попробуйте вычислить
виртуальную постоянную времени, предпола-
гая, что перепады усреднения имеют период
длительностью 100 мкс25.
сложения этого значения и значения новой вы-
борки (которое будет в аккумуляторе А) снова
помещается в аккумулятор. Пока что все пря-
молинейно. Но что если полученный резуль-
тат переполнит 8-разрядный аккумулятор?
Например, в 8-разрядном аккумуляторе сумма
значений 80h и 80h будет Oh. А половина этой
суммы (которую можно вычислить сдвигом
влево) тоже будет ноль! Как же можно решить
эту проблему?
Нужно учитывать бит переполнения, т. е. вы-
ходной перенос. Найдите команду, которая ис-
пользует это при делении на два, что должно
быть операцией сдвига, а не буквально деле-
нием. Подсказка: такая команда действительно
существует, мы не издеваемся над вами.
Настройка фильтра
Старому среднему и значению новой выборки
не обязательно присваивать одинаковый вес.
Деление на степень двойки можно быстро вы-
полнить посредством сдвига; но есть еще и опе-
рация умножения, которая может умножать
байт на байт. Значение новой выборки можно
поместить в регистр В, а значение ослабите-
ля — в А; старшая половина результата поме-
щается в В. Ослабитель работает следующим
образом: значение FFh соответствует самому
малому ослаблению26, Oh — ослаблению до
уничтожения, 080h — делению на два и т. д.
Старое среднее значение следует ослаблять на
взаимодополняющую дробную величину: если
новое значение ослабляется до 1/4, то старое —
до 3/4. Для выполнения всех этих вычислений
можно привлечь ассемблер. Например, можно
использовать команду MOV A, #(OFFh - NEW__
WEIGHT. Альтернативно, как это делается в сле-
дующей программе (листинг 23N.9), вычисле-
ние комплементарного значения можно предо-
ставить самой программе, применяя в данном
случае команду CPL А.
Некоторые размышления о возможном
способе реализации усреднения
Среднее — это, конечно же, просто сумма,
разделенная на два. Задача получения суммы
не представляет сложностей. Например, для
хранения текущей суммы можно использо-
вать любые из восьми регистров Rn. Результат
25 Согласитесь, это не такая и трудная задача. Поскольку
длительность каждого шага составляет 100 мкс, то посто-
янная времени будет приблизительно 140 мкс.
Листинг 23N.9. Программа усреднения
NEW_WEIGHT EQU 040h; Вес нового: 080h ==> равно
старому среднему,
; например: 040h дает новому одну третью веса старого
26 Было бы аккуратнее, если значение FFh означало полное
отсутствие ослабления. К сожалению, FFh означает умно-
жение на значение 255/256, которое очень близко к еди-
нице, но не дотягивает до нее около 0,4%. (Спасибо Маюн-
ги Киму (Myunghee Kim) за то, что обратил наше внимание
на эту разницу.)
974
23N. Микропроцессоры IV: прерывания; АЦП и ЦАП
M0VR3,#NEW_WEIGHT
FILTER: ACALL GETONE; Вызываем подпрограмму
; для получения значения выборки (в аккумуляторе)
MOV В,А; Подготавливаем его для умножения
; на значение веса
MOV A, R3; Устанавливаем (дробный) множитель
; для нового значения выборки
MUL АВ; Ослабляем новое значение, чтобы
; откорректировать его вес относительно старого.
Результат сохраняем в В
MOV R5,B; Сохраняем ослабленное новое значение
MOV В, R7; Получаем старое среднее
MOV A,R3; Устанавливаем вес старого
; как дополнение веса нового
CPLA
MUL АВ ; Корректируем вес старого
MOV A,R5; Достаем взвешенное новое
ADD A,B ; Формируем сумму из взвешенного
; нового и взвешенного старого
Значение Значение
ослабления = 80Ь ослабления = 40h
Входной
перепад
Использование операции умножения делает
фильтр более универсальным, но также вно-
сит погрешности округления. Полагая, что
прежде чем складывать новое и старое значе-
ния, вам нужно ослабить оба эти значения, вы
обнаружите (если ваша программа похожа на
написанную нами), что в результате сильно-
го ослабления нового значения выборки при
больших входных значениях, как положи-
тельных, так и отрицательных, конечное зна-
чение будет меньшим. Эта погрешность будет
заметна при установленном ослаблении, рав-
ном 020h — около одной восьмой. Округление
старшей цифры результата умножения (прове-
ряя старший бит младшего байта результата)
несколько помогает уменьшить погрешность.
Возможно, что вам удастся найти более ориги-
нальное решение.
Настраиваемый низкочастотный фильтр
На рис. 23N.14 изображено несколько нало-
женных друг на друга осциллограмм, отобра-
жающих реакцию на перепад27 для четырех раз-
ных значений ослабления. Данная программа
содержит команду умножения и применяет но-
вые значения ослабления величиной 1/2, 1/4,
1/8 и 1/16. Экспоненциальная форма сигнала
наиболее очевидна для самого легкого случая
ослабления величиной 1/2 (значение множи-
теля, равное 080h).
Рис. 23N.14. Реакция НЧ-фильтра на входной перепад при
наличии умножения для варьирования ослабления новой
выборки относительно текущего среднего
27 Данный входной перепад выглядит несколько странно
из-за усреднения осциллограммы. В действительности
входной перепад имеет четкую границу.
23L Лабораторное занятие:
микроконтроллеры 4. Прерывания; АЦП и ЦАП
23Ы.ЦАПиАЦП
Прерывания
Здесь мы опять будем работать с прерывания-
ми. На прошлом занятии мы использовали
прерывания для того, чтобы дать процессору
знать, когда мы хотели инкрементировать зна-
чение, которое затем выводилось на дисплей.
На этот раз мы несколько усложним задачу.
В частности, по каждому прерыванию мы бу-
дем выполнять преобразование аналогового
сигнала в цифровой, а затем восстанавливать
аналоговый сигнал из полученного цифрового
сигнала. Кроме того, вместо ручного тактиро-
вания прерываний посредством кнопки (кноп-
ки WR цифровой клавиатуры), как мы это де-
лали на лабораторном занятии 22L, на этот раз
сигнал тактирования прерываний мы получим
от встроенного в макетную плату генератора
сигналов с ТТЛ-выходом. Таким образом мы
сможем управлять частотой выборки.
Конечно же, эта программа не служит никаким
практическим целям. Действительно, если нам
нужен аналоговый сигнал, зачем утруждать
себя, преобразуя его в цифровую форму, а затем
восстанавливать заново? Но она предоставляет
рабочую платформу, которая позволит вам экс-
периментировать с частотой выборки, чтобы ис-
следовать ее влияние на восстановленный сиг-
нал. Вы сможете увидеть, а также и услышать,
побочные сигналы, образующиеся в процессе
дискретизации, а затем увидите, как эти паразит-
ные сигналы можно удалить с помощью высоко-
качественного настраиваемого НЧ-фильтра.
23L1.1. Подключаем ЦАП и АЦП
Первым делом мы добавим к нашему микрокон-
троллеру АЦП и ЦАП, чтобы он мог работать
с сигналами. Затем мы сначала напишем очень
простую программу, которая просто берет от-
счеты и сразу же передает на ЦАП. Сама по
себе программа не представляет ничего инте-
ресного, главное — понять ее функциониро-
вание. Поскольку процесс дискретизации так-
тируется сигналом прерывания, поступающим
от генератора сигналов, мы можем очень легко
управлять частотой выборки. Завершающим
элементом этой платформы является выходной
фильтр с крутым спадом амплитудно-частотной
характеристики.
Аппаратура АЦП-ЦАП
Преобразователь AD7569
Микросхема AD7569 представляет собой ком-
бинированный АЦП-ЦАП, с которыми очень
легко работать. Это 8-разрядное устройство
двоичного поиска (или РПП), подобное тому,
которое мы собрали на лабораторном заня-
тии 18L. Но данное устройство отличается от
собранного нами тем, что для него требуется
сигнал запуска. Иными словами, вместо рабо-
ты в режиме постоянных преобразований, на-
чиная новое преобразования сразу же после
завершения предыдущего, оно выполняет пре-
образования только тогда, когда поступает со-
ответствующее указание. Для реализации этой
возможности требуется пара дополнительных
строчек кода, но в результате можно управлять
выборкой от компьютера, позволяя принимать
данные только тогда, когда в наличии имеется
новая действительная выборка. На рис. 23L.1
изображена блок-схема этой микросхемы.
А на рис. 23L.2 показано подключение микро-
схемы АЦП-ЦАП AD7569 к нашему компью-
теру из дискретных компонентов. Сигнал за-
пуска преобразователя необходимо инвер-
тировать. Для этой цели подойдет один из
976
23L. Лабораторное занятие: микроконтроллеры 4. Прерывания; АЦП и ЦАП
напряжения, определяемого
шириной запрещенной зоны
Диапазон Управляющая
Рис. 23L.1. Блок-схема микросхемы АЦП-ЦАП AD7569
8,
'ШШ&ШШжШШШ№Ш$Ш£^^^
Шина данных ЦП
-f Щ\ |31 111 fOt э! В\ ?1 Ы
-%брос
Выбор
2S
О
Аналоговый вход
От 0 до +2,5 В
Диапазон
Pt
А/Ц
07/
V&s
Цифровая «земля»
й Запуск
преобразования
AD7569
Комбинированный
П/
Не используется ,3- Занят i комоиниро
{^Прерывание . АЦП/ЦАП
Сигнал «Земля»*
тактирования
^Земля»
ЦАП
Рис. 23L.2. Подключение микросхемы AD7569 8-разрядного АЦП-ЦАП к компьютеру из дискретных компонентов
незадействованных элементов микросхемы
инвертеров 74НС14, которую мы подключили в
схему на предыдущих лабораторных занятиях.
Некоторые подробности включения
преобразователя AD7569
У внимательных студентов определенные осо-
бенности подключения микросхемы преобра-
зователя AD7569 к компьютеру могут вызвать
некоторые вопросы. В частности:
1. Мы не используем сигналы INT* и BUSY*, ко-
торые могут информировать компьютер о
завершении преобразования. Можно было
бы ожидать, что компьютер должен прове-
рять сигнал BUSY*, беря выборку только при
должном уровне этого сигнала. (Такой под-
ход называется программируемым вводом-
выводом или вводом-выводом по запросу.)
Альтернативно процессор должен брать вы-
борку только по прерыванию от сигнала с со-
ответствующим названием INT*. Такие схемы
выглядят аккуратно, но не обладают необхо-
димой эффективностью в случае таких бы-
стрых преобразователей, каким является вы-
бранный нами. В частности, процессору по-
требуется приблизительно столько же време-
ни для проверки активирования сигнала INT*,
сколько АЦП занимает для выполнения пре-
образования. А реагирование ЦП на преры-
вание будет еще более медленным. Поэтому
мы предпочитаем простой подход: позволя-
ем процессору брать выборку в любое время,
но при этом при разработке нашей програм-
мы учитываем то, что нельзя предпринимать
попытку взятия выборки в течение 1,6 мке
после подачи преобразователю команды за-
23и.ЦАПиАЦП
977
пуска преобразования. Оказывается, что со-
блюдать это ограничение совсем не трудно;
более того, нужно хорошо потрудиться, что-
бы нарушить его.
2. Для сигнала выбора микросхемы CS* посто-
янно поддерживается низкий уровень. Это
всего лишь дублирующий сигнал, который
обрабатывается операцией И совместно с
сигналами RD* и WR* и ничего не делает сам
по себе.
3. Преобразователь мы запускаем по отрица-
тельному перепаду сигнала OUT3** (инвер-
тированный сигнал OUT3* декодера ввода-
вывода).
23L1.2. Программа для проверки
работоспособности ЦАП
Хотя ЦАП и АЦП содержатся в одной микро-
схеме, целесообразно проверить их работо-
способность по отдельности, поскольку АЦП
является более сложным устройством, чем
ЦАП. Проверку этих преобразователей начнем
с ЦАП. Если устройство работает должным об-
разом, это подтверждает, что большая часть
монтажа по подключению микросхемы выпол-
нена правильно.
Создайте программу, которая обнуляет ре-
гистр, подает его значение на ЦАП, инкремен-
тирует регистр и снова подает его на ЦАП, и
продолжает бесконечно инкрементировать ре-
гистр и подавать его на ЦАП. Если ЦАП рабо-
тает должным образом, такая программа долж-
на создать на выходе ЦАП циклический сигнал,
линейно нарастающий от 0 до приблизительно
2,55 В. В случае ступенчатого нарастания вы-
ходного сигнала определить причину можно,
быстро рассмотрев несколько возможных ва-
риантов. Предположим, что наблюдается сиг-
нал с неравномерным нарастанием, как пока-
зано на рис. 23L.3
^Полная
■ шкала
Полная
шкала
^Полная
'шкала
Бит D6 застрял
на низком
уровне
Бит D6 застрял
на низком
уровне
Линии битов D5, D6
перепутаны местами
Рис. 23L.3. Примеры неравномерно нарастающего выход-
ного сигнала ЦАП. Чтобы определить проблемный бит, счи-
тайте перерывы
По этим графикам можно как минимум увидеть
состояние самой старшей линии данных ЦАП,
на которую подается неправильный сигнал или
которая не ведет себя должным образом. Один
перелом (посередине диапазона) подразумева-
ет проблемы с самым старшим разрядом; два
перелома (в 1/4 и 3/4 диапазона) подразуме-
вают проблемы с линией d6 и т. д. Этот тип
информации дает нам подсказку, какие линии
нужно проверить в процессе поиска причины
неполадки. Но по ней мы не можем выяснить
более подробные аспекты, такие как застряла
ли линия на высоком или низком уровне или
находится в «плавающем» состоянии («пла-
вающие» состояния вызывают самые странные
формы сигнала).
23L1.3. Программа для проверки
работоспособности АЦП
Создайте программу, которая берет значение из
АЦП, отображает его на дисплее, снова берет
значение и отображает его и так далее до бес-
конечности. Подайте на вход АЦП постоянное
напряжение через потенциометр на макетной
плате номиналом 1 или 10 кОм, как показано
на рис. 23L.4.
ЮкОм
или меньше
>< На АЦП
I
Рис. 23L.4. Входной сигнал постоянного уровня для провер-
ки АЦП
При подаче на процессор сигнала тактирования
максимальной частоты (11 МГц) необходимо
принимать во внимание требования тактиро-
вания АЦП. В частности, необходимо обеспе-
чить интервал как минимум 1,6 мкс между от-
рицательным перепадом сигнала ST* (=OUT3**)
и активированием сигнала RD*, поскольку АЦП
не нравится, когда у него запрашивают данные,
прежде чем они готовы. Организуйте все таким
образом, чтобы команда запуска преобразова-
теля подавалась тогда, когда между запуском и
операцией чтения выполнялись какие-либо не-
обходимые операции. Если вам это удастся, то
вы сможете избежать необходимости устраивать
задержку, используя холостые команды (NOP)1.
1 Это можно легко сделать, поместив операцию запуска
сразу же после команды чтения, чтобы АЦП мог выпол-
нять преобразование в течение времени, когда программа
проходит цикл до следующей операции чтения.
978
23L Лабораторное занятие: микроконтроллеры 4. Прерывания; АЦП и ЦАП
АЦП-ЦАП: быстрое преобразование
и восстановление
Версия 1 с адресацией АЦП и ЦАП через
@Rn
Программа, приведенная в листинге 23.L1, при
каждом прерывании берет выборку в АЦП, ко-
торую затем отправляет на ЦАП. Главная про-
грамма не делает абсолютно ничего. Собствен-
но говоря, она эквивалентна соединенным по-
следовательно АЦП и ЦАП.
Обратите внимание на то, что частота прерыва-
ний должна равняться частоте дискретизации.
Чтобы задать частоту выборки, используйте
другой генератор сигналов, например генера-
тор сигналов с выходным сигналом с логиче-
скими уровнями вашей макетной платы. Также
обратите внимание на необходимость удаления
линии, которая на лабораторном занятии 22L
служила для подачи сигнала INTO* с линии KWR*
цифровой клавиатуры. Если этого не сделать,
то новое подключение, т. е. генератор сигналов,
будет конфликтовать со старым.
До настоящего времени для определения адре-
сов внешней памяти и операций ввода-вывода
мы полагались почти исключительно на ре-
гистр DPTR. Но для этого существует и другой
метод, который иллюстрируется далее. Эта
версия чуть более компактна, чем версия с ис-
пользованием регистра DPTR, которая приво-
дится после листинга 23.L1.
Режим адресации @Rn использует комбинацию
порта 2 (для старшего байта адреса, константы
80h) и регистров R0 и R1 (для младшего байта
адреса). Обратите внимание на то, что для это-
го кода требуются другие инициализации, чем
те, которые вы привыкли видеть в программах,
задействующих регистр DPTR.
Между прочим, микроконтроллер 8051 осна-
щен четырьмя банками рабочих регистров R0...
R7. Иногда в подпрограмме обработки преры-
вания полезно переключиться на другой банк
регистров. Такое переключение в этой про-
грамме позволило бы главной программе ис-
пользовать регистры R0 и R1.
Но здесь мы не делаем такого переключения
между банками рабочих регистров, поскольку
в данном случае нет надобности занимать ре-
гистры R0 и R1 двумя разными фрагментами
кода. Но вы можете оказаться в ситуации, когда
такое переключение на другой банк регистров
будет необходимым. Осуществляется оно запи-
сью соответствующего значения в двухбитовое
поле слова статуса программы.
Листинг 23L.1. Программа быстрого АЦП и ЦАП с адресацией через @Rn
05/05/04 16:06:07 PAGE I
MACRO ASSEMBLER ADCDACINT_RN_504
LOC OBJ LINE SOURCE
; ADCDACINT_Rn_504.a51 Передача значения с АЦП на ЦАП по прерыванию,
; Используем Р2 и Rn 5/04
; Считываем АЦП, записываем в ЦАП, запускаем АЦП по каждому прерыванию
1
2
3
4
5
6
172
196
197
198
199
200
201
202
00Е0 75817F 203
ООЕЗ 11ED 204
205
0080
0000
0000 01Е0
00Е0
SNOSYMBOLS
SINCLUDE (C:\MICRO\8051\RAISON\INQREG320.INC)
$INCLUDE (C:\MICRO\8051 \RAISON\INCWECTORS320.INC)
STACKBOT EQU 80H; Не обязательно, но хорошее место для него
ORG0H
AJMP STARTUP
ORG ОЕОН
STARTUP: MOVSP,# 128-1
ACALLINITDACPTRS; Инициализируем указатели для АЦП и ЦАП
23и.ЦАПиАЦП
979
00Е5
00Е7
00Е9
ООЕВ
OOED
OOFO
00F2
00F4
OOF5
ОООЗ
0003
0004
0005
0006
D288
D2A8
D2AF
80FE
75А080
7803
7902
F2
22
Е2
F2
F3
32
END
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
; —ТЕПЕРЬ РАЗРЕШАЕМ ПРЕРЫВАНИЯ —
SETBTCON.0; Делаем INTO чувствительным к перепаду
SETB IE.0; Разрешаем INTO
SETB IE.7; Разрешаем глобальные прерывания
STUCK: SJMP STUCK;ЖДЕМ ПРЕРЫВАНИЙ
;** ИНИЦИАЛИЗАЦИИ***************
INITDACPTRS: MOV Р2,#80Н ; Определяем старший байт адреса в качестве базового адреса
; ввода-вывода
MOV R0,#3H; Определяем 8-разрядный индексный регистр как указатель на АЦП
MOV R1,#2H; Определяем второй регистр как указатель на ЦАП
MOVX @R0,A; В первом проходе: посылаем что угодно — просто импульс для запуска АЦП
RET
;**ISR:ADC->DAC-*****
; ВЕКТОР ДЛЯ ПРЕРЫВАНИЯ:
ORG INT0VECTOR
ISR: MOVX A, @R0; Считываем АЦП (не совсем правильное хронирование в первом проходе
; но правильное во всех последующих проходах)
MOVX @R0,A; Запускаем АЦП для следующего прохода
MOVX @R1,A; Отправляем выборку на ЦАП
RETI
Версия 2 с адресацией АЦП и ЦАП через
регистр DPTR
В листинге 23L.2 приведена такая же програм-
ма, но только с использованием регистра DPTR.
Мы поместили ее в область памяти, занятую
предыдущей альтернативной версией, чтобы
можно было ввести сначала одну версию, а
затем вторую, которая затрет первую. Но мы
сомневаемся, что вам захочется вводить код
дважды. Если у вас действительно нет такого
желания, можете игнорировать эту версию.
Листинг 23L.2. Программа быстрого АЦП и ЦАП с адресацией через DPTR
LOC OBJ LINE SOURCE
1 ; ADCDACINT_504.a51 Передача значения с АЦП на ЦАП по прерыванию
2 ; 4/01: Использует другие назначения портов, и всего лишь один
3 ; указатель данных 5/04
4 ; Помещаем всю подпрограмму ISR по адресу вектора
5 ; Должна при каждом прерывании считывать АЦП, записывать значение в ЦАП и запускать АЦП
б
7 SINIOSYMBOLS
8 SINCLUDE (C:\MICRO\8051 \RAISON\1NC\REG320.INC)
174 $INCLUDE (C:\MICRO\8051\RAISON\INQVECTORS320.INC)
0080 198 STACKBOT EQU 80H ; He обязательно, но хорошее место для него
980
23L Лабораторное занятие: микроконтроллеры 4. Прерывания; АЦП и ЦАП
199
0000 200
0000 01 ЕО 201
202
ООЕО 203
204
ООЕО 75817F 205
ООЕЗ 11ED 206
207
208
209
00Е5 D288 210
211
00Е7 D2A8 212
00Е9 D2AF 213
214
ООЕВ 80FE 215
216
217
218
219
OOED 908003 220
OOFO F0 221
00F1 22
0003
0003 ЕО
0004 F0
222
223
224
225
226
227
228
229
0005 1582 230
231
0007 F0 232
0008 0582 233
ОООА 32 234
235
236
ORG0H
AJMP STARTUP
ORG ОЕОН
STARTUP: MOVSP,# 128-1
ACALLINITDACPTRS; Инициализируем указатели для АЦП и ЦАП
; —ТЕПЕРЬ РАЗРЕШАЕМ ПРЕРЫВАНИЯ —
SETB TCON.0 ; Первая попытка использовать битовую операцию:
; делаем INTO чувствительным к перепаду
SETB IE.0 ; И разрешаем прерывание INTO
SETB IE.7 ; Разрешаем глобальные прерывания
STUCK: SJMP STUCK; ЖДЕМ ПРЕРЫВАНИЙ
;** ИНИЦИАЛИЗАЦИИ***************
INITDACPTRS: MOV DPTR, #8003H ; Инициализируем указатель данных для АЦП
MOVX @DPTR, А ; В первом проходе: посылаем что угодно — просто импульс для запуска АЦП
RET
;** Подпрограмма ISR: АЦП ~> ЦАП
; ВЕКТОР ДЛЯ ПРЕРЫВАНИЯ
ORG INT0VECTOR
MOVX A, @DPTR ; Считываем АЦП (порт 3)
MOVX @DPTR, А ; Посылаем что угодно — просто импульс для запуска АЦП
; для следующего прохода
DEC DPL ; Теперь указываем на ЦАП (порт 2) (данная команда DEC работает только
; с младшим байтом)
MOVX @DPTR, A ; Отправляем взятую выборку на ЦАП
INC DPL ; Возвращаем указатель на АЦП для следующего прохода
RETI
END
Проверяем работоспособность каждой про-
граммы, подавая синусоидальный сигнал на
вход АЦП и наблюдая такой же синусоидаль-
ный сигнал на выходе ЦАП. При этом необхо-
димо смотреть за тем, чтобы амплитуда вход-
ного синусоидального сигнала была в пределах
диапазона рабочих напряжений АЦП: 0-2,55 В.
Также следует иметь в виду, что восстановлен-
ный на ЦАП синусоидальный сигнал будет
ступенчатым, если только не брать большое
количество выборок за период. Но эту ступен-
чатость можно несколько сгладить с помощью
НЧ-фильтра. Добавление такого фильтра рас-
сматривается в следующем разделе.
23L2. Лабораторное занятие SiLabs 4. Прерывания, АЦП и ЦАП
981
23L1.4. Низкочастотный фильтр
с коммутируемым конденсатором
на микросхеме МАХ294
Как уже упоминалось, качественный низкоча-
стотный фильтр на выходе ЦАП может сгла-
дить восстановленный ступенчатый сигнал.
Подключение микросхемы низкочастотно-
го фильтра МАХ294 показано на рис. 23N.9
в главе 23N.5 и применимо в обеих ветвях се-
годняшнего лабораторного занятия: как с ком-
пьютером из дискретных компонентов, так и
с компьютером на основе автономного микро-
контроллера C8051F410.
Усилитель звуковой частоты для
прослушивания эффектов выборки
В разделах 23N.5.2 и 23N.53 приводятся схе-
мы подключения усилителя звуковой частоты
для прослушивания эффектов выборки. Там
же предлагаются способы модификации вы-
ходных сигналов АЦП с последующей их пода-
чей на ЦАП: двухполупериодное и однополу-
периодное выпрямление и низкочастотная
фильтрация.
231.1.5. Изменение формы сигналов
Здесь вам предоставляется возможность са-
мостоятельной разработки кода. Программа
FULLWAVE_401Ь.а51 (которую можно загру-
зить с веб-сайта этой книги) реализует двух-
полупериодное выпрямление. Ваша задача —
написать программы для однополупериодного
выпрямления и фильтрации. Некоторые под-
сказки по этим небольшим программам обра-
ботки сигналов можно найти в разделе 23N.6.
Однополупериодное выпрямление
Несомненно, что код для этого упражнения мо-
жет быть очень похож на код программы двух-
полупериодного выпрямления. Разработку это-
го кода мы предоставляем вам.
Низкочастотный фильтр
Возможный подход к программированию та-
кого фильтра также описывается в главе 23N.
Протестируйте свою программу на низкоча-
стотном (100 Гц или ниже) прямоугольном
сигнале, наблюдая реакцию на входной пере-
пад. Выясните, имеет ли выходной сигнал фор-
му, которую можно приблизительно выразить
формулой
Цшх= Um[l-ap(t/RC)].
Настраиваемый низкочастотный фильтр
для желающих поэкспериментировать
Как упоминалось в главе 23N, если у вас есть
немного свободного времени, то его можно
потратить на разработку программы с исполь-
зованием операции умножения для настройки
амплитудно-частотной характеристики филь-
тра. Вы можете получить удовольствие, пыта-
ясь решить эту задачу, или наоборот, отказать-
ся от решения, поскольку на самом деле это
задача для специализированного процессора
цифровых сигналов.
23L2. Лабораторное занятие
SiLabs 4. Прерывания, АЦП
и ЦАП
Двухполупериодное выпрямление
В этом эксперименте преобразуем входной
синусоидальный сигнал (амплитуда которого
должна быть в пределах входного диапазона
АЦП от 0 до 2,55 В) в выпрямленный двухпо-
лупериодный выходной сигнал. Выпрямление
осуществляется относительно среднего уровня
диапазона напряжений АЦП и ЦАП, как пока-
зано на рис. 23N.12. Обратите внимание на то,
что среднее значение диапазонов АЦП и ЦАП
равно шестнадцатеричному 80h.
Выводы порта, используемые на этом
лабораторном занятии
Два вывода микросхемы микроконтроллера
служат для ввода аналогового сигнала в АЦП
и вывода аналогового сигнала из ЦАП. Под-
ключенный к выводу РО.О АЦП заменяет све-
тодиод, который был подключен к этому вы-
воду на лабораторных занятиях 20L.3 и 21L.2.
Не забудьте отключить этот светодиод сейчас.
Прерывание INT1* (рис. 23L.5) потребуется
нам только на этом лабораторном занятии,
982
23L Лабораторное занятие: микроконтроллеры 4. Прерывания; АЦП и ЦАП
а прерывание INTO* мы будем использовать
снова на лабораторном занятии 25L.2.
К
g
РО,
in
РО.
РО,
РО.
м
РО.
V)
5
РО.
у
б
РО,
Рис. 23L5. Использование вывода РО.О на этом лаборатор-
ном занятии
23L2.1. Прерывания
Как упоминалось в главе 23N, чтобы разрабо-
тать программу, в которой прерывания опреде-
ленно приносят пользу, требуется приложить
некоторые усилия. Многие из программ с пре-
рываниями на наших лабораторных занятиях
выполняют странный маневр, позволяя пре-
рыванию устанавливать программный флаг,
который опрашивается основной программой.
Такой метод выглядит как лишение прерыва-
ния его достоинства, но это не совсем так.
В частности, кроме того, что значение можно
вставить в исполняющуюся программу, пре-
рывание также полезно тем, что оно предо-
ставляет встроенный триггер, который может
зафиксировать событие запроса прерывания.
Наличие такого триггера позволяет получить
два полезных результата.
♦ Триггер равнозначен флагу, который будет
оставаться в установленном состоянии до
тех пор, пока прерывание не будет принято
на обработку. Если полагать, что прерывание
всегда обслуживается быстро, то это может
выглядеть излишним, но некоторые обстоя-
тельства могут не позволить получить такое
быстрое обслуживание. Чаще всего встреча-
ются следующие два обстоятельства:
• прерывания могут быть временно отклю-
чены в основной программе. Этот случай
рассматривается в упражнении с запоми-
нающим осциллографом на лабораторном
занятии 24L.2;
• процессор может быть просто занят обра-
боткой другого прерывания, при этом на-
стройки могут не позволять ему ответить
на новое прерывание до тех пор, пока он
не завершит обслуживание текущего. Это
всегда происходит в случае прерываний,
работающих с естественным приоритетом.
Также это случается, когда прерывание с
более низким приоритетом происходит
тогда, когда процессор обрабатывает пре-
рывание с более высоким приоритетом
(что может совпадать или не совпадать
со случаями прерываний с естественным
приоритетом).
♦ Активирование внутреннего триггера по пе-
репаду облегчает задачу реализации одно-
разового реагирования на перепад уровня
на линии запроса прерывания, тогда как для
реализации опроса обычно требуется допол-
нительный программный код, чтобы полу-
чить нечто похожее на определение перепа-
да. Во всех наших программах с прерывания-
ми на этом лабораторном занятии мы будем
пользоваться преимуществом прерывания,
активируемого перепадом.
Демонстрация прерывания:
инкрементирование или
декрементирование значения,
отображаемого на дисплее
Предположим, что нам нужно отслеживать
количество пассажиров на платформе огра-
ниченной емкости. Например, на стеклянной
платформе, установленной на консоли над
Большим каньоном. Входной турникет создает
отрицательный перепад при входе посетителя
на платформу, а выходной делает то же самое
при выходе с платформы. Количество посети-
телей на платформе отображается на дисплее.
(Ради простоты, мы допускаем отрицательное
количество посетителей на платформе2.)
Прерывание 0 инкрементирует значение, пре-
рывание 1 декрементирует его, а основная про-
грамма просто исполняется в цикле, отображая
текущее число. Сначала рассмотрим, какое обо-
рудование нам потребуется, а затем перейдем
к программированию.
Оборудование: две кнопки с приемлемой
защитой от дребезга
Как мы знаем, дребезг на входе, активируемый
перепадом, может создавать проблемы, по-
скольку это выглядит как множество запросов.
У вас может возникнуть мнение, как в ситуации
2 Такая ситуация невозможна в действительности. Разве
что если кто-то перепрыгнет через входной турникет, а за-
тем выйдет, как полагается, через выходной.
23L2. Лабораторное занятие SiLabs 4. Прерывания, АЦП и ЦАП
983
на рис. 22W.10, что в данном случае дребезг
можно игнорировать, поскольку он длится
всего лишь несколько миллисекунд. Но, как
было показано в ситуации на рис. 22W.11, это
ошибочное мнение, поскольку мы имеем дело
с микроконтроллером, который способен реа-
гировать в течение микросекунд. Поэтому за-
щита от дребезга является обязательной.
Но, оказывается, что в данной ситуации можно
обойтись псевдозащитой, которая была бы не-
достаточной в случае со входом, по настоящему
активируемым перепадом (как, например, вход
сигнала тактирования триггера или счетчика).
Для нашей же ситуации достаточно простой
схемы защиты на основе RC-цепочки, которая
показана на рис. 23L.6.
„to INT*X
X
о.пр
Рис. 23L.6. Псевдозащита от дребезга для линий подачи
сигнала запроса прерывания: просто инерционная схема на
основе RC-цепочки
В данной схеме RC-цепочка состоит из резисто-
ра номиналом 10 кОм и конденсатора емкостью
ОД мкФ. Резистор номиналом 4,7 кОм служит
для защиты микроконтроллера C8051F410,
ограничивая ток разряда конденсатора при вы-
ключении питания3.
Но почему в данном случае достаточно просто-
го увеличения длительности сигнала, вносимо-
го RC-цепью? Это можно понять, если вспом-
нить, почему простого замедления было недо-
статочно в случае входа, по-настоящему акти-
вируемого перепадом. В такой ситуации мед-
ленный перепад вызывал проблемы, поскольку
реагирование на перепад было достаточно
быстрым и возникала неопределенность при
прохождении медленного перепада через по-
роговую область. Быстрое реагирование на по-
ложительный перепад вызывало переключение
выходного сигнала триггера; это событие соз-
давало помехи на линиях питания, что, в свою
очередь, заставляло входной каскад изменить
свое решение. Этот процесс повторяется бес-
конечно, создавая паразитные автоколебания,
3 Мы позаимствовали этот прием из схемы набора раз-
работчика для микроконтроллера C8051F410 компании
Silicon Laboratories.
пример которых мы видели на лабораторном
занятии 8L (см. рис. 8L.3), когда подавали на
компаратор 311 входной сигнал с медленным
перепадом.
Входы микроконтроллера, на которые подает-
ся сигнал прерывания, описываются как чув-
ствительные к перепаду, но это не совсем так.
В действительности микроконтроллер берет
выборки на этих входах в нескольких последо-
вательных циклах внутреннего сигнала такти-
рования. Реагирование на запрос прерывания
не настолько быстрое, чтобы создавать помехи
на линиях питания и сопутствующие колеба-
ния в принятии решения, перешел ли входной
сигнал пороговый уровень. Поэтому в данном
случае достаточно простой замедляющей схе-
мы на основе RC-цепочки, которая устраняет
большие перепады сигнала в течение дребезга.
Данное прерывание, псевдоактивируемое пере-
падом, нельзя сбить с толку медленным пере-
падом, как в случае с входом, по-настоящему
активируемым перепадом.
Подключите кнопки, оснащенные псевдозащи-
той от дребезга, к каждому из двух входов за-
проса прерывания: INTO* и INT1*.
Код подпрограммы I5R для
инкрементирования или
декрементирования отображаемого
значения
Данная программа необычна: основной цикл
просто бесконечно выводит на дисплей значе-
ние в регистре А:
STUCK: MOV DISPLAY, A ; Отображаем постоянное
; значение, пока оно не будет инкрементировано
; прерыванием
SJMP STUCK
Все действие происходит в двух крошечных под-
программах ISR: одна инкрементирует значение
в регистре А, а другая декрементирует его.
В разделе 143.8 книги АоЕ не рекомендуется
выполнять слишком большой объем работы
в подпрограмме ISR. Мы полагаем, что эти две
подпрограммы ISR полностью отвечают этому
требованию: каждая из них состоит всего лишь
из одной линии кода, после которой следует ко-
манда RETI для возвращения из подпрограммы
ISR в главную программу.
984
23L Лабораторное занятие: микроконтроллеры 4. Прерывания; АЦП и ЦАП
Таблица 23L.1. Параметры инициализации регистров
Регистр
IT01CF
TCON
IE
IP
Значение бита/байта
d7 (= IN1PL)
d6...d4(=INlSLx)
d3 (= INOPL)
d2...dO (= INOSLx)
d2,d0(=ITl,IT0)
d7,d2,d0(=EA,EXl,EX0)
d2 (=PX1)
Функция
0 ==> INT1 активируется низким уровнем
111b ==> прерывание INT1 * присваивается выводу Р0.7
0 ==> INTO активируется низким уровнем
101Ь ==> прерывание INTO присваивается выводу Р0.5
lib ==> Оба прерывания активируются перепадом
1 ==> Разрешение прерываний: глобальных, внешнего 1,
внешнего 0
1 ==> Присваиваем INT1 высокий приоритет
В табл. 23L.1 приводится информация по ини-
циализации регистров, которая на этот раз
довольно трудоемкая. При этом в данную та-
блицу не включены инициализации регистров,
которые осуществляются в процессе обычной
инициализации USUAL_SETUP. Как обычно, вы
можете проигнорировать эти побитовые под-
робности инициализации и выполнить ее с по-
мощью Мастера настроек.
Организация прерываний с помощью
Мастера настроек
Трудоемкую работу по организации прерыва-
ний можно значительно облегчить, используя
Мастер настроек, графические окна которого
напоминают пользователю, какие опции следу-
ет выбрать. На рис. 23L.7 показано окно Мас-
тера настроек, содержащее основные опции,
5 1 Xi
Г TO 1
IE,
1С:
OF,
#0*75}
#06 Si'
Рис. 23L.7. Настройку прерываний можно также реализовать с помощью Мастера настроек
23L2. Лабораторное занятие SiLabs 4. Прерывания, АЦП и ЦАП
985
включая присвоения прерываний определен-
ным выводам. (В другом окне, не показанном
здесь, можно изменить естественный приори-
тет источников прерываний.) Мы присвоили
INTO* выводу Р0.5, a INT1* - выводу Р0.7. Мы
оставили без изменений естественные прио-
ритеты источников прерываний.
Достаточно странно, но, по-видимому, Мастер
настроек не предоставляет опции выбора меж-
ду активированием прерываний по перепаду
или уровню. А активируемые по перепаду пре-
рывания полезны. Реализовать такие преры-
вания можно следующим кодом (как можно
увидеть в полном листинге программы на веб-
сайте книги):
SETBIT0 ; Делаем INTO чувствительным к перепаду
;(ITO=TCON.O)
SETB IT1 ; То же самое и для INT1
Но мы пойдем трудным путем ручной на-
стройки прерываний
С некоторым сожалением мы должны сказать,
что, показав вам чудесный способ легкой и
быстрой организации прерываний с помощью
Мастера настроек, в данном случае предпо-
чтительнее организовать их вручную. Делаем
мы это частично потому, что Мастер настро-
ек не содержит возможности выбора между
способом активирования запроса прерыва-
ния (перепадом или уровнем), но в большей
степени потому, что мы полагаем, что будет
легче разобраться в коде, если его реализовы-
вать и объяснять (комментариями в листинге)
для одного действия за раз. Но это всего лишь
учебное упражнение, поскольку мы ожидаем,
что вы будете пользоваться Мастером настроек
во всех возможных случаях. Полный листинг
программы int_inc_deca51 можно загрузить на
веб-сайте данной книге.
Исполнение программы
Проверка с пошаговым исполнением
Сначала проверьте программу, исполняя ее
в пошаговом (или многошаговом) режиме.
Программа должна итерироваться в главном
цикле STUCK до тех пор, пока не будет нажа-
та одна из кнопок прерываний. Удерживайте
кнопку нажатой, по крайней мере» в течение
пары циклов многошагового исполнения. Это
объясняется тем, что короткий импульс не бу-
дет иметь эффекта прерывания, поскольку, как
отмечалось в разделе 23L2.1, эти входы преры-
вания реагируют не на настоящие, а на псевдо-
перепады.
В зависимости от нажатой кнопки, ход испол-
нения программы перейдет к одной из двух
подпрограмм ISR. Удерживание кнопки нажа-
той не должно вызывать никаких дальнейших
реагирований на данный запрос прерывания:
хотя эти прерывания и не реагируют на крат-
ковременный импульс, в нашем контексте они
активируются перепадом.
При нажатии кнопки прерывания INTO* в про-
цессе пошагового исполнения подпрограммы
обработки прерывания INT1* выясните, пре-
рывается ли исполнение этой подпрограммы,
чтобы начать обработку нового прерывания?
Хотя прерывание INTO* имеет более высокий
приоритет, чем прерывание INT1*, его запрос
не должен прерывать исполняющуюся подпро-
грамму обработки прерывания INT1*. Данный
тип приоритета, называющийся естественным,
определяет, какое прерывание обрабатывается
первым при одновременном запросе больше
чем одного прерывания.
Непрерывное исполнение
Теперь запустите программу на исполнение в
непрерывном режиме и экспериментируйте с
ней, нажимая кнопки прерываний. Как и при
работе в одношаговом режиме, нажатие кнопки
должно вызывать одноразовое инкрементиро-
вание или декрементирование отображаемого
на дисплее значения, что возможно благодаря
активированию этих прерываний по перепаду.
Проверка псевдозащиты от дребезга
Если вам интересно знать, каким образом ра-
ботает применяемая здесь псевдозащита от
дребезга, попробуйте удалить замедляющий
конденсатор из схемы одной из кнопок. Вы
должны увидеть, что нажатие на кнопку при
исполнении программы в непрерывном режи-
ме иногда вызывает изменение отображаемого
значения на несколько единиц в ту или другую
сторону.
Изменяем естественный приоритет
прерываний
В разделе инициализации прерываний заком-
ментирована эта строка кода: SETB PX1. Если
986
23L Лабораторное занятие: микроконтроллеры 4. Прерывания; АЦП и ЦАП
данный комментарий убрать, то последствия
будут следующими:
♦ приоритет прерываний INTO и INT1 меняется
на обратный;
♦ запрос прерывания INT1 сможет прерывать
исполнение подпрограммы обработки пре-
рывания INTO, тогда как при естественном
приоритете прерываний обработка прерыва-
ния даже с более низким приоритетом будет
завершена, прежде чем микроконтроллер бу-
дет реагировать на запрос прерывания с бо-
лее высоким приоритетом.
Если вы хотите увидеть эти эффекты в дей-
ствии, удалите точку с запятой, которой за-
комментирована эта строчка кода, и исполните
программу в одношаговом (или многошаго-
вом) режиме. Прерывает ли теперь прерывание
INT1* подпрограмму ISR для прерывания INTO*
(назовем ее ISRO)? Если запрос на прерывание
INTO* поступает в процессе исполнения подпро-
граммы ISR1, что происходит после возвраще-
ния из ISR1 в главную программу?4
23L2.2. ЦАП
Было бы хорошо, если можно было устано-
вить рабочие диапазоны АЦП и ЦАП одина-
ковыми. К сожалению, этого нельзя сделать.
Диапазон напряжений входного сигнала АЦП
составляет 0-2,2 В (значение Uon), а диапазон
устойчивости по напряжению выходного сиг-
нала ЦАП еще меньше: 0-1,3 В. Кроме того,
мы установим немного меньший верхний пре-
дел ЦАП: 1,2 В5.
Выходной сигнал ЦАП является не сигналом
напряжения, а токовым сигналом, который
ЦАП поставляет в режиме источника тока.
Самый простой способ преобразовать этот ток
в напряжение — пропустить его через резистор
на «землю», как показано на рис. 23L.8. Чтобы
получить больший размах сигнала, его необхо-
димо подать на операционный усилитель.
4 Поскольку мы сделали запросы на прерывания чувстви-
тельными к перепаду, запрос на прерывание INTO* будет
сохранен триггером и будет обработан после возвращения
из подпрограммы ISR1.
5 Верхний предел диапазона рабочих напряжений ЦАП
в худшем случае составляет +17 - 1,2 В = 1,3 В (согласно
табл. 6.1 IDAC Electrical Characteristics [Электрические
характеристики соединительного цифроаналогового пре-
образователя], на с. 75 справочного листка на микрокон-
троллер C8051F410).
410
Выходной сигнал ЦАП —"
Рис. 23L.8. Чтобы преобразовать выходной токовый сигнал
ЦАП в напряжение, его нужно пропустить через резистор на
«землю»
Мы установим ток полной шкалы ЦАП вели-
чиной 1 мА (наше любимое значение) и про-
пустим его на «землю» через резистор номина-
лом 1,2 кОм.
Левое и правое выравнивание значения
выборки в слове регистра
Подобно многим ЦАП и АЦП, наш ЦАП по-
зволяет выровнять свое входное 12-разрядное
значение по левому или правом краю двух-
байтового регистра, в котором он хранится.
Подробности такого выравнивания показаны
на рис. 23L.9.
IDAlH
i—8—
IDA1L
У/////Л У//Л \
У//А У/////Л
Выравнивание
по левому краю слова
Выравнивание
по правому краю слова
При левом выравнивании старший байт
;ет использоваться сам по себе
Рис. 23L9. Подобно выходному значению АЦП, входное 12-
разрядное значение ЦАП можно выравнивать полевому или
правому краю двухбайтового слова
Мы решили выбрать левое выравнивание, по-
скольку это позволяет нам использовать во-
семь старших битов сами по себе, т. е. работая
с ЦАП (а позже и с АЦП), как будто бы это
было 8-разрядное устройство. Игнорирование
младших четырех битов не искажает значение
старших восьми, а просто снижает разрешение
преобразователя. В следующем далее упраж-
нении (в разделе 23L.2.7) выравнивание по
левому краю входного значения ЦАП облег-
чает переключение с 12-разрядного вывода на
8-разрядный.
23L2.3. Не совсем 12-разрядное
разрешение
Как уже упоминалось в главе 23N, используе-
мые нами устройства ЦАП и АЦП поддержи-
вают более высокое разрешение, чем мы мо-
жем реализовать в наших схемах, собранных
23L2. Лабораторное занятие SiLabs 4. Прерывания, АЦП и ЦАП
987
на макетных платах: влияние младших двух
или трех разрядов из двенадцати возможных
«глушится» искажениями. Но просто для того,
чтобы показать вам, что такое 12-разрядное
разрешение, мы поэкспериментируем, работая
с ЦАП в пошаговом режиме и наблюдая его вы-
ходной сигнал посредством цифрового вольт-
метра. Цифровой вольтметр выбран по той
причине, что его усреднение позволит увидеть
даже перепады младшего разряда.
Как обычно, прежде чем задействовать это пе-
риферийное устройство, необходимо выпол-
нить большое количество инициализационных
настроек. Нам нужно было даже указывать со-
бытие, по которому выполнять обновление со-
стояния ЦАП. Для этого события обновления
мы решили делать запись в регистр ЦАП, по-
скольку этот подход выглядел наиболее прямо-
линейным. Мы решили вместо обновления по
переполнению любого из четырех счетчиков
выполнять обновление по перепаду входного
сигнала, называющегося CNVSTR.
23L2.4. Инициализация ЦАП
с помощью Мастера настроек
Запустив Мастер настроек, выберите в меню
Peripherals опцию DACs, а в открывшемся
диалоговом окне DAC выберите ЦАШ, выбрав
вкладку IDA1. Мы предпочитаем использовать
DAC1 по причине его жесткой привязки к вы-
воду РОЛ, что оставляет вывод РО.О свободным
для других задач (рис. 23L.10).
На вкладке IDA1 диалогового окна DAC вы-
полните следующие настройки:
♦ разрешите DAC1, установив флажок IDA1;
♦ выберите опцию выравнивания по левому
краю слова, включив переключатель IDA1H:
IDA1L is left justified в разделе Right Justify
Select;
♦ задайте выходной ток величиной 1 мА, вклю-
чив в разделе Output Mode переключатель
1.0 mA full-scale output current6;
♦ задайте обновление вывода ЦАП по собы-
тию записи в старший байт, включив в раз-
деле DAC output updates on переключатель
write to IDA1H;
♦ нажмите кнопку Configure Port I/O и в от-
крывшемся диалоговом окне Port I/O уста-
новите флажок Pin Skip для IDA1. Таким
образом мы оставим вывод РОЛ свободным
для его использования ЦАШ;
♦ затем установите для этого вывода анало-
говый режим, щелкнув его флажок Analog/
Digital, чтобы его значение изменилось с
буквы D на букву А.
I 0 я А
Л >,' №
04} И
I.UIH
bdii.A;}itO\ifjKiMiKt4
•Г/А51.. Wif»;'«4
*.«| I <)«'«! ftjK4
r "y:\.iif.: .by
СъгЫЫ,
.>
P./.-MJ-.e'-iii-tj f
iEiElj
!iH
^»^. c^ ->тщщщшщшщщщш}щщщшщ
р'У.лСвк - iVf D
1 e*«*
Рис. 23L.10. Конфигурирование DAC1 в окне настроек DAC
(слева). В окне настройки портов ввода-вывода (справа)
вывод DAC1 конфигурируется для работы в аналоговом
режиме
6 Конечно же, потому что мы, как всегда, предпочитаем зна-
чение 1. Это значение делает вычисления очень легкими.
988
23L Лабораторное занятие: микроконтроллеры 4. Прерывания; АЦП и ЦАП
Подключите выход DAC на «землю» через ре-
зистор номиналом 1,2 кОм. Таким образом мы
сможем преобразовать выходной токовый сиг-
нал ЦАП в напряжение.
23L2.5. Параметры DAC1
из Мастера настроек
Результатом выбранных нами опций в Мастере
настроек будет файл с набором инициализаци-
онных команд (листинг 23L.3), которые нуж-
но добавить в неполный листинг программы
в разделе 23L2.6.
Листинг 23L.3. Параметры инициализации
DACJnit:
movlDA1CN,#0F2h
ret
PortJOJnit:
; PO.O - Unassigned, Open-Drain, Digital
; P0.1 - Skipped, Open-Drain, Analog
; P0.2 - Unassigned, Open-Drain, Digital
; РО.З - Unassigned, Open-Drain, Digital
; P0.4 - Unassigned, Open-Drain, Digital
; P0.5 - Unassigned, Open-Drain, Digital
; P0.6 - Unassigned, Open-Drain, Digital
; P0.7 - Unassigned, Open-Drain, Digital
mov POMDIN, #OFDh
mov POSKIP, #002h
movXBR1,#040h
ret
; Initialization function for device,
; Функция инициализации устройства,
; Call lnit_Device from your main program
; Вызов Init.Device осуществляется из вашей главной
программы
lnit_Device:
Icall DACJnit
Icall PortJOJnit
ret
end
Добавьте эти инициализационные команды в
неполную программу dac_test_12_junel5.a51
в разделе 23L.2.6.
23L2.6. Начало программы для
проверки ЦАП, которую вам нужно
будет завершить
В листинге 23L.4 приводится цикл, который
инкрементирует 12-разрядное значение ЦАП
при каждой итерации. (Подробности этой опе-
рации инкрементирования 12-разрядного зна-
чения излагаются после листинга.) Инициа-
лизационные параметры можно получить с по-
мощью Мастера настроек, а затем добавить их
в программу.
Листинг 23L.4. Программа тестирования ЦАП
; dac_test_12Junei 5.a51 12-разрядное разрешение: видимое только при наблюдении с помощью цифрового
; вольтметра при пошаговом исполнении
; Переход на ЦАП1; назначения выводов отмечены в комментарии
; Обратите ВНИМАНИЕ на то, что это не полная программа: вам нужно выполнить настройку параметров ЦАП1
; (возможно, используя для этого Мастер настроек)
SNOSYMBOLS ; Сокращаем объем кода в листинге
SINCLUDE (C:\MICRO\8051 \RAISON\INC\c8051 f410.inc)
STACKBOT EQU 080h ; Размещаем стек в начале рабочего косвенно адресуемого блока памяти (80h и дальше)
; Вывод ЦАП1 на порт Р0.1, преобразовываем ток в напряжение, подключив вывод на «землю»
; через резистор номиналом 1 кОм
ORGOh
UMP STARTUP
ORG080h
STARTUP: MOV SP, #STACKBOT-1
ACALL USUAL_SETUP
ACALLANALOG.SETUP
23L2. Лабораторное занятие SiLabs 4. Прерывания, АЦП и ЦАП 989
ACALL Init.Device ; Вызываются инициализационные параметры, созданные Мастером настроек, предполагая,
; что вы далее вставили их в программу
; 12-разрядный равномерно нарастающий сигнал
CLRA
CLR С; Обнуляем бит переноса
MOV IDA1L, А ; Первый проход, чтобы узнать напряжение при нулевом токе ЦАП1
MOVIDA1H,A
RAMP_12: MOV A, IDA1L ; Извлекаем младший полубайт
ADD A, #1 Oh ; Инкрементируем младший полубайт с выравниванием по левому краю (обновляя бит переноса)
MOVIDA1UA ; Обновляем младший байт ЦАП
MOV A, IDA1Н ; Извлекаем старший байт
ADDC А, #0 ; Используем выходной перенос из младшего байта для обновления старшего байта
MOVIDA1H,A
SJMPRAMPJ2
; ИНИЦИАЛИЗАЦИИ
USUAL_SETUP: ANL PCAOMD, #NOT(040h) ; Отключаем сторожевой таймер, обнуляем бит разрешения
; сторожевого таймера
; Конфигурируем генератор тактовых колебаний
ORL OSCICN, #04h ; Частота системного тактового сигнала = 25,5 мГц / 8
; Разрешаем матричный переключатель портов входа-выхода
MOV XBR1, #40h ; Разрешаем матричный переключатель
RET
ANALOG_SETUP: SETB PO.O ; Обеспечиваем высокий выходной уровень защелки
RET
; СЛЕДУЮЩИЙ РАЗДЕЛ ПРОГРАММЫ НЕЗАВЕРШЕН:
; (вставьте здесь инициализационные команды, созданные в Мастере настроек)
; Следующие четыре линии использовать не обязательно;
; эти и другие требуемые строки кода должен сгенерировать Мастер настроек
;НАСТРОЙКА.ПОРТА
; Задаем иэтпн величиной 2,2 В (необходимо для АЦП, но для ЦАП, скорее всего, нет)
; MOV P0MDIN, ; Задаем аналоговый режим работы для вывода ЦАП 1
MOV POSKIP, ; Даем указание матричному переключателю пропустить бит ЦАП1 (Р0.1)
; MOV IDA1CN, ; Разрешаем DAC1
; обновление вывода ЦАП по событию записи в старший байт
; выравнивание по левому краю слова 1 мА полной шкалы
; RET
END
Некоторые подробности 12-разрядного байт, благодаря приему, который мы рассмо-
иыкпрмрытмппияымя трешл в разделе 21N.6. В частности, выполняя
инкрементирование командой ADDC А, #0, если
Цикл для работы с 12-разрядным линейно на- установлен бит переноса. На первый взгляд ин-
растающим сигналом может выполнять инкре- крементирование младшего полубайта может
ментирование значений, больших чем один выглядеть странным.
990
23L Лабораторное занятие: микроконтроллеры 4. Прерывания; АЦП и ЦАП
Следует иметь в виду, что команда INC А непри-
годна ни для каких операций со значениями
больше чем один байт, поскольку эта команда
не модифицирует флаги. Таким образом, мы
бы не смогли использовать эту команду для
данной операции с 16-разрядным значением,
которая задействует флаг переноса в своем вто-
ром шаге7.
Еще один момент: если необходима команда
ADD, а не INC, тогда зачем для инкрементирова-
ния добавляем 10h, а не Olh? Потому что самый
младший полубайт (т. е. самые младшие четыре
бита) нашего 12-битового значения хранится в
старшем полубайте регистра IDA1L Добавление
значения 10h может выглядеть странно, но это
действительно просто инкрементирует млад-
ший полубайт нашего 12-разрядного значения.
Проверяем 12-разрядный линейно
нарастающий сигнал
Обратите внимание, что данная программа не
содержит никаких задержек, поэтому не ожи-
дайте увидеть что-либо вразумительное, ис-
полняя ее в непрерывном режиме. Крошечные
инкрементирования младшего байта 12-раз-
рядного значения можно исследовать следую-
щими двумя способами:
♦ исполнять программу в пошаговом режиме,
чтобы дать цифровому вольтметру время
установиться и устранить шум посредством
усреднения входных значений;
♦ установить контрольную точку в каком-либо
месте цикла. Подробности этого решения
рассматриваются чуть далее.
Любой из этих методов должен позволить уви-
деть инкрементирование младшего бита.
Значение младшего бита в терминах
напряжения
Какая величина шага в терминах напряжения
самого младшего бита данного 12-разрядного
ЦАП, которую вы можете наблюдать? Если зна-
чение полной шкалы выходного сигнала равно
1,2 В, какую величину шага можно ожидать?8
Настройте окно мониторинга регистров
Watch
Значение IDA1 можно наблюдать одним из двух
способов. Более трудоемкий способ, который
обеспечивает лучший контроль, состоит в том,
чтобы настроить окно мониторинга регистров
Watch для требуемых регистров. Таким обра-
зом вы сможете наблюдать только выбранные
регистры.
Настройка окна мониторинга регистров
Watch для требуемых регистров
На рис. 23L.11 мы начали процесс отображе-
ния в виде отдельных элементов двухбайтовых
входных регистров IDAC1. Как показано на ри-
сунке, мы выбрали младший байт.
На рис. 23L.12 отображены результаты монито-
ринга обоих байтов: IDA1Н (старший) и IDA1L
(младший).
Установка контрольной точки
Когда процесс исполнения программы дости-
гает контрольной точки, исполнение програм-
мы останавливается в этой точке. Это позво-
ляет нам увидеть изменения входного значе-
Для мониторинга требуемого регистра •'
выделите его, а затем щелкните по нему i _ ;;i,a,
правой кнопкой мыши
ili ■■^-^;;•■ -
Затем нужно выбрать правильный тип данных регистра -
(в случае неправильного выбора система об этот НЕ сообщает)
Рис. 23L.11. Настройка окна мониторинга регистров Watch
7 Данная информация спрятана глубоко в описании ко-
манды INC в руководстве программиста 48051 Programmer's
Guide and Instruction Set» компании Philips, доступном по
адресу: http://www.keil.com/dd/docs/datashts/philips/
p51_pg.pdf
ния IDAC1 после каждой итерации цикла. При
каждом нажатии кнопки запуска программы
Go можно видеть, как значение регистра IDA1L
8 1,2 в/212.
23L.2. Лабораторное занятие SiLabs 4. Прерывания, АЦП и ЦАП
991
Значение младшего байта входного регистра ЦАП
после двух итераций цикла. Это значение 2, а не 20h,
поскольку младший полубайт входного значения ЦАП
хранится в битах 67...64
\Курсор (синяя линия): текущая точка в исполнении — остановлено в контрольной точке
Рис. 23L.12. Использование контрольных точек делает легкой задачу наблюдения влияния инкрементирования входного
значения ЦАП
Шаги линейно нарастающего сигнала,
очищенные от шума, используя
усреднение
То же ссилог, с еще большим усреднением
Рис. 23L.13. Восьмиразрядный линейно нарастающий входной сигнал ЦАП, в котором можно видеть шаги младшего бита.
(Вертикальный сдвиг на правом рисунке является побочным эффектом измененного напряжения запуска развертки.)
инкрементируется. (Но своим особым спосо-
бом: значение регистра увеличивается на 10h,
но это означает увеличение на единицу самого
младшего байта значения во входном регистре
ЦАП.) На рис. 23L.12 показано содержимое
обоих входных регистров в окне мониторинга
регистров Watch.
Кроме просмотра содержимого входных ре-
гистров ЦАП в окне мониторинга регистров
Watch, это можно также делать, выполнив по-
следовательность команд меню средства разра-
ботки View/Debug Windows/SFR's/IDAC.
Наблюдайте значение ЦАП на цифровом
вольтметре; при этом можно также определить
величину шага младшего бита в терминах на-
пряжения. На рис. 23L.12 отображено входя-
щее значение ЦАП, равное 2 (чей младший бит
хранится в бите d4 регистра IDA1L). Для этого
значения мы наблюдали выходное напряже-
ние, равное приблизительно 0,9 мВ.
Между прочим, цифровой вольтметр необходи-
мо подключать на «землю» как можно ближе к
выводу «земли» микроконтроллера C8051F410.
Это объясняется тем, что несколько сантиме-
тров линии «земли» макетной платы могут
создать падение напряжения величиной в не-
сколько младших битов. Мы наблюдали паде-
ние напряжения величиной около 3 мВ вдоль
линии «земли» макетной платы длиной 18 см.
23L2.7. Восьмиразрядное
разрешение
В случае схемы, собранной на макетной плате,
более полезным будет задать 8-разрядное раз-
решение. Отдельные перепады 8-разрядного
линейно нарастающего входного сигнала ЦАП
можно наблюдать на осциллографе; с этого вре-
мени мы будем конфигурировать наши ЦАП и
АЦП как 8-разрядные устройства. Для этого
мы просто будем игнорировать младшие четы-
ре бита, используя только регистр IDA1Н ЦАП
и эквивалентный регистр старшего байта АЦП.
На рис. 23L.13 показаны осциллограммы 8-раз-
рядных входных сигналов ЦАП, по которым
можно видеть, что при усреднении шаг млад-
шего бита составляет около 5 мВ.
992
23L Лабораторное занятие: микроконтроллеры 4. Прерывания; АЦП и ЦАП
Разработайте программу для цикла
обработки линейно нарастающего
входного сигнала ЦАП
Это очень простая программа, не содержащая
трудоемкого кода, требуемого для реализации
инкрементации 12-разрядных значений. Цикл
обработки линейно нарастающего сигнала дей-
ствительно такой короткий, как намекается в
следующих далее комментариях. Написание
этого кода мы предоставим вам. Обратите вни-
мание на то, что для 8-разрядного управления
ЦАП запись нужно выполнять только в регистр,
в котором хранятся старшие 8 битов обрабаты-
ваемого значения. Это регистр IDA1Н.
В качестве рабочего регистра для реализации
инкрементирования будем использовать акку-
мулятор.
EIGHT_BIT: ; Перемещаем текущее значение линейно
; нарастающего сигнала в ЦАП1
; Инкрементируем это значение
; Берем небольшую паузу
; Повторяем до бесконечности
23L2.8. Полный код программы
за исключением цикла обработки
входного линейно нарастающего
сигнала
Полная программа (листинг 23L.5) содержит
код задержки, чтобы ее можно было исполнять
в непрерывном режиме и наблюдать линей-
но нарастающий сигнал на осциллографе. Как
обычно, код для инициализации параметров
намного более трудоемкий, чем собственно код
для выполнения задачи.
Листинг 23L.5. Программа обработки линейно нарастающего входного сигнала ЦАП
; dac1_8bit_wizard_MT.a51 Восьмиразрядное разрешение
SNOSYMBOLS ; Сокращаем объем кода в листинге
SINCLUDE (C:\MICRO\8051\RAISON\INC\c8051f410.inc)
STACKBOT EQU 07Fh ; Размещаем стек в начале рабочего косвенно адресуемого блока памяти (80п и дальше)
; DAC1 at P0.1
ORGOh
UMP STARTUP
ORG080h
STARTUP: MOV SP, #STACKBOT
acall USUAL.SETUP
acall lnit_Device ; Предоставляем Мастеру настроек делать нашу работу
setb р0.1 ; Обеспечиваем высокий выходной уровень ЦАП
; Код цикла обработки 8-разрядного равномерно нарастающего сигнала
CLRA
EIGHT.BIT:
.; Перемещаем текущее значение линейно нарастающего сигнала (старший байт) в ЦАП1
.; Инкрементируем это значение
.; Берем небольшую паузу (используйте подпрограмму DELAYSHORT)
_; Повторяем до бесконечности
DELAYSHORT: PUSH ACC
MOV A, #1 ОН
DJNZACC,$
POP ACC
RET
23L2. Лабораторное занятие SiLabs 4. Прерывания, АЦП и ЦАП
993
USUAL_SETUP: ANL PCAOMD, #not(040h)
ret
/ ———————————————— ———
;- Сгенерированный файл инициализаций -
; Отключаем сторожевой таймер
; Функция инициализации устройства,
; Вызов lnit_Device осуществляется из вашей главной программы
Init.Device:
Icall DACJnit
Icall PortJOJnit
ret
; Функции инициализации для конкретного периферийного устройства
; Вызываются с метки Init.Device
DACJnit:
movlDA1CN,#0F2h
ret
PortJOJnit:
; PO.O - He присвоенный, открытый сток, цифровой режим
; РОЛ - Пропущенный, открытый сток, аналоговый режим
; Р0.2 - Не присвоенный, открытый сток, цифровой режим
; РОЗ - Не присвоенный, открытый сток, цифровой режим
movP0MDIN,#0FDh
mov POSKIP, #002h
movXBR1,#040h
ret
end
Значение самого младшего бита в терминах на-
пряжения (инкремент, который можно наблю-
дать, если исполнять программу в многошаго-
вом режиме с небольшой задержкой) можно
увидеть с помощью цифрового вольтметра.
В нашем случае это значение было приблизи-
тельно 8 мВ. Но интереснее наблюдать это зна-
чение на осциллографе. В этом случае для чет-
кого отображения отдельных ступеней сигнала
может потребоваться ограничить полосу про-
пускания (скрыть шумовые пульсации).
23Ь2.9.АЦП
Оборудование для источника сигнала
Для первой проверки работоспособности АЦП
лучше подать входной сигнал постоянного
уровня. Источником такого сигнала может
служить потенциометр (рис. 23L.14), с макси-
мальным значением, чуть большим, чем значе-
ние полной шкалы, и умеренным #ТЕВ.
-На мультиплексор АЦП
Рис. 23L.14. Потенциометр может служить в качестве источ-
ника входного сигнала постоянного уровня для АЦП
Каково максимальное i?TEB для этой схемы?
Несомненно, этот вопрос вызовет у вас много
приятных воспоминаний, унося вас к началу
этого курса9.
9 Если воспоминания даются вам с трудом, мы напомним,
что максимальное значение RTEB будет при нахождении
движка потенциометра в самом верхнем положении. Тогда
Rj.EB = (1 кОм || 1 кОм) = 0,5 кОм. При всех других положе-
ниях движка потенциометра это значение будет меньше.
994
23L Лабораторное занятие: микроконтроллеры 4. Прерывания; АЦП и ЦАП
Программа
Задача настройки АЦП похожа на настройку
ЦАП: множество параметров требуют мно-
жества решений. Наша первая программа для
проверки работы АЦП выводит 8-разрядное
выходное значение АЦП на ЖКД. Данная про-
грамма такая же простая, как и большинство
других наших программ. Листинг 23L.6 содер-
жит код (который мы уже рассматривали в раз-
деле 23N.4.3), который берет значение выборки
у АЦП.
Листинг 23L.6. Программа тестирования АЦП
GET.SAMPLE: CLR CNVRT.START
; Низкий уровень на AD0BUSY
; (чтобы разрешить положительный перепад)
SETB CNVRT.START
; Положительный перепад на ADOBUSY
; начинает процесс преобразования
JNB CNVRSN_DONE, $ ; Ждем здесь, пока не будет
; установлен флаг завершения преобразования
MOVSAMPLE_HI,ADC0H
; Теперь берем старший байт из АЦП
; и сохраняем его
RET
Функция GET_SAMPLE содержит пару команд,
формирующих положительный перепад по
биту, который запускает АЦП. Мы рассмотрели
подробности этого кода в разделе 23N.4.3.
23L2.10. Конфигурирование АЦП
с помощью Мастера настроек
Мы рассмотрели другой процесс инициали-
зации АЦП в разделе 23N.4.3. Но настройки
порта для АЦП сложнее, чем для предыдущих
программ. Настройки ЦАП мы оставим преж-
ними, с выходом на порт Р0.1, но добавим вход
для прерывания, а также установим эталон-
ное напряжение. Матричный переключатель
позволяет задать аналоговый режим работы
для выводов ЦАП и АЦП (вскоре мы будем
использовать оба устройства в программе), а
также позволяет задать эталонное напряже-
ние, выведенное на вывод Р1.2. Для этого пор-
та установлен аналоговый режим работы, и
его сигнал выводится наружу, хотя в АЦП он
используется только внутренне (рис. 23L.15).
Инициализация параметров АЦП и ЦАП при-
ведена в табл. 23L.2.
Предварительная проверка АЦП
посредством вывода на дисплей
напряжения с потенциометра
Даная проверка работы АЦП эквивалентна
демонстрации цифрового вольтметра. Лис-
тинг 23L.7 содержит только основной код про-
граммы; код для инициализации АЦП можно
сгенерировать с помощью Мастера настроек.
Рис. 23L.15. Настройка параметров АЦП и ЦАП в окне матричного переключателя
23L2. Лабораторное занятие SiLabs 4. Прерывания, АЦП и ЦАП
995
Таблица 23L.2. Инициализация параметров АЦП и ЦАП
Регистр/порт
ADC0CN
...
...
...
...
...
ADC0MX
ADC0TK
...
ADC0CF
...
РО
P0MDIN
POSKIP
P1SKIP
REFOCN
Значение байта
d7
d5
d4
62
dl,dO
00b
OOh
d3...dO
FBh
d2,dl
00b
dl,dO
OFCh
23h
04h
13h
Функция
Разрешение ADCO: 1 ==> разрешен
ADOINT: 1 ==> Выборка готова (это флаг, который мы проверяем)
ADOBUSY: Положительный перепад начинает процесс преобразования
ADOLJST: 1 ==> Выравнивание по левому краю
Выборка события, запускающего преобразование
Выборка положительного перепада на ADOBUSY как события,
начинающего процесс преобразования
Назначение мультиплексора ADC0 ==> биту РО.О
Режим отслеживания
Двойной режим (режим работы по умолчанию)
Количество преобразований за цикл «запуск — преобразование»
==> одна выборка/цикл «запуск — преобразование»
Установлены оба бита, чтобы разрешить использование в аналоговом
режиме
Для выводов АЦП и ЦАП задан аналоговый режим (Р0.0, РОЛ)
Пропускаем INTO*, АЦП и ЦАП, dl, dO
Пропускаем вывод 17ЭТ
Разрешение 17ЭТ, установка полной шкалы на 2,2 В
Листинг 23L.7. Программа предварительной проверки АЦП
; adc_wizard_apr11 .a51; Проверка АЦП выполнена, используя Мастер настроек, 11 января: выводы переназначены
; АЦП в качестве вольтметра (отображение 8 битов на ЖКД), вход на РО.О
$NOSYMBOLS; Сокращаем объем кода в листинге...
$INCLUDE(C:\MICRO\8051\RAISON\INQc8051f410.inc)
;... а не то эта строка может создать громадный список
; определений идентификаторов (все они для регистров 8051)
SINCLUDE (C:\MICRO\8051\RAISON\INCWECTORS320.INC) ; Файл тома определения векторов
STACKBOT EQU 080h ; Размещаем стек в начале рабочего косвенно адресуемого блока памяти (80h и дальше)
DISPLAY_LO EQU P2
DISPLAYJHI EQU P1
; Использование порта: ADC0 на РО.О
ORGOh
UMP STARTUP
ORG080h
STARTUP: MOVSP,#STACKBOT-1
acall USUAL_SETUP
acall SETUP.ANALOG
acall Init Device
START_ADC: mov ADCOCN, #84h
movADC0CN,#94h
jnbADC0CN.5,$
mov DISPLAYJHI, ADCOH
movDISPLAYJ_O,ADC0L
sjmp START.ADC
; Низкий уровень на ADOBUSY
; Высокий уровень на ADOBUSY начинает процесс преобразования
; Ждем здесь, пока не будет установлен флаг завершения преобразования
; Выводим выходное значение АЦП на дисплей
- ИНИЦИАЛИЗАЦИИ
USUAL_SETUP: anl PCA0MD, #NOT(040h); Отключаем сторожевой таймер
ret; Обнуляем бит разрешения сторожевого таймера
SETUPJ\NALOG: setb РО.О
ret
; Установка высокого уровня, чтобы позволить использовать вывод в аналоговом
; режиме (для АЦП)
- Инициализации Мастера настроек (значения этих параметров можно получить с помощью Мастера настроек)
996
23L Лабораторное занятие: микроконтроллеры 4. Прерывания; АЦП и ЦАП
Удовлетворившись тем, что ЦАП и АЦП рабо-
тают должным образом, можно подавать вы-
ходной сигнал АЦП на вход ЦАП, чем мы и
займемся дальше.
23L2.11. Программа передачи
значения с АЦП на ЦАП
по прерыванию
Программа adc_dac_intjanll.a51 берет вы-
борку с АЦП по каждому прерыванию микро-
контроллера C8051F410. Затем это 8-разрядное
значение выборки отображается на ЖКД, а
также отправляется на вход ЦАП. Программа
слишком большая для ручного ввода, поэтому
загрузите ее на веб-сайте книги.
23L2.12. Подача выходного сигнала
АЦП на ЦАП
Последовательное преобразование
синусоидального сигнала АЦП и ЦАП
Эта программа предоставляет хорошую плат-
форму для испытания рассмотренных нами
правил выборки, когда мы собрали схему АЦП
на лабораторном занятии 18L. В качестве ис-
точника входного синусоидального сигнала для
преобразования в АЦП используйте генератор
сигналов. При этом обеспечьте, чтобы размах
этого сигнала не превышал входной диапазон
АЦП: от 0 до 2,2 В.
А чтобы задать частоту выборки, возьми-
те прямоугольный ТТЛ-сигнал от генератора
сигналов макетной платы или от отдельного
генератора сигналов в качестве источника за-
проса прерывания INTO*. Для первого тести-
рования наблюдайте с помощью осциллогра-
фа входной и выходной аналоговые сигналы.
Если задать частоту выборки, кратную трем и
четырем значениям частоты входного сигнала,
то наблюдаемые осциллограммы должны быть
наподобие показанных на рис. 23L.16.
Экспериментируя с соотношением между ча-
стотой входного сигнала и частотой выборки,
можно подтвердить, по крайней мере грубо,
правило Найквиста. При частоте дискретиза-
ции, меньшей, чем двойная частота входного
сигнала, должны наблюдаться побочные сиг-
налы. Но восстановленный сигнал может быть
настолько странным, что его будет трудно рас-
познать как синусоидальный. Предлагаемый
нами далее фильтр поможет сделать побочные
сигналы более очевидными.
Фильтрация выходного сигнала ЦАП
Хороший низкочастотный восстанавливаю-
щий фильтр обеспечивает эффективную вы-
борку с частотой дискретизации чуть выше
двойной максимальной частоты входного сиг-
нала. Вспомните, что самый первый побочный
сигнал имеет частоту^ЫБ -fBX_MAKC Имеющийся
в нашем распоряжении качественный НЧ-
фильтр МАХ294 ослабляет сигналы более
-60 дБ (меньше одной тысячной) с частотой
всего лишь 20% выше^тс */3лЪ. Таким обра-
зом, мы можем безопасно выполнять выборку
на частоте, равной 292х/вх.шкс или выше. Вам
вряд ли захочется вычислять эту безопасную
частоту выборки, когда можно просто экспери-
ментировать с частотой выборки, поворачивая
ручку установки частоты выходного сигнала
Тактовый сигнал выборки
(запрашивает прерывание INTO*)
Входной аналоговый сигнал
(на АЦП)
Выходной аналоговый сигнал
(из ЦАП)
1 5.00 V
л J f 360mV
Рис. 23L16. Синусоидальный сигнал, подаваемый на АЦП, и выходной синусоидальный сигнал, восстановленный ЦАП
23L2. Лабораторное занятие SiLabs 4. Прерывания, АЦП и ЦАП
997
генератора сигналов и одновременно наблюдая
результаты на осциллографе.
В главе 22N мы изложили подробности схемы
фильтра и усилителя звуковой частоты, кото-
рый позволяет прослушивать восстановленный
сигнал, поэтому мы не будем останавливается
на этих моментах здесь. Но для подачи сигнала
тактирования на фильтр МАХ294 вам потре-
буется еще один, третий, генератор сигналов.
Если у вас нет лишнего генератора сигналов
для этого, соберите генератор на таймере 555
с прямоугольным выходным сигналом с часто-
той, регулируемой от 5 кГц до 1 МГц (см. лабо-
раторное занятие 8L).
Прослушивание восстановленного
сигнала
Мы надеемся, что вы соберете усилитель зву-
ковой частоты, рассмотренный в разделе 23N.5,
и прослушаете восстановленные сигналы. Ин-
формация, полученная своими ушами, допол-
нит информацию о сигнале, полученную по-
средством наблюдения их на осциллографе.
23L2.13. При желании можете
изменить форму сигналов
В главе 22N мы описали некоторые изменения,
которые микроконтроллер 8051 может внести в
дискретизированный сигнал перед тем, как по-
давать его на ЦАП. Например, с помощью не-
скольких строчек кода можно выполнить двух-
полупериодное или однополупериодное вы-
прямление этого сигнала. Но, возможно, более
интересным будет цифровой низкочастотный
фильтр, реализуемый взвешенным усреднением
текущего значения выборки и текущего среднего
значения. Несомненно, что интереснее прослу-
шивать сигнал, обработанный таким фильтром.
Но, как мы признаем в главе 22N, эти упражне-
ния являются, по сути, развлечением, посколь-
ку микроконтроллер 8051 обладает очень сла-
быми возможностями обработки сигналов. Но
они позволят вам немного попрактиковаться в
программировании, одновременно доставляя
вознаграждение в виде конкретных результа-
тов, которые можно наблюдать на осциллогра-
фе и, возможно, прослушивать.
23S. Дополнительный материал:
микроконтроллеры 4
23S.1. Использование
ассемблера/компилятора
и симулятора RIDE
23S.1.1. Установка RIDE
Ассемблер/компилятор RIDE1 предоставляет-
ся бесплатно для проектов с объемом кода до 8
Кб. Ассемблер состоит из двух модулей: инфра-
структуры, называющейся RIDE7 (на момент
подготовки данной книги), которая поддержи-
вает множество микроконтроллеров, и модуля
для конкретного микроконтроллера. Модуль
RIDE, требуемый нам для микроконтроллера
8051, называется RKit51.
Чтобы получить доступ для загрузки этих двух
компонентов, необходимо зарегистрироваться
на сайте компании. После этого вышлют код
регистрации, который позволит работать с лю~
бительской версией модуля RKit51. После уста-
новки Ride7 и модуля RKit51 среду разработки
можно будет использовать без регистрации в
течение недели. Но мы рекомендуем не мед-
лить с регистрацией и выполнить ее как можно
быстрее.
Процесс регистрации следующий. В меню Help
выберите опцию License, а затем опцию Se-
rial activation и введите код регистрации.
Щелкните по ссылке Get Activation code on-
line, чтобы получить код второй регистрации,
который будет выслан на вашу электронную
почту. Получив этот код, введите его, и на этом
процесс лицензирования будет завершен.
Между прочим, при установке RIDE запом-
ните папку установки. Эта информация вам
1 Сокращение от Raisonance Integrated Design Environment
(интегрированная среда разработки Raisonance). Raiso-
nance - это французская компания.
потребуется позже, когда нужно будет сооб-
щить RIDE, где находятся ваши файлы equates
для регистров микроконтроллера. Например,
на нашей машине папка INC, содержащая фай-
лы equates для микроконтроллера C8051F410,
находится по такому пути:
C:\Program Files\Raisonance\Ride\inc\51 XSilabs
А для версии микроконтроллера DS89C420
путь такой же, но только заканчивается не-
много по-другому: ...\51\Dallas. В вашем случае
папка INC может находиться по другому пути,
в зависимости от диска и папки установки.
Поэтому запомните, куда вы устанавливаете
RIDE, чтобы потом знать, где искать эту папку.
23S.1.2. Создание проекта в RIDE
Среда RIDE хранит файлы с исходным кодом и
параметры отладки (которые мы рассмотрим
далее в разделе 23S.2.1) в папке проекта.
Чтобы создать проект, выберите в меню Project
опцию New. В открывшемся диалоговом окне
создания проекта (рис. 23S.1) укажите пап-
ку, в которой нужно сохранить проект (поле
Location), название проекта (поле Name), a
также версию микроконтроллера 8051, на ко-
торой будет исполняться код проекта (поле
Processor).
Выбор правильной версии микроконтролле-
ра важен, поскольку, хотя все перечисленные
в поле Processor микроконтроллеры являют-
ся модификациями микроконтроллера 8051,
определенные новые версии содержат некото-
рые возможности и регистры, отсутствующие
в оригинальном микроконтроллере 8051. Для
проекта компьютера из дискретных компонен-
тов выберите в узле Dallas версию микрокон-
троллера DS80C320. Среда RIDE не предлага-
ет используемую нами версию 89С430, поэтому
23S.1. Использование ассемблера/компилятора и симулятора RIDE
999
микроконтроллера. При этом мы знаем, что
кроме перечисленных в списке RIDE на рынке
предлагаются другие версии этого микрокон-
троллера, как можно судить по отсутствию в пе-
речне применяемого нами микроконтроллера
производства компании Dallas Semiconductors.
Рис. 23S.1. Выбор папки, названия и версии контроллера
при создании проекта
выбираем наиболее близкую к ней. А для про-
екта компьютера на автономном микрокон-
троллере выберите в узле SiliconLaboratories
версию C8051F410.
Если просмотреть список производителей ми-
кроконтроллера 8051 и список версий этого
микроконтроллера, предлагаемых каждым из
производителей, то доступное разнообразие
вариантов очень впечатляет. Вот поэтому мы
и выбрали контроллер 8051, так как это наи-
более распространенный на рынке микрокон-
троллер. Список RIDE содержит 19 произво-
дителей. А лишь для одного производителя,
Silicon Laboratories, RIDE содержит 244 версии
23S.1.3. Создаем исходный код
на ассемблере (расширение
файла *.а51)
Создайте файл исходного кода на языке ассем-
блера или, что намного легче, откройте уже
существующий файл этого типа, полученный
от кого-либо, чтобы быть уверенным, что это
заведомо правильный файл. Такой файл мож-
но добавить в проект, выбрав в меню Project
опцию Add Item, в открывшемся диалоговом
окне навигации по файловой системе найти
требуемый файл и нажать кнопку Открыть.
На рис. 23S.2 показан снимок экрана открытой
в RIDE программы из лабораторного занятия
по компьютеру из дискретных компонентов
для ввода значения и вывода его на дисплей.
Во вставке на рисунке показан код цикла соб-
ственно программы, выполняющей полезные
операции.
Данная программа просто принимает байт с
цифровой клавиатуры, а затем выводит его на
дисплей. На нынешнем этапе вам не нужно по-
нимать, как работает данная программа. Все,
что интересует нас в текущий момент, — это
формат отображения исходного кода в RIDE.
Некоторые особенности этого формата упоми-
наются чуть далее.
Рис. 23S.2. Окно проекта среды RIDE, содержащее файл исходного кода на языке ассемблера
1000
23S. Дополнительный материал: микроконтроллеры 4
Директивы для ассемблера
(а не для микроконтроллера 8051)
Исходный файл содержит несколько команд,
предназначенных для ассемблера или компиля-
тора, а не для исполнения микроконтроллером.
Такие команды называются директивами. Мы
рассмотрели большинство из этих директив в
разделе 20N.7, а сейчас только бегло пройдемся
по ним.
♦ Директива NOSYMBOLS - избавляет
нас от необходимости генерировать много-
страничный перечень названий регистров и
выводов микроконтроллера DS80C320 при
каждой распечатке файла .1st. Это файл ма-
шинного кода, создаваемый ассемблером из
исходного кода на языке ассемблера.
Среда RIDE предоставляет альтернативу
этой директиве в виде окна свойств проекта,
в котором свойствам Symbol table и Display
includes можно присвоить значение No (это
значение по умолчанию) (рис. 23S.3).
Альтернатива
директиве
-NOSYMBOLS/uw
устранения вывода на
экран эквивалентных
обозначений
(включаемых
файлов)
Рис. 23S.3. Альтернативный способ избавиться от обшир-
ных листингов
Директива INCLUDE — эта директива рас-
сматривается главе 21N; для теперешней
очень простой программы она не нужна. Но
мы вставляем эту директиву вместе с соответ-
ствующими параметрами на случай, если она
требуется для какой-либо другой програм-
мы. На рис. 23S.4 включенный файл отобра-
жается в узле Dependencies (Зависимости) в
правой верхней панели среды RIDE.
♦ Директива ORG — подробно рассматрива-
ется в главе 21N, сообщает ассемблеру адрес
ячейки памяти, в которой поместить код, ко-
торый следует за этой директивой.
Листинги и машинный код
Наши лабораторные занятия по микрокон-
троллерам включают много листингов про-
грамм, которые кроме исходного кода (коман-
ды на языке ассемблера типа MOV A, DPTR, как
на рис. 23S.2) также содержат результат работы
ассемблера: исполняемый машинный код (типа
шестнадцатеричного значения Е0 в этом ли-
стинге).
Способность ассемблера преобразовать пони-
маемый людьми код на языке ассемблера типа
MOV А... в труднопонимаемый для людей экви-
валентный исполняемый машинный код типа
Е0 является его основной функцией. Человек
мог бы посмотреть для каждой команды на
языке ассемблера ее эквивалентный машинный
код в специальной таблице; мы даже пару раз
дадим вам задание сделать это. Но люди не мо-
гут быстро справиться с этой задачей, и к тому
же им не очень нравится выполнять ее. При
вводе программ в память RAM, как нам часто
приходится делать при работе с компьютером
из дискретных компонентов, мы набираем их в
шестнадцатеричном машинном коде на цифро-
вой клавиатуре.
Но при работе с компьютером на автономном
микроконтроллере C8051F410, а также с ком-
пьютером из дискретных компонентов на бо-
лее поздних лабораторных занятиях, мы не
будем утруждать себя подобным трудоемким
занятием, а просто загрузим исполняемый код
в микроконтроллер, используя компьютер.
•^gej№^^
^-^Зависимости^ включенный файл
Рис. 23S.4. Отображение включенных файлов в окне среды RIDE
23S.1. Использование ассемблера/компилятора и симулятора RIDE
1001
23S.1 А Выполняемые ассемблером
замены, позволяющие
использовать символические
идентификаторы
Иногда для того, чтобы преобразовать команду
на языке ассемблера в эквивалентный машин-
ный код, требуется промежуточная операция.
Например, при работе со встроенными порта-
ми, а не внешними шинами, может потребо-
ваться обращаться к этим портам через такие
идентификаторы, как Р1 или Р2.
С этой задачей справится следующая строчка
кода, в которой предполагается, что цифровая
клавиатура и дисплей подключены к портам Р2
и Р1 соответственно:
TRANSFER: MOV Р1, P2; Копирование байта с цифровой
клавиатуры на дисплей в одну операцию
Чтобы этот код работал должным образом,
в программу необходимо подключить файл
REG320.INC, который позволяет ассемблеру
вычислить, что означают идентификаторы Р1
иР2.
Ассемблер находит адреса этих символиче-
ских идентификаторов в подключенном фай-
ле и подставляет их в создаваемый им испол-
няемый код. Далее приводится строка кода,
в которой показано значение, подставленное
ассемблером вместо идентификаторов Р1 и Р2
в соответствующий машинный код. Для порта
назначения Р1 ассемблер подставляет значе-
ние 144, а для порта Р2 — 160 (оба десятичные
значения).
85А090
TRANSFER: MOV 144,160
Эти значения отображаются ассемблером в
шестнадцатеричном формате в машинном коде
в левом столбце листинга после кода операции
85: А016 для 16010 и 9016 для 14410.
На снимке экрана на рис. 23S.4 в узле Depen-
dency в верхней левой панели показан вклю-
ченный файл REG320.INC. Такие включен-
ные файлы отображаются в этом окне только
после выполнения ассемблирования (см. раз-
дел 23S.1.7).
23S.1.5. Еще одна замена,
выполняемая ассемблером
с использованием символических
идентификаторов
Как упоминалось в разделе 21N.1.3, еще более
понятными, чем криптические идентифика-
торы типа Р1 и Р2, являются мнемонические
названия типа PORT I P0RT2. Такие описатель-
ные идентификаторы становятся возможными
благодаря директиве EQU. Определить такие
идентификаторы можно с помощью ассембле-
ра, после чего такие мнемонические идентифи-
каторы позволят нам сделать код для операции
перемещения данных TRANSFER почти не тре-
бующим разъяснений. В частности, ее можно
будет представить следующим образом:
TRANSFER: MOV DISPLAY, KEYPAD
Листинг 23S.1 иллюстрирует первый этап двух-
этапного процесса замены, который позволяет
обращаться к портам таким образом: ассемблер
заменяет указанный нами описательный иден-
тификатор DISPLAY символическим идентифи-
катором Р1. Мы уже рассмотрели ранее многие
подробности такой замены.
Листинг 23S.1. Пример замены идентификаторов
; byte_in_out_ports.a51
SNOSYMBOLS; Сокращаем объем кода в листинге
SINCLUDE (C:\MICRO\8051\RAISON\INC\REG320.inc)
KEYPAD EQU P2
DISPLAY EQU P1
ORGOh
SJMP TRANSFER
ORG 02 Oh
TRANSFER: MOV DISPLAY, KEYPAD
SJMPTRANSFER
После этого, на втором этапе замены, трансля-
тор сверяется с подключенным файлом .INC и
заменяет идентификатор Р1 адресом AOh, как
рассматривается в разделе 23S.1.4.
85А090 178 TRANSFER: MOV 144,160
Те, кто привык к программированию на языках
высокого уровня, скорее всего, не будут особо
удивлены такими возможностями. Но, согла-
ситесь, что такие замены могут сделать код на
языке ассемблера более понятным.
1002
23S. Дополнительный материал: микроконтроллеры 4
235.1.6. Ассоциируем файл типа
.а51 с проектом
В среде RIDE этот шаг называется добавле-
нием элемента. Для этого в меню Project вы-
полните команду Add Item. Откроется диало-
говое окно навигации по файловой системе, с
помощью которого найдите требуемый файл
на вашем компьютере и выполните по нему
двойной щелчок кнопкой мыши или нажмите
кнопку Открыть.
235.1.7. Ассемблируем программу
.а51
В меню Project выберите команду Build. Ко-
манда Build выполняет две операции. Сначала
она осуществляет компиляцию (для исходного
кода на языке С) или ассемблирование (для
исходного кода на языке ассемблера). Затем
выполняется компоновка ассемблированных
модулей с присвоением адресов, чтобы разме-
стить код должным образом.
Обнаружение ошибок
Если ассемблер обнаружит ошибку в коде, то он
выводит соответствующее сообщение об ошиб-
ке в панели Build Log, расположенной внизу
основного окна среды RIDE. Для демонстра-
ции этой возможности ассемблера мы внесли
ошибку в программу из раздела 23S.1.3. При
сборке программы ассемблер указал на эту
ошибку в листинге программы, подчеркнув
красной линией команду с ошибкой, и вывел
объяснительное сообщение об этой ошибке
в панели Build Log (рис. 23S.5).
Полный листинг вывода ассемблера может
иногда помочь прояснить ошибку, предостав-
ляя для нее определенный комментарий.
23SJ .8. Просмотр файла .1st
Иногда по какой-либо причине вам может за-
хотеться просмотреть листинг программы на-
подобие тех, которые мы показываем на ла-
бораторных занятиях по микроконтроллеру.
В частности, листинг, который содержит не
только исходный код на языке ассемблера, но
также адреса, по которым размещаются коман-
ды кода, а также исполняемый машинный код,
сгенерированный из исходного кода.
Для просмотра листинга в таком формате выбе-
рите в меню View опцию View Listing. Если про-
грамма содержит ошибку, то в листинге будет
отображено сообщение об этой ошибке после
строки кода, содержащей ее (листинг 23S.2).
Листинг 23S.2. Пример сообщения об ошибке
в программе
0030 175ORG30H
176 STARTUP: MOV DPTR, 8000H
; point to keypad and display
*** ERROR #23 IN LINE 11 OF C:\micro\8051\raison\lab_
programs\in_put\in_out.a51:
EXPRESSION TYPE DOES NOT MATCH INSTRUCTION
0030 E0 177 COPY: MOVX A, @DPTR
; pick up keypad value...
0031 F0 178 MOVX @DPTR, A ; ...and send it to display
0032 8000 F179 SJMP COPY ; keep doing this forever
180 END
В данном случае ошибка состоит в пропу-
щенном символе # перед операндом 8000Н.
Наличие этого символа является обязатель-
ным, и не только для того, чтобы выполнить
требуемую нам операцию (иногда ассемблер не
достаточно умный, чтобы распознать наши на-
мерения), но также и для того, чтобы команда
A53EKS"/ COMPCETC. 0 ИАРШЙСЧЗ) I ERROfljS
Рис. 23S.5. Ассемблер обнаруживает ошибки в программе
23S.2. Отладка
1003
имела разрешенный формат. Когда программа
ассемблируется без ошибок, ее можно испытать
в эмуляторе, который запускается по команде
Start меню Debug.
23S.2. Отладка
Ассемблер выявляет и сообщает о синтаксиче-
ских ошибках в коде, но он ничего не говорит
о логической правильности программы, т. е.
будет ли она делать то, что вы хотите. Этот про-
бел заполняет среда RIDE, которая предостав-
ляет возможность исполнения программы в
эмуляторе.
Чтобы запустить программу на исполнение в
эмуляторе, выполните команду Start в меню
Debug. Откроется окно, во многом похожее на
окно редактора исходного кода, в котором на-
против первой исполняемой строки кода будет
установлен курсор в виде синей стрелки. Здесь
программу можно запустить на исполнение в
пошаговом режиме, нажав клавишу F11 или
выполнив команду Step Into в меню Debug.
Обратите внимание на то, что режим пошаго-
вого исполнения имеет три варианта:
♦ Step Into — подпрограммы исполняются по-
шагово, как и главная программа2.
♦ Step Over — подпрограммы исполняются
в безостановочном режиме, но пошаговый
режим возобновляется при возвращении в
основную программу.
♦ Step Out — осуществляется немедленный
выход из подпрограммы (т. е. сразу же ис-
полняется команда возврата из подпрограм-
мы RETURN).
Но пошаговое исполнение не очень интересно,
если не воспользоваться возможностью эмуля-
тора отображать содержимое регистров микро-
контроллера 8051. Таким образом эмулятор
делает работу микроконтроллера прозрачной.
На рис. 23S.6 показано окно эмулятора после
пошагового исполнения трех строк кода про-
граммы ввода/вывода in_out.a51, а также ин-
формационные окна для элементов микрокон-
троллера (выбранные из списка в левой панели
главного окна):
♦ Основные регистры (окно Main Regis-
ters) — это окно содержит огромный объем
информации, и поэтому будет всегда полез-
ным открыть его. Оно отображает информа-
цию не только о содержимом основных ре-
гистров, но также и о содержимом регистра
указателя данных DPTR.
♦ Внешние порты (окно XdataView) — это
окно мы настроили для отображения ячеек
памяти с адресами 8000h no 8003h, которые
выделены для операций ввода-вывода в ком-
пьютере из дискретных компонентов.
Рис. 23S.6. Окно отладчика-эмулятора и панели, отображающее содержимое регистров после нескольких шагов исполнения
программы
2 В программах на языке С подпрограммы называются
функциями.
В левой нижней панели главного окна эму-
лятора отображается подробный листинг
1004
23S. Дополнительный материал: микроконтроллеры 4
программы (как листинг 23S.2). В этой пане-
ли можно видеть, например, что следующая
команда для исполнения находится по адресу
34h.
♦ Регистр PC (program counter — счетчик ко-
манд) вверху окна Main Registers содержит
такое же значение, какое он и должен содер-
жать.
♦ Содержимое остальных регистров отобража-
ет, что наша программа успела сделать после
выполнения трех команд:
♦ Регистр DPTR содержит значение 8000h, ко-
торое было загружено строкой кода, обозна-
ченной маркером STARTUP.
♦ Регистр АСС (также называется регистр А
или аккумулятор) содержит значение ABh,
которое также отображается по адресу 8000h
в окне Xdata, а также (равнозначно) в поле
@DPTR, представляющем адрес, на который
указывает регистр DPTR.
♦ Регистр АСС содержит это значение пото-
му, что оно было помещено в него из порта
ввода-вывода командой, помеченной в ли-
стинге маркером COPY, а именно MOVX А,
@ DPTR. Как мы знаем, регистр А — это то же
самое, что и регистр АСС, т. е. аккумулятор3.
23S.2.1. Что просматривать
при отладке
В левой панели окна отладчика отображает-
ся иерархический список элементов, который
Oats VV-v
Ров. ?
UAPTO
Рис. 23S.7. Дерево элементов, доступных для просмотра
при отладке программы
можно просматривать в соответствующем окне
(рис. 23S.7).
Некоторые из этих элементов требуют просмо-
тра только в редких случаях, тогда как элемент
Main Registers при отладке следует просматри-
вать всегда. Если ваша программа выполняет
операции ввода-вывода, используя внешние
шины, а не встроенные порты микроконтрол-
лера 8051, тогда, наверное, также будет полез-
ным просматривать содержимое так называе-
мой внешней памяти, поскольку порты ввода-
вывода выглядят для процессора как внешняя
память. Для просмотра этого элемента выбе-
рите в узле программы подузел Data Dump,
Введите в поле справа от значка бинокля
адрес внешней памяти (т. е. порта)...
...а затем уменьшите окно, чтобы
показывать только требуемые вам данные
Рис. 23S.8. Просмотр данных порта в окне внешних данных Xdata
3 Как уже упоминалось ранее (в частности, в главе 22N),
такое неприятное усложнение возникает из-за двух раз-
ных способов адресации аккумулятора. Дело в том, что
ассемблер требует, чтобы в разных контекстах использо-
валось одно или другое обозначение аккумулятора (см.
главу 21N). В частности, например, в команде MOV А,
@DPTR нужно указывать название А, а не АСС, а для сохра-
нения содержимого аккумулятора в стеке нужно указывать
название АСС, т. е. PUSH АСС.
а в нем подузел Xdata View и дважды щелкните
по нему мышью. В результате откроется окно,
отображающее содержимое блока адресов, как
показано на рис. 23S.8.
При наблюдении операций ввода-вывода на
своем компьютере в это окно можно ввести
23S.2. Отладка
1005
интересующий вас адрес, скажем, 8000h. Можно
также ввести любое значение в любой порт,
щелкнув отображаемое значение, введя но-
вое значение, а затем нажав клавишу <Enter>.
Таким образом можно эмулировать ввод дан-
ных, например, с цифровой клавиатуры или
АЦП.
Конечно же, в окне Xdata можно просматривать
содержимое памяти, а не только портов ввода-
вывода, поскольку микроконтроллер 8051 не
различает память и порты ввода-вывода, как
это любим делать мы, люди.
компьютере из дискретных компонентов это
делается подачей отрицательного перепада на
бит 2 встроенного порта 3.
Чтобы эмулировать этот запрос прерыва-
ния, дважды щелкните подузел Port 3 в узле
Peripherals в левой панели окна отладчика.
В результате откроется окно для этого порта,
показанное на рис. 23S.10. В этом окне щелк-
ните правой кнопкой по биту 2 и в открыв-
шемся контекстном меню выберите опцию
Ground. Программа отреагирует на следую-
щем шаге.
Окно мониторинга регистров Watch
Это многофункциональное средство, позволяю-
щее посредством одного окна наблюдать раз-
нообразную важную информацию. Например,
с его помощью можно просматривать опреде-
ленный сигнал или регистр, выбрав требуемый
элемент в коде программы, затем щелкнув по
нему правой кнопкой мыши и выбрав в открыв-
шемся контекстном меню опцию Add Watch
(рис. 23S.9). Между прочим, окно мониторинга
регистров Watch среды RIDE работает точно
так же, как и одноименное окно среды разра-
ботки Silicon Laboratories.
Эмуляция прерываний
Чтобы смоделировать прерывание (т. е. тип,
который инициируется подачей сигнала на
Таймеры
При работе с таймерами очень полезно окно
таймера4, в котором можно наблюдать следую-
щую информацию:
♦ регистр управления таймерами (T2CON: con-
trol);
♦ значения таймеров (NHL2, 16-разрядное те-
кущее значение для таймера Timer2);
♦ регистр захвата/перезагрузки (RCAP2) толь-
ко для таймера Timer2. Здесь отображается
значение, которое будет перезагружено, ког-
да таймер будет в режиме автоматической
перезагрузки;
♦ флаг переполнения (TF2 для таймера Timer2);
♦ бит исполнения (TR2 для таймера Timer2):
установлен для разрешения таймера.
Рис. 23S.9. Окно мониторинга регистров Watch позволяет наблюдать требуемые
переменные
Рис. 23S.10. Чтобы эмулировать запрос
прерывания, заземлите бит 2 порта 3
вывод микроконтроллера 8051), необходимо
эмулировать запрос прерывания. На нашем
4 По состоянию на май 2015 г. эмуляция таймеров в RIDE7
отсутствовала. Мы надеемся, что компания Raisonance
вернет обратно эту полезную возможность.
1006
23S. Дополнительный материал: микроконтроллеры 4
16-разрядное значение
работающего таймера
16-разрядное значение
для загрузки в таймер
после переполнения
Регистр управления для
данного таймера (№ 2):
определяет, например,
использовать ли режим
автоматической перезагрузки
Рис. 23S.11. Окно для таймера Timer2 (который более универсален, чем таймеры TimerO или Timer!)
Разрешение таймера
" (управление ходом работы)
Флаг переполнения таймера
. (слева — переполнения нет;
справа — только что произошло
переполнение, вызвав
перезагрузку)
На рис. 23S.11 показано окно эмуляции тай-
мера Timer2 до и после переполнения, которое
вызвало перезагрузку исходного значения5.
Последовательный порт
Состояние последовательного порта (ми-
кроконтроллер DS89C420 компании Dallas
Semiconductors оснащен двумя последователь-
ными портами, а микроконтроллер C8051F410
компании Silicon Laboratories — одним) и его
регистров можно наблюдать с помощью окна
UART. На данном этапе мы не будем рассма-
тривать последовательный порт; он будет пред-
ставлять для нас интерес только тогда, когда вы
решите использовать его, возможно на поздних
этапах курса. На рис. 23S.12 показан снимок
экрана с окна просмотра последовательного
порта при эмуляции исполнения программы в
среде RIDE6.
Рис. 23S.12. Окно просмотра последовательного порта при
эмуляции исполнения программы в отладчике среды RIDE
5 На рис. 23S.11 показан снимок экрана версии Ride 6.1,
которая больше не предоставляется компанией Raisonance,
но ее можно загрузить на веб-сайте книги АоЕ. Мы ис-
пользовали эту более старую версию, поскольку текущая
версия Ride 7 при эмуляции не поддерживает таймеры для
микроконтроллеров компании Dallas Semiconductors.
6 Изображение взято из руководства компании Raisonance
по средствам разработки для микроконтроллеров 80С51 и
80С51ХА «80С51 and 80C51XA Development Tools», part 2:
Debugging, § 333.3 (часть 2: Отладка, § 3333).
Как и следовало ожидать, в этом окне эмулятор
может отображать значение, посылаемое или
получаемое от УАПП, а в режиме приема REC
позволяет отображать последовательный по-
ток данных.
23S.2.2, Много других
возможностей
Если вы хотите стать экспертом по работе со
средой RIDE, начните с изучения документации
по этому средству, которую можно найти в меню
справки Help среды RIDE. Развлекайтесь!
23S.3. Изменение формы
сигнала
На данном этапе мы располагаем (или очень
скоро будем располагать) подключенными к
нашему лабораторному компьютеру АЦП и
ЦАП. Это дает нам возможность изменять фор-
му сигналов; результаты этой деятельности за-
нимательно наблюдать на экране осциллографа
или прослушивать через усилитель звуковой
частоты. Вкратце освежим, что мы проходили о
таких модификациях формы сигнала.
Микроконтроллер 8051 не очень хорошо при-
способлен для обработки сигналов. Для вы-
полнения этой задачи применяются специаль-
ные процессоры цифровой обработки сигналов
ЦОС. Такие процессоры оснащены быстродей-
ствующими многоразрядными умножителями
и аккумуляторами, а также обычно используют
конвейеризацию для ускорения обработки. Тем
не менее полезно и увлекательно попробовать
разработать несколько небольших программ
для обработки сигналов как часть эксперимен-
тов с вашими АЦП и ЦАП.
23S.3. Изменение формы сигнала
1007
23S.3.1. Выпрямление
Однополупериодное выпрямление
Как только мы определим форму цифрового
выходного сигнала АЦП, задача реализации
однополупериодного выпрямления становит-
ся прямолинейной. Подключенный нами на
лабораторном занятии АЦП питается от одно-
полярного источника и работает в смещенном
двоичном коде. Пример смещенного двоичного
кода показан слева на рис. 23S.13.
FFh
80h
00h
1111
1000
0000
1111
0000
0000
<—TOP —i
<—MID —з
► 7Fh
► OOh
<- BOTTOM -► 80h
0111
0000
1000
1111
0000
0000
Смешенный
двоичный код
Дополнительный
двоичный код
Рис. 23S.13. Два разных двоичных формата данных
Таким образом, чтобы реализовать выпрямле-
ние, мы можем наблюдать самый старший бит,
который указывает, по какую сторону от сред-
него уровня находится напряжение входного
сигнала. В частности, в смещенном двоичном
коде 0 в этом бите означает нижнюю половину,
а 1 — верхнюю. В обратном двоичном коде зна-
чения самого старшего бита имеют обратные
значения.
Код для однополупериодного выпрямления
В листинге 23S.3 приводится код програм-
мы для однополупериодного выпрямления
(используя смещенный двоичный код).
Листинг 23S.3. Пример программы
jb acc.7, ASJS; Если самый старший бит установлен,
; ничего не делаем (сигнал уже в верхней половине)
mov a, #80h ; Но если старший бит нулевой,
; принудительно устанавливаем средний уровень
ASJS:... ; Когда управление программы оказывается
; здесь, регистр А содержит значение, равное
; среднему уровню или выше
Версия программы для дополнительного
двоичного кода
Программу однополупериодного выпрямления
с использованием смещенного двоичного кода
легко модифицировать для дополнительного
двоичного кода. Для этого требуется лишь одна
дополнительная строчка кода:
cpl асс.7; Меняем значение самого старшего бита
; на обратное, чтобы перейти из смещенного двоичного
; кода в дополнительный
Альтернативным способом получения до-
полнительного двоичного кода будет под-
ключить вывод Uss преобразователя ADC7569
(с компьютером из дискретных компонен-
тов) к напряжению питания -5 В (это доста-
точно «умный» преобразователь). Восполь-
зовавшись любым из этих способов, можно
получить выходной сигнал в дополнительном
двоичном формате.
Двухполупериодное выпрямление
В данном случае простое инвертирование зна-
чений смещенного двоичного кода не будет
работать. Далее рассматривается, что происхо-
дит, когда сигнал поступает на максимальном
размахе, а затем инвертируется (относительно
своего среднего уровня) двумя разными спосо-
бами:
♦ операция CPL (инвертируется каждый бит)
и
♦ операция NEG (дополнение до двух: инвер-
тируются все биты и прибавляется единица7)
(рис. 23S.14). Операция NOT сохраняет ноль.
Полный размах
Среднее значение /\j\ /\j\
диапазона
Полный размах -~г к к к
Среднее значение J \-У у V/ [_
диапазона
CPL
Рис. 23S.14. Инвертирование с дополнением значения до
двух в смещенном двоичном коде не дает желаемого ре-
зультата
Данная трудность указывает на необходимость
быть осторожным при выполнении двухполу-
периодного выпрямления. Подумайте, какая
будет разница в коде программы при использо-
вании АЦП смещенного двоичного кода и до-
полнительного двоичного кода?8
23S.3.2. Фильтры
БИХ-фильтр
В главе 23N для реализации низкочастотного
фильтра предлагалась схема усреднения ново-
го значения выборки с текущим средним всех
предыдущих значений выборки. Такой фильтр
7 Набор команд микроконтроллера 8051 не содержит опе-
рации NEG. Чтобы получить эквивалентный результат,
нужно выполнить две операции: CPL А, а затем INC А.
8 Для дополнительного двоичного кода используется
операция NEG, а для смещенного — операция CPL.
1008
23S. Дополнительный материал: микроконтроллеры 4
называется фильтром с бесконечной импульсной
характеристикой (БИХ-фильтр), поскольку
его импульсная характеристика никогда полно-
стью не спадает. Вскоре мы рассмотрим проти-
воположный случай.
Имеет ли значение формат?
Будет ли этот метод работать одинаково хоро-
шо как со смещенным двоичным кодом, так и
с обратным двоичным кодом? Будет ли код на-
шей программы зависеть от выбранного пред-
ставления? (Для меня всегда трудно дать ответ
на этот вопрос!) На рис. 23S.15 изображена
блок-схема такого фильтра.
Примечание
Входное
значение
(новое)
Входное
значение
(новое)
Сохраненное
среднее
охраненное среднее;
[ модифицированное
новым знамени
Рис. 23S.15. БИХ-фильтр
Если новому и старому значениям выборки
присвоить вес, как предлагается в разде-
ле 23N.6, то можно будет вычислить эффектив-
ную частоту УздБ- Аргументация будет следую-
щей: представьте ступенчатый входной сигнал
в диапазоне от 0 до 1В в момент времени, когда
долгосрочное среднее равно нулю. Наблюдайте,
что происходит на правильно работающем
фильтре.
Любую из этих схем можно с легкостью реа-
лизовать на вашем лабораторном компьютере.
В главе 23N мы видели осциллограмму сигнала
с переходной характеристикой, наподобие по-
казанной на рис. 23S.16.
Формирование нового текущего среднег§>
Рис. 23S.16. Реакция фильтра на ступенчатый входной сигнал
Если новому и старому значению присвоить оди-
наковый вес, то каждое новое значение выборки
будет поднимать выходной сигнал на половину
от начального значения (на момент после пре-
дыдущей операции выборки и усреднения) по
направлению к напряжению входного сигнала
(которое в данном случае составляет 1 В).
Вспомните, что эти числа в точности описывают по-
ведение 1/конд в схеме с таймером 555. Весь проход
займет 0,7 постоянной времени RC (как вы помни-
те из вашего опыта работы с таймером 555).
Таким образом, мы можем вычислить частоту
Например, при частоте выборки величиной
8 кГц время между выборками будет 1/8 кГц =
= 0,12 мс = 120 мкс, что, в свою очередь, должно
быть 0,7jRC. Отсюда, RC = (1/0,7) х 120 мкс =
= 170 мкс, а частота/^ для этого фильтра долж-
на быть 1/(2я х 170 мкс) = 900 Гц.
Частоту £ Б можно изменить, поменяв частоту
выборки (легкий, но грубый способ) или из-
менив относительные величины весов, при-
сваиваемые новому значению выборки и зна-
чению текущего среднего. Как упоминалось в
главе 23N, чтобы изменить эти веса, нужно вос-
пользоваться командой умножения. Хотя это
медленная команда, возможно, что она подой-
дет для звуковых сигналов. В частности, выпол-
нение команды умножения занимает 5 команд-
ных циклов, или 20 циклов сигнала тактиро-
вания, что равно приблизительно 2 мкс. Этого
вполне достаточно для частоты дискретизации
8 кГц, которая предполагалась чуть ранее.
Цифровой процессор обработки сигналов
(ЦПОС) выполняет операции такого типа без
малейшего напряга, и мог бы без труда спра-
виться с такой задачей цифровой фильтрации.
Цифровой фильтр с жесткой прошивкой, напо-
добие используемых в микросхемах ЦАП для
воспроизведения цифрового аудио (типа КИХ,
который рассматривается в следующем разде-
ле), будет самым простым и быстродействую-
щим решением.
23S.3.3. КИХ-фильтр
Фильтр с конечной импульсной характеристи-
кой (КИХ-фильтр) представляет собой фильтр,
который «не помнит» никаких прежних вход-
ных сигналов (как это делал бы аналоговый
фильтр), но обладает знаниями о нескольких
выборках, которые обычно, но не всегда, яв-
ляются уже выполненными выборками9. Он
9 Как он может знать значения будущих выборок? Позво-
ляя нам обрабатывать выборку, которая является не самой
последней, но такой, которая находится между более позд-
ними и более ранними выборками.
23S.3. Изменение формы сигнала
1009
позволяет им входить на конвейер и выходить
из него и умножает их на веса разных значений,
чтобы сформировать взвешенное среднее, ко-
торое является его выходным сигналом.
Например, мы могли бы создавать выходной
сигнал из среднего значения последней и пред-
последней выборок, как показано на рис. 23S.17.
Это будет не очень консервативный низкоча-
стотный фильтр.
g Значение предпоследней выборки
значение
(новое)
-•Выходной сигнал
Рис. 23S.17. Низкочастотный фильтр КИХ-фильтр
Альтернативно мы могли бы создавать вы-
ходной сигнал из разницы между значениями
последней и предпоследней выборок, как по-
казано на рис. 23S.18. Это будет дифференциа-
тор или очень примитивный высокочастотный
фильтр. Более длинный конвейер позволил бы
реализовать более точный фильтр.
Входное
значение-
(новое)
Значение предпоследней выборки
-•Выходной сигнал
Рис. 23S.18. Высокочастотный КИХ-фильтр
23S3A Реверберация
Этот эффект очень интересно прослушивать
и экспериментировать с ним. Если в качестве
источника входного сигнала использовать ми-
крофон, то можно заставить выходной сигнал
звучать так, будто вы находитесь в большой
трубе, цистерне, зале или каньоне, варьируя
длительность эха и скорость затухания.
Для реверберации требуется кольцевой буфер,
представляющий собой таблицу в памяти RAM,
которая создает конвейер такой длины, как
требуемая длительность эха. Каждая входящая
выборка объединяется с ослабленной верси-
ей старого значения текущей суммы (которое
извлекается из позиции в конвейере, опреде-
ляемой значением задержки), затем эта сумма
выводится на динамик и сохраняется. При от-
сутствии входного сигнала старое значение те-
кущей суммы будет постепенно затухать.
Кольцевой буфер представляет собой просто
таблицу со скользящим указателем, который
реинициализируется, когда доходит до конца
таблицы. Алгоритм, который извлекает старое
значение, должен быть достаточно «интеллек-
туальным», чтобы также переходить в нача-
ло таблицы по достижении ее конца. Во всем
остальном реализация этого эффекта является
прямолинейной задачей.
24N. Микроконтроллеры V. Перемещение
указателей, последовательные шины
Содержание
24N.1. Перемещение указателей 1010
24N.1.1. Копирование таблицы на языке ассемблера 1011
24N.1.2. Копируем таблицу на языке С 1012
24N.1.3. Альтернатива регистру DPTR 1013
24N.1.4. Программа для сохранения и последующего воспроизведения сигнала
(для компьютера из дискретных компонентов) 1014
24N.2. Регистр DPTR также может быть полезным и для микроконтроллера
C8051F410 1015
24N.3. Определение достижения конца таблицы 1015
24N.3.1. Посредством подсчета количества обменов 1015
24N.3.2. Определение конца таблицы посредством проверки значения указателя 1015
24N.4. Последовательные шины 1017
24N.4.1. YAnn/RS232 1017
24N.4.2. Протокол USB 1019
24N.4.3. Интерфейс SPI 1020
24N.4.4. Периферийное устройство SPI: цифровой потенциометр 1022
24N.4.5. Другие последовательные протоколы 1024
24N.5. Материал для чтения в АоЕ 1025
Цель этой главы
Мы хотим научиться сохранять цифровые данные, включая аудиозапись, в таблицах и извлекать
сохраненную таким образом информацию.
24N.1. Перемещение
указателей
До сих пор в нашем компьютере из дискрет-
ных компонентов и с внешними шинами мы
использовали регистр указателя данных DPTR
почти во всех операциях передачи данных.
Это не совсем удобный способ, но так работает
микроконтроллер 8051, и нам приходилось ми-
риться с этим. Но сегодня мы рассмотрим ме-
тоды работы с регистром DPTR, которые позво-
лят вам увидеть его положительную сторону.
В частности, как только указатель данных на-
чинает перемещаться в программе, его неуклю-
жая косвенность превращается в очевидную
полезность.
Чтобы оценить полезность косвенной адре-
сации, которую налагает регистр DPTR, пред-
ставим, что нам нужно скопировать таблицу
небольшого размера, не используя для этого
указатель. Такую задачу нельзя выполнить на
микроконтроллере 8051, но ее можно изложить
в виде псевдокода, который можно будет реа-
лизовать на большинстве компьютеров и ми-
кроконтроллеров.
Псевдокод для копирования данных без
использования указателя
Предположим, что исходные данные находятся
в таблице, первый элемент которой хранится
в ячейке RAM с адресом 400h, а дубликат та-
блицы следует сохранить в области памяти с
24N.L Перемещение указателей
1011
начальным адресом 800h. Алгоритм для реше-
ния этой задачи следующий:
берем значение по адресу 400п
записываем его по адресу 800п
берем значение по адресу 401 h
записываем его по адресу 801 h
берем значение по адресу 402h
записываем его по адресу 802h ...
Если для копирования каждого элемента ис-
пользовать новую строку кода, то процесс бу-
дет вызывать ужас. В таком случае нужно обя-
зательно применить цикл, в каждой итерации
которого будет выполняться инкрементация
адресов. А этот процесс требует использовать
указатели (предполагая отсутствие попыток
создать самомодифицирующийся код, что яв-
ляется пугающей альтернативой).
24N.1.1. Копирование таблицы
на языке ассемблера
Поэтому резонный подход к решению этой за-
дачи будет таким: задействуем регистр DPTR и
станем инкрементировать его при каждой ите-
рации цикла:
STARTUP: mov dptr, #400h; Инициализируем указатель
начальным адресом таблицы
movx a, @dptr; Берем значение из таблицы
movx; Вот те раз! А теперь что? Требуется второй
указатель данных?
Начало было неплохое, но очень быстро после
начала нам потребовался второй указатель. Как
же решить эту проблему? На ум приходит пара
возможных решений.
STARTUP: mov dptr, #0800h; Инициализируем указатель
начальным адресом вставляемого дубликата таблицы
mov гб, dph; сохраняем регистр DPTR для дубликата
таблицы (по байту за раз:\\
mov r7, dpi; сначала старший байт, затем младший)\\
mov dptr, #0400h ; Инициализируем указатель
; начальным адресом исходной таблицы\\
mov r4, dph ; Сохраняем указатель для исходной
; таблицы\\
mov r5, dpi
mov r3, #1 Oh ; Инициализируем счетчик
; для дубликата таблицы для 16 операций
; копирования\\
AGAIN: mov dph, r4 ; Загружаем указатель
; для исходной таблицы\\
mov dpi, r5\\
movx a, @dptr ; Берем значение из таблицы\\
inc dptr ; Инкрементируем указатель\\
mov r4, dph ; сохраняем регистр DPTR для исходной
; таблицы (по байту за раз:\\ \\
mov r5, dpi ; сначала старший байт,
; затем младший)\\\\
mov dph, гб ; Загружаем указатель для дубликата
; таблицы\\
mov dpi, r7\\
movx @dptr, a ; Сохраняем значение в дубликате
; таблицы\\
Inc dptr ; Инкрементируем указатель\\
mov гб, dph ; Сохраняем указатель для дубликата
; таблицы\\
mov r7, dpi W
djnz r3, AGAIN ; Выполняем операцию копирования
;10праз\\
DONE: sjmp DONE ; После завершения копирования
; переходим в бесконечный цикл\\
Используем один указатель, повторно
инициализируя его
Указатель DPTR можно заново инициализи-
ровать каждый раз, когда нам нужно пере-
ключиться с адресации исходного элемента
на адресацию вставляемого, а затем обратно.
Но код будет довольно уродливым и трудоем-
ким. В листинге 24N.1 приводится пример, как
он мог бы выглядеть (приблизительно таким
способом компилятор языка С делает свою
работу).
Используем другой указатель
микроконтроллера 8051
Немного лучшим подходом будет задейство-
вать два указателя. Оригинальный микрокон-
троллер 8051 был оснащен всего лишь одним
регистром DPTR, но некоторые более новые
версии этого микроконтроллера, как и вы-
бранный нами микроконтроллер DS89C420
компании Dallas Semiconductor, имеют два та-
ких регистра, что облегчает нашу задачу ко-
пирования. Это хорошая новость. Плохая же
1012
24N. Микроконтроллеры V. Перемещение указателей, последовательные шины
новость состоит в том, что этот второй указа-
тель данных также называется DPTR. Поэтому
на программиста возлагается ответственность
управления битом, который различает эти два
регистра с одним названием. Это самый млад-
ший бит регистра выбора указателя данных
DPS. Пример программы для копирования
16-байтовых значений из одного места в другое,
используя эти два регистра DPTR, иллюстриру-
ет листинг 24N.2.
Листинг 24N.2. Пример программы
копирования с двумя регистрами DPTR
START:
MOV DPTR, #400h ; Инициализируем главный
; указатель начальным адресом исходной таблицы
; (указатель источника)
MOV DPS, #1 ; Переключаемся на другой указатель
MOV DPTR, #800h ; Инициализируем вторичный
; указатель начальным адресом дубликата
; таблицы (указатель назначения)
MOV DPS, #0 ; Восстанавливаем главный указатель
MOV R0, #01 Oh ; Инициализируем счётчик
; копируемых значений
COPY: MOVX A, @DPTR ; Берем значение из исходной
таблицы
INC DPTR ; Инкрементируем указатель источника
MOV DPS, #1 ; Переключаемся на указатель
;назначения
MOVX @DPTR, A ; Сохраняем значение
; в дубликате таблицы
INC DPTR ; Инкрементируем указатель назначения
MOV DPS, #0 ; Восстанавливаем указатель источника
DJNZ R0, COPY ; Повторяем, пока не будут
; скопированы все значения
STOP: SJMP STOP ; После завершения копирования
; переходим в бесконечный цикл
END
В главе 24W мы рассматриваем еще несколько
других способов решения этой задачи. Но кому
могут нравиться все эти хлопоты с переключе-
нием указателей? Давайте посмотрим, как мо-
жет выглядеть код для решения этой задачи на
языке С.
24N.12. Копируем таблицу на языке С
Программа для копирования таблицы значе-
ний на языке С требует выполнения определен-
ных, довольно трудоемких инициализирующих
объявлений, но код для собственно копирова-
ния очаровательно простой {листинг 24N.3).
Листинг 24N.3. Пример программы
/*tblcopy_804.c*/
// Используем компактное представление для
// копирования 16 байтов
#include<Z:\MICRO\8051 \RAISON\INC\REG320.H>
void main()
{
xdata char *ORIG; // Объявляем байтовый тип данных
// ("char"), хранящихся во внешней памяти ("xdata")
// по адресу, определяемому указателем
xdata char *DUP; // То же самое для другого указателя
int i; // Просто значение счетчика, используемое
// в цикле FOR
ORIG = 0x400; /* Начальный адрес копируемой таблицы:
загружается указатель */
DUP = 0x800; /* Начальный адрес дубликата таблицы:
загружается другой указатель */
for (i=1; k=16; i++) // Всего лишь 1 б операций
// копирования (чтобы облегчить отладку)
{
*(DUP++) = *(ORIG++); /* Одношаговое копирование
с автоматическим инкрементированием указателей,
хотя микроконтроллер 8051 сам этого делать не может
V
Некоторые моменты этого кода требуют объяс-
нения. В частности:
♦ xdata char *ORIG; Данная строчка кода выражает
несколько параметров:
• операнд *orig является указателем, что
обозначается символом *;
• он указывает на внешние данные, что обо-
значается символом х в команде xdata;
• разрядность данных составляет один байт
(данные типа char).
♦ *(DUP++) = *(ORIG++); Чрезвычайно компакт-
ный способ выразить операцию, требующую
много линий кода на языке ассемблера.
• знак равенства = реализует копирование, а
символ *, как вы уже знаете, означает, что
данные идентификаторы являются указа-
телями, используемыми для копирования;
• двойные плюсы ++ после dup означают, что
после использования указателя его значе-
ние следует инкрементировать.
24N.I Перемещение указателей
1013
Между прочим, создаваемый компилятором
языка С код на языке ассемблера для этой про-
граммы не отличается особой элегантностью
(листинг 24N.4). Он выглядит даже несколько
хуже, чем созданный нами код для метода копи-
рования с использованием одного указателя.
Листинг 24N.4. Код программы копирования,
сгенерированный компилятором С
ASSEMBLY LISTING OF GENERATED OBJECT CODE
; FUNCTION main (BEGIN)
; R4R5 is assigned to ORIG
; SOURCE LINE \#14\\
0000 7C04 MOV R4,\#004H\\
0002 E4 CLRAW
0003 FD MOV R5,A\\
; R6R7 is assigned to DUPW
; SOURCE LINE \#15\\
0004 7E08 MOV R6,\#008H\\
0006 FF MOVR7,A\\
; SOURCE LINE \#17 \\
0007F500R MOVi,A\\
0009 750001 R MOV i+01 H,\#001 H\\
000C?FOR1:\\
; SOURCE LINE \# 19 \\
000C8C83 MOVDPH,R4\\
000E 8D82 MOV DPL,R5\\
0010 0D INCR5W
0011 ED MOVA,R5\\
0012 7001 JNZ7LAB5W
0014 0C INCR4W
0015?LAB5:\\
0015 E0 MOVX A,@DPTR\\
0016 FA MOVR2,A\\
0017 8E83 MOVDPH,R6\\
0019 8F82 MOVDPLR7W
801В OF INCR7W
001С EF MOVA,R7\\
001D 7001 JNZ7LAB6W
001 FOE INCR6W
0020 ?LAB6:\\
0020 EA MOVA,R2\\
0021 FO MOVX@DPTR,A\\
; SOURCE LINE \#17\\
0022 0500 R INC i+01 H\\
0024E500R MOVA,i+01H\\
0026B411E3 CJNEA,\#011H,?FOR1\\
; SOURCE LINE \#22\\
0029 22 RETW
; FUNCTION main (END)W
Но прелесть использования языка высшего
уровня наподобие языка С состоит в том, что
нам безразлично уродство создаваемого ком-
пилятором кода на языке ассемблера, если
только не требуется высокая скорость испол-
нения. В таком случае можно самостоятельно
реализовать критическую область программы
на языке ассемблера.
24N.1.3. Альтернатива регистру DPTR
Теперь вернемся обратно к языку ассембле-
ра. Использованию регистра DPTR для обмена
данными с внешней памятью и устройства-
ми ввода-вывода есть альтернатива. Большим
преимуществом второго подхода является то,
что этот регистр высвобождается для других
целей. Эта альтернатива особенно полезна для
версии микроконтроллера DS89C420. (Если
вы внимательно прочитали материал разде-
ла 21S.1.4 по режимам адресации, то уже долж-
ны догадаться, что это за альтернатива.) Это
высвобождение становится особенно важным
в сегодняшнем материале, когда регистр DPTR
будет, скорее всего, занят чтением и записью
данных таблиц.
Данная альтернатива состоит в применении ко-
манды типа MOVX @R0, А. Можно также задей-
ствовать регистр R1 и, конечно же, выполнять
обмен в противоположном направлении.
Чтобы реализовать этот режим адресации, сна-
чала необходимо загрузить в порт Р2 старший
байт 16-разрядного адреса. На рис. 24N.1 пока-
зана организация этого режима адресации.
AIS.4I
Старший байт адреса
берется из порта P0RT2
Рис. 24N.1. При обмене данными с использованием внеш-
них шин старший байт адреса предоставляется портом
P0RT2 микроконтроллера
1014
24N. Микроконтроллеры V. Перемещение указателей, последовательные шины
В нашем компьютере этот режим адресации
удобен для работы с устройствами ввода-
вывода. Для этого в порт Р2 загружается значе-
ние 80h для старшего байта адреса, а младший
байт адреса предоставляется регистром R0 или
R1. В показанном здесь случае (взятом из лабо-
раторного занятия 23L) эти регистры содержат
значения 02h и 03h, которые формируют 16-
разрядные адреса АЦП и ЦАП. Более подроб-
но адресация с помощью команды MOVX @Ri,...
рассматривается в разделе 21S.1.4.
А пример его использования можно най-
ти в листинге программы MACRO ASSEMBLER
ADCDACINT_RN_504 в разделе 23L1.3, где он
служит для обращения к АЦП и ЦАП.
24ISL1.4. Программа для сохранения
и последующего воспроизведения
сигнала (для компьютера
из дискретных компонентов)
При работе с АЦП и ЦАП этот режим адреса-
ции упрощает задачу заполнения таблицы вы-
ходными значениями АЦП или чтения входных
значений из таблицы в ЦАП. В листинге 24N.5
приводится часть программы из лабораторно-
го занятия 24L для компьютера из дискретных
компонентов, которая сохраняет в таблице ре-
зультаты дискретизации сигнала, а затем счи-
тывает эти значения в ЦАП. Программа так-
тируется прерыванием, которое задает частоту
выборки.
Листинг 24N.5. Программа передачи данных
из АЦП в ЦАП
;TABLEINT_Rn_408.A51 Сохраняет выходные данные
АЦП в таблицу, затем подает данные из таблицы на ЦАП.
Тактируется прерыванием
.; Подробности опущены касательно разрешения
; прерывания и использования флага прерывания
STARTUP: ACALLINITPTR ; Инициализируем указатели
; для данных АЦП и ЦАП и т. п.
MOV DPTR, #800h ; Инициализируем главный
; указатель адресом первой записываемой ячейки
ACALL OKINT ; Разрешаем прерывания
FILLTABLE: SETB IE.7 ; Повторно разрешаем прерывания
JNB SAMPLEFLAG,FILLTABLE ; Ждем здесь, пока
; не нужно будет делать выборку
CLR SAMPLEFLAG ; Обнуляем флаг, установленный
; подпрограммой ISR
CLR IE.7 ; Отключаем прерывания до тех пор,
; пока не выполним задачу
ACALL GETSAMPLE
MOVX @DPTR, A ; Сохраняем выборку
INC DPTR
ACALL COMP_PTR ; Проверяем, дошли ли до
; последнего адреса
JC FILLTABLE ; ...если нет, повторяем операцию
; (с ==> movx ptr < ref)
REINIT: MOV DPTR, #800h ; Инициализируем главный
; указатель адресом первой записываемой ячейки
PLAYBACK: SETB IE.7 ; Повторно разрешаем прерывания
JNB SAMPLEFLAG,PLAYBACK ; Ждем здесь,
; пока не нужно будет воспроизвести выборку
CLR SAMPLEFLAG ; Обнуляем флаг, установленный
; подпрограммой ISR
CLR IE.7 ; Отключаем прерывания до тех пор, пока
; не выполним задачу
MOVX A,@DPTR ; Извлекаем значение выборки
; из таблицы
MOVX @R0,A ; Отправляем выборку на ЦАП
INC DPTR ; Инкрементируем указатель таблицы
ACALL COMP_PTR ; Проверяем, дошли ли до
; последнего адреса
JC PLAYBACK ; ...если нет, повторяем операцию
SJMP REINIT ; В противном случае снова
; выполняем инициализацию и воспроизведение
Как можно видеть, работа с регистром DPTR
в высшей степени прямолинейна: используется
только один указатель, который инкременти-
руется до тех пор, пока таблица не будет полно-
стью заполнена или воспроизведена, после чего
он снова инициализируется. В листинге 24N.6
опущены некоторые подробности, чтобы луч-
ше показать простоту использования регистра
DPTR.
Листинг 24N.6. Пример использования
регистра DPTR
MOVX A,@DPTR ; Извлекаем значение выборки из таблицы
MOVX @R0,A ; Отправляем выборку на ЦАП
INC DPTR ; Инкрементируем указатель таблицы
ACALL COMP_PTR ; Проверяем, дошли ли до последнего
; адреса
JC PLAYBACK; ...если нет, повторяем операцию
Кроме того, благодаря наличию команды MOVX @Ri...
для адресации АЦП, подпрограмма для получения вы-
борки GETSAMPLE также получается на удивление про-
стой:
GETSAMPLE: MOVX A, @R1 ; Считываем АЦП
MOVX @R1, A ; Посылаем что угодно — просто
; импульс для запуска АЦП
RET
24N.2. Регистр DPTR также может быть полезным и для микроконтроллера C8051F410
1015
24N.2. Регистр DPTR также
может быть полезным
и для микроконтроллера
C8051F410
До сих пор у нас не было надобности в реги-
стре DPTR при работе с микроконтроллером
C8051F410, поскольку мы не использовали
с ним команды MOVX. Но такие команды мож-
но задействовать с этим микроконтроллером
для обращения к его встроенной памяти RAM
объемом 2 К. Эта память иногда называется
памятью MOVX RAM. В отличие от версии ми-
кроконтроллера DS89C420 с его 32 К внешней
памяти SRAM, во внутренней памяти микро-
контроллера C8051F410 мы не можем создать
большую таблицу, а способны сохранить всего
лишь 2 К данных. В разделе 24L2 мы сохраняем
в памяти MOVX RAM значения выборок АЦП.
Конечно же, в этой памяти можно создать таб-
лицу для хранения данных любого типа. Объем
памяти величиной 2 К может выглядеть более
внушительным, если эту память использовать,
например, в качестве буфера для данных, по-
ступающих с клавиатуры. Вспомните, что в гла-
ве 23N мы упоминали возможность реализации
кольцевого буфера совместно с прерыванием, в
частности, добавление символа в буфер при на-
личии символа, готового для добавления или
считывания символа из буфера, когда процес-
сор готов принять его. Такой кольцевой буфер
подойдет, например, для развязки по времени
ввода с клавиатуры (выполняемого с непред-
сказуемой скоростью печати пользователя) и
исполняемой программы.
В разделе 24L2 рассматривается программа
Ram Store, в которой во внутренней памяти
RAM микроконтроллера хранятся значения
выборок, полученные с АЦП. В частности, мы
сохраняем 2 К значений выборок, а затем бес-
конечно подаем эти сохраненные значения на
ЦАП, реализуя таким образом так называемый
эффект запоминающего осциллографа. Если вы
чувствуете себя способным, то можете попро-
бовать модифицировать программу воспроиз-
ведения, оснастив ее возможностью создавать
эффект реверберации, используя встроенную
память RAM в качестве кольцевого буфера, в
котором новое входное значение объединяет-
ся с ослабленным старым. Но, скорее всего, на
данный момент вы вряд ли располагаете доста-
точным для этого временем, и лучше оставить
реализацию этой идеи на потом.
24N.3. Определение
достижения конца таблицы
24N.3.1. Посредством подсчета
количества обменов
Определить достижение конца небольшой таб-
лицы легче всего методом подсчета количества
выполненных обменов. Мы применили этот
метод в нашем примере программы в разде-
ле 24N.1.1, декрементируя 8-разрядный регистр:
MOV R0, #01 Oh ; Инициализируем счетчик
; копируемых значений
COPY: MOVX A, @DPTR ; Берем значение из исходной
; таблицы
DJNZ R0, COPY
; Повторяем, пока не будут
; скопированы все значения
А в эквивалентной программе на языке С всего
одна строка кода:
for(i=1;k=16;i++)
// Всего лишь 16 операций копирования
(чтобы облегчить отладку)
При небольшом количестве элементов таблицы,
или если есть основания рассматривать задачу
как выполнение определенного количества ци-
клов, использование счетчика имеет смысл.
Замечание
В программе на языке ассемблера реализация
счета, превышающего 8-разрядное двоичное зна-
чение, требует немного дополнительного кодиро-
вания; в программе на языке С повышение разряд-
ности не влечет за собой необходимости дополни-
тельного кода.
24N.3.2. Определение конца
таблицы посредством проверки
значения указателя
Но лучшим способом определения завершения
обработки всех данных таблицы может быть
проверка значения адреса. Мы использовали
1016
24N. Микроконтроллеры V. Перемещение указателей, последовательные шины
этот метод в программе запоминающего осцил-
лографа в разделе 24N.1.4 вызовом подпро-
граммы COMP_PTR:
ACALL COMP_PTR; Проверяем, дошли ли до послед-
него адреса
Данная подпрограмма сравнительно сложная,
выполняющая проверку на точное совпадение
16-разрядных значений перемещающегося
указателя DPTR и конечного адреса таблицы.
Полный листинг этой подпрограммы можно
найти в описании лабораторного занятия 24L
для компьютера из дискретных компонентов.
Но чаще для такой проверки достаточно срав-
нивать 8-разрядные значения. (Разрядность
сравниваемых значений важна в коде на языке
ассемблера, а при работе с кодом на языке С это
обстоятельство нам безразлично.)
Например, в программе запоминающего осцил-
лографа, где целью является использовать всю
имеющуюся в наличии внутреннюю память
RAM, нужно проверить только старший байт пе-
ремещающегося указателя, чтобы определить,
пересек ли он конечный адрес RAM (адресное
пространство RAM простирается до адресно-
го пространства устройств ввода-вывода, на-
чальный адрес которого равен 8000h). Таким
образом, если инкрементировать указатель до
проверки, можно проверить на значение 80h
в старшем байте, регистре DPH, и когда значе-
ние указателя равно этому значению, остано-
вить дальнейшие операцию с обменом данных
таблицы.
Листинг 24N.7 содержит код на языке ассем-
блера для сравнения 8-разрядных адресов.
Конечное значение находится в регистре R6.
Пока значение указателя не равно конечному
значению, данная подпрограмма устанавлива-
ет флаг переноса.
Листинг 24N.7. Пример сравнения 8-разрядных
адресов
; -Сравнение указателя: данная подпрограмма изменяет
флаг переноса
COMPJHI: ХСН A,R5 ; Быстрый способ сохранить
; регистр А (быстрее, чем операция PUSH ACC)
CLRC
MOVA,DPH
SUBB A, R6; Проверяем, меньше ли значение
; указателя, чем конечное: да, если флаг
; переноса установлен
ХСН A,R5 ; Восстанавливаем старое значение
; регистра А
RET
Как вы уже, возможно, знаете, операцию обну-
ления флага CLR С необходимо предварительно
выполнять по той причине, что единственная
команда вычитания в наборе команд микро-
контроллера 8051 принимает в качестве неяв-
ного операнда флаг переноса. Это обозначается
кажущейся ошибкой в названии команды SUBB.
В действительности же это не ошибка, а это вто-
рое В означает флаг займа, borrow по-английски
(что то же самое, что и перенос), над которым
оперирует данная команда. Поэтому, прежде
чем выполнять операцию вычитания, которую
мы используем в качестве своеобразной опе-
рации сравнения, необходимо обнулить флаг
переноса.
Можно было бы выполнить проверку
на равенство
Для проверки значения указателя на равенство
с конечным адресом таблицы вместо операции
вычитания можно использовать команду CJNE
А, #КОНЕЧНЫЙ_АДРЕС Но эта команда не сде-
лает код проще (листинг 24N.8).
Листинг 24N.8. Сравнение с проверкой
на равенство
; -СРАВНЕНИЕ УКАЗАТЕЛЯ: Данная подпрограмма могла
бы управлять программным флагом, называющимся
ALL_DONE
COMPJHI: ХСН A,R5 ; Быстрый способ сохранить регистр А
;(быстрее, чем операция PUSH ACC)
MOV A, DPH
ONE A, R6, NOT_YET ; Проверяем, меньше ли
; значение указателя,
; чем конечный адрес
SETB ALL_DONE ; Если дошли до предела,
; устанавливаем программный флаг, чтобы
; сообщить об этом программе
SJMP EXIT
CLRALL_DONE
EXIT: ХСН A,R5; Восстанавливаем старое значение
; регистра А
RET
Проверка значения указателя на языке С
При использовании языка С реализация срав-
нения значения указателя с требуемым значе-
нием намного проще, чем на языке ассемблера.
24NA. Последовательные шины
1017
Соответствующий код будет почти такой же,
как комментарий на обычном языке, объясня-
ющий выполняемое действие.
// Часть программы для заполнения таблицы: сохраняем
одно значение выборки по каждому прерыванию
while (STORE_POINTER <=TABLE_END)
В этом коде значение TABLE_END играет роль
регистра R6 в версии сравнения 8-разрядных
значений в программе на языке ассемблера в
разделе 24N.3.2. Работа с 16-разрядными зна-
чениями не представляет для программиста
никаких трудностей.
24N А. Последовательные
шины
Наш лабораторный компьютер из дискретных
компонентов взаимодействует с периферийны-
ми устройствами посредством своих шин (ко-
торые, конечно же, представляют собой просто
набор параллельных проводов) или через свои
встроенные порты, каждый из которых предо-
ставляет восемь параллельных линий1. Но до
сих пор компьютер на автономном микрокон-
троллере C8051F410 использовал для этой цели
только свои параллельные порты. Благодаря
этим возможностям сопряжение микрокон-
троллера с периферийными устройствами
очень упрощается.
Но при всем этом удобстве, предоставляемом
шинами и портами, следует также знать еще
один способ обмена данными, который приме-
няется для реализации сопряжения в большом
количестве случаев. Этот метод — последова-
тельный обмен данными. Последовательная
связь завоевывает все больше позиций в пол-
номасштабных компьютерах, но она еще боль-
ше привлекательна для микроконтроллеров
по причине хронического недостатка выводов
у них2. Последовательные шины достигли до-
1 АоЕ §14.6.3.
2 Этот аспект можно рассматривать с другой стороны:
пользователи микроконтроллеров страдают хронической
скупостью, поскольку они с легкостью могли бы иметь
большое количество выводов, если бы были готовы пла-
тить за них. Но низкая цена является основной составляю-
щей привлекательности микроконтроллеров. Например,
микроконтроллер PIC24F04KA200 компании Microchip
очень «разговорчивый», но только благодаря его пораз-
ительным трем протоколам последовательной связи: SPI,
I2CHRS232/YAnn.
статочно высокой скорости передачи данных,
и даже такие устройства, как FPGA, которые
раньше требовали большого количества парал-
лельных линий, теперь могут оснащаться бло-
ком сериализатора-десериализатора (СерДес)3.
24NA1.yAnn/RS232
Рассмотрим вкратце несколько последователь-
ных протоколов4. Самым старым из стандарт-
ных последовательных протоколов является
протокол RS2325 (или УАПП6). Это сравни-
тельно сложный, хотя и самый медленный по-
следовательный протокол. Данный протокол
используется в устаревших портах СОМ ком-
пьютеров. Большинство микроконтроллеров
оснащены портом RS232, и микроконтроллер
8051 входит в их число. Версия микроконтрол-
лера DS89C420 производства компании Dallas
Semiconductors содержит два таких порта, а вер-
сия C8051F410 производства компании Silicon
Laboratories — один. Эти порты полезны для
взаимодействия с полномасштабным компью-
тером (обычно ПК), но не очень широко при-
меняются для взаимодействия с периферийны-
ми устройствами (например, последовательной
RAM, последовательными АЦП, часами реаль-
ного времени, последовательными датчиками,
и т. п.).
Протокол RS232 требует, чтобы приемник обла-
дал определенный уровнем «интеллектуально-
сти», поскольку в нем присутствует только одна
сигнальная линия (или две для дуплексного ре-
жима связи) плюс шина «земли»7. Отсутствие
отдельного синхронизирующего сигнала (сиг-
нала тактирования или строб-импульса) озна-
чает, что прежде чем приступать к обмену
данными, для приемника нужно задать при-
близительную скорость обмена в бодах. Кроме
этого, приемник должен синхронизировать
себя со скоростью передачи, чтобы принимать
3 Касательно общего рассмотрения сериализаторов/десе-
риализаторов см., например: http://citeseerx.ist.psu.edu/
viewdoc/download?doi=10.1.1.173.4371&rep=repl&typ
e=pdf.
4 АоЕ §14.6.3Н.
5 Универсальная асинхронная приемопередача (или прие-
мопередатчик).
6 Англ. Recommended Standard (рекомендуемый стандарт)
#232. Более подробную информацию см. в § 14.7.8 книги
АоЕ.
7 В течение многих лет для RS232 применялся стандарт-
ный разъем с 25 выводами. Позже количество выводов
было уменьшено до 9 по той причине, что удаленные вы-
воды не требовались пользователям.
1018
24N. Микроконтроллеры V. Перемещение указателей, последовательные шины
ОтПК(УАПТТ) гт
Ответ
микроконтроллера в
Передача по про- &
токолу (дифферен-
циальному) USB от
ПК — преобразован- и
hcwbRS-232
микросхемой FTDI
Рис. 24N.2. Обмен сигналами между ПК и микроконтролле-
ром через последовательные протоколы RS-232 и USB
сигнальные уровни битов в соответствую-
щих временных рамках. Приемник запускает-
ся стартовым битом, после чего берет отсчет
уровня сигнальной линии в момент времени,
которая согласно его внутреннему сигналу так-
тирования находится посередине временного
интервала каждого бита передаваемого байта.
Передача байта завершается стоповым битом8.
Отсутствие отдельной линии тактирования не
является уникальной особенностью протоко-
ла RS23, но также присуще таким протоколам,
как USB, Firewire, SATA и PCI-E. Но отсутствие
отдельного сигнала тактирования усложняет
аппаратное обеспечение, требуемое для реали-
зации связи, в противоположность, например,
протоколу SPI (см. раздел 24NA.3).
Если для передачи данных требуется только
семь битов (что достаточно для представления
всех символов стандартного набора ASCII),
тогда восьмой бит может служить в качестве
бита четности для выявления ошибок: уста-
новленный бит четности означает нечетное ко-
личество установленных битов данного байта.
Но обычно АСПП использует восемь битов для
передачи данных. Таким образом, для передачи
семи или восьми битов данных АСПП требует-
ся десять битов.
8 Один из моих студентов однажды спросил, каким обра-
зом можно отличить стартовый бит от битов данных, если
между передачами байтов не вставляется интервал свобод-
ного времени. Это хороший вопрос, ответ на который со-
стоит в том, что потеря синхронизации была бы вскоре об-
наружена из-за отсутствия стопового бита. Тогда приемник
может запросить повторную передачу искаженных данных.
Возможно, что вас интересует, не может ли несинхронизи-
рованный набор битов случайно содержать бит, который
выглядит как правильный столовый бит. Да, может. Но это
очень редкое событие, которое будет вскоре выявлено, ско-
рее всего в следующем байте. После этого синхронизация
будет восстановлена, сработает процесс выявления ошибки
и искаженный байт будет передан повторно. Более подроб-
но об этом см. § 14.7.8 книги АоЕ.
Верхняя осциллограмма на рис. 24N.2 ото-
бражает сигнал передачи данных по протоко-
лу RS232 от компьютера на микроконтроллер
DS89C420 (который может принимать код, за-
гружаемый в этом формате). А вторая осцил-
лограмма отображает ответ микроконтролле-
ра, который он выдает сразу же по обнаруже-
нии символа ASCII9 для возврата каретки10 CR
(carriage return).
Если исследовать битовый поток на верхней
осциллограмме на рис. 24N.3, то можно раз-
личить определенную закономерность, кото-
рой является следование символа перехода на
новую линию (LF — line feed) за символом воз-
врата каретки. Эти символы имеют шестнадца-
теричные значения 0А и 0D соответственно.
CR LF
Рис. 24N.3. Два символа RS-232, выделенные из потока битов
Ответ микроконтроллера, отображенный вто-
рой осциллограммой на рис. 24N.2, более
длинный, информирующий, что поступает от
микроконтроллера DS89C420. На рис. 24N.4
этот ответ показан в текстовой форме, как он
отображается на мониторе компьютера, веду-
щего обмен с микроконтроллером.
|DS89C420 tOAOCft VERSION 1 0 COPYRIGHT (С) 2000 DAltAS SO^KONOUCTOR
Рис. 24N.4. Текстовая форма ответа микроконтроллера ПК
На рис. 24N.5 показано несколько версий
осциллограммы передачи от микроконтролле-
ра C8051F410 на ПК по протоколу RS-232, взя-
тых с нарастающей частотой развертки.
На рисунке осциллограф декодирует посту-
пающий сигнал потока 8-битовых значений в
соответствующие символы ASCII. При самой
9 Англ. American Standard Code for Information Interchange —
Американский стандартный код для обмена информаци-
ей. — Примеч. пер.
10 Анахронизм из ранних времен истории компьютеров,
когда в качестве принтеров использовались чуть более
продвинутые печатающие машинки.
24N.4. Последовательные шины
1019
Н 5.00 V
1Z 4,00ms 0.00000$
к
5.00 V
г
t
>
t 1 h
_PS~
X
1(21.00ms
-_n__
0,00000 $](
h
UVL
1 s I
i
t $
5.00 V
Рис. 24N.5. Декодированная осциллограмма передачи по протоколу RS-232, взятая с нарастающей частотой развертки
start stop
I 4 7 Г
П TU—'J
0 0 10 1110
'^lJW
5.00 V
Р400Д» 0,00000 s]
Рис. 24N.6. Подробность битового потока передачи по протоколу RS-232 с расшифровкой символа t в шестнадцатеричное
значение 74
высокой частоте развертки (осциллограмма
для которой показана в самом низу рисунка)
можно попробовать расшифровать двоичный
код, используемый для представления пере-
даваемых символов. Но это будет задача не из
легких. Прежде всего, осциллограф нужно на-
строить так, чтобы он инвертировал поступаю-
щие на него логические уровни, чтобы высокий
логический уровень отображался высоким гра-
фическим уровнем. Затем восемь битов данных
дополняются в конце двумя лишними битами.
Это стартовый бит (который на осциллограмме
отображается графическим низким уровнем) и
столовый бит (отображается графическим вы-
соким уровнем).
Данные передаются в порядке, где самый млад-
ший бит следует первым, поэтому четырехби-
товые кластеры нужно считывать в обратном
порядке (т. е. начиная с самого старшего бита
справа). На рис. 24N.6 символы обозначены их
соответствующими шестнадцатеричными зна-
чениями11, что позволяет увидеть, что шестнад-
цатеричное значение символа, например, Нрав-
но 74h, каким оно и должно быть. Попробуйте
расшифровать битовый поток для символа h
в шестнадцатеричное значение 68h. Нашему
осциллографу12 эта задача расшифровки дается
намного легче, чем вам или нам.
24NA2. Протокол USB
Поскольку в настоящее время протокол RS-
232 не применяется в обычных компьютерах13,
ЖКД плата, которую мы используем на наших
лабораторных занятиях по микроконтролле-
рам, принимает входные данные по протоколу
USB14, преобразуя их в формат RS-232, который
понимают обе версии нашего микроконтрол-
лера 8051. Последовательный протокол USB
намного сложнее протокола RS-232. Данный
протокол обладает хорошей помехоустойчиво-
стью благодаря дифференциальной передаче
11 Код ASCII использует только семь младших битов для
представления символов, и в данном случае восьмой бит,
самый старший, просто обнулен.
12 Для взятия этих осциллограмм мы использовали
осциллограф MSO2014 компании Tektronix совместно с
модулем декодирования протокола RS-232.
13 АоЕ § 14.6.3М.
14 Англ. Universal Serial Bus - Универсальная последова-
тельная шина.
1020
24N. Микроконтроллеры V. Перемещение указателей, последовательные шины
сигнала, в отличие от протокола RS-232, по-
мехозащищенность в котором обеспечивается
очень широким размахом уровней сигнальных
напряжений. В исходной спецификации указы-
вались уровни величиной ±12 В, хотя выбран-
ный нами RS-232 преобразователь использует
только стандартные логические уровни вели-
чиной 5 В.
Шина USB не является настоящей шиной в
том смысле, что к ней нельзя одновременно
подключать несколько устройств. Но эквива-
лентный результат можно получить благодаря
дополнительному оборудованию. Это оборудо-
вание называется концентратором (или хабом)
и раздает сигнал с USB шины на несколько под-
ключенных к нему устройств, а также передает
сигналы с устройств на USB шины. Протокол
USB первого поколения (так называемый пол-
носкоростной USB — full-speed USB) определя-
ет максимальную скорость передачи данных в
12 Мб/с; второго поколения (так называемый
высокоскоростной USB — high-speed USB) —
480 Мб/с; а третьего поколения (так называе-
мый сверхскоростной USB или USB3 — Super-
Speed USB) - 5-10 Гб/с.
На рис. 24N.7 показано подробное представле-
ние осциллограммы нескольких пачек обмена
по USB-протоколу, который на рис. 24N.2 вы-
глядит, как мелкая бахрома.
RS-232
От ПК
От микроконтроллера
USB
Двухпроводная
дифференциальная
передача сигналов
Рис. 24N.7. Подробности дифференциальной передачи сиг-
налов по протоколу USB
Осциллограмма обмена USB на рис. 24N.7 по-
казывает состояние двух линий, применяемых
в USB для дифференциальной передачи сигна-
лов. Сигнал в одной линии является дополне-
нием сигнала в другой, за исключением двух
случаев, один из которых находится посереди-
не сигнала, а другой — у его правого края. Эти
отступления от нормы вызваны сигналами со-
стояния шины, такими как, например, сигнал
сброса устройства.
If
J \
Г fm')f\p fin
Шина USB постоянно загружена, в результате
чего она создает много помех, которые могут
представлять проблему, если, например, сигнал
с нее подается на схему, содержащую аналого-
вые функции.
24N A3. Интерфейс SPI
Интерфейсы RS-232 и USB слишком сложны
для взаимодействия с периферийными устрой-
ствами микроконтроллеров15, и для этого раз-
работано несколько других, более простых ин-
терфейсов16. В упражнении 24N.4.4 по цифро-
вому потенциометру и лабораторном занятии
24L мы познакомимся с одним из таких интер-
фейсов, который, наверное, считается самым
простым и наиболее распространенным. Это
последовательный синхронный периферийный
интерфейс (или интерфейс SPI17).
Интерфейс SPI был разработан и представлен
компанией Motorola; другие производители
предложили свои последовательные шины.
В частности, компания Philips предложила ин-
терфейс I2C (Inter-IC). Это более сложный ин-
терфейс, чем интерфейс SPI: в нем всего четы-
ре линии (для сигнала тактирования, по одной
линии передачи данных в каждом направлении
и линия «земли»), а также допускается нали-
чие на шине нескольких «хозяев» шины (bus
masters). Шина I2C является настоящей шиной,
допускающей одновременное подключение
к ней множества устройств, не требуя отдель-
ной линии выборки устройства для каждого
подключенного устройства, как это необходи-
мо делать в интерфейсе SPI. Более подробная
информация по этому вопросу приведена в раз-
деле 24N.4.5.
Принцип работы интерфейса SPI
По шине SPI передается сигнал тактирования
и данные, которые считываются по одному из
перепадов сигнала тактирования. Какой имен-
но перепад используется (положительный или
15 АоЕ § 14.7.1.
16 Но интерфейс RS-232 все же используется несколь-
кими периферийными устройствами. В частности, он
применяется в ЖКД, а также в микросхеме обработ-
ки звука, которая есть в нашей университетской лабо-
ратории. См.: https://www.parallax.com/sites/default/
files/downloads/30016-Emic-2-Text-To-Speech-
Documentation-vl.2.pdf
17 SPI - Serial Peripheral Interface.
24NA. Последовательные шины
1021
Главный последовательным тактовый сигнал
SCK
(Собственно шиной
являются эти линии)
MOSI
MISO
Рис. 24N.8. Псевдо-шина SPI
Байт даннь
Байт командь
Данные передаются, начиная
со старшего бита: 0001 0001г
для этой команды
Рис. 24N.9. Сигналы передачи двух байтов по интерфейсу SPI на цифровой потенциометр. Сигналы сверху вниз: тактовый
сигнал, сигнал выбора микросхемы, данные
отрицательный), определяется конкретным
типом или режимом работы интерфейса SPI.
Таким образом, в отличие от интерфейса RS-
232, интерфейс SPI синхронный. Кроме того,
для каждого подключаемого к шине перифе-
рийного устройства к шине необходимо до-
бавлять линию выборки этого устройства, по-
скольку интерфейс не использует адреса для
идентификации требуемых устройств. Данное
требование дополнительной линии для каждо-
го подключенного периферийного устройства
делает его не настоящей шиной. (Но шина USB
также не является настоящей, поэтому не стоит
удивляться такой неэлегантности интерфей-
са SPI.)
Такая синхронная схема делает задачу обме-
на данными по интерфейсу SPI очень легкой.
Количество передаваемых битов не фикси-
ровано, как, например, в интерфейсе RS-232.
Для устройств на наших лабораторных заня-
тиях (цифровой потенциометр на лаборатор-
ном занятии 24L и SPI RAM на лабораторном
занятии 25L.2) данные передаются, начиная
с самого старшего бита. В других приложениях
порядок передачи битов может быть изменен
на обратный. Никакие стартовые или стопо-
вые биты или биты четности не усложняют эту
схему обмена данными (и не защищают ее от
ошибок). Конечно же, скорость обмена зависит
от имеющегося оборудования. В случае нашего
микроконтроллера DS89C420, в котором ин-
терфейс SPI реализован программно, скорость
передачи битов составляет приблизительно
120 кГц. Это демонстрируется осциллограм-
мами на рис. 24N.9, отображающими передачу
двухбайтовых значений: сначала llh, а затем
EEh.
Микроконтроллер C8051F410 оснащен встро-
енным аппаратным портом SPI, поэтому его
скорость передачи битов может достигать не-
скольких мегагерц {ом. раздел 23.5 справочного
листка по этому микроконтроллеру).
Достоинство интерфейса SPI — его низкие тре-
бования к периферийному устройству, которое
должно обладать только сдвиговым регистром.
Алгоритм функционирования ведущего устрой-
ства прост:
♦ выбирает требуемое ведомое устройство,
активировав его личную линию разрешения
(выбора микросхемы);
♦ подает битовый уровень на линию передачи,
называемую MOSI (Master Out Slave In —
Выход ведущего, вход ведомого);
♦ затем предоставляет перепад сигнала такти-
рования (для одних периферийных устройств
требуется положительный перепад, а для
других — отрицательный);
1022
24N. Микроконтроллеры V, Перемещение указателей, последовательные шины
♦ тем временем ведущее устройство может
принимать данные с линии MISO (Master In
Slave Out — Вход ведущего, выход ведомого)
одновременно с передачей данных по линии
MOSI. Такой режим обмена данными назы-
вается полнодуплексным.
На одном из следующих лабораторных заня-
тий мы предложим вам управлять цифровым
потенциометром посредством интерфейса SPI.
Этот потенциометр принимает 8-битовое сло-
во команды, за которым следуем 8-битовое
значение данных. Значение команды llh дает
указание цифровому потенциометру исполь-
зовать следующий байт данных, чтобы устано-
вить себя в одну из 256 возможных позиций.
На рис. 24N.9 показана осциллограмма сигна-
ла передачи определенных данных цифровому
потенциометру.
Значение llh команды отображается на осцил-
лограмме возле левого края экрана, а значение
EEh данных — возле правого. Два значения Е
представлены в виде двух длинных последова-
тельностей высоких уровней, за которыми сле-
дует низкий уровень младшего бита.
24N.4.4. Периферийное устройство
SPI: цифровой потенциометр
Здесь мы излагаем такие подробности, которые
обычно оставляем для лабораторных занятий.
Делаем мы это во избежание повторения, по-
скольку данное периферийное устройство SPI
используется в обоих ветвях сегодняшнего ла-
бораторного занятия.
Мы предлагаем вам попробовать поработать
с шиной SPI, позволив своему микроконтрол-
леру 8051 управлять цифровым потенциоме-
тром, используя для этого три линии шины
SPI. Данный цифровой потенциометр в виде
микросхемы МСР41100 компании Microchip
представляет собой потенциометр номиналом
100 кОм, «ползунок» которого перемещается
от одного фиксированного вывода к другому
в диапазоне 256 шагов под управлением полу-
чаемого байта.
С помощью этого потенциометра мы будем
управлять усилением инвертирующего опера-
ционного усилителя. Инвертирующий режим
работы усилителя выбран для того, чтобы схе-
ма могла или усиливать, или ослаблять входной
сигнал. Одним из возможных применений та-
кой схемы может быть саморегулирующийся
входной каскад АЦП, который при полном раз-
махе входного сигнала будет уменьшать уси-
ление и повышать его, когда уровень входно-
го сигнала становится меньше определенного
минимального значения. Иными словами, это
будет нечто вроде автоматической регулировки
усиления, полезной в некоторых приложениях
(например, при записи звукового сигнала). На
рис. 24N.10 приводится общая схема, которую
мы предлагаем вам собрать. Цоколевку микро-
схемы цифрового потенциометра и номиналы
компонентов схемы можно найти в материале
лабораторного занятия 24L.
Цифровой потенциометр с интерфейсом SPI
Входной
сигнал
Выходной
сигнал
(Смещен по постоянному току для работы
с одно полярным источником питания)
Рис. 24N.10. Схема использования цифрового потенциомет-
ра МСР41100 для управления усилением операционного
усилителя
Управляемый операционный усилитель досту-
пен в виде микросхемы с большими возмож-
ностями LMH6881 компании Texas Instruments.
Это высокоскоростной операционный усили-
тель (с рабочей частотой 2,5 ГГц, да, именно
гигагерц), чей коэффициент усиления можно
программировать через интерфейс SPI инкре-
ментами по 0,25 дБ. Поскольку нам не требу-
ется такое быстродействие, мы не будем иметь
ничего против использования операционного
усилителя 358, когда вы будете собирать схему
на рис. 25N.10.
АРУ как возможное применение для
операционного усилителя, управляемого
через интерфейс SPI
Как мы уже упоминали, эта схема подойдет
для автоматической регулировки усиления,
чтобы поддерживать амплитуду выходного
сигнала более-менее постоянной при меняю-
щейся амплитуде входного сигнала. Такие схе-
мы (рис. 24N.11) стандартно применяются
24N.4. Последовательные шины
1023
в автомобильных радиоприемниках (посколь-
ку при движении автомобиля, спускающегося
во впадины рельефа и поднимающегося на воз-
вышенности, уровень сигнала колеблется в ши-
роком диапазоне) и в устройствах записи речи
(говорящий может повышать или понижать
голос, но пользователь не хочет постоянно на-
страивать входной уровень). Датчиком средне-
го уровня выходного сигнала будет служить
диод, выход которого подключен на «землю»
через конденсатор и резистор.
Диод Шотки
IN5711
УГТУ*
г
i
на АЦП
~RC »тСИГН
*Усилитель
с программируемым усилением
Рис. 24N.11. Усреднитель амплитуды: выходной сигнал мож-
но подавать на АЦП, чтобы позволить микроконтроллеру
регулировать усиление
На рис. 24N.12 изображена осциллограмма вы-
ходного сигнала усилителя и выходного сигна-
ла такой усредняющей схемы. Этот усреднен-
ный выходной сигнал можно подавать на АЦП
микроконтроллера, который будет реагировать
должным образом: повышать коэффициент
усиления при слишком малой амплитуде вы-
ходного сигнала и наоборот.
ITrig'd
ЬХОДиОИ СИ1!"ИОЛ HifCXiiNW
"1 Ch3 Mean
1.806 V
{ Chi Amp!
f 2.060 V
СИ2 Ampi
2.029 V
Ch3 Pk-P
104mV
4 Apr 2004
Рис. 24N.12. Осциллограмма входного и выходного сигна-
лов схемы усреднения
Простейшая программа для микроконтролле-
ра для реализации такого АРУ инкрементиру-
ет или декрементирует коэффициент усиления
операционного усилителя в зависимости от
того, выше или ниже целевого значения на-
ходится усредненное значение. Регулировать
коэффициент усиления такая программа бу-
дет медленно, поскольку ей нужно будет ожи-
дать стабилизации усредненного уровня при
каждом новом выходном значении усиления.
Реакцию можно улучшить, объединив быстрый
отклик на нарастание с медленным откликом
на спад. Или же вы можете изобрести новый
метод, например, двоичный поиск наилучшего
значения усиления.
Инфракрасный пульт дистанционного
управления устройствами
В пультах дистанционного управления для
многих бытовых электронных устройств ис-
пользуется схема, во многом похожая на RS-
232. Приемник и передатчик должны работать
с одинаковой скоростью обмена. Стартовый
импульс синхронизирует приемник, который
берет выборку уровня битов через регулярные
интервалы времени. Мы научили наш микро-
контроллер 8051 распознавать десять кнопок
дистанционного пульта управления компании
Sony. Но передатчик посылает не двоичные
уровни, как это делает УАПП, а пачки коле-
баний с частотой 40 кГц. Схема формировате-
ля сигнала интегрирует амплитуду этих пачек
(в схеме, во многом похожей на усредняющую
схему на рис. 24N.11 и наподобие любого де-
модулятора АМ-сигналов) и передает полу-
ченный результат на компаратор. Компаратор
выдает двоичные уровни, примеры которых
показаны на нижних трех осциллограммах на
рис. 24N.1318. Нижние осциллограммы отобра-
жают три последовательных нажатия кнопок.
Программа, которая декодирует полученное
сообщение, сначала ищет стартовый импульс, а
затем делает выборку четырех последователь-
ных импульсов, получая коды кнопок от 0 до 9.
Исходная ИК-передача
(пачки импульсов
с частотой 40 кГц)
Логические уровни, —
извлеченные из Ул
ИК-пачек импульсов/*
Пачка импульсов/ hf
с частотой 40 кГц //•-
Стартовый импульс ^^„,
Кнопка 1
Кнопка 2
Кнопка 3
Рис. 24N.13. ИК-пульт дистанционного управления посыла-
ет пачки импульсов с частотой 40 кГц, которые приемник
преобразует в логические уровни
На рис. 24N.14 изображена макетная плата со
схемой приемника сигналов ИК ПДУ, которую
мы использовали в своих экспериментах.
18 На рисунке показаны три переданных кода; только
нижняя осциллограмма совпадает с последовательностью
пачек импульсов, показанных на верхней осциллограмме
(в инвертированной форме).
1024
24N. Микроконтроллеры V. Перемещение указателей, последовательные шины
Преобразователь ИК-сигналов^
в логические уровни
(фототранзистор включен в схему, __*
чтобы иметь возможность наблюдать
пачки импульсов с частотой 40 кГц)
(Две линии прерываний,
-активируемых противоположными
фронтами)
** Дисплей
Рис. 24N.14. Макетная плата со схемой ИК-приемника с преобразователем ИК-сигналов в логические уровни и микрокон-
троллером
24N.4.5. Другие последовательные
протоколы
Мы не будем пытаться подробно рассмотреть
все последовательные протоколы, оставляя эту
задачу для книги АоЕ. Но рассмотрим вкратце
несколько основных протоколов.
На наших лабораторных занятиях мы не ис-
пользуем элегантный, но сложный протокол
12С даже с микроконтроллером C8051F410,
который реализует этот интерфейс аппаратно.
Даже в таком случае мы держались от протоко-
ла 12С подальше, предпочитая простоту прото-
кола SPI.
Протокол 12С
Как уже упоминалось ранее19, протокол 12С
представляет собой более утонченную схему
для взаимодействия микроконтроллера и пе-
риферийных устройств20. Это настоящая шина,
состоящая из трех линий (сигнальной, тактиро-
вания и «земли»), по которой посылаются как
адреса, так и данные. Таким образом этот про-
токол устраняет необходимость в отдельных
линиях выбора микросхемы, как в протоколе
SPI. Но данный протокол требует довольно
высокого уровня «интеллекта» как от передат-
чика, так и от приемника. Это объясняется не-
обходимостью извлечения адресов устройств
из последовательного потока данных. Хотя это
оригинальный подход, его довольно сложно
реализовать в коде.
Микроконтроллеры компании Philips (где был
изобретен этот протокол) и многие перифе-
рийные устройства содержат встроенную под-
держку протокола 12С. Сопряжение устройств,
оснащенных таким аппаратными возможно-
стями, представляет собой простую задачу, тог-
да как реализовать все это программно значи-
тельно труднее. А вот протокол SPI мы смогли
реализовать программно для компьютера из
дискретных компонентов приблизительно в
40 строчек программного кода.
19 АоЕ § 14.7.2.
20 Англ. Inter Integrated Circuit Bus — шина для соединения
ИС. Компания Philips предлагает подробное описание это-
го протокола (совместно с его продвижением), которое
можно загрузить по адресу: https://www.nxp.com/docs/
en/application-note/AN10216.pdf.
Еще нескольких других
последовательных протоколов
И совсем кратко рассмотрим несколько других
последовательных протоколов.
Однопроводный протокол
Действительно однопроводный21? Ну, это не-
большое преувеличение, или преуменьшение,
поскольку в действительности для этого прото-
кола нужны две линии: одна сигнальная линия
и линия «земли». Но и это тоже довольно впе-
чатляюще. Все устройства подключаются к сиг-
нальной линии, на которой обычно поддер-
живается высокий уровень (и которая служит
линией питания для всех ведомых устройств).
Ведущее устройство посылает адрес и данные,
закодированные в виде импульсов низкого
уровня разной длительности. Периферийное
устройство, распознавшее свой адрес, отвечает,
подавая низкий уровень на линию (в течение
низкоуровневых импульсов на линии устрой-
ства питаются от конденсаторов). В качестве
примера этого интерфейса можно привести си-
стему для фиксации обхода охранником объек-
та. При обходе объекта охранник прикасается
специальным устройством к установленным на
стене кнопкам из нержавеющей стали. Таким
образом на устройство записывается иденти-
фикационный код кнопки, подтверждающий
факт прохода охранником данной точки, а так-
же время прохода.
21 АоЕ § 14.7.3.
24N.5. Материал для чтения в АоЕ
1025
Протокол JTAG22
Последовательный протокол JTAG23 изначаль-
но предназначался для тестирования печатных
плат посредством проверки всех установлен-
ных на них микросхем. Все микросхемы соеди-
няются последовательно, через них пропуска-
ется тестовый сигнал и считывается результат.
Впоследствии использование протокола JTAG
было распространено как на программирова-
ние устройств (посредством модуля програм-
мирования, подобного тому, которым мы про-
граммируем наши устройства ПМЛ на лабора-
торных занятиях), так и на отладку схем, таких
как микроконтроллеры (которые в противном
случае полностью непрозрачны для пользо-
вателя). Например, процессор или микрокон-
троллер можно разработать с внутренними
регистрами, которые считывать посредством
интерфейса JTAG, что позволит исследовать их
содержимое и даже переводить микроконтрол-
лер в пошаговый режим, не извлекая его из схе-
мы.
Протокол JTAG используется в некоторых
микроконтроллерах производства компании
Silicon Laboratories, обычно в тех, которые име-
ют много выводов. Применяемый нами микро-
контроллер этой компании, C8051F410, не
оснащен этим протоколом, чтобы не тратить на
него свои бесценные выводы.
24
Протокол Firewire: IEEE 1394:
Протокол Firewire или IEEE 1394 был пред-
ложен компанией Apple. В настоящее время
этот протокол не используется в компьюте-
рах данной компании; его заменил протокол
Thunderbolt. Для протокола 1394а заявлена та-
кая же номинальная скорость, как и для USB2,
приблизительно 480 Мб/с, но на практике он
более быстрый, приближаясь к своему полно-
му потенциалу ближе, чем USB. Протокол под-
держивает полнодуплексный режим обмена
данными.
Протокол Ethernet: 10-100-1000 Мб/с
Этот протокол применяется для объединения
компьютеров в проводные сети25.
22 АоЕ § 14.7.4.
23 Англ. Joint Test Action Group — Объединенная рабочая
группа по автоматизации тестирования. Протокол на-
зван по имени промышленной группы, создавшей данный
стандарт.
24 АоЕ § 14.7.14.
25 АоЕ § 14.7.6.
В табл. 24N.1 приведены характеристики раз-
личных протоколов.
Таблица 24N.1. Характеристики
последовательных протоколов обмена
Протокол
RS-232
RS-422HRS-485
USB1
USB2
USB3.0
USB3.1
Thunderbolt
Firewire: 1394a
Ethernet
Скорость
19,2 кбит/с на расстояние
до 15 м (скорость соответствует
заявленной в исходной специ-
фикации; в настоящее время,
возможно, до 100 кбит/с)
Дифференциальная версия:
100 кбит/с на расстоянии
до 1200 м; 10 Мбит/с
на расстоянии до 15 м
12 Мбит/с
480 Мбит/с
5 Гбит/с
10 Гбит/с
10 Гбит/с
400 Мбит/с
10 Мбит/с до 1 Гбит/с
24ISL5. Материал для чтения
в АоЕ
♦ Глава 14. Компьютеры, контроллеры и ка-
налы передачи данных.
• Раздел 14.7. Последовательные шины и ка-
налы связи.
♦ Справочник по микроконтроллеру 8051
(http://www.8052mcu.com/tut8051):
• Таймеры: с. 20-29;
• Прерывания по таймеру: с. 35;
• Приоритеты прерываний: с. 36-37.
♦ Руководство пользователя по микроконтрол-
леру DS89C420:
• Таймеры: с. 96-107;
• Timer2, особенно с. 99-105;
• Timer2, режим автозагрузки, особенно
с. 100-102.
24L Лабораторное занятие: микроконтроллеры V.
Перемещение указателей, последовательные шины
На сегодняшнем лабораторном занятии мы
попытаемся рассмотреть несколько приложе-
ний для микроконтроллера 8051. При этом мы
предполагаем, что у большинства учащихся не
будет времени опробовать их все. Далее приво-
дится краткий обзор задач, которые мы попы-
тается выполнить сегодня.
♦ Добавить оборудование загрузчика —
подробное описание выполнения этой задачи
приведено в главе 24S.
♦ Запоминающий осциллограф - возмож-
ность использовать компьютер для хранения
сигналов. Данную программу можно загру-
зить на сайте этой книги. Вместо того чтобы
тратить свое время на разработку кода про-
граммы, в этом упражнении мы хотим, чтобы
вы сразу имели возможность поэксперимен-
тировать с частотой выборки. Наличие всего
лишь 30 К памяти для хранения значений вы-
борок предрасположит вас к рачительности
в вопросе выбора частоты дискретизации.
♦ Последовательная шина — с помощью
микроконтроллера 8051 управляем коэффи-
циентом усиления усилителя через трехпро-
водную последовательную шину. Возможно,
что вам удастся придумать какое-либо прак-
тическое применение для этой возможности.
Одним из возможных применений может
быть автоматическая регулировка усиления.
♦ Таймеры — далее у вас будет возможность
испытать два таймера микроконтроллера в
одной или двух программах:
• Первая предлагаемая нами программа не
делает ничего особенного, а просто инкре-
ментирует отображаемое на дисплее зна-
чение при каждом переполнении таймера.
Цель этой программы — продемонстриро-
вать работу таймера, но ее можно также
использовать, например, для установки
частоты выборки. Программа «АЦП-на-
ЦАП» уже должна находиться на вашем
компьютере (это программа adcdacint_
rn_504.a51, с которой мы работали в раз-
деле 23L.1.3), поэтому вам нужно только
реализовать вызов этой программы под-
программой обработки прерывания в про-
грамме таймера. Тогда эти две программы
будут осуществлять выборку с частотой,
задаваемой таймером микроконтролле-
ра 8051. Это более практичная схема, чем
та, которая была у нас в прошлый раз, где
для задания частоты выборки мы выдели-
ли внешний генератор колебаний.
• Во второй программе функционируют два
таймера. Эта программа более длинная и
поэтому ее более трудно вводить вручную
с клавиатуры. Один из таймеров (более
медленный) предоставляет прерывания с
частотой несколько раз в секунду. А второй
таймер (более быстрый) задает длитель-
ность импульса высокого уровня, который
создается при каждом переполнении мед-
ленного таймера. Длительность задерж-
ки быстрого таймера задается значением,
вводимым с цифровой клавиатуры. Таким
образом, у нас получилась управляемая с
цифровой клавиатуры схема ШИМ, хотя и
с необычайно низкой частотой.
Мы предлагаем использовать этот импульс-
ный выходной сигнал для управления по-
ложением сервомашинки наподобие тех,
которые имеются в радиоуправляемых моде-
лях. Мы надеемся, что вам будет интересно
посмотреть, как ваш компьютер заставляет
что-то двигаться.
На лабораторном занятии 25L мы задействуем
микроконтроллер 8051 в автономном режиме.
Это будет последнее лабораторное занятие по
программе, но мы надеемся, что после него
вы самостоятельно разработаете какой-либо
проект, пусть и очень скромный. Заниматься
24L1. Таблица данных, шина SPI, таймеры
1027
собственными разработками гораздо инте-
реснее, да и процесс обучения с ними более
быстрый. Мы понимаем, что для работы над
своими проектами вам, возможно, нужно будет
отказаться от некоторых проектов из этого ла-
бораторного занятия. Мы не видим в этом ни-
каких проблем — отказывайтесь, если нужно.
24L.1. Таблица данных, шина
SPI, таймеры
Введение
Программы на этом лабораторном занятии бо-
лее длинные, чем те, которые вам приходилось
вводить на предыдущих лабораторных заняти-
ях по микроконтроллерам. Поэтому мы начнем
с предложения потратить немного времени,
чтобы оснастить ваш самодельный компьютер
возможностью загрузки в него кода из ПК. Мы
надеемся, что вам не придется потратить слиш-
ком много времени: когда все идет должным
образом, то это должно занять около пяти ми-
нут. Но, конечно же, ошибки в программе мо-
гут замедлить этот процесс.
Между прочим, программный код для всех
упражнений можно загрузить на веб-сайте
этой книги. С помощью среды RIDE выполнить
сборку требуемого загруженного файла, чтобы
получить исполняемый файл (с расширением
.HEX), который потом загрузить в ваш само-
дельный компьютер. На этом веб-сайте можно
также загрузить и некоторые готовые испол-
няемые файлы.
Для первого упражнения этого лабораторного
занятия, проекта так называемого запоминаю-
щего осциллографа, не требуется почти ника-
кого нового оборудования при условии, что у
вас уже установлен фильтр на коммутируемом
конденсаторе (на микросхеме МАХ294), что,
мы надеемся, вы сделали на предыдущем лабо-
раторном занятии. Вам потребуется усилитель,
чтобы оценить эффекты дискретизации с ми-
нимальной частотой выборки. Для этой цели
подойдет усилитель, который вы установили
на прошлом лабораторном занятии. В качестве
источника входного сигнала возьмите микро-
фонный усилитель, который вы собрали на ла-
бораторном занятии 7L.
Для второго и третьего упражнений потребует-
ся немного нового оборудования.
24L1.1. Используем загрузчик
При подключении компьютера к шинам платы
USB/ЖКД будьте внимательны и не перепу-
тайте проводники: последовательные линии
шины обозначены названиями сигналов, кото-
рые передаются по ним на стороне ПК1:
♦ DTR (Data Terminal Ready — готовность тер-
минала данных) — это сигнал с активным низ-
ким уровнем, подаваемый на вывод LOADER*
устройства GLUEPAL (ПМЛ связывающей
логики), на который до этого времени пода-
вался постоянный сигнал высокого уровня.
♦ TXD (Transmit exchange Data — передача
данных) — сигнал с этой линии подается на
вывод RxD микроконтроллера (вывод 10),
который также называется РЗ.О.
♦ RXD (Receive exchange Data — прием дан-
ных) — на эту линию подается сигнал TxD
микроконтроллера (вывод 11), который так-
же называется Р3.1.
24L1.2. Небольшая программа
для проверки загрузки
Прежде чем приступать к основным упражне-
ниям, неплохо сначала протестировать вашу
платформу, загрузив в компьютер какую-либо
простую и небольшую программу. Выберем для
этой цели программу,
которая просто мигает
светодиодом несколько
раз в секунду. А в каче-
стве схемы светодиода
для мигания используем
схему, которую вы со-
брали на лабораторном
занятии 22L (рис. 24L.1).
Будем надеяться, что вы
ее не разобрали.
Рис. 24L.1. Простая схема для управления светодиодом по-
средством микроконтроллера 8051
£3,3
I
V*
кОм
1
8051
Р1.0 /
1 Эта возможная неопределенность возникает по той при-
чине, что как ПК, так и микроконтроллер могут играть
роль отправителя или оконечного оборудования обработки
данных (DTE) на профессиональном жаргоне. Направле-
ние сигналов определяется с точки зрения устройства DTE,
поэтому TxD означает сигнал, передаваемый с устройства
DTE. В однозначном случае приемником будет перифе-
рийное устройство, которое определенно не может быть
устройством DTE. Такое устройство называется устрой-
ством передачи данных (DCE). Микроконтроллер и ПК
устройствами DCE не являются.
1028
24L Лабораторное занятие: микроконтроллеры V. Перемещение указателей...
Мы создали две версии программы: одну на
языке ассемблера, а другую на языке С. Неза-
висимо от версии, вам, возможно, понадобится
среда RIDE, чтобы создать исполняемый файл
(с расширением .HEX), который принимает за-
грузчик.
Программа для мигания светодиодом
на языке ассемблера
Листинг 24L.1 содержит код программы на язы-
ке ассемблера для мигания светодиодом. Но эта
программа исполняется слишком быстро, что-
бы заметить мигание светодиода, поэтому ее
следует исполнять в пошаговом режиме.
Листинг 24L.1. Программа на языке ассемблера
для мигания светодиодом
; bit_flip_assy.a51 Небольшая программа для проверки
загрузки.
; Мигает светодиодом, подключенным к порту Р1.0
микроконтроллера.
; Необходимо исполнять ее в пошаговом режиме
SNOSYMBOLS ; Сокращаем объем кода в листинге...
SINCLUDE (C:\MICRO\8051\RAISON\INC\REG320JNC)
; ...а не то эта строка может создать громадный список
SINCLUDE (C:\MICRO\8051\RAISON\INCWECTORS320.INC)
; Список определений идентификаторов (все они для
; регистров 8051)
ORG0
UMP START
ORG480h
START: MOV0C4h,#04h ; Включаем сигнал ALE при
; проходе по ROM (бит 2, ALEON, регистра PMRf C4h)
FLIPIT: CPL P1.0; Инвертируем бит управления светодиодом
SJMP FLIPIT ; Повторяем до бесконечности
END
Программа для мигания светодиодом
на языке ассемблера с задержкой
Эта программа (листинг 24L.2) вызывает под-
программу задержки DELAY, которую мы созда-
ли на лабораторном занятии 21L. Это позволит
исполнять ее в безостановочном режиме.
Листинг 24L.2. Программа на языке ассемблера
для мигания светодиодом с задержкой
; bit_flip_assy.a51 Небольшая программа для проверки
загрузки
; Мигает светодиодом, подключенным к порту Р1.0,
несколько раз в секунду
SNOSYMBOLS ; Сокращаем объем кода в листинге...
SINCLUDE (C:\MICRO\8051\RAISON\INC\REG320.INC);...
; а не то эта строка может создать громадный список
ORG0
UMP START
ORG480h
START: CLRA
MOV R2, A ; Оригинальный способ обнуления
; регистров задержки,
MOV R3, А ; для максимальной длительности
; задержки (поскольку декрементация
; выполняется до тестирования)
FLIPIT: CPL P1.0 ; Инвертируем бит управления
; светодиодом
LCALL DELAY ; Это подпрограмма задержки,
; которую создали на лабораторном занятии 21L.
; Ее начальный адрес 100h
SJMP FLIPIT ; Повторяем до бесконечности
; На случай, если у вас еще нет этой программы задержки:
ORGIOOh
DELAY: PUSH PSW ; Сохраняем содержимое
; регистров, которые будут изменены
PUSH ACC
PUSH В
MOV A,R2 ; Получаем значение задержки
; внешнего цикла
INITINNER: MOV B,R3 ; Инициализируем счетчик
; внутреннего цикла
INLOOP: DJNZ В, INLOOP ; Декрементируем счетчик
; внутреннего цикла, пока не станет нулевым
DJNZ ACCJNITINNER ; ...затем декрементируем
; счетчик внешнего цикла и снова запускаем
; внутренний цикл
POP В ; Восстанавливаем содержимое
; сохраненных регистров
РОРАСС
POP PSW
RET ; Возвращаемся в основную программу
END
Программа для мигания светодиодом
на языке С
Листинг 24L.3 содержит код программы
мигания светодиодом с задержкой на языке С.
Листинг 24L.3. Программа на языке С для мига-
ния светодиодом с задержкой
/*delay_bitflip_408.c*/
// Мигает светодиодом с задержкой
#indude<Z:\MICRO\8051\RAISON\INC\REG320.H>
// Используется для определения "Р1"
24L1. Таблица данных, шина SPI, таймеры
1029
// Порт Р1.0 управляет светодиодом
sblt volatile OUT_BIT = PI A0;
int n; // Это 16-разрядное значение предоставляет
// задержку в около 0,5 секунды.
void delay (void); // Объявляем функцию, следующую
// за главной программой
void main (void) // Главная программа должна
// называться main, чтобы удовлетворять требованиям
//файла setup.a51
{
while(1)
{
delayO;
OUT_BIT = ~OUT_BIT;
void delay (void)
{
for(n= 0; n< 0x8600; n++)0 // Значение задержки 2 Гц
// (задержка в 250 мс)
Скомпилируйте эту программу в среде RIDE.
Совет
Для этого вам нужно будет исправить путь к фай-
лу REG320.H, чтобы он отражал местонахождение
этого файла на компьютере, на котором исполня-
ется среда RIDE.
Загрузите полученный исполняемый файл (с рас-
ширением .HEX) во внешнюю память RAM сво-
его самодельного компьютера. С кодом во внеш-
ней памяти RAM легче выполнять отладку.
24L1.3. Запоминающий
осциллограф
Убедившись, что загрузчик работает должным
образом, его можно использовать для загрузки
на ваш самодельный компьютер более интерес-
ных программ. Программа, с которой мы будем
работать здесь, может заполнить всю доступ-
ную память RAM. Поэтому целесообразно на-
чать с небольшой таблицы, скажем, размером
в два байта. Это позволит вам протестировать
программу в эмуляторе RIDE в пошаговом ре-
жиме исполнения.
Удовлетворившись, что программа работает,
замените значение конечного адреса таблицы
(значения в регистрах R7, R6) на значение 8000h.
Операция заполнения таблицы остановится на
самом последнем доступном адресе RAM —
7FFFh, не доходя один байт до этого адреса.
Это происходит потому, что проверка на до-
стижение конечного адреса выполняется перед
операцией сохранения значения в таблицу. Для
пользователя доступно 30 К памяти RAM из
общих 32 К, поскольку ее нижние 2 К защище-
ны от записи. В этих 2 К защищенного адрес-
ного пространства хранится сама программа
(в компьютере из дискретных компонентов).
Альтернативно, программу можно сохранять
и исполнять из памяти ROM, используя внеш-
нюю память RAM для хранения данных.
После заполнения таблицы в RAM значениями
выборок программа в бесконечном цикле на-
чинает подавать эти сохраненные значения на
ЦАП для их воспроизведения. Поскольку наше
приложение может записывать сигналы, мы на-
зываем его запоминающим осциллографом.
Замечание
Конечно же, на данном этапе вы можете быть на-
столько привычными к цифровым осциллографам,
что полагаете, что все осциллографы могут сохра-
нять сигналы. Это не всегда было так, как вы мо-
жете вспомнить по своему опыту использования
аналогового осциллографа ранее в этом курсе.
Частота, с которой программа дискретизиру-
ет и воспроизводит сигнал (частота выборки)
задается сигналом, снимаемым с ТТЛ-выхода
внешнего генератора сигналов и подаваемым
на вход прерывания 0. Подпрограмма обра-
ботки прерывания просто устанавливает про-
граммный флаг (бит в памяти RAM процессо-
ра), а главная программа выполняет ветвление
по состоянию этого бита, ожидая, пока этот бит
не будет активирован. Таким образом, мы при-
знаем, что такое прерывание скорее похоже на
опрос, но его легко реализовать.
24L1.4. Бонусная программа
переводчика со шведского языка
Просто ради шутки мы добавили в схему пере-
ключатель, который позволяет воспроизводить
сохраненный сигнал в обратном порядке. Чтобы
установить, в каком порядке воспроизводить
сохраненный сигнал, программа определяет
уровень на выходе порта Р3.4. При установлен-
ном бите порта (значение 1) воспроизведение
1030
24L Лабораторное занятие: микроконтроллеры V. Перемещение указателей...
выполняется в прямом порядке, а при сброшен-
ном (значение 0) — в обратном. Управление со-
стоянием бита Р3.4 осуществляется с помощью
подключенного к нему ползункового переклю-
чателя. Схема подключения этого переключа-
теля показана на рис. 24L.2.
Как обычно, частота выборки задаётся}
-сигналом генератора сигналов^/
+51
8051
Прямой/обратный
Рис. 24L.2 Управление порядком воспроизведения (пря-
мой/обратный*) сохраненного сигнала осуществляется с по-
мощью ползункового переключателя
Возможность обратного воспроизведения мы
включили в этот проект в честь Алехандро
Дженкинса (Alejadro Jenkins), одного из наших
бывших студентов и помощника преподавате-
ля, который создал незабываемый «перевод-
чик со шведского языка». Его «переводчиком»
был просто компьютер, оснащенный большим
объемом памяти, чтобы справиться с длинны-
ми орациями, и с программой для воспроизве-
дения записанного сигнала в обратном порядке.
Но большое достижение Алехандро состояло не
столько в разработке оборудования и програм-
мы, а в его поразительной способности говорить
наоборот. Когда он удостоверился, что никто из
студентов в классе не знал шведского языка, он
записывал в компьютер речь на испанском язы-
ке, но наоборот, утверждая, что эта речь была на
шведском языке и что компьютер переведет ее
на испанский. При воспроизведении этой бели-
берды в обратном порядке она становилась по-
нимаемой (хотя с трудом, вследствие комбини-
рования эффектов обратного воспроизведения
и его значительного коста-риканского акцента).
Тем не менее, эффект был впечатляющий.
Убедившись в том, что оборудование загрузчи-
ка работает должным образом, программу за-
поминающего осциллографа можно загрузить
в микроконтроллер за пару секунд, а сэконом-
ленное время потратить на эксперименты с ней.
В эту программу мы включили подпрограм-
му для сравнения 16-битовых указателей. Это
большая точность, чем необходимо, поскольку
было бы достаточным сравнивать только 8 би-
тов старшего байта адреса. Тем не менее вам
может быть интересно посмотреть один-два
случая, демонстрирующих, как 8-разрядный
процессор способен соединять последователь-
но 8-битовые операции для обработки значе-
ний разрядностью выше байта.
Исходный код и листинг программы можно
загрузить на сайте этой книги. Листинг может
быть полезным в том случае, если вы желаете
подробно разобраться с программой и, воз-
можно, вручную внести в нее какие-либо из-
менения после загрузки в микроконтроллер.
(Предполагается, что программа будет загру-
жаться и исполняться из внешней памяти RAM
микроконтроллера, а не его внутренней памя-
ти ROM.) Например, на нашем самодельном
компьютере из дискретных компонентов легко
изменить размер таблицы. Для этого нужно
просто взять управление шиной и изменить ко-
нечные значения. Далее приводятся две стро-
ки кода, которые реализуют эту модификацию
(они обрабатывают значения, определенные в
заголовке программы, которые задают макси-
мальный размер таблицы):
MOV R7, #END_HI; Устанавливаем базовый адрес
(конец таблицы: последний адрес ниже пространства
в вода-вы вода))
MOV R6, #END_LO; То же самое - младший байт
В листинге программы можно видеть, что эти
значения загружаются по адресам 146h и 148h.
Чтобы задать крохотную двухэлементную та-
блицу для отладки, значения полноразмерной
таблицы в регистрах R7 и R6 можно заменить
на 08h и 02h соответственно. Тогда таблица бу-
дет начинаться по адресу 800h и заканчиваться
по адресу 801h. Эту модификацию можно вы-
полнить вручную намного быстрее, чем по-
вторным ассемблированием программы. В по-
следнем случае нужно изменить исходный код,
ассемблировать его, а затем загрузить из ком-
пьютера в микроконтроллер.
24L1.5. Простая последовательная
шина SPI
Синхронный интерфейс SPI существенно облег-
чает задачу обмена данными. Этот интерфейс
подробно рассматривается в разделе 24N.4.3.
Периферийное устройство SPI: цифровой
потенциометр
Мы предлагаем вам попробовать поработать с
шиной SPI, позволив своему микроконтроллеру
24LI Таблица данных, шина SPI, таймеры
1031
МСР41100
МСР41100
Входной сигнал
Сигналы шины 5PI
(U+ = 8, gnd = 4)
Рис. 24L.3. Схема включения цифровогапотенциометра МСР41100 для управления усилением операционного усилителя
8051 управлять цифровым потенциометром по
трем линиям шины SPI. Микросхема МСР41100
от компании Microchip представляет собой
цифровой потенциометр номиналом 100 кОм,
«ползунок» которого перемещается от одного
фиксированного вывода к другому в диапазоне
256 шагов под управлением получаемого байта.
Эта схема подробно рассматривается в разде-
ле 24N.4.3 и показана с дополнительными объ-
яснениями на рис. 24L.3.
Код для микроконтроллера 8051
для обмена по шине SPI
Данная программа передает два байта при каж-
дом прерывании INTO*. Кроме этого, она счи-
тывает последовательные два байта на входной
линии и сохраняет их. В описываемом далее
лабораторном упражнении используется фик-
тивный вход, поскольку данное периферийное
устройство не создает никаких выходных дан-
ных для передачи микроконтроллеру 8051. Но
в другой обстановке возможность одновремен-
ной передачи и приема данных может быть по-
лезной.
Прежде чем передавать байт для регулировки
цифрового потенциометра, программа пере-
дает байт команды, который сообщает ему, что
следующий байт нужно рассматривать как ре-
гулировочный. Шестнадцатеричное значение
этой команды равно llh. Мы уже видели это
значение llh в двухбайтовой последователь-
ности, отображенной на самой нижней осцил-
лограмме сигналов шины SPI, помеченной «SI
(данные)» на рис. 24N.9.
Поскольку код этой программы довольно за-
путанный, мы сначала рассмотрим ее исходный
код. Этот код находится в файле с расширением
.а51, и с ним легче разобраться, чем с кодом
в файле с расширением .1st (особенно по той
причине, что в последнем файле некоторые
символы преобразованы в простые числа).
Файлы с кодом программы для обмена по
шине SPI
Файлы с исходным кодом (sPI_digipot_int_504.
а51) и листингом (sPI_digipot_int_504.1st) про-
граммы для работы с шиной SPI можно загру-
зить на веб-сайте этой книги.
Возможное применение
для операционного усилителя,
управляемого через интерфейс SPI
Автоматическая регулировка усиления
Как отмечалось в главе 24N, эту схему можно
использовать для автоматической регулировки
усиления, чтобы поддерживать амплитуду вы-
ходного сигнала более-менее постоянной при
меняющейся амплитуде входного сигнала. Если
у вас есть настроение попробовать реализовать
это приложение, обратитесь к главе 24N для
разъяснений.
24L1.6. Использование таймера
микроконтроллера 8051
Подобно большинству микроконтроллеров,
микроконтроллер 8051 оснащен довольно впе-
чатляющими аппаратными возможностями.
К сожалению, работать с ними не так просто,
поскольку предварительно необходимо вы-
полнить массу мелких и трудоемких настроек.
Примером самого трудоемкого аппаратного
средства являются, наверное, таймеры (после-
довательный порт, тоже серьезный конкурент
1032
24L Лабораторное занятие: микроконтроллеры V. Перемещение указателей...
по степени трудоемкости). Микроконтрол-
лер 8051 оснащен тремя таймерами, и все они
с разными характеристиками. Мы не распола-
гаем достаточным временем, чтобы рассмо-
треть все подробности этих таймеров, поэтому
только приведем пример программы, который
демонстрирует одну из многих возможностей
таймера. Мы надеемся, что, получив уверен-
ность в своих способностях запускать таймер
в действие, вы сможете найти для него какое-
либо применение, когда перейдете к этапу раз-
работки своих схем в оставшееся время этого
курса.
Счетчик/таймер2, который мы будем исполь-
зовать в данном случае, обладает более высо-
ким уровнем интеллектуальности, чем подоб-
ные устройства в более ранних версиях микро-
контроллера 8051. В частности, его разрядность
составляет 16, а не 13, как раньше. Но, что более
важно, он «знает», как при переполнении авто-
матически перезагружать себя предварительно
запрограммированным начальным значением.
При переполнении данный таймер может или
подать сигнал на выход, или сгенерировать за-
прос на прерывание процессора. Мы задейству-
ем это устройство для генерирования прерыва-
ний. Как упоминалось ранее, мы не способны
придумать что-либо захватывающее в качестве
реакции на прерывание, поэтому просто инкре-
ментируем отображаемое на дисплее значение.
Возможно, вам удастся придумать что-то более
оригинальное.
Установка длительности повторяемых
импульсов с помощью двух таймеров
Программа servopulseJJI 2.a51 (которую можно
загрузить на веб-сайте книги) также использу-
ет Timer2 в режиме автоматической перезагруз-
ки для генерирования несколько раз в секунду
запросов на прерывание при каждом переполне-
нии таймера. Все, что Timer2 делает при этом, так
это устанавливает бит флага во внутренней па-
мяти микроконтроллера. Главная программа
отслеживает состояние этого флага, и когда он
устанавливается, программа запускает TimerO,
загрузив его значением задержки, вводимым с
цифровой клавиатуры. Таймер TimerO выдает на
порт РЗ импульс, длительность которого также
задается с цифровой клавиатуры. Эта програм-
ма довольно объемная и содержит большое
количество нудных операций инициализации
и обнуления причудливых флагов. Если вам не
терпится заняться разработкой своих проектов,
то можете спокойно пропустить ее.
Чтобы предоставить вам возможность полу-
чить удовольствие увидеть, как что-то начина-
ет двигаться в ответ на сигнал управления от
вашего самодельного компьютера, мы предла-
гаем подавать выходной импульс на сервома-
шинку, подобную тем, которые установлены в
радиоуправляемых моделях (рис. 24L.4).
Программа для работы счетчика Timer2
в режиме автоматической перезагрузки
Данная программа (TMR800.a51) слишком ве-
лика для ручного ввода, поэтому загрузите ее
на веб-сайте книги. Обратите внимание, что
файл символов, предоставляемый компанией
Dallas Semiconductor, несколько облегчает нашу
работу. В частности, вместо того, чтобы искать
адрес и позицию бита разрешения счетчика
Timer2, можно просто обращаться к нему та-
ким образом: SETB ET2 ; Timer2 interrupt enable.
Тем не менее код все равно довольно сложный:
неудобочитаемый и не доставляющий удоволь-
ствия при написании. Но мы надеемся, что его
результаты будут удовлетворительными.
2 Оба названия правильны, поскольку это устройство мож-
но настроить для подсчета на входе или перепадов, или
циклов сигнала тактирования процессора (замедленных
предварительным делителем частоты). В первом случае
оно будет счетчиком, а во втором, где частота сигнала так-
тирования постоянна, лучше подходит название таймер.
Рис. 24L.4. Сервомашинка для радиоуправляемых моделей
Сервомашинка представляет собой электро-
двигатель, ротор которого занимает угловую
позицию, определяемую длительностью пода-
ваемого импульса управления. Этот электро-
двигатель имеет три вывода: красный, белый
и черный. На красный подается напряжение
+5 В, черный подключается на «землю», а на
белый подается управляющий импульс логиче-
ского уровня с порта Р1.0 вашего самодельного
компьютера.
Внутри сервомашинки установлен одновибра-
тор. При поступлении на вход сервомашинки
управляющего импульса ротор электродвига-
24LI Таблица данных, шина SPI, таймеры
1033
теля вращается в ту или другую сторону в те-
чение времени, когда импульс одновибратора и
входной импульс не совпадают. Длительность
импульса одновибратора задается позицией
ротора электродвигателя (двигатель вращает
потенциометр, подключенный как переменный
резистор), в результате чего длительность им-
пульса одновибратора корректируется, чтобы
совпадать с длительностью входного управ-
ляющего импульса. Если длительность вход-
ного импульса превышает длительность им-
пульса одновибратора, то в течение времени
несовпадения импульсов ротор сервомашинки
вращается в одном направлении, а если наобо-
рот — в другом. Процесс корректировки и по-
следующий выход ротора на целевое положе-
ние обычно требует большого количества по-
вторяющихся импульсов. Данное решение не
очень быстрое, но изящное и отличается очень
простым сигналом управления.
Таймер Timer2 задает частоту следования им-
пульсов (рис. 24L.5).
Рис. 24L.5. Частота следования выходных импульсов про-
граммы таймера определяется таймером Timer2
А второй таймер, TimerO, длительность импуль-
сов которого задается с цифровой клавиатуры,
определяет длительность импульсов, создавае-
мых по каждому импульсу таймера Timer2. На
рис. 24L.6 приведена осциллограмма, отобра-
жающая варьирование длительности импуль-
сов, получаемое программой для диапазона
значений, вводимых с цифровой клавиатуры.
24L1.7. Программа для
генерирования импульсов
управления сервомашинкой
с помощью таймеров
Загрузите программу servopulse_512.a51 на веб-
сайте этой книги. Программа использует одно
значение, вводимое с цифровой клавиатуры,
О КТ/ИШКОЛЛ KODOT-.Hi:' £?.ОЕ-ЮЛлОЦгИН*С ,.ИГ^;ЛО'
Рис. 24L.6. Осциллограммы длительностей импульсов для
управления сервомашинкой, задаваемых таймером TimerO
для задания длительности импульса, который
определяет положение ротора сервомашинки.
Диапазон значений длительности импульса,
соответствующий пределам вращения рото-
ра сервомашинки, охватывает значения от 4
до F (при этих значениях ротор сервомашин-
ки упирается в ограничители вращения). При
значениях 5 и Е ротор останавливается, чуть не
доходя до ограничителей. Диапазон длитель-
ности импульсов составляет приблизительно
0,5-2 мс. Частота импульсов составляет при-
близительно 30 Гц, для показанных значений
таймера Timer2.
Пытаясь определить влияние вводимых значе-
ний на длительность импульсов, мы добавили
в программу команду умножения, чтобы слегка
уменьшить диапазон значений длительности
импульсов, определяемый введенным значени-
ем, сдвинутым влево четыре раза. Множитель
ODCh позволяет оставить приблизительно 85%
этого сдвинутого значения. Теперь, когда мы
рассмотрели все аспекты таймера, возможно,
вы сможете придумать приложение для его
применения. Если вам это не удастся, взгля-
ните на материал лабораторного занятия 25L,
где мы предлагаем вам воспользоваться воз-
можностью микроконтроллера 8051 работать в
автономном режиме, а не как мозговой центр
компьютера из дискретных компонентов, со-
бранного вами на большой макетной плате.
24L1.8. Код программы для обмена
пошинеБР!
Программу spi_digipot_int_504.a51 и файл spi_
digipot_int_504.1st с ее листингом можно загру-
зить на веб-сайте этой книги.
1034
24L Лабораторное занятие: микроконтроллеры V. Перемещение указателей...
24L1.9, Код запоминающего
осциллографа на языке ассемблера
и языке С
Загрузите на веб-сайте книги код программы на
языке ассемблера table_bidirectionaLdec10_wL
ale.A51 и файл ее листинга table_bidirectional_
dec10_wiJst.A51, а также код на языке С store_
and_playback_bidirectional.c. В коде на языке С
вы увидите несколько расширений языка С
наподобие языка ассемблера для указания вы-
водов портов, вектора прерывания и для ра-
боты с внешней памятью (xdata char *STORE_
POINTER)3.
24L.2. Последовательные
шины микроконтроллера
C8051F410
24L2.1. Использование
выводов порта на сегодняшнем
лабораторном занятии
На этот раз нам предстоит использовать семь
из восьми выводов порта Р0. Вам нужно будет
удалить все другие подключения к этим выво-
дам, сделанные на предыдущих лабораторных
занятиях, чтобы не создавать конфликтных
ситуаций. На рис. 24L.7 показан сигнал MISO
шины SPI, хотя он необходим нам на лабора-
торном занятии 25L.2, а не на сегодняшнем. Но
мы решили, что логично представить все сигна-
лы шины SPI на данном этапе.
Р0.7
Р0.6
РОЗ
Р0.4
РО.З
Р0.2
Р0.1
РО.О
NSS (CS*) -- INT1*
MOSI
RXD \
TXD /
MISO (не используется на сегодняшнем занятии)
SCK
ЪАС1
АЪСО
Рис. 24L.7. Подключение выводов порта Р0 на этом лабора-
торном занятии
На этом лабораторном занятии вывод Р0.5 за-
действован двумя разными способами. Не за-
будьте отсоединить от него подключение для
3 По-видимому, команда XDATA информирует компиля-
тор о том, что для данного указателя требуется не команда
MOV, a MOVX.
первого использования (INTO*) при переключе-
нии на другое (RxD).
24L2.2. Таблица данных в RAM
Микроконтроллер C8051F410 оснащен неболь-
шим объемом встроенной памяти RAM — 2 К.
Этой памяти недостаточно для хранения значи-
тельного объема данных от АЦП, чем мы будем
заниматься сегодня. Лучше отвести этой памя-
ти роль буфера для данных, вводимых с кла-
виатуры. Но для того, чтобы продемонстриро-
вать вам работу со встроенной памятью RAM,
или, как она еще называется, MOVX RAM, мы
сохраним в ней пару тысяч значений выборок
от АЦП, а затем будем в бесконечном цикле по-
давать сохраненные значения на ЦАП для вос-
произведения. В данном применении она будет
функционировать как запоминающий осцил-
лограф небольшой емкости.
Данная программа обращается к подпрограм-
ме GETSAMPLE для работы с АЦП, которую мы
применяли в прошлый раз, и отправляет зна-
чения выборок, взятых с АЦП, на ЦАП, как и
в прошлый раз. Но сегодня мы будем впервые
использовать 16-разрядный регистр указате-
ля данных DPTR микроконтроллера 8051. Мы
обсуждали этот регистр в материалах занятий,
начиная с главы 22N, но, может быть, вы не
уделили ему должного внимания, поскольку он
не был задействован ни в каких программах на
лабораторных занятиях. Регистр определяет
адрес для обмена данными с внешней памятью.
В случае компьютера из дискретных компонен-
тов это обычный способ чтения и записи дан-
ных через шины и внешнюю память RAM срав-
нительно большого объема (32 К). Но в случае
компьютера на автономном микроконтроллере
C8051F410 эта внешняя RAM, или MOVX RAM,
в действительности не является внешней, но
при обращении к ней микроконтроллер рас-
сматривает ее, как будто бы она была таковой.
Подпрограмма STOREJT сохраняет одно значе-
ние выборки в память RAM по адресу, опреде-
ляемому содержимым регистра DPTR. Затем она
инкрементирует указатель и проверяет, запол-
нена ли таблица полностью (листинг 24L.4).
Листинг 24L.4. Подпрограмма STOREIT
STOREJT: MOV A, SAMPLEJHI ; Если еще не дошли
; до конца RAM, сохраняем значение выборки
Общие сведения о последовательных шинах
1035
MOVX @DPTR, A ; Сохраняем значение выборки
INC DPTR
MOV A, DPH ; Вышли за предел RAM&
ONE A, #08h, OK
SETBTABLEFULL ; Если таблица заполнена,
; извещаем об этом
OK: R0ET
Этот код проверяет заполнение таблицы не-
привычным способом: поскольку встроенная
память RAM занимает диапазон адресов от 0
до 7FFh, факт ее заполнения можно определить
по состоянию старшего байта регистра DPRT.
(Этот байт называется регистром DPH: data
pointer high.) Когда в результате очередной ин-
крементации регистра DPTR значение регистра
DPH становится 8h, следовательно, значение
указателя вышло за верхний предел адресного
пространства RAM, что, в свою очередь, озна-
чает, что пора завершать цикл ее заполнения4.
Такой подход используется и при считывании
сохраненных в таблице данных.
Код программы
Листинг кода для этой программы, adc_store_
on_chip_apr15.a51, можно загрузить на веб-
сайте книги. Возможно, еще один момент мо-
жет потребовать объяснения: отключение пре-
рываний в подпрограммах сохранения STOREIT
и воспроизведения PLAYBACK. Это делается для
того, чтобы программу можно было исполнять
в пошаговом режиме, даже когда она получа-
ет запросы на прерывание с обычной высокой
частотой: подпрограммы можно отслеживать
в медленном режиме, без постоянного отвлече-
ния на обслуживание прерываний.
Общие сведения
о последовательных шинах
Контроллерам всегда не хватает выводов.
Чем меньше размер контроллера, тем более
острой становится задача эффективной рабо-
ты с доступными выводами. На лабораторном
4 В данном случае значение DPTR «заворачивается» об-
ратно на 0, и последующие операции записи выполнялись
бы поверх действительных данных. Но это обнуление ре-
гистра DPTR не представляет никакой проблемы, поскольку
проверка его значения выполняется после его инкремента-
ции, но до его использования. Поэтому ничего поверх уже
записанных данных не записывается.
занятии 21L.2 мы познакомились с общим
использованием выводов интерфейса, приме-
няемого во избежание выделения даже двух
линий для интерфейса отладки. В некоторых
ситуациях скорость передачи последователь-
ных шин приносится в жертву ради экономии
выводов.
Примечание
Это относится к микроконтроллерам, но не к пол-
норазмерным компьютерам, в которых скорость
обмена последовательных каналов может превы-
шать скорость параллельных.
В крайнем случае, вся информация может пере-
даваться по одной линии (при этом всегда пред-
полагается наличие линии «земли»). Примером
такого интерфейса является однопроводной
интерфейс микроконтроллера DS89C420.
Однопроводным интерфейсом также является
привычный интерфейс RS-232, с которым мы
будем работать позже на этом лабораторном
занятии. Но начнем мы с последовательной
шины, которая менее эффективна, но легко
реализуема: шины SPI разработки компании
Motorola.
24L2.3. Последовательная шина SPI
Как упоминалось в главе 24N, шина SPI не яв-
ляется настоящей шиной, поскольку, кроме
линий, общих для всех подключенных к ней
устройств (что является определением шины),
каждое устройство требует отдельной линии,
посредством которой осуществляется его вы-
бор. Это можно сравнить с выделенной линией
звонка для каждого абонента и одной общей
телефонной линией. Абонент, чей звонок сра-
батывает, поднимает трубку общей телефонной
линии и осуществляет обмен аудиоданными по
ней. Эта шина рассматривается более подробно
в главе 24N.
Оборудование для управления
цифровым потенциометром через SPI
В данном примере к шине SPI подключено
только одно периферийное устройство — по-
тенциометр с цифровым управлением. С помо-
щью цифровых сигналов, подаваемых на этот
потенциометр через интерфейс SPI, его средний
контакт можно установить в любом из 256 по-
ложений между фиксированными контактами
1036
24L Лабораторное занятие: микроконтроллеры V. Перемещение указателей...
постоянного сопротивления (номинал которо-
го в данном случае составляет 100 кОм)5.
Организация тестирования
Цоколевка микросхемы МСР41100 цифрового
потенциометра показана на рис. 24L.8.
ЮОкОмф
V\Ar
CS SCK SI
MCP41100
(U+ = 8, gnd = 4)
Сигналы шины SPI
Рис. 24L.8. Цоколевка микросхемы МСР41100 цифрового
потенциометра
В микроконтроллере C8051F410 функции вы-
водов для SPI зафиксированы на аппаратном
уровне, поэтому от этих выводов нужно от-
ключить все конфликтующие подключения.
Подключение выводов порта на этом лабора-
торном занятии показано на рис. 24L.7.
Первое тестирование: просто переменное
сопротивление
Первым делом просто проверим работоспо-
собность цифрового потенциометра. Для это-
го с помощью цифрового вольтметра измерим
сопротивление между ползунковым выводом и
одним из крайних выводов цифрового потенци-
ометра. Посредством ввода соответствующего
значения на цифровой клавиатуре программа
должна установить сопротивление в диапазоне
от значения, близкого к нулю6, до 100 кОм.
На осциллографе можно наблюдать сигналы
шины SPI: разрешение микросхемы NSS (P0.7),
тактирование SCK (P0.2) и MOSI (P0.6)7. Попро-
буйте определить значения передаваемых бай-
тов. Байт команды с постоянным значением llh
может помочь вам сориентироваться во време-
ни при наблюдении изменения байта данных.
Настройки регистров для порта ввода-
вывода
С этой задачей за нас справится Мастер настро-
ек, как показано на рис. 24L.9.
Рис. 24L.9. Настройка порта с помощью мастера настроек для работы с интерфейсом SPI
Код программы
Листинг кода для этой программы, SPL_digipot_
silabs_apr14.a51, можно загрузить на веб-сайте
книги.
В действительности 100 кОм + гигантские 30%!
6 Всегда присутствует остаточное сопротивление анало-
гового переключателя, коммутирующего сигнал. Поэтому
минимальное сопротивление будет не 0 Ом, а вплоть до
100 Ом (100 Ом — максимальное значение, 52 Ом — ти-
пичное).
7 На рис. 24L.8 сигнал MOSI (Master Out Slave In - Выход
ведущего, вход ведомого) обозначен как SI.
Общие сведения о последовательных шинах
1037
Настройки регистров для SPI
Для работы с шиной SPI необходимо задать
некоторые параметры для этого интерфейса.
К счастью, эту задачу для нас также может вы-
полнить мастер настроек. На рис. 24L.10 пока-
заны установленные параметры для SPI.
Рис. 24L.10. Установка параметров SPI с помощью Мастера
настроек
24L2.4. Применение цифрового
потенциометра
Убедившись, что цифровой потенциометр ра-
ботает должным образом, попробуйте найти
ему более полезное применение: регулировка
коэффициента усиления инвертирующего уси-
лителя. Схема подключения потенциометра
для реализации этой задачи изображена на
рис. 24L.8.
Как предлагалось в главе 24N, добавление
к цифровому потенциометру возможности
усреднения амплитуды выходного сигнала
(просто диод и RC-цепочка) реализует опера-
цию автоматической регулировки усиления.
Микроконтроллер C8051F410 позволяет де-
лать это также и в цифровой форме, используя
его оконную функцию. В частности, микрокон-
троллер отслеживает уровень входного сигнала
АЦП и информирует программу, когда он вы-
ходит за пределы определенного разрешенного
диапазона. Но программа для реализации ана-
логового усреднителя кажется более простой.
Решайте сами, какой из этих подходов вам
больше по душе.
24L2.5. Последовательный
интерфейс RS-232
Практически все микроконтроллеры оснаща-
ются портом последовательного интерфейса
RS-232 (который отсутствует в большинстве
современных персональных компьютеров), ко-
торый предоставляет микроконтроллеру пря-
молинейный способ взаимодействия с полно-
масштабным компьютером. Микроконтроллер
может обращаться к ПК (например, чтобы вос-
пользоваться его более мощными возможностя-
ми манипулирования и отображения данных),
и ПК может обращаться к микроконтроллеру
(например, для управления исполнением про-
граммы, скажем, руководить процессом приема
данных микроконтроллером). В этом разделе
мы попробуем реализовать двунаправленный
обмен данными. Программа не будет выпол-
нять никаких особенных операций, но покажет
некоторые необходимые инициализации.
Оборудование для реализации канала
RS-232 между ПК и микроконтроллером
Традиционный канал RS-232 обеспечивает хо-
рошую помехозащищенность за счет большого
размаха сигналов. А в упрощенном интерфейсе
RS-232 используются ТТЛ-уровни. Мы будем
применять упрощенный вариант RS-232, поль-
зуясь преобразователем USB/RS-232, встроен-
ным в нашу плату ЖКД дисплея. Этот преоб-
разователь работает по протоколу RS-232, но
с ТТЛ-уровнями. Это удобное свойство, по-
зволяющее избежать преобразования уровней,
что иногда приходится делать8.
Более того, плата ЖКД дисплея содержит два
преобразователя RS-232/USB. Один из них
является автономной микросхемой FTDI232R,
которую можно задействовать в качестве
устройства общего назначения и которая тре-
буется для взаимодействия с микроконтрол-
лером DS89C420 (на лабораторных занятиях
8 Приходится только иногда, поскольку простого ограни-
чителя напряжения будет достаточно вместо настоящего
преобразователя уровней, наподобие рассматриваемых в
§ 12.10.4 книги АоЕ.
1038
24L Лабораторное занятие: микроконтроллеры V. Перемещение указателей...
с компьютером из дискретных компонентов).
А другой преобразователь встроен в микро-
контроллер C8051F410 платы ЖКД: это такая
же микросхема, как и та, которая выполняет
преобразование USB/C2 для среды разработки
Silicon Laboratories.
Устройство УАПП микроконтроллера C8051F410
использует выводы Р0.4 и Р0.5 (сигналы ТХО и
RXO соответственно). Это назначение выводов
зафиксировано аппаратно. Подключите эти ли-
нии (направление сигналов которых обозначе-
но с точки зрения микроконтроллера) к лини-
ям RXD и TXD платы ЖКД. Эти выводы платы
ЖКД обозначены с точки зрения ПК, который
подключается через нее. Иными словами, вы-
воды ТХО и RX0 микроконтроллера C8051F410
подключаются к выводам RXD и TXD платы
ЖКД соответственно. На рис. 24L.11 показана
реализация этого подключения в нашей схеме
на макетной плате.
Микроконтроллер принимает
данные от ПК (на линии RX)...
Или микроконтроллер
передает данные на ПК
24L2.6. Программа монитора порта
среды Silicon Laboratories
Самой простой программой для сопряжения
ПК с микроконтроллером будет программа
терминала Toolstick Terminal среды Silicon
Laboratories. Прежде чем запускать эту програм-
му, загрузите требуемый код в микроконтрол-
лер C8051F410, а затем отключитесь. Теперь
запустите программу терминала. Проверьте,
что в настройках программы задано значение
скорости обмена 9600 бод, а для всех других
параметров оставьте значения по умолчанию
(рис. 24L.12, слева).
После загрузки программы в микроконтрол-
лер C8051F410 и отключения загруженная
программа начинает исполняться, постоянно
обращаясь к последовательному порту ми-
кроконтроллера. Выполнив подключение к
микроконтроллеру посредством программы
терминала Toolstick Terminal, посылаемые
микроконтроллером данные можно наблюдать
в панели Recieve Data главного окна. В этой
панели также отображается и один символ, со-
ответствующий шестнадцатеричному значе-
нию, вводимому в порт Р2 микроконтроллера,
к которому подключена цифровая клавиатура.
На рис. 24L.11 подключение цифровой клавиа-
туры не видно; это подключение было показано
на рис. 21L.15.
Обратите внимание на то, что линии
RX микроконтроллера соответствует
линия ТХ на плате ЖКД и ПК
Рис. 24L.11. Реализация канала последовательной связи
с платой ЖКД
данные
Рис. 24L.12. Окна программы терминала Toolstick Terminal: настройки порта (слева) и главное окно, отображающее обмен
между ПК и микроконтроллером (справа)
Двунаправленный последовательный интерфейс
1039
Таблица 24L.1. Настройки регистров
Регистр
SC0N0
CKCON
TMOD
TCON
XBR0
Т1Н
Значение бита/байта
67 (= S0MODE)
d4 (=REN0)
d1 (=TI0)
dO (= RIO)
d3(=T1M)
d1/d0(=SCA1/SCA0)
OOh
d6(=CЯ1)
d5,d4(=T1M1,T1M0)
20h
d7(=TF1)
d6(TR1)
40h
dO (= UARTOE)
01h
d7...dO (= значение пе-
резагрузки таймера)
Функция
0 ==> 8-битовый последовательный режим
1 ==> приемник включен
Флаг прерывания передатчика: установлен по завершении передачи;
нужно обнулить
Флаг прерывания приемника: установлен по завершении приема;
нужно обнулить
0 ==> используйте SCA1, SCA0 для установки частоты таймера Timeii
00 ==> Частота сигнала тактирования микроконтроллера = систем-
ная частота /12
Системная частота /12 (это значение сброса)
0 ==> сигнал тактирования таймера Timeri определяется битом Т1М
(CKCON.4)
доь ==> 8-битовая перезагрузка
То же самое
1 ==> Переполнение таймера Timeii (выполняйте ручной сброс,
если только не используется прерывание)
1 ==> Разрешение таймера Timeii
Таймер Timeii включен
1 ==> маршрутизация сигналов УАПП ТХО, RX0 на Р0.4, Р0.5
То же самое
96h ==> 9600 бод, когда частота сигнала тактирования микрокон-
троллера = системная частота /12
Двунаправленный
последовательный
интерфейс
24L.2.7. Микроконтроллер может
обращаться к ПК
Программа, результаты исполнения которой по-
казаны на рис. 24L.12, предназначена только для
демонстрации того факта, что микроконтрол-
леры действительно могут взаимодействовать
с полномасштабными компьютерами. Файл
листинга этой программы seriaLmessage_si-
Iabs_apr11.a51 можно загрузить на веб-сайте
данной книги. Программа повторяет текст, со-
держащийся в строке кода db (define byte), на-
ходящейся после подпрограммы GETSPEECH.
Подробности работы подпрограммы GETSPEECH
рассматриваются в разделе 24L.8.
Настройки регистров
В табл. 24L.1 приводятся инициализационные
параметры регистров.
На рис. 24L.13 показан снимок экрана Мастера
настроек, с которого можно взять значения для
предыдущей таблицы, если вы не хотите прове-
рять побитно каждый регистр. В нашем случае
нам пришлось вставить одно значение вруч-
ную — значение перезагрузки, #096h, скорости
в бодах9.
24L2.8, Подробности работы
подпрограммы GETSPEECH
Программа seriaLmessage_silabs_apr11.a51 ис-
полняется микроконтроллером, бесконечно
посылая ПК фиксированное сообщение посред-
ством подпрограммы, для реализации которой
был использован прием программирования,
не встречавшийся ни в каких других случаях
на наших лабораторных занятиях по микро-
контроллерам. Эта крошечная подпрограм-
ма GETSPEECH берет по одному символу ASCII
передаваемого сообщения. Новой командой
является команда MOVC: GETSPEECH: MOVC А,
9 Когда мы попытались получить значение перезагрузки
из скорости в бодах, Мастер настроек выдал неправиль-
ный результат. Мы так и не смогли выяснить причину это-
го.
1040
24L Лабораторное занятие: микроконтроллеры V. Перемещение указателей..
Рис. 24L13. Конфигурирование последовательного порта с помощью Мастера настроек
@ А+РС Эта команда означает «переместить
код» (move code), а операндом источника слу-
жит адрес, формируемый суммированием зна-
чения регистра PC (счетчик команд) и регистра
А (аккумулятор). При этом операндом назначе-
ния, как можно видеть, является аккумулятор.
Мы уже упоминали этот режим адресации в
разделе 21S.1.5.
Таким образом, при каждом вызове подпро-
грамма GETSPEECH загружает в аккумулятор
значение, находящееся по адресу, определяемо-
му значением PC + А, где PC означает значение
счетчика команда в данный момент. Иными
словами, аккумулятор играет роль индекса та-
блицы данных, начальный адрес которой ука-
зывается значением PC.
Текущее значение счетчика команд PC явля-
ется адресом следующей команды (в данном
случае команды RET)10. Таким образом, чтобы
получить первый символ сообщения (который
является буквой «t» в тексте «this value is the
410...»), значение индекса, содержащееся в ре-
гистре А, должно быть равным 1, чтобы в ре-
зультате суммирования PC + А получился адрес
ячейки памяти, в которой хранится символ «t».
Вот почему в регистр а загружается значение 1
этой строчкой кода:
10 Если вы помните, определение текущего значения счет-
чика команд PC дается при обсуждении команды CALL,
где оно является значением, которое сохраняется в стеке,
а также при вычислении адреса для команды перехода
JUMP, где текущее значение PC — второй адрес после адре-
са самой команды JUMP.
START_OFFSET EQU 01 h; Начальное смещение в таблице
сообщения
Значение 1 загружается в аккумулятор в два
этапа: сначала в регистр R2, а уже оттуда — в ре-
гистр А. А после его использования в качестве
индекса аккумулятор служит хранилищем для
символа, извлеченного из таблицы.
Такое интенсивное применение аккумулятора
характерно для микроконтроллера 8051. Как
мы уже упоминали ранее, более поздние ми-
кроконтроллеры распределяют работу между
множественными регистрами. Но в ранних
микроконтроллерах, включая микроконтрол-
лер 8051, аккумулятор был «центральной стан-
цией», куда стекались результаты выполнения
всех арифметических и булевых операций, а
также служил источником и назначением для
операций MOVX обмена данными с внешней
памятью.
Чтобы сделать эту программу еще более инте-
ресной, чуть похожей на разработанную вами
самостоятельно, мы предлагаем вам изменить
текст сообщения, следующего после команды
db. Это может позволить вам лучше оценить
возможность, предоставляемую микрокон-
троллеру последовательным портом: взаимо-
действовать с полномасштабным компьюте-
ром. Каким образом реализовать эту возмож-
ность, мы, как обычно, оставим на ваше усмо-
трение. Возможно, вы найдете ей применение
для какого-либо из проектов, предлагаемых в
конце нашего курса.
Двунаправленный последовательный интерфейс
1041
24L2.9. Последовательный канал
беспроводной связи Bluetooth
Удовлетворившись, что программа последо-
вательной связи работает должным образом
и микроконтроллер может взаимодействовать
с ПК, можете, если у вас есть такое желание,
маршрутизировать этот сигнал через беспро-
водный канал Bluetooth. Посредством этого
канала ваш микроконтроллер сможет общать-
ся с ПК или (что, наверное, более интересно)
со смартфоном на Android. Но не с iPhone, по-
скольку компания Apple не позволяет обыч-
ным гражданам, как мы, экспериментировать с
их устройствами.
разует последовательные сигналы протокола
RS-232 в радиосигналы протокола Bluetooth.
Это модуль Roving Networks WRL-12579, выпу-
скаемый компанией Sparkfun.
Отключите питание 5 В и подключите 33 В
Для питания модуля требуется напряжение
3,3 В (а не 5 В), которое подается на него через
кабель платы ЖКД (это кабель с разъемом 5x2).
Способ подачи питания на модуль Bluetooth по-
казан на рис. 24L.14.
Напряжение 3,3 В можно также использовать и
для питания микроконтроллера C8051F410.
Оборудование
Модуль Bluetooth — автономное устройство,
содержащее микроконтроллер, который преоб-
Отключите обычную шину питания
напряжением +5 В с платы ЖКД, чтобы можно
было подать питание напряжением 3,3 В
Замечание
Линия напряжения 3,3
предоставляет напряжение питания
для микроконтроллера и SPI RAM
Рис. 24L.14. Организация питания напряжением 3,3 В для
модуля Bluetooth и для микроконтроллера
Такой способ организации питания также исполь-
зуется на лабораторном занятии 25L, где мы будем
работать с другим устройством, требующим пита-
ния 3,3 В: последовательной памятью RAM.
Подключение сигнальных линий
Bluetooth
Теперь подключите линии Тх и Rx микрокон-
троллера (хотя в данном случае мы не будем
использовать режим приема для микрокон-
троллера) к линиям Rx и Тх модуля Bluetooth
соответственно. Вспомните, что на каждом
устройстве эти линии обозначены с точки
зрения данного устройства, т. е. когда микро-
контроллер ведет передачу по своей линии Тх,
модуль Bluetooth принимает данные по своей
линии Rx.
Jm: 3,3 В, «земля»
Скорость передачи в бодах:
высокий уровень для 9600, низкий для 115 к
Rx
(подключается
к линии Тх
'Тх | \
(подключается Разрешение
к линии Rx передатчика
микроконтроллера
C8051F410)
Светодиод состояния (мигает, когда модуль
в режиме обнаружения; постоянно включен,
когда установлено подключение)
Рис. 24L.15. Подключение сигнальных линий модуля Bluetooth. (Используется модуль Roving Networks WRL-12579 компании
Sparkfun)
1042
24L Лабораторное занятие: микроконтроллеры V. Перемещение указателей...
Подключение к смартфону
Когда микроконтроллер бесконечно подает на
модуль Bluetooth последовательное сообщение
«this is the 410 talking...», процедура для под-
ключения модуля к смартфону на Android до-
вольно проста.
Светодиод индикации состояния будет мигать
со скоростью 1 раз в секунду.
♦ Включите возможность Bluetooth на смарт-
фоне.
♦ Выполните сканирование на присутствие
устройств Bluetooth.
♦ Модуль, скорее всего, идентифицирует себя
как Шгфу...
♦ При выборе этого устройства откроется окно
для ввода пароля; введите пароль 1234.
♦ После приблизительно 30 секунд размыш-
лений смартфон должен выдать сообщение
об установлении сопряжения с устройством
Firefly, а светодиод индикации состояния
должен прекратить мигать и начать светить-
ся постоянно.
♦ После этого на экране смартфона должно
выводиться повторяющееся сообщение от
микроконтроллера. Если сообщение не по-
мещается по ширине экрана смартфона, в
программе для микроконтроллера, отправ-
ляющей сообщение, вставьте возврат карет-
ки посередине сообщения.
Подключение к ПК
Подключение к ПК требует больше усилий, чем
к смартфону.
♦ Здесь также нужно выполнить сопряжение
ПК и модуля Bluetooth и ввести пароль мо-
дуля. После установления сопряжения ПК с
Firefly компьютер выведет сообщение, ин-
формирующее, какой порт СОМ он будет ис-
пользовать для Bluetooth. Далее приводится
более подробное описание этого процесса:
• щелкните правой кнопкой мыши по значку
Bluetooth;
• в открывшемся контекстном меню выбе-
рите опцию Добавить устройство;
• откроется окно, содержащее список уст-
ройств Bluetooth, обнаруженных Windows;
• щелкните в этом списке по устройству
Firefly, а затем нажмите кнопку Далее;
• введите код сопряжения устройства, 1234,
а затем нажмите кнопку Далее;
• в области задач отобразится значок в виде
корпуса компьютера типа башня, внизу ко-
торого будет круглый вращающийся зна-
чок. По истечении приблизительно одной
минуты круглый значок исчезнет, означая,
что сопряжение модуля Bluetooth и ПК
было выполнено успешно;
• теперь выполните двойной щелчок по
значку корпуса-башни;
• в списке устройств будет показано, какой
порт COM Windows присвоила устройству.
♦ Выполните двойной щелчок по значку про-
граммы PuTTY11:
• в разделе Connection type открывшего-
ся окна PuTTY Configuration установите
переключатель Serial;
• в разделе Serial line введите номер пор-
та СОМ, присвоенного Windows данному
устройству;
• далее в иерархическом списке Category
выберите узел Translation и выпадающем
списке Remote character set выберите оп-
цию ISO-8859-4:1998 (Latin-4, North
Europe)12;
• в этом же списке выберите узел Session, в
разделе Saved sessions выберите опцию
Default settings и нажмите кнопку Save.
Это сохранит выполненные настройки
СОМ порта и отображения текста до сле-
дующего раза.
24L2.10. Микроконтроллер может
принимать обращения от ПК
Последовательный порт также позволяет ПК
обращаться к микроконтроллеру, чтобы, на-
пример, давать ему указания, что ему делать.
Комбинация этой возможности с той, которая
демонстрируется в разделе 24L2.7, позволяет
совместить знакомый интерфейс полномас-
штабного компьютера с уникальными возмож-
ностями выделенного микроконтроллера. На
11 PuTTY - свободно распространяемый клиент для раз-
личных протоколов удаленного доступа, включая SSH,
Telnet, rlogin. Также имеется возможность работы через
последовательный порт (https://ru.wikipedia.org/wiki/
PuTTY).
12 Наверное, будет все же более практично выбрать опцию
UTF-8.
Двунаправленный последовательный интерфейс
1043
веб-сайте книги можно загрузить программу se-
rial_receive_silabs.a51, которая представляет со-
бой простейшую демонстрацию возможности
приема микроконтроллером сообщений от ПК.
Как применить эту возможность для практиче-
ских целей, оставляем на ваше усмотрение.
Эта программа использует такие же инициа-
лизационные настройки, как и рассмотренные
в разделе 24L.2.7, но цикл программы намно-
го проще: микроконтроллер просто выводит
на дисплей все символы, посылаемые ему ПК.
Практическая версия подобной программы
могла бы применить получаемые данные для
более интересных целей, например направляя
микроконтроллер выполнить то или иное дей-
ствие.
Рассмотрим код цикла этой программы:
SHOW_ONE: JNB RIO, $; Ожидаем получения байта от
УАПП
CLR RI0; Обнуляем флаг после его активирования
MOV DISPLAY, SBUFO; Берем принятые данные
SJMP SHOW_ONE; Повторяем до бесконечности
Он почти такой же, как и для цикла в разде-
ле 24L2.7, с единственной разницей, что в нем
выполняется проверка состояния флага приема
символа (RIO), а не передачи (ПО), как это де-
лается в цикле SENDIT в разделе 24L2.7. Далее
приводится код этого цикла, в котором выпол-
няется проверка флага ТЮ:
SENDIT: MOV SBUFO, A; Помещаем символ в буфер (пере-
даем его)--УАПП 1
LINGER: JNBTIO, LINGER; Ожидаем здесь, пока не полу-
чим подтверждение передачи
CLRTIO
RET
Чтобы сделать подобную программу действи-
тельно полезной, а не просто пригодной только
для демонстрационных целей, исполняющаяся
на микроконтроллере программа, вероятно,
должна содержать специальный модуль, кото-
рый мог бы анализировать полученный текст и
на основе его содержимого давать указание вы-
полнять то или иное действие. Например, этот
модуль может проверять, получен ли символ С
или D. Если получен символ С, то следующий
байт сохраняется в качестве команды для циф-
рового потенциометра. А если получен символ
D, то следующий принятый байт сохраняется
как данные для передачи на цифровой потен-
циометр. Затем микроконтроллер передает оба
байта и возвращается обратно к задаче про-
верки входа УАПП. Таким образом можно с по-
мощью ПК управлять состоянием цифрового
потенциометра. Опять же, мы привели только
грубый набросок решения. Если вы полагаете,
что можете реализовать эту идею, то вам при-
дется самому продумать все детали.
Взаимодействие с микроконтроллером
посредством терминала
Программа терминала ToolStick, которую мы
использовали в разделе 24L2.6 для приема на ПК
данных от микроконтроллера (см. рис. 24L.12),
подойдет также и для передачи данных с ПК на
микроконтроллер. На рис. 24L.16 показан сни-
мок экрана окна этой программы после пере-
дачи с ПК четырех значений; пятое значение
было введено, но еще не передано. Переданные
значения являются кодами ASCII для симво-
лов Р123, которые связаны с названием нашего
курса в Гарвардском университете.
,•;■"
Данные только введены,
но еще не переданы
Четыре байта, переданные с ПК на микроконтроллер
и отправленные им обратно на ПК
Рис. 24L.16. Программа терминала ToolStick среды Silicon
Laboratories осуществляет взаимодействие ПК с микрокон-
троллером через последовательный порт
Программа для приема
микроконтроллером данных от ПК
Подобно другим программам программу seriaL
receive_silabs.a51 можно загрузить на веб-сайте
этой книги.
24S. Дополнительный материал.
Загрузчик программ для микроконтроллеров
компании Dallas Semiconductor
24S.1. Загрузчик программ 24S.2. Оборудование
Встроенную память ROM микроконтролле-
ров 89С420/30/50 производства компании
Dallas Semiconductor можно загружать из ПК
через последовательный интерфейс RS-2321.
Встроенная память ROM этих микроконтрол-
леров содержит программу монитора, которая
обычно скрыта. Сделать эту программу доступ-
ной можно, активировав вывод PSEN одновре-
менно с выводами RESET и ЕА микроконтрол-
лера (рис. 24S.1).
Конфигурация оборудования для
последовательной загрузки Figure 15-2
Подается сигнал
высокого уровня -
kin * on | *
T Oil TJ'J ;4
Подается сигнал
низкого уровня
Подается сигнал
низкого уровня
Рис. 24S.1. Подключения для активирования загрузчи-
ка (рисунок взят из справочного листка компании Dallas
Semiconductor)
Активирование этих выводов осуществляется
устройством ПМЛ GLUESTEP нашего компью-
тера из дискретных компонентов при подаче
сигнала низкого уровня на его вывод LOADER.
До сих пор этот вывод был деактивирован под-
ключением к шине положительного питания.
1 Рассматриваемая здесь программа загрузчика работает
только на компьютерах под Windows. Насколько нам из-
вестно, компания Dallas Semiconductor/Maxim Integrated
не предоставляет версий программы для Linux или Macin-
tosh.
Для реализации загрузчика не требуется до-
бавлять почти никакого нового оборудования,
поскольку устройство GLUEPAL настроено для
работы с загрузчиком.
24S.2.1. Преобразователь USB/RS-232
Печатная плата ЖКД дисплея также содержит
преобразователь USB/RS-232, который позво-
ляет ПК взаимодействовать с микроконтролле-
ром 8051. Между прочим, для RS-232 он выдает
ТТЛ-уровни, а не уровни большого размаха тра-
диционного RS-232. Используются три сигнала:
TXD (передача от ПК), RXD (прием, опять же, с
точки зрения ПК) и DTR (сигнал разрешения для
управления загрузчиком). Кстати, этот канал
USB/RS-232 пригоден для любого взаимодей-
ствия ПК и микроконтроллера, а не только для
реализации функции загрузчика, описываемой
здесь. На рис. 24S.2 изображена плата ЖКД
Сигнал TXD T7K: к RXD микроконтроллера
(РЗ.О, вывод 10)
Сигнал RXD ПК: к TXD микроконтроллера
(Р3.1, вывод И)
^-Сигнал DTR*: на сигнал LOADER*
I (вывод 8 ПМЛ 6LUE3TEP}
Рис. 24S.2. Плата ЖКД с выводами трех сигналов преобразо-
вателя USB/RS-232
24S3. Два способа использования загрузчика
1045
с преобразователем USB/RS-232 с обозначен-
ными выводами интересующих нас сигналов.
Обратите внимание на то, что сигналы TXD и
RXD отображают направление обмена с точки
зрения ПК и подключаются к своим противо-
положным сигналам на микроконтроллере.
Иными словами:
♦ сигнал TXD от ПК и преобразователя USB/
RS-232 на плате ЖКД подключается к сигна-
лу RXD на микроконтроллере;
♦ сигнал RXD от ПК и преобразователя USB/
RS-232 на плате ЖКД подключается к сигна-
лу TXD на микроконтроллере.
24S.2.2. Сигнал DTR активирует
загрузчик
Управление загрузчиком на микроконтроллере
осуществляется сигналом DTR, который, в свою
очередь, управляется программой загрузчика,
исполняемой на ПК. Сигнал DTR (инвертиро-
ванный преобразователем) подается на вывод
сигнала LOADER устройства ПМЛ GLUESTEP.
Подача сигнала низкого уровня на вывод
LOADER активирует несколько выводов устрой-
ства GLUEPAL, переводя микроконтроллер
в режим загрузки. В частности, активируется
сигнал RESET51 и сигнал PSEN* (включая тре-
тье состояние этого вывода). До сих пор линия
PSEN* использовалась только в качестве выхода
для микроконтроллера. Сигнал LOADER также
активирует постоянный сигнал тактирования
микроконтроллера, необходимый для того,
чтобы он реагировал на особенные сигналы,
которые запускают его встроенную программу
монитора/загрузчика.
Примечание
Не забудьте удалить провода, подключающие вы-
вод LOADER устройства GLUESTEP к шине положи-
тельного питания.
24S.3. Два способа
использования загрузчика
Для взаимодействия с загрузчиком можно
использовать одну из двух прикладных про-
грамм. В настоящее время компания Dallas
Semiconductors/Maxim Integrated разработа-
ла программу МТК (Microcontroller Took Kit).
Раньше они предлагали программу Loader420,
обладающую интерфейсом, который мы пред-
почитаем. Хотя они больше не поддерживают
эту программу, на момент подготовки данной
книги ее можно было еще найти в Интернете2.
Сначала мы рассмотрим программу Loader420,
а затем - МТК.
По результатам наших последних испытаний
этих двух программ для работы с загрузчиком,
мы склоняемся к мнению, что программа МТК
более надежная. Тем не менее мы рекомендуем
вам также просмотреть материал по програм-
ме Loader420, чтобы получить представление о
возможностях обоих программ. Мы не излага-
ли подробно все возможности для каждой про-
граммы для работы с загрузчиком. Программа
МТК может показать вам возможности про-
граммы Loader420.
24S.3.1. Программа Loader420
Загрузите и установите программу Loader420.
После запуска программы откроется окно,
содержащее кнопку OPEN в левом нижнем
углу и пустое текстовое поле, как показано на
рис. 24S.1. Прежде чем выполнять какие-либо
дальнейшие действия с программой, нужно
инициализировать последовательный порт.
Для этого в меню Ports выберите опцию Select
Port Settings и в открывшемся диалоговом
окне Select Port and Baudrate укажите в соот-
ветствующих полях необходимый СОМ-порт
и скорость обмена в бодах. Нам нравится
порт COM3 и скорость обмена 9600 бод. Порт
COM3 является виртуальным портом СОМ, но
Windows не против считать его обычным по-
следовательным портом (хотя иногда она пута-
ется; эта тема более подробно рассматривается
в разделе 24S.5).
Установив параметры для СОМ-порта, нажмите
кнопку OPEN, а затем нажмите кнопку Loader
на нижней панели программы. В результате
должен загореться красным цветом индикатор
DTR SET, расположенный посередине нижней
части главного окна. Сигнал DTR (с низким ак-
тивным уровнем) подается на вход LOADER*
устройства GLUEPAL, что дает указание
2 Мы смогли найти эту программу на Codeforge. Ее также
можно загрузить на веб-сайте этой книги.
1046 24S. Дополнительный материал. Загрузчик программ для микроконтроллеров компании Dallas...
. Port кате
" Baud Raie
Рис. 24S.3. Главное окно программы LOADER420 с открытым
диалоговым окном инициализации последовательного порта
микроконтроллеру активировать свою про-
грамму монитора и загрузчика. На плате ЖКД
также должен загореться индикатор DTR.
Если все работает должным образом, то в тек-
стовом окне программы работы с загрузчиком
должно отобразиться сообщение, пример кото-
рого показан на рис. 24S.4. Это сообщение было
отправлено микроконтроллером DS89C420 и
служит индикатором, что микроконтроллер
должным образом подключен к ПК и что он
успешно получил от ПК комбинацию сигналов,
которые запускают программы монитора и за-
грузчика на нем.
Рис. 24S.4. Сообщение от микроконтроллера означает, что
подключение работает должным образом. Это хорошая но-
вость
Теперь осталось задать еще один настроечный
параметр, и можно будет приступать к загрузке
программы.
ЙУЙ PU PI
При установленной опции Flash
(опция по умолчанию) данные
загружаются во внутреннюю память
микроконтроллера 89С430
Выбор опции External позволяет загружать
. программу во внешнюю память ЙДАЛ вашего
■компьютера из дискретных компонентов
: (а также отображать ее содержимое)
Рис. 24S.5. Выбор внешней памяти для загрузки программ
24S.3.2. Указываем тип памяти,
в которую необходимо загружать
программу
В отличие от микроконтроллера DS80C320, с
которым мы работали все это время, микро-
контроллер 89С420 содержит встроенную па-
мять ROM (так называемую флеш-память:
перезаписываемую, но энергонезависимую па-
мять, во многом похожую на память EEPROM
(ЭСППЗУ), которую вы использовали в устрой-
ствах ПМЛ). Поскольку нам нужно загружать
программы не во внутреннюю память ROM ми-
кроконтроллера, а в его внешнюю память RAM,
то следует оговорить это требование в програм-
ме Loader420. Для этого нужно в меню Options
программы выбрать пункт Memory Type, а в
этом меню — пункт External (рис. 24S.5).
24S3.3, Загружаем файл из ПК
С помощью программы RIDE создайте файл
типа .HEX; это файл с машинным кодом в фор-
мате для процессоров Intel. Чтобы создать та-
кой файл, щелкните значок справа от значка,
используемого для ассемблирования файла.
Скопируйте этот файл типа .HEX в папку, в ко-
торой находится программа Loader420.
Например, файл типа HEX для программы
KEYSUM из лабораторного занятия 20L выгля-
дит следующим образом:
Ю2000000802Е50
:0D0030009080007800E8F0F8E0280080F9EA
:00000001FF
Формат довольно непонятный, и вряд ли вы за-
интересованы в его понимании.
Но в случае, если же у вас такой интерес все же
имеется, попробуем дать краткое объяснение.
♦ Каждая новая строка начинается с двое-
точия.
♦ После двоеточия следует двухразрядное зна-
чение количества байтов кода или данных.
♦ Далее идет четырехразрядное значение на-
чального адреса.
♦ После начального адреса следует двухраз-
рядное значение типа записи: 00 для кода
или данных, 01 для адреса исполнения.
24S3. Два способа использования загрузчика
1047
♦ Последнее двухразрядное значение является
контрольной суммой, в частности битовой
суммой всех байтов строки в дополнитель-
ном двоичном коде, за исключением началь-
ного двоеточия и байта самой контрольной
суммы.
Если этих сведений вам недостаточно, то можете
навестить сайт http://www.keil.com/support/
docs/1584.htm, чтобы узнать больше.
24S.3.4. Процедура для загрузки
файла в микроконтроллер
Файл шестнадцатеричных значений можно за-
грузить из ПК в микроконтроллер следующими
двумя способами.
Способ 1
♦ В меню File программы Loader420 выберите
пункт Load File. В открывшемся окне нави-
гации по файловой системе вашего компью-
тера выберите файл, который вы хотите за-
грузить.
Способ 2
♦ В окне ввода терминала введите команду L
или LX для загрузки файла во внутреннюю
или внешнюю память соответственно.
♦ В меню File выберите пункт Send File to
Serial Port. В открывшемся окне навигации
по файловой системе выберите требуемый
файл для загрузки.
Просмотр загруженного кода
с помощью ПК
При желании можно проверить, что загру-
женный в память RAM микроконтроллера
код программы совпадает с кодом в исходном
файле. Но это будет очень трудоемкая работа,
требующая особой внимательности. Более ин-
тересно исследовать содержимое RAM, чтобы
удостовериться в том, что загруженный в нее
код выглядит как код в исходном файле (шест-
надцатеричные значения без заполняющих
символов, содержащихся в самом файле .HEX).
Чтобы исследовать содержимое определенного
блока памяти RAM, введите начальный адрес
диапазона в поле Begin, а конечный — в поле
End (рис. 24S.6).
; Затем нажмите кнопку !>?spicy
Рис. 24S.6. Просмотр содержимого области RAM микрокон-
троллера с помощью программы Loader420
В нашем случае мы просматриваем содержимое
области RAM просто ради интереса. Но эту воз-
можность можно применить в более полезных
целях. В частности, можно вручную откоррек-
тировать код в памяти RAM, загрузить его на
компьютер, а затем с помощью среды RIDE
дизассемблировать его в листинг. (Мы еще не
пробовали выполнять этот прием.)
На рис. 24S.7 показан снимок экрана с отобра-
жением содержимого области памяти RAM в
диапазоне адресов от 0 до 18h после загрузки
в нее тестовой программы из лабораторного
занятия 18L. Эта программа должна быть вам
знакома.
ОСИ, АСОМ СМХЖ РМй
"
к Адрес
Преобразование кош программы
в коды ASCII. В данном случае
довольно бесполезное занятие
Рис. 24S.7. Отображение в программе Loader420 загруженной во внешнюю память RAM микроконтроллера тестовой про-
граммы из лабораторного занятия 20L
1048 24S. Дополнительный материал. Загрузчик программ для микроконтроллеров компании Dallas...
24S.3.5. Исполнение программы
на микроконтроллере,
подключенном к ПК
Чтобы микроконтроллер мог исполнять при-
кладные программы (а не свою внутреннюю
программу монитора/загрузчика), необходимо
деактивировать сигнал DTR. Все, что для это-
го нужно сделать, так это нажать кнопку Run в
нижней части окна программы Loader420. Но
это действие не запустит программу на исполне-
ние, как можно было бы ожидать. Нужно вруч-
ную подать и снять сигнал сброса. Следует иметь
в виду, что микроконтроллер может не работать
должным образом, если закрыть программу
Loader420, оставив при этом последовательное
соединение подключенным. Это объясняется
тем, что в таком случае на линии DTR не просто
устанавливается высокоимпедансное состояние,
а может появиться низкий уровень, в результате
чего микроконтроллер окажется в постоянном
режиме загрузки. Чтобы после нажатия кнопки
Run (что дезактивирует сигнал DTR) микрокон-
троллер мог исполнять прикладные программы,
необходимо не закрывать программу Loader420.
Если от микроконтроллера отключить плату
USB, то он будет продолжать работать, посколь-
ку внутренний повышающий резистор в устрой-
стве ПМЛ должен дезактивировать сигнал
LOADER*. Тем не менее благоразумнее подать
на его линию высокий уровень, подключив ее к
шине положительного питания через резистор с
номиналом в несколько килоом.
Если, например, выбрать для отображения об-
ласть памяти в диапазоне адресов от 0 до 10h,
то в программе Loader420 должно отобразиться
содержимое первых 16 ячеек внешней памяти
RAM. Вы, наверное, в любом случае знаете, что
представляют собой первые два или три байта,
поскольку они содержат команду перехода к на-
чалу последней программы, с которой вы рабо-
тали: 80 хх, если выполнялся короткий переход,
или 02 хх хх в случае длинного перехода.
Если вы все еще настроены скептически, то
можете загрузить в нижнюю область памя-
ти легко распознаваемую последовательность
(например, 0123456...), а затем просмотрите эту
область с помощью программы Loader420.
контроллера 8051 обеспечивает функциональ-
ность, подобную программе Loader420, но об-
ладает менее удобным интерфейсом и не под-
держивает некоторые возможности, такие как
отображение содержимого RAM или ROM про-
граммируемого микроконтроллера.
Где взять МТК
Программу МТК можно загрузить на веб-сайте
компании Maxim Integrated по адресу: https://
files.maximintegrated.com/microcontroller/
devtoolsoftware/mtk/obsolete/. Эта пап-
ка содержит несколько версий этой програм-
мы, не все из которых являются рабочими.
Загрузите версию программы МТК2 Install-
2.4,12.
Выбор микроконтроллера и настройка
последовательного порта
Как и в случае с программой Loader420, для
программы МТК необходимо выполнить не-
которые предварительные настройки. В част-
ности, при запуске программы сначала откры-
вается диалоговое окно Select device со спи-
ском микроконтроллеров, поддерживаемых
программой. Выберите в нем свой микрокон-
троллер и нажмите кнопку ОК. В открывшем-
ся главном окне программы выберите в меню
Options пункт Configure Serial Port и в по-
явившемся диалоговом окне Serial Port вы-
берите в соответствующих полях выпадающих
списков последовательный порт COM3 и ско-
рость 9600 бод (рис. 24S.8).
24S.3.6. Программа МТК
Программа МТК (Microcontroller Tool Kit)
для работы с монитором/загрузчиком микро-
Рис. 24S.8. Выбор микроконтроллера и настройка последо-
вательного порта в программе МТК
24S А Диагностика проблемы с записью во флеш-память программой Loader420
1049
Открытие порта и подключение
микроконтроллера к загрузчику
Так же как и в программе Loader420, снача-
ла открываем последовательный порт, а затем
подключаемся к загрузчику микроконтролле-
ра (рис. 24S.9).
го в меню Target выберите пункт Disconnect
from Loader (рис. 24S12).
Рис. 24S.9. Открытие порта и подключение микроконтрол-
лера к загрузчику в программе МТК
После успешного подключения, как и в случае
с программой Loader420, в окне сообщений
программы МТК отобразится сообщение от
микроконтроллера, означающее, что последо-
вательный канал работает должным образом.
Теперь нужно выбрать тип памяти, в которую
загружать программу: внешнюю RAM или вну-
треннюю ROM (флеш-память) (рис. 24S.10).
Рис. 24S.10. Выбор памяти для загрузки прикладной про-
граммы микроконтроллера в программе МТК
Выбор и загрузка файла программы
Далее нужно выбрать и загрузить файл при-
кладной программы в формате HEX.
Phc.24S.12. Для исполнения загруженной прикладной про-
граммы отключитесь от программы загрузчика микрокон-
троллера
Отключение от программы загрузчика микро-
контроллера деактивирует линию DTR и вход
LOADER* устройства GLUEPAL, к которому под-
ключена эта линия. Это возвращает наш са-
модельный компьютер в стандартный режим
работы. Теперь программу можно исполнять
обычным образом, или в пошаговом, или не-
прерывном режиме.
24S.4. Диагностика
проблемы с записью
во флеш-память
программой Loader420
Иногда в ответ на попытку выполнить запись во
флеш-память из программы Loader420 выдает-
ся загадочное сообщение об ошибке «Cannot
write l's to 0's» (Нельзя записывать единицы
в нули). Эта проблема решается просто — вы-
бором в меню Options пункта Load Blind to
Flash (Загрузка вслепую во флеш-память).
Сообщение об ошибке и соответствующее ре-
шение показаны на рис. 24S.13.
Сообщение об ошибке,
Рис. 24S.11. Выбор файла для загрузки в память микрокон-
троллера в программе МТК
Выбрав требуемый файл, отправьте его микро-
контроллеру. Чтобы исполнить загруженный
файл на микроконтроллере, необходимо от-
ключиться от программы загрузчика. Для это-
Решение проблемы -
Рис. 24S.13. Проблема записи во флеш-память и ее ре-
шение
Загрузка вслепую (Load Blind) означает невы-
полнение двух операций проверки в процессе
1050 24S. Дополнительный материал. Загрузчик программ для микроконтроллеров компании Dallas...
записи в память. Мы не понимаем, почему это
решение работает, поскольку неясно, чем вы-
зывана исходная ошибка. На рис. 24S.14 пока-
зано сообщение об успешной записи во флеш-
память после первой неудачной в результате
применения опции Load Blind to Flash.
Рис. 24S.14. Загадочное но эффективное решение пробле-
мы записи во флеш-память
помощью дополнительного оборудования мо-
гут взаимодействовать с устройствами, осна-
щенными стандартным последовательным пор-
том RS-232. Компьютер эмулирует стандарт-
ный последовательный порт, но отправляет
сигналы в формате USB на внешний порт USB.
Подключенный к этому порту специальный
преобразователь преобразует исходящие от
ПК USB-сигналы в сигналы RS-232, а входящие
сигналы RS-232 — в сигналы USB.
Иногда при открытии программы Loader420
или МТК выводится сообщение об ошибке, что
порт СОМ занят другим приложением. Похоже,
что причиной данной ошибки является ава-
рийное отключение платы преобразователя
USB/RS-232 (это плата, на которой также раз-
мещен ЖКД).
24S.5. Диагностирование
проблем присвоения порта
СОМ
24S.5.1. Самое простое решение,
хотя и примитивное
Иногда проблему можно решить, просто сме-
нив порт USB на ПК. Это не совсем утонченное,
но зато быстрое решение, которое можно по-
пробовать, если программа работы с загрузчи-
ком микроконтроллера сообщает вам, что она
не может подключиться к нему. Но, скорее все-
го, проблема так не решится, и в таком случае
читайте дальше.
24S.5.2, Проблема
Персональный компьютер взаимодействует с
вашим самодельным компьютером посредст-
вом микросхемы, которая преобразует сигналы
USB в сигналы RS-232 (но с TTL-уровнями) и
наоборот. Для этого ПК создает виртуальный
последовательный порт. Современные ПК
не оснащаются физическим разъемом СОМ-
порта3, но они способны его эмулировать и с
3 Более старые ПК оснащались разъемом последователь-
ного порта (он же порт СОМ и RS-232), который пред-
ставляет собой 9-контактный разъем DE-9. На контакты
разъема выводятся полноуровневые сигналы TXD и RXD,
а также некоторые сигналы управления, которые иногда,
24S.53. Решение проблемы
Поскольку ПК «думает», что порт COM3 (кото-
рый мы обычно используем) все еще использу-
ется каким-то другим приложением, он автома-
тически присваивает плате USB-преобразовате-
ля другой порт СОМ. Но номер этого порта не
совпадает с номером порта, указанным в пара-
метрах программы Loader420 или МТК.
В следующем примере ОС Windows присвои-
ла преобразователю USB/RS-232 порт СОМ6.
Нам нужно возвратить обратно порт COM3,
чтобы восстановить связь между ПК и нашим
самодельным компьютером.
Замечание
Иногда возникает разновидность этой проблемы:
плате преобразователя присваивается порт COM3,
но тем не менее выводится сообщение о недоступ-
ности этого порта. В таком случае необходимо сна-
чала принудительно присвоить плате другой СОМ-
порт, а затем снова присвоить ей порт COM3.
Первый шаг: Открываем Диспетчер
устройств
Выполните последовательность команд Пуск |
Панель управления | Система | Обору-
дование | Диспетчер устройств. Открыв-
шееся окно Диспетчер устройств содержит
но не всегда, использовались. В нашей схеме требуется
один из этих сигналов управления - DTR (Data Terminal
Ready — готовность терминала данных), означающий, что
компьютер готов к приему данных.
24S.5. Диагностирование проблем присвоения порта СОМ
1051
список категорий устройств, включая катего-
рию Порты (СОМ & LPT), которая содержит
порты СОМ (скорее всего только один), пола-
гая, что плата преобразователя USB/RS-232 все
еще подключена к ПК4. На рис. 24S.15 можно
видеть, что плате преобразователя был присво-
ен последовательный порт СОМ6. Нам нужно
изменить его на порт COM3.
Второй шаг: принудительно присваиваем
плате порт COM3
В диспетчере устройств щелкните правой кноп-
кой виртуальный порт СОМ, присвоенный
преобразователю, в контекстном меню выбе-
рите опцию Свойства, в окне Свойства выбе-
рите вкладку Параметры порта, а на ней на-
жмите кнопку Дополнительно. В поле Номер
порта СОМ увидим, что устройству присвоен
порт СОМ6 (рис. 24S.16).
Щелкните направленный вниз треугольник
справа от поля и в выпадающем списке выбери-
те порт COM3. Нажимайте кнопку ОК, чтобы
закрыть все открытые диалоговые окна до окна
Диспетчер устройств.
ш$щщщж
fte A««>fi V»>a Help
1 if # if S "ill
J Ports (COM &IPT)
General Port Settings Drive* Delate
USB Sena! Рой (CGMS)
i Device type: Potts (COM t LPT)
Manufacturer: ffOf
Location on USB Send Converter
TNs device ss wotking property
If you ate having prebietM wtlh INs device, click Tfoubieshoot to
$\&l the tfoybfeshooler.
Device usage:
Use this device tenable)
\ OK . I Cancel
Рис. 24S.15. Первый шаг в восстановлении присвоения порта COM3 плате преобразователя USB/RS-232
Si's pet second1 |Щ
Ftov? contco!' Non»
Advanced . • [ Restore Defaults j
Рис. 24S.16. Второй шаг в восстановлении присвоения порта COM3 плате преобразователя USB/RS-232
4 Виртуальный СОМ-порт не отображается в диспетчере
устройств современных компьютеров, если только после-
довательное устройство не подключено к разъему USB.
1052 24S. Дополнительный материал. Загрузчик программ для микроконтроллеров компании Dallas...
Последний шаг: Подтверждаем успешность
присвоения устройству порта COM3
Вашей первой мыслью, наверное, будет, что пе-
реназначение порта COM3 не было успешным,
поскольку в окне диспетчера устройств будет
отображаться старое назначение — порт СОМ6,
как показано слева на рис. 24S.17.
Не отчаивайтесь. В меню Действие окна
Диспетчер устройств выберите опцию Об-
новить конфигурацию оборудования, и
после нескольких секунд присвоение порта
будет обновлено до COM3, как можно видеть
справа на рис. 24S.17.
:;;::;;,
* ., Mof
J
Coco ;.>-;-ь-;глг vt'f i Adaptet
P.ibrfeli- НсФ/''Of}. Adfip?.fif
IJ58 Senal Port (C0M6) ^~
У Ports (COM & LPT) Г
УIUS8 Serial Port (C0M6)|
Рис. 24S.17. Успешное переназначение порта COM3 преобразователю USB/RS-232
24W. Пример с решениями. Четыре способа
копирования таблицы
Задача
Создайте программу на языке ассемблера для
копирования 80 последовательных байтов из
области памяти с начальным адресом 100h в
область памяти с начальным адресом 800h.
Решение № 1. Используем один указатель
Текст программы приведен в листинге 24W.1.
24W.1. Несколько способов
скопировать таблицу
Ранее мы упоминали, что существует несколько
способов для копирования табличных данных
из одной области памяти в другую. Здесь мы
приводим листинги четырех программ для ре-
шения этой задачи. Если у вас нет настроения
вводить эти программы вручную, то файлы ли-
стингов также доступны на веб-сайте книги.
Листинг 24W.1. Программа копирования байтов (вариант 1)
;TABLECOPY__ONE_PTR_403.A51 Используем один указатель DPTR для копирования таблицы 8/6/02,4/03
SNOSYMBOLS; Сокращаем объем кода в листинге...
SINCLUDE (C:\MICRO\8051\RAISON\INC\REG320.INC); ...а не то эта строка может создать громадный список
SINCLUDE (C:\MICRO\8051\RAISON\INQVECTORS320.INC); определений идентификаторов (все они для регистров 8051)
ORG0
AJMP START
ORG 200h
START: MOVR6,#08
MOV R7, #00
MOV DPTR, #100h
MOVR0,#080h
COPY: MOVXA,@DPTR
INC DPTR
ACALLGETOTHER
DJNZR0,COPY
STOP: SJMP STOP
; Задаем начальный адрес конечной таблицы
; То же самое - младший байт
; Инициализируем главный указатель начальным адресом исходной таблицы
; Инициализируем счётчик копируемых значений
; Берем значение из исходной таблицы
; Берем другой указатель и используем его для записи
; Повторяем, пока не будут скопированы все значения
; После завершения копирования переходим в бесконечный цикл.
; Сохраняем первый указатель
GETOTHER: PUSH DPH
PUSH DPL
MOVDPH,R6
MOVDPL,R7
MOVX @DPTR, A ; Сохраняем значение
INC DPTR
MOVR7,DPL
MOVR6,DPH
POP DPL ; Восстанавливаем первый указатель
POP DPH
RET
END
; Восстанавливаем второй указатель
; Сохраняем обновленный второй указатель
1054 24W. Пример с решениями. Четыре способа копирования таблицы
Решение № 2. Используем два указателя
Текст программы приведен в листинге 24W.2.
Листинг 24W.2. Программа копирования байтов (вариант 2)
;TABLECOPY_TWOPTRS_403.A51 ИСПОЛЬЗУЕМ ДВА УКАЗАТЕЛЯ DPTR ДЛЯ КОПИРОВАНИЯ
; ТАБЛИЦЫ 4/22/03
SNOSYMBOLS; Сокращаем объем кода в листинге...
$INCLUDE (C:\MICRO\8051\RAISON\INC\REG320.INC) ; ...а не то эта строка может создать громадный список
SINCLUDE (C:\MICRO\8051\RAISON\INCWECTORS320.INC) ; определений идентификаторов (всех регистров
; микроконтроллера 8051)
ORG0
AJMP START
ORG160h
START:
MOV DPTR, #100h; Инициализируем главный указатель начальным адресом исходной таблицы (указатель источника)
INC DPS ; Переключаемся на другой указатель
MOV DPTR, #800h ; Инициализируем вторичный указатель начальным адресом дубликата таблицы
; (указатель назначения)
DEC DPS ; Восстанавливаем главный указатель
MOV R0, #080h ; Инициализируем счётчик копируемых значений
COPY: MOVX A, @DPTR ; Берем значение из исходной таблицы
INC DPTR ; Инкрементируем указатель источника
INC DPS ; Переключаемся на указатель назначения
MOVX @DPTR, A ; Сохраняем значение в дубликате таблицы
INC DPTR ; Инкрементируем указатель назначения
DEC DPS ; Восстанавливаем указатель источника
DJNZ R0, COPY ; Повторяем, пока не будут скопированы все значения
STOP: SJMP STOP ; После завершения копирования переходим в бесконечный цикл.
END
Решение № 3. Меняем местами старшие байты
Текст программы приведен в листинге 24W.3. Этот метод годится только для таблиц небольшого
размера.
Листинг 24W.3. Программа копирования байтов (вариант 3)
; tablecopy_DPH_swap_405.A51 Копирует 80h значений из одной области памяти в другую;
; Использует метод обмена регистров DPH, разработанный Полем (4/28/05)
SNOSYMBOLS ; Сокращаем объем кода в листинге...
SINCLUDE (C:\MICRO\8051\RAISON\INC\REG320.INC) ; ...а не то эта строка может создать громадный список
SINCLUDE (C:\MICRO\8051\RAISON\INCWECTORS320.INC) ; определений идентификаторов (всех регистров
; микроконтроллера 8051)
ORG0
UMP START
ORG400h
START: MOV R6, #01 Oh ; Инициализируем счетчик
MOV DPL, #0h ; Инициируем младший байт обоих указателей (по границе 256)
24W. I Несколько способов скопировать таблицу 1055
MOV R0,#01 h ; Инициируем старший байт указателя источника
MOV R1 ,#08h ; To же самое с указателем назначения
COPY: MOV DPH, R0 ; Загружаем указатель источника (старший байт)
MOVX A, @DPTR ; Берем байтовое значение
MOV DPH,R1 ; Загружаем указатель назначения (старший байт)
MOVX @DPTR,A ; Сохраняем это байтовое значение
INC DPL ; Инкрементируем оба указателя (младший байт общий)
DJNZ R6, COPY ; Повторяем, пока не скопируем все значения
STUCK: SJMP STUCK ; После завершения копирования переходим в бесконечный цикл
END
Решение № 4. Используем смещения от значения указателя DPTR
Текст программы приведен в листинге 24W.4.
Листинг 24W.4. Программа копирования байтов (вариант 4)
;TBLCOPY_OFFSET_403.A51 Копирование таблицы, используя прием со смещением
SNOSYMBOLS; Сокращаем объем кода в листинге...
SINCLUDE (C:\MICRO\8051\RAISON\INC\REG320.INC) ; ...а не то эта строка может создать громадный список
SINCLUDE (C:\MICRO\8051\RAISON\INC\VECTORS320.INC) ; определений идентификаторов (всех регистров
; микроконтроллера 8051)
ORG0
BLOCKSTART EQU 100h ; Начальный адрес исходной таблицы
BYTECOUNT EQU 6h ; Здесь произвольное предположение: должно отражать количество байтов в блоке,
; который нужно скопировать
OFFSET EQU 07h ; Смещение (старший байт): разница между адресами исходной таблицы и ее дубликата
AJMP START
ORG 260h
START: MOV R0, #BYTECOUNT ; Инициализируем счётчик копируемых значений
MOV DPTR, #BLOCKSTART ; Инициализируем главный указатель начальным адресом исходной таблицы
MOV R1 ,#OFFSET ; Задаем постоянную смещения (старший байт)
NUDGE: MOVX A,@DPTR ; Берем байтовое значение, которое нужно скопировать
MOV R2,A ; Сохраняем рабочий регистр, используемый в вычислениях
MOV R3,DPH ; Сохраняем старший байт главного указателя
MOV A,DPH ; Берем байт указателя, который нужно модифицировать
ADDA,R1
MOV DPH,A ; Теперь указывает на дубликат таблицы
MOV A,R2 ; Восстанавливаем значение
MOVX @DPTR,A ; И сохраняем его в дубликате таблицы
MOV DPH,R3 ; Восстанавливаем исходный указатель
INC DPTR ; ...и инкрементируем его
DJNZ R0,NUDGE ; Повторяем, пока не будут скопированы все значения
STOP: SJMP STOP ; После завершения копирования переходим в бесконечный цикл
END
25N. Микроконтроллеры VI. Таблицы данных
Содержание
25N.1. Устройства ввода и вывода для микроконтроллера 1056
25N.1.1. Несколько простых примеров интерфейса устройств ввода 1057
25N.2. Задача для пользователей компьютера из дискретных компонентов:
работа с автономным микроконтроллером 1058
25N.3. Задача для пользователей компьютера на основе автономного
микроконтроллера: использование внешней памяти RAM 1059
25N.3.1. Последовательный доступ к памяти 1059
25N.3.2. Запись и чтение одного байта 1059
25N.3.3. Запись и чтение нескольких байтов 1060
25N.3.4. Код программы для работы с памятью RAM с интерфейсом SPI 1060
Цель этой главы
Эта глава содержит два довольно разных проекта для двух версий наших самодельных компьюте-
ров. В частности, проект для компьютера на автономном микроконтроллере C8051F410 состоит в
вводе и выводе данных из компьютера, используя ограниченное количество линий и последова-
тельный протокол. А проект для компьютера из дискретных компонентов реализует дизайн, ха-
рактерный для однокристального микроконтроллера (что, конечно же, является привычным де-
лом для тех из вас, кто работает с компьютером на автономном микроконтроллере).
25N.1, Устройства
ввода и вывода для
микроконтроллера
Как вы знаете, кроме собственно контроллера
микросхемы микроконтроллеров могут содер-
жать много других встроенных периферий-
ных устройств. Микроконтроллер DS89C420
производства компании Dallas Semiconductor
содержит минимальный набор таких перифе-
рийных устройств: таймеры, два последова-
тельных порта и параллельные порты. А вот
микроконтроллер C8051F410 компании Silicon
Laboratories более совершенен в этом отноше-
нии. Он оснащен АЦП, ЦАП, ШИМ, последо-
вательными портами разных типов (SPI, 12С,
RS-232), таймерами, а также часами реаль-
ного времени, которые способны обеспечить
длительный отсчет времени (т. е. реализо-
вать задержки большой продолжительности
или предоставлять временные маркеры для
данных).
Но довольно часто встроенных периферий-
ных устройств недостаточно, и к микрокон-
троллеру требуется подключить, по крайней
мере, пару кнопок и несколько светодиодов.
Взаимодействие с микроконтроллером для бо-
лее «продвинутых» периферийных устройств
реализуется с помощью одного из последова-
тельных протоколов, скорее всего, SPI или 12С.
Но для несложных устройств такие мощные
интерфейсы не требуются и используются бо-
лее простые, несколько примеров которых мы
рассмотрим далее.
Книга АоЕ содержит более обширный набор
примеров в § 15.8. В частности, на рис. 15.20-
15.22 показано около 60 периферийных уст-
ройств с интерфейсами разных типов: парал-
лельным, SPI и PC (для некоторых из этих
устройств также указан номер детали).
25N.L Устройства ввода и вывода для микроконтроллера
1057
25N.1.1. Несколько простых
примеров интерфейса устройств
ввода
На рис. 25N.1 показано несколько наиболее
распространенных устройств ввода.
RC-цепочку, которая работает потому, что дат-
чик перехода в действительности таковым не
является, а просто определяет уровень после-
довательных периодов сигнала тактирования.
Благодаря этому медленному процессу удается
избежать появления паразитных автоколеба-
ний, подобных возникающим в компараторе.
/При
уповь
отсутствии внутреннего
ышения по напряжению
Микроконтроллер
<*>INT LHeA°Poroe средство
^ "[ устранения дребезга
Датчики угла поворота
Оптический прерыватель
Два оптических прерывателя
Определяет абсолютное
положение (угловое)
[ ® Подсчитывает
> I число оборотов
пу ( (=> скорость вращения)
р 1 (?) Кроме скорости также
па I определяет
РпЬ \ направление вращения
)(|) Несколько оптических
прерывателей
Рис. 25N.1. Примеры устройств ввода и их интерфейсов
Некоторые из этих устройств необходимо до-
полнять программными интеллектуальными
возможностями. Например, чтобы придать
датчику вращения возможности большие,
чем просто подсчет числа оборотов, его нуж-
но снабдить соответствующей программой.
Другие устройства могут работать самостоя-
тельно. Например, средство устранения дре-
безга представляет собой просто замедляющую
Еще одно устройство ввода:
цифровая клавиатура
Задача сканирования выводов матрицы цифро-
вой клавиатуры не представляет для микрокон-
троллера никаких трудностей. На рис. 25N.2
показано оборудование, необходимое для ска-
нирования выводов матричного коммутатора
размерностью 4x4, подобного имеющемуся
в цифровых клавиатурах, которыми мы поль-
зуемся на наших лабораторных занятиях.
Матричный коммутатор
цифровой клавиатуры
0 «
снннь
(ИНН*—♦
<нхх>
Микроконтроллер Л
5
► 4 выхода...
. ...4 входа
Рис. 25N.2. Микроконтроллер' может сканировать цифро-
вую клавиатуру (представляющую собой матрицу переклю-
чателей). См. также рис. 15.8 в книге АоЕ
При нажатии одной кнопки цифровой клавиа-
туры происходит соединение линий опреде-
ленного ряда и столбца. Таким образом, ска-
нирующий алгоритм должен постоянно одно-
временно активировать только одну из четы-
рех выходных линий устройства, определяя
при этом состояние четырех входящих линий1.
Если ни одна из четырех линий не активирова-
на, это означает, но не нажата никакая кнопка.
При активировании одного из входов програм-
ма смотрит, какой выход был активирован и
каким активированным входом. Полученная
комбинация активированного входа и выхода
позволяет определить нажатую кнопку и на-
править программу в таблицу для выбора со-
ответствующего значения кнопки. Защиту от
дребезга можно реализовать, вставив задержку
1 Ко всем четырем входным линиям должен быть под-
ключен повышающий резистор. Микроконтроллер 8051
оснащен встроенными резисторами для небольшой под-
тяжки по питанию, но для других микроконтроллеров
может потребоваться повышающий резистор номиналом
около 10 кОм.
1058
25N. Микроконтроллеры VL Таблицы данных
после начального определения нажатия кноп-
ки, а затем проверив, все ли еще она нажата.
Несколько примеров интерфейса
устройств вывода
Некоторые из показанных на рис. 25N.3
устройств вывода вам уже знакомы, тогда как
другие, в особенности ЖКД, наверное, нет.
Микроконтроллер
Тодтяжка по
I напряжению,
| чтобы обеспеч
точное U.
7 линий
(А
Многие выходи
подобны ТТЛ в том
отношении, что их ток
в режиме потребления
намного больше, чем
в режиме выдачи
Электродвигатель
г/
Нагрузка с
I большим
▼ потреблением
тока
ЖКД
^ Разрешение
Рис. 25N.3. Примеры устройств вывода и их интерфейсов
Жидкокристаллический дисплей оснащен зна-
чительным интеллектом. Он использует стан-
дартизированный интерфейс и реализует набор
команд, включающий команды очистки и пере-
хода на новую строку. Дисплей также содержит
встроенный счетчик, который служит для вы-
вода следующего символа рядом с предыду-
щим. Он также способен принимать 8-битовые
команды и данные порциями по 4 бита, чтобы
уменьшить количество линий, требуемых для
его интерфейса2. В случаях, когда выделение
семи линий под дисплей является слишком за-
тратным (выводов микроконтроллера всегда
не хватает), можно воспользоваться одним из
ЖКД, оснащенных последовательным интер-
фейсом: RS232, SPI или 12С3.
2 Можно обойтись без линии R/W* дисплея, если для
тактирования микроконтроллер использует задержки, а не
полагается на считывание с ЖКД сигнала занятости.
3 Компания Newhaven Display International выпускает
ЖКД, оснащенные всеми тремя последовательными ин-
терфейсами: SPI, PC и RS-232. Компания Adafruit предо-
ставляет плату преобразователя между интерфейсом SPI
25N.2. Задача для пользо-
вателей компьютера из
дискретных компонентов:
работа с автономным
микроконтроллером
На этом занятии мы предлагаем пользовате-
лям разных ветвей компьютеров поменяться
ролями.
В частности, мы хотим, чтобы те из вас, кто
до сих пор работал с компьютером из дис-
кретных компонентов, узнали, как легко мож-
но загрузить код во встроенную память ROM
микроконтроллера. Конечно же, пользователи
компьютера на автономном микроконтролле-
ре C8051F410 делали это на протяжении всего
курса. Мы не хотим, чтобы пользователи ком-
пьютера из дискретных компонентов вынесли
из нашего курса представление о микрокон-
троллере как о схеме размером приблизитель-
но 75x35 сантиметров с подключенной к ней
цифровой клавиатурой.
Теперь, получив опыт построения большого
«прозрачного» компьютера на основе микро-
контроллера 8051, мы хотим, чтобы вы полу-
чили удовольствие от работы с компактным и
простым микроконтроллером. Мы хотим, что-
бы вы смогли увидеть его в работе без какого-
либо дополнительного внешнего оборудования
(хотя к нему нужно подключить внешний квар-
цевый или керамический резонатор).
Мы надеемся, что у вас была возможность по-
экспериментировать с программой загрузчи-
ка на лабораторном занятии 24L. Если нет, то
вы можете попробовать работать с ней сейчас.
Хотим вам напомнить о двух альтернативных
способах программирования микроконтролле-
ра 8051 (которые подробно рассматриваются
на лабораторном занятии 25L):
♦ Программировать на платформе из дискрет-
ных компонентов, как вы это делали все это
время. Как вы знаете, этот подход возможен
благодаря устройству GLUEPAL.
или PC и стандартным интерфейсом ЖДК. Плата задей-
ствует шесть из стандартных 16 выводов ЖКД. (Шесть
линий вместо семи, показанных на рис. 25N.3, возможны
вследствие неиспользования линии R/W*.)
25N3. Задача для пользователей компьютера на основе автономного микроконтроллера..
1059
♦ Установить немного оборудования на макет-
ную плату и программировать микрокон-
троллер 8051 на ней. Подробная информа-
ция об этих подходах к программированию
микроконтроллера 8051 излагается на лабо-
раторном занятии 25L.
Мы надеемся, что как те из вас, кто работает
с компьютером из дискретных компонентов,
так и те, кто работает с компьютером на базе
автономного микроконтроллера, придумают
какую-либо небольшую задачу, которую мож-
но решить с помощью своего компьютера.
Решение какой бы то ни было задачи становит-
ся более интересным, если вы сами ее поста-
вили перед собой. Задача должна быть более
сложной, чем простое мигание светодиодом,
но, наверное, не слишком сложной. Полезно
заглянуть наперед в содержимое главы 26N, ко-
торая содержит список устройств, использова-
ние которых в качестве периферийных может
быть интересным. Это такие устройства, как
акселерометры, электродвигатели, микросхема
синтеза речи.
25N3. Задача для
пользователей компьютера
на основе автономного
микроконтроллера:
использование внешней
памяти RAM
В обеих ветвях лабораторного занятия 24L мы
сохраняли значения в таблицах в памяти RAM
прямолинейным способом с помощью переме-
щающегося указателя DPTR для записи и счи-
тывания данных по одному байту за раз. При
этом микроконтроллер DS89C420 компании
Dallas Semiconductors имел доступ к 32 К па-
мяти RAM, что было достаточно для хранения,
например, многих секунд аудиоинформации.
А вот микроконтроллер C8051F410 компании
Silicon Laboratories в реализации этой задачи
выглядел несколько слабовато, поскольку все,
что ему было доступно для хранения данных,
так это 2 К встроенной памяти RAM.
Однако он может восполнить этот недостаток
отсутствия шин для доступа к внешней па-
мяти, используя для этого последовательный
интерфейс. Но программный код для реали-
зации последовательного доступа к внешней
памяти RAM намного сложнее, чем код для па-
раллельного доступа к ней через шины. И это
несмотря на то, что микроконтроллер содер-
жит аппаратную поддержку последовательного
протокола SPI.
25N.3.1. Последовательный доступ
к памяти
Память RAM с последовательным доступом
микроконтроллера C8051F410 оснащена аппа-
ратным оборудованием, обеспечивающим этот
доступ, несмотря на возможность использо-
вания всего восьми выводов. Подобно другим
периферийным устройствам с интерфейсом
SPI (включая даже простой цифровой потен-
циометр с интерфейсом SPI, упоминаемый на
лабораторном занятии 24L), устройству с по-
следовательным доступом необходимо указы-
вать, что ему нужно делать с отправляемыми
значениями. Для этого требуется небольшой
набор команд.
Память RAM объемом 32 К и с интерфейсом
SPI может записывать или считывать байт по
указанному адресу. Но для выполнения этих
операций в блоке последовательных ячеек па-
мяти (т. е. в таблице) достаточно внутреннего
счетчика, автоматически инкрементирующего-
ся после каждой операции записи или чтения.
Для обоих типов многобайтных операций не-
обходимо указать только начальный адрес,
а всю остальную работу RAM выполняет по
большому счету автономно.
25N.3.2. Запись и чтение одного
байта
Прежде чем отправлять информацию по SPI-
интерфейсу в память RAM, нам нужно сооб-
щить ей, каким образом она должна обраба-
тывать данные, которые мы ей предоставим.
В данном случае команда записи состояния Olh
информирует RAM, что следующий байт будет
командой установки режима. Следующий байт
задает режим, в нашем случае один байт Olh.
Проинструктировав RAM о необходимости
принять один байт, можно выдавать команду
записи (02h), а после нее — адрес и данные.
1060
25N. Микроконтроллеры VI. Таблицы данных
На рис. 25N.4 показано начало временного ин-
тервала, в течение которого осуществляется за-
пись данных.
["[Выбор микросхемы* f~~~ |
Команда записи <
Л—I
Команда;
записи данных
SCK , 41
MOSI
Рис. 25N.4. Сначала в память RAM с интерфейсом SPI посы-
лается команда, указывающая, какой из ее режимов нужно
использовать
На рис. 25N.5 показан процесс записи одного
байта по произвольному адресу, а затем считы-
вание данных из этого адреса. Микроконтрол-
лер записывает значение данных АВ в ячейку с
адресом 24 45, а затем считывает это значение
из этой ячейки памяти.
Как и следовало ожидать, самый первый эле-
мент в каждом временном интервале (начало
которого отмечается активированием сигнала
CS*) является командой: сначала записи (02h),
а затем чтения (03h).
25N.3.3. Запись и чтение
нескольких байтов
Когда нужно сохранить данные в таблице, а за-
тем прочитать эти данные обратно из таблицы,
способность памяти RAM работать с длинны-
ми последовательностями байтов — это как раз
то, что нам нужно. На рис. 25N.6 показано, как
микроконтроллер передает три байта данных
(значения AAh, BBh, CCh) в три ячейки памяти
RAM с последовательными адресами, начиная с
нулевого адреса.
25N.3.4. Код программы для работы
с памятью RAM с интерфейсом SPI
Последовательные операции записи выполня-
ются быстро благодаря автоматической инкре-
ментации адреса. В отличие от операции записи
одного байта рассмотренной в разделе 25N.3.2,
в данном случае после указания первого адреса
указывать последующие адреса нет необходи-
мости.
Из микроконтроллера (выход ведущего...)
v Команда записи Адрес Данные (один байт) Команда чтения
Адрес Данные (входные из RAM)
{ 00 ^^а^^ш^ —»—|v
7
Z
JiiLJil
JIML
~LJ Ш1_ОГ"
_J ШП1—L_
:На микроконтроллер (вход ведущего...) I
Рис. 25N.5. Запись и чтение последовательной памяти через интерфейс SPI
Команда Начальный
записи адрес
Три байта данных для Команда Начальный Три байта данных для
записи (в адреса 0,1, 2) чтения адрес чтения (из адресов 0,1, 2)
"ЯП ^Vr
IP^ra^G^
Рис. 25N.6. Запись и чтение трех последовательных байтов в память RAM с интерфейсом SPI с указанием только начального
адреса
25N.3. Задача для пользователей компьютера на основе автономного микроконтроллера...
1061
Листинг 25N.1 содержит текст программы, ко-
торая записывает последовательность байтов
в память RAM с интерфейсом SPI. Хотя концеп-
туально это простая программа, ее реализация
изобилует сложными подробностями.
В листинге не приводятся непривлекатель-
ные подробности нескольких подпрограмм.
Полный листинг кода для этой программы,
spi_ram_adc_dacjncomplete.a51, можно загру-
зить на веб-сайте книги. Слово incomplete (не-
завершенная) в названии программы означает,
что вам нужно самим написать небольшой блок
кода, который реализует проверку завершения
записи и чтения таблицы.
Листинг 25N.1 Программа записи последовательности байтов в память RAM с интерфейсом SPI
; Теперь запишем несколько байтов
WRITE.SEVERAL: a call START_VALS ; Инициализируем счётчик копируемых значений
acall INIT_ADDRESS ; Задаем начальный адрес
movR7,#WRITE_COM
acall STARTJDPERATION
acall SEND_ADDRESS
; Подпрограмма START_OPERATION будет использовать это для отправки
; соответствующей команды
; Активируем сигнал CS*, посылаем сигнал
SENDJDNE: acall GET.SAMPLE
acall SENDJDATA
acall CHECK.END
; Получаем байт из АЦП
; Проверяем, заполнена ли таблица (данная подпрограмма устанавливает флаг
; ALL_done при заполнении таблицы)
jnb ALL_DONE, SEND_ONE ; Если не заполнена, отправляем следующее значение
clr AILDONE ; Если заполнена, обнуляем флаг и идем дальше
setb NSSMD0 ; Деактивируем сигнал CS* в конце записи
; Считываем записанные данные
READ_SEVERAL: acall START.VALS
acall INIT_ADDRESS
movR7,#READ_COM
; Задаем начальный адрес
; Считываем значение из RAM
acall START_OPERATION
acall SEND ADDRESS
; Активируем сигнал CS*, посылаем команду
READ.ONE: acall GET.DATA
mov DISPLAY, R3
movlDA0H,R3
; Показываем, что нам выдала RAM (только для режима пошаговой отладки)
; Отправляем считанное значение на ЦАП
acall CHECK_END
jnbALL_DONE,READ_ONE
clr AILDONE
setb NSSMDO
; Проверяем, считаны ли все данные из таблицы
; Если нет, считываем следующее значение
; Если заполнена, обнуляем флаг и идем дальше
; Деактивируем сигнал CS* в конце считывания
sjmp $ ; Это для проверки передачи одного байта
sjmp WRITE_SEVERAL ; Это для передачи множества значений
25L Лабораторное занятие: микроконтроллеры VI.
Автономный микроконтроллер
Напоминание
Для тех из вас, кто до сих пор работал с ком-
пьютером из дискретных компонентов, у нас
есть хорошая новость: работа с микроконтрол-
лером может быть намного легче. Опять же, мы
говорим (после того как вы вложили много вре-
мени и усилий в это предприятие), что, конечно
же, у вас никогда не возникнет желания снова
работать с микроконтроллером таким образом.
Сначала мы поступили с вами таким образом
после того, как вы научились разрабатывать
схемы из дискретных компонентов: транзисто-
ров, диодов, резисторов, конденсаторов и т. п.
Затем мы повторили этот трюк после того, как
вы проделали значительную работу по сборке
логических схем из отдельных микросхем се-
мейства 74хх. И наконец, после того, как вы со-
брали компьютер из дискретных компонентов
на большой макетной плате и работали с ним,
в большинстве случаев вводя код программ
вручную, мы снова поступаем с вами, как и в
предыдущих двух случаях. Теперь мы хотим
перед завершением этого курса напомнить вам
о нормальном способе использования микро-
контроллера. А именно то, что мы программи-
руем его с помощью ПК и предоставляем ему
работать самостоятельно, без какого-либо до-
полнительного оборудования или с очень ма-
лой его толикой. Это подход, который пользо-
ватели компьютера на автономном микрокон-
троллере C8051F410 применяли на протяжении
всего нашего курса. (Но они упустили возмож-
ность поиска интересных аппаратных проблем,
которыми вы насладились вполне.)
Для этого лабораторного занятия мы предла-
гаем скелетное приложение, чтобы у вас нако-
нец была возможность поэкспериментировать
с микроконтроллером в качестве автономного
устройства, собранного на одной макетной пла-
те. У вас может возникнуть желание не ограни-
чиваться этими начальными экспериментами,
а сделать что-либо большее. Это полностью на
ваше усмотрение. С другой стороны, вы може-
те захотеть возвратиться к компьютеру из дис-
кретных компонентов и реализовать на нем
какой-либо проект своей разработки.
Если проект измерения длительности импуль-
са, который рассматривается в разделе 25L.1.3,
вам не по душе, возможно, вам больше понра-
вится одна из следующих программ:
♦ работа с ЖКД. Эти дисплеи последователь-
но отображают символы при подаче кодов
ASCII на один порт;
♦ сканирование цифровой клавиатуры. Фор-
мирует значение кнопки, нажатой на базовой
цифровой панели 4x4, наподобие панелей,
на основе которых собраны цифровые кла-
виатуры, используемые на наших лаборатор-
ных занятиях.
Сами по себе эти программы не представля-
ют никакого интереса, но любая из них может
быть полезной в качестве интерфейса в каком-
либо разработанном вами приложении.
25L.1. Два способа записи
во флеш-память
25L1.1. Предпочитаемый способ:
используем компьютер с внешними
шинами
Используя компьютер из дискретных компо-
нентов, загрузите программу в его внешнюю
память RAM и запустите его на исполнение, как
обычно в пошаговом режиме. Удостоверившись,
что программа работаем должным образом, за-
грузите ее опять, но на этот раз во внутреннюю
25LI Два способа записи во флеш-память
1063
память ROM микроконтроллера (так называе-
мую флеш-память). Далее извлеките микро-
контроллер с загруженной в него программой
из большой макетной платы и установите его на
одной обычной макетной плате, где он может
работать в автономном режиме. Загруженную
в память ROM программу можно попробовать
исполнить, не извлекая микроконтроллер из
платы компьютера из дискретных компонен-
тов. Для этого на вывод ЕА* микроконтроллера
нужно подать постоянный высокий уровень,
как показано на рис. 25L.1.
Автономный режим
А_ С использованием внешних шин
Рис. 25L.1. Тумблер позволит вам исполнять программы из
внутренней памяти ROM
Загрузка в память ROM возможна благодаря
наличию устройства GLUEPAL. Для того чтобы
исполнить программу из внутренней памяти
ROM микроконтроллера, нужно только устано-
вить тумблер, посредством которого можно по-
давать постоянный сигнал высокого уровня на
вывод ЕА* микроконтроллера. Проще и быть
не может.
Между прочим, программа будет исполняться в
среднем в три раза быстрее из внутренней па-
мяти ROM микроконтроллера, чем из внешней
памяти RAM. Это объясняется тем, что в этом
режиме многие команды выполняются за один
цикл сигнала тактирования, а не за четыре, как
при исполнении из внешней памяти RAM. Но
в большинстве случаев это обстоятельство не
будет важным, если только ваш код не требует
программного тактирования.
допускает их отладку, наблюдая за состоянием
шин при пошаговом исполнении программы.
Автономный микроконтроллер не использу-
ет внешних шин, и эта непрозрачность может
быть досадным недостатком, когда программа
не работает должным образом. Этот недоста-
ток можно частично компенсировать, эмулируя
исполнение программы в среде RIDE.
Когда микроконтроллер установлен на боль-
шой макетной плате, в пошаговом режиме
можно исполнять даже программы из его вну-
тренней памяти ROM. Пошаговый режим мож-
но разрешить, установив бит ALEON микро-
контроллера. Это можно сделать посредством
команды MOV 0C4h, #04h. В результате акти-
вируется сигнал ALE, который используется
функцией пошагового исполнения устройства
GLUEPAL для тактирования. В программах
для исполнения на автономном контроллере
мы активировали сигнал ALE, установив бит
ALEON. Тем не менее отладка программ оста-
ется трудной задачей, когда нельзя наблюдать
состояние шин.
Схема для разрешения загрузки
автономного микроконтроллера
На рис. 25L.2 показана схема, разрешающая
выполнять загрузку программ в автономный
микроконтроллер 8051.
Последовательные подключения должны быть
вам знакомы, а вот использование сигнала DTR,
возможно, нет. В данном случае сигнал DTR пе-
реводит микроконтроллер в особое состояние,
в котором в него можно загружать программы
через последовательный порт2. В результате ак-
тивация сигнала DTR:
25L1.2. Альтернативный способ:
программируем микроконтроллер
на отдельной макетной плате
В течение приблизительно пяти минут можно
собрать схему на макетной плате, на которой
программировать микроконтроллер, не при-
бегая к помощи вашего компьютера на боль-
шой макетной плате. Но хотя этот метод хо-
рошо подходит для загрузки программ1, он не
1 С этой схемой удобнее работать, чем выполнять загрузку
программы в микроконтроллер с помощью компьютера из
дискретных компонентов. Это объясняется тем, что здесь
мы обходим стороной большое «минное поле» потенци-
альных аппаратных неисправностей, например неспособ-
ность компьютера из дискретных компонентов выполнять
запись в RAM. До сих пор нам никогда не требовалось
выполнять эту операцию на лабораторных занятиях, и
поэтому возможность компьютера в этом отношении не
была испытана. Поэтому существует вероятность, что
ваш вполне исправный компьютер может отказаться вы-
полнять загрузку во внешнюю память RAM, при этом не
испытывая никаких проблем с загрузкой во внутреннюю
память ROM.
2 В вашем компьютере из дискретных компонентов на
большой макетной плате устройство GLUEPAL реагирует
на сигнал DTR, устанавливая эти сигналы таким же обра-
зом. Вентильная схема на рис. 25L.2 служит еще одной по-
лезной цели: она управляет сигналом ЕА*. На полном ком-
пьютере сигналом ЕА* необходимо управлять вручную.
1064
25L Лабораторное занятие: микроконтроллеры VI. Автономный микроконтроллер
8051
(Маркировка на плате ЖКД —
направление передачи с точки I
зрения ПК) [
2,2 кОм
1/4 74НС125
2,2 кОм|
DTR (активный 1
TXD (P3.1)
RXD (РЗ.О)
ЕА (высокий уровень для исполнения
с внутренней памяти)
PSEN
, (ручной сброс)
низкий уровень,
подается с платы
ЖКД)
Рис. 25L.2. Оборудование для разрешения загрузки программ в автономный микроконтроллер 8051
♦ устанавливает высокий уровень сигнала RST;
♦ устанавливает низкий уровень сигнала
PSEN*, в результате чего микроконтроллер
включает свою внутреннюю память ROM и
разрешает последовательный порт;
♦ устанавливает низкий уровень сигнала ЕА*,
чтобы разрешить загрузку.
Деактивация сигнала DTR отключает линии
всех этих сигналов, позволяя микроконтролле-
ру исполнять загруженный в его память ROM
код программы.
Монтажная схема
На рис. 25L.3 показано, как выглядит макет-
ная плата с монтажной схемой для работы с
микроконтроллером в автономном режиме.
Эта схема «слепая, глухая и немая», так что
сама по себе она бесполезна. Но мы, конечно
же, надеемся, что вы попытаетесь добавить
к запрограммированному микроконтроллеру
какое-либо оборудование для выполнения не-
которой полезной задачи.
Загадочным устройством, подключенным к
выводам XTAL1 и XTAL2 микроконтроллера,
является кварц, который необходим для встро-
енного генератора колебаний микроконтрол-
лера3. Это менее дорогой и компактный генера-
тор колебаний, чем генератор, установленный
в полном компьютере. Альтернативно для так-
тирования микроконтроллера подойдет гене-
ратор колебаний, который вы применяли на
предыдущих лабораторных занятиях.
Добавляем светодиод для проверки
оборудования
Для проверки работы оборудования загруз-
чика можно подключить светодиод к выво-
ду Р1.0 микроконтроллера. (Для ограничения
тока через светодиод включаем последователь-
но резистор номиналом 3,3 кОм.) Загрузите в
микроконтроллер один из файлов .HEX про-
граммы для мигания светодиода с задержкой
Рис. 25L.3. Собранная на макетной плате схема для раз-
решения загрузки программ в автономный микроконтрол-
лер 8051
3 Вдаваясь в технические подробности, микроконтрол-
лер ожидает параллельный резонансный кварц АТ-среза,
работающий на основной частоте. См. раздел описания
выводов микроконтроллера DS89C430 на с. 12 его спра-
вочного листка.
25LI Два способа записи во флеш-память
1065
(доступные на веб-сайте книги). Отключите
загрузчик и проверьте, мигает ли светодиод.
Если не мигает, попробуйте выполнить руч-
ной сброс микроконтроллера. Когда светоди-
од начнет мигать, указывая таким образом на
правильное функционирование оборудования
для загрузки, можете приступать к поиску под-
ходящего применения для своего автономного
загружаемого микроконтроллера.
Далее предлагаем немного поэксперименти-
ровать с вводом-выводом для автономного
микроконтроллера, а также предоставляем го-
товый код программы, который можно приме-
нить для развлекательных целей.
25L.13 Схема для измерения
длительности импульса
На рис. 25L.4 изображена схема, которую мож-
но использовать для измерения и отображения
длительности импульса посредством автоном-
ного микроконтроллера. На схеме показаны
шестнадцатеричные семисегментные светодиод-
ные индикаторы, но при желании можно взять
ЖКД из предыдущих лабораторных занятий.
+5
31
Генератор
колебаний
с частотой
И МГц
В качестве дисплея
подойдет наша плата
DS89C430 ЖКД или семисег-
ментный индикатор
Рис. 25L.4. Схема для измерения длительности импульса с
помощью микроконтроллера DS89C420
25L1А Код программы для работы
со схемой
Изображенная на рис. 25L.1.4 схема довольно
общая, в результате чего ее можно применить
для выполнения многих задач. Она хорошо
подходит для приложений ведения счета, ко-
торыми мы и намереваемся заняться. Далее
мы предоставим две версии программы для
записи (и вывода на дисплей) длительности
логического импульса низкого уровня. Одна
программа отображает длительность в деся-
тичном формате и тактируется программно4.
А другая версия отображает длительность в
шестнадцатеричном формате и задействует
внутренние таймеры микроконтроллера 8051.
Десятичная версия лучше подходит для тех слу-
чаев, когда длительность импульса в основном
предназначена для отображения; а шестнад-
цатеричная версия (которая использует свои
биты для счета более эффективно) лучше под-
ходит для тех случаев, когда значение длитель-
ности предназначено не для отображения, а для
передачи в другую программу.
На веб-сайте книги размещены файлы исход-
ного кода программ (с расширением .а51), а не
файлы листингов (с расширением .1st), как для
предыдущих лабораторных занятий. Это объяс-
няется тем, что мы предполагаем, что на данном
этапе вы предпочитаете не вводить код в микро-
контроллер вручную, а загружать его из ПК.
Замечание
Эта возможность вам будет необходима, если вы
хотите загружать код в автономный контроллер.
Для этого с помощью среды RIDE нужно будет вы-
полнить ассемблирование и компоновку исходно-
го кода из файла .а51, создав файл .hex, который за-
гружается в микроконтроллер. Но на случай если
вы не хотите заморачиваться с ассемблированием,
мы также предоставляем и файл .hex.
Десятичная версия программы
измерения длительности импульса
Отрицательный перепад входного импульса ак-
тивирует вход прерывания INTO*, чья подпро-
грамма ISR запускает программный счетчик.
А положительный перепад входного импульса
активирует ввод прерывания INT1 *, чья подпро-
грамма ISR останавливает счет и выводит полу-
ченное значение на дисплей. При исполнении
в ее текущем виде на полной скорости данная
программа способна отображать длительность
импульсов в диапазоне 100 отсчетов, или при-
близительно от 0,3 мс до 30 мс. При перепол-
нении счетчика загорается светодиодный ин-
дикатор, предупреждающий о недостоверности
отображаемого значения.
4 Данная программа исполняется на полной скорости; что-
бы измерять более длительные импульсы без переполнения
счетчика, вставьте вызов подпрограммы задержки DELAY.
1066
25L Лабораторное занятие: микроконтроллеры VI. Автономный микроконтроллер
25L1.5. Шестнадцатеричная
версия программы измерения
длительности импульса
Эта программа также использует отрицатель-
ный и положительный перепады входного
сигнала для активирования соответствующих
прерываний: INTO и INT1. Но считает она по-
другому. В частности, подпрограмма ISR пре-
рывания INTO запускает внутренний 16-би-
товый таймер, предварительно обнулив его.
А конечный перепад импульса запускает два
события. Во-первых, как и в предыдущей про-
грамме, он активирует прерывание INT1, под-
программа ISR которого выводит на дисплей
результат измерения. Во-вторых, он активи-
рует операцию захвата счета таймера, в ре-
зультате которой его значение записывается в
16-разрядный регистр захвата. В данном слу-
чае этот прием нам ничего не дает, поскольку
мы могли бы с таким же успехом сами считать
регистры таймера после его остановки. Мы
просто хотели испытать возможность захвата
значения счета.
Чтобы настроиться для удобного диапазона
длительности импульса, можно поэкспери-
ментировать со скоростью инкрементирова-
ния внутреннего таймера. При работе таймера
на полной скорости диапазон отображаемых
значений (старший байт 16-битового счетчи-
ка) составляет от 40 мкс до приблизительно
бмс.
25L1.6. Несколько возможных
применений этих программ
Прежде всего проверим наше
оборудование
Если загрузить одну из описанных программ
в микроконтроллер DS89C430, а затем вста-
вить эту микросхему в макетную плату с под-
ключенным дисплеем, в качестве источника
прямоугольного сигнала для измерения можно
использовать выход с ТТЛ-уровнями генерато-
ра сигналов. Убедившись таким образом, что
аппаратное и программное обеспечение рабо-
тает как следует, можно начинать искать для
измерения что-то более интересное, чем вы-
ходной сигнал генератора сигналов.
Измеритель емкости
Возможно, что вы уже занимались этим про-
ектом на предыдущих лабораторных занятиях,
и он вам больше не интересен. В таком случае
можете заняться реализацией какого-либо при-
ложения своей собственной разработки. В про-
тивном случае можете подать прямоугольный
сигнал для измерения от генератора колеба-
ний на таймере 555 с однополярным питанием.
Вспомните из лабораторного занятия 8L, что
длительность части сигнала с низким уровнем
(что приблизительно равно его полупериоду)
составляет 0,7 постоянной времени RC-цепи.
Значение постоянной RC-цепи можно выбрать
таким, которое дает значение измерения, близ-
кое к значению полной шкалы. Затем в контур
подключаем конденсаторы меньшей емко-
сти, наблюдая, вызывает ли это значительное
уменьшение значения счета.
Если начать со значения счета полной шка-
лы для конденсатора емкостью, например,
0,33 мкФ, то в схему следует включить под-
строечный потенциометр, чтобы можно было
откорректировать длительность импульса для
получения счета, близкого к 33. Затем в схему
вставляется конденсатор емкостью 0,1 мкФ и
проверяется, будет ли значение счета для него
близким к 10. Эксперименты со значениями
емкости конденсатора цепочки продолжают-
ся в подобном духе. Если в цепь подключить
другой конденсатор емкостью 0,33 мкФ па-
раллельно первому, создаст ли это ожидаемый
эффект?
Если у вас есть желание и время, диапазон из-
мерений можно увеличить, добавив в дисплей
третий разряд. В таком случае нужно будет мо-
дифицировать код программы измерения, что-
бы учитывать четыре старших бита младшего
байта значения счета, измеряющего длитель-
ность импульса.
Измеритель скорости реакции
Этим проектом мы также уже занимались, но
реализовывали аппаратно, а не программно с
помощью микроконтроллера. Опять же, если
он не представляет для вас интереса, можете
пропустить его.
Если переключателем с защитой от дребезга по-
дать на вход запроса прерывания INTO* сигнал
25LI Два способа записи во флеш-память
1067
низкого уровня, а затем на вход запроса пре-
рывания INT1* подать другим переключателем
другой сигнал низкого уровня, то микрокон-
троллер сможет измерить время между этими
двумя событиями. Эту способность микрокон-
троллера можно использовать как измеритель
скорости реакции. Но для версии программы
десятичного формата необходимо замедлить
счет, а именно нужно увеличить диапазон пол-
ной шкалы длительности импульса приблизи-
тельно в 10 раз, до 300 мс.
Считыватель сигналов ИК-пульта
дистанционного управления
Это более интересный проект. Когда у вас есть
возможность измерять длительность инфра-
красного импульса, вы только на расстоянии
нескольких шагов от создания приспособления
для чтения последовательностей битов, посы-
лаемых любым ИК-пультом дистанционного
управления. На рис. 25L.5 показана осцилло-
грамма трех кодов, отправленных ИК-пультом
дистанционного управления для телевизоров
Sony.
Необработанные сигналы ПДУ, на основе ко-
торых были созданы эти логические уровни,
изображены на рис. 25L.7. Полные последова-
тельности кодов намного длиннее, чем пока-
зано на рисунках. Но и той информации, что
показана, достаточно для того, чтобы позво-
лить программе, по крайней мере, различить
эти три кода. (Этот рисунок является частью
рис. 24N.13.)
Начальная часть кодов трех кнопок
ИК ПДУ для телевизоров Sony
ZJ>
ы i.ooms A' chi \ 1.60'
Рис. 25L.5. Коды трех кнопок И К ПДУ для телевизоров Sony
(детектированы микросхемой ИК-приемника)
Микросхема ИК-приемника/преобразователя этих
импульсов в соответствующие логические уровни
(предоставляется компанией Vishay Semiconductors)
«Земля»
Выходной сигнал
(логические уровни)
Рис. 25L.6. Микросхема ИК-приемника/преобразователя
р- Подробный вид ИК сигнала до его преобразования
j в логические уровни
•Mi
! • | \ '■ U.,f • ■•■ 1.1 * I | *, ч !< \ I •• .
О
Микросхема ИК-приемника/
преобразователя
Пульт дистанционного управления выдает не
аккуратные сигналы логических уровней, а пач-
ки импульсов частотой 40 кГц. Эти пачки им-
пульсов преобразуются в соответствующие ло-
гические уровни микросхемой ИК-приемника
(фотодиода). На рис. 25L.6 показан пример та-
кого ИК-приемника/преобразователя.
На рис. 25L.7 изображен сигнал частотой в рай-
оне 40 кГц, посылаемый ИК ПДУ. Этот сигнал
интегрируется микросхемой приемника, а ре-
зультат подается на компаратор в этой же ми-
кросхеме, который и создает выходной сигнал
• Логические уровни,
выдаваемые преобразователем
Ml.OOms A
\ 2.20 V
Рис. 25L.7. Пачки импульсов с частотой 40 кГц ИК-сигнала
ПДУ и полученный из них сигнал логических уровней
логических уровней, показанный на самой
нижней осциллограмме на рисунке.
Сигнал ИК ПДУ очень устойчив к искажени-
ям, поскольку в нем нужно только детекти-
ровать наличие пачки импульсов частотой
1068
25L Лабораторное занятие: микроконтроллеры VI. Автономный микроконтроллер
40 кГц, а не каждый переход, как в проекте по
передаче звукового сигнала на лабораторном
занятии 13L.
Программная стратегия
Для синхронизации нашей программе требует-
ся детектировать длинный стартовый импульс
низкого уровня (длительность 2,5 мс). Чтобы
детектировать этот импульс, запускаем нашу
программу измерения длительности импуль-
са и сравниваем полученное значение счета с
эталонным значением минимальной длитель-
ности. Значение счета длительности стартово-
го импульса ПДУ Sony составляет около 6Dh
при измерении программой захвата из раз-
дела 25L.1.5, исполняющейся с таймером, ра-
ботающим на полной скорости. Поэтому ми-
нимальное эталонное значение должно быть
с надежным запасом ниже этого типичного
значения.
Определив стартовый импульс низкого уровня,
измеряем длительность следующего импуль-
са. Этот следующий импульс является первым
импульсом, несущим кодовую информацию;
его длительность составляет или 600 мкс, или
вдвое больше, 1200 мкс. Поэтому эталонное
значение длительности импульса данных долж-
но быть где-то посередине. Значение таймера
для 600 мкс будет lAh и вдвое больше для бо-
лее длительного импульса.
Когда программа определит, что импульс длин-
ный или короткий, она может выполнить пере-
ход к подпрограмме, которая помещает 1 или
0 в регистр. После четырех таких операций у
нас будет достаточно информации, чтобы раз-
личить кнопки от 0 до 9.
Применение считывателя сигналов
ИКПДУ
В настоящее время все бытовые устройства
управляются дистанционно, но, возможно, вам
захочется управлять каким-либо лабораторным
устройством в другом конце комнаты. Например,
заставить электродвигатель вращаться в пря-
мом или обратном направлении или остановить
его. Или, возможно, выбрать один из несколь-
ких источников звука для подачи на динамик.
Признаемся, что с воображением у нас плохо-
вато. Но удовольствие доставляет именно де-
кодирование сигнала ИК ПДУ, а не управление
чем-то посредством этого сигнала. В настоящее
время ПДУ встречаются повсеместно.
25L1.7. Программы для измерения
длительности импульса
Две программы для измерения длительности
импульса и перевода в 16-битовое значение
счета можно загрузить на веб-сайте этой книги.
Одна из этих программ выдает значение в де-
сятичном формате, а другая — в шестнадцате-
ричном.
Это программы pulse_measure_dedmaL
standalone_505.a51 и pulse_measure_capture_
standalone_505.a51 соответственно.
25L2. Лабораторное
занятие SiLabs6: память RAM
с интерфейсом SPI
Выводы порта, используемые на этом
лабораторном занятии
На этом лабораторном занятии вам потребу-
ются практически те же выводы (см. рис. 25L.8),
что и на лабораторном занятии 24L.2. Так-
тирование программы опять реализовано с по-
мощью прерывания INTO*. Это прерывание за-
меняет сигнал RXD, который использовал порт
Р0.5 на лабораторном занятии 24L.2.
Рис. 25L.8. Использование выводов порта PORTO на сегод-
няшнем лабораторном занятии. Запрос прерывания INTO*
возвращен на вывод Р0.5
25L2.1. Последнее предписанное
упражнение: таблица большого
размера в RAM
Это короткое упражнение, в котором мы пред-
лагаем загрузить довольно объемный код,
25L2. Лабораторное занятие SiLabs6: память RAM с интерфейсом SPI
1069
позволяющий вашему микроконтроллеру
C8051F410 обращаться к достаточному объему
памяти RAM (32 КБ), чтобы сохранить звуко-
вые данные. На понятийном уровне это такое
же приложение, как и то, с которым мы работа-
ли последний раз, используя встроенную память
RAM. Но на практике оно имеет три отличия:
♦ больший объем памяти RAM обеспечит вам
больше возможностей: вы сможете произне-
сти короткую речь или спеть отрывок песни,
а затем прослушать ее воспроизведение;
♦ внешняя RAM позволит вам познакомиться
с еще одним периферийным устройством по-
следовательного доступа (первым был циф-
ровой потенциометр с последовательным
интерфейсом SPI);
♦ впервые вам придется обращать внимание на
особые требования устройства по питанию:
память SPI RAM не может работать с пита-
нием напряжением 5 В, а должна питаться от
3,3 В.
Для микропроцессора C8051F410 питание на-
пряжением 3,3 В не представляет никаких про-
блем, и он будет с готовностью работать при
таком питании. Но при сборке схемы следует
быть внимательным, чтобы случайно не под-
ключить микроконтроллер C8051F410 или па-
мять RAM к питанию напряжением 5 В.
Подключаем микроконтроллер
С8051F410 и память RAM к питанию 3,3 В
Вам нужно отключить линию, которая до сих
пор подавала питание USB, получаемое из адап-
тера для программирования, на микроконтрол-
лер C8051F410. Эта линия теперь будет просто
висеть неподключенной, а вместо нее подклю-
чается линия питания напряжением 3,3 В, нахо-
дящаяся в левом нижнем углу кабеля, которая
и будет подавать питание на микроконтроллер
C8051F410 и память SPI RAM. Монтажная схе-
ма этой модификации показана на рис. 25L.9,
а принципиальная — на рис, 25L.10.
Подключаем микроконтроллер
C8051F410 к памяти SPI RAM
Для подключения микроконтроллера к памяти
RAM используются четыре линии шины SPI —
две линии данных (по одной для каждого направ-
ления), линия сигнала тактирования и линии
разрешения микросхемы. Сигнал прерывания
Линия подачи питания напряжением +5 В
с ЖКД платы отключается, чтобы обеспечить
подачу питания напряжением 3,3 В
Линия напряжением 3,3 В с пп
предоставляет напряжение питания для
микроконтроллера и SPI RAM
Рис. 25L.9. Вместо 5 В с кабеля платы ЖКД берется напряже-
ние 3,3 В для питания как микроконтроллера С8051F410, так
и памяти SPI RAM
(Частота fBbrf5 задается
сигналом от генератора
сигналов с TTL-
Рис. 25L.10. Подключаем микроконтроллер С8051F410 и па-
мять RAM к питанию 3,3 В. При этом в обязательном порядке
отключите питание 5 В, используемое до этого времени
подается на микроконтроллер от внешнего ге-
нератора сигналов (см. рис. 25L.10).
Резистор номиналом 1 кОм, подключенный
последовательно линии прерывания (сигнал на
которой задает частоту выборки), предназна-
чен для ограничения тока в случае превышения
входным сигналом напряжения питания 3,3 В5.
Обратите внимание, что назначения выводов
порта Р0, показанные на рис. 25L.11, отличают-
ся от предыдущих лабораторных занятий.
Выполните необходимые изменения. В особен-
ности не забудьте, что выходной сигнал ЦАП
на выводе Р0.1 является токовым (0-1 мА).
Поэтому для преобразования его в напряже-
ние данный вывод необходимо подключить на
5 Мы не думаем, что такое превышение на этом выво-
де порта с открытым стоком доставит микроконтролле-
ру какие-либо неприятности. На с. 151-152 справочного
листка для микроконтроллера указывается: входы и выхо-
ды порта Р0 могут выдерживать напряжение 5 В в рабочем
диапазоне напряжений ввода-вывода. Но мы предпочита-
ем перестраховаться.
1070
25L Лабораторное занятие: микроконтроллеры VI. Автономный микроконтроллер
«землю» через резистор номиналом 1,2 кОм,
как показано на рис. 25L.12.
+33V
h
■ i
6 6 4 3
РО
1 О
РОЗ
Рис. 25L.11. Сопряжение микроконтроллера с памятью RAM
реализуется посредством четырех линий шины SPI
410 Р0.1
Выходной
сигнал ЦАП
1,2 кОм
Рис. 25L.12. Чтобы преобразовать выходной токовый сиг-
нал ЦАП в напряжение, нужно подключить его выход через
резистор на «землю»
25L2.2, Пробуем работать
с памятью SPI RAM
Наблюдаем сигналы SPI
Некоторые из вас захотят сразу же начать ис-
пользовать память RAM для записи в нее зву-
ковых сигналов. Но если вам интересно пона-
блюдать сигналы шины SPI, это можно сделать
с помощью более простой программы, которая
записывает в RAM только один байт, а затем
считывает его. Эту программу, spi_single_byte.
а51, как всегда можно загрузить на веб-сайте
этой книги. Выполняет она эту операцию толь-
ко один раз, поэтому снимок экрана осцил-
лограммы нескольких сигналов (рис. 25L.13)
вполне объясним. В главе 25N мы уже узнали,
что следует ожидать: сначала идет команда, за
ней адрес, а затем байт данных.
Чтобы наблюдать протокол SPI в действии, за-
пуск развертки нужно выполнять по сигналу
CS* (отрицательный перепад) в нормальном
режиме (чтобы сохранить одну зафиксирован-
ную осциллограмму). При наличии четырех-
канального осциллографа можно наблюдать
все сигналы: CS*, MOSI и MISO. (Вспомним, что
последние два сигнала обмениваются между
микроконтроллером и SPI RAM и означают
«Выход ведущего, вход ведомого» и «Вход ве-
дущего, выход ведомого» соответственно.) На
рис. 25L.15 показана такая осциллограмма,
взятая с рис. 25N.4.
2 О
Рис. 25L13. Осциллограмма сигналов протокола SPI
25L2.3. Более интересная
программа, использующая 32 КБ
памяти
Более интересно, чем наблюдать сигналы про-
токола SPI, будет поэкспериментировать с за-
писью и воспроизведением звукового сигнала.
Как обычно, для этого нам потребуется хоро-
ший восстанавливающий фильтр, а именно
8-полюсный эллиптичный низкочастотный
фильтр на микросхеме МАХ294. В качестве
источника сигнала тактирования для этого
фильтра используйте выходной сигнал с TTL-
уровнями внешнего генератора сигналов. В гла-
ве 23N мы познакомились со схемой подключе-
ния этого фильтра, а также со схемой УНЧ для
усиления выходного сигнала ЦАП.
Сегодня мы впервые имеем достаточный объ-
ем памяти (32 КБ) для записи звука, так что
можно вытащить из прошлых проектов микро-
фонный усилитель, который мы собрали на ла-
бораторном занятии 7L. Выходной сигнал это-
го усилителя отцентрирован по напряжению
1,25 В, и его можно подавать напрямую на вход
АЦП микроконтроллера. (Рабочий диапазон
входных напряжений этого АЦП составляет
0-2,2 В, поэтому напряжение 1,25 В достаточ-
но близко к средней точке этого диапазона. Но
если вы перфекционист, то можете сдвинуть
напряжение покоя до 1,1 В, переместив смеще-
ние усилителя на неинвертирующем входе.)
Объем памяти величиной 32 КБ позволит вам
записать много секунд речи или пения: для
речи мужского голоса частота выборки величи-
ной 1 К выборок в секунду будет достаточной.
Но, конечно же, для такой низкой частоты вы-
борки требуется хороший восстанавливающий
фильтр (МАХ294). Для записи и воспроизве-
дения пения частота выборки должна быть не-
много выше.
25L2. Лабораторное занятие SiLabs6: память RAM с интерфейсом SPI
1071
Если у вас есть такая возможность, настройте
три генератора сигналов:
♦ Один будет служить в качестве источника те-
стового синусоидального сигнала, подавае-
мого на АЦП (мы ожидаем, что позже вы его
замените на свой микрофонный усилитель).
♦ Другой будет предоставлять сигнал с ТТЛ-
уровнями для тактирования выборки; этот
сигнал подается на вход INTO* микрокон-
троллера C8051F410. Последовательно реко-
мендуется подключить резистор номиналом
1 кОм, поскольку напряжение питания ми-
кроконтроллера C8051F410 составляет 3,3 В.
♦ А третий генератор сигналов будет служить
в качестве источника сигнала тактирования
(с ТТЛ-уровнями) для фильтра МАХ294.
Вспомним, что фильтр МАХ294 является
фильтром с коммутируемым конденсато-
ром, т. е. его частота отсечки^ Б составляет
/такт/100.
На рис. 25L.14 показана блок-схема подключе-
ния всего необходимого оборудования для за-
писи и воспроизведения звукового сигнала.
8051
МАХ 294 LM386
Генератор
сигналов
№1
'ВЫБ
f unc gen #2
unc gen #3
Рис. 25L.14. Три генератора в качестве источника входного
сигнала и сигналов тактирования выборки и фильтра
Несомненно, что лучше всего начать работу со
схемой, подавая в качестве входного сигнала
синусоидальный сигнал от генератора сигна-
лов. Но, мы надеемся, что, поэксперименти-
ровав с частотой выборки, чтобы определить,
настолько низкой она может быть, благодаря
хорошему восстанавливающему фильтру вы
возьмете входной сигнал от микрофонного уси-
лителя и начнете разговаривать со своим ком-
пьютером (или петь, если вы уверены в своих
способностях на этом поприще).
25L2.4. Завершаем программу
запоминающего осциллографа
Данная программа почти полностью готова.
Код для работы по протоколу SPI делает ее
слишком большой и сложной, и мы не желаем
задерживать вас изучением всех ее подробно-
стей. Вместо этого мы хотим, чтобы вы почув-
ствовали себя немного разработчиком данной
программы, и с этой целью приглашаем вас
создать подпрограмму, которая определяет со-
бытие полного заполнения таблицы.
В данном случае вам нужно занять всю доступ-
ную SPI RAM. Поскольку нам доступно 32 КБ
этой памяти, то ее диапазон адресов составляет
от 0 до 215 - 1 = 32 787. Следующим адресом за
пределами этого диапазона (вспомним наши
многочисленные примеры на компьютере из
дискретных компонентов, в которых верхняя
половина адресного пространства предназна-
чена для устройств ввода-вывода) является
шестнадцатеричное значение 8000h.
Для определения полного заполнения памяти
программа использует 16-разрядный счетчик.
Поскольку микроконтроллер 8051 оснащен
только одним таким регистром, которым явля-
ется регистр DPTR, мы задействуем этот регистр,
но нестандартным образом: не для указания
адресов, а просто для ведения счета. В листин-
ге 25L.1 приводится заготовка подпрограммы
CHECKJEND для проверки заполнения всей до-
ступной памяти, которую вам нужно реализо-
вать на языке ассемблера.
Листинг 25L.1. Заготовка подпрограммы
CHECK_END
CKECK_END: ; Сохраняем регистры, содержимое
; которых будет изменено подпрограммой
; Инкрементируем 16-разрядный счетчик
; Вышли за пределы RAM?
; Если нет, обрабатываем другой байт
; Если адрес 8000И, т. е. за пределами RAM,
; тогда устанавливаем флаговый бит, который
; проверяет главная программа
GO_AHEAD: ; Восстанавливаем сохраненные регистры
; Возвращаемся в основную программу
Подпрограмма CHECK_END вызывается после
каждой операции записи в память RAM и чте-
ния с нее. Одной из инициализаций, выполняе-
мых в программе, является обнуление регистра
DPTR перед началом записи в память и его по-
вторное обнуление перед началом чтения из
памяти.
Чтобы реализовать проверку значения реги-
стра DPTR, следует принять во внимание огра-
ничения доступных вам операций сравнения:
1072
25L Лабораторное занятие: микроконтроллеры VI. Автономный микроконтроллер
♦ микроконтроллер 8051 не оснащен командой
16-битового сравнения;
♦ доступная 8-битовая команда сравнения
CJNE наиболее универсальна при работе с
аккумулятором (или регистром А, как он еще
называется).
Флаговый бит, который дает главной програм-
ме знать, что память полностью заполнена, на-
зывается ALL_DONE. Он был определен в нача-
ле программы, поэтому код может обращаться
к этому биту по присвоенному ему названию
переменной. Таким образом, вам не нужно
смотреть, где находится данный бит. В этом,
конечно же, и состоит прелесть описательных
идентификаторов сигналов.
Созданную вами подпрограмму вставьте в код
программы spi_ram_adc_dac_incomplete.a51,
файл которой, как обычно, можно загрузить на
веб-сайте этой книги.
25L.3. Ссылки на листинги
программ
На веб-сайте книги можно загрузить следую-
щие программы:
Запись и чтение одного байта: spi_single_
byte.a51.
Заполнение и последующее чтение 32 КБ
памяти RAM: spi_ram_adc_dacjncomplete.a51.
Две версии программы измерения длительно-
сти импульса:
pulse_measure_decimaLstandalone_505.a51;
pulse_measure_capture_standalone_505.a51.
Программа для работы с памятью SPI RAM:
spLram_adc_dac_incomplete.a51.
26N. Потенциальные проекты.
Игрушки на любой вкус
Содержание
26N.1. Еще один микроконтроллер, который может быть вам интересен 1074
26N.1.1. Конфигурирование микросхемы PSOC - 1075
26N.2. Проекты: приглашение и предостережение 1076
26N.3. Несколько примеров впечатляющих проектов 1077
26N.3.1. Символьный лазерный дисплей 1077
26N.3.2. Определитель источника звука 1078
26N.3.3. Волшебный экран, управляемый компьютером 1079
26N.3.4. Гигантский волшебный экран 1079
26N.3.5. Попытка создать насекомое 1080
26N.4. Несколько других выдающихся проектов 1080
26N.4.1. Координатные осциллографические дисплеи 1080
26N.4.2. Усложнения и улучшения 1081
26N.4.3. Управление размером и масштабирование 1082
26N.4.4. Настоящее векторное рисование 1085
26N.4.5. Анимация 1085
26N.4.6. Вычисляемая графика 1085
26N.4.7. Лазерный координатный дисплей 1086
26N.4.8. Простой до очарования светодиодный дисплей 1086
26N.4.9. Мобильные платформы 1087
26N.4.10. Интересное применение для шасси, управляемого независимыми
приводами 1088
26N.4.11. Игрушечный автомобиль, управляемый компьютером 1089
26N.4.12. Вечная проблема обратного маятника 1090
26N.5. Игры 1093
26N.5.1. Пакман на экране осциллографа 1093
26N.5.2. Астероиды на экране осциллографа 1093
26N.5.3. Другие великолепные игры 1094
26N.6. Датчики, приводы, другие приспособления 1094
26N.6.1. Поставщики датчиков, приводов и прочих устройств 1094
26N.6.2. Поставщики небольших механических деталей 1095
26N.6.3. Механические детали: электродвигатели 1095
26N.6.4. Сервоприводы 1096
26N.6.5. Мускульные провода Nitinol 1096
26N.6.6. Датчики 1097
26N.6.7. Дисплеи 1100
26N.6.8. Устройства сопряжения 1100
26N.7. Драйвер шагового двигателя 1101
26N.8. Идеи для проектов 1103
26N.8.1 Оригинальные новые и неиспытанные идеи для вашего вдохновения 1103
26N.9. Две потенциально полезные программы: драйвер ЖКД
и сканер цифровой клавиатуры 1104
26N.10. Множество других примеров в книге АоЕ 1104
26N.11. А теперь вперед, к новым приключениям 1105
1074
26N. Потенциальные проекты. Игрушки на любой вкус
26N.1. Еще один
микроконтроллер, который
может быть вам интересен
У нас не было времени поработать с микросхе-
мами PSOC1, но, возможно, в дальнейшем вы
захотите испробовать их. Они содержат в одной
микросхеме микроконтроллер (8051 в пока-
занном далее примере) с аналоговыми устрой-
ствами, которые можно конфигурировать про-
граммно. Эти микросхемы производства ком-
пании Cypress Semiconductor предоставляют
возможность запрограммировать аналоговые
компоненты, которую мы привыкли видеть в
устройствах ПМЛ.
Далее приводится несколько страниц из спра-
вочного листка одной из таких микросхем
CYPRESS
PSOC, в которых описывается совмещение
в одной микросхеме довольно стандартно-
го микроконтроллера, пары операционных
усилителей, а также нескольких компарато-
ров. (Последнее решение не совсем новое, по-
скольку микроконтроллер C8051F410 компа-
нии Silicon Laboratories содержит встроенный
компаратор.) Но новшество состоит не только
в самой интеграции операционного усилителя
в микросхему микроконтроллера; само по себе
это вряд ли было бы большим достижением.
Настоящее новшество состоит в том, что кон-
фигурация схемы операционного усилителя яв-
ляется в некоторой степени программируемой:
для операционного усилителя можно задавать
разные коэффициенты усиления, или настро-
ить его как преобразователь «ток — напряже-
ние» (трансимпедансный каскад), или даже,
как схему выборки и хранения.
PSoC4" 3: CY8C38 Family
Data Sheet
1. Architectural Overview
Introducing the CY8C38 family of ultra low-power, flash Programmable System-on-Chip (PSoC*) devices, part of a scalable 8-bit
PSoC 3 and 32-bit PSoC 5 platform. The CY8C38 family provides coofigurabte Modes of analog, digital, and intecconnect circuitry
around a CPU subsystem. The combination of a CPU with a flexible analog subsystem, digital subsystem, touting» and I/O enables
a high level of integration in a wide variety of consumer, industrial, and medical applications.
Figure 1*1. Simplffitd Block Diagram
Обычные
компоненты
Особые
компоненты
Рис. 26N.1. Логическая блок-схема микросхемы PSOC: микроконтроллер 8051 и стандартные цифровые устройства и преоб-
разователи, а также операционные усилители. (Воспроизведение с разрешения компании Cypress Semiconductor Corporation.)
1 Англ. Programmable System On Chip - программируемая Мы надеемся, ЧТО ЭТО ТОЛЬКО начало более ШИ-
система на кристалле (чипе). - Примеч. пер. рокого набора программируемых аналоговых
26N.1. Еще один микроконтроллер, который может быть вам интересен
1075
функций. Такие устройства уже пользуются ком-
мерческим успехом.
Аналоговые компоненты показаны более под-
робно в блок-схеме на рис. 26N.2.
Блоки переключаемых конденсаторов SC/CT2
реализуют эффективный эквивалент резисто-
2 Похоже, что обозначение СТ (непрерывное время) рас-
сматривается как эквивалент, а не противоположность.
ров в аналоговых элементах. Их можно исполь-
зовать, чтобы, например, задавать коэффици-
ент усиления операционных усилителей, как
показано на рис. 26N.3.
26N.1.1. Конфигурирование
микросхемы PSOC
На рис. 26N.3 приводится отрывок из справоч-
ного листка микросхемы PSOC, объясняющий,
CYPRESS
PSoC® 3: CY8C38 Family
Data Sheet
Port
Блок-схема аналоговой подсистемы
Reference
phub
«*—|»
CPU
1 I I
081
Ctocfc
Dsstrsfoutson
Deeim&tcc
GPIO Port — Порт ввода-вывода общего
назначения
Analog routing — Аналоговая
маршрутизация
Op Amp — Операционный усилитель
Del Sig ADC — ЦATT типа дельта-сигма
Precision Reference — Точно опорное
напряжение
SC/CT Block — Блок SC/CT (переключаемых конденсаторов и непрерывного времени)
Comparators — Компараторы
CapSense Subsystem — Подсистема CapSense (емкостного датчика)
Analog Interface — Аналоговый интерфейс
Config A Status Registers — Конфигурационные регистры и регистры состояния
DSI array — Массив DSI (цифровая интерполяция речи)
Clock distribution — Распределение сигнала тактирования
Decimator — Прореживатель
PHUB — Периферийный хаб
CPU - ЦП
Рис. 26N.2. Подробная блок-схема аналоговой части микросхемы PSOC (Воспроизведение с разрешения компании Cypress
Semiconductor Corporation.)
1076
26N. Потенциальные проекты. Игрушки на любой вкус
: CY8C56LP Family
Datasheet
flHOli
$.6$ PGA
w$m Ы m Ism m ИнЛ mmm» Iht fcMN**t far «tub 91*1
юоь
20
40
60
250
1006
1
24
4$ ^
50
«JOMKZ j
220 km
1 iis Ш
Fi^yf© 8^9. PGA Resi*tOf Settings
V<*i$
Рис. 26N.3. Коэффициенты усиления для выбранных схем операционных усилителей микросхемы PSOC задаются с помощью
цифровых кодов. (Воспроизведение с разрешения компании Cypress Semiconductor Corporation.)
как задать коэффициент усиления для схемы
операционных усилителей. Допустимы только
конкретные указанные значения.
26N.2. Проекты:
приглашение
и предостережение
В нашей собственной версии этого курса толь-
ко небольшая часть студентов выбирает воз-
можность заниматься проектами. Но работа
над проектом может доставить много удоволь-
ствия. Чтобы помочь вам придумать идею для
проекта, далее приводится некоторая информа-
ция по устройствам и идеи, которые могут об-
легчить эту нелегкую задачу. С этой же целью
даются наброски некоторых замечательных
проектов, разработанных студентами наших
прошлых курсов.
Общий совет
♦ Расскажите о проекте кому-либо более опыт-
ному и дайте возможность оценить ваши
идеи на ранней стадии процесса разработки.
Такой человек может отговорить от гранди-
озного проекта, который невозможно реали-
зовать. Иногда он может дать вам знать, что
ваше изобретение слишком скромное, чтобы
его можно было назвать проектом.
♦ Задуманный вами проект должен соответ-
ствовать параметрам вашего скромного
самодельного компьютера, а не требовать
возможностей полномасштабного компью-
тера. Это означает, среди прочего, не очень
разгоняться с программной частью. Можно
ограничиться, например, вращением элек-
тродвигателя, а не выполнением вычислений
и отображением результата.
♦ Постарайтесь сопровождать программное
обеспечение своего проекта аппаратными
26N3. Несколько примеров впечатляющих проектов
1077
приставками. Этот пункт является частично
следствием предыдущего, но также отобра-
жает другую цель: проект часто помогает вам
закрепить свое понимание идей, предостав-
ляя возможность выполнять определенное
конструирование. Такое конструирование
может служить своего рода оценочной ста-
дией вашего проекта. Подобная расширен-
ная оценка лучше, чем простое упражнение
в программировании.
♦ Подходите к реализации своего проекта по-
следовательно, а не на основе «все или ниче-
го». Например, студенты, которые собрали
проект автомобиля, управляемого по радио
от компьютера (см. раздел 26N.4.11), снача-
ла предложили игру, в которой управляемый
компьютером автомобиль догонял бы авто-
мобиль, управляемый человеком. Мы убеди-
ли их применить поэтапный подход к реали-
зации своего проекта:
• прежде всего проверить, сможет ли ком-
пьютер управлять автомобилем (может с
большой легкостью);
• затем проверить, смогут ли ультразвуко-
вые датчики извлечь достаточную инфор-
мацию из значений задержки между уль-
тразвуковыми сигналами автомобиля и их
приемом тремя ультразвуковыми датчика-
ми компьютера;
• наконец, создать сопряжение между своим
самодельным компьютером и ПК.
♦ Такая, в общем, идея. В действительности
эти студенты смогли заставить работать
большую часть своей исходной задумки. Но
решение задач почти всегда занимает больше
времени, чем изначально ожидается, и мы
хотим, чтобы вы почувствовали удовлетво-
рение от завершения скромного проекта, чем
получили разочарование от начатого и неза-
вершенного грандиозного проекта.
26N.3. Несколько примеров
впечатляющих проектов
Далее в этой главе, начиная с раздела 26N.4,
мы рассмотрим некоторые замечательные
проекты, реализованные студентами нашего
курса. Начиная с раздела 26N.6, мы приводим
список поставщиков оборудования любитель-
ской электроники и роботехники, а затем рас-
сматриваем некоторые из предоставляемых
ими устройств. В этом же разделе, с целью воз-
будить ваши амбиции, мы предлагаем вашему
вниманию краткий обзор некоторых интерес-
ных устройств, созданных теми немногими
студентами наших прошлых курсов, которые
смогли найти время для этих проектов.
26N.3.1. Символьный лазерный
дисплей
Автор этого проекта упорно продолжал рабо-
тать над ним, несмотря на наш совет попробо-
вать что-то менее амбициозное. Его исходная
идея выглядела слишком сложной: вращая на-
бор зеркал с разными углами наклона и вклю-
чая и выключая лазер в нужные моменты вре-
мени, отображать на экране символы.
Мы онемели от изумления, когда он принес го-
товый проект. Мы также испытывали чувство
беспокойства за это великолепное устройство,
заметив, что оно было собрано с помощью пла-
стилина. Даже подстройка направления луча
лазера достигалась, подминая комочек пласти-
лина туда или сюда.
На рис. 26N.4 показан этот набор зеркал, каж-
дое из которых снабжено палочкой для указа-
ния положения.
Палочка для указания
положения отдельного
зеркала /
" f Л - -Л'" \
Палочка для указания одного
оборота сборки зеркал
Рис. 26N.4. Механизм вращающихся зеркал лазерного дис-
плея
Еще одна общая палочка служит для указания
полного оборота. Эти палочки прерывают луч
света в двух оптических прерывателях, состоя-
ние которых считывается микроконтроллером.
1078
26N. Потенциальные проекты. Игрушки на любой вкус
Винты, расположенные вверху и внизу зеркал,
позволяют регулировать угол наклона каждого
зеркала. Еще более тонкую настройку можно
было осуществлять программно, чтобы компен-
сировать небольшие погрешности в боковом
расположении каждого зеркала. На рис. 26N.5
показано это устройство в действии.
- Лазер
Рис. 26N.5. Проекция текста на лист бумаги с помощью ла-
зера и вращающегося набора зеркал (на фотографии текст
неразборчивый)
На фотографии текст виден плохо, но вживую он
был полностью разборчивым. Отображаемый
таким образом текст содержал длинное сооб-
щение, начинающееся с названия курса и закан-
чивающееся фамилией автора, г-на Ушинского
(Uscinski). За такое устройство он заслужил ме-
сто в нашей памяти!
26N.3.2. Определитель источника
звука
Данный проект был реализован на компьюте-
ре из дискретных компонентов, а не на авто-
номном микроконтроллере, как другие проек-
ты. Собран он был с удивительной скоростью:
всего за полдня. Он выжил в сборе частично
по той причине, что его разработчики, Сиань
Клайдинст (Sian Kleindienst) и Кристофер Гаук-
шейм (Kristoffer Gauksheim), потрудились, со-
брав его на большом куске пенопласта.
Он определяет азимут громкого звука (обычно
хлопка в ладоши). В компьютер вводятся три
двоичных сигнала, поступающие с микрофон-
ных усилителей и компараторов. Микрофоны
расположены на расстоянии нескольких сан-
тиметров друг от друга. Компьютер определя-
ет приблизительное направление на источник
звука, просто анализируя порядок срабаты-
вания компараторов. Он выдает более точ-
ное направление в секторе круга с углом в 60°.
Студенты-разработчики решили, что пора
было заканчивать с этим проектом и начи-
нать готовиться к экзаменам. Схема, выдаю-
щая более точное направление, осуществляет
это, определяя задержку между сигналами трех
микрофонов.
На рис. 26N.6 показана организация этого
проекта: три макетные платы с микрофонны-
ми усилителями и плата большого компьюте-
ра, на дисплее которого отображено значение
320, означающее азимут последнего хлопка
в ладоши.
Показания ^
азимута
(320 градусов)
Рис. 26N.6. Внешний вид устройства определения источника звука
26N.3. Несколько примеров впечатляющих проектов
1079
■щ
члт
Рис. 26N.7. Осциллограф, подключенный к схеме определения источника звука, показывает осциллограммы выходных сиг-
налов схем микрофонов-компараторов
На рис. 26N.7 показан экран осциллографа, со-
держащий осциллограммы смещенного прихо-
да сигналов от трех микрофонов, по которым
было получено данное значение азимута после
хлопка в ладоши.
26N.3.3. Волшебный экран,
управляемый компьютером
Данный проект реализует менее оригиналь-
ную идею, чем два предыдущих: два шаговых
двигателя, управляемые от компьютера, враща-
ют ручки детской игры, называющейся волшеб-
ным экраном3. Реализация механической части
проекта была сложной задачей, поскольку оси,
на которые насажены ручки игрушки, вращают-
ся довольно туго и с небольшим биением. Тем
не менее приспособление позволило с трудом
начертить на экране текст «Р123» Возможно,
что это не выглядит особым достижением. Но,
будучи свидетелями предшествующих усилий
разработчиков по программной реализации
драйвера шаговых двигателей, включая тон-
кую настройку полушага, мы были полностью
впечатлены, когда увидели появление номера
нашего курса на экране (к сожалению, не пока-
занного на рис. 26N.8).
Рис. 26N.8. Волшебный экран, приводимый в действие ша-
говыми двигателями
26N3A Гигантский волшебный
экран
Несколько похожее на предыдущее устрой-
ство для рисования было создано на основе
массивного координатного стола, который мы
отыскали на мусорной свалке. Это устройство
обладает фантастическим разрешением, но в
данном проекте оно было применено для на-
писания короткого сообщения в стиле преды-
дущего проекта волшебного экрана.
Один из последующих студентов добавил к
нему соленоид, позволяющий поднимать сти-
лус. Было бы хорошо, приспособить этот за-
мечательный координатный стол для разводки
https://ru.wikipedia.org/wiki/BoAme6Hbiii__3KpaH.
1080
26N. Потенциальные проекты. Игрушки на любой вкус
дорожек печатных плат. Но программная часть
такого проекта оказалась бы чрезмерно слож-
ной для наших студентов.
Рис. 26N.9. Большой координатный стол, приводимый в
действие шаговыми двигателями наподобие проекта вол-
шебного экрана
26N.3.5. Попытка создать насекомое
Не все проекты были успешными, что не долж-
но быть удивительным. Но нас вполне удовлет-
воряют даже неудавшиеся проекты, если неуда-
че предшествовали интеллектуальные усилия.
На рис. 26N.10 показан один из таких неосу-
ществленных проектов: добротно исполненное
шестиногое насекомое.
на землю. В своем текущем виде создание, изо-
браженное на рис. 26N.10, не могло идти, а
было способно только поднимать и опускать
свое тело, как будто бы оно било поклоны. Но
оно не могло передвигаться ни вперед, ни на-
зад. Разработчики насекомого компании Radio
Shack, показанного на рис. 26N.11, понимали,
что создание должно быть способным под-
нимать некоторые из своих ног при их посту-
пательном движении, а затем опускать их при
движении назад.
Установка средней ноги на эксцентрике позволяет
ей подниматься и опускаться, в результате чего
при ее движении поднимаются передние и задние ноги.
Рис. 26N.11. Ноги насекомого с более продвинутой эволю-
цией могут подниматься и отрываться от земли при посту-
пательном движении
Средняя нога насекомого установлена на экс-
центрике, который периодически отрывает
переднюю и заднюю ноги от земли. Когда ноги
подняты над землей, они двигаются вперед, а
когда они начинают двигаться относительно
тела насекомого назад, то снова опускаются на
землю, в результате чего насекомое передви-
гается вперед. Но даже если устройство, изо-
браженное на рис. 26N.10, и не было успешным
проектом, смотрится оно красиво и собрано хо-
рошо. Мы не сомневаемся, что в следующий раз
оно обзаведется коленями.
Рис. 26N.10. Насекомое с шестью ногами, приводимыми в
действие сервомашинками, нуждается в доработке
Каждая нога насекомого приводится в действие
сервомашинкой (угловое положение вала ко-
торой определяется длительностью управляю-
щего импульса). Плоская батарея напряжением
6 В для питания насекомого закреплена на его
брюшке. Установленный на плате стабилизатор
понижает его до 5 В.
Когда разработчики попытались заставить свое
устройство идти, они обнаружили, что ему тре-
буются колени, или какая-либо другая схема,
позволяющая ноге подниматься и опускаться
26N.4. Несколько других
выдающихся проектов
Большинство выдающихся проектов, которые
мы видели, выглядят не слишком изящно, по-
этому далее мы полагаемся больше на их опи-
сание, чем на фотографии.
26N.4.1. Координатные
осциллографические дисплеи
Это самый быстрый и легкий способ рисо-
вать изображения на экране осциллографа.
В описываемых здесь проектах использовались
26Л/.4. Несколько других выдающихся проектов
1081
аналоговые осциллографы с электронно-лу-
чевой трубкой, а не цифровые осциллографы
с ЖКД экранами.
Используя ЭЛТ, можно применить замедляю-
щую RC-цепочку (по сути, низкочастотный
фильтр), чтобы соединить точки, выдаваемые
программой. В результате получим векторный
дисплей, хорошо подходящий для рисования
линий, включая диагонали. А обычный дис-
плей растрового сканирования (наподобие
телевизионного) рисует линии с трудом в виде
последовательности точек, и, между прочим,
эти линии выглядят ужасно, когда их крутизна
стремится к вертикальной или горизонтальной
(эффект, называемый ступенчатостью).
Необходимое оборудование
Вам нужно будет оснастить свой самодельный
компьютер дополнительным ЦАП (или двумя,
если вы решите реализовать аппаратное мас-
штабирование, как рассматривается в разде-
ле 26N.43). Дополнительные мелочи, предлагае-
мые в последующих подразделах, требуют еще
больше необходимого оборудования. Но основ-
ная работа заключается в программировании и
создании таблиц данных, которые программа
посылает на осциллограф. Но все ваши труды
вознаграждаются, когда вы сможете отобразить
на экране осциллографа все, что пожелаете.
Два типа ЦАП
В нашей лаборатории мы используем два типа
ЦАП:
Совместимый с микроконтроллером с
однополярным питанием. Это микросхема
AD7569 (АЦП, ЦАП в одном корпусе), а микро-
схема AD558 8-битового ЦАП. Последнюю мы
использовали на лабораторном занятии 17L,
где она обеспечивала обратную связь для АЦП
последовательных приближений. Избегайте
ЦАП на микросхеме AD558 в любом приложе-
нии, в котором ввод осуществляется напрямую
из шины данных, из-за его неприемлемо дли-
тельного времени установки.
Перемножающий ЦАП (ПЦАП). Выходной
сигнал этого ЦАП является произведением
его цифрового входного сигнала и аналого-
вого входного тока. Мы пользуемся этой ха-
рактеристикой для реализации возможности
масштабирования, рассматриваемой более по-
дробно в разделе 26N.4.3.
Если вам по душе аппаратный подход, то нужно
с самого начала решить, будете ли вы реализо-
вывать возможность масштабирования, чтобы
выбрать соответствующий ЦАП.
Массив точек 16x16
Для массива точек размерностью 16x16 доста-
точно двух 4-битовых ЦАП. Эти ЦАП удобны
тем, что сигнал на них можно подавать с одного
8-битового порта, также доступен их внутрен-
ний регистр. На рис. 26N.12 показана самая
простая схема, которая не требует отключения
линий от используемого ЦАП-АЦП.
-<ЭХ
/
л (
oufa
/4
i
8
Г"
АР
-iv -© Y
Рис. 26N.12. Карта экрана осциллографа для простого коор-
динатного дисплея
Если вас не беспокоит погрешность величиной
приблизительно в 1 младший бит, то эта схема
будет достаточно хороша.
Замечание
Значение координаты /изменяет четыре младшие
бита, подаваемые на ЦАП координаты X. Обратите
внимание на то, что эти четыре бита подаются на
четыре старших разряда ЦАП координаты Y.
Эта программа должна извлекать по одному
байту из последовательных ячеек в таблице
значений координатного дисплея и выводить
их на дисплей. Включив в программу вызов
подпрограммы задержки, вы сможете коррек-
тировать скорость рисования.
26N.4.2. Усложнения и улучшения
Соединяем точки
Как вас научили в детском садике, соединив
точки, можно получить понятную картинку.
1082
26N. Потенциальные проекты. Игрушки на любой вкус
Поэтому, приложив сравнительно неболь-
шое усилие по программированию (поскольку
ваша таблица не содержит много координат),
вы сможете рисовать рисунки с прямыми ли-
ниями. Чтобы соединить точки, выходной
сигнал каждого ЦАП нужно пропустить через
низкочастотный фильтр. Попробуйте для на-
чала взять фильтр с постоянной времени ве-
личиной в несколько микросекунд (например,
R = 2,3 кОм, С = 0,01 мкФ). Но нужно будет по-
экспериментировать со значениями резисто-
ра и конденсатора; визуальный эффект будет
разным для различной частоты обновления
рисунка и для разных постоянных времени
RC-фильтра. Конечно же, фильтр замедляет из-
менение выходных напряжений, поэтому пере-
мещение луча осциллографа становится види-
мым. Обратите внимание на то, что новая схема
требует учитывать последовательность вывода
программой этих точек.
Массив точек 256x256
Можно, конечно же, использовать два вы-
ходных порта и подавать все восемь битов на
каждый ЦАП. Но при этом необходимо поза-
ботиться о том, чтобы новая информация по-
ступала на оба ЦАП одновременно. Для этого
следует использовать 8-битовый регистр из
D-триггеров. В данном случае может быть легче
подключить ЦАП AD558, на который подается
выход регистра D-триггеров, чем ЦАП AD7569.
Разбираться с подробностями этого оборудова-
ния мы предоставим вам самим. (Используйте
Шина
данных
Рис. 26N.13. Аппаратное обеспечение координатного дис-
плея размерностью 256x256 точек. Для одновременных об-
новлений используется регистр триггеров
микросхему 74НСТ574 восьмибитового реги-
стра D-триггеров и поддерживайте его трех-
стабильные буферы постоянно включенными.)
Чтобы получить из ЦАП AD558 такое же напря-
жение полной шкалы, как и предоставляемое
ЦАП AD7569 (0-2,55 В), нужно откорректиро-
вать его коэффициент усиления. (Подробности
см. в материалах лабораторного занятия 18L
и в справочном листке по ЦАП AD558.)
Если ввести в программу большое количество
точек, то экран начнет мерцать, даже если про-
грамма не содержит подпрограмму задержки.
Чтобы избежать раздражающего мерцания
экрана, он должен обновляться приблизитель-
но 30 раз в секунду. Приемлемое количество
точек можно рассчитать, или просто работать
с большой таблицей и смотреть, насколько за-
метное мерцание создается.
26NA3. Управление размером
и масштабирование
Как уже упоминалось, масштабирование мож-
но реализовать программно. Но если вы хоти-
те облегчить себе задачу программирования
и реализовать возможность сохранения сим-
метричности изображения при изменении его
размеров, то рассмотрите возможность приме-
нения аппаратного масштабирования, рассма-
триваемую чуть далее.
Вспомним, что масштабирование представля-
ет собой операцию, которая может восполь-
зоваться возможностями умножения, кото-
рыми обладают некоторые устройства ЦАП.
Наиболее прямолинейный подход — исполь-
зовать микросхему двойного перемножающего
ЦАП, как рассматривается в следующем раз-
деле. В альтернативном подходе задействова-
ны три ЦАП: один из которых масштабирует
выходные сигналы двух других ЦАП (которые
определяют значения X и Y).
Масштабирование с помощью двойного
ПЦАП
Микросхема DAC8229 компании Analog Devi-
ces представляет собой устройство с потенци-
альным выходным сигналом, вход опорного на-
пряжения которого осуществляет масштабиро-
вание. Данная микросхема хорошо подходит
для масштабирования значений координат Х- Y,
26NA. Несколько других выдающихся проектов
1083
поскольку содержит два ЦАП в одном корпусе.
Выходные сигналы X и Y представляют собой
произведение данного опорного напряжения и
8-битового входного цифрового сигнала. Для
микросхемы требуется двуполярное питание,
поскольку для положительного входного опор-
ного напряжения она выдает отрицательный
выходной сигнал.
Микросхема LTC7545A похожа на предыду-
щую — двойной ПЦАП с однополярным пи-
танием, но требует двуполярного источника
питания для обеспечения входного опорного
сигнала, поскольку, опять же, для положитель-
ного опорного входного сигнала она выдает от-
рицательный выходной сигнал. Это 12-битовое
устройство, но его можно использовать как
8-битовое, подавая входные данные только на
восемь самых старших битов.
Масштабирование с помощью трех ЦАП
На рис. 26N.14 изображена подробная схема
для масштабирования на основе трех ЦАП,
в данном случае МС14084. Между прочим, если
вы решите модифицировать эту схему, учтите
то обстоятельство, что ток опорного сигнала
протекает по направлению к суммирующему
соединению внутреннего операционного уси-
лителя. Поэтому при желании вместо опорно-
го тока можно использовать опорное напряже-
ние. В таком случае сигнал на вывод 14 ЦАП
МС1408 подается через соответствующий по-
следовательный резистор (например, 7,5 кОм
от линии с напряжением +15 В).
В схеме на рис. 26N.14 постоянный опорный
ток подается только в самый верхний из трех
ЦАП — ЦАП, определяющий размер изобра-
жения. На два других ЦАП подается не посто-
янный опорный ток, а выходной ток ЦАП раз-
мера (пропущенный через сдвоенное токовое
зеркало). Таким образом, компьютер может с
помощью ЦАП размера масштабировать вы-
ходные сигналы ЦАП X и У. При номинале
резистора масштабирования RUACU19 например,
7,5 кОм максимальный выходной ток ЦАП X и
Убудет составлять 2 мА.
Токовое зеркало (схема, работу которой мы
предпочитали не рассматривать в этой книге)
+1$
Рис. 26N.14. Перемножающий ЦАП может масштабировать координатное изображение
4 Возможно, что вам больше понравится работать с бо-
лее современным перемножающим ЦАП с однополярным
питанием, например AD7524. В таком случае вам нужно
будет должным образом переделать схему на рис. 26N.14,
в которой предполагается ЦАП МС1408.
выдает ток масштабирования ЦАП, получае-
мый из шины положительного питания, что-
бы поставлять ток на два входа опорного тока
ЦАПХиУ.
1084
26N. Потенциальные проекты. Игрушки на любой вкус
На рис. 26N.15 показано на удивление изыскан-
ное изображение, прорисованное с использо-
ванием описанного устройства. Пирамида вы-
глядит, как будто бы на нее были искусно нало-
жены тени, постепенно переходящие из одного
оттенка в другой. В действительности же это
изображение представляет собой всего лишь
уменьшающийся квадрат. Квадрат был нарисо-
ван как обычно, определив четыре точки, а за-
тем соединив их и замедлив выходной сигнал
каждого ЦАП с помощью RC-цепи.
Рис. 26N.15. Уменьшающийся квадрат, нарисованный коор-
динатными ЦАП с масштабируемыми выходными сигналами
От ЦАП
размера
\S _____
1408
САС
у —
1408
к нулевой, когда точка приближается к своему
конечному положению), осциллограмма стано-
вится все более яркой.
Расположение масштабируемого
изображения по центру экрана
Далее предлагается улучшение схемы, состоя-
щее в придании ей возможности располагать
изображение по центру экрана ЭЛТ, независи-
мо от его размера. Без такой переделки изме-
нение размера изображения также перемеща-
ет его: поскольку значения X и Y всегда отри-
цательные, визуальный эффект будет таким,
как будто бы увеличивающееся изображение,
кроме приближения к наблюдателю, также
движется по направлению к левому нижнему
углу экрана. Для того чтобы увеличивающие-
ся изображения приближались без смещения,
схему нужно модифицировать, добавив опе-
рационный усилитель на выходы ЦАП X и Y.
Операционные усилители позволять поддер-
живать выходные сигналы координат по цен-
тру экрана (в точке 0 В).
-'вы:
:ху
Рис. 26N.16. Обработка выходного сигнала ЦАП операционным усилителем позволяет всегда удерживать его в точке 0 В
Эффект, который на рис. 26N.15 выглядит как
затенение, создается в результате постепенного
замедления луча ЭЛТ, по мере того, как он пере-
мещается из исходного положения в конечное.
Поскольку перемещение точки замедляется
экспоненциально (со скоростью, стремящейся
В схеме, изображенной на рис. 26N.16, поло-
вина входного тока ЦАП подается на выход
суммирующего соединения5 операционного
5 Резисторы номиналом 1 кОм включены в схему для
того, чтобы ток разделялся между двумя ЦАП поровну
26N.4. Несколько других выдающихся проектов
1085
усилителя, в результате чего этот ток вычита-
ется из выходного сигнала, удерживая это на-
пряжение по центру при варьировании тока
масштабирования6.
26N.4A Настоящее векторное
рисование
В таблице рисунка не обязательно хранить абсо-
лютные позиции на экране. Вместо этого в ней
можно сохранять векторы: направления и дли-
ну относительно текущей позиции на экране7.
Показанные на рис. 26N.16 относительные век-
торы обозначены наподобие направлений ком-
паса. Например, ВЮВ = Восток-Юг-Восток.
5,ВЮВ
г, юз
5,303
Рис. 26N.17. Рисование векторами: относительное переме-
щение
Этот подход будет работать с 4-битовым
определением направления (16 направлений).
Остальные четыре бита можно использовать
для определения величины вектора и растяги-
вать вектор единичной длины командой умно-
жения (единичная длина может быть прибли-
зительной).
Этот способ определения фигуры позволяет
вращать ее без особых трудностей. Несколько
примеров вращения показаны в разделе 26N.4.6.
Но программирование векторного рисования
намного сложнее, чем рисование абсолютных
координатных фигур.
26N .4.5. Анимация
Если сохранить в памяти координаты двух
или больше похожих, но слегка отличающих-
ся изображений, а затем прорисовать эти изо-
бражения на экране быстро друг за другом
(меняя изображения, скажем, каждую десятую
долю секунды), то мы получим анимированное
даже при разных значениях напряжения смещения Ucu,
при которых напряжения на суммирующих соединениях
были бы слегка разными.
6 Благодарим Д. Дурлах (D. Durlach) за это удачное до-
полнение.
7 Наши благодарности Скотту Ли (Scott Lee) за его пред-
ложение и демонстрацию этого подхода.
изображение. Очевидно, что для анимации
даже простой фигуры, потребуется большой
объем данных, поэтому начинайте с задачи
поскромнее. Для того чтобы минимизировать
количество точек для одного изображения,
рекомендуется метод соединения точек. На
рис. 26N.18 показан грубый пример анимации:
нарисованный вручную эскиз существа с дву-
мя положениями ног (слева) и изображение на
экране осциллографа его реализации (справа),
которое было чуть более амбициозным.
Рис 26N.18. Анимация с помощью векторной графики:
эскиз {а) и его реализация (б)
Похоже, что на экране существо превратилось
из лошади в терьера, а процесс реализации по-
зволил собаке качать головой вверх-вниз и ви-
лять хвостом.
26N.4.6. Вычисляемая графика
Утомительная загрузка значений в память, не-
обходимая в рассмотренных схемах чтения та-
блицы, наверное, вызвала у вас страстное жела-
ние передать компьютеру задачу определения,
какие точки рисовать. Конечно же, это можно
сделать. Можно создать программу, которая
1086
26N. Потенциальные проекты. Игрушки на любой вкус
будет рисовать прямоугольник, инкрементируя
регистр X в течение нескольких шагов, не ме-
няя при этом значения У, а затем инкременти-
руя регистр У, не меняя при этом значения X,
затем декрементируя регистр X, и т. д.
Два довольно опытных программиста исполь-
зовали координатное оборудование, чтобы
рисовать кубики, которые они затем могли
вращать вокруг любой из трех осей8. Мно-
гочисленные кубики на рис. 26N.19 в дей-
ствительности являются многократным экспо-
нированием вращающегося кубика. Реализа-
ция такого эффекта требует весьма высокого
уровня мастерства программирования, а так-
же слишком объемного кода, чтобы быть под
силу простым смертным.
Phc.26N.19. Вычисляемая графика: два варианта кубика, ко-
торый можно вращать вокруг его осей
8 Впервые этот эффект реализовал Грант Шюмейкер
(Grant Shumaker) в 1986 г., и сделал он это полностью на
языке ассемблера, причем программа была набрана вруч-
ную. Этот подвиг можно грубо сравнить с восхождением
на один из средней высоты гималайских пиков без кисло-
родных баллонов. Давид Джингоулд (David Gingold) по-
вторил этот подвиг, поместив фигуры внутри кубов. Но
Давид использовал «кислородный баллон» в виде компи-
лятора С, как отмечается в рассмотрении его выдающейся
астероидной игры в разделе 26N.5.2.
26NA7. Лазерный координатный
дисплей
Зеркало, которое можно наклонять по лю-
бой из его ортогональных осей, способно
управлять лазерным лучом, чтобы проеци-
ровать изображение на экран (или потолок).
Первые два студента, которые попытались ре-
ализовать эту затею, создали замечательную
конструкцию из двух автомобильных дина-
миков, как показано на рис. 26N.20.
Показанный на рис. 26N.20 массивный меха-
низм работал, но только отчасти. Зеркало на-
клонялось в ответ на сигналы от двух ЦАП, в
результате чего проецируемый лазерный луч
можно было направить под программным
управлением в требуемую точку на потолке. Но
как средство рисования графики это было пе-
чальное зрелище. Механизм был очень массив-
ным и соответственно слишком медленным.
Позже другой студент заставил схему работать,
как задумывалось, радикально уменьшив габа-
риты механизма. Восьмидюймовые вуферы он
заменил крошечными динамиками из наушни-
ков, к которым прикрепил осколок зеркала.
26N.4.8. Простой до очарования
светодиодный дисплей
Вам, наверное, приходилось видеть дисплеи из
вращающихся или качающихся светодиодных
лент: прикрепленные к велосипедному колесу,
к лопастям вентилятора или качающейся план-
ке. Один из наших студентов хотел сделать что-
то подобное, но на первых порах застопорился
в связи с трудностью подачи электрических сиг-
налов на вращающееся устройство9. Возможное
решение — оснастить каждый светодиод щет-
кой для скользящего контакта — выглядело
проблематичным. (В настоящее время такая
специализированная электропроводка доступ-
на на рынке, но в то время у нас ее не было.)
Он поступил по-умному, не уделяя слишком
много усилий на изготовление устройства.
Его решением было вращать все конструк-
цию: не только светодиоды дисплея, но также
и управляющий компьютер и его источ-
ник питания (батарею). Такое устройство не
9 Этим студентом был Раян Джамйолковски (Ryan Jamiol-
kowski) из курса 2008 г.
26N.4. Несколько других выдающихся проектов
1087
Рис. 26N.20. Сборка коорди-
натного лазерного зеркала
(габариты, к сожалению, слиш-
ком большие)
Рис. 26N.21. Вращающийся дисплей: вместе с компьютером и батареей
было слишком «разговорчивым»: оно про-
сто вело счет от 0 до 9. Но оно работало, как
задумывалось, что доставляло удовольствие
(рис. 26N.21).
26N.4.9. Мобильные платформы
Двухколесные платформы
с независимыми приводами
Установив два электродвигателя с колесами
по сторонам платформы, получим мобильную
платформу, которой можно управлять наподо-
бие бульдозера или танка, независимо приво-
дя в движение каждое колесо. Такая платформа
обладает полезной возможностью разворота
на месте.
На рис. 26N.22 справа показана коммерчески
доступная версия такой платформы. Данная
модель больше не выпускается, но существует
много подобных10. Наши студенты использо-
10 Компания Parallax (www.parallax.com) предлагает круг-
лую платформу, SEN-13285. А компания Pololu (www.
вали ее, чтобы создать самоходное шасси, спо-
собное следовать вдоль линии, а также танце-
вать, обучаясь танцевальным движениям, ска-
нируя находящуюся вблизи радиометку.
Два амбициозных студента (Майк Паре — Mike
Pahre и Дэнни Вандеррин — Danny Vanderryn)
разработали самодельное шасси, показанное
слева на рис. 25N.22, для прохождения лабирин-
та. Оно было оснащено единственным датчиком
в передней части — кнопкой, срабатывающей
при столкновении с препятствием. Но этого
было достаточно, чтобы шасси, после того как
оно с большими усилиями нашло дорогу к вы-
ходу лабиринта из ящиков и книг, вернулось
обратно, не заезжая ни в какие тупиковые на-
правления. Оно безостановочно проехало весь
путь, избегая всех тупиков, которые были об-
наружены при первом прохождении лабиринта.
По завершении прохождения шасси станцевало
танец победы, наподобие футболиста, только
pololu.com) предлагает подобную платформу с вырезами
по бокам для колес (Pololu 5" Robot Chassis RRC04A). Лю-
бую из этих платформ нужно самостоятельно оснастить
подходящими электродвигателями и колесами.
1088
26N. Потенциальные проекты. Игрушки на любой вкус
Рис. 26N.22. Шасси, управляемые колесами с независимым приводом
Сервомашинка непрерывного вращения
(одна из двух), вторая не видна
Хобот с направленным
вниз дальномером
Переключатель выбора аналогового
у или цифрового режима
- Аналоговая плата
\ Цифровая плата
(наличие микроконтроллера очевидно)
Рис. 26N.23. Интеллектуальное шасси с чувством самосохранения
- Край стола (опасный обрыв)
что забившего гол. Мы считали, что оно было
вправе быть довольным собой.
Это был трудный проект, и сама сборка ме-
ханического шасси требовала значительных
навыков работы с инструментами. Поскольку
электродвигатели потребляют большой ток,
питание на шасси подавалось по кабелю, по ко-
торому также передавались управляющие сиг-
налы.
А предлагаемое на рынке шасси снабжено сер-
вомашинками с малым энергопотреблением,
модифицированными для непрерывного вра-
щения. Более подробную информацию см. в
разделе 26N.6.4. Эти электроприводы спокой-
но работают от плоской батарейки для фото-
аппарата «Поляроид» или от трех батареек
типа ААА, установленных на шасси. Но отсут-
ствие шагового привода, который позволяет с
легкостью повторить ранее пройденный путь,
означает, что для составления маршрута через
лабиринт требуется какой-либо вид обратной
связи и способ записи получаемых данных.
26NA10. Интересное применение
для шасси, управляемого
независимыми приводами
Два студента (Люкас Коция — Lucas Kocia и
Феррел Хелблинг — Ferrel Helbling) восполь-
зовались готовым шасси, чтобы создать лов-
кую машинку, обладающую неким интеллек-
том. Идея была несложной, и они ее реализо-
вали за полдня: шасси получилось достаточно
«умным», чтобы не переехать через край «про-
пасти» (через край стола в данном случае).
Они оснастили свое шасси длинным «хобо-
том», на котором разместили оптический даль-
номер (инфракрасный модуль с диапазоном из-
мерений от 4 до 30 см производства компании
Sharp11), направленный вниз. Таким образом,
дальномер может определять, когда «хобот»
выходит за край стола (рис. 26N.23).
11 Номер артикула компонента GP2Y0A41SK0F, предо-
ставляется компанией SparkFun, которая также предлагает
версию с расширенным диапазоном измерений.
26N.4. Несколько других выдающихся проектов
1089
л(^ Яв^а
Рис. 26N.24. Управление игрушечным радиоуправляемым автомобилем с помощью компьютера
Дальномер работает в синхронном режиме,
чтобы игнорировать общее освещение. Он по-
дает прямоугольный разрешающий сигнал на
свой ИК-излучатель. Пока излучатель включен,
интегратор накапливает отраженное излучение
и свет окружающей среды. А когда излучатель
выключен, приемник инвертирует сигнал, по-
лученный за счет общего света, прежде чем по-
давать его на интегратор. Таким образом свет
окружающей среды аннулирует сам себя.
Эти два студента продемонстрировали нам свое
шасси, всегда вовремя поворачивающее от об-
рыва, а затем ошарашили нас, открыв, что они
реализовали его за счет чисто аналоговых ме-
тодов (за исключением, возможно, цифрового
включения микросхемы 555 в качестве однови-
братора). Наверное, мы выглядели разочаро-
ванными, что они не воспользовались микро-
контроллером, который изучали в нашем курсе.
На следующий день они пригласили нас снова
наблюдать за тем, как их шасси ходит по краю.
Но на этот раз они решили задачу с помощью
автономного микроконтроллера C8051F410.
При этом они также оставили и аналоговую
схему и установили переключатель для выбора
аналогового или цифрового режима управле-
ния шасси. Мы были очарованы их искусным
способом демонстрации широкого круга на-
выков, которыми, мы надеемся, все студенты
овладеют по завершении этого курса.
26NA11, Игрушечный автомобиль,
управляемый компьютером
Два студента Джонатан Вольф Qonathan Wolff)
и Джордж Маркус (George Marcus) предложи-
ли проект, который мы посчитали чрезмерно
объемным: они хотели использовать свой са-
модельный компьютер для управления радио-
управляемым игрушечным автомобилем, кото-
рый бы преследовал такой же автомобиль, но
управляемый человеком. (Мы упомянули их
амбиции в разделе 26N.2.) Мы рекомендовали
начать с более легкой части: проверить, сможет
ли компьютер просто управлять автомобилем.
Они неохотно, но согласились, всем своим ви-
дом показывая, что они считали это скучной и
тривиальной задачей. Так мы им испортили их
забаву.
Много дней спустя они продемонстрирова-
ли такую конструкцию, и это оказалось очень
трудной задачей. Часть с «догонялками» так
никогда и не была реализована. Их проект тре-
бовал решения нескольких сложных задач:
♦ Самой трудной была задача определения
компьютером местонахождения автомоби-
ля. Они решили ее, установив на автомобиль
ультразвуковой излучатель, сигналы кото-
рого затем улавливались тремя ультразвуко-
выми датчиками. Компьютер давал команду
1090
26N. Потенциальные проекты. Игрушки на любой вкус
издать ультразвуковой сигнал12, и местопо-
ложение автомобиля определялось методом
триангуляции по времени прихода этого сиг-
нала на ультразвуковые датчики.
♦ Триангуляция?! Тригонометрия на языке ас-
семблера на карликовом компьютере? Они
осознали, что это требовало больших усилий,
и решили передать задачу сложных вычисле-
ний настольному ПК. С этой целью они соз-
дали интерфейс между своим самодельным
компьютером и ПК (что уже само по себе
было бы приличным проектом). Самодель-
ный компьютер отправлял на ПК исходные
данные в виде временных задержек, ПК на
основе этих данных вычислял координаты
местонахождения автомобиля и передавал
эти координаты назад.
♦ Получив эти координаты, самодельный ком-
пьютер мог вычислить, как ему доставить
автомобиль оттуда, где он находится сейчас,
туда, где он должен быть.
♦ Наконец, самодельный компьютер вел ав-
томобиль к месту назначения. Для этого он
управлял кнопочными переключателями,
которые предназначались для человека. За-
дача управления переключателями не была
трудной, но задача управления автомобилем
была таковой. Они приобрели самый деше-
вый автомобиль, предлагаемый в магазине
Radio Shack, и этот автомобиль не мог про-
сто, например, повернуть налево. Чтобы по-
вернуть налево, ему нужно было повернуть
передние колеса направо, а затем сдать на-
зад. Только после этого он мог ехать вперед
и налево.
26NA12. Вечная проблема
обратного маятника
Подобную задачу регулярно предлагают в
курсах по системам управления. Это также
очень трудная задача, которую в нашем курсе
мы решаем, действуя по наитию13. Некоторые
12 С грустью отметим, что поскольку они испытывали
острый дефицит времени, команда для издания сигнала пе-
редавалась на автомобиль по проводу, а не радиосигналом.
13 Два хороших примера успешного решения этой задачи
показаны на YouTube. Но если эти ссылки окажутся больше
недействительными, просто выполните поиск по словам «об-
ратный маятник» или «inverted pendulum». См.: http://www.
youtube.com/watch?v=MWJHcI7UcuE (Указка балансиру-
ется на основании наподобие принтера); http://www.you-
tube.com/watch>v=d 8RYpHfRK4&feature=related (Авто-
мобиль Lego Mindstorm балансирует на двух колесах).
студенты были близки к успеху, но настоящего
успеха пока еще никто не добился.
Безумству храбрых поем мы песню
Первый студент, который попытался решить
данную проблему, подошел к этому таким об-
разом, который делал успешное ее решение
чрезвычайно маловероятным. Тем не менее его
подход был очень впечатляющим. Он не изучал
теорию систем управления и, наверное, не знал,
какую трудную задачу поставил перед собой.
Поскольку, если бы он знал, разве бы пытался
решить ее в двух измерениях, а не в обычном
одном?
Он применил простые и полностью аналого-
вые методы, чтобы балансировать карандаш
на его острие. Использование карандаша вме-
сто более привычной длинной указки делало
его задачу еще труднее. Тем не менее его при-
митивное устройство было в силах балансиро-
вать карандаш на острие в течение нескольких
секунд, перемещая платформу, на которой он
находился, по гладкой поверхности.
В его разработке стоящий вертикально каран-
даш освещался светодиодом, а пара фотодатчи-
ков наблюдала за наличием отклонения каран-
даша от вертикали. Сигналы с фотодатчиков
подавались на дифференциальный усилитель,
который управлял электродвигателем, реакция
которого и восстанавливала вертикальное по-
ложение карандаша. Электродвигатель вращал
шкив с намотанной на него ниткой, прикреплен-
ной к платформе, на которой был установлен
карандаш, в результате чего платформа переме-
щалась по базовой площадке туда или сюда, как
требовалось, чтобы сбалансировать карандаш.
Две пары таких связок светодиода и фотодат-
чика наблюдали за отклонениями карандаша
по осям Хи Y. Отрицательная обратная связь
в этой конструкции обеспечивала довольно
хорошую работу механизма, несмотря на то,
что его исполнение было до предела простым:
швейная нитка, деревянные шкивы, базовая
площадка из древесно-стружечной плиты, а
также обрезки изоляционной ленты.
Примечание
Создателем этого балансировочного механизма
был экстраординарный энтузиаст-самоделкин
Поль Титком (Paul Titcomb). Еще один из его по-
разительных проектов заслуживает упоминания
26Л/.4. Несколько других выдающихся проектов
1091
Карандаш
*ТТара фотодатчиков Двигатель X
Двигатель У
Перемещающаяся
платформа
Подробное
устройство
платсрормы
/V/fc
Рис. 26N.25. Замечательный частичный успех: балансировщик карандаша
Оси
здесь; возможно, что он может вдохновить кого-
либо на подобный подвиг. Используя свой само-
дельный компьютер, Поль создал устройство,
повторяющее процесс рисования, выполненный
человеком. Он соорудил двухшарнирную «руку»,
к которой прикрепил карандаш. В каждый шарнир
он поместил потенциометр, а затем перемещал
«руку» с карандашом, рисуя какую-либо картин-
ку. При этом компьютер регулярно периодически
считывал показания потенциометров в шарнирах
«руки». Завершив рисование, Поль давал указание
компьютеру воспроизвести движения, которые
тот определил в процессе исходного рисования,
управляя парой шаговых двигателей на шарнирах
другой руки, подобной первой, к которой также
был прикреплен карандаш. Это устройство никог-
да не работало должным образом: его рисунки вы-
глядели так, как будто бы вышли из под руки кого-
то, серьёзно страдающего болезнью Паркинсона.
Возможно, что причиной этому была предельная
простота его механического исполнения, а также
то, что в нем (в отличие от устройства балансиро-
вания карандаша) не использовалась обратная
связь с ее магией прощения ошибок. Тем не менее
это была впечатляющая штуковина, и «рука», и ее
дрожащие «шедевры» собирают пыль где-то на
задворках нашей лаборатории в ожидании кого-
либо, кто усовершенствует эту схему.
Механизм работал достаточно хорошо до тех
пор, пока балансировочная платформа не при-
ближалась к какому-либо краю базовой пло-
щадки. Тогда карандаш падал. Чего всему это-
му устройству не хватало, так это осведомлен-
ности о местонахождении перемещающейся
балансировочной платформы на базовой пло-
щадке. Кроме того, медленность реагирова-
ния делает его уязвимым к нестабильностям,
подобным тем, которые мы видели в случае с
ПИД-управлением электродвигателем. После-
дующие попытки решения этой задачи были
более утонченными, но ни одна из них не ока-
залась такой захватывающей, как у Поля.
Одномерный обратный маятник
После этой первой попытки все пробовали ре-
шить задачу в более осуществимой форме: в
одном измерении, используя детали старого
принтера для перемещения основания длин-
ной указки. Мы начали собирать выброшенные
принтеры, и оснастили некоторые из них дру-
гим потенциометром, который предоставлял
данные о местонахождении перемещающейся
базы в дополнение к информации о наклоне,
предоставляемой первым потенциометром.
Эта информация давала предупреждение о том,
когда приближался предел корректировочного
диапазона.
Год спустя два студента, Джастин Альберт
(Justin Albert) и Парфа Саха (Partha Saha) были
более успешными, применив чисто аналого-
вый подход. Эти студенты были достаточно
умудренными и прекрасно знали о неизбеж-
ных проблемах со стабильностью, в связи с
1092
26N. Потенциальные проекты. Игрушки на любой вкус
w$
измеряет наклон указки
Рис. 26N.26. Оборудование обратного маятника: внутренности старого матричного принтера... Результаты были неодно-
значными. Один студент, чей компьютер не смог справиться с управлением этой конструкцией, сочинил исчерпывающий
и наполненный формулами отчет с выводом, что причиной неудачи было слишком медленное реагирование электродвига-
теля, в результате чего он не успевал откорректировать падающую указку14. Он предположил, что задача не будет решена до
тех пор, пока мы не обзаведемся более мощным электродвигателем.
Рис. 26N.27. Две студентки и плод их умственных усилий
чем попробовали суммировать сигналы рас-
согласования разных типов, создав петлю ПИД
наподобие той, которую вы собрали на лабо-
раторном занятии 10L. Их схема работала на-
столько хорошо, что мы попросили их показать
ее студентам нового курса в первый день заня-
тий. В сентябре они вытащили свое устройство,
которое работало в мае, и не смогли заставить
14 Имеет ли какое-либо значение тот факт, что этот парень
был выпускником Массачусетского технологического ин-
ститута?
его функционировать снова. Грустная история.
Можно ли считать такое развитие событий
доводом против аналоговых схем, корректи-
руемых потенциометрами, и доводом в пользу
цифровых методов?
В недавней повторной попытке решения этой
задачи была применена цифровая реализа-
ция ПИД-контура. Модифицированное таким
образом устройство проявило поразитель-
ные способности, гоняя базу туда и обратно,
26N.5.№pbi
1093
Здесь ТТакман
s немного откушал
Рис. 26N.28. Два снимка экрана осциллографа с игрой Пакман
стараясь удерживать указку в вертикальном
положении. Но после нескольких секунд оно
проигрывало, не в силах обеспечить достаточ-
ные корректировки. Но было очевидно, что
оно очень старалось. Дразнящий но неполный
успех устройства можно видеть на фотографи-
ях, изображенных на рис. 26N.27: сначала раз-
работчики, переполненные тревогами и опасе-
ниями, запускают устройство в действие (слева
на рисунке)15, а затем радуются, когда оно не-
истово выполняет небольшие корректировки,
поддерживая линейку вертикально в течение
нескольких секунд. Мы не сочли нужным по-
казывать фотографию более грустного завер-
шающего события падения указки.
26N.5. Игры
Мы бы хотели показать вам эту игру в действии,
но однажды кто-то отключил от нее питание
и оставил на все лето, а мы до сих пор были
слишком ленивыми, чтобы снова вводить код
вручную. Но у нас не поднимается рука, что-
бы разобрать саму схему. Так что, возможно,
в какой-нибудь из дней...
26N.5.2. Астероиды на экране
осциллографа
В игре Пакман применялся дисплей с растро-
вой разверткой, а лабиринт в основном был
статическим. В игре Космические захватчики
(Space Invaders) использовалась векторная гра-
фика наподобие рассмотренной ранее в разде-
ле 26N.4.616.
26N.5.1. Пакман на экране
осциллографа
Это был безумно сложный и трудоемкий про-
ект: для него потребовалось собрать специ-
альную видеоплату, чтобы обновлять экран
осциллографа. Микроконтроллер просто не
успевал постоянно обновлять содержимое все-
го экрана. Вместо этого сначала в RAM записы-
валась разметка экрана, а затем ее содержимое
быстро обновлялось с помощью аппаратных
счетчиков.
Таким образом, обязанности компьютера по
дисплею были сведены к записи только изме-
нений: рот Пакмана открывался и закрывался,
и он перемещался, как и монстры.
15 Этими разработчиками были студентки Эмили Рассел
(Emily Russell) и Лусанн Вэнг (Lusann Wang) из класса
2012 г. Их соавтор, Том Димидюк (Tom Dimiduk) не по-
казан. Они использовали не микроконтроллер 8051, а Аг-
duino, поскольку у Тома был опыт работы с этим микро-
контроллером.
Рис. 26N.29. Астероиды на экране осциллографа
В проекте было гравитационное поле, как в
настоящей игре космических захватчиков.
Смотреть эту игру было одно удовольствие.
Схему мы также сохранили, не в силах поднять
руку, чтобы разобрать ее.
16 Этим проектом занимался Давид Джингоулд (David
Gingold). Проект был настолько амбициозным, что засчи-
тался ему за два курса (второй курс был по компьютерной
анимации).
Он не только создал программную часть, но также обору-
дование для рисования линий постоянной яркости. Когда
он скомпилировал код на языке С на ПК, ему нужно было
загрузить полученный исполняемый файл в свой самодель-
ный компьютер. Эта надобность возникла на выходных,
поэтому вместо того, чтобы попросить нас помочь ему най-
ти микросхему УАПП, он написал программу последова-
тельного интерфейса, как будто бы ему требовалось сделать
проект еще сложнее. Его программный последовательный
интерфейс работал так же хорошо, как и игра.
1094
26N. Потенциальные проекты Игрушки на любой вкус
26N.5.3. Другие великолепные игры
Наши студенты разработали и другие чудесные
игры, но у нас нет их фотографий, поэтому при-
дется ограничиться описанием.
Виртуальная реальность
Стефан Райдер (Stephane Ryder) вычислил, как
расшифровать сигналы сенсорной управляю-
щей перчатки из игры Nintendo. Эта перчат-
ка может определить свое местонахождение
и пространственную ориентацию, а также дей-
ствия сгибания пальцев. Он использовал эти
сигналы, чтобы создать игру на своем само-
дельном компьютере. Компьютер издавал зву-
ковые сигналы, частота которых повышалась
по мере приближения перчатки к трехмерным
координатам виртуального объекта, просто
некой произвольной точки X, У, Z в простран-
стве. Когда перчатка находилась в целевой
точке, пользователь мог «захватить» ее, сжав
руку в кулак, а затем переместить ее в дру-
гую позицию и оставить ее там, разжав кулак.
Великолепная игра!
Боксерский интерфейс
Студенты Ноа Хельман (Noah Helman), Самир
Бхалотра (Sameer Bhalotra) и Клэй Скат (Clay
Scott) заменили цифровую клавиатуру игры в
бокс компании Ninitendo массивом фотодатчи-
ков, установленных в пустую рамку, наподобие
рамки для картины. Позади рамки с датчиками
они установили телевизор, на котором показы-
вались боксеры. Чтобы нанести удар боксеру из
телевизора, пользователю нужно было нанести
удар в пределах рамки с датчиками. Внутреннее
пространство рамки было поделено на девять
сегментов, каждому из которых была присвоена
функция, которая ранее была назначена кнопке
на цифровой клавиатуре: апперкот, удар в кор-
пус и т. п. Хотя проект и не был завершен, он
был довольно увлекательным.
Лабиринт на экране осциллографа
В этой игре компьютер управлял выводом на
экран, но выводимые изображения хранились
в виде конечных автоматов в микросхемах
ПМЛ. Таким образом, можно было менять ла-
биринт (набор комнат в виде прямоугольников
с проходами к другим прямоугольникам), ме-
няя микросхемы ПМЛ. Авторы этого проекта:
Мередит Траунер (Meredith Trauner) и Робби
foiami(Robby Klein).
Тетрис на светодиодной матрице
Автор проекта: Курт Шелтон (Kurt Shelton).
Микроконтроллер 8051 исполнял программу,
загруженную во флеш-память. Для реализации
проекта потребовалось выполнить громадную
работу по программированию, но проект рабо-
тал, как задумывалось.
26N.6. Датчики, приводы,
другие приспособления
На данном этапе нашего университетского кур-
са мы предлагаем студентам список устройств,
которые есть в нашей лаборатории, надеясь, что
они смогут придумать новые способы исполь-
зования этих устройств. В этой книге, которая
должна пережить любой список устройств, до-
ступных на момент ее подготовки, кажется, что
целесообразнее предоставить читателю список
поставщиков оборудования, которых мы счи-
таем полезными. Конечно же, в Интернете вы
сможете найти много других источников.
26N.6.1. Поставщики датчиков,
приводов и прочих устройств
Мы находим следующих поставщиков обору-
дования одними из лучших на рынке.
Adafruit
(www.adafruit.com)
Действительно хороший сайт, основанный се-
рьезным и вдумчивым фанатом электроники,
который часто устанавливает детали на по-
лезные адаптерные платы, в результате чего
их легко монтировать. Это важный аспект, по-
скольку многие новые компоненты выпуска-
ются только в корпусах для поверхностного
монтажа. Благодаря установке таких деталей
на адаптерные платы с ними можно работать,
как с обычными деталями, включая установку
их на макетную плату. Компания Adafruit часто
предоставляет код со своими программируемы-
ми устройствами. В настоящее время эта ком-
пания склоняется к программам и интерфейсам
для Arduino.
26N.6. Датчики, приводы, другие приспособления
1095
Sparkfun
(www.sparkfun.com)
Похожа на компанию Adafruit, но с более ком-
мерческой атмосферой. Также часто предостав-
ляет детали на адаптерных платах.
Parallax
(www.parallax.com)
Хороший источник деталей для роботехники,
таких как шасси, а также предлагает обшир-
ный выбор датчиков.
Pololu
(www.pololu.com)
Источник деталей для роботехники, хотя ас-
сортимент несколько меньший, чем у Sparkfun.
All Electronics
(www.allelectronics.com)
Это магазин товарных излишков, поэтому ас-
сортимент неорганизованный и непредска-
зуемый. Но здесь можно найти необычные
устройства по низким ценам, которые могут
вдохновить на изобретение. Например, ленточ-
ный тормоз для электрического скутера.
eBay
И, конечно же, не забывайте о eBay, где иногда
предлагают товары по очень низким ценам.
26N.6.2. Поставщики небольших
механических деталей
Специальные механические детали, такие как
подшипники, шестерни, приводные ремни и
карданные шарниры, предлагаются в магазине
Sparkfun, а также в магазине индустриальных и
научных товаров (Industrial and Scientific Store)
компании Amazon.
Amazon Industrial & Scientific Store
(www.amazon.com/industrial)
Сайту не хватает уютности магазина Small
Parts, Inc., который был приобретен компанией
Amazon, но он предоставляет доступ к большо-
му разнообразию деталей.
Stock Drive Products
(htty://www.sdp-si.com/)
Веб-магазин меньшего размера, менее ошелом-
ляющий.
26N.6.3. Механические детали:
электродвигатели
Шаговые двигатели
Привлекательность шаговых двигателей со-
стоит в том, что для прецизионного управле-
ния позиционированием не требуется обратная
связь.
Существуют два типа шаговых двигателей по
полярности: униполярные и биполярные.
Униполярные шаговые двигатели. Унипо-
лярными шаговыми двигателями легче управ-
лять; для них требуется только один транзи-
стор, подключенный к обмотке каждой фазы.
Обычно он играет роль переключателя на
«землю», как показано на рис. 26N.31. Обмотки
униполярного шагового двигателя имеют шесть
выводов: по выводу от каждого конца двух об-
моток и еще по одному выводу от середины
каждой обмотки. Иногда два центральных вы-
вода соединяют вместе, что сокращает количе-
ство выводов до пяти.
Биполярные шаговые двигатели. Обмотки
этих двигателей не имеют центральных отво-
дов, в результате чего для них требуется пара
драйверов, которые могут работать в токовом
режиме как источника, так и потребителя тока.
Такие драйверы выпускаются в виде микро-
схем и называются Н-мостами. Хотя интерфейс
биполярных шаговых двигателей сложнее, эти
двигатели более эффективные, чем униполяр-
ные, у которых в любое время задействуется
только половина обмоток.
1. Разрешение и мощность. Типичные шаго-
вые двигатели поддерживают 200 шагов на
оборот и потребуют ток значительной силы:
0,3-1 А при напряжении в районе 12 В17.
17 Например, биполярный шаговый двигатель типа
NEMA-17 компании Adafruit поддерживает 200 шагов на
оборот, потребляя ток 350 мА при напряжении 12 В. Похо-
жие шаговые двигатели стоят меньше в магазине All Elec-
tronics, но ассортимент там небольшой.
1096
26N. Потенциальные проекты. Игрушки на любой вкус
2. Малогабаритные шаговые двигатели. Мало-
габаритные шаговые двигатели имеют более
грубое разрешение. Например, компания
Sparkfun предлагает малогабаритный шаго-
вый двигатель, поддерживающий 48 шагов
на оборот18. Самый маленький шаговый дви-
гатель, который нам попадался, имел диа-
метр меньше 1 см.
Драйверы шаговых двигателей
Как отмечается в разделе 26N.7, работы по на-
писанию программы для управления шаговым
двигателем можно избежать, используя специ-
альную микросхему драйвера шагового двига-
теля.
26N.6A Сервоприводы
Эти электродвигатели, управляемые длитель-
ностью импульса, хорошо подходят для под-
ключения к компьютеру, поскольку длитель-
ность импульса легко регулировать с помощью
микроконтроллера. Существуют два основных
типа сервоприводов.
С управляемым угловым положением вала
Такие сервоприводы наиболее часто приме-
няются в радиоуправляемых моделях, где они
еще называются сервомашинками. (Принцип
работы сервомашинок рассматривается на ла-
бораторном занятии 24L.) Вал сервомашинки
вращается в пределах сектора величиной 270°
и удерживается в установленном положении,
которое определятся длительностью импуль-
сов, посылаемых на сервомашинку в виде непре-
рывной последовательности. Сервомашинки
выпускаются, по крайней мере, трех стандарт-
ных размеров, не потребляют много мощности
и создают значительный вращающий момент
(хотя электродвигатель сервомашинки и не-
большой, крутящий момент с него снимается
через редуктор с очень большим понижающим
коэффициентом).
Сервомашинки в основном применяются для
привода в действие элементов радиоуправляе-
мых моделей: руля автомобиля, элеронов само-
лета и т. п. Но они достаточно мощные, что по-
зволяет их использовать, например, в неболь-
шом манипуляторе (руке-роботе).
С управляемой скоростью и направле-
нием непрерывного вращения
В этих сервомашинках длительность импульсов
определяет не угловое положение вала, а его на-
правление и скорость вращения. При импульсе
длительностью 1,5 мс вал сервомашинки не
вращается; более короткие или более длинные
импульсы вызывают вращение вала в одном
или другом направлении. При этом скорость
вращения вала приблизительно прямо пропор-
циональна разнице между длительностью по-
даваемых импульсов и длительностью импуль-
сов покоя. Импульсы длительностью 1 мс вы-
зывают вращение на максимальной скорости в
одном направлении, а длительностью 2 мс — на
максимальной скорости в противоположном
направлении. Такие сервомашинки использо-
вались в проекте мобильного шасси, который
рассматривался в разделе 26N.4.9, где каждое из
двух колес шасси приводилось в движение сво-
ей сервомашинкой непрерывного вращения.
26N.6.5. Мускульные провода
Nitinol
По крайней мере, одна компания так и называет
эти устройства — мускульные провода (muscle
wires)19. Но по-научному они называются про-
водами с эффектом памяти или нитиноловые20
провода. При нагреве такие провода сжимают-
ся (на 3-7%) со значительной силой, если до
нагрева они был растянуты.
Такой небольшой процент сжатия подразуме-
вает, что для того, чтобы получить более-менее
значительный приводной ход, потребуется до-
вольно длинный отрезок провода. Небольшая
компания Miga Motors производит оригиналь-
ный удлинитель хода, который, по сути, со-
держит длинный отрезок провода, сложенный
в несколько раз. Устройство размером с кре-
дитную карточку, реализованное по этой схеме,
позволяет получить ход длиной около 7,5 мм.
На рис. 26N.30 показан пример одного такого
устройства — MigaOne-1521. Оно оснащено кон-
тактом, который используется схемой управле-
ния для определения полного хода, чтобы от-
ключить питание и не допустить повреждения
вследствие перегрева.
18 Номер компонента R0B-10551B магазине Sparkfun.
19 www.musclewires.com.
20 Нитинол — никель-титановый сплав.
21 Это изящное, но дорогое устройство, стоимость которо-
го составляет около 50 долл. См.: migamotors.com.
26N.6. Датчики, приводы, другие приспособления
1097
26N.6.6. Датчики
Рис. 26N.30. Устройство MigaOne увеличивает длину хода
привода из нитинолового провода
Для приводов из нитинолового провода требу-
ются очень большие токи, поскольку ток дол-
жен нагревать провод, расходуя мощность PR.
Но если достаточно только кратковременного
сокращения, то и подача тока будет кратковре-
менной. Таким образом, при коротком рабочем
цикле устройства для его питания подойдет ба-
тарея небольшой емкости, что позволит умень-
шить габариты всего устройства.
Применение: крошечные роботы
Два наших студента собрали шестиногого жука
с движителем из нитиноловых проводов. В ре-
зультате они пришли к выводу, что никогда
больше не притронутся к таким компонентам:
они просто пожирают ток, не создают доста-
точного усилия, а также с ними очень сложно
работать. В частности, требуется выполнять
множество корректировок натяжения. Тем не
менее более легкого привода, чем нитиноло-
вый провод, не найти.
Эти провода можно использовать для подража-
ния работе сухожилий, например, в грубой мо-
дели руки, способной шевелить пальцами22.
Звуковые
Сборка ультразвукового динамика с ми-
крофоном
Представляет собой диафрагмы небольшого
размера, прикрепленные к фрагменту пье-
зоэлектрического материала, которые резо-
нируют на частоте около 40 кГц. Передатчик
и приемник или одинаковые, или очень по-
хожи друг на друга.
Применяются в дальнометрии (передатчик
посылает пакет звуковых импульсов, прием-
ник ловит эхо), связи (данные передаются в
виде последовательностей пачек ультразву-
ковых импульсов).
Интегрированные ультразвуковой датчик
и усилитель
Этот метод был разработан компанией Polaroid
для использования в качестве дальномера в
выпускаемых ими фотокамерах. Такой способ
также копируется в дальномерах компании
MaxBotix23. Например, диапазон измерений
дальномера EZ1 составляет от 0 до 250 см, в
инкрементах величиной 2,5 см. Дальномер пре-
доставляет три типа выходного сигнала: анало-
говый, широтно-импульсный код и RS-232. На
рынке предлагаются дальномеры такого типа с
разными уровнями чувствительности. Следует
также отметить альтернативный метод опреде-
ления расстояния, в котором используется ин-
фракрасный свет. Этот метод упоминается в
разделе 26N.4.10. Инфракрасные дальномеры
обладают лучшим разрешением, но меньшим
диапазоном измерений.
Инфракрасные
Преобразователь ИК импульсов в логиче-
ские уровни
Эта микросхема рассматривалась в главе 24N.
Она преобразует каждую пачку импульсов
частотой 40 кГц, посылаемую типичным ИК-
пультом дистанционного управления, в соот-
ветствующий логический уровень. (В приме-
ре, описанном в главе 24N, пачка импульсов
создает низкий логический уровень, а отсут-
ствие ИК-сигнала соответствует высокому
логическому уровню.)
22 Набор для такой руки предлагается компанией
MuscleWires (www.musdewires.com).
23 Такие дальномеры предлагаются компанией Sparkfun.
См., например, дальномер MaxBotix LV-MaxSonar-EZl.
1098
26N. Потенциальные проекты Игрушки на любой вкус
Выдаваемая преобразователем последова-
тельность логических уровней может обра-
батываться с помощью микроконтроллера,
который, в зависимости от ее содержания,
будет выполнять ту или иную операцию.
Должным образом тактируемый 8-битовый
сдвиговый регистр, реализованный про-
граммно или аппаратно, может теоретически
обеспечить 256 разных операций.
Пассивный дифференциальный
ИК-датчик движения
При изменении ИК-образа пространства под
наблюдением активируется сигнал управле-
ния. Напряжение питания от 3,3 до 12 В, вы-
ходной сигнал логического уровня"
Г24
Различитель цветов
Различитель цветов представляет собой ми-
кросхему матрицы датчиков, каждый из кото-
рых оснащен фильтром определенного цвета.
Два изобретательных человека соединили это
устройство с оптоволокном, пытаясь считывать
цветовые коды резисторов. Цвета резисторных
кодов были плохого качества, и их устройство
не справилось с данной задачей. Но вот цвета
плоского кабеля оно могло различать в боль-
шинстве случаев, что тоже довольно впечатля-
ет. Возможно, что вам захочется улучшить их
устройство для автоматической сортировки
резисторов25. В таком случае спецификации
для данного датчика можно найти на веб-сайте
компании Parallax26.
Датчики ускорения (акселерометры)
и скорости вращения
Большой выбор акселерометров предостав-
ляют компании Adafruit, Parallax и Sparkftm.
Исследуйте их веб-магазины, и вы, скорее всего
сможете найти там даже лучшие устройства, чем
те, которые заметили мы. Эти компании обыч-
но предлагают для своих устройств адаптерную
плату для установки на макетную плату.
Скорее всего, вам будет достаточно устройства с
диапазоном измерений всего лишь в несколько
24 SparkfunSEN-13285.
25 Прежде чем вы приступите к этой тяжелой работе,
должны ли мы напомнить вам о наличии более легкого
способа определения значения сопротивления резистора?
Будем надеяться, что нет.
26 См.: https://www.parallax.com/product/28302 (Но-
мер артикула детали: TAOS TCS3200-DB).
единиц g27. А акселерометр с двумя осями мо-
жет определять наклон.
Компания Sparkfun на своем веб-сайте предла-
гает полезное описание многих разных акселе-
рометров:
,28
Трехосевой акселерометр с выходным
аналоговым сигналом
Микросхема ADXL335 с диапазоном измере-
ний ±3g и напряжением питания 3,3 В. Иногда
хорошо иметь аналоговый сигнал, что позво-
ляет наблюдать на экране осциллографа вы-
ходные сигналы устройства в режиме реаль-
ного времени. Также эти значения можно счи-
тывать, используя АЦП микроконтроллера; но
для чтения сигналов всех трех осей посредством
одного АЦП требуется наличие аналогового
мультиплексора. Микроконтроллер C8051F410
оснащен встроенным аналоговым мультиплек-
сором, что позволяет его одному АЦП последо-
вательно считывать выходные сигналы акселе-
рометра для всех трех осей. Компания Adafruit
предлагает адаптерную плату для этой микро-
схемы акселерометра, которая также содержит
стабилизатор напряжения, позволяющий по-
низить 5 до 3,3 В.
Акселерометры с цифровым выходным
сигналом (SPI или 12С)
Пример такого акселерометра — микросхема
ADXL 345 с диапазоном измерений, настраи-
ваемом от +2 до 16 единиц g, и напряжением
питания 3,3 В. С интерфейсом SPI легко рабо-
тать, особенно с его аппаратной реализацией
компании Silicon Laboratories (см. лаборатор-
ное занятие 24L). Хотя цифровые выходные
сигналы этого акселерометра нельзя просма-
тривать на экране осциллографа, их значения
можно выводить на экран компьютера с по-
мощью среды разработки Silicon Laboratories.
Кроме того, принимать сигнал акселерометра
в цифровой форме легче и удобнее, чем в ана-
логовой. Интерфейс SPI делает ненужными
последовательные операции с АЦП, включая
переключение входных выводов АЦП.
27 Как вы, наверное, знаете, одна единица g соответствует
ускорению свободного падения, вызываемому силой при-
тяжения (гравитацией) планеты Земля.
28 См. руководство этой компании для покупателей ак-
селерометров и гироскопов Accelerometer, Gyro and IMU
Buying Guide (https://www.sparkfiin.com/pages/accel_
gyro_guide).
26N.6. Датчики, приводы, другие приспособления
1099
Гироскопы
Небольшой полупроводниковый гироскоп вы-
дает аналоговый сигнал, пропорциональный
угловому ускорению. В данном случае одной
оси может быть достаточно; аналоговый вы-
ходной сигнал бывает удобнее, чем цифровой.
Примером одноосевого гироскопа с анало-
говым выходным сигналом может служить
микросхема LY530AL (напряжение питания
3,3 В). Предлагается компанией SparkFun.
А микросхема L3GD20H производства ком-
пании STMicro (предоставляется компанией
Adafruit) будет примером трехосевого гироско-
па с цифровым выходным сигналом (12С и SPI).
Предоставляемая адаптерная плата позволяет
использовать напряжение питания и сигналы
управления величиной 5 В.
Комбинированный модуль
акселерометра и гироскопа
На рынке доступны микросхемы, содержа-
щие как акселерометр, так и гироскоп. Одним
из примеров такой микросхемы будет микро-
схема MPU-6050 (предоставляется компанией
SparkFun). При стоимости 40 долл. это доволь-
но дорогое устройство.
Несомненно, что в будущем на рынке будут до-
ступны многие улучшенные модели, поэтому
рассматривайте наш список только как краткий
обзор того, что было доступно в 2015 г.
Магнитометры
Существуют два основных типа: простые и за-
мысловатые.
Простые
Это просто датчик эффекта Холла с линейным
выходным сигналом, пропорциональным току.
Примером такого датчика будет микросхема
ACS712, предоставляемая на адаптерной плате
компанией SparkFun. Еще более простые датчи-
ки просто выдают сигнал определения да/нет.
Примером такого датчика будет микросхема
US 1881 (предоставляется компанией SparkFun).
Замысловатые
Магнитометрами этого типа являются циф-
ровые компасы. Например, микросхема трех-
осевого магнитометра НМС5883 производства
компании Honeywell, поставляемая компанией
Adafruit, установленная на адаптерную плату,
совместимую с питанием 5 В. Микросхема со-
держит две ортогональные катушки для опре-
деления вариаций в ориентации магнитного
поля Земли относительно каждой из катушек.
Полученные трехосевые показания предостав-
ляются через интерфейс 12С.
Тензометрические датчики
Представляют собой гибкие панели неболь-
шого размера, создающие разность потенциа-
лов при изгибе. Пример такого датчика можно
найти на https://www.parallax.com/product/
30056.
Синтезатор речи
Модуль синтеза речи DEV-11711 на чипсете
Emic-2 (предоставляется компанией Sparkfun
по цене 80 долл.). Данный модуль берет в каче-
стве входных данных (через УАПП) последова-
тельность символов ASCII и пытается наилуч-
шим образом произнести введенный текст.
Те, кто не боится немного потрудиться, могут
собрать свой синтезатор из двух микросхем по
25 долл.: микросхемы TTS256 для преобразо-
вания последовательности текстовых символов
в представление аллофон и микросхемы синте-
за речи Speakjet. Обе микросхемы предостав-
ляются компанией SparkFun.
Распознаватели речи
Эта очень трудная задача легко решается с
помощью переходной платы для Arduino
EasyVR Shield 3.0. Предоставляется компани-
ей SparkFun, артикул номер СОМ-13316. Плата
поддерживает 23 встроенные команды, а также
позволяет пользователю задать свои собствен-
ные 32 команды.
Просто заставить такую плату работать, про-
ектом считаться не будет. Настоящая зада-
ча — придумать для нее какое-либо интерес-
ное применение. Благодаря своим небольшим
габаритам (приблизительно 2,5x5 см) плату,
в принципе, можно установить, например, на
игрушечный автомобиль (возможно, но не
обязательно, управляемый с помощью микро-
контроллера), что позволило бы управлять ав-
томобилем с помощью голосовых команд.
1100
26Л/. Потенциальные проекты. Игрушки на любой вкус
26N.6.7. Дисплеи
Жидкокристаллические дисплеи (ЖКД)
Практически все ЖКД оснащены стандарт-
ным интерфейсом в виде одного адреса ввода-
вывода. Компьютер последовательно подает по
этому адресу коды ASCII (7- или 8-битовые),
а схема дисплея размещает их должным обра-
зом на экране. Для этого, как отмечалось в гла-
ве 25N, требуется шесть или семь линий ввода-
вывода, хотя с помощью платы расширения
этот параллельный интерфейс можно преобра-
зовать в последовательный29.
Применяются ЖКД для оснащения разных
устройств текстовым выводом. Это может быть
не очень интересно, поскольку такой визуаль-
ный дисплей сильно проигрывает намного бо-
лее информативным ЖКД, к которым мы при-
выкли на полномасштабных компьютерах.
Растровый дисплей на органических
светодиодах
Такие дисплеи позволяют отображать изобра-
жения или текст, обычно довольно малых раз-
меров, с высоким разрешением. Но на момент
подготовки этой книги реализация интерфейса
для таких дисплеев являлась трудной задачей.
Для ее облегчения компания Adafruit предо-
ставляет библиотеки кода. Одним из примеров
такого дисплея будет предоставляемый компа-
нией Adafruit монохромный дисплей под на-
званием Monochrome 128x32 SPI OLED graphic
display, артикул номер 661. Эти дисплеи также
предоставляются обычными поставщиками,
включая компанию Digikey.
Умные 2- или 4-символьные буквенно-
цифровые светодиодные дисплеи
Это малогабаритные дисплеи, каждый символ
которых имеет свой адрес ввода-вывода, по
которому подается код ASCII. Примером та-
кого дисплея будет привлекательный, но уста-
ревший дисплей PD2435 компании Siemens.
Попробовать найти поставщика можно на сай-
те octopart.com. Такие дисплеи подходят для
вывода небольших текстов, которые должны
быть хорошо заметными.
29 Такая плата расширения предоставляется компанией
AdaFruit под названием PC/SPI Character LCD Backpack,
артикул номер 292.
Гистограммные дисплеи
Светодиодные
Вам, наверное, приходилось видеть подобные
дисплеи, применяемые в качестве индикато-
ров уровня громкости на аудиооборудовании.
В простых дисплеях данные подаются индиви-
дуально на каждый светодиод. Примером та-
кого дисплея будет KWL-R1025BB (предостав-
ляется компанией Adafruit). В более сложных
имеется последовательный интерфейс. Такие
дисплеи также предоставляются компанией
Adafruit.
Электростатические E-Ink
Дисплеи E-Ink привлекательны тем, что после
записи уровня их энергопотребление равно
нулю. А недостатком являются необычные
требования к сигналу управления: кратковре-
менный импульс напряжением ±15 В, чтобы
включить или выключить сегмент. Но вам, воз-
можно, захочется похвастаться своими навы-
ками и создать свой драйвер. Компания при-
держивается особого принципа, состоящего
в том, что требования их устройств касательно
драйвера являются конфиденциальной инфор-
мацией. Они даже требуют, чтобы пользовате-
ли подписывали соглашение о неразглашении!
Но эти требования не являются никаким секре-
том, и драйвер для нескольких сегментов очень
легко реализовать.
Компания Digikey предоставляет 14-сегмент-
ный гистограммный дисплей (номер артикула
SC002221), а также трехсимвольный числовой
дисплей (номер артикула SC004221).
26N.6.8. Устройства сопряжения
Выходные
Полупроводниковые реле
Такие реле могут включать или выключать
устройства с питанием переменного тока боль-
шой мощности (электродвигатели, лампы, элек-
троприборы), используя в качестве управляю-
щего сигнала логический уровень. Например,
поставляемое компанией SparkFun полупро-
водниковое реле (номер артикула СОМ-10636)
может управлять устройствами, потребляющи-
ми ток до 8 А. Логический вход и высоковольт-
ный выход оптически развязаны, так что управ-
ляющая схема не подвергается опасностям, при-
сущим работе с сетевым напряжением.
26Л/.7. Драйвер шагового двигателя
1101
Входные и выходные
Последовательный радиоканал
Простой радиоканал может осуществлять об-
мен цифровыми данными. Самая простая
идея — включать и выключать передатчик в
соответствии с определенной схемой кодиро-
вания. А самым простым передающим устрой-
ством будет включаемый и выключаемый
высокочастотный генератор колебаний логи-
ческого уровня. Для управления питанием та-
кого передатчика подойдет МОП-транзистор.
Самым простым приемником будет усилитель
с выходом на детектор огибающей, которой мо-
жет служить простой однодиодный амплитуд-
ный детектор, подобный тому, с которым мы
познакомились на лабораторном занятии 3L.
Усилитель можно собрать самому или же взять
готовый усилитель на микросхеме. Затем ком-
паратор может определить, что выявил детек-
тор огибающей: присутствовал ли сигнальный
импульс (1) или нет (0).
В самом простом виде такое наличие/отсут-
ствие входного сигнала могло бы создать им-
пульс логического уровня, управляющий по-
ложением вала сервомашинки для руления
игрушечным автомобилем. В более амбициоз-
ном проекте по этому радиоканалу можно ор-
ганизовать передачу последовательных данных
посредством одного из стандартных последова-
тельных протоколов, например обычного RS-
232 или же 12С.
А самый простой способ реализовать радио-
канал — приобрести для этого готовые модули
передатчика и приемника. Компания SparkFun
предлагает большой выбор плат для реализа-
ции радиоканала, некоторые из которых до-
вольно просты, например передатчик WRL-
10534 и приемник WRL-10532. Это так назы-
ваемые неразборчивые устройства, поэтому
интеллектуальность им должны обеспечить
вы, разработчик. Некоторые из таких радио-
устройств содержат встроенный последова-
тельный интерфейс RS-232.
Еще легче работать с платами радиоустройств
с USB-интерфейсом, хотя для них требуется
значительное программное обеспечение. Ком-
пания SparkFun предлагает широкий ассорти-
мент модулей радиоканала, например, модуль
Wixel, номер артикула WRL-10665 . Но мы не
пробовали работать с этими устройствами.
26N.7. Драйвер шагового
двигателя
Общие сведения
Шаговый двигатель состоит из двух обмо-
ток статора и ротора с постоянным магнитом.
Ротор по форме похож на шестерню, зубья ко-
торой стремятся выровняться с одной или дру-
гой слегка смещенной обмоткой, в зависимости
от протекания тока в обмотках. Протекающий в
этих обмотках постоянный ток удерживает ро-
тор в фиксированном положении. Изменение
протекания тока на обратное в любой из обмо-
ток перемещает ротор на один шаг по часовой
стрелке или против нее.
Примечание
Ротор шагового электродвигателя с низким разре-
шением за один шаг может провернуться на десят-
ки градусов, тогда как для двигателя с умеренно
высоким разрешением проворачивается на 1,875°,
что составляет 200 шагов на один оборот.
Последовательность изменения направления
протекания тока (так называемый код Грея)
определяет направление вращения30. На рис.
26N.32 сигналы на обмотках А и В обозначены
как D1 и D2.
Микросхемы драйверов шаговых
двигателей
Микросхемы драйверов шаговых двигателей
делают задачу управления такими двигателями
очень легкой. Подобная микросхема обычно
представляет собой просто двунаправленный
счетчик/сдвиговый регистр, способный вы-
давать и поглощать намного большие токи,
чем обычные логические элементы. Более
«продвинутые» микросхемы, такие как, на-
пример, микросхема A3967SLB31 компании
Allegro Microsystems, обладают возможностью
управления с более высоким разрешением: так
30 На веб-сайте http://www.pcbheaven.com/wikipages/
HowStepperMotorsWork можно найти полезное учеб-
ное пособие, объясняющее принцип работы шаговых дви-
гателей, сопровождаемое анимационной иллюстрацией.
31 Компания SparkFun предоставляет эту микросхему для
поверхностного монтажа на удобной адаптерной плате под
названием EasyDriver Stepper Motor Driver, артикул номер
ROB-10267.
1102
26N. Потенциальные проекты. Игрушки на любой вкус
называемыми микрошагами32. Данная микро-
схема драйвера поддерживает точность в 1/8
шага. Эта микросхема также содержит драй-
верные транзисторы, токовые возможности
которых больше, чем можно было бы ожидать
от скромной микросхемы с 20 выводами: до
750 мА при напряжении до 30 В (хотя не оба
эти параметра одновременно). Хотя этого не-
достаточно для управления мощным шаговым
двигателем, такие токовые характеристики,
действительно, впечатляют.
Подобные драйверы понижают нагрузку на
микроконтроллер в области определения на-
правления вращения и частоты шагов (перепад
сигнала на выводе микросхемы запускает один
шаг).
Микроконтроллер может управлять
шаговым двигателем
Но для управления шаговым двигателем не
обязательно использовать микросхему драй-
вера, поскольку эту задачу можно выполнить
Обмотка
электродвигателя
с помощью микроконтроллера и нескольких
силовых транзисторов. В качестве таких тран-
зисторов можно использовать силовые МОП-
транзисторы. Например, подойдут транзи-
сторы IRLZ34 (55 В, 30 А макс), с которыми
мы работали на лабораторном занятии 12L33.
Схема подключения микроконтроллера и тран-
зисторов к шаговому двигателю показана на
рис. 26N.3.
Микросхемы драйверов шаговых двигателей
обычно также обеспечивают ограничение тока.
Схема нашего самодельного драйвера такого
ограничения не предоставляет, поэтому следует
поддерживать умеренное напряжение питания,
чтобы не перегреть двигатель. При этом двига-
тель может нагреваться до некоторой степени
без вредных последствий.
Одним из способов создания последовательных
комбинаций для управления шаговым двигате-
лем будет циклический сдвиг загруженного в
регистр значения путем подачи сигналов двух
смежных битов на драйвер управления обмот-
ками двигателя (рис. 26N.32).
От 5 до 12 В. Используйте внешний
V* источник питания, а не встроенный
| в макетную плату
j
Обмотка В
Выход 2
Рис. 26N.31. Схема драйвера шагового двигателя
32 Микрошаговый режим шагового двигателя (величина
дробления которого может достигать 1/256 шага) реализу-
ется, подавая на обе обмотки двигателя плавно изменяю-
щиеся разные по величине токи. Но за такое повышение
разрешения приходится расплачиваться резким падением
крутящего момента, поэтому не следует полагаться на ми-
крошаговый режим для получения чрезвычайно высоко-
го разрешения. Более подробную информацию по этому
вопросу можно найти на веб-сайте http://www.micromo.
com/microstepping-myths-and-realities.
33 Демпфирующие диоды, показанные в схеме на рис.
26N.31, предназначены для защиты транзисторов от
всплесков напряжения, возникающих при их выключе-
нии. Это должны быть мощные диоды, например Ш400х
(где х обозначает максимальное обратное напряжение, ко-
торое в данной схеме не является критичным). Диоды для
слабых сигналов, такие как наши обычные диоды 1N914,
здесь не подойдут.
26N.8. Идеи для проектов
1103
Г
По часовой стрелке Против часовой стрелки
Двухбитовое
число:
231023 13ZO132
Циклический
Циклический сдвиг
значения регистра:
\ 4 Ч Выходной
J сигнал
Циичесий
иг /^?*~ сдвиг —*рч
а: i 1 V 1 1 ° ° 1
Рис. 26N.32. Последовательность двухбитовых комбинаций
для управления шаговым двигателем можно создать с помо-
щью циклически сдвигаемого регистра
Применение шагового двигателя
Задачу придумать, как применить шаговый
двигатель, мы оставим на ваше усмотрение. Но
чтобы дать вам определенную идею, далее при-
водятся два примера, придуманных нашими
студентами.
Подъемный кран
На валы двух шаговых двигателей, установлен-
ных на краю стола, установлен шкив с отрез-
ком шнура. Концы шнуров обоих двигателей
соединены вместе, и к ним прикреплен груз.
Работая совместно, оба двигателя могут подни-
мать, перемещать или опускать груз. Эту схему
легко реализовать для простых операций, но
будет трудно для таких операций, как, напри-
мер, поднять груз вертикально, затем переме-
стить его горизонтально, а затем снова поднять
вертикально. Можно использовать небольшой
электромагнит для подъема небольших грузов
(например, гаек или шайб). Такой электромаг-
нит легко соорудить, намотав изолированный
провод на обычный железный болт. Один из
наших студентов, Дилан Джоунз (Dylan Jones),
изготовил такой электромагнит, установил его
на лебедку, приводимую в действие шаговым
двигателем, а затем закрепил всю эту конструк-
цию на мобильном шасси, подобном описанно-
му в разделе 26N.4.10.
Машина для рисования
Как упоминалось в разделе 26N.33, два шаго-
вых двигателя могут вращать ручки осей X и У
детской игрушки для рисования.
26N.8. Идеи для проектов
26N.8.1 Оригинальные новые
и неиспытанные идеи для вашего
вдохновения
Распознавание речи
Определенно будет неразумным с вашей сто-
роны применить к этой задаче стандартный
полноценный подход: преобразовывать в ча-
стотную область, а затем сравнивать с шабло-
ном. Это сложная программная задача, кото-
рая плохо подходит для нашего самодельного
компьютера и других наших инструментов.
(Но обратите внимание на простую уловку,
Обмотка Ах\
V На
_. о / Драйверы
Обмотка Вх / г
Волшебный экран
Обмотка Ау
Обмотка By
Двигатель X
Двигатель У
Выход У
Рис. 26N.33. Два шаговых двигателя могут приводить в действие игрушку «Волшебный экран»
ПРИМЕР МАКРО:
Диагональ: юго-восток
I
Хпо часовой стрелке
1
/против часовой
стрелки
I
ВОЗВРАТ
1104
26N. Потенциальные проекты. Игрушки на любой вкус
предлагаемую в конце раздела 26N.6.6 в под-
разделе Распознавание речи: использовать го-
товую микросхему, выполняющую всю тяже-
лую работу.) Мы хотим предложить быстрый и
простой метод, пусть и не обязательно самый
результативный.
Одной из стратегий может быть метод, исполь-
зуемый в старой микросхеме компании Radio
Shack, которая могла различать слова «Стоп» и
«Идти» для управления игрушками. Он заклю-
чается в простом обнаружении пресечения ну-
левого уровня, или, иными словами, нахожде-
ния доминирующей частоты. Такой способ мо-
жет, например, определять звук «Сссс» в слове
«Стоп». Подсчитываем пресечения нулевого
уровня аппаратно или программно и сверяемся
с несколькими эталонными точками диапазо-
на: 5 кГц = «Сссс» и т. д.
Более продвинутый способ — использовать
высокочастотный и низкочастотный фильтры
с крутыми характеристиками, которые немного
накладываются друг на друга, и сверять ампли-
туды (которые, наверное, следует усреднять по
времени) выше и ниже этой частотной грани-
цы. В Лабораториях Белла экспериментирова-
ли с этим методом в начале 1950-х гг., с грани-
цей, равной приблизительно 900 Гц, и обнару-
жили, что можно достаточно хорошо различать
10 цифр.
Шифрование аудиоданных
Идею простого шифрования речи мы обнару-
жили в одном из отраслевых журналов. Суть ее
состоит в инвертировании спектра речи.
Для этого нужно нарушить правило Найквиста:
умножить речевой сигнал (в цифровом форма-
те) на прямоугольный сигнал с частотой чуть
большей, чем самая высокая частота входного
сигнала. В результате по причине наложения
спектров получится инвертированный частот-
ный спектр. Дешифрование выполняется умно-
жением на такую же самую частоту. Вообще то,
«умножение» является более простой операци-
ей, чем она звучит: просто инвертируем самый
старший бит данных на частоте умножения
(подаем 1, затем 0, затем 1 и т. д. на один вход
элемента ИСКЛ-ИЛИ, на другой вход которо-
го подается старший бит данных). То же самое
можно выполнить с помощью аналоговых ме-
тодов.
Музыкальные эффекты типа хора и т. п.
Вспомним фазовращетель, с которым мы ра-
ботали на лабораторном занятии 7L. Это
устройство может изменять фазу сигнала, ме-
няя значение сопротивления подключенного
к «земле»34. С помощью цифрового потенцио-
метра, с которым мы работали на лаборатор-
ном занятии 24L, можно создать фазовраща-
тель, управляемый компьютером.
Альтернативный способ получить такой же ре-
зультат — использовать перемножающий ЦАП,
который можно описать как аттенюатор с циф-
ровым управлением, выходной сигнал которого
является произведением входных аналогового
и цифрового сигналов.
В принципе, совместив любую их этих схем
фазовращателя с суммирующей схемой, мож-
но получить генератор интересных эффектов
рок-н-ролла, несколько напоминающих эф-
фекты, упоминаемые в главе 7L. Примеры та-
ких звуков можно прослушать на веб-странице
http://www.harmony-central,com/Effects.
Этот веб-сайт также содержит схемы и полез-
ные ссылки.
26N.9. Две потенциально
полезные программы:
драйвер ЖКД и сканер
цифровой клавиатуры
Эти аппаратные интерфейсы рассматривают-
ся в главе 24N. Если вы захотите использовать
их в своем проекте, программный код для их
реализации можно загрузить на веб-сайте этой
книги.
26N.10. Множество других
примеров в книге АоЕ
Мы предложили лишь несколько возможных
периферийных устройств для совместной рабо-
ты с микроконтроллером35. В книге АоЕ можно
найти множество других примеров.
34 Это была вторая из двух рассмотренных схем фазо-
вращателей.
35 АоЕ § 15.8.
26Ш1. А теперь вперед, к новым приключениям
1105
26N.11. А теперь вперед,
к новым приключениям
Мы надеемся, что завершение изучения мате-
риала этой книги подвигнет вас на создание
какого-либо проекта. Но нашей более глубо-
кой надеждой для этого курса является то, что
полученные здесь знания по электронике вы
будете использовать во множестве разных си-
туаций. Мы также надеемся, что электроника
будет оставаться для вас интригующим и при-
носящим удовольствие занятием. Покупатель
на рис. 26N.34 немного отступает от нашего
идеала: мы не хотим, чтобы создаваемые вами
устройства были бесполезными. Но мы вос-
хищаемся его энтузиазмом. Наверное, все мы,
кто помешан на электронике, храним на пол-
ках какие-либо штуковины, наподобие той,
которую он покупает, — классные вещи, кото-
рые нам просто необходимо иметь.
Рис. 26N.34. Образец энтузиазма для электроники
ПРИЛОЖЕНИЯ
Приложение А. Язык HDL Verilog
Как вы, возможно, знаете по своему опыту ра-
боты с другими языками программирования,
для них существует множество усовершенство-
ваний, а выбор дополнений может быть весьма
обширным1. Но наша цель в этом курсе скром-
ная: просто дать вам возможность испробовать
некоторые возможности языка HDL Verilog и
микросхем PLD, для программирования кото-
рых он применяется. Впоследствии, когда вы
будете разрабатывать более амбициозные про-
екты, вы, несомненно, захотите приобрести не-
сколько справочных пособий по языку Verilog
и изучить все его богатые возможности2.
АЛ. Проектный файл Verilog
Файл Verilog использует некоторые жесткие ко-
довые конструкции, которые лучше показать,
нежели обсуждать. Пример содержимого фай-
ла Verilog показан на рис. А.1. Мы предполага-
ем, что при создании своей первой программы
вы просто скопируете код (который в первых
примерах мы предоставляем почти в полном
объеме) в свой файл, чтобы не морочиться
с соблюдением требований для его создания,
а просто добавив собственный фрагмент: урав-
нения, описывающие логику, которую вы наме-
реваетесь создать. На рис. А.1 приводится пер-
вый пример такого файла, который реализует
двухвходовый логический элемент И и двух-
входовый логический элемент ИЛИ3.
1 АоЕ § 11.3.4В.
2 Можем посоветовать вам две следующих книги в этой
области:]. Bhasker «VerilogHDL Synthesis» (1988), чрезвы-
чайно немногословное пособие, содержащее очень краткое
обсуждение, но, по крайней мере, по одному примеру для
каждой рассматриваемой темы; S. Palnitkar «Verilog HDL»
(2003), более обширное пособие, хотя содержащее мень-
шее количество примеров, но при этом с более подробным
обсуждением примеров.
3 Этот код создан в среде разработки Xilinx ISE 11.1. Фор-
мат слегка меняется с каждым последующим обновлением
среды. Последняя версия среды разработки Design Suite —
14.7. Следующих версий этой среды разработки больше
не будет, поскольку компания Xilinx переходит на среду
module and_or(
input x1,
input x2,
output and2,.
output or2
assign and2 = х1 & х2;
assign or2 = х11 x2; ^
endmoduie
- Перечисляем все входы..
.... и выходы
Данная секция что-то делает:
- ее уравнения сопоставляют
выходы входам
Рис. А.1. Исходный файл программы на Verilog для реализа-
ции функций И и ИЛИ
Код файла состоит из следующих элементов:
♦ ключевое слово module;
♦ за ним следует название файла4: and_or;
♦ далее, в следующих строках идет список
входных и выходных переменных: х1, х2,
and2, or2;
♦ строка кода модуля завершается точкой с за-
пятой; так требуется завершать большинство
строк кода.
Все эти сигналы принадлежат к типу по умол-
чанию — wire (проводник). Но вскоре (в раз-
деле A3) мы познакомимся с другим важным
типом — reg (регистр).
После объявления переменных можно при-
ступать к настоящей работе, которая выпол-
няется двумя строками кода assign. Ключевое
слово assign определяет логическую связь вы-
хода (например, and2) с соответствующими
входами (в данном случае х1 и х2). Символ &
означает операцию И, а символ | — операцию
ИЛИ. Ключевое слово assign уместно для ис-
пользования с комбинационной логикой (хотя
доступны и другие методы). Вскоре мы увидим,
что для разработки последовательностных
разработки Vivado. Но эта среда разработки не поддержи-
вает более ранние устройства FPGA, чем седьмая версия
(Series 7).
4 Это формат файла для наших простых проектов. Но
файл может содержать несколько модулей.
1110
Приложение А. Язык HDL Verilog
х1
and2
: Х2 _-Г ОТ?
Выберите требуемый выход, а затем
ог2
or2jmp_or21
- {добавление входной воронки
нажмите кнопку Add Input Cone
(добавить входную воронку)
отображает логику, которая создает
выход ог2)
Выберите выход, для которого вы хотите Добавление входной воронки (кнопка Add Input Cone) отобразит
просмотреть логику только ту логику, которая создает данный выходной сигнал
Рис. А.2. Выбор сигнала для отображения на схеме
схем лучше выбрать другие директивы. После
компиляции проекта среда разработки Xilinx
ISE создаст результирующую схему. В среде
разработки ISE 12 можно задать по умолча-
нию опцию, чтобы отображать схему верхнего
уровня. Мы рекомендуем воспользоваться этой
возможностью.
В небольшом проекте необходимость всегда
указывать интересующие сигналы может быть
излишней. Но в сложном проекте полезно
иметь возможность просмотреть среди множе-
ства цепей только ту цепь, которая дает один
или небольшое количество выходных сигна-
лов. Далее описывается процесс, который по-
зволяет указать, какие сигналы необходимо
отображать в схеме.
♦ Сначала выбираем и добавляем порты высо-
кого уровня.
♦ Затем отображаются сами сигналы, как пока-
зано на рис. А.2, но не связывающая логика.
Затем можно щелкнуть по требуемому выводу,
чтобы увидеть «воронку» (рис. А.З), которая
отображает всю логику, создающую данный
выходной сигнал (это единственный способ по-
лучения схемы).
ч- __ Используя инструмент выделения,
укажите оба входа.
х1
х2
3iid2
0Г2
Затем щелкните по кнопке Add Output Cone
(добавить выходную воронку), чтобы отобразить все
элементы, на которые воздействуют входы xl и х2
Рис. А.З. Отображение логической схемы, создающей опре-
деленное выходное состояние
Созданная средой ISE схема (рис. А.4) не содер-
жит никаких сюрпризов, но все-таки убеждение
в том, что схема выглядит правильно, добавляет
уверенности в способности этой среды.
and2
|Х2>-
- and2>
and2jmp_and21
or2jmp_or21
Рис. А.4. Схема, созданная в результате компилирования ис-
ходного файла Verilog: то, что и ожидалось
А.2. Созданная Verilog схема
может пригодиться при
отладке
Иметь перед собой наглядную схему полезно
не только для начинающих разработчиков, но
и для любого другого, чтобы быстро оценить,
скомпилировался ли проект должным обра-
зом. Это относится и к тем случаям, когда про-
ект далеко не простой. Среда разработки ISE
позволяет исследовать только ту составляю-
щую логической схемы, которая создает опре-
деленную часть выходного состояния сложно-
го проекта. В проекте, содержащем большое
количество выходов, можно выделить так
называемую входную воронку (input cone),
для определенного выхода, чтобы выделить
все элементы, воздействующие на данный
выход.
Например, в приложении Б показывается, как
выделение логики, связанной с одним выходом,
может укротить сбивающую с толку путаницу
логических связей. В приведенном там приме-
ре используется микросхема ПМЛ, создающая
большое количество выходов связывающей ло-
гики GLUEPAL, которая помогает реализовать
компьютер из дискретных компонентов.
A3. Эмуляционный файл Verilog testbench
1111
A3. Эмуляционный файл
Verilog testbench
После создания файла проекта Verilog обычно
возникает желание выполнить его эмуляцию,
чтобы проверить, работает ли проект, как ожи-
дается. В этом курсе мы эмулируем все наши
проекты. Но мы можем позволить себе это по
причине простоты наших разработок. В ре-
альных ситуациях существуют веские причи-
ны не выполнять эмуляцию проекта целиком.
Некоторые разработчики сложных схем для
микросхем FPGA считают, что быстрее просто
загрузить разработку в устройство и проверить
ее работоспособность. Такой метод называется
«прожигание и сбой», но такое умаляющее на-
звание метода не всегда соответствует действи-
тельности.
Эмуляционные файлы трудно создавать, и для
сложных проектов они не могут быть всеохва-
тывающими: проверить каждую возможную
ситуацию практически невозможно. Это осо-
бенно касается разработок последовательност-
ной логики. Файл эмуляции Verilog называется
testbench5 и представляет собой текстовый файл,
в котором описывается функционирование
разработки. Для нашей разработки логических
элементов И и ИЛИ эмуляция вряд ли требует-
ся, но чрезвычайная простота этой разработки
позволит легко разобраться со структурой фай-
ла testbench.
Файл эмуляции testbench начинается, как и
файл разработки, с перечисления входных
и выходных переменных и указания их типа:
wire или гед. В случае, если вы думаете, что на-
чинаете понимать разницу между типами wire и
гед, обратите внимание на то, что в файле эму-
ляции входные переменные всегда имеют тип
гед, а выходные — wire. Различие между этими
типами трудно определить. Тип гед имеет неко-
торое отношение к соответствующему аппарат-
ному элементу «регистр», но только очень от-
даленное. Переменная типа гед имеет значение,
которое «остается в памяти... до тех пор, пока не
будет изменено последующим присвоением»6.
Это звучит, как будто набор триггеров, но ни
в коем случае не является таковым и даже не
подразумевает использование триггеров. На
рис. А.5 показано содержимое файла testbench
для проработки логики проекта И-ИЛИ.
Результаты эмуляции
Результат эмуляции показан на рис. А.6, и вы-
глядит он так, как и ожидалось. Выход ИЛИ вы-
глядит как результат операции ИЛИ на входах
// Inputs
Название общего блока логики, к которому мы
сейчас прикрепляем сигналы
Названия сигнала в данном конкретном случае
Название сигнала в логическом блоке
// display variables as
initial
xa binary toe»
-Уровни, присвоенные данным входным
сигнала в данное время (начало отсчета)
// «ait 100 й« tot aiobal reset to tini»H
// #190; // we won't do Un», because it mke» %h» display clu»»y
// JUW stimulus h*r«
x2 » 0; xl • 1; it *itec a delajp of 10 ti»e unite, apply n&tr iaj>\jt levels
#10 xa • i? xt • 0;
Задержка относительно*^ ^^4*;.хг *1;
предыдущей строки кода
Рис А.5. Содержимое файла эмуляции testbench на языке Verilog
Строго говоря, в Verilog такие файлы называются Test x1 И х2, а ВЫХОД И - как результат операции И
р р
Fixture. Слово testbeenh является жаргоном языка VHDL,
но мы употребляем его, поскольку данный термин чаще
встречается, чем термин test fixture, особенно в литературе
компании Xilinx.
на этих входахч
6 См. с. 77 книгиJ. Cavanagh «VerilogHDL» (2007).
7 Средство эмуляции в версиях 11 и 12 среды ISE имеет
1112
Приложение А. Язык HDL Verilog
m л!
Vie. Ы2
шшшш
0
0
0
о
i p OCO ps
1
j
1
i j
ijoccops
i
1
115 OOD ps
pO 000 P5
125 teO ps
1
j
1
30 C'DO p5
1
Рис. А.б. Выходные сигналы, полученные в результате исполнения файла эмуляции Verilog
Создание экземпляра
Некоторые элементы файла эмуляции testbench
требуют объяснения. Одним из таких элемен-
тов является блок создания экземпляра (ли-
стинг А.1).
Листинг А.1. Блок создания экземпляра
// Instantiate the Unit Under Test (UUT)
// Создаем экземпляр испытываемого устройства
and_or uut (
jc2(x2),
.and2(and2),
.or2(or2)
);
endmodule
Необычный термин «создание экземпляра»
(англ. instantiation) обозначает не такое уж и
странное понятие. Это просто процесс исполь-
зования определенного логического блока
(в данном случае это блок, предоставляющий
логические элементы И и ИЛИ) для обработ-
ки сигналов в конкретном экземпляре. Данный
термин был выбран, чтобы показать переход от
высокого уровня абстракции проекта к «экзем-
пляру», который превращает проект в реаль-
ность.
Фрагмент кода (.and2(and2)) в блоке создания
экземпляра показывает, что происходит в дан-
ном случае: обычная операция связи конкрет-
ного названия в этом экземпляре (and2) с на-
званием переменной, выходящей из логическо-
го блока (.and2).
Но тот факт, что эти две переменные имеют
почти одинаковое название — одно из блока
проекта, а другое из конкретного экземпля-
ра, — скрывает то обстоятельство, что они пред-
ставляют совершенно разные, независимые
понятия. Чтобы подчеркнуть важность этого,
мы создали другой файл эмуляции, используя
«глупые» названия сигналов. На рис. А.7 по-
казан эскиз, с помощью которого мы пытаем-
ся подчеркнуть тот факт, что когда логический
блок and_or вызывается конкретным процес-
and2
ог2
Элемент логики, описываемый
файлом и2_или 2.v
and2
ог2
и мэри
ИЛИ ЛЮСИ
Сигналы, которые файл
эмуляции применяет к тем \
общим входным переменным, \
доказанным в прямоугольникеЗ
/Мы могли бы присвоить этой
/ переменной любое название,
I связывающее ее в данном i
Экземпляре с общей переменнойи2^
Рис. А.7. Иллюстрация создания экземпляра: в конкретном экземпляре сигналам основного логического блока можно при-
сваивать любые названия
досадный недостаток: на первый взгляд выглядит, как буд-
то бы ничего не было сделано, поскольку отображаются
постоянные уровни. Это объясняется тем, что среда ISE
отображает сигналы с максимальным увеличением и уста-
навливает курсор с правого края окна. Чтобы получить
разборчивое представление сигналов, нужно щелкнуть по
значку Zoom to Full View (Масштабировать для отобра-
жения полного представления), который в нашей версии
среды ISE выглядит, как спасательный круг.
сом использования или создания экземпляра,
его входным и выходным сигналам можно при-
сваивать любые желаемые названия.
В листинге А.2 приводится список сигналов и
раздел создания экземпляра с использованием
забавных названий.
A3. Эмуляционный файл Verilog testbench
1113
// Входные сигналы
reg harry;
reg bill;
// Выходные сигналы
wire and тагу;
wire ormaude;
// Instantiate the Unit Under Test (UUT)
// Создаем экземпляр испытываемого устройства
and_or uut (
.x1 (harry),
.and2(andmary),
.or2(ormaude)
Этот файл эмуляции работает точно так же, как
и первый. Результаты эмуляции, показанные
на рис. А.8, точно такие же, за исключением за-
бавных названий сигналов.
// Отображаем любые изменения в перечисленных пере-
менных в двоичной форме
Ключевое слово initial означает, что операция
выполняется только один раз. А оператор $то-
nitor отображает перечисленные сигналы при
любом их изменении. Символы %Ь означают,
что задан двоичный числовой формат. А сим-
волы \t вставляют табуляцию, чтобы таблицу
было легче читать. Если вам понятны результа-
ты эмуляции в виде временной диаграммы, то
можете не заморачиваться с представлением в
виде таблицы.
Входные значения управляющего
воздействия и времена задержки
В центральной части кода эмуляции мы подаем
на схему проекта управляющее воздействие в
виде указанных уровней входных переменных
(листинг A3).
i Cyrrent Simulition
• Time: 2000 ns
I «40 stficlrrtaiy
!
1
h _ >
0
Q
0
3
<
_1
20
j
Ill^llllll
■ 40
_=_J
■■~T__
0 m
jv] and2_<M2_nemedJb.v ■'• [j and2_or2.rpl
Finished circuit initialization process.
1<
arry
и*
0,0
0,1
1, О
1,1
Simutalion
andrnarf = О, orroaude = О
andrnary ~ 0/ огшшйе = 1
arnUmar^ - 0, orraaucie - 1
= lf ocrnaucie ~ 1
- О,, о г Maude = О
Рис. А.8. Результаты эмуляции такие же, как и для сигналов экземпляра с забавными названиями
Отображение результатов в виде таблицы
В отличие от автоматически выводимого ком-
пилятором Xilinx графического отображения
сигналов, отображение в текстовом виде воз-
можно благодаря следующему коду:
// Отображаем переменные в текстовом виде
initial
$monitor(«x1# х2 = %b,%b, \t and2=%b, \t or2 =%b», x1, x2, and2, or2);
Листинг А.З. Реализация управляющего
воздействия
initial begin
// Инициализируем входы
х1 = 0;
х2 = 0;
// Ждем 100 не для завершения глобального сброса
#100; // Мы не будем делать этого, поскольку
// в результате возникнут проблемы с дисплеем
1114
Приложение А. Язык HDL Verilog
II Добавляем здесь управляющее воздействие
#10 х2 = 0; х1 = 1; // После задержки длительностью
// в 10 временных единиц применяем новые входные
//уровни
#10х2 = 1;х1=0;
#10x2 = 1;х1 = 1;
#10$finish;
end
Значения #10 означают, что нужно выдержать
паузу длительностью в десять временных
единиц, прежде чем применять следующие за
лими входные урони. Длительность самой вре-
менной единицы определяет файл эмуляции.
Примечание
Обычно эта длительность имеет порядок наносе-
кунд, но для настоящего случая это не имеет зна-
чения, поскольку нас интересуют только выход-
ные состояния без учета тактирования.
Таким образом, показанный в листинге А.З на-
бор управляющих воздействий меняется каж-
дые 10 не. Эти временные задержки содержатся
в графическом отображении результатов эму-
ляции, как на рис. А.8. Наконец, ключевое сло-
во initial в начале блока опять означает, что он
исполняется только один раз при запуске.
АА Проверочный файл
эмуляции
Хорошо потрудившись, можно создать файл
эмуляции, предсказывающий результаты для
каждой функции и сравнивающий эти предска-
занные значения с действительными значения-
ми проектируемой схемы. Мы создали такой
файл для проекта схемы устройства GLUEPAL,
которое связывает микроконтроллер с его пе-
риферийными устройствами в компьютере из
дискретных компонентов. В листинге А.4 при-
водится отрывок из файла эмуляции: таблица
истинности и задача или функция, ссылающая-
ся на нее.
Листинг А.4. Фрагмент файла эмуляции
// В таблицах истинности перечисляются ожидаемые
// выходные состояния (в правом столбце)
// и вызываются определенные функции
// (называемые Task — задача) для сравнения
// предсказанного значения
// с результатом логических операций в исходном файле
//Таблица истинности для CTR__OE_bar: f(br, loader)
check_CTR_OE_bar(0,0, 1);
check_CTR__OE_bar(0,1 ,0);
checkJITR__0E_bar(1,0,1);
checkJZTR_0E_bar(1,1,1);
// Набор задач (tasks) или функций, вызываемый
//таблицами истинности
task check_CTR_OE_bar;
input i_BR_bar;
input i_LOADER_bar;
input expect_CTR_OE_bar;
begin
#25; BRJ>ar = LBR_bar; LOADER_bar = LLOADER_bar;
#25;
if (CTRJDE.bar !== expect_CTR_OE_bar)
begin
$display(«\t CTR_OE_bar ERROR: at time=°/odns \t INPUTS:
BR_bar=%b, LOADER_bar=%b,
\t OUTPUT: CTR_OEJ>ar=%b, \t expected=%b», $time,
BR_bar,LOADER_bar,
CTR_OE_bar, expect_CTR_OE_bar);
errors = errors +1;
end
end
endtask
Мы не будем пытаться дать полное объяснение
этой схеме, а удовлетворимся следующим на-
броском: таблица истинности для CTR_OE_bar
содержит два входных уровня и ожидаемый
выходной уровень. Задача с названием check_
CTR_OE_bar проверяет наличие несовпадения
между предсказанным таблицей истинности
состоянием выхода и значением, в действи-
тельности создаваемым функцией CTR_OE_bar.
Любое несовпадение, когда действительное и
предсказанное значения отличаются друг от
друга:
CTR_OE_bar !== expect_CTR_OE_bar
вызывает вывод подробного описания несов-
падения: что ожидалось и что было получено:
if (CTRJDE_bar !== expect_CTR_OE_bar)
begin
$display(
AS Триггеры в Verilog
1115
Данная возможность проверки будет для нас
полезной в этом курсе. Например, когда мы
дадим задание студентам разработать схе-
му связывающей логики GLUEPAL, эмуляция
разработанной схемы предупредит студента о
каждом случае, когда она не дает ожидаемый
результат.
Сложный файл эмуляции трудно
использовать без флагов ошибок
На рис. А.9 показан результат моделирования
схемы связывающей логики GLUEPAL: набор
сигналов, по которым трудно определить, есть
ли в схеме какие-либо ошибки или нет.
Но наш файл эмуляции содержит возможность
самопроверки, которая выводит на экран одну
функцию, результаты исполнения которой не
совпали с ожидаемыми. Это сообщение по-
казано внизу на рис. А.9, но слишком мелким
шрифтом, который невозможно прочитать. На
рис. А.10 это сообщение показано в более удо-
бочитаемой форме.
А.5. Триггеры в Verilog
Проверка изменения указанной
переменной
В разделе АЛ мы реализовали комбинацион-
ную задачу (И и ИЛИ), используя для этого
ключевое слово assign. При разработке по-
следовательностных схем, в которых присут-
ствуют триггеры, полезно другое ключевое
слово:
always@(nEPEMEHHAfl)
Это ключевое слово дает указание компилято-
ру выполнять проверку на изменение значения
переменной ПЕРЕМЕННАЯ и при наличии изме-
нения исполнять код, следующий за этой стро-
кой. Это ключевое слово можно использовать
также и для разработки комбинационных схем,
но для разработки схем на триггерах, активи-
руемых перепадом, требуется его другая, спе-
циальная форма.
Рис. А.9. Определить наличие логических ошибок по одним сигналам результата эмуляции схемы может оказаться трудной
задачей
CSim>
# run all
lSim>
CTRjOE_bar ERROR: at time*
CTRJDE J>ar ERROR: at time«
Sim faied with 2 errors
1120ns INPUTS: BRJ>ar*Q^ADERJ>ar«l,
1220ns INPUTS: BRjttr»!, LOADERj>ar»t,
OUTPUT: CTRjC€jbar«l,
OUTPUT: CTR J)Ej>ar»Q,
expected»Q
expected»!
Рис. А.10. Проверочный файл эмуляции находит функцию, результаты эмуляции которой (показанные на рис. А.9) не совпали
с предсказанными
1116
Приложение А. Язык HDL Verilog
Проверка изменения значения
переменной по положительному
перепаду
Для такой проверки применяется следующая
конструкция:
always@(posedge ПЕРЕМЕННАЯ)
В данном случае проверка выполняется на из-
менение значения переменной по положитель-
ному перепаду. Для отрицательного перепада
указывается параметр negedge. Мы вскоре
будем иметь дело с осложнением, состоящим
в том, что эта конструкция может указывать
поведение, чувствительное или к перепаду, или
к уровню. Конкретное поведение, применяемое
к отдельной переменной, определяется поряд-
ком переменных в списке.
В качестве нашего первого примера рассмотрим
настолько простую последовательностную схе-
му, насколько возможно: один D-триггер с
асинхронным сбросом. По положительному
перепаду сигнала тактирования переменной q
присваивается значение d; если активирован
сигнал reset_bar (низкий уровень), перемен-
ной q присваивается значение 0 (несмотря на
ключевое слово negedge далее в тексте про-
граммы, это представляет собой асинхронный
сброс). Применение Verilog для создания этой
крошечной схемы, одного D-триггера, можно
сравнить со стрельбой из пушки по воробьям,
но для простого начального примера можно
позволить себе такое расточительство (ли-
стинг А.5).
Листинг А.5. Пример программы, реализующей
D-триггер
module flop(d, clock, reset_bar, q);
input d;
input clock;
input reset_bar;
output q;
wire d,clock,reset_bar;
reg q;
always @(negedge reset_bar or posedge clock)
if (!reset_bar) // Использование скобок обязательно.
(Кстати, несмотря на ключевое слово negedge, это асин-
хронный сброс.)
q<=0;
else
q <= d;
endmodule
Даже эта простая разработка требует некото-
рых новых конструкций Verilog. В частности,
следующих:
♦ Тип гед для выходных сигналов требуется
вместе с конструкцией always®. (Для дру-
гих сигналов мы указали тип wire, но делать
так было необязательно, поскольку это тип
по умолчанию, чем мы и воспользовались в
примере И-ИЛИ в разделе АЛ.) В разделе A3
мы отметили, что гед не означает аппарат-
ный регистр или триггер, а то, что сигнал со-
храняет свое значение до тех пор, пока оно
не будет изменено.
♦ Символ =, который указан вместе с ключе-
вым словом assign, после выражения always©
(posedge...) нужно заменить комбинацией
символов <= (которые означают неблокиру-
ющее присваивание). Это, казалось бы, не-
значительное изменение в действительности
очень важное и довольно мудреное. В разде-
ле А.13 мы рассмотрим более подробно раз-
ницу между блокирующим и неблокирую-
щим присваиваниями. Но это тонкое раз-
личие можно игнорировать, если следовать
правилу, что неблокирующее присваивание
<= используется для триггеров8.
♦ Конструкция if...else. Следующая за этим
выражением строка кода исполняется при
удовлетворении условия if; в противном слу-
чае исполнение переходит к части else. (До-
пускаются вложенные выражения if...else.)
♦ Чувствительные к перепаду или к уровню
входы. Это очень тонкий и трудный для по-
нимания момент.
• вход clock чувствительный к перепаду;
• вход reset_bar чувствительный к уровню
(несмотря на ключевое слово negedge).
8 Если вам необходимо точно знать разницу между не-
блокирующим (<=) и блокирующим присваиванием, то
в общих чертах блокирующие конструкции исполняются
последовательно (как в обычной компьютерной програм-
ме), тогда как неблокирующие конструкции исполняются
параллельно, все в указанное время. В нашем примере
этот означает «если уровень сигнала тактирования меня-
ется на высокий или уровень сигнала reset.bar меняется
на низкий». Использование блокирующего присваивания
после конструкции always @ (posedge...) разрешается, но не
рекомендуется по причине потенциальных проблем с так-
тированием. См. с. 68 ранее цитируемой книги J. Bhasker
«VerilogHDL Synthesis» (1988).
AS Триггеры в Verilog
1117
Изо всех сигналов, перечисленных в операто-
рах if... else... else, только последний обраба-
тывается как чувствительный к перепаду и как
событие тактирования9; все остальные сигналы
чувствительные к уровню
10
Показанная на рис. А.11 схема реализации
только что описанного триггера, созданная
Verilog, подтверждает, что по настоящему чув-
ствительным к перепаду является только вход
тактирования.
JME/
FDC
Рис. А.11. Созданная Verilog схема подтверждает, что пере-
падом активируется только вход тактирования
И конечно же, результат эмуляции соответст-
вует созданной Verilog схеме: сброс выполня-
ется в асинхронном режиме, когда выход Qo6-
нуляется сразу же при активировании сигнала
сброса reset*, не дожидаясь перепада сигнала
тактирования (рис. А.12).
ключевого слова always@(...) содержится лишь
переменная сигнала тактирования clock, чтобы
только этот сигнал мог вызывать изменение
состояния схемы. Соответствующий код про-
граммы приведен в листинге А.6.
Листинг А.6. Пример программы, реализующей
триггер с синхронным сбросом
module flop(d, clock, reset_bar, q);
input d;
input clock;
input reset_bar;
output q;
wire d,clock,reset_bar;
reg q = 0; // Указание уровня инициализирует
// выходной уровень триггера для эмуляции
always @(posedge clock)
if (!reset_bar) // Этот сброс синхронный:
// он не применяется до тех пор, пока не будет
// положительного перепада сигнала тактирования
q<=0;
else
q <= d;
endmodule
Current Simulation
Time: 140 us
Sflclk
58 reset
Начальные состояния
входов определяются
здесь
Состояние выхода (С?)
определяется здесь
L
Активирование сигнала сброса reset* устанавливает на
выходе Q низкий уровень (очевидно, что сброс выполняется
асинхронно), не ожидая перепада сигнала тактирования
Рис. А.12. Эмуляция триггера показывает, что сброс выполняется асинхронно
Триггер с синхронным сбросом
Можно создать триггер с синхронным сбро-
сом. Мы с таким триггером не встречались, но
Verilog позволяет реализовать его. Разница в
проекте состоит лишь в том, что в параметрах
9 См. с. 78 ранее цитируемой книги J. Bhasker «VerilogHDL
Synthesis» (1988).
10 Возможно, что мы придаем слишком большое значение
слову «перепад» или требуем слишком много, ожидая от
Verilog использовать этот термин в его обычном цифро-
вом смысле. Чтобы быть справедливым с Verilog, можно
сказать, что в этом языке слово «перепад» означает про-
сто «изменение». В этом смысле не будет ошибкой сказать,
что схема Verilog реагирует на «перепад» на своей линии
сброса: она реагирует на изменение уровня на этой линии.
На рис. А.13 изображена схема, созданная
Verilog для этой разработки. Она подтверждает
ожидаемый результат: сигнал reset_bar может
принудительно установить низкий уровень на
входе Д но любое изменение состояния выхода
Q будет ожидать следующего положительного
перепада сигнала тактирования.
Как можно видеть по результатам эмуляции
триггера на рис. А.14, сброс ожидает следую-
щего положительного перепада сигнала такти-
рования. В принципе, это и не удивительно. Но
все же приятно знать, что у нас есть выбор как
синхронного, так и асинхронного сброса.
1118
Приложение А. Язык HDL Verilog
LPM DFF 1:1
and2
i iCD^—|
_andO00OJmp andOOOOl [ 0
Ц
LPM_DFF_:1
fd
>
""** ~
0
-a.
0
A
Рис. А.13. Схема триггера с синхронным сбросом, созданная Verilog
100 ns
120 ns
140 ns
160 га
180 ns
Перепад сигналаГсброса /
Перепад выходного сигнала соответствует
не сигналу сброса, а тактовому сигналу
Рис. А.14. Результаты эмуляции триггера показывают, что синхронный сброс выполняется только по следующему перепаду
сигнала тактирования
А.5.1. Эмуляция
последовательностной схемы
должна начинаться из известного
состояния
Если в файле эмуляции не указать начальное
состояние схемы, то эмуляция может завер-
шиться неудачно. В принципе, вопрос началь-
ного состояния не представляет важности для
комбинационных схем, но требует особого
внимания в последовательных схемах. Если,
например, при тестировании схемы делителя
на два не сообщить эмулятору исходное состоя-
nodule cHv_2_s1w_«xa«ip1«(
input elk,
output reg Q
ние схемы, то эмулятор откажется работать и
не выдаст никаких результатов.
Начальное состояние схемы можно
указать в файле разработки
На рис. А.15 показаны результаты эмуляции
без указания начального состояния схемы
(вверху) и с указанием такового (внизу). Без
указания начального состояния эмуляция за-
вершается ошибкой, а после добавления ин-
формации о начальном состоянии в файл раз-
работки (не в файл эмуляции) эмуляция вы-
полняется успешно.
a1ways«(posedge elk)
cndnodule
^Эмуляция завершается ошибкой, поскольку
"неизвестно начальное состояние
module div_2_$i«_examp1e(
input elk,
output reg Q •> a // initialized, to allow si «illation
""4^ // to start in known state
alwaysOKposedbe cikT*
О <« ~Q;
«ndnodule
Указание в файле разработки начального
уровня выхода триггера...
...позволят эмуляции выполняться: начальное состояние
известно, переключение может быть показано
Рис. А.15. Для эмуляции последовательностных схем необходимо указывать начальное состояние схемы
А.6. Поведенческое и структурное описание схемы
1119
Аппаратная инициализация,
как правильный метод
Указание начального состояния в файле раз-
работки позволяет исполняться эмуляции, но
не влияет на реализацию схемы, поскольку
в действительности начальное состояние не-
предсказуемо. Поэтому в схему необходимо до-
бавить возможность аппаратного сброса (ли-
стинг А.7).
Листинг А.7. Пример аппаратной инициализации
module div_2_sim_example_better(
input elk,
input reset_bar,
output reg Q
always@(posedge elk or negedge reset.bar)
if(!reset_bar)
Q <= 0;
else
Q<="Q;
endmodule
Такой аппаратный сброс будет влиять не толь-
ко на эмуляцию, но также и на поведение про-
граммируемого устройства.
А.6. Поведенческое и струк-
турное описание схемы
Средство Verilog позволяет проектировать схе-
мы, как последовательностные, так и комбина-
ционные, подробно описывая их внутреннее
устройство, как будто бы рисуя логические
вентили и триггеры. В следующем разделе мы
спроектируем крошечный двухразрядный син-
хронный счетчик, описывая его внутреннюю
структуру. Но это трудный способ решения за-
дачи. Вскоре мы решим ее легким способом.
Структурное описание схемы
Подавая сигнал на второй триггер через логи-
ческий вентиль ИСКЛ-ИЛИ, можно создать
Т-триггер, выходное состояние которого изме-
няется только по указанию. В данном случае мы
дадим ему указание изменять состояние, когда
на выходе Qq присутствует высокий уровень, по
перепаду сигнала тактирования (в течение вре-
мени установки). В листинге А.8 приводится
код Verilog для реализации такого проекта.
Листинг А.8. Пример программы, реализующей
двухразрядный счетчик методом структурного
описания
module ctr_boolean_2bit(clk, reset_bar, Q);
input elk;
input reset_bar;
output [1:0] Q;
wire elk, reset_bar;
reg Q;
always@(posedge elk or negedge reset_bar)
iffreset_bar)
Q[1:0] <= 2'bO; //Синхронныйсброс
else // Эти события происходят по положительному
// перепаду сигнала тактирования
begin
Q[0] <= ~Q[0]; // Состояние выхода Q0 всегда
// переключается
Q[1] <= Q[0]A Q[1]; // Состояние выхода Q1
// переключается,
// если на выходе Q0 присутствует высокий уровень
// (это достигается посредством использования функции
// ИСКЛ-ИЛИ)
end
endmodule
На рис. А.16 показана схема, созданная Verilog
для этого проекта, которая выглядит, как и
ожидалось.
Рис. А.16. Созданная Verilog принципиальная схема двухразрядного счетчика, разработанного методом подробного булева
описания
1120
Приложение А. Язык HDL Verilog
Поведенческое описание схемы
Но мы можем разработать такую же схему, при-
ложив минимум усилий, предоставив компи-
лятору выполнить большую часть работы. А в
случае нашего простого счетчика его разработ-
ка методом поведенческого описания смехо-
творно проста. Мы просто формулируем требу-
емое нам поведение схемы, а затем предостав-
ляем Verilog делать все остальное (листинг А.9).
Листинг А.9. Пример программы, реализующей
двухразрядный счетчик методом поведенческого
описания
module two_bit_simplest_ctr(clk, reset_bar, count);
// Перечисляем сигналы,
input elk; // ...указываем, входные ли они или выходные
input reset_bar;
output [1:0] count;//Двухбитовая переменная
wire elk, reset_bar; //Термин, применяемый для входов
reg count = 0; // и выходов при использовании
// конструкции always@(...) (в данном случае
// инициализированная в нулевое состояние)
always@(posedge clk,negedge reset_bar)
// Несмотря на posedge, вход reset_bar нечувствительный
// к перепаду
if freset_bar) // Чувствительный к перепаду
count <= 2'ЬОО;
else
count <= count +1; // Вход сигнала тактирования
//действительно чувствительный к перепаду
endmodule
Созданная Verilog принципиальная схема для
этого проекта такая же, как и для предыдущего.
(Прямоугольник, подающий сигнал на второй
триггер, содержит один логический вентиль
ИСКЛ-ИЛИ, в чем можно убедиться, исследо-
вав этот прямоугольник.) Скорей всего, вас не
нужно убеждать, что целесообразнее исполь-
зовать поведенческий подход к разработке во
всех возможных случаях.
А.7. Verilog позволяет
иерархические проекты
Когда проект становится сложным, хорошо
иметь возможность разрабатывать его мето-
дом «от простого к сложному». Иными слова-
ми, сначала создаем сравнительно простой мо-
дуль «нижнего уровня», наподобие D-триггера
со сбросом (пример которого рассматривается
далее), а затем используем этот модуль в более
сложном модуле. (Таким модулем в рассма-
триваемом далее примере является триггер,
меняющий выходное состояние на обратное
при каждом импульсе сигнала тактирования.)
Повторяем этот процесс, сколько требуется,
в конечном итоге создавая сложную схему, ко-
торая является набором сравнительно простых
составляющих модулей.
Этот метод похож на наш подход с использо-
ванием модулей для разработки аналоговых
схем. В случае с аналоговыми схемами мы при-
меняли правило десятикратного импеданса,
поскольку это позволяло нам разработать мо-
дуль А, а затем подключить его к модулю Б без
необходимости повторно анализировать рабо-
ту подключенного модуля А. Иными словами,
нам не нужно было анализировать сложный
супермодуль АБ. Таким образом, помодуль-
ный подход к разработке позволял упростить
как саму разработку, так и анализ. Подобный
метод можно также применять при разработ-
ке схем на Verilog. Он иллюстрируется далее
на очень подробном примере, взятом из книги
S. Palnitkar «VerilogHLD» (2003).
Разрабатываемой в данном примере схемой
является трехразрядный счетчик со сквозным
переносом. В качестве рабочих элементов это-
го счетчика используются D-триггеры, выход
Q* каждого из которых подключен к его входу
D. Ничего особенно сложного здесь нет. Но эта
простота и делает данный пример полезным,
предоставляя возможность показать каждый
блок, составленный из субблоков более низко-
го уровня. В частности:
♦ D-триггер создается «на чистом листе», без
использования более простых элементов.
♦ Триггер с переключающимся выходом11 соз-
дается из этого D-триггера, путем подачи ин-
вертированного значения выхода Q, обратно
на его вход D. Даже инвертированный сигнал
создается с помощью примитива Veribog —
субмодуль НЕ.
♦ А трехразрядный счетчик создается из трех
переключающихся триггеров, на вход такти-
рования каждого из которых подается сигнал
с выхода (^предыдущего триггера.
Далее приводятся листинги программ для всех
этих модулей.
11 Это не Т-триггер, а простой делитель на два: триггер,
выходное состояние которого переключается на обратное
по каждому импульсу сигнала тактирования.
Л.7. Verilog позволяет иерархические проекты
1121
D-Триггер
К настоящему времени этот элемент уже дол-
жен быть вам полностью знаком: обнуление
при сбросе, сигнал с входа D передается на вы-
ход Q.no отрицательному перепаду сигнала так-
тирования (листинг А.10).
Листинг А.10. Модуль D-триггера
module D_FF (q, d, elk, reset);
output q;
input d, elk, reset;
reg q;
always @(posedge reset or negedge elk)
// Используется отрицательный перепад сигнала
//тактирования, чтобы создать суммирующий счетчик
if (reset)
q<=1'bO;
else
q <= d;
endmodule
not n1 (d, q); // Вентиль НЕ (not) является встроенным
// примитивом Verilog
// В данном случае мы присвоим ему произвольное
//название п1.
// Его выходом является d, а входом — q.
// Мы подаем сигнал с названием q на вход
// примитива НЕ и берем его выходной сигнал
//с названием d
// Иными словами, элемент ni инвертирует сигнал q,
// подавая свой выходной сигнал на вход d элемента D_FF
// В случае, если использование элемента НЕ выглядит
// слишком сложным, такой же результат можно
// получить более знакомым способом:
// оператором assign d = !q;
endmodule
В данной программе даже инвертирование
сигнала осуществляется с помощью модуля
более низкого уровня, которым в нашем слу-
чае является примитив Verilog HE (NOT). Его
выход указывается первым, а вход — вторым:
not n1 (d, q). Такой способ передачи или опреде-
ления параметров рассматривается более под-
робно в разделе А.9.
Триггер с переключающимся
выходным состоянием по каждому
импульсу сигнала тактирования
(DIV2)
Это просто D-триггер, на вход D которого по-
дается инвертированный сигнал с выхода Q,
чтобы вызывать переключение его выходного
состояния по каждому импульсу сигнала такти-
рования (листинг А.11). (Как уже отмечалось
ранее, это более простой подход, чем использо-
вание Т-триггера.)
Листинг А.11. Модуль DIV2
module DIV2_FF(q, elk, reset); // Это новое устройство,
создаваемое с использованием модуля D_FF и встроен-
ного примитива Verilog — базового логического элемен-
та НЕ, функционирующего, как можно ожидать по его
названию
output q;
input elk, reset;
wire d;
D_FF dffO(q, d, elk, reset); // Создаем экземпляр модуля D_FF
// и называем его dffO.
// Выбор названия dffO не имеет абсолютно никакой
// важности; оно никогда нигде не используется
Счетчик со сквозным переносом
Этот счетчик создается из трех триггеров счет-
чика-делителя на два DIV2, подключая выход
On предыдущего к входу тактирования Clkn+V
как показано в листинге А.12.
Листинг А.12. Модуль счетчика со сквозным
переносом
module ripple_carry_counter_3bit (q, elk, reset);
output [2:0] q;
input elk, reset;
// Четыре экземпляра делителя на два DIV2_FF
DIV2_FF div2_0(q[0],dk, reset);
// Подает сигналы elk и reset на входы
//счетчика-делителя на два DIV2, принимает выход q
// счетчика DIV2 более высокого уровня и называет
//eroq[0]
DIV2JT div2 J (q[1],q[0], reset);
// Наподобие предыдущего экземпляра, но здесь
// со сквозным переносом: сигнал тактирования
// для этого триггера DIV2 не elk, а выходной сигнал
// триггера более низкого уровня — q[0]
DIV2JT div2_2(q[2],q[1], reset);
endmodule
1122
Приложение А Язык HDL Verilog
Наверное, самым удивительным в этом проек-
те является тот факт, что модуль наивысшего
уровня (который мы называем счетчиком со
сквозным переносом), который по всем ожида-
ниям должен быть наиболее сложным элемен-
том, выглядит самым простым.
Еще раз повторим потенциально сбивающий с
толку момент: названия, присваиваемые сигна-
лам при создании экземпляра — div2_0, div2_1,
div2_2, — не играют абсолютно никакой роли и
в этом проекте нигде больше не используются.
В проекте высшего уровня присутствуют толь-
ко сигналы, перечисляемые в скобках, такие
как (q[o],cik, reset). Выходными сигналами трех-
разрядных счетчиков являются только эти три
значения q[n].
Снова о создании экземпляра
На первый взгляд строки кода в модуле верхне-
го уровня, которые присваивают сигналы вхо-
дам и выходам модулям нижнего уровня, могут
выглядеть незнакомыми:
// Четыре экземпляра делителя на два DIV2_FF
DIV2.FF div2_0(q[0],dk, reset);
// Подает сигналы elk и reset на входы счетчика DIV2
АА DIV2.FF div2_1 (q[1 ],q[0], reset);
// Наподобие предыдущего экземпляра, но здесь со
сквозным переносом: сигнал тактирования для этого
триггера DIV2 не elk, а выходной сигнал триггера более
низкого уровня — q[0]
Снова напомним о списке сигналов счетчика
DIV2.FF:
ВВ module DIV2_FF(q, elk, reset);
Сложив эти два выражения вместе (строки
кода, обозначенные АА и ВВ), мы увидим, что
определенный экземпляр div2_1 подает опреде-
ленный сигнал сброса на вход сброса в счетчи-
ке DIV2_FF. Более интересными и познаватель-
ными являются подача выходного сигнала q[0]
на вход elk счетчика DIV_FF и присвоение назва-
ния выходного сигнала q[1] выходу q счетчика
DIV_FF.
Это будет выглядеть более знакомо, если дан-
ное создание экземпляра выполнить в виде, с
которым мы знакомы по файлам эмуляции.
Иерархия
На рис. А.17 изображено дерево иерархии объ-
ектов проекта в среде ISE. Узел последнего триг-
гера DIV2 показан развернутым, чтобы можно
было видеть простую конструкцию D_FF, из ко-
торой он создан.
Рис. А.17. Иерархия модулей проекта Verilog: модуль верх-
него уровня состоит из модулей нижнего уровня
Схема модулей
Нижний уровень: DIV2_FF
Модуль самого нижнего уровня — D-триггер -
слишком хорошо нам знаком, чтобы его нужно
было отображать. Устройство модуля счетчика
DIV2_FF довольно очевидно, но, возможно, вам
будетприятноувидеть, что Verilog создал его схе-
му должным образом, как показано на рис. А.18.
и*4™-
Рис. А.18. Схема модуля DIV2_FF, созданная Verilog:
D-триггер, инвертированный выходной сигнал которого по-
дается обратно на его вход
Более знакомый способ разработки
триггеров с переключающимися
выходными состояниями
Возможно, что мы зашли слишком далеко,
возвратившись к проектированию D-триггера
заново и создавая из него триггер с переклю-
чающимся выходным состоянием. Если пропу-
стить данный этап, то код программы для соз-
дания триггера, выходное состояние которого
по сигналу тактирования всегда переключается
на обратное, выглядит более знакомым (ли-
стинг А.13).
А.8. Счетчик ДДК
1123
Листинг А.13. Модуль триггера
с переключающимся состоянием
always @(negedge elk or negedge reset)
if(lreset)
q <= 0;
else
q <= !q;
Счетчик со сквозным переносом
На рис. А.19 изображена схема из трех таких
счетчиков-делителей на два, соединенных по-
следовательно, чтобы создать счетчик со сквоз-
ным переносом. Но эта схема, на которой пока-
заны только загадочные прямоугольники, вы-
полняющие работу счетчиков DIV2, не очень
наглядна. А вот если вместе с ней рассматри-
вать подробное содержимое одного из этих
прямоугольников (счетчика DIV2 из рис. А.18),
то она становится намного понятнее. Опять же,
этот результат очевидный, но снова вам будет
приятно увидеть, что Verilog создал то, что от
него ожидалось.
Понять эту схему будет легче, если не приме-
нять строгий иерархический подход, пока-
зывая только прямоугольники для устройств
более низкого уровня. На рис. А.20 показана
схема трехразрядного счетчика со сквозным
переносом, в которой подробно изображены
составляющие ее D-триггеры.
А.8. Счетчик ДДК
Двоичный счетчик относится к числу самых
простых. Как вы знаете, язык Verilog позволяет
создать суммирующий счетчик простой стро-
кой кода count <= count+1. Но иногда (когда
результаты предназначаются для просмотра
людьми), будет лучше использовать счетчик-
делитель на десять, или счетчик, работающий
в двоично-десятичном коде (ДДК).
Создание такого счетчика в Verilog требует
больших усилий, чем обычного двоичного
счетчика, а последовательное соединение не-
скольких каскадов требует иерархического
подхода, подобного применяемому для разра-
ботки счетчика со сквозным переносом, кото-
рая была рассмотрена в разделе А. 7.
Одноразрядный счетчик ДДК
(модуль самого нижнего уровня)
Счетчик ДДК выглядит подобно обычному
двоичному счетчику, с тем лишь исключением,
что после счета 9 ему нужно указывать начи-
нать новый цикл счета с 0.
Также следует уточнить более тонкую разницу,
поскольку этот счетчик будет модулем в иерар-
хии. Так как каждый счетчик является звеном
последовательного каскада, выходной перенос
одного разряда должен зависеть не только от
Рис. А.19. Схема верхнего уровня проекта: соединенные последовательно триггеры DIV2 образуют счетчик со сквозным пе-
реносом
<и I «_
DJ=F
А. . —
j
Рис. А.20. Схема счетчика со сквозным переносом с подробным изображением устройства составляющих ее DIV2 счетчиков
1124
Приложение А. Язык HDL Verilog
состояния данного разряда, но также и от со-
стояния всех остальных младших разрядов.
Иными словами, выходной перенос данного
разряда также зависит и от входного переноса
из предыдущего разряда. В приводимом далее
листинге А.14 эти сигналы обозначаются cin
для входного переноса и cout — для выходно-
го. Вопрос необходимости включения в расчет
входного переноса, чтобы обеспечить каскад-
ное соединение, подробно рассматривается
в главе 16N.
Листинг А.14. Одноразрядный счетчик ДДК
module bcd_counter(
input elk, cin, reset_bar,
output reg [3:0] count,
//Тип reg потому, что будет использоваться
// неблокирующая конструкция always@(...);
// Инициализация = 0 для чистого запуска при
// эмуляции
output cout
assign c_out = cin & (count == 9);
// Состояние cin реализует зависимость от младших
// разрядов:
// Все они должны быть заполнены, чтобы создать
// выходной перенос
always @(posedge elk, negedge reset_bar)
begin
iffreset.bar)
count<=0; //Асинхронныйсброс
else // Здесь начинаем переходы, зависящие
// от сигнала тактирования (т. е. те, которые являются
// синхронными)
if (cin & (count ==9))
// Данная линия кода делает этот счетчик типа ДДК,
// в отличие от обычного двоичного счетчика:
count <= 0;
// Начинаем новый цикл только тогда, когда
// установлен данный разряд и все младшие разряды
// (значение девять), если таковые имеются
else
if(cin)
count <= count +1;
else
count <= count-
end
endmodule
На этот раз у нас есть аппаратный сброс, по-
этому мы не использовали подход с инициа-
лизацией устройства, который упоминается в
разделе А.5.1. В частности, мы не выполнили
инициализацию выходного состояния output
reg [3:0] =0. Вместо этого мы реализовали аппа-
ратный сброс, следуя совету, который мы дали
в том разделе.
Соединяем последовательно
несколько счетчиков ДДК, чтобы
создать многоразрядный счетчик
Рассматриваемый здесь счетчик ДДК создает-
ся подобно 4-разрядным счетчикам на старых
микросхемах, упоминаемых в главе 16N (на-
пример, 74НС161), соединяя последовательно
необходимое количество базовых счетчиков,
чтобы получить счетчик-делитель на сто, де-
литель на тысячу и т. д. Это каскадное соеди-
нение можно реализовать с помощью соот-
ветствующего модуля Verilog. Например, в
листинге А.15 приводится код программы для
счетчика-делителя на сто, создаваемого из двух
базовых счетчиков ДДК.
Листинг А.15. ДДК-счетчик делитель на сто
module div_1 OO_bcd(
input elk,
input cin,
input reset_bar,
output [7:0] count,
output c_out
bcd_counter units (elk, cin, reset_bar, count[3:0],c_outO);
// Создаем один экземпляр счетчика div-10
bcd_counter tens (elk, c_outO, reset_bar, count[7:4],c_out);
// Создаем еще один такой экземпляр, только
// на его cin подается cout счетчика разряда единиц
// (экземпляр которого был создан как coutO)
endmodule
Опять же, подобно счетчику со сквозным пере-
носом, этот модуль высшего уровня намного
проще, чем элемент нижнего уровня, из кото-
рых он состоит.
Aft Два альтернативных способа создания экземпляра субмодуля
1125
А.9. Два альтернативных
способа создания
экземпляра субмодуля
Передача параметров по позиции
Использование в коде для создания каскада
определенного разряда, например единиц, суб-
модуля с названием bcd_counter позволяет сде-
лать этот код компактным:
bcd_counter tens (elk, c_outO, reset_bar, count[7:4],c_out);
// Создаем еще один такой экземпляр, только на его cin
подается cout счетчика разряда единиц (экземпляр кото-
рого был создан как c_outO)
Это хорошо, но за компактность приходится
расплачиваться. Сигналы elk и c_outO подаются
из модуля более высокого уровня (divj OO_bcd)
на модуль более низкого уровня (bcLcounter),
полагаясь на их позицию в списке. Например,
сигналу c_out из модуля более низкого уровня
присвоено название c_outO. Это допускается по
той причине, что параметр c_out является по-
следним в списке в модуле bcLcounter. Но при
неправильном порядке параметров в списке
полученная схема будет нерабочей. Если бы,
например, мы полагали, что параметр reset__bar
находится на последнем месте в списке сигна-
лов модуля bcLcounter, мы бы связывали его с
сигналом c_out субмодуля. Такая связь не име-
ла бы смысла.
Передача параметров по названию
Менее компактным, но более ясным способом
связывания сигналов с сигналами субмодуля
(т. е. более однозначный способ создания эк-
земпляра субмодуля) будет указание в списке
обоих сигналов рядом друг с другом, как это
делалось в файлах эмуляции:
bcd_counter units(
.clk(clk),
.cin(c_outO),
.reset_bar(reset_bar),
.count(count[7:4]),
\c_out(c_out)
Передача параметров по имени,
а не по позиции: второй счетчик
ДДК
Например, сигнал входного переноса cin на этот
счетчик подается из вывода сигнала выходно-
го переноса c_outO счетчика младшего разряда.
Если использовать этот подход, то нам не нужно
помнить порядок размещения в списке сигналов
модуля bcLcounter, поскольку указаны явные
связи. Для простого модуля, например модуля
НЕ из раздела А.79 у которого только один вход
и один выход, передача параметров по позиции
довольно легко осуществима. Но в случае боль-
шего количества сигналов более полезным будет
подход явного перечисления.
АЛО. Конечные автоматы
Реализация счетчика с помощью
конструкции условия case
Для простого счетчика нет более легкого ме-
тода разработки, чем рассмотренное ранее по-
веденческое описание. Но для более сложных
устройств, которые переходят из одного состоя-
ния в другое (под «состоянием» имеются в виду
уровни триггеров устройства), может быть по-
лезным другой подход, например вложенные
операторы условия if или case. Автоматом
с конечным числом состояний, или просто ко-
нечным автоматом, называется схема, кото-
рая под управлением подаваемых на нее извне
сигналов пошагово проходит через последова-
тельность состояний. Счетчики являются са-
мым простым примером конечного автомата.
Предмет конечных автоматов рассматривается
более подробно в главе 17N.
Каким же образом выполняется разработка та-
ких устройств? Для сложных ветвлений можно
использовать вложенные условные операторы
if...else, но когда нужно просто протестировать
несколько состояний, более подходящим будет
условный оператор case. Например, суммирую-
щий или вычитающий счетчик в виде конеч-
ного автомата можно разработать следующим
образом. Мы можем перечислить каждое воз-
можное текущее состояние счетчика как си-
туацию (case), влекущую за собой то или иное
последующее состояние. Поскольку мы знаем
1126
Приложение А. Язык HDL Verilog
о существовании более легкого способа созда-
ния счетчики и нам вряд ли понравится пред-
лагаемый способ, внесем в разрабатываемый
счетчик небольшое дополнительное свойство.
В частности, мы позволим ему проходить толь-
ко через три состояния, а также сделаем после-
довательность этих состояний несколько не-
обычной. (Обычный двоичный код мы заменим
кодом Грея12.) Придание нашему счетчику этих
необычных свойств почти оправдывает приме-
нение подхода конечного автомата для его раз-
работки. (Вскоре мы рассмотрим пример, для
которого этот подход определенно оправдан.)
Кроме того, мы также оснастили наш счетчик
двумя нестандартными элементами, подроб-
ное объяснение которых приводится далее. Это
выходной перенос, значение которого меняет-
ся соответствующим образом для выбранного
типа счета, а также названия состояний, чтобы
сделать текст программы более понятным.
В листинге А.16 приведена первая версия про-
граммы, реализующая суммирующий/вычитаю-
щий счетчик с асинхронным выходным пере-
носом посредством условных операторов case.
Листинг А.16. Программа, реализующая
счетчик с помощью операторов case
module up_down_state_machine(dk, startup_bar,up,c_out,
state);
// Код для создания малоразрядного счетчика
// в виде конечного автомата
input elk, startup_bar, up;
output c_out; // Выходной перенос: активируется при
// нулевом значении для вычитания и при значении 11
//для суммирования
output [1:0] state;
wire dk,startup_bar,up, c_out;
reg[1:0]state;
parameter A = Ъ00, В = Ъ01, С = Ъ11; // Делаем счетчик-
делитель на 3
assign c_out= ((up & (state == С)) | ("up & (state == A)));
// Выход типа Мили, поскольку он зависит
// от входа (up), так же как и от состояния
always @(posedge elk, negedge startup_bar)
begin
iffstartup.bar)
state <= A;
else
case (state)
A:
if (up)
state <= B;
else
state <= С; // Меняем направление счета
// на обратное
В:
if (up)
state <= С;
else
state <= A; // Меняем направление счета
// на обратное
С:
if (up)
state <= А;
else
state <= В; // Меняем направление счета
// на обратное
endcase
end
endmodule
Как уже упоминалось, код программы данного
счетчика содержит два новых элемента:
♦ Параметр — позволяет присваивать состоя-
ниям описательные названия, чтобы сделать
код более удобочитаемым13.
♦ Активирование сигнала с out зависит от
типа счета. При суммирующем счете сигнал
выходного переноса c_out активируется при
максимальном значении счета (11), а при вы-
читающем — при минимальном (00). В этом
нет ничего нового, но эту особенность счет-
чиков мы не рассматривали ранее.
Такой перенос является асинхронным, поэтому
может засбоить в процессе изменения состоя-
ния, в котором триггеры синхронизированы не
совсем точно, вследствие незначительной раз-
ницы в длительности их задержки. Если сигнал
выходного переноса c_out подается на син-
хронный вход, например, входного переноса
синхронного счетчика, то такой сбой будет без-
вредным. Но если же использовать сигнал c_out
для определения переполнения, например, по-
давая его для тактирования триггера перепол-
нения, то сбой может создавать проблемы.
12 В коде Грея между двумя последовательными состоя-
ниями допускается изменение только одного бита. Это
правило предотвращает ложные переходные состояния.
См. § 10.1.3Е книги АоЕ.
13 Область действия этого определения является локаль-
ной для данного модуля. Один авторитетный профессио-
нал рекомендует вместо параметров использовать дирек-
тиву компилятора define. Но директива define не входит в
состав Verilog, и поэтому ее нужно использовать вне любо-
го модуля Verilog (см. с. 36 книги Monte Dahymple «Micro-
processor Design Using Verilog HDL» («Проектирование ми-
кропроцессоров, используя язык HDL Verilog»), 2012 г.).
А 70. Конечные автоматы
1127
Реализация суммирующего/
вычитающего счетчика, используя
оператор условия case. Версия 2
с синхронным выходным
переносом carry_out
Рассмотренный в разделе АЛО суммирующий/
вычитающий счетчик можно реализовать
с синхронным сигналом выходного переноса
c_out. Теперь сигнал выходного переноса не
будет подвержен сбоям, поскольку подобно
другим сигналам он станет изменять состоя-
ние только спустя короткое время после сиг-
нала тактирования. В периоде времени меж-
ду сигналами тактирования, подобно любой
другой синхронной функции, он будет вести
себя должным образом: соблюдать спокой-
ствие.
Добавление сигнала c_out к информации о сле-
дующем состоянии принуждает его ожидать
сигнал тактирования14. Затем уровень сигнала
cout указывается для каждого состояния
(листинг АД7).
Листинг А.17. Фрагмент программы
case (state)
А:
if (up)
begin
state <= В;
c_out <= 0; // Это уровень, который мы получим по-
сле следующего импульса сигнала тактирования
end
В листинге А.18 приводится полный код прог-
раммы для суммирующего/вычитающего счет-
чика, за исключением информации в начале
файла. Мы не повторяли эту информацию по
той причине, что она выглядит подобно соот-
ветствующей информации в файле счетчика с
асинхронным выходным переносом в листин-
ге А.16.
14 Также в начале файла сигналу c_out потребовалось при-
своить тип reg:
wire clk,startup_bar,up;
reg [l:O]state;
reg cout;
Листинг А.18. Полный код программы
суммирующего/вычитающего счетчика
module up_down_state_machine_sync_carry(clk, startup.
bar,up,c_out, state);
// Код для создания малоразрядного счетчика в виде
// конечного автомата
// [Начальный код пропущен, поскольку он такой же,
// как и для счетчика с асинхронным выходным
// переносом]
always @(posedge elk, negedge startup_bar)
begin
if fstartup_bar) // Обычная функция асинхронного
// сброса
begin
state <= A ;
c_out <= 0;
end
else
case (state)
A:
if (up)
begin
state <= B;
c_out <= 0; // Это уровень, который мы получим
// после следующего импульса сигнала тактирования
end
else // Вычитающий режим счета
begin
state <= С;
c_out <= 0;
end
В:
if (up)
begin
state <= С;
c_out <= 1; // Проверяем наличие
//синхронизирующего переноса (следующеесостояние,
// максимальное для суммирующего счетчика)
end
else // Вычитающий режим счета
begin
state <= A;
c_out <= 1; // Проверяем наличие
// синхронизирующего переноса (следующее состояние,
// максимальное для вычитающего счетчика)
end
С:
if (up)
begin
state <= A;
c_out <= 0;
end
else // Вычитающий режим счета
begin
state <= В;
c_out <= 0;
end
endcase
end
1128
Приложение А Язык HDL Verilog
A.11. Устройство, более
подходящее для реализации
в виде конечного автомата:
арбитр шины
Только что рассмотренный пример был непло-
хим подходом к реализации устройства, но не
совсем подходящим для реализации счетчика.
Этот подход был вполне приемлем для крошеч-
ного счетчика-делителя на три: три случая с
двумя ветвлениями для каждого. Но, например
для 8-разрядного суммирующего/вычитающе-
го счетчика этот подход был бы очень плохим:
256 случаев с двумя ветвлениями для каждо-
го. Но применение метода конечного автомата
подходит как по заказу для реализации устрой-
ства с более сложной моделью поведения, чем
счетчик. В этом разделе мы проиллюстрируем
подход с использованием конечного автома-
та для создания арбитра шины. Арбитр шины
представляет собой устройство, которое обе-
спечивает двум пользователям (необязательно
людям, а, скорее всего, микропроцессорам) со-
вместный доступ к одному ресурсу (например,
памяти или периферийному устройству).
На рис. А.21 отображена блок-схема такого
устройства для двух запросчиков: ARQST и
B_RQST.
A_RQST >
К А <
Сигнпп
тактирования
Арбитр
шины
А
< B_RQST
> К_В
Общий
ресурс
Рис. А.21. Блок-схема арбитра ресурса
Разрабатываемая схема должна принуждать
пользователей следовать правилу, знакомому
нам с детского сада. Вот правила для игры в пе-
сочнице:
1. Не держи лопатку у себя, если ты нею не
пользуешься.
2. Не хватай лопатку у своего одногруппника,
если он использует ее.
3. Работайте лопаткой по очереди.
Схема последовательности операций
Создадим схему последовательности операций
для выражения изложенных правил. Сколько
состояний нам потребуется? Определенно, что
нам нужно состояние, в котором мы предостав-
ляем шину запросчику А, и другое состояние, в
котором она предоставляется запросчику В. Но
более тонким моментом является то, что в слу-
чае двух одновременных запросов нам потре-
буются еще два состояния, определяющие, кто
получит доступ к ресурсу следующим.
На рис. А.22 изображена такая предваритель-
ная схема последовательности операций, где
показаны только состояния, которым присвое-
ны названия, грубо описывающие значение
каждого состояния.
Wait (Ждать)
A_Next
(А_Следующий)
Wait (Ждать)
B_Next
(В_Спедующий)
Grant__A
(ТТредоставляем_А)
Grant_B
(ГТредоставляем_В)
Рис. А.22. Предварительная схема последовательности опе-
раций, содержащая только состояния без правил для пере-
хода
Два состояния, изображенные слева, описыва-
ют состояние ожидания, когда шина не предо-
ставлена никому из запросчиков. А названия
состояний GRANT_A и GRANT_B означают
выходной сигнал или действие — предоставле-
ние шины.
Правила перехода
Чтобы завершить схему последовательности
операций, в нее нужно добавить обозначения,
показывающие, какие входные условия долж-
ны вызывать переход из одного состояния в
другое. Такие обозначения входных условий,
вызывающих переход в другое состояние, по-
казаны на рис. А.23.
Обозначение А означает запрос ресурса пользо-
вателем А, а обозначение АВ — одновременный
A.I I Устройство, более подходящее для реализации в виде конечного автомата: арбитр шины
1129
А*В
А
Grant__A
(Предоставляем_А)
В
Grant_B
(Предоставляем__В)
сигналы схемы показаны в том состоянии, в ко-
тором они активированы
15
Рис. А.23. Полная схема последовательности операций ар-
битра ресурса
В этой блок-схеме делается выбор, который не
требуется в постановке задачи. В частности,
общий ресурс никогда не передается сразу от
пользователя А пользователю В, а только после
задержки длительностью в один период сиг-
нала тактирования. Возможно, что в будущем
мы дадим вам задание модифицировать схему
и убрать эту задержку. Но реализовать это из-
менение будет совсем не трудно.
А.11.1. Эмуляция, демонстрирующая
поведение арбитра
На рис. А.24 изображен снимок экрана с сигна-
лами арбитра в процессе эмуляции схемы. Это
может сделать поведение данной схемы более
наглядным.
Код программы арбитра ресурсов приведен в
листинге А.19.
ТТервыь одновре/v^: '^
запросы создают
г г -бытие t ive__A (дать
Вторые одновременные
запросы создают
событие £ive_B (дать В)
Рис. А.24. Эмуляция работы схемы арбитра ресурса
Когда В прекращает запрашивать, А все еще хочет
ресурс, поэтому получает G\ve__A
запрос обоими пользователями. Конечно же,
это синхронно тактируемая схема, поэтому пе-
реход из одного состояния в другое происходит
по импульсу сигнала тактирования. Выходные
15 Выходные значения сигналов данной схемы зави-
сят только от ее текущего состояния, а не от состояния и
присутствующих входных значений. На языке конечных
автоматов это делает ее автоматом Мура, а не автоматом
Мили.
1130
Приложение А. Язык HDL Verilog
Листинг А.19. Программа, реализующая арбитр
шины
module bus_arbiter(clk, startup, A_rqst, B_rqst, state,
Give__A, Give_B);
input elk;
input startup;
input A_rqst;
input B_rqst;
output [1:0] state;
output Give_A;
output Give_B;
wire elk, startup,A_rqst,B_rqst;
wire Give_A, Give_B; // Для assign тип wire
reg [1:0] state;
parameter waitA = ЪОО, waitB = fb01, GrantA = Ъ10,
GrantB = 'Ы1;
// Присваиваем состояниям описательные названия,
// чтобы сделать код более удобочитаемым.
assign Give_A = (state == GrantA);
// Неуклюжий способ получить выходной сигнал после
// неудачи с подходом по Муру
assign Give_B = (state == GrantB);
// Простой способ реализации автомата Мура (который
// не зависит от входных сигналов)
assign A_only = A_rqst & ~B_rqst;
assign B_only = Bjrqst & ~A_rqst;
assign no_rqst = ~B_rqst & ~A_rqst;
always @(posedge elk, posedge startup)
if (startup)
state <= waitA;
else
case (state)
if(B_rqst)
state <= GrantB;
else
if(A_only)
state <= GrantA;
end
GrantA:
begin
if (A_rqst) // Ждем здесь, пока А не потеряет интерес
state <= GrantA;
else
state <= wait В;
end
GrantB:
begin
if (B_rqst) // Ждем здесь, пока В не потеряет интерес
state <= GrantB;
else
state <= waitA;
end
endcase
endmodule
Сама по себе схема арбитра ресурса не пред-
ставляет ничего особенного, но мы надеемся,
что в процессе ее разработки вы смогли почув-
ствовать силу возможностей, которые предо-
ставляет использование метода конечного ав-
томата для создания большого разнообразия
устройств, которые могут решать задачи до-
вольно элегантно.
waitA:
begin
if (no_rqst) // Ждем здесь, пока не запросит А или
// не запросит В без запроса А
state <= waitA;
else
if(A_rqst)
state <= GrantA;
else
if(B_only)
state <= GrantB;
end
waitB:
begin
if (no_rqst) // Ждем здесь, пока не запросит А или
// не запросит В без запроса А
state <= waitB;
else
A.12.CpeflalSEXilinx
предлагает помощь
в разработке
Когда у вас нет настроения разрабатывать схе-
му своего собственного устройства, можно вос-
пользоваться значительной библиотекой гото-
вых схем, доступных в среде разработки ISE.
Библиотеки содержат много элементов: логи-
ческие вентили, триггеры, мультиплексоры,
счетчики, конечные автоматы. Все эти элемен-
ты предоставляются в виде шаблонов, которые
также содержат код программы (но без инфор-
мации заголовка файла).
Предположим, например, что вы забыли,
как проектировать простой суммирующий/
А.13. Блокирующие и неблокирующие присваивания
1131
вычитающий счетчик. Стандартный шаблон
проекта такого счетчика можно найти в среде
разработки ISE, следуя такой процедуре:
♦ в навигаторе по проектам Project Navigator
выполните команды меню Edit => Language
Templates;
♦ в левой панели открывшего окна разверните
узел Verilog;
♦ а в нем разверните последовательно узлы
Synthesis Constructs > Coding Examples.
В показанном далее примере мы последова-
тельно развернули следующие узлы:
♦ Counters (счетчики).
♦ Binary (двоичные).
♦ Up/Down Counters (суммирующие/вычи-
тающие счетчики).
В последнем узле мы выбрали элемент Simple
Counter (простой счетчик), в результате чего
программа вывела в правой панели код для та-
кого счетчика, как показано на рис. А.25.
Листинг А.20.8-битовый суммирующий/вычи-
тающий счетчик
гед [7:0] count;
always <5>(posedge clock)
begin
if (up)
count <= count + 1;
else
count <= count-1;
end
А.13. Блокирующие
и неблокирующие
присваивания
Хотим обратить ваше внимание на один аспект,
который не следует игнорировать. Это пример
для тех, кто испытывает трудности с различием
между этими двумя типами присваивания, ко-
торое уже упоминалось в разделе А.5.
' Common CtM«t<u<te
Device №»€t iratontiaUon
' Osvke primitive Instantiate
■ Simulation Constructs
> Syrrthes» OjftStcurts:
;' ; fttwayi
' "• Attributes
>,S Gicling Examples
t; "..' Accumulator
«cj (<upper>t 0)
/ load, CE and Async Active low Reset
/ Iwd, CC «ftd Sync Active High ftes<R
Active low Reset
Рис. А.25, Пример одного из многих шаблонов стандартных логических элементов, доступных в среде разработки ISE Xilinx
Мы можем сделать этот шаблон менее абстра-
ктным, заменив в нем заполнители дейст-
вительными переменными, требуемыми для
реализации конкретной схемы, например,
8-разрядного суммирующего/вычитающего
счетчика. Сначала нужно ввести обычную ин-
формацию заголовка файла, а затем модифици-
руем шаблон, как показано в листинге А.20.
Мы попробуем на этом примере сделать эту
разницу очевидной. Разработаем в Verilog трех-
разрядный сдвиговый регистр, схема которого
изображена на рис. А.2616.
16 этот пример приводится в примечаниях ко второму
семестру 2004 учебного года курса 6.11 Массачусетско-
го технологического института. Он также приводится
в докладе Клиффорда Каммингса (Clifford Cummings)
1132
Приложение А. Язык HDL Verilog
IN.
D0Q0
А
Dl Q1
Л
ак.
г т
D2Q2
А
Листинг А.21. Программа сдвигового регистра
с блокирующими присваиваниями
Рис. А.26. Трехразрядный сдвиговый регистр, который мы
намереваемся разработать
Мы выполним разработку этого устройства
дважды: первый раз неправильно, как будто
мы не понимаем разницу между блокирующим
и неблокирующим присваиванием, а второй
раз правильно.
Неправильный подход
с блокирующими присваиваниями
Блокирующие присваивания исполняются в
том порядке, в котором они перечислены в по-
следовательном блоке. Данное присваивание
называется блокирующим по той причине, что
оно завершает присваивание левой стороны с
правой стороны, не позволяя прерывания какой
бы то ни было другой операцией Verilog. Как го-
ворится в докладе Каммингса: «Блокирующее
присваивание "блокирует" выполнение замы-
кающих присваиваний в том же самом блоке
assign до тех пор, пока не будет выполнено те-
кущее присваивание»17. Блокирующие присва-
ивания ведут себя таким образом, как мы при-
выкли видеть в коде компьютерных программ:
сначала исполняется одна строка кода, затем —
следующая.
Давайте разработаем сдвиговый регистр, ис-
пользуя блокирующие присваивания, позволяя
по импульсу сигнала тактирования входному
сигналу IN создавать выходной сигнал Qo, сиг-
налу Qo создавать сигнал Q1 и т. д. Код для тако-
го регистра приведен в листинге А.21.
«Nonblocking Assignments in Verilog Synthesis, Coding Styles
that Kill» («Неблокирующие присваивания в синтезе Ver-
ilog, убойные стили кодирования»), доступном по адресу:
http://homepages.cae.wisc.edu/~kime/554/s02/ma-
terials/CummingsSNUG2000SJ_NBA revl_2.pdf. А в
ранее цитируемой книге J. Bhasker «Verilog HDL Synthesis»
этот предмет рассматривается в разделе 2.18.
17 Раздел 3 доклада Клиффорда Каммингса (Clifford Cum-
mings) «Nonblocking Assignments in Verilog Synthesis, Coding
Styles that Kill».
module shift_reg_blocking(
input elk,
input in,
output reg qO,
output regqi,
output reg q2
);
always@(posedge elk)
begin
qO = in;
q1=qO;
q2 = ql;
end
endmodule
Этот код скомпилируется без проблем. Но он
не создаст схему, которую мы хотели разрабо-
тать. Операция always@(...) исполняется по по-
ложительному перепаду сигнала тактирования
elk. Все несколько присваиваний выполняются
в ответ на один перепад импульса сигнала так-
тирования. Пока что все хорошо.
Тогда по одному импульсу сигнала тактиро-
вания сигнал IN должен пройти полностью до
выхода Q2, а это совсем не то, чего мы хотели.
На рис. А.27 показана схема, созданная Verilog
по приведенному коду программы. Это вовсе
не сдвиговый регистр, а триггер, единствен-
ному выходу которого присвоены все три
названия.
shiftjregj>locking
Рис. А.27. Схема реализации Verilog проекта трехбитового
сдвигового регистра с блокирующими присваиваниями
А.13. Блокирующие и неблокирующие присваивания
1133
Правильный подход: используются
неблокирующие присваивания
При использовании неблокирующих присваи-
ваний по каждому положительному перепаду
сигнала тактирования на выходах трех тригге-
ров устанавливаются уровни, присутствующие
на их входах непосредственно перед переходом
сигнала тактирования на высокий уровень.
В ранее цитируемых примечаниях МИТ это
описывается следующим образом: все присваи-
вания откладываются до тех пор, пока не будут
вычислены все правые стороны (конец такта
эмуляции)18. Листинг А.22 иллюстрирует этот
подход.
Листинг А.22. Программа сдвигового регистра
с неблокирующими присваиваниями
module shift reg non blocking!
input elk,
input in,
output reg qO,
output reg q1,
output reg q2
);
always@(posedge elk)
begin
qO <= in;
qK=qO;
q2<=q1;
end
endmodule
18 Страница 7 примечаний ко второму семестру 2004 учеб-
ного года курса 6.11 Массачусетского технологического
института. Употребление слова «эмуляция» в данном кон-
тексте выглядит странным и напоминает о том неудобном
факте, что Verilog был создан как программа для эмуля-
ций. Только позже он начал применяться для синтеза.
LPM DFF 1:1
LPM DFF 1:2
LPM DFF 1:3
Рис. А.28. Схема реализации Verilog проекта трехбитового
сдвигового регистра с неблокирующими присваиваниями.
На этот раз то, что и имелось в виду
Поскольку каждое присваивание принимает
старый уровень, присутствующий до сигнала
тактирования, этот проект действительно соз-
дает сдвиговый регистр, как и подтверждает
схема, показанная на рис. А.28.
Данный пример служит доводом в пользу
утверждения, в котором вы, скорее всего, и так
не сомневались, что при проектировании по-
следовательностных схем необходимы небло-
кирующие присваивания.
Приложение Б. Работа с логическим
компилятором Xilinx
Б.1. Краткий обзор Xilinx,
Verilog и ABEL
По мере развития языков описания аппаратных
средств (HDL1) языки Verilog и VHDL почти
полностью вытеснили более старые аппарат-
ные языки компилятора, такие как ABEL. Эти
два новых широко распространенных языка
изучать2. Здесь мы представим вам основные
понятия языка Verilog. Мы не будем использо-
вать ни VHDL, ни ABEL. На рис. Б1 приведена
базовая структура ячейки микросхем семейства
XL/XC95xx компании Xilinx.
Независимо от устройства, выбранного для
реализации разрабатываемой схемы, будь то
СПЛУ (меньшая и более жесткая структура)
При необходимости каждая переменная
доступна в инвертированной форме
Установка сомножителя
Сигнал тактирования
сомножителя
Сбоос сомножителя
ение вывода
сомножителя
Дополнительные
сомножители
(от других
макроячеек)
Глобальная Глобальные
установка/сброс сигналы тактирования
Инвертируется или пропускается
Сигнал тактирования может быть
глобальным (общим для всех триггеров)
или отдельным для данного триггера
То же самое для сигналов
/ установки и сброса
К матричному
-коммутатору
FastCONNECT
Базовая структура
ячейки — сумма
произведений
(операция ИЛИ
над результатами
операций И).
(Это схема
устройств ТТМЛ)
Выходной^
сигнал
РТОЕ*
>То I/O Blocks
Этот 2:1 мультиплексор позволяет
выбрать, использовать ли триггер,
или обойти его
Тристабильный выход,
управляемый логической схемой
Количество входов ИЛИ можно увеличить
больше, чем емкость одной макроячейки
*РТОЕ (Разрешение выходе сомножителя)
Рис. Б.1. Устройство логической ячейки (макроячейки) семейства микросхем Х!_/ХС95хх компании Xilinx
выглядят больше похожими на языки програм-
мирования высокого уровня. Язык VHDL, мо-
жет быть, чуть более мощный, но его труднее
1 Англ. Hardware Description Language - язык описания ап-
паратных средств. — Примеч. пер.
2 Если вас интересует более подробная информация
по этому вопросу, то вы сможете найти ее на веб-сайте
https://homepages.thm.de/~hg53/hes-wsl819/
aufgabel/Cooley-VHDL-Verilog.html. (Ссылка действи-
тельна на момент перевода. Если больше недействительна,
то можно попробовать выполнить поиск по фразе «Cooley-
VHDL-Verilog».)
Б.1 Краткий обзор Xilinx, Verilog и ABEL
1135
или FPGA (большая и очень гибкая структура,
имеющая таблицы соответствия для сопряже-
ния входа с выходом), процедура использова-
ния средств Xilinx по существу одинакова.
актуальном состоянии. По завершении уста-
новки на рабочем столе будет создан ярлык
Project Navigator, двойной щелчок по которому
запусти средство ISE.
Б.1.1. Загрузка установочного
пакета среды ISE Xilinx
На веб-сайте компании Xilinx щелкните по
ссылке Support и в открывшемся меню вы-
берите ссылку Downloads & Licensing. В от-
крывшемся окне Downloads под заголовком
Version щелкните по ссылке ISE Archive и вы-
берите в нем для загрузки самую последнюю
версию ISE — 14.7 для Windows. Компания
Xilinx продолжает поддерживать среду разра-
ботки ISE, но больше не выпускает новых вер-
сий для нее, предпочитая развивать средство
разработки Vivado (которое, к сожалению, не
поддерживает ПЛУ)3. Для загрузки выберите
так называемую опцию WebPACK. Это большой
файл, свыше 3 ГБ, а установленная программа
занимает на диске свыше 8 ГБ.
Распакуйте загруженный архив, найдите файл
XSETUP.EXE и запустите его на исполнение.
Хотя версия WebPACK предоставляется бес-
платно, для ее установки требуется лицензия.
Данная лицензия предоставляется бесплатно
после регистрации и действительна в тече-
ние одного года, после чего нужно получить
новую бесплатную лицензию. Возможно, что
компания Xilinx хочет, чтобы пользователи ее
продуктов поддерживали свою регистрацию в
Б.1.2. Создание исходного файла
в Verilog
Присвоение проекту названия
и указание папки для хранения
В меню File выберите команду New Project и
присвойте проекту название. По умолчанию но-
вый проект помещается в корневую папку уста-
новки среды ISE, но будет разумным указать для
хранения проекта какую-либо другую папку.
Выбор устройства и языка
В следующем окне Project Settings предлага-
ется выбрать семейство устройств (Family),
устройство (Device) и язык (Synthesis Tool).
Мы выберем семейство самых простых и самых
маленьких устройств, которых будет достаточ-
но для реализации всей логики, требуемой на-
шим лабораторным компьютером: семейство
СХ9500 CPLDs4. Для целей первой части этого
раздела предположим, что будем использовать
язык Verilog. А работать мы будем с конкрет-
ной микросхемой XC9572XL с напряжением
питания 3,3 В. Обратите внимание на то, что
для эмулятора (Simulator) следует выбрать
ISim, а не Modelsim (рис. Б.2).
Рис. Б.2 Присвоение названия проекту, выбор устройства и компилятора
3 Если в среде ISE вы хотите использовать компилятор
ABEL, то нужно установить не самую последнюю версию
среды, а версию 10.1, которая содержит этот устаревший
компилятор.
4 Самое меньшее устройство из этого семейства, микро-
схема ХС9536, содержит 36 триггеров и около 800 логиче-
ских элементов.
1136
Приложение Б. Работа с логическим компилятором ХШпх
Создание исходного файла
При работе с файлом шаблона, который мы пре-
доставляем в этом курсе, мы будем добавлять в
проект исходный файл, а не создавать его. Тем
не менее рассмотрим процедуру создания ново-
го исходного файла. Щелкните по значку New
Source, в открывшемся окне Мастер созда-
ния исходного файла выберите опцию Verilog
Module (рис. Б.З) и в поле File name присвойте
ему название.
Содержимое исходного файла
Компилятор предоставляет возможность за-
дать необходимые входные и выходные сиг-
налы, которые могут быть однобитовыми или
многобитовыми (рис. Б.4). Затем компилятор
выводит шаблон исходного файла, в котором
уже выполнена некоторая предварительная
работа. Шаблон исходного файла показан по-
середине на рис. Б.4.
В файле шаблона выполнена большая часть
подготовительной работы, включая следую-
щее:
♦ перечислены все входные и выходные сиг-
налы;
♦ для каждого сигнала указан его тип: входной
или выходной;
♦ переменным сигналов присвоены типы: wire
(по умолчанию) или гед (менее часто исполь-
зуемый тип, который сохраняет присвоенное
значение).
Затем в файл шаблона мы добавляем нашу раз-
работку, как показано справа на рис. Б.4.
Синтез (компиляция) исходного файла
Завершив создание кода модуля Verilog и сохра-
нив исходный файл, компилируем его. Для это-
го в панели Processes в узле Implement Design
Рис. Б.З. Создание нового исходного файла (модуля Verilog)
\:
;:
in., . ..],„
•i /> £'tvcsjri#er:
? //14
: f/, 1ч
9 If
■■! eacte,
5
►vision: !
' Hi,
асйк
t,,i , ( 1M i ., ">«*» Tit ,
Определение сигналов
Рис. Б.4. Три этапа создания исходного файла Verilog
Пустой файл шаблона,
созданный автоматически
Файл шаблона с добавленными
в него уравнениями разработки
6.7. Краткий обзор Xilinx, Verilog и ABEL
1137
выбираем узел Synthesize и выполняем двой-
ной щелчок по нему. На данном этапе нам не
требуется полностью выполнять реализацию,
и мы не будем делать этого, пока не настанет
время исполнять программу. Процесс синтеза
может занять минуту-другую даже для очень
простой схемы. Успешно выполненный этап
синтеза или реализации отмечается галочкой в
зеленом кружочке, как показано на рис. Б.5.,
♦ Представление RTL — сокращение RTL
означает register transfer level Это жаргон
языка HDL, значение которого мы сейчас не
будем рассматривать. Само же представление
является общей принципиальной схемой,
независимо от конкретного используемого
устройства.
♦ Представление Technology Schematic —
данное представление показывает реализа-
цию разрабатываемой схемы на основе кон-
кретной микросхемы.
Оба представления принципиальной схемы
разрабатываемого устройства показаны на
рис. Б.6. В данном случае представление RTL
проще, но иногда представление Technology
Schematic более понятное5.
Ptocesse? for andLof
С Add Eating Soutce
^ Cieale New Source
(: } Cuftiigyie Taigel Device
Рис. Б.5. Компилирование исходного файла разработки
схемы
Просмотр схемы разработки
Просматривать схему разработки, созданную
Verilog, нет никаких веских причин, но это за-
нятие может доставить удовольствие, так как
предоставляет существенное доказательство,
что компилятор действительно что-то сделал.
Впрочем, иногда просмотр схемы может быть
полезным, поскольку по ней можно увидеть,
что компилятор не совсем правильно понял
наши намерения. Но для простой схемы И и
ИЛИ мы не даем компилятору больших воз-
можностей для фантазирования, поэтому вряд
ли в этой схеме будут какие-либо сюрпризы.
Два типа представления
принципиальной схемы
Для просмотра созданной Verilog схемы раз-
рабатываемого устройства предлагаются два
представления:
anchor
and or
Рис. Б.б. Логический блок разрабатываемого устройства
(слева) и два представления его принципиальной схемы
(справа)
Показанные на рис. Б.б принципиальные схе-
мы логики И-ИЛИ выглядят, как и ожидалось.
В случае сложных проектов полная схема мо-
жет быть не очень полезной. Вместо нее целе-
сообразнее просмотреть только интересующую
часть схемы, чтобы не потеряться в деталях.
Эта возможность рассматривается далее.
Просмотр части принципиальной схемы
Средство просмотра схемы позволяет выбрать,
для какой части разрабатываемого устройства
создавать схему. Эта возможность предостав-
ляется при первом запросе создания схемы; ее
также можно открыть позже, выполнив после-
довательность команд меню Edit | Preferences |
RTL | Technology Viewers.
5 Мы обнаружили, что иногда представление RTL может
быть неправильным. В частности, строка кода COUNT <+
<+ COUNT + 1 разрабатываемого счетчика в нем была реа-
лизована как сумматор, а не счетчик. А в представлении
Technology Schematic такая ошибка отсутствовала.
1138
Приложение Б. Работа с логическим компилятором ХШпх
Представление полной схемы
Просмотр полной схемы лучше подходит для
простых устройств. Установить этот режим про-
смотра по умолчанию можно, выбрав опцию
Start with a schematic of the top-level block
(Начинать со схемы блока верхнего уровня),
как показано на рис. Б.7.
andhor
and or
многом похожую на такую же схему на рис. Б.7.
Но в этом «черном ящике» можно выбирать
сигналы, для которых нужно создать принци-
пиальную схему. Для этого нужно выполнить
щелчок правой кнопкой по требуемому вход-
ному сигналу и в контекстном меню выбрать
опцию Add Output Cone (Добавить выходную
воронку), и среда ISE создаст схему всех элемен-
тов, на которые подается этот сигнал. Но часто
полезнее выбрать выходной сигнал и создать
для него входную воронку (Add Input Cone).
Результат такого действия изображен справа на
рис. Б.9, где показана только функция ИЛИ раз-
рабатываемой схемы, но не ее функция И.
Рис. Б.7. Установка просмотра всей схемы по умолчанию
Изначально схема отображается в виде «черно-
го ящика», как показано на рис. Б.7 справа, но
двойной щелчок по нему отображает его вну-
треннее устройство, как показано на рис. Б.6
справа. Более сложные проекты могут содер-
жать дополнительные слои, отобразить кото-
рые можно так же двойным щелчком по ним.
Частичное представление схемы
Это представление хорошо подходит для слож-
ных схем. Чтобы создать принципиальную схе-
му только для части разрабатываемого устрой-
ства, выберите опцию Start with explorer
wizard (Начинать с мастера просмотра), как
показано на рис. Б.8. В данном случае мы вы-
брали создание схемы только для портов верх-
него уровня (top level ports).
Рис. Б.9. Среда ISE может создавать принципиальную схему
только для части разрабатываемого устройства
Пример создания частичной схемы
Для схематики И-ИЛИ нашего примера трудно
найти практические причины для просмотра
только части ее принципиальной схемы. На
рис. Б.10 приводится более убеждающий при-
мер полезности этой возможности. В частно-
сти, это схема связывающей логики GLUEPAL,
Х^ Запустите Мастер
просмотра схем
Затем выберите сигналы,
для которых нужно создать схему
Рис. Б.8. Мастер просмотра принципиальных схем позво-
ляет выбрать сигналы, для которых необходимо создавать
схему
Щелчок по кнопке Create Schematic (Создать
схему) открывает окно, содержащее схему в
виде «черного ящика» (слева на рис. Б.9), во
Рис. Б.10. Полная принципиальная схема может содержать
слишком много информации
5.7. Краткий обзор Xilinx, Verilog и ABEL
1139
используемой для связи элементов лаборатор-
ного компьютера из дискретных компонентов.
Хотя полная схема вполне понятна, она содер-
жит слишком много информации, чтобы ее
можно было всю охватить.
На рис. Б.11 иллюстрируется пример создания
принципиальной схемы только для одной инте-
ресующей нас функции, а не для всего устрой-
ства. Несомненно, эта схема намного легче под-
дается восприятию.
присвоить ему название и далее следовать ин-
струкциям Мастера.
В листинге Б.1 приводится пример шаблонного
файла эмуляции для нашей схемы И-ИЛИ.
Листинг Б.1. Пример шаблонного файла
эмуляции схемы И-ИЛИ
module and_or_tb;
ог2Ь2
ramce_impjramce1
RAMCEJ»rjmp_RAMeEJ>ar1
G5S>
ESS>
ШШ>
Рис. Б.11. Принципиальная схема только одной интересую-
щей нас части разрабатываемого устройства, легче поддаю-
щаяся восприятию
// Входные сигналы
гед а;
гед Ь;
// Выходные сигналы
wire out^and;
wire out_or;
// Создаем экземпляр тестируемого устройства (UUT)
and_or uut (
.out_and(out_and),
.out_or(out_or)
Б.1.3, Эмуляция разрабатываемой
схемы
Функционирование разрабатываемой схемы
можно проверить с помощью файла эмуля-
ции (testbench6) Verilog. Такой файл позволяет
смоделировать подачу стимулов (т. е. входных
сигналов) на схему и наблюдать вызываемые
ими выходные сигналы. В результате эмуляции
создается диаграмма входных и выходных сиг-
налов, которые при желании можно также ото-
бразить в виде таблицы.
Процесс эмуляции
Для эмуляции работы схемы в проект нужно
добавить новый исходный файл с названи-
ем ..._tb.v. Шаблон такого файла, содержащего
большую часть подготовительного материала,
для нас создаст среда ISE. Чтобы создать файл
шаблона эмуляции, нужно выполнить последо-
вательность команд меню Project/New Source,
в открывшемся окне Мастер создания исходно-
го файла выбрать опцию Verilog Test Fixture,
initial // Следующая строка кода выводит результаты
// эмуляции в табличной форме
// (По умолчанию результат также выводится
// в виде графика)
$monitor("(a, b) = %b,%b, out_and = %b, out_or = %b", a,
b, out_and, out_or);
+
initial begin
// Инициализируем входы
a = 0;
b = 0;
// Ждем 100 не для завершения глобального сброса
#100;
// Добавляем здесь управляющие воздействия
end
endmodule
Этот шаблонный файл выполняет работу по со-
поставлению данного файла эмуляции с соот-
ветствующим файлом проекта:
// Создаем экземпляр тестируемого устройства (UUT)
and_or uut(
Также он создает экземпляры необходимых
входных и выходных сигналов:
6 Строго говоря, на языке Verilog этот файл следует назы-
вать Test Fixture. Термин testbench взят из языка VHDL, но
употребляется в обоих этих языках.
1140
Приложение Б. Работа с логическим компилятором ХШпх
.out_and(out_and),
.out_or(out_or)
Шаблонный файл также «помнит» то, что мы
сами могли бы и забыть, а именно, что для
файла эмуляции переменные входных сигна-
лов должны быть типа REG, чтобы они могли
сохранять свои значения, пока не будут переза-
писаны новыми значениями. А вот переменные
выходных сигналов должны быть типа WIRE.
Завершаем файл эмуляции
В данном шаблонном файле мы указываем
входные уровни и моменты времени, когда они
должны меняться. Например, в листинге Б.2
выражение #10 означает, что данная операция
должна выполняться 10 временных единиц по-
сле выполнения операции в предшествующей
строке кода7. В листинге Б.2 мы вставили в ша-
блонный файл четыре возможные комбинации
входных сигналов для двух входов логической
схемы И-ИЛИ.
Листинг Б.2. Завершенный файл эмуляции
module and_or_tb;
// Входные сигналы
reg a;
reg b;
// Выходные сигналы
wire out_and;
wire out_or;
// Создаем экземпляр тестируемого устройства (UUT)
and_or uut (
.out_and(out_and),
.out_or(out_or)
initial // Следующая строка кода выводит результаты
эмуляции в табличной форме
// (По умолчанию результат также выводится в виде
графика)
$monitor("(a, b) = %b,°/ob, out_and = %b, out_or = %b" a,
b, out_and, out_or);
initial begin
// Инициализируем входы
a = 0;
b = 0;
// Ждем 100 не для завершения глобального сброса
#100;
// Добавляем здесь управляющие воздействия
#10 b = 1; // Выражение #10 определяет задержку от-
носительно
// предыдущей строки кода
#10Ь = 0;
а = 1;
#10Ь = 1;
#10 а = 0;
Ь = 0;
end
endmodule
Эмулятор ISim автоматически выводит резуль-
таты в виде графика сигналов, задействованных
в эмуляции. Но в файле эмуляции мы добавили
строку кода $monitor..., которая также выводит
результаты эмуляции в виде таблицы. Иногда
результаты моделирования в табличной форме
могут быть более информативными, чем в виде
временного графика сигналов, хотя данная схе-
ма настолько проста, что результаты в таблич-
ной форме определенно не являются необхо-
димыми.
Выполняем эмуляцию
Исполнение файла эмуляции дает результаты,
показанные справа внизу на рис. Б.13: времен-
ная диаграмма входных и выходных сигналов.
Но сам процесс исполнения эмуляции несколь-
ко запутанный.
Б.1 А Процесс выполнения
эмуляции
Чтобы запустить готовый файл эмуляции на
исполнение, установите переключатель Simu-
lation, как показано на рис. Б.12.
7 Величину временной единицы можно определить, как
вам нравится. В данном файле величина временной еди-
ницы определена (в строке кода в самом начале файла) как
одна наносекунда.
Рис. Б.12. Для запуска файла эмуляции нужно установить
переключатель Simulation
БЛ. Краткий обзор XHinx, Verilog и ABEL
1141
После запуска эмуляции в окне эмулятора
не отображаются ожидаемые результаты
Двойным щелчком
запускаем эмуляцию X
)
Чтобы отобразить правильные результаты, выберите в меню Simulotion команду Run All,
о затем щелкните по значку Zoom to full View
Рис. Б.13. Процедура получения результатов эмуляции
Затем в панели Processes выполните двойной
щелчок по узлу Simulate Behavioral Model.
В результате будет запущено приложение эму-
лятора ISim, в котором вместо ожидаемых сиг-
налов с перепадами отображены только гори-
зонтальные линии, как показано на рис. Б.13.
Но не стоит впадать в отчаяние. Чтобы эмуля-
тор ISim отобразил правильные сигналы (ко-
торые он по умолчанию не отображает, что до-
статочно странно), выберите в меню Simulation
команду Run All, а затем щелкните по значку
Zoom to Full View. В результате должны ото-
бразиться правильные прямоугольные входные
и выходные сигналы. Если в файле эмуляции
вы вставили код для отображения результатов в
табличной форме, вместе с результатами в фор-
ме сигналов в нижней панели окна эмулятора
(которая называется Console) будут отображе-
ны результаты эмуляции в табличной форме.
Иногда результаты эмуляции легче понять, если
они приведены в табличной форме. Например,
это может быть в случае результатов эмуляции
схемы И-ИЛИ, как показано на рис. Б.14. Но это
уже дело личных предпочтений.
Проверочный файл эмуляции
Для сложных схем может быть полезным соз-
дать проверочный файл эмуляции, который
содержит ожидаемые результаты и сверяет их
с полученными. Но создание таких файлов яв-
ляется трудной задачей. Более подробно этот
вопрос рассматривается в приложении А.
This is a Lite version of ISE S
:? 10 fit I ;■;< tOf ).:"
finished с ire
( a, fe; ■■■00r our
i a, Ы »10, mjr
{ a, b} •■•-11, out
ing rircuit initialisation
t in it. xaiii^rtt ion proc&Sc,
d -" О, о и t о г - О
о u t о t ~: 1
ont ox -■ 0
Рис. Б.14. Результаты эмуляции в графической и табличной
форме
Устранение неполадок
Иногда вследствие ошибок при компиляции
происходит искажение файлов и компилятор
начинает выдавать загадочные сообщения об
ошибках типа Could not link simulation (He уда-
лось сопоставить эмуляцию). В таком случае
попробуйте выполнить очистку файлов проек-
та, выполнив в меню Project команду Cleanup
Project Files.
Приложение В. Линии передачи
Содержание
8.1. Тема, от которой мы до сих пор уклонялись 1142
В.1.1. Правила для импеданса, когда сигнал устройства А подается
на устройство Б 1142
8.2. Линия передачи 1143
8.2.1. Использование частотной характеристики для синусоидальных сигналов 1143
8.2.2. Использование временной характеристики 1144
8.3. Отражения 1145
8.3.1. Импульсы, а не синусоиды 1145
8.3.2. Случаи неправильной оконечной нагрузки 1145
8.4. Почему мы беспокоимся об отражениях? 1147
8.4.1. Оконечная нагрузка решает проблему отражений 1147
8.4.2. Классическое решение посредством согласованной оконечной нагрузки 1148
ВАЗ. Последовательная оконечная нагрузка 1148
8.5. Влияние линии передачи для синусоидальных сигналов 1150
8.5.1. Знакомый эффект низкочастотного фильтра 1150
8.5.2. Новые эффекты в линии передачи 1150
8.5.3. Частичное рассогласование импедансов 1151
В.1. Тема, от которой мы
до сих пор уклонялись
На наших лабораторных занятиях нам не при-
шлось встретиться с высокими частотами, ког-
да необходимо принимать во внимание свой-
ства линии передачи. Поэтому по завершении
данного курса вы можете не знать об этом ме-
тоде рассмотрения вопросов, связанных с им-
педансом. Описанный здесь метод понадобит-
ся, когда вам придется работать с частотами,
значительно превышающими те, с которыми
мы имели дело в нашем курсе. Мы работали
с сигналами с частотой всего лишь несколько
мегагерц, с единственным исключением: часто-
та высокочастотных паразитных автоколеба-
ний в эмиттерном повторителе из дискретных
компонентов в некоторых случаях приближа-
лась к 100 МГц. Еще мы использовали сигнал
тактирования для микроконтроллера часто-
той 11 или 24,5 МГц (для микроконтроллера
C8051F410), но никакого участия в обработке
этого сигнала не принимали.
В.1.1. Правила для импеданса,
когда сигнал устройства А подается
на устройство Б
Самый распространенный случай:
источник напряжения умеренной
частоты
В самый первый день занятий мы начали все-
сторонне рассматривать тему, когда сигнал из
части А схемы подается на часть Б той же схемы.
Мы постоянно напоминали, что нужно следить
за тем, чтобы выходной импеданс каскада А был
низким по сравнению с входным импедансом
каскада Б. Мы также возвели в статус основного
правила понятие, что отношение этих импедан-
сов должно быть в пропорции 10 к 1:
0,lZ
вх Б*
Это правило проектирования не утрачивает
свою полезность и при рассмотрении свойств
линий передачи.
6.2. Линия передачи
1143
Менее распространенный случай:
источник тока умеренной частоты
Иногда нам приходилось иметь дело с сигнала-
ми в виде токов, а не напряжений. Предпочтения
для источника тока, наподобие фотодиода из
лабораторного занятия 6L (схема которого при-
водится на рис. В.1), противоположны предпо-
чтениям для источника напряжения.
1М0м
ЛЛ/V—|
Освещение
Фототранзистор
Эмиттер не подключен
Рис. В.1. Для подключения источника тока требуется низкий
входной импеданс
Фотодиоду в схеме на рис. В.1 «нравится» по-
давать свой выходной сигнал на нагрузку с низ-
ким входным импедансом, а его «любимой» на-
грузкой будет (кто бы мог подумать!) короткое
замыкание. Операционный усилитель преобра-
зователя «ток - напряжение» в схеме на рис. В.1
(который иногда называют трансимпедансным
усилителем) обеспечивает почти идеальный
входной импеданс для сигнала в виде источ-
ника тока. При виртуальной «земле» входной
импеданс очень мал; золотым правилом будем
считать его равным нулю1. (Надеемся, вам не
нужно напоминать, что входной импеданс этой
схемы не равен 1 МОм.)
В.2. Линия передачи
На протяжении этого курса мы работали с ко-
аксиальными кабелями (которые мы часто на-
зываем BNC-кабелями, по названию исполь-
зуемых с ними разъемов). Эти кабели обычно
служили нам, не требуя к себе какого-либо осо-
бого внимания. Но иногда приходилось учи-
тывать емкость коаксиальной линии (около
30 пФ на 30 см). Обычно так было в тех случа-
ях, когда сигнал на кабель подавался не от ге-
нератора сигналов, а от схемы со значительным
выходным сопротивлением. До сих пор это был
предел сложностей, доставляемых кабелями.
Но такое «кроткое» поведение знакомого нам
коаксиального кабеля меняется в худшую сто-
рону, когда на довольно длинный кабель по-
дается сигнал с частотой выше, чем сигналы, с
которыми мы работали в этом курсе.
Примечание
Этот эффект свойствен не только кабелю, но его
легче всего рассматривать на кабелях по причине
их стандартных характеристик.
В частности, мы получаем новые результаты,
которые можно описать, используя частотные
или временные термины. Случаи, в которых
тракт сигнала необходимо рассматривать как
линию передачи (длинную линию), можно
описать двумя способами2:
1. С помощью частотной характеристики —
когда длина линии3 составляет, цитируя кни-
гу АоЕ: «значительную часть длины волны с
наивысшей частотой».
2. С помощью временной характеристики —
когда время прохождения сигнала в прямом
и обратном направлениях составляет значи-
тельную долю общего времени нарастания
сигнала.
В.2.1. Использование
частотной характеристики для
синусоидальных сигналов
Попробуем применить первый из этих крите-
риев (частотный) к сигналам, с которыми нам
приходилось работать в этом курсе. Проверим,
в частности, можно ли доверять нашим впечат-
лениям от работы с этими сигналами и не заме-
тить никакого влияния линии передачи.
При какой длине кабеля должны мы начинать
беспокоиться о влиянии линии передачи?4
1 Но вы-то знаете лучше, чем верить этому. Вспомним,
что действительное значение R^ = JR0C/A, где А обознача-
ет коэффициент усиления с разомкнутой цепью обратной
связи. Таким образом, на частоте, при которой значение А
будет, например, 10 000, величина Двх = 1 МОм/10 000 =
100 Ом.
2 АоЕ §Н.2.
3 Как говорится в книге АоЕ, важным фактором является
«электрическая длина», которая учитывает замедление
распространения сигнала в диэлектрике кабеля. См. также
раздел В.2.1.
4 В табл. В.1 предполагается, что скорость распростране-
ния сигнала составляет 2/3 скорости света, что более или
менее правильно для кабеля с твердым полиэтиленовым
диэлектриком.
1144
Приложение 8. Линии передачи
Ответ на этот вопрос дан в табл. В.1. Мы при-
меняем эмпирическое правило, гласящее, что
следует беспокоиться, если длина кабеля (элек-
трическая длина, с учетом диэлектрика кабеля)
составляет приблизительно 1/10 длины волны
подаваемого в него сигнала.
Таблица В.1. Параметры линии передачи
Частота,
МГц
1
3
10
30
100
Длина
волны
300
100
30
10
3
Физическая
длина волны
в кабеле, м
200
66
20
6,6
2
Пороговая дли-
на линии пере-
дачи, м
(кабель = Х/Ю)
20
6,6
2
0,66
0,2
Для конкретной частоты физическая длина
волны в кабеле меньше, чем в вакууме из-за
меньшей скорости распространения сигнала
в диэлектрике. Таким образом, проблемы на-
чинают возникать при более коротком кабеле,
чем можно было бы ожидать.
Но из таблицы ясно видно, как нам удавалось
избегать влияния линии передачи в этом курсе:
мы использовали генераторы, частота сигна-
лов у которых не превышала 3 МГц. А в редких
случаях, когда синусоидальные сигналы имели
более высокую частоту, мы не передавали их по
7-метровому кабелю.
В.2.2. Использование временной
характеристики
Это все, что касается синусоидальных сигналов
(за исключением еще одного взгляда в разде-
ле В.5). Но цифровые сигналы с крутыми фрон-
тами могут вызывать проблемы при передаче
по линии даже при низкой частоте следования
импульсов. При работе с цифровыми сигналами
в этом курсе иногда встречалась потенциально
проблематичная ситуация: крутые перепады и
довольно длинные линии. Но нас эти эффекты
не беспокоили, поскольку их результатом было
только некоторое искажение логических сиг-
налов, но не до такой степени, чтобы создавать
ложные переходы логических пороговых уров-
ней. Высокая помехоустойчивость цифровых
схем является одним из их достоинств.
Мы не передавали логические сигналы по
длинным коаксиальным кабелям, но в компью-
тере из дискретных компонентов подавали та-
кие сигналы на дорожки печатных плат длиной
до 30 см. В этих случаях возникали отражения
сигналов, но они не создавали проблем, по-
скольку требования к сигналам были не очень
жесткими. Мы передавали только такие циф-
ровые сигналы, как данные и адреса, у которых
было достаточно времени, чтобы стабилизиро-
ваться после перехода. Вспомните, что мы не
передавали по этим шинам никаких сигналов
тактирования.
Далее мы рассмотрим такие сигналы в разде-
ле ВАЗ. Но сначала изложим некоторые эмпи-
рические правила, которые могут помочь нам
сопоставить время нарастания сигнала и длину
тракта сигнала, чтобы узнать, когда нам следу-
ет беспокоиться о проблемах линии передачи.
Сопоставление времени нарастания
длине тракта
Причина проблемы
Легче всего увидеть причину проблемы можно,
рассмотрев тип отражений, которые не создают
проблем: отражения в коротких линиях, кото-
рые возвращаются к точке подачи сигнала, пока
источник сигнала все еще находится в процессе
перехода. Такие отражения могут немного ис-
казить перепад, но обычно не причиняют ему
существенного вреда. Таким образом, когда
время нарастания значительно превышает вре-
мя прохождения сигнала в прямом и обратном
направлениях, влиянием линии передачи мож-
но пренебречь5.
Эмпирические правила, касательно ситуации,
когда следует беспокоиться о влиянии линии
передачи, можно сформулировать нескольки-
ми способами. Далее приводится очень простое
правило для определения приблизительной
длины линии, при которой следует ожидать
начала возникновения нежелательных эффек-
тов. Данное правило описывает длину дорожки
печатной платы, в которой отражение сигнала
возвратится к источнику как раз к завершению
нарастания передающего импульса6.
5 Более подробную информацию по этому вопросу мож-
но найти на веб-сайте http://www.ultracad.com/mentor/
transmission%201ine%20critical%20length.pdf
6 Данное правило применимо к печатным платам из мате-
риала FR-4 (http://www.ultracad.com/mentor/transmis-
ВЗ. Отражения
1145
Дорожку печатной платы следует рассматри-
вать как линию передачи, когда ее длина со-
ставляет
75 мм • f^p,
где tHA? — время нарастания сигнала в наносе-
кундах.
Данное правило основано на аргументе, что
такая длина позволяет отражению возвратить-
ся к источнику в течение времени нарастания.
Например, время нарастания длительностью
1 не допускает линию длиной приблизительно
15 см.
Примечание
Скорость распространения сигнала на печатной
плате из материала FR-4 принимается равной при-
близительно половине скорости света в вакууме,
которая составляет приблизительно 30 см/нс.
Таким образом, время прохождения сигналом
дорожки печатной платы длиной 7,5 см долж-
но составлять 1 не. На этом и основано данное
правило. А время нарастания длительностью
3,5 не (почти такое же, как и время нарастания
сигналов микросхем семейства 74НС7) уве-
личит критическую длину линии передачи до
приблизительно 25 см.
Еще одно эмпирическое правило сопоставляет
время нарастания самой высокой частоте, при-
сутствующей в сигнале:
Ширина полосы пропускания
(т. е. максимальная частота синусоидального
сигнала)» 0,35/^,
где £НАР — время нарастания сигнала.
Таким образом, время нарастания, например,
3,5 не допускает частоту 100 МГц. Тогда, со-
гласно данным из табл. В.1, можно предполо-
жить, что для импульса с временем нарастания
длительностью 3,5 не влияние линии передачи
sion%201ine%20critical%201ength.pdf). Доходчивое не-
формальное объяснение можно найти по адресу: http://
www.ultracad.com/articles/criticallength.pdf.
7 См. руководство пользователя компании Philips: http://
www.nxp.com/documents/usermanual/HCTUSER
GUIDE.pdf, в котором указывается время нарастания дли-
тельностью 4 не для микросхем-драйверов шины и 6 не
для обычных микросхем семейства 74НС. Время нарас-
тания более современных микросхем семейства НС может
быть еще меньше.
проявится при длине линии приблизитель-
но 20 см для коаксиального кабеля или около
15 см для дорожки печатной платы. Это более
консервативное правило, чем более простое
правило времени нарастания (75 мм • fHAP), по
которому устанавливается предельная дли-
на величиной приблизительно 25 см. Но оба
правила дают примерно одинаковые значения
критической длины.
ВЗ. Отражения
В.3.1. Импульсы, а не синусоиды
Поведение импульсов в линиях передачи легче
поддается пониманию, чем поведение синусои-
дальных сигналов, поэтому начнем с рассмо-
трения первых. Поведение синусоидальных
сигналов будет рассматриваться далее, в раз-
деле В.5. Когда все делается должным образом,
как мы увидим в разделе ВАЛ, при прохожде-
нии импульса даже по длинному кабелю не
происходит ничего особенного. Интересное и,
что более важно, проблемное поведение, на-
зываемое «отражением», возникает в резуль-
тате неправильной оконечной нагрузки линии.
Отражение сигнала в линии можно сравнить
с отражением вносимых колебаний в слегка
провисшем шнурке, который вам, несомненно,
приходилось видеть8. Мы начнем с рассмотре-
ния исключительных примеров неправильной
оконечной нагрузки длинного кабеля, на кото-
рый подается сигнальный импульс.
В3.2. Случаи неправильной
оконечной нагрузки
Случай № 1: разомкнутый конец линии
Если конец линии передачи оставить разом-
кнутым (что в электрических терминах эквива-
лентно подаче сигнала на нагрузку с импедан-
сом более высоким, чем импеданс линии пере-
дачи), то подаваемый в такую линию импульс
отражается на ее конце назад. Этот импульс
8 На веб-странице http://www.animations.physics.unsw.
edu.au/jw/waves_superposition_reflection.htm#reflections
можно найти хорошее объяснение этого эффекта, иллю-
стрируемое анимационным роликом. Эффект отражения
импульса также рассматривается в Википедии (http://
en.wikipedia.org/wiki/Pulse %28physics%29), но не
так хорошо, как в предыдущем источнике.
1146
Приложение В. Линии передачи
имеет такую же полярность, как и падающий
импульс (достигая, таким образом, двойного
уровня входного импульса), и движется обрат-
но к началу линии9. Рассмотрим следующий
пример этого эффекта. Длительность импуль-
са на рис. В.2 достаточно мала, поэтому отра-
женный импульс приходит значительно поз-
же, после затухания исходного импульса. Два
импульса в конце подачи сигнала — исходный
и отраженный — находятся на временном ин-
тервале приблизительно 32 не друг от друга.
Это примерно соответствует тому, что можно
было бы предсказать для кабеля длиной 3 м10.
&: плт
О
Рис. В.2. Для кабеля длиной 3 м с разомкнутыми концами
неинвертированный отраженный импульс приходит после
исходного импульса через интервал, равный времени рас-
пространения сигнала туда и обратно. (Настройки осцилло-
графа: 2 В/дел., 20 нс/дел.)
Случай № 2: замкнутый конец линии
Другой крайностью будет случай с замкнутым
дальним концом линии. В данном случае им-
пульс также отражается, но при этом инверти-
руется. На рис. В.З показан эффект подачи им-
пульса на кабель длиной 3 м.
9 Это поведение, подобное такому же эффекту в случае
с закороченным концом линии, является результатом
принципа сохранения энергии. При разомкнутом конце
линии ток нулевой, а при закороченном нулевым является
напряжение. Индуцированное отражение рассеивает энер-
гию в линии и импедансе источника сигнала. См.: http://
www.ti.com/lit/an/snlaO27b/snlaO27b.pdf.
10 Длина тракта прохождения сигнала туда и обратно со-
ставляет 6 м. Скорость распространения сигнала в этом
коаксиальном кабеле составляет 0,66 от скорости его рас-
пространения в вакууме, или около 20 см/нс. Таким об-
разом, время прохождения туда и обратно равно около
30 нс.
Передающий
конец кабеля с
Рис. В.З. При подаче сигнала в кабель длиной 3 м с коротко-
замкнутым приемным концом отраженный сигнал приходит
инвертированным. (Разрешение осциллографа: 500 мВ/дел.,
40 нс/дел.)
Крутой входной сигнал при замкнутом
конце
Интересную версию этой схемы можно ис-
пользовать для создания короткого импульса
из входного сигнала с крутым перепадом. Если
рассматривать, как будет выглядеть сигнал на
стороне передачи при замкнутом принимаю-
щем конце, то первой мыслью может быть, что
ничего мы на нем не получим, если #вых = 50 Ом,
поскольку мы имеем дело с делителем между
50 и 0 Ом. Это будет почти правильно: мы ни-
чего не получим в стабильном состоянии. Но
на передающей стороне потребуется некоторое
время, чтобы «обнаружить», что принимаю-
щий конец замкнут. Тем временем, напряжение
выглядит так же, как и напряжение запускаю-
щего сигнала (или, более точно, как £/источ/2,
поскольку #вых создает делитель совместно
с волновым сопротивлением кабеля величи-
ной 50 Ом). Только по прибытии отраженно-
го сигнала напряжение становится нулевым.
Длительность импульса равна времени про-
хождения сигнала туда и обратно. На рис. В.4
Крутой сигнал,
нагрузка отсутствует
Крутой входной
сигнал, приемный
конец кабеля замкнут
накоротко
Рис В.4. Подача крутого сигнала в кабель (длиной 3,5 м) с ко-
роткозамкнутым приемным концом приводит к появлению
импульса малой длительности. (Разрешение осциллографа:
500 мВ/дел., 40 нс/дел.)
В А. Почему мы беспокоимся об отражениях?
1147
импульс начинает спадать где-то через 30-
40 не после нарастания до полной амплитуды.
Величина вычисленного времени прохождения
сигнала туда и обратно приблизительно равна
рассчитанной в разделе В.3.2.
В А Почему мы беспокоимся
об отражениях?
Можно привести правдоподобное рассужде-
ние, что отражения сигнала могут быть без-
вредными. Подайте выходной импульс с логи-
ческого элемента (низкий выходной импеданс)
через длинный коаксиальный кабель на вход
другого логического элемента (высокий вход-
ной импеданс). Что произойдет в этом случае?
Данный случай, когда сигнал в кабель пода-
ется не от генератора сигналов, а с выхода ло-
гического элемента, отличается от ситуации
с разомкнутым концом, рассматриваемой в
разделе В.3.3, в том отношении, что источник
сигнала здесь не согласован с кабелем, как был
согласован генератор сигналов. Генератор сиг-
налов имеет встроенную выходную нагрузку
величиной 50 Ом, как и другое лабораторное
оборудование. Импеданс источника величиной
50 Ом поглощал отраженный сигнал, в резуль-
тате чего происходило только одно отражение.
А вот низкий выходной импеданс логического
элемента должен создавать новое отражение
(инвертированное), которое снова проходит по
кабелю и опять отражается. Похоже, что ситуа-
ция может оказаться запутанной и сложной.
В действительности такой она и будет. На
рис. В.5 изображена осциллограмма сигнала,
Передающий
конец кабеля
Принимающий
конец кабеля
подаваемого в коаксиальный кабель длиной
приблизительно 180 см без оконечной нагруз-
ки с параллельно соединенных выходов не-
скольких логических элементов 74НСТ для
обеспечения достаточного тока11. Довольно не-
привлекательное зрелище...
Сигнал не только имеет уродливую форму, но
всплеск амплитудой 8 В на дальнем конце кабе-
ля может повредить логические элементы, ра-
бочее напряжение которых составляет 5 В. На
первый взгляд, осцилляции сигнала выглядят
похожими на резонансные колебания, кото-
рые, как мы видели, создавались паразитными
индуктивностями и емкостями. Подобные бес-
форменные сигналы можно наблюдать, если,
например, не заземлить щуп осциллографа. Но
природа этих колебаний иная. В действитель-
ности они создаются в результате отражений
сигнала от принимающего (дальнего) кон-
ца кабеля, затем от передающего, затем снова
от принимающего и т. д. Когда импульс отра-
жается от низкого импеданса на передающем
конце, он инвертируется, что объясняет отри-
цательное смещение на принимающем конце,
которое возникает приблизительно через 30 не
(что равно длительности одного прохождения
туда и обратно) после достижения этого конца
первоначальным положительным импульсом.
Самым лучшим свидетельством того, что такие
искажения сигнала вызываются отражениями,
является тот факт, что эти искажения устраня-
ются при надлежащей оконечной нагрузке ка-
беля. Этот момент подробно рассматривается
в разделе ВАЗ и иллюстрируется на рис. В.7.
В.4.1. Оконечная нагрузка решает
проблему отражений12
Эффекты отражения, описанные в разде-
лах В.3.2 и В.3.3, могут выглядеть в некоторой
степени интересными. Но, конечно же, они
являются нежелательными, за исключени-
ем случая с генератором коротких импульсов
(см. рис. В.4), который может быть полезным.
Искажения сигналов малой длительности мож-
но устранить с помощью надлежащей оконеч-
ной нагрузки кабеля.
2",'fto"v >|;4(Г1'5' а; Он I ?20tnvi
Рис. В.5. Осциллограмма сигнала, подаваемого в разомкну-
тый коаксиальный кабель длиной приблизительно 180 см от
запараллеленных логических элементов микросхемы 74НСТ.
(Настройки осциллографа: 2 В/дел., 40 нс/дел.)
11 Мы использовали все восемь логических вентилей ми-
кросхемы 74НСТ541, чтобы получить ток величиной при-
близительно 50 мА, достаточный для установления полно-
ценного высокого логического уровня в кабеле с волновым
сопротивлением 50 Ом.
12 АоЕ §Н.5.
1148
Приложение В. Линии передачи
В.4.2. Классическое решение
посредством согласованной
оконечной нагрузки
Оконечная нагрузка кабеля реализуется под-
ключением его дальнего конца к «земле» или
к источнику напряжения через резистор. Если
сопротивление этого резистора равно волно-
вому сопротивлению кабеля, то с точки зре-
ния электротехники кабель будет выглядеть
бесконечным. В результате волна или импульс
сигнала никогда не встретит разрыва в кабеле.
Таким образом, если коаксиальный кабель дли-
ной 3,5 м, в котором возникал двойной импульс
(см. рис. В.2), оснастить оконечной нагрузкой,
в нем больше не будет возникать отражений. На
рис. В.6 для сравнения показаны осциллограм-
мы сигналов в таком кабеле для двух случаев:
без оконечной нагрузки (слева) и при наличии
таковой (справа).
■*•■
Разомкнутый
принимающий конец
Кабель оснащен оконечной
нагрузкой величиной 50 Ом
Рис. В.б. Сравнение сигналов в кабеле длиной 3 м без око-
нечной нагрузки и с таковой: оконечная нагрузка устраняет
отражения. (Настройки осциллографа* 2 В/дел., 20 нс/дел.)
Такое же решение — подключение дальнего
конца линии передачи на «землю» через рези-
стор номиналом 50 Ом — устраняет импульс
отражения сигнала, подаваемого в кабель с вы-
хода логических элементов, осциллограмма ко-
торого была показана на рис. В.5 (рис. В.7).
Передающий
конец кабеля
Принимающий
конец кабеля
\/у
Ch2, 2'oo'v""'iM:4p."dris:1 A- ciit I 3©S«V
Рис. В.7. Оснащение оконечной нагрузкой величиной 50 Ом
устраняет отражения в коаксиальном кабеле, в который по-
дается сигнал с выходов логических элементов микросхемы
74НС. (Настройки осциллографа: 2 В/дел., 40 нс/дел.)
Хотя подключение оконечной нагрузки устра-
няет отражения в кабеле, она повышает токо-
вые требования к источнику сигнала. В част-
ности, если резистор оконечной нагрузки
подключается на «землю» и на нем создается
напряжение 5 В, то источник сигнала должен
обеспечить ток величиной вплоть до 100 мА13.
ВАЗ, Последовательная оконечная
нагрузка
Менее идеальной, но более практичной защи-
той от отражений будет просто подключение
выхода источника сигнала к кабелю через по-
следовательный резистор, сопротивление кото-
рого равно волновому сопротивлению кабеля14.
Пример реализации этого решения показан на
рис. В.8. Это настолько стандартный прием,
применяемый с генераторами сигналов, что его
даже трудно рассматривать как решение. Но
включение последовательного сопротивления
для подачи сигнала в кабель чрезвычайно эф-
фективно.
Л open
(or high-Z load)
Рис. В.8. Последовательная нагрузка на передающем конце
кабеля поглощает отражения
Этот прием не предотвращает отражение
от приемного конца (как мы видели в разде-
ле В.3.2), но устраняет второе отражение от
передающего конца, а также все последующие
отражения от обоих концов. Такая нагрузка по-
глощает все отраженные сигналы, предотвра-
щая «столкновение» сигналов, пример которо-
го приводится на рис. В.5. Она также ослабляет
сигнал, подаваемый в кабель, в результате чего
на дальний конец приходит сигнал с обычным,
а не двойным уровнем.
Для логических элементов это решение пред-
почтительнее по сравнению со стандартной
оконечной нагрузкой на дальнем конце, для
13 Ток можно уменьшить больше чем наполовину, если
использовать делитель окончательной нагрузки, создаю-
щий напряжение величиной в половину напряжения ис-
точника питания, делая его RTEB = 50 Ом. Такую оконечную
нагрузку подключить немного сложнее. От постоянного
тока можно избавиться посредством оконечной нагрузки
со связью по переменному току, реализованной с помо-
щью разделительного конденсатора.
14 АоЕ § Н.5.
6.4. Почему мы беспокоимся об отражениях?
1149
которой требуются большие токи покоя. На
рис. В.9 демонстрируется, как подача выход-
ного логического сигнала микросхемы 541 на
вход кабеля длиной приблизительно 180 см
через резистор номиналом 47 Ом обеспечивает
чистый сигнал.
Передающий
конец кабеля
Принимающий
конец кабеля
Рис. В.9. Подача логического выходного сигнала микросхе-
мы 541 на вход кабеля через последовательный резистор
номиналом 47 Ом довольно хорошо очищает передавае-
мый по кабелю сигнал. (Настройки осциллографа: 2 В/дел.,
40 нс/дел.)
Передача сигнала по дорожкам печатных
плат
Подача входного сигнала через последова-
тельный резистор также хорошо помогает и
при передаче сигналов по дорожкам печатных
плат. На рис. В.10 изображена осциллограмма,
демонстрирующая улучшение в случае подачи
выходного сигнала логических элементов на
дорожку шины длиной 25 см. Слева на рисун-
ке показана осциллограмма сигнала, переда-
ваемого по кабелю без нагрузки на передаю-
щем конце, а справа — с нагрузкой в 100 Ом.
Источником сигнала являются логические эле-
менты микросхемы 74НСТ54115.
■■ А/ \
driv*lhrai«M00ebms
Рис. В.10. Согласованная нагрузка на передающем конце
очищает сигнал, передаваемый по дорожке печатной платы
длиной 25 см. (Настройки осциллографа: 2 В/дел., 20 нс/дел.)
15 В качестве источника сигнала опять используются во-
семь логических элементов с параллельно соединенными
выходами, чтобы получить ток, необходимый для пере-
дачи сигнала по дорожке печатной платы со стандартной
оконечной нагрузкой на принимающем конце.
Семейство логических микросхем для
дифференциальной передачи LVDS со
встроенной оконечной нагрузкой
Цифровые микросхемы для дифференциальной
передачи, с которыми мы познакомились в гла-
ве 14N, решают проблему отражений довольно
элегантным способом. На первый взгляд может
показаться, что быстрые перепады длитель-
ностью вплоть до 0,25 не при передаче LVDS
могут создавать проблемы16. Но на принципи-
альной схеме типичной организации передачи
LVDS на рис. В.11 можно видеть, что эти опасе-
ния необоснованны17.
350 мВ
Приемник
Рис. В.11. Принципиальная схема подключения передатчи-
ка и приемника LVDS
Волновое сопротивление дорожек печатных
плат составляет приблизительно 100 Ом, и ре-
зистор на входе приемника выглядит очень по-
хожим на резистор оконечной нагрузки, сопро-
тивление которого согласовано с импедансом
линии передачи. Так оно и есть, и это не слу-
чайность. Данный резистор номиналом 100 Ом
требуется не только для оконечной нагрузки,
но и для создания сигнала на входе приемника.
Ток передатчика, подаваемый на приемник по
одному проводу и снимаемый с другого, создает
Входной импульс
амплитудой 5 В
Дифференциальные
сигналы:
(амплитуда каждого
равна 350 мВ)
Рис. В.12. Встроенная оконечная нагрузка устройств пере-
дачи LVDS обеспечивает чистые сигналы на дорожке печат-
ной платы длиной 25 см. (Настройки осциллографа: 2 В/дел,
(входной сигнал), 500 мВ/дел. (дифференциальные сигналы);
100 нс/дел.)
16 http://www.ti.com/lit/an/sUaO14a/sllaO14a.pdf.
17 Сравните с рис. 1-1 руководства по LVDS компании Na-
tional Semiconductor, доступного по адресу: http://www.
ti.com/lit/ug/snlal87/snlal87.
1150
Приложение fi. Линии передачи
на этом резисторе дифференциальный сигнал
напряжением 350 мВ.
На рис. В.12 показана осциллограмма сигналов
дифференциальной передачи по прибытии на
принимающий конец дорожки печатной платы
длиной 25 см: хотя амплитуда невелика, но ис-
кажений почти нет.
В.5. Влияние линии
передачи для
синусоидальных сигналов
Когда в линию передачи подается не импульс,
а синусоидальный сигнал, это вызывает еще
более странные эффекты, чем те, которые мы
наблюдали в лаборатории. В лаборатории мы
экспериментировали с цифровыми сигналами
с крутыми перепадами, но никогда не могли
добраться до высокочастотных синусоидаль-
ных сигналов. Если бы мы могли, то увидели
бы результаты, удивительно отличающиеся от
тех, которые наблюдали для низкочастотных
сигналов.
В.5.1. Знакомый эффект
низкочастотного фильтра
При передаче сигналов с более-менее низки-
ми частотами поведение коаксиального кабеля
можно сравнить с поведением конденсатора ма-
лой емкости, подключенного на «землю». Если
подавать сигнал в длинный кабель (скажем,
длиной 3,5 м, который мы использовали в боль-
шинстве экспериментов с импульсными сигна-
лами) от генератора с выходным импедансом
величиной 50 Ом, то ослабление сигнала обыч-
но не наблюдается. Это то, к чему мы привыкли
в наших лабораторных экспериментах.
Но на определенной высокой частоте мы бы
начинали наблюдать эффект низкочастотного
фильтра, создаваемого RC-цепью, состоящей
из волнового сопротивления величиной 50 Ом
и паразитной емкости кабеля величиной 30 пФ
на 30 см. Если выполнить расчет для коакси-
ального кабеля типа RG58 длиной 3,5 м, то по-
лучим частотуУздБ приблизительно 9 МГц. Такая
сравнительно высокая частота объясняет, по-
чему мы не наблюдали никаких эффектов на
наших лабораторных занятиях: наши генера-
торы не выдают сигналы с такой высокой ча-
стотой, или мы никогда не использовали их на
таких частотах. И определенно, мы никогда не
пытались передавать высокочастотный сигнал
по коаксиальному кабелю длиной 3 м или око-
ло того.
В.5.2. Новые эффекты в линии
передачи
Если частота синусоидального сигнала, пода-
ваемого на коаксиальный кабель длиной 3,5 м,
будет выше частоты, с которой мы работали на
лабораторных занятиях, то будет наблюдаться
незнакомое нам до сих пор поведение, вызы-
ваемое эффектами линии передачи. В частно-
сти, по мере повышении частоты сигнала и ее
приближения к значению, при котором длина
кабеля составляет 1/4 длины волны сигнала,
амплитуда сигнала на передающем конце начи-
нает снижаться, что внешне выглядит подобно
поведению низкочастотного фильтра. Когда же
частота сигнала достигает значения, при кото-
ром длина кабеля равна точно четверти длины
волны сигнала, амплитуда сигнала падает до
нуля. Это происходит на частоте приблизи-
тельно 16 МГц. Если частота сигнала продол-
жает увеличиваться, также начинает возрас-
тать и его амплитуда, достигая максимума на
частоте, когда длина кабеля равна 1/2 длины
волны сигнала. С этим поведением нам еще не
приходилось встречаться. Чем оно вызвано?
Отражениями сигнала от конца кабеля, не на-
груженного должным образом.
На рис. В.13 изображена осциллограмма сигна-
ла, частота которого меняется вручную от 1 до
приблизительно 110 МГц. На осциллографе на-
блюдается сигнал на передающем конце кабе-
ля без оконечной нагрузки. На осциллограмме
можно ясно видеть, когда сигнал имеет нулевую
амплитуду. Первый такой случай наблюдается
на частоте около 16 МГц.
При частоте сигнала, на которой длина кабеля
равна 1/4 длине волны сигнала, отраженный
сигнал приходит обратно на передающий конец
в момент времени, когда передаваемый сигнал
находится в точке половины периода. Тогда от-
раженный сигнал является инвертированной
версией передаваемого сигнала, и оба сигнала
аннулируют друг друга. При частоте сигнала, на
которой время его прохождения туда и обратно
6.5. Влияние линии передачи для синусоидальных сигналов
1151
Рис. В.13. Сигнал с повышающейся частотой содержит не-
сколько точек с нулевой амплитудой, в которых входной и
отраженный сигналы нейтрализуют друг друга. (Разрешение
осциллографа: 5 В/дел., 2 с/дел.)
равно целой длине волны (32 МГц), помехи от-
сутствуют, и мы снова наблюдаем полную ам-
плитуду сигнала.
Попробуем делать вычисления, чтобы посмо-
треть, имеют ли смысл точки осциллограм-
мы на рис. В.13, в которых амплитуда сигнала
равна нулю. Для кабеля длиной 3,5 м время
прохождения сигнала равно интервалу вре-
мени, в течение которого сигнал распростра-
няется на расстояние, равное 7 м. Скорость
распространения сигнала в кабеле равна при-
близительно 2/3 скорости распространения
сигнала в вакууме; таким образом, для прохож-
дения расстояния в 7 м сигналу требуется при-
близительно 7 • 5 не » 35 не. Амплитуда сигнала
должна быть нулевой, когда это время равно
половине периода, что делает полный период
равным около 70 не. Эта длительность периода
соответствует частоте нулевой амплитуды рав-
ной 1/70 не = 0,015 ГГц = 15 МГц, что мы и на-
блюдали на осциллограмме на рис. В.13. Вроде
бы все сходится.
Поскольку причина данной проблемы такая
же, как и причина отражений импульса, ко-
торые мы рассматривали ранее, решается она
аналогично: путем согласования импедансов
источника сигнала и нагрузки с кабелем.
В.5.З. Частичное рассогласование
импедансов
Мы рассмотрели только крайние случаи рассо-
гласования импедансов: разомкнутый дальний
конец кабеля и замкнутый. Менее экстремаль-
ные рассогласования создают, как можно дога-
даться, частичные отражения. Но даже частич-
ные отражения нежелательны. Однако здесь
мы не будем рассматривать такие случаи.
Приложение Г
Советы по работе с осциллографом
Содержание
Г.1. Что не следует делать
Г.2. Что нужно знать в первую очередь
Г.2.1. Запуск развертки
Г.2.2. Ложные осциллограммы на цифровых осциллографах
1152
1152
1152
1155
Г.1. Что не следует делать
Невозможно научиться работать с осциллогра-
фом только по книгам и техническим описа-
ниям. Работе с осциллографом, как и с любым
другим инструментом, обучаются, используя
его на практике и обращаясь за советом в про-
блемных ситуациях к опытному человеку, на-
ходящемуся рядом (если вам повезет). Тем не
менее несколько моментов работы с осцилло-
графом стоит описать и проиллюстрировать.
Г.2. Что нужно знать
в первую очередь
Г.2.1. Запуск развертки1
Выбор режимов развертки — наиболее сложная
часть работы с осциллографом. Запуск разверт-
ки представляет собой включение механизма
осциллографа для синхронизации прохож-
дения луча через экран слева направо. Такая
синхронизация необходима для отображения
устойчивого изображения, а не перепутанного
набора осциллограмм. При каждой последую-
щей развертке осциллограмма сигнала долж-
на прорисовываться в таком же положении
на экране, как и при предыдущей развертке.
В противном случае осциллограммы смеща-
ются по горизонтали, как показано на рис. Г.1.
Наблюдать такую картинку на экране крайне
неприятно.
Неправильный запуск развертки:
на цифровом осциллографе...
...и на аналоговом
осциллографе
Книга АоЕ, Приложение О: Осциллограф.
Рис. Г.1. Неправильный запуск развертки создает неразбор-
чивое изображение накладывающихся друг на друга осцил-
лограмм
Выбор правильного сигнала запуска
развертки
Не будем отвлекаться рассмотрением узко-
направленных вопросов, а начнем с наиболее
общих.
Не пытайтесь исправить изображение, настраи-
вая уровень сигнала запуска развертки
Новички часто пытаются стабилизировать
изображение, вращая ручку настройки уровня
LEVEL. Это в корне неправильно и не даст ни-
каких ожидаемых результатов. Эта ситуация де-
монстрируется на рис. Г.2 и Г.З для аналоговых
и цифровых осциллографов соответственно.
Г.2. Что нужно знать в первую очередь
1153
Вращение ручки уровня сигнала
-запуска развертки LEVEL не даст
никаких результатов
...поскольку переключатель
выбора источника сигнала
развертки SOURCE установлен
в неправильное положение.
В частности, выбрана подача
внешнего (EXT — external)
сигнала запуска развертки,
а на соответствующий вход
не подается никакого сигнала
Рис. Г.2. Не начинайте настройку отображения осцилло-
граммы, вращая ручку уровня LEVEL. Сначала установите
переключатель выбора ввода сигнала запуска развертки
SOURCE в правильное положение
Мы наблюдаем
сигнал
в канале 2
...однако в качестве
источника запуска
развертки выбран канал 1
Поэтому изменение уровня сигнала запуска LEVEL вряд
ли решит возникшую проблему запуска развертки (если
только сигналы в каналах 1 и 2 не синхронизированы,
что может быть в случае, когда один из них порождает
другой). Скорее всего, нам нужно установить в качестве
источника сигнала запуска развертки канал 2
Рис. Г.З. Корректировка уровня LEVEL в цифровом осцилло-
графе также не решит эту проблему
для подачи исследуемого сигнала. Почти
всегда это будет правильный выбор.
Опция LINE — обозначает запуск развертки
от сети электропитания. Этот режим хоро-
шо подходит для стабилизации любого сиг-
нала, синхронизированного с напряжением
электросети с частотой 60 Гц3. Данной опци-
ей можно воспользоваться, чтобы выяснить,
например, не являются ли причиной низко-
частотной помехи или колебаний исследуе-
мого сигнала наводки с частотой сети, кото-
рыми обычно заполнены помещения. В част-
ности, если при запуске сигнала развертки
от источника LINE колебания исследуемого
сигнала прекращаются, то это указывает, что
причиной действительно были помехи, соз-
даваемые источником питания. Таким обра-
зом, опция LINE может быть полезной, но не
очень часто, а только в некоторых случаях.
Опция ЕХТ — означает external т. е. внешний
источник сигнала запуска развертки, кото-
рый подается на отдельный BNC-разъем4.
Эта опция полезна в тех случаях, когда обыч-
ный источник сигнала запуска развертки
(один из каналов подачи исследуемого сиг-
нала INT) сильно зашумлен, что может отри-
цательно влиять на запуск развертки.
Первым делом нужно выбрать
правильный источник сигнала развертки
Прежде чем заниматься тонкой настройкой
развертки (например, регулировкой уровня
сигнала синхронизации), нужно правильно вы-
брать источник сигнала запуска развертки. На
осциллографах наиболее часто предусмотрены
три опции выбора источника сигнала разверт-
ки, обозначенные INT/LINE/EXT2.
♦ Опция INT — означает internal т. е. внутрен-
ний запуск, но, несмотря на такое название,
относится к каналам INPUT осциллографа
2 На отечественных приборах эти опции обозначены
ВНУТР./СЕТЬ/ВНЕШ. - Примеч. ред.
Рис. Г.4. Внешний источник сигнала запуска развертки (ЕХТ)
может быть полезен в тех случаях, когда входной сигнал
сильно зашумлен
3 В Европе и большинстве стран бывшего СССР частота
электросети составляет 50 Гц.
4 Обычно, в старых аналоговых осциллографах этот разъ-
ем находится на передней панели; в цифровых осцилло-
графах TDS3013 компании Tektronix он расположен на
задней панели.
1154
Приложение Г Советы по работе с осциллографом
Затем выбираем конкретный внутренний
источник сигнала запуска
В качестве источника сигнала запуска разверт-
ки мы почти всегда будем использовать один из
каналов исследуемого сигнала (т. е. INT), а не
источник электропитания (LINE) или внешний
источник (ЕХТ). Но теперь нам нужно решить,
какой канал использовать, и здесь тоже таится
опасность.
Но если использовать этот режим, будь то в
аналоговом или цифровом осциллографе, от-
носительные временные соотношения между
входными каналами будут отображаться не-
правильно. Например, на рис. Г.6 показаны
осциллограммы сигналов, снимаемых с выво-
дов MAIN и SYNC генератора сигналов и ото-
бражаемых на цифровом осциллографе в этом
режиме.
Остерегайтесь опции VERT MODE
Кроме двух позиций СМ или Ch2 (рис. Г5)
переключатель выбора канала имеет еще и тре-
тью - VERT MODE (VERT означает vertical но
что именно подразумевается под этим обозна-
чением в данном случае — мы не знаем).
Остерегайтесь опции
-VERTICAL MODE
Рис. Г.5. Опция VERTICAL MODE может ввести в искушение
несведущих
При установке данной опции в качестве источ-
ника сигнала запуска развертки выбирается тот
канал, который будет запускаться следующим.
В результате теряется относительное фазовое
соотношение между двумя каналами. Для циф-
ровых осциллографов, используемых в нашей
университетской лаборатории (TDS2014), эта
опция называется Alternating, и чтобы найти ее,
нужно пройти через несколько уровней меню.
Это значительно уменьшает возможность ее
случайного выбора. Не следует путать данную
опцию с режимом отображения аналоговых
осциллографов, называемым ALT5.
5 Напомним различие между режимами отображения
ALT и CHOP аналоговых осциллографов: в режиме ALT
оба канала прорисовываются попеременно, каждый от-
Эквивалент режима VERT MODE аналогового
осциллографа, и такой же коварный
Обратите внимание на то, что синусоидальный и
прямоугольный сигналы не согласованы должным
образом: в действительности перепады прямоугольного
сигнала должны совпадать с пиками и впадинами
синусоидального сигнала
Рис. Г.6. При использовании опции VERT MODE (Alternating в
цифровых осциллографах) нарушаются временные соотно-
шения между отображаемыми осциллограммами каналов
Мы знаем, что временные соотношения между
осциллограммами на рис. Г.6 неправильны, по-
тому что синхронизация по фазе сигналов вы-
водов MAIN (синусоидальный) и TRIG_SYNC
(прямоугольный) является запроектированной
характеристикой генератора сигналов: перепа-
ды прямоугольного сигнала должны совпадать
с пиками и впадинами синусоидального. Здесь
это отношение отсутствует. Осциллограф ото-
бражает относительные временные соотноше-
ния этих двух сигналов неправильно.
Вы можете спросить, почему разработчики
осциллографа создали такую коварную ловуш-
ку? Как и можно было ожидать, существует си-
туация, для которой режим VERT MODE явля-
ется полезным. Это очень редкий случай, когда
сигналы в нескольких каналах не синхронизи-
рованы. Тогда режим VERT MODE позволяет
получить стабильное отображение осцилло-
грамм всех каналов за счет потери информации
об относительном временном соотношении
дельно за полный проход развертки. А в режиме CHOP
оба канала прорисовываются одновременно за один и
тот же проход развертки за счет быстрого переключения
между каналами.
Г2. Что нужно знать в первую очередь
1155
между ними. Поэтому следует помнить об этой
особенности режима VERT MODE, так как в
противном случае он может ввести вас в за-
блуждение. Но на всех лабораторных занятиях
у вас вряд ли возникнет надобность в данном
режиме.
Опции AUTO и NORM
Определившись с источником сигнала запуска
разэертки, нужно сделать следующий выбор:
между опциями AUTO и NORM. Опция AUTO
допускает отображение осциллограмм даже при
неправильно установленном уровне сигнала за-
пуска; а опция NORM этого не позволяет: если
не подать правильный сигнал запуска разверт-
ки, то на осциллографе ничего отображаться не
будет. Поскольку темный экран — или в случае
цифрового осциллографа, который способен
запоминать последнее захваченное изобра-
жение, неподвижный экран — намного хуже,
чем экран с искаженной осциллограммой, мы
рекомендуем вам считать NORM сокращением
ABNORMAL, т. е. ненормальный. Мы исполь-
зуем этот режим только в исключительных слу-
чаях.
На рис. Г.7 демонстрируются разные результа-
ты использования режимов AUTO и TRIG для
случая слишком высокого уровня (LEVEL) сиг-
нала запуска развертки. (Выше самого высо-
кого уровня сигнала канала Ch2, выбранного
в качестве источника сигнала запуска разверт-
ки. Этот уровень показан стрелкой для каждой
осциллограммы.)
Левое изображение, для режима AUTO, содер-
жит пересекающиеся осциллограммы, тогда
г 4-4lV UHoldOff;
Режим AUTO при слишком высоком уровне
запуска развертки
как на правом, для режима NORM, нет ничего.
Обычно лучше видеть хоть что-либо, чем во-
обще ничего.
Когда использовать режим NORM
Режим NORM превращается из раздражающе-
го в полезный, когда нужно отобразить сигнал
с редкими событиями запуска развертки. В та-
ких случаях режим AUTO теряет «терпение»
и запускает развертку, когда он полагает, что
прошло достаточно времени. А режим NORM
терпеливо ожидает наступления события запу-
ска развертки. Случаи, требующие использова-
ния режима NORM, можно распознать при их
возникновении. Но обычно такие случаи будут
исключениями.
Г.2.2. Ложные осциллограммы
на цифровых осциллографах
Цифровые осциллографы практически безу-
пречны, но они подвержены одному «глюку»,
который довольно загадочен для тех, кто никог-
да ранее с ним не сталкивался (а иногда даже и
для тех, кому уже приходилось его наблюдать).
Это создание ложных осциллограмм при недо-
статочно высокой частоте дискретизации ис-
следуемого сигнала.
Вопрос дискретизации и побочных сигналов,
создаваемых в ее процессе, рассматривает-
ся довольно подробно в главах 18N и 18S. Но,
если вы читаете данное приложение перед тем,
как изучили материал этих глав, то можете не
понять полностью эффекты дискретизации.
Поэтому мы ограничимся одним примером и
ж
ЗуИ з.оо v
•М 200ps A
U 0.000 е»
Holtloit
Xut record
12.3401%
'[ Set to win
Режим NORMAL при слишком высоком
уровне запуска развертки
Рис. Г.7. Результаты использования режимов развертки AUTO и NORMAL при слишком высоком уровне сигнала запуска раз-
вертки
1156
Приложение Г Советы по работе с осциллографом
щиллограмму
на как частота
ктвительности
90 кГц)
(ТГосле изменения параметров захвата осциллографа
4 с Sample на Peak ложный сигнал исчезает, подтверждая
недействительность осциллограммы частотой 10 Гц
Рис. Г.8. При низкой частоте развертки цифровой осциллограф может создавать осциллограмму сигнала с более низкой ча-
стотой, чем частота исследуемого сигнала
кратким объяснением причины возникновения
ложных осциллограмм. Если вы прочитаете
главу 18, а затем возвратитесь к этому прило-
жению, то мы надеемся, что изложенный мате-
риал будет более понятным.
Ложные осциллограммы возникают вследствие
нарушения стандартного правила дискретизации
(которое часто называется теоремой дискретиза-
ции Найквиета или Шеннона). Данное правило
гласит, что для того, чтобы получить достаточ-
ную информацию о дискретизируемом входном
сигнале, частота выборки должна быть несколь-
ко выше, чем две выборки за период входного
сигнала. При более низкой частоте выборке не
только пропускаются некоторые данные о сигна-
ле, но также формируется ложная информация
о нем, которая проявляется в виде ложного дис-
кретизированного сигнала (в данном случае это
неправильная осциллограмма).
Например, частота выборки синусоидально-
го сигнала частотой 5 кГц должна быть чуть
выше, чем 10 кГц. Частота самого первого соз-
даваемого дискретизацией ложного сигнала
составляет/ВЫБ -fBXe. Таким образом, при дис-
кретизации сигнала частотой 5 кГц, используя
частоту выборки 7,5 кГц, будет создан ложный
сигнал с частотой 2,5 кГц. В примере, который
иллюстрируется на рис. Г.8, мы увидим подоб-
ный эффект.
Ложные сигналы и цифровой
осциллограф
Ложные сигналы могут создавать странную
низкочастотную осциллограмму на цифровом
6 В более широком аспекте, при дискретизации создаются
б б
осциллографе. Чтобы продемонстрировать эту
опасность, мы подали синусоидальный сигнал
с частотой чуть ниже на цифровой осцилло-
граф7, на котором была установлена довольно
низкая частота развертки (200 мс/деление).
Полученные осциллограммы показаны на
рис. Г.8.
Десять герц, когда частота подаваемого на
осциллограф сигнала составляет почти 5 кГц?
Более точно, 5 кГц без 10 Гц. Эта подробность
окажется очень важной8. Неужели наш осцил-
лограф сошел с ума?
Нет, не сошел, а просто не может ничего поде-
лать с тем, что он является дискретизирующим
устройством. Чтобы создать осциллограмму
сигнала, заполняющую весь экран, осцилло-
граф берет 10 000 выборок значений этого сиг-
нала. Таким образом, при масштабе развертки
200 мс/деление длительность полной раз-
вертки (через весь экран) составляет 2 секун-
ды. Следовательно, эти 10 000 выборок нужно
взять при частоте выборки величиной 5 кГц.
Это слишком низкая частота выборки, чтобы
получить правдивый образ сигнала, частота
которого составляет почти 5 кГц. В результа-
те осциллограф отображает ложный сигнал с
частотой 10 Гц. Частота этого ложного сигна-
ла соответствует формуле побочных сигналов:
/выб ~/вх = 5 кГц - 4,990 кГц = 10 Гц.
Осциллограмма справа на рис. Г.8 показывает,
что происходит, когда мы, столкнувшись со
побочные сигналы на частотах п -/В
. Но обычно нас
ВЫБ ^
интересует только ложный сигнал с самой низкой часто-
той.
7 Осциллограф TDS3014 компании Tektronix.
8 Ложный синусоидальный сигнал, осциллограмма ко-
торого изображена на рис. Г.8, а не просто искаженная
осциллограмма, создается вследствие близости частоты
входного сигнала к частоте выборки. Но подобный эф-
фект возникал бы и при других частотах входного сигна-
ла. В частности, частота входного сигнала, близкая к зна-
чению, кратному 5 кГц, тоже будет создавать подобную
странную осциллограмму.
Г.2. Что нужно знать в первую очередь
1157
странным сигналом частотой 10 Гц, меняем ре-
жим захвата входного сигнала осциллографа
с обычного Sample (выборка) на Peak. Тогда,
несмотря на низкую частоту развертки, осу-
ществляется выборка только самых высоких и
низких значений сигнала с высокой частотой
дискретизации.
Мы не хотим напугать вас этим примером по-
бочных сигналов. Вам не придется часто стал-
киваться с этим явлением, а если и придется,
то оно вряд ли введет вас в заблуждение. Ведь,
несмотря на показания осциллографа, вы же не
поверите, что сигнал с частотой 5 кГц выглядит
как сигнал с частотой 10 Гц? Но знать о возмож-
ности возникновения ложных сигналов полез-
но. Когда ваш цифровой осциллограф вдруг
начнет отображать абсурдные осциллограммы,
особенно если это осциллограммы с низкой
частотой, мы надеемся, что вы вспомните, что
может быть причиной этого.
Приложение Д. Перечень и описание
необходимых компонентов
Далее приводится перечень и краткое описа-
ние компонентов, используемых на лабора-
торных занятиях, описываемых в этой книге.
Приобрести все эти компоненты за один прием
трудно, поэтому мы планируем разделить их по
наборам, отдельно для аналоговых и цифро-
вых схем. Информацию о таких наборах можно
найти на веб-сайте этой книги по адресу: www.
learningtheartofelectronics.com.
Если вам не удается отыскать какой-либо ком-
понент (а некоторые из компонентов в этом
списке обязательно будет трудно найти в буду-
щем), попробуйте найти требуемое с помощью
замечательного средства для поиска компонен-
тов OCTOPART (www.octopart.com).
Компонент
Лампы
#47
#344
Катушки
индуктив-
ности
10 мГ
100 мкГ
На ферритовом
каркасе
Трансфор-
матор
6,3 В, трансфор-
матор тока
Описание
Лампа
Лампа
Q.= 150
Длина
4,3 мм,
внут-
ренний
диаметр
1,5 мм,
тестовая
частота
100 МГц
1,2 А
Дополнительные
сведения
(корпус и т.п.)
ТЗ-1/4
ТЗ-1/4
Радиальная
Радиальная
Цилиндрическая
—
Произво-
дитель
Visual
Communi-
cations
Company
JKL
Compo-
nents
Murata
Panasonic
Kemet
Stancor
Номер
детали
47
344
13R106C
ELC-
12D101E
B-20F-
46
P-6134
Постав-
щик
D
M
D
M
D
N
Номер
детали
постав-
щика
CM47-ND
344
811-2058-
ND
67-ELC-
12D101E
399-
10820-ND
16P8886
Цена
(1),
долл.
1
1
0,59
1,28
0,25
16
Цена
(25),
долл.
0,65
0,85
0,58
0,83
0,18
15
Компонент
Теплоотвод
ТО-92
Переключатели
Ползунковые
Тумблерные
Кнопки
Однополюсная
однопозиционная
Однополюсная
двухпозиционная
DIP-переклю-
чатели
4-позиционный
8-позиционный
Описание
Надеваемый
Однополюсный двух-
позиционный
Однополюсный двух-
позиционный
Квадратная, монтаж
заподлицо
Квадратная
Однополюсный одно-
позиционный
Однополюсный одно-
позиционный
Дополнительные
сведения (корпус и т. п.)
ТО-92
Расстояние между выво-
дами 2,5 мм
Расстояние между выво-
дами 5 мм
Расстояние между выво-
дами 5 мм
Расстояние между выво-
дами 2,5 мм
Расстояние между выво-
дами 2,5 мм
Расстояние между выво-
дами 2,5 мм
Произво-
дитель
Aavid
E-switch
С&К
Aspem
ТЕ
ТЕ
Alco
Номер детали
575200B00000G
EG1218
ZMA00A150L04PC
MJTP1212
KS12-R22CQD
1825057-3
ADE0404
Постав-
щик
М
D
D
D
D
D
N
Номер детали
поставщика
532-575200В00
EG1903-ND
CKN10157-ND
679-2424-ND
CKN1595-ND
450-1364-ND
68К9398
Цена
(1).
долл.
0,68
0,58
0,73
0,36
0,81
0,81
Цена
(25),
долл.
0,63
0,55
0,69
0,35
0,67
0,75
Поставщики:
А=Avnet Express, Arizona; ADI=Analog Devices Inc.; D=Digikey; J=Jameco; M = Mouser; N=Newark;
PA is Proto Advantage (Ontario): PA/D означает, что компонент предоставляется компанией Digikey; Q=Quest Components Inc. (Калифорния);
R=Rochester Electronics (Массачусетс); S=Sparkfun; TTI=TTI Inc. (Техас).
U1
Компонент
Потенциометры
Подстроенный
С приводом
от мотора
Микрофон
Диоды
Обычные крем-
ниевые
1N914
1N4004
Стабилитрон
1N5232
Диоды Шоттки
1N5817
1N5711
Описание
Металлокерами-
ческий, один
оборот
Поворотный
потенциометр
Ползунковый
потенциометр
Электретный,
всенаправлен-
ный
Кремниевый
диод, 0,3 А
Импульсный
кремниевый
диод, 1А
Стабилитрон,
5,6 В
Диод Шоттки,
1А
Диод Шоттки,
15 мА, с малой
емкостью
Дополнительные
сведения
(корпус и т. п.)
0,5 Вт
4-6 В,
обратная логариф-
мическая зависи-
мость
ВЗ
10 В, обратная ло-
гарифмическая за-
висимость 15 А
Расстояние между
выводами 2,5 мм
DO-35
DO-41
1/2W
—
1кОм
ЮкОм
100 кОм
1М0м
100 кОм
ЮкОм
—
—
—
—
Производитель
Bourns
Alps
Top-up Industry
PUI Audio
Fairchild
Diodes, Inc.
Vishay
Diodes, Inc.
STM
Номер детали
3352T-1-102LF
3352T-1-103LF
3352T-1-104LF
3352T-1-105LF
RK16812MG099
«100mm»
AOM-6738P-R
1N914BTR
1N4004-T
1N5232B-TR
1N5817T
1N5711
Источ-
ник
D
D
D
D
M
S
D
D
D
D
D
N
Номер детали по-
ставщика
3352T-102LF-ND
3352T-1-103LF-ND
3352T-1-104LF-ND
3352T-1-105LF-ND
688-
RK16812MG099
COM-10734
668-1296-ND
1N914BCT-ND
1N4004DICT-ND
1N5232BVSCT-ND
1N5817DICT-ND
89К1806
Цена
(1),
долл.
1,53
1,53
1,53
1,53
9,61
19,95
1,65
0,1
0,13
0,19
0,44
0,86
Цена
(25),
долл.
1,22
1,22
1,22
1,22
8,58
18,95
1,18
0,06
0,11
0,15
0,25
0,5
Компонент
Светодиоды
HLMP-4700
C566C-AFS-
CU0W0252
HLMP-3950
LNG995PFBW
LTL-30EHJ
TSTS7100
TIL311
Описание
Красный, слабо-
точный
Желтый, яркий
Зеленый, высо-
кой эффектив-
ности
Синий, широко-
угольный
Красно-зеле-
ный, с тремя вы-
водами
ИК,9850нм,
угол 10°
Светодиодный
шестнадцате-
ричный дисплей
с декодером
Дополнительные
сведения
(корпус и т. п.)
5 мм
5 мм
5 мм
5 мм
5 мм
ТО-18
DIP, 14 выводов
Производитель
Avago
Сгее
Avago
Panasonic
Lite-On
Vishay
TI
Номер детали
HLMP-4700-
C0002
C566C-AFS
CU0W0252
HLMP-3950
LNG995PFBW
LTL-30EHJ
TSTS7100
TIL311
Источ-
ник
D
D
D
D
D
D
J
Номер детали по-
ставщика
516-2483-1-ND
C566C-AFS-
CU0W0252CT-ND
516-1347-ND
P468-ND
160-1057-ND
TSTS7100-ND
TIL311
Поставщики: А=Avnet Express (Аризона); ADI=Analog Devices Inc.; D-Digikey; J=Jameco; M = Mouser; N=Newark;
Цена
долл.
0,6
0,18
0,6
2,1
0,5
3,45
19,95
Цена
(25),
долл.
0,4
0,17
0,4
1,7
0,4
2,42
19,95
PA=Proto Advantage (Онтарио): PA/D означает, что компонент предоставляется компанией Digikey Q=Quest Components Inc. (Калифорния);
R=Rochester Electronics (Массачусетс); S=Sparkfun; TTI=TTI Inc. (Техас).
Компонент
Транзисторы
биполярные
2N3904
2N3906
MJE3055T
MJE2955T
Транзисторные
сборки
СА3096
HFA3096
Оптоэлектронные
приборы
BPV11
QSD124
Описание
NPN, малосигнальный
PNP, малосигнальный
Силовой NPN (10 А),
мин. бета 20, ток 4 А
Силовой PNP (10 А),
мин. бета 20, ток 4
Сборка биполярных
транзисторов,
3NPN,
2PNP
Сборка биполярных
транзисторов,
3NPN,
2PNP
Переходник SOIC-16
на DIP
Фототранзистор,
видимый спектр
Фототранзистор, ИК
Дополнительные
сведения
(корпус и т. п.)
ТО-92
ТО-92
ТО220
ТО220
16 DIP
16-SOIC
16 DIP
видимый спектр,
5 мм
ИК,5мм
Производитель
Fairchild
Fairchild
ON
Fairchild
Intersil
Intersil
Proto
Advantage*
Vishay
Fairchild
Номер детали
2N3904TFR
2N3906TFR
MJE3055TG
MJE2955TTU
CA3096CM96
HFA3096BZ
PA0005
BPV11
QSD124
Источ-
ник
D
D
N
D
R
D
PD
N
D
Номер детали по-
ставщика
2N3904D26ZCT-ND
2N3906D26ZCT-ND
45J1504
MJE2955TTUFS-ND
CA3096CM96
HFA3096BZ-ND
PA0005
32C9138
QSD124-ND
Цена
(1).
долл.
0,21
0,21
0,97
0,64
0,88
6,38
5,09
0,68
0,51
Цена
(25),
долл.
0,18
0,18
0,75
0,5
0,81
5,43
5,09
0,64
0,33
Компонент
МОП-транзисторы
BUK9509
IRLZ34
2N7000
BS250P
DG403
Транзисторные
сборки
CD4007
Полевые транзи-
сторы с управляю-
щим переходом
2N5485
1N5294
Описание
Силовой МОП-тран-
зистор, л-канал, иш
логического уровня
Силовой МОП-тран-
зистор, л-канал, иш
логического уровня
л-МОП
р-МОП
Аналоговый
переключатель
Сборка МОП-транзис-
торов, 3 я-канальных,
3/7-канальных
Полевой транзистор
с управляющим
переходом
Полевой транзистор
с управляющим пере-
ходом, источник тока,
0,75 мА
Дополнительные
сведения
(корпус и т. п.)
ТО220
ТО220
Т092
Т092
16 DIP
14 DIP
ТО-92
DO-35
Производитель
NXP
IR
Fairchild
Diodes Inc.
Maxim
TI
Central
Solid State
Поставщики: A=Avnet Express (Аризона); ADI=Analog Devices Inc.; D=Digikey; J=Jameco; M=
Номер детали
В1Ж9509-40ВД27
IRLZ34NPBF
2N7000TA
BS250P
DG403CJ+
CD4007UBE
2N5485
1N5294
=Mouser; N=Newark;
Источ-
ник
D
N
N
D
D
N
M
N
Номер детали по-
ставщика
568-5727-5-ND
63J7705
31Y5851
BS250P-ND
DG403CJ+-ND
4C7958
610-2N5485
79T5011
PA=Proto Advantage (Онтарио): PA/D означает, что компонент предоставляется компанией Digikey; Q=Quest Components Inc. (Калифорния);
R=Rochester Electronics (Массачусетс); S=Sparkfun; TTI = TTI Inc. (Техас]
1.
* Компания Proto предоставляет услугу приобретения микросхем и впаивания их на переходную плату.
Нам нравится компания Proto за то, что они предоставляют услугу установки компонентов для поверхностного монтажа на переходную плату.
Цена
(1).
долл.
1,6
1,75
0,12
8,43
0,48
1Д9
Мин.
заказ
25 шт.
Нет
дан-
ных
Цена
(25),
долл.
1,28
1Д
0,12
7,47
0,37
0,98
4,43
I
о-
с:
Компонент
Тиристор
Операционные
усилители
LF411
LM741
LM358
LMC6482
LMC662
Компараторы
LM311
TLC372CP
Описание
100 В, 8 А
Операционный усили-
тель, входной каскад
на полевом транзисторе
с управляющим
р-л-переходом, 3 МГц
Операционный усили-
тель, на биполярных
транзисторах, 1,5 МГц
Операционный уси-
литель, двуполярное
и однополярное питание
Операционный
усилитель, входной
и выходной сигналы
полного размаха
напряжения питания,
КМОП-технология
(16 В макс. U+ до U-)
Операционный
усилитель, однополяр-
ное питание, выходной
сигнал полного размаха
напряжения питания,
КМОП-технология
Компаратор
Компаратор,
однополярное питание
Дополнительные
сведения
(корпус и т. п.)
ТО220
8 DIP
8 DIP
8 DIP
8 DIP
8 DIP
8 DIP
8 DIP
Производитель
ON
TI
TI
TI
TI
TI
TI
TI
Номер детали
MCR218-4G
LF411CP
LM741CN
LM358P
LMC6482IN/
NOPB
LMC662CN/NOPB
LM311PE4
TLC372CP
Постав-
щик
D
N
N
D
D
N
M
N
Номер детали по-
ставщика
MCR218-4GOS-ND
60K6163
97K3586
296-1395-5-ND
LMC6482IN/
NOPB-ND
41K2696
595-LM311PE4
36K3644
Цена
(1).
долл.
1,29
1,69
0,73
0,49
1,78
1,69
0,61
1,14
Цена
(25),
долл.
1,03
1,35
0,58
0,33
1,4
1,32
0,47
0,9
Компонент
Стабилизаторы
напряжения
LM317T
LM385-2.5
LM78L05
LT1073
Генераторы
колебаний
TS555IN
Кварцевые
генераторы
11,0592 МГц
8 МГц
Кварц
11,0592 МГц
Фильтр
МАХ294
Описание
Регулируемый стабили-
затор напряжения, 1,5 А
Источник опорного
напряжения
Стабилизатор напряже-
ния, три вывода, 100 мА
Импульсный стабилиза-
тор напряжения, пони-
жающий/повышающий
Таймер/генератор
колебаний,
КМОП-технология
Металлический корпус
половинного размера
Металлический корпус
половинного размера
Расстояние между
выводами 2,5 мм
Эллиптический,
8-полюсный НЧ-фильтр
с коммутируемым кон-
денсатором
Дополнительные
сведения
(корпус и т. п.)
ТО220
ТО-92
ТО-92
8 DIP
8 DIP
8 DIP
8 DIP
Два вывода,
запаяны
8 DIP
Производитель
TI
TI
Fairchild
Linear
TI
ECS
CTS
ECS
Mx
Номер детали
LM317HVT/ NOPB
LM385LPR-2-5
LM78L05ACZ
LT1073CN8#PBF
TLC555CP
ECS-2200B-110.5
MXO45HS-3C-
8M0000
ECS-110.5-S-4X
MAX294CPA
Постав-
щик
D
D
D
D
D
D
D
D
D
Номер детали по-
ставщика
LM317HVT/NOPB-
ND
296-31451-1-ND
LM78L05ACZFS-ND
LT1073CN8#PBF-ND
296-1857-5-ND
XC268-ND
CTX743-ND
X1064-ND
MAX294CPA+-ND
Цена
a>.
долл.
2,42
0,66
0,43
5,53
0,85
3,68
2,07
0,81
5,66
Цена
(25),
долл.
1,93
0,51
0,25
3,67
0,68
3,15
1,9
0,69
5,44
о»
1
as
Компонент
УНЧ
LM386N
LM4667
Описание
Усилитель мощности
(однополярное питание,
выходной сигнал можно
подавать на динамик
с сопротивлением
катушки 8 Ом)
Импульсный УНЧ
Переходник
MSOP-10 на DIP
Дополнительные
сведения
(корпус и т. п.)
8 DIP
10 TSOP
10 DIP
Производитель
TI
TI
Proto Advantage*
Номер детали
LM386N-1/NOPB
LM4667MM/
NOPB
РА0027
Постав-
щик
D
D
PD
Номер детали по-
ставщика
LM386N-1/
NOPB-ND
LM4667MM/
NOPBCT-ND
РА0027
Цена
(1),
долл.
0,98
1,2
10,99
Цена
(25),
долл.
0,79
0,9
10,99
Поставщики: A=Avnet Express (Аризона); ADI=Analog Devices Inc.; D=Digikey; J=Jameco; M = Mouser; N=Newark;
PA=Proto Advantage (Онтарио): PA/D означает, что компонент предоставляется компанией Digikey; Q=Quest Components Inc. (Калифорния);
R=Rochester Electronics (Массачусетс); S=Sparkfun; TTI=TTI Inc. (Техас).
* Компания Proto предоставляет услугу приобретения микросхем и впаивания их на переходную плату.
Нам нравится компания Proto за то, что они предоставляют услугу установки компонентов для поверхностного монтажа на переходную плату
Компонент
Цифровые
компоненты
ТТЛ (LS -низко-
скоростные)
74LS00
74LS503**
кмоп
(НС-высоко-
скоростные)
74НС00
74НС02
74НС04
74НС74
Описание
Четыре элемента И-НЕ
8-разрядный регистр
последовательных приближений
Четыре элемента И-НЕ
Четыре элемента ИЛИ-НЕ
Шесть элементов НЕ (инвертер)
Двухэлементная микросхема
D-триггеров
Дополнительные
сведения
(корпус и т. п.)
14 DIP
16 DIP
14 DIP
14 DIP
14 DIP
14 DIP
Произво-
дитель
TI
Fairchild
TI
TI
TI
TI
Номер детали
SN74LS00N
DM74LS503N
SN74HC00N
SN74HC02N
SN74HC04N
SN74HC74N
Постав-
щик
N
R
D
N
D
D
Номер детали по-
ставщика
60K6847
296-1563-5-ND
67K1077
296-1566-5-ND
296-1602-5-ND
Цена
(1),
долл.
1,18
поза-
просу
0,52
0,49
0,56
0,52
Цена
(25),
долл.
0,94
поза-
просу
0,35
0,33
0,43
0,35
Компонент
74НС86
74НС125
74НС175
Счетчики
КМОП: 74НС
74НС160
74НС161
74НС163
74НС390
74НС393
74НС4040
ФАПЧ
74НС4046
КМОП: 74НСТ
74НСТ14
74НСТ125
74НСТ139
74НСТ541
74НСТ573
74НСТ574
Описание
Четыре элемента ИСКЛ-ИЛИ
Четыре тристабильных буфера
Четыре D-регистра
Четырехразрядный ДДК-счетчик
с асинхронным сбросом
Переходник с TSSOP 16 на DIP
Четырехразрядный двоичный
счетчик с асинхронным сбросом
Четырехразрядный двоичный
счетчик с синхронным сбросом
Сдвоенный десятичный счетчик
со сквозным переносом
Сдвоенный двоичный счетчик
со сквозным переносом
12-разрядный счетчик
со сквозным переносом
Микросхема фазовой
автоподстройки частоты
Шесть инвертеров с входом
на триггере Шмитта
Четыре тристабильных буфера
Два декодера 2:4
Восемь тристабильных буферов
Восемь триггеров-защелок
с тристабильными выходами
Восемь D-регистров
с тристабильными выходами
Дополнительные
сведения
(корпус и т. п.)
14 DIP
14 DIP
16 DIP
16 DIP (запланировано
снятие с производства)
16TSSOP
16 DIP
16 DIP
16 DIP
16 DIP
16 DIP
16 DIP
16 DIP
14 DIP
14 DIP
16 DIP
20 DIP
20 DIP
20 DIP
* Компания Proto предоставляет услугу по приобретению микросхем и впаиванию i
Произво-
дитель
TI
TI
TI
NXP
Proto
Advantage*
STM
TI
STM
TI
TI
TI
TI
TI
TI
TI
TI
TI
Номер детали
SN74HC86N
SN74HC125N
SN74HC175N
74HC160N,652
74HC160PW,118
РА0034
M74HC161B1R
CD74HC163E
M74HC390B1R
SN74HC393N
SN74HC4040N
CD74HC4046AE
SN74HCT14N
SN74HCT125N
SN74HCT139N
SN74HCT541N
SN74HCT573N
SN74HCT574N
их на переходную плату.
Постав-
щик
D
D
D
М
D
PD
D
D
D
N
D
D
D
D
D
D
D
D
Нам нравится компания Proto за то, что они предоставляют услугу установки компонентов для поверхностного монтажа на i
** Данная микросхема снята с производства, но предоставляется несколькими поставщиками. Если вы не сможете найти ее,
эквивалент на устройстве ПМЛ.
Номер детали по-
ставщика
296-8375-5-ND
296-1572-5-ND
296-8257-5-ND
771-74HC160N
568-8860-1-ND
РА0034
497-1787-5-ND
296-33033-5-ND
497-7370-5-ND
60К6838
296-8324-5-ND
296-9208-5-ND
296-8394-5-ND
296-8386-5-ND
296-8390-5-ND
296-1619-5-ND
296-1621-5-ND
296-1623-5-ND
тереходную плату.
Цена
(1),
долл.
0,42
0,45
0,52
1,65
0,62
4,19
0,96
0,88
1,07
0,48
0,71
0,66
0,59
0,42
0,63
0,68
0,61
0,76
Цена
(25),
долл.
0,33
0,35
0,4
1,32
0,48
4,19
0,76
0,7
0,85
0,37
0,54
0,53
0,45
0,33
0,51
0,52
0,49
0,61
мы предлагаем функциональный
I
I
о-
с
I
I
S
ON
J
Компонент
Микросхема
ПМЛ
XC9572XL
Процессоры/
контроллеры
C8051F410
DS89C430 или
DS89C450
Память RAM
CY62256NLL-
70РХС
ЦАП
AD558JN
DAC08
AD7524JN
DAC8229
Описание
Адаптер 44 TQFP-Ha-DIP
Контроллер, 50 МГц
Контроллер, 33 МГц
Память SRAM, 32 Кх8, с малым
энергопотреблением, 55 не.
Широкий корпус, что хорошо
для прикрепления наклейки.
Подойдет любой эквивалент
ЦАП, 8-разрядный, однополярное
питание, выходной сигнал —
напряжение
Перемножающий ЦАП, параллель-
ный вход, выходной сигнал - ток
Перемножающий ЦАП, параллель-
ный вход, выходной сигнал — ток
Двойной ЦАП, параллельный
вход, выходной сигнал — напря-
жение
Дополнительные
сведения
(корпус и т. п.)
44TQFP
32 LQFP
32 DIP
40 DIP
28 DIP, 15 мм
(ширина корпуса)
16 DIP
16 DIP
16 DIP
20 SOIC
20 DIP
Произво-
дитель
Xilinx
Silicon Labs
Proto
Advantage*
Maxim/
Dallas
Cypress
Analog
Devices
Analog
Devices
Analog
Devices
Analog
Devices
Proto
Advantage*
Номер детали
XC9572XL-
10VQG44C
PA0093*
C8051F410-GQ
PA0091
DS89C430-MNG
DS89C430-MNG+
DS89C430-MNL
DS89C430-MNL-K
или DS89C450:
DS89C450-MNL+
CY62256NLL-
70PXC
AD558JN
DAC08CP
AD7524JN
DAC8229FSZ
PA0008
Постав-
щик
D
PD
D
PD
R
D
R
D
D
N
D
D
D
ADI
PD
Номер детали по-
ставщика
122-1448-ND
PA0093
336-1318-ND
PA0091
DS89C430-MNG
DS89C430-MNG+-ND
DS89C430-MNL
DS89C430-MNL+
DS89C450-MNL+-ND
48W3332
AD558JN-ND
DAC08CP-ND
AD7524JN-ND
DAC8229FSZ-ND
PA0008
Цена
долл.
2,86
10,49
6,02
10,99
19,54
21,31
15,42
21,31
28,29
4,88
18,2
3,22
10,74
11,16
4,69
Цена
(25),
долл.
2,86
10,49
5,8
10,99
17,13
18,69
14,31
18,69
24,81
4,88
15,31
2,59
St8
10,15
4,69
Компонент
МАХ5102
АЦП
AD7569
Описание
Двойной ЦАП, параллельный
вход, выходной сигнал —
напряжение
АЦП, ЦАП, совместимый
с микроконтроллером
Дополнительные
сведения
(корпус и т. п.)
16 TSSOP
16 DIP
24 DIP
Произво-
дитель
Maxim
Proto
Advantage*
Analog
Devices
Номер детали
MAX5102BEUE+
PA0034
AD7569JNZ
Постав-
щик
D
PD
M
Номер детали по-
ставщика
MAX5102BEUE+-ND
PA0034
584-AD7569JNZ
Цена
долл.
3,24
4,19
20,42
Цена
(25),
долл.
3,11
4,19
17,36
Поставщики: A=Avnet Express (Аризона); ADI=Analog Devices Inc.; D=Digikey; J=Jameco; M = Mouser; N=Newark;
PA=Proto Advantage (Онтарио): PA/D означает, что компонент предоставляется компанией Digikey; Q=Quest Components Inc. (Калифорния);
R=Rochester Electronics (Массачусетс); S=Sparkfun; TTI=TTI Inc. (Техас).
* Компания Proto предоставляет услугу приобретения микросхем и впаивания их на переходную плату.
Нам нравится компания Proto за то, что они предоставляют услугу установки компонентов для поверхностного монтажа на переходную плату.
Компонент
Шестнадцате-
ричный дисплей
TIL311
Прочие
периферийные
устройства
23K256-I/P
MXD1210
5103310-1
СЕМ-1205С
Описание
Светодиодный шестнадца-
теричный дисплей с декоде-
ром и защелкой
Цифровой потенциометр с
интерфейсом SPI, 100 кОм
Память RAM, 32 К, с ин-
терфейсом SPI и резервным
питанием от батареи
Контроллер источника пи-
тания памяти RAM
Модуль ИК-приемника
Разъем, 10 выводов
Зуммер, 5 В
Дополнительные
сведения
(корпус и т. п.)
16 DIP
8 DIP
8 DIP
8 DIP
Три вывода
5X2
Расстояние между
выводами 7,6 мм
Произво-
дитель
TI
Microchip
Microchip
Maxim
Vishay
ТЕ Connectivity
CUI
Номер детали
TIL311
MCP41100-I/P
23K256-I/P
MXD1210CPA+
TS0P31240
5103310-1
CEM-1205C
Постав-
щик
J
D
D
D
D
D
D
Номер детали по-
ставщика
TIL311
MCP41100-I/P-ND
23K256-I/P-ND
MXD1210CPA+-ND
TS0P31240-ND
A33179-ND
102-1124-ND
Цена
(i).
долл.
19,95
1,61
1,34
9,08
1,45
1,25
2,51
Цена
(25),
ДОЛЛ.
17,95
1Д1
1,08
6,29
0,98
1Д9
2,08
Компонент
Микросхема ПМЛ
XC9572XL
Специальные
компоненты
Плата ЖКД
РПП (для лаб. заня-
тия по АЦП)
Конденсаторы
керамические
СК05
Полиэстерные
(майларовые)
Танталовые
OS-Con/
проводящий
полимер
Описание
ПЛУ с 72 ячейками, напря-
жение питания 3,3 В
32-битовый ЖКД
Преобразователь
USB<=>UARTh
USB<=>Silabs C2
Функциональный эквива-
лент микросхемы 74LS502,
которая устарела, вслед-
ствие чего ее трудно найти
10 пФ
68 пФ
100 пФ
470 пФ
0,01 мкФ
0,1 мкФ
0,223 мкФ
1мкФ
4,7 мкФ
15мкФ
100 мкФ
100 мкФ, малое последова-
тельное сопротивление
Дополнительные
сведения
(корпус и т. п.)
44-PLCC
24 DIP
0,2"
С аксиальными
выводами, 630 В
С аксиальными
выводами, 50 В
С аксиальными
выводами, 400 В
С аксиальными
выводами, 35 В
С аксиальными
выводами, 20 В
С аксиальными
выводами, 20 В
С аксиальными
выводами, 20 В
С аксиальными
выводами, 16 В
Произво-
дитель
Xilinx
**
**
AVX
Cornell-
Dubilier
Cornell-
Dubilier
Cornell-
Dubilier
Kemet
Vishay
Vishay
Kemet
Panasonic
Номер детали
XC9572XL-10PCG44C
CK05BX100K
150103K630BB
WMF05P1K-F
150224J400FE
T322B105K035AT7200
173D475X9020VE3
173D156X9020XE3
T322F107K020AT
667-16SEPC100MW
Постав-
щик
N
M
N
TTI
N
D
N
N
A
M
Номер детали по-
ставщика
98K3382
581-CK05B100K
93B3223
WMF05P1K-F
91B1397
399-11374-1-ND
06X1297
06X1292
T322F107K020AT
16SEPC100MW
Цена
(1).
долл.
8,91
0,2
0,62
1,4
1,67
1Д
1,94
9,53
0,82
Цена
(25),
долл.
8,91
0,18
0,57
1Д4
1,4
0,97
0,85
1,56
6,47
0,35
Поставщики: А=Avnet Express (Аризона); ADI=Analog Devices Inc.; D=Digikey; J=Jameco; M = Mouser; N=Newark;
PA=Proto Advantage (Онтарио): PA/D означает, что компонент предоставляется компанией Digikey; Q=Quest Components Inc. (Калифорния);
R=Rochester Electronics (MA); S=Sparkfun; TTI=TTI Inc. (Техас).
** См. релевантную информацию на сайте книги: www.learningtheartofelectronics.com
Компонент
Резисторы
композиционные,
0,25 Вт
мощный резистор,
проволочный
Описание
1,10,47,100,
150,220,240,
270,330,390,
470,560,620,
680,750,820
1 кОм, 1,5 кОм, 2,0 кОм,
2,2 кОм, 2,7 кОм, 3,3 кОм,
4,7 кОм, 5,6 кОм, 6,2 кОм,
6,8 кОм, 7,5 кОм, 8,2 кОм,
10 кОм, 12 кОм, 15 кОм,
20 кОм, 22 кОм, 33 кОм,
47 кОм, 56 кОм, 68 кОм,
82 кОм, 100 кОм, 120 кОм,
150 кОм, 220 кОм,
330 кОм, 470 кОм, 560 кОм,
1 МОм, 3,3 МОм, 4,7 МОм,
ЮМОм
10 Ом, 25 Вт
Дополнительные
сведения
(корпус и т. п.)
С аксиальными
выводами
С аксиальными
выводами
Производитель
Allen-Bradley
или SEI
TE-connectivity
Номер детали
1625971-5
Постав-
щик
Q
D
Номер детали
поставщика
A102130-ND
Цена
(1).
долл.
Нет
инфор-
мации
3,05
Цена
(100),
долл.
0,10
ДО
0,3
2,08
Поставщики: А=Avnet Express (Аризона); ADI=Analog Devices Inc.; D=Digikey; J=Jameco; M = Mouser; N=Newark;
PA=Proto Advantage (Онтарио): PA/D означает, что компонент предоставляется компанией Digikey; Q=Quest Components Inc. (Калифорния);
R=Rochester Electronics (Массачусетс); S=Sparkfun; TTI=TTI Inc. (Техас).
%
ь
о-
i
!
О
Приложение Е. Перечень и описание
необходимых компонентов
ж дане
Uk^Jttf W
Рис. Е.1. Полная принципиальная схема компьютера из дискретных компонентов
Приложение £ Перечень и описание необходимых компонентов
1173
Подписи к рис. E.I
Reset (on keypad) — Сброс (на цифровой клавиатуре)
Keypad, 6 — Цифровая клавиатура, вывод 6
Glue - Схема связывающей логики
From keypad — С цифровой клавиатуры
From LCD board -С платы ЖКД
i/Oport7(ba7e=8000h) - Порты ввода-вывода
(базовый адрес = 8000Н)
Keypad - Цифровая клавиатура
Fla9 ~флаг
Clear flag - Сброс флага
Display LO — Младший байт дисплея
Display HI - Старший байт дисплея
DAC -ЦАТТ
ADC Start - Запуск АЦП
Address display (LCD) - Дисплей отображения
адресов (ЖКД)
External keypad — Внешняя цифровая клавиатура
Signals and power v\a external DIP ribbon — Сигналы
и питание подаются через DIP-шлейф
Data display (LCD) — Дисплей данных (ЖКД)
Data bus — Шина данных
Latched/Continuous — Вывод данных через
триггер-защелку/Непрерывный вывод данных
Address bus — Шина адреса
I/O decoder - Декодер адресов ввода-вывода
Address counter PAL - Счетчик адреса на микросхедле ПААЛ
Same +3, GND for GLUEPAL — Те же выводы для
DIP Switch - DIP-переключатель
Keypad dafa bus _ Шина даннь1Х цифровой клавиатуры
ЫАА £гееп _ Зеленый светодиод индикации
прямого доступа к памяти
Octal 3-state buf — Восьмиэлементная микросхема
тристабильных буферов
32k х 8 static RAM — Статическая память RAM, 32 Кх8
Ready Flag -Флаг Ready
Analo9 'n " Входной аналоговый сигнал
° то 25у " ° до 2'5 В
Not used — Не используется
Combined ADC/DAC - Комбинированный АЦП/ЦАТТ
Analog out — Выходной аналоговый сигнал
0 to 2.5v - 0 до 2,5 В
Приложение Ж. Где приобретать электронные
компоненты?
Хороший вопрос. Далее приводится несколько советов, основанных на нашем опыте в этой
области.
партии компонентов, что обычно не подходит
для разработки прототипов или производства
небольших партий устройств.
I. По почте и через Интернет
Digi-KeyCorp
(Thief River Falls, MN: 1-800-digikey)
Раньше мы говорили: «Закажите их каталог», но,
к сожалению, они больше не предлагают бумаж-
ного каталога своих товаров, заменив его впе-
чатляющим онлайновым каталогом с возмож-
ностью поиска. У них можно приобрести любой
компонент, даже в небольших количествах, с бы-
строй доставкой. Зачастую очень удобно разра-
батывать устройство, открыв их веб-страницу
каталога и заказов: www.digikey.com.
Mouser Electronics (www.mouser.com)
Это дистрибьютор с широким ассортиментом
компонентов и перечнем услуг, сравнимых с
компанией Digi-Key, включая готовность про-
дажи в небольших количествах. Предоставляет
хороший выбор прецизионных пассивных ком-
понентов. Также все еще выпускает всеохваты-
вающий печатный каталог своих товаров.
Newark Electronics + Farnell
(1-800-2-newark; www.newark.com)
Дистрибьютор с собственным складом, предла-
гающий широчайший ассортимент компонен-
тов, включая хороший выбор инструментов.
Предоставляет услуги, сравнимые с услугами
компании Digi-Key, а также все еще выпускает
печатный каталог.
Дистрибьюторы с собственными складами
Это обычный источник для приобретения ком-
понентов в больших количествах. В качестве
примера поставщиков данного типа можно
назвать компании Allied (которая продолжает
издавать свой печатный каталог), Arrow, Avnet,
FAI, Heilind, Insight, Pioneer, Wyle. Но они выдви-
гают требование приобретения значительной
Покупка напрямую от производителя
Многие производители полупроводниковых
компонентов (например, Analog Devices, TI,
Maxim и т. п.) не только предоставят вам бес-
платные образцы по малейшему намеку о заин-
тересованности в их продукции, но также про-
дают их в небольших количествах с оплатой
кредитной карточкой. Компания Mini-Circuits
специализируется на компонентах для радио-
устройств, a Coilcraft — на катушках индуктив-
ности, трансформаторах и ВЧ-фильтрах.
Нестандартные компоненты
Компании Marlin PJones, Jameco, B&cD, Herbach &
Rademan, Omnitron, ABRA, All Electronics предла-
гают постоянно меняющийся набор складских
излишков, некоторые по очень низким ценам.
eBay (www.ebay.com)
Если вы не знаете про eBay, вы, наверное, толь-
ко что прибыли с Марса. На этом онлайновом
аукционе на продажу предлагается невероятно
большое количество товаров, буквально мил-
лионы изделий. Здесь также можно приобре-
сти много электронных компонентов, но при
этом имея в виду, что здесь принцип CAVEAT
EMPTOR1 особенно уместен. В этом отношении,
прежде чем совершать покупку, полезно изучить
отзывы о данном продавце и его товаре.
Alibaba
Небольшие компании стран тихоокеанского
кольца избавляются от своих складских из-
лишков и устаревших запасов на этой торговой
1 Лат. «пусть покупатель будет бдителен», качество товара
оценивает сам покупатель, действуя на свой страх и риск.
Приложение Ж. Где приобретать электронные компоненты?
1175
площадке. Разместив здесь запрос цены на ком-
понент, можно получить десятки предложений
по разумной цене.
II. Каталоги и поисковые
системы
Octopart, FindChips, NetComponents
(octopart.com, findchips.com,
netcomponents.com)
Введите в строку поиска одной из этих систем
номер детали, и она выполнит ее поиск по де-
сяткам дистрибьюторов, выдавая информацию
(иногда не особенно надежную) о наличии то-
вара и его цене.
ЕЕМ (https://www.eem.com)
Поисковая система, в которой можно или вы-
полнить поиск по компоненту, или просматри-
вать компоненты по категориям.
Google (www.google.com)
Поисковый портал по умолчанию, который
«читает ваши мысли» и направляет вас туда,
где находятся требуемые вам вещи. Иногда по-
лезен для поиска компонентов и их производи-
телей и поставщиков.
III. Местные источники
При всем удобстве онлайновых источников
иногда полезно иметь возможность самому по-
сетить магазин. Далее приводится список обыч-
ных радиомагазинов.
Radio Shack (www.radioshack.com)
Сами они называют себя американским элек-
тронным супермаркетом, мы же называем их
постоянно открытым микрорайонным мага-
зином электронных компонентов. Их магази-
ны находятся повсюду и содержат несколько
необычный ассортимент компонентов и рас-
ходных материалов неизвестного качества или
срока службы. Но в современном постоянно
меняющемся мире бытовой электроники их бу-
дущее неясно.
«Блошиные» рынки
Еще называются толкучками или барахол-
ками2, и в настоящее время, возможно, их
2 В США это не совсем «барахолка» в нашем понимании,
а, скорее всего, встреча многочисленных энтузиастов для
обмена знаниями, достижениями, а также для продажи/
покупки интересных устройств/компонентов.
популярность идет на убыль. По одному боль-
шому «блошиному» рынку находится на каждом
побережье США. На западном побережье ме-
роприятия проводятся в колледже Де Анза (De
Anza Colledge) в городе Купертино (Cupertino),
штат Калифорния, каждую вторую субботу с
марта по октябрь. А на восточном побережье
эти встречи проводятся в Массачусетсом тех-
нологическом институте в городе Кембридже
(Cambridge), штат Массачусетс, каждое третье
воскресенье с апреля по октябрь. Здесь встре-
чаются три культуры: электронщики, компью-
терщики и радиолюбители. Торговаться обяза-
тельно, принцип caveat emptor также применим
в большой степени.
Магазины по продаже товарных излишков
У этих магазинов какая-то особая атмосфе-
ра! Среди наиболее известных можно назвать
Halted (www.halted.com), который официаль-
но называется HSC Electronics Supply, в Санта-
Клара (Santa Clara), Сакраменто (Sacramento)
и Санта-Роза (Santa Rosa), и Murphy's Surplus
Warehouse (www.murphyjunk.bizland.com)
в Эль-Кахон (El Cajon). Все они находятся в
Калифорнии.
IV. Прочее
Устаревшие микросхемы
Самым лучшим местом для поиска устаревших
микросхем будет компания Rochester Electronics
(www.rocelec.com), которая, по всей видимо-
сти, скупает складские запасы компонентов,
снятых с производства. Компания Jameco так-
же является хорошим источником устаревших
компонентов. А компащш Freetradezone пред-
лагает списки брокеров устаревших компонен-
тов. Компания Interfet (www.interfet.com) про-
изводит малосигнальные полевые транзисто-
ры, включая снятые с производства большими
компаниями.
Изготовление печатных плат
Для решения этой задачи нам нравится компа-
ния Advanced Circuits (www.4pcb.com). У них
можно получить онлайн-информацию о цене,
они выпускают качественную продукцию и до-
ставляют ее в кратчайшие сроки. Канадская
компания Alberta Printed Circuits (www.
apcircuits.com) также известна своими либе-
ральными ценами и быстрой доставкой.
Приложение 3. Программы, доступные
на веб-сайте книги
Далее приводится список программ, которые можно загрузить с веб-сайта книги. Этот сайт может
содержать и другие программы, которые мы иногда добавляем. Мы сочли ненужным выкладывать
для загрузки очень короткие программы для начальных лабораторных занятий по компьютеру из
дискретных компонентов.
Лабораторное занятие 20L
Компьютер на автономном микроконтрол-
лере C8051F410
♦ bitflip.a51
♦ bitflip_delay_inline.a51
Лабораторное занятие 21L
Компьютер из дискретных компонентов
♦ 16_sum_02.a51
♦ keysum_delay_inline_4 O2.a51
♦ keysum_delayroutine_4 O7.a51
Компьютер на автономном микроконтрол-
лере C8051F410
♦ bitflip_delay_subroutine.a51
♦ byte_in_out_ports.a51
♦ bitflip_if.a51
♦ byte_in_out.a51
♦ keysum_8bit.a51
♦ keysum_16bit.a51
Лабораторное занятие 22L
Компьютер из дискретных компонентов
♦ getready_12 O8.a51
♦ intdsply_12 O4.a51
♦ timer2_bitflip.a51
♦ pwmbywizard.novlO.a51
♦ comparator_oscillatorjanll.a51
♦ comparator_osc_displayjanll.a5
Лабораторное занятие 23L
Компьютер из дискретных компонентов
♦ adcdacint_Rn_504.a51
♦ adcdacint_504.a51
♦ fullwave_4 01b.a51
♦ int_inc_dec.a51
Компьютер на автономном микроконтрол-
лере C8051F410
♦ adc_dac_intjanll.a51
♦ dac_test_12Junel5.a51 (incomplete)
♦ dacl_8bit_wizard_MT.a51
♦ adc_wizard_aprll.a51
♦ adc_dac_intjanll.a51
Лабораторное занятие 24L
Компьютер из дискретных компонентов
♦ bit_flip_assy.a51
♦ tmr8 00.a51
♦ servopulse_512.a51
♦ spi_digipot_mt_504.a51
♦ delay _bitflip_4 O8.c
♦ table bidirectional declO wi ale.a51
Приложение 3. Программы, доступные на веб-сайте книги
1177
♦ table.bidirectional declOwiale.lst
♦ storeandjplaybackbidirectional.c
Компьютер на автономном микроконтрол-
лере C8051F410
♦ adc_store_on_chip_mayl5.a51
♦ spi_digipot_silabs_aprl4.a51
♦ serial_message_silabs_aprll.a5
♦ serial_receive_silabs.a51
Лабораторное занятие 25L
Компьютер из дискретных компонентов
♦ pulse.measure_decimal_standalone_505.a51
♦ pulse.measure_capture_standalone_505.a51
Компьютер на автономном микроконтрол-
лере C8051F410
♦ spi_ram_adc_dac_incomplete.a51
♦ spisingle.byte.a51
Глава 26N
Компьютер из дискретных компонентов
♦ lcd_4bit_4 O7.a51
♦ keypad_encoder_6 O6.a51
Программы на языке Verilog
Программы для микросхемы ПМЛ связы-
вающей логики (GLUEPAL)
♦ stepglue_qfp_octl5.v
♦ stepglue_qfp_octl5_tb.v
♦ stepglue_qfp_octl5.ucf
♦ stepglue_qfp_octl5.xise
Программы реализации счетчика
♦ ctr_16bit_ud_3stt_10data.v
♦ ctr_16bit_ud_3stt_10data_tb.v
♦ ctr_16bit_ud_3stt_10data.ucf
♦ counter.micro_16bit_qfp_octl5.xise
Приложение И. Оборудование
И.1. Для кого будет полезна
эта информация
Мы убеждены, что при оснащении домашней
мастерской или учебной лаборатории трудно
заранее знать, какое именно оборудование не-
обходимо приобрести в первую очередь. И мы
надеемся, что разделы этого приложения, в
котором описывается понравившееся нам обо-
рудование, помогут вам в решении данного во-
проса. Несомненно, что в течение нескольких
лет, прошедших после издания этой книги, по-
явятся дополнительные хорошие альтернативы
описанному в ней оборудованию. Поэтому не
считайте, что изложенная далее информация
является исчерпывающей. Но, между прочим,
обратите внимание, что здесь мы указываем
цены, которые были приведены на соответ-
ствующих веб-сайтах. Вам, возможно, удастся
получить лучшую цену, особенно если вы при-
обретаете оборудование для учебного заведе-
ния, поскольку довольно много компаний де-
лают скидки в таких случаях.
которыми нам пришлось работать (включая
цифроаналоговую модель MSO2014 компа-
нии Tektronix), мы склоняемся к мнению, что
осциллографы компании Rigol дают наилучшее
соотношение цена/возможности. По поводу
осциллографов модельного ряда MSO, если вы
можете позволить приобрести их себе, можно
сказать, что цифровые каналы иногда бывают
полезными, а полоса пропускания шириной
100 МГц выглядит привлекательно, но далеко
не всегда необходима.
И.2.1. Цифровые осциллографы
Rigol DS1054Z. Полоса пропускания 50 МГц,
4 канала. Очень хорошее соотношение цена/
возможности, 399 долл.
Rigol MSO1104Z. Цифроаналоговый осцилло-
граф с полосой пропускания 100 МГц, 4 анало-
говых канала1,16 цифровых, 997 долл.
Tektronix DPO2014B. Полоса пропускания
100 МГц, 4 канала, 2074 долл.
И.2. Осциллограф
Это самый важный инструмент в нашей лабора-
тории, и наиболее дорогой. В течение тридцати с
лишним лет мы использовали в основном осцил-
лографы производства компании Tektronics. Мы
пробовали работать с осциллографами других
компаний: HP (которая затем стала Agilent, a
теперь Keysighf), Hameg, LeCroy. Но мы все-
гда возвращались к оборудованию компании
Tektronix. В основном мы работали с аналоговы-
ми осциллографами 2213 (2-канальный, полоса
пропускания 60 МГц) и цифровыми TDS3014
(4-канальный, полоса пропускания 100 МГц).
Последние мы продолжаем с удовольствием
применять и в настоящее время.
На сегодняшний день обе эти модели сняты с
производства. Из современных приборов, с
И.2.2. Аналоговые осциллографы
Далее приведен список аналоговых осцилло-
графов, которые предлагаются двумя из по-
следних компаний, все еще изготавливающими
подобные приборы. Мы не пробовали работать
ни с одним из них.
В & К Precision 2160C. Полоса пропускания
60 МГц, 2 канала, 1119 долл.
Instek 6051. Полоса пропускания 50 МГц, 2 ка-
нала, 832 долл.
1 Эти четыре «аналоговых» канала в действительности
являются дискретизированными каналами. Аналоговыми
их можно назвать в том смысле, что на дисплее отобража-
ется почти непрерывное изменение напряжения, тогда как
шестнадцать цифровых каналов отображают только дво-
ичные уровни — высокий и низкий.
И А. Макетная плата со встроенным источником питания
1179
Instek GOS6103. Полоса пропускания 100 МГц,
2 канала, вывод данных на экран, 1493 долл.
Обратите внимание, что стоимость перечислен-
ных аналоговых осциллографов превышает сто-
имость цифровых осциллографов, обладающих
очень хорошей функциональностью. Поэтому
вы, несомненно, не захотите сделать новый
аналоговый осциллограф своим единственным
осциллографом. Но не стоит забывать, что мож-
но купить подержанные и снятые с производ-
ства аналоговые осциллографы наподобие Tek-
tronix 2213 за очень небольшую сумму (иногда
200 долл. или даже меньше). Это может быть
особенно привлекательно для любителей.
ИЗ. Генератор сигналов
Нам не очень нравится направление, в кото-
ром, эволюционировали генераторы сигналов.
В большинстве современных генераторов сиг-
налов настройки задаются с помощью цифро-
вой клавиатуры или кнопок, что мы считаем
менее удобным, чем вращающиеся ручки ана-
логовых генераторов сигналов, которыми мы
пользовались в течение долгого времени. Но
указанная далее модель генератора сигналов от
компании В & К во многом похожа на приборы
старого образца, которые нам нравятся.
В & К Precision Model 4017А. Выходной сиг-
нал с частотой до 10 МГц, линейная и логариф-
мическая зависимость качания частоты, циф-
ровая индикация, 449 долл.
Более современные цифровые генераторы сиг-
налов обладают функциями, отсутствующими в
старых аналоговых моделях, включая возмож-
ность формирования сигналов произвольной
формы. Но в нашем курсе не нужны эти воз-
можности, поэтому более простой генератор
сигналов будет вполне приемлемым.
И.3.1. Можно обойтись и без
отдельного генератора сигналов
Осциллограф со встроенным
генератором сигналов
Для некоторых осциллографов, включая упо-
мянутую ранее модель MSO1104Z от компании
Rigol, предоставляется опция оснащения гене-
ратором сигналов. Такая модель этого осцил-
лографа, оснащенного генератором сигналов
с частотой до 20 МГц, называется MSO1104Z-S
и стоит на 232 долл. дороже, чем версия без та-
кового. Хотя совмещение на передней панели
органов управления осциллографом и генера-
тором сигналов менее удобно, чем отдельный
генератор сигналов, цена такого комбиниро-
ванного устройства очень привлекательна.
Генератор сигналов, встроенный
в макетную плату с источником питания
Любитель-электронщик, планирующий приоб-
рести макетную плату со встроенным источни-
ком питания наподобие платы РВ-503 (которая
рассматривается чуть далее), может обойтись
без отдельного генератора сигналов, поскольку
генератор сигналов встроен в саму макетную
плату. Этот генератор сигналов не поддержива-
ет смещение постоянной составляющей, форма
создаваемых им сигналов не такая идеальная,
как у лабораторного генератора сигналов, и мак-
симальная частота его выходного сигнала со-
ставляет всего лишь 100 кГц2. Несмотря на это,
его будет достаточно для целей нашего курса.
И .4. Макетная плата
со встроенным источником
питания
Макетная плата, выполненная заодно с ис-
точником питания, наподобие платы РВ-503
производства компании Global Specialties, кото-
рую мы использовали несколько десятилетий,
очень удобна во многих случаях, а для нашего
курса кажется почти незаменимой.
Для электронщика-любителя более дешевой
альтернативой будет приобретение источника
питания с тремя выходными напряжениями
(+5, ±15 В) и отдельных макетных плат, или
набора из трех макетных плат наподобие РВ-
105 от компании Global (стоимость 54 долл.).
2 Другой способ обойтись без отдельного генератора
сигналов - приобрести промышленный осциллограф со
встроенным генератором сигналов. Такой дополнитель-
ной функциональностью (а также встроенным анализато-
ром спектра) обладает, например, осциллограф MDO3014
от компании Tektronix, но при его стоимости свыше $4000
это вряд ли будет разумным решением для любителя или
для начинающего профессионала.
1180
Приложение И. Оборудование
В таком случае вам придется самостоятельно
обеспечить другие функции макетной платы
РВ-503 (стоимость 433 долл.), которые мы счи-
таем удобными:
♦ простой генератор сигналов. Мы нечасто
пользуемся генератором сигналов, встроен-
ным в макетную плату РВ-5033. Но в тех ред-
ких случаях, когда нам требуется второй сиг-
нал, наличие этого генератора очень удобно;
♦ переключатели с противодребезговой за-
щитой;
♦ два потенциометра;
♦ светодиоды.
Но самостоятельная реализация этого функ-
ционала не должна представлять больших
трудностей.
И.5. Авометр и цифровой
мультиметр
И.5.2, Цифровой мультиметр
На рынке существует большой выбор цифро-
вых мультиметров. Нам нужен простой прибор
без экзотических функций.
В & К Precision 2704C. Очень простой прибор
с дисплеем на 3,5 цифры. Кроме базовых функ-
ций измерения (напряжение, ток, сопротивле-
ние) предоставляет возможность определения
коэффициента передачи тока транзисторов
(коэффициента Р), емкости конденсаторов и
частоты сигналов. Нам нравится этот недорогой
(стоимость 66 долл.) инструмент. Его возмож-
ности измерения частоты и бета-коэффициен-
та являются приятным бонусом, что не часто
встречается в недорогих приборах.
Amprobe 37XR-A. Больше функций и более
дорогой прибор. Дисплей на 4,5 цифры, изме-
рение истинного действующего значения на-
пряжения, емкости, индуктивности, частоты,
152 долл.
И.5.1. Авометр (аналоговый
мультиметр)
Аналоговый мультиметр 260-8 производства
компании Simpson (стоимость 267 долл.) явля-
ется роскошью, без которой можно обойтись.
Мы показываем его на первом занятии потому,
что хотим, чтобы наши студенты знали, как ис-
пользовать этот инструмент, который требует
больших умственных усилий, чем цифровой
мультиметр. Но обычно мы работаем не с ним,
а с цифровым мультиметром. Авометр превос-
ходит цифровой мультиметр только в одной ис-
ключительной ситуации, когда нужно быстро
получить графическую индикацию медленно
меняющегося процесса, например спада тока
в транзисторном источнике тока по мере при-
ближения схемы к режиму насыщения.
Любители могут прекрасно обойтись без аво-
метра или же приобрести небольшую и. недо-
рогую модель наподобие Тешпа 72-8170 (сто-
имость 31 долл., предоставляется компанией
Newark).
3 Наиболее часто мы используем встроенный генератор
сигналов в качестве источника прямоугольного сигнала
с логическими уровнями. А на лабораторном занятии 5L
мы задействуем его в качестве второго источника синусои-
дального сигнала, когда подаем два таких сигнала на диф-
ференциальный усилитель.
И.6. Источник питания
Из двух источников питания, перечисленных
далее, мы работали только с одним: моделью
компании Keysight (бывшая Hewlett-Packard).
Но мы находим впечатляющими характеристи-
ки модели производства компании Rigol.
Keysight (formerly HP) E3630A. Три выход-
ных напряжения, 35 Вт, напряжение до 20 В
при токе до 0,5 А, 670 долл.
Rigol DP832. Три выходных напряжения,
195 Вт, напряжение до 30 В при токе 3 А,
450 долл.
И.7. Логический пробник
Tenma 72-500. Комбинированный логический
пробник и импульсный датчик. Определяет им-
пульсы длительностью до 10 не. Обеспечивает
переключение между уровнями ТТЛ и КМОП,
27 долл.
И.8. Магазин сопротивлений
Из перечисленных далее магазинов сопротив-
лений мы предпочитаем устройство с меньшим
И.11 Провода
1181
количеством значений, поскольку так легче из-
менять номинал. Но иногда бывает полезным
разрешение в 1 Ом, которое обеспечивает дру-
гой магазин сопротивлений. Для оснащения
учебного класса, возможно, будет разумным
приобрести несколько устройств RS4000 и одно
устройство RS5000.
Elenco RS4000. 24 значения в диапазоне от
10 Ом до 1 МОм, 17 долл. (Amazon).
Elenco RS5000. Значения от 0 до 11 МОм, с
шагом в 1 Ом, 24 долл. (Robotshop.com).
И.9. Модуль
программирования ПЛУ
nFPGA
Мы используем модуль DLC9G компании Xilinx
стоимостью 47 долл. (Amazon). К компьютеру
он подключается с помощью интерфейса USB.
Модуль оснащен выводами для подачи сигна-
лов интерфейса JTAG на микросхему ПМЛ. Для
подключения программируемых устройств мы
используем разъемы с нулевым усилием уста-
новки, подключенные к этим выводам, а также
к напряжению питания (+5 В и «земля»). Но
такие гнезда (например, компонент 44-6551-10
производства компании Aries, предоставляе-
мый компанией Digikey) не продаются в еди-
ничных экземплярах. Такое гнездо можно за-
менить обычным гнездом на 44 вывода с рас-
стоянием 15,24 мм между рядами выводов.
И.10. Ручные инструменты
И.10.1. Плоскогубцы
Мы предпочитаем небольшие плоскогубцы, так
называемые тонконосы, длиной 13 см, которые
удерживаются пружиной в открытом положе-
нии. Из перечисленных в следующем списке
инструментов нам нравятся плоскогубцы фир-
мы С & 1С, но недавно мы переключились на ме-
нее дорогой инструмент фирмы Excelta.
Excelta. Модель 2644 с гладкой поверхностью
или модель 2644D с рифленой поверхностью,
17 долл.
С&К. Модель 3772D, обычные длинногубцы,
52 долл.
И.10.2. Инструмент для снятия
изоляции с проводов
Ideal 45-12S. Толщина обрабатываемых про-
водов от 22-го до 30-го калибра4 по системе
стандартов проводов AWG5,12 долл.
И.10.3. Отвертка
Xcelite R3324. Плоское жало шириной 2,5 мм,
длиной 15 см, 3,50 долл.
И Л1. Провода
Изолированный одножильный монтаж-
ный провод калибра 22 по системе AWG.
♦ Alpha. 3051/1 ВК005, одножильный провод
калибра 22 по системе AWG, катушки прово-
да длиной 33 м (8 цветов; черный цвет здесь
указывается кодом ВК. Коды для других цве-
тов см. по справочнику. Красный, например,
будет RD005,20 долл. (Allied).
♦ Techedco. Катушки провода длиной 330 м
(8 цветов), 49 долл. (ebay).
Диагностические провода со штыревым
разъемом типа «банан» на обоих концах
длиной 45 см. Мы разрезаем такие провода
посередине и припаиваем на обрезанный ко-
нец короткий отрезок одножильного провода
для вставки в гнезда на макетной плате. Мы
используем такие провода красного и черного
цвета.
♦ Pomona. B-18-0 (черный), В-18-2 (красный),
5,22 долл./шт. при покупке 25 шт. (Digikey).
4 Соответствует диаметру провода от 0,644 до 0,255 мм. -
Примеч. ред.
5 American Wire Gage — Американский сортамент прово-
дов. — Примеч. пер.
Приложение К. Цоколевка компонентов
К.1. Аналоговые компоненты
ТО-92:
2N3904
(при)
2п3906
(рпр)
ТО-220:
IRLZ34
(nMOS)
MJE3055
(рпр)
MJE2955
(рпр)
ТО-220:
SCR
м
И
6 — Управляющий электрод
6-"
13
J
lo-
J
12
ТО-92:
2N5485
(JFET)
f 2N7000
(nMOS)
I BS25O
I (pMOS)
13
15
CD4007 Сборка
МОТТ-транзисторов
3 NPN's 2 PNP's
СА 3096 (DIP) Сборка биполярных (Подложка
HFA 3096 (SO-16) транзисторов подключена
к выводу 16)
Плоская
грань
BPV11 (Фототранзистор) Вид снизу
э к
TSTS7100 QSD124
ИК-светодиод ИК-срототранзистор
Светодиод (видимого спектра)
Рис. К.1. Транзисторы
К.1. Аналоговые компоненты
1183
C311 компаратор
D
TLC 372 компаратор
TRIG (2
OUT
©THRESH
555 таймер
Рис. К.2. Аналоговые микросхемы: операционные усилители, компараторы и т. п.
35& 1 Операционный
LMC6482 ^усилитель
LF411 1
LM741 V Операционный
LTC1150 И
с
€
V-
©PJN-
t i
и
О1ЛГ
ъ
НЧ-<рильтр
с коммутируемым конденсатором
МАХ 294
ТО-220
LM317
стабилизатор
напряжения
Вход
1 Общий
Выход
ТО-92:
78L05
Рис. КЗ. Стабилизаторы напряжения
LT1073 Импульсный
стабилизатор
напряжения
LT1073 Импульсный стабилизатор
напряжения
D6403 Аналоговый
переключатель
(2
€
LM4667 Импульсный
усилитель
LM386 УНЧ
Рис. К.4. Прочие аналоговые микросхемы
1184
Приложение К. Цоколевка компонентов
К.2. Цифровые компоненты
'02 ИЛИ-НЕ
u) <&T @ © <§) ©
'00 И-НЕ
'08 И
'32 ИЛИ
'10 И-НЕ
'27 ИЛИ-НЕ
'04 Инвертер
' 14 Инвертер с входом
на триггерах Шмитта
Рис. К.5. Логические вентили
Vf
v
ж
б*3>
' 125 Тристабильный буфер
<Й)
ЙЭ
Д Si fil
74 Два D-триггера
Рис. К.б. Регистры
'175 Четыре D-регистра '573/* 574 Восьмиразрядный регистр-защелка
12 и
со
тт
тттт
тт
'16 Четырехразрядные счетчики '393 Сдвоенный
'160,162: BCD
'161, '163: Двоичный
'160,161: Асинхронный сброс
'162,163: Синхронный сброс
Рис. К.7. Счетчики
двоичный счетчик
со сквозным
переносом
'390 Сдвоенный '4040 12-разрядный
десятичный счетчик счетчик со сквозным
со сквозным переносом переносом
С©
I*
Ох.
V* с$ се
Ок
@ <&
V* *ft ^ * Q5 <3ч ST
Сс QO
AD558 8-разрядный ЦАП
74 LS 503 Регистр последова-
тельных приближений (РТТТТ)
'4046 Схема ФАПЧ
AD7569 8-разрядный комбинированный ЦАТТ/АЦТТ
Рис. К.8. Преобразователи: АЦП, ЦАП и РПП, схема ФАПЧ
К.2. Цифровые компоненты
1185
ok \b Y< Уг Уз YV Yy Yfe
А7
6E Ao At Аг Аз
'541 Восемь тристабильных буферов
Рис. К.9. Тристабильный буфер, декодер
IV
ad м уь Ц
Y3
'139 Два декодера 2:4
(£>
out
V^ D?
1>^ ^
1>з
Кварцевый генератор
колебаний
DIP-разъем для подключения
шлейфа цифровой клавиатуры
Рис. К.10. Разные цифровые микросхемы
(Г
DIP-кнопка
А •
TTL311 Шестнадцатеричный
дисплей
Микросхема ПМЛ счетчика адресов (компонент для поверхностного монтажа
с 44 выводами, установленный на DIP-переходник)
Микросхема ПМЛ связывающей логики (GLUEPAL)
Рис. К.11. Две микросхемы ПМЛ
1186
Приложение К. Цоколевка компонентов
to Э» 38 У! & 3S ЗЬ » зг Э| Зо 2» га t? г^ z5 а» » г» w
7 e ^ с и л i)
Dallas (Maxim) DS89C430/450
го
Микроконтроллер C8051F410, установленный на DIP-переходнике
Статическая RAM объемом 32 кБ SPI RAM, 32 кБ
23К256
Рис. К.12. Микроконтроллеры, память RAM, цифровой потенциометр с интерфейсом SPI
J2>
Ч
1в 8
МСР 41100
Цифровой
потенциометр
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Авометр 56
Автомат конечный 683,692,694, 797,1125
Мили 684
Мура 684
на основе памяти 694
Адрес
декодирование 705
Адреса
совмещение 706
Адресация
индексная 906
косвенная 865,902
непосредственная 841,864,902
прямая 905
Адресное пространство 706
Амплитудная модуляция 153
боковые полосы 775
Анализатор дифференциальный 793
Аналоговые
коммутаторы 495
системы 542
Аналоговый
коммутатор 514
модулятор дельта 743
Аналого-цифровое преобразование 723
параллельное 732
Апертура триггера 668
Аппаратные прерывания 870
Аппаратный флаг 925
Арбитр шины 1128
Арифметико-логическое устройство 591
Архитектура
гарвардская 809
фон-неймановская 807
Асинхронное обнуление счетчика 641
Ассемблер
директива 891
$INCLUDE 859
EQU 859
ORG 859
директивы 815
команда
ACALL 889
ADD 872,881
ADDC 872,881
CALL 868
CPL 838
DA A 880
DJNZ 876
MOV 864
MOVX 865
POP 889
PUSH 889
RET 868,889
RETI 958
SJMP 857,838
АЦП
дельта-сигма 738,740
конвейерное 734
База транзистора
модуляция ширины 249
Байт 543
Биполярные транзисторы 180
Бит 542
Т2МН 937
стартовый 1018
стоповый 1018
Блокирующие присваивания 1132
Боковые полосы 775
частота 776
Броски тока 103
Буфер
ИБО 955
кольцевой 1009
с тремя состояниями 573
1188
Предметный указатель
В
Вход осциллографа «X» 122
Вектор
прерывания 816,956
сброса 857
Вентиль дополнительный 635
Вентильные матрицы программируемые 553
Вина мост 437
Виртуальная «земля» 279
Вольт
определение 35
Вольтаж 34
Воронка входная 1110
Время
нарастания 62,168
распространения 630
удержания триггера 630
установки триггера 630-632
Всплески напряжения 103
Выборка ложный сигнал
удаление 746
частота 745
Выпрямитель двухполупериодный мостовой 147
Высокоскоростной USB 1020
Выходной импеданс 55
Гальванометр 56
Гарвардская архитектура 809
Генератор
колебаний с мостом Вина 437
сигналов 60, 61
Гироскоп 1099
Гистерезис 355
вне области электроники 354
компаратора 354
побочный эффект задержка 355
Графики логарифмические 92
Дальномер EZ1 1097
Двигатели шаговые 1095
биполярные 1095
униполярные 1095
Двоично-взвешенная сумма 280
Двоичный код
Обратный 546
дополнительный 546
Двуоксид кремния 495
Двухполюсный фильтр 383
Действующее напряжение 168
Декодер 580
Декодирование адреса 705
«ленивое» 706
Делитель напряжения
на конденсаторах 90
регулируемый 40
смещения 190,191
Детектор пиковый 157
Децибел 92
Дешифратор команд 797
Динамическое сопротивление 36
Диод
Зенера. См. Стабилитрон
катод обозначение 161
напряжение пробоя 145
прямое напряжение 145
паразитный 496,497,503
Диодный мост 169
Директива
EQU 1001
ассемблера 815,891
$INCLUDE 859
EQU 859
ORG 859
Дискретизация
побочный сигнал 727
Дифференциальное усиление 255
формула 231
Дифференциальный
анализатор 793
усилитель 216
Дифференциатор 84-86
усиление 460
Длина электрическая 1143
Добротность 142,143
формула 168
Доступ к памяти прямой 676
Драйвер
шагового двигателя A3967SLB 1101
ШИМ 369
Дребезг контактов
устранение 608,609
Дрейф электронов 35
Дроссель 168
Загрузка
«вслепую» 1049
счетчика синхронная 641
Предметный указатель
1189
Задание смещения 258
Задержка обработки прерывания 955
Замок
схема управления 708
Запас по фазе 392, 443
операционного усилителя 413
Запуск по фронту 631
Заряд инжекция 508
Захват
единиц 605
тока биполярным транзистором 498
Защелка 607
SR тактируемая 604, 605
прозрачная 604-607
Звон щупа осциллографа 145
Звуковая частота
усилители класса D 731
«Земля»
виртуальная 279
сигнальная 49
Зеркало токовое Уилсона 259
Знаковый разряд 858
И
Идентификаторы 890
Измеритель периода 660
Импеданс
выходной 55
источника тока 246
низкочастотного фильтра 96
индуктора 139
конденсатора 139
вычисление 88,89
формула 88
Импедансы
преобразование 179
Импульс пробирующий 804
Импульсный стабилизатор 481
Индуктивность паразитная 103
Инжекция заряда 508
Инициализация регистра DPTR 902
Интегратор 84,86,87
Интерфейс
I2C 832,1020
SPI 832,1020
С2 833,835
Искажения переходные 193
Источник питания
двухполярный 147,258
однополярный 258
Источник тока 199
импеданс выходной 246
на биполярных транзисторах 238
рабочий диапазон 258
К
Каскод 258
Каскодная схема 251
Категории операционных усилителей 309
Катод диода
обозначение 161
Катушка привода жесткого диска 332
Качающаяся частота 121
Квантование
погрешность 725
Ключевое слово assign 1109
Ключи силовые 495
Код
Грея 1101
двоичный
дополнительный 546
обратный 546
объектный 829
операции 864
Колебания собственные 442
период 459
Команда ассемблера
ACALL 889
ADD 872, 881
ADDC 872,881
CALL 868
CPL 838
DA A 880
DJNZ 876
MOV 864
MOVX 865
POP 889
PUSH 889
RET 868,889
RETI 958
SJMP 857
дешифратор 797
формат 864
Коммутатор аналоговый 495,514
Компаратор
гистерезис 354
как операционный усилитель 349 >.
отличие от операционного усилителя 349
Компенсирование 242
Компилятор логический 554
Комплементарная структура 502
1190
Предметный указатель
Конденсатор
блокировочный 102,103
импеданс 139
вычисление 88,89
накопительный 151
плавающий 520
развязочный 103
развязывающий 102
шунтирующий 165
Контроллер ПИД 451
Контрольные точки 842,847
Контур 38
ПИД 437
резисторный Т-образный 321,323
Концентратор USB 1020
Корпус Mini-DIP 286
Коррекция частотная 483
операционных усилителей 409
Косвенная адресация 865,902
Коэффициент
бета 185
заполнения сигнала ШИМ 369
подавления синфазной составляющей 228,237,
262
усиления транзистора по току 182,185
Крутизна 258
л
Линейная область транзистора 225
Линия
MISO 1022
MOSI 1021
передачи эффекты 1150
Логика программируемая матричная 623
Логические устройства программируемые 553
Логический компилятор 554
Логический элемент универсальный 549
Ложный сигнал выборки
удаление 746
частота 745
м
Магнитометр 1099
Макроячейка 624
Маска прерываний 959
Маскирование 921
Материнская плата 795
Матрица резисторов R-2R 729,730
Матрицы вентильные программируемые 553
Матричная логика программируемая 623
Матричный переключатель 814,815,917
Метка перехода 856
Микроконтроллер
6805 796
8048 795
8051 795
Микропроцессор
6052 795
8008 794
8080 794
C8051F410 646
Микросхема
74НС14 558
LF411 287
LM741 286
LT1150 286
REF200 253
USB/RS-232FTDI232R 1037
акселерометра
ADXL335 1098
ADXL345 1098
активного фильтра UAF42 384,385
аналогового коммутатора DG403 517
аналогового переключателя
ADG1211 509
DG403 509
АЦПАБиС848 753
АЦП-ЦАП AD7569 726,975
буфера 74НС125 789,790
вентилей И-НЕ
74LS00 567
74НС00 567
выборки и хранения LF198 509
генератора колебаний
ICM7555 370
LMC7555 370
TLC555 370
генератора сигналов
LTC6906 360
генератора синусоидальных колебаний
ICL8038 363
гироскопа
L3GD20H 1099
LY530AL 1099
декодера
74НС138 789
74НС139 789,790,861
74НСТ139 558
дифференциального усилителя
INA105 296
INA149 299,296,327
INA194 326
драйвера шагового двигателя A3967SLB 1101
Предметный указатель
1191
импульсного стабилизатора LT1073 488,489
импульсного усилителя LM4667 524,969
инвертора CD4007 571
источника тока REF200 473,493
компаратора 311 349
контроллера энергонезависимой RAM MXD1210
873
магнитометра
ACS712 1099
НМС5883 1099
US1881 1099
микроконтроллера DS89C430 824
ограничителя тока LT3092 472
операционного усилителя
324 335
358 335
411 409
741 409
LM358 343,482
LMH6881 1022
LMP2015 345
LTC1150 331
LT1215 407
опорного напряжения LM385-2.5 481
памяти
CY14B101KA 682
М48Т35 681
ПМЛ XC9572XL 844
преобразователя логических уровней МАХ3370
723
регистров 74НСТ573 824
регистров последовательного приближения
74LS502 759
74LS503 759
стабилизатора напряжения 78L05 469,485,486,
485
сумматора
74НС83 590
74LS83 590
счетчика
74НС161 662
74НС163 662,663,787
74НС390 787
74НС393 790
74НС1600 787
счетчика со сквозным переносом
74НС74 610
74НС393 610
транзисторной сборки
СА3096 234
HFA3096 234
триггера
74НС74 614
74НСТ573 825,826
74НСТ574 1082
триггера Шмитта 74НС14 357,827
усилителя звуковой частоты
LM389 968
LM4667 523
фазового детектора 74НС4046 750,766
фильтра МАХ294 772,967,1070
ЦАП
AD558 758,1081
AD7569 1081
DAC8229 1082
LTC7545A 1083
МС1408 1083
ЦАП/АЦП
ADC7569 962
цифрового потенциометра МСР41100 1022
Микросхемы
ASIS 624
LF411 253
специализированные 553
Множители 590
Модель обратной связи 426
Модулирование 153
Модуль
Bluetooth Roving Networks WRL-12579 1041
RIDERKitSl 998
Модулятор
дельта аналоговый 743
дельта-сигма 740,741
Модуляция
амплитудная 153
боковые полосы 775
длины канала полевого транзистора 530
импульсно-шютностная 501
частотная 532
ширины базы биполярного транзистора 249
широтно-импульсная 369
МОП-транзистор 180
Мост
Вина 437
диодный 169
Мощность 36
Мультивибратор одноходовый 360
Мультиметр
функция тестирования диодов 196
Мультиплексирование 505
Мультиплексор канала осциллографа 505
1192
Предметный указатель
И
Нагрузка оконечная 1145
Наложение спектров 521,727,770
Нанофарада 114
Напряжение 34
всплески 103
выходное скорость нарастания 315
действующее 168
диода
обратное 145
пробоя 145
прямое 145
линейное 135
отключения 483
стабилизатора 468,484
сети 135
смещения 190,191
Неблокирующие присваивания 1133
Непосредственная адресация 841,864,902
Непрерывная развертка 121
Несущая частота 153
Нитиноловые провода 1096
Обмотка
привода жесткого диска 332
трансформатора
вторичная 168
первичная 168
Обнуление счетчика 641
Оборудование 440
Обратная связь 241
модель 426
разделенная 390
Ограничение
выходного тока 315,316
П-усиления 437
Одновибратор 621
Окно для мониторинга регистров Watch 849
Операционный усилитель 216,274,309,409
запас по фазе 413
как компаратор 349
псевдо 455,456,457
Остаточная погрешность 461
Осциллограмма 26
Отображение портов ввода-вывода в память 804
Отражение сигнала 1145
Отсечка 258
п
Память
EEPROM 680
EPROM 680
MOVXRAM 1015,1034
PROM 680
RAM 680
динамическая 681
синхронная 681
статическая 681
ROM 680
время доступа 682,683
прямой доступ 676
теневая RAM 682
энергозависимая 681
энергонезависимая 681
Пара
Дарлингтона TIP110 379,380
Шиклаи 380
Парадокс Зенона 82
Паразитная индуктивность 103
Паразитные колебания незатухающие
условия возникновения 385
Паразитный диод 496,497,503
Передискретизация 724,727,742,770,773
Переключатель
транзисторный 256
матричный 814,815,917
Переполнение 583
Переход
метка 856
относительный смещение 857
частота 138
Переходные искажения 193
Период
измеритель 660
собственных колебаний 459
Петлевое усиление 396,428
ПИД-контур 437
Пиковый детектор 157
Пикофарада 115
Плавающий уровень 702
Плата
дочерняя 833
материнская 795
Плоскости комплексные 99
ПМЛ 624
Побочный сигнал при дискретизации 727
Погрешность 65
квантования 725
Предметный указатель
1193
остаточная 461
резисторов 65
Подпрограмма 868
USUAL_SETUP 887
обработки прерывания 926
Подстройка смещения 310
Поле электрическое 34
Полевой эффект 496
Полевые транзисторы 180
Полнодуплексный режим связи 1022
Полноскоростной USB 1020
Полный сумматор 584
Полоса пропускания 95
Полосовой фильтр 141
Полосы боковые
частота 776
Помехи линейные 112
Помехозащищенность 229
Помехоустойчивость 594
Порты ввода-вывода
отображение в память 804
Последовательностные схемы 601,602
Постоянная времени 83,84,107
Потенциалы электрические
разность 34
Потенциометр 40
Поток тепловой
скорость 471
Правила «Золотые» 429,430
Программа comparator_osc_displayjanll.a51 947
Преобразование
аналогово-цифровое 723
аналого-цифровое параллельное 732
импедансов 179
с двукратным интегрированием 643
с однократным интегрированием 643
цифроаналоговое 723
метод дельта-сигма 732
Прерывание
аппаратное 870
вектор 816,956
задержка обработки 955
маска 959
подпрограмма обработки 926
приоритет
естественный 958
запрограммированный 958
Прилипание 449
Присваивания
блокирующие 1132
неблокирующие 1133
Пробой тепловой 265
Провисание 168
Провода
мускульные 1096
нитиноловые 1096
с эффектом памяти 1096
Проводник общий 49
Программа
adc_dac_intjanll.a51 996
bit_transfer_port.c 919
comparator_pscfflatorjanll.a51 946
FilterPro 384
full_wave_silabs.a51 971
GETREADY_1208.a51 930
GET_SAMPLE 965
int_inc_dec.a51 985
Loader420 1045
maskingjf.c 923
MTK 1045,1048
ч pulse_measure_capture_standalone_505.a51 1068,
1072
pulse_measure_decimal_standalone_505.a51 1068,
1072
pwm_by_wizard_novl0.a51 942
serialjnessage_silabs_aprll.a51 1039
servopulse_512.a51 1032,1033
sPI_digipot_int_504.a51 1031
spi_digipot_int_504.a51 1033
SPI_digipot_silabs_aprl4.a51 1036
spij:am_adc_dac_incomplete.a51 1072
spi_single_byte.a51 1070
spi_single_byte.a51. 1072
table_bidirectional_declO_wi_ale.A51 1034
tblcopy_804.c 1012
TMR800.A51 1032
для разработки фильтров FilterPro 418
определение 688
цикл 856
Программная функция 870
Произведение усиление — полоса пропускания 315
Проникновение сигнала емкостное 243
Пространство адресное 706
ПротивоЭДС 438
Проходной транзистор 251,468
Процессор
4004 794
слово состояния 956
Прямой доступ к памяти 676
Псевдооперационный усилитель 455,456,457
Пульсации 168
1194
Предметный указатель
Рабочий диапазон источника тока 258
Развертка непрерывная 121
Разделенная обратная связь 390
Разность
потенциалов электрических 34
температур 471
Разрешение выходное ЦАП 731
Разряд знаковый 858
Регистр 621
АСС 889
Accumulator 863
AD0CN 964
CKCON 937
DPH 1035
DPS 1012
DPTR 863,902,1010,1034
инициализация 902
PSW 889
TMR2CN 934,937
аккумулятор 868
сдвиговый 612,621
указателя данных 875
<|wiaroB_PSW 885
Режим
насыщения транзистора 183,194
покоя 259
разделения времени 506
связи полнодуплексный 1022
синфазный 231
хранения 614
Резистор 35
разрядный 169
шунтирующий 71
Резисторы
металлопленочные 35
погрешность 65
угольные композиционные 35
Резонанс 140
Резонансная частота 101,141
Реле 514
Ряд Е12 66
Самозагрузка 798
Сборка транзисторная
HFA3096 234
СА3096 230,234
Сброс
вектор 857
синхронный 607
Сверхскоростной USB 1020
Связь обратная 241
следящая 259
Сдвиг фазовый в RC-цепях 97,98
Сигнал
DTR 1027
RXD 1027
SYNC 62
TXD 1027
время нарастания 62
займа 664
отражение 1145
псевдодифференциальный 244
рассогласования 438
тактирования 606
Сигнальная «земля» 49
Силовые ключи 495
Символ
возврата каретки 1018
перехода на новую строку 1018
Синфазная составляющая
коэффициент подавления 228,237
Синфазное усиление 255
Синфазный
режим 231
шум 228
Синхронная загрузка счетчика 641
Синхронный сброс 607
Системы
аналоговые 542
цифровые 542
Скорость
нарастания выходного напряжения 315
теплового потока 471
Следящая связь 259
Слово
ключевое assign 1109
состояния процессора 956
Смещение
задание 258
напряжение
делитель 190,191
перехода 857
подстройка 310
Собственное сопротивление эмиттера 217
Собственные колебания 442
период 459
Совмещение адресов 706
Соединение суммирующее 279
Создание экземпляра 1112
Предметный указатель
1195
Сопротивление
динамическое 36
дифференциальное 36
малое гэ 201
реактивное 87
тепловое 472
расчет 472
теплопередаче 471
удельное 36
эмиттера собственное 217
эффективное определение 211
Состояние
безразличное 685
третье 675
Спад
усиления 314
частотной характеристики фильтра 102
Спектр частотный 776
синусоидального сигнала 776
Спектры
наложение 521,727,770
Специализированные микросхемы 553
Стабилизатор 170
импульсный 481
линейный 481
потеря мощности 474
напряжение отключения 468,484
с малым падением напряжения 386
Стабилизация нуля прерыванием 311
Стабилитрон 465
Стек
указатель 868
Сторожевой таймер 815,954
Стробирующий импульс 804
Структура комплементарная 502
Сумма двоично-взвешенная 280
Сумматор 584
полный 584
Схема
каскодная 251
монтажного ИЛИ 561
тактирования 80
тактируемые 602
управления замком 708
усредняющая 731
эквивалентная источника тока 248
Схемы
последовательностные 601,602
тактируемые 602
Счетчик делитель на два 616
загрузка синхронная 641
обнуление
асинхронное 641
синхронное 641
со сквозным переносом 609
Счетчики программируемые 933
Таблица эквивалентов 816
Таймер
Timer2 935
сторожевой 815,954
Тактирование
сигнал 606
фронт медленный 633
Теорема де Моргана 598
Тепловое сопротивление 472
расчет 472
Теплоотвод 471
Тиристор 487
Ток
броски 103
выходной ограничение 315,316
источник 199
поглотитель 199
сдвига 313
смещения 308
трансформатора действующий 151
Токовое зеркало Уилсона 259
Точка/3дБ 91
Точки контрольные 842,847
Транзистор
1N5294 238
2N3904 249
2N3906 295
BS250P 295
DG403 504
MJE2955 453
MJE3055 453
MJE3055T 201
с изолированным затвором 500
МОП 180
BUK9509-40B 514,515
IRLZ34 514,515
обедненный 527
обогащенный 525
проходной 251,468
режим насыщения 183
усиление коэффициент 182
Транзисторная сборка
СА3096 234
HFA3096 234
СА3096 230
1196
Предметный указатель
Транзисторы
биполярные 180
полевые 180
Трансформатор
обмотка первичная 168
ток действующий 151
Трение статическое 449
Третье состояние 675
Триггер
D 606,608
JK 615
MS 605
SR 619
Т 617
апертура 668
время
удержания 630
установки 630-632
запускаемый по фронту 605
Шмитта 354,357
Удаление ложного сигнала выборки 746
Удельное сопротивление 36
Указатель 902
данных регистр 875
стека 868
Универсальный логический элемент 549
Уровень
активный низкий 550
плавающий 702
Усиление
дифференциальное 255
формула 231
дифференциатора 460
коэффициент бета 185
петлевое 396,428
петли 426
по току 185
синфазное 255
спад 314
Усилители
звуковой частоты класса D 731
операционные 309
Усилитель
дифференциальный 216
операционный 216,274
трансимпедансный 1143
Условия
для незатухающих паразитных колебаний 385
покоя 205
Устройства логические программируемые 553
Устройство
DCE 1027
DTE 1027
арифметико-логическое 591
управляемое 440
ф
Файл
.1st 1000
testbench 1111
Фарада 115
Фильтр 81
LC задерживающий 100
RC 80
активный RC двухполюсный 102
Баттерворта 383,418
Бесселя 383,418
двухполюсный 383
низкочастотный импеданс выходной 96
полосовой 141
Саллена - Ки 384,416
с бесконечной импульсной характеристикой 1008
с конечной импульсной характеристикой 1008
Чебышева 383,418
Флаг аппаратный 925
Формат команд
языка ассемблера 864
Формула
дифференциального усиления 231
добротности Q 168
импеданса конденсатора 88
Фототранзистор BPV11 293,294
Функция
программная 870
экспоненциальная 83
Характеристика
полосового фильтра 141
режима покоя 259
ЦАП
микросхема AD558 758
разрешение выходное 731
с коммутируемыми конденсаторами 730
Цепочка Т-образная резистивная 321,323
Цикл программы 856
Предметный указатель
1197
Цифроаналоговое преобразование 723
Цифровые системы 542
Частота
боковых полос 776
единичного усиления 315
качающаяся 121
несущая 153
перехода 138
резонансная 101,141
сигнала выборки ложного 745
Частотная
коррекция 483
операционных усилителей 409
модуляция 532
Эффект
Миллера 259,400
модуляции ширины базы 200
полевой 496
самообеспечения 427
Эрли 200,246,259,281
квантификация 254
Эффективное сопротивление
определение 211
Эффекты линии передачи 1150
А
ASIS 624
характеристика фильтра lUz
Часы реального времени 955
ш
Шаговые двигатели 1095
биполярные 1095
униполярные 1095
ШИМ-драйвер 369
Шина 573,578
арбитр 1128
питания 675
Широтно-импульсная модуляция (ШИМ) 369
Шум
напряжения 316
синфазный 228
токовый 316
Шунтирование 259
Щ
Щуп осциллографа
звон 145
э
Эквивалентная схема источника тока 248
Эквиваленты
таблица 816
Экземпляр создание 1112
Электрическая длина 1143
Электрокардиограф 228
Электроны дрейф 35
Эмиттер
сопротивление собственное 217
EEPROM 680
EPROM 680
F
FPGA 623
G
GAL 624
н
HFA3096 235
Р
PROM 680
R
RAM 680
динамическая 681
синхронная 681
статическая 681
теневая .682
ROM 680
и
USB
высокоскоростной 1020
концентратор 1020
полноскоростной 1020
сверхскоростной 1020
Arduino. Базовый набор 2.0 + КНИГА
ISBN 978-5-9775-3756-8
Если вы хотите не только изучить теоретически основы использования попу-
лярной микроконтроллерной платформы Arduino для разработки электронных
проектов, но и получить первичные практические навыки, то этот комплект
для вас.
В набор входят:
• популярная книга Дж. Блума «Изучаем Arduino: инструменты и методы
технического волшебства» (2-е изд.);
• плата, совместимая с Arduino Uno, и кабель для подключения к ПК;
• беспаечная макетная плата и провода;
• электронные компоненты;
• брошюра с упражнениями.
Вы научитесь:
• программировать контроллер Arduino;
• собирать электрические схемы на макетной плате;
• подключать датчики;
• осуществлять обмен информацией между Arduino и ПК.
«Пятьдесят лет назад для разработки программного обеспечения вам тре-
бовалась команда людей в белых халатах, которые знали все об электронных
лампах. Но теперь даже моя мама может программировать. Мы позволили
множеству людей создавать электронные устройства самостоятельно».
Массимо Банци, один из создателей платы Arduino
ИНТЕРНЕТ И BLUETOOTH
• Передача данных по каналу Bluetooth
• Управление по каналу Bluetooth
• Wi-Fi и облачные хранилища
• Веб-сервер на ESP32
• Более Ы) экспериментов из книги
. * Более 30 примеров на сайте разра- '
! ботчика Afdtiino ■
. * Более 90 компонентов
ПРОЕКТЫ
• Самоходный робот
на алюминиевом
шасси
• Хронометр
• Регулятор темпе-
ратуры и др.
Изучаем Arduino. Учебный набор
+ КНИГА
ISBN 978-5-9775-6739-8
Это наиболее полный в России набор электронных ком-
понентов, который поможет вам быстро и основательно
освоить работу с контроллером Arduino и начать созда-
вать собственные электронные проекты. В набор входят
популярная во всем мире книга Дж. Блума «Изучаем
Arduino: инструменты и методы технического волшеб-
ства» (2-е изд.), микроконтроллеры Arduino Uno и ESP32S,
электронные компоненты, двигатели и макетная плата для
выполнения экспериментов, а также алюминиевое шасси
с колесами для сборки самоходного робота.
В процессе чтения книги вы сможете собирать электриче-
ские схемы и проводить эксперименты, чтобы облегчить
освоение изучаемого материала.
ОСНОВЫ РАБОТЫ
• Цифровые сигналы, широтно-импульстная модуля-
ция (ШИМ)
• Сигналы аналоговых датчиков
• Сдвиговые регистры
• Работа со звуком
ГЛУБОКОЕ ИЗУЧЕНИЕ
• Управление редукторными, серво-
и шаговыми двигателями
• Шины PC, SPI, Serial Bus
• Чтение/запись карты SD
Умный дом на базе Arduino.
Большой набор + КНИГА
ISBN 978-S-9775-3988-3
Набор поможет вам с головой окунуться в удиви-
тельный мир Arduino. Вы научитесь подключать
к плате Arduino.и программировать различные
датчики и модули, соберете макет «Умного до-
мика» и разместите в нем собственную «систе-
му умного дома», которую можно впоследствии
частично реализовать и у себя в квартире или
на даче.
Набор будет интересен как начинающим раз-
работчикам, у которых еще нет опыта создания
проектов Arduino, так и тем, кто уже сделал пер-
вые шаги в разработке электронных проектов.
В набор входят:
• плата Arduino Uno;
• датчики;
• модули;
• светодиоды и дисплеи;
• серводвигатель и микронасос;
• блок питания 9 В и 4 батерейки АА;
• популярная книга Дж. Блума «Изучаем
Arduino: инструменты и методы техниче-
ского волшебства» (2-е изд.);
• макет фанерного домика.
Электроника для начинающих 2.0.
БОЛЬШОЙ НАБОР + КНИГА
ISBN 978-5-9775-3831-2
В процессе выполнения 28 экспериментов вы поймете, что
такое электрический ток, изучите на практике основные за-
коны электричества, познакомитесь с принципом работы
электронных компонентов и устройств от резисторов до ин-
тегральных микросхем, научитесь паять, соберете учебные
и практические электрические схемы, создадите проекты
с использованием платы Arduino, а также научитесь работать
с мультиметром.
В набор входят:
• более 300 компонентов;
• мультиметр;
• инструменты (паяльник, держатель проводов «третья
рука», нож, плоскогубцы);
• элементы и блок питания;
• макетная плата;
• плата, совместимая с Arduino Uno;
• книга Ч. Платта «Электроника для начинающих»
(2-е изд.).
рухторз ^Электроника дня начинающих 2,0
МАЛЫЙ НАБОР--