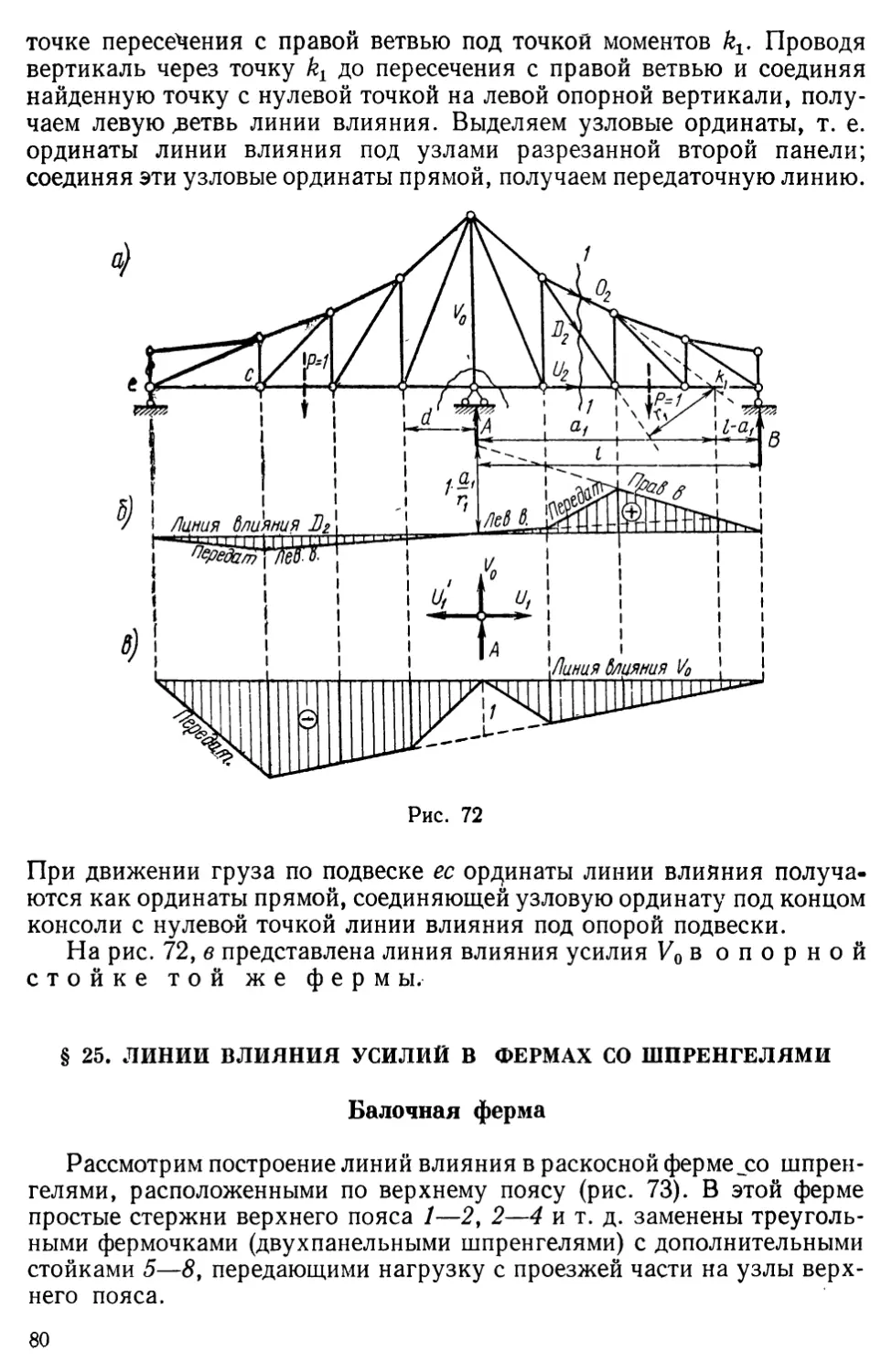
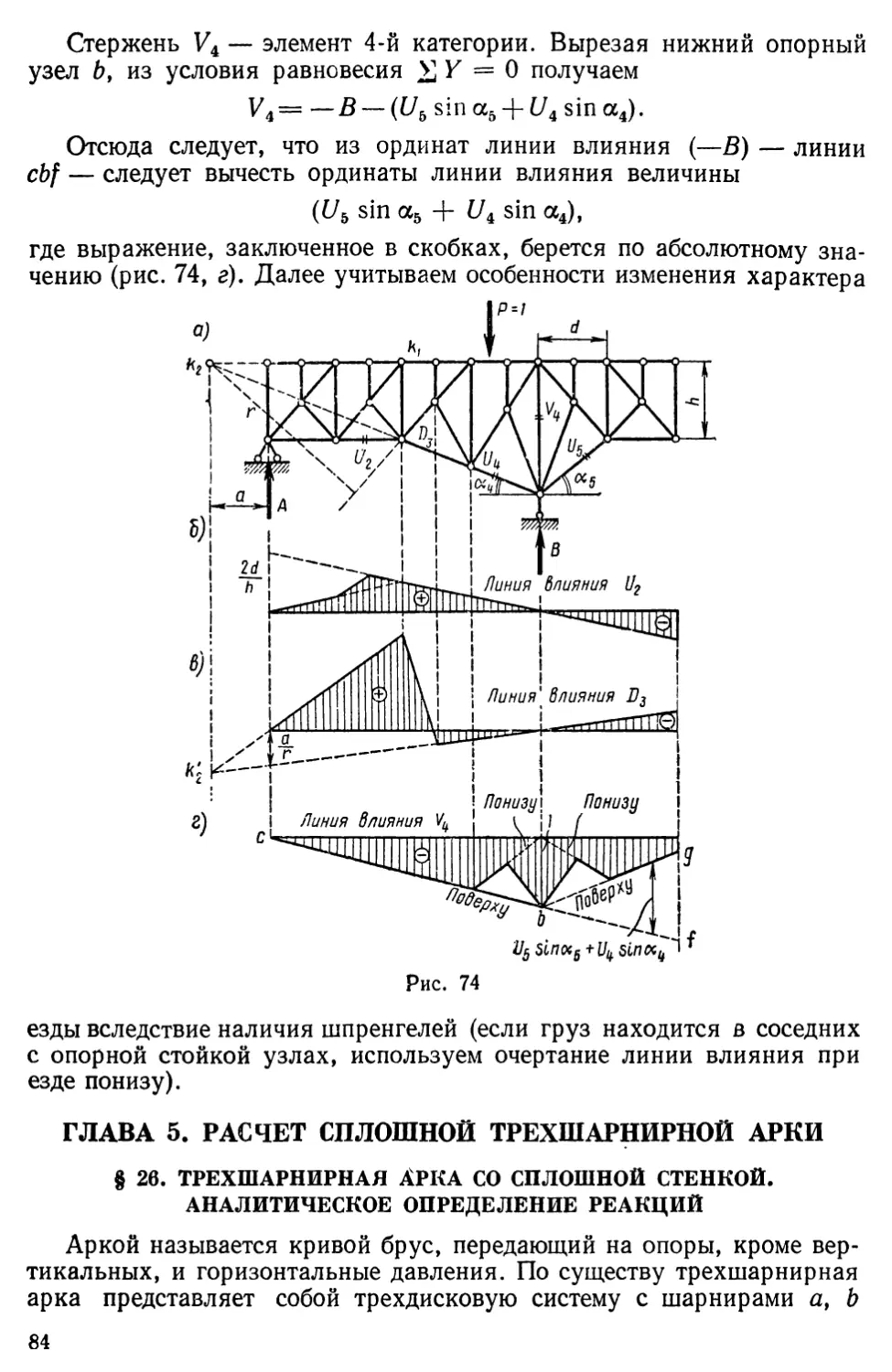
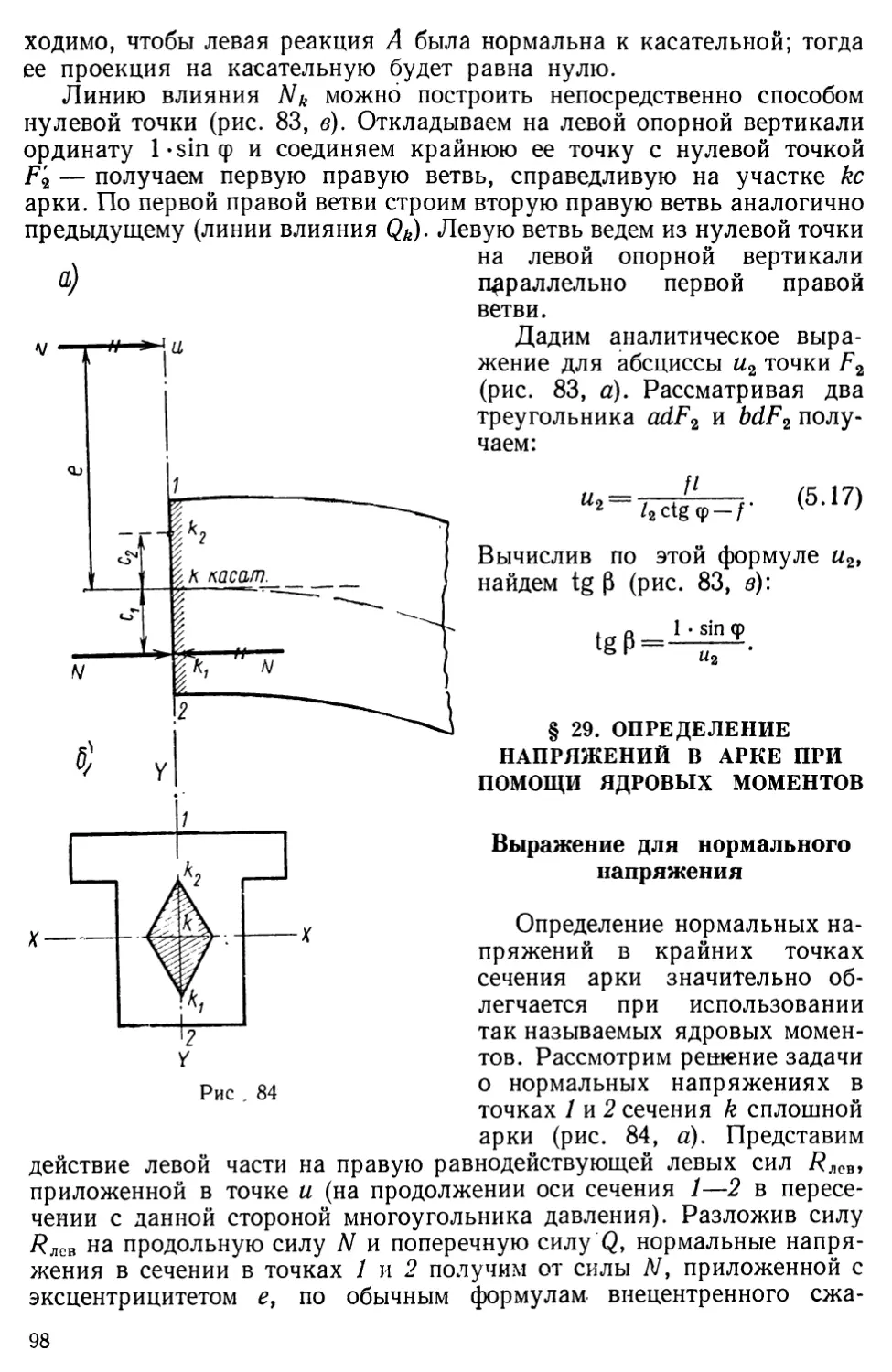
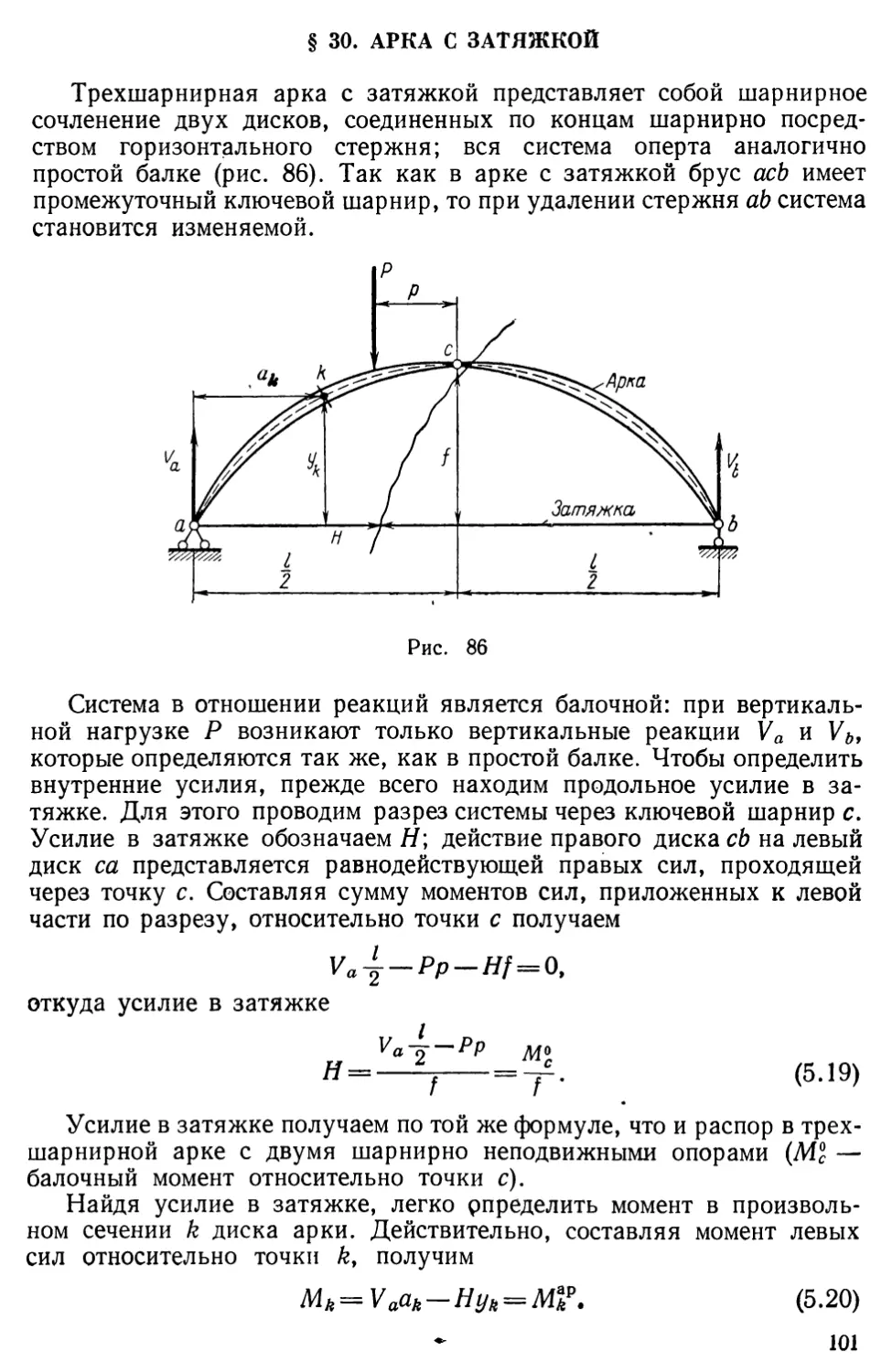
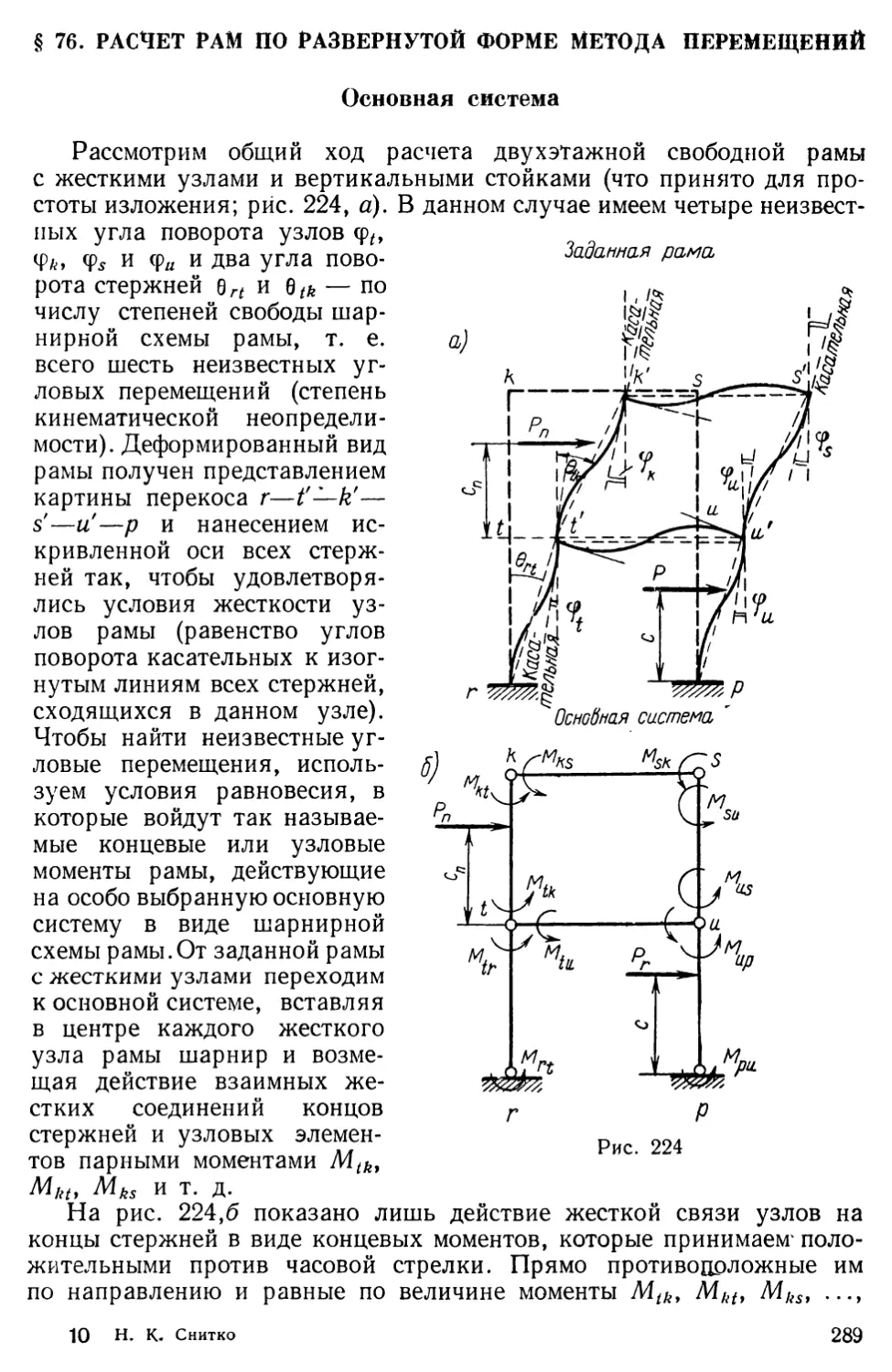
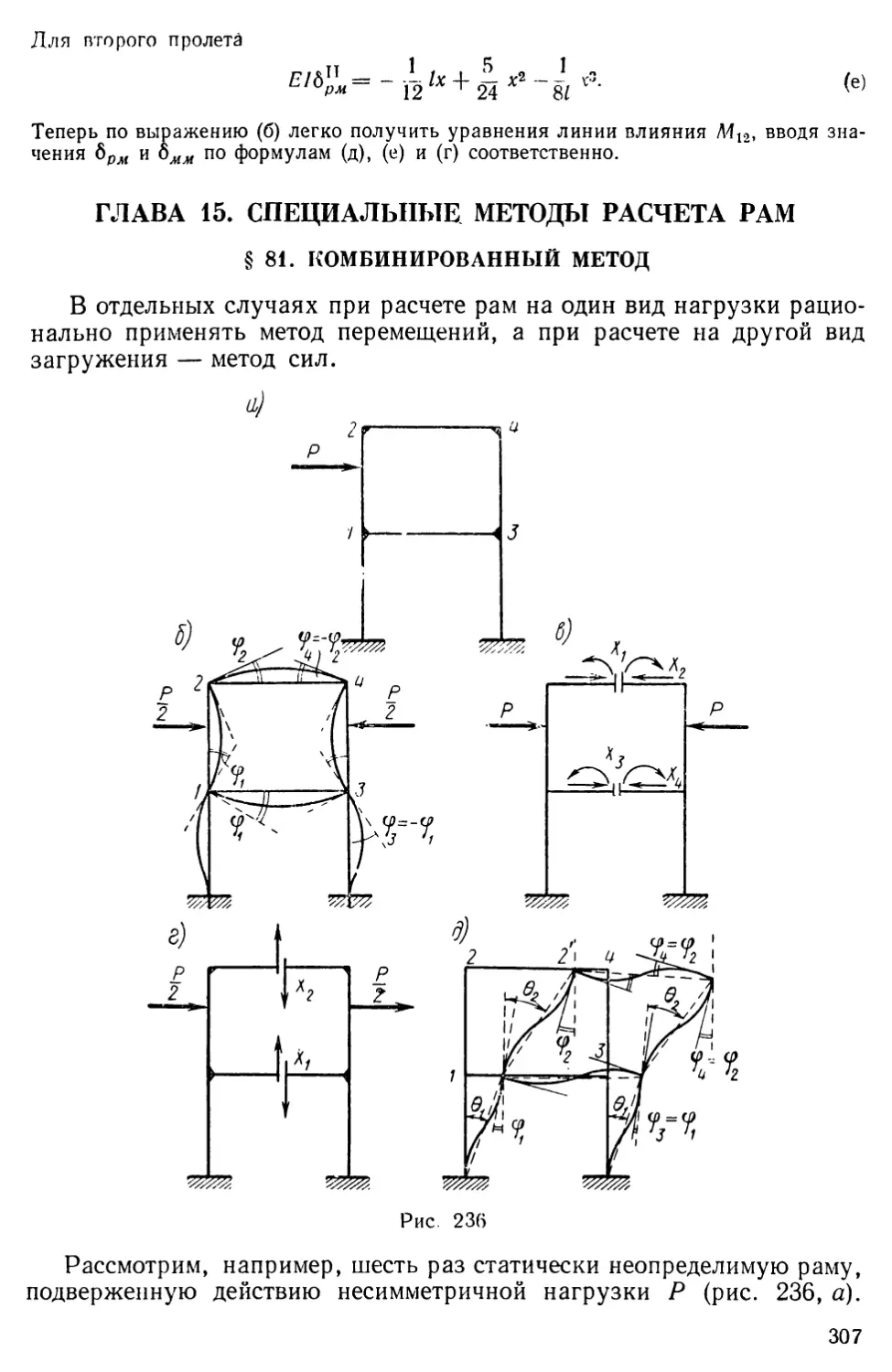
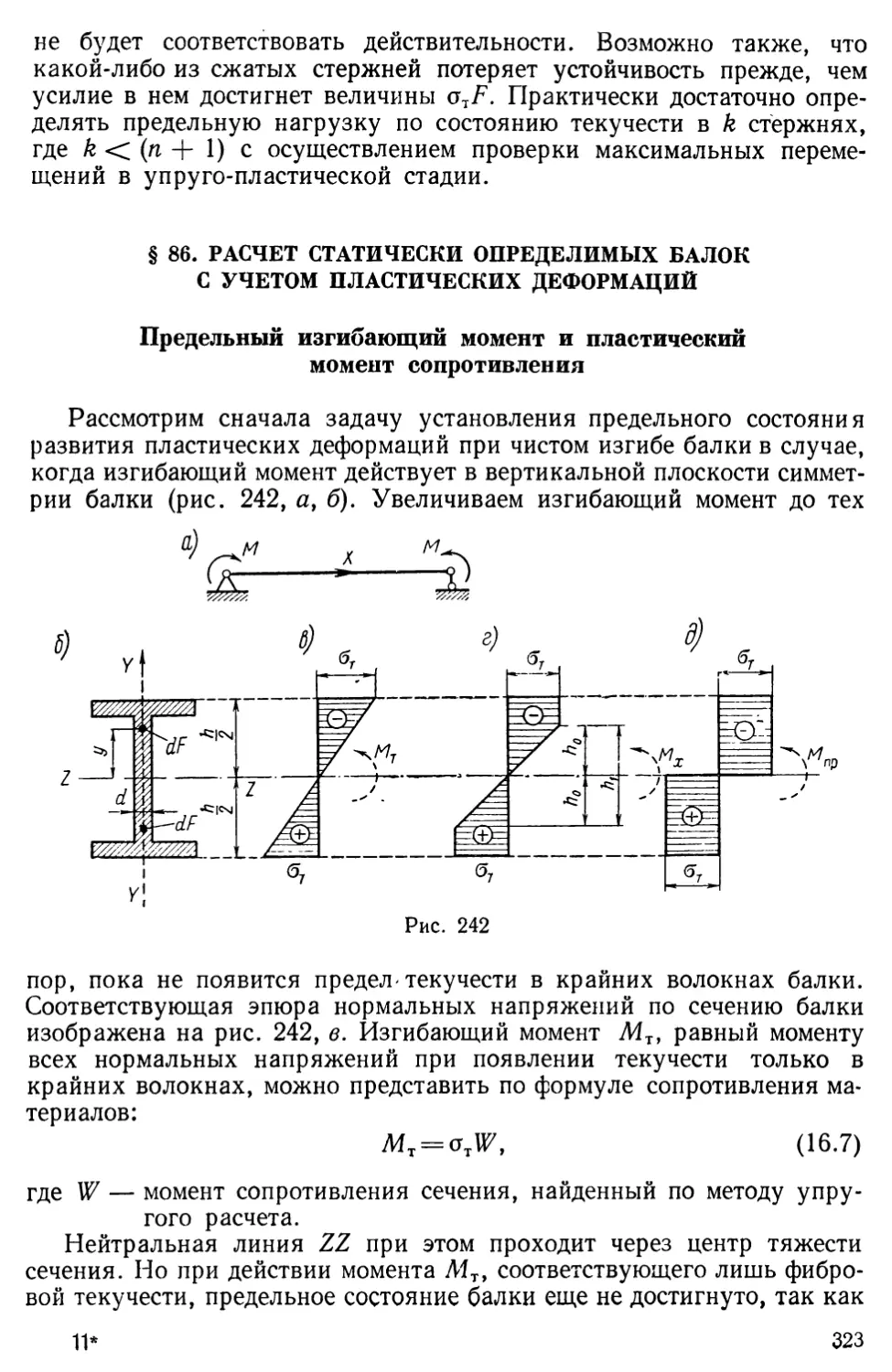
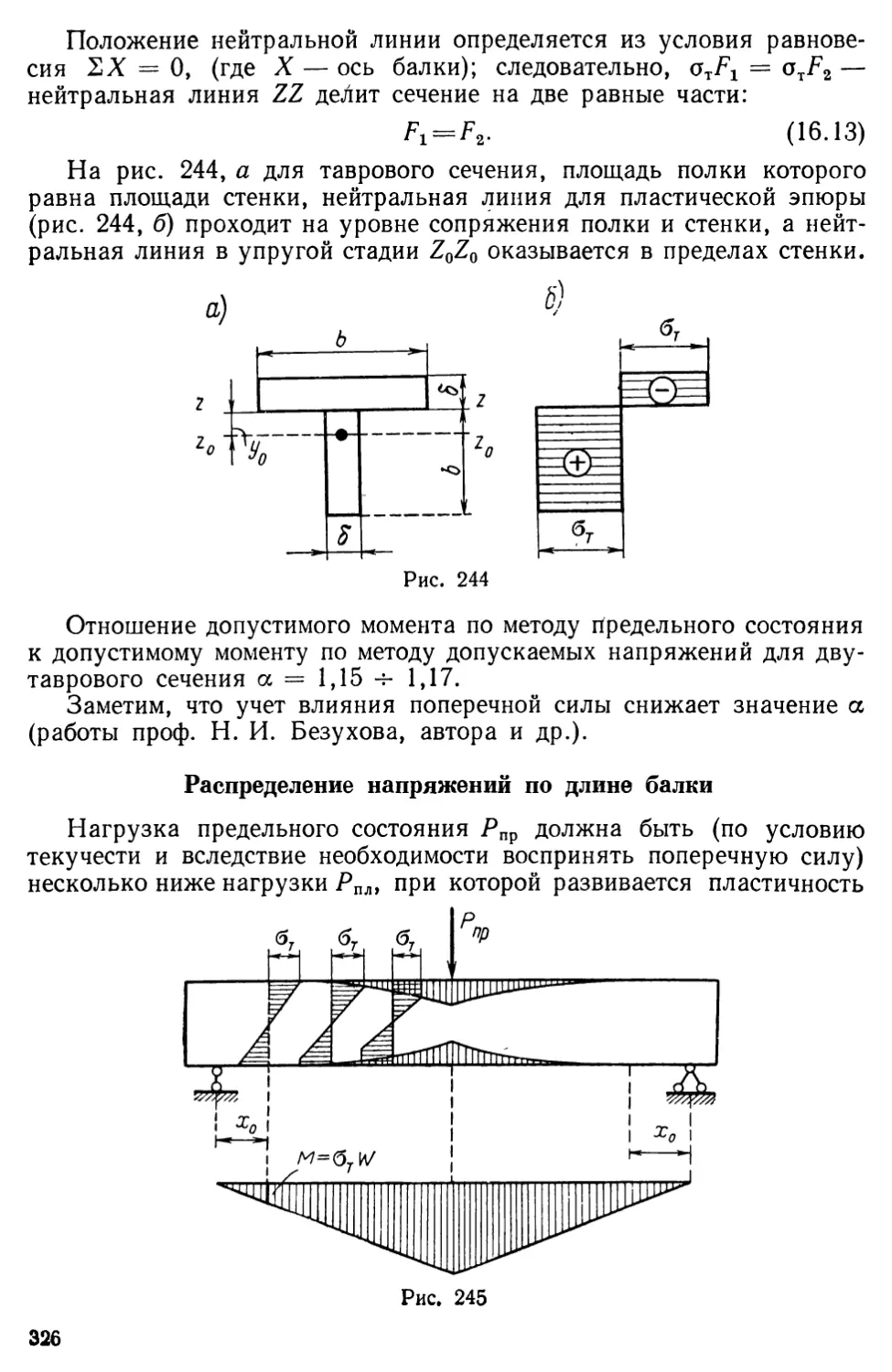
Text
н. к. снитко
Заслуж. деят. науки и техники РСФСР Проф., докт. техн. наук
СТРОИТЕЛЬНАЯ МЕХАНИКА
Допущено Министерством высшего и среднего специального образования СССР в качестве учебника для студентов строительных специальностей вузов
Издание 2-е, переработанное
ИЗДАТЕЛЬСТВО «ВЫСШАЯ ШКОЛА»
МОСКВА — 1972
Снитко Н. К.
С53 Строительная механика. Учебник для втузов.
Изд. 2-е, доп. М., «Высшая школа», 1972.
488 с. с илл.
Книга представляет собой курс строительной механики и содержит изложение основных методов расчета статически определимых и неопределимых стержневых систем, а также расчета конструкций на устойчивость и основы динамики. В последней части курса даны методы расчета пластинок и оболочек. В учебнике приведены примеры, иллюстрирующие применение теории.
3-2-5
82—72 6С1
Рецензент — кафедра строительной механики Московского инженерно-строительного института
ПРЕДИСЛОВИЕ
Широкое развитие строительства в нашей стране, намеченное Директивами XXIV съезда КПСС по пятилетнему плану, требует дальнейшего совершенствования подготовки инженера-строителя. Высокий уровень подготовки инженера может быть обеспечен лишь разносторонней самостоятельной его работой с использованием учебных пособий как для усвоения теории, так и для приобретения важных практических навыков в решении задач по расчету сооружений на прочность, жесткость и устойчивость.
В настоящее время особенно большое значение приобретает использование современной вычислительной техники, значительно ускоряющей расчеты сложных сооружений и облегчающей труд инженера-вычислителя. Значительное распространение получают континуальные системы (пластинки и оболочки). Им в настоящем издании уделено особое внимание.
Содержание данного курса соответствует последней программе по строительной механике. Автор изложил материал, который необходим для прохождения этого курса как по специальности «Промышленное и гражданское строительство» (материал третьей части программы, освещающей устойчивость и динамику стержневых систем), так и по специальности «Гидротехническое строительство» (расчет круговых арок).
Курс содержит основы расчета статически определимых и статически неопределимых стержневых и континуальных систем, матричную форму определения усилий, основы расчета на устойчивость и колебания, а также основы теории расчета пластинок и оболочек. Настоящее второе издание курса значительно переработано по сравнению с первым изданием, вышедшим в 1966 году. В ряде глав сделано сокращение, за счет чего введены главы по расчету пластинок и по моментной теории оболочек,
3
Учебник предназначен для студентов инженерно-строительных вузов. Он может быть также полезен инженерам всех специальностей.
Автор выражает большую благодарность проф. Н. И. Безухову, проф. Д. В. Вайнбергу, проф. П. М. Варваку, а также кафедре МИСИ во главе с профессором Г. К. Клейном за их ценные замечания, сделанные при рецензировании настоящего курса.
ЧАСТЬ ПЕРВАЯ
СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ СИСТЕМЫ
ГЛАВА 1. ВВЕДЕНИЕ
§ 1. СТРОИТЕЛЬНАЯ МЕХАНИКА КАК НАУКА. КРАТКИЙ ИСТОРИЧЕСКИЙ ОБЗОР
Задачи и методы строительной механики
Всякое сооружение должно быть прочным, жестким и устойчивым, т. е. оно не должно разрушаться от действия внешних сил и должно иметь необходимый запас прочности; в нем недопустимы перемещения, нарушающие нормальную эксплуатацию сооружения; кроме того, должна быть исключена возможность потери сооружением устойчивости заданной формы.
Строительная механика занимается разработкой методов статических и динамических расчетов сооружений на прочность, жесткость и устойчивость. Статика сооружений изучает их работу при статическом действии нагрузки — медленном ее приложении в определенный конечный промежуток времени. При динамическом действии нагрузки, меняющейся во времени, учитываются динамические эффекты нагрузки и вводятся в рассмотрение силы инерции. Расчеты на динамическую нагрузку освещаются динамикой сооружений.
Задачи строительной механики состоят в разработке рациональных методов определения усилий в сооружениях и их перемещений; методов расчета сооружений на прочность, жесткость и устойчивость, а также в установлении наивыгоднейших форм сооружений, удовлетворяющих требованиям экономичности.
Строительная механика широко использует методы теоретической механики, изучающей равновесие и движение твердых тел, но в отличие от последней она рассматривает деформации сооружения (упругие или упруго-пластические). Большую роль в решении современных проблем строительной механики играют аналитические выражения расчетных величин или в замкнутой форме, или в дискретной (численной). Аналитические численные методы получили в настоящее время большое распространение при подготовке к вычислениям на электронно-счетных машинах. Характерно для последнего времени использо¬
5
вание матричного исчисления, теории вероятности, статистической механики, итерационных методов. Широко применяются графо-аналитические методы, основанные, с одной стороны, на исходных аналитических зависимостях, с другой, — на графических представлениях. Большое распространение в настоящее время получили такие новые конструктивные формы сооружений как пластинки и оболочки, а также пластинчато-стержневые системы. Поэтому в данном курсе уделяется внимание и теории расчета континуальных систем.
Краткий исторический очерк развития строительной механики
Развитие строительной механики тесно связано с прогрессом строительной техники и сменой общественных формаций.
Основы строительной механики были созданы лишь в XIX в. в связи с появлением железных дорог и строительством мостов и крупных гидротехнических и промышленных сооружении.
Первые большие достижения отечественной строительной механики связаны с деятельностью русских инженеров-мостовиков, строителей первой железной дороги Петербург — Москва.
Можно указать на работы следующих русских ученых: профессора Д. И. ЖУРАВСКОГО (1821—1891 гг.), автора первой теории раскосных ферм; профессора Ф. С. ЯСИНСКОГО (1856—1899 гг.), предложившего первые решения по различным задачам устойчивости стержней и по теории пространственных ферм; почетного академика, крупного инженера В. Г. ШУХОВА (1853—1939 гг.), создавшего ряд новых плоских и пространственных ферм (сетчатые перекрытия, башни в виде сетчатого однополостного гиперболоида), и Н. А. БЕЛЕЛЮБСКОГО (184.5—1922 гг.), создавшего полный курс строительной механики.
Важную роль в популяризации новых методов строительной механики сыграли работы В. Л. КИРПИЧЕВА (1845—1916 гг.), в которых наиболее полно изложены графическая статика и анализ основных положений теории статических неопределимых систем.
Значительное развитие теории шарнирно стержневых ферм было достигнуто благодаря работам Л. Д. ПРОСКУРЯКОВА (1858— 1926 гг.) и почетного академика В. Г. ШУХОВА. Замечательный конструктор и изобретатель, почетный член Академии Наук СССР В. Г. ШУХОВ предложил ряд новых решений металлических конструкций. Известна его сетчатая ферма со схемой в виде двух дисков, связанных тремя стержнями. Замечательны также гиперболические башни ШУХОВА (маяк высотой 80 ж, мачта радиостанции высотой 160 ж, многочисленные водонапорные башни), использующие простое свойство совмещения на поверхности однополостного гиперболоида прямолинейных элементов.
Большой интерес представляли работы профессора С. И. БЕЛЗЕЦКОГО по расчету арок и труб: «Теория рациональных форм цилиндрических сводов» (1902 г.), «Рациональные формы сплошных упругих арок в железнодорожных мостах и трубах» (1905 г.) и «Типы
6
каменных труб под насыпями» (1912 г.). Ценный вклад в развитие строительной механики корабля сделан профессором И. Г. БУБНОВЫМ, которому принадлежит оригинальное исследование устойчивости равнопролетного стержня на упругих опорах (1912 г.). К этому же периоду можно отнести капитальные исследования по устойчивости стержней переменного сечения академика А. Н. ДИННИКА и многочисленные его решения по устойчивости арок.
Среди работ многих советских ученых можно указать на труды академика А. Н. Крылова (1863—1945 гг.) по строительной механике корабля, теории продольного изгиба, теории вынужденных колебаний и расчету балки на упругом основании; академика Б. Г. ГАЛЕРКИНА (1871—1945 гг.), давшего ряд решений по плитам, собранных в его капитальном труде «Упругие тонкие плиты», а также разработавшего общие методы решения задач устойчивости и теории упругости; члена-корреспондента АН СССР, профессора Н. С. СТРЕЛЕЦКОГО, внесшего большой вклад в строительную механику мостов и конструкций, теорию расчета сложных статически неопределимых систем и теорию надежности конструкций; профессора И. М. РАБИНОВИЧА, создавшего теорию вантовых многопоясных систем и сделавшего много ценных обобщений и исследований по статике и динамике сооружений, опубликованных в его капитальном труде «Строительная механика стержневых систем» и в других работах; профессора В. 3. ВЛАСОВА, предложившего новую стройную математическую теорию оболочек и тонкостенных стержней; профессора Н. В. КОРНОУХОВА, разработавшего теорию устойчивости каркасных рам (в особенности метод перемещений); профессора А. А. ГВОЗДЕВА, разработавшего смешанный метод расчета рам и развившего теорию расчета сооружений по предельному состоянию; профессора К. С. ЗАВРИЕВА, впервые предложившего метод расчета сжато-изогнутых стержней по предельным состояниям и профессора А. Ф. СМИРНОВА, разработавшего матричную форму решения различных задач статики, устойчивости и динамики сооружений. Большую роль в решении различных задач строительной механики сыграли также В. В. НОВОЖИЛОВ, П. Ф. ПАПКОВИЧ, Н. И. БЕЗУХОВ, В. В. БОЛОТИН, А. А. УМАНСКИЙ, А. П. СИНИЦЫН, Д. В. ВАЙНБЕРГ, В. А. КИСЕЛЕВ,
А. Р. РЖАНИЦЫН, Г. К. КЛЕЙН, А. П. ФИЛИН и многие другие.
Из зарубежных ученых, внесших свой вклад в развитие строительной механики в XIX в., следует назвать ДАЛАМБЕРА, ЛАГРАНЖА, КУЛОНА, НАВЬЕ, ЛАМЕ, СЕН-ВЕНАНА, ЭЙЛЕРА, МАКСВЕЛЛА, МОРА и других.
§ 2. НОВЫЕ ЗАДАЧИ СТРОИТЕЛЬНОЙ МЕХАНИКИ В СВЯЗИ С РАЗВИТИЕМ СТРОИТЕЛЬНОЙ ИНДУСТРИИ.
РАСЧЕТНАЯ СХЕМА
В настоящее время в инженерной практике находят применение новые типы сложных строительных конструкций больших пролетов и высоты, требующие применения более совершенных методов рас¬
7
чета. Поэтому возрастает роль тех аналитических методов в строительной механике, которые обеспечивают применение новых вычислительных средств (электронных цифровых вычислительных машин — ЭЦВМ).
В связи с применением легких ответственных конструкций и механизацией производственных процессов особенно большое значение приобретают динамические расчеты и анализ устойчивости сооружений. Современный инженер должен уметь рассчитывать не только плоские, но и пространственные системы, мачты, пластинки, складки и оболочки, а также уметь оценить действие динамической нагрузки и знать методы анализа устойчивости сложных конструкций. Вследствие этого исключено параллельное изложение решения задач и аналитическими и графическими методами и отдано предпочтение применению аналитических методов.
В Советском Союзе за годы пятилеток и в последнее время построены многие замечательные гидротехнические сооружения, крупнейшие промышленные сооружения, новые города, развернуто огромное жилищное строительство. Развитие нового строительства в СССР требует решения важнейших задач строительной механики по созданию новых методов расчета крупнейших стержневых и пластинчатых сооружений.
В связи с распространением электронных счетно-решающих устройств и кибернетики должны быть развиты соответствующие новейшие методы расчета сооружений, удобные для использования машинной техники. Важнейшим инструментом этой вычислительной техники является аппарат матричной алгебры. Матричная форма расчета сооружений получила большое распространение при расчете сложных статически неопределимых систем, при анализе устойчивости сооружений и в динамике сооружений. Применение матриц позволяет обобщить ряд задач расчета и статически определимых систем. Основным преимуществом матричной формы является то, что одна и та же последовательность матричных операций применяется в расчете самых различных систем — плоских и пространственных, стержневых и пластинчатых.
В развитии современных методов расчета пространственных конструкций ярко выделяется тенденция к синтезу методов теории упругости, общей теории оболочек и строительной механики стержневых систем.
При решении задач расчета реального сооружения упрощают его и оперируют так называемой расчетной схемой. Расчетной схемой называют идеализированную, упрощенную схему действительного сооружения, в которой отражаются только его основные свойства. В расчетную схему сооружений вводят идеализированные опоры.
Выбор расчетной схемы основывают на изучении действительной конструкции, вида узловых соединений в сооружении, особенностей работы данного материала, конструкции опор и фундамента и т. д. Так, при расчете стальных конструкций в соответствии с приближением свойств металла к идеализированной схеме вполне возможно
8
применение уточненных расчетных схем. При расчете же деревянных конструкций в связи с отклонением свойств материала от схемы упругого изотропного тела естественно использование приближенных расчетных схем. Например, расчет многопролетных деревянных конструкций можно выполнять, принимая шарнирные соединения ригелей со стойками и подкосами. Применение уточненной расчетной схемы должно быть логически увязано с необходимой точностью расчета, степень которой определяется свойствами материала, эксплуатационными требованиями и др.
Переход к расчетной схеме является необходимой идеализацией реального сооружения. По мере накопления новых результатов испытаний сооружений совершается переход от одной расчетной схемы к другой, более точно отражающей реальное поведение материала.
Основные элементы плоских сооружений — стержни (или брусья) и пластинки. Стержнем называют элемент, размеры поперечного сечения которого малы по сравнению с длиной. Фермы и рамы представляют собой сочленения стержней. Ферма при узловом действии нагрузки рассматривается в расчетной схеме как система стержней, связанных идеальными шарнирами. Под идеальным шарниром понимают узловое соединение стержней, в котором не возникает сил трения и усилия на стержни передаются строго через центр шарнира. Пластинкой называют элемент, один размер (толщина) которого мал по сравнению с двумя другими (шириной и длиной). Следует заметить, что пластинка может быть и основной несущей конструкцией. Пластинку с криволинейным очертанием срединной поверхности принято называть оболочкой.
§ 3. ОПОРНЫЕ УСТРОЙСТВА. ВИДЫ НАГРУЗОК
Для прикрепления сооружения к основанию служат опоры, обеспечивающие неподвижность опорных точек конструкции. Рассмотрим основные типы опор плоских сооружений, для которых применяют следующие опорные устройства:
1) шарнирно подвижную опору; 2) шарнирно неподвижную опору; 3) защемляющую неподвижную опору.
На рис. 1 изображена простейшая схема устройства шарнирно подвижной опоры (а) и условное изображение этой опоры (б). Подвижная опора допускает вращение вокруг оси, проходящей через центр шарнира а опоры, и поступательное перемещение по линии аЬ. Шарниры а я с предполагаются идеальными, вследствие чего реакция со стороны опоры проходит по линии ас. В шарнирно подвижной опоре возникает реакция, нормальная к направлению перемещения катков.
о)
9
Шарнирно неподвижная опора (рис. 2, а) обеспечивает вращение верхнего балансира А вокруг определенной оси, проходящей через центр шарнира а, и не допускает линейных перемещений. В условной схеме она заменяется двумя опорными стержнями. В неподвижной опоре возникают две составляющие реакции Ка и На (рис. 2, б). Абсолютное защемление (рис. 3, а) не допускает каких-либо линейных перемещений и поворота (оно эквивалентно трем опорным стержням;
рис. 3, б). В защемлении возникают две составляющие реакции На, На и реактивный момент Ма.
Нагрузки можно разделять по характеру действия во времени, по способу их приложения, в зависимости от назначения при эксплуатации самого сооружения и т. д.
По характеру действия во времени различают статические и динамические нагрузки. Статическую нагрузку принимают независящей от времени, она передается на сооружение спокойно, плавно, без толчков и вибраций, ее считают медленно возрастающей от нуля до конечного значения. Динамическая нагрузка быстро меняется со временем; при расчете сооружения на динамическую нагрузку необходимо вводить силы инерции системы, возникающие при колебаниях, и динамические.
эффекты действия нагрузки, о) р а По способу приложения различают сосредоточенный груз и сплошную нагрузку, распределенную по площади или по линии.
Сосредоточенный груз — нагрузка в виде силы, приложенной в одной точке.
Сплошная нагрузка — распределенная непрерывно поданной площади или по данной линии. Линейная сплошная нагрузка, распределенная по длине, измеряется интенсивностью ее, т. е. нагрузкой, приходящейся на единицу длины в данной точке. Поверхностная нагрузка измеряется нагрузкой, действующей на единицу поверхности в данной точке. Интенсивность линейно распределенной нагрузки измеряется в килоньютонах на метр погонной длины, а интенсивность поверхностно распределенной нагрузки — в килоньютонах на квадратный метр.
В зависимости от назначения различают постоянную, временную и подвижную нагрузки. Постоянная нагрузка — нагрузка,
Я МгХ:
К г
Рис. 3
Рис. 2
10
которая постоянно действует на сооружение (собственный вес, усилия предварительного натяжения и т. п.). Времён пая нагрузка действует на сооружение в отдельные промежутки времени, в другие же периоды она может отсутствовать (давление ветра, снега; полезная нагрузка, воспринимаемая сооружением). Подвижная нагрузка — та, которая занимает различное положение на сооружении (поезд, автомобиль, толпа людей). По действующим нормативным документам различают основные сочетания нагрузок (состоят из постоянных и временных), дополнительные сочетания (включают и кратковременные нагрузки) и особые сочетания нагрузок (сейсмические, аварийные и др.).
§ 4. КЛАССИФИКАЦИЯ СООРУЖЕНИЙ И ИХ РАСЧЕТНЫХ СХЕМ.
ОСНОВНЫЕ ПОЛОЖЕНИЯ
Виды сооружений
Ниже рассматриваются лишь идеализированные расчетные схемы сооружений. Различают сооружения плоские и пространственные, которые подразделяют по виду соединений в узлах; по геометрическому типу элементов, составляющих сооружение; по особенностям работы сооружения и т. д.
ф ф
Рис. 4
Все сооружения, в действительности пространственные, имеют три измерения, однако в ряде случаев заменяют пространственное сооружение плоскими сооружениями, представляющими данное пространственное. Плоским сооружением называют систему, осевые линии всех элементов которой расположены в одной плоскости.
По геометрическому типу элементов сооружения могут быть стержневыми, пластинчатыми и массивными. Сооружения, составленные из стержней (два основных размера которых малы по сравнению с третьим), называют стержневыми (рис. 4, а). Сооружения, представляющие собой систему пластинок, будем называть пластинча¬
11
тыми (пластинка — элемент, два основных размера которого значительны по сравнению с третьим; рис. 4, б). Сооружения, три основных размера которых одного и того же порядка, называют массивными (например, подпорная стенка; рис. 4, в).
По виду соединений в узлах сооружения делятся на системы с шарнирными и с жесткими узлами. В качестве примера первой системы можно указать ферму с шарнирными узлами, в качестве примера второй — раму с жесткими узлами.
По особенностям работы сооружений различают балочные, рамные, арочные и висячие системы. Балка представляет собой прямолинейный брус, работающий на изгиб. Балка при наличии обычной горизонтально подвижной опоры является безраспорной системой, в которой вертикальная нагрузка вызывает только вертикальные опорные реакции. В распорной системе с криволинейным или многоугольным очертанием оси (арка, рама) вертикальная нагрузка, помимо вертикальных, вызывает и горизонтальные составляющие реакций — распоры. При наличии идеально шарнирного соединения стержней во всех узлах систему называют шарнирно стержневой фермой, или просто фермой. Все стержни фермы при узловой нагрузке работают только на осевое действие сил.
Рамой называют стержневую, систему преимущественно с жесткими соединениями в узлах; стержни рамы работают одновременно на изгиб и осевое действие сил, причем изгибная деформация в раме преобладает.
Аркой называют криволинейный брус, закрепленный неподвижно двумя концами. Арка со сплошной стенкой работает на осевое сжатие и изгиб.
Часто применяют висячие системы, в которых цепи или кабели поддерживают балочную часть. В идеальной гибкой цепи или гибком кабеле возникает только растяжение.
Сооружения можно разделить на статически определим ы е, усилия в которых определяются только с помощью одних уравнений статики, и статически неопределимые, расчет которых производится с дополнительным использованием уравнений связности деформаций. Применяются также методы расчета сооружений по допускаемым напряжениям и по предельным состояниям, методы расчета на основе точной и приближенной теорий и т. д.
Основные положения строительной механики
Основные исходные положения строительной механики при решении задач упругого расчета сооружений те же, что и сопротивления материалов:
1. Предположение об идеальной упругости и непрерывности материала, из которого состоит сооружение. Однако в специальном разделе курса рассматриваются методы расчета сооружений с учетом развивающихся и пластических деформаций. В настоящее время ряд конструкций рассчитывается по методу предельных состояний, в част¬
12
ности, расчет железобетонных конструкций ведется у нас с 1939 г. по стадии разрушения (использование криволинейной эпюры сжимающих напряжений при наличии пластических деформаций в области сжатого бетона).
2. Применение линейной связи между напряжением и деформацией (закон Гука). Отметим, что существуют тела, поведение которых в известных границах можно считать нелинейно упругим, т. е. в которых остаточных деформаций не возникает, но зависимость между напряжением и деформацией нелинейна.
3. Применение принципа независимости действия, согласно которому результат действия систем сил равен сумме результатов действия отдельных сил. Этот принцип применим только к относительно жестким сооружениям и использование его при расчете существенно гибких систем в области больших деформаций недопустимо.
ГЛАВА 2. АНАЛИЗ НЕИЗМЕНЯЕМОСТИ ПЛОСКИХ СООРУЖЕНИЙ
§ 5. ПРОСТЕЙШИЕ ПРИЗНАКИ НЕИЗМЕНЯЕМОСТИ ШАРНИРНО СТЕРЖНЕВЫХ СИСТЕМ
Системы, геометрически изменяемые и неизменяемые
Сооружение должно быть геометрически неизменяем ы м, т. е. постоянно сохранять ту геометрическую форму, которая ему задана при возведении. Изменяемые системы недопустимы, так
как они резко меняют форму, получая произвольные перемещения без изменения длин стержней. Неизменяемые же системы могут менять форму только в результате деформаций стержней. Примером простейшей неизменяемой системы является шарнирно стержневой треугольник (рис. 5, а), по заданной длине трех стержней которого можно построить единственный шарнирный треугольник. Простейшей изменяемой системой является шарнирный четырехугольник (рис. 5, б), в котором перемещения узлов 1 и 2 могут быть конечными без изменения длин стержней системы.
-у
Рис. 5
13
При расчете сооружений нередко используют основную схему в виде так называемой кинематической цепи — изменяемой системы. Важно знать число степеней свободы кинематической цепи и уметь перейти от нее к неизменяемой системе путем введения соответствующих связей. Степенью свободы системы называется количество независимых геометрических перемещений, определяющих положение системы (например, линейных перемещений узлов). Для шарнирного четырехугольника по рис. 5, б имеем одну степень свободы (достаточно поставить раскос 02, чтобы обратить систему в неизменяемую).
Формула для определения числа связей плоской стержневой системы
Рассмотрим плоские шарнирно стержневые системы стержней или дисков. Пусть задана шарнирно стержневая система по рис. 6, в е ь с которой шесть шарнирных уз¬
лов связаны стержнями аЬ, ас, ай,. Установим соотношение между числом узлов системы к и числом стержней
5. Под к понимаем число узлов без опорных, а под 5 — число стержней вместе с опорными. При отсутствии всех 5 стержней система будет обладать 2к степенями свободы, так как каждый узел имеет на плоскости две степени свободы. При наличии связей числом 5 2к система может быть неподвижна, если стержни расположены целесообразно. Условие неизменяемости системы будет
з 2к. (2.1)
Рис. 7
Для системы по рис. 6: 5 12, к 6.
Мы получили аналитический признак геометрической неизменяемости, согласно которому число связей между узлами равно числу возможных степеней свободы узлов. Если 5 с 2к, система изменяема; она не имеет необходимого количества связей. Если 5 2к, система может быть неизменяема; она обладает достаточным количеством связей для создания геометрически неизменяемой системы. Если же связи расположены нецелесообразно, система может оказаться изменяемой. Итак, соотношение 5 2к является необходимым, но недостаточным условием геометрической неизменяемости. То же можно сказать и относительно соотношения: 5 2к.
В качестве примера приведем ферму, в первой панели которой имеется два раскоса, а во втброй раскоса нет (рис. 7). Общее число стерж¬
14
ней и узлов в данном случае 5 12; к 6, т. е. 5 2к. Однако система изменяема, так как она сводится к шарнирному четырехугольнику (имеем диск аЬе[, который заменяем одним стержнем).
Формула для определения числа степеней свободы кинематической цепи. Перемещения цепи
Дадим формулу для подсчета числа степеней свободы любой плоской кинематической цепи, которая может быть получена непосредственно из условия (2.1). Рассматривается случай, когда связей недо-
Рис. 8
статочно для создания неизменяемой системы, т. е. когда 5 2к. Следовательно, число степеней свободы Ссв системы будет
Ссв 26-5. (2.2)
Так, для цепи стержней по рис. 8, а имеем
Ссв 24 —5 3.
Для обращения системы в неизменяемую (рис. 8, б) достаточно ввести три дополнительных опорных стержня а, Ь и с в узлах 1, 2, 3. На рис. 8, а представлена картина возможных перемещений цепи, определяемая тремя независимыми перемещениями узлов 1, 2, 3: Д2, Л2 и А3. Под независимыми перемещениями понимают перемещения тех узлов цепи, посредством которых определяется положение всех остальных ее узлов. Число независимых перемещений совпадает
15
с числом степеней свободы цепи. Отложив вектор Дх 11р произвольной величины перпендикулярно к 01, проводим линию 12", параллельную 12; далее откладываем вектор Д2 2"2 также произвольной величины, затем проводим отрезок 23", равный и параллельный отрезку 23 и откладываем вектор А3 ЗЗ" снова произвольной величины. Точка 4 находится на пересечении перпендикуляров к отрезкам 34" и 45. Перемещение узла 4
Д4 Й.
Простейшие геометрические признаки неизменяемости систем
Как мы уже указывали, аналитический признак 8 2к является недостаточным для окончательного суждения о неизменяемости си¬
стемы; поэтому необходимо провести соответствующий анализ её геометрической структуры. Наиболее целесообразным и общим является
геометрический метод исследования неизменяемости, основанный на использовании свойств геометрических фигур.
Первый признак геометрической неизменяемости: ферма неизменяема, если она составлена из шарнирных треугольников (рис. 9), поскольку треугольник— неизменяемая геометрическая фигура. В данном случае к исходному треугольнику аЬс каждый последующий узел 1, 2, 3, 4 и т. д. прикрепляется двумя стержнями, вследствие чего создается новый треугольник. Прикрепление узлак узлам Ь и с двумя стержнями 1Ь и 1с, не лежащими на одной прямой, равносильно созданию шарнирно стержневого неизменяемого треугольника.
Более общий признак геометрической неизменяемости ферм следующий: ферма неизменяема, если каждый последующией узел прикрепляется к двум предшествующим узлам двумя стержнями, осевые линии которых не лежат на одной прямой. Такой структурой обладают
16
все простейшие фермы, представляющие собой совокупность диад (диада — пара наклонных стержней, связанных общим узлом).
На рис. 10 изображена консольная ферма с ромбической решеткой, к узлам а, Ь, и с которой двумя стержнями каждый прикрепляются узлы 1, 2, 3, 4, 5, 6 и т д.
На рис. 11 приведен ряд ферм, образованных по указанному общему правилу. Выделен основной треугольник — геометрический базис, к которому присоединяются все остальные узлы фермы; последовательность их прикрепления отмечена цифрами. На рис. И, а показана полураскосная ферма, в которой каждый узел
1, 2, 3, 4, 5 и т. д. последовательно прикреплен к основному базису — треугольнику аЬс и к последующим треугольникам. На рис. 11, б дана простейшая схема висячей системы аЬс с балкой 1—2—3; каждый узел последовательно прикреплен двумя стержнями: узел а — к узлам Ь и с;
узел 1 — к узлам а и 2;
узел 3 — к узлам 1 и 4.
На рис. 11, в приведена вантовая ферма, стержни которой составлены из вант (работающих только на растяжение); узел а прикреплен к узлам Ь и с двумя стержнями; к узлам а и Ь последовательно прикрепляются узлы, 2иЗ, а к узлам а и с — узлы 4, 5 и 6 внизу расположена проезжая часть 0—7—14.
Указанные два правила создания геометрически неизменяемых шарнирно стержневых систем, однако, не применимы для анализа геометрической неизменяемости любых ферм (см. § 9, где дан общий метод исследования неизменяемости).
Мгновенно изменяемая система
Выше было установлено, что при прикреплении данного узла двумя стержнями осевые линии стержней не должны располагаться на одной прямой, иначе говоря, не должны находиться на одной прямой три шарнира. Случай прикрепления узла двумя стержнями аЬ и ас., лежащими на одной прямой (рис. 12, а), дает мгновенно изменяемую
Рис. И
17
систему: точка а вследствие фиксации ее положения касающимися цугами окружностей радиусов аЬ и ас может получить бесконечно малое смещение. Конечное же смещение этой точки возможно лишь в результате удлинения стержней; при этом система обращается в неизме-
а)
яь
а ----ч;- —
няемую, так как три шарнира а, Ь и с уже не будут лежать на одной прямой.
М гновенно изменяемой называют систему, которая оказывается изменяемой лишь в первый момент приложения соответствующей нагрузки.
Дадим статическую характеристику мгновенно изменяемой системы для данного частного случая. Предположим, что стержни аЪ и ас не лежат на одной прямой (рис. 12, б) определим усилия X для случая симметричного расположения стержней. Проектируя все силы, приложенные к узлу а, на вертикальную ось, находим
2Х зт ос — Р 0,
откуда
Х--
2 81П а
(2.3)
При стремлении а к нулю усилие X стремится к бесконечности. При малом значении а усилие X получает конечное очень большое значение. Когда же точка а незначительно отклоняется от прямой Ьс, в стержнях аЪ и ас возникают усилия, вызывающие если не разрушение, то во всяком случае значительные деформации, что сопровождается резким опасным смещением точки а.
§ 6. АНАЛИЗ ГЕОМЕТРИЧЕСКОЙ СТРУКТУРЫ СООРУЖЕНИЙ РАСЧЛЕНЕНИЕМ НА ДИСКИ
Сочленение двух дисков
Система может представлять собой сочленение отдельных неизменяемых частей (дисков), связанных между собой различно расположенными стержнями. Для анализа неизменяемости таких систем необходимо:
1) выделить неизменяемые части системы — диски;
2) провести анализ системы соединения дисков между собой.
Ниже остановимся на правилах соединения дисков, начиная с простейшей системы двух дисков:
18
1. Сочленение двух дисков образует неизменяемую систему, если диски связаны между собой тремя стержнями, осевые линии которых не пересекаются в одной точке или не параллельны между собой.
2. Соединение двух дисков составляет неизменяемую систему, если диски связаны шарниром и стержнем, причем центр шарнира не лежит на осевой линии стержня.
Схема соединения по первому признаку приведена на рис. 13. При отсутствии стержня 3 возможно вращение дисков относительно точки а — мгновенного центра вращения; при наличии третьего стержня, осевая линия которого не проходит через точку а, система неизменяема. Однако если три стержня пересекаются в одной точке
(рис. 14), система будет мгновенно изменяема, так как возможно бесконечно малое смещение диска путем вращения его вокруг мгновенного центра вращения а. Рассмотрим этот частный случай.
Мгновенную изменяемость системы по рис. 14 можно показать и с помощью статического метода. Если к диску I приложена сила Р, линия действия которой не проходит через точку а, то система не может находиться в равновесии. Беря сумму моментов всех сил, приложенных к диску I, относительно точки а, получим
Если предположить, что осевая линия опорного стержня 3 образует небольшой эксцентриситет А относительно точки а пересечения стержней и 2, то из условия 2Л1а 0 найдем
Л
Рис. 13
Рис. 14
ЪМа Риф 0.
Ри—Яъ Д 0,
откуда
(2.4)
При Д 0, оо; при Д 0иР 0по формуле (2.4) получим
г» 0
т. е. в мгновенно изменяемой системе при отсутствии нагрузки усилия получают неопределенные значения, при наличии конечной нагрузки— бесконечно большие значения. В частном случае параллельности трех опорных стержней (рис. 15) при действии любой нагрузки получается
изменяемая система, так как вертикальными реакциями невозможно уравновесить горизонтальную силу Рх.
На рис. 16 приведен ряд ферм, представляющих собой сочленение двух дисков, связанных тремя стержнями.
На рис. 16, а два диска аЬс и йе связаны между собой тремя стержнями 1, 2 и 3. На рис. 16, б представлена простейшая схема фермы Шухова, в которой два треугольника аЬс и с1е[ взаимно соединены тремя стержнями аД, еЬ и с. На рис. 16, в малый треугольник соединен с большим треугольником аЬс тремя стержнями еЬ, ас1 и с. На рис. 16, г дана простейшая трехпоясная вантовая ферма Рабиновича, все элементы которой работают на растяжение. Ферма аЬ представляет собой два диска и II, связанные между собой тремя стержнями 1, 2 и 5, не пересекающимися в одной точке.
Многие стержневые системы представляют собой сочленение двух дисков шарниром и стержнем (рис. 17). Очевидно, треугольник 1а2 можно отнести к нижнему диску II, к которому узел а прикреплен двумя стержнями а1 и а2. В результате получается соединение двух дисков шарниром а и стержнем Ъс, образующим так называемый фиктивный треугольник аЬс. При расположении шарнира а на осевой линии стержня Ьс система становится мгновенно изменяемой. На при¬
20
мере рис. 17 иллюстрировано применение эффективного при исследовании неизменяемости способа замены связей: для перехода к фиктивному треугольнику аЬс диск заменяем одним стержнем аЬ, диск а 2с— стержнем ас.
На рис. 18 приведены примеры ферм, представляющих собой соединение двух дисков шарниром и стержнем. На рис. 18, а изображена простейшая статически определимая комбинированная система и виде сочетания раскосной фермы с параллельными поясами и гибкой арки (верхний третий пояс). Система сводится к фиктивному треугольнику аЬс. На рис. 18, б показана шарнирно стержневая система, образующая шарнирный пятиугольник; диск прикреплен к земле шарниром а и стержнем Ьс, диск же II к неизменяемой левой ча-
Рис. 17
сти и к земле — тремя стержнями 1, 2 и ?, осевые линии которых не пересекаются в одной точке. Нередко применяются фермы, представляющие собой последовательное соединение двух дисков.
Образование многопролетных статически определимых балок
Стремление перекрыть большие пролеты, естественно, вызвало применение многопролетных консольно-подвесных балок, представляющих собой сочленение ряда двухопорных консольных балок с разрезными, так называемыми подвесными балками.
Можно предложить ряд целесообразных схем консольно-подвесных балок (рис. 19). При наличии шарнирных опор для д-пролетной балки, чтобы превратить ее в статически определимую, необходимо дать (п — 1) промежуточных шарниров. Для каждого шарнира можем написать условие, что момент левых сил равен нулю. Учитывая эти условия, для всех введенных шарниров составляют (п — 1) дополнительных уравнений. Так, для трехпролетных балок по рис. 19, а,
б, в, вводим два промежуточных шарнира с и Л, а для трехпролетной балки (рис. 19, г), имеющей одну заделку, — три промежуточных
шарнира. Заметим, что вводить промежуточные шарниры нужно в полном соответствии с требованиями геометрической неизменяемости. В связи с этим важно правильно разместить промежуточные шарниры, введение которых обращает первоначальную неразрезанную балку в статически определимую многопролетную. В любой схеме такой балки диск должен быть последовательно прикреплен шарниром и стержнем или тремя стержнями.
Рассмотрим неизменяемость четырех видов многопролетных консольно-подвесных балок по рис. 19. В первой схеме (рис. 19, а) главная поддерживающая балка ей (диск I) неизменяемо прикреплена к
а) е Л с I Ш Г
ф
1 1
Ь с
ф
ф
Рис. 19
земле шарнирно неподвижной опорой а и шарнирно подвижной опорой Ь; к диску присоединены диски II и III, каждый шарниром и стержнем. Во второй схеме (рис. 19, б) диск неподвижно связан с землей тремя опорными стержнями; диск II (третий пролет) прикреплен непосредственно к земле двумя стержнями е и и к неподвижному диску — третьим стержнем сЛ — система неизменяемая. Третья схема (рис. 19, в) характерна последовательным сочленением одноконсольных балок: к диску I, прикрепленному тремя опорными стержнями в точках а и Ь, следующий диск II прикреплен шарниром с и стержнем е; новый диск III присоединен шарниром Л и стержнем. В четвертой схеме (рис. 19, г) исходной неизменяемой частью является балка аЪ, защемленная левым концом; диск II опирается шарниром Ь и стержнем с; диск III прикреплен к диску II и к земле тремя опорными стержнями — система неизменяемая.
22
О фиктивном шарнире и стержне
_-о
Рис. 20
Отметим, что незагруженный диск, шарнирно неподвижно присоединенный концами к остальной части конструкции, можно заменить стержнем, расположенным по оси диска, соединяющим концевые шарниры. Этот стержень, заменяющий диск, называют заменяющим (фиктивным). Анализ неизменяемости и расчет ряда ферм при введении фиктивных стержней упрощается. Система по рис. 20 неизменяема: два диска I и II соединены двумя реальными стержнями 1 и 2 и третьим фиктивным стержнем 3, эквивалентным диску. Соединение дисков I и II двумя стержнями 1 и 2 можно заменить фиктивным шарниром с. Рассмотрим подробнее эту систему в виде двух дисков
и II, связанных между собой тремя стержнями 1, 2, 3, причем стержни 1 и 2 не соединены в точке пересечения их осевых линий (рис. 21).
Точка с в статическом и кинематическом отношениях играет ту же роль, что и центр шарнирно неподвижной связи; равнодействующая 7?пр усилий и 52 в стержнях 1 и 2, обнаруженных
разрезом тт, должна проходить через точку их пересечения с, аналогично реальному шарниру в этой точке; перемещение диска II относительно диска при наличии связи их только двумя стержнями и 2 совершается как вращение вокруг точки с. Можно сформулировать следующее положение: связь двух дисков двумя стержнями, с шарнирным прикреплением их концов к дискам, эквивалентна соединению их шарниром с центром в точке пересечения осевых линий стержней. Точку с в дальнейшем будем называть фиктивным шарниром. Схема системы по рис. 21, таким образом, сводится к шарнирному треугольнику аЬс, стороны которого соединяют реальные шарниры а, Ь и фиктивный шарнир с. В общем случае фиктивный стержень есть элемент, соединяющий фиктивные шарниры.
Используя принцип замены связей введением фиктивных шарниров и стержней, можно упростить анализ неизменяемости большого класса сложных ферм.
23
§ 7. СИСТЕМЫ В ВИДЕ СОЧЛЕНЕНИЯ ТРЕХ ДИСКОВ
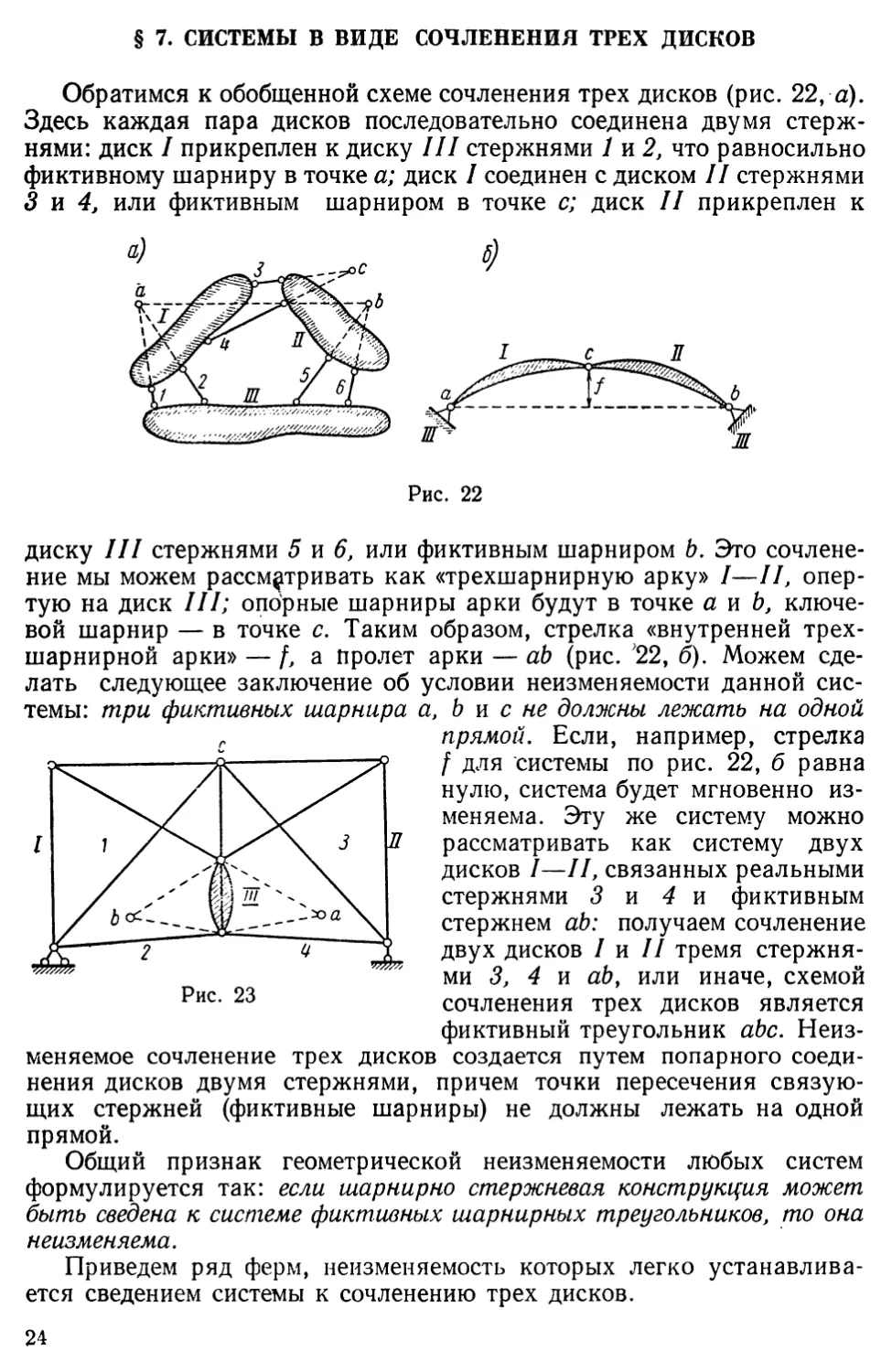
Обратимся к обобщенной схеме сочленения трех дисков (рис. 22, а). Здесь каждая пара дисков последовательно соединена двумя стержнями: диск I прикреплен к диску III стержнями 1 и 2, что равносильно фиктивному шарниру в точке а.; диск I соединен с диском II стержнями
3 и 4, или фиктивным шарниром в точке с; диск II прикреплен к
Рис. 22
диску III стержнями 5 и 6, или фиктивным шарниром Ь. Это сочленение мы можем рассматривать как «трехшарнирную арку» —II, опертую на диск III; опорные шарниры арки будут в точке а и Ь, ключевой шарнир — в точке с. Таким образом, стрелка «внутренней трехшарнирной арки» — Да пролет арки — аЬ (рис. 22, б). Можем сделать следующее заключение об условии неизменяемости данной системы: три фиктивных шарнира а, Ъ и с не должны лежать на одной
прямой. Если, например, стрелка для системы по рис. 22, б равна нулю, система будет мгновенно изменяема. Эту же систему можно рассматривать как систему двух дисков —II, связанных реальными стержнями «3 и 4 и фиктивным стержнем аЬ: получаем сочленение двух дисков I и II тремя стержнями 3, 4 и аЬ, или иначе, схемой сочленения трех дисков является фиктивный треугольник аЬс. Неизменяемое сочленение трех дисков создается путем попарного соединения дисков двумя стержнями, причем точки пересечения связующих стержней (фиктивные шарниры) не должны лежать на одной прямой.
Общий признак геометрической неизменяемости любых систем формулируется так: если шарнирно стержневая конструкция может быть сведена к системе фиктивных шарнирных треугольников, то она неизменяема.
Приведем ряд ферм, неизменяемость которых легко устанавливается сведением системы к сочленению трех дисков.
г
24
Ферма по рис. 23 встречается как ячейка многорешетчатых ферм; средний вертикальный стержень принимаем за диск ; диски и II соединены между собой реальным шарниром с, диски I и III — фиктивным шарниром а, а диски II и III — фиктивным шарниром Ь.Три шарнира а, Ь и с образуют шарнирный треугольник, следовательно, система неизменяема.
На рис. 24 показана мгновенно изменяемая система: диски и сочленены реальным шарниром с, диск
I соединен с диском III стержнями 1 и 2 — фиктивный шарнир а; диск II связан с диском стержнями 3 и 4, что равносильно фиктивному шарниру Ь, но все три шарнира а, Ь и с лежат на одной прямой.
На рис. 25 показана трехопорная ферма со средним опорным шарнирным четырехугольником. Такая ферма легко может быть сведена к трехдисковой по схеме рис. 22, если применить способ «расщепления» треугольного диска 5——4 и ввести опорный диск III. В качестве дисков самой фермы вводят стержень 1—2 (диск ) и треугольник 4—3—Ь (диск II). Диски I и II соединены стержнями 1—4 и 2—3 — фиктивный ключевой шарнир с. Диск I опирается на диск III стержнями 1—5 и 2—6 — фиктивный опорный шарнир а. Диск II опирается на землю стержнями 4—5 и Ь—7; эти связи можно заменить неподвиж¬
25
ным шарниром в точке Ъ. Три шарнира а, Ъ и с не лежат на одной прямой — система неизменяема.
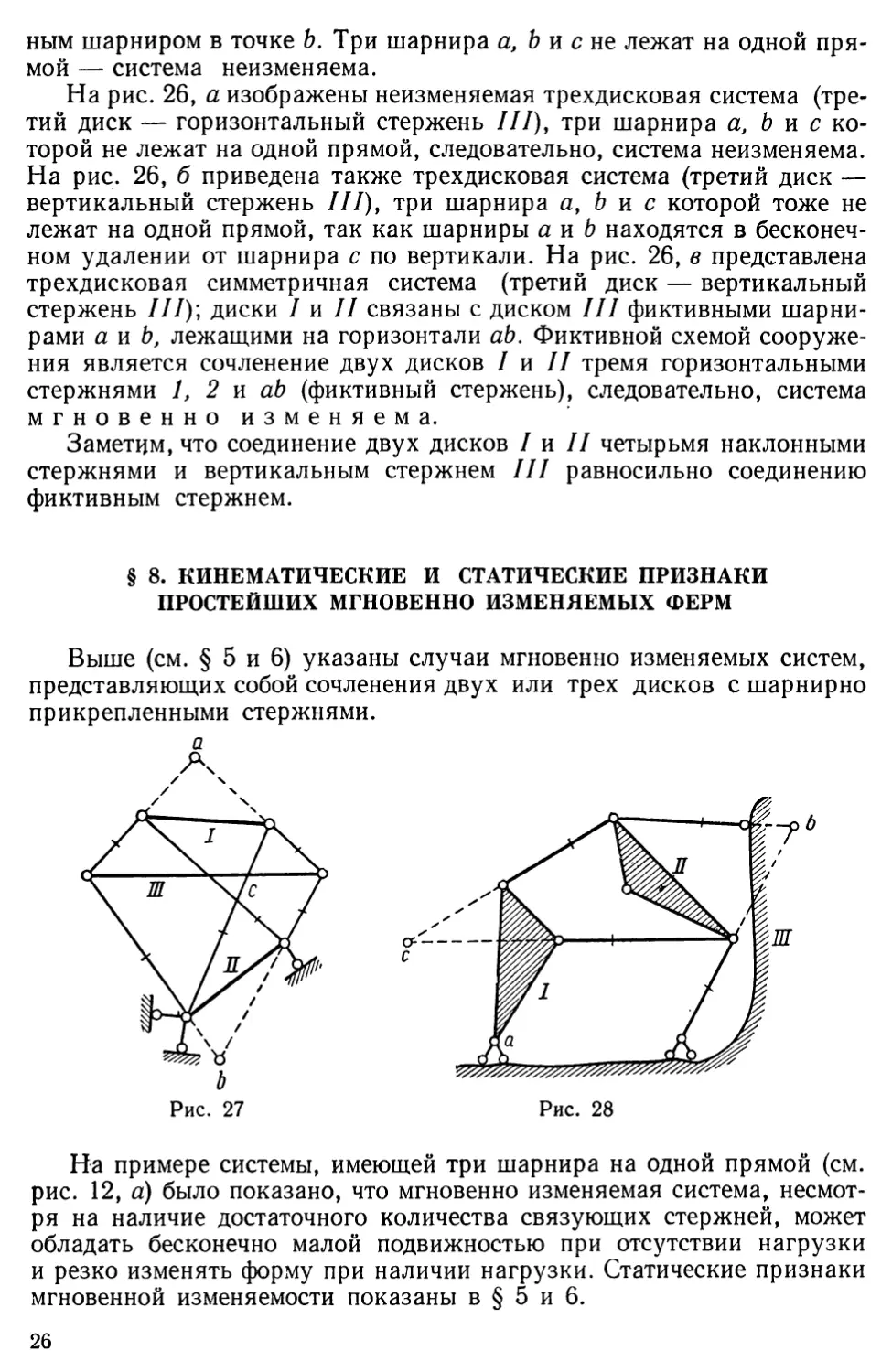
На рис. 26, а изображены неизменяемая трехдисковая система (третий диск — горизонтальный стержень III), три шарнира а, Ь и с которой не лежат на одной прямой, следовательно, система неизменяема. На рис. 26, б приведена также трехдисковая система (третий диск — вертикальный стержень ), три шарнира а, Ь и с которой тоже не лежат на одной прямой, так как шарниры а и Ь находятся в бесконечном удалении от шарнира с по вертикали. На рис. 26, в представлена трехдисковая симметричная система (третий диск — вертикальный стержень ); диски I и II связаны с диском III фиктивными шарнирами а и Ь, лежащими на горизонтали аЬ. Фиктивной схемой сооружения является сочленение двух дисков и тремя горизонтальными стержнями 1, 2 и аЬ (фиктивный стержень), следовательно, система мгновенно изменяема.
Заметим, что соединение двух дисков I и II четырьмя наклонными стержнями и вертикальным стержнем III равносильно соединению фиктивным стержнем.
§ 8. КИНЕМАТИЧЕСКИЕ И СТАТИЧЕСКИЕ ПРИЗНАКИ ПРОСТЕЙШИХ МГНОВЕННО ИЗМЕНЯЕМЫХ ФЕРМ
Выше (см. § 5 и 6) указаны случаи мгновенно изменяемых систем, представляющих собой сочленения двух или трех дисков с шарнирно прикрепленными стержнями.
На примере системы, имеющей три шарнира на одной прямой (см. рис. 12, а) было показано, что мгновенно изменяемая система, несмотря на наличие достаточного количества связующих стержней, может обладать бесконечно малой подвижностью при отсутствии нагрузки и резко изменять форму при наличии нагрузки. Статические признаки мгновенной изменяемости показаны в § 5 и 6.
26
Для фермы, которую можно свести к сочленению двух или трех дисков, задача установления мгновенной изменяемости сводится к простому геометрическому анализу системы, к рассмотрению взаимного расположения фиктивных шарниров или связующих стержней. Так, на рис. 27 представлена ферма, структура которой сводится к сочленению трех дисков — стержней, II, III (показаны толстыми линиями); каждая пара дисков соединена двумя стержнями, что эквивалентно соединению фиктивными шарнирами а, Ь и с. В случае если три шарнира а, Ь и с лежат на одной прямой, ферма мгновенно изменяема (см. также рис. 22). Для фермы гго рис. 28 целесообразно включить в качестве третьего диска III землю; в этой ферме диски I и II соединены фиктивным шарниром с; диск II с диском III — шарниром Ь; диск с диском III — реальным шарниром а. В случае расположения трех шарниров а, и с на одной прямой получим мгновенно изменяемую систему. Если расстояние шарнира с от линии аЪ незначительно, ферма близка к мгновенно изменяемой системе и обладает большой деформируемостью. В дальнейшем все фермы, образованные последовательным прикреплением каждого узла двумя стержнями или представляющие сочленения двух и трех дисков, будем называть простейшими.
§ 9. АНАЛИТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ НЕИЗМЕНЯЕМОСТИ ФЕРМ
Общий аналитический метод
Общим методом исследования неизменяемости является анализ определителя системы уравнений для всех усилий в стержнях данной фермы при действии на нее произвольной нагрузки.
Применяя метод вырезания узлов, известный из теоретической механики, составляем для п неизвестных усилий в стержнях данной статически определимой фермы уравнения равновесия, которые будут содержать п неизвестных усилий Х1у Х2, Х3,., Хп и отражать влияние заданной нагрузки. Эти уравнения можно представить в следующей форме:
111 0122 211 а22%2
л11 ап22 • • • аппХп — Упру
а1пХп у1р,
2пХп Учр
(2.5)
где а,к — коэффициент при неизвестном усилии (косинус составляющего угла);
у1р — грузовой член, отражающий влияние заданной нагрузки (составляющая узловой нагрузки).
27
Систему уравнений (2.5) можно представить в виде матричного уравнения (см. Приложение):
АХ1Р.
(2.6)
Систему (2.5) рассматриваем как преобразование от вектора усилий в стержнях фермы X (Х1 Х2у Хп) к вектору внешних сил
Ур (У1Р Уър •••» УпР)- Обращенная матрица от матрицы А и будет матрицей влияния осевых усилий в ферме.
Решая систему уравнений (2.5), получаем по Крамеру следующее выражение для любого неизвестного Х:
где О — общий определитель из коэффициентов а1к системы уравнений (2.5);
О — определитель, отражающий влияние заданной нагрузки; он получается из общего определителя О заменой столбца коэффициентов Щь при искомом неизвестном столбцом свободных членов (—У(р).
Если по выражению (2.7) для всех усилий Хь получены конечные и определенные значения, приходим к заключению о неизменяемости фермы. При этом следует исключать такое загружение фермы, при котором получается мгновенно-равновесная система.
Если при Д 0 (на ферме имеется нагрузка) определитель О равен нулю, то для усилия Хь получаем бесконечное значение
Условие (2.8) является признаком изменяемости фермы. Если и числитель и знаменатель в формуле (2.7) равны нулю, для усилия Хг получаем неопределенное значение:
Итак, если для данной фермы определитель системы уравнений равен нулю, ферма изменяема. Указанный общий аналитический метод исследования слишком громоздкий, так как требует решения сложной системы алгебраических уравнений (раскрытия определителя ).
Способ нулевой нагрузки значительно проще предыдущего общего метода. Сущность способа нулевой нагрузки заключается в следующем.
Рассмотрим ферму, освобожденную от нагрузки. Если при действии конечной нагрузки в неизменяемой ферме все усилия Х должны иметь конечные значения, то при нулевой нагрузке усилия в статически оп¬
у Л
И ’
(2.7)
(2.8)
Способ нулевой нагрузки
28
ределимой ферме должны иметь нулевые значения. Такой ответ для всех усилий свидетельствует о неизменяемости данной фермы. Если же в каком-либо стержне или в группе стержней фермы усилия Х( оказываются неопределенными, система изменяема.
В качестве примера проанализируем ферму по рис. 29. В этой ферме нет ни одного узла, где сходятся два стержня. Докажем, что при отсутствии нагрузки усилия во всех стержнях фермы равны нулю.
Сначала выделим узел 1; проекта- Рис 2д
руя все усилия, действующие на этот
узел, на вертикаль, найдем, что усилие 512 0. Затем вырежем узел
2, в котором имеется два новых стержня и нет нагрузки, поэтому5240, 523 0. После этого перейдем к узлам 3 и 4 и, удовлетворяя тому же условию (в каждом узле два новых стержня, а усилие в среднем стержне равно нулю), получим:
•46 «5з6 0, 37
Теперь рассмотрим узел 5:
356 0, 557 0.
Выделяя узлы 7 и 6, находим:
517 0, 316 0.
Усилия во всех стержнях данной фермы при отсутствии нагрузки нулевые, следовательно, ферма неизменяема.
Значительно проще задача решается рассмотрением трех дисков (два треугольника и стержень 1—2).
Способ замены стержней
Способ замены стержней представляет большой теоретический интерес. Его следует применять к анализу сложных систем. Способ этот основан на следующем: 1) отбрасывают какой-либо стержень фермы (по рисг 30, а — стержень еЬ) и заменяют его другим стержнем аЬ так, чтобы получилась простая ферма; 2) воздействие отброшенного стержня представляют силами Х;Ъ) определяют усилие в заменяющем стержне от X 1 (рис. 30, б) и от нагрузки Р; если первое усилие обозначить Ызх, а второе Ызру то полное усилие в заменяющем стержне бу¬
дет
М3 МзхХ Мзр. (2.9)
Но это усилие должно быть равно нулю, так как заменяющего стержня в заданной ферме нет; следовательно,
Лд Л, 0, (2.10)
29
откуда
Х -5.
ал,.
(2.11)
Графическое определение Ызх показано на 30, в; как видно из рисунка, Ызх Ф 0, следовательно, система неизменяема.
Если Ызх 0, получим при Ызр Ф 0, X оо, что является признаком изменяемости системы.
Рис. 30
Недостатком этого способа является его громоздкость для сложных ферм, преобразование которых в простейшие возможно лишь введением нескольких заменяющих стержней; в этом случае приходится составлять систему уравнений с неизвестными усилиями X в заменяющих стержнях.
ГЛАВА 3. ТЕОРИЯ ЛИНИИ ВЛИЯНИЯ И ЕЕ ПРИМЕНЕНИЕ К СТАТИЧЕСКИ ОПРЕДЕЛИМЫМ БАЛКАМ
§ 10. ПОНЯТИЕ О лшдии влияния
Расчет сооружений на действие вертикальной подвижной нагрузки проводится с использованием линий влияния. Обычная подвижная и0 нагрузка для мостов — движу¬
щийся железнодорожный состав (рис. 31)— представляет собой систему постоянных вертикальных сосредоточенных сил с неизменным расстоянием между грузами а 1, а2, а3. и т. д. Эта нагрузка движется по пролетному строению моста с известной скоростью V, занимая различные положения на сооружении. Аналогичны автомобильные и гусеничные нагрузки.
Решая статическую задачу, пренебрегают динамическим действием нагрузки, т. е. исключают силы инерции, которые возбуждаются при
Г Я
аз
%
у К
5
ав
; к
д7
у V
а8
Ре
рэ
Рис. 31
30
вибрации самой балки и подвижного груза, и пренебрегают скоростью движения груза. Применяя принцип независимости, изучают сначала действие лишь одного груза Р1, после чего легко получить значение усилия от груза поезда Р ф 1, увеличивая усилие от единичного груза в Р раз.
Дадим определение линии влияния усилия: линией влияния какоголибо усилия для определенного сечения сооружения называется графическое изображение закона изменения данного усилия в этом сечении при перемещении груза Р 1 по длине сооружения.
Линия влияния (инфлюэнтная линия) представляет собой диаграмму, при построении которой функцией является изучаемая величина усилия, а независимой переменной — абсцисса груза Р 1. Каждая ордината линии влияния численно равна значению изучаемого усилия для положения груза Р 1 на сооружении над этой ординатой.
Сравним линии влияния моментов с эпюрами моментов. При построении линии влияния сечение неподвижно, положение груза меняется; при построении эпюры моментов меняется положение сечения, нагрузка неподвижна.
Для построения любой линии влияния усилия в данном месте сооружения применяем следующий статический метод: поставив груз в произвольное положение, определяемое переменной абсциссой х, и применяя условия равновесия, даем аналитическое выражение данного усилия; затем представляем это выражение в графической форме. Кроме статического метода построения линий влияния, для получения общего вида линии влияния применяют кинематический метод (§ 15). При расчете на подвижную нагрузку пластинок и других конструкций с двумя переменными координатами точки приложения груза строят так называемые поверхности влияния.
§ И. ЛИНИИ ВЛИЯНИЯ УСИЛИЙ В ПРОСТЫХ БАЛКАХ Балка на двух опорах
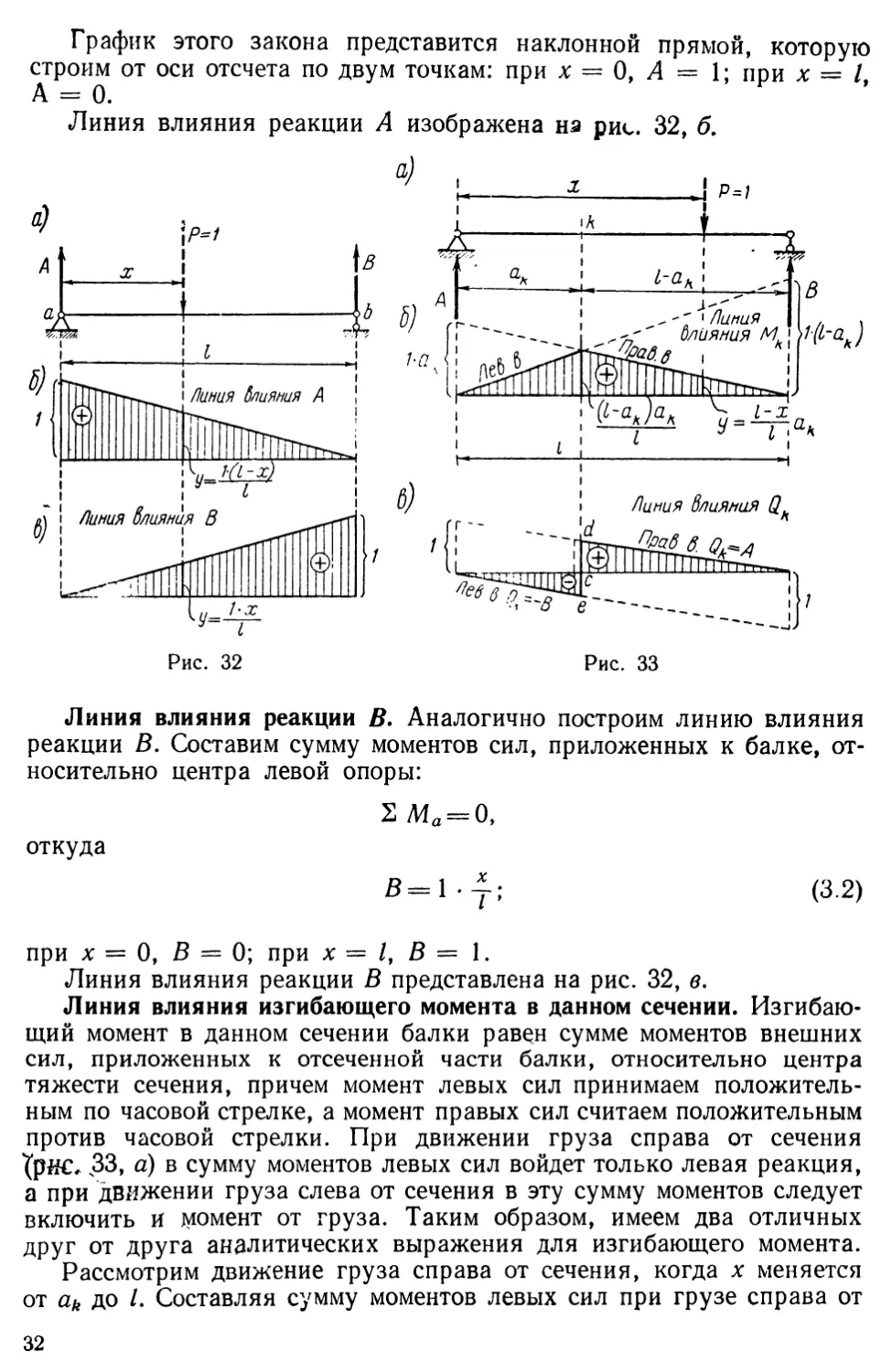
Линия влияния реакции А. В соответствии с указанным выше порядком, поставив груз Р 1 в произвольное положение (рис. 32, а), находим выражение для левой опорной реакции А в функции от х. Применяем условие равновесия в виде равенства нулю суммы моментов сил, приложенных к балке, относительно центра правой опоры:
ЪМЬ О,
или иначе, раскрывая левую часть уравнения,
А1 — Р(1 — х) О, откуда, принимая во внимание, что Р 1,
1 — х
График этого закона представится наклонной прямой, которую строим от оси отсчета по двум точкам: при х О, А 1; при х А 0.
Линия влияния реакции А изображена на рис. 32, б.
Рис. 32 Рис. 33
Линия влияния реакции В. Аналогично построим линию влияния реакции В. Составим сумму моментов сил, приложенных к балке, относительно центра левой опоры:
2 Ма 0,
откуда
В-; (3.2)
при 0, В 0; при х I, В 1.
Линия влияния реакции В представлена на рис. 32, в.
Линия влияния изгибающего момента в данном сечении. Изгибающий момент в данном сечении балки равн сумме моментов внешних сил, приложенных к отсеченной части балки, относительно центра тяжести сечения, причем момент левых сил принимаем положительным по часовой стрелке, а момент правых сил считаем положительным против часовой стрелки. При движении груза справа от сечения 33, а) в сумму моментов левых сил войдет только левая реакция, а при движении груза слева от сечения в эту сумму моментов следует включить и момент от груза. Таким образом, имеем два отличных друг от друга аналитических выражения для изгибающего момента.
Рассмотрим движение груза справа от сечения, когда л: меняется от ак до. Составляя сумму моментов левых сил при грузе справа от
32
сечения, получаем
Мк Аак 1 1--ак.
(3.3)
По этому уравнению строим правую ветвь линии влияния, умножая все ординаты линии влияния А на ак. Откладываем на левой опорной вертикали ординату, равную 1 -ак и соединяем верхнюю ее точку с нулевой точкой на правой опорной вертикали (рис. 33, б).
Рассмотрим теперь движение груза Р 1 слева от сечения, т. е. когда х меняется от 0 до ак. Определяем изгибающий момент Мк по правым силам. Принимая во внимание формулу (3.2), получаем:
Мк В(1-ак) ±-(1-ак), (3.4)
т. е. закон изменения изгибающего момента при Движении груза слева от сечения получается как закон правой реакции В, все значения которого увеличены в ( — ак) раз. Отложив на правой опорной вертикали ординату 1 • ( — ак) и соединив ее с нулевой точкой на левой опорной вертикали, построим левую прямую. Левая ветвь линии влияния момента пересекается с правой ветвью под сечением й.
Линия влияния поперечной силы (к. Аналогично строится линия влияния поперечной силы (алгебраической суммы сил, приложенных к отсеченнойчасти балки относительно сечения) с рассмотрением двух положений груза. Поперечную силу считаем положительной, если равнодействующая левых сил направлена вверх от оси балки или равнодействующая правых сил направлена вниз от оси. Если груз движется справа от сечения, сумма левых сил относительно сечения к составляет
3 А. (3.5)
Правая ветвь линии влияния ф получается по закону изменения левой опорной реакции А. Этот закон справедлив, очевидно, лишь для участка изменения х от ак до I (рис. 33, в). Если груз движется слева от сечения, то сумма левых сил, определяемая по правым силам, будет равна
0.к — В
т. е. левая ветвь линии влияния поперечной силы получается по закону изменения правой опорной реакции В, взятой с обратным знаком. Линию (—В) используем только на участке оси балки с абсциссами от 0 до ак.
Двухконсольная балка
Линии влияния опорных реакций. При произвольном положении груза, составляя уравнение равновесия по сумме моментов сил относительно центра правой опоры (рис. 34, а).
%МЬ О,
2 Н. К, Снитко
33
получаем
А1 — Р (I — х) 0у
откуда находим следующее выражение для реакции:
Л. (3.6)
Абсцисса груза х, отсчитываемая от центра левой опоры, меняется в пределах от 0 до ( с2) и от 0 до (—сг) (рис. 34, б).
Аналогично строится линия влияния реакции В (рис. 34, в).
1с2
I
Линия влияния момента И. При положении груза справа от сечения (рис. 35, а) изгибающий момент в сечении к междуопорной части будет
Л1к Аак
Правая ветвь следует закону изменения левой опорной реакции А с множителем ак (рис. 35, б). При положении груза слева от сечения сумму моментов левых сил в сечении к найдем по моменту правых сил:
Мк В(1—ак).
Левая ветвь получается по закону изменения правой опорной реакции с коэффициентом пропорциональности 1 •( — ак).
Линия влияния поперечной силы ()к. При положении груза справа от сечения поперечная сила в сечении междуопорной части как сумма левых сил будет
--А.
34
При движении груза слева от сечения сумма левых сил, полученная по правым силам, составит
Левая ветвь меняется по закону правой реакции, взятой с обратным знаком (рис. 35, в). Замечаем, что для консольных участков ветви линии влияния получаются простым продолжением основных ветвей.
Линии влияния для сечения консольной части.
Рассмотрим теперь построение линий влияния усилий в сечении къ взятом на левой консоли одноконсольной балки (рис. 36).
Линия влияния поперечной силы (2. При движении груза Р 1 справа от сечения кх как на консоли, так и в между опорной части, сумма левых сил равна нулю (слева сил нет):
О-
Правая ветвь линии влияния нулевая. При положении груза Р 1 слева от сечения кх сумма левых сил
(2ь-Р - 1.
Левая ветвь — горизонталь, расположенная от оси абсцисс на расстоянии, равном 1 (рис. 36, а).
Линия влияния момента Мкг При положении груза Р 1 справа от сечения кх
Мк 0.
Правая ветвь линии влияния нулевая. При движении груза Р 1 слева момент левых сил
Мкх — Рх — 1 • х.
Левая ветвь — наклонная прямая с ординатами (рис. 36, б): при х 0, Мкх 0; при х ак Мкх —1 -ак.
Линии влияния от движущейся пары. Пусть на балке на двух опорах движется пара, момент которой т 1. Построим линии влияния опорных реакций и усилий в сечении (рис. 37, а).
а) л
Линия
1 1 1
о
1-аК
В
1
блияния МК
] Линия блияния • г -
ч ГПТТтг» 1
1
1
1
1
1
цгв
1
Рис. 35
2
35
Линию влияния опорной реакции А получим, применяя условие равновесия
2МЬ О,
или откуда
так как т 1,
А1 -- ш О, А
т
Т
Л--)- -В.
Линия влияния левой опорной реакции представлена на рис. 37, б.
р
р1 1
Пинии влияния 0.
а)
Ф
1-а,
Лед в.
Прав. в.
Линия влияния М
Прав.
Рис. 36
Рассмотрим построение линии влияния поперечной силы. Положение движущейся пары не влияет на изменение С1к и при любом приложении пары пг 1 имеем
з,л_-.
Линия влияния С1к изображена на рис. 37, в.
При построении линии влияния изгибающего момента Мк существенное значение имеет положение движущейся пары т. Если пара движется справа от сечения,
Мк Аак - ак.
36
При движении пары слева от сечения по правым силам получаем МкВ(1-ан) (1-ал).
Линия влияния Мк представлена на рис. 37, г. Она имеет характерный скачок в величине ординаты под сечением к.
Отметим связь между ординатами линий влияния усилий от движущейся вертикальной силы и движущейся пары: производная от
1 Линия Влияния С-
1—гттгттТТПТПТ[Т.
в
ш
Линия
иггГГГППТ
влияния МК
ик
ц
зг
Рис. 37
Рис. 38
ординаты линии влияния какой-либо величины для движущейся силы Р 1 по независимой переменной равна ординате линии влияния этой же величины для движущейся пары с моментом, равным единице. Так, для реакции Ар от силы (см. рис. 32, б) было получено
Дифференцируя это выражение по х, получим ординату линии влияния А от пары с моментом, равным 1.
Трехопорная балка
Рассмотрим балку на трех подвижных опорах, две из которых направлены под углом 45° (рис. 38, а). Линию влияния реакции А получим, составляя сумму моментов относительно точки пересечения линий В и С
37
(рис. 38, б). Линию влияния реакции С найдем, составляя сумму моментов относительно точки й (рис. 38, в). По этим линиям влияния найдена линия влияния момента в сечении над промежуточной опорой (рис. 38, г).
§ 12. ОПРЕДЕЛЕНИЕ УСИЛИЙ ПО ЛИНИЯМ ВЛИЯНИЯ
Рассмотрим использование линий влияния усилий для отыскания величины их полных значений при действии на сооружение системы
вертикальных сил или распределенной вертикальной нагрузки. При этом изучаем линии влияния, построенные от вертикального груза Р, равного единице.
Пусть требуется определить по линии влияния полное значение изгибающего момента в сечении к при действии на балку системы сосредоточенных сил Ръ Р2,., Рпу занимающих определенное положение. В данном случае вместо любого усилия 5д. изучаем изгибающий момент в сечении Мк (рис. 39). Каждая ордината линии влияния 8к, обозначенная уи численно равна значению усилия 5Л, когда груз Р 1 находится на балке над этой ординатой.
При действии на сооружение одного груза Р усилие будет
(а)
При загружении балки системой сил Ръ Р2,., Р,., Рп полное усилие 8ь получим по принципу сложения действия, суммируя усилия, вызванные отдельно действующими силами:
или
5г — РхУх Р2У2 • • • Р1У1 Ь • • • 4“ РпУп
8к— Р1У1-
1 1
(б)
(3.7)
Пусть на сооружение действует сплошная неравномерно распределенная нагрузка интенсивностью () (рис. 40). Для определения полного значения усилия заменим сплошную неравномерную нагрузку системой бесчисленного количества бесконечно малых сосредоточенных сил. Выделим на расстоянии а: от левого конца элемент балки длиной йх, в центре которого приложена нагрузка йР цхйх.
I»
38
Элементарное усилие получим по формуле (а):
(18к чх(1х)ух.
Полное усилие найдем интегрированием:
Сз
ЦхУхХ
(3.8)
Очень часто на сооружение действует равномерно распределенная нагрузка постоянной интенсивности:
ЯхЯ сопз.
Вынося постоянную ц в правой части формулы (3.8) за знак интеграла, получаем
уЛх.
С1
Но произведение ухйх равно площади одной из элементарных полосок, на которые расчленяется вся площадь участка линии влияния. Следовательно,
с2
5 ухЛхсо12,
39
где а12 — площадь, ограниченная линией влияния и осью абцисс на участке действия нагрузки (площадь участка линии влияния).
Итак, полное усилие определяется формулой
3 7(012, (3.9)
т. е. чтобы получить полное усилие от сплошной равномерно распределенной нагрузки по линии влияния, необходимо интенсивность нагрузки умножить на площадь данного участка линии влияния.
Размерность ординаты линии влияния может быть найдена по выражению:
размерности данного усилия
размерность ординаты линии влияния - -.
размерность груза
Для опорных реакций и поперечных сил размерность ординаты линии влияния — величина отвлеченная. Для изгибающих моментов ординаты линии влияния выражены в единицах длины.
§ 13. ЛИНИИ ВЛИЯНИЯ ПРИ УЗЛОВОМ ДЕЙСТВИИ НАГРУЗКИ
В конструкциях часто действие нагрузки узловое, т. е. она передается на узлы главной балки, перемещаясь по системе продольных балок проезжей части (рис. 41, а). Для простоты расчета примем продольные балки 0—1У 1—2, 2—3 разрезными, шарнирно опертыми в соседних узлах на главную балку АВ. Рассмотрим построение линии влияния изгибающего момента в сечении к главной балки АВ, если груз Р 1 движется по разрезной системе продольных балок. В этом случае линия влияния изгибающего момента будет ограничена многоугольником, вершины которого находятся под узлаМи — опорами продольных балок (Оу, 2, 3). Если груз Р 1 находится в узлах, он непосредственно действует на главную балку АВ. Поэтому прежде всего строим линию влияния момента при непосредственном действии груза и отмечаем ординаты ее ух и у2 под узлами. При положении груза
Р на расстоянии х от опоры 1 продольной балки 1—2 момент Ми по
ординате линии влияния ее, взятой под грузом (рис. 41, б), согласно определению линии влияния будет
Мк Ру. (а)
То же усилие Мк можно получить, отбрасывая продольную балку 1—2 и представляя ее действие на главную балку в Еиде опорных давлений Р± и Р2, причем
Рг Р(б)
Используя линию влияния в случае действия системы двух сосредоточенны сил, согласно формуле (3.7) получаем
Ми — РхУх I РгУг- (в)
40
Приравнивая одни и те же значения момента Мк по формулам (а) и (в), получаем
РуРуУг РъУг или, внося Рг и Ра по формуле (б), находим
ру р±у1 ру2.
Сокращая на Р, получаем уравнение ординаты линии влияния при произвольном положении груза:
У а-У1 у. (3.10)
Отсюда следует, что при движении груза между узлами линия влияния в главной балке имеет вид прямой, соединяющей узловые
Рис. 41
ординаты уг и у2. Пользуясь первоначальной линией влияния при непосредственном действии груза (рис. 41, б), достаточно найти узловые ординаты и далее соединить концевые точки этих ординат прямыми.
Заканчивая построение линии влияния момента в сечении главной балки, учтем, что при положении груза над крайними опорами 0 и 3 груз Р 1 воспринимается опорами и момент равен нулю.
41
Итак, линия влияния какого-либо усилия при узловом действии нагрузки в случае разрезной системы продольных балок всегда ограничена многоугольником, вершины которого располагаются под узлами главной балки.
Рассмотрим построение линии влияния поперечной силы в сечении к (рис. 41, в). Предполагая непосредственное действие нагрузки, получаем линию влияния поперечной силы, очерченной двумя параллельными прямыми г—д—е—ж. Отмечаем узловые ординаты у и у и проводим прямую, соединяющую концевые точки этих ординат, так как при движении груза по средней продольной балке 1—2 поперечная сила меняется по линейному закону. Затем из нулевых точек линии влияния под узлами 0 и 3 проводим крайние прямые.
§ 14. ЛИНИИ ВЛИЯНИЯ УСИЛИЙ ДЛЯ МНОГОНРОЛЕТНЫХ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ БАЛОК
Каждую многопролетную балку расчленяем на отдельные простые балки, линии влияния усилий для которых уже изучены. Пользуясь схемой образования системы, устанавливаем предварительно, какая часть конструкции является основной, главной, балкой, которая поддерживает подвески (см. рис. 19, а, б) или одноконсольные балки (см. рис. 19, в). В подвесках возникает усилие только тогда, когда они несут на себе нагрузку, передавая ее на главные балки и на опорные части. Поддерживающая балка работает при воздействии нагрузки на нее и при приложении нагрузки к подвескам, которые оперты на главную балку (см. рис. 19, а, б). Рассмотрим построение линий влияния опорных реакций и усилий в консольно-подвесной балке по первой схеме (рис. 42).
Линии влияния реакций А и В. Систему можно расчленить на главную балку е и две подвески се и (рис. 42, а). Если проведем разрезы в точках е и и отбросим подвески, то получим простую двухконсольную балку, линия влияния реакции А для которой имеет известное очертание е11 (рис. 42, б). Теперь рассмотрим закон изменения реакции А при перемещении груза Р 1 по левой подвеске се. Воздействие со стороны подвески се на главную балку е[ представится, очевидно, опорным давлением Е, которое меняется по закону
опорного давления разрезной балки се.
Отбросив подвеску се и представив ее действие на главную балку силой Е, найдем реакцию А из условия
ЪМЬ О,
или иначе
А1 — Е(1 сг) О,
42
откуда
А Е
Подставляя выражение для Еу получим
Л 1
1-с 1 ;
1
при х О, Л 0; при х 1Ъ А
Полученные ординаты определяют участок линии влияния при движении груза по подвеске, когда реакция А меняется по закону прямой.
е
Ф
Ф
А.
г
I
I
.лтптШТМ
1
лтгМИ I
1 Лини
1в
1
я блияния Е 1. ‘
11 1 1 7 1 Линия блияния А
[МШШгтттт
1 1 1 1 1 "т 1 1 ; 1 Линия
1
1
1 1 I 1
I
1 Линия блияния Мк
I
I
I
I
7
1 Щ
4
Линия блияния к
1т Это общее свойство, которым пользуются для построения участка линии влияния при перемещении груза по подвеске для любого усилия в главной балке.
Аналогично строится линия влияния реакции В (рис. 42, в).
43
Линия влияния момента Мк в междуопорной части балки. При положении груза Р 1 справа от сечения к,(рис. 42, а)
Мь Аак.
При положении груза Р 1 слева от сечения к
Мк — В (1 — ак)-
По этим уравнениям правой и левой ветвей построена линия влияния Мк. Для движения груза по подвеске й линия влияния представляет собой прямую 2й2, а при движении груза по подвеске се, поскольку момент Мк меняется по закону изменения правой реакции, — прямую 2 (рис. 42, г).
I Р1
Рис. 43
Линия влияния поперечной силы в междуопорной части балки.
При движении груза справа от сечения к поперечная сила
0.к — А.
При движении груза слева от сечения к
(2ь -в.
По этим уравнениям построена линия влияния на рис. 42, д.
Линии влияния и кг на консольной части балки. Рассматриваем сначала движение груза по двухконсольной балке, отбрасывая подвески (рис. 43). При положении груза справа от сечения (от кг и до й — опоры правой подвески)
(21 0; Мих 0.
При движении груза слева от сечения
0.кх 1» М.кх: 1 ’ х»
44
Получив очертание линий влияния и для участка движения
груза по левой части консоли, переходим к ветви линии влияния, соответствующей движению груза по подвеске се.
При движении груза по подвеске усилия в сечении главной балки меняются по закону наклонной прямой, соединяющей крайнюю точку ординаты для конца консоли и нулевую точку для опорной вертикали подвески.
Линии влияния С?и Мк% представлены на рис. 43, а, б.
§ 15. КИНЕМАТИЧЕСКИЙ МЕТОД ПОСТРОЕНИЯ ЛИНИЙ ВЛИЯНИЯ
Весьма ценно использование кинематического метода построения линии влияния. По этому методу каждую линию влияния усилия или реакции находят по эпюре перемещений основной системы, полученной отбрасыванием той связи, в которой возникает рассматриваемое усилие. При этом применяют принцип возможных перемещений, согласно которому, если данная система находится в равновесии, сумма работ всех сил, действующих на систему, на любых малых возможных перемещениях должна быть равна нулю.
Найдем, например, л инию влияния опорной реакции левой опоры балки АВ (рис. 44, а).
Поместив груз Р в произвольное положение, отбрасываем опорный стержень в точке А и заменяем его действие силой X. Далее представляем картину возможных малых перемещений полученного механизма — бруса АВ, прикрепленного лишь одним правым концом посредством шарнирно неподвижной опоры в точке В (рис. 44, б). Возможное перемещение бруса получаем как перемещение жесткого диска, вызванное поворотом вокруг шарнира
В. При этом по малости угла поворота а все перемещения точек оси бруса можно принимать вертикальными. Обозначаем через 8рх перемещение точки приложения силы Р, через 8 перемещение точки приложения силы X. Устанавливаем следующее правило знаков: перемещение 8рх принимаем положительным по направлению силы Р. Согласно началу возможных перемещений работа сил, приложенных к брусу
РЬрх—Х6хх 0. (а)
Работа силы X взята со знаком «минус», так как сила X противоположна направлению перемещения Ьхх.
а)
ф.
р
с
1
X
Л.
1
Р—1
«А—•-"
охх Ь Линия
Рис. 44
45
Из уравнения (а) получаем:
X 1
ирх
(3.11)
Так как Р 1 при построении линии влйяния перемещается по балке, то Ьрх переменно, меняясь от 0 (при х 0) до 8 (при х I). Перемещение же 6ХХ не меняется. Следовательно, линия влияния X может быть получена как эпюра перемещений 6рх, все ординаты
а)
а
А
Р 1
X
р—
1-а
которой разделены на постоянное перемещение 6 по направлению X. Перемещение Зможно принять за масштаб для ординат линии влияния.
Из рис. 44, б имеем
брх хдаха 6хх 1ёаъ и по выражению (3.11) получаем окончательно
(б)
(3.12)
Аналогично найдем линию влияния изгиб а ю щ е г о момента для какого-либо сечения к балки АВ (рис. 45, а). Переходим к основной системе, отбрасывая в сечении к ту связь, которая передает изгибающий момент Мк X, т. е. снимаем жесткое соединение соседних сечений. Оставляя лишь шарнирное соединение в сечении к, жесткое соединение соседних сечений возмещаем парными моментами X (рис. 45, б).
Картина малых возможных перемещений полученного четырехшарнирного механизма АкВС определяется поворотом звена Ак на угол 3 и звена Вк на угол а. Согласно началу возможных перемещений
46
сумма работ силы Р 1 и моментов X на возможных перемещениях системы равна нулю:
Ррх — Ха — Х 0. (в)
Моменты X противоположны направлениям углов поворота аир. Из уравнения (в) имеем:
Х Р- Рг- ь-, (3.13)
а Р °хх О XX
где
б — X
°Р 1 — ах
6Йь • 6ь
хх 1— Ь •
1 — а[а
(3.14)
Мы вновь пришли к тому, что закон изменения X (линия влияния Мк) получается как эпюра вертикальных перемещений 6рдг, все ординаты которой разделены на постоянную 8ХХ (масштаб ординат линии влияния). Линия влияния X представлена на рис. 45, в.
Подставляя в выражение (3.13) значения (3.14), получаем
Х М
— известное уравнение правой ветви линии влияния изгибающего момента Мк-
§ 16. НЕВЫГОДНОЕ ЗАГРУЖЕНИЕ ЛИНИЙ ВЛИЯНИЯ Аналитическое условие максимума усилия
Полное усилие 5П в данном месте сооружения при движении подвижной нагрузки в виде системы сосредоточенных сил Р меняется по достаточно сложному закону, график,
которого имеет ряд переломов. На рис. 46 на оси абсцисс откладываем абсциссу х системы сосредоточенных сил (поезда), на оси ординат—значения полных усилий 5П. График изменения полного усилия прерывный. При х х0 усилие 5„ имеет местный максимум, условие для которого
при Д, Д5„-; -1 при Ах-, Д5П —. ( Как при положительном, так и при отрицательном приращении абсциссы поезда Ах приращение полного усилия Д5„ должно быть отрицательным.
47
Критерий невыгодного положения системы грузов для многоугольной линии влияния
Невыгодным положением подвижной системы сосредоточенных сил называем такое положение ее, при котором усилие в данном элементе конструкции принимает наибольшее абсолютное значение. Для стержня, имеющего двухзначную линию влияния, рассмотрим два возможных невыгоднейших положения поезда: при загружении положительного и отдельно отрицательного участков линии влияния. Дадим аналитический критерий для определения того положения системы сосредоточенных сил Р, для которого получаем максимум усилия 5П, используя линию влияния этого усилия. Пусть линия влияния усилия 5 ограничена многоугольником (рис. 47). Прямолинейные участки линии влияния составляют с осью абсцисс углы а2 и аз-
Заменим каждую группу сил Р на данном прямолинейном участке линии влияния их равнодействующей 7?,. Для данного случая линии влияния получаем три равнодействующие: ?2, Яз-
Полное усилие 5П можно определить по равнодействующим:
5П Я1У1 К2У2 К2У3 И • (а)
После сдвижки поезда на Ах все равнодействующие также сдвинутся на Ах. Получим новое значение полного усилия с приращением Д5П:
5П А 5П (ух 4 А уг) ?2 (у2 А у2) ?3 (у3 — А у3). (б)
Для третьего участка имеем отрицательное приращение, так как ординаты линии влияния с увеличением х уменьшаются.
Вычитая из выражения (б) выражение (а), находим приращение полного усилия:
А5П Агх - [- К2Ау2— КзАу3. (в)
48
Согласно рис. 47 находим:
Ау1 Ахёа1; Ау2 Аха2; Ау3 Ах%а3.
Подставляя эти значения Ауь в выражение (в), получаем после вынесения Дл; за скобку
Ах 1 ?2 2 ?8 з)’ (О
при наличии п прямолинейных участков линии влияния
(3.16)
п
Применим теперь аналитический критерий максимума (3.15). Согласно первой строке выражения (3.15) при Ах положительном
2 18 «• О-
(л)
Если поезд сдвигается влево (Дл; отрицательно), Д5П также должно быть отрицательным, а потому согласно второй строке выражения (3.15)
в«1о.
(«
Объединяя обе строки критерия, получаем
Ч--
(3.17)
(л)
т. е. при переходе через опасное положение должна менять свой
знак на обратный, что вполне соответствует условию максимума функции 5П, поскольку дает приближенное выражение
первой производной от 5П по х.
Так как 1§аг — величины постоянные, то, для того чтобы согласно формуле (3.17) менялась по величине и знаку, необходимо,
чтобы при сдвижке поезда резко менялись величины равнодействующих 1. Это возможно лишь тогда, когда один из грузов поезда находится у самой вершины линии влияния (на рис. 47 груз Ркр)- Этот груз условно называют критическим.
Необходимым условием опасного положения системы сосредоточенных грузов является такое ее положение, при котором один из грузов (критический) расположен у вершины линии влияния.
Этот признак необходим, но недостаточен, так как возможен случай, когда после такой установки при сдвижке поезда меняется лишь величина, но не знак
Задачу определения опасного положения поезда решают способом последовательных попыток: поставив поезд так, чтобы один из грузов его находился у вершины, по формуле (3.17); проверяем,
49
выполняется ли условие максимума; если это условие выполняется, имеем местный максимум для функции полного усилия.
Величину максимального усилия 5„ определяем по формулам:
5П ЯРУР ЯЪУ1- (3.18)
Критерий невыгодного положения для треугольной линии влияния
Рассмотрим какую-либо треугольную линию влияния усилия 5, вершина которой от опорных вертикалей находится соответственно на расстоянии а и Ь (рис. 48). Выделим из всей системы грузов %Р9 размещенной по длине а Ь и установленной в опасное положение, критический груз Ркр- Равнодействующую всех грузов слева от критического обозначим ?ЛРВ, равнодействующую всех грузов справа от критического назовем ?пр. Тогда, очевидно
2-Р лев -Ркр 4“ Япр- (3.19)
Применим теперь к опасному положению поезда выведенный выше критерий (3.17). При сдвижке поезда вправо по первой строке критерия, приняв во внимание введенные обозначения, получим
Рис. 48 Ялев 1 (2 Р лев)
Объединяя члены с ?лев и перенося в правую часть, получим
Ялев (1е ах 18 а2) «2 2 р- (3.20)
Внося выражения тангенсов
I Ь Н
8«. 5-
и сокращая на й, находим:
п ь а _1_ у р
Клев аЬ С ь Ь И
или окончательно:
Ялов у 2 я. (3.21)
Аналогично развернем вторую строку критерия (3.17) для случая
сдвижки поезда влево, когда на первом участке равнодействующая
будет равна
Р. л ев 1 кр
Линия влияния 5
I
] 1 И ♦
1 ♦
лед
I м
м 1
р 1 %
1
и изменится знак неравенстсва формулы (3.17). Теперь
СвТЯкРу2Р. (3.22)
Используя полученные неравенства, легко найти опасное положение поезда. Задачу решаем в следующем порядке:
1) по данной длине I однозначного участка линии влияния находим %Р (имея расчетную схему поезда);
2) проверяем выполнение неравенств (3.21) и (3.22);
3) выясняем, не изменяется ли величина после установки поезда в опасное положение, когда весь поезд сдвигается так, что критический груз становится у вершины линии влияния и часть грузов может выйти за пределы пролета; для нового значения %Р расчет повторяем.
§ 17. ОПРЕДЕЛЕНИЕ УСИЛИЙ ПО ЭКВИВАЛЕНТНОЙ НАГРУЗКЕ
Значительно упрощается определение усилий по линиям влияния с использованием эквивалентной сплошной нагрузки, заменяющей действие системы сосредоточенных сил поезда. Согласно действующим ТУП СН—200 для железнодорожных мостов расчет производится только по эквивалентным нагрузкам.
Эквивалентной называют равномерно распределенную нагрузку, приложенную на длине однозначного участка линии влияния, усилие от которой равно усилию от системы сосредоточенных сил поезда, помещенных в невыгоднейшее положение.
Дадим аналитическое выражение для интенсивности эквивалентной нагрузки 7эКВ, заменяющей
систему сосредоточенных сил (рис. 49). Усилие от действительной системы сосредоточенных сил по линии влияния будет
5„ 2Р1-. (а)
Заменив систему грузов поезда равномерной нагрузкой интенсивностью дэкв, то же усилие определим, умножая дэкв на площадь линии влияния:
Зпэкв со (б)
Приравнивая выражения (а) и (б), находим выражение для интенсивности эквивалентной нагрузки:
ЪРгУ1
I (экЬ
1пни1тниии
Рис. 49
7экв (3.23)
51
Заметим, что при увеличении максимальной ординаты Н треугольной линии влияния в п раз, во столько же раз увеличивается площадь линии влияния о и, следовательно, при постоянном положении вершины (невыгоднейшее загружеиие то же) 7ЭКВ не меняется. Таким образом, эквивалентная нагрузка постоянна для различных линий влияния (с различными значениями Л), но при равных длинах I и одинаковом положении вершины. С учетом этого свойства составлены таблицы эквивалентных нагрузок для простейших, часто встречающихся треугольных линий влияния (см. табл. 1). Параметрами, от которых зависит эквивалентная нагрузка, являются:
1) длина загружаемого участка I (основание треугольника);
2) положение наибольшей ординаты (вершины).
Если длина I и положение вершины данной линии влияния не совпадают с табличными, производят линейную интерполяцию по соседним табличным значениям. Найдя по данному положению вершины и длине I из таблицы эквивалентную нагрузку, приходящуюся на одну ферму, получают усилие по формуле (б).
Таблица 1
Равномерно распределенные эквивалентные нагрузки к Тм железнодорожного пути
м
К
1
1
м
К-
1
а 0
а 0,5
а 0
а 0,5
1
5,000
5,000
5
2,077
1,817
1,5
3,992
3,493
8
1,868
1,634
2
3,115
2,726
10
1,781
1,558
3
2,464
2,156
14
1,651
1,444
4
2,212
1,936
20
1,505
1,317
к — класс нагрузки; а
а- положение вершины линии влияния.
§ 18. МАТРИЧНАЯ ФОРМА ИСПОЛЬЗОВАНИЯ ЛИНИЙ ВЛИЯНИЯ. МАТРИЦА ВЛИЯНИЯ
В ряде задач строительной механики большое применение получила матричная форма расчета (см. Приложение). Матрицы применяются для решения системы линейных алгебраических уравнений (определение усилий в сложных системах), определения перемещений и в частности для определения усилий по линиям влияния от системы связанных грузов. Остановимся на решении последней задачи.
Пусть требуется определить моменты в узловых сечениях 1, 2, 3 и 4 балки на двух опорах при действии в узлах главной балки системы сил Р0, Р1У Р2, Р3, Р4, Р5 (рис. 50). По формуле (3.7) момент в каждом сечении найдем как сумму произведений каждого груза Р на соответ¬
52
ствующую ординату линии влияния 11. Обычно при узловой передаче нагрузки длины панелей одинаковы; в данном случае принимаем 1п 15.
а)
1-с
Рис. 50
Для момента Мг получим (рис. 50, а)
М1 (4Р1 ЗР2 2Р3 Р,) или иначе в матричной форме
гРг
Рг
Рь
Р
(3.24)
Момент Мг получаетсй как произведение «строки» узловых ординат линии влияния на «столбец» узловых грузов (с множителем IIп2 25). В краткой матричной записи момент Мг можно представить так:
(3.25)
где Ь[ — вектор-строка ординат линии влияния момента Мх; р — вектор-столбец грузов.
53
Для моментов М.2, Мя, М4 (рис. 50, б-
М,±ь,р
М, ЫР;
-г) соответственно получим: Мл ЬкР.
25
6 4
2 3
2];
4].
где для векторов-строк имеем:
; [4 3 2 1]; Ь; [3
6з [2 4 6 3]; ; [1
В целом определение всех узловых моментов по линиям их влияния от данной системы узловых грузов Р можно представить таким матричным равенством:
_ - (3 26)
М ЬиР Р,
где Ьп —21 представляет собой матрицу из узловых ординат всех
линии влияния моментов в сечениях центробежная матрица порядка п 5.
4
1, 2, 3 и 4, а — натуральная В данном случае
(3.27)
Матрица Ьм носит название матрицы влияния моментов. Каждый столбец этой матрицы соответствует столбцу коэффициентов узловых ординат всех линий влияния моментов (см. рис. 50). Числа этой матрицы обладают свойством взаимности, т. е. числа, расположенные симметрично относительно главной диагонали (4, 6, 6, 4) равны между собой. Выражение (3.26) для всех моментов при действии системы сосредоточенных сил Р дает возможность использовать при вычислении моментов в различных сечениях электронно-счетные машины, так как легко можно получить общее выражение матрицы влияния моментов без построения линий влияния.
Выражение (3.26) формулирует также решение задачи о семействе так называемых обобщенных линий влияния. Пусть требуется построить закон изменения момента при движущейся системе грузов Р. Тогда, оставляя вектор-строку Ь в выражении (3.25) постоянным, будем считать вектор-столбец Р меняющимся. Отсюда следует, что выражение (3.26) при переменном Р (вследствие перемещения поезда) дает семейство обобщенных линий влияния Мъ М2У М3 и т. д.
ГЛАВА 4. БАЛОЧНЫЕ И КОНСОЛЬНО-БАЛОЧНЫЕ ПЛОСКИЕ ФЕРМЫ
§ 19. ПОНЯТИЕ О ФЕРМЕ. СТАТИЧЕСКАЯ ОПРЕДЕЛИМОСТЬ ФЕРМ
В фермах стержни соединены в узлах или заклепками или сваркой, т. е. жестко. Однако, как показывают сравнительные расчеты, при действии на стальные фермы с обычной решеткой узловой
54
нагрузки усилия в стержнях фермы с жесткими узлами мало отличаются от усилий в стержнях идеально-шарнирной фермы. В дальнейшем будем рассматривать ферму, все элементы которой связаны в узлах идеальными шарнирами (рис. 51, а). В таких фермах при узловом приложении нагрузки каждый стержень подвергается лишь осевому действию силы. Так как нагрузка приложена в узлах (рис. 51, б), то по условию равновесия любого невесомого стержня аЬ на него со стороны узлов а и Ь действуют две равные и противоположные по направлению силы 8аЬ и 8Ьа и в нем возникает лишь продольная сила.
Дадим аналитический признак статической определимости в форме алгебраической связи числа стержней фермы и числа узлов ее к. Положим пока, что ферма имеет обычное опирание на левую шарнирнонеподвижную опору, в которой возникают две составляющие реакции, и на правую шарнирно-подвижную опору, которая дает одну неизвестную реакцию. В таком случае общее число неизвестных будет 3), где 5Х — число неизвестных усилий в стержнях фермы, а 3 — число неизвестных реакций. Для каждого стержня имеем только одно неизвестное — величину усилия (положительным его считаем, если усилие вызывает растяжение стержня). Для определения усилий в любой шарнирно-стержневой ферме применим общий метод вырезания узлов, а именно последовательно выделяем каждый узел фермы (рис. 51, в) и составляем для сил, сходящихся в точке, два условия равновесия в форме суммы проекций:
%Х 0; ;к о.
Всего уравнений равновесия, очевидно, будет 2к, где к — число узлов фермы. Сопоставляя число неизвестных (5Х 3) с числом уравнений 2к,
55
получаем аналитическое условие статической определимости фермы:
1 Ь 3 2 к, (а)
откуда
81 2к—3. (б)
Это критерий статической определимости шарнирно-стержневой фермы, опертой на одну неподвижную и одну подвижную опоры (или на три опорных стержня). Если ферма имеет больше, чем три опорных стержня условие статической определимости можно представить несколько иначе. Обозначая 3 5, где 5 — общее число стержней фермы вместе с опорными, вместо выражения (а) получим:
5 2.
Если 5 2к, число неизвестных больше числа уравнений равновесия, следовательно, нельзя найти неизвестные из условий равновесия — система статически неопределима. Если 5 2к, число неизвестных меньше числа уравнений. В этом случае задача по отысканию усилий становится неопределенной и условиям равновесия удовлетворить нельзя.
§ 20 КЛАССИФИКАЦИЯ ФЕРМ
Фермы классифицируют:
1. По назначению на: фермы пролетных строений мостов, фермы каркасов промышленных зданий, стропильные фермы.
2. По характеру опорных закреплений на: а) балочные (рис. 51, а) и консольно-балочные, б) арочные и висячие
I I
ТуШТ
ПТТТТТП ГТТП ППП1ЛТП ГПТП1ТПТ
Рис. 52
фермы, в опорах которых в отличие от балочных систем при вертикальной нагрузке возникают и горизонтальные реакции; так, на рис. 52 представлена схема моста с трехшарнирной аркой со сплошной стенкой, а на рис. 53 показана висячая винтовая система; со стороны наклонных тяг сооружения действуют наклонные реакции, горизонтальные составляющие которых — распоры; в) разрезные (см. рис. 51) и неразрезные (рис. 54) фермы, перекрывающие несколько пролетов, а также консольные фермы (рис. 55), один конец которых оперт, другой свободен.
56
3. По очертанию поясов на: фермы с параллельными поясами (рис. 56, а) и фермы с полигональными поясами (рис. 56, б, в). На рис. 56, б показана балочная ферма с одним верхним полигональным
поясом. На рис. 56, в представлена двухшарнирная арочная ферма с двумя полигональными поясами, так называемая серповидная арочная ферма.
- 4. По системе решетки на: фермы с раскосной решеткой (рис. 56, а, б и 55); раскосной называют решетку, при наличии которой в каждой половине двухопорной фермы направления раскосов идентичны; фермы с треугольной решеткой (рис. 51, а и 56, в) треугольной решетка называется тогда, когда раскосы попеременно меняют направление; фермы С двухраскосной решеткой (рис.
57, а); в каждой панели этой фермы два раскоса одинакового направления; фермы с полураскосной решеткой (рис. 57, б); такая ферма в каждой панели имеет два разных по направлению раскоса, идущих к стой- Рис. 55
ке; двухрешетчатые фермы (рис. 57, в);
разновидностью двухрешетчатых ферм являются двухрешетчатые фермы башенного типа (рис. 58), однако в большинстве случаев такие фермы входят в состав пространственных ферм; фермы с ромбической решеткой (рис. 57, г); многорешетчатые фермы (рис. 57, д) и фермы с составной решеткой (шпренгелями); составной называют решетку,
57
которая, кроме основной треугольной или раскосной решетки, включает дополнительные малые фермы (шпренгеля), разделяющие большую панель на малые (рис. 57, е).
5. По особенностям структуры на: простые (балочные, консольно-балочные, арочные, висячие) фермы, перечисленные выше, и комбинированные, представляющие собой сочленение простых
Рис. 59
систем (например, балочной фермы и гибкой арки; рис. 59). В системе, изображенной на рис. 59, а, гибкая арка (верхний пояс) концами связана с балочной фермой; в системе же, показанной на рис. 59, б, гибкая арка (нижний пояс) отделена опорными концами от верхней балочной фермы. Если перевернуть последнюю систему относительно горизонтальной оси на 180°, получим цепь с балкой жесткости.
§ 21. СПОСОБЫ ОПРЕДЕЛЕНИЯ УСИЛИЙ В ФЕРМАХ Общие соображения
Ниже рассмотрим применение наиболее общего аналитического метода. В основу расчета усилий в стержнях фермы можно положить общую систему уравнений статики для узлов фермы и отдельных ее частей.
Определение усилий основано на общем методе отделения части фермы и рассмотрения ее условий равновесия аналогично методу разрезов, применяемому в сопротивлении материалов. Главнейшая задача статики ферм заключается в применении таких способов расчета, которые избавляют от решения системы совместных уравнений (проведение так называемой ортогонализации, обеспечивающей равенство нулю ряда неизвестных).
59
Способ моментных точек
Этот способ в наиболее простой форме применяется к фермам, в которых можно провести разрез только через три стержня.
Определим усилия 02, Д2, И2 в элементах фермы с треугольной решеткой (рис. 60). Предварительно находим опорные реакции А и В. Проводим разрез п—п через три стержня, усилия в которых определяются, и действие частей фермы представляем соответствующими векто¬
рами 02, Д2 и ]2 полагая усилия растягивающими. Рассматривая равновесие левой части (где меньше сил), составим три уравнения, каждое из которых включает только одно неизвестное. Для этого вместо трех классических уравнений равновесия
%М 0; ЦХ 0; %У 0
получим для левой отсеченной части уравнения следующего вида:
%Мк1 0; 0; 0, (4.1)
где в сумму моментов не войдут усилия 02 и 02, проходящие
через моментную точку кг сумма моментов Мь2 не содержит усилий Ц2 и 02; сумма з не включает усилий 02 и 02. Каждое уравнение (4.1) будет содержать только одно неизвестное усилие, что позволит легко и точно его найти. Для определения У2 составляем сумму моментов сил, приложенных к отсеченной левой части фермы, относительно точки кх — точки пересечения направлений 02 и 02:
2о,
или
Аа1 — Р1 ах — 6) — 12г 0,
откуда
У _ Аах — Р (Д1 — а)
2 гх
Здесь числитель не что иное, как момент левых внешних сил относительно точки кг (изгибающий момент в сечении воображаемой балки со сплошной стенкой).
60
Таким образом, получаем
П _м%г и2 — г »
где Мх — момент левых внешних сил относительно кх гг — плечо усилия.
Найдем теперь усилие 02, составляя сумму моментов сил, приложенных к левой отсеченной части фермы, относительно точки к2 — точки схода 02 и И2
%Мк0,
или
Ай -- 02г 2 —
откуда
0 - А- -
Щ2
(4.2)
Для определения П2 выбираем точку моментов в к3 — точке пересечения направлений 02 и И2. Рассматривая равновесие левой части, находим
2Мк з 0,
или
—А а3 Рг (а3 ф—й2г3 «О, откуда
■ Ааг (а3 с1) Мк%
Гз
(4.3)
Как видим, при применении способа моментных точек усилие всегда выражается
отношением момента внешних сил, приложенных к левой отсеченной части, к плечу усилия г.
Так, для определения усилия в элементе нижнего пояса Ц2 полураскосной фермы (рис. 61) проводим зигзагообразный разрез п—п, пересекающий четыре стержня. Но направления трех усилий 02, и У2 пересекаются в одной точке. Ее и принимаем за точку моментов для определения У2:
откуда
2МГо,
Ай — 12А 0; У2 А
А
Аналогично определяется усилие 02 с использованием моментной точки кх.
61
Замкнутый разрез применяем для отыскания усилий в стержнях фермы Шухова и других подобных системах (рис. 62). Положим, требуется определить усилие 0± в первом элементе верхнего пояса фермы Шухова.
Для определения усилий в стержнях Ох, 03 и 05, связующих два основных треугольника, проводим разрез, который рассекает стержни верхнего пояса по одному разу и раскосйГ и В2 — по два раза. Рассматривая равновесие части фермы, расположенной внутри разреза п—п, составляем условие равновесия в виде равенства нулю суммы моментов относительно к — точки пересечения осевых линий стержней 03 и 06:
или
откуда
%мГо,
— 01Г1 — ВЬ О,
ог —в 1 1
Способ проекций
Способ проекций применяют, когда моментная точка оказывается в бесконечности, т. е. при параллельности двух стержней из трех рассеченных. Допустим, требуется определить усилие в раскосе 03 фермы с параллельными поясами (рис. 63). Проводя разрез п—п, рассекаем три стержня, усилия в которых 03, 03 и (У3. Но направления усилий
03 и 173 параллельны; следовательно, моментная точка для 03 будет в бесконечности. Задача определения усилия 03 легко решается применением уравнения проекций всех сил, приложенных к отсеченной части, на вертикальную ось, перпендикулярную к направлениям 03 и И3:
2 у лев __ О,
или
А — Р — 03 зт а 0,
откуда
(4.4)
81П а 81П а 4 7
62
где д — р (пп — поперечная сила в сечении п —п воображаемой балки со сплошной стенкой.
Раскос фермы с параллельными поясами работает на восприятие поперечной силы. Закон изменения усилий в раскосах легко установить по эпюре поперечных сил.
Способ вырезания узлов
Способ вырезания узлов наряду со способом моментов является одним из самых общих способов определения усилий. Для каждого узла фермы составляют два условия равновесия в виде двух уравнений проекций на две непараллельные оси. Целесообразно поэтому начинать с узла, где сходятся два стержня. Покажем применение способа вырезания узлов для определения усилий в элементах фермы, представленной на рис. 64, а. Для определения усилия 0г проще всего вырезать опорный узел фермы (рис. 64, б). Проектируя все силы, действующие на узел, на вертикаль, получим:
откуда
Ог 8111 а Л О, А
Ог --г
X С1
(4.5)
т. е. усилие в опорном элементе верхнего пояса фермы пропорционально опорной реакции.
Для определения усилий в стойках 1х и У2 вырезаем соответственно узлы 1 и 3 нижнего пояса фермы. Вырезая нижний узел 1 и проектируя все силы, приложенные к нему, на вертикальную ось, получаем (рис. 64, в) Уг 0.
Отсюда можно сделать следующее заключение: если в узле сходятся три стержня,, из которых два направлены одинаково (IIх и II2) и нет наг-
63
рузки, то усилие в отдельно направленном стержне (Уг) равно нулю. Такой стержень называют нулевым. Указанное правило распространяется также на узлы, к которым приложена нагрузка, не имеющая составляющей, нормальной к двум другим стержням одного и того же направления.
в д)
Рис 64
Предположим, что к узлу, в котором сходятся два поясных усилия 1» 2 и усилие в раскосе О, приложена горизонтальная сила Р (рис. 64, г). Проектируя все силы, действующие на узел, на вертикаль, находим:
О соз а О,
откуда
0 0.
Отдельно направленный стержень имеет нулевое усилие и в случае приложения нагрузки, действующей по оси одинаково направленных стержней.
Вернемся теперь к рассмотрению фермы (рис. 64, а) и определим усилие в средней стойке У3. Вырежем для этого средний узел нижнего пояса, где сходятся только три стержня (рис. 64, 5). Проектируя все
64
силы, приложенные к узлу, на вертикальную ось, получим
— Р 0,
откуда
У9 Р.
Следовательно, если в узле сходятся три стержня, из которых два направлены одинаково3 и (У4) и есть нагрузка Р, направленная по оси третьего стержня У3, то усилие в отдельно направленном третьем стержне равно нагрузке.
Способ вырезания узлов целесообразно также применять для получения соотношения между усилиями в трех стержнях при наличии перелома пояса. Покажем применение способа вырезания узлов для получения выражения усилия в стойке У2 через усилие в верхнем поясе 02 (рис. 64, а). Вырезая верхний узел 2 фермы, прежде всего проектируем все силы на горизонталь (рис. 64, е):
02 соз а2 — 03 соз а3 О,
откуда
(4.6)
Теперь проектируем все силы, приложенные к узлу 2, на вертикальную ось:
0381па3—02 81па2— У2 0,
откуда
У2 — (02 81П а2 — 03 8111 а3),
или, подставив значение 03 из выражения (4.6), получим
У 2 — О2 (зт а2 — соз а2а3). (4.7)
Для определения 02 применяем способ моментной точки, проводя разрез фермы по второй панели.
§ 22. РАСЧЕТ ТРЕХДИСКОВЫХ ФЕРМ НА НЕПОДВИЖНУЮ НАГРУЗКУ Способ равнодействующих
Трехдисковые фермы (анализ неизменяемости их приведен выше, см. § 7 и 8) рассчитывают с полным разделением неизвестных при учете положения основных фиктивных шарниров а, с и Ъ. От заданной системы с реальными связями переходим к трехдисковой системе, установив положение основных шарниров а, с и Ь. Затем определяем реакции шарниров а и Ь, а по реакциям фиктивных шарниров легко находим реакции реальных закреплений.
Рассмотрим в качестве первого примера графическое определение опорных реакций двухпролетной фермы со средним опорным четырех-
3 Н. К. Снитко
65
угольником (рис. 65, а) при действии вертикальной нагрузки Р, приложенной к левому диску. При действии вертикальной нагрузки Р и одинаковом направлении средних опорных стержней (угол а) усилия в них одинаковы. Поэтому реакции этих стержней В и В на диски
I и II равны между собой. Так как нагрузка приложена к левому диску, а диск II не загружен, равнодействующая реакций В[ и И — сила Нь должна пройти по Ьс. Продолжая направление Нь до пересечения
с линией действия силы в точке получаем направление равнодействующей На двух реакций А и Вх левого диска — линия ас1. В плане сил (рис. 65, б) уравновешиваем силу Р равнодействующими реакциями Кь и На- Получив На и Нь, заменяем их составляющими: силу Ка — составляющими Л и Въ силу Нъ— составляющими В[ ий.
Расчет фермы с полным разделением неизвестных способом двух сечений
Рассмотрим определение усилий в стержнях трехдисковых ферм на примере решетчатой фермы (рис. 66 а). Ферма загружена вертикальной силой Р, приложенной к правой узлу диска III. Пусть плечо силы Р относительно центра левой оп®ры будет р. Тогда балочные
реакции: В Р А Р 1—. Отсекаем диск, проводя первое
66
сечение п—п. Действие рассеченных стержней, 2, 3 и 4 представляем усилиями 5Х, 52, 53 и 34. Усилия 5г и 52 заменяем силами Уа и На, усилия 53 и 54 — силами Уь и Нь.
Рис. 66
По условию равновесия системы дисков I и II имеем
На Нь Н.
Составляя условие равновесия нижней части системы —II в форме
%МНЬ О,
получаем
А I -- и) Вы — Vа1 О,
откуда
гг А (1-и)--Ви V а— Из условия равновесия той же части 2У 0 находим Уь. Рассматриваем теперь равновесие одного диска, проводя второе сечение к—к через средний шарнир су и составляем условие равновесия:
3 67
что дает
А 2 — Уа (2и) Я 0, откуда и находим Н:
н-НЧ1“)--4т]-
Теперь легко определить усилия в стержнях 1 и 2 данной фермы хотя бы графическим построением. В плане сил (рис. 66, б) откладываем векторы Уа и Н и находим равнодействующую 12 этих «внутренних реакций». Исходя из того, что силы Уа и Н — заменяющие сил и 52, разложим равнодействующую ?12 на направления усилий и 52. Решение, таким образом, полностью расчленяется.
§ 23. РАСЧЕТ ФЕРМ С СОСТАВНЫМИ ЭЛЕМЕНТАМИ
Фермой с составными, или сложными, элементами называют такую ферму, в которой ряд прямолинейных стержней заменен составными стержнями в виде фермочек. В ферме, изображенной на рис. 67, а, вместо простых элементов по нижнему поясу даны сложные элементы Оа, аЬ, Ь[. Заменяя составные стержни прямолинейными, получаем первоначальную, так называемую основную ферму, из которой образована ферма с составными элементами. Узлы основной фермы называют главными; узлы, расположенные между главными, — дополнительными. При отсутствии составных элементов и том же приложении нагрузки стержень основной фермы аЬ испытывал бы, кроме действия осевой силы, еще поперечный изгиб от силы Р.
Рассматриваем два случая действия нагрузки: 1) нагрузка не приложена в дополнительных узлах данного сложного элемента и 2) нагрузка имеется и в промежуточном узле фермочки.
В первом случае (элемент Ь на рис. 67, б), выделяя фермочку разрезами у главных узлов, получаем из условия равновесия фермочки, что по концам ее со стороны главных узлов будут воздействовать только осевые силы (У3, направленные по прямой, соединяющей главные узлы. Эти осевые силы легко определить способом, известным для простых ферм.
Рассмотрим теперь определение усилия 12 в стерженьке составного элемента аЬ, к промежуточному узлу 2 которого приложена вертикальная нагрузка Р. Выделим этот элемент из фермы разрезами у узлов а и Ь (рис. 67, в). Реакции со стороны узлов а и Ь представляем каждую в виде двух составляющих Уа, и Ум из которых составляющие 2 направлены по оси составного элемента, т. е. по линии аЬ.
Из условия равновесия фермочки 2Х 0 получаем, что правая горизонтальная реакция (У2 равна по величине и противоположна по направлению левой реакции (У2; найти же величину (У2 из условия равновесия фермочки невозможно. Вертикальные реакции фермочки Уа и Уь легко находятся. Составляя условие равновесия в виде суммы
68
моментов относительно точки Ь.
2М О,
получаем
уаа-рРо9
откуда
(а)
Составляя условие равновесия в виде суммы моментов относительно точки а, получаем
Вертикальные реакции Уа и Уъ малой фермочки от местной нагрузки находят так же, как реакции простой балки с пролетом й. Можно считать фермочку аЬ опертой статически определимо на главные узлы. Усилия в стерженьках этой фермочки можно найти, зная все внешние силы для нее, в том числе и осевые силы У2.
Для определения осевых сил рассмотрим равновесие части всей фермы (рис. 67, г). Выделив сложный элемент аЬ из заданной фермы, возмещаем его связи в а и Ь опорными давлениями Уа и У ь и осевыми силами 1]ъ направленными от узлов. Опорные давления Уа и Уь по величине равны вертикальным опорным реакциям фермочки и определяются формулами (а) и (б). Рассекая всю ферму разрезом т—т и рассматривая равновесие левой части ее, составляем условие равновесия:
где М% —,момент левых вертикальных сил относительно точки г. Выражение (в) показывает, что осевая сила сложного элемента вычисляется так же, как в элементе простой фермы, но особенностью является разложение промежуточной нагрузки на составляющие Уа и УЬу приложенные к главным узлам.
После определения осевой силы [2 возвращаемся к рассмотрению фермочки аЬ (рис. 67, в). Найдем усилие во втором элементе нижнего пояса фермочки 512. Для этого проводим разрез п—п и рассматриваем равновесие левой части фермочки:
-уьаР(1-р)о,
откуда
(б)
2МР0
или в развернутом виде
откуда
Ас-Уа(с-й)-Угк О,
,, _ Ас-уа(с-й) _ Мк
и - к 7Г’
(в)
69
или
УА21 — 51гг 0,
откуда
5ггУаС и, (г)
Первый член правой части представляет собой усилие в стерженьке
1—2 составного элемента от местной вертикальной нагрузки; назовем его Второй член правой части можно рассматривать как усилие
70
в том же стерженьке 1—2 от осевых сил 12; обозначим второй член Получаем следующее общее выражение для полного усилия
в любом стержне фермочки:
с -12 —
: 5?
(Д)
где в данном случае
•мес
Т С1. СОС тт ГА_
V а 12 — и 2 г •
Усилие от местной нагрузки возникает только тогда, когда загружен данный сложный элемент, и это воздействие называют потому местным. Усилие от осевых сил может быть равно осевой силе, если гх г.
Рассмотрим частный случай ферм с составными элементами, в которых осевая линия сложного элемента аЪ совпадает с осью пояса малой фермочки (рис. 68, а). В этом случае сложный элемент будем называть шпренгелем.
Выделив составной элемент аЬу подверженный действию местной вертикальной нагрузки (рис. 68, б), получиц по общей формуле (г) следующее выражение для усилия в стерженьке 1—2 шпренгеля:
12
:5М6С
12
5° 5Г 2.
(е)
Заметим, что в данном случае усилие от осевых сил равно осевой силе, которая воспринимается нижним поясом шпренгеля, и, следовательно, усилия от осевых сил Ц2 в элементах а—3, 3—4, 4—5, 5—Ьу 3—У, 1—4, 4—2 и 2—5 равны нулю. Эти элементы получают усилия только от местной вертикальной нагрузки, т. е.
г» г«мес
34 34 •
Будем различать две фермы по рис. 68 стержни трех категорий: стержни первой категории, в которых возникают усилия только от осевых сил (стержни основной фермы, например, 6—7, 6—Я, 6—5, 6—3); стержни второй категории, которые получают усилия только от местной вертикальной нагрузки и входят лишь в состав шпренгеля (стерженьки 3—У, 3—4, 4—5, У—4 4—2, 2—5); стержни третьей категории, которые входят в состав основной фермы и в состав малой фермочки (а—У, У—2, 2—Ь, а—3, Ь—5), причем усилия в таких стержнях определяют по общей формуле (г) путем суммирования усилий от осевых сил и от местной вертикальной нагрузки.
В фермах, в которых шпренгеля меняют характер воздействия груза на главны узлы (если происходит изменение «положения езды»),
71
очертание линий влияния усилий в стойках основной фермы также изменяется, и такие стойки относят к элементам особой, четвертой, категории.
§ 24. ЛИНИИ ВЛИЯНИЯ УСИЛИЙ В ПРОСТЫХ БАЛОЧНЫХ ФЕРМАХ
Перед построением линии влияния данного усилия следует выбрать наиболее целесообразный способ отыскания этого усилия на основе ортогонализации (см. § 21).
Рассмотрим построение линии влияния усилий в стержнях балочной фермы с треугольной решеткой при езде понизу (рис. 69). Положение езды на чертеже отмечено пунктиром. Усилие в любом стержне фермы будем выражать через опорные реакции А и В. Усилие 02 находим, применяя способ моментной точки. Проводя указанный на чертеже фермы разрез, отмечаем точку моментов с абсциссой, равной длине панели й находим плечо усилия 02, равное гх. При положении груза Р 1 справа от разрезанной панели рассматриваем равновесие левой отсеченной части и составляем сумму моментов относительно точки кг:
2МГ 0,
или
Ас1 02г1 О,
откуда усилие в элементе верхнего пояса
02 — А у-. (а)
Г1
Мы получили аналитическое выражение правой ветви линии влияния 02. Усилие 02 меняется по закону изменения левой опорной реакции Л, все значения которого умножены на постоянную 1Ди взяты
со знаком «минус». Строим правую ветвь линии влияния 02, отклады-
, Л
вая на левой опорной вертикали ординату —1 • — и соединяя ее с нулевой точкой на правой опорной вертикали. Полученную правую прямую используем на участке движения груза справа от разрезанной панели.
При положении груза слева от разрезанной панели составляем условие равновесия правой отсеченной части как условие равенства нулю суммы моментов относительно точки кх
2КР0,
или
— В (1 — й)—С2г1 О,
откуда
Ое -В(б)
72
Усилие 02 меняется по закону изменения правой реакции, все орди-
1 — й
наты которой увеличены в —— раз и взяты со знаком «минус» (рис. 69, а).
Левую ветвь линии влияния можно построить и непосредственно по правой ветви, учтя, что лерая ветвь линии влияния момента пересекается с правой ветвью ее подточкой моментов кг. Левая ветвь используется на участке первой левой панели фермы. При движении груза между
3
узлами разрезанной панели (участок 1—2 по ездовой линии) линия влияния очерчивается прямой (передаточной), соединяющей узловые ординаты левой и правой ветвей.
Линия влияния 02 подобна линии влияния момента М1Г При определении усилия И2 моментной точкой будет к2 — точка пересечения осевых линий стержней 02 и Д2. Составляя сумму моментов левых сил относительно точки к2 при положении груза справа от разрезанной панели, т. е.
2МГ 0,
получаем
Аа2 — Ц2Н 0, (в)
где а2 — абсцисса моментной точки к2.
Уравнение правой ветви линии влияния будет
(г)
На левой опорной вертикали откладываем ординату -° вверх
и соединяем ее концевую точку с нулевой точкой на правой опорной вертикали. Используем правую ветвь на участке движения груза справа. Левую ветвь линии влияния Ц2 получим непосредственно по правой ветви. Для этого проводим через моментную точку к2 вертикаль до пересечения с правой ветвью линии влияния, получаем точку, принадлежащую и левой ветви. По этой точке и нулевой точке на левой опорной
вертикали строим левую ветвь. Передаточная линия — прямая, соединяющая узловые ординаты и соответствующая участку 1—2 ездовой линии на ферме, в данном случае не совпадает с продолжением левой или правой ветви. Заметим, что передаточная линия для участка движения груза по перерезанной панели не совпадает с продолжением левой или правой основной линии (рис. 69, б), если моментная точка к2 не совмещается ни с одним из узлов разрезанной панели по ездовой линии (узлы 1 и 2).
Аналогично, применяя способ моментных точек, строим линию влияния усилия 02, пользуясь тем же разрезом. Точка моментов теперь к3 — точка пересечения усилий 02 и 02 за пределами фермы. Рассматривая равновесие левой части фермы при движении груза Р 1 справа от разрезанной панели, получаем
2С о,
или в развернутом виде
— Аа3 — Я2г2 0,
где а3 — абсцисса точки моментов к3. Уравнение правой ветви линии влияния
Оя-А%. (д)
74
Правая ветвь линии влияния строится по линии влияния левой
опорной реакции А, все ординаты которой умножены на 1 - у- и взяты
со знаком минус (при любом положении груза справа раскос сжат).
На левой опорной вертикали откладываем ординату — 1 • — и, соединяя
Г 2
с нулевой точкой на правой опорной вертикали, получаем правую ветвь.
Переходим к построению левой ветви линии влияния 02 при положении груза Р 1 слева от разрезанной панели.
Рассматривая равновесие правой части фермы и составляя сумму моментов всех сил, приложенных к правой части относительно точки моментов к3, получаем
— В ( а3) 2 0,
откуда имеем следующее выражение для усилия:
0 В1-. (е)
Усилие 02 ПРИ движении груза слева от разрезанной панели меняется по закону изменения правой реакции, все ординаты которой увеличены в раз, причем усилие 02 теперь растягивающее. Поэтому Г2
левую ветвь строим в виде прямой, имеющей на правой опорной верти-
, 4-а, 0 „
кали ординату 1-—1—а на левой опорной вертикали — нулевую г 2
точку (рис. 69, в). Левая ветвь линии влияния 02 при продолжении должна пересекаться с правой ветвью под точкой моментов к3. Как видим, линия влияния двузначна. При удалении точки моментов к3 за пределы фермы все далее перемещается точка пересечения левой и правой ветвей к и для случая параллельности поясов ветви линии влияния становятся также параллельными.
Рассмотрим решение задач по построению линии влияния усилий в решетке фермы с параллельными поясами, когда при определении усилий в раскосах и стойках целесообразнее всего применять способ проекций (рис. 70, а).
Для построения линии влияния усилия Б3 проводим разрез 1—, выявляя усилия 03, Е3 и 113. Угол наклона раскоса к горизонтали обозначим а. Рассматриваем произвольное положение груза Р 1 справа. По условию равновесия отсеченной части
2 улев 0,
или
А — з5па 0,
откуда
Оа -Д—. (ж)
3 81П (У. 75
Правую ветвь линии влияния усилия 03 строим по линии влияния
1
раз.
левой опорной реакции, все ординаты которой увеличены в
81П а
При произвольном положении груза слева по условию равновесия правой части фермы
ЦУП р 0,
или
В 03з1па 0,
откуда
В
81П а
Левую ветвь линии влияния усилия строим по линии влияния правой реакции, все ординаты которой умножены на— Отметив
узловые ординаты, проведем передаточную линию под разрезанной
76
панелью (рис. 70, б). При любом положении груза
о3 4-. (и)
3 81П а 4
Раскос работает на поперечную силу множитель
Аналогично строится линия влияния усилия в стойке фермы с параллельными поясами. Рассмотрим построение линии влияния усилия У4 при езде понизу (расположение ездовой линии будет влиять на очертание линии влияния У4). Проведя разрез
2—2, полагаем груз Р 1 справа от разрезанной четвертой панели (по нижнему поясу). Рассматривая равновесие левой части, получаем
Л-У4_0,
откуда
Уа А.
Как видим, правую ветвь линии влияния усилия в стойке можно построить по закону изменения левой опорной реакции А.
Аналогично при положении груза слева из рассмотрения равновесия правой части находим
У, — В.
Левая ветвь подчиняется закону изменения правой реакции, но с обратным знаком (рис. 70, в).
При построении линий влияния усилий в стойках фермы с треугольной решеткой целесообразно применять способ вырезания узлов. Рассмотрим в качестве примера ферму с треугольной решеткой и дополнительными стойками (рис. 71, а). Построим линии влияния усилий У0, У1у У2 и У4 при езде понизу. Вырезая верхний узел О и принимая во внимание отсутствие нагрузки в узлах верхнего пояса, получаем
Уо 0.
Линия влияния У0 нулевая.
Вырезая нижний узел Г при положении груза Р 1 в этом узле, получаем
1.
Если груз расположен в одном из соседних узлов, из рассмотрения равновесия узла находим
0.
По полученным значениям строим линию влияния Уи которая имеет вид «местного» треугольника (рис. 71, б).
Перейдем к построению линии влияния У2, применяя последовательно способ вырезания узлов и способ моментных точек. Вырезая узел 2 и имея в виду отсутствие нагрузки в этом узле (езда понизу),
77
составляем условие равновесия 2Х 0 или (рис. 71, в)
02 соз ах — 03 соз а2 О,
откуда
(К)
Проектируя все силы, действующие на узел 2, на вертикальную ось, получаем
Подставляя значение 03 из соотношения (к), получаем следующее выражение для усилия:
Усилие в стойке прямо пропорционально усилию в поясе (рис. 71, д). Следовательно, ординаты линии влияния У2 можно получить по ординатам линии влияния усилия 02, умножая их на коэффициент (это —
— созо).
Применяя способ моментных точек, строим линию влияния 02 (точка моментов к) при этом опорная ордината для правой ветви будет
—. Изменив знак на обратный и умножив все ординаты этой линии г 1
влияния на множитель согласно выражению (л), получим линию влияния У2 (рис. 71, ё). При движении груза Р 1 по верхнему поясу очертание линии влияния устанавливают так: от полученной ранее ординаты линии влияния под узлом 2 следует вычесть единицу и провести две соседние передаточные линии (пунктиры на рис. 71, е).
Аналогично строится линия влияния усилия У4 (рис. 71, г, ж). Рассмотрим еще построение линии влияния усилия в раскосе И 2 одноконсольной фермы. Применяя способ моментных точек (рис. 72, а), проводим разрез 1—1 для обнаружения усилий 02,
О 2 и (У2. Точка моментов для усилия )2 будет кг абсцисса ее — ах. При положении груза Р 1 справа от разрезанной панели из уравнения равновесия левой отсеченной части
Строим график правой ветви, откладывая на левой опорной верти-
откуда
02 81П ах — 03 8Ш а2 О,
V2 — (О2 81П а± — 03 81П а2).
V2 — О2 (§ т % —а2 соз а).
(л)
(м)
кали опорную ординату 1 -у (рис. 72, б). Левую ветвь получаем по ее
79
точке переселения с правой ветвью под точкой моментов кг. Проводя вертикаль через точку кх до пересечения с правой ветвью и соединяя найденную точку с нулевой точкой на левой опорной вертикали, получаем левую.ветвь линии влияния. Выделяем узловые ординаты, т. е. ординаты линии влияния под узлами разрезанной второй панели; соединяя эти узловые ординаты прямой, получаем передаточную линию.
Рис. 72
При движении груза по подвеске ес ординаты линии влияния получаются как ординаты прямой, соединяющей узловую ординату под концом консоли с нулевой точкой линии влияния под опорой подвески.
На рис. 72, в представлена линия влияния усилия У0 в опорной стойке той же ферм ы.
§ 25. ЛИНИИ ВЛИЯНИЯ УСИЛИЙ В ФЕРМАХ СО ШПРЕНГЕЛЯМИ
Балочная ферма
Рассмотрим построение линий влияния в раскосной ферме_со шпренгелями, расположенными по верхнему поясу (рис. 73). В этой ферме простые стержни верхнего пояса 1—2, 2—4 и т. д. заменены треугольными фермочками (двухпанельными шпренгелями) с дополнительными стойками 5—5, передающими нагрузку с проезжей части на узлы верхнего пояса.
В соответствии с указаниями § 23 в этой ферме имеются элементы первой категории: 7—9, 5—9 и другие, элементы второй категории: 5—4, 5—8 и другие, элементы третьей категории: 2—3, 3—4, 2—5 и другие, элементы четвертой категории: 2—7, 4—9 и др.
Линии влияния усилий в элементах первой категории строятся так же, как и для основной фермы, которая получается отбрасыванием шпренгелей, с проведением передаточных линий на участках больших разрезанных панелей. Длину малой разрезанной панели, образованной
81
вспомогательными узлами 6, 8 и т. д., обозначим с1. Построим линию влияния в элементе второй категории — раскосе Л54 (рис. 73, а).
Рассмотрим положение груза в узле 5, когда работает малая фермочка 2—4—5, и положения груза в соседних узлах 7 и 9, когда фермочка не работает. Очевидно, что в двух последних случаях
ям0.
При положении груза в узле 8 (рис. 73, б) проводим разрез второй панели и рассматриваем равновесие правой части фермочки, составляя сумму моментов сил, приложенных к узлу 4, относительно точки 3:
О,
или
ПыГ1 — ;А Ъ
откуда
Отложив под узлом 8 ординату и соединив крайнюю ее точку
с нулевыми точками под соседними узлами 7 и 9, получим линию влияния Оъ± (рис. 73, в).
Построим теперь линию влияния усилия в стержне 3—4У входящем в состав основной фермы и шпренгеля. Как уже указывалось, этот стержень является элементом третьей категории. В случае двухпанельных шпренгелей при определении усилия 034 в стержне третьей категории нет необходимости в расчленении системы на основную ферму и малые фермочки шпренгеля и, следовательно, отпадает необходимость в использовании формулы наложения. Усилие 034 можно найти непосредственно, оперируя с заданной составной фермой. Прежде всего, вырезав узел 3, где нет перелома пояса, получим 034 023. Переходим к построению линии влияния усилия 023, которое легко найдем способом моментных точек, рассекая ферму разрезом I—I через малую панель 7—8. В этой малой панели разрез пересекает только три стержня, выявляя усилия 023, Ц78 и б2Ь. Точка моментов для 023 будет к (узел 9). При положении груза справа от узла 8 уравнение моментов будет
%мГо,
или
А. • 5(I 023г О,
откуда
023-Л-. (б)
Мы получили уравнение правой ветви линии влияния 023. Откладывая на левой опорной вертикали вниз ординату 1— и соединяя крайнюю точку ее с нулевой на правой опоре, получаем правую ветвь. Правую ветвь еЬс используем на участке движения груза справа
82
от узла 8. Левую ветвь аЬ получим по правой ветви, имея в виду общее свойство пересечения левой и правой ветви под точкой моментов. Передаточная линия 6,, очевидно, соответствует малой разрезанной панели (рис. 73, г). Ординаты треугольника АЬ и отражают влияние 0“ес на общее усилие в стержне 023. Если бы шпренгелей не было, мы имели бы очертание линии влияния по аЬс.
Стойка, усилие в которой У27, является элементом четвертой категории. Очертание линии влияния для нее меняется по сравнению с очертанием линии влияния для элемента 2—7 основной фермы. Решаем задачу так: находим два варианта линии влияния — при езде понизу и при езде поверху, и используя их, устанавливаем окончательное очертание линии влияния. Предполагая отсутствие шпренгелей и считая, что груз находится справа от большой разрезанной панели 7—9 (разрез II—), рассматриваем равновесие левой части фермы в форме
1Жво,
где к — точка пересечения осевых линий стержней 1—2 и 7—9, или
— Аак — У27 (ак Ь Зй) О, откуда получаем следующее выражение для правой ветви:
у”А-т- в
Отложив на левой опорной вертикали ординату 1 - д 3, строим
правую ветвь линии влияния.
По правой ветви находим левую ветвь, пользуясь моментной точкой кх (точка пересечения правой и левой ветвей к на рис. 73, д). При езде понизу линия влияния У21 для основной фермы имеет очертание аЬсд,, а при езде поверху — аей.
Переходим к учету наличия шпренгелей, меняющих характер езды для нашей фермы. При положении груза в узлах 6 и 8 он воспринимается шпренгелями и передается на узлы верхнего пояса; поэтому используем линию влияния ае§М, отмечая ординаты для точек и к. При положении груза в узлах 10,7 и 9 шпренгеля не работают и ординаты линии влияния берут из линии влияния для Движения груза понизу (точки е, Ь и к на рис. 73, д). Соединяя соседние ординаты прямыми (е[, Ь, Ьк, кс), находим окончательное очертание линии влияния У27.
Аналогично получим линии влияния усилий для стоек — 1—10 и 4—9.
Консольно-балочная ферма
Построим линии влияния усилий Ц2, й3 и У4 для фермы, изображенной на рис. 74, а.
При построении линии влияния У2 (рис. 74, б) используем моментную точку кх. Так как У2 — элемент третьей категории, то передаточная линия проводится на длине малой панели.
То же имеем для линии влияния Оъ. При построении линии влияния 03 (рис. 74, в) используем моментную точку к2:
83
Стержень У4 — элемент 4-й категории. Вырезая нижний опорный узел 6, из условия равновесия V] V 0 получаем
У4 — В — (11ь 8па5 [4з1па4).
Отсюда следует, что из ординат линии влияния (—5) — линии сЬ[ — следует вычесть ординаты линии влияния величины
(Ць 51П а5 У4 51П а4),
где выражение, заключенное в скобках, берется по абсолютному значению (рис. 74, г). Далее учитываем особенности изменения характера
езды вследствие наличия шпренгелей (если груз находится в соседних с опорной стойкой узлах, используем очертание линии влияния при езде понизу).
ГЛАВА 5. РАСЧЕТ СПЛОШНОЙ ТРЕХШАРНИРНОЙ АРКИ
§ 20. ТРЕХШАРНИРНАЯ АРКА СО СПЛОШНОЙ СТЕНКОЙ. АНАЛИТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ РЕАКЦИЙ
Аркой называется кривой брус, передающий на опоры, кроме вертикальных, и горизонтальные давления. По существу трехшарнирная арка представляет собой трехдисковую систему с шарнирами а, Ь
84
и с (рис. 75), если в рассмотрение ввести и опорный диск. Горизонтальные давления арки на опоры, а также противоположные им реакции называют распорами. Недостатком трехшарнирных арок по сравнению с двухшарнирными является меньшая их жесткость в виду наличия ключевого шарнира. Статическая определимость трехшарнирных арок обеспечивает отсутствие дополнительных напряжений от температуры и горизонтального смещения опор.
В отличие от свода арка имеет небольшую ширину сечения и потому относится к виду брусьев. Пролетом арки называют расстояние между опорными вертикалями, стрелой подъема ее — расстояние от наиболее удаленной точки оси
арки (ключа) до линии, соединяющей центры опор. В строительной практике встречаются арки трех основных видов: трехшарнирная, двухшарнирная и бесшарнирная. Последние два вида статически неопределимые и будут рассмотрены во второй части курса.
Так как обе опоры арки шарнирно неподвижны, имеем всего четыре составляющие реакций, которые легко определяются, если применить три условия равновесия всей системы (см. рис. 75):
%мь 0, %Ма О, 2Х 0
и четвертое дополнительное уравнение 2 М?ев О, отражающее наличие ключевого шарнира. Это последнее уравнение составляем на том основании, что равнодействующая левых или правых сил в сечении, проведенном через шарнир с, должна проходить через центр шарнира. Для удобства раздельного отыскания неизвестных реакций каждую реакцию неподвижной опоры для несимметричной арки с опорами на разных уровнях представляем в виде двух составляющих: вертикальной Уа, Уь и по линии опоры (Та, Ть — наклонные распоры).
Полагаем, что на арку действует Рх — вертикальная и Р2 — горизонтальная силы. Составляя сумму моментов относительно центра правой опоры Ь, находим
Уа,1 — 1 (2 Рг) Р2Р2 “ О» откуда вертикальная составляющая левой опорной реакции т 1 (2 Р1) — Р2Р2
у а ——. (а)
80
Составляем теперь сумму моментов относительно центров левой опоры а:
— У Ь1 Рх (1Х — рх) Р2 (Л8 ® Рг) 0
откуда
1 М(р)
Уь-т [Р1 (кРг) Р. (Д8« Р«)1 -т-• (б)
Применяем третье общее уравнение равновесия системы в форме
2 Х 0:
Та сох а—Тг, сох а Р2 О, имея в виду, что Р2 — горизонтальная сила,
Т Т“ 1Ш- Правый наклонный распор Ть можно найти, зная левую реакцию Та, для отыскания которой составляем четвертое дополнительное уравнение:
В развернутом виде получаем
V а1 Р1Р1 — Та1 О,
откуда
„ Уак-РгРх Щ
(5.1)
где М1 — момент всех левых внешних сил относительно точки с за исключением распора Та.
Значение распора Та обратно пропорционально стреле подъема. Определив Та по формуле (5.1), по формуле (в) найдем Ть. Теперь определим горизонтальные распоры Яа и Яй:
НаТасо а;
НЬ ТЬ соз а. Полные вертикальные составляющие реакций Уа и Уь будут:
УаУа Тата;
УЬУЬ — ТЬ та.
(Д)
Распоры при действии вертикальной нагрузки равны между собой.
В частном случае, когда трехшарнирная арка имеет опоры, расположенные на одном уровне, и нагрузка вертикальна (рис. 76),
м°
На Нь Н -±9 (5.2)
86
где Мс — балочный момент относительно точки с (момент левых вертикальных сил):
М1Уак-РиЪ
— расстояние по вертикали от ключевого шарнира до линии опор (стрела подъема арки).
Заметим, что вертикальные реакции трехшарнирной арки Vа и Уъ при вертикальной нагрузке определяются так же, как реакции в простой балке — см. формулы (а) и (в).
§ 27. ОПРЕДЕЛЕНИЕ УСИЛИЙ В СЕЧЕНИИ ТРЕХШАРНИРНОЙ АРКИ. ЭПЮРЫ МОМЕНТОВ
Изгибающий момент
Определим усилия в сечении к, центр которого имеет координаты ук и ак (рис. 77, а).
Для определения изгибающего момента Мк составляем выражение суммы моментов сил, приложенных к отсеченной части, относительно точки к — центра сечения:
Мь (Уаак — РгР] — Ну и- (а)-
Выражение в круглых скобках правой части представляет собой сумму моментов левых вертикальных сил, равную изгибающему моменту в сечении к простой балки М%.
Введя это обозначение изгибающего момента в балке (рис. 77, б), получим следующее окончательное выражение изгибающего момента в сечении арки:
Мк Мк — Нук. (5.3)
Изгибающий момент в сечении арки Мк равен разности моментов в соответствующем сечении балки М% и от распора Нук
Эпюра моментов. Рациональная ось
Эпюру моментов в арке легко построить, используя формулу (5.3). Строим эпюру моментов в балке М% и, наложив на нее эпюру Нук (эпюру ординат оси арки, увеличенных на Я), отмечаем разности ординат этих двух эпюр (рис. 77, в). Предварительно необходимо найти распор Н от данной вертикальной нагрузки.
87
Пользуясь формулой (5.3), находим выражение для ординаты кривой давления или многоугольника давления; подними понимают линии.
для всех точек которых изгибающий момент равен нулю. Следовательно, приравняв Мк нулю, получаем
М%-Нук О, (5.4)
откуда выражение для ординаты многоугольника давления будет
(5.5)
Ук м%
Н •
Ордината кривой давления может быть получена как ордината эпюры изгибающих моментов в простой балке, разделенная на значение распора (при этом рассматривается случай действия вертикальной нагрузки).
На рис. 78, а представ- а лена та же эпюра моментов в арке, полученная из рис.
77, в, причем ординаты этой эпюры отложены от горизонтальной оси отсчета.
Поперечная сила
Найдем теперь поперечную силу 0,ь в сечении к арки (см. рис. 77, а). Для этого, пользуясь проведенным сечением, составляем сумму проекций сил, приложенных к отсеченной левой части, на направление сечения, т. е. на направление перепендикуляра к касательной в данной точке оси арки; получаем, применяя указанное выше правило знаков:
С1ь Vа СОЗ фл — 1 СО8 ф — Я 81П фЛ.
Объединим первые два члена правой части:
0.к(Уа —Рт) СО фк — Н 8Ш ф. (б)
г
Выражение в круглых скобках правой части, не что иное, как поперечная сила 0% в сечении к простой балки (см. рис. 77, б). Поэтому окончательно получаем следующее выражение поперечной силы в сечении арки:
Як 0% СОЗ фь — Н 81П ф. (5.6)
На рис. 78, б представлена эпюра 2, построенная с использованием
формулы (5.6) для случая, изображенного на рис. 77, а. При этом
соблюдается дифференциальная зависимость между М и ф — см. формулу (5.8).
Продольная сила
Продольную силу Ык в сечении к арки определяем как сумму проекций сил, приложенных к отсеченной части, на направление касательной в данной точке оси арки (см. рис. 77, а). Составляя эту сумму проекций для сил Уа, Р и Я, действующих на левую отсеченную часть арки, и считая сжимающую продольную силу положительной, получаем
Мк Vа 31П ф — фа Я С05 фл,
или
Л (Уа — Рх) 81П фл ЯС08 фл.
89
Так же, как и в предыдущем случае, выражение в круглых скобках представляет собой поперечную силу в простой балке, т. е. 2. Таким образом, окончательно получаем следующее выражение продольной силы в сечении арки:
Ык (2°к 81Пфк Н С08ф. (5.7)
Эпюра продольных сил также может быть построена непосредственно по этому выражению (рис. 78, в).
Дифференциальные зависимости между усилиями
При расчете арочных плотин часто рассматривается действие радиальной нагрузки в виде гидростатического давления.
Дадим основные дифференциальные зависимости между моментом М, поперечной силой (2 и продольной силой N при наличии сплошных радиальной и тангенциальной нагрузок, интенсивности которых соответственно обозначим и Положение сечения к определяем полярным углом а (рис. 79, а).
Составим первое условие равновесия элемента длиной бк, а именно приравняем нулю сумму моментов всех сил, приложенных к элементу, относительно точки 0Х пересечения соседних касательных (рис. 79, б):
м-(мам)г((3с1(я§ 0,
откуда, пренебрегая малой второго порядка, получаем
5-8)
Поперечная сила есть первая производная от момента по длине дуги оси арки (г — радиус кривизны первоначальной оси в данной точке).
Спроектируем все силы, действующие на элемент, на направление кУ левой касательной (рис. 79, б):
N — (Ы ЛЩ С05 (йа) — ((2 (10) §т (йа) сА соз (с1а) 0.
Отсюда, пренебрегая малыми второго порядка, получаем
% —7’7с (5-9)
Производная продольной силы по длине оси прямо пропорциональна поперечной силе, разделенной на радиус кривизны оси.
90
Составим теперь третье уравнение равновесия элемента, проектируя все силы, действующие на элемент, на ось к2
( — ((2 (10) сов (с1а) (ДО с?ДО) вт (йа) — дгй со - 0,
или
— б ДО йа 9Г5,
откуда находим
§«-«,г. (5.10)
При отсутствии радиальной нагрузки
§ 28. ЛИНИИ ВЛИЯНИЯ РЕАКЦИЙ И УСИЛИЙ В АРКЕ
Линии влияния реакций
Рассмотрим построение линий влияния составляющих реакций Уа, и Я для трехшарнирной арки (рис. 80, а). Построим, например, линию влияния левой реакции Уа. При произвольном положении груза Р 1, составляя Мь 0, получаем
Уа1 — Р(1 — х) 0,
откуда
(а)
Выражение для вертикальной реакции то же, что и в случае простой балки. Линии влияния Уа и Уь представлены соответственно на рис. 80, б и 80, в.
Линия влияния распора Н имеет две ветви, так как распор Н согласно выражению (5.2) прямо пропорционален балочному моменту относительно точки с. Пусть груз Р 1 перемещается справа от ключевого шарнира. Рассматривая левую часть арки, составляем уравнение равновесия ее:
%МГ0,
или
Уак-Щ 0,
откуда уравнение правой ветви линии влияния распора
НУа±. (б)
91
Отложив на левой опорной вертикали ординату 1 • у и соединив
найденную точку с нулевой точкой на правой опорной вертикали, получим правую ветвь (рис. 80, г).
При движении груза слева от шарнира с рассматриваем равновесие правой части арки и составляем уравнение равновесия
2С о,
или
-Уь1г Щ 0,
откуда уравнение левой ветви
(в)
Левую ветвь линии влияния распора строим, по ординате 1-2, которую откладываем на правой опорной вертикали. Соединяя край¬
92
нюю точку этой ординаты с нулевой точкой на левой опорной вертикали, получим левую ветвь линии влияния распора.
Линию влияния распора можно, конечно, построить и по одной правой ветви.
Линия влияния изгибающего момента.
Матрица влияния моментов
Построим линию влияния изгибающего момента в сечении трехшарнирной арки (рис. 81, а). Координаты точки к (центра сечения) будут: ук — ордината, ак — абсцисса.
Изгибающий момент в сечении к арки при произвольном положении груза определяем по выражению (5.3):
Мк М%-Нук. (5.12)
Следовательно, ординаты линии влияния изгибающего момента в сечении к арки могут быть получены как разности ординат двух линий влияния Мк и Нук• Строим линию влияния момента в сечении арки по способу наложения:
1) вверх от оси отсчета откладываем ординаты линии влияния балочного момента М% (для чего на левой опорной вертикали откладываем ординату 1 (рис. 81, б), строим правую ветвь и по ней находим левую ветвь);
2) от той же оси отсчета откладываем ординаты линии влияния распора Я, увеличенные в ук раз; для этого достаточно получить левую ветвь линии влияния Нук ее строим по правой опорной ординате,
равной 1 уУь,
3) получаем разность ординат линий влияния М% и Нук.
При построении этого графика следует учесть, что левая ветвь линии влияния Нук должна пересекаться с правой ветвью линии влияния М% в так называемой нулевой точке линии влияния.
Положение нулевой точки линии влияния Р можно найти графическим построением на чертеже арки (см. рис. 81, а). Нулевое значение момента Мк получается при положении груза между сечением к и шарниром су т. е. когда груз Р 1 приложен к левому диску арки а — с и правее сечения. Так как груз приложен к левому диску арки, правая реакция В должна проходить через центр ключевого шарнира, чтобы выполнялось известное условие
%М?Р 0.
Так как груз справа от сечения, то слева от сечения к действует лишь полная левая реакция А; чтобы момент Мк был равен нулю, левая реакция должна иметь вполне определенное направление, а именно по линии ак.
Приводим линии Ъс и ак, под точкой пересечения которых Р находится нулевая точка линии влияния Р.
93
Ту же линию влияния Мк можно построить непосредственно способом нулевой точки.(рис. 81, в). Откладываем на левой опорной вертикали ординату 1 -ак, затем соединяем, концевую точку ее с нулевой точкой Р линии влияния — получаем первую правую ветвь. По пер-
Рис. 81
вой правой ветви строим вторую правую ветвь, проводя через шарнир с вертикаль до пересечения с первой правой ветвью и соединяя полученную точку с нулевой точкой на правой опорной вертикали. Левую ветвь линии влияния находим по первой правой ветви, пользуясь основным свойством линии влияния момента.
Дадим аналитическое решение задачи по отысканию абсциссы и точки Р (и тем самым нулевой точки линии влияния). Из треуголь-
94
пиков аРй и ЬР1 получаем
Л и -( — „)
а к к 7
откуда определяем абсциссу нулевой точки линии влияния
Линия влияния поперечной силы
При построении лрнии влияния поперечной силы в данном сечении к арки (рис. 82, а) используем общее выражение поперечной силы по формуле (5.6)
(3к 0.% С05 ф — Н 51П ф, (5.14)
где ф — угол наклона касательной в данной точке оси арки;
О% — балочная поперечная сила.
При движении груза будут меняться ОХ и Я, а соз ф и зт ф — величины постоянные. Следовательно, линию влияния С[к можно получить, складывая алгебраически две линии влияния: 0% соз ф и Я зт ф. Для этого (рис. 82, б):
1) строим линию влияния 0% соз ф, для чего проводим две параллельные прямые с опорными ординатами 1 - соз. ф с вертикальным уступом под сечением;
2) вверх от оси отсчета откладываем ординаты графика Я зт ф, которые получаем по левой ветви линии влияния ее (ордината на правой опорной вертикали 1•у зт ф);
3) отмечаем ординаты, равные разности полученных выше ординат.
В пересечении левой ветви линии влияния Я зт ф с правой ветвью
0% соз ф будет нулевая точка линии влияния Ри положение которой легко установить по чертежу арки (см. рис. 82, а).
Предположим, что груз находится где-то между точками с и к (точка Рг). Так как слева от сечения к имеем лишь полную левую реакцию А, то, чтобы получить сумму проекций левых сил на нормаль к касательной, равную нулю, необходимо, чтобы левая реакция была параллельна касательной. Проведя из точки а линию аРх параллельно касательной до пересечения с линией Ьс, получим точку Р19 определяющую положение нулевой точки линии влияния Р[. Пользуясь нулевой точкой Р1у можно непосредственно построить линию влияния (ркс. 82, в): откладываем на левой опорной вертикали ординату 1 - соз ф и соединяем найденную точку с нулевой точкой Р[ — получаем первую правую ветвь; проводим через шарнир с вертикаль до пересечения с первой правой ветвью и соединяем точку пересечения с нулевой на правой опорной вертикали — получаем вторую правую ветвь; левая ветвь параллельна первой правой ветви.
95
Абсциссу « точки Р1 легко найти аналитически из рассмотрения двух треугольников аРхй и ЬРгй:
ъ-тт- (5-16
Линия влияния продольной силы
Рассмотрим построение линии влияния продольной силы Ыь в данном сечении к арки (рис. 83, а). Для этого воспользуемся общим выражением продольной силы (5.7):
Мь 0.1 31П ф Я С05 ф. (5.16)
96
Линию влияния Ык можно получить, суммируя ординаты ЛИНИЙ влияния (1 51п ф и Н соз ф. При этом к положительным ординатам линии влияния (2 51П ф следует прибавить ординаты Н соз ф, что графически осуществляется приложением к графику СЭД зт ф перевернутого графика Н соз ф (рис. 83, б).
Линию ВЛИЯНИЯ (2 51П ф строим по опорной ординате 1-зшф, причем левый участок ее имеет отрицательные ординаты.
Линию влияния Н СОЗф получаем по левой ее ветви, которая отсекает на правой опорной вертикали
ординату 1 • соз ф. Произведя сложение ординат по формуле (5.16), получим линию влияния Л.
Характерно, что при продолжении левой ветви линии Н соз ф и правой линии 0% зш ф точка их пересечения Рг имеет вполне определенное положение под точкой Р2 на чертеже арки. Продолжением первой правой ветви в области, расположенной слева от опоры а арки, практически можно воспользо- ваться лишь при наличии особой консоли — ответвления от участка арки кс (пунктирные дуги на рис. 83, а). Первая правая ветвь 0% зш ф при продолжении влево пересекается с осью отсчета Нх X соз ф в точке Р’ъ—нулевой точке. Найдем то положение груза Р 1, приложенного к введенной консоли,
N. 0.
Правый диск арки не загружен, а потому правая реакция В проходит через шарнир с в направлении Ьс. Слева от сечения к имеем лишь полную левую реакцию А (груз Р 1 «справа» от сечения к — на консоли). Чтобы продольная сила в сечении к равнялась нулю, необ-
при котором
4 И. К, Снитко
97
ходимо, чтобы левая реакция А была нормальна к касательной; тогда ее проекция на касательную будет равна нулю.
Линию влияния Ыь можно построить непосредственно способом нулевой точки (рис. 83, в). Откладываем на левой опорной вертикали ординату 1 • 51П ср и соединяем крайнюю ее точку с нулевой точкой Р% — получаем первую правую ветвь, справедливую на участке кс арки. По первой правой ветви строим вторую правую ветвь аналогично предыдущему (линии влияния С1к). Левую ветвь ведем из нулевой точки
на левой опорной вертикали параллельно первой правой ветви.
Дадим аналитическое выражение для абсциссы и2 точки Р2 (рис. 83, а). Рассматривая два треугольника аЛР2 и ЬйР2 получаем:
«2 т-тг—?• (5.17)
2 2 с1ф — 4 7
Вычислив по этой формуле и2, найдем Р (рис. 83, в):
м и2
§ 29. ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ В АРКЕ ПРИ ПОМОЩИ ЯДРОВЫХ МОМЕНТОВ
Выражение для нормального напряжения
Определение нормальных напряжений в крайних точках сечения арки значительно облегчается при использовании так называемых ядровых моментов. Рассмотрим решение задачи о нормальных напряжениях в точках 1 и 2 сечения к сплошной арки (рис. 84, а). Представим действие левой части на правую равнодействующей левых сил Клев, приложенной в точке и (на продолжении оси сечения 1—2 в пересечении с данной стороной многоугольника давления). Разложив силу ?лев на продольную силу N и поперечную силу (2, нормальные напряжения в сечении в точках 1 и 2 получим от силы Л, приложенной с эксцентрицитетом е, по обычным формулам виецентренного сжа-
Рис, 84
98
тия:
(а)
_ Л_И °г Р 1Гг’
(б)
где Мк — момент относительного центра сечения;.
Р — площадь сечения;
1у №2 — моменты сопротивления сечения для точек 1 и 2 относительно главной оси инерции поперечного сечения, перпендикулярной к плоскости изгиба (для симметричного сечения XVг №)•
В формулах (а) и (б) сжимающее напряжение принимаем положительным. Преобразуем формулу (а) для нормального напряжения в крайней верхней точке сечения 1.
Воспользуемся для этого основным свойством ядра сечения: если продольная сжимающая сила приложена на контуре, ограничивающем ядро сечения, нормальное напряжение по граничной линии самого сечения равно нулю (рис. 84, б). Следовательно, если продольная сила приложена в крайней нижней точке ядра сечения къ нормальное напряжение в крайней точке сечения 1 равно нулю. Приложим в крайней точке кг ядра сечения две равные и противоположные по направлению силы N. Объединяя две силы N. дающие пару сил (на рисунке перечеркнуты), находим, что левая часть действует на правую:
1) сжимающей силой N, приложенной в точке кг и не дающей напряжений в крайней точке сечения 1
2) парой сил N. момент которой
Следовательно, напряжение ах будет выражено только через момент Мк1:
где Мкг — ядровый момент относительно нижнейточки ядра сечения. Момент левых сил по часовой стрелке вызывает сжимающие напряжения. Момент Мк± равняется моменту равнодействующей левых сил или ее составляющей N относительно нижней точки кх ядра сечения. Итак, нормальное напряжение в крайней точке сечения можно определить по ядровому моменту относительно крайней нижней точки ядра сечения. Аналогично
В данном случае момент Мкг вызывает растягивающее напряжение. Напряжение в крайней нижней точке сечения определяется по ядровому моменту относительно крайней верхней точки ядра сечения.
Мк N (е С).
(в)
М(е-с2)
4
99
Линия влияния ядрового момента
Рассмотрим построение линии влияния ядрового момента (рис. 85, а). Размеры сечения заданы, а потому известно положение крайней точки
кг ядра сечения. Пусть крординаты этой точки будут ух и аг. Составляя сумму моментов левых сил относительно точки къ получаем
Мкх Уаа1 — Нуг.
Но Уааг М%х — балочный момент относительно точки кг. Выражение ядрового момента окончательно будет
Мк1 М11-Ну1. (5.18)
Аналогия этого выражения с выражением для момента относительно центра сечения позволяет применять приемы построения линии влияния, установленные для момента относительно цецта сечения. Используя способ нулевой точки, проводим линии Ьс и акх — получаем точку Р, определяющую положение нулевой точки Рх (рис. 85, б). Откладывая на левой опорной вертикали 1аъ где ах — абсцисса точки к19 и соединяя крайнюю ее точку с нулевой точкой Р19 находим первую правую ветвь; затем обычным путем строим левую ветвь и вторую правую ветвь. Приводим здесь же очертание линии влияния момента Мк относительно центра сечения (пунктирные линии на рис. 85, б). При загружении линии влияния Мкх поездом получаем вполне определенное решение для напряжения ох.
100
§ 30. АРКА С ЗАТЯЖКОЙ
Трехшарнирная арка с затяжкой представляет собой шарнирное сочленение двух дисков, соединенных по концам шарнирно посредством горизонтального стержня; вся система оперта аналогично простой балке (рис. 86). Так как в арке с затяжкой брус асЬ имеет промежуточный ключевой шарнир, то при удалении стержня аЬ система становится изменяемой.
Система в отношении реакций является балочной: при вертикальной нагрузке Р возникают только вертикальные реакции У а и Уь, которые определяются так же, как в простой балке. Чтобы определить внутренние усилия, прежде всего находим продольное усилие в затяжке. Для этого проводим разрез системы через ключевой шарнир с. Усилие в затяжке обозначаем Я; действие правого диска сЬ на левый диск са представляется равнодействующей правых сил, проходящей через точку с. Составляя сумму моментов сил, приложенных к левой части по разрезу, относительно точки с получаем
Уа±-Рр-Н 0,
откуда усилие в затяжке
Я
Уа-Рр
Г
(5.19)
Усилие в затяжке получаем по той же формуле, что и распор в трехшарнирной арке с двумя шарнирно неподвижными опорами Щ — балочный момент относительно точки с).
Найдя усилие в затяжке, легко рпределить момент в произвольном сечении к диска арки. Действительно, составляя момент левых сил относительно точки к, получим
Мк—Уааь — Нуц М%р.
(5.20)
101
Выражение момента в сечении диска арки с затяжкой то же, что и выражение арочного момента. Аналогично вычисляют поперечную силу С1к и продольную силу Ык. Следовательно, расчет криволинейного бруса системы по существу ничем не отличается от расчета трехшарнирной арки.
При учете собственного веса затяжки в сечении ее, кроме продольной растягивающей силы, возникает изгибающий момент от распределенной нагрузки веса. Поэтому целесообразно ввести промежуточные узлы затяжки, связав их с жестким диском арки (см. § 32).
ГЛАВА 6. АРОЧНЫЕ ФЕРМЫ И КОМБИНИРОВАННЫЕ СИСТЕМЫ
§ 81. РАСЧЕТ ТРЕХШАРНИРНЫХ АРОЧНЫХ ФЕРМ
Трехшарнирная арочная ферма — распорная ферма с поясами в виде многоугольников, имеющая две шарнирно неподвижные опоры и промежуточный ключевой шарнир. Расчет трехшарнирных арочных ферм проводится на основе изложенных выше приемов расчета трехшарнирной арки со сплошной стенкой. Определение опорных реакций и построение многоугольника давления для трехшарнирной арочной фермы осуществляется так же, как для сплошной арки. Отличительной особенностью шарнирно-стержневой фермы является лишь то, что в каждом стержне фермы при узловой нагрузке возникает только осевое усилие; при расчете на подвижную нагрузку используем линии влияния усилий в стержнях фермы.
Построим линию влияния усилия 13 в элементе нижнего пояса трехшарнирной арочной фермы, высота которой возрастает от замка к пятам (рис. 87, а).
Проведем разрез, как указано на чертеже, выявляя усилия Ц39
03 и 03. Точка моментов для отыскания 3 будет кг — точка пересечения 03 и Оэ. Найдем аналитическое выражение для усилия (3, представляя его в зависимости от момента в точке оси воображаемой трехшарнирной арки со сплошной стенкой. При положении груза Р 1 справа от разрезанной панели, составляя сумму моментов всех сил, приложенных к левой части фермы относительно точки к1у получаем
2МГ О,
или, учитывая наличие распора Я,
Уаак, — Ну 1ц — ИЪГ О,
откуда
аакНу.
102
В скобки в правой части заключено выражение изгибающего момента в сечении кг трехшарнирной арки, стрела подъема которой та же, что и заданной фермы, а точка оси ее кх имеет те же координаты
укх и акхУ что и точка моментов для данной задачи. Итак, общее выражение усилия Ц3 будет
и3±м%. (6.1)
Линию влияния 13 можно получить по линии влияния арочного момента Мку все ординаты которой разделены на гх.
Применяя способ нулевой точки, проводим на чертеже фермы линии Ьс и ак1У в пересечении которых получаем точку Рг. На левой опорам
ной вертикали откладываем ординату 1-- и, соединяя крайнюю ее
точку с нулевой точкой Р[ (находится под точкой Рг), получаем первую правую ветвь; по ней определяем очертание всей линии влияния (рис. 87, б). Отдельные элементы фермы работают лишь на местную нагрузку (рис. 87, в).
юз
Рассмотрим теперь построение линии влияния усилия в раскосе И3 данной трехшарнирной фермы (рис. 88, а). Для линии влияния усилия 03 в виду несовпадения точки моментов к (точки пересечения
03 и II3) с любым из узлов разрезанной панели передаточная линия занимает особое положение.
Рассматривая положение груза Р I справа от разрезанной панели, составляем условие равновесия левой части фермы:
%мго,
или
V аОк — Нуь — й3г 0у откуда для П3 получаем следующее выражение:
А) тг(Уаак — Нук).
В скобки в правой части заключено выражение изгибающего момента Мр в сечении к трехшарнирной арки со сплошной стенкой (ось левого диска акс этой воображаемой арки на рис. 88, а указана пунктиром), причем стрела подъема арки та же, что и стрела подъема фермы. Окончательно для усилия в раскосе рассматриваемой фермы имеем
104
следующее выражение:
о-ОН
из— г
(6.2)
Линия влияния усилия в раскосе трехшарнирной арочной фермы может быть получена как линия влияния момента в сечении к воображаемой арки аксЬг все ординаты которой разделены на г.
Пользуясь способом нулевой точки для момента Мр, легко строим линию влияния (рис. 88, б). В пересечении прямых Ьс и ак на чертеже арки получаем точку Ръ на одной вертикали с которой имеем нулевую точку Р линии влияния. На левой опорной вертикали откладываем
1.
ординату
и, соединяя ее
с нулевой точкой Р[ получаем первую правую ветвь. Пользуясь точкой моментов к, по первой правой ветви, строим левую ветвь, которая пересекается с правой ветвью в точке к[. По первой правой ветви находим вторую правую ветвь.
§ 32. КОМБИНИРОВАННЫЕ СИСТЕМЫ. АРКА С ЛОМАНОЙ ЗАТЯЖКОЙ
Комбинированные системы получили значительное распространение в строительстве.
Основные виды комбинированных систем: арка или арочная ферма с затяжкой, цепь с балкой жесткости, балка с гибкой аркой. Комбинированная статически определимая система характерна сочленением каких-либо двух жестких дисков, связанных промежуточным шарниром (балочной фермы, балки
со сплошной стеной, арочного диска с ключевым шарниром), с кой частью в виде шарнирно стержневой системы стержней.
гиб-
105
Простейшей системой является арка с прямолинейной затяжкой в виде одного стержня, соединяющего шарнирные опоры конструкции. Арка, составленная из двух жестких дисков ас и сЬу связанных шарниром су при опирании на одну неподвижную опору а и другую подвижную опору Ь (рис. 89, а) не является неизменяемой системой. При большом пролете для уменьшения изгибающих моментов в затяжке от собственного веса необходимо поддержать затяжку в промежуточных узлах, вводя подвески. Очевидно, что при езде поверху подвески на подвижную нагрузку не работают, получая лишь усилия от веса соседних частей затяжки. В дальнейшем развитии конструкции прямолинейный стержень затяжки заменяют шарнирно-стержневым многоугольником (рис. 89, б). Стрелой подъема этой системы будет расстояние ключевого шарнира до среднего горизонтального элемента многоугольной затяжки. Введение переломов в узлах многоугольной затяжки 1, 2, 2, 1 целесообразно для использования подвесок шарнирно-стержневой части: в подвесках теперь возникают усилия и от временной нагрузки.
Покажем, как определить усилия во всехостальных стержнях шпренгельной части, т. е. в наклонных стержнях затяжки и в подвесках. Вырезая узел 2 затяжки (рису 89, в) и проектируя все силы на горизонталь, находим
Составляя то же уравнение равновесия для узла 1 затяжки (рис. 89, г)у получаем
5а1со8 аа1 512 сов а12 0 или, принимая во внимание выражение (6.3),
Горизонтальная проекция усилия в наклонном элементе шарнирностержневого многоугольника цепи (или арки) равна распору.
Любое усилие в наклонном элементе этого многоугольника стержней вычисляют по формуле, подобной (6.3). Так, для усилия 5Д1 имеем
Определим теперь усилие в вертикальном элементе шпренгельной части, т. е. в подвеске (рис. 89, г). Проектируя все силы, действующие на узел, на вертикаль, находим
(а)
откуда
5 - Н
О 1 9 хс ГП« П
соз а12
(6.3)
5а X С05 аа 1 513 С08 012 Н.
(б)
512 51П а12 —5а18Ш аа1 0,
откуда усилие в подвеске
—512 5Ш а1?
106
или, подставляя 5а1 и 512 по выражению (б), получаем
Уг Н( 1ёаа1-1§а12). (6.4)
Рассмотрим теперь построение линии влияния момента в сечении к жесткого диска арки с многоугольной затяжкой (рис. 90, а). Дадим выражение изгибающего момента в сечении к диска арки "с многоугольной затяжкой. Для этого, рассекая в точке к всю систему верти-
г
кальным разрезом, составляем сумму моментов всех сил, приложенных к отсеченной части, относительно точки к. При грузе Р 1, расположенном справа, слева от к будем иметь вертикальную реакцию Уа и усилие в наклонном элементе затяжки 312. Перенесем это усилие по оси стержня —2 в точку, являющуюся концом вертикального отрезка ук, и разложим его на вертикальную и горизонтальную составляющие, причем последняя согласно выражению (б) равна распору Н. Следовательно, момент Мк будет равен:
Мь—У аак — Нук — Мр.
107
Так как выражение для момента Мк аналогично выражению момента в сечении арки, которое возвышается над линией опор на величину ук, то для применения метода нулевой точки необходимо представить воображаемую арку, стрела подъема которой равна, а сечение к которой имеет ординату ук относительно линий опор. Даем новое положение опорных точек аг и Ьг арки и особое положение точки к с ординатой ук относительно линии а1Ь1. Проводим правую прямую Ь±с и левую прямую агк в пересечении которых получаем точку Р, определяющую положение нулевой точки влияния момента. Теперь обычным путем строим линию влияния Мк (рис. 90, б.) Первую правую ветвь этой линии влияния строим по левой опорной ординате 1 ак и нулевой точке Р.
Переходим к линии влияния для чего используем метод наложения. При произвольном положении груза справа от сечения составляем сумму проекций сил Vа и 512 на направление, перпендикулярное к касательной, проведенной в данной точке оси арки. Угол наклона касательной в точке к к горизонтали обозначим через ф, угол наклона элемента 1—2 к горизонтали — а12, угол между касательной и осью элемента —2 будет
Р12 Ф а12-
Составляя сумму проекций левых сил на нормаль к оси арки, находим
(2 Vа С08 ф — 12 зт р12 или, заменяя Vа 0% и 512, получаем следующее выра-
СОЗ СС12
жение для поперечной силы:
Э (со8ф-Я--. (6.5)
Т соз а12 4 7
Очертание линии влияния Ск определяем путем наложения: первый член представляется графиком Ле§Ну второй — треугольником сШг (рис. 90, в).
Аналогично строится линия влйяния продольной силы Ык путем суммирования двух линий влияния. Выражение продольной силы как суммы проекций левых сил на направление касательной в точке к (рис. 90, а):
Мк Уа 31П ф 312 СОЗ Р12
или, подставляя Уа СЦ, 812, получаем выражение для
СОЗ ССХ2
продольной силы:
б-е)
Изменение первого.члена правой части (по балочной поперечной силе) представлено графиком тпор (рис. 90, г); график изменения второго члена в соответствии с законом изменения распора, увеличенного
108
на изображен в виде треугольника тгр. Объединяя ординаты
этих двух составляющих графиков, получаем окончательные ординаты линии влияния продольной силы.
§ 33. БАЛКА С ГИБКОЙ АРКОЙ. ЦЕПЬ С БАЛКОЙ ЖЕСТКОСТИ
Балочная ферма с гибкой аркой
Рассмотрим задачи на построение линий влияния усилий в балке с гибкой аркой (рис. 91, а). Вместо балки со сплошной стенкой в данном случае имеем балочную ферму с раскосной решеткой и ключевым
Тис. 91
шарниром в точке с. Элементы шарнирно-стержневого многоугольника 0—3—3—0 работают на сжатие. Воображаемая трехшарнирная арка опирается в точках аи Ь и имеет фиктивный ключевой шарнир в точке сг.
Линия влияния И2. Проводим разрез через вторую панель балочной фермы и элемент 1—2 гибкой арки. Точка моментов для И2 будет к — точка пересечения В2 и 02: Усилие 312 элемента 1—2 перенесем в точку, расположенную над точкой моментов к на вертикали ук. Составляя сумму моментов сил, приложенных к левой части фермы,
109
относительно точки к, получаем
2МГ0,
или
Уаак — Нуь — игк О,
откуда
м?
(6-7)
т. е. усилие У2 выражается через арочный момент.
Линия влияния И2 получается по линии влияния момента в сечении воображаемой арки аспричем центр сечения этой арки кг должен возвышаться над линией опор аЬ на величину ординаты ук. Откладывая от первого промежуточного узла нижнего пояса ук, получаем точку кг соединяя точки а и кх прямой и продолжая ее до пересечения с прямой Ьси получаем точку Ри которая определяет положение нулевой точки линии влияния Р[. Затем строим линию влияния И2 по линии влияния Мьх (рис. 91, б).
Линия влияния И2. Ввиду параллельности поясов балочной фермы придется использовать способ проекций. Проектируя силы, приложенные к левой части фермы, на вертикальную ось (рис. 91, а), получаем
Vа — Н ф — В2 81П а 0, (а)
где Н ф — вертикальная составляющая усилия 512 в элементе 1—2 гибкой арки (горизонтальная составляющая Н — распор);
Ф — угол наклона оси элемента 1—2 к горизонтали.
Из выражения (а) получаем следующее выражение для 02:
О К-НЦф
81П ОС
или
О Уа С05Ф — 51пФ 2 С08 ф 81П а Числитель представляет собой выражение для поперечной силы в
сечении к2 воображаемой арки ак2сгЬу касательная к оси которой составляет с горизонталью угол ф.
Итак, можно записать вместо выражения (б)
2р
й2 ——. (6.8)
4 С08 ф 8111 а 4 Линию влияния усилия в раскосе фермы жесткости данной комбинированной системы можно построить по линии влияния поперечной силы (Щ, разделив все ее ординаты на (соз ф зта).
110
По методу нулевой точки проводим левую прямую параллельно осевой линии стержня 1—2, наклоненной под углом ф, до пересечения с правой прямой Ъсх в точке Р2 отложив на левой опорной вертикали
ординату соединим ее крайнюю точку с нулевой точкой Р —
получим первую правую ветвь; левая ветвь линии влияния В2 параллельна первой правой, ветви (рис. 91, в).
Цепь с балкой жесткости
Цепь с балкой жесткости представляет собой висячую систему, жесткость которой усилена благодаря введению балки (рис. 92, а). Цепь шарнирно-стержневого многоугольника работает лишь на растя-
Рис. 92
жение, что представляет большое преимущество по сравнению с аркой в виду меньшей затраты материала. Для усиления цепи вводится балка жесткости, воспринимающая изгибающие моменты и поперечные силы.
Ш
Особенность данной комбинированной системы по сравнению с предыдущими системами состоит в том, что опоры балки жесткости аг и Ьх отделены от опор цепи (точки 0 и 7). Эта система получена заменой стержней ах — 1 и Ъх — 6 соответственно стержнями 0—1 и 7—6. Горизонтальная проекция усилия в любом наклонном элементе цепи по доказанному выше свойству цепи стержней с вертикальными подвесками равна усилию Я в горизонтальном элементе цепи 3—4. То же значение имеет и горизонтальная реакция полной опорной реакции цепи. Проведем теперь разрезы опорных элементов цепи 1—0 и 6—7 и разложим усилия 501 и Зв7 соответственно на Уа, Н и VI, Н в точках пересечения, вертикалей, проведенных через ах и Ьх, и осевых линий 1—0 и 6—7. Со стороны опор балки жесткости возникают только вертикальные реакции, которые обозначим Уа и Уь соответственно.
Докажем, что сумма реакций Уа и Уа дает вертикальную реакцию Уа простой балки (аналогично сумма реакций Уь и VI дает вертикальную реакцию Уь простой балки). Составим общее уравнение равновесия системы в форме суммы моментов сил относительно точки Ь:
%МЬ 0.
В развернутом виде получаем
(Уа Уа)1-Рр 0,
откуда
УаГ Уа.
Имеем выражение левой реакции двухопорной простой балки Уа. Итак, доказано соотношение
Уа УаУа- (6.9)
Аналогично
Уь Уь Уь (6.9)
Выразим вертикальные реакции опорных стержней цепи Уа и Уь через распор Я. Так как горизонтальные проекции усилий 501 и 567 равны Я, то вертикальные их проекции будут:
У"а Н1ё рог; У; Я§ф67.
Таким образом, из выражений (6.9) и (6.9) получаем следующие выражения У а и Уь:
Уа Уа-Н 18 Фоь Уь Уь-Нё ф67. (6.10)
Задача сводится к отысканию распора. Для нахождения распора проводим разрез через шарнир с балки жесткости и горизонтальный элемент цепи 3—4 усилие в последнем и равно Я. Рассматривая равновесие левой части системы по проведенному разрезу и составляя сумму моментов всех сил относительно точки с, получаем
(Уа Уа)12-Щ 0,
112
откуда
и (К Уа) I Уа1 М
П ‘ 2 2 (
Распор в цепи определяется как отношение балочного момента Мс к стреле — понижению точки с относительно линии фиктивных опор аЬ (рис. 92, а). Следовательно, линия влияния распора цепи Н может быть найдена как линия влияния распора перевернутой трехшарнирной арки, опоры которой расположены в точках а и Ь, а ключевой шарнир — в точке с. Это позволяет просто решать все задачи определения усилий Мк и в балке жесткости и ее опорных реакций.
Линия влияния реакции Уа. Эту линию влияния можно получить, исходя из аналитического выражения (6.10):
УаУа-Н 1ёфо1.
Согласно этому выражению поступаем так: на график линии влияния Уа накладываем график линии влияния Н р01; в результате получаем линию влияния Уа (рис. 92, б). Ту же линию влияния можно построить способом нулевой точки. Находим то положение груза Р 1 (очевидно, на левом диске балки жесткости), при котором У’а 0 и, следовательно, полная левая реакция направлена по линии оси стержня 0—1. Продолжая. линию 0—1 до пересечения с линией Ъс получим то положение груза, при котором Уа 0 (точка Р0). Отложив на левой опорной вертикали ординату, соединяем крайнюю ее точку с нулевой точкой Р0 — получаем первую ветвь линии влияния; по этой ветви находим вторую ветвь, пользуясь наличием ключевого шарнира с
Линия влияния момента Мк. Построим линию влияния момента Мк в сечении к балки жесткости. В этом сечении возникают лишь момент Мк и поперечная сила (к. Проведя разрез балки жесткости в точке к и далее разрез элемента цепи 1—2 в точке к, разложим усилие 512 на две составляющие Н и Я1§ ср12. Составляя сумму моментов левых сил относительно точки к при грузе Р 1 справа, получаем
Мк Уа Уа) ак — Нук Уаак — Нук или окончательно
Мк М%-Нук. (6.11)
Момент в сечении балки жесткости находится так же, как и момент в сечении к перевернутой трехшарнирной арки аксЪ. Проведя линии ак и Ъс в пересечении их получим точку Ру а по ней найдем нулевую точку Р. Теперь обычным путем строим линию влияния Мк согласно известному правилу построения линии влияния арочного момента (рис. 92, в).
Линия влияния поперечной силы Ск. Линию влияния 0,к в сечении балки жесткости к строим по выражению для
113
нее, которое получаем, проектируя все левые силы на вертикаль:
Ч У.-НЧъ,-- (6.12)
Нулевая точка линии влияния С1к будет под точкой Рг (из точки а ведем линию, параллельную оси стержня цепи 1—2, до пересечения с линией Ьс).
На левой опорной вертикали откладываем ординату 1 • 1
(рис. 92, г). Соединяя крайнюю ее точку с точкой Р[, получаем первую правую ветвь. Левая ветвь линии влияния (2 параллельна, как обычно, первой правой ветви.
§ 34. ПОНЯТИЕ О ВАНТОВЫХ ФЕРМАХ И ИХ РАСЧЕТ
Вантовыми фермами называют такие геометрически неизменяемые шарнирно-стрежневые висячие системы, все элементы которых при суммарном воздействии постоянной и временной нагрузок основного направления получают лишь растягивающие усилия. Стержни таких ферм могут быть изготовлены из гибких стальных тросов — вант, почему эти фермы и называют вантовыми. Добиться возникновения во всех стержнях лишь растягивающих усилий при совместном действии постоянной и временной нагрузок возможно лишь при выборе определенного очертания поясов этих ферм и наличии относительно небольшого динамического эффекта временной нагрузки.
На рис. 93, а представлена схема простой вантовой фермы одного из мостов, построенных в СССР. В основе этой системы лежит перевернутая трехшарнирная арка, составленная из двух дисков-треугольников айс и Ьесу каждый из которых поддерживает по е радиальные фермы, состоящие из трех треугольников. Диски I и II связаны между собой ключевым шарниром и опираются на опоры двумя стержнями каждый, что равносильно наличию двух шарнирно неподвижных опор в точках а и Ь.
Таким образом, система представляет собой висячую трехшарнирную ферму, особенность которой заключается в том, что все стержни составлены из вант и работают на растяжение. К узлам нижнего пояса фермы посредством стоек подвешена разрезная проезжая часть. Усилия в стержнях радиальной фермы легко определяются путем вырезания узла и применения способа нулевой точки.
Так, для построения линии влияния поставив груз Р 1 в точку су установим, что работают лишь стержни и О;. Разложив силу Р 1 на направления и из силового треугольника (рис. 93, б) определим ординату линии влияния %. Затем находим нулевую точку Р1У продолжая направления 02 и 0. Соединяя верхнюю точку ординаты % и нулевую точку Р19 получаем первую правую ветвь до пересечения с вертикалью, проведенной через узел Л. Левая ветвь определяется ординатой под точкой й и нулевой точкой а,
114
Аналогично строим линию влияния 02, получая ординату т2 с помощью силового треугольника (рис. 93, в) и нулевую точку Р2 в пересечении усилий и 1)х.
Кроме определения растягивающего усилия (загружением временной нагрузкой положительного участка и всей линии влияния собствен¬
ным весом), необходимо отдельно загрузить временной нагрузкой отрицательный участок линии влияния и выяснить, не возникает ли (после добавления усилия от постоянной нагрузки) сжимающее усилие в стержне, которое не может быть воспринято вантой.
ГЛАВА 7. ТЕОРИЯ ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ
§ 35. ПЕРЕМЕЩЕНИЯ. РАБОТА ВНЕШНИХ СИЛ
Понятие о перемещении. Действительная работа внешних сил
Перемещения, вызванные деформацией элементов конструкции, определяют для проверки жесткости и устойчивости, а также для расчета статически неопределимых конструкций. Усилия в лишних
115
а)
р
1
1
Г
2
Ф
связях статически неопределимой системы находят, используя дополнительные уравнения деформаций, которые выражают соотношения между перемещениями и внешними силами. Поэтому теория определения перемещений стержневых систем имеет большое значение.
Рассмотрим общие методы нахождения перемещений, которые базируются на теории работы сил, приложенных к упругой системе. В основу определения перемещений в сооружениях кладем принцип
возможных перемещений для дефор мируемой системы.
Перемещением данной точки сооружения называется изменение ее координаты, вызванное деформацией сооружения. Будем определять перемещения в линейно-деформируемых системах, подчиняющихся закону Гука и принципу наложения, согласно которому результат действия системы сил равен сумме результатов действия отдельных сил. Далее в ряде задач, помимо перемещений отдельных точек оси сооружения (простых перемещений), будем находить так называемые групповые перемещения системы точек, представляющие собой совокупности перемещений ряда заданных точек сооружения.
Будем различать действительные и возможные перемещения, для силы Р. Под действительным перемещением понимаем перемещение, вызванное силой Р (рис. 94, а). Оно, согласно закону Гука, прямо пропорционально силе: Дрр кРу где к — коэффициент пропорциональности.
Рассмотрим статическое приложение силы, меняющейся от нуля до окончательного значения Р. Промежуточное значение силы обозначим РХУ а соответствующее ему перемещение Ах (рис. 94, б). При изменении силы на с1Рх получим приращение в прогибе ААХ и элементарную работу внешней силы:
бТр Рх йАх.
Полная работа силы при ее изменении от 0 до Р будет определяться интегралом
Тр Рхй Д„ (а)
116
где согласно закону Гука
Ах — кРх; йкх кйРх,
к — постоянная [для данной задачи к •
Подставляя выражение сЛх в выражение работы силы Р, получаем
ТркРх1Рх кР-. (7.1)
О
Действительная работа внешней силы Р равна половине произведения силы на перемещение точки ее приложения по направлению
силы (теорема Клапейрона). Эта работа внешней силы переходит
в потенциальную энергию деформации сооружения (работу внутренних сил, действующих на элементы сооружения). При наличии ряда сил Р1У Р2., Рп полная работа внешних сил будет
Тр42ЛА« (б)
Так как работа внутренних сил в линейно-деформируемой системе зависит только от начального и конечного состояния ее, то работа внешних сил не зависит от последовательности приложения внешних сил.
Возможное перемещение. Возможная работа внешних сил
Под возможным перемещением будем понимать весьма малое перемещение точки оси сооружения, допускаемое имеющимися связями и независящее от заданной системы сил.
Для конкретности представления возможных перемещений, не зависящих от заданной системы сил Р, рассмотрим процесс приложения двух систем сил в последовательные интервалы времени (рис. 95, а). Пусть на сооружение в первой стадии действует сила Р, приложенная статически и меняющаяся от нуля до конечного значения Р. При этом вертикальное перемещение точки приложения силы Р, которое обозначим Дрр, является действительным перемещением
Положим, что после действия силы Р на сооружение в указанном деформированном состоянии действует также статически новая сила К, которая вызывает дополнительные перемещения точек оси балки (на рис. 95, а заштрихованы). При этом точка приложения силы Р получает добавочное перемещение ДрА, величина которого соответствует окончательному значению силы К. Так как первоначальные перемещения, вызванные силой Ру считаем малыми, то добавочные перемещения, вызванные силой К,.можно определять от недеформированного состояния и потому их можно считать независимыми от силы Р. Перемещение обозначаем буквой Д а двумя индексами — ДрЛ: первый индекс р отмечает точку приложения и направление перемещения,
117
соответствующего силе Р второй индекс к указывает на причину, вызывающую данное перемещение (сила К). Перемещение ДрЛ, вызванное
в той же системе иной сир лой К, будет возможным
перемещением для силы Р.
Рассмотрим теперь понятие о возможной работе силы Р. Возможной работой силы называем работу этой силы на малом возможном перемещении точки приложения силы по ее направлению; для силы Р (рис. 95, а) возможной будет работа силы Р на возможном перемещении Арк, ремещение Д
от силы Р, то работа силы Р выразится простым произведением силы Р на перемещение Арк:
Ткр РАрк. (7.2)
Так как Арк не зависит от силы Р, то состояние действия силы К можно представить отдельно от состояния действия силы Р. На рис. 95, б показаны два независимых состояния одной и той же балки. Первое состояние — силовое, состояние действия заданной нагрузки Р и второе состояние — возмож-
Так как перк не зависит
Рис. 95
иое, состояние перемещение Д
действия силы К, на котором отмечаем возможное
рк
Пользуясь этими состояниями, можно определить возможную работу силы К второго состояния на перемещении по направлению этой силы в первом состоянии, т. е. на Акр:
Ткр Ккр-
(7.2)
Выражение для полной работы при последовательном загружении балки силой Р, а затем силой К (рис. 95, а) будет
ТР РАрь К
кк
(в)
118
Если изменить порядок приложения сил, а именно сначала приложить силу К, а затем силу Ру то получим следующее выражение для полной работы (рис. 95, в):
Т2 К КАкр Р. (г)
Но от порядка приложения сил величина работы не меняется. Приравняв выражение (в) выражению (г), получим:
РАрк КАрк. (7.3)
Равенство (7.3) формулирует теорему о взаимности возможных работ внешних сил.
Из предыдущего видно, что выражения возможной работы справедливы,.если:
1) заданная нагрузка в силовом состоянии вызывает малые перемещения (не только при расчете по недеформированному состоянию, но и в других случаях, например, при продольно-поперечном изгибе);
2) нагрузка в возможном состоянии также дает лишь малые перемещения, соответствующие связям системы (причиной, вызывающей перемещения, может быть не только нагрузка К, но также температура и осадка опор).
Определим возможную работу системы сил Р19 Р2 и Р3 для какоголибо сооружения (рис. 96, а). Возможное состояние сооружения от действия сил представлено на рис. 96, б. Возможные перемещения по направлениям сил Рг, Р2 и Р3 соответственно будут ДР1, АР2к и АРзк.
По принципу наложения возможная работа системы сил будет найдена как сумма работ каждой силы первого состояния на перемещениях точек их приложения во втором состоянии:
Трк Р Д Рхь Р 2 Дрй "Ь Р з (7 • 4)
И9
Вообще при наличии п сил возможную работу внеших сил можно представить выражением
Трк Р-Др,ь (7-5)
1 1
где Лр Л — возможное перемещение точки приложения силы Рь по направлению этой силы, вызванное силой К или группой сил К во втором возможном (виртуальном) состоянии.
Понятие об обобщенном перемещении
Любую систему сил Ръ Р2 и Р3,. можно представить как совокупность сил и принять за обобщенную силу. Такое представление позволяет переносить соотношения, выведенные для одиночной силы, на случай действия системы сил.
Поясним понятие об обобщенном перемещении на примере балки (см. рис. 96, а), подверженной действию системы сил Ръ Р2, Р3, которую характеризуем значением первой силы Рх и отношениями:
а — — • а «21 — рг, «31 рг-
Составим выражение для возможной работы внеших сил первого состояния на перемещениях по их направлению во втором состоянии по выражению (7.5) и вынесем за скобки Рх
ТрЬ Р 1рхк “Ь Р2ЬРгк Ь “ Р1 №рЬ 4“ “Ь а31 Рль) Р 1Рхк-
Здесь АР1ь можно рассматривать как обобщенное перемещение по направлению системы сил Ръ Р2, Рз-
Обобщенная сила при этом характеризуется значением и параметрами а21 и а31. Как видим, в данном случае обобщенное перемещение есть линейная функция простых линейных перемещений (см. рис, 96, б). Таким образом, возможную работу системы сил всегда можно представить в виде произведения одной обобщенной силы (определяемой каким-либо параметром системы сил) на обобщенное возможное перемещение, соответствующее данной системе сил.
§ 36. ТЕОРЕМА О РАВЕНСТВЕ ВОЗМОЖНЫХ РАБОТ ВНЕШНИХ И ВНУТРЕННИХ СИЛ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
Вывод формулы Мора
Используя принцип возможных перемещений применительно к упругим системам, получаем основное соотношение между возможной работой внешних и внутренних сил одного и того же состояния сооружения и общую формулу для определения перемещений.
120
Согласно принципу возможных перемещений для несвободной материальной системы., подчиненной идеальным связям, сумма работ всех сил, находящихся в равновесии, на любых малых возможных перемещениях равна нулю, что является необходимым и достаточным условием равновесия такой системы. Для деформируемой системы в аналитическом выражении начала возможных перемещений следует учесть работу как внешних, так и внутренних сил сопротивления деформации. Рассмотрим два состояния данного сооружения.
В первом состоянии (рис. 97, а) заданы внешние силы Рг Р2 и для любого бесконечно малого элемента сооружения длиной дк известны внутренние силы: изгибающий момент Мр9 поперечная сила и продольная сила (на рисунке указаны положительные их направления). Внутренним силам, действующим на элемент, отвечают противоположные по направлению и равные им внутренние силы сопротивления деформации
МрМр, Мр : N р»
Во втором возможном состоянии представим малые перемещения системы, вызванные действием какой-либо силы К (рис. 97, б). При этом каждый бесконечно малый элемент сооружения получает изменение
121
формы, соответствующее общему случаю действия сил (изгиб, сдвиг и растяжение). Пусть перемещения точек оси сооружения по направлению внешних сил Р1У Р2» ••• Рь во втором состоянии будут АРгк9 АРгку., Ар. Представим возможные перемещения, вызванные деформацией элемента по направлению внутренних сил сопротивления деформации (например, для моментов Мр— угол наклона соседних сечений йук рис. 97, б). Обозначим возможную работу внешних сил Р через Трк, а возможную работу внутренних сил сопротивления деформации Мр, р и через Урк. Тогда согласно началу возможных перемещений для сил первого состояния можно написать
Тркурк О, (7.6)
Трк — 1 Рг Рк- (я)
I состояние
к Л состояние
где
Л состояние
Но работа внутренних сил сопротивления деформации Мр, С[р и №р (рис. 98, а) как сил, равных по величине, но противоположных по направлению внутренним силам Мр, й Nр равна по величине, но противоположна по знаку возможной работе внутренних сил Мру (р и Ыр. Обозначая последнюю УРрку составим равенство
Урк-рк-
Подставляя значение Урк из последнего соотношения в выражение (7.6) и перенося №рк в правую часть, получаем
Трк №рк, (7.7)
т. е. возможная работа внешних сил Р первого состояния на перемещениях точек их приложения и по их направРис. 98 лению во втором состоянии равна
возможной работе внутренних сил первого состояния Мр, Nр и С?р на перемещениях по их направлению во втором состоянии. Эта теорема носит название основной теоремы строительной механики статически неопределимых систем. В наиболее общей форме она была сформулирована О. Мором (1874 г.). Левая часть соотношения (7.7) определяется по формуле (а).
Дадим теперь аналитическое выражение возможной работы внутренних сил для рамной системы, составленной из призматических
Л состояние
122
элементов. При этом внутренние силы берем из первого состояния (рис. 98, а), а перемещения по направлению внутренних сил — из второго состояния (рис. 98, б, в, г). Возможную работу внутренних сил для прямолинейных стержней можно определить, суммируя отдельно работу моментов, поперечных сил и продольных сил, т. е. применяя принцип сложения
Для брусьев большой кривизны такое разделение невозможно, так как при действии моментов возникает и удлинение по оси; а при действии продольных сил — взаимный поворот сечений.
Находим сначала возможную работу моментов Мр, приложенных к бесконечно малому элементу (см. рис. 98, а), на перемещениях во втором состоянии, вызванных деформацией элемента вследствие чистого изгиба (см. рис. 98, б). При этом по направлению каждого из моментов совершается поворот сечений, ограничивающих элемент,
на угол, где с1(рк — взаимный угол поворота соседних сечений
элемента во втором состоянии, вызванный действием внешних сил К. При этом совмещаем деформированный элемент с его начальным положением. Возможная работа левого момента Мр будет равна
правого момента Мр — также Мр, причем каждое из этих значений положительно. Таким образом, работа моментов, приложенных к соседним сечениям бесконечно малого элемента сооружения, будет
ЯР(“р) Мр Мр Мр1чк, (б)
т. е. возможная работа моментов Мр, приложенных к соседним сечениям элемента, равна произведению величины момента Мр на взаимный угол поворота сечений йф.
Для упругой области взаимный угол поворота соседних сечений йуь можно выразить согласно закону Гука линейно, через момент, возникающий во втором состоянии и действующий по граням того же элемента (см. рис. 98, б):
. МьС(8
йЧь ПП
где Е1 — жесткость при изгибе;
I момент инерции сечения.
Подставляя значение с1(рк в соотношение (б), получаем
ау1“г)мраркмрмк-.
Всю работу изгибающих моментов получим интегрированием элементарной работы по всей длине сооружений
Кмр) --2 5 мр 2 мрм ш - 7-9
о о
123
где каждый интеграл берется по длине непрерывного изменения подынтегральной функции.
Теперь определим возможную работу продольных сил. Найдем сначала элементарную работу продольных сил Ыр первого состояния (см. рис. 98, а) на перемещениях точек из приложения во втором состоянии (см. рис. 98, в). Возможным перемещениям для каждой продольной силы NР будет продольное перемещение центра тяжести сечения. Если обозначить абсолютное удлинение элемента во втором состоянии через дкк, то продольное перемещение центра тяжести каждого сечения составит Аку а потому выражение возможной работы продольных сил N р, приложенных к бесконечно малому элементу, будет
(в)
т. е. возможная работа продольных сил, приложенных к центрам тяжести соседних сечений А и В, равна произведению величины продольной силы Nр на изменение расстояния между точками А и В (удлинение элемента). Для упругой деформации во втором состоянии согласно закону Гука
Nк йз
и А к,
где ЕР — жесткость при продольном действии силы;
Р — площадь поперечного сечения.
Элементарная работа продольных сил
с]%р) NраXк NрNкр.
Возможную работу продольных сил для всего сооружения получим интегрированием
5 5
КУ2 5 мри4вг (7Л°)
о о
Определим возможную работу поперечных сил. Для этого представим во втором состоянии такое изменение формы элемента, при котором происходит возможное перемещение по направлению сил т. е. взаимный сдвиг соседних сечений, что осуществимо лишь при действии на элемент поперечных сил 0к (см. рис. 98, г). Обозначим взаимный сдвиг центров тяжести соседних поперечных сечений элемента с1уг (сдвиги по высоте сечения меняются неравномерно, и эта особенность их изменения далее будет учтена введением коэф фициента неравномерности сдвигов (х). Совмещая деформированное положение элемента с начальным, находим, что вертикальное смеще
ние центра тяжести каждого сечения будет у йук.
Сопоставляя первое состояние элемента (см. рис. 98, а) с его вто рым состоянием (см. рис. 98, г), получаем следующее выражение воз
124
можной работы поперечных сил, приложенных к бесконечно малому элементу:
кр)ррарЛук. (Г)
Для упругой области, принимая во внимание неравномерность сдвигов по сечению, взаимный сдвиг центров тяжести поперечных сечений можно представить следующим образом:
(Д)
гДе [х — коэффициент неравномерности сдвигов по сечению, зависящий от формы сечения (для прямоугольного сечения л 1,2), определяется из условия равенства работы поперечной силы С?, приложенной в центре тяжести сечения, сумме работ отдельных тангенциальных усилий ткйР, распределенных по сечению; значения коэффициентов 1 в дальнейшем не используются, так как влиянием поперечных сил, как правило, пренебрегаем; О — модуль поперечной деформации (можно принимать 0 Е. Внося выражение (1ук по формуле (д) в формулу
(г) и интегрируя, получаем возможную работу поперечных сил1 для всего сооружения:
71
О О
Подставляя выражения возможной работы моментов, продольных и поперечных сил в выражение (7.8), получаем аналитическое выражение полной работы всех внутренних сил на перемещениях в виртуальном состоянии:
«V2 Ир р2 2
ООО
Основная теорема (7.7) может быть представлена в следующей наиболее общей форме:
2 р‘ V2 5 лмф2 5 Мр 2 5 ?• 7-12)
ООО
Эту формулировку основной теоремы можно использовать в случае, рогда перемещения возникают и в упруго-пластической области или вызываются любой причиной. Если перемещения во втором состоянии происходят в чисто упругой области, применяя закон Гука, получаем
Кратко теорему Мора можно сформулировать так: возможная работа внешних сил Р на перемещениях по их направлению равна возможной работе внутренних сил Мр, Лр, 0Р на соответствующих им перемещениях в той же системе.
Потенциальная энергия системы
Соотношение (7.13) легко распространить на действительную работу внешних и внутренних сил, т. е. на работу сил, которая производится на вызываемых ими перемещениях. Принимая во внимание статическое действие внешних и внутренних сил, а именно нарастание перемещений в соответствии с ростом сил, во всех членах соотношения (7.13) нужно ввести коэффициент 12; кроме того, необходимо учесть, что йуь бфр» (1ь Ук АуР-
52532да 7
ООО
Правая часть выражения (7.14) соответствует потенциальной энергии УРр бруса при поперечном изгибе и растяжении. Это выражение легко распространить и на более общий случай.
§ 37. ТЕОРЕМЫ О ВЗАИМНОСТИ РАБОТ И ВЗАИМНОСТИ ПЕРЕМЕЩЕНИЙ Теорема о взаимности работ внешних и внутренних сил
Одним из основных положений теории работы упругих сил является теорема о взаимности возможных работ внешних сил. Выведем ее теперь непосредственно из теоремы Мора, сформулированной соотношением (7.13).
Рассмотрим два силовых состояния одной и той же конструкции (рис. 99). Внутренние силы и деформации в первом силовом состоянии обозначим соответственно:
Мру N ру
(1ру йур.
Внутренние силы и деформации во втором силовом состоянии
С1ь
С?фй, Ук
Составим уравнение работ по принципу возможных перемещений на основе выражения (7.13) для сил первого состояния, выбирая за возможные перемещения второго состояния:
Теперь поменяем указанные два состояния, рассматривая силы второго состояния, а возможные перемещения по их направлению возьмем из первого состояния:
СР
(б)
Но правые части равенств (а) и (б) равны между собой (взаимность работ вну.тренни х сил очевидна). Следовательно, равны и левые части этих равенств:
(7-15)
Соотношение (7.15) можно прочитать так: возможная работа внешних сил первого состояния Р данной конструкции на перемещениях во
Р
%?
" МР Ы1
I состояние "р"р,0р
Л состояние
лР,ь
Рис. 99
втором состоянии равна возможной работе внешних сил второго состояния К на перемещениях первого состояния. Полученное соотношение носит название теоремы Бетти, которая, как видно из вывода, справедлива лишь для линейно-деформируемых упругих систем.
Теорема о взаимности перемещений
Рассмотрим вновь два силовых состояния какой-либо конструкции (рис. 100). В первом состоянии к произвольной точке т системы приложена сила Р, во втором состоянии — к точке п сила К. Применим
к этим двум состояниям теорему о взаимности работ:
РАрП КАьР. (7.16)
Положим теперь, что силы Р и К численно одинаковы, т. е. Р К. Тогда из равенства (7.16) получаем
ЛрЛр. (7.17)
127
Это теорема Максвелла о взаимности перемещений: перемещение точки п от силы Р первого состояния, действующей в точке т, численно равно перемещению точки т от силы К второго состояния, действующей в точке п, если силы Р и К количественно одинаковы. Иначе говоря, перемещение по направлению первой силы Арк от второй силы К численно равно перемещению по направлению второй силы Акр от первой силы Р, если Р К.
Теорема Максвелла позволяет упростить вычисления перемещений; если мы знаем какое-либо перемещение Др, то известно и рк: величина перемещения не меняется от перестановки индексов, если численно равны силовые воздействия.
Пользуясь этой теоремой, легко получить линии влияния усилий в статически неопределимых системах путем построения линий прогибов. Этот способ основан на способе построения линий влияния перемещений (рис. 101). Пусть требуется найти линию влияния вертикального перемещения точки к при движении груза Р 1 по балке. В дальнейшем будем обозначать перемещение точки к, вызванное единичной силой Р 1, через 8кр в отличие от перемещения Ккру вызванного силой Р, не равной единице. Необходимо найти перемещение точки к, вызванное силой Р 1, т. е. 8кр при различных положениях груза Р 1 на балке. Заменим построение линии влияния перемещения Ькр нахождением эпюры прогибов Ьрк. В самом деле, согласно теореме о взаимности перемещений
®кр - рк
где 8рк — перемещение по направлению силы Р, вызванное неподвижной силой К 1, приложенной к точке к. Строя эпюру перемещений брА, тем самым определяем линию влияния 6кр. Итак, линия влияния прогиба в точке к получается как эпюра прогибов от силы К 1, приложенной в точке к.
1 состояние
Р.Дкр л-р п
1
1
1
1
1
1
Л состояние
1
1
к
т
П
-Д.
ЛР
Рис. 100
128
§ 38. ОБЩАЯ ФОРМУЛА ДЛЯ ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ
Вывод формулы для определения перемещений
Важнейшим приложением выведенной основной теоремы является общая формула для определения перемещений различных сооружений. Пусть требуется найти перемещение какой-либо точки сооружения по определенному направлению от заданной нагрузки (рис. 102, а). Эту задачу можно решить путем вычисления возможной работы внутренних сил второго состояния того же сооружения на перемещениях в заданном состоянии. Рассмотрим вспомогательное (единичное) состояние конструкции (рис. 102, б). В этом состоянии к сооружению, освобожденному от заданной нагрузки Р9 в точке к по
направлению искомого перемещения приложим соответствующую единичную силу К 1 (для линейного перемещения — сосредоточенную силу, для угла поворота — момент и т. д.). Единичное второе состояние будем рассматривать как силовое, а за возможное примем состояние действия заданной нагрузки Р. Так как сила К 1 выбрана по направлению искомого перемещения Акр, то работа силы К 1 на перемещении в первом состоянии будет -Акр.
В единичном состоянии для любого бесконечно малого элемента балки имеем внутренние силы Мк, №к и (к (черта означает, что внутренние силы вызваны силой К, равной единице).
В первом состоянии по направлению внутренних сил Мк, Ык и (±к происходят перемещения Лрр, Дкр, Аур, где йцр — взаимный угол наклона соседних сечений; акр — абсолютное удлинение элемента, с1ур — взаимный сдвиг соседних сечений.
Применяя теорему о равенстве возможной работы внешних сил второго состояния на перемещениях в первом состоянии — возмож¬
5 Н. К. Снитко
129
ной работе внутренних сил второго состояния, получаем
Перемещение Акр легко находится по правой части выражения (7.18), т. е. по величине возможной работы внутренних сил единичного состояния на перемещениях в действительном состоянии. Для упругого состояния сооружения выражаем деформации элемента через внутренние силы первого состояния по закону Гука:
Лр р
Мрс1з
ЁГ
ак
N рйв (ЗрЛз
: ЕР ’ Чр ОР •
Подставляя эти значения деформаций в правую часть выражения (7.18), получаем
кр(5
ОР •
(7.19)
Г
Мы получили общую формулу Мора для определения перемещения Акр т заданной нагрузки Р в упругой области работы сооружения. Этой формулой широко пользуются для отыскания упругих
перемещений любых пло ских стержневых конструк¬
ций: балок, рамных систем, арок и ферм.
Согласно формуле (7.19) подсчет любого перемещения сводится к вычислению определенных интегралов правой части, т. е. X возможной работы внут ренних сил единичного состояния на перемещениях в действительном состоянии.
Знак перемещения Акр определяется по знаку пра вой части, т. е. по знаку
возможной работы внутренних сил. Если правая часть выражения (7.19) дает знак «плюс», это означает, что работа силы К 1 на перемещении Акр положительна, т. е. перемещение Акр происходит по направлению действия силы К 1. Произведение МкМр считаем положительным, если моменты Мк и Мр вызывают растяжение крайних волокон с одной и той же стороны оси стержня. При построении эпюр моментов будем откладывать ординаты этих эпюр со стороны растянутого волокна стержня. Условимся всегда в единичном состоянии прикладывать силу К 1 отвлеченного изме¬
130
рения. Тогда левая и правая части выражения (7.19) дают величины,имеющиету же размерность, что и размерность искомого перемещения; при этом в правой части усилия ф и Ык при действии сосредоточенной силы К 1 будут выражены в отвлеченных единицах.
Формулу Мора для пространственного ломаного бруса, изображенного на рис. 103, можно получить, развивая соответственно выражение возможной работы внутренних сил.
Кроме изгибающих моментов в вертикальной главной плоскости Мр% в, в данном случае возникают изгибающие моменты в горизонтальной главной плоскости Мр г и крутящие моменты относительно оси каждого данного прямолинейного элемента бруса Мр ос. Пренебрегая влиянием поперечных сил, учтем, кроме указанных моментов, еще продольные осевые силы. При этом формула Мора для определения какого-либо перемещения точки к будет иметь следующий вид:
5 5
ьд2§ а.вМр.в-25 мк,гмр,гв
о г о в
5 5
2 5 Мк,осМр,осщ- 2 5 (7.19)
о кр о
где г, в — моменты инерции соответственно относительно горизонтальной и вертикальной главных осей сечений;.
О — модуль сдвига;
Лр — момент инерции кручения;
Ыру ос — продольная сила от заданной нагрузки Р;
ос — продольная сила в состоянии действия силы К 1, которую следует представлять во втором состоянии.
Формула для определения перемещений в частных случаях
Для плоских балок и рам при отношении высоты сечения к пролёту менее 15 можно отбросить влияние поперечных и продольных сил на величину перемещения и определять его по формуле
VI Г МкМр(1з
2 5 -1Г- 7-20
Для строительных арок малой кривизны (радиус кривизны более 5г, где к — высота сечения) перемещения с достаточной точностью определяются по формуле (7.19), выведенной для прямолинейных стержней. Для обычных пологих арок влияние поперечных сил на перемещения незначительно и им можно пренебречь; поэтому перемещения пологих арок мокно определять, учитывая лишь влияние
б
131
моментов и продольных сил:
МкМрйз
ЁГ
(7.21)
Для шарнирно-стержневых ферм при узловом действии нагрузки формула (7.19) значительно упрощается, так как исключаются члены
с влиянием М 0, (рис. 104, а, б). Поэтому вместо выражения (7.19) получаем
ЧР
(7.22)
где знак 2 распространяется на все стержни фермы.
Так как по длине каждого стержня фермы 5 продольные силы №к и и площадь сечения Р постоянны, то в правой части можно вы-
- 1 5 нести за знак интеграла и. Учтя также, что йз8, окон-
0
чательно для перемещения узловых точек шарнирно-стержневых ферм найдем _
(7-23)
(п)
где знак 2 относится ко всем стержням фермы.
Заметим, что, зная проекции вектора перемещения А какого-либо узла Ь фермы (рис. 104, в), представляющие собой удлинения стержней ЬЬ и ЬЬ", само перемещение находим, восставляя перпендикуляры к концам проекций вектора.
132
§ 39. УПРОЩЕНИЕ ТЕХНИКИ ВЫЧИСЛЕНИЯ ПЕРЕМЕЩЕНИЙ В БАЛКАХ И РАМАХ
Правило перемножения эпюр
Перемещения в балках и рамах определяем по формуле
кр
Е1
Обычно по длине данного стержня рамы жесткость стержня по-
1
стоянна, поэтому можно вынести за знак интеграла:
±кр
МкМр(1х.
Можно упростить вычисление интеграла функции МкМр в случае, если момент Мк в единичном состоянии подчиняется линейному затону, т. е. если эпюра моментов Мк по длине стержня ограничена прямой. Такой линейный закон изменения момента Мк в единичном состоянии действия сосре¬
доточенных воздействии и имеет место для рамных систем с прямолинейными стержнями. В этом случае, когда Мр — любая функция, а Мк — линейная функция, интеграл
8
8 )МкМрйх (а)
можно вычислить как произведение площади криволинейной или ломаной эпюры моментов - Мр на ординату прямолинейной эпюры Мк, взятую под центром тяжести эпюры моментов Мр.
Рассмотрим два состояния какого-либо стержня
1 состояние
Рис. 105
рамной конструкции (рис. 105). В первом состоянии построена эпюра моментов Мр от заданной нагрузки, которая очерчена произвольной кривой; ординату этой эпюры в любой точке обозначим ух. Во втором состоянии эпюра моментов Мк прямолинейна; О — точка пересечения линии моментов с осью стержня; ординату эпюры мо¬
133
ментов Мк в произвольной точке на расстоянии х от начала координат О обозначим у2. Вместо выражения (а) получаем
5
8 угу1с1х. (б)
О
Ординату у2 можно выразить через абсциссу х, введя угол наклона а линии моментов Мк к оси стержня:
у2 §а-х.
Вместо выражения (б) получим
5
5 а ■ х (ух). (в)
О
Но а — величина постоянная; кроме того,
уг (1х ар,
где — площадь элементарной полоски эпюры моментов Мр. Вместо выражения (в) теперь получаем
5
5 1бхййр- (г)
О
Интеграл § х др — статический момент площади эпюры моментов Мр
о
относительно точки О. Статический момент площади эпюры моментов Мр относительно точки О равен произведению всей площади эпюры моментов Мр, т. е. йр, на координату центра тяжести этой площади х0. Теперь вместо (г) получаем
5 а • х0р. (д)
Но согласно рис. 105
1а-х0 ук,
где ук — ордината эпюры Мк, взятая под центром тяжести эпюры Мр. Таким образом, окончательно из выражения (д) имеем
5 (7.24)
5
Интеграл МкМрх в случае, если Мк — линейная функция, можно
о
вычислить как произведение площади криволинейной эпюры на ординату прямолинейной эпюры уку взятую под центром тяжести криволинейной эпюры. Правило перемножения эпюр было дано А. Верещагиным в 1925 г.
Этот же способ применим и для случая, когда обе эпюры Мр и Мк прямолинейны; при этом сам порядок перемножения безразличен. В результате перемножения двух прямолинейных эпюр Мр и Мк,
134
представленных на рис. 106, получим:
5
МрМк йх (2ас 2Ьй ас Ьс). (7.25)
О
В скобках помещены удвоенные произведения ординат эпюр моментов, расположенных одна над другой, и ординат эпюр моментов, расположенных накрест. Формулу
(7.25) дал Мюллер-Бреслау в курсе «Графическая статика», т. II,
1905 г.
Пример. Определить горизонтальное перемещение подвижной опоры двухопорной рамы, подверженной действию равномерной нагрузки, приложенной клевой стойке (рис. 107, а). Интенсивность нагрузки р высота стойки к 2, момент инерции сечения стойки х 22) где 2 — момент инерции сечения ригеля.
Решение. Строим эпюру моментов Мр от заданной нагрузки (рис. 107, б).
Полевой стойке имеем эпюру моментов в виде параболы второй степени, по ригелю — в виде треугольника. Во втором состоянии (рис. 107, в) к подвижной споре прикладываем горизонтальную силу К 1, которая вызывает в неподвижной опоре равную ей реакцию; эпюра моментов Мк симметрична. Принимая во внимание, что площадь параболической эпюры по стойке в данном случае равна 23 к, а расстояние центра тяжести
эпюры до нулевой точки 5Л8, получим следующее значение АЛр, увеличенное в
Е1г раз:
или, подставляя 1Х 22, I 2г, находим окончательно
29 рг
24 Ех
135
Комбинированное применение формулы Мора и обобщенного уравнения упругой линии
В случае, если ригель рамы загружен сложной прерывной нагрузкой (рис. 108, а), дающей скачки в эпюрах М, ф и, способ перемножения будет слишком громоздким. Поэтому предлагается, построив эпюру моментов от заданной нагрузки, -выделить из нее со¬
ставляющую эпюру моментов только от опорных моментов и перемножить ее на единичную от силы К 1, приложенной в точке к. Тогда мы получим составляющую полного перемещения ДЛр, т. е.
ъсм0рпмк А Ар — 3 Е1 х"
о
Полное перемещение найдем как сумму
кр крЛ-Укру (е)
где укр определяется по обобщенному уравнению, предложенному автором для стержня постоянного сечения (рис. 108, б) [12];
1 а% Р3 Мст2 (а—а)I
Укр — Фо 5о зу Рс 2] 21 41 » ()
136
где 20 — начальная поперечная сила в простой балке (принимается со знаком «минус» при направлении ее вверх);
Фо — начальный угол поворота, который вычисляется из условия равенства нулю прогиба простой балки на правой опоре:
•1 Г 3
Ш [° ЗГ
рг тг
р А __ м Л. 0 3 1У1с 21
(3)
при этом расстояния до скачков в нагрузке отсчитываются от правой
опорной вертикали; положительные направления внешних сил указаны на рис. 108, б (сила Рс положительна при направлении вниз, момент Мс — против часовой стрелки).
Пример. Найти вертикальное перемещение середины ригеля рамы, загруженной по рис. 109, а, при Е сопз,
к.
Решение. Эпюра моментов от заданной нагрузки представлена на рис. 109, б. Разбивая эту эпюру моментов на шесть простейших и «перемножая» ее на единичную (рис. 109, в), получим по формуле (7.20) с использованием формулы (7.24)
_ 7 РАЗ
кр 384 ‘ Е1 •
Теперь применим решение (е). Перемещение от опорных моментов по эпюрам рис. 110, а и 109, в
; _ (Н_ Н 5_ РН _ _ 5 ЯЛ
кР 4 2 ] 16 ’ Е1 128 ’ Е1
137
Для двухопорного ригеля по рис. 110, б, пользуясь формулой (з), находим:
_Рк4ъ 1 (т) 1 (т) пу 1] 6№
Е1 8 ’ 6 6 2 2 2) 24“96ЕГ
По обобщенной формуле (ж) получаем
,, ‘ ь (Иг 111 -
2 Е1 6 6 “48Е
Полное перемещение
_ _ 5 ЯА ЯЛ3 _ 7 РА®
% 128‘ Е "Г48Е- 384 • Е •
Формула Симпсона. Формула трапеций
Весьма удобны для определения перемещений в случае переменного момента инерции сечения формулы приближенного определения интегралов. Наиболее точное решение получается по формуле Симпсона, применение которой в сложных случаях определения перемещений было разработано Н. В. Корноуховым [5].
Пусть требуется вычислить перемещение путем интегрирования
ММ ч
функции ух — ■ в пределах от ачдо Ь (рис. 111):
ь _ ь
С мкмр г
3 ЁТах уйх’ (и)
а а
где 1Х — переменный момент инерции.
Разобьем интервал изменения функции (Ь — о) на п равных частей, длиной А, и заменим действительную кривую ух рядом дуг парабол второй степени, проведя их через концы каждых трех ординат:
Уо Уоъ Уъ Уъ У12 У2 • • • » Уп-Ъ Уп-1, п Уп•
138
Вычисляя площадь каждого параболического участка с основанием Л, получаем по приближенной формуле Симпсона
ь
кр Ух(х 1Г 01 • "Ь
(Уп-1 4Уп-1, п Уп)]• (7.26)
В круглых скобках помещены множители при для каждого данного
параболического участка. В такой форме удобно применять эту формулу при наличии скачка в значении какой-либо ординаты на границе участков.
По формуле трапеций (когда узловые ординаты соединяются прямыми) интеграл Мора можно приближенно представить так:
Акр Л [-а У о Ух Уъ • • • Уп-1 Уп).
(К)
Матричная форма определения перемещений
Перемещение Акр представим вместо выражения (и) в форме ь ь
( М. йв Г Ар Мк Мкйфр я» 2 М6фр
а а
— к (у М0б0 1 • Лбх 1 • М282 • • • 1 • Мп_гЬп_ Мп8, (л)
где М0, М1 М2,., Мп — изгибающие моменты в узловых точках единичного состояния;
б0 б2,., 6п — взаимные углы поворота сечений в тех же точ¬
ках от заданной нагрузки Р.
Выражение (л) можно представить по аналогии с выражением
(3.25) в матричной форме:
Д кр мт, (7.27)
где М — вектор-строка моментов в единичном состоянии (транспонированный столбец);
б — вектор-столбец перемещений, соответствующих моментам М; № — весовая матрица формулы трапеций:
У к
12
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
12
(м)
Структура матрицы № определяется формулой (л) [8].
139
§ 40. ПЕРЕМЕЩЕНИЯ, ВЫЗВАННЫЕ ИЗМЕНЕНИЕМ ТЕМПЕРАТУРЫ
Перемещения в сооружениях вызываются не только внешними силами, но и температурным воздействием. Так как в статически
неопределимых системах усилия
а)
м
возбуждаются только вследствие изменения температуры сравнительно с начальной, соответствующей моменту постройки сооружения, то в дальнейшем будем рассматривать лишь действие приращений температуры. Температурные перемещения в статически определимых изотропных системах совершаются свободно и, следовательно, не возбуждают усилий: При равномерном нагревании прямолинейного стержня (одинаковое приращение температуры А по высоте сечения) он удлиняется без осевых напряжений (рис.
и
Л
и
V
М
12
ш,
1
лШ
-А1
ш
Рис. 112
?па.с1з
Рис. 113
112, а). Абсолютное удлинение при этом будет аА, где а — коэффициент линейного расширения.
При неравномерном нагреве такого стержня (нижние волокна нагреваются на А, верхние волокна охлаждаются на А) он искрив¬
140
ляется без изгибающих напряжений (рис. 112,6). При этом, если температурное воздействие постоянно по длине стержня, искривление аналогично деформации стержня при чистом изгибе.
Выясним, как использовать формулу (7.18) для определения температурного перемещения прямолинейного стержня при неравномерном нагревании его по высоте сечения и постоянном температурном воздействии по длине. Для простоты приращения температур Д в дальнейшем будем обозначать просто через (. Пусть верхние волокна балки нагреваются на нижние волокна — на 2, причем 2 (рис. 113, а, б). При этом неравномерном нагреве стержень искривляется и удлиняется вдоль оси. Изменение температуры по толщине стержня (рис. ИЗ, в) принимаем для простоты по линейному закону. Если центр тяжести сечения находится на расстоянии сх от нижнего волокна, то температура нагрева по оси («средняя» температура) будет
2 р
0 1 с с2 »
где с — общая высота сечения.
Если центр тяжести находится посредине высоты сечения, то
4- 4- 1 — 2 1 2
о 1 2 “ 2 ’
Рассмотрим взаимное смещение соседних сечений элемента бруса при данном температурном воздействии, полагая левое сечение закрепленным неподвижно. Если первоначальное положение правого сечения элемента АВ (рис. 113, г), то после деформации оно займет положение АгВг. Удлинение верхнего продольного волокна будет а5, удлинение нижнего продольного волокна 12аЛз. При принятом линейном распределении по высоте сечения удлинение по оси будет:
Угол наклона сечения А В при неподвижном положении левого сечения определяет взаимный угол поворота сечений
Лр, - « 8 -,
где 1Г — разность температур нагрева верхнего и нижнего волокон.
Для отыскания перемещения какой-либо точки к стержня от действия температуры рассмотрим второе единичное состояние (см. рис. ИЗ, б). Приложив в этом состоянии единичную силу по направлению искомого перемещения, применим теорему Мора к силам этого состояния. За возможные перемещения примем температурные перемещения (см. рис. 113, а). Согласно выражению (7.18)
1 • А2 5 2 5 ад.
о о
Работа поперечной силы равна нулю ввиду отсутствия взаимных сдвигов.
141
Подставляем найденные выражения температурных деформаций элемента:
5 5
(7.28)
О о
Мы получили формулу для определения температурного перемещения при переменном воздействии температуры. Если температуры 2 и высота сечения с постоянны по длине стержня, то формула (7.28) принимает следующий вид:
5 5
А2:сМкйз2 5 а • (7-29)
6 о
_ Интегралы правой части выражают соответственно площади эпюр Мк и Мк для данного стержня в единичном состоянии действия К 1.
Рис. 114
Обозначим эти площади соответственно через и. Таким
образом, окончательно
д»2тЧ2,ая,- 7-30
Для шарнирно-стержневых ферм при равномерном нагревании каждого стержня температурное перемещение определится так:
(7.31)
где 5 — длина стержня;
0 — температура нагрева данного стержня фермы (меняется от стержня к стержню).
Правило знаков установим, как и ранее, по знаку возможной работы МкЛ% или А7кдк(9 т. е.: 1) если единичный момент Мк того же
направления, что и взаимный угол поворота сечений от температуры, произведение Мкйф имеет знак плюс; 2) если единичная продольная сила Ык вызывает растяжение, а действие температуры дает удлинение элемента то произведение Мкй%1 положительно (положительна возможная работа сил А7).
142
Пример. Определить горизонтальное перемещение подвижной опоры рамы при
действии изменения температуры, указанного на рис. 114, а. Высота сечения с
Решение. Во втором состоянии к подвижной опоре приложим горизонтальную силу К 1. По внутренним силам единичного состояния находим площади и (рис. 114, б, в) для стойки и для ригеля:
к2
4г; 1 -к.
мк 2 ’ нк
Параметры температурного воздействия: для стойки
1Г—10°; 0159;
для ригеля
1Г 30°;
По формуле (7.30) находим
20а Л2
, о 10а, 30а Н „л и [
— (15аА 2Ъак) — у— • — • у) 40аг —
40аг — 200а к — 160а к.
Первый член правой части выражает влияние удлинений оси системы, второй—влияние искривлений, вызванных моментами. Влияние температурных удлинений оси, как видим, значительно: оно составляет 20°о от перемещений, вызванных искривлением.
§ 41. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИИ ОТ ОСАДКИ ОПОР Перемещения от случайных осадок опор
Осадки опор могут быть случайными (вызванными просадкой грунта, размывом, оползнем и другими причинами) при отсутствии нагрузки на сооружении или могут возникать под действием нагрузки в результате податливости основания. Рассматривая первый случай, будем считать, что трехшарнирная арка асЬ получает одинаковые горизонтальные смещения опор Д и вертикальное смещение левой опоры Дд, причем величины смещений заданы (рис. 115, а). От действия осадок опор в статически определимой системе внутренние усилия не возникают. Часто при этом требуется определить новое положение системы. Пусть нужно найти вертикальное и горизонтальное перемещения ключевого шарнира с арки. Для определения вертикального перемещения по формуле Мора представляем единичное состояние действия вертикальной силы К 1, приложенной к ключевому шарниру арки (рис. 115, б). Составляем сумму работ всех внешних сил единичного состояния на перемещениях в действительном состоянии, когда происходит осадка опор (см. рис. 115, а), и приравниваем ее нулю, так как возможная работа внутренних сил равна нулю:
1 • Ду— VаД0 - ЯДя - Я Дя 0, (а)
откуда искомое перемещение
АуУаАа 2НАн, (б)
143
т. е. перемещение данной точки арки от осадок опор есть линейная функция осадок опор и получается как сумма возможных работ реакций единичного состояния на смешения опор в действительном состоянии.
Рис. 115
Подставляя значения реакций (см. рис. 115,6) в выражение (б), получаем
2 у • (в)
Для определения горизонтального перемещения Д точки су вызванного осадками опор, рассматриваем второе единичное состояние (рис. 115, в). Применяя теорему Мора, получаем
1. Ах— КаДа-ЯДя Нан 0,
откуда
Д VаДа -у Аа. (г)
В данном частном случае перемещение точки сооружения полу¬
чается простым перемножением реакции га на осадку опоры. Заметим, что при односторонней вертикальной осадке опор трехшарнирной арки происходит и горизонтальное смещение ключевого шарнира.
Перемещения от нагрузки, вызывающей упругие осадки
Чаще всего в практике осадки опор возникают в результате действия нагрузки при наличии упругой податливости грунтового основания, на котором расположены опоры. Пусть под действием нагрузки р трехшарнирная рама получает равные вертикальные осадки опор
Д т—, где к0 — коэффициент оседания опоры, Уа (рис. 116, а).
К о 144
Найдем вертикальное перемещение ключевого шарнира, учитывая при этом влияние только изгибающих моментов Мр (рис. 116, б). Представляя единичное состояние действия силы К 1, приложенной к ключевому шарниру с (рис. 116, в), применяем теорему Мора
к внешним и внутренним силам этого состояния, принимая за возможные — перемещения в действительном состоянии (см. рис. 116, а). Тогда получаем
СД)
откуда
V ( МьМ0с18 —
Дс2Л-ж1- 21д- (е)
где Уа V,.
145
Таким образом, перемещение нагруженного сооружения при наличии осадок опор вычисляется через возможную работу внутренних сил единичного состояния на перемещениях в действительном состоянии и возможную работу реакций единичного состояния.
§ 42. ТЕОРЕМА КАСТИЛЬЯНО И ПРИНЦИП НАИМЕНЬШЕЙ РАБОТЫ
Сначала дадим выражение для перемещения по направлению какой-либо сиды Р1 (рис. 117, а) через частную производную от потенциальной энергии (см. 7.14). В выражении потенциальной энергии будем учитывать лишь влияние изгибающих моментов.
Момент в произвольном сечении от системы сил
Мр РМх-- Р2М2-. - Р1 - • РпМп,
(7.3?)
где М1у М2у Мь Мп — моменты в единичных состояниях действия отдельных сил Р1у Р2у., Л, •••, Рп-
Частная производная от момента Мр по Р будет (рис. 117, б)
дМг
дРг
м1.
(7.33)
Дадим выражение для перемещения Д по направлению силы Рь. Согласно формуле (7.20)
м
рТГг
или, подставляя значение М-ь из выражения (7.33), получаем
что иначе можно представить так:
-2 «(•
О
По теореме о дифференцировании интеграла по параметру
(7.34)
Но в квадратные скобки заключено выражение потенциальной энергии системы №р. Следовательно, окончательно
— частная производная от потенциальной энергии (как функции внешних сил) по данной силе равна перемещению по направлению этой силы (теорема Кастильяно).
Перейдем теперь к принципу наименьшей работы. Применительно к случаю, представленному на рис. 117, а, положим, что Рг — заданная нагрузка, а Р,- Хи Рп Хп — опорные реакции промежуточных опор неразрезной балки. Тогда перемещения по направлениям сил Хи Хп будут равны нулю, т. е.
Это условие минимума потенциальной энергии как функции неизвестных X, Хп. Следовательно, усилия в лишних связях статически неопределимой системы таковы, что они соответствуют минимуму потенциальной энергии (начало наименьшей работы).
§ 43. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ПРИ ПОМОЩИ УПРУГИХ ГРУЗОВ. МАТРИЧНАЯ ФОРМА
Когда речь идет о нахождении упругой линии арки или пояса фермы — целой совокупности перемещений различных точек сооружения, применение формул (7.19) сопряжено с очень большой вычислительной работой. В арках при произвольном законе изменения момента инерции сечения и произвольном очертании оси арки интегрирование приходится заменять суммированием, графо-аналитическую интерпретацию которого представляет собой метод упругих грузов. По наглядности операций и универсальности метод упругих грузов является одним из самых эффективных для определения перемещений.
(7.35)
(7.36)
Общие выражения для упругого груза
147
Заданный криволинейный стержень заменяем ломаным, каждый прямолинейный участок которого выбираем достаточно малым. Произвольную нагрузку, действующую на криволинейный стержень, заменяем эквивалентной узловой Рп-1, Рп, Рп1 (рис. 118, а). В общем
упругая линия стержня представляет собой совокупность слабо изогнутых линий отдельных ветвей для элементов (п — 1) ч- п, п ч- (п 1), связанных условиями неразрезности в узлах. Пренебрегая местным изгибом прямолинейных элементов за малостью их длин, представляем упругую линию системы в виде ломаной. Подберем такую фиктивную сосредоточенную нагрузку, которая будучи приложена к горизонтальной условной балке давала в виде эпюры
148
изгибающих моментов искомую Ломаную линию прогибов. Если принять ломаную линию прогибов сооружения за фиктивную эпюру моментов, то вызывающая эту эпюру моментов нагрузка должна представлять собой систему сосредоточенных сил, приложенных в точках перелома эпюры моментов.
Обозначим эти фиктивные силы, располагаемые на одних вертикалях с соответствующими узлами сооружения, И7,, №п1.
Направление фиктивных сил при отыскании вертикальных перемещений должно быть также вертикальным, иначе говоря, нормальным к оси условного сооружения (горизонтальной балки). Для сооружения, опертого на две шарнирные опоры, условным сооружением является балка на двух шарнирных опорах; для сооружения, заделанного левым концом, с другим свободным концом, заделка в условном сооружении переносится на свободный конец и т. д.
Обозначим ординаты линии прогибов заданного сооружения под узлами его через уп_1у уп, уп1 (рис. 118, б). Найдем выражение для одного из фиктивных грузов Уп всей системы. Так как эпюра фиктивных моментов принимается эквивалентной эцюре прогибов, то
Уп-1 М-1 Уп — Мп л1 М1.
Поперечную силу для условного сооружения в (п 1)-й панели можно представить через поперечную силу в п-й панели:
01 -№„; (а)
при этом поперечная сила принята положительной при направлении вверх, №п — положительна при направлении вниз. Из выражения (а) найдем значение Уп
«2-,. (б) Выразим поперечные силы через моменты (рис. 118, в):
„ф Уп-Уп-г
Чп К К ’
„Ф _М1-М _уп1-уп
1 л л
Ап1 л,г1
Подставляя эти значения в выражение (б), получаем
Уп Уп-1 У П- 1 Уп
п — Окончательно упругий груз
п — Уп-1 (т— Т ) Уп — Г Уп1. (7.37)
П Лп1 1 А,п
Задача определения фиктивного, или упругого, груза УУп сводится к определению обобщенного перемещения, включающего три узловых соседних перемещения уп_1у уп уп1. Однако упругие грузы Уп легко
149
выразить через внутренние силы заданного сооружения. Воспользуемся известным выражением работы двух единичных пар (- -г-.-М
Лл п
и ч- —) (рис. 118,3) на перемещениях в действительном соЛл1
стоянии. Обозначим внутренние силы действительного состояния Мру Мру С1Р. Внутренние силы единичного состояния (к — нагрузки) будут М1у Л7х, Принимая за силовое состояние воздействие двух единичных пар, возьмем возможные перемещения в первом действительном состоянии. По теореме возможной работы сил получаем, пренебрегая влиянием поперечных сил:
1,1,1 1 _ С МьМр, V С
К Уп Л КУп К1Уп К1Уп1 “ 2.1 Е1 2л Л
Таким образом, упругий груз УРп можно выразить только через внутренние силы системы в заданном и единичном состояниях:
р.з8)
Мы получили общее выражение упругого груза через внутренние силы двух состояний. Покажем, что для ломаного стержня при любом его очертании сумма интегралов правой части распространяется только на два элемента, смежных с узлом п.
В самом деле, жесткое сочленение двух соседних стержней (п — 1)-ь ч- п и п ч- (п 1) всегда можно представить в виде ломаной балки; при этом предполагаем, что в п-м узле нет шарнирного включения (рис. 119, а). К этой основной системе во втором состоянии прикладываем две единичные пары (рис. 119,6). В единичном состоянии только в ломаной балке (п — 1) -г- пу п -г- (п 1) возникают усилия. Таким образом, выражение (7.38) представится для многоугольного стержня так:
_ _ п — 1 п — 1
Дадим развернутую формулу для упругого груза, раскрывая значения интегралов внутренних сил для соседних стержней сочленения (п— 1) ч- л -г (п 1).
На рис. 119, а изображена эпюра изгибающих моментов от заданной нагрузки Р в сочленении. Здесь же представлены продольные и поперечные силы в элементах. Длины элементов обозначим з„1, моменты инерции сечений — „, 1п1у площади сечений — Рпу Р„1. На рис. 119, б изображена эпюра моментов в единичном состоянии.
Крайние силы и разлагаем каждую на составляющие — попе-
лп1
речную и продольную силы. Очевидно,
150
для стержня (п — 1) п
Н[п) — Д-81П рл ;
для стержня «т (я 1)
Мп 1) 5-зтрл4.
Лг1
Ординаты эпюры моментов в единичном состоянии для узлов (п— 1), я, (п 1) будут соответственно 0, 1,0.
Изгибающие моменты считаются положительными, если растягиваются нижние волокна для горизонтального стержня и правые для вертикального; продольные силы положительны, если они вызывают растяжение, поперечные левые силы — если они направлены вверх от оси стержня, поперечные правые — при направлении вниз от оси.
Применяя для моментов формулу (7.25) и подставляя значения продольных сил единичного состояния, получим вместо выраже¬
151
ния (7.39)
№ т-п 1ш") 6(Мп «2М«
Nп1 5п РяЛ Мп (5п Рг
ЕРМ К1 Гя1 ЕР„ к Подставляем обозначения относительных удлинений
8 2" ЕРп
X
в выражения работы продольных сил и, заменяя 8п - —, полу-
С05 р2
чаем для Ж7п окончательно
» Гп (Мп -1 2Мп) Шп1 2Мп) 4-
“1“ п1 Рл1 п Рг (7.40)
Это и есть развернутая формула упругого груза для сплошных многоугольных стержней при произвольном очертании их оси и люВом законе изменения момента инерции. Ее применяют при решении задач по построению линий прогибов арок со сплошной стенкой.
Для пологих тонких арок при
4 ’ Г 4
можно, как указано выше, пренебречь влиянием продольных и поперечных сил. Тогда выражение упругого груза будет
УРп. 6Е1П Ь2Мг) ёя7-“ (Лл1 Н2УИЛ). (7.41)
Остановимся на правиле знаков.
На эпюре фиктивных моментов, построенной со стороны растянутого волокна, линия прогибов соответствует действительному положению. Принимаем эпюру действительных моментов Мр положительной, если она построена от нижнего растянутого волокна (для горизонтальных стержней). Тогда вниз же будут направлены и упругие грузы.
Упругие грузы для ферм
Для построения деформированного вида шарнирно-стержневой фермы достаточно найти новое положение ломаной цепи стержней, преходящей через все узлы фермы (рис. 120, а).
На основе геометрического анализа устанавливаем, что перемещение шарнирной цепи стержней фермы является функцией: 1) изменений углов между стержнями цепи, 2) составляющих удлинений стержней цепи е. Зная изменения длин стержней фермы, легко построить
152
выбранную цепь стержней в деформированном виде. Линия прогибов для шарнирно-стержневой фермы представляет собой ломаную линию с переломами под узлами; искривление стержней шарнирной 4рмы в отличие от арочной конструкции отсутствует. Следовательно, эпюру вертикальных перемещений какого-либо пояса фермы получаем как зпюру фиктивных моментов от системы упругих грузов прило-
Заданная система,
женных на вертикалях, проведенных через узлы пояса (рис. 120, б). Пусть длина панели пояса будет X. Покажем, как для данной шарнирно-стержневой фермы вычислить упругий груз Рп У2 с целью дальнейшего построения эпюры вертикальных перемещений нижнего пояса фермы. Для этого во втором состоянии, т. е. в состоянии Я-нагрузки (рис. 120, в), к двум соседним стержням нижнего пояса фермы 1—2 и 2—3 прикладываем две равные и противоположные по направлению пары сил с моментом каждая, равным единице; следова¬
153
тельно, каждая из сил пары равна Как было указано выше, при
отыскании вертикальных перемещений упругий груз №п представляет собой взаимный угол поворота горизонтальных проекций элементов «цепи» стержней. При нахождении перемещений горизонтального пояса фермы упругий груз равен взаимному углу поворота соседних элементов пояса фермы. Величина его для шарнирно-стержневой фермы, очевидно, будет функцией лишь продольных сил в ее стержнях и выразится формулой
(7.42)
Матричная форма вычисления перемещений при помощи упругих грузов
Принимая во внимание, что прогибы уп (рис. 118, г) по методу упругих грузов могут быть определены как фиктивные изгибающие моменты от упругих грузов ИР,- ( 1, 2, г), получим для проги¬
бов у по аналогии с выражением (3.27) матричное уравнение
У (7.43)
где — матрица влияния моментов;
ИР — упругие грузы.
По А. Ф. Смирнову [8] можно дать следующее матричное выражение для упругих грузов. Учитывая влияние лишь моментов и деля брус на равные участки длиной 5, получим в соответствии с выражением (741)
(7.44)
где
4 1
1 4 1
1 4 1
В1
14
— якобиева матрица, так как согласно выражению (7.41) имеем трехчленное выражение.
ГЛАВА 8. ПРОСТРАНСТВЕННЫЕ ФЕРМЫ § 44. ПОНЯТИЕ О ПРОСТРАНСТВЕННЫХ ФЕРМАХ
Пространственные фермы — шарнирно-стержневые системы, элементы которых расположены не в одной плоскости. Все сооружения являются пространственными, но многие из них можно расчленить
154
на отдельные плоские системы, работающие независимо. Существуют все же такие пространственные системы, которые невозможно разложить на отдельные плоские системы (различные башенные и крановые конструкции, купола и др.).
Пространственные системы по характеру образования делятся на следующие основные виды: рамы, оболочки и фермы.
Рама (рис. 121) представляет собой пространственное жесткое сочленение стержней между собой в узлах.
Оболочка — пространственная тонкостенная конструкция, срединная поверхность которой криволинейна (см. гл. 21).
Пространственная ферма — геометрически неизменяемая система стержней, соединенных между собой пространственными шарнирами. На рис. 122 в двух проекциях показана пространственная шарнирностержневая статически определимая ферма в виде купола. От действия вертикальной силы Р, приложенной в узле п, возникают усилия в стержнях пт, по, пк, то, пр, ки Ы, ко и т. д.
Теория расчета и проектирования пространственных ферм существенно развита отечественными учеными. В частности, В. Г. Шухов предложил целесообразный тип водонапорной башни в виде сетчатой пространственной фермы, прямолинейные элементы которой располагаются на гиперболоиде вращения (рис. 123).
155
При расчете пространственных ферм предполагается, что все стержни фермы соединены в узлах идеальными шаровыми шарнирами, обеспечивающими вращение концов вокруг трех
взаимно перпендикулярных осей. Нагрузку, действующую на ферму, принимают узловой. Следовательно, в стержнях пространственной фермы возникают лишь продольные усилия.
§ 45. ВИДЫ ОПОР И НЕИЗМЕНЯЕМОСТЬ ПРОСТРАНСТВЕННЫХ ФЕРМ
Виды опор пространственных ферм и классическое опирание
Первый тип опоры — шарнирно неподвижная шаровая опора (рис. 124, а). Шаровой вкладыш этой опоры а находится в сферических углублениях верхнего и нижнего балансиров, неподвижно прикрепленных соответственно к узлу с пространственной системы и опорной подушке Ь. Реакция такой опоры проходит через центр шарнира и имеет три составляющие X, V,
2 (см. условное изображение этого типа опоры в виде трех стержней, не лежащих водной плоскости; рис. 124, а, справа).
Зная составляющие X, У, Ъ полной
реакции опоры ?, находим ее величину.
Второй тип опоры — подвижная цилиндрическая опора (рис. 124, б) — отличается от предыдущего тем, что нижняя подушка расположена на цилиндрических катках. Условно эту опору изображают в виде двух опорных стержней, нижние шарниры которых расположены на прямой ЬЬЪ параллельной оси X (рис. 124, б, справа). Такая опора может перемещаться перпендикулярно к плоскости чертежа. Реакция К действует в плоскости IX.
Третий тип опоры — подвижная шаровая опора
(рис. 124, в). Нижняя подушка опоры покоится на шаровых катках.
Реакция опоры имеет единственное направление, нормальное к плоскости катания XV.
Четвертый тип опоры — полное защемление (рис. 124, г), в котором возникают три составляющие сил 2, У и X и три момента защемления М2 (в плоскости XV), Му (в плоскости IX) и Мх (в плоскости 2У).
Условное изображение опоры четвертого типа можно представить в форме прикрепления тела шестью опорными стержнями.
156
4
Рис. 124
Рассмотрим сначала классическое опирание пространственной фермы (рис. 125, а), заменив ее твердым телом. Для неизменяемого прикрепления пространственной фермы (блока) к земле необходимо дать шесть опорных стержней, расположенных не менее чем в трех точках: в точке А — трехстержневую (шар- а) нирно неподвижную) опору; в точке В—двухстержневую подвижную опору с цилиндрическими катками, на- правление движения которых перпендикулярно к плоскости стержней 1 и
2, ив точке С — одностержневую опору (подвижную шаровую опору с шаровыми катками, плоскость движения которых перпендикулярна к условному стержню 3 этой опоры).
Таким образом, для неизменяемого прикрепления сооружения к основанию требуется шесть опорных стержней: в узле А — три опорных стержня, не лежащих в одной плоскости; в узле В—два стержня, плоскость которых не проходит через центр неподвижной опоры Л, и в
157
опоре С — один стержень, направление которого не пересекает линию АВ. Три точки Л, В и С не должны лежать на одной прямой. Вообще опорные стержни следует располагать так, чтобы нельзя было найти линию, пересекающую все шесть направлений стержней (линию, момент всех опорных реакций относительно которой равен нулю).
Определение опорных реакций
Опорные реакции для пространственной статически определимой системы (см. рис. 125, а) находят, используя шесть условий равновесия:
2Х 0; 2У 0; Ц2 0;
ЦМХ 0; %МУ 0; %Мг 0.) (вЛ)
Обычно стремятся оси моментов выбирать так, чтобы последние три уравнения содержали наименьшее число неизвестных. Так, предположив, что плоскость стержней опоры В параллельна направлению оси АС9 получим:
1) ЪМАс 0, так как Хь параллельна АС отсюда легко находим 1Ь
2) 2Мав 0; отсюда определяем 2С
3) 2Мас 0 (или 22 0); отсюда находим 1а
4) 2М?а 0 при условии, что вертикальная ось проходит через точку А; отсюда находим Хъ
5) 0 при условии, что ось VI] перпендикулярна к направлению АВ отсюда находим Ха
6) 2У 0; отсюда определяем Уа.
Первые четыре уравнения составлены по способу моментных осей, который часто используется для определения усилий в стержнях фермы.
Неизменяемое соединение двух блоков.
Случаи неправильного прикрепления
Остановимся на неизменяемом соединении двух блоков и, которые можно рассматривать как неизменяемые части фермы. Те же правила относятся и к способам неизменяемого прикрепления фермы к земле II (рис. 125, б). Для неизменяемого статически определимого соединения двух блоков I и II необходимо дать шесть стержней, причем:
1) три шарнира Л, В, С не должны лежать на одной прямой;
2) плоскость, в которой лежат стержни 4 и 5, не должна совмещать точку А;
3) направление стержня 6 не должно пересекать линию АВ.
В таком случае нельзя найти линию, пересекающую все шесть направлений стержней, момент опорных усилий относительно которой был бы равен нулю.
№
Перейдем теперь к случаям неправильного прикрепления пространственных ферм к земле.
На рис. 126 приведены первых два исключительных случая изменяемого прикрепления. На рис. 126, а линия ак, параллельная направлениям стержней 4, 5, 6 и проходящая через точку а, пересекает все направления. На рис. 126, б пять из шести направлений стержней располагаются в двух плоскостях, пересекающихся по линии, парал-
В)
Рис. 126 Рис. 127
лельной направлению стержня 6, и момент относительно оси стержня 3 всех опорных усилий равен нулю (стержни 1, 2, 3 лежат в одной вертикальной плоскости, стержни 4, 5 — в другой вертикальной плоскости, пересекающейся с первой по линии 3).
На рис. 127, а представлен случай, когда больше трех направлений лежат в одной плоскости. Найдем точки пересечения А и В плоскости, совмещающей направления стержней, 2, 3 и 4 с направлениями стержней 5 и 6. Линия АВ пересекает все шесть направлений и потому диск I к диску II прикреплен неправильно. На рис. 127, б представлен случай, когда больше трех направлений параллельны друг другу (или пересекаются в одной точке). В данном виде соединения четыре стер¬
169
жня 1,2, 3 и 4 параллельны друг другу, и, если за ось проекций выберем линию ак, а нагрузка действует вдоль оси ак, равновесие невозможно.
Опорное кольцо
Выше рассмотрен классический случай опирания блока или фермы на три точки, не лежащие на одной прямой (см. рис. 125). Для равномерности передачи усилий обычных мостовых конструкций целесообразно дать четыре опорных узла. Такой случай статически опреде¬
лимого опирания представлен на рис. 128, причем роль трехстержневого узла играет точка й пересечения стержней 1,2 и
3. Однако при этом имеем лишь три вертикальных опорных стержня и нет возможности выделить две балочные фермы аЬ и ей. Поэтому часто переходят к статически неопределимому опиранию блока на землю. Такие виды опирания при помощи опор-
Рис. 128
ного кольца представлены на рис. 129, а, б. Здесь в каждом углу блока имеется вертикальный опорный стержень, что обеспечивает симметричную передачу нагрузки на вертикальные фермы, располагающиеся в двух плоскостях ас62 и Ьй75. При действии вертикальной нагрузки, приложенной в вертикальных плоскостях ас и Ъй, усилия в горизонтальных опорных стержнях можно принять равными нулю и вести расчет, расчленяя систему на отдельные плоские фермы.
Простейшие фермы. Признаки их неизменяемости
Простейшие шарнирно-стержневые пространственные фермы имеют регулярную структуру в форме последовательного прикрепления каждого узла тремя стержнями, не лежа¬
160
щими в одной плоскости (рис. 130). На рис. 130, а узел О прикреплен тремя стержнями к шарнирно неподвижным узлам Л, В и Су каждый из которых закреплен трехстержневой опорой. На
рис. 130, б изображено простейшее опорное кольцо ЛВС, соединенное с фундаментом при помощи классического опирания; к трем неподвижным узлам прикрепляется четвертый узел О тремя стержнями. На рис. 131 приведен пример простейшей пространственной башни треугольного сечения, представляющей собой совокупность стержневых тетраэдров: узел 1 прикреплен тремя стержнями к узлам Л, В, С, узел
2 — тремя стержнями к узлам А,, В и т. д.
Можно дать следующий аналитический признак неизменяемости ферм в виде соотношения между числом их стержней 5Х и числом узлов к. Для взаимного соединения четырех узлов первого шарнирно-стержневого тетраэдра АВС1 с фундаментом (см. рис. 131) необходимо дать шесть стержней; для присоединения каждого последующего узла из оставшихся (к— 4) узлов — по три стержня на каждый узел. Общее число стержней
51 6 3(А — 4),
или
Зк — 6. (8.2) Рис. 131
Соотношение (8.2) можно представить так:
5 6 Зку
где 5Х 6 — общее число стержней вместе с опорными; обозначим его 5.
6 Н. К. Снитко
161
Аналитический признак неизменяемости представляем так:
5 3 к. (8.3)
Пространственная ферма, для которой соблюдается соотношение (8.3), может быть неизменяемой. Если 5 С 3к, система безусловно изменяема. Если 5 Зк, система имеет лишние связи. Так как условие неизменяемости (8.3) является необходимым, но недостаточным, то для окончательного заключения о неизменяемости необходимо провести соответствующий анализ структуры системы или дать аналитическое исследование определенности усилий при действии произвольной нагрузки.
Остановимся на основных геометрических признаках неизменяемости пространственных ферм:
1) ферма неизменяема, если каждый узел фермы последовательно прикрепляется к трем предыдущим узлам тремя стержнями, не лежащими в одной плоскости;
2) ферма неизменяема, если она составлена из блоков (неизменяемое тело), связанных между собой попарно шестью стержнями, расположение которых удовлетворяет условиям неподвижности соединений блоков (см. § 45).
Вообще, если имеем п блоков, то число связующих блоки стержней определяется по формуле
С 6(п—1). (8.4)
Сетчатые фермы
Сетчатой системой называем такую, в которой все стержни фермы расположены лишь на плоскостях граней многогранника, а все узлы —
на линиях пересечения граней (рис. 132). Для рационального прикрепления сетчатых ферм многоугольного сечения к земле необходимо использовать конструкцию в виде опорного кольца, причем под каждым вертикальным ребром сооружения располагается вертикальный опорный стержень (рис. 133). В первом варианте опорного кольца (рис. 133, а) каждый узел последовательно прикреплен тремя стержнями: в узлах 7, 2 и Зу расположенных через один, даны трехстержневые опоры в виде двух горизонтальных стержней и одного вертикального. В промежуточных уз¬
162
лах между трехстержневыми опорами, т. е. в узлах 4, 5 и 6У опоры имеют один вертикальный опорный стержень. Другой вариант опорного кольца представлен на рис. 133, б, где каждый опорный узел получает по два опорных стержня.
Докажем неизменяемость последней системы методом нулевой нагрузки. Заметим, что в каждом из шести узлов сходится по четыре стержня, но три из них лежат в одной плоскости. Вырезаем узел а и проектируем все силы, приложенные к узлу, на направление, перпендикулярное к плоскости стержней 7, 7 и 8. В полученное урав¬
нение проекций войдет только проекция усилия так как ось проекций перпендикулярна к направлениям стержней 7, 7 и 8. В результате составленного уравнения равновесия получим 56 0. Стержень 6 можно назвать «отдельно направленным». Подобным же образом получим, что усилия 52, 53, 54 и 50 равны нулю. Следовательно, в каждом узле остается по два опорных стержня, усилия в которых при отсутствии нагрузки равны нулю. Отсюда следует, что система неизменяема.
§ 46. РАСЧЕТ ПРОСТРАНСТВЕННЫХ ФЕРМ Сложение и разложение сил, сходящихся в одной точке
Способы сложения и разложения сил в пространстве известны из курса теоретической механики. Для системы сил, сходящихся в одной точке (рис. 134, а), последовательно применяем принцип параллелограмма сил: найдя равнодействующую сил и 52, складываем ее с силой 53; затем их равнодействующую — с силой 54 и т. д. Замыкающая пространственной системы векторов 5Ь 52,. дает равнодействующую всех сил 7?.
Разложение силы 7? на три направления в пространстве 7, 2, 3 (рис. 134, б) производим так: находим линию пересечения 0—4 пло¬
6
163
скости, проведенной через направления сил Р и Ръ с плоскостью, совмещающей направления усилий Р2 и Р3, и разлагаем силу Я на составляющие Рх и 5. Затем разлагаем силу 5 на две составляющие по направлениям Р2 и Р3.
Способ
проекции II моментов
способ
По способу проекций (рис. 135), вырезая узел О, где сходятся три стержня, проектируем все силы Р, 32 и 53 на направление, перпендикулярное к плоскости, совмещающей два других усилия, например 2 и 53. Пусть нормаль к плоскости 52 53 будет
Оп. Тогда уравнение проекций всех сил на ось Оп будет
5Х соз а — Р соз р О,
откуда
эсозр
51Я
соз а
(8.5)
По способу моментов для определения усилия составляем сумму моментов относительно оси АВ, пересекающей на-
Р
Рис. 135
правления 2 и 53. Тогда условие равновесия в виде суммы моментов относительно оси А В будет
8гг соз а — Рг соз р 0, где введены составляющие сил Р и на направление нормали Оп 164
к плоскости ОАВ, а г —- длина перпендикуляра, опущенного из точки О на ось АВ.
Способ моментных осей был применен в § 45 при определении шести составляющих реакций (см. рис. 125, а и формулы 8.1).
Расчет простейших пространственных ферм
Расчет пространственных ферм, расчленение которых на плоские невозможно, проводится аналогично расчету плоских ферм. Для простейших ферм можно указать на: 1) способ моментных осей и 2) способ проекций.
По способу моментных осей для независимого определения усилия в каком-либо стержне трехстержневого узла составляем сумму моментов относительно оси, пересекающей направления двух других стержней.
Усилия в простейших фермах легко определяются по способу вырезания узла последовательным разложением силы на три направления. Пусть, например, требуется определить усилия 5 и
52 53 в стержнях простейшей трехстержневой фермы по рис. 136 при действии на узел О вертикальной силы Р.
Проектируя все силы; действующие на узел О, на вертикальную ось, перпендикулярную к плоскости стержней 2 и 53, получаем
Р соз а 0,
откуда
1 соз а
Проектируя силы, действующие на узел О, на горизонталь ивводя равнодействующую сил 52 и 53, которую обозначим ?23, получаем
81П а 23 О,
откуда
23 — зт а Я а.
По равнодействующей сил 2 и 53, принимая во внимание, что 52 53, находим составляющую
?23 252 соз р,
откуда
о _ 23 __ Р
2 2 соз р 2 соз р •
165
Расчет стержневого купола Шведлера, ортогональные проекции которого даны на рис. 122, при действии вертикальной силы Ру приложенной в узле п (см. проекцию на вертикальную плоскость У)у ведем в следующем порядке.
Рассматривая равновесие узлов §, г, 5,, т по способу «отдельно направленного стержня», находим нулевые усилия во всех стержнях купола, показанных на рис. 122 тонкими линиями. Затем силу Р разлагаем на направления пт, по, пН усилие 8пт — на направления то и тр усилие 8пН — на направления Ъш, Ыу Но и т. д.
Расчет пространственных ферм путем разложения их на плоские
Нередко расчет пространственных, призматических ферм можно осуществлять путем разложения их на отдельные плоские фермы, причем нагрузка произвольного направления разлагается при этом на составляющие, действующие в плоскостях отдельных плоских ферм.
с
Рассмотрим, например, пространственную сетчатую ферму, представленную на рис. 137. Решетка дается лишь в вертикальных гранях этой пространственной фермы, никаких поперечных связей не требуется. Не трудно убедиться в неизменяемости данной фермы, применяя метод нулевой нагрузки. Определим усилия в стержнях этой
166
фермы, если на нее действуют горизонтальные силы по диагонали шестиугольного поперечного сечения фермы (а§, а). Каждую из сил разлагаем на две горизонтальные составляющие, например силу Р на Нас, Наъ расположенные в плоскостях плоских граней фермы ас[е и аЬАе. Первая плоская ферма прикреплена к земле тремя опорными
стержнями 3, 4, 5, вторая — также тремя опорными стержнями, 2, 3 (рис. 138). Внешние силы теперь действуют в плоскостях граней ас[е и аЬск. Следовательно, усилия возникают только в элементах этих плоских ферм. Очевидно,
Нас НаЬ На1С1 НахЬ1 Р•
Рассматривая теперь плоские фермы ас[е и аЪйе отдельно, определяем усилия в их элементах. Значения этих усилий указаны на рис. 138. Суммарные усилия стержней аа1у ахе и 3 пространственной фермы будут
аах — Р 5а1е 4Р; 53 —6Р.
ЧАСТЬ ВТОРАЯ
СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ
ГЛАВА 9. ОСНОВЫ ТЕОРИИ РАСЧЕТА СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ МЕТОДОМ СИЛ
§ 47. СТАТИЧЕСКАЯ НЕОПРЕДЕЛИМОСТЬ
Простейшие критерии
Статически неопределимой называют такую систему, которая не может быть рассчитана с использованием одних условий равновесия, так как она имеет лишние связи. За лишние принимают те связи, которые необходимо отбросить для получения статически определимой и геометрически неизменяемой системы. Количество лишних связей, которые следует удалить из статически неопределимой системы для обращения ее в статически определимую и геометрически неизменяемую, называют степенью статической неопределимости. Можно различать: 1) внешне статически неопределимые и 2) внутренне статически неопределимые системы Как выяснится из дальнейшего, это разделение является условным.
Внешне статически неопределимой называют такую систему, которая имеет только лишние внешние связи, т. е. лишние опорные закрепления. Примером внешне статически неопределимой системы является трехпролетная рама (рис. 139). Степень статической неопределимости подобной системы Сн легко установить по числу опорных стержней ее т, вычитая из него число необходимых стержней для неизменяемого прикрепления системы к земле:
С и т — 3, (9.1)
где т — общее число опорных стержней при замене шарнирно неподвижной опоры двумя стержнями, а защемления — тремя опорными стержнями.
Рис. 139
168
Для рамы, изображенной на рис. 139, заменяя защемление тремя опорными стержнями, получаем т — 8; Сн т — 3 5. Система пять раз статически неопределима.
Внутренне статически неопределимой плоской системой называют систему (прикрепленную к фундаменту лишь тремя опорными стерж-
у
I)
N.
ИЮ¬
НЯМИ), обладающую лишними а) связями, введенными для взаимного соединения частей системы.
Двухопорная рама с повышенной затяжкой (рис. 140, а) является системой внешне статически определимой, но внутренне однажды статически неопределимой. В этой раме, помимо соединения сечений а и Ь ломаным стержнем, имеется затяжка Рис 140
аЬ, шарнирно прикрепленная к
стойкам. На рис. 140, б показана статически определимая рама, полученная из заданной статически неопределимой системы путем разрезания затяжки аЬ, причем действие взаимной связи частей затяжки заменено неизвестными осевыми силами Получаем одно неизвестное — продольное усилие Мг в затяжке аЬ, соответствующее одной лишней связи.
При наличии замкнутого бесшарнирного контура получим трижды
статически неопределимую систему (рис. 141, а). Действительно, после разрезания затяжки аЪ перейдем к статически определимой системе — двухопорной раме с консолями ас и Ьс (рис. 141, б). Взаимную жесткую связь частей ас и Ьс нижнего ригеля рамы следует возместить усилиями (? и Мъ которые нельзя найти из условий равновесия. Итак, замкнутый бесшарнирный контур имеет три лишние связи (по числу трех лишних неизвестных, обнаруженных разрезом).
Если система содержит п замкнутых бесшарнирных контуров, то она, очевидно, будет 3п раз статически неопределима, так как каждый
169
замкнутый бесшарнирный контур дает три лишние связи. Так, переходя от рамы, имеющей три замкнутых бесшарнирных контура (рис. 142, а), к статически определимой системе (рис. 142, б), полупим, что система девять раз статически неопределима.
Заметим, что любую внешне статически неопределимую систему можно обратить во внутренне статически неопределимую. Для этого
достаточно ввести в рассмо-
а)
У
-(йд
м3 ЛА
-г—
Рис. 142
а)
трение опорный диск, кото рый полагаем прикрепленным к земле. Рассмотрим, например, раму, обе стойки которой защемлены (рис. 143, а). Система внешне трижды статически неопределима. Объединяя защемления А и В и вводя опорный диск А В в качестве элемента самой конструкции (рис. 143, б), получим внутренне статически неопределимую систему с тремя лишними связями.
Степень статической неопределимости для систем с соединениями различных видов
Установим простой критерий для определения степени статической неопределимости стержневой системы, имеющей любые замкнутые контуры с шарнирными включениями.
В сооружениях встречаются узловые соединения трех видов: 1) жесткая связь стержней в узле (рис. 144, а); 2) соединение полным шарниром (рис. 144, б), когда все стержни, сходящиеся в узле, связаны шарнирно; 3) соединение неполным шарниром (рис. 144, в), когда одна часть стержней в узле прикреплена шарнирно, а другая их часть — жестко.
При наличии шарнирного прикрепления конца стержня к узлу получаем добавочное условие равенства нулю изгибающего момента в центре шарнира. При этом нужно иметь в виду, что для любого узла можно составить общее условие равновесия:
2м,о, («)
(9.2)
170
Рис. 144
где М; — внутренний момент в сечении у узла для данного стержня. Это условие должно соблюдаться для узлов различного вида.
Для полного шарнира получаем столько добавочных уравнений равновесия, сколько стержней сходится в узле без одного. Принимая во внимание уравнение (9.2), для узла по рис.
144, б составляем четыре следующих дополнительных условия равновесия:
Ма Мь Мс Ма 0.
Условие же равенства нулю момента Ме вытекает из уравнения (9.2).
Для неполного шарнира (сравнивая это соединение с жестким) имеем столько условий равновесия, сколько всего стержней в узле прикреплено шарнирно. Так, для узла по рис. 144, в можно написать:
Мь 0; Мс 0; Ма 0.
Общий прием установления степени статической неопределимости любой стержневой системы со смешанными прикреплениями заключается в следующем. От данной системы (рис. 145), имеющей как
жесткие, так и шарнирные соединения в узлах (объединяя опорные
части в общий опорный диск), переходим к системе, содержащей лишь
замкнутые бесшарнирные контуры и определяем по числу п замкнутых ее контуров степень статической неопределимости преобразованной системы 3п. Наличие же в заданной системе шарнирных соединений позволяет составить добавочные условия равновесия вида:
Мь 0.
Подсчитываем общее число § добавочных условий равновесия, определяемых наличием шарниров. При этом принимаем во внимание указанные выше правила подсчета числа добавочных условий равновесия для полных и неполных шарниров. Для рамы, изображенной на рис. 145, имеем два полных и четыре неполных шарнира, над каждым из которых на рисунке указано добавочное число условий равновесия. Общее число добавочных условий равновесия § 10.
При п замкнутых контурах и § дополнительных степенях свободы, которые дают шарниры, степень статической неопределимости устанавливают по формуле
Сь Зп—§. (9.3)
171
Это наиболее простой критерий установления степени статической неопределимости плоской системы, состоящей из замкнутых контуров. Для рамы по рис. 145 получаем
Си 3п — — 3 ■ 5 — 10 5
— пять раз статически неопределимая система.
Для более сложных систем при совмещении контуров целесообразно применять общий метод, заключающийся в последовательном удалении всех лишних связей. Это удаление связей можно производить:
а) отбрасыванием лишних опорных стержней;
б) проведением разрезов, причем каждый разрез стержня, жестко прикрепленного к узлам, равносилен отбрасыванию трех связей;
в) включением шарниров и т. д.
§ 48. ОСНОВНЫЕ СВОЙСТВА СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ. МЕТОДЫ РАСЧЕТА
Основные свойства систем с лишними связями
Отметим следующие свойства статически неопределимых систем:
1. Статически неопределимое сооружение ввиду наличия добавочных лишних связей оказывается по сравнению с соответствующей статически определимой системой более жестким.
2. В статически неопределимой системе ввиду ее большей связности (сравнительно с соответствующей статически определимой системой) при той же нагрузке цолучаются меньшие усилия, следовательно, статически неопределимые системы более экономичны.
3. Нарушение лишних связей статически неопределимых систем (или их перенапряжение) не ведет к немедленному разрушению всего сооружения, так как удаление этих связей приводит к геометрически неизменяемой системе, в то время, как потеря связи в статически определимой системе лриводит к изменяемой системе.
4. Усилия в статически неопределимых системах зависят от размеров сечений и формы сооружения, а при различных модулях упругости — также от соотношения между ними. Изменение размеров сечений стержней статически неопределимой системы приводит к изменению усилий в связях и новому распределению усилий во всей системе.
Обычно сначала проводят ориентировочный расчет статически неопределимой системы, затем задаются отношениями жесткостей стержней, после чего осуществляют точный расчет системы.
5. В статически неопределимых системах температурное воздействие, осадка опор и неточность изготовления и сборки вызывают дополнительные усилия. Наличие стержней, длина которых не соответствует проектной, а также воздействие температуры, вызывающей перемещение по направлению избыточных связей, создают дополнительные усилия, которые могут быть весьма значительными.
172
Методы расчета статически неопределимых систем
Методы расчета статически неопределимых систем можно разделить прежде всего по характеру основных неизвестных, которые определяют все остальные усилия и перемещения. Различают следующие важнейшие методы расчета статически неопределимых систем: 1) метод сил; 2) метод перемещений (деформаций); 3) смешанный метод. При расчете по методу сил за основные неизвестные принимают усилия в лишних связях. При расчете по методу перемещений неизвестными являются перемещения, вызванные деформацией системы, знание которых достаточно для определения всех усилий. При применении смешанного метода за неизвестные выбирают частично силы, частично перемещения.
Кроме указанной классификации, методы расчета статически неопределимых сооружений можно расчленить по степени их точности, по области работы материала сооружений, по особенностям расчетных операций и т. д.
По степени точности различают точные и приближенные методы расчета.
Точные методы расчета базируются на обычных основных допущениях, принятых при расчете достаточно жестких сооружений (закон Гука, расчет по недеформированной схеме, принцип сложения действия сил). Приближенные методы расчета, кроме обычных упрощений, используют дополнительные допущения, что обусловливает заметное отклонение от результатов точных методов расчета.
По области работы материала различают расчет сооружений в упругой стадии и расчет сооружений за пределом упругости. По особенностям расчетных операций методы расчета можно разделить на вычислительные и экспериментальные.
§ 49. ОСНОВНАЯ СИСТЕМА ПРИ РАСЧЕТЕ РАМ МЕТОДОМ СИЛ. КАНОНИЧЕСКИЕ УРАВНЕНИЯ
Порядок расчета
Рассмотрим порядок проверочного расчета статически неопределимой рамы на действие неподвижной нагрузки. При расчете рам произвольного очертания целесообразно от заданной статически неопределимой рамы переходить к основной статически определимой системе. Основной называют такую систему, которая принимается в основу расчета данной статически неопределимой конструкции. По основной системе (обычно статически определимой) устанавливают перемещения и усилия, по которым находят лишние неизвестные, применяя уравнения деформаций; затем определяют окончательные усилия для заданной системы.
Общий порядок расчета рамы методом сил следующий:
173
1. От заданной статически неопределимой системы переходим к основной системе — статически определимой и неизменяемой, которая получается из заданной системы путем отбрасывания всех лишних связей.
2. Заменяем отброшенные лишние связи соответствующими им силами, называемыми лишними неизвестными Х19 Х2, Х3 и т. д.
3. Составляем уравнения деформаций, выражающие условия равенства нулю перемещений по направлению каждой лишней связи.
а) р
Ф
I А
сум
ь
Рис. 146
4. Определив все коэффициенты при неизвестных и свободные члены уравнений деформаций, решаем систему этих уравнений и находим лишние неизвестные, после чего строим эпюры Му (2 и ТУ для рамы.
Уравнения деформаций метода сил, написанные в определенной, раз навсегда установленной форме, называют каноническими уравнениями метода сил.
Рассмотрим порядок расчета простейшей несимметричной статически неопределимой рамы (рис. 146, а). В данном случае система дважды статически неопределима. От заданной статически неопределимой системы переходим к основной системе, отбрасывая шарнирно неподвижную опору (рис. 146, б). Получаем основную систему в виде рамы, защемленной правым концом, со свободным левым концом. Действие неподвижной опоры возмещаем силами Х± и Х2 — составляющими реакции неподвижной опоры. Это один из вариантов основной системы.
Можно предложить другой вариант основной системы — в виде двухопорной рамы; отбрасывая защемление правой опоры, заменяем
174
ее действие моментом Ху 4 ликвидируя горизонтальное закрепление левой опоры, возмещаем ее действие горизонтальной реакцией ХА (рис. 146, в).
И еще один вариант основной системы — в виде трехшарнирной рамы асЬ (рис. 146, г); действие лишних связей при этом возмещаем моментами Х[ и XI, где моменты Х заменяют жесткую связь соседних сечений в заданной системе. Меняя положение шарнира су получаем ряд вариантов основных систем. Наиболее простой является основная система в виде защемленной рамы (рис. 146, б), для которой проще всего строится эпюра изгибающих моментов. Р
Выбрав основную систему и представив действие лишних связей неизвестными сйлами Х1 и Х2, составляем канонические уравнения.
Каждое, уравнение деформаций, как было отмечено, выражает условие равенства нулю перемещения по направлению лишнего неизвестного. В заданной раме (см. рис. 146, а) вертикальное и горизонтальное перемещения центра неподвижной опоры а равны нулю.
Те же условия должны выполняться и для основной системы (см. рис. 146, б). Условия равенства нулю вертикального и соответственно горизонтального перемещений точки а можно выразить так:
(ххх2р)
А2 (ХгХ2р)
°; 0,1
(9.4)
где Д (.ххх2р) — вертикальное перемещение точки а, т. е. перемещение по направлению силы Хх от действия сил Х1у Х2 и нагрузки р АХг (Ххх2р) — горизонтальное перемещение точки а по направлению силы Х2 от действия сил Х1у Х2 и нагрузки р.
Чтобы выразить уравнения (9.4) в явной форме через лишние неизвестные, применим известный из предыдущего принцип независимости действия: перемещение, вызванное системой сил, представим в виде суммы перемещений, вызванных отдельными силами Х1у Х2 и нагрузкой р. Вместо уравнений (9.4) получим
АХ1хх Ах1х2 Д Ххр — 0; Х2хх “Ь Д22 Ах2р
°: 0, I
(9.5)
где первый индекс в выражении перемещения указывает, по направлению какой силы совершается перемещение, а второй индекс отмечает, какой силой вызвано перемещение.
Для краткости опустим в индексах при всех перемещениях букву х, оставив лишь номер лишнего неизвестного. Тогда вместо уравне-
175
(9.6)
ний (9.5) получим
Дц 12 Дц» 0;
21 22 2р
Перемещения Д1р и Д2р, вызванные нагрузкой р, изображены на рис. 147, а.
Для линейно-деформируемой упругой системы перемещения Ди, Д12, Д22, вызванные силами Хх и Х2, представляем по обобщенному закону Гука пропорциональными силами Хг и Х2 соответственно:
Дц 1бц; Д12 Х2б12;
Д22 -222»
где бп — перемещение по направлению силы Хъ вызванное единичной силой Хг 1 (рис. 147, б);
612 — перемещение по направлению силы Х1у вызванное силой 2 1;
621 — перемещение по направлению силы Х2у вызванное единич¬
ной силой Хх 1 (рис. 147, в)
622 — перемещение по направлению силы Х2, вызванное единич¬
ной силой Х2 1.
Уравнения деформаций (9.6) теперь можно представить в явной форме от лишних неизвестных:
111 212 Д1р 0; 1 ад1х2б22д2Ро. (У-7)
Здесь 8П, 612, б21, б22 — «единичные» перемещения; их легко определить по соответствующим эпюрам моментов, пользуясь формулами:
2 И
ЕГ
п О
п О
(9.8)
В выражениях (9.8):
М± — функция изгибающего момента в произвольном сечении основной системы от Хх 1;
М2 — изгибающий момент в том же сечении от Х2 1;
5 — длина стержня рамы; п — число ее стержней.
Свободные члены уравнений (9.7), так называемые грузовые члены, определяют по общей формуле для перемещений:
1Р
д2 р
п О
М1МР‘§1;
М2МР%.
(9.9
п 0
176
При этом в формулах (9.8) и (9.9), как обычно при расчете рам, учтено лишь влияние на перемещения изгибающих моментов. Найдя выражения изгибающих моментов Мр, Мг и М2 и вычислив перемещения по формулам (9.8) и (9.9), решаем канонические уравнения деформаций (9.7) и находим лишние неизвестные Хх и Х2.
Если стержни рамы имеют переменное сечение, меняющееся от стержня к стержню, при решении уравнений (9.7) вводят соотношения моментов инерции сечений стержней. _
Эпюры моментов Мр и от единичных неизвестных Мх и М2 даны на рис. 148, а, б, в.
Рис. 148
Свойства канонических уравнений. Построение эпюры моментов
Отметим следующие свойства коэффициентов при неизвестных канЪнических уравнений: _ __
1. Перемещения от единичных сил Хг 1 и Х2 1 с различными индексами равны между собой, т. е.
612 62Ъ (9Л0)
или иначе «единичные» перемещения не меняются от перестановки индексов (теорема о взаимности перемещений).
2. Перемещения от единичных сил Хх и Х2 с одинаковыми индек?алА1и всегда положительны (би, 622), что непосредственно следует из выражений (9.8) для этих перемещений, содержащих квадраты изгибающих моментов.
V
177
«Единичные» перемещения с одинаковыми индексами 6П, 622 называют главными перемещениями, поскольку они не могут быть равны нулю и всегда входят в уравнения. «Единичные» перемещения с различными индексами 612, б21 называют побочными перемещениями, так как при удачном выборе неизвестных они могут оказаться равными нулю.
Если наметим линию, соединяющую в уравнениях (9.7) главные перемещения 6П и 622 (главная диагональ), то побочные перемещения, расположенные симметрично относительно главной диагонали, согласно равенству (9.10) должны быть равны между собой. Найдя из канонических уравнений лишние неизвестные Х± и Х2, перейдем к построению эпюры моментов в заданной раме по основной системе. Эту эпюру моментов называют окончательной эпюрой моментов Л4сум. Ординату этой эпюры моментов в произвольном сечении находим, пользуясь принципом сложения (см. рис. 146, б):
Мсум Мр-- ХхМг Х2М2. (9.11)
По правой части выражения (9.11) момент в заданной статически неопределимой раме получается как сумма моментов от нагрузки Мр и от каждого_лишнего неизвестного Х1 и Х2. Увеличивая ординаты моментов от Хх 1 и Х2 1 соответственно в Хг и Х2 раз и складывая этот результат с ординатой эпюры моментов только от нагрузки Мр (см. рис. 148, а), получаем ординаты окончательной эпюры Мсум (рис. 148, д). На этой эпюре показано, как найти момент в середине ригеля.
Проверка вычисления перемещений
В случае дважды статически неопределимой системы, решая систему уравнений (9.7), выражаем лишние неизвестные так:
у 1 1 IX —
Ог
1 р
12
2р
б22
6ц
612
622
622
бп
1 р
612
2 р
I 6ц 12
I 21 22
1 р22 2 р12
611622 — б2
1р°12
(9.12)
где О — определитель системы, составленный из коэффициентов при неизвестных;
1» 2 — определители системы, которые получаются путем за мены соответствующего столбца членами Д1р и Д2р. Существуют специальные способы решения системы линейных алгебраических уравнений вида (9.7), которые будут рассмотрены ниже.
178
Характерно, что при использовании решения (9.12) нередко каждое лишнее неизвестное для систем уравнений определенного вида получается в форме отношения разностей чисел, близких друг к другу. Возьмем следующий численный пример: лишнее неизвестное
_ 160 — 158 0
1 “ 250-249 Допустим теперь, что в одном из чисел разности знаменателя допущена ошибка в 1250; тогда получим
у, _ 160— 158 _
1 “ 249 — 249 С°-
Ничтожная ошибка в одном члене знаменателя приводит к огромной ошибке в результате. Поэтому решение канонических уравнений в этом случае необходимо проводить с большой точностью, а каждую ступень вычислений подвергать тщательной проверке. Естественно избавиться от совместности канонических уравнений и сводить решение к определению неизвестных из одного уравнения с одним неизвестным. Если в системе уравнений (9.7) будет 612 0, то для Хг получим решение:
Лишнее неизвестное здесь выражено отношением двух перемеще: ний. Основная задача упрощения расчета сложных статически неопределимых систем и сводится к исключению совместности канонических уравнений деформаций путем специального выбора основной системы и лишних неизвестных. Для решения системы уравнений успешно применяются электронные счетно-решающие машины и новые приемы решения системы линейных уравнений.
Отметим важность осуществления контроля всех операций расчета статически неопределимой системы, в особенности при наличии совместности уравнений. Проведем проверку расчета рамы, изображенной на рис. 146, а. Для отыскания всех перемещений, входящих в_систему канонических уравнений, необходимо построить эпюры М19 М2 и Мр. Они изображены на рис. 148, а, б, в. Полагаем, что х 2. Проверив правильность построения всех эпюр, вычислим по правилу перемножения эпюр перемещения:
А А _-1.
Р 8 ЕГ 4Е1,
4 « 3. _ з
3 Е1; 12 2Е1 °223ЕГ
Далее производят так называемую построчную проверку единичных перемещений. Она состоит в следующем. Находят сумму перемещений (бп 612), которую можно рассматривать как_ перемещение по направлению силы Х19 вызванное системой сил Хх 1 и
179
Х2 1, действующих одновременно. Тогда
5
(6пМ61(1,2)2 (9-14)
П о
где_ М12 — изгибающий момент от действия системы сил Хг 1 и Х2 1 по рис. 148, г.
Назовем момент М12 моментом в суммарном единичном состоянии. (В общем случае этот момент обозначают через М5.) Итак, сумма «единичных» перемещений первого канонического уравнения может быть получена путем перемножения единичной. эпюры моментов на суммарную единичную эпюру моментов М12. Аналогично
(21 22) 2(1.2) 2И12 (9.15)
(п) О
— сумма единичных перемещений второго канонического уравнения получается перемножением эпюры М2 на эпюру М12. Кроме построчной проверки, проводим универсальную проверку всех единичных перемещений. Для этого найдем сумму левых частей выражений (9.14) и (9.15), применяя теорему о взаимности перемещений для групповых и простых перемещений при наличии единичных силовых воздействий:
(8ц б12) (621 б22) б1(12) б2(12)
(1.2)1 “Ь (1.2)2 (1.,3) (12) 12 -г. (9.16)
(п) о
«Перемножая» эпюру М12 на нее же, получаем сумму всех единичных перемещений. Для нашего примера (см. рис. 148, г)
2Г Г, 1 а 2 ;, 2 3 м 2 5 Л 8
) М12 Е1 Е1 2 3 2 2 3 ] — 3 Е1 1
П О
а сумма всех единичных перемещений
2б 611 2б12 б22(43У 3) ЕТ
1
— универсальная проверка соблюдается.
Проведем еще первую построчную проверку:
д д П 3
°11 °12 — 6ЁТ
С другой стороны, перемножая эпюры УЙХ и М12, находим
Таким образом, построчная проверка также выполняется. Кроме универсальной и построчной проверок, проводим постолбцовую проверку грузовых членов Д1р и Д2р, к которой приходим на основании следующих равенств:
5
1р 4“ 2р Др1 Ь р2 р(1,2) (1,2)р М±2Мр -гу, (9.17)
п О
т. е. сумму всех грузовых членов получаем «перемножением» эпюры моментов от нагрузки Мр на эпюру моментов М12 (см. рис. 148, а, г). В данном случае
т-г4) -т-
п о
Постолбцовая проверка выполняется. Проверив правильность всех предшествующих вычислений, перейдем к решению уравнений. В данном случае, подставляя численные значения перемещений в канонические уравнения (9.7) и умножая все члены на Е1, находим
43 Х2-- 0;
V Р I V Р П
1 2 2 Т 4
Решая уравнения способом исключения неизвестных, получаем
Ххр1 Х2 р1.
Проверка суммарной эпюры моментов
Применяя принцип сложения, получаем все ординаты «суммарной» эпюры моментов (см._рис. 148, д). При этом суммирование ординат эпюр Мр, ХхМъ Х2М2 проводим последовательно, вычисляя их для сечений, взятых по концам каждого стержня рамы и соединяя концы ординат соответствующими линиями (при отсутствии нагрузки — прямыми).
Получив суммарную (окончательную) эпюру моментов, проводим проверку правильности ее построения. Для этого выясняем, выполняется ли каждое условие деформаций вида (9.4), т. е.
1(хгхяр) 0; А(х1х2р) 0. (9.18)
Вместе с тем перемещения по направлениям Хг и Х2 от одновременного действия нагрузки и неизвестных Хъ Х2 можно найти, перемножая суммарную эпюру Л4сум на соответствующую единичную
181
эпюру моментов йли М2. Вместо выражения (9.18) получим
5 5
2 су-- °; 2 м2мсук г 0. (9.19)
ПО П О
Результат перемножения суммарной эпюры моментов на любую единичную должен равняться нулю. Заметим, что это соотношение не выполняется при действии на статически неопределимую систему температуры. _
В частном случае, если М,- сопз вдоль всех стержней рамы и
рассматривается случай действия нагрузки, вместо выражения (9.19)
получим
о 9-20
п о
( Мсум
— приведенная площадь эпюры моментов [ площадь —), подсчитанная
по всей длине оси рамы, должна быть равна нулю, если для какоголибо состояния X, 1 эпюра И,- постоянна (например, в случае замкнутого бесшарнирного контура).
§ 50. ПОСТРОЕНИЕ ЭПЮР ПОПЕРЕЧНЫХ И ПРОДОЛЬНЫХ СИЛ В РАМАХ
V
По суммарной эпюре моментов, ординаты которой отложены со стороны растянутых волокон рамы, строят эпюру поперечных сил. При сложном очертании оси рамы эту эпюру будем находить непосредственно по эпюре моментов. При этом используем основную схему рамы в виде системы стержней, шарнирно опертых на узлы рймы, а жесткость прикрепления конца каждого стержня рамы к узлу возмещаем моментом, действующим со стороны узла на стержень. Таким образом, стержень 1—2 рамы (рис. 149, а), жестко связанный с узлами
1 и 2 и подверженный действию равномерной нагрузки д, рассматриваем как балку, шарнирно опертую на узлы, заменяя при этом жесткое прикрепление концов стержня моментами УИ12 и М21 (первый индекс в обозначении моментов указывает номер узла, у которого действует момент, а оба индекса соответствуют наименованиям концов стержня). Найдя для простой балки 1—2 реакции Л12 и Б21из условия равновесия узлов 1 и 2 (рис. 149, б), получаем величины поперечных сил:
(212А12 (21 21 (а)
При этом придерживаемся правила знаков для поперечных сил, которое не связано с положением наблюдателя: знак поперечной силы у онца данного стержня рамы устанавливается по направлению того момента, который получается от поперечной силы, действующей со стороны стержня, относительно центра данного узла. Пользуясь
182
этим правилом, можно быстро установить направление действия поперечных сил со сторойы стержней рамы на узел, что упрощает отыскание продольных сил в стержнях рамы. Принимаем, например, поперечную силу (312 положительной, если она дает момент, вращающий относительно центра узла 1 по часовой стрелке. Поперечная сила ф21, действующая у правого конца стержня, должна быть взята со знаком минус, так как она дает момент относительно, центра узла 2, вращающий против часовой стрелки. Направление силы ф21, уравновешивающей реакцию В21, устанавливаем по направлению предварительно найденной реакции В21.
Отложив ординаты опорных поперечных сил ф12 и (321 и соединив их концевые точки прямой, получим эпюру ф для стержня 1—2 в случае действия равномерной нагрузки (нижняя схема рис. 149,6).
В случае отсутствия нагрузки на данном стержне рамы 1—2 (рис. 150, а) эпюра моментов очерчена наклонной прямой и реакции Л12 и В21 дают пару сил общим моментом (М12 М21); поперечная сила в стержне постоянна и равна
у (М12 М21) (рис. 150, б). Направление поперечной силы, действующей со стороны стержня на узел, в этом случае найти особенно просто: следует у данного узла провести на эпюре моментов вектор от очертания этой эпюры к оси стержня (см. рис. 150, а).
Пэ эпюре поперечных сил (2 строим эпюру продольных сил N.
Устанавливаем правило знаков: продольную силу, растягивающую стержень, считаем положительной. Для отыскания продольных сил в стержнях обычных каркасных рам по эпюре поперечных сил применяем способ вырезания узлов, известный из теории расчета статически определимых ферм. Расчет начинаем с узла, где сходятся лишь два стержня рамы. Зная узловые поперечные силы и нагрузку Р, определяем продольные силы в стержнях из условия равновесия в виде суммы проекций па выбранные оси координат. Затем переходим к следующему узлу рамы, где имеем два новых неизвестных усилия в стержнях, и определяем усилия в них из условий равновесия и т. д.
мг 0 ггтштпшииип?
.21
у.
Злюра (I
Рис. 149
183
Для простейшего случая — узел с взаимно перпендикулярными осями стержней (рис. 151, а), зная направления и величины поперечат
а1
р,
Ф
Рис. 151
ных сил (312 и (13, получаем для суммы проекций на ось X:
2 0,
Р 1 12 С13 0»
откуда
Л12 С13 Р (б)
из равенства нулю суммы проекций на ось У:
ЪУО,
Р 2 Лз — С12 0,
откуда
М13 С112 Р 2 (В)
В выражения (б) и (в) подставляем абсолютные значения узловых поперечных сил, направления которых должны быть найдены в соответствии с правилом знаков.
В более общем случае — произвольное направление стержней рамы (рис. 151, б) — получаем по уравнениям проекций 2]Х 0и2 0:
Ы12 соз а12 312 зт а12 — Ы1з соз а 13 — Э1з зт а13 0; (г)
Р Л12 зт а12 — 312 соз а12 Ыхз зт а13 — Э13 соз а13 0. (д)
184
I ®2и
Решая эти уравнения, находим Ы12 и Ы13. Затем переходим к следующему узлу рамы, где сходятся два новых стержня, и поступаем
аналогично. Если в раме нет ни одного узла, где сходятся лишь два
стержня, система будет статически неопределимой в отношении продольных сил и необходимо использовать соответствующие уравнения деформаций.
Пример. Для рамы, изображенной на рис. 152, а, в первом пролете которой действует равномерная нагрузка, построить эпюры О и N. Суммарная эпюра М дана на рис. 152, б. Интенсивность нагрузки 7 1 кнм.
Решение. Выделяя стержни рамы 1—2,2—5, 3—5, получаем расчетные схемы в виде простых балок (рис. 152, в). Определяем левые реакций для указанных схем:
Лх2 2,35 кн Л2з 0,57 кн
Лзб —0,145 кн Л24 0,145 кн.
Теперь находим для загруженного стержня узловые поперечные силы ф12 2,35 кн и С?21 — 3,65 кн и для стержней 2—5, 3—5 и 2—4 поперечные силы, постоянные по длине стержня. Эпюра представлена на рис. 152, г. Так как в узле 1 рамы подвижная опора, то УУ12 0. Вырезая последовательно узлы 2 и 3 рамы, находим N 2з, N 24 и N35.
Так, для узла 2 получаем (рис. 152, д)
ЦХ 0; А2з-(?24 0,
откуда
Л23 24 145 кн.
Е У — 0; (?21 (?23 24 0,
откуда
Л24 — ((?21 (?2з) —’ 4,22 КН.
Эпюра N изображена на рис. 152, е.
§ 51. РАСЧЕТ ПРОСТЕЙШИХ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ НА ДЕЙСТВИЕ ТЕМПЕРАТУРЫ И ОСАДКИ ОПОР
Действие температуры
При изменении температуры среды в статически неопределимых системах возникают дополнительные напряжения.
При равномерном нагревании всех элементов внутренне статически неопределимой системы дополнительных напряжений не возникает. При нагревании какого-либо одного или ряда элементов внутренне статически неопределимой системы (внешне статически определимой) возникают дополнительные напряжения, так как благодаря наличию лишних внутренних связей создаются препятствия температурной деформации.
В системах внешне статически неопределимых (внутренне определимых или неопределимых) при одновременном нагревании всех или части элементов возникают дополнительные усилия. Не возбуждаются усилия во внешне статически неопределимых системах лишь в том случае, когда температурное воздействие вызывает перемещение по
186
направлению безусловно необходимых связей, в которых возникают статически определимые реакции. Так, при равномерном нагревании неразрезной балки, имеющей одну неподвижную опору (рис. 153, а), температурная деформация происходит свободно и никаких усилий в системе не возбуждается; перемещение крайней подвижной опоры будет ос(Ьу где а — коэффициент линейного расширения, а — перепад температуры. В этом случае напряжения в балке равны нулю.
Иначе обстоит дело при неравномерном по высоте балки нагревании. Пусть, например, трехпролетная неразрезная балка постоянной высоты с подвергается нагреванию верхних волокон и охлаждению нижних волокон на ° (рис. 153, б). За лишнее неизвестное примем симметричную группу реакций, каждую величиной Хг. Составим каноническое уравнение деформаций для неизвестного Х±:
ХА1 Ьи 0, (9.21)
откуда
1—в. (9.22)
где Д — перемещение по направлению Хг от температуры.
По теории определения перемещений
и г
О
6ц — перемещение, соответствующее обобщенной силе, за которую принята группа сил Х1 в состоянии Хг 1; оно равно:
3 Е1
6 0 I”
11 — сТ •
187
Таким образом, по выражению (9.22)
12 а 1Е1
Хг
5 с1
Эпюру моментов в системе строим только от лишних неизвестных, так как в статически определимой основной системе усилий от воздействия температуры не возникает:
М МХхХгМ1
Эта особенность работы статически неопределимых систем на воз-
Зпюра Л,
“шш
действие температуры сказывается в том, что условие (9.19) не соблюдается:
2 ЯгМ -%-фО,
П О
так как правая часть этого неравенства представляет собой выражение перемещения по направлению Хъ вызванного только лишним неизвестным, и согласно уравнению деформаций (9.21)
(9.23)
Таким образом, результат перемножения суммарной эпюры моментов в статически неопределимой системе (при воздействии температуры) на какую-дабо единичную эпюру от Л",- 1 равняется (—Д,), где Д, — температурное перемещение по направлению X в основной системе. Деформированная ось системы получается суммированием
18а
действия температуры и лишних неизвестных и потому в указанном случае нет соответствия между положением растянутых волокон и ординат эпюры М (рис. 153, б, в).
Пример. Найти лишнее неизвестное и построить эпюру моментов в раме постоянного сечения (рис. 154, а), если наружные волокна нагреваются на 30°, а внутренние — на 2 Ю° Высота сечения стержня рамы I- При отыскании температурных перемещений учесть влияние удлинений по оси. Длина стержней рамы одинакова: I Н.
Решение. Перемещение от действия температуры для основной системы (рис. 154, б)
Аи 1 °о 2 (8 ) та —280а.
Единичное перемещение
© ___1 2 2 _ 4 3
11 Е1 2 3 3" Е1
Лишнее неизвестное по уравнению (9.22)
Аи_2ЮаЕ1
Х1-Ьп I(а)
Эпюра моментов в статически неопределимой системе показана на рис. 154, в. Она подобна эпюре моментов в единичном состоянии действия неизвестного. Деформированный вид рамы представлен на рис. 154, г.
Действие осадки опор
Осадка опор внешне статически неопределимых систем вызывает дополнительные усилия, если при этом происходят смещения по направлению лишних связей. Так, при осадке промежуточной опоры неразрезной балки в ней возникает статически неопределимая реакция (рис. 155, а) и создаются дополнительные усилия. Отбросив эту опору и возместив ее действие силой Хъ составим уравнение деформаций, учитывая, что в заданной системе в результате действия силы Хх и нагрузки Р происходит смещение опоры Д2 (рис. 155, б):
111 “Ь 1Р Дх, (9.24)
где Дх — осадка опоры;
Д1р — перемещение от нагрузки в основной системе; б 11 — единичное перемещение.
Из уравнения (9.24) получаем лишнее неизвестное:
Уравнение деформаций при наличии осадки всегда можно представить так, чтобы правая часть уравнения (9.24) оказалась равной нулю. Для этого за неизвестное принимаем усилие в опор-
189
ном стержне, смещение которого обусловлено отклонением опорной площадки с — с на величину Дх (рис. 155, в). Полагая взаимное смещение сечений разрезного опорного стержня равным нулю, имеем:
а)
I
С Т с Рис. 165
111 1, ос 1р 0, (9.26)
где Д1( ос - взаимное смещение сечений, вызванное действием осадки на основную систему.
Если обозначить смещение опорной площадки Ли то Д1ос можно выразить так:
1,ос—1- (б)
Подставляя это соотношение в уравнение (9.26), приходим к первоначальному уравнению (9.24).
Смещение опор, реакции в которых можно определить только из условий равновесия статики, не вызывают дополнительных усилий (например, вертикальные смещения опор двухшарнирной арки).
Пример. Определить лишнее неизвестное для рамы (рис. 156, а) и построить эпюру моментов в двух случаях:
1) при наличии осадки левой опоры, не зависящей от нагрузки и равной
А -_3
ЁГ ЁТ 9
2) при отсутствии осадки.
Длина стержней рамы одинакова: к. Сечение постоянно по длине.
Решение. За лишнее неизвестное принимаем реакцию подвижной опоры,
которую направляем вверх. Составляем каноническое уравнение по уравнению (9.24).
Осадка опоры происходит вниз, поэтому поставлен знак «минус» в выражении Д.
При наличии нагрузки и осадки опоры каноническое уравнение будет:
откуда
ХАх ДиДь А — Д 1р
1 -
(В)
По эпюрам моментов от нагрузки (рис. 156, б) ив единичном состоянии (см. рис. 154, б) получаем
к3
л 5 рк4
А1“8Ж;
с 4
11Тя7-
Подставляя эти значения и величину осадки‘Дг — —в выражение (в), находим
о к
(г)
190
а при отсутствии осадки реакция будет в 2,5 раза больше:
V 15 и
х,з-2рН.
Эпюра моментов при наличии осадки показана на рис. 156, в, а при отсутствии осадки — на рис. 156, г. В первом случае момент в узле увеличивается в 10 раз.
§ 52. РЕШЕНИЕ СИСТЕМЫ КАНОНИЧЕСКИХ УРАВНЕНИЙ СПОСОБОМ ГАУССА
Канонические уравнения для п раз статически недиределимой рамы
Рассмотрим задачу расчета п раз статически неопределимой рамы методом сил. Для основной системы, подверженной действию нагрузки и лишних неизвестных Хъ Х2, Х3,., составим уравнения деформаций, каждое из которых выражает условие равенства нулю перемещения по направлению I-го неизвестного (или г-ой лишней связи). Получим следующую систему канонических уравнений:
11 212 - • 121 222 “К •
Хп6пп -- Апр 0.
(9.27)
191
Первое каноническое уравнение деформаций выражает условие равенства нулю перемещения по направлению первой отброшенной связи; второе уравнение — условие равенства нулю перемещения по направлению второй отброшенной связи и т. д.
В системе уравнений (9.27) Д1р, Д2р,., Д„р — перемещения от нагрузки (грузовые члены); при действии температуры или осадки опоры они соответственно заменяются величинами Д1Л Д2,,. или Д10с, Д2.ос, ••• Коэффициентами при неизвестных являются перемещения в основной системе от единичных сил, приложенных по направлению отброшенных связей.
Система канонических уравнений (9.27) обладает симметрией в коэффициентах при неизвестных относительно так называемой главной диагонали, т. е. линии, соединяющей главные перемещения бц, 622,., 8пп. Это свойство взаимности позволяет воспользоваться одним из эффективных приемов решения системы уравнений (9.27) по сокращенному способу Гаусса.
Осуществив все проверки вычисления перемещений, решим систему уравнений (9.27) и найдем неизвестные Хх, Х2,., Х„.
Определяем действительный изгибающий момент в сечении рамы по формуле
М МР2ХД, (9.28)
1 1
где Мъ М_2,., Мп — моменты соответственно в состояниях действия Хг 1, Х2 1,., Хп 1; Мр — момент от заданной нагрузки.
Решение системы канонических уравнений
Систему канонических уравнений (9.27) представим несколько иначе:
Здесь:
Хбц Х2612 Х3613. • • ХпЬ1п — Дх; X 121 Х2622 хзб2з. Хп62п — 2у 131 Ь Х2б32 Х3б33. • Хп6зп Д3;
1 — Дг Дг р»
з р
(1)
(2)
(3)
(п)
(9.29)
192
— Д,
В матричной форме (см. Приложение) эта система представляется так:
где Л — квадратная матрица, составленная из единичных перемещений:
От системы (9.29) путем последовательного исключения неизвестных переходим к следующей преобразованной системе уравнений:
Таким образом, по методу Гаусса решение сводится к построению эквивалентной системы (9.32), имеющей треугольную матрицу из коэффициентов при неизвестных
В системе уравнений (9.32) первое уравнение то же, что и первое уравнение системы (9.29); второе уравнение получено из второго уравнения первоначальной системы исключением неизвестного Хх третье уравнение найдено путем исключения неизвестных Хг и Х2 и т. д. В последнем уравнении содержится лишь одно неизвестное Хп и все побочные коэффициенты равны нулю.
Из последнего (п-го) уравнения получаем
Затем переходим к предыдущему (п — 1) уравнению, содержащему два неизвестных Хп 1 и Хп, и, зная Хп% определяем Хп_г. Теперь переходим к уравнению (п — 2) и находим Хп _2 и т. д. Наконец, из
А-Х А,
(9.30)
,11и12и13
62122;
21и22и23
А
(9.31)
г1®г2®яЗ • • • ®пп
а X и Д — векторгы-столбцы.
111 212 313 • • • Хп61п— 1 0)
х№ Х8ва. Хп6 Да1’; (2(1))
адв«,.-адвп,Дз; (з(2)) (9.з2)
в
о о. ей,-”
(9.33)
7 Н. К. Снитко
193
первого уравнения определяем Хг. Задача состоит в том, чтобы найти преобразованную систему уравнений (9.32), содержащую последовательно уменьшающееся число неизвестных. Второе уравнение этой системы получается после одного преобразования (уравнение 21)), третье уравнение находится после двух преобразований (3(2)), четвертое уравнение — после трех преобразований (4(3)) и п-е уравнение — после (п — 1) преобразований. Первое уравнение (9.32) справедливо для основной статически определимой системы, второе — для основной однажды статически неопределимой, п-е — для основной (п — 1) раз статически неопределимой системы. Остановимся на составлении алгоритма Гаусса.
Все коэффициенты при неизвестных уравнения 2и) определяют по формуле
бзл 62л “Ь 0С12®1г, (а)
т. е. к коэффициенту второго уравнения системы (9.29) прибавляется произведение множителя а12 на коэффициент при данном неизвестном первого уравнения. Множитель а12 для исключения Хг должен быть равен:
«»—“• (б)
Аналогично свободный член уравнения 2(1) будет
ДДз аЛ. (в)
На этом основании таблицу получения преобразованных уравнений системы (9.32) сокращенного способа Гаусса (табл. 2) составляем так.
В левой части таблицы приводим коэффициенты при неизвестных, а в правой части ее — множители акп, свободные члены уравнений и для контроля — суммы коэффициентов при неизвестных Нередко в сумму 5 включают для контроля и свободный член. В пер¬
вом столбце указываем номер преобразования, во втором столбце — номер уравнения по системе (9.29) и (9.32). В первую строку таблицы в левой части вносим коэффициенты при неизвестных первого уравнения и затем вычисляем множители:
13
а12-_бй; ои-
614
“14 ёи:
61 п
а1 п д
Он
В последнюю графу включаем сумму коэффициентов: 31 бп 612 б13. 61п
— это контрольная сумма.
(г)
194
Решение системы уравнений способом Гаусса
7
195
Переходим к составлению уравнения (2(1)), пользуясь соотношением
(а). Для этого вносим во второй строке таблицы коэффициенты второго уравнения, затем в третьей строке — коэффициенты первого уравнения, помноженные на а12. Складывая в каждом столбце значения членов, входящих в эти две строки, получаем коэффициенты уравнения (2(1)), которое не содержит неизвестного Хг. Аналогично вычисляем свободный член этого уравнения До1 и сумму
Получив уравнение (21)), вычислим множители:
А1) Л1) Аа
°23 °24 ч
а2з — ТГ » а24 — 5ТГГ •••» а2 п — Щ- • (Л)
Теперь переходим к составлению уравнения (32)). Коэффициенты при неизвестных в этом уравнении находим по коэффициентам уравнений (3), (1), (2(1)) по следующей формуле:
ЗП 3 п а13® 1П а23® (е)
Аналогично получаем свободный член этого уравнения и сумму коэффициентов при неизвестных. Уравнение (3(2)) не содержит двух неизвестных Х1 и Х2.
Символически выражение (е) можно представить так:
3(2) 3 а1з • 1 а23 • 2а). (ж)
Коэффициенты нового уравнения получаем как сумму коэффициентов третьего уравнения, первого уравнения, умноженного на аши уравнения (2(1)), помноженного на а23. Получив коэффициенты уравнения (3(2)), вычислим множители:
Я2) Х(2) Л(2
ГУ — г —. ГУ — V
34— Я2) » а35— Л2) •••» 3п— 2) • 3)
°33 °33
Проверяем сумму коэффициентов уравнения (3(2)), сопоставляя ее с суммой, полученной непосредственно по формуле (ж).
Переходим к составлению уравнения (4(3)), коэффициенты которого получаем по символической формуле
4(3) 4 а14 • 1 а24 • 2(1) а34 • 3(2). (и)
Множители а14, а24 и а34 берем из третьего столбца коэффициентов а (см. табл. 2). Работу продолжаем до тех пор, пока не будет получено уравнение с одним неизвестным. Из этого уравнения находим:
д«-1
п Ь(п-1) (к)
ипп
после чего, идя в обратном порядке, найдем из преобразованных уравнений Хпъ Х1-2 Х3, Х2, Хг. Заметим, что при изменении
нагрузки меняется только столбец свободных членов.
Остановимся на сущности алгоритма Гаусса, т. е. самой логической последовательности перехода к системе уравнений
(9.32) с треугольной матрицей;
196
1) находят множители а,- путем деления побочных коэффициентов на главные; в ( — 1)-м преобразовании
в-‘
(9-34)
°и
где (г — 1) 0 относится к коэффициентам первоначального уравнения;
Таблица 3
Решение системы уравнений по способу Гаусса
Номер
преобра¬
зования
Номер
уравнения
Коэффициенты при неизвестных
Множители
Сво¬
бодный
член
д
Сумма о (А)
Хх
X,
X 4
°2
“аз
1
1
2
3
-3
— 2
-3а
32
1
— 5
0
II
2
3
2
-1
— 3
0
1
а12 ’ 1
-3
-02
е2
3
‘5з
0
2Ц
0
5 2
72
0
7 а
0
162
1
III
3
-3
— 1
3
2
10
1
а13 •
3
й2
-92
-3
152
0
«23 • 2“
0
72
4ую
0
212
V
З2
0
0
17а
-1
х,
13
1Уь
IV
ч
4
-2
-3
2
3
2
0
«м-
2
-3
-3
-2
— 5
0
«24 21’
0
0
0
0
0
0
«34 ■ 3»
0
0
1
-б,7
«Л,
12п
4131 о
.0
0
1217
14х,
12п
2) находят коэффициенты преобразованных уравнений и их свободных членов путем суммирования предыдущих строк граф II, III, IV и т. д. (табл. 2) по формулам:
к 1) 6;А а1?61д а2бб2А. 1-1,к1-1,к- (9.35)
Пример. Решить, пользуясь таблицей сокращенного алгоритма Гаусса (табл,3), систему уравнений:
2Х ЗЛ:2-ЗХз-2Х4-5; ЗХ1 2Х2— Х3-ЗХ4 0; I
— ЗА1— Х2 ЗХд -- 2X4 10; — 2X3 “I- ЗХ 2. )
197
Решение. Решение системы уравнений (л) ведем в табл. 3 по цриведенной выше общей схеме.
Из табл. 3 получаем преобразованную систему уравнений:
Способом Гаусса можно просто получить обратную матрицу на основе схемы с единственным делением. (О применении вычислительных машин см. гл. 17, § 88.)
§ 53. РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ СПОСОБОМ ИТЕРАЦИИ
В том случае, когда главный коэффициент при данном неизвестном больше суммы абсолютных значений всех побочных коэффициентов при остальных неизвестных в каждом уравнении системы, целесообразно применять способ итерации (способ последовательных приближений).
Выразим из системы канонических уравнений (9.27) каждое неизвестное через все остальные неизвестные и свободный член:
В первом приближении принимаем все неизвестные, входящие в правые части уравнений (9.36), равными нулю. Тогда получим первые грубо приближенные значения неизвестных:
Подставив значения первых приближений неизвестных в правые части выражений (9.36), получим значения вторых приближений для неизвестных:
(м)
Решая эти уравнения (ходом снизу вверх), находим
47в 3 2бв 2 17в» 1 2з-
(9.36)
(9.38)
198
Проще находить не полные приближенные значения неизвестных, а только поправки к ним, которые получаются из выражений
(9.38), если отбросить свободные члены. Поправки второго приближения будут:
дГ -
612 у 13 у 14 V
Л2— 7С7Л3— 7СГ Л4“ •••
д V-" 21 у 23 у V
А б22 л3 -б22 л4.
22 31 V Озз
32 V 34 V А2 А4
3
33
(9.39)
Поправки третьего приближения получим, если в правые части выражений (9.39) внесем вместо значений неизвестных поправки второго приближения, и т. д.
Если поправки какого-то приближения окажутся в пределах принятых отклонений, вычисляют полные значения неизвестных по формулам:
Хг- ЛХГ ЛГ.
8
лз р
ДЛ’зДз
(9.40)
ГЛАВА 10. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ АРКИ § 54. ЗАКОНЫ ИЗМЕНЕНИЯ СЕЧЕНИЙ АРОК
В этой главе рассмотрим расчет статически неопределимых двухшарнирных и бесшарнирных арок со сплошной стенкой.
Двухшарнирная арка — криволинейный брус на двух шарнирно неподвижных опорах, очевидно, однажды статически неопределима (рис. 157, а). Бесшарнирная арка — криволинейный брус, защемленный двумя концами (рис. 157, б). Обычно в силу криволинейности оси и переменности значения расчетных усилий по длине оси арки она имеет переменное сечение, что осложняет вычисление перемещений и не дает возможности применять правило перемножения эпюр. Поэтому при вычислении перемещений в арках используем непосредственно формулу Мора и проводим интегрирование по длине оси арки с учетом переменности сечений. Лишние неизвестные в арках зависят не только от закона изменения сечений, но и от очертания оси, которое должно быть задано. Ось массивной арки целесообразно задать по кривой давления в соответствующей трехшарнирной арке от собственного веса.
199
Рассмотрим законы изменения момента инерции по длине оси арки. Для двухшарнирной арки пользуются уравнением в форме
0со8ф, (а)
где 0 — момент инерции в замке;
Ф — угол, образуемый касательной к оси арки с горизонталью. Очевидно, уравнению (а) соответствует увеличение сечения от пяты к замку с наибольшим сечением в замке.
Для бесшарнирных арок нередко, чтобы упростить расчет, принимают такой закон изменения момента инерции:
--. (б)
С05ф 4 Этому закону соответствует увеличение сечений от замка к пяте с наибольшим сечением в пяте. Однако закон изменения по уравнению
(б) не удовлетворяет действительному распределению расчетных моментов в бесшарнирной арке. Риттер, Штрасснер, Маннинг и другие рекомендуют следующий закон изменения I для симметричных бесшарнирных арок:
- 5—, (10.1)
со3ф 1 р п
200
где ?, — длина полупролета;
х — абсцисса, отсчитываемая от замка;
Р — параметр закона изменения момента инерции: меняется от О до —1.
Для пяты, х 11г и вместо выражения (10.1) получаем
откуда
(в)
(10.2)
1к созф
Окончательное выражение для закона изменения момента инерции бесшарнирной арки
-. (10.3)
С05«Р 1-(1-л)
п
Зная отношение -р и соз ф (косинус угла наклона пяты арки к гори-
• к
зонтали), легко находим по выражению (10.2) параметр р или п. В среднем Р — 0,75.
При определении перемещений, вызванных влиянием продольной силы в арке, важно знать закон изменения площади сечения арки Р. Если ширина сечения арки постоянна, то переменную площадь сечения можно выразить так:
(Ю-4)
где Р0 — площадь сечения в замке.
§ 55. РАСЧЕТ ДВУХШАРНИРНОЙ АРКИ НА НЕПОДВИЖНУЮ НАГРУЗКУ
Общий ход расчета
Расчет двухшарнирной арки, как и других систем с криволинейными элементами, при заданном очертании оси производится по методу сил (рис. 158, а).
За лишнее неизвестное принимаем распор Хг — горизонтальную реакцию неподвижной опоры (рис. 158, б), за основную систему — криволинейную балку. В отдельных случаях используют основную систему в виде трехшарнирной арки (рис. 158, в).
Сначала рассмотрим общий ход расчета двухшарнирной арки при действии вертикальной неподвижной нагрузки Р с использова¬
201
нием первого типа основной системы (см, рис. 158, б). Отбросив горизонтальное закрепление правой неподвижной опоры, возместим ее действие распором Хг. Для отыскания распора Хх составляем канони¬
ческое уравнение, выражающее условие равенства нулю горизонтального перемещения подвижной опоры:
111 "Ь О»
где А1р — горизонтальное перемещение правой опоры, вызванное нагрузкой Р
202
8П — горизонтальное перемещение этой опоры от действия единичной силы Хх 1.
Из канонического уравнения получаем выражение для распора:
(10.5)
Определение перемещений
Если арка представляет собой кривой брус малой кривизны (ра-
р
диус кривизны ?0 велик, 8, где к — наибольшая высота сечения
бруса), применяем формулу, справедливую для прямолинейного стержня (рис. 159, а):
Ч ( МхМрс1з ЧЛ С ЫхЫрйз
а2 (1о-6)
Далее рассматриваем лишь пологие арки, для которых
В этом случае продольная сила в сечении к в основной системе от действия вертикальной нагрузки (рис. 159, б) выражается формулой
Л С51Пф,
где 0°ь — поперечная сила в простой балке.
Для пологой арки величина зт ф незначительна; поэтому можно пренебречь влиянием Nр в формуле (10.6) и вычислять Д1р по упрощенной формуле:
2, з -тг- 10-7
где Мр — различно на разных участках арки.
Пренебрегать же влиянием продольной силы при вычислении
горизонтального перемещения би не всегда возможно.
Единичное перемещение (см. рис. 159, б) определяем по формуле
(10.6):
5 5
(10.8)
0 0
где
М1 — -у Л11созф; (10.9)
5 — длина оси арки.
Сжимающую силу принимаем положительной. Подставляя значения усилий из выражений (10.9) в формулу (10.8), Получаем
12 12
бц 2 § У2 2 § с082ср-. (10.10)
о 0
Здесь учтена симметрия арки.
203
В ряде случаев для гибких арок при малом отношении в выражении (10.10) вполне можно пренебречь влиянием продольных сил.
Так, для одного из железобетонных мостов при у и Т 26 вто рой член в выражении (10.10) составил 0,2% от первого члена.
Частный случай параболической арки и закона изменения момента инерции по косинусу
Принимаем следующий закон изменения момента инерции:
СОЗ ф
204
Этот закон, хотя и не соответствует действительному распределению расчетных моментов в двухшарнирной арке, дает весьма простые выражения для перемещений и распора Хъ что используется в предварительных расчетах двухшарнирных арок. В этом случае имеем
йв Ах соз ф йх
0 соз ф 0
Следовательно,
1р2 § ХРТП1 5 УМрЛх. (а)
?
Для пологих гибких арок
1
б цщ)угах. (б)
о
(1 — х)
Если У -±-а-,2—то после интегрирования по выражению (б) получаем единичное перемещение
в„ в-й-
§ 56. ЛИНИИ ВЛИЯНИЯ РАСПОРА И УСИЛИЙ В ДВУХШАРНИРНОЙ АРКЕ. ЭПЮРЫ УСИЛИЙ
Линия влияния распора
Для построения линии влияния распора рассмотрим произвольное положение груза Р 1 на расстоянии а от левой опорной вертикали. Действие одного груза на основную систему представлено на рис. 159, а, действие силы Хг 1 — на рис. 159, б. Каноническое уравнение метода сил
-111 Н“ 1р 0 (а)
По теореме взаимности перемещений
1р — р1-
Учтя это равенство, из уравнения (а) найдем
т. е. линию влияния Хх можно получить по эпюре вертикальных перемещений бр1 основной системы от действия Х1 1. Деля все ординаты эпюры бр1 на 6и и меняя знак на обратный, находим ординаты линии влияния Хх (рис. 159, е). Задача, таким образом, сводится к построению эпюры вертикальных перемещений бр1, которую можно найти или аналитически, или способом упругих грузов.
205
Заметим, что влияние на ординаты линии влияния Хг для относительно гибких и подъемистых арок незначительно. Так, для
арки с у Т максимальные ординаты инфлюэнтной линии Х1
с учетом и без учета влияния отличаются на 0,6%. Для той же арки при замене закона изменения момента инерции 0соз ср на 0 соз ср получается разница в 4,2% (ордината линии влияния меньше в последнем случае).
Пример. Пренебрегая влиянием продольных и поперечных сил на деформацию, найдем уравнение линии влияния распора для параболической арки при законе изменения момента инерции
——.
СОЗ ф
Решение. Уравнение оси арки
У-Щ. (10.12)
Определим перемещения бр1 и 6П, входящие в выражение для инфлюэнтной линии Хг:
у р1
Перемещение бр1 можно найти непосредственно, применяя формулу Мора и проводя интегрирование по двум участкам (0 х а; 0 хх Ь):
? МрМ1Лв МрМЛв РЬх йх С Рах1 йх,
—ёт— —ёг- -) -ТуЕГ0) —уЁГ0-
0 0 0 0
Подставляя значение у и вынося постоянные за знаки интегралов, получаем
- а Ь
Р- 4
ЬхН1-х)-. ахи1-Х1)§.
»Р 1 3
Для случая изменения момента инерции по закону I
1_о о
о
СОЗ ф
ь
я. 4
х2 (I — х) йх а х (I — хх) д,хх
Р1 13Е1 ш
о о
Вычисляя интегралы, получаем при Р 1 4_
1 о
(в)
Заменим
Ь I — а 41 — ЗЬ 1 За.
Тогда после преобразований получим
V ЗШ,; а(1-а)(Ра1- а’-)
3 Е„ ‘ I (, Д 3 Е1йъ( 1)05 Е), (г)
а где Ъ-[. 200
Будем считать положение груза меняющимся. Следовательно, в уравнении (г) абсцисса переменна. Придавая различные значения получим все ординаты эпюры бр1. Значения функции 6(1 — (1 5 — I2) приведены ниже:
1 аЦ
0
0,10
0,20
0,30
0,40
0,50
?(1-Ш1 6-52)
0
0,0978
0,1855
0,2545
0,2975
0,3125
Теперь найдем перемещение 6И:
I I
0 0 о
Таким образом, уравнение инфлюэнтной линии Хг будет
6Р1 5 Инфлюэнтная линия Хх представлена на рис. 159, в.
(10.14)
Линия влияния и эпюры усилий в сечении арки
Имея линию влияния распора, легко получить линию влияния момента Мк, поперечной силы (±к и продольной силы Ык в любом сечении к арки (рис. 160, а), пользуясь принципом наложения.
Так же как и для трехшарнирной арки, изгибающий момент в сечении к представляем как момент левых вертикальных и горизонтальных сил:
Мк М%-Х1Уку (10.15)
где М% — балочный момент (момент левых вертикальных сил); при положении груза Р 1 справа от сечения
М% Уаак
Vа — левая вертикальная реакция;
Ххук — момент распора;
Ук — ордината точки к.
Следовательно, ординаты линии влияния Мк находят вычитанием ординат линии влияния момента от распора Ххук из ординат балочного
момента Мк (см. рис. 160, а). Линия влияния Мк показана также
на рис. 160, б, где ординаты ее отложены от горизонтали. Аналогично находят ординаты линий влияния поперечной силы Ск и продольной силы Ыку пользуясь формулами, известными из теории расчета трехшарнирной арки, с заменой Н на Хх.
Для поперечной силы имеем
Ъ Ук С08 цк — Хг 81П фь (10.16)
для продольной силы
— 2 1П фк хг С08 фь (10.17)
207
где 0% — балочная поперечная сила (при грузе справа от сечения 2 Уа) ср — угол наклона касательной к оси арки в точке к.
По выведенным уравнениям найдены линии влияния ф и Л., которые изображены на рис. 160, в, г. Эпюры Мк1 и Ык (при неподвижной нагрузке и переменности сечения к) легко построить, пользуясь теми же формулами (10.15)—(10.17). Вычислив распор Хг от заданной неподвижной нагрузки по выражению (10.5), построим эпюру
балочных моментов М и сложим ее алгебраически с эпюрой ординат ук) увеличенной в Хг раз. Аналогично поступаем для эпюр и Ык, вврдя законы изменения 51П фА И СОЗ фА.
а)
I
Р«7
I
§ 57. ПОСТРОЕНИЕ ЛИНИИ ВЛИЯНИЯ РАСПОРА ДВУХШАРНИРНОЙ АРКИ МЕТОДОМ УПРУГИХ ГРУЗОВ
Построение линии влияния Х1 сводится к отысканию линии прогибов основной системы, что в самом общем случае произвольного очертания оси легко проделать, используя метод упругих грузов:
1. Заменяем заданный криволинейный стержень ломаным, разбивая на равные части пролет арки или ее ось. На рис. 161, а пролет арки расчленен на 12 равных участков. Находим ординаты узловых точек ломаного стержня уп, значения тригонометрических функций углов наклона всех элементов 8п с осью абсцисс (углов фД моменты инерции и площади сечений л, Рп для средних (промежуточных) точек между узлами.
2. В общем случае учитываем влияние и продольных сил. Тогда для подсчета упругого груза №п пользуемся формулой
Жп 1Г (Мп-1 2Мп) (Мл1 2Мп)
л1 ЁГп пу 203
где Мп и — соответственно изгибающий момент и продольная сила в состоянии действия силы Хг 1;
Мп--уп, Мп — Ьсо8фл; (б)
рл — угол наклона элемента 8п с нормалью к направлению искомого перемещения (для вертикальных перемещений ф„; для горизонтальных — 90° — фл).
Обычно задается закон изменения момента инерции 1Х 10уху где ух — какая-либо функция от х (например, V соз ф), 0 —
момент инерции в замке. Тогда для случая арки, сечение которой имеет постоянную ширину,
Рп РоУп 1п 1(Рп-
Сделаем эти подстановки и, кроме того, умножив обе части выражения (а) на 6Е10:
6Е10№п (Мп_1 2Мп)-
1
СМл1 2Мп)
,60
0
Nп1 Р71 Nп п
(в)
V 1 V
Рассмотрим теперь развернутое выражение упругого груза для построения упругой линии арки в состоянии действия силы Х± 1. Подставим значения усилий по выражению (б)
Мы получили выражение для промежуточного упругогогруза.
В первых двух скобках правой части выражения (г) отражено влияние моментов, в третьей — влияние продольных сил. При отыскании вертикальных перемещений направляем грузы №п вниз, если выражение (г) дает знак «плюс» (рис. 161, б). При этом для случая вертикальных перемещений п ф„, т. е. углу наклона элемента 8п к горизонтали.
При отыскании горизонтальных перемещений используем то же
выражение (г), но с заменой 19"; меняется только влияние
продольных сил №ял", влияние же моментов остается постоянным. Таким образом (рис. 161, в), при отыскании горизонтальных перемещений имеем следующее выражение для упругого груза:
6Е1№‘ - (уп 2уя) - (уп1 2уп)
6о С08 фд1 С08 фц
Го V 1 Фп1 VЧп фп)
Для верхнего упругого груза учитываем только выражение, соответствующее элементу 8„1. Для среднего упругого груза влияние продольных сил берем в каждом члене с одинаковым знаком.
3. Определив величины всех упругих грузов переходим к построению линии прогибов бр1. Приложив систему вертикальных фиктивных сил к простой двухопорной балке, найдем эпюру фиктивных моментов Мф (см. рис. 161, б).
4. Отыскиваем бп — горизонтальное перемещение подвижной опоры. Для этого, используя симметрию в изогнутой оси арки (угол наклона упругой линии арки в замке равен нулю), представляем левуючветвь линии горизонтальных перемещений арки, вводя заделку в замке и освобождая левую опору (см. рис. 161, в). Горизонтальное перемещение свободного конца этой половины стержня и дает 12 6П. Для нахождения этого перемещения вводим условное сооружение — консоль с заделкой внизу и свободным концом в замке. Упругие грузы, подсчитанные по формуле (д), прикладываются по горизонтальному направлению. Средний упругий груз делится на 2.
Тогда фиктивный момент от горизонтальных сил иУп относительно точки О будет
м0 ф.
5. Деля ординаты эпюры фиктивных моментов Мф на значение 2Моф, получаем ординаты линии влияния Хх.
§ 58. АРКА С ЗАТЯЖКОЙ
Арка с шарнирно прикрепленной к ней затяжкой (рис. 162,,а) являете системой с одной лишней связью. За основную систему может быть принята криволинейная балка с перерезанной затяжкой
210
(рис. 162, б). Так как затяжка А В связана с аркой у опор шарнирно, в ней возбуждается только продольная сила X.
Перейдем к определению лишнего неизвестного — усилия в затяжке. Взаимное смещение сечений разреза для основной системы равно нулю. Поэтому каноническое уравнение имеет следующий вид:
Х8ц 1Р 0, (а)
где
6П — взаимное
смещение сечений разреза по горизонтали от действия силы X 1;
Д1р — то же, от приложенной нагрузки Р.
От действия нагрузки Р на основную систему работает только криволинейная балка, перерезанная же затяжка не имеет усилий. Следовательно, выражен ние для Дзр будет то же, что и для аналогичной двухшарнирной арки. Для перемещения 6П сравнительно с двухшарнирной аркой добавляется влияние
X 1, т. е. удлинение тУ-, где Е5Р8 — жесткость затяжки на ра-
8 8
стяжение.
Итак, для 6И имеем
удлинения затяжки в состоянии
(10.18)
При пренебрежении влиянием продольных и поперечных сил в арке значение усилия в затяжке или распора X будет
Х
С МР
-уе7
1Р
(10.19)
а распор в двухшарнирной арке
Хй-
1 р 11, а
(б)
Очевидно, распор в арке с затяжкой всегда меньше, чем распор в двухшарнирной арке, так как в первом случае увеличивается знаменатель
211
выражения (10.19):
Агр п, п
х -Ч- ха— (10.20)
Л I 1 °11»Я 1 1
п’аЕ3Р8 Л1,а
При Р3 Оу X 0, арка обращается в балку.
При Р8 оо, X Ха, имеем двухшарнирную арку.
При относительно небольшой площади затяжки быстро нарастает распор X.
Таким образом, чем меньше сечение затяжки Р8, тем меньше усилие в ней.
§ 59. РАСЧЕТ БЕСШАРНИРНОЙ АРКИ НА НЕПОДВИЖНУЮ НАГРУЗКУ
Основная система
Бесшарнирная арка трижды статически неопределима. Рассмотрим расчет симметричной арки в случае действия нагрузки в плоскости ее оси (рис. 163, а). За основную принимаем симметричную систему
в виде двух раздельных криволинейных консолей (рис. 163, б). Используя симметрию, разрезаем арку в замке и в качестве первых неизвестных принимаем силы и моменты взаимодействия: (продоль¬
ные силы), Ъ2 (моменты) и 23 (поперечные силы). Канонические уравнения для этих первых неизвестных будут иметь следующий вид:
%111 4" 212 4" 1р — 0; 121 4" 22б22 4“ А2р 0;
(а)
23633 4" Лзр 0.
Общая система трех канонических уравнений распадается на две группы: в первую группу входят симметричные неизвестные и вторая «группа» содержит лишь одно обратносимметричное неизвестное 23 (рис. 164, а, б, в).
Нетрудно видеть, что при данном выборе неизвестных 612 0. Поэтому переходим к новой системе неизвестных ХьХ2иХ3, несколько преобразуя основную систему. К сечениям проведенного в замке разреза присоединяем невесомые и абсолютно жесткие консоли длиной с. К концам этих консолей и прикладываем силы взаимодействия Х1у Х2 и Х3 (рис. 165).
Консоли считаем абсолютно жесткими и невесомыми, чтобы не вводить добавочных перемещений их концов сравнительно с замковыми
212
точками оси арки и добавочных усилий. Система сил Хх, Х2 и Х3 должна быть статически и кинематически эквивалентна системе сил
Ъ1% 22 и 23. Из сопоставления рис. 165 и 163, б получаем:
2г Х19 2ъ Х2 — Ххс9
23 Х3.
(б)
Таким образом, момент в замке 2® выражается как разность между моментом на конце консолей Х2 и моментом от горизонтальных сил
взаимодействия Хг. Так как из условия равновесия Хг Я, то неизвестное Хх называют распором. Длину введенных консолей с выбираем так, чтобы побочное перемещение 612 в системе уравнений
213
для симметричных неизвестных Хх и Х2
111 212 1р 0 1 121 4" Х222 2р 0
равнялось нулю.
Для вывода выражения 612 используем эпюру моментов в единичных состояниях Хг 1 и Х2 1. Если распор Хг будет приложен на
конце консолей (рис. 166, а, б), то при соответствующем выборе длины с легко добиться _равенства нулю 612. Моменты Мг и М2 в произвольном сечении бруса:
Л?1 — 1 -Уъ
м2 1,
где. — ордината оси арки от носительно линии действия распора Хг.
Выражение для 612 при подстановке Мг и М2 будет
б)
бх2м1м25- о о
-(с-у)т-
о
Выбираем длину абсолютно жесткой консоли так, чтобы побочное перемещение б12 равнялось нулю:
«-
й
еГ
0,
(д)
где 5 — вся длина оси арки.
Из выражения (д) получаем, принимая во внимание симметрию арки,
52 52
( с1з Г с1з п
С)ё1-)Уё1 °
откуда длина абсолютно жесткой консоли
Мы получили формулу для определения длины введенной консоли основной системы по рис. 165.
Примем йзЕ1 за величину фиктивной элементарной горизонтальной силы, сосредоточенной в центре элемента оси арки длиной (рис. 166, в). Тогда числитель формулы (10.21) будет представлять собой момент фиктивных горизонтальных сил ск 1Е1 относительно центра замка (точки 5), а знаменатель — сумму фиктивных сил по длине оси арки. Тем самым определяется вертикальная координата точки приложения равнодействующей фиктивных сил упругих грузов в состоянии Х2 1. Поэтому эту точку — центр тяжести упругих йз
грузов — часто называют упругим центром.
Положение упругого центра в различных случаях
Дадим определение координаты упругого центра в различных случаях.
Если момент инерции сечения параболической арки меняется по закону косинуса:
10-22
то координата упругого центра
с. (е)
Пусть ось арки — кубическая парабола, уравнение которой (по Маннингу)
»[(? (1-)] Л (10.23)
где — заданный параметр (1 меняется от 0 до 1,4); закон изменения момента инерции по Риттеру
- —, (10.24)
СОЗф ж- )
п
где р — заданный параметр закона изменения момента инерции (Р меняется от 0 до —1). При (5 0 момент инерции меняется по закону косинуса. Уравнение (10.23) охватывает большое семейство очертаний оси арок. Пользуясь формулой (10.21) и выражениями
(10.23) и (10.24), получаем после интегрирования следующее общее выражение для координаты упругого центра с в случае очертания оси по уравнению (10.23):
с 15-- 5р. -)- Р (124- Зц) 1Л пг
0 30(2 Р) •
215
Расчет арки на неподвижную нагрузку
После выбора лишних неизвестных с таким расчетом, чтобы все побочные перемещения были равны нулю, канонические уравнения принимают вид:
111 1р — 0; )
Х2622 Л2р 0; (10.26)
333 Азр 0. 1
Влиянием ф1э з и Ыру (р пренебрегаем.
По рис. 166, а, б и рис. 164, в находим выражения для внутренних сил в произвольном сечении основной системы:
М1 —1- у±; Лг1 —1-созф;
М2 1; Л?з1р1 ■.
Тогда единичные перемещения будут:
52 ф бц 2 У% 2 с082(РТГ
(Г о
52 52
б22 2 ; 633 2
ТГ’
(10.27)
где у — длина половины оси арки.
Перемещения от нагрузки, если пренебречь влиянием Ыр и ()р,
составят:
Д1р — § Мру
о
5
рмрШ (10-28)
о
5
Дзр “ МрХ.
о
Подставляя выражения для перемещений (определяемых способом точного или приближенного интегрирования) в канонические уравнения (10.26), находим лишние неизвестные, после чего переходим к отысканию усилий в произвольном сечении арки.
21а
§ 60. ЛИНИИ ВЛИЯНИЯ ЛИШНИХ НЕИЗВЕСТНЫХ для БЕСШАРНИРНОЙ АРКИ
Кинематический метод
Рассмотрим получение общего вида линий влияния лишних неизвестных. Каждую линию влияния будем находить по ее «модели» — эпюре вертикальных перемещений, полученной в единичном состоянии данного лишнего неиз¬
вестного.
Так как груз Р 1 (рис. 167), то канонические уравнения (10.26) принимают вид:
I я
111 1р — 222 Ь 2р
333 Н“ 3р 0
(а)
(б) (в)
Рассмотрим построение линии влияния Хг (рис. 168,а). Пользуясь теоремой взаимности перемещений, заменяем ®1р ®р1в Тогда вместо уравнения (а) получаем
111 вР1 0,
откуда неизвестное Х19 равное распору, будет
Рис. 167
а)
Хг -
Эр1
(г)
где бр1 — ордината эпюры вертикальных перемещений оси арки от действия Хг 1.
Эта ордината отмечается на линии действия груза Р 1, приложенного в произвольном месте (на расстоянии а от замка). От действия симметричной системы сил Хг 1 получим симметричную эпюру перемещений с максимальной ординатой для замка.
Так как 621 0, то жесткие консоли не получают поворотов и смещаются в положение, параллельное первоначальному. Перемещение 6П есть взаимное расхождение консолей по горизонтали. Эпюра 6р1 имеет у заделок горизонтальные касательные.
Рис. 168
217
Построив эпюру бр1 и деля согласно выражению (г) все ее ординаты на (— 6П), получаем ординаты линии влияния распор а Хх Н (рис. 168,6).
Переходим к построению линии влияния Х2 — момента в упругом центре (см. рис. 169,а). Пользуясь теоремой взаимности перемещений и учитывая, что 62р 6р2, из выражения (б) находим
Линию влияния Х2 получаем по_эпюре вертикальных перемещений
00рлпилй Л о Гглпггглаипп У —- 1 Попа тэг»а лпттниоти апхлру
6р2 на (—б22), находим ординаты линии влияния Х2. Очевидно, б22 — взаимный поворот жестких консолей. Заметим, что так как 612 О, то в состоянии действия Х2 1 нет взаимного смещения концов отростков и потому они перемещаются одинаково и по вертикали. Линия влияния момента в упругом центре симметрична (рис. 169,6).
Рассмотрим теперь построение линии влияния поперечной силы Х3, которую находим из канонического уравнения (в) заменой 63р 6р3:
Отсюда следует, что ординаты линии влияния Х3 могут быть получены путем деления всех ординат эпюры вертикальных перемещений 8р3 основной системы в состоянии действия Х3 1 (рис. 169,в) на
Здесь 633 — взаимное вертикальное смещение концов консолей, или замковых сечений разреза. Заметим, что 633 2у3, где у3 — прогиб в замке. Так как парные силы Х3 обратносимметричны, то эпюра 8р3 также обратносимметрична. При положении груза Р 1 у замка,
Рис. 169
218
очевидно, 8р3, а потому ордината линии влияния у замка согласно
выражению (е) будет: т]з,макс 0,5. Линия влияния Х3 обратносимметрична (рис. 169, г).
Аналитическое решение задач о линиях влияния
Для случая параболической арки (ось — квадратная парабола)
г о
и закона изменения момента инерции —— легко аналитически
Г СОЗ ф
по формуле Мора найти 6р1, 6р2 и 8р3 в функции от а (или лучше от -у, а также главные перемещения би, 622, б33. Пренебрегая влиянием в выражении 6П, получаем следующие уравнения для левой ветви линий влияния Х1у Х2, Х3:
V 15 1 (1 т22
1 Т71т“5)
(10.29)
где % меняется от 0 (замок) до 12 (пята).
При этом максимальные ординаты линий влияния:
— 1А. _Пг
1, макс — 0 2, макс — Лз. макс — ЛО.
Практически в приближенном решении выбор оси арки по уравнению (10.23) с произвольным параметром х и закона изменения момента инерции, выраженного уравнением (10.24) с произвольным параметром р, охватывает большую область очертаний оси и видов изменения жесткости арки по ее длине.
Уравнение для ординаты линии влияния момента в упругом центре в этом случае будет
. т(1-),В -з(1-Н)]- 10-30
где
с. а 2 а
“ Т-
Максимальная ордината линии влияния X2
Уравнение линии влияния поперечной силы в замке Ха 1 (6-2ф) р(Ч4-4Ч1»6ф»)
8 1 -Р
ъ
где Г-;
1
о — расстояние точки приложения груза до заделки;
1г — полупролет.
Линию влияния распора строим, пользуясь уравнением (г).
Построение линий влияния методом упругих грузов
Начинаем с построения простейшей линии влияния Х2 (рис. 170, а), для которой находим левую ветвь лии влияния. Загрузив левую криволинейную консоль моментом Х2 1, построим эпюру вертикальных перемещений как эпюру моментов от фиктивной нагрузки в виде вертикальных упругих грузов ИРЯ (рис. 170,6).
Рис. 170
Упругий груз при учете влияния только изгибающих моментов будет
И?» ощ Мп_х 2Мп) -(Мп1 2Мп), (10.32)
где зп — длина элемента арки между узлами (п — 1) и п.
В данном случае при действии Х2 1 нет продольных сил.
220
Принимая во внимание, что Мп 1, получаем для промежуточного узла
(3)
Так как упругие грузы положительны, направляем их вниз и прикладываем к фиктивной балке, защемление которой переносим на правый конец (см. рис. 170,6). Перемещение 6р2 определяем как момент левых сил:
б р2ед.
Как было показано на рис. 169,а, б22 2а есть взаимный угол поворота жестких консолей, а а — угол поворота элемента оси у замка, определяемый как фиктивная поперечная сила в защемлении фиктивной балки:
оь у б22 2НЛ.
Ординаты линии влияния Х2 могут быть получены делением момента на б22 22 №я.
Заметим, что так как для конца консоли (точка И) горизонтальное перемещение равно нулю, то для системы горизонтальных упругих грузов №п (рис. 170, в) должно быть
сШп ШпУп, (и)
откуда
шп (К)
Рассмотрим общий ход получения линии влияния Х3, которую находим, пользуясь уравнением (е), причем 833 равняется удвоенному прогибу замка в состоянии Х3 1 (см. рис. 169,в). В состоянии Х3 1 строим эпюру моментов М3 (рис. 171,а) и находим узловые моменты
Л4п 1 • хп. (л)
Вычисляем упругие грузы по формуле (10.32), подставляя значение Мп из выражения (л):
№п “6(1 -Хп ЪХп) - б1(1 Х11 2хп). (м)
Так как упругие грузы отрицательны, направляем их вверх. Построением эпюры моментов МПф и определяется эпюра бр3 (рис. 171,6):
8р3 Мпф.
Прогиб в замке у8 833 получается как момент в фиктивном
защемлении:
Уз — 2
221
Переходим к построению линии влияния распора Хи которая определяется уравнением (г); би есть горизонтальное расхождение
Рис. 171
концов бесконечно жестких консолей. В состоянии Х± 1 строим эпюру моментов, определяя все узловые моменты (рис. 172,а):
Мп 1 • Ут
где уп — ордината узла п относительно линии Действия распора
Хг; уп считаем положительным для узла п, расположенного выше линии действия Хх. Влиянием продольных сил будем пренебрегать.
222
Упругий груз, вычисляемый по формуле (10.32), составит
Г„ -
6 ЕГп
(1 -уп 2уп)
Ч
6Я„,
0 т Уп 14" 2(л).
(н)
Прикладывая упругие грузы к фиктивной горизонтальной балке, строим эпюру моментов Мп получаем эпюру 6р1 (рис. 172,6):
М лф бр1.
Заметим, что так как угол наклона упругой линии криволинейного бруса в замке равен нулю, то поперечная сила у фиктивной заделки для системы сил также равна нулю:
гвф 2И7л 0, (о)
т. е. сумма всех фиктивных грузов №п должна быть равна нулю.
Переходим к определению знаменателя в выражении Хг по формуле, (г). Определяем горизонтальное перемещение конца жесткой консоли или замка, которое можно найти как фиктивный момент нижних горизонтальных упругих грузов Уп по расчетной схеме рис. 172,в:
1
Прикладывая к вертикальной консоли, защемленной на уровне упругого центра, систему горизонтальных упругих грузов УРП, вычисляем момент этой системы сил относительно точки 5 — получаем бп2.
Деля все ординаты эпюры р1 на (—6П), находим ординаты линии влияния Хг.
§ 61. ЛИНИИ ВЛИЯНИЯ УСИЛИЙ В СЕЧЕНИИ БЕСЩАРНИРНОЙ АРКИ
Рассмотрим общий ход решения задачи по построению линий влияния момента Мк, поперечной силы Ск и продольной силы
Ык в произвольном сечении к арки по основной системе (рис. 173). Предполагаем, что линии влияния лишних неизвестных найдены и выражаем усилия Мк, Ск и Nк через лишние неизвестные и непо¬
м0
223
средственное влияние груза Р 1. Рассмотрим сначала построение линии влияния изгибающего момента в сечении к (рис. 173,а). Будем находить момент по силам, приложенным к правой части левой полуарки АЗ.
Когда груз находится справа от сечения к на участке кЗ, имеем по правым силам
Мк Х2 — Х1ук — Х3аъ—1 •хр, (а)
где ук — ордината точки оси арки относительно линии действия Хх; хр — переменное плечо силы Р 1 относительно точки к, для которой определяется момент.
Если груза на участке кЗ нет, то по правым силам получаем
Мк — Х2 — Хгук — Х3ак. (б)
По этим формулам и строим линию влияния момента Мк (рис. 173,6). Для построения линии влияния продольной силы Ык нахедим аналитические выражения ее при указанных выше положениях груза. В первом случае (груз на участке кЗ)
Мк Хг СОЗ Х3 51П ф 1 • 5Ш ф. (в)
Во втором случае (груза на участке кЗ. нет)
Ык Х соз ф Х3 51П ф. (г)
Линия влияния Ык представлена на рис. 173, в. Знак «плюс» соответствует действию сжимающей силы.
Переходим к построению линии влияния поперечной силы (к. При положении груза Р 1 на участке кЗ
Ск Х3 СОЗ ук — Х1 31П ф 1 - соз фл. (д)
Если груза на участке кЗ нет,
2 Х3 соз ф — X 81П ф. (е)
Линия влияния поперечной силы Ск представлена на рис. 173, г. Аналогично находим линии влияния усилий в других сечениях. Линия влияния вертикальной опорной реакции VА дана на рис. 173, д. По этим же формулам, считая переменными ак, ук и фл, строим эпюры усилий.
§ 62. РАСЧЕТ ВЕСШАРНИРНОЙ АРКИ НА ДЕЙСТВИЕ ТЕМПЕРАТУРЫ
И СМЕЩЕНИЯ ОПОР
Действие температуры
Рассмотрим случай равномерного нагревания арки по всей толщине и длине ее на 1° (рис. 174,а). Нетрудно показать, что из всех лишних неизвестных Х19 Х2 и Х3 неизвестные Х2 и Х3 равны нулю
224
(рис. 174, б). Вертикальные силы взаимодействия Х3 равны нулю, так как имеем случай симметричного воздействия. Момент в упругом центре Х2 следует определять из уравнения
(а)
(б)
где
Х2Й22 Д2 —
"5 М2(1з § Яга(0йз.
Но первый интеграл равен нулю, так как разность температур 1Г 0; второй интеграл равен нулю в виду нулевого значения Ы2 поэтому А2( 0. Следовательно, Х2 0.
Итак, при равномерном на- а) гревании арки возникает лишь распор Х19 определяемый из канонического уравнения
Хи ЛО, (10.33)
где
и Мг йз Ыга(0йз.
(5) («)
(в)
Так как
(г 0, —1-созф,
йх
(18
П.
то первый интеграл равен нулю и
I
и — йх — аЛ1. (г)
—дпюраМ1
Рис. 174
Учитывая лишь влияние моментов в выражении 6и, получаем из уравнения (10.33)
1 -
ай
о
(10.34)
8ц I _
3 4,1 Е1
(5)
При учете влияния продольных сил
йц С052 ф ■
Найдя распор, получаем изгибающий момент Мь (рис. 174,б)
и продольную силу N1 в произвольном сечении арки:
М1 — Х1у1 Л — ХхС08ф. (д)
8 Н. К. Снитко 225
си
ер-
Влияние смещения опор
Пусть под влиянием какой-либо причины защемления арки получили взаимное смещение по горизонтали на величину Д10 без поворота (рис. 175). Каждая из опор смещается на Д0. Требуется определить лишние неизвестные, вызванные таким смещением. Так как в основной
системе будем иметь лишь перемещение по направлению Х19 то неизвестные Х2 и Х3 равны нулю. Каноническое уравнение деформаций для Хх с учетом того, что изменение расстояния между концами жестких консолей равно нулю, будет
111 Дю 0» (е)
где
Дю 2До» (ж)
Так как перемещение Д10 происходит в направлении действия силы Х19 его берут со знаком «плюс». Из выражения (е) получаем
(10.35)
При смещении опор кнаружи пролета возникает растягивающая сила Хг.
§ 63. ПОПЕРЕЧНАЯ, ПРОДОЛЬНАЯ СИЛЫ И ИЗГИБАЮЩИЙ МОМЕНТ ДЛЯ КРУГОВОЙ АРКИ ПРИ РАДИАЛЬНОМ ДАВЛЕНИИ
При проектировании гидротехнических сооружений нередко приходится рассчитывать круговые арки на действие гидростатической нагрузки, направление которой нормально к оси (распределенная радиальная нагрузка; рис. 176).
Рассмотрим решение задачи по определению усилий и перемещений такой круговой арки, подверженной действию радиальной нагрузки интенсивностью д0 и по концам — действию поперечных сил ф0, продольных сил Ло, Ы и моментов М0, М.
226
Предварительно напомним основные зависимости между М, С и N (см. гл. 5) при действии постоянной радиальной нагрузки:
(а)
При определении усилий будем принимать такое правило знаков: поперечную силу ф и радиальную нагрузку считаем положительными при направлении к центру кривизны, момент М левых сил положи¬
тельным против часовой стрелки, продольную силу N положительной, если она вызывает сжатие.
Выделим элемент кругового бруса длиной йз, ограниченный соседними сечениями (рис. 177).
Спроектировав все силы, действующие на элемент, на ось 55, получим
-М у — Ы д0г,
(10.36)
Спроектировав все силы, приложенные к элементу, на ось, перпендикулярную к 55, найдем
Щ-Ь
(10.37)
Составляя сумму моментов сил, приложенных к элементу относительно его центра, получаем
(б
Подставляя сз гйр, получаем окончательно связь между ф и М в такой форме:
А АЛ
(10.38)
йМ п
УГ-
8
227
Дадим теперь выражения для усилий (, N и М в произвольном сечении арки, представляя их в зависимости от начальных значений (0, М0, М0 и нагрузки.
Дифференцируя обе части уравнения (10.36) по ф и учитывая выражение (10.37), получаем
а?--• в
Начальные значения производных поперечной силы по уравнению
(10.36)
фо —0,о — — 0,- (г)
Интегрируя дифференциальное уравнение (в), получаем следующее общее выражение для поперечной силы:
0 00 С08 ф 0Г 51П ф — Ы0 51П ср. (10.39)
Интегрируя дифференциальное уравнение (10.37), находим выражение для продольной силы:
N N0 С08 ф (2о 51П ф ч0г (1 —соз ф). (10.40)
Общее выражение для изгибающего момента М в зависимости от полярного угла ф получим, интегрируя дифференциальное уравнение
(10.38):
М Мо 20г з 1п ф (д0г2 — Ы0г) (1 — соз ф). (10.41)
§ 64. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ КРУГОВОЙ АРКИ
Общие уравнения
Обозначим: радиальное перемещение произвольной точки оси щ касательное перемещение (вдоль оси арки) и. Выразим сначала относительное удлинение по нейтральному слою для элемента арки СВ длиной (1з (рис. 178, а). Пусть перемещения соседних точек оси арки С и В по касательной к оси будут соответственно и и и йи.
Тогда относительное удлинение по оси
йи йи. ч
е1 йз
где г — начальный радиус кривизны оси арки,
(18 г Йф.
Радиальное перемещение элемента т (рис. 178, б) вызывает абсолютное сжатие величиной доЛр; относительное сжатие
до йу до
62 с1з г 9
228
Общее относительное удлинение элемента по нейтральному слою
(б)
йи
г с?ср г
Удлинение по нейтральному слою выразим через продольную сжимающую силу N1
N __ йи хю
8 ЕР г й(р г
Мы получили основное соотношение между перемещениями и продольной сжимающей силой:
йи Мг
й(р
(10.42)
Если влиянием продольной силы на деформацию пренебречь, т. е. считать арку несжимаемой, то
(в)
Установим связь изгибающего момента М с изменением угла 0 между соседними сечениями арки.
Для бруса малой кривизны получаем изменение угла 6 аналогично прямолинейному стержню:
М. М
йд г йф,
229
откуда
с(в _ Мг
(Г)
Найдем выражение угла 0 через и и полагая 0 положительным по часовой стрелке. Касательное перемещение точки и вызывает поворот на угол 0 (рис. 179, а):
л и
Рассмотрим влияние приращения в радиальном перемещении (рис. 179, б). Первое положение элемента определяется направлением
■ 0,1
I
О
касательной к оси в точке С (ось У) второе положение после совмещения точки С с начальным ее положением определяется положением оси Уг заметим, что точка В получает приращение в радиальном перемещении дхю.
Влияние приращения дш на угол поворота, т. е. 02, равно:
йт
Полный угол поворота сечения будет
Дифференцируем это выражение по ф:
ав_ __ 2
йу г
(д)
(е)
Рассматривая круговую ось арки и пользуясь формулой (е), приравниваем выражения (е) и (г); получаем следующее дифференциаль¬
230
ное уравнение:
Для несжимаемой арки согласно (в)
йи
-7-.10.
аф
(10.43)
(ж)
йи
Подставляя это выражение в формулу (10.43), получаем известное
дифференциальное уравнение радиальных перемещений круговой арки малой кривизны по Буссинеску (1883 г.):
5 ш ЁГ- 1044)
Рассмотрим теперь более общую задачу отыскания перемещений с учетом сжатия оси. Из уравнения (10.42) находим
N г л г
Ц г»-Ш. (10.45)
Подставляя это выражение в уравнение (10.43), получаем следующее дифференциальное уравнение радиальных перемещений учетом обжатия оси:
кругового бруса с
ЕР
(10.46)
Интегрируя дифференциальное уравнение (10.46), получаем радиальное перемещение хю в функции от ф. После этого переходим к отысканию касательного перемещения по уравнению (10.45), интегрируя которое, находим
и и0 йф — N йф. (10.47)
о о
Рассмотрим выражение начального значения первой производной от до, т. е. Доо через, начальное значение касательного перемещения и0 и угла поворота сечения в начале координат 0О (рис. 180).
Согласно соотношению (д) имеем
, йии
Следовательно, начальное значение первой производной радиального перемещения
тВ0г — и0. (10.48)
Найдем интеграл дифференциального уравнения (10.46) дя радиального перемещения с учетом обжатия. Представим это уравнение в виде
та) Мс Ик — 1ЮУ (10.49)
где
сй(ж); ]
01
КЕР Мн) ’ )
Интегрируя это уравнение с учетом уравнений (10.40) и (10.41), получаем уравнение радиальных перемещений (см. рис. 180)
1й) Щ СОЗ ф 0оГ 81П ф — и0 81П ф —— Л1()С (1 — СОЗ ф)
?, (сг А) гРЕ-Ф.аД,,, („«)(]-С05Ф-
д,ог«1_„(1_с»»_Ь1)], (10.51)
где в0г — и0 щ
Л10, 30, Ло, Яо — начальные значения усилий и нагрузки.
Зная начальные параметры М0, 20 0, щ, 0О, и0, из граничных условий по уравнению (10.51) находим радиальное перемещение в любой точке.
Перейдем к получению развернутого выражения касательных перемещений в функции от угла ф.
Подставляя выражение по уравнению (10.51) и N по уравнению
(10.40), после интегрирования получаем следующее уравнение касательных перемещений для кругового бруса:
и и0 соз ф 0ог (1 — соз ф) т0 зт ф М0с (ф — зт ф) 4-
о. [с. (1 - со. ф -11) -,„г [сг („ -1 И»
— (зШф —фС05 ф) — Л0 [сг — -зтф ф со28 --(51Пф фС08ф). (10.52)
В качестве начальных неизвестных при расчете кругового бруса, заделанного правым концом, свободного на левом, принимаем и0, 0О и ш0, которые находим из условий на правом конце при ф ф5: и 0, 0 0, т 0.
Кроме уравнений для перемещений хю и иу необходимо воспользоваться выражением для угла поворота сечения (см.
232
(и)
рис. 180). Из выражения (д) получаем
Г
Подставляя сюда значения и и ха из уравнений (10.52) и (10.51), имеем следующее выражение для угла поворота:
6 бо 7 [Л10ф Фог2 (1 — соз ф)
7(3 (ф —51П ф) —Л0г2 (ф — зт ф)]. (10.53)
По полученным уравнениям решают задачи на прочность и жесткость любого кругового бруса при действии постоянной радиальной нагрузки.
Случай равномерной радиальной нагрузки
В этом случае круговая ось арки при неучете обжатия будет кривой давления и потому в любом сечении (рис. 181)
М 0; (1 0.
По уравнению момента (10.41) получаем
М (7ог2 — Лг) (1 — соз ф) 0,
откуда
Л0 7о г.
(к)
Продольная сила в любом сечении арки будет равна интенсивности радиальной нагрузки, умноженной на радиус:
N N0 соз ф 70г (1 — соз ф) 70г. (л)
Пример. Определить распор двухшарнирной круговой арки постоянного сечения при действии вертикальной сосредоточенной силы посредине (рис. 182, а). Центральный угол между опорными нормалями 2фх 120°, -у- 3,464.
233
Решение. Разрезая арку по оси симметрии и принимая здесь начало координат, получаем (рис. 182, б)
Со 0,5 Р.
Начальные неизвестные М0, и Пограничные условия при ф фх:
0, 0, и» 0.
(рх » ср, I (р1
(М)
Момент, радиальное и касательное перемещения равны нулю.
По уравнению момента (10.41), исходя из первого условия (м), получаем
Ло (1 — созфх) —0,5Яг зт фх- (н)
Из уравнения радиального перемещения (10.51) согласно второму условию (м) находим
Ш0СОЗ фх М0С (1 — соз фх)
0,5Рсг(-1Шф1ф1СОЗР1)-
— Ы0СГ 1 — СОЗ фх
фх 81П фх
)0. (о)
По уравнению касательного перемещения (10.52), принимая во внимание третье условие, имеем
Щ 81П фх М0С (фх — 81П фх)
0,5Рсг (1 -соз ф1 - ?1С°3ф1) — ЛГ0сг ф - ЯП ф —С5 ф11 0. (П)
На оси симметрии угол поворота сечения и касательное перемещение и0 равны нулю. Подставляя в выражения (о) и (п) моРис. 182 мент М0 из выражения (н), получаем два
уравнения с двумя неизвестными щ и Д0, решая которые, находим их значения. При фх 60°, зт фх 0,866, соз фх 0,5 вместо выражений (о) и (п) имеем
щ сг
0,866йУо
-° 0,4080-0,262Р 0; сг
■ 0,082Ао — 0,056Я 0,
откуда распор а прогиб в замке арки
0,632Я, 0,004Рг3
Е1
234
ГЛАВА 11. РАСЧЕТ СЛОЖНЫХ РАМ МЕТОДОМ СИЛ
§ 65. УПРОЩЕНИЕ РАСЧЕТА СИММЕТРИЧНЫХ РАМ
Разделение системы канонических уравнений на две независимые группы
Расчет симметричных систем имеет большое практическое значение благодаря широкому распространению симметричных конструкций в строительстве. Симметричной конструкцией называют такую систему, которая обладает симметрией не только в очертании оси и в расположении опорных закреплений, но и в жесткостях элементов. Однопролетная рама прямоугольной формы (рис. 183, а) имеет одну вертикальную ось симметрии, так как одинаково очертание оси относительно линии п—п в левой и правой половинах рамы. Кроме
а)
Ф
Рис. 183
того, как в точке А, так и в точке В рама одинаково защемлена; симметрично расположенные сечения стоек рамы имеют равные моменты инерции 2, а сечения ригелей — равные моменты инерции 1г. Рама может обладать одной, двумя, многими осями и бесчисленным количеством осей симметрии (например, кольцо).
Важнейшим упрощением расчета симметричных статически неопределимых сооружений при действии любой несимметричной нагрузки является расчленение общей системы канонических уравнений для лишних неизвестных на две независимые группы. При этом разделении первая группа уравнений включает лишь прямосимметричные неизвестные, а вторая группа — обратносимметричные неизвестные. Прямосимметричным неизвестным называют такую совокупность усилий со стороны отброшенных связей, которая создает симметричную эпюру моментов. В прямосимметричной эпюре моментов соблюдается равенство моментов и по величине и по знаку. В обратносимметричной эпюре в симметрично расположенных сечениях моменты равны по величине, но противоположны по знаку.
Для упрощения расчета симметричной системы необходимо:
235
1) за основную систему принимать только симметричную систему;
2) лишние неизвестные выбирать только в виде прямосимметричных и обратносимметричных усилий.
Так, для заданной дважды статически неопределимой рамы, имеющей шарнир на оси симметрии п—п (см. рис. 183, а), в качестве основной системы принимаем симметричную же систему — две отдельные ломаные балки — консоли со свободными концами на оси симметрии (рис. 183, б). От заданной системы переходим к основной системе путем разрезания ее по оси симметрии. За лишние неизвестные принимаем горизонтальные и вертикальные силы взаимодействия в шарнире Х1 и Х2. Первое неизвестное является прямосимметричным, а второе — обратносимметичным. Эпюра моментов от Хг 1 симметрична (рис. 184, а), а эпюра моментов от Х2 1 обратносимметрична (рис. 184, б). Эпюра моментов от нагрузки Р не обладает какой-либо закономерностью и оказывается несимметричной (рис. 184, в). Если бы и лишние неизвестные были несимметричными воздействиями, то канонические уравнения деформаций имели бы общий вид:
1611 2612 Д1р 0;
ХЛ1 Х2б22 А2р 0, (11Л)
причем побочное перемещение 612 не равнялось бы нулю.
Заметим, что первое уравнение выражает условие равенства нулю взаимного горизонтального смещения сечений разреза, а второе — условие равенства нулю взаимного вертикального смещения сечений.
Докажем теперь, что при данном выборе неизвестных побочное перемещение 612 по направлению симметричного неизвестного, выз-
ис. 184
ванное обратносимметричным неизвестным Х2 1, В самом деле, по формуле для перемещения
равно нулю.
(11.2)
Но в данном случае Мг — функция симметричная, а М2 — обратносимметричная и потому интеграл их произведений по симметричному контуру равен нулю (рис. 184, а, б):
с _ 1 к2 I к.
Е1 У 2 2 2 ;
(а)
236
Это свойство равенства нулю побочного-перемещения 612 или 821 можно сформулировать и так: симметричная и обратносимметричная эпюры при перемножении дают нуль или, иначе, являются взаимно нулевыми. В результате система двух канонических уравнений (11.1) распадается на два отдельных уравнения:
(11.3)
из которых легко найти каждое неизвестное:
у 1Р у —“V
Лг“‘б1Г; Л2”“ 627-
(11.4)
В общем случае п раз статически неопределимой системы использование симметрии при выборе лишних неизвестных приводит общую
Рис. 185
систему п канонических уравнений к двум независимым группам уравнений, каждая из которых содержит лишь часть из п неизвестных, не обязательно равную половине их. Первая группа уравнений содержит лишь прямосимметричные неизвестные, вторая — только обратносимметричные неизвестные.
Рассмотрим, например, двухэтажную симметричную раму с шарнирами посередине каждого ригеля (рис. 185, а). В данном случае имеем четырежды статически неопределимую систему. В качестве основной системы выбираем две раздельные консоли, проводя разрезы ригелей по оси симметрии (рис. 185, б). В качестве неизвестных принимаем продольные силы Хг и Х2 и поперечные силы Х3 и Х4 в разрезах на оси симметрии.
237
Вместо совместной системы четырех уравнений с четырьмя неизвестными получаем две отдельные группы уравнений:
111 Х2612-(-Д1р 0
121 Ь 222 Ь 2р О
333 4® 34 ЗР О 343444 Д.
зр 0;
Ч, 0.
(11.5)
(11.6)
В первую группу уравнений (11.5) входят прямосимметричные неизвестные, во вторую группу уравнений (11.6) — обратносимметричные неизвестные.
Метод группировки неизвестных при расчете многопролетных симметричных рам
При расчете многопролетных симметричных рам за неизвестные следует принимать групповые неизвестные в виде системы сил, приложенных в различных симметрично расположенных точках оси сооружения.
а)
■
. я
1
1
ф
ч
—1
в.
Л ‘
.1
6)
Г;
Зпюра М,
11
Х,1 Х1
УЯ’Л
Зпюра М,
тгтп
1 1
Эпюра Й1
Ы
- ГШТПтттттг
н
11
х;
мг
Рис. 186
В виде примера рассмотрим двухпролетную симметричную раму, крайние стойки которой оперты на подвижные опоры А и В (рис. 186, а). За основную систему принимаем симметричную раму с защемлением нижнего конца средней стойки, отбрасывая крайние вертикальные опорные стержни. Первые неизвестные реакции крайних опор обозначим и 22. Они оказываются выбранными неудачно, так как в со-
238
стояниях 2Х — 1 и 22 1 (рис. 186, б) не получаем в эпюрах ни прямой, ни обратной симметрии.
Поэтому для выбранных неизвестных б12 Ф 0 и канонические уравнения являются совместными:
Естественно поэтому перейти к групповым неизвестным Хх и Х2.
Применяя принцип замены первых неизвестных и 2г новыми неизвестными Хг и Х2, им эквивалентными (рис. 186, в), поступаем так: реакцию заменяем суммой сил X и Х2, а реакцию 22 — разностью тех же сил Хх и Х2.
Таким образом, вместо двух сил 2Х и 22 вводим новые неизвестные из четырех сил, определяемых двумя параметрами Хг и Х2, причем Хх — значение каждой из сил симметричной группы (рис. 186, г), а Х2 — значение каждой из сил обратносимметричной группы; Хх — величина симметричного группового неизвестного, Х2 — величина обратносимметричного группового неизвестного. В единичном состоянии первого группового неизвестного, когда прикладываем силы Хг 1, эпюра моментов М1 симметрична; в единичном состоянии второго группового неизвестного Х« 1 эпюра моментов М2 обратносимметрична; поэтому теперь побочное перемещение равно нулю:
Первое уравнение выражает условие равенства нулю суммы вертикальных перемещений точек Л и В, а второе — разности тех же перемещений. Но так как отдельные перемещения равны нулю, то суммы и разности их также равны нулю. Находим групповые неизвестные Хх и Х2 обычным путем и строим полную эпюру моментов:
Пример. Построить эпюры М, 0 и N для симметричной рамы при действии равномерно распределенной нагрузки в первом пролете р 4 Мнм и внешнего момента т — 24 Мн-м, приложенного в конце второго пролета. Относительные значения моментов инерции указаны на рис. 187, а. Пролет рамы 12 лс, высоты стоек рамы к — Нг 6 м.
Решение. Заданная система трижды статически неопределима. Выбираем симметричную по своей конструкции основную систему (рис. Г87, б). В качестве лишних неизвестных принимаем вертикальную реакцию средней опоры Хх, группу симметричных составляющих реакций Х2 и группу обратносимметричных составляющих реакций Х3. Для симметричных неизвестных и Х2 составляем систему двух уравнений:
(11.7)
(11.8)
Неизвестные в уравнениях теперь разделяются:
(11.9)
М МрХ1М1 ХгМ9.
(11.10)
Ххбц Х2б12 1р 0; •121 222 1“ 2р 0.
(11.11)
239
Обратносимметричное неизвестное Х3 находим из уравнения
ззз Дзр 0. (11.12)
Для определения всех перемещений, входящих в канонические уравнения (11.11) и (11.12), находим эпюры моментов. Чтобы проще было отыскать грузовые члены,
О) р4Мнм т2иМн м
заданную нагрузку расчленяем на равномерно распределенную интенсивностью р и внешний момент т (рис. 187, в, г).
После построения эпюр моментов от действия единичных неизвестных 1, Х2 1 и Х3 1 (рис. 188, а, б, в) вычисляем единичные перемещения, применяя правило перемножения эпюр. Учитывая различие в сечениях стержней рамы, получим
240
при Е1г 1 Мнм2 (см. рис. 187, а):
°22
2 [5-1-5. — (
2 3 (
л 2 6-12 2 624Л то,АЛ
6ц • —2 ‘ “з 6 — 72, б12 — 2 Ю8 мМн;
п6-6 2 6 • 12 • б осп я,
§22 2 ( • у 6Н - ) 360 мМн;
6
6)]т
1 24-12 2
4 2-4 3 ”) т 4 2 3
Для простоты вычислений взято условное значение жесткости Ё1г.
241224 мМн.
Расчленяя нагрузку по схемам, изображенным на рис. 187,в,г, находим грузовые члены:
1р
1 Г144 - 12 2
— Т6
1Г141_12.6.72.12.6.
72-12 6-24-12
2
24-24
]
]-
1944 ж; 3024 м
--т[
т[
.„._(4.72.„9) 1[1(66)]_
_1[12.12.9 6 у6 - 1584 л».
Проведем универсальную проверку правильности определения перемещений в группе симметричных неизвестных. Для этого строим суммарную единичную эпюру моментов, полученную при одновременном действии Хх 1 и Х2 1 (рис. 189, а).
241
Перемножая ее на нее же, получим обобщенное перемещение, соответствующее силам Хг иХ„:
(л) 0 (б)
Сумма же всех единичных перемещений для симметричных неизвестных би
а)
5 рЦ Мни
ид,89
0))т2йМн
Рис. 189
2б12 622 72 216 360 648 м. Проверка выполняется. Аналогично проверяем грузовые члены:
(В)
Подставляем найденные значения перемещений в уравнения (11.11) и (11.12):
711082- 1944 0;
108 3602-3024 0;
12243-1584 0.
Решая эти уравнения, находим
1 262п Мн; Х2 6ц Мн; 3 1,294 Мн.
Переходим к построению суммарной эпюры моментов. Пользуясь основной системой (см. рис. 187,6), получаем следующее выражение действительного изгибающего момента М:
М Мрт 1 Мх- Х2М2 3М3.
Увеличив все ординаты эпюр моментов М1 М2 и М3 соответственно в ь 2 и 3 раз, найдем ординаты суммарной эпюры моментов (рис. 189,6). Эпюры М, 0 и N должны удовлетворять как условиям равновесия, так и условиям деформаций. Помимо выполнения условий равновесия всей рамы в целом (2 0, 2 К 0, 1М 0), должны удовлетворяться условия равновесия отдельных ее частей и? в частности,
243
условия равновесия узлов. Так, для узла
2М2 0; 12,84 31,06-43,890
— моменты в Мнм.
Для узла 3:
2М3 0; 24-4,49-19,510
— моменты в МнМ.
Кроме проверки эпюры М по условиям равновесия, важно установить, удовлетворены ли условия деформаций вида
Д, -2 -■
п 0
Проверим, например, равно ли нулю перемещение
2 С а А.йз 11,04-6 2. 4,49-6 2.,
2 ■ "3 6 2 ’ Т
п О
27.465-12 616Л75,2. 6 _ 726 _ 9179_9179 0.
Равенство нулю перемещения выполняется.
После проверки действительной эпюры моментов можно приступить к построению эпюры поперечных сил ф. Пользуемся новой основной системой в виде совокупности балок, шарнирно опертых на узлы, возмещая жесткость прикрепления стержней
к узлам моментами (рис. 190,а). Обозначая узлы 0,, 2, 3, 4, 5, выделяем последовательно каждый стержень и обычным путем строим эпюры поперечных сил для простых балок. Например, для стержня 1—2, принимая во внимание наличие равномерно распределенной нагрузки р, получаем схему, изображенную на рис. 190,6. Определяем левую опорную реакцию:
л1 -,•»-- 21,27 Мн.
Следовательно, поперечные силы у конца стержня:
12 А1 21,27 Мн
ф21 А — р1 21,27 — 48 — 26,73 Мн.
Учитываем при этом правило знаков для 0, изложенное выше. Так, 921 Дает момент относительно узла 2 против часовой стрелки, почему ее берем со знаком
243
«минус»; р12 дает момент относительно узла по часовой стрелке, поэтому считаем ее положительной (см. рис. 190,6). Для незагруженного стержня 2—4 ордината опорного момента отложена справа (см. рис. 189,6), поэтому поперечная сила ф24 направлена справа налево и, следовательно, дает момент против часовой стрелки.
В окончательном виде эпюра 0 изображена на рис. 190,а. Она должна удовлетворять соотношению:
(там, где 90, момент будет Ммакс).
мин
Пользуясь эпюрой (? и применяя метод вырезания узлов, строим эпюру продольных сил N. В данном случае последовательно вырезаем узлы, 2 и 3 (рис. 191,а,б,в).
а)
©
«)
©
35
0.75 ®
1,аи
кг
©,
Ф
©
"Ж
5? Эпюра N
Рис. 191
Согласно рис. 191,а имеем
1) 2Х 0; 0м Ли 0, откуда
N 12 — Фю — 1,84 Мн
2) 2К 0; Ло Э12 0
и
N10 — 12 — 2,27 Мн.
По рис. 191,6 получаем
1) 2Х 0; N N — 121 0, откуда
23 624-2 2,59-1,84 0,75 Мн;
2) 2 У — 0; N--(1 — (32з 0
и
N24 — э21 С223 — 26,74 0,56 — 26,18 Мн.
244
По рис. 191,в находим
2 У 0; Л35 (Зз2 0,
откуда
N35 — 32 — 0,56 Мн.
Знак «минус» соответствует сжимающей стержень силе, знак «плюс» — растягивающей.
Эпюра N изображена на рис. 191, г.
§ 66. ЗАМЕНА ПРОИЗВОЛЬНОЙ НЕСИММЕТРИЧНОЙ НАГРУЗКИ ПРЯМОСИММЕТРИЧНОЙ И ОБРАТНОСИММЕТРИЧНОЙ НАГРУЗКАМИ
Основной вывод
Используя свойство взаимно нулевых эпюр, можно добиться дальнейшего упрощения расчета симметричных рам при действии несимметричной нагрузки, преобразуя эту нагрузку в составляющие нагрузки закономерного вида: симметричную и обратносимметричную. При этом заданную несимметричную нагрузку определенной интенсивности заменяем двумя отдельно действующими нагрузками — симметричной и обратносимметричной — половинной интенсивности так, чтобы после сложения этих нагрузок получилась заданная нагрузка. Рассчитав раму на действие симметричной и отдельно на действие обратносимметричной нагрузок, найдем в каждом случае эпюры моментов — от симметричной нагрузки Мсим и от обратносимметричной нагрузки Мобр. Очевидно, эпюра моментов от заданной нагрузки Мзад будет получена суммированием отдельных эпюр от симметричной и обратносимметричной составляющих нагрузок:
зад М. сим Мобр-
Вместо одной эпюры Мзад по этому способу необходимо найти две эпюры моментов — от симметричной и от обратносимметричной нагрузок согласно приведенному выше выражению. Однако получение этих эпюр значительно облегчается.
Нетрудно показать, что при действии симметричной нагрузки возникают только симметричные лишние неизвестные, а при действии обратносимметричной нагрузки возбуждаются лишь обратносимметричные лишние неизвестные.
Рассмотрим простейшую дважды статически неопределимую раму (рис. 192,а). Рама имеет вертикальную ось симметрии, проходящую через центр шарнира С. При расчете на несимметричную нагрузку интенсивностью р будем искать два неизвестных Хх и Х2, где Хг — симметричное неизвестное, Х2 — обратносимметричное неизвестное (рис. 192,6). Вместо непосредственного расчета на несимметричную
нагрузку ведем расчет: 1) на симметричную нагрузку интенсивностью
(рис. 192,в) и 2) на обратносимметричную нагрузку интенсивностью
245
а)
Ж-1
6)
у (рис. 192,2). При этом для горизонтальных сил симметричная нагрузка имеет прямо противоположное направление, а обратносимметричная — одинаковое направление. Складывая нагрузки, приложенные в этих двух состояниях, по правой стойке получаем равнодействующую нулевую нагрузку, а по левой стойке — равномерную нагрузку интенсивностью р.
Нетрудно видеть, что при действии симметричной нагрузки обратносимметричные неизвестные должны быть равны нулю. На рис 192,6 показана основная система, деформированная симметричной нагрузкой, при этом
1р Д2р0
Система уравнений будет иметь следующий вид:
-111 Л1р 0;
Х2622 0,
откуда, так как 622 Ф О, Х2 О — обратносимметричное неизвестное равно нулю.
От действия обратносимметричной нагрузки (рис. 192,г) вследствие обратносимметричности деформированного вида в основной системе Д1р б и потому канонические уравнения имеют вид:
1 0;
Х2622 4 Д2р 0
— симметричное неизвестное Хг равно нулю, так как би Ф 0.
При расчете любой симметричной конструкции применяем указанное свойство: от симметричного загружения ищем лишь симметричные неизвестные, от обратносимметричной нагрузки определяем только обратносимметричные неизвестные.
У,
Ф
Общий случай разложения несимметричной нагрузки
В общем случае несимметричного загружения рамы вертикальной и горизонтальной силами Р и парой т (рис. 193,а) поступаем аналогично.
246
На рис. 193, б показано загружение рамы симметричной системой сил и парами, а на рис. 193,в — обратносимметричной нагрузкой. Сложение этих составляющих нагрузок приводит к загружению заданной нагрузкой.
Расчет на каждое симметричное или обратносимметричное загружение упрощается еще потому, что вычислять перемещения можно перемножением эпюр только по длине половины всей системы.
Пример. Построить эпюры моментов и продольных сил для двухъярусной симметричной рамы, подверженной действию горизонтальной узловой силы Р 20Т (рис. 194,а). Пролет рамы 6 м. Высота этажа Н 5 м. Сечения стоек: нижней 40Х 50 см, верхней 40Х 60 см. Сечения ригелей: нижнего ЗОХ 100, верхнего 30Х 70 см.
Решение. Сводим задачу к действию двух симметричных сил, вызывающих
Р Р
растяжение верхнего ригеля 0Т, и обратносимметричной нагрузки по
(рис. 194,6). На этом рисунке показана основная система и эпюра моментов только от нагрузки Мр. На рис. 194,в даны эпюры моментов в состоянии действия Хг 1 и Х2 1. От обратносимметричной нагрузки возникают лишь поперечные силы X я Х2.
По заданным размерам сечений находим моменты инерции
12х 0,4- 0,125 0,05 м;
12а 0,3 - 1з 0,3 м4;
12з 0,4. 0,63 0,0864 м;
124 0,3.0,73 0,1029 мК
Соотношения между моментами инерции
4 1 2,058: 1,728:6: 1.
Определяем перемещения
Е1гД1р - 2 75 • 5 • з) - 2684,028;
Е1хА2р — 2 • (75 • 5 • 3) — 2250;
В, А, -2 (3. 4. 3.5. з) - 150,8304;
Е1612 2-3-5-3 90;
Яге22 2 • • 3 • 5 • з) 93.
247
Решая канонические уравнения, находим: Хг 7,94877 Х2 16,5027 Суммарная эпюра моментов Мсум представлена на рис. 194Д По ней получена эпюра 0сум и затем эпюра ДОсум (рис. 194,е). На эпюре Усум по верхнему ригелю доба-
г 3
Шт
я,
г)
м,
3
уШу
Шж,
е) 10Т
3Е
77Ш
вочно показана эпюра N от действия растягивающих симметрично действующих сил р
10Г.
ГЛАВА 12. РАСЧЕТ НЕРАЗРЕЗНЫХ БАЛОК § 67. РАСЧЕТ НЕРАЗРЕЗНЫХ БАЛОК МЕТОДОМ СИЛ Введение -
Неразрезной балкой называют изгибаемый брус, перекрывающий ряд пролетов и неразрывно связанный с опорами. Неразрезные балки широко применяются в строительстве. Они экономичнее разрезных, так как значения изгибающих моментов в них меньше, чем в разрез¬
248
ных балках. Недостатком неразрезных балок, как и всякой статически неопределимой системы, является большая чувствительность их к неравномерной осадке опор, а также появление дополнительных напряжений при неравномерном изменении температуры. Расчет неразрезной балки на шарнирно неподвижных опорах на действие вертикальной нагрузки ничем не отличается от расчета такой же балки на одной неподвижной и остальных подвижных опорах. Неразрезная балка при отсутствии промежуточных шарнирных включений столько раз статически неопределима, сколько промежуточных опор (при условии шарнирного опирания концов).
Уравнение трех моментов как частный случай канонического уравнения
Расчет неразрезной балки можно выполнить по общим правилам расчета статически неопределимых систем, применяя метод сил. Вследствие простоты статической схемы неразрезной балки решение для нее можно дать в развернутой форме.
Рис. 195
Рассмотрим такой способ расчета неразрезной балки, изображенной на рис. 195,а. В качестве основной системы примем систему разрезных балок, полученную из заданной системы включением шарниров в опорные сечения (рис. 195,6). За неизвестные принимаем опорные изгибающие моменты. Очевидно, что число их равно числу промежуточных опор (при наличии крайних шарнирных опор). Преимущество выбранной основной системы заключается в том, что эпюры моментов от единичных усилий распространяются в ней только на два соседних пролета и, стало быть, большое число побочных перемещений обращается в нуль (рис. 196,а,б).
Для составления типового канонического уравнения в развернутом виде строим эпюры изгибающих моментов в основной системе от внешней нагрузки и единичных условий. Из рассмотрения этих эпюр
249
вытекает, что типовое п-е каноническое уравнение будет трехчленным следующего вида:
п-1п,п-Л МпЬп,п 16
п, п- 1
Д„,Р 0.
Коэффициенты в этом уравнении определяем по правилу перемножения эпюр:
п-Е1п
5 ——
пп Е1п
К
1_
пл1 Е1па
1 • 1п
1
2
3 ’
Ь 1п
.2. 1
2
3 1 Е1п,
1 •
’п1 1.
1 -1п1 1
Апо 1 пап I 1 П1П1
Л”Р Е1п 1п 1 Е1п.и 1п1 Подставив их в каноническое уравнение и перенеся свободные члены в правую часть, получим:
250
Л1 6 Е1п1 Е1п1п Е1п11п1-
В этом уравнении 0,п и йя1 — площади эпюр моментов в однопролетных балках п-й и (п 1)-й от внешней заданной нагрузки, а величины ап и „1 — расстояния от центров тяжести этих эпюр до опор (п—1)-й и (п 1)-й соответственно.
Выражение — В„ пред-
Т1
ставляет собой правую фиктивную опорную реакцию в
п-м пролете, а ®пЬп1. Л1
Л1
— левую фиктивную опорную реакцию в (п 1)-м пролете. Правая часть написанного выше уравнения есть угол перелома упругой линии на п-й опоре простых балок от действия на них внешней нагрузки.
Умножив правую и левую части рассматриваемого уравнения на 6Е1СУ где 1С — произвольный момент инерции, и введя так называемые приведенные длины пролетов:
1С
1п — 1п ; г1 —
п
Л1
1 п
получим
Мпп 2Мп (1п пг) Мп11п1
а
-шппп
-6Ц
■л1"
1п1
(12.1)
Это и есть уравнение трех моментов в общем виде. Уравнение трех моментов выражает отсутствие в упругой линии угла перелома на п-й опоре, т. е. представляет собой условие неразрезности балки на п-й промежуточной опоре.
Если неразрезная балка имеет постоянное сечение, т. е.
11 12 • - — Iп Iс
то Гп 1п Гпг л1 и т. д. и уравнение трех моментов будет иметь следующий вид:
пап
Мп-г1п 2Мп (1п 1пл1) Мл1Л1 - 6
п
а
П1°П1
11
В уравнениях (12.1) неизвестными являются опорные изгибающие моменты Мп_ъ Мп и т. д. Число этих неизвестных равно числу промежуточных опор неразрезной балки. Таким образом, для расчета неразрезной балки необходимо составить столько уравнений трех моментов, сколько промежуточных опор. Решая совместно эти уравнения, находим все неизвестные опорные моменты.
Если конец неразрезной балки защемлен, для применения уравнения трех моментов вводим дополнительный фиктивный пролет, как показано на нижнем рис. 197. При уменьшении этого пролета до нуля (0 -■ 0) переходим к абсолютно жесткому защемлению.
251
Для опоры О составляем первое уравнение трех моментов в следующем виде:
2М0(1, 1[) М1Г1-6.
Подставляя в предыдущее уравнение Г0 0, окончательно получаем
2М0 Мг-6.
При отсутствии внешней нагрузки на крайнем левом пролете неразрезной балки у защемленного конца ее ЯО и М0— М1у т. е.
изгибающий момент в заделке равен половине момента на первой промежуточной опоре с обратным знаком.
Определение усилий в сечениях неразрезной балки и построение эпюр усилий
Изгибающий момент М и поперечную силу ф в произвольном сечении неразрезной балки (рис. 198) определяют, как известно из курса сопротивления материалов, по следующим формулам:
ММЮ М Мг; (12.2)
"И
(1х(1хр) Х-:ПГ- 12-3)
В этих формулах Мх] и -- изгибающий момент и поперечная сила в рассматриваемом сечении шарнирно опертой балки с пролетом 1п от заданной внешней нагрузки. Опорная реакция Ап может быть
найдена как разность поперечных сил слева и справа от опоры п.
При расчете неразрезной балки на неподвижную нагрузку конечной целью является отыскание эпюр изгибающих моментов и поперечных сил.
Для получения эпюры моментов первоначально над опорами неразрезной балки откладываем в виде отрезков опорные моменты и концы отложенных ординат соединяем прямыми линиями. Это даст эпюру от опорных моментов. Затем в шарнирно опертых балках с пролетами 1г, 2 и т. д. строим эпюры моментов от заданной внешней нагрузки. Сложив последние эпюры с соответствующими участками эпюры опорных моментов, получим окончательную эпюру М в неразрезной балке.
Аналогично строим эпюру (
252
§ 68. РАСЧЕТ НЕРАЗРЕЗНЫХ БАЛОК МЕТОДОМ МОМЕНТНЫХ ФОКУСОВ
Фокусные отношения
Рассмотрим общий ход расчета неразрезной балки методом фокусов (рис. 199).
При загружении только одного какого-либо пролета неразрезной балки проявляется закон затухания влияния нагрузки и система обладает следующей характерной особенностью: в каждом незагруженном пролете возникает нулевая точка эпюры моментов, причем положение этой точки не зависит от величины и места приложения нагрузки Р в загруженном пролете; опорные моменты последовательно
Рис. 199
уменьшаются в сторону от нагрузки. В данном случае при загружении четвертого пролета постоянные нулевые точки будут в трех первых и трех последних пролетах.
Нулевые точки эпюры моментов в незагруженных пролетах, расположенные слева от загруженного пролета, называют левыми фокусными точками (на рис. 199 обозначены Ръ Р2, Р3 в соответствии с номером каждого пролета). Нулевые точки эпюры моментов в правых незагруженных пролетах называют правыми фокусными точками (Р Рв, Р,). Если фокусные точки не меняют своего положения при изменении нагрузки загруженного пролета, то положение нулевых точек эпюры моментов загруженного пролета зависит не только от величины, но и от вида действующей нагрузки Р. Положение фокусных точек определяется фокусным отношением. Под фокусным отношением понимают отношение длин частей данного незагруженного пролета, на которые онделится фокусной точкой. Так, левое фокусное отношение во втором пролете (см. рис. 199):
где у2 — большее, а и2 — меньшее расстояние фокусной точки до соответствующих опор.
253
Аналогично правое фокусное отношение в пятом пролете
» (а)
гдечгй, Уз отличаются от иъ, VI.
Из выражений (а) и (б) видно, что фокусные отношения всегда положительны. Иначе фокусное отношение к2 (из подобия соответствующих треугольников эпюр моментов) можно представить как абсолютное значение отношения опорных моментов по концам данного незагруженного пролета, например:
к —
м2
Мл
ж- (б)
Перед отношением берем знак «минус», так как моменты М2 и Мг разных знаков. Вообще для я-го левого незагруженного пролета
Мя
кп-
м
Д-1
мп
(12.5)
Установим значение к2 составляя уравнение трех моментов для точки оси балки над первой промежуточной опорой. Согласно уравнению трех моментов (12.1) для п 1
2 мг (; длу;о;
при этом учтено, что М0 0 (шарнирная опора).
Из предыдущего уравнения определяем отношение момента М2 к моменту Мг:
м%___?п ъ__к
мг— Т2 2’ (В)
откуда
(г)
Фокусное отношение к2 зависит лишь от геометрических размеров балки для первого и второго пролетов (приведенных длин). Чтобы
получить общую формулу для фокусного отношения, найдем сначала
выражение для й3, причем согласно выражению (12.5)
а 3-Жз. (д)
Составляем уравнение трех моментов для точки оси балки над второй промежуточной опорой:
2М2 (12 3) Луз 0.
Делим все члены на М2:
Ж2 2 ( з) 3’з 0,
откуда, принимая во внимание, что Мг—получаем
К 2
М3 г 2 (:;) : 1
Щ I. Ыг
254
или иначе
М3
—[2К2-й)Ь--
Мы получим выражение для левого фокусного отношения в третьем пролете:
(е)
1
2,
Обобщая это выражение, заменяя 3 на п и 2 на (п — 1), получаем
А„ 2 (2-). (12.6)
► п кп.—1
Это формула для левого фокусного отношения л-го незагруженного пролета, определяющая положение левой фокусной точки (рис. 200, а). Проверим общность этого выражения вычислением к2 по формуле (12.6) находим
А, 2 (2-1). (Ж)
Но
к,
мг
м0
оо,
так как М0 0 (шарнирный конец), и, следовательно, приходим к выражению (г).
Для определения всех левых фокусных отношений последовательно находим к2, къ и т. д., пользуясь формулой (12.6) для кп. В формулу (12.6) входит при этом отношение предшествующего пролета 1п_х к данному 1п. Заметим, что
для случая абсолютной заделки Хп- — 0 и фокусное отношение кп 2.
Аналогично получим правое фокусное отношение в п-ы правом незагруженном пролете, проводя последовательный расчет справа налево. Теперь предшествующий пролет при ходе справа налево будет (п 1)-й, а потому к’п (рис. 200, б) примет вид
Рис. 200
кп 2-
п1
Согласно рис. 199
п
Ме
М7
(12.7)
оо.
256
Для кь получим по формуле (12.7) выражение
66 2 2 2±.
Ч 0
Вычислив по формулам (12.6) и (12.7) необходимые фокусные отношения и определив по специальным формулам опорные моменты по концам загруженного пролета (М3 и М4), легко построить эпюру моментов.
Опорные моменты по концам загруженного пролета
Для вывода окончательных формул для опорных моментов по концам загруженного пролета рассмотрим сначала случай загружения четвертого пролета семипролетной балки (см. рис. 199). Составив уравнения трех моментов для точки 3 и 4 исключим моменты М2 и М5; в результате получим два уравнения двух моментов, решая которые и придем к фюрмулам для М3 и Л44.
Уравнение трех моментов для точки 3
М 2М3 ( 4) М4п - (3)
4
По формуле (з), выражая М2 через М3 и вынося за скобку М311, находим
м)(,[2(2-)]лад_“М (и)
Но в квадратную скобку заключено выражение для левого фокусного отношения в четвертом пролете к±. Поэтому получаем оконча¬
тельно
МАА4 (К)
Составляем уравнение трех моментов для точки 4:
МВГ, 2М4 (П в) МЪ1Ъ, -.
Принимая во внимание выражение Мъ и вынося за скобку МЛ:
- ладл«.« [ 2(2-1)]-
или, учитывая формулу (12.7) для кп, получаем
М9 ММ-Щ. (л)
Итак, для М3 и М4 имеем уравнения:
М3Ь4 М4-Ц;
60 а М)
М3 «Л-. ]
256
Переходим теперь к загружению одного п-то пролета (рис201).
Решая уравнения (м) и заменяя индекс 3 на (п — 1), а индекс 4 на п, приходим к следующим окончательным формулам:
Ь„кп—ап
м, — -. — -•
1У1П-1 12 У У 1 1п кпп 1
АЛ апп Ьп
1Пп И ■ КК- 1 •
(12.8)
Мы получили формулы для опорных моментов по концам загруженного п-го пролета. Теми же формулами можно воспользоваться для расчета несвободных рам.
При загружении ряда пролетов применяем принцип независимости действия, складывая эпюры моментов, полученные от отдельных загружений.
§ 69. ЛИНИИ ВЛИЯНИЯ ОПОРНЫХ МОМЕНТОВ И УСИЛИЙ В СЕЧЕНИИ НЕРАЗРЕЗНОЙ БАЛКИ
Построение линий влияния опорных моментов методом фокусов
Метод фокусов дает возможность быстро получить все линии влияния опорных моментов.
Рассмотрим пример построения линии влияния опорного момента М2 на второй промежуточной опоре пятипролетной неразрезной балки (рис. 202, а).
Решаем задачу, последовательно рассматривая движение груза по первому, затем второму, третьему, четвертому и пятому пролетам.
Пусть груз движется в первом пролете. При этом опорный момент Мх можно найти по второй формуле (12.8):
•
9 Н. К. Снитко
257
или, принимая во внимание, что кг оо и деля числитель и знаменатель второй дроби на ки получаем
ЛГ1) бйх (Ц
1 - 1 ик[
(б)
где — площадь эпюры моментов для простой балки от силы Р 1, приложенной на расстоянии х от левого ее конца (рис. 202, б). Индекс при Мх вверху указывает на номер загруженного пролета.
Площадь Абсциссы центра тяжести
(1 — х) X
13- (1 х);
1
Ьг (21г-х).
Подставляем выражения для 1 и аг в формулу (б):
(1 — ) х (1 )
к
(в)
(г)
(д)
(е)
258
Обозначим:
х и — х 1
и -г V — —.— 1 — и
,«ц
где и и у — «относительные абсциссы» и меняется от 0 до 1). Подставляя значения величин из выражения (ж) в формулу (е), получаем следующее уравнение линии влияния момента Мх при движении груза в первом пролете:
— ои(1 «)• (12.9)
1
Задаваясь значениями и (например, через 110 пролета: и 0;
0,1 ит. д.), находим различные значения ординат линии влияния М[1). Из эпюры моментов при произвольном положении груза (см. рис. 202, а) вытекает
М
к
Следовательно, уравнение линии влияния М при движении груза в первом пролете
МУ га(1н). (12.10)
По этому уравнению и построена первая ветвь линии, влияния М9 (рис. 202, в).
Рассмотрим произвольное положение груза во втором пролете (рис. 202, г). Момент М2 можно найти непосредственно по второй формуле (12.8):
ДД(2) 62 22
т2 “ ‘ к2к2- ‘
Подставляем выражения для Я2, а2, Ь2 из формул (в), (г) и (д):
м;1"тй)[(;ах)"(2,ах)1 (3)
Подставляя теперь обозначения относительных абсцисс из выражения (ж), получим вместо формулы (з)
м-Шл т К1 “)к °)]- 12-1 •)
Мы получили уравнение ветви линии влияния М2 при движении
груза Р 1 во втором пролете (рис. 202, д).
Переходим к установлению выражения для М2 при движении
груза в третьем пролете. Теперь момент М2 можно вычислить как ле¬
вый опорный момент третьего загруженного пролета. Поэтому поль-
9 259
зуемся первой формулой (12.8), заменяя в ней индекс (п — 1) на 2:
М?-1д±гVи[( V)к- и). (12.12)
При движении груза в четвертом пролете определяем сначала
момент Щ по первой формуле (12.8):
10 И) ;-(1 и)]. (12.13)
Затем находим момент М124:
При движении груза в пятом пролете прежде всего находим момент М45’:
Л45 -ш[(1 1);-(1и)]. (12.14)
После этого находим из эпюры моментов:
По приведенным аналитическим выражениям отдельных ветвей для М2 строим всю линию влияния М2 (рис. 202, е). Она имеет вид знакопеременного графика с последовательно затухающими ординатами к концам балки.
Построение линий влияния опорных моментов кинематическим методом
Вид линии влияния опорного момента непосредственно легко получить кинематическим методом. По этому методу для получения линии влияния какого-либо опорного момента, например М2 (рис. 203, а), переходят к основной системе, отбрасывая лишь ту связь, которая передает искомый момент. Для этого необходимо в сечении балки над второй промежуточной опорой вставить шарнир, заменяя отброшенную связь парными моментами М2 (рис. 203, б). Каноническое уравнение совместности деформаций, выражающее условие равенства нулю взаимного угла поворота элементов оси у шарнира, будет
М2д22 62р 0.
Но по теореме взаимности 62Р бр2. Учтя это в уравнении деформаций, получим
т. е. линию влияния момента М2 можно найти по эпюре вертикальных перемещений в состоянии действия парных моментов М2 1
260
на основную систему. Эпюра 6р2 изображена на рис. 203, в. Ее легко найти, решая задачу получения изогнутой оси двух отдельных неразрезных балок 0—2 и 2—5. Деля все ординаты эпюры бра на глав¬
ное перемещение (—622), определяем ординаты линии влияния М2 (рис. 203, г). Заметим, что б22 — взаимный угол поворота касательных к упругой линии чуть слева и чуть справа от шарнира; тогда
б22 а2 а2, (12.15)
где а2, с2 — углы поворота указанных касательных на второй промежуточной опоре.
Линии влияния усилий в сечении балки и опорной реакции
Рассмотрим построение линий влияния изгибающего момента Мк и поперечной силы в произвольном сечении к третьего пролета неразрезной балки (рис. 204, а). Расстояния центра сечения до левой
261
и ггравой опор соответственно а и 6. Переходим к основной системе в виде балки 2—3 на двух шарнирных опорах с пролетом 3, возмещая жесткость прикрепления концов ее опорными моментами М2 и М3. Линии влияния опорных моментов М2 и М3 предполагаем заданными (рис. 204, б, в).
Р1
Основная система в виде разрезной балки 2—3 изображена на рис. 204, г. Применяя принцип. независимости, момент в сечении к получаем, суммируя момент только от единичной силы Р 1 (в простой балке) с изгибающим моментом от опорйых моментов:
Лй МР, Ма Ама, (12.16)
где М[р) — момент в простой разрезной балке;
Ам — левая опорная реакция от опорных моментов;
л М8 — м2 — 1.
262
Подставляя выражение Ам Р формулу (.16), после преобразований
получим
Мк Мр) МЛ М3. (12.17)
Линия влияния М1Р) показана на рис. 204, д.
Рис. 205
Линия влияния М получится наложением трех линий влияния: М[р М2, увеличенной в раз, и М3, увеличенной в — раз. Линия влия-
3 3
ния Л4г приведена на рис. 204, е. В общем виде ее легко получить методом моделей, вставляя шарнир в сечении к и представляя упругую линию такой системы от действия парных моментов Мк 1.
263
Аналогично строим линию влияния поперечной силы используя нервоначальную основную систему по схеме рис. 204, г. По прин¬
ципу сложения имеем
ь Р) (12.18)
Линия ЕЛшния Скр) изображена на рис. 204, д.
Линия влияния поперечной силы в сечении к неразрезной балки может быть получена путем суммирования линии влияния поперечной силы в простой разрезной балке 0] и линии влияния левой опорной реакции Ам, выраженной через разность линий влияния опорных моментов М3 и М2, деленную на 3. В общем виде линия влияния Ск показана на рис. 204, ж.
Остановимся еще на построении линии влияния полной опорной реакции неразрезной балки для второй ее опоры (рис. 205, а). Используя предыдущее решение, выразим опорную реакцию через поперечные силы в сечениях к и къ расположенных чуть правее и чуть левее опорного сечения. По определению поперечной силы имеем
0.ь 0.кх
откуда
Д2 Са-Са,. (12.19)
Суммируя ординаты линий влияния (рис. 205, 6) и (—Ск1) (см. линию Ск1 на рис. 205, в), находим ординаты линии влияния опорной реакции (рис. 205, г).
Ту же линию влияния можно получить методом моделей по эпюре Ьрк для неразрезной балки с отброшенной второй опорой, реакцию которой ищем (рис. 205, д).
§ 70. НЕВЫГОДНЕЙШИЕ ЗАГРУЖЕНИЯ И ПОСТРОЕНИЕ ОБЪЕМЛЮЩЕЙ ЭГПОРЫ МОМЕНТОВ ПРИ ДЕЙСТВИИ РАСПРЕДЕЛЕННОЙ НАГРУЗКИ
Из рассмотрения линий влияния различных усилий можно установить следующие закономерности невыгоднейших загружений неразрезной балки временной нагрузкой:
1. Наибольший отрицательный момент в опорном сечении балки возникает при загружении обоих пролетов, прилегающих к данной опоре, и всех остальных пролетов через один.
2. Наибольший положительный момент в пролете балки возникает при загружении данного пролета и всех остальных пролетов через один.
3. Наибольшее абсолютное значение поперечная сила в сечении у опоры имеет при загружении обоих пролетов, прилегающих к данной опоре, и всех остальных пролетов через один.
4. Наибольшее значение реакция опоры получает при таком же загружении, как указано в п. 3.
264
Таблица 4
Значения опорных моментов в неразрезной балке от различных загружений
Характеристика загружения
Значение опорных моментов в кн • м
М
В
мс
Мт
Постоянная нагрузка 10 кнм
Загружены все пролеты
-47,45
-102,67
-104,16
Временная нагрузка р 7,5 кнм
Загружен 1-й пролет
-18,08
4,83
-1,21
Загружен 2-й пролет
-29,85
-32,55
8,14
Загружен 3-й пролет
14,48
-57,83
-52,95
Загружен 4-й пролет
-2,14
8,55
-32,1
Постоянная временная нагрузка
-51,05
1П.
а
То же
10
-79,44
-97,52
-62,82
-53,19
-155,67
-126,67
-121,84
-193,05
-147,12
-158,32
-128,12
-129,33
-148,97
— 190,42
Для составления проекта конструкции неразрезной балки необходимо знать величины наибольших и наименьших изгибающих моментов не только на опорах и у середины пролета, но и в промежуточных сечениях. Расчетные изгибающие моменты в ряде сечений неразрезной балки определяют по построенным для этих сечений линиям влияния моментов или по таблицам.
Если найденные для каждого загружения временной и постоянной нагрузками расчетные изгибающие моменты отложить от горизонтальной оси (отрицательные вниз, положительные вверх) и соеди-
265
нить концы отдельно отрицательных и отдельно положительных ординат моментов, то получим объемлющую эпюру моментов (рис. 206). Она имеет две ветви: ветвь, соответствующую закону
изменения наибольших по абсолютному значению отрицательных моментов, и ветвь
II, соответствующую закону изменения наибольших расчетных положительных моментов в различных сечениях. На некоторых участках (.Аа, Ьс и др.) имеются лишь расчетные моменты одного знака; на других же участках (например, ай) для сечений балки получаем два расчетных момента — положительный и отрицательный. Объемлющая эпюра моментов дает полную картину изменения Мтах и Мпйп для всех сечений балки от действия расчетной нагрузки —временной совместно с постоянной. Следует иметь § в виду, что постоянная на64 грузка расположена на всех У пролетах балки, а временная
а устанавливается в соответст¬
вии с видом линий влияния момента в данном сечении. Например, для отыскания
максимума момента в среднем сечении первого пролета Мх временной нагрузкой
загружаем первый и третий пролеты, для определения _ максимума момента в среднем сечении второго пролета Мь2 загружаем второй и четвертый пролеты, для нахождения минимума Мц загружаем первый, второй и четвертый пролеты и т. д. (
Построение объемлющей эпюры моментов сводится к следующему. Строят эпюры моментов для загружения каждого пролета в отдель-
266
ности; на их основе находят эпюры моментов от расчетных загружений для отдельных сечений — М4, М2, Мв, Мс, М0 (см. рис. 206). Объемлющие очертания построенных эпюр сверху и снизу от оси и образуют объемлющую эпюру моментов.
Пример. Пусть требуется построить объемлющую эпюру моментов для неразрезной балки, изображенной на рис. 206, со следующими пролетами и моментами инерции сечений: 6 м 2 9 м; 8 12 м; 48 м х 2; 2 3; 8 4; 4 2,67. Постоянная нагрузка 10 кнм; временная нагрузка р 7,50 кнм.
Решение. В табл. 4 приведены значения опорных моментов такой балки для отдельных и расчетных загружений.
Расчетные опорные моменты Мв, Мс и Мй получаем для 8, 9 и 10-го видов загружений. Отдельные эпюры моментов рис. 206 построены по загружениям 6— 10 табл. 4. Объемлющая эпюра моментов в общем виде представлена на рис. 206.
ГЛАВА 13. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ ПЛОСКИХ ФЕРМ
§ 71. ОБЩИЙ ХОД РАСЧЕТА ФЕРМЫ ПРИ ПОСТОЯННОЙ НАГРУЗКЕ
Виды ферм
Ниже рассматривается расчет статически неопределимых шарнирно-стержневых плоских ферм на действие узловой нагрузки. В действительности, соединение стержней фермы в узлах жесткое, в результате чего во всех узлах фермы возникают моменты аналогично рамной конструкции. Эти моменты по концам стержней в ферме и в случае узловой нагрузки при большой жесткости узлов и наличии эксцентриситетов в прикреплениях могут быть весьма значительными. В особенности существенны дополнительные напряжения от неразрезности очень мощных поясов и от жесткости узлов в фермах со сложной решеткой. Однако расчет ферм с жесткими узлами крайне сложный и может быть рационально проведен лишь методом деформаций (см. ниже) или специальными приемами. В этом разделе мы остановимся на об¬
Рис. 207
267
щепринятом расчете ферм как систем с идеально-шарнирными узлами.
Различают два вида статически неопределенных ферм — внешне и внутренне статически неопределимые. Примерами внешне статически неопределимых ферм являются: неразрезная ферма (дважды статически неопределимая; рис. 207, а) и двухшарнирная арочная ферма (однажды статически неопределимая; рис. 207, б). К внутренне статически неопределимым фермам относятся некоторые комбинированные системы (например, балочная ферма с гибкой аркой; рис. 208) и различные фермы со сложными решетками (крестовой, многорешетчатой).
Расчет ферм на действие неподвижной нагрузки
Общий ход расчета статически неопределимой фермы при заранее заданных размерах поперечных сечений стержней тот же, что и для
рамных систем. Следует лишь иметь в виду особенность определения перемещений узлов шарнирно стержневых ферм, в элементах которых возникают только продольные силы N.
Порядок расчета однажды статически неопределимой фермы следующий.
Освобождаем заданную ферму от лишней связи (рис. 209, а). В данном случае отбрасываем промежуточную опору неразрезной фермы и реакцию этой опоры принимаем за лишнее неизвестное Хг. Для основной системы (рис. 209, б) составляем каноническое уравнение деформаций, формулирующее условие равенства нулю перемещения точки 1 по направлению отброшенной связи от действия лишнего неизвестного Хх и силы Р:
Ххбц Д1р 0,
откуда
1-
1Р
()
(13.1)
где 6П — перемещение по направлению Хг в состоянии действия Хх 1 (рис. 210, а)
Д1р — перемещение по направлению Хг от действия заданной нагрузки Р (рис. 210, б).
Обозначая продольные силы в произвольном стержне основной системы в состояниях действия Хх 1 и нагрузки Р соответственно
268
и А1р, получаем по формуле Мора — Максвелла следующие выражения для перемещений:
п
«и "20
(б)
д1р2л,.
1
где 5 — длина стержня;
Р — площадь поперечного сечения стержня;
2 — знак суммы, распространяющийся на все стержни фермы.
Лишнее неизвестное найдем подстановкой значений величин из выражения (б) в формулу (13.1):
2-1?
1--4 • (13.2)
1
Если ферма внутренне статически неопределима, то суммирование в знаменателе распространяется и на рассеченный стержень.
Из выражения (13.2) видно, что лишнее неизвестное зависит от соотношения в площадях сечений стержней. Суммарные значения величин, входящие в выражение (13.2), вычисляют табличным путем. Определив лишнее неизвестное Хи находим усилие в любом стержне фермы, суммируя влияние нагрузки Р и лишнего неизвестного Хг:
Лсум Nр X1N. (13.3)
26У
Аналогично проводится расчет п раз статически неопределимой фермы; лишние неизвестные Хъ Х2, Х3, Хп определяют, исполь¬
зуя систему канонических уравнений, а суммарное усилие в стержне фермы вычисляют по формуле
Лсу „ ЛГр‘2Хл (13.4)
1
Пример. Найти лишнее неизвестное для неразрезной фермы, подверженной действию сил Р 600 кн (рис. 211).
Решение. За лишнее неизвестное принимаем усилие Хг в среднем стержне верхнего пояса. Определяем перемещения 6П и Д1р по табл. 6. Из табл. 5 получаем
уЕбц 50,09; у ЕА1р -30100.
Лишнее неизвестное
30100 -лп 1юд)9 кн-
Заметим, что в данном случае напряжения во всех стержнях фермы одинаковые, следовательно, ферма равного сопротивления.
Таблица 5
Перемещения 6ц и Д1р
Обозначение
стержня
Длина в см
Площадь сечения в см2
Усилие
Ъ
_ 5
N1 рг см
"р.
кн
4г.
Р Р" кнсм
0
500
.11,17
0,625
28,4
17,75
-500
— 14 200
о,
400
53,6
1,00
7,46
7,46
0
0
V
800
8,94
-0,50
—44,75
22,38
400
— 17 900
1
500
78,2
-0,625
-4,0
2,50
-500
2 000
2
50,09
2
—30 100
§ 72. ЛИНИИ ВЛИЯНИЯ ЛИШНИХ НЕИЗВЕСТНЫХ И УСИЛИЙ В СТЕРЖНЯХ ФЕРМ
Так как усилие в ряде стержней статически неопределимой фермы согласно формуле (13.3) выражается через лишнее неизвестное, то при расчете фермы на подвижную нагрузку прежде всего строят линию влияния лишнего неизвестного Хг.
Рассмотрим общий ход получения линии влияния Хх для двухпролетной неразрезной фермы (рис. 212). Полагаем, что груз Р 1 движется по проезжей части, расположенной на уровне нижнего пояса фермы. Отбрасывая промежуточную опору фермы, заменяем ее воз¬
270
действие силой Хи линию влияния которой требуется найти (рис. 212, а) При произвольном положении груза Р 1, приложенного в точке ;, составляем каноническое уравнение метода сил
откуда
-111 “Ь — О,
у 1р
бп’
(13.5)
где б1р — перемещение среднего узла основной системы от силы Р 1, поставленной в произвольное положение; би — перемещение по направлению Хх от силы Хг 1.
Так как решается задача о линии влияния, то груз Р 1 подвижный и, следовательно, 61р — величина переменная. гу задачу можно заменить задачей построения эпюры перемещений 6 точек приложения силы Р от неподвижной силы Хг 1. В самом деле, согласно теореме о взаимности перемещений
б1р 8Р1, (а)
где 6р1 — вертикальное перемещение точки приложения силы Р 1 при данном ее положении, вызванное действием неподвижной силы Хг 1 (см. рис. 212, б).
Применяя метод упругих грузов, легко построить эпюру прогибов точек оси нижнего пояса от действия силы Х11. Это и будет эпюра бр1 (рис.
212, в). Пользуясь соотношением (а), находим для Хх выражение
V _ р1
Х1 бхГ
(13.6)
Рис. 212
Отсюда следует, что линия влияния лишнего неизвестного Хг может быть построена как эпюра вертикаль- _
ных перемещений грузового пояса фермы от действия силы Хг 1 делением всех ординат ее на главное перемещение (—6П). Главное перемещение ищем по формуле
(13.7)
где А? — усилие в стержне фермы для основной системы в состоянии действия силы Хг 1.
Ординаты эпюры бр1 легко определить, пользуясь методом упругих грузов по известным усилиям Л. Каждый упругий груз №п находят по возможной работе внутренних сил в состоянии действия двух равных и противоположных по направлению пар сил с моментом,
271
равным 1. Из выражения (13.6) вытекает, что поскольку линия влияния Хг определяется законом изменения 6р1 путем деления любого значения 6р1 на постоянную (—6П), то эпюра бр1 представляет м одель линии влияния. Таким образом, модель линии влияния Хх получается по эпюре вертикальных перемещений основной системы в состоянии действия силы Х1 1. Деля ординаты модели (эпюры 6р1) на постоянную (—6П), получаем ординаты линии влияния (рис. 212, г).
Линию влияния усилия в произвольном стержне статически неопределимой фермы N1 легко получить по линии влияния лишнего неизвестного Х19 пользуясь формулой (13.3):
А МР) ВД, (13.8)
где р) — усилие в 1-том стержне фермы от груза Р 1 в статически определимой ферме;
N1 — усилие в -том стержне фермы для основной системы от силы Хг 1 (постоянная величина).
Так как при движении груза Р 1 будут меняться значения Ыр) и Хи то выражение (13.8) можно сформулировать так: линия влияния усилия в произвольном стержне фермы получается путем суммирования двух линий влияния — линии влияния усилия в статически определимой ферме и линии влияния лишнего неизвестного Хг, все значения которой умножены на N В отдельных случаях 0 и линия влияния N1 совпадает с линией
Пример. Построить линии влияния лишнего неизвестного Хх и усилий 03 и для двухпролетной неразрезной фермы (рис. 213, а). Длина панели с1 8 м, высота фермы Н 4 м. Площади сечений всех элементов поясов, за исключением крайних,7
272
ри1 200 см2. Площади сечений крайних элементов нижнего пояса Ри 100 см2. Площади сечений всех раскосов и крайних элементов верхнего пояса 70,7 см2.
Решение. Определяем усилия во всех элементах фермы в основной системе для вспомогательного состояния действия силы Хг (табл. 6)
Рис. 214
По методу упругих грузов вычисляем упругие грузы №п и №П1: ЕУР - 0,225 кнсм,
ЕФи — 0,4 кнсм
ЕЧ7т — 0,95 кнсмг.
Система грузов, приложенных к фиктивной балке, изображена на рис. 213, б. Если № положительные, направляем их вниз. По системе упругих грузов строим
273
эпюру моментов. Ординаты эпюры бр1 получаем по формуле
Р1— ф
где Мф—фиктивный момент в сопряженной балке; Е 2- 04кнсм2.
Таблица 6
Значения усилий
Обозначение стержня
Усилие N.
Обозначение стержня
Усилие N.
01
0,707
—2,500
02
1,000
-0,707
Оз
2,000
0,707
о4
3,000
Оз
-0,707
-0,500
04
0,707
-1,500
Об
—0,707
Эпюра 6р1 представлена на рис. 213, в. Заметим, что пренебрежение деформацией решетки при определении 6р1 может привести к существенной ошибке (более 20%). Для данного случая неразрезной фермы главное перемещение
б11 б,1111 0,098.
По формуле (13.6) получаем ординаты линии влияния Хг (рис. 214, а). Ординаты линии влияния Хг для положения груза в узлах,, соответственно будут: 0,449; 0,806; 1,00. Применяя формулу (13.8), строим линии влияния 03 и )3. Подставляя значения «единичных» усилий для этих элементов, получаем
03 0(р2Х1;
030(р)-0,707Х1.
Линия влияния 03 изображена на рис 214, б. Отыскание линии влияния иллюстрировало рис. 214, в. Линия влияния с ординатами, отложенными от горизонтали, представлена на рис. 214, г.
§ 73. МАТРИЧНАЯ ФОРМА РАСЧЕТА ФЕРМ
В связи с распространением электронных цифровых вычислительных машин широкое применение получает матричная форма расчета
статически неопределимых систем. Достоинством матричной формы расчета является ее компактность, стандартность и общность. Одна и та же последовательность матричных операций может быть использована для расчета самых различных систем (рам, арок, ферм).
Рассмотрим ход расчета статически неопределимой фермы, изоРис. 215 браженной на рис. 215. За лишнее
274
неизвестное примем реакцию X в вертикальном опорном стержне. Усилия 5,- в каждом из остальных стержней фермы линейно связаны с удлинениями V стержней:
(а)
1 • 52
ЕР
1 у
удлинения стержней от единичных усилии
(податливости); длины стержней;
Ри Р2 — площади поперечных сечений.
В матричной форме соотношения (а) можно записать так:
или кратко:
IIп 0II
II51
II о и II
II 52
(б)
(в)
где V — матрица удлинений стержней;
— матрица податливости;
5 — матрица усилий.
Отбросив лишний стержень и приложив внешнюю силу Р 1 (рис. 216, а), найдем перемещение гхр по направлению лишнего не-
I
известного. Усилия в этом состоянии будем далее обозначать Ь1р. Для этого вводим состояние действия силы Хг 1 и применяем принцип возможных перемещений (рис. 216, б). Получаем
1 ?хр (г)
где 5 — усилие в г-том стержне от силы X 1,
1Р— удлинение стержня в состоявши действия силы Р 1. Усилия в состоянии действия силы X 1 будем обозначать Ъ1Х. Иначе правую часть соотношения (г) представим так:
2 §1х1р 1x1 р “1“ 2x2р “Ь ■ • • 1Х2Х Р
’Нр
(д)
275
Следовательно, равенство возможных работ по соотношению (г) будет
и2 р
Ьх1)1р,
(е)
где Ъх — транспонированная матрица от матрицы столба Ь1Х
— матрица-столбец удлинений, которая представляется по матричной форме (б) так:
1р 1р —
г О
О,
(ж)
После подстановки выражения (ж) в равенство (е) получаем для перемещения матричное выражение
ГХр Ьх1Ь1р (3)
или в развернутом виде
ГхР Ь1хЬ2х
АО
0[2
и1р
Ь2р
1х1р? 1 “Ь 2Х2р?2
(и)
Аналогично определяем перемещение гхх в состоянии действия силы X 1 (рис. 216, б), выбирая за возможное состояние то же действие единичного неизвестного:
А о
ь1х
Г XX 1 1хЬ2х
о к
2Х
— Ь[х Ь 1x2-
(К)
Каноническое уравнение будет
ххХ г хрР О, откуда лишнее неизвестное
Х-ГР-г2гхрР. (л)
XX
Полное усилие в стержне статически неопределимой фермы (см. рис.215)
5т Ь1рР ЬхХ. (м)
Как видим, чтобы найти X, необходимо получить обратную матрицу от гхх.
ГЛАВА 14. РАСЧЕТ РАМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ § 74. КИНЕМАТИЧЕСКАЯ НЕОПРЕДЕЛИМОСТЬ РАМ Общие сведения
До сих пор мы рассматривали расчет различных статически неопределимых систем (рам, арок, балок, ферм) по методу сил, принимая за основные неизвестные силы или моменты.
Если при расчете статически неопределимых систем по методу сил выбирают силы (усилия в лишних связях) и для их отыскания используют уравнения совместности деформаций, причем применяют обычно основную геометрически неизменяемую систему, то при расчете по методу перемещений за неизвестные принимают перемещения, а для их нахождения используют условия равновесия. В случае свободной, незакрепленной, рамы шарнирная схема рамы (полученная введением во всех жестких узлах полных шарниров) оказывается геометрически изменяемой. Шарнирная схема рамы используется для установления числа неизвестных перемещений.
Метод перемещений (или метод деформаций) в настоящее время получил большое распространение, особенно при расчете сложных статически неопределимых систем с большим количеством лишних связей, обладающих малой подвижностью узлов (сложные каркасные рамы, фермы с жесткими узлами и т. д.). Метод перемещений явился основой для разработки ряда ценных приближенных методов расчета рам (метод Кросса, Кани и др.). Метод перемещений с большим успехом применяется при решении задач устойчивости и динамики.
Существует две формы решений задач по методу перемещений: каноническая и развернутая. Развернутая форма применена Гелерсм, Манном, Б. Н. Жемочкиным, Н. В. Корноуховым, автором и распространена за рубежом.
Каноническая фэрма записи уравнений метода перемещений аналогична той же форме записи уравнений метода сил (см. Приложение).
Степень кинематической неопределимости
Степенью кинематической неопределимости называется число тех неизвестных перемещений, знание которых определяет деформированный вид системы и, следовательно, все усилия в ней. Часто степень кинематической неопределимости не совпадает со степенью статической неопределимости. Для установления степени кинематической неопределимости — числа независимых неизвестных перемещений — необходимо рассмотреть особенности деформаций рам. При представлении деформированного состояния рам будем пренебрегать, как это принималось и при расчете рам методом сил: 1) продольными деформациями, вызванными осевыми силами в стержнях (влиянием Ы) 2) разницей длин искривленного стержня и проекцией его на первоначальное направление стержня; 3) влиянием поперечных сил на деформацию. При расчете же на действие температуры продольные деформации учитываются.
При указанных выше предположениях для плоской рамы (рис. 217,а), каждый узел которой прикрепляется последовательно к двум другим узлам двумя стержнями, не лежащими на одной прямой, линейные смещения узлов отсутствуют. В самом деле, стержни рамы считаются нерастяжимыми, а система ее узлов образует треугольники (1—6—0, 2—5—1Х 3—4—2), длины сторон которых не меняются и потому ли¬
277
нейных смещений не происходит. При этом шарнирная схема рамы (рис. 217, б) неизменяема. Такие рамы,-шарнирная схема которых неизменяема, относятся к первому виду закрепленных, или несвободных, рам. Расчет рам этого вида особенно прост по методу перемещений. За неизвестные перемещения, определяющие всю картину деформаций рамы и, следовательно, все усилия в системе,
для рам этого типа принимают у глы поворота жестких свободных узлов. Для рамы, изображенной на рис. 217, а, эти углы обозначены рх, р2 иср3. Кинематическая неопределенность системы для этого случая равна трем. При расчете, как обычно, исходят из предположения об абсолютно жестком взаимном соединении стержней в узле; концы всех стержней, связанных в данном жестком узле (, 2, 3), поворачиваются поэтому на один и тот же угол (см. рис. 217, а).
Ко второму общему виду рам относятся рамы, имеющие линейные смещения узлов. Такие смещения возникают вследствие того, что в рамах этого типа нет последовательного прикрепления каждого узла двумя стержнями и, следовательно, шарнирная схема рамы изменяема. В качестве примера рассмотрим простейшую раму прямоугольного очертания (рис. 218, а). Идя слева направо,
6)
Рис. 217
замечаем, что узел 1 рамы прикреплен лишь одним вертикальным стержнем, почему для этого случая возможно горизонтальное перемещение узла А 1 — Г (нет горизонтального закрепления). Узел 2 рамы прикреплен двумя стержнями 1—2 и 2—4, и так как узел 1 перемещается, то узел 2 также получает линейное смещение 2—2. Смещения узлов 2 и 1 должны быть одинаковыми, поскольку стержень принят нерастяжимым: 2—2 1—Г А. Деформированный
276
вид рамы, так же как и для предыдущего типа, характерен тем, что проекции искривленных линий каждого стержня на первоначальное направление равны начальным длинам стержней и узлы рамы остаются жесткими — углы фх или р2 одинаковы для концов ригелей и концов стоек.
Для рам данного типа за неизвестные при расчете методом деформаций принимают как углы поворота жестких узлов фх и ф2, так и линейные смещения узлов А. В данном случае мы получили одно неизвестное линейное смещение А, и нетрудно видеть, что шарнирная схема рамы (рис. 218, б) имеет одну степень свободы в отношении произвольных линейных смещений. Действительно, для обращения шарнирной схемы в неизменяемую систему необходимо ввести один дополнительный опорный стержень.
Число степеней свободы шарнирной схемы рамы всегда совпадает с числом неизвестных линейных смещений узлов заданной рамы или со степенью линейной подвиоюности узлов рамы. Это позволяет легко4 установить число неизвестных линейных смещений узлов А или им пропорциональных углов поворота стержней б (по рис.
218, а 0 для любой рамы.
Рассмотрим, например, раму, изображенную на рис.
219, а. Переходя к шарнирной схеме рамы (рис. 219, б), получаем кинематическую цепь стержней 1—2У 2—3 3—4, 4—7 — систему с двумя степенями свободы (в отношении линейных смещений). К этому заключению приходим, устанавливая число добавочных опорных стержней, необходимых для обращения шарнирной схемы в неизменяемую. Для этого прежде всего нужно закрепить узел добавочным опорным стержнем I (кроме стержня 1—5) узел 2 теперь прикреплен неподвижно двумя стержнями 1—2 и 2—6 для закрепления узла 3 следует ввести дополнительный опорный стержень, после чего узел 3 оказывается прикрепленным двумя стержнями; двумя стержнями прикреплен и узел 4.
Использование кинематической цепи — шарнирной схемы рамы — важно и для установления неизвестных линейных смещений узлов, точнее, взаимных линейных смещений концов стержней данной рамы
279
или неизвестных углов поворота рамы 0 в картине ее перекоса. Картиной лерекоса рамы называют многоугольную линию, вершинами которой являются центры узлов, рамы в деформированном состоянии (на рис. 219, а это контур 5—Г—2—3—4—7).
Так как в шарнирной схеме дополнительным стержнем подкреплен узел 1У то первым неизвестным линейным смещением является Д2 — смещение узла 1 относительно узла 5 в направлении, перпендикулярном к стержню 1—5. Поскольку же второй подкрепляющий стержень дан в узле 3, вторым неизвестным линейным смещением следует выбрать смещение Д2 узла 3 относительно узла 2 по нормали к первоначальной оси стержня 2—3 (см. рис. 219, а). Положение дополнительных опорных стержней дает возможность установить, взаимные смещения концов каких именно стержней следует принимать за неизвестные (в данном случае стержней 1—5 и 2—3). Вместо взаимных линейных смещений концов стержней в развернутой форме метода перемещений целесообразно принимать углы поворота.стержней рамы в картине перекоса (точнее — углы поворота хорд изогнутых линий стержней). Эти углы, очевидно, линейно связаны со смещениями:
где 15, 23 — первоначальные длины стержней.
Если теперь нанести на картину перекоса рамы искривленные линии стержней, то углы 0 будут углами поворота хорд изогнутых линий стержней рамЫ. Введение в качестве неизвестных углов б особенно удобно для представления деформированного вида рамы, когда естественно сопоставление углов поворота стержней 0 с углами поворота узлов ф. Это одно из преимуществ развернутой формы метода перемещений.
Для рассмотренных свободных рам за неизвестные по методу перемещений в развернутой форме принимают: 1) углы поворота жестких свободных узлов и 2) углы поворота тех стержней рамы, положение которых определяет картину перекоса рамы. Так, для рамы, изображенной.на рис. 219, а, неизвестными угловыми перемещениями будут: четыре угла поворота узлов фх, ф2, ф3 и ф4 и два угла поворота стержней 0 и 02. Для зависимых углов поворота 03 и 04 получаем
О _02к; 04 ±(01и 0яи8та).
‘34 ‘47
§ 75. СООТНОШЕНИЯ МЕЖДУ КОНЦЕВЫМИ МОМЕНТАМИ И УГЛОВЫМИ ДЕФОРМАЦИЯМИ
Стержень, жестко приклепленный к узлам двумя концами
Важной частью всей операции расчета рам по методу перемещений является выражение концевых моментов М,к и Мкь через угловые перемещения и члены, отражающие влияние нагрузки.
280
Составим соотношения между концевыми моментами и угловыми перемещениями прямолинейного стержня рамы постоянного сечения в предположении, что концы стержня и к жестко прикреплены к узлам (рис. 220). В результате общей упругой деформации всей рамы ее узлы получают неравные смещения — и кк которые в общем случае наклонены к первоначальной оси стержня, и стержень рамы искривляется. Полное перемещение стержня —к в положение —к можно представить как поступательное перемещение в параллельное положение I—к1у затем поворот на угол вк и искривление. В основной системе (нижний рисунок) отбрасываем жесткое прикрепление концов и возмещаем его моментами Мк и Мк(. Отмечаем углы поворота касательных по концам к изогнутой линии стержня от начального направления его оси ср, и срА; они равны углам поворота
узловых элементов I и к. Проведя хорду изогнутой линии 1к у укажем также углы а(к и аш между хордой и касательными по концам к изогнутой линии стержня.
Принимаем следующее правило знаков. Концевые моменты М1к и Мкь считаем положительными при действии их против часовой стрелки; углы поворота узлов ср, и фЛ, а также угол поворота хорды изогнутой линии §(к принимаем положительными по часовой стрелке. Углы поворота касательных к изогнутой оси стержня по концам его, отсчитываемые от хорды, считаем положительными против часовой стрелки.
Дадим выражение для углов а1к и аы через концевые моменты М1ку Мы и нагрузку Р.
Перемещения, отсчитываемые от хорды изогнутой линии и к, а также углы поворота а1ку ак1 определяем по схеме простой балки с горизонтальной осью, пренебрегая влиянием поворота на угол в1к за его малостью. Так же кас и при выводе выражения для углов поворота по концам простой балки от опорных моментов и нагрузки, для а(к и ак( при постоянном сечении имеем
Рис. 220
(а)
281
где аь а — углы поворота по концам простой шарнирно опертой балки только от действия нагрузки Р
Е11к — жесткость балки на изгиб.
Первые два члена правой части выражения (а) отражают влияние на углы поворота неизвестных концевых моментов.
Введем для краткости записи понятие погонной жесткости, т. е: жесткости на единицу длины стержня, обозначая ее через ь1к
_ Е1Ь (х
—(б) Вместо выражения (а) можем написать:
Мк Мм, о.
а-з-еа«
М(и мм
Чк Чк
ак‘1С 1 а«-
(в)
Решая эти уравнения относительно моментов М1к и Мы получаем Чк (4оьл 2а) — 1[Ь (4а?г 2оф);
Мы — Чк 2Х(ь) — ь1к (4а 2а?) •
(г)
Первые члены правой части этих выражений содержат статически неопределимые угловые деформации а1к и ак1 вторые же члены включают лишь углы поворота по концам простой балки ок и а% от заданной нагрузки.
При действии сплошной равномерной нагрузки р по всей длине балки
п0 — р1к - гс0 — Р1к (п)
Щк 24Е1(к ак124Е1ш где учтено принятое правило знаков для углов а1ку ак:.
При расчете рам методом перемещений необходимо выразить углы поворота а(ку акь отсчитываемые от хорды изогнутой линии, через углы поворота узлов ф,, фй и угол поворота хорды в1к. Из рис. 220 получаем
Щк Ък — фь 1
— Чк- )
Подставляя значения а1к и аг из выражений (е) в формулы для концевых моментов (г), находим
М(к — Чк (4ф 2фк — 60,) — Ь1к (4а?Л 2аЪ) Мк1 — 11к (4фк 2ф — 60А) — Ь1к (4а -- 2а?)
(14.1)
Мы получили выражения для концевых моментов стержня рамы I—жестко закрепленного в узлах и к.
282
Заметим, что узлы рамы являются упругими защемлениями для данного стержня. В самом деле, концы стержня получают повороты фьу Фк и помимо того, происходят взаимные линейные смещения вследствие податливости узлов, из чего и складывается угол смещения Ъ(к для всего стержня.
Если же упругость защемлений концов стержня исключить, т. е. если положить в выражениях (14.1) ср, 0, фЛ О, 0,Л 0, то получим схему стержня в виде балки, абсолютно жестко защемленной двумя концами (рис. 221, а). Так как
на стержне имеется нагрузка Р, то от нее возникают концевые моменты, выражения для которых имеют вид последних членов формул (14.1). Обозначая эти моменты, вызванные только нагрузкой Р через Мк и М., согласно формулам (14.1) получаем
Мк — 1ьк (4о 2а);
М°и - 11к (4а?г 2а?). (142)
Моменты Мк и М%1 только от нагрузки для балки 1—к, абсолютно
жестко защемленной двумя концами, легко вычислить, пользуясь формулами (14.2), по известным углам поворота ок и ак( шарнирно
опертой балки при действии на нее той же нагрузки. В случае загру-
жения стержня равномерно распределенной нагрузкой д, подставляя
283
Таблица 7
Реакции для балок с защемленными концами
Схема
Реакции
V 1 п »М,
-й)
4Е
М-аЪ— »
2Е1 ; МЬ ;
• ? 6Е
На1Г
I
"аЬ
а Ь 8-1-1
я0 —Л
I
х°
ДЛ ЛЛ еЕ о
Маь — Мьа— — --—
я м
и1
Г ьш
МаЬ —МV(Ъи—) Мда —Ми(3и—1)
Продолжение табл. 7
Схема
Реакции
Р
Маь(4а Ьу,
Если а — 2» то:
МЬа--(6а 4аЬ Ь)
значения углов из выражения (д), согласно формулам (14.2), полу чаем
В табл. 7 указаны значения моментов М% и реакций для различных типов нагрузки.
Подставляя краткие обозначения от нагрузки из формул (14.2) в выражения (14.1), окончательно получаем следующие выражения для концевых моментов в стержне рамы с упруго-податливыми заделками:
Этими формулами далее и пользуемся при расчете рам, стержни которых жестко прикрепляются к упруго-податливым узлам рамы двумя концами. Влияние упругой податливости узлов выражается первым членом правой части; влияние нагрузки, приложенной непосредственно к стержню, — последними членами. На рис. 221,а показаны моменты от нагрузки, на рис. 221,6 — моменты от поворота левой заделки на угол ф,, на рис. 221,в — моменты от поворота правой заделки на угол фЛ и на рис. 221,г — моменты от взаимного смещения заделок, соответствующего углу 0. Эти моменты рассматриваются как «упругие реакции» при применении канонической формы метода перемещений.
Пусть стержень рамы (рис. 222) жестко прикреплен к ее узлу и шарнирно — к узлу к. Тогда в месте шарнирного прикрепления момент Мк( 0, и после отбрасывания жесткого прикрепления в узле I
(ж)
Мм — — (4ф 2фб — 6Ь1к) М%
Мы — 1(к (4фк 2ф — 6в) Мы-
(14.3)
Стержень, жестко прикрепленный одним концом и шарнирно другим
265
получаем расчетную схему в виде простой двухопорной балки, подверженной действию лишь одного момента М1к и нагрузки, непосредственно приложенной к стержню.
Перемещение стержня г, так же как и в предыдущем случае, представляется поступательным в параллельное положение, затем в форме поворота на угол смещения в1к без искривления и далее в виде искривления стержня (изогнутая линия 1к). Выражаем угол поворота а(к в месте жесткого прикрепления стержня к узлу, отсчитываемого от хорды, через единственный концевой момент М1к и нагрузку:
Щъ-
3 Е1(к
1цг "Ь
(3)
где ок — угол поворота только от нагрузки для разрезной балки. Вводя погонную жесткость, вместо выражения (з) получаем
М
(к
■ щк.
Отсюда находим момент М1к:
А16 1к ’ — 1(к 30С.
Заменяем в первом члене правой части а1к на (0 — ср,): М.1к Ь(к (Зф 30) — 3гСХ.
(14.4)
Мы получили выражение момента М1к в стержне рамы I — к, упруго заделанном в узле I и шарнирно опертом в узле к. Выражение (14.4) представлено в виде суммы влияний: упругости заделки и взаимного смещения концов (первый член) и действия нагрузки, непосредственно приложенной к стержню (второй член). Если заделка абсолютно жесткая (ф, 0 и Ь(к 0), то в заделке стержня I — к возникает момент, вызванный лишь нагрузкой (рис. 223,а). Из формулы (14.4) этот момент будет
МЧ’к —
Зная а%, легко определить момент М% — момент в защемлении от заданной нагрузки для стержня рамы, абсолютно жестко заделанного одним концом в узле I и шарнирно опертого другим концом в узле к. Значения моментов М)к от нагрузок разных видов приведены в табл. 8.
286
Таблица 8
Реакции в защемлении балки, заделанной одним концом
Схема
Реакция
О- 3 Е1
■ к:
3 Е1
Л М I М I I
м°
1
Мкг
р12 8
ПБ Лц;
к 1
а
6
Г
- Э. (
п
гг
Т а
И
Ь
г
Р
-
а
Ь
и_1
1
м”
— (4а
м,
Я4
287
Продолжение табл. 8
Окончательно момент М1к для жесткого конца стержня, шарнирно опертого другим концом, согласно формуле (14.4) будет
М.1Ь — г (Зф— 30й) Л1А. (14.5)
Мы получили выражение концевого момента в зависимости лишь от одного угла поворота жесткого узла ср, и угла смещения 0. Угол
Рис. 223
поворота касательной в месте шарнирного прикрепления в данном случае знать не требуется, поэтому в дальнейшем при расчете рам, имеющих и жесткие и шарнирные узлы, за неизвестные принимают лишь углы поворота жестких узлов. Первый член правой части формулы (14.5) дает момент со стороны защемления от поворота на угол ф, (рис. 223, б) и от поворота всего стержня на угол 0ь (рис. 223, в). Эти реактивные моменты от защемления, вызванные его упругостью и взаимным смещением опор, называют упругими реакциями. Их значения используются и в канонической форме метода.
288
§ 76. РАСЧЕТ РАМ ПО РАЗВЕРНУТОЙ ФОРМЕ МЕТОДА ПЕРЕМЕЩЕНИЙ
Основная система
.
Рассмотрим общий ход расчета двухэтажной свободной рамы с жесткими узлами и вертикальными стойками (что принято для простоты изложения; рис. 224, а). В данном случае имеем четыре неизвестных угла поворота узлов ср,,
Фь ф и ф„ и два угла пово- Заданная рама
рота стержней 0Г, и д(к — по числу степеней свободы шарнирной схемы рамы, т. е. всего шесть неизвестных угловых перемещений (степень кинематической неопределимости). Деформированный вид рамы получен представлением картины перекоса г—I—к—
5—и—р и нанесением искривленной оси всех стержней так, чтобы удовлетворялись условия жесткости узлов рамы (равенство углов поворота касательных к изогнутым линиям всех стержней, сходящихся в данном узле).
Чтобы найти неизвестные угловые перемещения, используем условия равновесия, в которые войдут так называемые концевые или узловые моменты рамы, действующие на особо выбранную основную систему в виде шарнирной схемы рамы.От заданной рамы с жесткими узлами переходим к основной системе, вставляя в центре каждого жесткого узла рамы шарнир и возмещая действие взаимных жестких соединений концов стержней и узловых элементов парными моментами М1ку мк1, Мкх и т. д.
На рис. 224,6 показано лишь действие жесткой связи узлов на концы стержней в виде концевых моментов, которые принимаем положительными против часовой стрелки. Прямо противоположные им по направлению и равные по величине моменты М1ку Мки Мк8У.,
Рис. 224
10 Н. К. Снитко
289
действующие от концов стержней на узлы, называется узловыми моментами (на рис. 224, б не показаны).
Основная схема рамы является кинематической цепью балок, обладающей определенным количеством степеней свободы по числу произвольных поворотов узловых элементов относительно концов стержней (таких степеней свободы данная рама имеет 4) и по числу произвольных взаимных смещений концов стержней или произвольных поворотов стержней шарнирной схемы, т. е. по числу дополнительных опорных стержней (таких степеней свободы 2). Полное число степеней свободы основной системы (4 2 6) совпадает с числом неизвестных угловых перемещений. Заданная же жесткая рама неизменяема и находится в равновесии. Действие жесткости в соединении стержней рамы в узлах нами возмещено в основной системе концевыми и узловыми моментами Мьк9 Мк1. Эти моменты следует подобрать так, чтобы они удовлетворяли условиям равновесия основной системы, отрицающим произвольные малые перемещения системы: повороты узлов и повороты стержней шарнирной схемы.
Всю систему уравнений равновесия делим на две группы: основные и дополнительные уравнения. Основные уравнения составляются как условия равновесия узлов в форме равенства нулю суммы узловых моментов. Дополнительные уравнения формулируются как условия равновесия шарнирной схемы рамы в целом.
Представляем сначала общий вид основного уравнения метода перемещений для -того узла в первом предположении отсутствия внешнего момента (рис. 225, а, б).
На рис. 225, а выделена часть рамы у узла I и показаны как концевые, так и равные им узловые моменты М1к, Мип Мгг. Отбрасывая стержни рамы, рассматриваем равновесие узла, предполагая размеры его ничтожными (рис. 225, б). Считая, что в узле I сходится п стержней (к19 62, з,., составляем условие равновесия в виде равенства нулю суммы всех узловых моментов:
Основные уравнения
7
Рис. 225
Цм.-о,
п
290
т. е. сумма всех узловых моментов, действующих со стороны всех стержней, связанных с -тым узлом рамы, должна быть равна нулю.
Таков простой смысл основных уравнений при отсутствии внешнего момента.
Нередко к данному -тому узлу рамы бывает присоединена консоль, несущая какую-либо нагрузку. Тогда на центр узла консоль оказывает воздействие в виде силы и пары сил, момент которой т1 должен быть учтен при составлении суммы моментов (рис. 225, в).
Выделяя в этом случае узел, подверженный действию внешнего момента т1У а также действию узловых моментов от стержней числом п, получаем
М(к т( 0. (14.6)
П
Таково основное уравнение метода перемещений в общем случае. Очевидно, вместо узловых моментов в уравнении (14.6) можно внести концевые моменты, так как они равны между собой. Основных уравнений можно составить по числу свободных жестких узлов, т. е. по числу неизвестных углов поворота узлов ф.
Заменяя теперь в уравнениях (14.6) все моменты М1к перемещениями, получаем уравнения (14.6) относительно углов поворота ср, и 0 (Ь-
Для возможности отыскания и углов поворота 0А необходимосоставить группу дополнительных уравнений.
Дополнительные уравнения
Дополнительные уравнения, выражающие общие условия равновесия рамы по основной системе и отрицающие произвольные линейные смещения ее (или повороты стержней), проще всего составить, применяя начало возможных перемещений. Это наиболее общая форма записи дополнительного уравнения для рам с любыми наклонными элементами без введения поперечных и продольных сил в элементах рамы, что обычно делается в канонической форме.
Согласно началу возможных перемещений, когда данная система находится в состоянии равновесия (см. рис. 224, б), сумма работ всех сил и моментов, находящихся в равновесии на любых малых возможных перемещениях, должна быть равна нулю. Если задаться для основной системы — кинематической цепи — картиной малых возможных перемещений и составить сумму работ всех сил Рп и концевых моментов М1к% Мк1 на виртуальных перемещениях основной системы (рис. 226, а, б), то должен получиться нуль. В картине возможных перемещений кинематической цепи (например, в первом состоянии по рис. 226, а) имеются лишь перемещения стержней цепи как элементов твердого тела без упругих деформаций и усилий в стержнях. Картина возможных перемещений для каждого элемента линейна и легко определяется «независимыми» виртуальными углами поворота стержней.
10
291
Виртуальные углы поворота стержней обозначаем и принимаем их (так же как и углы 0) положительными по часовой стрелке. Задаваясь в первом виртуальном состоянии цепи малым поворотом первого «независимого» стержня (например, I—к), равным 1, и полагая повороты остальных стержней равными нулю, получаем наиболее простую картину возможных перемещений (см. рис. 226, а). Составляя сумму работ
Рис. 226
концевых моментов М, Мы на поворотах и сумму работ нагрузки Рп на перемещениях бРл, получаем по началу возможных перемещений
2 рЛря - 2 ма)о
или, вынося за скобку:
рпЬРп-(М1к Мк1)Ьи 0, (14.7)
где первая сумма выражает возможную работу заданной нагрузки на виртуальных перемещениях, а вторая — возможную работу концевых моментов (см. рис. 224, б) на виртуальных углах поворота (см. рис. 226, а).
Уравнений (14.7) можно составить столько, сколько независимых друг от друга картин возможных перемещений кинематической цепи в отношении линейных смещений, т. е. по числу неизвестных углов поворота 0,Л. В данном случае для системы с двумя степенями свободы имеем два независимых виртуальных состояния: в первом состоянии (см. рис. 226, а) сообщаем возможный угол поворота стойке верхнего зтажа, равный 1, 1 и % 0; во втором состоянии (рис. 226, б)
принимаем возможный угол поворота стойки первого этажа равным 1, чрг( 1 и г)1к 0. При таком задании в каждое уравнение будет входить наименьшее количество неизвестных. Составив группу дополнительных уравнений (14.7) по числу неизвестных углов 0, заменим в этих уравнениях все концевые моменты угловыми перемещениями р,, 0 и получим всю систему основных и дополнительных уравнений, содержащих лишь неизвестные перемещения и влияние нагрузки.
292
§ 77. УРАВНЕНИЯ МЕТОДА ПЕРЕМЕЩЕНИЙ В РАЗВЕРНУТОЙ ФОРМЕ
Развернутая форма уравнений. Основные уравнения
Рассмотренными выше уравнениями (14.3) — (14.7) исчерпываются все необходимые соотношения для проведения расчета рамы методом перемещений. В этих уравнениях коэффициенты при неизвестных перемещениях получены в готовом виде. При наличии внешнего момента в узле I (см. рис. 225, в) основным уравнением метода перемещений является (14.6).
Если рама имеет все жесткие прикрепления концов стержней в узлах, для концевого момента М1к применяем выражение (14.3):
2 [— к (ф 4“ 2фг — б9г) Мг] 4" — О
п
или после переноса известных членов вправо и умножения на (—1)
2 [« (4Ф 2ф — 60«е)] 2 Шк пи (14.8)
п п
— абсолютное значение суммы реактивных моментов, вызванных упругими поворотами, равняется сумме реактивных моментов от нагрузки и внешнему моменту.
Аналогично, подставляя в формулу (14.6) выражение момента М(к из выражения (14.5) для случая стержней рамы с одним шарнирным концом, получаем основное уравнение в виде
(Зф-Зе«)] 2]Л (14.9)
п п
Дополнительное уравнение
Общий вид дополнительного уравнения метода перемещений по началу возможных ‘ перемещений согласно выражению (14.7)
- 2 (Мш Мы) ъ Ц РпЬРп о, (а)
т
где т — число стержней рамы, получающих повороты в возможном состоянии (см. рис. 226).
Для случая жестких прикреплений концов стержней к узлам, составляя сумму моментов М1к и Мы по выражению (14.3), находим
Мм “Ь Мм — (6ф 6ф — 12д(к) Мш, (б)
где
М°ш Мк М1 (в)
— сумма моментов по концам стержня от нагрузки. Подставляя выражение суммы концевых моментов из выражения (б) в уравнение (а),
293
получаем после преобразований
2 кн (6ф, 6фА -126,) Ьи - 2 РпЬря (14 10)
71 71 Ш
— дополнительное уравнение метода перемещений в развернутой форме для любой рамы с жесткими прикреплениями. Левая часть выражения (14.10) представляет собой абсолютное значение суммы работ концевых моментов, вызванных упругими поворотами (узлов и стержней), правая часть — виртуальную работу нагрузки и реактивных моментов от нагрузки на перемещениях в возможном состоянии кинематической цепи.
Подставляем в уравнение (а) Мн 0, а вместо М1к — его выражение из формулы (14.5), получаем
2 Нк (Зф, -30,) Ьк 2 М?Л - 2 рпЬРп (14.11)
т т т
— дополнительное уравнение виртуальных работ для случая рамы со стержнями, имеющими односторонние шарнирные прикрепления. Решая систему уравнений (14.9) и (14.11), получим угловые перемещения, после чего по выражению (14.5) вычислим все концевые моменты и построим суммарную эпюру моментов.
Проверку суммарной эпюры моментов можно осуществлять так же, как это делалось при расчете рам по методу сил: при выборе основной системы по методу сил и перемножении суммарной эпюры моментов на единичную должен получиться нуль согласно условиям совместности деформаций. Кроме того, необходимо проверить, соблюдаются ли для полученной суммарной эпюры моментов, а также для эпюр (2 и N условия равновесия.
Пример. Построить эпюру моментов для свободной рамы при действии на нее узловой горизонтальной силы Р — рН и равномерно распределенной нагрузки р, приложенной к ригелю (рис. 227, а). Размеры к Зж; сопз; погонная жесткость стержней I соп1. Интенсивность нагрузки р — 30 кнм.
Решение. Устанавливаем степень кинематической неопределимости системы: имеем один угол поворота узла фх и один угол поворота стержня б01 0 (шарнирная схема обладает одной степенью свободы). Находим соотношение между принятым за неизвестное углом 0О1 и углом 012: так как длины стержней 0—1 и 1—2 одинаковы, то
012 — 0. (г)
Заметим, что в узле 1 сходятся два стержня с жесткими концами и один стержень с шарнирным концом. Поэтому основное уравнение составляем, комбинируя выражения (14.8) и (14.9):
01 (4Ф1 2Фо — 6001) 12 (4ф 2ф3 — 601Й) 11Л (ЗфА — 3018) Мз, (д)
где М°п берут из табл. 8, третья строка сверху:
До — Е—
М13" 8 ‘
Учтя, что ф0 0, ф2 0, 013 0; 0О1 0, 012 —0, получим
4фх • 21 Зф — 60 60 —.
294
В данном частном случае 0 исключается; окончательно
р2
Пф1 -
Угол поворота узла будет
Ф1 -
Р12
88
30 • 32 88
270 88
(е)
Составляем дополнительное уравнение как сумму работ концевых моментов стоек и нагрузки Р (рис. 227, б) на виртуальных перемещениях в возможном состоянии кинематической цепи (рис. 227, в).
Рис. 227
Задаваясь возможным углом поворота ф01 — 1 находим г)12 —1; виртуальное перемещение узла 1 будет
60Ьг.
Непосредственно по уравнению (а) находим
— (Мы М01) г)01 — (М12 М2) ’ф12 — Л4зФз4 — Рр 0»
(ж)
где г01 принимаем по часовой стрелке.
Подставляя выражения концевых моментов, значения виртуальных углов и возможного перемещения 6р 1 «Л, получаем
-27 Ы рН,
295
Откуда
0
рк 271
30 • 32 27
10
(з)
При этом учтено, что вертикальная равномерная нагрузка не совершает работы на виртуальных перемещениях (они горизонтальны).
Стойка 0—1 поворачивается против часовой стрелки (см. рис. 227, а).
По найденным перемещениям можно представить деформированный вид рамы
(рис. 228, а); углы поворота стержней 0—1 и 3—4 равны 0— и направлены
против часовой стрелки, угол поворота узла рх — также против часовой стрелки, но меньше по абсолютному значению, чем угол 0.
Переходим к вычислению концевых моментов по формулам (14.3) и (14.5):
Лл[ 27(Л а 101 1050
Мп-ч4 г т8 т) --й-
30-З2
1590
22
540
КН • м
8 22 Сумма моментов для узла 1 равна нулю:
(159-105-54)-10
мим10м18± Определяем моменты М0ь М2ъ М43:
кн • м.
22
0.
1185
М„1 — (2ф — 66) 22” кн-м;
14с
М21 — (2ф1 66) —22“ КНМ
., ОЙЧ 660 М43 — I (— 30) — -22 кн-м.
Эпюра моментов в раме изображена на рис. 228, б.
296
Пример 2. Получить эпюру моментов и представить деформированный вид рамы, если к I 8 м. Погонные жесткости стержней:
12 г23 0,5;
25 гзв 14;
114 18
Интенсивность распределенной нагрузки ц 3 гж. Горизонтальная сила Р 5 г (рис. 229, а). Жесткость Е1и 1.
а) о
и
ЛИШНИ
6
Зпюра м в) Деформированный вид
Рис. 229
Решение. Погонные жесткости вычислены по значениям моментов инерции (показаны на рис. 229, а). Концевые моменты в стержнях рамы
121 — 112 Зф2 — — 1,5фа;
о12
М2з — 23 (4фг 2ф3) — 2ф3 ФзЬ 16;
М25 — 125 (4ф2 — 60) — фа1,50;
3
МЗб —фз1,50; Л41 0;
МЬ2 — 0,5ф2 -- 1,50;
М бз — 0,5ф3 1,50;
М 32 — 2ф3 — ф2— 16.
Основные уравнения:
1) ЦЛ12 0; 21 Н- М25 “I- М2з 0.
Внося значения моментов, получаем
— 4,5ф2 — фз Ь 1,50 —— 16 0;
2) ЕЛ1з 0; Лз2“Ьзб 0
или
— р2 — фз "1“ 150 — 16 0.
(и)
(К)
(л)
297
Дополнительное уравнение
-Л41. 1-(М2б М52). 1_(М3в Мвз)- 1—5 8 0 или после внесения значений моментов
1»5ф2 1,5ф3 — 6,3750 — 40 0. (м)
Решая систему уравнений (к), (л) и (м), получаем:
ф2 3,21; ф3 — 10,385, 0 — 7,963.
По найденным угловым перемещениям вычисляем концевые моменты (эпюра М изображена на рис. 229, б).
Деформированный вид дан на рис. 229, в. В стойках 3—6 и 2—5 имеются точки перегиба в сечениях, где Мх 0.
§ 78. ИСПОЛЬЗОВАНИЕ СИММЕТРИИ ПРИ РАСЧЕТЕ РАМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
Использование симметрии позволяет значительно упростить расчет рам и по методу перемещений. При действии симметричной нагрузки на симметричную раму деформированный вид рамы будет симметричным, углы поворота симметрично расположенных узлов равны по величине и обратны по направлению, в ряде случаев (при наличии сквозных ригелей) углы смещений равны нулю. При действии обратносимметричной нагрузки на симметричную раму деформированный вид рамы обратносимметричен (углы поворота симметрично расположенных элементов равны и по величине и по знаку).
Пример 1. Построить эпюры моментов, поперечных и продольных сил для двухэтажной рамы по рис. 230, а. Размеры рамы и соотношения в моментах инерции сечений стержней даны ниже. Учесть симметрию в деформационном виде рамы. Данные: 6 м к 5 м, Р 52 Т, р 6 Тм. Размеры сечений см. на рис. 194.
Решение. Погонные жесткости стержней:
1с. 1,728 л олся. • сс 1. • 2,058 л
1о1“151 12 —г— 0,3456, 13 66—1) 24 —ъ— — 0,343.
о о
Выражения концевых моментов после подстановки значений
М12 — 0,3456 (4ф 2ф2) — 1,3824фх — 0,6912ф2;
Мю 0,2 (4фх) — 0,8фь
п2 О
М13 - 1 (2ф1) з- - 2ф, 57;
М21 — 0,3456 (4ф2--2ф1) — 1,3824ф2 — 0,6912фх;
М24 —0,343 (2ф2) — 0,686ф2 18.
По симметрии в изогнутых осях ригелей получаем: ф3 — фг; ф4 — ф2.
Имеем только два неизвестных ф и ф2. Составляем два основных уравнения:
21 0; ЦИ2 0.
298
Внеся выражения моментов, получим:
— 4,1824ф - 0,6912ф2 57 0;
— 0,6912фх — 2,0684ф2 18 0,
откуда
ф1 12,9028, ф2 4,3913.
б)
Рис. 230
Эпюра моментов представлена на рис. 230, б. Эпюра поперечных сил дана на рис. 230, в. Эпюра продольных сил изображена на рис. 230, г. В нижних стойках получаются значительные продольные силы, а изгибающие моменты больше в верхних стойках.
Пример 2. Построить эпюру моментов для безраскосной двухпанельной фермы. Погонная жесткость всех стержней сош (рис. 231, а).
299
Решение. При действии несимметричной нагрузки кинематическая неопределимость рамы равна 8 (шесть углов поворота узлов и два линейных смещения: горизонтальное смещение узла и вертикальное смещение узла ?),
При симметричной нагрузке
Ф5 — фЪ Ф4 — ф2;
углы поворота стоек равны нулю.
Рис. 231
Имеем три неизвестных: р2, фх и 0 (угол поворота ригелей —2 и 0—3).Концевые моменты:
М12 --(4ф1-60)
12
М21 -г-(2ф1-60)-;
Мю — (4ф 2ф2); Мо1— I (4Ф2 2Ф);
Моз — (4ф2 —60); М30 — г (2ф2 — 60).
Основное уравнение для узла : М12 М10 О приводится к следующему:
8ф1 2ф2— 6В.
Основное уравнение для узла 2: М0г Моя 0 приводится к виду:
2ф1 -)- 8ф2 — 60 0.
300
(а)
(б)
Дополнительное уравнение (возможная работа моментов и нагрузки для одной панели) будет:
(12 21) • 1 “(оз М30) • 1 2
или после внесения значений концевых моментов:
6ф1 6ф2 — 240 — г-. (в)
Решая систему уравнений (а), (б) и (в), получаем:
__31_ ?2 Л_ 31 дР
41 1008 I ’ ф2 —1008 ’ 1008 7 ‘
На рис. 231, 6 представлена эпюра моментов, все ординаты которой для получения действительных значений следует шножать на 250Ф.
§ 79. РАСЧЕТ РАМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ НА ДЕЙСТВИЕ ТЕМПЕРАТУРЫ И ОСАДКУ ОПОР
Расчет на действие температуры
Рассмотрим расчет рам на действие температуры по методу перемещений, применяя развернутую его форму. При расчете закрепленных рам (рис. 232, а) в качестве неизвестны принимаем лишь углы поворота узлов ср, а углы поворота стержней 0 определяем непосредственно по картине перемещений неизменяемой шарнирной схемы рамы.
а)
г Г
5)
ХИ
Й
4%
I
I
а11
:
С.
) -1
%
1-—л
ф
?,5и
Зпюра
е)
ЗссН
Рис. 232
Пусть, например, ригель рамы нагревается на °. Тогда для шарнирной схемы имеем картину, изображенную на рис. 232, б. Горизонтальное перемещение узла 1 будет а°, что соответствует углу поворота
301
стойки 612 ос(°. Таким образом, в закрепленных рамах углы поворота сержней находят непосредственно по картине перемещений шарнирной схемы рамы по известным удлинениям стержней от изменения температуры среды. Эти известные углы поворота стержней подставляют в основные уравнения, из которых определяют углы поворота узлов, после чего вычисляют концевые моменты.
Так, для рамы, изображенной на рис. 232, а, при I сопз и I к имеем
4фх • 21— 6 б12 0,
откуда при 012
3
ф1
■а°.
Эпюра М
Затем вычисляем концевые моменты по формуле (14.3). Эпюра моментов представлена на рис. 232, в.
Если свободная рама и температурное воздействие симметричны, задача сводится к рассмотрению закрепленной рамы. Пусть в прямоугольной раме (рис. 232, г) нагреванию подвергается только ригель. Из состояния основной системы (рис. 232, д) получаем при к угол поворота левой стойки
я - а1°
Ю “2“-
Составляем основное уравнение равновесия левого узла :
Мю Мц 0
или
— I (4фх — 601О) — I (2фх) 0,
откуда
л (
: У10 — ф:
аР_
2 Рис. 233
Теперь определяем концевые моменты по формуле (14.3).
Эпюра моментов изображена на рис. 232, 2.
Для свободных, незакрепленных рам расчет на действие температуры проводим, принимая в качестве неизвестных как углы поворота узлов, так и углы поворота стержней. Полный угол поворота данного
302
стержня рамы получаем как сумму двух углов: угла поворота стержня закрепленной шарнирной схемы от действия температуры и угла поворота, вызванного подвижностью узлов рамы, 0[Л). Угол б[° определяем по картине перемещений закрепленной шарнирной схемы от действия температуры, а угол 0д) от подвижности узлов находим из системы дополнительных уравнений метода перемещений. Так, для рамы,
показанной на рис. 233, ау при нагревании ригеля и правой стойки на ° из схемы по рис. 233, б получаем
6 — а(°; в х(°. (а)
Принимая в качестве неизвестного угол поворота стержня, т. е.
001, находим
023 02 23 ] ®01 а°• (б)
Составляя основные уравнения, получаем
10 12 0; Д214230
или, подставляя выражения моментов,
— I (4ф — 60о1) — I (4ф 2ф2 — 6б0)) 0;
— I (4ф2 2фх — б0(,2’) — I (4ф2 — 6023) 0.
Подставляя значения величин из выражений (а) и (б), окончательно находим
8фх 2ф2 — 60О1 6а1° 0; 1
2ф1 8ф2 —60о1 О. )
Дополнительное уравнение составляем как сумму работ «стоечных» моментов на виртуальных перемещениях-шарнирной схемы:
(М10 М01) • 1 (Л42з М32) • 1 0, (г)
или, подставляя значения моментов в уравнение (г) и учитывая выражение (б), получаем
6ф1 6ф2 240()1— 12а° 0. (д)
Решая систему уравнений (в) и (д), определяем углы поворота
ф — ф2 — 0О1 —ЦаГ.
Деформированный вид рамы представлен на рис. 233, в.
По формулам (14.3) вычисляем концевые моменты. Например,
Мг)1 I (2фх 6001) 32 I (2ф2 6023)
Эпюра моментов изображена на рис. 233, г.
303
Расчет на осадку опор
Расчет на заданную осадку опор осуществляется аналогично расчету рамы на действие температуры.
Пусть требуется построить эпюру моментов для прямоугольной рамы при наличии случайной осадки правой заделки на величину Д (рис. 234, а).
а)
1 2 г—— —
1
-О-
"■91 г
•с
о
ШЪ.—Г
ф
Ф
У, 2
ТПТТТтг
у ы.1
ой
§ои
Рис. 234
Из картины перемещений закрепленной шарнирной схемы рамы (рис. 234, б) получаем
где а — заданная величина угла.
К углам поворота стержней закрепленной шарнирной схемы рамы прибавляем неизвестные углы поворота стержней от подвижности узлов. Таким образом, в данном случае имеем
дп--а; 623 — 6 01. (е)
304
Основные уравнения имеют вид:
Ч- М12 0
М21 “Ь 423
или, подставляя4 значения моментов из формул (14.3) и учитывая выражение (е), получаем
8фх 2ф2 60 ох 6 ; 1
А (ж)
2ф1 8ф2 — 6001 6 у. Дополнительное уравнение виртуальных работ
(Мю М0х) • 1 (М23 М32) -10
или после подстановки значения моментов
бфх 6ф2 — 24001 0- (з)
Решая систему уравнений (ж) и (з), получаем углы поворота
6 6 0 3
Ф1 уа; ф2 у а; 0О1 уа.
Деформированный вид рамы изображен на рис. 234, в.
По формулам (14.3) вычисляем концевые моменты. Эпюра моментов представлена на рис. 234, г. В соответствии с характером перекоса рамы от вертикальной осадки одной из опор получаем обратносимметричную эпюру моментов; каждый узловой момент
6. 6 Л.
М(к у си 7 Т1.
§ 80. ПОСТРОЕНИЕ ЛИНИЙ ВЛИЯНИЯ КОНЦЕВЫХ МОМЕНТОВ С ПРИМЕНЕНИЕМ МЕТОДА ПЕРЕМЕЩЕНИЙ
Наиболее целесообразно при расчете рам на подвижную нагрузку строить линии влияния по схеме, аналогичной решению этой задачи для неразрезных балок: сначала находить линии влияния опорных (концевых моментов), а затем по этим линиям влияния строить линии влияния в произвольных сечениях.
Линии влияния концевых моментов проще всего находить, применяя кинематический метод. После вставления шарнира в опорное сечение к стержня выражение момента Мк по каноническому уравнению метода сил получаем в форме
(а)
иММ
где 8рм — эпюра вертикальных перемещений ригеля основной системы, к сечениям у шарнира которой приложены парные моменты Мк — 1;
§мц — главное перемещение (по направлению моментов).
305
Для получения деформированного вида рамы (перемещений дрм применяем метод перемещений.
Ьмм)
Пример. Построить линию влияния МХ2 для двухпролетной рамы (рис. 235, а), применяя кинематический метод — метод моделей. Принять Е сопз, I к, I сопз.
Решение. Модель линии влияния М12 найдем по деформированному виду
основной системы, полученной вставлением шарнира в узле (рис. 235, б). Уравнение линии влияния будет
Чрм
где
ММ — Ф12Ф14-
(б)
Проще всего деформированный вид основной системы получить, применяя метод перемещений. Имеем три неизвестных р2, ф3 и б. При постоянной погонной жесткости уравнения метода перемещений будут следующие:
11 ф2 4 2ф3 — 66 —1—— 0;
2ф2 -- 8ф3 — 66
0;
1,5
6ф2 6ф3 — 276 0.
(в)
Решая систему уравнений (в), получаем:
ф2 —-
_1_
12г
1_
241
1_
12Г
Углы ф2 и б равны между собой по абсолютному значению. Деформированный вид рамы приведен на рис. 235, б.
По найденным углам поворота находим концевые моменты; эпюра моментов, построенная на рис. 235, в, соответствует деформированному виду. Выделяя каждый стержень рамы и рассматривая его как балку на двух опорах, получаем:
Рис. 235
ф2:
7
:24Г
фы 241
Л -1
°ММ — ш.
Итак,
(г)
По обобщенному уравнению изогнутой оси для первого пролета имеем:
Для второго пролета
2С--й Я-й А (е)
Теперь по выражению (б) легко получить уравнения линии влияния Л412, вводя значения 6РМ и омм по формулам (д), (е) и (г) соответственно.
ГЛАВА 15. СПЕЦИАЛЬНЫЕ МЕТОДЫ РАСЧЕТА РАМ
§ 81. КОМБИНИРОВАННЫЙ МЕТОД
В отдельных случаях при расчете рам на один вид нагрузки рационально применять метод перемещений, а при расчете на другой вид загружения — метод сил.
а)
Рассмотрим, например, шесть раз статически неопределимую раму, подверженную действию несимметричной нагрузки Р (рис. 236, а).
307
Применяя способ разложения нагрузки на составляющие закономерно действующие нагрузки, ведем расчет отдельно на симметричное загружение двумя силами по Р2 разного направления и на обратносимметричное загружение силами по Р12 одинакового направления. При действии симметричной нагрузки (рис. 236, б) по методу, перемещений получается более простое решение, так как всего будет только два неизвестных фх иф2. В самом деле, углы поворота симметрично расположенных узлов равны по величине, но противоположны по знаку:
Никаких линейных смещений узлов в данном случае не возникает. При расчете по методу сил (рис. 236, в) получим четыре симметричных неизвестных: момент и продольную силу в сечении верхнего и нижнего ригелей: Хи Х2, Х3 и Х4. Применение метода сил в этом случае дает более сложное решение задачи.
При расчете на обратносимметричную нагрузку, наоборот, целесообразнее применять метод сил (рис. 236, г). В данном случае при расчете по методу сил будет два неизвестных: поперечные силы и Х2 в нижнем и верхнем ригелях. Использование метода перемещений приводит к более трудоемкому решению. В самом деле (рис. 236, д), теперь получаем четыре неизвестных перемещения рх, ф2, 0Х и б2. Прежде всего отметим наличие в этом случае действия нагрузки линейных смещений и, следовательно, углов поворота стержней б1и б2. По условию обратной симметрии в деформированном виде рамы углы поворота симметрично расположенных узлов равны между собой по величине и по знаку:
При расчете симметричных конструкций часто используют комбинированный метод: при расчете на симметричную нагрузку применяют метод перемещений, а при расчете на обратносимметричную нагрузку — метод сил. Заметим, что и при симметричном воздействии могут возникать линейные смещения узлов, если“ симметрично расположенные узлы рамы не связаны между собой сквозным ригелем.
Комбинированный метод в ряде случаев применяют и при расчете несимметричных рам.
Большое распространение в практике получили приближенные методы расчета рам. Обычным расчетом рам при ориентировочном задании сечений можно найти лишь приближенные значения усилий,
(а)
(б)
§ 82. ПРИБЛИЖЕННЫЕ МЕТОДЫ
Расчет несвободных рам
308
так как усилия ё статически неопределимой системе зависят от соотношений в размерах поперечных сечений. Важно достаточно обоснованно задаться размерами поперечных сечений, для чего и служат приближенные методы расчета. Приближенность «точного» метода определяется неучетом ряда факторов: влиянием размеров узловых соединений, влиянием пространственности каркаса соору- а)
жения, податливости опор и т. д.
Приближенными методами расчета называют такие, при применении которых вводятся дальнейшие упрощения, что дает возможность сократить объем вычислений и полностью исключить решение систем канонических уравнений.
Укажем на некоторые из приближенных методов расчета рам.
При расчете сложных закрепленных рам на загружение одного пролета при первом ориентировочном расчете возможно пренебречь влиянием всех углов поворота узлов, за исключениём двух углов поворота узлов рамы по концам загруженного пролета (рис. 237, а). При этом в противоположных по отношению к загруженному стержню 1—2 узлах а, Ь, с, й, е, вводим абсолютно жесткие защемления.
В случае загружения ряда пролетов рамы (рис.
237, б) используется метод расчета рам на «узловое загружение моментами». Вводя фиктивные защемления в узлах 1 и 2, находим реактивные моменты в защемлениях от нагрузки М1р и М2р. На стержнях 1—2 и 2—4 строим эпюру моментов от местной нагрузки Мр. Затем «раскрепляем» раму, отбрасывая защемления, и прикладываем к узлам ее моменты, равные и противоположные моментам М1р и М2р (активные узловые моменты). Строим эпюры моментов от узловых моментов М1Р (рис. 237, в) и М2р
1 2 И
т
0
3
Эпюра Мгр
Рис. 237
309
(рис. 237, г) отдельно. В приближенном решении расчет можно вести путем итерации, распределяя каждый момент только на стержни, сходящиеся в загруженном узле (в первом случае — стержни 1—2 и —0 во втором случае — стержни 2—, 2—4 и 2—3). Таким образом, расчет несвободных рам легко осуществляется по методу последовательного распределения узловых моментов, предложенному в 1922 г. проф. К. А. Малышевым [10]. Метод этот был далее развит Харди Кроссом, Кани и проф. Гофманом.
Порядок расчета свободных рам следующий. Расчетом закрепленной рамы находят реакции со стороны введенных горизонтальных опорных стержней, которые затем отбрасывают, и раму рассчитывают на действие узловых горизонтальных сил, равных по величине и направленных противоположно реакциям от опорных стержней [10].
Расчет свободных рам распределением этажных моментов
Первый ориентировочный расчет свободной каркасной рамы на узловое действие горизонтальных сил достаточно прост. Вычисляют так называемые этажные моменты и°, т. е. моменты всех внешних сил, расположенных выше нижних концов стоек данного этажа относительно этих точек. Так, для рамы, изображенной на рис. 238, а, верхний этажный момент
Щ Р2к2, (а)
нижний этажный момент
УР Р2 (к2 кг) Р1 кг. (б)
Полагают, что нулевые точки эпюры моментов во всех не опорных стойках рамы находятся посередине, а нулевые точки эпюры моментов в опорных стойках — выше середины стоек и отношение верхнего концевого момента к нижнему лежит в пределах 0,75—0,95. В среднем можно принимать последнее отношение равным 0,85. Составляют условие уравновешивания этажного момента внешних сил суммой концевых моментов стоек данного этажа. Так, для стоек верхнего этажа
2 (М41 Мл2) т, (в)
для стоек нижнего этажа
(Мб3 Мзв) (М74 М47) (М8Ъ МЬ8) Г °, (г)
или, подставляя соотношения между верхним и нижним концевыми моментами, для опорных стоек вместо выражения (г) получаем
1,85 (М63 М74 М9г0) П. (Д)
Концевые моменты в стойках данного этажа предполагают прямо пропорциональными погонным жесткостям стоек, следовательно,
И41: Мъ2 14 1 52;
М6з : М74: М8Ь 163 : 74: 85.
310
Из уравнений (в), (д) и (е) легко вычислить все концевые моменты в стойках. Моменты в ригелях для узла, где сходится более трех стержней (узел 4 для рамы, изображенной на рис. 238, б), определяют
а)
г
о I
И I 6
Р2
%;®
©
©
©
©
©
53
ТЯГ
по суммарному моменту в стойках, который распределяют пропорционально жесткостям ригелей. Так, для узла 4
М43 М45 Ма М47;
М45 43 45 • 43‘ Получив первые значения концевых моментов, далее применяем итерационный способ, при котором находятся новые значения моментов или их поправок (см. способ Кросса—Кани, описанный в нашей работе [10]).
311
Наиболее целесообразна итерационная схема расчета по Зейделю, развитая у нас проф. Ш. М. Гофманом [10].
Пример. Рассчитать раму: Рг 27 кн, Р28,7 кн, Ь.х 4,34 м, Н2 3,0 м. Погонные жесткости стержней указаны в кружках на рис. 238, а.
Решение. Этажные моменты согласно выражениям (а) и (б):
№2 26,1 кн-м § 155 кн-м.
Из уравнения (в), принимая во внимание соотношение (е), получаем:
1,67М52 --№5; М52 7,98 кн - м.
Из уравнения (д) с учетом соотношения (е) находим:
1,2 155 1СОО 3 155
63 62 Г85 ’ кн-м; М74 —.- 40,5 кн-м;
Мд-Ш27° кнм-
Вычислив верхние концевые моменты УИ36, УИ47, М78 (как 0,85 от нижних моментов), наХодим по соотношениям (ж) концевые моменты в рцгелях. Эпюра моментов, полученная описанным способом распределения этажных моментов, изображена на рис. 238, б. Концевой момент М85 27 кн-м отличается от точного значения
(25,7 кн-м) на 7,15% (см. работу [10]). Максимальные моменты М74 почти совпадают
(приближенное значение 40,5 кн-м, точное — 40,3 кн-м).
ГЛАВА 16. РАСЧЕТ СООРУЖЕНИЙ ПО НЕСУЩЕЙ СПОСОБНОСТИ
§ 83. РАСЧЕТ ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ Основные сведения
С 1955 г. в СССР в качестве основного принят метод расчета строительных конструкций по расчетным предельным состояниям. Этот метод существенно отличается от применявшегося ранее обычного метода расчета по допускаемому напряжению (частное от деления опасного напряжения на общий условный коэффициент запаса).
Основными недостатками старого метода при расчете на прочность являлись: введение общего нерасшифрованного коэффициента запаса; применение оценки прочности по образцам материала; неучет изменчивости механических характеристик материала; представление о постоянстве расчетных нагрузок; отсутствие учета пластических свойств материала. Недооценивался тот факт, что прочность материала конструкции неодинаковее прочностью материала образца, которая в свою очередь не отвечает нормативной прочности (изменчивость свойств материала). Кроме того, сооружение реально подвергается действию различных перегрузок в зависимости от назначения (изменчивость нагрузок).
При расчете по предельным состояниям (с введением расчленных коэффициентов запаса) вводится новый принцип оценки надежности
313
сооружения с использованием статистических данных о прочности материала и о расчетных нагрузках, в соответствии с которым наибольшее вероятное (за все время эксплуатации) расчетное усилие в элементе конструкции не должно превышать предельного сопротивления его (несущей способности).
Предельными состояниями конструкции называют такие, при достижении которых невозможна дальнейшая нормальная эксплуатация ее. Различают три предельных состояния:
первое — по несущей способности (прочности, устойчивости, выносливости);
второе — по развитию чрезмерных деформаций (перемещений);
третье — по образованию трещин или повреждений. При использовании метода расчета по предельным состояниям равновесия учитывают и пластические свойства материалов, при этом проектируемые сооружения получаются более экономичными и в ряде случаев достигается большая простота расчета. По новому методу расчета по предельным состояниям общий коэффициент запаса расчленяется на три:
1) коэффициент перегрузки п, оценивающий изменчивость нагрузки и учитывающий неизбежное превышение (а иногда и уменьшение) нагрузок по сравнению с их нормативными значениями, т. е. вероятное отклонение нагрузки от нормативной; обычно п 1;
2) коэффициент неоднородности материала к, учитывающий возможную изменчивость свойств материала, возможность снижения прочности материала и влияние отклонений в форме и размерах сечения; коэффициент г 1;
3) коэффициент условий работы конструкции т, оценивающий влияние на работу конструкции различных неблагоприятных факторов, не поддающихся точному учету (например, влияние агрессивной среды, концентрации, неточности сопряжений элементов в узлах и т. д.); коэффициент т может быть больше и меньше 1.
Предельным состоянием называют такое состояние сооружения, когда вследствие достижения сооружением чрезмерных напряжений или перемещений оно становится непригодным для нормальной эксплуатации. Таким образом, здесь вводится критерий пригодности сооружения к нормальной эксплуатации. Предельное состояние является не состоянием разрушения сооружения, а состоянием недопустимых для эксплуатации напряжений или деформаций. При этом расчетное предельное состояние сооружения может наступить и до исчерпания так называемой несущей способности сооружения.
Под пределом несущей способности сооружения понимают ту наибольшую нагрузку, которую сооружение еще может выдержать. Отметим различие между пределом прочности и пределом несущей способности, который нередко оказывается меньше разрушающей нагрузки. В ряде конструкций при переходе за предел упругости
313
(в область текучести) быстро возрастают деформации, что приводит к значительным перемещениям, опасным для дальнейшего использования сооружения. Для конструкций из пластичных материалов опасные перемещения возникают задолго до разрушения.,
Потеря устойчивости конструкции, которая наступает при нагрузке, меньшей предела прочности, также относится к случаям потери несущей способности: сооружение теряет форму и получает настолько большие перемещения, что не в состоянии воспринимать нагрузку.
Под пределом эксплуатационной способности понимают ту предельную нагрузку, при действии которой сооружение получает предельные пёремещения или напряжения; при превышении последней эксплуатация сооружения становится невозможной. Деформация предела эксплуатации несколько меньше деформации потери несущей способности (например, предельный прогиб верха мачты может быть принят в 1100 высоты, однако пределу эксплуатации может соответствовать прогиб лишь в 1150 высоты). Пределом несущей способности является наивысший предел потери эксплуатационной способности. Под расчетным предельным состоянием и понимают предельное состояние потери эксплуатационной способности.
Нормативные и расчетные нагрузки. Сопротивления
Нормами предусматривается наибольшая «нормативная» нагрузка Я, возможная при.эксплуатации данного типа сооружения. Однако расчет производится не на нормативную нагрузку Я, а на большую, которая получается умножением Р на коэффициент перегрузки п и носит название расчетной нагрузки:
где п — коэффициент запаса по нагрузке, назначается в зависимости от вида нагрузки (собственная, крановая, снег и др.).
От расчетной нагрузки Ррас, вычисленной по формуле (16.1), находят в сооружении наибольшее расчетное усилие Лрас.
Требуется, чтобы наибольшее расчетное усилие в сооружении было меньше предельного усилия, определенного по расчетному сопротивлению 7?рас. Обозначим предельное усилие в конструкции, являющееся функцией геометрических размеров, расчетного сопротивления материалов и коэффициентов условий работы конструкции Ар. Формула обеспечения прочности по первому предельному состоянию имеет следующий вид:
где Ыир — минимальное значение усилия в предельном состоянии сооружения.
Расчетное усилие Лрас определяется как суммарное от постоянной •Лп и временной Лр нормативных нагрузок; при этом каждую из этих
рас Р П,
(16.1)
пр
(16.2)
314
нагрузок умножают на коэффициент перегрузки п. Для нагрузок разных видов установлены свои коэффициенты перегрузки (табл. 9). Таким образом, для расчетного усилия можно написать:
Лрас “Ь Лврвр- (16.3)
Таблица 9
Коэффициенты перегрузки п по СНиП П-А. 11
Вид нагрузки
"п
"вр
Постоянная.
1,1-1,2
Снег —
1,4
Ветер. —
1,2—1,5
Полезная 1,2—1,4
Нормативной нагрузкой называют ту наибольшую нагрузку, которая еще не нарушает нормальных эксплуатационных условий (задается нормами).
При определении предельного усилия Лпр сопротивление ?рас находят по нормативному сопротивлению пользуясь формулой
Ярас НЪП, ‘ (16.4)
где ?н — нормативное сопротивление;
ка — нормативный коэффициент неоднородности материала; т — коэффициент условий работы конструкции.
Если, например, нормативный предел текучести для стали Ст. 3 ?п 290 Мнм2 (2900 кГсм2), то расчетное сопротивление
?рас 290 • 0,9 261 Мнм2.
Предельное сопротивление конструкции Ып? находят по размерам конструкции и материалу ее как возможное наименьшее сопротивление. При этом учитывают:
а) особенности работы конструкции, оцениваемые статистическими коэффициентами условий работы л, которые приведены ниже:
т
Сплошные балки и сжатые элементы ферм перекрытий; подкрановые балюи,
колонны 0,9
Сжатые раскосы пространственных решетчатых конструкций 0,8—0,9
Сжатые элементы из одиночных уголков 0,75
б) вероятное понижение расчетного сопротивления 7?рас материала сравнительно с нормативным ?п, которое вычисляют по формуле (16.4).
Для бетона при сжатии и изгибе еп 0,6, для стали в среднем 0,9. Расчетные сопротивления ?рас Кик1 для некоторых материалов приведены ниже:
315
Мнм2
Ст. 3, Ст. 4 — растяжение, сжатие, изгиб 210
Ст. 3, Ст. 4 — срез 130
Ст. 3, Ст. 4 — смятие торца 320
Сосна: изгиб; сжатие и смятие вдоль волокон 13
растяжение 10
скалывание 1,2
сжатие и смятие поперек волокон 1,8
Кирпичная кладка при марке кирпича и раствора 75 1,4
Бетон и железобетон:
осевое сжатие 6,5— 9,0—12,5
изгиб ч 7,5—10,5—14
осевое растяжение 0,4
Арматура в железобетоне:
Ст. 3 210
Ст. 5 240
Выбрав в соответствии с особенностями материала и условиями работы конструкции коэффициенты кн и т, зная нормативное сопротивление 7?н и геометрическую характеристику сечения, вычисляют предельное сопротивление для элемента конструкции:
ЛПр РткпНи РтН рас, (16.5)
где в данном случае (для ферм) Р — площадь сечения.
Можно выразить расчетное условие (16.2) по несущей способности через напряжения, подставляя вместо Nп? его выражение по соотношению (16.5) и деля обе части на площадь сечения:
0рас -рас Ну
где (Трас — определяется от расчетной нагрузки (с учетом коэффициентов перегрузки);
Н — расчетное сопротивление, полученное после введения коэффициента условий работы (СНиПП-В.З).
Расчетная формула по второму предельному состоянию имеет вид:
ЛрасШ (16.6)
где Драс — действительное наибольшее перемещение конструкции, определяемое от нормативной нагрузки;
[] — перемещение, допускаемое нормами.
§ 84. РАСЧЕТ ПРОСТЕЙШЕЙ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ СТЕРЖНЕВОЙ СИСТЕМЫ ПО ПРЕДЕЛЬНОМУ СОСТОЯНИЮ
Диаграммы стч-е зависимости напряжений от деформации
Нередко пользуются упрощенной расчетной схемой для идеального упруго-пластического материала, подчиняющегося идеализированной диаграмме Прандтля (рис. 239, а). При этом полагают, что
316
в упругой области диаграмма о -5- е имеет вид прямой ОА вплоть до предела текучести, а в области упруго-пластической деформации она ограничена горизонтальной прямой А В, причем предел текучести ат совпадает с пределом пропорциональности апц, что является грубым приближением.
Многим материалам больше отвечает билинейная ломаная диаграмма ОАВ (рис. 239, б). Упругой области соответствует наклонная прямая ОА с наибольшей ординатой апц и тангенсом угла наклона Е, где Е — модуль упругой деформации. Упруго-пластиче¬
ской области отвечает наклонная прямая А В, тангенс угла наклона которой Еъ где Ех— модуль упруго-пластической деформации. При использовании билинейной (и вообще криволинейной диаграммы) вполне осуществим расчет по второму предельному состоянию, так как Для билинейной зависимости (см. рис. 239, б) легко получить, что приращение пластической деформации йепл прямо пропорционально приращению упругой деформации уп:
где к 1 — §-•
Расчет простейшей статически неопределимой стержневой системы
Для статически определимой системы, имеющей лишь осевые усилия, расчет по допускаемым напряжениям и по предельному состоянию дает одни и те же результаты при расчете на прочность. В случае рассмотрения второго предельного состояния и применения схемы по рис. 239, б (при расчете на жесткость) результаты расчетов по этим двум методам различны. Расчет же статически неопределимой системы по первому предельному состоянию дает иные результаты по сравнению с расчетом по методу допускаемых напряжений.
317
Рассмотрим ход расчета диска ВР, прикрепленного четырьмя стержнями (рис. 240, а), из которых горизонтальный стержень считается жестким. При действии вертикальной нагрузки УУ4 0. Однажды статически неопределимая система подвергается действию вертикальной силы Р9 приложенной по середине жесткой плиты ВР. Полагаем, что все стержни А5, СО и ЕР выполнены из одного и того же материала,
крайние стержни А В и ЕР имеют длину а и одинаковую площадь сечения Рдлина среднего стержня Ь, площадь его сечения Р2. По способу допускаемых напряжений расчет ведем на основе двух уравнений: уравнение равновесия ( У 0)
2 Л ЛЛ Р (а)
и уравнение совместности перемещений
«»
или иначе
Рф
Ч
Из выражений (а) и (б) получаем
1 2Рф Рца Р 2 2Р1Ь Р„р Р’ Так как Ь а, то о1 меньше, чем о 2- и средний стержень
более напряжен:
°1 2Р1Ь Р2а Р ] °2 2Рф Р Р Подставим соотношения в длинах стержней Ь 23 а и в площадях
сечений Рг 2Рг. Допускамое напряжение обозначим [ст]. Тогда
318
по формулам (в) получим
ЫХ 0,2Р; Л2 0,6 Я;
При этом в стержнях будут следующие напряжения:
а2 [а]; а1[о],
т. е. имеет место неравнопрочность стержней системы.
При возрастании силы Р предельное напряжение появится прежде всего в среднем стержне. Заметим, что именно проведенный «упругий» расчет позволяет установить наиболее напряженный из всех стержней конструкции. Полагая, что стержни выполнены из пластичной стали, приходим к заключению, что при возрастании нагрузки усилие в среднем стержне, где предельное напряжение текучести ат появляется прежде всего, будет отР2. Появление предела текучести в среднем стержне соответствует значению нагрузки Рл, а на диаграмме зависимости между переменной силой Р и вертикальным перемещением плиты Д (рис. 240, б) этому состоянию отвечает точка А. Участок О А соответствует упругой области работы конструкции. При увеличении силы Р выше значения Рл средний стержень «потечет» и его удлинение будет нарастать без увеличения усилия Ы2т отР2 увеличение нагрузки вызовет возрастание усилий в крайних стержнях, а вертикальнее смещение плиты будет вследствие текучести среднего стержня нарастать больше, чем в упругой области. Поэтому диаграмма зависимости между Р и Д теперь представится линией АВ, наклоненной к оси абсцисс под меньшим углом (см. рис. 240, б). Приращение нагрузки (Р — РА) будет восприниматься двумя крайними стержнями, и общую нагрузку можно увеличить до значения Рпр, соответствующего появлению текучести в крайних стержнях. При этом согласно условию равновесия будет соблюдаться равенство:
В дальнейшем при увеличении деформации несущая способность будет исчерпана, так как конструкция получит недопустимые перемещения; в условиях идеализированной диаграммы большая нагрузка воспринята быть не может. Этому состоянию отвечает горизонтальный участок ВС диаграммы. Для пластичного материала нарушение прочности или разрушение еще не происходит.Поэтому предельная нагрузка согласно равенству (д) может быть приравнена расчетной (16.1):
Предельная нагрузка Рп может быть найдена непосредственно по условию равновесия.
Если подставить в выражение (е) оТ п [а], то получим
Рпр (2Р1 Р2) ат.
(Д)
Рпр Ррас РП (2Рг Р2) СТТ.
(е)
Рп(2Р1 Р2) п [а],
319
откуда находим
21 72 [-. (ж)
Сравним расчеты по методу предельного состояния и по методу допускаемых напряжений. Подставляя то же соотношение в площадях, что и ранее, т. е. Р2 2Рг в выражение (ж), получаем
г‘°’25Рг
Площади сечений стержней, полученные расчетом по методу предельного состояния, оказались меньше, чем по методу «упругого» расчета; при этом действительные напряжения от нормативной нагрузки по выражению (г)
ст21,2[а]; т1 0,8 [а].
Резюмируя изложенное, можно указать следующий порядок расчета по методу предельного состояния (на прочность):
1. Предварительно проводится обычный «упругий» расчет, что позволяет определить наиболее напряженные (и следующие за ними) стержни конструкции. Однако в ряде случаев такого расчета можно не проводить, так как выбор предельного состояния оказывается очевидным.
2. Пользуясь результатами первого расчета, устанавливают предельное состояние конструкции, полагая, что в наиболее напряженных стержнях напряжения при расчете сооружения из пластичного материала равны пределу текучести и, следовательно, продольные силы
N рас ?Р •
3. Число стержней, в которых предполагается опасное состояние, должно быть на единицу больше числа лишних связей. В этом случае статически неопределимая конструкция обращается в механизм.
4. Для полученного предельного состояния по прочности составляется уравнение равновесия, из которого и определяется площадь наиболее напряженного стержня. В это уравнение включаются разрушающая сила и предел прочности, которые можно выразить через допустимую силу и допускаемые напряжения, вводя коэффициенты запаса.
§ 85. МЕТОДЫ РАСЧЕТА СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СТЕРЖНЕВЫХ СИСТЕМ ПО ПРЕДЕЛЬНОМУ СОСТОЯНИЮ
Расчет сооружений можно вести по двум основным методам:
1) по методу непосредственного рассмотрения высшего предельного состояния, соответствующего потере несущей способности;
320
2) по методу исследования сооружения в упруго-пластической стадии работы.
В первом случае сооружение рассматривается только в момент, непосредственно предшествующий потере несущей способности, а работа конструкции до этого момента не исследуется.
Можно при этом применять или статический или кинематический метод. Статический метод изложен выше (см. § 84). По кинематическому методу рассматриваются различные схемы равновесия механизмов, которые могут быть получены из заданного сооружения при возникновении текучести в (п 1) стержнях, где п — число лишних связей.
Для системы с двумя лишними связями (рис.
241, а) представляют возможные схемы перемещений механизмов при появлении текучести в какихлибо трех стержнях. Таких возможных схем можно дать в данном случае по числу комбинаций из четырех стержней по три, т. е. четыре. На рис. 241, б, в даны две из этих четырех схем. Для первой схемы предполагается, что.три -стержня У, 2 и 3 перешли в область текучести; при этом предельная нагрузка будет
Рпр 1,5т 1,5(7.
Для второй схемы считаем, что текучесть имеет место в стержнях, 2 и 4, при этом
Рп р 1,33?т 1,33(7ТР.
Из всех возможных схем выбираем ту, для которой получается наименьшая предельная нагрузка. В данном случае
Лтр. мин1,33(ТтЛ
Однако это решение неверно, так как стержень 4 с ж а т и критическая сила Якр меньше усилия ?т огР.
Если ?кр 0, 9?,, то действительное предельное значение силы РПр будет найдено из уравнения моментов
%мво
11 Н. К, Снитко
321
или
Рпр • За — 2 Кга — ?та — 0,9 Я,а 0,
откуда
Рпр1,зят.
Предельное усилие в стержне 3
Л3 0,2ЯТ.
Схема действия всех усилий с поправкой на критическое усилие в сжатом стержне дана на рис. 241, г.
К недостаткам кинематического метода следует отнести его громоздкость и сложность установления схемы образования механизмов; для ферм с лишними стержнями необходимо наметить большое количество схем разрушения.
Утверждение, что п раз статически неопределимая система превращается в механизм при появлении текучести в п 1 стержнях, неправильно. Заметим, что быстрое увеличение перемещений в системе, имеющей текучесть в ряде стержней числом к, меньшим п, может привести к потере несущей способности. Более обоснованно осуществлять расчет сооружений в предположении развития текучести в к стержнях, где к (п 1). Таким образом, расчет может осуществляться и в предположении выпадения вследствие текучести лишь нескольких связей. Расчет по стадии развития пластических деформаций вполне осуществим лишь тогда, когда при определенной таким образом нагрузке не возникает значительных перемещений или не происходит потери устойчивости сжатых элементов в местах, где возникает текучесть.
Для упрощения часто прибегают к методу «упругого» расчета в предположении последовательного появления текучести во всех наиболее напряженных стержнях в каждой расчетной схеме. При этом изучают процесс последовательного нарастания нагрузки. Проводят расчет п раз статически неопределимой системы в упругой стадии, используя систему п канонических уравнений, и определяют самый напряженный стержень, который «потечет» в первую очередь. Предполагается, что этот стержень при дальнейшем увеличении нагрузки сохраняет состояние текучести, поэтому его удаляют, заменяя внешней силой, равной ат Для полученного (п— 1) раз статически неопределимого сооружения вновь проводят упругий расчет с усложненной внешней нагрузкой. Расчет доводят до последней стадии, когда появляется текучесть в (п 1)-й связи и, следовательно, в наиболее напряженном стержне статически определимой системы при действующих в п лишних связях усилиях аТр1. Соответствующую нагрузку принимают предельной (равной несущей способности).
Этот метод расчета обладает следующим недостатком: при переходе от одной стадии к другой какой-либо стержень, принятый в состоянии текучести, на самом деле станет разгружаться и усилие в нем будет падать по закону упругости; следовательно, степень статической неопределимости системы повысится на единицу и принятая расчетная схема
322
не будет соответствовать действительности. Возможно также, что какой-либо из сжатых стержней потеряет устойчивость прежде, чем усилие в нем достигнет величины от Практически достаточно определять предельную нагрузку по состоянию текучести в к стержнях, где к (п 1) с осуществлением проверки максимальных перемещений в упруго-пластической стадии.
§ 86. РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ БАЛОК С УЧЕТОМ ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ
Предельный изгибающий момент и пластический момент сопротивления
Рассмотрим сначала задачу установления предельного состояния развития пластических деформаций при чистом изгибе балки в случае, когда изгибающий момент действует в вертикальной плоскости симметрии балки (рис. 242, а, б). Увеличиваем изгибающий момент до тех
а) и (я—
М.
пор, пока не появится предел - текучести в крайних волокнах балки. Соответствующая эпюра нормальных напряжений по сечению балки изображена на рис. 242, в. Изгибающий момент Мт, равный моменту всех нормальных напряжений при появлении текучести только в крайних волокнах, можно представить по формуле сопротивления материалов:
Л1т хтИ7, (16.7)
где № — момент сопротивления сечения, найденный по методу упругого расчета.
Нейтральная линия 22 при этом проходит через центр тяжести сечения. Но при действии момента Мт, соответствующего лишь фибровой текучести, предельное состояние балки еще не достигнуто, так как
11
323
во всех остальных точках сечения напряжения меньше предела текучести. Возможно дальнейшее увеличение момента М Мт. При этом считаем, что материал подчиняется идеализированной диаграмме Прандтля и соблюдается гипотеза плоских сечений. При последовательном возрастании момента М Мт текучесть появится в других волокнах, кроме крайних (рис. 242, г); останется лишь часть балки высотой 2Н01 работающая в упругой стадии. Эта упругая область сечения балки называется упругим ядром. При последующем возрастании момента до предельного значения текучестью будут затронуты все волокна балки и дальнейшее увеличение момента окажется невозможным (рис. 242, д). Сечение уже не в состоянии воспринять большего момента, и при М М11р будут быстро нарастать прогибы балки. Следовательно, значению момента Мпр соответствует исчерпание несущей способности балки.
Состояние сечения, при котором напряжение в каждом волокне равно пределу текучести, называют пластическим шарниром. Отличие его от обычного шарнира состоит в том, что к соседним сечениям после включения шарнира прикладываются две взаимно противоположные пары, момент которых М Л4пр.
Предельный момент можно определить в данном случае как равнодействующий момент всех элементарных усилий ойР относительно оси II:
Л2 Л2 Л2
Мпр уо-,йР2 уот (1Р 2от уйР 2от80, (16.8)
— Л2 О О
где 50 — статический момент половины сечения относительно нейтральной оси 21, положение которой соответствует переходу от сжатой к растянутой зоне сечения (см. рис. 242, д).
Для прямоугольного сечения Ь х к
с ш ч
5о ■-§-. (а)
Аналогично работе балки в упругой области представим выражение
(16.8) в форме
Мпр ат117пл, (16.9)
где №пл 250 — «пластический» момент сопротивления сечения.
Пластический момент сопротивления прямоугольного сечения
И7ПЛ 250. (б)
Упругий момент сопротивления для того же сечения
(В)
Отношение пластического момента сопротивления №Пл к упругому моменту сопротивления ЦР и показывает, во сколько раз предель¬
324
ный момент Мпр больше упругого момента Мт, соответствующего фибровой текучести:
м
а
пр
М т
№
(16.10)
Для прямоугольного сечения а 1,5, т. е. в этом случае расчет с учетом распространения пластичности по всему сечению при изгибе позволяет повысить момент на 50%. При расчете же по методу допускаемых напряжений полагают, что несущая способность балки исчерпана уже при появлении текучести только в крайних точках сечения. Это предположение, как видим из изложенного, не соответствует действительности. Для двутаврового сечения а 1,16, т. е. несущую способность балки можно повысить на 16%.
МП
пр
Рассмотрим теперь определение положения нейтральной линии и пластического момента сопротивления для сечения, несимметричного относительно горизонтальной оси 11 (рис. 243, а). Предельный изгибающий момент определится по моменту всех внутренних сил, интенсивность которых для сжатой и растянутой зон будет равна пределу текучести (рис. 243, б). Следовательно,
Нг Н2
МПр ат (х йу) У ат (Ьг йу) у, (г)
о о
где первый интеграл относится к сжатой зоне, второй — к растянутой, причем каждый интеграл представляет собой статический момент относительно оси 11.
Выражение (г) можно представить так:
Л1„р ат51 ат5а ат (5х 52) атГпл. (16.11)
Таким образом, пластический момент сопротивления №пл равен сумме
статических моментов соответственно сжатой и растянутой зон:
V (16.12)
326
Положение нейтральной линии определяется из условия равновесия 2Х 0, (где X — ось балки); следовательно, отРг отР2 — нейтральная линия 21 делит сечение на две равные части:
Рг Р2. (16.13)
На рис. 244, а для таврового сечения, площадь полки которого равна площади стенки, нейтральная линия для пластической эпюры (рис. 244, б) проходит на уровне сопряжения полки и стенки, а нейтральная линия в упругой стадии 2020 оказывается в пределах стенки.
а)
а)
7
У
бт
Рис. 244
Отношение допустимого момента по методу Предельного состояния к допустимому моменту по методу допускаемых напряжений для двутаврового сечения а 1,15 1,17.
Заметим, что учет влияния поперечной силы снижает значение сс (работы проф. Н. И. Безухова, автора и др.).
Распределение напряжений по длине балки
Нагрузка предельного состояния Рпр должна быть (по условию текучести и вследствие необходимости воспринять поперечную силу) несколько ниже нагрузки Рпл, при которой развивается пластичность
б7
пр
по всему сечению. Поэтому зона пластичности в действительности в предельном состоянии не распространяется до нейтрального слоя (рис. 245). Распределение напряжений по длине оси зависит от эпюры изгибающих моментов. Для балки с шарнирно опертыми концами, нагруженной в середине пролета сосредоточенной силой, диаграммы нормальных напряжений имеют вид изображенных на рис. 242, д. с 2ат№
В сечениях на расстоянии х0 —-р— эпюры напряжении имеют вид
треугольника (см. рис. 242, в). На участках длиной х0 имеем чисто упругие деформации балки.
§ 87. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ БАЛОК И РАМ С УЧЕТОМ РАЗВИТИЯ ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ
Расчет однопролетных балок
Расчет статически неопределимых балок по высшему предельному состоянию образования пластических шарниров (без учета влияния поперечной силы) может быть в ряде случаев осуществлен.по одним лишь условиям равновесия без применения уравнений деформаций.
Пусть, например, требуется найти момент сопротивления балки, защемленной одним концом и шарнирно опертой другим концом, по методу предельного состояния развития пластических деформаций. Это состояние наступит тогда, когда в какихлибо двух сечениях появятся пластические шарниры.
Как показывает «упругий» расчет (рис. 246, а), наибольший отрицательный момент возникает в сечении А у защемления, где прежде всего и образуется пластический шарнир. Пластический шарнир на рис. 246, б отмечен кружком.
Однако при этом несущая способность балки не будет исчерпана, а наличие пластического шарнира у заделки не вызовет значительных прогибов. Поэтому можно увеличить нагрузку Р до
Рис. 246
327
значения Рпр, при котором появляется пластический шарнир под грузом в сечении В, где возникает наибольший положительный момент (рис. 246, в). В момент исчерпания несущей способности, т. е.
0. р
появления второго пластического шарнира, система обращается в механизм (три шарнира на одной прямой). Составляем условие равенства момента в сечении В предельному моменту (рис. 246, г):
Рпр
2 пр -Мпр
откуда
Мп
Рпр1
1ПР“ 6 “
Следовательно, предельная нагрузка
Лг
пр-
(16.14) (а)
(16.15)
Найдем момент сопротивления балки считая, что ах п[о и Рпр пРу где п — коэффициент запаса:
пР--
откуда
6г [а] аИ7 Р1
где а -
6 [а] а’
(б)
№
По методу допускаемых напряжений при применении расчета в упругой, области
мА
и?уп-г4
3 Р1
Р1
[а] 16 [а] 5,33 [а]
При расчете по методу предельных состояний достигается экономия в моменте сопротивления сечения.
328
. Однако в формулу (б) следует ввести какой-то дополнительный коэффициент запаса, так как состоянию образования второго пластического шарнира соответствует значительный прогиб балки и, кроме того, формула (а) не учитывает влияние поперечной силы.
Пример. Найти сечение двутавровой балки по рис. 247, а если Р 100 кн, [а] 14 кнсм2, 5 м груз Р приложен на расстоянии 3 м от заделки. Решение. Составляем условие «выравнивания» моментов (рис. 247, б):
6 Мпр • 2
пр —пр (г)
где сомножитель при Рпр выражен в метрах.
Из условия (г) получаем:
пр — ёпр—
или при Рпр пР ах п [а];
Р [а]а
О
требуемый момент сопротивления
гтгт т гт?-530 см3■
7 [а] а 7 14 • 1,16
Берем балку двутаврового сечения № 28в, 565 см3.
По методу упругого расчета требуется двутавр № ЗОв.
Расчет мнбгопролетных неразрезных балок
В й-пролетной неразрезной балке число лишних связей п к—1. Поэтому для обращения ее в механизм и полного исчерпания ее несущей способности можно допустить в ней образование к пластических шарниров. Однако это условие не является обязательным; несущая способность балки может быть потеряна ранее, чем при образовании к пластических шарниров (например, при наличии трех шарниров на одной прямой в данном пролете балки).
Рассмотрим частный случай такой нагрузки на неразрезную балку, для которой при к пролетах несущая способность может быть исчерпана при появлении к пластических шарниров.
Пусть, например, двухпролетная неразрезная балка (рис. 248,а) подвергается действию сосредоточенной силы Р по середине первого пролета. Требуется найти предельное значение нагрузки Япр, соответствующее исчерпанию несущей способности балки. Проведя упругий расчет балки, установим, что наибольший положительный момент под грузом (рис. 248, б)
Опорный момент
р 4 64 64
М — — Р
оп — 32
329
а)
Ф
Устанавливаем, что первый пластический шарнир появится под грузом Р, после чего дальнейшее возрастание нагрузки вызовет рост
прогибов балки в первом пролете и последовательное развитие пластических деформаций в сечении балки на промежуточной опоре. Если нарастание перемещений под грузом не опасно, то можно допустить состояние образования второго пластического шарнира над промежуточной опорой (оба пластических шарнира показаны на рис. 248, в кружками).
Итак, высшим предельным состоянием (при наличии значительных прогибов в первом пролете) будет система-механизм по рис. 248, в. При этом в сечениях балки под грузом и на опоре Ь моменты принимают предельное значение
Мпр отРпд ота№. (16.16)
г)
Рис. 248
По эпюре моментов, изображенной на рис. 248, г, составляем условие образования второго пластического шарнира:
Р пр
м
пр
откуда
4 2
6МП р
р —
Считая Рпр пР от п [а], находим из выражения (д)
№
Р1
(Г)
(д)
(е)
что аналогично решению по формуле (б).
По упругому же расчету получается следующий момент сопротивления:
13Р Р1
и?уп
64 [о] 4,9 [ст] ‘
(Ж)
Расчет по предельному состоянию дает более экономичное реше-
о Р1
ние («допускаемый» момент равен
330
Определение несущей способности рам
Аналогично определяется несущая способность для рамных конструкций включением (п 1) шарниров. Так, для рамы, изображенной на рис. 249, а, при действии нагрузки Р на точки В и С оси рамы
получаем после обычного расчета эпюру М приведенного вида. В предельном состоянии двухшарнирная рама обращается в четырехшар-
I)
5;
о - -V 1
о
1
ц
пр
1
1
1
1—1
и?
1
1
р
гпр
нирную (рис. 249, б). Исходя из условия выравнивания пролетного (в точке С) и опорного (в узле ) моментов (см. рис. 249, а), получаем
Рк м-мп
пр У
2 2
откуда предельная нагрузка несущей способности
о
(16.17)
где УИпр вычисляют по формуле (16.16). Для шесть раз статически неопределимой рамы по рис. 250, а рама с семью пластическими шар¬
331
нирами показана на рис. 250, б, причем, как следует из «упругой» эпюры моментов, последний пластический шарнир создается в точке Э.
Анализ последовательности образования пластических шарниров, произведенный по эпюре моментов, показывает, что сначала создается пластический шарнир в точке Л, затем в точке О, после этого в точке С, потом в точке Р, далее в точке Е, затем в точке В и, наконец, в точке Ь. В момент появления пластического шарнира в точке О предельная нагрузка
11 Мпо
Р"Р “8ТГ- 16Л8
При этом взаимные углы поворота в пластических шарнирах будут:
66 МпрН 62 МпрН
АРл —-72 Е1 ; Дфо —72 Е
60 М прН 44 М„рН
Афс —72 Е 72 ЁТ
35 М прЛ 12 уМпрА
Афя — 72 ; Дфв — 72“Ё7 ’
Афо 0.
5 М №
Горизонтальное перемещение. Все перемещения
найдены применением уравнений виртуальных работ.
ГЛАВА 17. ПРИМЕНЕНИЕ СОВРЕМЕННЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИН
§ 88. ЭЛЕКТРОННЫЕ ЦИФРОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ Общая характеристика ЭЦВМ
В настоящее время широко используются вычислительные машины автоматического действия, существенно ускоряющие расчеты сложных сооружений. Имеется два принципиально отличных друг от друга типа вычислительных машин: электронно-цифровые вычислительные машины (ЭЦВМ) и аналоговые вычислительные машины (АВМ). Остановимся сначала на ЭЦВМ, которые предназначены для решения весьма трудоемких инженерных задач (решение систем линейных алгебраических уравнений с числом неизвестных до 800, расчеты траекторий космических кораблей и т. д.). Основные особенности ЭЦВМ следующие:
1. Автоматичность, которая выражается в выполнении всех вычислений в заданной последовательности по подготовленной исходной информации.
2. Быстродействие, т. е. производство огромного количества арифметических операций за малый промежуток времени (от 30 до МО6
332
действий в секунду). Чаще всего применяются машины, выполняющие несколько тысяч арифметических действий в секунду. В США плоская 40-этажная 39-пролетная рама (1640 неизвестных перемещений) на ЭЦВМ типа 1ВМ-7090 с учетом влияния продольных сил и применением метода итераций по Зейделю рассчитывается за 7 мин.
3. Электронность в устройстве. Основные устройства ЭЦВМ построены на электронных лампах, полупроводниковых диодах и триодах. Основным элементом машины является триггер, состоящий из двух ламп, анодов и сети, по которой передаются импульсы. Исходными данными служат параметры электрической цепи, ее схема, значения электродвижущих сил и токов источников.
4. ЭЦВМ оперируют величинами, которые представляются только цифрами в отличие от аналоговых вычислительных машин (АВМ — машины непрерывного действия).
5. ЭЦВМ — машины с программным управлением. Они работают по программе, которая представляет последовательность специальных закодированных указаний (команд), устанавливающих, в каком порядке необходимо выполнить все арифметические операции.
В машине осуществляются следующие основные операции: хранение информации, выполнение арифметических действий (переработка информаций) и управление процессом. В соответствии с этим в ЭЦВМ имеются следующие основные устройства: 1) запоминающее устройство, или «память», 2) арифметическое устройство (электронный арифмометр), 3) устройство управления и 4) устройство ввода и вывода. Связи между основными устройствами ЭЦВМ представлены на рис. 251.
Запоминающее устройство разделено на перенумерованные ячейки, в каждой из которых может быть записано одно число; номер ячейки называется ее адресом. В машине имеются: 1) оперативная память,
2) промежуточное запоминающее устройство, 3) внешнее запоминающее устройство. Оперативная память (ЗУ, рис. 251) — совокупность ячеек, в каждой из которых представляется определенное число, причем в процессе работы машины это число может быть взято и в данную ячейку (имеющую определенный адрес) занесено другое число. Некоторая ячейка обычно обозначается р, а управляющая ячейка (в которой образуется ±1) — б.
Внешнее запоминающее устройство (работающее сравнительно медленно) может хранить большое количество чисел. Внешняя память разделяется на память на перфоленте (перфокартах) и на магнитной ленте (накопитель). На перфоленте посредством специальных устройств в виде кОхМбинаций отверстий записывается информация, которая далее переносится в оперативную память машины. Устройство вывода печатает результаты вычислений.
Арифметическое устройство способно выполнять четыре арифметических действия и различные логические операции. Устройство управления, объединяя работу отдельных частей машины, настраивает их на выполнение различных операций. Устройства ввода и вывода служат для обмена информацией с внешней средой. Устройство ввода представляет собой перфоленту с закодированными пробивками, кото¬
333
рая протягивается с большой скоростью между лампой и фотоэлементами. При пробегании через отверстие создается электрический импульс, который передается в запоминающее устройство. Совокупность импульсов создает запись числа в памяти. Устройство вывода может быть в виде электрифицированной пишущей машины (телетайпа), управляемой импульсами от вычислительной машины [11].
Электронные цифровые вычислительные машины общего назначения разделяются на малые, средние и большие. Примером малой машины является машина «Урал-1», команда которой содержит один адрес, быстрота работы — 100 операций в секунду. К средним вычислительным машинам относится «Урал-2», который имеет ско-
Рис. 251
рость 300 операций в секунду и внутреннее быстродействующее запоминающее устройство емкостью в 2047 чисел. Примером большой вычислительной машины является трехадресная машина БЭСМ-2М, которая работает со скоростью 10 000 операций в секунду, имеет запоминающее устройство на ферритах емкостью 2047 чисел и внешние запоминающие устройства на магнитных барабанах и лентах емкостью 12 288 чисел («память» машины). Передача цифр в цепях машины производится либо импульсами, либо потенциалами. Часто на ЭЦВМ используется двоичная система чисел. При двоичной системе любое число представляется комбинацией только двух цифр: единицы и нуля. За основание при этом принимают число 2 и любое число выражают как сумму соответствующих степеней этого числа. Например: 7 1 - 22 1- 21 1 -2° 0111.
Выполнение расчетов на ЭЦВМ. Программирование
Приступая к выполнению расчетов на ЭЦВМ, расчетчику необходимо проделать ряд подготовительных работ:
1) установить метод расчета, расчетные формулы и дать алгоритм решения, причем предпочтение следует отдавать таким методам, которые обеспечивают цикличность расчета. Алгоритм — система
334
предписаний для выполнения в установленном порядке определенных логических и вычислительных операций по решению задач данного типа;
2) разбить расчет на части, каждая из которых выполняется по своей программе;
3) составить программы для каждой части расчета;
4) произвести отладку программы на машине.
Каждая программа (последовательность цифр) содержит нередко несколько сотен команд (закодированных указаний). Некоторые из основных команд машины БЭСМ-2М приведены в табл. 10.
Таблица 10
Главнейшие команды машины БЭСМ-2М
Вид команды
Операция
Условное
обозначение
код
опера¬
ции
I
адрес
II
адрес
III
адрес
Пояснения
Сложение
а--Ь — с
01
а
Ь
С
Сумма
Вычитание
а — Ь с1
02
а
Ь
01
Разность
Умножение
а • Ь с2
03
а
ь
С2
Произведение
Деление
о,: Ь — С3
04
а
ь
Сз
Частное
Пересылка
а—»с4
00
а
0000
С4
Содержимое одной ячейки передается в другую
Каждой команде соответствует свой код (цифровое изображение команды). Простейшая задача программирования — это вычисление усилий по готовым формулам. Рассмотрим, например, определение изгибающего момента в заданном сечении двухопорной балки по формуле Мх дх Это вычисление разбивают на четыре операции,
Таблица 11
Программа вычисления
Условное
обозначение
команды
Адрес
команды
Команда
ч
Код
I адрес
II адрес
III адрес
1 — X — Г
0001
02
0010
.0012
0014
С4
II
0002
03
0012
0014
0014
ЯГ Г%
0003
03
ООП
0014
0014
г2 -2 Мх
С004
04
0014
0013
0017
Стоп
0005
33
0000
0000
0000
335
определяя сначала I—х г, потом хг гъ затем г2 и, наконец, г2 : 2 УИд.
Программа вычисления момента Мх по данной формуле приведена в табл. 11.
Пролет I дается в ячейке 0010, ц — в ячейке ООН, х — в ячейке 0012, константа 2 — в ячейке 0013, результаты г — в ячейке 0014, момент Мх — в ячейке 0017.
При решении уравнений по способу Гаусса задача сводится к переходу от полной квадратной матрицы к треугольной.
Остановимся на программе вычисления треугольной матрицы по данной квадратной матрице при решении по способу Гаусса:
1 1
5м
.11
ч,ь
А
бц б12 б1з 691 б «о 6 оо
6-1 б
п 1 ия2
(а)
Рис. 252
Необходимо обратить в нуль все элементы матрицы, лежащие ниже главной диагонали (рис. 252). Чтобы обратить в нуль коэффициент б(2У в преобразованном уравнении, необходимо вычислить коэффициент б21
а12 и затем вычесть из элементов второй строки соответствующие
элементы первой строки, умноженные на этот коэффициент. Когда будут обращены в нуль все коэффициенты, стоящие ниже диагонали в 1,2,., (г—1)-м столбцах, нужно обратить в нуль коэффициент б7.
б
Для этого вычисляют коэффициент т- и вычитают из элементов -той
строки соответствующие элементы г-той строки. Следовательно, при применении способа Гаусса вводят два следующих оператора счета:
п - 6
В —оператор, вычисляющий множитель ау7 --;
— оператор, вычисляющий значения коэффициентов преобразованных уравнений 6 и свободных членов их А)н, причем
бл бй — 8м.
(б)
Используя эти операторы, схему счета по приведению матрицы к треугольному виду можно представить так:
П
П В и и
I 1 I г 1 Н — I 1
где П — произведение операторов,
336
ул
(в)
Под элементы матрицы выделяются ячейки памяти машины, причем элементы матрицы располагаются в последовательных ячейках запоминающего устройства в порядке следования по строкам матрицы (а). Все действия на машине производятся в соответствии со схемой счета (в). Заметим, что операторы Вц и меняются не в одном, а в нескольких циклах (каждому индексу соответствует свой цикл в программе). В схему программы вводят соответствующие обозначения счетчиков у(9 уЛ у,г для индексов,, к. Схема счета не исчерпывает всей программы, так как, кроме команд по реализации счета и логических операций, программа включает ряд команд по подготовке ячеек машины, переадресации команд и т. д. Схема программы, помимо схемы счета, содержит и все то, что относится к управлению действиями. Поэтому в схему программы входят еще следующие операторы:
— оператор восстановления, который приводит в первоначальное состояние команды (зависящие от индекса I), преобразованные в процессе счета;
Рг — оператор подготовки счетчика; этотоператор-засылает в счетчик начальное значение индекса 1
Р(1) — оператор переадресации, который преобразует команды, зависящие от индекса I, на п единиц;
— логическое условие проверки индекса г
Т — оператор передачи, который выбирает из всего набора данных нужную группу и передает ее в рабочие ячейки;
1(1) — оператор, прибавляющий единицу в счетчик индекса I.
Простейшая схема программы вычисления полинома
Ф (Х) — а0 а1х 4" • • • ”Ь агХП
имеет такой вид:
Т — Аь -Р (1) — — Стоп,
Г 1
I П
где А; — оператор, прибавляющий в ячейку р коэффициента и умножающий содержимое этой ячейки на я.
Аналогично в более усложненном виде составляется программа вычисления треугольной матрицы способа Гаусса в соответствии с выражением (в).
Очень часто для программ применяют геометрические схемы действий над формулами. Приведем такую схему для итерационного цикла. Решение уравнения х (х) можно искать в форме последовательных приближений, вычисляя:
1(о); г(■); з(«); •••; хЛ1(), где х0 — произвольно выбранное начальное значение. Процесс последовательных приближений останавливают, когда
а1 — лг е,
где е — наперед заданная малая величина, и л:1 тогда принимают за окончательное решение. В изложенной форме итерационный про-
337
цесс представляется такой программой:
х0-хк
Счет
А1 ()
(17.1)
Хк1 — ХгГг
Х1 — Хк I в ГХ I Стоп
Если программа содержит огромное количество команд, то для облегчения программирования переход от алгоритма к программе производится через блок-схему, причем блок представляет собой логически законченную часть программы [11]. Для сокращения записи большой программы применяется операторная с и м в о л и к а. Оператором называется часть программы, соответствующая блоку. Каждый тип оператора обозначают определенной буквой, например: А — арифметический оператор, О — оператор восстановления, Р —
оператор переадресации, Р— оператор проверки логического условия, Я — оператор «стоп» и т. п. Операторная схема программы сложения п чисел кратко будет выглядеть так:
л
ш
ш
7
ОхА2А3РРьЯ%, (17.2)
.
Рис. 253
где 0Х — оператор восстановления оператора Л3; оператор А2 суммирует первые два числа;, оператор А3 добавляет очередное число; оператор Р± осуществляет переадресацию оператора А3; оператор Р5 проверяет, все ли числа просуммированы; оператор Я6 отражает конец счета — «стоп». Блок-схема программы сложения п чисел представлена на рис. 253 с введением операторной символики [11].
При использовании ЭЦВМ особенно удобна матричная форма расчета, которая хорошо приспособлена к расчету на машинах, обеспечивает компактность записи формул и позволяет разбить весь расчет на две части: в первой производится выбор метода и дается построение алгоритма расчета, во второй выполняется вычислительная работа на основе выбранного алгоритма. При этом используются матричные соотношения между усилиями и перемещениями. Так, при расчете по методу перемещений и выборе в качестве неизвестных углов поворота узлов ф„, срт и взаимного линейного смещения Д„т узлов применяют связь между концевыми моментами, поперечной си¬
338
лой (упругими реакциями) и перемещениями в следующей форме:
Мпт
М.тп
0.ПТТ1
к пт 2 пт 21
-к о Кпт
пт
3
к пт о кпт
™п
21
пт
3 и Ъ_
пт о Кпт.2 кп пт 1пт 1пт
фг
фт
Для
(17.3)
где
4ЯЛ
Кратко соотношение (17.3) можно представить так:
Япт К
7
птпт
(17.4)
где Япт — упругие реакции, вызванные в дополнительных связях по направлению введенных концевых закреплений;
2пт — неизвестные перемещения;
Кпт — матрица жесткости для данного стержня, определяемая по правой части соотношения (17.3).
Для всей рамной конструкции расчет по методу перемещений в матричной форме можно сформулировать следующим образом. За неизвестные принимаем всю совокупность неизвестных перемещений 2, по направлениям которых вводим дополнительные связи Я К2, где К — общая матрица жесткости всей системы. Обозначив матрицустолбец реакций в дополнительных связях от внешней нагрузки через Р (матрица нагрузки) и приравняв сумму реакций в дополнительных связях нулю, получим матричное уравнение для всей системы
или
К2 — Р 0 Р К2,
из которого и определяем все перемещения:
гк1Р.
(17.5)
(17.6)
Задача сводится к обращению матрицы жесткости всей системы, что легко реализовать на ЭЦВМ (см. Приложение). Можно применить также итерационный процесс по Зейделю (см. § 89).
§ 89. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ С ПРИМЕНЕНИЕМ ЭЛЕКТРОМОДЕЛИРУЮЩИХ УСТРОЙСТВ
Применение электрической модели МЛ-2 для решения системы линейных уравнений
В настоящее время существуют электрические модели — аналоги различного типа. Дадим описание электрической модели МЛ-2 (на рис. 254 изображена часть схемы). К узловым точкам сети (указаны
339
кружками) присоединены источники токов; в сеть включены омические сопротивления (показаны прямоугольниками); величины токов могут регулироваться с панели управления, а величины омических
сопротивлений сети уста-
3
ь-
-ь-
-4-
-0-
-3-
Рис. 254
навливаются поворотом ручек на панели сопротивлений. Даны сумматоры или усилители (показаны треугольниками со знаками V)). Все блоки схемы обладают направленным действием (указано стрелкой). Основные операции выполняются посредством усилителей постоянного тока. Модель МЛ-2 дана для решения системы 12 линейных уравнений с 12 неиз¬
вестными хл
42»
причем искомые неизвестные изображаются потенциалами. В модели имеется 12 усилителей тока, каждый из которых суммирует 12 членов уравнений; кроме этого, 12 усилителей, работающих в режиме перемены знаков. В модели МЛ-2 вмонтировано 144 схемы установки коэффициентов при неизвестных и 12 схем установки свободных членов. Каждое неизвестное х1у 2, х12 определяется питанием шин. Задача сводится к опреде¬
лению сил токов. Модель МЛ-2 предназначена для решения системы линейных уравнений:
0111 0120. аь 1212 а21Х1 а22х2. а2 12х12 Ь2
(а)
12, 11 “Г 12. 22 4 • • ■ 4 12.1212 — 12 )
Применяя способ итерации, можно представить эту систему так:
— --0г Л 122 132 - •• 1»
2 —21 4“ 0 —1— Л233. •. “Ь В2
— 3 311 А322 4 0 • • -г З3;
— 12 — 12, 11 4 12, 22 4" • • • 4" 0 4" В12,
(б)
Значения А и и В1 очевидны из выражений (а).
В соответствии с этими выражениями для неизвестных и осуществляется электрическая схема по рис. 254, причем неизвестные определяются питанием шин хи 2,., а потенциал шин устанавливается при помощи делителя напряжений. Метод моделирования по данной
340
схеме применим, если выполняется одно из следующих условий:
2 Атя1 (т 1, 2, Л);
п — I к
У А-тп 1 (л 1, 2,., ),
т 1 к
Л тп 1 •
т 1 я 1
По первому условию сумма коэффициентов для каждой строки системы (б) должна быть меньше единицы; по второму условию сумма коэффициентов для каждого столбца должна быть меньше единицы, по третьему условию сумма квадратов всех коэффициентов должна быть меньше единицы. Если ни одно из этих условий не выполняется, применяем способ итерации по Зейделю.
Применение многополюсников
Решение задач по расчету сложных статически неопределимых систем требует осуществления большего объема вычислительных операций. Вследствие этого в последнее время все более широкое применение в строительной механике находят как малые, так и мощные электронные вычислительные машины.
Использование электронных вычислительных машин типа ЭМСС-7 и ЭМСС-8 основано на различных электрических аналогиях, состоящих в замене механических систем (балок, рам, ферм) соответствующими электрическими схемами в виде многополюсников, под которыми понимают часть электрической цепи, присоединяющуюся к остальным частям цепи в нескольких точках. Г. Е. Пуховым [61 для замещения изгибаемого стержня предложен электрический трехполюсник, что позволяет упростить и ускорить расчеты плоских стержневых систем, применяя методы исследования электрических цепей непосредственно в лаборатории. Вычисления изгибающих моментов и углов поворота сечений стержней по концам заменяют измерением соответствующих токов и электрических напряжений. Для электрического моделирования рам со смещающимися узлами им же была применена более сложная П-образная электрическая схема и для реализации дополнительного уравнения метода перемещений построена так называемая схема перекоса.
Приведем известные из электротехники понятия о двухполюснике и трехполюснике. Простейшим многополюсником является двухполюсник (рис. 255, а) — цепь, рассматриваемая по отношению к ее двум зажимам а и Ь. Характеристиками активного двухполюсника являются: напряжение 00 холостого хода, т. е. напряжение между его разомкнутыми зажимами, и ток короткого замыкания, проходящий
341
О I 1
между короткозамкнутыми зажимами двухполюсника. Отношение
и гг
— гв выражает внутреннее сопротивление двухполюсника. По отношению к внешней цепи активный двухполюсник ведет себя как источник энергии, обладающий электродвижущей силой 10 и внутренним сопротивлением гв. При замыкании зажимов двухполюсника на некоторое внешнее сопротивление в последнем возникает ток
Уо
а) гГ
[У
I
I
г гв
Т-образная схема замещения — аналог изгибаемого стержня — изображена на рис. 255, б. Цепь этого трехполюсника вполне определяется электродвижущими силами и сопротивлениями; для каждой пары зажимов схемы имеются три входных сопротивления. Токам в схеме замещения соответствуют усилия в сооружении, а электрическим напряжениям V — углы поворота узлов.
Расчет на АВМ состоит из следующих операций:
1) набор схемы на наборном поле машйны, ввод характеристик системы, ввод исходных данных и снятие результатов с приборов;
2) аналитическая часть расчета — перевод механических величин в электрические и обратно.
Общая характеристика АВМ
Как видно из изложенного, в собственно аналоговых вычислительных машинах (АВМ) осуществляются процессы, аналогичные изучаемым закономерностям в строительной механике. Каждый параметр и переменная в АВМ математически эквивалентны параметру и переменной в изучаемой системе. Так, сила тока и напряжения в электрической сети (включающей, кроме того, индуктивности, сопротивления и емкости) эквивалентны силам (концевым моментам) и перемещениям (углам поворота концов стержня). В настоящее время нашей промышленностью серийно выпускаются наиболее совершенные машины ЭМСС-7М. В весьма целесообразной электрической модели ЭМСС-7М применена несимметричная П-образная схема-аналог изгибаемого стержня с 50 схемами аналогов стержней. Машина осуществляет расчет не только плоских нерегулярных многоэтажных рам, но и пространственных свободных ортогональных рам. АВМ позволяет решать и дифференциальные уравнения как с обыкновенными, так и с частными производными; находят применение и функциональные аналоговые вычислительные машины (ФАВМ). В них обеспечивается не взаимно однозначное соответствие между изучаемой физической и аналоговой системами, а соответствие между необходимой математической операцией и компонентами машины [6].
ЧАСТЬ ТРЕТЬЯ
УСТОЙЧИВОСТЬ и ОСНОВЫ ДИНАМИКИ СООРУЖЕНИЙ
ГЛАВА 18. УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ § 90. ЗАДАЧИ И МЕТОДЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ
Основные понятия
Исследование Эйлером явления выпучивания в сторону сжатого в продольном направлении стержня (рис. 256, а) привело к созданию большой области строительной механики — теории устойчивости стержневых систем.
Рассмотрим задачу об устойчивости сжатого прямолинейного стержня, подверженного действию осевой сжимающей силы Р. При отсутствии побудительных причин центрально приложенной осевой силе Р соответствует лишь прямолинейная форма равновесия. При достижении сжимающей силой Р критического значения возможны две формы равновесия — прямолинейная и криволинейная, вызванная искривлением стержня (рис. 256, б), причем прямолинейная форма равновесия оказывается неустойчивой. Стержень в этих условиях остается искривленным и после удаления причины, вызвавшей искривление. Существуют и высшие формы потери устойчивости стержня, когда для шарнирно опертого стержня возникает ряд полуволн искривленной формы.
Задачу о потере устойчивости прямолинейной формы сжатого стержня впервые решил Л. Эйлер в 1759 г., установив, что «сжимающая сила конечной величины может вызвать искривление стержня при наличии любого незначительного начального отклонения». Если
Рис. 256
343
определить критическое значение сжимающей силы точнее, чем это сделал Эйлер (который исходил из приближенного дифференциального уравнения упругой линии), критической.нагрузкой следует назвать такую, при очень незначительном превышении которой возможно появление новой, искривленной формы равновесия. Вторым примером может являться потеря устойчивости плоской формы изгиба полосы при действии момента М, приложенной в плоскости по¬
лосы (плоскость ХУ). При достижении определенного значения момента силы М Мкр происходит выпучивание полосы в сторону (из
плоскости ХУ), сопровождаемое скручиванием (§ 101, рис. 281).
Различают потери устойчивости первого и второго родов.
Примером потери устойчивости первого рода является продольный изгиб прямолинейного стержня, сжатого осевой силой (см. рис. 256)
или потеря устойчивости плоской формы изгиба балки; примером потери устойчивости второго рода — продольный изгиб внецентренно сжатого стержня или продольный изгиб при наличии поперечной нагрузки (рис. 257), потеря устойчивости сжатоизогнутой рамы или арки и т. д.
Потеря устойчивости первого рода для сжатого стержня (см. рис. 256) сопровождается возникновением нового вида деформации изгиба вместо сжатия, имевшего место до РРкр. При потере устойчивости плоской формы изгиба тонкостенной балкой, подверженной действию поперечной нагрузки, в случае достижения нагрузкой критического значения стенка балки поворачивается и возникает скручивание балки, сопровождающее боковой изгиб ее. При потере устойчивости второго рода вид деформации не меняется, но перемещения стержня при Ря«0,8 Ркр начинают возрастать. Например, при продольно-поперечном изгибе стержня, сжатого силой и одновременно подверженного действию поперечной нагрузки д (см. рис. 257), за особым пре¬
Рис. 253
344
дельным значением силы Рпр при нарастающих прогибах величина сжимающей силы падает, т. е. стержень полностью теряет свою несущую способность (см. график зависимости прогиба у от нарастающей силы Р рис. 258). Однако и до достижения силой предельного значения возникает опасное состояние по прогибам (Роп по рис. 258), причем
где уоп — недопустимые по условиям эксплуатации прогибы.
Основными методами отыскания критических нагрузок являются статический, динамический и энергетический.
Статический метод. При использовании этого метода получают характеристические уравнения для возможных форм статического равновесия системы. Предполагая, что нагрузка незначительно превышает критическую, и представляя себе искривленную форму равновесия, используют уравнения для перемещений и усилий в этом отклоненном состоянии системы. Применяя граничные условия, по уравнениям деформационной теории сжато-изогнутых систем составляют характеристическое уравнение. Для прямолинейных, ломаных и круговых стержней удобно использовать метод начальных параметров, по которому основные уравнения содержат лишь начальные элементы изгиба. Для сложных стержневых систем весьма эффективно применение уравнений виртуальных работ кинематической цепи, полученной включением во всех узлах рамы шарниров, и использование метода перемещений. Имеются и другие варианты статического метода исследования устойчивости (способ последовательных приближений; применение уравнений в конечных разностях; матричная форма решения задач устойчивости; способ интегральных уравнений и т. д.).
Динамический метод. Применяя динамический метод, составляем уравнение собственных колебаний сжатого осевой силой Р стержня и определяем то значение силы Ркр, при котором частота собственных колебаний будет равна нулю. Так, для сжатого шарнирно опертого стержня постоянного сечения с распределенной массой частота поперечных колебаний выражается формулой
где со0 — частота поперечных колебаний при отсутствии сжимающей
Если Р Ркр, то о) - 0 и период колебаний становится бесконеч¬
ным, т. е. стержень, колебавшийся около своего положения равновесия, не возвращается к первоначальному состоянию. Найдя общее выражение частоты поперечных колебаний сжатого стержня, приравни¬
Методы исследования устойчивости. Действие распределенной нагрузки
(а)
силы Р.
345
вают его нулю, откуда и находят критическое значение сжимающей силы.
Энергетический метол, или метод потенциальной энергии. Он основан на известном принципе Дирихле, согласно которому в устойчивом состоянии равновесия потенциальная энергия системы П имеет значение минимум, а в безразличном состоянии разность двух соседних значений потенциальной энергии АП равна нулю:
АП АЦ — АТ 0, (б)
где 1 — потенциальная энергия внутренних сил;
Т — потенциальная энергия внешних сил.
Согласно выражению (б) приращение потенциальной энергии для
двух смежных положений в безразличном состоянии должно быть равно
нулю, следовательно,
АЦ АТ. (в)
Для устойчивого состояния А1 АТ, для неустойчивого состояния, наоборот, А11 Д71, т. е. приращение работы внутренних сил меньше приращения работы внешних сил.
Хорошие результаты дает метод потенциальной энергии, если удовлетворяются не только граничные условия задачи (условия на концах стержня), но и эпюры С и М для заданной формы отклонения приближаются к действительным эпюрам усилий. Рассмотрим, например, случай действия равномерно распределенной продольной нагрузки сопз на стержень постоянного сечения (рис. 259, а). Поперечная сила в произвольном сечении для искривленной формы равновесия равна
I
ф31П Лг.
х
346
Для случая малых деформаций, заменяя зт ср ф ух, получаем
I
0х Ухягйг у(1 — х). (г)
а:
Вводим фиктивную распределенную поперечную нагрузку рх (рис. 259, б), интенсивность которой находим как производную от поперечной силы ф, задаваясь при этом приближенной формой искривленной оси (удовлетворяя для ух граничным условиям):
Фх ч
(д)
По найденной поперечной нагрузке вычисляем начальные значения поперечной силы и изгибающего момента (рис. 259, в, г), г также Ух и Мх Е1ух. Затем определяем левую часть соотношения (б), т. е. приращение потенциальной энергии:
1 г» М1Ах О
Элементарную работу силы дх йх на продольном перемещении [х стержня подсчитываем по формуле (рис. 259, а внизу)
X X
Ях йх-х дх йх йх дхйх (йх—йх соз ф) о о
Х ( 2 • цхйх 2 51П2 -5- йх дхйх 2 йх дхйх -йх. (ж)
ООО
Полная работа всей продольной нагрузки при искривлении стержня на продольных перемещениях будет
I Гх
йх. (3)
АГ
Перейдем к решению данного примера, когда дх Задаемся формой отклонения в виде параболы 2-й степени ух кх2, ух 2кх. Подставляя значение ух в выражение (г), получаем
С1Х 2кхд ( — х) ах ( — ), (и)
где а 2 кд — произвольно.
Интенсивность фиктивной распределенной нагрузки по выражению (д):
Рх (1- 2х).
При а 2 эпюра нагрузки имеет вид двух треугольников (см. рис. 259, б).
347
Начальные значения ф0 и М0:
2о 0; М0 -.
Уравнение изгибающего момента
Мх 1х2-х3 — -.
Уравнение углов наклона
«-“-зет
По выражению (з) получаем
2АТ щрр ■ 0,005247.
По выражению (е) находим
0,04127.
Из равенства работы по выражению (в) вычисляем
(70кР 7,866.
Точное решение с применением функций Бесселя дает
(70кР 7,87
§ 91. ОБЩЕЕ УРАВНЕНИЕ УПРУГОЙ ЛИНИИ СЖАТО-ИЗОГНУТОГО СТЕРЖНЯ
Действие распределенной поперечной нагрузки и осевой сжимающей силы
При решении самых различных задач по анализу устойчивости и несущей способности сжатых гибких стержней используют основные выражения перемещений при их деформации, вызванной одновременным действием сжимающей силы и поперечной нагрузки.
Применение общего уравнения упругой линии сжато-изогнутого стержня в форме метода начальных параметров позволяет значительно упростить решение ряда задач определения перемещений при одновременном действии поперечной нагрузки и продольной силы. Выведем это уравнение, используя приближенное дифференциальное уравнение
У" -ЁЪ (18-1)
Получаемое решение дает достаточно точные результаты при действии сжимающей силы 5 0,85 5Э, где 5Э — эйлерово критическое значение [12].
348
Рассмотрим сначала случай действия распределенной поперечной нагрузки и продольной силы 5 на стержень, левый конец которого оперт на вертикально-податливую опору (рис. 260). На концах стержня приложены моменты М0 и М[. Интенсивность сплошной поперечной нагрузки дх меняется по степенной функции п-й степени:
. х, »Х2,, „V X1
Ях — 7о Яо тт Яо о7 • • • Яа
п
(18.2)
[ТШПТШХШ
Рис. 260
На рис. 260 показана ось стержня в деформированном виде. Пренебрегая продольными перемещениями при изгибе в области малых деформаций, а также влия- нием продольных деформаций сжатия, будем считать, что каждая точка оси стержня получает лишь перемещение, нормальное к 5 первоначальной оси. Выразим ординату упругой линии у в функции от х, учитывая влияние продольной силы 5 на искривление, и следовательно, в выражении изгибающего момента Мх, кроме момента от поперечной нагрузки, войдет и момент силы 5 относительно любой точки деформированной оси. Применяем следующее правило знаков: направляя ось У вниз, ось X вправо и помещая начало координат в центре левой опоры балки, считаем изгибающий момент Мх положительным при направлении его против часовой стрелки, поперечную силу —при направлении ее вниз. Ввиду наличия левой податливой опоры получаем начальный прогиб у0. Мы имеем дело со случаем действия непрерывной нагрузки и потому законы изменения у, у Мх и ф выражаются также непрерывными функциями.
Для получения уравнения упругой линии представим изгибающий момент в произвольном сечении в виде суммы:
Мх Мя -- МУ
где Мд — изгибающий момент только от поперечной нагрузки;
М —5 (у — Уо) — изгибающий момент от действия продольной силы.
Подставляя значение М5, получаем полный изгибающий момент Мх Мд-8(у-у0). (18.3)
Дифференцируя Мх по х, получаем согласно известному соотношению поперечную силу в произвольном сечении
■8у.
йх
349
Первый член правой части представляет собой поперечную силу от поперечной нагрузки второй член — поперечную силу от осевой силы «5:
где 0.я — поперечная сила, перпендикулярная к недеформированной
Первая производная поперечной силы д (вызванной действием только поперечной нагрузки 9) согласно известному соотношению из теории изгиба равна интенсивности поперечной нагрузки:
Подставим теперь выражение изгибающего момента Мх из формулы (18.3) в дифференциальное уравнение (18.1):
Рассматривая случай балки постоянного сечения и обозначая
получаем дифференциальное уравнение упругой линии сжато-изогнутой балки в окончательном виде:
Используя приведенные выше дифференциальные зависимости, находим последовательно производные высшего порядка по выражению (а):
Ях — производная от дх (п — 4)-го порядка.
При нахождении начальных значений производных уХ9 ух,., у№примем во внимание дифференциальные соотношения между изгибающим моментом от поперечной нагрузки и поперечной силы, а также поперечной силой С1Я и интенсивностью поперечной нагрузки. Очевидно, при х О согласно рис. 260
(18.4)
оси.
(18.5)
М о 8, ч
Ух Ё7 (у у®) ’
к2 — — - М —О — -®9 к ЕГ тд—Е1, Е1,
(18.6)
Ух Мд—к2(у — у0).
(а)
Ух (ч — к2у УхЧ Ях-у";
(б)
где
,(п-4)
Е1
А4ц — М0, Чх—Чо
(в)
350
Кроме того, по общему выражению для интенсивности нагрузки
(18.2) при х 0:
Ях — Яо
Ях — Я о»
-4)с4)
(Г)
где я0п4) — начальное значение (п — 4)-й производной интенсивности сплошной нагрузки.
Учитывая приведенные соотношения, найдем начальные значения всех производных ух согласно выражению (б).
Подставляя начальные значения производных из выражения (б) в члены разложения функции ух в ряд Маклорена и объединяя все члены с одинаковыми параметрами у)у Л40, Я о и т. д., получаем следующее решение:
„ „, У (кх кЧ з ТЙо (кЧ кх уу» т 1 ■71 ” "зг • • •) 1 [2Г 4Г • • • ]
. Оод [х кьхь ?о №х кх6.,
-гзГ“-5Г •••; гЧт--бГ.
дЫ Г (кх)™ (кх)«, I
•" кп [(л 4) (п 6) ]» где Ма М0Е1 Зод 2одЕ1.
Обозначая сумму членов ряда, стоящего при у[ через Вх, где Вх
8пх ? и учитывая интегральные зависимости между рядами при у0,
Мо, §од и т. д., получаем выражение для ух в замкнутой форме:
х (1) _ х (2)
Ух Уо УВх М0 5 Вхйх С1о? 5 ВхАх
0 о
х (3) (л 3)
7о 5 Вх(1х. дЪп 5 (е)
о о
Произведем подстановку В и интегрирование:
., 8117 кх. тГл [ 1 — СОЗ,
У Уо Уо—ь М0 ( ]
соз кх — 1 3
о
Мы получили основное уравнение упругой линии сжато-изогнутого стержня при действии сплошной нагрузки, меняющейся по степенной функции п-й степени, которым далее будем пользоваться для решения различных задач.
351
По уравнению (18.7) заходим общее уравнение для тангенса угла наклона упругой линии в произвольной точке ее:
Ух Фа У С05 кх Мй х(п--2)
. 1 —соз кх. _ (кх — т кх,. С т кх
Цод( р )7о( я ) к
йху
(18.8)
где
Уо — Фо-
Дифференцируя уравнение (18.8) и умножая на Е1, получаем уравнение изгибающего момента для сечения с абсциссой х:
Мх Е1ух — уъкЕ 81пЛл: Л10со8 кх
х(п )
. зш кх, 1—-соз кх., „ч ( зш кх.
?о —р—) • • • -1- Яо — Лх.
о
(18.9)
где М0 и С0д — момент и перерезывающая сила от поперечной нагрузки и нормальных к оси стержня реакций.
Еще раз Дифференцируя, находим общее быражение для поперечной силы:
Сх — уок2Е1 соз кх — М0к зш кх (3од соз кх д0
31 п кх
Х(п)
. 51П кх,
гйх-
(18.10)
Пользуясь найденными выражениями, легко построить эпюры ух,
х(п)
ух, Мху ф. Под йх понимают г-кратный определенный ин¬
теграл от 0 до х функции
зш кх
. В эти уравнения входит значение начальной поперечной силы которое при наличии осадки опоры го будет включать, конечно, и дополнительную реакцию от правых сил 5, равную
5у. Нетрудно установить возможность применения принципа сложения влияния отдельных факторов при 5 сопз. Выведенные общие выражения применяем для отыскания ординат эпюр перемещений и эпюр усилий от действия непрерывной нагрузки и приложения сосредоточенных воздействий по концам, а также для эффективного анализа устойчивости стержней.
352
Пример 1. Определить максимальный изгибающий момент в заделанной балке
от действия пары сил и осевой сжимающей силы (рис. 261). Момент М0 возникает
от эксцентричного приложения силы
М0 5е,
где е — эксцентрицитет.
Решение. Принимая начало координат в центре тяжести левого крайнего сечения и направляя ось X по линии действия осевой силы после деформации, составляем выражение для тангенса угла наклона по уравнению (18.8):
,, 0 зт кх.
ух ф0 соз кх М0 —г—. (ж)
Используем условие для заделки, а именно, что при х I, ух 0, что дает
зт к1
ф0 соз 6 М0
откуда получаем начальный угол наклона
фо — М0
- 0,
к1
(з)
Максимальный момент будет в заделке; по уравнению (18.9) при х— I
Миакс — фокЕ1 зт к1 -(- М0 соз к1 М0 ( к1 зт к1 соз Ы)
М о
соз к1
(и)
Для стержня, шарнирно опертого пролетом, в случае симметричного загружения максимальный момент будет посередине пролета:
Мы
М о
Ы
(Ю
Максимальный прогиб по уравнению (18.7) для стержня, изображенного на рис. 261,
М0 1 — соз Ы
макс
Е1к 2
соз Ы
(л)
Пример 2. Найти максимальный момент в случае одностороннего эксцентричного приложения сжимающей силы к шарнирно опертому стержню (по рис. 262).
Рис. 262
Решение. (20. Граничное условие: при х, у1 0, или
откуда
(тйг)-
12 Н. К. Снитко
353
Подставляя это значение в формулу (18.9) для Мх, получаем
М0 [к1 — вт Ы.,. М0 зт кх
МТ1 (-ШГ-)81П кхТ • —•
(Н)
Приравняв С? по формуле (18.10) нулю, найдем, что для Ммакс должно быть соз кх 0, зт кх 1.
Отсюда вместо выражения (н) получим
Ммак с —
М о
МаКС_ 81ПЛ •
(о)
Общее уравнение упругой линии при наличии прерывной нагрузки
Рассмотрим теперь действие прерывной нагрузки (рис. 263). При наличии х с скачков в эпюре моментов величиной Мс, в эпюре поперечных сил значением РСУ в эпюре интенсивности величиной цс
применяем метод учета скачков в аналитических функциях, известный из курса сопротивления материалов, и получаем
. Гл Г 1 — сов к (х — с) 1. тг Г к (х — с) — зт к (х — с),.
Уг(х) Угх) Мс [ г. рс_4 — 1 к2х-с)2
соз к (х — с) — 1
2
(18.11)
Здесь влияние момента Мс, приложенного на расстоянии с от начала координат, учитывается с функциональным множителем
1 — соз к2
—р, где г х — с, причем вид этой функции тот же, что и в
уравнении (18.7) при начальном моменте.
Аналогично учитывается влияние скачков в поперечной силе и интенсивности нагрузки.
Соответственно составляем выражения для тангенса гла наклона, изгибающего момента и поперечной силы на втором участке оси балки.
354
Так, для момента имеем
М2 (х) М1 (х) МС соз к (х — с) 81П кх—с) [1 — С05(л: —с),
где
М± (х) — кЕ1у0 пкх (18.12)
§ 92. ОПРЕДЕЛЕНИЕ КРИТИЧЕСКИХ СИЛ МЕТОДОМ НАЧАЛЬНЫХ ПАРАМЕТРОВ
Одноконсольный стержень
Применим способ начальных параметров к нахождению критической силы для одноконсольного стержня, подверженного действию сжимающей силы на конце консоли (рис. 264) [12].
Представляя возможную форму искривления стержня О — Ь — си получаем два неизвестных начальных параметра: начальный угол поворота ф0 и начальную реакцию (20. Из уравнения суммы проекций
получаем, что реакция правой опоры равна (—ф0).
Выражение ординаты упругой линии для участка балки О — Ь по уравнению (18.7)
81П кх. 0п « • г
Уг Фо (кх — 51П кх) (а)
и выражение изгибающего момента на втором участке по уравнению (18.12)
■ я иг? • и, 51П кх 31П к (X — )
М2 —рикЕ1 ыпкх ао— 20 1(б)
где первые два члена составляют уравнение момента на участке балки О — Ь, третий член учитывает влияние скачка в эпюре поперечных
сил вследствие наличия правой опорной реакции.
Далее составляем граничные условия:
при х I уг 0;
при х I а М2 0.
12
355
Третье уравнение О]У 0) использовано для определения правой реакции. Заметим, что на свободном конце консоли деформационная поперечная сила не равна нулю.
На основании уравнений (а) и (б) с учетом обозначений Ы V, ка — а граничные условия будут
81П V. ?о ч А р«пг тт-5т°’
О (в)
— ф0кЕ181 п (V а) [§т(г а) — зта] 0.
Если произошло искривление стержня, ф0 и ф0 получают конечное произвольное значение, что возможно для системы однородных уравнений (в) только при условии равенства нулю ее определителя, т. е.
81П V [зШ (V а) — 5Ш а] (V — 81П V) 81П (V а) 0. (г)
Мы получили уравнение неустойчивого состояния для прямолинейного стержня. Решая это трансцендентное уравнение относительно V г, находим критическое значение сжимающей силы:
р _
“ 2 •
Уравнение (г) после простых преобразований примет вид:
V (18 1еа) 1§а. (д)
Рассмотрим частный случай, когда я у и, следовательно,
а у. Решая уравнение (д) способом попыток, получим значение
наименьшего корня его:
1,802,
откуда
р (е)
кр— р » Vе;
в то время как для шарнирно опертого стержня без консоли получаем из уравнения (д) при а 0
V V 0,
что дает наименьший корень, отличный от нуля: V я и известное эйлерово значение критической силы для шарнирно опертого стержня:
0 п2Е1. ч
ркр -р. (ж)
Определение приведенной длины стержня
Все случаи определения критической силы могут быть сведены к основному случаю шарнирно опертого стержня введением так называемой приведенной длины 0 (я:
п п2Е1 п2Е1 Е1 2Е1 10 1о
Рч1Г (18ЛЗ)
356
где 0 — приведенная длина стержня;
ау — коэффициент устойчивости, зависящий только от условий закрепления кондов; ау V2;
1 — коэффициент приведенной длины.
Решая соответствующее уравнение неустойчивого состояния, находим коэффициент устойчивости ауу зная который, вычисляем приведенную длину данного сжатого стержня конструкции:
и-
(18.14)
после чего находим приведенную гибкость для данного случая:
и
где I — радиус инерции при изгибе в данной плоскости. По приведенной гибкости можно определить коэффициент уменьшения допускаемого О
напряжения ф.
§ 93. УСТОЙЧИВОСТЬ СТОЕК СТУПЕНЧАТОГО СЕЧЕНИЯ И СТЕРЖНЕЙ С ЛЮБЫМИ ГРАНИЧНЫМИ УСЛОВИЯМИ
Стойки ступенчатого сечения при действии системы сосредоточенных сил
Задачу анализа устойчивости многоэтажной колонны переменного сечения со ступенчатым законом изменения сечения при действии системы конечного числа сосредоточенных сил, точки приложения которых совмещаем с точками оси стержня с резким изменением сечений (рис. 265), легко решить, применив наше обобщенное уравнение упругой линии для сжато-изогнутого стержня.
Последовательно идя от свободного конца стержня, находим выражения для угла поворота и момента в конце данного участка [12]. Для первого участка:
Ф1 Фо соз 01;
М12 —(р011015[пу01,
где у01 с01"-;
Е1 ох
С01
357
для второго участка:
, М12 81П VI©
Фг Ф1 СОЗ У12 у
И
12
а12
. 101
где а12 -г — отношение погонных жесткостей;
12
V -ЛГР» Р1.С гм- V Ям 12-
Принимая во внимание обозначение для а12, получаем:
ф2 ср1С08г12.а12,
м23 — Фх У12 81П У)2 М1г С08 У12. Аналогично для пн- (п -- 1) участка:
Мл.,, „ 8ШГ,и,л,
51П У12
фЛ фл-1 С05
01
01
П-1УП
Мп,п1 — — фл-1 I л-1,п 51П Vп-1,п ”Ь Мп-п С08 Vп-1,п•
ап-1, п
(а)
Переходим к последнему участку и составляем условие деформации для заделки. В данном случае, пользуясь выражением угла для четвертого участка, получаем
0
, М34 8Ш Г34
ф4 ф3 соз -г а34 — -И,
(б)
что после сокращения на ф0 дает так называемое условие продольного изгиба.
Решаем задачу численным способом. Задаваясь каким-либо значением г01, последовательно выражаем ф„ и Мп п1 через ф0, пользуясь приведенными цепными зависимостями метода начальных условий. Продолжая эти вычисления, приходим к последнему участку упругой линии, для которого составляем условие продольного изгиба по типу уравнения (б) в соответствии с характером закрепления. Это уравнение можно представить так:
ф0до,
откуда получаем условие продольного изгиба:
Дч 0. (в)
Если задавшись у01 получим Л, 0, следует увеличить V,), и наоборот. Аналогично поступаем для стержня, шарнирно опертого двумя
358
концами. Принимая за начальное неизвестное угол наклона ф0 на левой опоре, последовательно выражаем прогибы, углы наклона и моменты в конце данного участка (они же в начале следующего участка). Для последнего участка составляем условие равенства прогиба на правой опоре нулю, причем все члены этого уравнения будут содержать ф0. Отсюда, сокращая на ф0, получаем характеристическое уравнение.
Пример. Составить условие продольного изгиба для защемленного одним концом одноступенчатого стержня, подверженного действию двух сосредоточенных сил Р0 и Рх (рис. 266).
Решение. Составляем выражения для рх и М12:
ф1 Фо соз г0х;
12 — фМ101 Г01
и условие для заделки
, М12 зт г12 Л
вфСОЗ Ч12 -. —°,
г12 12
откуда получаем условие продольного изгиба
Фо (соз У01 СОЗ V2 — зт г01зт г12) 0
11212 I
или иначе после сокращения на ф0:
01 § Л,12 1 (Г)
Г12
Для двухступенчатого стержня 0—1—2—3:
ап г011§ г,2 V,, г23 а23 г0] г2Г) 1
12 23 а12 23
Стержень с любыми граничными условиями
Часто, рассматривая локальную потерю устойчивости (одного наиболее сжатого стержня), приходится решать задачу устойчивости прямолинейного сжатого стержня с упругими (на поперечное перемещение У1 и на поворот ф,) опорами (рис. 267, а). Для такого стержня, при¬
нимая установленное правило знаков, имеем следующие начальные условия:
I У лг—0 Уоу Л4оофо I У и-о Фо; Фо —коУо
где г0 — коэффициент осадки опоры на поворот ее (опорный момент, соответствующий ф0 1);
к0 — коэффициент осадки опоры на поперечное перемещение ее (опорная реакция, соответствующая смещению у0 1).
Граничные условия для правого конца стержня:
при I ух.1 у, Мд_, Оф,; при у’ и- ф ? — %;, ) ’
где гг и — те же коэффициенты осадки для правой опоры.
359
В соотношениях (е) приняты: угол наклона ф—по часовой стрелке, К1 — опорная реакция правой опоры. Имея два начальных параметра у0 и фо, выражаем (по уравнениям § 91), и ф,, а также Мг и Н1 через у0 и ф0 и получаем два однородных уравнения относительно начальных параметров у0 и ф0. Приравняв определитель этих уравне¬
ний нулю, получим характеристическое уравнение. Для стержня, жестко защемленного левым концом и упруго опертого правым концом (рис. 267, б; коэффициент осадки 6), характеристическое уравнение будет:
1 - а м
§ 94. УСТОЙЧИВОСТЬ СТЕРЖНЯ В УПРУГО СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ Стержепь конечной длины
В практике расчета башен и мачт на часто расположенных упругих опорах, а также верхнего пояса открытого моста нередко применяют упрощенную расчетную схему сжатого стержня в упругой среде. При постоянном сечении стержня и постоянном коэффициенте податливости упругой среды с (рис. 268, а), применяя гипотезу Винклера, можно получить точное решение задачи путем интегрирования соответствующего дифференциального уравнения.
Рассматриваем общий случай продольно-поперечного изгиба стержня на упругом основании; по концам стержня действуют осевые сжи¬
360
мающие силы 5, моменты М0 и Мь и поперечные силы ф0 и ф. Интенсивность распределенной реакции упругой среды при введении гипотезы Винклера (рис. 268, б).
Х СУ 9 (з)
где с — коэффициент осадки упругого основания.
Полагаем, что упругая среда может давать реактивное давление разных знаков. Принимая начало координат в центре свободного ле¬
вого стержня и учитывая влияние на изгибающий момент сжимающей силы 5 с плечом (у — у0), где у0 — начальный прогиб, получаем следующее его выражение:
X
Мх М0 Я0х — 8 (у—Уо) (и(х—и) йи, (б)
О
где 1и — интенсивность реакции упругой среды для сечения с текущей абсциссой и; 0 и х.
Выражение для поперечной силы (2Х и ее производной по х согласно выражению (б) имеют вид:
X
2хС1о — 8у (и1и; (в)
О
-8у" 1х -8у"-су. (г)
Дифференциальное уравнение упругой линии
-7м0 3о- — 8 (у — у0) 1и(х — и)йи.
б
361
Дифференцируя его дважды, получим
X
"[20-5 Ми;
у" ±(-8у"-су).
(д)
Имеем следующее дифференциальное уравнение упругой линии сжато-изогнутой балки в упругой среде при отсутствии активной распределенной нагрузки:
У Ш’ ГУО. (е)
Введя обозначения:
V 2Ё; 2 Ш получим окончательное исходное дифференциальное уравнение задачи
у 2уу"у 0. (18.15)
Решение этого дифференциального уравнения будет различно в зависимости от корней характеристического уравнения:
№ 2ук2 62 0. (з)
Корни этого уравнения
Ч2,3.4 ±1А— У±УУ2 б2 (И)
могут быть: 1) чисто мнимыми, сопряженными первой кратности, если у2 б2; 2) мнимыми, сопряженными второй кратности, если
V2 б2; и 3) комплексными сопряженными, если у2 С б2. Первый
случай соответствует гибким стержням на слабом упругом основании,
т. е. при малом значении б2. Чаще всего, однако, встречается третий
случай — достаточно жесткого основания (значительное б2).
Первый случай. При у2 б2 корни характеристического уравнения представим так:
к ±и7Я, (к)
где вещественные значения корней
71 — ЯзГу Ууг — б2;
7г — Я Уу— Уу2 — б2-
Решение дифференциального уравнения (18.15) будет
у Ах соз д1х В18Ш дхх А2 соз д2х В2 тд2 х, (18.16)
где Аъ В1У А2у В2 — произвольные постоянные. Для шарнирно опертого стержня в упругой среде, принимая во внимание граничные условия: при х 0, у0 0, у 0, а при, 0,
362
уI 0, получим условие неустойчивого состояния
51П дп1 0, (м)
откуда
Я л пл (н)
(п1, 2, 3, 4,.).
Подставляя значение из выражений (л) в первое выражение (ж), получаем следующее значение критической силы:
с п2Е1 [ о. а, ч
•кр— (°)
где а — коэффициент жесткости системы;
с4.
аШ1- п)
То же решение дает метод потенциальной энергии (по С. П. Тимошенко).
Если, например, Е1 4 • 105 т -ж2, 100 м с 360 тж2, то а 900, п 5, Ркр 34400 сг.
Второй случай. При у2 б2 корни характеристического уравнения
71,2. 3.4 ± У У- (Р)
Для шарнирно опертого стержня
81П 0
и критическая сила
5 гч
-кР— р • Iе;
Третий случай. При у2 б2 согласно выражениям (л) корни характеристического уравнения
Х1,2,3,4 ±]"— 7± Уу2 — б2
± КО,5 (6—7) ±1 КО,5-(8 -у) а 1‘Р,
где
а :± 0,5 (б — у);
р ±0,5(6 т). 1 (Т)
В этом случае интеграл дифференциального уравнения (18.15):
у А сЬ ах соз х А2 сЬ ал: зт 3х
Л3 зЬ ах соз р-1-Л4 зЬ ах зт рлс. (18.17)
Для шарнирно опертого стержня при действии только осевых сжимающих сил 5 (устойчивость первого рода) применяем условия, что при х 0, у0 0, го 0 и для правого конца
стержня, что при, уг 0, (Г 0.
При наличии начального момента М0 и начальной поперечной силы Со имеем начальные значения второй и третьей производной от у
Пользуясь решением (18.17) и подставляя начальные значения Уо Уо Фо» Уо и Уп » получаем следующие произвольные постоян-
Подставляя эти значения произвольных постоянных в решение
(18.17), получаем следующее уравнение упругой линии сжатоизогнутого стержня в упругой среде:
Пользуясь этим уравнением, можно провести деформационный расчет и анализ устойчивости стержня в упругой среде для различных случаев закрепления.
Найдя по уравнению (18.19) у" и применив граничные условия для шарнирно опертого стержня, получим при М0 О, С0 0 следующие характеристические уравнения:
что справедливо при наличии двусторонней реакции упругой среды. В случае одностороннего опирания на грунтовую среду второй член правой части формулы (18.22) следует отбросить.
Из выражения (18.21) можно получить
У0М0; Уо о—2уф0-
(18.18)
ные:
Уо» 2(5 2(36
у сЬ ах 81П Рл: зН ах соз Рл; ах 5п х
2Ш" (]Гах 8п х■■зЬадссоз Рх I. (18.19)
(18.20)
откуда
соз р 0
(18.21)
или
зН а 0.
(18.2Г)
Для критической силы из выражения (18.21)
РР, --2УсЕ1,
(18.22)
Ркр 2 УсЕ.
(18.23)
364
Бесконечно длинный стержень на упругом основании
Для сжатого бесконечно длинного стержня на упругом основании при наличии в начале координат усилий М0 и ф0, пользуясь уравнением (18.19) и применяя условие, что при х оо, у О, получаем следующее уравнение упругой линии:
, а. 0. _аХ 81П Влг
р зт Рх) ф0е
(18.24)
где начальные перемещения: ».1Г55(.-)
Фо 2у б
(18.25)
Перемещения беспредельно нарастают, если б—2 70, откуда и получаем критическое значение силы
Ркр УсЕ1.
(18.26)
§ 95. УСТОЙЧИВОСТЬ СОСТАВНЫХ СТЕРЖНЕЙ
Составные стержни, состоящие из отдельных ветвей, связанных планками или решеткой, обладают меньшей жесткостью, чем цельные. Решетка должна воспринять действие поперечной силы,
влияние которой можно учесть, введя выражение для угла сдвига соседних элементов
,, Фх. (мх
у— ОР — ОР Ох »
где х — коэффициент неравномерности сдвигов. Влияние поперечной силы для сжато-изогнутого стержня учитываем, принимая во внимание влияние «единичного» угла сдвига
[I
365
В результате этого учета критическая сила составного шарнирно опертого стержня может быть выражена по А. Ф. Смирнову так:
5кр 59—I—, (18.27)
КР 175 ’
где 5Э — критическая эйлерова сила для сплошного стержня;
5кр — критическая сила для составного стержня;
у — «единичный» угол сдвига от поперечной силы ф 1.
Для стержня с раскосной решеткой (рис. 269, а)
7 4(т-т Ь г—-—К (18.28)
г Е 1 7со52азша х
где — площадь сечения двух распорок (по двум плоскостям, параллельно оси У — У);
Ра — площадь сечения двух раскосов; а — угол наклона раскоса к оси.
Для стержня с планками (рис. 269, б)
М 2Ш (18.29)
12:р
где р — момент инерции сечения двух планок относительно оси 22 (при изгибе в вертикальной плоскости);
с — момент инерции сечения одной ветви стойки относительно оси 2Х2Х.
§ 96. УСТОЙЧИВОСТЬ МНОГОПРОЛЕТНОГО СТЕРЖНЯ НА ЖЕСТКИХ ОПОРАХ
Углы поворота стержня, не имеющего линейных смещений концов
Ниже рассматриваем задачи устойчивости стержневых систем при узловом действии нагрузки, когда сжатый стержень подвергается лишь действию сжимающей силы и концевых моментов.
Составим выражения для углов поворота по концам сжато-изогнутого стержня, подверженного действию опорных моментов М12 и М21 при одновременном приложении сжимающей силы 5. Направле¬
366
ния моментов М12 и М21 принимаем такими, при которых растянутые волокна оказываются снизу.
Полагаем, что концы стержня не получают линейных смещений (рис. 270). Углы поворота от моментов при действии осевой сжимающей силы находим из обобщенного уравнения; для определения угла поворота а1м от опорных моментов используем выражение (18.7) для ординаты упругой линии, предполагая действие лишь моментов М12 и М21:
кх — 81П кх
(а)
где
Л?21 — М12 С?ом
Ом » 4:0м •
Но при х, ухм 0, что дает при V к1
1—С08У М21 — М12 V— 81п л
к ) I- ) к,»■
откуда
а1м81П
Л12 I (1 — СОЗ V) V
V — ЗШ V
где 1 -— погонная жесткость стержня. Для угла а1м из выражения (б) получаем
(18.30)
Окончательно для углов а1м и а2м имеем
(18.31)
где и 5, — функции Жуковского (1918 г.):
(18.32)
При V 0 (сжимающей силы нет) функции 1, 5, 1.
367
Многопролетный стержень на жестких опорах (метод сил)
Рассмотрим многопролетный стержень со ступенчатым изменением момента инерции при постоянном значении его по длине данного пролета (рис. 271, а).
Продольная сжимающая сила меняется от пролета к пролету:
“Ь пЪ
5л2 Р п1 Р пу ч
Для искривленной формы стержня, соответствующей потере устойчивости (рис. 271, б), получим следующие опорные моменты:
Мл-1 МПУ Л4. п1
которые принимаем положительными соответственно рис. 271, в. Для основной системы —серии разрезных шарнирно опертых балок —
Рис. 271
составляем выражения для углов поворота у п-й промежуточной опоры п-го и (п 1)-го пролетов по формулам (18.31):
Ф _ Мп I -I Мп-1 5.
фл“зя ып Ч
(г)
3 п I 1 П1 б? 1_1 П
_. ”п1
Я п1 ’п1 6„1
По условию неразрезности стержня у п-й промежуточной опоры
ф п фп- (Д)
368
Подставляя выражения для р„ и цп по формулам (г), получаем Жл_1 2Мя( ) Мл1±1 0. (18.33)
п 1П 1П1 1П1
Это уравнение трех моментов искривленной формы равновесия многопролетного стержня на неподатливых опорах; функциональные множители
и п находят по формулам (18.32) в зависимости от продольной силы 5„ и жесткости Е1п для п-то пролета:
чп кп1п У §±-п-1п. (е)
Изложенный метод можно назвать методом сил (моментов), так как в качестве неизвестных искривленной формы приняты опорные моменты [12].
Составив уравнения трех моментов неустойчивого состояния, приравниваем, пользуясь соотношениями (18.33), определитель из коэффициентов при неизвестных моментах нулю — получаем характеристическое уравнение относительно неизвестного критического параметра V,, выражаемого через 8п по формуле (е). Все остальные V можно представить в зависимости от п.
Решая характеристическое уравнение, определяем критические значения параметра пу из которых выбираем наименьшее значение.
Заметим, что уравнение (18.33) для несвободных рам переходит в уравнение четырех моментов; для свободных рам в качестве дополнительных неизвестных вводим углы поворота стержней. Проще в этом случае применять метод перемещений (см. § 98 и 99).
§ 97. РАСЧЕТ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ ПРИ УЧЕТЕ ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ
Приближенное решение
Учет пластических деформаций в стержнях в виду сложности точного решения задачи обычно осуществляется приближенно, простым введением переменного касательного модуля, соответствующего упруго-пластическим деформациям. Имея критическое значение продольР1
ной силы 8кр 2 акрЛ найденное расчетом устойчивости по
упругой стадии, определяют приведенную гибкость стержня из формулы
1. (18.34)
где X— действительная гибкость стержня.
Пользуясь графиком акр X, находят критическое напряжение акр, 1. Таков приближенный способ учета пластических деформаций.
369
Однако сама критическая нагрузка зависит от закона изменения переменного модуля по оси сооружения. Вводя определенную для данного материала аналитическую зависимость между переменным модулем и критическим напряжением и задаваясь, последним в каком-то элементе сооружения, принятом за исходный, вычисляем основные параметры, входящие в характеристическое уравнение, и проверяем его тождественность. Найдем уточненное по сравнению с предыдущим значение а,.г1 (с учетом предложения Энгессера — Шенли) методом последовательных приближений. Получив из первого упругого расчета
из полной аналогии дифференциальных уравнений изогнутой оси весьма слабо искривленного стержня в упруго-пластической области, когда напряженное состояние полностью определяется осевым напряжением акр (рис. 272). К этому же предложению пришел американский ученый Шенли (1947), отметив, что при последовательном нагружении стойки с возрастанием силы при Р Ркр и осевом напряжении акр, соответствующим касательному модулю 1§а, происходит потеря устойчивости.
Модуль аналитически выражается для углеродистых сталей по предложению Шенли так:
Заметим, что эта формула является эмпирической, в ней сгт — предел текучести, апц — предел пропорциональности.
Подставляя это выражение Е в выражение (б), получим следующее квадратное уравнение относительно акр:
откуда и определяется уточненное значение критического напряжения в пластической области. Для мягкой углеродистой стали марки Ст. 3
б
устойчивости критическую силу для данного стержня, найдем
5кр ч2Е я 2Е
С другой стороны, критическое напряжение можно представить через касательный модуль Е( по Энгессеру — Шенли:
С
О
Упруго - пластическая область
Рис. 272
Упругая
оЬласть
Это решение было получено немецким ученым Энгессером (1891), исходя
(в)
(18.35)
370
(а, 235 Мнм2; апц 196 Мнм2) можно аппроксимировать уравнение Шенли (18.35) прямой в системе СИ:
стКр — 235 -
-О.ЗЭ Мнм2,
(18.36)
в технической системе единиц
акр 2400 -
кГсм2.
(18.37)
Имея указанное значение сткр для какого-либо исходного элемента сложной рамной или арочной конструкции 0—1, получим коэффициент
01
а01
01
01 01 ’
(г)
где а01 — первое значение критического напряжения;
101 — наименьший радиус инерции;
5о1 — продольная сила в стержне.
Тот же коэффициент для любого другого стержня будет
кп
Екп.1 кп
•I
кп
-1 °кп.
У Екп 1пк
(д)
Модуль Екп вычисляем по формуле (в) или (точнее) по (18.38) (см. ниже) по величине напряжения аАл, действующего в стержне кп.
Зная соотношение между усилиями 501, 8кп и площадями сечений Р01, Ркп, легко найдем выражения для всех кп через г01:
Vлл
кп
о
(е)
Еп,1
011 01
2
01 о1 01 Г 501 Екп I ьл
Далее проводим уточненное решение. Задаваясь ч01, вычисляем все кп и подставляя эти значения в характеристическое уравнение, проверяем его тождественное удовлетворение. Так, найдем критическое значение нагрузки в пластической области при переменности модуля. При этом может оказаться, что часть стержней сооружения работает в упругой, а часть в пластической области. Рассмотрим это на примере.
Пример. Определить критический параметр для ступенчатой стойки в упруго-пластической области работы ее (рис. 273).
Даны: соотношения между силами Рх — 2Р0 и размеры стойки — длины с01 с12 2 м моменты инерции сечений (минимальные) 01 3040 см4, 12 5450 сж4; площади сечений Р01 46,8 см2, Р12 98 см2; радиусы инерции 01 8,07 см, 12
10,55 см. Материал— сталь марки Ст. 3; отношение 1,792.
01
Решение. Действительные гибкости участков:
Рп Р г0 1
Рис. 273
Со, _ _200 _ ■»01 “8,07
к -С12 —
2 — —
200
12 10,55
: 18,925.
371
Ке зная критического параметра, предполагаем сначала, что потеря устойчивости происходит только в упругой области.
Применяем уравнение (г) § 93:
V», 8 V,, 4Ф- ■ — • — Г2 1.792
01 01 01 С12 0101 1
При заданных значениях моментов инерции
5- 294”“-
Характеристическое уравнение (г) § 93 в упругой области
1,294г01 1,792- 1,294 2,319, (ж)
откуда способом попыток получаем:
■у01 0,862;,12 1,115.
Теперь.в первом приближении упруго-пластического расчета определяем приведенные гибкости для участков стержня по формуле (18.34):
"нр ш‘24,7 90: 18.925 53,1.
По формуле (18.36) находим
а°‘ 235—0,39-90 200 Мнм11;
кр
акр2 : 235 —0,39 • 53,1 214 Мнм2.
По формуле Шенли (в) этого параграфа получаем Е01 0,99Е; Е12 0,75Е.
Теперь находим по формуле (е) новое соотношение между у12 и у01:
л ГЛ 1 0101 1 С01-.
2 1 I —п • ъ 1 1,581 г01-
г г0 С121 12
Характеристическое уравнение (г) § 93 принимает следующий вид:
1,5801 2,121. (з)
Решая его, получаем новые значения:
■Уо1 0,737; У].2 1,165.
Переходим ко второму приближению, определяя прежде всего приведенные гибкости:
“•"""(Щ- -24’7- № ""ШТ •8,95 - 50,5.
Верхний участок стержня — в упругой области, нижний — в пластической области. Теперь по формуле (18.36) находим
о™ 235 — 0,39 50,5 215 Мнм2.
По формуле (в) этого параграфа имеем
Е12 0,755Я.
Соотношение между параметрами
■12 1 0,755-1,792 1,49’У°1-
372
Характеристическое уравнение (г) § 93 принимает новый вид: 01 1,4901 0,755- 1,792 - 1,49 2,016.
Решая это уравнение [оно существенно отличается от уравнения (ж)], получаем
Критический параметр во втором приближении на 13% отличается от его значения, полученного методом упругого расчета.
Вместо эмпирической формулы Шенли (в) можно дать более точное решение задачи на основе изучения последовательного развития пластических деформаций агрегата монокристаллов, составляющих поликристалл. Если обозначить скорость роста пластической зоны по сечению (е) в зависимости от е е0, где е0 — деформация предела упругости, то для
выражения для площади пластической зоны и для касательного модуля будут следующие:
Принимая для (е) линейный закон (в области от е0 до ет), получаем:
для площади пластической зоны
р р во (в 8р)2
пл“ «т —во (ет-е0)2’
для касательного модуля
что заметно отличается от формулы Шенли (при X 60 значение Ет менее на 18%). Соответственно решению (18.38) имеем следующее выражение для а в упруго-пластической области:
о1 0,759; У12 1,131.
Точное решение
е0 е ет
е
Л.Л 5 I (е) °е; ЕГ Е (1 — Рпл).
(18.38)
(18.39)
При этом для стали марки Ст. 3
ет (3ах—2а0).
(18.40)
373
Задавшись (после первого расчета Хг) по формуле (18.37) значением о и решая кубическое уравнение (18.39), находим е, которое вносим в уравнение (18.38), определяя Ет.
§ 98. ВЫРАЖЕНИЯ КОНЦЕВЫХ МОМЕНТОВ СТЕРЖНЯ ЧЕРЕЗ УГЛОВЫЕ ДЕФОРМАЦИИ
Основным методом при анализе устойчивости сложных систем является метод перемещений [4].
Выделим какой-либо стержень рамы после ее искривления, вызванного потерей устойчивости в данной плоскости.
Для применения метода перемещений составим выражения углов поворота касательных по концам сжато-изогнутого стержня от действия концевых моментов при учете действия продольной силы 512 и наличия взаимного смещения концов стержня на величину б (рис. 274).
Обозначим фх и ф2 углы поворота касательных к изогнутой оси, отсчитываемые от первоначального положения оси стержня; 012 — угол поворота хорды 1—2, вызванный смещением концов стержня; аг и а2 — углы поворота касательных к изогнутой оси, отсчитываемые от хорды 1—2.
Применяем особое для метода перемещений правило знаков: углы О и ф считаем положительными при вращении по часовой стрелке; концевые моменты М12 и М21 — положительными при действии их против часовой стрелки; углы и а2 — положительными по направлению положительных концевых моментов, т. е. при вращении против часовой стрелки. На рис. 274 отмечены положительные направления указанных углов поворота и концевых моментов.
В соответствии с видом изогнутой оси стержня имеем следующие соотношения между углами ф, 0 и а:
ф1 012 — а1; ф2 012 — а2. (а)
Углы поворота и а2 от действия концевых моментов М12 и М21 с учетом влияния сжимающей силы на искривление можно получить
374
по формулам (18.30):
(б)
где ь12 — погонная жесткость стержня. Согласно выражениям (18.32):
— 3111 V
(в)
V2 8111 V
Подставляем выражения углов и а2 из формулы (б) в соотношения (а):
Это основные выражения, устанавливающие соотношения между углами поворота концевых касательных фх и ф2 стержня сжато-изогнутой рамы (при наличии жестких прикреплений обоих концов стержня) и концевыми моментами М12 и М21, а также углом смещения 012.
Решив уравнения (г) относительно моментов М12 и М21, получим выражения моментов через деформации:
Приведем выражения (д) к виду, более удобному для использования таблиц, обозначив функциональные множители при Фх12, ф22» 61212 соответственно 2ау, 2(3,, 2у, тогда окончательно получим
Мы получили выражения концевых моментов стержня рамы через основные деформации с учетом влияния сжимающих сил на искривление. В формулах (18.41) функции 2а„ 23,, 2уV имеют следующие значения:
М12 — — — “Ь ф2 — 12 (а )]I
V V
(д)
М1 — [фаа рА — 012 (а, М-
41
Мц — 212 (фха, ф2р, — 012у,); М1г — 2г12 (ф2а, фхР, — 012уч)-
(18.41)
а,
Ь,
После подстановки в выражения (е) значений функций и из выражений (в) получим
V — V
а„
21
2 81П V
2182-г
V — 81Г1 V
уч а,-)-РуЕсли сжимающей силы нет, то
(ж)
0; ач
Ь
6 ;
а, 2; рч1; у, 3
и выражение для момента М12 принимает обычную форму М12 — 12 (4ф 2ф2 — 6б12).
Таблицы функций, определяемых выражениями (ж), приведены в работах Н. В. Корноухова и А. Ф. Смирнова [4,8].
Для стержня, жестко прикрепленного одним концом и шарнирно опертого другим, момент М21 в месте прикрепления может быть представлен так:
М21 (ф2 12)» (18.42)
где основная функция влияния сжимающей силы
1 V2 V
а„ —
V—V
(з)
§ 99. УРАВНЕНИЯ МЕТОДА ПЕРЕМЕЩЕНИЙ ДЛЯ СЖАТО-ИЗОГНУТЫХ РАМ
Основная система
Ниже рассматривается расчет плоских р-ам на устойчивость при узловом действии нагрузки. В первом приближении продольные силы в стержнях рамы находим по недеформированной схеме рамы так же, как и для многопролетных стержней на упругих опорах.
Распространение метода перемещений на случай рам. со сжатоизогнутыми элементами производится подстановкой более общих соотношений между моментами и перемещениями с учетом влияния ежимающих сил (см. § 98).
В качестве основной системы применяем шарнирную схему балок — кинематическую цепь. Такая схема удобна для рам со смещающимися узлами, так как позволяет применить общую форму дополнительного уравнения, полученного по началу возможных перемещений. При расчете рамных систем, имеющих наклонные элементы, можно сократить число неизвестных, входящих в дополнительное урав¬
376
нение, составляя сумму работ заданной нагрузки, концевых моментов и моментов продольных сжимающих сил на виртуальных перемещениях кинематической цепи.
Для получения основной системы от рамы с жесткими узлами (рис. 275, а) переходим к совокупности балок, опертых на узлы ста¬
тически определимо, причем для сжатых стержней принимаем один конец опертым шарнирно неподвижно, другой — шарнирно подвижно (рис. 275, б), но продольное перемещение конца считаем равным нулю.
Жесткое прикрепление концов стержней к узлам заменяем концевыми моментами, например, для стержня 1—2 моментами М12 и М21, которые принимаем положительными при действии их против часовой стрелки. Продольное закрепление подвижного конца стержня в узле
377
возмещаем продольной силой, например в узле 2 силой 312. В выражение для работы силы сжатых стоек при взаимном смещении их концов войдут продольные силы 5 (дающие момент пары 56), концевые моменты и местная нагрузка, приложенная к данному стержню.
Основные уравнения метода перемещений
На основе предварительного расчета рамы находят соотношения между продольными силами 5Л. Принимая в качестве неизвестных углы поворота узлов фл и углы поворота хорд изогнутых стержней 0Я, составляют основные и дополнительные уравнения для отыскания этих перемещений.
Основное уравнение метода перемещений выражает условие равенства нулю суммы моментов, действующих на узел к (см. рис. 275, б):
%Мкп 0. (а)
Для элемента рамы с жесткими узлами после подстановки выражений (18.41) основное уравнение принимает вид:
1’йЛау 2 2 фл1йяр„ — 2 2 Вкч1кпУч 0. (18.43)
Для элементов рамы, сходящихся в жестком узле к и с шарнирными связями в противоположных узлах, основное уравнение после подстановки в него выражения (18.42) будет
ФА 1] 1кпкп® (18.44)
Дополнительные уравнения метода перемещений
Составление дополнительных уравнений по принципу виртуальных перемещений основной системы — кинематической цепи — позволяет исключить деформационные поперечные и продольные силы, возникающие в стержнях рамной конструкции с наклонными элементами. Дополнительные уравнения содержат лишь концевые моменты, вычисленные с учетом влияния сжимающих сил, деформационные моменты пар продольных сил 56, нагрузку и осевые продольные силы.
При деформационном расчете сжато-изогнутой рамы методом перемещений снова используется основная система в виде кинематической цепи. Рассмотрим общий случай рамы с наклонными элементами (см. рис. 275, а).
Основная система для заданной рамы с жесткими узлами изображена на рис. 275, б: на каждый сжатый стержень в смещенном положении действуют осевая сила 8пк и концевые моменты МкП9 Мпк. Противоположно направленные воздействия следует представить действующими на узлы (моменты не показываем; узловые давления на рис. 275, б изображены пунктиром). На рис. 275, в показано вирту¬
378
альное состояние кинематической цепи; г)лА — виртуальный угол поворота стержня п — к. Работа осевых сил 8пк воздействия на стержни на возможных перемещениях, определяемых углами может быть представлена выражением
пФппкпк»
Помимо работы осевых сил 8пк (что ясно видно из рис. 275, б, в) часть узловых давлений 8пк также совершает работу на составляющих 8упк виртуальных перемещений узлов.
Узловые давления 8пк не производят работы только в том случае, если соответствующие узловые диски смещаются по нормали к направлениям сил 8пк (в данном случае силы 8п и 5д4 не производят виртуальной работы, сила же 8 ее совершает). Таким образом, в общем случае для рамы произвольного очертания, кроме работы пар сил 8пкВпк1пк необходимо в уравнение начала возможных перемещений включать виртуальную работу осевых сил 8пку действующих на узловые диски основной системы. Заметим, что если система симметрична и симметрично загружена, а многоугольный контур рамы имеет четное число сторон, то при обратносимметричной форме возможных перемещений в случае анализа устойчивости первого рода для рам и арок виртуальная работа узловых давлений на оси симметрии равна нулю.
В общем случае, кроме работы осевых сил 8пку воздействующих на сжатые стержни, следует ввести еще работу узловых давлений
Ц5М.
За положительные принимаем: концевые моменты Мпк против часовой стрелки, действительные углы бпк и виртуальные углы г)пк поворота стержней по часовой стрелке.
В связи с особым правилом знаков для концевых моментов дополнительное уравнение виртуальных работ, как условие равенства нулю возможной работы концевых моментов Мпку моментов пар смещенных продольных сил 8пквпк1пк, узловых давлений 8пк и нагрузки Р(, представится применительно к схемам рис. 275, б, в в форме
2 8пкЪпк1пкпк — 2 Щпк Мкп) пк 2 2 Р16р1 0у (18.45)
где первый член левой части представляет возможную работу моментов пар осевых сжимающих сил, второй — работу концевых моментов, третий — виртуальную работу узловых осевых давлений и последний — виртуальную работу нагрузки.
Подставляем в уравнение (18.45) выражения концевых моментов через деформации: углы поворота узлов ср и углы поворота стержней 0.
Решая указанные уравнения относительно углов ср и 0, находим эти углы, а затем определяем концевые моменты.
Использование уравнений виртуальных работ (18.45) избавляет.от необходимости вводить в расчет узловые поперечные силы и деформационные продольные силы в стержнях статически неопределимой системы. Можно составить столько уравнений, сколько степеней свободы шарнирной схемы рамы в отношении • линейных смещений ее
379
узлов. Каждую картину возможных перемещений получаем, придавая угол поворота ) 1 какому-либо независимому стержню шарнирной схемы и полагая углы поворота всех остальных независимых стержней равными нулю. Составив все основные и дополнительные уравнения, получим при узловом действии нагрузки систему однородных уравнений. Отличные от нуля значения угловых перемещений ср и 0 будут в том случае, если общий определитель из коэффициентов при неизвестных системы основных и дополнительных уравнений равен нулю:
Д (18.46)
Решая это характеристическое уравнение относительно параметра
V продольных сил, находим критическое значение параметра.
Пример. Найти критическое значение нагрузки для симметричной бесшарнирной рамы 12 «01 ПРИ обратносимметричной форме искривления (рис. 276, а). В этом случае будет наименьшее значение критической нагрузки.
Решение. Для обратносимметричной формы имеем два неизвестных: угол поворота узла фх и угол смещения 0О1. По основной системе в стойке находим два концевых момента; по формулам (18.41) получаем
—«1о (ф1 • 2аю — 6012710); 1 М01 — 1ю (ф1 • 2Рю — 001 • 27ю)
Момент в ригеле
Мц — 6ф1‘12.
Согласно основному уравнению метода перемещений (а)
Мц Мю 0.
После подстановки выражений моментов находим
Ф1 аЮ “Ь 3 —001710 (в)
01
где осю и ую — функции от у01.
380
Для исключения 601 составляем дополнительное уравнение, используя уравнение (18.45) и основную систему (рис. 276, б):
(01®01Ь) • 1 — (Мю М01) • 10.
Подставляя выражение
с 0101 01—““
и значения концевых моментов из выражений (б), находим окончательно
ф17ю — 601(2710 — 0.5у51) 0. (г)
Приравняв определитель системы уравнений (в) и (г) нулю, получим уравнение неустойчивого состояния
(аю зИ(2ую-0,5г11) у1о.
101
Решая это уравнение при 12 101, находим
7 2,717.
Критическое значение нагрузки для данной обратносимметричной формы
Р -7’37 Е1
кр —“дг01-
§ 100. ОПРЕДЕЛЕНИЕ КРИТИЧЕСКИХ НАГРУЗОК ОДНОПРОЛЕТНЫХ СИММЕТРИЧНЫХ МНОГОЭТАЖНЫХ РАМ
Анализ устойчивости однопролетных симметричных многоэтажных рам при симметричном загружении проводим при помощи одного уравнения неустойчивого состояния, представляя все концевые моменты у узлов нижнего ригеля рамы —1 через угол поворота фх (рис. 277, а) и применяя способ функциональных множителей. Возможность составления одного уравнения неустойчивого состояния имеет большое принципиальное значение, так как при приближенном расчете многопролетную многоэтажную симметричную раму можно расчленить на однопролетные равноустойчивые рамы. Характерно, что для свободных однопролетных рам узловые моменты выражаются при этом только через углы поворота узлов ф и не содержат углов смещений 0 [12].
Рассматриваем обратносимметричную форму отклонения оси рамы (см. рис. 277, а). Поэтому дополнительные моменты по концам каждого ригеля равны по величине и одинаковы по направлению. Выделяя любую часть рамы горизонтальными разрезами у узлов стоек, из условия равновесия отсеченной части рамы получаем, что нормальные реакции со стороны узлов рамы на концы стоек равны нулю.
Проведя разрез рамы у нижних концов стоек 1—0, получим из условия равновесия 0 поперечную силу от опорных моментов, равную нулю:
где индекс 7 указывает на то, что речь идет о поперечной силе от опорных моментов данного стержня.
381
По разрезу рамы у нижних концов стоек 2—1 из рассмотрения равновесия верхней отсеченной части найдем
Вассмотрим теперь стержень 1—2 стойки рамы в основной системе (рис. 277, б). По концам стойки действуют моменты М21 и М12 и продольные силы 512; опорная поперечная сила в стержне равна нулю.
В этом случае угол смещения легко исключить, выразив его через концевые моменты. В самом деле, уравнение равновесия моментов для стержня 1—2 дает
Для ригеля 2—2 (рис. 277, в) для обратносимметричной формы упругой линии получим:
М22 — Ы22ц2.
Для случая сжатой стойки, упруго заделанной обоими концами, дадим выражения для углов поворота срх и ср2 через концевые моменты
I
Рис. 277
561 — МХ2 -- М21,
откуда
(а)
382
и для концевых моментов через углы фх и ср2 (рис. 278). Принимая начало координат в узле 1, составляем выражение для изгибающего момента в пройзвольной точке:
Мх — кЕI [пкх М12 со кх;
при х к изгибающий момент Мх —УИ21, откуда — М21 — фгкЕ1 §1П V М12 С08 V,
где кЕ1 IV.
Из уравнения (б) получаем
и аналогично
ф
ф2
Мл
М«
" IV V
Мп
’ V V 1 IV 31П V
Мл
(б)
(в)
(г)
Решая эти уравнения относительно концевых моментов, получаем выражения для концевых моментов упрощенного способа перемещений:
Л12 -
1 Г§ Ф1
М 21 -(Ф2
(18.47)
Как и следовало ожидать, выражения концевых моментов М12 и М21 не включают углов смещений 6 (см. рис. 278) [4].
383
Остановимся теперь на случаях стоек рамы нижнего этажа, заделанной или шарнирно опертой в узле 1.
1. Стержень,
жестко заделанный в узле 1 и упруго заделанный в узле 2. Из формулы (18.47) при 0 получаем (рис. 279, а):
т __ V Фз—,
‘ ф2»
(Д)
(е)
(ж)
2. Стержень, опертый в узле го заделанный в выражений (г) и (в) при (рис. 279, б):
Ф- ”
Ф1
м2
IV V
мп.
IV 5111 V ’
шарнирно 1 и упруузле 2. Из М12 0 имеем
(з)
(и)
М21 П?ф2 V ГУфх 81П V. (К)
Эти выражения применяем для составления уравнений неустойчивого состояния однопролетных рам и в особых случаях равноустойчивых рам по отношению к многопролетным рамам. При использовании выведенных формул, очевидно, полностью отпадают дополнительные уравнения способа деформаций.
Пример. Найти критическое значение нагрузки для двухэтажной рамы (рис. 280). Погонные жесткости всех стержней одинаковы. Рама в деформированном виде изображена на рис. 277.
Решение. Применяем упрощенный способ деформаций. По выражениям (ж) и (18.47) для концевых моментов имеем: для стоек:
УИ1о_‘ф1:
. ( V V
М12 — I I т ф1 : ё V 81П V
М21— I
для ригелеи
Ми — бф, Условия равновесия узлов и 2 будут
ф1
М2 2 — — бГф2.
2V
Приравняв определитель из коэффициентов при неизвестных углах и р2 нулю, получаем уравнение неустойчивого состояния:
Решая уравнение (л) способом попыток, находим
V 2,272.
Критическая нагрузка
V2ЕI _ 5,15Е1 КР“ к2 к2
§ 101. УСТОЙЧИВОСТЬ ПЛОСКОЙ ФОРМЫ ИЗГИБА ПОЛОСЫ
Чистый изгиб полосы
При определенном значении поперечной нагрузки, действующей на тонкостенные балки, последние могут выпучиться из плоскости изгиба — возникает изгибно-крутильная форма потери устойчивости. Рассмотрим сначала простейшую за¬
дачу об устойчивости плоской формы изгиба полосы с узким прямоугольным поперечным сечением под влиянием изгибающих моментов М, действующих в вертикальной плоскости УХ и вызывающих явление чистого изгиба (рис. 281, а). Такая полоса при некотором особом критическом значении моментов М может потерять устойчивость плоской формы изгиба, т. е. искривиться в боковом направлении с одповременным скручиванием. Получается изгибно-крутильная форма
13 Н. К. Снитко
385
потери устойчивости, возникающая при малой боковой жесткости полосы и отсутствии промежуточных закреплений, препятствующих этой форме деформации.
Критическое значение моментов найдем, предполагая, что при наличии в вертикальной плоскости пар М происходит незначительное пространственное искривление полосы, сопровождаемое скручиванием; из дифференциальных уравнений равновесия, как обычно, находим критическое значение моментов М. Составляющие ординаты упругой линии в вертикальной плоскости обозначим через V, а в горизонтальной плоскости — через и. Угол закручивания полосы на расстоянии х от начала координат обозначим 6 и будем его принимать положительным по часовой стрелке (что соответствует вращению сечения в направлении от оси 1 к оси У). Используем две системы координатных осей: первоначальную систему осей 2, У и X, связанную с главными осями сечения и осью полосы до деформации, и вторичную подвижную систему осей I, т] и выбранную так, что оси I и г направлены по главным осям сечения после его поворота, а ось принята по касательной к искривленной оси полосы (рис. 281, б).
Таким образом, вторичная система осей координат смещается и поворачивается в связи с пространственной деформацией полосы. При составлении дифференциальных уравнений равновесия разложим вектор момента М на три составляющих вектора, соответствующих моментам относительно осей т) и С, е. ММ и Мс, причем, так как перемещения V, и и 0 малы, то пренебрегаем малыми высшего порядка, считая соз 0 1 и соз а 1, где а — угол наклона касательной к проекции упругой линии на горизонтальную плоскость 2Х:
йи. ч
а Шс а)
Дифференциальное уравнение упругой линии в вертикальной плоскости имеет обычный: вид:
Вгё-М. (б)
г, г? йг3 где Е "у2 — жесткость полосы относительно оси 2.
Составим теперь дифференциальные уравнения бокового изгиба и скручивания полосы. Обозначим
.
12
В2 Е-Т7Г
— жесткость полосы при боковом изгибе и примем, что кривизна в плоскости IX имеет то же значение, что и кривизна в переменной плоскости — С- Моменты относительно осей т и С как составляющие полного момента, вызванные деформацией, обозначим соответственно Мп и Мг Тогда дифференциальное уравнение бокового изгиба при пренебрежении малыми второго порядка примет вид:
Вг% Мг (в)
386
Проектируя вектор момента М на оси г) и 5 (рис. 281, в) получаем МГ1 М 81П 0 МО.
Таким образом, дифференциальное уравнение бокового изгиба имеет следующий вид:
В ЪМ. (г)
Характерно, что это уравнение содержит угол закручивания б.
Дифференциальное уравнение скручивания полосы, если относительный угол закручивания обозначить, по теории кручения будет
-«• «
где М: — переменный по длине стержня крутящий мо¬
мент относительно оси С 01 а — жесткость при кручении;
О — модуль сдвига;
-1—0,63 — момент инерции кручения для сечения по л осы.
Крутящий момент М легко находим непосредственно по рис. 281, б, проектируя вектор момента М на оси и
М: — М §ш а — аМ или, учитывая выражение (а)
М, §М. (е)
Подставляя выражение (е) в (д), получаем дифференциальное уравнение скручивания полосы в окончательной форме:
п йЬ йи ЛА. ч
СТХТХМ- (ж)
Дифференцируя обе части последнего уравнения по а: и йсключая при помощи уравнения (г) производную и"х, находим
Введем обозначение
г РЪ _ М2
С йх2 Во
М2
тогда дифференциальное уравнение скручивания при наличии бокового изгиба будет
ахг - кь- (и)
13 387
Мы получили однородное дифференциальное уравнение для деформации при потере устойчивости плоской формы изгиба. Заметим, что рассматривается задача о потере устойчивости первого рода.
Общее решение для угла закручивания 0 находим из уравнения (и):
б Ах 81П кх А2 соз кх.
Предполагая, что на концах полосы (л; 0 и х ) угол закручивания равен нулю, получим, что потеря устойчивости полосы возможна, если
§ш к1 0, (к)
откуда по наименьшему корню находим согласно выражению (з) критическое значение момента:
Мкр уКв. (л)
Критическое значение момента УИкр зависит от произведения наименьшей жесткости при изгибе В2 на жесткость при кручении С и от длины стержня. При малых длинах (наличие ребер жесткости) следует проверять возможность появления пластических деформаций.
Действие сосредоточенной силы на двухопорную балку прямоугольного сечения
Аналогично решается задача о критическом значении вертикальной сосредоточенной силы Р, приложенной в центре тяжести среднего поперечного сечения балки на двух шарнирных опорах, если сечение балки — узкий прямоугольник. Составив подобные уравнениям (ж) и (з) дифференциальные уравнения бокового изгиба и скручивания и используя то же решение в бесконечных рядах, получают следующее критическое значение нагрузки:
Ркр Ув. (м)
ГЛАВА 19. ОСНОВЫ ДИНАМИКИ СООРУЖЕНИЙ
§ 102. ВИДЫ КОЛЕБАНИЙ
При рассмотрении динамического действия нагрузки, меняющейся со временем и вызывающей заметные ускорения движения элементов сооружения, будем учитывать возникающие силы инерции, скорость движущейся нагрузки и кинетическую энергию, передающуюся сооружению при ударе. Различают кратковременно приложенную нагрузку, когда продолжительность действия ударной нагрузки т мала по сравнению с периодом собственных колебаний сис-
388
темы Т если -т Т) или продолжительную динамиче-
(■
4
скую нагрузку если
Все динамические нагрузки вызывают колебания, т. е. движения, обладающие известной повторяемостью. Колебания различают: 1) в зависимости от наличия динамической нагрузки; 2) по виду деформаций, возникающих при колебаниях; 3) в зависимости от учета сил сопротивления; 4) по виду функции отклонений при колебании; 5) по характеру закона изменения восстанавливающей силы при колебании; 6) в зависимости от числа степеней свободы. Частые колебания нередко называют пульсацией.
По первому признаку колебания подразделяют на собственн ы е, которые совершаются при отсутствии непрерывно действующей силы, под влиянием какого-либо начального воздействия, и вынужденные, характерные непрерывным действием возмущающей силы. По второму признаку (по виду деформаций) различают продольные, поперечные и крутильные колебания. Нередко встречаемся со смешанными и з г и б н о - к р утилбными колебаниями (пространственные системы). По третьему признаку имеем затухающие и незатухающие колебания. По виду функции отклонений при вибрации различают периодические и непериодические колебания. Периодическими колебания называют в том случае, когда каждое значение отклонения повторяется неограниченное число раз через равные промежутки времени, называемые периодом. Если восстанавливающая сила при вибрации линейно зависит от отклонения, имеем линейные колебания; если эта сила нелинейно связана с отклонением, возникают нелинейные колебания (например, колебания в упруго-пластической области работы конструкции, колебания при больших отклонениях и др.). По числу степеней свободы различают системы с одной степенью свободы (одна точечная масса для балки), со многими степенями свободы (ряд точечных масс) и с бесчисленным количеством степеней свободы (распределенная масса по длине стержня).
Рассмотрим в качестве примера собственные продольные колебания стержня, на конце которого подвешен груз весом Р т§, где т — масса груза, —ускорение силы тяжести. Имеем систему с одной степенью свободы, поскольку состояние ее вполне определяется вертикальным перемещением груза (рис. 282, а). Отклонение центра массы груза, вызванное каким-то начальным воздействием, для произвольного момента времени I обозначаем у. При этом отклонении воз-
§ 103. СОБСТВЕННЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
Отклонение при колебании. Частота
389
никает упругая сила Руп, которая возвращает груз в состояние равновесия и потому называется восстанавливающей силой. Полагаем, что
а) I)
связь между силой Руп и динамическим перемещением у та же, что и статической задачи:
Уст Р6, (19.1)
где б — перемещение точки приложения груза от действия единичной
силы Р 1 в данном случае б
Е — модуль продольной упругости;
Р — площадь сечения).
В случае консоли, несущей груз на свободном конце (рис. 282, б),
где — момент инерции сечения балки.
Выражение (19.1) можно представить так:
У РТ (19-2)
откуда получаем выражение для силы Р, соответствующей упругому перемещению уст:
Р суст, (19.3)
где с — жесткость системы, т. е. сила упругости, соответствующая перемещению, равному 1.
Из сравнения выражений (19.1) и (19.3) имеем:
с4- (19.4)
390
В процессе колебаний отделяем груз и прикладываем, кроме восстанавливающей упругой силы Руп су и силу инерции по Далам-
беру:
н — ту".
Составляя условие равновесия для сил Руп и н, получаем
РУп-н 0. (19.5)
Очевидно, при этом был использован метод перемещений. Подставляя значение сил, находим
су ту 0, (19.6)
где у" — ускорение при колебании.
Деля обе части выражения (19.6) на т и обозначая
получаем дифференциальное уравнение собственных незатухающих колебаний системы с одной степенью свободы без учета сопротивлений
" ю2 0, (19.8)
где со — круговая частота собственных незатухающих колебаний системы.
По Международной системе единиц (СИ) масса т имеет раз-
н • сек2
мерность —-—.
Пусть в начальный момент времени при 0 начальное отклонение у0 и начальная скорость у0 известны. Интегрируя дифференциальное уравнение (19.8) по методу начальных условий, получаем решение для отклонения у в произвольный момент времени:
л. 8Ш л г г
уу0соа) V0—— (19.9)
— начальное отклонение умножается на соз со, начальная скорость —
8Ш Ш
на (интеграл от соз со).
Это решение можно представить в более сжатой форме, введя замены:
у0 АпХ; А соз Я. (19.10)
Подставив эти соотношения в выражение (19.9), получим
у А зтЯсозоо Л соз К зш со _(19.11)
или иначе
у А зт (со А). (19.12)
391
Уравнение (19.12) выражает процесс чисто периодического собственного колебания системы.
Напомним связь между периодом и частотой. Если для первоначального момента времени I отклонение у, то и для момента времени
1
1 1 со
ИЛИ
со 2 л
по уравнению (19.12) получим то же отклонение. Поэтому период колебаний, т. е. время, в течение которого совершается одно колебание, будет
Г. (19.13)
Если Т — время одного колебания (в 1 сек совершается -
Т 2к
колебаний, то в 2я сек будет происходить со колебаний, почему со
и носит название круговой частоты (в отличие от техничес-
1 кои частоты V — I.
Для круговой частоты со по выражениям (19.3) — (19.6) имеем:
Пример. Определить круговую частоту колебаний балки на двух опорах, несущей груз Р 0,981 кн посередине пролета, если I 1 м Е 1,962 10б Мнм2; I 8-107 ж4.
Решение. Находим жесткость системы с:
48Е1 48 • 1,962 • 10» • 8 • 10“» _,
с —7— 7,534 Мн м 7534 кнм.
I6 1Л
По формуле (19.14) круговая частота
лГё ЛГ 7534-9,81 0_. 1;
“У « У -ода-276 х,сек•
Метод инерционной нагрузки
Рассмотрим сначала систему с одной степенью свободы (см. рис. 282, б). Применяя принцип Даламбера, отклонение у при свободных колебаниях можем получить как результат действия силы инерции
н и, следовательно, в линейной области
у 1аЬ. (а)
Подставляя выражение силы инерции
1а — — ту", (б)
392
получаем дифференциальное уравнение свободных колебаний:
у — ту" б, (в)
что совпадает с выражением (19.6). В данном случае был применен метод сил.
Подставим теперь в уравнение (в) решение (19.12):
у у° зш (со Я), (г)
где у0 А — амплитуда колебаний.
Имея в виду, что у" —со2°5т (со А,), вместо уравнения (в) получаем
у0 зт (со К) тсо20 зт (со К) б или после сокращения
у° (т(й2у°)8. (д)
Но согласно выражению (б) величина та2 у0 есть значение максимальной силы инерции:
н.макс 1г тсо V. (19.15)
Таким образом, для максимального отклонения при колебании получаем
у° г1 б. (19.16)
Амплитуду колебаний можно получить как перемещение, вызванное статическим действием максимальной силы инерции (рис. 283):
2Х тсо2у°.
2тсо2у°
у
1
1
2
2
Рис.
283
Составляя по формуле (19.16) выражение для перемещения у0, получаем уравнение (д); после сокращения на у°9 находим
1 тоо2б,
откуда и получаем квадрат круговой частоты
1
СО
тд
(19.17)
§ 104. СОБСТВЕННЫЕ КОЛЕБАНИЯ СИСТЕМЫ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ
Метод инерционной нагрузки
Рассмотрим собственные поперечные колебания балки или рамы, несущей я точечных масс (рис. 284, а). Отклонение центра каждой массы можно получить как результат действия системы сил инерции 1н,
393
2Н Л)Н ••• 1п
У1 11н®11 1-1Н12 Ь • • • Н“ пнш"’ Уг 1 1н21 12нб22 ••• ян2я
(19.18)
Уп — 1н®я1 “Ь 12ня2 Н" пяпп •
При составлении уравнений в этом случае использован метод сил.
Подставляем выражение каждой силы инерции 1н — щу, 2„ — ?;2г2,., —т„уп и частное решение системы дифферен¬
циальных уравнений вида:
У1 У 5Ш (со Я.); у2 — у1т (© Я,);
упупйп («о А),
(а)
полагая, что все отклонения происходят в одной фазе. Тогда после сокращения на 1п (со к) приходим вместо выражений (19.18) к соотношениям:
У со26и щувЧ1г. тпуппа)281п;
У Ш1У®2вгх т2г2б22 уЪ т2у1а26п2 тпуЪиЧгп-, тпу°паЧпп.
(19.19)
Мы получили систему линейных однородных алгебраических уравнений относительно амплитуд колебаний у9 у, у°п. Конечные зна-
394
чения эти амплитуды имеют лишь тогда, когда определитель системы уравнений равен нулю. Объединяя члены с одинаковыми амплитудами, вместо соотношений (19.19) получаем
(т1со2б11 — )у т2(о2612 • • • тпа281пу°п 0; тЬпу] (т2со2б2г — 1) у. т„со2б2л 0;
тха)2бп, у щай8п2у1. (т„о26яп — 1) 0.
(19.20)
Уравнение частот находим, приравнивая определитель системы
(19.20) нулю. Так получается частотное, или вековое, уравнение, которое оказывается алгебраическим уравнением п-й степени относительно со2. Корни этого уравнения находим или способом попыток, или графическим способом, или способом А. Ф. Смирнова.
Заметим, что уравнениям (19.19) можно придать силовой характер, выделив максимальные инерции:
тгу°2;
22 я202;
(б)
2п гппу°п(й2.
Тогда вместо уравнений (19.19) получим
У -2x6ц 22612 • • • У 621 22б22.
(19.21)
Каждую амплитуду колебания сложной системы узловых масс можно получить по принципу наложения как результат действия системы максимальных сил инерции (рис. 284, б).
Система с двумя степенями свободы
Для системы с двумя степенями свободы вместо уравнений (19.21) имеем
Уи — “Ь 2б12,
У%1 — %121 222 или, подставляя силы инерции [см. также систему (19.20)]
(т2бп —1)1 т2со28125 0; ) тх(2821уи (тасо2б22 — 1) 0.
395
Приравняв определитель системы уравнений (в) нулю, получим
(т2би — 1) (т2со2б22 — 1) т1т2(йъ О
или, раскрывая скобки после приведения,
со4пхт2 (бцб22 — б) — со2 (т1811 т2822) 1 0. (19.22)
Обозначая й 8п822 — 6;2; В т1б11 т2622, вместо уравнения
(19.22) получаем
со4т1т20 — со2В 1 0, откуда для со2 находим
шкщ [В±Ув-40тхт2]. (19.23)
Получаем два значения частоты: низшую сох и высшую со2. Для вычисления со корень квадратный в выражении (19.23) берется со знаком «минус», для со2 — со знаком «плюс».
Главные формы колебаний
Общее решение системы дифференциальных уравнений собственных колебаний складывается из частных решений вида (а). Так, для системы с двумя степенями свободы путем сложения влияний двух форм получим
У У и 51П («М 1) 41-2 51П (®2 1
у2 °2) 3111(0 ) 4- 1ЗШ(С02 Я2). Каждой форме отвечает своя частота колебаний; уи у — частные амплитуды колебаний, соответствующие первой форме колебаний
с частотой сог (рис. 285, а) уъ Ум — частные амплитуды колебаний, соответствующие второй форме колебаний с частотой со2 (рис. 285, б). Под главной формой колебаний понимают ту форму отклонений системы, соответствующую данной частоте, для которой 51П (со, А,) 1.
Следовательно, каждую из главных форм можно получить как деформированный вид от системы максимальных значений сил инерции: для первой формы
— от сил, изображенных на рис. 285, а, для второй формы — от сил, представленных на рис. 285, б. Главные формы взаимно
°)
т,ьу°
тгшу1
Пербая
форма
п
У 2%
г У
Оу
и0
щ
Уц —
У°21
Вторая
формо
ЧЫгУ,?
Рис 285
о9б
ортогональны (возможная работа сил первой формы на перемещениях для второй формы равна нулю). Амплитуды уи уъ а также фазы Хг и находятся из начальных условий. Амплитуды уЧп и у%2 легко выражаются через у°п и у% из любого уравнения (в) следующим образом:
у1 _ т1с°1и 1. УЬ _ т1п — 1
уЪ т2(0] 612 ’ уо т2со;;6 12
Эти отношения называются характеристиками форм и обозначаются Р21 и Р22 соответственно.
§ 105. КОЛЕБАНИЯ РАМ. ПРИВЕДЕННАЯ МАССА Частоты собственных колебаний рам
При определении частот свободных колебаний рамной системы с распределенной массой по длине каждого стержня достаточно точным является метод стержневых масс. Обычно равномерно распределенную массу каждого стержня рамы сосредоточиваем в середине длины стержня. Рассматривая деформированный вид оси рамы, устанавливаем
число степеней свободы системы по количеству возможных перемещений центров масс. В ряде случаев возможно упростить картину перемещений; так, в обратносимметричной форме колебаний рам можно отбросить вертикальные перемещения в ригелях и учитывать лишь горизонтальные перемещения.
Пример. Найти низшую круговую частоту колебаний двухшарнирной симметричной рамы, полагая жесткость Е1 и погонную массу т постоянными (рис. 286, а), а I к.
Решение. Рассматриваем обратносимметричную форму колебаний рамы, которая дает низшую круговую частоту колебаний. Используя обратносимметричность формы отклонений и разрезая раму по оси симметрии, получаем схему по рис. 286, б с горизонтально подвижной опорой для конца ригеля. Пренебрегаем про¬
397
дольными деформациями стержней рамы, а также вертикальными перемещениями точек ригеля 6 Тогда приходим к системе с двумя степенями свободы: масса тг
— тк имеет амплитуду горизонтальных колебаний масса т2 — т у имеет
амплитуду у%. Это состояние максимальных перемещений «вызывается» силами инерции:
21т1со2у1.
22 т2со2-
Обозначая
я202,
получаем
ху1; 2 0,5 ху.
По рис. 286, б составляем уравнения (19.21):
У1 хуЬц ЪМуАъ у ху[Ьг10, Ьху1Ь.
Приравниваем определитель системы из коэффициентов при у и у1 нулю:
(дгбц-1) 0,5л:612 0
21 (0,5x622—1)
Развертывая определитель, получаем
0,5я2 (бцбгг — 62) — х (6ц Ь 0,6622) “” 1 0. (а)
По правилу перемножения эпюр находим
А 5 А3 А Л3 Л 5 Л3 — 24 ‘ Е1 ’ 22 2Е1 ’ 12 _ 16 ’ ЕГ
Подставим эти значения в выражение (а) и, обозначив
хк
Е1 ’
получим уравнение
522-70421536 0.
Решая это уравнение, находим
гх 2,218; г2 138,52.
Низшая круговая частота колебаний будет
1,489 ЛГШ
Щ яГ
Приведенная масса
Для приближенного решения многих динамических задач применяют метод приведения масс, который заключается в приведении системы, имеющей п степеней свободы, к подобной же системе (по очертанию и упругим свойствам), но с одной степенью свободы. Это необходимо для вычисления приведенной маес ы тпр, т. е. той сосредоточенной массы (взятой в определенной точке
398
приведения), при введении которой данная система получает ту же частоту колебаний, что и действительная. Конечно, при такой замене не достигается полного подобия действительных масс и приведенной массы.
Отношение приведенной массы тпр к полной массе системы называется коэффициентом приведения:
пр —
пр т
Часто, не зная точного значения частоты, приведенную массу получают, приравнивая кинетические энергии действительной и приведенной систем. Найдем выражение приведенной массы через точное
значение круговой частоты сот, полагая его известным из частотного уравнения типа (19.22). Приравниваем точное значение частоты сот к значению частоты системы с одной степенью свободы, имеющей приведенную массу в выбранной точке а:
т пР 1Л — л —к—, V тпр У тпраа
(19.24)
где даа — единичное перемещение для точки а от действия силы 2а 1. Из выражения (19.24) находим выражение для приведенной массы:
тир —
(19.25)
Имея точное значение круговой частоты колебаний и единичное перемещение, определяем тпр.
Пример. Найти приведенную массу системы для обратносимметричной формы колебаний рамы (рис. 287, а), используя результат предыдущего примера. Решение. Единичное перемещение по эпюре Мх (рис. 287, б)
ь - Н3 аа2В1 ’
399
Точное значение квадрата частоты по формуле (б)
2_ 1,4892 Е1 _ 2,22 Е1_
0)7 г4 т Н4 Ш
Приведенная масса по выражению (19.25)
71Пр — тттё 0,901 шН.
Коэффициент приведения для данного случая (рамы)
тп0 0,901йЛ
пр — -гтТ- °,6. (В)
пр т,ЬтН у
Коэффициент приведения для балки на двух опорах
Апр 0,493. (г)
При этом -приведенная масса предполагается сосредоточенной посередине пролета (см. рис. 283). Для консоли с грузом на свободном конце (рис. 282, б)
кп р 0,243.
§ 106. ВЫНУЖДЕННЫЕ ПЕРИОДИЧЕСКИЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ. РЕЗОНАНС
Система с одной степенью свободы
Разберем сначала общий случай действия любой возмущающей силы Р, на систему с одной степенью свободы (рис. 288), вызывающей вынужденные колебания. В качестве примера рассмотрим продольные колебания стержня, причем не будем принимать во внимание затухание. В произвольный момент времени отклонение центра массы т будет у, которое является искомой функцией времени.
Выделив груз, к которому приложена возмущающая сила Ри учтем еще наличие восстанавливающей
силы Руп и силы инерции н. Составляем динамиче¬
ское условие равновесия по методу перемещений:
Руп-1а-Р 0. (19.26)
Подставляя выражения сил
Руп су у I н ту
и деля все члены уравнения (19.26) на т, находим
у" Л 1 Р(. (19.27)
Мы получили дифференциальное уравнение вынужденных незатухающих колебаний системы с одной степенью свободы. Здесь со2 —-, где со — частота собственных колебаний.
400
Рассмотрим теперь частный случай действия периодической синусоидальной силы (вертикальная составляющая центробежной силы от неуравновешенности двигателя):
Р Р0 8Ш0, (19.28)
где Р0 — постоянная амплитуда силы;
0 — частота изменения возмущающей силы.
Дифференциальное уравнение колебаний при подстановке значения Р( из выражения (19.28) и обозначении
Ро— т
будет
у" --2у р0 зт 0. (19.29)
Общий интеграл этого дифференциального уравнения, как известно, равен
У 1П0 —-8ШЮ). (19.30)
Это решение удовлетворяет дифференциальному уравнению (19.27). Множитель при скобке правой части обозначим С:
с щ- 19-31)
Решение (19.30), выражающее отклонение при действии периодической синусоидальной силы, представится так:
у С ш 0— С-- зт со. (19.32)
Заметим, что первый член правой части с переменным множителем 51П0 соответствует чисто вынужденным колебаниям с частотой самой
0
возмущающей силы 0, а второй член с множителем — шсо—вынужденным колебаниям с г частотой собственных со. Иногда второй член называют выражением «свободных» колебаний.
Анализ показывает, что с течением времени колебания с частотой собственных («свободные» колебания) затухают и для этого установившегося процесса движения можно пренебречь вторым членом уравнения (19.32), ограничиваясь чисто вынужденными колебаниями. Итак, имеем
гС51П0, (19.33)
где С — амплитуда чисто вынужденных колебаний (наибольшее динамическое перемещение). Величину амплитуды чисто вынужденных колебаний по выражению (19.31) представим так:
Р° - Р° 1 -Уст—,,ТстЦ, (19.34)
т( 0)2 — 02) 720)2 02 Уст д2
О)2 0)2
где Уст — статическое перемещение, вызванное силой Р0
401
1 — динамический коэффициент, показывающий, во сколько раз динамическое перемещение больше статического.
Динамический коэффициент установившихся периодических колебаний по выражению (19.34) равен
-□?• (19-35)
По мере увеличения частоты возмущающей силы 0 и приближения ее к значению со (рис. 289) динамический коэффициент нарастает. В случае
6 0) (19.36)
динамический коэффициент х становится бесконечно большим:
[Д, сю.
Этот случай совпадения частот 0 и со соответствует резонансу.
Явление резонанса весьма опасно для сооружения, поскольку в области резонанса наблюдается значительное увеличение амплитуд колебаний. Поэтому, чтобы резонансная область не оказывала влияния на сооружение, должно быть
0 0,8со
— формула расчета на резонанс.
При 0 со чисто вынужденные колебания и 1 имеют отрицательное значение; выше рассмотрен график абсолютного значения ц (кривая, рис. 289). При учете затухания в зоне резонанса получают конечные,
402
но весьма значительные величины амплитуд (кривая, рис. 289). Заметим, что как только перемещения становятся значительными, уравнение, из которого найдено решение, теряет силу и необходим учет затухания.
Учет затухания
В случае учета сопротивлений динамический коэффициент
Ц ■ 1 ■ (19.37)
л е2а, Ле202 У (‘-р) 4г
где е гсо — коэффициент затухания; к находят экспериментальным путем; для стальных конструкций к 0,02 -г- 0,08.
В случае резонанса (б со) динамический коэффициент
2е
(19.37)
Сведя сложную систему к системе с одной степенью свободы и применив формулу (19.37), легко учесть явление затухания.
Определение амплитуд вынужденных колебаний методом инерционной нагрузки
Рассматривая случай установившихся вынужденных незатухающих колебаний, определяем отклонение при колебании как результат действия возмущающей силы и силы инерции (рис. 290, а):
У(Р 1 „)«,
где б — единичное перемещение.
Подставляя выражение силы инерции, получаем
уР1-ту")Ь. (19.38)
Рассматривая при действии периодической силы
Р( — Р051П Ы
чисто вынужденные колебания, подставляем решение
У У° 31П0,
причем где у° -
У" — °02 8Ш Ы, амплитуда колебаний; получаем вместо выражения (19.38) у0 зт 0 (Р0 зт 0 у°02т зт 0() 6. (19.39)
403
Сокращая обе части выражения (19.39) на зтб, находим
У° (Ро У0Ъ2т) б. (19.40)
Но у°в2т — максимальное значение силы инерции. Вводя это
обозначение, получаем
у (Р0 г1)6. (19.41)
Амплитуду чисто вынужденных периодических колебаний можно получить как результат статического действия амплитуды силы и максимальной силы инерции 2г у°2т (рис. 290, б).
Из выражения (19.40) имеем
о РоЬ Ро
у°г —1-у
со2
что совпадает с выражением (19.34).
§ 107. ВЫНУЖДЕННЫЕ ПЕРИОДИЧЕСКИЕ КОЛЕБАНИЯ СИСТЕМЫ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ
Применим изложенный выше метод инерционной нагрузки к системе с п степенями свободы. В качестве примера рассмотрим балку, несущую п точечных масс (рис. 291, а).
Изучается действие периодической силы Рг Р0тЪ причем ищем решение для установившегося процесса чисто вынужденных колебаний, когда каждое перемещение центра точечной массы можно представить выражением
уг у 51П 0, (а)
где у — амплитуда колебаний.
Применяя принцип Даламбера, вводим силы инерции ь 2,., 1п и каждое перемещение находим по принципу наложения, используя
404
метод сил:
У 11111 212 4" • • • Ал Р р
у2 I 1621 222 • • • I П2П Р 2р
(б)
Уп 11®л1 1П2 • • • Iппп РАр,
где 6Л1, бя2,., 8пр — единичные перемещения. Подставляя решение (а) и значения сил инерции:
. П-02 81П Ы,
а также
и сокращая уравнения (б) на т0 получаем
Каждое перемещение у°п в его амплитудном значении можно получить как результат действия системы максимальных сил инерции 21у 22у 2п и силы Р0 в ее наибольшем значении; значения сил 2г
Систему уравнений (19.42) можно представить, объединив члены с одинаковыми амплитудами:
Р1 Р §1П Ы
У°1 т1г;е2611 т2у1Ъ2 б12. Я0б1р; у ШхуЧы т2уЬ2Ь22 4-. -)- Р082р;
(19.42)
21 т1[02; 2,2 т2у62;
(19.43)
2п — тпу%62.
М2? («и — 2612612 • • • РсАр 0;
тф2у (Ь22 —. Р062р 0;
405
Подставляя обозначения сил 2, из выражений (19.43), получаем систему канонических уравнений для максимальных сил инерции:
11—“Ь • • “Ь %п1п Р01р 0;
121 4" 2 (22 02 ) “Ь • • • "Ь %п§2п Р()§2р Ф _ тф (19.44)
%1п1 22бп2 • • • бпл — тр) °®ЛР Решая эту систему уравнений при заданном значении 0, отличном
от частот собственных колебаний,©,-, находим конечные значения максимальных сил инерции 2.
0) Р1 Рг
ЛА—ЛЛЛЛ ■ »■
В случае если частота возмущающей силы 0 совпадает с какой-либо из частот собственных колебаний а, имеем явление резонанса — неограниченное нарастание амплитуд кблебаний. Найдя из системы канонических уравнений (19.44) все силы инерции 2, строим эпюру моментов в состоянии наибольших отклонений (рис. 291, б), пользуясь формулой
ЛСум Мрв :Е2,УЙ,. (1945)
Затухание приближенно можно учесть методом приведения масс.
Пример. Построить эпюру моментов в состоянии наибольших отклонений при действии на раму обратносимметричной системы вибрационных сил (рис. 292, а).
406
Число оборотов двигателя в минуту: п 250. Амплитуда возмущающей силы Р 5 кн. Размеры рамы Н 4,35 ж, Е1 449-103 кн-м2у погонная масса ригеля и стойки т 0,025 кнСек2м2.
Решение. Переходим к расчетной схеме по рис. 292, б, учитывая обратную симметрию в форме колебаний. Массы стержней тг и т2:
т1 т1 0,025 • 4,35 0,1088 кн • сек2м
т2 т 2 0025 • 0,0544 кн • сек2м.
Низшая частота собственных колебаний
1,489 ЛГШ 0_. 1
(01 —— у — 35,4 1 сек.
Частота возмущающей силы
9 -250 26,17 1сек.
Канонические уравнения (19.44) для данной системы (рис. 292, в)
1 11 — 02 ) 12 Р1Р 0;
121 ( б22 — тф) 2р
По примеру § 105, имеем
(Г)
Шп 17,149; Е622 41,156;
Е161г № 25,723;
10
РЕ1 б1р Р№ 25.723Р;
РНб2р 41,156Я;
-г 62,512; --125,024.
Л02 т2 в2
Решая уравнения (г), получаем
2Х 1,023 Р; 22 0,805 Я.
Эпюра моментов изображена на рис. 292, в.
Узловой динамический момент будет
Мдин 2,316 ЯЛ,
а узловой статический момент Таким образом, динамический коэффициент л 2,316.
§ 108. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ ПРИ ДЕЙСТВИИ НЕПЕРИОДИЧЕСКОЙ НАГРУЗКИ
Общее уравнение вынужденных колебаний
Рассмотрим случай незатухающих колебаний системы с одной степенью свободы при действии возмущающей силы по степенной функции
Р( Ро РоГ Р --- Р°П)Ш- 19-46
407
Составим общее выражение для вынужденных колебаний в этом случае по методу начальных параметров.
Считаем для простоты, что в начальный момент масса груза находится в покое и потому отклонение в произвольный момент времени зависит исключительно от возмущающей силы. Это отклонение будем называть чисто вынужденным ув у. В случае если в начальный момент масса не находится в покое, полное отклонение упол будет
У пол Уев “Ь Ув Уев У
где первый член — выражение свободных колебаний, вызванных начальным отклонением и начальной скоростью:
, 8Ш со
св о СОЗ Ы V0--.
Расчленение полного отклонения на два слагаемых — свободного и вынужденного закономерно в силу линейности дифференциального уравнения колебаний. Для получения выражения ув у составим дифференциальное уравнение чисто вынужденных колебаний.
Выделим массу т, к которой непосредственно приложена возмущающая сила Р, и составим дифференциальное уравнение колебаний согласно уравнению (19.27):
(а)
Интегрируем это дифференциальное уравнение по методу начальных параметров при следующих начальных условиях: при О
уго 0, у0 0. (б)
В результате интегрирования уравнения (а) получим
Р0 1 — С08 СО. Р0 СО—■81П ©А.
У т со2 у т со3 ”•
ж (С05••• 5 — (19-4?)
о
ЦП)
где условимся обозначать — М — г-кратный определенный
о
интеграл от нуля до функции:
(19-48)
Р09 Р(), Р[п) — начальные параметры возмущающей силы.
При помощи уравнения (19.47) решаются различные задачи дина¬
мики системы с одной степенью свободы. При наличии затухания функция Аь включает влияние сопротивления и ее вид меняется.
408
Действие постоянной по времени силы
Считаем, что при I — О приложена постоянная сила Р( Р сопз. Так как все производные Р равны нулю, то в уравнении (19.47) следует сохранить лишь первый член и потому отклонение
Р 1 — созсо, ч
Ут——- (В
Р
Учитывая, что псо2 с и, кроме того, — уСТ, получим окончательно
У Уст( 1—созсоО (19.49)
— система колеблется по синусоиде относительно положения равновесия (уср уст). При л, макс 2уст.
Действие мгновенного элементарного импульса
При I О прикладывается внезапно сила Р, после чего при 6,1 сила Р внезапно снимается. Имеем случай действия элементарного (мгновенного по времени действия) импульса АР
йР Р Н. (г)
По методу учета скачков в нагрузке после действия импульса при произвольном I имеем:
ЛуШ(1 _008 — Ш [ -со8 ® VШтМ з1п ы
или, подставляя значение Р из выражения (г), находим
, йР зт со 1Л СЛЧ
(19-5°)
Мы получили формулу для элементарного перемещения при действии мгновенного импульса йР. Отклонение, как видим, меняется по закону синуса.
Действие мгновенного конечного импульса
Пусть импульс конечной величины Р0 приложен в начальный момент времени почти внезапно (Д очень мало). Тогда динамическое перемещение
19.51)
409
Действие любой возмущающей сосредоточенной силы
Рассмотрим теперь действие любой возмущающей сосредоточенной силы приложенной к данной массе. Предполагаем, что закон изменения силы Р( в зависимости от времени известен (рис. 293).
Найдем выражение для отклонения у центра массы в момент времени
считая, что динамическое давление приложено в начальный момент времени 10 0.
Для отыскания перемещения в момент применим принцип наложения, определяя перемещение у как результат действия системы бесчисленного количества элементарных импульсов
йР Р(11) Л1
и используем решение (19.50). Выделим промежуточный момент времени и определим влияние импульса йР на перемещение в момент I за интервал времени ( — 1Х) отсюда согласно решению (19.50)
Р Цг) Н §ш со (? — х) т со
йу-
(д)
Полное же отклонение как результат действия всех элементарных импульсов будет найдено интегрированием:
Увш 5 — )сИи (19.52)
О
где 1г — текущее значение независимого переменного.
Эта формула предложена проф. И. М. Рабиновичем для решения различных динамических задач [7].
§ 109. УДАР ГРУЗА ПО СООРУЖЕНИЮ Общее решение
Будем рассматривать систему с одной степенью свободы, считая, что приведенная масса балки т2 (рис. 294, а) сосредоточена в месте удара падающего груза массой тг. Явление удара характерно быстрым уменьшением скорости движения ударяющего тела с момента первого его контакта с балкой до установления скорости, соответствующей конечной местной деформации в области контакта. Пренебрегая последней, будем считать, что ударяющее тело является абсолютно жестким и ударяемое тело не получает местных деформаций. Итак, рассматривается «абсолютно жесткий удар», но само сооружение считается упругим. При таком предположении явление удара будет считаться проис¬
410
ходящим мгновенно: скорость V1 падающего груза в начальный момент контакта мгновенно уменьшается до скорости V0, являющейся общей начальной скоростью движения груза и балки (общей массой М т1 т2). Заметим, что скорость соответствует высоте падения к:
V У 2§Н.
В момент встречи груза и балки, приведенная масса которой т2, к сооружению мгновенно присоединяется масса груза т1 — сразу же после встречи груза и балки устанавливается общая скорость их движения V0. Скорость и соответствует моменту времени I 0, который принимаем за начало оси времени. Для упрощения анализа удара считаем, что после встречи груза с балкой обе массы перемещаются, не отделяясь друг от друга (неупругий удар). Полагаем, что в конструкции возникают только упругие деформации.
Дальнейшее движение системы общей массой М т1 т2 представляет собой колебание от действия приложенной постоянной силы Р (рис. 294, б), причем начальной скорости соответствует мгновенно приложенный импульс Р0, который можно представить, как передающееся от груза балке количество движения:
Р0 тг.
Начальную скорость движения системы находим из закона сохранения количества движения, считая, что до удара балка находилась в покое.
Массу и скорость груза перед ударом обозначим тл и приведенную массу балки т2 тпр.
Приведенная масса есть та точечная масса в месте удара, которая заменяет действительную распределенную массу; ее находят из условия динамической эквивалентности масс, например, по равенству частот или по равенству кинетических энергий данной системы и системы сприведенной массой.
Для определения V0 напишем, что количество движения перед самым ударом равняется количеству движения непосредственно после удара:
72 (тх Н- т2) Vо,
откуда
тх 4- т2
VI
(19.53)
411
Но т1 т2 М — общая масеа балки и груза, поэтому начальная скорость
_т1у1
у°— м АГ (19.54)
Уравнение движения системы после падения груза на балку, считая у0 О и принимая во внимание схему рис. 294, б, можно написать по нашей обобщенной формуле
81П О) Р л,Л Гг
д(1-созсо0, (19.55)
где частота собственных колебаний системы
1956
Заметим, что по выражению (19.54)
_ ШхУх _ Ру±со СОУх
со Мсо §Мсо2 ст §
Внося это выражение в уравнение (19.55), получаем
У Уст 5Ш со 1 — С08 (О) устц„ (19.57)
где переменный по времени динамический коэффициент при ударе
51п со 1 — соз со.
Теперь легко найти тот момент времени для которого получим максимум 1Ы.
Найдем максимальное значение динамического коэффициента 1маКс» дифференцируя л( по :
ф С02Ух,. Л
СОЗ (01 4- (О 81П (010,
(И ц 11 1 откуда
Из этого уравнения определяем 1и соответствующее [ямакс. Из формулы (19.58) находим:
соз со 1
8
81П(01
С01
V
У[Т.
412
Внося в выражение (19.57) эти значения зт и соз после преобразований находим:
Ц»акс Цд1 1 )2- (19-59)
Представим теперь 1)2 через к и отношение
йюЛ2 С02У? Р 2Н __ 2Н 71
Т ёг Муст 8 -ум-
Для наибольшего значения динамического коэффициента при ударе окончательно получаем следующее выражение:
». •,“ «9-М)
Таково выражение хд с учетом массы конструкции.
В формуле (19.60) Сп? — приведенный вес сооружения; фпр т, где т2 — приведенная масса балки.
Если т2 оо, то М оо и динамический коэффициент при любой высоте падения равен двум (массивная стенка). Определив наибольшее значение динамического коэффициента, находим динамическое напряжение
О дин МдОсТ
Конечно, к динамическому напряжению от падающего груза прибавляем статическое напряжение от собственного веса сооружения. Заметим, что учет массы сооружения имеет существенное значение.
Из формулы (19.60) видим, что с увеличением уст при прочих равных условиях уменьшается. При Л 0, что соответствует внезапному действию силы, ыд 2. С возрастанием к значение динамического коэффициента быстро увеличивается.
Общее решение в форме (19.55) дает возможность решать различные задачи и, в частности, задачу о действии повторных ударов, когда новый удар может произойти в произвольный момент времени, не соответствующий максимуму перемещения от первого удара.
Формула (19.60) конечно применима как при поперечном, так и при продольном ударе. Ею часто пользуются в практике расчетов на удар.
Приведенные массы
Для расчета балки на поперечный удар груза в среднем сечении балки на двух опорах, пролетом, в случае распределенности массы балкиее приводят к центру удара — посредине пролета. При этом так называемая «приведенная», т. е. сосредоточенная, динамически эквивалентная распределенной, масса будет
т2 0,493л, где л — масса единицы длины балки.
413
Для защемленной балки при приведении массы к свободному ее концу
т2 0,243я.
Для приближенного решения сложных динамических задач часто применяют метод приведения масс. Он состоит в замене
системы со многими степенями свободы системой с одной степенью свободы с приведенной массой тпкр в заданной точке сооружения к (рис. 295, а). Приведенной массой будем называть такую сосредоточенную массу п”Р, для которой полученная система с одной степенью свободы динамически эквивалентна заданной системе со многими степенями свобо-
м0ч
р
Рис. 295
Рис. 296
ды. Условие эквивалентности можно выбрать в форме равенства кинетических энергий. Для системы со многими степенями свободы:
2Гд 25
(19.61)
где VI — скорость точки приложения г-тои элементарной массы. Для системы с одной степенью свободы
2 тт1
Приравняв выражения (19.61) и (19.62), получим:
тпкр-
(19.62)
(19.63)
Однако выведенной формулой (19.63) воспользоваться затруднительно, так как неизвестны скорости движения точек 1, 2,., к. Приближенно отношение скоростей заменяют отношением единичных пере¬
414
мещений, вызванных статическим действием силы Рк 1 (рис. 295, б). Тогда окончательно получим
тР б(19.64)
Пример. Найти приведенную массу, помещая ее на свободном конце в случае распределенной массы, погонное значение которой т сопз (рис. 296). Балка защемлена одним концом.
Решение. Пользуемся формулой (19.64), считая 6,, кк Ук — перемещения (прогибы ) от силы Р 1.
Имеем:
_ 2 _3_ 3
Ух 2Е1 6Е1 Ук ЪЕ1 ’
I
С _ 0,0262ш’
ту (Е1)2 ’
1 9 (Ер
У 1° ■
Приведенная масса по формуле (19.64)
тР 0,236т.
Точное значение приведенной массы для этого случая
тпр 0,243т,
где пг1 — масса всей балки.
§ 110. ПОПЕРЕЧНЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ С РАСПРЕДЕЛЕННОЙ
МАССОЙ
Общий интеграл дифференциального уравнения собственных колебаний
Рассмотрим задачу о свободных колебаниях балки с распределенной массой, предполагая, что малые колебания ее происходят в главной плоскости изгиба и размеры поперечного сечения незначительны по сравнению с длиной стержня.
Считаем, что ось балки прямолинейна и масса ее распределена по заданному закону:
где т — погонная масса балки;
р — вес единицы длины балки;
§ — ускорение силы тяжести.
Так как рассматривается случай малых колебаний, можем применять обычные соотношения теории изгиба балок и, в частности, приближенное дифференциальное уравнение упругой линии. Пусть под влиянием какой-то причины балка получает в момент времени смеще-
(
415
ние в вертикальной плоскости (рис. 297). Ординаты динамической упругой линии балки д будут функцией двух независимых переменных — абсциссы л; и времени :
где у отсчитывается от положения оси балки в ее статическом состоянии. При таком движении балки каждый ее бесконечно малый элемент находится под действием: 1) сил упругости, возникающих при поперечном динамическом изгибе; 2) сил инерции, приложенных к каждому элементу и пропорциональных ускорению движения.
Для данной системы с бесконечным числом степеней свободы вертикальное отклонение произвольной точки балки будет сложной гармонической функцией времени и абсциссы. Внутренние силы — динамические моменты и поперечные силы также будут сложными функциями от двух независимых переменных л; и I.
Выделяя бесконечно малый элемент балки, ограниченный двумя сечениями (см. рис. 297), представим действие ееотброшенных частей в момент времени внутренними силами Мх, 3 и
Кроме того, на элемент действует сила инерции, при вертикальном смещении равная
При этом ввиду малости углов поворота сечений не учитываем влияния инерции поворотов сечений и сдвигов их. Проектируя все силы, действующие на элемент, на вертикальную ось, получаем
Рис. 297
416
Подставляем выражение для 11 и делим на 6х
Щ- тШ0-
Но поперечная сила связана с моментом известным соотношением
П -дМ
Чх— дх •
Подставляя это соотношение в уравнение (а), получаем
дМх. ду Л дХ2 тдр
Теперь воспользуемся дифференциальным уравнением упругой линии балки при чистом изгибе:
ду _ Мх дх2 “ ЯГ»
откуда
тх — п1 дх2.
Подставляя это выражение в уравнение (б), получаем следующее дифференциальное уравнение поперечных колебаний балки при переменном сечении ее:
— (е1
дх2
Щт0- (в
Это приближенное дифференциальное уравнение поперечных колебаний балки с распределенной массой.
Рассмотрим далее балку постоянного сечения, т. е. Е1 соп1. Деля обе части уравнения на ту окончательно находим
0 (г)
д№ т дх "
Вместо бесконечной системы обыкновенных дифференциальных уравнений имеем одно линейное дифференциальное уравнение в частных производных 4-го порядка. Здесь у — функция двух независимых переменных х и I.
Так как дифференциальное уравнение (г) линейно, то линейная совокупность частных интегралов этого дифференциального уравнения также будет его решением. Общий интеграл этого дифференциального уравнения получим как сумму отдельных решений его:
00 оо
5Е91 Е(х, I), (д)
1 1
где — частное решение дифференциального уравнения (г) или выражение так называемой -той формы колебаний.
Применяя метод Фурье, представим каждое частное решение в виде произведения двух функций, полагая первую зависящей только от ху а вторую — только от I:
уХ (х) 7 (0. (е)
ла14 Н. К. Снитко
417
Выражения частных производных, входящих в дифференциальное уравнение (г):
—у (х Т (0. т а () ч
—Л х) ж • дх 1 V № Частные производные функции у представлены через полные производные функций Т и X. Подставляя выражения (ж) в дифференциальное уравнение (е), находим
М? П1®-0. (3)
Отсюда можно получить следующее равенство отношений:
Е1 Ах4 йР „ ч
Левая часть равенства (и) зависит только от х, а правая часть выражена только в функции от, и все же имеем постоянное равенство этих двух различных функций от отдельных переменных. На основании этого считаем, что как левая, так и правая часть равенства (и) не зависит соответственно от л: и I и потому каждая из них равна постоянному числу. Обозначим это постоянное отношение со2.
Таким образом, вместо равенства (и) получаем
5 ®гГ0; (к)
(ИХ О т V А Ч
(л)
Перейдем теперь к решению дифференциальных уравнений (к) и (л). Интегрируя первое дифференциальное уравнение (к), аналогичное уравнению для свободных колебаний системы с одной степенью свободы, находим
Т () А1 зш (со,- X), (м)
где А — постоянная;
со — частота свободных колебаний для г-той формы.
Решим второе дифференциальное уравнение, применяя метод начальных условий. При постоянной массе и жесткости — величина
постоянная и уравнение (л) в известной степени аналогично дифференциальному уравнению упругой линии для балки на упругом основании, но с изменением знака перед у на обратный.
Подставляя в выражение (е) решение (м), получаем
У1 А1Х (х) 81П (СО; Я) ЗШ (СО; X), (й)
где
уь А(Х(х).
Если для функции X (х) соблюдается дифференциальное уравнение (л), то и для у1 имеем аналогично
3?-(тг)- °
418
Найдя решение дифференциального уравнения (о), получим уь из выражения (н) и полное решение из выражения (д). Очевидно, если
51П (,• X,-) 1,
то I-тая форма колеблющейся балки дь становится равной ус.
У1 Уг 1-,
т. е. -тая форма колебаний обращается в функцию лишь абсциссы х, не зависит от времени и дает амплитуды ординат упругой линии. Поэтому у1 будет выражением нормальной формы колебаний, т. е. выражением формы изогнутой оси, которая соответствует значению
81П (С0 ) 1.
Можем отметить, что полное решение дифференциального уравнения свободных колебаний
, §1. 1 о
д(2 т дх
следует искать в форме
Я («. М. (19.65)
I 1
где -тая нормальная форма колебаний определяется из дифференциала ного уравнения (о).
Обозначая
(н)
окончательно получаем дифференциальное уравнение для вместо уравнения (о):
Йг-,-0. (р)
где уь — функция лишь абсциссы х.
Интегрирование дифференциального уравнения нормальной формы колебаний
Для получения уравнения ь-той нормальной формы колебаний балки применяем метод начальных параметров, полагая, что при х О имеются начальный прогиб г0 начальный угол наклона динамический изгибающий момент М01 и поперечная сила С101.
Принимаем начало координат в центре левой опоры балки. Ось У направляем вниз; изгибающий момент, действующий против часовой стрелки, считаем со знаком «плюс»; поперечную силу, направленную вниз, принимаем положительной (см. рис. 297). Последовательное дифференцирование уравнения (р) дает
у? у;, у] к%; у к%-, УГ %■,
‘.14
419
Для начальных значений производных имеем:
УыкУы’ У1 к%п У% ЬМЫ;
у1"к%г СЧ.-: х%- •••-
где
0‘ ТГ: « §р у; Моь
М0, Со — начальные моменты и поперечная сила «-той нормальной формы динамической изогнутой оси.
Раскладывая уь в степенной ряд Маклорена, получаем
., Ьх, кх,,, х, гл ч
о; (1 -4Г -8Г -) Т1 "5Г Г --) . л:2. кх«, кх™,. г дЗ. Их’.,)П сс
ог(2Г -бГ -тоГ -.)?о(з[гтГГ - -)- 19-66) Из теории рядов известно, что разложение функции
5у (сЬ кх соз х)
будет
4И Ь12«42
5. 1 -. (19.67)
Таким образом, выражение (19.66) можно представить в следующей общей форме:
(1) _ х (2) х(3)
У1Уо1х Уо1 5 8хёх М0, 5 8хах 0ы 5 8хйх, (19.68)
где
8Х—у (сЬ кх С08 кх)
По правилам интегрирования функций окх и соз кх находим (1)
8хйх
» (2) И
йх
О
х(3)
О х (4)
8хйх
зЬкзтх
Тх.
2 к
к
сЬ кх — соз кх
и».
2к2
А
зЬ кх— зт кх
V
2к3
к ’
сЬ кх -- соз кх
5,
2 к
к ■
(19.69)
420
Пользуясь этими обозначениями для определенных интегралов функции 5, окончательно получаем следующее выражение для -той нормальной формы колебаний:
У, Уоёх УоТ Т? 01 Ж 19-70)
Это уравнение для ординаты динамической упругой линии балки с распределенной массой в зависимости от абсциссы х в состоянии наибольших отклонений.
Найдем теперь уравнения амплитуд угла наклона изгибающего момента и поперечной силы для -той формы, для чего последовательно дифференцируем выражение (19.70). При этом, как нетрудно видеть из выражения (19.69),
8х кУх; 8" кЩх, 8хкТх.
Учитывая эти соотношения, получаем амплитуду угла наклона для I-той формы:
у У«кУх у;и8х М01 Ц (19.71)
Амплитуда изгибающего момента
Мг уо1Е1кЦх у91Е1кУх Мо18х Тх. (19.72) Амплитуда поперечной силы
(1 Уо1Е1кТх уцЕ1кихМ01кУх (013х. (19.73)
Пользуясь полученными выражениями для амплитуд колебаний и усилий, легко решить задачу о нахождении частот свободных колебаний в соответствии с характером опорных закреплений балки. Условия на конце балки, которые можно составить по уравнениям (19.70) — (19.73), не будут включать свободных-членов, а поэтому не нулевые значения начальных элементов динамической упругой линии (например, для шарнирно опертой балки у0 и 20) имеют место, если определитель системы уравнений равен нулю:
Д« 0. (с)
Из этого уравнения и находят корни его й,- и, следовательно, по выражению (п) значения частот колебаний балки со,- в зависимости от условий закрепления ее концов:
(19-74
Свободные колебания однопролетных балок
Определим частоты колебаний балки на двух шарнирных опорах (рис. 298). Задача сводится к анализу I-той стоячей формы колебаний, уравнение ординаты которой (19.70), По условию закрепления началь¬
14 Н. Кч Снитко
421
ный прогиб у01 0; ввиду наличия шарнирной опоры Мог 0. На правом конце балки равны нулю прогиб и момент:
У 1 0; Мь 0.
Пользуемся уравнениями (19.70) и (19.72); так как у01 0 и М01 0, получим
Т_а 0.01 У_а Л.
У°‘ к Е1 к2 ’ у’о1Е1кУа Та 0,
(19.75)
где Та и Уа — значения соответствующих функций при М а.
Для начального угла наклона и начальной поперечной силы, возникающих при колебаниях системы, имеем ненулевые значения, если
детерминант системы (19.75) из коэффициентов при неизвестных у и 20 равен нулю. Умножая первое уравнение на А, а второе на
получаем: или иначе
Ь„Т1-У1 0 Уа 0;
.у.о. 1
Подставляем значения функций:
Т.
т„
(19.76)
зЬ а 8т а
зЬ а 81П а
зЬ а — 81п а
зЬ а—81П а
2 2 после преобразований получаем:
81П сс 0; зЬ (
0; :0;
1х 0; 1 а 0. )
(19.77)
Первое уравнение и дает спектр частот свободных колебаний балки. Из условия, что 51П а 0:
а к1 — пл,
где п 1,2, 3, 4,.
422
Частоты колебаний будут
ос2 1 Е1 п2л2 -шГЕ1 1Л точ
м»рУ т1гУ т- 09 78)
Второму уравнению зЬа 0 соответствует а 0, т. е. отсутствие колебаний. Итак, частоты колебаний получаем только из первого уравнения (19.77) по формуле
где
сол а 2а,
1 ЛГЕ1 ар] т•
Наинизшая частота со0 9,87 а, первый обертон сс 39,48 а, второй обертон со2 88,83 а и т. д. Например, для стальной балки двутаврового сечения № 226 при 4,35 ж, т 20,4 н-сек2м2; 2,16-10_5ж4; Е 21,091010нм2 а 24,9 сек со0 246 1сек.
Балка, заделанная одним концом
Найдем частоты колебаний балки, заделанной одним концом, с другим свободным (рис. 299). Теперь граничные условия при х I
Мг 0; (1 0.
Пользуясь уравнениями (19.72) и (19.73), получаем
М0,-5о Та 0;
Л«в. %5в 0.
к
Приравниваем детерминант этой системы нулю:
5 —Га1а 0, (т)
где
а к1.
Подставляем в уравнение (т) значения функций из выражений (19.69) и после простых преобразований получаем
1 —сЬ а соз а 0.
Пользуясь таблицами гиперболо-тригонометрических функций, решаем это уравнение путем подбора. Находим
а0 к01 1,875; 0 4,694; аг л.
Частоты колебаний будут
со0 3,51 а; о1 22а; а2 61,6а;
14 423
Первая частота о0 колебаний балки, заделанной одним концом, почти в три раза меньше частоты со1 для балки на двух шарнирных
опорах. Зная низшую частоту колебаний
„ 3,515 ЛГШ
У т’
найдем приведенную точечную массу для защемленной балки, если
з
приведение дается к свободному концу балки, для которого бт
‘3 ЕГ
тп
1
тЗЕ1
""Р 06 “ (3,515)2Е3
Выше мы пользовались этим значением приведенной массы.
2
МП
и
о
1-И‘
Рис. 300
На рис. 300 приведены первые формы колебаний для балки, защемленной двумя концами.
§ 111. ПРОДОЛЬНЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ С РАСПРЕДЕЛЕННОЙ МАССОЙ
Дифференциальное уравнение свободных колебаний
Рассмотрим собственные продольные колебания прямолинейного стержня постоянного сечения (рис. 301, а).
Обозначим продольное смещение в произвольной точке на расстоянии х от начала координат их19 относительное удлинение гх1, продоль¬
424
ную силу N1. Для упругих деформаций имеем по закону Гука
„ Л
х1 рр •
Известно, что [см. формулу (а) § 112]
о _ дих1 х дх •
(а)
(б)
Рис. 301
Следовательно, согласно выражению (а)
N х1 ЕРех( — ЕР
ди
хЬ
дх
х( рр д2иХ1
дх дх2 ‘
(в)
Пусть масса единицы длины стержня т. Тогда сила инерции, приложенная к бесконечно малому элементу стержня,
й1п -(тйх).
(г)
Составляя по Даламберу условие равновесия элемента (рис. 301, б), получаем
Л1 н
дх
с(х 0.
(Д)
Подставляем в уравнение (д) значения величин из выражений (в) и (г) и делим на т:
д2их( ЕР_ дыхЬ дР т дх2 •
Обозначая
ЕР 2 — а2,
т
(е)
(ж)
где а — скорость распространения упругой волны деформации при колебании, получаем окончательно следующее дифференциальное уравнение свободных продольных колебаний стержня с распределенной массой:
дих1
дР
а2
дх2
(з)
425
Выражение для продольных колебаний по методу начальных параметров
Полное решение линейного дифференциального уравнения (з) будет:
00 со
и (2и,-28‘пИм. (и)
1 1
где иХ1 — ь-тая форма продольных колебаний.
Очевидно, о — частота колебаний, соответствующая -той форме; иХ1 — выражение -той нормальной формы продольных колебаний — функция только х.
Подставляя один член ряда (и) в уравнение (з) и опуская индекс I, получаем
— со2их зш (со Я) а2 5111 (со X),
или после сокращения на зш (со к)
а1г аи- (к)
Для отыскания выражения нормальной формы колебаний пользуемся обыкновенным дифференциальным уравнением (к).
Деля обе части выражения (к) на а2 и обозначая
1 о (О2 СО2 _. ч
а? ЕР ()
получаем окончательно для дифференциального уравнения нормальной формы колебаний
(М)
Пусть при х 0 начальное отклонение их_0 и0 и начальное значение продольной силы Л0, определяющее начальное значение относительного удлинения при колебании
еп
ди
дх
Ао ЕР
Интегрируя дифференциальное уравнение (м) по методу начальных параметров, получаем
,, 81П к;Х. ч
их и01 соз кгХ еог. (н)
Таким образом, общее решение дифференциального уравнения (з) будет
оо
их1 2 (ио соз кх е0(- зш (ог К). (о)
426
Пример. Найти настоты продольных колебаний стержня длиной Ь со свободными концами (рис. 301).
Решение. На свободных концах стержня продольные силы равны нулю; поэтому имеем следующие граничные условия:
0;
)
0.
Эти условия справедливы для любой -той формы колебаний:
зт к;Х
ди
ео
дх
-о
ди
е1
дх
х-Ь
(п)
(Р)
«ЛГ соз к IX е0; :
Поэтому согласно уравнению (п) для их имеем
их и0( соз к(Х.
Находим выражение для удлинения
дих и •
8Ж “°181П
Применяем теперь второе граничное условие, т. е. уравнение (р):
0 — к 1 зт кЬ.
Для г,-, отличного от нуля, получаем
зт к(1 0,
откуда
кЬ пл (п 1, 2, 3, 4,.).
Частоты колебаний находим из выражения (л):
(с)
(т)
пп - Г ЕР
ЩТ У Ш
(У)
ЧАСТЬ ЧЕТВЕРТАЯ
ПЛАСТИНКИ И ОБОЛОЧКИ
ГЛАВА 20. ТЕОРИЯ ТОНКИХ ПЛАСТИН § 112ч ОБЩИЕ ПОЛОЖЕНИЯ
Соотношения между деформациями и перемещениями
Рассмотрим элемент упругого тела в виде параллелепипеда, выделенного у произвольной точки А (рис. 302). Размеры ребер его пусть будут йх, йуу йг.
Обозначим составляющие перемещения точки А вдоль осей координат X, У9 2 через и, V и т соответственно. Предполагаем, что перемещения являются непреры-
0 вными функциями коорди¬
нат:
У, г);
0М. У г):
йУ М У у г).
Под действием внешних сил тело меняет свою форму и объем и каждый его элемент дефор ми р у ется.
Деформацию тела в данной точке представляем как относительные удлинения ребер параллелепипеда (е, еу, гг) и как относительные сдвиги — изменения углов между ребрами АВУ АЕу АСУ СИу. в плоскостях XV, 2Х и 2У (изменения углов Ф, 6, по рис. 302). Изменение этих углов (углов сдвига) обозначим через ухУу у2Х и угу.
Найдем соотношения между деформациями и перемещениями. Рассмотрим (рис. 303) изменение формы грани АВСО параллелепипеда, которое происходит в плоскости 2Х. В результате общей деформации упругого тела точка А получает в плоскости 2Х составляющие пере¬
Рис. 302
428
мещения и и до, а точка В, находящаяся на расстоянии Ах от точки А перемещения
, ди,, ди),
И ДО Ш рГ й?-
дх
Приращение в перемещении точки В дает абсолютное удлинение ребра АВ:
— и с1х.
Относительное удлинение ребра АВ
ди
8 — -
дх Х ди
йх дх
Аналогично для ребер АС и Л5
ду
ту-
(а)
(б)
Рассмотрим теперь изменение угла между ребрами А В и Л С, которое, очевидно, равно:
7 а Р, (в)
где аир соответственно углы сдвига для ребер АВ и АС (рис. 303). В виду малости деформаций принимаем а 1§а; р р.
Из рис. 303
а-
ВВ"
АВ :
СС" АС
дш, з- йх дх
йх
ди
дг
йг
йъ
дхю дх9
ди дг
429
Сложив а и р, получим Аналогично
где
ды), ди
Угх дх дг
ди, о г
ху ду дх9
д-о, ди)
Чудг ду ’
Тху туг гх
УХУ 1Т Чуго ’ гх С
(г)
(д)
(е)
Зависимости (а) и (б), а также (г) и (д) непосредственно используются в теории пластинок.
Понятие о пластинке
Под тонкой пластинкой понимаем тело, один размер которого, высота Л, мал по сравнению с двумя другими — длиной а и шириной Ь
(рис. 304). Пластинку можно считать тонкой, если
Ь, где Ьса. Ограничиваемся рассмотрением пластинок постоянной толщины. Срединной плоскостью пластинки называем плоскость, которая делит высоту к пополам. Вертикальные перемещения то-
1 чек срединной плоскости
рис 304 называем прогибом т (в на¬
правлении оси 2). Деформации пластинки с известным приближением описываются через прогиб пластинки т. Выбираем прямоугольные координаты XVI. Нагрузку предполагаем действующей нормально к срединной плоскости.
О
х
1
‘ Ь2
§ ИЗ. НАПРЯЖЕНИЯ И УСИЛИЯ В ПЛАСТИНКЕ.
УРАВНЕНИЯ РАВНОВЕСИЯ
Представим бесконечно малый элемент пластинки, на поверхности которого действует распределенная нагрузка, интенсивностью р р (х, у) (рис. 305). Укажем напряжения в точках к и кг сечений параллельных плоскостям VI и XI соответственно. Точки к и кг расположены на расстоянии г от срединной плоскости пластинки. В точке к действуют нормальные напряжения ах и касательные напряжения %хг и %ху
430
в точке кг — нормальное напряжение ау и касательные напряжения %г и тух. Для каждого касательного напряжения первый индекс соответствует направлению нормали к сечению, по которому действует напряжение, а второй индекс указывает на направление действия напряжения. Согласно закону парности касательных напряжений
хХу Хух. (а)
Рассматриваем действие нагрузки, нормальной к срединной плоскости. Поэтому равнодействующие всех усилий, определяемых напряжениями аХ1 ау птху,
Рис. 305
равны нулю и соответствующие усилия, вычисляемые по этим напряжениям, приводятся только к моментам. Напряжения ох сводятся к моменту Мх, а напряжения о у — к моменту Му (см. рис. 305). Все усилия (и моменты) вычисляем как результирующие напряжений на единицу длины. Напряжения ох и оу дадут изгибающие моменты
Мх охгАг Му оугсг.
(б)
Момент Мх действует в плоскости XI, а момент Му — в плоскости У2. Напряжения хху и тух приводятся к крутящим моментам:
МХу — МуХ— тхуг Аг
(в)
Крутящий момент Мхх действует в плоскости 2У. Вертикальные касательные напряжения %Х2 и хуг дадут поперечные силы
: Аг
(Г)
Поперечные силы С1Х приложены в плоскостях У2, поперечные силы С1У — в плоскостях XI. На рис. 306 представлен выделенный элемент — элемент пластинки йх х Ау и показаны положительные направления усилий (2, 0,уу Мх Му, Мух, Мху. Проектируя все силы, прило-
431
лЗенные к элементу пластинки на вертикальную ось 2, получим по условию равновесия:
рахйу--Щйхйу--Щйуйх О,
откуда
%-р°- (20Л
О у йх
Рис. 306
Составляя условия равновесия в форме суммы моментов относительно осей 1 и 2, параллельных осям X и У, получаем:
Пренебрегая малыми второго порядка и имея в виду, что Мух Мху, получим вместо (д) и (е):
дУИ у
Отсюда выразим (±у и 2
п дМху
дх
дМхг
-аг
дМу
1 ду дМх
(20.3)
Вносим выражения
2 и дМх
Су в условие равновесия (20.1); получаем
дМх„
2—
дуг
(20.4)
Му и Мху одного уравнения (20.4)
дх2 дх йу
Для определения трех моментов М недостаточно и для решения задачи необходимо рассмотреть деформации пластинки, выразив моменты через вторые производные от прогиба (как это имело место в теории изгиба балок).
§ 114. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ИЗОГНУТОЙ ПОВЕРХНОСТИ ПЛАСТИНКИ
Для тонких пластинок вводим следующие предположения.
1. Считаем, что все друг против друга лежащие по вертикали точки
пластинки получают одинаковый прогиб, не зависящий от координаты г, т. е. с хю хю(х, у).
Взаимным сжатием слоев пластинки, таким образом, пренебрегаем.
2. Нормали к срединной плоскости пластинки (с—с) остаются после деформации перпендикулярными к искривленной поверхности (деформированной срединной плоскости; рис. 307). Это предположение носит наименование «гипотезы о прямолинейном элементе нормали» и является перенесением гипотезы Бернулли для балок на теорию пластинок.
3. Пренебрегаем нормальным напряжением о2 сравнительно с ах и оу. Поэтому относительные деформации ех и гу записываем в форме:
где V — коэффициент Пуассона.
433
Кроме того, по формулам (е) § 112:
ху ьху
Ь-2(у)
(б)
Соотношения (а) — известны из курса сопротивления материалов для плоской задачи. Разрешая уравнения (а) и (б) относительно напряжений, получаем
Е (ди, дV
°х 1 — V2 дх Л? ду) Е (дV, ди
1 — V2 ду Л? дх
Е Iди, дV I
тлгу 2 (1 V) ду дх) )
(20.5)
Пользуясь 1-м ц 2-м предположениями, выразим перемещения и и V черз т и координату г. По рис. 307 можно написать:
дт
дх
Аналогично (из сечения в плоскости VI)
дгю
V — г
ду
(20.6)
(20.7)
Внося эти выражения в формулы (20. 5), получаем следующие окончательные соотношения между напряжениями и прогибом пластинки:
л Ег (д2ш, л д2ш
°х—— 2 Г Щр ) •
Ег д2т, д2ш
1 — V2 ду2
О г
тху — —20гдхду
дхг Ег д2ш 1 V дх ду
(20.8)
В последнее соотношение подставлено выражение О через Е. Выражения (20.8) вносим в соотношения (б) и (в) § ИЗ и после интегрирования по высоте сечения получаем для моментов Мх, Му и Мху:
"(г-З):
с
Мху— (1 —V) О
дх2 д2ю
(20.9)
дхду 1
где О — так называемая «жесткость» пластинки:
Е№
О--
12 (1 — V2)
(20.10)
434
Пользуясь соотношениями (20.3) и внося в них выражения (20.9), получаем формулы для поперечных сил Сх и С1у:
п _ п д д2хю I д2® п д,А.
дх [дх2 ду2 ) дх
п п д (д2и). д2хю п д л ч [ (20.11)
э (а )
где Доу — линейный дифференциальный оператор с частными производными второго порядк а:
А д2ш, д2т.
Аы) д1ё ду2- (в)
Таким образом, все усилия выражены через производные от прогиба пластинки ы). Обращаясь теперь к условию равновесия (20.4) и внося в левую часть его выражения для моментов (20.9), после преобразова,ний получаем:
д4оу. п. д4ш А А р ГЛ,
дх дх2 ду2 ду4 “ ДДйу — • (20.12)
Это и есть известное дифференциальное уравнение изогнутой срединной поверхности пластинки, полученное Софи Жермен и представленное к опубликованию Лагранжем в 1811 году. Оно является неоднородным бигар моническим уравнением. Его коротко можно записать так:
Д Дш 0-, (г)
где в левой части имеем бигармонический оператор над хю.
Заметим, что бигармоническому уравнению удовлетворяют как гармонические, так и бигармонические функции (например, хсЪахсозау, хЪах созау и др.). Применяя уравнение (20.12), мы сталкиваемся с трудностями в нахождении соответствующего решения, которое должно удовлетворять условиям закрепления пластинки по краям, — так называемым краевым условиям [1].
§ 115. КРАЕВЫЕ УСЛОВИЯ ДЛЯ ПЛАСТИНОК В РАЗЛИЧНЫХ СЛУЧАЯХ
Основные положения
Решение дифференциального уравнения (20. 12) существенно зависит от краевых условий. Будем различать следующие три случая закрепления края пластинки (рис. 308):
1) шарнирно опертый край (АВ),
2) защемленный край (АО),
3) свободный край (ВС, СЬ).
435
Шарнирно опертый край
Напишем аналитические выражения для шарнирно опертого прямолинейного края АВ пластинки (см. рис. 308). Для всех точек этого
Рис. 308
края равны нулю прогибы хю и изгибающие моменты МУ9 т. е.
и)(х9 0) 0; Му(ху 0) 0.
(а)
Второе условие из равенств (а) по формуле (20.9) можно записать
так:
дх2
х, 0
0.
Но так как хю (х, 0) 0, то и
д2и)
дх2
о.
(20.13)
(б)
Поэтому из формулы (20.13) следует:
д2ы)
ду2
о
0.
Внося же эти значения в первую формулу (20.9), получим, что и
Мх(х, 0) -0
д2и, д2ш дх2У ду2
х, 0
0.
(в)
(г)
Итак, вдоль шарнирно опертого края и момент Му, и момент Мх равны нулю. Следовательно, равна нулю и сумма моментов
откуда
А4 Мх-1 МУу Дау 0.
(д)
Итак, вдоль шарнирно опертого края пластинки возникают только поперечные силы и крутящие моменты. По предложению ряда авторов,
436
крутящие моменты на шарнирно опертом краю возмещаются непрерывно распределенными «силовыми» парами (рис. 309). На левом элементе Ах вместо крутящего момента Мхус1х дается пара вертикальных сил Мху с плечом Ах. Аналогично преобразование крутяще-
Ах
I, емху го момента I Мху --дх
Ах для правого элемента края А В пластинки. Такое преобразование (предложено Томпсоном и Тайттом в 1876 г.) основано на принципе Сен-Венана, по которому влияние характера приложения сил сказывается в узко ограниченной области (вблизи приложения сил). Указанные на рис. 309 сплошными линиями пары сил
дМху
Рис. 310
у границы между элементами создают приращения —-йх, которые
дополнительно нагружают опорный край. Таким образом, полная опорная поперечная сила на единицу края
I
(е)
Используя формулы (20.9) и (20.11), получаем:
?,(, 0) -о[(2-»)
Важно еще рассмотреть шарнирно опертый угол пластинки (рис. 310) и обратить внимание на то, что у угла пары сил Мху дают суммирующееся опорное давление Р 2Мху.
Защемленный край
Для защемленного края (см. рис. 308) в любой точке края равны нулю прогибы и углы наклона касательных вдоль оси X, т. е.
И°, у) 0; [50 0. (Ж)
Кроме того,
По условию (20.13) получаем:
о
т. е., принимая во внимание третье соотношение (20.9), найдем, что крутящий момент вдоль защемленного края равен нулю. Очевидно,
4Ь1
изгибающие моменты в защемлении возникают. Для момента Мх (0, у) имеем, принимая во внимание (з),
МАО. У) 0(20.14)
Для момента Му вдоль края АО МАО. «)-вт’т1.--,-УМАО, у). (20.15)
Для поперечной силы
о, (0.,) - О [ Ц) - - О У. (20.16)
Свободно опертый край
Для свободно опертого края ОС (у Ь по рис. 308) равны нулю изгибающий момент Му (.х, Ъ) и опорная поперечная сила (х, Ь). В развернутом виде получаем по формулам (20.9) и (20.11) соответственно:
Ь)ШЩ,,ь0- (20.17)
,. ») [ (2-)г]х,.-0.- (20.18)
Для края ВС имеем
Мх(а9 у) 0; х(ау у) 0.
§ 116. ПРОСТЕЙШИЕ СЛУЧАИ
Цилиндрический изгиб пластинки
Пусть прямоугольная пластинка, имеющая размер а, существенно меньший размера Ь (рис. 311), подвергается действию нагрузки, постоянной вдоль оси У и являющейся лишь функцией координаты л;:
р р(х).
Пусть и закрепления краев будут одинаковы вдоль оси У. При этом прогиб хю будет, очевидно, функцией лишь абсциссы а: и не зависит от у. Следовательно, упругую поверхность можно считать цилиндрической, и по уравнению (20.12) для нее получаем:
что представляет собой дифференциальное уравнение изогнутой оси
438
«полочной балки». В отличие от простой балки (ось которой — вдоль оси X) нагрузка р (х) понимается на единицу площади, и кроме моментов Мх возникают моменты Му, причем:
А АЛ лл
7 0; Мх — — 0-т2 — —
ду
МХу — 0; (2 — О ; 0у — 0.
Таким образом, все случаи цилиндрического изгиба легко разрешаются, исходя из дифференциального уравнения (20.17), аналогично решению задачи о балках. Для случаев а и б по рис. 312 соответственно имеем:
•и-г(1г-т-1г, (а,
О V 24 2 2А )
Эллиптическая и круговая пластинки, защемленные по краям, при действии равномерно распределенной нагрузки
Для эллиптической пластинки, загруженной равномерно распределенной нагрузкой интенсивностью р (рис. 313, а), решение для хю можно представить в форме
ш(х, у) а(% — 1) (20.20)
а2 1 Ь2
где А — произвольная постоянная, причем уравнение эллипса
2 у1 _ 1 о
а2 т- 1 и.
439
Краевые условия будут:
ш°; ж0: ?-о.
Внесем выражение (20.20) в дифференциальное уравнение (20.12), в результате получим
дд1»84[з(1 1)-].
откуда и определяем А, внося значение которого в уравнение (20.20), окончательно находим:
Л,,(Х 2, у2,2
ра (о Р Ш 80 [3 (а2 2)2 - (2абр]“• (20.21)
Для случая круговой пластинки (рис. 313, б) Ъ — а и из формулы (20.21) имеем
ш6( ?-“)• (20-22) По выражениям для т легко определить все усилия.
Шарнирно опертая по краям прямоугольная пластинка при действии синусоидальной нагрузки
Пусть прямоугольная пластинка размером а X Ь (рис. 314), шарнирно опертая по краям, подвергается действию синусоидальной (в каждом направлении X и У) нагрузки
, ч. лх. ли
Р(Х У)Ро 31П — 81П
440
Решение для прогиба пластинки будет
ГГ—Гу
(зг Й
Прогиб в центре пластинки
Ы0 -
. пх. пу 81П — 81П а Ь
Ро
Ь2
(20.23)
(20.24)
117. ШАРНИРНО ОПЕРТАЯ ПО КРАЯМ ПРЯМОУГОЛЬНАЯ ПЛАСТИНКА ПРИ ДЕЙСТВИИ ПРОИЗВОЛЬНОЙ РАСПРЕДЕЛЕННОЙ НАГРУЗКИ
Рассмотрим решение Навье, данное им в 1821 г. Если все края пластинки шарнирно оперты (рис. 315), то при действии произвольной распределенной нагрузки интенсивностью р (х, у) выражение для прогиба по Навье берется в силу линейности дифференциального уравнения (20.12) в виде двойного тригонометрического ряда вида
У
у--Ь
2 2
т — 1,.п 1,.
-. тпх. ппу
Атп ЗШ — 51П,
(20.25)
1 X
X я Г
X 0
Рис. 315
где ы)тп — произвольный член ряда;
Атп — постоянная произвольного члена ряда.
Разложив далее нагрузку р (ху у) в двойной тригонометрический ряд, найдем значение каждой произвольной постоянной.
Заметим, что при принятом выражении каждого произвольного члена ряда
I Ап
. тпх. ппу 1 81П —а— 8Ш Т
(20.26)
удовлетворяются краевые условия (см. рис. 315), т. е. при 0 и х а
Мх 0; Му 0; Дау 0; ш 0; при у 0 и у Ь
Мх 0; Му 0 АйУ 0; ш 0.
В самом деле, по выражению (20.26) имеем:
тпх
Iт2п2 Д а2
Аы (Атп 81П -г— 81П
плу
(20.27)
441
Находим по выражению (20.25) производные от хю (х, у), содержащиеся в уравнении (20.12), и, внося их в последнее, получаем после умножения на О:
п% 2
_ ипа
т 1. п 1.
тпх. I
51П -,
а Ъ
. тпх. ппу. ч ЛЛ ЛОЧ
X З1п т-т-р (х, у). (20.28)
Задача состоит в отыскании всех произвольных постоянных Ат,и что позволит найти окончательное решение в форме (20.25). Разложив нагрузку р (х, у) в двойной тригонометрический ряд того же вида, найдем значения Атп (см. далее выражение 20.30). Перепишем уравнение (20.28) для краткости так:
ци ци
2 п ±т2 I п22 а т71Х • ппу
2 ««5111—8Ш--
т,. п,.
оо оо
2 2 р;п тля ппу
Гт„51П—31П-у
т 1,. п 1,.
откуда получаем
г„т 5) (20.29)
Для отыскания Атп сначала приводим левую часть уравнения (20.28)
к одиночному ряду, для чего умножаем левую и правую
части уравнения (20.28) на зт 1 йх, где — какое-либо целое число,
и интегрируем в пределах от 0 до а:
оо оо а
гл л л яг2. п22. ппи ?. тлдс. лдс,
2 0п4А’Пп[-2-) ЗШ- ЗШ — ЗШ — йх 721,. п1,. х 0
а
Р(. У)8п. (а)
л: О
Нетрудно установить, что интеграл в левой части соотношения (а) представляет собой постоянную. Действительно, при т I
-11 а а 2
х 0
тпх. тх, а
81П — йх Д-, (б)
а при т Ф I интеграл этот обращается в нуль:
а
. тпх. тх, Л ч
81П 81П йх0. (В)
х0
442
Таким образом, из всех членов суммы пот, содержащейся в левой части выражения (а), остается лишь один член, равный
который можно вынести за знак 2; получаем вместо выражения (а)
при т I
2 ОпА„ )2 51П ( р (X, у) 51П — Ох. (в)
п 1,. О
В левой части соотношения (в) имеем ординарный ряд. Умножаем
теперь левую и правую части уравнения (в) на зт -У-йу, где к—
какое-либо целое число, и интегрируем левую и правую части в пределах от 0 до Ьу получаем
т2°ЯМЛ(5 5)2 у о
Ь г- а
§ рх, у)
У 0 О
Но при п к имеем
кпу, 31П —-йу.
(г)
ппу. кпу, Ь 81П т 31П —гг с1у—,
а при пфк
У о
ь
у0
ппу
Т
кпу
Ь
81П —г31П — 0.
В левой части выражения (г) вместо суммы имеем один член с коэффициентом А1к (или Лт„): I
ь
откуда при Ак А„ 4
у 0 _х 0
кпу,
31П —г-йу,-
ъ л Л"2, П
ОпаЬ (-аТя 0 -0
о г- а
5 р (х, у)
. тпх ■,
З1п ах
зт У-йуу (20.30)
а №
где множитель при интеграле ниже, будем обозначать 5.
Теперь известны и коэффициенты гтп для разложения по формуле (20.29). Коэффициенты разложения Атп согласно формулы (20.29) выражаются через двойной интеграл 5 правой части формулы (20.30)
с множителем Для Атп имеем
Определив из формулы (20.30) все коэффициенты Атт получаем развернутое выражение для т в виде двойного тригонометрического ряда. Если ряды быстро сходящиеся, можно ограничиться первыми четырьмя членами ряда, например при р сопз
ш (х, у) Ап зт ™ зт А31 зт зт Ц-
Л13зт8т-. Л3з51п81п. (20.31)
§ 118. РАСЧЕТ ШАРНИРНО ОПЕРТОЙ ПЛАСТИНКИ НА ДЕЙСТВИЕ РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ НАГРУЗКИ
Нагрузка действует по всей поверхности пластинки
Рассматриваем пример равномерно распределенной нагрузки, действующей по всей поверхности а X Ь пластинки, шарнирно опертой краями (см. рис. 315). Интенсивность нагрузки р (х, у) р соп1. Легко найти выражение для коэффициента Атп ряда, применяя формулу (20.30) и проводя интегрирование. Двойной интеграл, входящий в формулу (20.30) будет
а Ь
8-.
(. тлх, С, пт.
-- р 51П ——йх 51П -у-ау
п Ь
р — (1 — соз шл) — (1—со§ пл). (20.32)
71Л 13Т
При четных значениях т и п (0, 2, 4,.) это выражение обращается в нуль, а при нечетных их значениях получаем
3 р ■ —. (20.33)
г тп пк 4 7
Поэтому коэффициенты ряда Атп будут
4» (20-34)
Сяотп ьг
Теперь легко получить общее решение для т (х, у). Следует иметь в виду, что в формуле (20.34) тип равны 1, 3, 5, и т. д.
Общее решение для хю (х, у) будет
оо оо
11
. птх. пли
1 С Г
И. 1г- (20-35)
т 1,3,.п1, 3,
Обычно применяют выражение для ы (.х, у), беря первые члены, так как имеем быстро сходящиеся ряды,
444
Нагрузка действует на малую прямоугольную область пластинки
Нагрузка действует внутри прямолинейной области со сторонами а0 и Ь0, причем координаты средней точки х0 и у0 (рис. 316). Теперь
по формуле (20.30) выражение двойного интеграла будет
У о "
У — 1 4раЬ
, I °°
°2
тлх. пли,,
31П 51П -г-ах ау
п Ь
Ьо Оо
У Уо — 2- х х0 —
. тлхп. тла0. плу0. плЬ0 81П — 81П -тг-2- 81П —г- 31П
тпл2 а 2а Ь
По условию действия сосредоточенной силы
и из выражения (а) находим:
тла0
тлх0. ппуп. 2а
-зт —тр- Ьт 31П пт
2 • (а)
Пт (а„Ь0р) Р,
а о —0, —• 0 4 аЬ
■- 5" 31П
тпл2 а
ао
плЬ0
“2Т
Пт5 Рзт5т (»).
а I
Для коэффициента Атп по формуле (20.30) получим
1
А -?—
тп ОлаЬ
т2
а2 Т)2
тлхп. (плу0 п25Ш 1)5Ш пг)-
Пт (а060р);
Со-» 0
(б) (в)
Прогиб ш (х, у) пластинки в любой точке при действии сосредоточенной силы, после подстановки формул (в) в уравнение (20.25), будет:
ю(х, у) -
4 Р
Ил аЬ
. тлхп. плип. тлх. плу
81П 81П - - 81П 81П
а о а о
т2 ту
а? Р
. (20.36)
т 1,. п 1,
В сложных случаях замкнутое решение задачи невозможно, и чаще всего применяют метод конечных разностей или метод Ритца.
445
§ 119. ОБЩЕЕ РЕШЕНИЕ ДЛЯ КРУГЛОЙ ПЛАСТИНКИ
Рассматриваем случай осесимметричной нагрузки и того же вида опирания. Пусть элемент круглой пластинки, ограниченный двумя соседними цилиндрическими сечениями на расстоянии г и г йг
от оси 2 (рис. 317), двумя вертикальными радиальными сечениями, угол между которыми йф, и двумя соседними горизонтальными сечениями, расстояние между которыми йг. Так же, как и для прямоугольной пластинки, будем пренебрегать напряжениями аг, вводя лишь радиальные нормальные ог и окружные нормальные О; напряжения, а также касательные напряжения т. Для данного случая осесимметричного нагружения крутящие моменты МГ(р и М?г равны нулю и по вертикальным сечениям аЬ и ей возникают лишь вертикальные касательные напряжения, результирующие которых дают вертикальные поперечные силы (2Г. По вертикальным граням элемента будут возникать еще изгибающие моменты Мг (результирующие радиальных нормальных напряжений) и М1 (результирующие окружных нормальных напряжений).
Согласно рис. 318 связь между результирующими усилиями и напряжениями ог, а и т будет следующая:
2
(20.37)
Перейдем к выражениям напряжений аг и ст, через прогиб до пластинки, выраженный очевидно лишь в функции от г. Принимая ось г за ось Ху можем вместо первого выражения (а) § 112 написать;
ди 1,
ед7Ё
(а)
446
Выразим теперь относительную деформацию е, в окружном направлении через радиальное перемещение и (рис. 319). Длина элементарной
Рис. 318
дуги до деформации г йср, после деформации (г и) йу. Следовательно:
(г и)р — г йу и
е1 г г
Присоединяя к выражению (а) выражение для е
и решая эти два уравнения, получаем:
ог
Е (е,е,) Е
1 — V2
1 — V2 дг и
Е,. ч Е [ и. ди
Т т(уЛ’
(б)
(в)
Связь между и ишпо формулам (20.6) при замене х на г устанавливается соотношениями:
с1хю
и — г-
Хг
Ъг гТг
г йю г йг
(Г?
Внося выражения (г) в соотношения (в), получаем:
Ег ( й2ш V я’аЛ
°г — _г,2 у • ); I
1 йш
У ’ йг) )
Ег [ с12и)
1 — V2 V
(20.38)
447
Для изгибающих моментов Мг и М, получим по формулам (20.37) и
(20.38):
(20.39)
От2
сРчм
г йг 1 с1т
г
Выразим теперь поперечную силу 2, через моменты, составляя условие равновесия элемента пластинки в форме суммы моментов
относительно оси, перпендикулярной к направлению радиуса (рис. 318). Принимая моменты, направленные против часовой стрелки, с. плюсом и имея в виду, что а, составляет с
осью моментов угол (рис. 317), получим: у (гМг) йг йц — 2М(йг — 22гг 0,
Рис. 319 откуда имеем
(20.40)
Я:(гМг)-М,-0гГ 0. (20.41)
Из формулы (20.41) после внесения выражений (20.39) поперечная
сила
п п 1.,1 п а сРш 1 йш 9П 9
Чг и1м-72--фГ т -М)--° аР ? Т - а7- 20-42)
кйг3
Окончательно:
(20.42)
Из условия равновесия элемента в форме суммы вертикальных сил (см. рис. 318) имеем:
ЬГГ) — Р(Г)Г.
(20.43)
Внося сюда выражение поперечной силы по формуле (20.42), получим
сРю 1 й2ю 1 сШ) р (г)
йг г2 йг2 -з л п •
№ 2 йг •" г
йг
И
(20.44)
Это дифференциальное уравнение для круглой пластинки выведено Эйлером. Его можно переписать и так, вынеся за скобки дифференциальный оператор Лапласа:
; 7-)( 4-»-4А»,-еМ. да.45,
г йгI йг 1 г йг I Дифференциальное уравнение (20.44) запишем в форме
IV I ЧП " I 1г I ЧЯГ Л Р
Решение этого обыкновенного дифференциального уравнения 4-го порядка можно представить как сумму решений однородного уравнения щ (г) и частного ы)р (г):
т щ (г) ы)р (г). (20.47)
Решение однородного уравнения (20. 46) (без свободного члена) будет
щ (г) Сг С21п г С3г2 С4г21п г. (20.48)
Произвольные постоянные Съ С2, С3 и С4 легко определяются из условий на краях пластинки и требования конечности значения прогиба.
В ряде случаев легко определяется поперечная сила 0 (г), действующая по боковой цилиндрической поверхности пластинки радиусом г сопз. Очевидно,
2 (г) 2яг2г (г);
Теперь из выражения (20.42) получаем
1 йт _ а 1 й ( Лу1 __ (? (г) ( Л
д?3 г с1г2 г2 I л йг ) 2пгй ’ § 120. СВОБОДНО ОПЕРТАЯ ПО КРАЯМ КРУГОВАЯ ПЛАСТИНКА ПРИ ДЕЙСТВИИ РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ НАГРУЗКИ И СОСРЕДОТОЧЕННОЙ СИЛЫ
Распределенная нагрузка
Для цилиндрического сечения радиусом г (рис. 320, а) имеем следующую суммарную поперечную силу:
г
(2 (г) — § (р 2лг) с1г — лг2р. (20.50)
г 0
Дифференциальное уравнение (20.49) будет теперь иметь вид (рис. 320, б):
Интегрируем это дифференциальное уравнеттае, принимая во внимание решение (20.48). Для краткости вместо пишем С[:
ш ГГ (й с;-2 С21п г Сз), (20.52)
где Сь С2 и С3 — произвольные постоянные.
При г 0 пластинка дрлжна иметь конечный прогиб (рис. 320, б) поэтому С2 0. Таким образом, вместо выражения (20.52) получаем
449
для прогиба и его производных:
т (г)й-(й2СИ;
®(г) Ты С,г С3);
“’"Н 24
(20.53)
(20.54)
(20.55)
5)
8
ППППМ1Т
1,
Рис. 320
Применяем теперь граничные условия, что при г 0 (опорный край):
аг (а) 0; (а)
тг (а) 0. (б)
Первое условие (а) с учетом того, что
Ег,,. V,
ти),
приводит к значению
с;-
д2 (3 у)
(в)
(г)
32(1г) ‘
Из второго условия находим значение С3:
г __а (5 у)
3 64 1 V
Внося эти значения С[ и С3 в выражение (20.53), получаем следующее уравнение для упругой поверхности пластинки:
20-56
450
Сосредоточенная сила
Рассмотрим еще действие сосредоточенной силы Р в центре пластинки (рис. 320, в). Теперь суммарная поперечная сила в сечении радиусом г
2(г) -Р.
Вместо уравнения (20.49) имеем
[_ а_( ЛиЛ1 _ Р
с1г г Лг Лг ] 2пгЭ ’
После интегрирования получаем
ш Ш (т 1п г Сг с21п г С,). (20.57)
Учтя, что Птг2 1п г 0 и что при г 0 прогиб имеет конечное зна¬
чение, получим С2 из выражения (20.57) находим
ау(г)2Но (т1пг С1г2 Сз). (20.58)
Из условия, что при г а, ог 0, получаем
С1 -1п а—(д) Из условия, что при г а, до 0, имеем
_д2 з у,.
8 1у- Окончательно для до (г) согласно выражению (20.57) получаем:
ш - [т1п г - (т1п °4 • Ш)г2? (Ш)] • (20-59)
В случае защемленной по краям пластинки при г а:
т (а) 0; хю (а) 0. (20.60)
ГЛАВА 21. РАСЧЕТ ОБОЛОЧЕК
§ 121. РАСЧЕТ СИММЕТРИЧНОЙ ОБОЛОЧКИ ВРАЩЕНИЯ НА ОСЕСИММЕТРИЧНУЮ НАГРУЗКУ
Пластинки с криволинейным очертанием срединной поверхности называются оболочками (рассматриваем незамкнутые оболочки).
Проследим сначала за ходом расчета очень тонких оболочек вращения по мембранной теории на действие осесимметричной нагрузки, распределенной по поверхности оболочки. При этом будем предполагать, что оболочка имеет (во избежание местного изгиба)
451
плавно изменяющуюся непрерывную поверхность и нагрузка, действующая на оболочку, непрерывна. Края оболочки считаем свободно перемещающимися в направлении нормали к поверхности; при невыполнении этого условия будет происходить изгиб оболочки.
Остановимся на геометрии оболочки вращения (рис. 321, а). Радиус основания оболочки А В обозначаем ?. Срединная поверхность ее получается вращением кривой ОВ вокруг оси вращения О А. Кривые ОВ, ОВ и т. д., расположенные в вертикальных сечениях, называются меридиональными кривыми. Меридиональная кривая задана уравнением в виде функции г (г) (рис. 321, б), где г—радиус горизонтального сечения оболочки на расстоянии г от ее вершины О. Соседние горизонтальные сечения образуют на поверхности оболочки широтные окружности (1—4, 3—2 на рис. 321, а). Обозначим радиус кривизны меридиональной кривой ?, радиус кривизны дуги аЪ (длиной йз2) — ?2 Как видно из рис. 321, б,
Я 2
Рис. 321
(а)
51П ф
где ф — угол между радиусом Я2 и осью 02. Обозначим меридиональное усилие, действующее на длине Лз2 через с1Ы1у окружное усилие, действующее на длине дя1у через йЛ2. Эти усилия выражаем так:
N, N3,;
лу2лг2а5; (
где Ы2 — соответственно погонные меридиональное и окружное нормальные усилия (на единице длины меридиана и окружности). В силу симметрии системы и симметричности нагрузки элемент
452
1—2—3—4 (см. рис. 321, а), ограниченный соседними меридиональными сечениями и широтными кольцевыми сечениями, не получает сдвигающих усилий й8 (они возникают лишь при действии обратносимметричной нагрузки).
Радиальное давление на элемент поверхности
Рг 62,
где рг — радиальная составляющая интенсивности по поверхности. Проекция усилий (рис. 322, а) на нормаль V
Проекция усилий с1Ы2 (рис. 322, 6) на нормаль V
2 [йЫг зш) ЛУ24а2 ЙЛ2
Сумма проекций всех усилий, действующих на элемент,
Рг сз, о,
(б)
(в)
453
или, подставляя значения величин из выражений (б) и (в), получаем уравнение Лапласа:
(21.1)
Это первое уравнение для определения нормальных меридиональных и окружных усилий.
Рис. 323
Для получения второго уравнения проведем горизонтальное сечение оболочки вращения радиусом г (рис. 323, а) и спроектируем все силы, действующие на верхнюю отсеченную часть, на вертикальную ось 22. Вертикальная проекция всех меридиональных усилий по сечению пп равна
2ягД 81П ф.
Равнодействующая нагрузки, распределенной по поверхности выделенной части оболочки, будет где Р — площадь поверхности выделенной части оболочки (пОп, рис. 323, а).
Условие равновесия (1,2 0) отсеченной части оболочки
281П ф Цр 0,
откуда
Ыь-
2ПГ 8Ш ф
(21.2)
454
Усилия Ыг получаются сжимающими (нагрузка действует вниз). Подставив значение N яз выражения (21.2) в уравнение Лапласа (21.1), найдем окружное усилие Ы2.
Пример. Определить усилия Ц М2 для сферического купола при действии вертикальной распределенной по поверхности купола нагрузки собственного веса интенсивностью 7. Радиус сферы Я (рис.
323, б).
Решение. Для сферы 1
2 Поверхность отсеченной горизонтальной плоскостью пп части оболочки
Р 2пКк — 2л?2 (1 — соз ф).
Меридиональное усилие по выражению (21.2)
Я2(1
2л?2 (1— созф) _ 2лг зт ф П
— СОЗ ф)
К зт2 ф
-7 -
1 соз ф
(21.3)
Усилие N1 сжимающее.
Подставляя найденное значение N1 в уравнение (21.1), получаем
N2 — дЯ (соз ф-
1
1 соз ф
(21.4)
Рис. 324
В вершине купола, где Ф 0, имеем
На рис. 323, в даны эпюры меридионального и окружного (кольцевого) усилий по высоте купола. Если купол задан в виде полусферы, то усилие Ы2, сжимающее у вершины, с увеличением ф меняет свой знак и в нижней части становится растягивающим. Приравняв усилие Ы2 по формуле (21.4) нулю, получим предельный угол фпо, при увеличении которого появляется растягивающее кольцевое усилие; фпр 51°49
§ 122. РАСЧЕТ ОБОЛОЧЕК ВРАЩЕНИЯ НА ПРОИЗВОЛЬНУЮ НАГРУЗКУ
Геометрия оболочек
При расчете оболочек вращения очень удобно применять сферические координаты, определяемые углами 0 и ср (рис. 324). Угол 0 — между вертикальной плоскостью, совмещающей данный меридиан СВ с координатной плоскостью 10Х он определяет положение данного меридиана. Угол ср определяет направление радиуса кривизны Я2 для элемента параллели ОЕ в заданной точке а. Этот угол отсчиты-
455
вается от вертикальной оси 1. Радиус г окруйюсти данной параллель есть заданная функция 2. Рассмотрим бесконечно малый элемент по верхности оболочки аЬсй, выделенный двумя соседними меридианами Оа и ОЬ и двумя соседними параллелями аЬ и йс (рис. 325, а).
Из чертежа легко установить, что
г ?2 31Пф, (а)
где ?2 — радиус кривизны дуги параллели. Длина дуги аЬ где
аЬ й2 г (б)
г — радиус параллельного круга.
Длина элемента дуги по меридиану (рис. 325, б)
ас1 с1з1 К1с1 ф, (в)
где ?х — радиус кривизны меридиана.
Вывод основных дифференциальных уравнений мембранной теории
Пусть оболочка подвергается действию любой распределенной нагрузки, составляющие интенсивности которой
Р» Ръ Рз» где рг — составляющая по касательной к меридиану (см. рис. 325, а)
р2 — составляющая по касательной к данной параллели;
р3 — составляющая, нормальная к меридиану (см. рис. 325, б). Применяем мембранную теорию оболочки, считая, что в оболочке не возникает ни изгибающих моментов, ни поперечных сил. Следовательно, элементы оболочки получают только нормальные ох, а2 и касательные т12 напряжения. Нормальным напряжениям соответствуют нормальные усилия на единицу длины и М2 — меридиональное и кольцевое (окружное). Касательным напряжениям отвечают
Рис. 325
456
вдвигающие усилия на единицу длины 512 и 521. Из условия равновесия элемента оболочки аЬсА получим, что касательные усилия 512 и 521, действующие по взаимно перпендикулярным направлениям, равны,ежду собой:
512 521 5.
Составляем теперь три условия равновесия бесконечно малого элемента оболочки аЬсА (см. рис. 325, а): 1) сумму проекций всех усилий на направление нормали к меридиану; 2) сумму проекций всех усилий на направление касательной к меридиану; 3) сумму проекций всех усилий на направление касательной к параллели.
Первое уравнение равновесия будет иметь тот же вид, что и уравнение (21.1), а именно:
1 Лг 1 т- —Рз 81 йз2 0, (21.5)
малыми высшего порядка пренебрегаем. Из уравнения (21.5), сокращая на А81А82, получаем
ё- 0. (21.6)
Составляем второе уравнение равновесия элемента аЬсс оболочки как равенство нулю суммы проекций всех сил, приложенных к элементу, на направление касательной к меридиану в центре элемента. Учитывая, что величины (Лг) и (5г) при переходе от верхней площадки аЬ к нижней Ас, а также величины (Л0) и (8 Аь) при переходе от левой площадки аА к правой Ьс меняются в зависимости от ф и от 0, получаем для площадок Ас и Ьс соответствующие бесконечно малые приращения, указанные на рис. 325, а. Составляющая нагрузки по меридиану для элементарной площадки будет:
рг Азг Аз2.
От меридиональных усилий по площадкам аЬ и Ас в уравнение войдет приращение
От касательных усилий по площадкам аА и Ьс войдет приращение
(1 ср.
Кроме того, в уравнение равновесия войдет составляющая по меридиану нормального усилия Ы2ЦА по стороне Ьс, «развернутой» по отношению к стороне аА на угол (рис. 326). Эта составляющая равна
— ЛЛр-г), (г)
где угол можно найти как тангенс г(у.
а”
(Д)
15 Н. К. Снитко
457
Подставляя значение э из выражения (д) в выражение (г), получаем составляющую от кольцевого усилия на меридиан:
(е)
Заметим, что из рис. 325, б
дг дг п (Ш п, ч
Таким образом, окончательно составляющая кольцевого усилия будет
— N2% 1 С03ф-Йф Ад.
Второе условие равновесия (сумма проекций всех усилий на меридиан):
дф- — 21 С08 ФФ Ад рхГ Аф Ад 0.
Сокращая на Лр Ад, окончательно получаем
-- 1§-адсо8ф р1?1г 0. (21.7)
Переходим к составлению третьего уравнения равновесия — суммы проекций всех усилий, приложенных к элементу аЬсА, на
а
Рис. 326
направление касательной к средней параллели элемента. При этом в уравнение войдет составляющая нагрузки, действующая вдоль параллели:
Р2 А1 А8%,
Эта нагрузка, очевидно, вызывает скручивание оболочки вокруг оси 2. Результирующая сдвигающих усилий по сторонам аЪ и Ас
458
равна приращению (5г)
Приращение от кольцевых усилий по сторонам ай и Ьс
Проекция сдвигающего усилия по стороне йс, развернутой по отношению к стороне аЬ на угол г(?2 (см. рис. 326), будет
(5гй0) (5гйГ0)-. 5йФйв 5йФае;
сейа по малости принимаем за ромб; тогда для составляющего кольцевого усилия имеем согласно выражению (ж)
соз ф ф с1д.
Подставляя найденные составляющие в уравнение суммы проекций на касательную к параллели, находим
д ф йЬ ? ф ЛЬ ? С08 ф ф Р21Г с1ус№ 0
или, сокращая на йф Й0, получаем окончательно для третьего уравнения
Я1Г Я1со8ф Л1г 0. (21.8)
Итак, уравнения равновесия элемента оболочки имеют вид:
?1§-ЛУ?1с°8ф М1 °; (21.9)
•- х1 51со8ф р2?1г 0; (21.10)
%Рг 0. (21.11)
§ 123. РАСЧЕТ СФЕРИЧЕСКОЙ ОБОЛОЧКИ НА ВЕТРОВУЮ НАГРУЗКУ
Рассмотрим действие на оболочку ветровой обратносимметричной (относительно оси ОУ) нагрузки. Считаем, что составляющие р± и р2 нагрузки равны нулю и,имеется лишь нормальная составляющая р3.
В общем случае интенсивность ветровой нагрузки р3 раскладываем в ряд Фурье [11]:
?з 2Рлс°8лб. (21.12)
(П)
где 1 0, 1, 2,.;
Рп — функция распределения нагрузки по ф, не зависящая от 0.
10’
459
Рассмотрим решение в случае нагрузки, представленной одним членом ряда, имея в виду возможность сложения решений для общего случая нагрузки по выражению (21.12). Если нагрузка дана в виде периодической по
ра р„сопв, (21.13)
то и усилия Ыи и 5 будут выражаться периодическими законами:
Л1 Л1„со8пб;
М2 Л2ЯС05 л0; (21.14)
5 5„зтг6, ;
где Л1л, Ы2п, 8п — функции лишь угла р.
Подставляем значения величин из выражений (21.14) в выражения (21.9) — (21.11); получаем соответственно:
д дф1” 008 1 Пп с05 п® — 1 соз ФМ2п со8 пЬ 0; (а)
—81П П0 — «Л2Я 81П пв СОЗ ф5„ 31П п8 0; (б)
4- СОЗ П0 соз «6 рп СОЗ П0.
А1 2
(в)
Уравнения (а) и (в) сокращаем на созя0, уравнение (б) — на 51П п0 и, кроме того, учитываем, что имеем дело с системой обыкновенных дифференциальных уравнений:
а (гы1я)
- КгпЗп — соз фЛ2Л 0;
- К1ПЫы ?, СОЗ ф5„0;
N1 п I N 2п кГ Ърп
Для сферической оболочки (см. рис. 323) имеем ?1 ?2 ; г ?зтф.
Из третьего уравнения (21.15) легко выразить А2л
N 2п — Рп N 1п.
(21.15)
(г)
(21.16)
Подставляем значение УУ2л из выражения (21.16) в первые два уравнения (21.15); учитывая соотношения (г) и подставляя производную от г по ф, получаем
Яп5л Я 2- 51П ф 2КЫ1п СОЗ ф к2 СОЗ ф • Рп,
Я зт ф 23„ соз ф ЯяЛ1п Я2пр„.
460
Делим все члены этих уравнений на ? т р:
п
" 81П ф Л т м1п
ЛУ,
с1(р
-2Л1пс1§ф с1ёф-рп;
, - 25лс1§ф 7?-Д-ря.
8111 ф (1(р 1 П Ь Т 8Ш ф
Сложим почленно эти уравнения и вычтем второе уравнение из первого. Тогда получим
№ 1 п 8п)
81П ф
(Мщ—Зп) [ —
2 с§ ф)
Ш
81П ф
Крп [с1§ ф
2с1§ф
Ш,
П
81П
Ветробоя нагрузка р3р зспУсовд
У
Меридиан Номр
V, для В-О,Я
ф
15 п йф 1
81П ф
(21.17)
Щ для 90, я
Примем за нёизвртные суммы и разности Ы1п и 5л:
Л1л 5„ Ф1; М1п—„ Ф2. (21.18)
Тогда вместо уравнений (21.17) получим два несовместных уравнения
л, 0., йф. „. п
01
81П ф
Ф, -
-2с1вф) я«(сёф-. 8Шф
П I О А I ф2 Г» I П
— 1-2 сйф -- -тЛ НРп Ф ——
5Ш ф Ь 1 ф П Ь 81П ф
(21.19)
461
Интегрируя дифференциальные уравнения (21.19), получаем выражения для функций Фх и Ф2 и, учитывая условия для вершины оболочки, определяем произвольные постоянные Сх и С2, входящие в выражения Фх и Ф2. После этого находим из выражений (21.18) Ы1п и 5Л, а из (21.16) — Ы2п.
Пример. Пусть сферическая оболочка в виде полусферы подвергается действию ветровой нагрузки вида [11]
р3 — 7 81П ф соз 0 рп соз б,
где
7 81Пф, 11.
Эпюры нагрузки для главного меридиана (в плоскости ХТ) и нижней параллели (рис. 327, о) представлены на рис. 327, б.
Решение. Интегрируя уравнения (21.19), получаем:
_ 1 соз ф Г „ соз3 ф 2 1
ф1-нмГ и Г8 ГЧ - Т
_ 1 — соз ф Г [ соз3 ф, 2
I - (со8 —з )т «4
Из выражений (21.18) находим
1 — (2 сов ф - 3 С053 фС084 ф); (21.20)
5—•(2-Зсофсо83ф), (21.21)
Из выражения (21.16) получаем
М2 — Я зт фсозб — Л.- (21.22)
Эпюры Ы1у N2 и 5 для некоторых сечений даны на рис. 327, в.
§ 124. РАСЧЕТ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК ПО БЕЗМОМЕНТНОЙ ТЕОРИИ
Условия равновесия
Рассмотрим еще часто встречающийся случай цилиндрической оболочки, подвергающейся действию произвольной распределенной нагрузки, составляющие которой р1у р2 и р3 (рис. 328, а), где рг — нагрузка, направленная по меридиану, р2 — по параллели, р3 — по нормали к поверхности. Применяя цилиндрическую систему координат, положение данной точки а оболочки определяем координатами: углом 0, радиусом соп1 и абсциссой х. Сопоставляя этот случай цилиндрической оболочки с предыдущим более общим случаем оболочки вращения (см. рис. 325), находим:
? оо; К2 Я; ф
Толщину оболочки обозначим К
462
Уравнения равновесия в этом, случае проще всего получить, выделяя элемент аЬей оболочки, для чего проводим два соседних меридиональных и два соседних нормальных к оси цилиндра сечения, отстоящих друг от друга на расстоянии йх. Размеры элемента аЬей будут: по окружности Я йВ, по меридиану кх. На рис. 328, а показаны интенсивности нагрузки, приложенной к центру элемента поверхности. На рис.
328, б изображены усилия, действующие по сечениям элемента: нормальные Л, Ы2 и сдвигающие 5 на единицу длины. По площадкам Ьс и ей усилия получают бесконечно малые приращения в соответствии с приращениями координат йВ и йх.
Составляем первое уравнение равновесия как сумму проекций всех усилий, приложенных к элементу аЬсй, на нормаль к поверхности элемента; получаем по рис. 328,6 йхйВ — р3йХйВ О, откуда
Лр3Я. (а)
Составляем второе уравнение равновесия в форме суммы проекций всех усилий на направление образующей цилиндра (меридиана):
Рис. 328
или
йхН йВ йВ йх рх йх йВ • ? О
ае
(б)
Составляем третье уравнение равновесия как сумму проекций всех усилий, действующих на элемент, на направление касательной к окружности (параллельно аЬ, ей); получаем
-йВ ах — ахК йВ р2 йх йВ-К 0,
откуда
дМй ЯЛЯ 0.
дЬ
(в)
463
Итак, уравнения равновесия элемента цилиндрической оболочки имеют вид:
-1г жлЯо; 21-23
Г Ж °; (21.24)
Л р3Я. (21.25)
Из уравнения (21.24) находим сдвигающее усилие, подставляя из уравнения (21.25):
5 - Рг ЪЩ1х С1 (6) - (л Сб), (21.26)
где Сх (6) — некоторая произвольная функция от 0.
Найдя 5 из уравнения (21.26), подставляем его значение в урав¬
нение (21.23):
Л- 5(л-ж)с0) 21-27)
где С2 (0) — вторая произвольная функция от 0.
Выражения для деформаций
Функции Сх (0) и С2 (0) находятся из граничных условий для упругих перемещений. Чтобы составить эти условия, необходимо иметь выражения для относительных удлинений ех (по образующей), в2 (по кольцевому направлению) и относительного сдвига у.
Очевидно,
■-8Г-Ж 21-28»
где V — коэффициент Пуассона;
и — перемещение вдоль образующей (оси X).
Найдем теперь выражение е2 через перемещения V и хю, где V — перемещение в кольцевом (тангенциальном) направлении, хю — перемещение, нормальное к поверхности цилиндра. Для определения в2 рассмотрим элемент сечения оболочки аЪ длиной Н с1в (рис. 329, а).
Пусть точка а получит перемещение V, точка Ь — с(0
в тангенциальном направлении. Тогда часть относительного удлинения в этом направлении будет ду 1 1 ду, ч
6-2 — Ш К дЪ От радиального перемещения хю (рис. 329, 6) получим
(Я до) 0 — Я АЬ до тЛ
е«— — 7Г 464
Полное относительное удлинение в кольцевом направлении
Р-М)
Выделим элемент аЪсй оболочки на поверхности (рис. 329, в). Относительный сдвиг у будет
у а-- р,
где
ду йх ду д ди йО 1 ди
адх0х дх’ ЯЖ Ж Окончательно
до. 1 ди _ 8 _ 2(1у)5 о 1 30
дх Я дв Ск ЕН ’ (1.)
Мы получили три уравнения, связывающие деформации и усилия — уравнения (21.28—21.30).
Определение усилий в оболочке разложением нагрузки в ряд Фурье
При наличии произвольной распределенной нагрузки, имеющей
составляющие р1у р2 и ?3, разлагаем последние в ряды Фурье следую¬
щего вида [11]:
СО СО СО
рх ргпСОп% р2 ]р2п5тп0; р3 ]рзпсо5 лв, (21.31)
0 1 0
где р1п, р2пу Рзп — коэффициенты разложения интенсивностей, являющиеся функциями только х.
465
Аналогично представлению нагрузки разложим в ряды Фурье усилия (нормальные — по косинусам, сдвигающие — по синусам). Рассмотрим п-й член разложения нагрузки и найдем соответствующие ему усилия; для всей нагрузки полные усилия получим суммированием результатов влияния отдельных членов разложения.
Для п-то члена разложения нагрузки имеем
р3 рзпсопВ р2 р2п §1п л0; 1 (2132)
Р1 Л„созл0. )
Подставляя значение р3 из выражения (21.32) в уравнение (21.25), получаем кольцевое нормальное усилие:
М2 р3г?созг0; дМ, о • 0 (21.33)
— РзлЛЯзтлО. ]
Подставляем значения величин из последнего выражения в дифференциальное уравнение (21.24) и интегрируем:
5 — 51ПП0 (Р2п — прзп)с1х С1(В)9 (21.34)
(X)
где Сх (0) — произвольная функция от 0.
Найдем производную 5 по 0:
§ -лсоз Л0 ? (р2п — прзп)(1х Р-
(X)
и подставим ее в уравнение (21.23):
- соз пО
Рхп
соз пЬ
(х)
1 асх (а) к ав •
дх
Интегрируя, получим 1 — созлб --(р2п — пр3п)йх йх—±.Мх С2(в),
(X) [ (X) ]
(21.35)
где С2 (0) — новая произвольная функция от 0.
Рассмотрим теперь частный случай, когда
р1п 0 р2„ сопз1; р3„ сопз1.
Зададим функции Сх (0) и С2 (0) как периодические с постоянными коэффициентами и Д2:
С1(д) 018ШЯ0; С2(0) О2созАг0. (21.36)
Применяя выражение (21.34), получим для сдвигающего усилия
5 — 81П пВ [р2п — прзп) —Ях]. (21.37)
Нормальное усилие по уравнению (21.35) будет
N1, 1- [(р2п—прзп) х — д соз пЬ. (21.38)
466
Определение перемещений железобетонной оболочки
Для железобетонной оболочки определим перемещения при нагрузке вида, рассмотренного в предыдущем разделе.
Для случая железобетонной тонкостенной трубы можно положить коэффициент Пуассона равным нулю [11]; тогда вместо уравнений
(21.28), (21.29) и (21.30) получим следующие соотношения между пере¬
мещениями и усилиями:
1 (21.39)
1 (21-40)
I КМ 2 Гк1,и
Ш тЕГ (21-41
Подставляя в соотношение (21.39) решение для из выражения (21.38) и интегрируя по х, находим
ыт[(-п) т]яМ- (21-42)
При интегрировании вошла третья произвольная функция
В3С где 13 — третья произвольная постоянная.
Зная функцию и, обращаемся ко второму геометрическому уравнению (21.40):
до _ 25 1 ди
дх Ёк “ 7? дЬ
Подставляя значение усилия 5 из выражения (21.37), значение перемещения и из выражения (21.42) и интегрируя по х, получаем
Г гРх х пЧз 2лЛ,
(Р п Прзп) ЕН) 6фЕН Н )
ш[1Г1) п0’х 0)]ШЬ’ (2143)
где пО Оь — произвольная функция от 0;
Г4 — произвольная постоянная.
Из уравнения (21.41), подставляя значения величин из выражений (21.43) и (21.33), находим перемещение хю:
ш -п (р2п-прзп)(0 - ж) - ж (щ2х)
т,(г°п°х°) ег005 л6 • (21 -44
467
§ 125. РАСЧЕТ ТОНКОСТЕННОЙ ТРУБЫ НА ИЗГИБ ОТ СОБСТВЕННОГО ВЕСА
Рассмотрим действие собственного веса на тонкостенную горизонтальную трубу длиной при интенсивности нагрузки д (рис. 330, а). Составляющие нагрузки будут:
р1 0; р2 81П0; р3 — 7соз0. (21.45)
Сравнивая эти выражения с выражением (21.32), получаем
п 1; р2п — Рзп д соп5, (21.46)
где — нагрузка от веса на 1 см2 площади оболочки (кнсм2). Прежде всего необходимо установить, каковы опорные закрепления трубы
В)
Зпшра V,,
РЩЩ 1
1
1
)Р777777777777777777777ТГ77
4?
0
"р “4
[-с ■ 1
ШШтттттг.,
X
V-?
Рис. 330
по концам. Считаем, что опоры по краям трубы воспринимают сдвигающие вертикальные силы (абсолютно жесткие в своей плоскости и подвижные в направлении оси ОХ рис. 330, б). Так как опоры по-
46Ь
движны в направлении оси ОХ, то нормальные силы в краевых сечениях равны нулю:,
Перемещения на опорах в кольцевом направлении V и нормальные к поверхности оболочки хю также равны нулю.
Так как радиальное перемещение т на опорах принимается равным нулю, то безмоментное напряженное состояние оболочки у опор будет нарушено, однако оно носит местный характер.
Для определения усилий в произвольном сечении л; для произвольной точки оболочки (угол 6) применяем выражения (21.38), (21.33) и (21.37); получаем, подставляя значения из выражений (21.46):
Найдем произвольные постоянные. Из условия (21.47) получаем:
Из условия (21.48), пользуясь первым уравнением (21.49), находим
М2 определяется из уравнения (21.49).
В кольцевом направлении и У2 меняются по закону косинуса 0. Для 0 я (соз 6 —1) на рис. 330, б построена эпюра меридиональной нормальной силы Ыг.
Максимальное ее значение
Верхние волокна трубы от сжаты (выше линии ЛВ), нижние — растянуты.
при х 0 Л 0; при х — 1 Л 0.
(21.47)
(21.48)
N2 -К соз 0;
5 _ 8Ш 0 [(д д) X — Ох],
или
(21.49)
Я2 0.
Ог д1.
Подставляя в уравнения (21.49), получаем
А1тг(х — 1) СО5 0;
4 — ч и ’
5 — д (2х—) зш 0.
(21.50)
(21.51)
Л —
1, макс 4, •
(21.52)
469
То же самое можно сказать о действии кольцевой нормальной силы N2 — соз е.
Сдвигающая сила 5 меняется по сечению в соответствии с законом изменения синуса 0. На рис. 330, б под продольным разрезом
трубы показана эпюра 5 по длине трубы при когда 5 —7 (2х — ).
Наибольшие значения 5 — по краям трубы (7). Эпюра 5 по сечению дана справа от продольного разреза трубы.
Ниже рассматриваем подробнее изгиб цилиндрических оболочек.
§ 126. МОМЕНТНАЯ ТЕОРИЯ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
Краевые условия в общем таковы, что они приводят к изгибному эффекту; в ряде случаев необходимо применение моментной теории оболочек. При действии на оболочку прерывной нагрузки в окрестности ее будут также возникать изгибающие моменты и поперечные силы. Поэтому нельзя ограничиться определением усилий в оболочке только по мембранной теории [1].
Сначала рассмотрим круговую цилиндрическую оболочку, которая подвергается действию сил, симметрично распределенных относительно оси цилиндра. Нагрузка может быть в виде давления жидкости или пара, а также в виде собственного веса (при вертикальном положении цилиндра). Решение этой задачи применяется при расчете котлов, резервуаров и труб.
Составим основное дифференциальное уравнение для определения перемещения гюу происходящего нормально к цилиндрической оболочке. Выделим элемент оболочки, размеры которого йг — вдоль оси 2 (цилиндра) и а й ср — в окружном направлении (рис. 331а) а — радиус срединной поверхности. Напряженное состояние
470
элемента характеризуется продольными силами и 2, поперечными силами и моментами Мг и М2, которые принимаются на единицу длины соответствующего размера (на рис. 331, а показаны величины усилий, действующих на сеыения длиной а йфи). В связи с тем, что рассматривается осесшшетричная задача, мембранные силы сдвига 8уг 5 оказываются равными нулю, а усилия Ы2 будут пойЙроянными вдоль окружности. Очевидно, в силу симметрии поперечные "силы по вертикальным площадкам окажутся равными нулю, также обращаются в нуль крутящие моменты Мг? М?г, а изгибающие моменты М? М2 будут постоянными по окружности. Задача сводится к отысканию поперечных сил (2Ъ моментов Мх и М2 п продольных сил и Ы2. Для определения этих усилий составляем три уравнения равновесия элемента и два соотношения для деформаций, выражая их через следующие компоненты перемещений: составляющую т нормально к поверхности цилиндра и составляющую и вдоль оси цилиндра. Составляющая перемещения вдоль окружности V по условию симметрии равна нулю. Влиянием собственного веса цилиндрической оболочки пренебрегаем; соответствующие напряжения от этой нагрузки можно учесть дополнительно, простым наложе? нием.
Рассматривается нагрузка в виде нормального давления интенсивностью р2 (является функцией координаты г). Выпишем приращения в значениях Л, С1 и М2 в связи с приращением йг (см. рис. 331):
Составляем три условия равновесия: 22 О, 2Х О, 0.
Они представляются так:
Из первого уравнения получаем, что силы постоянны. В дальнейшем изложении, пренебрегая влиянием этих сил на изгиб, будем считать их равными нулю:
Второе и третье уравнения после деления на (а Лр йг) принимают вид:
(■37-2) айу М2йхй(р ргай(рйг 0; ■
(а)
0.
(б)
Уравнения (в) содержат три неизвестных Л2, и
471
Вместо первого уравнения можно написать «1, ЛЛ,
Чг Т -Р- (21.53)
Для исключения М2 воспользуемся соотношениями между деформациями ёх и е2 и усилиями Ыг и принимая согяяшо формул (21.28)
и (21.29) 4
Ли, и)
е1_37’ е2 ер а- (г)
При этом считаем, что при положительном хю в направлении к оси цилиндра 22 окружное относительное удлинение будет со знаком минус (см. рис. 331).
По формулам, аналогичным (21.8) получаем выражения для продольных сил:
аг л I ЕЬ (Ли Ы) (е1 )т(аг-У -) 0;
кг ЕН., ч ЕН ( ш, с1и
(««480- -- у ж,
(д)
где V — коэффициент Пуассона.
Из первой формулы имеем
Ли г Л? а ’
а внося во вторую, получаем
ЕН
N.г -хю. (е)
В случае, если Ф 0 (например, Ых —ук ( — г) — от собственного веса, где V — объемный вес материала оболочки, г 0 для днища), пишем выражение для е2:
е2 — —V), (ж)
откуда
ЛГ, ——ууй ( —г). (з)
Теперь найдем выражение для момента М1г входящего в уравнение (21.53). Оно может быть получено аналогично формулам (20.9) для моментов по теории тонких пластинок. Момент М1у действующий в плоскости 2ХУ будет зависеть от кривизны в этой плоскости
с12ы) л
и, кроме того, от изменения кривизны Дх? в плоскости срл (см. рис. 331, б)
М х — О (к2 V Дх), (и)
где О берется по формуле (20.10),
472
Очевидно, изменение кривизны при увеличении радиуса от а до (а — ш) будет
1 1 Ы)
а а — а2
Таким образом, выражение момента
(К)
За малостью радиальных перемещений и при больших радиусах а часто пренебрегают вторым членом в скобках формулы (к). После подстановки выражений (к) и (з) в уравнение (21.53), получаем
тл V I ЕН
Ба2
О
— V
уН (I—г)
Оа
. (21.54)
При отбрасывании второго члена в выражении момента Мх и не учете влияния собственного веса сосуда получаем:
уты- (21-55
При этом хю принимается положительным при смещении в направлении к оси цилиндра. Уравнение (21.55) аналогично дифференциальному уравнению изогнутой оси балки на сплошном винклеровском основании. Дифференциальное уравнение (21.55) можно записать так:
ш1У 40%, (21.56)
где
Р4
ЕН
3(1—V2)
4 йа2
(21.57)
цилиндрическая жесткость:
ЕН3
12(1 — V2)
(л)
473
Применяя дифференциальное уравнение (21.56), находим изгибающий момент в меридиональной плоскости по формуле
Мг — 01ю" — Иау
где а — угол наклона изогнутой поверхности в меридиональной плоскости, а — производная угла наклона.
Если р2 — интенсивность давления жидкости на глубине г (рис. 332, а), то:
7В — объемный вес жидкости.
Дифференцируя обе части уравнения (21.56) и принимая во внимание выражение рг по формуле (м), последовательно получаем:
Уравнения (21.57) — (21.59) применяют при исследовании изгибного напряженного состояния любых оболочек вращения в первом приближении.
Рассмотрим решение задачи определения перемещений и усилий в стенке цилиндрического сосуда конечной длины, подверженного действию давления жидкости, меняющейся по линейному закону (рис. 332, а). Дифференциальное уравнение задачи по уравнению (21.56) для радиального перемещения:
где И — цилиндрическая жесткость;
Р — определяется по формуле (21.57).
Интеграл этого дифференциального уравнения, как известно из теории расчета балки на упругом основании, при использовании записи через начальные параметры изгиба (щ, а0, УИ0, ф0), будет:
где
Рг Тв( — 2) Ро г,
Ро — Тв
(м)
М.
эу 41 0.
(21.58)
(21.59)
§ 127. РАСЧЕТ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК ПО МОМЕНТНОЙ ТЕОРИИ
Оболочка конечной длины
(21.60)
474
где Аг, В,, Сг, и имеют следующие выражения: Аг соз Рг сЬ рг;
Вг (з1п Рг сЬ (к соз Рг зЬ рг); сг - 31П Р2 зЬ р2;
Ц 4- (зш рг сЬ рг — соз рг зЬ Рг).
(21.62)
Таблицы этих функций приведены, например в работе К. Гогенемзера и В. Прагера. Дифференцируя выражение (21.61), получаем уравнения для угла наклона, момента и поперечной силы:
Л О П I Л Л1п С
аг — 0-4рОг а0Лг — у “ Р Ро
Ь
Р
1-Аг
4
Мг — щ-42ОСг — а04ООг — М0Аг — С,
п Ь._
Чо р
"Ро
Р2
, Ро_ Рг. г рз.
2г — Щ ■ 4р3ОВ; — а„ • 4р2ОСг
М0-4рОг-(30Лг-р0 -.
(21.63)
(21.64)
(21.65)
Положительные направления М0 и С0 указаны на рис. 332, б. Два начальных неизвестных в этих уравнениях находятся из граничных условий. Так, для сосуда с водой (см. рис. 332, а) имеем: при г, Мг О, Э2 0 и из уравнений (21.64) и (21.65), принимая, что стенки сосуда жестко защемлены в днище (щ 0, а0 0), получаем:
— М0АЬ—0.0- — Ро у • з0; М0 • 4рЯ, - 2 - р0 Ь- • 0,
откуда
М,
фф-СМ-шМ-ОА)
40,6, Л
(а)
(б)
(21.66)
Пример 1. Найти момент защемления и напряжения от изгиба для сосуда при
I Юм, а 5 м, Л 70 см, V 0,3.
Решение. Определяем по формуле (21.57) Р 0,69; Р2 0,47; Р3 0,324; Р 6,9. Момент по формуле (21.66) М0 11 Т — 11000 кГ-смсм. Напряжение
0 113,5 кГсм.
К. Гогенемзер и В. Праге р. Динамика сооружений, Стройиздат, Л. —М., 1936, стр. 310.
476
Оболочка бесконечной длины
При больших значениях р необходимо переходить к расчетной схеме бесконечно длинной оболочки, так как иначе в решение входят отношения разностей больших чисел.
Внося в решение (21.61) значения гиперболо-тригонометрических функций и учтя, что множители при возрастающих функциях ег соз рг и е г 51П рг должны быть равны нулю (при г- оо, хю- 0), получим из решения (21.61) после нетрудных преобразований следующие выражения для начальных щ и а0:
Щ — -Що (ро 2о щ а "1“ •
Общее уравнение для щ:
™г -2ю(Мо 2о)е-?гсог -фп Мзшрг-. (21.68)
Дифференцированием легко получить выражения для угла наклона, момента и поперечной силы. Заметим, что углом наклона весьма пологой эпюры рг в данном решении мы пренебрегаем (см. рис. 332, б).
Для случая защемления стенок сосуда в днище получаем при г 0, ш0 0, а0 0 и из решения (21.67) находим:
М„г, (21.69)
2о -Рр. (21.70)
Пример 2. Для тех же данных, что и в примере 1, найти И0.
Решение. Для Р2 0,47, р0 10 Тм2, момент 10,65 Т-смсм, что отличается всего на 3% от решения по схеме конечной балки. Однако решение (21.66) не применимо при обычных малых толщинах стальных сосудов.
Пример 3. Найти момент защемления стенки сосуда при к 1 см и тех же других данных, что и в примерах 2 и 1. Определить М0 и а.
Решение. Теперь Р 5,74 1 му р2 32,86 1 м2, момент
М° Щ 2-32,86 0152 тсмсм•
Окончательно
М0 152 кГ • смсм
6 М0 6-152 Л1П п, а — цГ —уГ "912 кГсм.
(21.67)
Близкое к этому решение получается и из более точного дифференциального уравнения (21.54).
ПРИЛОЖЕНИЕ
МАТРИЧНАЯ ФОРМА РАСЧЕТА СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ
1. ПОНЯТИЕ О МАТРИЧНОЙ ФОРМЕ РЕШЕНИЯ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Эффективное применение электронных цифровых вычислительных машин (ЭЦВМ) к расчету сложных статически неопределимых систем получило широкое распространение благодаря существенной экономии труда проектировщика. При этом используется матричная форма решения, развитая у нас благодаря работе А. Ф. Смирнова [8] и далее коллектива, им возглавляемого [9].
Дадим основные понятия о матрицах, применяемых при решении задач расчета статически неопределимых систем [11]. Определение лишних неизвестных (например, по методу сил) сводится, как известно, к решению системы уравнений
0111 0122 0133 • 02110222 233 •
• 01 пхп — Аь
• 02 22 2»
(а)
0г11 0222 0233 ••• 0г2г — Аг
где ак — коэффициент при неизвестном хк
Д,- — Др — грузовой член канонического уравнения.
Система уравнений (а) выражает собой линейное преобразование неизвестных хк в величины Д. Система коэффициентов составляет матрицу А из чисел а[к:
А
011
012
013 •
•• 012
021
022
023 •
. 0,2п
021
022
023 •
•• 022
(б)
Полагаем, что матрица А не особенная, для которой определитель Ое1 А не равен нулю. Кроме того, считаем, что коэффициенты а-1к обладают свойством взаимности:
а1каЫ (в)
В матричной форме систему уравнений (а) записывают так:
А-Х А,
где X — матрица-столбец величин неизвестных, а свободных членов;
1
Дх
2
; Д
42
хп
д »
(Г)
Д — матрица-столбец величин
(Д)
477
Решение уравнения (г) в матричной форме можно записать так:
Х Б • Д Л-1 • А,
(е)
где В Л-1 — обратная матрица по отношению к матрице А. Задача решения уравнения (г) или системы уравнений (а) сводится, таким образом, к определению обратной матрицы.
Покажем,- как найти обратную матрицу для системы трех уравнений:
а11Х1 122 133 1» а21Х1 222 233
а31Х1 “Ь а32Х2 4 а33х3 3
Дх; Д2; [
д3. )
(ж)
Решение этой системы уравнений можно представить по Крамеру в форме, содержащей так называемые миноры Л, матрицы Л:
у А 11, Л21, д Л31
жа Д1 Д2 Д8; х3 Д1 Дз Дз,
(3)
где миноры Лм — алгебраические дополнения матрицы Л или определителя вычеркиванием -го столбца и к-й строки, взятый с множителем (—)к1:
Ак (- 1)(
ац
а12.
. аи
. а1п
а21
а22 •
. а2
. а2л
ак1
а2 •
,. ам
. акп
аП1
ал2 •
• аП1
. алг
(и)
Для трех уравнений (ж) в решении (з) имеем:
Ли —
22 23 32 а33
Л12(-1),12
13
— 2233 28»
а21 23
а31 а33
— 312э) — 21
21 а2 2 з1 а32 ац а13
а31 азз
Л 22
Л23 (-1)(23
33
2132 — 3122 — ЗЪ
— ц88 1
аи а12
31 32
ац а12 а21 а22
(ацазг — а31а12) Л32;
а11а2о 12
При этом учтено свойство взаимности.
Решение системы уравнений (ж) вместо развернутой формы (з) можно дать в матричной форме:
х-я.дл-.д,
(к)
478
где
В
О
11
А 21
31
А12
А 22
А 32
13
А 23
33
(л)
Итак, получить обратную матрицу В можно, вычислив определитель Э матрицы А и миноры Ам по формуле (и). Эти вычисления легко осуществляются на ЭЦВМ.
"(Я и±-
Рис. 333
После вычисления обратной матрицы В, согласно решению (к), чтобы установить значения лишних неизвестных, необходимо квадратную матрицу В умножить на столбцовую матрицу А. Умножение квадратной матрицы из коэффициентов ак1 на столбцо-
479
вую матрицу Д для трех неизвестных производится так:
аП 012 13 а21 22 а23
031 а32 а33
X
А
Дг
Дз
(аи Дх а12Дг Я13Д3) (21Д1 Л2гД 2 Я23Д3) (а31Дх Я32Д2 Я33А3)
(м)
Как видим, члены каждой строки квадратной матрицы умножаются последовательно на элементы столбцовой матрицы. Матричная форма решения в виде (к) удобна тем, что для данной конструкции раз навсегда вычисляется влияние жесткостных факторов на величину матрицы А, а влияние нагрузки отражается столбцовой матрицей. В случае расчета рамы методом перемещений матрица, содержащая упругие реакции, носит название матрицы жесткости.
2. МАТРИЧНЫЙ РАСЧЕТ РАМЫ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
Будем применять каноническую форму метода перемещений, значительно развитую И. М. Рабиновичем, А. Ф. Смирновым и другими [7]. Основную систему выбираем в виде рамы с фиктивными защемлениями всех жестких не опорных узлов и с введенными дополнительными опорными закреплениями по числу независимых линейных смещений узлов. В качестве примера рассмотрим раму, изображенную на рис. 333, а. Размеры рамы и вертикальная нагрузка те же, что и в работе [4], но добавлена горизонтальная нагрузка для получения более общего случая наличия свободного члена и для составления третьего канонического уравнения. Первый пролет загружен равномерно распределенной нагрузкой 7,2 Тм, второй — сосредоточенной силой Р 32 Г по середине пролета; вторая стойка загружена горизонтальной силой Рг 18 Т. Пусть отношение моментов инерции стойки и ригеля будет стУр 45. Пролет I — 5 м, высота стойки к 4 м. При данных размерах отношение погонных
жесткостей 1, и можно ввести постоянную погонную жесткость 1. Основная 1Р
система с введенными фиктивными закреплениями на поворот узлов 1 и 2 и на смещение узла 3 представлена на рис. 333, б. В этих фиктивных закреплениях полные реакции з равны нулю. Условия равенства нулю реакций и ?3 и дадут
нам канонические уравнения метода перемещений, которые будут включать перемещения 2. Углы поворота узлов 1 и 2 в действительной раме обозначим через и Ъ2 линейное смещение узла 3 назовем 23 (положительные их направления указаны на рис. 333, б). Пусть реакции со стороны закреплений в состоянии 7,г 1 будут
Г1Ъ Г21 У31» в состоянии 12 1 — г12, г22, г32, в состоянии 23 1 — г13, г23, г33. Для
упругих реакций соблюдается свойство взаимности г — г. Реакции в указанных трех единичных состояниях вычисляются по эпюрам моментов, представленным на рис. 333, в, гид соответственно. Эпюра моментов от нагрузки в закрепленной раме изображена на рис. 333, е. Из этих эпюр получаем «единичные реакции»:
п 8г,.г12 а21 2г, г13 3 1 —— —1,5;
т22 4 Ъь 4 11; г23 — 32 — — 1
121, 12;,
ГязЖ ж ’ :
реакции в закреплениях от нагрузки:
,1р — 15; 2, 15-30 9 —6; ?3р — 9.
Полные реакции равны нулю; поэтому канонические уравнений имеют вид:
2111 2212 13 1 р 0‘, 2121 2222 23Г3 7?2р 0; (Н)
%1Г 31 %%г 32 %3Г 33 Н Кзр 0 ]
480
или в матричной форме
Решение для неизвестных
Аг-2 Я 0; Аг2 -Я.
(о)
• Я — Вг • Я. (п)
Для отыскания обратной матрицы Вг вычисляем определитель матрицы жесткости Аг по упругим реакциям г1к:
8 2-1,5
Аг 1 2 11 - 1,5 86,25г.
— 1,5 — 1,5 1,5
Обратная матрица Вг вычисляется по формуле (л), содержащей миноры, определяемые по формуле (и):
14,25
— 0,75
13,5
1
19
— 1
18
р г 86,25
— 0,75
9,75
9
1
тж
— 1
13
12
13,5
9
84
18
12
112
Решение для неизвестных по (п) представим в виде:
•7 1
12 123
19
— 1
18
15
1
“ 123
441
— 1
13
12
X
6
171
18
12
112
9
1350
Отсюда имеем:
147 57 7 450
21 ф14ТГ; 2 Ф24Т7;
Для угла поворота стойки получаем
112,5
к 4 И
Окончательная эпюра моментов и деформированный вид рамы изображены на рис. 333 ж и з соответственно.
ЛИТЕРАТУРА
1. Вайнберг Д. В., Вайнберг Е. Д. Пластины, диски, балки-стенки. Госстройиздат, УССР, Киев, 1952.
2. Дарков А. В., Кузнецов В. И. Строительная механика. Изд. «Высшая школа», 1962.
3. Киселев В. А. Строительная механика. Госстрой издат, 1960.
4. Корноухов Н. В. Прочность и устойчивость стержневых систем. Госстрой издат, 1949.
5. Митропольский М. Н. Применение теории матриц к решению задач строительной механики. Изд. «Высшая школа», 1969.
6. Пухов Г. Е. Электрическое моделирование задач строительной механики. Изд. АН УССР, Киев, 1963.
7. Рабинович И. М. Курс строительной механики. Госстрой издат, ч. I и ч. II, 1960.
8. Смирнов А. Ф. Статическая и динамическая устойчивость сооружений. М., Трансжелдор издат, 1947.
9. Смирнов А. Ф., Александров А. В., Шапошников Н. Н., Лащенников Б. Я. Расчет сооружений с применением вычислительных машин. М., Издательство литературы по строительству, 1964.
10. Снитко Н. К. Расчет рамных сооружений итерационными методами. Госстройиздат, 1962.
11. Снитко Н. К. Строительная механика. Изд. «Высшая школа», 1966.
12- Снитко Н. К. Устойчивость стержневых систем в упруго-пластической области. Госстройиздат, 1968.
ОГЛАВЛЕНИЕ Стр.
Предисловие 3
Часть первая Статически определимые системы
Глава 1. Введение 5
§ 1. Строительная механика как наука. Краткий исторический обзор 5
§ 2. Новые задачи строительной механики в связи с развитием строительной индустрии. Расчетная схема 7
§ 3. Опорные устройства. Виды нагрузок 9
§ 4. Классификация сооружений и их расчетных схем. Основные положения 11
Глава 2. Анализ неизменяемости плоских сооружений 13
§ 5. Простейшие признаки неизменяемости шарнирно стержневых систем 13
§ 6. Анализ геометрической структуры сооружений расчленением на
диски 18
§ 7. Системы в виде сочленения трех дисков 24
§ 8. Кинематические и статические признаки простейших мгновенно изменяемых ферм 26
§ 9. Аналитические методы исследования неизменяемости ферм 27
Глава 3. Теория линий влияния и ее применение к статически определимым балкам 30
§ 10. Понятие о линии влияния 30
§ 11. Линии влияния усилий в простых балках 31
§ 12. Определение усилий по линиям влияния 38
§ 13. Линии влияния при узловом действии нагрузки 40
§ 14. Линии влияния усилий для многопролетных статически определимых балок 42
§ 15. Кинематический метод построения линий влияния 45
§ 16. Невыгодное загружение линий влияния 47
§ 17. Определение усилий по эквивалентной нагрузке 51
§ 18. Матричная форма использования линий влияния. Матрица влияния 52
Глава 4. Балочные и консольно-балочные плоские фермы 54
§ 19. Понятие о ферме. Статическая определимость ферм 54
§ 20. Классификация ферм 56
§ 21. Способы определения усилий в фермах 59
§ 22. Расчет трехдисковых ферм на неподвижную нагрузку 65
§ 23. Расчет ферм с составными элементами 68
483
Стр.
§ 24. Линии влияния усилий в простых балочных фермах 72
§ 25. Линии влияния усилий в фермах со шпренгелями 80
Глава 5. Расчет сплошной трехшарнирной арки 84
§ 26. Трехшарнирная арка со сплошной стенкой. Аналитическое определение реакций 84
§ 27. Определение усилий в сечении трехшарнирной арки. Эпюры моментов 87
§ 28. Линии влияния реакций и усилий в арке 91
§ 29. Определение напряжений в арке при помощи ядровых моментов 98
§ 30. Арка с затяжкой 101
Глава 6. Арочные фермы и комбинированные системы. 102
§ 31. Расчет трехшарнирных арочных ферм 102
§ 32. Комбинированные системы. Арка с ломаной затяжкой 105
§ 33. Балка с гибкой аркой. Цепь с балкой жесткости 109
§ 34. Понятие о вантовых фермах и их расчет 114
Глава 7. Теория определения перемещений 115
§ 35. Перемещения. Работа внешних сил 115
§ 36. Теорема о равенстве возможных работ внешних и внутренних сил.
Потенциальная энергия 120
§ 37. Теоремы о взаимности работ и взаимности перемещений 126
§ 38. Общая формула для определения перемещений 129
§ 39. Упрощение техники вычисления перемещений в балках и рамах 133
§ 40. Перемещения, вызванные изменением температуры 140
§ 41. Определение перемещений от осадки опор 143
§ 42. Теорема Кастильяно и принцип1 наименьшей работы 146
§ 43. Определение перемещений при помощи упругих грузов. Матричная форма 147
Г л а в а 8. Пространственные фермы 154
§ 44. Понятие о пространственных фермах 154
§ 45. Виды опор и неизменяемость пространственных ферм 156
§ 46. Расчет пространственных ферм 163
Часть вторая Статически неопределимые системы
Глава 9. Основы теории расчета статически неопределимых систем методом сил 168
§ 47. Статическая неопределимость 168
§ 48. Основные свойства статически неопределимых систем. Методы расчета 172
§ 49. Основная система при расчете рам методом сил. Канонические
уравнения 173
§ 50. Построение эпюр поперечных и продольных сил в рамах 182
§ 51. Расчет простейших статически неопределимых систем на действие
температуры и осадки опор 186
§ 52. Решение системы канонических уравнений способом Гаусса. 191
§ 53. Решение системы линейных уравнений способом итерации. 198
Глава 10. Статически неопределимые арки 199
§ 54. Законы изменения сечений арок 199
§ 55. Расчет двухшарнирной арки на неподвижную нагрузку 201
§ 56. Линии влияния распора и усилий в двухшарнирной арке. Эпюры
усилий. 205
§ 57. Построение линии влияния распора двухшарнирной арки методом упругих грузов 208
484
Стр.
§ 58. Арка с затяжкой 210
§ 59. Расчет бесшарнирной арки на неподвижную нагрузку 212
§ 60. Линии влияния лишних неизвестных для бесшарнирной арки 217
§ 61. Линии влияния усилий в сечении бесшарнирной арки 223
§ 62. Расчет бесшарнирной арки на действие температуры и смещения
опор 224
§ 63. Поперечная, продольная силы и изгибающий момент для круговой
арки при радиальном давлении 226
§ 64. Определение перемещений круговой арки 228
Глава И. Расчет сложных рам методом сцл 235
§ 65. Упрощение расчета симметричных рам 235
§ 66. Замена произвольной несимметричной нагрузки прямосимметричной и обратносимметричной нагрузками 245
Глава 12. Расчет неразрезных балок 248
§ 67. Расчет неразрезных балок методом сил 248
§ 68. Расчет неразрезных балок методом моментных фокусов 253
§ 69. Линии влияния опорных моментов и усилий в сечении неразрезной балки. 257
§ 70. Невыгоднейшие загружения и построение объемлющей эпюры моментов при действии распределенной нагрузки 264
Глава 13. Расчет статически неопределимых плоских ферм 267
§ 71. Общий ход расчета фермы при постоянной нагрузке 267
§ 72. Линии влияния лишних неизвестных и усилий в стержнях ферм 270
§ 73. Матричная форма расчета ферм 274
Глава 14. Расчет рам методом перемещений 276
§ 74. Кинематическая неопределимость рам 276
§ 75. Соотношения между концевыми моментами и угловыми деформациями 280
§ 76. Расчет рам по развернутой форме метода перемещений 289,
§ 77. Уравнения метода перемещений в развернутой форме 293
§ 78. Использование симметрии при расчете рам методом перемещений 298
§ 79. Расчет рам методом перемещений на действие температуры и
осадку опор 301
§ 80. Построение линий влияния концевых моментов с применением
метода перемещений 305
Г л а в а 15. Специальные методы расчета рам 307
§ 81. Комбинированный метод 307
§ 82. Приближенные методы 308
Глава 16. Расчет сооружений по несущей способности 312
§ 83. Расчет по предельным состояниям 312
§ 84. Расчет простейшей статически неопределимой стержневой системы
по предельному состоянию 316
§ 85. Методы расчета статически неопределимых стержневых систем по
предельному состоянию 320
§ 86. Расчет статически определимых балок с учетом пластических деформаций 323
§ 87 Расчет статически неопределимых балок и рам с учетом развития
пластических деформаций 327
485
Глава 17. Применение современных вычислительных машин
§ 88. Электронные цифровые вычислительные машины § 89. Расчет статически неопределимых систем с применением электромоделирующих устройств Часть третья Устойчивость й основы динамики сооружений
Глава 18. Устойчивость стержневых систем § 90. Задачи и методы исследования устойчивости § 91. Общее уравнение упругой линии сжато-изогнутого стержня. § 92. Определение критических сил методом начальных параметров § 93. Устойчивость стоек ступенчатого сечения и стержней с любыми
граничными условиями § 94. Устойчивость стержня в упруго сопротивляющейся среде.
§ 95. Устойчивость составных стержней § 96. Устойчивость многопролетного стержня на жестких опорах. § 97. Расчет стержней на устойчивость при учете пластических деформаций § 98. Выражения концевых моментов стержня через угловые деформации § 99. Уравнения метода перемещений для сжато-изогнутых рам. § 100. Определение критических нагрузок однопролетных симметричных многоэтажных рам § 101. Устойчивость плоской формы изгиба полосы Г л а в а 19. Основы динамики сооружений § 102. Виды колебаний § 103. Собственные колебания системы с одной степенью свободы. § 104. Собственные колебания системы со многими степенями свободы
§ 105. Колебания рам. Приведенная масса § 106. Вынужденные периодические колебания системы с одной степенью свободы. Резонанс § 107. Вынужденные периодические колебания системы со многими степенями свободы § 108. Вынужденные колебания системы с одной степенью свободы при
действии непериодической нагрузки § 109. Удар груза по сооружению § 110. Поперечные колебания стержней с распределенной массой. § 111. Продольные колебания стержней с распределенной массой.
Часть четвертая
Пластинки и оболочки
Глава 20. Теория тонких пластин § 112. Общие положения § 113. Напряжения и усилия в пластинке. Уравнения равновесия. § 114. Дифференциальное уравнение изогнутой поверхности пластинки
§ 115. Краевые условия для пластинок в различных случаях § 116. Простейшие случаи § 117. Шарнирно опертая по краям прямоугольная пластинка при действии произвольной распределенной нагрузки § 118. Расчет шарнирно опертой пластинки на действие равномерно
распределенной нагрузки § 119. Общее решение для круглой пластинки Стр. 332
332
339
343
343
348
355
357
360
365
366
369
374
376
381
385
388
388
389 393 397
400
404
407
410
415
424
428
428
430
433
435
438
441
444
446
486
Стр.
§ 120. Свободно опертая по краям круговая пластинка при действии
равномерно распределенной нагрузки и сосредоточенной силы 449
Глава 21. Расчет оболочек 451
§ 121. Расчет симметричной оболочки вращения на осесимметричную
нагрузку. 451
§ 122. Расчет оболочек вращения на произвольную нагрузку 455
§ 123. Расчет сферической оболочки на ветровую нагрузку 459
§ 124. Расчет цилиндрических оболочек по безмоментной теории. 462
§ 125. Расчет тонкостенной трубы на изгиб от собственного веса 468
§ 126. Мрментная теория цилиндрических оболочек 470
§ 127. Расчет цилиндрических оболочек по моментной теории 474
Приложение 477
Литература 482
Николай Константинович С н и т к о
СТРОИТЕЛЬНАЯ МЕХАНИКА
Редактор Т. М. Минаева Переплет художника В. В. Казакевича Худож. редактор Н. К. Гуторов Техн. редактор С. П. Передерий Корректор Г. А. Кулаева
Т-17616. Сдано в набор 7У1 1971 г. Подп. к печати 27Х 1971 г. Формат 60X90Чв. Объем 30,5 печ. л. Уч.-изд. л. 25,58.
Изд. № 0т-15670. Тираж 88 000 экз. Цена 83 коп.
План выпуска литературы для вузов и техникумов изд-ва «Высшая школа» на 1972 г. Позиция № 82. Москва, К-51, Неглинная ул., д. 2914,
Издательство «Высшая школа»
Ордена Трудового Красного Знамени Ленинградская типография № 1 «Печатный Двор» им. А. М. Горького Главполиграфпрома Комитета по печати при Совете Министров СССР, г. Ленинград, Гатчинская ул.-, 26.
За к. 1777