Теория и расчёт авиационных лопаточных машин - Холщевников К.В.

Author: Холщевников К.В.

Tags: авиация и космонавтика летательные аппараты ракетная техника космическая техника пневмоэнергетика машины и инструменты холодильная техника холодильное оборудование машиностроение авиация авиастроение

Year: 1970

Similar

Теория и расчёт авиационных лопаточных машин

Теория и расчет авиационных лопаточных машин

Теория лопаточных машин авиационных газотурбинных двигателей. Курс лекций

Проектный термогазодинамический расчет основных параметров авиационных лопаточных машин

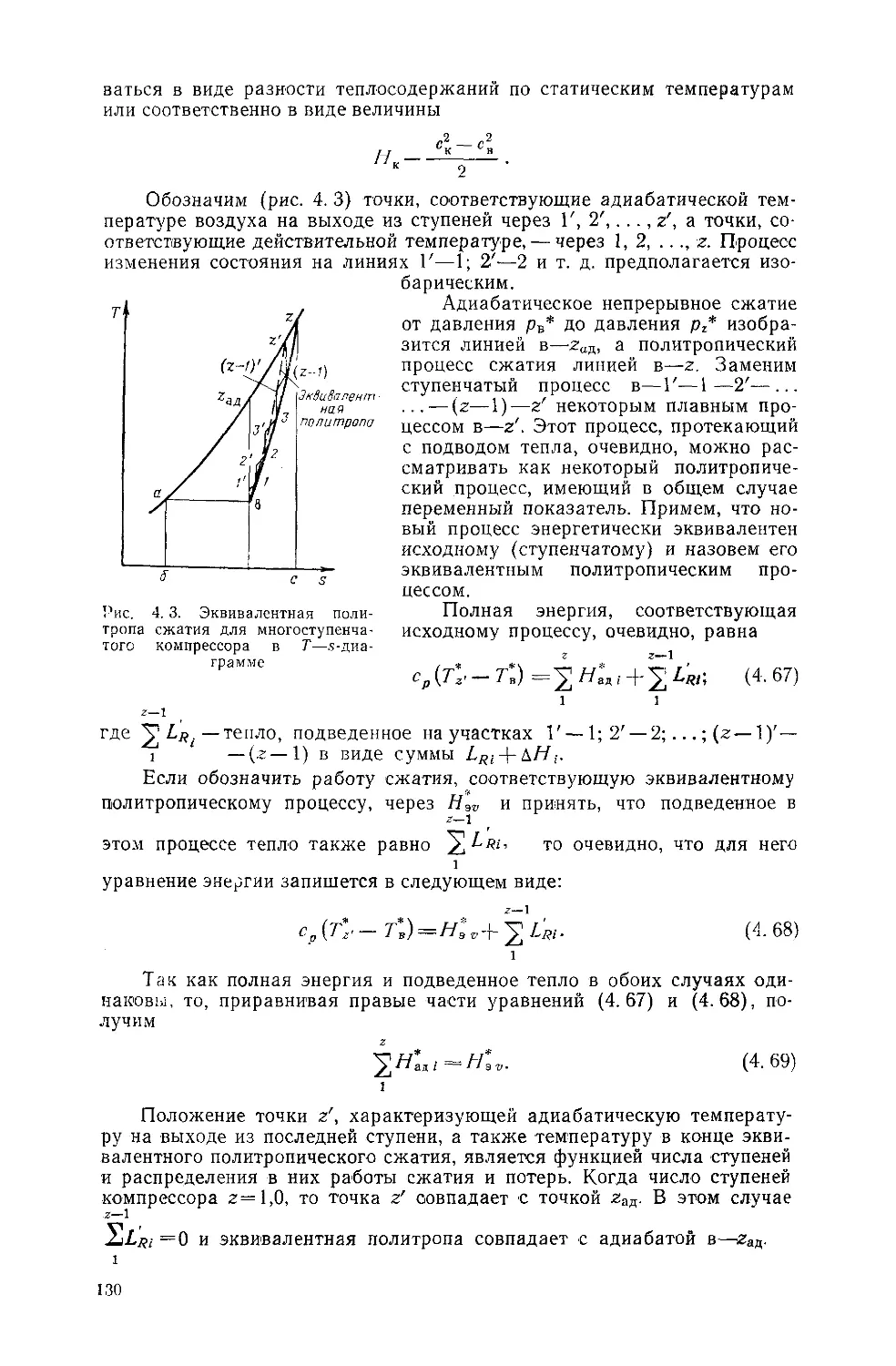
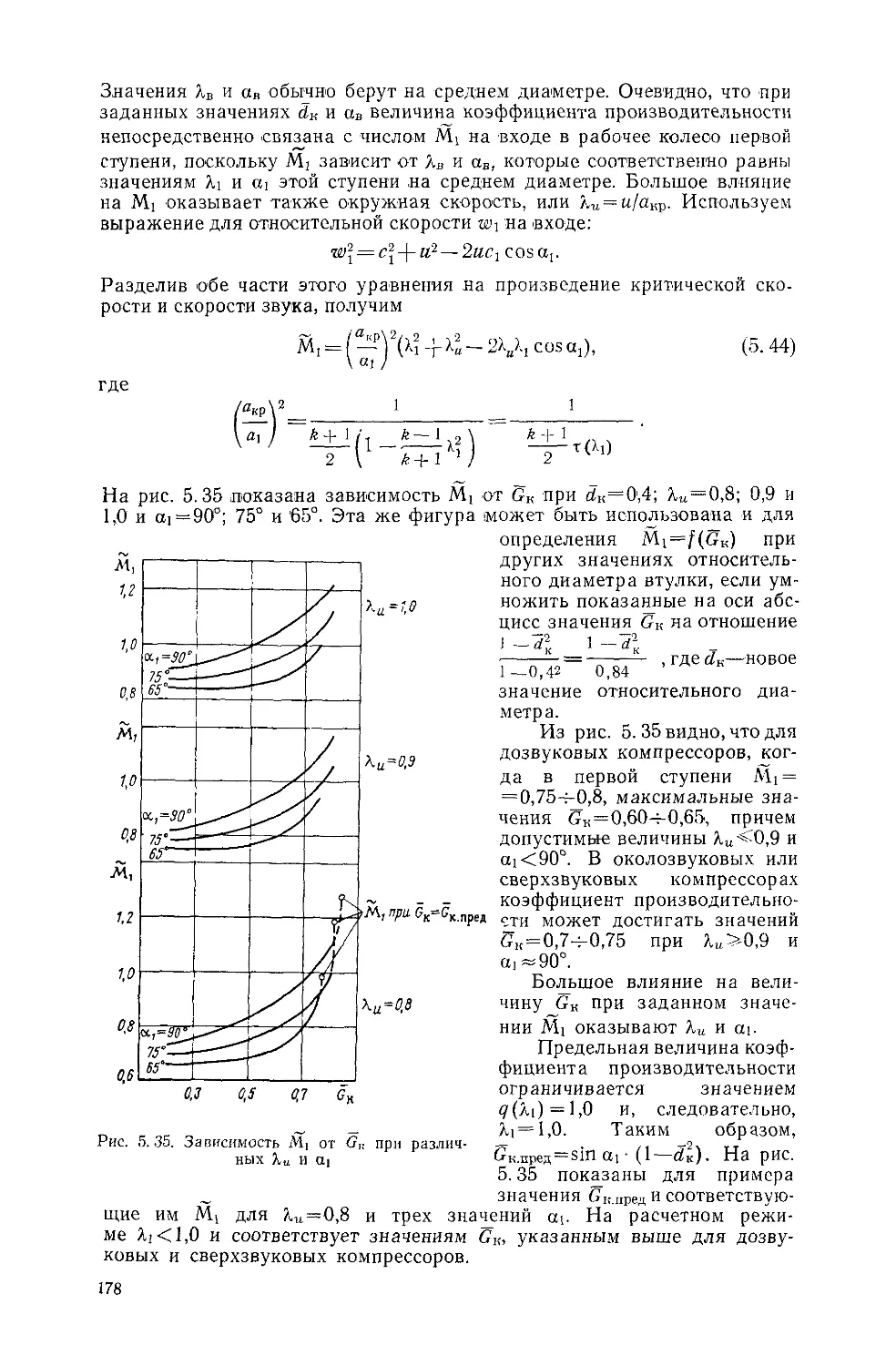
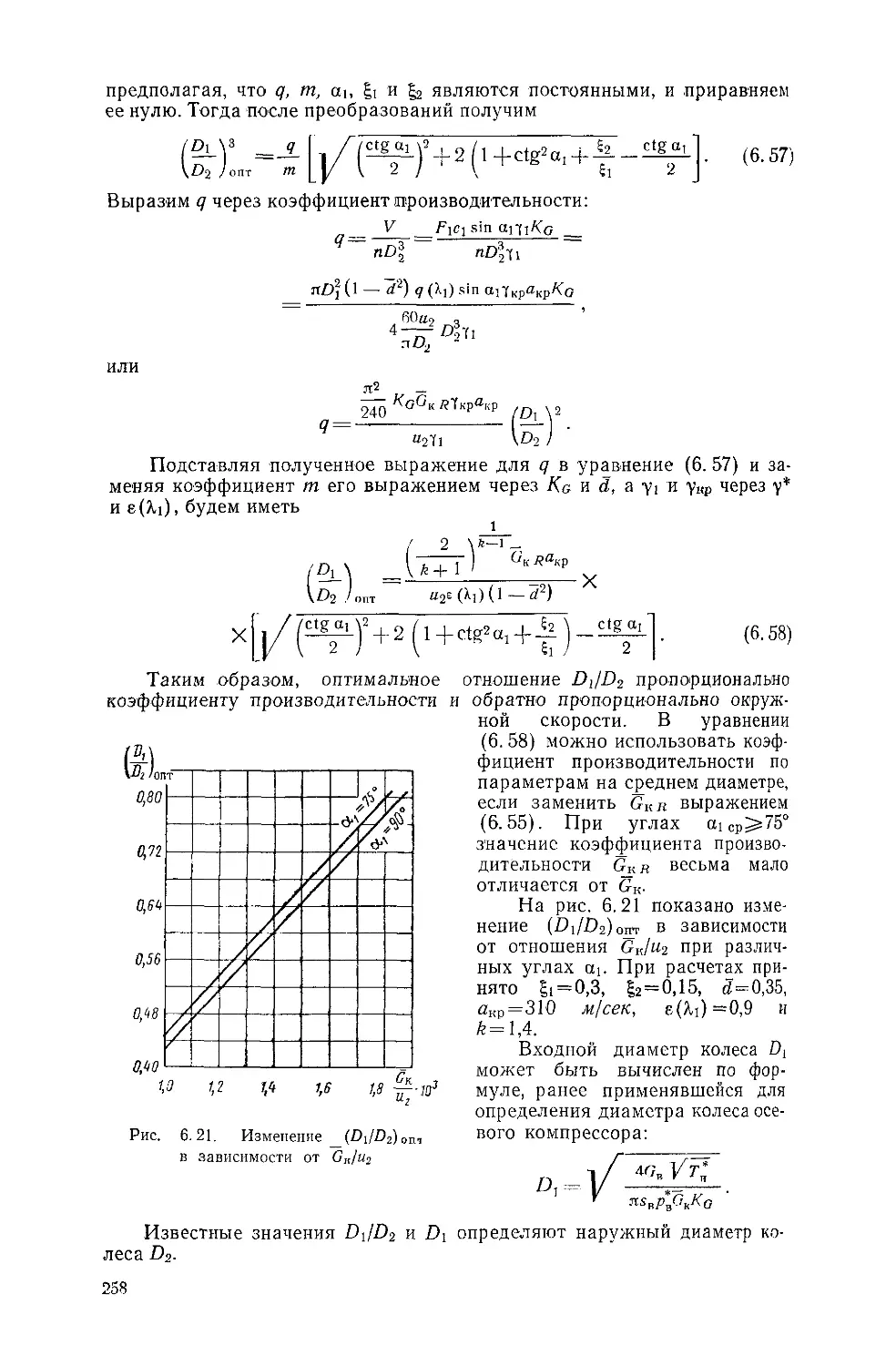
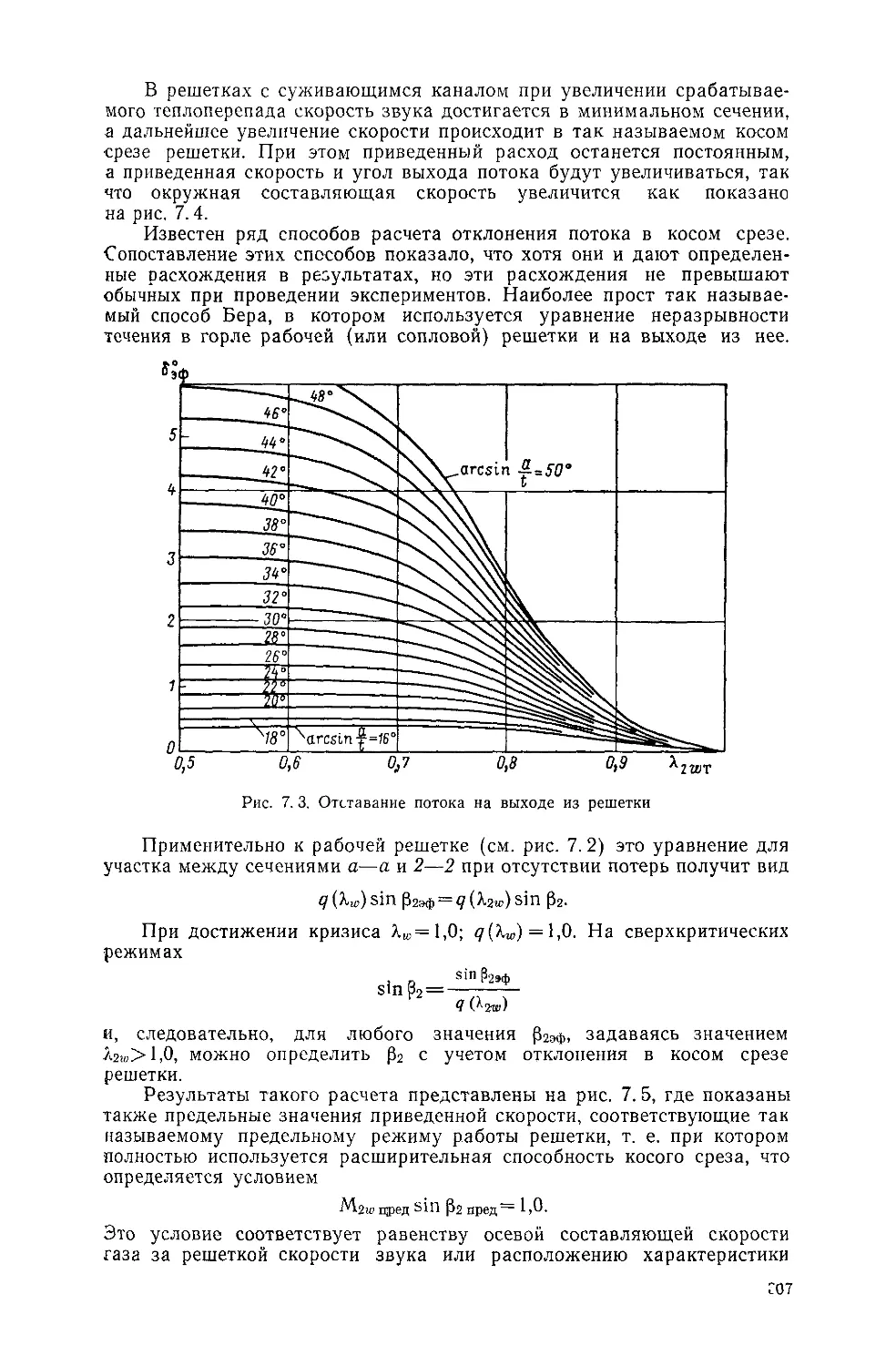
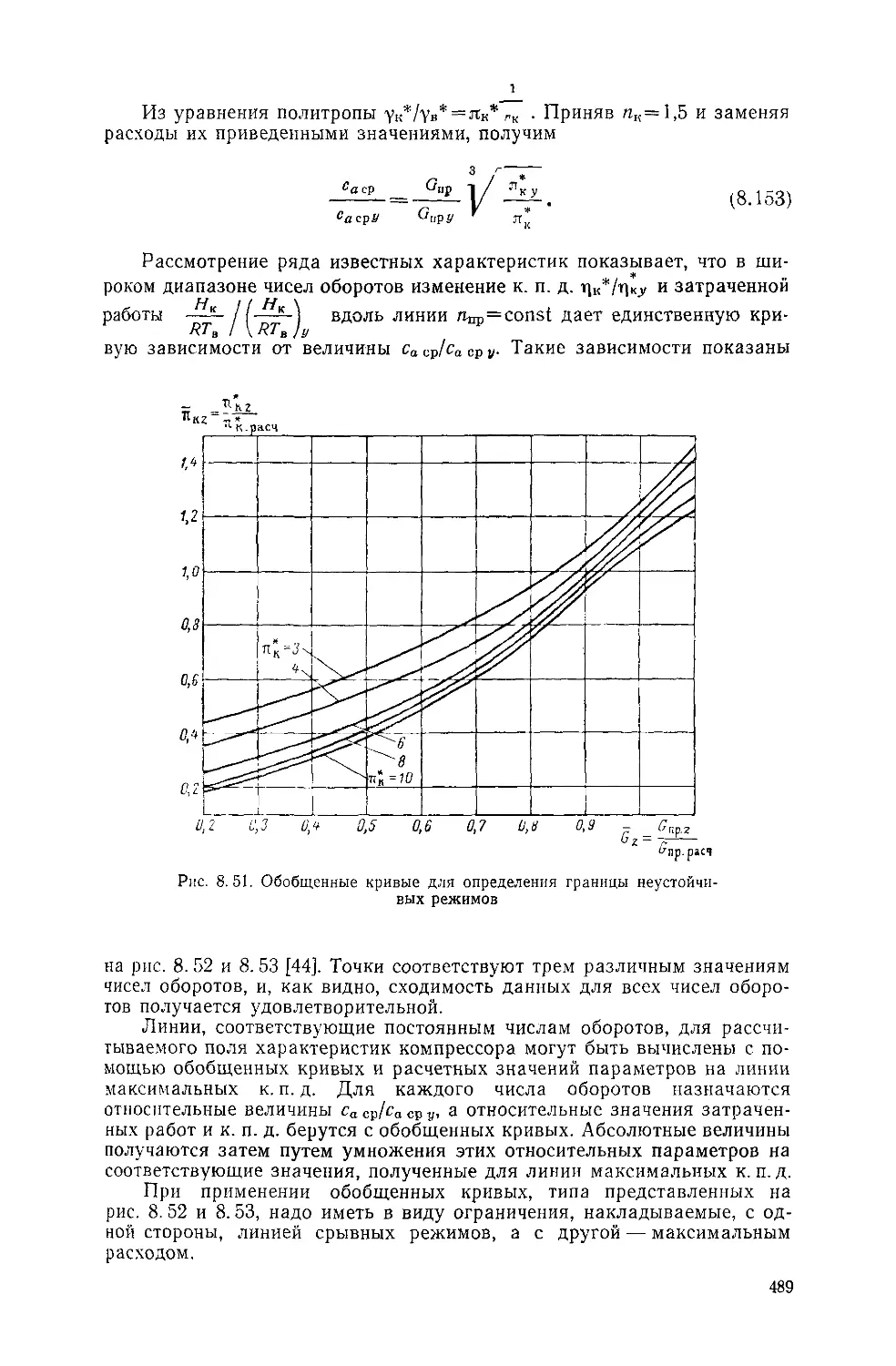
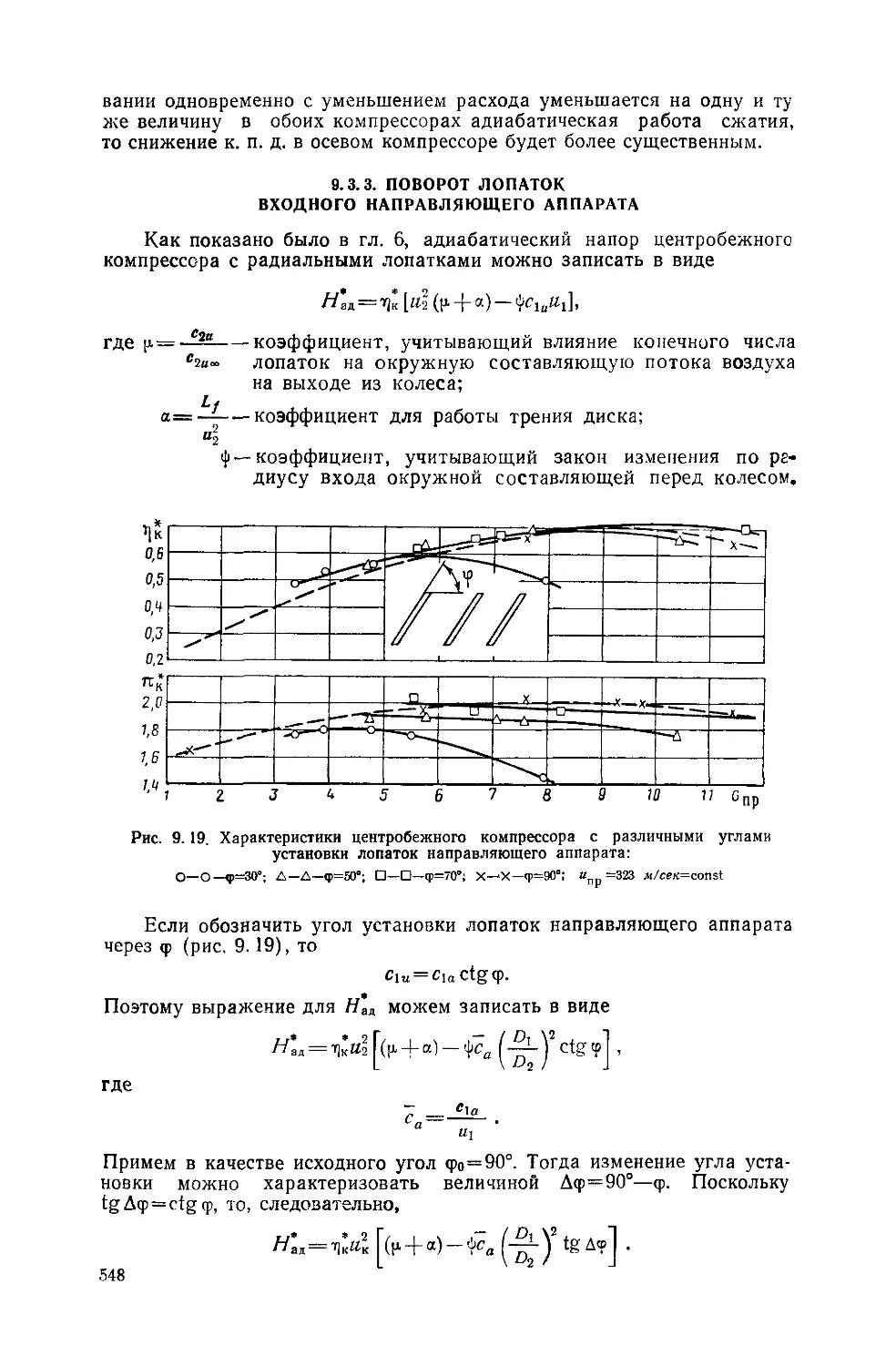
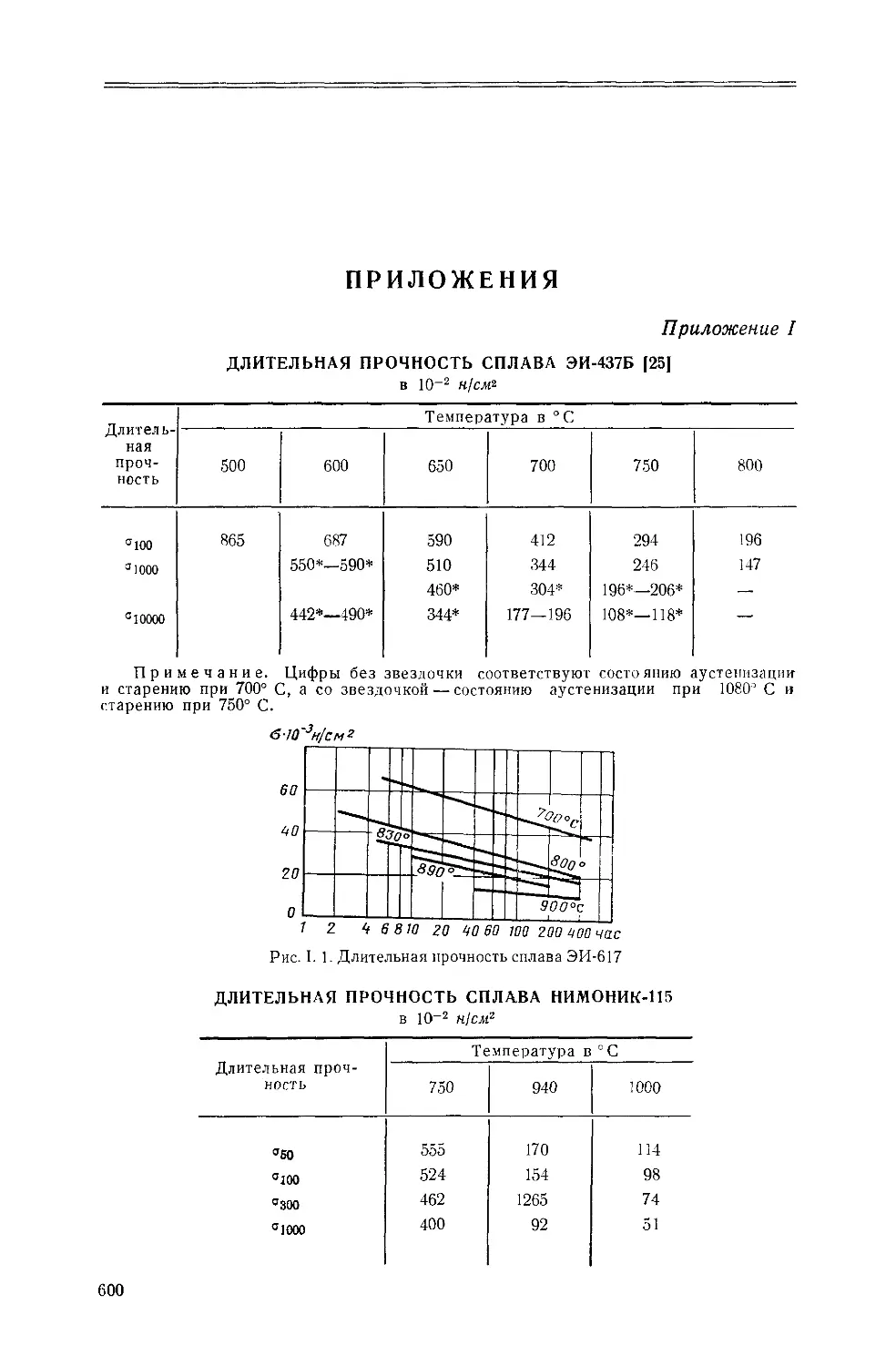
Text

К. В. ХОЛЩЕВНИКОВ
ТЕОРИЯ И РАСЧЕТ
АВИАЦИОННЫХ
ЛОПАТОЧНЫХ МАШИН
Допущено
Министерством высшего и среднего
специального образования РСФСР
в качестве учебника
для авиационных вузов и факультетов
ИЗДАТЕЛЬСТВО «МАШИНОСТРОЕНИЕ»
Москва 1970
УДК 629.7.036 : [621.438+621.51J.001 (075.8)
В учебнике рассмотрены основы теории лопаточных машин,
а также схемы и принципы работы лопаточных машин различ-
ного типа — осевых, центробежных и комбинированных ком-
прессоров и осевых турбин. Значительное внимание уделено
характеристикам и регулированию турбин и компрессоров,
а также вопросам согласования их параметров в системе газо-
турбинного двигателя.
Учебник предназначен для студентов авиационных вузов
и факультетов. Он может быть использован также инженерно-
техническими работниками авиадвигателестроения.
Табл. 57, иллюстр 3'56, библ. 67 назв.
Рецензенты: академик А. М. Люлька
и кафедра авиационных турбомашин Казанского авиационного института
Редактор инж. М. А. Колосов
3-18-6
345-69
ПРЕДИСЛОВИЕ
Книга «Теория и расчет авиационных лопаточных машин» написана
в соответствии с учебной программой одного из основных профилиру-
ющих курсов для студентов, специализирующихся по авиационным га-
зотурбинным двигателям, и включает теорию и расчет компрессоров и
турбин.
Основам теории лопаточных машин уделено значительное место в
известных курсах прикладной газовой динамики и посвящено большое
количество специальных книг. Тем не менее выпуск учебника, соответ-
ствующего учебной программе и согласованного с дисциплинами, как
предшествующими изучению курса лопаточных машин, так и изучаемы-
ми после него весьма необходим.
В чисто теоретическом аспекте ряд вопросов, имеющих непосредст-
венное отношение к лопаточным машинам (например, теория решеток,
теория пограничного слоя, диффузоров, сопел), рассматриваются в кур-
се газовой динамики, предшествующем курсу лопаточных машин, а
вопросы, относящиеся к применению лопаточных машин в газотурбин-
ных двигателях и к их конструированию, — в курсах теории и конструк-
ции двигателя, читаемых после данного курса. Поэтому в настоящем
учебнике наибольшее внимание уделено вопросам общей теории лопа-
точных машин и их отдельных видов, а также выбору исходных пара-
метров и инженерным методам расчета, которые не рассматриваются в
курсе газовой динамики, но связаны с ним рядом положений и урав-
нений.
Связь курса «Теория и расчет авиационных лопаточных машин» с
курсами по теории и конструкции газотурбинных двигателей выявля-
ется при рассмотрении исходных параметров и методов расчета, и осо-
бенно, в главах, посвященных характеристикам и регулированию лопа
точных машин (гл. 8 и 9) и согласованию параметров компрессоров и
турбин (гл. 10). Вопросы согласования, разработанные впервые авто-
ром, изложены применительно к различным типам газотурбинных авиа-
ционных двигателей и сопровождаются практическими рекомендациями.
Для иллюстрации отдельных вопросов теории и методов расчета
лопаточных машин, а также для облегчения выполнения курсовых и
дипломных проектов в учебник включены примеры расчета на базе про-
извольно взятых исходных величин.
Предлагаемые методы расчета не являются единственно возмож-
ными. В практике работы исследовательских институтов и конструктор-
ских бюро могут применяться и другие методы расчета, основанные на
результатах специальных испытаний, однако, как показывает опыт, усво-
ение в учебном процессе теории и упрощенных методов расчета позволя-
3
ет инженерам быстро освоить конкретные методы, применяемые в той
или другой организации.
В книге применена международная система единиц измерения СИ.
В приложении дана таблица перевода некоторых единиц измерения, вы-
раженных в других, еще применяемых в практике системах, в систе-
му СИ.
Разделы 7.2 и 8.10—8.13 написаны под руководством автора
и совместно с ним доц., канд. техн, наук О. Н. Еминым, которым также
выполнен пример расчета многоступенчатой турбины.
Расчеты, относящиеся к распределению осевых скоростей по радиу-
су в осевом компрессоре, и примерный расчет многоступенчатого комп-
рессора сделаны доц., канд. техн, наук Е. В. Солохиной. Инж. Д. П. Ха-
силева произвела большое количество расчетов, относящихся к различ-
ным разделам курса.
Автор выражает признательность рецензентам — академику
А. М. Люлька и сотрудникам кафедры Казанского авиационного инсти-
тута за ряд ценных замечаний по рукописи.
Автор благодарит также за полезные советы и замечания профес-
сора, д-ра техн, наук В. И. Дмитриевского и кандидатов техн, наук
В. М. Микиртичана, В. И. Дышлевского и Г. А. Комиссарова, а также
т.т. Л. Р. Стойкого и И. И. Дунского.
Автор с благодарностью примет пожелания и критические замеча-
ния, которые следует направлять по адресу: Москва, К-51, Петровка, 24,
издательство «Машиностроение».
ОСНОВНЫЕ УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
а — скорость звука в м/сек;
лкр—критическая скорость в м/сек;
в—хорда профиля в м;
в/<— густота решетки в ступени компрессора или турбины;
с—скорость воздуха или газа в абсолютном движении в м/сек;
D—диаметр в м;
d— относительный диаметр втулки;
F— площадь проходного сечения в м2;
G— массовый расход в кг/сек;
Q— коэффициент производительности;
Нк—удельная работа, затрачиваемая в компрессоре, в дж/кг;
Нт—'удельная работа, получаемая в турбине, в дж/кг;
Нth — теоретический напор компрессора в дж/кг;
Н-!л — теоретическая работа турбины в дж/кг;
Hth—коэффициент теоретического напора ступени компрессора;
Н — коэффициент адиабатического напора ступени компрессора;
77та— коэффициент теоретической работы (коэффициент нагрузки) ступени
турбины;
Л,— высота лопатки в м;
k—показатель адиабаты для воздуха;
kr—показатель адиабаты для газа;
~ М—число Маха воздуха или газа в абсолютном движении;
М или М®—число Маха воздуха или газа в относительном движении;
пк— показатель политропы сжатия в компрессоре;
лт—показатель политропы расширения в турбине;
N — мощность в кет;
п— число оборотов в об/мин;
р — давление в бар (105 Па);
R—-универсальная газовая постоянная в дж/кг-град;
s— осевая ширина лопатки в м;
Т—температура в °К;
t— температура в °C;
и—окружная скорость колеса в м/сек;
V—объемный расход в м3/сек;
w — скорость воздуха или газа в относительном движении в м/сек;
z—число ступеней;
а— углы потока и лопаток в проточной части компрессора и турбины
в абсолютном движении в град;
р — углы потока и лопаток в проточной части компрессора и турбины
в относительном движении в град;
у — плотность (объемная масса) в кг/м3;
5
S—коэффициент полного давления;
г)—коэффициент полезного действия;
X— приведенная скорость в абсолютном движении;
х— теплопроводность в вт/л град\
\ или Хш— приведенная скорость в относительном движении;
р. — динамическая вязкость в н сек/м2 (Па сек.);
лк— степень повышения давления в компрессоре;
лт—степень понижения давления в турбине;
ар— растягивающее напряжение в н1см2',
/_— отношение площади концевого поперечного сечения лопатки к плошади
сечения у основания.
Индексы
в — вход в компрессор; воздух;
к — компрессор и выход из компрессора;
т — турбина и выход из турбины;
г — вход в турбину; газ;
с — реактивное сопло и выходное его сечение (или горловина);
кр — критические параметры;
ад — адиабатический процесс.
Глава 1
СХЕМЫ И ОБЛАСТИ ПРИМЕНЕНИЯ
ЛОПАТОЧНЫХ МАШИН
1.1. НАЗНАЧЕНИЕ И ОБЛАСТИ ПРИМЕНЕНИЯ
АВИАЦИОННЫХ ЛОПАТОЧНЫХ МАШИН
Лопаточными машинами называют компрессоры и турбины, в ко-
торых передача энергии газу для его сжатия (компрессоры) или отбор
энергии от газа для получения полезной работы на валу (турбины) про-
исходят в результате взаимодействия с газом лопаток специальной
формы, размещенных на вращающихся дисках или барабанах.
Существуют машины, в которых газ сжимается или совершает
работу и без применения лопаток (в частности, поршневые или другие
объемные машины), но в настоящей книге эти машины не рассматри-
ваются.
Лопаточные машины находят широкое применение в авиационной
и в других областях техники. В авиационной технике лопаточные ма-
шины используются в первую очередь как основные элементы газотур-
бинных двигателей различного типа, в которых с их помощью осущест-
вляются подача и процессы сжатия воздуха и расширения газа в рабо-
чем цикле для получения заданной тяги или мощности.
Кроме того, лопаточные машины применяются во вспомогатель-
ных агрегатах (пусковые устройства, питание кабин сжатым воздухом
и др.), а также в качестве оборудования испытательных высотных
станций.
Для иллюстрации функций, выполняемых лопаточными машинами
в газотурбинном двигателе, рассмотрим схему турбореактивного дви-
гателя (ТРД) с осевым компрессором (рис. 1.1). Воздух поступает из
атмосферы в компрессор 2, ротор которого 3 вращается турбиной 6.
В компрессоре воздух сжимается, и его давление возрастает в 8—15 и
более раз. Из компрессора воздух попадает в камеру сгорания 5, куда
впрыскивается через форсунки 4 жидкое топливо. Сгорание топлива
происходит при почти постоянном давлении. При этом часть воздуха
поступает непосредственно к форсункам в количестве, необходимом
для сгорания при примерно стехиометрическом составе, а остальной
воздух постепенно подмешивается к продуктам сгорания для их охлаж
дения до заданной температуры, которая в современных двигателях
достигает 130'0—1500° К. С этой температурой и давлением, близким к
давлению за компрессором, газ поступает в турбину и расширяется в
7
00
Рис. 1. 1. Схема турбореактивного двигателя:
/—входной патрубок; 2—многоступенчатый компрессор; 3—ротор компрессора; 4—форсунки; 5-камера сгорания; 6—турбина;
7—реактивное сопло
ней, передавая одновременно часть своей энергии с помощью лопаток
на вал для вращения компрессора.
В турбине ТРД газ расширяется до давления, при котором мощ-
ность турбины равна мощности, потребляемой компрессором. Это дав-
ление больше атмосферного, и в реактивном сопле 7 происходит даль-
нейшее расширение газа, в результате чего газ вытекает со скоростью,
критической или больше критической в зависимости от типа сопла и
располагаемого перепада между давлением на входе в сопло и атмос-
ферным давлением, создавая реактивную силу тяги. В турбовинтовом
двигателе большая часть тяги получается от винта, и турбина развива-
ет мощность, требующуюся не только для вращения компрессора, нс
и для вращения винта. Следовательно, в турбине ТВД срабатывается
больший перепад давлений, чем в ТРД, а на долю реактивного сопла
остается только небольшая часть общего перепада давлений р*1рн,
где р* —полное давление перед турбиной и рн — атмосферное давление.
Аналогичные функции выполняют компрессоры и турбины и в дру-
гих типах газотурбинных двигателей. Это краткое рассмотрение пока-
зывает, что турбина и компрессор являются основными элементами
газотурбинных двигателей, обеспечивающими протекание рабочего
процесса.
1.2. ОСНОВНЫЕ ТРЕБОВАНИЯ
К АВИАЦИОННЫМ ЛОПАТОЧНЫМ МАШИНАМ
К числу основных требований, которым должны удовлетворять
авиационные лопаточные машины, относятся:
1) минимальные габариты и масса;
2) высокий к.п.д.;
3) благоприятное протекание характеристик;
4) высокая надежность.
1.2.1. МИНИМАЛЬНЫЕ ГАБАРИТЫ И МАССА
Эти требования, являющиеся основными для любой авиационной
конструкции, имеют для газотурбинных двигателей особо важное зна-
чение, поскольку двигатели должны обеспечить полеты на больших
скоростях и высотах. Выполнение их в значительной степени зависит
от габаритов и массы лопаточных машин, поскольку габариты комп-
рессора и турбины определяют в большой степени диаметр и длину
двигателя, а их масса составляет 60—70% массы двигателя. Чтобы
обеспечить получение минимальных габаритов и массы авиационных
лопаточных машин, их проектирование основывают на ряде принци-
пов, к числу которых, в частности, относятся:
1) применение больших скоростей воздуха и газа по тракту комп-
рессора и турбины;
2) уменьшение числа ступеней за счет увеличения аэродинамичес-
кой нагруженности каждой ступени и окружных скоростей рабочих ко-
лес турбины и компрессоров;
3) применение лопаток с большим удлинением (малой относитель-
ной шириной);
4) использование легких материалов (алюминиевые, магниевые и
титановые сплавы) и жаропрочных сплавов.
Применение этих принципов привело к значительному усовершен-
ствованию лопаточных машин, что видно из сопоставления современных
значений некоторых параметров с их значениями в начале развития га-
зотурбинных двигателей (табл. 1.1).
9
Уменьшение удельной массы (г. е. отнесенной к 1 н тяги) лопаточ-
ных машин может быть косвенно иллюстрировано уменьшением удель-
ной массы всего двигателя. Как видно из табл. 1. 1, за период 1945—
1970 гг. удельная масса ТРД уменьшилась в 3—4 раза; расход воздуха,
отнесенный к площади миделя компрессора, возрос в 2—21/2 раза.
Следует одновременно отметить, что уменьшение удельной массы
двигателей происходило не только за счет снижения удельной массы
лопаточных машин, но еще и из-за роста рабочей температуры газа
перед турбиной, благодаря чему росла удельная тяга.
1.2.2. ВЫСОКИЙ К. П. Д.
Высокий к.п.д. лопаточных машин требуется не только в авиацион-
ной технике. Однако в связи с применением в авиационных лопаточ-
ных машинах больших скоростей воздуха и газа и больших окружных
скоростей, а также в связи с высокой аэродинамической нагруженностью
ступеней достижение высоких к.п.д. в авиационных лопаточных машинах
сопряжено со значительными трудностями и требует проведения специ-
альных исследований.
Величина к.п.д. лопаточных машин оказывает существенное влия-
ние на к.п.д. цикла двигателя и, следовательно, на его экономичность.
В частности, в ТРД ухудшение на 1% к.п.д. компрессора или турбины
увеличивает удельный расход топлива примерно на 1%. В турбовин-
товом двигателе ухудшение к.п.д. турбины на 1% увеличивает удель-
ный расход топлива на 2—2,5%.
К.п.д. лопаточных машин оказывает влияние также и на массовые
характеристики двигателя, так как от значения к.п.д. зависит тяга, по-
лучаемая от одного килограмма воздуха (удельная тяга), а следова-
тельно, расход воздуха, габариты и масса. Рост адиабатического к.п.д.
компрессора и турбины на 10—13% за период 1945—1970 гг. (см.
табл. 1.1) является также результатом совершенствования авиационных
лопаточных машин.
Степень повышения давления в компрессорах возросла за это же
время с 3—4 до 10—20, а это, в свою очередь, вызывало дополнительные
трудности для получения более высоких к. п. д. В дальнейшем потребу-
ется иметь еще большие степени повышения давления (25—30), однако
для получения при этом высоких к.п.д. необходимы дополнительные
исследования.
1.2.3. БЛАГОПРИЯТНОЕ ПРОТЕКАНИЕ ХАРАКТЕРИСТИК
Авиационные газотурбинные двигатели в эксплуатации работают
в широком диапазоне режимов по оборотам, а также по высоте и ско-
рости полета и, следовательно, по температуре и давлению воздуха на
входе.
Таблица 1.1
Параметр 1945 г. J970 г.
Удельная масса ТРД в кг!н 7—8,5 1,6—2,0
Отношение расхода воздуха к миделю ком- 70—80 160—170
прессора в кг]сек-м2 Адиабатический к.п.д. компрессора 0,75—0,80 0,85—0,88
турбины 0,8—0,85 0,90—0,94
Степень повышения давления 3—4 10—20
10
В связи с этим при неудовлетворительной характеристике может
сильно снижаться к.п.д., а компрессор может попадать в область, где
он работает неустойчиво и где нормальная работа двигателя невозмож-
на из-за резкого уменьшения расхода воздуха, давлений и колебания
этих параметров. Поэтому благоприятное протекание характеристик ло-
паточных машин, в первую очередь компрессоров, является весьма
важным.
1.2.4. ВЫСОКАЯ НАДЕЖНОСТЬ
Выполнение этого требования обеспечивается правильным констру-
ированием, выбором материалов, соответствующих условиям работы и
нагрузкам, и рациональных запасов прочности, что подробно рассматри-
вается в курсах конструкции двигателей.
С точки зрения газовой динамики лопаточных машин это требова-
ние связано с устранением опасных колебаний лопаток, часто вызываю-
щих их поломку. Эти колебания могут быть устранены соответствующим
благоприятным регулированием лопаточных машин и отдельными кон-
структивными решениями (например, шарнирный замок лопаток, бан-
дажные полки и т. п.).
1.3. СХЕМЫ И ОСНОВНЫЕ ДАННЫЕ
АВИАЦИОННЫХ ЛОПАТОЧНЫХ МАШИН
1.3.1. КЛАССИФИКАЦИЯ ЛОПАТОЧНЫХ МАШИН
Наиболее общей является классификация лопаточных машин по на-
правлению потока, согласно которой машины делятся на:
а) осевые;
б) радиальные (центробежные и центростремительные);
в) диагональные;
г) смешанные.
К осевым относят машины, в которых направление потока в
среднем параллельно оси. Если же направление потока в среднем ра-
диальное (т. е. перпендикулярно оси), то такие машины называются
радиальными. Причем в зависимости от того, протекает ли газ от
центра к периферии или наоборот, радиальные машины делятся еще
на центробежные и центростремительные.
Смешанными, или комбинированными, машинами, т. е. осецентро-
бежными или оседиагональными, называют сочетания машин указан-
ных выше типов. Эта классификация несколько условна, так как в дей-
ствительности в осевых и радиальных машинах значительная часть
линий тока отклоняется от указанных средних направлений. Наряду с
классификацией по направлению потока все лопаточные машины могут
подразделяться в зависимости от числа ступеней на:
а) одноступенчатые;
б) многоступенчатые.
К общей классификации относится также разделение лопаточных
машин в зависимости от отношения скоростей потока на входе в рабо-
чее колесо к местной скорости звука.
В связи с этим могут быть машины:
а) дозвуковые;
б) околозвуковые («трансзвуковые»);
в) сверхзвуковые.
Все многоступенчатые машины могут быть:
а) одновальные;
б) двухвальные;
в) трехвальные.
11
Наряду с общей классификацией, относящейся ко всем лопаточ-
ным машинам, существует еще классификация частная, относящаяся
к отдельным видам лопаточных машин. Так, например, турбины могут
быть:
а) с охлаждаемыми лопатками;
б) с неохлаждаемыми лопатками.
Центробежные компрессоры встречаются:
а) с односторонним входом;
б) с двухсторонним входом.
Частная классификация используется при изучении отдельных
типов лопаточных машин.
Ниже рассматривается ряд схем компрессоров и турбин, применя-
ющихся в авиационных газотурбинных двигателях и агрегатах.
1.3.2. СХЕМЫ И ОСНОВНЫЕ ДАННЫЕ КОМПРЕССОРОВ
1.3.2.1. Осевые многоступенчатые компрессоры
Осевые многоступенчатые компрессоры состоят из чередующихся
рядов неподвижных лопаток, расположенных на корпусе, и вращаю-
щихся, расположенных на дисках или на барабанах (рис. 1.2, а). По
тракту такого компрессора воздух движется в направлении, в среднем
а)
Рис. 1.2, Осевой компрессор с ротором дискового типа:
а—продольный разрез; б—развертка на плоскость
1—воздухозаборник; 2—рабочее колесо; 3—неподвижный спрямляющий аппарат; 4—полная и
элементарная ступень; .5—входной направляющий аппарат; 5—3—рабочие колеса ступеней I и II;
7—9—спрямляющие аппараты ступеней I и II
близком к осевому, чем и обусловлено его название. Вращающиеся
ряды лопаток называются рабочими колесами или иногда роторами,
а неподвижные ряды лопаток — спрямляющими аппаратами или ста-
торами. Совокупность одного рабочего колеса и расположенного за
ним спрямляющего аппарата называется ступенью. В первую ступень
часто входит еще направляющий аппарат, расположенный перед ра-
бочим колесом.
Сущность работы каждой ступени компрессора состоит в том, что
лопатки рабочего колеса, вращающегося от постороннего источника
мощности, увеличивают момент количества движения и энергию про-
ходящего через них воздуха, вследствие чего возрастает его скорость и
давление. В неподвижных аппаратах происходит только преобразова-
ние энергии. Например, в спрямляющем аппарате, расположенном по-
сле колеса, как правило, за счет торможения скорости возрастает дав-
ление, а в направляющем аппарате перед колесом первой ступени про-
исходит увеличение скорости за счет снижения давления.
12
Для того чтобы в рабочих колесах передавать энергию, а в направ-
ляющих аппаратах ее преобразовывать с минимальными потерями, лопат-
ки рабочих колес и направляющих аппаратов представляют собой со-
вокупность аэродинамических профилей, расположенных по радиусу
под различными углами к оси машин. Построение профилей и выбор
углов их установки являются основной задачей расчета осевого комп-
рессора.
Если рассечь ступень (или несколько ступеней) цилиндрической
поверхностью и затем развернуть ее на плоскость, то получим так на-
зываемые плоские решетки профилей рабочих колес и спрямляющих
аппаратов (рис. 1.2,6), из которых образуются «элементарные ступе-
ни». Для получения достаточно высоких к.п.д. приходится ограничивать
энергию, передаваемую воздуху в каждой ступени, что характеризует-
ся величиной теоретического напора в ступени, достигающего 30 000—
40000 дж/кг. Нагруженность решетки рабочего колеса можно еще ха-
рактеризовать углом отклонения потока или так называемой кривизной
профиля, находящимися в пределах 20—30° (см. гл. V).
Вследствие указанных ограничений достижимая степень повыше-
ния давления в каждой ступени невелика и в первой и средних ступе-
нях находится примерно в пределах л^=1,3—1,4, а в последних — снижа-
ется до 1,2. Поэтому для получения требующихся для двигателя степеней
повышения давления л* =10—15 и выше требуется иметь достаточно
большое число ступеней, достигающее в отдельных двигателях z=15—
17. При этом в одной ступени удается получить к.п.д. т] = 0,88—0,9, а
во всем компрессоре в зависимости от суммарной степени повышения
давления к.п.д. достигает значений 0,85—0,88.
Иногда применяют ступени с околозвуковыми и сверхзвуковыми
скоростями потока на входе в рабочую лопатку. Такие ступени позво-
ляют получать более высокие степени повышения давления, но к.п.д.
их несколько ниже, чем у дозвуковых ступеней.
Для сокращения числа ступеней в современных авиационных осе-
вых компрессорах применяются достаточно большие окружные скорос-
ти, которые на периферии рабочих колес достигают значений пк = 330н-
350 м/сек, а иногда и выше (370—400 м/сек). В последнем случае пер-
вые ступени, как правило, околозвуковые или сверхзвуковые.
Для получения при заданном расходе воздуха минимально воз-
можных диаметральных габаритов компрессора применяются на входе
большие осевые скорости потока, характеризующиеся значением приве-
денных скоростей = 0,65—0,7, а также малые относительные диаметры
втулок d = Z)BT/DI; ~ 0,35—0,4, где DBT— диаметр втулки колеса, a DK —
его наружный диаметр.
Вдоль компрессора осевые скорости постепенно уменьшаются с
целью постепенного снижения их значений до величин, приемлемых
для входа в камеры сгорания, и для того, чтобы высота лопаток послед-
них ступеней была не слишком малой—обычно не менее 15—20 мм.
В связи с возможностью получать достаточно высокие к.п.д. и степени
повышения давления при относительно малых диаметральных разме-
рах осевые компрессоры в настоящее время являются основными для
газотурбинных двигателей.
Вместе с тем следует отметить и некоторые их недостатки.
1. Сравнительно узкий диапазон рабочих режимов, особенно при
больших степенях повышения давления, что заставляет применять слож-
ную систему регулирования (перепуск воздуха, поворот лопаток на-
правляющего аппарата).
2. Большое число ступеней, что увеличивает длину компрессора и
усложняет его производство.
13
3. Чувствительность к забоинам на входных кромках лопаток и
ухудшению их поверхности из-за попадания посторонних частиц в
компрессор.
В процессе совершенствования осевых компрессоров некоторые из
этих недостатков частично устраняются.
1. 3. 2. 2. Двухкаскадные многоступенчатые осевые компрессоры
С увеличением степени повышения давления диапазон рабочих
режимов многоступенчатого осевого компрессора сокращается, и при
уменьшении приведенных оборотов компрессор попадает в область не-
устойчивой работы.
Для того чтобы избежать этого, приходится, как уже отмечалось,
применять на компрессорах специальные способы регулирования. Почти
такой же эффект можно получить, применяя двухкаскадный (двухваль-
ный) многоступенчатый компрессор (см. рис. 10.7), в котором каждый
из каскадов вращается своей газовой турбиной. Распределение общей
степени повышения давления между каскадами и их числа оборотов оп-
ределяются в процессе согласования параметров компрессора и турбины
с учетом характеристик каждого из каскадов. В остальном параметры
этих компрессоров Ха, ик, d и др. и методы их расчета остаются такими,
как и для одновального многоступенчатого компрессора.
1. 3. 2. 3. Центробежные компрессоры
Так как в центробежном компрессоре поток воздуха в колесе про-
текает в основном в радиальном направлении от центра к периферии,
то, следовательно, на поток воздуха в числе других сил воздействуют
еще центробежные силы.
Центробежный компрессор может быть как одноступенчатый, так и
многоступенчатый.
В авиационной технике широко применяется только одноступенча-
тый и двухступенчатый компрессоры.
Одноступенчатый центробежный компрессор имеет следующие эле-
менты (рис. 1. 3, а):
1) входной патрубок и направляющий аппарат;
2) рабочее колесо;
3) безлопаточный диффузор;
4) лопаточный диффузор;
5) выходные устройства.
Основным элементом является рабочее колесо, в котором, как и в
осевом компрессоре, с помощью лопаток увеличиваются момент коли-
чества движения и энергия протекающего воздуха и вследствие этого
его скорость и давление. В диффузоре, как и в спрямляющем аппарате
осевого компрессора, часть скорости на выходе из колеса преобразует-
ся в давление Для уменьшения потерь при входе воздуха в колесо
входные кромки рабочих лопаток загнуты. В одноступенчатом центро-
бежном компрессоре при окружных скоростях п2 = 350—370 м/сек до-
стигаются к.п.д. 0,82—0,83 и степень повышения давления л* =2,5—3,0,
т. е. примерно в два раза больше, чем в ступени осевого компрессора
при тех же примерно окружных скоростях. При окружных скоростях
450—480 м/сек, применяющихся в ТРД с центробежными компрессора-
ми (двигатель ВК-1 и др), л* = 4,5 при к.п.д. 0,76—0,78. В эксперимен-
тальных центробежных компрессорах достигнуты степень повышения
давления л* =6,0 при окружной скорости п2 = 530 м/сек и к.п.д. г)*—
= 0,81 [62].
14
Дальнейшее увеличение степени повышения давления связано с
ростом окружной скорости и числа ступеней, что приводит к усложнению
конструкции и некоторому снижению к.п.д.
Для уменьшения диаметральных размеров применяются центро-
бежные компрессоры с двухсторонним колесом (рис. 1,3,6). Центро-
бежные компрессоры успешно применялись в агрегатах наддува авиа-
ционных поршневых, двигателей, а также на первых советских и англий-
ских турбореактивных двигателях. Однако в связи с большими диамет-
Рис. 1.3. Схемы центробежных компрессоров:
а—с односторонним входом; б—с двухсторонним входом.
1—входной патрубок с неподвижным направляющим
аппаратом; 2—рабочее колесо; 3—безлопаточный диффу-
зор; 4— лопаточный диффузор; 5—выходное устройство
ральными размерами и ограниченной степенью повышения давления
на более поздних конструкциях авиационных газотурбинных двигателей
с большими расходом воздуха и тягой центробежные компрессоры не ис-
пользуются. Вместе с тем они пригодны для применения на транспорт-
ных и учебно-тренировочных самолетах, в двигателях с осецентробеж-
ными компрессорами, а также в наземных транспортных установках и
др. Этому способствуют их положительные особенности, к числу кото-
рых, в частности, следует отнести:
1) относительно большую степень повышения давления в одной
ступени;
2) достаточно широкий диапазон рабочих режимов, позволяющий
в газотурбинных двигателях обходиться без регулируемых элементов;
3) простота конструкции и производства, а также надежность в
эксплуатации.
1.3. 2. 4. Диагональные компрессоры
Малая степень повышения давления в ступенях осевого компрессо-
ра и большие диаметральные размеры центробежного компрессора при-
вели к схеме диагонального компрессора (рис. 1.4), в котором поток
направлен под углом к оси машин. Являясь промежуточным типом, этот
компрессор имеет и промежуточные свойства. В частности, степень по-
вышения давления может доходить в нем до 2,5—3,0 в зависимости от
окружной скорости при значениях к. п. д. 0,84—0,85.
15
Однако поскольку степень повышения давления в одной ступени
все же невелика, применение этого компрессора в качестве самостоя-
тельного может быть весьма ограниченным и, по-видимому, оно вероят-
но лишь в сочетании с осевым компрессором.
1.3. 2. 5. Комбинированные компрессоры
(осецентробежные или оседиагональные)
Применение осевого компрессора при небольших расходах воздуха
и достаточно высокой степени повышения давления неэффективно, так
как лопатки последних ступеней получаются весьма короткими. Так,
например, если принять расход воздуха GB = 2,5 кг/сек и степень повы-
шения давления л* =7,5, то при постоянном внешнем диаметре компрес-
сора высота лопаток последней ступени должна составлять ~8 мм, что
Рис. 1.4. Схема диагонального
компрессора:
/—входной направляющий аппарат;
2—диагональное рабочее колесо;
5—осевой диффузор
Рис. 1.5. Схема комбинированного осецент-
робежного компрессора:
А—осевой околозвуковой компрессор; В—центро-
бежный компрессор.
1—стойка; 2~рабочее колесо осевого компрессора;
3— первый спрямляющий аппарат; 4—второй
спрямляющий аппарат; 5—«опорные стойки; 6—
вращающийся направляющий аппарат; 7—рабо-
чее колесо центробежного компрессора; 8—ра-
диальный диффузор; 9—осевой диффузор
неприемлемо. С другой стороны, центробежный компрессор достаточно
удовлетворительно работает при малых расходах, но получение в нем
степеней повышения давления больше 4—4,5 конструктивно сложно.
В связи с этим рациональной является схема осецентробежного компрес-
сора (рис. 1.5), в котором вместо последних ступеней осевого компрес-
сора используется центробежный компрессор.
Такие комбинированные компрессоры получили в настоящее время
широкое применение на двигателях с небольшим расходом воздуха.
В них окружная скорость центробежной ступени находится в широких
пределах: «2 = 300—450 л//сек.
В двигателе «Протей» фирмы Бристоль, являющемся одним из
ранних образцов двигателей с комбинированным компрессором, при-
меняется 12 осевых ступеней, которые вместе с центробежной ступенью
дают л* =7,2. В нем окружная скорость центробежного компрессора
составляет ~300 м!сек, т. е. близка к окружной скорости первой сту-
пени осевого компрессора. Доля центробежного компрессора в общей
работе сжатия не превышает 30%. В более поздних двигателях окруж-
ная скорость центробежного компрессора, а следовательно, и приходя-
щаяся на него доля общей работы сжатия увеличивается. Например,
в двигателе Т-63 (США) окружная скорость центробежного компрес-
сора 360—380 м/сек, а осевого — 280 м/сек и на центробежный компрес-
сор приходится 42—52% общей работы сжатия при л* =6,2. Встреча-
ются также двигатели, в которых работа сжатия в центробежном комп-
16
рессоре доходит до 70—75% общей работы. В них комбинированный
компрессор с общей степенью повышения давления л* = 5,5-4-6,0 со-
стоит из одной центробежной и одной околозвуковой осевой ступени,
как показано на рис. 1.5. К таким двигателям, например, относятся
английский ТРД «Континентл» [55] и «Астазу» {52]. В них степень повы-
шения давления в осевой ступени доходит до 1,6, а для получения об-
щей степени повышения давления л* =5,5—6,0 необходимо иметь в
центробежном компрессоре окружную скорость 4501—475 м/сек, т. е.
близкую к верхнему пределу окружных скоростей, применяемых в цент-
робежных компрессорах.
Комбинированный компрессор может также состоять из осевых
ступеней и ступени диагонального компрессора, что позволяет умень-
шить диаметральные размеры. При этом встречались схемы таких ком-
бинированных компрессоров, в которых осевые ступени размещались
после диагонального компрессора, что позволяло иметь в этих ступе-
нях высокую окружную скорость и повышенный напор при дозвуко-
вых и околозвуковых скоростях потока на входе.
1.3.3. СХЕМЫ И ОСНОВНЫЕ ДАННЫЕ ГАЗОВЫХ ТУРБИН
1. 3. 3. 1. Одноступенчатые осевые турбины
На рис. 1.6, а показана принципиальная схема ступени осевой
газовой турбины. Ступень состоит из рабочего колеса, аналогичного
колесу осевого компрессора, и расположен-
ного перед ним направляющего аппарата,
который в данном случае принято называть
сопловым аппаратом. В рабочем колесе
ступени газовой турбины в результате
взаимодействия газа с лопатками происхо-
дит уменьшение момента количества движе-
ния и энергии газа на некоторую величину,
которая передается рабочему колесу и при-
водит его во вращение вместе с компрессо-
ром, винтом и другими агрегатами.
Таким образом, в ступени турбины
протекает процесс, обратный процессу
в ступени осевого компрессора, и обе ма-
шины в принципе обратимы. Однако,
тогда как одноступенчатая турбина приме-
нялась и применяется до сего времени на
некоторых двигателях с достаточно высо-
ким к. п. д., одноступенчатый осевой ком-
прессор из-за малой степени повышения
давления в двигателях применяться не мо-
жет. Это является следствием того, что
из-за высоких температур в ступени тур-
бины, даже при передаче от газа доста-
точно большой энергии, получаются уме-
ренные числа М потока и связанные с ними
умеренные потери. Кроме того, поскольку
в турбине давление и температура пони-
жаются (процесс расширения), то значитель-
но меньшую роль играют потери в погранич-
ном слое даже при большом отклонении
потока в канале между лопатками.
Рис. 1.6. Ступень газовой тур-
бины:
а—принципиальная схема; б—раз-
вертка на плоскость.
/—сопловой аппарат; 2—рабочее ко-
лесо; <3—решетка соплового аппа-
рата; 4—решетка рабочего колеса;
5~элементарная ступень
17
Если рассечь ступень турбины цилиндрической поверхностью, ко-
торую затем развернуть на плоскость, то получим решетки профилей
соплового аппарата и рабочего колеса, образующих вместе элементар-
ную ступень (рис. 1.6, б). В принципе эти решетки идентичны решеткам
осевых компрессоров, но отличаются от них значительно большей кри-
визной профилей и соответственно большим углом отклонения потока.
В одноступенчатых газовых турбинах, применяющихся в газотур-
бинных двигателях, процесс расширения осуществляется как в сопло-
вом аппарате, так и в рабочем колесе, т. е. они относятся к так называ-
емым реактивным ступеням.
Современная одноступенчатая турбина может характеризоваться
следующими данными:
окружная скорость на внешнем диаметре uT = 3504-400 м!сек\
степень понижения давления л* = 2,0н-2,5;
коэффициент полезного действия т]* =0,88-4-0,9;
температура газа перед турбиной Т* = 1200-4-1300° К.
В дальнейшем значение температуры газа будет увеличиваться. Одно-
ступенчатые турбины в настоящее время встречаются относительна
редко, так как с увеличением степени понижения давления в этих тур-
бинах снижается коэффициент полезного действия. Однако они вероят-
но найдут применение в будущем в так называемых «подъемных»
двигателях для самолетов с вертикальным взлетом и посадкой, в неко-
торых транспортных двигателях и т. п.
1.3. 3.2. Многоступенчатые осевые турбины
Многоступенчатые авиационные осевые турбины (рис. 1.7) пред-
ставляют собой последовательное соединение ступеней турбин, рассмот-
ренных выше. Такие многоступенчатые турбины принято называть
турбинами со ступенями давления в отличие от турбин со ступенями
скорости (ступени «Кертиса»), в которых все расширение газа происхо-
дит в первом сопловом аппарате, а в рабочих колесах изменяются толь-
ко скорости без изменения статического давления. Турбины со ступеня-
ми скорости встречаются в паротурбинной технике и в турбинах приво-
да различных авиационных агрегатов и насосов жидкостных ракетных
двигателей. При выборе надлежащего числа ступеней многоступенча-
тые турбины со ступенями давления всегда могут обеспечить мощность,
необходимую для привода компрессоров и винтов с высоким к.п.д.
В многоступенчатых турбинах современных двигателей число сту-
пеней находится в пределах 2—8, причем последние цифры относятся к
двухконтурным двигателям с высокой степенью повышения давления
и с большой степенью двухконтурности.
Отдельные ступени многоступенчатой турбины работают в различ-
ных условиях. Так, например, первые ступени работают при наиболее
высокой температуре газа, и лопатки этих ступеней часто специально
охлаждаются.
Выбор числа ступеней, их окружных скоростей, диаметральных
размеров и других параметров турбины согласовывается с газодинами-
ческими параметрами и размерами компрессоров.
Коэффициенты полезного действия современных многоступенчатых
турбин находятся приблизительно в пределах 0,90—0,94.
1.3. 3.3. Радиальные турбины
Осевые турбины, одноступенчатые и многоступенчатые, получили
преимущественное применение благодаря их высокому к.п.д. и хоро-
шим весовым и габаритным характеристикам. Однако при небольших
18
Рис. 1.7. Трехступенчатая турбина ТВД
расходах газа иногда отдают предпочтение более простым и дешевым
радиальным турбинам, которые в этих условиях могут и по к.п.д. не
уступать осевым турбинам. Радиальные газовые турбины, в частности
центростремительные, в последнее время все чаще стали применяться
в малоразмерных ГТД, предназначенных для привода различного рода
агрегатов, а также в турбонасосных агрегатах жидкостных ракетных
двигателей.
На рис. 1.8, а изображена схема центростремительной радиальной
турбины и на рис. 1.8,6 — центробежной. Обе турбины состоят, как и
турбина осевая, из соплового аппарата и рабочего колеса.
Рис. 1. 8. Схемы радиальных турбин:
а—'центростремительная; б—центробежная.
1—рабочее колесо; 2—сопловой аппарат
В центростремительной турбине рабочее колесо аналогично колесу
центробежного компрессора, причем центробежные силы в колесе, дей-
ствующие на поток, преодолеваются за счет срабатываемого в турби-
не теплоперепада. Однако это мало влияет на величину полезной ра-
боты турбины и сказывается, в основном, на ее степени реактивности.
В то время как в ступени центробежного компрессора величина
напора в два-три раза больше, чем в ступени осевого компрессора, сту-
пень центростремительной турбины по величине полезной работы не
превосходит одноступенчатую осевую турбину.
Центробежная турбина, в которой было несколько рядов рабочих
и сопловых лопаток, впервые разработана в 1897 г. русским инженером
П. Д. Кузьминским в связи с постройкой им газотурбинной установки.
В дальнейшем фирма «Юнгстрем» (Швеция) применила паровые
турбины такого же типа, но с двумя дисками, вращающимися в проти-
воположные стороны, что увеличивало срабатываемый теплоперепад.
1.4. КРАТКИЙ ИСТОРИЧЕСКИЙ ОБЗОР РАЗВИТИЯ
АВИАЦИОННЫХ ЛОПАТОЧНЫХ МАШИН
Газотурбинные двигатели, для которых потребовались эффектив-
ные лопаточные машины, разрабатывались еще в конце прошлого и в
начале 20-го века. К ним относились уже упоминавшийся газотурбин-
ный двигатель русского инженера И. Д. Кузьминского (\897 г.), дви-
гатели французских инженеров Арменго и Лемаля (1903—1906 гг.) и
др. Однако все эти двигатели предназначались для стационарного
применения. Поэтому началом развития авиационных лопаточных ма-
шин можно считать появление агрегатов наддува, применявшихся для
20
увеличения земной и высотной мощности авиационных поршневых дви-
гателей. В конце войны 1914—1918 гг. А. Рато предложил в качестве
Рис. 1.9. Турбокомпрессор «Рато» для мотора мощностью
300 л. с.
агрегата наддува использовать так называемый турбокомпрес-
сор, состоящий из центробежного компрессора и газовой турбины, ра-
ботающей от выхлопных газов двигателя (рис. 1.9). В этом турбокомп-
рессоре окружная скорость на внеш-
нем диаметре колеса компрессора
достигала 360—380 м/сек и лопатки
турбины работали при температуре
750—800° С. Турбокомпрессор был
испытан в полете в 1918 г. и это
было, по-видимому, одним из пер-
вых испытаний турбокомпрессоров
в полете. По схеме Рато турбоком-
прессоры строились в ряде стран и
в том числе в США. Позднее в США,
примерно в 1926—1927 гг., фирма
«Дженераль электрик» начала раз-
рабатывать собственную конструк-
цию турбокомпрессора для мотора
мощностью около 450 л. с. (рис.
1.10).
Почти в то же время были раз-
работаны турбокомпрессоры и в
других странах. Например: турбо-
компрессор Лоренца (Германия)
с пустотелыми лопатками турбины,
через которые проходил воздух, вы-
ходящий из каналов колеса центро-
бежного компрессора; турбоком-
прессор RAE к мотору Бристоль-
Юпитер (Англия) и др. [13].
Рис. 1.10. Турбокомпрессор фирмы
«Дженераль электрик»
21
Вначале применение турбокомпрессора носило большей частью
экспериментальный характер, и практическое применение они получи-
ли в военной авиации во время войны 1941 —1945 гг., когда турбокомп-
рессорами были снабжены двигатели самолета США В-27 «Летающая
крепость», благодаря чему они могли летать на высотах Н~^ 11 км.
На большинстве поршневых авиационных двигателей применялись
приводные центробежные нагнетатели. В качестве примера на рис. 1. 11
Рис. 1.11. Двухскоростной центробежный нагнетатель «Рато»
показана конструкция приводного нагнетателя «Рато». Этот нагне-
татель был снабжен двухскоростным механизмом, с помощью которо-
го на земле и малых высотах поддерживалось пониженное число обо-
ротов рабочего колеса («1=22000 об/мин), а при максимальном числе
оборотов (« = 27500 об/мин) нагнетатель мог поддерживать земное
давление до высоты 6000 м.
В СССР нагнетатели и турбокомпрессоры начали исследоваться
и создаваться с начала 30-х годов. На двигателях, созданных под ру-
ководством А. А. Микулина, применялся разработанный в 1934—
1935 гг. центробежный нагнетатель (рис. 1. 12), который в последних
модификациях имел окружную скорость — 450 м/сек и входной направ-
ляющий аппарат с поворотными лопатками для регулирования его на-
порности. Приводные центробежные нагнетатели с двухскоростными
механизмами, обеспечивающие необходимую высотность, были разра-
ботаны для двигателей, созданных под руководством В. Я. Климова и
А. А. Швецова.
22
Проф. В. И. Дмитриевским был разработан и создан турбо-
компрессор, успешно прошедший все летные испытания.
Турбокомпрессор специальной конструкции был разработан в
1938—1940 гг. автором этой книги (рис. 1. 13). Для получения большой
окружной скорости (~400 м/сек) и высокого напора центробежного
компрессора при умеренных числах оборотов турбины между турбиной
Рис. 1. 12, Приводной центробежный нагнетатель двигателя АМ-34
и компрессором был поставлен мультипликатор с передаточным чис-
лом 1 — 2. Турбокомпрессор обеспечил проектный прирост высоты и ско-
рости полета самолета.
В целях создания авиационных лопаточных машин за границей и
в СССР проводились специальные исследования, так как стационар-
ные компрессоры и паровые турбины не имели столь больших окруж-
ных скоростей рабочих колес (до 400—450 м/сек) и таких высоких тем-
ператур газа, как авиационные компрессоры и турбины.
Следует отметить работы академика Б. С. Стечкина и проф.
В. И. Дмитриевского, которым также написана первая монография,
посвященная теории высотных авиадвигателей и агрегатов наддува,
главным образом, центробежных компрессоров [13].
Большие работы по центробежным компрессорам проведены канд.
техн, наук М. Н. Этингофом и другими советскими учеными.
23
Рис. 1.13. Турбокомпрессор ТК-2
Несмотря на значительный объем исследований, к.п.д. и напор соз-
данных компрессоров и турбин для агрегатов наддува были относи-
тельно невысоки. Так, например, к.п.д. центробежных компрессоров
были равны 0,60—0,70 при степенях повышения давления л* =2,0—3,0;
к.п.д. турбин был не выше 0,7—0,75.
Низкие к.п.д. компрессоров и турбин агрегатов наддува авиацион-
ных двигателей объяснялись, с одной стороны, относительно малыми
их размерами и, с другой стороны, несовершенством методов расчета
и проектирования лопаточных машин.
Такие к.п.д. и степени повышения давления были недостаточны
для создания газотурбинных двигателей. Кроме того, для газотурбин-
ных двигателей большой интерес представляли еще осевые многосту-
Рис. 1. 14. Турбореактивный двигатель Роллс-Ройс «НИН»
пенчатые компрессоры, которые в агрегатах наддува не применялись.
Поэтому, когда вплотную возникла задача создания авиационных газо-
турбинных двигателей, потребовалась большая работа по усовершенст-
вованию методов расчета и проектирования центробежных компрессо-
ров и газовых турбин и по разработке основ расчета и проектирования
осевых компрессоров.
Разработка авиационных газотурбинных двигателей с центробеж-
ными и осевыми компрессорами началась в СССР (В. В. Уваров,
А. М. Люлька) и за границей еще до войны 1941—-1945 гг.
В. В. Уваровым на созданном им турбовинтовом двигателе с цент-
робежным компрессором и осевой газовой турбиной с охлаждаемыми
лопатками была применена еще центробежная турбина, работающая
от потока воздуха, выходящего из колеса центробежного компрессора,
и передающая свою мощность на винт.
На базе опыта, накопленного при создании центробежных компрес-
соров агрегатов наддува, удалось относительно быстро решить задачу
повышения их к.п.д. (до 0,76—0,78) и степени повышения давления (до
4,0—4,5), в результате чего в 1945—1946 гг. в Англии и в СССР были
созданы турбореактивные двигатели с центробежными компрессорами
(рис. 1. 14), имеющими двухстороннее колесо (двигатели «Дервент» и
«НИН» английской фирмы Роллс-Ройс, отечественный двигатель ВК-1).
Первые турбореактивные двигатели с осевыми компрессорами
ЮМО-004 и БМВ-003 были созданы в Германии в конце войны 1941 —
1945 гг. (рис. 1.15).
В связи с несовершенством осевых компрессоров и турбин (низкие
к.п.д. и степень повышения давления, а также невысокая температура
газа) эти двигатели имели большой удельный расход топлива, относи-
тельно большие удельные габариты и массу. Тем не менее по удельной
25
массе и габаритам они были значительно лучше поршневых двигателей и
обеспечили резкое увеличение скоростей полета.
В 1945—1946 гг. появились первые турбореактивные двигатели с
осевыми компрессорами в СССР (А. М. Люлька и А. А. Микулин), в
Англии и США. Дальнейшее усовершенствование осевых компрессо-
ров и газовых турбин привело к существенному улучшению экономич-
ности, а также массовых и габаритных данных авиационных газотур-
бинных двигателей. Появились турбовинтовые двигатели в СССР
(Н. Д. Кузнецов, А. А. Ивченко) и в Англии.
Разработка новых типов двигателей (двухконтурных, а также для
самолетов с вертикальным взлетом и посадкой), предъявила к лопа-
точным машинам новые требования по массовым показателям и по
производительности. В частности, для самолетов с вертикальным взле-
том и посадкой потребовались двигатели с удельной массой 0,5—0,6 кг!н,
Рис. 1. 15. Газотурбинный реактивный двигатель БМВ-003
что вызвало необходимость применения новых конструктивных и тех-
нологических решений и новых материалов. Улучшение параметров
лопаточных машин и газотурбинных двигателей непрерывно продол-
жается, и в этом отношении большая заслуга принадлежит коллективам
научно-исследовательских институтов ЦИАМ и ЦАГИ и конструктор-
ских бюро, руководимых С. К- Туманским, А. М. Люлька, Н. Д. Кузне-
цовым, П. А. Соловьевым, а также кафедр проф. Т. М. Мелькумова,
проф. Г. Н. Абрамовича и др.
В СССР разработка методов расчета осевых компрессоров и тур-
бин производилась на основе классических работ Н. Е. Жуковского и
С. А. Чаплыгина по аэродинамике крыла и решеток и по вихревой тео-
рии винта. Большой вклад в разработку гидродинамической теории
решеток внесли советские ученые И. Н. Вознесенский, Л. Ф. Лесохин,
Л. И. Седов, Л. А. Симонов, Г. Ю. Степанов и др. Весьма существенное
значение в этой области имели также теоретические и эксперименталь-
ные работы зарубежных ученых (Вейнига, Хауелла и др.).
Основные труды по теории решеток перечислены в библиографии
книги Г. Ю. Степанова [42].
В разработке методов расчета осевых компрессоров большую роль
сыграли работы Б. С. Стечкина, К. А. Ушакова, К- К- Баулина,
Л. А. Симонова.
Принципиальное значение для развития авиационных лопаточных
машин имели работы проф. В. В. Уварова по теории газовых турбин,
по способам их охлаждения и по профилированию длинных лопаток
газовых турбин на основе закона постоянства циркуляции по высоте
лопаток.
Большой вклад в развитие теории газовых турбин внесли проф.
Г. С. Жирицкий, И. И. Кириллов, П. К. Казанджан, В. X. Абианц.
Глава 2
ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ
ЛОПАТОЧНЫХ МАШИН
2.1. ОБЩИЕ СВЕДЕНИЯ О ПАРАМЕТРАХ ВОЗДУХА (ГАЗА)
В СТУПЕНИ ЛОПАТОЧНОЙ МАШИНЫ
Ступень лопаточной машины в общем случае состоит из направля-
ющего аппарата, рабочего колеса и спрямляющего аппарата. Если
ступень рассечь меридиональной плоскостью, то получим ее меридио-
нальное сечение (рис. 2. 1).
Возьмем какую-либо точку А в зазоре между направляющим аппа-
ратом 1 и рабочим колесом 2, находящуюся на расстоянии г от оси.
Точка А лежит на некоторой линии тока, меридиональная проекция
которой на участке зазора обозначена через b—d.
Предположим, что движение установившееся; тогда линии тока
должны совпадать с траекториями частиц. Касательная к линии тока
в точке А будет давать направление меридиональной проекции скоро-
сти потока в этой точке. Обозначим меридиональную проекцию скорости
через ст и разложим ее в свою очередь по направлению радиуса г и по
направлению х оси машины. Эти проекции принято называть радиаль-
ной составляющей скорости потока — сг и осевой составляющей — са.
Кроме них полная скорость потока может иметь составляющую,
перпендикулярную радиусу, которая называется окружной составляю-
щей и обозначается через си.
Разложение скорости потока с в точке А по всем указанным на-
правлениям показано на рис. 2. 2.
Значение полной скорости потока и ее составляющих по радиусу
в осевом зазоре может изменяться различным образом в зависимости
от принятого способа профилирования лопаток рабочего колеса, при
котором сохраняются условия равновесия частиц по нормалям к лини
ям тока или по радиусу.
Обычно предполагается, что в окружном направлении на каждом
данном радиусе скорости потока не изменяются, т. е. течение является
осесимметричным. Однако такое предположение справедливо только
на некотором расстоянии от кромок лопаток: теоретически — на беско-
нечном удалении, а практически — на расстоянии примерно одного
шага. В непосредственной же близости от кромок скорости в окруж-
ном направлении будут изменяться на участке в пределах шага между
27
соседними лопатками. Это изменение скоростей будет периодически по-
вторяться при переходе от одного канала к другому.
Давление и температура воздуха по радиусу будут изменяться в
соответствии с изменением скоростей, а по окружности на данном ра-
диусе в случае осесимметричного течения должны оставаться неиз-
менными.
В направляющем аппарате при установившемся движении условие
осесимметричности скоростей, температуры и давлений, естественно,
соблюдаться не может, так как по ширине канала между лопатками
все эти параметры изменяются, периодически повторяясь при переходе
от канала к каналу.
Рис. 2. 1. Меридиональное сечение сту-
пени лопаточной машины:
У—направляющий аппарат,- 2—рабочее колесо;
3—спрямляющий аппарат
Рис. 2.2. Разложение полной скорости
в точке А по трем направлениям
В связи с этим на участке a—b (см. рис. 2. 1), соответствующем
направляющему аппарату, линии тока могут быть различными в зави-
симости от их положения по ширине канала. Иногда в расчетах опери-
руют некоторыми средними значениями скоростей и соответствующей
им линией тока. В этом случае течение и в направляющем аппарате
рассматривается как осесимметричное.
Очевидно, что изложенное выше применительно к направляющему
аппарату и зазору между ним и рабочим колесом, остается в силе и
для спрямляющего аппарата и зазора между ним и рабочим колесом.
Иная картина, однако, будет получаться при рассмотрении линий тока
в рабочем колесе. Во-первых, применительно к неподвижным аппара-
там и зазорам речь шла только об абсолютном движении, так как рас-
сматривалась скорость потока в определенных точках неподвижного в
данном случае относительно земли пространства, в которых как бы на
ходился наблюдатель. Абсолютное движение можно определять также
как движение по отношению к неподвижной системе координат.
Если лопаточная машина перемещается относительно земли вмес-
те с летательным аппаратом, то, обращая движение, будем рассматри-
вать неподвижный летательный аппарат в потоке воздуха, имеющем
скорость, равную скорости полета, и применять понятие об абсолютном
движении. При этом необходимо учитывать влияние скорости полета
на значения абсолютных скоростей и других параметров воздуха и га-
за в лопаточной машине.
28
Применительно же к рабочему колесу, наряду с абсолютным дви-
жением необходимо рассматривать еще относительное движение, ког-
да скорости потока определяются в точках пространства, вращающего-
ся вместе с колесом. Очевидно, что это соответствует условию, когда
наблюдатель перемещается вместе с движущимся телом, т. е. с колесом.
Иными словами, относительное движение можно определить как
движение по отношению к системе координат, вращающихся вместе с
колесом. Во-вторых, все частицы в колесе наряду со скоростью относи-
тельно колеса имеют еще так называемую переносную скорость, которой
в данном случае является окружная скорость колеса в данной точке.
Таким образом, абсолютная скорость частиц газа складывается
из скоростей переносной и относительной (по отношению к колесу) и
является их геометрической суммой:
с=« + ш,
(2.1)
где с — вектор абсолютной скорости;
w—вектор относительной скорости;
и — вектор переносной скорости (окружная скорость колеса в дан-
ной точке).
Уравнение (2.1) изображается треугольником скоростей (рис. 2.3),
в котором вектор скорости с является замыкающей стороной.
Окружная скорость колеса в данной точке
может быть записана так:
и=Г(о, (2.2) УЧ
где м — угловая скорость вращения колеса. с .у /и>
Если рассматривать в относительном дви- ^У /
жении меридиональную, осевую и радиальную
составляющие скорости w, то они по величине _______г \
будут такими же, как и в абсолютном движении, и
так как проекции скоростей w и с на каждое из
этих направлений равны между собой. Поэтому
wm=cm; wr=cr и wa = ca. (2.3)
Рис. 2. 3. Треугольник
скоростей в рабочем
колесе
Окружные же составляющие скоростей w и с, являющиеся их про-
екциями на направление окружной скорости, будут различны и связа-
ны между собой соотношением
cu = u±wu.
(2.4)
Знак плюс в этом уравнении берется, когда направление скорости
совпадает с направлением окружной скорости.
При равномерном вращении колеса и определенном расходе воз-
духа (газа) относительное движение будет установившимся. Следова-
тельно, линии тока в каналах между лопатками не будут зависеть от
времени, а должны определяться только положением частиц по отно-
шению к поверхности лопаток.
Кроме того, на линию тока должно влиять расстояние от оси ко-
леса, поскольку от этого расстояния зависят ширина канала и форма
профиля. Однако абсолютное движение частиц, наблюдаемое в какой-
либо неподвижной точке пространства, ометаемого лопатками, являет-
ся неустановившимся, так как мимо этой точки будут проходить раз-
личные относительные линии тока и, следовательно, при одной и той
же переносной скорости абсолютные скорости будут переменными во
времени.
Если в определенный момент времени провести для ряда точек
пространства, ометаемого лопатками, направления абсолютных ско-
29
ростей, то можно получить мгновенную картину абсолютного движения
во всем рассматриваемом пространстве, представленную мгновенными
абсолютными линиями тока. Если относительное движение установив-
шееся, то картина мгновенных абсолютных линий тока как бы прохо-
дит мимо неподвижной точки пространства с переносной скоростью.
Для иллюстрации изложенного на рис. 2. 4 показана решетка, дви-
жущаяся с равномерной скоростью и. Такая решетка может быть по-
лучена сечением колеса осевой ступени цилиндрической поверхностью
с последующей разверткой этой поверхности на плоскость. При этом
предполагается, что газ течет параллельно оси колеса.
На входе в решетку с помощью направляющего аппарата обеспе-
чивается протекание газа под углом си (рис. 2.4,6). Принято, что на-
Рис. 2.4. Течение газа через плоскую прямую равномерно движущуюся
решетку
правление и величина скоростей по всей ширине решетки постоянны
(течение осесимметричное), так что расход газа будет вполне опреде-
ленным. Поскольку при этом скорость и постоянна по времени, то отно-
сительное движение будет установившимся. Линии тока в относитель-
ном движении показаны на рис. 2. 4, а.
Если геометрически сложить относительные и переносные скорос-
ти, то получим абсолютные скорости с и мгновенные абсолютные ли-
нии токов (см. рис. 2.4,6). Следует отметить, что по всему контуру ло-
пасти нормальная составляющая с„ мгновенной абсолютной скорости с
должна быть равна проекции ип окружной скорости и на направление
нормали в соответственной точке контура, т. е. сп = ип. Это показано
для одной точки на рис. 2. 4, 6. Картина мгновенных абсолютных линий
тока в каждый момент времени имеет один и тот же вид и то же рас-
положение по отношению к решетке; она передвигается вместе с решет-
кой, как если бы была с ней жестко связана.
Таким образом, наблюдатель, находящийся в неподвижной точке
пространства непосредственно у входа в решетку, будет видеть пери-
одические по времени изменения абсолютной скорости. Это сказывает-
ся и на траектории отдельной частицы. В зависимости от того, близко
или далеко от точки наблюдения находится в это мгновение лопасть,
частица описывает совершенно различные траектории.
Таким образом, из одной и той же точки пространства исходят пе-
риодически колеблющиеся траектории; на рис. 2.4, а обозначена циф-
рой I истинная траектория частицы, которая в относительном движе-
нии проходит вдоль вогнутой стороны лопасти, и цифрой II—-траекто-
рия частицы, движущейся вдоль ее выпуклой стороны. Наконец, циф-
30
рой III обозначена траектория частицы которая движется в середине
между лопастями.
Обратимся опять к схеме рис. 2. 1. Заменим действительное течение
в рабочем колесе некоторым осредненным по времени и шагу течением
[42] и проведем через некоторую среднюю относительную линию тока в
канале этого рабочего колеса поверхность вращения, на которой можно
рассматривать двумерные решетки. Эту поверхность назовем осреднен-
ной осесимметричной поверхностью тока.
Меридиональная проекция этой поверхности изобразится в общем
случае кривой d—е, которая может рассматриваться как меридиональ-
ная проекция абсолютных мгновенных и относительных линий тока, ле-
жащих на той же поверхности.
Если продолжить указанную поверхность тока в неподвижных
аппаратах и в зазорах между ними и рабочим колесом, то в результате
меридиональная проекция поверхности тока для всей ступени может
быть изображена некоторой кривой а—b—d—е—f—g, проходящей через
окружность, соответствующую точке А.
Статические значения давлений, температур и плотности в относи-
тельном и абсолютном движении равны.
Что же касается температур, давлений и плотности, соответствую-
щих адиабатически заторможенным скоростям, то они в относительном
и абсолютном движениях неодинаковы. Действительно, обозначая за-
торможенные параметры, соответствующие абсолютным скоростям, ин-
дексом с и относительным скоростям — индексом w, будем иметь:
(2. 5)
(2. 6)
(2.7)
* . w2
= 7 + — ,
2ср’
откуда
]С-—
1 с-' W И “
или
7л ___________________________с2 —
/ w —- / с ' ~ •
2ср
Скорости с и w не равны, что очевидно, в частности, из треугольника,
показанного на рис. 2. 3.
Соотношение между этими скоростями зависит от окружной скорос-
ти и типа машин. Например, для турбины на входе в колесо w<c и, сле-
довательно, T*W<T* .
Давления заторможенного потока связаны с соответствующими
температурами законом адиабаты:
fe—1
\ к
с2 — т- ) (2. 8)
Т* /
ZCP2 с /
Я—1
2.2. ОБЩИЕ СВЕДЕНИЯ О РЕШЕТКАХ
И ЭЛЕМЕНТАРНЫХ СТУПЕНЯХ
Как следует из изложенного ранее, важным элементом лопаточной
машины является плоская решетка, позволяющая пространственную
кольцевую решетку, соответствующую рабочему колесу или неподвиж-
ному аппарату, расчленить на элементы с двумерным (плоским) пото-
31
ком. Плоская решетка получается в результате сечения кольцевой ре-
шетки поверхностью с последующей разверткой этой поверхности на
плоскость, если секущая поверхность сама не является плоскостью.
В качестве секущей поверхности берется поверхность вращения,
проходящая через некоторую среднюю линию тока и являющаяся, та-
ким образом, некоторой осредненной поверхностью тока *).
В осевой лопаточной машине осредненные поверхности тока близки
к соосным круговым цилиндрам. В этом случае в плоскости развертки
любого из этих цилиндров получаются плоские прямые решетки с
бесконечным числом профилей (см. рис. 1.2).
Аналогично в радиальных лопаточных машинах в плоскостях, пер-
пендикулярных к оси вращения, образуются плоские круговые
(или радиальные) решетки с конечным числом профилей (см. рис. 6.27).
Рис. 2. 5. Основные параметры профиля
В диагональной лопаточной машине в случае, когда осредненная
поверхность тока является поверхностью круглого конуса, в развертке
ее на плоскость можно получить плоскую решетку с конечным числом
профилей.
Рассмотрим подробнее плоскую прямую решетку. Она состоит из
бесконечного числа одинаковых профилей, расположенных эквидистант-
но вдоль прямой, которую условимся называть фронтом решетки.
Рассмотрим основные геометрические параметры профиля и ре-
шетки.
На профиле 1 (рис. 2.5) различают выпуклую сторону, или спин-
ку 2, вогнутую сторону, или корыто 3, входную (переднюю) кром
ку 4 и выходную (заднюю) кромку 5. Кромки могут быть радиус-
ными и угловыми с углом схождения у. Геометрическое место центров
окружностей, вписанных в профиль, называют его средней линией.
Прямая, соединяющая концы средней линии у входной и выходной
кромок, называют хордой профиля с длиной Ь. Диаметр стах наиболь-
шей из вписанных окружностей называют толщиной профиля;
диаметры Д и d2 крайних вписанных окружностей — толщинами
кромок.
Профиль часто задается двумя координатами его точек: абсциссой
х, отсчитываемой по хорде обычно от входной части к выходной, и ор-
динатами точек, образующих вогнутую ук и выпуклую ус стороны.
Обычно профиль характеризуется относительными значениями его
основных параметров, иногда выраженными в процентах от хорды:
а) относительная абсцисса
*) Высота плоской решетки (постоянная или переменная) соответствует сечению
кольцевой решетки двумя близкими поверхностями тока с последующей их разверткой.
32
б) относительные ординаты
СПИНКИ ус = £^--
корыта г/к=-^-;
ь
в) относительная толщина профиля
сшах .
b ’
г) относительная вогнутость (кривизна) профиля
~7_ f max .
J b ’
д) относительная абсцисса места максимальной толщины профиля
е) относительная абсцисса места максимальной вогнутости
а
~Ь
В случае если профиль образуется сопряжением дуг окружности и
прямых линий, то его очертания могут задаваться координатами цент-
ров окружностей, их радиусами и координатами точек сопряжения.
Рис. 2.6. Геометрические параметры рабочей решетки:
а—турбинная; б—компрессорная
Профиль в рабочей решетке (рис. 2. 6) характеризуется следующи-
ми углами:
Ул и Х2 — углы изгиба входной и выходной кромок профиля, обра-
зуемые направлением хорды и соответствующими каса-
тельными к средней линии профиля;
&— угол выноса (угол установки профиля), образуемый на-
правлением хорды и фронтом решетки;
Pi —угол потока на входе в решетку;
2 546
33
₽2 — угол потока на выходе из решетки;
P'j и Р2 — входной и выходной углы профиля, образуемые соответ-
ствующими касательными к средней линии профиля и
фронтом решетки *>;
9—угол кривизны, или угол изгиба, профиля; 9=xi + X2, а
также 6=Рз—Pi Для компрессоров и 9=180°—(pj )
для турбин;
I — угол атаки; —Pi;
б — угол отставания потока на выходе из решетки; б = р2—Рг
Исходя из общего уравнения параболы, по которой изгибается
средняя линия профиля, можно установить следующую связь между
углами Xi и Х2 и отношением а/Ь:
а _ 3ctgxi + Ctg х2
ь 4 ctg Xi + ctg Х2 '
Ограничиваясь первыми членами разложения котангенса в ряд и учи-
тывая, что Х2 = 9—Хь получим с точностью до полградуса:
= Г1+2(1 —2 —)] ; Х2=— h-2/l-2~'ll .
1 2 L 1 \ b JJ ’ 2 [ \ b /]
При
.£-=0,45, Xi —0,6 6 и Х2=О,4 9.
ь
Углы отставания б потока на выходе определяются для компрессорных
и турбинных решеток по эмпирическим зависимостям, которые приве-
дены в гл. 5 и 7.
Для профилей и решетки неподвижного аппарата углы потока и
профиля обозначаются буквами а с соответствующими индексами. На-
пример, для решетки спрямляющего аппарата осевого компрессора
приняты обозначения:
аг и аз — углы потока на входе и на выходе соответственно;
а2 и Из —входной и выходной углы профиля соответственно.
Для решетки направляющего и соплового аппаратов приняты обоз-
начения:
ао и oi — углы потока на входе и на выходе соответственно;
ад и ctj — входной и выходной углы профиля соответственно.
В многоступенчатом компрессоре только первая ступень имеет са-
мостоятельный направляющий аппарат. В остальных ступенях роль
направляющего аппарата играет спрямляющий аппарат предыдущей
ступени.
Решетка характеризуется следующими параметрами:
s — ширина решетки;
t — шаг решетки, равный расстоянию между двумя одноименны-
ми точками соседних профилей;
Ь , л
-----густота решетки (обратная величина называется относитель-
ным шагом);
Ар — угол отклонения потока в рабочей решетке, образованный
векторами скоростей Wi и w2;
Да—угол отклонения потока, образованный векторами скоростей
с2 и с3 в спрямляющем аппарате компрессора или с0 и Ci в
сопловом аппарате турбины.
*) В дальнейшем из соображений удобства углы лопаток будут иногда обозна-
чаться индексом «л».
34
Как видно из рис. 2.6,6, Др = р2—Pi и для решетки рабочего колеса
турбины (рис. 2,6,а)
Д0=18Оо-(₽1 + ₽2).
Углы отклонения потока в турбинной решетке, как правило, сущест-
венно больше, чем в решетке компрессорной. Так, например, в турбин-
ной решетке в среднем Др = 50°-ь80°, а в компрессорной— Д£= 15° : 25°.
Турбинные решетки реактивного типа имеют непрерывно сужаю-
щиеся каналы, а активного типа составлены из более изогнутых и утол-
щенных профилей, образующих каналы с приблизительно постоянным
проходным сечением. Компрессорные решетки в отличие от турбинных
имеют расширяющиеся межлопаточные каналы, менее изогнутые, и
более тонкие профили, напоминающие профили крыла самолета. В тур-
бинных решетках имеют место конфузорные процессы в отличие от
диффузорных процессов в решетках компрессоров. Этим и объясняет-
ся возможность применения больших углов поворота потока в турбин-
ных решетках. Решетка, являясь наиболее общим объектом гидроди-
намического исследования, переходит в одиночный профиль или канал
соответственно при t—*оо (при b = const) и при b-^оо (при t~ const).
Другим важным предельным случаем является бесконечно густая ре-
шетка, которой соответствует t—>-0 при 6 = const и c/t = const.
Наиболее исследован установившийся поток через плоские решет-
ки в слое постоянной толщины, называемый просто плоским установив-
шимся потоком. В большинстве теоретических исследований такого
потока через решетку предполагается, что поток безвихревой (потенци-
альный) и жидкость несжимаемая.
Течение вязкой жидкости изучается при больших числах Рейнольд-
са, когда влияние вязкости сводится к образованию на профилях по-
граничного слоя и турбулентных следов за решеткой.
Наряду с теоретическими исследованиями решеток большое вни-
мание уделяется экспериментам, которые наиболее полно позволяют
изучить влияние различных факторов и в том числе влияние вязкости
и сжимаемости. Вследствие этого экспериментальные данные широко
используются в инженерных расчетах. Применяемые методы построения
решеток в турбинах и компрессорах практически несколько различны.
2-3. УРАВНЕНИЯ МОМЕНТА, МОЩНОСТИ
И УДЕЛЬНОЙ РАБОТЫ
2.3.1. УРАВНЕНИЕ МОМЕНТА
ДЛЯ РЕШЕТКИ РАБОЧЕГО КОЛЕСА
Мощность и удельную работу, получаемые с колеса или затрачи
ваемые на его вращение, следует определять, используя в качестве ис-
ходной величины момент колеса. Последний удобно находить с по-
мощью теоремы о моменте количества движения. Для этого требуются
только данные о состоянии потока на граничных поверхностях рассмат-
риваемой области, но не внутри области. Это значительно упрощает
задачу, так как позволяет не рассматривать сложные гидродинамичес-
кие явления в колесе. Согласно теореме о моменте количества движе-
ния его производная по времени относительно какой-либо точки (или
оси) равна главному моменту относительно той же точки (или оси)
всех внешних сил, приложенных к массе. Вырежем сначала решетку
из колеса, показанного на рис. 2. 1, двумя весьма близкими конически-
2*
35
ми поверхностями, предполагая, что они совпадают с поверхностями
тока, и развернем ее на плоскости (рис. 2. 7).
Применение теоремы о моменте количества движения к такой ре-
шетке проще, чем для всего колеса, так как из-за малости высоты решет-
ки можно считать скорости постоянными по высоте. Кроме того, рас-
сматривая поток на некотором расстоянии от решетки, можно также
считать распределение скоростей вдоль нее равномерным, что следует
из условия осесимметричности.
Определение моментов необходимо производить для абсолютного
движения. Действительно, как видно из дальнейшего, момент зависит
от произведения разности окружных составляющих абсолютных ско-
Рис. 2. 7. Решетка с контрольными поверхностями
ростей на входе в решетку и на выходе из нее на соответствующий ра
диус, или от дифференциала произведения сиг. Так как окружная сос-
тавляющая в относительном движении отличается от аналогичной ско-
рости в абсолютном движении на величину окружной скорости [см.
уравнение (2.4)], то только при постоянстве окружной скорости для
всех точек решетки моменты в абсолютном и относительном движениях
будут одинаковы. В частности, это должно иметь место в плоской пря-
мой решетке, рассмотренной на рис. 2. 4, для которой предполагалось,
что она движется с постоянной скоростью и, одинаковой для всех точек.
Для применения теоремы о моменте количества движения в ре-
шетке, показанной на рис. 2. 7, выделим для определенного мгновения
около одной лопатки контрольное пространство, ограниченное двумя
поверхностями а—а' и b—Ь', отстоящими друг от друга на длину одно-
га шага t = 2 nrfz и совпадающими с относительными линиями тока, и
цилиндрическими поверхностями 1—1 и 2—2. Кроме того, поверхности
профиля лопатки также являются границами контрольного прост-
ранства. Наконец, в качестве границ следует рассматривать две по-
верхности, лежащие в плоскости чертежа и ограничивающие высоту
решетки. Для каждой частицы жидкости с массой Ат, находящейся в
этом пространстве, на основании теоремы о моменте количества дви'
жения относительно оси колеса может быть написано уравнение
(2.9)
dx
36
Суммируя эти выражения для всех находящихся в пространстве час-
тиц, получаем
Едт^Г=£дЛ1’ (2.10)
где ДЛ1 — момент внешних сил относительно оси.
В правой части уравнения (2. 10) сокращаются моменты всех сил,
действующих между частицами, включая силы трения, так как все эти
силы являются внутренними, и остаются только моменты сил на гра-
ницах и моменты силы тяжести частиц. Последние обычно не учитыва-
ются вследствие их незначительности.
На поверхностях 1—1 и 2—2 появляются моменты от сил трения,
касательных к элементам поверхности и перпендикулярных к радиусу.
Вследствие малой вязкости трение между частицами невелико и в даль-
нейшем не принимается в расчет. Давление газа на эти поверхности на-
правлено по нормали к ним и, следовательно, не создает момента.
Давление газа на границах поверхностей а—а' и b—Ь' дает момен-
ты относительно оси, но так как поле течения и поле давления именно
тем и характеризуются, что на расстоянии шага t моменты на поверх-
ности а—а' повторяются на поверхности b—Ь', то каждому элементу
на а—а' с моментом +ДЛ4 соответствует на b—Ь' противоположный
момент —ДЛ1, так что обе эти поверхности не дают никакого дополне-
ния к сумме моментов.
На поверхностях, ограничивающих высоту решетки и по которым
вырезана решетка из колеса, в принципе существуют моменты от тан-
генциальных сил на торцах лопаток и от тангенциальных составляю-
щих сил трения в потоке. Разность моментов от тангенциальных сил на
торцах лопатки по условиям равновесия, очевидно, будет в точности рав-
на моменту сил давления и трения, действующих на поверхности пера ло-
патки между плоскостями, ограничивающими ее высоту, и потому ничего
к сумме моментов не добавляет. Что касается моментов от тангенци-
альных сил трения в потоках на ограничивающих плоскостях, то они,
вообще говоря, будут оказывать некоторое влияние на си и сиг. Однако
вследствие малой вязкости влияние это невелико и его можно не учи-
тывать, как это делалось выше для поверхностей 1—1 и 2—2.
В результате остаются только моменты сил давлений и сил трения
на поверхности пера лопатки, суммируя которые, мы получаем равнодей-
ствующий момент.
Для того чтобы определить численное значение левой части урав-
нения (2. 10), рассмотрим элементарную струйку в относительном дви-
жении.
Принимая, что вращение колеса равномерное и расход газа имеет
определенное значение, получим, что относительное движение будет
установившимся.
Поскольку меридиональные скорости и плотности в относительном
и абсолютном движении равны, то и расход газа в струйке в относи-
тельном и абсолютном движении через единицу площади будет одина-
ковым.
Для элементарной струйки уравнение (2. 10) запишем в виде
Mn(cur) = dM, (2.11)
где dM — момент внешних сил, действующих на струйку.
Левая часть уравнения (2.11) представляет собой изменение в
единицу времени момента количества движения массы SAm, находя-
щейся в элементарной струйке. За время dr рассмотренная масса пере-
местится из положения ABCD в положение A'B'C'D'. Изменение мо-
37
мента количества движения этой массы равно разности моментов ко-
личества движения масс в объемах ABCD и A'B'C'D'. Так как движе-
ние установившееся, то эта разность равна моменту количества движе
ния массы в объеме CDC'D' минус момент количества движения мас-
сы в объеме АВА'В'. Обозначим массы и моменты количества движе-
ния элементарных объемов CDC'D' и АВА'В' через Дт2, Ат.\, c2ur2 и
с\игх. Тогда вместо уравнения (2.11) можем написать
(Дт2с2иг2—дт^г = dMb
ах
Но так как массы объемов CDC'D'=Дт2 и АВА'В'= Ат, представля-
ют соответственно массы газа, вышедшего из концевого сечения струй-
ки и вошедшего в начальное сечение струйки за промежуток времени
dx, то следовательно, Am2=df2Y2cm2dT; &mi=dFiyiCmidx, где dF2, dFi,
Y2, Yi, cm2 и cmi — площади сечения, плотности и меридиональные ско-
рости струйки на выходе и на входе соответственно. Но dF2y2cm2=dG2,
dF1ylcmi=dGi, где dG\ и dG2—массовый секундный расход газа, поэ-
тому Am2=dG2dx; Ami = dGidx.
Так как движение установившееся, то
Ami = Am2 = Am; dG\=dG2=dG и Дт — dG • Ах.
В результате для всей струйки вместо уравнения (2. 11) будем
иметь
dG(c2ur2—ciuri) —dM. (2.12)
Распространяя на все контрольное пространство около лопатки,
получаем
(l-?S
Ж
Мя= J dG(c2ur2 — c^rj. (2.13)
о
При интегрировании рассматривается сечение входа и предполагается,
что высота решетки равна единице.
Так как на поверхностях 1—1 и 2—2 скорости распределены рав-
номерно, то
•'Мл = Сл(с2Иг2—с1иг1) = СЛ1Д(^аг), (2. 14)
где бл и А1Л соответственно расход и момент для одной лопатки.
Если уравнение (2. 12) распространить на всю решетку, то полу-
чим
2icrx
Mi= ( й!О2д(свг),
о
или
Mi = Gn^ (сиг), (2.15)
где Mi и Gi — момент и расход для всей решетки.
Полученные уравнения можно представить еще в другом виде.
Для контура, охватывающего контрольное пространство вокруг ло-
патки, составим интеграл J с cos a ds, где с — скорость в точках конту-
ра, ds — элемент кривой и а — угол между ними. Величину J с cos а ds для
замкнутой кривой называют циркуляцией по замкнутому кон-
туру Ге. Если обозначить составляющую скорости в направлении s че-
рез c(s), интеграл вдоль замкнутого контура через то
rs= c(s)ds.
38
Рассматривая отдельные участки всего контура, можем написать
Ь Ъ' а' а
а b Ь' а ’
Очевидно, что на границах поверхностей а—а' и b—Ь' величины интег-
ралов будут равны по абсолютной величине и противоположны по зна-
ку. На участке а—b величина интеграла запишется
2лг1С1О
в виде

Z
на участке а'—Ь'
г 2лг2с2И
1 2Л —
откуда
.
2л ’
Следовательно, для лопатки получим
2Л
Wi =
Г2лг
С2аГ2=~-
2л
(2.16)
Z=O/-!-Z.
л2я
Для решетки имеет Мг=Млг; Gi — G^z; Г\=Гяг.
(2.16) можно придать вид
Ml=Gl^—^ = Gi^- .
1 2л 1 2л
В данном случае циркуляция вычислена исходя из
ны течения. Она может быть вычислена также и для
картины течения. В общем случае для рассмотренного замкнутого кон-
тура можно написать
Г, =$>с (s) ^5 = (f) м(5) + w (s)ds.
В случае, когда окружная скорость является постоянной по величине и
направлению
вательно,
Тогда уравнению
(2.17)
абсолютной карти-
относительной
для всех точек контура, интеграл u(s)tZs=O и, следо-
Z
Учитывая это,
фс (s) ds — w (s) ds.
можем для плоской прямой решетки написать
rs = i (^2а — flo) = t (® Iti — W2u'l,
где t — шаг решетки.
Полученные уравнения будут справедливыми и для решеток непод-
вижных аппаратов (направляющего и спрямляющего). В этих случаях
контрольные пространства около лопатки на ширине шага будут огра-
ничиваться линиями тока в абсолютном движении и таким же линиям
будут соответствовать элементарные струйки. Изложенные выводы также
показывают, что за моменты Ciuri и с2иг2 принимаются те, которые
имеет поток перед колесом и после колеса в области, где поле скорос-
тей равномерно. В связи с этим возникает вопрос, будут ли справедли-
вы эти уравнения, если рассматривать сечения в непосредственной бли-
зости к колесу, где, как уже отмечалось, наблюдается неравномерное
поле скоростей.
Следует отметить, что на участках перехода от равномерного пото-
ка к неравномерному или наоборот непосредственное воздействие ко-
леса на поток еще отсутствует. Поэтому выравнивание потока (за ко-
39
лесом) или деформация поля скоростей (перед колесом) происходят
за счет энергии самого потока. Поэтому если, например, в контрольном
пространстве (см. рис. 2. 7) выделить участок 1—1 и Г—Г, располо-
женный до колеса, то для этого участка момент внешних сил будет ра-
вен нулю и момент количества движения следует записать в виде
z
о
Принимая во внимание, что на поверхности 1—1 поле скоростей равно-
мерное, можем написать
Z
о
Если на поверхности Г—Г принять среднее значение окружной состав-
ляющей скорости, то получим
С, г, —С, г'.
Следовательно, изложенные выше выводы будут справедливы, если на
поверхностях, где поле скоростей неравномерное, рассматривать сред-
ние скорости.
Номера точек
Рис. 2.8. Распределение давлений по профилю конфузорной
решетки
Момент на отдельной лопасти решетки и на всей решетке, вырезан-
ной из колеса, можно также определить, зная распределение давления
по профилю. При этом под распределением давления понимается за-
висимость давления р на профиле от длины его дуги s. Конкретный вид
этой функции определяется формой профиля, углами его установки и
шагом решетки, а также условиями обтекания данной решетки, харак-
теризуемыми чаще всего величинами угла атаки и скорости на входе.
С распределением давления однозначно связано и распределение ско-
рости на профиле. На рис. 2. 8 показано для примера распределение
давления на профиле лопатки осевой турбины, построенное для раз-
личных точек на выпуклой и вогнутой поверхностях профиля. Если
обозначить длину контура профиля через L, то результирующую силу
40
давления газа, приходящуюся на единицу высоты лопатки, можно вы-
разить в виде
Проекция результирующей силы на плоскость, перпендикулярную осн
колеса, будет являться ее тангенциальной составляющей, которая
для вращающейся решетки будет совпадать с направлением окружной
скорости.
Рис. 2. 9. Схема сил, действующих на профиль в решетке
Обозначая проекцию дуги s на указанную плоскость через su, мо-
жем проекцию результирующей силы записать в виде
Ra = fLP(s)dsu.
Тогда момент лопасти будет равен
= rdsu.
Момент решетки, состоящей из z профилей, очевидно, выразится так:
Мг-=Млг.
Если профиль соответствует такой решетке осевой турбомашины,
в которой все поверхности тока являются концентричными цилиндрами,
то для всех элементов профиля радиус г будет одинаковым, и момент
можно записать в виде
Мл=7?иг=г (j) Lp(s)dsu.
Очевидно, что вычисление момента с помощью результирующей силы
давления на профиль будет представлять значительные трудности по
сравнению с методом, основанным на теореме о моменте количества
движения. Результирующую силу давления на профиль плоской пря-
мой решетки, соответствующий осевой машине, можно связать с цирку-
ляцией вокруг профиля с помощью теоремы Жуковского.
Применим теорему о количестве движения к контрольному конту-
ру а—b—а'—Ь', проведенному вокруг профиля плоской прямой решет-
ки (рис. 2. 9), принимая для простоты жидкость несжимаемой и пренеб-
41
регая трением. Согласно этой теореме изменение количества движения
во времени, т. е. производная по времени, равна равнодействующей
всех внешних сил, действующих на выделенный контур. В рассматри-
ваемом случае внешними силами будут являться силы давления на по-
верхностях а—Ь, а'—Ь' и на поверхности профиля. Силы же давления
на поверхностях а—а и b—Ь, будучи равными и противоположно на-
правленными, взаимно сокращаются. Выберем оси координат и и а так,
что ось и совпадает по направлению с окружной скоростью (или с
фронтом решетки), а ось а — с направлением осевой скорости. Все рас-
суждения, относящиеся к составлению уравнения (2. 14) на основе те-
оремы о моменте количества движения, остаются справедливыми и при
использовании теоремы о количестве движения. Поэтому в соответст-
вии с этой теоремой в проекции на ось а получим
G„(w2a—wla) = t(p2—Pl)— Ra, (2.18)
где
JRa=<$p(s)dsa.
Таким образом, Ra— проекция на осевое направление результирую
щей силы давления жидкости на лопатки, приходящейся на единицу ее
высоты.
Из уравнения равенства расхода через входные и выходные сече-
ния получаем,что
G„ = ytwla=ytw2a,
откуда
W}a = W2a = Wa.
Вследствие этого уравнения (2. 18) примет вид
Ra=t(p2—Pl)-
Выразим давления через скорости, используя интеграл Бернулли, ко-
торый при отсутствии потерь и при постоянстве для всех точек окруж-
ной скорости будет для относительного движения иметь вид
—-ф— =const.
2 ' у
Тогда получаем
-^(®2-w2) = -^(®22k-®2„),
или
Используя уравнение для циркуляции вокруг профиля, получим
/?0 = - yrs W1“ . (2.19)
В проекции на ось и по теореме о моменте количества движения полу-
чаем аналогично:
(w2„-®i„) =-/?„,
где
Ra = (£ Р («) dsa,
откуда
Rtr= — yi^2a — wla)wa=— yFswa. (2.20)
Отношение
= __ «’ig / _
Ra 2 / °’
42
вытекающее из формул (2.19) и (2.20), показывает, что равнодейству-
ющая сил Ra и Ru перпендикулярна к результирующей скорости

получающейся при геометрическом сложении скоростей
В этом легко убедиться, рассматривая соответствующие подобные
треугольники на рис. 2. 9. Вектор скорости wm делит пополам отрезок,
соединяющий концы векторов скоростей Wi и w2. Каждая из этих поло-
вин численно равна , а для прямой плоской решетки — одно-
временно равна -2ы ~С1а . Поэтому вектор скорости wm является
средним арифметическим векторов скоростей w1 и w2, т. е.
Учитывая, что равнодействующая сил Ra и Ru равна /? = У Ra-[-Ru,
мы вместо уравнений (2. 19) и (2. 20) можем написать одно уравнение
R=yrswm.
(2. 18) —(2.20)
проекции заменяются абсолютными ско-
(2.21)
к неподвижной решетке
При применении уравнений
относительные скорости и их
ростами и их проекциями.
Уравнение (2.21) и указание о направлении равнодействующей
силы, действующей на профиль, составляет содержание теоремы
Н. Е. Жуковского, полученной им как для одиночного профиля (кры-
ла), так и для решетки профилей. Если увеличивать шаг между двумя
соседними профилями, сохраняя при этом циркуляцию r=\t(w2u—
—W\u) постоянной, то разность скоростей w2u—wiu будет уменьшаться,
и в пределе для t—>оо, т. е. для одиночного профиля, она становится
равной нулю. Следовательно, на достаточном расстоянии перед одиноч-
ным профилем и позади него скорости потока будут совпадать и поэто-
му среднюю скорость wm можно принять равной скорости невозму-
щенного потока в бесконечности.
Для дозвуковых скоростей практически используется теорема
Н. Е. Жуковского в ее формулировке для несжимаемой жидкости,
причем в качестве плотности у берется средняя арифметическая вели-
чина
1 _
Y . .. .
Вектором средней скорости считается по-прежнему средний вектор
= -~-(®1 + «’2) для вращающейся решетки или cm=_L- (Ci-j-c2)
для неподвижной решетки [42]. При отсутствии потерь равнодействую-
щая сила R является одновременно и подъемной силой профиля и, сле-
довательно, может быть выражена уравнением
Y = -|“(Yj Ц-у2) или, более точно, средняя гармоническая величина
1 / 1 . 1 \
— ---1---из значении плотности перед решеткой и за ней.
(2.22)
где b—хорда профиля;
Су—коэффициент подъемной силы.
43
С учетом вязкости появится еще сила лобового сопротивления про-
филя, направленная противоположно скорости wm и равная по величине
где Сх—коэффициент лобового сопротивления.
Возьмем дополнительные координаты х и
у так, что ось х направ-
лена по скорости wm, а ось у перпендикулярна ей и, следовательно, со-
впадает по направлению с силой R
Рис. 2. 10. Схема сил, действующих
на профиль в решетке, с учетом
потерь
(рис. 2.10). Примем, что при наличии
вязкости сохраняются неизменными
треугольники скоростей и окружная
составляющая Ru результирующей
силы давления. Тогда, нанося силу ло-
бового сопротивления, получим новую
подъемную силу Ry и равнодействую-
щую силу Rp, а также осевую силу
Rap. Все эти силы меньше по величине
соответствующих сил, получавшихся
без учета вязкости.
Подъемная сила Rv может быть
также выражена уравнением (2. 22), но
с другим (меньшим по величине)
коэффициентом подъемной силы:
wL
Ry=CyP\b-^.
Обозначим через ф угол между равнодействующей силой Rp и подъ-
емной силой Ry. Тогда нетрудно видеть, что
где ц—величина, обратная качеству профиля.
2.3.2. УРАВНЕНИЯ МОЩНОСТИ И УДЕЛЬНОЙ РАБОТЫ
ДЛЯ РЕШЕТКИ РАБОЧЕГО КОЛЕСА
Для единичной струйки получим мощность, если момент умножим
на угловую скорость:
dN = dMuy=dO (с2и«2—cia«i)=dO\^(cuu).
Мощность, отнесенную к расходу, принято называть удельной работой
лопаточной машины. Для элементарной струйки получаем
,, dN 2 . /У a(j (2. 23)
Для решетки имеем
N t = ^dMu = Gi(c2!lii2 + cluu,) (2. 24)
и соответственно
N- 2 Gi (2. 25)
Таким образом, удельная работа для струйки и для всей решетки
одинакова.
44
Если решетка осевая, то ui = u2 и, следовательно,
Н = и (с2а — cJa) = iiiAcu. (2.26)
Если сии при прохождении газа через решетку увеличивается, то и
Н возрастает (действие компрессора, насоса); если оно уменьшается,
то падает и Н (действие турбины).
Таким образом, при принятом обозначении скоростей и радиуса
на выходе из колеса и на входе в него мощность и удельная работа для
решетки компрессора в соответствии с уравнениями (2. 24) и (2. 25)
будут иметь положительное значение, а для турбины—отрицательное.
Для получения в турбине положительных значений N и Н меняют
местами члены в скобках. В дальнейшем удельная работа по уравнению
(2.25) называется теоретическим напором решетки для ком-
прессора Hth и теоретической работой решетки турбины Нти.
Такое наименование, однако, не означает, что речь идет о величи-
нах, соответствующих идеальному процессу без потерь. В действитель-
ности, как следует из выводов, теоретический напор и теоретическая ра-
бота учитывают потери на трение между частицами и на поверхности
профиля. Трению могут сопутствовать вихревые движения и отрывы по-
тока. Если эти явления возникают внутри контрольного пространства,
то в выводах ничего не меняется. Если же они выходят за пределы кон-
трольного пространства, то должны быть приняты во внимание при вы-
числении J CuUdG.
Для удельной работы мы также можем ввести понятие циркуляции
и записать уравнение (2. 25) в таком виде:
(2.27)
Как установлено в разд. 2. 5, удельная работа характеризует изме-
нение энергии в лопаточной машине. Из уравнения (2. 25) получаем
dH=d(cuti). (2.28)
Таким образом, для движущейся частицы в каждой точке энергия
течения меняется в той же мере и в том же направлении, в каком ме-
няется произведение сии.
Очевидно, что удельная работа существует только в потоке, движу-
щемся через вращающееся колесо. При этом, как уже указывалось,
абсолютное движение будет неустановившимся.
Следовательно, увеличение (в компрессоре) или уменьшение (в тур-
бине) энергии движущегося потока возможно только, если его абсо-
лютное движение неустановившееся. Для такого движения полное мгно-
венное изменение энергии частицы потока в элемент времени dx будет
происходить вследствие изменения скорости и давления во времени в
каждом данном месте потока и продвижения частицы на величину ds в
направлении мгновенной абсолютной линии тока. Это изменение для
направления касательной к линии тока запишется так:
Для идеальной несжимаемой жидкости
у 2
Подставляя, получим
— = А + Н — + — + с — .
dx дх у \ ds у д~ ds J
45
Но выражение в скобках равно нулю, так как оно представляет со-
бой уравнение Эйлера в направлении касательной, которое, как извест-
но, имеет вид
дс , д ______ д р
~ --------- ‘~ •
от cs 2 ds 1
Поэтому получаем
dE _ д
dx дт
(2.31)
\ V / '
Следовательно, общее
изменение энергии течения отдельной части-
цы равняется локальному
д I рп
ся движении“ — и
изменению величины р/у. При установившем-
и поэтому Е = const.
В этом случае удельная работа будет равна нулю.
Уравнения (2.25) и (2. 26) принято называть уравнениями Эйлера.
Этим уравнениям можно придать еще другой вид, если ввести относи-
тельные скорости. Из треугольников скоростей (см. рис. 2. 7) для входа
и выхода получаем
wf= — 2и1с1 cos Qj = и2 -ф с2 — 2«jClu;
Отсюда
Wl — U2 + С2 ~ ^U2C2 COS И2 = И2 + С2 ~ 2и2с2а-
W] — W22
«2е 2и — И\С\и =-----------
Следовательно, уравнение для теоретического напора решетки компрес-
сора можно записать в таком виде:
__w2~w2 U2—U.\ t С2-с\
72 + 2 -1 ~
Соответственно для турбины
/Ут и
2 2
“1 —“2
2
г2 — с2
С1 — С2
2
(2. 32)
(2.33)
W2~^l ।
2
Таким образом, уравнения (2.32) и (2.33) показывают изменения,
которые должны происходить в потоке, протекающем через решетку ра-
бочего колеса при затрате энергии (компрессор, насос) или при полу-
чении от потока энерии (турбина).
В зависимости от типа колеса и способа его проектирования отдель-
ные члены в уравнениях (2. 32) и (2. 33) могут иметь различное значе-
ние. Так, например, в осевых машинах исчезает второй член. При про-
ектировании осевых машин иногда принимают, что Wi = tO2, и тогда ки-
нетическая энергия в относительном движении не будет изменяться
(так называемые «активные» колеса). В этом случае вся энергия, сооб-
щаемая в компрессоре или получаемая в турбине, будет соответствовать
только изменению кинетической энергии в абсолютном движении.
Наряду с абсолютными значениями Hth и Н?и в расчетах компрес-
соров и турбин широко применяются следующие безразмерные коэффи-
циенты, характеризующие удельную работу решеток лопаточных машин:
коэффициент теоретического напора Hth =—
коэффициент теоретической работы //ти = ^т —
Последний часто называется также коэффициентом нагрузки.
46
2.3.3. УРАВНЕНИЕ МОМЕНТА ДЛЯ РАБОЧЕГО КОЛЕСА
Полученные для решетки уравнения момента, мощности и удельной
работы не могут быть безоговорочно применены для всего колеса вслед-
ствие наличия дополнительных явлений на внешних границах колеса и
переменного по радиусу поля скоростей и давлений. Для получения мо-
ментов и удельной работы для колеса в целом воспользуемся снова тео-
ремой о моменте количества движения. Выделим около колеса контроль-
ное пространство, которое в данном случае ограничено замкнутой по-
верхностью вращения А (рис. 2. И). На этой поверхности можно выде-
лить следующие части:
1) а—а' и b—Ь', пересекающие
поток на входе в колесо и выходе из
него;
2) а'—а' и Ь'—d, соответствующие
диску колеса;
3) а—Ь, соответствующая бан-
дажу лопаток колеса;
4) d—d, соответствующая пересе-
чению контрольной поверхности с ва-
лом. (Если колесо расположено не-
консольно, то пересечение происходит
в двух местах.)
В частях а'—а', Ь'—d и а—b конт-
рольные поверхности должны вплот-
ную примыкать к поверхности колеса,
так как в дальнейшем будет идти
речь о силах, приложенных на этих
Рис. 2.11. Контрольные поверхности
вокруг рабочего колеса
поверхностях к колесу.
Если лопатки колеса не имеют бандажей, то на участке а—b кон-
трольная поверхность также, в основном, будет проходить в потоке
газа. Отметим, что в противоположность выводам в разд. 2. 3. 1. поверхно-
сти лопаток в данном случае не рассматриваются как поверхности кон-
трольного пространства.
Применим для определенного момента времени для жидких и твер-
дых частиц, находящихся в контрольном пространстве, теорему о мо-
менте количества движения. Тогда для жидких частиц получим
дт - (СиГ) — AM,
dx
а для твердых частиц
A A rf (Г2®) ..
Дщ —-—ьт ——-= д/И,
1В dx ™ dx
где и—окружная скорость на данном радиусе;
со—угловая скорость колеса.
Суммируя эти выражения для всех частиц, находящихся в конт-
рольном пространстве, получаем
+ (2'34’
Рассмотрим сначала правую часть уравнения. Отметим, что по-
скольку колесо симметричное, то центр тяжести всех масс, находящих-
ся в контрольном пространстве, лежит на оси, поэтому в целом сила тя-
жести не дает момента. Все внутренние силы, т. е. давление и трение
между жидкими частицами или напряжения между твердыми частица-
ми, при сложении взаимно уничтожаются. Точно так же, пока частицы
находятся внутри контрольного пространства, выпадают силы давления
47
и трения между жидкими и твердыми частицами и, следовательно, меж-
ду потоком с одной стороны и поверхностью лопаток и других частей
колеса с другой. Однако это не противоречит результатам, полученным
в разд. 2. 1 при выводе момента для решетки, откуда вытекало, что мо-
мент определяется силами давления и трения на поверхности лопатки.
При рассмотрении колеса момент от сил на лопатках проявляется в се-
чении d—d вала контрольной поверхностью. Кроме того, в момент внеш-
них сил входят моменты от сил давлений и трений на остальных поверх-
ностях контрольного пространства. При этом момент сил трения на по-
верхностях а—а' и b—Ь' можно не учитывать, так как эти поверхности
находятся в газе и вследствие малой вязкости силы трения будут незна-
чительны.
Момент сил трения на поверхностях диска и бандажа (части кон-
трольной поверхности а'—а', Ь'—d и а—Ь) должен приниматься во вни-
мание. Обозначим этот момент через М/. Он действует всегда противо-
положно вращению. Следует отметить, что при отсутствии бандажа
момент трения на этой поверхности уменьшается, но зато появляются
потери в зазоре. Наличие бандажа полезно при длинных лопатках для
уменьшения в них вибрационных напряжений, а при коротких лопатках —
для уменьшения потерь, обусловленных радиальным зазором. Величи-
ну крутящего момента в сечении вала d—d, передаваемого от внешней
части вала на внутреннюю (или наоборот), обозначим через Mz и будем
считать его положительным, если он действует в направлении вращения
колеса. В частности, этот момент должен иметь в компрессоре положи-
тельный знак и отрицательный в турбине. Таким образом, получаем
£ A.M = AK-A?Z. (2.35)
Для определения значения левой части рассмотрим в первую оче-
редь твердые частицы. Сумму моментов количества движения для них
можно записать в виде
У ДЩ1В \ гЧтп = (2.36)
dт t/т J dx
где J—момент инерции массы колеса.
Полученное выражение имеет существенное значение для неустано-
вившихся режимов лопаточных машин (запуск, разгон) и на этих режи-
мах вводится в расчет.
В дальнейшем мы ограничимся рассмотрением установившихся ре-
жимов, когда и можно считать постоянной величиной, и поэтому момент
от массы колеса будет равен нулю.
Для жидких частиц мы должны иметь в виду, что момент скорости
сиг изменяется по двум причинам. Во-первых, потому что частицы в
мгновенной картине течения двигаются по какой-либо линии тока (кон-
вективное изменение). Именно такого рода изменения рассмотрены бы-
ли выше при составлении уравнения моментов для решетки. Во-вторых,
сиг изменяется потому, что из-за нестационарности потока изменяются
во времени скорости в каждом данном месте потока (локальное изме-
нение). Это второе изменение для частицы выражается в виде
Am , т. е. частной производной момента количества движения по
ОТ
времени.
Для всех частиц, находящихся в контрольном пространстве, полу-
чаем
dz
48
где V—является полным объемом жидкости (газа), находящегося в кон-
трольном пространстве. Но так как одно и то же распределение скоро-
стей периодически повторяется, то этот интеграл, когда хотят получить
среднюю картину течения, можно приравнять нулю. Следовательно, в
левой части уравнения (2. 34) необходимо учитывать только конвектив-
ное изменение момента количества движения. Для элементарной струй-
ки было получено уравнение (2. 12). Если распространить его на поверх-
ность входа (или выхода), то получим момент количества движения для
потока в колесе:
Р или F
* вх И,1И вых
А1= у dQ(c7ur2 — с1игг), (2.37)
выходе из него соот-
поверхности а—а' и
знать распределение
где Евх и ЕВых — сечение на входе в колесо и на
ветственно частям контрольной
Ь—Ь'.
Уравнение (2. 37) можно записать еще в виде
F F
вых ВХ
М = J dGciar2— dQciurv
При применении этого уравнения достаточно
скоростей, давлений и температуры отдельно в каждой точке на входе
и на выходе, независимо одно от другого, тогда как в уравнении (2. 37)
параметры в каждой точке на входе (или выходе) должны быть взаим-
но связаны с параметрами на выходе (или входе), так как речь идет об
одной струйке.
Применяя для входа или выхода систему полярных координат, мы
можем рассматривать скорости и др. параметры как функции радиуса и
полярного угла ср, вследствие чего расход через струйку будем выражать
зависимостью
(2.38)
dG=cmyrdifdr.
Поэтому выражение для момента количества движения можно записать
в виде
2« 'к
= dG(c2ar2 — ciarx),
° гвт
где rBT и гк—радиусы втулки и периферийного сечения лопатки на входе
в колесо и на выходе из него.
Если учесть принимавшееся выше условие, что поток является осе-
симметричным, то вместо двойного интеграла в уравнении (2. 39) мож-
но брать интеграл только по радиусу и, следовательно, в подынтеграль-
ном выражении величины dG и си будут соответствовать решеткам, на-
ходящимся на различных радиусах:
(2.39)
/14 = J dCiic^—с1игх).
(2. 40)
Аналогично изменится и уравнение (2. 38):
^к2 Гк1
/И= у dGi(c2llr2) — У dGi(ciari), (2.41)
гвт2 гвт1
где dGi=2nrcmydr—расход через решетку на данном радиусе (на входе
в колесо или на выходе из него).
49
В результате уравнение (2. 34) с учетом уравнения (2. 35) мы можем
записать в виде
М=Мг—Мь (2.42)
где М то же, что и в уравнениях (2.37) — (2.41).
Из уравнения (2. 42) следует, что момент на валу будет выражаться со-
отношением
MZ=M+Mf. (2.43)
В этом уравнении Mf всегда считается положительным. Если
C2uf2>Ciuri, то и Mz положительно, т. е. вал приводит в движение рабо-
чее колесо и к валу должен быть приложен вращающий момент; в таком
случае это есть компрессор (насос). Если, наоборот, C2Ur2<Ciuri, то по-
скольку Mf составляет не более 10% правой части, Mz отрицательно.
Следовательно, вал приводится в движение рабочим колесом, т. е.
мы имеем турбину. Учитывая, что применительно к турбине Mz и Л)
имеют отрицательный знак, уравнение (2. 43) можно написать в виде
~MZ=—M + Mf. (2.44)
Переходя к положительным величинам, получим
MZ=M—Mf
или
M = Mz-\-Mf. (2.45)
Момент М появляется в результате взаимодействия лопаток и по-
тока. В турбине этот момент приводит в движение колесо (момент Мг)
и затрачивается на преодоление момента трения Mf [см. уравнение
(2.45)]. В компрессоре (насосе) на создание момента М расходуется
внешний момент Mz, часть которого одновременно затрачивается на пре-
одоление момента трения Mf [см. уравнение (2.43)].
Все полученные в разд. 2. 3. 3. уравнения применимы и для непод-
вижных направляющих и спрямляющих аппаратов, но момент Mf при
этом всегда равен нулю.
2.3.4. УРАВНЕНИЯ МОЩНОСТИ И УДЕЛЬНОЙ РАБОТЫ
ДЛЯ РАБОЧЕГО КОЛЕСА
Если уравнения для моментов умножить на угловую скорость ко-
леса oj, то получим уравнения для мощностей. Мощность на валу, соот-
ветствующую моменту Mz, обозначим в турбине NT и в компрессоре NK-
Таким образом, для турбины [из уравнения (2.44)]—
NT=N—Nf, (2.46)
для компрессора [из уравнения (2.42)]—
NK=N+Nf. (2.47)
Следовательно, в этих уравнениях
N—мощность, обусловливаемая взаимодействием потока и лопаток
рабочего колеса;
Nf—мощность, затрачиваемая на трение диска и обода колеса («бо-
ковое» трение).
С использованием уравнения (2. 40) величину N для колеса турбины
можем записать в виде
N — \ dGi(cluu1-\-c2uti2). (2.48)
50
При этом учтено, что окружная составляющая скорости за колесом
ступени обычно направлена в сторону вращения и поэтому она записы-
вается со знаком плюс. Для получения положительного значения 7V из-
менен знак у величины ciuUi.
Для колеса компрессора аналогично получаем
гк
J dOi^Uz — (2. 49)
гвт
В этом уравнении принято, что окружная составляющая скорости на
входе направлена в сторону вращения колеса. В соответствии с уравне-
нием (2. 25) мы можем выражения в скобках под интегралом уравнений
для N заменить удельной работой и, обозначая ее индексом i, записать
эти уравнения:
для турбины
2V= J dGztfT„z; (2.50)
ГВТ
для компрессора
гк
N= (2.51)
гвт
В уравнение для W в общем случае должны входить действительные
скорости Ciu и с2и на различных радиусах, отличающихся от расчетных
в силу ряда причин, в том числе в силу влияния радиального зазора,
уменьшающего циркуляцию вокруг профиля в верхних сечениях и изме
няющего соответственно углы выхода потока. Это явление вызывается
перетеканием (при отсутствии бандажей) газа с вогнутой стороны про-
филя, где высокое давление, на выпуклую сторону с низким давлением.
Существенное влияние, и особенно в средних и последних ступенях
компрессора, оказывает также деформация поля скоростей по радиусу
перед колесом из-за наличия пограничного слоя на периферии и v
втулки. Это также вызывает уменьшение удельной работы.
Влияние этих и других факторов на расчетные значения окружных
составляющих скоростей и удельной работы для решеток на различных
радиусах условимся учитывать с помощью коэффициента Qj, который
применительно к компрессору называется коэффициентом за-
траченной работы, а применительно к турбине — коэффици
ентом уменьшения работы.
Таким образом, для турбины вместо уравнения (2. 50) получаем
гт
J//TJfZ2zrfGz. (2.52)
гвт
Для компрессора вместо уравнения (2. 51) будем иметь
N= J H^dO^ (2.53)
гвт
Если ввести средние по радиусу значения теоретической работы,
теоретического напора и коэффициентов Q, то можем написать
N = GHlaQ (2.54)
и
N = GHihQ. (2.55)
51
Средние значения //Tu и Hih должны, очевидно, подчиняться уравне-
ниям
J —с2и«2)
Н =-^1____________________
11 т и ~
и
гк
j (C2uu2 — с1мц1)
(2. 56)
(2. 57)
В частности, если в исходных условиях для профилирования лопа-
ток колеса принимается постоянство теоретической работы или теоре-
тического напора по высоте лопаток, то в уравнения (2.54) и (2.55)
должны входить эти расчетные значения НТи и Hth-
Рис. 2.12. Схема перетекания воздуха через ра-
диальный зазор и обозначение сечений:
а—турбина, б—компрессор
Необходимо подчеркнуть, что коэффициент Q не является коэффи-
циентом потерь, связанных с ростом энтропии, а учитывает лишь сте-
пень отклонения теоретической работы и теоретического напора от их
расчетных величин, которые фактически не реализуются вследствие
того, что при реальных условиях обтекания претерпевают изменения
окружные составляющие скорости. Таким образом, рабочие поверхно-
сти лопаток не передают газу или не воспринимают от него предпола-
гаемой энергии.
Уравнения баланса мощностей (2. 46) и (2. 47) можно записать че-
рез удельные работы. Предварительно необходимо отметить, что в тур-
бине расход газа непосредственно через рабочее колесо несколько мень-
ше полного расхода, вследствие того, что часть газа проходит через ра-
диальный зазор. Таким образом (рис. 2. 12. а),
G = GT—G3,
где G —расход газа через колесо;
Gr—общий расход, полезно используемый за колесом;
G3—расход через радиальный зазор.
В отличие от турбины, расход G через рабочее колесо компрессора
превышает полезно используемый за колесом расход GB, вследствие
того что часть сжатого в колесе воздуха вновь возвращается на всасы-
вание из-за наличия радиального зазора (рис. 2. 12,6). Поэтому для
колеса компрессора получим
G = GB + G3. (2.58)
52
Разделим обе части уравнения (2. 46) на используемый расход Gr и
обозначим
Ят

и Lf
Nf
Очевидно, что 7/т представляет собой удельную работу на валу турби-
ны, a Lf—удельную работу бокового трения. В дальнейшем Нт будем
называть сокращенно работой турбины. При делении мощности М на
расход Gr получим, принимая средние значения Нти и Q:
N _ OH-ruQ __ Gr —G3 н Q
Gr Gr Gr т “
Gr
Обозначив — Л/ТОЙ через L3 и произведение Нги2 через Н' получим
(7 г
H1=HtU — L3 — Lf. (2.59)
Если уравнение баланса мощностей для колеса компрессора (2. 47)
разделить на полезно используемый (за колесом) расход GB, то анало-
гично получим
HK=H'th + Ls + Lf, (2.60)
где
м (1 Nr
L3=--^-HthQ; Lf=—; Hfh=HihQ.
(/ R Cz в в
Величина Нк представляет собой удельную работу, затрачиваемую в
компрессоре и учитывающую все потери, за исключением механических.
В дальнейшем Нк будет сокращенно называться «работа, затрачивае-
мая в компрессоре». Величины Н'ти и H't/l могут быть соответственно
названы теоретической работой турбины и теоретическим напором ком-
прессора с учетом действительных значений окружных составляющих
скорости.
2.3.5. ЧАСТНЫЕ СЛУЧАИ ПРИМЕНЕНИЯ ОБЩИХ УРАВНЕНИЙ
МОМЕНТА, МОЩНОСТИ И УДЕЛЬНОЙ РАБОТЫ
В ряде случаев уравнения момента, мощности и удельной работы
могут быть упрощены. Рассмотрим несколько примеров, ограничив-
шись уравнениями для М, N и Hth или Нти, т. е. величин, обусловленных
только взаимодействием потока и лопаток, и без учета коэффициента Q.
Пример I. Центробежное колесо насоса с радиальным вхо-
дом (рис. 2. 13).
В этих случаях в сечениях 1—1 и 2—2 ri = const и r2 = const. Кроме того, предпо-
лагается. что поток осесимметричен, т. е. по окружности распределение скоростей рав-
номерное. Поэтому можно принять, что clu = const и C2u=const. Вследствие этого урав-
нения для М, N и Hth получат вид
M=G(c2ur2—cluri);
N == G (С2иМ2-С] цЩ) J
Н th — C2uU2 Cl
Таким образом, уравнения имеют такой же вид, какой получался выше для ре-
шеток. Если на входе не будет закрутки потока, т. е. если ciu = 0, то второй член
во всех уравнениях исчезнет.
Пример II. Центробежное колесо с осевым входом (рис. 2. 14).
В этом случае входные кромки лопаток расположены, как в осевых машинах,
а выходные кромки — как в предыдущем примере.
53
В связи с этим уравнения в общем случае будут иметь вид
M = Gc2ur2 — J rfOciar5;
'вт
гк
N = Gc2ua2 — J dGc\uuY,
ГВ1
J dGc\uui
Н th — с2ии2 — .
G
Если на входе поток не будет закручен, то вторые члены в этих уравнениях
исчезнут.
С другой стороны, закрутка на входе может подчиняться различным законам.
В частности, встречается изменение С\и по закону вращения «твердого тела» — =
Рис. 2. 13. Центробежное колесо с ра-
диальным входом
Рис. 2. 14. Центробежное колесо
с осевым входом
= const и по закону постоянства циркуляции А=const или Ciuri = const. В последнем
случае уравнения примут такой же вид, как и в предыдущем примере:
Л1 = G (c2ur2—ciuri);
N=G{c2uu2—c\uUi.)\
Нth — C2u U2-—Cl и Щ.
Рабочие колеса, рассмотренные в примерах I—II, применяются и в турбинах, причем
газ входит с периферии к центру. Следовательно, для турбины параметры в перифе-
рийном сечении должны иметь индекс 1. В уравнениях М, N и Н члены, соответствую-
щие выходу (индекс 2), будут иметь знак плюс.
Пример III. Осевое колесо (рис. 2.15).
В общем случае уравнения М, N и Н для осевого колеса будут иметь вид, рас-
смотренный выше [уравнения (2.37) — (2.40)], но в предположении чисто осевого на-
правления потока Г1=г2=г и иг = и2=и.
В осевых колесах компрессоров и турбин часто окружные составляющие скоро-
стей на входе в колесо и на выходе из него подчиняются закону постоянства цирку-
ляции: .Ti=const и T'2=const или Ciuri=const и c2ur2=const. В связи с этим уравнения
М, N и Я приобретают в таких колесах простой вид. Так, например, для компрессора
будем иметь
M=G(c2u—Ciu)r;
N=Gu(c2u—cm);
tit ь—u (c2«—Ciu) •
54
При этом очевидно, что на каждом радиусе значения Hth будут одинаковыми и
следовательно, равны средним значениям этих величин для колеса в целом. Следует
отметить, что и в том случае, когда струйки в ко-
лесе не будут иметь чисто осевого направления,
указанные уравнения должны оставаться справед-
ливыми, так как независимо от радиуса выхода
произведения с2цг2 или с2ии2 сохраняют свою ве-
личину.
Наряду с осевыми колесами, имеющими по-
стоянную циркуляцию в потоке на входе и на вы-
ходе часто применяются колеса с переменной цир-
куляцией, но с постоянными по радиусу теоретиче-
ским напором и теоретической работой. В этом
случае произведения cluUi и c2uu2 порознь не яв-
ляются постоянными по радиусу, но их разность
(например, для компрессора) или сумма (для
турбины) будет на всех радиусах одинаковой. То-
Рис. 2. 15. Осевое колесо
гда уравнения М, N и Н будут такими же, как и
при законе постоянства циркуляции.
2.4. УРАВНЕНИЯ ДЛЯ ОПРЕДЕЛЕНИЯ ОСЕВЫХ СИЛ,
ДЕЙСТВУЮЩИХ В КОЛЕСЕ
Для расчета подшипников и их опор необходимо знать осевые силы,
действующие в лопаточной машине. Для определения этих сил в общем
виде воспользуемся теоремой о количестве движения, согласно которой
изменение количества движения во времени, т. е. его производная по вре-
мени, равно результирующей всех сил, приложенных к массе.
Рассмотрим колесо, показанное на рис. 2. 11, с выделенным около
него контрольным пространством. Применим для определенного мо-
мента времени для жидкой или твердой частицы, находящейся в кон-
трольном пространстве, теорему о количестве движения в проекции на
ось колеса. Тогда получим
Ып^- = ьРа,
dx
где Дт—масса частицы;
са—составляющая скорости по направлению оси;
ДРа—составляющая вдоль оси равнодействующей всех внешних
сил, действующих на частицу.
Суммируя эти выражения для всех частиц, находящихся в конт-
рольном пространстве, получаем
Рассмотрим сначала сумму сил в правой части уравнения (2.61). Ради
общности не будем ограничивать положение вала; ось его может со-
ставлять любой угол с вертикалью.
В связи с этим в качестве составляющей суммы сил ЛРа должны
быть учтены осевые составляющие силы тяжести всех жидких и твер-
дых частиц, находящихся в контрольном пространстве. Обозначим их
соответственно через (2Д/иж-g)a и (2Дттв • g) а-
В общем случае надо учесть еще осевые силы, возникающие вслед-
ствие движения вместе с летательным аппаратом с ускорением или за-
медлением твердых и жидких частиц, находящихся в контрольном про-
странстве.
Если обозначить проекцию ускорения на ось машины через ja, то
осевая составляющая силы инерции может быть выражена произведе-
нием массы всех твердых и жидких частиц на это ускорение:
2Д/77тв • ja И 2Дшж • /а-
55
Все указанные составляющие считаются положительными, если они
совпадают по направлению с осевой составляющей скорости потока.
Аналогично тому, как было показано при составлении уравнения момен-
тов (см. разд. 2. 3. 3), учитывается, что внутри контрольного пространства
давление и трение между жидкими частицами, а также давление и трение
между жидкими и твердыми частицами взаимно уничтожаются и остают-
ся только действия сил давления, трения и напряжения на поверхности
контрольного пространства.
На части этой поверхности, пересекающейся с валом (часть d—d),
появляются осевые напряжения и их равнодействующая 7? от действия
внешней части вала на внутреннюю, которую считаем положительной в
направлении текущего вдоль оси газа. На всех остальных частях по-
верхности контрольного пространства должна быть рассмотрена осе-
вая составляющая равнодействующей всех сил давления. Обозначая
элемент этой поверхности через dF и давление на этот элемент через р,
можем в общем виде осевую составляющую равнодействующей сил
давления записать в виде интеграла J (j)dF)a, где F—вся поверхность
контрольного пространства, за исключением ее части d—d, относящейся
к пересечению с валом. Таким образом, правая часть уравнения (2.61)
может быть записана в виде
S д^а=(2дтж-^)а+(2дш™‘^)в+2дтж'Уа+
+ 2L д'ГСтв-Л + Я + ]’ (pdFV (2.62)
Рассмотрим теперь левую часть уравнения (2.61). Пренебрегая
локальным изменением количества движения, может рассмотреть
его конвективное изменение сначала для элементарной струйки, а затем
для решетки, совершенно аналогично тому, как это делалось при опре-
делении момента (в разд. 2.3. 1). Распространяя затем конвективное
изменение количества движения для решеток на всю поверхность входа
и выхода, можем написать
Гк1
\ rfG/(c2fl-q0) (2.63)
dx J
ГВТ1
ИЛИ
гк2 Гк1
Едт^-= c^dG,- \ c,adGh (2.64)
dx J J
гвт2 гвт1
где dGi = 2n.rcaydr—расход через решетку на данном радиусе (на входе
в колесо или на выходе из него);
гвт2 и гВТ1—радиусы втулки колеса на выходе и входе;
гк2 и rKi—радиусы по концам лопаток на выходе и входе.
Используя полученные выражения и учитывая, что сила 7? проти-
воположна и равна силе 7?подп, с которой нагружается упорный подшип-
ник (подпятник), можем для этой силы написать
/?подп = (2 дтж • F)tt+ (2 Д"2™’ g}a + (2 Дт* + Д/М ja +
4-J {pdF)a — j dG^cai, (2.65)
гвх
где Acoi = c2a—Cia для данного радиуса.
56
Величину J dGiAcai принято называть динамической частью
осевого усилия, а сумму остальных членов правой части уравне-
ния (2.65) — статической частью этого усилия.
Для лопаточных машин, работающих на газе и воздухе, значения
(2Дтж • g)a и 2Дтж • /а можно не учитывать.
F
Интеграл J (pdF)a можно выразить в виде суммы интегралов, пред-
ставляющих осевые составляющие равнодействующих сил давлений,
действующих на отдельные части поверхности контрольного простран-
ства:
F ^вх ^вых Рд
^padF = ^<pdF^a+ j (^Двых)а+ J (pdFд)аД- ^(pdFб)0,
где РЕХ и FBbix—поверхности, соответствующие входу и выходу потока
(части а—а' и b—Ь') контрольного пространства;
Fn—поверхность диска (части а'—а' и Ь'—d контрольного простран-
ства) ;
Fa—поверхность бандажа.
Для каждой из этих поверхностей можно брать некоторое среднее-
значение давления. Если направление осевой составляющей сил дав-
ления на данную поверхность совпадает с направлением осевого пото-
ка, то соответствующий интеграл берется с положительным знаком.
Осевое давление обычно уменьшается с помощью специальных
конструктивных мер. В частности, поскольку в газотурбинных двига-
телях осевые усилия компрессора и турбины направлены в противопо-
ложные стороны, то при надлежащем соединении валов существенно
уменьшается результирующее усилие, действующее на упорные под-
шипники. Для этой же цели уменьшают разность давлений действую-
щих на передний и задний диски компрессора и турбины [40].
В многоступенчатых лопаточных машинах полное осевое усилие,
действующее на упорные подшипники, является суммой осевых усилий,
возникающих на рабочих колесах отдельных ступеней.
Таким образом,
^ПОДП 2^' подл-
Осевое усилие на каждом колесе определяется с помощью приве-
денных выше уравнений по известным из расчета отдельных ступеней
давлениям, скоростям и размерам.
Уравнение (2. 65) пригодно также для неподвижных аппаратов и
физически будет представлять собою осевое усилие, воспринимаемое
корпусом, в котором размещается аппарат. Покажем применение урав-
нения (2. 65) на некоторых простейших примерах.
Пример I. Колесо центробежного компрессора с двухсторон-
ним входом (рис. 2. 16).
Примем, что ось компрессора расположена горизонтально и движение летатель-
ного аппарата установившееся. Тогда первые члены в уравнении (2.65), учитывающие
силу тяжести и силы инерции, выпадут. Так как ось выходного сечения совпадает
с осью колеса, а входные сечения и параметры потока воздуха в них (давление, ско-
рость) одинаковы, получаем
F 'к!
J (р dF)n = 0 и J dGikcai = 0.
гвт
Следовательно, для этого колеса
^?подп =0.
В действительных условиях из-за влияния силы тяжести, сил инерции и неравномер-
ного распределения расхода воздуха по входам в таком колесе будет существовать осе-
вое усилие, хотя и относительно небольшое.
57
Пример II. Колесо промежуточной ступени многоступенча-
того осевого компрессора с креплением лопаток
на поверхности барабана (рис. 2. 17).
Принимаем, как и в предыдущем примере,
(]£ Дтж' ")д = (^ Д/Птв'" )а=° И (2Д/кж+2Дтгв)/а=°-
Так как ось внешней поверхности колеса совпадает с осью барабана и в данной сту-
пени отсутствуют торцовые поверхности барабана, то осевые составляющие сил давле-
Рис. 2. 16. Схема центробежного
колеса с двухсторонним входом
Рис. 2. 17. Схема промежу-
точной ступени многосту-
пенчатого осевого компрес-
сора с креплением лопаток
на барабане
ния возникнут только на поверхностях входа потока в колесо и выхода из него. При-
нимая средние значения давления в этих сечениях, получим
У (pdF) а = ^выхРв ы х—Т^вхРвх.
Если на входе в колесо и на выходе из него принять также среднее значение осевых
скоростей, то получим
\ dGi&Cai~ G (Са вых—Са вх).
В результате
Rao дп ы хРв ы х—Т’вхРвх—G(Ca вых—Са вх).
Если 7ВЫх и ЛВх близки по величине, то тогда
Rao дп — F (Рв ы х—Рвх)—G(ca вых—Са вх).
Направление усилия противоположно направлению движения потока, при этом
усилие от изменения количества движения имеет такой же знак, как и от перепада
давления, вследствие того что, как правило, са вых<са Вх.
2.5. УРАВНЕНИЯ ЭНЕРГИИ ДЛЯ СТРУЙКИ
И РЕШЕТКИ В КОЛЕСЕ И В СТУПЕНИ
2.5.1. УРАВНЕНИЯ ЭНЕРГИИ
ДЛЯ СТРУЙКИ И РЕШЕТКИ В КОЛЕСЕ
Под ступенью компрессора принято понимать сочетание рабочего
колеса и расположенного за ним спрямляющего аппарата. Для турбины
ступенью является сочетание соплового (направляющего) аппарата и
рабочего колеса.
Примем обозначения сечений согласно рис. 2. 12 и разд. 2. 2. Рас-
смотрим сначала элементарную струйку, протекающую через канал
между лопатками рабочего колеса (рис. 2. 18). Как и ранее, будем счи-
тать, что струйка ограничена относительными линиями тока. Однако
для определенного мгновения мы можем рассматривать параметры ча-
стиц этой струйки (скорости, температуры торможения и др.) в абсо-
лютном движении.
58
Рис. 2. 18. Элементарная струйка
в канале рабочего колеса
Энергетический баланс струйки необходимо рассматривать именно
в абсолютном движении, так как удельная работа, передаваемая газу
лопатками или воспринимаемая ими от газа, изменяется, как показано
выше, в соответствии с изменением d(cuu). В относительном же движ?
нии окружная скорость и колеса, а сле-
довательно, и удельная работа, будут рав-
ны нулю. Принимаем, как и ранее, что
границами струйки до входа в колесо и
после выхода из колеса являются поверх-
ности, где скорости, давления, темпера-
туры уже выравнены. Реально это про-
исходит примерно на расстоянии шага
от решетки. Для струйки ABCD измене-
ние энергии за промежуток времени dr,
когда она передвинется в положение
A'B'C'D', можно написать в виде разно-
сти внутренней и кинетической энергий в
объемах CDC'D' и АВА'А'. Эти объемы
равны расходу газа через струйку за промежуток времени dx, т. е. dGdx.
Таким образом, обозначая сумму внутренней и кинетической энергий для
объема АВА'В' через Е} и для объема CDC'D' через Е2, можем измене-
ние энергии записать в виде
/ с1 \ / с9 \
Е2 —Д1— (CVT2 +-у- \dGdx — l‘Gdx.
Это изменение энергии вызвано следующими факторами.
1. Работой, полученной газом от действия лопаток или, наоборот,
переданной лопаткам от газа. Обозначая удельную работу через Н, мо-
жем всю работу записать в виде ±HdGdx.
2. Работой, совершенной силами давления в сечениях 1—1 и 2—2.
Эту работу можно записать в виде
PidFiCmldx-~ p2dF2cm2dx,
где dFi и dF%—сечения струйки на входе в колесо и на выходе из него;
pi и ст1—давления и скорости на входе в колесо;
р2 и ст2—давления и скорости на выходе из колеса.
Умножив и разделив члены этого выражения на плотность у, получим
— dQdx —dGdx.
У1 У2
3. Работой, затраченной на преодоление потерь. Если удельную ра-
боту потерь обозначить через LRk, то всю работу можно записать в виде
LRvdGdx.
4. Теплом, эквивалентным потерям и подведенным к газу,
QRKdGdx,
где QRk—удельное тепло.
5. Теплом, отведенным во вне от газа или, наоборот, подведенным к
нему от внешнего источника,
± QqKdGdx.
59
Знак плюс соответствует подводу тепла и знак минус—отводу тепла.
Учитывая изложенное выше, можно написать для уравнения энергии
следующее выражение (сократив все члены на произведение dGdx)-.
—
cv(T7-T^ + -^-^^-^^H-LRK + QRK±QqK. (2.66)
2 V1 У?
Так как LRk=-QRk
и
то после преобразований получим
/y = ^(T2-TI)±Q9K + -2F^. (2.67)
Это уравнение не зависит от размеров струйки или расхода через
нее газа, поэтому оно полностью пригодно и для решетки, поскольку в
ней значения температур и скоростей на входе и на выходе для всех
струек одинаковы.
Применительно к компрессорной решетке удельная работа Н равна
теоретическому напору Hth и берется со знаком плюс; температура
Т2>Т,- кроме того, в компрессорах, как правило, может идти речь толь-
ко об отводе тепла либо с помощью специального охлаждения, либо
путем отвода конвекцией и излучением во внешнюю среду. Поэтому в
уравнении (2. 67) перед QqK должен быть знак плюс [с учетом измене-
ния знаков при переходе от уравнения (2.66) к уравнению (2.67)]. Та-
ким образом, применительно к компрессорной решетке получим
cl — с,
Hth = cp(T2-Ti) + Q9K+^-r^. (2.68)
В турбине величина удельной работы Н соответствует теоретической ра-
боте Н^и со знаком минус. Температура Т2<1\, и тепло в процессе рас-
ширения может в принципе как отводиться (во внешнюю среду или за
счет охлаждения лопаток), так и подводиться (например, за счет дого-
рания несгоревших в камере частиц топлива). Если и для Яти принять
положительное значение, то можем написать
H.!U=cp(T1-T2)±Qt,K + -2^.---. (2.69)
В дальнейшем и для турбины будет в основном рассматриваться,
как наиболее вероятный, случай с отводом тепла и поэтому перед QgK
будет ставиться знак минус.
В случае действия на данную решетку факторов, уменьшающих
теоретические значения напора или работы, левая часть уравнений
(2. 68) и (2. 69) должна быть умножена на коэффициент Q, учитываю-
щий влияние этих факторов. Следовательно, с учетом этой поправки из-
менение температур и скоростей в данной решетке должно уменьшаться.
Если ввести температуры, соответствующие изэнтропически затор-
моженным скоростям потока
то уравнения (2. 68) и (2. 69) примут вид
Hih = cp(T*-T*) + QqK; (2.70)
(2.71)
60
Из уравнений (2.70) и (2.71) следует, что в компрессоре и в тур-
бине при отсутствии подвода или отвода тепла удельная работа зави-
сит только от разности температур торможения в выходном и входном
сечениях. Полученные уравнения баланса энергии в элементарной
струйке и в решетке можно записать еще в другом виде. Согласно пер-
вому закону термодинамики
dQ = cdT — .
Y
Теплом, сообщаемым воздуху или газу в колесе, является тепло трения
и др. потерь минус тепло, отведенное во вне. Таким образом,
dQRK^dQqK = cpdT-d-^
или
dQ*K + ~ ^cpdT+dQqK.
у
Интегрируя это уравнение в пределах от сечения входа (7—/) до
сечения выхода (2—2) и заменяя QHK через LRk, получим
2
Lr к + = СР (^ - T'l) + к- (2- 72)
1
Подставляя полученное уравнение в уравнения (2.68) и (2.69), будем
иметь
2 г2
+^к + -^; (2.73)
1
1 2 2
—~^к+ (2-74)
♦ 7
2
При подстановке уравнения (2.72) в уравнение (2.69) в нем изменены
знаки на обратные и переставлены местами пределы интегрирования.
Уравнения (2.73) и (2.74) называют обобщенными уравнениями Бер-
нулли [1].
Если жидкость несжимаемая, то эти же уравнения примут вид
Hth - + Lr к + ; (2. 75)
Y 2
2 2
и = - LRk + -1" Сг- . (2. 76)
Т и К > \ /
Y 2
Уравнения (2. 68) и (2. 69) сохраняются и для несжимаемой жидкости.
Однако при отсутствии потерь и подвода или отвода тепла в строго не-
сжимаемой жидкости изменение температур происходить не будет.
Действительно, из уравнения первого закона термодинамики при
y=const следует
dQR±dQq = cvdT.
Поэтому если QR=0 и Qg = 0, то изменения температуры жидкости быть
не может. В общем случае, когда жидкость не является строго несжи-
маемой, то при изэнтропическом процессе (Qb=0; Qg = 0) температура
будет повышаться или понижаться, что должно определяться по табли-
цам или Т—s-диаграмме при заданном подводе или отводе работы co-
al
ответственно. Однако изменение температуры при изэнтропическом про-
цессе невелико. Например, для воды при повышении давления в насосе
от 1 до 300 бар температура возрастет приблизительно на 0,5°, если на-
чальная температура 20° С.
При той же величине затраченной работы на 1 кг жидкого водоро
да и начальной температуре 20° К изэнтропическое повышение темпе-
ратуры составит около одного градуса. Повышение температуры при
наличии потерь может быть значительно более существенным.
Полезно еще получить уравнение энергии решетки в относительном
движении. Сопоставляя уравнения (2.68) и (2.73) с уравнением (2.32),
получаем
9 О 9 о 2 ®Г“да2 . «2~ “1 [dp . , 2’2 i у + 1 (2. 77)
и 9 9 2 9 w;—w; u;- и. .... » ,А + _2_^=Ср(Г2_Г1) + (??к. (2.78)
В эти уравнения не входит работа, передаваемая от лопаток газу, что и
должно быть для относительного движения.
Из сопоставления уравнений (2.69) и (2. 74) с уравнением (2. 33)
можно получить и для турбинной решетки уравнения энергии в относи-
тельном движении:
О 9 9 9 1
WZ—Wi U7—U-, ! Ян
(2-79>
9
В осевых компрессорах и турбинах, когда ui = u2 и ±Q?k=0, изме-
нение давления и температуры в решетке будет определяться только
изменением кинетической энергии в относительном движении.
2.5.2. УРАВНЕНИЯ ЭНЕРГИИ ДЛЯ РЕШЕТКИ
НЕПОДВИЖНЫХ АППАРАТОВ И ДЛЯ ЭЛЕМЕНТАРНОЙ СТУПЕНИ
Полученные в предыдущем разделе уравнения энергии справедли-
вы и для решеток неподвижных аппаратов, но удельные работы Hth и
ЯТи в этом случае равны нулю. Поэтому для решетки спрямляющего
аппарата компрессора получим
или
„2 .2
Со — С г)
Ср (Т3 - Г2) + Qq с + = 0.
(2.81)
(2. 82)
Для соплового аппарата турбины соответственно будем иметь
0 2 2 f^-ist + ^=0 1 (2.83)
или (2.84)
62
В неподвижных аппаратах происходит только преобразование энер-
гии потока без изменения ее величины. Например, в сопловом аппарате
турбины значительно растет скорость при соответствующем уменьше-
нии температуры и давления. В спрямляющем аппарате компрессора,
наоборот, в большинстве случаев имеет место уменьшение скорости
при росте температуры и давления. Как известно из газовой динамики
[1] и [4], в случае отсутствия подвода или отвода тепла температура тор-
можения в неподвижных аппаратах остается постоянной. Это непосред-
ственно следует и из уравнений (2.82) и (2.84), если в них считать
QqC и ввести температуры торможения
2ср ’
Уравнение энергии для элементарной ступени, состоящей из решеток
рабочего колеса и неподвижного аппарата, можно вывести, связывая
между собой уравнения энергии, полученные для решеток. Так, напри-
мер, для вывода уравнения энергии элементарной ступени компрессора
в правой части уравнения (2.68) прибавим и вычтем член Сз/2.
Тогда получим
но из уравнения (2.81) находим, что
Подставляя это выражение в предыдущее уравнение, будем иметь
- 3 2 2
J У J У 2
1 2
Вводя суммарные величины
3 2 3
С_ц ( dp .
J у J у ' J у
1 1 2
получим
3 2 2
Н —С dp | . сз— С1
1
Аналогично можем получить
с2 —с2
HtK=cp (7'3— Л) + Qg + —-„-1 •
(2. 85)
(2. 86)
Таким образом, уравнение энергии для элементарной ступени по форме
совершенно идентично уравнению энергии для решетки рабочего колеса,
но в него входит изменение температур, давлений и скоростей, соответ-
ствующее всей ступени, и суммарные значения потерь и отведенного
63'
тепла. Не повторяя выводов, напишем уравнения энергии для элемен-
тарной ступени турбины:
О 2 2
(2.87)
с2—С2
(2.88)
2.5.3. ОБЩАЯ КЛАССИФИКАЦИЯ ПОТЕРЬ И ПОЛНОЕ УРАВНЕНИЕ
ЭНЕРГИИ ДЛЯ РЕШЕТКИ РАБОЧЕГО КОЛЕСА
И ЭЛЕМЕНТАРНОЙ СТУПЕНИ С УЧЕТОМ Lf И La
Рассмотренные выше уравнения энергии учитывали потери, имею-
щие место при обтекании профилей решеток и непосредственно на вхо-
де и на выходе из них. Эти потери будут в общем случае различны для
решеток, расположенных на разных радиусах. Особенно должны отли-
чаться от потерь на среднем радиусе потери вблизи внешнего и внутрен-
него радиусов лопатки, где добавляются трение на поверхности втулки
между лопатками и с внутренней стороны бандажа, потери от «парного
вихря» (см. разд. 7.2.3), а при отсутствии бандажа—потери, обуслов-
ленные завихрениями, возникающими при перетекании газа с вогнутой
стороны профиля на выпуклую.
Принципиальной особенностью всех этих потерь является то, что
они относятся к пространству, которое при выводе уравнений моментов
ограничивалось контрольными поверхностями и поэтому не входили в
явном виде в уравнения моментов и удельных работ. Эти потери, обо-
значавшиеся выше через LRk и LRc, принято разделять на профиль-
ные и вторичные.
К профильным потерям относятся:
1) потери на трение и вихреобразование в пограничном слое на
профиле;
2) кромочные потери, возникающие у задней кромки при смеше-
нии потоков, сходящих с вогнутой и выпуклой частей профиля; если
учесть, что контрольные поверхности проводятся на некотором расстоя-
нии от решетки, то кромочные потери по существу включают в себя
также потери в осевом зазоре между двумя рядами венцов и не включа-
ют потери на трение на внутренних поверхностях корпусов и втулок в
осевом зазоре;
3) волновые потери, возникающие при околозвуковом и сверхзву-
ковом обтекании профиля с образованием местных скачков уплотнения,
головных и ударных волн.
К вторичным потерям в рабочих и неподвижных лопатках относят:
1) потери отпарного вихря, обусловленного наличием пограничного
слоя у торцовых стенок и неравномерностью поля скоростей перед ко-
лесом;
2) потери от вихреобразований, возникающих при перетекании газа
через торцовые поверхности лопаток (от корыта к спинке) в радиаль-
ном зазоре (при отсутствии бандажей);
3) потери, связанные с перетеканием пограничного слоя вдоль об-
разующих вращающихся лопаток к периферии и наличием радиальных
течений;
4) потери из-за нестационарное™ потока, обтекающего рабочие
лопатки, как из-за наличия закромочных следов на выходе из преды-
дущего неподвижного лопаточного венца, так и в силу окружной не-
равномерности потока на входе в рабочее колесо.
64
Приведенная классификация профильных и, особенно, вторичных
потерь является ориентировочной. Как видно из определения, значитель-
ная часть вторичных потерь связана с влиянием концов лопаток и по-
этому существенно зависит от длины лопаток. Более подробно отдель-
ные виды профильных и вторичных потерь и их зависимость от чисел М
и Re рассматриваются в разделах, посвященных компрессорам и тур-
бинам.
Для оценки профильных и вторичных потерь применяются коэффи-
циенты потерь в виде
\р*
где Др* — потеря полного давления;
у* — плотность:
С] — скорость на входе в решетку.
В таком виде коэффициент потерь применяется в решетках осевьп
компрессоров. В турбинах под коэффициентами потерь часто понимают
величины:
где L'Rc и L'r— потери, выраженные в виде работы;
С1ад — скорость на выходе из решетки соплового аппарата и
к>2ад — на выходе из решетки рабочего колеса в пред-
положении адиабатического процесса в них.
В расчетах газовых турбин профильные и вторичные потери часто
учитывают с помощью коэффициентов скорости:
Cl
для решетки соплового аппарата ® =----;
с1аД
для решетки рабочего колеса ф ——— .
^2ал
Коэффициенты скорости связаны с коэффициентами потерь, запи-
санными через работу потерь, соотношениями:
<Р2=1— ic; ф2=1— £к.
Иногда потери в решетках характеризуют коэффициентами полного
давления б, т. е. отношением полного давления на выходе из решетки к
полному давлению на входе в нее; например, для соплового аппарата
имеем
для решетки рабочего колеса соответственно
Легко показать, что потери полного давления при течении без теплооб-
мена являются мерой возрастания энергии. Так, например, рассматри-
вая в относительном движении решетки рабочего колеса, мы можем при
отсутствии теплообмена принять
7 — Т211)=7 7 щ,.
3 546
65
Тогда возрастание энтропии можно подсчитать по формуле для изотер-
мического процесса:
ДХ = 52_51 = —1П1П 8р к.
Pin
Применительно к турбинам связь 6Р.К (или 6с.а) с коэффициентами скоро-
сти ф или ф определится формулой
где X2w
приведенная скорость.
w2
Эта зависимость показана графически на рис. 2. 19.
Рис. 2. 19. Зависимость коэффициента полного давления
от коэффициента потери скорости и коэффициента скоро-
сти за решеткой
Для оценки профильных потерь главным образом в осевых компрес-
сорах применяются коэффициенты лобового сопротивления
У —
2
Я.,=Схр
где Rx— сила лобового сопротивления решетки;
С\р— коэффициент лобового сопротивления;
wm — среднее значение относительной скорости;
Fu — суммарная поверхность профилей в решетке (при высоте ре-
шетки, равной единице);
2у1Уо
У = —!— — среднее значение плотности.
Y1+Y2
66
Наконец, при теоретическом изучении профильных потерь использу-
ются применяемые в теории пограничного слоя характерные толщины
вытеснения [42]
М(1----------
Л1
и потери импульса
J \ wa* / Ya*
nt
В этих формулах ось п направлена по нормали к скорости потока; п2—пл—
ширина следа за кромками. С коэффициентами ф и ф величины 6* и &**
связаны соотношениями
, < 8** . 1 8**
ф== 1----------; <р = 1---------•,
Рок* sin ?2 Pec* sin Я]
где рок и рос — коэффициенты расхода, представляющие собой отноше-
ния действительного расхода через выходное сечение решетки к расходу
в изэнтропическом процессе при равномерном полном давлении по шагу.
1 8* . 1s*
Р*ОК * , g ’ P'Oe * ,
t sin flo t sin ai
Наряду с профильными и вторичными потерями, учитываемыми
уравнениями энергии для решеток, имеются потери, относящиеся ко
всей ступени и обусловленные боковым трением диска и бандажа и пе-
ретеканием газа (воздуха) через радиальные зазоры. Удельная вели-
чина указанных потерь обозначена выше через Lf и L3. Эти потери свя-
заны в первую очередь с увеличением (в компрессоре) или уменьшением
(в турбине) работы на валу и изменяют в основном средние параметры
потока, получаемые на некотором расстоянии за ступенью в результате
смешения всех струек. Условимся потери Lf и L3 называть концевыми*\
главная особенность которых состоит в том, что они являются внешними
по отношению к пространству, ограниченному контрольными поверхно-
стями, и потому входят в уравнения моментов и удельных работ. Отме-
тим, что в потери Lf должны входить и потери трения на той части коль-
цевой поверхности, которая находится в осевом зазоре. Что же касается
трения диска, то в осевых турбинах и осевых компрессорах авиационных
двигателей относительная доля затрачиваемой на это мощности неве-
лика и обычно отдельно она не учитывается. В центробежных компрес-
сорах потери Lf и L3 объединяют и подсчитывают по формулам, соответ-
ствующим трению диска (см. гл. 6), с использованием эмпирического
коэффициента. Как уже отмечалось выше (см. рис. 2.12), потери L3
соответствуют перетеканию части газа через радиальный зазор, что свя-
зано с потерей соответствующей работы в турбине или с затратой до-
полнительной работы в компрессоре. Потери L3 и Lf в осевых лопаточ-
ных машинах оцениваются с помощью коэффициентов т)3 и г)/, численное
значение которых дано в гл. 4 и 5.
Повлиять непосредственно на параметры потока в отдельных ре-
шетках и, особенно, тех, которые более удалены от концов лопатки, потери
L3 и Lf физически не могут. Однако в расчетах условно принимают, что
эти потери относятся к потоку во всех решетках, и определяют пара-
метры газа на выходе из них и к. п. д. решеток с учетом и этих потерь.
*) Это название неполностью характеризует их сущность, и к концевым потерям
некоторые авторы относят еще часть вторичных потерь.
3* 67
В первую очередь это относится к решетке, расположенной на сред-
нем радиусе, по параметрам которой производится предварительный
расчет ступени. С учетом рассмотренных потерь уравнения энергии для
решеток рабочего колеса компрессора и турбины по аналогии с урав-
нениями (2.73) и (2.74) примут вид:
2 2 2
\ 7Г + к + Н----”7—~
Г Y 2.
(2. 89)
(2.90)
Таким образом, в эти уравнения войдут полная работа, затрачи-
ваемая в компрессоре, и полезная работа, получаемая в турбине. Сопо-
ставляя эти уравнения с уравнениями (2.73) и (2.74), следует иметь
в виду, что интегралы J — , являющиеся политропическом работой
сжатия и расширения, должны быть в них равны несмотря на то, что
показатель политропы будет изменяться от дополнительных потерь Lf и
L3. Чтобы показать это, вычтем из обеих частей уравнения (2.89) сумму
Lf + L3. Тогда получим (при Q = 1,0)
2 2 2
HK-(L3 + Lf) = Hth^^ + LR^^^- (2-91)
1
Если принять, что в уравнениях (2.91) и (2.73) скорости одинаковы,
io должны быть равны и интегралы J— . Однако показатель политропы
1 1
в уравнении (2.91) будет больше, чем в уравнении (2.73), поскольку
процесс сжатия происходил при наличии дополнительных потерь L3 и
Lf. Поэтому отношение давлений р^р^ в интеграле \ — для уравнения
1 Ч
(2.91) будет меньше, чем в уравнении (2.73). Так, например, если пред-
положить, что в уравнении (2.73) п=1,5 и p2/pi = 10, а в уравнении
(2.91) и=1,55, то будем иметь p2/Pi~9,57. Если уравнения энергии Hv
и 7/т записать в зависимости от разности теплосодержания, то очевидно,
что, поскольку и Н^<Нти, температура на выходе из колеса
должна быть выше.
В уравнении энергии для всей элементарной ступени значения Hth,
Нт. v, Lf и L3 (а следовательно, Як и 7/т) остаются без изменения. В ре-
зультате процессов, происходящих в неподвижном аппарате, в правой
части уравнений (2.89) — (2.91) изменится величина , добавятся
яотери Ад с в неподвижном аппарате и изменится член, учитывающий
разность кинетических энергий, как было показано при выводе уравне-
ний (2.85) — (2.88). Кроме указанных выше потерь, в ступенях компрес-
сора и турбины могут иметь место так называемые дополнительные по-
тери.
1. Потери от перетекания газа через лабиринтные уплотнения и
щели. Лабиринтные уплотнения могут стоять между ступенями, а также
:в начале и в конце многоступенчатой машины. Не приводя выводов, да-
68
дим окончательную формулу для определения расхода через лабиринт-
ное уплотнение [2]:
Здесь р — коэффициент расхода;
/ — площадь проходного сечения, равная л£>бо, где D — диаметр
лабиринта, б0 — зазор между гребешками лабиринта и ва-
лом;
Ро И рг — давление перед и за лабиринтом;
z — количество гребешков в лабиринтном уплотнении;
По —удельный объем жидкости (газа) перед лабиринтом.
По исследованиям С. М. Шляхтенко величина коэффициента рас-
хода находится в пределах 0,7—1,27. Поскольку расход через лабиринт
пропорционален /, а значит и D, то уплотнение следует размещать на воз-
можно малом диаметре. При перетекании газа через лабиринтное уплот-
нение и отводе его наружу в количестве Gs к.п.д. компрессора или
турбины уменьшается на величину GS&.H/GH, где ДЯ— напор (или ра-
бота), соответствующая 1 кг перетекающего газа.
2. Потери от парциальности.
Эти потери встречаются в малоразмерных турбинах, которые иногда
выполняют парциальными, т. е. с использованием только части полной
окружности соплового венца, для того чтобы увеличить высоту лопатки.
Потери, связанные с парциальностью, рассмотрены в гл. 9.
3. Потери от двухфазности потока. Эти потери встречаются только
в случае, когда турбины работают на двухфазном рабочем теле, т. е.
когда в основном потоке пара или газа имеются жидкие или твердые
частицы. При течении двухфазного потека возникает ряд дополнитель-
ных потерь. Основными из них являются:
а) потери на «удар» жидких капель о стенку рабочих лопаток вслед-
ствие их отставания от потока и на отбрасывание жидкой пленки на
периферию;
б) увеличение профильных потерь в сопловом аппарате из-за трения
потока о жидкую волнистую пленку, текущую по поверхности лопаток.
Эти потери трения в основном зависят от вязкости жидкой фазы.
В авиационных газотурбинных двигателях потерь, связанных с двух-
фазностью, как правило, не наблюдается, и поэтому они в настоящей
книге не рассматриваются.
2 5.4. УРАВНЕНИЯ ЭНЕРГИИ ДЛЯ КОЛЕСА, ПОЛНОЙ СТУПЕНИ
И МНОГОСТУПЕНЧАТОЙ ЛОПАТОЧНОЙ МАШИНЫ
В связи с тем, что значения отдельных параметров, входящих
в уравнения энергии для решеток и элементарных ступеней, состоящих
из решеток, в общем случае существенно изменяются по радиусу, урав-
нения энергии для всего колеса и полной ступени должны иметь инте-
гральную форму; так, например, принимая, как и ранее (см. 2.5.3), по-
ток осесимметричным, можно для колеса компрессора написать
'к гк /'2 д А
j HKldG=\ + + +
гвг гвт \1 / I
ИЛИ
гк Гк
J Нк tdG = J (срД7+ Q?k + 4"\ d0'
гвТ гвт
69
где индексом «i» обозначены величины, соответствующие отдельным
решеткам;
dG=2n.rycadr— расход через решетку.
Если в эти уравнения ввести средние значения величин Hit ДГ, Ас2,
то уравнения энергии примут вид, какой был дан выше для решеток и
элементарных ступеней.
Средние значения всех параметров потока в данном сечении должны
быть такими, чтобы расход, энергия и момент количества движения,
определяемые по ним и по действительным параметрам, были одинако-
выми. Иными словами, должны соблюдаться соотношения:
GCP=J dG
гвт
= 2nr2J cayrdr
7вт
1
J T*dG
T* ___ zar
7 cp----i ,
J*?
(2. 92)
J AfaG
—
j dG
гдеГвтиг — относительные радиусы у втулки и текущий, являющиеся от-
ношениями соответствующих радиусов к радиусу гк у конца
лопатки;
Г* — температура, соответствующая изэнтропическому торможе-
нию скорости неравномерного потока и характеризую-
щая полное теплосодержание (или энергию) потока (при
ср = const);
Л4ср — момент количества движения в осредненном неравномерном
потоке.
Если в потоке нет закрутки, то вместо момента количества движения сле-
дует соблюдать в исходном неравномерном потоке и в осредненном
равенство энтропий или количеств движения. Определение таких средних
величин достаточно затруднительно и не всегда имеет существенное прак-
тическое значение. Однако в дальнейшем при изучении отдельных
свойств ступеней мы в ряде случаев будем применять уравнения, соот-
ветствующие средним параметрам на входе и выходе, предполагая, что
эти средние параметры удовлетворяют уравнениям (2.92).
При расчетах ступеней их часто характеризуют параметрами на так
называемом среднем диаметре. В качестве среднего диаметра иногда
принимают среднюю арифметическую величину между значениями диа-
метра втулки и наружного диаметра, т. е.
Dcp^+D^=DK^, (2.93)
где d= ——-относительный диаметр втулки.
DK
Иногда под средним диаметром понимают величину, соответствую-
щую окружности, которая делит пополам рассматриваемое кольцевое
сечение. В этом случае средний диаметр выражается формулой
Р-94)
70
Средний диаметр, определяемый по формуле (2.93), несколько
меньше среднего диаметра, соответствующего формуле (2.94). Напри-
мер, при <2 = 0,5 их отношение равно 0,95. С увеличением d это отноше-
ние стремится к единице, а при уменьшении d уменьшается. Наименьшее
значение оно имеет при d=0 и равно —0,7.
В некоторых случаях поток на входе в ступень и на выходе из нее
является достаточно равномерным, вследствие чего средние значения
параметров можно считать весьма близкими к истинным. Такое поло-
жение, например, будет, если поток на входе в ступень и на выходе из
нее не имеет закрутки, канал прямолинейный и расстояние от лопаток
достаточно большое для выравнивания потока. Тогда уравнение энергии
для всей ступени можно и для действительных параметров написать
в виде, ранее записанном для элементарной ступени. Изменение энергии
в многоступенчатой машине, очевидно, должно определяться суммой
изменений, имевших место в отдельных ступенях. Поэтому для много-
ступенчатой лопаточной машины будем иметь:

где индексом «2» обозначены величины, относящиеся к отдельным
ступеням.
В дальнейшем применительно к одно- или многоступенчатым ком-
прессорам ГТД обозначим параметры на входе в компрессор индексом
«в» и на выходе из компрессора индексом «к»; на входе в одно- или
многоступенчатую турбину — индексом «г» и на выходе из турбины
индексом «т». Тогда если рассматривать в каждой ступени средние
заторможенные параметры или параметры в элементарных ступенях,
имеющих общие линии тока, то, очевидно, можем написать:
Ср (Г;-71) = £ срД7’*; ср (Т'г - 7^) = J срД?'’;
где дГ* — разность температур в отдельных ступенях.
Следовательно, уравнение энергии примет вид, рассмотренный ра-
нее для отдельных ступеней, но с использованием в нем суммарных зна-
чений Нк, Lr к, разности температур и других величин.
Для определения общих параметров многоступенчатых компрес-
соров и турбин и, в частности, при рассмотрении их в системе двигателя,
как правило, исходят из условий достаточной равномерности потока на
входе и на выходе и для этих условий применяют уравнения энер-
гии.
Однако следует иметь в виду, что в действительных условиях поля
скоростей, температур и давлений достаточно неравномерны и поэтому
для правильного определения затраченной или полезной работы и к.п.д.
в существующей машине необходимо по данным измерений осреднять
эти величины.
71
2.6. УРАВНЕНИЯ ДВИЖЕНИЯ ГАЗА
В ПОЛОСТЯХ ЛОПАТОЧНЫХ МАШИН
Скорости и другие параметры газа на различных радиусах и, сле-
довательно, в отдельных решетках и элементарных ступенях связаны
между собой соотношениями, которые в первую очередь определяются
условиями равновесия частиц при их движении в полостях лопаточных
машин.
Эти полости могут находиться: а) в зазорах между неподвижными
и вращающимися лопатками, т. е. в пространстве, не занятом лопат-
ками; б) в каналах между неподвижными лопатками; в) в каналах
Рис. 2.20. Проекция на меридио-
нальную плоскость сил, действую-
щих на элементарный объем газа
в канале рабочего колеса
между вращающимися (рабочими) ло-
патками.
В первом случае поток можно при-
нять осесимметричным, установившим-
ся и движущимся без воздействия
внешних сил. Во втором случае поток
также будет установившимся, но не
осесимметричным, и находящимся под
действием силы от лопаток. Наконец,
в каналах между лопатками рабочего
колеса — абсолютное движение неуста-
новившееся и неосесимметричное, со-
вершающееся под действием сил от
лопаток.
Рассматривая поток в полостях,
где расположены лопатки (неподвиж-
ные или рабочие), можно считать его
осесимметричным, если наложить
условие, что число лопаток беско-
нечно велико, или введя осреднение
по шагу. Если для рабочих лопаток
ввести осреднение по времени, то мож-
но движение через них принять в сред-
нем установившимся. Поверхность
лопаток рассматривается при этом как поверхность разрыва всех функ-
ций, по нормали к которой на жидкость действуют поверхностные силы
Принципы осреднения по шагу и по времени, возможные при этом упро-
щения и погрешности подробно рассмотрены в работе [42].
Используя эти принципы, рассмотрим осредненный по шагу и вре-
мени поток в каналах между рабочими лопатками *’.
Применим естественную систему координат (п, tn, s), в которой
ось m направлена по касательной к линии тока (рис. 2.20). Ось п орто-
гональна к линии тока и расположена в меридиональной плоскости и,
наконец, ось s — ортогональна к осям пиши направлена в сторону
вращения. Для установления условий равновесия газа достаточно рас-
смотреть уравнение равновесия в направлении нормали п. Что касается
уравнений в направлении осей m и s, то они будут соответствовать урав-
нениям энергии и момента количества движения для струйки, подробно
рассмотренным выше.
В направлении оси п на частицу газа с массой Ат действуют сле-
дующие силы.
1. Проекция сил давления pAfn и —(p + Ap)Af„, где Afn — боковые
поверхности элементарного объема, перпендикулярные к оси п;
*> Эти выводы будут соответствовать также предельному случаю бесконечно боль-
шого числа бесконечно тонких лопаток.
72
2. Центробежная сила инерции Д/2=--, обусловленная движе-
Rm
нием газа по криволинейной линии тока, имеющей в рассматриваемой
точке радиус кривизны Rm, совпадающий с осью п. Эту силу будем счи-
тать положительной, если радиус кривизны направлен по оси п вверх
от начала координат.
3. Проекция A/i =- cos-ф центробежной силы инерции, обуслов-
ленной движением газа вокруг оси машины с окружной составляющей
скоростью си.
4. Проекция Fnk.m на нормаль распределенной (объемной) силы дей-
ствия лопаток на газ, где Fn сила, приведенная к единице массы (в меж-
венцовых зазорах Fn равна нулю).
Уравнение равновесия в проекции на ось п приобретает вид
Д/2 + ДЛ — Д/?Д fn + MnFn=0
или
9 2
Д/пс“ ктс„ „
------1----cos Ф — Д/2Д /„ + kmFn = 0.
Rm r
Разделив на Am и заменяя Am=yAfnAn, получим, переходя к пределу,
2 °
— = cos^ + F„. (2.95)
у дп г
В таком виде это уравнение пригодно и для потока в неподвижных ло-
патках. Если же в нем положить Е„ = 0, то оно будет соответствовать
потоку в зазорах между неподвижными и вращающимися лопатками.
Для течения несжимаемой жидкости при цилиндрической форме
проточной части и постоянном значении са меридиональные линии тока
параллельны друг другу и оси лопаточной машины.
Для течения сжимаемой жидкости радиальное распределение линий
тока в зависимости от расстояния по оси машины характеризуется та-
кой величиной г, для которой справедливо следующее выражение:
Г
j 2nycardr = const.
Ат
Радиальное расстояние г линии тока больше при малых значениях
у и наоборот. Это приводит к искривлению линий тока. В общем случае
их кривизна зависит еще и от других факторов (форма проточной части,
толщина лопаток и др.).
Применительно к рабочим лопаткам уравнение (2.95) можно запи-
сать еще в относительном движении. Для этого перейдем в нем к относи-
тельным скоростям w и заменим
cm=wm=w sin Р
и
Cu = U±W cos р,
где знаки зависят от типа машины (турбина, компрессор) и от направ-
ления закрутки потока в абсолютном движении. Так, например, если
принять, что окружная составляющая си является положительной, когда
73
она совпадает по направлению с окружной скоростью, то перед рабочим
колесом турбины всегда (см. рис. 7.1)
Clu = u + Wi COS Pl,
а за рабочим колесом турбины
C2u = U~W2 COS р2.
Знак с2и будет определяться численным соотношением между окружной
скоростью и и проекцией относительной скорости на направление ско-
рости и: w2u=w2cosfi2. В компрессоре (см. рис. 5.1 и 5.2) для окруж-
ной составляющей на выходе из колеса получаем
c2v = u±w2 cos р2.
При этом с2и всегда совпадает по направлению с окружной ско-
ростью; на входе в рабочее колесо
Ciu = U—КУ1 cos Pi = и—W\u-
Знак с1и может быть положительным или отрицательным, что опре-
деляется соотношением между значениями и и W\ cos В каналах между
рабочими лопатками в общем случае мы получаем
Cu = U±W COS P = U±U>u.
Подставив выражение для си в уравнение (2.95), получим
1 др W2 sin2 3 . и2 -|- w2 COS2? ± 2wu COS 3 . Д. n_.
— =—7,—- H------------C1 cos Ф + Fn. (2. 96)
Y dn Rm r
Силу Fn можем выразить в виде
Fn=Fu tg б,
где Fu — окружная составляющая силы действия лопаток;
б — угол между нормалью п и средней поверхностью лопатки,
в качестве которой можно брать поверхность, образуемую
совокупностью по радиусу средних линий профилей.
Величину Fu можно выразить исходя из уравнения момента коли-
чества движения, которое для рассматриваемой частицы, как и ранее,
запишется так:
д?И = дщ .
dx
Заменим dx=dlmlcm и AAf = AFur, где dlm — элемент длины координат-
ной линии в меридиональном направлении, &FU— окружная сила, дейст-
вующая со стороны лопаток на частицу. Тогда получим
_с d(car)
&т ~ т dlm
Так как &Ful&m=Fu, т. е. является объемной окружной силой действия
лопаток, отнесенной к единице массы, то, разделив обе части уравнения
на радиус г, будем иметь
Р d[(u ± wu)r]
“ г dlm ~ г dlm
В таком виде это уравнение пригодно как для рабочих, так и для непо-
движных лопаток.
74
Если правую часть этого уравнения умножить и разделить на угло-
вую скорость вращения колеса, то применительно к рабочим лопаткам
его можно записать еще в виде
р d(cau) _wm d{(u ± wa) u]
“ и dlm и dlm
Уравнения равновесия (2.95) и (2.96) относятся к так называемой
прямой задаче расчета осесимметричного потока через турбомашину.
Эта задача соответствует определению параметров потока через данную
лопаточную машину при заданных граничных условиях. Действительно,
в эти уравнения входят как известные величины углы потока и радиус
кривизны линии тока, являющиеся функцией параметров потока и гео-
метрии ступени.
В начальной стадии расчета многие из этих величин неизвестны и
по существу решается обратная задача, заключающаяся в построении
решеток и ступени, удовлетворяющих определенным заданным условиям
(например, заданы расход, напор, окружная скорость, предельные числа
М и др.). Обратная и прямая задачи должны дополнять друг друга.
Вначале может решаться обратная задача в упрощенной постановке
(например, Rm= <х при заданном законе изменения циркуляции по ра-
диусу). По этим данным профилируют лопатки ступеней, добиваясь
выполнения определенных требований к углам и скоростям потока в ре-
шетках на отдельных радиусах. После этого в качестве поверочного
расчета следует решать прямую задачу с использованием полученных
выше уравнений. При этом может оказаться целесообразным внести не-
которые уточнения в параметры профилей.
Отметим также, что при решении прямой задачи краевые условия
необходимо задавать не только для рабочего колеса, но включать
и неподвижный аппарат, а также подводящий и отводящий каналы, так
как их форма во многих случаях существенно сказывается на потоке
в ступени. Кроме того, такое совместное рассмотрение дает возможность
учитывать взаимное влияние венцов, подводящих и отводящих каналов.
Прямая задача решается путем последовательных приближений,
причем в качестве исходного приближения используются результаты
одномерного расчета. Применение принятой для уравнений (2.95) и
(2.96) естественной системы координат связано с некоторым неудобст-
вом, так как эта система заранее неизвестна и должна определяться
в процессе решения путем последовательных приближений. В связи
с этим применяется и другой метод, при котором в начале расчета за-
дается определенная фиксированная система координат [42]; [39].
Для получения некоторых общих соотношений рассмотрим уравне-
ние (2.95) в предположении, что Fn —О, т. е. применительно к зазору
между неподвижным и рабочим колесом. В отдельных случаях получен-
ные результаты будут близки и к осредненному потоку в каналах между
лопатками. Отметим предварительно, что для конических течений, когда
Rm— <z>, из уравнения (2.95) получим
— d£_=^.C0S(1) (2.97)
у дп г
При цилиндрическом течении, когда Rm= <*> и ф=0, ось п будет совпа-
дать с осью г, и это уравнение примет вид
(2.98)
у dr г
75
Это уравнение иногда называют уравнением радиального равновесия.
Оно показывает, что для устранения перетекания частиц в радиальном
направлении изменение давления по радиусу однозначно определяется
законом изменения по радиусу окружной составляющей.
Так, например, при cu = const получаем
= с2 In — ,
" г
' к
где гв — внешний радиус колеса;
г — текущий радиус колеса.
Принимая, что давление и плотность в различных точках по радиусу
связаны адиабатической зависимостью, получим
будем иметь
Обозначив —— =
kRTK
Р
Рк
к
1 + (£-i)mL in —
г к J
(2.99)
В случае, когда изменение окружной составляющей по
подчиняется закону постоянства циркуляции, т. е. cur = const,
радиусу
получим
const2 /1 1
2 ( /-2 г2
Заменяя const2 через Сик^к
чим после преобразований
п к 1
и вводя обозначения -------— М;
kRTK
.«К,
полу-
к
ft
-^=(1-~ м;
РК I 2

(2.100)
Наконец, при изменении окружной составляющей по
Си
закону —=
= const, т. е. по закону вращения твердого тела, будем иметь
(2.101)
На рис. 2.21 показано изменение р/рК в зависимости от отношения
г/гк. При подсчетах принимается Мик=0,35. Как видно из графика, при
уменьшении радиуса давление также уменьшается и особенно резко
в случае, когда cur = const. Последнее является следствием возрастания
си при уменьшении радиуса, и, как будет показано в гл. 5 и 7, это огра-
ничивает применение закона cur — const в ступенях осевых компрессоров
и турбин с малым относительным диаметром втулки. Для межвенцового
76
зазора или для осредненного потока в каналах между неподвижными
лопатками параметры газа в рассматриваемой точке можно выразить
с помощью уравнения энергии для линии тока, к которой рассматривае-
мая точка относится:
где Lr — потери на линии тока до рассматриваемой точки.
Рис. 2.21. Изменение давления в межвенцовом
зазоре по радиусу для различных законов изме-
нения закрутки по радиусу:
/— cw=const; 2— cur=const; 3—<?u/r=const
Дифференцируя по нормали и предполагая, что поток уравновешен
по нормали, вследствие чего составляющая скорости вдоль нормали
равна нулю, получим
(?£_ 1 I с дСа
дп у дп'тдп'идп
dLR
дп
Используя уравнение (2.95) и принимая, что работа силы Еп=0,
находим
дЕ
дп
। । &С[п । дси
cos^4-cm-^+cB-^
дп дп
dLR
дп
г
Если учесть, что cos ty = dr/dn, то сумма второго и четвертого членов в
правой части может быть записана в виде
си дг_ . дси___1__д(сцг)2
г дп'Садп~~2г^ дп
В результате получаем
=Д_ бст I , 1 д(сцг)2 . dLR
дп 2 дп Rm 2г"2 дп дп
(2. 102)
По отношению к меридиональной скорости ст это уравнение будет
являться линейным дифференциальным уравнением первого порядка.
Исходя из этого для меридиональной скорости получаем выражение
с2т = е "° т ГТ—f f 1 । dn ,
J \ r2 dn dn dn J
_ Л 0 -
(2. 103)
где C — постоянная интегрирования.
77
Если принять, что вдоль нормали E = const, а также EH=const или
£д = 0 (идеальный поток), то предыдущее уравнение примет вид
С — ) [ 1 d<caH2 '
j [ г2 dn
J тл
еп° dn
(2. 104)
Если Ед = 0, то параметры газа (д, у, Т) по радиусу связаны между
собой изэнтропической зависимостью. Когда LR — const, то эти же пара-
метры связаны между собой политропической зависимостью, причем
показатель политропы п в общем случае будет переменным по радиусу.
В зависимости от исходного положения, принимаемого для коорди-
наты «о, постоянная интегрирования С будет равна квадрату меридио-
нальной скорости на среднем, внутреннем или внешних радиусах канала.
Следует отметить, что постоянство Е имеет место для всех точек
потока при потенциальном установившемся движении.
В случае вихревого движения величина Е является постоянной для
точек, находящихся на одной линии тока; для разных же линий тока
она будет в общем случае иметь разные значения. Для потока в межвен-
цовом зазоре можно принять, что значение Е будет постоянным по нор-
мали, т. е. для различных линий тока, в следующих случаях:
1) если рассматриваемый зазор находится после первого направ-
ляющего аппарата компрессора или первого соплового аппарата тур-
бины, т. е. при всасывании из атмосферы или при поступлении газа
из камеры сгорания;
2) если этот зазор находится после рабочего колеса, в котором на
каждом радиусе сообщается (или отнимается) одинаковая энергия
(/f(h = const или /7Tu = const) при постоянстве энергии перед колесом.
Рассмотрим в качестве примера распределение меридиональных
скоростей для некоторых частных случаев.
Предположим, что cur=const и /?т= со, тогда из уравнения
(2.104) получаем
cm=C=const.
В частности, для осевой машины, когда можно принять, что нормаль
совпадает с радиусом, получаем
са=const.
Применительно к осевым турбинам иногда рассматривают случай, когда
угол потока на выходе из соплового аппарата ai=const. Принимая и
в этом случае Rm= <х> и ст=са, запишем уравнение (2.104) в диффе-
ренциальной форме:
..rf(c»£>2, =о. (2.105’
dr 7-2 dr
Так как ra==catga1, то
tg2a-
г dr
ИЛИ
откуда
78
Решение этого уравнения имеет такой вид:
Из этого также следует
c„rC08’“* =const.
carC0S,“‘ = const.
В некоторых случаях для центробежных и осевых компрессоров может
представлять интерес закрутка потока перед колесом по закону
fu/r=const. Принимая и в этом случае Rm=oo, получаем для распреде-
ления осевой скорости по радиусу выражение
Са — б’дкН- 2C1 ы к
(1 -г2),
где сак и сын — соответствуют внешнему радиусу колеса, a r = rlrK.
Если рассматривать канал между рабочими лопатками, то постоян-
ство энергии будет сохраняться только для линии тока в относительном
движении:
dp
У
W2
2
\-LR = E = const.
Если продифференцировать Е по п и подставить в уравнение (2.96),
то получим
дЕ w2sin2|3 . u2-j-w2 cos2 3 ± 2wm cos Й , .
---—-------------- -4----—--------------------— cos Ф 4-
дп Rm 2 т ‘
+ Л. + ® + . (2. 106)
on on on
Это уравнение является нелинейным.
Уравнения (2.95) и (2.96) могут быть выражены еще с помощью
газодинамических функций. Так, В. М. Акимовым дано уравнение
(2.95) для абсолютного движения при Fn — 0 в виде
dX2__ /cos2 cos ф .sin2 а. Л—1 dlnp*\ . й+1
dn \ г Rm 2k dn ) k
d In p*
dn
(2. 107)
где p*— давление заторможенного потока в абсолютном дви-
жении;
а — угол между векторами абсолютной и окружной скорости.
Интеграл этого линейного уравнения будет иметь вид
— С p(n)dn Г Г f p{n}dn
k2 = e J [jQ(/z)eJ dn-\-C
(2.108)
где
p(n)=2
cos2 a cos ф
r
sin2 a k — 1 din p*
~R~m ^~2k~ dn
а
д(л)==Ш 112^
k dn
79
Уравнение равновесия в относительном движении при Fn = 0 при-
обретает с использованием газодинамических функций следующий вид:
d/.w2
dn
2 Л о « \2 ,
— (ATOCOSd----------cos^ —
Г \ #кр w /
sin2 3 ь । i d In л*
-2^—— + ^±±t(Xw)—(2.109)
Rm k dn
где
— ; aKpw—1/ , , ; r(Xw)—-j- ;
«кр® V Tw
3— угол между относительной и окружной скоростью;
Т — термодинамическая температура;
Tw и pw — температура и давление заторможенного в относительном
движении потока.
Уравнение (2. 109) является нелинейным и его следует решать
численным образом.
Уравнения равновесия в безразмерном виде с использованием газо-
динамических функций и с учетом Fn в относительном движении даны
в книге [42].
Применение уравнений равновесия при расчетах компрессоров и
турбин дополнительно рассматривается в гл. 5 и 7, соответственно
относящихся к этим машинам.
Глава 3
ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ
В ЛОПАТОЧНЫХ МАШИНАХ И ИХ РАССМОТРЕНИЕ
В p—v-, Ts- и Z—s-ДИАГРАММАХ
Этот раздел расширяет сообщаемые в курсах термодинамики све
дения по процессам работы компрессоров и турбины и их графическому
изображению в р—v-, Т—s- и i—s-диаграммах.
3. 1. КОМПРЕССОР
3.1.1. ИЗОБРАЖЕНИЕ ПРОЦЕССА СЖАТИЯ
В КОМПРЕССОРЕ В р—^-ДИАГРАММЕ
Процесс сжатия воздуха в компрессоре можно разделить на три
этапа:
а) всасывание воздуха;
б) повышение давления;
в) подача воздуха к месту потребления.
Эти три этапа составляют цикл сжатия воздуха в компрессоре и
могут быть изображены в р—б'-диа-
грамме (рис. 3.1).
Будем оперировать средними значе-
ниями параметров воздуха на входе
в компрессор и на выходе из него. Усло-
вимся называть отношение давлений
Рк/Рв = лк степенью повышения
давления, а отношение удельных
объемов vB/vK=eK степенью сжатия. Ра-
Рис. 3.1. Изображение работы
компрессора в р—о-диаграмме
боту всасывания, представляющую со-
бой работу сил давления на входе в ком-
прессор, можем для промежутка времени
т сек написать в виде
Бвс — Рв^вСвХ PbCbGbX, (3.1)
где FB— площадь компрессора на входе (перед колесом) в м2-,
съ — средняя скорость воздуха на входе в м/сек-,
GB — секундный массовый расход воздуха в ке/сек-,
рв и ов — средние значения давления и удельного объема воздуха
перед колесом в н/м2 и м3/кг.
81
Разделив уравнение (3. 1) на GBt, т. е. отнеся работу к 1 кг воздуха,
получаем
Т.Вс = Рв^в* (3.2)
В р—^-диаграмме эта работа изобразится площадью, ограниченной кон-
туром в—1—2—3—в. Для повышения давления 1 кг воздуха требуется
работа
К
£C«=J Pdv- (3.3)
В
В р—и-диаграмме эта работа изобразится площадью к—в—1—5—к.
Работа сил давления на выходе из компрессора для 1 кг воздуха
по аналогии с работой сил давления на входе запишется в виде
1"J1'=PkVK- (3.4)
Эта работа, изображаемая площадью к—5—2—4—к, может быть
названа работой выталкивания или подачи, так как она связана с пода-
чей воздуха к месту потребления.
Работы £Сж и £п совершаются внешними силами, приложенными
к газу, а работа Авс — силой наружного давления перед компрессором.
Если всасывание воздуха производится из атмосферы, то это давление
непосредственно связано с атмосферным давлением рв соотношением
к
у-1,
Рн \ k + 1 J
где лв = св/аКр— приведенная скорость на входе в компрессор.
Поскольку работу всасывания можно рассматривать как работу
сил давления перед компрессором (в частности, атмосферного давления),
то ее следует считать отрицательной по отношению к работам LCHt и Ln-
Поэтому суммарная работа выразится уравнением
Ls = — pBvB + ] pdv + pKvK. (3.5)
В
Очевидно, что эта работа выразится площадью к—в—3—4—к и мо-
жет быть записана так:
Lz — \vdp=A—, (3.6)
J J V
В в
а полная работа, затрачиваемая на сжатие воздуха в компрессоре
[см. уравнение (2.89)], в виде
К 2 2
.
^ = ^4-^4-^-^. (3.7)
в
Таким образом, в р—и-диаграмме изображается только часть пол-
ной работы, затрачиваемой на компрессор, а именно: политропическая
К
работа сжатия Zs = \—. Эта работа будет выражаться различно
J у
В
в зависимости от того, по какому закону идет сжатие.
82
В общем случае процесс сжатия протекает с подводом тепла трения
и отводом гепла во внешнюю среду. Поэтому все подведенное тепло
может быть в дифференциальной форме записано следующим образом:
dQ = dQR—dQq=dLR—dQq, (3.8)
где Q — тепло, подведенное к воздуху в процессе сжатия, в дж)кг-,
Qr = Lr — тепло трения и других потерь в дж!кг\
Qq — тепло, отведенное во вне, в дж!кг.
Представим тепло dQ в виде
dQ = cnd7’,
где сп — теплоемкость процесса. Напишем для dQ уравнение первого
закона термодинамики в двух следующих видах:
dQ = cndT=Cj>dT—vdp; (3.9)
dQ = cndT~c,dT+ pdv (3.10)
или
(cn—cp)dT = —vdp\
(cn—cv)dT=pdv.
Разделим последние уравнения одно на другое. Тогда
с п с г) d р/р
—------=—— . (3.11)
сп— cv dv[v
Обозначим отношение
с п Ср
--------= п,
С п — Су
тогда уравнение (3.11) примет вид
dv dp
п —-------— .
V р
Принимая, что п — величина постоянная, получаем
pvn = const.
Величина п представляет собой показатель политропы сжатия
в компрессоре.
Отметим, что условие п = const справедливо для процесса сжатия
с бесконечно малым изменением параметров. В действительности, пока-
затель п будет переменным и различным на отдельных участках про-
цесса сжатия. Однако в теоретических исследованиях и в расчетах часто
оперируют некоторым средним значением показателя п, принимаемого
постоянным для всего процесса сжатия.
Проанализируем возможные значения п в зависимости от величины
и знака тепла dQ.
Из уравнения для п находим
, 1 — (сп!с р)
tl — k ------------ .
1 • k (с njc р)
Так как cn = dQldT, то
n — k
dQ
с pdT
(3. 12)
(3.13)
83
Возможны следующие случаи.
1. Если dQ>0, то n>k. Допустим, что dQlcvdT=G,3 и k= 1,4. Тогда
из уравнения (3. 13) получаем
,0,7 1 СП
n = k—— = 1,69.
0,58
Если -^- = 0,2, то п = k = 1,55.
с pdT 0,72
В этом случае либо dQn>4ZQg, т. е. тепло, подводимое от трения
и других потерь, больше тепла охлаждения, либо dQg = 0 при и,
следовательно, dQ = dQR. Случай, когда </Q>0, соответствует реальным
процессам в компрессоре.
Энтропия воздуха в компрессоре при этом возрастает, так как
, dQ ... п
ds=—- >0.
Т
В современных компрессорах средний показатель п= 1,45=1,55.
2. Если Q = 0, то dQ = 0 и n=k. Это возможно, когда dQR = dQq или
dQB = dQg = 0 (идеальный изэнтропический процесс). В обоих случаях
процесс сжатия воздуха происходит по адиабате. Однако такое охлаж-
дение, при котором отводится тепло в количестве, равном теплу потерь,
в авиационных компрессорах не применяется*). Идеальный изэнтропи
ческий процесс используется в качестве эталона для оценки эффектив-
ности компрессора. В дальнейшем и этот процесс называется адиабати-
ческим, хотя для адиабатического процесса достаточно лишь условия
dQg=0, т. е. отсутствия отвода тепла во внешнюю среду.
3. Если 7'=const и dT = 0, то из уравнения (3.13) получаем
n = k/k=\,0. В изотермическом процессе должно отводиться тепло при
сжатии в количестве, определяемом соотношением dQ=dQR—dQq =
=—vdp или dQg=dQRi-vdp.
Для всего процесса
В
Таким образом, в изотермическом процессе отводится тепло, экви-
валентное теплу трения и политропической работе сжатия. Этот процесс
практически в авиационных компрессорах невозможен и представляет
только теоретический интерес.
4. Если в уравнении (3. 13) положить 1 — k-^—==Q, то
Ср dT
П= (k—1)/0 = оо.
Процесс изменения состояния, соответствующий п = оо, может быть, как
известно, найден следующим образом. Из уравнения политропы pvn =
= const получаем, извлекая корень n-й степени,
1
рп v = const,
откуда при п = ос находим v = const. Для воздуха или газа этот процесс
возможен лишь при нереально большом подводе тепла в процессе
сжатия.
*) При применении в двигателях в качестве топлива жидкого метана или водорода
возможно и в авиационных двигателях иметь интенсивное охлаждение.
84
Из уравнений первого закона термодинамики при v = const
получаем Л с„ dQ + va'p dQ = cv dT = -p- dT=———— , v k k
откуда dQ=^_ k—\
и dQR=^ + dQq.
Интегрируя и принимая k= 1,4, получаем
—2,5
J у
Таким образом, при &=1,4 тепло трения и других потерь должно
в 2,5 раза превышать работу сжатия и, кроме того, компенсировать
тепло, отводимое во вне. Очевидно, что случай с такими большими поте-
рями нереален. Однако процесс v = const или у — const имеет и для газов
практическое значение для случаев, когда степень повышения давления
в компрессоре невелика (рк/рв^1,05—1,10). В частности, при таких
значениях рк1ръ ступень осевого компрессора иногда подвергают ана-
лизу при v = const, поскольку погрешность при предположении, что воз-
дух ведет себя как несжимаемая среда, при таких значениях рк/рв
весьма невелика.
Насосы для жидкостей в большинстве случаев можно достаточно
точно рассчитывать в предположении отсутствия сжимаемости, т. е.
при у=const.
Из изложенного видно, что показатель процесса п непосредственно
связан с величиной подводимого тепла Q. Поэтому приведем еще фор-
мулы, которыми можно пользоваться для определения среднего значе-
ния п в отдельных элементах компрессора или для всего компрессора:
k — 1 LR — Qq
п = k
1 k R&.T
Lr — Qq
1 — {k — 1)———
' 7 RbT
(3.14)
где ДГ — повышение температуры в данном элементе или во всем ком-
прессоре.
Удобной для применения является также формула
п k LR — Qq k г Lr — Q?i
-----=-------------------- 1----------. (3. Io)
n—1 k—1 R\T k—1[ c p\T J
Рассмотрев реальные и теоретически возможные процессы измене-
, л f dp
ния состояния, выведем формулу для определения работы сжатия I — ,
изображаемой в р—n-диаграмме. Если принять, что п=const, то можем
написать
п
п — 1
п —1
(3.16)
85
Это же уравнение можно написать еще в следующих видах:
или
TR(rK-rB).
(3. 17)
(3. 18)
Уравнения (3. 16)—(3. 18) позволяют вычислить политропическую
работу сжатия, если известен показатель п, начальная и конечная тем-
пературы или степень повышения давления.
Для адиабатического процесса все эти уравнения сохраняют свою
силу при замене показателя п показателем k и температуры Тк — ее
адиабатическим значением. Таким образом, адиабатическую работу
сжатия можно вычислять по одной из следующих формул:
— RTB
k — l в
В компрессоре могут сжиматься как воздух, так
имеющие различные значения k и R, показанные для
в табл. 3. 1.
(3. 19)
(3. 20)
и другие газы,
некоторых газов
Таблица 3.1
Наименование газа k R дж/кг-град k R—E дж{ кг • г рад k—1 Е
Ев
Воздух 1,4 287 1005 1,0
Водород 1,4 4160 14580 14,4
Гелий 1,66 2080 5240 5,2
Неон 1,66 416 1048 1,035
Аргон 1,66 208 524 0,52
Таким образом, при одной и той же степени повышения давления
для сжатия 1 кг водорода потребуется затратить работу, превышающую
в 14,4 раза работу сжатия воздуха.
Для изотермического сжатия, когда п=1,0, из уравнений (3.16) —
(3. 18), получаем неопределенность 0/0. Поэтому для изотермической
работы сжатия находим выражение непосредственным интегрированием.
Так как для этого процесса соблюдается условие pv—p3v3,
то v= ^в —. Следовательно,
Р
К к
\ vdp = pBvB \— = pBvB In—= /?Гв In
J J P Рз Рв
в в
(3.21)
86
Работа сжатия для v = const найдется по очевидной формуле
Рк -Рп

(3.22)
Из этого уравнения видно, что работа, затрачиваемая при v= const,
существенно зависит от плотности рабочего тела. Так, например, для
воды при условиях р = 0,981 бар и Т=273° К у = 1000 кг/л3, а для жидкого
водорода при р = 0,981 бар и 7=40° К — у=70 кг 1м3. Таким образом, при
одинаковом повышении давления работа водородного насоса будет
в 14,3 раза больше, чем насоса водяного.
Насосы, используемые для повышения давления жидких металлов,
приближаются по затрачиваемой ими работе к водяным насосам. Так,
например, жидкий натрий имеет плотность у = 800 кг/м3, т. е. 0,8 плот-
ности воды.
Сопоставление работ сжатия при различных значениях показателя
политропического процесса п показано на рис. 3.2, откуда следует, что
минимальной является изотермическая работа сжатия, а максималь-
ной— работа сжатия при o = const. При n>k работа сжатия больше
адиабатической и может быть записана в виде
+ Д// ИЛИ +
3.1.2. ИЗОБРАЖЕНИЕ ПРОЦЕССА СЖАТИЯ
В КОМПРЕССОРЕ В Т—« ДИАГРАММЕ
3.1.2.1. Основные свойства Т—«-диаграммы
Для графического изображения процесса сжатия в компрессоре
более удобной является Т—«-диаграмма, которая позволяет представить
все величины, входящие в полную работу компрессора.
Напомним кратко основные свойства Т—«-диаграммы, используе-
мые в дальнейшем при рассмотрении работы компрессора.
В Т—«-диаграмме площадью, ограниченной кривой процесса, осью
абсцисс и крайними ординатами, измеряется в некотором масштабе ко-
личество подведенного или отведенного тепла в данном процессе. Дейст-
вительно, если тело переходит из состояния 1 в состояние 2 по кривой
1—2 (рис. 3.3), уравнение которой T=f(s), то согласно определению
энтропии
откуда
Q = j7</«.
1
Это количество тепла соответствует площади внутри контура
1—2—3—4—1.
87
Для процесса с постоянным давлением
следовательно,
Если ср = const, то
Q=\cpdT.
1
Q = cp(7’2—
Для изобары изменение энтропии
С ат
S2~ S1— ср
1
Так как для газа теплоемкость ср есть функция только температуры, то,
следовательно, приращение энтропии в изобарическом процессе зависит
Рис. 3. 2. Сравнение в р—V-
диаграмме работ сжатия
при различных показателях
политропы п
Рис. 3. 3. Изображение произволь-
ного процесса в Т—s-диаграмме
исключительно от изменения температуры и не зависит от давления.
Поэтому для всех изобар приращение энтропии в данных пределах тем-
пературы будет одинаковым. Отсюда, следовательно, все изобары дан-
ного газа одинаковы и лишь смещены относительно друг друга в гори-
зонтальном направлении, т. е. являются эквидистантными относительно
оси абсцисс s. При постоянной теплоемкости
S2_S1 = ^ln
Таким образом, изобара является логарифмической кривой. Для
изохорического процесса при постоянной теплоемкости аналогично
получаем
1 т2
s2-sx = cv In -4.
11
Следовательно, и изохора является логарифмической кривой и все
изохоры будут эквидистантными относительно оси абсцисс s. Если
в Т—s-диаграмме из одной точки выходят изохора и изобара, то в слу-
чае возрастания энтропии изохора будет располагаться выше изобары,
а в случае уменьшения энтропии — ниже изобары, поскольку cp>cv.
Если dQ = G, то для этого процесса
, dQ „
ds ~ ——=0.
Т
88
Следовательно, s = const, т. e. процесс является изэнтропическим
и изображается в Т—s-диаграмме вертикальной прямой.
Если dQ>Q (при подводе тепла), то процесс будет протекать с воз-
растанием энтропии, так как
ds=—^- > 0.
Т
Соответственно при c?Q<0 будет rfs<0, т. е. энтропия уменьшается.
Поэтому при наличии подвода тепла за счет трения процесс расшире-
ния (АВ) или сжатия (ВС) изобразятся в Т—s-диаграмме некоторыми
кривыми с соответствующим увеличением энтропии (рис. 3. 4).
Для удобства процесс сжатия в компрессоре в Т—s-диаграмме рас-
смотрим сначала без отвода тепла и без учета скоростей потока, затем
при отводе тепла и, наконец, с учетом скоростей.
Рис. 3.4. Изобра-
жение в Т—s-диа-
грамме процесса
сжатия и процесса
расширения с под-
водом тепла тре-
ния
Рис. 3.5. Изображение в
Т—s-диаграмме работы ком-
прессора при Qg=0 и без
учета скоростей потока
3. 1. 2. 2. Изображение процесса сжатия в компрессоре
в T’-s-диаграмме без отвода тепла и без учета скоростей потока
Предполагая, что Q9 = 0 и обозначая работу, затрачиваемую на
компрессор, без учета скорости потока на входе и на выходе через Нкх
получим
к
HKX=\d-^ + LR, (3.23)
J Y
В
ИЛИ
Дкх = ср(Ек Ев). (3.24)
Запишем последнее равенство в виде
Нкх = ср(Тк—0)— ср(7'в—0).
По смыслу Т—s-диаграммы начальное теплосодержание tB =
= ср(Тъ—0) измеряется площадью треугольника в—1—3 под изобарой
в—1 (рис. 3.5). Аналогично конечное теплосодержание
jk = Ср (Тк 0)
измеряется площадью треугольника к—2—4. В действительности изо-
бары в—/ и к—2, будучи логарифмическими кривыми, асимптотически
89
приближаются слева к оси абсцисс, и поэтому точки 1 и 2 в действи-
тельности находятся в бесконечности. Для удобства рассуждения эти
точки на рис. 3.5 показаны в пределах чертежа.
Однако полученной результирующей площадью к—2—1—в—3—4—к
для измерения величины Нкх пользоваться неудобно. Проведем изо-
терму в—5; тогда ввиду эквидистантности кривых к—2 и в—1 площадь
в—1—3—в можно заменить равновеликой ей площадью треугольника
5—2—6. В связи с этим Якх = площадь (к—2—4—к)—площадь (5—2—
6—5) = площади к—5—6—4—к. Рассмотрим отдельные элементы этой
площади. Между точками в и к проходит политропа сжатия в—к. Пло-
щадь, ограниченная этой политропой и изэнтропами в—3 и к—4, будет
представлять тепло, подведенное в процессе сжатия к воздуху. В рас-
сматриваемом случае, когда Qg = 0, тепло, подведенное к воздуху, равно
теплу трения и других потерь. Следовательно, площадь в—к—4—3—в =
= Qr—Lr.
В соответствии с уравнением (3.23) оставшаяся часть площади бу-
дет равна политропической работе сжатия:
К
площадь к — 5 — 6 — 3— в — к =\ — .
J у
В
Если бы процесс сжатия происходил без потерь, то политропа в—к
превратилась бы в изэнтропу или, так как Qg=0 — в адиабату в—кад.
кал
R
3
соответствовать площади кад—5—6—3—кад. Разница между политропи-
ческой и адиабатической работами сжатия будет измеряться площадью
к—кад—в—к; следовательно,
Следовательно, адиабатическая работа сжатия
будет
Разность между работами, затрачиваемыми в компрессоре при поли-
тропическом и адиабатическом сжатии, выразится величиной
к /КаЛ \
= + \~ =^ + Д/7=^.
•> Y I J У /
В \ в / ал
Таким образом, при наличии потерь работа, затрачиваемая на ком-
прессор, при одинаковом конечном давлении возрастает на величину
большую, чем требуется непосредственно для преодоления потерь. Фи-
зически это обусловлено тем, что, кроме затраты работы на преодоление
самих потерь, необходимо еще при одном и том же конечном давлении
затратить дополнительную работу ДЯ в связи с ростом удельного объема
воздуха из-за подвода тепла трения. Вследствие возрастания работы,
затрачиваемой в компрессоре за счет потерь и ДЯ, увеличивается и тем-
пература воздуха (газа) на выходе по сравнению с адиабатическим
процессом. Если предположить, что при наличии и отсутствии потерь
будет затрачиваться одинаковая работа, т. е. Нкх = Нкхая, то из урав-
нений (3.23) и (3.24) следует, что при наличии потерь температура
„ Г dp
в конце сжатия останется неизменной, но уменьшатся — и конечное
давление рк. На рис. 3. 6 площадь кад—1—2—3—кад соответствует
исходной адиабатической работе сжатия Нкхая с конечным давлением
90
Рк.ад- При наличии потерь та же работа будет соответствовать давле-
нию рк<рк.ад и изобразится площадью к—4—5—6—к.
В Т—«-диаграмме могут быть показаны также работы всасывания
и выталкивания. Так, если из точки к (рис. 3.7) провести изобару
рк=const и изохору vK= const до условного пересечения с осью абсцисс,
то площадь треугольника к—6—5 и будет соответствовать работе вытал-
кивания ркик.
Действительно, имеем
PkVk — {RTk— (Ср Ct,) Тк.
Запишем это выражение в виде
pBvK=cv (Тк 0) сг (Тц- 0).
Но ср(Тк—0) изображается площадью треугольника к—6—1 и
cv(TK—0) —площадью треугольника к—5—1.
Рис. 3. 6. Изображение в Т—s-
диаграмме работы сжатия при
Нк=const в случаях LR=0
и
Рис. 3. 7. Изображение в Т—s-
диаграмме работы всасывания
и выталкивания
Разность этих площадей будет равна площади треугольника к—6—5
или, следовательно, равна pKvB.
Аналогично получим рБпв = площади треугольника в— 4—3.
Воспользовавшись тем, что изохоры так же, как и изобары, между
собой эквидистантны, получим (рис. 3.8)
(рк^к—Рв^в) =площади к—5—4—3—6—к.
Следовательно, площадь к—6—3—2—в—к будет равна J pdv.
В частном случае, когда процесс адиабатический, интеграл J pdv
будет изображаться площадью кад—7—8—2—в—кад. Согласно первому
закону термодинамики в этом случае J pdv будет равен одновременно
изменению внутренней энергии (UKaR—Us).
3. 1.2. 3. Изображение процесса сжатия в компрессоре
при отводе тепла и без учета скоростей
В авиационном компрессоре в процессе сжатия, как правило, отво-
дится некоторое количество тепла во внешнюю среду в силу разности
температур сжимаемого воздуха и воздуха, окружающего корпус ком-
прессора. Этот отвод тепла обычно относительно невелик и в расчетах
компрессора его не учитывают. Однако возможны случаи, когда приме-
няются специальные меры для охлаждения сжимаемого воздуха. Так,
например, с целью форсировать двигатель на входе в компрессор впры-
91
сживается вода или другая охлаждающая жидкость, которая испаряется
в процессе сжатия и отводит часть тепла.
В компрессорах неавиационных известны и более интенсивные ме-
тоды охлаждения, например введение промежуточных между ступенями
холодильников или охлаждение корпусов водой. Однако эти методы
связаны с увеличением массы и габаритов силовой установки и для
авиационных компрессоров непригодны *>.
Рис. 3.8. Изображение в Т—s-
диаграмме адиабатического про-
цесса всасывания и выталкивания
Рис. 3.9. Изображение в Т—s-
диаграмме работы компрессора
с охлаждением
Если в процессе сжатия будет отводиться тепло, то политропа в—к
(рис. 3.9) сдвинется влево и конечная точка процесса сжатия займет
некоторое положение к7. Площадь под линией политропы в—к' будет
представлять собою тепло, подведенное в рассматриваемом случае, т. е.
площадь к7—в—5—6'—к7 = QH—Qq = LR—Qq.
Так как при Q(/ = 0 приведенное в процессе сжатия тепло было равно L,,
и изображалось площадью к—в—5—6—к, то, следовательно, отведен-
ное тепло Qq будет измеряться разностью площадей к—в—5—6—к и
к7—в—5—6'—к7. Изменение величины работы Нкх при отводе тепла
можно получить следующим путем: при Qg = 0 Нкх = ср(Тк—
при Qo/0 ^ = r,(7'K-7;)-l-Q9.
Вычитая второе уравнение из первого, получим
х cp{T.-r}-Q4.
Так как ср(Тк—Тк7) =площади к—к7—6'—6—к, то, прибавляя к этой
площади — площадь к7—в—5—6'—к7, вычитая площадь к—в—5—6—к,
получим площадь к—к7—в—к.
Таким образом, НКХ>НКХ на величину площади к—к7—в—к, рав-
ной \Н—А.Н', где ДЯ7— разность между политропической и адиабати-
ческой работами сжатия в процессе с отводом тепла. Если тепло Qq, отве-
денное в процессе сжатия, будет равно по величине Qr = Lr, то точка к'
совпадает с точкой кад. Поскольку в этом случае ДЯ7=0, то выигрыш
в затраченной работе будет равен ДЯ, т. е. соответствовать площади
К—К а д в к.
*)См. сноску на пр. 84.
92
Если отведенное тепло будет по величине больше тепла QR, то ли-
ния политропического сжатия в—к" пройдет левее линии адиабаты
в—Над. Отведенное тепло в этом случае
Qq = QR + \Qq, (3.25)
где AQg = площади к"—в—5—6"—к".
Экономия в затраченной работе будет составлять
Н кх~ HrX = ^Н" = площади треугольника к —кад—- в-(-площадь
треугольника кад —к" —в.
В пределе, когда процесс сжатия будет изотермический, линия
сжатия совпадает с линией в—7 и отведенное тепло выразится также
уравнением (3.25), причем Дфд = площади в—7—8—5—в.
3.1.2.4. Изображение процесса сжатия в Т—«-диаграмме
с учетом скоростей потока
Работа Нкх может существенно отличаться от полной затраченной
работы Нк, вследствие того что разность кинетических энергий потока
воздуха на входе и на выходе из компрессора достигает значительной
величины. Так, если принять, что скорость на входе св = 180 м/сек и на
выходе ск=120 м/сек, то получим
cl -<?
-----— = — 9000 дж/кг.
Для компрессора с полной затраченной работой Як = 200 000 дж/кг
такая разность кинетических энергий будет составлять 4,5%. В компрес-
соре с меньшим значением Нк относительное значение разности кинети-
ческих энергий будет еще более существенным. Поэтому графическое
изображение процесса работы компрессора в Т—«-диаграмме без учета
скоростей является неполным.
Эти скорости можно учесть, если ввести параметры изэнтропически
заторможенного тока:
где л — приведенная скорость потока.
При использовании параметров заторможенного потока точка в
в Т—«-диаграмме переместится в точку в*, которая лежит на изобаре
* СВ
с давлением рв* и соответствует температуре 7 я — (рис. 3. 10).
Аналогично переместится и точка к, соответствующая параметрам по-
тока на выходе из компрессора. Применяя построения, аналогичные рас-
смотренным выше, получим, что вся затраченная работа Нк~ср(Тк —
— 7'в) изобразится площадью к*—7*—8*—6—к*, т. е. подобно тому, как
изображалась работа Нкх. Если предположить, что изменение пара-
метров заторможенного потока подчиняется некоторой непрерывной
политропической зависимости, то точки в* и к* можно соединить неко-
торой кривой, являющейся политропой сжатия по заторможенным пара-
метрам.
93
При этом можно записать
Рис. 3. 10. Изображение в
Т—s-диаграмме работы ком-
прессора с учетом скоро-
стей потока
к*
h-K = \^r + L*R, (3.26)
.) у *
в»
к»
где ~~ и L*r— политропическая работа сжатия и работа трения по
в* v параметрам заторможенного потока.
Тогда в соответствии с изложенным выше политропическая работа
сжатия изобразится площадью к*—7*—8*—5—в*—к*, работа тре-
ния — площадью к*—в*—5—6—к*.
Таким образом, при введении параметров торможения и политропы
изображение процесса работы компрессора
в Т—s-диаграмме становится совершенно
идентичным рассмотренному выше изобра-
жению при использовании статических па-
раметров. Необходимо, однако, подчеркнуть
следующие условности такого изобра-
жения.
1. Работа трения по параметрам затор-
моженного потока получается больше ра-
боты трения по статическим параметрам.
В действительности никаких оснований для
возрастания работы трения нет, так как
торможение по условию производится изэн-
тропически.
2. Возрастание работы трения является
условным и объясняется введением поня-
тия о политропическом процессе по затор-
моженным параметрам, которого физически
не существует.
Несмотря на отмеченные условности,
изображение процесса работы компрессора
в Т—s-диаграмме по заторможенным пара-
метрам представляет интерес, в первую очередь, потому, что позволяет
изобразить всю затраченную в компрессоре работу. Средний показатель
политропы сжатия по параметрам торможения может быть легко свя-
зан с показателем политропического процесса по незаторможенным
параметрам. Изменение энтропии для обоих политропических процессов
одинаково и может быть записано в виде
As=s6-ss = c„ In ;
1 в
т*
^S = S6-S& = C*n 1Пу£ ,
где сп* — теплоемкость политропического процесса в заторможенных
параметрах, принимаемая постоянной для диапазона температур от Тв*
до Тк*. Разделив одно уравнение на другое, получим
(3. 27)
94
Выражая сп* и сп через показатели процессов, будем иметь
л* — 1 п — 1 / т* \ '
'п| у*-|
откуда
га* = k----, (3. 28)
п — k
где
Воспользовавшись выражением для температур торможения, можем
записать следующее равенство:
(3. 29)
Если ХК=ХВ, то T*JT* = TKITB и, следовательно, 2? = 1,0. Тогда из урав-
нения (3.28) получаем га*=га. Как правило, Хк < Хв и поэтому га*>га.
В табл. 3.2 даны значения га* для нескольких значений лк в предполо-
жении, что п=1,5; А,в=0,65 и Х.к=0,4.
Таблица 3.2
Лк 1,5 2,0 3,0 6 10
п* 1,575 1,53 1,519 1,51 1,507
Показатель га* для отдельных элементов компрессора может суще-
ственно отличаться от среднего значения, определяемого для всего ком-
прессора. В частности, в неподвижных аппаратах показатель п* должен
быть равен единице, поскольку при отсутствии отвода тепла темпера-
тура торможения в этих элементах остается неизменной.
При изображении в Т—s-диаграмме адиабатической работы сжатия
по заторможенным параметрам наиболее естественно принимать, что
конечное полное давление в адиабатическом процессе будет таким же
по величине, как и в действительном. Поэтому точка кач будет лежать
на изобаре рк*. В этом случае статические давления в обоих процессах
могут приниматься одинаковыми лишь тогда, когда для адиабатиче-
ского процесса полное давление будет определяться с некоторой мень-
шей (адиабатической) скоростью. Действительно, принимая статическое
давление рк и полное давление рк* в адиабатическом и действительном
процессах одинаковыми, можем написать
Тк
т
* к.ад
к.аД
95
с другой стороны,
Тк k — 1 „
1------
k + I к
/'кал ,_______— 1-.2
k+ 1 к'ад
Следовательно,
или
\с ^к.ад
Так как Т*к ал<^Т*, то и адиабатическая скорость ск.ад должна быть
меньше действительной скорости ск. Хотя различие между ск и ск.ад
s
Рис. 3. 11. Изображение в i—s-
диаграмме работы компрессора
Рис. 3. 12. Изображение в i—s-
диаграмме работы компрессора
в параметрах торможения
относительно невелико, однако в принципе оно должно учитываться.
Адиабатическая работа сжатия по параметрам заторможенного потока
изобразится площадью кал — 7* —8* — 5 — кад. q использованием скоро-
сти ск.ад связь между адиабатическими работами сжатия по затормо-
женным и статическим параметрам можно выразить в виде
2 2
С — С
—- (3.30)
3. 1. з. изображение процесса сжатия
В КОМПРЕССОРЕ В Z—«ДИАГРАММЕ
В i—s-диаграмме, в отличие от Т—s-диаграммы, работы Нкх, НК1
//ад будут изображаться отрезками, а не площадями. В частности, ве-
личина Нк х может быть записана в виде
//к х=Ср (Тк Тв) = /к iB.
Следовательно, величина Нкх изобразится отрезком, равным
/к—iB (рис. 3.11). Аналогично адиабатическая работа сжатия изобра-
зится ОТреЗКОМ Гк.ад—/в-
96
Так как
Ннх ^к.ад— LR + l\H,
то, следовательно, отрезок 1К—1к.ад в I—s-диаграмме будет представлять
собой сумму (Лн + АЛГ) в дж/кг.
Таким образом, в i—s-диаграмме работа трения и величина ДЯ
отдельно не изображаются. Следовательно, не может быть изображена
и политропическая работа сжатия, если Ln или ДЯ неизвестны.
Если применить параметры торможения, то в I—s-диаграмме, так
же как и в Т—s-диаграмме, может быть изображена полная работа Нк,
а также адиабатическая работа сжатия по параметрам торможения
Я*ад (рис. 3.12). Одновременно будет изображаться сумма Ьд-\- &Н*.
3.2. ТУРБИНА
Графическое изображение процесса расширения в турбине в р—V-,
T—s- и 1—s-диаграммах во многом аналогично рассмотренному выше
процессу сжатия для компрессора.
3.2.1. ИЗОБРАЖЕНИЕ ПРОЦЕССА РАСШИРЕНИЯ
В ТУРБИНЕ В р—v-ДИАГРАММЕ
Процесс расширения газа в турбине можно разбить на три этапа:
а) подача газа к сопловому аппарату турбины,
б) процесс понижения давления,
в) выталкивание газа, вышедшего из турбины.
Эти три этапа легко изображаются в р—^-диаграмме (рис. 3.13).
Будем оперировать, как и в ком-
прессоре, средними значениями
параметров. Условимся называть
отношение давлений рт/рт = Лт—
степенью понижения
давления, а отношение удель-
ных объемов vT/vr= ет — сте-
пенью расширения. Рабо-
та подачи газа на входе в тур-
бину будет характеризоваться
работой сил давления, которую
для промежутка времени т сек
можем написать в виде
Ln ~ Рг-ЕрСрТ pr V-p G-^X,
где FT — площадь турбины на входе в м2;
сГ — средняя скорость газа в м/сек-,
Рт и цг — средние значения давления и удельного объема газа перед
сопловым аппаратом турбины соответственно в н/м2 и м?/кг\
бг— секундный массовый расход газа в кг/сек.
Разделив предыдущее уравнение на Grr, т. е. отнеся работу к 1 кг
газа, получаем
Ln рт^т. (3.31)
В р—^-диаграмме эта работа изобразится площадью г—1—2—3—г.
При понижении давления от рГ до рт будет совершаться работа рас-
ширения газа:
Zp = j/?a'T>. (3.32)
Г
В р—и-диаграмме эта площадь изобразится площадью г—т—6—
1-г.
Рис. 3. 13. Изображение работы
турбины в р—v-диаграмме
4 546
97
Работа выталкивания газа на выходе из турбины представляет
собой работу сил давления в выходном сёчении и по аналогии с работой
подачи запишется в виде
^выт — ptVf.
Эта работа изобразится площадью т—6—2—4—т.
Работа LTI, представляющая собой работу внешней силы над газом,
и работа расширения газа Лр используются для получения полезной
работы турбины и поэтому имеют одинаковый знак. Работа выталкива-
ния, совершаемая газом против внешней силы и служащая для удале-
ния газа из турбины, непосредственно в полезную работу турбины не
входит и поэтому должна иметь противоположный знак по сравнению
со знаком работ Ln и Ар. Таким образом, суммируя рассмотренные ра-
боты и принимая для Лп и Ар знак плюс, сможем написать
^3 = Р^Г + р - Р^у
т
Очевидно, что эта работа изобразится площадью г—т—4—3—г и мо-
жет быть описана выражением
L. = {vdp=^\^-. (3.33)
Таким образом, и для турбины в р—^-диаграмме изображается только
часть полной работы, которая в соответствии с изложенным выше
имеет вид
Г 9 9
т
Как и для компрессора, принимают, что связь между давлением
и объемом выражается так:
pvn = const,
где п — является показателем политропы процесса расширения.
Для определения п остаются в силе все выводы, сделанные выше,
в том числе и уравнение (3.13), только применительно к турбине член
dQlcpdT должен иметь знак минус, а поэтому уравнение (3.13) примет
вид
Если и в турбине dQ>0 и, следовательно, тепло трения и других
потерь больше отводимого тепла, то показатель политропы п будет
меньше показателя адиабаты k. Этот случай и является для турбин
наиболее характерным. Так, например, если показатель k в авиацион-
ных турбинах для средних условий часто принимают равным 1,33, то
показатель политропы п= 1,284-1,29.
При Q = 0, n = k, и такой процесс в турбинах, так же как и в ком-
прессорах, используется в качестве эталона для оценки эффективности
турбины и называется адиабатическим процессом. Что ка-
сается изотермического процесса, когда dT=O и я = 1,0, то к нему не-
сколько приближается процесс расширения в многоступенчатой турбине
98
с промежуточным (между ступенями) подогревом газа до одной и той
же температуры Тт*.
rr С dp
Для определения интеграла \ — справедливы выводы, сделанные
J у
цля компрессора. При этом, если рассматривать положительную ею
величину, можем написать
(3.34)
или
J у п—1
т
Для адиабатической работы расширения справедливы эти же урав-
нения с заменой в них показателя п показателем k. Разность между
политропической и адиабатической работами расширения, которую бу-
дем, как и для компрессора, обозначать ДЯ, изобразится площадью
Г—Т—Тад—г.
3.2.2. ИЗОБРАЖЕНИЕ ПРОЦЕССА РАСШИРЕНИЯ В ТУРБИНЕ
в Т—s-ДИАГРАММЕ
Так же как это было сделано применительно к компрессору, про-
цесс расширения в турбине в Т—s-диаграмме будем рассматривать
сначала при отсутствии отвода тепла и без учета скоростей потока,
а затем последовательно учтем и эти факторы.
3.2.2.1. Изображение процесса расширения в турбине в Т—s-диаграмме
без отвода (подвода) тепла и без учета скоростей
Для Qg = 0 и без учета скоростей потока обозначим
или
Н, х—Ср (Тт—Тт).
(3.35)
(3. 36)
Последнее равенство запишем в виде
Ятж = Ср(7’г—0)—Ср(Тт—0).
По смыслу Т—s-диаграммы начальное теплосодержание гг=
= ср(Тт—0) измеряется площадью треугольника г—1—2 (рис. 3.14) под
изобарой г—2, условно пересекающей ось абсцисс в точке 2. Аналогично
конечное теплосодержание /т = ср(7’т—0) изобразится площадью тре-
угольника т—3—4.
В силу свойства эквидистантности изобар может заменить площадь
треугольника т—3—4 площадью треугольника 5—2—6, вследствие чего
работа Нтх будет эквивалентна площади г—5—6—1—г. Работа трения
и других потерь (Ад) будет изображаться площадью г—т—4—1—г,
расположенной под кривой г—т политропического процесса расширения.
4*
99
Из исходного уравнения (3.35) следует
(3.37)
J у
т
Поэтому политропическая работа расширения (££. изобразится
•I Y
площадью г—т—4—6—5—г.
Если процесс будет происходить без потерь, то конечной точкой
процесса будет являться точка тад. Адиабатическая работа расширения
/ г \
I \ I изобразится площадью г—7—8—1—г, и эта площадь по ве-
U Y /
Vai / at
личине будет одновременно равна работе п т х ад-
Рис. 3. 14. Изображение в Т—s-диа-
грамме работы турбины при Qq=0 и
без учета скоростей потока
Рис. 3. 15. Изображение в Т—s-диа-
грамме работы подачи и выталкива-
ния в турбине
Из рис. 3.14 нетрудно видеть, что разность между Ятхад и Нгх
равна площади 5—6—8—7—5. С другой стороны, эта площадь равна
площади т—тад—1—4—т. Последняя представляет собой только часть
работы трения LR. Следовательно, остальная часть работы трения,
а именно площадь треугольника г—т—тад, полезно используется в тур-
бине. Эта площадь эквивалентна величине ЛЕГ, представляющей собой
разность между политропической и адиабатической работами расшире-
ния. Таким образом, в отличие от компрессора, в турбине потерянная
работа меньше работы, затраченной на потери, на величину ЛЯ. (Ср. на
рис. 3. 14 площади г—т—4—1—г и т—4—1—тад—т).
Так как
J V I J V /
т \тал / ал
то, следовательно, политропическая работа расширения изобразится
еще площадью г—7—8—1—тад—т—г.
Исходя из принципов, изложенных в разд. 3.1.2.2 применительно
к компрессору, в Т—s-диаграмме для турбины могут быть изображены
работы подачи, работы выталкивания и их разность. На рис. 3. 15 пло-
щадь треугольника г—2—3 между изохорой ог = const и изобарой
рг = const представляет собой работу подачи prvT. Соответственно пло-
100
щадь треугольника т—4—5 является работой выталкивания /?тут и,
наконец, площадь г—6—7—8—9—г эквивалентна разности работ по-
дачи и выталкивания (ртит—р^). Соответственно площадь г—9—8—
1—т—г будет изображать интеграл С pdv.
3.2.2.2. Изображение процесса расширения в турбине
в Т—s-диаграмме при отводе (подводе) тепла
и без учета скоростей потока
В реальных процессах турбины всегда существует некоторый отвод
тепла от газа через лопатки, диск и наружный корпус. Обычно этот
отвод относительно невелик и при расчетах турбины его не учитывают.
Однако в турбинах с лопатками, специально охлаждаемыми, отвод
тепла может составлять заметную величину, которую необходимо при-
нимать во внимание.
В турбинах процесс расширения может иметь место и при подводе
тепла. В частности, такой случай встречается при догорании топлива
в каналах сопел и рабочих лопаток. С подводом тепла протекает отме-
чавшийся выше процесс с промежуточным подогревом между ступенями
турбины.
Если процесс расширения будет происходить с отводом тепла, то
политропа г—т на рис. 3.16 сдвинется влево. Предположим, что конеч-
ная точка т' займет положение в промежутке между точками т и тад.
Площадь под линией политропы г—т', т. е. площадь г—т'—2'—1—г, бу-
дет представлять собою тепло, подведенное в рассматриваемом случае,
т. е. величину Qb—Qq = LR—Qg.
Так как при Qq = 0 подведенное тепло изображалось площадью
г—т—2—1—г, то, следовательно, отведенное тепло будет изображаться
разностью указанных площадей и будет эквивалентно площади
г—т—2—2'—т'—г.
Уменьшение величины Нгх при отводе тепла можно найти следую-
щим образом:
при Q?=0 Н,х = ср(Тг—Тт);
при H'TX = cp(Tr-T'T)-Qq.
Вычитая второе уравнение из первого, получим
НтХ-^х=ср(Гт-Тт) |-Q9 = Q9_Cp(7\-:Q. (3.38)
Так как ср(Гт— 7^) соответствует площади т—т'—2'—2—т, то, следова-
тельно, разность работ Нтх и Н'тх будет равна площади треугольника
г —т —т', которая, как нетрудно видеть, представляет собой разность
величин д/7 — дН', так же как было получено для компрессора.
Если отведенное тепло будет равно LR, то, следовательно, оно изо-
бразится всей площадью г—т—2—1—г, а уменьшение работы турбины
будет равно АН (площадь треугольника г—т—тад). Если в процессе
расширения в турбине будет подводиться тепло, то политропа процесса
расширения сдвинется на рис. 3. 16 вправо и займет положение г—т".
Применяя рассуждения, использованные выше, получим, что подведен-
ное тепло изобразится площадью г—т"—2"—2—т—г, а исходная (без
подвода тепла) работа 7/тж возрастет на величину площади треуголь-
101
ника г—т"—т. В пределе при изотермическом процессе подведенное
тепло изобразится площадью г—тиз—2ИЗ—2—т—г, а увеличение исход-
ной работы Ят х площадью треугольника г—тиз—т.
Рис. 3. 16. Изображение в Т—«-диа-
грамме работы турбины с охлажде-
нием и подводом тепла
Рис. 3. 17. Изображение в Т—s-диа-
грамме работы турбины с учетом ско-
ростей потока
3.2.2.3. Изображение процесса расширения в турбине
в Т—s-диаграмме с учетом скоростей газа
Работы Н? х и Ht х, как правило, значительно отличаются от полез-
ной работы турбины Нт, поскольку скорость на выходе из турбины
обычно велика, и поэтому разность кинетических энергий (сг2—ст2)/2
составляет значительную часть всей располагаемой энергии, особенно
при умеренном значении теплоперепада. Так же как и в компрессорах,
скорости потока могут быть учтены путем введения параметров затор-
моженного потока. При использовании этих параметров точка г переме-
стится в точку г*, которая лежит на изобаре рг* и соответствует темпе-
сг
ратуре 7’г* = 7’г-|-(рис. 3. 17). Аналогично переместится и точка т,
2ср
соответствующая параметрам на выходе из турбины.
Применяя построения, производившиеся при определении работы
7/тж, получим, что вся работа турбины HT = cp(Tv*—Тт*) изобразится
площадью г*—5*—3*—1—г*, т. е. подобно тому, как изображалась ра-
бота Ят X.
Если и для турбины предположить, что изменение параметров за-
торможенного потока подчиняется некоторой непрерывной политропиче-
ской зависимости, то точки г* и т* можно соединить некоторой кривой,
являющейся политропой расширения по параметрам заторможенного
потока.
При этом можно записать
(3.391
где
LR=L*R-bH*,
f и L*r — политропическая работа расширения и работа трения по
J V параметрам заторможенного потока.
102
Тогда в соответствии с изложенным выше политропическая работа рас-
ширения изобразится площадью г*—5*—3*—4—т*—г*, а работа тре-
ния—площадью г*—т*—4—/—г*.
Таким образом, при введении параметров торможения и политропы
по параметрам торможения изображение процесса расширения в тур-
бине в Т—«-диаграмме становится совершенно идентичным изображе-
нию при использовании статических параметров. Необходимо подчерк-
нуть, что и в данном случае существуют такие же условности, на кото-
рые уже обращалось внимание при рассмотрении процесса сжатия в ком-
прессоре по параметрам заторможенного потока (см. 3.1.2.4).
Уравнение (3.27), устанавливающее связь показателя политропы
по параметрам заторможенного потока с показателем политропы, соот-
ветствующим статическим параметрам, остается справедливым и для
турбины, если коэффициент В принять равным
Т'т
In zr
В = —
Т
In-?-
* г
В полной мере сохраняются и указания об условности показателя поли-
тропы п*, сделанные ранее для компрессора.
При изображении адиабатической работы расширения в Т—«-диа-
грамме по параметрам заторможенного потока также целесообразно
предположить, что конечное полное давление в адиабатическом процессе
будет таким же по величине, как и в процессе действительном. Поэтому
точка 7* будет лежать на изобаре рт*. В этом случае статические
давления в обоих процессах могут приниматься одинаковыми лишь
тогда, когда для адиабатического процесса полное давление рт* будет
определяться с некоторой меньшей (адиабатической) скоростью:
= (3.40)
Вывод этой формулы производится совершенно так же, как и вы-
вод формулы для скорости ск.ад в компрессоре. При этом, как и в ком-
прессоре, должно существовать условие
Хт = А<г.ад.
Адиабатическая работа расширения по параметрам заторможен-
ного потока, являющаяся одновременно и полезной работой турбины
в процессе без потерь, изобразится площадью г*—7*—8*—1—г*.
3.2.3. ИЗОБРАЖЕНИЕ ПРОЦЕССА РАСШИРЕНИЯ В ТУРБИНЕ
в i—«-ДИАГРАММЕ
Для графического изображения процесса расширения в турбине
наиболее часто применяется i—s-диаграмма, в которой работы или теп-
лоперепады Н^х, Нт, Ят.ад и др. будут изображаться отрезками*).
^Применительно к изображению процесса работы турбины в i—«-диаграмме вели-
чины Нт J, Дт, Дт.ад и соответствующие им отрезки принято называть теплоперепа-
дами, тогда как ранее мы называли их работами. Это объясняется различной размер-
ностью работы и теплосодержания в системе единиц, где калория является единицей
измерения количества теплоты, но в связи с распространенностью термина «теплопере-
пад» мы сохраняем его в данной книге.
103
Так, например, величина Нтх изобразится отрезком, равным /г—/т
(рис. 3.18). Аналогично адиабатический теплоперепад изобразится
отрезком, равным 1Г—/т.ад. Так как
НУХЪЛ — НУХ^=ЬК — =L'r,
то, следовательно, величина LR изобразится отрезком гг—г'т.ад- Таким
образом, для турбины, как и для компрессора, величины LR и АН в i— s-
диаграмме порознь не изображаются. Поэтому не может быть изобра-
жена и политропическая работа расширения, если не известны LR или
АН. Если применить параметры торможения, то в i—s-диаграмме может
Рис. 3. 18. Изображение
в i—s-диаграмме работы
турбины
5
Рис. 3. 19. Изображение в i—s-диаграмме
работы турбины в параметрах тормо-
жения
быть изображена полная работа турбины Нт, а также адиабатическая
работа расширения или теплоперепад по параметрам торможения
(рис. 3. 19). Одновременно будет изображаться
Ад-ДЯ*==Гл.
Перед турбиной в качестве исходных параметров часто принимают
параметры заторможенного потока, даже когда на выходе из турбины
рассматривают параметры статические. В этом случае процесс расши-
рения условно изобразится линией г*—т и работа Нтж выразится урав-
нением
2
Н^=сР(Т*~Т*)+-^=ср (Т*-ТТ) = (ГГ-
3.2.4. ВОЗМОЖНОСТЬ БОЛЕЕ ПОЛНОГО ИЗОБРАЖЕНИЯ
ПРОЦЕССОВ СЖАТИЯ В КОМПРЕССОРЕ И РАСШИРЕНИЯ
В ТУРБИНЕ В р—и-ДИАГРАММЕ
При некоторых дополнительных построениях в р—^-диаграмме воз-
можно изобразить не только политропическую и адиабатическую работы
сжатия и расширения в виде интеграла ^^-,но и работу трения и
учесть скорости потока. Для изображения работы трения наиболее
удобно воспользоваться сопоставлением процессов в р—v- и в Т—
диаграммах. Рассмотрим сначала компрессор, причем для простоты -
без отвода тепла и без учета скоростей.
В Т—s-диаграмме (рис. 3.20) адиабата, проведенная из точки к,
пересечется с изотермой Тв в точке в' и вместе с политропой в—к огра-
ничит площадь треугольника к—в—в', являющегося частью работы тре-
ния. Если в р—о-диаграмме также провести из точки к адиабату, а из
точки в изотерму, то после их пересечения в точке в' получим площадь
104
к—в—в —к, очевидно, эквивалентную соответствующей площади
в Т—s-диаграмме.
Оставшаяся часть площади работы трения в—в'—6—5—в может рас-
сматриваться как изотермическая работа сжатия (при переходе от точ-
ки в' к точке в), и в соответствии с этим она изобразится в р—о-диа-
грамме площадью в—в'—3'—3—в.
Рис. 3.20. Изображение в р—v и Т—s-диаграммах ра-
боты трения в компрессоре
Таким образом, полная работа трения для компрессора в р—п-диа-
грамме изобразится заштрихованной площадью к—в'—3'—3—в—к.
Применительно к турбине построение можно произвести следующим
образом (рис. 3.21). Проведем в Т—s-диаграмме из точки тад изотерму,
которая пересечет адиабату т—4 в точке т'. Тогда полная работа трения
будет разделена на следующие части: площадь треугольника г—тад—т,
эквивалентную величине ДЯ, площадь треугольника т—тад—т' и пло-
щадь 1—тад—т'-—4—1, представляющую собой изотермическую работу
Рис. 3.21. Изображение в р—v- и Т—s-диаграм-
мах работы трения в турбине
расширения. Проведя в р—п-диаграмме изотерму тад—т', адиабату т—т'
и изобару т—4', получим полную работу трения в виде площади
г—т—т'—4'—4—тад—г.
Вводя политропические процессы сжатия и расширения по пара-
метрам торможения, можно в р—v-диаграмме учитывать скорости по-
тока с рассмотренными выше ограничениями, которые налагает услов-
ность процессов по параметрам торможения.
3.2.5. ПРИМЕНЕНИЕ р—v-, t-s- И I—s-ДИАГРАММ
р—v-, Т—s-, i—s-диаграммы являются средством наглядного графи-
ческого изображения процессов в турбинах и компрессорах. Кроме того,
T~s- и i—s-диаграммы дают возможность относительно просто произ-
водить расчеты с учетом влияния переменной теплоемкости, необходи-
мость в чем увеличивается с ростом степени повышения давления, тем-
пературы воздуха на входе в компрессор и температуры газа перед тур-
биной. При этом зависимости i(s) и T’(s) могут быть даны не только
105
в виде диаграмм, но и в виде таблиц, что в ряде случаев более удобно.
Иногда также применяются диаграммы или таблицы i—Т или s—T.
С помощью указанных диаграмм или таблиц определяется с учетом
переменной теплоемкости ряд величин, встречающихся в расчетах
лопаточных машин и двигателей. Так, например, температура торможе-
ния воздуха перед компрессором определяется по полной энергии набе-
гающего потока (или энтальпии, соответствующей температуре тор-
можения) :
Г-i
1н~ 1нТ 2 ,
где
1н=срТц-
Степень повышения давления от скоростного потока без учета по-
терь находится с помощью разности энтропий:
Адиабатическая работа сжатия воздуха в компрессоре по парамет-
рам заторможенного потока
Энтальпия i * ая t соответствующая адиабатическому сжатию, опреде-
ляется с помощью энтропии в конце сжатия и степени повышения
давления:
^к-аД^^^ + lgJtK.
Аналогично определяется адиабатическая работа расширения в тур-
бине по параметрам заторможенного потока
Определение к. п. д. компрессора и турбины с учетом переменной тепло-
емкости при помощи i—s- и Т—s-диаграмм приведено в гл. 4.
Глава 4
КОЭФФИЦИЕНТЫ ПОЛЕЗНОГО ДЕЙСТВИЯ
КОМПРЕССОРОВ И ТУРБИН
Возможны различные виды коэффициентов полезного действия
компрессоров и турбин. Поскольку они могут существенно различаться
по величине, необходимо для правильной оценки лопаточных машин
произвести классификацию к. п. д. и выбрать те из них, какие наиболее
целесообразно использовать в расчетах авиационной техники.
4.1. КОЭФФИЦИЕНТЫ ПОЛЕЗНОГО ДЕЙСТВИЯ КОМПРЕССОРОВ
4.1.1. ОБЩЕЕ ПОНЯТИЕ О К.П.Д. КОМПРЕССОРА
Оценка эффективности компрессора по своему принципу отлична
от оценки эффективности двигателя или турбины, так как компрессор
только потребляет работу, но не совершает ее.
В применении к компрессору можно говорить не о полезной работе,
а о некотором полезном эффекте, характеризующем степень использо-
вания работы, затраченной на его вращение. Таким образом, к. п. д. т]в
компрессора можно выразить как отношение полезного эффекта ком-
прессора к затраченной работе.
Обозначая полезный эффект через Н и затраченную работу через
/7затр, получим общее выражение для к. п. д. компрессора в виде
(4.1)
//затр
В связи с различными определениями полезного эффекта и затра-
ченной работы возможны и различные виды к. п. д.
4.1.2. К. П.Д. КОМПРЕССОРА В ЗАВИСИМОСТИ ОТ ВИДА
ЗАТРАЧЕННОЙ РАБОТЫ
Если в качестве затраченной работы в ступени компрессора принять
средний теоретический напор, то получим к. п. д. ступени компрессора
в виде
107
Этот к. п. д. можно назвать лопаточным, так как он учитывает
профильные и вторичные потери, непосредственно связанные с обтека-
нием лопаток*),т. е. изолированно от прочих потерь. Лопаточный к. п. д.
имеет ограниченное применение — только в расчетах отдельных ступе-
ней компрессора. В насосах такой к. п. д. ступени принято называть
гидравлическим.
Если в качестве затраченной работы принимать величину Нк, учи-
тывающую все газодинамические потери в отдельной ступени (или
во всех ступенях), то получим так называемый внутренний к. п. д.
компрессора
Внутренний к. п. д. является основным как для отдельной ступени,
так и для многоступенчатого компрессора. Он находит преимуществен-
ное применение в расчетах, как отдельно компрессора, так и двигателя
в целом.
Следует указать на разновидность внутреннего к. п. д. Когда в ка-
честве затраченной работы принимается разность теплосодержаний
по статическим температурам
о 9
л “ _л z
/4—к-т^-=ср(,гк-тв),
то такой вид внутреннего к. п. д.**> называется к. п. д. п о статиче-
ским параметрам, так как в нем и напор выражается также в стати-
ческих параметрах.
Если кроме газодинамических потерь учитывать также потери меха-
нические (на трение в подшипниках и др.), то получим эффектив-
ный к. п. д.
Применительно к отдельной ступени между рассмотренными к. п. д.
можно установить связь с помощью частных коэффициентов. С этой
целью запишем выражение для 1)кев виде
У) НМ Н th + L3 Hth-^Ls + Lf /4 Ej\
Hth th~i~ L3 Hth + if + Lf Hth + is + Lf 4- Lm
Так как
H г n + L3+Lf~ HK
и
Hth + La + Lf + Lm = HK e,
то предыдущее уравнение примет вид
п —Hth— Hth + L3 Нк
K‘ HthHth + L3 Нк Нке ’
Обозначим
_ Н.!И -=Пз
Hth + is
Так как L3 = — Hth, то очевидно, что
Ся
*)В осевых компрессорах вместо Hth должна использоваться величина
Hth —HthQ.
**) Предложен акад. Б. С. Стечкиным.
108
Обозначим также
Як
и
(4.9)
Так как одновременно H/Hth = f]K.w, то получаем
Т]к е = Т1к.иТЫ1Л1т- (4-7)
Коэффициент г|з учитывает затрату дополнительной работы, обу-
словленную утечкой воздуха через радиальный зазор; коэффициент тц
учитывает трение диска и обода и коэффициент т],„ — механические по-
тери. Радиальный зазор, если нет бандажей или покрывных дисков (в
центробежных колесах), обусловливает еще перетекание газа поперек
лопаток со стороны высокого давления на сторону с низким давлением,
что вызывает дополнительные потери на вихреобразование и смешение,
учитываемые цк.и- Кроме того, в ступенях осевых компрессоров эти
перетекания вызывают изменение угла выхода потока в верхних сече-
ниях, что уменьшает теоретический напор.
Отсюда следует, что связь теоретического напора с внутренней ра-
ботой устанавливается зависимостью
= <4'8)
В осевых компрессорах дополнительно учитывается с помощью
коэффициента Q уменьшение теоретического напора из-за отклонения
действительных окружных составляющих скорости от расчетных вслед-
ствие влияния деформации поля скоростей перед колесом, радиального
зазора и других факторов. Тогда получаем
4.1.3. К.П.Д. КОМПРЕССОРА В ЗАВИСИМОСТИ ОТ ВИДА
ПОЛЕЗНОГО ЭФФЕКТА
Полезный эффект компрессора принято называть напором, под
которым понимается работа сжатия с учетом или без учета кинетической
энергии.
В зависимости от вида работы сжатия напоры и соответствующие
им к. п. д. могут быть политропические или адиабатические. Рассматри-
вая эти виды к. п. д., будем предполагать, что они являются внутрен-
ними, т. е. в качестве затраченной работы принимается полная работа
Нк, учитывающая все газодинамические потери. Поэтому все рассмотре-
ние относится в равной степени как к одноступенчатому, так и к много-
ступенчатому компрессору.
4.1. 3. 1. Политропический к. п. д.
Если в качестве напора взять политропическую работу сжатия по
статическим параметрам, то получим политропический к. п. д. в виде
К
( dp^
J V
^ = в-77~- (4.Ю)
109
Выражая политропическую работу сжатия и работу Нк через раз-
ность температур и предполагая, что отсутствует отвод тепла во внеш-
нюю среду, можем написать для постоянного показателя политропы:
---г^(Тк-Тк)
п — 1
k
'---R(TK-TB) + ~
k — 1
(4.Н)
Отсюда
В случае, если ск~св, получаем
И,
п — 1
(4. 12)
Таким образом, политропический к. п. д. будет зависеть только от
показателя политропы.
В табл. 4. 1 даны значения f]u по уравнению (4. 12) в зависимости
от величины п.
Таблица 4.1
п 1,4 1,5 1,6 1,7 1,8
1,0 0,858 0,764 0,695 0,644
Политропический к. п. д. с работой сжатия (напором) по статиче-
ским параметрам при ск=св может быть выражен и через степень повы-
шения давления. Так как
п
п — 1
то, следовательно,
1g —
Рв
Тк
1g ~
‘ в
Как правило, скорость на входе в компрессор (св) существенно
выше, чем на выходе (ск). Поэтому политропический внутренний к. п. д.
компрессора с напором по статическим параметрам [формула (4.11)]
имеет преувеличенное значение, особенно для компрессоров с малой
степенью повышения давления. В табл. 4.2 приведены значения поли-
тропического к. п. д. для различных степеней повышения давления по
статическим параметрам при п— 1,5; св=180 м/сек и ск= 120 м/сек.
110
Таблица 4.2
лк 1,5 2,0 з,о 4,0 6,0 10,0
* Як 1,33 1,765 2,62 3,475 5,18 8,57
п» 1,1 0,976 0,923 0,905 0,89 0,88
Из табл. 4.2 видно, что при малых степенях повышения давления
к. п. д. для принятых значений ск и св получается даже больше еди-
ницы. Избежать этой несообразности при применении напора по стати-
ческим параметрам возможно, если в знаменателе и при св¥=ск брать
только разность теплосодержаний по статическим температурам, т. е.
ь
Тъ). Это эквивалентно применению в качестве затраченной
работы величины Нк-----——, которая при св>ск больше действитель-
ной затраченной работы Нк.
В предыдущем разделе при рассмотрении процесса сжатия в ком-
прессоре в Т—s-диаграмме по статическим параметрам для величины
Нк ——применялось обозначение Нкх. В этом случае и при ск^св
к. п. д. будет выражаться уравнением
И =—— ---
v „_1/л—1
и, следовательно, не может быть больше единицы. Характерной осо-
бенностью этого к. п. д. является также то, что полезный эффект и за-
траченная работа (т. е. Нкх) целиком изображаются в диаграмме.
Поскольку в данном случае как числитель, так и знаменатель выра-
жены в статических параметрах, этот к. п. д. целесообразно называть
к. п. д. по статическим параметрам.
Когда в знаменателе применяется вся затраченная работа Нк, что
обычно и делается, то правильное представление о значении к. п. д.
можно получить, применяя в качестве напора величину
К
R
Величину Яюп принято называть полным политропиче-
ским напором. Он отличается от затраченной работы на величину
потерь Hvn = HK—Lr. Поэтому к. п. д. компрессора по полному
напору можно записать в виде
nvn = l-^-- (4.13)
Н к
В авиационной технике более употребителен политропический
к.п.д. по заторможенным параметрам
*
V
(4. 14)
111
Если политропическую работу сжатия по заторможенным парамет-
рам выразить с помощью показателя политропы п*, то при отсутствии
отвода тепла к. п. д. г]р* выразится следующим образом:
П* —-------------------
v ь
п
* 1
п — I
k
k — \
(4.15)
Таким образом, этот к. п. д. по форме идентичен к. п. д. по стати-
ческим параметрам при ск = св [см. формулу (4. 12)] или к. п. д. по стати-
ческим параметрам. Политропическая работа сжатия по параметрам
заторможенного потока отличается от затраченной работы на величину
условных потерь:
h*v=hk~l’r.
Следовательно, к. п. д. >]„* можно записать в виде
L*
n;=i-^-. (4.16)
Так как LR*>LR, то из сопоставления уравнений (4. 13) и (4. 16)
видно, что политропический к. п. д, по заторможенным параметрам будет
меньше к. п. д. по полным напорам. В табл. 4.3 даны для нескольких
як* значения к. п. д. по полным напорам и по заторможенным парамет-
рам при п—1,5; ск= 120 м!сек и св = 180 м/сек.
Таблица 4.3
лк 1,5 2,0 з,о 6,0 10,0
* як 1,33 1,765 2,62 5,18 8,57
'П® п 0,882 0,872 0,866 0,862 0,86
0,806 0,832 0,84 0,846 0,852
Как видно из табл. 4.3, различие между т]„* и т]гп уменьшается
по мере увеличения як*. Это следует из того, что с увеличением
(Тк—Тв) и Тк/Тв оба к. п. д. стремятся к = ~ .
k!{k— i)
4.1.3.2. Адиабатические к. п. д.
В авиационной технике наиболее часто применяются адиабатиче-
ские к. п. д., в которых в качестве полезного эффекта принимают адиа-
батические напоры. В зависимости от вида напора возможны и различ-
ные к. п. д.
Принимая в качестве полезного эффекта адиабатический напор по
статическим параметрам, получаем следующее выражение для внутрен-
него адиабатического к. п. д.:
112
При отсутствии отвода тепла этому к. п. д. можно придать следую-
щее выражение:
k—1
(4.17)
В случае, когда ск~св, получаем
й—1
(4.18)
Применение т]к по формуле (4.17) при существенном отличии в зна-
чениях ск и св нецелесообразно, так как этот к. п. д. будет иметь завы-
шенное значение и при малых лк может быть даже больше единицы
подобно политропическому к. п. д. с напором по статическим пара-
метрам. Поэтому такими к. п. д. при с^св не пользуются.
Если в качестве затраченной работы рассматривать только раз-
ность теплосодержаний по статическим температурам или соответст-
венно величину Нк--* - в~, обозначавшуюся ранее через Нкх, то адиа-
батический к. п. д. по статическим параметрам будет также иметь вид,
соответствующий уравнению (4.18). В этом случае полезный эффект
и затраченная работа (т. е. Нкх) целиком изображаются в Т—s-диа-
грамме, как установлено в предыдущем разделе для случая, когда от-
сутствует отвод тепла и не учитываются скорости на входе и на выходе.
Такой к.п.д. может быть назван к. п. д. п о статическим парамет-
р а м. Принимая в качестве полезного эффекта сумму адиабатической ра-
^2 _с 2
боты сжатия по статическим параметрам и величины ——2-, получим
адиабатический к. п. д. по полному напору
(аЛ \ 9 9
\ dp )|, Ск
J V I 2
1к.п=—---. (4.19)
Этот к. п. д. можно записать еще в виде
пк.п=1-^4г^- <4-20)
л к
Таким образом, в отличие от политропического к. п. д. по полному
напору, в адиабатическом к. п. д. по полному напору к числу потерь
относится и ДЯ.
В последние годы наибольшее распространение получил адиаба-
тический к.п.д. по заторможенным параметрам из-за
относительной простоты определения параметров заторможенного по-
тока и существенного упрощения расчетов двигателя:
(4.21)
113
При отсутствии отвода тепла этот к. п. д. можно записать так:
(4.22)
Таким образом, к. п. д. по параметрам заторможенного потока
имеет такой же вид, как и к. п. д. с напором по статическим парамет-
рам при ск~Св или когда, кроме напора по статическим параметрам
2 2
СК — Св
используется в качестве затраченной работы величина лк----------------
[уравнение (4.18)].
К. п. д. по полному напору немного выше к. п. д. по заторможенным
параметрам вследствие того, что значение полного адиабатического на-
пора больше адиабатической работы сжатия по заторможенным пара-
метрам. Действительно,
ТТ ____и I СК СЯ .
** ад.п пад । о >
н* =н.
ад <
Ск ач — св
2
Вычитая одно уравнение из другого, имеем
ад.п 77 ад
/?2 — с2
47 к с к. ад
так как
^к.ад <^. ^к’
ТО
^д.п>н:д.
Используя понятие о политропическом процессе по заторможенным
параметрам, можем этот к. п. д. записать еще в виде, аналогичном урав-
нению (4.20):
П*=1
4 + ДЯ*
(4. 23)
С помощью уравнения (4.22) можно установить связь между адиа-
батическим и политропическим к. п. д. по заторможенным параметрам,
так как
ft—1
п*—1 ’ ST
7к л*
—— = л — л ,
Следовательно.
П’
'к
й-1
» ft ,
Лк — 1
л*
(4. 24)
114
Когда л* = 1,0, то Л* = 0/0. Раскроем эту неопределенность обычным
путем:
d / г" , |
к /
limn; = lim-----------------Г =
<-i,o "к-*1'0 d I
--- 1 /
, » \ к-/
rfnK 4 '
Таким образом, при степенях повышения давления, мало отличаю-
щихся от единицы, разница между адиабатическим и политропическим
к. п. д. должна быть невелика.
В табл. 4.4 дано соотношение между адиабатическим и политропи-
ческим к. п. д. при различных лк* Для двух значений показателя поли-
тропы п*.
Таблица 4.4
* лк 1,0 1,2 1,5 2,0 4,0 6,0 10
(при п*=1,5) * 1,0 0,992 0,990 0,985 0,984 0,952 0,938
-Х(при л*=1,8) 1,0 0,991 0,971 0,945 0,888 0,853 0,812
Из табл. 4.4 видно, что разница между адиабатическим и политро-
пическим к. п. д. возрастает по мере увеличения лк*, а также при уве-
личении п*, т. е. с ростом потерь в компрессоре.
4. 1.3.3. Влияние теплоотвода на к.п.д.
Если при наличии теплоотвода определять адиабатический к. п. д.
по формуле (4.22), то он будет завышенным по сравнению с действи-
тельным значением, так как в затраченной работе не учитывается отвод
тепла. В частности, когда отводимое тепло будет равно теплу, эквива-
лентному потерям, то т]к* = 1Д так как в этом случае Гк* = 7'к.ад и, сле-
а- —i
довательно, Т'*1^*в=лк * • Чтобы при отводе тепла получить выра-
жение для к. п. д., характеризующего действительную эффективность,
надо затраченную работу Нк рассматривать с учетом отведенного тепла.
Запишем Нк в виде
где 7*'— температура заторможенного потока на выходе из компрессора
при отводе тепла;
Q9 — количество отведенного тепла.
115
Тогда адиабатический коэффициент полезного действия по пара-
метрам заторможенного потока запишется в виде
к Нк
cP(K-TfB) + Q9 ‘
(4. 25)
Если отведенное тепло будет равно теплу, эквивалентному работе,
затрачиваемой на потери, т. е. если Qq~LR, то и, следова-
тельно, получим
ч;=---------. (4.26)
1+'Ж.ад-71)
Поскольку применение формулы (4.22) при отводе тепла не дает
истинного значения к. п. д., то получаемый в этом случае к. п. д. следует
называть для отличия адиабатическим температурным, так как знаме-
натель учитывает только разность теплосодержаний, а не всю затра-
ченную работу.
В приведенных выше формулах для к. п. д. компрессора предпола-
галось, что теплоемкость воздуха (газа) в процессе сжатия остается по-
стоянной. Однако при больших степенях повышения давления, а также
при высокой температуре на входе (большие сверхзвуковые скорости
полета) изменение теплоемкости становится достаточно существенным.
В этих случаях целесообразно пользоваться i—s-диаграммой (или таб-
лицами) и определять к. п. д. с помощью значений энтальпий, получен-
ных из этих диаграмм и учитывающих изменение теплоемкости. В част-
ности, для адиабатического к. п. д. по заторможенным параметрам дол-
жно применяться выражение (см. рис. 3. 12)
•*
* 'к.ал гв ,л cyjx.
п к = —т»—— • (4. 27}
‘к в
При экспериментальном определении к. п. д., когда измеряется
температура торможения на выходе из компрессора и на входе в него,
а также степень повышения давления лк*, должно быть еще вычислено
i к.ал • Для этого вычисляется сначала энтропия, соответствующая I к.ад,
из соотношения
«(/*к.ад) = «(/в) + 1ёЛк, (4.28)
где
2,305/?
С помощью полученной энтропии находится либо температура Т к.ад
и затем 1к.зл , либо непосредственно г,*ад по i—s-диаграмме при извест-
ном давлении на выходе из компрессора.
4.2. КОЭФФИЦИЕНТЫ ПОЛЕЗНОГО ДЕЙСТВИЯ ТУРБИН
4.2.1. ОБЩЕЕ ПОНЯТИЕ О К. П. Д. ТУРБИНЫ
Коэффициент полезного действия турбины в общем случае может
быть записан как отношение полезного эффекта к располагаемой
энергии.
Для турбины в качестве полезного эффекта целесообразно прини-
мать в том или ином виде механическую работу. Однако, как показано
116
ниже, иногда встречается и другое содержание понятия о полезном
эффекте. Обозначая располагаемую энергию через Нр и полезный
эффект через На, запишем к. п. д. турбины в виде
л=-^. (4.29)
ир
Рассмотрим различные к. п. д. турбин в зависимости от различных
понятий На и Нр.
4.2.2. К. П.Д. ТУРБИНЫ В ЗАВИСИМОСТИ ОТ ВИДА
ПОЛЕЗНОГО ЭФФЕКТА
Если в качестве полезного эффекта ступени турбины принять тео-
ретическую работу, то получим к. п. д. ступени турбины в виде
Пт,и = ^-И. (4.30)
"р
Аналогично соответствующему к. п. д. компрессора этот к. п. д.
можно назвать лопаточным, так как он учитывает потери профильные и
вторичные, непосредственно связанные с обтеканием лопаток. Иногда
этот коэффициент полезного действия называется к. п. д. на ободе,
поскольку потери, имеющие место вне обода, в нем не учитываются.
Этот к. п. д. часто используется в расчетах ступеней турбин.
Если в качестве полезного эффекта принимать работу турбины на
валу (без учета механических потерь), то получим так называемый
внутренний к. п. д. турбины, учитывающий все газодинамические
потери:
Пт=-^. (4.31)
нр
Этот к. п. д. является основным при оценке эффективности как
отдельной ступени, так и многоступенчатой турбины. Если кроме газо-
динамических потерь учитывать также потери механические, то полу-
чим к. п. д., который можно назвать эффективным:
(4.32)
ир
Совершенно аналогично тому, как это было сделано для ступени
компрессора, можно и для ступени турбины внутренний или эффектив-
ный к. п. д. выразить в виде произведения частных коэффициентов:
VW/
(4. 33)
(4 34)
и
где
Я,,„-£3 G3 .
Н т.и GT
//Т.И Н3 Н ц
Нт.и ^*3 ^Т.И ^3
Коэффициент т)з учитывает уменьшение полезной работы турбины
из-за утечек газа через радиальный зазор. Как и применительно к сту-
пени компрессора, остальные потери, обусловленные этим зазором,
должны учитываться коэффициентом т]т.и.
117
Связь между теоретической и внутренней работой турбины будет
выражаться соотношением:
= (4.35)
Если учитывать уменьшение теоретической работы за счет факторов,
влияющих на отклонение действительных треугольников скоростей от
расчетных и оцениваемых коэффициентом Q (см. 2.3.4), то будем иметь
Н т
(4.36)
В дальнейшем применительно к турбине произведение -q3r|/Q обо-
значается через 6р.к. На расчетном режиме величина 6Р.К может прини-
маться равной 0,97—0,98.
Иногда в качестве полезного эффекта турбины принимают раз-
ность теплосодержаний по статическим температурам на входе в тур-
бину и на выходе из нее. В соответствии с уравнением энергии (2.69)
эта разность теплосодержаний связана с работой турбины и скоростями
на входе и на выходе соотношением
ср(Тг-Тг)=Нг
(^)
2
Следовательно, внутренний к. п. д. турбины при таком понятии
о полезном эффекте будет иметь вид
я
Пт=-----—2— • (4.37)
Яр
Таким образом, полезный эффект в этом к. п. д. включает не только
работу на валу, но и кинетическую энергию выходной скорости. Этот
вид к. п. д. в дальнейшем назван к. п. д. по статическим тепло-
перепадам, так как в нем располагаемая энергия тоже выражается
в виде разности теплосодержаний по статическим температурам. Этот
к. п. д. может представлять известный интерес тем, что он непосред-
ственно характеризует потери в проточной части.
Часто на входе в турбину рассматриваются параметры заторможен-
ного потока, тогда уравнение (4.37) будет иметь вид
(<?д
^т+ —
Пт =----(4.38)
Яр
Этот к. п. д. также будет называться к. п. д. по статическим теп-
лоперепадам.
4.2.3. К.П.Д. ТУРБИНЫ В ЗАВИСИМОСТИ ОТ ВИДА
РАСПОЛАГАЕМОЙ энергии
В зависимости от вида располагаемой энергии к. п. д. турбины мо-
гут быть политропические и адиабатические. В первом случае в качестве
располагаемой энергии принимается политропическая работа расшире-
ния, а во втором — адиабатическая работа расширения.
Как уже отмечалось, часто на входе в турбину принимаются пара-
метры, соответствующие заторможенному потоку. На выходе же из тур-
бины рассматриваются как статические, так и заторможенные пара-
метры. В последнем случае соответствующие к. п. д. называют к. п. д.
118
по заторможенным параметрам. В последующем изложении
будем рассматривать только внутренние к. п. д., учитывающие все газо-
динамические потери, и поэтому к. п. д., отличающиеся по виду распо-
лагаемой энергии, будут в равной мере относиться как к одноступенча-
той, так и к многоступенчатой турбинам.
4.2.3.1. Политропические к. п. д.
Эти к. п. д. в расчетах турбин применяется относительно редко.
Поэтому ограничимся рассмотрением только внутреннего политропиче-
ского к. п. д. по параметрам заторможенного потока. Общее выражение
для этого к. п. д. будет
(4. 39)
Если в формуле (4.39) заменить
п
и
то получим
(4. 40)
Таким образом, этот вид к. п. д. турбины, как и соответствующий
к. п. д. компрессора, зависит только от значений k и п*.
Для современных значений температуры газа перед турбиной пока-
затель адиабаты k для процесса расширения можно принять в среднем
равным 1,33. Среднее значение показателя политропы п*=1,29. Для
этих данных т)от =0,9.
4.2.3.2. Адиабатические к. п. д.
Если в качестве полезного эффекта принять внутреннюю работу
турбины, а в качестве располагаемой энергии — адиабатическую работу
расширения при заторможенных параметрах на входе и на выходе, то
получим внутренний адиабатический к. п. д. по параметрам затормо-
женного потока, выражение для которого будет иметь вид
(4.41)
Подставив
Н^с^Г-Г^,
119
получим
/ т* \
т*—т* 1 — \ Т* /
п* = г т — 4 г
’Т р*_____р* -I
1 г 1 т.ад 1 1
1 — ft-1
(4.42)
где л*=р*[р* — степень понижения давления в турбине по параметрам
заторможенного потока.
Если применить показатель политропы расширения по параметрам
заторможенного потока, то этот к. п. д. может быть записан только через
степень понижения давления:
(4.43)
С k
В табл. 4.5 даны значения этого к. п. д. в зависимости от лт* при
к= 1,33 и п* = 1,29.
Таблица 4.5
Ж Лт 2,0 4,0 6,0 8,0 10
ж п, 0,91 0,915 0,918 0,922 0,925
Как следует из табл. 4.5, к. п. д. турбины по параметрам затормо-
женного потока при постоянном значении п* относительно мало зави-
сит от лт*.
Если в качестве располагаемой энергии принять адиабатическую
работу расширения, определяя ее по статическому давлению и темпе-
ратуре на выходе из турбины, то получим следующий к. п. д.:
(4. 44)
где лт = р*//7т—степень понижения давления в турбине от полного дав-
ления на входе до статического давления на выходе.
Этот коэффициент полезного действия турбины может называться
внутренним адиабатическим к. п. д. по статическим
параметрам на выходе. Часто его сокращенно называют мощ-
ностной к. п. д. Однако это наименование не является строгим, так
как к. п. д. по заторможенным параметрам также является мощностным,
поскольку и в нем в качестве полезного эффекта принимается работа
на валу, соответствующая мощности, получаемой от 1 кг газа.
120
В соответствии с уравнением (4.38) адиабатический к. п. д. тур-
бины по статическим теплоперепадам имеет вид
(4. 45)
Лт.ад н т* Т 1
2 2 т.ад 1 г — 1 т.аД 1 —
Лт
В этом случае как в числитель, так и в знаменатель входит статиче-
ская температура на выходе из турбины в действительном или в адиа-
батическом процессах.
Чтобы объяснить различие между рассмотренными видами внутрен-
них к. п. д. по их физическому смыслу, целесообразно выразить все
к. п. д., введя в их уравнения потери.
Так, учитывая уравнения (4.45) и (2.90), адиабатический к. п. д.
по статическим теплоперепадам можно записать в виде
т.ад 22 т.ад п т.ад
где
kfl, L3 L3—Д//3; Lf = Lf — bJif,
или
Лт.ал = 1-^- (4.46)
Н т.ад
где 2сумма всех газодинамических потерь, включая и потери,
обусловленные радиальным зазором, а также трением диска
и обода.
Таким образом, к. п. д. по статическим теплоперепадам непосред-
ственно учитывает все газодинамические потери в турбине. Если анало-
гично рассмотреть мощностной к. п. д., то получим
н 2
Т1т=------=-----------------=1------------
^т.ал ^т.ад ^Тт.ад
Следовательно, в отличие от к. п. д. по статическим теплоперепадам
этот к. п. д. характеризуется тем, что кинетическая энергия выходной
скорости в нем относится к потерям.
В тех случаях, когда энергия выходной скорости после турбины не
используется, применение такого к. п. д. является правомерным. (Напри-
мер, стационарные турбины, турбины привода агрегатов и др.) В газо-
турбинных авиационных двигателях скорость после турбины исполь-
зуется в реактивном сопле, и поэтому в расчетах ГТД чаще всего при-
меняется к. п. д. по заторможенным параметрам. Используя уравнение
(3.39), этот к. п. д. можно записать в виде
л:
ад-< , LR
<ад
(4.48)
Таким образом, этот к. п. д. выражается аналогично к. п. д. по ста-
тическим теплоперепадам, если в формулу (4.48) включить условные
потери, введенные выше при рассмотрении процесса работы турбины
по заторможенным параметрам. Эти потери можно связать с действи-
121
тельными потерями следующим соотношением исходя из выражений для
работы турбины:
//_ =//т ад — AL — —Т-; Н=н* — L*'
т т.ад 2 т т.ад /? ’
откуда с2 H,a.-L’ - = Н* -L*' т*ад R 2 т.ад R
Так как lj* т_1 т.ад П т.ал Пт.ад g ,
то получаем 2 2 Ад ^r + 2 . (4.49)
Таким образом, условные потери Lr отличаются от действительных
потерь Lr' на величину разности кинетических энергий, соответствую-
щих действительной и адиабатической скоростям на выходе из турбины.
Рассматривая выражения для трех к. п. д. турбин, нетрудно
видеть, что
1I .оД Т 1
Только в пределе, когда ст—-0, все к. п. д. будут совпадать по величине.
Если пренебречь различием между ст.ад и ст, то коэффициенты по-
лезного действия Цт.ад, т|т и Т)т* можно связать между собой простым
соотношением.
Запишем выражение для т]т* в виде
Учтя также выражения для т]т.ад и т]т и произведя преобразования,
получим !-Пт
или <==r-r2h—г- (4-51) 1 — (Пт.ад — Пт)
Из этих соотношений следует, что можно произвольно принимать значе-
ния только для двух из рассмотренных к. п. д. Третий же к. п. д. дол-
жен при этом иметь вполне определенное значение. Так, например, если
принять -qT* = 0,9 и т]ад=О,92, то т]т=0,72. Увеличение т]т.ад при зафикси-
рованном значении т]т* приводит к резкому уменьшению г]т. Так, на-
пример, если г|т*=0,9 и т]т.ад=0,94, то г)т = 0,54. Такое изменение есте-
ственно, ибо рост т]т.ад при неизменном -qT* является следствием увели-
чения выходной скорости ст, что и приводит к снижению мощностного
К. П. Д.
В заключение покажем, как изображаются рассмотренные к. п. д.
газовых турбин с помощью I—«-диаграммы.
122
Так, к. п. д. по статическим теплоперепадам изобразится отноше-
нием (см. рис. 3. 19).
Лт.ад = 77
“т.ад
мощностной к. п. д.
Я.*
т «г—*Т
Пт 77 ~’
“ т.аД 1г ^т.аД
к. п. д. по параметрам заторможенного потока
Лт
п т.ад
.» .»
I —I
г *т
"7* ". '
Ч.ад
Так как значения tr*, /т*, г*.ад берутся обычно из i—s-диаграмм
(или таблиц), составленных с учетом зависимости теплоемкости от тем-
пературы для газа данного состава, то в этом случае получаемые к. п. д.
турбин будут учитывать влияние переменной теплоемкости и состава
газа в отличие от к. п. д., определяемых по уравнениям (4.42)—-(4.45).
При использовании i—s- и Т—s-диаграмм связь степени понижения дав-
ления в турбине с энтропией устанавливается зависимостью
S (f г) — S (г Т.ад) =
где
— $
5 =--------.
2,305R
При расчетах турбины, когда известны лт* и температура газа перед
турбиной, эта зависимость используется для определения энтропии,
соответствующей энтальпии I*ад , т. е. s(t*at ), и затем температуры
Т*л по Т—s-диаграмме (или таблицам) и величины г*ад. Можно опре-
делять г*ад и минуя нахождение температуры, если воспользоваться
i—s-диаграммой при известных значениях s(i*aa) и рт*. Аналогично
поступают, если при экспериментальном определении к. п. д. турбины
измеряется температура торможения газа на входе в турбину и степень
понижения давления. Для определения к. п. д. требуется еще измерять
температуру торможения на выходе из турбины и по ней находить зна-
чение iT* или же измерять работу турбины Нт по крутящему моменту
на валу, числу оборотов и расходу газа.
4.3. СВЯЗЬ МЕЖДУ К. П. Д.
МНОГОСТУПЕНЧАТОЙ ЛОПАТОЧНОЙ МАШИНЫ
И ОТДЕЛЬНЫХ ЕЕ СТУПЕНЕЙ
Все изложенное выше, относящееся к внутреннему к. п. д. компрес-
соров и турбин, в равной степени справедливо как для многоступенча-
тых, так и для одноступенчатых машин. Однако полезно рассмотреть
еще связь между к. п. д. многоступенчатой лопаточной машины и ее
отдельных ступеней, которую требуется учитывать при расчетах много-
ступенчатых машин. Хотя эта связь в компрессорах и турбинах имеет
много общего, из методических соображений целесообразно рассмотреть
отдельно каждый из этих типов машин.
123
4.3.1. МНОГОСТУПЕНЧАТЫЙ КОМПРЕССОР
Связь между к. п. д. многоступенчатого компрессора и отдельных
его ступеней существенно зависит от того, политропические или адиа-
батические напоры принимаются в качестве полезного эффекта ком-
прессора и, соответственно, рассматриваются ли политропические или
адиабатические внутренние к. п. д.
Рассмотрим сначала случай, когда принимаются политропические
напоры и к. п. д. Воспользуемся р—п-диаграммой и изобразим на ней
политропическую работу сжатия многоступенчатой машины, состоящей
из z ступеней. Обозначим пара-
метры перед компрессором, как
и ранее, буквой в, а на выходе
буквой z, а не буквой к, как обо-
значалось выше.
Соответственно политропиче-
ская работа сжатия всего ком-
прессора изобразится площадью
в—z—аг—аъ—в (рис. 4.1). Эта
Рис. 4. 1. Изображение в р—«-диаграмме
политропической работы многоступенчатого
компрессора
работа сжатия может соответст-
вовать статическим или затормо-
женным параметрам в зависимо-
сти от того, какие параметры
рассматриваются на входе и на
выходе. Будем в дальнейшем рас-
сматривать заторможенные пара-
метры и соответствующую им работу сжатия, поскольку к. п. д. по за-
торможенным параметрам является наиболее принятым. Участки поли-
тропы сжатия, соответствующие параметрам на выходе из отдельных
ступеней, обозначим цифрами 1, 2, 3,..., (z—1), z. Соответственно ра-
боты сжатия в отдельных ступенях изобразятся площадями
//vi=(b —1 — ах — а.л — в); /У^2=(1 — 2 — а2—аг — 1);
. . H*vz=[(z— 1) — z — аг — az^ — (z — 1)].
Обозначая работу сжатия всего компрессора через Hv*, имеем из
р—^-диаграммы
H*v=H*vl + H*v2 + Hl3+ . - +Я;2, (4.52)
или
И-53)
Таким образом, политропическая работа сжатия многоступенча-
того компрессора равна сумме политропических работ отдельных сту-
пеней. Очевидно, что это останется справедливым и для случая, когда
рассматривается работа сжатия по статическим параметрам. Наряду
с уравнением (4.53) должно, очевидно, соблюдаться условие, что ра-
бота, затраченная на весь компрессор, равна сумме работ, затраченных
на отдельные ступени, т. е.
HK=HKi + HB2+ + HKZ.
124
Заменяя затраченные работы через политропические напоры и соот-
ветствующие им к. п. д., получим
/у; _ я;2 н\г
* * ~I’ * | • • • | ' * Э
^2
откуда имеем
(4.54)
%1
Из этого соотношения, в частности, следует, что при равенстве
к. п. -д. во всех ступенях получаем
Так как политропический к. п. д. выражается уравнением —
ц* / k
=------ -----, то, следовательно, при одинаковых во всех ступенях к. п. д.
п* — 1 / k — 1
показатель политропы сжатия для всего компрессора и для отдельных
ступеней будет одним и тем же.
Условие п* = const иногда принимается в расчетах многоступенчатых
осевых компрессоров, что достаточно удовлетворительно соответствует
действительности.
При п* = const степень повышения давления в m-й ступени будет
равна
п *
/ г’
I т I
л = I —*--
т \ т /
> 1
Отношение температур может быть выражено через напор ступени:
Т н
1 т път ।
__ __ 1 #
т-1 п* V я*
1
Следовательно,
*
л
(4. 55)
Если во всех ступенях Я*. = const, то степень повышения давления
в m-й ступени можно выразить через степень повышения давления
в первой ступени.
В этом случае
125
Принимая во внимание, что
получим
(4. 56)
Когда т—\, то лт* = Л1*, а если т-^оо, то Таким образом, при
одинаковых значениях напора в каждой ступени степень повышения дав-
ления в последующих ступенях уменьшается. Если во всех ступенях бу-
дет одинаковая степень повышения давления, то напор в последующих
ступенях должен возрастать по закону геометрической прогрессии.
Действительно, в этом случае
п
п — 1
*
п
п — 1
-^-=л*п* = const
Тт-1 ‘
(4.57)
или
Hvm = A"1""1
где
п -1
yt=COnSt=Jl;
Когда для многоступенчатого компрессора и для отдельных его сту-
пеней принимается в качестве напора адиабатическая работа сжатия,
Рис. 4. 2. Изображение в р—и-диаграмме адиа-
батической работы многоступенчатого ком-
прессора
то связь между напором и
к. п. д. всего компрессора и от-
дельных его ступеней будет
более сложной. В р—и-диа-
грамме адиабатический напор
компрессора, имеющего z сту-
пеней, изобразится площадью
в—гая—az—ав—в (рис. 4.2),
где линия в—гад — адиабата,
соответствующая непрерывно-
му адиабатическому сжатию от
давления рв* до давления pz*.
С этой линией совпадает только
адиабата первой ступени, у ко-
торой начальный объем vB со-
ответствует начальному объему
адиабаты в—zan, в последую-
щих же ступенях начальными объемами для линий адиабатического
сжатия являются объемы vlt v2 и т. д., соответствующие точкам 1, 2 и т. д.
линии действительного (политропического) процесса сжатия. Поскольку
126
эти объемы больше объемов, соответствующих адиабате в—гая (напри-
мер, объем v2>v2"), то линии адиабатического сжатия для всех ступе-
ней, кроме первой, проходят на рис. 4.2 правее адиабаты в—zaK. Адиаба-
тические напоры ступеней выразятся соответственно: А7ад1 = площади
(в— Г — а, — ав— в); //^ — площади (1— 2'—а2——1) и т. д. При
этом непосредственно из диаграммы видно, что сумма адиабатических
напоров отдельных ступеней больше напора, соответствующего адиа-
бате в—гад. Таким образом, если обозначить этот напор через Н*л, то
очевидным является неравенство
Z
(4.58)
1
Исходя из равенства работы, затрачиваемой на
и суммы работ, затрачиваемых на отдельные ступени,
весь компрессор,
получаем
"ал __"а*д1 , <2
* * I *
Пк Чк! Пкг
"ал.
‘ ад i
*
Лк/
(4. 59)
где Нк — работа, затрачиваемая на весь компрессор;
Л/1Д; Лк —адиабатический напор и к. п. д. всего компрессора;
ал/! Лк/ — то же для отдельных ступеней.
Из уравнения (4.59) получаем
"ал
LH^i
</
(4. 60)
Если принять, что для
всех ступеней т)*;. — const, то будем иметь
nK
(4.61)
Так как Н* <у Я* .
ад 2-J ад »
Таким образом, адиабатический к.п.д. многоступенчатого компрес-
сора меньше к. п. д. отдельной ступени, если последние во всех ступе-
нях одинаковы. Аналогичный вывод можно получить, если при перемен-
ных напорах и к. п. д. в ступенях принять их средние значения. В общем
случае к. п. д. многоступенчатого компрессора должен определяться
с помощью уравнения (4.60).
Если при решении этого уравнения заданными будут являться число
ступеней, их адиабатические напоры и к. п. д., то предварительно следует
вычислить суммарный адиабатический напор с помощью уравнения
/ fe—1
где л* —общая степень повышения давления.
Нк
Z
1
, то и
♦
п < п ..
’к * 'к f
127
Значение л* в данном случае не является независимой величиной,
а должно вычисляться с помощью заданных значений Я* и г)* ., исходя
из следующих соотношений:
(4.62)
где л* , л* . . . л* —степени повышения давления в отдельных сту-
К1 ’ К-^ К Z J
пенях.
Значения л*р л*2, . . . л*г являются функциями напора и к. п. д.
данной и предшествующей ступеней. Например, для m-ой ступени мо-
жем написать
k
---------------------h 1 \ - (4. 63)
1 /
Если будут заданы значения //* л* и z, то для вычисления общего
к. п. д. компрессора должны быть предварительно найдены путем под-
бора значения Л/*дг и ц*., исходя из известных принципов распреде-
ления напоров по ступеням многоступенчатого компрессора и статисти-
ческих данных по к. п. д. ступеней, обеспечивая при этом получение
заданного л*.
Наконец, если при решении уравнения (4. 60) заданными будут зна-
чения 7)к,-, а также Н&л (и, следовательно, лк* при известном Тв*),
то предварительно должно быть определено число ступеней. Для этого
вычисляются с помощью соотношения (4.63) значения л* z в отдельных
ступенях, начиная с первой, и путем последовательного перемножения
находится число ступеней, обеспечивающее заданную общую степень
повышения давления.
Иллюстрируем примером последний случай для условия, когда
во всех ступенях значения Дадг и т]кг- одинаковы. Уравнение (4.60)
тогда примет вид
п
1 аД
гпак1
ц* ..
'К I
(4. 64)
Обозначив ----ZJ_L_
k »
С, из выражения (4.63) находим
(4. 65)
Величину С можно выразить через степень повышения давления
в первой ступени. Действительно,
С
k—i
k
-1
k-Л в
где Лк1 — степень повышения давления в первой ступени.
128
Следовательно, степень повышения давления в любой т-й ступени
может быть выражена как функция ад
к
(4. 66)
Воспользовавшись этими формулами, определим адиабатический к. п. д. много-
ступенчатого компрессора, имеющего при ТВ*=288°К степень повышения давления
Лк*=6,0. Примем, что Я*д;=29 700 дж!кг. Тогда при 7’В* = 288:,К nK)*=l,4. Зададимся
к. п. д. ступени т]*; =0,85. Применяя формулу (4.66), находим:
л*2= 1,352 и р- * = 1,893;
у3 = 1,318 и ®г* = 2,495;
<4= 1,293 И 4 * = 3,225;
,^5= 1,267 и 5 * 1як = 4,08;
<6=1 >238 и 6-* 1 лк = 5,05;
т*7= 1,226 и 7 * 14 = 6,19.
Следовательно, при z=7,0 степень повышения давления достаточно близко соот-
ветствует заданной. При большем различии необходимо было бы решать задачу путем
подбора величины Нл:[1 (или лк1 ). Если принять z=7 и лк*=6,19, то, воспользовав-
шись уравнением (4.64), можем вычислить к. п. д. всего компрессора:
1
* * k 1
* * 7/ял * ЛК 1
Пк = Пк I —— = Чк I —--------Го-----— =
гни1 ( * — ,)
-1/
. 6,19°-286—1
— 0,8а 70(4О,286 _ °’818'
Таким образом, к. п. д. всего компрессора приблизительно на 3—4°/о меньше
к. п. д. отдельной ступени.
Изложенное показывает, что связь между адиабатическими к.п.д. все-
го компрессора и к.п.д. его отдельных ступеней устанавливается зави-
симостями, требующими для решения, как правило, подбора отдельных
величин даже в простейших случаях, когда во всех ступенях
и ,• являются одинаковыми. В отдельных исследованиях по данному
вопросу даются приближенные соотношения между г>к и гк;.
Весьма удобными для употребления являются формулы, получен-
ные с помощью метода эквивалентной политропы, разработанного авто-
ром. Сущность этого метода состоит в следующем. Изобразим в Т—s-
диаграмме процесс сжатия в многоступенчатом компрессоре, пренебре-
гая отводом тепла. Как и ранее, принимаем значения давления и темпе-
ратуры, соответствующими полному торможению скорости. Отметим
также, что все выводы и формулы будут полностью применимы и при
использовании статических давлений и температур для адиабатического
напора и затраченной работы. Последняя должна при этом рассматри-
5 546
129
ваться в виде разности теплосодержаний по статическим температурам
или соответственно в виде величины
с2 — с2
ьк св
к
2
Обозначим (рис. 4. 3) точки, соответствующие адиабатической тем-
пературе воздуха на выходе из ступеней через Г, 2',..., г', а точки, со-
ответствующие действительной температуре, — через 1, 2, ..., z. Процесс
изменения состояния на линиях Г—1; 2'-—2 и т. д. предполагается изо-
Рис. 4. 3. Эквивалентная поли-
тропа сжатия для многоступенча-
того компрессора в Т—s-диа-
грамме
барическим.
Адиабатическое непрерывное сжатие
от давления рв* до давления рг* изобра-
зится линией в—-гад, а политропический
процесс сжатия линией в—г. Заменим
ступенчатый процесс в—Г—1—2'—...
... — (г—1)—г' некоторым плавным про-
цессом в—г'. Этот процесс, протекающий
с подводом тепла, очевидно, можно рас-
сматривать как некоторый политропиче-
ский процесс, имеющий в общем случае
переменный показатель. Примем, что но-
вый процесс энергетически эквивалентен
исходному (ступенчатому) и назовем его
эквивалентным политропическим про-
цессом.
Полная энергия, соответствующая
исходному процессу, очевидно, равна
М4- - т!) = 2 н:я: + 24/; (4.67)
1 1
Z—1
где 2 — тепло, подведенное на участках Г — 1; 2' — 2;...; (г— 1)'—
1 — (г—1) в виде суммы
Если обозначить работу сжатия, соответствующую эквивалентному
политропическому процессу, через H*v и принять, что подведенное в
S'—1
этом процессе тепло также равно т0 очевидно, что для него
1
уравнение энергии запишется в следующем виде:
ср - 7-;) =7/4+ 2^-- <4- 68>
1
Так как полная энергия и подведенное тепло в обоих случаях оди-
наковы, то, приравнивая правые части уравнений (4.67) и (4.68), по-
лучим
2^а«/=77^. (4.69)
1
Положение точки г', характеризующей адиабатическую температу-
ру на выходе из последней ступени, а также температуру в конце экви-
валентного политропического сжатия, является функцией числа ступеней
и распределения в них работы сжатия и потерь. Когда число ступеней
компрессора z = 1,0, то точка z' совпадает с точкой гад. В этом случае
z—1
^iLRl =0 и эквивалентная политропа совпадает с адиабатой в—гад.
1
130
При безграничном увеличении числа ступеней точка z' приближает-
ся к точке z, а эквивалентный политропический процесс — к действи-
тельному, характеризуемому линией в—z.
В пределе, когда z=oo, оба политропических процесса (эквивалент-
ный и действительный) совпадают.
Политропический к.п.д., соответствующий работе Н 3V, очевидно, вы-
разится уравнением
* __
где Нк — полная работа, затраченная в компрессоре и выражающаяся
в Т—s-диаграмме площадью z—а—б—с—г.
Так как
то, используя формулу (4.69), можем уравнение для цэг, привести к
виду
(4.70)
Исходя из равенства полной работы, затрачиваемой в компрессоре,
как в действительном процессе, так и при эквивалентном политропичес-
ком сжатии, можно написать
Лк I
У
л,
где т]v — некоторый к.п.д., соответствующий равенству затрачиваемой
работы в обоих процессах.
Из этого уравнения находим
ад i
= ---~
VI
ЛК(-
Z *
S''aaj
Л* i
(4-71)
Используя величины H3V
писать следующим образом:
и г],, можем уравнение (4.60) для т]к за-
* ад
Г!к = ^771-
V
(4. 72)
5*
131
Если с некоторым приближением принять, что показатель эквива-
лентной политропы на всем участке между точками виз' величина по-
стоянная, то уравнение (4. 72) можно привести к виду
(4.73)
где Лк = р*/рв — общая степень повышения давления в компрессоре;
«' — показатель эквивалентного политропического сжатия.
Величина «' связана с показателем k выражением ——-=
T1 -----
k-1
Используя эту зависимость вместо уравнения (4.73), получим
*
Пк= —
а—1
-1
fe—1
ТГ KTI ---- 1
К Э V
(4. 74)
Как показывают расчеты, уравнение (4.74) дает значения т]к, от-
личающиеся от действительных не более чем на 1-н2°/о в большом диа-
пазоне изменения и z. Точность этого уравнения немного понижается
только в случае весьма большого различия между напорами и к.п.д. в
отдельных ступенях компрессора.
Применение метода эквивалентной политропы значительно упрощает
определение к.п.д., подбор числа ступеней и решение некоторых других
вопросов, относящихся к многоступенчатому компрессору. Для примера
рассмотрим сначала наиболее простой случай, когда во всех ступенях
/У*л / =const и т]к / “Const. Из уравнений (4.70) и (4.71) получаем
ад i
гг*
“ад i
Z ---—
’Ik i
Уравнение для т>к можем записать в виде
(4. 75)
(4. 76)
(4. 77)
*
*
где пэ у — определяется из уравнения (4.76).
Таким образом, если заданы Як, v*Ki и г, то с помощью уравнений
(4. 77) и (4. 76) легко определить т]к.
Так, для рассмотренного выше примера, когда было задано л* =6,0 и г|*; =0,85,
можно сразу определить к. п. д. всего компрессора, принимая то или другое число
ступеней.
а 32
Например, при г=7 получаем
*
¥<Э V
7-0,85
7—14- 0,85
0,87;
, б0’286 - 1
т]к —0,85 , 0/286
0,87\6°’87 — 1
= 0,814.
Исходя из равенства работ находим: при 7’В*=288Р К
откуда
1005-288 (б0,286 — 1 )
0,814-7
Z Ок I
k *
= 34 100 дж/кг ,
34100-0,85
1005-288
Так же просто может быть произведен расчет и для другого числа ступеней.
Рис. 4. 4. Зависимость т;к/Пк г от числа ступеней
Следует отметить, что для заданных значений л^ и 1%-,- с ростом
числа ступеней отношение Ок/Ок/, а следовательно, и т]к, уменьшают-
ся. На рис. 4.4 показано изменение Ок/Окг в зависимости от z при
различных для т)*;=0,8. С ростом z величина т]к асимптотически
приближается к предельному значению, соответствующему условию
,г = схэ; в этом случае = и формула для т]к получит вид
-. (4. 78)
1
Нетрудно видеть, что эта формула идентична уравнению (4.24),
связывающему между собой адиабатический и политропический к.п.д.
Такое соответствие является закономерным, так как при z = oo эквива-
лентная политропа совпадает с действительной и к.п.д. ступени г] к i бу-
дет являться политропическим к.п.д. ступени и всего компрессора.
Применение формулы (4. 78) при конечном числе ступеней связано
с известной ошибкой, более существенной при высоконапорных ступе-
нях и пониженных к.п.д.
133
Так как к.п.д. ступени компрессора зависит от ее напора, то полу-
чить постоянное значение к.п.д. ступени для всех лк и г, приведенных на
рис. 4. 4, невозможно, ввиду того что напор ступеней будет при этом из-
меняться в больших пределах. Поэтому при решении задач, рассмотрен-
ных в предыдущем примере, необходимо для заданных значений лк и
рк i произвести вычисления для нескольких чисел ступеней с целью со-
гласовать значения т]к i и напор каждой ступени.
Реально, в многоступенчатом осевом компрессоре напор и к.п.д.
каждой ступени различны, а заданными, как правило, являются общая
степень повышения давления и к.п.д. всего компрессора и, следовательно,
при определенных внешних условиях известной является суммарная за-
траченная работа Нк.
Распределение общей затраченной работы по ступеням и изменение
к.п.д. ступеней производятся исходя из соображений, изложенных ни-
же, в разделе «Осевые компрессоры». Метод эквивалентной политропы
облегчает и в этом случае согласование к.п.д, ступеней и всего комп-
рессора.
Из уравнения (4. 74) получаем
Логарифмируя, находим выражение для политропического к.п.д.
соответствующего эквивалентному политропическому процессу:
(4. 79)
lgI 1 + *
Tj9 v
Отношение ть/Пэт- можно выразить в виде функции к.п.д. и затра-
ченной работы в последней ступени. С этой целью воспользуемся общи-
ми выражениями (4.70) и (4.71) для т], и ц’„. После преобразований
получаем
(4.80)
Если задаться значениями затраченной работы и к.п.д. последней сту-
пени, то можно вычислить отношение г],/т]эт» из уравнения (4.80), опре-
делить т)э v из уравнения (4.79) и затем найти т^. Отметим, что даже
при существенном изменении ркz (~ 10%) величина гр, определяющая
результаты расчета согласования к.п.д. ступеней, изменяется весьма ма-
ло (^0,5%). Это объясняется тем, что с ростом ijKz увеличивается отно-
шение но одновременно уменьшается Поэтому некоторый
произвол при выборе т)Кг относительно мало влияет на результаты рас-
чета.
Затраченные работы в отдельных ступенях должны подчиняться ус-
ловию

134
Значения к.п.д. отдельных ступеней должны удовлетворять уравне-
нию
Z
1
2 Мк1
1
Яэ р
(4.81)
При известных значениях Нк, Як i и это уравнение должно ре-
шаться путем подбора к.п.д. отдельных ступеней.
Известные значения Нк { и г]к t позволяют определить степени по-
вышения давления в отдельных ступенях по уравнению (4. 63). Точность
всех расчетов контролируется с помощью соотношения
4.3.2. МНОГОСТУПЕНЧАТАЯ ТУРБИНА
Если для многоступенчатой турбины и для ее отдельных ступеней
принимать в качестве располагаемой энергии политропическую работу
расширения и соответственно рассматривать политропический к.п.д., то
аналогично тому, как было показано для многоступенчатого компрессо-
ра, получим
1
и при Т1* .=const
г Т I
2 Т i Т i
П* =_!-----------
I# т Ш*
П V Т
’Лет ь
где Нот и — политропические работы расширения всей турбины
и отдельных ее ступеней по заторможенным пара-
метрам;
и t}*tZ —политропические к. п. д. всей турбины и отдельных
ее ступеней по заторможенным параметрам.
В связи с тем, что поли-
тропические к. п. д. приме-
няются в расчетах турбин
редко, рассмотрим более по-
дробно случай, когда в каче-
стве располагаемой энергии
принимается адиабатическая
работа расширения и соответ-
ствующие ей к. п. д. Условимся
и в данном случае рассматри-
вать заторможенные парамет-
Рис. 4.5 Изображение в р—и-диа-
грамме адиабатического процесса
расширения в многоступенчатой тур-
бине
ры, но все выводы будут при-
годны и для случая статиче-
ских параметров.
В р—о-диаграмме адиа-
батическая работа расширения
турбины, имеющей z ступеней, изобразится площадью г—гад—az—ат—г
(рис 4.5), где линия г—гал — адиабата, соответствующая непрерывному
адиабатическому расширению от давления рг* до давления pz*. С этой
линией совпадает только адиабата первой ступени, у которой началь-
135
ный удельный объем уг соответствует начальному удельному объему
адиабаты г—год.
В последующих ступенях начальными объемами для линий адиаба-
тического сжатия являются объемы v2, ..vz, соответствующие точ-
кам 1, 2, ..z,—линии действительного (политропического) процесса
расширения. Поскольку эти объемы больше объемов, соответствующих
адиабате г—дад, то линии адиабатического расширения для всех ступе-
ней, кроме первой, проходят правее на рис. 4. 5 адиабаты г—2ад. Адиа-
батические работы расширения ступеней выразятся соответственно пло-
щадями (г— Г— аг — аг — г) = /7т.ад,, (7— 2'~а2— ar — и т. д.
При этом непосредственно из диаграммы видно, что сумма адиа-
батических работ расширения отдельных ступеней больше адиабатиче-
ской работы, соответствующей адиабате г—гад. Таким образом, если
обозначить эту работу расширения через Ят.ад , то, очевидно, будем
иметь
/7*.ад< ^т.ад/. (4.82)
1
Следовательно, соотношение между адиабатическими работами рас-
ширения всей турбины и ее ступеней аналогично полученному ранее со-
отношению между адиабатическими работами сжатия (напорами) всего
многоступенчатого компрессора и его отдельных ступеней.
Суммарная внутренняя работа всей турбины будет, очевидно, равна
сумме внутренних работ ступеней, т. е.
/7Т=77т 1 + 77Т2Ч~ ••• +77тг.
Заменяя значения внутренних работ с помощью адиабатических ра-
бот расширения и коэффициентов полезного действия, получим
Z
f f* * f г* * I г г* ♦ . I у у * * I *
77т.адТ]т== Т7т>ад1 Т]т1-|- /7т,ад2Рт2 "г • • • “Г Т7т.адгТ]т г = Г1 т.ад ; V'iT;’,
1
откуда
2 ^т.адгПт/
= -----• (4.83)
1 т.ад
Если принять, что для всех ступеней т]*i—const, то будем иметь
* 2 H-t w
Пт 1
* Lf*
Пт i т.ад
Учитывая соотношение (4. 82), можем написать
г 1> л .
Таким образом, адиабатический к.п.д. многоступенчатой турбины
больше к.п.д. отдельной ступени, если последние во всех ступенях оди-
наковы. Аналогичный вывод получим, принимая при переменных к.п.д.
их среднее значение. Это соотношение между к.п.д. противоположно то-
му, какое ранее было получено для многоступенчатого компрессора.
Физический смысл полученного соотношения удобно пояснить с по-
мощью Т—s-диаграммы. Процесс политропического расширения в мно-
гоступенчатой турбине изобразится линией г—z (рис. 4.6), а адиабати-
ческого расширения — линией г—гад.
136
Потерянная работа L'R изобразится площадью зад—z—az—ат—гад.
Политропические процессы в отдельных ступенях будут соответство-
вать отрезкам г—/; 1—2\... ; (z—/)—z общей политропы. Адиабатиче-
ские процессы в ступенях изобразятся отрезками г—1—2' и т. д., а
потерянная в них работа изобразится площадями:
для первой ступени
LRl = площади Г — 1 — ах — аг — Г;
для второй ступени
LRt = площади 2'~ 2—а2 — ах — 2';
для z-ступени
LRz = площади z'— z — az — aXz-\)~z'.
С учетом этих соотношений из рис. 4. 6 следует, что работа, безвоз-
вратно потерянная во всей турбине, меньше суммы работ, потерянных в
отдельных ступенях, т.
е.
1
Следовательно, часть работы
потерь в предыдущих ступенях по-
лезно используется в последующих
ступенях турбины.
Так, например, в первой сту-
пени полезно используемая часть ее
потерь выразится площадкой
Г—1—В1—£ад—во второй ступе-
ни— площадкой 2'—2—вг—В!—2'
Рис. 4.6. Изображение в Т—s-диа-
грамме работы многоступенчатой
турбины
и т. д. Это использование проявляет-
ся в том, что теплосодержание газа
на входе в последующие ступени по-
лучается выше по сравнению с адиа-
батическим расширением, вследствие чего располагаемый тепловой пере-
пад в последующих ступенях и во всей многоступенчатой турбине воз-
растает.
Это явление в турбинах принято характеризовать коэффициентом
возврата тепла
(4. 84)
В общем случае к.п.д. многоступенчатой турбины должен опреде-
ляться с помощью уравнения (4.83). Принципы решения будут такими
же, как и для многоступенчатого компрессора.
Если будут заданы число ступеней, адиабатическая работа расши-
рения и к.п.д. в каждой ступени, то для вычисления общего к.п.д. тур-
бины необходимо еще знать суммарную адиабатическую работу расши-
рения. Последнюю можно вычислить по уравнению
/1------
I * ь
\ ят
где л*— общая степень понижения давления. Значение л* в данном слу-
чае не является независимой величиной, а должно вычисляться с по-
137
мощью известных значений /7*аа и т]*п используя следующие соотно-
шения:
зт —— ТС . ТС п • • • зт ,
а т! т2 • • • т z’
(4.85)
где л’р Яд,..., л* z —степени понижения давления в отдельных сту-
пенях. Значение степени понижения давления в любой m-й ступени мо-
жет быть вычислено по уравнению
к
(Н* \ S—1
1--------------\ • (4. 86)
7ГТ^-^<ад/п’т, I
1 /
Это уравнение следует из общего выражения для адиабатической рабо-
ты расширения в m-й ступени:
t_j * k туг* /1 1 \
** т.ад тп — ~ " К1 г m | 1 “ | >
I t I
\ ятт J
где
ад
i’ItZ
Рассмотренный случай для многоступенчатой турбины является
наиболее распространенным, так как обычно такая турбина рассчиты-
вается по ступеням с последовательным определением в каждой из них
Н*.ав.1, тю и I• В общих теоретических исследованиях могут встре-
чаться и другие случаи.
Так, например, если при
известной температуре газа
перед турбиной будут заданы
значения суммарной адиабати-
ческой работы турбины (а сле-
довательно, и лт*) и число
ступеней, то для определения
к.п.д. турбины адиабатическая
работа расширения и к. п. д.
каждой ступени могут быть
найдены только путем подбора
с учетом возможных значений
к. п. д. ступени в зависимости
Рис. 4.7. Эквивалентная политропа расшире- от ее нагруженности и извест-
ния в многоступенчатой турбине ных принципов распределения
общего теплоперепада по сту-
пеням.
Для общих теоретических исследований, а также и в отдельных
практических задачах полезным является метод эквивалентной поли-
тропы, рассмотренный выше применительно к многоступенчатому ком-
прессору.
Изобразим в Т—s-диаграмме процесс расширения в многоступен-
чатой турбине, имеющей с-ступеней (рис. 4.7). Как и ранее, принимаем
давления и температуры, соответствующие адиабатическому торможе-
нию скорости. Отметим также, что все выводы и формулы будут пол-
ностью приемлемы и при использовании статических давлений и темпе-
138
ратур, если рассматривать к.п.д., названные выше, как к.п.д. по полным
статическим теплоперепадам.
Обозначим, как и на рис. 4. 6,. точки, соответствующие адиабатиче-
ской температуре газа на выходе из ступеней, соответственно 2', ...,
г', а точки, соответствующие действительной температуре, — через 1,
2, ..., z. Процесс изменения состояния на линиях 1'—1; 2'—2 и т. д.
предполагается изобарическим. Адиабатическое непрерывное расшире-
ние от давления р* до давления р* изобразится линией г—гад, а поли-
тропический процесс расширения — линией г—z. Заменим ступенчатый
процесс г—Г—1—2'— .. .z' некоторым плавным процессом г—z'. Этот
процесс, протекающий с подводом тепла, очевидно, можно рассматри-
вать как некоторый политропический процесс. Предполагая, как это де-
лалось применительно к многоступенчатому компрессору, что процесс
г—z' энергетически эквивалентен исходному (ступенчатому), назовем его
эквивалентным политропическим процессом. Полная энер-
гия, соответствующая исходному процессу, может быть записана в виде
сД7';-7^ = £Я;.адг-2^-, (4.87)
1 1
Z—1
где у Lri— тепло, подведенное на участках Г—1-,2’—2;...; (г—1)'—
f -(г-1).
Очевидно, что L'Rl равно теплу или работе трения и других потерь
в отдельной ступени за вычетом тепла, соответствующего дополнитель-
ной объемной работе расширения (АН).
Если обозначить работу расширения, соответствующую эквивалент-
ному политропическому процессу, через Н*эт1 и принять, что подведен-
Z—1
ное в этом процессе тепло также равно то очевидно, что для
1
этого процесса уравнение энергии запишется в следующем виде:
ср (7’J - Г* ) = Z^LR!. (4. 88)
1
Из сопоставления уравнений (4. 87) и (4. 88) получаем
1
Очевидно, что при неограниченном увеличении числа ступеней точ-
ка z' будет приближаться к точке z и, следовательно, эквивалентный по-
литропический процесс будет стремиться к совпадению с действитель-
ным. При z= 1,0 точка z! совпадает с точкой гад.
Политропический к.п.д., соответствующий работе H*v , очевидно, вы-
разится уравнением
. = + , (4.89,
*Э Z, гг* г_т* у \ /
П 9 V ** Э V
где Ят — внутренняя работа многоступенчатой турбины, соответствую-
щая площади г—аг—4—5—г.
Так как
Z
— I И Cp(T*z — Г*') =//т.ад(1 — Т]*г)/
1
139
то выражение для tj9P можем привести к виду
(4. 90)
Исходя из равенства полной работы турбины как в действительном,
так и при эквивалентном политропическом процессах, мы должны напи-
сать
Z
Нт ===’ 2 т ад I z ==? 3 V ’
1
где —некоторый к.п.д., соответствующий равенству работ. Из’послед-
него уравнения имеем,, что
П,=-Ч-----------• (4.91)
2 ^т.ад/
1
Используя величины и т]„, мы можем выражения для к.п.д.
турбины записать следующим образом:
< = (4.92)
''т.ад
И
т]*=т],а. (4.93)
Если и для турбины с некоторым приближением принять, что пока-
затель эквивалентной политропы на всем участке между точками гиг' —
величина постоянная, то уравнение (4.92) можно привести к виду
(4.94)
где п'—показатель эквивалентного политропического расширения. Ве-
личина п' связана с показателем k зависимостью
1
П’ __ k
П'_1~ (£-1)^ •
Используя эту зависимость в уравнении (4.94), получим
1
SV
* k
т
k
* ’i,
Пэг,
(4. 95)
140
Из выражений (4. 93) и (4. 95) получим следующее уравнение для
определения коэффициента возврата тепла:
(4. 96)
Уравнения (4.95) и (4.96), являясь достаточно точными, упрощают
анализ к.п.д. многоступенчатой турбины и подбор числа ступеней. Рас-
смотрим для примера случай, когда во всех ступенях теплоперепады
/Д.ад i и к.п.д. одинаковы.
Из уравнений (4.90) и (4.91) находим
* _ ^^т.ад fИ* < (1 ~ г) , 1 ~ Ч* /
v ~тт* 'Т I "Г э
гНт.ал1 z
П»
(4.97)
гЯт.ад
гН
*
т.ад
(4.98)
Уравнение (4. 95) для т]*
можно написать в виде
(4. 99)
где Л* р — определяется из уравнения (4.97).
Если задано л*, г*, и z, то уравнение (4.99) позволяет легко оп-
ределить к.п.д. многоступенчатой турбины.
С помощью полученного к.п.д. легко находится величина адиабати-
ческой работы расширения в ступени:
т.ад
где
и
Зная /Ут.ад I , можно оценить нагруженность ступеней и реальность
принятого для них к.п.д. исходя из известных данных, приведенных в
гл. 7.
141
Обратим внимание на некоторые предельные значения п*. Из урав-
нений (4.97) и (4.99) следует, что когда z = 1,0, то 'П*Т!= 1,0 и т*=т*.;
когда z—oo, то п*ю=п*. и формула для н* получит вид
1
I —------—
* k
п;=—-—j--------. (4.1 оо)
Таким образом, с увеличением числа ступеней при заданном лт ве-
личина -Цт приближается к некоторому предельному значению, которое
зависит как от лт, так и от к.п.д. отдельной ступени.
На рис. 4. 8 показано изменение отношений Т)т/Пт t в зависимости от
числа ступеней при различных л* для двух значений к.п.д. ступени:
Цт/^0.80 и гт; =0,85, откуда следует, что при всех значениях лт число
ступеней целесообразно увеличивать, но лишь до некоторого предела,
сверх которого выигрыш в к.п.д. будет весьма небольшой. Чем выше
к.п.д. ступеней, тем быстрее достигается указанный предел, что естест-
венно, так как с ростом к.п.д. ступеней уменьшается выигрыш за счет
возврата в них тепла.
Практически стремятся иметь минимальное число ступеней, обеспе-
чивающее возможность получать в каждой ступени, а следовательно, и
во всей турбине максимальное для заданных условий значение к.п.д.
Глава 5
ТЕОРИЯ И РАСЧЕТ ОСЕВЫХ КОМПРЕССОРОВ
Проблема расчета осевых компрессоров, в конечном счете, сводится
к проблеме точного вычисления параметров потока, проходящего через
лопаточные венцы. Основные вопросы, возникающие при этом, являют-
ся общими для всех лопаточных машин и, как указывалось выше, свя-
заны в первую очередь с трудностями, возникающими вследствие того,
что поток является трехмерным, вязким и сжимаемым и в общем случае
нестационарным. Для получения приемлемых методов расчета вводятся
различные упрощения, к числу которых,, в частности, относятся: приме-
нение понятий об осредненном осесимметричном потоке, использование
двухмерных решеток и элементарных ступеней с плоским установившим-
ся потоком и др. Одновременно широко используются эксперименталь-
ные данные, полученные при продувке плоских решеток и при испыта-
нии отдельных ступеней и многоступенчатых компрессоров.
В гл. 2—4 были приведены общие уравнения для моментов, напора,
к.п.д., изменения скоростей и давлений в лопаточных машинах, в том
числе в полных и элементарных ступенях компрессоров, а также геомет-
рические параметры ступеней. Ниже рассматривается применение этих
уравнений для расчета осевых компрессоров с учетом их специфических
особенностей. При этом сначала рассматриваются решетки и элементар-
ные ступени компрессоров, а затем полные ступени и многоступенчатые
машины.
5.1. ОСНОВНЫЕ ПАРАМЕТРЫ РЕШЕТОК
И ЭЛЕМЕНТАРНЫХ СТУПЕНЕЙ
5.1.1. ТРЕУГОЛЬНИКИ СКОРОСТЕЙ И ЧИСЛА М
Предположим, что элементарная ступень состоит из рабочей решет-
ки и решетки спрямляющего аппарата за ней. Учитывая, кроме того, на-
личие спрямляющего аппарата предшествующей ступени в многоступен-
чатом компрессоре или входного направляющего аппарата в первой
ступени, можно показать треугольники скоростей, как изображено на
рис. 5. 1. Совмещая треугольники скоростей на входе в рабочую решетку
и на выходе из нее (рис. 5.2), получим треугольник скоростей рабочей
решетки, являющийся основным при изучении осевых компрессоров. Осе-
вые и другие скорости вдоль рабочей решетки будут изменяться не
только вследствие изменения углов и проходных сечений, но еще и вслед-
143
ствие сжимаемости. Поэтому для рабочей решетки с постоянной высотой
и радиусом треугольники скоростей будут характеризоваться тем, что
осевые скорости на выходе должны быть меньше, чем на входе, т. е.
C2a<Cia (рис. 5.2, а). В специальных
Рис. 5. 1. Треугольники скоростей эле-
ментарной ступени:
а—-на входе в рабочую решетку; б—на вы-
ходе из рабочей решетки; в—на входе
в спрямляющую решетку и на выходе
из нее;
Л—решетка входного направляющего аппа-
рата; В—рабочая решетка; С—решетка
спрямляющего аппарата
случаях, когда рассматриваются ре-
шетки с переменной высотой или рас-
положенные на конической поверхно-
сти с уменьшающимся к выходу ра-
диусом, может оказаться, что осевая
скорость на выходе больше скорости
на входе, т. е. c2a>cia (рис. 5.2,6).
В теоретических расчетах и в случаях
относительно небольших дозвуковых
скоростей рассматривается преимуще-
ственно треугольник скоростей, в ко-
тором осевые скорости до и после ра-
бочей решетки одинаковы, т. е. с2а =
— С\а (рис. 5.2,в). Величины скоро-
стей, характеризующиеся числами М,
играют большую роль в осевых ком-
прессорах. Наиболее существенное
влияние оказывают числа =
на входе в решетку рабочего колеса,
подсчитанные по относительной ско-
роста, и числа М2 = с2/а2 на входе
в решетку спрямляющего аппарата.
Эта числа М в каждой из указанных
решеток имеют наибольшее значение
именно на входе, так как скорости
потока и, следовательно, числа М в са-
мих этих решетках, как правило,
уменьшаются. В зависимости от значе-
ний чисел Mi и М2 компрессоры подразделяются на дозвуковые
(М<: 0,75-1-0,85), околозвуковые (М = 0,9ч-1,1) и сверхзвуковые
(М>1,1). При этом в околозвуковых и сверхзвуковых компрессорах ука-
занные значения могут иметь только числа Mi или М2 в зависимости от
схемы ступеней, как рассмотрено ниже. На рис. 5.3 для иллюстрации
Рис. 5. 2. Треугольники скоростей рабочей решетки
показан треугольник скоростей решетки рабочего колеса околозвукового
компрессора. Влияние на коэффициент потерь полного давления
g = Ap*/ ycj2 и чисел М на входе в решетку (т. е. Mi или М2) показано
на рис. 5.4 для решетки, состоящей из обычных 10% толстых профилей,
откуда следует, что, начиная с чисел М»0,74-0,75, коэффициент потерь
144
значительно возрастает. Число М, начиная с которого коэффициент потерь
резко возрастает, принято называть критическим числом М. Оно
характеризуется наличием местных сверхзвуковых зон на выпуклой по-
верхности профиля и скачков уплотнения. Таким образом, наряду с кро-
мочными потерями *>, потерями на трение и на вихреобразование появля-
ются еще и волновые потери, доля которых в общей величине профиль-
ных потерь возрастает с увеличением значения числа М выше критиче-
Рис. 5.3. Треугольники скоростей рабочей
решетки на среднем радиусе колеса около-
звукового компрессора
Рис. 5. 4. Влияние числа М
на коэффициент потерь
ского. Влияние чисел М на потери при различных углах атаки io показано
на рис. 5. 5, откуда видно, что при больших числах М на входе в решетку
сильно сужается диапазон углов атаки с малыми коэффициентами по-
терь. Если число М становится достаточно большим, решетка запирается,
образуются сильные скачки, вызывающие отрыв пограничного слоя при
всех углах атаки, и сильно возрастает коэффициент потерь. Числа М
на входе в решетку, при которых в узком сечении канала возникают
скорости звука и происходит запирание решетки, принято называть
максимальными числами М (Мтах)•
Рис. 5. 5. Влияние числа М на входе в решетку
на характеристики потерь в ней
Рассматривая процесс расширения воздуха при переходе от сечения
к сечению горловины Emm (рис. 5. 6) применительно к решетке рабо-
чего колеса, нетрудно установить связь между Мтах и Fmin/Ei.
Из уравнения неразрывности для сечений Е. и Emin имеем (без учета
потерь и рассматривая течение как одномерное)
Я Owi) __ Emtn
Я(*)Р . El
г min
*> Кромочные потери подробно исследовались применительно к турбинным решет-
кам и рассмотрены в разд. 7.2. 1.2.
145
При достижении максимального числа М — значение q(X) Frain = 1,0 и,
следовательно, получаем
«(^)м„„=-77- (5.1)
Так как
?(М
jfe—1
k + 1
a связано с числами Mi зависимостью
то, учитывая, что в данном случае М]=Мтах, получаем
__ F mln
~ Fl
(5.2)
Очевидно, что это уравнение справедливо и для решеток спрямляющих
максимально возможные числа МтаХтеор (линия 1) в зависимости от от-
ношения площадей Fmin/Fi при адиабатическом изменении состояния.
Поскольку одному и тому же значению <? (Х) отвечают, как известно,
два значения % или М, то теоретическая кривая на рис. 5.6 при
Fmm/Fi< 1,0 имеет две ветви: нижнюю — дозвуковую и верхнюю—сверх-
звуковую.
146
Рис. 5. 7. Зависимость критического
и максимального числа М от угла
атаки при а2=30°; в =28°; //6=1,0
и а/6 = 1О°/о
С учетом потерь уравнение (5. 1) получит вид
?(\ы)мтаХ= 8к.в,
где ^‘ — коэффициент полного давления во входном участ-
к’в га1п ке канала.
Кроме того, вследствие образования пограничного слоя сечение Fmm
уменьшается по сравнению с его номинальным значением.
Таким образом, в действительности при данном номинальном отно-
шении Fmtn/Fi значения <7(%wi) Мп1аХ будут всегда меньше теоретических.
Значения Мтах, полученные при экс-
периментальных исследованиях ком-
прессорных решеток, составленных из
обычных дозвуковых профилей, пред-
ставлены на рис. 5.6 кривой 2, откуда
следует, что в области Р^1ъ/Р\<б,96
значения Мтах относительно близки
к теоретическим, а в области
Тт1п/Л> 1,0 существенно отличаются.
При этом только когда Fmin/Fy =
= 1,44-1,5, Mmax может достигнуть зна-
чений, близких к единице. Это связано
с тем, что в профилях со значительной
кривизной и толщиной входного
участка, обычно используемых в ре-
шетках с дозвуковыми скоростями,
имеют место большие потери на входе
При околозвуковых скоростях (Хвх~
= 0,85—1,2). При использовании про-
филей лопаток, обеспечивающих ма-
лые потери во входном участке меж-
лопаточного канала, протекание кри-
вой Мтах может не очень сущест-
венно отличаться от протекания кри-
вой Мтах теор (кривая 3) .
Поскольку jFi = /sin pi = /sin (рj—z), то для данной решетки (т. е.
при заданных /’mm. t и pj) с увеличением угла атаки i должно увеличи-
ваться отношение FmtiJF\, вследствие чего будет возрастать и Мщах (рис.
5. 7). В то же время Мкр уменьшается как при уменьшении, так и при
увеличении угла атаки по сравнению с оптимальным.
Из изложенного следует, что увеличение Мтах может достигаться
как выбором надлежащего угла атаки (при допустимом Мкр), так и пу-
тем увеличения Fmln за счет применения более тонких профилей. Послед-
нее способствует увеличению Мкр, что используется в околозвуковых и
сверхзвуковых решетках. Во втулочных решетках из условия прочности
обычно применяются более толстые профили, что приводит к уменьше-
нию Мтах в этих решетках.
5.1.2. ЧИСЛА РЕЙНОЛЬДСА
Для осевого компрессора, равно как и для других лопаточных ма-
шин, имеет существенное значение число Рейнольдса, являющееся на-
ряду с числом М критерием подобия. Для решетки профилей компрес-
сора число Рейнольдса целесообразно определять по хорде профиля и
параметрам воздуха на входе в решетку. Поэтому для рабочей решетки
„ «'iVl^p.K
Re =---------.
I4!
147
Рис. 5.8. Влияние чисел Re, чисел М и толщины профиля на коэффициент
потерь (а) и угол отклонения _потока (б) в компрессорной решетке:
--------------------------------с=12%;
....с=4%
Исследования [j66] показывают, что при снижении чисел Re и уровня
турбулентности коэффициенты потерь полного давления в решетке воз-
растают, а углы отклонения потока уменьшаются. Указанные явления
обусловлены отрывом ламинарного пограничного слоя при малых числах
Re. При высоких же числах Re и в зависимости от уровня турбулентности
ламинарный пограничный слой переходит в турбулентный, вследствие
чего возможность отрыва пограничного слоя уменьшается.
Числа Re, при которых начинается значительный рост потерь, на-
зываются критическими числами. При характерном для осе-
вого компрессора уровне турбулентности потока критические числа ReKP
для различных компрессорных решеток находятся в пределах (2,0—.
3,0) • 105. На рост потерь при уменьшении чисел Re существенное влия-
ние оказывает также сжимаемость (числа и толщина профиля. На
рис. 5.8 показано влияние чисел Re, чисел М и толщины профиля на
коэффициент потерь полного давления и угол (отклонения потока для
компрессорной решетки с густотой b/t=\,0 и углом установки -0=60°.
Из этого графика видно, что при числах Re (2,0—2,5) • 10s существенно
растет коэффициент потерь и уменьшается угол отклонения потока, при-
чем более интенсивно при повышенных числах М и больших толщинах
профилей, поскольку эти факторы способствуют расширению области от-
рыва ламинарного пограничного слоя.
Выше рассмотрено влияние чисел М и Re на профильные потери в
компрессорных решетках. Что касается вторичных потерь, которые вклю-
чают в себя потери от парного вихря, влияние радиального зазора и не-
стационарности, то количественных данных для их оценки применительно
к компрессорным решеткам недостаточно *>.
Физическая природа парного вихря в компрессорных и турбинных
решетках одинакова, и качественно на компрессорные решетки можно
распространить результаты, полученные при исследовании парного вих-
ря в турбинных решетках (см. раздел 7.2.3). Однако количественные
данные для компрессорных решеток требуют уточнения.
Влияние на к. п. д. потерь энергии, обусловленных перетеканием в радиальном
зазоре с вогнутой на выпуклую поверхность профиля у периферии лопатки, теорети-
чески рассмотрено в работе [68]. При этом предполагалось, что вся кинетическая энер-
гия массы потока, связанная с составляющей скорости, нормальной к хорде, теряется
при этом перетекании. Однако данные, получаемые по теоретическим уравнениям,
не вполне согласуются с результатами экспериментальных исследований.
5. 1.3. СТЕПЕНЬ РЕАКТИВНОСТИ
Из уравнений (2. 32) и (2. 77) мы можем применительно к рабочей
решетке осевого компрессора написать:
2 2 9 О
W\ — Wn ci— с;
+ (5.3)
2 2 2
= (5.4)
J 7
i
При заданном теоретическом напоре работа сжатия в решетке рабочего
2
С ар
колеса, т. е. , может иметь различные значения в зависимости от
1
того, какую часть теоретического напора составляет член, характеризую-
щий изменение кинетической энергии в относительном движении.
*> При рассмотрении вторичных потерь как здесь, так и в гл. 7 предполагается,
что высота решетки имеет конечную величину.
149
Под степенью реактивности принято понимать отноше-
ние работы сжатия в решетке рабочего колеса при отсутствии потерь к
теоретическому напору:
2
(2 х
С dP |
J V у
Qk . Д г_т Q r_r
П th th
9 9
— 11}^
(5.5)
где Н — I —работа сжатия в решетке ротора при отсутствии потерь.
\i Y / О
В решетках выполненных компрессоров в зависимости от способа
профилирования лопаток и положения решетки по высоте лопатки сте-
пень реактивности рк.д находится в пределах 0,2—0,8.
Однако в принципе степень реактивности может равняться нулю и
даже быть отрицательной. В последнем случае статическое давление в
решетке рабочего колеса будет понижаться (конфузорный процесс). На
расчетном режиме отрицательная степень реактивности, как правило, не
допускается и встречается на нерасчетных режимах, сопровождаясь иног-
да переходом решетки с компрессорного режима на турбинный.
Степень реактивности может быть и больше единицы, когда в абсо-
лютном движении скорости потока в решетке рабочего колеса уменьша-
ются. Степень реактивности можно выразить еще через абсолютные ско-
рости, если в уравнение (5. 5) вставить относительные скорости из урав-
нения (5. 3):
___-I С2 С1
Рк.Д 1 с,,,
2-П th
(5.6)
Заменим c2 и Ci окружными и осевыми составляющими, тогда
и2 —г2 г2 —г2
„ , с2и Чи Ча Ча
. — 1 —--------------.
2Я/Й 2Hth
Во втором члене заменим Hth его выражением из уравнения (2.26)
с учетом того, что в этом уравнении окружная составляющая с1и поло-
жительная, когда ее направление совпадает с окружной скоростью, и от-
рицательная, когда Ciu направлена против окружной скорости. Тогда
2 __ 2
__-| _Ча ± С1ц _с2а с1а
Ук-Л~ 2а 2Hth
Первые два члена правой части уравнения (5.7) принято называть
кинематической степенью реактивности qk, т. е.
(5.7)
г __Ча±. Ч.» = ! Ча-Ча ,5 8)
2и 2 '
В дальнейшем в уравнениях (5. 7) и (5. 8) перед с1и будем писать
только знак плюс, а значение с1и принимать со своим знаком («плюс-
при закрутке по вращению и «минус» при закрутке против вращения).
Когда с2а=с1а, то рк = рк.д. Если c2a=^Cia, то кинематическая степень ре-
активности по физическому смыслу характеризует тип треугольника ско-
ростей. Прибавив и вычтя в правой части уравнения (5. 8) (при знаке
«плюс» перед ciu) величину ciu/2, получим также
ек=1 -с 1а - =1 - 71в - , (5.9)
так как Дси равно коэффициенту напора Hth-
150
5.1.4. ТИПЫ ДОЗВУКОВЫХ ЭЛЕМЕНТАРНЫХ СТУПЕНЕЙ
В ЗАВИСИМОСТИ ОТ СТЕПЕНИ РЕАКТИВНОСТИ
Как следует из уравнения (5.9), степень реактивности рабочей ре-
шетки зависит от относительного значения и знака окружной составляю-
щей скорости на входе и от коэффициента напора. Если принять один и
тот же коэффициент напора для всех степеней реактивности, то очевид-
но, что
Ск(ё1и<0) =ек(71о-0) + С1О;
ек(?1в>о)=ечё1в-о) — ciB,
Рис. 5.9. Треугольники скоростей элемен-
тарных ступеней с различной степенью
реактивности:
а—0к—1,0; 6—1,0> QK> 0,5; в—Q.{—0,5; г—ск=0.
рабочем колесе в результате тор-
спрямляющем аппарате должно
где qk (7щ-о) — соответствует осевому потоку (без закрутки) на входе
в рабочее колесо, а индексы ci«<0 и ciu>0 соответственно указывают,
когда окружная составляющая направлена против вращения и по враще-
нию. В частности, на среднем радиусе дозвуковой ступени коэффициент
теоретического напора Hth находится примерно в пределах 0,3—0,4.
Тогда QK(clu-o\ =0,85—0,8. Следовательно, при закрутке потока против
вращения степень реактивности будет больше, а при закрутке по враще-
нию меньше указанных значений.
При более высоких коэффициентах
напора, что имеет место, например,
в решетках, расположенных у втул-
ки, степень реактивности должна
уменьшаться. Наоборот, при более
низких коэффициентах напора сте-
пень реактивности должна возра-
стать. Специальным подбором изме-
нения окружной составляющей ciu
по высоте лопатки удается сохра-
нять qk = const, несмотря на измене-
ние коэффициента напора.
На рис. 5.9 показаны треуголь-
ники скоростей в рабочих решет-
ках для элементарных ступеней,
имеющих постоянный коэффициент
напора //^ = 0,4 и одинаковую
окружную скорость, но различные
степени реактивности от 1,0 до 0.
При qk=1,0 все повышение стати-
ческого давления достигается только в
можения относительной скорости. В
происходить только изменение направления скорости. Из сравнения тре-
угольников скоростей видно, что относительная скорость на входе в эту
ступень больше, чем у остальных, что является следствием закрутки по-
тока против направления вращения. Поэтому, если в различных ступе-
нях одинаковые числа Мь то в ступени, имеющей qk= 1,0, должна быть
ограничена окружная скорость, а следовательно, и напор.
В настоящее время такие ступени не применяются. В прошлом они
использовались на компрессоре первого немецкого турбореактивного
двигателя ЮМО-004. ~
В ступени, имеющей ciu = 0 (рис. 5.9,6), числа Mi также будут не-
сколько ограничивать окружную скорость. Эта ступень характерна тем,
что в ней степень реактивности всегда меньше единицы, так как ок=1,0
только при Hth = b. В случае возрастания коэффициента напора до
Hth= 1,0 степень реактивности будет равна qk = 0,5 и в этой ступени будет
получаться максимальный напор при заданном числе Mi (см. разд. 5.2. 1).
Ступени, имеющие с1и=0 или очень малую закрутку, находят примене-
151
ние при сверхзвуковых скоростях на входе в рабочее колесо, а также как
ступени вентилятора двухконтурного двигателя. Ступень (рис. 5.9,в),
имеющая ок = 0,5 при Ciu>0, т. е. при совпадении окружной составляю-
щей потока на входе в рабочую решетку с направлением окружной ско-
рости, имеет ряд характерных особенностей. Во-первых, треугольник ско-
ростей такой ступени является симметричным, т. е. W\ = c2 и ®i = Ci и, сле-
довательно, условия работы решетки рабочего колеса и решетки спрям-
ляющего аппарата одинаковы. Во-вторых, при относительно небольших
числах М1<1,0 в такой ступени можно иметь достаточно большие окруж-
ную скорость и напор. Наконец, как показано ниже, к.п.д. ступени, имею-
щей qk = 0,5, является максимальным. Этим объясняется, что в дозвуко-
вых компрессорах степень реактивности рк = 0,5 часто применяется на
среднем радиусе, а также и для всей лопатки, если она спрофилирована
по закону qk = const на всех радиусах. При сы-^О эта ступень прибли-
жается к предыдущей ступени.
Ступень с рк=0 (рис. 5. 9, а) по своему треугольнику скоростей про-
тивоположна ступени, имеющей qk=1,0. В таких ступенях в рабочем
колесе происходит только поворот относительных скоростей без измене-
ния их величины и сильно возрастает абсолютная скорость с2, впо-
следствии замедляющаяся в спрямляющем аппарате.
К таким ступеням иногда приближаются элементарные ступени во
втулочных сечениях.
5.1.5. ТИПЫ СВЕРХЗВУКОВЫХ (И ОКОЛОЗВУКОВЫХ)
ЭЛЕМЕНТАРНЫХ СТУПЕНЕЙ
Из уравнения для теоретического напора рабочей решетки
Н th — U(C2u Ciu)
следует, что в случае, когда Ci„=O или с1м<0, напор при данной окруж-
ной скорости будет возрастать. Однако с этим связано увеличение чисел
М] на входе в решетку. Поэтому применение профилей, эффективно ра-
ботающих при больших числах Mi, позволяет иметь ступень с большим
напором.
Исследования [66] показывают, что эффективность работы решетки
при повышенных числах М] может быть достигнута путем уменьшения
толщины лопаток и расположения максимальной толщины профиля бли-
же к середине хорды [66]. Последнее позволяет допускать малый угол
заострения входной кромки профиля, что ослабляет возможные голов-
ные ударные волны и уменьшает связанные с ними потери, так как из
газодинамики известно [1], что при сверхзвуковом обтекании клина, угол
которого больше предельного для данного числа М, образование косого
скачка становится невозможным и на некотором удалении от вершины
клина образуется отсоединенная, или головная, ударная волна. Напри-
мер, для М= 1,5 угол клина не должен быть больше 12°.
В выполненных сверхзвуковых и околозвуковых компрессорах [58]
поток на входе в рабочее колесо не имел окружной составляющей, т. е.
ступень по своему типу относилась к ступени, треугольники скоростей
которой показаны на рис. 5. 9, б. Типичный треугольник скоростей око-
лозвуковой ступени был показан на рис. 5. 3. В треугольнике скоростей
сверхзвуковой ступени рис. 5. 10 — сверхзвуковая относительная скорость
на входе в рабочее колесо и дозвуковая абсолютная скорость на входе
в спрямляющий аппарат. Относительная скорость на выходе из рабо-
чего колеса — дозвуковая, и переход от сверхзвуковой скорости к дозву-
ковой происходит в головной ударной волне или в системе скачков уп-
лотнения (см. разд. 5. 2. 4). На рис. 5. 11 показано течение на входе в ре-
152
щетку профилей, обтекаемую сверхзвуковым потоком с головными удар-
ными волнами.
Известный интерес могут представлять также ступени с дозвуковой
относительной скоростью на входе в рабочее колесо и сверхзвуковой
рабочих
ступени
Рис. 5. 10. Треугольники скоростей
решеток сверхзвуковой элементарной
Рис. 5.11. Обтекание сверхзвуковым
потоком решетки профилей:
/—головные волны; 2—волны разрежения:
3—линии перехода через скорость звука
скоростью на входе в спрямляющий аппарат, что достигается сужением
сечений проточной части [66]. Исследованная ступень такого типа (рис.
5. 12) имела пониженную кинематическую степень реактивности рабо-
Рис. 5. 12. Схемы проточной части ступени осевого компрессора
со сверхзвуковой скоростью на входе в спрямляющий аппарат:
а—меридиональное сечение; б—’схема решеток по среднему диаметру А—В;
в—треугольники скоростей на входе в рабочее колесо и на выходе из него;
г—треугольник скоростей на входе в спрямляющий аппарат
чего колеса (qk=0,328) и следующие числа М: в рабочей решетке на
среднем диаметре М[=О,73 и на входе в спрямляющий аппарат М2 =
= 1,334.
153
5.1.6. СТУПЕНИ С ПРОТИВОПОЛОЖНЫМ ВРАЩЕНИЕМ
РАБОЧИХ КОЛЕС
Наряду с обычными ступенями, состоящими из рабочего колеса и
неподвижного спрямляющего аппарата, в отдельных случаях встречают-
ся ступени, в которых два рабочих колеса вращаются в противополож-
ных направлениях. Кроме этих колес в ступени могут быть и неподвиж-
ные направляющие аппараты.
Рассмотрим сначала случай, когда неподвижные аппараты отсутст-
вуют и абсолютные скорости на входе в первое колесо и на выходе из
Рис. 5. 13. Треугольники скоростей ступени с противопо-
ложным вращением рабочих колес
второго колеса не имеют окружных составляющих (рис. 5. 13). Такая
ступень может применяться как самостоятельная. В треугольниках ско-
ростей векторы, относящиеся к первому колесу, имеют дополнительный
индекс (1), а ко второму колесу — дополнительный индекс (2).
Треугольник скоростей (рис. 5.13, а) показывает, что первая
рабочая решетка работает в этом случае по схеме рис. 5. 9, б, т. е. име-
ет 0,5<Qk<^1,0, а во второй решетке должна быть степень реактивности
рк>1,0, так как на входе в нее имеется закрутка против направления
вращения (с1и<0), а окружная составляющая на выходе (с2и) равна ну-
лю. Из треугольника скоростей также видно, что при одинаковых окруж-
ных скоростях относительная скорость на входе во вторую рабочую ре-
шетку, а следовательно, и числа М по относительной скорости должны
быть значительно больше, чем на входе в первую решетку.
J54
Если потребовать равенства чисел М, то непосредственно из тре-
угольника скоростей следует, что в этом случае должно быть
М(2)+С2и(1) = «(!)>
откуда
W(2)=U(1)—C2u(l)
или
М(2) _ 1 LJ
------1 — /7^(1).
“(1)
При этом, очевидно, Н th(y> —Н th(.2}=Н th, так как ift7i=c2u(i) = ciu(2).
В ступени с противоположным вращением рабочих колес можно
осуществить одинаковые числа М и при равных окружных скоростях,
введя промежуточный направляющий аппарат или создавая только ок-
ружные составляющие скорости на входе в первое колесо и на выходе из
второго колеса.
В последнем случае окружная составляющая ciU(d должна быть на-
правлена против вращения, так как иначе неравенство чисел М] при
«(i)=«(2) возрастет еще в большей степени, чем при ciu=O- На рис. 5. 13, б
показан треугольник скоростей, в котором скорости ah(i)=t0i(2) при iz(i)=
= U(2) = «. Для небольших степеней повышения давления можно считать,
что при toi(D = Wi(2) будут мало отличаться и числа Мц1) и Mip). В тре-
угольнике рис. 5. 13, б абсолютная скорость Сщ) равна и по направлению
симметрична скорости c2(ij. Следовательно, степень реактивности первой
рабочей решетки gK=l,O- Аналогичное положение будет и для второй
решетки при Др(2)=ДР(р. Как уже отмечалось выше, при qk=1 и задан-
ных числах Mi ограничивается величина окружной скорости, а следова-
тельно, и напор. Но когда Mi>l,0, то несмотря на эти ограничения воз-
можно получить достаточно высокие значения и и Hth- Создание много-
ступенчатого компрессора с противоположным вращением рабочих колес
связано с большими конструктивными трудностями.
5.1.7. СТЕПЕНЬ ДИФФУЗОРНОСТИ, ГУСТОТА
И УГОЛ ОТКЛОНЕНИЯ ПОТОКА В РЕШЕТКЕ
Важными параметрами решеток являются степень диффузорности,
густота b/t и угол отклонения или поворота потока Ар или Да, тесно
связанные между собой (см. рис. 2. 6).
Диффузорность канала решетки можно характеризовать с помощью
угла эквивалентного диффузора. Очевидно, что для каждой диффузор-
ной решетки, работающей на определенном режиме, можно построить
эквивалентный плоский диффузор, длина которого равна длине средней
линии канала, а площади входа и выхода равны соответственно живым
сечениям в потоке при входе и выходе из канала. На рис. 5.14 изобра-
жены три решетки и эквивалентные им плоские диффузоры. Решетки
типа а и б имеют одинаковую густоту и углы поворота потока, работа-
ют при одинаковом угле атаки, но у решетки б угол потока на выходе
р2 меньше, чем у решетки а. Из рис. 5. 14 видно, что решетке б соответ-
ствует эквивалентный диффузор со значительно большим углом раскры-
тия. Так, если для решетки а принять угол 9Д за единицу, то в решетке б
9д=1,43. В решетке в густота и углы потока на выходе оставлены та-
кими же, как и в решетке а, но угол поворота потока в решетке увели-
чен за счет уменьшения угла потока на входе Pi при том же угле атаки.
В результате угол раскрытия в решетке в по сравнению с углом в решет-
ке а возрастет примерно в два раза. Принимая высоту решетки равной
155
Рис. 5. 14. Эквивалентные диффузоры b/t=l,O; 1=2’
единице, угол раскрытия эквивалентного диффузора можно записать в
виде
о 180 /(sin 32 — sin pi)
= Т--------i-----•
Значение 0Д можно выразить еще в виде
g _180 _b_ sin (ДР ч- 81) — sin pi
д л I _Ь_
t
Из уравнения (5. 10) следует, что угол раскрытия диффузора дол-
жен при заданном значении 0! возрастать с увеличением угла поворота
потока. Одновременно 0Д увеличивается с уменьшением густоты решет-
ки. Как известно из газовой динамики, сопротивление диффузора сла-
гается из потерь на трение и на вихреобразования. Вихревые потери вы-
зываются отрывом пограничного слоя от стенок диффузора, что в пер-
'тах
Поверхность
'^разрешения
-_____
Поверхность
сжатия
0 50 100
% хорды
Рис. 5. 15. К выводу коэффициента диффузорности
вую очередь определяется углом раствора диффузора. Оптимальными
углами являются углы 0д=6-нГО°. В этой области не наблюдается види-
мого отрыва струй от стенки диффузора. Таким образом, выбор углов
поворота потока и густоты, а в конечном итоге, и напора решетки необ-
ходимо согласовать с допустимым углом раствора диффузора, как рас-
сматривается ниже.
Применяется оценка допустимой диффузорности еще в форме так
называемого коэффициента диффузорности [66], который
также является критерием допускаемой расчетной нагрузки на лопатку.
В основе этого параметра лежит торможение скорости на выпуклой по-
верхности профиля. На рис. 5. 15 приведено типичное распределение ско-
рости на поверхности профиля в компрессорной решетке. Вблизи перед-
ней кромки на верхней поверхности профиля наблюдается увеличение
скорости до значения wmax, превышающего скорость набегающего пото-
ка W\. Затем скорость непрерывно падает и у задней кромки мало отли-
чается от скорости потока за решеткой. Уменьшение скорости сопровож-
дается отклонением потока из-за циркуляции скорости вокруг профиля,
равной r=&wut.
Циркуляция проявляется в увеличении скорости на спинке профиля
и в уменьшении ее на нижней поверхности. Пренебрегая отличием дуги
верхней и нижней поверхности от хорды (для малоизогнутого профиля)
и принимая линейное изменение скоростей на этих поверхностях, можем
приближенно циркуляцию вокруг профиля записать в виде
Г = ~~ - W2) - (®t - ®2)] = (®max - wj,
где к — некоторый поправочный коэффициент.
157
Заменяя Г через произведение &wut, получим
- W2 . , е, bwa W2
— =1+ it. - — — = а„
®1----------------------------(ЬЦ) wi wi и
Коэффициент aD называют коэффициентом диффузорно-
ст и. По данным различных исследователей, 2х=0,4-т-0,6, т. е. в сред-
Рис. 5. 16. Зависимость коэффициента
потерь от коэффициента диффузорности:
А—периферийные решетки рабочего колеса;
В—втулка рабочего колеса и направляющий
аппарат
нем 0,5.
Для неподвижной (спрямляю-
щей) решетки этот коэффициент
будет иметь вид
I Сд
+ 2(Й/0С2 ~ с2 ’
где с2 — скорость на входе в непо-
движную решетку.
Таким образом, коэффициент
диффузорности при заданных значе-
ниях скоростей на входе возрастает
с увеличением Awu (а следова-
тельно, ДР) и с уменьшением гу-
стоты.
Зависимость коэффициента потерь полного давления в решетке
5=Др* I -i- от коэффициента диффузорности для сечений рабочего
колеса и направляющего аппарата показана на рис. 5. 16, откуда оче-
видно, что можно ожидать весьма больших потерь, если коэффициент
диффузорности для периферийных рабочих решеток превосходит величи-
ну, равную приблизительно 0,4.

Гцсто та b/t о- 0,5 п-0,15 0- 1,0 ь-1,25 v- f,5 0 V
V 0 7
. «а
Т V ооОо 0^ I
6**
0,03
о,ог
0,01
о
1,0 1,2 1,0 7,5 1,8 2,0 2,2 0Cj,e
Рис. 5. 17. Зависимость толщины потери импульса от
эквивалентного коэффициента диффузорности при
оптимальных углах атаки
При исследовании потерь и помпажных характеристик компрессор-
ных решеток пользуются и другими определениями коэффициента диф-
фузорности. В частности, применяется параметр, представляющий отно-
шение максимальной скорости на поверхности профиля к выходной -ско-
рости:
®'пих _ । т
--------------р 1= а„ .
W2 D W2-------De
Как показано в работе [65], с использованием теории пограничного -слоя
этот параметр дает общее соотношение между толщиной потери импуль-
158
са и геометрией решетки (рис. 5. 17). Найдено, что указанные выше па-
раметры обычно применимы, пока максимальное местное число М на по-
верхности лопатки соответствует дозвуковой или околозвуковой области
(числа М на входе в решетку примерно 1,1 —1,2).
5.2. ВЛИЯНИЕ ОСНОВНЫХ ПАРАМЕТРОВ
НА ТЕОРЕТИЧЕСКИЙ НАПОР РЕШЕТКИ
И ЭЛЕМЕНТАРНОЙ СТУПЕНИ
5.2.1. ВЛИЯНИЕ СТЕПЕНИ РЕАКТИВНОСТИ И ЧИСЕЛ М.
СТУПЕНЬ МАКСИМАЛЬНОГО НАПОРА
Запишем коэффициент теоретического напора в виде
Кй (5.11)
где
г ____с2и .
с2и------->
и
окружные составляющие, связанные
ческую степень реактивности зави-
симостью
к 2
откуда
с2« = 2(1 — ек) — с1а. (5.12)
Подставив выражение (5. 12)
в уравнение (5.11), получим
^ = 2[(1-qk)-c1u]. (5.13)
Так как clu = cia ctg си, то можем
также написать
77/л = 2[(1 — qk)— c^ctgaj. (5.14)
На оис. 5.18 показано изменение Н
г ____с\и
с1и-------
и
Рис. 5. 18. Зависимость Hth от ок
И С[ и
в зависимости от qk при различных
значениях ciu, откуда видно, что значение Hth может в принципе изме-
няться в весьма широких пределах. При qk=0,5, например, Яг/1 = 0,5, если
ciu=O,25, и Д\л=1,0, когда ciu=0. Величина Hth будет больше единицы,
когда окружная составляющая на входе направлена против вращения
(cia<^0). Для примера на_рис. 5. 19 показан треугольник скоростей при
с\и= 1,0 и qk = 0,5, когда Zfth=3,O. Однако получение столь высоких ко-
эффициентов напора даже при умеренных окружных скоростях будет
связано с большими значениями чисел Mi на входе в рабочую решетку
(а также и в решетку спрямляющего аппарата). Из треугольника скоро-
стей, приведенного на рис. 5. 19, имеем
®i = ^ + (2zz)2 = c^4„2
или
Л11 = ]/‘м„+4Ми2.
Примем, что и=29О м/сек, са = 170 м/сек и а=340 м/сек. Тогда Мм=0,85 и Ма=0,5.
Следовательно,
Mi = КО,25+ 2,89=1,775.
159
Интересно отметить, что если бы компрессор работал в системе с замк-
нутым контуром, заполненным гелием, в среде которого скорость звука
(при 7'н=288° К) составляет 1000' м/сек, то при тех же значениях и и c,t
число М! равнялось бы 0,6. Однако угол отклонения потока в рабочем
колесе этой ступени настолько велик (Др=130°), что даже и при малом
значении Mi такая ступень не может быть практически использована и
представляет лишь теоретический интерес.
Рис. 5.19. Треугольники скоростей для с1и=—1,0 Рис- 5.20. Треугольники ско-
и qk = 0,5 ростей
Таким образом, напор ступени в первую очередь ограничен числами
Mi и М2 и при заданных числах М может иметь некоторое максимальное
значение. Из треугольника скоростей (рис. 5. 20) имеем:
тогда Дси=х—н.
Следовательно,
Hth = и^са = «у — и? (5. 15)
и
(5.16)
и
Величина / представляет собой функцию чисел Mb М2, MQ. Действи-
тельно,
infra = w2i — с2а^=а2 (Ml — М?а);
clu = cl — cla=al(Mi— Mia).
Следовательно,
X = ai ]/м?-мГвД-a2(5.17)
Примем, что в уравнении (5. 15) величины % и, следовательно, чисел М
заданы, а переменной будет окружная скорость и. Дифференцируя урав-
нение (5. 15) по и и приравнивая производную нулю, получим
-^- = (Х-2«) = О,
du
откуда
___ и —р А с
Подставляя значение х, получаем м = —— , или и=Дси. Следова-
тельно, при заданных числах М максимальному напору соответствует
условие «=Аси, а сам напор выражается уравнением и коэффи-
циент напора будет равен единице. Численная величина максимального
160
напора будет определяться абсолютным значением окружной скорости
и, следовательно, чисел М в соответствии с уравнением (5.17).
Поскольку в этой ступени для получения максимального напора
должно быть ы=х/2, то, следовательно:
и=/М? - ML + VMo-ML. (5.18)
Из уравнения (5.18) следует, что окружная скорость будет иметь наи-
большее значение, когда числа Mi и М2 будут одинаковыми и равными
числу М, принятому в качестве предельно допустимой величины.

Рис. 5.21. Треугольники скоростей ступеней, имею-
щих Ac„ = ti
Если приближенно принять, что одинаковыми являются скорости
звука «1 и а2 и числа М!а и М2а,. то получим
и=а]Лм1-Ма.
Следовательно, для ступени с максимальным напором имеем
Hth=u2=a- (Mi —Мй).
(5. 19)
Для принятых условий (u = Acu; ах = а2\ Mi = M2 и Mia=M2a) треуголь-
ник скоростей будет симметричен, причем закрутка на входе отсутствует
и ®2=са (рис. 5.20, а). Степень реактивности при этом равна рк=0,5.
В двух верхних строчках табл. 5. 1 приведены сравнительные данные
ступени такого типа для чисел Mi = 1,50; Mi =0,85 и a = 340 м!сек.
6 546
161
Таблица 5.1
6к Mi ма Нth дж)кг Hth и м]сек Д?° 31 02 Прикечание
0,5 1,5 0,72 200 000 1,0 445 61° 19' 28°41' 90° ] Ступени с > максималь-
0,5 0,85 0,6 42 200 1,0 205 45° 45° 90° J ным напором
0,735 1,5 0,72 52 500 0,265 445 8° 12' 28°41' 36° 53'
0,5 0,85 0,6 33 000 0,368 300 20° 45° 65°
0,735 0,85 0,6 22 200 0,53 205 20° 45° 65°
Из табл. 5. 1 видно, что сверхзвуковая ступень максимального на-
пора имеет напор примерно в пять раз больше, чем ступень дозвуковая.
Обе ступени характеризуются большими углами поворота потока. В до-
звуковой ступени с максимальным напором окружная скорость полу-
чается низкой.
Условие и=Дси, характеризующее ступень с максимальным напо-
ром, может реализоваться и при степенях реактивности qk§0,5. Тре-
угольники скоростей таких ступеней показаны на рис. 5.21, б, в. В этих
ступенях напор также подчиняется выражению Hth = u2, но окружные
скорости будут меньше, чем при рк = 0,5, если наложить условие, что
наибольшее число М (Mi при рк>0,5 или М2 при qk<^0,5) по величине
одинаково с числами Mi и М2 в ступени с qk = 0,5. Ступени, в которых
реализуется условие и=Дси, не находят применения вследствие больших
углов поворота потока, трудности получения высоких к.п.д. при сверх-
звуковых скоростях, как на входе в рабочее колесо, так и на входе в
спрямляющий аппарат, и из-за малой окружной скорости при заданных
числах Mi и М2 в дозвуковой ступени. Последняя может встретиться
только во втулочных сечениях лопаток с постоянной степенью реактив-
ности по высоте, поскольку в этих сечениях небольшая окружная ско-
рость и повышенный угол Д|3. Реально же используются ступени с ко-
эффициентами теоретического напора Я<л<^1,0. Для иллюстрации в
табл. 5. 1 помещены данные сверхзвуковой и дозвуковой ступеней с та-
кими же значениями Mi и Ма, которые приняты для соответствующих
ступеней с максимальным напором, но с коэффициентами напора
При этом сверхзвуковая ступень ограничена условием, что на
входе в спрямляющий аппарат число М2 = 0,8 и ее треугольник скоростей
аналогичен треугольнику, показанному на рис. 5. 10. По величине окруж-
ной скорости и числа Mi данные такой элементарной сверхзвуковой сту-
пени соответствуют периферийным сечениям полной ступени. Реально
в этих сечениях значения 11ц, у сверхзвуковых ступеней находятся в пре-
делах 0,2—0,4, а числа Mi<l,3—1,5 [66].
Дозвуковая ступень ограничена так называемым номинальным углом
поворота потока.
Из табл. 5. 1 также видно, что переход от ступеней с максимальным
напором к ступеням с связан с существенным уменьшением на-
пора, но при этом одновременно уменьшается и угол поворота потока.
В дозвуковых ступенях при Ягд<(1,0 и одинаковых углах поворота пото-
ка большая окружная скорость и больший напор получаются в ступени
со степенью реактивности qk = 0,5.
162
5.2.2. ВЛИЯНИЕ НА ТЕОРЕТИЧЕСКИЙ НАПОР
УГЛОВ ОТКЛОНЕНИЯ ПОТОКА И УГЛОВ ПОТОКА
НА ВХОДЕ В РАБОЧУЮ РЕШЕТКУ И НА ВЫХОДЕ ИЗ НЕЕ
Запишем уравнение для теоретического напора в виде
Ям = ы(ш1ц—ау2и).
Заменим
Wiu = Са Ctg Pi И W2u = Cadig Р2,
тогда
Я№=uca (ctg Pi—ctg р2).
Заменив разность котангенсов известным выражением, получим
или
,, sin Д8
п th==ucn---------------- .
sin-sin (₽2— Д₽)
Это уравнение можно записать еще в виде
Н______ sin Др
са sin₽2-sin(₽2 —ДЗ)
(5. 20)
(5.21)
Из уравнений (5.20) и (5.21) следует, что при заданных значениях ок-
ружной и осевой скоростей или коэффициента расхода теоретический
напор и коэффициент теоретического напора возрастают при увеличении
угла отклонения потока Др и при уменьшении угла р2. Для примера в
табл. 5. 2 показано изменение различных параметров и в том числе тео-
ретического напора и коэффициента напора при постоянном угле откло-
нения потока Др = 25° и различных углах р2, а также при постоянном
р2=65° и переменном Др.
При расчетах принято рк=0,5; « = 300 м/сек; са= 187 м/сек и &Д=
= 1,3.
Таблица 5.2
д 3° 25 25 25 20 25 30
65 60 55 65 65 65
40 35 30 45 40 35
с2и в м/сек 223 266 324 187 223 266
с1а в м/сек 86,5 108 131 86,5 86,5 86,5
кси в м/сек 136,5 158 193 100,5 136,5 179,5
Hth в дж/кг 41000 47500 58000 30200 41000 53800
0,455 0,528 0,65 0,335 0,455 0,598
7/ th'ca 0,728 0,845 1,04 0,535 0,728 0,958
11,7 12,9 14 8,8 11,7 14,6
Однако, как уже рассматривалось выше [см. (5. 17) и рис. 5. 14], умень-
шение угла р2 при заданном Др или увеличение Др при заданном р2
влечет за собой рост угла расширения эквивалентного диффузора решет-
ки 0Д, что связано с увеличением потерь. Изменение углов 0д также при-
ведено в табл. 5. 2.
6*
163
Если величину угла расширения эквивалентного диффузора ограни-
чить пределами, обеспечивающими низкий уровень потерь, то углы откло-
нения потока Ар и углы выхода потока будут при каждой густоте решет-
ки связаны однозначной зависимостью, которая должна ограничивать ве-
личину теоретического напора в ступени.
Для дозвуковых решеток углы отклонения, связанные с углами вы-
хода потока условием малых потерь, получены в результате многочислен-
ных продувок и дают возможность производить подбор решеток для за-
данных условий.
Рис. 5. 22. Типичные результаты испытаний реше-
ток при малых скоростях:
а'=47,5°; ^-7.5": o/ft-0,5; Z/5-0 94; 9 = 40°
Для испытаний решеток применяются аэродинамические трубы ти-
па рассмотренных в разд. 7. 2.
При заданной геометрической форме решетки и данных значениях
критериев М и Re углы отклонения потока Ар (Да), повышение давления
Ар и потеря полного напора (давления) зависят только от угла атаки i.
Типичные результаты испытаний решеток изображены на рис. 5. 22, где
по оси абсцисс отложены значения угла атаки I, а по оси ординат—из-
меряемые параметры потока: угол отклонения потока Ар или Аа, ко-
эффициент подъемной силы Су, коэффициент лобового сопротивления Сх
и потеря полного напора ALR, отнесенная к скоростному напору на
входе.
При увеличении угла атаки i отклонение потока Др (Да) возраста-
ет до некоторого максимального значения, а затем вновь начинает умень-
шаться.
Угол атаки, соответствующий максимальному углу отклонения по-
тока, называется критическим. Уменьшение угла отклонения потока при
увеличении угла атаки выше критического обусловлено отрывом потока
от поверхности профиля. При этом резко увеличиваются гидравлические
потери вследствие неизбежного вихреобразования при отрыве. Испыта-
ния показывают, что при критическом обтекании потеря полного напора
увеличивается приблизительно вдвое по сравнению с ее минимальным
164
значением, соответствующим оптимальному углу атаки гОпт. Угол атаки
iH.o, при котором только начинается резкое увеличение потери полного
напора, по-видимому, соответствует началу отрыва потока и располо-
жен примерно посредине между углом /опт, соответствующим минималь-
ному сопротивлению, и гкр. При расчетах компрессора обычно выбирают
такой наибольший угол отклонения потока, который может быть достиг-
нут в решетке без значительного увеличения потерь, т. е. при угле атаки
Рис. 5.23. Зависимость номи-
нального угла отклонения по-
тока в решетках от густоты и
угла выхода потока
Таким углом отклонения, или пово-
рота, условно считают Др = 0,8Дртах (или
Да=0,8Датах) и называют его номиналь-
ным. Как показали результаты испытаний,
при постоянных числах Re и М номиналь-
Рис. 5.24. Зависимость номинального отклоне-
ния от густоты решетки
ный угол отклонения потока практически зависит только от двух пара-
метров: от густоты решетки b/t и от угла выхода потока р2. Это можно
объяснить тем, что при заданных р2, b/t и максимально допустимой диф-
фузорности однозначно определяется угол Pi, а следовательно, и Др. Та-
кая зависимость показана на рис. 5. 23 при различных значениях густо-
ты решетки [50]. Эта зависимость справедлива как для рабочих, так и
для неподвижных решеток. Если с помощью рис. 5. 23 определить для
различных значений р2(а2) соответствующие номинальные отклонения,
то оказывается, что отношение этих отклонений к отклонению при b/t—
= 1,0 не зависит от угла выхода потока р2, а зависит только от густоты
с ДЗ с. Да
решетки. Обозначая это отношение через L = ----• или с — ,
можно построить график зависимости Е от b/t (рис. 5. 24).
Как следовало ожидать, номинальные режимы характеризуются от-
носительно небольшими углами расширения эквивалентного диффузора,
близкими к оптимальным углам, указанным выше (5.17). В табл. 5.3
приведены значения 0Д, соответствующие номинальному режиму при
различных р2 для решетки с густотой b/t= 1,0.
Таблица 5.3
Д8°(Д а) — 10 0 10 20 30 40 50 60
?2(а2) 39 33 28 24 19,5 15,5 12,0 8,8
0д 6,2 9,2 11,3 12,7 12,4 11,5 9,9 7,9
При заданных углах ₽i и р2 (или си и а2) входной угол ₽’ (ар
165
лопатки определяется углом атаки г, а выходной угол pj (а^) —
углом отставания потока & согласно уравнениям
= i- =
Для угла атаки на номинальном режиме можно ориентировочно указать
оптимальный диапазон:
0<г<5°.
Для номинального режима величина & подчиняется уравнению
8 = т9 , (5.22)
где
т=0,23 (2— Y+0,1 .
\ Ь ) \ 50J
Обычно
alb=0,40—0,45.
Далее для номинального режима мы можем написать
9 = ^1 — рг = /1 — i — Р2 == Д? — гЧ~ 5,
откуда
9 — &=Д₽—I.
Заменяя 9 из уравнения (5.22), получим
ж|/т (ЛЗ“°
2!_ г
Следовательно, если при заданных для номинального режима величинах
р2(а2) и Др (Ла) выбирается угол атаки i, то тем самым предопределяет-
ся и величина угла отставания &. Данные по величине углов i, р), РД 5
требуются для построения профиля. Более подробно сведения о технике
построения даны в разд. 5. 6.
Для околозвуковых и сверхзвуковых решеток обобщенных зависимо-
стей типа показанных на рис. 5. 20 не существует, и выбор угла откло-
нения потока и густоты решеток производится по известным из опыта
средним данным в зависимости от числа Мь
В ступенях с околозвуковой и сверхзвуковой скоростью на входе в
рабочее колесо и дозвуковой скоростью на входе в спрямляющий аппа-
рат значения Др в решетках, соответствующих среднему диаметру, не-
велики и находятся в пределах 10—20° [66], но у втулки они имеют по-
вышенные значения (30—60°). Для околозвуковых решеток
(Mi< 1,1 ч-1,2) угол отставания мало зависит от чисел Mi и в первом
приближении может определяться по формулам для дозвуковых реше-
ток.
5.2.3. ОБОБЩЕННАЯ ЗАВИСИМОСТЬ НАПОРА ОТ ЧИСЛА М,
И е„ ПО ДАННЫМ ПРОДУВКИ РЕШЕТОК
Данные продувки рабочих решеток целесообразно изображать еще
в виде связи Hth с са и ок. Если учесть, что на номинальных режимах
угол отклонения Др при данной густоте однозначно определяется вели-
чиной угла выхода потока, то левую часть уравнения (5.21) можно за-
писать в виде функции только от р2, т. е.
4^-=/(р2).
165
Однако часто более удобно эту зависимость выразить в другом виде.
Из треугольника скоростей получаем
ctg?2=^^
Са
Прибавим и вычтем в числителе величину ctu и воспользуемся уравне-
нием (5. 9) для степени реактивности; тогда получим
и — С%д — с1и 4~ С!и Ч (1 Н th) Qk Чth
Са Са Са ^Са
(5. 23)
Следовательно, для нош^нальных условий, т. е. при изменении Др по
рис. 5.23, зависимость Hthlca=f($2) может быть с учетом влияния гу-
стоты решетки изображена в виде
Н th у / (?к . \
Са \ Са t J
На рис. 5. 25 показана эта зависимость для различных густот.
В связи с тем, что при подборе параметров рабочих решеток часто в
Рис. 5. 25. Зависимость Hthlca от Qv!ca
качестве исходных величин принимают степень реактивности и коэффи-
циент расхода, график, приведенный на рис. 5. 25, позволяет при вы-
бранной густоте непосредственно определить коэффициент напора. Вы-
ше отмечалось, что отношение угла отклонения при любой густоте к уг-
лу отклонения при для всех углов выхода потока остается по-
стоянным. Аналогично ведет себя и отношение
Hth И Hth \
са / \ са )о
Поэтому, обозначая это отношение через J, можно изображать его в за-
висимости от bit одной кривой для всех углов 02(а2) (рис. 5.26). Непо-
средственно из_рис. 5.25 видно, что в некотором диапазоне величин
бк/ёа функция Hthlca изменяется очень мало и, следовательно, при за-
167
данном значении са коэффициент напора от степени реактивности не за-
висит. Этот диапазон приблизительно подчиняется соотношению
Hth
са
(5. 24)
Соотношение (5. 24) рекомендуется применять только в диапазоне от
1 — ^th I (
Сд / \ а /
в зависимости от густоты решетки
= 1,2 до -^=------Ь?-----.
С а С а 1 + 1,5«/6)
При отклонении рк/са от указан-
ных _предельных значений функ-
ция Нth/ca возрастает, что свиде-
тельствует об увеличении коэф-
фициента напора при данном
коэффициенте расхода.
При заданном Hth величина
теоретического напора найдется
исходя из допустимой окружной
скорости и чисел Mi на входе
в рабочую решетку. Эти пара-
метры также можно для номи-
нального режима выразить в
виде функции от QK/ca и b/t. За-
пишем выражение для относи-
тельной скорости в виде
+ “ Ой)2=^ + («-О« +
Учитывая уравнение (5.9) для степени реактивности, получаем
2 / ‘
откуда
или
Учитывая, что = ), можно, следовательно, написать
Са \ С a t /
Ml
МцСд \ Са t )
Эта зависимость показана на рис. 5. 27. Для всех густот получается поч-
ти одна кривая. Таким образом, выбор значений степени реактивности,
коэффициента расхода и густоты решетки однозначно определяет коэф-
фициент напора, а также отношение Mi/Mu; выбирая значение Мь нахо-
дим допустимую окружную скорость ы=Мма и теоретический напор
Hth=Hthu?.
Из рис. 5. 27 следует, что с увеличением рк при заданном са отноше-
ние М1/Ми возрастает, что приводит при заданном Mi к уменьшению Ми
и, следовательно, окружной скорости и напора (рис. 5.28). Такое влия-
ние степени реактивности отмечалось и выше. Оно связано с тем, что
168
по мере роста степени реактивности окружная составляющая на входе в
решетку, первоначально направленная по вращению, уменьшается, а за-
тем изменяет свое направление, т. е. против вращения.
В результате при заданном числе
Mi уменьшаются окружная скорость и
напор, хотя по данным продувок ре-
шеток коэффициент напора несколько
возрастает.
Рис. 5. 28. Зависимость теорети-
ческого напора от степени реак-
тивности при постоянном зна-
чении М1 и b]t
Рис. 5. 27. _3ависимость_параметра
Mi/caMu ОТ QK/Ca И bit
Следует отметить, что рост Hth при уменьшении qk связан с увели-
чением чисел М2 на входе в спрямляющий аппарат, которые при по-
строении рис. 5. 28 не были ограничены по величине.
5.2 4. ВЛИЯНИЕ ОСНОВНЫХ ПАРАМЕТРОВ РЕШЕТОК
И ЭЛЕМЕНТАРНЫХ СТУПЕНЕЙ НА ИХ К.П.Д.
Рассмотрим закономерность изменения к.п.д. решеток и элементар-
ных ступеней в зависимости от их основных параметров. Запишем к.п.д.
элементарной ступени в виде
„ __I ___ L-r_____ 1 _ Lr к __ Lr с
Лк“ Hth Hth Hth ’
(5.26)
где Lr к — профильные потери в рабочей решетке;
LRc — профильные потери в решетке спрямляющего аппарата.
Используя теорему Жуковского и рис. 2. 10 (см. 2.3. 1), выразим
теоретический напор через коэффициент подъемной силы и степень реак-
тивности для рабочей решетки, высота которой равна единице. В соот-
ветствии с теоремой Жуковского и с учетом потерь
9
W2, „
Ry-Cypy^Fn.
При этом суммарную поверхность Fn всех профилей можно записать в
виде Fn=b-z. Тангенциальная составляющая результирующей аэроди-
намической силы, характеризующая крутящий момент и теоретический
напор, выразится через подъемную силу уравнением
Так как
/?й = cos (90° - - ф)=Rp sin (Pm + ф).
^=^/С08ф,
169
то, следовательно,
2 2
= С»У F. iin<^+<,) = С,Р1 F„ sin (1 + ctgft,tg4).
Но
sMm=-^- и tg^ = —^ = |ЛК,
Wm Ry
где цк — величина, обратная качеству профиля в решетке. Следова-
тельно,
^B=G^^nMl+!\ctg^). (5.27)
С другой стороны, из проекции уравнения количества движения на на-
правление окружной скорости имеем
RU @i (^2и Ciu) tzyca (^2и ^1в)>
где Gi — расход через решетку.
Умножив и разделив правую часть на окружную скорость и, получим
Ra=tzy~caHtha.
Подставив это выражение для Ru в уравнение (5. 27), получим
Hth = Cyp±- ^(l-HKctg3m). (5.28)
Следует отметить, что ctg Pm=QK/ca- Действительно, из треугольника ско-
ростей на рис. 2.10 и с учетом уравнения (5. 9) имеем
Дси
g тти 2 tlQK Ск
ca ca ca
Выразим потери в решетке рабочего колеса через коэффициент лобово-
го сопротивления и wm:
wL
Rx=Cxpy-^Fn.
Тогда мощность, затраченная на преодоление потерь, будет равна
Np=RxWm=Cxpy-^F„,
но
wm
_Np _С*рЧ 2 bz b Kn 1
Rli Qi t2cay xp t 2 ct
Аналогично для спрямляющего аппарата получим
г ___Ь т 1
t — —.
(5. 29)
(5. 30)
Используя уравнения (5.28) и (5.29), заменяя ctg $т = Qjca
= «2(сд + бк), получим
и гт =
”2 2
__ Р-к са 8- ек
77th са , , Qk
са
(5.31)
170
Принимая для спрямляющего аппарата c3u = ciu и учитывая, что при
этом условии степень реактивности спрямляющего аппарата qc=1—Qk,
можем теоретический напор выразить через параметры спрямляющего
аппарата:
Htfl ==СУр±-и-^-(\+ К 1^) (5. 32)
и так как
то, используя уравнения (5. 30) и (5. 32), получим
с Р-с c2 + (l— бк)2
В результате к.п.д. элементарной
ступени можно записать в виде
1 Р-К (са + бк)
1 — 6к
Са
(5. 34)
Таким образом, к.п.д. элементарной ступени является функцией степени
реактивности, коэффициента расхода и коэффициентов ик и цс- Послед-
ов
Рис. 5.29. Зависимость коэффициента р. от 6/1 и =~по дан-
Са
ным продувки плоских решеток
ние, в свою очередь, зависят от чисел М на входе в решетки, густоты ре-
шетки, а также степеней реактивности и коэффициента расхода.
На рис. 5.29 показано изменение ц в зависимости от b/t и qk/ci
для номинальных режимов при небольших значениях чисел М. Очевид-
но, что этот график справедлив и для спрямляющих аппаратов, если
заменить о|; на qc.
При некоторых допущениях из уравнения (5. 34) можно выяснить
условия, при которых достигаются максимальные значения -рк и.
В связи с относительно небольшой величиной коэффициентов |iK и
бв 1 - бв
цс можно пренебречь членами рк и р-с — , стоящими в знаменате-
са Са
лях правой части уравнения (5. 34). Допустим также, что можно принять
коэффициенты цк и цс постоянными при изменении qk и са. Тогда, взяв
171
частную производную от i-|KU по степени реактивности qk и приравняв ее
нулю, получим
Qk опт ; • (о. 35)
'’к + Р-с
Если взять частную производную от т]к и по коэффициенту расхода и при-
равнять ее нулю, то получим
-2 Ркбк + Pc G — 6к)2
£ Д О П Т-
+ Ис
Подставляя в это выражение значение еКопт, получим значение с00пт>
соответствующее минимуму т]к и по двум переменным:
- УркРс
Са опт
Рк + Рс
При Цк=Цс будем иметь Саопт = 0,о и Qkoht~0,5. Для Qk~0,5 условие
цк=Цс обеспечивается и, следовательно, при qk=0,5 и са = 0,5 будет
Рис. 5.30. Зависимость ц от са при &/£=1,0
действительно существовать максимум к.п.д. элементарной ступени по
двум переменным (qk и са). Подставляя в уравнение (5.34) qk = 0,5;
са = 0,5 и цк=Цс, получаем
В частности, при ц=0,05 будем иметь т]к и=0,905.
При степенях реактивности qkS0,5 коэффициенты цк и цс не будут
одинаковыми, что непосредственно следует и из рис. 5. 29, если учесть,
что степень реактивности решетки спрямляющего аппарата qc связана
со степенью реактивности рабочей решетки соотношением qc=1—Qk-
На рис. 5.30 и 5.31 показана для b/t=\,0 зависимость ц и цс/цк от с,л
при различных значениях qk (или qc). При степенях реактивности, не
существенно отличающихся от 0,5, отношение цс/цк мало отличается от
единицы.
На рис. 5. 32 показано изменение т]ки в зависимости от са при b/t=
= 1,0 и нескольких значениях степеней реактивности qk. На каждой кри-
вой в скобках поставлены значения степени реактивности, для которой
эти кривые также действительны вследствие симметричности треуголь-
ников скоростей, а следовательно, и изменения т]к и- Из рис. 5. 32 видно,
что с увеличением (и с уменьшением) qk по сравнению с qk=0,5 к.п.д.
уменьшается и его максимум перемещается на большие значения са-
Наивысшее значение т]Ки достигается при qk = 0,5 и са = 0,5, как было
показано выше.
Из рис. 5. 32 также видно, что при уменьшении са по сравнению с
оптимальным значением к.п.д. уменьшается более резко, чем при уве-
личении са. Это объясняется тем, что при са<са опт уменьшается теоре-
тический напор п несмотря на некоторое уменьшение потерь их отноше-
112
ние к теоретическому напору возрастает быстрее. Рассмотрим для при-
мера случай, когда рк = 0,5. В этом случае потери в рабочем колесе и в
спрямляющем аппарате одинаковы и поэтому достаточно рассмотреть
Рис. 5.31. Зависимость от са при
b/t= 1,0
только изменение отношения LRKIHth. Если пренебречь произведением
Ок-
, то оно запишется в виде
Са
Производная по са имеет вид

н
de а
При рк=Са производная равна нулю, т. е. LRKIHth имеет минимум, как
и должно быть для этого соотношения, а при qk = 0,5 Lr к/Нth — 1,0ц. При
са= 1,5qk (Дса=+0,25) получаем, что отношение LRKIHth= 1,085ц, а его
Рис. 5. 32. К. и. д. элементарной ступени в зави-
симости от Си и gK при b/t=l,0
производная равна 0,555ц. При са = 0,5ек(Дса=—0,25) отношение
£вк/Я*й=1,25, а производная равна —Зц, т. е. для меньших са как от-
ношение потерь к Hth, так и его производная существенно больше, что
и приводит к более резкому падению к.п.д. в этой области.
Отметим, что если принять для всех степеней реактивности ц1;=цс - ц
при рк=0,5, то к.п.д. относительно мало отличаются от их значений, под-
считанных при Цк=АЦс (см. рис. 5.32). Это объясняется тем, что разли-
чие между цк и це в широком диапазоне с и рк относительно невелико
(см. рис. 5.31), а на величину к.п.д. оказывает превалирующее влияние
абсолютное значение qk (qc)- Поэтому в первом приближении оптималь-
173
ный коэффициент расхода можно, исходя из уравнения (5.36), опреде-
лять для каждой степени реактивности по формуле
(5. 38)
В частности, если qk=0,9, то са опТ= ] 0,41 =0,64, что достаточно близко
К са опт при Pk=/-Pc- Кроме qk и са, важное значение для к.п.д. имеют чис-
ла М и густота решеток. Влияние чисел М на потери в решетке было
показано выше (см. рис. 5.4). Можно считать, что, начиная с чисел
М«0,7, уже будет проявляться заметное влияние дальнейшего роста
этого параметра на потери и к.п.д. Как уже отмечалось, рост этих по-
терь замедляется при применении так называемых околозвуковых про-
филей, характеризующихся малой толщиной профиля и более острой
входной кромкой.
Рис. 5.33. Влияние густоты ре-
шетки на к. и. д. ступени
Головная волна.
Рис. 5. 34. Влияние густоты на
потери в околозвуковой ре-
шетке
Для дозвуковых решеток уменьшение густоты положительно влияет
на |1с и цк, как видно из рис. 5. 29, и, следовательно, повышает к.п.д., что
показано на рис. 5. 33.
В околозвуковых и сверхзвуковых решетках, наоборот, установлено,
что при уменьшении густоты потери возрастают (рис. 5. 34, а). Исследо-
вания показали, что увеличение потерь является следствием, главным
образом, потерь в скачке, связанном с числом М на поверхности профи-
ля [66]. Было обнаружено, что при уменьшении густоты место пересе-
чения головной ударной волны с поверхностью профиля перемещается
назад вдоль лопатки, как это показано схематически на рис. 5. 34, б.
В результате этого смещения местное число М на спинке профиля воз-
растает и, следовательно, возрастают потери, вызываемые скачком и
взаимодействием скачка с пограничным слоем. Было обнаружено, что
потери при малой густоте решетки значительны, даже когда околозву-
ковые числа М на входе относительно малы.
Поэтому для уменьшения потерь, связанных с возникновением го-
ловных волн, необходимо применять достаточно густые решетки, как
указано ниже (см. 5.3.3).
Однако -исследования этой схемы течения показывают, что при на-
личии головных волн обтекание решетки всегда происходит с положи-
тельными углами атаки и что даже при больших густотах местное число
М перед замыкающим скачком остается -больше, чем Mi, что приводит
к увеличению потерь и заставляет ограничивать число Mj.
Ограничения чисел Mi вызываются также возможностью отрыва
пограничного слоя на спинке профиля в месте расположения замыкаю-
щего скачка.
174
Поэтому для получения достаточно высоких значений к.п.д. в сту-
пенях, работающих с системой головных волн перед лопатками рабоче-
го колеса, целесообразно иметь Mi не более 1,3—1,4 (в периферийных
сечениях). ~
Ступени, работающие при более высоких числах Мь имеют пони-
женные к.п.д. Избежать появления головных волн и осуществить сжатие
в системе скачков внутри канала теоретически возможно при наличии
очень острых входных кромок и путем соответствующего профилирова-
ния углов заострения кромки (углов клина) на входном участке лопа-
ток. В этом случае числа Mi, имеющиеся на входе, будут снижаться до
минимального значения в узком сечении за счет системы косых скачков
уплотнения, распространяющихся от входной кромки и замыкающихся
прямым скачком. В такой системе скачков потери оказываются меньше,
чем при наличии головных волн. Однако практически такую систему
трудно реализовать из-за необходимости выполнения очень острых кро-
мок и неустойчивости замыкающего скачка, расположенного в узком се-
чении канала. На к.п.д. решеток и элементарных ступеней должно ока-
зывать также влияние число Рейнольдса, если оно становится меньше
критической величины Re = (2н-3) • 105.
С уменьшением чисел Re убывает и коэффициент адиабатического
напора, так как при неизменном Аси повышение полного давления и ко-
эффициент напора зависят от к.п.д. ступени. Испытания изолированных
профилей показывают, что с повышением турбулентности, так же как и с
ростом чисел Re, увеличивается максимально достижимое значение ко-
эффициента подъемной силы. Физические причины этого явления заклю-
чаются в том, что при турбулентном движении к замедленному слою у
стенки подводятся новые импульсы от главного потока, вследствие чего
отрыв появляется при больших углах атаки, что увеличивает коэффици-
ент подъемной силы. Такой же эффект появляется и у решетки профи-
лей.
Увеличение коэффициента подъемной силы влечет за собой возра-
стание максимального значения коэффициента напора.
Выше профильные потери характеризовались коэффициентом ц.
Имеются и другие рекомендации для определения этих потерь. В рабо-
те [14] приводится зависимость
сЛт1п=0,012-]-0,042/+0,0023 -у,
где Cxmin — минимальное значение коэффициента профильных потерь,
соответствующее режиму безотрывного обтекания.
Формула справедлива для решеток, составленных из профилей с от-
носительной толщиной 5% <с< 10% при 45°<О< 100°.
Для расчета потерь на режиме максимального качества решетки ре-
комендуется формула [28]
. °-оге+2(аГ
100/ /"sin 3]
, -
где $ =------е —угол поворота потока (ЛЗ или да).
УД
175
Для расчета потерь при оптимальном угле атаки и числе М набегающего
потока, равном критическому, предлагается использовать соотношение
1—8 = 0,06 — [0,27(90°-&) + 0,01е fl6—Д-9^ +11,
t L \ ь / ]
где б — отношение полного давления за решеткой к полному давлению
до решетки [28].
Поскольку расчет производится обычно для случая, когда М~Мкр, то
применение последней формулы более целесообразно.
5.3. ОСНОВНЫЕ ПАРАМЕТРЫ И ТИПЫ ЛОПАТОК
ОСЕВЫХ КОМПРЕССОРОВ
5.3.1. ОБЩИЕ ПОЛОЖЕНИЯ
Рабочие и неподвижные лопатки ступеней осевых компрессоров
можно рассматривать как совокупность бесконечно большого числа ре-
шеток, связанных между собой определенными условиями, и характери-
зовать их некоторыми средними параметрами, к числу которых, в част-
ности, относятся:
средний теоретический напор
J Hthi dG
Hthcv = -^—------, (5.39)
(j
средний лопаточный к.п.д.
г
j ^KiHthidG
nK,cp = ^----------, (5.40)
J Hthi do
rBT
средняя степень реактивности
гк
J HthiQx i dG
Qk.c₽=-^-----------• (5-41)
J HthidG
rBT
К числу средних параметров можно также отнести среднюю осевую
скорость и ряд других.
В частном случае, когда во всех решетках
Hthi — const; т|к; = const; qkZ = const,
получаем
th ср ~ thi' Лк.ср Лк I Ок.ср t?K t-
5.3.2. ОТНОСИТЕЛЬНЫЙ ДИАМЕТР ВТУЛКИ
И КОЭФФИЦИЕНТ ПРОИЗВОДИТЕЛЬНОСТИ
Как рассмотрено ниже, закономерность изменения отдельных пара-
метров по радиусу и значения средних величин зависят от выбранного
175
типа лопаток и относительной высоты лопаток 7гв=Л/£>ср, где Dcp — сред-
ний диаметр, делящий пополам высоту лопаток.
Отношение DBT./DK=dK называется относительным диаметром втул-
ки. Относительная высота лопатки и относительный диаметр втулки свя-
заны между собой соотношением
/Д==^Т- (5.42)
1 + dK
Величина относительного диаметра втулки различных ступеней много-
ступенчатого компрессора изменяется в широких пределах от dK=
= 0,35=0,4 в первой ступени до 0,90-5-0,92 в последней ступени.
Малые значения dK в первой ступени многоступенчатого компрессо-
ра, где низкая плотность воздуха, позволяют при заданном расходе воз-
духа уменьшать диаметр первой ступени и всего компрессора или уве-
личивать расход воздуха при заданных диаметральных габаритах. Тот
и другой эффект означает увеличение производительности компрессора,
т. е. увеличение расхода воздуха через единицу входной площади.
Производительность компрессора в большой степени зависит не
только от относительного диаметра втулки, но и от скорости воздуха на
входе и характеризуется коэффициентом производительности. Этот ко-
эффициент представляет собой отношение действительного расхода воз-
духа к теоретическому расходу, достижимому в случае отсутствия втул-
ки (dK=0), а также при скорости воздуха на входе, равной критиче-
ской скорости, и при отсутствии окружной составляющей. Обозначая па-
раметры, относящиеся к теоретическому расходу, индексом «0» можем
выражение для коэффициента производительности написать в виде
_ GB _ ^вРв9(хв)я1пав-^в]/ Т*„
Оно V 7'*/?B0sinaB0-jp
в0^ ^в0
где д(Хв) =——----газодинамическая функция, выражающаяся через X
Ykpckp уравнением
1 1
ЦХН*-1/ Ь_______ 1 \k~1
(i-[—Д)
[Для воздуха при k = 1,4 и R = 287,3 дж1кг-град sB = 0,0404
кг - град/дж)0'5].
Так как
а также
Р\=Р*^ К=-Ко, sb = sb0, <7(Хв)0 = 1,О
и sinaB0=l,0,
то получаем
GK=^(XB)(l-^)sinaB. (5.43)
177
Значения лв и ав обычно берут на среднем диаметре. Очевидно, что при
заданных значениях dK и ав величина коэффициента производительности
непосредственно связана с числом Mi на входе в рабочее колесо первой
ступени, поскольку Mj зависит от Лв и ав, которые соответственно равны
значениям М и cti этой ступени на среднем диаметре. Большое влияние
на Mi оказывает также окружная скорость, или T.u = u/aKp. Используем
выражение для относительной скорости wi на входе:
W2 = 6?2-|-«2 —2МЩ COS dp
Разделив обе части этого уравнения на произведение критической ско-
рости и скорости звука, получим
(5. 44)
где
Рис. 5.35. Зависимость Mi от GK при различ-
ных И Q]
На рис. 5.35 показана зависимость Mi от GK при dK=0,4; Хм=0,8; 0,9 и
1,0 и ai = 90o; 75° и 65°. Эта же фигура может быть использована и для
определения Mi=f(GK) при
других значениях относитель-
ного диаметра втулки, если ум-
ножить показанные на оси абс-
цисс значения GK на отношение
1 — d2K 1 — rf2
--------------------------------------------= , где dK—новое
1 —0,42 0,84
значение относительного диа-
метра.
Из рис. 5. 35 видно, что для
дозвуковых компрессоров, ког-
да в первой ступени Mi =
=0,75~-0,8, максимальные зна-
чения GK = 0,60-4-0,65, причем
допустимые величины Х„<0,9 и
Oi<90°. В околозвуковых или
сверхзвуковых компрессорах
коэффициент производительно-
сти может достигать значений
Gk = 0,7h-0,75 при Лм>0,9 и
о,—90°.
Большое влияние на вели-
чину GK при заданном значе-
нии Mi оказывают Хиии|.
Предельная величина коэф-
фициента производительности
ограничивается значением
<7(Л1) = 1,0 и, следовательно,
Xi = l,0. Таким образом,
С^к.пред^зш oi (1 dyz). На рис.
5.35 показаны для примера
значения Ск.пред и соответствую-
щие им Mi для /.„,=0,8 и трех значений аь На расчетном режи-
ме Xi < 1,0 и соответствует значениям GK, указанным выше для дозву-
ковых и сверхзвуковых компрессоров.
178
При прочих равных условиях рост коэффициента производительно-
сти позволит уменьшить диаметр первой ступени и всего компрессора,
так как обычно' диаметр первой ступени одновременно является и наи-
большим. Связь диаметра первой ступени с коэффициентом производи-
тельности определяется уравнением расхода через входное сечение ком-
прессора:
„ г'аР.,Я (лв)81пав-«вКо
О в =-----------,
ю-.
где Kg — коэффициент, учитывающий 'неравномерность поля скоростей
по высоте лопатки и влияние пограничного слоя у наружной и внутрен-
ней стенок (см. разд. 5. 5. 4). Заменяя
и
— rf^sin ав —С7К,
получим
Л 4ОпУт1
Ок=]/ • (5-45>
’ 7tSKp,(iKK(}
Иногда производительность компрессора оценивают, относя расход воз-
духа к лобовой площади колеса компрессора на входе, т. е. в виде
О„ (7В , „
———V кг сек-м2.
F„ 1
4
Обозначив эту величину через блоб, нетрудно показать, что она связана
с коэффициентом производительности соотношением
7=Г __73 Рп SR
илоб —A-Z--
Таким образом, при заданном значении GK величина (?лоб будет зави-
сеть от условий работы компрессора, т. е. от высоты и скорости полета.
Для ориентировки в табл. 5.4 приведены соотношения между <?Лоб и GK
для стандартных земных условий, т. е. р„ =1,014 бар и ТВ = 288°К.
Таблица 5.4
^лоб 120 130 140 150 160 170 180 190
Ок 0,496 0,538 0,58 0,621 0,662 0,704 0,745 0,785
5.3.3. УДЛИНЕНИЕ ЛОПАТОК И ГУСТОТА РЕШЕТОК
Важным параметром ступени является удлинение лопаток, под кото-
рым понимается отношение высоты лопаток к хорде на среднем ра-
диусе:
179
Большие значения этого параметра соответствуют узким лопаткам, что
уменьшает массу ступени и ее продольные размеры. Наоборот, малые
значения h соответствуют ступени с широкими лопатками, что не только
увеличивает ее массу, но и уменьшает ее к.п.д. из-за роста потерь на
трение.
В первых дозвуковых ступенях значения h доходят до 3,5-?-4,5.
В последних ступенях й=2,0-н2,5. Это объясняется тем, что в первых
ступенях, где лопатки имеют большую высоту, весьма важно увеличивать
их удлинение как с точки зрения массы, так и с точки зрения продоль-
ных габаритов компрессора. В последних ступенях относительно малые
удлинения оправданы рядом соображений; к числу их, в частности, от-
носится стремление уменьшить число лопаток. Действительно, число ло-
паток можно записать в виде
— ь h ~ jt £ р _ b Л — л
h IlD
При относительно малой абсолютной и относительной высоте лопаток h
и йс в последних ступенях выбор больших удлинений h может при дан-
ной густоте привести к из-
Рис. 5.36. Влияние удлинения лопаток на харак-
теристику компрессора:
а—Л =1,5; б—h=3,0
130 КО 150
S)
лишне большому и практи-
чески нецелесообразному чи-
слу лопаток с весьма малы-
ми хордами и пониженными
числами Re. Кроме того,
большие удлинения снижают
запас устойчивой работы в
этих ступенях. Действитель-
но, с ростом удлинения угол
раскрытия круглого диффу-
зора, эквивалентного криво-
линейному диффузору всего
межлопаточного канала, должен увеличиваться, что может приводить
к более раннему срыву в этих ступенях. В околозвуковых и сверхзвуковых
ступенях требуется иметь несколько меньшие удлинения, исходя главным
образом из получения канала с малым углом расширения на участке
торможения скоростей после завершающего скачка. Однако, как пока-
зали испытания [66], при умеренных числах Mi, можно спроектировать
рабочее колесо с малой хордой, обладающее удовлетворительными дан-
ными как на расчетном, так и на нерасчетном режимах.
На рис. 5.36 сравниваются к.п.д. околозвуковых рабочих колес,
имеющих удлинение лопаток й = 3,0 и h = 1,5. К.п.д. даны для разных рас-
ходов воздуха при постоянном числе оборотов.
Оба рабочих колеса имели лопатки, построенные с помощью двух
дуг окружности, относительный диаметр втулки dK = 0,5, степень повы-
шения давления л* = 1,35, окружную1 скорость ик=300 м/сек и числа
М1раСч=1,1. Как видно, и при удлинении й = 3,0 можно получить к.п.д.,
не уступающие по величине к.п.д. колеса с удлинением й=1.5
Влияние густоты решеток на коэффициент диффузорности, коэффи-
циент напора и к.п.д. рассмотрено было выше. Величина густоты выби-
рается для первых дозвуковых ступеней на среднем диаметре в пределах
6Д=0,6н-1,0.
В средних и последних ступенях b]t=1,2—1,4. В околозвуковых и
сверхзвуковых ступенях густота решетки увеличивается и достигает на
среднем диаметре значений 1,4—1,6, а у втулки 2,0-н2,2 [66].
Для спрямляющих аппаратов h/b и b/t могут иметь такие же зна-
чения, какие принимаются для рабочих колес соответствующих ступе-
ней.
180
5.3.4. ТИПЫ ЛОПАТОК РАБОЧИХ КОЛЕС И СТУПЕНЕЙ
Тип лопаток рабочих колес в первую очередь определяется законом
изменения циркуляции (см. разд. 2. 3) по их высоте, от чего зависит из-
менение по высоте теоретического напора, степени реактивности, чисел
Mi, осевых скоростей и к.п.д.
Различные законы изменения циркуляции по радиусу можно выра-
зить зависимостью.
camrm = const, (5.46)
где
(5-47)
Скорость сит является окружной составляющей скорости ст, непо-
средственно связанной со скоростью wm, определяющей в соответствии с
теоремой Жуковского величину равнодействующей силы на профиле ре-
шетки [см. уравнение (2.21)]. Скорость ст связана со скоростью со-
отношением
ст=Vwl + ti(a.-‘2wum) = ]/^2m + «(cum-w„m).
Для симметричного треугольника скоростей, когда cum=wUm, cm=wm.
Для неподвижной решетки скорость ст заменяет скорость wm. Величи-
на показателя т характеризует свойства различных типов ступеней
компрессора.
Используя выражения (5.46) и (5.47), а также уравнение для тео-
ретического напора, получаем
I ^7th Ifth
c2u = ^Um 4“ 'T " ’ CT.u — ctim 9 •
2u 2u
Заменяя cum из уравнения (5. 46), получаем
const . Hth . const Hth
(5. 48)
С помощью этих соотношений находим выражение для кинематической
степени реактивности:
где
1 const 1 В
const ситгт
0) со
(5.49)
В настоящее время известны следующие типы лопаток и соответст-
вующих им ступеней, получившие практическое применение:
а) с постоянной по радиусу циркуляцией, у которых показатель
т=1,0;
б) с постоянной по радиусу кинематической степенью реактивности,
для которых т=—1,0;
в) лопатки промежуточного типа, для которых 1,0>т>—1,0'.
Ниже рассматриваются основные свойства этих лопаток и ступе-
ней.
5.3.4.1. Лопатки и ступени с постоянной по радиусу циркуляцией
Такие лопатки и ступени иногда в литературе называют лопатками
(ступенями) «со свободным вихрем» или просто «вихревыми». Они ха-
181
растеризуются тем, что на входе в рабочие лопатки и на выходе из них
выдерживается на всех радиусах постоянство циркуляции:
Т,г1 = 2лг1с1и = const;
Г;-2=2лг2(?2и = const.
Эти условия соответствуют значению показателя т=1,0 в уравне-
нии cumrm~const. Действительно, умножив на г обе части соотношения
(5. 47), получаем
СтГ~ const,
что соответствует показателю т= 1,0.
Постоянство значений ciur или C\uti, а также с2иг или с2ии обуслов-
ливает и постоянное значение теоретического напора по радиусу, т. е.
Hth, = const. Коэффициент теоретического напора будет изменяться об-
ратно пропорционально квадратур радиуса. Так, например, если в каче-
стве исходного взять значение Hth ср на среднем радиусе, то величина
Hth на любом другом радиусе будет связана с Hth ср соотношением
Нth / гср \ /гср \
Hth ср \ г / \ Г /
где
Гер - г
гср = — И Г=—.
Гк гк
На рис. 5.37 показано изменение этого отношения в зависимости от от-
носительного диаметра втулки для периферийных и втулочных решеток,
откуда следует, что при нормальных коэффициентах напора на среднем
радиусе втулочные решетки при <7к=0,4 ? 0,5 могут быть по коэффициен-
ту напора в два с половиной — три раза перегружены. Это вызывает не-
обходимость уменьшения коэффициента напора в первых ступенях осе-
вых компрессоров с постоянным напором по радиусу, имеющих малый
относительный диаметр втулки.
Как было показано в гл. 2, при постоянстве циркуляции по радиу-
су будут постоянными и осевые скорости по радиусу:
С1а=const; с2а = const.
Однако, если учесть взаимное влияние всех лопаточных венцов, а также
влияние формы проточной части компрессора, изменение полного напо-
ра по радиусу и другие факторы, то и в данном типе ступени осевые ско-
рости несколько изменяются по радиусу, что, однако, в расчетах часто не
учитывают.
Ступени с постоянной циркуляцией характеризуются существенным
изменением по высоте лопатки степени реактивности и чисел Mi на входе
в рабочее колесо и М2 на входе в спрямляющий аппарат. Это видно из
рис. 5. 38, где показаны треугольники скоростей при профилировании ло-
паток по закону cur=const. Из выражения (5. 49) для кинематической
степени реактивности получаем при т = 1,0
1 в
—’
(5.50)
где
g ситг + Г1цГ
О) 2со
Из этого выражения следует, что при постоянной циркуляции на входе
и на выходе степень реактивности должна уменьшаться от периферии к
182
корню. Только при В = 0, когда с2иг =—ciur или c2u =—С\и степень реак-
тивности является величиной постоянной (рк =1,0). Степень реактивно-
сти на среднем радиусе выразится уравнением
1 В 4
(1+7к)2 •
(5. 51)
Степень реактивности на текущем радиусе можно связать со степенью
реактивности на среднем радиусе соотношением
6к=1 - ci -oKrcp)(l_^2i, (5.52)
где г = г!гк.
Чем меньше относительный диаметр втулки, тем значительнее сте-
пени реактивности на внешнем радиусе (г=1,0) и у втулки (r = J) отли-
Рис. 5.37. Изменение коэффи-
циента напора на внешнем ра-
диусе и у втулки в зависимости
от относительного диаметра
втулки
Рис. 5. 38. Треугольники скоростей при профи-
лировании лопаток по закону постоянства цир-
куляции:
а—на периферии лопаток; б—на среднем диаметре;
в—у втулки лопатки
чаются от степени реактивности на среднем радиусе, как показано в
табл. 5. 5 при QKrcp = 0,5.
Как видно из табл. 5. 5, при значениях dK=0,4—0,5, характерных
для первых ступеней многоступенчатого компрессора, степень реактив-
ности у втулки становится
отрицательной, а у вершины
приближается к единице.
Это вызывает резкий рост
чисел М] на входе в рабо-
чее колесо и чисел М2 на
входе в спрямляющий аппа-
рат у втулки, так как с уве-
личением степени реактив-
ности возрастают относи-
тельные скорости Wi, а при
уменьшении степени реак-
Таблица 5.5
dK гср 9к Гк Qk гвТ
0,85 0,5 0,5725 0,41
0,6 0,5 0,68 о,н
0,5 0,5 0,718 -0,132
0,4 0,5 0,755 —0,53
тивности возрастают скоро- ~
сти на выходе из колеса. Отношение чисел Mi и М2 на внешнем диа-
метре и у втулки к числу Мир и М2ср на среднем диаметре в зависимо-
сти от относительного диаметра втулки показано на рис. 5. 39. Расчеты
183
произведены для ступени, имеющей на среднем диаметре ркср=0,5;
Саср = 0,76; Hth ср = 0,33; М1ср=0,75; М2ср = 0,74.~
Из рис. 5.39 видно, что увеличение чисел Mi и М2 при малых отно-
сительных диаметрах весьма велико, что препятствует их применению.
На рис. 5. 40 показаны результаты экспериментальных исследова-
ний ступени с постоянной циркуляцией в виде зависимости от чисел Mi
к. п. д. г)ст и коэффициента напора Н для
оптимального режима в процентах от со-
ответствующих величин при наименьшей
окружной скорости. Ступень имела на
расчетном режиме на внешнем диаметре
са = 0,5, пк = 250 м/сек и Mi = 0,72.
Из графика видно, что рост чисел М,
сверх значения 0,72, являющегося для
данного профиля критическим, вызывает
существенное снижение к. п. д. и напора.
Иногда исходят из предположения, что
оптимальная конструкция ступени с по-
стоянной циркуляцией получается в слу-
чае равенства относительной скорости на
Рис. 5.39. Изменение отноше-
ния чисел Mi и М2 на внешнем
диаметре колеса и у втулки
к числу Micp и М2Ср на сред-
нем диаметре в зависимости от
относительного диаметра втул-
ки для ступеней с постоянной
циркуляцией
Рис. 5.40. Экспериментальные
зависимости параметров сту-
пени с постоянной циркуляцией
Цтах и //опт от числа Ml
входе в колесо на внешнем радиусе и
абсолютной скорости на входе в спрям-
ляющий аппарат у втулки, т. е.
^1к— С2вт-
Это условие приблизительно соответствует равенству чисел М в этих
сечениях, т. е. М1К^М2Вт, которые в частном случае могут быть равны
их максимально допустимым значениям. Воспользовавшись треугольни-
ками скоростей, мы можем для указанных двух скоростей написать:

С2 вт ~ С2а “Ь (С2и вт 4" Дси вт)2*
Принимая с1а = с2а, получаем
Ык С1и к = С1ц вт + Ас„ вт*
При законе cMr=const
С\и К=С1и вт^к *
(5. 53)
184
кроме того,
ВТ
Hth
uKdK
Подставляя эти значения ciuK и ДсМвт ® уравнение (5. 53), получим
Hth
UK — =—
«А
Следовательно,
« _ Hth
- I . „ ик^к । Нth цк 0 4~ Hfh)
с 1и вт ~Г —с и вт ‘ 1 , Т I „ 1 1 Т
1 + dK WjA 1 + dK
Таким образом, окончательно можем написать
или, разделив на пк,
®1к ^2вт
цк (1 + 7/th к)
1 + dK
(5.54)
2
Таким образом, для получения равенства между WiK и с2вт или прибли-
зительно между М1к и М2вт необходимо для каждого dK иметь опреде-
ленные соотношения между коэффициентом расхода и коэффициентом
напора на внешнем_радиусе. На рис. 5.41 даны значения wik(c2BT)_b за-
висимости от (1+Я/йк)/(1+йк) при различных сак и значения Hth.K в
зависимости от (14-Яц1К)/(1-Мк) при различных dK. Этими графиками
как номограммой можно пользоваться при подборе параметров ступени
с постоянной циркуляцией, если наложить условие, что WiK==c2BT. При
этом в качестве исходных следует принимать данные для номинального
режима (см. рис. 5. 25).
Пример. Для промежуточной ступени многоступенчатого компрессора заданы за-
висимости по рис. 5. 25 и
d„=0,652; Нгк сР = 0,443; cL сР=0,648;
wCp=289 м!сек-, aj=355 м!сек.
Определяем:
Са к—ГдсрГср — Са ср 2 —0,536;
«к = “ср/гср = 350 mJcbk-,
Нth к — Нth сргср = 0,302;
1 +^«-0,780;
1 4- dK
w1K= /0,5362 + 0,7892“= 0,955;
и,1к= ®]кик = 0,955-350 = 334 м]сек-,
334
М1К= — = 0,94.
ООО
По графику рис. 5.39 находим для заданных условий MiK/Micp=l,2. Следовательно,
М1Ср=0,785. Значения Мюр и MiK являются еще приемлемыми при соответствующем
185
подборе профилей. Следовательно, при заданных условиях возможно реализовать
к|1к = с2Вт, в противном случае могло бы потребоваться изменить окружную скорость,
степень реактивности на среднем радиусе или Hih и са.
На среднем радиусе ступеней с постоянной циркуляцией часто при-
нимается элементарная ступень со степенью реактивности рк = 0,5. Пере-
мещая эту элементарную ступень по направлению к внешнему диаметру
(т. е. уменьшая степень реактивности на среднем радиусе), можно умень-
шить число Mik у вершины. Однако
это может привести к увеличению чис-
ла М2 у втулки направляющего аппа-
рата, если не выполнить условий,
соответствующих уравнению (5.541.
Углы выноса, или углы установки, се-
чений лопатки на различных радиусах сильно изменяются от вершины
к основанию. Углы установки в основном определяются углами потока
Pi и р2- Исходя из рис. 2. 6 получаем
р. й1 + 32 I XI — 7.2 । 8 ± i
2 2 ' 2
Так как значения ——— и относительно
2 2
приближении можно считать
<1 31 + 32
2
невелики, то в первом
2
В связи с этим угол установки можно характеризовать величиной угла
|Зт (см. рис. 5. 38 и 2. 10), который связан с углами Pi и р2 зависимостью
t 8 +ctgg2 =sin (8, + з2)
' т 2 2 sin 8j • sin 82
Как уже было показано (см. 5.2.4), величина ctg pm связана простым
соотношением со степенью реактивности и коэффициентом расхода:
« — cia — —
ctg^ =------------
са са
Так как по направлению от вершины к втулке ок уменьшается, а коэф-
фициент расхода возрастает, то угол 0т (и, следовательно, угол установ-
ив
ки) уменьшается, причем особенно сильно при малых значениях d.
Вследствие этого лопатка получается сильно перекрученной, что под-
тверждается данными рис. 5.42, где_приведены значения углов ртВт,
ртк и их разность в зависимости от rfK при степени реактивности и ко-
эффициенте расхода на среднем радиусе дКСр = 0,5 и саСр = 0,76. При
уменьшении dK у основания лопатки уменьшается степень реактивности
и поток на выходе из колеса может изменить свое направление по отно-
шению к осевой скорости, вследствие чего угол (32 следует считать отри-
цательным (см., например, на рис. 5.9 qk=0). Такое явление в связи с
неблагоприятной формой канала нежелательно, и поэтому при профили-
ровании лопаток с постоянной циркуляцией следует иметь 0°<Р2<^90°
и положительным по величине. Использовав выражение (5. 23) для ctg 02
и наложив указанные выше условия для решетки у основания, получаем
соотношение
п вт
Ук.ВТ г,
Выразив с помощью выражения (5. 52) qk. ,ът и Нth вт чсре.3 степень» реяк."
тивности и коэффициент напора на среднем радиусе, получаем
. 1 ср
ек.еР>1+— (1+7ку
(5. 55)
Таким образом, чем меньше относительный диаметр втулки <2К, тем боль-
ше должна быть при заданном значении Hth степень реактивности на
среднем радиусе, удовлетворяющая требование
0°<(32<90°.
Поскольку это-Связано с ростом чисел_М1к у периферии и М2 у втулки,
то при малых d требуется уменьшать Hth, а следовательно, и напор сту-
пени.
Все изложенное выше показывает, что ограничения по числу MiK и
М2вт и по углу выхода потока у втулки становятся особенно заметными
при 5к<0,6, которые обычно требуются для первых ступеней компрессо-
ра. Поэтому применение лопаток с постоянной циркуляцией является
целесообразным только в ступенях с относительным диаметром втулки
Г7|;'~'О,6.
Лопатки рассматриваемого типа можно характеризовать еще средней интеграль-
ной степенью реактивности, которая с помощью уравнения (5.41) при //(/u = const за-
писывается в виде
J
______ гвт______
бк.ср —
к
Jd0
гвт
Заменим в этом уравнении ок из выражения (5.50), а значение dG исходя из уравне-
ния (2.100) запишем в виде
1
[ k — 1 , Г/ г.. \2 1)*~1
dG = 2nrycadr — 2пгсаук 1Л——-—М„ к I—1 —1 1 dr,
где
М2 =
kRT\ '
187
Разложив выражение, стоящее в фигурных скобках, в ряд и ограничившись первыми
двумя членами, получим для QK.cp уравнение
Ск.ср ~ 1
После интегрирования и преобразований получим
(5. 56)
При М„ к=0, т. е. при отсутствии закрутки на входе в колесо, получим
1
Bln —
Ск.ср — 1 -7 (5.57)
тО-О
Это же выражение справедливо для QK.cp в случае, когда при наличии закрутки можно
приближенно принять, что по радиусу у=const. Разложив в ряд и пренебрегая
членами второго и более высокого порядков, получим
Используя это выражение, будем иметь
6К-С₽ (1+?к)2 Г2 •
Это значение средней интегральной степени реактивности равно степени реактивности
на среднем радиусе, делящем пополам высоту лопатки [см. (5.51)].
При М1и1.=л0 Qk.cp^Qktcp , но при d^0,6 различие между этими ве-
личинами относительно невелико, как показано на рис. 5.43 при QKrcp =
= 0,5. Поскольку значения qk и са являются переменными по радиусу,
то переменными должны быть и к.п.д. элементарных ступеней. Поэтому
ступень в целом должна характеризоваться средним интегральным зна-
чением к.п.д., который на основании уравнения (5.40) при Hth — const
может быть записан в виде
J r^idG
к.ср г
\dG
гвт
Расчеты показывают, что даже при учете только профильных потерь
среднее интегральное значение к.п.д. с уменьшением относительного диа-
метра втулки несколько уменьшается по сравнению с к.п.д. на среднем
188
радиусе. Причиной этого является снижение к.п.д. элементарных сту-
пеней, расположенных в сечениях, отличных от среднего, вследствие из-
менения степени реактивности и коэффициента расхода (рис. 5.44). К.п.д.
полной ступени существенно зависит еще от вторичных и концевых потерь,
влияние которых будет особенно заметно в периферийных сечениях из-
за утечек и перетеканий в радиальном
зазоре. По экспериментальным данным
увеличение относительного радиально-
го зазора б/йл на 1 % приводит к сни-
жению к.п.д. ступени на 2—3%, т. е.
влияние этого зазора достаточно вели-
ко *>. Очевидно, что этот вид потерь
имеет наибольшее значение для по-
следних ступеней, где высота лопаток
уменьшается. Трение диска, являющее-
Рис. 5.44. Зависимость Г]к г/Лк top от г при
от Ма к и dK различных значениях dK
ся также составной частью концевых потерь, оказывает на к.п.д. ступеней
второстепенное влияние по сравнению с потерями, обусловленными ра-
диальным зазором. Примерный характер изменения клт.д. ступени с уче-
том вторичных и концевых потерь показан на рис. 5. 48.
5. 3.4.2. Лопатки и ступени с постоянной по радиусу
кинематической степенью реактивности
Лопатки ступени, спрофилированные с сохранением по радиусу по-
стоянной кинематической степени реактивности, часто называют ступе-
нями и лопатками с постоянной степенью реактивности. Однако такое
их наименование не является точным, поскольку, как показано ниже,
на всех радиусах (исключая средний) осевые скорости на входе в коле-
со и на выходе из него должны быть не равными, вследствие чего дейст-
вительная степень реактивности существенно отличается от кинематиче-
ской. Из уравнения (5.49) получаем, что если т=—1,0, то
рк = 1 — В== const.
Таким образом, при т— —1,0 на всех радиусах кинематическая сте-
пень реактивности будет одинаковой. Одновременно из уравнений (5. 48)
при —1 получаем
-^2-= const 4~-Hth—;
г
-^- = const —
Г 2г^а
В данном случае речь идет о суммарном влиянии радиального зазора, а не
только о потерях из-за утечек, оцениваемых работой La и т]3 [уравнения (2. 60) и (4. 7)]
189
Рассмотрим применительно к этим лопаткам два случая.
1. 1'1 const по высоте лопатки; тогда очевидно, что c2u/r-Aconst и
Ciu/r^const, хотя
-£2u_ _J_ S1!L — с on st.
г г
2. Нconst-г2 по высоте лопатки; тогда с2и/г = const и с1и/г =
— const.
Следовательно, во втором случае поток до и после колеса закручен
по закону твердого тела. Характерной особенностью этих лопаток являет-
ся постоянство коэффициента теоретического напора по радиусу. Дейст-
вительно, исходя из условия /f<h=const • г2, получаем
= и = const.
Г2М2 «2 “
При этом теоретический напор будет уменьшаться от конца лопатки
к ее основанию. Средний интегральный теоретический напор выразится
уравнением
Г
WfW J u-dG
U ЛВТ
22 th ср т
[ dQ
гвт
Чтобы сравнить его с теоретическим напором лопаток, имеющих Hth =
=const, отнесем средний интегральный напор к напору элементарной
ступени на внешнем радиусе, где он имеет максимальное значение. Тогда
после преобразования получим
1.0
J еауг3 dr
Нth- ср J"
(5. 58)
J сауг dr
1
где г=г/гк.
Если пренебречь изменением у по радиусу, которое для закона cu/r—const
относительно невелико (см. рис. 2.21), и для определения си в зависи-
мости от радиуса применить уравнение, полученное выше для Дт = оо,
то можно получить следующее выражение для Hthcp/HthK-
MthK ’ b
(5. 59)
где alb=1^0,5(caJciuKy.
Результаты расчетов по уравнению (5.59) показаны на рис. 5. 45.JIpn
расчетах принято, что у периферии са=128 м/сек, с1и=146 м/сек и М]=
= 0,73. Как видно, при небольших dK существенно уменьшается напор,
190
достижимый в ступени с такими лопатками, по сравнению со ступенью,
имеющей по всей высоте лопатки постоянный теоретический напор. Не-
равномерность распределения напора по радиусу неблагоприятна для
последующих ступеней. Поэтому предпочитают лопатки с постоянным
теоретическим напором по радиусу. В отдельных случаях, в частности,
в вентиляторных ступенях компрессора двухконтурного двигателя, воз-
Рис. 5. 45. Изменение
Hth cp/HtK к в зависимости от
относительного диаметра втул-
ки для лопаток, спрофилиро-
ванных по закону ciu/r=^const
Рис. 5.46. Изменение числа Mi по радиусу
в ступени с лопатками, спрофилированными
по закону QK = const; Ht л = const:
wK=350 м/сек;
H^~20 00Q дж/кг
можно и //tzt=Aconst по радиусу. При этом изменение напора по радиусу
может существенно отличаться от рассмотренного, например, —быть
линейным или ступенчатым, а степени реактивности по радиусу не будут
постоянными. Лопатки с постоянной степенью реактивности и постоян-
ным теоретическим напором по радиусу характеризуются малым изме-
нением числа Mi по высоте лопатки (рис. 5. 46). Это объясняется тем, что
осевая скорость уменьшается от втулки к концу лопатки, а окружная со-
ставляющая возрастает. Треугольники скоростей при профилировании
лопаток для условий gK=const и Ягл=соп51 по радиусу показаны на
4)
Рис. 5.47. Треугольники скоро-
стей при профилировании лопа-
ток по закону qk = const:
#tzt=const:
а—на периферии лопаток; б-—на
среднем диаметре; в—у втулки
рис. 5.47. Вследствие малого изменения Mi и qk=const коэффициент по-
лезного действия элементарных решеток и ступеней должен несущест-
венно изменяться по радиусу, если не учитывать вторичных концевых
потерь, даже при реальных изменениях коэффициента расхода са. На
рис. 5. 48 показано относительное изменение по радиусу к.п.д. решеток
рабочего колеса, подсчитанное по выражению рр.к=1—LR1JHth для сту-
пени, имеющей QK = 0,5=const, d = 0,4 и cia, изменяющееся как показано
191
на рис. 5.49 при т— — 1 „О’. Однако с учетом вторичных концевых потерь
изменение к. п.д. будет более значительным.
Несмотря на существенное изменение коэффициента расхода по ра-
Рис. 5.48. Зависимость Т]г/Т]г ср от г для лопаток
с постоянной степенью реакции:
без учета концевых потерь-------с учетом кон-
цевых потерь
новки лопаток по радиусу (или углы рт и Д0т) изменяется значительно
меньше, чем при cur—const, как показано в табл. 5. 6 для лопаток, имею-
Таблица 5.6
dK Лопатки са r=const Лопатки qk = const
?т к Р/72 ВТ к \Jm вт А ?т
0,6 48° 83° 50' 35’50' 33° 30' 61’20' 27’50'
0,4 54°38' —68° 20' 122’58' 33’30' 70'48' 37°18'
щих dK=0,6 и dK=0,4. Таким образом, лопатки, имеющие QK=iconst, ме-
нее закручены по радиусу. Изложенное выше показывает, что ступени с
Рис. 5. 49. Изменения осевой скорости на входе в колесо (а) и сте
пени реактивности у втулки (б) при различных значениях показа-
теля т
постоянной степенью реактивности и постоянным напором по радиусу
более пригодны при малых относительных диаметрах втулки. Однако
и они имеют серьезный недостаток, выражающийся в значительном из-
192
менении осевой скорости по радиусу (рис. 5.49 и 5.50), которое увели-
чивается с ростом коэффициента напора. Это ограничивает напорность
ступени, так как в области малых са будут требоваться нереально высо-
Рис. 5.50. Изменение c2a=f(r) на выходе из рабочего ко-
леса при различных значениях показателя т
кие углы поворота потока. Кроме того, при больших коэффициентах на-
пора осевые скорости на периферии могут по расчетам получаться даже
отрицательными, что явно невозможно.
5.3.4.3. Лопатки и ступени промежуточного типа.
Комбинированные лопатки
В ступенях промежуточного типа показатель 1,0>т>—1,0, и при
требующейся величине напора его значение определяется в конечном ито-
ге допустимыми числами Mt у конца лопатки, степенью реактивности у
основания ее и степенью неравномерности поля осевых скоростей на
входе.
В качестве примера на рис. 5. 49 и 5. 50' показано изменение осевой
скорости и чисел М] на периферии на входе в рабочую лопатку и М2 на
выходе из нее у втулки, подсчитанные для различных значений т по
упрощенному уравнению (5.62) при постоянных значениях qk.cp = 0,5,
Hth ср=0,33 и ык=350 м/сек.
На рис. 5.49 показано также изменение степени реактивности у
втулки. Как видно из этих кривых применение промежуточных значе-
ний т значительно' уменьшает степень неравномерности поля осевых
скоростей по радиусу. В то же время возрастают числа М] у периферии
по сравнению со случаем, когда т=—1,0 (gK=const, Ягд—const), до-
стигая максимального значения при m=l,0 (cur=const). Одновремен-
но уменьшаются степени реактивности у втулки, оставаясь все же по
величине значительно больше, нежели при т=1,0. Поэтому лопатки со
значениями 1,0^>т>1,0 могут быть использованы и при относительно
небольших диаметрах втулки.
В отдельных случаях возможно применение «комбинированных» ло-
паток, в которых используется не один, а два или более законов профи-
лирования. Так, например, если от среднего до внешнего радиуса приме-
нить профилирование с показателем т = —0,5, а от среднего радиуса до
втулки профилировать с показателем т=+0,5, то поле скоростей ста-
нет более равномерным, нежели при т~—0,5 для всей лопатки (см.
рис. 5. 49 и 5. 50). При этом можно обеспечить приемлемые числа АК у
периферии и числа М2 у втулки.
7 546
193.
5. 3.4. 4. Сравнение ступеней различных типов
Из изложенного вытекают следующие различия между ступенями
с разными законами профилирования. Если все ступени будут иметь
одинаковые степени реактивности на среднем радиусе, то степень реак-
тивности на периферии у лопаток с т^>—1,0 возрастает. Вследствие это-
го при равных числах Mj в ступенях с т>—1,0 окружная скорость дол-
жна быть меньше, чем в ступени с постоянной степенью реактивности
(т = —1,0), либо в этих ступенях будут больше числа Mt (см. рис.
5.49). Если же ступени с т>—1,0 будут первыми, то пониженная ок-
ружная скорость будет и во всех последующих ступенях, вследствие че-
го потребуется увеличивать число ступеней. Когда значения т относи-
тельно близки к т= —1,0 (например, т=—0,54—0,75), то указанные
различия в числах Mi и в окружной скорости не столь велики и в то же
время обеспечивается более равномерное поле скоростей. В случае же,
когда m=l,0 (cur = const), числа Mi у периферии или окружные ско-
рости должны значительно отличаться от чисел Mi и и в ступени, имею-
щей лопатки с постоянной степенью реактивности или с показателем т,
близким к минус единице, особенно при малых относительных диамет-
рах втулок.
Поэтому лопатки с постоянной циркуляцией применяют обычно в
средних и последних ступенях осевого компрессора, где относительные
диаметры втулок <?^0,6н-0,65; в первых же ступенях более целесообраз-
ны лопатки с т=(—0,5н—0,75) или «комбинированные». Окончательно
значение т уточняется в зависимости от получающихся чисел Mi на пе-
риферии и М2 у втулки.
В первых околозвуковых или сверхзвуковых ступенях может ис-
пользоваться закон постоянства циркуляции при осевом входе воздуха.
Однако в этих же ступенях могут применяться лопатки и с переменной
циркуляцией при наличии предварительной закрутки, что наиболее важ-
но для внешнего радиуса, поскольку позволяет уменьшить числа Mi при
достаточно больших окружных скоростях.
5.3.5. ОПРЕДЕЛЕНИЕ ПОЛЯ ОСЕВЫХ СКОРОСТЕЙ
В СТУПЕНЯХ С ЛОПАТКАМИ РАЗЛИЧНЫХ ТИПОВ
В гл. 2 были рассмотрены некоторые примеры упрощенного опре-
деления поля осевых скоростей в зазорах между рабочими и неподвиж-
ными лопатками, когда радиус кривизны линии тока /? —оо, что равно-
сильно условию dca!dx = 0, а также когда Е—const и LR=const по ра-
диусу колеса. Если применить эти же условия в общем случае, ког-
да окружные составляющие абсолютных скоростей на входе в рабочее
колесо и на выходе из него подчиняются уравнениям (5.48), то можно
получить в общем виде уравнение для распределения осевых скоростей
при условии, что Hth = const по радиусу:
Суд
С la ср
т — 1 (1— QK. ср)2
т с la ср
(5. 60)
194
Формула для определения cirJcia ср имеет такой же вид, но перед третьим
членом должен стоять знак плюс. В случае, когда m=0 (cum=const), то
уравнение приобретает такой вид:
^ = 1/1-2 (1_/"»),lnX+ <'_ig-») 77„1р(1-<-). (5.61)
Clacp ' С1аср гср С1дср \ ' 5гср /
Это же уравнение справедливо и для определения с2а1с2а ср при условии,
что перед третьим членом будет стоять знак минус. Для значения т =
=—1 (QK=QK.cp=const) уравнение 5. 60 будет иметь следующий вид:
С1и
С1а ср
(1 - щ)2
72
с 1а ср
(1-Ск.ср) 1п^--
г ср
(5. 62)
Для определения осевых скоростей потока за колесом в уравнении
(5.62) перед третьим членом должен стоять знак минус. Результаты
расчетов по уравнениям (5.60), (5.61) и (5.62) для сечений на входе в
рабочее колесо показаны были на рис. 5.49, а на выходе — на рис. 5. 50.
Из сопоставления этих графиков видно, что при уменьшении т поле ско-
ростей становится все более неравномерным, причем в сечении за рабо-
чей лопаткой оно более неравномерное, чем на входе, и поэтому на всех
радиусах, исключая средний, cia=#=C2a. В связи с этим, как уже отмеча-
лось выше, при QK = const по радиусу (т = —1,0) действительная сте-
пень реактивности существенно отличается от кинематической. Это лег-
ко показать и в общем виде. С этой целью выразим с помощью уравне-
ния (5.62) С1йи с2а и, приняв, что на среднем радиусе CiaCp = C2acp,
получим после вычитания одного уравнения из другого:
С~Ча С\а' ^Иср^Мср(^ 6к) -
г ср
Используя выражение (5. 7) для степени реактивности, можем на-
писать
2 2
___с2а с\а
Qk. д Qk г) гг
th
। 4ис pH th Ср . , < г
QK Н------77— (1 - ек)111 --- - ,
ш th ^ср
или, так как и? Hth<.v==Hth,
6к.*=0к + 2(1-ек) 1п~
1 + а
(5.63)
Если принять d = 0,4 и qk=0,5, то получим значения дк.д на различных
радиусах, как показано в табл. 5. 7.
Таблица 5.7
Г 0,4 0,6 0,7 0,8 0,9 1,0
Ок.д —0,0586 0,3457 0,5 0,633 0,75 0,8577
Таким образом, действительная степень реактивности у втулки име-
ет отрицательное значение и, следовательно, в относительном движении
имеет место понижение давления, а у периферии большая часть повы-
шения давления в ступени приходится на рабочее колесо. Упрощенные
уравнения для определения поля скоростей в принципе пригодны для
1
применения, лишь когда кривизна линий тока km = ~z~ <0,1. В лопатках
Кт
с малыми относительными диаметрами втулок при переменной циркуля-
7* 195
ции по радиусу колеса линии тока имеют значительную кривизну, вслед-
ствие чего упрощенные уравнения дают существенную погрешность.
Более точные методы расчета, о которых упоминалось выше (см.
гл. 2), достаточно сложны и трудоемки. Правда, при использовании
электронно-вычислительных машин эти трудности преодолеваются. Од-
нако в учебной практике применение этих машин не всегда возможно.
Иногда это может быть неудобно и при предварительных расчетах в
ОКБ. Поэтому применяются приближенные методы расчета, но с учетом
влияния кривизны.
Ниже излагается один из таких методов*), согласно которому рас-
сматривается осесимметричный поток в межвенцовом зазоре без учета
вязкости воздуха в уравнениях движения. Предполагается, что энергия
потока и работа, затрачиваемая на потери, постоянны по радиусу.
Так как в общем случае в осевом компрессоре меридиональная со-
ставляющая скорости будет наклонена к его оси, то дифференциальное
уравнение радиального равновесия в проекции на направление радиуса
г будет аналогично уравнению (2. 95):
2 2
I др , си. । ст „„„
— -----h-д-COST
Q dr г Rm
dCm . _
---sincp=O,
di
где cm — меридиональная составляющая абсолютной скорости;
Rm — радиус кривизны меридиональной проекции линии тока;
<р — угол между направлением оси компрессора и меридиональной
составляющей скорости, равный углу ф по рис. 2.21.
Пренебрегая членом dcmldt sin <р, так как он мало влияет на поле
скоростей, и заменяя, как делалось при выводе уравнений (2. 103) и
(2. 104), др]дг с помощью уравнения энергии **>, получим после интегри-
рования (при Е = const и Z.fl=const):
dr
Вводя пределы интегрирования от гСр ДО г, можем заменить постоян-
ную С меридиональной скоростью на среднем радиусе. Учитывая также,
что cm = ca/cos<p=ca}/ 14-tg2% а Rm может иметь знак плюс и минус,
получим
1
±2 J
гср т
(1 + tg2?)e
(l+tg2<prCp)c2 ср-
d(car)i
dr
(5. 64)
Данное уравнение может быть решено методом последовательных при-
ближений, так как заранее нельзя определить кривизну меридиональ-
ных проекций линий тока \/Rm как явную функцию независимой пере-
менной г.
*> Метод разработан в МАИ аспирантом Я. Трачек под руководством автора.
**> в уравнении энергии радиальную составляющую скорости не учитываем в связи
с относительно небольшим значением угла <р.
196
Однако при некоторых упрощающих предположениях задача может
быть решена в первом приближении. В общем случае кривизна мери-
диональных проекций линий тока может быть представлена следующим
образом:
кт ~ -----F д^т л + Д^т Т + Д^тр+ Д^Ш Г’
Ат Кт прот
1
где----------кривизна меридиональной проекции линии тока, обуслов-
Яотгрот ленная только формой проточной части компрессора;
—учитывает приращение кривизны линии тока, обусловлен-
ное конечной толщиной лопаток;
д£тГ—учитывает влияние изменения радиального градиента
плотности газа вдоль линии тока;
Lkmp— учитывает изменение радиального градиента полного
давления вдоль линии тока;
д£тГ —учитывает влияние изменения радиального градиента
циркуляции вдоль линии тока.
Весьма трудоемко определение ДАтти &kmr, которые в общем слу-
чае могут быть найдены только методом последовательных приближе-
ний. Однако, если ограничиться рас-
смотрением только дозвуковых первых
ступеней, то задача может быть упро-
щена, так как эти ступени проекти-
руются с относительно небольшим гра-
диентом плотности газа, вследствие
чего влияние Akml незначительно.
С достаточной степенью точности
Aktm может быть выражено эмпири-
ческой формулой
Д^тТ—±Д^л(-т) •
\ h J
На поле осевых скоростей сущест-
Рис. 5.51. Схема проточной части
осевого компрессора
венно влияет изменение кривизны ли-
нии тока, вызванное радиальными градиентами циркуляции, в данном
и смежных с ним сечениях. Это влияние целесообразно учитывать не пу-
тем изменения кривизны линии тока с помощью Д/гтт, а внося поправку
непосредственно в уравнение для определения са. Поправка вносится
добавочным членом, который на основе теории вихревого диска запи-
шется в виде
j-i
где I—расчетное сечение, которое берется в межвенцовом зазоре (рис.
5.51);
/ — порядковый номер межвенцового зазора;
1 — интеграл от радиального градиента циркуляции в межвенцовом
зазоре:
,1 г2 дг
'’ср
Kj — коэффициент, учитывающий затухание возмущений в потоке:
—cos2®-e h ;
7 2 r
197
Xj — расстояние вдоль оси х от межвенцового расчетного сечения до
аэродинамической оси решетки, расположенной между межвен-
цовыми зазорами / и (/—1);
г — г/гк — относительный радиус.
Добавочный член Ф учитывает взаимное влияние всех лопаточных
венцов на поле осевых скоростей в расчетном сечении. Так как коэффи-
циенты Kj очень быстро убывают с ростом х, то для инженерных рас-
четов достаточно учесть влияние только двух ближайших лопаточных
венцов, лежащих слева от расчетного сечения и двух справа. С учетом
указанных выше преобразований можно получить следующую прибли-
женную формулу для определения ноля осевых скоростей в расчетном
межвенцовом зазоре:
Г
1 и д I ~
\ ТТ^гЬ7(/ + ФТг
_ са ср (* + ‘g2 ?Гср) 'ср
С —--------------------1 , (О. OOJ
У У
где
г ь
±2 J cos ? [??,„/ +(1+ л+дГ^* ] d?
У = Гср ;
— Rm прот
I'm прот ~ ’
kk.
&kmp*
Гк
„ , Г 1
Величину интеграла /= \ —
J г2
(5.64), приняв в нем /?т=со
Тогда получим
<5 (cjr)2
_ dr можно выразить из уравнения
дг
и <р = 0.
I = с1
а ср
ср
При указанных условиях значения (cjcacv)2 для различных значений
показателя т были даны в уравнениях (5.60)— (5.62), с помощью ко-
торых и может быть получено значение I до и после колеса. Так, напри-
мер, для значения т =—1 (gK=const) получим с помощью уравнения
(5. 62)
{, — \ 21 _ — \
-2(l-QK)2l-p +2Яй(1-ек)1п^ .
уср/ J гср]
При профилировании по закону постоянства циркуляции 1=0.
В предварительных расчетах величину 7 + Ф можно определить с
помощью приближенной эмпирической формулы
' 1 4 1100
Л-i + Л+1 /1 _ К°/о А
2 100 J ’
где
/С = 50 + 30
h, 7c,a(i—1)
2
198
Для простоты расчета условно принимаем, что лопатки бесконечно тон-
кие. Поэтому Д£тл = 0. Кроме того, для рассматриваемого наиболее
простого случая, когда теоретический напор и потери по радиусу явля-
ются постоянными, получаем

Примечание. Для первых двух ступеней, у которых толщина лопатки играет
существенную роль, надо брать уменьшенное значение (/+Ф). Рекомендуется принять
для первой ступени (/+Ф)Расч=0,9(/+Ф), для второй ступени (/+Ф)раоч =
=0,95(/+Ф).
Для последующих ступеней влияние толщины лопатки менее значительно и по-
этому (1+Ф)расч« (/+Ф). Таким образом, косвенным путем учитывается влияние
конечной толщины лопаток на поле осевых скоростей в межвенцовом зазоре.
В результате произведенных преобразований приближенное урав-
нение для определения эпюры осевых скоростей в данном сечении имеет
вид
г (/ + Ф); + 4 (1 + tg2 ? )
с2 =-----------------—--------, (5. 66)
у
где
2) z/ = (l+tg2?-)e 'ср
3)?- +
1 — d 1 — d
rcp
4- D,< COS ?nep
nep 1 fl
Здесь /?mBT — средний радиус кривизны проточной части у втулки;
-Rjnnep — средний радиус кривизны периферийного контура про-
точной части.
В формуле (5. 66) знак плюс, если /?топер, /?твт положительны, и знак
минус, если /?тПер, вт отрицательны (рис. 5. 52).
На рис. 5. 53 и 5. 54 дано сравнение расчетов по формуле (5. 66)
и по формулам (5.60)—(5.62) для различных значений показателя т.
Как видно, поле скоростей по формуле (5. 66) получается более поло-
гим и, особенно, при т =—1,0 (QK=const, Hth — const). При т>—1,0 раз-
личие в расчетах, по указанным формулам уменьшается. Это различие
можно еще уменьшить, если для принятого значения показателя т поле
осевых скоростей определять по упрощенным формулам (5.60) — (5.62)
с показателем т'=рт. Примерное соотношение между т' и т дано на
рис. 5. 55, а, в. Сравнение расчетов по формуле (5. 66) и по формулам
(5.60) — (5.62) с использованием показателя т' показано на рис. 5.55,
б, г, из которых видно, что расчеты с показателем т' мало отличаются
от расчетов по формуле (5. 66), будучи в то же время проще.
199
Рис. 5. 53. Сравнение упрощенных и_уточ-
ненных расчетов изменения cia = f(r) при
различных значениях показателя т:
------- по уточненному расчету; ---------но
уравнениям (5.62), (5.63), (5.64)
Рис. 5. 54. Сравнение упрощенных и уточненных расчетов измене-
ния c20 = f(r) при различных значениях показателя т:
------по уточненному расчету,
------по уравнениям (5.62), (5.63), (5.64)
200
Приведенное соотношение между т и т' соответствует определен-
ным параметрам и в дальнейшем должно быть уточнено. Поэтому та-
кой метод может быть рекомендован только для предварительных рас-
четов.
Рис. 5. 55. Зависимость показателя т' от показателя т для входа
в колесо компрессора и выхода из него: а и в.
Определение осевых скоростей: биг;
------по формуле (5. 66) для случая «г=—1,0; т=—0,5 и /«=+0,5
по формулам (5. 60)—(5. 62) с показателем т'<т
Б. 3.6. ПОРЯДОК РАСЧЕТА ПАРАМЕТРОВ ПОТОКА
ПО РАДИУСУ ДЛЯ СТУПЕНИ с постоянной ЦИРКУЛЯЦИЕЙ
Расчет параметров потока по радиусу колеса (по высоте лопатки)
производится не менее чем для пяти сечений.
При профилировании по закону Г—const теоретический напор по
высоте лопатки не меняется, т. е.
Hth=const.
Параметры потока определяются следующим образом.
1. Осевая составляющая абсолютной скорости потока на входе в
рабочее колесо — по упрощенному уравнению радиального равновесия:
Ciar~ Cia cp=COnst.
Однако, если учесть взаимное влияние всех лопаточных венцов, а
также влияние формы проточной части компрессора, то осевая скорость
переменна по высоте лопатки. Методика учета этого влияния изложена
в разд. 5.3.5* >.
После уточнения эпюры осевых скоростей следует проверить расход
воздуха через ступень осевого компрессора. Если окажется, что расход
*) Для ступеней с постоянной циркуляцией обычно ограничиваются условием
Са=const, а методику, изложенную в разд. 5.3.5, применяют для ступеней с QK = const
или с промежуточным законом профилирования.
201
через ступень меньше или больше расчетного, то следует изменить внут-
ренний и наружный диаметры компрессора, соответственно увеличив
или уменьшив площадь проходного сечения.
2. Окружная составляющая абсолютной скорости потока на входе в
рабочее колесо
Г СР
С Хиг ^\и ср ~ •
3. Абсолютная скорость газа на входе в рабочее колесо
с1г—']/' с2. 4-с? .
if у lar I 1иг
4. Угол потока на входе в рабочее колесо по абсолютной скорости
пг
alr = arc sin .
С1г
5. Окружная скорость на входе в рабочее колесо
«1г=«1ср —•
/•ср
6. Угол потока на входе в рабочие лопатки по относительной ско-
рости
plr = arc tg--.
«1Г -с1иг
7. Относительная скорость потока на входе в рабочие лопатки
sin 3ir
8. Окружная скорость на выходе из рабочего колеса
и2г — и2ср-.
Если проточная часть осевого компрессора выполнена при Dcp=
= COnst, ТО М1ср=П2ср.
9. Окружная составляющая абсолютной скорости потока за рабо-
чим колесом
___ /*2ср
<-2иг— ^2ucp •
10. Осевая составляющая абсолютной скорости потока на выходе из
рабочего колеса
С2аг— ^2а ср — COBst.
11. Угол потока на выходе из рабочего колеса по абсолютной ско-
рости
a2r= arc tg^-.
dur
12. Угол потока на выходе из рабочих лопаток по относительной ско-
рости
в2г = агс tg -2пг- -.
м2г с2иг
13. Относительная скорость потока на выходе из рабочих лопаток
^2, = -^-
Sin P2r
202
14. Угол отклонения потока в решетке рабочего колеса
—?2г ?1г-
15. Скорость звука на входе® рабочее колесо
а1г~ ако1/ —1------------,
1Г кр |/ 2 \ Л + 1 1 /
где
1 с^г
V 18,3]/7f’
16. Число Mi по высоте лопатки
М,=^.
а1г
Число М] на периферии в дозвуковой ступени должно быть <0,84-0,85.
17. Кинематическая степень реакции
„ _ 1 + с2иг
«к г— 1 с,
2ur
18. Принимается угол атаки по высоте лопатки: на среднем радиусе
в первых ступенях i°=+2°~.—Н3°; на последних ступенях — до —2°; на
периферии углы атаки увеличивают, а у втулки уменьшают на Г-г-20.
19. Входной угол профиля по высоте лопатки
₽1Г = ₽1Г +г'г-
20. Угол кривизны профиля
где
mr=0,23 ^2 —У+0,1 (—.
I bt J \ 50 J
Обычно а/й=0,4-н0,45,
где а — расстояние точки максимальной вогнутости от передней кром-
ки профиля;
b — хорда профиля.
21. Угол отставания потока на выходе
22. Выходной угол профиля fijr = fer + ^-
23. Угол изгиба входной кромки профиля (см. гл. 2)
Zlr=A [1 +2 (1 _ 2 .
1 2 L \ b ) J
24. Угол изгиба выходной кромки профиля
%2г= 9 т Х1г-
25. Угол выноса профиля на радиусе г
&2=Xlr + ?U-
203
Все расчеты по пп. 18—25 производятся для спрямляющего аппа-
рата по тем же формулам. Обозначение углов в решетке спрямляющего
аппарата см. разд. 2.2. Величины углов потока для спрямляющего ап-
парата берутся из расчета параметров потока по высоте лопатки.
5.3.7. ПОРЯДОК РАСЧЕТА ПАРАМЕТРОВ ПОТОКА
ПО РАДИУСУ ДЛЯ СТУПЕНЕЙ
С ПОСТОЯННОЙ СТЕПЕНЬЮ РЕАКТИВНОСТИ
И СТУПЕНЕЙ ПРОМЕЖУТОЧНОГО ТИПА
Параметры потока по высоте лопатки рассчитываются не менее, чем
для пяти значений радиусов.
При профилировании ступеней компрессора как по закону qk =
=const, так и по промежуточным законам обычно принимают, что тео-
ретический напор по высоте лопатки не меняется, т. е.
Hth=const.
Параметры потока определяются следующим образом.
1. Окружные составляющие абсолютных скоростей потока на входе
и выходе из рабочего колеса по высоте лопатки находятся по уравнениям
(5. 48).
2. Осевые составляющие скорости на входе и на выходе из рабочего
колеса вычисляются по формуле (5.66). Предварительные расчеты мо-
гут быть произведены по уравнению (5.60) при m'<m (см. рис.
5. 55, а, в).
При вычислении осевых скоростей по высоте лопатки для проверки
сходимости заданного и полученного расходов необходимо рассчиты-
вать осевые скорости не менее, чем в пяти сечениях по радиусу.
Данные расчета осевых скоростей по формуле (5.66) для каждого
из сечений целесообразно свести в таблицу по образцу табл. 5. 8.
Дальнейшие расчеты производятся так же, как и для ступени с по-
стоянной циркуляцией (см. разд. 5. 3. 6).
В ступенях с промежуточным законом профилирования
(1>т>—1,0) эпюры осевых скоростей и другие величины вычисляются
так же, как показано в табл. 5.8, но постоянная в уравнении
Cmurm=|const и показатель т в этом случае подбираются исходя из за-
данного напора и степени реакции на среднем радиусе при условии по-
лучения допустимых значений чисел Mi и М2 у периферии и втулки ло-
паток и удовлетворительной эпюры осевых скоростей. Как уже отмеча-
лось, для ступеней с малыми значениями d рациональными являются
значения щ = —0,54-0,75, а также комбинированные лопатки.
5.3.8. ПРОВЕРКА РАСХОДА ВОЗДУХА
ЧЕРЕЗ СТУПЕНЬ КОМПРЕССОРА
После определения расчетного поля осевых скоростей можно вы-
числить расход воздуха через данное сечение:
Ск
Gs = 2nfep. \ \cardr,
ГВТ
где feu.— коэффициент, учитывающий влияние пограничного слоя на
проходное сечение; на первых ступенях fe ,, = 0,97= 0,98; на по-
следних — fep. =0,95-4-0,96.
204
№ п о
лор.
1
2
3
4
5
6
7
8
9
Учет
10
11
12
13
14
15
16
17
18**
19
20
21
22
Таблица 5.8
К расчету осевых скоростей (сечение I)
Параметры ^2 <3 Г4 Г5
П редварительные вычисления 1-7 _ ?вт _ _ ?пеР tg?; tg2?; >-^ср 72 ?2 - 7зср r Гер 1пЛ Г ср влияния закрутки потока, формы проточной части и взаимного влияния лопаточных венцов >-72ср) (7-Гср)--|-(72-72р) х = ± ТГ~ Гт [(' ~ - Т & ± I COS<pnep / t 1 - \| р . - 1 9 V /’2ср) й\Г ГСр)1 Кт пер 1 — (1 - к ех у(1+ех) = г 1 + tg2<p- p = ex(l+tg2!p7) №/0 = 504-15 +1^-1 4-30^ _\ h !v.ki \ h /с.а (Z—1) ] h (1 4- Ф), о/„ 4- Zz~I-+ /t + 1 | 1 — % | v H 1 100 /0 2 100 / z(Z 4- Ф)1 г(/4-Ф)/4-е2ср(1 4-tg2?7cp) „2 z (j 4* Ф)/4-(14- tg2?zcp) C2acp v ar У
>06 определении Ц, Ц—\, li+\ см. стр. 198.
205
где
Так как
Y=Y* (]~|ЗЛХ2Г 1 =V*e(X),
RT* '
то после несложных преобразований получим
Gs
где
= ^4 \ Се(Х)^г==Ту V^cpA^ s ) f f(r)dr,
V * ^t\ Л - Г л)
После вычисления расхода через данное сечение необходимо про-
верить совпадение расходов (полученного и заданного) и вычислить от-
ношение
где GB— заданный расход.
Вычисляют Gz методом численного интегрирования, т. е. делят в
данном сечении проточную часть на 10—16 колец, равновеликих по пло-
щади, и, найдя расход через каждое кольцо, определяют Gz .
Можно построить функцию f(r) по г и графически определить зна-
чение интеграла, а затем вычислить Kgs .
Теоретическое значение Kgs =1,0. Можно считать допустимыми от-
клонения, не превышающие 1 „Он-1,5%. Если же отклонение величины
Kgs от 1 получается больше 1—=—1,5%, то следует в соответствии со зна-
чением Kgs изменить скорость са на среднем радиусе и вновь рассчи-
тать поле скоростей по высоте лопатки, добиваясь путем последователь-
ных приближений совпадения Gz и GB.
После определения необходимой величины са следует внести уточ-
нения и в расчет данной ступени. Такие уточнения не потребуются, если
увеличить (или уменьшить) площадь проходного сечения до некоторой
величины F' и продлить (или сократить) полученное в первом расчете
поле скоростей до новых значений наружного и внутреннего диаметра.
При этом предполагается, что значения углов проточной части <р и ра-
диусов кривизны Rm остаются неизменными. Также предполагается, что
средний диаметр не меняется и высота лопатки равна
Соответственно
h’
F'
л/Эср
/Л=-Оср~ТА/; DBT~ Dcp — h’\
dK——r.
203
Такой расчет производится до получения равенства между Gs и GB.
Сохранение значений и Rm при изменении площади, как показывают
расчеты, не вносит сколь-нибудь существенных погрешностей.
В первом приближении можно определять .площадь из соотношения
Р, F FG*
K-G a Fiy. ’
где F — площадь, вычисленная ранее по параметрам потока на среднем
радиусе.
Расчеты показывают, что этого приближения, как правило, оказы-
вается достаточно.
5.4. СХЕМЫ МНОГОСТУПЕНЧАТЫХ ОСЕВЫХ КОМПРЕССОРОВ
И ПАРАМЕТРЫ ОТДЕЛЬНЫХ СТУПЕНЕЙ И ЛОПАТОК
5.4.1. ОБЩИЕ ПОЛОЖЕНИЯ
В современных многоступенчатых осевых компрессорах число сту-
пеней доходит до 17 и, следовательно, столько же имеется рядов рабо-
чих и неподвижных лопаток. В дальнейшем с ростом степени повыше-
ния давления число ступеней, по-видимому, будет возрастать. Выше рас-
сматривались некоторые характерные особенности отдельных ступеней
многоступенчатого компрессора (например, значения относительного
диаметра втулок, удлинения лопаток, законы их профилирования и др.).
Кроме этого, весьма важно знать закономерность изменения по ступе-
ням напора, осевых скоростей, степени реакции. Изменение этих пара-
метров тесно связано с принятой схемой компрессора, характеризую-
щейся в первую очередь формой проточной части в меридиональном
сечении.
5.4.2. ФОРМЫ ПРОТОЧНОЙ ЧАСТИ
На рис. 5. 56 показаны некоторые типичные формы проточной ча-
сти в меридиональном сечении многоступенчатого осевого компрессора.
Рис. 5.56. Типичные формы проточной части осевого многоступен-
чатого компрессора
При условии £>к=const (рис. 5. 56, а) окружные скорости во всех сту-
пенях имеют максимальное значение на периферии, а на среднем диа-
метре и у втулки они возрастают от первой ступени к последней. Все это
207
позволяет увеличивать напор ступеней и уменьшать их число по сравне-
нию с другими схемами при той же окружной скорости на первой сту-
пени. Однако при высоких значениях лк, особенно когда расход воздуха
относительно небольшой,, лопатки последних ступеней могут получаться
слишком короткими, что будет отрицательно- влиять на к.п.д. этих ступе-
ней и всего компрессора в целом.
В выполненных компрессорах лопатки последней ступени имеют вы-
соту не меньше 15—20 мм. Если высота лопаток последних ступеней по-
лучается меньше 15—20 мм, то следует выбрать проточную часть мно-
гоступенчатого осевого компрессора, имеющую £)K=#const, например,
Dcp = const (рис. 5.56,6). Что касается формы проточной части, имею-
щей Dbt — const (рис. 5. 56, в), то в связи с малой окружной скоростью
у втулок напор ступеней будет относительно небольшой и потребуется
значительно увеличивать число ступеней. Поэтому такую форму проточ-
ной части можно рекомендовать только в особых случаях, когда другим
путем получить приемлемую высоту лопатки не представляется возмож-
ным. Иногда бывает целесообразным применение комбинированных
форм проточной части (рис. 5. 56, г).
5.4.3. РАСПРЕДЕЛЕНИЕ НАПОРА И ИЗМЕНЕНИЕ К. П. Д.
ПО СТУПЕНЯМ КОМПРЕССОРА
В многоступенчатом осевом компрессоре, как правило, напор рас-
пределяется по ступеням неравномерно. В дозвуковых компрессорах
наименьший напор назначается в пеовых ступенях, что обусловлено ог-
раничениями, налагаемыми числами Mi, малым относительным диамет-
ром втулки и густотой, а также соображениями, связанными с расши-
рением диапазона рабочих режимов. Значение Нм можно определить с
помощью коэффициента теоретического напора и окружной скорости
на среднем радиусе. При этом коэффициент теоретического напора вы-
числяется по формуле (5. 14) с последующим согласованием с данными
продувки решеток (см. рис. 5. 25 и 5. 26) и числами Мь Окружная ско-
рость на среднем диаметре связана с окружной скоростью на внешнем
диаметре соотношением
Окружная скорость на внешнем диаметре принимается для дозвуковых
компрессоров 330—360 м/сек. Для околозвуковых и сверхзвуковых пер-
вых ступеней ик может быть увеличена до 3701—380 м/сек, а в отдель-
ных случаях и выше. Число ступеней в первом приближении целесооб-
разно выбирать, пользуясь средней величиной затраченной работы, ко-
торая в современных компрессорах находится в пределах 20 000—
35000 дж/кг и определяется выражением HK.CV—HK/z, где z — число сту-
пеней и Ни — полная работа, затрачиваемая на компрессор:
Минимальная величина Як.ср соответствует компрессорам, имеющим
большое число ступеней [47]. Затраченная работа в первой дозвуковой
ступени связана со значением Як.ср следующим приближенным соотно-
шением:
Як1== (0,5-г-0,6)Як.ср.
Если первые ступени —околозвуковые или сверхзвуковые, то вели-
чина НК1 может достигать значений (0,75—0,85) Як.ср [66]. Затраченная
208
работа в средних ступенях на 15—20% больше средней работы, а в по-
следних ступенях примерно равна ей, причем она будет выше в компрес-
сорах с формой проточной части, показанной на рис. 5. 56. В первом
приближении изменение Нк{ по ступеням на отдельных участках может
быть принято линейным, как показано на рис. 5. 57. При этом в качестве
средней ступени (с0) для четного числа ступеней можно принимать z0=
—z/2, а для нечетного числа ступеней z0=(2+l)/2. Для ступеней от Zo
до (zq + 2) можно принять HKi~HKimax. После построения графика,
подобного приведенному на рис. 5.57, уточняются значения Нк { для
отдельных ступеней с целью обеспечить соблюдение равенства
2^=^к-
Коэффициенты полезного действия в отдельных ступенях, как правило,
не являются одинаковыми. В первой ступени значения =0,84-М),86.
В средней ступени т]к доходит до 0,89—0,90; в последней — до 0,86—0,87.
К.П.Д. отдельных ступеней можно согласовать с к.п.д. всего компрес-
сора методом эквивалентной политропы (см. разд. 4. 3. 1).
Рис. 5.57. Распределение
затраченной работы по сту-
пеням компрессора
Рис. 5.58. Распреде-
ление осевой скорости
по ступеням компрес-
сора
5.4.4. ИЗМЕНЕНИЕ ОСЕВОЙ СКОРОСТИ
ВДОЛЬ ТРАКТА КОМПРЕССОРА
Осевая скорость на входе в первую ступень находится по заданному
расходу воздуха и принятым величинам коэффициента производительно-
сти, относительного диаметра втулки и числа Mi на входе в рабочее ко-
лесо. Вопрос о величине коэффициента производительности рассмотрен
в разд. 5. 3.2. Он выбирается в начале расчета и затем уточняется в про-
цессе согласования параметров компрессора и турбины. После проведе-
ния расчетов по уравнениям (5. 43) и (5. 44) определяются значения Мь
Mai и Xa='Xsin ai, а следовательно, и Cia = ZaaKp.
Характер изменения осевой скорости в последующих ступенях мно-
гоступенчатого компрессора представлен на рис. 5. 58 кривыми 1, 2, 3.
Изменение осевой скорости по кривым 2 и 3 в принципе целесообразно,
так как при этом в группе ступеней, где са постоянно или возрастает,
можно увеличить напор при принятых для них значениях густоты ре-
шетки или уменьшить требующуюся для этих ступеней густоту при -при-
нятом напоре. Однако такие решения и, особенно, при изменении по
кривой <3 ограничиваются допустимой величиной чисел Mj и М2 в этой
группе ступеней и прежде всего на нерасчетных режимах.
Кроме того, может оказаться, что в ступенях, расположенных в об-
ласти, где са уменьшается, градиент уменьшения осевой скорости Аса
в отдельных ступенях превысит желательные пределы порядка 10—
15 м/сек. Распределение осевых скоростей по ступеням должно также
позволять получать плавную проточную часть. После выбора осевых
209
скоростей при известных значениях окружной скорости на среднем диа-
метре становятся известными коэффициенты расхода по ступеням на
среднем диаметре са ср, которые могут находиться в пределах 0,9—0,5.
При этом меньшие цифры соответствуют последним ступеням. Величи-
ны са<0,5 г0,4 нежелательны, так как это приводит к снижению к.п.д.,
который для каждого са зависит еще от степени реактивности (см. рис.
5. 32).
5.4.5. ИЗМЕНЕНИЕ СТЕПЕНИ РЕАКТИВНОСТИ
ПО СТУПЕНЯМ МНОГОСТУПЕНЧАТОГО КОМПРЕССОРА
Рис. 5.59. Зависимость коэф-
фициента напора от степени
реактивности (&//=1,0)
Учитывая, что рк=0,5 является наиболее благоприятной величиной
с точки зрения к.п.д., можно ее принимать во всех ступенях для всей
лопатки или на среднем диаметре. Однако это значение рк может огра-
ничивать напор средних и последних ступеней при выбранных для них
значениях осевой скорости (или со) и гу-
стоты решетки. На рис. 5.59 показано
изменение коэффициента напора элемен-
тарной ступени в зависимости от степени
реактивности при различных са и при
b/t=i,O, найденное по данным, приве-
денным на рис. 5. 25, т. е. для номиналь-
ного режима. Как видно, при qk = 0,5 и
пониженных значениях са = 0,44-0,6, бо-
лее характерных для средних и послед-
них ступеней многоступенчатого компрес-
сора (на среднем и других радиусах),
коэффициент напора значительно ниже,
чем при более высоких са, свойственных
первым ступеням. Однако, если при по-
ниженных са увеличивать степень реак-
тивности сверх 0,5, то коэффициент на-
пора возрастает. Увеличение степени
реактивности одновременно влечет за
собой и рост относительной скорости wit
но числа М] в ступенях даже при рк>0,5 могут остаться в допустимых
пределах вследствие роста местной скорости звука. Так, например, со-
гласно рис. 5.27, приняв для промежуточной ступени са = 0,5, 6/7= 1,0 и
Ми = 0,78, при ок = 0,5 получим Mi = 0,624, а если qk=0,7, то Mi = 0,781,
что является допустимым. При этом согласно рис. 5.59 коэффициент
теоретического напора возрастает с 0,3 до 0,33, т. е. на 10%. Поэтому
в некоторых случаях увеличение степени реактивности в средних и пос-
ледних ступенях может оказаться целесообразным.
5.5. РАСЧЕТ МНОГОСТУПЕНЧАТОГО
ОСЕВОГО КОМПРЕССОРА
5.5.1. ОСНОВНЫЕ ЭТАПЫ РАСЧЕТА
Расчет многоступенчатого осевого компрессора является сложной
задачей и состоит из следующих этапов.
1. Выбор расчетного режима и определение расчетных условий (вы-
сота и скорость полета, степень повышения давления и др.).
2. Согласование параметров компрессора с параметрами турбины
(в газотурбинных двигателях) и определение ряда исходных данных,
которые должны быть положены в основу расчета компрессора.
3. Расчет компрессора по среднему диаметру.
210
4. Предварительный расчет характеристик компрессора, определе-
ние запасов устойчивой работы и выбор системы регулирования на раз-
личных режимах; уточнение характеристик с принятой системой регу-
лирования.
5. Пространственное профилирование лопаток.
Содержание данного раздела в основном посвящено расчету ком-
прессора по среднему диаметру.
5.5.2. ОБОЗНАЧЕНИЯ РАСЧЕТНЫХ СЕЧЕНИЙ
Для первой ступени примем следующие обозначения основных кон
структивных размеров многоступенчатого осевого компрессора.
£>ki I — наружный (периферий-
ный) диаметр на входе
в рабочее колесо;
Z)cpi I — средний диаметр на
входе в рабочее колесо;
DBTt I — внутренний (втулочный)
диаметр на входе в ра-
бочее колесо;
Дк2 1 — наружный диаметр на
выходе из рабочего ко-
леса;
ДСр21 — средний диаметр на
выходе из рабочего ко-
Рис. 5.60. Схема проточной части
осевого многоступенчатого компрес-
сора
леса;
DBt2i — внутренний диаметр на выходе из рабочего колеса;
E>3i — наружный диаметр на выходе из спрямляющего аппарата;
Дсрз! — средний диаметр на выходе из спрямляющего аппарата;
Двтз I — внутренний диаметр на выходе из спрямляющего аппарата.
В последующих ступенях изменяется лишь дополнительный индекс,
который соответствует номеру ступени (II, III и т. д.) (рис. 5.60).
5.5.3. ВЫБОР РАСЧЕТНОГО РЕЖИМА
Расчетный режим компрессора выбирают исходя из условий рабо-
ты двигателя либо при Я=О; Мн = 0, либо на некотором режиме, проме-
жуточном между режимами с максимальными и минимальными приве-
денными оборотами. Таким образом, для расчетного режима компрессо-
ра задаются следующие параметры.
1. Высота полета Н км.
2. Скорость полета VH км/час или число Мн полета (Мн=1/н/ан).
3. Расход воздуха GB кг/сек.
4. Степень повышения давления лк.
5. Коэффициент полезного действия т]к •
6. Коэффициент полного давления во входном устройстве 6ВХ-
Расход воздуха, известный для некоторых значений Н и Мн, может
быть пересчитан и для условий Н=0 и Мп = 0 по методике, указанной
ниже [см. гл. 10, формулы (10.40)]. Значения лкодля Н = 0 и Мн=0 оп-
ределяются по статистическим данным или по характеристике компрес-
сора (см. гл. 10).
5.5.4. ИСХОДНЫЕ ДАННЫЕ, ПОЛУЧЕННЫЕ ПРИ СОГЛАСОВАНИИ
ПАРАМЕТРОВ КОМПРЕССОРА И ТУРБИНЫ
После согласования параметров компрессора и турбины на расчет-
ном режиме (см. гл. 10) становятся известными окружная скорость и
коэффициент производительности компрессора, которые должны удов-
211
летворять диапазону значений чисел М, допустимых для выбранного
типа первой ступени компрессора (см. 5.3.2), и обеспечивать требова-
ния по прочности и эффективности турбин. Если компрессор двухкас-
кадный или двухкаскадный и двухконтурный, то в результате согласо-
вания параметров компрессора и турбины будет известно распределение
работ между каскадами, соотношение чисел оборотов и т. д. При согла-
совании параметров компрессора и турбины одновременно определяются
следующие данные по первой ступени компрессора.
1. Внешний диаметр первой ступени, вычисляемый по формуле
(5.45), причем значения коэффициента Kg в этом уравнении могут
приниматься исходя из следующих соображений: в первых ступенях с
лопатками с постоянной степенью реактивности 7G; = 0,93-:-0.95; если в
первых ступенях применяют лопатки с постоянной циркуляцией, то в
основном будет сказываться влияние пограничного слоя и Kg~
— 0,97—0,98; для первых ступеней с промежуточным законом профили-
рования Kg=0,95—0,97. Известные значения диаметра и окружной ско-
рости позволяют определить число оборотов п = 00uK/nDK.
2. Осевая скорость, коэффициент расхода и числа Mi на входе в ко-
лесо первой ступени компрессора, находятся по формулам (5.43),
(5.44), исходя из принятого коэффициента производительности и отно-
сительного диаметра втулки.
3. Коэффициент теоретического напора в первой ступени, опреде-
ляется по формуле (5.14), с использованием коэффициента расхода,
полученного в п. 2, и принятой степени реактивности. Полученный ко-
эффициент напора согласовывается с данными продувки решеток путем
проверки по данным графиков рис. 5. 25 и 5. 26 густоты решетки, тре-
бующейся для обеспечения номинального угла поворота потока. Как
уже отмечалось, для дозвуковых ступеней желательная густота решеток
на среднем диаметре находится в пределах 0,6—1,0. Для околозвуковых
и сверхзвуковых ступеней график рис. 5. 25 не может применяться. Огра-
ничение в этом случае накладывается числами Mi и величинами коэф-
фициента теоретического напора и густоты решетки.
В околозвуковых ступенях числа Mi на внешнем диаметре рабочего
колеса могут быть <1,1, а в сверхзвуковых ступенях достигать значе-
ний 1,4—1,5 и более, но с одновременным снижением к.п.д. Коэффициент
теоретического напора в околозвуковых и сверхзвуковых ступенях на
внешнем диаметре может быть в пределах 0,2—0,4, а на среднем диа-
метре 0,3—0,6. Густота решетки в ступенях этого типа может быть раз-
личной:
на внешнем диаметре (b/t) к<0,9-4-1,1;
на среднем диаметре (&/0ср<1,4н-1,6;
у втулки (bit) вт <2,0-4-2,25.
При известных коэффициенте напора и окружной скорости находит-
ся величина теоретического напора
Н th~uwH th.
Затраченная работа в первой ступени определяется по уравнению(4.9):
уу 77 thl&
Для первой ступени можно принять г)3г)/ = 0,97н-0,98 и й = 0,98-4-1,0.
В результате
/7К1= (1,0-4-1,03)/Дм-
212
Иногда для первой ступени берут г)з'П/== 1,0; тогда
#к1= (1,0^0,98)
4. Учитывая приведенное выше соотношение между средней рабо-
той /Ук.ср и работой, затраченной в первой ступени, можно определить
//к.ср и число ступеней z:
для дозвуковой первой ступени
Н ~ ~ •
к,с'р 0,5 ч- 0,6 ’ " /7к.сР ’
для сверхзвуковой первой ступени
Н =______—
к'с₽ 0,7 ч-0,8’
Полученные данные позволяют произвести подробный расчет компрес-
сора.
5.5.5. РАСЧЕТ КОМПРЕССОРА ПО СРЕДНЕМУ ДИАМЕТРУ
5.5.5.1. Расчеты распределения затраченной работы,
теоретического напора, к. п. д. и осевых скоростей
в ступенях компрессора
По данным, полученным в разд. 5. 5.3 и 5. 5. 4, расчет компрессора
по среднему диаметру может производиться в такой последовательно-
сти.
1. Распределение полной затрачиваемой работы по ступеням произ-
водится по рекомендациям, данным в разд. 5. 4. 4. Принятые значения
затрачиваемой работы Як; в отдельных ступенях с учетом работы в пер-
вой ступени (см. разд. 5.5.4) должны подчиняться условию
1
2. Теоретический напор в первой ступени известен из расчетов разд.
5.5.4. В остальных ступенях значение HtM определяется по уравнению
Н thi— Q
Значения произведения ЛзЛ/ и величины Q для первой ступени указаны
были выше. В последних ступенях, где относительная величина радиаль-
ного зазора возрастает, произведение т]зЛ/ уменьшается и достигает зна-
чений 0,95—0,96. Значения Q для последних ступеней также уменьша-
ются. Можно принять, что величина Q уменьшается линейно до значе-
ния 0,86—0,9 в последней ступени. Иногда линейный характер измене-
ния Q принимается только для ступеней от первой до средней, а для
остальных Q имеет постоянное значение, равное указанному для по-
следней ступени.
3. Адиабатические коэффициенты полезного действия для отдель-
ных ступеней должны соответствовать рекомендациям, данным в разд.
213
5.4.4, и одновременно обеспечивать при принятом распределении рабо-
ты заданный желательный к.п.д. всего компрессора. Эти расчеты целе-
сообразно производить по методу эквивалентной политропы [см. разд.
4.3.1 и формулы (4.79)—(4.81)].
4. Полученные значения Нк i и к.п.д. позволяют определить темпера-
туры торможения и степени повышения давления по ступеням:
а) температура торможения на входе в первую ступень
7'1=7':= К;
б) температуры торможения на входе в последующие ступени рав-
ны соответственно температурам на выходе из предыдущих ступеней:
Тц = Тз(1-1)- Температура на выходе из данной ступени равна
* -г* । Т7К1-
3/ — I и 4----------
— 7?
k—\
в) степень повышения давления в отдельных ступенях
л . = /----------
к‘ £ *
ft—1
После окончания расчета степени повышения давления в отдельных
ступенях компрессора необходимо проверить его правильность. Для
этого вычисляется общая степень повышения давления, которая равна
произведению z отдельных ступеней и должна совпадать с заданной:
$ * * * *
Лк= ЛК1Лк2Лкз ... лкг.
Во всех ступенях, кроме первой, степень повышения давления яв-
ляется отношением полного давления на выходе из спрямляющего ап-
парата к полному давлению перед колесом:
Для первой ступени под начальным давлением понимают давление
перед направляющим аппаратом и поэтому
В частном случае, когда направляющий аппарат отсутствует, давление
рв будет являться одновременно и давлением перед колесом.
5. Распределение осевых скоростей по ступеням выбирается по ре-
комендациям, рассмотренным выше. При этом значение са на входе
в первую ступень определено ранее при согласовании параметров комп-
рессора и турбины. Значение осевой скорости на выходе из компрессора
может контролироваться величиной Хк, рекомендуемой в пределах 0,35—
0,45, и коэффициентом расхода са, который, как уже отмечалось, неже-
214
лательно иметь на среднем диаметре последней ступени меньше 0,45—
0,5. Одновременно для последней ступени определяющим параметром
является высота лопатки, связанная как с величиной Ха(и c<j), так и с
формой проточной части компрессора, в связи с чем требуется проведе-
ние вариантных расчетов. При этом предварительно определяются пло-
щадь сечения и скорость воздуха на выходе из компрессора, т. е. из
спрямляющего аппарата последней ступени, в предположении, что ско-
рость потока не имеет окружной составляющей и направлена по оси:
F - а‘Уг:
3 ’
где
»*== р*л
к "в
Высота лопатки спрямляющего аппарата на выходе из компрессора оп-
ределяется в зависимости от принятой формы проточной части по приве-
денным ниже формулам. Принимая в первом приближении, что высота
рабочей лопатки последней ступени и ее средний диаметр равны высоте
лопатки и среднему диаметру спрямляющего аппарата, можно опреде-
лить окружную скорость и коэффициент расхода на среднем диаметре
последней ступени.
1. При постоянн ом среднем диаметре (£>ср = const и
Mcp=const):
высота лопатки л3=—— ;
л£>ср
наружный диаметр £>кз=£>ср+Лз;
внутренний диаметр D^—D^—h3-,
относительный диаметр втулки ;
А<3
коэффициент расхода са=-^-,
иср
ГДС £а~А<к£Хкр-
2. При постоянном наружном диаметре (DK—
= const):
/i w.
1 — -^2;
диаметр втулки ПВтз=-Окйз;
средний диаметр £>ср3 — •р,<+^вт3;
высота лопатки А3 = —~£>вт ;
3 2
л£)СрП
окружная скорость на среднем диаметре иср=- ;
коэффициент расхода са—-^.
Ucp
215
5. 5.5. 2. Расчеты треугольников скоростей, густот решеток
и проходных сечений в отдельных ступенях
Порядок расчетов для первой ступени
Часть параметров потока на среднем диаметре входа в рабочее ко-
лесо первой ступени, а также густота решетки колеса (&Д), наружный
диаметр и проходное сечение на входе определяются выше. Далее на
среднем диаметре определяются следующие параметры *).
1. Угол потока на входе в рабочее колесо в относительном движе-
нии
2. Окружные составляющие на входе и на выходе из рабочего колеса
[по уравнениям (5. 12) и (5. 13)]
С]в = И]Ср ^(1 Qk) ’
<'2« = ^1ср [(1 Qk) Н J •
3. Осевая скорость на выходе из рабочего колеса
__01а + Сза
2
Если при распределении осевых скоростей принято, что в первых
ступенях осевые скорости на среднем диаметре остаются постоянны-
ми, то
С2а~С1а~ ('За-
4. Абсолютная скорость и приведенная скорость на выходе из ра-
бочего колеса
акр2 у й-t-i
Величины акр2 и Т\ будут соответственно равны акр3 и Тз на выходе из
спрямляющего аппарата.
5. Угол выхода потока из рабочего колеса по абсолютной скорости
sina2=— .
02
6. Полное давление на выходе из колеса
где 6С — коэффициент полного давления в спрямляющем аппарате;
6С=0,98-^0,99;
рз—полное давление на выходе из спрямляющего аппарата;
* * Й--
РЗ == рв^к!*
*) В последующих формулах индекс 1, обозначающий номер ступени, для про-
стоты опускается.
216
Полное давление на выходе из рабочего колеса может быть опреде-
лено еще с помощью адиабатического к.п.д. рабочего колеса исходя из
соотношения
k
(Ц * \ Й—1
4^^+Л .
п'гг‘ '
k—1 /
где г] р.к—к.п.д. рабочего колеса, который на среднем диаметре можно
принять равным 0,92—0,94 *>.
7. Площадь на выходе из рабочего колеса
Р О. У7*
Л о ---.
р2 q (k2) sin а2-snKa
В зависимости от принятой формы рабочего колеса размеры на вы-
ходе из рабочего колеса (высота лопатки, относительный диаметр втул-
ки и др.) определяются по формулам, приведенным выше для расчета
размеров на выходе из компрессора.
8. Относительная скорость на выходе из рабочего колеса
®2 = V С2а + («ср — ^2И)2-
9. Угол потока на выходе из рабочего колеса
/1 • ^2/7
32= arc sin .
w2
10. Задаваясь удлинением лопатки hlb = h, определяют число лопа-
ток по формуле
_ Ь
Z —---------- .
h.
Полученное значение округляется до целого числа и уточняются
значения h/b.
11. Угол отклонения потока в рабочем колесе
Д^=₽2 — ₽1-
12. Номинальный угол отклонения потока в спрямляющем аппара-
те при д//=1,0 определяется с помощью графиков рис. 5.22 и 5.23 по
углу выхода потока из спрямляющего аппарата аз = аш. Этот угол
(т. е. eti п) становится известным после расчета второй ступени.
13. Угол отклонения потока в спрямляющем аппарате
Д(Х = 0] и — <^2 !•
14. Отношение
Да
и по этой величине с помощью рис. 5.24 определяется густота решетки
спрямляющего аппарата.
*) После определения р2* надо проверить величину дс=р3*/р2*.
217
15. Задаваясь удлинением лопатки h/b для спрямляющего аппара-
та, определяем число лопаток аппарата
h?.
Порядок расчетов для последующих ступеней
Если проточная часть компрессора имеет Dcp=const, то по приня-
тым для всех ступеней значениям Hth, са и других величин расчет этих
ступеней производится совершенно так же, как и расчет первой ступени.
Когда форма проточной части отлична от случая Z>Cp=const, то средний
диаметр неизвестен и поэтому вначале ступени рассчитываются методом
последовательных приближений. При расчетах должны использоваться
все ранее выбранные для отдельных ступеней величины: Hthi, ркь cai,
* —*
Лк/, Ти, Тъ1.
1. Определяют площадь на входе в ступень в первом приближении,
предполагая, что отсутствует закрутка потока, т. е. Ci«=0:
I/
где
Ри q (ha)i SBKa
М2,
2. По величине площади на входе находится Dcp i так же, как это
делалось для первой ступени в зависимости от формы проточной части.
3. Находятся окружная скорость на среднем диаметре при извест-
ном числе оборотов и окружная составляющая скорости на входе в сту-
пень:
Иц/ ~ ^ср i' Г О 6к) ГУ thi
4. Вычисляются абсолютная и приведенная скорость и угол потока
на входе:
cu = Ve2ai + c2u[-, Н/=^; aH = arctg^-.
акр i с1и1
Примечание. Угол на входе ан является углом выхода потока из спрямляю-
щего аппарата предыдущей ступени, т. е.
ан = аз(г_1).
По углу ан и углу а2(;_1) (предыдущей ступени) рассчитывается и профилируется
спрямляющий аппарат предыдущей ступени, как было показано в расчете первой
ступени.
5. По н'айденному углу ан и величине кц определяется площадь на
входе в ступень во втором приближении:
11 Pul (M)/sina]Z-sKaz
6. Повторяются все расчеты и определяется угол ан во втором при-
ближении. Если полученная величина отличается более чем на 1° от ве-
личины, полученной в первом приближении, то расчет производится еще
раз. Обычно двух приближений бывает достаточно.
218
7. Проверяется число Ми для ступени на среднем диаметре:
Mu-=-----,
где
^iz=ria<- + («cPi—cu/)2;
8. Задаваясь степенью реактивности, проверяют густоту решетки
рабочего колеса на среднем диаметре с помощью графиков рис. 5.26.
для чего находятся отношения
Hfh . Ок .. г Hth Hth]
— ’ —— И L = -= I —=— (
с а С а Са I \ С а /b/t^l,0
Для получения приемлемой густоты может понадобиться изменить
значения qk, са и величину теоретического напора. Весь последующий
расчет производится так же, как было показано выше для первой
ступени.
5.5.6. ПРИМЕР РАСЧЕТА МНОГОСТУПЕНЧАТОГО КОМПРЕССОРА
ПО СРЕДНЕМУ ДИАМЕТРУ
Используя изложенный выше порядок расчета и соответствующие уравнения, рас-
считаем многоступенчатый осевой компрессор ТРД для следующих исходных условий:
высота полета Я=0;
скорость полета Рн=О (Мн=0);
расход воздуха GB = 70,5 кг!сек-,
степень повышения давления лк* = 7,5;
адиабатический к. п. д. по параметрам торможения т]к* = 0,85;
коэффициент полного давления во входном устройстве 6вх=0,98.
Этим условиям соответствуют:
адиабатическая работа сжатия в компрессоре по параметрам торможения
. / й-1 \
Я* =-------ЛТ*(< k —1 =Ю05-288 (7,5°’286 — 1) = 225000 дж/кг-,
полная работа, затрачиваемая на компрессор,
H*ai 225 000
Нк = —- =-----------= 265 000 дж/кг.
Т)к 0,85
В результате расчетов по согласованию параметров компрессора и турбины
получены:
окружная скорость первой ступени компрессора_ик = 350 м/сек-,
коэффициент производительности компрессора GK = 0,66;
диаметр колеса первой ступени £)Ki=0,78 м;
число оборотов компрессора и=8570 об/мин-,
осевая скорость и коэффициент расхода на среднем радиусе на входе в первую
ступень со=187 м/сек-, са = 0,763;
теоретический напор и коэффициент напора первой ступени на среднем радиусе
Я«м=19 800 дж/кг-, //4ftl=0,33;
работа затрачиваемая в первой ступени (при Q/r|3ii/ = 1,0), HKi =19 800 дж/кг-,
число Mi на входе в рабочее колесо первой ступени на среднем радиусе Mi =0,75;
густота решетки рабочего колеса на среднем радиусе Ь/1=0,63;
средняя работа 7/к.Ср=33 200 дж/кг;
число ступеней г=8,0.
Результаты расчета всех ступеней по среднему диаметру сведены в табл. 5.9.
В расчетах принят линейный закон изменения S2 по ступеням от 0,98 в первой до 0,91
в последней. Уменьшение т]3 принято так же по линейному закону от 0,98 в первой
ступени до 0,96 в последней. Распределение Нк , и т]к , по ступеням произведено в со-
ответствии с разд. 5. 5. 5. 1.
Предполагается, что лопатки первой ступени будут профилироваться по промежу-
точному закону; для нее и всех последующих ступеней принят коэффициент Ло = 0,97.
219
Таблица 5.9
Сводная таблица расчета компрессора по среднему диаметру
№ по пор. Параметр Размер- ность № ступени
I II III IV V VI VII VIII
1 HKi дж/кг 19800 27200 33800 38200 39240 38200 36300 32400
2 * ПК/ 0,865 0,872 0,885 0,892 0,892 0,892 0,882 0,865
3 ЛГ»* rnt Т"* 1 3 i~‘ 2 1~-1 1(1 + 1) °К 307,6 334,6 368,3 406,3 445,3 483,3 519,3 551,3
4 1,222 1,292 1,347 1,362 1,335 1,29 1,25 1,2
5 clai м/сек 187 187 187 182 177 172 167 163
6 Пз-П/ 0,98 0,977 0,974 0,971 0,968 0,965 0,962 0,96
7 S 0,98 0,97 0,96 0,95 0,94 0,93 0,92 0,91
8 дж/кг 19800 27400 34330 39100 40500 39600 38000 34200
9 ик 1 м/сек 350 350 350 350 350 350 350 350
10 wicp i м/сек 245 269 288 301 312 319 324 328
11 Qk i 0,5 0,5 0,52 0,54 0,56 0,59 0,62 0,65
12 Ka i 0,97 0,97 0,97 0,97 0,97 0,97 0,97 0,97
13 Fu м2 0,4 0,339 0,28 0,229 0,1865 0,155 0,1327 0,116
14 d\i 0,4 0,539 0,644 0,721 0,781 0,822 0,85 0,871
15 ^btI i м 0,312 0,42 0,502 0,563 0,61 0,641 0,664 0,68
16 e1ui м/сек 82 83,4 78,4 73,4 72,8 68,7 64,5 62,7
17 C}1 м/сек 204 204,7 202,7 196,2 191,2 185,2 179 174,6
18 щг град 66° 18' 65° 54' 67° 22' 67° 49' 67° 49' 68° 08' 68° 45' 68° 45'
19 W\l м/сек 248 263,4 280,9 291,4 297,5 303,6 308,5 311,4
20 aU м/сек 330 340 355 374 395 413 432 450
21 Ml,- 0,75 0,775 0,792 0,783 0,754 0,735 0,715 0,693
22 cai 0,763 0,695 0,65 0,606 0,568 0,54 0,515 0,497
23 HtM 0,33 0,38 0,414 0,43 0,415 0,38 3,362 0,317
24 Л 0,702 0,895 1,04 1,148 1,16 1,092 1,062 0,94
25 (»/Ор.к l 0,63 0,86 1,06 1,19 1,2 1,12 1,08 0,93
26 Ai, м 0,234 0,18 0,139 0,104 0,085 0,075 0,058 0,05
27 (Л/6),- 4,И 3,78 3,61 3,1 2,8 2,68 2,49 2,3
28 zi 19 34 56 75 86 96 105 98
29 c2ui м/сек 163 185,4 197,6 203 201,2 193,3 181,5 166,5
30 C2i м/сек 248 263,3 270,3 270,9 266,4 257,1 245,3 232,1
31 a2i м/сек 334 348 368 386 405 426 445 460
32 ^21 0,74 0,755 0,735 0,705 0,655 0,602 0,55 0,505
33 «21 град 49° 45° 12' 43° 05' 41° 32' 40° 55' 41° 18' 42° 13' 44°
34 ^2/ М2 0,365 0,312 0,251 0,206 0,169 0,1425 0,122 0,1065
35 d2i 0,485 0,59 0,689 0,754 0,804 0,838 0,863 0,881
36 W2l м/сек 211 208,7 208,7 207,5 208,9 213,4 220 229,7
37 hi град 62° 30' 63° 42' 62° 59° 54' 56° 42' 52° 39' 48° 36' 44°50'
38 ₽!/ град 49° 45° 12' 41°46' 38° 42' 36° 30' 34° 31' 32° 45' 31°36'
39 д₽ град 13° 30' 18° 30' 20° 14' 21° 12' 20° 12' 18° 08' 15° 51' 13° 14'
40 аз, = И1(,- + 1) град 65° 54' 67° 22' 67° 49' 67° 49' 68° 08' 68° 45' 68°45' 90°
41 Аа=<хЯ(-—а2,- град 16° 54' 22°10' 24° 44' 26°17' 27° 13' 27° 27' 26° 32' 48°
220
Продолжение
№ по пор. Параметр Размер- ность № ступени
I II III IV V VI VII VIII
42 El 0,735 0,936 1,038 1,1 1,14 1,13 1,09 1,34
43 0,63 0,91 1,04 1,16 1,25 1,24 1,15 1,68
44 (№)i 4,05 3,79 3,5 2,98 2,78 2,6 2,31
45 h2i 0,2015 0,16 0,121 0,095 0,077 0,063 0,053 0,047
46 ?Ci 23 42 61 78 100 116 114
Примечание. В связи с большим углом поворота потока и большой потреб-
ной густотой в последнем спрямляющем аппарате целесообразно поставить на вы-
ходе из компрессора два последовательно расположенных спрямляющих аппарата.
5.6. ПРОФИЛИРОВАНИЕ ОТДЕЛЬНЫХ ЭЛЕМЕНТОВ
ПРОТОЧНОЙ ЧАСТИ ОСЕВОГО КОМПРЕССОРА
5.6.1. ПРИНЦИПЫ ПОСТРОЕНИЯ ПРОФИЛЕЙ ЛОПАТОК
ОСЕВОГО КОМПРЕССОРА
При конструировании лопаток за расчетные сечения у периферии
и втулки обычно принимают сечения, отстоящие на 2ч-4 мм от радиаль-
ных границ потока по направлению к среднему диаметру.
Профили лопаток строятся по данным газодинамического расчета
компрессора по среднему диаметру и расчета параметров потока по вы-
соте лопатки.
Существует ряд методов построения профилей лопаток, основан-
ных на положениях гидродинамической теории решеток [42]. Одновре-
менно в инженерной практике широко применяются графические и ана-
литические методы, использующие некоторые исходные аэродинамиче-
ские профили, характеристики которых известны из экспериментальных
данных. Ниже излагается один из таких методов.
Задачи профилирования лопаток компрессора на базе исходных
аэродинамических профилей может быть разделена на две части: по-
строение средней линии профиля и построение профилей лопаток.
5. 6.1.1. Построение средней линии профиля лопатки
Среднюю линию исходного профиля изгибают по дуге круга или по
параболе так, чтобы углы у передней и задней кромок xi и /2 соответ-
ствовали расчету.
Для повышения точности среднюю линию профиля лопаток ком-
прессора (как и всего профиля) следует строить в большом масштабе
(М=10:1). При чисто графическом построении средней линии прово-
дятся отрезки АВ и СВ из концов хорды АС = Ь под углами %i и /2
(рис. 5. 61, а). Отрезки АВ и СВ разбиваются на равное число частей.
Одноименные точки соединяются прямыми, затем проводится огибающая,
которая и является искомой средней линией, изогнутой по параболе.
Так как чисто графический способ построения средней линии недоста-
точно точен, то часто прибегают к графоаналитическому построению
по уравнению
Ьх — №
ц=--------.
у ЧАх + С
где
А =0,5 (ctg /г — ctg /л); С = b ctg ул.
Связь между углами и /2 дана в гл. 2.
221
5. 6.1.2. Графическое построение профиля лопатки
Перед построением профиля задаются максимальной относительной
толщиной профиля по высоте лопатки
^тах=--— 100%,
Шал »
где стах —• максимальная толщина
Ь — хорда профиля.
Обычно принимают Стах — 18ч-
= 54-6% у конца ее. Для коротких
5)
Рис. 5.61. Построение средней линии
и профиля лопатки на заданном
радиусе
данную максимальную толщину
на рис. 5.62, а, б, в и приведенные таблицы). При определении с/2 ве-
личина Ун берется со знаком плюс. Для симметричного исходного профи-
профиля;
12% У основания лопатки и стах =
лопаток (d>0,75) можно принимать
Cmax = const ПО ВЫСОТв ЛОПЭТКИ
(стах = 8—Ю%), так как числа Ml
мало изменяются и центробежные
силы относительно невелики.
Для графического построения
профиля полученная средняя линия
разбивается на большое число рав-
ных отрезков так, чтобы длина каж-
дого отрезка составляла целое
число процентов (2ч-4%) от длины
средней линии.
После этого по обе стороны
средней линии по нормалям к ней,
восстановленным в конце каждого
отрезка, откладывается половина
толщины с/2 = (t/в + Ун) /^, где уъ и
ун берутся из таблиц для исходного
профиля после пересчета их на за-
профиля стах (см. примеры профилей
ля у = Ун=Ун- Когда исходный профиль несимметричный, такое построе-
ние является приближенным, поскольку в этом профиле перпендикуляр к
хорде не является одновременно перпендикуляром и к его средней линии.
Однако, поскольку кривизна средней линии в несимметричном исходном
профиле обычно весьма невелика, погрешность при таком построении не-
Профиль №1 (fmax=P,O%) Профиль №2 (cmax -12 %) Профиль N>3 (стах = 107^
О 1020304050 60 70 80 90 100
О)
0 Ю203040 50 60 70 80 90 100 0 10203040 50 60 70 80 90 100
6) 6)
Рис. 5. 62. Примеры геометрических характеристик профилей
* Ун 1/ср с
0 0 0 0 0
1,25 1,42 -1,42 0 2,84
2,5 1,96 -1,96 0 3,92
5 2,67 -2,07 0 5,34
7.5 3,15 —3,15 0 6,30
10 3,51 —3,51 0 7,02
15 4,01 —4,01 0 8,02
20 4,30 —4,30 0 8,60
25 4,46 —4,46 0 8.92
30 4,50 —4,50 0 9,00
40 4,35 —4,35 0 8,70
50 3,97 —3,97 0 7,94
60 3,42 —3,42 0 6,84
70 2,75 —2,75 0 5,50
80 1,97 — 1,97 0 3,94
90 1,09 —1,09 0 2,18
95 0,60 -0,60 0 1,20
100 0 0 0 0
S52
X Ув Ун ^ср с
0 0 0 0 0
1,25 1,89 — 1,89 0 3,78
2,5 2,62 —2,62 0 5,24
5 3,56 —3,56 0 7,12
7,5 4,20 —4,20 0 8,40
10 4,68 —4.68 0 9,36
15 5,34 —5,34 0 10,68
20 5,74 —5.74 0 11,48
25 5,94 —5,94 0 11,88
30 6,00 —6.00 0 12.00
40 5,80 —5,80 0 11,60
50 5,29 —5,29 0 10,58
60 4,56 —4,56 0 9,12
70 3,66 —3,66 0 7,32
80 2,62 —2,62 0 5,24
90 1,45 -1,45 0 2,90
95 0.81 —0,81 0 1,62
100 0 0 0 0
(в процентах от хорды)
Ун 0Н ^ср с
0 0 0 0 0
1,25 2,01 — 1,03 0,49 3,04
2,5 2,92 — 1,52 0,70 4,44
5 4,02 — 1,95 1,03 5.98
7,5 4,83 —2,17 1,33 7,00
10 5,51 —2,47 1,52 7,98
15 6,40 —2.60 1,90 9,00
20 6,78 —2,78 2,00 9,56
25 6,93 —2,95 1,99 9,88
30 6,97 —3,03 1,97 10,00
40 6,75 —2,95 1,90 9,70
50 6,16 —2,72 1,72 8,88
60 5,34 —2,30 1,52 7,64
70 4,29 —1,81 1,24 6,10
80 3,19 —1,41 0,89 4,60
90 1,60 —0,74 0,43 2,34
95 0,92 -0,42 0,25 1,34
100 0 0 0 0
значительна. Полученные точки соединяются плавной кривой, которая и
представляет собой очертание профиля (см. рис. 5. 61, б).
Далее все профили, составляющие данную лопатку, координи-
руются относительно некоторой базовой системы осей, используемой
в дальнейшем при обработке лопатки на станке.
Изложенный графический способ построения профиля является
приближенным, так как графическое восстановление нормалей к кривой
довольно неточно. Кроме того, метод графического построения профиля
еще и непроизводителен, что особенно проявляется, когда необходимо
строить большое количество профилей. Поэтому часто пользуются ана-
литическими методами расчета*’. В современных условиях аналитиче-
ские методы часто сочетаются с использованием электронных вычисли-
тельных машин.
5.6.2. АНАЛИТИЧЕСКИЙ МЕТОД РАСЧЕТА ПРОФИЛЕЙ
ЛОПАТОК ОСЕВОГО КОМПРЕССОРА
На рабочих чертежах компрессорных лопаток профиль обычно за-
дается координатами точек спинки и корыта. При этом если точки
спинки А и корыта D задавать так, чтобы они имели одну и ту же абс-
циссу хА, D (рис. 5. 63), то возможен аналитический расчет геометриче-
ских характеристик профиля (площади, центра тяжести, моментов инер-
ции), необходимых для дальнейшего прочностного расчета. Графическое
и аналитическое построение профиля производится обычно по плоским
сечениям, тогда как в действительности газ движется по цилиндриче-
ской поверхности. При достаточно больших удлинениях (6Л^ 1,54-2,0)
построение лопаток по плоским сечениям обеспечивает получение пара-
метров ступени, близких к расчетным [7].
Рис. 5.63. К расчету профиля лопатки Рис. 5. 64. Некоторые обозначения,
принятые при расчете профиля ло-
патки
5. 6. 2.1. Исходные данные первичного профиля
Идея аналитического метода расчета заключается в том, что гео-
метрические размеры заданного профиля определяются путем пере-
счета размеров некоего первичного профиля. В данном случае в каче-
стве первичного профиля взят один из симметричных профилей с отно-
сительной толщиной 10%, но изогнутый таким образом, чтобы угол из-
гиба у передней кромки профиля /10=arc ctg 0,505. Последнее эквива-
лентно заданию угла кривизны профиля, так как /1 = 0,60 для отношения
«/6 = 0,45 (см. разд. 2.2).
Все параметры, относящиеся к этому профилю, в дальнейшем обо-
значаются индексом «0». Зададим профиль точками с относительным
интервалом между абсциссами этих точек Дх=Дх/Ь = 0,1 по всему про-
филю; из-за большей кривизны профиля в области передней кромки
Дх = 0,05.
Все исходные и расчетные данные сводятся в таблицу по образцу
табл. 5. 10, в том числе следующие исходные.
*) В излагаемом ниже аналитическом методе расчета профилей лопаток осевого
ксмпрессора использованы разработки инж. Л. М. Титова.
223
й
Расчет координат профиля
1. 6= Сечение .... tgxi
п , . 6. х = ------
2. 6= 4. tgxi= tgxio
•3-7i= 5. tg хю=0,5055 7. cmax=
Таблица 5.10
1 xa=x 0,02 0,05 0,10 0,15 0,20 0,25 0,30 0,40 0,50 0,60 0,70 0,80 0,90
2 УсрО 0,0098 0,0234 0,0431 0,0591 0,0727 0,0880 0,0907 0,0989 0,0985 0,0905 0,07(0 0,0557 0,0301
3 c0>2 0,0176 0,0263 0,0348 0,0398 0,0443 0,0468 0,0488 0,0500 0,0488 0,0453 0,0380 0,0280 0,0168
4 tg ao 0,4744 0,4296 0,3596 0,295 0,2355 0,1802 0,1289 0,367 —0,0419 —0,1122 — 1756 —0,2304 —0,2791
5 6 7 8 9 10 11 12 13 14 15 16 17 ( \ dx)fi x=xb xtg a0=tg a cos a C CO cmax 2 ~ 2_ 10 Уср=У cpO^x dy _ Стах/ dy\ dx 10 \ dx)p c Ttga C dy — tga — 2 dx c dy y^+'2^Tx c 1 2 cos a Усп Укор 0,3598 0,2875 0,1350 0.0950 0,0700 0,0450 0,0288 0 -0,0238 —0,0538 —0,0862 —0,1012 —0,1188
1. Относительные абсциссы выбранных точек. Очевидно, что отно-
сительные абсциссы сохранятся и для проектируемого профиля,
т. е. х=хо.
2. Относительная высота средней линии (рис. 5. 64)
- _г/сРо
УсрО ’
где г/сро — ордината точки средней линии первичного профиля;
Ьо — хорда первичного профиля.
3. Относительная толщина первичного профиля
Так как профиль симметричный, то
Со
Для удобства расчетов в табл. 5. 10 вносится половина толщины
профиля с0/2.
Рис. 5.65. Некоторые параметры исходного
симметричного профиля
4. Тангенс угла наклона касательной к средней линии первичного
профиля tg «о-
5. Величина dyjdx, рассчитанная для неизогнутого первичного про-
филя с= 10%.
Как видно из рис. 5.65, величина dy!dx характеризует изменение
толщины симметричного профиля в данной точке.
5.6.2.2. Расчет профилей лопаток проектируемого компрессора
Хорда Ь, угол изгиба 0 и относительная толщина профилей лопаток
проектируемого компрессора находятся путем пересчета соответствую-
щих параметров первичного профиля.
Так, например, для каждого значения х=хо находим следующие
величины (х0 изменяется в диапазоне от 0 до 1,0).
1. Абсциссы задаваемых точек искомого профиля
x = xb.
2. Ординаты средней линии искомого профиля
Уср==2/сро^к,
где уСро — относительная высота средней линии первичного профиля
для данного значения жо-
Значение коэффициента х вычисляется по формуле
tgXio ’
где хю — угол изгиба у входной кромки первичного профиля;
Xi — угол изгиба у входной кромки искомого профиля (задан газо-
динамическим расчетом).
8
546
225
Данные расчета сведены в табл. 5. 10.
3. Толщина искомого профиля
с.Ь^-,
° 10
где со —• относительная толщина первичного профиля при том же
значении х (см. табл. 5. 10) ;
Стах — максимальная относительная толщина искомого профиля
в процентах.
Для удобства расчета в табл. 5. 10 вносится половина толщины
искомого профиля.
4. Искомые ординаты точек спинки и корыта для выбранных значе-
Рис. 5.66. к вычислению координат
спинки и корыта искомого профиля
лопатки
ний хо запишутся соответственно
(рис. 5.66):
Усп^Уср + д Н~Ау;
г 2 cos а
Укор У ср' Т" У ^У-
1 2 cos а
Для того чтобы найти выраже-
ние для Ду, рассмотрим исходный
неизогнутый профиль (см. рис.
5.65). На основании ряда Тэйлора
имеем для любой выбранной точки
» (dy \ « I /' d^u \ Дх2
7 \dxj / 2
Пренебрегая вторым
членом, так как Дх2 мало, получим

(/ I
Для изогнутого профиля (см. рис. 5.66), откуда
где Ду характеризует изменение ординаты, обусловленное переменной
толщиной профиля.
Величина dyjdx изменится по сравнению с (c/y/dx)0 пропорцио-
нально отношению максимальных относительных толщин:
dy /dy \ Стах
dx \dx J о 10
где (dy/dx)o — величина, подсчитанная для первичного профиля. Вводя
полученное выражение для Ду, можем написанные выше уравнения для
Ус-п и уМр записать в виде
। с
у ср 4" q
F 2 cos а
с с
Укор У ср Л
F 2 cos а 2
226
5. Для определения а имеем на основании свойств параболы
tga = tgaoz,
где tg ао —тангенс угла наклона касательной к средней линии в дан-
ной точке первичного профиля;
tga — тангенс угла наклона касательной к средней линии искомого
профиля для того же значения То=Т.
5. 6. 2. 3. Вычисление геометрических характеристик профиля
Для определения площади профиля, его моментов инерции и коор-
динат центра тяжести необходимо вычислить соответствующие инте-
гралы при изменении х от 0 до 1,0.
Площадь профиля можно определить с помощью выражения
х2 = 1,0 _
J (z/сп— yKO^dx.
Для решения этого интеграла применяем формулу Симпсона
Z К^/сп J/корО + (^сп .Vkdp)1 + (Усп Укор)2 “Ь 4 ( £/сп I/КОр)з ~
о
-р . . . -р 2 (усп ~р Укор)л—2 “Р 4 (z/cn //кор)л—1 (Уси Z/l{(,p)„],
где Ах — относительные интервалы между абсциссами точек, при-
нимаемые одинаковыми;
0, 1, 2...П — номера точек (я — четное).
С увеличением числа выбранных точек точность формулы растет.
Для расчетов составляется табл. 5.11.
Так как при определении площади профиля точки по профилю за-
даны с различным интервалом АТ, при решении интеграла численным
методом суммировать нужно по частям, а именно;
х=1,0 х = 0,2 jr=l,0
^2 Укор) (Усп 1/кор) -р (z/сп Укор)-
х=й х=0 х = 0,2
Коэффициент 1/2, стоящий перед первой суммой, учитывает, что точки
в области передней кромки (до Т=О,2) взяты по оси абсцисс в 2 раза
чаще (АТ = 0,05), чем по всему профилю (АТ = 0,1).
Граничная точка Т = 0,2 входит в общую сумму 2 раза:
_ х-0,2 _ х=1,0
F = £ (z/cn-i/KOp)-p^- £(z/cn-z/KOp) =
О ,5 мм
J=0 х=0,2
х-0,2 х=1,0
___0,05* VI / , । °, !* V?
3 \Усп Укор) Г з (1/сп Укор.
х~0 х=0,2
8*
227
Геометрические характеристики сечения лопатки рабочего колеса (статора) на радиусе
Таблица 5.11
1 *0 0 0,05 0,1 0,15 0,2 о,з 0,4 0,5 0,6 0,7 0,8 0,9 1,0
2 3 4 5 6 7 8 9 10 И 12 13 14 15 15 17 X У сп Укор У сп—Укор //спЧ“//кор 2 2 У СП У Kt р ^(Усп—Укор) У сп—Уп.т Укор Уи.х (.У СП //ц.т)3 (//кор //ц.т)3 (Усп //ц.т)3 (//кор //ц.т)3 ^2.5) 2 [8] , *°° -’ц.т — b _ 2 [5] х_=0 Х=1 2 pi 1 х=0 ^ц-т = Т 7-1 2 [5] х-0 х-1 90 2"’1" л-=0
Координаты центра тяжести профиля вычисляем по формулам
Уц.т р ; -y«.t р >
где 5Л: и Sy — статические моменты площади относительно осей у и х,
соответственно:
Л-1,0 №1,0
(Усп УкОр) Уср^Х 2 (Усп Укор) dx\
№0 №0
№1,0 _ _
= J (Усп Укор)Х^-Х.
№0
Применяя формулу Симпсона, получим
। х (Усо Укор)
хцг=Ь -----------------
ц-т х=1,0
2 (усп Укор)
х— 0
№1,0
2 (yL-Hop)
2 У (Уеп — Укор)
х-0
Моменты инерции профиля можно определить по формуле
7=1
d (Усп Уц.т) (Укор Уц.т) •
х-0
При ориентировочных расчетах геометрических характеристик изо-
гнутого профиля можно пользоваться некоторыми упрощенными фор-
мулами:
F=0,741 У2стах (ошибка <Д%);
J=0,045У2стах (А2 4- Стах) (ошибка + 5),
где J — минимальный момент инерции профиля;
h — ордината средней линии в точке максимальной вогнутости;
Уц.т = 0,772 h (ошибка < 1 %);
Хц.т = 0,456А (ошибка < 0,5 %).
5.6.2.4. Порядок расчета
Принятые для выбранных сечений лопатки хорда профиля Ь, угол
кривизны профиля 0, относительная толщина Стах и величины, получен-
ные последующим расчетом, вносятся в табл. 5.10.
Пункты 2, 16 и 17 табл. 5.10 дают искомые координаты точек про-
филя, по которым можно построить профиль лопатки на данном радиусе.
Далее с помощью табл. 5.11 определяют координаты центра тяжести
и площадь профиля.
229
Рассчитав 3—5 профилей лопатки на различных радиусах, можно
построить перо лопатки, совместив профили в первом приближении по
центру тяжести с учетом углов установки профиля на каждом радиусе.
Если необходимо точно определить геометрические координаты про-
филя, то производятся расчеты по формуле Симпсона методом числен-
ного интегрирования.
5.6.3. НЕКОТОРЫЕ ОСОБЕННОСТИ ПОСТРОЕНИЯ ПРОФИЛЯ ЛОПАТКИ
ОКОЛОЗВУКОВОЙ И СВЕРХЗВУКОВОЙ СТУПЕНИ
Изложенные принципы построения профиля в основном могут быть
использованы также для околозвуковых и сверхзвуковых ступеней.
Основными особенностями профилей для этих ступеней являются,
во-первых, их меньшая относительная толщина, которая может на конце
лопатки достигать 2—2,5%, и, во-вторых, заостренные входные кромки
с углом заострения у=4°—6° и радиусом скругления входных и выход-
ных кромок 3—10% от величины хорды.
Угол атаки на входе в рабочее колесо принимается положительным
и составляет 2°—-4° [66]. Угол отставания несколько меньше на перифе-
рии, а у втулки достигает 9°—10°, изменяясь примерно по линейному
закону.
В некоторых околозвуковых и сверхзвуковых ступенях использова-
лись профили, состоящие из дуг окружности [58].
Средняя линия такого профиля также представляет собой дугу
круга с радиусом к, — и стрелой прогиба f — о —2~Тт~ё/2~ ' ‘
Если максимальная толщина профиля равна стах, то спинки и ко-
рытце профиля образуются дугами окружности, опирающимися на хорду
и имеющими стрелу прогиба соответственно /+стах/2 и [—стах/2.
Г лава 6
ТЕОРИЯ И РАСЧЕТ ЦЕНТРОБЕЖНЫХ
КОМПРЕССОРОВ
6. 1. ВВЕДЕНИЕ
Возможные схемы центробежных компрессоров были описаны в гл. 1.
При рассмотрении основных уравнений теории лопаточных машин (см.
гл. 2) уже отмечались отдельные особенности, свойственные центробеж-
ным компрессорам. Дополнительно целесообразно рассмотреть еще не-
которые вопросы. Коэффициент производительности центробежного ком-
прессора, определяемый по входному сечению, практически равен коэф-
фициенту производительности осевого компрессора, так как значения
относительного диаметра втулки и приведенной скорости воздуха на
входе Xi могут быть у них одинаковыми. Однако по производительности,
отнесенной к лобовой площади, центробежный компрессор существенно
уступает осевому. Как уже отмечалось, в осевом компрессоре
производительность, отнесенная к площади колеса, связана с
циентом производительности соотношением
лобовая
коэффи-
'Люб. о с С К
В центробежном компрессоре это же соотношение будет иметь
вид
с — с PbSr
лоб-«
Следовательно, при равных значениях р*а и Т*а получаем
Сдоб.ц ID1 \2
^лоб.ос '
Так как Z>i/Z>2 = 0,554-0,65, то, следовательно, лобовая производи-
тельность центробежного компрессора в 2'/2—3 раза меньше, чем у осе-
вого. Если учесть, что габаритный диаметр центробежного компрессора
в 1,7—1,8 раза больше диаметра колеса, а осевого компрессора только
в 1,1 —1,2 раза, то лобовая производительность центробежного компрес-
сора, отнесенная к полной площади миделя, будет еще больше уступать
производительности компрессора осевого.
231
По величине напора, достигаемого в ступени, центробежный ком-
прессор существенно превосходит компрессор осевой. Иногда это объяс-
няют действием центробежных сил. Однако в уравнение Эйлера для
теоретического напора центробежные силы в явном виде не входят.
Поэтому, рассматривая, например, случай, когда отсутствует закрутка
на входе, всегда можно представить, что в осевом и центробежном ком-
прессорах окружная скорость колеса и окружная составляющая на вы-
ходе из него практически одинаковы, вследствие чего будут равны и зна-
чения теоретического напора Htu. Однако в осевой ступени в этом слу-
чае будут большие числа М как на входе в рабочее колесо, так и на
входе в спрямляющий аппарат.
Кроме того, в рабочей решетке
должен быть больший угол пово-
рота потока. В результате повы-
шенный теоретический напор бу-
дет достигаться при более низ-
ких к. п. д. В центробежном же
компрессоре числа Mi на входе
в колесо будут умеренными из-за
более низких окружных скоро-
стей во входном сечении колеса.
Числа М, получаемые после ко-
леса, могут быть снижены прак-
Рис. 6. 1. Схема центробежного компрессора тически без скачков В безлопа-
с радиальными лопатками точном диффузоре. Таким обра-
зом, центробежный компрессор
по своей газодинамической схеме лучше приспособлен для получения
повышенных напоров в одной ступени. В отличие от колеса осевого ком-
прессора, в колесе центробежного компрессора при передаче энергии
воздуху существенную роль играют еще кориолисовые силы.
Рассмотрим колесо центробежного компрессора с радиальными ло-
патками (рис. 6. 1). Известно, что при движении материальной частицы
по вращающейся траектории, помимо ускорений в относительном и пере-
носном движениях, частица обладает так называемым ускорением Ко-
риолиса, величина которого применительно к рассматриваемому случаю
равна
Укор — 2щсо,
(6.1)
где w — относительная скорость воздуха;
и — угловая скорость колеса.
Вектор кориолисова ускорения перпендикулярен вектору относитель-
ной скорости w и оси вращения х, вдоль которой направлен вектор
угловой скорости со. Для рассматриваемого движения, происходящего
в плоскости, перпендикулярной оси колеса, вектор / направлен в сто-
рону вращения колеса под углом 90° к вектору w. Поскольку в рассмат-
риваемом случае элементарная частица движется по радиусу от центра
к периферии, то вектор кориолисова ускорения совпадает по направле-
нию с окружной скоростью, а кориолисова сила инерции dPK0V, дейст-
вующая на частицу, направлена в сторону, обратную вращению колеса,
и по величине равна
ЛРкор——2w(£>dm, (6.2)
где dm — масса элементарной частицы.
232
Массу элемента представим в виде
dm=ybrd^dr,
«де b — ширина колеса вдоль оси;
<76—центральный угол, соответствующий элементарной частице;
у — плотность газа.
Но ywbrdQ=dG,
где dG — расход газа через поверхность элементарной частицы.
Следовательно,
dPw>v=—2d Gasdr. (6.3)
Удельная работа колеса, затрачиваемая на преодоление действия
кориолисовых сил, равна
, j г dN dP
^кор=-------=——— = 2г<<Л/г. (6.4)
dG dG
После интегрирования в пределах от г\ до г2
HKOp=ul—ut (6.5)
Сопоставим уравнение (6.5) с уравнением Эйлера для теоретическо-
го напора:
= C{uU{. (6.6)
В частном случае, когда с2и = и2 и ciu = U[, что соответствует радиаль-
ному направлению относительной скорости на входе в колесо и на вы-
ходе из него, вместо уравнения (6. 6) получим
Hth = u2-—ii\. (6.7)
Таким образом, в этом случае теоретический напор равен удельной ра-
боте, затрачиваемой колесом на преодоление кориолисовых сил, которые
создают соответствующую разность скоростей и давлений на обеих сто-
ронах лопаток. В остальных случаях эта работа составляет значитель-
ную часть теоретического напора. Следует отметить, что поскольку
в осевом компрессоре кориолисовы силы инерции направлены в основ-
ном по радиусу, то они не влияют на распределение давлений на лопат-
ках и, следовательно, на величину теоретического напора, так как это
распределение определяется только условиями обтекания лопаток. Пре-
валирующее влияние на величину теоретического напора действия корио-
лисовых сил инерции не отражается на к. п. д. центробежного компрес-
сора, который зависит от относительного значения потерь.
Как было показано в разд. 1.1, одноступенчатый центробежный ком-
прессор состоит из следующих основных элементов:
1) входного патрубка;
2) рабочего колеса;
3) диффузора;
4) выходного устройства.
Ниже рассматриваются эти элементы.
6.2. ВХОДНОЙ ПАТРУБОК
На входе в центробежный компрессор применяются различные вход-
ные патрубки (рис. 6.2). Для компрессоров газотурбинных авиационных
двигателей характерными являются патрубки типа а и г, причем тип г
применяется на компрессоре с двухсторонним колесом (см. рис. 1.14).
Входной патрубок служит для подвода воздуха к колесу и должен обес-
печить осесимметричность потока относительно оси колеса и равномер-
ное и правильное заполнение всех каналов колеса. Иногда во входном
233
патрубке ставятся еще лопатки неподвижного направляющего аппарата,
создающего закрутку потока перед рабочим колесом в сторону враще-
ния колеса. Такая закрутка, как и в осевом компрессоре, в первую оче-
редь служит для уменьшения относительной скорости и числа Mi =
= wi/a! на входе в рабочее колесо при заданных значениях абсолютной
Рис. 6.2. Формы входных патрубков:
а—осевой вход; б—коленообразный вход; в—входная улитка;
г—осесимметричный коленообразный вход
и окружной скоростей. Для определения скоростей на входе в колесо и
в любом кольцевом сечении, перпендикулярном к направлению потока
в патрубке, показанном на рис. 6.2, г и 6.3, б', можно применить уравне-
ние (2.104). На рис. 6.3 J—Н—Н; G—G и т. д. — нормали к мери-
диональным линиям тока.
Примем в уравнении (2. 104), что нижний предел интегрирования пп
равен нулю и соответствует внутренней стенке канала т0, а верхний
предел интегрирования п соответствует внешней стенке тк.
а)
Рис. 6.3. Изменение скоростей в канале входного
компрессора при закрутке потока по закону
(сиг = const):
б)
патрубка центробежного
постоянства циркуляции
а—по нормалям к меридиональным линиям тока; б—канал
Вдоль нормалей и в сечении перед колесом в общем случае (при
наличии на входе в патрубок направляющих лопаток) может быть пере-
менная циркуляция (cur=£const), т. е. поток будет вихревым. В то же
время вдоль меридиональной линии тока произведение c„r=const и,
следовательно, исходя из этого условия должна устанавливаться связь
между окружными составляющими вдоль меридиональных линий тока.
Если в патрубке отсутствуют окружные составляющие скорости (си = 0)
[ d(cur) 1
или вдоль каждой нормали циркуляция постоянна =0 , то поток
234
будет безвихревым. Таким образом, во втором случае во всех точках
потока будет соблюдаться условие cur = const. Для безвихревого потока
уравнение (2.104) получит вид
г J т
о , (6.8)
ст0
где CmQ— меридиональная составляющая скорости у внутренней стенки
канала.
Другое частное решение получается из уравнения (6.8), если для
безвихревого потока предположить, что центры кривизны всех меридио-
нальных линий, проходящих через нормаль, совпадают. В этом случае
нормаль есть прямая линия и dn = dRm. Поэтому
CmRm— COHSt,
(6.9)
где RmQ— радиус кривизны внутреннего контура канала. Следовательно,
в этом случае не только циркуляция скорости относительно оси симмет-
рии величина постоянная, но также постоянной является и циркуляция
скорости с„ относительно центра кривизны.
При любых условиях во всех сечениях патрубка должно соблю-
даться уравнение неразрывности. Рассматривая поверхность, проходя-
щую через нормаль, можем записать расход воздуха в виде
р7к
= \rcmdti. (6 10)
о
С учетом уравнения (2. 104) можем написать
где
(6.И)
d (саг)2
dn
Для несжимаемой жидкости имеем у = у* = const.
Для изэнтропического процесса совершенного газа получим
где
(6. 12)
Поле потока в данном канале должно быть определено методом после-
довательных приближений, так как меридиональные линии тока в на-
чале расчета неизвестны.
235
Сначала наносят приблизительно меридиональные линии тока,
исходя из кривизны внешней и внутренней стенок канала и соблюдая
условие, чтобы между двумя соседними меридианными поверхностями
тока проходили одинаковые расходы. Далее графически определяются
радиусы кривизны меридиональных линий вдоль
В качестве первого приближения можно принять,
тока вдоль нормалей изменяется линейно:
i_\ _п_
Rm ^тк) h-
где h — длина всей нормали от внешнего до внутренней стенки канала;
JRmK — радиус кривизны внешней стенки;
радиус кривизны внутренней стенки.
Тогда для некоторой промежуточной точки нормали имеем
п
С dn ____________________ п , /?2
J
о
Для всей нормали от внешней до внутренней стенки канала
I к dn _ h
J ~R^~2
о
различных нормалей,
что кривизна линий
т0
(6.13)
1______1_
m0 RmK
(6.14)
(6.15)
к
Скорость ст 0находится из уравнения (6.11) путем последовательного
приближения до совпадения с принятой вначале величиной; зная вели-
чину сто,можно определить значения скорости ст в точках пересечения
меридиональных линий с нормалями с помощью уравнения (2. 104),
в котором постоянная интегрирования С принимается равной Ст0. В ча-
стном случае безвихревого потока для определения сгг по величине с,„0
используется уравнение (6.8). Для примера на рис. 6.3, а даны резуль-
таты расчетов по определению отношения скоростей ст1сто,си1с-ца и углов
потока а для нескольких сечений входного патрубка, меридиональное
сечение верхней части которого показано на рис. 6.3,6 [61]. При-
нято, что перед сечением J—J канал состоит из двух стенок, перпенди-
кулярных оси, между которыми расположены по окружности направ-
ляющие лопатки, создающие постоянную тангенциальную скорость
вдоль сечения J—J. Во всех. остальных сечениях cur = const. Из рис.
6.3, а видно, что в сечениях Е—Е и А—А, несмотря на постоянство цир-
куляции, меридиональная скорость существенно возрастает по направ-
лению от внутренней к внешней стенке канала, что является следствием
кривизны линий тока.
Очевидно, что, если не учитывать указанное изменение скоростей,
неизбежно несовпадение расчетных и действительных углов атаки на
входе в рабочее колесо и соответствующее возрастание потерь и сни-
жение к. п. д.
При проектировании коленообразных входных патрубков целесо-
образно принимать входное сечение (Fo) и выходное (Л) такими, чтобы
F0/Fi>ly2. Вследствие конфузорного течения потери в патрубке будут
меньше. Температура торможения принимается в патрубке постоянной
и равной температуре торможения атмосферного воздуха. Среднее дав-
ление заторможенного потока в конце патрубка (перед колесом) под-
считывается по соотношению
Рв Р1 ЛАх-
В зависимости от конструкции входа в компрессор коэффициенты пол
ного давления бвх могут иметь следующие значения:
236
а) при отсутствии лопаток, закручивающих поток,
— для осевого входного патрубка dBX = 0,984-0,99;
— для коленообразного входного патрубка 6пх=0,974-0,98;
б) при наличии лопаток, закручивающих поток,
— для осевого входного патрубка двх = 0,97-4-0,98;
— для коленообразного входного патрубка бвх = 0,964-0,97.
Потери во входном самолетном устройстве, расположенном перед вход-
ным патрубком, должны учитываться отдельно.
6.3. РАБОЧЕЕ КОЛЕСО
6.3.1. ВХОДНАЯ ЧАСТЬ КОЛЕСА
Входная часть рабочего колеса конструктивно выполняется обычно
в виде отдельного элемента, называемого вращающимся направляющим
аппаратом (ВНА). Входные кромки лопаток ВНА изогнуты под утлом
р/ (рис. 6.4), что обеспечивает поступление воздуха с заданным углом
атаки. Как и в осевом компрессоре, углы потока и лопаток связаны
с углами атаки соотношением
~ + Л
где Pi — угол потока;
i — угол атаки.
Величина угла потока на входе существенно зависит от величины окруж-
ной составляющей скорости на выходе из патрубка. Когда C\ujul = Q
Рис. 6. 4. Треугольники скоростей на входе в колесо центробежного ком-
прессора на диаметре Dr.
о — без закрутки 1их =0); б — с закруткой (ctjilux =0,5); в — с закруткой (С1и/аг = 1,0)
относительная скорость Wi и число N[1 = wi/al имеют максимальное зна-
чение (рис. 6. 4, а). По мере роста Ciu/ui уменьшаются Wi и М|. Мини-
мальное значение Wj будет при C)U/ui = l,0 (рис. 6.4, в). В этом случае
угол потока 01 на входе равен 90° и, следовательно, входная кромка
лопатки может быть не изогнута (при угле атаки г=0). Однако большое
значение окружной составляющей будет отрицательно влиять на теоре-
тический напор ступени.
Углы потока (и лопаток) будут различны по радиусу ВНА вслед-
ствие изменения си и и. Принимая, что на входе меридиональная со-
ставляющая параллельна оси колеса, получим *>
= -. (6.17)
с1и;
*)Текущее промежуточное сечение обозначается индексом «й»; параметры для вту-
лочного сечения индексом «вт», а для среднего сечения «ср».
237
Следовательно,
tgPu =...igg^- (6.18)
C1U,;
На рис. 6.5 дано изменение по радиусу углов аи и в сечении
перед колесом для коленообразного входного патрубка, показанного
на рис. 6. 3, б, и углов ацс и Рнс для осевого патрубка (осевая скорость
постоянна по радиусу) при таком же изменении окружной составляю-
щей. Из сопоставления углов щ и Pi для этих двух патрубков видно, что
влияние коленообразного патрубка на углы потока весьма значительно,
и не учитывать этого влияния нельзя, так как в противном случае дей-
Рис. 6.6. Измерение числа Mi на
входе в рабочее колесо с предвари-
тельной закруткой и без нее:
1—направляющие поверхности; 2—без
предварительной закрутки; 3—*с предвари-
тельной закруткой
Рис. 6. 5. Изменение углов as и Pi по
радиусу вращающегося направляю-
щего аппарата центробежного ком-
прессора:
«1 и $Чс —ПрИ ПОСТОЯНИОЙ скорости по
радиусу (осевой патрубок);
и Pi; — при переменной скорости по
радиусу (коленообразный па-
трубок)
ствительные углы атаки будут сильно отличаться от назначенных при
расчете.
Закон закрутки потока перед рабочим колесом и абсолютное зна-
чение окружных составляющих скоростей оказывает заметное влияние
на величину теоретического (и адиабатического) напора центробежного
компрессора.
Как было показано в разд. 2.3.5, теоретический напор центробеж-
ного компрессора с осевым входом в общем случае выражается урав-
нением
j ciu^ndG
Н th~C 2иИ2---11 Q (6.19)
Это уравнение можно записать в виде
Нth~ С2ии2 — U1 >
ИЛИ
(6-20)
Коэффициент ц учитывает влияние конечного числа лопаток. Величина
коэффициента ф зависит от закона изменения окружной составляющей
238
на входе. В случае, когда реализуется закон cur = const, коэффициент
ф = 1,0. Такой закон не всегда может быть признан достаточно рацио-
нальным. При ф = 1,0 и повышенных значениях ciu = ciu/«i теоретический
напор будет значительно меньше, чем когда закрутка на входе отсут-
ствует. Так, например, если принять, что О1/П2 = 0,6, то при различных
значениях с1и получим величины Hth!(Hth) =о, показанные в табл. 6. 1.
Таблица 6.1
С lit 0 0,1 0,2 0,5 0,75 1,0
Н thW th)ciu=0 1,0 0,934 0,928 0,82 0,73 0,64
Для предотвращения значительной потери напора обычно величина
с1и<0,15-М),2, что соответствует примерно углам а,>-70о-э75° и дик-
туется допустимыми числами Mi на диаметре Di (Mi 0,9).
При применении закона постоянства циркуляции будут иметь место
значительная закрутка лопатки ВНА и существенное изменение чисел
М] по радиусу, которые, имея допустимое значение на диаметре D\
входа, становятся у втулки излишне малыми. Для уменьшения коэффи-
циента ф и для получения меньшей закрутки лопаток ВНА иногда при-
меняют другие законы изменения окружной составляющей на входе. На
рис. 6.6 показано изменение чисел на входе в рабочее колесо при
наличии предварительной закрутки и без нее. В этом случае на внутрен-
них радиусах закручивание было уменьшено, так как снижение чисел
Mi в этой части не дает преимуществ, вызывая излишнюю потерю на-
пора. При этом входной канал с помощью трех направляющих поверх-
ностей был разделен на четыре полости (см. рис. 6.2, г). Уменьшение
коэффициента ф достигается также при закрутке потока по закону вра-
щения твердого тела, т. е. c«/r=const. В этом случае выражение для
второго члена в уравнении (6. 19) будет иметь вид
О
J Cla(«HdG
CaNr^dr
Следовательно, коэффициент ф выражается соотношением
Если принять приближенно, что сау = const, то получим
ф=1±£2
‘ 2
(6.21)
где d = D^/Di — относительный диаметр втулки. Например, при d = 0,4
коэффициент ф = 0,58, т. е. почти вдвое меньше, чем при cur = const.
В действительности при cjr=const са и у в общем случае являются
переменными по радиусу и их произведение не является постоянным.
Однако в коленообразном патрубке из-за влияния кривизны изменение
ст (или са на входе) может быть незначительным. На рис. 6.7 дано
изменение ст и си в различных сечениях входного патрубка (см.
239
рис. 6.3, б) для случая, когда закрутка потока в нем осуществляется
по закону culr=const. Из графиков видно, что изменение меридиональ-
ных скоростей в различных сечениях и, в частности, в сечении А—А1
(перед колесом), весьма невелико. Кроме того, при закрутке потока по
закону cufr~const относительно мало изменяются давление и плотность
по радиус)' (или по нормали) (см. рис. 2.21). Поэтому коэффициент ф
будет близок по величине к значению, соответствующему формуле
(6.21). Обычно входные кромки лопаток вращающегося направляю-
щего аппарата изгибаются по дуге окружности, радиус которой не дол-
жен быть малым, так как в противном случае возникнут большие потери
вследствие резкого возрастания сечений (большая диффузорность) и
крутого поворота.
нале входного патрубка центробеж-
ного компрессора при закрутке по-
тока по закону твердого тела
Рис. 6.8. Параметры лопатки ВНА,
изогнутой по окружности
Радиус R окружности, по которой изогнута средняя линия лопатки
ВНА (рис. 6.8) и хорда b связаны между собой соотношением
/? =---------, (6.22)
6
2 sin —
2
где
9 = = + в з; = з2=90о.
Хорду b на среднем диаметре входа можно в первом приближении опре-
делять, находя густоту b/t по кривой рис. 5.24 и вычисляя шаг исходя
из принятого для колеса числа лопаток*’. При определении густоты сле-
дует иметь в виду, что для ВНА
Ар = 90°—pi.
Предварительная закрутка увеличивает угол Pi, в результате чего
уменьшается угол изгиба 0 лопаток ВНА. С этой же точки зрения может
являться полезным некоторое увеличение углов атаки (до 4°—5°). Тре-
буемый угол поворота потока в ВНА значительно выше, чем принимают
в практике проектирования осевых компрессоров и на ^диаметре Di до-
стигает 50°—60°, что в сочетании с большими числами Mi может приво-
дить к отрыву потока в ВНА.
*) Иногда число лопаток в ВНА принимают меньше чем в колесе с целью избе-
жать загромождения входного сечения.
240
Отрыв потока отрицательно отражается на течении через все эле-
менты центробежного компрессора и, особенно, его диффузора, вызывая
неравномерность потока на входе, при наличии которой диффузор не
может работать с высоким к. п. д. Поэтому при профилировании ВНА
необходимо иметь большую густоту решетки, чтобы угол расширения
канала находился в допустимых пределах на всех радиусах входного
сечения.
6.3.2. ТИПЫ КОЛЕС
6.3.2.1. Конструктивные формы
По конструктивному выполнению колеса могут быть закрытыми,
полуоткрытыми и открытыми (рис. 6.9). Наибольшее распространение
в авиационных газотурбинных двига-
телях получили полуоткрытые колеса,
обеспечивающие высокую надежность
при больших окружных скоростях и
достаточно хороший к. п. д. При не-
больших зазорах между лопатками
и корпусом закрытые колеса позво-
ляют получать несколько более высо-
кий к. п. д., но они более сложны в из-
готовлении и менее пригодны для боль-
ших окружных скоростей. Открытые
колеса встречались только в ранних
конструкциях. Колеса с двухсторонним
входом (см. гл. 1) могут быть и за-
крытые, но практического применения
они не получили.
а) 5) 6)
Рис. 6.9. Конструктивные формы
колес центробежного компрессора:
а—открытое; б—полуоткрытое; в—за-
крытое
6.3.2.2. Формы лопаток колес
Как рассмотрено выше, углы относительной скорости на входе
в рабочее колесо определяются значениями скоростей са, си и и на раз-
личных радиусах входного отверстия. Угол |32 выхода из рабочего
колеса может выбираться произвольно. Поэтому необходимо исследо-
вать зависимость основных параметров колеса от угла выхода |32.
Для упрощения предположим, что рабочее колесо имеет бесконеч-
ное число лопаток. Следовательно, линии тока и углы будут совпадать
с контурами лопаток, и поток на входе в колесо и после, выхода из него
будет равномерен. Эти предположения соответствуют струйной теории
Эйлера.
Многообразные формы лопаток центробежных компрессоров можно
разделить на три основные группы в зависимости от выходного угла р2,
а именно (рис. 6. 10):
а — лопатки, загнутые против вращения (р2<90°);
б — радиально оканчивающиеся лопатки (р2 = 90°);
в — лопатки, загнутые по вращению (р2>90°).
Для упрощения предполагается, что вход в колесо радиальный, но
на конечные выводы это не оказывает влияния.
Если предположить также, что поток входит в рабочее колесо без
предварительной закрутки, т. е. с1м=0, то выражение для теоретиче-
ского напора будет иметь вид
Hth=u2c^, (6.23)
241
где индекс оо означает бесконечное число лопаток. Коэффициент теоре-
тического напора соответственно выразится так:
/у _
ttl “2
Из треугольников скоростей имеем
tg 02
<?2г С2г
откуда
М2 С2В~ 1 th™
(6.24)
(6. 25)
Нth™ —
С?г
tg₽2
Таким образом, теоретический напор и соответствующий коэффи-
циент теоретического напора являются функцией с%г и угла выхода по-
тока 02.
Рис. 6. 10. Треугольники скоростей для различных форм
лопатки центробежного компрессора
Когда 02 = 90 , то Я«л«,= 1,0 независимо от ^величины с2г; когда ло-
патки загнуты против вращения, то tg 02>О и Я//1со<1,0; при наличии
лопаток, загнутых по вращению, tg 02<О и Яйм>1,0. На рис. 6. 11 пока-
Рис. 6. 11. Зависимость Hth™ от р2 при
различных значениях с2г.‘
с2г-0,2; 2—с2/.=.0,25; 3-с2г = 0,3
зано изменение Hthoo в зависи-
мости от р2 при различных значе-
ниях с2г. В авиационных газотур-
бинных двигателях нашли приме-
нение только компрессоры с ра-
диальными лопатками, обеспечи-
вающими хорошую надежность
при больших окружных скоро-
стях и достаточно высокие к. п. д.
Центробежные колеса с лопат-
ками, загнутыми против враще-
ния, встречаются часто в жидко-
стных насосах, где не требуется
высоких коэффициентов напора.
Колеса с лопатками, загнутыми
по вращению (0г>9О°) дают воз-
можность иметь высокие коэффи-
циенты теоретического напора и
получать большие степени повы-
шения давления в одной ступени
по сравнению с колесами, имею-
щими 02 = 90°. Однако вследствие
больших потерь в колесе, а так-
242
же и в диффузоре из-за более высоких скоростей в колесе и на входе
в лопаточный диффузор к. п. д. такого компрессора должен быть ниже.
Значительно труднее обеспечить в нем необходимый запас устойчивой
работы. Поэтому такие колеса не нашли применения в центробежных
компрессорах ГТД.
К центробежным компрессорам можно применить использованное
в осевых компрессорах понятие о степени реактивности:
2
С dP
__1 (»!~»2)+(Ц2 —Ц1)
6к- Hth ~ wth
2
где — работа сжатия в колесе без учета потерь. Так
J Y
1
но уравнению (2.32)
9 9 9 2 2 2
Htn = 7, I й I й >
то
„2 2 2 _ 2
с2 С1 _____ | _С2и + C1U 1 62г 11г
4Hth ~ 2и ' 2Htn
(6. 26)
как соглас-
(6.27)
Если принять, что радиальные скорости на входе с1г в колесо и
на выходе из него с2г одинаковы, получим выражение, аналогичное
уравнению (5.8) для кинематической степени реактивности в осевом
компрессоре:
с211 + Пи
а при отсутствии закрутки на входе
ек-(6.28)
В колесе с бесконечным числом радиальных лопаток и р2 = 90° (?к=
= 0,5, так как C2u<x>=_U2 и Я;лоо=1,0. При р2>90° степень реактивности
уменьшается и при Hth—^fi будет равна нулю, т. е. в этом случае повы-
шения статического давления в колесе не будет (активное колесо).
В случае, когда р2<90°, степень реактивности увеличивается и в пределе
стремится к единице при Hth—-0. Отметим особенность изменения теоре-
тического напора в зависимости от объемного расхода воздуха через
колесо. Из треугольника скоростей (см. рис. 6.10), учитывая, что c2ttoo =
-=и2—c2rctgp2, получаем
„ = с2ц ~и2 = «2 — С2гМ2 Ctg ₽2 = «2 — «2 Ctg fa,
где V2 — объемный расход воздуха на выходе в м?1сек.
Принимая, что радиальные составляющие абсолютной и относи-
тельной скорости на выходе из колеса и на входе в него одинаковы,
можем написать
= и* - и2 ctg 32 = ul - ТПГ «2 ctg fa. (6. 29)
Г l ejYi
213
На рис. 6.12 показана зависимость Hth«>=f(Vi), из которой видно,
что при р2 = 90° теоретический напор не зависит от расхода, при
р2>90° — возрастает с увеличением расхода и при р2>90°— уменьша-
ется с ростом расхода. Реальное протекание зависимости напора от
расхода несколько иное.
Рис. 6. 12. Зависимость теоретического напора от
объемного расхода и угла (32:
при «2=300 м!сек\ F\~\
6.3.3. ВЛИЯНИЕ КОНЕЧНОГО ЧИСЛА ЛОПАТОК
К выводу
распределе-
Рис. 6. 13.
уравнения
ния скоростей в канале
центробежного компрес-
сора
При рассмотрении движения газа в рабочем колесе в предположе-
нии бесконечного числа лопаток (струйная теория) принималось, что
все линии тока имеют одинаковую форму, а лопатки представляют со-
бой отрезки линий тока. Отсюда следует, что скорость на каком-либо
радиусе рабочего колеса постоянна по всей окружности. Однако для
передачи энергии от лопаток рабочего колеса к потоку необходима раз-
ность давлений между обеими сторонами лопатки, что возможно лишь
при разности скоростей на этих сторонах.
Таким образом, в противоположность струй-
ной теории скорость движения непостоянна по
окружности и периодически изменяется, так как
в каждом канале, ограниченном двумя сосед-
ними лопатками, картина течения должна быть
одинакова. Покажем причину неравномерного
распределения относительных скоростей по сече-
нию канала колеса, а также аналитическую за-
висимость между шириной канала и величиной
относительной скорости воздуха, рассматривая
для простоты вращение канала с радиальными
лопатками (рис. 6.13).
Используя полярную систему координат,
применим рассуждения, аналогичные приведен-
ным в гл. 2 при выводе уравнений равновесия.
В направлении оси г на частицу газа с массой
Ат действуют следующие силы:
а) проекции сил давления рДД. и (р+Ар)\frr
где А/г = гА0Ь — поверхность элементарного объ-
ема, перпендикулярная г;
б) центробежная сила Amr<o2;
в) сила инерции от ускорения
движении Am dwfdx.
В направлении полярного угла
силы:
а) проекция сил давления рД^
вая поверхность элементарного объема;
частицы воздуха в относительном
О на частицу действуют следующие
и (р+Ар)Д/а > где Afe = \rb — боко-
244
в) проекция сил Кориолиса /\m2aw, направленная перпендикулярно
оси г против вращения.
Написав уравнение равновесия для оси г, получим
дтгш- — Ltn —— \pLf2 = 0.
dr
Разделив на \т и учтя, что &fr/Am= 1/уЛг, переходя к пределу, можем
написать
(6.30)
у dr dr
Аналогично для проекции в направлении полярного угла получим
— — =— 2<ow (6.31)
У rdO
Отметим, что в уравнения (6.30) и (6.31) в отличие от уравнений
(2.95) и (2.97) не вошли проекции объемной силы действия лопаток на
воздух. Это объясняется тем, что в гл. 2 рассматривалось осесимметрич-
ное течение (осредненное или при бесконечном числе лопаток), при ко-
тором отсутствует разность давлений по обе стороны лопаток и, следо-
вательно, не получает физического объяснения момент, прилагаемый
к колесу. В связи с этим требовалось введение сил Fn действия лопаток
на поток. При выводе же уравнений (6.30) и (6.31) осесимметричности
потока не предполагалось. В связи с тем, что скорость w имеет только
одну составляющую вдоль оси г, можем написать
dw dw , dw
—---f-w---.
dr-------------dr ' dr
Полагая относительное движение установившимся, получим выражение
dw dw
----------— W------- .
dr--------dr
Подставляя его в уравнение (6.30), будем иметь
Интегрируя равенство (6.32) в пределах от Г\ и г2, получаем
Г % о о 2 9
г dp _ , ^1-^2
J 7 2 2 ’
Это уравнение соответствует ранее полученному уравнению энергии
(2.77) для относительного движения при Ля=0. Если начальная полная
энергия струек одинакова, то из уравнения (6.32) для r = const полу-
чаем выражение
— = — wdw.
7
Подставляя его в уравнение (6.31), будем иметь
dw = 2ardQ.
Считая, что начало координат лежит на передней по вращению
кромке, где относительная скорость w равна некоторой скорости
при 0 = 0, получаем после интегрирования
w = a>o+2cor0=Wo+2u9, (6.33)
где и — окружная скорость на данном радиусе.
245
Из уравнения (6. 33) следует, что в канале вращающегося колеса
с конечным числом лопаток благодаря ускорению Кориолиса относи-
тельные скорости на дуге данного радиуса изменяются по линейному
закону в-зависимости от полярного угла. Вследствие этого у передней
стороны лопаток скорости меньше и давления выше, а у задней стороны —
наоборот (рис. 6.14). Если обозначить угол, соответствующий одному
каналу, через 0О, то максимальная относительная скорость (у задней
стенки) будет равна
®maX = ®o + 2u0o.
Так как 0о=2л/г, где z— число лопаток, то получим
®тах = ®о + 4я-у (6.34)
Для средней относительной скорости можем написать
wcp==w0-l-2n—. (6.35)
z
Из выражения (6. 34) следует, что чем меньше число лопаток, тем
больше различие в скоростях у передней и задней стенок лопаток. Рас-
Рис. 6. 14. Изме-
нение скоростей и
давления в канале
центробежного
компрессора
Рис. 6. 15. Схема возникновения неравномерности
потока в канале колеса центробежного компрессора
смотренные выше общие положения показывают, что основные черты
потока во вращающемся центробежном колесе обусловлены главным
образом ускорением Кориолиса, благодаря которому нарушается равно-
мерность поля относительных скоростей между лопатками. Это различие
скоростей, а соответственной давлений и обусловливает передачу энергии
от колеса к воздуху. Полученный характер потока в относительном дви-
жении позволяет при изучении применять принцип наложения, т. е. рас-
сматривать поток во вращающемся канале как результат сложения дви-
жения воздуха с одинаковыми скоростями во всех точках между лопат-
ками на окружности данного радиуса (рис. 6. 15, а) и вращательного
движения внутри канала с угловой скоростью со (рис. 6.15,6). Эпюра
скоростей суммарного потока показана на рис. 6. 15, в. Скорость посту-
пательного движения приравнивается средней скорости, определяю-
щейся расходом воздуха в неподвижном колесе. Угловая же скорость
обусловлена вращением колеса. В чистом виде это вращательное дви-
жение имеет место в колесе с замкнутыми со всех сторон каналами
(нулевой расход воздуха). Вращательное (циркуляционное) движение
газа (относительный вихрь) со скоростью имеет на периферии на-
правление, противоположное вращению рабочего колеса, и создает на
246
выходе из лопаточного рабочего канала дополнительную окружную
составляющую wuz относительной скорости ау2<», направленную против
вращения (рис. 6.16). Появление дополнительной окружной составляю-
щей Wuz можно объяснить также, рассматривая процесс выравнивания
скоростей на выходе из колеса, где поток течет свободно, без воздейст-
вия внешних сил. При выравнивании скоростей струи, обладающие
большей скоростью, уменьшают свою скорость до некоторой средней
величины, а струи, обладающие меньшей скоростью, увеличивают ее
до этой средней величины. В результате происходит некоторое переме-
щение масс воздуха на периферии в направлении, противоположном
вращению колеса, вследствие чего и появляется некоторая окружная со-
ставляющая wuz.
по направлению вращения
Из-за наличия wU2 уменьшается C2U = C2U<X—wuz и, следовательно,
уменьшается теоретический напор, или работа, сообщаемая 1 кг воздуха,
проходящего через колесо. Уменьшение окружной составляющей (щ ра-
боты) принято учитывать с помощью коэффициента ц = С2и/с2иоо*).
Коэффициент у. можно выразить следующей приближенной форму-
лой, вытекающей из предположения о постоянной нагрузке по длине
лопатки [32]:
^='+2т—(6'36)
1 “ (г>2 У
где х — коэффициент, зависящий от выходного угла лопаток р/ и вы-
числяемый для колес центробежных насосов по соотношению
х = 0,6 (1 +sin 0/) •
*) Теоретическому и экспериментальному исследованию коэффициента р посвя-
щено большое количество работ, в которых осуществлялся различный подход для
определения р. Так, например, проф. Стодола рассматривал лишь относительное вих-
ревое движение. Б. Экк при определении р учел, кроме того, влияние центробежных
сил в поперечном направлении. Теоретическое определение зависимости напора от числа
лопаток было произведено проф. Кухарским, акад. Проскура, проф. Уваровым и Пфлей-
дерером [32]. Экспериментально р определялся В. И. Дмитриевским.
247
Из формулы (6.36) следует, что зависимость коэффициента ц от 0/
протекает симметрично относительно точки р2/ = 90° (радиальные ло-
патки). Однако теоретические исследования [27] показывают, что угол
отставания у реактивного колеса (р2'<90°) всегда меньше, чем у актив-
ного (р2>90°) вследствие уменьшенной нагрузки на лопатку. Следова-
тельно, при одинаковых диаметрах, числе лопаток и режимах работы
значение коэффициента ц для реактивного колеса существенно выше,
чем для активного. Экспериментальные значения ц для колеса с ра-
диальными лопатками [13] даны в табл. 6.2.
Таблица 6.2
Z 2 4 7 10 14 16
р 0,52 0,67 0,77 0,82 0,87 0,89
Для подсчета коэффициента ц в случае радиальных лопаток может
быть рекомендована формула [44]
(6.37)
где z — число лопаток;
гСр — средний радиус входа.
На рис. 6. 17 приведен график значений коэффициента ц, подсчи-
танного по формуле (6. 37) для различного числа лопаток в зависимости
от относительной длины лопа-
ток гср/г2. Как видно из гра-
фика, коэффициент ц растет
с увеличением числа и относи-
тельной длины лопаток. Это
соответствует приведенным вы-
ше объяснениям причин откло-
нения потока на выходе из
колеса. Чем меньше длина и
чем больше относительная ши-
рина межлопаточного канала
колеса (т. е. чем меньше число
лопаток колеса), тем больше
отклонение относительной ско-
рости воздуха на выходе из
колеса от направления выход-
ных кромок лопаток, вызван-
ное наличием циркуляционного
течения или выравниванием
Рис. 6.17. График для определения коэф- скоростей на выходе из колеса,
фициента ц по формуле (6. 37) Рост отклонения потока приво-
дит, очевидно, к уменьшению
коэффициента ц и теоретического напора. При отсутствии окружной
составляющей на входе теоретический напор запишется для колеса
с радиальными лопатками в виде
Н tfl — Н — y-ti?,
где Нц10О — соответствует бесконечному числу лопаток.
248
При наличии закрутки на входе получим
Hth=p.ul — = — Ф— . (6.38)
\ “2 D2 J
Если ввести ciu = Ciu/«i, то это уравнение будет идентично уравне-
нию (6. 20).
6.3.4. ПОТЕРИ В КОЛЕСЕ И ИХ ВЛИЯНИЕ
НА ЗАТРАЧЕННУЮ РАБОТУ
И ПАРАМЕТРЫ ВОЗДУХА ЗА КОЛЕСОМ
В соответствии с общей классификацией потерь (см. разд. 2.5)
потери в колесе центробежного компрессора можно разделить на про-
фильные, вторичные и концевые. К профильным и вторичным потерям,
которые обычно рассматриваются совместно, относятся:
а) потери во вращающемся направляющем аппарате, обусловлен-
ные трением, поворотом потока и местными скачками уплотнения при
сверхзвуковом обтекании;
б) потери, связанные с поворотом потока из осевого направления
в радиальное;
в) потери на трение и вихревые течения в радиальной части колеса,
в том числе потери от вихреобразований, обусловленные перетеканием
воздуха через торцовые поверхности лопаток в зазоре между лопатками
и корпусом (при открытом или полуоткрытом колесе).
К концевым потерям в центробежном колесе относятся потери от
перетекания воздуха через боковые зазоры и от трения диска.
В отличие от осевых машин, в центробежном компрессоре эти потепи
рассматривают совместно.
6.3.4.1. Профильные и вторичные потери
Эти потери во вращающемся направляющем аппарате принято опре-
делять по соотношению
(6-39)
где Wi — относительная скорость на диаметре Di.
Как правило, значение w< — наибольшее.
Для расчетного режима можно принимать gi = 0,20—0,3.
Следует отметить, что значение gi для расчетного режима должно
являться функцией числа Mi, угла атаки на входе в направляющий
аппарат угла поворота потока и связанной с ним диффузорности канала
ВНА. В частности, значение вблизи нижней границы указанных зна-
чений соответствует более умеренным числам Mi =0,84-0,85 при нормаль-
ных углах уширения канала. Однако в связи со специфическими осо-
бенностями ВНА центробежных компрессоров требуются эксперимен-
тальные исследования для определения gi применительно к конкретным
условиям и, в частности, при наличии на выходе радиальных лопаток.
Потери, связанные с поворотом потока из осевого направления
в радиальное, определяют по формуле
с2
(6.40)
Эта формула соответствует предположению, что относительная
скорость после поворота равна абсолютной осевой скорости на входе
в рабочее колесо. Если осевая скорость на входе является переменной
по радиусу, то в уравнении (6.40) берется на диаметре Di.
249
В соответствии с опытными данными принимают
12 = 0,1^0,15.
Потери, обусловленные трением и вихревыми течениями в радиаль-
ной части колес, принято, как относительно небольшие, включать в ЛДк;
следовательно, коэффициент оценивает и эти потери. Однако при не-
которых условиях потери, связанные с вихреобразованием, могут воз-
расти. В колесе полуоткрытого типа (см. рис. 6.9) эти потери возни-
кают в основном из-за перетеканий воздуха поперек лопаток со стороны
с высоким давлением на сторону с низким давлением. При недостаточ-
ном числе лопаток или при малом отношении czrlu?. в межлопаточном
канале могут и на
Рис. 6. 18. Обрат-
ные течения в ко-
лесе центробежно-
го компрессора
расчетном режиме возникнуть обратные перетекания,
обусловленные тем, что циркуляционная скорость
w будет больше радиальной скорости (рис. 6.18).
Такое перетекание приводит к образованию
вихревых полостей в канале и к резкому увеличе-
нию гидравлических потерь. Отрыву потока от ло-
патки соответствует значению вуо^О в уравнении
(6.35).
Следовательно, условием безотрывного обте-
кания является
2л
г
Для внешнего радиуса
получаем
Г2 (где U = «2, WCp = W2r)
- 2л
— Д — или
«2 z
С2г \ 2Л
и--) '' Z
Соответственно определяется минимальное
число лопаток рабочего колеса, при котором не дол-
жен происходить отрыв потока:
г0>2л^_.
В колесе с радиальными лопатками относительные скорости ш2ср
или Wvt соответствуют средней радиальной скорости, определяющейся
из расхода воздуха. Поскольку на выходе из рабочего колеса направле-
ние относительной скорости отклоняется от направления лопаток, то
радиальная составляющая выразится в виде (см. рис. 6.16)
w2r = --2“ =
сtg а2 ctg а2
(6-41)
Следовательно,
г0 > 2л
ctg а2
(6.42)
Так как p.=f(z), то вычисление Zo по формуле (6.42) должно про-
изводиться последовательным приближением. Так, например, для реаль-
ного диапазона углов 02=16°—25° и /'ср//'2=0,4, воспользовавшись
рис. 6. 17, получим
2о=244-16.
В выполненных газотурбинных двигателях с центробежными (или
осецентробежными) компрессорами число лопаток находится в преде-
лах 2=164-29, что близко к полученному диапазону значений z0. При
этом меньшие числа лопаток (z= 164-19), как правило, относятся к ком-
250
прессорам с относительно небольшим расходом воздуха (G=l,5—
4,0 кг!сек) и диаметром, так как применение в них большого числа
лопаток вызывает вредное загромождение входного сечения. В отдель-
ных случаях встречаются конструкции, где г>29 даже при сравнительно
малых расходах воздуха, но по причинам, отличным от рассмотренных
выше при выводе уравнений (6.41) и (6.42). Так, например, колесо
центробежной ступени в двигателе Даймлер-Бенц [54] с расходом воз-
духа G--6 кг/сек вначале имело 17 лопаток, но при этом наблюдался
отрыв пограничного слоя в месте перехода от ВНА к рабочему колесу,
что объяснялось в основном неудовлетворительной работой диффузор-
ных каналов ВНА. На рис. 6. 19 показано изменение расчетного стати-
ческого давления в центре канала колеса и измеренного вдоль наружной
стенки канала по всей его длине.
Рис. 6. 19. Изменение статического давления в канале колеса цент-
робежного компрессора:
I — расчетное в центре канала; II — колесо с 17 лопатками; III — колесо
с 34 лопатками
На рис. 6. 19 отчетливо видно местное падение измеренного давле-
ния, обусловленное срывом пограничного слоя в зоне перехода с ВНА
на колесо для компрессора с 17 лопатками (пунктир). При переходе
к колесу с 34 лопатками падение давления почти полностью преодолено.
При этом в ВНА дополнительные лопатки были на входе укорочены,
чтобы избежать сильного загромождения входного сечения.
Так как W2r = c2r, то из уравнения (6.41) получаем
«2 Ctga2 "
Для указанного выше диапазона углов а2 и значений =24-1-16 полу-
чаем с2г/н2 = 0,26—0,4.
Обычно принимают, что с2,—с1а, и поэтому указанное отношение
характеризует производительность компрессора по входу. Таким обра-
зом, компрессор с меньшей производительностью требует применения
большего числа лопаток, чтобы обеспечить отсутствие отрыва. Однако
при выборе числа лопаток все же определяющим является получение
более высокого коэффициента напора, в связи с чем и при больших
отношениях с2г/н2 применяют большое число лопаток, если этому не пре-
пятствуют другие соображения (загромождение входа, усложнение тех-
нологии, удорожание и др.).
6.3.4.2. Концевые потери
Концевые потери представляют собой сложное сочетание потерь,
обусловленных перетеканием воздуха из диффузора через зазоры между
колесом и корпусом, и потерь на трение диска. На рис. 6.20 дана кри-
251
(L3) и из-за трения диска
сг м/сек
Рис. 6.20. Кривая радиальных
составляющих сг абсолютной
скорости воздуха после вы-
хода его из колеса
вая радиальных составляющих сг абсолютной скорости воздуха после
выхода его из колеса на разных точках по ширине канала. Как видно,
около стенок сг<0. Следовательно, воздух движется к центру колеса.
Чем больше зазор между колесом и стенкой корпуса, тем интенсивнее
обратное перетекание воздуха.
Затрата дополнительной мощности в связи с перетеканием воздуха
(Lf) имеет различную физическую природу,
но эти оба процесса связаны между собой.
В частности, перетекающий по зазору воз-
дух приводится во вращение колесом вслед-
ствие трения. Однако в центробежном ком-
прессоре потери Lf относительно значитель-
но больше, нежели в компрессоре осевом.
Поэтому можно считать оправданным,
когда в теории и расчетах центробежных
компрессоров потери L3 условно включают-
ся в работу трения диска Lf. В связи с этим
полная работа, затрачиваемая на враще-
ние колеса, запишется в виде
Нк = Hth + Lf.
Работа трения вычисляется исходя из
мощности трения гладкого диска, вращаю-
щегося в неподвижном корпусе, и расхода
воздуха через колесо.
Мощность трения определяется следую-
щим образом.
Сила трения, действующая на элементарное кольцо поверхности
писка dF = 2nrdr, равна
dR = С — tiHlnrdr = n^vLr3dr н,
где £— коэффициент трения;
у — плотность воздуха;
и — окружная скорость на радиусе г;
о — угловая скорость диска.
Момент от трения всего диска (с двух сторон) равен
т, гъ
Mf=2 rdR^= 2л£а)2уср Hdr = 2лС<о2уср -у- дж,
о о
где Yep — некоторое среднее значение плотности.
Мощность трения диска равна
Л4/М 2л _ , Г2 ПС , Г-.9
Nf = -L- = — C<03Yco—=—YcoMq^o Ktir-
f 103 103 ,CP 5 104 ,c₽ 2 2
Обычно это уравнение записывают в виде
N f = 10-6^Y2M2O2,
где
8 = 'Z^L
Р Ю272 '
252
Следовательно, работа трения диска выразится уравнением
103Д'г/ о 72И?/Э2
Lf=-------— — ------— дж1кг. (6.43)
7 Он 103 Ов ' V
Часто Lf выражают в виде
Lf = aul (6.44)
где
В 72“ 2^?
а=—-----------—.
юз Ов
Безразмерный коэффициент (3 есть функция числа Рейнольдса
Ке=и2О2у2/р2 [33]. Однако значения £, приводимые из экспериментов
для гладких дисков в зависимости от числа Re, не согласуются с данны-
ми для колес центробежных компрессоров, тем более что коэффициент
|3 должен учитывать еще дополнительные потери мощности от перетека-
ний. Опыт дает различные значения для коэффициента р. Для закрытых
колес его можно брать равным 1,0—1,5; для полузакрытых 2,0—3,0.
Выразив GB в виде
GB = n.D2b2y2c2r,
получим
U,- — --- . IU. *Т'Л
103 Ь2 с2г 103 ь.>
я — •— я ——
О2 «2 D2 u2
Из выражений (6.43), (6.44) и (6.45) следует, что коэффициент а
и, следовательно, относительные потери на трение диска уменьшаются
с ростом производительности, характеризующейся отношением С\а/н2,
и с уменьшением диаметра при заданном расходе и окружной скорости,
так как в этом случае увеличивается отношение в b2/L)2. Работа трения
диска Lf и, следовательно, коэффициент a = Lflu22 уменьшаются при при-
менении двухстороннего колеса в связи с тем, что при тех же размерах
увеличивается расход воздуха через колесо. Используя выражение L;
через коэффициент а и уравнение (6. 38) для теоретического напора по-
лучим полную работу, затрачиваемую на вращение колеса центробеж-
ного компрессора, в виде
//к = «Ь^+а)-ф—(6.46)
“2 L>2
Температура торможения на выходе из колеса определится из урав-
нения энергии:
71 = 7U—.
Статическая температура
Д
Т2 = Т*2-----2—, (6.47)
k
где
2 „2,2 ,2.2
С2 — С2и -ф С.2г — p2ZZ2 -ф С2т.
253
Статическое давление и плотность на выходе из колеса можно опре-
делить с помощью показателя политропы сжатия в колесе пк:
п 1
Рч = Pl
Y2 = Y1
Величина показателя политропы пк определится из уравнения
(3. 14). Применительно к рассматриваемому случаю это уравнение за-
пишется в виде
п,
пк — 1 & — 1
k— 1
k 11 4+ 2j lr<< \
k
---R\T /
где — сумма профильных и вторичных потерь в колесе.
Повышение статических температур AT заменим выражением
(2 2 \ / 2 2 \
с2 — cr \ k—1 / с с2 С] \
//„-------=------и21р.4-а — Ф— —---------— .
к 2 / kR 2\ «2 ©2 2а2 /
Приняв с2,.~с1а, можем член (с2—с2)/2«2 написать в виде
с2— С1 u.2 1 /cincpj2
2и2 2 2 \ и2 /
(6.48)
2
Следовательно,
2
«2 ©2
Подставляя эти выражения в уравнение (6.48), получим
образований
k— 1
/С “ “ А 2 I
и2 а —
«2
(6.49)
после пре-
где
п.
пк — 1 k — 1
р.2 1 ( «1и ср V
2 2
“2
«2 ©2
(6.50)
“2
k

И2
При отсутствии закрутки на входе уравнение (6. 50) упрощается:
Р2 V* 7
и — 2 ' - к
пк k
1
пк — 1 k — 1
р2
2
(6.51)
После вычисления статического давления за колесом может быть
определено полное давление р2 по обычному газодинамическому соот-
ношению:
*
Рч
Рч.
где
Лкр2
254
(6.52)
К.п.д. колеса компрессора выражается отношением
и. ’
где 7/алр.к подсчитывается с помощью полного давления за колесом.
К.п.д. компрессора в целом запишется в виде
м*
* ''ал
пк
где //ал подсчитывается с использованием полного давления на вы-
ходе из компрессора, т. е. с учетом потерь в диффузоре и в
выходном устройстве. Поэтому
•к 'р к
Записывая //аД в виде //*,= ii'.LI и заменяя Нк из уравнения (6.46),
получим соотношение
Н / , , ciu. Di
— = !^+а-ф— ~
П,< \ «2 D4
Это соотношение показывает, что коэффициент напора и к.п.д. не
могут приниматься независимо друг от друга, что и должно учитывать-
ся в расчетах. В выполненных компрессорах отношение Я/t]* находит-
ся в пределах 0,85—1,1. При этом более низкие цифры соответствуют
компрессорам с закруткой потока на входе и высоким к.п.д. Верхняя
граница относится к компрессорам без закрутки потока и с относительно
малой производительностью (си/ыг), что приводит к повышенным зна-
чениям а и более низким к.п.д. В компрессорах без закрутки, но с до-
статочно высоким к.п.д., большим числом лопаток и высокой производи-
тельностью отношение Н/т]*к =0,95-4-1,0.
Коэффициент напора мало зависит от работы трения диска и, сле-
довательно, коэффициента а. Легко показать, что коэффициент напора
можно записать в виде
тт 1 а R
П I и 2 I ’
X \ “2 /
где 27д — сумма всех потерь в колесе и в диффузоре без работы тре-
ния диска Lf [см. формулу (8. 11)].
Таким образом, Lf не входит непосредственно в число потерь, опре-
деляющих коэффициент напора Н, а влияет только косвенно через ко-
эффициент 1/х, зависящий от показателя политропы.
Коэффициент же полезного действия непосредственно зависит от ра-
боты трения диска Lf, выраженной через коэффициент а:
*
Пк =
2_
X
2
6.3.5. ВЫБОР ОКРУЖНОЙ СКОРОСТИ И ОТНОШЕНИЯ £>1/£>2
В центробежных компрессорах окружную скорость колеса при за-
данном адиабатическом напоре по заторможенным параметрам принято
определять с помощью коэффициента адиабатического напора
255
Следовательно,
и2 =
(6.53)
Для колес с радиальными лопатками коэффициент напора находит-
ся в пределах Н~ 0,65-4-0,75.
Величина Н и окружная скорость зависят от наличия окружной
составляющей скорости (закрутки потока) на входе в рабочее колесо.
Связь между окружными скоростями колеса при наличии и отсутствии
закрутки можно получить следующим путем. Адиабатическую работу
сжатия для случая, когда имеется закрутка потока перед колесом, мож-
но записать в виде
/7аЛ= Якг]к= Lf)v*K,
или
#ад= и1(р.-фа) Пк —
В случае отсутствия закрутки потока перед колесом получим
(fi'4-а')^*'-
Так как рассматривается расчетный режим, когда Н*ал в обоих слу-
чаях одинаково, то, приравнивая правые части, получим
и2(р- + “) ,Пк = (и2)2(р.' + а') Цк'-Н<олХ-
Значения у. и а практически от закрутки не зависят, поэтому можно при-
нять
н'

Тогда получим
«2 =
Если допустить, что то будем иметь
и2 =
77/ ’«К *
(6.54)
Новой окружной скорости соответствует коэффициент напора
г/ *
77=—^-.
“2
Следует отметить некоторую условность предположений, принятых
при выводе уравнения (6.54). В действительности при отсутствии за-
крутки числа М( и потери должны быть больше, что вызовет снижение
к.п.д. Равные же числа Mi при отсутствии и наличии закрутки возмож-
ны, если в первом случае будет принята пониженная производитель-
ность cijuz или GK, что при требующейся окружной скорости приведет к
увеличению входного диаметра D\, а также диаметра колеса Di и к уве-
личению Lf и а. Несмотря на отмеченную условность, применение фор-
мулы (6. 54) полезно, так как позволяет в первом приближении опреде-
лить окружную скорость компрессора при наличии закрутки потока и
затем произвести уточненный расчет. Окружная скорость и производи-
тельность компрессора определяют оптимальное значение Z)i/Z)2, при
котором потери в колесе будут минимальны. При заданной окружной
256
скорости производительность центробежного компрессора (по входу)
может характеризоваться отношением С\а1ч2- Одновременно по аналогии
с осевым компрессором целесообразно применять коэффициент произво-
дительности по параметрам на среднем диаметре входа:
GK = <7(ki)cp (1—^2) sina]cp.
В дальнейшем коэффициент производительности будет определять-
ся и по параметрам, соответствующим диаметру D\. Обозначая
эффициент производительности индексом R, можем написать
74 ?(Л1) sin И]
этот ко-
(6. 55)
входе и
радиусу
в преде-
q (М)ср s’n Щср
В частном случае, когда отсутствует закрутка потока на
входной патрубок не коленообразный, параметры воздуха по
входа (Xi, ai) будут одинаковыми и GkR = Gk.
Значение коэффициента производительности можно брать
лах 0,6—0,65.
Используя уравнения (6.39) и (6.40) и учитывая, что wi=CiaL-
4- (и\—Cm)2, запишем суммарные потери в колесе в виде
Г t Cla I t (И1 с1и)2 । е С1а
Li - ?! — + ~-----+ Ъ —
Разделив обе части уравнения на и2 и заменив С\и—С\а ctg си, бу-
дем иметь
2 к
"2
7?к~
10’
у.
И2 U2 2 \ U2 /
Исходя из уравнения расхода через входное сечение
6?==F1V1cla = ^- (1-
заменим Cia/u2 следующим выражением:
G=V
где Kg — коэффициент, учитывающий неравномерность поля осевых
скоростей и плотности по радиусу входа и влияние погранич-
ного слоя на наружной и внутренней стенках;
G и V — массовый и объемный расход воздуха в 1 сек на входе.
В данном случае коэффициент Ка соответствует условию, когда
расход определяется по значениям осевой скорости с1а и плотности
у, на диаметре Dr, а не на среднем диаметре. Обозначим Дг= q и
п£)2
(6. 56)
Ka{\—d2) = m. Тогда
240
с1а ____ Я
«2 ~~ ID\ V *
/п — I
\d2)
Подставляя это выражение в уравнение (6.56) и заменяя в нем
отношение ui/u2 через DJD2, возьмем производную от по D1/D2,
9 546 257
предполагая, что q, т, си, Bi и являются постоянными, и приравняем
ее нулю. Тогда после преобразований получим
\Z)2 / опт fn. I/ \ 2 / \ 2
Выразим q через коэффициент производительности:
__ V _^ici sin ariiKg __
nDf nD\-\\
(6.57)
лО](1 — d2) ?(X])sin апкракр/<о
ИЛИ
я2
240 "сК'к Я^кракр \9
q =--------------- 7Г I '
«271 \О2 )
Подставляя полученное выражение для q в уравнение (6. 57) и за-
меняя коэффициент т его выражением через Kg и d, а уг и укр через у*
и e(Xi), будем иметь
1
/ 2 \»-1_
/А\ A^+l) G^p
\^2 ' опт ^2£ (М) 0 )
X ]/ )’ + 2 (1 + cig» а, + Д ) - £!SA1. (6.58)
Таким образом, оптимальное
коэффициенту производительности
Рис. 6.21. Изменение _(Di/f>2) от
в зависимости от GKju2
Известные значения D-JD2 и D\
леса D2.
отношение Di/D2 пропорционально
I обратно пропорционально окруж-
ной скорости. В уравнении
(6. 58) можно использовать коэф-
фициент производительности по
параметрам на среднем диаметре,
если заменить GkR выражением
(6.55). При углах си ср^75°
значение коэффициента произво-
дительности G_kR весьма мало
отличается от GK.
На рис. 6.21 показано изме-
нение (Z?i/D2)oar в зависимости
от отношения GK/u2 при различ-
ных углах И). При расчетах при-
нято gi = 0,3, ^2=0,15, d = 0,35,
пкр=310 м/сек, e(A,i)=0,9 и
k=l,4.
Входной диаметр колеса Dt
может быть вычислен по фор-
муле, ранее применявшейся для
определения диаметра колеса осе-
вого компрессора:
” nsKp3GKKa
определяют наружный диаметр ко-
258
Поскольку известна окружная скорость и2 на внешнем диаметре, то
могут быть найдены окружная скорость щ на диаметре DL и число обо-
ротов.
В двухстороннем колесе расход для каждой стороны составляет по-
ловину исходного расхода и поэтому из уравнения (6. 58) следует, что
при том же GK отношение £>1ДВ/.О1одн=]/0,5=0,707. Еслипри этом со-
хранится также и отношение D1/D2, то и Оздв/ЕЬоди=0,707.
6 3 6. ПРОФИЛИРОВАНИЕ КАНАЛА КОЛЕСА
Профилирование канала колеса имеет целью обеспечить на расчет-
ном режиме минимальные потери в нем, а значит в первую очередь не
допускать срывов потока в ВНА, в зоне поворота потока из осевого на-
правления в радиальное и у передних поверхностей лопаток колеса. Для
этого необходимо выбрать закон изменения проходных сечений, исклю-
чающий наличие местных расширений и сужений, и рациональное чис-
ло лопаток. Определение необходимых сечений в общем случае затруд-
нительно в связи с тем, что параметры потока в относительном движе-
нии в колесе, т. е. скорости, температуры и плотности, зависят от трех
координат.
Имеется ряд упрощенных методов определения сечений канала ко-
леса центробежного компрессора [32], [50], [24], [26]. Рассмотрим один из
них, характеризующийся тем, что он аналогичен рассмотренному выше
методу расчета входного патрубка. С этой целью поток в колесе осред-
няем и, рассматривая в относительном движении осесимметричный двух-
мерный поток, используем уравнение (2. 104). В этом случае также тре-
буется построить линии тока и нормали, подобные показанным на рис.
6. 3. Отличие от входного патрубка будет состоять в том, что поток в
канале колеса, по сравнению с рис. 6. 3, имеет противоположное направ-
ление и при применении радиальных лопаток окружная составляющая
относительной скорости вдоль меридиональной линии тока равна нулю.
При satt = O из уравнения (2. 104) получим *>
п
_ Г dn
J Rm
ют—‘Штае 0 , (6.59)
где ^та — меридиональная составляющая скорости у внутренней стен-
ки колеса.
Уравнение (6.59) совпадает с уравнением (6.8), полученным выше
для входного патрубка. Принципиально таким же должно быть и его
решение. В частности, скорость подбирается путем последователь-
ных приближений так, чтобы в результате расчетов получить заданный
расход в каждом сечении колеса. Для определения wm<> может быть ис-
пользовано уравнение (6. 11), которое с учетом условия wu = 0 примет вид
Wm=-^----------, (6.60)
J 2n~[rAdn
о
где
п
С dn
*) В уравнениях (6.59) — (6.64) для общности с уравнениями (6.8) — (6.11) ско-
рости в колесе имеют индекс т, так как только часть из них направлены по радиусу.
9*
259
Для определения величины А в качестве первого приближения мож-
но принять, что кривизна 1/Rm линий тока вдоль нормалей изменяется
линейно, и тогда справедливы будут уравнения (6.13) — (6.15). Плот-
ность воздуха в различных
уравнений
сечениях может вычисляться с помощью

( Т
Y = Yicp — ;
V 1 Ср '
^Icp—6-1 ц2~~ц1ср
2 ' kR 2
(6.61)
(6.62)
где у, Т и wm — плотность, температура и относительная скорость воз-
духа в рассматриваемой точке потока;
Yicp, Лер и да1ср — плотность, температура и относительная скорость
потока перед колесом (на среднем радиусе входа);
и и utep — окружная скорость колеса на текущем радиусе и на
среднем радиусе входа;
пк — средний показатель политропы, определяемый по
уравнению (6.50).
Так как согласно уравнению (6. 59) wm=wmA, то у должно опре-
делиться в процессе последовательного приближения при решении урав-
нения (6.60), в результате чего становятся известными значения wm„,
wm и у для точек пересечения каждой нормали с меридиональными ли-
ниями и с внутренней и наружной границами канала. При этом, как и
при расчете канала входного патрубка, сначала меридиональные линии
тока ‘наносят приблизительно, исходя из первоначального очертания
внешней и внутренней стенок канала и соблюдая условие, чтобы между
двумя соседними меридиональными поверхностями тока проходили оди-
наковые расходы AG = Glim, yrs. lm — число промежутков между меридио-
нальными поверхностями.
Исходная ширина промежутка подбирается по уравнению
,
2nrCp7cpm’m(.p
где гСр — радиус, соответствующий пересечению средней линии канала
и данной нормали;
уср — средняя плотность, соответствующая гСр и определяемая по
уравнениям (6.60) и (6.61);
®тср — средняя скорость в сечении, соответствующем радиусу гср.
Принимается, что wmCp = ciaCp&, где &=t!(t—А) учитывает
уменьшение рассматриваемого проходного сечения с шагом
лопаток t за счет их толщины А. В среднем можно принять
е=1,04—1,05.
При нанесении первоначального меридионального сечения колеса
(рис. 6.22, б) можно использовать следующие положения: относительный
диаметр втулки в сечении 1к—1к на выходе из ВНА определится из вы-
ражения;
51к=1/--------------• (6.63)
lK J/ к 1
При этом в первом приближении предполагается, что внешний диаметр
ВНА по всей ширине остается постоянным и равным диаметру входа О(.
Плотность у определяется с помощью уравнений (6.61) и (6.62), в ко-
торых принимается, что« = «1Ср
1 + ^1к
1 + Л
а скорость
Wm— Wm 1к — Cla cp£-
260
Внутренний контур втулки от d\ до d\K предполагается прямолинейным.
Высота лопатки ВНА на выходе или лопатки рабочего колеса на входе
Aik = ^k=Y
Ширина направляющего аппарата Si определяется в соответствии с
рис. 6.8 по отношению s\ — b sin ft. Ширина колеса (без направляюще-
го аппарата) в первом приближении может быть принята равной s2—
= (0,15—0,20) £>2*’.
Величина s2 оказывает определяющее влияние на внешний (7?тк)
и внутренний (Rma) радиусы канала. Чтобы избежать чрезмерного уве-
личения скорости, срывных явлений и роста потерь на внешнем радиусе
f)
Рис. 6.22. Меридиональное сечение колеса центробежного ком-
прессора
Ширина канала
первого приб-
лижения (d[)
Ширина канала
второго приближения
Приближен-
ная замена
нормали к яи~
ниям тока
в)
входа, величина RmK должна быть достаточно большой, хотя это и свя-
зано с некоторым увеличением габаритов ступени вдоль оси (размер s2).
Ширина колеса на выходе определяется по уравнению
Ь2=—°”— ,
Т2лД2С2г
где c2r = w2r— радиальная составляющая абсолютной и относительной
скорости за колесом. В выходном сечении канала колеса
средняя относительная скорость
'a'm2 = c2rs,
где
Выбор скорости wm2(H с2г) и принципа ее изменения вдоль канала
колеса тесно связан с понятием о диффузорности потока в колесе, ха-
рактеризуемым отношением wm2/wm, или диффузорностью канала колеса
(F2IF1). Если принять, что на протяжении всего канала средняя относи-
тельная скорость wm=const, то очевидно, что проходные сечения в ка-
нале колеса будут к выходу уменьшаться в соответствии с ростом плот-
ности. Следовательно, при неизменной скорости канал будет конфузор-
ным. Если относительная скорость будет уменьшаться в такой же сте-
пени, в какой возрастает плотность, то проходные сечения будут оста-
ваться неизменными. При дальнейшем уменьшении скорости начнут воз-
растать и проходные сечения, т. е. канал будет становиться диффузор-
*) В двухстороннем колесе эти цифры соответствуют половине колеса.
261
ным. Увеличение диффузорности потока и сопутствующий ему рост диф-
фузорности канала (A/^i) увеличивает зону, занятую обратными тока-
ми, и снижает к.п.д. [24]. В авиационных центробежных компрессорах
наиболее часто применяются колеса с постоянной скоростью wm^ с 1а
или с относительно небольшим уменьшением скорости (на 10-4-20%).,
при котором каналы еще остаются конфузорными, поскольку плотность
на расчетном режиме возрастает в таком колесе в 1,5—2,0 раза. Более
существенное уменьшение скоростей может представлять интерес лишь
для колес малых размеров, поскольку это позволяет увеличить ширину
колеса (высоты лопаток) на выходе. Диффузорность потока можно ха-
рактеризовать градиентом давления dpfdl или градиентом относитель-
ных скоростей dwjdl, где I — длина канала. В принципе возможно про-
филировать каналы так, чтобы один из этих градиентов оставался по-
стоянным [24]. В авиационных компрессорах эти способы еще не иссле-
довались.
Исходя из прочностных соображений угол уширения внутренней
стенки диска 02 (рис. 6.22, а) принимается 5°—7°, с последующим
уточнением после расчета на прочность.
Относительная толщина диска А» на диаметре D2 составляет А2 =
=А2/Р2=0,00754-0,01.
Контур втулки ВНА и прямолинейная часть внутренней стенки со-
прягаются окружностью с радиусом Дто. Если принять, что эта окруж-
ность касается контура втулки ВНА в крайней точке А и внутреннего
контура канала колеса в точке В, находящейся на окружности с диа-
метром DB, то согласно рис. 6. 22, а
Rrna = sin 9[ + s2 — -rr2-°B- tg 92 — / cos 02.
Принимая cos 02~ 1,0 и s2 = xD2> получим
Как уже отмечалось, z = 0,154-0,20 и A2/D2=0,0075h-0,01.
Можно принять Db/D2 = 0,75-4-0,85. Угол 0j определяется графиче-
ски или с помощью соотношения
ctgQi =^-1 (d1K-dd-
Можно также принимать 0] = 1О4-2ОР. Тогда величина Е>вт.к и di,f
определятся при построении колеса.
Так, например, если х=0,2; £)в/£>2=0,75; 91 = 15°; 92 = 7°; А2 = 0,01,
то/^mo = O,236D2~ l,18s2- Таким образом, ширина колеса определяет
величину радиуса Дт„. Внешний контур канала можно получить, прове-
дя ряд вспомогательных окружностей, касательных к внутреннему кон-
туру, которые одновременно должны быть касательными к внешнему
контуру. Обозначим через Di диаметр, соответствующий одной из точек
касания, и через 0 г- угол между вертикалью и линией, касательной к
окружности с радиусом Rm0 (или прямолинейным участком внутренней
стороны диска, где 0г = 02). В качестве ширины канала (£>,-), являющей-
ся нормалью к средней скорости, можно принять в первом приближении
диаметр di вспомогательной окружности, проведенной через точку ее
262
касания с внутренним контуром (рис. 6. 22, в). Тогда диаметр di вспо-
могательной окружности определится из уравнения
оя=л (D; 4- di sin 0 z) z
или
sin 6,- л sin fiiiiWmi
откуда
di = bi = i / (——Уч---------—-----------— (6.64)
у \2sin0t-/ nw„ii'(Z sin di 2sine(-
Угол 0j определяется графически.
При этих расчетах также целесообразно принимать скорость wmi —
~ciaCpE или изменять ее по линейному закону от Wicp на входе до
(0,85—0,9)tOicP на выходе из колеса. Плотность уг в первом приближе-
нии можно принять равной плотности в центре предыдущей окружности
или на среднем диаметре выходного сечения ВНА (для первой окруж-
ности). После нахождения di со значением у» первого приближения ста-
новится известным диаметр и окружная скорость в центре окружности
dt, после чего вычисляются вновь значения у, по уравнениям (6.61) и
(6. 62) и dt во втором приближении, которое можно принять как окон-
чательное.
Проведя прямую и окружность (или несколько окружностей), оги-
бающую вспомогательные окружности с диаметрами di, получим внеш-
ний контур. Можно уточнить расчет, приняв в качестве ширины канала
во втором приближении прямую, проведенную через точки касания вспо-
могательной окружности данного диаметра di с внешним и внутренним
контурами. При этом целесообразно, сохраняя полученный канал, огра-
ничиться лишь определением уточненной скорости wmi из уравнения
расхода:
W j ' )
л/?ср / Тер Z bi
где Dcpi и усРг относятся к середине новой ширины канала bi.
В дальнейших расчетах в полученном канале наносятся линии тока
указанным выше методом, и очертания контура последовательно уточ-
няются. При этом с достаточным приближением нормаль к линиям то-
ка заменяют линиями, показанными на рис. 6.22, в.
6.4. ДИФФУЗОР ЦЕНТРОБЕЖНОГО КОМПРЕССОРА
6.4.1. НАЗНАЧЕНИЕ И РОЛЬ ДИФФУЗОРА
В диффузоре центробежного компрессора происходит преобразова-
ние кинетической энергии, имеющейся на выходе из колеса, в статиче-
ское давление. Аналогичный процесс происходит и в спрямляющем ап-
парате осевого компрессора, но величина преобразуемой в нем кинети-
ческой энергии существенно меньше. Вследствие этого целесообразно
рассмотреть более подробно, нежели это было сделано в гл. 5, некото-
рые вопросы, относящиеся к диффузору.
Как уже рассматривалось, в колесе с радиальными лопатками при
z = oo и с]и=0 степень реактивности рк = 0,5, т. е. только половина
всей подведенной энергии преобразуется в колесе в статическое давление
и, следовательно, остальное преобразование происходит в диффузоре.
263
С учетом влияния конечного числа лопаток и соотношения c2u = p»2
уравнение (6. 28) для степени реактивности колеса выразится в виде
₽к=1-— -
Так как р< 1,0, то рк>0,5.
С другой стороны, энергия, преобразуемая в статическое давление
в диффузоре, может характеризоваться степенью реактивности диффу-
зора:
1
О 1 — Л — ---- .
1 л ‘к 2
Следовательно, отношение адиабатических работ сжатия в диффу-
зоре и в колесе опишется выражением
77,а-1.л _ Р-
77ад .к 2 ’х
Значения этого отношения для нескольких величин ц представлены
в табл. 6. 3.
Таблица 6.3
Iх 1 0,9 0,8 0,7
н ад.д Н ад.к 1 0,8:9 0,666 0,538
Таким образом, при всех значениях ц<1,0 адиабатическая работа
сжатия в диффузоре значительно меньше адиабатической работы сжа-
тия в колесе. В действительном компрессоре это отношение еще мень-
ше, так как относительные потери в диффузоре больше, чем в колесе.
Диффузоры авиационных компрессоров характеризуются большими при-
веденными скоростями на входе Ла, часто превышающими единицу. Ве-
личину на выходе из рабочего колеса, являющейся одновременно при-
веденной скоростью на входе в диффузор, можно записать так:
где
с2г
«2
Таблица 6.4
«2 300 350 400 450 500
Л2 0,808 0,906 0,994 1,065 1,135
В табл. 6.4 приведены значения л2 в зависимости от «2 при ц=0,9;
с2г=0,3; ТГ=288°К и а=0,05.
Так как в авиационных газотурбинных двигателях часто окружная
скорость m2>400 м!сек, то и Х2> 1,0.
264
6.4.2. ПОТЕРИ В ДИФФУЗОРЕ. К.П.Д. ДИФФУЗОРА
В расширяющихся каналах источником потерь кроме трения яв-
ляются колебания потока и отдельные срывы вихрей, которые предшест-
вуют началу отрыва. Отрыв появляется, когда запас кинетической энер-
гии частиц пограничного слоя становится настолько незначительным, что
он оказывается недостаточным для преодоления того положительного
градиента давлений, который образуется вдоль диффузора вследствие
расширения сечений. Под действием этого градиента появляются обрат-
ные токи и образуются вихревые зоны. Описанная картина течения пре-
пятствует повышению давления и свя-
зана со значительными потерями
энергии.
Представляется удобным общие
потери в диффузоре разделить на по-
тери от трения и потери на расшире-
ние, т. е. рассматривать их как сумму.
Lr д — Lr тр + Lr расш
ИЛИ
= 5тр + брасш,
где
С2
2
Рис. 6. 23. Потери в диффузоре
На рис. 6. 23 показано изменение коэффициентов потерь в зависи-
мости от угла расширения канала при постоянной степени расширения
F^/F^ откуда видно, что потери на трение уменьшаются с увеличением
угла 6, так как при этом уменьшается длина диффузора, а потери на
расширение — возрастают. Оптимальный угол в для диффузора кругло-
го и квадратного лежит в пределах 6°—7°, а для прямоугольного (пло-
ского) диффузора — 10°—12°. На работу диффузора оказывает также
влияние величина и неравномерность скоростей на входе.
В табл. 6.5 приведены результаты испытаний круглых диффузоров
[1], показывающие зависимость коэффициента потерь ^x=LR[clf2 от чис-
ла М] и угла расширения диффузора 9.
Таблица 6.5
Ml
6=4° 6=5° 6=8° 6=10°
0,3 0,145 0J55 0,17 0,2
0.5 0,14 0,145 0,159 0,18
0,7 0,135 0,14 0,16 0,19
0,9 0,141 0,2 0,22 0,23
0,95 0,24
Коэффициенты потерь диффузора, приведенные в табл. 6. 5, полу-
чены для случая, когда потери относятся к квадрату входной скорости.
Как следует из табл. 6. 5, при числах М|=0,3-т0,7 на входе в диффузор
коэффициенты потерь изменяются незначительно, наблюдается даже не-
существенное их снижение с увеличением Mi до 0,5, а при 9 =4°—6° и
до 0.7, что можно объяснить ростом чисел Рейнольдса. При увеличении
265
же числа Mi до 0,9—0,95 в диффузорах с углами 9 =6°н-10° коэффи-
циенты потерь заметно возрастают.
Испытываемый диффузор имел степень расширения ~ 5,0, и
поэтому непосредственно использовать эти данные для расчета диффу-
зоров центробежного компрессора не представляется возможным, так
как в этих диффузорах такие большие степени расширения не применя-
ются. Приближенно эти данные можно пересчитать на другие степени
расширения, если воспользоваться эмпирической формулой для коэффи-
циентов потерь диффузора, связанных с расширением [43]:
фасш — С I 1
где_ 9°—угол расширения диффузора;
J = F F t —степень расширения;
С=3,2-: 6,4 — коэффициент, зависящий от 9, от степени неравномерно-
сти потока на входе в диффузор и от формы канала.
Применяя эту формулу к двум диффузорам с одинаковым углом
расширения, но с различными значениями / и С, получим
г С1
Ч расш
2
Д’расш £ /j_________ 1 V
Так как коэффициент потерь на расширение в 3—5 раз превышает
по величине коэффициент потерь на трение, то это отношение можно с
некоторым приближением распространить и на полный коэффициент
потерь в диффузоре.
В случае применения этого пересчета при переходе от испытывае-
мого (круглого) диффузора к лопаточному (прямоугольному) диффузо-
ру центробежного компрессора со свойственной ему неравномерностью
потока на входе должно быть учтено различие в коэффициентах С, вы-
званное этими факторами. Для лопаточного диффузора значение С может
быть принято на 35—40% больше.
Часто потери в диффузоре оценивают с помощью коэффициента
полного давления Ьа = р2/Р1, где р\ и р, полное давление на входе в
диффузор и на выходе из него. Коэффициенты бд и сд могут быть связа-
ны между собой следующим соотношением:
St St S' h S' Z
A J» =P1~P2 = i^2 ~
ИЛИ
(1-М = £л
st
Pl
PT*2P*
2
2
Правую часть запишем в виде
Поэтому
k <,
2
266
Эффективность диффузора можно оценивать также с помощью адиа-
батического или политропического к.п.д.
(f—)
»i.»= ; (6.65)
С1 с2
2
С dj>_
—гЛ—• <6-66)
С1 ~С2
2
Величина (ci —сг)/2 является располагаемой энергией в диффузоре,
как следует из уравнения энергии:
2 2
^2 С dp , г tС7\
—о— = \-------(6.67)
2 J 7
Так как
2 2
V д>д7’ и С1~С.2.= —— ^дТ,
J 7 лд — 1 2 k — 1
ТО
<6-68)
Яд — 1 / k — 1
где лд —показатель политропы в диффузоре.
Если потери в диффузоре определять в виде
с2 —с2
ЬКя^л^~, (6.69)
то исходя из уравнений (6. 66) и (6.67) получим
йг,= 1- 1д.
Используя выражение (6.68), получим
В табл. 6. 6 приведены данные, показывающие связь £ц, пя и г],,.
Таблица 6.6
«д 0 0,2 С, 25 0,43
'Hz' 1,0 0,8 0,75 0,57
Пд k 1,56 1,615 2,0
Реальным пределам коэффициентов потерь £д=0,2-д-0,25 соответст-
вует показатель политропы п=1,5-н1,6. Потери в диффузоре с неболь-
шой степенью расширения могут определяться по уравнению
(6.70)
р STp С'2
= \ — — dl,
х. * Jr
где ?тр —~~—коэффициент трения (X — коэффициент сопротивления
4
при течении в трубе), являющийся функцией числа Re
и степени шероховатости [1] (см. рис. 8.3);
рг —гидравлический радиус;
/—длина диффузора.
267
Если приближенно определить £Лд из уравнения (6.70), считая
плотность постоянной, то для круглого диффузора, заменяя
получим [43]
D , 160*
— ; с2 =---------
4 л2Д472
,, dD , 6
и dl=------tg— ,
2 2
_ 16G»Sip t 9 Г dD
~ Л2у2 g 2 J £>5 ’
1
откуда
Lrh
?тр
2tg —
S 2
Это соответствует уравнению (6.69), если принять, что
г ______________________________ £тр
Д— о 6
2 tg —
2
Уравнение (6. 70) используется в дальнейшем в основном для оп-
ределения потерь в безлопаточном диффузоре, в котором степень рас-
ширения, как правило, невелика (F2/Fi = 1,14-1,3) и при этом небольшие
углы расширения (<3°—4°), соответствующие эквивалентному кругло-
му диффузору. Степень повышения статического давления в диффузоре
определяется числом М. на входе, степенью расширения F2jFx и уров-
нем потерь, определяющим показатель политропы сжатия. Связь между
этими величинами устанавливается уравнениями энергии и неразрыв-
ности.
Из уравнения энергии получаем
с2 —с2
С1 — с2
/ д \
/?М«дЛд -1.
k — 1 1 д
где пл=р21рх— степень повышения статического давления в диффузоре.
Заменяя
рывности
и взяв выражение c2jcx из уравнения нераз-
I2 —
2/пл
яд Л
получим
k — 1 >.2
------Mi
2
”д
"д-1
При
тельным
нимать
, _ / \2____1_
\Р2 I
известных Mi, FxfF2 и пя это уравнение решается последова-
приближением. В качестве первого приближения можно при-
(6.71)
k— 1 ><2
------Mi
2
1-
"д
23 "д-1
Р-1
(6.72)
2
д
При параметрах диффузоров центробежных компрессоров уравне-
ние (6. 72) дает результаты, отличающиеся от точных [по уравнению
(6.71)] не более, чем на 3—4% и, особенно, при Mi<l,0 (рис. 6.24).
При Fx/F2=0 (F2=oo) и пл=к получаем известное из газодинамики от-
268
ношение давления изэнтропически заторможенного потока к статическо-
му давлению:
л
( — )=(Z l + , (6.73)
причем р*= р*.
Таким образом, уравнение (6. 73) характеризует предельный режим
работы идеального диффузора. В соответствии с уравнениями (6.71) и
(6. 72) можем написать уравнения для отношения плотностей:
или
Mi
k— 1
2
(6.74)
(6.75)
На рис. 6.24 показано изменение лд в зависимости от F2IFX при
различных числах Mt при показателе пд=1,6, откуда видно, что увели-
Рис. 6.24. Изменение степени повы-
шения давления в диффузоре в за-
висимости от F2IF\ и Mi при «д=1,6:
-----по формуле (6.71);
-----по формуле (6. 72)
чение степени расширения диффузора F2IFt сверх 4—4,5 малоэффектив-
но даже при числах Мь близких к единице.
6.4.3. БЕЗЛОПАТОЧНЫЙ ДИФФУЗОР
6.4.3.1. Структура потока в безлопаточном диффузоре
Безлопаточный диффузор (рис. 6.25) представляет собой кольце-
вую щель с параллельными или расходящимися стенками. При одних и
тех же скоростях на выходе диффузор с параллельными стенками дол-
жен иметь больший наружный диаметр, чем диффузор с расширяющи-
мися стенками. Однако к.п.д. последнего, по данным опытов, меньше
[24], [50] и поэтому чаще применяется диффузор с параллельными стен-
ками.
269
Для потока в безлопаточном диффузоре можно применить уравне-
ние моментов количества движения, приводившееся в гл. 2 для колеса.
Однако в связи с тем, что из моментов внешних сил в данном случае
остается только момент сил трения, уравнение для частицы с массой Дт
примет вид
дт d(cuR) = _ дуи
dt г
(6.76)
Если пренебречь трением, то для потока в диффузоре получаем
Ca/?=ICOnst.
(6. 77)
Из уравнения расхода получаем для среднего значения радиальной
скорости
где b — ширина диффузора.
Рис. 6. 25. Безлопаточный диффузор: траектория частицы газа
при течении без трения
Если принять, что by = const, что соответствует сходящимся стенкам
(или b = const и y=const), то получим
cTR = const. (6.78)
Из уравнений (6. 77) и (6. 78) следует
— tga= const.
cu
Следовательно, без учета трения и изменения плотности (при Ь=
=const) траектория движения будет логарифмической спиралью. В дей-
ствительности из-за влияния трения окружная составляющая скорости
будет уменьшаться быстрее, чем по уравнению (6.77). Условие by = const,
соответствующее сходящимся стенкам, требует увеличения диаметра
диффузора и редко применяется. В случае же b=oonst радиальная ско-
рость не будет подчиняться уравнению (6. 78) из-за изменения плотно-
сти. Поэтому траектория действительного потока будет отклоняться от
логарифмической спирали, особенно вне ядра потока, где влияние тре-
ния проявляется сильнее.
Рассмотрим уравнение движения потока в безлопаточном диффу-
зоре с учетом трения. Работа трения массы Ат на участке А1
£тр Г2 .
ДтдА^д = Дт------— Д/.
Рг 2
270
Сила трения
ДтД/.,, 5ТР с2
др =----------ДШ _2_ __ ,
f Рг 2
а момент этой силы, отнесенный к единице массы,
sPfR cos АЛЬ с2 ;тр
---------=------=--------R с os а.
Am Дт 2 рг
Гидравлический радиус для безлопаточного диффузора равен
_ _Г _ 2лР» __ Ь_
‘ г ~ П ~ 2л/? + 2п/? — 2 ’
где F — проходное сечение;
П — периметр.
Тогда из уравнения (6. 76) получим
</ (с„/?) $тр
= c-R cos а,
d~.------------b
Но
1/2,2 Си
С=У Cu-\-Cr; cosa= — ;
с
dx
dR
cr
G __ Q
2xRb-( R
где
G
Подставляя эти выражения, получим
d(cuR) V(cuR)* + W^RdR
b £2
ИЛИ
R
C _____d RuR)
£ RUR) V(cuRy + Q2
£Tp dR
~T Q
(6.79)
Решение этого уравнения в общем случае с учетом изменения плот-
ности представляет известные трудности. Поэтому введем ряд упро-
щающих допущений.
Если учесть, что Q = c,R~ (cuR)tg а, то левую часть уравнения
(6. 79) можно выразить в виде
R R
(• d (cuR)Г d (cuR)
R RuR) \ RuR)2 + RuR) 1 + tg2 a
Так как угол a изменяется вдоль диффузора относительно немного
и tga<l,O, то можно с небольшой погрешностью принять, что
К1 -|~tg2a —V 1-t-tg2a2= const.
Поэтому интеграл в левой части уравнения (6. 79) решается в виде
2?
С dRuR) 1 / 1_______1_\
£ RuRP 1^1 + tg2 а У1 Ttg2a2 V C“R C-‘^ '
271
Если в правой части уравнения (6.79) величину й заменить ее
значением
2 л if
то правая часть запишется в виде
Vh —= \dR. (6.80)
J Ь 2 G„ J
/?2 Т?2
Используем уравнение (6. 75), причем заменим отношение квадратов
площадей отношением квадратов радиусов (/?2/Д)1 2, и, разложив уравне-
ние в ряд, ограничимся первыми двумя членами. Тогда получим
Подставив это выражение для у в уравнение (6. 80) и интегрируя, по-
лучим
Н[1 I k~X f
GB J GB \ /?2 ) L ид-1 2 \
«2
Или умножив и разделив на c2rb2, будем иметь
Используя полученные выражения, получим уравнение (6. 79) в виде
С2и^1
, г---------- -тр ( R \
1 + С2и/?2Г 1 + *К2а2 7 (“ТТ-1 I
»2с2г \ л2 /
-----------------------, (6.81)
М2 / /?2\
пд-1 2 V R ).
учитывая, что c2r/c2u==^g а2„ получим
cuR =-----------------------.
/?2 ( R \ Г k — 1 М? / fi>\
P6oSina2 \ /?2 . L Яд—1 2 \ R /
Таким образом, циркуляция в безлопаточном диффузоре уменьшает-
ся вследствие трения независимо от наличия или отсутствия сжимаемо-
сти. Вместе с тем, чем больше число М2 или больше отношение R2!b2
и меньше угол а2, тем значительнее будет влияние трения при данном
коэффициенте трения.
При отсутствии трения (|Тр = 0) получаем уравнение (6.77)
cuR = c2uR2=const.
Для несжимаемой жидкости (М2 = 0), а также приняв К1 -4- tg2а2
^1,0, получим из уравнения (6.81) уравнение [13]
1 1 2j* Btd
— =—J--------1----^-(R-R2),
cuR c2aR2 У
где V= 2nR2b2c2r — объемный расход воздуха, являющийся для несжи-
маемой жидкости постоянным по всей длине диффу-
зора.
272
Показатель политропы сжатия в уравнении (6.81) можно брать в
пределах пд=1,5н-1,6 или среднее значение пд=1,55. Умножив и разде-
лив левую часть уравнения (6. 81) на ст и учтя, что , по-
Rb^
лучим выражение для угла потока на окружности с радиусом R-.
{tg«2 +ю W, [1 + ( 1 -^)]l
b'l \ b? L n'i — i \ X / )
(6.82)
Из уравнения (6.82) следует, что угол а в безлопаточном диффузо-
ре изменяется как вследствие трения, так и вследствие сжимаемости.
В случае постоянства произведения by угол потока а при наличии тре-
ния будет определяться выражением, стоящим в фигурных скобках в
уравнении (6.82). Если в уравнении (6.82) принять постоянными b и у,
К1 +tg2a2— 1,0, то получим известное [13] выражение, учитывая,
что при этом иМ2 = 0:
tga = tga2-|- -^-(/? —/?2).
Если £Тр = 0, то в несжимаемой жидкости
tga=tg ct2 и a=a2,
а в сжимаемой среде так будет только при бу = const. В случае же, когда
только b = const, а y = var получаем
tga = tga2 .
7
Так как у>у2, то с увеличением радиуса угол а уменьшается, т. е.
траектория становится более пологой. Хотя трение действует на величи-
ну угла в противоположном направлении, однако и с учетом его угол a
несколько уменьшается.
Как показали эксперименты [4], распределение окружной и ради-
альной составляющих скорости, а также углов потока а по ширине диф-
фузора весьма неравномерно, и особенно вблизи колеса (рис. 6. 26). Не-
равномерность радиальной составляющей скорости была показана и
ранее, на рис. 6.20. Указанную неравномерность можно объяснить тре-
нием в пограничном слое, а также некоторой неравномерностью потока
на выходе из колеса, обусловленной наличием вихревых зон на выходе
из ВНА и в колесе. В связи с трудностью учета имеющейся неравномер-
ности расчет ведется по некоторым средним величинам.
Важной особенностью безлопаточного диффузора является воз-
можность преобразовывать в нем сверхзвуковую скорость в давление без
скачка уплотнения*’ Это объясняется тем, что в безлопаточном диффу-
зоре может иметь место только косой скачок (по нормали к поверхно-
сти cu=const) и, следовательно, в нем может претерпевать разрыв толь-
ко радиальная составляющая скорости, нормальная к фронту скачка,
которая обычно меньше критической величины. В данном случае при-
*) Было впервые показано В. П. Никольским.
273
Рис. 6. 26. Изменение направления потока, а также радиальной и окружной составляющих скорости по ши-
рине безлопаточного диффузора:
7—1,02270,: 2—1,040,; 3—1,080 ; 4—1,08650,: 5 — 1,11250,;
6—1,160,; 7—1,1960,; 6-1,'.'240,; 9—1,230,
менимы соотношения для косого скачка, которые для сечения после вы-
хода из колеса имеют вид:
где
2 k — 1 2
С2гСг= ^КР + |
сг — радиальная составляющая после пересечения струей фронта
косого скачка.
Предыдущее выражение можно записать еще в виде
СЧгС г—
где дкрг — условная критическая скорость, соответствующая температу-
ре частичного торможения [1]
*'2«
Скачок уплотнения может быть только в случае, когда с2г>акрг,
что в современных компрессорах не встречается.
Безлопаточный диффузор характеризуется еще малыми углами
расширения, вместо которых можно брать углы расширения эквивалент-
ного круглого диффузора, т. е. имеющего такую же степень расширения
и длину [24]. Для круглого диффузора можем угол расширения выразить
формулой
tg fl = Г? У У (У7-1)
Z |/ л Z V л
где I — длина диффузора;
^У/У — степень расширения.
Если подставить в эту формулу параметры безлопаточного диффу-
зора, в частности,
Fi = nD2b2 sin а2, = s’n аз и =5~
2 sin acp
Oto -|- Clo
где acp —•’ , то получим
у
Для компрессора, расчет которого дан в примере 6. 4.7. 2 и у кото-
рого />2 = 0,0316 м; D2 = 0,806 м; -^=1,12; а2=20°10' и аз=18°40', полу-
чаем 0Экв=1°ЗО'.
275
Если пренебречь изменением угла а2 за счет трения и сжимаемости,
то формула для эквивалентного угла упрощается [24]:
0Э
tg-^ = 2
—— sin3/2 <х2
А
Однако для рассматриваемого примера расчет по этой формуле да-
ет почти вдвое больший угол расширения.
6.4.3.2. Определение размеров безлопаточного диффузора
и потерь в нем
Определение диаметральных размеров безлопаточного диффузора
подчиняют иногда условию, чтобы число Мз было меньше единицы (М3=
= 0,85^-0,95) во избежание повышенных потерь в лопаточном диффузо-
ре. Запишем температуру торможения в конце диффузора в виде
Т*3 = Т3 (1 +Ml).
Аналогично для температуры торможения на выходе из колеса (у
входа в диффузор) получаем
= 14-~^-м1).
Так как Т*3=7'*2, то, следовательно,
Но
Т2 _
7'3 «1
Если без учета трения и сжимаемости приближенно принять
с3==;с2-^- ,
3 D3 ’
тогда для k — 1,4
Г 1 + °’2М«
£>2 Мз J/ 1 + 0,2М2
или при заданных D3/D2 и М2 получаем значение М3:
(6.83)
(6.84)
С учетом трения и сжимаемости скорости и числа М3 будут умень-
шаться быстрее, поэтому формулы (6. 83) и (6. 84) могут быть исполь-
зованы только в качестве первого приближения, так как действительное
276
значение М3, получающееся при заданном D3/D2, будет приблизительно
на 5% меньше значений, получаемых по формулам, не учитывающим
трения и сжимаемости.
Потери в безлопаточном диффузоре можно определять по уравне-
нию (6.70). интегрируя его графически, или по упрощенной формуле, в
которой площадь интеграла заменена площадью трапеции:
, / 2 2 '
?тр / с2 । С3
----- I-------1------
4 \ Рг2 РгЗ>

— /??
. ач + я3
sin----------
2
(6.85)
Учитывая достаточно большие числа Re в безлопаточном диффузо-
ре на расчетном режиме (Re>106), а также достаточно гладкую поверх-
ность, малые степени расширения (Fz/Fi —1,1—=—1,3) и отсутствие скач-
ков при числах М2> г,О, величину коэффициента сопротивления Хтр мож-
но брать с достаточной точностью в пределах Хтр = 0,030-4-0,040. Следо-
вательно, 1тР = = (0,75н-1,0) • 10“2. Гидравлические радиусы рг2 и
Ргз соответственно равны Ь2/2 и Ь3/2 и будут одинаковыми, когда b2 = b3.
Параметры на выходе из безлопаточного диффузора определяются
последовательным приближением, которое целесообразно выполнять
следующим путем.
Используя упрощенное уравнение (6.75) изменения плотности в
диффузоре и принимая приближенно F2/F3~R2IR3, получим
УТ’1-
72 12 L ^3 / JJ
Задаваясь отношением R2/R3 и показателем политропы пд, пределы
значений которых указаны выше, получим в первом приближении плот-
ность уз на выходе из диффузора. После этого можно определить угол
а3 по уравнению (6.82). Вычисляем затем радиальную и полную ско-
рость в конце диффузора:
‘ ----, L-.J--------------- .
п/??Уз7з sin а3
Полученные данные позволяют вычислить LR д по уравнению (6. 85),
повышение температуры Д7'=(<?2 — сз) /----R и 73=7'2-|- ДГ. В резуль-
тате определяются показатель политропы из уравнения
ид ____________________________ k________
Пд — 1 k — 1 RST
и уточненное значение плотности
1
/ Л \ "л-1
Тз = Т2
\ 1 2 !
Так как полученные значения пд и у3 будут, как правило, отличать-
ся от величин, принятых в первом приближении, то, используя их, вновь
определяют а3, с3 и остальные величины. Это второе приближение в
большинстве случаев является достаточно точным.
Потери в безлопаточном диффузоре сильно возрастают с увеличе-
нием его радиальной протяженности из-за роста длины траектории, ко-
торая при а = О2—const может быть записана в виде
Кг
£ С rf/? 7?3 — Т?2
j sin а2 s'n а2
Кг
277
Угол а2 обычно невелик и на расчетном режиме равен 14°—16°. Сле-
довательно, длина траектории приблизительно в четыре раза превышает
радиальную протяженность диффузора. Поэтому относительную ради-
альную протяженность безлопаточного диффузора ограничивают значе-
ниями /?з/Т?2= 1,05ч-1,15, возлагая на него функции снижения чисел Мз
и некоторого выравнивания потока на входе в лопаточный диффузор, от-
чего существенно зависит эффективность последнего. С ростом произво-
дительности компрессора на расчетном режиме угол а2 увеличивается и
может достигать 18°—20°. В этом случае эффективность безлопаточного
диффузора возрастет, но все же нельзя считать целесообразным увеличи-
вать относительную радиальную протяженность безлопаточного диффу-
зора /?з/Т?2 выше 1,15, так как степень расширения 'при этом возрастает
медленней, чем габариты, и поэтому становится выгоднее использовать
лопаточный диффузор.
6.4.4. ЛОПАТОЧНЫЙ ДИФФУЗОР
6.4.4.1. Общие сведения
В лопаточном диффузоре (рис. 6. 27) в силу воздействия лопаток по-
ток не подчиняется закону cur=const и окружная составляющая сни-
жается более интенсивно, чем в безлопаточном диффузоре. На входе в
лопаточный диффузор угол потока аз = 12°-т-18°, а на выходе из него
Рис. 6. 27. Колесо центробежного компрессора с безлопато�