СБОРНИК
ЗАДАЧ
ПО МАТЕМАТИКЕ
ДЛЯ ВТУЗОВ
МЕТОДЫ ОПТИМИЗАЦИИ
УРАВНЕНИЯ
В ЧАСТНЫХ ПРОИЗВОДНЫХ
ИНТЕГРАЛЬНЫЕ
УРАВНЕНИЯ
СБОРНИК
ЗАДАЧ
ПО МАТЕМАТИКЕ
ДЛЯ ВТУЗОВ
МЕТОДЫ ОПТИМИЗАЦИИ
УРАВНЕНИЯ
В,ЧАСТНЫХ ПРОИЗВОДНЫХ
ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Под редакцией А. В, ЕФИМОВА
ИЗДАНИЕ ВТОРОЕ, ПЕРЕРАБОТАННОЕ
Допущено Государственным комитетом
по народному образованию в качестве учеб/
для студентов высших технМескцх учебны
МОСКВА «НАУКА»
1//7/ ГЛАВНАЯ РЕДАКЦИЯ
кгГ7/1 ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
РШШ Л 9 9 О
ББК 22.11
С23
УДК 51(075.8)
Коллектив авторощ
Э. А. ВУКОЛОВ, А. В .< ЕФИМОВ, В. Н. ЗЕМСКОВ,
А. Ф. КАР АКУЛИН, В. В. ЛЕСИН, А. С. ПОСПЕЛОВ,
А. М. ТЕРЕЩЕНКО
Сборник задач по математике для втузов. Ч. 4. Методы оптими-
зации. Уравнения в частных производных. Интегральные уравнения:
Учеб. пособ./Вуколов Э. А., Ефимов А. В., Земсков В. Н. и др.;
Под ред. А. В. Ефимова,'—2-е изд., пере раб.-- М.: Наука. Гл. ред.
физ.-мат. лит., 1990.—304 с.—ISBN 5-02-014457-6 <4. 4).
Сборник содержит задачи и упражнения по специальным кур-
сам математики: методам оптимизации, уравнениям математичес-
кой физики и интегральным уравнениям. Во всех разделах при-
водятся необходимые теоретические сведения. Все задачи снабжены
ответами, а наиболее сложные*-решениями. Решение части задач
предполагает использование ЭВМ.
1-е изд.— 1984 г.
Для студентов втузов.
Рецензен т
кафедра специальных курсов высшей математики
Московского энергетического института
(заведующий кафедрой профессор С. А, Ломов)
1602070000—016 -6 0О
С 053(02)-90
ISBN5-02-014457-6(4. 4)
ISBN5-02-014338-3
© «Наука».
Физматлит, 1990
ОГЛАВЛЕНИЕ
Предисловие ко второму изданию	6
Глава 16. Методы оптимизации ........................  7
§ 1, Численные методы минимизации функций одной
переменной ...................................  7
1. Основные понятия. Прямые методы минимизации
(7). 2. Методы минимизации, основанные на ис-
пользовании производных функции (20).
§ 2.	Безусловная минимизация функций многих пере-
менных ............. ........	23
1.	Выпуклые множества и выпуклые функции (23).
2.	Методы безусловной минимизации, основанные
на вычислении первых производных функции (26).
3.	Методы безусловной, минимизации, использую-
щие вторые производные функции (32).
§ 3, Линейное программирование..........  .	. . ,	34
1. Постановки задач линейного программирования.
Графический метод решения (34). 2. Симплекс-ме-
тод решения задачи линейного программирования
(45). 3. Целочисленное линейное программиро-
вание (58).
$ 4. Нелинейное программирование.................. 68
1. Задачи, сводящиеся к нелинейному программиро-
ванию (68). 2. Методы возможных направлений
(75). 3. Градиентнце методы решения задач нели-
нейного программирования (84). 4. Методы Штраф-
ных и барьерных функций (91).
§ 5. Дискретное динамическое программирование . . *	96
§ 6, Вариационное исчисление..................... Ill
1. Предварительные сведения. Простейшая задача
вариационного исчисления (111). 2. Обобщения про-
стейшей задачи вариационного исчисления (117).
3. Задачи с подвижными границами (121). 4. Задачи
на условный экстремум (125). 5. Прямые методы
вариационного исчисления (130).
Глава 17. Уравнения в частных производных........... 138
§ 1, Основные задачи и уравнения математической фи-
зики .................. . . . . ............. 138
1. Вывод уравнений и постановка задач математи-
ческой физики (138). 2. Приведение уравнений к
каноническому виду (141).
§ 2. Аналитические методы решения уравнений матема-
тической физики	145
3
L Метод Далацбера (145). 2. Гильбертовы прост»
рЪЙсШ. Ортогональные системы (148). 8. Ортого*
бальные ряды (154). 4. Метод Фурье решения урав-
ЙеЯйи математической физики (156).
| в. Приближенные методы решения дифференциальных
уравнений в частных производных.............. 169
1. Основные понятия метода сеток (169). 2. Числен-
ное решение краевых задач методом сеток (183).
Глава 18. Интегральные уравнения............  .	* • •	188
§ L Интегральные уравнения Вольтерра .......	188
1. Уравнения Вольтерра 2-го рода: основные по-
нятия, связь с дифференциальными уравнениями
(188). 2. Метод последовательных приближений.
Решение с помощью резольвенты (194). 3. Уравне-
ния Вольтерра 2-го рода типа свертки (198).
4. Уравнения Вольтерра 1-го рода (202).
$ 2. Интегральные уравнения Фредгольма	207
1. Основные понятия. Метод последовательных при-
ближений и резольвента для уравнений Фредголь-
ма 2-го рода (207). 2. Решение уравнении Фред-
гольма 2-го рода с вырожденным ядром (213).
3. Характеристические числа и собственные функ-
ции. Теоремы Фредгольма (216). 4. Уравнения
Фредгольма 2-го рода с симметричным ядром (223).
§ 3, Численные методы решения интегральных уравнений 229
Ответы ............................................. 236
Список литературы..............................    •	299
Содержание частей 1—3............................... 300
4
Светлой памяти
Анатолия Федоровича
Каракулина
посвящается
5
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
Настоящая четвертая часть сборника задач по мате-
матике для втузов содержит существенно переработанные
главы 16—18 первого издания третьей части сборника
(специальные курсы). Глава 16 «Методы оптимизации»
написана заново. Во всех главах более четкими и лако-
ничными стали теоретические введения. Значительно уве-
личено число простых типовых задач. Исправлены неточ-
ности и опечатки в условиях задач, примерах и ответах.
В главе 16 «Методы оптимизации» расширен круг
рассматриваемых методов одномерной минимизации, без-
условной минимизации функций многих переменных, не-
линейного программирования, включен материал по
целочисленному линейному программированию, а также
некоторым задачам вариационного исчисления. Большее
внимание уделено методической стороне изложения мате-
риала: более простыми и полными стали теоретические
введения, увеличено число разобранных примеров, в каж-
дом разделе теперь предлагаются как простые, так и
сложные задачи.
Изменения в главах 17 и 18 относятся в основном к
численным методам. Более систематичным и полным стало
изложение метода сеток в § 3 главы 17. В главу 18 до-
бавлен § 3 «Численные методы решения интегральных
уравнений».
Во время подготовки рукописи настоящего тома к
изданию скоропостижно скончался один из членов автор-
ского коллектива доцент, кандидат физико-математических
наук А. Ф. Каракулин, активно и плодотворно работав-
ший над рукописью всех четырех частей задачника.
В частности, им был подготовлен материал главы 18’
«Интегральные уравнения».
6
Глава 16
МЕТОДЫ ОПТИМИЗАЦИИ
§ 1. Численные методы минимизации функций
одной переменной
1. Основные понятия. Прямые методы минимизации. Пусть на
множестве U с R определена функция f (х). Под минимизацией
функции f(x) на множестве U будем понимать решение следую-
щей задачи: найти хотя бы одну точку минимума х* и минимум
f* = f(x*) этой функции на множестве U.
Задача нахождения точки максимума и максимального значе-
ния функции f(x) сводится к задаче минимизации заменой f (х)
на — / (х), поэтому ниже будут рассматриваться только задачи
на минимизацию.
Напомним» что число x*gi/ называется точкой абсолютного
{глобального) минимума или просто точкой минимума функции f (х)
на множестве (/, если f(x*)^f (х) для всех x£U. Значение /* =
= min f(x) называется абсолютным (глобальным) минимумом или
и
просто минимумом f{x) на U. Множество всех точек минимума
функции f(x) на множестве U будем обозначать (7*.
Число x^U называется точкой локального минимума функции
f (х), если существует такое число б > 0, что f (х) f (х) для всех
х £	= {х | х g Ut I х—х ] < 6}. Значение f (x) называется локаль-
ным минимумом f (х). Всякая точка глобального минимума /(х)
является и точкой локального минимума этой функции. Обратное,
вообще говоря, неверно.
В задачах 16.1—16.4 найти множество точек мини-
мума U* функции f(x) на множестве U.
16.1.	f(xj = sin^nx,	=
16.2.	f(x) = |x—х?[. [/ = [— I; 2].
16.3.	f(x) = COS-2-, [/ = (0; 1].
( x’ при Ixl > 1,
16.4. f(x) = < . H '	l/==R.
'v ’ (1 при |x|< 1,
16.5. Доказать, что линейная на отрезке [а; Ь] функ-
ция f(x) = Ах+В, Д ¥=0, достигает минимума на этом
отрезке только в точке х — а или х—Ь.
7
Отметим, что минимум функции f(x) на множестве U может
и не существовать, т. е. множество £/♦ может быть пустым. В этом
случае используют обобщение понятия минимума*-точную ниж-
нюю грань функции f(x) на множестве U. Пусть f(x) ограничена
снизу на U, т. е. f(x)^X>«oo для всех x£U. Число f9 назы-
вается точной нижней гранью функции f(x) на множестве U
= f(х)), если f(x)^fe при всех x£U и для любого 8>0
найдется точка х8 С/ такая, что f(*8 )</*+*» Для неограни-
ченных снизу функций f(x) полагают со. Если £/* # Н, то
«inf f (х) ==/*== nUn f (x).
Пример 1. Пусть f(x)=l/x, £7==Ц; 4-оо). Показать, что
множество U* точек минимума функции f (х) на множестве U пу-
сто и f* = inf /(х)=0.
Предположим, что U* & 0, т. е. существует хотя бы одна
точка минимума x*gl/ функции / (х) на U, Возьмем произволь-
ное число х > х*. Тогда x£U и f (х*) = 1/х* > l/x = f (х), т. е. х* не
является точкой минимума f (х) на U. Полученное противоречие и
доказывает, что множество £/* точек минимума пусто.
Покажем, что f* == inf / (х) = 0. Очевидно, для произвольного
х<(1; +«о) справедливо неравенство f(x) = l/x> 0. Далее, пусть
8 > 0. Возьмем произвольное xe>max(i/8, 1). Тогда xe и
/(х8) < е = 04-е. Поэтому /# = 0. ►
Пример 2. Пусть /(x)==lnx, C/=s(O; 1J. Найти /% = inf/(x).
Функция /(х) не ограничена снизу на множестве (/, поэтому
пегопределению точной нижней грани полагаем оо.
В случае под задачей минимизации f (х) на множестве
U понимают определение fe = inf/(x), полагая	При этом
точка минимума х* не ищется.
В задачах 16.6—16.11 убедиться, что множество точек
минимума функции f (х), заданной на множестве I/, пусто,
и найти fe = inf/(x).
16-6.	= U = R.
16.7.	f(x) = 2x»—9x?+12x4-5, (7 = (— oo; 5).
16.8.	f(x)=xsinx, l/ = R.
Ю. /(x) = arctgx, l/ = (—oo; —1].
16.10.	f(x)=tgx, (/ = [—2; 2].
16.11.	/W—a) t/ = (0; 1); 6) I/ = (l; 4-oo).
16.12.	Показать, что если minf(x) существует, то
и
inf / (х) — minf(x).
и и
Существование локальных минимумов функции /(х), отлич-
ных от абсолютного, почти всегда затрудняет поиск точек х*^(/*э
поэтому многие приближенные методы минимизации применимы
только^ тогда, когда любой локальный минимум f (х) является
8
одновременно и глобальным. Один из классов функций, удовлет-
воряющих этому условию, составляют унимодальные функции.
Функция f(x) называется унимодальной на отрезке (a; 6J, если
она непрерывна на [а; Ь] и существуют числа а и ₽,
такие, что:
1)	если а < а, то на отрезке [а; aj f (х) монотонно убывает;
2)	если 0 < Ь, то на отрезке [0; 6] f (х) монотонно возрастает;
3)	при xg[a; ₽] f(x) = /*= minf(x).
[а;Ч
Отметим, что возможно вырождение в точку одного или двух
из отрезков [а; а}, [а; 0| и (0; bj. Некоторые варианты располо-
жения и вырождения в точку отрезков монотонности и постоян
ства унимодальной функции показаны на рис, 204*—207.
Множество функций, унимодальных на отрезке [а; 6], будем
обозначать Q [а; 6].
Для проверки унимодальности функции /(х) на практике
обычно используют следующие критерии:
1)	если функция f (х) дифференцируема на отрезке [а; Ь] и
производная f (х) не абываёт на атом отрезке, то f(x)^Q(a*
2)	если функция f (х) дважды дифференцируема на отрезке fcr, 6J
и Г(х)^0 при х£[а; 6J, то f(x)$Q (а; Ы.
Пример 3. Показать, что функция /(х)==х4*—10х34-36хЦ-5х
унимодальна на отрезке [3; 5].
9
«4 Вторая производная функции /(х) равна /®(х)«12х*—60x4-72.
Корни полученного квадратного трехчлена xj =2 и х2=3. Следо-
вательно-, f*(x>s=0, если и, в частности, при xg|3; 5].
Используя второ* критерий унимодальности, получаем, что
/(*)€<? (3: 6]. ►
В задачах 16.13—16.16 убедиться в унимодальности
функций f(x) на указанных отрезках [а; Й.
16.13.	f(x)==x?—3x4-xlnx, [1; 2]. .
16.14.	/(х) = 1п(1 4-х*)—sinx, [0; я/4].
16.15.	f(x)=4x*+x?—*»+12, [0; 2].
16.16.	f(x) = lx?—sinx, [0; 1].
16.17.	Показать, что любая из точек глобального мн- '
нимума функции f(x)GQ[a; Ь] является и точкой ее ло-
кального минимума.
16.18.	Показать, что если f(x)GQ[a\ 6] и аСс<
<d^b, то Цх)€Ф[с; dj.
16.19.	Пусть f (х) € Q (а; Ь] и а Схг < х2 ^Ь. Показать,
что	!
а)	если f (xt) > f (х2), то U*c[x}; fr], а если /(х2)<
</(х2), то U*<z[a; x2j;
б)	если f(xi) = f (х2), то отрезок [х2; х2] содержит хо- '
тя бы одну точку x*€i/**,
в)	если f (xi)’</(x2), то л*€[о; х2], а при f(xt)>
>/(х2) имеем x*€[xj; Ь], где х*—одна из точек мини-
мума /(х) на [а; Ь].
16.20.	На какие 3 части следует разбить отрезок
[—1; 2], чтобы на каждой из них функция /(х) =
= ||х(х—1)|—1| была унимодальной?
16.21.	Найти максимальное значение Ь, при котором
функция f(x) ——х?4-бх—6 унимодальна на отрезке
[—5; Ь].
16.22.	Будет ли функция f(x) = ax8—Зх?—10 унимо-
дальной на отрезке [1; 2J при а>3?
Большую группу приближенных методов минимизации функ-
ций составляют прямые методы минимизации, основанные на вы-
числении только значений минимизируемой функции в некоторых
точках и не использующие значений ее производных.
Метод перебора является простейшим из прямых методов ми-
нимизации. Пусть [a; 6) и требуется найти какую-либо из
точек минимума х* функции f (х> на отрезке (a; с абсолютной
погрешностью в > 0. Разобьем [а; 6} на п равных частей точками
деления	(6—a)/nt i = 0, 1,2, п, где	а)/е.
Вычислив значения f (х) в этих точках, путем сравнения найдем
точку для которой
/(*«>“ mln	(1)
о<;
10
Далее полагаем х* «	Ири этом максимальная по»
грешность еЛ определения точки ж* равна 8я»(б-*а)/л.
; F Пример 4. Найти минимальное значение f* н точку мини*
{ мума л* функции / (х)===х*4-8х3—6х2—72х на отрезке (1,5$ 2].
Точку х* найти а погрешностью 8=0,05.
f (x)CQ U,5; 2J, так как Г (х) = 12х*4~48х—12 > О ври xg
g(l,5’, 2| (проверьте!^
Выбрав Лвя’у^"^1^ вычислим значения /<хД ^«НЛЧ*
4-1*0,05, i«0,1, Ю, поместив их в таблице 1.1.
Таблица 1.1
XI	1,50	1,55	1,60	1,65		1,70		1,75
l(Xi)	—89,4	—90,2	—91,2		91,8	—92,08		—92,12
Xi	1,80	1,85	1,90		1,95		2,00	
f м	—91,9	-91,4	-90,5		-89,4		—88,0	
Из таблицы 1.1 находим х*« 1,75, f* » —92,12.
16.23*	. Пусть f(x)gQ[a; 6], хт—точка, найденная
из условия (1), х*—одна из точек минимума f(x) на
[а; Ь]. Показать, что если l^m^n—1, то x*g
I €[xm-n	если ^=0, ТО [Хо? «СЛИ .^ = Я,
ТО x*G[x„_l; х„].
16.24.	Пусть отрезок (а; &] разбит на п частей точ-
. ками x(=a-|-(t>—a)i/n = a+А£, i = 0, 1, ..., п. Рас-
смотрев функцию
' — д4й(х—х«+1 + б)	ПРИ	*€[°; хт+1—Ч»
Л*)М 2
-g-(x—x^i + б)	при х€[хл+$—б; 6],
где 1^/пСп—1. 0<;6<Д, показать, что абсолютная
погрешность определения точки минимума унимодальной
функции, методом перебора может быть как угодно близ-
кой к А =	= е„.
16.25.	Составить блок-схему алгоритма минимизации
функции Цх) на отрезке [а; 5] методом перебора в по-
мощью ЭВМ.
В задачах 16.26—16.33 методом перебора найти точку
минимума х* функции f (х) на отрезке [а; Ь] в точностью
в и минимум /*.
11
е=0,05.
в = 0,03.
16.26.
16.27.
16.28.
16.29.
16.30.
16.31.
16.32.
16.33.
f(x) = x?—2x4-е**, Fl; 1,5
/(х)= tg х—2sinx, [0; л/4'
/(x) = Kl 4-x2+e’“, (0; 1], e = 0,1.
f(x)==x4 + 4x«—32x4-1, [1,5; 2], e=0,05.
f(x) = yx’—x’4-y*?—[И 1.5], e=0,05
f(x)~x?—3sinx, [0,5; 1], e = 0,05.
f(x) = 5x2—8xbfi—20x, [3; 3,5], e = 0,02.
f (x)==jx8—5x4-xlnx, [1,5; 2], e = 0,02.
16.34.	Пусть /(x)—-унимодальная дифференцируемая
на [а; Ь] функция, причем | /' (х) | С М при х£[а; Ь].
Оценить погрешность нахождения минимума f* мето-
дом перебора при разбиении отрезка [а; Ь] на п частей.
Метод перебора, предполагающий предварительный выбор то-
чек X/, i«=0, 1, п, называется также пассивной стратегией
поиска точки минимума х*. На практике точки х/выбираются за-
ранее, когда удобно провести п+1 независимых экспериментов
по измерению значений f(x), а последовательное измерение этих
значении трудоемко или невозможно, например ввиду нехватки
времени. Однако использование уже полученной в предыдущих
экспериментах информации о функции f (х) для выбора очередной
точки X/ измерения (вычисления) f (х) приводит к более эффектив-
ному поиску точки х*. Методы минимизации, в которых точки х/
определяются в процессе поиска точки минимума с помощью най-
денных ранее значений функции f(x) называются последователь-
ными методами.
Метод деления отрезка пополам является простейшим после-
довательным методом минимизации. Он позволяет для любой функ-
ции f(x)^Q(a;b] построить последовательность вложенных от-
резков [а; б) Г) 1«г, М Э ... Z)	Г) [аЛ; 6Я), каждый из
Af(x)

f 1-----4	Ь—— | 1
ап а?* ол	ап а* Ьа
Рис. 208	Рис. 209
которых содержит хотя бы одну из точек минимума х* функции
f(x). Пусть е > 0—требуемая точность определения точки 'Л
Выбрав 6g(0; 2в), построим последовательности {ап}, {бд}>
и {4Й>}» ««0, 1» «о, используя рекуррентные формулы
12

^«-»в(вв_,+6я_1-в)/2, хГю = (а„_1+6„_14-6)/2|	(2)
au^an-it Ьп = Я~1\ если f (хГ*’)<f (хП
ап = хГ\ Ъп=Ьп-Ь если /(хГ«) > f (хГw).
Переход от отрезка [art-i; ^n-il к отрезку [ап; Ьп] методом
деления отрезка пополам иллюстрируется на рис. 208, если
f (х!л”п) < f (*з’~1>)» и на рис. 209, если f (xil“*1)) > f (хз,“1)).
Полагая x* ж (art4-6rt)/2, находим x* с абсолютной погреш-
ностью, не превосходящей величины
8й = (дп^ай)/2 = (Ь-а-6)/2«+1+б/2.	(3)
Используя условие 8п^в, из последнего выражения можно
найти необходимое число шагов п для обеспечения требуемой точ-
ности е. Однако на практике часто поступают иначе: определив
границы отрезка [ап; Ьп], вычисляют 8П по формуле (3) и сравни-
вают с заданной точностью 8.
Пример б. Решить пример 4 методом деления отрезка по-
полам.
Положим 6 = 0,02 < 28 = 0,1. Построим последовательность
вложенных отрезков [ай; Ьп] по формулам (2), записывая резуль-
таты вычислений в таблицу 1.2:
Таблица 1.2
л	ап	Ьп	е о 1 tt	сч	х™	Jn) *2	1(х<Л		Примечание
			II е ю						
0	1,5	2	0J&		1,74	1,76	—92,135	—92,096	&1в*8в)
1	1,5	1.76	0,13		1,62	1,64	—91,486	—91,696	ва = х<1)
2 3	1,62 1,68	1,76 1.76	0,07 0,04		1,68	1,70	—91,995	—92,084	от е,<е, точность достигнута
Следовательно, х* « 1,72, и « f (1,72)=92,13.
Для увеличения скорости сходимости метода величину 6$
g(0; 2е) целесообразно выбирать как можно меньшей, однако
этот выбор ограничен снизу используемым количеством верных
десятичных знаков при задании аргумента х. В любом случае 6
должно быть больше машинного нуля применяемого вычислитель-
ного средства»	г	.
13
16.35.	Показать, что каждый из отрезков [а„; &п],
я==1, 2, .... полученных методом деления отрезка по-
полам, содержит хотя бы одну из точек минимума функ-
ции f(x)GQ[a-, 6].
16.36.	Показать, что для /(x)GQ[<J; 6] п шагов мето-
да деления отрезка пополам обеспечивает вычисление
точки минимума х* на отрезке [а; Ь] с абсолютной по-
грешностью, не превосходящей
— ^~“а I (1____1 \
ел — 2» + Х ' 2 V 2В/
16.37.	Найти число шагов п метода деления отрезка
пополам, необходимое для определения точки минимума
функции f (х) € Q [а; &] на отрезке [а; Ь] с точностью е > 0.
16.38.	Достаточно ли вычисления 10 значений функции
f(x)€Q[O; 1] для определения ее точки минимума на от-
резке [0; 1] с точностью е = 0,02 методом деления отрезка
пополам?
16.39*	. CpdBHHTb необходимые количества вычисленных
значений Л\ и N„ функции /(х) при поиске ее точки мини-
мума на отрезке длины 1 с точностью е—10-6 методами
деления отрезка пополам и перебора соответственно.
16.40.	Составить блок-схему алгоритма метода деления
отрезка пополам, рассчитанную на использование ЭВМ.
В задачах 16.41 —16.48 методом деления отрезка попо-
лам найти точку минимума х* функции f (х) на отрезке [а; Ь]
с точностью е и минимум /*.
16.41.	f(x) = xsinx4-2cosx, [—5; —4], е = 0,02.
’ 16.42. f(x) = x44-8x’—6x2—72x4-90, [1,5; 2], 6 = 0,05.
16.43.	f(x) = x64-3x?4-6x— 1, [—1; 0], е = 0,1.
16.44.	/(x) = 10xlnx—у, [0,5; 1], е = 0,05.
16.45.	f(x) = x?4-2(xlgy— 2), [1,5; 2], 8 = 0,01.
’ 16.46. /(х) = Зх‘—10х»4-21х84-12х, [0; 0,5], е = 0,01.
16.47.	/(х) = -^—2х\ [3,5; 4,5], е = 0,02.
16.48.	f(x) = ex~xa + 2x, [—1,5; —1], е = 0,01.
Метод золотого сечения также является последовательным мето-
дом минимизации. Опираясь на свойства золотого сечения отрезка,
этот метод использует найденные значения f U) более рационально,
чем метод деления отрезка пополам (см. задачу 16.53), что позво-
ляет иереходить к очередному отрезку, содержащему точку ж* после
вычисления одного, а не двух значений f (х). Деление отрезка на
две неравные части так, что отношение длины всего отрезка к длине
14
большей его части равно отношению дли вы большей части к длине
меньшей части, называется золотым еечением этого отрезка, -
Золотое сечение отрезка [а; ft) осуществляется двумя точками
(6—а),	' (4)
причем *i есть вторая точка "золотого сечения отрезка {а; х8),
а х2—первая точка золотого сечения отрезка (х<; ft). -
Зная одну из точек золотого сечения отрезка (a; ft), другую
можно найти по одной из формул
Xj»a-|-ft —х2,	х2=а+^~ хь	(5)
Пусть /(x)(£Q[fl; ft] и требуется найти точку минимума х*функ-
ции f(x) на [a; ft). Построим последовательности {ап}> {Ьп} и{хп},
л = 1, 2, .следующим образом:
если/(хГ^Х/СхГ1’);
в„-хГм, Ьа~Ь„.ь 7„ = хГи, если / (жГ-1’) > f (хГ1’).	(6)
n=»2, 3, ...» где ах —a, fti=ft, Xin"1) и Хз1"1*—-первая и вторая
точки золотого сечения (4) отрезка [ал-1; ftn-tL
Для определения чисел ал, ftrt, хп по найденным ап-Т» ft«»t,
jTr-i необходимо выполнить следующие операции:
I)	найти одну из точек золотого сечения отрезка (ая-Г> ftrt-tl
по известной другой точке используя формулы (5) *);
2)	вычислить значение f (х) во вновь найденной’точке золотого
сечения (значение в другой точке xn~i уже вычислено на одном
из предыдущих шагов);
3)	сравнить значения /(xf*1*) и /(хГ"1>) и найти ап, bni хйпо
формулам (6).	*
Таким образом, на каждом шаге определения ал, ftB и ха
п=2, 3, .требуется вычислений одного значения / (х). Положив
х* «х*л, найдем точку минимума х* с точностью ел:
(i/’r?_। \п
Г -р--) (Р-а),
откуда следует, что число шагов п метода золотого сечения, обеспе-
чивающее заданную точность е нахождения точки Xе, должно удовле-
творять неравенству
Пример 6. Решить пример 3 методом золотого сечения.
*) При определении х* с большой точностью, чтобы избежать
накопления ошибок округления, обычно точки золотого сечения
отрезка {ал; _ftB] находят по формулам (4) и в качестве Xi1”^ и х?*0
используют хп-х и ту из найденных точек, которая больше отли-
чается от Xn_f.
И
Вычисления проведем по формулам (6), представив результаты
в таблице 1.3, где стрелками отмечены сохраняющиеся при пере-
ходе к следующему шагу значения.
Таблица 1.3
п		ап	Ьп	х{»>	Г(Л) Х2			Примечание
1	0,309	1,5	2 »	1,691	1,809	-92,049	“91,814	
2	0,191	1,5	1,809	1,618	1^691	“91,464	“92,049	1	4'01
3	0,119	1,618	1,809	1,691	1,736	-92,049	“92,138	
4	0,073	1,691	1,809	1,736	1,764	“92,138	“92,083	
5	0,045				V36		“9^,138	en<e , точность
	-							достигнута
Из таблицы 1.3 получаем х* « хб= 1,736,	(х5)==—92,138.
Заметим, что если воспользоваться формулой (7), то необходимое
число шагов п можно определить заранее. В нашем случае п^4,79,
т. е. п=5, и отпадает необходимость во втором столбце таблицы 1.3
16.49.	Показать, что каждая из точек --
ю Q $ (&_0) и х2=а+^-^=2-(Ь—а) осуществляет
золотое сечение отрезка [а; Ь].
16.50.	Пусть хх и х2—точки золотого сечения отрезка
[а; Ь]. Показать, что х, является второй точкой золотого
сечения отрезка [а; х2], а х2—первой точкой золотого
сечения отрезка [х,; &].
16.51.	Пусть Xf и х2—точки золотого сечения отрезка
[«; Ч-
а)	Доказать, что справедливы равенства х1 = а 4-Ь—х2,
xa—fi+b—xt.
6)	Найти длины отрезков [а; х2] и [хх; 6].
16.52.	Найти длину Ап отрезка [п„; Ьп], полученного
методом золотого сечения при поиске точки минимума х*
функции на отрезке [а; Ь], и показать, что |х*—х„|
\» —
—$—I (Ь—а), где хп—одна из точек золотого сече-
ния отрезка [а„; Ь„].
16.53.	Сравнить необходимые количества вычисленных
। значений N* и Ne функции f(x) при ее минимизации на
! отрезке длины 1 с точностью е=10~5 методами деления
I отрезка пополам и золотого сечения соответственно.
I 16.54. Составить блок-схему алгоритма метода золотого
। сечения, рассчитанную на применение ЭВМ.
I 16
В задачах 16.55 —16.62 методом золотого сечения найти
точку минимума х* функции f (х) на отрезке [а; Ь] с точ-
ностью 8 И минимум f*.
16.55.	f{x):=x* + 2x2 + 4x+ 1, [—1; 0], 8 = 0,1.
16.56.	/(х) = х5—5х3 + 10х?—5х, [—3; —2], е = 0,1.
16.57.	/(х) = х2 + 3х(1пх—1), [0,5; 1], е = 0,05.
16.58.	/(х) = х2 —2х—2cosx, [0,5; 11, е = 0,05.
16.59.	/(х) = (х + 1)4—2х2, [—3; —2Т, 8 = 0,05.
16.60.	f(x) = 3(5—х)4/3+2х2, [1,5; 2], 8 = 0,025.
il6.61.	f (х) = — х3 + 3 (1 4~ х) [In (1 +х)— 1], [-—0,5; 0,5],
е = 0,05.
16.62.	Дх) = 2 + х?4-хг/3 —ln(l -f-x2/3)—2xarctgx1Z\
[0,5; 1], 8 = 0,025.
В прямых методах [минимизации, рассмотренных выше, тре-
буется, чтобы функция f (х) была унимодальной. Если f (х) этим
свойством не обладает, то применение указанных методов приво-
дит, вообще говоря, к неверному результату. Кроме того, во многих
случаях доказательство унимодальности функции f (х) бывает за-
труднительно.
Метод ломаных является последовательным методом, рассчитан-
ным на минимизацию произвольных (не обязательно унимодаль-
ных) функций, удовлетворяющих условию Липшица. Говорят, что
функция f (х) удовлетворяет на отрезке (а; Ь] условию Липшица,
если существует такое число L > 0 (константа Липшица), что
lf(xW(x')l<b]x'~x'|	(8}
для всех х', х*£[а; ft].
Для проверки условия Липшица на практике используют сле-
дующий факт: если функция f (х) имеет на отрезке [а; ft] ограниченную
производную, то она удовлетворяет условию (8), еде L max | f' (х) |.
(«; *1
Пусть функция f (х) удовлетворяет на [a; ft] условию Липшица
с константой L, Опишем метод ломаных для минимизации f(x).
Положим
* == 2Г if (a)-f (6) + L (a-f-й)!,	[f (a) + f (b)+L(a-t>)]
и реализуем следующую схему вычислений:
Шаг 1. Вместо пары чисел (xj, pi) образуем двг«овыеявр«к
(*ь Pi) и (хъ pi) следующим образом:
Af,	Р1«>у [/(**)+/>*]»
гд? а< = 2т;|7(х*)—р*]-
Ш а г 2. Из полученных двух пар (xj, Pi) и (хи'рх)“В«верем 
ту, у которой вторая компонента минимальна. Обозначим ев
pl) и исключим из рассматриваемого множества (очевидно, на
данном male в качестве (xj, pl) можно взять любую из пар (xt, pt),
IT ,
(xit Pi))- Вместо дары (xl, pl) добавляем две новые пары (х£, р8)
и (хз» Ps)> компоненты которых находятся по формулам
XaesxJ—Да, Ха«Ха + Да, Ра«у D W)—Д*]>
где Да=«^-[/(х*) —Ра]-
В результате получим множество, состоящее из трех пар чи-
сел (х, р).
Шаг п. Из п полученных на предыдущих шагах пар (х, р)
выбираем ту, у которой вторая компонента р минимальна. Обо-
значим ее (хп, рд). Исключаем эту пару из рассматриваемого мно-
жества в добавляем вместо нее две новые пары чисел (хд, рп)
и (хп9 Рп) по формулам
k х; = Хп—А„, Хп=Хп+Д„, рп=у [/(х„)—рД, (9)
/
где’’Ап=[/ (х„)—р„].
Полагая х* « Хд, f*«f(x«), получим приближенное решение
задачи минимизации. Точность определения f* характеризуется
неравенствами 0 < f (хд) — /• < 2LAп.
Геометрически метод ломаных состоит в построении последо
вательности ломаных, приближающихся к графику функции f {хг
Рис. 210
снизу и имеющих угловые коэффициенты всех звеньев, равные ± L
(рис. 210).
Пример 7. Методом ломаных найти минимум /* функции
f (Х) =	на отрезке [ 10; 15] с точностью 0,01 и точку минимума х*.
Функция f(x) дифференцируема на указанном отрезке. Так как
tf' {х}ijxcosx-stox| < xlcosxl+lsinxl < х+1 <011 пра
<€(10; 15], то f (х)' удовлетворяет условию Липшица с константой
lt=0,Н.
18
Найдя х* = 12,056, pl <=—0,281, продолжим вычисления, исполь-
вуя соотношения (9). Результаты вычислений представим в таб-
лице 1-4.
Таблица 1.4
n	Исключаемая пара Ur Д)			Включенные пара (x, p)		
	xn			xn	xn	?n
1	12,056	—0,281	0,240	10,963	13.149	—0,161
2	10,963	—0,161	0,070	10,646	11,280	—0,126
3	13,149	—0,161	0,203	12,227	14,071	-0,096
4	10,646	—0,126	0,038	10,474	10,818	—0,107
5	11,280	—0,126	0,041	11,094	11,466	—0,106
6	10,474	-0,107	0,024	10,364	10,584	-0,095
7	10,818	—0,107	0,160	10,745	10,891	—0,099
8	11,094	—0,106	0,016	11,020	11,168	—0,098
9	11,466	—0,106	0,028	11,338	11,594	—0,092
10	10,891	-0,099	0,008<e	—	—	—
Из таблицы 1.4 находим х* я 10,89, /* « f (10,89) =0,091. Отме-
тим, что f ,(х) £ Q [10; 15], поэтому из методов минимизации, рас-
смотренных выше, в данном случае применим только метод лома-
ных. ►
16.63.	Показать, что если функция f (х) удовлетворяет
условию Липшица (8), то модуль углового коэффициента
любой хорды или касательной к графику f (х) не превосхо-
дит константы Липшица L.
16.64.	Показать, что если функция удовлетворяет усло-
вию Липшица (8), то она непрерывна на [а; Ь].
16.65.	Найти наименьшую из констант Липшица функ-
ции / (х) = ух®4-2х2—5x4-6 на отрезке: а) [0; 1]; б) [0; 10].
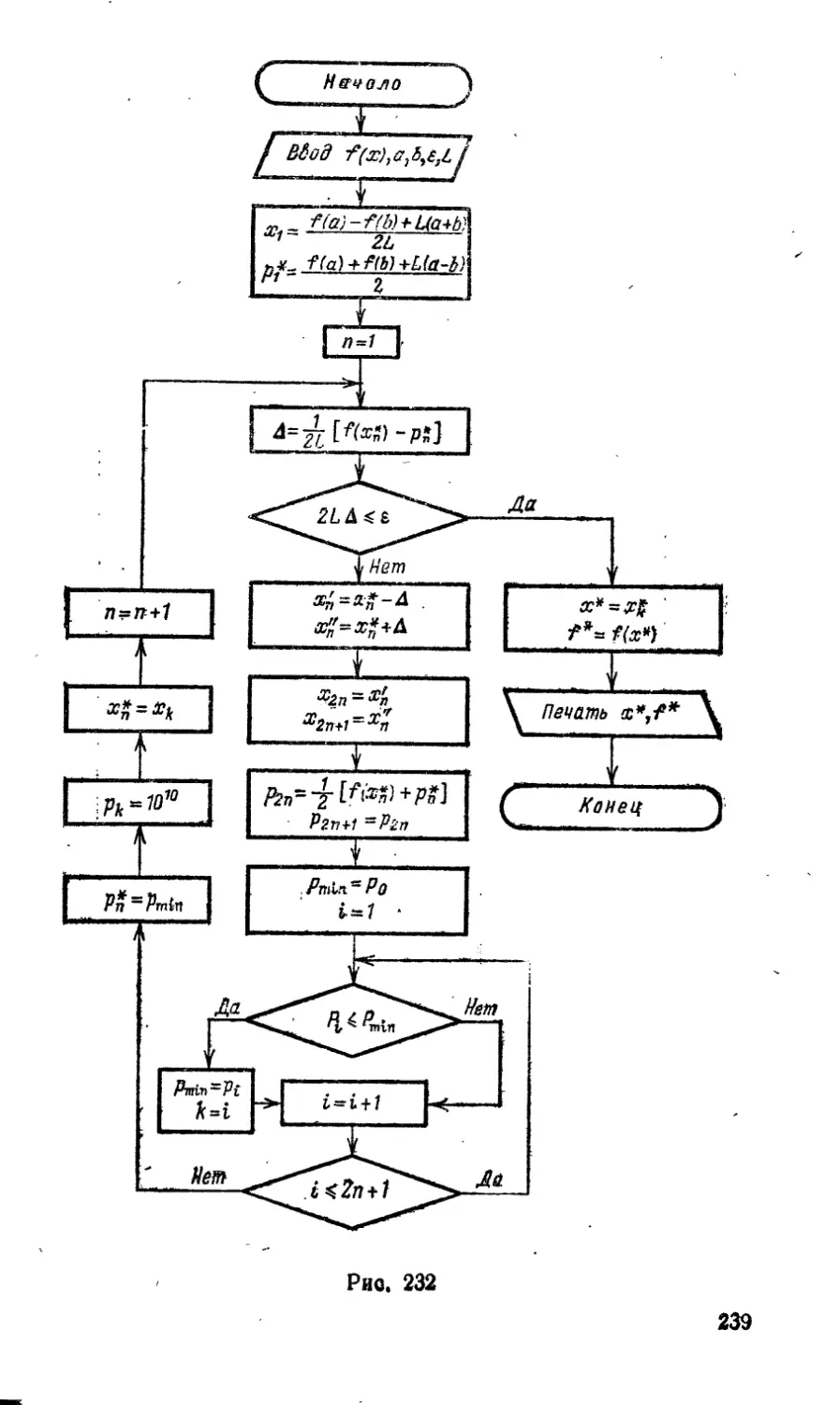
16.66.	Составить рассчитанную на использование ЭВМ
блок-схему алгоритма метода ломаных.
В задачах 16.67—16.71 методом ломаных найти мини-
мум f* функции f(x) на отрезке [а; Ь] с точностью е.
16.67.	/(х) = ^, [7; 11], е = 0,01.
16.68.	/(х) = —К20х—х?4-0,01 sinx, [9; 11], е = 0,05.
16.69.	/(х) —(0,1х—5)84-cos(0,02x), [49; 51], е = 0,02.
16.70.	f(x) = lnx 4-0,1 sin(0,lx), [10; 12], s=0,01. ,
16.71. f(x) = (x—0,9)a4-(x—1,1)‘, [0,8; 1,2], e«=0,05.
19
2. Методы минимизации, основанные на использовании производ-
ных функции. Если вычисление или измерение производных функ-
ции f(x) не представляет больших затруднений, то при решении
задачи минимизации можно применять непрямые методы, основан-
ные на использовании производных f (х). Во многих случаях эти
Рис. 211
методы обеспечивают более быструю
сходимость, чем прямые методы ми-
нимизации.
Метод касательных применяет-
ся для минимизации выпуклых диф-
ференцируемых функций. Функция
f (х) называется выпуклой на отрез-
ке [а; £], если
f [ах' + (1 — а) хяX af (х') +
-Н1-а)/(х")	(10)
для произвольных х', хя(£[а; Ь] и
аёЮ; И-
Проверка условия (10) почти
всегда вызывает затруднения, по-
этому на практике используют следующий критерий выпуклости:
Для того, чтобы дважды дифференцируемая на отрезке [а; /?]
функция f(x) была выпуклой на отрезке [a; Z?], необходимо it доста-
точно, чтобы Г(х)^0 при всех xg[a; 6].
Опишем метод касательных. Пусть f (х)—выпуклая дифферен-
цируемая на отрезке [а; функция, причем/' (a)'f‘ (b) < 0. Построим
последовательности {ая}, {6Я} и {ся}, п=1, 2, ..., в соответствии
с рекуррентными соотношениями
6О = 6,
„ * bn~if'(bn~i)~an-tf'(an-i) + f	(bn~i) ,ln
(tf)
=	при f' (Сп-1)^0,
fin==Cn-i, bn^bn^i при f'(cn^) < 0.
После п шагов полагаем х*«ся, « f (сп). Требуемая точ-
ность минимизации f(x) считается достигнутой, если производная
Г (ся) достаточно близка к нулю, т. е. \f' (ся) |<е> где е>0 —
заданное число, характеризующее точность.
20
Метод касательных имеет простой геометрический смысл: вели-
Af яз (11)—это абсцисса точки пересечения касательных
»Игпа*ик¥ / (*)• проведенных в граничных точках отрезка [an_i; &n_d
/пис 211). Рис. 212 и 213 поясняют формулы (11) для случаев
(Че «) >0 и f (c„_i) < 0 соответственно. Отрезок [а„; ЬП1 выби-
вается так, чтобы х*(£[Лв,
р Если условие f (a) f (6) < 0 не выполняется, то
а)	х»=а при f (а) > 0, f (b) > 0;
б)	х*=Ъ при Г (а) < О, Г {Ь) <0;
в)	х’=<1, если f (а)=0, и х*=6, если (&)=0.
Пример 8. Убедиться, что функция f(x)—x*4-е* выпукла
на [—1; 1] и минимизировать ее методом касательных о точностью
1Г («в) I <0,05.
Так как Г (х)=24-е* > 0, то /(х)—выпуклая функция; кроме
того, Г (а) Г (5) < 0. Проведем вычисления по формулам (11), (12),
поместив результаты вычислений в таблицу 1.5.
Т а б л и ц а 1.5
п	ап	Рп	сп	Г'(еп)	Примечание
0	-1	1	0,11586	1,35	Z’(^o)>O,
1	—*4	0,11586	—0,41637	—0.173	г ta)<of
2	—0,41637	0,11586	—0,14313	0,58	f (^й)^О, Ьд-—
3	—0,41637	—0,14313	—0,27806	0,02	|/'(*«)!<0.05, точ- ность достигнута
Из таблицы 41.5 находим х* я с8 =0,278; f* « f (с8) «0,835.
16.72	. Показать, что если функция f(x) выпукла на
отрезке [а; Ь], то на любом отрезке [х'; л?]с [а; Ь] график
f(x) лежит не выше хорда, проходящей через точки гра-
фика с абсциссами х' и х".
16.73	**. Показать, что если /(х)—выпуклая диффе-
ренцируемая функция, то любая касательная к графику
f(x) лежит не выше этого графика.	- • •
16.74	. Показать, что выпуклая дифференцируемая на
отрезке, [а; &] функция унимодальна на этом отрезке,
16-75. Составить блок-схему алгоритма метода каса-
тельных, рассчитанную на использование ЭВМ.
В задачах 16.76—16.83, убедившись в выпуклости
функции f(x) на отрезке [а; 6], найти ее точку минимума] X*
и минимальное значение /• методом касательных, исполь-
зуя в качестве условия достижения требуемой точности
неравенство I /' (с„) I 0,01.
16.76.	f(x) = x—1пх, [0,1; 2].
16.77,	/(х)«=х?—sinx, [0; я/2].
16.78.	/(х)-х‘+х?+хЧ-1, [—1; 2].
16.79,	f[x)=-£—cosx, [0; 3].
16,80.	f(x) = KIT** +«"**, [0; 1].
18.81.	/<х)=^4-1, [0J; 2].
16.82.	/(л) = ^-4у + 1п^ ГЗ; 51
16.83.	f(x) — x*+e~x, {0; 1].
Метод Ньютока, использующий не только первую, но я вто-
рую производные функции f (х), ври определенных условиях обеспе-
чивает значительно более высокую, чем рассмотренные выше методы
минимизации, скорость сходимости к точке минимума х*.
Пусть J (х) — выпуклая дважды дифференцируемая на R функ-
ция. Выбрав начальное приближение х0, построим последователь-
ность
я=1,2, ...	(13)
Считая неравенство |/' (хй) |<е (е—достаточно малое число) усло-
вием достижения требуемой точности вычислений, положим х* « хП9
При неудачном выборе х0 последовательность (13) может рас-
ходиться, Если же точка х0 достаточно близка к л*, то эта последо-
вательность сходится к х* достаточно быстро.
Оценка скорости сходимости может быть сформулирована сле-
дующим образом. Пусть /(х)—дважды дифференцируемая на R
функция, причем /• (х)^р. > 0 при всех xgR и /й(х) удовлетво-
ряет условию Липшица на R с константой L. Тогда, если началь-
ное приближение х0 удовлетворяет условию <7 = ^21/'(х0) | < 1,
то последовательность (13) сходится к единственной точке мини-
мума х* функции /(х) на R, причем ]х*—хп	/1=0,1, ...
1л
Пример 9. Методом Ньютона найти точку минимума х*
и минимальное значение /* функции f (х) =(х—2)4—In х с точностью
|Hx»)l<10-7-
Выберем х0=3 и проведем вычисления по формуле (13), запи-
сывая результаты в таблице 1.6.
Таблица L6
п	хп	/ и„)	ru„)
0	3	—9,8640-*	3,67
1	2,6972477	—0,7558859	0,985
2	2,5322701	—0,8488508	0,208
3	2,4736906	—0,8553636	2,Ь10-а
4	2,4663735	—0,8554408	3.10-*
5	2,4662656	—0,8554408	5.10-9< 10-т
Окончательно х* « 2,4662656, f* « —0,8554408.
Метод Ньютона часто используется на завершающем зтопе
минимизации, когда точка минимума х* грубо найдена другим,
менее трудоемким методом и требуется найти х* с большой точ-
ностью.
22
В задачах 16.84—16.89 минимизировать функцию/(х)
на всей числовой оси методом Ньютона. Критерием достн-
неравен-
жения требуемой точности считать выполнение
ства |fz(^n)l^ Ю”*.
16.84. /(х)«х»+е-*
16.85.	.
16.86.	f(x)s=x? + x-+-sinx.
16.87.	f(xy=x?—х+е~*.
16.88.	/(х) = е*4-е"’* + 2х.
16.89.	f(xj = 2x,4rx-f-cos®x.
16.90.	Найти точку мининума х* функции /(х) одной
из задач 16.76—16.83 методом Ньютона, используя в ка-
честве начального приближения решение, найденное методом
касательных. Вычисления закончить при |Г(хв)|^'10"Л
§ 2. Безусловная минимизация функций
многих переменных
1. Выпуклые множества и выпуклые функции. Пусть ^в—м-мер-
ное евклидово пространство арифметических векторов х=(Х£, хг, ...
.... хя). Множество Uc:£n называется выпуклым, если вместе
с любыми двумя точками	оно содержит и отрезок','
соединяющий эти точки, т. е.	,
ах«1>4-(1—для всех agfO; 1|.	(1)
Пример 1. Показать, что множество точек *=(Х£; х»} пло-
скости t/={(xt; х») | xi+x* < О выпукло.
4 Пусть x<1) = (xiI). Х2Ъ) и x<s>«=(xi, Xz^U, a X=(Xf, х2) =
= ах(11 Ч- (1 —а) jfW—точка отрез-
ка, соединяющего точки х11* и хт.
Покажем, что x£U. Имеем
М1' 4-(1 —а>Х1®’]’+
+[ах<1>+0-.а)х?>У=
+ (1~а)«[(х13>)Ч(хГ,)*] +
+2а(1-а)[хГх1в>+^?>1-
Используя неравенства
Н-(4°)2<1, *=1, 2 (так как
и
+W2>)?, получим
+ (1~-а)*4-2а(1— а)== I, т. е»
х^и.
Рис. 214
Выпуклость множества U ясна и из рис. 214. Так как (7 —
круг, то отрезок, соединяющий любые две точки
Целиком лежит в (/. ►
Проверка условия (1) в большинстве случаев требует громозд-
ких выкладок, поэтому иа практике при исследовании выпуклости
множеств в пространствах и £з часто используют геометриче-
ские иллюстрации, подобные рис. 214.
В задачах 16.91—16.100 установить, являются ли выпук-
лыми множества U.
16.91.	U = {(Xj, x2)|2xj+x2<2, 2х2—х2>—2, х2>0}.
=	х2)
(Xt, х2)
[(Xi, х2)
(Xf, Х2)
Х2,
(Х(, х2,
(Xf, х2,
(Xf, х2>
16.92.
16.93.
16.94.
16.95.
16.96.
16.97.	V-
16.98.	U =
16.99.	(7 =
16.100.	U~ |(хй х2, х,)|х?+4+т
и=
и=
Функция f (ас), веданная на выпуклом множестве (/cz^n, назы-
вается выпуклой на этой множестве, если для любых точек х(1),
x{i}£U и произвольного чмсла а^{0; 1) справедливо неравенства-
f[ax«>+(l~a)	(^) + (l-*a)/(^S))-	(2)
На практике обычно используют следующий критерий выпук-
лости функции:
Если f (х) —дважды дифференцируемая на выпуклом множестве
U С £п функция и матрица ее вторых производных f" (х)=*
»(даТ(х)/дх/Яху) (гессиан) положительно определена при всех x£U,
то функция f(x) является выпуклой на множестве U,
Применяя критерий Сильвестра к матрице вторых производных,
можно сформулировать это утверждение в более удобном для про-
верки виде:
Если все^лавыеминорыматрицы f”(х)положительны при x£U,
то функция f(x) выпукла на множестве U.
Пример 2. Выяснить, является ли функция f(xlt x2)~2xi+
+ xa4-8in(xi+x2) выпуклой в пространстве
Запишем матрицу вторых производных
rd*f(x) &f(xV
dxj dxt дх2	/4—sin (xf 4- x2) — sfn (xt + x2) \
d*f (x) g2/(x)	\ — sin (xi+x2) 2—sin (Xi +x2))
k gx2 dxt dxl ,
Найдя угловые миноры этой матрицы Д1 «==4 —sin (Xj-J-Xg),
|4-sta(xij-x2)	,
I — sin (xj 4-x2) 2—sln(xi + x2)|	7
убеждаемся, что Дх- > 0, i«= 1, 2, при всех х^^г, т« е* Функция f (х)
выпукла. ►
Выпуклые функции играют большую роль во многих вопросах
оптимизации в связи е тем, что всякий локальный минимум выпук-
лой функции является одновременно и глобальным.
24
в задачах 16.101—16.106 убедиться в выпуклости функ-
ции во всем пространстве <£„.
16.101.	f(xit х2) = 44+4—2х,ха + 6xt—х2—2.
16.102.	f(xit х2)=/1+ 4+4.
16.103.	f(xit яа)=4+4—cos-^-^.
16.104.	f(xit х2)=4+4+4+4+44-
16.105.	f(Xi, 'x2, х3) = г*+**+ж’.
16.106.	f (xt, хг, Xa) = 5xi+54 + 4x^+4xIx2+2x2x9.
В задачах 16.107—16.110 указать множества U, на
которых функции f(x) являются выпуклыми.
16.107.
16.108.	f(x) = sin(Xj + x2).
16.109.	/(х) = 4 + 24—sin(Xi—х2).
16.110.	f(x)=4+4+^.
Во многих задачах оптимизации рассматриваются квадрата*
п	п
ные функции, т. е. функции вида /(х) = 2	^сли
/./«1	5=1
положить <7//в с//+сд, то получим симметрическую матрицу
~ с помощью которой можно представить квадратичную функ-
цию в виде
M*)=y(Q*. 4+(г, х),	(3)
где х = (*1> *2» •••>	r = (fi, *8» «••> векторы-столбцы,
(х, у)—скалярное произведение векторов х и
Градиент и матрица вторых производных функции (3) равны
grad f (х) =/' (х) = Qx+ г, f" (х) = Q - (qtj).
Таким образом, для того чтобы функция (3) была выпуклой
в достаточно, чтобы матрица Q была положительно определена.
Пример 3. Пусть f (х) = 2х?—2xiXaH“ Зххх3 4- х% -*-2х2^з +
4е 4хз4-хх 4-2x2 4“ Зх3.
а)	Найти матрицу Q и вектор г в представлении (3) функции /(х).
б)	Найти градиент f (х).
в)	Выяснить, является ли функция /(*) выпуклой.
< а) В данном случае сц—2, сХ2=—2, сХз = 3, с22=1,	2,
( 4 2	3)	А
^8з~4, fj»!, г2 = 2, /з==3, поэтому Qa== —2	2 —2 , г«= |2|
( 3 —2	8)	(з>
б) Используя найденные матрицу Q и вектор г, запишем
/' W=Qx+r=!
(4—2	3) (Xi
—2 2 —2 ‘
3 —2 8) (х8,
г2 | 4* 121 =»
з)
/ 4x1 *•“ 2х3 4" 4* О
I — 2х^ 4~ 2х3 2х3 4" 21
I Зхх •*2х24”8хэ 4“ 3/
26
в) Найде» угловые миноры Л/ матрицы /"(•*) = Ф
At=4, Ла=|_2 ||=4. &»=
4—2 3
—2 2 —2
3 —2 8
=22.
Так как А/ > 0, 1=1, 2, 3, то фувкция f(x) выпукла в ►
16.111.	При каких а, бивфункция f (х)=axf -f-bxtx2-l-
4- cxf является выпуклой в #2?
16.112.	При каких значениях а функция /(х)=х?4-*а+
4-Хз-4-0*1*» выпукла в ^,?
В задачах 16.113—16.116 выписать матрицу Q квадра-
тичной функции f(x), найти ее градиент/' (хт) в точке х<0‘
и убедиться в выпуклости f(x) в <£п.
16.113.	Дж)-^+5*л + 3х|4-*!—*», ж<0> = (1, 1).
16.114.	f(x) = xf—ЗххХ24-10x^4-5*!—Зх2. х(0) = (2, 1).
16.115.	f (x) = xj 4- 2x1 4- Зх! 4- 2xiX2—х»х» 4-2х, 4-х„
*”> = (!, О, —1).
16.116.	f(х) = xj4-ух%4-44-*1*» 4"xix*+4- 5X1 —
-хг-3х„ х1«» = (1, 2, 3>.
2.	Методы безусловной минимизации, основанные на вычисле-
нии первых производных функции. Постановка задачи минимизации
функции п переменных f (х) = /(*ь	...»хп) на множестве Uczd>n
не отличается от постановки в одномерном случае. Если
то говорят о безусловной минимизации функции f(x).
Для решения задачи безусловной минимизации функции f(x\
наиболее часто применяют приближенные методы, в основе кото-
рых лежит вычисление производных f(x) первого порядка. Такие
методы обычно называют градиентными. В ряде других методов
требуется вычисление не только первых, но и вторых производных
функции f (х).
Метод градиентного спуска. Пусть /(л)-* выпуклая дифферен-
цируемая во всем пространстве $п функция и требуется найти ее
точку минимума х*. Выбрав произвольное начальное приближение
построим последовательность
x(*+i>=x(W— akf(x№)t k^Q, 1,	(4)
где величины ад (параметрические шаги) выбираются достаточно
малыми для того, чтобы выполнялось условие
f(x<*+U) < f(x^), fc==O, 1, ...	(5)
В качестве условия окончания вычислений обычно используется
близость к нулю градиента /' (х(Л>), т» е» выполнение неравенств
|^|<6.	1=1,2.....п,
I дх{ I
или I/' (*<*>)| = j/"У,	]2 <8 (6>
28
(е—'заданное достаточно малое число), после чего полагают	х^>
Если при некотором kt условие (5) нарушается, то шаг а* в (4)
уменьшают (дробят) в заданное число раз до выполнения неравен-
ства (5) и продолжают вычисления.
Пример 4. Минимизировать в <£а функцию =
= xl + 2xi + exi+x* методом, градиентного спуска, завершив вычис-
ления при 1^/(л<л’)7^7К0,&, /=1, 2.	Р
<4 Выбрав начальное приближение х(0)==(О, 0) и а0=х1, построим
последовательность (4), записывая результаты вычислений в таб-
лице 2.1.
Таблица 2.1
Примечаете
0
—0,25
0
-0,25
11 11
3,145 —	—
1 1
1J18
1 1
0,794 0,106
1	Ю,5
1
-0,393
-0,2766326 -0,1516326 0,774 0,0983
—0,3012259 —0,1629096 0,772 0,0262
0,0451
—0,023
(0,25
Условие (5) на*
рушено. Умень-
шаем «ц в 2 ра-
за
Условие (5) на-
рушено. Умень-
шаем в 2 ра-
за
Условие (5)
выполнено
То же
Точность дос-
тигнута
1
2
3
Итак, х* « (—0,301, —0,163), /* « 0,772.
Для квадратичной функции (3) формула (4) принимает вид
х<^^ = х<^-аА((?х<Л)4-г),	£«0, 1,	(7J
В задачах 16.117—16.120 совершить один шаг гради-
ентного спуска (4) из точки жсо) с шагом ав и сравнить
значения f(x(0)) и /(х(1)).
16.117.	/(*)==*? +24+^<+Ч	1), а)а0«=0,1|
б) а0== 0,265; в) ав==0,5.
16.118.	}(х)~2х%+х1+Х1Х2 + Х1 + х21 лг<0> = (0, 0),
а) ао = О,1; б) ао = 0,5; в) а0==1.
16.119.	f Сг) = 4+*2+*!+*1*2+*2*з, х(0) = (0, I, 0),
а) ас = 0,1; б) «0 = 0,638; в) <^ = 10.
16.120.	!(х)~ех*+(Х1 + х,+х^	1, О.
а) о^ = О,1; б) <х8 —0,21268; в) «0=1.
27
16.121.	Составить блок-схему алгоритма метода гради-
ентного спуска, рассчитанную на использование ЭВМ.
Метод наискорейшего спуска отличается от метода градиентного
спуска способом определения величины а^, которая находится из
условия
фл(ал)в пн’п ФЛ(а), где ФЛ(а) = Н^>—(8)
а > О
Такой выбор а# обеспечивает максимально возможное уменьшение
функции f(x) вдоль направления ее антиградиента—/'
в точке
Таким образом, для определения а* на каждом, шаге метода
наискорейшего спуска решается одномерная задача минимизации
(8), для чего можно использовать методы, рассмотренные в § 1.
Пример 5. Решить пример 4 методом наискорейшего спуска.
Шаг 1. Положим = (О, 0), тогда/'(лЯ)==(1; 1), ФоС»)^
= /(0—а-1,0-*а« 1)^3а2,+в“2а. Для нахождения точки минимума
функции Ф$(а) используем метод перебора:
а	0,18	0,20	0,22	0,24	0,26
Ф«(а)	0,7949	0,7903	0,7892	0,7916	0,7973
т. е. а«аб«0,22, откуда х<««(0, 0)—0,22.(1, !)=»(—0,22, -0,22),
Шаг 2. Г(лЯ)»=(0,204, —0,236), Ф£ (а) ==(-0,22 —0,204а)*+
+ (—0,22 +0,236а)а+е-°»44+0»032с% Минимизируем Ф1(а):
а	0,28	0,30	0,32	0,34	0,36
®f(a)	0,77401	0,77384	0,77380	0,77387	0,77408
т.е. а =»«!=>0,32, откуда х{2)= (—0,22, —0,22)—0,32-(0,204, —0,236) =
«(-0,2853, —0,1445).
Ш а г 3. f «(8,007, 7,268) • 10“*, Ф2 (а)«(—0,2853—8,007X
К 10“*)*4-(—0,1445-^7,268«10"*-а)»+в“о,*‘*~1*’вп'10"‘. Миними-
зируем Ф, (а):
а	0,20	0,22	0,24	0,26	0,28
Ф,(а)	0,77273	0,77241	0,77240	0,77241	0,77244
t. е. а-а,-0,24, х”> = (—0,3045, —0,1619), /'(*<») -(1,821,
—2,061) • 10“*, поэтому требуемая точность достигнута и ж* и х<”—
- (-0,305, -0,162), /* « f (х<»)=0,772. >
Есля /(х)—квадратичная функция (3), те величина ад может
< быть найдена в явном виде
«*=’ Где f <А> = QX<*>+ Г'	(9)
Таким образом, для квадратичной функции метод наискерей-
i щего спуска состоит в построении последовательности {*<*>} по
' формулам (7), (9).
16.122*	. Показать, что градиенты f (x<ft)) и f (x<A+1)
в последовательных точках итерационного процесса ме-
тода наискорейшего спуска ортогональны, т. е. (/'(<*’**)»
/'(х(*+1))=0. ^=0, I, ...
16.123.	Составить блок-схему метода наискорейшего
спуска.
16.124.	Составить блок-схему алгоритма метода наиско-
рейшего спуска минимизации квадратичных функций.
В задачах 16.125—16.128 для функции f (х) найти ве-
личину шага а0 метода наискорейшего спуска из точки х<0>.
16.125.	/г(х) = х1 + 2х1+«х<+«», xw) = (l, 1).
16.126.	f(x) = 2x?+xl4--x1x2+xi+x2, х<0) = (0, 0).
16.127.	f (x) — xl4-xH- xl+XiXt + x2x3, x(0) = (0, 1, 0).
16.128.	/(x) = ^+(xi + x2+x8)’, x‘0, = (l, 1, 1).
В задачах 16.129—16.144 минимизировать квадратич-
 ные функции методом наискорейшего спуска, заканчивая
вычисления при j6 ^*^|^0,01, 1 = 1, 2......л.
16.129.	/ (х) = 7x1 + 2xtxa + 5ха + xt— 10х8.
16.130.	f (х) =? 3x'l—Зххх8 4- 4x1—2Xj+хг.
16.131.	f (х) = х? + 4ххх2 + 17x1+Фя^-
16.132.	f (х) = 5xi—4хгХа+5х1—Хд—х2.
16.133.	f(x) = 4xt+4XiXa + 64—47Xi.
,16.134. f(x) = 2xl — 2XiX24-3x2+xi—Зх8.
16.135.	f(x) = 10x?+3xxXa+xl + 10x2.
18.136.	f (x) = x?—2xiX2 + 6x14- xi—x2.
16.137.	f (x) =4x'l + 5x1 + 7x|—2xxx2+XiXi+ Xi —-х#4-х$.
16.138.	f (x) = 3xl + 4x1 + 5x3 + 2xxx2— ВД- 2x»xs +
+ Xi—3xg.
16.139.	f (x)—xf + 5x?2+8x1—xxx2+XfXi—x2xa+—
~3x2-|-xa.
16.140.	f (x) = 2X1 -h 4x1 + 8x! + 2x^2— XfXi 4- 2Xa*i 4-
+ 6xj—7x8.
16.141.	f (x) = 7x1+ 4x1 4- M— 3xjX2+ Xjx8— x8x8 +
+ xj—x2 + x8.
16.142.	f (X)=5xi+3xl+2xl+2x1x2+x1xg+x2x8+5xi+x8.
16.143.	f(x)=3x1+5x1+4xl4- 2x!X8—XiX8—XaX8+7xi4-x;8.
29
16.144.	f(x)*=4xi+44+4—*ixs4-2xtx«4-x»**--xi +
+ X,—x,.
Метод сопряженных направлений состоит в построении после*
довательных приближений к точке минимума функции f(x)
следующим образом:
^+X) = x(ft)_aAp(W й«0, 1,	(Ю)
где х(0)—заранее выбранное начальное приближение, шаг ад выби-
рается аналогично (8):
Фд(а*)в mln фНа)« W Фд(а)«=/(^—ар<й>)|	(11)
а>0
а направление спуска —р<*’ определяется по формуле
Й®1, 2,	/*°>;=/'(*Ч
где
_ <-4 dXl J	{12)
₽*“ I/'(**-«)	'
М дх{ )
It* 1
Таким образом, метод сопряженных направлений отличается
от метода наискорейшего спуска только выбором направления
уменьшения функции иа каждом шаге (—•р№ вместо —/' (лс<л>)).
Отметим, что р№ из (12) определяется не только антиградиентом
но и направлением спуска — />(*-« на предыдущем
шаге. Это позволяет более полно, чем в градиентных методах, рас-
смотренных выше, учитывать особенности функции f (х) при построе-
нии последовательных приближений (10) к ее точке минимума.
Критерием достижения заданной точности вычислений в методе
сопряженных направлений обычно служат неравенства (6). Часто
для уменьшения влияния накапливающихся погрешностей вычис-
лений через каждые W итераций (10) полагают 0, m«0,1, .. м
т. е. производят обновление метода (N —параметр алгоритма).
Для минимизации выпуклой квадратичной функции в $п тре-
буется не более п итерации метода сопряженных направлений.
Пример 6. Методом сопряженных направлений найти точку
минимума х* функции f (x)==xi+2xt + xixa‘— 7xi—7ха.
<< / (х)—квадратичная функция, заданная в ^2. Поэтому точка х*
будет найдена после двух шагов метода сопряженных градиентов.
Шаг 1, Выбрав начальное приближение-х(0)=(0, 0), по фор-
мулам (9)—(11) находим
^>«Z(xC»>)«(2xi+xa-7, xi4-4xa—7)1ж<о)=(—7, -7),
ф0(а)=98 (2 а*—а). Из условия Фо(ао) = О минимума Фо (а) полу-
чим Отсюда х(1)==(0, О)-— •(—7, -—7)=Г~,
/	7 7 \
Шаг 2./'(х(Х))=(—-у!, откуда с учетом (12) имеем
₽i=jg. ^=(-7. т)+15(“7’	is)’ Поэтому
зо
49 / 7	\
(«)=32	4а—392J
„ (L	21 \
~\4’ 4 J 7 { 16’ к)
4
ai=y. Окончательно
1) = х*. >
и
= (3,

16.145.	Показать, что при обновлении метода сопряжен-
ных направлений на каждом шаге (т. е. если 0ft«=O, Л =
=-1,2, ...) он переходит в метод наискорейшего спуска.
16.146.	Составить блок-схему алгоритма метода сопря-
женных направлений.
16.147.	Минимизировать одну из квадратичных функ-
ций задач 16.129—16.136, совершив две итерации метода
сопряженных направлений из произвольного начального
приближения
16.148.	Минимизировать одну из квадратичных функ-
ций задач 16.137—16.144 а помощью трех итераций Мето-
да сопряженных направлений, используя произвольное
начальное приближение хы>
В задачах 16.149—16.174 минимизировать функцию
f(x) методом сопряженных направлений, заканчивая вы-
числения при I	Ю~3,	2, ...» я.
2	2
16.149.	/(х)=х?4-2х?4-е*1+**—Х! + 2хл.
16.150.	f(x) =	+	1 +1^—1 ха.
16.151.	+	+	+
16.152.	/(х) — Х14-Зхг-}-cos(Xi+x2).
16.153.	f(х) = И1 + 2х? 4-4 + е*+**—Х1—Хг
3	2
16.154.	Дх) = х1 + 5х24-еХ1та.
16.155.	/(х) = Х?4-Хг + К2 + .Х?4-Ла—Зх^ЗХу
16.156.	f(x) = 2x? + 3xi—2sin(i4p) + xs.
16.157.	/(х) = ln[l +3xi4-5xf 4-cos(Xi—ха)].
4	16.158.’ f (x) = 4+/+ж| + 4xt + 3xr
16.159.	f (x) = xt 4- 2xs 4- 4 К1 4- x? + 4.
16.160.	^(x) — 2xi—5x2 + e*1+ s *2,
16.161.	f (x) = 2 ИЗ 4- x? 4- 2x14- 4 -Xi—x,.
16.162.	f (x) = xi 4- 2x1 4- xlxl 4- x# 4- exl+xl-x3 4- xg.
16.163.	f (x) = 4 И1 4- 4 + xi 4- 3x14- Xf-2x2.
16.164.	/(х) = 2х?4-х!4-х?^4-х1+^х|4-Х14-х1.
16.165.	f (x) == x’ 4- 5x14- 2x| 4- cos (Xi—x, 4- x,).
81
16.166.	f(x)=e4+*l + In(4+^+2^).
16.167.	-5х34-Л*Ч
16.168.	f (x)—xJ-bxl4-XiX2 4-K5+x2 4-2xl+xi+xs.
16.169.	f(x) = 2x?4-xl+4x^—2sin	.
16.170.	f (x)» 2	4- 3*a 4- 3 4-x^xf—xt—xt.
16.171.	/(х)=х|4-^4-ех?+**+*’4-Х1—xs.
16.172.	f(x)>=xf4-^4-X3 4-3Kxt4-x|4-14-e^.
16.173.	f(x)e=2x?4-4 4-sin(xf 4-х,)4-K34-j44- 4
16.174.	H-v)t=^i4-10x2—3x*4-ex?+xl+*1.
3.	Методы безусловной минимизации, использующие вторые
производные функции. Если при построении последовательности ;
приближений к точке минимума функции f (х) использовать инфор-
мацию, содержащуюся в значениях не только первых, но и вторых f
производных f(x), то при определенных условиях можно обеспе- |
чить более быструю, чем в градиентных методах, сходимость этой I
последовательности.	I
Метод Ньютона применяется для безусловной минимизации
выпуклых дважды дифференцируемых функций. В этом методе по- ;
следовательные приближения х<Л) к точке минимума функции f (х)
строятся с использованием первых и вторых производных следую-
щим образом:
(х<*)),	fe=0, 1...... (13)
где х(0)ё^ и ••начальное приближение, [Г (х(Л))]“1*—матрица, об-
ратная матрице вторых производных функции f(x) в точке х№. |
Критерием достижения требуемой точности вычислений обычно
служат неравенства (б).
Если начальное приближение х<0) достаточно близко к точке
минимума х*, то метод Ньютона сходится, как правило, гораздо
быстрее методов минимизации, использующих первые производные
fix), поэтому его часто используют на завершающем этапе мини-
мизации при уточнении приближения к точке х*, найденного дру-
гим, более простым методом.
Пример?. Используя решение примера 4 в качестве на-
чального приближения метода Ньютона, найти точку минимума
функции f (х)==%14-2x2с точностью | д{ (х<*>)/дх/К 10"Л
(«1, 2.
Используя результаты решения примера 4, запишем
/-о.»122№	/ «да»ую...
0,1629096/ J ' ' \—2,296005/ .
К» /0,3931915 1 0,628678354
'	)-\0,62867835 0,22329787/*
Найдем
« _j /—0,39319151	—5.3404226.10"»
(Г(*°)Г в^_5,3404226«10-»	0,22329787
32
откуда
/-0,30122594 / 0,39319151	—5,3404226.10"» \
=	0,1629096/	5,3404226.10"» 0,22329787	/ *
/ 2,6226554	. /—0,31276414
VI	|.Ю-»=(	I.
\—2,296005/	\—0,1563821/
Вычислив f (х<1)) = (7,9.10-в, 7,9.10-“), убеждаемся, что условие
точности выполнено, т. е. х* « *» = (—0,3127641, —0,1563821). >
Модифицированный метод Ньютона обеспечивает более устой-
чивую сходимость последовательности приближений к точке мини-
мума, чем метод Ньютона.
J Если начальное приближение х*0' выбрано недостаточно близ-
ким к точке минимума х*, то даже для выпуклой функции f(x)
последовательность (13) может не сходиться к X*. Этот недоста-
ток метода Ньютона будет устранен, если последовательность
приближений {x(ftl} строить по модифицированной формуле
=	аНГ(х(*>)]-»/'(х<*>),	Л=0, 1......... (14)
где а* находится подобно (8) и (11):
®fe(aft) = min®ft(a),
,	<Х>0
Ф4 (а) = f {х<*> -а (Г	(х<*>)}.
Кроме того, для последовательности (14) всегда выполняется не-
равенство /(x*ft+1))<f (х'й)), k=0,1,.,,, которое может нарушать-
ся в случае (13).
16.175.	Показать, что точка минимума выпуклой квад-
ратичной функции находится с помощью одной итерации
метода Ньютона из произвольного начального приближе-
ния х(0)€<^„.
16.176.	Используя результат задачи 16.175, показать,
что для нахождения точки минимума выпуклой квадра-
тичной функции достаточно одной итерации модифициро-
ванного метода Ньютона при произвольном х<0> €©„.
16.177.	Составить блок-схему алгоритма метода Нью-
тона.
16.178.	Построить блок-схему алгоритма модифициро-
ванного метода Ньютона.
16.179.	Минимизировать одну из квадратичных функ-
ций задач 16.129—16.144 о помощью одной итерации
метода Ньютона.
16.180.	Используя в качестве начального приближения
решение одной из задач 16.149—16.174, полученное ме-
тодом сопряженных градиентов, уточнить это решение с
помощью метода Ньютона, заканчивая вычисления при
I df (x^)/dxi | < Ю"6, f«1, 2...n.
2 Под ред. А. В, Ефимова, ч. 4.
16.181 • Выбрав произвольное начальное приближение,
минимизировать одну из функций задач 16.149—16.174
модифицированным методом Ньютона, используя критерий
точности решения 15/(x(A))/5xz|< 10~&, 1 = 4, 2, п.
§ 3. Линейное программирование
1. Постановки задач линейного программирования. Графический
метод решения. Задача минимизации функции п переменных f(x)~
== f (хи ..хп) на некотором множестве U с не совпадаю-
щем со всем пространством £п и заданном ,с помощью ограниче-
ний (равенств и неравенств) на координаты х/ точки xg^n> на-
зывается задачей математического программирования. При этом функ-
цию f (х) называют целевой функцией, а множество U — допустимым
множеством..
Решение задач математического программирования, как пра-
вило, связано со значительно ббльшими трудностями, чем реше-
ние задач безусловной минимизации, рассмотренных в § 2.
Простейшим частным случаем задачи математического програм-
мирования является задача линейного программирования, состоящая
в минимизации линейной целевой функции 7(х) = /(хь хп) =
п
*=	на множестве	заданном системой линейных
/»1
ограничений (равенств и (или) неравенств) на координаты X/
(/ = 1,2...л).
Задача линейного программирования формулируется следую-
щим образом.
Среди точек x=(xi, .. м хп)£$п, удовлетворяющих ограниче-
ниям
п
^ailXj = bi,	i=l,2...... l\	(I)
/=i
п
^ai/Xj^bj,	i = l+l,..,tm;	(2)
/м
n
найти me, в которых функция f(x)~ У, с/Х/ принимает мини*
а	7=1
малъное значение, и определить это значение.
Отметим, что в условии задачи линейного программирования
могут содержаться неравенства и противоположного, чем в (2), знака,
однако такие неравенства легко сводятся к виду (2) умножением
на —1.
Если в условии задачи линейного программирования не содер-?
жатся ограничения-неравенства (2), т. е. в (1) Z—т, то она назы-
вается задачей линейного программирования в каноническом виде»
34
Вводя дополнительные переменные хп+/^0, /==7-М, .... т,
ограничения-неравенства (2) можно записать в виде равенств
п
< = /4-1, .11, Ш.
/«1
Таким образом, любая , задача линейного программирования
может быть записана в каноническом виде
п
f W =• У, С/*/ -* mln »)»	(3)
/«1
п
t—1. ...» т,	(4)
/=i
ху>0.	(5)
Часто используется векторная запись задачи (3)~*(5)>
f(x) = (c, х) —>min,
Дх=д,	(6)
х>0,
где х = (х{, . *», xrt) —вектор неизвестных, =	...» вектор
коэффициентов целевой функции из (3), Д=(а, у)—прямоугольная
матрица размер^ тХп, Ь=(6ь . bm)—вектор правых частей
системы (4), а х^ 0—* краткая запись условий неотрицательно-
сти (5).
Математические модели многих важных для практики задач
оптимизации представляют собой задачи линейного программиро-
вания.
Пример 1. Составить математическое описание следующей
задачи об оптимальном составе сплава и представить полученную
вадачу линейного программирования в каноническом виде.
Для приготовления bQ кг сплава с заданными свойствами
используют вещества Ду, /=1, ,п, В х кг вещества Ду содер-
жится ацх кг химического элемента В/, <«=1, .*«, т. Содержание
элемента В/ в сплава должно заключаться в пределах от 3/ до
кг. Стоимость 1 кг вещества Ду составляет су руб.
Требуется определить такой состав для приготовления спла-
ва, при котором общая стоимость израсходованных веществ мини-
мальна.
◄ Обозначим ху количество кг вещества Ду, используемое для
приготовления сплава (очевидно Ху^О, /»!, 2, ..., п). Тогда
п
содержание элемента В/ в сплаве составит а//х/ кг» а стой-
Mi
п
мость израсходованных веществ будет равна У^о/Х/ руб.
/==1
4)	Символ f (х) min в записи условия задачи математического
программирования используется вместо слов «минимизировать
Функцию f(x)>. Далее указываются^ ограничения, определяющие
допустимое множество.
Поэтому» с учетом ограничений на содержание элементов В/ в
•плаве, для величин xj получим следующие неравенства;
п
aijXj<bi, iel, ...» т,
i=i
Кроме того, количество сплава должно составлять кг, поэтому
п
У\х/=Ь6.
/«I
Таким образом, математическое описание задачи об оптималь-
ном составе сплава принимает вид
п
/<«)-£ сух/—>min,
/“1
п
^оцх/СЬц	(7)
/-1
п
У tiijXj 2s Р/	(i •= 1..т),	(8)
/=1
п
(9)
Х;^09 /=1> •• м П.
Запишем эту задачу линейного программирования в канониче-
ском виде*
Среди ограничений (7) —(9) на переменные xj содержится 2m
неравенств (7), (8). Для преобразования их в ограничения-равен-
ства введем 2m дополнительных неотрицательных переменных хп+/
и Хп±т+Ь ^««1» • • •» т*
Прибавив переменные xn+t к левым частям соответствующих
неравенств (7) и вычтя переменные xn+m+i из левых частей нера-
венств (8), получим задачу линейного программирования в кано-
ническом виде
п
/ (х)=У 9х/ —♦ т1п»
/-1
л
7=1
п
п
ж/^0, /=1» •••, п. >
36
Составить математическое описание задач оптимиза-
ции 16.182—16.187, представив полученные задачи ли-
нейного программирования в каноническом виде.
16.182	. Для изготовления сплава из меди, олова и
цинка в качестве сырья используют два сплава тех же
металлов, отличающиеся составом и стоимостью. Данные
от этих сплавах приведены в таблице 3.1.	х'-
Т аблица.3.1
Компоненты сплава	Содержание компонентов в %	
	сплав № 1	сплав № 2
Медь	10	10
Олово	10	30
Цинк	80	60
Стоимость 1 кг	4	6
Получаемый сплав должен содержать не более 2 кг
меди, не менее 3 кг олова, а содержание цинка может
составлять от 7,2 до 12,8 кг.
Определить количества Ху, /=1, 2, сплавов каждого
вида, обеспечивающие получение нового сплава с мини-
мальными затратами на сырье.
16.183	*. Для изготовления двух видов изделий Ai и
Аг завод использует в качестве сырья алюминий и медь.
На изготовлении изделий заняты токарные и фрезерные
станки. Исходные данные задачи приведены в таблице 3.2.
Таблица 3.2
Виды ресурсов	Объем ресурсов	Нормы расхода на 1 изделие /	
		изделие Л1	изделие Л?
Алюминий (кг)	570	10	70
Медь (кг)	420	20	50
Токарные станки (станко-час.)	5600	300	400
Фрезерные станки (станко-час»)	3400	200	100
Прибыль на 1 изделие (тыс. руб.)		3	8
37
Определить количества Xj, j = 1, 2, изделий Aj, ^ото-/
рые необходимо изготовить для достижения максимальной
прибыли.
16.184	. Из одного города в другой ежедневно отправ-
ляются. пассажирские и скорые поезда. В таблице 3.3
указаны: состав поезда каждого типа, количество имею-'
щихся в парке вагонов различных видов для формиро-
вания поездов и максимальное число пассажиров, на ко-
торое рассчитан вагон каждого вида.
Таблица 3.3
Поезда	Вагоны				
	багаж- ный	почтовый	плац- картный	купейный	мягкий
Скорый	1	- 1	5	6	3
Пассажирский	1	—--	8	4	1
Число пассажиров	——	—	. 58	40	32
Парк вагонов	12	8	81	70	26
Определить число скорых xt и пассажирских ха поез-
дов, которые необходимо формировать ежедневно из имею-*
щегося парка вагонов, чтобы число перевозимых пасса- !
жиров было максимальным.	j
16.185	. Завод производит продукцию двух видов Л, й
Ла, используя сырье, запас которого составляет b т. <
Согласно плану выпуск продукции At должен составлять
не менее 60% общего объема выпуска. Расход сырья на
изготовление 1 т продукции At и Ла составляет соответ-
ственно at и аа т. Стоимость 1 т продукции Лу и Ла со-
ставляет соответственно руб. и с2 руб. Определить план
выпуска продукции At и Ла, при котором стоимость вы- 
пущенной продукции будет максимальной.
16.186	. В начале рабочего дня автобусного парка на
линию выходит xt автобусов, через час к ним добавляется
ха автобусов, еще через час—дополнительно х3 машин.
Каждый автобус работает на маршруте непрерывно в
течение 8 часов. Минимально необходимое число машин
на линии в i-й час рабочего дня({ = 1, 2, ..., 10) равно
Превышение этого числа приводит к дополнительным
издержкам в течение i-го часа в размере Q руб. на каж- |
дый дополнительный автобус.	%
Определить количества машин xit ха, ха, выходящих *
на маршрут в первые часы рабочего дня, с таким расче- |
88	.	1
том, чтобы дополнительные издержки в течение всего
рабочего дня были минимальными.
н 16.187, Процесс изготовления изделий двух видов со-
стоит в, последовательной обработке каждого из них на
трех станках. Время использования i-го станка состав-
ляет bi часов в сутки, i = 1, 2, 3. Время обработки каж-
дого изделия j-ro вида, /=1, 2, на i-м станке равно
часам. Прибыль от реализации одного изделия /-го вида
составляет с} руб. Составить план суточного выпуска из-
делий так, чтобы прибыль от их производства была мак-
симальной.
Если задача линейного программирования содержит только
две переменные, и в ее условии нет ограничений-равенств (1), то
такую задачу можно исследовать и решить графически.
Рассмотрим задачу
f W—CfXi+caXs —* min,	(10)
a/i*i+0/2*2 <	i * 1, ..., m,	(11)
xi^O, xa>6.	412)
На плоскости (xf, x2) любое из. неравенств (11) определяет
полуплоскость, лежащую по одну из сторон от прямой ацх^ -f-
+ а/2х2 = ^/. Для того чтобы определить расположение этой полу-
плоскости относительно граничной прямой, можно подставить
координаты какой-либо точки (при 6/ # 0 проще всего взять начало
координат) в соответствующее неравенство (11) и проверить его
выполнение.
Таким образом, допустимое множество U задачи (10)-*(12)
является пересечением первого квадранта Xf^sO, х2^0 и Нолу.
плоскостей, соответствующих неравенствам (И). Поэтому множе-
ство U представляет собой либо;
„ а) пустое множество, тогда задача (10)—(12) не имеет реше-
ний из-за несовместности ограничений (И), (12);
б)	многоугольник (рио. 215);
в)	неограниченное многоугольное множество (рис. 216).
39
Для решения задачи (10)—(12) в случае. U 0 рассмотрим
семейство линий уровня функции f (х) из (10)
cixi-|-c2x2 ®С, С «х const,
(13)
которые являются параллельными прямыми. Антиградиент
—(х)==(—cj, —с2) = я перпендикулярен прямым (13) и указывает
направление убывания f(x). Если перемещать параллельно самой
себе произвольную прямую (13), проходящую через допустимое
множество Ut в направлении е убывания f(x) до тех пор, пока
эта прямая будет иметь хотя бы одну общую точку с множеством
Ut то в своем, крайнем положении указанная прямая пройдет
через точку множества (7, в которой целевая функция f (х) при-
нимает минимальное на U значение.
Пример 2. Используя графический метод, найти решение
следующей аадачи линейного программирования
f (х) = —Зхх—2х$	пип,
xj+2x2<7,
2xi-f-x2<8,
х2 3,
Xf, х2^0.
«4 Изобразим на плоскости (xj, х2) допустимое множество U дан-
ной задачи (многоугольник
3

3 4 \
~Л»,-2а?2=17
Рис. 217
ABCDE) и одну из линий уровня
— 3xi—2х2 = С целевой функции
(рис. 217). Направление убывания
/(х) указывает вектор ^ = (3, 2). Со-
вершая параллельный перенос ли-
нии уровня вдоль направления е>
находим её крайнее положение. В
этом положении прямая — 3xi—2х2 —
проходит через вершину D (3, 2)
многоугольника ABCDE. Поэтому
целевая функция /(х) принимает
минимальное значение f* в точке
х* = (3, 2), причем /*=/(3, 2) =
в=—13.
Задача линейного программи-
рования (10)—(12) может иметь
и бесконечное множество решений.
Пример 3. Решить задачу линейного программирования с
целевой функцией f(x)~—хх—2х2 и ограничениями на допусти-
мое множество (/, взятыми из примера 2.
Множество U построено при решении примера 2. На рис. 218
изображена линия уровня —xi—2х2 = С целевой функции /(х).
В своем крайнем положении при параллельном переносе вдоль
направления £ = (1, 2) она содержит сторону CD многоугольника
ABCDE. Таким образом, все точки отрезка CD являются точками
минимума функции /(х) на множестве U. Так как концы С и D
этого отрезка имеют координаты (1, 3) и (3, 2) соответственно, то
любая точка минимума f(x) представима в виде х*=а(1, 3) +
+ (1—а)(3, 2) = (3—2а, 2-|-а), где а£[0; 1]. Минимальное зна-
чение целевой функции /♦ = /(х*) = — 7. >>
В случае неограниченного допустимого множества U задача
линейного программирования (10)—(12) может не иметь решения.
40
так как целевая функция яа таком множестве может быть не ог-
раниченной снизу.
Пример 4. Решить графическим методом задачу линейного
программирования
f (х) =з —Xi—2х2 —► min,
Xi + *2	1,
2Xf—*2^—1»
Xi—2х2<0,
xt, х2^0.
Допустимое множество U данной задачи представляет собой
неогран и ченвоемного угольное множество (рис. 219). Функция f (х)
Рис. 219
убывает в направлении £ —(1, 2). При параллельном переносе ли-
нии уровня — Xi—2х2==С вдоль направления е она всегда пере-
секает множество U, а целевая функция f(x) неограниченно убы-
вает. Поэтому рассмотренная задача не имеет решений.
Решить задачи линейного программирования 16.188 —
16.200 графическим методом.
16.188.	f(x)==Xi—2ха—>min,
—Xi+x,<0,
2xj -J* x2 3,
Xj—Xg<l,
Хъ *2>°-
16.189.	f[x\——xt—3xa—*-min,
2xi+xs<2,
Xi—x4>0.
Xj-’Xg 1.
Xf, xt>0.
41
ст
'*х
‘Х’Х + Jxg
*6>rx
‘g > *x + *x
'щш <-8x—ix —= (r)/ '261’91
‘0 *x '*x
'{—^’x—Jx
‘0>’xg—*x
‘Q<tx—ixZ
‘щш-ь-’х—»xg — = (*)/ W9I
•(X’x **x
‘g>’x
‘g>’x
‘I > ’*—T*
*1—^’x — Jx
‘l < ®x + JX
‘ига-»—*x—*x— = (*)/ *861’91
0^”x <Jx
‘g>sx + Jx
‘g>’x
,Z<*xZ+ix
‘g>’x
‘щш <•—’xt-—fx —= (x)./ ’661’91
‘0^?af ,fx
‘l ^’хЧ-1^
‘g>’x
‘g>JX
‘ujui«—*x—Jx — ;=(x)/ Ч6Г91
’0^8x *Jx
*Z^*xf—^x
‘l—гх—Txg
’I^’x+’xs
‘uim*-*x—ixg— = (x)/ '061’91
16.196.	Решить задачу 16.182 об оптимальном составе
сплава.
16.197.	Найти оптимальный план выпуска продукции
в задаче 16.183.
16.198.	Определить число формируемых пассажирских
и скорых поездов в -задаче 16.184.
16.199.	Найти оптимальный план выпуска товаров
в задаче 16.185, полагая «1 = 2» 02=1» Ь = 390, ^ = 2,
г2 = 3.
16.200.	Решить, задачу 16.187 со следующими исход-
ными данными:
/0,1 0,2\	/bt\	/12\
Д = («..)= 0,2 0,1 V Л =	Ю),
\0,3 0,3/	Ъ3/	\21/
а) С1 = 65, $2 = 80; б) Cf = 85, са = 60.
Графический метод используется также для решения задачи
линейного программирования в каноническом виде (3) — (5) с про-
извольным числом переменных Ху, если число свободных перемен-
ных системы уравнений (4) не превосходит двух.
Пусть ранг г матрицы системы ограничений (4) (т. е. мат-
рицы А из (6)) равен рангу расширенной матрицы (А | Ь) этой
системы. В противном случав система (4) несовместна и задача
линейного программирования (3)—(5) не имеет решения, так как
ее допустимое множество U пусто.
Выберем произвольный базисный минор матрицы А. Для опреде-
ленности будем считать, что этот минор порядка г соответствует
первым г столбцам и строкам матрицы А. Если г < т, то уравне-
ния (4) с номерами i = г4~ 1, ..., т являются следствиями осталь-
ных уравнений и их следует опустить. Поэтому будем считать,
что г=т.
Предположим, что п — т~2 или n—т=1. Считая перемен-
ные Ху, / = 1, ...» т, базисными, а остальные—свободными, ре-
шим систему (4), т. е. выразим базисные переменные через свобод-
ные, после чего исключим базисные переменные из условия за-
дачи (3) —(5). Для этого полученные соотношения для базисных
переменных подставим в выражение (3) целевой функции и запи-
шем условие неотрицательности (5) для всех переменных.
В результате получим задачу линейного программирования
вида (10)— (12), эквивалентную исходной задаче и содержащую
только свободные переменные исходной задачи, а их число не
превосходит двух. Для решения полученной задачи можно исполь-
зовать графический метод.
Пример 5. Используя графический метод, найти решение
следующей задачи линейного программирования в каноническом
виде:
f (х) = Xi + 9х3+5х3 4- Зх4+4хб +14хв —* min,
Xi4-x4 = 20,
*2 + *5 = 50,
х3 4" Xq = 30,
х4 4“Яб4“*б==69>
Ху^О, /=1,	6.
43
В данном случае матрица системы ограничений-равенств имеет вид
/1 0 0 1 0 0\
(0100101
А 0 0 1 0 0 1 Г
\о 0 0 1 1 1/
Ее ранг г«к4^т, причем минор, образованный первыми четырьмя
столбцами, может быть выбран в качестве базисного (проверьте!).
Число свободных переменных я—/и=2, поэтому для решения за-
дачи можно использовать графический метод.
РеШив сис&му ограничений-равенств относительно базисных
переменных х/, /=1, •	4, получим
Xi=—40 -f- Xg ~f- Хе,
xa=50—хб,
Ki « 30—xe,
К4«б0*-Х6 —xe.
(В)
Исключая с помощью (14) переменные Xf, х4 из выраже-
ния для целевой функции, находим
f(x)«740-7x5+7xe.	(15)
С учетом условия неотрицательности ху^О, /=1, <»«> 6, и
равенств (14), (15) получаем следующую задачу:
f (х)=740*-7хб4-7хв —> min,
х»+хе^40,
xs<50,
Хе 30,
к5+хв<60,
х5, Хе^О.
Допустимое множество U последней задачи изображено на
рис. 220. Это многоугольник ABCDE. Перемещая линию уровня
—7хб + 7хе = С функции (15)
по направлению вектора
=(7, —7), находим точку
минимума f(x)—вершину
D (50,	0) многоугольника
ABCDE. Подставив значения
х§ = 50, х8=0 в равенства
(14), окончательно находим
х* = (10, 0, 30,10, 50,0), f=
= 390. >
Решить задачи линей-
ного программирования в
каноническом виде 16.201—
16.206 графическим мето-
дом.
16.201«	f(x)== — Xi + xa—>min,
2xi—4х2—xs + х4 = — 3,
4xf—Зх2—х9 +-х4+хб == 6,
*i + 4x2 + x8 + x6=15,
*/>0, /-1....5.
44
16.202.	f(x)==4Xi—3x2—x4+x8-*min,
"~“Xj "4” 3x2 *4“ x4 ,==— 13,
4Xi4-Xs+x5==26,
2xj 4" x3 4“ x8 — 1,
x,—3xa4-xe=0,
x7>0, j=l, ..., 6.
16.203.	/(x) = Xi4-2x2 4-x8—x4 —> min.
10x2 4-x3 4- 2x4 4- 3x5 e= 25,
—Xt+5xa 4- x8 4- x4 4- xs = 10,
2xi—xa 4- x3—3x4 == 6,
Xy>0, / = 1, .... 5.
16.204.	f(x) = — 4xt4-2xa—x84-x4—>min,
3xi4-2x2—x84-4xt = 3,
*i—x» + 4x3—2x4 — 2,
xz>0, /= 1, .... 4.
16.205.	/ (x) —— x,—3xa —»-min,
2xi—x24-x84-x8 = 10,
2xi 4-2x2 4-x4 4-x8 = 25,
—2xi 4- 3x2 4- x8—x6 = 9,
6x24-x84-x4 = 36,
xz>0, /=1, ...» 6.
16.206.	f(x) — — 3xi4-2x24-3x4—x8 —»min,
3xi—2xa—xs 4- x4 = 2,
Xi4-*2—x« = 3,
4xj—x24-x4+x5= 19,
4xj—xa—x4 4- xf = 13,
Xj^Q, i—l, .... 6.
2. Симплекс-метод решения задачи линейного программирова-
ния. Общим методом решения произвольной задачи линейного
программирования является симплекс-метод, рассматриваемый
ниже.
Пусть ранг г матрицы Я »(azy) системы ограничений-равенств (4)
задачи линейного программирования в каноническом виде^совпадает
с рангом расширенной матрицы (Л | Ь).
Выберем какой-нибудь базисный минор матрицы Л. Для опре-
деленности будем считать, что он соответствуем первым г столб-
цам и строкам этой матрицы. Если г < т, то уравнения с номе-
рами J=aг4-1,	/п, являющиеся следствиями остальных урав-
нений системы, отбросим, полагая в дальнейшем г=/п.
45
Для решения системы уравнений (4) относительно базисных
переменных Ху, /=1, ...» mt с помощью эквивалентных преобра-
зований приведем ее к виду
+ • • • +«<’>пхи = Pf”,
+°Cm+lX«+i+ ••• +a2?n*'‘ = ₽?”»	()е)
+°С гп+1*« +»+•”+“«.’ п*п = ₽£’•
Тогда общее решение системы (4) запишется следующим образом:
Xi...
ж»вр20>—’ a8?m+lx®+<““	a»?n*(i.	(17)
...
где свободные переменные xm+i, •хп могут принимать произ-
вольные значения.
Положив их равными нулю, получим частное решение
Xf=s Pj0)»	+ i ~^/п+2= ••• =^:==^
ИЛИ
₽<о>,	Р<£>, О, О, ...,0),	(18)
которое назовем базисным решением системы (4). Каждому выбору
базисных переменных соответствует свое базисное решение си-
стемы (4).
Если все компоненты базисного решения (18) удовлетворяют •
условию неотрицательности, т. е. если Р(Р>0, i = l, ...» /п, то
такое решение называют допустимым базисным решением системы (4)
или угловой точкой допустимого множества U задачи линейного
программирования (3)—(5). Если среди неотрицательных чисел (^0) :
в (18) есть равные нулю, то допустимое базисное решение назы- ’
вается вырожденным (вырожденной угловой точкой), а соответст- 'i
вующая задача линейного программирования также называется
вырожденной.	|
В основе симплекс-метода лежит следующий факт:	f
Евли задача линейного программирования (3)—(5) разрешима, j
то минимум целевой функции f(x) из (3) достигается хотя бы I
в одной из угловых точек допустимого множества U этой задачи.
Так как различные базисные решения системы (4) соответст- i
вуют различным вариантам выбора т базисных из общего числа п |
переменных X/, то число допустимых базисных решений (угловых i
точек) не превышает Cff. Поэтому задачу линейного программиро- S
вания можно решать посредством перебора конечного числа угло-
вых точек допустимого множества U, сравнивая значения целевой J
функции в этих точках. Однако при большой размерности п за- 4
дачи линейного программирования этот подход затруднителен. 5
Идея симплекс-метода состоит в направленном переборе угловых *
точек допустимого множества U е последовательным уменьшением т
целевой функции f(x).	|
Описание симплекс-метода.	!
“Предположим, что задача линейного программирования (3)—(5} |
является невырожденной, а базисное решение (18) ««допустимым. |
46	?
Используя соотношение (17)> выразим целевую функцию из (3)
! через свободные переменные х/, / = т-|-1, ..., п:
2	<19)
/=т + 1
где
т	т
№= 2 с$0); ₽/0,=с/—2	/=от+1.........
<=i	i=i
Справедливы следующие утверждения:
а)	Если в выражении (19) все коэффициенты М°>, /=«+!,.««
п, неотрицательны, то в угловой точке (18) достигается ми»
нимум целевой функции f (л) из (3) на допустимом множестве U
задачи (3) — (5) и этот минимум равен ро.
б)	Если среди отрицательных коэффициентов 0, из (19)
есть такой (например pfy), что в (16) все коэффициенты
i==l, ...» т, то целевая функция f (х) не ограничена снизу на
допустимом множестве U и задача (3)—(5) не имеет решений.
в)	Если хотя бы один из коэффициентов р^\ j в (19) отри-
цателен (например р(р < 0) и при этом "среди коэффициентов ag>
а (16) есть хотя бы один положительный, то существует угловая
точка множества U такая, что f (х№) < f (#°>).
В случаях а) и б) процесс решения задачи линейного програм-
/ мирования на этом заканчивается. Рассмотрим подробнее алучай в).
Пусть в (19) коэффициент р<°> < 0 и в (16) имеются положитель-
ные коэффициенты а$\ Найдем номер k базисной переменной
из условия
«ж Ж
“k?	> 0 V.4 *
(20)
где минимум берется по всем номерам 1 = 1, т, для которых
<$’ > 0.
Найдем решение системы (4), считая свободными переменные
х/л+!» JQ-f, *k>	хп, т. e. поменяв местами свобод-
ную переменную Xi с базисной переменной х^ Система уравнений
вида (16) в этом случае запишется следующим образом:
п /	~(0) \	</°>
1 ‘ z	\ aij	„(0) Iх/ (0) *k — vi aU „(0)1
мТ+1\	. “«/
№t
4=1,,,,, m,	(21)
V х .и 1	_ С.
Z=m + 1 “«	“М
I
47
а зависимость целевой функции от новых свободных переменных
[Примет вид
,	П /	(0) \	(О)
! /w- £	™
/=т+1 '	akl /	М
Компоненты нового базисного решения можно найти, при-
равняв нулю свободные переменные Ху, /»/«+!, п, / # /,
м Xk и найдя при атом условии значения базисных переменных
?яз (21). Базисное решение х(Х) является допустимым, т. е. угловой
точкой множества U9 причем f (xJ)) < f (Xе0*).
По знакам коэффициентов в системе (21) и выражении для
; целевой функции (22) можно сделать одно из трех приведенных
? выше заключений, как это было сделано для угловой точки х<0>.
В случае в) следует совершить переход к очередной угловой
точке х(8), аналогичный переходу от х(0> к х(*\ и т. д.
Так как число угловых точек допустимого множества U не
превышает С"1, то случай в) может повторяться конечное число
раз, т. е. в результате конечного числа шагов перехода к новой
угловой точке будет либо найдено решение задачи, либо сделано
ваключение о том, что она не имеет решений.
Реализация описанного выше симплекс-метода значительно
упрощается при использовании симплекотаблиц. Записав коэффи-
циенты уравнений (16) и целевой функции (19) соответствующим
образом (см. таблицу 3.4), получим симплекс-таблицу задачи
(3)—(5) для угловой точки xt0) из (18).
Таблица 3.4
хт+1 ••• х( ... хп
XI
Xk
Г
9
Й1
Хщ
а(°)
m+i
„(о)
ат, I • * •
Л1, ...	...
-р'."'
Рассмотрим переход от симплекс-таблицы, соответствующей
угловой точке х(0), к симплекс-таблице для угловой точки х(1).
Пусть номера k и I определены так, как это сделано выше.
Элемент а$>, а также строка и столбец таблицы 3.4, на пересе-
чении которых он стоит, называются разрешающими или опорными,
48
ЛИз формул (21) и (22) следует, что преобразование исходной симп-
лекс-таблицы с опорным элементом (см. таблицу 3.4) приво-
дит к новой симплекс-таблице (таблица 3.5), для определения
элементов которой необходимо выполнить следующие операции:
1.	Поменять местами переменные хь и X/, остальные перемен-
ные оставить на прежних местах, см. таблицу 3.5.
Таблица 3.5
хда+1 ... xk ... хп
Pmk ••• Pft’ •••
— Ро1’
2.	На место опорного элемента поставить число
3.	На остальных местах разрешающей строки записать соот-
ветствующие элементы исходной таблицы, деленные на опорный
элемент.
4.	На свободные места разрешающего столбца поставить со
знаком минус соответствующие элементы исходной таблицы, делен-
ные на опорный элемент.
5.	Оставшиеся свободные места в новой симплекс-таблице
заполнить построчно следующим образом: из строки элементов
исходной таблицы вычесть произведение ее элемента из разрешаю-
щего столбца на уже заполненную разрешающую строку новой
таблицы.
Например, для строки с i-й базисной переменной имеем
(знак ш стоит на месте элемента разрешающего столбца, запол-
ненного согласно определению операции 4):
— LJ.......
....«а* ₽п*-
......LJ....₽п.
Пример 6. Решить задачу линейного программирования из
примера 5 симплекс-методом, используя в качестве начальной
угловой точки х(0) базисное решение, соответствующее свободным
переменным Xf и х§.
49
Столбцы с номерами 2, 4, 5 и 6 матрицы А системы ограниче-
ний-равенств данной задачи образуют базисный минор (проверьте)).
С помощью эквивалентных преобразований приводим эту систе-
му к виду (16), где базисными являются переменные х2, х4,
и хв:
х2	-f-Xi-f-Хз = 40
х4 -|- Xi = 20
хб —Xi—х3=10
%в 4-х3 = ЗО
(23)
Полагая в равенствах (23) свободные переменные хх и х3 рав-
ными нулю, находим х2 = 40, х4==20, х5=10, хб = 30, т. е. базис-
ное решение л<0) = (0, 40, 0, 20, 10, 30). Так^как все базисные пере-
менные в xV» положительны, данное базисное решение является
допустимым (т. е. угловой точкой) и невырожденным.
Исключив с помощью (23) базисные переменные в выражении
для целевой функции, получим
f(x) = 880--7x1—14x3.
(24)
С помощью равенств (23) и (24) составляем снмплекс-таблицу,
соответствующую угловой точке
	xi	*3	
х2	1	1	40
х4	1	0	20
*5	-1	-1	10
*6	0	1	30
	—7 -	14	—880
Среди коэффициентов р(Р>, / 0, из (19) есть отрицательные —
это элементы —7 и —14 последней строки симплекс-таблицы. Сле-
довательно, угловая точка не является решением задачи.
Для каждого из отрицательных элементов р(у0) среди соответ-
ствующих коэффициентов из (16) (т. е. [элементов симплекс-
таблицы, стоящих в том же столбце, что и р<.°>) есть положительные,
значит, возможен переход к новой угловой точке х(Х) с меньшим
значением f (л).
Найдем разрешающий элемент. В качестве опорного можно
взять любой из столбцов таблицы, соответствующих свободным
переменным Xf и х8. Выберем, например, столбец при свободной
переменной х8.
Разрешающую строку находим в соответствии с (20): так как
min (40/1, 30/1) = 30/1, то разрешающей является строка, соответ-
ствующая базисной переменной хв. Итак, опорный элемент найден,
в симплекс-таблице он обведен рамкой.
50
Заполнив новую симплекс-таблицу по правилам, описанным
выше, получим	Xi	х9	
Xi	1	-1	10 -
Х4	1	0	20
х6	— 1	1	40
х3	0	1	30
	—7	14	—460
Отметим, что значение f (х) в новой угловой точке уменьшилось
по сравнению со значением в исходной: 460 вместо 880 {см. эле-
менты в правых нижних углах симплекс-таблиц).
В нижней строке последней таблицы есть отрицательный эле-
мент —-7, стоящий в столбце при свободной переменной хр Кроме
того, в этом столбце имеются положительные элементы, поэтому
возможно дальнейшее уменьшение f (х) с помощью очередного
шага симплекс-метода.
На данном шаге выбор опорного столбца однозначен и опре-
деляется отрицательным элементом —7 последней строки. Разре-
шающая строка находится из условия (20): так как min (10/1, 20/1)=
= 10/1, то это строка при базисной переменной х2. Опорный эле-
мент в последней таблице обведен рамкой.
Как и на предыдущем шаге, находим очередную симплекс-
таблицу по общим правилам:
	Xi	Хз	
Г1	1	—-1	10
Х<	—I	1	10
Хц	1	0	50
Хз	0	1	30
	7	7	—390
В этой симплекс-таблице оба коэффициента j 0, в по-
следней строке положительны. Поэтому угловая точка х(2), соот-
ветствующая свободным переменным х2ихв> является точкой мини-
мума целевой функции /(х): х* = х<2) = (10; 0; 30; 10; 50;0). Мини-
мальное значение f (х) со знаком минус записано в правом ниж-
нем углу симплекс-таблицы, поэтому /* = 390. Сравните эти резуль-
таты с решением той же задачи, полученным графическим методом,
см. пример 5.
Замечание. Если задача линейного программирования
(3) —(5) вырождена, то возможны холостые шаги симплекс-метода,
т. е. шаги, в результате которых значение целевой функции не
изменяется. При этом теоретически возможно и зацикливание, т. е.
61
бесконечное повторение холостых шагов. Для того чтобы избежать
зацикливания, разработаны специальные алгоритмы (антицик-
ли ны). Однако на практике зацикливание происходит крайне
редко, поэтому антициклины мы здесь не рассматриваем.
Решить задачи линейного программирования 16.207 —
16.212 симплекс-методом, используя х<0) в качестве на-
чальной угловой точки.
16.207.	/ (х) — —5X14-4*2—*8—Зх4—5х, —► min,
3xt—х,4-2х44-х8 = 5,
2Xi—Зх, 4-х, 4- 2х4 4-х, «= 6,
3x1—х, 4- *э 4- Зх4 4- 2х, == 9,
Ху>0, / = 1, .... 5; х(о) = (О, 0, 1,2, 1).
16.208.	f(x) ——Xj—х2—х3—х44-4х, —> min,
3xf 4-*, 4-*8—6*8 = 7,
2xi 4" *2 "Ь Зх, 4- 3*4—7х, = 10,
—3xi 4- х, 4-*8—6х4 = 1,
х7>0, / = 1, ...» 5; х(0) — (1, 2, 2, 0, 0).
16.209,	f(x) = 2xi4-x,4-*8 + 7x4—2х,—> min,
*i+*2—х,4-*4=1,
2x14- *2 4- *s—*8=7,
Xi 4- 2Х,+*е—7х4 4- *8 = 6,
ху>0,	.... 5; х« = (2; 1; 2; 0; 0).
16,210.	f (х) = Xi—Зх,—Зх3 4- 6х4 4- Зх, —► min,
—2X14” Зх,—4х, 4- Зх4 4* 2х, = 1,
—8xi + 2х, 4- Зх,—4х4—4х, = 1,
—Xi—4х, 4- 2х,—Зх4 4- Зх, = 1,
*/>0, / = 1....5; х(0) = (0; 1; 1; 0; 1).
16,211,	f (*) = — 2xt4-*2+4*8—*4—*, —» min,
х,4-2х4—х,«=1,
*!—*,—*,==1,
2*,4-х,4-2х, = 4,
*/>0, / = 1, .... 5; х«» = (1; 1; 2; 0; 0).
16,212,	f(x)—xt—х,—х,—х4—Зх, —> min,
2xi 4* 2х, 4- х4 4* *8=: 3,
3*1—*24-2х4—2х,= 1,
•—3X14“ 2х,—х4 4- 2х, = 1,
х7>0, / = 1, .... 5; лг"» = (О; 1; 1; 1; 0).
62
Решение задачи линейного программирования симплекс-мето-
дом начинается с поиска какой-либо угловой точки х^} допусти-
мого множества U этой задачи.
Метод искусственного базиса нахождения начальной угловой
точки состоит в следующем. Пусть в ограничениях задачи
линейного программирования (3) —(5) все 6/^0, t==l, т.
Если это не так, то умножим соответствующие уравнения (4) на —L
Введем т дополнительных переменных xrt+f-, iel, ..., m, и рас-
смотрим вспомогательную задачу линейного программирования
т
?(*) = 2 m‘n’	(25)
1	= 1
л
2	а'7х/+*»+'=<-»Ь ...» т»	(26)
k — \9 ...*п+т.	(27)
Одной из угловых точек допустимого множества О этой задачи,
очевидно, является точка х<0) = (0;	; 0; fy;..,; Ът). Поэтому
для решения задачи (25)—(27) можно использовать симплекс-метод
со следующей начальной симплекс-таблицей:^
	Х1	xi	• • • xn		
хп+1	аИ	O£2	♦ ♦ ♦	ain	bi
#й + 2 • • •	a2f	aa2	• » »	ain.	bt * •
хп+т		ami			
	Pi	Pi	• ♦ •	Pn	—P#
т	т
где pj = — 2а'7- /=1......«г — Ро=— 26‘-
1=1	t=l
Отметим, что решение задачи (25) — (27) всегда существует, так
как ее допустимое множество U непусто (x<0)g(7), а целевая
функция (25) ограничена снизу на U (/(х)^0).
Пусть/*==minj(x). Рассмотрим возможные случаи.
О
1. /* > 0. Тогда допустимое множество U исходной задачи
линейного программирования (3)—(5) пусто, т. е. эта задача не
имеет решений.
о 2. /*=0 и минимум целевой функции / (х) достигается в угло-
вой точке
Хп\ xn+s; £n+w)	(28)
Допустимого множества U вспомогательной задачи, Тогда
xtf ..И Хп1	(29)
53
есть угловая точка допустимого множества U исходной задачу
(3) —(5) и ее можно использовать в качестве начальной угловой
тойки при решении этой задачи симплекс-методом.
Йз (25) видно, что равенство f	возможно только
тогда, когда все координаты хд+г-, i = l, ..., /п, в (28) равны нулю.
Ёсли задача (25) — (27) невырождена, то это означает, что все
переменные x«+t- для угловой точки (28) являются свободными.
Опустим столбцы, соответствующие этим переменным в окончатель-
ной симплекс-таблице, составленной при решении задачи (25) — (27).
Полученная в результате этого таблица будет соответствовать
системе уравнений (4), разрешенной относительно т переменных х/,
являющихся базисными для угловой точки (28). Поэтому остается
заменить в этой таблице последнюю строку на строку коэффи-
циентов целевой функции (3) исходной задачи и продолжить ее
решение симплекс-методом из начальной угловой точки (29).
Если вспомогательная задача (25) —(27) вырождена, то в угло-
вой точке (28) некоторые из переменных xrt + f, i»i, ..., /п, могут
оказаться базисными. Тогда эти переменные следует перевести
в свободные с помощью холостых шагов симплекс-метода, выбирая
в качестве разрешающих произвольные элементы симплекс-таблиц,
отличные от нуля. После этого исходная задача (3) — (5) решается
симйлекс-методом так, как описано выше.
Пример 7. Методом искусственного базиса найти какую-
либо угловую точку допустимого множества задачи линейного
программирования, рассмотренной в примере 5, и записать соот-
ветствующую этой угловой точке симплекс-таблицу. .
Введем дополнительные переменные х?, ..., Х{0 и запишем уело- ;
вие вспомогательной задачи линейного программирования (25)— .
(27) для рассматриваемого случая:
? (х) = х, + х3 + х9 + Xjo —* min,
*1 + *4Ч~*7 = 20,
*2 Ч" *5 + *8 = 50»
Хз + Х* Ч" х9 = 30,
*4+*б + *вЧ- *10 = 60,
хл^0, 6=1,	10.
Считая дополнительные переменные х7, Хю базисными,
запишем симплекс-таблицу этой задачи, соответствующую угловой
точке i<°^==(0; 0; 0; 0; 0; 0; 20; 50; 30; 60):
	*1	*2	*3	*4	*5	*e	
*7	1	0	0	1	0	0	20
*8	0	1	0	0	'I	0	50
*9	0	0	1	0	0	1	30
*16	0	0	.0	1	1	1	60
	—1	—1	— 1	—2	—2	—2	— 160
54
Любой столбец этой симплекс-таблицы может быть выбран
качестве разрешающего, так как элементы, ее последней строки
отрицательны. Выберем, например, столбец, соответствующий сво-
бодной переменной х4. Тогда разрешающим будем элемент этого
столбца, стоящий в первой строке, так как min (20/1, 60/1)==20/1.
Производя преобразования симплекс-метода, получим такую
последовательность симплекс-таблиц (рамками обведены разре-
шающие элементы):
*8
#9
*5
**1	#3	*^10
10 0 о
1 [7] о -1
G 0 1 0
-10 0 1
-1 -1 -1 2
В нижней строке последней симплекс-таблицы нет отрицатель-
ных элементов, а в правом нижнем углу стоит нуль. Следовательно,
минимум ^*==0 вспомогательной целевой функции достигнут и
х«»==(0; 40; 0; 20; 10; 30)	(30)
есть угловая точка допустимого множества U исходной задачи
линейного программирования из примера 5.
4)	Столбец симплекс-таблицы, соответствующий вспомогатель-
ной переменной хп+/, вводимой в свободные на каждом шаге метода
искусственного базиса, удобнее вычеркивать на данном шаге вместо
того, чтобы исключать такие столбцы одновременно в окончатель-
ной симплекс-тсблице.
55
Заменив нижнюю строку последней симплекс-таблицы на строку
коэффициентов целевой функции исходной задачи, получим симп-
лекс-таблицу этой задачи, соответствующую угловой точке х<0)
из (30):
х8
X4	1	0	20
X2	1	1	40
x9	0	1	30
x9	—1	—1	10
	—7	— 14	—880
Отметим, что другие варианты выбора разрешающих элемен-
тов в ходе реализации метода искусственного базиса могли при-
вести к другим угловым точкам допустимого множества U исход-
ной задачи.
Использование х*0) из (30) в качестве начальной угловой точки
симплекс-метода в рассматриваемой задаче иллюстрирует решение
примера 6.
Решить задачи линейного программирования 16.213 —
16.225 симплекс-методом, находя начальную угловую точку
методом искусственного базиса.
16.213.	f (ж) =—3xt 4-2xg—2ха + 2xt—xs —► min,
Xi + Xg—x8 = l,
— X2 + x3 + *4= 1,
*a+*s-Ks = 2,
Xy^O, /!, ..5.
16.214.	f (x) = — 6xi—8x2 —* min,
2xi4-5x24-x8 = 20,
12xi+6x2 + x4 — 72,
*/>0, /=1, .... 4.
16.215.	f(x) = — Xi—4x4—*min,
—Xf—2x2 4- 2хэ 4- x4 4- 5xe =s 13,
—2xf 4- 2x2 4- 4x4 4- x8 == 5,
xi—x24-x,—x44-2x8 = 5,
X/^0, /=“1, ..., 5.
16.216,	/(x) =— 34xi4-x24-3x8—3x4—►min,
3xf—2x2-}-3x84-2x4=9,
xt4-2x2—x84-x4=0,
—xt—x2 4- 2x8 4- x4 = 6,
X/>0, 1 = 1......4.
56
16.217.	/(х) = — ^Ч-Хг + ^з—x4-> min,
xi4-x24-x34-x4<=7,
—3xj Ч_х2 Ч~2х3 4~ х4 ~ ®>
2х1 + х2 + х3—х* = 2,
*/>0, /=1, .... 4.
16.218.	/(*) =—Зх44-х4—2x4-r>min,
15xi+2х2—Зх3—7х4 + х5 = 4,
2xi + х2 + х3—2х4 = 3,
х3 + 5х4Ч-2х# = 7,
Х/^0, / = 1, .... 5.
16.219.	/(х) = — хг —>min,
Х1+х2>1,
—Х1 + х2>—1,
2xi—х2^0,
Xi, х2 0.
16.220.	f (х) = 3xi—2х2+х3 —* min,
3xj + x2—2х8 = 2,
4х4 4~ Зх2 4е 2х3 1,
ху>0, / = 1, 2, 3.
16.221.	f(х) = — 2х1Ч-х2—x34»xs —► min,
—2х2Ч-х4Ч-х5 = — 3,
х3 2х4 ~= 2,
х4 Ч*3х2—х4 ^5,
Х1Ч-х2^—3,
*/>0, /=1.....5.
16.222.	f(x) = — 8x1—2x24*5xt— 15x4-»-min,
—Xj 4- Зх2 Ч- х3 Ч- Юх4	25,
2X14- х2 4- х3 4* бх4 < 10,
1 Oxi 4- 2х2 4- 2х3—5х4 ^26,
х7>0ъ /=1..........4.
16.223.	Предприятие, располагающее ресурсами сырья
трех видов Bh i=l, 2, 3, может производить продукцию
четырех видов At, / = 1, .... 4. В таблице 3.6 указаны
затраты ресурсов В; на изготовление 1 т продукции Aj,
объем ресурсов и прибыль, получаемая от изготовления
1 т продукции А;.
67
Таблица 3.6
Вид сырья	Вид Продукции				
		А,	А»	а4	Объем ресурсов, т
Bt	4	5	2	3	60
В»	30	14	18	22	400
В»	16	14	8	10	128
Прибыль, руб.	48	25	56	30	
Определить ассортимент выпускаемой продукции, при
котором полученная прибыль будет максимальной, при
условиях:
а)	продукции Аг необходимо выпустить не менее 8 т,
продукции Л4—— не более 5 т, а продукции Л4 и Л8—
в отношении 2:1;
б)	производственные издержки на 1 т продукции Л/,
/ = 1, ..., 4, составляют соответственно 3, 9, 12 и 6 руб.,
а суммарные издержки не должны превышать 96 руб.
16.224.	Завод получает 4 вида полуфабрикатов В{
в количествах! Bt—400 т, Вг—250 т, В3—350 т и
В, —100 т.
В результате смешения, этих компонентов получают
3 вида продукции Aj. Пропорции смешиваемых полуфаб-
рикатов следующие: для At—2:3:5:2, для Л,—3:1:2:1,
для Л3—2:2:1:3. Стоимость 1 т продукции Лу состав-
ляет: Л—12 руб., Л2—10 руб., Л,—15 руб.
Составить оптимальный план выпуска продукции по
критерию;
а) максимальной стоимости выпущенной продукции;
б) максимального использования полуфабрикатов.
16.225.	Решить задачу 16.186 об оптимальном графике
работы автобусного парка при следующих исходных
данных:
i	1	2	3	4	5	6	7	8	9	10
bt	10	20	22	23	25	22	20	15	10	5
<4	5	5	6	6	6	8	10	15	15	20
3.	Целочисленное линейное программирование. Во многих слу- ;
чаях на допустимое множество задачи линейного программировав :
ния (3)—>(5) накладывается дополнительное требование целочис- i
58
ленности переменных Ху. Если этому требованию должны удовлет-
ворять все переменные, то получаем полностью целочисленную
задачу линейного программирования, которая в каноническом виде
записывается следующим образом:
п
f (*) = 2 cjxj min'
i=i
п
1 = 1, to» m,
Xy^O,
*y(EZ, /=1,	«	(31)
где 2 —множество целых чисел.
Полностью целочисленную задачу с двумя переменными можно
решить графически/учитывая, что допустимое множество U этой
задачи состоит из точек целочисленной координатной сетки, при-
надлежащих допустимому множеству U задачи линейного програм-
мирования без дополнительного требования (31).
Решить полностью целочисленные задачи линейного
программирования 16.226—16.234 графическим методом.
16.226.	—20х2—>min,
—Xi+lOxg^^O,
4хх + 2х2 29,
*у>0,	/ = 1, 2.
На плоскости (xf, х2) построим допустимое множество U рас-
сматриваемой задачи линейного программирования без требования
целочисленности (многоуголь-
ник ABCD на рис. 221) и от-
метим точки множества U с
целочисленными координата-
ми. Совокупность этих точек
представляет собой допустимое
множество U полностью цело-
численной задачи.
Перемещая линию уровня
целевой функции f (л) в направ-
лении £ = (—1,20) убывания
/(л), находим крайнее поло-
жение этой линии, в котором
она еще имеет непустое пересечение с множеством U. В этом по-
ложении линия уровня проходит через точку В (0, 4), Поэтому
решение задачи имеет вид л* =(0,4), f* = min f (л) = — 80.
и
Отметим, что, как видно из рис. 221, точкой минимума f(x)
в данной задаче без требования целочисленности является точка
С(5; 4,5), т. £. л* = (5; 4,5), /* = тш f (л) = — 85. Отсюда следует,
что точкой минимума целевой функции на допустимом множестве U
Целочисленной задачи не обязательно является ближайшая к реше-
нию х* обычной (нецелочисленной) задачи точка множества U
$ Целочисленными координатами.
59
16.227.	f(x) = — Xi—xa —► min,
2x£ -f- 3x2 < 36,
<13,
3x£4-x2>6,
xz>0, xz£Z, /—1, 2.
16.228,	f (x) = — 9xf—1 lx2 —* min,
4x£4-3x2<10,
Xt < 5,
x£+2x2<8,
xz>0, xz6Z, /-1, 2.
16.229. f(x) = —4x£—3x2-> min,
4x£ 4* x2 < 10,
2x£4-3x2<8,
xz^0, xz£Z, f/el, 2.
16.230,	f (x) =—Xi—x, -► min,
2x£4-3xa<5,
X| < 2,
Xy^&O, xz6Z, /sl, 2.
16,231,	f(x)—xt—x#—► min,
3x2 + x8-f-x4==3,
Xi—2x84-xs = 1,
Xy>0, Xy€Z, j — 1, 2.
16,232.	f(x) =—x2 —*• min.
3x£ 4* x2 + xa = 12,
—8x£4-3x2+x4 = 24,
Xy^O, XygZ, / = 1, 2.
16.233.	В цехе площадью 74 м? необходимо установить
станки, на приобретение которых отпущено 42 тыс. руб.
Существует два типа станков. Станок первого типа
стоимостью 6 тыс. руб., требующий 12 м? производствен-
ных площадей, обеспечивает изготовление 70- изделий
в смену. Аналогичные характеристики станка второго
типа составляют соответственно 4 тыс. руб., 6 м?, 40 изде-
лий в смену.
Найти оптимальный вариант приобретения станков,
обеспечивающий максимальное производство изделий
в цехе.
60
16.234.	Решить задачу 16.182 об оптимальном составе
сплава, предполагая, что сырье каждого вида приобре-
тается в количествах, кратных 1 кг.
Для решения полностью целочисленных задач линейного
программирования с произвольным числом переменных исполь-
еуется метод Гомори. Он состоят в последовательном отсечении
от допустимого множества U нецелочисленной задачи частей, не
содержащих точек с целыми координатами. Эти отсечения произ-
водятся включением в задачу дополнительных ограничении на
переменные Xj.
Опишем алгоритм метода Гомори, использующий симплекс-
метод.
1.	С помощью симплекс-метода находится решение х* задачи
линейного программирования без учета требования целочислен-
ности (31). Если для х* условие (31) выполняется, то задача
решена. В противном случае среди чисел 0, последнего столбца
симплекс-таблицы, определяющей решение х*, есть такие, что
{0/}>О1).	' а
2.	Среди нецелых элементов 0/ выбирается произвольный
элемент 0Г (например, с максимальной дробной частью {0Г})«
По г-й строке симплекс-таблицы составляется дополнительное
п	»
ограничение вида 2 {аг/}ху<—{₽,} (здесь, как и выше, для
/=т+ 1
определенности мы полагаем, что свободные переменные X/ имеют
номера	..., л). С помощью вспомогательной переменной
это ограничение представляется в виде равенства хп+1 —
п
— 2 e** {04 и вводится в симплекс-таблицу дополни-
/=т+ 1
тельной строкой
Я/1+f I an+i, т+1 • • • п I Рп+Ь	(32)
где an+ft7=—{ar> ;},/== т+1, п; 0П4Л=— {0г}.
Так как Ри+1=—{₽/•} <0, то после дополнения строкой (32)
симплекс-таблица перестает соответствовать допустимому базис-
ному решению задачи линейного программирования, которую она
описывает.
3.	Для перехода к допустимому базисному решению произво-
дятся следующие операции:
а)	строка с отрицательным свободным членом 0^ считается
разрешающей (на первом шаге, очевидно, fc=n4-l);
б)	если все коэффициенты а*/ > 0, то задача не имеет реше-
ния, в противном случае номер I разрешающего столбца нахо-
дится из условия
 min -£/_ •
I	I /: аь/ <0 I I
в)	совершается преобразование симплекс-таблицы с опорным
элементом сцр Если в новой таблице по-прежнему есть хотя бы
один отрицательный свободный член, то описанная процедура
повторяется, начиная с операции а), необходимое число раз.
;) Напомним, что всякое действительное число а можно пред-
ставить в виде a = la]+{a}, где [а]**целая часть числа а, а
W = a*»[a]«.ero дробная часть.
61
Если все элементы ₽/ вновь полученной симплекс-таблицы
неотрицательны, то допустимое базисное решение найдено. Отме-
тим, что выбор опорного элемента гарантирует неотрицатель-'
ность коэффициентов р/ новой симплекс-таблицы. Поэтому найден-:
ное допустимое базисное решение является и оптимальным»
4.	Если найденное в разделе 3 решение задачи линейного
программирования удовлетворяет условию целочисленности, то
вычисления завершаются, а если нет, то продолжаются переходом
к разделу 2 описания алгоритма.
Описанный алгоритм позволяет найти решение полностью |
целочисленной задачи линейного программирования или устано- |
вить отсутствие решений за конечное число итераций.	J
Пример 8. Решить задачу 16.226 методом Гомори.	|
Введя дополнительные переменные х8, х<^0, запишем эту задачу *
в каноническом виде:
f (Х)=х1—20х2 —> min,
***Xf -|- 10X2 “Ь *3 ® 40,
4х{ 2xg 4“ в 29,
х/^0, X/gZ, /==1, 2.
Отметим, что так как все коэффициенты ограничений-равенств
данной задачи целые, то целочисленность исходных переменных
хг х8 влечет целочисленность и дополнительных переменных х8, л
х4. Поэтому и после перехода к каноническому виду можно рас-
сматривать данную задачу как полностью целочисленную и при-
менить для ее решения метод Гомори.
Одна из угловых точек допустимого множества нецелочислен-
иой задачи очевидна: х(0) = (0, 0, 40, 29). Запишем симплекс-таб-
лицу для этой угловой точки:
	xt	ха	
*9			4»
*4	4	2	29
	1 —20		0
Решение нецелочисленной задачи находится за две итерации
симплекс-метода:	ч
	Xi	*3		Xi		
Х9	-Q10	1/10	4	X»	1/42	4/42	9/9
Х4	42/10	—2/10	21	Xi	10/42		5
	-1	2	80	10/42	82/42	85
62
Это решение х*=(5, 9/2, 0, 0), /*==—85 не удовлетворяет
условию целочисленности, поэтому дополняем последнюю сим-
1 плекс-таблицу строкой (32):
	х4	х3	
х2	1/42	4/42	9/2
XI	10/42	—2/42	5
Хъ	— 1/42	—4/42	-1/2
	10/42	82/42	85
Для перехода к допустимому базисному решению находим
разрешающий элемент по описанному правилу и преобразуем
симплекс-таблицу:
	Х5	Хз	
х2	1	0	4
Х1	10	—1	0
х4	—42	4	21
	10	1	80
Последняя симплекс-таблица не только соответствует допусти-
мому базисному решению, но и дает решение рассматриваемой
задачи: х* = (0, 4), /* = —80.
Отметим, что дополнительное ограничение, введенное в симп-
лекс-таблицу, имеет вид —^-х4—1/2, С помощью уравне-
ний x3 = 40+xi—10х2, х4 *=29 — 4xi—2х2 перепишем его для пере-
менных Xi и х2: х2^4. Отсюда видно, что дополнительное огра-
ничение соответствует отсечению от допустимого множества U
(многоугольника ABCD на рис. 221) части, содержащей точку
•**=(5, 9/2) (вершину С этого многоугольника).
Решить полностью целочисленные задачи линейного
программирования 16.235—16.250 методом Гомори.
16.235.	/(х) = —Xi + x4-> minf
—2Xf + х4+Xg = 1,
Xj Н-х2—2х4 = 2,
Xi + 4" Зх4 = 3,
Ху>0, Ху € Z, /^=1, •••> 4.
63
16.236.	f (x) = — 2x, + 2xa—3x8 4- 3x4 —min,
Xi—2xa4-x4 = 3,
xa + x3—2x4=5,
3x2 4* xt -J- x6 — 4,
Xy>0, Xy^Z, / = 1. ...» 5.
16.237.	/(x) = — Xt + x2—x34-x4—>• min,
Xi 4-2x84-x4 = 8,
xr4-x8—x4 = 4,
—Xi 4- 2xa 4- xs 4- 3x4=6,
xy^O, xy^Z, /—1, ...» 4.
16.238.	f (x) =—Xi—xa —* min,
2х14-ха4--*а = 5,
2xa *4” 3xa 4“ *4 = 9,
*y>0, XZ€Z, / = 1, ..., 4.
16.239.	f (x) = xt 4- 2xa 4- x5 —»• min,
Xi 4- *2 4“ *s 4" xi 4* *« = 5,
*a + *84-*4—xs=2,
x8—x44-xb=1,
*y>0, Xy€Z, /=1» ...» 5.
16,240.	f(x) = — 4xi—3xa—> min,
2x1 + ^^2 4“ x3 == 8,
4xf4-xa4-x4= 10,
Xy^sO, Xy£Z, j—l, ...» 4.
16.241.	f (x) = — X,—x2 —> min,
Xi4-2xa4-xs = 6,
3xi 4~ 2xa 4- x4 == 9,
xy>0, Xj^Z, j — 1, ...» 4.
16.242.	f (x) = — xa —> min,
—6xa4-5x84-x8 = 6,
7x2—4x84-x4 = 4,
*14-*2 4-*з = 9,
Xy>0, Xy^Z, j — l, ...» 5.
Отметим, что переход к каноническому виду в полностью
целочисленной задаче линейного программирования, содержащей
64
ограничения-неравенства
(33)
/=1
не приводит, вообще говоря, к полностью целочисленной задаче
в каноническом виде, так как в преобразованных ограничениях (33)
2	Xn + i^bi
7=1
вспомогательные переменные xrt+- не подчинены требованию цело-
численности.
Однако если все коэффициенты a/у, bi в (33) — целые числа, то
условие целочисленности можно распространить и на хд+/, как это
сделано при решении примера 8.
Полностью целочисленную задачу в каноническом виде можно
получить также, если в (33) a/у, Ь/— рациональные числа. Для
этого следует умножить (33) на общее кратное знаменателей
коэффициентов a/у, bi (т. е. перейти к целым коэффициентам в (33))
и лишь после этого ввести вспомогательные переменные хд + (*.
16.243.	/(x) = 3x1 + 2x2 + x8~^min,
X] •-{- Зх2 ~Ь* х3 10,
2xi + 4x3^14,
2х2+х3^7,
Xy>0, XygZ, / = 1, 2, 3.
16.244.	f(x) =—2х2—х2—х3—>min,
Xj + 2х2 + 2х3 = 16,
Xi + *2	7,
Зхх + 2х3	18,
Xy>0, xzgZ, / = 1, 2, 3.
16.245.	f(x) =—4xt—3x2—*min,
4Xi + x2^44,
Xi 22,
x2< 18,
xz 0, Ху (E Z, / = 1,2.
16.246.	f(x) =x1 + 2x2 + x3—> min
1	।	1	- । 2	i
2	3 '^2 "T" 3	* »
' 2Xi + x2 > 1,
1	. 3
2	4	»
Xy>0, xz6Z, / = 1, 2, 3.
з
Под ред. А. В. Ефимова, ч. 4
65
16.247.	fW.^ — Xi—2xa—3x3-
,2	.1	_-25-
%i 4* з ^2 + 2 ^8 g >
%i 4~ П-* ^2 4" “g* *^s	3,
Xy^O, Xj (• 7jу / = 1, 2, 3.
16.248.	В цехе размещены 100 станков 1-го типа
и 200 станков 2-го типа, на каждом из которых можно
иреизводить детали Аг и Л2. Производительность станков
в сутки, стоимость 1 детали каждого вида и минимальный
суточный план их выпуска представлены в таблице 3.7.
Таблица 3.7
Детали	Производительность дет./сут		Стоимость 1 детали, руб.	Минималь- ный суточ- ный план
	Тип 1	Тип 2		
А	20	1 15	1 6	1510
я.	35	30	4	4500
Найти количества х^ станков i-ro типа, i=l, 2, ко-
торые необходимо выделить для производства деталей A/t
/ = 1, 2, с таким расчетом, чтобы стоимость продукции,
производимой в сутки, была максимальной.
16.249.	Решить задачу 16.183, считая, что в резуль-
тате усовершенствования технологического процесса рас-
ход меди на изготовление одного изделия А2 снизился
с 50 до 40 кг.
16.250.	Решить задачу 16.199 в предположении, что
товары /If и А2 выпускаются в количествах^
а)	кратных 1 кг;
б)	кратных 2 кг.
Если требованию целочисленности подчинены не все пере-
менные задачи линейного программирования, то такая задача на-
зывается частично целочисленной.
Для решения частично целочисленных задач также исполь-
зуется метод Гомори, но его алгоритм в этом случае отличается
видом коэффициентов aw+f, у в дополнительной строке (32), а именно
। —ary,	если azy^0,
«» +1,7 = |	«г/. если a/7<°>
66
если переменная Я/ подчинена требованию целочисленности» я
	( —{«г/}.	если
,7 I	е^и М>»А
для х/, свободных от этого требования.
Разумеется, вычисления заканчиваются, когда целыми явля-
ются не обязательно все коэффициенты р/ симплекс-таблицы,
а только те, которым соответствуют переменные х/, подчиненные
требованию целочисленности.
Решить частично целочисленные задачи линейного
программирования 16.251—16.256 методом Гомори.
16.251.	f(x)=xt—10ха—>min, 3Xi+*2 С 12, —8х,4-3ха<24, ’ xz>0, x2£Z.
16.252.	f(x) = — х,—xa — min, xt4-2x2sC4, 2x, H-xa< 4, X/^0, x(£Z.
16.253.	f(x) = —Xi—4xa —> min. xa4-xs=7/2, хг + х2 + х4 = 7, — x1+x2 + x6==2, X/ 0, x, € Z.
16.254.	f(x) = — 10Xf + 5xa + 7x3—3x4 —> min, — x, — 2xa 3xs -|- 3x4 = 3/2, xi 4* x2 "b ^xa + 2x4 — 7/2, 2xj -r 2xa + 8xs+Xx = 4, xz>0, хй xagZ.
16.255. Решить задачу 16.182 об оптимальном составе
сплава, предполагая, что сырье второго вида приобретается
в количествах, кратных 1 кг, а сырье первого вида —
в произвольных количествах.
3*
67
16.256, Решить задачу 16.199 в предположении, что:
а) товар At выпускается в количествах, кратных 1 кг,
а товар Л2—в произвольных количествах;
б) товар At выпускается в произвольных количествах,
а товар Аг—в количествах, кратных 1 кг.
§ 4. Нелинейное программирование
1. Задачи, сводящиеся к нелинейному программированию. В наи-
более общей постановке задача нелинейного программирования
формулируется следующим образом:
f (х) —> min,
gi(x)=bb	Z==l, 2....Z,
gi(x)*£bb	i==/+l, ...» m,
(1)
(2)
(3)
где f(x), gi(x), Z = l, m,— заданные (не обязательно линей-
ные) функции п переменных. Отметим, что условие неотрицатель-
ности переменных Ху>.0, /=1, п, входящее в постановки
многих задач нелинейного программирования, можно записать
в виде неравенств (3), положив £у(х)~ — ху, &у = 0.
Некоторые задачи нелинейного программирования сводятся
к задачам линейного программирования, методы решения которых
описаны в § 3.
Рассмотрим задачу дробно-линейного программирования
п
2 CjXj+c6
-------------> min,	(4) 
2 4/Х/+
7 = 1	»
п '
/jj	1, ./,	(5)
/ = 1
n
2 aijxj^bh Z = Z+1, m,	(6)
/ = 1
xy>0,	z (7)
Будем считать, что на допустимом множестве U задачи
(4) —(7) знаменатель целевой функции из (4) не обращается в нуль
и, следовательно, сохраняет знак. Если этот знаменатель отри-
цателен, то умножим числитель и знаменатель дроби из (4) на — 1
п
и будем в дальнейшем считать, что 2	> 0 для всех
J==f
х € U.
f п	\
Обозначим 1/( 2	) (очевидно, у§ > 0 при x£U)
* \/ = 1	J
и введем новые переменные yj~y$Xjt j=l, t99, п.

В новых переменных / = 0, 1, • л, задача (4)*»(7) при-
нимает следующий вид:
п
Т(У)1^ S	—►min,
/==О
п
2	= О* f=»l» мм Ц
/ = 1
п
2aWefcMo<°r < = /+1, mt
7 = 1	W
п
i=o
yj^Q,	/ = О, ...» n,
t. e. превращается в задачу линейного программирования (см. § 3).
Отметим, что требование #о^О> включенное в условие задачи (8);
не ограничивает возможного изменения переменной у^ так как
Уо > 0 при x^U.
Найдем решение	...» y„)t )* задачи линейного про-
граммирования (8) и, используя равенства
Х/==Д-. /=1......П,	f* = minf(x) = T*,	(9)
уо	и
получим решение исходной задачи дробно-линейного программи-
рования (4) —(7).
Если #о=О, то допустимое множество U задачи (4)—(7) не
ограничено и минимум целевой функции f(x) на нем'не дости-
гается.
Решить задачи дробно-линейного программирования
16,257—16.266.
16-257- н*)~ .~+w!r-mln’
Xi—2ха^2,
2xi + x2 + x3 = 6,
Лу>0, / = 1, 2, 3.
^Знаменатель х,+2х2+1 целевой функции положителен при
всех х из допустимого множества U, так как xt, х2^0.
Вводя переменные j/0 = 1/(xi+2x2+ 1), <//={/ох/. / —1» 2, 3,
получим следующую задачу линейного программирования:
,	Ну) — —tyt 4- yt —* min,
{«—2у2—2t/0<0,
-2//1—Уо. + Уз—6^0 = 0,
Vi + 21/2+1/0= Is
j/y^O, /=0,	3.
69
Приведя эту задачу к каноническому виду и решив ее си'мп-
лекс-методом, находим у*— 1/3, у* = 2/3, уз—0, //* — 2/3,—4/3,
откуда, используя формулы (9), получаем решение исходной
задачи: х*=(2; 0; 2), /* =—4/3.
16.258.	=	- min,
Xi4-2x2^16,
Х1 + й^<10,
х4^6,
х2 7,
х„ х2^0.
16.259.	—min,
'v '	2х24-х3+1
— x14-x,4-3xs = 8,
2xj — х2—х3 = 4,
Xj 0, / = 1, 2, 3.
16.280.	=	rain, .
*1—-^ + 2х3 = 4,
— х4 + 2х2 4“ хз + х4 — 6,
х/^- 0, 7 = 1,..., 4.
юле!. /w = Jii±a5-.mi«,
xi 4"хг + хъ — 3>
Sx^Xj—х3 = 4,
— xt + Зх2 + х4 = 6,
•*7>0> /== 1, ..5.
,6'262-
6х,—Зх2 4~ х3 + = 12,
7х!—x2-|-2xg^ 12,
—4х14-2х2—хл—х5= 1,
xz>0, / = 1,..„ 5.1
16-263-7^=зЙ£тг-min,
Xi -j“ Х2 4“ Хд = 6,
Зхх—2х24- х4 = 9,
—х14-2х24-х5= 10,
xj^Q, / =	5.
70
16.264.	f (x) = —Д^2 min»
Xj -f- 0X2
4xt—xs^5,
Xj + ЗХг—X3 = 7,
—3x, + 4xa + x4 = 17,
X/^0, / = 1, ..., 4.
16.265.	f(x) = --^ + 2^+1 -^min,
X] 4- X2 -f- о
— Xt4-3xa—x4= 10,
2x, + 4xa—x#—x4 = 20,
5xt 4- 2x2 4- xs = 35,
—3X| -j* 2x2 4- xe — 11,
Xj 0, / = 1, ..., 6.
16.266.	f (x) =	— min
XiH-x2—xs = 5,
— xt + 2x2 > 1,
—3xj + xa + x4 = 1,
*/>0, /=!,..., 4.
Другой важный класс задач нелинейного программирования,
решение которых можно найти методами линейного программиро-
вания, образуют задачи квадратичного программирования, в которых
требуется минимизировать выпуклую квадратичную функцию
(см. § 2) на допустимом множестве, заданном линейными ограни-
чениями, т. е.
f (X)—у (Qx, Х)4-(Г, х) —► min,	(10)
п
2	(=1, ,.м т,	(11)
/ = 1
Ху^о, /==1, ...» п.	(12)
Здесь Q = (qt/) — симметричная матрица размера яхя, г®
= (гь Гд) — заданный вектор. Напомним, что. если матрица Q
положительно определена, то квадратичная функция f(x} из (10)
является выпуклой в ^п.
На основании известной теоремы Куна«-Таккера (1J точка
минимума х* —(х*,	х«) целевой функции f (х) из (10) на до-
пустимом множестве U (11), (12) может быть найдена как реше-
ние следующей системы уравнений с дополнительными перемен-
ными X/, х„ + /, i=l, т\ цу, /«1, л:
п	пг
S <и/х‘+г/+ 2 М//—н/=°»	/=1. ••••«.	(,3>
<=г	i=i
2 а//*/ + *п+<=г&б	1=1,.,., т,	(14)
i = I
^«4-1=0, t = l, m; |хуХ/ = 0,	/«= 1> »tM nt (15)
П
удовлетворяющее условию неотрицательности
х7-^0, цу^О, /=1, п\ Х/^0, 7=1, •»>» т. (16)
Для решения системы (13) —(16) можно использовать метод
искусственного базиса (см. § 3), позволяющий найти одну из угло-
вых точек множества, заданного ограничениями (13), (14), (16),
Так как эта точка принадлежит указанному множеству, то она
удовлетворяет перечисленным ограничениям.
При реализации метода искусственного базиза следует учи-
тывать и условия (15), т. е. не включать в базисные одновременно
переменные X/ и хп+; с одним и тем же индексом i и перемен-
ные Ху, ру с одинаковым номером /.
Пример 1. Решить задачу квадратичного программирования
f (х) = х!-|-2х2 — 2х1х2—2X1 — 6х2 —* min,
Xi4*^a<£2,
— xi + 2x2^2,
Xi, x2^0.
[2 ____21
квадратичной функции f (x) положи-
—4 J
тельно определена (проверьте самостоятельно!). Система (13)— (16)
в данном случае принимает вид
2X1 —2х2-Ь Xi—Х2 —Ц1 = 2,	(И)
—2Х1 + 4х2 + М + 2^2—р2 = 6,	(13)
Xi -j~ Х2“|“ Хд = 2,	(19)
— Х14“ 2х24> х4 = 2,	(20)
ИЛ =Ф 2*2 == М*з — А2х4 = 0,	(21)
*1, »»., х4^0; pi, р20; Аь А2^0.
Будем искать угловую точку множества, определяемого этой
системой, методом искусственного базиса. При этом, гак как урав-
нения (19) и (20) легко разрешаются относительно переменных
х3 и х4, для уменьшения размера симплекс-таблиц дополнительные
переменные (хб и хб) вводим только в уравнения (17) и (18), считая
базисными переменными начальной угловой точки х3, х4, х5 и хв.
Вспомогательную целевую функцию J(x) = xs4-xe выразим
через свободные переменные х1} х2, Xi, Х2, pi и р.2 с помощью
уравнений (17) и (18): f (х) = — 2Х] — 2Xj—A,2+Hi4-Hs4-8.
Последовательность симплекс-таблиц, приводящих к решению
задачи, приведена ниже. Рамками обведены опорные элементы,
а те свободные переменные, которые на данном1 шаге нельзя пере-'
водить в базисные из-за условий (21), обведены кружками.
В последней таблице элементы нижней строки неотрицательны,
следовательно, минимум вспомогательной целевой функции /*=0
достигается в угловой точке, соответствующей этой таблице.
Поэтому искомое решение задачи квадратичного программи-
рования имеет вид х* = (4/5, 6/5), /* = / (х*) = 36/5.
Замечание. Если задача квадратичного программирования
наряду с ограничениями-неравенствами (11) содержит и равенства
п
2	то для преобразования их к виду (И) следует вы-
/ = 1
72
Xt x2 (5)(J?) Mi Мг
0-2-2 4 1 1 -8
Х1 xi (^) ^2 F1 /‘•г
— - - .	-х"о	~7"
.^••Гв 0-2	12	0-1	2
Уз ^‘1/2	О	0	0 0	1’
х2 -1/21/2	0	0	0 0	1
-11-2-11 1 -6
хз х4 I'j lj{ /4 рг
х5 -2/34/3 1 4 -1 0 10/3
хв 0 -2 [1]	2	0	4	2
Xi 2/3-УЪ 0	0	0	0	2/5
Х2 1/31/3 0	0	0	Q	4/3
.2/32/3-2’4	1	1	4t/3
Х3 Х4 Xg Л2 H1(S)
Xs -2$0/$-1 -3 -1 1 4/3
*1 0 -2 «1 2 0 4 2
xt 2/34/3 0 0 0 0 2/3
х2 1/31/3 0 0 0 0 4/3
2/3-10/5 2" 3* 1“4'
разить из этих равенств какие-либо базисные переменные через
остальные и записать условие неотрицательности для базисных
переменных.	4	,
Например, преобразуем ограничения-равенства
3xi+ *a+#3”b*4= 16,
Xi + 3^2—Хз+Х4 = 4
к виду (11). Разрешив их относительно х$ и Х4, находим х3 = 6 —
— Sxx + xs, х4= 10—Х£*-2х2. Учитывая условие неотрицательности
х3^0, х4^0, получим ограничения-неравенства (11): 2xf*»X2^6,
^i + 2x2<10.
Решить задачи квадратичного программирования
16.267—16.276.
16.267.	/(х) = х;+^—10^—15xa->min,
2X|-J-Зха 16.
2xi4-x2C 10,
Xj, x2 0.
73
16.268.	f (x) = x1+xl—20Xj—30x2 —>• min,
5xi + 13x2C51,
15xi+7x2< 107,
Xu xs>0.
16.269.	f(x) — xl—2xi—x2 —>min,
2xj 4* 3x2 6,
, 2xf4-x2^4,
Xf, Xj^sO.
16.270.	f(x) = xl+x%— lOXj—20x, —► min,
9xj4-8x2C 72,
Xf + 2x»< 10,
Xi, x2>0.
16.271.	f (x) = x?+j4—10Xi—8x2 —► min,
2х^ 4" 3x8 -f- x8 = 6,
xz>0, /=1,2,3.
16.272.	f(x) = 3x? + *l + 3Xi—2x2—min,
Xj -J- 3x2 + x8 4- x4 = 16,
3xi —-x2—x, + x4 = 4,.
x,^0, j =» 1, ..., 4.
16.273.	/(х) = хЦ-х1 + х!4-х2—2x8 -> min,
Xi + x2 4- 2xs C 6,
3xi 4-2x24-x8^ 12,
Xj^fi, /вЪ 2, 3.
16.274.	/(x) = (xi4-x24-x8)?—» min,
Xi4-2x84-3x8<6,
Xt 4- хг < 1,
x2 4~x3 < 1,
Х/>0, /=1,2,3.
16.275.	f (x) = x|4- 2ХЛ—x8 —< min,
*14-= 4,
x2 + xs = 8,
X/>0, /=1,2,3.
16.276.	/(x) = x?4-*2—*i—2x8—*min,
Xi X2 4* 2x3 = 6,
*/>0, /=1, 2, 3.
74
Минимизировать в многоугольнике с вершинами (0, 0),
(0, 4), (5, 8), (10, 4), (6, 0) следующие функции!
16.277.	f(x) = x? + xf—4xi—6х2.
16.278.	f(x)=xl+x?t—20Xi— 16х,.
16.279.	f(x) —— XjXs.
16.280.	f (x) = 2x1 + 3x1—40xi—48x2.
2.	Методы возможных направлений. Основная идея этой группы
методов решения задач нелинейного программирования заклю-
чается в построении последовательных приближений к точке
минимума х* целевой функции f (х) на допустимом множестве С7:
6 = 0,1............. aft>0.	(22)
Эти методы напоминают безусловную минимизацию f(x) гра-
диентными методами (см. § 2).	*
Вектор определяющий направление перемещения (22) из
точки хш в точку x(ft+1), должен удовлетворять следующим двум
требованиям.
1. Для достаточно малых а* > 0 точка х(*+1> из (22) принад-
лежит множеству U (т. е. задает возможное направление).
2. Для достаточно малых а* > 0 выполняется неравенство
f(x(*+1)) < f (xlfe) (т. е. определяет направление убывания f (х)).
Первое условие означает, в частности, что для граничных
точек х{к} допустимого множества U векторе^ направлен внутрь U.
Величина сц > 0 в (22) выбирается из условия наибольшего
убывания целевой функции в направлении с учетом требова-
Рассмотрим сначала метод возможных направлений решения
задачи минимизации выпуклой дифференцируемой нелинейной
функции f (х) на допустимом множестве U, заданном линейными
ограничениями
f(x)—>min	(23)
2	1 = 1. .... m.	(24)
/ = !
ху^О, /=1, п.	(25)
Опишем выбор вектора e^^=(e(iy*t .епУ) из (22), опреде-
ляющего возможное направление убывания функции f (х)
в точке х(/г>. Рассмотрим возможные случаи.
1. Пусть в точке х(Л) все неравенства (24) и (25) выполняются
как строгие. Это означает, что х(А0 — внутренняя точка допусти-
мого множества U. Тогда
<?<*> = -/'(*(Л,)>	(24
т. е. определение очередного приближения хСА+1) из (22) совпадает
с итерацией градиентного метода (см. § 2).
2. Пусть хотя бы одно из неравенств (24), (25) в точке х(*
обращается в равенство, т. е; х<А) является граничной точкой
допустимого множества U. Тогда выбор e(fi) в соответствии о (26)t
вообще говоря, невозможен, так как может оказаться; чтх)
А) Если среди этих ограничений есть равенства, то преобра*
вовать их к виду (24) можно описанным выше способом (см. заме»
чание на с, 72).
П
точка Х'л+1) из (22) при любом а* > 0 не принадлежит множеству U
(е™ из (26) не является возможным в точке х№ направлением).
Опишем, как определять возможное направление убывания е‘п)
в этом случае.
Обозначим через Ik и множества индексов; соответствующих
ограничениям (24) и (25), которые в точке x{k) обращаются в ра-
венства, т. е.
=	=	(27)
I / = 1 J
Представим компоненты вектора е1 * з) * * **’ для / $ в виде
e’ft)=e^)+ —(28
где
е(*)+=/ 4*’’ «ли
1	\ О, если < 0;
°> если 4^°’
1	\ —4**. если < 0.
Очевидно, , e^~^0, и	для всех /£
Вектор	&'} из (22) ищется как решение сле-
дующей задачи линейного программирования:
^(^«(/«(xU)), ^))«
zeJft 1 i$-Jk 7
(аЧе<«)= 2 МА)+ 2 а,у(ер+-е^-)<0, i£lk, (30)'
/6Jft	i$Jk
214*4=2 4fr>+ S (4*,++4*)')<1’	<31>
/=i	iejk i$jk
4*^0, i£Jk,	(32)
4*)+, 4*>-&o, t$jk,	(зз)
4ft)+.4ft)"=o, /£ла),	(34)	
где = (g/i, ain).
x) Такое представление для j позволяет находить
вектор е{к) как решение задачи линейного программирования,
содержащей условие неотрицательности переменных, несмотря
на то, что его компоненты могут быть отрицательными.
Для j^Jk представление (28) не используется, так как у век-
тора определяющего возможное направление, компоненты
с номерами / g не могут быть отрицательными.
з) Для учета дополнительного условия (34) при решении за-
дачи (29) — (33) симплекс-методом следует не включать переменные
е^+ и с одинаковым номером / в число базисных одновре-
менно.
76
Поясним смысл соотношений (29) —(33).
1. Минимуму целевой функции	из (29) соответствует
минимально возможный с учетом ограничений (30)—*(34) угол
между искомым вектором и антиградиентом *-/'(х(*}), опре-
деляющим направление скорейшего убывания f (х) в точке
2. Ограничение (30) для каждого означает, что вектор
^(/г) составляет угол	с вектором а(х>, нормальным к гра-
п
ничвой гиперплоскости 2 aijXj — bi допустимого множества и
/=1
направленным вне (/.
Так как точка х(Л) принадлежит этой гиперплоскости, то усло-
вие (30) для любого гарантирует, что направление яв-
ляется возможным по отношению
к i-му ограничению (24) исход-
ной задачи. Рис. 222 поясняет
смысл ограничений (30) в двумер-
ном случае.
3/Условие (31) является ог-
раничением на длину вектора
и обеспечивает ограниченность
снизу целевой функции fk (в(Л))
из (29).
4. Неравенство (32) для каж-
дого	гарантирует, что на-
правление искомого вектора
является возможным по отношению к /-му ограничению (25) ис-
ходной задачи.
5. Соотношения (33) и (34) следуют из представления (28) ком-
понент 4*’, i&h, вектора
Опишем теперь, как определить величину перемещения
вдоль направления е(к} из (22). Для найденного вектора она
находится из условия
/(х(Л) + а^Л>)= min f (х(А) + ^(Л)),
а> 0, х^ +	е и
Т. е.
aft==min(aM, аЛл, ak£, akni а£),	(35)
где и а#/ —максимальные перемещения, при которых для точ-
ки ^^+1) из (22) выполняются соответственно i-e ограничение (24)
и /-е ограничение (25), т. е.
— __ ( 4~оо,	если (#<*>,*<*>)< О,
а&' = I 1&(—(аф,	й<»), если (а‘‘К	>0;	(3 *
-	( Н-оо.	если 4А>^0,
"у~ I -xflef, есме<р<0,	()
а а* находится из условия наискорейшего спуска вдоль направ-
ления вектора e{ky без учета ограничений (24), (25), т. е.
фл(ал) = т1п Фе(а), где Фй(а)=/(*<*>+ав'Л>).	(38)
а>0
77
Приведем описание fc-ro шага решения задачи (23) —(25) мето-
дом возможных направлений.
1.	Подставить х(Л) в неравенства (24) и (25) и определить
множества индексов /#, по формулам (27).
2.	Если	найти вектор е№ из (26), в противном
случае определить из решения задачи линейного программи-
рования (29)—(33) с помощью формулы (28).
3.	Для найденного вектора е^к} определить а^ из формул
(34)—(37).
4.	Найти очередное приближение х*А+1) подформуле (22).
При выполнении хотя бы одного из условий (х(А))или
[| х(А~”— х(А) || е, где 8 > 0—число, определяющее точность реше-
ния задачи, вычисления завершают, полагая x*»xtA), /*»/(х(Л)).
Любое из равенств (х<А))| = 0, Ц х^-” —х(А) |] = 0 означает,
что точка минимума х* функции /(х) на множестве U найдена
точно: х*===х(А>.
Пример 2, Решить следующую задачу нелинейного про-
граммирования с линейными ограничениями методом возможных
направлений, завершая вычисления при	или
II х'*-”— x^>J<0,01.
f (х) = (Xi — 4)3 4- (х8—2)2 —> m in.
Xf + x2^3,
Х14-2х8^4,
4	Xi, x2^0.
В качестве начального приближения выберем, например, точку
Х(0) —(0,4; 1,4) (убедитесь, что x(0)g(/).
Шаг1.	.
1.	Ограничения (24) и (25) в точке х(0) выполняются как-
строгие неравенства (проверьте!), т. е. х<0> — внутренняя точка
множества U, т. е. /0= J0 = 0.
2.	В соответствии с (26) находим
е“» = — f’ (х<^) = (7,2; 1,2).	(39)
3.	Из формул (36), (37) получаем aOi = 1/7, a02 = 1/12, ctOi =
= afi2=4'00'
Определим a<* в соответствии с (38), используя условие мини-
мума Ф^(а) = 0:
Фо (а) = / (х«» 4-ае(о)) == (0,44-а• 72— 4)2 4- (1,4+а• 1,2 — 2)2,
Фо (а) = 107,04а—53,52 = 0, откуда а&=1/2.
Из (35) окончательно находим
ao=min(l/7, 1/12, 1/2, 4-00)= 1/12.	(40)
4.	Используя равенства (22), (39) и (40), получим
*<1> = (0,4; 1,4)+-1(7,2; 1,2) = (1; 1,5).	(41)
Шаг 2.
1.	В точке Xе” из (41) второе из ограничений задачи выпол-
няется тсак равенство, поэтому Xй*— граничная точка множества (Л
пр ичем =	/1==0.
?8
2.	Задача (29)—(33) для определения принимает вид
fi (e(i>) = -6ei<1>+4-6e?,_—41, + 4-е*1,_ —> min,
4,)+-^'“4-241)+-24u-<o.
е<1)+, e(1)"SsO; е^1>+-е^>“==0, /=1, 2.
Записав эту задачу в каноническом виде G помощью дополни-
тельных переменных и выбрав эти переменные в качестве базис-
ных, в результате двух шагов симплекс-метода получим = 2/3»
g<n- = l/3, g(D-= g(D+= о, т. е.
(о 1 \
у>—у)-	(42>
~3. По формулам (36), (37) находим ап = 3/2, cqa=s=9/2,	=
= ап = +оо, aj = 156/85, поэтому в соответствии о (38)
. /3 9 156 г \	3
а1=га,п	,+eoj=_.	(43)
4.	Очередное приближение х<2) находим по формуле (22) е
учетом (41), (42) и (43):
*,а>=(1;4)+4(т;-у)“(2; f)-	(44>
Шаг 3.
Как и на втором шаге, для определения е(2) получаем задачу
линейного программирования
7	/2 (^3))==—4^<а>+ + 4е<3)- — 2^<2>+4-2e<s2>- —> mitf»
е<2> + — е<2>~ + 42>+ ~ е™~ < °*
е(2)+ _ ею- + 2е<3) < — 2г<2)~ < 0,
е(2)+ + е(2)-+е(2)-ь +	i t
е<-2)+, e<2)_SsO; ej2)+.^2)"=0, /=1, 2,
решив которую, получим
*,г,=(т;-4У	<45’
Как и на предыдущем шаге, находим a2£==a22 = a2f = 4~оо ’
а22 = «2 = 1, т. е.
а2 = min (1,+ оо) = 1.	(46)
Из формул (22), (44) —(46) получаем
(1	1 \	/ к 1 \
2;~2-) = (т4)-
Ш а г 4.
Находя £13) по общему правилу, получим ^3> = 0, т. е. х(4) = х<^,
и || х(4) — х(3>|| = 0. Это означает, что точка минимума х* найден^
точно: х* = х(4) = (5/2; 1/2), /* = / (х(4)) =9/2.
79
Рис. 223 дает геометрическую ^иллюстрацию хода решения
задачи. На нем штриховыми линиями показаны линии уровня
f(x) (окружности с центром в точке (4,2)).
Рис. 223
Решить задачи нелинейного программирования с ли-
нейными ограничениями 16.281—16.290 методом возмож-
ных направлений, завершая вычисления при ||/' (x(ftl) || <
<0,01 или Цх'*-”—x,ft)||<0,01.
16.281.	f(x) = x\ + 2x1—16xt—20х2 —* min,
2xj4-5x2 < 40, z
2x14-x,<16,
хъ x2^0.
16.282.	f(x)~x^-f-xi—18xx—20x2—> min,
xl + x2<15,	"
2xi-|-5x2<60,
Зх^ + x2 30,
xx, x2^0.
16.283.	/(x) = (Xj —16)? + (x2—9)? -> min,
5x1 + 2x2<60,
Xj + x2<15,
Xj + 4x2 < 40,
xlt x2^>0.
16.284.	f(x) = x? + x?—xxx2—3x2—► min,
Xi + x2^4,
Xt, x2>0.
16.285.	/(x) = x, + x|—4х4—8x2—► min,
6хх + llx2 + xs + 2x4 = 96,
—2xi + 3x2—2xs + x4 = 8,
Xj>0,	....4.
80
16.286.	f(x) = xi + 2xi—x2 —> min,
Xi + x2 15,
Xi 4° Зх2 Ч~ X3 = 30,
5xj + 3x2 + x4 = 60,
Xj > 0, / = 1, ..., 4.
16.287.	f (x) = x\ + 2xl — 6xi—32x2~* min,
3%i 4~ X-2 “I- x$ = 30,
Xi + ^ + ^=15,
2xj 4- 3x2 4- = 60,
xf^0, /=U, ...» 5.
16.288.	f(x)=2x? + 3xi + 2x2 + 4x8->min, .
-Xi 4“ 3x2-f~ 2xg 15,
3xj + x2-h x3 20,
> x7 > 0, / = 1, 2, 3.
16.289.	f (xj^xl + xl + xl + xj—2x2 —► min,
Xi + 2x2 4~ 3x3	1.8,
2xi 4“ x2 4“ x$ 20,
xz>0,’ / = 1, 2, 3.
16.290.	/(x) = Xi—2xi + 2x24-x3 —> min,
Xi 4~ 3x2 4” 2x3 7,
3xi 4~ x2 4- x3 3,
xz>0, /=1, 2, 3.
Метод возможных направлений используется также для реше-
ния задачи нелинейного программирования более общего, чем
(23)-—(25), вида, а именно
f (х) —► min,	(47)
g/(x)<0,	1=1, ..., tn,	(48)
где f(x), gt(х) — выпуклые дифференцируемые в $п функции.
Опишем один из вариантов определения необходимого для
решения этой задачи вектора e{k) из (22) методом возможных на-
правлений, а также укажем критерий окончания вычислений.
1.	Выбор вектора е{®. Если внутренняя точка до-
пустимого множества (/, г. е. £/(х(Л>) <0, i=l, то вектор
определяется так же^ как в рассмотренном выше случае ли-
нейных ограничений (24), (25), т. е. = —/'(х(Л)).
Если же	—граничная точка множества Ut т. е. множество
нндексов
/»=(Пг/(*,й)=о}	(49)
непусто, то компоненты вектора e{k} [представляются в виде
—и находятся из решения следующей задачи
линейного программирования с переменными	t
81
J L ..л;
fft = ——min,
. n
i =1	7
Z -^Л>) (^)+-4*)')+p*<0, i^lk, (50)
2 (^++^-)<i,
/=i
Oft. <?p+• 4** ~ 3s °> 4*)+ ’ 4*>” = °’ / = 1.«•
Замечание. Для ускорения сходимости метода возможных
направлений множество индексов (49) иногда определяют не по
точному, а приближенному равенству £/(х(Л))==0 со все возрас-
тающей точностью еЛ, т. е. вместо используют множество
^л(М = {<| — 8*<£/С*1А))<0}> где е^—>0 при k —*оо.
2.	Выбор величины перемещения^, Величина сц
находится по авалогии со случаем линейных ограничений (24),
(25) на допустимое множество U, т. е.
aft = min (afef.akmi a*),
где a* определяется из (37), а a^, i=l, ...» /п,—максимально
возможное перемещение вдоль направления с учетом Z-го огра-
ничения (48), найденное из условия g/(х(Л)4-а^в(Л)) = 0.
3.	Критерий окончания вычислений. Условием
достижения заданной точности решения 8 > 0 задачи (47), (48) ме-
тодом возможных направлений служит выполнение хотя бы одного
из неравенств ||/' (х{®) |]«Се, о^^Се. При выполнении этого усло-
вия полагают х*»х'й), /*«/(х(Л))-
Любое из равенств f (х(Л)) = 0, од = 0 означает, что . точка
минимума х* функции f (х) на множестве U найдена точно: x*=x(ft).
Пример 3. Решить следующую задачу нелинейного про-
граммирования методом возможных направлений, завершая вы-
числения при J/'(х(/г))1 или а*«С0,1:
f (х) = — Xi—х2 —-> min,
gi(x) = x* + xi— 25<0.
Функции f (х) и gi (х) являются выпуклыми (проверьте!) и диф-
ференцируемыми в £п, поэтому можно использовать метод воз-
можных направлений.
Выберем начальное приближение х(0) == (0; 1). Очевидно, х(0) £ £/.
' Шаг 1.
1.	Так как gi (х(0)) = — 24 < 0, то х(0) является внутренней
точкой множества U и Ik = 0. .
2.	Вектор £(0) находим по формуле е(0) = — /' (х(0)) = (1, 1).
3.	Найдем максимально возможное перемещение aOi из усло-
вия g1(xfo)+a01^o))=0: (0 + ссог 1)а+(1+«01-1)2-25 = 2а|1 + 2ао1-
— 24 = 0, откуда a0i = 3.
Определяя aj из (38), получим а*=>4~оо, так как функция
<I)o(a)=/(JC(9) + a^(^))=—2a— 1 неограниченно убывает при a —►+00t
82
Отсюда находим величину перемещения на первом шаге: а0 =•
min (3,+оо) = 3.
4.	Найдем следующее приближение (22):
х^ = (0,1)4-3(1, 1) = (3, 4).
Ш а г 2.
2.	Поскольку gj(x(n) = O, то — граничная точка множества
(/иЛ = {1}- (1,
2.	Вектор е(1) находим из решения задачи линейного програм-
мирования (50):
fi = —- at —* min,
e(i)+ — e(D- 4- e<v+ — ecu- 4. q1 < 0,
6e?>4 _4-4-01 < 0,
e(n+ 4- >- 4- eu)+ 4. g(i>- < 1,
Qb	/ = 1,2.
PeiujiB ее симплекс-методом, получим &£ = 1/8, г^+ = 9/16,
^(i)- = 7/16, <>a>- = e(i>+ = 0, т. e. £«>==(£«)+—
1 (9/16, —7/16).
3.	Величину перемещения at находим, как и на предыдущем
шаге: ап = 16/65, а* = 4~<», т. е. «1=16/65.
4.	Очередное приближение х<2> находим на (22):
Шаг 3.
Так как gi (х(г,) = 0,'то точка х<*’является граничной. Находя
е'2, и а2 по общему правилу, получим: о2 = 0,125, «<2) = (0,547;
—0,453), а2=0,186. Отсюда х'3’= (3,240; 3,809).
Переходя к следующему шагу, найдем ог8=0,094 < 0,1, т. е.
требуемая точность достигнута и х*«х*3| = (3,240; 3,809), f*«f(X8,)=
=—7,049.
Решить задачи нелинейного программирования 16.291—
16.298 методом возможных направлений, завершая вычис-
ления при (x(ft)) IIC0.01 или ufcC0,01,
16.291;	f (х) = 2х, -|-х2 —* min,
gr (x)==x?-|-xl—9CO-
16.292.	1(х) — х1 + х%—12х,—6x2—«-min,
gi (x) = x- -j- x*—16 C 0.
16.293.	f(x) = — Xj—2x2 —► min,
g,(x) = x? + xl—1 <0,
gr2(x) = —X,—x2<0.
16.294.	f(x) = xi—2xj — x2—♦ min,
gi (x) = 2xj 4- 3x1—6 < 0.
16.295.	/(xj — 4x| 4-x2 + 2x2 —♦ min,
gt (x) = xj + xl—4x2 < 0,
g2(x) = — х,4-х2 — 2 CO.
83
16.296.
16.297.
16.298.
f(x) = 10xj — x, —min,
gi (x) = xl—4xj + xi + 3	0,
g2 (x) = x? + 4x1— 4x; — 4 < 0.
f x) — 4xi + x2 —* m>n,
gi(x) = x? + x2 —1 <0,
g2(x) = X!—x2<0.
f (x) — x'f—3Xi + xl —► min,
gi (x) = x'i—2x2 < 0,
g2 (x) == — Xj + x2 < 0.
3. Градиентные методы решения задач нелинейного программи-
рования. Один из подходов к решению задач нелинейного про-
граммирования состоит в такой модификации градиентных методов
безусловной минимизации (см. § 2), чтобы в процессе построения
последовательных приближений к точке минимума учитывались
ограничения на допустимое множество.
Ниже рассматриваются два метода минимизации, основанных
на этом подходе применительно к решению гладкой задачи выпук-
лого программирования
/(*)—*min, x£U,	-(51)
где Ucz£n~-выпуклое замкнутое множество, /(л)—выпуклая диф-
ференцируемая на U функция.
Первый метод (метод проекции градиента). На каждой
итерации этого метода предусмотрена процедура возврата очеред-
ного приближения градиентного спуска х(Л+1)== х(Л)—-(x,Ji')
на допустимое множество U, если х(Л+1) £ U. Такой возврат произ-
водится посредством проектирования x(*+i) на U, т. е. замены
х(Л+1) на ближайшую точку множества U.
Т)пределение. Пусть заданы замкнутое множество
и точка zf^Sn* Точка Z[j—P[j(z) называется проекцией точки z
на множество £/, если
р(*г7, £) = minp(x, z)s
хе и
где р (х, j) = |] х-^у || — расстояние между точками хи ув про-
странстве $п.
Очевидно, для точки z^U проекция Py(z) совпадает с Z.
Таким образом, в методе проекции градиента последователь-
ные приближения х™ к точке минимума х* целевой функции / (х)
на множестве U вычисляются по формулам
х<л+1)==Р£;[х^—«^/'(х^)!,	^ = 0, 1, ,..,х<°)€гЛ	(52)
В зависимости от способа вычисления из (52) различают
несколько вариантов метода проекции градиента, самыми распро-
страненными из которых являются следующие.
1. а* находится, как в методе наискорейшего спуска безуслов-
ной минимизации (см. § 2), т. е. (а^)==т1п Ф* (а), где Ф^ (а) =
а>0
= f \x™-af (х<*>)].
2. В предположении, что градиент /' (х) целевой функции
удовлетворяет на множестве U условию Липшица, т. е.
Я/' (X')	(х") II с L || X’ - х" II	(53)
S4
для всех х'у x"£Ut полагают Odessa, 1, ..., где а—про-
извольное число из интервала (0; 2/L). Если известна минималь*
пая константа Липшица L из (53), то выбирают, как правило,
х= 1/L.
Вычисления по формуле (52) завершаются при выполнении
одного из неравенств |!/' (х(Л))||«Се или ||х(Л)*“Х(й_Х) ||< е, где
величина 8 > 0 опреде ляет точность решения задачи. Окончательно
полагают X* «	f (х(*>).
Отметим, что определение проекции Ру (%) Для точки z$U
является самостоятельной задачей нелинейного программирования
7(х) = ||х-2|Р= 2(ху-гу)« —min, x£U, (54)
/= I
решение которой может вызвать затруднения,
В частном случае, когда множество U определяется лишь
линейными ограничениями, задача (54) представляет собой задачу
квадратичного программирования. Ее решение может быть най-
дено зЭх конечное число шагов, как описано выше.
Особый интерес при использовании метода проекции градиен-
та представляют такие множества U, для которых задача проек-
тирования решается в явном виде.
Пример 4. Найти проекцию Py(z\ точки z^Sn на мно-
(	п	Л
жество 4/==/|||х[|2=2	(замкнутый шар радиуса
I	/ = 1	J
/?о с центром в точке 0 в пространстве $п).
Запишем условие задачи (54) для рассматриваемого случая?
7(х) =
/=1
2
/=и
(55)
Рассмотрим возможные случаи.
1. z£U, т. е. 2	Тогда Рг/(г) = £.
/= 1
п
2 z$U, т. е. 2г/~^2>^о* Запишем ограничение-нера-
/=1
венство (55) в виде равенства, добавив в его левую часть допол-
нительную переменную Хпм=£/2^0. В результате получим за-
дачу на условный минимум (см. т. 1, с. 363):
7(х)= 2<х/~гДа min-
/=|
<р(X, ^)= 2 х7+{/’•“#0=0.
/= •
85
Для ее решения запишем необходимые условия экстремума |
л	/ п	\ 1
функции Лагранжа L(x, Х)= 2	2	): Я
/=1	\/=1	7 ;
^=2(xy~2y) + 21x/ = 0,	7=1............  '
2 xj+y^R2^0.
Решив эту'систему л + 2 уравнений с учетом предположения
л	р	р
2«/-*l> Ro, находим х,=—г/,/=1,	Х =-5—. 1, у = 0, -
К	Ао
т. е. ж=^л»/?ог	2(г/-
Проверим выполнение достаточного условия минимума L‘(x, у, А)
в найденной точке. Для этого найдем все частные производные
" • ^=2Д
Изу «о’
-1Y ;по<
(р
J^-=0, /=1............  **	О, 15^/;
dxjdy	dxidxt	"
D ”	/	p
этому d2L = 2T-V dxJ-j-2 (
AO	\	*\Q
т. e. достаточное условие минимума
Окончательно
г> °; 'ro 1
^_2 (I
ду* \1
\ п
— Ijdy* > О при dx* + dy*
выполняется/

n
если 2 г/ <
/ = 1
(56)
Pui^
\
п
если 2 г/ > ^ ►
/=1
Если проекция точки яа допустимое множество задачи
нелинейного программирования находится в явном виде, то ис-
пользование метода проекции градиента для. ее решения значи-
тельно упрощается.
Пример 5. Решить следующую задачу нелинейного про-
граммирования методом проекции градиента, завершая вычисления
ври выполнении одного из условий [I/' (х(Л))||х(л*Х) —
—	>1КО,01:
/ (х) = —xt+ %2 —> min,
+
В качестве начального приближения возьмем, например, точку
х<о) = (О; 0,5) ё</.
86
Градиент f‘ (х)=(—1,2х2) удовлетворяет условию Лившица (53)
с константой L = 2, так как
л/ (х')-Г (*”) || = К(-1+1)« + (2х2-2х;)2 =
= 2|х2«-Х2|<2[| х' —хп||.
Поэтому в (52) можно положить oc^ = ag(0; 1), ^ = 0, 1, ...»
например, <х% = 0,75.
Шаг 1. Так как ff (х<0>) = (—1, 1), по формуле (52) находим
=	(ж(о,)) = ^1(О; 0,5)—0,75 (—1» 1)] =
«=Р£7((0,75; —0,25)].
Точка (0,75; —0,25) принадлежит множеству U, так как 0,752 +
4-0,252 = 0,625 < 1, поэтому х(1^ = (0,75; —0,25).
Требуемая точность не достигнута, так как J	— ха) [|»
= 1,06 >0,01.
Шаг 2. Как и на предыдущем шаге, находим
f (Х<1)) = (—1; —0,5),	-0,25) —0,75 (—1; —0,5)] =
==РИ(1>5; 0,125)].
Точка (1,5; 0,125) допустимому множеству не принадлежит, по-
тому что 1,524-0,1252 = 2,266 > 1. Так как множество U представ-
ляет собой замкнутый шар радиуса Ра=1 с центром в точке 0
в пространстве ^2> то, используя результат примера 4, по фор-
муле (5G) находим
Х 2) = ри [(1,5; 0,125)|=Uk5;:,^125) = (0,9965; 0,08304).
К 1,5*4-0,125»
Требуемая точность не достигнута, так как ||х(О—х(2>|| =
= 0,298 >0,01.
Результаты остальных шагов метода проекции градиента при-
ведены в следующей таблице:
k		|М*-1)_Ж(*)||	Г (*<*>>	*(&)—а/*
2	(0,9965; 0,0830)	0,298	(—1; 0,1661)	(1,7465; —0,0415)
3	(0,9997; —0,0238)	0,107	(-1; —0,0476)	(1,7497; 0,0119)
4	(0,99998; 0,00679)	0,031	(—1; 0,0136)	(1,74998; —0,00339)
5	(0,99998; -0,00194)	0,0087	Точность достигнута	
Из таблицы следует, что х* « х(В) = (0,99998; —0,00194), f* «
f (х<5>) = —1. Отметим, что точное решение рассматриваемой за-
дачи х* = (1, 0), f* =—1. >
В задачах 16,299—16.303 найти проекцию 2'y=Pc(z)
точки z^Sn на указанные множества Uc.Sn.
87
16.299.	U = {х€^>„|х/>0, /==1, ...,л} (неотрица-
тельный октант пространства $п).
16.300.	U —	j — 1, ...,«} (n-мер-
ный параллелепипед).
{п
х € <§п | 2 (-4—х)0))г С	f (замкнутый
/= 1	J
шар радиуса 7?d с центром в точке х<0)).
(	п	1
16.302,	(7 = <x€<£n| 2«+/ = ^ а = (.аь • ••, йп)^=0(
I	/=1	)
(гиперплоскость с нормальным вектором а).
(	п	1
16.303,	U = < x€<£n|2a/x/^^ =	..., ап)=И=0?
(полупространство в <§п).
Используя результаты решения подходящих задач
16.299—16.303, решить задачи нелинейного программиро-
вания 16.304—16.313 методом проекции градиента. Вы-
числения завершить при ||x(ft-l)—х‘*’ || 0,01.
16,304.	f (х) = х%+4х| 4- Зххх2 + 2xt +16х2 —► min,
*(>0, х2>0.
16,305.	f (х) = Эх, 4-х?—54хх 4- 4х2 —* min,
*i^s0, х2>0.
16.306.	/(х) = х? + 9х?—12хх—36х2—> min,
—1 X, ^4, 1 ^х2^ 2.
16.307.	f (х) = 2К 1 + х? + 24+хх + х2 —► min,
5<xf<8, 1<х2<10.
16.308.	f(x) = 2xi+x2—► min,
(^-4)« + (х2-2ГС1.
16.309.	/(x) = Xj—8xf + xi—> min,
•	x? + (x2-4)«<9.
16.310.	/(x^xj+xi+xl+xj+xj+xs—» min,
xx+x2+xg = 3.
16.311.	/(x) = х,+4+Хз—4xt—6x2—2xa—► min,
2xi+x8 = 2.x
16.312,	f(x) = (xx—2)4 + (xa—I)4—> min,
2Xi+x2<2.
16.313,	/(x) = x;—x2—> min,
2xx—2x2	1.
Второй метод (метод условного градиента). Пусть x(ft) g U —
очередное приближение к решению гладкой задачи выпуклого
программирования (51), причем /'(х(Л))Й0. Тогда* в окрестности
точки функция /(х) представима в виде
f (х)=/(х^)) + (/? (Х{®)> Х-Х<*>)+0(11 х-х<*)||),
и линейная функция
fe(x) = (/'(*•*’), X-*»)
88
является приближением разности f(x) — f(x{k}} с точностью до
величины о (|| х—- х<*> Ц) в некоторой окрестности точки х{кК
Поставим вспомогательную задачу минимизации на множестве
U линейной функции fk(x)t т. е.
fkW — if' (х(А)), х —х(Л))—►min,	x^U. (57)
Пусть х(/г) —решение этой задачи. ^Следующее приближение
х(й+1) к точке минимума х* функции f (х) на множестве U най-
дем по формуле
x^+1) = x^+aft(x^> — х<*>),	a*€(0; 1).	(58)
В силу выпуклости допустимого множества х(А+1)££Л
Величина из (58) в различных вариантах метода условного
градиента вычисляется по-разному. Опишем два способа опреде-
ления а&.
1. a£ = min(l, а&), где а,* найдено из условия наискорейшего
спуска по направлению x(ft) —х(Л): Ф^(а^) = minФ^(а), где ФЛ(а)=
_ а>°
=/[х'^ + а(х(А5> — х<*))Ь
2. В начале выполнения итерации (58) полагают ^=1, после
чего проверяют условие
/ (х<л+1)) < / (Л^Л)).	(59)
Если оно нарушается, то a# уменьшают (дробят) в 2 раза и
повторно проверяют (50). Дробление ak производят до выполнения
неравенства (50), после чего переходят к следующей итерации (68).
" Условие окончания вычислений по методу условного градиента
совпадает с аналогичным условием метода проекции градиента.
Отметим, что вспомогательная задача (57) является, вообще
говоря, задачей нелинейного программирования. Укажем случаи,
когда поиск ее решения х{® не представляет затруднений.
1.	Допустимое множество U задано линейными ограничениями
и условием неотрицательности переменных. Тогда (57) — это задача
линейного программирования и ее решение можно найти с по-
мощью симплекс-метода (см. § 3).
2.	Допустимое множество U={x£$n I	/=1, ,,», л}—
n-мерный параллелепипед. Тогда,
/	ajt	если	df	(x®)/dxj > О,
bjt	если	df	<	О,
,	если	df	(х{Л))/дх7- = 0.
(60)
( п
3.	Допустимое множество
I
шар радиуса Ro с центром в точке #(0). Тогда
£*>=><» _£0
Л(х(Л>)
II/' (*(Й)|Г
Пример 6. Решить следующую задачу нелинейного про»
‘Раммирования методом условного градиента, завершая вычисления
89
При If x(*_J>*~ x<*> |[ < О, I:
/(x) = Xj — 4xi+xl —2x2 —* min,
0<*i< 1, 0<x2<2, :
В качестве начального приближения выберем, например, точку
х«» = (0, 0)££7.
Шаг 1. Найдем градиент f (x) = (2xi —4, 2х2 — 2) в точке х(0):
/'(х*0*) == (—4, —2). Запишем вспомогательную задачу (57):
fk (*) = (/' (^0>), х—х<0)) =—4X1 — 2х2 -* min,
0<Х1< I, 0«^х2<2.
Это задача линейного программирования, ее можно решить
симплекс-методом. Однако проще воспользоваться соотношениями
(60), откуда следует х(0) = (1,2).
Найдем а0 первым способом. В данном случае
Фо (а) = f 1*0)+«(хw—х«»)) = f (а, 2а)=5а2—8а.
Из условия Фо(а)=О находим а = ао —0,8.	Поэтому Оо =
= min(l, 0,8) =0,8.
Вычислим очередное приближение х(1) по формуле (58): Xй* =
«=(0, 0)+0,8(1, 2)«=(0,8; 1,6).
Так как ||х(0)'—х(Х) ||= 1,79 > 0,1, то требуемая точность не
достигнута.
Результаты вычислений на следующих шагах метода условного
градиента приведены в следующей таблице.
k				“fr
1	(0,8; 1,6)	1,789	1 (1.0)	1 0,462
2	(0,892; 0,861)	0,745	(1.2}	0,212
3	(0,915; 1,103)	0,213	(1.0)	0,168
4	(0,929; 0,917)	0,187	(1.2)	0,140
5	(0,939; 1,069)	0,152	(1.0)	0,121
6	(0,947; 0,940)	0,129	(1.2)	0,106
7	(0,952; 1,053)	0,113	(1.0)	0,095
8	(0,957; 0,953)	0,1	Точность достигнута	
Окончательно х* ге х<8) = (0,957; 0,953), f* « f(xt8,) = —3,91.
Решить задачи нелинейного программирования 16.314—
16.322 методом условного градиента, завершая вычисле-
ния при ||х(Л~1) —
16.314.	f(x) = x? + xl — 6X1—4х2“> min,
*i + *2 С 2,
90
16.315.	/(x)=xl + 4xf—8хг—8x2 —► min,.
—2 sC	2,
0<x2<3.
16.316.	/'(x) = e(M*-*’>*+xt + xf—4*i—4x2 —> min,
0 < Xj < 1,
—2	x2 3.
16.317,	f (x) =z In (2+4+xt—2x2)+e<*«-— mln,
%i>3,
x2 > 0.
16.318.	f (x) = xt4-*a + 6xi—2x2 —> min,
xt+xt<l.
16.319.	7 (x) = xl+*1—8X1 + 4xamin,
(x1-l)8+(xe-l)s<l.
16.320.	f (x)=ln (xl+xl—4xx—6x2+13)—2x<—x2 —> min,
(Xi+2)8+xl <4.
16.321,	f(x) = J^+xi—6xx—3x2 + 5 —> min,
*i+x2<3,
2xj+x2 4,
xb x2^0.
16.322.	/(x)=ln (xl + xl—8x!—6x2+26)—xx—x2 —+ min,
x, + x2 < 4,
х0<хх<3,
0 «С x2 2.
4.	Методы штрафных и барьерных функций. Один из подходов
к решению задачи нелинейного программирования /(х)—>-min,
x£U основан на ‘замене этой задачи последовательностью задач
безусловной минимизации
М*) = /W+фНх)—*-min, х£$п, ft-1,2,,,,,	(61)
где ф/, (х)—функции, которые с ростом k во все большей степени
учитывают ограничения, определяющие допустимое множество U
исходной задачи.
В методе штрафных функций функции <рд (х) подбираются так,
чтобы при больших k функция /Их) из (61) мало отличалась от
I (х) при x£U и быстро возрастала при удалении точки x^U от
допустимого множества U.
Определение. Пусть Uc$n—заданное множество. По«
следовательность функций (<рНх)}, определенных в и обла-
дающих свойством
1.ШфА(Х) = / °- если х^и'
j+°°> если
называется последовательностью штрафных функций множества V»
91
st (*)=•{
Рассмотрим один из вариантов метода штрафных функций
приближенного решения задачи нелинейного ^программирования
f (х) —► min,
gz(x)«0,	/==1.....I,	(62)
g/(X)<0,
считая, что функции f(x)t gi(x)t i=l, tn, заданы во всем
пространстве
Положим
фЛ(х)=6ф(х),	6=1, 2, <1О	(63)
где
I	т
S fe<+(«Я1»
i~l	i=/+l
О, если g/(x)<0,
gi 1.x), если gi (x) > О*
Равенства (63) определяет последовательность штрафных функ-
ций допустимого множества задачи (62) (проверьте!).
При определенных условиях последовательность решений за-
дач J6esyc лов ной минимизации (61), (63) сходится к решению х*
задачи (62), поэтому для достаточно больших k полагают х* « х(Л\
Г «/(*<*>).
Критерием достижения требуемой точности решения задачи (62)
может служить неравенство
||х^-Х<^||<8,	(64)
где 8 > 0 —число, характеризующее точность, четное число.
Для решения задач (61) можно использовать методы безуслов-
ной минимизации, рассмотренные в § 2.
Если в задаче (62) / (х) —выпуклая квадратичная функция,
a gi(x)> t=l, ..., m,— линейные функции, то точное решение
вспомогательной задачи (61) можно найти из системы линейных
уравнений %(х)/^х7- = 0, /=1, . п, определяющих стационар-
ную точку функции fk(x).
Пример 7. Методом штрафных функций решить следующую
вадачу нелинейного программирования:
f(x)==2xl+xl—►min,
gi (•*) = — xi—x2 + 2<0, ’
g2 (x) = Xi — 2x2 + К 0,	(65)
gs (x)=— 2xi+x2 < 0.
4$ Целевая функция f (x) является выпуклой (проверьте!) квадра-
тичной функцией, а ограничения, определяющие допустимое мно-
жество задачи, линейны. Поэтому решение х(Л) вспомогательной
задачи (61) для любого 6=1, 2, ... может быть найдено точно из
условия /^(Х<А))=0.
Так как функция ф^(х)- из (63) в различных областях про-
странства <§п задана по-разному, то при составлении вспомога-
тельной функции ffc (х) следует сделать определенное предположе-
ние о расположении ее точки минимума
92
1.	Предположим, что в точке безусловного минимума функ-
ции fk (х) все ограничения задачи (65) нарушаются, т. е. gi (ж**>) >0»
i=l, 2, 3.
Тогда gt (x(A))==j?z (х<Л>),	2, 3, поэтому считаем, что
fk (x)~f(x)+k [g? (X) + gl (x)+gl (x)]~
= (2 + 6k) xj + (1 + 6&) xl6£xxx2 ** 2kxi — 8kx$+5£.
Решив систему уравнений ’
^-^=(44-12й)х1—6b2—2й = 0,
OX}
——6b:, + (2 + 12k) x2—8k=0,
OX3
находим
<fr)_	18fe2 + *	27b 4-86
X1 —27fe2+18fe+2’ *2	27fe2+18fe + 2‘
Так как g3(x<*>) = —2x^4-xa*’=^5q^q^ < 0 при веех
k — 1, 2, ..., то предположение g3 (x<A>) > 0 не подтвердилось.
2.	Предположим, что gz(*<A))>0, i = l, 2, gsC^XO- Тогда
g? (x(A))=g/(х(А)), 1 = 1, 2, £з (х(й))=0, поэтому считаем, что
f k (X) = f (х) + k [g? (x) 4- gl (x)] = (2 4- 2fe) xl 4- (14- 5k) xl - 2k x,x2 -
— 2&Xi«— 8&X2 + 5k, откуда находим
(fe) _ 9k* + k	<k)_ 9k*+8k
1	9&2+12&+2’	2 ^9/s2+12^+2*
(66)
Легко проверить, что сделанное предположение подтвержда-
ется, т. е. равенства (66) определяют точку безусловного мини-
мума х(А) вспомогательной функции fk (х) из (61).
Окончательно находим х*~ Пт х(А) = (1; 1), f*t=f(x*) — 3.
k-+ со
Отметим, что для решения вспомогательных задач (61) можно
было использовать н приближенные (например, градиентные) ме-
тоды безусловной минимизации (см. § 2). Тогда, если требуемая
точность решения задачи нелинейного программирования (65) за-
дана числом е из (64), равным, например, 0,01, то получим х*а»
~ ХЦ2О)И (0,9899;	0,9963),	/ (х<120>) = 2,9524, так как
||х<12°) —x<W)||=0,01. >
Решить задачи нелинейного программирования 16.323 —
16.332 методом штрафных функций, полагая
при ||хш—-л:да2)|| <0,05.
16.323.	/(х) = Xj 4-*2—20х,—30ха —> min,
2xi4-3x2—13<0,
2х, 4-х2—Ю <0.
16.324.	f(x) — xl +xl—10x1—15ха—»• min,
5xi 4- 13ха—51 <0,
,	15X14-7ха—107<0.
93
16.325.	f(x)=x?4-*l—5xf—4x2 —> min,
2xt -4* 3x2 -4- Xg ® 6.
16.326.	f (x) = Xj + xi—5x1—10x2—
9xi + 8x2—72 <0,
Xf4-2x2—10 <0.
16.327.	/(ж) = Х1—2xt—x2—«-min,
2xf + 3x2—6<0,
2xi-j-x2—4<0.
16.328.	f(x) — x%—2xt + 2xi + xi—>-min,
xt + 3x2 + 2x,—6 < 0,
3xi+**+*$—2 <0.
16.329.	f(x) = —Xf+xl—2x2 —* min,
3x?4-2x|—6<0.
16.330.	f(x)=xl-^x£—6xi—3x2—«-min,
хЦ-х|—9^0.
16.331.	f(x)—xl+x%—3x2—► min,
—2xt+xl^0,
xi—2x2^0.
16.332.	f(x)——xt—4x2—>min,
Xi4-x!— 1 <0,
В методе барьерных функций исходная задача нелинейного
программирования также сводится к последовательности задач
безусловной минимизация {61), но функции ф^(х) выбираются та-
ким образом, чтобы при больших k функции fn(x) из (61) мало
отличались от f(x) во внутренних точках х допустимого множе-
ства U и в то же время при приближении точки x£U к границе
множества U эти функции неограниченно возрастали.
Определение. Пусть множество U<z@n задано. Последо-
вательность функций {фд (*)}> определенных во всех внутренних
точках множества U, называется последовательностью барьерных
функций этого множества, если выполняются условия:
*1. lim <Pj(x)=0 для любой фиксированной внутренней точ-
с©
ки х множества U\
2.	lira (x<r)) = + 00 для любой последовательности {л(г)}
Г-> СО
внутренних точек множества U, сходящейся к какой-либо гра-
ничной точке этого множества.
Рассмотрим некоторые варианты метода барьерных функций
решения следующей задачи нелинейного программирования:
Положим
ф*(х) = уф(х), *«=1,2.............................. (68)
где
ф(х) = 2 lg<(*)l ~р> Р>0,	(69)
i-i
или
т
ф(*)=—2 м—&(х)].
i=l
(70)
Выражения (68)~—(70) определяют последовательности барь-
ерных функций допустимого множества U задачи (67) (проверьте!).
Пусть —решение задачи безусловной минимизации (61),
где функция (л) определена равенствами (68), (69) или (68),
(70). Полагая х* « л(Ч f*&f(x№) для достаточно большого k,
находим приближенное решение задачи нелинейного программи-
рования (67) методом барьерных функций. Для контроля достиг-
нутой точности решения можно использовать критерий (64).
Пример 8. Решить следующую задачу нелинейного про-
граммирования методом барьерных функций, полагая х*«
при ||л^~х^>1|< 0,002:
f (x)=x?-f-2x2 -.min,
gi('x) = —Xi + x2<0,
g2 (х) = 1 — — х2 <0.
Используем последовательность барьерных функций (68), (70).
Тогда задача (61) принимает вид
f*(*)=xi+2xf —y(ln (Xi—x2) + ln(xj+xi—1)] —*min, х£<§п.
Решая ее методом Ньютона (см. § 2) при k ==500 и А = 1000, по-
лучаем х<в00) = (0,6696; 0,3319), х<^00> = (0,6682; 0,3326). Так как
»д^ьоо, ц_ 1>65. ю-s < о,002, полагаем X* х х’«00’ =
= (0,6696; 0,3319), /*«f(x<we«’)=0,6687. >
Решить задачи нелинейного программирования 16.333—.
16.339 методом барьерных функций, полагая х* & х'м
при ||x,w—х<*/*>К0,05.
16.333.	f (x) = xi—2х2—min,
xi+xl—4^0.
16.334.	f (x) = Xi + x‘j — IO*!—8x2 + 3-*min,
Xi + 2x2—2^0,
2xt+x2— 2^0.
16.335.	f(x) = —2xi+xf—x2 + 2—>min,
2x? + 3xt—6^0.
16.336.	/(x)=x;+x2—8xx—4x2 + 3—> min,
xj-t-xj—8^0.
16.337.	f.(x) — xi+x%,—3xj + l—*min, '
x2—2x2 CJO,
—2x1+x2 s^O.
16.338.	f(x) = — xx—5x2 —► min,
Xj+x-2 —1<0,
— Xj + 2x2	0.
16.339.	f (X) - 9 (x, -5)2 + 4 (Xj—5)?	min,
xj — 2xj—Xj + 1^0,
— Xi+x2—K0,
Xi—x2^0.
95
§ 5. Дискретное динамическое программирование
В этом параграфе рассматриваются многошаговые задачи опти-
мизации, т. е. задачи, оптимизацию в которых можно представить
в виде ряда последовательных этапов (шагов).
Предположим, что состояние некоторого процесса или объек-
та описывается n-мерным вектором х = (хь х2, ...» хп), или, что
то же самое, точкой х пространства <§п, которое называют фазо-
вым пространством.
Будем считать, что процесс является Af-шаговым, т. е. его
эволюция происходит в N этапов (шагов) в соответствии со сле-
дующей схемой:
в в, —>> я(Л~1) —>	111 —>.
начальное '	'	конечное
состояние	4-й шаг	состояние
Переход между состояниями на &-м шаге происходит в соот-
ветствии с уравнением состояний
x№=fW(x^\ #<*>),	(1)
где	есть /n-мерный вектор управления, выбираемый на
6-м шаге, /<*>(х, и) — заданная n-мерная вектор-функция аргумен-
ТОВ X^Sn,
Таким образом, предполагается, что в результате &-го шага
процесс переходит в состояние х(Л), которое определяется только
начальным состоянием х(Л~1) этого шага и выбранным на нем
вектором управления и{М и не зависит от «предыстории» процесса
до k-ro шага, т. е. от х<0>, ...» x(ft*2) и й(1>, ...,
Показателем эффективности &-го шага является заданная чис-
ловая характеристика (целевая функция этого шага) Jk —
^Jfe(x'b-»t 6=1, 2, ..., N.
Предположим, что эффективность всего процесса в целом ха-
рактеризуется целевой функцией вида
N
J (х, и)= 2	«'*’).	(2)
4=1
где х = {х(0>, х(1>,	х(^>} —набор состояний, называемый фазо-
вой траекторией процесса, а 2 = {а(1), и{2), .— набор век-
торов управления, который называется управлением процессом.
Таким образом, рассматриваются только аддитивные целевые
функции J, представимые в виде суммы целевых функций шагов
Предположим далее, что на фазовую траекторию и выбор уп-
равлений наложены ограничения
x^gX*, k=\, ..., JV-1,	(3)
«<*>g£/*(x<*-x,)>	4=1, N,	(4)
где Xk и	—заданные множества в пространствах (§rt и
$т соответственно, причем множество U зависит, вообще говоря,
от начального состояния x{k~1} 4-го шага.
Ограничения па начальное и конечное состояния процесса
х(0,€Х0, xW>$XN
называются начальными и конечными условиями. При этом множе-
ства Хо и	во многих случаях содержат по одной точке
(начало и конец фазовой траектории).
96
Пусть и —{#а), й(2), ...» к(ЛГ)}— управление процессом, удов-
летворяющее ограничениям (4) и переводящее его из некоторого
начального состояния л?(0>£Х0 в некоторое конечное состояние
в соответствии с уравнениями (1) с учетом ограниче-
ний (3). Обозначим множество всех таких управлений буквой U.
Многошаговая задача оптимизации формулируется следующим
образом: среди всех управлений u£U выбрать такое («* =
=	я(2)*, ...» а(ЛГ)*}), для которого целевая функция (2) при-
нимает минимальное или максимальное (в зависимости от смысла
задачи) значение. ~
Управление w* и соответствующая ему фазовая траектория
х* называются оптимальными.
Условие многошаговой задачи оптимизации будем записывать
следующим образом:
N
J (X, и) = 2 h «'*’) -> extr*),	(5)
k=l
й(Л))г	bl,	....	N,	(6)
x^£Xk,	6=1....../V — 1,	(7)
tt^£Uk(x^-V),	6 = 1,	N,	(8)
x^gX0, x^X„.	(9)
К многошаговым задачам оптимизации сводятся многие при-
кладные задачи.
Пример 1. Сформулировать следующую задачу в виде мно-
гошаговой задачи оптимизации (5) — (9).
С помощью М-ступенчатой ракеты с заданной стартовой мас-
сой М в космос запускается межпланетная станция массой т.
За время работы каждой ступени ракета получает добавочную
скорость &v — F(y, г), где у—масса, разгоняемая этой ступенью,
г —масса самой ступени. Найти такое распределение общей мас-
сы М ракеты между ее ступенями, при котором конечная скорость
станции будет максимальной.
Обозначим U'to, 6=1, ..., Af, массу 6-й ступени, считая от
межпланетной станции (т. е. на старте работает ступень массой
u{N\ а в конце разгона — ступень массой и{1>).
Массу станции вместе с примыкающими к ней 6 ступенями
ракеты обозначим 6 = 0, 1, N. Тогда, очевидно,
x^) = x^’i> + ^4	6=1, ЛГ;
х<0) = т, = М + т.
Из условия задачи вытекают следующие ограничения на мас-
сы х'й) и	+ Q^u{k) т. е.
х(б)^хЛ=[/п; М+т], 6 = 1,	2V—1,
=	М],	6 = 1,	W.
х) Символом extr мы будем обозначать минимум или макси-
мум соответствующей функции, в зависимости от смысла задачи.
Несмотря на то, что задачу на максимум целевой функции J
всегда можно свести к задаче минимизации — / —► min, мы будем
рассматривать и задачи на максимум, используя обозначение
/ ► шах, чтобы математические постановки этих задач соответ-
ствовали их прикладному смыслу.
4 Под ред. А. В. Ефимова, ч. 4	97
В результате работы &-й ступени ракеты приращение скорости
станции составит F	поэтому ее конечная скорость
N
будет равна 2 F u’*>).
Л=1
Таким образом, рассматриваемую задачу можно сформули-
ровать как многошаговую^ задачу оптимизации следующей:
вида:
N
J (х, «)= 2 С*’*-1’.	—* П1аХ,
=	fe=l.....ДГ,
х<*’£[т; m-j-M],	k=l,	....	Л’ —1,
H(e)g[Oj Л4],	fe=l.....N,
x*Oj=т, х*-М=М т. ►
Сформулировать задачи 16.340 —16.349 в виде много-
шаговых задач оптимизации вида (5)—(9).
16.340.	Сумма средств S распределяется между N
предприятиями. Выделение А-му -предприятию средств в
размере и приносит, доход Jk (и), k—\, 2, .... N. Опре-
делить, какое количество средств необходимо выделить
каждому предприятию, чтобы суммарный доход всех
предприятий был максимальным. '
. 16.341. Сумма средств S выделяется предприятию в
течение W лет. Прибыль, получаемая предприятием в ре-
зультате выделения ему средств и в течение Л-го года,
составляет Jk(u), k—\, ..., ЛЛ Распределить выде-
ляемые средства по годам таким образом, чтобы сум-
марная прибыль предприятия за N лет была максималь-
ной.
16.342.	Найти N неотрицательных чисел utk\ k =
= 1, ..., N, сумма которых равна S, а произведение
максимально.
16.343.	Совхоз производит посевной материал. Еже-
годно часть семян продается потребителям, а оставшаяся
их часть используется для воспроизводства. Доход от
продажи и т семян составляет F (и) руб. Количество по-
севного материала, оставленное в совхозе, в следующем
году увеличивается в А раз (А > 1). В начале первого
года имеется ат семян. В конце 7V-ro года их производ-
ство прекращается. Сколько семенного материала следует
продавать каждый год, чтобы доход совхоза за N лет был
максимальным?
16.344.	Рассмотреть задачу 16.343 в предположении,
что в конце ЛГ-го года производство семян не прекраща-
ла
•йен и минимальное планируемое их количество к началу
м/4-’1)-го года составляет Ьт.
16.345.	Планируется производство на двух предприя-
тиях в течение W лет. Начальные средства, предназна-
ченные для выделения предприятиям, составляют S руб.
Средства в размере U руб., вложенные в производство
нз\м предприятии в начале каждого года, приносят к
концу этого года доход Jz(u)py6., а также сумму fz(u),
оставляемую для финансирования дальнейшего производ-
ства, 1 = 1, 2. Пр истечении каждого года все предназна-
ченные для дальнейшего производства средства перерас-
пределяются между предприятиями.
Найти такой способ распределения средств предприя-
тиям, при котором суммарный доход двух предприятий
за N лет будет максимальным.
16.346.	Оптовая база вмещает Р т продукции. Запасы
продукции могут пополняться и продаваться в начале
каждого из /V месяцев, причем пополнение предшествует
продаже. Хранение 1 т продукции в течение k-vo месяца
обходится в ак руб., а продажа того же ее количества в
начале Л-го месяца приносит доход руб. Начальное ко-
личество продукции на базе составляет ат.
Определить количества продукции, которые в начале
каждого месяца, следует принимать на хранение и про-
давать, чтобы суммарная прибыль базы за М месяцев
была максимальной.
16.347.	Рассмотреть задачу 16.346 в предположении,
что в начале каждого месяца продажа продукции пред-
шествует ее пополнению.
16.348.	Г(й)= 2 /ч («<*>)-► min,
N
fe=i
' «<*>>0, u<ft)£Z, £=1........N,
где ак^0, k=\, .... N, b^O (сепарабельная* 1) задача
целочисленного программирования е одним линейным
ограничением).
п
1) Функция п переменных вида	#«)=2 Ф/WI на-
вывается сепарабельной.
Если все функции, входящие в условие задачи математиче-
ского программирования, сепарабельны, то такую задачу назы-
вают сепарабельной.
4*	*	99
N
16.349.	F(u)= 2 Л —mln,
£= 1
N
aiku{k) ^bi9 i = l, ..., m.
u™^0. u™£Z. k=\. .... N.
где aik. Ь{^09 /=1, .... tn. &=1, .... N (сепарабель-
ная задача целочисленного программирования с tn линей-
ными ограничениями).
Для решения многошаговой задачи оптимизации (5) — (9) ис-
пользуется метод динамического программирования, основанный на
принципе оптимальности Веллмана:
Оптимальная траектория в задаче (5)—-(9) обладает тем свой-
ством. что любая ее завершающая часть, начинающаяся с k-го шага,
й=1, .... TV—1, является оптимальной для остающихся шагов
процесса.
Опишем метод динамического программирования.
Заметим прежде всего, что в формулировке многошаговой за-
дачи оптимизации (5) —(9) ограничения на фазовую траекторию
(7) и на конечное состояние (9) можно включить в ограничения
на выбор управлений, заменив соотношения (7) и (8) следующим
эквивалентным ограничением:
u^)£Xk},	(10)
6 = 1, .... N.
С учетом этого перепишем формулировку	задачи (5) —(9) в
следующем виде:
J (х. и) =2	я(А))extr,	(11)
Х(Л) =/А)	k^\,...,N.	(12)
£=1, .... N.	(13)
x^£X0.	(14)
Предположим, что в результате начальных -1 шагов про-
цесс перешел в состояние Рассмотрим задачу оптимизации
оставшихся N — k+l шагов, аналогичную задаче (11)—-(14). Пусть
оптимальное управление и*(k) = {«<*>*, .... u(N)*} последних N —
— &4-1 шагов и оптимальная траектория этих шагов =
=	...» начатая из состояния найдены.
Целевая функция J<k)(x(k), «(&)) = 2	#(Л)) послед-
них /V—&+1 шагов при х (^)=Г: (k), u(k)~u*(k) принимает оп-
тимальное (т. е. минимальное или максимальное) значение, зави-
сящее от начального состояния фазовой траектории этих
шагов, т. е.
extr (х (k), и (&)) =	(£* (k), 2* (k)) = Bk (x(*-i>).	(15)
Функция Вь(х&~1)) из (15) называется функцией Веллмана
последних N^k^l шагов.
100
Очевидно,
Вдг(х^1>)= extr	U{N}).	(16)
«(^ 6 UN (х{^~ Х))
Кроме того, функции Веллмана связаны между собой следующими
рекуррентными соотношениями, вытекающими из принципа опти-
мальности:
ВИ*(А-Х>)= ib- jxtr {BA+i (х^, #<*>)) +
«<Л) € Uk (х(Й“Х)
+ ЛС*(**Х\ «(А))Ь	*=1> ...» Af—1.	(17)
Соотношения (16) и (17), позволяющие последовательно найти
функции Веллмана Вдг(х(ЛГ-х>), BN_X (х^-2))>	В1(^о)), назы-
ваются уравнениями Веллмана.
Находя функции B*(xlft~l)), k^N, ...» 1, из(16) и (17),
мы одновременно определяем и управления и(й)* (х<А“Х)), которым
отвечают оптимальные значения соответствующих величин Z\r~
=	И	+	+	ДО»),
£ —N —1, Л/—2,	1, из правых частей равенств (16) и (17):
ZNl*H-i\ ^ЛО*(д<лг.1))]=г
== extr ZN(x^~*\	(18)
ZkWk~i\ «<*>*(х<*~1,)1=*
« b ~extrfe ,	(19)
k=JV—1,	1.
Управления а(Л)*(x(A“J)), k~\, ...» АГ, называются условными
оптимальными управлениями, а процесс их нахождения-*условной
оптимизацией. Отметим, что управления я(Л)* (х<*"1)), найденные
в соответствии с (19), удовлетворяют принципу оптимальности,
т. е. в зависимости от начального состояния x(ft“X) управление
#(£)*(х(Л“Х))э £=1, .Л/—.1, учитывает оптимизацию не только
&-го шага, но и следующих за ним /V—& шагов.
Итак, в результате условной оптимизации находятся функции
Веллмана Вь(х^-1Т\ и условные оптимальные управления
^*(^-1)), &=1,
После этого можно осуществить безусловную оптимизацию
в задаче /11)—(14), т. е. определить искомые оптимальное управле-
ние процессом и*—{и{1}\ ..., u(N}*} и оптимальную фазовую траек- -
торию £*={х(0)*, ...» следующим образом.
Так как функция Веллмана Bi (х;0)) для каждого начального
состояния x(0)gX0 равна оптимальному значению целевой функ-
ции /V шагов, т. в. всего процесса, начатого из состояния х(0\ то
оптимальное начальное условие х(О>*^^о находим из соотношения
Вх(х^*)® extr Bi(x(0>)	(20)
*(0)ех0
(если множество Хо из (14) состоит из единственной точки х(0\ то
полагаем х(б)*=х((>)).
101
Далее, используя найденные условные оптимальные управле-
ния, а также уравнения состояний (12), последовательно находим
gO)*,	н{2)*, х121*, ...» x{Ny* из следующих соотношений:
д(1)* — иа}* (х(0)*),	х<Д)* =/(Х) (х(0)*,
ЯС2)* = ^2)*	=f&> (Х<Х)*, Л<^*),	(21)
(x(JV"X)*, я(ЛГ>*)*
Алгоритм метода динамического программирования.
Этап I (условная оптимизация).
Ша г 1. Находим условное оптимальное управление tt(Af)*(x<jV”X))
и функцию Веллмана Вдг (х^”1*) в соответствии с (16), (18).
III а г 2. Используя результаты первого шага, находим
дсЛГ-хн^ЛГ-й) и	с помощью равенств (17) и (19) при
6 = /V — l.
Шаг N. Используя результаты (А—1)-го шага, определяем
д(1)*(х(0)) и Bi(x<0)) в соответствии с (17) и (19) при 6=1.
Этап II (безусловная оптимизация).
Шаг 0. Находим оптимальное начальное состояние х(0)* в соот-
ветствии с (20).
Шаг 1. Определяем оптимальные управление д(1)* и конечное
состояние х(Х)* первого шага процесса по формулам (21).
Шаг 2. Используя результаты предыдущего шага, находим
и х<2>* в соответствии с (21). .
Шаг С помощью результатов (JV — 1)-го шага определяем
и x(N)* по формулам (21).
Окончательно имеем =	х* = {х(0)*, ...,xtiV,s‘}.
Пример 2. Методом динамического программирования ре-
шить задачу из примера 1 со следующими исходными данными:
JV = 3, Л1 = 63, m=l, F (у, z)~z/y.
Для указанных исходных данных многошаговая задача оптими-
зации примера 1 формулируется следующим образом:
з
JCx, S)=£
fe=l
=	+ «(*>, 6=1, 2, 3,	(22)
x^g(l; 64],	6=1,2,
63],	6=1, 2,3,
^ = 1, '	^ = 64.
Определим множества Uиз (10)4
£Л(х<*-а>) = {ц<А>€[0; 63! I	64]}=Ю; 64—x<*-q,
6=1, 2, 3, так как /Л“Х)^1.
Проведем вычисления по методу динамического программиро-
вания в соответствии с описанным выше алгоритмом.
Этап I (условная оптимизация).
\	М3)'
Шаг 1. Из (16) находим В3 (х<^)= max -757. Так как
«<?>€ [0; 64-х<2)] Х ~
= при всех	64] является возрастающей
102
функцией аргумента м(3), тоее максимум достигается при макси-
мально возможном значении т. е.
(Х<2>) ~ 64 — X 2).	(23)
Тогда
В3 (**>) = Z3 и™*.	(24)
Ша г 2. В соответствии с (17) при 6 = 2 с учетом (24) и (22)
получаем
В2(х{1})— шах
tf(2,€ lO; 64-х(1)]
64—х*1' — ^
I Ifi* \
х<*J •
Найдем точку
64— х*1*—
ЛЧ А) 4-^(2)
максимума tz(2)* (х*^) функции Z2 (х(1), и(2)) ==
2)
на отрезке (0; 64—х(1)} в зависимости от х(Х).
Для определения стационарных точек функции	п(2>)
решим уравнение
__(и(2))г+2ц(2)ха) —(Xе11)8—64Х11* _
ди(2}	х11'(ха,4~ и'2))а	~ ’
а(2)£(0; 64 —х<*>|,
откуда получим
«<« (^1)0=8 К*17—	(25)
(очевидно, и{2} (x^^gfO; 64—x(1)J, так как х(Х)<;64).
Сравним значения функции Z2 (x<w, н(?>) в точке (x^fo из (25)
и на концах отрезка (0;64—х^}:
a) Za(x<4 0)=-^--1; б) 2а(хЧ 64—x(J))=0;
в) Z, (*», и™ (*»),) = 2 ( -£= -1У
\у х^ /
Отсюда следует, что Z2(xtlJ, 64—x(1J) Z2 (хц>, О)<
<Z2(x<4 w(2)(x(1%) при x(X)g[l; 64J (проверьте!). Поэтому
«<«>* (л<1>) = и<?) (л>х>)0=?8 УТ*7— х<1>	(26)
И
68 (х<»>)«Zt (х<», «<»•	.2 (-Д=^~ 1У (27)
\К x(i) /
Шаг 3. Учитывая равенства (27) в (22), из (17) при &«1
получаем
[/ я \
2( г,_—I }4-~й» L
Как и на втором шаге, исследуя функцию Z1-(x(e\ и(1)) =
(8	\
о) 4-	1 на максимУм по м<1> на отрезке
IV; 64 —хс>] (проведите исследование самостоятельно!), получим
ию* (х‘*>) = 4 (х<*)2'3—х<°>,	(28)
В1(^О)) = 12(х4°>)-1/зявЗ.	(29)
103
Этап II (безусловная оптимизация).
Шаг 0. Так как множество Хо состоит из единственной точки
х(0>=1, то полагаем
(30)
Шаг 1. Из формул (21) с учетом (28), (30) и (22) находим
(1) = 3,	0)*+м(1)* = 4.
Шаг 2. Аналогичным образом из формул (21), (26) и (22)
получаем
W(2)»= w<2)» (4) == 12,	16.
Шаг 3. Используя равенства (21), (23) и (22), находим
w(3)*=	(16) = 48,	г?3>* = 64.
Окончательно получаем н*={3, 12, 48}, х*={1, 4, 16, 64}.
Таким образом, массы верхней, средней и нижней ступеней ракеты
должны равняться соответственно 3\ 12 и 48 единицам.^ При этом
межпланетная станция достигнет максимально возможной в данных
условиях скорости, равной В1(х(0)*) = 9 единицам (см. формулы
(29), (30)). >
Задача, рассмотренная в примере 2, свелась к непрерывной
модели многошагового процесса оптимизации. В этой модели управ-
ления векторы состояний х№ и другие величины могут не-
прерывно изменяться на соответствующих множествах.
Для многих экономических и производственных задач харак-
терной является дискретная модель, предполагающая, что величины,
описывающие процесс, могут принимать только дискретный ряд
значений. Функциональные зависимости в таких задачах задаются,
как правило, в виде таблиц, а не аналитически. Однако общая
схема их решения методом динамического программирования
остается без изменений.
Пример 3. Общая сумма в 4 млн. руб. распределяется между
тремя предприятиями в количествах, кратных 1 млн. руб. В резуль-
тате выделения средств £-му предприятию в размере и оно дает
доход J#(u), £=1> 2, 3, величина которого может быть найдена
из таблицы 5.1.
Таблица 5.1
и	0	1	2	3	4
А(«)	0	5	9	11	12
(«)	0	4	8	12	14
Л(“)	0	7	9	10	И
Распределить средства между предприятиями так, чтобы их
суммарный доход был максимальным.
<4$ Обозначив средства, выделенные £-му предприятию (£ = 1,2,3),
символом а сумму средств, выделенных предприятиям с номе-
рами от 1 до £, символом х№> сформулируем рассматриваемую
104
задачу как многошаговую задачу оптимизации (11)^-(14):
з
J(x, 2)=2	max,
Л;(А)==Х(А-1)4.иШ>	^=г1> 2, 3,
u(A)g[O; 4—%<*-*)] Л z, Ы, 2, 3,
х(О)=о,	х<3) = 4.
Для решения этой задачи применим метод динамического про-
граммирования.
Этап I (условная оптимизация).
Шаг 1. Найдем В3(х№)*= max	Так как
«<8><= [0; 4-х<2>1 п
функция Z3 (х(2>, ru(3)) = J3 (w(S)) является возрастающей функцией
аргумента м(3) (см. таблицу 5.1), то ее максимум достигается при
максимальном допустимом значении и№, т. е.
а(3)* (х<?)) = [4 —*(?)] 1).	(31)
Отсюда В3 (х<2)) ==Z8 (tf2), и(3)* (х<2>)) = J3 ([4—tf2)]). Значения
В3(х<2)), найденные с помощью таблицы 5.1 представлены в табли-
це 5.2.
Таблица 5.2
х<2>	0	1	2	3	4
Вз (*<2))	11	10	9	7	П
Ш а г 2. Вычислим
В2 (х<*>) =	max	{В3 (х™ + и&) + /а (^2>)}.
«(2, «[0; 4-*(1)] п Z
Для нахождения максимума функции Z2	(*(X)+^U))+
+ J%(u(2)) составляем таблицу 5.3 значений этой функции, исполь-
зуя данные таблиц 5.1 и 5.2.
В таблице 5.3 рамками обведены максимальные по зна-
чения функции Z2(*(X)> u(?))> соответствующие различным зна-
чениям х(1).
Используя таблицу 5.3 находим функции В2(х<1)) и (x(i))»
представив их значения в таблицах 5.4 и 5.3.
Ш а г 3. Так как множество Хо состоит из единственной точки
х(0) = 0, то найдем только (0) и и<1)*(0):
Bi(0)= max	(B3(0 + u^) + Ji(u^)}.
e [0; 4]^n 25
Для определения максимума в правой части последнего равенства
составим таблицу 5.6 значений функции Z2 (0, «(1))=»Ва (и(Х,)+Л («(1))>
которые найдем с помощью таблиц 5.1 и 5.4.
Из таблицы 5.6 видно, что Bi(0) = 20, причем ^1,*(0) = 1 или
и(1)*(0) = 2, т. е. в данной задаче существует два оптимальных
управления и две оптимальные траектории.
х) Напомним, что символом [а] обозначается целая часть числа а.
105
Т а б л и ц а 5.3
Этап II (безусловная оптимизация).
Шаг 1. а) Пусть	Тогда xa>* = x(°)*4-u<1>* = 1.
б) Пусть п'Х)*=2. Тогда x(1)*=xl0):5 + u(1>-=2.
Шаг 2. а; Для	имеем и(2,*=г/(?)*(1) = 2 (см" табли-
цу 5.5),
б) Дли х'1* = 2 получаем	(2)= I (см. таблицу 5.5),
Шаг 3. Так хак для обеих оптимальных фазовых траекторий
то из (31) находим w<®*=u^(3)~l, хс^*==х(®*4^*=4.
Окончательно получаем 2*={1, 2, 1} или 2*«={2» 1, 1} и соот-
ветственно х*=={0, 1, 3, 4} или х*«я{0, 2, 3, 4}.
Таким образом, существуют два оптимальных варианта рао
пределения средств предприятиям:
106
Первый вариант: первому предприятию выделяется 1 млн. py6<f
второму—2. млн. руб. и третьему — 1 млн. руб.;
Второй вариант: первому’—2, второму—1 и третьему—1 млн. руб*
В обоих случаях суммарный до ход предприятий составит
в 20 млн. руб. ►
В условиях задачи 16.340 решить задачи 16.350—16.351
об оптимальном распределении средств предприятиям со
следующими исходными данными.
16.350.	S = 5 млн. руб., # = 4. Средства предприятиям
распределяются в количествах, кратных 1 млн. руб. Функ*
ции Л(и)> k—\,	4, заданы следующей таблицей:
и (МЛН. руб.)	0	1	2	3	4	5
	0	1,5	2	3.5	5,5	9
7?	0	3	4,5	5,5	5,5	7,5
7 з (и)	0	4	5	5,5	6	9
(«)	0	2	3	4	6,5 '	. 8
16.351. S — 5 млн. руб., N—5. Средства распределяются
в количествах, кратных 1 млн. руб. Функции
А — 1,	4, заданы таблицей из условия задачи 16.350,
а функция Js (и)—следующей таблицей:
и (млн. руб.)	9	1	2	3	4	5
Л (и)	0	3	4,5	6	7,5 i	3,5
16.352. 5 = 100 тыс. руб., N—4. Средства каждому нред-
приятию выделяются в количествах, ^кратных 25 тыс. руб.,
но не могут превосходить 50 тыс. руб. Функции /*(«),
Л=1, ... 4, заданы следующей таблицей:
(тнс. руб.)	0	25	50	75	100
J1(M)	0	12	14	20	28
J2 (W)	0	12	18	24	30
А («)	0	12	16	24	30
7 4 (я)	0 ,	8	12	16	24
107
В условиях задачи 16.341 решить задачи 16.353 —
16.357 об оптимальном выделении средств предприятию
в течение N лет со следующими исходными данными.
16.353.	5 = 500 тыс. руб., М = 4. Средства, выделяемые
в течение каждого года, кратны 100 тыс. руб. Функции
Jk(u) представлены в таблице.
и (тыс. руб.)	0	100	200	800	400	600
А(«)	0	40 ,	70	104	120	136
J2 (U)	0	50	80	96	112	124
J»(u)	0	34	76	100	НО	120
Ji («)	0	60	90	100	110	136
16.354*	. Найти решение задачи 16.353, если начальная
«умма S
а)	уменьшена на 100 тыс. руб.;
б)	увеличена на 100 тыс. руб. при следующих допол-
нительных данных о прибыли предприятия при выделе-
нии ему в течение k-ro года средств в размере 600 тыс. руб. 5
k	1	2	3	4
At (600)	146	132	130	144
16.355, 5=400 тыс. py6.,Af = 4. Выделяемые в течение
k-ro года средства кратны 20 тыс. руб. и не могут пре-
восходить 200 тыс. руб. Функции /6(«) заданы таблицей
и (тыс. руб.)	0	20	40	60	80	100	120	140	160	180	200
Ji («)	0	10	20	40	100	160	180	190	200	210	215
J2 (U)	0	20	40	60	80	95	101	102	103	104	105
	0	5	10	15	25	37	69	140	225	280	300
Jl{u)	0	30	68	95	140	160	170	175	176	177	178
16,356, 5 = 300 тыс. руб., N = 3, функции Jk («), k =
el, 2, 3, определяются следующим образом:
a)	(и) = Jt (и) = Jk (w) = 10 — 10-а. (W _i oo)?;
108
б)	Л (м) = J. (и) = 24—Q- 10-* (и — 200)2,
7я(м) = 16—4-10-1(и—200)2.
16.357.	S= 150 тыс. руб., jV = 3, Jj(m) = 0,12u, J2(m)=j
= 0,0012м2, J3(и) = 0,36a —0,0024м?.
16.358.	Найти решение задачи 16.342, если/7 = 3, S = 9.
16.359.	Найти решение задачи 16.342 с произвольными
исходными данными.
16.360.	Найти решение задачи 16.343, если F(u) — cu,
с > 0.
16.361.	Найти решение задачи 16.343 при следующих
исходных данных: F (м) = 0,1м?, 4 = 5, а = 4, N = 3.
16.362.	Найти решение задачи 16.344, если F(u) = cu,
с > 0, Ааа > Ь.
16.363.	Найти решение, задачи 16.344 при следующих
исходных данных: Р(н) = 0,1м?, Л = 5, м = 4, b = 5, N = 3.
16.364.	Найти решение задачи 16.345 со следующими
исходными данными: W = 4, S = 200 тыс. руб., J1(m)=0,3m,
72(м) = 0,4м, /1(м) = 0,8м, /2(м) = 0,5м.
16.365.	Найти решение задачи 16.345 при следующих
исходных данных: N = 3, S— 120 тыс. руб., /1(м) = 0,4м,
/2(м) = 0,6м. Выделение средств предприятиям происходит
в количествах, кратных 20 тыс. руб., а функции Ji(u)
и J2(m) заданы следующей таблицей:
и (тыс. руб.)	0	20	40	6С	80	100	120
71 (и)	0	5	8	12	14	15	16
и)	0	3	5	8	12	14	15
16.366.	Найти решение задачи 16.346 со следующими
исходными данными: Р=10, М = 4, а = 0. Коэффициенты
ак и &=!,..., 4, представлены в таблице:
k	1	2	о	
	10	15	10	6
	7	12	9	8
Считать, что к концу рассматриваемого периода база
должна быть освобождена от продукции.
16.367.	Найти решение задачи 16.346 при следующих
исходных данных: Р— 12, М = 4, а = 5. Значения коэффи-
109
циентов aft, pft, k=\, ..., 4, приведены в условии зада-
чи 16.366.
Считать, что- к концу рассматриваемого периода на базе
должно остаться 4 т продукции.
Используя результат решения задачи 16.349, решить за-
дачи целочисленного линейного программирования 16.368 —
16.371 методом динамического программирования.
16.368.	F(u) —— 4и{1}—3«(?>—» min,
4 u(l)+	10,
2 «(u-|-3u<?’<8,
иа\	m,2)€Z.
16.369.	F(«) = —uU)—u(?’—»min,
иш<2,
2 ыа> + 3м(?’<5,	. "
ua\ ua>, u<?’£Z.
16.370, F(») =—llu<?’-^ min,
ua,<5,
4mu> + 3m<?) < 10,
u<«4-2m<S><8,
uU),	un), a«’€Z.
16.371.	F(tl) =— uwr—2u^}—3m<?) —> min,
6 u<i> + 4«<?’ + 3u(3’<25,
5 «<«+3w<?) + 2u<»’<15,
a'»>0; u<*>eZ, k=l, 2, 3.
16.372.	Имеется 7 т сырья, пригодного для производ-
ства изделий трех видов. Для изготовления одного изде-
лия каждого вида требуется соответственно 1, 2 и Зтсырья.
Расходы Jk (и) на производство и изделий k-ro вида,
k—l, 2, 3, приведены в таблице (значения Jк (0) характе-
ризуют штраф, выплачиваемый в случае, если изделие
k-vo вида не производится).
и	0	1	2	3 z	4	5	6	7
h («)	40	30	25	21	17	14	11	2
' 72 °0	55	40	29	I1	—	—	—	—
J 3 (w)	70	50	35		—	—	—-	—
Спланировать выпуск изделий так, чтобы затраты на
их производство были минимальны.
16.373.	Судно грузоподъемностью Ют загружается кон-
тейнерами трех типов. Массы контейнеров различных типов
110
и стоимости грузов в них составляют соответственно 860 кг,
720 кг, 600 кг и 516 руб., 360 руб,, 240 руб.
Найти количества контейнеров каждого типа, которые
необходимо загрузить, чтобы стоимость грузов на судне
была максимальной.
16.374.	Имеется 9 однотипных станков, каждый из
которых можно наладить на производство изделий одного
из трех видов. Зависимость количества изделий каждого
вида, изготовленных за смену, от количества станков, за-
нятых для их производства, приведена в таблице.
Число станков
Вид изделия	1	4	3	4	5	6	7	а	9
1	14	18	22	26	32	38	42	48	50
II	Ю	18	24	28-	30	36	40	44	54
ш	12	20	26	30	32	36	42	44	50
Найти количества станков, которые необходимо исполь-
зовать для изготовления изделий каждого вида, чтобы
общее число произведенных изделий было максимальным.
§ 6. Вариационное исчисление
I. Предварительные сведения. Простейшая задача вариационного
исчисления. Существует ряд прикладных задач оптимизации, в кото-
рых качество выбранного решения не удается охарактеризовать
с помощью целевой функции. Числовой показатель качества в этих
задачах зависит от функции (а не от одной или нескольких пере-
менных), определить которую необходимо так, чтобы этот показа-
тель принял минимальное или максимальное значение. Числовыми
показателями в указанных задачах являются функционалы.
Определение. Если каждому элементу у = у(х) множест-
ва G из некоторого функционального пространства X поставлено
в соответствие определенное число /, то говорят, что на множестве
G cz X задан функционал J (у) sb J [у (х)].
В качестве функциональных пространств X в вариационном
исчислении используются пространства Сд[а; 6J, которые опре-
деляются следующим образом.
Линейное нормированное пространство Сп[а*, 6], n==0, 1,
состоит из функций у(х), имеющих на отрезке [а; Ь] непрерывные
производные && (х) до п-ro порядка включительно1), с нормой
п
вуи«= S max
__	/?=о х € ь]
*) Под производной {х) нулевого порядка здесь понимается
сама функция у (л).
Ш
Расстояние р(уъ Уъ) между функциями (кривыми) yi (х) и у2 (х)
в пространстве Сп [а; 6] определяется формулой
п
р(У1, У2)п = ИУ1 — Ып = 2 max	wl. П—О, 1. ...
k=Ox^l“i Ь]
Пусть функция у* (х)£Сп(а\ 6] и е > 0 —произвольное число.
Множество функций (кривых) у (х)£Сп(а9, Ь], для кот?фых выпол-
няется неравенство
Р (у*. У)п < 8.
называется окрестностью п-го порядка кривой у*(х).
Говорят, что функционал J[#(x)J достигает на кривой у* (х)
локального или относительного минимума (максимума), если для
всех у (х) из некоторой е-окрестности кривой у* (х) выполняется
неравенство
J ly* Wl < J \у W] (/ {у* W1 J 1у (х)]).	(1)
Локальные минимумы и максимумы функционала I [у (х)] назы-
ваются его локальными экстремумами.
Если (1) выполняется для всех кривых у(х), принадлежащих
некоторому множеству G cz Сп [а; 6], то говорят^ что на кривой у* (х)
достигается абсолютный экстремум функционала J [у (x)J на мно-
жестве G.
Пусть функционал J (х)] определен на множестве G с Cf [а; 6].
Функции y(x)£G можно рассматривать не только как элементы
пространства Ci [а; 6], но и как элементы Со [а; Ь]. Локальный
экстремум функционала J [у (x)J в пространстве Со [а; 6] называется
сильным, а в пространстве Ci [а; 6]—слабым локальным экстрему-
мом. Всякий сильный экстремум функционала является и слабым,
а обратное, вообще говоря, неверно.
Отметим, что всякий абсолютный экстремум функционала
J [у W1 является сильным и слабым локальным экстремумом, но
не всякий локальный экстремум будет абсолютным.
Сформулируем простейшую задачу вариационного исчисления.
Пусть функция F (х, у, г) имеет непрерывные частные произ-
водные до второго порядка включительно по всем своим аргумен-
там. Требуется среди всех функций y(x)£Ci[a\ &], удовлетворя-
ющих граничным условиям
У(а)—Уо> y(b)=yi,	(2)
найти ту функцию, на которой достигается слабый экстремум функ-
ционала
ь
J \у (*)] = J Р (X, у, у') dx.	(3)
а
Другими словами, простейшая задача вариационного исчисле-
ния состоит в отыскании на множестве всех гладких кривых, про-
ходящих через точки /Ио (о, yQ) и Mi (b, уг), той кривой, на которой
функционал (3) достигает слабого экстремума.
При решении простейшей задачи вариационного исчисления
используется следующая теорема.
Теорема 1. Для того чтобы функционал (3) достигал на функ-
ции у (x)gCi [а; Ь] слабого экстремума, необходимо, чтобы эта функ-
112
ци» удовлетворяла уравнению Эйлера
f«-S^=o.	«I
Решения (интегральные кривые) уравнения (4) называют экстре-
малями функционала (3).
Уравнение (4) в развернутом виде записывается следующим
образом:
У* W Fy'y + у' (х) Fyy> + Fxy — = 0.
Если	то оно представляет собой обыкновенное дифферен-
циальное уравнение второго порядка, поэтому его общее решение
зависит от двух произвольных постоянных, которые находятся
с помощью граничных условий (2).
Отметим, что так как всякий сильный экстремум функционала
является и слабым, то теорема 1 дает необходимое условие и силь-
ного экстремума функционала (3).
Кроме того, так как абсолютный экстремум функционала (3)
на множестве
G = {у (х) g Ct [а; b] | у (а) = у0, у (b) = yt}	(5)
является и локальным экстремумом (сильным и слабым), то тео-
рема 1 определяет необходимое условие абсолютного экстремума
функционала (3) на множестве (5).
Таким образом, решение краевой задачи
F(a) = Fo> ytty — yi
позволяет найти все кривые возможного экстремума функционала (3)
на множестве функций (5).
Пример 1. Найти гладкие экстремали функционала
I
J 1у (*)1= $	12*f) dx>
о
удовлетворяющие граничным условиям f/(0)=0,
В данном случае F (х, у, /) == у'212ху, поэтому уравнение
Эйлера (4) имеет вид z/"4-6x—0. Era общее решение у(х) = —х3+
+ Cix+C2. Из условий у (0) = 0,	= 1 получаем систему урав-
нений для определения С\ и С2:
у(0) = С2 = 0,
у (i)=-—i	с*2=1,
откуда находим Cf=2, С2 = 0. Следовательно, в рассматриваемой
задаче существует единственная экстремаль у(х)==— х?+2х, ►
Решение задачи (6) существует не всегда, а если оно сущест-
вует, то может быть не единственным?
Пример 2. Найти гладкие экстремали функционала
2
(*)]=»{ (4x-y}ydx,
1
удовлетворяющие граничным условиям у(1)==1, у(2]==3.
113
Уравнение Эйлера имеет вид х —// —0. Так как функция у(х)^х
условию у (2) = 3 не удовлетворяет, данная задача не имеет решений.
Пример 3. Найти гладкие экстремали функционала
л
J 1У (*)]= $ (у'*~У*)4х,
о
удовлетворяющие граничным условиям у(0) = 1, #(л) =—1.
<4^ Уравнение Эйлера имеет вид у*+у = О, а его общее решение
у (x) = Ci cos х + С2 sin х.
Используя условия t/(0) = l, £/ (jt) = —1, находим #(x) = cosx +
4~Csinx, где С—произвольная постоянная.
Таким образом, данная задача имеет бесконечное множество
решений. ►
В задачах 16.375—16.384 найти все экстремали функ-
ционала J (у), удовлетворяющие указанным граничным
условиям.	j
16.375.	J(y)=i(y't + xy)dx-, (/(0) —г/(1) = 0.
о
Л,-
16.376.	J(y)=^(4ycosx + y'i—yi)dx-, у (0) = у (л) = 0.
о
е
16.377.	J(y)=^(2y-x*y'*)dx-, у(\) — е, г/(е) = О.
1
1
16.378.	J(«/)=$(/’ + уу' + I2xy)dx; у (0) =//(1) = 0.
О
1
16.379.	J(у) = § (е« + ху') dx-, у(0) = 0, «/(!) = 1.
О
1
16.380.	J (у) — (у'*+у-+ ху) dx; г/(б) = у(1) = 0.
О
1
16.381.	J (у) = $ (у'г + уг+Ьу sh 2х) dx", у (0) = 0, у (1) = 1.
о
1
16.382.	/(«/) =	+	У(0)=0,«/(1) = -^.
О
'	hi 2
16.383.	Цу)~ J W' + W^dx-, £f(0)«=0,y(ln2)=^.
О
ь
16.384,	J{у) = $ (у'* +у-—4у sin x)dx-, у(0) «О, y(b) = yf.
О
114
16.385.	Показать, что функционал j [р(х)/+ <?(*)#+
а
4.	г (х)] dx, где р (х) € С\ [a; b], q (х), г (х) £ Со [а; &], не имеет
экстремумов.
Уравнение Эйлера (4) не ^всегда интегрируется в квадратурах,
а в ряде случаев его решение может вызвать затруднения. Пере-
числим частные случаи, в которых решение уравнения Эйлера
упрощается по сравнению с общим случаем.
1.	Функция F из (3) не зависит от /, т. е. F = F(x, у). Урав-
нение (4) в этом случае принимает вид Fy (х, е/)=0. Это конечное
(не дифференциальное) уравнение, его решение не содержит про-
извольных постоянных и, следовательно, удовлетворяет условиям
(2) только в исключительных случаях.
2.	Функция F зависит только от у'". F = F(y'). Уравнение Эй-
лера принимает вид F^/-/' = 0, а его общее решение у (х)=Схх + С2.
Таким образом, в данном случае экстремалями функционала J (х)]
являются всевозможные прямые.
3.	Функция F не зависит от yt т. е. F = F(x, у'). Тогда урав-
нение (4) записывается в виде ^F^'(x, Р*) —0» откуда получаем
первый интеграл уравнения Эйлера Fy> (х, /) = Cf, т. е. дифферен-
циальное уравнение первого порядка, решив которое, найдем экстре-
мали функционала.
4.	Функция F не зависит явно от х, т. е. F~F(y, у'). Урав-
нение Эйлера принимает вид Fy—Руу’у' —Fy'y>y"=Q или (после
умножения обеих частей этого равенства на у') ^(F-—/F^)—О,
откуда получаем первый интеграл уравнения Эйлера F—yfFy — Ci.
Это дифференциальное уравнение первого порядка можно проин-
тегрировать, разрешив его относительно у1 и разделив переменные,
или путем введения параметра.
Найти экстремали следующих функционалов J (у),
удовлетворяющие указанным граничным условиям.
16.386.	=	1/(0) = 1, у(1)=е.
о
1
16.387,	J (у) — J (е*+»~у—sinx)dx; #(0) = 0,#(1) = —1.
о
1
16.388.	=	f/(0) = 0, у(1) = 1.
о
1 ._______
16.389.	•/(//)=[ V ^У'г dx-, t/(-l) = 0, г/(1) = 1.
-1 у
3/2
16.390.	J (i/)=| (/’ + 2x)dx; t/(0) = 0,
115
1
16.391.	/(«/)= $ (xy' + y'^dx-; y(-l) = l, y(l)-0.
— 1
2
16.392.	J(y) = §xny’*dx, n^N, n^l; «/(1) = -^,
1
16.393.	J(t/) = $(t/-y'a)rfx; y(0) = y(l) = 0.
0
1
16.394.	J(y)^yy'dx-, t/(0) = l, z/(l)=p/4.
0
л/2
16.395.	J(y)= j (2y + y*-y's)dx-, z/(0) = ^(y)=0.
0
В ряде случаев существование абсолютного экстремума функ-
ционала (3) на множестве функций (5) и его характер (минимум
или максимум) бывают очевидны из физических или геомет-
рических соображений. В таких случаях необходимое условие
экстремума, сформулированное в теореме 1, позволяет найти функ-
цию у(х), дающую абсолютный минимум или максимум функцио-
налу (3) на множестве (5).
Пример 4. Найти гладкую кривую на плоскости, соединяю-
щую две данные точки MQ (а, А) и Mi (b, В) и имеющую минималь-
ную длину.
Длина дуги гладкой кривой, описываемой уравнением у~у(х)
и проходящей через точки с абсциссами а и Ь, равна V l-\-yf2dx.
а
Поэтому данную задачу можно сформулировать следующим
образом: найти функцию у(х), минимизирующую функционал
ь _____
Цу(х)]=^1 + у'*<1х	(6)
а
и удовлетворяющую условиям у (а) —А, у(Ь)~В.
Уравнение Эйлера для этой задачи имеет вид ^"(х) = 0, откуда
=	Найдя Ci и С2 из условий на функцию у (х) при х~а
и получим	(х —<z)4-At т. е. необходимое условие
экстремума функционала (6) выполняется на прямой, соединяющей
точки Мо и Мр
Из геометрических соображений ясно, что среди гладких кри-
вых, соединяющих данные точки, кривая минимальной длины должна
существовать, а кривая максимальной длины —нет. Поэтому упо-
мянутая прямая и является искомой кривой.
116
16.396.	Материальная точка перемещается вдоль плоской
кривой у — у (х), соединяющей точки Ма(а, Л) и Mi(b, В)
со скоростью v — ky'. Найти гладкую кривую, время дви-
жения вдоль которой из точки Мо в точку Mi будет мини-
мальным.
16.397.	Решить задачу 16.396, если А4о = (О, 0), Mf=*
= (1, 1), и = х.
16.398.	Среди гладких кривых, соединяющих точки
Мо(О» 1) и Alj(1, 1), найти ту, которая при вращении
вокруг оси Ох образует поверхность наименьшей площади.
16.399*	*. Задача о брахистохроне. Найти гладкую кри-
вую, соединяющую точки М„ (0, 0) и (xit z/i), при ска-
тывании вдоль которой под действием силы тяжести мате-
риальная точка, зафиксированная первоначально в точке Мо,
переместится в точку Afj за минимальное время (трением
и сопротивлением воздуха пренебречь).
2.	Обобщения простейшей задачи вариационного исчисления.
Ниже рассмотрены два обобщения простейшей задачи вариацион-
ного исчисления. Первым из них является задача на экстремум
функционала J [у (х)], зависящего от производных высших поряд-
ков функции у(х):
ь
Jly(x)] = ^F(x, у, £<» y(n))dx,	(7)
а
гд& функция F (х, у, ♦	имеет непрерывные частные произ-
водные вплоть до (п+1)-го порядка по всем аргументам, а у(х]£
£Сп[а',Ь].
Граничные условия в этой задаче имеют вид
у(а)=уо. =	.... ^»>(а) = А
У (Ь) = У(, j/l> (ft) = .У™ (*) = уГ\	' '
Приведем обобщение теоремы 1 применительно к рассматривае-
мой задаче.
Теорема 2. Для того чтобы функционал (7) достигал на функ-
ции у (х)£Сп[я; локального экстремума, необходимо» чтобы эта
Функция удовлетворяла уравнению Эйлера—Пуассона
d	d2	Я»
FV F ~d^	‘	275	(9)
Подобно случаю простейшей задачи вариационного исчисления,
решения уравнения (9) (экстремали функционала (7)), удовлетворяю-
щие граничным условиям (8), являются кривыми возможного абсо-
лютного экстремума этого функционала на множестве
G={'/W€cn[o; ftll^(a)=ffo, ....	У(Ц=У1, ...
.... «<•> ДО-*«’}•
117
Пример 5. Найти экстремали функционала
1
/(*<*)] = piaoxy-/')<&,
0
удовлетворяющие граничным условиям
^(0) = /(0)-0, ^(1)= 1, /(1)=6,
Запишем уравнение Эйлера — Пуассона: ^ = {20х. Его общее
решение у (x)=x^CiX3-^С2х2+ С9х+С4. Отсюда с помощью гра-
ничных условий получаем систему уравнений для определения
остоянных Ci, ,**, С4:
С4=0,
с3=о,
£i 4* 4~ Сз 4~ == о,
3Ci -|- 2С3 -j- С3 = 1,
из которой находим Сх = 1, С2 = —1, С3 = С4— 0. Поэтому экстремум
функционала может достигаться на кривой у (х)—х^х3—х2.
В задачах 16.400—16.411 найти все экстремали функ-
ционала J (у), удовлетворяющие указанным граничным
условиям.
16.400.	J (у) = $ tf dx-, у (0) = у (1) = у' (1) = 0, у' (0) = 1.
о
I
16.401.	J (у) = j (48//-/‘) dx-, у (0) = у' (0) = 0,у (1) = 1,
0’(1) = 4.
1
16.402.	J (у) ~ J (/‘-24х//) dx; у (0)«у' (0)_0, у (1)«
О
я/2
16.403.	J(y)= $ (y^—yl*)dx; #(0) = «/'(0)=0,	)=
Л f / JT \	/4
-2’ « ' \2 )-0-
b
16.404.	J (y) - $	+y!2) dx;	у (0) ~ у' (0) == у (b) =
о
16.405.	J(y)^e’*!fdx; !/(0)=0, /(0) = 1, y(l)=e,
/(1)=^. , °
lie
16.406.	J(y) = \(x+tfy^dx', [/(O) = l, /(O) = —I,
0
/14	1	*
У (1) — 2 » У ~~	4 ’
л/2
16.407.	J (y) = J 0,”1	у (0) = 1, у' (0) -
О
/ Л \ Г\ f / Л \	«
~^2j=0, Ц2-)=-1.
1
16.408.	J (y) = J y"’* dx; у (0) = у' (0)« у" (0)=0, у (1) -
О
₽1,/(1)=4./(1)=1.2.
1
16.409.	J(y) = J(/"1-/g)dx; z/(0) = /(0)^0,j/'(0)“
О
= 1, 0(l) = /(l)=shl, /(l) = chl.
Я
16.410.	J (у) = $ (y',fl-y^ dx; у (0) = / (0) = / (0) = О,
О
г/(л) = л, /(л) = 2, /(л) = 0.
Л
16.411.	J(y) = l (y'^-y'^dx; i/(0)~/(0)~У(0) = 0,
о
#(n) = «/*(n)==sh л, /(n) = chn-|-l.
Другим обобщением простейшей задачи вариационного исчис-
ления является задача об экстремуме функционала, зависящего От
нескольких функций:
ь
J IУ1 W....Уп (*)) = $ F (х, д± (х).уа (х), д[ (х).. (х)) dx,
а
(W
где функция F(...) имеет непрерывные частные производные до
второго порядка включительно по всем своим аргументам й уь{х)£
£С1[а; &J, £==1, .п.
Граничные условия в этой задаче имеют вид
«?*(“) = Л0)’ Vk4>Y=y$\ fe = l, .... п.	(И)
Теорема 1 для данного случая обобщается следующим образом.
Теорема 3. Для того чтобы набор функций yi (х)> * •., у№ (х) £
£Ci [а; 6] доставлял слабый экстремум функционалу (10), необходимо9
чтобы эти функции удовлетворяли системе дифференциал ь-
и-ых уравнений Эйлера
Fu -%-F ,=0.	&=1, .<> я.	[12)
dx	,
119
Пример 6. Найти функции yt(x) и уг(х)^Су\а\ Ь], на кото-
рых может достигаться экстремум функционала
Л/2
Ы*)]= J Gi +у^^У1Уг)^х
О
при граничных условиях yi (0) = у2 (0)»0,	(л/2)==#2 (л/2)== 1.
Система уравнений Эйлера имеет вид
^' + {/2 = 0.
Исключая из второго уравнения функцию у2 =— Уъ получим
i/i4)—У1 = 0. Общее решение этого уравнения имеет вид у± (х) «а
« Сце* 4- С2е + С$ cos х+С4 sin х. Отсюда находи м
у2 (х) = — у" (х) == — Cte*—С2е“*+С2 cos х-f- С4 sin х.
Из граничных условий следует, что Ci=C2 = C3 —0, С4 = 1,
поэтому yt (х) = sin х, у2 (х) = sin х.
В задачах 16.412—16.419 найти функции у± (х) и у2 (х) £
gCf[a; Ь], на которых может достигаться экстремум функ-
ционала J (уи Уъ) при указанных граничных условиях.
Л/2
16.412.	J(yt, y2)= l [y'l +y'i +2y1yi)dx; yt(0) =
о
= уа(0) = 0, ^(л/2) = 1, t/s(n/2) = —1.
1
16.413.	J (yit y2) = J (y[+y'*—2угуг) dx-, yi (0) = y2 (0) =
0
= 0, i/i(l) = shl, z/2(l) = -shl.
n/2
16.414.	J (yt, y2)= j (.У1У'1—У1У2^х\ t/i(0) = {/2(0) = 0,
0
#1(л/2)я=1, г/2(л/2) = —1.
1
16.415.	J (yb y2) = J (y\y'i+yiy2) dx; yt (0) = y2 (0) = 0,
0
У1 (l). = e, #2(l) = l/<?.
1
16.416.	J(yt, y2'j=^(y'1y'i+Qxyi+l2x2y2)dx; yi(0)~
0
₽l/2(0) = 0, й(1) = !/а(1) = 1.
3
16.417.	J(yif Уг\=\(ху'^-Vy'i +хууу2)^Х, У1(Г).= 1,
У2(3)^0, ^(3)^ In3 + 1.
120
л
16.418.	J (ylt уг) = $ (yf—y‘' + 2y[y!i + 2ylcosx + 2yl)dx,
0
z/i(°) = —УЛ0) = УЛп) = °> !/1(л)=1+л.
16.419.	J (yit y2) = $ (yi + y‘* + 2yJdx, yt (0) ~ y2 (0)’ »= 1,
0
z/i(l) = 3/2f f/2(l) = l.
3.	Задачи с подвижными границами. В задачах вариационного
исчисления с подвижными границами в отличие от ранее рассмот-
ренных задач граничные условия на функцию у(х), xg(a; 6] на
концах отрезка [а; не зафиксированы.
Простейшая задача вариационного исчисления с подвижными
границами состоит в определении функции у (x)gCi [а; Ь] и точек
х0, xig[a; &], xQ < Xi, для которых функционал
J {у (*)]= $ (х* У> У'}dx	(13)
ХО
достигает слабого1) экстремума при условиях
^(Хо)=»фо(^о)>	(И)
(Здесь ф0(х), Ф1(х)ёС1[а; b], F(x, у, г) —заданные функции
и F (х, yt z) имеет непрерывные частные производные до второго
порядка включительно по всем аргументам.)
Эту задачу можно сформулировать и следующим образом.
Пусть на плоскости заданы гладкие кривые ух: г/=®Фо(х) и {/ =
= ф1 (х), xg [а; 6]. Требуется найти такую гладкую кривую у*4у (х),
которая соединяет какую-либо точку кривой yi с какой-либо точкой
кривой уг и доставляет слабый экстремум функционалу (13).
Приведем обобщение теоремы 1 для простейшей задачи вариа-
цонного исчисления с подвижными границами.
Теорема 4. Для того чтобы функционал (13) достигал на
функции y(x)gCi[a; b] слабого экстремума при условиях (Х^Гнеоб*
ходимо, чтобы эта функция удовлетворяла уравнению Эйлера
и условиям трансверсальности
[Г (фо —	/1К\
[F+(ф1—/)' Fy~]XSSXl == 0.
х) Напомним, что слабым называется локальный экстремум
в пространстве Ci [а; Ь]. В задаче с подвижными границами на
кривой у*(х) с абсциссами концов Хо и xl функционал (13) дости-
гает локального экстремума в Ct [а; 6], если существует число
в > 0 такое, что для всех кривых у(х)£С±{а\ д] и точек xQ и Xf,
удовлетворяющих неравенствам [| у* — рОх < е, | Хо — Хо| < 8,
1*1 — Xi | < е, справедливо J (х)] J [у (х)] (локальный минимум)
или J (х)] J [у (х)] (локальный максимум).
121
Таким образом, для определения экстремалей в простейшей
•адаче с подвижными границами необходимо найти общее решение
у(х, Cf, С2) уравнения Эйлера, после чего из условий (15) и урав-
нений
р(*о. Ci, C2) = <p0(x0), y(xi, Ci, C2) = <P1 (*1)	(16)
определить постоянные С± и С2 и концы отрезка [xff; хх].
' Если на одном из концов искомой кривой у(х) задано обыч-
ное граничное условие (у(а) = Уо или y(b) — z/i), то условие транс-
версальности (15) следует записать только для другого конца
кривой.
Частным случаем задачи с подвижными границами является
вадача, в которой задана абсцисса одного из концов кривой у (х),
например х2~ Ь, но граничное условие для х=д отсутствует. Это
означает, что граничная точка (Ь, у (/?)) кривой у(х) может пере-
мещаться по вертикальной прямой х—Ь, и вместо второго условия
Трансверсальности (15) следует записать естественное граничное
условие
[VUb=°-	<17>
Пример 7. Найти экстремали функционала в следующей за-
даче с подвижными границами:
_____
J [у Wl«J К1 +у'2 у М = х*+2> у (*i)=ч*
Так как функция F (х, у, К 1 + у‘2 зависит только от у’„
то общее решение уравнения Эйлера имеет вид
р(х) = С1х+С2.
(18)
Запишем условия трансверсальности (15):
=0,
=0.
Из (18) находим у’ (x0)^yf (xi)=»Cf. Отсюда с учетом равенств
(16) получаем систему четырех уравнений для определения Сь Са,
*о и xt	_____
V l+CH(2s»-Ci) ,/U—.
V i+cf
V i+ci+(i- —£i=^-o,
ri+ci
CiX$ -J- C2 = xi-j" 2>
CfXi C2 ~ Xif
решив которую, находим C5=5—1, C2=ll/4, xB=l/2, xi=»ll/8.
Следовательно» уравнение экстремали имеет вид у(х)=з
, П 1 П
Отметим, что функционал J [# (х)] в данной задаче с подвиж-
ными границами представляет собой длину дуги кривой между

точками (х0, y(xQ)) и (хь у(хх)). Поэтому геометрический смысл
этой задачи состоит в определении гладкой кривой минимальной
длины, соединяющей параболу = и прямую у = ж. Найден-
ное решение позволяет определить расстояние S между указанны-
, 1V8	_______ 7
ми параболой и прямой: 5= \ Y 14-(—IJMxss-s-1^2 < ►
J	о
1/2
Пример 8, Найти экстремали функционала в следующей за-
даче:
Л/4
/[</(*)]= j (/WM*. P(O)-1.
о
В этой задаче отсутствует граничное условие при х-п/^, сле-
довательно, правый конец кривой у(х) может перемещаться по
прямой х=п/4, и необходимо использовать естественное граничное
условие (17).
Уравнение Эйлера имеет вид */"-|-у = 0, а его общее решение
t/(x) = Cxcosx+C2sin х. Из условия p(0)»Ci=l находится по-
стоянная Cf, а из условия (17) 2у'	— sin
=s О — постоянная С2=1, откуда у (x) = cos x-j-sinx.
Найти экстремали функционала в следующих задачах
с подвижными границами.
Xi
16.420.	J (у) — у’1 dx; у (0) = 0, у(х$ = —х^— L
о
Xt
16.421	./(«/) = JZdx; 9(0) =0, у(х^_*
\	Х1 у,— —
16.422.	J(9) = $y l+Z^;9(0) = 0. 9(^х) = 4-.
0
16.423.	=	+	—	5-
Хо
4i
16.424.	J(9) = $ (y-y*)dx; у[0) = 0.
D
16.425.	9(l)>0.
о
16.426.	J(y)= J (у,г-у*)<1х; 9(0) = 0.
о
16,427.	=	^(0) = 0, ^(^) = 1.
о
123
16.428.	/(//) = $	dx-, у (0) = 1, у (Xi) = Xi-1.
0 У
3T/4
16.429.	J (t/)=|j (/’—t/a4-4ycosx)dx; г/(0) = 0.
0
К задачам вариационного] исчисления с подвижными грани-
цами относится и задача Больца, состоящая в определении функции
y(*)£Ci[a; 6], доставляющей слабый экстремум функционалу
ъ
3 [у (*)1 - $ F (*> У> У') dx+f (у (а), у (&)),	(19)
а
Где f(u, о)-»*заданная функция, имеющая непрерывные производ-
ные по и и V,
Необходимое условие экстремума функционала (19) формули-
руется следующим образом.
Теорема 5. Для того чтобы функционал (19) достигал на
функции y(x)£Ci\cr, b] слабого экстремума, необходимо, чтобы эта
функция удовлетворяла уравнению Эйлера
и условиям трансвереальности длязадачи Больца
Условия (20) используются для определения постоянных Cj и
и$ общего решения у(х, Ct, С2) уравнения Эйлера.
Пример 9, Найти экстремали функционала
J [у (Х)]= $ (/2-У?) dx-y* (0) + 2у ( «.).
о	4	'
Уравнение Эйлера уп-[-у~Ц имеет общее решение
у (x)==Ci cos х-\-С2 sinх.	(21)
Записав условия трансверсальности (20)
[2z/' +2y]Xss0 «2 [—Cj sin х + cos x+Ci cos x+C2 sin x]x~ 0»
«2Ci+2C2=0,
(2/+2)хял/2 = 2 [—Ci sin x+Ca cos	l]x=Jt/2 = —2Ct+2 = 0,
находим Ci= 1, C2 =—1. Таким образом, функция y(x) = cosx—sinx
является единственной кривой возможного экстремума функционала
/1Я*)1 ►
Найти экстремали следующих функционалов.
16.430, /(«/) = $ у'гйх+уЦ0)—2у»(1).
124
16.431.	/((/) = $(/+f/2)tto-2shl«/(l).
О
16.432.	J (у) = $ (y,*+y»-4ysinx)dx+2y*(Q)_ +
+ 2i/(n) — у2 (л)..
16.433.	J(y) = J 4/Vdx + ^(0)-8^(3)'.
О
16.434.	/(«/) = $ 2y'(xy' + y)dx+3y^l)-y4e)-4y(el
1
1
16.435.	J (y) = $ e*« (/’ + 2y*) dx + 2y (1) (y (0) +1).
0
16.436.	J(y) =	dx+4e»«« + 32e-»U).
0
Л/2
16.437.	J(^)=
4. Задачи на условный экстремум. Задачи вариационного ис-
числения, е которых на искомые функции накладываются, помимо
граничных условий, дополнительные ограничения, называются за-
дачами на условный экстремум.
Рассмотрим следующую задачу об экстремуме функционала,
зависящего от нескольких функций,
ъ
<f[yi(x)...Уп (*)] =	J/1W> .... Уп(х), yi(x)..y'n(x))dx
(22)
с граничными условиями
УкЮ^уФг Ук(Ь) = Ук\ fe=l, п,	(23)
при дополнительных ограничениях, заданных уравнениями связи
Ф/(х, уъ уп, y’v ^) = 0, 1 = 1, т, т < л. ,	(24)
Эта задача вариационного исчисления называется задачей Лаг-
ранжа.
Введем функцию Лагранжа рассматриваемой задачи
L(x, yt....Уп, у'1, .... Уп, ....	=
= F (х, У1> yrt, yi, •«,, Уп)"^9
+ 2 Мх)ф/(*, yt, .... Уп, У и .... УпЪ (25)
1 = 1
где X/ (x)gCi[a; 6J—произвольные функции (множители Лагранжа),
125
При решении задачи Лагранжа используется следующее необ-
ходимое условие экстремума функционала (22).
Теоремаб1). Если функции yi(x), .уп (х) доставляют
слабый экстремум функционалу (22) при условиях (24), (25), то су-
ществуют множители Лагранжа Х,(х), i=l, .т, при которых
эти функции удовлетворяют системе уравнений Эйлера
LVu~4~L '-°-	ft=1> •••• п'	<26>
vk dx yk
b
записанных для функционала /(yt, . y^—^Ldx.
а
С помощью теоремы 6 решение задачи об условном экстремуме
функционала J (ytf .уп) сводится к исследованию экстремума
функционала / (уь .уп) без дополнительных условий (24).
При использовании теоремы б для решения задачи Лагранжа
искомые функции Уь(х)> k—\, ...» п, и множители Лагранжа
Х/(х), /«1, «... т, определяются из системы п-\-т уравнений (26)
и (24).
Пример 10. Найти функции у± (х), у2 (х), на которых может
достигаться экстремум функционала J (уь у2) в следующей задаче
Лагранжа:
- 1 .
. J(yt, У&^ (У1 +у-1 )dx-,
Pi(0) = ya(0) = 0, у}(l) = 2cb 1„ p2(l)=2sbl;
Pi—р2=0.	* •
Функция Лагранжа данной задачи имеет вид £ =	+
+ МУ1-~№)‘ Для определения функций Ух(х), у2(х) и К(х) запи-
шем систему, состоящую из уравнений Эйлера (26) и уравнения
связи:
2yi+A/ = 0,
2у;+А«0,
' Ух—Уг-Ъ. -
Исключая из этой системы сначала функцию Х(х), азатем yi(x),
получим у'^^у^ — Ъ. Обозначим у' буквой г. тогда
Общее решение этого уравнения z(x)==Cie*4-C2e-*. Отсюда после-
довательно находим
^(х)ов^
У1 W == $ Р2 («) ^=С1е*+С2е-*+С8х+С4.
Для определения постоянных Cj, из граничных усло-
вий получаем следующую систему уравнений:
У1 (0)==С1+С2+С4 = 0,
У2(0) = С1-С2+Сз=0,
У1 (1) =	Сав''1-)-Сз4-С4=2 ch 1,
y^l) == Cie—С2е-1+=2 sh 1.
1) Эта теорема обобщает соответствующий результат для задачи
на условный экстремум функции п переменных (см. т. I, стр. 363)
126
откуда находим	С3 = С4==0» т. е. в данной задаче функ-
ционал J (Уъ Уг) может достигать экстремума при (х) =е*+ «-*==
ss= 2chх,	<?“x = 2sh*. ►
Найти функции у2 (х), уг (х), на которых может дости-
гаться экстремум функционала J (уъ у2) в следующих
задачах Лагранжа.
Я/2
16.438.	J (ylt у2)= J (у1+у1—У'*—yf 4-cos х) dr;
{/1(0) = У2(0) = У1(л/2) = 1, уа(л/2) = —1;
yi—у2—sinx = 0.
16.439.	J (уь у2) = $ (у* + 2у'* + yl) dx\
Уг (0)=-°2, й(0)« !,?,(!) = -е~\ у2(1) = 0;
У1—yi = 0.
16.440.	J (У!, уг) = ^ (у'* + у2 4- х3) dx\
Л(0) = Уа°(1) = 2. ^(0)«^.(1Ы,	,
Ух—2у24-Зх = 0.
16.441.	J (yt, уг) == $ (у'* 4- у'* 4-1) dx\
l/i(0) = t/2(0) = f/a(l). = 0, ^(1) = 2;
У1+У2—2х2 = 0.
16.442.	J (yit у2) = J (у'*+у$ dx,
1/х(0) = 1/2О(1) = 0, &(0)=М1)«1.
*/а=о.
16.443.	J(yit У2) = 1(У1— y»)dx; -
У1 (0) = УI (0) = у! (л) = 0, у2 (л) = л/2;
У1—ya4-cosx = 0.
16.444.	J(yit у2)= $ (y'l+yf*+2yiy2)dx;
Л(0) = 1, Уа(0) = —1,
f я>\
У^Г—~1:
1/1‘4-Уа — 4x^=0.
127
&
16.445.	J (yt, у2) = $ (t/j + уг + y't) dx;
У1(а)=У^, уЛа)=У2\ У1(Ь)==у?\ у2(Ь)=*у<£>;
y't+yi—1=0.
Задача на условный экстремум функционала (22) с гранич-
ными условиями (23) при дополнительных условиях
b
уи Уп> у'ъ ...» yn)dx^C[t i=l, ml)t (27)1
а
называется изопериметрической задачей.
Функция Лагранжа данной задачи имеет вид
£(«. Щ, ...» Уп, yi, .... Уп, U..М= '
т
•=F(.X,yi,y„,yi, 0n)+ 2 VM*. Vi, .... Уп, yi...........Уп},
i~ i
(28)
где множителями Лагранжа 1/, i = 1,..., mt являются произволь-
ные вещественные числа.
При решении изопериметрической задачи используется сле-
дующее необходимое условие экстремума, подобное условию, сфор-
мулированному в теореме 6 для задачи Лагранжа.
Теорема 7. Если функции у\ (х), ..., уп(х) доставляют сла-
бый экстремум функционалу (22) при условиях (23), (27), то сущест-
вуют числа	(множители Лагранжа), при которых эти
функции удовлетворяют системе уравнений Эйлера
^yk~dx~Ly'k~Q' fe==1.......П’	(29)
где L—функция Лагранжа (28).
При использовании теоремы 7 для решения изопериметриче-
ской задачи функции уь(х), 6=1, ...» п, и множители Лагранжа
К/, i = l, ...» m, находятся из системып + т уравнений (29) и (27).
Пример 11. Найти функцию y(x)t на которой может дости-
гаться экстремум функционала J (у) в следующей изопериметри-
ческой задаче:
л
•Ну) = J y’*dx;
о
л
$г(0) = 1, у(п}=—1; J 0cosxdx=y.
о
Функция Лагранжа данной задачи имеет вид L = /2+cos х.
X
Из уравнения Эйлера X cos x-*2z/"=0 находим у (х) = — -5- cos х+
1) В данном случае, в отличие от задачи Лйгранжа, число до-
полнительных ограничений не ограничивается условием т < п.
128
+ Ci^+C2. Для определения множителя Лагранжа к используем
я
дополнительное условие J cos x+Cix +Са) 008 х dx
e=s —~ к —2Cf = у , откуда находим Хад —2— ~ Ср Таким обра-
зом, общее решение уравнения Эйлера имеет вид y(x) = cosx +
Ci cos AC-f-Citf-j-Ca*
Постоянные С/ и С2 определяем из граничных условий у(0)=з
== 1+~7 +	1, . у(л)=—1 + (л—~^Cf+C2=—1,	откуда
л	\ л у
С1=С,»0.
Итак, функционал J (у) может достигать экстремума при
p(x) = cosx. >
Найти функции, на которых может достигаться экст-
ремум функционала J (уt, .... уп) в следующих изопери-
метрических задачах.
1 . .
16.446.	Цу) = ^y'*dx;
О
1
£/(0)=0, у(1) = 1; ^xydx=Q.
О
1
16.447.	J(y) = \y'*dx-,
О
1 1
i/(0) = 1/(1) = 0; ( ydx— 1, ^xydx—0.
о	о
л
16.448.	J (y)=^ty''dx-,
О
п
0(О) = О, #(л) = 1; Jf/sinxdx —0.
О
л
16.449.	J (у) ~ у sm х dx-,
о
Л
У (0) = о, у (л) = л; $ у'* dx = л.
О
1
16.450.	/(«/)=$(/‘ + i/4)dx;
о
1
У (0) =» о, у (1)»j е-ху dx -1 (1 -Зе-8).
О
5 Под ред. А. В. Ефимова, я. *
129-
16.451.	J yj^ylyldx;
t/i(O)“//s(O)’ = ^(l) = O,
1	1
^y3dx=Q.
0	0
1
16.452.	J(yit У^=\{У1+У^Лх",
4)
^(0) = ^(0} = 0,	=	---3;
1
$ y'^dx^Q.
0
1
16.453.	J\yit yj~\y&dx;
0
1
^1(O)“^(O)=^(1) = O,	$x^dr=O,
0
1
Jxt/adx=O.
0
1
16.454.	J (yu y3) = J (y? 4- y'*) dx;
0
1
Vi (0) *= У» (0) = Vi (1) = У» 0) = °; $ y^dx=— 2.
0
1
16,455.	J [yIt y2) = $ x (У1—уг) dx;
0
Л(0)=^(0)»^(1) = 0, У1(1) = 2;
1
0
5. Прямые методы вариационного исчисления. Обычные методы
вариационного исчисления, при использовании которых задача
минимизации функционала сводится к интегрированию уравнений
Эйлера—Лагранжа, как правило, приводят к трудоемким вычис-
лениям и поэтому являются малоэффективными. Приближенные
численные методы, дающие непосредственное решение вариацион-
ной задачи, называются прямыми методами вариационного исчис-
ления. Основная идея прямых методов заключается в том, что
вариационная задача рассматривается как предельная для неко-
торой задачи на экстремум функции конечного числа переменных.
130
Наиболее известными среди них являются методы, Ритца, Канто-
ровича и Галёркина. Следует отметить, что прямые метода вариа-
ционного исчисления являются также и приближенными методами
решения краевых задач дифференциальных уравнений.
Метод Ритца. Пусть требуется найти минимум функцио-
нала
6
•Ч9)=^(*. 9.	Р(а)=Уб, ?(&)«=?£•	(30)
а
Идея метода Ритца состоит в том, что значения функционала
J (у) рассматриваются не иа произвольных допустимых кривых
вариационной задачи (30), а лишь на всевозможных линейных
комбинациях вида '
п
Л(*)-Ф»(*)+2СМ(*Ь	(31)
где ф^(а)=эу(5,	и ф/(х)-* последовательность линейно
независимых функций, причем <р/(а) = срг-(д)=0.	1, 2» п-
Эти функции называются координатными.
На функциях вида (31) функционал (30) превращается в функ-
цию, зависящую от п переменных Ct, С2, «.»> Сп:
/(^«М)«Ф(С£, С2, Сй).
Значения С£, С2, .Сп выбираются так, чтобы функция
Ф(С1, С2, ...» Сп) достигала экстремума, т. е. Cf, С& ««., Сп оп-
ределяются из системы уравнений
|®=0,	(-1.2, ...» П.	(32)
При найденных из системы (32) значениях С/, /=□!, 2, ...» п,
приближенное решение вариационной задачи (30) запишется в виде
Уа (*) — фо (*)+2 С/* W W’	(33)
Вопросы сходимости минимизирующей последовательности
{^(х), ngN} являются сложными. Они изучаются в специальной
литературе. Для оценки точности результатов, полученных мето-
дом Ритца или другими прямыми методами, обычно пользуются
следующим практическим правилом. Вычислив уп (х) и (х),
сравнивают их между собой в нескольких точках отрезка (а, 6].
Если в пределах требуемой точности их значения совпадают, то
считают, что с требуемой точностью решение рассматриваемой ва-
риационной задачи (30) равно гм(х). Если же значения у«(х) и
^+i(x) хотя бы в некоторых из выбранных точек отличаются
значительно, то вычисляют рл+г(х) и сравнивают теперь значения
Уп+1 (х) и ул+2 (х). Этот процесс продолжается до тех пор, пока
значения уп+ь(х) и yn+k+i (х) не совпадут в пределах заданной точ-
ности.
5*
131
Пример 12. Найти экстремаль функционала
1
(34)
О
при граничных условиях у(0)«=0, #(1)=0 методом Ритца.
Полагаем фо (л) аз 0. В качестве координатных функций выби-
раем ф^(х)«=хЛ+д—х\ Эти функции удовлетворяют гранич-
ным условиям ф*(0) = фЛ (1) =0. Выберем и=2. Тогда в соответ-
ствии е (33)
р2 (х)=С1 (х2—х)+С2	(35)
я
^(x)=Ci(2x— 1)4-Са(Зх2—2х).	(36)
После подстановки (35) и (36) в (34) и интегрирования получим
Ф (Ci, C2)=J (St	с? + Д CA+l Cl -1 Ct—1 ct.
OU	OU	<	U	1U

Воспользовавшись необходимыми условиями экстремума функции
Ф (СЪ С^, находим
’-О
—g—0.
дФ_11	2	1
йё;"зоС1+7Сг_То~0-
(37)
Решая систему (37), получим С1 = 69/473, С* « 7/43. Следова-
тельно, приближенное выражение у! (х) для экстремали у(х) имеет
®»Д
р» W=S {xi^x) + Й (х3""%2) ” 4Тз (77*s-8*a-69jc>-
В данном случае существует точное решение поставленной
вадачи:
(«*•“«“*)—х.
Сравним полученное методом Ритца приближенное решение у? (х)
и точное при некоторых значениях аргумента:
X	0,0	0,2	0,4	0,6	0,8	1,0
У(х).	0,0000	—0,0287	-0,0505	—0,0583	—0,0444	0,0000
У\ W	0,0000	—0,0285	—0,0506	—0,0585	—0,0442	0,0000
Сравнение показывает, что точное и приближенное решения
совпадают с точностью до 0,0002. ►
В вадачах 16.456—16.460 методом Ритца найти приближенное
решение вадачи об экстремуме указанных функционалов.
,. ,132
2
16.456	*. J [у (x)] = $ (у1* 4- у*- + 2ху) dx, у(О) = у (2) = О,
О
п = 2.
2
16.457	*. J [у(х)] = j ^ху'*-±=±у»-2х^ dx,
‘	у(1) = «/(2) = 0, of=2.
16.458	*. ^[t/(x)] = J(/*—z/2—2xy)dx, J/(O) = у(1) = О,
о
п — 2.
W.459.. 7[U(x, 0] = Щ(£)' + (-£)!)<^.
D — {(x, У)\х^ О, «/>0, х+#с 1}, «|гп = *?+{/\ п=3.
I6.4W*	. /[«(х, у)]-ДО
D
D = {(x, t/)|—2<x<2, —2<#<2}, u|rD = 0, n = 2.
16.461	. Найти методом Ритца приближенное решение
дифференциального уравнения у”+х2у=х, t/(O) = y(l) = 0.
Определить yl(x) и yl(x) и сравнить их значения в точ-
ках х=0,25 и х=0,5.
Метод Канторовича; Этот метод применяется для приближен*
ного решения вариационной задачи, когда функционал зависит
от функции нескольких переменных. Пусть
Jlu(x,	У’ и‘ IF’ ^}dxdyf (38}
D
D = {(r, у) |аОСЬ, at(x)<y<a2(x)}, и|г^=ф(^ у).
При применении метода Ритца к функционалу (38) (см. за-
дачи 16.459—16.460) выбирается следующая система координат-
ных функций: ф0(х, у), ф1(х, у), .ф«(х, у). Решение ищется
в виде
«п(*. р) = фо(*. 0)+2С*фНж. У)>
где неизвестные постоянные. В методе Канторовича выраже-
ние для экстремали берется в виде
«п (X, у) = 2 “й (*) Фй (X, у),	(39)
й = 1
где иь (х) — неизвестные функции, определяемые таким образом,
чтобы функционал (38) достигал экстремального значения. Отыс-
кание решения в виде (39) позволяет расширить класс экстремалей.
'133
I-
После подстановки (39) в (38) и интегрирования полученного |
выражения по у получается следующий функционал:	X
ь
»iW» ♦..» «nW, и\(х), u'n(x))dx.
а
Функции ul(x), 6=»1, 2, ...э л, должны удовлетворять системе
уравнений Эйлера—- Лагранжа
ф	*,6=0, Л— 1» 2, л,
“k dx »k
а приближенное решение и* (х, у) вида (39)*-*заданным гранич-
ным условиям на прямых х = д и х~Ь.
Пример 13. Методом Канторовича найти экстремаль функ-
ционала
D
где D = {(x, у)|—и|г^=0, л = 1.
Решение будем искать в виде
ui(xt £/)^Д1(х)
Граничные условия на прямых у i b выполняются. После под-
становки ut(x, у) в (40) и интегрирования по у получаем
(х)]= J (jf +
«-а
Уравнение Эйлера для этого функционала имеет вид
М** 2J2 ai	»
Находим общее решение этого уравнения:
ut (x)«Ci ch у 4-Cs sh /2?5 у+0,5.
Постоянные С$ и С2 определяем из граничных условий, т. е.
«1 (—й) = «I (a) s= 0, откуда Ct == 0 и Ci ==-**^2 ch 1^2,5-у	t
Окончательно получаем следующее приближенное выражение
для экстремали функционала (40):
(ch /2^4 \
1----------L ). >.
ch/2,5 4 /
В задачах 16.462 и 16.463 найти приближенное ре*
шение методом Канторовича. Положить п«=»1.
134
16.462*. J [и(х, «/)] = $$ (и** +и^—-2u)dxdy, где D =*
D
= {(*. fdlkICi. M<i}, «|г=о.
16.463*. J[u(x, 1/)] = $$ (uxx + ufg—2xy) dxdy, где D
D
= {(x,	1, O<«/< 1}, u|r=O.
Метод Галёркина. Этот метод применяется для опус-
кания приближенных решений как вариационных задач, так и
краевых задач для обыкновенных дифференциальных уравнений
и уравнений в частных производных, в частности, уравнений
Эйлера—Лагранжа.
Пусть неизвестная функция и (Р) удовлетворяет в некоторой
области D следующей краевой задаче:
Ни (P))-f(P), р^а,
Г(и(Р))~$ на у (у—граница G).
Здесь £—некоторый линейный дифференциальный оператор, Г —
линейный оператор граничных условий. Приближенное решение
краевой задачи (41) ищется в виде суммы
6=1
где Cfc—неопределенные коэффициенты, фд (Р)—система линейно
независимых непрерывно дифференцируемых функций, удовлетво-
ряющих однородным краевым условиям. Обозначим б/ невязку
6f-£(«n(P))-f(P).
Коэффициенты определяются из условия ортогональности в об-
ласти D невязки 6/ к функциям фд(Р), 6=1, 2, п:
[lL(u„(P))-f(P)]<fk(P)dP=O,	6 = 1. 2, .... п. (42)
D
Так как оператор L линеен, то (42) запишется в каноническом
виде, удобном для вычислений с/:
2 С/ U (ф< (Р)) ф* (Р) dP = Г f (Р) <pft (Р) dP,
i	= i G	G
или в виде
2	<7 $ fr (Р) Ф* (Р) <*Р = р (Р) ф» (Р) dP,
i-l О	G
где Л (Р)^Ь(Ф/(Р)).
Замечание. Можно использовать ортогональность невязки
к другой линейно независимой системе функций ф* (Р) выбирае-
мой из удобства вычислений получаемых интегралов (см. решение
примера 14).
135
Пример 14. Найти экстремаль функционала
1
/($/)“ J (у'*™2xy)dx
о
при граничных условиях у(0)®0, у(1) = 0.
Составив уравнение Эйлера F'y F*~ = 0,|имеем
£у = /(х), т. е. у"«=—х.	(43)
Краевые условия остаются прежними: у(0)®0, у(1)«0. Исходная
задача сводится к эквивалентной краевой задаче:
/=-х, у(0)«0, у(1)«0.
Решение будем искать приближенно методом Галёркин», записы-
вая искомую функцию в виде
у (х)=X (1 — х) (А + Вх) = Ах (1 —х) + Вх2 (1 — х),	(44)
где (pf (х)=х (1—х) и фг (х)=х2 (1 *-х). Вычисляя у* и подставляя
Н левую часть уравнения (43), запишем выражение для невязки 6:
б/ = —24 + В(2—6х)+х.
Вместо условий ортогональности невязки б/ к функциям epi (х) и
ф2 (х) коэффициенты А и В определены из условия ортогональ-
ности б/ к функциям iff (х)=»1 и ф2(х) = х (функции ф1(х) и фа(*>
линейно независимы на [О, 1] с <pi (х) и <р2 (х):
1 1 1
A J —2 dx-^B J (2—6x)dx = '— J xdx,
°!	°1	° 1	(45)
A C — 2xdx + B J (2*-6x)xdx®—J x2dx.
oo	о
Вычисляя интегралы в (46), получим систему уравнений
24 +В «1/2,
А + В^\/3.
Решая эту систему относительно А и В, получим
А «= 1/6, В хх 1/6.
Подставив найденные коэффициенты А, В в формулу (44), найдем
искомое приближение для экстремали:
у* со «1 х (1 -х) 4-1 х» (1 _Х)-.
Заметим, чтохв данной задаче найденное приближение совпадает
с точным решением у?*=х (1 —-х2)/6. ►
Методом Галёркина найти решение следующих вариа-
ционных задач. Ограничиться приближениями искомой
136
экстремали в виде
Уп (х) = ф (х) (а6+atx+а2х’ +... + а„хп),
где ф(х) выбирается из условия выполнения граничных
условий, ап=1.
2
16.464.	J(y) = $ (xy'+y^dx, у(0)-0, у (2) = 0.
О
1
16.465.	J(z/) = $(^+^’-2z/sinx)dx, у(0)=0, j/(l)=0.
О
1
16.466.	/(«/)=$ (у? +/+2уе*) dx, р (0) = О, у (1)=0.
о
16.467.	Составить на фортране подпрограмму-функцию
для вычисления функций <рЛ+1 (х) = ф(х)х*, 6 = 0, 1, ...
.... п—1, используемых при решении задач 16.464 —
16.466. В качестве параметров выбрать FIK—идентифи-
катор подпрограммы-функции, X—аргумент функции,
параметр К на единицу меньше номера функции.
16.468*	. Составить подпрограмму-функцию для вычис-
ления функций fk(x) в задачах 16.464—16.466. В каче-
стве параметров выбрать FK—идентификатор подпрограм-
мы-функции, X—аргумент функции, п=3.
16.469.	Используя формулу Симпсона, составить под-
программу-функцию для вычисления интегралов
ъ
/=1, 2, ..., п. В качестве парамет-
а
ров взять А, В—начало и конец отрезка интегрирования,
Fl, FT—идентификаторы соответствующих функций, К на
единицу меньше номера функции, EPS—абсолютная по-
грешность вычислений.
46.470*	. Составить на фортране подпрограмму реше-
ния задач 16.464 —16.466, используя подпрограммы, по-
лученные при решении задач 16.467—16.469, а также
подпрограмму решения системы линейных уравнений ме-
тодом Жордана—Гаусса, выбирая при этом для уа(х)
порядок n = 4, EPS = 0,05.
Г лава 17
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ
§ 1. Основные задачи и уравнения математической
физики
1. Вывод уравнений и постановка задач математической физики.
Многие задачи механики, физики,^широкий круг инженерно-техни-
ческих задач приводят к исследованию дифференциальных урав-
нений с частными производными второго порядка, являющихся
частным случаем так называемых уравнений математической фи-
зики.
Их вывод опирается на механические или физические законы.
Из всего многообразия таких задач мы ограничимся лишь не-
сколькими простейшими, иллюстрирующими некоторые методы
построения математических моделей реальных физических или ме-
ханических процессов.
Пример 1. Вывести уравнение распространения тепла в
изотропном твердом теле.
Обозначим температуру тела в точке М (х, г) в момент вре-
мени t символом и (х, у, г, /). Как известно, в теле происходит
движение тепла от более нагретых частей к менее нагретым.
В теории теплопроводности принято, что количество тепла AQ,
проходящего через некоторый элемент поверхности До, лежащий
внутри данного тела, пропорционально ДПА/, где ДП—поток век-
тора grad и через элемент До, т. е.
Дфзк&ДПА/.	(1)
Здесь k = k(x, yt г) — коэффициент теплопроводности тела.
Выделим внутри тела произвольный объем V, ограниченный
гладкой замкнутой поверхностью 2, и составим уравнение тепло-
вого баланса для выделенного объема. Пусть Qi—количество
тепла, входящего в V через поверхность 2 за промежуток време-
ни (/, /-f-Д/). Тогда из (1) следует, что
Q1 = k (41} ^grad do) Д/.

Обозначим Qa количество тепла, выделяемого или поглощаемого
в объеме V за промежуток (/, / + Д/) вследствие имеющихся в
этом объеме источников (или стоков), плотность которых, т. е.
количество поглощаемого или выделяемого тепла за единицу вре-
мени в единице объема, обозначим F (х, у, г, /). Ясно, что
v
138
а тогда, используя формулу Гаусса—Остроградского, для общего
количества тепла, приходящего в объем V за промежуток време-
ни (/, / + Д/), получаем выражение
Qi+ @2= J J J div (k grad и) dv Ы +	J F (x, yt г, l)dv&t,
(2)
С другой с1ороны, на изменение температуры объема тела V за
время (t, ? + &/) на величину Д/« = « (х, t/, г,/ + Д/)—и (х, у, г, t) «
ди (Л4, t)
«----необходимо затратить следующее количество тепла:
^8= П <*• 9> г+АЧ~« (*• У' г> 0] V (*. У> г) Р (*> У< dv «
v
(3)
V
где у==у(Л1) — теплоемкость вещества, а р —р (М)—его плотность.
Но Qi + Qa^Qa» а потому из (2) и (3) следует соотношение

div (k grad u)—>F (x, yt z, t) Lfo=0.
Так как объем V произволен, а подынтегральная функция непре-
рывна, то отсюда следует, что в любой момент времени / должно
выполняться соотношение
ди •
yp-^- = div(£gradu)+F(Af, /).	(4)
у, г, t),	(5)
Это уравнение (4) называется уравнением теплопроводности неод»
народного изотропного тела. Если тело однородно, то у, р и k
постоянные и уравнение (4) запишется в виде
ди — 2 (aJ^U
li~a + dt/a + dt*
где	__
а = f(X’ V' *’ 0=4F(X’ У’ г> °- ►.
Для вычисления температуры тела и (х, yt г, t) в любой точке
тела и в любой момент времени t недостаточно решения уравне-
ния (4) или (5). Из физических соотношений следует, что необхо-
димо знать еще распределение температуры внутри тела в началь-
ный момент времени (начальное условие) и тепловой режим на
границе тела (граничное условие). Точно так же и для решения
других задач математической физики требуется знание начальных
(если процесс нестационарный) и граничных условий. Поэтому под
постановкой задачи в дальнейшем подразумевается выбор функции,
характеризующей исследуемый физический процесс, вывод (или
выбор) соответствующего этому процессу уравнения, установление
граничных условий и формулировка начальных условий.
Пример *2. Поставить задачу об определении температуры
однородного изотропного стержня 0^х«с/с теплоизолированной
боковой поверхностью, если его начальная температура есть неко-
139
юрая функция х, а на концы стержня подается извне заданный
тепловой поток.
Температура стержня зависит только от координаты точки
xg|0, I] и времени t, т. е. «=*и(х, /). Внутри стержня источники
тепла отсутствуют, т. е. F (х, у, г, /)азО. Поэтому уравнение (5)
ди(х, 0	9д2и(х, t)	*
принимает вид —~—-=а9— *  , где л —— • Начальное
н	dt	дх2	ур
условие записывается в виде и(х, О)=ср(х), 0<х</, где ср(х) —
заданная функция. Граничные условия имеют вид
«;(о, п=-^«(о. «;(/, п=^<7а(О.	о<<<«о,
где а—площадь поперечного сечения стержня, qt(t) и (^)—
тепловые потоки (количество тепла, поступающего в единицу вре-
мени) в стержень через его концы. Таким образом, имеем задачу:
Найти решение и(х, t) уравнения,
аг=-,	0<х<1,	0 < Z < оо, (6)
dt	дх2	ур
удовлетворяющее условиям:
и(х, 0) —ср(х) (начальное условие),
«»• о—
•	(граничные, или краевые, условия). (7)
Рассмотренная в примере 2 задача относится к так называемым
смешанным задачам, в которых участвуют как начальные, так и
граничные условия. Граничные условия (7), наложенные на значе-
ние производной их(х, t), называют условиями второго рода. Рас-,
сматриваются также задачи с условиями первого рода, наложенными
на значения функции и(х, t),
«(О, 0=Ф1 (0> «(*> *) = <М0	(8)
и с условиями третьего рода, наложенными как на значения функ-
ции и(х, t), так и на значения производной и'х(х, t),
(9>
Условие (9) означает упругое закрепление в точках х=0 и х = 1.
Кроме смешанной задачи достаточно часто встречается задача
Коши, состоящая в отыскании решения и(х, t) в области — оо < х <
<оо, 0</<оо, удовлетворяющего только начальным [условиям
(например, условию и(х, 0) = ф (я) для уравнения (6)).
17.1	**. Вывести уравнение малых колебаний закреплен-
ной на концах х — 0 и x=Z натянутой струны, т. е. сво-
бодно изгибающейся в плоскости горизонтальной тонкой
нити. Действующая на струну сила натяжения Т значи-
тельно больше силы тяжести, т. е. действием силы тяжести
можно пренебречь.
17,2	. Используя уравнение задачи 17.1, поставить
вадачу о вынужденных колебаниях закрепленной на концах
140
х=0 и х = ( горизонтальной однородной струны, если
в момент 1 = 0 струна имела форму ф (х), 0 х /, и ско-
рость струны в каждой ее точке задается функцией ф (х).
17.3	*. Используя уравнение задачи 17.1, поставить
задачу о свободных колебаниях закрепленной на конце
х = I горизонтальной однородной струны, левый конец
которой (при х = 0) движется так, что касательная в этом
конце (при х—*4-0) в любой момент времени горизон-
тальна. В момент t = 0 струна имела формулу Ф(х), а
скорость каждой точки равна нулю.
17.4	**. Рассматривая однородную двухпроводную ли-
нию равномерно распределенных индуктивностей, сопро-
тивлений, емкостей и утечки, вывести волновое уравнение,
называемое также уравнением длинной линии. (Ввести
величины: L—коэффициент индуктивности, С—емкость,
R—сопротивление, G — коэффициент утечки, которые счи-
тать отнесенными к единице длины.)
17.5	. Используя уравнение задачи 17.4, поставить за-
дачу об отыскании закона изменения напряжения и силы
тока в длинной линии (0^х< оо) без потерь (т. е. R =
= G = 0), если известны начальные напряжение ф (х), сила
тока ф(х), а напряжение в точке х — 0 постоянно и
равно Ео.
17.6	*. Воспользовавшись уравнением (6) примера 2,
поставить задачу о распределении температуры внутри
однородного изотропного стержня, начальная температура
которого равна и0, при свободном внутреннем теплообмене,
если в левом конце его (при х = 0) поддерживается посто-
янная температура ы0, а через правый конец (при х=/>0)
происходит теплообмен с окружающей средой, темпера-
тура которой задана функцией ф(/).
17.7	. На границе бесконечного изотропного однород-
ного цилиндра, направляющая которого—кривая L—ле-
жит в плоскости, перпендикулярной образующей, поддер-
живается температура, зависящая только от положения
точки на L. Используя уравнение (5) примера 1, поставить
задачу об установившемся стационарном распределении
температуры внутри цилйндра (плоская задача Дирихле). -
2.	Приведение уравнений к каноническому виду. Общее уравне-
ние второго порядка относительно функции a(xf, х2, .... х„) неиз-
вестных X], х-i, ..., хп имеет вид
V<	д2и , , (	ди	ди \ п
....Ха’и' W ВД=0-
141
Методы решения таких уравнении и характер описываемых этими
уравнениями процессов вависят от вида квадратичной формы
£ a//U хй)М/	(П)
г, /«1
в каждой точке Ма(х?, ».», Хп) некоторой области D а-мерного
пространства.
Как известно, выбором линейного преобразования матрица
...» Хп))”/~1 квадратичной формы (11) может быть приве-
дена к каноническому (диагональному) виду, причем согласно
закону инерции число положительных, отрицательных и равных
нулю коэффициентов канонического вида матрицы не зависит от
способа диагонализации.
В соответствии с этим уравнение (10) в точке М$ (в области D)
называется уравнением эллиптического типа, если все п коэффи-
циентов канонического вида квадратичной формы одного знака,
т. е. квадратичная форма (11) является положительно либо отри*
цате ль но определенной в точке Л1о (соответственно в области D).
К уравнениям эллиптического типа обычно приводят задачи
о стационарных тепловых процессах, об отыскании гармонических
в области D функций.
Уравнение (10) имеет гиперболический тип в точке /Ио (в об-
ласти D), если в точка Мо (соответственно в области D) п—1
коэффициент канонического вида квадратичной формы (11) имеет
один знак, а один коэффициент противоположен им по знаку.
К уравнениям гиперболического типа приводят различные задачи
о колебательных процессах. В более общем случае уравнение (10)
имеет улътрагиперболическай тип, если т коэффициентов канони-
ческого вида квадратичной формы одного знака, а остальные
п —т—противоположного.
Наконец, уравнение (10) имеет в точке Л40 (в области D) пара-
болический тип, если в точке Л1о (соответственно в области D)
котя бы один из коэффициентов канонического вида квадратичной
формы (11) равен нулю. Такие уравнения описывают процессы
распространения тепла, диффузии и некоторые другие.
В случае двух независимых переменных х и у уравнение (10)
обычно записывается следующим образом:
л	t ль / ч 1	/ ч б2и . . /	ди ди \ л
J?)-^+2* (ж, ц)^+в(х,	(х, g. и, ^,^=0.
(12)
Соответствующая ему квадратичная форма имеет вид
а(х, y)ti + 2b(xt yJMa+H*» У) 4.
Тип уравнения (12) может быть определен и без приведения квад-
ратичной формы к каноническому виду. Именно: уравнение (12)
имеет в точке Л1о (х0, у$ (в области D)
эллиптический тип, если ас~*Ь2 > ОЛ
гиперболический тип, если аг—&2<0,
параболический тип, если ас—Ь2 —0
в точке Мо (соответственно в области D).
, Уравнение
а (х, у) dy*~*2b (х, у) dxdy^c (х, у) dx2 = 0	(13)
142
называется характеристическим для уравнения (12), а его общие
интегралы
<р(ж, у) = С, ф(х, = C
— характеристиками.
Характеристики линейного уравнения в частных производных
второго порядка (12) используются для приведения его к канони-
ческому виду. Для уравнения гиперболического типа (ас—/?2 < 0)
характеристики действительны и различны. Полагая £==эф(х, у) и
т) = ф(х, у), приводим уравнение (12) к виду
или
д2и
ди
д2и дги
да2 ”“д£2
+-Ф1 ( а, Р, и,
ди ди \
да ' др
(14)
(И')
W 6, п. «.
если положить дополнительно а=у (£+л)» Р=='^“
Для уравнения эллиптического типа (ас—Ь* > 0) характе-
ристики комплексные и комплексно сопряжены (ф (х, у)==ф(х, у)).
Полагая £=у(ф(х, y)+^f(x, у))«Reф(х, у) и
—	у)) = 1тф(х, у), уравнение (12) приводим к виду
д2и । д2и । К ди ди \ л
В случае уравнения параболического типа (ас—62=0) имеется
только одна характеристика ф(х, у)=С. Полагая g=<p(x, у) и
Т|=ф(х, у), где if (х, у) —произвольная функция, независимая
с <р(х, у) ( т. е. якобиан /=
0 ) , получаем
%
0*11 I A ft	\ л
^+ФФ’ П’ Я- • «J-0,
(16)
Уравнения (14), (14'), (15), (16) называются каноническими.
Рассмотренный метод приведения уравнения (12) к канони-
ческому виду (14) —(16) и решение полученного уравнения носит
название метода характеристик.
Так как для каждого типа канонических уравнений разрабо-
таны определенные методы как аналитического, так и численного
решения, то задача приведения уравнений (12) к каноническому
виду представляет практический интерес.
Заметим, .то в различных областях тип одного и того же урав-
нения (12) может быть различным.
Пример 3. Определить тип уравнения
y‘>uXx-{-x2Uyy——Uy — ^—ux = 0	(17)
У Л
и привести его к каноническому виду.
Так как ас--Ь2 — у2х2 > 0 во всех точках, не лежащих на пря-
мых х=0 или у==0, то в любом открытом квадранте заданное
143
уравнение имеет эллиптический тип. Составим характеристическое
уравнение
Оно имеет ^комплексно сопряженные общие интегралы =
и f/2-—/х2 = &. Поэтому полагаем £=#2 и т) = х2. Тогда имеем
и-х ==	= #тр2х,
Ug=U<gy + Wr^== й|’2у.
ихх =	4- Uflnni) • 2*+«П •2=«лч •4х*+2«п»
«до=(“й^+ «Sn%)-2y+«V2e«U‘4z/2+2«5.
Подставив эти значения в исходное уравнение, получим
/	w	г у2 / W2 ,
у* (4х2«^ + 2«J)) + х2 (4уги к 4-2/4)-- 2уи% -~-2хип=0,
У	*
т. е. 4х2у2 (^пп4“ии)~0. Сокращая на 4Л/2#0, приходим к урав-
нению канонического вида	— Отсюда заключаем, что
решение уравнения является * гармонической функцией по пере-
менным 5 и Т). ►
В задачах 17.8—17.18 определить тип уравнений и
привести их к каноническому виду.
17.8. ^±4-5^-4-4^-=0.
дх* 1 дх ду 1 ду2
1-7 п д2и । л	\ л \	\ а$и л
17.9. -з-т -4- 4	4- 4 -s-т 4- 3 з~ + 6 — =0.
дх2 ‘ дхду 1 ду2 1 дх ‘ ду
17.10.	-Д-— б^-4-13-^4 = 0.
дх2 дх ду ‘ ду2
17.11.
дх2 ’ г & дхду 1 я ду2 2 \ К «	$ )ду
17.12.	z/2f|—2xt//^-4-x2-f( = 0.
47 дх2 9 дхду ' ду2
- я, 1 о 2 д2и , д2и а ди п
17	1	। I ди 1 ди п -	Л
17.14. Ху^ + -^ + -у----^0 в области х>0,
у>о.
17.15. g-4-2^J-4-cos2xj4—ctgxf^+^Ko.
дх* ' дхду г ду2 & \дх ' ду)
17 ia	д2и	а
17.16,	тт-%тт = 0.
дх2	ду2
4 7 17	d2U		d2U	г\	л
17.17. dja+* в области х>0.
17.18. ж*^ + 2х^Д4-^ = 0.
144
17.19*	*. Найти общее решение уравнения из за-
дачи 17.8.
17.20.	Найти общее решение уравнения из задачи 17.9.
17.21.	Найти общее решение уравнения из задачи 17.11.
17.22.	Найти общее решение уравнения из задачи 17.15.
17.23.	Найти общее решение уравнения из задачи 17.18.
§ 2.	Аналитические методы решения уравнений
математической физики
1.	Метод Даламбера. Одним из широко используемых способов
решения уравнений колебаний струны является метод характе-
ристик, называемый в этом случае методом Даламбера. В основе
его лежит тот факт, что с помощью замены g=jt4-otf, r\=x—ai
уравнение
<Ри -д«а
а дх*
(D
д2и
преобразуется в уравнение ^-=0 (см. зяДачУ 17.5), которое
имеет общее решение «(£, Т)) = Ф (Ь + F (Л)> где Ф и F—произволь-
ные дважды дифференцируемые функции. Для определения этих
функций Ф и F, т. е. для определения закона колебаний струны,
требуется использовать начальные условия, а для некоторых задач
и граничные. Если вернуться к старым переменным х и /, то
решение имеет вид
и(х, 0 = Ф (x + at) + F (х—at).
Здесь F(x —at) характеризует прямую, волну (кривая F (х) сме-
щается вправо со скоростью а), а Ф (х-|-а/)—обратную волну
(кривая Ф(х) смещается влево со скоростью а).
Если рассматривается задача Коши для бесконечной струны
— оо < х < оо, то по заданным начальным условиям
и (х, 0) == ф (х), щ (х, 0)«ф(х)	(2)
определяются функции Ф и F и искомое решение (формула Далам-
бера)
x+at
U(x, о = у 1ф(*~оО + <Р(*+«ОГ+^- J Ф(г)*.	(3)
Пример 1. Найти решение и (х, t) задачи Коши (—- оо < х<
< оо, 0 < t < оо)
д2и д2и	ди(х, 0) л
dt2 ~дх2' 0)~cosx» Qt —°-
Используя формулу Даламбера (3), имеем
а(х, /)=у [cos (х—• Z) + cos(x+OJ = cosxcos t. >
Используя формулу Даламбера, найти решения и (х, 0
следующих задач Коши (— оо < х < оо, 0 < / < oo)j
де
17.24.	Найта решение уравнения uti — uxx при началь-
ных условиях «(х, 0) = ^-^-, «,'(х, 0)=0.
17.25.	Найти решение уравнения = ихх при началь-
ных условиях и(х, 0)=^у^, «;(х, 0) = у^5-'
17.26.	Найти решение уравнения и’и — и.хх при началь-
ных условиях и(х, 0) =, u't(x, 0) = sinx.
* *Т *
17.27.	Найти решение уравнения u"lt = ихх при началь-
ных условиях п(х, 0)=-гт—в-, u’t(x, 0)=cosx.
J -f-X
17.28.	Найти решение уравнения utt = uxx при началь-
ных условиях и(х, 0)=с~х1, u't(x, 0)=-г^-5.
1 -р X
17.29*. Найти закон свободных колебаний бесконечной
струны, если начальная скорость каждой ее точки равна
нулю, а начальное отклонение задается функцией
!0 при х€(—оо» 0)и(2/, со),
х при х€(0, /)»
21—х при х€(/, 21).
Построить на чертеже профиль струны в моменты времени
t — l/2a и t — 1{а (а—входящая в уравнение (1) посто-
янная) .
17.30*# Найти решение уравнения и"ц = а*ихх при на-
чальных условиях и(х, 0)=<p(x)ss0,
нДх, 0) = ф(х) =
0 при |х | > h,
—а при —Л<х<0,
а при 0 < х < h.
Построить профиль струны в моменты времени t — h/(2a)
и t = 3h/(2a).
В случае полубесконечной струны кроме начальных усло-
вий (2), заданных при 0<х< оо, необходимо добавить еще гра-
ничное условие (конец струны предполагается в точке х=0)
«(0,0=0	(4)
для закрепленной в точке х=0 струны,
«х(0, 0 = 0	.	(5)
для .свободного конца в точке х=0,
«х(0, i)—hu(b, 0 = 0
для упругого закрепления в точке л = 0.
146
Из условий (2) и (4) следует, что ф(0)==0.
В случае однородных граничных условий (4) или (5) решение
задачи о колебании полубесконечной струны сводится к решению
задачи о колебании бесконечной струны путем продолжения на-
чальных условий на всю ось нечетным образом для условия (4),
т. е. <р(—х)=—ф(х), ф(— х)=—ф(х), и четным образом для
условия (5), т. е. ф(— х)«=ф(х), \р(-х)=ф(х).	'
Пример 2. Найти решение уравнения	> 0 < х <
< оо, С < t < оо, удовлетворяющее условиям а(х, 0)«х8»	==
= sin2x, и (О, /) = 0.
Продолжим функции ф(х)=х8 и ф(х) = sin8х на отрицательную
полуось нечетным образом:
, v ( х8 при х^0>
Ф1 (*) — ^ __ пр1Г х < 0;
z ( sin8x при х^О.
W = I — sin2 х при х < б.
Тогда по формуле Даламбера (3) решение запишется следующим
образом:
x+at
«(«.О—j-IW(«4-вЧ+Ф<(*—«01+-^ j frC?)dr=
x-at
x+at
1	t P	x
s-[lx+at)»+(x—at)*] + — sta«zd2 при /<-£-.
а	J	а
x-at
1[(х+а0г-(х-о0а1 +
при/ >	> О,
х*4-а*/*+-^—cos 2х sfti 2а/ при t<L^,
I	4»
Saxt +	[2х—sin 2х cos 2o/J при > О. ►
3	а м е ч а н и е. Как следует из формулы Даламбера (3) и урав-
нения (1), входящая в условие (2) функция ф(х> должна иметь
вторую производную, а функция ф(х) — первую. Однако в после-
дующих задачах мы будем рассматривать функции ф (х) с угло-
выми точками, а функции ф(х) — с точками разрыва, предполагая
тем не менее, что определяемая по формуле (3} функция является
решением (вообще говоря, обобщенным) исходного уравнения (1).
Это объясняется тем, что путем незначительных изменений функ-
ции ф и ф можно сделать достаточно гладкими и полученные для
этих сглаженных функций по формуле (3> решения м*(х, t) будут
мало отличаться от и (х, О-
Н7
Используя метод продолжения и формулу Даламбера,
найти решения следующих задач!
17.31,	В области О^х < оо, 0 < / < оо найти реше-
ние уравнения (1), удовлетворяющее условиям
и(х, 0) = 0, Ui(x, 0) = sinx, и* (О, /) = 0.
17.32.	В области 0^х<оо, 0 < / < оо найти реше-
ние уравнения (1), удовлетворяющее условиям
«Нх’°)=0’ “(°. 0=0-
17.33.	В области 0<х < оо, 0 < /< оо найти реше-
ние уравнения (1), удовлетворяющее условиям
u(x, 0) = 0, и'Дх, 0)-!^, «(0,0 = 0.
17.34.	В области0 <х < оо, 0 < / < оо найти решение
уравнения (1), удовлетворяющее условиям
«(*. 0) = ь£г,	«(0,0 = 0.
17,35.	В области 0<х< оо, 0 < / < оо найти решение
уравнения (1), удовлетворяющее условиям
и (х, 0) «= «J (х, 0) = sin х, «(0, 0 = 0.
17.36.	В области 0^х<оо, 0</<оо найти реше-
ние уравнения (1), удовлетворяющее условиям
„(х,0)4 Si" T ”Р»
V 0 при х£(/, оо),
«J(x, 0) = 0, «(0, о = о.
Построить графики решения в моменты t == //(4«) и i =
= 3Z/(4a).
17.37.	Полуограниченная струна (м(0, 0 = 0) в на-
чальный момент имеет форму ы(х, 0)==0 и начальную
скорость
ы*. 0)-Г„ пр" °:
(0 при х£[/, °°).
Найти форму струны для момента времени t—lfa и / =
===== 5Z/a, где а—входящая в уравнение (1) константа.
2. Гильбертовы пространства. Ортогональные системы. Одним из
наиболее распространенных аналитических методов решения урав-
нений математической физики является так называемый метод
Фуръе> который опирается на свойства ортогональных систем и
МГ
ортогональных разложений. Поэтому изложению метода Фурье*
мы предпосылаем ряд задач на свойства ортогональных систем/
ортогональных рядов и на решение краевых задач обыкновенных
дифференциальных уравнений.
Пусть в векторном пространстве Я& введено скалярное (внут-
реннее) произведение (х, >) векторов x(^lL и (см. ч. 1, глава 4,
§ 1, п. 3), удовлетворяющее условиям
1)	(л,	х),
2)	(Xf+x2, » = (xi, «у) + (х2, У),
3)	(hx, >)=Mx, y), ^€0»
4)	(x, x)^0, причем (x, x)=0$x==0.
Нормой элемента x^U, обозначаемой ||х||, называется число, рав-
ное К(х> т. е. ||х||2==(х, х). Последовательность векторов {хл}с:
сЭД называется фундаментальной, если она удовлетворяет условию:
для всех 8>0 существует Я«зЯ(8) такое, что для любых nj,
п2 > Я (в) выполняется неравенство ||хП|**хП| |] < в. Пространство
<U называется полным, если любая фундаментальная последова-
тельность векторов {х„} этого пространства имеет предел Хб(5ЭД.
Полное линейное векторное пространство со скалярным произве-
дением называется пространством Гилъберта и обозначается бук*
вой Я.
17.38*	. Доказать, что удовлетворяющее условиям 1)—
4) скалярное произведение есть непрерывная функция
относительно сходимости по норме, т. е. если ||хЛ—ж||—>0
И ILy»—Х|-*0 при п —со, то и 1(хп, уп)—(х,д»)|-*0
при п,—► СО.
17.39.	Доказать, что линейные операции над векто-
рами гильбертова пространства Н непрерывны, т. е. если
||ж„—х||—►О, ||_уп—у J —► 0 и последовательность чисел
L —А, (п —со), то ||(4r„+j>„)—(*+.?) 11=^0 и ЦМп —
— Хх||—-0.
17.40*	. Доказать, что конечномерное евклидово про-
странство является полным.
17.41.	Пусть Z2—векторное пространство бесконечных
последовательностей	хг, ..., хп, ...) о дейст-
вительными (комплексными) компонентами хя, п € N,
QO
причем 2 |х„|2< оо. Доказать, что соотношение (ж,^)=*
1
«О _
®= 2 хпУп задает скалярное произведение в пространстве 1г.
п = 1
17.42,	Доказать, что счетное множество $™{en,
е„ = (0, •••> 0, 1.0. •••)} образует ортонормированный
базис в пространстве Z2 относительно скалярного произ-
ведения задачи 17.41.
17.43*	. Доказать, что Z2 является пространством Гиль-
берта.
14$,
17.44.	Пусть La(a, ^—пространство заданных на [a, Ь]
ь
комплекснозначных функций f(x) таких, что J |f(x)|2dx<
а
b
< со. Считая известным, что из условия J | f (х) |2dx — О
• а
следует /(х) = &(х), где 0(х)—нулевой элемент простран-
ства L2 (о, Ь), доказать, что если f (х) С (а, Ь), g (х) С
ь
Ъ), то соотношение (/, g) = J f (x) g (x) dx опреде-
Л
ляет скалярное произведение в Lj(a, b). Написать нера-
венство Коши—Буняковского ъ Ц(а, Ь), называемое так-
же неравенством Шварца (см. ч. 1, с. 164).
17.45*	. Доказать, что последовательность непрерыв-
ных функций
{—1 ври <€[—1, —1/л],
nt при /£(—1/п, 1/п),
1 при /€[1/п, 1]
фундаментальна в пространстве непрерывных на отрезке
[—1, 1] функций с нормой J (/(0—g(0)2^) . но не
имеет предела. Таким образом, это пространство не яв-
ляется полным.
17.46.	Пусть Ц (а, Ь)—пространство заданных на [а, Ь]
ь
функций /(х) таких, что |/(x)|*p(x)dx< оо, где весовая
а
функция р (х)	0 и может обращаться в нуль только
в отдельных точках. Доказать, что если /(х)€Ц(а, Ь),
g(x)£L%(a, b), то соотношение
ь
(f, g)=\fWg(x)p(x)dx
а
определяет скалярное произведение в 1&(а, Ь) (см. усло-
вие задачи 17.44).
Система функций {<р„ (х)}^. заданных на отрезке (а, t], на-
зывается ортогональной на [а, £], если
а)	фп(х)€^(а- ь)> « = 0> !»•••;
ь
. С > ч х .	( 0 при m / п,
6}(ФП. <pe.) = j4>nW<pra(x)dr = j	^ри т^п
а
150
Система функций {<prt называется ортогональной на [а, 5J
с весом р(х), если
«) Фл(х)€^(в, b), n~Q, 1,
б)	(<pn, <pm)=f фп W<?m(x)p(x)^=| °
J	V ®n 9* V При Л1 = П.
a
Если dn=l для всех л=0, 1, ..., та система называется
ортонормированной на (а, 6] или соответственно ортонормировак-.
ной на (а, 6} с весом р(х).
На примерах следующих задач убедиться в сущест-
вовании ортогональных и ортогональных с весом систем
функций.
17.47.	Доказать, что тригонометрическая система функ-
ций
1cosх, sinх, cos2х, sin2х, ..., cosпх, sinпх, ...
ортогональна на отрезке [—я, я], а система
1 саз х slnx	СОЗ их sin пх
V л *	я *	У" л	У" я
ортонормирована на [— я, я].
17.48.	Доказать» что система'функций -{cos
ортогональна на отрезке [0, /].
17.49.	Доказать, что система функций |sln
ортогональна на отрезке [0, 1/2].
17.50.	Пусть система функций/в(х), Д (х), ...,f„(x),...
из L2(a, b) линейно независима на [а, &]. Доказать по
индукции, что построенные по рекуррентной формуле
функции
<Ро(х)=КГ’
П-1
<₽„(*)-
»-1, 2, .
п-1	|	’
fn—	<Pfe)<Pftl
k = 0	II
образуют ортонормированную на [а, 6] систему (метод
ортогонализации Шмидта).
17.51.	Используя метод ортогонализации Шмидта (см.
задачу 17.50), найти первые четыре функции {ортонор-
мированые полиномы Лежандра Pt(x), Рх(х), Ра(х) и Ра(х)),
151
полученные при ортогонализации системы степеней 1, х,
х*, ... на отрезке [—4, 1].
17.52.	Используя метод ортогонализации Шмидта '(см.
задачу 17.50), найти первые 4 функции, получаемые при
ортогонализации системы степеней 1, х, х?, ... на отрез-
ке [—1, 1] с весом р (х)» J= (ортонормированные по-
линомы Чебышева).
17.53*	. Ненормированные полиномы Чебышева с коэф-
фициентом 1 при старшей степени имеют вид
70 (х)  1, Тп (х) =	cos (n arccos х), —1 < х <1
(n^N). Доказать, что система {^(х)}^ ортогональна на
[—1, 1] о весом р(х) = р==.
17.54.	Используя метод ортогонализации Шмидта (см.
задачу 17.50), найти первые 3 функции, полученные при
ортогонализации системы степеней 1, х, х2, ... на отрез-
ке [0, 1]'.
Функции Радемахера гя(х) определяются следующим
образом:
гя(х)«= sign sin 2"+хях,	n=0, 1, ...,
где
(1 при х > 0,
0 при х=0,
—1 при х < 0.
17.55.	Построить графики функций Радемахера г„(х)
для n»0, 1, 2, 3.
17.56.	Показать, что при p>v каждый интервал
постоянства функции rv(x) содержит четное число 2Ц_*
интервалов постоянства функции гц(х).
17.57.	Доказать ортонормированность	системы
{гя(х)}я_0 на отрезке [0, 1].
Функции Уолша lFn(x), xg(0, 1], в нумерации Пэли опре-
деляются следующим образом:
Го(х)«1, Wtk(x)^rk(x), fe=0, 1.........
и если ««2п,+2П2+ ,,,+2п*, щ > л2 >...> nv3*0, то
“1 « * *
Д62
где гл(х) —функции Радемахера, причем в точках разрыва
(х)IF„ (х+0) + Wa (x-O)J.
17.58.	Построить графики функций Уолша 1Гц (х) для
п = 0, 1, ..,, 8.
17.59.	Доказать ортонормированность системы
{^Л(х)}£=о на отрезке [0, 1].
17.60*	*. Пусть Jv(x)—решение уравнения Бесселя
+	+	v2)z/»0, a {|AV)}£=i—корни Jv(x). Дока-
зать, что система функций	ортогональна на
отрезке [0, 1] с весом р(х)«х.
Отыскание решения у(х)9 Ч* уравнения
(k (х) у' (x))'^q (х) у (х) 4-Лр (х) у (х) ® 0,	(6)
удовлетворяющего однородным краевым условиям одного из типов
1)
2)	у'(я)«^(*)«0,
3)	у(х) ограничено при х—иа+0 и х—0, будем назы-
вать задачей штурма—Лиувилля. При этом предполагаем, что
функции k (х), q(x) и р(х) непрерывны на отрезке {а, &], причем
Л(а) = Л(6)®0 в случае условия типа 3), k (х) > 0, у(х)^0,
р(х) > 0 и р(х) ограничена для х(£[а, &].
В общую задачу Штурма—Лиувилля краевые условия 1)—3)
могут входить и в некоторых линейных комбинациях.
Нетривиальные решения у(х)=£0 уравнения (6), удовлетво-
ряющие одному из краевых условий 1)—3), существуют не при
всех X. Значение 1*, при котором существует нетривиальное ре-
шение у*(х) задачи Штурма —Лиувилля, называется собственным
числом уравнения (6), а соответствующее ему решение у* (х) — соб-
ственной функцией.
Заметим, что собственные функции yt (х) и у2 (х) задачи
Штурма—Лиувилля, соответствующие различным собст-
венным числам	ортогональны на [a, с весом
Р(х),.т. е.
ь
(У1, Уз)«» $ У1 (х) у2 (х) Р (х) dx = 0.
а
Найти собственные числа и собственные функции сле-
дующих задач:
17.61*	*. у"—А,0 = О, t/(O) = t/(O = O.
17.62.	/—^ = 0, (/'(0) = у'(/) = 0.
17.63.	/—Х// = 0, (/(0) = 1/'(;) = 0.
17.64.	у"-Ъу = О, /(0) = 0(0 = 0. .
17.65*	*. у"(г) + ±У' (г) + <о»0 (г) = б, у (Я) = 0.
153
3.	Ортогональные ряды. Пусть Ф = (фп(х)}п=о ** орто нор миро-
ванная на [а, система функций, а функция	b). Тогда
существуют числа
,	ь
Сп—Сп (/) = (/. <P»)=J/ (х) <р„ (х) dx, n«=0, 1, ...»
а
называемые коэффициентами Фурье функции f(x) по системе Ф.
Ряд с этими коэффициентами
н*)~
п=0
называемые ортогональным разложением или рядом Фурье функции
f(x) по системе Ф.
Если система Ф только ортогональна, а не нормирована, то
ь
сп=-Б— --------J f (х)фп(х)dx, n = 0, 1, ,,,
J<j>n(x)dx °
17.66.	Используя результат задачи 17.60 (см. решение),
найти выражение коэффициентов Фурье—Бесселя функ-
ции f(x)£L£(O, 1) (р(х) = х) по системе Pv(14v>*)hsN-
17.67*	. Нормированные полиномы Лежандра Р„(х)
(см. задачу 17.51) можно определить также соотношением
(формула Родрига)
Р Ж (-1)" <** (»-**)"
»W“n!2» dx»
Они образуют ортогональную на
А	(О
\Pu(x)Pm(x)dx~< 2
-1	2п+ 1
n = 0, 1, ...
[—1, 1] систему, т. е.
при т=&п,
при /п = п.
Найти первые 4 коэффициента разложения функции /(х) —
==|х|, —1 <х<1, если известно, что Р0(х)==1, Рг(х)—х,
Р2 (х) - 3x42—1/2, Р, (х)- 5х3/2—Зх!2.
17.68.	Записать выражение коэффициентов Фурье функ-
ции f(x)€ £§(—!, 1) (р(х)==рг====0 по системе полино-
мов Чебышева (см. задачу 17.53).
17;в9. Для функции f(x) — x на отрезке [0, 1] вычис-
лить первые четыре коэффициента ее разложения по си-
стеме Уолша в нумерации Пэли.
п
17.70*	. Доказать, что частные суммы Sn(f, х)— 2сйФ*(х)
fe = 0
разложения функции f(x) по системе Ф дают решение
154
следующей задачи о наилучшем среднеквадратичном при-
ближении: в множестве

«полиномов». Т№ (х) по системе Ф порядка не выше п найти
тот, который дает минимум интегралов
ь
min
TnGM
$ V (X)-Tn(x)]’dx
по
17.71.	Используя результат задачи 17.70, вывести не-
равенство Бесселя для конечных сумм:
п »
а
и для бесконечных рядов
оо ?
д
. 17.72. Написать неравенство Бесселя задачи 17.71 для
коэффициентов Фурье функции f(x) периода 2л по три-
гонометрической системе {1, cosnx, sinnx}n6|^:
Ортогональная система Ф = {фи(*)}£_о называется полной, если
из равенств
ь
(f, фп)==$/(x)q>n(*)dx=0,	n=0, 1, ,,,т
а
следует, что f (х) = 0 почти во всех точках отрезка {а, $]♦
Для полных ортонормированных систем неравенство Бесселя
обращается в равенство Парсеваля
09	а
2с*=\
*=о	;
Рассмотренные ранее тригонометрические системы, система
Уолша, система функций Бесселя, системы полиномов Лежандра
и Чебышева являются полными.
17.73,. Каков смысл неравенства Бесселя и равенства
Парсеваля в конечномерном евклидовом векторном про-
странстве?
17.74*. Доказать, что система функций Радемахера не
является полной на отрезке [0, 1].
155
4. Метод Фурье решения уравнений математической физики. Метод
Фурье, широко используемый при решении ряда задач математи-
ческой физики, состоит в следующем. Искомая функция, завися-
щая от нескольких переменных, ищется в виде произведения функ-
ций, каждая из которых зависит лишь от одной или нескольких
переменных. После подстановки этого произведения в исходное
уравнение получается несколько обыкновенных дифференциаль-
ных уравнений, часть из которых вместе с краевыми условиями
исходной задачи являются краевыми задачами Штурма'—Лиувилля.
Искомое решение представляется рядом по произведениям соб-
ственных функций этих задач Штурма—Лиувилля.
Пример 3. Найти отклонение и(х, /) от положения равно-
весия закрепленной на конце х = 0 однородной горизонтальной
струны, правый конец которой при х=>/ перемещается так, что
касательная к струне остается постоянно горизонтальной. В на-
ч	.	1 । Иях _ 4лх
чальный момент времени струна имела форму sin ——cos
начальные скорости отсутствовали.
Прёдполагая, что струна совершает малые колебания, получаем
следующую смешанную краевую задачу: найти решение уравнения
свободных колебаний струны
д*и
dt*
д*и
дх* *
(7)

2 Tfl
--------
р
удовлетворяющее начальным условиям
, м 1,14лх ди (х, 0) л	/ov
«(x.0)«=Issto-^-CO3-5r, -^-2=0	(8)
я граничным условиям
w(0, 0 «0, ux(lt 0=0.	(9)
(Ю)
Решение этой задачи ищем в виде произведения а(х, /)
с» X (х) Т (/), подставляя которое в (7), находим
Х(х)Т^(0=паХ^(х)Т(0.
Разделив обе части этого уравнения на а*Х (х) Т (0, получаем
T№(t) _Х№(х)
a*T(t)~~ X (х) ‘
Каждое отношение в (10) зависит от своей переменной, поэтому
равенство возможно только в том случае, когда каждое из этих
Х"(х) ,
отношений постоянно. Полагая	и используя граничные
условия (9), получаем задачу Штурма—Лиувилля
Х"(х)—%Х(х)«0,	Х(0) = Х<(/)«0,
собственными числами’которой являются числа	\ ,
. 1
а собственными функциями**функцин Х*(х)==51п —лх, 6®1,
2, (см. задачу 17.63).
ч 156
Xff (%)
Подставив в (10) вместо отношения *v, г его значение
Л (X)
. 1 \» t '
Лд==—I	л I , получим при каждом й=1, 2, •«« уравнение
Т»(П+(^1яа)*Г(0-0.
общим решением которого является функция
Таким образом, решениями уравнения (7), удовлетворяю-
щими граничным условиям (10), являются функции
f л 26—1	< . D а 26—1 Л , 2&*-*1
= А* 008 ~w	+Вк sto ~~2Г~	)sln ~2i~
Л=1, 2, ...
Из линейности уравнения (7) следует, что любая линейная ком-
бинация этих уравнений, т. е. формально составленный ряд
/ V* (л ‘2k—\	4 । п , 2Zs~l X , 2fc—1
u(x, /)=^( Hftcos—ла/+ В sin—gy— nat j sin -	- лх
fe=i '	'
(11)
при условиях на, коэффициенты А* и Вд, допускающих возмож-
ность его двукратного почленного дифференцирования по i и по х,
также является решением уравнения (/), удовлетворяющим гра-
ничным условиям (9).
Потребуем, чтобы представленное рядом (11) решение н(х, /)
удовлетворяло также граничным условиям (8), т. е. чтобы
•о
. Лх 1 Л Илх 4лх Vя я , 26—1
«(х, 0) =I5 sin т cos -1Г=Х Л* sta -2Г ™
fe=l
И
ди(х, 0) Л \^2&—1 D 2^-«м1
—3/=°=L ~2Г Sto ~2Г
fees 1
Из этих равенств заключаем, что если числа Лд являются
коэффициентами Фурье функции
, ч	1 . Плх 4лх 1 ( я 7лх , ж 15лх\
ф W 8Ш — cos -^-=^ ^sta-2i-+sin )
( 2k" 1 Iе®
по системе <sin—ху—лх>	, т, ем если ЛА=»0 при k 4 и
(	J л® 1
k Ф 8, а Л4 = Л8 = 1/30 и если ьВдееО для всех 6»1, 2, .то
функция
z .v 1 / 7nat . 7лх .	15ла/ , 15лх\
U(z, 0 = зо(с08 — sin-^+cos-^—sln-^-j
является искомым решением уравнения (7). ►
' 157
17.75.	Найти отклонение и(х, I) от положения равно-
весия закрепленной на концах х—О и х=/ однородной
горизонтальной струны, если в начальный момент струна
имела форму -|-sin а начальные скорости отсутство-
вали.
17.76.	Найти отклонение «(х, t) от положения равно-
весия закрепленной на концах х=0 их«1 однородной
горизонтальной струны, если в начальный момент точки
струны находились в положении равновесия и ей была
придана начальная скорость ysin-^p.
17.77.	Найти отклонение ц(х, t) от положения равно-
весия закрепленной на конце х—1 однородной горизон-
тальной струны, левый конец которой при х=0 переме-
щается так, что касательная к струне остается горизон-
тальной, если в начальный момент струна имела форму
1 Злх
-g-cos-^j-, а начальная скорость отсутствовала.
17.78.	Найти отклонение и(х, t) закрепленной на кон-
цах х=0 и х=/ однородной горизонтальной струны от
положения равновесия, если в начальный момент струна
имела форму параболы с вершиной в точке х = 1/2 и от-
клонением от положения равновесия h, а начальные ско-
рости отсутствовали.
Решить уравнение колебаний закрепленной на концах струны
иц=а*и’хх при начальных условиях
. Л, 4hx (I— х) ди (х, 0). л
«(х. 0)- —у—L’	.'=0.
17.79.	Найти колебания закрепленной на концах х=0
и х=1 однородной горизонтальной струны, находящейся
в положении равновесия, если в начальный момент вре-
мени ударом молоточка в точке х —Z/3 ей сообщается
постоянная начальная скорость
(I П '
Vt при х—з.|<2Л»
о при X—Я>^,
где л/Л—ширина молоточка.
17.80.	Найти закон свободных колебаний закрепленной
на конце х=0 однородной горизонтальной струны, если
правый ее конец при х = 1 перемещается так, что каса-
тельная к струне остается постоянно горизонтальной.
158
В начальный момент струна находилась в положении рав-
новесия и ей была придана начальная скорость u't (х, 0)==
= sin пх/1.
ф Граничными условиями в данном случае являются условия
/А -А ЁН (.1Э	а	.	«	«а
ы(С, г)=—g”1 =0, а системой собственных функций является
система <sln	 п.—— > ...
1	2/ p«N
17.81.	Закрепленной в точке х=*1 однородной горизон-
тальной струне, левый конец которой в точке х=0
может перемещаться с горизонтальной касательной,
X (I**** х} ТТ О
придана начальная скорость	—L, Наити закон ее
свободных колебаний, если в начальный момент она имела
форму <р(х)х= sin 2^-.
• Системой собственных функций задачи является система
V 2/ faelM'
17.82.	На концах однородного изотропного стержня
длиной / поддерживается нулевая температура. Предпо-
лагая, что стенки стержня теплоизолированы от окружаю-
щей среды, найти закон распределения температуры в стерж-
не, если известно, что в начальный момент имелось
.	x(Z-—х)
следующее распределение температуры: и (х, 0) = и0 —>
где ы0 = const.
ф Решить уравнение распространения тепла o;=a’a«.
17.83.	Один конец стержня (при х«0] поддерживается
при постоянной нулевой температуре, а второй (при х=1)
теплоизолирован от окружающей среды (т. ё. производ-
ная от и (х, t) по х на этом конце равна нулю: и"х (/, t) = 0).
Найти закон распределения температуры внутри стержня,
если начальная температура задана функцией
и(х, 0) = <p(x)=J у
Uq При \ X 4*
• Системой собственных функций является система
Г 21 JkeN'
17.84	**. Однородная прямоугольная мембрана (0 x^Z,
закрепленная вдоль всего контура, лежащего
|S9
в горизонтальной плоскости, и имеющая в начальный
момент форму и (х, у, 0)= <р (х, у), начала колебаться
с начальной скоростью u't (х, у, 0) = ф (х, у). Найти закон
свободных колебаний мембраны. Получить решение в слу-
чае ср (х, у) =* sin -^25. sin , ф (х, у) = 0, если натяжение
мембраны Т6 равно ее поверхностной плотности р, т. е.
Р
17.85	*. Точкам закрепленной по контуру однородной
квадратной мембраны со стороной I, находящейся в на-
чальный момент в положении равновесия, придали началь-
ные скорости щ(х, у, 0) — sin sin . Найти закон сво-
бодных колебаний мембраны.
17,86	*. Закрепленной по контуру однородной квадрат-
ной мембране со стороной I придали форму и (х, у, 0)«
= sinsin-2г . Найти закон свободных колебаний, если
начальная скорость точек мембраны постоянна и равна
а/l, где а—входящая в уравнение колебаний постоянная.
17.87	**. Найти стационарное распределение температуры
в прямоугольнике D = {(x, i/)|0<x^a, O^y^.b], если
на границе прямоугольника поддерживается заданная тем-
пература:
и (х, 0) «= и (х, Ь) = 0, х б (0, о),
«(0, у) = ф=	t/), и(а, у) — фО/) = sin
У$(Р,Ь).
17.88	*. Найти решение и (х, у) уравнения Лапласа
Ди sa ихх 4- и"у№=0 в прямоугольнике D — {(х, у) 10 < х < а,
*<У<Ь}, удовлетворяющее следующим краевым усло-
виям:
«(0. У)~У(Ь-у\ и(а,	=	=
17.89	. Найти решение и(х, у) уравнения Лапласа
Дг/ = 0 в прямоугольнике D = {(х, у) 10 < х < а, 0 < у < Ь},
удовлетворяющее условиям
«(0. »)"«. и(а.у}-ау. ^-^-=0.
17.90	**. Найти свободные колебания'закрепленной по
краю однородной круглой мембраны радиуса Z, если в на-
чальный момент отклонение в каждой точке определялось
160
равенством и (г, <р, C)=a/0(^J, в котором цх—первый
положительный корень, /0 (х), а начальная скорость мем-
браны равна са, где а—постоянная, входящая в уравне-
ние колебаний мембраны.
17.91	**. Найти закон стационарного распределения тем-
пературы внутри бесконечного кругового цилиндра ра-
диуса /?, если на его поверхности поддерживается задан-
ная температура:
«О'. Ф)[,=/?==/(ф) = sin<р.
В случае, когда исходное уравнение в частных производных
является неоднородным, т. е. в характеризуемом этим уравнением
физическом процессе имеются внешние силы и источники, предва-
рительно находится система собственных функций соответствую-
щего однородного уравнения и решение ищется в виде ряда по
этим собственным функциям с переменными коэффициентами.
Пример 4. Найти форму и (х, t) (отклонение от положения
равновесия) закрепленной на конце х = 0 однородной струны, пра-
вый конец которой имеет горизонтальную касательную и на кото-
рую действует внешняя сила с плотностью F (х, В началь-
ный момент ^ = 0 струна имела форму <р(х) и каждая точка имела
скорость ф(х). Найти и (х, t) при условии, что <р (х) = ф (х)==0.
a F(x,
Предполагая, что струна совершает малые колебания, имеем
следующую первую краевую задачу: найти решение и (х, t) урав-
нения вынужденных колебаний струны
^=a«^4-F(x, 0, аа = -^,	(12)
dt2 дх8 1	1	'	р 9	' '
удовлетворяющее граничным условиям
и (0,0 = 0,	^}=0	(13)
и начальным условиям
и(х, 0) = <р(х),	ди -)=>[> (х).	(14)
Чтобы найти собственные функции однородного уравнения
иц =sa2u'xX с граничными условиями (13), положим и (х, 0=Х (х) Г(0
и после разделения переменных получим уравнения
Тп Хп
<15>
с граничными условиями
X(0)x=X40 = 0.	(16)
Решая уравнение XX =0 с краевыми условиями (16), нахо-
—» ду-"" - ) и соответствующие
/
6 Под ред. А. В. Ефимова, «.4	WI
собственные функции
ХЙ(Ж) = 81ПМ2^1!^, fe€N	(17)
(см. задачу 17.63>.
Рассматривая t как параметр, разложим функцию F (х, /)
( . л (2&—1) х)
в ряд по системе <sln ——2Z
л V1 л /л • л(2&—1)х
F (*» 0 = 2л А* (0 skl "2/ — •
k~\
где
I
Л 2 Р_.	.. , зт(2А?— 1)о ,	--.л
лИ0в71 F (». Оsin ' 2i '' dv*
Будем искать решение уравнения (12) в виде ряда
00
. ’ V1 /Л , л(2&— 1)х
И (*» 0=2й sin ' 2~ " •	(18)
*=1
подставляя который в (12) (считаем, что таковы, что воз-
можно двукратное почленное дифференцирование по х и по t) и
сравнивая коэффициенты при одинаковых гармониках, Йолу чаем
бесконечную систему дифференциальных уравнений второго по-
рядка относительно функций сь (/):
ck (04----—-^(0“>*л(0.	(19)
Из начальных условий (14) следует, что функции Ck(t) должны
удовлетворять условиям
00
/ л\ / ч	, л (26 — 1)х
и (х, О) = Ф (х) =2rf с к (0) sin — 2J—- 
fes 1
и
оо
'/ ЛЧ .74 V? ' /ЛЧ х Л (2&-— 1)Х
«/ (*, 0) = Ц> (х) = 2^ Ck (0) sin 2/	.
kss 1
Пусть
С к (0) = 4 ф (0 sin 3T(2fe~‘,P? dv	(20)
0
и
I
4 (0) = 4 J Ф sin 2"2f ~^ Vdv’ *€N>	(21)
о
t. e. cjt (0) и (0) являются коэффициентами Фурье соответствен*
но функций <р(х) и ф(х) по системе (17). Найдем теперь решения
162
уравнений (19), удовлетворяющие условиям (20) 9 (21), и,
подставляя их в ряд (18), получим искомое"решение и(х,
По условию <р(х) = ф (х)==0, поэтому
сЛ(0)=4 (0) = 0 для всея
Далее, так как F(x, /) = а2, то
Z-
Л /А А 2 С 2 . я(2&—1)о .
Ак (О = Л* = у j _а» sin	2f do=
о
— 2а*	21 я (2k— 1)оК 4а»
I л(2й—1) 008	21	|0=овЛ(2й—1) *
Поэтому	требуется	найти решения дифференциальных	уравнений
ck (О +	4р	(22)
удовлетворяющие 'условиям
^(0)=4(0)«0.	(23)
Корни характеристического уравнения для	уравнения	(22) мнимые,
поэтому частные решения уравнений (22) ищем в виде Од (/) =»
Подставив эти значения в (22), найдем, что
16Z*
П“л*(24-1)? ’
а поэтому общее решение каждого на уравнений (22) запишется
в виде
...	яа(2&—l)f . о	ла(2й—1)( .	16Z2	,	.
Q (/)==адсоз 2/ +P*sin 2/	"^лЗ(26—I)3’
и из условий (23) получим
16Z2
C*(°)=a*+«»(2fe— 1)'J==°’
* /ги о jux(2&«—1) ft
£fe(u)ePfc 21	—О»
т. е.	и «*“-^2^—., fegN.
Таким образом,
ек =
-	16/4 fl	32Л -ln*na(2fe~1)f
~n»(2fe—1)« V	Sl / я3(2*”1)’	41
и искомое решение имеет вид
,	32/» Vя 1	, .ла(2А—1)/ , я{2&—1)х .
1 *
6*
163
17.92*	. Для O^x^l и Z>0 решить уравнение
д2и д2и . ‘ , Л
dt2 в ах» +х(х О
при нулевых начальных и краевых условиях
н(х, 0) = «;(%, 0) = u(0, Z) = u(Z, 0 = 0.
17.93*	. Для O^x^Z и Z>0 решить уравнение
а»и - а«и . в» . ла<
-^“0?ajr+7rsin —
при нулевых начальных и краевых условиях
«Jx, 0) = иДх, 0) = ц(0, Z) = u(Z, 0 = 0.
17.94.	Найти температуру стержня при 0 с теп-
лоизолированной боковой поверхностью, если начальная
температура его концов равна нулю, а в точке x«€(0,.Q’
находится сосредоточенный источник е постоянной мощ-
ностью Q.
ф Требуется найти решение уравнения
dt дх*~ '
в нулевыми начальными и граничными условиями и (х, 0)==а (0, 0е
е«(|, 0««0, в котором f (xt O=B=Q6(*’~**o)/cp> 6(х)—дельта-функ-
ция Дирака, с**-удельная теплоемкость и р-—удельная плотность.
2 f*	jtkt)
При вычислении коэффициентов ЛА(/)=у \ f(vt t)sm -p-du ис-
о
пользовать следующее свойство 6-функции:
если f[x) определена и непрерывна в точке х0, то*
+ ®
j f(x)6(x—xa)dx—f (х0).
— 60
17.95.	Для 0<х<2 и Z>0 найти решение уравнения
ди д2и . . пх
dt "’Sc« + sin 4 ’
удовлетворяющее начальному условию и(х, 0)=0 и гра-
ничным условиям н (0, Z)—0 и Ux(2, /) = 0.
В примерах 3 и 4 краевые условия являлись однородными
(см. определение задачи Штурма-*Лиувилля перед задачей 17.61).
Если же рассматривается задача с неоднородными краевыми усло-
виями, то с помощью замены u = путем надлежащего выбора
функции U задача сводится к решению уравнения относительно
164
функции р.уже с однородными краевыми условиями. Выбор функ-
ции U определяется видом заданных краевых условий.
Пример 5. Найти закон свободных колебаний горизонталь-
ной струны, правый конец которой при закреплен, а левый
при х== 0 движется по закону u(0, Z) = sin2y. Начальные ско-
рость и отклонение равны нулю.
«4 Имеем уравнение и^==а2а"^ с начальными условиями и (х, 0) =
= lz'(x, 0)=0 и неоднородными граничными условиями п(0, О®
s=sin^, и(1, 0=0. Произведем замену п(х, /) = р(х, /)+
, Z—х , nat _	,
Н---j—sin—р . Тогда относительно функции v(x, t) получим- не-
однородное уравнение
г	/ л л / лч	ла(/—-х)
с начальными [условиями v(x, 0)=0» с^(х, 0) = —jg- «  < и одно-
родными граничными условиями у(0,	/)=0- Однородное
уравнение с^=а20"х с этими граничными условиями имеет систему
nkx 1
sin—т—>	поэтому ищем решение не-
* J леГ1
однородного уравнения в виде
оо
/ ач V /ч /дч « П^Х
V(X,	с»(0sto-7~-
*=|
Подставив это выражение в неоднородное уравнение, получим
бесконечную систему уравнений
^(0 + (-^)*С*(0=Л*(0. *€N,	(24)
I
л 2 Сп?а2(1—х) t nat , nkx . 2ла2 4 nat
где Ak(t)==-^----~----isin-y-sin--prfx=-^-sin-y , причем
о
из начальных условий следуют следующие условия на (0) и
»
Са(0):	0)=Ц	(0) sin	т. е. Сй(0)=0 для всех AgN,
k = i
00
,, Vя /лч . nkx na(l—x)
и v't (xt 0) =»2u Gk (°)	-----15—L * T‘ e’
I
/>г/Лч	2 Г na(l—x) , nkx ,	!2a	.
C'(0) =--J- \---—-Sin-y-dxsa—!— для всех fcgN.
о
При &®1 в уравнении (24) имеет меето резонанс (см. указание
к задаче 17.93), поэтому частное решение ищется в форме
165
Ci(Z) = / (zxcos^+^sin^) j подставив его в уравнение, най-
дем, что Ci (/)=—-у-cos. Используя затем условия Cf(O)=O
fr у*-*"**
и Ci (0)« —j । находим, что
_ ZJX 1 f nat at nat
Ci (/) = -“ Sin --fCOS-p.
Далее, используя условия С*(0) = 0 и С'(0) =-—, при ^>2
получаем следующие решения уравнений (24):
Л	2 nkat .	12	. nat
Ck(t)	n(fc2 —l)sin I + nk(k*- l)Sta I*
Подставив эти коэффициенты в ряд для v(xt /), получим искомое
решение
и(х, f)=-^~!-sln^-}-o(x, t). >
17.96.	В области О^.х^.1 и Z^sO найти решение
уравнения u't — а*ихх при начальном условии и (х, 0) = х{1
и граничных условиях и(0, 0 = 0 и u(l, t) = e~*.
ф Для приведения неоднородных граничных условий^ однород-
ным произвести замену и(х, t) = v(x, t)+xe~t/l.
17.97.	В области О^.х^.1 и /^0 найти решение
уравнения u't = ихх при начальном, условии и (х, 0) = 1 и
граничных условиях и(0, t)=e *1* и ди^ ^=0.
• Для приведения неоднородных граничных условий к однород-
ным произвести замену и(х, /)=р(х, /)+« il> •
17.98.	Найти закон свободных колебаний горизонталь-
ной струны, левый конец которой при х=0 закреплен,
а правый движется по закону u(l, l)-sin^~-. Началь-
ные уклонения и скорость равны нулю.
ф Для приведения неоднородных граничных условий к однород-
ным произвести замену и(х, i)*»v(x, t)+4-sin^.
17.99.	В области O^x^Z, i0 найти решение урав-
нения и1еяа9ихх при начальном условии и(х, 0)=-^- и
граничных условиях u(0,	u(l, Z)ss0.
166
17.100.	В области 0^x<U, /^0 найти решение
уравнения u’t = ихх при начальном условии и (х, 0) = 1 и
граничных аДО, 0=Д и (Л
При решении задачи Коши (в этом случае краевые условия
заменены ограниченностью решения на бесконечности) метод
Фурье приводит к использованию интеграла Фурье.
Пример 6. Найти закон распределения температуры u(xt t)
в длинном однородном стержне, боковая поверхность которого
теплоизолирована и известно начальное распределение темпера-
туры и(х, 0) = <р (х) = е~*г.
Пренебрегая влиянием температурных условий на концах длин-
ного стержня, будем считать его бесконечным. Поэтому мы имеем
следующую задачу Коши: найти решение уравнения
ди	(У2 и
-оо<х< + оо, 0</< + о»4	(25)
удовлетворяющее начальному условию
и(х, 0) = ф(х)=е-**.	(26)
Предполагаем, что ф(х) абсолютно интегрируема на оси(— оо, оо).
Ищем решение в виде произведения Га (х, $) = Х (х)Т (/), поэтому
уравнение (25) преобразуется к виду
Т' X"
<27>
причем отношение отрицательно в силу того, что при t —► оо
функция Т (t) = e~aW не должна возрастать до бесконечности.
Правое из отношений (27) приводит к уравнению Х"-|-со2Х=0,
решениями которого являются функции
(х) ® А (СО) COS СОХ + В (со) sin сох,
а потому решениями уравнения (25) являются функции
и® (х, /)=е“а2й)2/ (Л (со) cos сох+В (со) sin сох).
Если Л (со) и В (со) абсолютно интегрируемы для cog[0, -f-oo),
то интеграл
+ »	+ »
и(х, /)= J Иа)(х, J е"°8ш8/(Л (со) coscox+ В (ш) sin со х) dco
о	о
(28)
можно дифференцировать по параметрам t и х и мы имеем
+ 0О
ut (х, /) = —- а2 со2е-a2w2/ ^4 cos	sto WX) rfco,
о
+ а>
uxx(x> t)~— J а~ав£°8/сог(Л (со) cos cox-J-B (со) sin<ox)4co.
О
167
Следовательно, определяемая интегралом (28) функция и{х, t} яв-
ляется решением уравнения (25), поэтому, если мы выберем
+ оо
Л (со) ea-jL У ф (т) cos сот dx
-00
и
+ оо
В((о)=~ у ф (т) sin (от^т,
— 00
то определяемая интегралом (28) функция и (х,. t) будет удовлет-
ворять и условию (26). Таким образом, искомым решением яв-
ляется функция
+ »	+00
U (х, /) = — (* е-а*<иМ fa С ф |C0S cos Sjn Sjn ют] fa в
Л J	v
О	о
+ оо	+оо
C-X-L С ф(т)(/т С	COS G) (Х — Т)£?(0.
Л
-»	О
Используя формулу (см. задачу 8.192)
+ « _______________________________________ б2
J e“v<°8 cos&odo)==y j/"е *v ,
о
вычисляем внутренний интеграл
+ сю
С	t ГТ (*~т)‘
I е“в*»,<СО8<в(х«.т)</© = -г)/ —57 е 4аЧ .
Л	г CL*
о
а потому
и(Х, /) =-^г=
2а V nt
В нашем случаеф (т)=е“х. поэтому
1 V*
U(x,0=—Л J dt. >
2а У nt J
В задачах 17.101 —17.104 найти решение задачи Коши
ди___д^и
dt дх? ’
—:©6<х<4-оо, 0^/<4~°о,
при указанном начальном условии и(х, 0).
( А9 IxKft,
17.101.	и(х, 0) = <	’
168
17-102. и(х,0) = е-»*4,
17.103. u(x, 0) = < ’ 1
I 0» 1*1 > А
( х, IxKA,
17.104. и(х, 0) = < л
I 0» * > А.
§ 3. Приближенные методы решения
дифференциальных уравнений в частных производных
1. Основные понятия метода сеток. В большинстве случаев
получить решение дифференциального уравнения в частных про-
изводных с помощью элементарных или специальных функций
невозможно. В связи с этим важное значение приобретают при-
ближенные методы его решения. Ниже мы ограничимся рассмотре-
нием краевых задач для уравнений математической физики с двумя
независимыми переменными в области D с границей у, т. е.
Lu^a(x, у)и'хх-\-2Ь{х, у) Wxy-}-c(x, y)u’y+d(x, у)и'х +
+«(«. y)u’y+g(x, y)u = f(x, у),	(х, y)£D, (1)
Га = <р(х, у),	(х,	(2)
где а (х, у), b (х, у), с (х, у), d (х, у), е (х, у), g (х, у), f (х, у) —
известные функции переменных х и у, определенные в области D,
Г—некоторый линейный (в общем случае дифференциальный) опе-
ратор граничных условий и ф(х, у)— известная функция, задан-
ная на границе у.
Наиболее часто используемым методом численного решения
краевой задачи (1), (2) является метод сеток, (метод конечных раз-
ностей), В методе сеток замкнутая область D=D|J Т заменяется
конечным множеством точек—сеткой Da = Da|JYA‘ Точки этого
множества называются узлами сетки. Параметр h = (ht т), шаг
сетки, характеризует ее плотность в области D. Обычно при
| h | —рЛ/124-т2 —* 0_последовательность сеток стремится запол-
нить всю область D. Производные, входящие в левые части соот-
ношений (1) и (2), заменяются на сетке соответствующими
разностными отношениями. В результате получается система ли-
нейных алгебраических уравнений
LhPh^fhtyin*	УпУ^Е^Л*
ГЛн& - Фа (хт, уп)>	(хм, уп) € уА,	•
где (хт, уп), (хт, #n)gDA—искомая сеточная функция, fh уп),
4h(xm> у»)—сеточные функции, заданные^ на множествах Dh и уА
соответственно, и Lh, ГА—разностные операторы. Сеточная функ-
ция пА, являющаяся решением системы уравнений (3), называется
приближенным решением краевой задачи (1), (2) на сетке Dh. Ее
значения итл Л	Уп) приближенно заменяют в узлах сетки
Dh соответствующие значения точного решения и (хт, уп)
исходной краевой задачи б некоторой погрешностью дЛ>
= «и, (хт уп},
169
Семейство систем уравнений
ft==(/i, т), называется разностной
иногда удобно записывать в виде
(3), зависящее от параметра
схемой. Разностную схему (3)
где
^huh — fh (хт > Уп)»
(хт> Уп)£&Ь>
Гй» (хт* Уп)(£Хк>
/ /й» (хт» Уп)^®11*
I Фй, (хт» Уп)$Уь-
(4)
(хт> yn)£Dk>

Построение разностной схемы (3) или (4) для краевой задачи (1),
(2) начинается с выбора сетки, т. е. указывается правило замены
области D и границы у сеточной областью D^. Чаще всего сетка
выбирается прямоугольной и равномерной. Для этого проводятся
два семейства параллельных прямых: x = x0 + m/i и у=у^+пх и
рассматриваются всевозможные точки попарных пересечений пря-
мых из этих семейств, т. е. точки вида (х/Л, ^n) = (x0 + m/i, у0 + пт).
Точки (хот, Цп)> которые принадлежат замкнутой области Dt обра-
зуют сетку Dft, являясь ее узлами. У каждого узла (хт, уп)
имеется четыре соседних точки: (xw_f, уД (хЛ+х, уп), (хт,
(хт, Уп+1)- Если все эти соседние точки также принадлежат
сетке Dh, то узел (хот, уп) называется внутренним^ в противном
случае узел (хт, уп) называется граничным. Совокупность внут-
ренних узлов образует множество а граничных — множество у^
(так что Dh = DMyfi). Следует отметить, что множество гранич-
ных узлов уь не обязательно является подмножеством точек гра-
ницы у, что приводит к погрешностям при построении сеточной
функции фА из (3). На_рис. 224 приведен пример прямоугольной
и равномерной сетки построенной для заданной области D
170
(внутренние узлы сетки здесь отмечены символом *, а.граничные —
символом •).	__
После выбора сетки Dh проводится построение сеточной функ-
цииФл) и разностного_оператора Lh==(Lh9 1\) из (4). Для
определения в узлах сетки Dh полагают fA(xm, уп)~ f (хт, уп),
если (хт, yn)^Dhf fh(xm, yn) = q>(xm, уп), если (хЛ, yrt)gyA и
(хЛЛ, Уп)$Ъ если же граничный узел (хЛ, уп) $ у, то в качестве
f(xm, Уп) выбирается значение функции ф (х, у) в произвольной
точке (х, у)$Ъ отстоящей от узла (хш, уп) на величину, мень-
шую |Л|. Для построения разностного оператора Lh все известные
функции, участвующие в явной записи операторов L и Г (напри-
мер, а (х, 0, b (х, у) и т. д.), заменяются своими значениями в уз-
лах сетки Dh и обозначаются соответственно через ат* nt bm^n
и т. д., а частные производные 1-го и 2-го порядков неизвестной
функции «(х, у) приближенно заменяются соответствующими раз-
ностными отношениями. В результате получаем разностную схе-
му (4), соответствующую краевой задаче (1), (2).
Пример 1. Построить разностную схему для краевой за-
дачи распространения тепла в конечном стержне ((Хх^О
“t—aXx = ^X>	“(х> °) = <Р(*)«
«(О, 0=1^1(0.	«(/.<)='МП.
Заметим, что область определения{(х, /) 10<х<1, 0</<-f-oo}
данной краевой задачи является неограниченной. Поэтому для
построения равномерной прямоугольной сетки Т)А (которая всегда
является конечным множеством точек) поступим следующим обра-
зом. Проведем два семейства прямых x~mh и / = /гт для некото-
рых заданных h и т. Очевидно, что точка (xw, tn) принадлежит
области определения исходной задачи, если /п=±=0, 1, г, где
г = (//&), и n = 0, 1, ... Положим
Он = {(хи, /„)|m=0, 1.....г, п = 0, 1...$},	(5)
где целое s выбирается так, чтобы интервал 0</Cts перекры-
вал тот временной диапазон, в котором изучается распростране-
ние тепла в стержне. Множество внутренних узлов ^имеет вид
^A = {(xw> tn) I т=1, 2, ..., г—1; л«1, 2, ..., з. В это множе-
ство входят и узлы вида (хЛ, ts), /п=1, 2, ..., г—1, которые мы
считаем внутренними, так как наше о£раничение t st является
искусственным! Соответственно ?А=^А\^А или в явном виде
=	0) |/п==0» 1,	r}U{(0, /Л)|п«1, 2,	s}U{(^Jw)|,
Да1, 2,	$}.
Далее полагаем иА =»{uMt п},
^п) —
f f (хт> $
Ф (Хт)>
Ф1 (*п),
фз(и.
(хт*
n=0; m=0, 1, •««, г,
m=0; /is=l, 2,	$,
т~г, п=з 1> 2, ♦ «,, $.
(6)
Отметим, что в случае; когда l/h не является целым числом,
т. е. r=a[ljh] < l/h9 узлы (хг, /„), п=1, 2, ..., s, не принадлежат
граничной полупрямой х = /, yjbsO. Вместе с тем эти узлы яв-
171
, ляются граничными, поэтому значения сеточной функции fA в них
перенесены с границы.
Для получения разностного уравнения заменим производные '
разностными отношениями (см. задачи 17.105 и 17.108):
ut (х/л> ?п) & ~г(ит, n+V—Umt п)»
**хх (хл, /п) «	(#м+2, п"**2мт> п4“^1Я-1» п)»
где (жт,	Следовательно,
1	а2
(w«> n+i***w«,	(Йл+Х, п**2цл> п“Н*л-Х» п)>
т«1, ..., г—1; п=0, 1, s— 1,
m««0, ...» г,
п=®1, ...» з,
п=®1, ..., 3.
выражения (6) и (7) в (4), получаем искомую раз-
которая представляет собой следующую систему

(7)
И/я, 0»
n»
'. wr, n>
Подставляя
ностную схему, л . .
линейных алгебраических уравнений:
1	а2
~ (^т, п+1—“а, nV № (ил+1, п
/я=1, ...» г—
Um,0 = <P(*m).
«О, п = Ф1 (*п)>
ur, «“t»Gn)>
%umt	n)saf (хmt ^n)t
1; л=0, ..., s— 1,
m=0,	r,
n=»l,	s,
n»l, ...» s.
Эта система состоит из («+1) (г+1) уравнений. Решив ее относи-
тельно неизвестных ит*п> т = 0, ..., г; и=0, ...» з, найдем се-
точную функцию uh— {aWt п}, значения которой в узлах сетки при-
ближенно заменяют значения искомого решения исходной краевой
вадачи для уравнения теплопроводности. ►
Естественно, наибольшие трудности в построении разностной
схемы (4) вызывает замена дифференциального оператора L исход-
ного дифференциального уравнения в частных производных (1)
разностным оператором LA из (3).
Пусть Uh~~конечномерное нормированное пространство сеточ-
ных функций заданных на сетке Dht с 1|	||—max | uv|,
V
где «V—координаты вектора иА (индекс v последовательно про-
бегает все пары индексов (т, п), нумерующих узлы сетки). Будем
говорить, что разностный оператор LA приближает дифференци»
алъный оператор L, если для любой функции и (ж, р), дифферен-
цируемой достаточное число раз, норма сеточной функции
(Lu)a^Laua стремится к нулю при |й|—► 0, т. е.
|(Mb-Lb«h|| —о,	|ft|—* о.
Если, кроме того, выполняетея неравенство
О (Ма-Ьл«а I <С (| h |Р+1 т Р),
где С—константа, не зависящая от Л, то порядок приближения
разностным оператором равен р по переменной х и q по перемен-
ной у.
172
В частном случае, когда шагнсетки связаны соотношением т=0 (h)
(т. е. не являются независимыми) и
ULu)h^Lhuh^C\h^t
говорят, что разностный оператор Lh приближает оператор L
с порядком приближения и.
Для определения порядка приближения обычно используется
формула Тейлора;
Пример 2. Определить порядок приближения дифферен-
циального оператора Ьи~щ — а2иХх разностным оператором из
примера 1.
В примере 1 был построен разностный оператор
1	а2
(^fi^h)m, п=~ (^/я,	(W/e+i,	п)«
Используя формулу Тейлора, находим
“ (wm, n+i~" п) (^л,	’"* И (Хл, tn)аа
I	т
=«/ (хт, ta)+у u'tt (Хт, Г),
где tm < V < tm+т, и
^2” (um+i, п 2ит,	п) =
=4 (т(и (х»+л’ /п)—“ /я)+4(и (*«• *»)))=
=="^	*») +"g" ихх (хл, /п)-|—иххх(хт, *п)+
Uxxxx	—ux(xmt	ихх (xmt tn)~
h2 ///	h3	\\
--------------------------6* Uxxx ^Xmt ^n)”F”24* Uxxxx (**> tn) j j 9
где xm—h < xn < xm < xf < xm+h. Приводя подобные члены
в правой части последнего выражения, получаем
‘д2“(ида+1, n”"2wOTj	n) = Mxx (^m,
+‘24’ \uxxxx (* » tn)'kUxxxx(x\ tn))*
Следовательно,
(^А^л)лв, n= ul (xm> ?п)'~"а2ихх (xm> /n)H (xmt t')-—
---2^~ (uxxxx (x’, tn) + uxxxx (xat tn))*	(8)
Используя выражение (8), разность между исходным диффе-
ренциальным оператором L и заменяющим его разностным
в узлах сетки можем представить в виде
п'вЯк(^Л^л)т» n=’^’utt (хт> tf)^^^‘(uXxxx(x,i tn)JT^xxxx(x,\ tn})
173
! для некоторых f (*»<*'<*»гИ) и х',h<x" <хт<х' <xm+fy.
j Если теперь | иц (х, t) | < Mf и | ихххх (*> О I < М2, то выполняется
неравенство
|1 (Luj^^L^U^ IIеniax | (Lu) т,	nl^
m. n
X	14
Следовательно, использованный в примере 1 разностный опе-
ратор приближает исходный дифференциальный и порядок при-
ближения по переменной х равен двум, а по / — единице.
Отсюда, в частности, следует, что для того, чтобы порядок
приближения был равен двум, необходимо шаги h и т сетки свя-
зать соотношением t=/i2.
Замечание. Для облегчения запоминания построенного
разностного оператора полезно поставить в соответствие ему
«шаблон»-—геометрическую картинку расположения узлов сетки,
значения в которых связывает разностный оператор при некоторых
фиксированных значениях тип. Для разностного оператора из
примера 1 шаблон изображен на рис. 225 (проверьте!).^
В задачах 17.105—17.107 определить порядок прибли-
жения дифференциального оператора частной производ-
ной и'х указанным разностным оператором LA.
17.105.	(Мл)«. n=4 («m+i. п—иа, „)—оператор пра-
восторонней разности.
17.106.	(Lhuk)a, „=j (ит,	„)—оператор лево-
сторонней разности.
17.107.	(Laua)ot,„=^(h„+i,	— оператор
центральной разности.
В задачах 17.108—17.111 определить порядок прибли-
жения заданного дифференциального оператора L второй
частной производной указанным разностным оператором Lh.
17.108.	Lu*=uXX9 « =
в А2	п-j- ит~1, й).
17.109.	Lu*=Uyy9 (Lhuh)mt п =
17.110.	Lu — uxy, (Lhuh)mt п =
=	+ n-i	n-i)*
17.111,	Lu~Uxy9
— 1 /
л+1 ч» + 1. n i n »+v
i 174
17.112.	Построить разностную схему для краевой за-
дачи из примера 1, используя оператор правосторонней
разности и оператор, аналогичный приведенному в за-
даче 17.109. Определить порядок приближения получен-
ного разностного оператора Lh (шаблон приведен на
рис. 226).
.	(т.п+1)
Z7+/-I-------------*----------—•
\	л	(т-1,п+1)	(Л+^п+0
v (т-1,п) (т,п) (т+1,п)	п+1—------------*----------------
л у j т
h 	„	(т,п)
Рис. 225
Рис. 226
В задачах 17.113 и 17.114 определить, какой диффе-
ренциальный оператор и с каким порядком приближается
заданным разностным оператором Lh.
17.113.	п п) +
4" 2т (2“«. п+1 ^m + i, п 4" Чп-i, п)'
17.114.	=
“дг (Цт—i, п4" “л, п-1 4" ^и+f, п 4“ ^т,	п)"
17.115.	Определить при каком а порядок приближения
дифференциального оператора L: Lu = u't— и"хх разност-
ным Lh
(LfiU/ijg!, п (Цт, п+1	^т, п) ~~
д? (а («п»+1, п+1 —	B+i	n+i) 4-
4" 0 ~а) (мя + 1, п 2uCTt п—в))
будет четвертым по h и первым по т.
Составить разностные схемы для следующих краевых
задач.
17.116.	^•s=a?-g- + f(x,/),u(x,0) = (P(x),-g-(x1 0) =
=ф (х), и (0, 0=Ф1 (0, «<Ь, t) =ф2 (0, D = {(х, 0 10<х<6,
17.117.	c-^4-d-^=/(x,t/),c>0,d>0)zz|v = i|>(x,z/),
D={(x, i/)|0<x<&,
Более общим способом построения разностных операторов,
приближающих заданный дифференциальный, является метод
175
неопределенных коэффициентов. Этот метод состоит в том, что при-
ближается не каждая производная в отдельности, а сразу весь
оператор. Для замены дифференциального оператора разностным
в узле (хт, уп) рассмотрим АГ соседних узлов. Узел (xMt уп) обоз-
начим индексом 0, а остальные рассматриваемые узлы занумеруем
w
числами 1, 2, . N. Составим линейную комбинацию 2 ckuh
с неопределенными коэффициентами где иц — значение и (х, у)
в узле k.
Предполагая функцию и(х, у) дифференцируемой л+1 раз,
разложим и^ по формуле Тейлора в окрестности узла 0. Считая
сетку квадратной (т = /г), имеем

О)
Коэффициенты линейно выражаются через с^. Выберем коэф-
фициенты Ck так, чтобы правая часть в равенстве (9) отличалась
возможно меньше от значения дифференциального выражения Lu
в узле 0, т. е. чтобы коэффициенты при производных в уравне-
нии (1) совпадали с коэффициентами при соответствующих произ-
водных в правой части (9), а коэффициенты при старших произ-
водных порядка г(2 < г<д) в (9) приравняем нулю, т. е.
для 2<1’ + /5=г<п.	(10)
Учитывая, что выражаются через имеем систему уравнений
относительно решив которую, мы получим приближение опера-
тора Lu в узле (т, я):
N
4>=0
Система уравнений <10) относительно с% может иметь несколько
решений, однако достаточно взять одно из них. Используя в слу-
чае необходимости достаточно большое число узлов /V, можно
получить хорошее приближение Lu в узле (т, л).
В задачах 17.118 и 17.119 построить соответствующие
разностные операторы методом неопределенных коэффи-
циентов.
17,118.	+	+ Порядок приближения
равен двум (шаблон указан на рис. 227).
176
П&Строим квадратную сетку Dft, т. ё. выбираем шаг как по
переменной х, так и по переменной у равным h. В качестве сосед-
них берем 8 узлов (см. рис. 227), т. е. N=8. Имеем линейную
8
комбинацию 2 <Ws(b«)o*
Разлагая uk по формуле Тейлора в окрестности узла 0, будем
иметь
«1=«(х0+Л, у0) = «о+«^+-^ М+-^Л«4-О(Л4),
«а = «(«о.	Л*+-^Л«+О (Л«),
«з = «(хо-Л. Уо) = ио-ихН+^- h^-^-hi+Olh^,
«4 = «(х«> У»—Л) = «о—u'yh+л»—h»+О (h*),
«5 я» u(Xq 4~ ht уъ~{-Ь)=*Щ>-]г uxh~[- uji+(ихх+2aw'+ uyy)+
+“зГ (Uxxx4"3Ux*v4“4”
sa U (Xo—•&> Fo +Л) ® Ho —W^)*4*
h9 /	,/r
4" "зр (""" иххх4*3uxtg ~~ 3uXyi +	+ О (ft4),
w?=w (Хо—ft, ffo—h)=»uq—uxh—Uyh-f*-jp (uxx4~2uxy-f-Uyy) —
"“Jp (uxx^+3Mx^+3ux^ + w^p)+O (ft4b
u9=u(Xb+ht уо*-Л) = «о+"хЛ—u^+
+-g- («xx*-2u^+u^)+-gp (wXxx**3wx^+3«X£/l—(ft4).
Подставим эти выражения в (Lu)0:
{Lu)t  Uq (Co + Qi + Ci + c3 + ^4 + cb + c« + + fy) +
4“U^ft (С1-*-С34-С5-*Сб—1?7+С8) + «^ (C2-*^4+^б4"св**^7*^8) +
+#xx	(Pi+сз + c6+Ce+Cy+c8) + Uyy -jp (Cj+q+c#+ee+^+^e) +
+“^-Л2(с5—^xxx (£1вм-,£з) +
+ 3f “m (°2 ~ c4) + 3j- Of (“x*x+3«x»s+3«жу1 + Uygg) 4-
I 31 °9 (*“ UXXX 3ttx*^““* 3wxjre + Uyyyi
"" *3p (j^xxx 4" &Ux*g 4" Змхр*+ttyyy) 4*
*1"3|‘св(“***“Зал‘4/+Змед’“и4/г₽)*Ь^ (el’ c»’ •••• c8)“=*
e Uxg + 2«ед 4- 5uvg.
177
Сравнивая коэффициенты при соответствующих производных,’? по-
лучим систему линейных уравнений для нахождения ck, выбирая
при этом
С0 4” ££ 4” С2 +	+ £« + С7 + С8 =
ц	— с3	4-с6—с6—с7+с8=0,
С% -"£44-£б4’£б — С1—с8~^>
2
Ci	+С5 + Св4"С7+С8 — *^2»
Й 4’С4 + С54“Св + с7+С8 = '^Г»	0Q
,	2
с8 —С6 — С7+С8 = ^|-,
ci	**^з4"с44“с5—£в—*£7 4’с8==0>
с5+св—С7—с8 = 0,
С5 —Се ~“С7 4~^8~ О»
с3	*B’Q4"^54"Ce — с7—“С8 = 0.
Систему уравнений 4И) решаем методом исключения. Из послед-
вих четырех уравнений получим cg=c7, с2^с4. Используя эти
равенства, из второго и третьего уравнения системы установим,
«то св=с8, С1 = Сз. Можно переписать систему уравнений (11)
в следующем виде:
с3 -f- 2с£ 4"	-|“	= О,
2cf	-|~ 2с8 = 2//i2,
2са+2с6+2сб=: 10/ft2,
2с6 —2св = 2/Ла,	(12>
1	с4==0,
с2 = 0.
Решая систему (12), получим следующие значения для искомых
постоянных:
с0 = —2//i2, ci = — 4/А2, е2 = 0, с3 = —4/Я2,
е4=0, c6=3//i2, ce = 2//iar c7s=3//i2, с8 = 2/Л2.
Окончательно для узла 0 получим
(Lu)o » (—**»4и£ «•4^3 -|" 3«54-2н6 -f- 3w7-|-2h8),
т. е. для всех внутренних узлог сетки имеет место формула
(^Л^л)а» » =	n + 4wze+fi n4"4uze_il n —
n+i—*2мл_1} я+i—3uw_if »-1"~2плв) rt f-i-
Порядок аппроксимации второй: г—1 ==п-*1 = 2. ►
178
17.119.	Lu~'uxx + uyy. Порядок приближения равен
двум (шаблон указан на рис. 228).
Пусть, как и выше, иь=*{иА (т, п)} — решение 'разностной
схемы, т. е. системы линейных алгебраических уравнений (4).
Применение разностной схемы к решению краевой задачи (1), (2)
оправдано, если величины «д(т, п) являются приближенными
значениями сеточной функции и(хт, уп), представляющей собой
значения неизвестного решения и (х, у) вадачи (1), (2) в узлах
сетки.
Будем говорить, что разностная схема (4) является сходящейся
на решении и(х, у) задачи (1), (2), если при h —* 0 выполняется
условие х)
!«(*»> Уп)—(т, п) | -» 0.
Если дополнительно выполняется неравенство
II и (xmt yn) — uh(mt n)\\^Ahs9	(13)
где А—константа, не зависящая от Л, то говорят, что скорость
сходимости имеет порядок s относительно к.
Сеточная функция и (хт, уп), вообще говоря, не является
решением разностной схемы. Поэтому при подстановке ее в левую
часть (4) получается выражение
Lk(u(xmi У п) ~ fh>
где называется невязкой или погрешностью аппроксимации.
Если II|| —*0 при Л —>0, то говорят, что разностная
схема (4) аппроксимирует краевую задачу (1), (2) на решении й (х, у).
При выполнении дополнительного условия
(14)
где С—константа, не зависящая от Л, число ст > 0 называется
порядком аппроксимации.
Наконец, не менее важным свойством разностных схем яв-
ляется понятие их устойчивости. Разностная схема (4) называется
устойчивой, если существует такое Ло, что для всех h < Ло и лю-
бых fa она имеет единственное решение и
11М<С[1М,	_	(15)
где С—константа, не зависящая от h и правой части fa.
Между рассмотренными понятиями сходимости, аппроксима-
ции и устойчивости существует тесная связь.
Теорема 1. Пусть устойчивая разностная схема (4) аппро-
ксимирует краевую задачу (1), (2) на решении и(х, у) с порядком
аппроксимации о > 0. Тогда эта схема является сходящейся и по-
рядок ее сходимости совпадает в порядком аппроксимации.
Пример 3. Для задачи Коши
— Ux~f(xt t)9	—оо < х < Ч-оо, О «С/«С Г,
и (х, 0)==ф (х),	— оо < х < 4-оо,
Л) Здесь и в дальнейшем будем считать шаги Лит зависи-
мыми, т. е. т = 0 (Л).
179
построена разностная схема
~ (^/я, п + 1 —п)	+ п — Um п)~{т, nt
т = 0, ±1.....±М; п = 0, 1......[Т/т]	— 1,
«1в,о = фл>. ш = 0± 1, .... ±Л1,
где т=%Л и постоянная Л.< 1. Определить порядок аппроксимации
этой схемы и исследовать ее на устойчивость.
Сначала покажем, что построенная разностная схема аппрокси-
мирует исходную краевую задачу и определим порядок аппрокси-
мации. Предполагая, что решение и(х, у) задачи Коши имеет огра-
ниченные вторые производные, по формуле Тейлора имеем
“д’(um+i, п*~ит, п)~-^(и	tn)^U (xmt tn))***
t	h »
s‘Ux{Xm, ^n)4—jj"uxx (xm + £> ^n)>
r:	0<g<ft,
4-(«л,п+1—«л, n)=-7<“<x'»> <»+T)—«(*<». U) =
¥	v
^UtlXmt tn) + ~Uft(Xm, G + rj).
0 < T| < t.
Учитывая соотношение т=АЛ, получаем
1 ** - 1 *• - .
~ \ит, n + i~um>	+	=
=(«/ (Хт, tn)—ux(xm, tn))+h (у ~utt (Хт, *„+т))—у uxx (Xra-H,
Погрешность аппроксимации Гт, n—Lh («(xm, yrt))—f»,n, сле-
довательно, принимает вид
лТ f h(^~u"tt(xm, tn + 4)-^Uxx(xm + l, /„)),
ofm, r» = j ./	2
Ho 'um> о-фй = О для любого m в силу граничных условий. По-
этому норма bfMtn оценивается следующим образом:
II С., Л И < max | у utt(xm, tn+11) —у ~ихх (х + g, t„) | < hM ^i-1,
где Ммаксимальное значение вторых производных функции
и(х, у) в области D. Полагая здесь В	приходим к нера-
венству (14). Следовательно, рассматриваемая разностная схема
аппроксимирует исходную задачу Коши и порядок аппроксимации
равен единице. (Конечно же, на решении и (х, у), обладающем
ограниченными вторыми производными.)
Отметим, что метод проверки свойства аппроксимации разно-
стной схемы во многом повторяет метод определения порядка при-
ближения разностным оператором дифференциального.
180
Теперь проведем исследование разностной схемы на устойчи- ,
вость. Снова используя соотношение т = ХЛ, перепишем исходную
разностную схему в виде
ит, п+1=(1 —X) «1», n-№um+i,	n,	qgv
«/n.0 = <P«,	1 '
где, как и выше, m = 0, ±1,	±Л1; n==0, 1, [T/(Xft)J —1.
По условию Х<1, поэтому 1—Х^О. В этом случае справед-
лива оценка
| (1 — X) ит> n~l“Xwm+i> п | < (1 — X) | ит п |4-Х | um+it п | «с
< (1-X) max {| uMf п I,
I “m+i, п 1}+*- max {| ит, п |, | um+if п [}=> -
= тах {| ит> п |, |нл+1,п|}< max \ит> д|. ,
Используя эту оценку, из (16) находим:
I ит, п+11 < 1 (1	ит, п4“^л + 1, п 14" W*. п 1<
< Лах^«|Ил- »I+WA||. (17)
где J fh | = max | fm, п |. Правая часть неравенства (17) от т не за-
т, п
висит, поэтому выполняется неравенство
т.а* I< max J«»,B| + W*o (18)
для любого n=0, 1, ..., (T/(Xft)J — 1.
Используя неравенство (18) для оценки первого слагаемого
в его правой части, последовательно находим
max \ит, в+1|< max |ue> „-i |+2X/i|IM<-..
‘'W 11M<•• •
' ’	“«- °1 + (n+	11 M =
-	(19)
так как um,o = (pw из (16). Теперь заметим, что max |фЛ|<
___	_	~М<т<М
/л11 и ||/д|К||/лО* Подставляя эти неравенства в (19), получим
max |ии,„+1 |<(1+(п4-1) ХЛ)[)ТЛ||<
< (I+1Т/М] щ iiTft II < (14- Т) II т„ и.
Правая часть полученного соотношения от h не зависит. Следо-
вательно,
max max |«Л, П<Л I<U +Milfoil-
0<п<[Г/(Хй)1-2 -Л1<т<А(
Г. е.
ом«1+г) им.
и мы получили искомое неравенство (15) (с Cel-j-Т), означающее
по определению, что разностная схема устойчива при Х<1.
181
Так как заданная разностная схема аппроксимирует на реше-
нии исходную краевую задачу и устойчива, то при она
является сходящейся и скорость сходимости по теореме 1 имеет
первый порядок. ►
17.120	. Доказать теорему 1.
17.121	. Показать, что рассмотренная в примере 3 раз-
ностная схема неустойчива при % > 1.
17.122	**. В области D={(x,	1,
построить разностную схему первого порядка, аппрокси-
мирующую первую краевую задачу для уравнения гипер-
болического типа
г д2и ,д2и , ди , .ди . _	, Л « . п
Lu=!‘adx2~b^ + cdx + ddy+SU=:t' а>0’ fc>0’
|f|i)=0='l’W. «к=о=Ф(!/). u\XBll^F(yl
17.123	*. В области D из задачи 17.122 построить раз-
ностную схему второго порядка, аппроксимирующую пер-
вую краевую задачу.
17.124	*. В области D построить разностную схему пер-
вого порядка, аппроксимирующую третью краевую задачу
17.125	**. Построить разностную схему второго поряд-
ка, аппроксимирующую третью краевую задачу.
17.126	*. Определить порядок аппроксимации разност-
ной схемы задачи 17.117.
В задачах 17.127—17.129 для заданных задач Коши
и соответствующих им разностных схем выполнить следую-
щие задания!	_	_
1)	Выписать разностный оператор Lh и правую часть /fti
возникающие при записи этой схемы в виде (4).
2)	Нарисовать шаблон для разностного оператора Lh.
3)	Показать, что разностная схема аппроксимирует
соответствующую краевую задачу с первым относительно
h порядком на решении и(х, /), имеющем ограниченные
вторые производные.
4)	Исследовать разностную схему на устойчивость в
зависимости от значений параметра т = Х7г.
182
17.127.	u't — ux — f(x, t), —oo <x< +<x>,
и (x, 0) = <p (x); x
~(“ffl. n+1	к	e) = Zm. n»
m = 0, ±1, ...» ±M,
um.t-=9m, n = 0, 1, .... [Т/т]—1.
17.128.	u't + u'K — f (x, t), —oo < x <4-00, 0</<T,
ы(х, 0)=<p(x);
(®«rt n+I n) + ft’ (um, n	n) в»
ffl = O, ±1» ..., iAi,
««.«“Фт. »“0> 1> ...,[Т/Т]—1.
17.129.	u't-\-u'x = f(x, t), —oo<x<4-oo, 0</^T,
и (x, 0) = <p (x);
(^я, n+l~^«. в) + у (^m+I, в n) = Zm. в»
т = 0, ±1, ..., ±/И,
“я.О^Фя. Л»0, 1, .... [Т/т]— 1.
17.130.	Исследовать устойчивость разностной схемы из
примера 1.
17.131.	Исследовать устойчивость разностной схемы из
задачи 17.112.
17.132.	Исследовать устойчивость разностной схемы из
задачи 17.116.
17.133.	Исследовать устойчивость разностной схемы
n+i .п—1) де	п -|- ил+^ я),
m = 0, 1, ...» М—1, n = 0, 1, ...» N—1,
^льО^Ф/я»	«О,
2.	Численное решение краевых задач методом сеток. Все разно-
стные схемы, применяемые при решении краевых задач матема-
тической физики, делятся на два больших класса—*явных и не-
явных схем.
Под слоем разностной схемы понимается совокупность точек
сетки В, лежащих на некоторой горизонтальной (или вертикаль-
ной) прямой. Если значения сеточной функции ит> n+it заданные
на (п-р1)-м слое, выражаются в явном виде через значения этой
же функции на слоях с меньшими номерами, то такая схема на-
зывается явной. В противном случае схема называется неявной.
Например, разностная схема, полученная в примере 1, является
явной, так как может быть записана следующим образом (см.
183
выражение (7)):
umt nil**™», п + ~№‘ (w^+l, n^^umf п + ил-1, n)4“/m, n,
n = 0, 1, ...» <—1; /n=l, r—1,
^,о = фй,	m=0, 1, ♦,,, r,
Mo, ne^i(^n),	n»l, 2, ,«., s,
urt n= Фа (^n),	n=l, 2, ..., s.
Решение получающейся системы линейных алгебраических урав-
нений трудностей не представляет и осуществляется последова-
тельно, переходом от слоя к слою.
Сложнее обстоит дело с неявными схемами (как в задаче 17.112,
например). Для решения соответствующих им систем уравнений
удобно применять метод прогонки, т. е. модифицированный метод
исключения для решения системы линейных уравнений. Суть этого
метода разберем на основе неявной разностной схемы для уравне-
ния теплопроводности (см. задачу 17.112). Введем обозначения
2о^т
ат> n+l5®--^т, и+1 = 1 + да , ёт, п+1 = ит, n + Van п + 1*
(20)
Разностную схему из задачи 17.112 перепишем в виде
Чп = ^.П>,
ат, n+lum-lt n+1 + ^m, п^лв, п+1+алв, п+1мда+!» п+1 — ёт, п+1, (21)
ukfnsss^2tnt Л = 0,	S—*1,
^лв,0 = флп /И=1, «•	1.
Система уравнений (21) при^ каждом фиксированном значении п
совпадает с системой
и0==<р,	'
an«n-l+Mn+^n«»+i=^n, n=l, TV—1,	(22)
^№=<Ф»
для которой справедлива следующая
Лемма. Система уравнений (22), коэффициенты которой удов-
летворяют неравенствам | bn | 1 +1 ап | +1 сп |, разрешима при лю-
бых правых частях, и для ее решения справедлива оценка
|»|<тах{|<р|, |й|,	|-ф|}.
Для системы (21) условия леммы выполнены. Систему уравне-
ний (21) удобно решать с помощью метода, который называется
методом прогонки. Будем искать решение системы уравнений (21)
при каждом фиксированном п в виде
wjn-lt n+1= Qm, n+lwza, n+l + ^ze, п+1»	m*=kj ,,,, 2* (23)
Исключая um_it n+i из системы (21), получим
ат, п+1
п+1 = — а п.,Ом	Um+^ n+1 +
l*jn2 n+lxm, n+lT17/», n+X
^ёт, п+1^а/л. n+i^m. n+1
ft+lQm, n+l + ^jn2 n+i
184
Соотношение (24) сцдаывает значения функций ит> n+j, ит+ь n+i9
поэтому можно записать
ит, n + l==Qz»+l, п+1ида+1, п + 1 + ^/л + 1, »+!•	(25)
Сравнивая соотношения (24) и (25), имеем
_	ат, п+1
m+it n+1	n+iQint л+14“^л», п+1	(26)
, „	gm, п+1— ат,п+1^т,п+1
Лffl + 1, П + 1““л	н	tfc	*
ат, п + 1Чт, п+1"Г°хя, п+1
Соотношения (26) определяют значения всех прогоночных коэффи-
циентов Qm> „, Нт п. С помощью этих соотношений сетка проходит-
ся вверх по т от значения 1 до значения 1 при фиксированном
значении п. При этом определяются все значения Qm, п, Нт* п на
сетке (прямая прогонка). Определив все прогоночные коэффициенты
#ю,п, проходят сетку вниз от значения k до 2, последова-
тельно определяя значения ит, п из уравнения (23) (обратная
прогонка). Граничное условие при т=0 определяет начальные
значения Qi, n+f, Н1>п+1, а граничное условие прит=4 в общем
случае определяет первое значение и^. Метод прогонки обладает
тем свойством, что ошибки округления, получаемые на каждом
шаге, не нарастают. Это свойство служит основанием ее широкого
применения.
17.134*	*. Определить начальные значения прогоноч-
ных коэффициентов и значение uk для решения парабо-
лического уравнения в случае граничных условий
В задачах 17.135—17.147, используя разобранные вы-
ше разностные схемы, найти приближенной численное ре-
шение.
17.135.	2^-2^-/х2 = 0, D = {(x,0|0<x<2,
0</<1},	u|tB0=x2,	^|/=0=sinx»	1»
«U=2 = 4cos t.
17.136.	g2-p-8^ = 0, D = {(x, y)|0<x<l, 0<
<I/<1}, «(0, x) = x, «(0, y\ — y, g(x,O) = O, ul\,y)=*
= 1— У-
17.137.	uxx—4uyy = xy, D = {(x, #)|0^x<2, 0<
<1/<1}, и|„.о=х« + 1, «Я»=й = у + 6» «U=o = sin^+1,
MIa:=2 = 5cOS^.
17.138.	uxx—iugy—xys=0, D = {(x, i/)|0C*Cl, 0C
185
17.139.	ихх—^иуу = ех«, D = {(x, «/)|0<x<2, OCy<
ci}, «U-4X+5,.	(^+sin^)ko = ^‘
(S+H Lecos*'-
Задачи 17.140—17.143 решить, используя явную или
неявную схемы.
17.140.	|-2^-х = 0, D = {(x,t/)|0CxC2, ОС
<У<1}, «lv=o=l— у, и|х=о = созг/, «|x=2 = siny.
17.141.	§-2| + 1=0. D = {(x, </)|0<хС1, ОС
u(x,0) = x’, u|xeI»^, (Й+")ко==0-
17.142.	4u(—2uxx+x/ = 0, D~{{x, /)|0СхС2, ОС
(- + Й) ,., = <>•
17.143.	g = g+8x2/\D={(x, /)|0Сх<1,0С*<1},
aL_0==sinnx,	—0,5u) I	=0, (^4-0,5иМ =0.
Il-B	\ox ) |x=0	’ \ox - } |*=1
Решить следующие задачи Дирихле.
17.144.	2ux;( + tzwr=x? + 2xy, D={(x, |/)|0СхС2,
0<#С1}, и|(Я,= 1+х, «|х=2 = 3—у*, и|хж0=1+5^,
«Ui = 6—х2.
17.145.	д^+д^---х*-у\ D = {(x,z/)|0C*Cl,0C
1}, «и=о = 2г/?, «|хя1 = ^ + 4г/, и|y=0 = 0, и|и =
» x?+2x-t-2.
17.146.	g + 4g = sinx^ D = {(x, t/)|0CxCy+l,
0<у<1}, м|у=о = *, «Ux-I = ^+1, | «Ь«1 = 5—х,
17.147.	2«хж + Ч!,+ух=0, _D={(x, 0)|ОСхС2,
0<^<1}, «|х=о = 5«/, н|₽я0 = Их, ы|у=1 = 5—х2, и|х=2=
= V^ri-
В задачах 17.148—17.155 составить на фортране под-
программы для численного решения уравнений в частных
производных методом сеток, используя разобранные выше
разностные схемы. В качестве параметров подпрограмм
использовать: F, FI, PSI1, PSI2, DLT1, DLT2 ит. д.—
индентификаторы подпрограмм-функций, вычисляющих
значения правых частей уравнений, а также начальные
и краевые условия соответственно.
186
17.148.	Составить подпрограмму для решения уравне-
ния параболического типа	(*> 0,	{(*• У) 10^
1}, и|/=о = ф(х), «U=0 = %(0.
₽ф2(/) явным методом, используя схему примера 1.
17.149.	Составить подпрограмму для решения первой
краевой задачи, используя разностную схему из за-
дачи 17.123.
17.150.	Составить подпрограмму для решения третьей
краевой задачи, используя разностную схему из за-
дачи 17.125.
17.151*	. Составить подпрограмму для решения урав-
нения Пуассона, используя разностную схему из за-
дачи 17.117.
17.152.	Составить подпрограмму для решения уравне-
ния теплопроводности методом прогонки, используя раз-
ностную схему из задачи 17.112i а) граничные условия
не содержат производных; б) граничные условия общего
вида (см. задачу 17.134).
17.153.	Составить на фортране подпрограммы-функции
для вычисления функций правых частей уравнений
17.135—17.147.
17.154.	Составить на фортране подпрограммы-функции
для вычисления начальных и краевых условий в задачах
17.135—17.147.
17.155*	. Составить на фортране программы решения
задач 17.135—17.147, используя подпрограммы, получен-
ные при решении задач 17.148—17.154.
187
Глава, 18
ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
§ I.	Интегральные уравнения Вольтерра
1.	Уравнения Вольтерра 2-го рода? основные понятия, связь с диф-
ференциальными уравнениями. Линейным интегральным уравнением
Вольтерра 2-го рода называется уравнение
X
У(х)»/(х)+$ К (х, t)y(t)dt,	(1)
а
где г/(х) —искомая функция, a К(х, t) и f (х)-*-известные~функции,
определенные соответственно в треугольнике а^х<&,
и на отрезке [а, М. Функция К (х, t) называется ядром интеграль-
ного уравнения (1), функция f(x)«*свободным членом этого урав-
нения.
Решением уравнения (1) называется всякая функция у(х), х£
€1а> подстановка которой в это уравнение обращает его 6 тож-
дество. Вопрос о существовании и единственности решения ре-
шается различным образом в зависимости от свойств ядра К(х, t)
и свободного члена f (х), а также от того, в каком классе функций
ищется решение. Всюду в дальнейшем, если не оговаривается
противное, мы будем предполагать, что функции K(xt I) и f (х)
непрерывны в своей области определения. При этом условии урав-
нение (1) имеет, и притом единственное, решение в классе функ-
ций, непрерывных на [а, 6].
Интегральные уравнения Вольтерра 2-го рода используются
обычно при описании динамики различных процессов в системах.
В частности, всякая задача Коши для линейного дифференциаль-
ного уравнения
W + • • • +а»	(*).
У {X^yv у' М~У1, .... у"1-» (Х0)=^п-1
может быть сведена к решению некоторого линейного интеграль-
ного уравнения Вольтерра 2-го рода.
Пример 1. Составить интегральное уравнение, соответ-
ствующее задаче Коши
и"+2и' + и=х\ ц(0)8»1,	«'(0) —0.
Положим

(2)
188
Интегрируя (2) с учетом начальных условий, последовательно
находим
X	X
и' (х) = и' (0) + J у (0 dt U (0 dt,
О	о
(3)
X S	X
и (х) = и (0) + J ds J у (t) dt=1 + J (х-/) у (/) di, (4)
0	0	о
Подставляя (2)— (4) в [исходное дифференциальное уравнение,
получаем
X	/	х
У (х)+2 J у (О Л + ( 1 + J (x—t) у (/) dt
о	\	о
или
X
У (х)=х«-1-$(2+х-П ?(/)<«.	(5)
О
Таким образом, показано, что если и (х)** решение исходной
вадачи Коши, то функция у (х) = и" (х) удовлетворяет интеграль-
ному уравнению (5). Обратно, если у (х)-*решение этого уравне-
ния, то функция ц(х), определяемая соотношением (4), удовлетво-
ряет как исходному дифференциальному уравнению, так и началь-
ным условиям. Следовательно, рассматриваемая задача Коши
эквивалентна интегральному уравнению (5). ►
Проверить, что данные функции являются решениями
соответствующих интегральных уравнений:
х
18.1.	у(х)=е^х, y(x)-e»+^-*y(t)dt.
о
18.2.	у(х) = хех9!\ y[xj^x+^xty[t)dit
18.3.	у(х)«е-*(£ + 1).
X
y(xj=e~* +	sin(x—f)y'(t)dt.
о
Составить интегральные уравнения, соответствующие
следующим задачам Коши-
18.4.	и'4-2хы=е*, z/(0) = 1.
18.5.	2ы'+« = 0, «(2) = 1, и’ (2)= —2.
18.6.	и"—sinx-w' +е*и = х, и(0) = 1, «'(0)» — 1.
18.7.	uf'+xu^e*, ы(0) = 1, и' (0) = и"(0) = 0.
18,8,	и(0)=и?	(0)^0, и"\(0>1.
189
18.9*	. Показать, что задача Коши для линейного
дифференциального уравнения с постоянными коэффициен-
тами
fan + ai dxn-l + • • • + апУ — f (x)>
Уо (*o) = ya, у' (x0) = yu .... y{n~" (x0) = y„_t
сводится к интегральному уравнению вида (1) с ядром
К(х,	а*( (fe_>i)f ♦
зависящим лишь от разности к—t своих аргументов
{интегральное уравнение типа свертки, см. п. 3).
Задача Коши для произвольного дифференциальвого уравнения
Л-го порядка вида
у),	=
эквивалентна в общем случае нелинейному интегральному урав-
нению Вольтерра
У («)=?•+ У(О)Л-
Аналогично, задача Коши для произвольного дифференциального
уравнения n-го порядка, разрешенного относительно старшей
производной,
y™**f (xt yt у\ ...» У*""1*), £(Хо)==Уо,
может быть сведена к системе нелинейных интегральных уравне-
ний Вольтерра.
Пример 27 Составить систему интегральных уравнений,
соответствующую задаче Коши
tf^2y^yf\ у (0) — 1, у’ (0)=0.
4 Полагая yt (х) = д (х),	сведем исходную задачу
к задаче Коши для нормальной системы 2-го порядка
У1—Уо,	yi = 2yi—yl, #i(0)=l>3 У»(0)=0.
В свою очередь, полученная система дифференциальных уравнений
а учетом начальных условий эквивалентна системе интегральных
уравнений
И М=1т j Уо (О#. Уо (*) = $ (2и (0—»?(0) <Н- ►
о	о
Составить интегральные уравнения или системы урав-
нений, соответствующие следующим задачам Коши»
190
18.10.	y' = l 4-xsin«/, у(л) = 2л.
18.11.	/ = —14-3*? + ^,
18.12.	у” = х + у\ г/(0) = 1, /(0) = 2.
18.13.	Г =	у(0)-----3, t/'(0) = l, /(0) = -1.
18.14.	£f' = x+xz/»-A у(0) = 1, /(0)>/(0) = 0.
Во многих случаях решение интегрального уравнения Воль-
< терра 2-го рода (или системы таких уравнений) в свою очередь
может быть сведено к решению некоторой задачи Коши для
обыкновенных дифференциальных уравнений. Укажем здесь два
способа, посредством которых это может быть сделано.
а)	Если в исходном интегральном уравнении (1) ядро К(х, t)
и свободный член f (х) имеют непрерывные производные К' (х, t)
и /' (х), то это уравнение может быть продифференцировано (один
или несколько раз), что и позволяет в ряде случаев свести его
к задаче Коши для некоторого обыкновенного дифференциального
уравнения.
Пример 3. Решить интегральное уравнение
X
y(x) = slnx+ J sln(x—t)y(t)dt.	(6)
о
4 Последовательно дифференцируя интегральное уравнение, полу-
чаем
х
у'(х) <= cos х+ J cos (х—t) у (t) dt,	(7)
х
У (х) — sin х+у (х) — f sin (х— 0 у (t) dt.	(8)
*
Исключая из уравнений (6) и (8) интеграл J sin (х*»у)у(/) rf/, полу-
о
чаем для неизвестной функции у(х) дифференциальное уравнение
у"(х)==О. Из (6) и (7) находим начальные условия: у(О)«=б,
у'(0)=1. Следовательно, у(х)«х. ►
Рассмотренный прием всегда приводит к цели в том случае,
когда ядро К (х, I) имеет вид многочлена по степеням бинома х**/
(см. задачу 1.9).
Пример 4. Решить интегральное уравнение
X
х £ (x) = x-j-2 sin х—1 —(х—t)	(9)
о
Дважды дифференцируя уравнение (9), получаем
х у' (х) == 1 + 2 cos х— J у (/) dt, 0 / (х) = — 2 sin х—-у (х).	(10) (И) 191
Уравнение (11). или в стандартной форме
2sinx,	(12)
и есть дифференциальное уравнение для функции у(х). Началь-
ные условия найдем из (9) и (10) при х=0:
У(0)«—1, /(0)^3.	(13)
Уешая задачу Коши (12), (13), находим
г/(х) = 2 sin х+(х— 1) cos х,
что и является решением исходного интегрального уравнения. ►
б)	Пусть исходное интегральное уравнение (1) имеет вид
FW = /W+jf ^Pi(x)qiff)\y(t)dl	(14)
о \i=l	/
[уравнение о вырожденным ядром).
Запишем его следующим образом:
П	Л
У (X) - f (х) + 2 Pi (X) J q, (О У (t) df.	(15)
0
Вводя функции
Ut(x)= ^qi(t)y(t)dt,
0
................................. (16)
«n(x)= j qn(t)y(t}dt
о
и подставляя их в (15), заключаем, что решение интегрального
уравнения (14) имеет вид
р(х).= /(х)4-2 р|(*)«< (х).	(17)
i = I
Далее, дифференцируя соотношения (16) и подставляя вместо у(х)
выражение (17), получаем для неизвестных функций п/(х) систему
дифференциальных уравнений
«1 (х) =»« (х) f (х) + 2 qt w Pi w “< (*)>
i == 1
Un (x) — qn (x) f (x) + 2 qn (x) Pi (x) ui to’
i=l
Из (16) при X=0 находим начальные условия: Ui(0)==. = ип(0)=0.
Определив функции и/(х) и подставив их в (17), получим решение
у(х) интегрального уравнения (14).
192
Пример 5. Решить интегральное уравнение
X
Полагая а(х)=»^ ch/ y(i)dt, получим
о
/Ws=1+dT7“<*’-
Далее, дифференциальное уравнение для и(х) имеет вид
и' (х)=ch х у (х)« ch х ( 1	«(X))
иля
и'*~и=ch х.
Решая это уравнение с учетом начального условия «(0)=0.
находим и (х) = ~ {xe*+sh х)> откуда
, ч , , 1 xe*+sbx
Решить интегральные уравнения, сведя их предвари-
тельно к обыкновенным дифференциальным уравнениям!
18.15.	y(x)—ex + ^y(t)dt.
О
18.16.	^(х) = 1 + $^(/)Л.
О
18.17.	«/(х)==-|-^- + pin(х—t)y(t)dt.
18.18.	у (х) s= е~* cos х—$ cos хе" {x~t} у (f)dt.
о
18.19.	у (х) = 4е* + Зх—4—J (х—0 у (t) dt.
е
18.20.	^(x) = x—l-bj(x—/)0(/)d/.
О
18.21.	у (х) = sin х + у j (х—0? У (0 dt.
(93
Под ред. А. В. Ефимова* ч. 4
X
18.22.	i/(x)=chx— Jsh(x—i)y(f)dt.
о
18.23,	y’(x)’-*+f(4 sin (x—t)—x + i]y(t)dt.
0
x
18.24.	у (x)«1 + $ ((x—О2- (x- П) У (П dt.
О
2, Метод воследовательных «приближений. Решение с помощью
резольвенты. Метод последовательных приближений применительно
к линейному интегральному уравнению Вольтерра 2-го рода
»(х) = /«+$>(*. t)y(i)dt
а
заключается в следующем. Строится последовательность функ-
ций уо(х), yt(x), »*., уп(х), • где нулевое приближение #0(х) —
произвольная функция, а последующие приближения определяются
с помощью рекуррентного соотношения
Уп(х) = 1(х)+\К(х,	п-1, 2, ...
а
Если ядро К (л, 0 и свободный член f(x) непрерывны соответ-
ственно при a^x^b, a<,i^x и на отрезке [а, 6], то построен-
ная таким образом последовательность приближений уп (я), п =
s=0, 1, ...» при п—► со сходится к единственному непрерывному
решению интегрального уравнения.
Обычно полагают г/0(х) = /(х), однако это вовсе не обязательно:
удачный выбор нулевого приближения часто позволяет ускорить
сходимость последовательности уп(х) к точному решению.
Пример 6. Методом последовательных приближений решить
уравнение
о
Положим
Уо(*)=1-
Тогда
О
 х	'
о
194
Для л-го приближения получим
, . , х’ х* к* ,	, ,	V' .	х**
(х)-1 - аГ+4Г~ бГ+...+(- 1)” (2^Т=Ъ (“ О* (2Щ’
k «о
откуда
со
?И=Ви?в(х)=£(-1)‘^гЯСМ1. ►
Решить интегральные уравнения методом последова-
тельных приближений]
X
18.25,	у(х)-1 + $у(/)Л, у.(х)-=0.
О
х
18.26. y(x)~£+x-^y(t)dt,
а)	б) jr.(x)—£+х.
X
18.27.	у (х) ~ 1 — х? + J ху (0 dt,
О
а) У» (х) — 1 — х*, б) у, (х) =» I.
X
18.28.	у (х) =» 1 + $ ху (t) dt, у. (х) = 1.
О
х
18.29. у (х)«1 + $ ty (0 dt, у, (х) == 1.
О
х
18.30.	Р^Ор 1,2, ...
X
18.31.	у(х)«=х—^(х—t)y(t)dt, &(*)=0.
X
18.32.	yixj^l + ^x—tjyftjdt, jfe(x)«O.
0
X
18.33.	у(х)-2* + $2*-^(0Л, Vo(x)=O.
О
х
18.34.	0(x) = l+x»-4jl±£HO<tt. У«(*)“0-
В задачах 18.35—18.37 методом последовательных
приближений найти для заданных нелинейных уравнений
7‘	195
Вольтерра второе приближение уа (х); в качестве нулевого
приближения взять г/0 (х) = 0:
X
18.35.
о
X
18.36.	у (х) = х—п + J t sin у (/) dt.
0
X
18.37.
р
Часто вместо одного уравнения рассматривают семейство урав-
нений
X
г/(х) = /(х) + Х$К(х, t)y(t)dt,	(18)
а
соответствующих различным значениям числового параметра X.
Предполагая, ..что X фиксировано, будем решать уравнение (18)
методом последовательных приближений, взяв в качестве нулевого
приближения $/о(х) = /(х). Тогда получим
г/>W=/w+xJ Л(х, /)/(п;л=/(х)+х
а	а
где
К1(х, /)==Л(х, /);
X	X	/ $	ч
Уг (х) = /(х)+Х J К(х, t)f(t)dt + №^K(x, s)f Jtfifs,
= /(х) + ЦЯ1(х,	$Л'(х. s)J<i(s. /)Л)/(0Л«
а	а X/
х	х
= /(*) + Ц Ki (X, /) / (О Л + Xs J Л'2 (X, I) f (/) dt,
а	а
/)==^7<(х, s)Kt(s, t)ds.
где
Вообще
п г
Уп W=/W+2 V\/Cy(x, о/ю^==
/«i а
=/(х)+Ц^2 t]^f(t)dt, (19)
196
где
К) (X. О - J к (х, s) Kj.a (s, t)ds,	I=2, 3, ..(20)
t
Ki(xt t)=K(x, 0.
Ядра Kj{x> 0 называются повторными или итерированными.
Если ядро К (х, 0 непрерывно, то ряд
/?(Х,	Х)=2 V-iKy(x, 0	(21)
/=1
при любых фиксированных значениях X сходится (равномерно
относительно х£[а, 6] и /£[0, х]) к функции Я(х, 0 X), назы-
ваемой резольвентой ядра К (х, 0. Следовательно» соотношение (19)
в пределе при п —► » переходит в формулу
У (X) = f (х) +1J /? (х, t, М f (/) dt,	(22)
а
выражающую решение интегрального уравнения через резольвенту.
Пример 7. Найти резольвенту /?(х, 0 X) ядра Kfa
и, используя ее, решить интегральное уравнение
X
v(x)=x—-±-§xg(t)dt.
о
Из рекуррентных соотношений (20) получаем
К1(х, 0=х,
X	X
Р	р	уЗ — П
К2(х, 0«\ К(х, s)Ki(s, t)ds^\xeds^x——‘9
t	*
К»(х, t)=$K(x, s)K»(s,
Вообще, можно проверить (например, методом математической
индукции), что
*/(*. 0«х——1—, /=1, 2, ...
Подставляя это выражение для итерированных ядер в форму-
лу (21), найдем резольвенту
R(x, t, l)=*2u(/_l)f	2 )
/=1
Найдем теперь решение заданного интегрального уравнения. В
рассматриваемом случае Х=—у и /(х)»х, поэтому на оонования
t9T
(22) получаем
i р х*~ **	х* р I — ।	х*
у (x) = x—_L V хеГ < 4d/=x—хе" 4 \d\e * ] =хе
о	о
18.39. K(xt t) = t.
18.41. Л(х, i) = xt.
18.43. К(х, 1)=ех~*.
18.45. Л (х,
18.47. К (х, О=аНк
произвольного ядра вида
Найти резольвенты для следующих ядер:
18.38.	К(х, /) = 1.
18.40.	К(х, /) = *-•
18Л2. К(х, 0 = ^?.
18.44.	К(Х, 0 = 2sh*~sh/.
18.4в.Л(х,()=5=1±1.
18.48.	Показать, что для
К (х, /) = х?/9, где р и q—некоторые положительные целые
числа, резольвента имеет вид
xjp+?+i_ tp+g+i
R(x, t, Ь)^ХРРе ₽+«+1	.
18.49.	Показать, что для произвольного ядра вида
Л (х, /) —	» Я (/) =5^0, резольвента имеет вид
/?(х,	=
Найти с помощью резольвенты решения следующих
интегральных уравнений:
18.50.	t/(x) = l — \ty(t) dt.
о
18.51.	y(x)=^x+^xiy(t)dt.
е
18.52.	у (х) ==sinx + 2
о
х
18.53.	i/(x)=chx + j^j:(/)d/.
X
18.54.	1/(х) = Г{Ь- +
о
3.	Уравнения Вольтерра 2-го рода типа свертки. Интегральное
уравнение Вольтерра 2-го рода вида
?(*)-/(«)+$	(23)
 а
198
в котором ядро К (х,	зависит лишь от разности a pry*
ментов, называется дразнением типа свертки. Если в (23) а—ко-
нечное число, то, не ограничивая общности (см. задачу 18.65),
можно считать о=0, что мы и будем предполагать в дальнейшем.
Для решения уравнений типа свертки используется преобра-
зование Лапласа.
Предположим, что функции f(x) и К (и)—оригиналы (см. ч. 2,
глава 13, § 1, п. 1). Можно показать, ч:о в этом елучае решение
у {к} также будет оригиналом и, следовательно, к обеим частям
уравнения (23) можно применить преобразование Лапласа. Полагая
У W Y (р), fW^F (р), К(и) = К (р)
и используя теорему о свертке, согласно которой (х—О у (t) dt ==
о
== К 00 К (р), получим
rtrt-FW+ltwyW.
откуда
У(р)а,
l-K(P)
Оригинал ри для У (р) будет решением интегрального уравнения.
Пример 8. Используя преобразован ив Лапласа, решить
интегральное уравнение
ж
If (к)—1 + £ ch (г—0 К (0 dt.
О
Так как 1=~ и ch ц JTf * то, применяя к обеим частям
заданного уравнения преобразование Лапласа я используя теорему
о свертке, получим
Отсюда
' W •	Р»_
р»-!	-1
г 1Я~Р(Рг-Р-1)~Р
р
1-
1 v 5
2	/
и, следовательно, у(х)=> Н—е*'* $h —— х. >>
Y 5	2
С помощью преобразования Лапласа найти решения
заданных уравнений типа свертки:
X
18.55.	у(х)=е*—х—
о
ОЭ
X
18.56.	у (xj = j 4- j (x-1)у (/) dt.
X
18.57.	у (x)=xe2x — $ e?<x~»y (/)dt.
0
x
18.58.	у (x) = sin'x 4- J cos (x— t) у (t) dt.
о
X
18.59.	Jsin(x— t)y(t)dt.
о
x
18.60.	£/(x}= sinx— J sh (x—t)y(t)dt.
о
x
18.61.	у(х)-4+тЙж-^<0Л.
0
x
18.62.	y(x) = e?* + $(x—t)e*-*y(t)dt.
о
x
18.63.	f/(x) = 1 + J cos(x—/) sin (x—0 у (t) dt.
0
x
18.64.	y(x)=l 4-xcosx—sinx4- $ (x—t)x.
о
xsin(x—t)y(t)dt.
18.65.	Показать, что если у (х)—решение уравнения (23)
с 0^=0, то функция у* (х) = у (х 4- а) удовлетворяет урав-
нению
X
У* (х) = /• (х) 4- $ К (х-1) y*(t) dt,
О
где f*(x) = f(x4-a).
18.66.	Показать, что для ядра К(х, t) = K(x—t) все
итерированные ядра, а следовательно, и резольвента
также зависят лишь от разности аргументов х—t.
Решение уравнений типа свертки можно провести и несколько
иным способом, а именно—путем использования преобразования
Лапласа для нахождения резольвенты. В самом деле, резольвента
ядра K(xt	зависит лишь от разности аргументов (см.
задачу 18.66), и, следовательно, решение уравнения
х
у х)=/(х)4-Ск(х-/)у(0Л	(24)
> 200
можно записать в виде
(28*
О
где /? (я—/)==/?(*, /, I), a R(x9 /, к)—резольвента ядра К(х, /)ж
==/((х—Z). Применяя к обеим частям уравнений (24) и (25) пре-
образование Лапласа, получим
Г (p)»F (pH К <Р) Y (р), Y(p)~F (р)+Й(р) F (р),
откуда
₽(Р)
К(Р)
1-К(р)‘
(20)
Оригинал /?(«)== /?(р) определяет резольвенту R(x-»(),. зная ко
торую, из (25) найдем и решение уравнения.
Пример 9. С помощью резольвенты найти решение уравнения
У (0-1
2
КЗ
x-t
§ е 4 sin • (х—/)’</ (/) dt.
о
2	/	V”3
В рассматриваемом случае К (и)= -	e~u/8sln и и
УЗ	2
1
рЧ-р+1
Из (26) получим й(р)=—1—т. е.
(х-—/)== 1е~'х~ь. Учитывая, что f(x)«l, с помощью (25) на-
водим решение
X
о
Найдя резольвенту о помощью преобразования Лап-
ласа, решить следующие интегральные уравнения:
X
18.67.	у(х) = 1 + 5	dt.
О
х ♦
18.68.	y(x) = 2 + -L{(x-t)ty(t)dt.
X
18.69.	у (л) = е~х + $ «-<*-«sin (х—/) у (/) dt.
о
X х
18.70.	у(х) =е~~+ J (1— e-<x~ir)y(i)dt.
о
201
X . jf-1	i/"~~
18.71.	y(x) = 1 + j e ~cos	(x—t) у (t) dt.
о
Используя преобразование Лапласа, решить системы
уравнений типа свертки!
Гж	«
18.72.	у, (х) = -1 + $ у2 (0 dt, yt (х) = х- J yt (0 di.
о	о
х
18.73.	yt(x)—х + $У.(0Л,
о
х	х
У» (х)=—Зх8 + X—5 $ ух (0 dt + 2 J yt (О dt.
9	О
х
18.74.	у1(х) = х+$у,(/)<
О
х
yt(x) = ^ + ^-l-^(x-t)yAt)dt.
Q
х	х
18.75.	yt (х)=е* - J yt (О dt+4 $ е*-< у, (/) dt,
О	о
л	х
Ул W = 1 - $ У1 (О dt + J у, (О dt.
О	S
х	х
18.76.	yl(x)«=x+ $yt(O<tt. у,(х)-1-5й(0Л.‘
о	о
х
yt (х) = sin X	j (X— О У! (О dt.
О
4.	Уравнения Вольтерра 1-го рода. Линейным интегральным
уравнением Вольтерра 1-го рода называется уравнение вида
х
jK(x, Лу(04/«=Нх),	(27)
а
где у (х)—искомая функция, а К(х, t) и f (х)—заданные функции,
определенные соответственно в треугольнике а<х, t^b9 t<,x и
на отрезке [а, &]. Классическим примером уравнения этого типа
является уравнение Абеля
J У х—1
202
а также его обобщение с ядром вида К(х, flsss?—0 < а < 1,
имеющим интегрируемую особенность при х = Л В настоящем пункте
ограничимся рассмотрением уравнений, для которых ядро К (х, /)
и свободный член f(x) непрерывны всюду в своей области опреде-
ления*
К уравнениям Вольтерра 1-го рода приводит, например, сле-
дующая важная задача, часто встречающаяся на практике. Пусть
задана некоторая линейная динамическая система, х(/)—ее вход-
ной, а #(/)*•* выходной сигналы. Тогда, как известно, зависимость
у (0 от х (/) может быть записана в виде
У (0- $«(*, r)x(t)dT,	(28)
— а»
где g(t, т)~-весовая функция, определяемая свойствами системы.
Если, в частности, выполнено условие физической реализуемости
(т. е. т)«=0 при т > 0 и система находилась в покое до мо-
мента времени (т. е. х(/)«=0 при i < /0)> то (28) принимает вид
t
4/(0=$«(Л T)x(T)dr.	(29)
*0
Если теперь требуется по известному выходному сигналу восста-
новить внешнее воздействие, то мы приходим к уравнению Воль-
терра 1-го рода (29) относительно х(/) при заданной функции y{t}.
В отличие от уравнений Вольтерра 2-го рода, решение урав-
нения Вольтерра 1-го рода (27) существует только в том случае,
когда свободный член /(х) удовлетворяет ряду дополнительных
условий, зависящих в каждом конкретном случае от свойств
ядра К(х, 0.
В частности, каково бы ни было ядро, необходимым условием
существования решения, как это видно из (27) при х=0, является
равенство /(а)=0.
Пример 10. Найти условия разрешимости в классе непре-
рывных функций и решение уравнения
X
«=1. 2, ...» «ёЮ, е).	(30)
Предположим, что непрерывное решение у(х) существует. Тогда
из (30) следует, что f(0)==0 и существует непрерывная производ-
ная (х), х(У0, с]. Дифференцируя (30) последовательно п раз,
получаем
X
р (х t\n~*
о
я
о
y(xW>(x).
203
1аким образом* если непрерывное решение у(х) существует» то
функция f(x) имеет непрерывные производные до л-го порядка
включительно» причем
f (0) з= (0) = .,, = f«(0)=0;	(31)
при этом решение единственно и должно иметь вид У (х) = ^п) (х).
Подставляя в (30) у (х) =» ({п} (х) и л раз интегрируя по частям
с учетом соотношений (31), найдем, что функция у (х)=^п) (х)
действительно является решением исходного уравнения (про-
верьте!). ►
Если ядро К (х, 0 и свободный член f (х) (f (а)==0) уравне-
ния (27) таковы, 470 существуют непрерывные производные * х
и f' (х) и, кроме того, функция К (х, х) 0 всюду на
la, М, то уравнение (27) эквивалентно уравнению Вольтерра 2-го
рода и, следовательно (см. п. 1), имеет единственное непрерывное
решение. В самом деле, предполагая существование непрерывного
решения и дифференцируя (27) с учетом перечисленных условий,
получаем
X
К (х, х) у (х)4- j —у (/) di = /' (X)
а
или
у (*) ~ ir'i 'f F/1 -	1*’	У <Z) dt-	(32)
9 ' К (х, х) 1 J К (х, X)	дх	*'	’	v '
а
т. е. у(х) есть решение уравнения Вольтерра 2-го рода (32).
Обратно, непосредственной проверкой убеждается, что решение
уравнения (32) при условии /(а) = 0 удовлетворяет и исходному
уравнению (см. задачу 18.77).
Пример 11. Решить уравнение
х
J (24-х*—/»)у(/)<«“Х*,
о
сведя его к уравнению Вольтерра 2-го рода.
4 Дифференцируя это уравнение, получаем
X
2y(x)4-§ 2xy(t)dt^2x
О
иля
х
у (х)«х—ху (t)di
о
— уравнение Вольтерра 2-го рода. Ядро #(х, х вырождено
X
и, полагая и(х) = ^(0^. получаем
у(х)«=х—хи(х),
«' Ив»И-«-хи W
204
или
а' + х«=х, u(0)=0.
Отсюда и (х) = 1	н у (х)=хе~х*^.
Если в исходном уравнении Вольтерра 1-го рода (27) Д’ (х, х)^0
на |а, Ц, то после дифференцирования этого уравнения снова
получается уравнение 1-го рода, и—при выполнении соответ-
ствующих условий— можно повторить описанный выше прием.
При этом, однако, следует всякий раз внимательно учитывать
отмеченные выше ограничения на свободный член, необходимые
для разрешимости уравнения.
Пример 12. Решить уравнение
х
J sln(x— f)y(t)dt=e*— 1.	(33)
о
<4 Условия существования и непрерывности производных для ядра
и свободного члена здесь выполнены. Дифференцируя дважды*
получаем
J cos (х— t) у (/),<«=е*,	(34)
О
у(х) — J sin (x—i)y(t)dt = e*.	(35)
Уравнение (35) есть уравнение Вольтерра 2-го рода и оно имеет
единственно непрерывное решение у (х)»2ех—х—1, которое может
быть найдено, например, операционным методом. Однако функция
у (х)~2ех—х— 1 не удовлетворяет исходному уравнению, в чем
можно убедиться непосредственной подстановкой. Дело здесь в том,
что уравнение (34) не имеет решения, так как e*|x=o== 1	0. А по-
скольку решение уравнения (33) должно удовлетворять уравнению
(34), то и исходное уравнение (33) не имеет решения. ►
18.77.	Доказать, что решение уравнения (32), в кото-
ром / (а) = 0, является решением и уравнения (27).
Решить заданные уравнения Вольтерра 1-го рода, сводя
их к уравнениям 2-го рода.
X
18.78.	J (х—f)y	х— 1.
‘ о
х
18.79.	( в*’* у(0 #-=£•
V	*
X
18.80.	^3x-ty(t)dt^x.
о
х
18.81.	Jsin(x—0у	—cosx.
о
205
18.82.	J sh(x—t)y(t)dl=>$hx—x.
о
18.83.	J(x—O*i/(Od/ = x8.
о
18.84.	J (x— t)*y (П dt = x* + x?.
0
18.85.	j(14-x—t)y	e-xsinx.
18.86.	j(l—xt + ti)y(t)dt = ^-:.
18.87.	$ (2t —x)y(t)dt = x»-l.
i
Решить уравнения Вольтерра 1-го рода типа свертки,
применяя преобразование Лапласа непосредственно к за-
данному уравнению (см. также п. 3)1
18.88.	$(х—t) y(t)dt — ch х— 1.
0
18.89.	jsin(x—tjy^dl^^-x*.
18.90.	Jcos(x—t) у (0 dt == x sin x.
0
18.91.	Jsh(x—0y(/)<ft = 2sin‘y.
18.92.	J(x—/)sln(x—t) у (t)dl=sin* x.
0
18.93.	f (x—=	rex—4-.
18.94.	Je*“»cos(x— t)у(t)dt=x^.
0
18.95.	(е*-»81Цх—t)y(t)dt=4-^—J-.
206
18.96.	J (х—/)sh(x—t)y(t)dj=xehx—shx.
e
X
18.97*	. J Vx—ty(i)di*=x*Vx.
о
§ 2. Интегральные уравнения Фредгольма
1. Основные понятия. Метод последовательных приближений и
резольвента для уравнений Фредгольма 2-го рода. Линейными инте-
гральными уравнениями Фредгольма называются уравнения вида
ъ
y(x)-^K(x,t)9{t}dt~l(x)	(I)
а
(уравнения 2-го рода} и
ь
^K(x,i)9(l)dt~l(x)	(2)
а
(уравнения 1-го рода). В (1) и (2) у (х)—искомая функция, а ядро
д (х, О и свободный член f (х) предполагаются заданными соответ?
ственно в квадрате а^х, i^b и на отрезке [а, £]. Если, в част-
ности, К(х, 1)^=0 при а<х<£, то уравнения (1) и (2} превра-
щаются в уравнения Вольтерра 2-го и 1-го рода соответственно.
Мы ограничимся рассмотрением уравнений Фредгольма 2-го
рода, наиболее интересных и важных для приложений.
Далее будем предполагать, что пределы интегрирования а и
b в (1) — конечные числа, а функции К (х, t) и f (х) либо непрерывны
в своей области определения, либо, в более общем случае, удов-
летворяют условиям ъ
$ J И (X, t) Is dx dt^ Bk < + оо.	(3)
а а
Ъ
J (x)|*d« <4-00.	(4)
а
Если f(x)=O всюду на (a, &J, то уравнение Фредгольма 2-го рода
U) называется однородным, в противном случае оно называется
неоднородным. Решением уравнения (1) будем называть всякую функ-
цию у (х) класса (а, Ъ), обращающую это уравнение в тождество
относительно х£ [a, frj.
Обычно рассматривается не одно уравнение (1), а семейство
уравнений
(5)
а
зависящих от числового параметра 1, который может принимать
как действительные, так и комплексные аначения. В отличие от
207
уравнений Вольтерра 2-го рода, существование и единственность
решения уравнения (5) существенно вависят от значения парамет-
ра к (см. подробно об этом в п. 3). В настоящем пункте рассмот-
рим случай, когда число 1 удовлетворяет условию
, Ъ Ь	. — 1/8
У |К(ж. ОРЛсл)	. (6)
'а а	'
(точнее, |X|<ltal’ W наименьшее по модулю характерис-
тическое число уравнения (5), см. п. 3).
При условии (6) уравнение (5) имеет единственное решение (не-
прерывное, если непрерывны К (xf t) и f(x)), которое может быть
найдено методом последовательных приближений подобно тому, как
это делается в случае уравнений Вольтерра 2-го рода (см. п. 2§ 1).
А именно, перепишем уравнение (5) в виде
ь
И*Н«+ф(х, t)y(t)dt
а
и далее, выбрав произвольно нулевое приближение у0 (*)» построим
последовательность уп(х), 2, . полагая
УпМ^((х) + к $tf(x, i)yn-at)dt, ngN.
a
Если число X удовлетворяет условию (6), то при п —*оо последо-
вательность уп (х) сходится (в общем случае в метрике L2(#> &), а
в случае непрерывного ядра и равномерно на [а, 6]) к точному
решению у(х).
Пример 1. Методом последовательных приближений решить
уравнение
1
у (*)*•* У (0 sin
случае, полагая Х=1/2 и Л(х, /)==!, имеем
В данном
1 1
J J |К(х, t)\ldxdt^B\^ \ и, следовательно, условие |Х| < !/£/<
о о
выполнено. Приняв у^ (х)«= sin лх, последовательно находим
1 1
1 С	1 С'	1
(x)«sinnx+y \ Уо(Od/=»sin лх4-у \ sin n/d/«=sinax4-------,
о	о	Я
1
yi(0d/ —
ya(x)=sto
1	I
Уз (x) «sinnx-f-l j yt (*) di «sin ях-J-y J (sin л<4—4-2^) di«
, 1 . 1 , 1
e=Sin ЛХЧ-4*-я-Ьггт-»
гл^2л ‘ 22я
Вообще,
п-1
j/„(x)=sta«x+l+^-+.;,4.§;l--=sin3xx+lS 1,
fe=0
откуда
оо
МШ0„ (X)=sin лх+4-^2 X—sinях+-£-.
п-»оо	Л f"-*. 2*	Л
кяО
Поэтому решением уравнения является функция
₽(x)=sin ях+у,
в чем можно убедиться непосредственной проверкой. ►
Методом последовательных приближений найти реше-
ния заданных уравнений Фредгольма 2-го рода, предва-
рительно убедившись, что условие (6) выполнено:
1
18.98.	у(х)— $ xty (0 dt = 2х.
О
п
18.99.	у{х) + -i- J cos? ty (t)dt=>l.
О
1
18.100.	y(x)—л С (1 —x)sin2nty(/)d/ = -5-(l—х).
V	*
о
л
18.101.	у(х)—sinху(t)tdt = 2sinx.
о
Л
18.102.	у (x)+2^ J (cos (x-|-04-cos(x— t))y(t)dt ==COS X.
0
Если в качестве нулевого приближения выбрать свободный
член уравнения (5), т. е. ^0(х)в/(х), то для n-го приближения
получается общая формула (см. также § 1, п. 2)
п п
f»w=/w+2
/я1 а
if п \
t^f(t)dt, «€N.	(7)
20»
«де итерированные ядра определяются соотношениями
ь
Ki (х, t)**К (х, t), /(/ (х, /) = J К (х, s)	j (s. t) ds, i=2, 3, ... (8)
a
При |X| < 1/Вк ряд
R(x, /,!)-> 2	(9)
i = 1
сходится к функции R (я, /, X), называемой резольвентой ядра
К (х, /). Следовательно, (7) в пределе при п —► оо переходит в формулу
ь
»W=fW+ljR(x,U)/(/)«,	(10)
а
выражающую решение интегрального уравнения через резольвенту.
Замечание. Понятие резольвенты как функции R (х, X),
с помощью которой по формуле (10) определяется ‘решение интег-
рального уравнения, сохраняет смысл для любых значений 1, при
Которых это уравнение однозначно разрешимо. Метод последова-
тельных приближений и формула (9*) дают представление для ре-
зольвенты в виде ряда по степеням л (называемого рядом Ней мана),
годное лишь в области |Х| < 1/Вд^.
Существует, однако, общий метод нахождения резольвенты —
метод определителей Фредгольма, который в принципе позволяет
построить резольвенту для любого значения Л, при котором ин-
тегральное уравнение имеет единственное решение. Этот метод
здесь не рассматривается.
П р'и м е р 2. С помощью итерированных ядер найти резоль-
венту и решение интегрального уравнения
1
fW-Ш2 $ Тр» У(/) Л=°1+Л
X
В данном случае К(х, О=тп“75 и для
I -р*
на основании (8) получаем
итерированных ядер
Ki(x,t)*=K(x, 0—^.
1 1
Я,(х, 0-j К(х, s) Kt (s. /) ds=|	dsJ^
1	I
„ . Л f xv t In 2 С X S .	/1п2\2 x
*« (X, i)= J К (x,s)	(s, /) ds--T J _ —	) да
Kj(x, 1) = ^ 2 j
210
Поэтому резольвента ядра равна
S(x.ч-f,)
причем этот ряд сходится в области
Заметим, что в рассматриваемом случае
it	11
Й-Jjnc,
т. е. условие (6) приводит к неравенству
(12)
видно,
-/б	2
Так как 2 у 5F+2<^п"2, Т0 й3 сРавнения 00 и 02)
что в рассматриваемом случае область сходимости ряда Неймана
для резольвенты шире, чем это гарантируется условием (6) (в со-
ответствии с замечанием на с. 210).
Далее, для заданного уравнения —гД, и, следовательно,
1П £
• Решение уравнения на основании (10) равно
R х, /,
о
Ч+'Ч^'-'+И
о
।
Методом итерированных ядер найти резольвенту и
решение заданных интегральных уравнений:
л
18.103.	у(х) —l-Jt/(O^ = sinx.
о
I
18.104.	y(x)-~§2*+‘y(t)dt = x.
о
1
18.105.	у (х) 4- л $ х sin 2nty (/) dt = cos 2лх.
о
i
18.106.	у(х)-~$хе‘у (0 dt = е-*.
и
я/2
18.107.	у(х)— 5 81пх<м»<у(0Л—1.
о
211
Ядра К (х, /) и L (х, t) называются ортогональными в квадрате
а^,х, t^bt если выполняются условия
b	ь
J Я(х, s) L (s, /)ds== J L (х, s)/((s,/)ds = O
а	а
для всех а^х, t^b. Если, в частности, ядро К (xtt) ортогонально
самому себе, то для него второе итерированное ядро К2(*> 0==^
всюду в квадрате асх, i^b. Следовательно, для такого ядра
ряд Неймана для резольвенты сходится при любых значениях X,
а сама резольвента совпадает о ядром К (х, /).
Примерз. Методом итерированных ядер найти резольвенту
и решение интегрального уравнения
1
#(х) — ^со^лх cos Зл/1/(/)<//== cos Злх.
— I
Ядро /С(х, f) = cos лх cos 3л/ ортогонально самому себе:
1 1
J К s) X (s, t) ds ж С (cos лх cos 3ns) (cos ns cos 3n/) ds~ 0.
«> 1 •*» 1
Поэтому резольвента R (x, t, X) — cos их cos Зл/ и решение заданного
уравнения имеет вид
1
у (х) = СОЗ Зпх 4- \ cos лх cos’ Зл/ dt = СОЗ Злх 4- COS ЛХ. ►
-1
18.108.	Доказать, что если ядра L(x, t) и М(х, /) ор-
тогональны, то резольвента ядра Л (х, t) — L (х, t) 4- М (х, t)
равна сумме резольвент ядер L (х, /) и М (х, /), т. е.
/?к(х, /, Л)==/?£ (х, /, 1)4-Ям (х, t, 1).
Используя ортогональность ядер и результат зада-
чи. 18.108, решить интегральные уравнения:
1
18.109.	у (к) —jx(l-уt\y(t)dt — i.
о	'
1
18.110.	у(х)—J sin 2лху (/) idt — х.
о
п
18.111.	у(х)—J sin(х4-2/)y(f\dl = х.
-Л
1
18.112.	у(х)—у J (x?+l+x/)//(/)d/ = l.
— I
21$
18.113.	у(х) + -^ у (xsin/ + sin 2х) z/(/)d/ = s'inx.
-Л
2.	Решение уравнений Фредгольма 2-го рода с вырожденным
ядром. Ядро К (х, 0 называется вырожденным, если оно имеет вид
К(х,	<?/(/)•
Соответствующее интегральное уравнение
У(*)“S (;2» Р/(*) Я/ю)У	(13)
решается путем сведения к системе линейны» алгебраических
уравнений следующим образом.
Перепишем уравнение (13) в виде
у (*) — 2 pj ws/" f	<I4)
где неизвестные sj определяются через искомое решение р(х) ра-
венствами
ь	,
/-1,2, ..„п.	(1S)
а
Умножая тождество (14) последовательно на ?/(*), /’=»!, 2,
и далее интегрируя обе части на отрезке [а> 6], с учетом (15) по-
лучим для неизвестных чисел $/ следующую систему линейных
алгебраических уравнений:
п f*	\ Ъ
s'~~ 2 ( J qi Pj <х) ) s/m ) <*) /(«)<**• <-1,2,,n. (16)
/ sI	J а
Введем обозначения
в	ъ
aij— Jqi(x)pj(x)dx,	(17)
Ь	л
Тогда система (16) запишется в виде
S/— 2	2t ...t Я»	(18)
или в матричной форме
(F—A)S^P.	(19)
где единичная матрица, Л«а(а/у)" , , £«>(зь ..<« ам)т,
213
Если st, sn*~какое-нибудь решение системы (18), то &
соответствии с (14) функция
9 W—/ (X) + 2 Д/ (*)s/	(20)
будет решением исходного интегрального уравнения (13). Если же
система (18) несовместна, то и интегральное уравнение не имеет
решения.
Этот метод применим, конечно, и в том частном случае, когда
уравнение (13) однородное, т. е. f(x)=O.
Пример 4, Решить уравнение
J sin xsin/ + у (/) d/=»sln2x.
—я
◄ Ядро К(х, 0=~ sin х sin / + / вырожденное. Полагая
Pi(x)=^-slnjr, р,(х)=1,

но формулам (17) вычисляем
'	я
Сц = I — sin3xdx=xl,
J л
-я
л
Лй«э Г -Х-xsin Х4й=«Я
J л
л
/<=□ J sin xsin 2х dx=0,
-л
Сн== 1 slnxdx»O,
-я
л
J xdx~O,
-л
л
=	х-5ш2х</х= —л.
-л
Система (19) принимает вид
Г OOWstX { 0\
\-2 iAsJ~v~*r
ее общее решение: st==C, s2=—л+2С, где С—произвольная по-
стоянная. Следовательно, любая функция вида
0(x) = sin 2хЦ-~- sin х—fl+2C«esln 2х+С f-i-sin x-f-aj—л
есть решение заданного интегрального уравнения л других реше-
ний это уравнение не имеет.
Пример 5. Решить уравнение
1
y(M)-2^Tty(i)dt=x.
о
214
4 Следуя изложенному выше общему методу, вапишем это урав-
нение в виде
^(х) — 2УЪ=:Х>
1
где s=$	Умножая обе части на К* и интегрируя,
о
получаем
1 1
s—2 J xdx-s=* Г x3/2dx,
о о
или s-s=2/5, Последнее уравнение не имеет решения относи-
тельно s, следовательно, исходное интегральное уравнение также
не имеет решения. ►
Найти все решения или установить неразрешимость
заданных уравнений Фредгольма 2-го рода с вырожденным
ядром:
2л
18.114.	у (к)—J cos х sin 0/(0 Л = sin х.
।
18.115.	у(х)-^-^chxy{t)dt — \,
I	—
18.116.	=
1
18.117.	g(x)—J(1 4-х)соз2я^(/)Л==х.
о
Л/4
18J18. y(x)— J tg/y(0^«cosM.
0
I
18.119.	y(x)—4^xt*y(t)dl = 0.
о
i
18.120.	у(х)4-$е*/у(0Л-О.
0
1
18.121.	y(x)~ $(2x—f} у (t) di cos 2ях.
о
i
18.122.	у (x)—| (1 + 2x0 у (0 dt» — (x + 3)_.
1
t8.123. y(x}— j	1))4ФИ*=0.
— 1
18.124.	y(xj—-^-^cos?(x—/)г/(/)d/= sin 2x.
о
i
18.125.	y(x) + j (x—K7)у'(0Л—|x+K«—J-«
18.126.	y'(x]—§ cos(x -t)y(t)dt—Q.
-Л
1
18.127.	y\x}—3 J (Л?-|-4я/+ \}-y\t)dt = 2n*cos2nx.
0
* 1
18.128.	y(x)— J (х/+л»)у(0Л-0.
— 1
3. Характеристические числа и собственные функции. Теоремы
Фредгольма» Значения параметра Л, при которых однородное урав-
нение
ь
9(х)-Х J К (х, t) д (0 dt = 0	(21)
а
имеет ненулевые (нетривиальные) решения у (х) 00, называются
характеристическими числами этого уравнения или ядра Л(х, /),
а каждое ненулевое решение—собственной функцией, соответству-
ющей характеристическому числу X. Заметим, что число 1 = 0 не
является характеристическим, так как при 1=0 уравнение (21)
имеет лишь нулевое решение. Если 1—характеристическое число,
то число р.=»1/Х называется собственным числом интегрального
уравнения. При этом ц # 0.
Из результатов п. 2 следует, что в случае уравнения е вырож-
денным ядром
₽ (х)-Х J	р} (х) <?/(/)) у (/) dt =0	(22)
всякое решение имеет вид
(23)
где S=($i, ..., sn)*r*—решение однородной системы
(£—M)S=0	(24)
216
b
с матрицей Л = (п/у), «//= J <н (х) pj (х), tt j-l, п. Заметим.
а
что если ваменить X ва 1/ц, то система (23) принимает вид
(Л —рЕ)$«0,	(25)
Отсюда следует, что собственные числа интегрального уравнения
(22) совпадают с отличными от нуля собственными числами мат-
рицы Л, а собственные функции определяются соотношением (23),
где 5— (sf,	— соответствующие собственные векторы этой
матрицы.
Пример 6. Найти характеристические числа и собственные
функции уравнения
j (х/-2х2)г/(0Л = 0.
О	!
Ядро К(х, /) = х/—2х2 вырожденное. Полагая
Pt(x)==x,	р2(х) = —2ха,
<72 (0=1.
найдем элементы матрицы А в
1
С ал 1
flu — \ хМх=-—,
м	**
О
1
С ;	1
«21 = \ xdx^-j,
о
(25):
1
«12 = —2	—у,
о
1
С	2
«22 ==	2 I Х^ dx я* “5**
М	’Э
Характеристическое уравнение для определения собственных чисел
матрицы А имеет вид
det (Л—р£) =
1	1
3 11	2
1	2
2	3И
, , 1	.1	/ .1 V А
=м24-з и+зб=^+б-j -О,
откуда ц«=—1/6— единственное собственное число матрицы А.
Соответствующие собственные векторы находим из системы урав-
нений
\2	2/
общее решение которой sj=C, s2«=C, где С—произвольная посто-
янная. Следовательно, окончательно получаем, что заданное инте-
гральное уравнение имеет единственное характеристическое число
Х=—=—6, а соответствующие собственные функции имеют вид
У (х) = —6 (sp:—2s2x2)«=C (х—2х2)»
где С—произвольная постоянная. ►
217
Интегральное уравнение может вообще не иметь характеристи-
ческих чисел (например, в том случае, когда ядро К(х, /) Воль-
тер ровское или, в случае вырожденного ядра, матрица А в (24)
нулевая) либо не имеет действительных характеристических чисел.
Пример 7. Найти характеристические числа и собственные
функции уравнения
л
у(х}—X х cos/у (/) df ==0.
•я
Имеем
л
y(jr)—lxs=0, s= J eosty(t)dt,
-я
откуда
я
s—ks J xcosxdx = 0,
-л
л
Но J xcosxdx=0, поэтому при любом 1 последнее уравнение
-л
имеет только одно решение: $=0. Следовательно, при любом X
интегральное уравнение имеет только тривиальное решение, т. е.
не имеет характеристических чисел. ►
Пример^. Найти характеристические числа и собственные
функции уравнения
л
’ J 81п(*-Пу(0Л=0.
-я
4 Ядро
K(xf O=sin(x—O=sln xcos/ —cos xsin /
вырожденное, причем можно положить
pi(x) = skix, р2 (х) = •—cos х,
9l(f)a»cost, 9t(/)»sin/;
;	/Я	1 S
; матрица Л = I а/у = V (х) р/ (х) dx I имеет вид
i	( -а	//,/«1
’ характеристическое уравнение
имеет только комплексные корни	Найдем соответству-
ющие собственные векторы. Для =
I
(26)
218
Для ра = — in
(о)-
C:)»=4‘)- m
Окончательно заключаем, что заданное интегральное уравнение
действительных характеристических чисел не имеет, но имеет два
комплексных характеристических числа Xf>a=——= ЯР	Соот-
ветствующие собственные функции имеют вид (см. (26) и (27))
У! (X)=Х1 (Ct sin х—iCi cos х) «= Л
У2 (X)«1а (Са sin х +1<?2 cos х)» А 2е
тж Ai и Л2~ произвольные комплексные постоянные. ►
Найти характеристические числа и собственные функ-
ции заданных интегральных уравнений с вырожденным
ядром (ограничиться случаем действительных характери-
стических чисел)!
1
18.129. £(х)—Ц(1+2х)/И0<«=«.
о
1
18.130. у\х)—Л 5 (1— xt)y(i)di = Q.
о
1
18Л31. у(х)—1 $ |х|//(/)Л = 0.
— 1
л
18.132.	jr(x)—ijxsinty(t)dt — O.
О
л
18.133. у{х)—1 cosxcos/z/(/)d/ = 0.
о
1	1
18.134.	y(x)—l\(x + t)y(t)dl = b.
о
1
18.135.	y(x)—l\(xe' + 2t)y(t)dt~Q.
о
1
18.136.	у(х)~Xj(xsin2n/—y(t)dt~O.
о
п
18.137.	у (х)—1 $ sin (х +1) у (0di = 0.
о
219
18.138.	у(х)—XJcos(x—t}y(t)dt*=O.
Для уравнений Фредгольма 2-го рода вида
ь
д(х)-Ь^К(х, t)y(t)dt = f(x),	(28)
а
где а и 6—конечные числа, а ядро К(х, t) и свободный член f (х)
интегрируемы с квадратом в области а*£х, i^b и на отрезке
(а, (в частности, непрерывны), справедливы следующие тео-
ремы Фредгольма (при формулировке которых мы ограни-
чимся случаем действительного ядра К (х, /))•
1.	Однородное уравнение
ь
у(х)-К^К(х, t)y{t)dt=O	(29)
а
имеет либо конечное, либо счетное множество характеристических
чисел] евли тих чисел счетное множество, то они стремятся к бес-
конечности.
2.	Если X**характеристическое число, то уравнение (29) и сопря-
женное ему однородное уравнение
ь
у{х)-К^К*(х, t)y(t)dt~O,	(30)
а
еде К*(х, t)«K(t» х), имеют одно и то же, и притом конечное,
число линейно независимых решений.
3.	Альтернатива Фредгольма: либо неоднородное урав-
нение (28) имеет одно и только одно решение для любой функции
f(x)^Li(a, b), либо соответствующее однородное уравнение (29) имеет
по крайней мере одно нетривиальное решение. (Другими словами,
если число X не является характеристическим, то уравнение (28)
имеет, и притом единственное, решение для любой функции f (x)g
£)•)
4.	Если Л*~характеристическое число, то для того чтобы урав-
нение (28) имело решение, необходимо и достаточно, чтобы свободный
член f (х) был ортогонален любому решению у * (х) однородного сопря-
женного уравнения (30), т. е.
ъ
$/(*)/(») Л-0.
а
Проиллюстрируем теоремы Фредгольма на примере интеграль-
ного уравнения с вырожденным ядром.
Пример 9. Исследовать «решения интегрального уравнения
л
р(х)—X J (х8cosi^xsin0уcoax (31)
-я
• зависимости от значений параметра X.
120
4 Решение интегрального уравнения сводится к решению неодно-
родной системы
(£—M) S=F,
(32)
где
и F=(/i.
b
Л »(a/7), a,7 = J qi (x) py (x) dx, I, /«I, 2, , n> n,
a
( Ь
fn)T A = Qi (x) f (x) dx . В рассматриваемом случае
имеем
а
pi(x)=x2,
Qi (/)==cos /,
я
«й = J cosX‘X2dx=»43i,
*л
я
021= J sin x-xadx»0,
-л
Рг(х)=*х,
</a(x) = sin t,
Я
а1аЯЯ J cosx-xdx=0,
*я
fi== cos2xdx = n,
-Л
Система (32) имеет вид
/1-4лХ
\ 0
a2a« J sin x-xdxs= — 2n,
-л
n
f2= J sin x cos x dx » 0.
—я
1-}-2лХ
(33)
Характеристическое уравнение
det (£—Ы) = (1 +2л1) (1 — 4лЛ)=0
имеет корни Xi=— и л2= — являющиеся характеристи-
ческими числами соответствующего однородного уравнения.
При любом	система (33) имеет единственное
решение
®1=таИ’ s’e0:
соответствующее решение интегрального уравнения:
p(x) = cosx+1-^.^.
При X = из (33)’ получаем
221
Эта система, а вместе с неё и исходное интегральное уравнение»
решения не имеют.
При К==—1/(2лс) система (33) принимает вид
»:)
и имеет решения sf = n/3, st-»C. Соответствующие решения интег-
рального уравнения таковы:
у {к) «а cos х+(si*’+ $&)*= 00s х**-х’4- Сх,
где С— произвольная постоянная. ►
Исследовать решения заданных уравнений с вырожден-
ным ядром при различных значениях параметра К:
1
18.139. у(х)— Х$х(Ц-0у(0Л=«х«.
О
t
18Л40. у(х)—ху (0di«sui2nx.
1
18.141, у(х)—X | (1 +2х) ty(t)dt~\ —|х.
1
16.142,	^(х)—X^xsin2n/y(0d/=x.
2L
4
18.143,	у(х\— X $ tgty(O<ft“Ctg».
я
“Т
1
18.144,	у(х)—Х^ агссоз ty (/) dt = p-gj-p
Я
18.145,	y(x)—Кj sinxeos///(0d/=cosx.
i
18.148.	y(x)—X J (1 + xt) у(t)dt=3 sinnx,
i
18.147,	jr(x)-X J (х4-/)у(0Л=4+тж-
18.148,	if(x)—X(cos(x+/)i/(0d/ = l.

4.	Уравнения Фредгольма 2-го рода с симметричным ядром. Ядро
К(х, 0 называется симметричным, если оно удовлетворяет условию
для всех а^х, КЪ<
Для симметричных ядер» удовлетворяющих условию
ъ ь
$$ !*(*> < + *»
х	л а
дополнительно к основным теоремам Фредгольма (см. п. 3) спра-
ведливы следующие утверждения:
1. Симметричное ядро, отличное от тождественного нуля, имеет
по крайней мере одно характеристическое число,
2. Характеристические числа симметричного ядра действительны,
а собственные функции, соответствующие различным характеристи-
ческим числам, ортогональны.
На практике часто встречается случай, когда интегральное
уравнение с симметричным ядром является решением некоторой
самосопряженной однородной краевой задачи для обыкновенного
дифференциального уравнения. В таких случаях нахождение харак-
теристических чисел и собственных функций ядра сводится к реше-
нию указанной краевой задачи.
Пример 10. Найти характеристические числа и собственные
функции ядра
◄ Заметим, что ядро (34) симметричное. Действительно, из (34)
следует
*<*.*)-( (х+1)4 0<х<1<1.	(35)
Сравнивая (34) и (35), видим, что К(х, — х} для любой
пары (х, О-
Однородное интегральное уравнение
1
0(х)-Цк(х, t)y(t)dt = Q	(36)
о
с ядром (34) запишем следующим образом:
(х	1	\
Д (/+1)*(0<#+(*+1Л	(37)
О	х	'
Далее, дважды продифференцируем (37):
P'W-X^J(/4-1)^a)d/+x(x + ,)y(x)4.
° 1 \
-р J	(38)
У" (х) = А((*+ !)&(*)—. (39)
223
Таким образом» число 1 и функция у(х) таковы, что
у"—(40)
Найдем теперь краевые условия, которым должна удовлетво-
рять искомая функция у(х). Для этого, подставляя в (37) и (38)
х = 0 и х=1, получим
1 1
y(O)^K^ty{f)dt, у(1)=Ц(/+1)у(0<«.
О	о
1 1
У' (0) = К $ 1у (0 dt, у’ (1)« X $ (/+1) у (0 dt,
Q	О
откуда
г/(0)=/(0), у(1)«/(1).	(41)
Соотношения (40) и (41) образуют в совокупности однородную
краевую задачу, решая которую, найдем характеристические числа
и соответствующие им собственные функции исходного интеграль-
ного уравнения.
Рассмотрим три случая
1)	Х®=0. Уравнение (40) принимает вид
/'==0,
его общее решение:
y(x)=iCi+C2x.	(42)
Используя краевые условия (41), получим для нахождения постоян-
ных Ci и Ссистему
С1 = С2,
Ci+Ca«Ca,
которая имеет единственное решение Ci =»0, С2»0. Следовательно,
краевая задача—а вместе с ней и уравнение (36)-*при Х=0 имеют
лишь тривиальное решение у (x)es0, т. е. Л = 0 не является характе-
ристическим числом. Впрочем, это можно было заметить сразу из
уравнения (36): если в нем %=0, то у(х)®я0.
2)	> 0. Уравнение (40) имеет вид
у"—(О8У=з0,
его общее решение:
^(x) = Cie^ + C2e'-®x.
Краевые условия (41) приводят к системе
Cf+C2 = coCi—(оС2,
С^®+С8е~®=oCiew »шС2е-®
или, в матричной форме,
f I-® 1+со	бгп
сое®	} \С$) \ 0 /	' '
Эта система имеет нетривиальные решения в том и только в том
случае, когда выполняется условие
I 1—со 1+со I	11 1	|
|aw—сое®
= — 2(l—со) (l+<d)shft)=Of
т. е. co=»i 1 (со8 > 01), или Л = со2 = 1.
224
При (0=1 из (43) получаем
° 2 W^W0^ и
Oi/eJyCiJ \OJ \С2)~\0)>
откуда y(x) = Ctex, Ci —произвольная постоянная.
Аналогично, при ю = — 1 получаем
(44)
откуда у	С2—произвольная постоянная.
Таким образом, А= 1—характеристическое. число ядра (35),
соответствующая ему линейно независимая система собственных
функций состоит из двух функций У{ — ех y2=^e-xt а любая соб-
ственная функция имеет вид г/(x; = Ciex +С2е~х, где Ct и Са—
произвольные постоянные.
3)	Л = —со2 < 0. В этом случае уравнение (40) имеет вид
у" + й)2У = О,
его общее решение:
у (х) = Ci cos шх+С2 sin ох.
Краевые условия (41) приводят к системе
Ci=соС2,
Ci cos (о + С2 sin со =s— coCi sin со+фС2 cos со
или, в матричной форме,
1	\/СЛ /0
cos соф-со sin со sin со—со cos со/ \С2/	\0
Эта система имеет отрицательные решения в том и только в том
случае, когда со2sin(о = 0, т. е. (оп=»лп, п=± 1, ±2, или
Zn= —((£ = —л2л2,
При со==соп = л/г, л = ± 1, ±2, из системы (44) получаем
/ 1 —яд \ /С^Х f°\
k(— 1)" -лп(-1)" )\С9) \о)>
откуда С^лпС, С2 = С и у (х)«=С(лп cx)S n/?x4-sin лях), где С —
произвольная постоянная и п=£1, 4-2, ,Заметим, однако, что
в этом выражении для у(х) переход от п к г-я приводит лишь
к смене знака, т. е. к изменению константы С. С учетом этого
получаем, что каждому из характеристических чисел Хл = — л2л2,
соответствует одна базисная собственная функция yrt =
=лп cos mix-psin лпх, а любая собственная функция имеет вид
у (х)=С (пп cos лпх 4- sin япх),	п £ N,
С—произвольная постоянная.
Подводя итог, заключаем, что для заданного ядра задача
о характеристических числах и собственных функциях имеет сле-
дующее решение:
^=1, Уод=е*, ^о,2=е"*\
Хп = —л2я2,	=ля cos лях+sin лях,	►
8 Под ред. А. В. Ефимова, ч. 4	225
Для заданных симметричных ядер найти характеристи-
ческие числа и соответствующие им собственные функции,
сводя интегральное уравнение к однородной краевой за-
даче для обыкновенного дифференциального уравнения.
18.149. К(х, /) = (	[ (/ — l)x, 0<x</, [ /(x—1), /<х<1.
18.150. К(х, /) = J	[ —x, O^x^/. [ — /, / 1.
18.151. К(х, /) = (	V/ V/ V/ V/ О -К. 7 7 1 1
( cos t sin х, O^x^t, 18.152. К (x, /) = < . ,	. .	. '	(sin/ cos X, t^.x^.n.	
18.153. K(x, /) = <	[ sin t cos x, 0 X c /, [ cos/sinx, / -Сх^л.
18.154. K(x, /) = •	' sin(Z— l)slnx Sinl	’ sin t sin(x— 1)	.	. sinl	’ г^=х=^‘-
18.155. K(x, /) =	Г sh(f —l)shx n. j ‘ shi	’ sh/sh (/—1) k	shl ’ 1
18.156. K(x, /) = y sinjx—/|, 0<х</<л.	
18.157. K(x, /)=J	( —e_fchx, O^x^/, (—ch te~xt /^x^2.
Если задано неоднородное интегральное уравнение
ь
у(х)—Х. J К(х, t)y(t)dt=sf (х)	(45)
а
с симметричным ядром К (х,	л), удовлетворяющим условию
4 ъ
$ jl#(x, ty^dxdl <+<ю,
а а
то его решение в общем случае может быть найдено следующим
образом.
Пусть
*1.	.....(«)
— последовательность характеристических чисел ядра К. (л, I), а
И (•*). 9» W. • <.. fa (4	(47)
226
— соответствующая ортонормированная последовательность собст-
венных функций. При этом в последовательности (46) каждое харак-
теристическое число выписывается Столько раз, каков его ранг,
т. е. число линейно независимых функций, соответствующих этому
характеристическому числу.
Если параметр % в уравнении (45) не совпадает ни с одним
из характеристических чисел 7irt, л = 1, 2,,.., то решение этого
уравнения (существующее и единственное в силу 3-й теоремы Фред-
гольма для любой правой части f(x)) дается формулой
00
г/W=/«+?-Z	(48>
n=i п
где
ь
л«1, 2, ...	(49)
а
Если же параметр X совпадает с одним из характеристических
чисел, имеющим ранг г, т. е.
= л/7/ 4 1 “	+ 2 ж • • • “ +Г
для некоторого т, то решение существует в том и только в том
случае, когда функция f (х) ортогональна ко всем собственным
функциям, соответствующим данному характеристическому числу,
т. е. выполнены г условий
ь
J=0, n==m + l, /п-ф2,	/n+г.	(50)
а
В этом случае уравнение имеет бесконечное множество решений,
имеющих вид
во
«/(*) = /(*) +* У. у^-У»М + С1Уи+1(х) + ...
П=1	*
п W+1, ../п + г
• * *СгУт+г (*)•	(51)
где Си Сг—произвольные постоянные.
Пример 1L Найти все решения неоднородного интегрально-
го уравнения
я
^ = 7~sin j.
(52)
cos i sin xt 0 < x t9
sin/ COSXt
при различных значениях параметра Л.
Характеристические числа и соответствующие нм собственные
функции ядра (52) имеют вид (см. задачу 18,152)
''Ут в“°« 1» 2» •••
К(Х, 0“
8*
227
Заметим, что в данном случае каждое характеристическое число
имеет ранг, г=1, а последовательность собственных функций "орто-
гональна, но не нормирована на отрезке [0, л]: нормированные
собственные функции имеют вид
/2 . 2п 4“ 1	л 1 о
— sin——х, п=0, 1,2,
л X
По формулвхМ (49) для f (x) = y~ sin получаем
При X / ХЛ, л —О,
решение
L 2, уравнение имеет единственное
00
, . Л . « И V 1
n-Q
. 2л+ 1
Sin--х
2л4Н
При Х~Л0=—3/4 в силу ортогональности f (х) к собственной
функции yQ (х) = sin получаем бесконечное множество решений
вида
Л . 2л+ 1
_ л х . X 3 V Sin 2 Х • х
4 2 sin 2	4 2- n(n + l)(2n4-l) +Csin 2 »
гДе С «—произвольная постоянная.
Наконец, при	л=1, 2, уравнение решения не
имеет.
Найти решения неоднородных уравнений Фредгольма
2-го рода с симметричным ядром при различных значе-.
ниях параметра X (характеристические числа и собствен-
ные функции соответствующих ядер см. в задачах 18.149 —
18.157).
I
18.158.	у(х)~Х$Л(х, t)y(t)dt = 1,
О
к. J {t— i)x,
К1 tlx— 1), /<х<1.
928
1
18.159.	f/(x)—t)y(t)dt = sin jTxcos-yX,
я
18,160.	y\x)—X^/C(x, i)y(t)dt = x—я,
0	/
I sin/cosx, Q^x^t,
К (x, t)«s
( cost sin X, t-^x^n.
n
18.161.	y(x)—к j у sin | x—t\y(t\dt==\.
о
§ 3.	Численные методы решения интегральных
уравнений
Существуют различные методы численного решения интегралы
ных уравнений: метод конечных сумм. метод моментов, метод кол-
локации и др. Ниже будут рассмотрены два из них—метод конеч-
ных сумм и метод моментов.
Пусть задано интегральное уравнение Фредгольма второго рода
(ср. § 2, п. 1 настоящей главы)
ь
у(х)-Л^К(х. t)y(t)dt = f(x).	(у
а
где у (х) —искомая функция, К (х, i) и /(*)—известные функции,
определенные в прямоугольнике а^х. t^b и на отрезке [а. ЭД
соответственно, К—параметр, не равный собственному числу соот-
ветствующего однородного уравнения.
Метод конечных сумм. Этот метод основан на прибли-
женном вычислении определенного интеграла с помощью некоторой
квадратурной формулы
ь	п
J F (х) dx = У2 AiF (xf) dx + Rf,	(2)
a	bi
где х/. / = 1, 2,	точки отрезка [а, ЭД, Л/, i==l, 2,	л,—
числовые коэффициенты, не зависящие от выбора функции F (х),
и ошибка формулы (2), порожденная приближенным вычисле-
йием интеграла. В случае равноотстоящих узлов x/s=a-J-(t —1) ft,
i = l, •«.? п, где	коэффициенты Л/ в приближенных фор-
мулах (2) имеют следующие значения:
1)	для формулы прямоугольников
Ai—ht i»lf 2|	Лц«0|
229
2)	для общей формулы трапеций
Ai = An = H/2, Аа= ... = Ад-!==&;
3)	для общей формулы Симпсона при п = 2/и-|-1	/
At = А^+^ — Ь/З, Аа = А4= .,. = ASm ~ 4h/3, Аз = Аб =...=
^2zm-i = 2А/3»
Вводя обозначения
y(Xi) = yi, K(xit xj)^Ki/t f(Xi). = fb	f, /±=1, 2, п9
интегральное уравнение (1) на основании формулы (2), в которой
ошибка Rf отброшена, можно заменить системой п линейных
алгебраических уравнений относительно неизвестных у[—прибли*
жецных значений точного решения у (к) в узлах х,:
п
jyj=fit t == 1, 2, •«., н.	(3)
/=1
Система (3) может быть решена' одним из численных методов
линейной алгебры, например, методом Гаусса.
Найдя yt из (3), для решения ^(х) получаем из уравнения (1)
приближенное аналитическое выражение
п
,М = /(х)+1£лЛ(х, x/)yj-
Пример 1. Используя квадратурную формулу Симпсона, ме-
тодом конечных сумм найти приближенное решение уравнения
1
f(x)—- 0,5 J xety(t)dt — е~х. В вычислениях положить /1 = 3.
о
Выбираем равноотстоящие узлы Xi = 0, х2 = 0,5, Xa=L Значе-
ний ядра Z((x, /) = хе* и правой части /(х)=в~х в тачках (х/, /у)
я х/ соответственно оформим в виде таблиц:
Таблица значений Kij—K(xb if)
	xi	0	0,5	1
0		0	0,5	1
0,5		0	0,8244	1,6487
1		0	1,3592	2,7183
Таблица значений // = f(x/)
Xi	0	0,5	1
h	1	0.6065	0,36l9
230
Квадратурная формула Симпсона (см. (3)) в нашем случае
имеет вид
F(x)dx к l(F(0)4-4F(0,5)+F(l)),
О
так как ft=l/2, Л1 = &/3= 1/6, Л2= 4/г/3 = 4/6, Л3 = /1/3=1/6.
Для определения приближенных значений yi, 1 = 1, 2, 3, ре-
шения у (к) в узлах X/ согласно (3) получим, используя таблицы
значений Kij и следующую систему линейных уравнений:
</1=1.
Уг	(0.5^ 4- 3,2976у2 +1,35920,) = 0,6065.	(4J
У»(yi + 6,594802+2718303) = 0,3679.
После упрощения система (4) перепишется в виде
У1=1,
О,725202- 0,11330,=0,6482,	(5)
0,549602 —0,773503=-0,4512,
Решая систему (5), находим
yi=»sl, У2 — 1» 1079, уз =ss 1,3706.
Следовательно, приближенное решение интегрального уравне-
ния выражается формулой
=	4-1,003%.
Заметим, что точное решение уравнения есть у (х) = г~*4-х.
Изложенный выше метод применяется также для приближен-
ного решения интегрального уравнения Вольтерра второго рода
у(х) — К^ К (х, /) у (t) dt = f (х), a<x<fr.
а
В последнем случае полагают, что
/>1.
Действительно, уравнение Вольтерра с ядром К (х, I) можно свести
к уравнению Фредгольма с ядром К*(х5 /) вводя функцию
Л	0, х<1.
Метод моментов. В методе моментов приближенное ре-
шение у интегрального уравнения ищется в виде суммы [(х)' и
линейной комбинации линейно независимых на отрезке [а, 6]
функций фх(х), фа(х), ...» ф#(х), т. е.
0(Х)а»0я(Х)=/ W+£CW(«),	(6)
/1
231
где с2, •••» некоторые постоянные. Подставляя (6) в (1),
получаем невязку
п	п	ъ
t = l	/=1	а
Г]&
Ь
ф/(х) = J К(х,	i—1, 2, .Si> n.
a
Согласно методу моментов коэффициенты с/, i=l, 2, ...» п,
определяются из условий ортогональности невязки ко всем функ-
циям Ф1 (х), <р2 (*)» •••> Фп (*)• Эти условия дают следующую систе-
му линейных уравнений:
ь
$ R [уп W1Ф/ (*) dx—0, i=l, 2..п,
а
или в силу (7)
п
cj (tyj—Хр/у) = Ху/,	i == 1, 2, ,.,, п,	(8)
/=х
где	'
ъ
«//=$ ф/Wt/ W dx>
а
Ъ Ъ
₽«7=$ $ К (*• О Ф< (О Ф/ (0 <й>
а а
Ъ Ь
4i=^dx^K(x,
а а
Если определитель D (X) = det (aij—ХР/у) системы (8) отличен
от нуля, то коэффициенты ct, ?2» •••> сп определяются однозначно.
Подставляя их найденные значения в (6), получаем приближен-
ное решение исходного интегрального уравнения.
Замечание. Для удобства вычислений интегралов систему
(8) иногда формируют, используя условие ортогональности невяз-
ки (7) к некоторой иной системе функций, отличной от системы
Ф1(х), ф2(х), ...» фп(х).
Пример 2. Найти приближенное решение уравнения
1
у(х)=$К(х, t)g(i)dt = l,
О
где
К4\______0^х</,
232
4 Используя выражение для ядра К (х, /)> перепишем уравнение
в виде
fх	1	\
)=1.
\о	х	/
Положим уН = ^И=1тС1х+с2х2. Тогда невязка R [у2 (х)] имеет
вид
R (Уз (х)] = С!х+с2хг— £(х— 1) (ct	+* ( — —
( х3 х*Л с2 ।	/ Л4 х3 \\1	(х—1)х2 . х(х—ГЛ
-СЦ—}~+сЦ—;Л—— +—
Из условия ортогональности невязки R [у2 (х)] к функциям х
и х2 получаем следующую систему:
1
J R [г/2 (х)] Хб/Х = О,
о
1
$ /?(уз(*)]*2<Ьс=»0.
°
После вычисления интегралов и некоторых преобразований
получим следующую систему линейных уравнений [для определе-
ния Ci и с2:
0,3555с<+0,3146е2 = —0,1167,
0,2638^+0,2417с2 « —0,025.
Решая эту систему, находим Ci== 0,027, е2«—0,029. Приближен-
ное решение исходного интегрального уравнения имеет вид
^(х)==1 + 0,027х—0,029х2. >
Замечание. Мы не приводим оценок точности приближен-
ного решения для изложенных методов ввиду довольно громозд-
ких выкладок. Изложение этих вопросов можно найти в специаль-
ной литературе1).
Решить интегральные уравнения методом конечных сумм, либо
методом моментов. В методе моментов использовать функции
фЛ(х)=вХй, &=з0, I, 2, .п.
1
18.162.	у(х)—4 J sin2(x/a)#(/)d/==2x—л.
о
р i ~
18.163,	у(х)—Jearcsn2 y(t)dt — \£x.
о
1
18.164.	у (х\— $ tge0’1 <**+о у (t).dt = ctg (х + 5).
о
*) См., например, Березин И. С., Жидков Н. П. Методы
вычислений.—Т. 2.—М.«- Физматгиз, 1962, гл. 10, § 10.
233
1
18.165.	у(х\— sin(x-f- Vf y{t)dt = x2 + 5.
о
i
18.166.	y[x)—~^(x* + s\nxt) y(t)dt==cos2x.
° о
i
18.167.	y(x) + y $xln(x2+10^ + 3)y(0^ = x2 + 3x.
• о
i
18.168.	«/(x)—5 J tge0,lb7/(f)d/=cosax.
о
i
18.169.	у (x)— $ (1 + sin e*0 у (t) dt = | (x + 8)'.
0
1
18.170.	у (x)—3 J (xs/! + 6х1 +1) у (/) dt = cos 2x.
0
1
18.171.	z/(x) + 5 $e*!+t\/(/)d/ = In(!+*)•
&
1
18.172.	y(x) + J (xsin/ —К/)уcos3x.
о
i
18.173.	у (x)—$ (xt + x2 cos 0 y(f) dt = x—2.
g
i
18.174.	y(x)— J (x4 3)^f+f‘z/(0d/ = x(e*4-2).
0
1
18.175.	y(x)—cosln((/ 4-5)x)#(/)d/=^sinx.
° о
i
18.176.	у (x) — J (5x arcsin t—In (/ + 8)) у [t) dt~x*-±&
q
i
18.177.	у (x)—4 $ xe**+txy (/) dt =	+ 8.
G
1
18.178.	y(x) + J cos2n(x2+/x)/(/)tft=*x2 + sinx.
G
i
18.179.	y(x)—4 J (x?/+sinx/+ln(/+4))^(Qrf/=se*ll+8.
234
X
18,180.	у(х)— (х—sin xt) у (t)dt = sin х, O^x^l,
о
X
18.181.	y(x)—J(l+x2/—etx)y(t)dt=*eix+x, 0<x<l<
0
18.182.	y(x)—J sin(3x—8tx) y(t)dt — l—2cosx,
о
0<x<l.
X
18.183.	y(x)—~ $е^г--»^(0^ = езх + 9, 0<х<1.
0
x
18.184.	y(x)— J(xf0(/ + 8)—^)y(Z)d/ = le»* + x,
о	*
0<x<l.
18.185.	Составить на фортране подпрограмму для ре-
шения интегрального уравнения Фредгольма второго рода
(1). В качестве формальных операторов использовать:
N — количество узловых точек, С=*%, X—одномерный
массив размера N, который перед обращением к, подпрог-
рамме содержит значения узловых точек хк, k — 1, 2, ...
..., N, А—одномерный массив размера N, который перед
обращением к подпрограмме содержит коэффициенты квад-
ратурных формул А,л, т = 1, 2, ..., N, RK—промежу-
точный двумерный массив размера NxN,R—одномерный
массив размера N, в котором до обращения к подпрог-
рамме находятся значения правых частей, а после окон-
чания работы—решение системы линейных уравнений, F и
EF—имена подпрограмм-функций,,вычисляющих значения
К (х, I), f(x) соответственно.
• Для решения системы линейных уравнений можно
использовать подпрограмму EXCLUS(A, В, N) (см. ч. 2,
с. 178) или стандартную подпрограмму математического
обеспечения ЭВМ серии ЕС.
18.186.	Используя подпрограммы задачи 18.185 и-квад-
ратурную формулу Симпсона, найти решения задач
18.162—18.184. Число точек деления выбрать равным
п = 21.
235
ОТВЕТЫ
ГЛАВА 16
16.1. l/»=Z. 16.2. (/*={1. 2}. 16.3. ^*=<|2ГП’
16.4. {/*=[-1; 1). 16.6. f* = 0. 16.7. f, = -oo.' 16.8. f# = —oo.
16.9. f»«= — л/2. 16.10. f« = -oo. 16.11. a)/t = —oo; 6)^=0.
16.20. (—1; 0], [0; I J, Ц; 2]. 16.21. i!>=2,5. 16.22. Да. 16.23. • Вос-
пользоваться результатом задачи 16.19. 16.25. См. рис. 229.
Рис. 229
236
16.28. **=1,156, /*=0,6609.	16.27. **=0,6605, /*=—0,4501,
16.28. **=0,6565, /*=1,4653,- 16.29. х*= 1,6702, /*=—33,5064?
16.30. **=1,2963, /*= — 1,7557. 16.31. **=0,8241, /*=—1,6421/
16.32. **=3,3532, /*=—47,1447. 16.33. **=1,8411, /*=—6,0016?'
16.34. 6„=С — (6—а). 16.37. n^loga	16.38. Да. 16.39. ЛГД=
= 32, tf„ = 100001; Nn/Na = 3125. ® Использовать результат за«
дачи 16.37, полагая 6я0. 16.40. См. рис. 230. 16.41.**=—4,4934,
Рис. 230
/*=—4;8206. 16.42. **=1,6030, /*=—2,1376. 16.43. **=—0,7549,
/* = —3,6347. 16.44. **=0,3822,/* = —3,7491. 16.45. **=1,7556, /* =
= 2,4154. 16.46. ** = 0,3684, /* = 2,4154. 16.47. **=4, /*=—8,9169.
16.48.	**=—1,5,	/*= — 1,6519. _ 16.51. б)	*а—я=5—*( =
= ~	—°)’ 18.52.	= J 18.53. Nд=32, jVc=
= 24; /Уд/Л?с=1,33, 16.54. См. рис. 231. 16.55. **=-0,6823, /* =
237
«= —0,5814. 16.56. х*=—2,2340, /*=61,1806. 16.57. х*=0,6488, /*=
«=—2,3675. 16.58. х*=0,5110, /*=—2,5054. 16.59. х*=—2,3247,
/*=—7.7290. 16.60. х*= 1,5160, /*=20,4415. 16.61. х*=0, /* = —3.
Рис. 231
16.62. х* = 0,7339, /*=1,6796. 16.65. а) 1 = 5; б) L=135. 16.66. См.
пне. 232. 16.67. /*= 1.152Х10-2. 16.68. /*=—10,006. 16.69. /* =
= 0,523. 16.70. /*=2,387. 16.71. /*=1,393Х1О~*. 16.73. Урав-
нение касательной к графику /(х) в точке (хв, /(х0)) имеет вид
238
Рио. 232
239
y~~ f (xe)+/' (x0) (x—x0). По формуле конечных приращений f (х)=
==/(*«)+/'(g)(*—*o), где g заключено между х и х0. Поэтому
/(х)—у= [/'(g)—/'(*<>)](*—*o)Ss=O> так как f (х) не убывает. >.
16.75. См. рис. 233. 16.76. х*=1, /*=1. 16.77. х*=0,4502, /' =
= —0,2325. 16.78. х*=—0,3855, /*=0,7852. 16.79. х*=0, /*=—1.
16.80.	х*=0,6501,	/*=1,6951.	16.81.	х*=0,7035,	/*=3,4422.
16.82.	х* = 3,8708,	/*=1,3702.	16.83.	х*=0,5283,	/*=0,6675.
16.84. х*=0,351734, /*=0,827184. 16.85. х*=—0,693147, /* =
= 0,6137064. 16.86. х*= —0,835430, /*=—0,879073. 16.87. х* =
= 0,738835, /*=0,284712. 16.88. х*=—0,175203, /*=1,908524.
16.89. х*=—0,443931, /*=0,765751.
16.91.	Да. 16.92. Да. 16.93. Да. 16.94. Нет. 16.95. Да.
16.96. Да. 16.97. Нет. 16.98. Да. 16.99. Да. 16.100. Нет. 16.107. U =
= {(хь х2) | х2 > 0}. 16.108. U = {(xi, х2) | (2£— 1) п < Х14-х2 < 2йл,
16.109. U = <£2- 16.110. t/ = {(Xi, х2)|х1+ха > 0}U{(xi, Х2)|
XiS-Xj < —1^2}. 16.111. а > О, 4ас—> 0. 16.112. ag(—2; 2).
16.113.	/'(х*’>) = (^).
16.114.	/'(*») = ({).
240
4\
3 )•
—5/
(Ч 2 0\
16.115.	Q =12	4—1), /'(*(»>) =
\0 —1	6/
/2 1 1\	'	/12>
16.116.	Q= 1 1 1 ), /'(х<®>) = 5
\1 1 2/	\ 6,
16.117.	а) х(1) = (0,0б11; —0,1389), f (х<«) < f (х’°>); б) х'1’=
= (—1,4881; —2,0181), f (x‘l>) = f (х<®’); в) х(1> = (—3,6945; —4,6945),
f (х'1') > f(x<°>). 16.118. а) хЧ> = (—0,1; —0,1), f (х«>) < f (х[0>);
б) х11,=(—0,5; —0,5), f(x<1>) = f(x(0»); в) х'« = (—1, —1), f(x4’)>
>/(х^). >6.119. х<1’ = (—0,1; 0,8; —0,1), f (х<»>) < f (х<°>); 6)x>« =
= (—0,638;—0,276;—0,638), f (x<!>) = f (х<®>); в) х<1> = (—10, —19,
Рис. 234
-10), f(x'«) > f (х<«>). 16.120. а) х<*’ = (—0,1437; 0,4; 0,4), /(х<»>) <
<f(x<®>); б) х(1> = (—1,4323; —0,2761; —0,2761), /(х<1>)=/(х’®>);
в) xd> = (—10,4366; —5; —5), f (х<«) > f(x<’>). 16.121. См. рис. 234.
16.122. ф Воспользоваться необходимым условием минимума функ-
ции Фй(а) = /[х(А,—о^' (xlft,)l в точке а*: Ф*(аА)=0. 16.123. См.
241
Рис. 235
Рио. 236
242
рис. 235. 16.124. См. рис. 236. 16.125. а»=0,НЗ. 16.126. ао = О,25.
16.127. ао = 0,236. 16.128. ао=О,119. 16.129. ** = (—0,2206; 1,0441),
/* = —5.3309. 16.130. ** = (0,3333; 0), /*=0,3333. 16.131. ** =
= (0,3846; —0,1923), /* = -0,4877. 16.132. ** = (0,1667; 0,1667),
/* = -0,1667. 16.133. **=(2,55; —0,85), /* = —21,675. 16.134. ** =
= (0; 0,5), /* = —0,75. 16.135. ** = (0,9677; —6,4516), /* = —32,2581.
16.136. ** = (—0,5; 0), /* = —0,25. 16.137. **=(—0,1053 ; 0,0789;
—0,0639), /* = —0,1207. 16.138. ** = (—0,1538; 0,1154; 0,3077), /* =
= —0,5385. 16.139. ** = (—2,6028; —0,0198; 0,1050), /*=—6,4658.
16.140. **=(—1,5865; 0,3221; 0,2981), /*=—5,8029. 16.141. ** =
= (-0,1112;—0,0292; 0,0308), /*=—0,4435. 16.142. **=(-0,5236;
0,2028; —0,1698), /*=—1,3939. 16.143. **=(—1,2867; 0,2317; —0,2569),
/•=—4,6319. 16.144. **=(—0,0732; —0,2195; 0,6830), /* = —0,4146.
16.146. См. рис. 237. 16.149. **=(0,2310; —0,3160), /*=0,5565.
Начало
. 11/*7д?)н2
Z Jl/'(y)ilf


Мцнимцзщии функции.
а>0
Q Конец
Рис. 237
х'-х,
16.150. **=(—0,7071; 0,7074), /*=—0,7071. 16.151. **=(—0>7592;
—0,4053), /*=—1,4428. 16.152. **=(0; 0), /*=1. 16.153. ** =
= (0,2420; 0,1829), /*=1,7814. 16.154. **=(—0,1918; —0,9596),
/*=—2,3843.	16.155.	**=(0,7358;	—0,8580),	/*=—1,4001.
16.156. ** = (0,2400; —0,3267), /*=—0,4504. 16.157. **=(0; 0),
/* = 0,6931. 16.158. **=(—0,6132;—0,6633), /*=—1,805. 16.159.** =
= (—0,3015; —0,6031), /* = 3,3166. 16.160. ** = (—0,2990; 1,4952),
/*=—4,7299. 16.161. **=(1,2248; 0; 1,2248),/* = 2,4495. 16.162. ** =
= (0; 0,1555; —0,4119), /*=0,6949. 16.163. **=(—0,3016; 0,6030; 0),
243
/* = 3,3166. 16.164. x* = (—0,4446; —0,5778; 0,0010), /* = —0,7668.
16.165. x*=(0; 0; 0), /*=1. 16.166. x*=(0', 0°, 0), /*=2,3863.
16.167. x* = (—0,1907; —0,0954 ; 0,9535), /* = —2,4321. 16.168. x* =
= (—0,6300; 0; —1,5811), /*= 1,1087. 16.169. x* = (0,2300; 0,4600;
—0,1150), /*=—0,4131. 16.170. x*= (1,0610; 0,3539; 0,0011), /* =
= 2,8284. 16.171. x*==(—0,4041; 0,2235; 0), /* = 0,6600. 16.172. x* =
= (—0,1912; —0,4081; —0,3602), /* = 3,5056. 16.173. x* = (—0,2136;
—0,3328; 0), /*= 1,4461. 16.174. x* = (—0,1154; —1,1544; 0,3463),
/*==—8,3670. 16.177. См. рис. 238. 16.178. См. рис. 239.
16.182.	/ (x) = 4xj 4-6x2 —* min,
0,1X14-0,lx2<2,
0,1х| 4-0,3x2 3,
0,8x14~ 0,6x2	7,2,
0,8xi 4-0,6x2 < 12 8,
Xi, x2^0.
16.183.	/(x) = —3xi—8x2 —* min,
10xi4-70x2<570,
20xi 4-50x2 < 420,
300x14- 400x2 5600,
200x14-100x2 <3400,
*1, x2^0. ® Максимуму прибыли Зх/4-8*2 соответ-
ствует минимум противоположной величины.
16.184.	/(х) = —626X1—656х2 —► min,
Xi4”*2^ 12,
Xj<8,
5xi 4" 8х2 81,
6x1+ 4х2 *5» 70,
3xi 4“ *2	26,
Хъ х2^0.
16.185.	/ (х) == — СгХ! — С2х2—> min,
0,4X1—0,6x2^5 0,
агХ1 + «2*2 < Ь,
Xi, х2^0.
8	9	10	10
16.186.	Дж) = Х12	С(-+хз2 CA-*min,
1=1	i=2	i=3	i=l
Xi^bt,
Xi + *2^^2>
xi4-x24-*3^ max b[,
3 <i<8
*2 4- x2	dg,
x3 bio,
x7^0, /=1.2,3.
16.187.	/ (x)=—Crxf—C2x2 —► min,
atiXi 4" #12*2 bi,
«21*1 4“ #22*2 ^2»
#31X14“ «32*2 < *3,
Xi, x2 0.
16.188.	x*=(l; 1); /*=—1. 16.189. x*=(2/3; 2/3); /*=-8/3.
16.190. Нет решений. 16.191. Бесконечное множество решений:
ж*=(<х; 1—Ct), где а€1°; П:	16.192. х* = (1; 2); /* = -9.
16.193. х* = (2; 2); /* = —4. 16.194. Нет решений. 16.195. Бесконеч-
ное множество решений: х*=(2—а; &4-1), где aG[0; 1]; /*==—3.
16.196. х*=(2; 28/3). 16.197. х*=(1; 8). 16.198. х* = (5; 7).
16.199. х*= (146,25; 97,5). 16.200. а) х*=(20; 50); б) х*=(30; 40).
16.201. Л*=(4; 1; 7; 0; 0); /* = —3. 16.202. х*=(5; 6; 5; 0; 0; 13);
244
Рис. 238
Рис. 239
245
16.203. х*=(Ю/3; 7/3; 5/3; 0; 0); /*=29/3. 16.204. x* =
= (0; 2; 1; 0); /*=3. 16.205. Бесконечное множество решений:
X*=(6—За; 5+а; 6—6а; 0; За; 3+4а), где а£[0; 1J; /*=—21.
16.206. х*=(1; 2; 0; 3; 14; 0): /* = —4. 16.207. х*=(1; 0; 2; 0; 2);
/* =—17. 16.208. Нет решений. 16.209. х*=(3; 0; 2; 0; 1); /*=6.
16.210. Нет решений. 16.211. х* = (9/2; 0; 0; 3/2; 2); /* = —25/2.
16.212. х*=(0; 0; 11/10; 12/5; 3/5); /*=—5/3. 16.213. х*=(2; 0; 1;
0; 1); /*=—9. 16.214. х*=(5; 2; 0; 0); /*=—46. 16.215. х* =
= (1/2; 0; 6; 3/2; 0); /*=—65. 16.216. х*=(0; 1; 3; 1); /* = 7.
16.217. х*=(Г, 0; 3; 3); /*=2. 16.213. х* = (1/5; 27/5; 0; 7/5; 0);
/*=—17/5. 16.219. Нет решений. 16.220. Нет решений. 16.221. х* =
= (0; 2; 4; 1; 0); /*=—2. 16.222. х*=(3; 0; 0; 4/5), /*=—36.
16.223. а) х*=(0,9; 8; 0,45; 0); б) х* = (4,71; 0; 6,82; 0).
16.224. а) х*=(600; 0; 0); б) х*=(0; 700; 0). 16.225. х*=(15; 5; 5).
16.227. х*=(13; 3), /*=—16. 16.228. х* = (1; 2). /*=—31.
16.229. х*=(2; 1), /*=—11. 16.230. Два решения: х*=(2; 0), х* =
= (1; 1);/*=—2. 16.231. х*=(0; 0; 1; 2), /*=—1. 16.232. х* =
= (1; 9; 0; 5), /*=—9. 16.233. х*=(3; 6). 16.234. Х* = (3; 9).
16.235. х*=(0; 4; 0; 1; 0), /*=1. 16.236. х* = (0; 0; 11; 3; 1),
/*=—24. 16.237. х* = (3; 2; 2; 1), /*=—2. 16.238. х*=(0; 3; 2; 0)
или х*=(1; 2; 1; 1) или х*=(2; 1; 0; 2), /* = —3. 16.239. х* =
= (1; 3; 0; 0; 1), /*=8. 16.240. х* = (2; 1; 1; 1), /*=—11.
16.241. х* = (2; 1; 2; 1) или Х*=(1; 2; 1; 2) или х*=(3; 0; 3; 0)
или х*=(0; 3; 0; 3), /*=-3. 16.242. х* = (1; 3; 5; 3), /*=—5.
16.243. х* = (1; 2;-3), /*=10. 16.244. х*=(6; 1; 4), /*= — 17.
16.245. х*=(6; 18), /*=—78. 16.246. х*=(0; 1; 1), /* = 3.
16.247. х*=(0; 0; 7), /* = —21. 16.248. хц = 7&, х12 = 24, х?1 = 0,
хм = 200. 16.249. х*=(7; 7). 16.250. а) х* = (146; 97); б) х* =
= (146; 96). 16.251. х*=(3/8; 9), /*₽=-’717/8. 16.252. х»=(1; 3/2),
/♦=—5/2. 16.253. х*=(3; 7/2; 0; 1/2; 3/2), /*=—17. 16.254. х* =
= (1; 0; 1/6; 2/3), /*=—65/6. 16.255. х*=(3; 9). 16.256. а) х* =
= (146; 292/3); б) х*=(293/2 ; 97). 16.258. х*=(6; 0), /* = 2.
16.259. х*=(6; 14; 0), /*=—8/29. 16.260. х*=(0; 0; 2; 4), /* =
= —2/3. 16.261. х*=(3/5; 11/5; 0; 1/5), /*=5/6. 16.262. х* =
= (5/2; 11/2; 0; 27; 0), /*=—21/38. 16.263. х* = (0; 0; 6; 9; 10),
/*=—3. 16.264. х*= (12/5; 23/5; 46/5; 29/5), /*=—1/91. 16.265. х* =
= (5; 5; 10; 0; 0; 16), /*=—4/13. 16.266. Нет решений. 16.267. х* =
= (2; 3), ./*=—52. 16.268. х*=(5; 2), /*=-131. 16.269. х" =
= (2/3;	14/9), /*=—22/9. 16.270.	х*=(2;	4), /* = —80.	16.271. х* =
= (33/13; 4/13; 0), /*=—273/13.	16.272.	х*=(1/2; 1;	9/2; 8), /* =
= —7/4. 16.273. х*=(0; 0; 1), /*=—1. 16.274. х*=(0;0;0), /*=0.
16.275.	х*=(0; 4; 4), /*=12.	16.276.	х*=(0; 0;	3), /* = —6.
16.277.	х*=(2; 3), /*=—13. 16.278. х*=(8; 28/5),	/*= — 154,24.
16.279. х*=(15/2; 6), /* = 45. 16.280. х*=(10; 4), /*=—344.
16.281. х*=(29/5; 22/5), /*=—108,44. 16.282. х* = (7; 8), /*= — 173.
16.283. х’=(10;5), /*=52. 16.284. х*=(1;2), /*=—3. 16.285. х* =
= (2; 4; 8; 16), /*=—20. 16.286. х* = (0; 10; 0; 30), /*=-10.
16.287. х*=(3; 8; 13; 4; 14), /*=—137. 16.288. х*=(0; 0; 0),
/*=0. 16.289. х*=(0; 1; 0), /» =—1. 16.290. х* = (1; 0; 0),/* = -2.
16.291. х*=(—2,683;—1,342), /*=—4,025. 16.292. х*= (3,578; 1,789),
/*=—37,667. 16.293. х’ = (0,447; 0,894), /» =—1,4. 16.294. х* =
= (0,791; 1,258), /* = —2,214. 16.295. х*=(0; 0), /*=0. 16.296. х* =
= (1,005; 0,099), /*=9,95. 16.297. х’ = (0,618; 0,618), /*=4,090.
16.298. Х*=(1;0,5), /*=—1,75. 16.299. гу/ = тах (0, гу), /=1, .... п.
246
| а/, если Zf <
16.300.	2^/=| bjt если zj > bjt / = 1» »&*» th
\ zjt если
{Zj если z LA,
x(0> + Ro (z — x<“>)/|| z—x<»> ||, если z$U.
is.soz.	Z(j=z—[(a,	z)—ft] a/||a||.	16.303. zy=z+
+ max{0, ft—(а, z)}a/!|a||. 16.304. x*=(0; 0), /*=0. 16.305. x* =
= (3; 0), /6=—81. 16.306. x*=(4; 2), /*=±—68. 16.307. x* = (5; 1),
/*=11,29. 16.308. x*=(3,1056; 1,5528), /*==7,764. 16.309. x* =
= (2,1213; 1,8787), /*=—8,9411. 16.310. x*=(l; 1; 1), /*=6.
16.311. x*=(0,8; 1; 0,4), /* = —8,2. 16.312. x*=(0,8; 0,4), /* =
= 104,987. 16.313. x*=(l; 0,5), /*=0,5. 16.314. X* = (l,5; 0,5),
/* = —8,5. 16.315% x’=(2; 1), /*= — 16. 16.316. x*==(l; 2), /*=—3.
16.317. x* = (3: 1), /* = 2,3026. 16.318. x‘=(—0,9487; 0,3162), /* =
= —5,3246. 16.319. x*=(l,7071; 0,2929), /*=—9,4858. 16.320. x* =
= (—2,111:0,8944), /*=1,7603. 16.321. x*=(l,6; 0,8), /*=—3,8.
16.322. x’ = (2; 2), /*=—2,2082. 16.323. x*=(2; 3), /*=—117.
16.324. x” = (5; 2), /* = —51. 16.325. x*=(33/13; 4/13; 0), /* =
= —7,385. 16.326. x* = (2; 4), /* = —30. 16.327. x*= (2/3; 14/9),
/*=—2,444. 16.328. x* = (0; 1; 1), /*=—1. 16.329. x*=( 1,258; 0,791),
/*=-2,214. 16.330. x*=(2,684; 1,342), /*=—11,125. 16.331. x» =
= (0,5; 1), /*=—1,75. 16.332. x*=(0,618; 0,618), /*=4.090.
16.333. x*=(l,8388; 0,7862), /*=—2,7933. 16.334. x*=(0,6667; 0,6667),
/* = -8,1111. 16.335. x’=(0,791; 1,258), /*=—0,214. 16.336. x* =
= (2.530; 1,265), /*=—14,299. 16.337. x*=(l; 0,5), /*=—0,75.
16.338. x*=(0,8284; 0,4142), /*=—2,8995. 16.339, x*=(3; 4), /*=40t
w
16.340.	J (x, «)= 2 Л (и(Л)) —► max,
Л=1
+ Ul, .... N,
x^£[0; S}, k~lt
«(А)ёЮ; S], Ы, N,
x^>~S,
где — средства, выделенные k-му предприятию, сумма
средств, выделенных предприятиям с номерами от 1 до k.
16.341.	См. ответ к задаче 16.340, где средства, выделен-
ные предприятию в &-м году, а х(/г'—средства, выделенные ему за
первые k лет, A?==l, N,
16.342.	J (х, и)= 2	(^Л~Х)е ^Л>) —* max,
л=1
/?’=х<»-1> + и^>,	ft=l, N,
х^€(0; S], А=1,	R—1,
и<*>€10; S], Jfe=l.....N,
v<0)^-n
Xi =U, *2 I» X1 =»<>,
k	k
TBfi x?*=2	^-П «u,;/ft(x<*“l*.«(W)=‘Q. *-l. ....tf-t,
"	i= i
J^(x<^-«, «‘Л'^хГ*1’.^.
N
16.343.	J (x, u) = 2 F («'*’) -♦ mta,
*=i
x>*’ = 4x<*-1'—в<», fe=l, .... N,
' x^^O, 6=1, R—1,
247
6=1, ..., N,
х<°> = а, х<^ = 0,
где u<A>—количество семян, проданных в 6-м году, —их коли-
чество, оставленное в совхозе к концу 6-го года, 6=1, N.
16.344.	В ответе задачи 16.343 заменить конечное условие
х<^0 = 0 на условие xuV)^d.
N
16.345.	J(x, u)=S +	—► max,
^> = fl(u^)-r/2(^"'X) — «<*>), 6=1, ..., Nt
1Л*>ёЮ; **-*>], 6=1, ..., N,
x{ 0) = S, x^> 0,
где x<средства, перераспределяемые в начале 6-го года,
средства, выделяемые первому предприятию в 6-м году.
N
16,346.	/ (х, «)«» 2	шах,
6=1, N,
x(A>g[O; Р], 6=1,	Л/-1,
^€10; Р—х<А-1>1, «^€[0; х<*-»+«{*>],6=1,
х«» = а, х<лг>^[0; Р],
где «запасы продукции в начале 6-го месяца, и$у и —
количества продукции, принятой и проданной в начале 6-го ме-
сяца соответственно.
16.347.	В ответе задачи 16.346 заменить ограничения на управ-
ления следующими ограничениями:	x(A-i)J, uik)£
g[0; P~xf*-» + u^]t 6=1, tf.
N
16.348.	J (x, «)=» 2	<“**’) min,
A=1
x<*> = x<*-i>.-aku™, 4=1.....N,
**>S&0, 4=1, .... N—l,
«‘ft’SaO, u^fZ, 4=1, N,
X<0’ = 6, X^'^O,
k
где x<*>=6«-2
;=1
N
16.349.	J(x, u)= 2 Fft ~+min,
Л=1
x<»ex(ft-1>—u(ft'a’to, 4=1......N,
i*=l........ 4=1, ..,, N—l,
и(Ю>0, u<*’€Z, 4=1..........N,
j№*ab<ss(bi, .... bm), XfV>^0, 1=1, ..„ m,
где x*® и а‘*’=т-мерные векторы о компонентами х{А) = 6; —
k	I
— 2 aUu^} и	соответственно, 6 = 1, N.
/=1 Л Л
16.350.	#*={!, 2, 1, 1},/*=12. 16.351. Три решения: й* =
= {0, 2, 1, 1, 1}, 2*«{1, 1, 1, 1, 1}, «*={0, 1, 1, 1, 2}, /*=13,5.
16.352. «*={25, 25,25,25}, /*=44. 16.353. «*={100, 100, 200, 100},
/*=226. 16.354. а) «*={100, 100, 200, 0}, /*=186; б) «* =
= {100, 100, 300, 100}. ф использовать результаты условной оп-
248
тимизации, полученные при решении задачи 16.353. 16.355, Семь
решений: в* = {100, О, 200, 100}, в*={100, 40, 180, 80}, «*-
= {120, 0, 200, 80}, «*={120, 0, 180, 100}, «*={120, 20, 180, 80},
«*={100, 20, 200, 80}, «*={100, 20, 180, 100}; /*-620.
16.356. а) «*={100, 100, 100}, /*=300; б) «*={114,3; 114,3; 71,4},
/*=48,6. 16.357. «*={0, 150, 0}, /*=27. 16.358. «*={3, 3, 3},
/* = 27. 16.359. u*={S/N, S/N..S/N}, J*=(S/N)X. 16.360. «* —
= {0, 0, .... О, aAN}, J*=caAN. 16.361. «*={19,2; 3,84; 0,768},
/*=38,402. 16.362. «*={0, 0, .... О, aAN— b}, J*=caA^--cb.
16.363. «*={19,01; 3,802 ; 7,604}, /*=37,638. 16.364. «‘—
= {200, 160, 128, 0}, «* = {0;0;0; 102,4}, /*=187,36, где «I и«‘ —
средства, распределенные первому и второму предприятиям. соот»
ветственно. 16.365. «J = {40; 64; 25,6}, «1={80, 0, 0}, /*=99,84.
16.366. at = {10, 0, 10, 0}, «1 = {0, 10, 10, 0}, /*=90. 16.367. «I —
= {7, 0, 12, 4}, «: = {0, 12, 12, 0}, /*=111. 16.368. и*=(2, П.
F*=—11. 16.339. Два решения: «*={2, 0}, «*={1, 1}; F*—2.
16.370. «*={1, 2}, Г*=—31. 16.371. «*={0, 0, 7}, F*—21.
16.372. «*={2, 1, 1}, /*= 115. 16.373. «*={10, 1, 1}, /*-5760,
16.374. Четыре решения: в*={2, 3, 4}, «*={3, 3, 3}, «*={!, 4, 4},.
«* = {2, 4, 3}; /* = 72. 16.375. у=^(х3—х). 16.376. Бесконечное
множество решений: ^ = (C+?f)sinx, CgR. 16.377. у=»е/х**1пл.
16.378. у = х^—х. 16.379. Нет решений. 16.380. у =
16.381. y=sh2x—$^shx. 16.382. y=±-xex—shx. 16.383. 9 —
= ex—e~3x. 16.384. y=^-—^^shx-}-sinx. 16.386. Нет решений.
16.387. y=— x. 16.388. y=x. 16.389. jz=y(14-x). 16.390. p —
= (2x/3)3/2. 16.391. y=-£—у+т- l6,392, У==*1-п/(1—n).
16.393. y=-l (x—xs). 16.394. Два решения: р=(х-{-1)2/8  p —
= (3x—I)2'3. 16.395. {/=cosx4-sinx—l. 16.396. р=£^(х—«)4-Л.
16.397. {/= KT^T24-1. 16.398.y=ch ^x—l^ch-1. 16.399.^H«.
правим ось Оу вертикально вниз. Скорость материальной точки
ds/dt = V2gy, поэтому время ее движения из точки Af0 в точку
..	.	1 С 1 + /‘ А ' *Г	ж
Mf t— ______ \—ax. Так как подынтегральная функция
V 2g J V у
не зависит явно от х, то уравнение Эйлера имеет первый интеграл
1/* 1 I .,f2
•---у=------=-.„ “	:——С или y(l-t-y'z)=Ci. Введем параметр 1,
У у Кип-/1)	г
полагая /-ctgt Тогда «/ = 7-^72“.=^^1'-,cos2z):
249
шСх (l—»cos2f)4ff, x = y (2^ —sin 2/)-J-C2. Из условия прохожде-
Гя кривой д[х) через точку Л40 (0, 0) находим: С2 = 0. Обозначив
через получим уравнения семейства циклоид: х =
^уft), р=у (1 —-cos	Таким образом, искомая кри-
|ая является циклоидой. Постоянная Cf может быть найдена из
условия ее прохождения через точку (х& yt). 16.400. у~х (х — ip.
16.401. 9-х*. 16.402. у=1(х»4-3х«—2х2). 16.403. у=х+созх.
16.404. 9 — 0. 16.405. 9—хе*. 16.406.	16.407. 9 = cosx,
| 16.408. 9—х*. 16.409. 9=shx. 16.410. 9==х—sinx. 16.411. 9 =
•mshx—sinx. 16.412. r/! = sin х, = —sin х. 16.413. 0i~shx, y2 =
R—shx. 16.414. 0i = sinx, 02 = —sinx. 16.415. yi = ex, y^er*.
•416. yi=x4, gz — x3. 16.417. f/i = lnx+l, 02ssO. 16.418. Беско-
нечное множество решений: 0i~ — у sinx — cos x—Csin x-J-x, y&=
jp	x®
=—у sin x-f-Csln x, CgR. 16.419. yi = ~2—H>	16.420. у=
= —2x, Xi=»l. 16.421. Два решения: f/==±4x, xx = y. 16.422. y =
-x/К?. xi-J/?. 16.423. 9«-x+3/4, x0=1/2, x1 = 23/8.
16.424. 9—-|-x (1—x). 16.425. 9 = (x2—1)/4. 16.426. Бесконечное
множество решений: z/«Csinx, CgR, 16.427. Нет решений.
16.428. р = У2 —(x —Ip, Xi«b2. 16.429. 0= ^x—-y — 1 sin x.
16.430. y«0. 16.431. y—shx. 16.432. 0=/?*+sinx. 16.433. Два
решения:	и у— j/^yx8* 16.434. у** In x+ 1. 16.435. у=
e—exy(g8^_ijB 16.436. # = 2 In(x+1). 16.437. 0 = sinx4~cosx.
16.438. gi««cosx4-sinx, 02= cosx—sinx. 16.439. 0X = (x—2)е“«#
p2 = (l—x)e~*. 16.440. 0i = 2—x, 02 = x4~1. 16.441. 0i = x24-x,
р2«х2—x. 16.442. Нет решения. 16.443. 0i«=y5inx, p2 =
ку (sinx-»xcos x). 16.444. 0i=xa+cosx4-sinx, 02=x2—cosx —
— sinx. 16.445. Бесконечное множество решений: 0i = i|>(x), 02 =
= x—i]5(x)+0^) + 0iO)—a, где Ap(x)gCf[a; b]f если 0^1)-0<iu —
— Ы0)*в₽10))яш&*’а‘» нет решений при 021>~0i1>-~(0-’O)-*0ih) #
*b—a. 16.446. 9=yx2—yx.	16.447.	9=60x3-96x2+36x.
16.448. p«(x**2sinx)/n. 16.449. Два решения: 0=x4-sinx, 0 =
= x—sinx. 16.450. 0 = xe“*. 16.451. 0i = —6x2 + 6x, 02 = 3x2—2x.
16.452. Два решения: 0i = 3x2—2x, 02=3x2—6x и y3 =— 3x2+ 4x,
02«o—3x?. 16.453. 01^0, 02=yx8—yx. 16.454, Бесконечное мно-
жество решений: yi = 2 sin knx, 02 = —2sin ^nx, ^^2. 16.455. Два
решения; ш=3х—x3, 02=x3—x и 01—х3+х, 0a==— x3+*»
16.456. pj(x)«ax(2—x)(—1,35514-0,ЗОЗх). ф Искать решение
MO
yi{x) = x&—x)(C1-}-Cix). 16.457. $£ (л)=0,3215 (л— 1)(л—2). О
Решение искать в виде yi(x) — Ci(x—V)(x—2). 16.458. у*(х)=я
х (1 — л) (0,192+0,171л). ф Решение искать в виде уя(х)^л
^x(l-x)(Ci + C2x).	16.459. иЦх, $/) = л2 + $,2 + л$-(1-л-г,)>|.
Х(3,0401—0,0562л (1 +*)). ф Решение искать в виде «3(л, у)£
= л2 + у2 + Сгху(Г— х — {/) + С2л2у(1— л —у) + С3л3и(1 — л — у}.
16.460. и* (л, $0 = 0,0037 (л2 — 4) (у2—4). ф Решение искать в виде
«I (х, y)=Ct (л2—4) (j,2—4). 16.461. у'г (л)=л (л-1) (0,1708+0, р44л),
У1 = х(х— 1) (0,1705 + 0,176л —0,002л2). ф Решения искать £ виде
у8(л) = л(л—l)(Ci + C2x), у3(л) = л(л—l)(Cf+Cax+CsA В з0
данных точках значения у* и г/* совпадают с ФоТн остью дд
0,0001.	16.462. и* (л, $.)= 0,3125 (л2—1) ($,«—!). ф Решений
искать в виде щ[ (х, у)~Сг (х2—1) (у2 — 1). 16.463. м*(х, у)=»
яя0,3125л'д/(х — 1) (#— 1). Q Решение искать в виде Ui(x, у)=я
0t3125x^/(х—	1). 16.464. р(х)« х(2—х)/4. 16.4$5. у (х)=-
(1—х) (0,140—0,144х). 16.466. у (х) = х (1 —х) (-0,655—0,277х).
16.467. Для задачи 16.464 функции Ф^+1 (х) имеют вид
Фл+1	(2—х)хл,	& = 0, 1,2, 3,4-
Ответ записывается следующим образом!
FUNCTION FIK(X, К)
IF (X.EQ.OOR.X.EQ.2.) GO ТО 1
FIK=X*(2._ Х)*Х**К.
RETURN
1 FIK —0
RETURN
END
Для остальных задач ответы отличаются вторым оператором
и оператором, определяющим значение функции Фл+<(х).
16.468. Для задачи 16.464 ответ записывается следующим
образом
FUNCTION F1(X)
Fl =—2.
RETURN '
END
FUNCTION F2(X)
F2=4.—6.*X
RETURN
END
FUNCTION F3(X)
F.3=12.*(X—X**2)
RETURN
END
Уравнение Эйлера в данной задаче имеет вид у*4-1/2=0,
следовательно, Ly—y", f(x)=—-1/2 и’/д (х)«(х), £=1, 2, 3, 4, 5.
Для остальных задач ответы отличаются только вторым опера-
тором.
16.469.
FUNCTION SIMPiA^Fl.FT^EPSl
261
б Н=(В—A)N
Р1=0.
Р2=0.
Y —Д
DO 1 J=l, N
х=х+н
P1=P14-F1(X,K)*FT(X)
х=х+н
1 P2=P2+F1(X,K)*FT(X)
P3=(F1(A,K)*FT(A)-F1(B,K)*FT(B)+
*2.»Р2+4.»Р1)*Н/3.
IF (I.EQ.I) GO TO 2
I=I-H
8 Y=P3
N=N*2
GO TO 5
2 EPS1=ABS ((P3-Y)/15.)
IF (EPSI—EPS) 10,10,12
12 1=0
GO TO 3
10 SIMP-P3
RETURN
END
16.470.
DIMENSION Al (5, 5), ВЦ5)
EXTERNAL FIK,F1,F2,F.3,F4,F5,F
DATA A/О./, B/2./
EPS-.05
J=1
DO 3 1=1,5
Al (I,J) = SIMP(A,B,FIK,F1,I—l.EPS)
Al (I,J+1)=SIMP(A,B,FIK,F2.I-1.EPS)
Al (I, J-|-2)=SIMP(A,B,FIK,F3,I— l.EPS)
A1(I,J-|-3)=SIMP(A,B,FIK, F4.I-1.EPS)
A1(I,J4-4)=SIMP(A,B,FIK,F5,I—I,EPS)
8 B1(I)=SIMP(A,B,FIK,F,I—l.EPS)
CALL EXCLUSE (Al,В 1,5)
PRINT 2, Bl
2 FORMAT (//lnX,5F9.4)
STOP
END
ф Задание для ЭВМ должно содержать 9 программных единиц-*
указанную здесь основную программу и другие подпрограммы,
подпрограммы-функции, а именно: FIK(X,K), F1(X), F2(X), F4(X),
F5(X), SIMP(A,B,F1,FT,K,N, EPS), EXCLUSE(A,B,N), а также
подпрограмму-функцию F(X), вычисляющую значения функции
правой части £у=/(Р), в данном хлучае
FUNCTION FIX)
F=—.5
RETURN
END
При решении задачи 16.464 для функций F1(X), F2(X), F3(X),
F4(X), F5(X) использовать решение задачи 16.468. При решении
остальных (задач необходимо составить подпрограммы-функции,
вычисляющие соответствующие значения /*(х).
252
ГЛАВА Г/
, д-и (х, t) 9 д2и(х, t) , I с,	..	. .ч
пл- ----572--*’ Z ’ Где U (Х’	~~ откло<
нение точки струны с абсциссой х от положения равновесия в мо-
мент времени /, а3 = 77р, р — плотность струны, F (х, /) —плотность
распределения действующих на струну внешних сил. Пусть
а = а(х, /)—острый угол между осью абсцисс и касательной
к струне в точке с абсциссой х в момент времени t. Условие
малости колебаний означает, что величиной а2(х, t) можно пре-
-	.	< ди
небречь, а потому имеем sma«a, cosa«l, —=tga«a.
Длина любого участка МгМ2 струны в момент времени t выра-
жается формулой
Л 2	~ .
Xt
( ди \2
а так как -тг— х сг » 0, то
\ дх )
| М^М21 ~ х2— Х1=Дх.
Согласно второму закону Ньютона сумма всех сил, действующих
на участок струны М1Л12, равна по величине и по направлению
вектору ускорения ^того участка, умноженному на его массу. Вы-
числим все силы, действующие на этот участок. Плотность рас-
пределения внешних сил обозначим через F (х, /), тогда внешняя
сила, действующая на MxM2t равна F (х, 1} &х. Далее, силы на-
тяжения 7\ и Г2, действующие на концах Mi и М2, направлены
по касательным к дугам в соответствующих’ точках. Из малости
колебаний и из того, что равнодействующая этих сил вызывает
только вертикальные перемещения, заключаем, что горизонталь-
ная составляющая равнодействующей равна нулю, т. е. —cos at+
+ Т2 cos a2==0. Так как cos at « cos a2 w 1, то отсюда выводим
равенство 7\~T\~T. Следовательно, вертикальная составляю-
щая сил натяжения дается выражением Тsln^T sina* и сумма
всех сил FjfjMr действующих на участок AfiAf2t равна
т (sin a»—sin ai)+F (x, t) Ax.
Но в момент времени t a=a (x) = arctg u'x, а потому
sin a2—sin «! — sin a (xi + Ax)—sin a (xt) ®
== cos a (Xi -j- 0 Ax) (a (xf+Ax)—a (Xi))»
= cos a (Xi+0 Ax) (arotg u'x)'x |X=X1+01 &x Ax =
e cos a (Xi + 0 ДX) Г -rr-'-r-u" 1	Ax
[K!+(»;)* **JUr1+e.Ax
(o < e < i, о < ex < i).
При наших предположениях cosa(x3+0 Дх)«1 и (м’)?|^я^1+01Дл«О,
Таким образом,
р- Td2u(xi+eiAx, i)Ar,p,r ЛА„
1----------------Ах+г (х, 1)Ах.	(*)
253
С другой стороны, считая участок материальной точкой
(при достаточно малом Дх), имеем
d^u
— (**)
Приравняв согласно закону Ньютона выражения (*) и (**) и пере-
водя к пределу при Дх —* 0, для искомой функции и (х, t) полу,
чаем дифференциальное уравнение	F (х, I). ►
17.2.	Найти функцию и (х, t), определенную при 0<x^Z, я
O^Z^+oo, являющуюся решением уравнения
д*и «, д2и . 1 г /
^=e’^+-pf(x’°’
(а’^Г/р, Т—натяжение струны, р—* плотность струны, F (х, O'-
плотность распределения внешних сил) и удовлетворяющую
условиям
и (0, /)=«(/, /) = 0 (граничные условия),
и(х, 0)=ф(х),
ди (х, 0)	(начальные ус лов и я).
dt
17.3.	Найти функцию u(xt l)t определенную при 0^х>С/ я
А « №
0«С/<4*оо, являющуюся решением уравнения -^-==а’-—.
(Г	\
а2 = -^-, Т—натяжение, р—плотность струныу и удовлетво-
ряющую условиям
и(1, 0~0,
ди(О> t) п . (граничные условия)»
дх ж
м(х, 0)==ф(х),
0ц(х, 0)^.0 (начальные условия).
dt
• Граничное условие при х=0 получить из отсутствия на этом
конце внешней силы и, следовательно, равенства нулю силы на-
„	ч <М0, О
тяжения Т, пропорциональной —
17.4.	Напряжение u(x, /) и сила тока 1(х, t) в точках линии
в любой момент времени t должны удовлетворять волновому
уравнению
+(ЬС+ RC) dWft’ t}' + RGw (х, t).
Рассматриваем двухпроводную линию как систему равномерно
распределенных индуктивностей, сопротивлений, емкостей и утечки
(см. рис. 240). Согласно первому закону Кирхгофа (алгебраиче-
ская сумма токов, сходящихся в узле, равна нулю) имеем
. 1(х, о—0=СЛ*-^-4-ОДх«(х, о,
254
где СДх~ — ток через конденсатор, a Gkxu(xt /)—-ток утечки.
Разделив это равенство на Дх и переходя к пределу при Дх —» 0.
получим уравнение
а«^п с
дх	dt v ’	'
Далее, согласно второму закону Кирхгофа падение напряжения
и (х, I) на участке между х и х-(-Дх состоит из падения напря-
а?, Да? । а?+Д#
—-------^7	*
г д	0
жения на индуктивности L Дх—~—- и из падения напряжения
на сопротивлении R Axi (х, /), т. е.
и (х, 0—и (х+Дх, t)» L Дх	# Axi (х, /)*
Разделив на Дх и переходя к пределу при Дх —* 0, получим
уравнение
L	Ri-(x, П.	<**)
Уравнения (*) и (**) называются уравнениями длинной линии»
Исключая из этих уравнений i(x, t), приходим к уравнению
^=LC^+(LC+RG)^+RGu,	(**»)
а.исключая и (х, /) —к уравнению
g-=LC-g-+(LC+/?G)g-+«Gi.	(****)
Уравнения (***) и (****) называют также телеграфными уравне-
ниями. ► 17.5. Найти функции u(xt t) и i(x, /)» определенные
при 0< + оо и 0^/< + оо, являющиеся решениями урав-
нения
d2w(x, 0_гГ d*w(xt t)
дх*	д&
и удовлетворяющие условиям
u(xt	0) = ф(х),	я	ч
Z(x,	O)-f(x)	(начальные	условия),
и (О,	Л —^о>	/	I
А_;r_L L	л-п	(Граничные	условия)
255
(условия при х== + оо следуют из физических соображений).
17.6. Найти функцию и (х, /), являющуюся решением уравнения
ди __ 2 д2и
dt ~~а дх2
и удовлетворяющую условиям
и(х, О) = по
и (0, /) = н0,
O+Ytw(Л О—Ф(/)]=о
(начальное условие),
(граничные условия),
где у—коэффициент теплообмена между стержнем и средой. Q
Для получения граничного условия при х = / заметим, что коли-
чество тепла, проходящего через конец стержня за время Д£, равно
Д<7 = — k 4^-	S А/, где S—площадь поперечного сечения стержня,
а коэффициент теплопроводности материала стержня. С другой
стороны, Д? пропорционально произведению разности температур
u(lt 0-*ф(0 на площадь S и на время А/, т. е. А^=^й[«(/, !) —
— cp(01SAf, где зависит от качества теплоизоляции конца
стержня от окружающей среды. Сравнивая оба выражения дляД^
h
и обозначая у = -£- > приходим к написанному граничному условию.
17.7. Пусть система координат выбрана так, что ось Ог парал-
лельна образующей. Область, ограниченную кривой L в плоско-
сти Оху, обозначим через D. Найти функцию и (х, у), которая для
всех точек М (х, y)£D удовлетворяет уравнению
д2ц . д2и __ п
т. е. является гармонической в области D, а па границе области,
т. е. на кривой удовлетворяет условию
“(*. У)1(Х, y)eL^f(X, у),
где f(x, у) —заданная на L непрерывная функция. Для установив-
шегося теплового процесса —~-=0. 17.8. Гиперболический,
17.9. Параболический. Выбирая £(х, #) = 2х—•у и т) (х, у) = х, после
преобразования получаем уравнение	=	17.10. Эллипти-
ческий, Ugg + uyv = 0, где ,и(х, у)~ —Зх—y=Reg(x,y)HVjx,y)^
= 2x=img(x, у). 17.11. Параболический. Выбирая g = YУ—V *
и т]=х, после преобразования получаем уравнение ^-§=0.
17.12.	Параболический. Выбирая g=sx2+y2, г|=х при
при у / 0, получаем уравнение	+ g'^~~2 *4 0 > При t/=0 имеем
д^и	п
уравнение	а при х=0* уравнение ихх=0. 17.13. В об ла-
сти О={(х, у) I х £ О, у 5*0} гиперболический,	—
— —J—--w^aaO.	При х=0 или у=0 параболический.
2(ga«**tp)
256
17.14. В области D={(x, у) |х > 0, у> 0} эллиптический,
При х = 0 или у» 0 параболический. 17.15. Гиперболический, и|п=0.
„ 1
17.16. В области D =»{(*, у) | х & 0} гиперболический,	----X
о(§«*ту
х(н|--*и^)=з0. При х = 0 параболический. 17.17. В области
О —	У) | х £ 0} эллиптический, +	При х=»0
дТ]
параболический. 17.18. Параболический. Выбирая % (%, у)^у!х
и Л (*» #)=fZ> после преобразования получаем уравнение (§, т))==0.
17.19. и(х, ^) = ф(4х —у) + Шх~*У)* где ф(и) и ^(^ — произволь-
ные дважды дифференцируемые функции. Выбирая g (х, у) =»
— 4х*—у и Т|(х, у)~х —у, приводим уравнение к виду «^=50
(см. задачу 17.8), последовательно интегрируя которое, находим
«* = фо(Б) и и (I, I])™ J Фо (£)<*£+ф(п)==Ф(В)+ Ф(п)-	Подставив
сюда выражения для £ (х, у) и т) (х, у), получим искомое решение.
17.20. и (х, #) = ф(2х—#)е~зх + ф(2х —#), где ф (с?) и ф(о)—-про-
извольные дважды дифференцируемые функции. 17.21. «(х, у) =
-*<р (К 1— К ~х)+Ф (/Т— /"*). где ф(у) и ф(я)—произвольные
дважды дифференцируемые функции. 17.22. и (х, ^)=ф(у—х+соз х)+
+ ^0/——cosx), гдеФ(0 и У (у) — произвольные дважды диф-
ференцируемые функции. 17.23. п(х, у) = у

где
ф(р) и ф(о)— произвольные дважды дифференцируемые функции.
„ х sin х cos at — at cos x sin at
17.24. н(х, 0 е-----5---27a-------•
v '	x2—a2t2
лв % z .. x sin x cos at—at cos x sin at . 1 , l+(*+a02
,7-25- “ <*•	1п тН-аГ
17.26.	u(x, 0 = у [ i4-(x+/)a+l + (*—0a] + sm xsln*•
17.27.	u(x,	[14-(х4-/)«"^1 + (х—/)«]+ slnxcos**
17.28.	u(x, /) = e-<x‘+^.ch2x/+4-1п|Фт^-К5- *7-29- Если
v '	‘4	l + (x—02
o<«^. TO
u(x, /)==
у(х+а0	при	— at < х ^att
X	при	at ^х ^l--at,
/—а/	при	I —— at	x I -j- at,
2Z—х	при	l+at <x^2Z—аЦ
/-у(х-а0	при	2l^at ^x^2Z+a/,
0	при	остальных x.
9 Под ред. А. В. Ефимова, ч. 4
257
Если	то
2а а
	4(*+ао ~	при	— at ^x^l—at.
	/-1(х+а/)	при	l-^-ai^x^at,
	l^at	• при	at ^x^2l-^att
	1		
	у(х+аП	при	2l—at^x^l-}-at,
	Z—y(x—aZ)	при	l^at^tx<2l-Yat^
	> 0	при	остальных x.
1
Еели —</< + «>, то
а
п(х, /)«=<
у(*+«0
Z--1(х-|-а/)
1 .
, 2-(*—«О
при	—-а/«Сх<С/—at,
при I—at^x^2l—at,
при at^x^l-^at,
при l+at ^x^2l^at,
при остальных х\
у(х+у)при
I	1	31
у при —
5,1	3Z _ 5Z
при —<х< —
О	при остальных х;
г 4-(ж+/)
3/	х
2	2
V О
при	—/<х<0,
при	0<x<Z,
при	/<х<2/,
при	2/<х^З/,
при остальных х.
• Рассмотреть случаи различного возможного расположения зна-
чений х—at и x+at на оси х, а именно: если х—а/ < 0, тоточка
х+а/ может лежать в промежутках (— оо} 0), (0, I), (I, 21)
и (21, +«>); еели 0 < х**а/ < Л то точка х+а/ может лежать в
промежутках (0, /), (I, 21} и (2/, + оо); еели Z < х—а/ < 2/, то точка
х + а/ может лежать в промежутках (/, 2/) и (2Z, + °о}> если
258
21 < х —а/<-|-оо, то их + а/£(2?, 4-00). 17.30. ЕслиО^/«С^, то
	0	при	— оо < %<; — h — at
	и	при	A4~af<;x< + oo,
	-y(x+a/ + A)	при	— h—at ^x^at —A,
«(«. t) = <	— at	при	at~h ^x C—at,
	X	при	*—at ^x^at,
	at	при	at ^x^h—at.
	±-(-x + at+h)	при	h—at <x < h-±at.
Если	< — , TO a		
	0	при	— oo < x< — A—at
	и	при	h + at^x < + oo,
	— у (x+at+h)	при	—A—at ^x^,—at,
Щх, t)=*<	•^(x + at—h)	при	*~at ^x^at—h9
	X	при	—h + at «С x < A—at,
	j-(x—at + h)	при	h—at ^x^at.
	±(-x+at + h)	при	at x^h^ at.
При	имеем		
1	0	при	— oo < x^—h—at
	и	при	h + at^x < + oo,
	— у (x + aZ+ft)	при	—A — at ^x^—at,
и (x, t) = <	у (х + л/— А)	при	—at^x^h — at,
	0	при	h—at ^x^at —A,
	y(x-aH-A)	при	at-^h^x^at,
	у(-х + а/+Л)	при	at x^h-^at.
9
259
и
ф Рассмотреть случаи различного возможного расположения зна-
чений х—at и x-\-at*. если х—at <—h, то x+at может лежать
в промежутках (—со, — Л), (—/г, 0), (0, h) и (А, 4-оо); если
— h < x*~at < 0, ’то x-\-at может лежать в промежутках (—/г, 0),
(О, h) и (Л,+©о); если 0 < х—а/ < А, то x-\-at может лежать
в промежутках (0, h) и (А, 4~ °0); если А<х—а/<4-<ю» то
и х4~^€(Л» +00)* 17*31.
— sin х sin at, at<x< + <n,
a	1
1
— (1 —-cos x cos а/), 0*Сх«са/.
17.32.
(2
2
1
“2
при x^at,
при O^x^at.
м	1 . 14-(х4-аО3
17.33. и(х, 0- 4а In 1 + (x_0/)a-
17.34. и(х,
'	7 4а l-j-fx—at)2
при
при
O^x^at,
17.35. и (ж, /) = е-<*г+°г»2> ch axt +
1
— (1 — cos х cos at)
+ 1
— sin x sin at
\a
i?c36. Если	to
a
{. nx nat
sin — cos —j-
|#ГпДи-аО
A I
0
при
при
при
при
при
at.
l — at ^х«С l~^ati
l^at<x <4-00.
0<х<а^
260
Если у^/’<4“ао> то
г 0	при
при
при
0<х<о/—Z
I -|- at х < 4* °®,
at—l<x*£at + l.
и(х, /) = 5
и
1 . л ,
у sin у (х — at)
при 0<x<-y,
3*	_ 5/
при —<x^_t
ы
при -<х<4-00,
I
при
при
7/	’
при у <х <4-00.
17-37. Если <~, Т0
	' ct	при	0«Сх < 1 —aty
О(Х, 0='	£-(l + at—x)	при	l—qt^x < l-^at,
	u 0	при	l^at^x <4-со.
Если — < / < д	: «о, то		
	f cl	при	
и(х, П = |	±U + at-x)	при	at—x < at 4-/,
	I 0	при	aZ4“^<x <4-oo.
0<х < 2/,
2/<х < + «>;
OsCx < 4Z,
4/<х <6/,
6/ <х < 4- 00 <
при
при
при
при
при
17.38. Выражение (Хл,.Гп)—(Х,Я записать в виде [хп>уЛ— у)+
+ (xn—xt у) и 'воспользоваться неравенством Коши—Буваков-
ского. 17.40. Ц Показать, что в произвольном ортонормированием
базисе фундаментальность последовательности векторов {*n}ne^
эквивалентна фундаментальности числовых последовательностей
их координат. 17.43. ® Воспользовавшись результатами задач 17.41
и 17.42, доказать полноту пространства /$.
261
I ь	Г 6	6
17.44. I f (x)g (x) dxI < /(*) l*dx |g (x)|arfx.
I о	I fl	a -
17.45. 0 Пусть произвольная функция из 0*4—1, 1J
в h (/) — разрывная функция, равная —1 при I < 0 и 1 при
Из неравенства Коши —Бун яковского для интегралов (неравенства
Шварца, см. задачу 17,44) следует, что
i / ’	\1Z*
I ( $(/(0-фп(П)2л) s*
1	/1	\1/«	/ 1	\ 1/2
fe»( $а(с-л(О)’л) -( $(фв(о-л(П)*л) •
1	/ 1	/
Показать, что
1
11m ( (<рй(0«*Л(0)2^ = 0,
и в силу непрерывности
1
$(Д0-Л(0)4Л>0.
-1
1
Отсюда следует, что интеграл j (/ (/) —• <рп (/))2 dt не может стре-
1
миться к нулю при л —* оо, какова_бы ни была f(t)£C{i> (—1, lj.
17.51. P,W=p=-.	P2(x)=	y)>
Го&}

Рв(х)= l/”^(x3 —	.
17.52.	f0(x) = -7L,	f£(x) =
— к Л _
Л(Х)= ]/^(4x3-3x)/17.53. е
При вычислении интегралов
произвести замену переменной
arccosx = 0.	17.54.	<p0(x)=l,
<Pi (х) = 2 \/"з^х — 2-у <р2(х) =
= 6 V 5 ( х3—х+4-). 17.55. См.
\	Ь /
рис. 24L Вертикальные прямые
в точках разрыва проведены толь-
ко для наглядности. 17.58. См.
рис. 242. Вертикальные прямые
в точках разрыва проведены для
наглядности. 17.60. 40 Учитывая,
262
Рис. 242
что lv(ax) есть решение уравнения + / + ^а2х —= ^см‘
ч. 2, гл. 12, задача 12.338), т. е. уравнения
и полагая Za = /V(ax) и «/v V)x)» можно записать
4- (xZa) + ( а2х — — Za » О
dx \ х}
и
Ил	\	Л /
Умножая первое равенство на второе на Za, вычитая из
первого полученного равенства второе и принимая во внимание
соотношение
Ut £ (xZa) —2a A (xU'i) = £ (ZaxU 't -xU^'J,
их	их	их
получим
A (xZ,.U't -xUiZ'J + х ((gP)2 -a2) 2aUl =0.
dX
Интегрируя это равенство в пределах от 0 до 1 и учитывая, что
-£(2a)==-^-/v(ax)==a/v(ax), приходим к равенству
dx dx
1
((gp’’)2—a2) J / (gr’x)/v(ax)xdx = —gjv’/v(a)/vWV,).j]
о
Отсюда при а<=^т получаем
J /v(gzV)x) /v(gm’x) xdx^O,
263
<v>	**
а переходя к пределу при а—►р/, найдем
v (иГ,ж)]’ж dx= lim ®»
а-*- ц('
- Um ^V)/v	pl ШУ * 0. >
a-»H<v>	а2—(Ц/ )-	4
17.61.	Xj=— (^“У. ykW^sto-j!*’ «< Из общего реше-
ния уравнения y(x) = CjeVi'x-{-cte~V"ij‘ приХ>0 или у(х)*вС1Х-^-с9
при Х = 0 и из граничных условий следует, что отличное от тож-
дественного нуля решение этой задачи возможно только при А < 0
/	( С1+С2 = 0,	( С\ = 0,
( системы -	1/Г. и < _ , Л имеют нулевое реше-
\	I Cievu+Cte~V*i~0	I с*/в°
ниеС1=С2=0^. Поэтому полагаем —со* и общее решение
уравнения запишем в виде у (x) = Ci cos (ох + С2 sin сох. Из гранич-
ных условий следует, что Cj«=sOvh C2sincoZ=O. Это означает, что
отличное от тождественного нуля решение задачи возможно только
в случае sin со/ = 0, т. е. при cox=(oft®— ,k £N- Отсюда в находим
собственные числа. Функции у^(х) = sin	являются собст-
венными функциями этой задачи.	17.62. Хо=О, ^0(х)=1,	=
f kn V / ч fa1* tz-iM iino	7(2/? —1)л\*
= •*(—) • ^««cos —,	17.63.	*
. v . (2&—1)лх	-	/2^—1 V
^(x) = sini-__2—t fcgN. 17.64. Цх=—, УьМ=*
9b 1	✓ (<b\2	/ti<0) \
= cos*i^nx, *€N. 17.65.	) , gk(r)~lJ El-г), где
Zo (г) —функция Бесселя порядка нуль, a цГ’,	—ее нули,
т. е.	Если со*=0, то получаем уравнение у(гу"(г)+
+ у' (r))s=sOt или Jy (гу‘) = 0,. решая которое, находим сначала
ry'(r) = ci и, наконец, y~ci In г^с^. Из ограниченности решения
при л = 0 следует, что с5~0. Используя далее граничное условие
находим, что ^ = 0, т. е. y(r)ss0. Последнее означает,
что (0 = 0 не является собственным числом. Пусть теперь со 0.
Произведем в исходном уравнении замену переменной г)=оп
Так как ~	=== Уггe й>2#ггп> то уравнение преобразуется
к виду
(Л/	1	*	\
FrniOlH — Уг)(П) + ^(П) )=0,	(.)
которое является частным случаем (при v=0) уравнения Бесселя
у"+^у'А-^-^У)у^о.
264
Следовательно, решением уравнения (*) является функция
Бесселя «МлЬ т. е. решением исходного уравнения является
ФУНКЦИЯ у(Г}*=16((йГ).
Из граничного условия у (R)70 (соЯ)«=О находим, что «/?==
е» р40>. Таким образом, собственными значениями нашей задачи
(<о>\2
, &&N, а собственными функ-
((О) ч
Г ) .
л. /
Замечание. У равнение
^+4- /—®2</=о
(**)
заменой f/f —приводится к виду у\+ ®s£/i ®®0» откуда
выключаем,
потому для
собственные
2
что уравнение (**) имеет решение у~—1ь (cor), а
краевой задачи с уравнением (**) легко находим
числа и собственные функции. ► 17*66. £>==
- г,- / <v>\i2 f f МlvW'x)хdx, *€N. 17.67. c, = c9=0, Co=4,
I'm JJ J	z
§
C2==-g . <1 Воспользоваться четностью функции |x| и четностью
или нечетностью соответствующих полиномов. 17.68. Со =
Р ., . dx
соответствующих полиномов.
л Сх/ v cos(karccosх) .
с*=т у(х).....4—— ft€N-
-JL С2==—1 е8=о, 17.70. ф Воспользо-
4	о
вавшись ортонормированностью функций {<рп (х)}“-о, записать
интеграл в виде
Л	л	П	П
\ lH*)-TnM}2dx~\P(x)dx^^ ak(f, ФА)+2
а	а	^0	^«0
=л
17.69. с0=у, Cf =
„2
Л	п	п	
= W»(X) dx- 2 &+ 2 (<*-«»)’•
a	k=0	ЛаО
2	«	1 Г
17.72.	ZL+ 2 (al-b2k)<-±- J ?(x)dx.
17,73.	Равенство Парсева ля означает, что квадрат модуля
вектора равен сумме квадратов всех его координат (в ортонорми-
рованием базисе), а неравенство Бесселя-*-что квадрат модуля
вектора не меньше суммы квадратов некоторых из его координат.
17.74. ф Воспользоваться тем фактом, что функции Уолша Wk(x)
при Л^З" (см. определение перед задачей 17.58 и задачу 17.59)
ортогональны функциям Радемахера гт (х) —	(*)•
17.75.	и(х, 0=4-cos?^-sln^-x.
О	I	I
265
I . 5шт/ t 5лх
17.76.	u(x, t)=—-sul—-siIt-r.
17.77.	u(x, «)=4coscos-—.
« сояя(2*+1)а/
n 32h V	I  (2*4-1) nx
17.78.	u(x, t)= n9 (2A-4-1)3	Sln /
k=0	'	1
а	Jl2&
W V sinTsin 2lh , nkal. t nkx
17.79.	u(x, X----------p-------3111 — sto —•
k = 1
17.80.	«(я, 0-^2- (2* — 1) (2Лг+ 1) (2* + 3) X
k =0
Х51п^.-ь;.!"'51ддц.;>".
.	..	4 V (	2	(2k—I) nat .
17.81.	u(x, /)= 2-<! (2А+1)(2Л—3)C0S	21	+
. 42 f_ i I 4(— 1)*+*]	1 (2k—l}nat\ (2k-.\)nx
+iiia|. + (26—1) л J (26—I)3	21 fCS 21
17.82.	u(x,
0»	-	/(2W+l)Jto\2.	I
8u0 V 1	/(. I ) ‘.(2т + 1)ях
“ «3 2- (2т+1)зв	I
m—u
17.83.	«(x, 0»
• ent 1) Я /(2fe+i)na\s,
^£2_4_еЧ-Т-) 'sin(2i+l)^
л	2«+l	21
k^O 1
17.84.	u(x, y, 0eS Л \Ak.«cosna у (4) +(^У* +
f П\2Л s s ППУ
-)	/Jsin-y-sin-^,
где
tn I
a 4 f f .	. . nkv . mz , ,
A*' n^Tm \ J ф(^ *)sln~sm—dvdzt
ml.
------: V	^!!T‘,"Srd’d’-
и (т) +U) •»
n^N- В случае, когда ф(я, r/)=sin-^~-sin, ф(х, t/)=iO и
а==1, и (л, &, О^созл у -дsin-у-sinПредпола-
гая, что мембрана совершает малые колебания, 'имеем первую
краевую задачу; найти решение и(х, gt /) уравнения свободных
266
колебаний мембраны
удовлетворяющее начальным условиям
и (к, у, 0) = <j (ж, у}, -	°) =1|)(х, у)	(2)
и граничным условиям
«(О» У> i) = u{lt yt t) = u(x, 0, 0®u(xt mt t)~0.	(3)
Ищем решение в виде произведения
u(xt у, t)=*X (x)Y (у)Т (t)t
подставив которое в (1), получаем
XYT"~a* (XffYT + Y"XT).
Разделив это равенство на a2XYT\ имеем
ааТ X “ Y	' '
Каждое отношение здесь зависит от своей переменной, а потому
равенство возможно только в том случае, когда каждое из этих
отношений постоянно. Полагая XW/X=X,	и используя
граничные условия (3), получаем две задачи Штурма—Лиувилля:
Г-М=0, Х(0)®Х(/) = 0	(5)
и
Г"-|хУ = 0, У (0) = У (т)==0.	(6)
Рассмотрим сначала задачу (5). Как показано в задаче 17.61»
собственными числами задачи (5) являются числа —(л£//)а,
а собственными функциями —функции
Xfc(x)®sin Ttkxjl,	(7)
Аналогично, собственными значениями задачи (6) являются
числа рп = — (лп/т)\ ngN, а собственными функциями — система
функций Yn (y) = sin nnyjtn, ngM- Подставив в (4) вместо отноше-
ний Х№/Х и Y"/Y их значения — (rcfc/Z)2 и —(лп/т)а, получим
уравнения
Т'+я»а»[(|)Ч(-£)*]т=0,
решениями которых при различных k и п будут функции
Tk, «(0 = 4*,„cos ла ]/"
+ Bfti„sinna	(у)2’•’(йг)*6
Таким образом, решениями уравнения (1), удовлетворяющими
граничным условиям (3), являются функции
/ fe \2	/ п \2
Akincosnay 1 +( —] < +
,	,	1/7 i \2 , Гп \2Л , nkx , лпд
+ ЯЛ>„81П ла у	7SlnTSta т •	®
267
Из линейности уравнения (1) следует, что и любая линейная ком-
бинация-решений (8), т. е. формально составленный двойной ряд
и(х, у, 0=52 52 Г^*,вСО8ла ]/" ULV 1+
fe= 1 П= 1 '	4	7	\	/
+ 3*,п81пла у	-Ц —j /SU1~Sinm’ (9)
при условии возможности его двукратного почленного дифферен-
цирования также является решением уравнения (2), удовлетво-
ряющим условиям (3). Потребуем, чтобы представленное рядом (9)
решение и Ос, у, t) удовлетворяло условиям (6), т. е. чтобы
00 со
, ЛЧ	Л , Л^Х . МУ /
и(х, у, о)=2- 2йл*. »81П“8Ш от =^(х>
Г(=1
И
u't(x, у, 0) =
-£ £ в,..™ /(Ау+^у^Л^, »>.
Л=1 л=1	'	'
Из этих равенств заключаем, что если числа ЛЛ> Л являются коэф-
фициентами Фурье функции ф(х, у), т. е. если
т I
л 4 СС / ч , nkv 3U12 , .
Л*, n=-^ J J Ф (»• *>8|»^sin — du<i2, k, Л£|Ч,
а числа В*, „ла у	^—коэффициентами Фурье функ-
ции ф(х, £/), т. е. если
т I
~	4	f С . / ч , лАхг , лпг . ,
Въ п —---------z- .........— \ \ I’U'» г)sin -г-sin — dvdz9
n
k, n€N,
то ряд (9) является искомым решением задачи 17.84 в общем слу-
чае. Если же ф(х, у)*=0> то все В^ п = 0, kt ngN, а для ф(х, у) —
= sin^psin^^ имеем Л„«0. при (k9 п) & (3,8) и H8i8 = !< ►
17.85.	н(х, #,/) = —^r=sin22j^ / sin-у* sin^, • Вовполь-
ла у 5	*	♦	•
зоваться формулами для коэффициентов п“и В^ п> полученными
в задаче 17.84.
268
17.86.	и (х, yt t) =
( na^^2t t 16	. naV"2t\ , лх ny ,
= ( cos 7----1---7= sin —7 ) sin	sin -r4-
\ l л3 /2 I /	1 I ~
„ _	/(2fe+l)2 + (2n+l)31
co	sin_	—। - j
xstojB+asslnei+Ji«.
Воспользоваться формулами для коэффициентов п и B^nt
полученными в задаче 17.84.
, nky
oo sin-r-2 _	. ,	. _
>7.87. в (х, 9)=S	‘	.. sb	+t, sh >£],
*=>sh—
где
ь	ь
2 C / x , nkv j 2 f	nkv .
аь=~ J <Hu)sln — dv~T J v)sin — dVs=t
о	о
= ( H°(2m-1)3 "PH * = 2m-l,
V 0	при k~2m,
ь	: '	 •
, 2 f . ny . nky . ( 1 при £ = 1,
^=*77 \ sln-^Sin-~ dz/=< Л K . *
K b J b b ' I 0 при Л^2.
Определение стационарного распределения температуры сво-
д^и д^и
дится к решению уравнения Лапласа Д/^=^4*др=0 с заданными
граничными условиями. Решение ищется в виде и (я, у)=*Х (я) Y (у).
Тогда имеем уравнения -у’=—и граничные условия
К(0)=К(&)=0. Таким образом, задача	Y (0)=У (fe)==0
приводит к собственным функциям (см. задачу 17.61) Уц (y)=sin
AjgN. Решения уравнений X"—
и собственным числам
/ nk \ 2
— ( — \ л==0 запишем через гиперболические функции:
v / % .nkx t R , stkx
*k W=ак ch -g- ^bk sh -y-.
Тогда решение исходного уравнения Ды=0, удовлетворяющее
всем граничным условиям, запишем в виде
/ ч V5 ( ,nkx , , . nkx\ , nky
269
Для определения чисел а* и Ь^ получаем соотношения
во
«(О, Й = Ф(Й==£ aksln^~
Ь=1
и
во
. ж L ч Vя / к nka . L . nka \ , nky
«(«, 0 = W = 24»S<* — +&fe sh-y- )sin—,
fe=i4	'
из которых находим, что
ь	ь
2 С / к > j 2 Г /L nkv .
пЛ=у \ <p(0sin у^у \ v(b—и) sin у
о	о
(	8Ь*	. о
I 77Г~—V при £ —2/л — 1,
=	(2/и—1)3л3 г
V 0	при	&	= 2m, mgN
и
I
, nka r t . nka 2 С , . . ,	,
ak ch у + bk sh у=у I ф (о) sin — dv.
Из последнего равенства находим Ь%:
г ь	ъ
,	1	2 Р z . , nkv ,	2 Р , v , nkv . . nka
Ь^—ЦГа T	d»-T U (CO sin-j-Л, eh-у- .
sh —L	J
Подставляя зна ения и в ряд для и (х, у), получаем
и(Х, 0 = ^2
feel
/L4 . nkv , , nkx .
ф (b) sin у dv ch -у 4*
b
ф(о) sin —г-dv—-г- \ ф(и)8к1—r- ctoch-—
Y' ' b b j v \ ' ь b
0
, nkx\
sh—I
. nka
sb— J
oo / b
_ . nky 2v C / v , nkv . Г t-nkx ,nka .nka . n&xl ,
xs,n ь T J J *₽{0) 8in—d4ch “sh ~b "ch —sh — J +
b
4 С r / V .	J L
•Г \ “Ф (°)stn sh -y
, nky
Sin-T_
. nka
sh—
nk (a—*x)
b
270 —
» sh2^(x-a)
. 17.88. Мх,у) = -^х+^4-^У —2----------cos?^.
ba 1 6 л2 Xu , . 2тла Ъ
т^\ m2sb—£—
ф Собственными числами соответствующей задачи Штурма^ Лиу-
(nk \2 , л ,
билля являются числа — I — \ , fc==0, 1, ..., а соответствующие
им собственные функции имеют вид Уь (#) = cos-У-, k = 0, 1, ...
о
Поэтому уравнение X"—	Х = 0 имеет систему решений
X0(x)=a0x+60 и Xfc(*) = aAch^+*ftsh^p,
17.89. «(ж. у)=а+2^£,>
X —
(2т — 1) их
_*______соя(2от~1)лу
I — 1) ла с Ъ
b
о,	sh 1
4а6	1__________
л2 Хи (2/и—I)2 . (2/п
ms=i	sn----
17,90. u(rt ф, /) = «(г, /) = acos^j^
/о -I
Sin^/O
+2cl У !-------
М-аЛ<м*)
Уравнение а^ = а2Д«, Где u = u(x, у, t) и &u — uxx*\-Uyy, в по-
лярных-координатах (/, ф) записывается в виде (см. задачу 10.168
при и (х, у, z, t) = и (х, у, /)):
d2a_ 2 (д2и । 1 ди\ 1 д*и А
дР~~а \дг* +г,дг + г* frf )’
Начальные условия не зависят от ф, поэтому колебания ра-
диальные, и уравнение принимает вид .
д2и . (д2и . 1 ди \
№=а \^+уд?)-	<*>
Требуется найти решение^«и (г, /)»	уравнения (*)
при начальных условиях
и(г, О) = а/о (7-)»
и]	Q) = са
и граничном условии w(Z, f) = 0.
Ищем решение в виде произведения и (г, t)» (/) Т (/), под-
ставив которое в (*}, получаем:
T^H^a^^TR"
т. е.
г„т Я'ЧО+т-Я'Ю
—«й—-к
271
Отсюда получаем уравнение
/?"(r)+-J-/?<(r)-X/?(r) = Q
е граничным условием /?(/) = 0. Собственными числами этой крае-
вой задачи (см. ответ к задаче 17.65) являются числа =
«= —а собственными функциями-*функции Rk(r) =
Решая уравнение
Пю+а^угно-о,
получаем
7\(/)—cc^cos +sssin га'.
Следовательно, искомое решение представляется в виде ряда
«(6 С = У (aAcos-^+Mln-^Vo
\	* J \ I J
fe»l
Используя начальные условия, находим
«(г, O) = aZo(-til/AeV а*/0(.£1Д	(*=*) .,
«*(*» 0)=са=^Г /Д-Й&Д
£=1 ' '
Из ортогональности с весом р (х)=х (см. задачу 17.60) системы
*€*•} на промежутке [0, /] и из соотношения (**)
шеем af=a и а^=0 при k^2. -
Учитывая равенства
I	1
j {^гг)1б r)r dr^12 5'° °**о) ,о (gm0) vdvsa
( 1 Р	m«fe,
CS \
(о,	т kt
находим выражения коэффициентов Фурье—Бесселя функции
f(r) по системе </$	на отрезке [0, /] (ср. задачу
17.66):	1	J
I
z° r)dTf
272
а тогда из второго начального условия имеем
i
о 1	2 С , (цл \ .
•	/»(/,; (|Xt)P J Г’са-1й[ / rjdr»
О
LLft	Mfc
“татет$ (йг)	S	о/«^4°-
(;	о
Но (см. часть 2. задачу 12.335) vl6 (о)»-~ (v/f (0) я It (о) =
«—!'0(v)t а потому
Цй
== НйЛ (Ий) .W'
9
•'*	'Ч
У о/о (о) dv— (vli (о)) dv — vfi (о)
о	О
•*—й&э-  ‘«!*
Следовательно» г
со
17.91.	и(г9 ф) = До+52(^й^йсозйф4-В^гйз1пйф)5=^81Пф,где
1 *
2Л
Лояв2??У /(Ф)<*Ф-О,
О
гл
^(ф)cos	*€N.
о
гл	гл
eie^J Нф} sin ф rfcp =-^-, Bk—%gb§ /(ф)81п fopd(p«O. fe2.
О	о
Уравнение Лапласа в полярных координатах имеет вид
^+7^+72	(« не зависит от г). Решение и(г9 ф)
должно быть ограничено при 0<г<7? и периодично по ф, т. е.
ы(г, ф4-2л)=5«(г, ф). Полагая и (г, ф)«Х (г) Ф (ф), приходим к
О Под ред. А. В. Ефимова» ч. 4	273
уравнениям
ф.(
J.XW Ф№)
Решение уравнения Ф" (ф)-|-ХФ (ф) = 0 должно иметь период 2л, а
потому X —/г2, 6=0, 1, ...» и мы имеем
ФЛ (ф) = cos k<p + bk sin fop.
При X==A2 из левой части (*) получаем уравнение Эйлера
г2Х" (г) 4-гХ' (г) — k*X (г) = 0,
которое путем замены г~ev сводится к уравнению X"(t») = 0 при
6=0 и к уравнению X" (v)— &2Х(и) = 0 при решениями ко-
торогобудутфункцииХо(4=^+^ Xk>i (v) = ekv = rk и Xk^(v) =
s = е"“Лс' = г~Л. При а0 # 0 решение Хо GO не ограничено при
п—►—оо, также не ограничены и решения 2 G) ==Г-Л при
О < г < R. Следовательно, будем иметь w0 (г> ф) = ^о» ф) =
== rk (ak cos fop + bh sin kq). [Выберем ak и b^ так, чтобы функция
00
u (г, ф) = 60+ 2 fk (ak cos sin Ьф) удовлетворяла условию
k=i
00
u(Rt ф)=/(ф), т. e. чтобы f (ф) = &о+ 2 (ak cos fop+&fe sin fop).
/?=!
2Л
Для этого следует выбрать ^==='2л	/(ф)^ф, ak~
о
2Л	2Л
,=лЯ* У / (ф) cosfepdcp,	У f (ф) Sin top dtp,
о	о
В нашем случае /(ф) = 81п(ф), а потому &о = О, а^ = 0,
^1=s_ и /?^ = 0 при k^2.
К
(2m—1) л/
о /4	00 COS-----Z-----— 1 .о
пл» / /ч —V	1	. (2m—1)лх
17.92.	u(x, t) n5	(2m—I)5 sin I —
т- 1
(2m — 1) л/
8Z4 Д, C0S I (2m— 1) лх x
S (2m —1)? sln I 12(* -2x Z4-Z).
tn =U
О Последнее выражение получено путем двукратного почлен-
ного интегрирования:
X Xt	»	X Xi
СС	8/2 V 1 С . С (2m—1)лп^
\ dXi \ у (a—l)dv=—	(2m—TFj dxi J sin------1---dV'
О ;//Я	W = 1	0 Hi
274
17.93.
t ..	2 / 1 nat at nat X t лх ,
«(X, n»—^_8to_----cos—jSIn_+
I Г__________1	(2m —1) ла/
m(m**ij [	(2m—i)2 s I
2m 4-1
t nat 1 ,
sin — sin
(2m -*• 1) nx
I
О При решении системы уравнений	С#(0=» Ak(t)t
&— 2m—1 — нечетные числа, следует учесть, что частота амплитуды
внешней силы совпадает с частотой амплитуды первой гармоники,
т. е. имеет место резонанс и частное решение следует искать в
форме
л / j (	, not . q nat \
Ci (О®8* { »i sin —у—4-^j cos-—1.
«>	/ JikaX* -»
'7-м- '>
fc=l	J
Г /Лба\8	|
»	“(т) ‘
_L^_y	-«"‘J sin Я**
-Г Я	t •
t
17.97. н(х, П«е 4-
ж. stn 1?*+*2л* г _ > ./.г.ш+оу/1
। 'l у —_________________I е -е tl / I.
-t-Jf Z- (2*4-1) |л(2*4-1|2 —1)L	J
А>= о
(7.98. и {к, sin
4-ЛУ 1=221
Зл k
ferrl
17.99. u(xt t)**
Ы + 1	о ла/ \ nkx
___ sin __ -2 sin J sin -J-.
т-1
2m—1
ла	л
1 )
I
~ fe(naZ?4-l) (nak-~l)
sin —-— .
10»
275
17.100. «U, О-г’иЧ
17.101. я (х, 1)« —
л
2
17.102. и(х, /)»~
’ '	31
е \ и	9ft-» 1
п772*-1 V У08—пх-
Loo
(* tt sin <nh
\e	—“— cos ©x da>.
J 05
о
QO
।	— costoxdco.
к
о
17.103. и
о
. ш/l
sin —
tft________
to
ю/i 1 . &h\ _
С03 — __sin_Jx
X cos (ах dco.
e~®f*	—ft cos 0ft) sin 0X d(&.
nJ ш \	<0
17.105. Первый. 17Л06. Первый. 17.107. Второй. 17.108. Вто-
рой. 17.109. Второй. 17.110. Второй, если т=АЛ. 17.111. Первый,
если x«==Xft.
17112.
17.104; и
Lhuhяш
um, n + l~~Um п	+ n+i*“2«OTi п+1 + «/д-1, п+1
-----------------а2	-----
X
Л7» 1,
/п=«0, .
о>
wo, л»
/1*
ft—1, л==0, s—1,
k.
п«0
s;
«Л, л»
' fm л + 1»
. Ф/я>
$1, П>
. 4'2. И»
Л2» 1,
т«=0.
п«=0,
& —1, л<«0,
k9
S— 1,
S,
Порядок приближения разностным оператором ^—вто-
рой по Л и первый по х. 17.113. Lu^u'x + u'yt порядок приближе-
ния—первый по h и второй по т, если т2 = ХЛ. 17.114. Lussu^-f-
1
+ и'уу, порядок приближения второй. 17.115. as=s-.—
17.116. Разностные схемы могут быть следующими:
«/»,» + ! —	n4“wm. п-1	9 ит+1,	лЧ* ат^1, п
а	—	t
k—1, я= 1> ...» S— 1,
kt

х»
1
<*♦	Л
.. \	т=0,
^т, 1	0
т
wo, п>
Uki nt
Л е= 0 j «0 4>
276
um, n + 1	W/я, n-£	w/» + l\ n— ^Um> n4~	j n
T2	—a	-------------—>•
m=l, ♦ .., k— 1, /1=1, ..., s—-1,
Циле
2т
/2=0, ...» s;
"o.m
> W,
fm,n + i>
Фяп
Ф1, п»
4'2, П»
m=l, ..., 6—1, /г=0, .... s— 1,
m = 0, ...» kt
n = 0, ...,
17.117. т=Я, LhUh*3
um 4-1, n %ит,	n	Um n + f —	п4*и/я( n-i
cm, n	№	T“m, n	Д2	•
m=l, ..., k— 1, /2=1, S—1,
<um,n (xm> Уп)&Ук>
t__( fm.n» m==l’ •••>	1» n = l, ...» S—l,
l Фя», П» Уп)^УЬя
Замечание. В случае данной области разностные уравнения
составляются и для точек у^.
17.119.	Um + it п + 1 + «я»-1, П + 1 + w«-i, П-1+wm + l, П-f — ^um,n~
= 2h2fm,n- Порядок аппроксимации равен двум, ф (£и)0=с0//0 +
+ ^iMi Ч*с2М2Ч-Сз^з4 с4«4- В силу симметрии уравнения и симмет-
рии шаблона положить С1==с2 = с9 = С4—Ь:
17.120.	По определению аппроксимации имеем (см. соотно-
шение (14))
цад<вл<4	(*)
где §7л	(и (Хт, Уп)) ~-7л«_
Положим e/i(xm, Уп) — и(хт, yn)—umtn. Здесь, как и ранее,
н (х, ^) —решение краевой задачи (1), (2), а {ит> n} = w^—решение
разностной схемы (4). В силу линейности оператора имеем:
(ей) = ^*Л (w (Хщ, Уп) —Um, п)
^^к(и(хт, уп)) Lh(Um, n)~Lfo(u (хл, уп)) fh~$ffi9
т. е. сеточная функция ел(хт, уп) является решением разностной
схемы LhUfy^bffy. В силу устойчивости этой разностной схемы
(соотношение (15)), а также используя неравенство (*), находим:
II еЛ {xmt уп) |< С [| 6ГЛ [I < СВ№ = Ah*,
где А==ВС. Тем самым неравенство (13) установлено, что и дока-
зывает теорему.
17.121.	ф Для доказательства неустойчивости достаточно рас-
смотреть разностную схему при некотором выборе правой части
277
Положить /да, п = 0 для всех тип nq>OT = (—ly® е, 8 > 0 —некоторое
число. Тогда разностная схема запишется в виде:
^ОТ, й+1 = (1— WOT,	П>
«от,о = (—О* е-
Получить отсюда, что
^,л = (1-2Х)«(~1)«8.
Затем показать, что
1-2М|37(ХА)]е-
Если [ИИ= max I Фот | = &» то, следовательно, выполняется
- М< т < М
равенство
0^11=1 i-2X|t7’/()A)1-il7ft II-
Сравнивая это равенство и соотношение (15) и учитывая, что
11 —2Х	+ оо
при h —> 0, получаем, что исходная разностная схема неустойчив».
17.122.
Ат, пит, п + 1 + ^i», пия, n-14* nUm+ii ."t* 
+	„« от-1, п + Еа, дмлв, д»
П=1, ..., 3—1, /п==1, k—1,
m = 0, ..., k,
1^11^==^ wot, о*
мот, i>
: %, Д,
I Д»
f f т, т
I
/л = < фя+'П’ж
I
I Fn,
п = 0
и = 0.
з;
., s—l, m = l
з,
л = 1
., 1,
т = 0, ..., k,
где
п
Tf*! I* .	//* Э 99	99	fn 9 99
72-H	2Г» ^От,п= ^2	2F>
n
^am,n cm,n	_am,n cm,n
2h~>	2fT
r	^am, n	n
Вт, n------/^“ + 2 "^2-Г^Л, n-
17.123.
Am, n^m, n + i-i-Bm, n^m, n-i + ^ot, num + 1, д +
»мл-1, »4"^ot, nu m, m
wot, б>
TAUAae
a*
278
Фж»
д 1 л Ifm, $ 4~ т	+ 1
&т, оФот-1 Ет, офт],
*п,
где значения коэффициентов те же, что и в задаче 17.122. ф При-
влекая еще один горизонтальный ряд, соответствующий п =—1,
ди\
производную j заменить разностным отношением
wлй, 1 ит, -1 __
------2^----. Промежуточные значения ит> исключить, исполь-
зуя разностное уравнение
=	Л^/И, Л^14~^й2, пит, л-i 4-С/л, «млч-1, п4~
п^/а-1, п4“^*/л, пи/я, n — fmt «.
При исследовании порядка аппроксимации учесть, что порядок
аппроксимации уравнения равен двум. Для исследования порядка
аппроксимации разностной схемы необходимо определить порядок,
аппроксимации начальных и граничных условий.
17.124.	Атл nUm„n+l 4" ^л®, ntlmy л-1 + ^/л. пм« + 1, п 4*
4~ В/п, пит-1> Я 4~ Е т э	n~fm, п->	1» •	£ 1» Ц — 1» •••» S-—I.
«»,.=<₽«• me0 k
«тЛ = Фда + т<1».
/1	1, а
«1.« = (1 -«!«*) и», » + ЛФП, ик, „-и+6гпЛ) FП	+
Здаачеияя коэффициентов те же, что и в задаче 17.122.
17.125. Ат. пи,„ „., + /? т, п^ту п~1 4~£/л, гай/я + 1, га 4~
4"	га^/л-1, я4*^м, nllrn a ~fm. л» т ~ 1» - • •» — 1, Л =1, ..., S — С
....
W/л, I j----~Г~Р---17/д, о 4“ оЧ/n	офт + 1
оН" ^т, о
E^ni, оф/я -1 Е т t ],
А®,	4“ Ец> аиъУ п -14~ (£о. я4'^о, я) и1, п4- (^оп4~2/г61Л00< п)	п=
“ /о, п 4*2^^ft, п^га» (♦
(Ло. о4~$о, о) tti>, I = ^о, о4“2тво. офо 4"2hO0< 0Ф0 — (Се, о4"^о, о) ф1 —	)
e + ^Zi^le^o,») ф^
о4“ ^ky о) uky i =	л4~2тб^	qFо — (Скз о4* Dfct 0) ф^_1 —
— (£fe, o~'2A62oC^i о)
n^k, n+i+ Ek, nuky n-l 4-	n4~^, в) »4“
4-(£\ n + U^nCk, ж) n^tkt n-^ckt nFn.
Схема (*) имеет второй порядок аппроксимации на решении, об-
ладающем ограниченными четвертыми производными. Заменим
входящие в начальные и граничные условия производные централь-
ными разностями. Для аппроксимации граничных условий в узлах
279
(О п) и ik, л) привлечем еще узлы вертикальных рядов, соответ-
ствующие m = —1 и т = А>+1 (см. рис. 243), и запишем следующие
соотношения:
#i, п — п я	_
----------------п —
(**)
И/гМ, n — uk-i, п
----------------\-V2nuk, п — гп.
Разностные уравнения, аппроксимирующие дифференциальное урав-
нение задачи. 17.122 в узлах (0, п) и (£, л), имеют вид
Д), 71и0, Я + 1"Ь #0, ПМ0, n-i + Со, n«l, rt+ Do, П^-1, w+ D0, ntt0, n~fo, П*
Aj^ n^k, n + l+^fc, nuk, n-14”Cfc, nuk + l, n+Dft, n+Dfc, n^k, n~fk, n>
Исключая из. этих уравнений n_j, rt, Ufc+i, n c помощью выражений
(**), получим	’ _
Д, nuo, n+i“h^o, nwo, n-i + (C0, n+D0, n)	rt + (Do, rt+2/idiwDo, n) wo, »=
fo, n “b 2/iDo,	ti» (**♦)
n^kt w+1 + ^Л, nukt n-i + (C.v, п + &ь, n) uk-i, » +
4~(Dft, n—2/ц%пСд;, n) Uk4 n~fk, n~“~2hCk' nF2, n,
Значения решения в узлах (О, 1) и (&, 1) определяются из (***)
при л = 0. Исключая величины u0^ _t, _i с помощью начальных
Ио, 1 — wo,-1 uk, i—uk, -i
условий -------------=фо,------2i---------получим выражения
для определения u0, i, WA, i:
(Ло, о + ^о, о) «о, 1 = /о,о + 2тВо, о4о + 2W0, о®о —
—	(Со, о + Do, о) Ф1 — (Dq, о + 2/zdloDo, о) Фо-
(^Л, o-'hDfc, о) 1 =	о4"2тВ^ офй 2/iC/j, о^о~~
—	(С^, o + D^ о) Чк-1 — (Еь, о —2/i62oCft, о)Фл- ►
17.126.	Порядок аппроксимации равен двум, ф Для замену
частных производных и^х, и"уу использовать разностный оператор
из задачи 17.108. Положить т=А.
280
17.127.	1)
( 1 1 / 1 . .1
Lbub = | й“и’ п+1-Т	) Um' "+»•
V wzn, 0>
*T ___J fm, ni
l Фт-
2)	Шаблон изображен на рис. 244. 4) Схема неустойчива при лю*
бом X. ,
17.128.	1)Тйий =
( 1	1 (Л \	1	'
= ’!мИст’п+1 h \ х	д «» у J/л>, ш
« «	I
\ ит, о*
2)	Шаблон тот же, что и в задаче 17.127. 4) Схема устойчива
при Х«С 1.
( 1	1/1 , Л , 1
17.129.	1) Lbub~ [ Mi“m'n+l h Ц"Г J “«>»* hum+i,n,
V И/Д, о»
/л = <''я’п’ 2) Шаблон изображен на рис. 245. 4) Схема неустой-
1Ф/Я*
h2
чива при любом X. 17.130. Схема устойчива при условии	•
п+7				(1П)П+1)	п+1	(т,п+1)	
7) —	3		(т,г^			(т^п+1)
т	-F	л Рис. 244	1	 1 7	п	г—— 3 7	т Рис. 24£			
17.131. Схема устойчива при любых ft, т. 17.132. Схема устойчива
при условии ат «С ft. 17.133. Схема всегда устойчива. 17Д34. Про-
^1, п	ЛФ1 rt
гоночные коэффициенты	п = —	, Hi, ----------— >
"Р1, п--«J, п	ftPl, п-а1, п
п=1, s. Значение решения на правой границе, необходимое
для обратной прогонки,
а2, пНfc, п+ft^2«
Ufi'n «2,1(1----Qfe,n) + ft₽2,ne
Аппроксимируем граничные условия задачи 17.134 разностными
соотношениями
Uf м ““ На л
«1, п "fa F Pi, д^о, п= Ф1Э п>	(*)
«2, П-----g---------F Ра, пик, п == ®2, П» ««0, S, (**)
281
Полагая в формуле (25) /и = 0, запишем следующее равенствсг
wo, »== Q1, n +#1, л, п = 1,	(%**)
Сравнивая равенства (♦) и (*♦*), получим начальные значения
прогоночных коэффициентов
Л	а1,|»	u	Лф1,п
Qi, П “ ~ Го „	»	^1, П - 1.0	„	> п ---- Ь . . . , S.
«Pl, п"“а1, п	"Р1, п а1, п
Для обратной прогонки необходимо внать значение решения на
правой границе п- Для определения этого значения запишем
равенство (23) в узле (k, п):
Uk-1, Qk + nuk, п~\~ Hk, п* /1=1, ...» s. (****)
Заметим, что все прогоночные коэффициенты определены по фор-
мулам (24). Сравнивая равенства (****)	получим систему
линейных уравнений
Qk, nUk, п-Uk-i, П~--- Н*' п*
(&г, д +	$)	й — о&2, feWA-i, д	п-
uk п получим как решение этой системы. ►
’ 17.135. 7i = 0,02; т = 0,01;
	Л					
	0,0	0,40	0.80	1,20	1,60	2.00
0,0	0.0	0,16	0,64	1,44	2,56	4,00
0,2	0,22	0,28	0,82	1,67	2,80	3,98
0.4	0,49	0,48	1,08	1,96	3,10	3,68
0,6	0,82	0,92	1.41	2,33	3,19	3,30
0,8	1,23	1,42	1,82	2,76	3,11	2,79
1,00	1,72	1,97	2,46	2,97	2,88	2/16
17.136. 6 = 0,01; т = 0,01;
У	А					
	0,0	0,20	0.40	0,60	0,80	1,00
0.0	0,0	0,20	0,40	0,60	0,80	1,00
0,2	0,20	0,20	0,40	0,60	0,80	0,80
0,4	0,40	0,20	0,39	0,59	0,78	0,60

У	X					
	0,0	0,20	0,40	0,60	0,80	1,00
0,6	0,60	0,39	0,37	0,56	0,54	0,40
0,8	0,80	0,57	0,34	0,49	0,28	0,20
1,00	1,00	0,73	0,47	0,20	0,00	0,00
17.137. /г = 0,02; т = 0,01;
У	X					
	0,0	0,40	0,80	1,20	1,60	2,00
0,0	1,00	1,16	1,64	2,44	3,56	5,00 •
0,2	1,20	2,42	2,94	3,82	5,06	4,90
0,4	1,39	3,73	4,33	5,29	6,57	4,61
0,6	1,56	4,15	5,80	6,82	6,53	4,13
0,8	1,72	4,53	7,31	8,37	6,23	3,48
1,00	1,84	4,91	7,94	8,38	5,74	2,70
17.138. /1 = 0,01; т = 0,01;
У	X					
	0,0	0,20	0,40	0,60	0,80	1,00
0,0	0,0	0,04	0,16	0,36	0,64	1,00
0,2	—0,42	—0,03	0,41	0,93	1,53	3,01
0,4	— 1,14	—0,08	0,68	1,52	2,44	7,28
0,6	—3,28	—0,14	0,97	2,12	4,18	14.60
0,8	-10,87	-0,51	1,27	2,75	8,14	26,44
1,0	—40,84	—2,30	1,56	4,20	15,18	44,60
17.139. /1 = 0,02; т = 0,01;
У	X					
	0,0	0,40	0,8С	1,20	1,60	2 00
0,0	5,00	6,60	8,20	9,80	11,40	13,00
0,2	5,30	6,79	8,39	9,99	11,59	13,12
0,4	5,65	6,98	8,58	10,17	11,77	13,18
0,6	6,19	7,15	8,74	10,33	11,92	13,18
0,8	7,26	7,32	8,89	10,46	12,04	13,09
1,00	9,61	7,57	9,01	10,57	12,03	12,87
283
17.140. /1 = 0,02; т = 0,01;
Ш-			X					
У	0,0	0,40	0,80	1,20	1,60	2,0
0,0	1,00	0,80	0,60	0,40	0,20	0,0
0,20	0,98	0,84	0,72	0,58	0,42	0,20
0,40	0,92	0,87	0,81	0,72	0,59	0,39
0,60	0,83	0,88	0,88	0,83	0,73	0,56
0,80	0,70	0,86	0,91	0,92	0,86	0,72
1,00	0,54	0,80	0,92	0,98	0,96	0,84
17.141. Л = 0,02; т = 0,01;
У	X					
	0,0	0,20	0,40	0,60	0,80	1,00
0,0	0,0	0,04	0,16	0,36	0,64	1,00
0,20	—0,17	0,01	0,01	0,01	0,01	0,00
0,40	—0,72	0,04	0,02	0,01	. 0,00	0,00
0,60	—1,63	0,10	0,04	0,00	0,00	0,00
0,80	0,97	0,17	0,00	0,00	0,00	0,00
1,00	1,00	0,00	0,00	0,00	0,00	0,00
17.142. Л = 0,02; т = 0,01;
У	X					
	0,0	0,40	0,80	1,20	1,60	2,00
0,0	0,0	0,16	0,64	1,44	2,56	4,00
0,2	0,28	0,46	0,83	1,28	1,52	1,27
0,4	0,30	0,42	0,53	0,60	0,54	0,38
0,6	—0,03	0,05	—0,05	—0,24	—0,43	—0,44
0,8	—0,67	—0,61	—0,87	—1,23	—1,47	—1,29
1,0	-1,57	— 1,52	—1,90	—2,38	—2,62	—2,21
17.143. Л = 0,01; т = 0,01;
t	X					
	0,0	0,2	0,4	0,6	0,8	1,00
0,0	0,0	0,59	0,95	0,95	0,59	0,00
0,2	0,50	0,54	0,57	0,58	0,57	0,53
0,4	0,60	0,70	0,88	1,10	1,29	1,31
0,6	2,01	2,51	3,54	4,88	6,08	6,31
0,8	8,05	9,90	13,58	18,31	22,41	23,03
1,0	25,35	30,58	40,44	52,78	63,21	64,34
284
17.144. Л = 0,02;
У	x	'					
	0,0	0,4	0,8	1,2	1,6	2,00
0,0	1,00	1,40	1,80	2,20	2,60	3,00
0,2	2,00	1,05	0,95	1,06	1,44	2,96
0,4	3,00	1,02	0,60	0,59	0,93	2,84
0,^	4,00	1,36	0,76	0,67	0,93	2,64
0,8	5,00	2,76	2,12	1,81	1,64	2,36
1,0	6,00	5,84	5,36	4,56	3,44	2,00
17.145. /1 = 0,02;
‘ У		.	 — 	— 		 			 к					
	0,0	0,20	0,40	0,60	0,80	1,00
0,0	0,0	0,0	0,0	0,0	0,0	0,0
0,20	0,08	0,32	0,51	0,72	0,99	0,84
0,40	0,32	0,72	1,07	1,41	1,78	1,76
0,60	0,72	1,23	1,68	2,12	2,56	2,76
0,80	1,28	1,82	2,65	3,22	3,82	3,84
1,00	2,00	2,44	2,96	3,56	4,24	• 5,00
17.146. h=0,02;
У	X					
	0,0	0,40	0,80	1,20	1,60	2,00
0,0	0,0	0,40	0,80	1,20	1,60	2,00
0,20	1,00	0,24	0,35	1,24	0,0	0,0
0,40	2,00	0,34	0,10	0,82	0,0	0,0
0,60	3,00	0,66	0,19	0,47	1,96	0,0
0,80	4,00	1,92	1,34	1,25	2,04	0,0
1,00	5,00	4,60	4,20	3,80	3,40	3,00
17.147. ft = 0,02;
У	X					
	0,0	0,40	0,80	1,20	1,60	2,00 ,
0,0	0,0	0,63	0,89	1,10	1,26	1,41
0,20	1,00	0,36	0,44	0,54	0,64	1,29
0,40	2,00	0,32	0,26	0,28	0,32	1,20
0,60	3,00	0,83	0,66	0,56	0,45	1,12
0,80	4,00	2,86	2,06	1,69	1,19	1,05
1,00	5,00	4,84	4,36	3,56	2,44	1,00
285
17.148.
SUBROUTINE PARAB(A,F,FI,PSI1, PSI2,
* Kl.NSl.X.T.U)
COMMON Yl, В
DIMENSION X(K1),T(NS1),U(K1,NS1)
HT=Y1/(NSI-1)
HX=B/(K1-1)
DO 21=1, KI
' X(I)=HX*(I-1)
2 U(i,I)=FI(X(I))
DO 3 J=l, NSl
T(J)=HT*(J-1)
U(l,J)=PSll(T(J))
3 U(NS1,J)=PSI2(T(J})
A1=HT*A/HX**2
A2=l.—2* Al
K=K1—1
NS=NS1—1
DO 5 J=2, NS
DO 5 1=2, К
6 U(1,J4-1)=AUU(T+I ,JH-A2*U(I,J)+
• A1*U(I—1,J)4-HT»F(X(1),T(J))
RETURN
END
17.149.
SUBROUTINE GIPERl(A,F,FI,PSI,EFL,EFR.
» Kl.NSl.X.Y.U)
DIMENSION X(Kl), Y(NS1), U(Kl,NSl)
COMMON /С/ Yl, В
HY=Yl/(NSl—I)
HX=B/(Kl-l)
7 FORMAT (///10X,,HX=’.F7.4,10X,’HY=’,F7.4)
PRINT 7, HX, HY
HY2=HY**2
A1=HY2/(A*HX»*2)
DO 3 J=l, NSl
Y(J)=HY*(J—1)
U(1,J)=EFL(Y(J»
U(K1,J)=EFR(Y(J))
3 CONTINUE
DO 101=1, KI
X(I)=HX*(I-1)
DO 2 1=1, KI
U(I,1)=F1(X(I))
IF (I.EQ.l) GO TO 2
IF (I.EQ.KI) GO TO 2
U(I,2)=—.5*(HY2/A)*F(X(I),
Y(1))+HY*PS1(X(I))+.5»A1
(F1(X(I4-1))+FI(X(I-!)))+(!A1)*FI(X(D)
CONTINUE
K=K1-1
NS=NS1—1
DO 5 J=2, NS
DO 5 1=2, К
5 U(I,J+1)=-(HY2/A)»F(X(I), Y(J))—
♦ U(I,J-lH-Al*fU(I+l,JHU(I-l);J)>
10
2
286
RETURN
END
17.150.
SUBROUTINE GIPER3(A,F,FI,PSI,ELF,EFR,DLT1,
*  DLT2,K1,NS1,X,Y,U)	’	’	'
DIMENSION X(K1), Y(NS1), U(Kl.NSl)
COMMON /С/ Yi, В
HY=Y1/(NS1—I)
HX=B/(K1-1)
7 fORMAT (///10X,'HX=’,F7.4,10X,'HY=‘,F7.4)
PRINT 7, HX, HY
HY2=HY**2
A1=H¥2/(A»HX»*2)
NS=NS1—1
K=K0—1
DO II 1=1, KI
10 X(I)=HX*(I-1)
DO 2 J = i, NS1
2 Y(J)=HY*(J-1)
DO 3 1=1, KI
U(I, 1)=FI(X(I))
IF (I.EQ.l.OR.I.EQ.Kl) GO TO 3
U(l,2)=—5.*^HY2/A)»F(X(I), Y(1))4-HY*PSI(X(I))
• H-.5*AI*(F1(X(I-H))+FI(X(I—!))
* +(1—AI)*F1(X(IJ))
3 CONTINUE
Tl = l.— A14-HX»A1»DLT1(Y(1))
T2= 1A1—H X»A 1*DLT2(Y(1))
U( 1,2)=—.5*(H Y2/A)*F(X( 1), Y(1 ))+
•	HY*PSI(X(1))-HX*A1*ELF(Y(1))4-A1»
« FI(X(2))+T1*FI (X(I))
U(K1,2)=—.5*(HY2/A)*F(X(K1),
•	Y(1))+HY*PSI(X(K1))
* +HX*AI*EFR(Y(1))4-A1*FI(X(K))+T2*FI(X(K1»
DO 6 J=2, NS
DO 5 1=2. К
U(I,J+0=-(HY2/A)*F(X(I),Y(J)H
» U(I,J-lH-Ab(U(I+l,J)+U(J-l,J))+
*	2.*(l.—A1)*U(I,J)
U(l, J+l)=—U(l, J-l)+2.*Al*U(i,JH-
*	2.*(1.—A14-AbHX»DLTl(Y(J)))*U(l,J)—
•	(HY2/A)»F(X (1), Y(J))—2.»A1*HX»ELF(Y(J))
U(K1, J+1)=—U(K1, J—1)4-2.»A1*
* U(K,J)4-2.*(l.-Al— HX*AI**DLT2(Y(J))»U(K,J)—
* (HY2/A)*F(X (K),Y(J))-h2.»Al*EFR(Y(J))
6 CONTINUE
RETURN
END
17.151.
SUBROUTINE ELIPT(F.FI,EFL,EFV,EFR,K1,
» NSl'.X.YU)
DIMENSION X(K1), Y(NS1), U(K1,NS1)
COMMON /W/ A, KT, AMO, EPS
COMMON /С/ В
HX=B/(K1-1)
287
17 FORMAT (///10X,’HX=’,F7.4)
PRINT 17, HX
HX2=HX**2
K=Kl-l
NS=NS1—1
DO 6 J=l, NS1
Y(J)=HX*(J—1)
K2=KT*(J-1)+K1
DO 6 1=1, K2
X(I)=HX*(I— 1)
IF (I.GT.l.AND.l.LT.K2)U(I,J)=AM0
IF (I.EQ.1)U(I,J)=EFL(Y(J))
IF (I.EQ.K2)U(I,J)=EFP(X(I),Y(J))
IF (J.EQ.1)U(I,J)=FI(X(I)\
IF (J.EQ.NS1)U(I,J)=EFV(X(I))
6 CONTINUE
4 D=0
DO 3 J=2, NS
M=KT*(J-1)+K
DO 3 1=2, M
R=(U(I+1,J)+U(I-1,J)+A*(U(I,J+1)4-
* U(I,J-1))-HX2*F(X(I),Y(J)))/(2.*(1 ,+A)>
D1=ABS(R—U(I,J))
IF (D1.GT.D)D=D1
3 U(I,J)=R
IF (D.GT.EPS)GO TO 4
RETURN
END
ф При численной реализации разностной схемы для краевой
задачи 17.117 необходимо привести уравнение к виду
д2и . д2и . .	.
дх*+а ду2 ~
Для решения системы линейных разностных уравнений применить
метод простой итерации по формулам:
„F + D —	1	/„(О	.„(О A-a(u(i) 4-и(П	) —
“и, п ~2(1-1-а) \И/п+1.	\ит, n + n-v
—h2ft(xm, уп».
где i — номер итерации. Пусть 8—абсолютная погрешность вычис-
лений. Будем считать, что решение получено с заданной точ-
ностью, если выполнено соотношение
tn, п	х
При написании программы использовать указанное выше правило.
Использовать идентификаторы: F—правые части, FI, EFL, EFP,
EFV—идентификаторы функций, вычисляющих краевые условия
на нижней, левой, правой, верхней границе соответственно.
АМО —возможная вариация для значения п; КТ = 0 для пря-
моугольной области, КТ — 1 для трапецеидальной области.
17.152.
a)	SUBROUTINE PROGN1 (A,F,FI,PSI 1, PSI2,
* K1,NSI,X,T,U,Q,H)
COMMON Yl, В
288
KK	U(K1’NSlbQ(K1’NSl). H(K1.NS1>
A2=(HX**2)/(A*HT)
K=K1-1
DO 2 1=1, KI
X(I)=HX*(I—I)
2 U(I,1)==F1(X(!))
DO 3 J=l, NSl
T(J)=HT^(J—1)
Q(1,J)=O
H(1,J)=PSI1(T(J))
U(K1,J)=PSI2(T(J))
3 U(1,J)=H(1,J)
DO 20 J=2, NSl
DO 7. 1=1, К
Q(l+l,J)=l./(2.+A2-Q(I,J))
7 H(1+U)=Q(I +1, J)*(A2*U(I,J—1)+
* HT*F(X(I),T(J))+H(I,J))
I=K1
8 U(I-1,J) = Q(I,J)*U(I,J)4-H(I,J)
IF (3—1) 15, 20, 20
15 1=1—1
GO TO 8
20 CONTINUE
RETURN
END
6)	SUBROUTINE PROGN2(A,F,FI,ALF1,BET1,
*	ALF2,BET2,EF1,
*	EF2,K1,NS1,X,T,U,Q,H)
COMMON /С/ Yl, В
DIMENSION Q(K1,NS1), H(K1,NS1)
DIMENSION X(K1), T(NS1L U(K1, NSl)
HT=Y1 NSl—1)
HX=B/(K1—1)
17 FORMAT (///10X, ’HX=\ F7.4J0X, ^7=’, F7.4)
PRINT 17, HX, HT
A2=(HX**2)/(A*HT)
K=K1-1
DO 2 1=1, KI
X(I)=HX*(I-1)
2 U(I,1)=FI(X(I))
DO 3 J==l, NSl
T(J)=HB(J-1)
Q(l,J)=—ALFI(T(J))/(HX*BET1(T(J))—ALF1(T(J)))
H(1,J)=HX*EF1
* (T(J))/(HX*BET1(T(J))—ALF1(T(J)))
3 CONTINUE
DO 20 J=2, NSl
DO 71=1, К
Q(I+l,J)=l./(2.+A2-Q(I,J))
7 H(I + 1,J)=Q(I+1,J)*(A2*U(I,J—1)+
* HT*F(X(I),T(J))+H(I,J))
1=KI
U(I,J)=(ALF2(T(J))4:H(K1,J)+HX*
* EF2(T(J)))/(ALF2(T(J))*(1.-Q(K1,J))+
289
* HX*BET2(T(Jn)
8 U(I—
IF (2—1) 15, 20, 20
15 1=1—1
GO TO 8
20 CONTINUE
RETURN
END
17.153.	Для задачи 17.135 ответ записывается следующим
образом:
FUNCTION (Т.Х)
F=—.5*Т*Х**2
RETURN
END
Ответы для остальных задач отличаются только вторым операто-
ром, определяющим значение F.
17.154.	Ответ к задаче 17.135:
FUNCTION FI(X)
FI=X**2
RETURN
END
FUNCTION PSI(X)
PSI=SIN(X)
RETURN
END
FUNCTION EFL(T)
EFL=EXP(T)-1
RETURN
END
FUNCTION EFP (T)
EFP=4.*COS(T)
RETURN
END
Ответы к другим задачам отличаются вторыми операторами.
17.155.	Ответ к задаче 17.135:
EXTERNAL F,FI,PSI,EFL,EFP
DIMENSION Х(101), T(101), 0(101,101)
COMMON /С/ Yl, В
Yl=l
B=2
DATA A /1./, KI /101/, NS1 /101/
CALL GIPER1(A,F,FI,PSI, EFL, EFP,
«	K1,NS1,X,T,U)
25 FORMAT (50X, ’ТАБЛИЦА РЕШЕНИЯ’ /ДОХ,
*	110(’—*)/15X, >T/X\ 2X, 11F8.2/(11X,R8.2,
*	IX, 11F8.2)))
PRINT 25, (X(I), 1=1, KI, 10), (T(J), (U(I,J),
*	1=1, KI, 10), J=l, NS1, 10)
STOP
END
•	Задание для ЭВМ должно содержать 7 программных единиц:
указанную здесь основную программу, а также программы, полу-
ченные при решении задач 17.149, 17.153, 17.154. Программа
решения любой другой задачи отличается от приведенной операто-
рами, содержащими обращение к соответствующим подпрограммам.
290
ГЛАВА 18
х
18.4. у(х) = ^—2х—рхр(/)Л.
О
18.5. у(х) = 2х-9+ J (2-х+Лу «)Л.
2
ЮЛ. (х)==»е* (х— 1)— sin * + *+ J (sin л — е*(х — tyyftdt.
о
х
18.7. t/(x) = ^—х-~ ^*<х~	-
188. V(xl=—~x-^x-t—
О
18.9. • Воспользоваться формулой
С <ип_г... G(nd<e_L—С(х-.ов‘ху(ол.
V	м	J	Vя"* */* J
ала	а
18.19. ^(х)=хх + л+^/sin ultydt.	18.11. v(x) = xs—х+< +
п
+ jj/ЧОЛ.
18.12. W(x)»l + p,(/)d/, у»(х)=-у + 2+(у1(0Л.
е	о ‘
X	X
18.13. t/i(x) = —3+^ 0	yAt)dt, ^(х)=1+5«/з(ОЛ. 0
-i +4p’(o<«.	X 18.14.	(x)« 1 + J (/) tUt y* (x) «
0	X	X
Уз(0<Й, y8W=-y+	j /y?(/)d/-f^ (t)dt. 18.15. y(x) = 0	0
==е«(х+1). 18.16. у(х)=ех'/г. 18.17. 9(x)=-r-!?-_+xarc!g х-
I -р хл
— yln(l + x2). 18.18. ^(x)«cos хе" (x+sin х). 18.19. у(х) = 2ех —
— 2 cos x + 5sin х. 18.20.	^(х)« — е~х. 18.21. у(х) =
== ~^е*+3 cos х4-3 sin х—4e"x/scos xY 18.22. f/(x)= 1.
291
18.23» y(x) = xchx.
18.24.	0(х)=-1 ex+-
/1 V 7	V 7 '
X ( —ry sin Jy-x+3cos-!^-x
18.25. у (x)=ex. 18.26. у (x)=x.
18.27. y(x)=l. 18.28. y(x)=l+xV r9f * Vi i =1 +	f e~ dt-
“Г Ч’1	v
= O	0
x‘	xP+1
‘18.29. y(x)=e2.	18.30. y(x) = e
x*-t*
2 . 18.40. x2e 8 .
»
18.43.
18.31.	i/(x) = sinx.
-±x
18.32.	u(x) = chx. 18.33. y(x) = (2e)x. 18.34. y(x) = (14-x2)e 2 .
18.35.	U2 (x)=-^- —	.	18.36. y2 (x)==x + x cos x —-sin x.
О OO
л x’~p i х’~*’
18.37.	yi(x)=l—e~ 2 .18.38. eX(Z-x). 18.39. te
, x>-t>	л x*-f>
18.41.	xie 8 .	18.42. xt2e 4 .
18.44. 2,h*~sh teK(-x~fl. 18.45. 44 J г U~°- 18.46. C - -—1 ex<*~0.
1 + /2	~2 '' ' 1
X2	X3
18.50. e 2 . 18.51. xe 8
ex
ex ch x. 15.54^ ч-т—r .
1 + x2
18.57. e2*—18.58.
*8.47. •4rT«M’t_ °-
ch t
9
sin x. 18.53.
о
18.56. chx— 1.
x2—x+r
. 18.52. 4 e2x — 4- cosx-f-
О	О
18.55. e*(x—1)4-1.
2	e*/« Sjn 3 x
V “3	sln-2~*-
18.59.	2e*—x—l. 18.60. 2 sinx—x. 18.61.#(x)=4- e 2 X
о о
XSlnf^x+^Y 18.62.4 e2x(2x +3)4-4-• 18.68.4-4 cos/3x.
tt	OO
/ v2 \
18.64.	1. 18.67. 2—e~*. 18.68. chx4-cosx. 18.69. e~* ( l-|-±-h
18.70.	4е 8fl + 4ch-^.x\ 18.71. 2—cos^x4-K2sin^*«
18.72.	yj (x)= I —2 cos x, y3 (x) = 2 sin x. 18.73. 1/1(х)=Д—4-х—
ZD D
— e* (3 cos 2x—4 sin 2x),	y2 (x)=—r+~F eX (cos 2x-{-2 sin 2x).
20	О 0
18.74.	yi(x) = x+e~x—e*/2(cos-^-x-—=-sin4-1 x), y2(x) =
= —e~x4—4=e*/2 sin^4~ *• 18-75. #i(x) = (x4-2)sinx4-(2x4-l)cosx,
V з
y2(x) = ~	sinx+(4’x+1^ COSX. 18.76. i/i (x)“2 sin X,
\ Z )	\ Z i
x%
y,(x) = 2cosx—1, y3(x) = x. 18.78. e*. 18.79.x—у . 18.80. 1—xln3.
292
18.81.1. 18.82.x. 18.83.3. 18.84.Решения нет. 18.85.	(-i—sinx j.
18.86.хе*2.18.87.3(2х—1). 18.88. chx. 18.89.	х4). 18.90.2 sin *.
18.91. 2cosx—1.	18.92. Решения нет. 18.93. -g-(e4x —1).
18.94. е*^14-ух4). 18.95. 1. 18.96. 1. 18.97. ^х. • Воспользо-
2
ваться формулой Г (z+l)==*r (г). 18.98. Зх. 18.99.-^-. 18.100. 1—X.
о
2	I
18.101. 4sinx. 18.102. —cosx. 18.103. /?(х, 1, 1)=;-
о	1
y(x) = sinx. 18.104. R(x, t, 1)=2*+<---Цг—, у(х)=^?7~1 X
. ол	1П Z
2hT2
X 2^+х + х.
18.106. fl(x, t,
18.105.
хе*
1— к
R(xt tt Х) — х sin 2л/, у (х)» cos 2лх.
, 0(х)=е~* + х. 18.107. Я(х, /, Х)=«
2	1
«=-к—г-sinxcos/,	(х)—I+2slnх.	18.109.	1+~-х.
Z — A	. 4 -•
18.110. +4-СО82лх«	18.111. х—ncosx. 18.112. 7+бх*.
о	,
18.113. sinx — lx. 18.114. sinx + cosx. 18.115. Решения нет.
о

18.116.	х + С(1— х2).	18.117. х. 18.118. cos2x+»-/ft ,	.
2(2 —In 2)
18.119.	Сх. 18.120. 0.	18.121. соз2лх. 18.122. x-f-y.
(К	\
yx+x2J. 18.124. Решения нет. 18.125. 1 + К7.
5
18.126.	Сх cos х + С2 sin х. 18.127. 2л2 cos 2лх-|-—(2х2—1). 18.128. 0.
о
18.129.	1=-|, у(х)=С(1 + 2х).	18.130.1=4, у (х)=С(1-х4).
I	л	I
1	9
18.131. 1=1, у(х)=С|х|. 18.132. 1=—, у(х)=Сх. 18.133.1=—,
Л	л
y(x) = Ccosx. 18.134. gi, 2=у±-уД=-; >1, s(x) = c(/"3x ± 1).
18.135. gi,2=l± ]/1(е-1), М,г(х) = С^|/у(е-1)х± 1).
О
18.136. к ==—2л, у (х) = С. 18.137. Xft 2 —	» yit 2 (x)==C(sin x±cos х).
18.138. Х = у (х) = Cr cos х+С2 sinx. 18.139. При й#-г#(х)==
==x2 + ~-g-^^x, при ^==-|- решения нет. 18.140. При к 2
^(х) = 81п2лх, при Х = 2 r/(x) = sin 2лх-|-Сх. 18.141. При	у (х; =
293
«=1— -~х, при Л=у (х)= 1—у С(!+2х). 18.142. При A
2л
—2л у (х)«ж2л4-Л х' ПРИ ^в""2л решения нет. 18.143. у(х)=э
-elg«+f М *еи. «МИ. Пр. 1 # 1 ,w = -nL= + sJ!^i.
18.145. у (x) = cosx4-^sln х<	18.146. При к # 2., ^у (х) =
£Х
лл	1	3	3
x=slnnxj----П₽и ^“®“2 Hx)eSin ^x+^x-J-C, при
!-уХ
решения нет. 18.147. При Л # ± Хг- (х) = -!--}-А х-|-
1—1X2
О
/	2 \	1/*3
х( (1+2Х)х+1 4~з,М > ПРИ ± -у решения нет. 18.148. При
4	2	2Х	2
1#± — у(х)==1 —-----r-SlHX, ПРН ^"7 jz(x)=l—Sinx+Ccosx,
Л	« । лл	л
2
при А»— — решения нет. 18.149. Ал = —л2п2, t/n = sln ппх, ngN.
18.150.	Ап=«— ~(2Л+1)2, r/rt = sinn^t^x, л==0, 1, 2, ...
18.151.	Ап=— ®2, где соп—корни уравнения co = ctg(D, уп~
e=cos0n(x—1),	18.152.	1 +	^rt = sin^ilx,
л=0, 1, 2, ... 18.153. Х„=1 — (^y-^у. izn = cos?^tlx, л«0.1,
2,... 18.154.л2п2, u„=sin ллх, ngN. 18.155.Xn =—1— яМ,
дп*=81пяпх, п(EN. 18.156. Ао=1, ^0 = 1; Ап=1 — 4п2, уп^Сг cos2ax+
+ C2sin2nx, ngN- 18,157. Хя®1+©2, где корни уравнения
®=ctg2©t z/rt = coscortx, n^N. 18.158. При Х#Ад = *-л2л2, zigN,
/ч i । а X? *	4 sin л (2k4- l)x
p(x) = l+*2u , +i_x«	„(2*4-1) '•
ХеяХал, /ngN>
, . . , л к? 1 4sinn(2&+l)x . n t o
к W-l+^L ---------------------(2*4-1) *Csto 2nmx'
при X»X2m+I» Л1а=»0, 19 i.a> решения нет. 18.159. При A 5^ An =
„-0.1,2, ...
/ .	. ’ я л /	1	1 . л 1	1 3л \
у (x)=sin лхсоз Tx-% ( —J . у sin у x4 —. T Sin - x\ 5
\^*r 4	^*F 4	J
294
при Х = Л0 = —— и Л =	----— решения нет; при Л = ^, п—2,
3. ...,
/V !	Л 1/	1 -	« 1 ж Я ,	1	1 , Зя \ ,
у (x)=sin nxcos-x—> '--у2 + у sin у *+--• yStoyX\+
\^л+у	^в+~4"	/
_	я(5л+!)
•j-C sin""  2 "' 'Ху
18.163. При X X„=l-^^tiy, л=0, i, 2.....
при % = Xn решения нет. 18.161. При Х = ЛЯ= 1 — 4л2л2, л = 0,
1, 2, ...» у (х} = (1— К)*1; при Х = 1в=1 решения нет, при Х = АЙ,
у {X) = -----г~ 4- С, COS 2пх + С2 Sifi 2пх.
1 — Лп
18.162 !).	18.163.	18.164.	18.165.	18.166.	18.167.
—3,1459	-4,3533	0,5335	63,0353	1,0000	0,0000
—3,0518	—4,3578	0,3333	63,9561	1,0135	0,2209
—2,9692	—4,3631	0,1614	64,8184	1,0172	0,4469
-2,8983	—4,3688	0,0109	65,6236	1,0111	0,6780
—2,8387	—4,3747	—0,1233	66,3731	0,9955	0,9442
-2,7903	-4,3806	—9,2448	67,0681	0,9709	1,1557
-2,7527	—4,3863	—0,3566	67,7100	0,9376	1,4025
—2,7257	-4,3914	—0,4608	68,2999	0,8963	1,6546
—2,7088	-4,3956	—9,5594	68,8388	0,8476	1,9121
-2,7015	-4,3985	—п,6535	69,3277	0,7921	2,1751
-2,7033	-4,3998	—9,7444	69,7680	0,7306	2,4436
-2,7137	— 4,3988	—0,8332	70,1604	0,6641	2,7176
—2,7321	-4,3950	— ',9209	70.5С58	0,5933	2,9972
-2,7577	-4,3877	— 1,0082	70,8054	0,5192	3,2825
-2,7900	-4,3759	— 1,0959	71,0600	0,4428	3,5734
-2,8282	— 4,3585	—1,1848	71,2707	0,3651	3,8701
-2,8715	— 4,3341	- 1,2758	71,4384	0,2870	4,1726
-2,9193	-1,3008	-1,3695	71,5642	0,2096	4,4809
-2,9707	-4,2563	-1,4668	71,6409	0,1340	4,7950
-3,0247	—4,1974	-1,5688	71,6940	0,0610	5,1159
-3,0811	—4,1198	-1,6765	71,6998	—0,0083	5,4410
1) Ответы к задачам 18.162—18.184 приводятся в виде значе-
ний функции у(х} в точках отрезка 10» 1}» выбранных с шагом
Дх—0,05, т. е. уь=*у {xk)~y (kbx), & = 0, 1, ... 20. При решении
этих задач методом конечных сумм, ‘либо моментов следует срав-
нить значения полученного решения с приведенным в точках вида
= Ь0.05. /г = 0, 1, .... 20.
18.168.	18.169.	18.170.	18.171.	18.172.	18.173.
0,3123	2,4334	—1,1130	0,9897	—0,1988	0,8313
0,2985	2,3247	— 1,0644	0,9686	—0,1636	0,8287
0,2796	2,1981	— 1,0122	0,9376	—0,1312	0,8039
0,2555	2,0532	—0,9562	0,8970	—0,1016	0,7577
0,2264	1,8890	—0,8963	0,8469	—0,0744	0,6912
0,1925	1,7072	—0,8322	0,7879	—0,0497	0,6G62
0,1539	1,5056	—0,7639	0,7202	—0,0273	0,5048
0,1111	1,2843	—0,6910	0,6446	—0,0071	0,3894
0,0641	1,0430	—0,6134	0,5617	0,0110	0,2629
0,0134	0,7813	—0,5308	0,4722	0,0270	0,1281
—0,0407	0,4988	—0,4431	0,3768	0,0410	—0,0116
—0,0978	0,1951	—0,3500	0,2763	0,0530	—0,1528
—0,1575	—0,1303	—0,2513	0,1719	0,0630	—0,2922
—0,2192	—0,4778	—0,1466	0,0643	0,0711	—0,4265
—0,2827	—0,8480	—0,0358	—0,0455	0,0774	—0,5526
—0,3472	— 1,2413	0,0815	—0,1565	0,0818	—0,6672
—0,4125	—1,6584	0,2056	—0,2675	0,0842	—0,7678
—0,4780	—2,0997	0,3369	—0,3777	0,0848	—0,8518
—0,6076	—2,5659	0,4755	—0,4860	0,0834	—0,9172
—0,6708	—3,0576	0,6220	—0,5914	0,0802	—0,9623
	-3,5754	0,7766	—0,6929	0,0750	—0,9859
18.174.	18.175.	18.176.	18.177.	18.178.	18.179.
—2,0000	—2,8204	4,7481	9,0060	—0,7005	2,0380
—2,0579	—2,7112	4,9997	9,6196	—0,5713	1,8073
—2,1294	—2,5946	5,2563	10,4009	—0,4441	1,5597
—2,2145	-2,4700	5,5178	11,3784	—0,3191	1,2958
—2,3133	—2,3366	5,7844	12,5934	—0,1964	1,0164
—2,4257	-2,1938	6,0560	14,0952	—0,0760	0,7219
—2,5517	—2,0408	6,3326	15,9423	0,0420	0,4131
—2,6913	—1,8768	6,6142	18,2048	0,1574	0,0909
—2,8446	—1,7009	6,9008	20,9^59	0,2702	—0,2436
—3,0114	—1,5122	7,1924	24,3244	0,3804	—0,5896
—3,1920	—1,3096	7,4890	28,3977	0,4878	—0,9456
—3,3861	—1,0922	7,7906	33,3252	0,5923	—1,3104
—3,5938	—0,8587	8,0971	39,2718	0,6938 >	—1,6823
—3,8152	—0,6050	8,4087	46,4331	0,7924	—2,0595
—4,0502	—0,3388	8,7252	55,0407	0,8879	—2,4400
—4,2988	—0,0497	9,0468	65,3683	0,9802	—2,8212
—4,5610	0,2607	9,3734	77,7398	1,0693	—3,2004
—4,8369	0,5939	9,7050	92,5376	1,1552	—3,5743
—5,1263	0,9518	10,0416	110,2132	1,2376	—3,9390
—5,4294	1,3351	10,3832 ,	131,3000	1,3167	—4,2900.
—5,7462	1,7488	10,7297	156,4264	1,3923	—4,6216
296
18.180.	18.181.	18.182.	18.183.	18.184.
0,0000	1,0000	— 1,0000	10,0000	0,2500
0,0501	1,1550	— 1,0087	11,0564	0,3279
0,1004	1,3207	— 1,0196	11,6033	0,4112
0,1517	1,4969	— 1,0398	12,5516	0,5029
0,2027	1,6862	—1,0515	13,1184	0,6005
0,2556	1,8859	—1,0674	14,0373	0,7127
0,3076	2,1029	—1,0692	14,5906	0,8301
0,3625	2,3292	—1,0641	15,4312	0,9712
0,4151	2,5790	— 1,0452	15,9774	1,1155
0,4717	2,8354	— 1,0042	16,7572	1,2966
0,5247	3,1245	—0,9569	17,3502	1,4771
0,5823	3,4152	—0,8761	18,1492	1,7136
0,6349	3,7512	—0,8027	18,8795	1,9427
0,6926	4,0800	—0,6992	19,8175	2,2555
0,7443	4,4708	—0,6154	20,7997	2,5495
0,8008	4,8389	—0,5200	22,0172	2,9672
0,8508 .	. 5,2909	—0,4442	23,3845	3,3491
0,9053	5,6921	—0,3751	25,0395	3,9123
0,9535	6,2067	—0,3108	26,9496	4,4129
1,0059	6,6194	—0,2539	29,2271	5,1786
1,0499	7,2710	—0,1807	31,8675	5,7222
18.185.				
SUBROUTINE INTEGR (N, С, X, A, RK. R, F, EF)
DIMENSION X(N),A(N),RK(N,N)jR(N)
DO 5 1=1, N
DO 6 J=l, N
6 RK(I,J)=—C*A(J)*F(X(I), X(J))
RK(I,I)=I.+RK(I, I)
6 R(1)=EF(X(1))
CALL EXCLUS(RK, R, N)
RETURN
END
Подпрограмма для решения уравнения Вольтерра второго род»
отличается от вышеприведенной следующими операторами;
RK(I, J)=—C*A(J)*F(X(I),X(J))
IF (J.GT.I) RK(I, J)=0.
IF (I.EQ.l.AND.J.EQ.l) RK(I,J)=O.
6 CONTINUE
RK(I,I)=l.-f-RK(I,I)
15.188. Ответ приводится для решения задачи 18.162;
. EXTERNAL Fl, FF1
DIMENSION X(21), A(21), RK(21,21), R(21)
N=21
A 1=0.
B=l.
H=(B—A1)/(N— 1)
N1=N—1
C=4.
DO 5 1=1, N
6 X(I)=(I—1)*H
DO 6 J=2, Nl, 2
A(J)=4.*H/3.
lF(J.NE.Nl)A(J+l)=2.*H/3.
297
6 CONTINUE
A(l)=H/3.
A(N)«A(1)
CALL INTEGR (N, С. X, A, RK, R, FFt, Fl|
PRINT 9, (X(I), R(I), 1=1,N)
9 FORMAT (50X, ’РЕШЕНИЕ’ //10.X, ’X’,
* ЮХ, JY7(lH0, 2F15.6))
STOP
END
> Задание для ЭВМ должно содержать 3 программных жюдул я:
указанную здесь основную программу, а также программа. реа-
лизующие соответствующие подпрограммы-функции. Для рассмат-
риваемой задачи 18.162 они имеют вид:
- FUNCTION F1(X) FUNCTION FFi(X,T)
PI=3.14593	~ ~ ~
F1=2.*X—PI
RETURN
END
FF1=SIN(X*T**2)**2
RETURN
ENO
298
СПИСОК ЛИТЕРАТУРЫ
1.	Васильев Ф. П. Численные методы решения экстремаль-
ных задач.-—М.: Наука, 1980.
2.	Ку з и н Л. Т. Основы кибернетики.— Т. I: Математические
основы кибернетики.— Мл Энергия, 1973.
3.	Ефимов А. В. Математический анализ (специальные раз-
делы).— Ч. I: Общие функциональные ряды и их приложения.—
Мл Высшая школа, 1980.
4.	ЕфимовА. В.,Золотарев Ю. Г.,ТерпигореваВ.М.
Математический анализ (специальные разделы).— Ч. II: Примене-
ние некоторых методов математического и функционального ана-
лиза.— М.: Высшая школа, 1980.
5.	Гачев Э. М., Кушниренко А. Г., Тихомиров В. М.
Сборник задач по оптимальному управлению.— Мл Изд. МГУ, 1980.
6.	К о л и х м а н И. Л., ВойтенкоМ. А. Динамическое
программирование в примерах и задачах.— М.: Высшая школа, 1979.
7.	О ч а н Ю. С. Методы математической физики.—М.: Высшая
школа, 1965.
8.	О ч а н Ю. С. Сборник задач по методам математической
физики.— М.: Высшая школа, 1967.
9.	Б у д а к Б. М., Самарский А. А., Тихонова. Н.
Сборник задач по уравнениям математической физики.— Мл Нау-
ка, 1972.
10.	Араманович И. Г., Левин В. И. Уравнения матема-
тической физики.— Мл Наука, 1964.
11.	Смирнов М. М. Задачник по уравнениям математической
физики.— Мл Наука, 1968.
12.	Д ь я ч е н к о В. Ф. Основные понятия вычислительной
математики.—Мл Наука, 1977.
13.	К а л итки н Н. Н. Численные методы.— Мл Наука, 1978.
14.	Марчук Г. И. Методы вычислительной математики.— Мл
Наука, 1989.
15.	Краснов М. Л. Интегральные уравнения. Введение в
теорию.—Мл Наука, 1975.
16.	Краснов М. Л., Киселев А. Н., Макаренко Г. И.
Интегральные уравнения.—2-е изд.—'Мл Наука, 1976.
содержание частей t—3
ЧАСТЬ 1
ЛИНЕЙНАЯ АЛГЕБРА И ОСНОВЫ МАТЕМАТИЧЕСКОГО
АНАЛИЗА
Предисловие
Глава 1. Введение в анализ
$ 1. Действительные числа. Множества. Логическая символика
f 2. функции действительной переменной
f 3. Предел последовательности действительных чисел
§ 4. Предел функции. Непрерывность
f 5. Комплексные числа
Глава 8. Векторная алгебра и аналитическая геометрия
f 1. Векторная алгебра
2. Линейные геометрические объекты
3. Кривые на плоскости
f 4. Поверхности и Кривые в пространстве
Глава 3. Определители и матрицы. Системы линейных уравнений
§ 1.	Определители
§ 2.	Матрицы
§ 3.	Пространство арифметических векторов. Ранг матрицы
§ 4.	Системы линейных уравнений
$ 5.	Некоторые вычислительные задачи линейной алгебры
Глава 4. Элементы линейной алгебры
§ 1.	Линейные пространства и пространства со скалярным
произведением
§ 2.	Линейные операторы
§ 3.	Билинейные и квадратичные формы
300
Глава 5. Дифференциальное исчисление функций одной перемен*
ной
§ 1.	Производная
§ 2.	Дифференциал
§ 3,	Теоремы о дифференцируемых функциях. Формуле Тей*
лора
§ 4.	Исследование функций и построение графиков
§ 5.	Векторные и комплексные функции действительной пере»
менной
§ 6.	Численные методы функции одной переменной
Глава 6. Интегральное исчисление функций одной переменной
• • § 1. Основные методы вычисления неопределенного интеграла
§ 2.	Интегрирование основных классов элементарных функций
§ 3.	Смешанные задачи на интегрирование
§ 4.	Определенный интеграл и методы его вычисления
§ 5.	Несобственные интегралы
§ 6.	Геометрические приложения определенного интеграла
§ 7.	Приложения определенного интеграла к решению некото-
рых задач механики и физики
§ 8.	Численное интегрирование функций одной переменной
Глава 7. Дифференциальное исчисление функций нескольких пере*
менных
$ 1.	Основные понятия
$ 2.	Дифференцирование сложных и неявных функций
§ 3.	Приложения частных производных
§ 4.	Приближенные числа и действия над ними
Ответы
ЧАСТЬ 2
СПЕЦИАЛЬНЫЕ РАЗДЕЛЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА
Предисловие
Глава 8. Кратные интегралы
§ 1.	Двойной интеграл
§ 2.	Тройной интеграл
§ 3.	Несобственные кратные интегралы
§ 4.	Вычисление интегралов, зависящих от параметра
801
Глава 9. Дифференциальные уравнения
§ I.	Уравнения 1-го порядка
§ 2,	Дифференциальные уравнения высших порядков
§ 3»	Системы дифференциальных уравнений
§ 4.	Элементы теории устойчивости
§ 5.	Численное интегрирование обыкновенных дифференциаль-
ных уравнений
Глава 10. Векторный анализ
§ 1.	,Скалярные и векторные поля. Градиент
§ 2.	Криволинейные и поверхностные интегралы
§ 3.	Соотношения между различными характеристиками ска-
лярных и векторных полей
$ 4.	Специальные виды векторных полей
§ 5.	Применение криволинейных координат в векторном ана-
лизе
Глава 11. Основные понятия теории функций комплексной пере-
менной
§ 1.	Элементарные функции
§ 2.	Аналитические функции. Условия Коши-*Римана
§ 3.	Конформные отображения
§ 4.	Интеграл от функции комплексной переменной
Глава 12. Ряды и их применение
§ 1.	Числовые ряды
§ 2.	Функциональные ряды
§ 3.	Степенные ряды
§ 4.	Применение степенных рядов
§ 5.	Ряды Лорана
§ 6.	Вычеты и их применение
§ 7.	Ряды Фурье. Интеграл Фурье
Глава 13. Операционное исчисление
§ 1.	Преобразование Лапласа
§ 2.	Восстановление оригинала по изображению
§ 3.	Применения операционного исчисления
§ 4.	Дискретное преобразование Лапласа и его применение
Ответы -
802
ЧАСТЬ 3
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИС-
ТИКА
Предисловие
Глава 14. Теория вероятностей
§ 1.	Случайные события
§ 2.	Случайные величины
§ 3.	Случайные векторы
§ 4.	Функции случайных величин
§ 5.	Закон больших чисел и предельные теоремы теории веро-
ятностей
§ 6.	Случайные функции (корреляционная теория)
Глава 15. Математическая статистика
§ 1.	Методы статистического описания результатов наблюдений
§ 2.	Статистическое оценивание характеристик распределения
генеральной совокупности по выборке
§ 3.	Интегральные оценки
§ 4.	Проверка статистических гипотез
§ 5.	Однофакторный дисперсионный анализ
§ 6.	Критерий %2 и его применение
§ 7.	Элементы регрессионного анализа и метод наименьших
квадратов
§ 8.	Непараметрические методы математической статистики
Ответы
Приложения
Список литературы
Учебное издание
СБОРНИК ЗАДАЧ
ПО МАТЕМАТИКЕ
для втузов
МЕТОДЫ ОПТИМИЗАЦИИ
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ
ИНТЕГРАЛЬНЫЕ УРАВНЕНИЙ
Под редакцией А. В. Ефимова
Заведующий редакцией С. И. Зеленский
Редактор В. В. Донченко
Художественный редактор Т. Н. Кольченко
Технический редактор С. Я. Шкляр
Корректор Н. Б. Румянцева
ИБ № 41097
Сдано в набор 05.05,89. Подписано к печати
22 01.90. Формат 84x108/32. Бумага тип. № 2.
Гарнитура литературная. Печать высокая. Усл.
печ. л. 15,96. Усл. кр.-отт. 16,17.
Уч.-изд. л. 20,76. Тираж 49 000 экз.
Заказ № 3439. Цена 90 коп.
Издательско-производственное
и книготорговое объединение «Наука».
Главная редакция
физико-математической литературы,
117071, Москва В-71, Ленинский проспект, 15
Набрано и сматрицировано в
Ордена Октябрьской Революции и ордена
Трудового Красного Знамени МПО «Первая
Образцовая типография Государственного
комитета СССР по печати
113054, Москва, Валовая, 28
Отпечатано в типографии
издательства «Коммуна»,
г. Воронеж, пр. Революции, 39
90 коп.