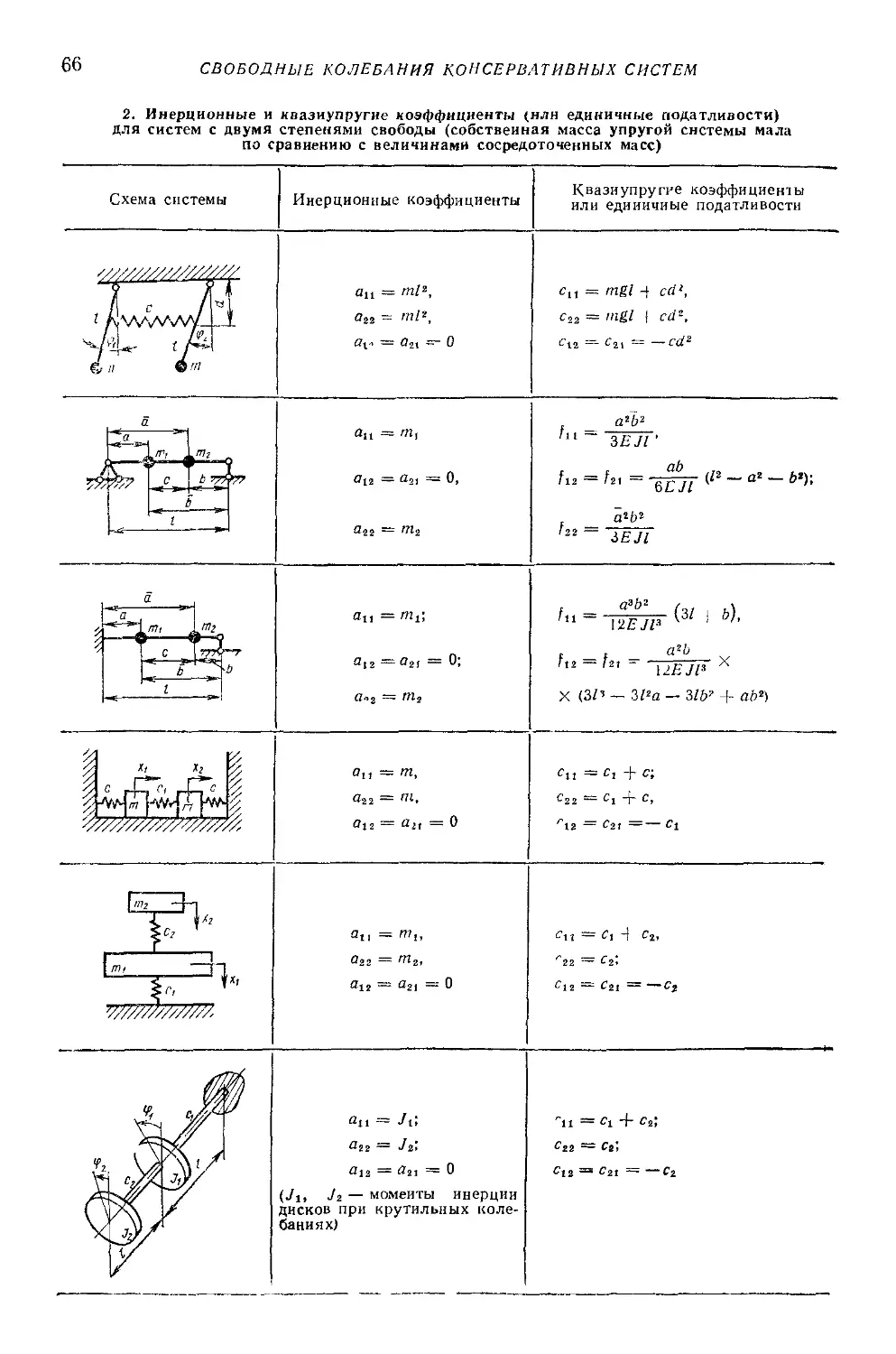
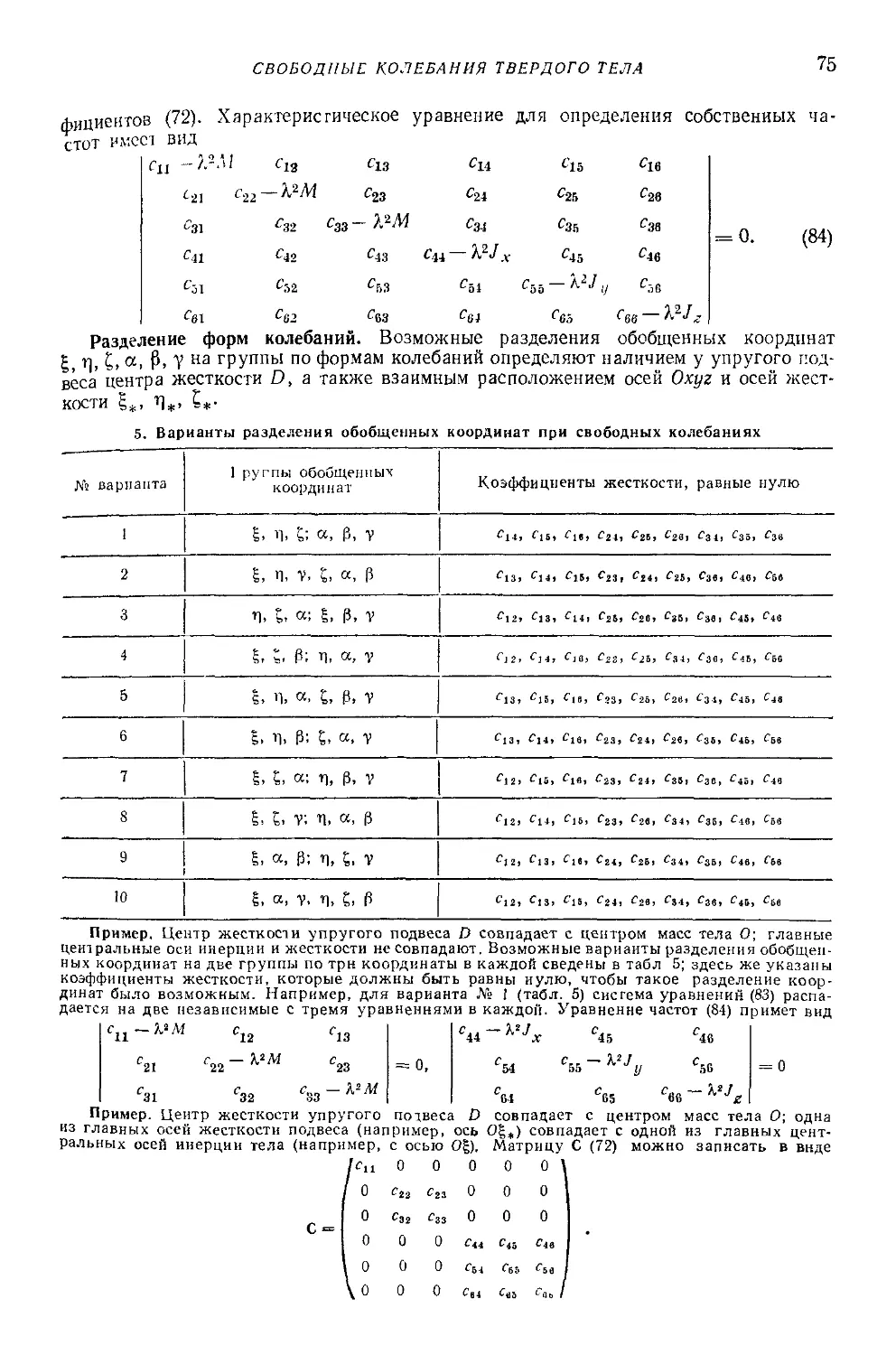
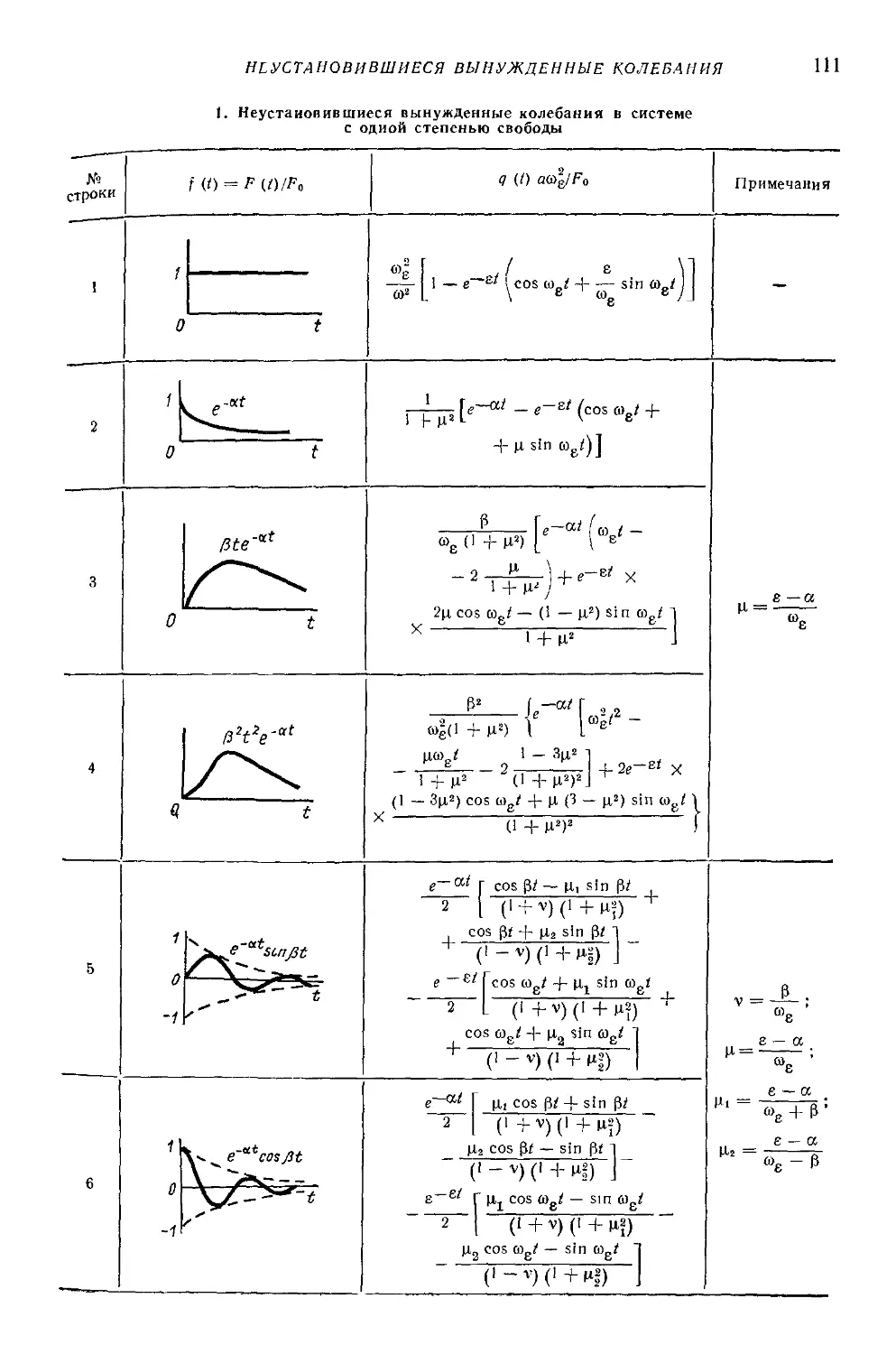
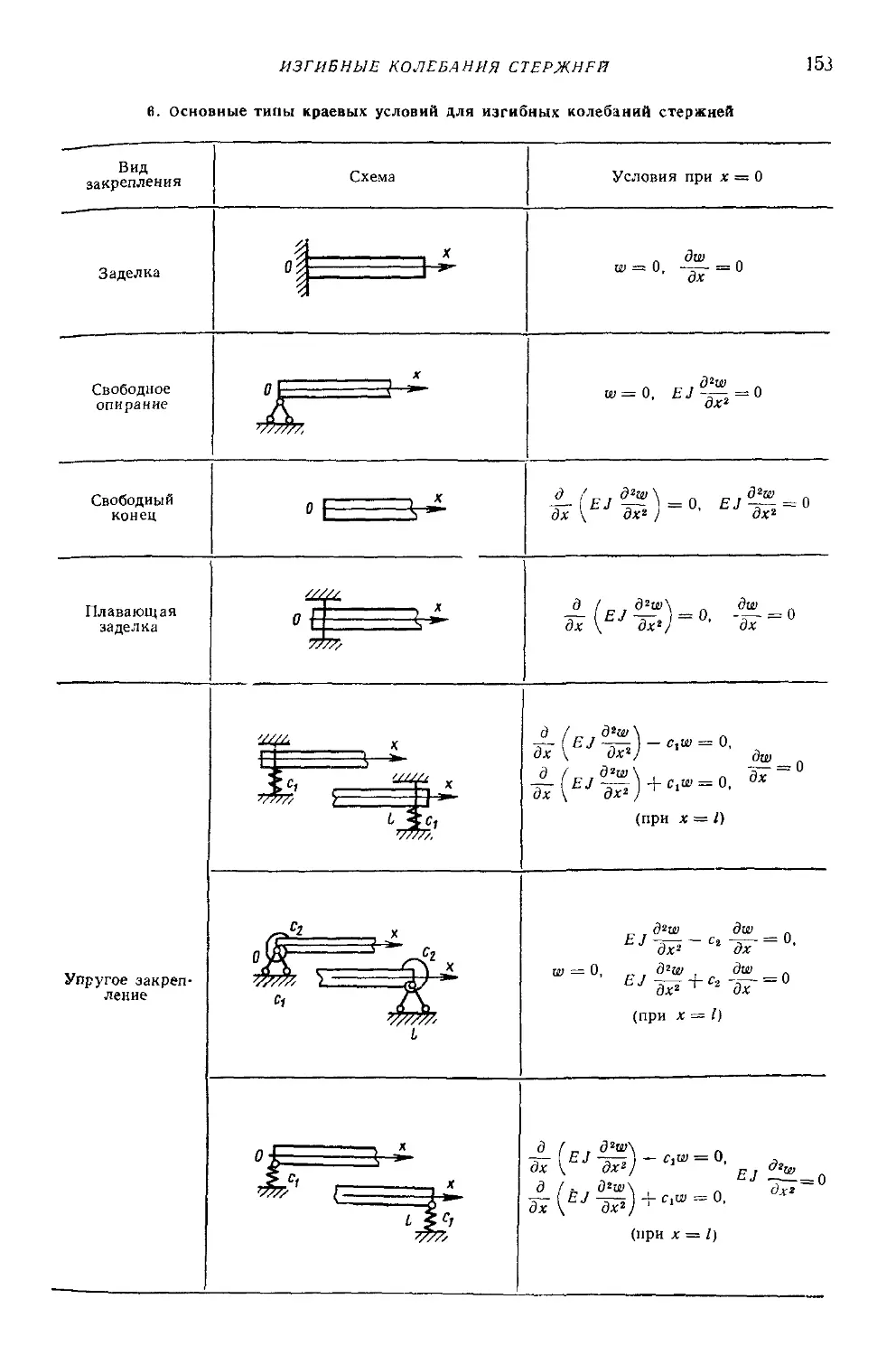
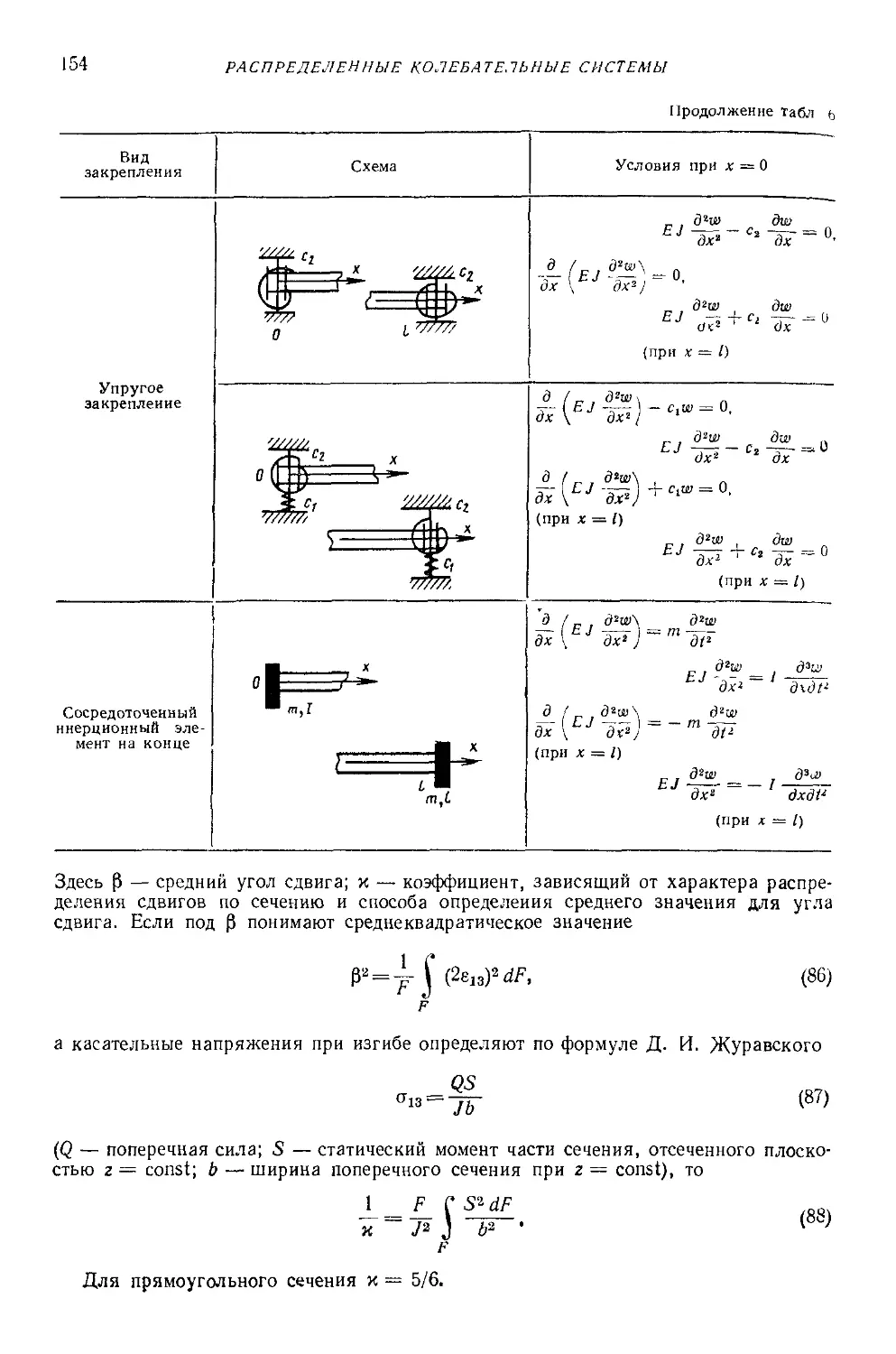
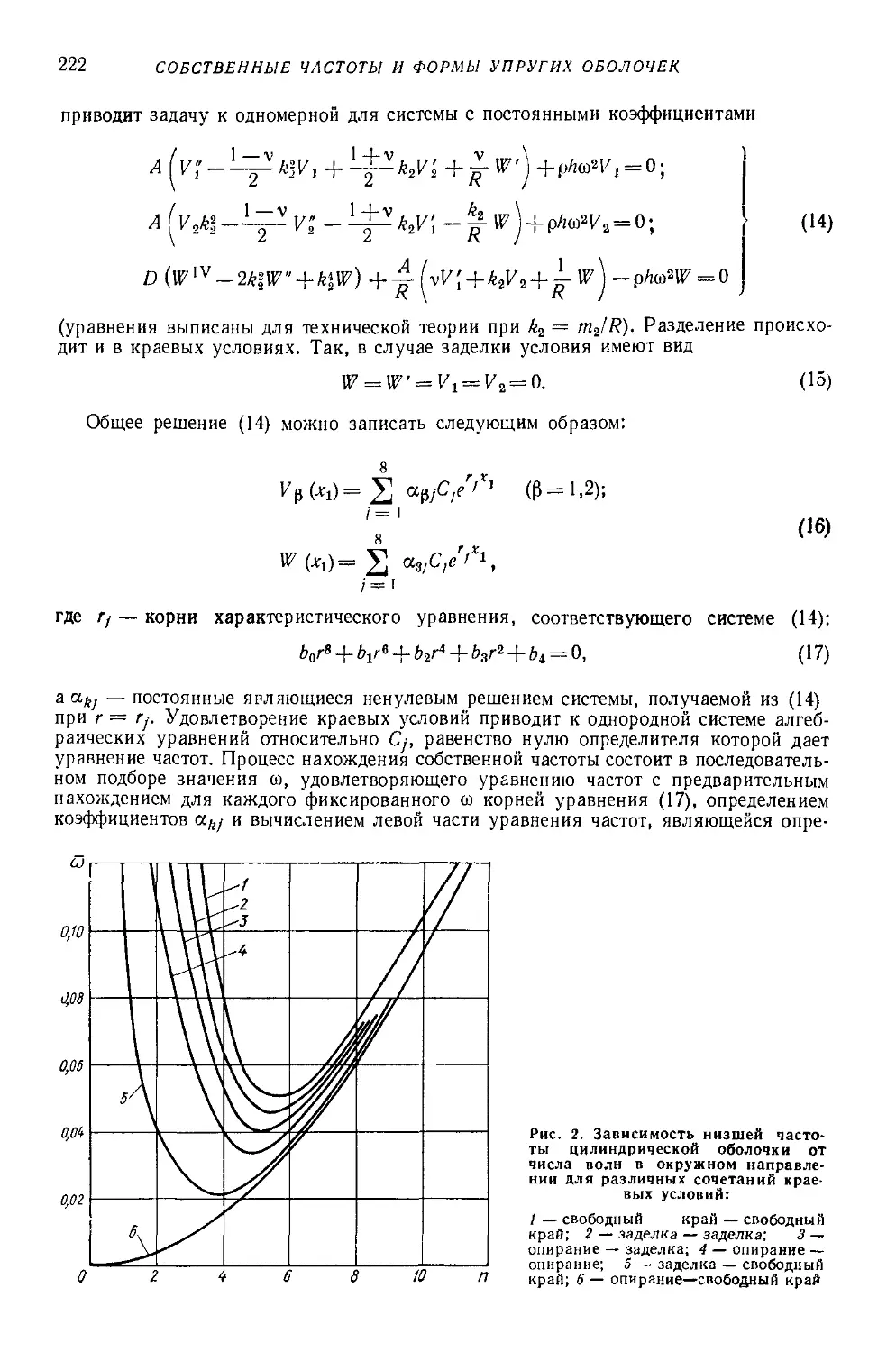
Text
ВИБРАЦИИ
В ТЕХНИКЕ
СПРАВОЧНИК
6
В 17 ТОМАХ
Редакционный совет
Председатель— В. Н. Челомей (главный редактор издания)
Члены В. С. Авдуевский, Й. И. Артоболевский/ И. И. Блехиан,
А. Н. Боголюбов, Н. Н. Боголюбов, В. В. Бойцов, В. В. Болотин,
Н. В. Бутенин, И. И. Быховский, Р. Ф. Ганиев, М. Д. Генкин,
Э. И. Григолюк (зам председатели и главного редактора),
Ф. М. Диментберг, А. Е. Кобринский, К. С. Колесников,
М 3. Коловский, Э. Э. Лавендел, А. И. Лурье, Ю. А. Митропольский,
Я. Г. Пановко, К. М. Рагульскис, В. В. Румянцев, Л. И. Седов,
) С. В. Серенсен), К- В. Фролов (зам. главного редактора)
Москва « Машиностроение » 1978
КОЛЕБАНИЯ
ЛИНЕЙНЫХ
СИСТЕМ
том
1
Под редакцией чл.-корр. АН СССР
В. В. БОЛОТИНА
Москва « Машиностроение »1978
ББК 34.41
В41
УДК 62-752@31)
Авторы:
И. И. Артоболевский, А. Н. Боголюбов, В. В. Болотин, В. Ю. Волоховский,
Н. И. Жинжер, Г. В. Мишенков, В. Г. Москвин, Ю. Н. Новичков, Ю. А. Окопный,
В. В. Парцевский, К. В. Фролов, В. П. Чирков
Вибрации в технике: Справочник. В 6-ти т. / Ред. совет:
В41 В. Н. Челомей (пред.). — М.: Машиностроение, 1978— —
Т. 1. Колебания линейных систем/Под ред. В. В. Болотина.
1978. 352 с, ил.
В пер.: 1 р. 70 к.
На обороте тит. л. авт.: И. И. Артоболевский, А. Н Боголюбов, В. В. Болотин
(и ДР ).
В первом томе изложены современные методы аналитического исследования колеба-
колебательных систем с конечным числом степеней свободы и линейных систем с распреде-
распределенными параметрами. Дана теория устойчивости колебательных систем, приведены
методы аналитического описания и анализа колебательных процессов. Приведены ре-
результаты новейших достижений, методы определения собственных частот и форм ко-
колебаний систем сложной структуры. Большое внимание уделено параметрическим и
случайным колебаниям, ударным процессам и распространению волн, а также теории
вибрационной надежности.
Справочник предназначен для инженерно-технических работников, занятых про-
проектированием, изготовлением и эксплуатацией современной техники,
ББК 34.41
31301-601
В подписное
038@1)-78 6П5.1
© Издательство «Машиностроение», 1978 г.
ОГЛАВЛЕНИЕ
Предисловие к справочнику „Вибрации в технике" 11
Предисловие к 1-му тому , . , ,,,...,. 14
ЧАСТЬ ПЕРВАЯ
КОЛЕБАНИЯ ЛИНЕЙНЫХ СИСТЕМ
С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
Глава I. Введение. Основные понятия (И. И. Артоболевский, А. Н. Бого-
Боголюбов, В. В. Болотин, К- В. Фролов, Ю. А. Окопный) 15
1. Предмет теории колебаний . , , 15
2. Классификация колебательных систем 16
3. Классификация колебательных процессов 18
4. Кинематические характеристики периодических колебательных
процессов 18
5. Кинематические характеристики непериодических колебательных
процессов 26
6. Другие характеристики колебательных процессов 28
Глава 11. Математическое описание колебательных систем с конечным
числом степеней свободы (В. В. Болотин, Г. В. Мшиенков,
10. А. Окопный) 31
1. Основные теоремы классической механики , 31
2. Принцип Гамильтона и уравнения Лагранжа для механических
систем 36
3. Распределение масс в абсолютно твердом теле 40
4. Уравнения динамики абсолютно твердого тела 48
5 Аналогии в динамике. Электрические и электромеханические
системы .,,.,.,..,,,.,..,,..,,,.,,..,,., 51
ОГЛАВЛЕНИЕ 7
Глава VII. Параметрические колебания (В. В. Болотин) 116
1. Общие сведения 116
2. Параметрические резонансы 117
3. Системы с одной степенью свободы. Области неустойчивости урав-
уравнения Матье — Хнлла 121
4. Области неустойчивости для систем с конечным числом степеней
свободы 126
5. Свойства параметрически возбуждаемых систем 131
ЧАСТЬ ВТОРАЯ
КОЛЕБАНИЯ ЛИНЕЙНЫХ РАСПРЕДЕЛЕННЫХ СИСТЕМ
Глава VIII. Математическое описание распределенных колебательных сис-
систем (Ю. Н. Новичков) 135
1. Принцип Гамильтона — Остроградского для упругих распреде-
распределенных систем 135
2. Уравнения динамики упругих тел 137
3. Учет диссипации в уравнениях движения. Вязкоупругое пове-
поведение деформируемых материалов 140
4. Колебания струны. Продольные и крутильные колебания
стержней 145
5. Изгибные колебания стержней 152
6. Изгибные колебания пластин 15?
7. Колебания тонких упругих оболочек 160
Глава IX. Общие свойства собственных частот и собственных форм
упругих систем (В. В. Болотин) 166
1. Основные соотношения 166
2. Свойства собственных частот и собственных форм 168
3. Вариационные принципы в теории собственных колебаний упру-
упругих систем . , 171
4. Структура спектра собственных частот 172
5. Плотность собственных частот 273
Глава X. Определение собственных частот и собственных форм упругих
систем A0. Н. Новичков, В. В. Парцевский) 177
1. Точные методы 177
2. Метод малого параметра (метод возмущений) 179
3 Метод последовательных приближений 180
4. Методы теории линейных интегральных уравнений 180
5. Асимптотический метод 181
6. Метод Релея и родственные методы 182
а ОГЛАВЛЕНИЕ
7. Методы Ритца, Бубнова — Галеркина, коллокаций и родствен-
родственные методы 183
8. Метод конечных разностей 185
9. Метод конечных элементов , 187
10. Методы динамических жесткостей и податливостей 189
Глава XI. Собственные частоты и собственные формы упругих стержней
и стержневых систем G0. Н. Новичков, 10. А. Окопный) . . . 190
1. Продольные и крутильные колебания стержней 190
2. Изгибные колебания стержней 193
3. Изгибно-крутильные колебания стержней 200
4. Расчет собственных частот и собственных форм колебаний по мето-
методам динамических жесткосгей и динамических податливостей 201
Глава XII. Собственные частоты и собственные формы упругих пластин
G0. Н. Новичков) •. . . 203
1. Пластины, прямоугольные в плане 203
2. Круговые и кольцевые в плане пластины 206
3. Применение асимптотического метода к упругим пластинам .... 209
4. Многопролетные пластины 212
5. Расчет собственных частот и собственных форм на основе уточ-
уточненных теорий ,.,.,...........,.,... 215
Глава XIII. Собственные частоты и собственные формы упругих оболочек
(ТО. Н. Новичков) 218
1. Классификация собственных форм колебаний 218
2. Круговые цилиндрические оболочки 219
3. Сферические оболочки 223
4. Конические оболочки 226
5. Пологие криволинейные панели 228
6. Применение асимптотического метода к расчету собственных
частот и собственных форм колебаний , 229
7. Плотность собственных частот 232
Глава XIV. Вынужденные колебания упругих систем (Ю. А. Окопный) 234
1. Установившиеся вынужденные колебания недиссипативных сис-
систем под действием периодических внешних сил , 234
2. Вынужденные колебания стержней 235
3. Метод разложения по собственным формам . , 236
4. Применение вариационных методов к расчету вынужденных коле-
колебаний , , 237
5. Неустановившиеся вынужденные колебания 238
6. Вынужденные колебания в диссипативных системах .,,,,,, 238
ОГЛАВЛЕНИЕ 9
Глава XV. Динамическая устойчивость распределенных систем (В. В. Бо-
Болотин) 210
1. Свободные колебания распределенных неконсервативных систем 240
2. Устойчивость распределенных систем 241
3. Методы исследования устойчивости 243
4. Параметрические колебания распределенных систем 245
5. Уравнения динамической устойчивости 246
6. Методы сведения к системам обыкновенных дифференциальных
уравнений 248
7. Построение областей неустойчивости 254
Глава XVI. Распространение волн и ударные процессы в упругих системах
(Ю. Н. Новичков) 256
1. Волны в неограниченной упругой среде 256
2. Поверхностные волны Релея 258
3. Упругие волны в стержнях 259
4. Соударение двух упругих шаров 261
5. Продольный удар в упругих стержнях 262
6. Поперечный удар по упругим балкам 265
ЧАСТЬ ТРЕТЬЯ
КОЛЕБАНИЯ ЛИНЕЙНЫХ СИСТЕМ ПРИ СЛУЧАЙНЫХ
ВОЗДЕЙСТВИЯХ
Глава XVII. Сведения из теории случайных процессов и полей (В. В. Во-
лотин, В. Ю. Волоховский) 268
1. Методы описания случайных функций 268
2. Стационарные случайные процессы 271
3. Многомерные случайные процессы 275
4. Марковские случайные процессы 276
5. Вероятностные характеристики случайных полей 278
6. Статистическое моделирование случайных процессов и полей 280
Глава XVIII. Случайные колебания систем с конечным числом степеней
свободы (В. В. Болотин, В. П. Чирков) 286
1. Задачи теории случайных колебаний 286
2. Метод дифференциальных уравнений относительно моментных
функций 287
3. Метод функций Грина (импульсных переходных функций) 288
4 Метод спектральных разложений 289
5. Стационарные колебания линейных систем 290
10 ОГЛАВЛЕНИЕ
6 Методы теории марковских процессов 294
7. Метод статистического моделирования в задачах случайных коле-
колебаний 296
Глава XIX. Параметрические колебания при случайных воздействиях
(В. В. Болотин, В. Г. Москвин) 299
1. Определения стохастической устойчивости 299
2. Метод стохастических функций Ляпунова 301
3. Метод моментных функций 303
4. Системы, возбуждаемые белыми шумами 306
5 Системы, возбуждаемые процессами с конечной дисперсией .... 308
Глава XX. Случайные колебания распределенных систем (В. Ю. Воло-
ховский) 310
1. Метод моментных функций 310
2. Методы спектральных представлений . 312
3. Метод разложения по собственным формам 315
4. Широкополосные случайные колебания 318
Глава XXI. Основы теории вибрационной надежности (В. В. Болотин,
В. П. Чирков) 319
1. Основные понятия 319
2. Критерии вибрационной надежности 322
3. Методы аналитической оценки функции надежности . 324
4. Теория выбросов случайных процессов 326
5. Расчет вибрационной надежности 332
Список литературы 335
Предметный указатель 341
ПРЕДИСЛОВИЕ К СПРАВОЧНИКУ
„ВИБРАЦИИ В ТЕХНИКЕ"
Цель издания настоящего справочника — дать читателю необходимые сведения
из важнейшей сферы современной физики, механики и техники — теории колебаний.
Можно без преувеличения сказать, что методы теории колебаний являются одними
из самых важных и общих при исследовании в различных областях естествознания.
В настоящее время колебания приобретают особое значение в связи с бурным
ростом мощностей машин, скоростей движения их агрегатов и механизмов, умень-
уменьшением относительной массы, увеличением их долговечности и надежности, обеспе-
обеспечением устойчивости и управляемости систем Значительную роль в технике играют
механические колебания, многие виды которых часто называют вибрациями.
Большое, еще недостаточно изученное влияние оказывают колебания на живые
организмы.
В ряде случаев колебания чрезвычайно опасны. Вследствие непредвиденных
колебаний возникают погрешности в работе машин и механизмов, увеличивается
износ и заметно понижается их надежность, возможны разрушения и аварии.
В других случаях колебания могут оказаться весьма полезными. Целые области
современной техники (радиотехника, акустика, вибротранспорт, вибрационная
технология) построены на основе использования различных колебательных про-
процессов.
Уметь рассчитать колебания различны* объектов машиностроения, приборостро-
приборостроения, транспортной и строительной техники, правильно оценить их воздействие
на изучаемые системы, экспериментально исследовать параметры колебаний и долж-
должным образом толковать результаты наблюдений — необходимые качества современ-
современного квалифицированного инженера.
Справочник рассчитан на широкий круг читателей. В основном, однако, мы пред-
предназначаем его инженерам, работающим в области создания новой техники и техно-
технологии.
Каждый том в рассматриваемом аспекте является самостоятельным и закончен-
законченным руководством.
Том первый посвящен колебаниям линейных систем. Здесь формулируются и
рассматриваются методы изучения колебательных процессов механических систем
с конечным числом степеней свободы, а также систем с распределенными парамет-
параметрами. Рассмотрены консервативные и неконсервативные системы, анализируются
вопросы устойчивости решений.
Наряду со свободными колебаниями с одной, двумя и многими степенями сво
боды освещены также вынужденные колебания с диссипацией и без нее. Изложена
теория параметрических колебаний. Применительно к упругим системам обсу-
обсуждаются общие свойства собственных частот и собственнь х форм колебаний, точные
и приближенные методы их определения. Представлены методы вычисления собствен-
собственных форм и частот упругих стержней, пластин и оболочек2 рассмотрены вопросы
12 ПРЕДИСЛОВИЕ К СПРАВОЧНИКУ
динамической устойчивости и теории удара упругих систем. Изложены методы иссле-
исследования колебаний при случайных возбуждениях систем с конечным числом степе-
степеней свободы и некоторых упругих систем с распределенными параметрами. Дана
оценка вибрационной надежности.
Том второй посвящен нелинейным колебаниям механических систем. В нем при-
приведены сведения о нелинейных колебаниях систем и рассмотрены их основные
модели (консервативные, диссипативные, автоколебательные системы, системы
с заданным внешним воздействием). Изложены математические методы изучения
нелинейных колебаний, в том числе важнейшие методы исследования устойчивости.
В отличие от известных руководств по нелинейным колебаниям том содержит раздел,
в котором рассмотрены задачи о взаимодействии нелинейных колебательных систем
с источниками возбуждения, проблемы синхронизации колебательных и вращатель-
вращательных движений, виброперемещение и виброреология, теория виброударных и электро-
электромеханических систем, колебания сосудов с жидкостью, колебания твердого тела
на нелинейно-упругих опорах.
Оба первых тома носят не только характер справочного руководства, но и дают
достаточно подробное представление о математи'еских методах, применяемых
в современной теории колебаний.
Том третий посвящен расчету колебаний элементов и систем упругих конструкций.
В нем даны методы расчета систем, состоящих из прямых и криволинейных стерж-
стержней, пластин и оболочек, расчет важнейших конструктивных элементов — валов,
пружин, турбинных и компрессорных лопаток, дисков, колец. Описаны способы
оценки выносливости конструктивных элементов, подверженных вибрациям, методы
определения вибраций в газовых и паровых турбинах, двигателях внутреннего
сгорания, станках, автомобилях и в других машинах и агрегатах. Рассмотрены
методы построения расчетных моделей.
Том четвертый посвящен полезному применению вибраций в современных техно-
технологических процессах. В нем описаны системы возбуждения колебаний, широко
используемые в промышленности, — пневматические, гидравлические, электромаг-
электромагнитные и инерционные. Рассмотрены кинематические и силовые методы возбуждения
вибраций. Даны сведения о некоторых типах вибрационных машин.
Том пятый посвящен современным методам экспериментального определения
характеристик колебательных процессов. В нем дан анализ гармонических, полигар-
полигармонических, нестационарных и случайных колебательных процессов. Приведены
сведения о виброизмерительной аппаратуре для всестороннего исследования слож-
сложных колебательных систем, даны характеристики виброизмерительных приборов
и методы обработки результатов наблюдения.
Рассмотрены вопросы вибрационных испытаний механических систем, подго-
подготовка и проведение испытаний, их автоматизация и использование результатов
испытаний в задачах идентификации и диагностики систем.
Том шестой посвящен вопросам, связанным с методами защиты от воздействия
вибраций. В нем рассмотрены системы и механизмы, которые следует предохранить
от динамических воздействий, обсуждены в этой связи вопросы проектирования
таких систем и механизмов. Изложена теория упругих подвесов, упругих вибро-
виброизоляторов и динамических гасителей. Описаны схемы и конструкции динамиче-
динамических гасителей, предохраняющих и защищающих машину и человека от воздействия
вибраций. Рассмотрены также некоторые вопросы биодинамики человеческого орга-
организма. Приведены допускаемые уровни вибрационного воздействия на человека.
Таким образом, справочный материал, заключенный в шести томах, должен дать
достаточно полную информацию о проблемах вибраций при проектировании, изго-
изготовлении, испытаниях и эксплуатации различного рода машин, аппаратов и соору-
сооружений. Изложение построено так, чго для решения этих проблем могут быть исполь-
использованы современные электронно-вычислительные машины.
Это издание мы рассматриваем как первый опыт создания уникального справоч-
справочного руководства. В дальнейшем целесообразно будет дополнить его такими глу-
глубоко связанными с теорией колебаний проблемами, как сложный удар, взрыв, аэро-
гидроупругость, построение и исследование моделей, правильно отражающих дина-
динамические характеристики реальных конструкций.
ПРЕДИСЛОВИЕ К СПРАВОЧНИКУ 13
К написанию и редактированию томов справочника были привлечены крупные
научные силы нашей страны. Для настоящего издания большую помощь оказал
академик И. И. Артоболевский.
Можно надеяться, что предлагаемый справочник окажется полезным читателям
в их практической работе. В этом случае цель, которую ставили перед собой авторы
и редакционный совет, будет достигнута.
Председатель редакционного совета
Академик В. Н. Челомей
ПРЕДИСЛОВИЕ К 1-му ТОМУ
В данном томе приведены основы теории колебаний линейных систем, методы этой
теории, наиболее существенные аналитические и численные результаты. Материал
изложен в последовательной, единой и методически отработанной форме, чтобы спра-
справочником могли пользоваться как инженеры-конструкторы и инженеры-исследова-
инженеры-исследователи, так и студенты и аспиранты высших технических учебных заведений. Авторы
постарались в максимальной степени отразить современную терминологию, современ-
современные формы исследования и подачи материала, а также применение электронных
вычислительных машин для решения инженерных проблем.
Большое внимание уделено основным понятиям теории колебаний и смежных
разделов механики, выбору и обоснованию моделей колебательных систем, методам
их аналитического и численного анализа; приведено большое количество справоч-
справочного материала, который может быть непосредственно использован в вибрационных
расчетах.
В этом томе рассмотрены эффективные численные методы и алгоритмы, рассчитан-
рассчитанные на применение ЭВМ; в отдельных случаях даются указания на возможность исполь-
использования стандартных программ из библиотеки математического обеспечения для
ЭВМ серии ЕС.
Том состоит из трех частей. В первой части изложена теория колебаний линейных
систем с конечным числом степеней свободы, во второй — теория колебаний линейных
распределенных систем. В них подробно рассмотрены методы расчета собственных
частот и собственных форм колебаний, вынужденных и параметрически возбуждаемых
колебаний, методы исследования устойчивости неконсервативных линейных систем.
В третьей части изложена теория колебаний линейных систем с конечным числом
степеней свободы и распределенных систем при случайных воздействиях.
Редактор чл.-корр АН СССР В. В.Болотин
Часть первая
КОЛЕБАНИЯ ЛИНЕЙНЫХ СИСТЕМ
С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
Глава I
ВВЕДЕНИЕ. ОСНОВНЫЕ ПОНЯТИЯ
1. ПРЕДМЕТ ТЕОРИИ КОЛЕБАНИЙ
Понятие о колебаниях. Рассмотрим некоторую систему, т. е. совокупность объектов,
взаимодействующих между собой и с окружающей средой по некоторому закону. Это
может быть как механическая система материальных точек, абсолютно твердых тел,
упругие и вообще деформируемые тела и т. п., так и электрическая, биологическая
и смешанная (например, электромеханическая) системы. Пусть состояние системы
в каждый момент времени t описывается некоторым набором параметров. Задача тео-
теории состоит в том, чтобы предсказать эволюцию системы во времени, если задано
начальное состояние системы и внешнее воздействие на нее.
Возьмем один из числовых параметров системы, обозначив его через и. Это может
быть скалярная величина, одна из компонент вектора или тензора и т. п. Рассмотрим
изменение этого параметра на некотором отрезке времени, например, при te @, оо).
Это изменение может быть монотонным, немонотонным, существенно немонотонным
(рис. 1). Наибольший интерес представляет последний случай.
Процесс изменения параметра, который характеризуется многократным поочеред-
поочередным возрастанием и убыванием параметра во времени, называется колебательным
процессом или просто колебаниями, а соответствующий параметр называется колеблю-
колеблющейся величиной.
Невозможно установить четкую границу, отделяющую колебательные процессы
от неколебательных. Например, в экономике процесс такого типа, как на рис. 1,6,
может быть отнесен к колебательным процессам. Можно сформулировать более общее
определение колебательного процесса: параметр u^t) совершает на заданном отрезке
времени колебания относительно параметра u2(f) (и наоборот), если разность и^(() —
— u2(t) на этом отрезке многократно изменяет знак (рис. 1,г). Например, можно гово-
говорить о колебательном изменении угла cp(f) вращения диска относительно равномер-
равномерного вращения ф = со^ -f- const с постоянной угловой скоростью ш.
Если все или наиболее существенные параметры системы — колеблющиеся вели-
величины, то говорят, что система испытывает колебания. Система, способная при опреде-
определенных условиях совершать колебания, называется колебательной системой. Строго
говоря, под это определение подходит любая система, так как для любой системы
можно выбрать такое воздействие, при котором она будет совершать колебательное
движение. Поэтому обычно используют более узкое определение: система называется
колебательной, если она способна совершать колебания при отсутствии внешних
воздействий (только за счет первоначально накопленной энергии).
Место колебательных процессов в науке и технике. Большинство наблюдаемых в
природе и технике процессов являются колебательными. К колебательным процессам
относятся самые разнообразные явления: от ритмов головного мозга и биения сердца
до колебаний звезд, туманностей и других космических объектов; от колебаний атомов
или молекул в твердом теле до климатических изменений на Земле, от вибраций зву-
звучащей струны до землетрясений. Все акустические явления и явления, связанные с
распространением электромагнитных волн, также сопровождаются колебательными
процессами.
16
ВВЕДЕНИЕ ОСНОВНЫЕ ПОНЯТИЯ
\i\iw
aj б> 6) г)
Рис. I. Изменение параметра и (t):
а—монотонное; б — немонотонное; в — существенно немонотонное; г — относительное изме-
изменение параметров ut(t) и u2(t)
В данном томе будут рассмотрены в основном механические системы. Колебатель-
Колебательные процессы, происходящие в этих системах, называются механическими колебаниями.
В технике, особенно в машиностроении, широко применяют также термин вибрация.
Он является почти синонимом терминов механические колебания или колебания меха-
механической системы. Термином вибрация чаще всего пользуются там, где колебания
имеют относительно малую амплитуду и не слишком низкую частоту (например, едва
ли можно принять термин вибрация, говоря о колебаниях маятника часов или о рас-
раскачивании качелей).
Прикладная теория колебаний и вибротехника. Совокупность методов и средств
для измерения величин, характеризующих колебания, называется виброметрией.
Совокупность методов и средств для уменьшения вредного воздействия вибрации
на человека, приборы и механизмы называется виброзащитой. Совокупность техно-
технологических приемов, основанных на целенаправленном использовании вибрации,
называется виброобработкой, а использование вибрации для перемещения материалов,
изделий и т. п. называется вибротранспортировкой. Для обеспечения способности
объектов выполнять свои функции и сохранять параметры в пределах установленных
норм, а также сохранять прочность в условиях вибрации необходимы расчеты на
виброустойчивость и вибропрочность или, в более общей постановке, на вибронадеж-
вибронадежность. Задачей виброиспытаний является изучение виброустойчивости, вибропроч-
вибропрочности и эффективности объектов в условиях вибраций, а также изучение эффектив-
эффективности виброзащиты; задачей вибродиагностики — изучение состояния объекта на
основе анализа эксплуатационных или искусственно возбуждаемых вибраций.
2. КЛАССИФИКАЦИЯ КОЛЕБАТЕЛЬНЫХ СИСТЕМ
Понятие об уравнении системы. Классификация колебательных систем связана со
свойствами операторного уравнения, устанавливающего зависимость между вектором
состояния системы и@ и вектором q(^) воздействий на систему со стороны окружаю-
окружающей среды:
Lu = q. A)
Здесь L — оператор системы, включающий в себя все уравнения и дополнительные
условия, необходимые для однозначного описания поведения системы и@ при внеш-
нгм воздействии q(^).
Для механических систем операторное уравнение A), как правило, сводится
к совокупности некоторых дифференциальных уравнений с граничными и начальными
условиями, а также с дополнительными соотношениями типа уравнений связи.
Системы с конечным числом степеней свободы и распределенные системы. Класси-
Классифицировать колебательные системы можно по различным признакам. Одним из
важнейших признаков является число степеней свободы системы, т. е. количество
независимых числовых параметров, однозначно определяющих конфигурацию сис-
системы в любой фиксированный момент времени t. Понятие конфигурации само по себе
КЛАССИФИКАЦИЯ КОЛЕБАТЕЛЬНЫХ СИСТЕМ 17
нуждается в определении. Здесь ограничимся указанием на то, что для механических
систем под конфигурацией понимается положение всех точек системы в простран-
пространстве.
Различают системы с конечным и бесконечным числом степеней свободы. В послед-
последнем случае множество степеней свободы может быть либо счетным, либо континуаль-
континуальным. Системы, обладающие континуальным множеством степеней свободы, называют
распределенными (континуальными). Число степеней свободы зависит от характера
идеализации реальной системы. Упругие системы с распределенной массой являются
распределенными системами; заменяя распределенную массу конечным числом сосре-
сосредоточенных масс, получим систему с конечным числом степеней свободы. С математи-
математической точки зрения колебания систем с конечным числом степеней свободы описы-
описываются обыкновенными дифференциальными уравнениями; колебания распределенных
систем — дифференциальными уравнениями в частных производных. Математическое
описание весьма широкого и наиболее важного для приложений класса распределен-
распределенных систем может быть сведено к бесконечным системам обыкновенных дифферен-
дифференциальных уравнений. Этот класс распределенных систем эквивалентен, таким обра-
образом, системам с бесконечным счетным числом степеней свободы. Приближенная трак-
трактовка последних приводит к системам с конечным числом степеней свободы.
Линейные и нелинейные системы. Принцип суперпозиции. Система называется
линейной, если ее оператор является линейным, т. е. удовлетворяет условию
L(a1u1 + a2u2) = a1Lu1 + a2Lu2 B)
для любых допустимых законов изменения состояния u^t) и и2@ и любых числовых
множителей^ иа2. Если условие B) не выполняется, система называется нелинейной.
Соотношение B) содержит в себе принцип суперпозиции для линейных систем. Пусть
при внешнем воздействии qt(t) поведение системы описывается вектором u^t), а при
внешнем воздействии q2(/) описывается вектором и2@- Тогда при внешнем воздейст-
воздействии qx@ + q2(/) поведение системы будет описываться вектором щ(() + и2@- Прин-
Принцип суперпозиции — одно из важнейших свойств линейных систем — широко ис-
используется как при теоретическом исследовании, так и в технических приложе-
приложениях.
Стационарные и нестационарные системы. Если свойства системы не изменяются
на данном отрезке времени, то систему называют стационарной на этом отрезке.
Отрезком времени, в частности, может быть вся числовая ось (— оо, оо). Если свой-
свойства системы изменяются во времени, то ее называют нестационарной. Процессы,
происходящие в стационарных системах, описываются дифференциальными урав-
уравнениями с постоянными коэффициентами; процессы, происходящие в нестационарных
системах, — дифференциальными уравнениями с переменными коэффициентами.
В литературе встречаются также термины система с постоянными параметрами и
система с переменными параметрами.
Автономные и неавтономные системы. В операторном уравнении A) для автономной
системы следует положить q = 0. Колебательные процессы в автономных системах
могут происходить лишь за счет внутренних источников энергии либо энергии, сооб-
сообщенной системе в виде начального возмущения. Остальные системы называются
неавтономными. Различие между автономными и неавтономными системами условно,
поскольку граница, отделяющая систему от окружающей среды, выбирается при
формулировке математической модели.
Консервативные и неконсервативные системы. Система называется консерватив-
консервативной, если ее полная механическая энергия остается постоянной при колебаниях.
В противном случае система называется неконсервативной. В свою очередь, среди
неконсервативных систем могут быть выделены системы, обладающие определенными
характерными свойствами. Так, система называется диссипативной, если полная
механическая энергия при любом движении соответствующей автономной системы
убывает. Систему называют автоколебательной, если она стационарна и автономна
и если при определенных условиях в ней возможно самовозбуждение колебаний.
Автоколебательные системы характеризуются наличием в них источника энергии
неколебательной природы, причем поступление энергии регулируется движением
самой системы.
18
ВВЕДЕНИЕ. ОСНОВНЫЕ ПОНЯТИЯ
3. КЛАССИФИКАЦИЯ КОЛЕБАТЕЛЬНЫХ ПРОЦЕССОВ
Свободные колебания. Колебания, которые совершаются при отсутствии перемен-
переменного внешнего воздействия и без поступления энергии извне, называются свободными
колебаниями. Они происходят за счет первоначально накопленной энергии, величина
которой определяется перемещениями и скоростями, заданными системе в некоторый
на4альный момент времени. Свободные колебания могут происходить лишь в авто-
автономных системах.
Вынужденные колебания. Колебания, которые вызываются переемнным внешним
воздействием, называют вынужденными колебаниями. Они характерны для неавто-
номьых систем.
Параметрические колебания. Колебания называют параметрическими, если они
вызываются изменением во времени параметров системы. Такие колебания возможны
лишь в нестационарных системах.
¦ Автоколебания (самовозбуждающиеся колебания). Колебания называют самовоз-
самовозбуждающимися или автоколебаниями, если они возникают и поддерживаются от
источника энергии неколебательной природы, причем этот источник включен в сис-
систему. Поступление энергии регулируется движением системы. Автоколебания воз-
возможны лишь в неконсервативных стационарных системах. Часто под автоколеба-
автоколебаниями понимают установившиеся колебательные процессы, которые поддерживаются
источниками энергии неколебательной природы; при этом параметры установившихся
автоколебаний в существенной степени определяются нелинейными свойствами
системы.
В колебательных системах возможны процессы смешанного характера, которые
представляют собой результат наложения свободных колебаний, колебаний, воз-
возбуждаемых внешними воздействиями, параметрически возбуждаемых колебаний
и колебаний, возбуждаемых внутренними источниками энергии.
4. КИНЕМАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЕРИОДИЧЕСКИХ
КОЛЕБАТЕЛЬНЫХ ПРОЦЕССОВ
Дадим кинематическое описание колебательных процессов для случая, когда
процесс характеризуется одной скалярной переменной u(t). Пусть эта переменная —
перемещение; тогда ее первая производная по времени — скорость и вторая произ-
производная — ускорение.
Рис. 2. Реализация периодического процесса ы(<) с периодом Т
Периодические колебания. Колебания называются периодическими, если любые
значения колеблющейся величины повторяются через равные отрезки времени. Более
точно, колебания называются периодическими, если существует такое число Т, что
для любого t выполняется условие (рис. 2) u(t + Т) = u(t). Наименьшее из этих
значений называется периодом колебаний. Обозначим его через Т. Величина, обратная
периоду колебаний, называется частотой колебаний: f = \/T. В технике период
колебаний обычно измеряется в секундах; частота f, следовательно, имеет размер-
КИНЕМАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ
19
ность с. В теоретические формулы входит величина
_ ,_2л_
Т '
C)
называемая угловой (циклической) частотой. Она также измеряется в с1. Эта частота
равна числу периодов колебаний, которые укладываются на отрезке времени продол-
продолжительностью 2л с. Необходимо остерегаться смешения частот / и ш. Частоту /
обычно измеряют в герцах (Гц). Для угловой частоты наряду с размерностью с часто
используют размерность рад/с.
Гармонические колебания. Простейшим (и наиболее важным) видом периодических
колебаний являются гармонические (синусоидальные) колебания, при которых колеб-
колеблющаяся величина изменяется во времени по закону
u(t) = A sin М+ф) D)
Здесь А, со, ф — постоянные параметры. Параметр А равен наибольшему значению
колеблющейся величины и называется амплитудой гармонических колебаний или
просто амплитудой. Постоянный параметр ф называется начальной фазой колебаний,
Рис. 3. Круговая диаграмма
Для простых гармонических
колебаний
Рис. 4. Круговая диаграмма
для суммы двух гармониче-
гармонических колебаний
у i
0
А j
А
\
А
X
а аргумент cat -f- ф называется фазой колебаний в момент времени t. Параметр со
является угловой частотой. Период гармонических колебаний выражается через
угловую частоту:
Для наглядного представления гармонических колебаний можно использовать
круговую диаграмму (рис. 3). Для этого на плоскости вводится вектор длиной А,
который вращается с постоянной угловой скоростью, равной со (отсюда происходит
термин угловая скорость). Начальное положение вектора задается углом ф. Проекти-
Проектируя конец вектора на вертикальную ось, получим закон движения в форме D).
Скорость при гармонических колебаниях
а ускорение
_du_
~ dt
d2u
IF"
(л)A COS
— оА4 sin
F)
G)
Таким образом скорость v{t) и ускорение w(t) при гармонических колебаниях
также изменяются во времени по синусоидальному закону с той же частотой, что и
перемещение u(f). Амплитуды скорости и ускорения равны соответственно соЛ и шМ.
В технической литературе перемещение, скорость и ускорение при колебательном
движении называют соответственно виброперемещением, виброскоростью и вибро-
ускорением.
20 ВВЕДЕНИЕ. ОСНОВНЫЕ ПОНЯТИЯ
Часто удобнее пользоваться следующей записью гармонических колебаний:
и (t) = A cos(co^+i|3), (8)
где вновь введенная начальная фаза т|з связана с фазой <р в формуле D) соотношением
ф = ф—— Иногда начальная фаза вводится с противоположным знаком.
Сумма двух гармонических колебаний с одинаковыми частотами будет гармони-
гармоническим колебанием с той же частотой:
/J1cos«^ + <42cos (Ы-\-ty) = A cos {a>t-\-y). (9)
Амплитуда А и фаза у результирующих колебаний могут быть найдены, например,
из круговой диаграммы (рис. 4):
Комплексное представление гармонических колебаний. Формула Эйлера
' A1)
(i — мнимая единица) дает удобную интерпретацию закона гармонических колебаний
D) на комплексной плоскости. Так, используя формулу A1), представим выражение
D) в виде
ц=Л sin (cof-f <p) = Im [Aeiiai+4"]. A2)
Это тождество соответствует интерпретации гармонических колебаний при помощи
круговой диаграммы (см. рис. 3).
Возможны другие варианты комплексного представления гармонических колеба-
колебаний. Например, закон колебаний в форме (8) получается из комплексного представ-
представления
и = A cos (<о/ + ф) = Re [Ael <">'+$>]. A3)
В формулах A2) и A3) амплитуда А является действительным числом. Наряду
с действительной амплитудой используются также комплексные амплитуды, равные
в зависимости от способа задания гармонических колебаний Ae'f или Ае'^. Рассмот-
Рассмотрим, например, выражение и = Re (Acelu>l), где Ас — комплексное число, действи-
действительная и мнимая части которого равны соответственно Аг и Л;. Тогда с учетом выра-
выражения A1) приходим к формуле (8), причем амплитуда и начальная фаза равны
соответственно
A=y~Af+A>=\Ae\; tg* = -^-. A4)
Полигармонические колебания. Следующий вид периодических колебаний — это
полигармонические колебания. Полигармоническими называют колебания, которые
могут быть представлены в виде суммы двух или более гармонических колебаний
с частотами (периодами), находящимися между собой в рациональном соотношении.
Примером может служить колебательный процесс
и @ = А1 coscoj^-f- Л2созш2^. A5)
который является суммой двух гармонических процессов типа (8). Существенно, чтобы
отношение частот щ1щ было рациональным числом. Пусть а>1 и ш2 выражаются через
некоторую частоту со так, что и>1 = ти>, со2 = п(Л- гДе тип — целые числа, причем
КИНЕМАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ
2!
mjn _ несократимая дробь. Тогда сумма A5) будет периодической функцией с пери-
периодом 2я/со.
Ряд Фурье для периодического процесса. В общем случае периодические функции
с периодом Т могут быть представлены в виде ряда Фурье:
u(t)=-y-ао-\- У а k cos k at + У bits
A6)
k= i
A,
Этому разложению соответствует представление периодических колебаний в виде
суммы гармонических колебаний с частотами, кратными основной частоте ш = 2п/Т.
Для представления функции u(t) в форме A6) она должна удовлетворять условиям
Дирихле, т. е. быть ограниченной и иметь конечнсе число максимумов, минимумов
и точек разрыва первого рода на любом
конечном интервале.
Коэффициенты а0, аъ аъ ..., Ьъ Ь2, .
называются коэффициентами Фурье. Коэф-
Коэффициент — аа характеризует среднее зна-
значение колеблющейся величины; коэффи-
коэффициенты flj и t1 — компоненту движения
с основной частотой со. Эта компонента
называется первой или основной гармони-
гармоникой колебательного движения. Компонен-
Компоненты движения с частотой ke>, где k > 1,
называются высшими гармониками, а чис-
число k — номером гармоники. Ряд Фурье
для колебательного процесса может быть
как бесконечным, так и конечным. Так,
колебательный процесс A5) содержит
лишь две гармоники: та и fiw.
Совокупность частот гармонических составляющих, расположенных в порядке
их возрастания, называется частотным спектром данного периодического
процесса. Каждой частоте соответствуют амплитуда Ад, и начальная фаза ср^:
О
Uz CJj
Рис. 5. Амплитудный спектр колебательно-
колебательного процесса
bk
A7)
Совокупность амплитуд, характеризующих гармонические колебания и располо-
расположенных в порядке возрастания частот, называется амплитудным спектром периоди-
периодического процесса. Совокупность начальных фаз, характеризующих гармонические
колебания и расположенных в порядке возрастания частот, называется фазовым
спектром. Понятие амплитудного спектра проиллюстрировано на рис. 5.
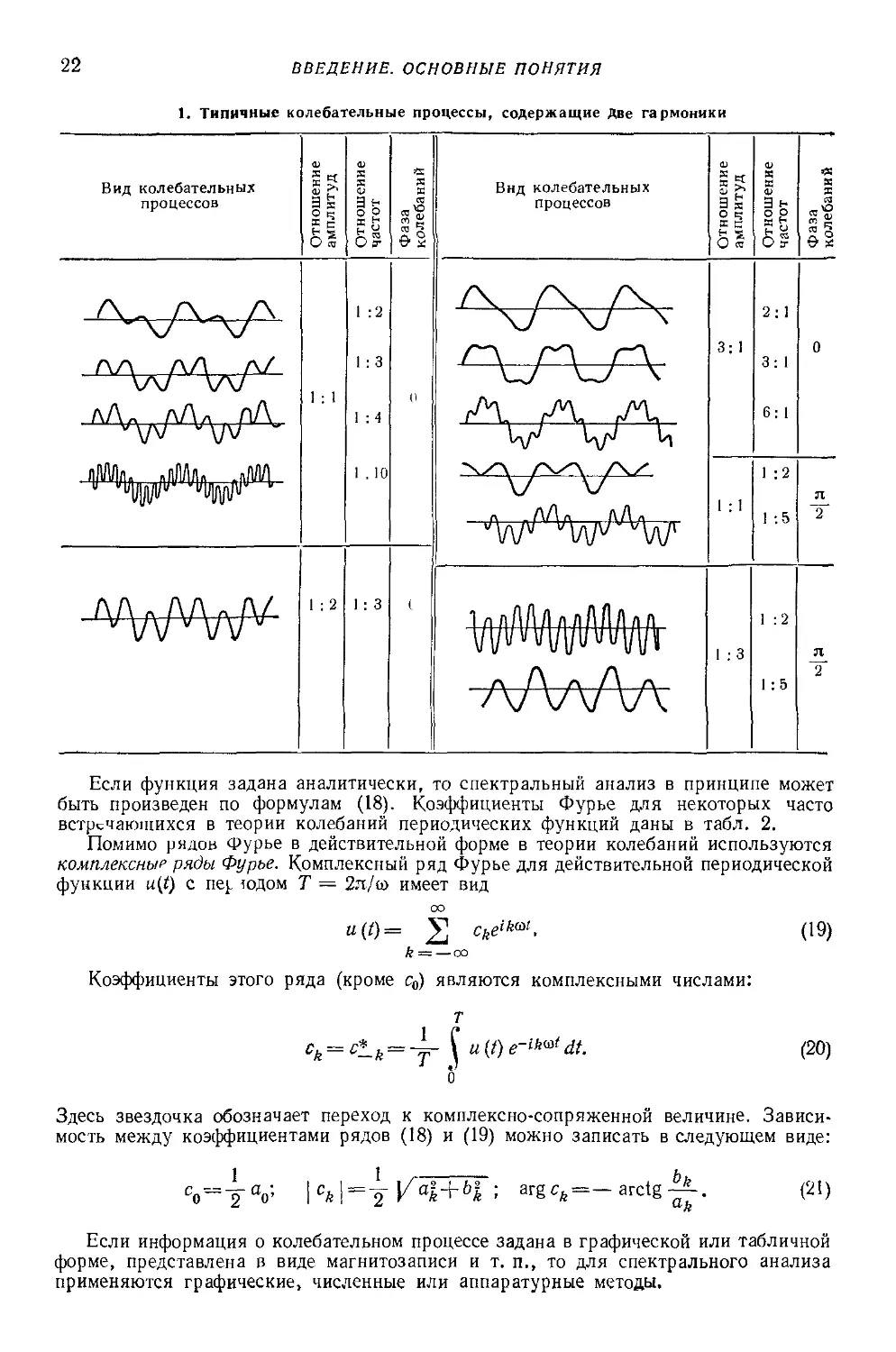
Примеры типичных колебательных процессов, содержащих две гармоники, при-
приведены в табл. 1. Существенно, что вид колебательного процесса зависит не только
от соотношения между частотами и амплитудами гармоник, но и от фазовых соотно-
соотношений.
Спектральный анализ периодических процессов. Определение спектра частот и ко-
коэффициентов Фурье по заданным периодическим функциям называется спектральным
анализом. Коэффициенты Фурье связаны с функцией u(f) следующими соотношениями:
я* = -=- \ u(t)coska)tdt (fe = (
2,
2 С „i
=l, 2,
A8)
22 ВВЕДЕНИЕ. ОСНОВНЫЕ ПОНЯТИЯ
1. Типичные колебательные процессы, содержащие две гармоники
Вид колебательных
процессов
51
Вид колебательных
процессов
Is
О г;
О я
S
is
о?
11
- \у Л/
лД- л
А л пЛ
1 : 1
1 :2
I : 3
1 :4
1 .10
\7
V V и
Л /
V V
1 : 2
1 : 3
3: 1
2:1
3: 1
6:1
1 :1
1 :2
1 :5
1 :3
:2
1:5
Если функция задана аналитически, то спектральный анализ в принципе может
быть произведен по формулам A8). Коэффициенты Фурье для некоторых часто
встречающихся в теории колебаний периодических функций даны в табл. 2.
Помимо рядов Фурье в действительной форме в теории колебаний используются
комплексны'' ряды Фурье. Комплексный ряд Фурье для действительной периодической
функции u{t) с nej- годом Т = 2л/ш имеет вид
"@= 2 cfte'*m'.
k= — оо
Коэффициенты этого ряда (кроме с0) являются комплексными числами:
A9)
~
B0)
Здесь звездочка обозначает переход к комплексно-сопряженной величине. Зависи-
Зависимость между коэффициентами рядов A8) и A9) можно записать в следующем виде:
B1)
Если информация о колебательном процессе задана в графической или табличной
форме, представлена в виде магнитозаписи и т. п., то для спектрального анализа
применяются графические, численные или аппаратурные методы.
КИНЕМАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ
23
2. Коэффициенты Фурье Для некоторых периодических процессов I б (х)
sin пх
Периодическая функция / (/) — f (t + Т)
Прямоугольный импульс
Коэффициенты Фурье
Симметричный треугольный
импульс
Симметричный трапецеидаль-
трапецеидальный импульс
2Г
Полусинусоидальный
импульс
. Го Г. Г 1 /2л Г„
ап-А~Т |бЫ— ~
— I
Срезанная синусоида
- 2 cos^J б (-у
Треугольная форма сигна
L
24
ВВЕДЕНИЕ ОСНОВНЫЕ ПОНЯТИЯ
Численная реализация преобразования Фурье. Чтобы осуществить спектральный
анализ колебательных процессов на ЭВМ, применяют численное преобразование
Фурье. Для этого процесс u(t) подвергается дискретизации, т. е. процесс u(t) на основ-
основном периоде Т задается N + 1 его значениями в моменты времени t0, tu ..., tN (рис. 6).
Обычно выбирают равноотстоящие интервалы h = TIN, причем число N выбирают
0
У
из
т
/
t
Рис. 6. Дискретизация колебательного процесса
таким образом, чтобы частота a>h = 2л/ft = 2nN/T превышала максимальную ожи-
ожидаемую частоту процесса u(t) в 1,5—2 раза. Частота (Од называется частотой среза
или частотой Котельникова—Найквиста. Для определенности примем, что N —
четное число и что t0 — u(t0) = 0. Кроме того, введем обозначения
B2)
Дискретный аналог преобразования Фурье A6) имеет вид
4 = 1
4= 1
B3)
причем для выполнения однозначности преобразования в правой части сохранены
частоты, не превышающие половины частоты среза <Вд. Для коэффициентов дискрет-
дискретного преобразования Фурье имеем формулы
2 V 'V1 2 V
= ~тт- 7 Un\ а — -ту 7 и„ cos ал; аь=*—гт- / и„ cos
а=1 2 а=1 а=1
"aSm
/V
a=i
¦=1, 2, .... yJV-l).
B4)
КИНЕМАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ 25
Алгоритм вычислений содержит следующие операции: вычисление величин 8 ка =
=2nka/N при различных значениях Ьа; вычисление cos Ь ка и sin 6ta; вычисление
выражений «acos6;;a и uasin9 fta; суммирование этих выражений. Этот алгоритм тре-
требует примерно N2 операций сложения и умножения. Объем вычислений можно умень-
уменьшить, используя идею быстрого преобразования Фурье [4].
Понятие о быстром преобразовании Фурье. Идея этого преобразования вытекает
из рассмотрения комплексного аналога формул B3) и B4):
— + 1 )
'2шаН
\ B5)
с*'
Н
1 .,
2niak \
а= 1
При вычислении правых частей в этих форм>лах многократно используются раз-
различные комбинации произведений чисел с# и иа на экспоненциальные функции. Если
N — составное число, т. е. может быть представлено в виде произведения целых
чисел: N = г1-г2 ¦¦¦¦гр, то многократного повторения операций можно избежать.
Количество операций сложения и умножения имеет при этом порядок N (г1 -\- гг-\-
+ ... гр). Обычно берется N = 2Р, что приводит к уменьшению объема вычислений
примерно в N/2p раз. Один из вариантов быстрого преобразования Фурье известен
под названием метода Кули и Тьюки [6].
Стандартные программы для численного анализа Фурье периодических функций.
Для численного анализа Фурье заданной периодической функции в области @, 2л)
в математическом обеспечении ЭВМ серии ЕС предназначена подпрограмма FOR IF
[60], которая осуществляет вычисление заданною числа коэффициентов ряда Фурье
^] sinfet),
k=i
аппроксимирующего заданную периодическую функцию. Обращение к подпрограмме
FOR IF осуществляется следующим образом:
CALL FORIF (FUN, N, М, А, В, IER).
Здесь FUN — имя внешней подпрограммы-функции пользователя, использующейся
для вычисления функции в заданных точках, параметр FUN должен быть описан
оператором EXTERNAL; N — число, определяющее подынтервал таким образом,
что 2N + 1 точка содержится на интервале [0, 2я), т. е. подынтервал равен 2n/BN +
+ 1); М—-максимальный порядок аппроксимирующих гармоник; А —вычисленный
вектор коэффициентов Фурье при косинусах размерности М+ 1: Ао, Аи ..., Ам;
В — вычисленный вектор коэффициентов Фурье при синусах размерности М + 1:
Во, Вг В№; IER — код ошибки. Внешняя подпрограмма-функция FUN должна
быть составлена пользователем.
Для вычисления коэффициентов Фурье периодической функции, заданной табли-
таблицей ее значений с постоянным шагом 2n/BN + 1), предназначена подпрограмма
FORIT [СО]. Обращение к подпрограмме FORIT осуществляется следующим обра-
образом:
CALL rORIT (ENT, N, At, A, B, IER),
26
ВВЕДЕНИЕ ОСНОВНЫЕ ПОНЯТИЯ
где ENT — входной вектор табличных значений функции размерности 2N + 1;
N — число, определяющее подынтервал таким образом, что N + 1 точка содержится
на интервале @, 2л); М — максимальный порядок аппроксимирующих гармоник;
А, В — вычисленные векторы коэффициентов Фурье размерности М+ 1: Ао, А1; ...,
Ам; Во, Bj, ..., Вм; IER — код ошибки. Подпрограмма FORIT не требует использо-
использования никаких других подпрограмм и подпрограмм-функций.
Фигуры Лиссажу для полигармонических процессов. При геометрическом сложе-
сложении двух процессов Ui(t) = А^ sin (pat -f- ф); u2(t) = A2 sin qa>t получаются плоские
кривые, называемые фигурами Лиссажу. Для получения уравнения кривых, описы-
описывающих траекторию движения точки на плоскости (иъ и2), необходимо рассматривать
выражения для Ui(t) и u2(t) как уравнение кривой, заданной в параметрической форме.
В общем случае вид траекторий, описываемых точкой, зависит от соотношений между
частотами, амплитудами и фазами слагаемых процессов.
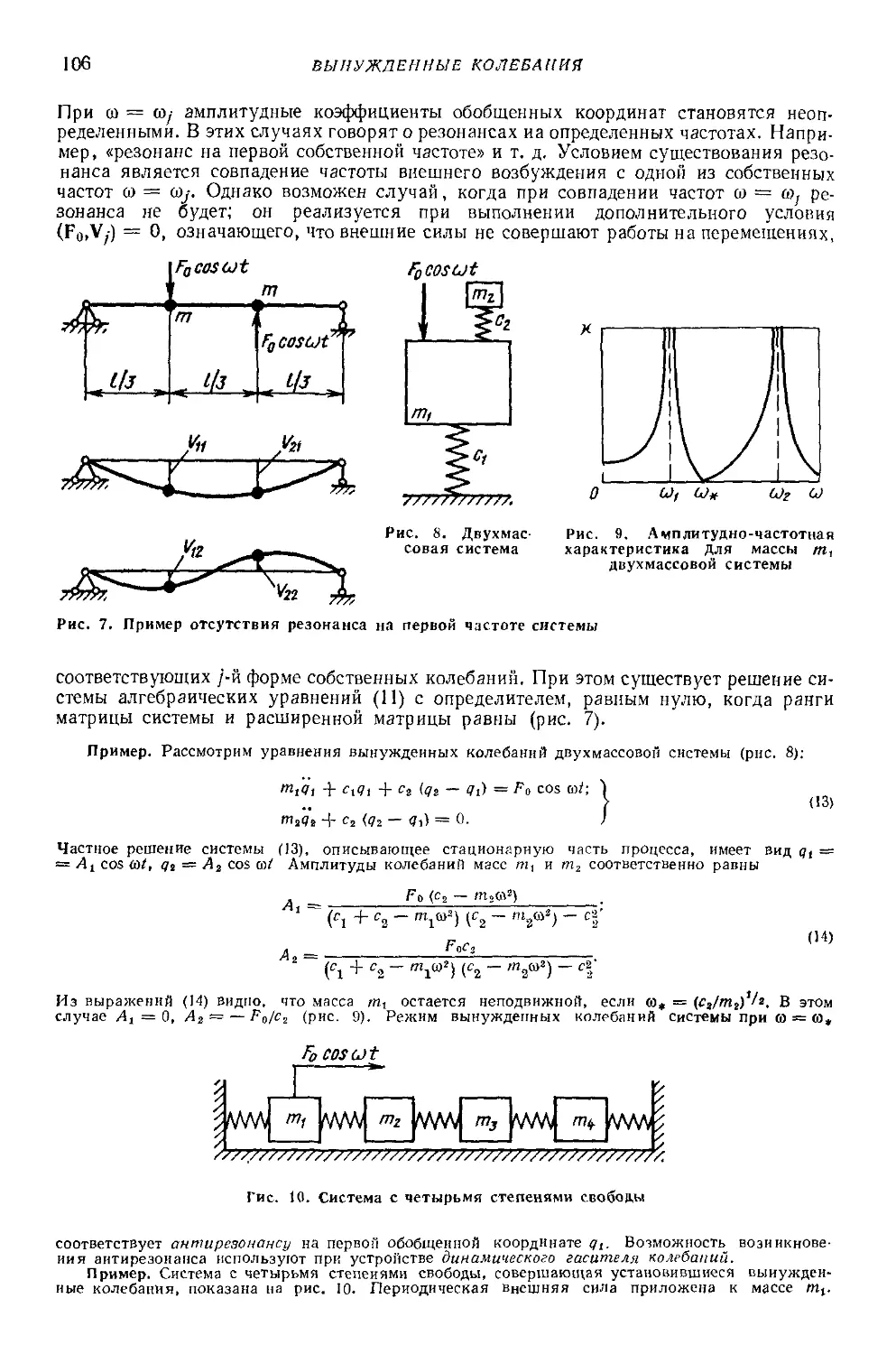
Пример. На рис. 7 показаны траектории, описываемые точкой при различных р, q и ф.
Принято, что Ai = А2= 1, так как изменение соотношений между амплитудами процессов Ui (t)
и ы2 (t) влияет на пропорции фигур Лиссажу, не изменяя общего характера форм кривых.
0
~у^
/
a) Uf
/
у
с
1
е)
Рис. 7. Фигуры Лиссажу:
а — (о, = @2, Ч> = 0; б — а, = <о2, Ф = я/3;
г — 2й>1 = (й2. ф — я/3; 3 — Зш, = 2(й2, ф = 0; е
— 2ю, = <о2. ф = 0;
StUx = 2(о2, ф = я/3
Траектории движения точки могут быть незамкнутыми кривыми; это наблюдается
в случае, когда частоты суммируемых процессов несоизмеримы, т. е. число plq не
является рациональным. По фигурам Лиссажу достаточно просто находят отношения
частот и сдвиг фаз суммируемых процессов [751.
5. КИНЕМАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ НЕПЕРИОДИЧЕСКИХ
КОЛЕБАТЕЛЬНЫХ ПРОЦЕССОВ
Классификация непериодических колебаний. Непериодические колебания могут
быть стационарными и нестационарными. Стационарные (установившиеся) колебания
по определению заданы на отрезке — оо <^ t <[ оо. Их можно определить как коле-
колебания, происходящие около постоянного среднего значения, причем максимальные
КИНЕМАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ 27
и минимальные значения колеблющейся величины, достигаемые на некотором доста-
достаточно большом отрезке времени, относительно мало изменяются при перемещении
этого отрезка по временной оси. Периодические колебания можно трактовать как
частный случай стационарных колебаний.
Среди колебательных процессов, которые нельзя отнести к стационарным, разли-
различают затухающие и расходящиеся колебания. Колебания называют затухающими,
если максимальные по модулю значения колеблющейся величины убывают (не обя-
обязательно монотонно) во времени, причем при t -*¦ оо эти значения стремятся к|
нулю.
Почти периодические колебания. Примером стационарных колебаний, не являю-
являющихся периодическими, могут служить почти периодические колебания. Строгое
определение почти периодических колебаний базируется на понятии почти периоди-
периодических функций.
Колебания называют почти периодическими (квазипериодическими), если для лю-
любого е > 0 можно найти такое число / > 0, что любой интервал оси t длиной / содер-
содержит хотя бы одно значение т, для которого при всех t выполняется неравенство
|к(<+ т) — u(t)\ <| е. Числа т называют квазипериодами почти периодических коле-
колебаний.
Почти периодическим процессом будет, например, процесс, представляющий собой сумму
двух гармонических колебаний, отношение частот которых не является рациональным числом
Так, в случае
и Ц) = А1 cos at + Л2 cos V? Ш B6)
нельзя подобрать такого числа Т, чтобы при любом t выполнялось условие u(t -\-Т) = и (i)
Тем не менее через достаточно большие отрезки времени параметры движения будут с большей
или меньшей точностью повторяться Более того, если аппроксимировать V^2 при помощи
рациональной дроби, например дроби J41/100, то можно построить периодический процесс,
достаточно хорошо воспроизводящий заданный почти периодический процесс при не слишком
больших t
Периодические колебания являются идеализацией колебательных процессов,
которые протекают в природе и технике. Достаточно ввести малые флуктуации час-
готы, фазы или амплитуды, чтобы нарушить строгую периодичность процесса.
Спектральное представление почти периодических колебаний. Большинство почти
периодических колебаний можно представить в виде ряда Фурье. Запишем комплекс-
комплексную форму этого ряда:
оо
«(9 = У) скеШ" . B7)
Здесь cjj — комплексные коэффициенты Фурье. Частоты а>ъ ш2, ... в отличие от ряда
Фурье A9) для периодических функций не находятся между собой в простом кратном
отношении. Представление B7) соответствует колебаниям с дискретным спектром.
Спектр почти периодических функций может быть также и непрерывным.
Почти гармонические колебания. Колебания называют почти гармоническими,
если закон изменения колеблющейся величины может быть представлен в виде
u(t) = A cos(utf — у) B8)
Здесь А (с), (u(t), y(t) — медленно меняющиеся функции по сравнению с функцией
cos cot, т. е. функции, удовлетворяющие неравенствам
dA
dt
da
<а>2;
B9)
Некоторые из этих функций могут быть постоянными. В частности, фазу y(t)
Можно выбрать так, что частота со будет постоянной. В этом случае будем называть
28
ВВЕДЕНИЕ. ОСНОВНЫЕ ПОНЯТИЯ
ее несущей частотой колебательного процесса. В радиотехнике колебательные про-
процессы типа B8) называются модулированными. В зависимости от того, какая из трех
перечисленных величин медленно изменяется во времени, говорят об амплитудной,
частотной или фазовой модуляции.
Биения. Биениями называют почти гармонические колебания, амплитуда A(f)
которых является колеблющейся функцией времени с квазипериодом, большим по
сравнению с квазипериодом 2я/со несущего колебательного процесса. В простейшем
случае биения можно получить при наложении двух гармонических колебаний с близ-
близкими частотами coj и ш2. Пусть частоты удовлетворяют условию
1 — со2
C0)
Применяя формулы (9) и A0), найдем
u(t) = A1 cos CO]/ +
= Аг cos a
2 cos ((oxt—г|)),
где сдвиг фазы т|) = (щ — «2)< в силу условия C0) можно трактовать как медленно
изменяющуюся по сравнению с cosoV функцию времени. Применяя формулу (9),
найдем
u(t) = A (Ocos[co^-y@], C1)
где амплитуда и фаза результирующих колебаний являются медленно изменяющимися
функциями времени:
A (t) =
(wj-co2) t
Аг sin (cot — ю2) *
I + Л2 COS (COj — Ш2) ^ "
C2)
C3)
1>ис. 8. Биения, возникающие при наложении двух
близких по частоте колебаний (Т — период биений)
Изменение u(t) согласно формуле C1) при выполнении условия C0) представлено
на рис. 8. Амплитуда A(t) периодически изменяется во времени с частотой loo, — со„|
и периодом
6. ДРУГИЕ ХАРАКТЕРИСТИКИ КОЛЕБАТЕЛЬНЫХ
ПРОЦЕССОВ
Пиковые значения и размах колебаний. Рассмотрим реализацию некоторого,
вообще говоря, непериодического колебательного процесса. Длина реализации
Т(Т — н& обязательно период колебаний). Абсолютные значения максимума и
ДРУГИЕ ХАРАКТЕРИСТИКИ КОЛЕБАТЕЛЬНЫХ ПРОЦЕССОВ
29
минимума колеблющейся величины на рассматриваемом отрезке Т = [О, Т]
Л,=|тах и (t) I;
t<=T
min u(t)\
называются пиковыми значениями. Разность max и @ — пип и (t) называется
t ет г е г
размахом колебаний на отрезке Т (рис. 9).
iu(t)
Рис. 9. Пиковые значения и размах реализации колебательного
процесса
Осредненные характеристики колебательного процесса. Используя операции осред-
осреднения по времени t на отрезке Т, запишем выражение:
для среднего значения
для среднего абсолютного значения
5
о
и (t) | dt
и для среднего квадрэтического значения
Иср.кв=[-^- ^ "'P
0
C5)
колеблющейся величины u(t) на отрезке Т. Для гармонического процесса, заданного
2 1
в виде D), эти значения равны соответственно нулю, — А и Л (А — амплитуда
я У 2
колебаний).
В приложениях особый интерес представляют средние квадраты и^ кв, которые
обычно оказываются пропорциональными энергии процесса или его средней мощности.
Если процесс u(f) периодический и его можно представить в виде ряда Фурье A9),
то, применяя формулу C5), можно записать
и
ср.'кв = 2
У Л|.
C6)
Здесь принято а0 = 0. Эта формула справедлива также для почти периодических
процессов, представимых в виде обобщенного ряда Фурье B2). При этом в формуле
C5) должен быть проведен предельный переход при Т -*¦ оо.
30 ВВЕДЕНИЕ. ОСНОВНЫЕ ПОНЯТИЯ
Уровень вибраций. Уровень интенсивности колебаний характеризуется соотноше-
соотношением между измеренным значением параметра процесса и некоторым стандартным
значением, которое соответствует нулевому уровню. Поскольку параметры вибраций
могут изменяться на несколько порядков и даже более, то удобно пользоваться лога-
логарифмической шкалой, принимая за уровень вибраций десятичный логарифм отноше-
отношения измеряемой величины к ее стандартному значению. Логарифмическая единица
измерения называется белом (Б), а ее десятая часть — децибелом (дБ). Возрастание
уровня на 1 Б означает, что параметр увеличился в 10 раз, а увеличение на 1 дБ —
в 10 оД xz 1,57 раз. Если измеряется энергетическая величина V (энергия, средняя
мощность и т. п.), то логарифмический уровень (в децибелах)
L = 101g^-, C7)
где Vo — значение, соответствующее нулевому уровню. Если измеряется виброуско-
виброускорение, виброскорость, виброперемещение и т. п., то логарифмический уровень
?- = 20 lg^, C8)
где а0 — начальное значение параметра а, соответствующее нулевому уровню. При
V = const-a2 определения C7) и C8) эквивалентны. За стандартное значение вибро-
виброускорения, т.е. за опорное виброускорение, принимают а0 = 9,81 м-с. Нулевому
уровню акустического давления соответствует значение р0 = 2-10Н-м~2.
Пример. Рассмотрим гармонические колебания с частотой /= 1000 Гц и амплитудой А= 1 мм.
Лмплитуда виброускорашя
а = Bя?J А = F,28-1000J- Ю-3 = 39,4-10= м^С.
Отсюда уровень виброуспарения
Уровень вибраций, отнесенный к полосе частот. Интенсивность вибрационных
воздействий на человека, приборы и другие объекты зависит от частоты. Поэтому
при оценке уровня вибраций целесообразно разбивать ось частот на отрезки (полосы
частот) и вычислять уровни вибраций для каждой полосы в отдельности. Рассмотрим
полосу частот со,, «? со <с сов, где сон и сов — граничные частоты. Будем учитывать
в правой части формулы C6) только те гармоники, частоты которых удовлетворяют
условию со^е[сон, сов). Отсюда найдем средний квадрат величины и для полосы
[сон, сов):
ср, кв ~2
При виброизмерениях выделение из спектра процесса тех составляющих, которые
принадлежат данной полосе частот, обычно осуществляется автоматически введением
в измерительную схему соответствующих полосовых фильтров.
В качестве стандартных частотных полос берут либо декадные полосы, у которых
отношение верхних граничных частот к нижним равно десяти, либо октавные полосы,
у которых это отношение равно двум. В случае необходимости октавная полоса делится
на полуоктавные полосы с соотношением граничных частот, равным }^2, на треть-
октавные полосы с соотношением р 2 и т. д. Частоты стандартных октавных диапазо-
диапазонов приведены в табл. 3.
ОСНОВНЫЕ ТЕОРЕМЫ КЛАССИЧЕСКОЙ МЕХАНИКИ
3. Верхние и нижние частоты стандартных октавных диапазонов (Гц)
Октавы
Первая
Вторая
Третья
Четвертая
Пятая
'в
22
44
83
176
352
'в
44
88
176
352
704
Октавы
Шестая
Седьмая
Восьмая
Девятая
'И
704
1408
2816
5632
'в
1 408
2 816
5 632
11 264
Замечание о многомерных колебательных процессах. Пусть поведение системы
во времени описывается совокупностью параметров tii(f), u2(t) un(t). Введем не-
некоторые понятия, относящиеся к многомерным колебательным процессам. Пусть
) = At sin
) = A2 sin
Если все частоты равны между собой, т. е. Wj = ш2 = ... = ш„, то колебания
называются синхронными (одночастотными). Если, кроме того, равны между собой
все начальные фазы, т. е. <pt = <р2 = ... = фл, то колебания называются синфазными.
Пусть п = 2, cl>i = ш2, ф2 = фх + л. Тогда ux(t) = А± sin (w^ + фх); u2(f) =
= —А2 sin (a.j + фх). Такие колебания называются антифазными.
Глава II
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ КОЛЕБАТЕЛЬНЫХ СИСТЕМ
С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
1. ОСНОВНЫЕ ТЕОРЕМЫ КЛАССИЧЕСКОЙ МЕХАНИКИ
В настоящей главе изложены методы математического описания механических
систем с конечным числом степеней свободы. Существование аналогий между матема-
математическим описанием механических, электрических и тому подобных систем позволяет
переносить результаты, сформулированные для механических систем, на системы
иной природы.
Уравнения динамики системы материальных точек. Рассмотрим систему N мате-
материальных точек с массами тъ тг, ...,mN (рис. 1). Радиус-вектор массы /л,- относи-
относительно некоторой инерциальной системы координат Охуг обозначим через г; (; =
^ 1, ..., /V). Векторы скоростей и ускорений обозначим соответственно через \; и w,.
32
СИСТЕМЫ С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
Внешние силы, характеризующие взаимодействие системы с окружающей средой,
обозначим через F(<f) (/ = 1 N). Внутренние силы, т. е. силы взаимодействия между
точками системы, обозначим через Fy/,, где первый индекс указывает номер массы m/t
на которую действует сила, второй индекс — номер массы т^, со стороны которой эта
сила действует. Всюду в дальнейшем полагаем, что справедлив третий закон Ньютона
г /к — г к] • \1)
Главный вектор всех внутренних сил, действующих на /-ю массу, обозначим через
F*''. Третью группу сил образуют реакции связей, т. е. силы, действие которых на
систему эквивалентно действию рас-
рассматриваемых связей. Главный век-
вектор всех реакций, действующих на
(е) массу mJt обозначим через R/.
(е) Уравнения динамики системы
г ¦ т(е) материальных точек имеют вид
F}
гШ Fi
а)
(/=1, 2,
Л).
B)
Эта система уравнений не яв-
является замкнутой, поскольку со-
содержит неизвестные реакции свя
зей.
Классификация связей. Связи
описываются при помощи равенств
и неравенств относительно коорди-
координат и скоростей точек, образующих
систему Различают связи удержи
воющие, условия которых выра-
выражаются в виде равенств, и неудер-
живающие, условия которых за
писываются в виде неравенств.
Уравнение удерживающей связи, наложенной на движение системы, имеет вид
f(*V Г2 ГМ> VV V2' - V)-0 C)
Связь называют стационарной (склерономной), если время t не входит явно в урав-
уравнение связи; в противном случае она нестационарная (реономная). Связь называют
геометрической, если она накладывает ограничения только на положение (на коор-
координаты) точек системы; в уравнение геометрической связи не входят векторы скоро-
скоростей. В противном случае ее называют кинематической или дифференциальной. Связь
называют голономной, если она является геометрической или интегрируемой диффе-
дифференциальной связью, т. е. уравнение связи может быть приведено к виду
Рис. I. Система Л' материальных точек
f(rv
'Л"
О=о.
D)
Неинтегрируемые дифференциальные связи называют неголономными.
Малые перемещения точек системы, совместимые с уравнениями связей, называют
виртуальными или возможными перемещениями системы. Они обозначаются через
Ьгъ бг2 бгуу. Связь называют идеальной, если работа ее реакции на любых вирту-
виртуальных перемещениях равна нулю. Если все связи, наложенные на систему, идеальны,
то для любых виртуальных перемещений системы будет выполняться условие
R,.6r,
E)
В дальнейшем будем полагать все связи удерживающими и голопомными.
ОСНОВНЫЕ ТЕОРЕМЫ КЛАССИЧЕСКОЙ МЕХАНИКИ 33
Замкнутая система уравнений динамики. Пусть на систему наложено s связей,
выражаемых равенствами типа D). Добавляя к уравнениям B) уравнения связей,
получим замкнутую систему
m,w = F(-e)+ FA)+ R,; \
i i I I I i F)
Mrr r2 rN< 0 = ° (/ = '. 2, ... , /V; k = \, 2 s), j
содержащую ЗЛ/ + s неизвестных функций C<У координат материальных точек
системы и s составляющих реакций).
Основные теоремы динамики системы материальных точек. Введем вектор
и псевдовектор (аксиальный вектор)
2 //,
/= 1
Вектор Q называют количеством движения (импульсом) системы, а псевдовектор
К — главным моментом количества движения (кинетическим мочентом, моментом им-
импульса) системы относительно начала выбранной системы координат. Из уравнений
B) следует теорема об изменении количества движения системы
и теорема об изменении главного момента количества движения системы
Здесь F — главный вектор всех внешних сил и всех реакций, действующих на си-
систему, a G — главный момент перечисленных сил относительно начала координат.
В соотношениях (8) и A0) вместо начала координат можно взять любую точку, непо-
неподвижную относительно выбранной системы координат. Существенно, что внутренние
силы, связанные соотношением A), в правые части уравнений (9) и A0) не входят.
Введем скалярную величину
N
называемую кинетической энергией системы. Из уравнений B) следует математическая
формулировка теоремы об изменении кинетической энергии системы:
^=Ц (F<e)+F<!) + R;)'rfr;.. A2)
/ = 1
В правой части уравнения A2) записана работа всех внешних и внутренних сил
и всех реакций связей на элементарных перемещениях йг} точек системы. Если все
связи идеальные, т. е. выполняется условие E), то работа реакций в правую часть
формулы A2) не входит.
Пусть все связи идеальные, а элементарная работа всех внешних и внутренних сил
является взятым с обратным знаком полным дифференциалом некоторой функции
координат:
2 (F<e>+F}'>)-dr;=-<tf/. A3)
/ — 1
2 п/р. Болотина В, В, т. 1
34
СИСТЕМЫ С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОВОДЫ
Функцию U (гь г2, ..., ГдГ) называют потенциальной энергией системы. Из A2
и A3) следует математическая формулировка теоремы о сохранении полной механиче-
механической энергии:
? = Г + (/ = const. A4)
Силы, удовлетворяющие условию A3), называют потенциальными или консерва-
консервативными, а механические системы, для которых выполняется теорема о сохранении
полной механической энергии, называют консервативными.
Принцип Даламбера. Составление уравнений динамики для конкретных механи-
механических систем значительно облегчается, если использовать принцип Даламбера:
Рис. 2. Инерциальная и подвижная системы координат
уравнения динамики механической системы формально совпадают с уравнениями равно-
равновесия этой системы, если к действующим внешним силам, внутренним силам и реак-
реакциям связей добавить фиктивные (даламберовы) силы инерции:
(/ = 1,2 N). A5)
1у = — m)v/;
С учетом A5) уравнения B) принимают вид
N).
A6)
Общее уравнение динамики Даламбера—Эйлера. Уравнения динамики системы
материальных точек и уравнения связей F) эквивалентны следующему утверждению:
движение системы происходит так, что в любой момент времени сумма работ всех
внешних и внутренних сил, реакций связей и даламберовых сил инерции на любых вирту-
виртуальных перемещениях равна нулю. Аналитическая запись этого утверждения имеет вид
2] (Ff+Ff + Rj-hi^-br^O A7)
и называется общим уравнением динамики. Если все связи идеальные, то работа реак-
реакций связей в общее уравнение динамики не входит.
Уравнения динамики относительного движения. Пусть движение системы описы-
описывается в некоторой подвижной (неинерциальной) системе отсчета Охуг. Наряду с этой
системой введем неподвижную (инерциальную) систему 0%ц1, (рис. 2). Движение по
ОСНОВНЫЕ ТЕОРЕМЫ КЛАССИЧЕСКОЙ МЕХАНИКИ 35
отношению к подвижной системе отсчета будем называть относительным, движение
по отношению к неподвижной системе — абсолютным. Движение подвижной chctjmu
отсчета по отношению к неподвижной системе называется переносным. Движение мате-
материальной точки ту в системе отсчета Охуг будем характеризовать радиус-вектоосм
г и относительным ускорением w'^. Абсолютное ускорение
w( = wf + wf -f- wjc\ A8)
где w^'и w'c' —соответственно переносное и кориолисово ускорения.
С учетом выражений B) и A8) уравнения динамики относительного движения
принимают вид
m/Wy>= ?f + Ff + R,+ if + if (/ = 1, 2, ... , N), A9)
где в правой части стоят переносные и кориолисовы силы инерции, приложенные
к массе mf.
](«) = _ m.w(.«); i<c> = _ m.w(c). B0)
Принцип Даламбера для относительного движения формулируется следующий
образом: уравнения динамики для относительного движения формально совпадают
с уравнениями равновесия этой системы, если к действующим внешним силам, внутрен-
внутренним силам и реакциям связи добавить фиктивные (даламберовы) силы инерции относи-
относительного движения, а также переносные и кориолисовы силы инерции.
Движение системы материальных точек относительно центра масс. Центром масс
называется точка, радиус-вектор которой
N
Д] mirl
N '
B1)
Движение центра масс определяется теоремой, вытекающей из уравнений (9)
и B1): центр масс движется так, как двигалась бы материальная точка, масса которой
равна суммарной массе системы, под действием силы, равной главному вектору всех
внешних сил и реакций, действующих на систему.
Движение в системе отсчета, которая перемещается поступательно вместе с цент-
центром масс, происходит так, что выполняются следующие две теоремы (в аналитической
формулировке): теорема об изменении главного момента количества движения в отно-
относительном движении
%--*' B2)
и теорема об изменении кинетической энергии в относительном движении
N
dT' = Д] ( Ff + ?f + R,.) • dr'j. B3)
Здесь
N
К'=2 (r;xm,v;) B4)
/¦=1
— главный момент количества движения относительно центра масс; Гу и v(' — соот-
соответственно радиус-векторы и скорости материальных точек в системе координат, кото-
которая движется поступательно вместе с центром масс; G' — главный момент всех внеш-
внешних сил и реакций связи относительно центра масс; V — кинетическая энергия си-
системы, соответствующая скоростям материальных точек в движении отно,сительнд
Центра масс.
г*
36 СИСТЕМЫ С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
2. ПРИНЦИП ГАМИЛЬТОНА И УРАВНЕНИЯ ЛАГРАНЖА
ДЛЯ МЕХАНИЧЕСКИХ СИСТЕМ
Обобщенные координаты. Рассмотрим систему N материальных точек с s удержи-
удерживающими голономными идеальными связями (некоторые ограничения на свойства
связей могут быть в дальнейшем смягчены). Движение этой системы описывается
уравнениями F), число которых равно 3jV -f- s. Если при помощи уравнений связей
удастся исключить из системы F) все реакции связей и, кроме того, s координат мате-
материальных точек, то система F) будет сведена к системе 3N — s дифференциальных
уравнений относительно оставшихся координат. Уменьшение числа неизвестных до
3jV — s может быть достигнуто и другим путем — введением некоторых взаимно одно-
однозначных функций координат материальных точек, определяющих в каждый момент
времени положение системы в пространстве с учетом наложенных связей. Эти вновь
введенные переменные, называемые обобщенными координатами системы, обозначают
<?i @> Яг @ °n W" Число обобщенных координат
n = 3W— s B5)
равно числу степеней свободы системы.
Обобщенные скорости и ускорения. Пространства аналитической механики. Про-
Производные qlt <72, ..., Цп от обобщенных координат по времени называют обобщенными
скоростями, а вторые производные q\, g2,..., qn— обобщенными ускорениями. Обобщен-
Обобщенные координаты однозначно определяют положение всех точек системы в каждый мо-
момент времени, т. е. конфигурацию системы. Пространство п измерений, элементами
которого являются совокупности обобщенных координат
<7 = (?„ <ь ... , qn), B6)
называют пространством конфигураций (конфигурационным пространством). До-
Дополняя пространство конфигураций временной осью, получим (п + 1)-мерное про-
пространство переменных qlt q2, ..., qn; t, которое называют расширенным пространством
конфигураций. Пространство 2/г измерений, элементами которого являются совокуп-
совокупности обобщенных координат и обобщенных скоростей
u = (qlt q2, ... , qn; qlt q2, ... , qn), B7)
называют пространством состояний. Простейшим примером пространства состояний
может служить плоскость (q, q) для системы с одной степенью свободы. Эту плоскость
называют фазовой плоскостью.
Вариационный принцип Гамильтона (общий случай). Общее уравнение динамики
Даламбера—Эйлера является вариационным принципом механики, выраженным в
дифференциальной форме. Важнейшим интегральным вариационным принципом
аналитической механики является принцип Гамильтона, который может быть выведен
из общего уравнения динамики. Пусть все связи, наложенные на систему, — идеаль-
идеальные. Уравнение A7) принимает вид
^(F^+Fj'l + I^.er^O. B8)
/= 1
Рассмотрим движение системы на некотором отрезке времени (^0, t{). При этом
истинном движении в каждый момент времени удовлетворяются как уравнения дви-
движения, так и уравнения связей. Наряду с истинным движением рассмотрим совокуп-
совокупность бесконечно близких движений, для которых уравнения связей удовлетворены
(в силу выбора обобщенных координат), а уравнения движения не удовлетворяются.
Эти движения будем называть смежными. Соответствующие приращения обобщенных
координат будем называть вариациями обобщенных координат и обозначать 8<7ъ bq2,
..., 6qn. Существенно, что при вычислении этих вариаций время t не варьируется, т. е.
смежные конфигурации должны удовлетворять уравнениям связей в тот же момент
времени (эта оговорка имеет значение только для нестационарных связей). Вариации,
ПРИНЦИП ГАМИЛЬТОНА И УРАВНЕНИЯ ЛЛГРАНЖА
37
удовлетворяющие поставленному условию, называют изохронными. На концах вре-
временного отрезка (t0, ti) движение варьировать не будем, т. е. в моменты времени t0
и tt все bqj = 0. Введенные представления проиллюстрированы на рис. 3, где пока-
показаны истинная и смежные траектории в расширенном пространстве конфигураций для
случая, когда п = 2.
Из уравнения B8) следует Ч
утверждение: истинное движение
системы происходит так, что
при любых изохронных вариа-
вариациях, обращающихся на концах
отрезка (t0, tx) в нуль, выпол-
выполняется условие
= 0 B9)
to
Здесь 8Т — вариация кинетиче-
кинетической энергии системы, т. е. при-
приращение кинетической энергии
при отклонениях от истинного
движения; б'Л — сумма работ
всех внешних и внутренних сил
системы на вариациях &qlt 6q2,
..., qbn (штрих в б'Л поставлен
для того, чтобы подчеркнуть, что б'Л не является, вообще говоря, вариацией
некоторой функции Л).
Знак вариации в первом члене подынтегрального выражения B9) может быть
вынесен за знак интеграла. В результате получаем соотношение
Рис. 3. К формулировке принципа Гамильтона
to
C0)
которое выражает вариационный принцип Гамильтона, сформулированный при отно
сительно общих предположениях о характере действующих на систему сил и о харак-
характере связей.
Существенно, что кинетическая энергия Т и виртуальная работа б'Л, входящие
в соотношения типа C0), должны быть выражены через обобщенные координаты и ско-
скорости. В частности, выражение для виртуальной работы имеет вид
б'Л =
Q,6q,,
C1)
где коэффициенты Q,{qi, q2 qn'< <7i> Ч\ Яп'< 0 при вариациях обобщенных коорди-
координат называют обобщенными силами.
Принцип Гамильтона для консервативных систем. Пусть все действующие на си-
систему внешние и внутренние силы консервативны, так что выполняется условие
б'Л = — bU. C2)
Здесь bU — вариация некоторой функции обобщенных координат U (</j, q2, ..., qn)
называемой потенциальной энергией системы. Тогда вместо соотношения C0) полу-
получаем
б \ (Т — U) dt = 0. C3)
to
Выражение, стоящее под знаком интеграла, называют функцией Лагранжа или
Аагранжианом:
1-T-U, 134)
38 СИСТЕМЫ С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
Соотношение C3) можно записать в виде
h
C5)
Интеграл от лагранжиана по времени, входящий в соотношение C5), называют
интегралом действия. Принцип Гамильтона для консервативных систем может быть
сформулирован таким образом: истинное движение системы под действием консерва-
консервативных сил происходит так, что на любых изохронных вариациях, обращающихся
в нуль на концах отрезка (t0, t^), вариация от интеграла действия обращается в нуль
(или, иначе, интеграл действия принимает для истинного движения стационарное зна-
значение).
Рис. 4. Движение материальной точки по
жесткой сфере
щд\
Рис. 5. Двойной маят-
маятник
Уравнения Лагранжа. Дифференциальные уравнения, соответствующие вариаци-
вариационному принципу Гамильтона, называют уравнениями Лагранжа (второго рода). Сово-
Совокупность уравнений Лагранжа для рассматриваемой механической системы описы-
описывает движение этой системы наиболее экономным образом и является основным рабо-
рабочим аппаратом аналитической механики.
В зависимости от характера ограничений, наложенных на силы и связи, уравнения
Лагранжа могут иметь различный вид. Пусть действующие на систему силы некон-
неконсервативны. Исходя из принципа Гамильтона в форме C0) и учитывая выражения C1),
приходим к уравнениям
дТ
(/ = 1, 2, ... , п)
C6)
Если все силы консервативны, то, применяя принцип Гамильтона в форме C3),
получим
{)W{T-U)=0 °' = 1>2> -•л) C7)
В тех случаях, когда некоторые силы, действующие на систему, консервативны,
целесообразно учесть влияние этих сил через их потенциальную энергию U. Осталь-
Остальные силы войдут в уравнения Лагранжа через обобщенные силы Qj. Такая трактовка
целесообразна, например, если внутренние силы консервативны, а внешние неконсер-
неконсервативны. Тогда в уравнениях Лагранжа вклад внутренних и внешних сил естествен-
естественным образом разделяется:
-^(Г-^ u=h2 п]- C8)
ПРИНЦИП ГАМИЛЬТОНА И УРАВНЕНИЯ ЛАГРАНЖА 39
Примеры составления уравнений Лагранжа. В первом примере рассмотрим движение мате-
материальной точки по жесткой сфере радиуса R (рис. 4). 3d обобщенные координаты примем угол
широты ф и угол долготы ф. Тогда кинетическая анерия Т = m [(r'i)' -\ (Rty sin ф)г]. Вир-
Виртуальная работа силы F, приложенной к материальной точке, 6'А = F R6ff -f F^R sin фб!|), где
Р tl p проекции силы на направления касательных к меридиану и параллели соответ-
твенно. Отсюда 0 „ = ^„R, О* = 'V^ sin Ч>- Лагранжиан просто равен Т. Подстановка выра-
выражений для кинетической энергии и обобщенных сил в уравнение C6) дает
mR (ф — ф2 sin ф cos ф) = F ; mR (ф sin ф +2фг1; )
( ) ^
Во втором примере рассмотрим плоские колебания двойного маятника. Пусть масса маят-
маятника сосредоточена в двух точках (рис. 5). Сила тяжести направлена вдоль оси Ог. Кинети-
Кинетическая энергия системы
Т = -J mi/i4>i + 2" m-> l'i<Pi + 2'1'»Ф1ф2 cos (qu — ф2) -f /?<pl]- C9)
D1)
Силу тяжести можно ввести в уравнения движения либо через обобщенные силы, либо
через потенциальную энергию. Введем силу тяжести через потенциальную энергию
U = mig/! (I —cos ф,) + m2g [/,A — cos<pO + l2 A — соэф,)]. D0)
Подставляя выражения C9) и D0) в уравнения Лагранжа в форме C7), получим
-^ [(m] + m2) /)ф1 + mj/t/гфг cos (ф, — ф,) — m2liU4>i<t2 sin (ф, — ф2)] -
= — («'l + "'г) fi'i sin ф,;
-JJ- 1!'1фа + тА'гф! COS (ф, — фа) + т^/аф^а sin (ф! — фа)] =
= — m2g/2 sin ф2.
Учет диссипативных сил. Диссипативная функция Релея. Процесс рассеяния
(диссипации) механической энергии проще всего учитывается введением сил, пропор-
пропорциональных обобщенным скоростям. В общем случае системы с п степенями свободы
диссипативные силы
п
Q/ = - 2 Mft (/ = 1. 2 n), D2)
А= 1
где bjk — некоторые числовые коэффициенты. Чтобы эти силы действительно описы-
описывали рассеяние механической энергии, необходимо, чтобы их виртуальная работа
почти на всех совместимых со связями перемещениях была отрицательная. Удобнее
говорить о мощности диссипации
^=2 2 bikq,qk. D3)
/= 1 к= 1
Матрицу
(>bu bi2 ... ?
b2i b22 ... btn
Ьп2 ... Ь
называют матрицей коэффициентов диссипации. Если соответствующая ей квадратич-
квадратичная форма мощности диссипации D3) является положительно определенной, то дисси-
диссипация называется полной (в том смысле, что любое допустимое перемещение будет со-
сопровождаться рассеянием энергии). При этом все диагональные элементы матрицы
В. а также все главные миноры, включая определитель матрицы, положительны.
Если же квадратичная форма, соответствующая матрице В, является неотрицатель-
неотрицательной, то возможны движения, не сопровождаемые рассеянием механической энергии.
Знакопеременность квадратичной формы указывает на возможность автоколебаний
в системе.
40 СИСТЕМЫ С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
Диссипативные силы могут быть введены в уравнения Лагранжа либо непосред-
непосредственно (т. е. через обобщенные силы), либо через квадратичную форму
п п
f=4 ^ 2 b'k^k' D5)
которую называют диссипативной функцией Релея
-* "-¦• -¦ D6)
Уравнения D6) содержат диссипативные силы в левых частях.
Циклические координаты. Обобщенную координату, которая не входит явно в
функцию Лагранжа, называют циклической. Пусть в системе с п степенями свободы
г циклических обобщенных координат. Соответствующие им уравнения Лагранжа
имеют вид
п)
и легко интегрируются относительно циклических координат.
Циклические координаты обычно соответствуют монотонным движениям, происхо-
происходящим по инерции, например, равномерному поступательному движению или равно-
равномерному вращению, происходящему в силу начальных условий.
3. РАСПРЕДЕЛЕНИЕ МАСС В АБСОЛЮТНО ТВЕРДОМ ТЕЛЕ
Предварительные замечания. Абсолютно твердым телом называют материальное
тело, в котором расстояние между двумя любыми точками всегда остается неизмен-
неизменным. Тело, не удовлетворяющее этому условию, называют деформируемым телом.
В дальнейшем для краткости абсолютно твердое тело будем называть просто твердым
телом.
Твердое тело является континуумом материальных точек. Поэтому использование
теорем классической механики в применении к твердому телу требует предельного
перехода, в частности, замены суммирования по материальным точкам системы интег-
интегрированием по объему, занятому телом. Распределение массы в теле характеризуется
функцией р (г), равной плотности тела в точке с радиус-вектором г.
Свободное твердое тело имеет шесть степеней свободы. Его движение описывается
шестью уравнениями динамики, в качестве которых можно взять, например, вектор-
векторное уравнение (9), выражающее теорему об изменении количества движения, и вектор-
векторное уравнение A0), выражающее теорему об изменении главного момента количества
движения твердого тела. Поскольку уравнение (9) определяет закон движения центра
масс тела, то в качестве второго векторного уравнения целесообразно взять уравнение
B2), описывающее изменение главного момента количества движения относительно
центра масс. В связи с этим в динамике твердого тела особое значение приобретают
центр масс и распределение массы тела относительно этого центра.
Центр масс твердого тела. Центр масс системы материальных точек вводится со-
согласно формуле B1), которая для твердого тела принимает вид
\ гр (г) dV
D7)
где интегрирование распространено по всему объему V, занятому телом. Запишем
эту формулу в составляющих
$ хр (г) dV $ ур (г) dV j гр (г) dV
V V V
х ; уг = —? ; zr = —7: , D8)
{r)dV ' *с $P(r)dV ' с $()dV
РАСПРЕДЕЛЕНИЕ МАСС В АБСОЛЮТНО ТВЕРДОМ ТЕЛЕ
41
Величины, стоящие в числителях, называют статическими моментами массы.
Во многих случаях тело может быть разбито на части, массы и положения центров
масс которых известны или легко определяются. Пусть V = V\ U V2 U ••• (J У и- Массу
объема Vk обозначим через М^, радиус-вектор центра масс этого объема обозначим
через i> Для центра масс тела
TjM/
D9,
М,
Данные о положении центра масс некоторых однородных тел простейшей геомет-
геометрической формы можно найти в табл. 1. Отыскание центра масс упрощается, если тело
обладает симметрией (как в геометрическом смысле, так и в смысле распределения
массы в теле). Если тело имеет плоскость симметрии, то центр масс лежит в этой пло-
плоскости; если оно имеет ось симметрии, то центр
масс лежит на этой оси. Если тело имеет центр
симметрии, то центр масс совпадает с этим цент-
центром. Поле плотности р (г) должно удовлетворять
при этом соответствующим условиям симмет-
симметрии.
Моменты распределения масс в твердом теле.
Введем систему координат Oxyz, начало которой
совмещено с центром масс тела (рис. 6). Соответ-
Соответствующие оси координат называют центральны-
центральными. Для удобства написания общих формул бу-
будем пользоваться также индексными обозначе-
обозначениями: х = хъ у = хг, г = х3.
Распределение масс в теле может быть опи-
описано как скалярной функцией р (г), так и пос-
последовательностью интегралов
\xi9(r)dV, \
V V
Хг*У
(r)dV,
х,*х
Рис. 6 Распределение маге в
дом теле
твер
Здесь Xj, xk, x/, ... — координаты точек тела, включая повторяющиеся. Эти интегралы
называют моментами распределения масс. Моменты первого порядка — это введенные
ранее статические моменты. Относительно центральных осей эти моменты тождественно
равны нулю.
Для выбранных координатных осей главная информация о распределении масс
в теле содержится в моментах второго порядка
v
=1, 2, 3).
E0)
Моменты второго порядка составляют симметричную квадратную матрицу (/.-^ =
= hj)
/hi 112 Iia\
'81 '32 'зз
Совокупность этих моментов характеризует некоторый тензор второго ранга по отно-
отношению к ортогональному преобразованию системы координат.
42 СИСТЕМЫ С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
1. Положение центра масс, объем и моменты инерции однородных тел
Схема тела и расположение
системы координат
Координата
центра масс
Объем тела
Моменты инерции
Тонкий стержень
Тонкое кольцо
MR';
= MR"
¦ ~ 2 '
Тонкая кольцевая
ппостина
/Не
Тонкая прямоугольная
пластина
!/ 12 "г 12
я треугольная
пластина
РАСПРЕДЕЛЕНИЕ МАСС В АБСОЛЮТНО ТВЕРДОМ ТЕЛЕ 43
Продолжение табл. 1
Схема гела и расположение
системы координат
Координата
центра масс
Объем тела
Моменты инерции
V = abd
_ d
2с "'I
ьг)
У
Чоуговои и.ипиид^
M /„»
12 '
°^ Кругодой тор
(г -радиус крдгоВаео сечений,
R расстояние центра сечения
от центра кольца)
V =
2r-6 j''
• = Ус = 0;
О
1 г~ 5
Полый шар
44
СИСТЕМЫ С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
Продолжение табл. 1
Схема тела и расположение
системы координат
Координата
центра масс
Объем тела
Моменты инерции
Эппипсаид
(ar b, й- попу оси зяяит
V = -=- ziabd
О
'г = Т
- лЯ"
• j,-tmjp
По/гушар
. = 0;
«sine
г„ = 0
Jx= MR':
_ MR'(Q—sin6cos0)
Vc^ 26 ;
MR'(e+ sin 9 cos 6)
26
Сегмент кольцевой
ппостинки
Моменты инерции твердого тела. Сумму диагональных элементов матрицы I
/о=/п + Лм + /эз = $(*? + *§ + *!)р(г) dV E1)
v
называют полярным моментом инерции твердого тела относительно начала координат
(в данном случае — центра масс). Образуем из моментов второго порядка E0) новые
величины
Jik = Jit>ik-lik. E2)
Здесь bjk — символ Кронеккера F,^ = 1, если / = k, и 6/ft = 0, если / Ф k). В развер-
развернутом виде формулы E2) с учетом E1) принимают вид
(г) dV;
(r) dV
E3)
РАСПРЕДЕЛЕНИЕ МАСС В АБСОЛЮТНО ТВЕРДОМ ТЕЛЕ
45
Эти величины называют моментами инерции тела относительно координатных
осей' при эгом моменты Jn, J22 и /зз> равные суммам произведений элементарных масс
а квадраты расстояний от этих масс до осей 0xlt 0x2 и 0х3 соответственно, называют
осевыми моментами инерции. Остальные моменты У12 = /21, J13 = J3l J23 = J32,
содержащие произведения неодинаковых координат, называют центробежными мо-
моментами инерции. Осевые моменты инерции положительные; центробежные моменты
могут принимать положительные, нулевые и отрицательные значения.
Матрица моментов инерции
/ / /
J — I J2\
'•"si
E4)
характеризует (в приближении вторых моментов) распределение масс в твердом теле.
Она является симметричной и положительно определенной.
Технические обозначения для моментов инерции. Возвращаясь к обозначениям
х, у, г, запишем моменты инерции в виде
{r)dV;
« = ./«= $«P (г) dV;
v
уг = j = f угр (г) dV.
E5)
Выражения для осевых моментов инерции отличаются от E3) только обозначени-
обозначениями; для центробежных моментов, кроме того, знаком. В матрице моментов инерции
целесообразно сохранить знак, который содержится в формулах E3), т. е.
1 __ I _ /
•I — | •> у
У*
— J xy — J xz
, -JyA.
E6)
Отказ от этого знака нарушает тензорные свойства моментов инерции.
Тензорные свойства моментов инерции. Перейдем от «старой» системы координат
к «новой» системе 0x'Lx'2x's с помощью ортогонального преобразования. Это
преобразование характеризуется косинусами углов между координатными осями
"/<* = «*(*/•*«). <57)
Формула перехода от моментов инерции J,-^ в системе Ох±хгх3 к моментам инерции
JjK в системе Ох'^х'^х'^ имеет вид
2 S
а = 1 |i = 1
(/, k=\, 2, 3).
E8)
Формула E8) означает, что совокупность моментов инерции относительно коорди-
координатных осей, имеющих общее начало, образует тензор второго ранга.
46
СИСТЕМЫ С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
Формула преобразований E8) позволяет вычислять моменты инерции относительно
осей, полученных из исходных п^тем вращения. Приведем формулы для частного слу-
случая, когда вращение осуществляется относительно одной из координатных осей, на-
например, оси Ох3. Матрица косинусов из выражения E7)
имеет вид
/ cos ф sin ф 0\
Уф = [—sin<p соэф О), E9)
\ 0 0 1/
где ф — угол поворота на плоскости Оххх2 (рис. 7).
Применяя формулы E8), получим
J'n = Ju cos2 ф -f- J2i sin^p — Jl2 sin 2ф;
J'i% = /n sin2 ф -f /22 cos2 ф + 712 sin 2ф;
¦sin
F0)
с. 7. Вращающаяся
система координат
Остальные моменты инерции остаются без изменения.
Некоторые знаки в системе F0) могут не совпадать со
знаками, приводимыми в отдельных руководствах, что
связано как с использованием технических обозначений
E5), так и с выбором правила знаков для ф. В данной книге всюду используется
правая система координат, а знаки псевдоскаляров и псевдовекторов согласованы
с выбранной системой координат.
Главные оси и главные моменты инерции. Оси координат, в которых матрица E4)
или E6) приводится к диагональному виду
0 0
]2 0
0 J
F1)
называют главными осями инерции. Иначе, главные оси инерции — это те, относитель-
относительно которых центробежные моменты инерции обращаются в нуль.
Моменты инерции относительно главных осей называют главными моментами инер-
инерции. Они обычно упорядочиваются по убыванию:
¦¦и
F2)
Главные моменты инерции обладают экстремальными свойствами: момент инерции
Jf является максимальным, а ]3 — минимальным среди всех осевых моментов инерции
относительно осей, проходящих через то же начало координат.
Определение главных осей и главны* моментов инерции сводится к алгебраиче-
алгебраической задаче о приведении матрицы моментов инерции к диагональному виду. Так,
главные моменты инерции равны корням характеристического уравнения
det (J—УЕ)==О, F3)
где Е — единичная матрица. В развернутом виде уравнение F3) имеет вид
У„-У J,
= 0.
F4)
Если положение одной из главных осей известно (например, из соображений сим-
симметрии), то задача нахождения двух других главных осей упрощается. Пусть ось
Ог — главная. Положение двух других главных осей будем характеризовать углом ф
РАСПРЕДЕЛЕНИЕ МАСС В АБСОЛЮТНО ТВЕРДОМ ТЕЛЕ
47
(см. рис. 7). Угол наклона главных осей к оси Ох (в технических обозначениях)
2/,
' ху
Г J
а главные моменты инерции
J
F5)
:у • F6)
Пусть тело обладает геометрической симметрией и симметрией в распределении
масс. Если тело имеет плоскость симметрии, то любая ось, перпендикулярная к ней,
будет главной осью; если тело имеет ось симметрии, порядок которой выше двух, то
одна из главных осей совпадает с этой осью.
Моменты инерции тонких и тонкостенных тел. Рассмотрим тонкое тело (стержень)
с массой на единицу'длины т (s). Здесь s — длина дуги, отсчитываемая вдоль, вообще
Рис. 8. К приближенному вычислению моментов инерции тонких (о) и
тонкостенных (б) тел
говоря, криволинейной оси стержня (рис. 8, а). С погрешностью порядка А2//2 (А —
характерный размер поперечного сечения тела, / — его длина или характерный радиус
кривизны оси) можно записать
Jx='ji(y2 + zi)m(s)ds, F7)
1
где у (s), г (s) — декартовы координаты точек оси тела относительно системы коорди-
координат Охуг. Аналогично вычисляются остальные моменты инерции.
Для плоского тонкого тела (пластины) с массой на единицу срединной плоскости
т (хъ х2) и площадью срединной плоскости Q имеют место приближенные соотноше-
соотношения
Q
Jy= $ *"
й
й
x2)dQ;
F8)
Здесь x (xj, x2), у (xi, x2) — декартовы координаты точек срединной плоскости отно-
относительно системы Охуг; хъ хг — координаты на срединной плоскости (рис. 8, б).
48
СИСТЕМЫ С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
Вычисление моментов инерции. Для тел простейшей формы моменты инерции опре-
детяются непосредственным интегрированием по формулам E5), F7) и F8). Данные
об осевых и центробежных моментах инерции некоторых тел содержатся в табл. 1.
Если оси главные, то значения центробежных
моментов инерции не выписываются. Вычисле-
Вычисление моментов инерции составных тел произво-
производят с учетом следующих двух положений:
1) моменты инерции аддитивны по области,
занятой телом, т. е. моменты инерции тела
равны сумме моментов инерции его частей от-
относительно тех же осей;
2) при переходе от центральных осей Схоуого
к произвольным параллельным осям (рис. 9)
моменты инерции преобразуются по формулам
Штейнера
Z I
(
0
Г
J
с
v/
V
\
\
Уо
с
У
JX=J,
= J +аЬМ;
Jцг= Jy
F9)
Рис. 9. К формулам преобразования
моментов инерции при переходе к
параллельным осям
Здесь а, Ь, с — расстояния между осями; М —
масса тела. В формулах F9) использованы тех-
технические обозначения E5) для моментов инерции .
4. УРАВНЕНИЯ ДИНАМИКИ АБСОЛЮТНО ТВЕРДОГО ТЕЛА
Кинематическое описание конечных перемещений твердого тела. Любое конечное
перемещение твердого тела эквивалентно поступательному перемещению вместе с не-
некоторым полюсом с последующим вращением относительно этого полюса (теорема
Шаля). Любое конечное вращение твер-
твердого тела относительно неподвижной
точки эквивалентно вращению относи-
относительно некоторой оси, проходящей
через эту точку (теорема Даламбе-
ра—Эйлера).
В динамике твердого тела движе-
движение тела представляется в виде сово-
совокупности поступательного движения
с центром масс и вращений относи-
относительно центра масс. Для кинематичес-
кинематического описания конечных вращений
обычно используют углы Эйлера.
Способ введения углов Эйлера по-
показан на рис. 10. Рассмотрим три пос-
последовательных вращения системы ко-
координат, «вмороженной» в тело. На-
Начальному положению тела соответствует
система координат О|г|?. Эта система
переводится в положение О|'т\'?' вра-
враРис 10. Введение эйлеровых углов ф,
щением относительно оси UQ на угол
гM (угол прецессии). Затем система
О\'г(^ поворачивается на угол 6 (угол
нутации) относительно оси О|' (оси узлов). В результате система координат пе-
переводится в положение О|"т)"^". Третье и последнее вращение на угол ф (угол
собственного вращения) производится относительно оси Ot," = Ог. Этим последним
вращением определяется конечное ютожение системы координат Охуг.
УРАВНЕНИЯ ДИНАМИКИ АБСОЛЮТНО ТВЕРДОГО ТЕЛА 49
Операции конечного вращения некоммутативны, а тройка углов ср, \р, 6 не обра-
т вектора. Аналитическое описание вращений производят при помощи ортого-
ортогональных матриц. Вектор декартовых координат р = (%, r), Q в система 0|т)^ связан
с соответствующим вектором г = (х, у, г) в системг Охуг соотношением г = Vp, где
G0)
Матрицы, входящие в правую часть выражения G0), описывают три последова-
последовательных вращения на углы г|), б , ф. Эти матрицы имеют специальную структуру. На-
Например,
/ cos ф sin ф 0\
Уф = — sin ф cos ф 0 ].
\ 0 0 1/
Распределение скоростей и ускорений в твердом теле. В отличие от конечных вра-
вращений бесконечно малые вращения и, следовательно, угловыг скорости абсолютно
твердого тела обладают векторными свойствами. По формуле Эйлера скорость любой
точки тела
v = vc + wxr, G1)
где vc — скорость центра масс; г — радиус-вектор рассматриваемой точки, отсчитывае-
отсчитываемый от центра масс; ш — псевдовектор мгновенной угловой скорости тела. Ускорение
в любой точке тела
w = wc + e х г+ш X (<а X г), G2)
где wc — ускорение центра масс; е — мгновенное угловое ускорение. Первый член
в правой части представляет собой ускорение поступательного движения, второй —
тангенциальное ускорение, третий — осестремительное ускорение.
Кинематические уравнения Эйлера. Обозначим проекции вектора ш на подвижные
оси координат Охуг через юх, шу, coz. Связь между этими составляющими и углами
Эйлера дается уравнениями
со д. = \р sin В sin ф + б cos ф;
®y = i\> sin В cos ср — б sin ф; G3)
сог = ф cos 6 + ф
Уравнения динамики твердого тела. Примем за обобщенные координаты тела три
координаты х^, ус, гс его центра масс и три угла Эйлера ф,^, 6. Движение центра
масс описывается уравнением (9) теоремы об изменении количества движения. Для
твердого тела это уравнение приводится к виду
d"-rr
М — = F G41
где М — масса тела; гс — радиус-вектор центра масс относительно некоторой непо-
неподвижной точки; F — главный вектор активных и реактивных сил, приложенных к
телу. В проекциях на неподвижные координатные оси это уравнение принимает вид
G5)
50
СИСТЕМЫ С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
Еще три уравнения дает векторное уравнение B2) теоремы об изменении момента
количества движения относительно центра масс. Совершая предельный переход в фор-
формуле B4), находим
K=_\'(rxv)p(r)dl/.
v
Отсюда с учетом формул E3) и G1) К = Jo>, где произведение тензора инерции E4)
на вектор угловой скорости to понимается как результат матричного умножения.
В технических обозначениях E5) и E6) это соотношение имеет вид
= J'X(OX —
G6)
К г — — Jix<i>x — J ziftly
z<*>z-
Динамические уравнения Эйлера. Уравнение B2) в системе координат Охуг,
«вмороженной в тело», имеет вид]
Здесь
dK
dK,
dt
XK = G.
dKu dK,
G7)
dt
dt
Подстановка в G7) выражений G6) дает динамические уравнения Эйлера. Обычно
уравнения Эйлера выписывают для случая, когда Oxyz — главные оси инерции:
Jx
J,J ¦
Jz-^ + (Jy-Jx)<
G8)
I
Теорема об изменении кинетической энергии твердого тела. Аналитически теорему
об изменении кинетической энергии A2) применительно к твердому телу можно запи-
записать так:
dr=F-6rc + G-6<p, G9)
где бгс — виртуальное перемещение центра масс; бф — виртуальный угол поворота.
Кинетическая энергия Т — -~ (Jw) • <», или в развернутом виде
T=Y(J*(a** + Jy(uv+J*<°i*-2J'y<o*(Oy-2J*'(u*(u*-2Jy*(Oy@<')- (80)
Частные случаи движения абсолютно твердого тела. Плоскопараллельное движе-
движение твердого тела (рис. 11) описывается системой уравнений
(81)
АНАЛОГИИ В ДИНАМИКЕ
51
где ф — угол поворота тела; Jс — момент инерции тела относительно оси, проходя-
проходящей через центр масс перпендикулярно плоскости движения; 0с — момент всех актив-
активных и реактивных сил относительно этой оси.
У'
Рис. II. Частные случаи движения твердого тела:
— плоскопараллельное; бив — соответственно вращение относительно неподвиж-
неподвижной оси и неподвижной точки
Движение относительно неподвижной оси описывается уравнением
(82)
где ф — угол поворота тела; Jг и Gz — соответственно момент инерции и момент всех
активных и реактивных сил относительно оси вращения Ог.
Движение относительно неподвижной точки описывается уравнениями Эйлера
G3) и G8) с выбором начала координат в неподвижной точке.
Оставшиеся уравнения динамики твердого тела могут быть использованы для
нахождения реакций связей.
5. АНАЛОГИИ В ДИНАМИКЕ.
ЭЛЕКТРИЧЕСКИЕ И ЭЛЕКТРОМЕХАНИЧЕСКИЕ СИСТЕМЫ
Существование динамических аналогий между механическими, электрическими, аку-
акустическими и тому подобными системами основано на формальном сходстве диффе-
дифференциальных уравнений, описывающих колебательные движения этих систем. Вы-
Выводы, полученные путем исследования дифференциального уравнения движения си-
системы, могут быть распространены на динамически аналогичные системы иной при-
природы. Рассмотрим аналогии между механическими системами и электрическими
цепями.
Аналогия «сила — напряжение». Для механической системы с п степенями сво-
свободы кинетическая энергия, потенциальная энергия, виртуальная работа и диссипа-
гивная функция определяются соотношениями A1), A3), C1) и D5).
Рассмотрим гс-контурную электрическую цепь, состоящую из источников напряже-
напряжения е,, активных резисторов R,-^, конденсаторов емкостью Cik и катушек индуктив-
индуктивности Ljlr Ток в /-м контуре
dq.
(83)
52 СИСТЕМЫ С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
где q/ — количество электричества. Энергия магнитного поля такой цепи
(84)
/=1к = \
энергия электрического поля
п п
У -^-Я,Як', (85)
диссипативная функция, характеризующая потери энергии на активном сопроти-
сопротивлении,
п п
Обобщенная сила и диссипативная функция связаны соотношением
О- —Е±- «7)
а виртуальная работа напряжений в электрической цепи
п
SM = ^ и,- б(?;-. (88)
Рассмотренные характеристики механической и электрической систем подобны.
Для составления динамических уравнений электрической цепи могут быть приме-
применены уравнения C6) Лагранжа второго рода (уравнения Лагранжа—Максвелла),
если за обобщенные координаты принять количества электричества q,- (/ = 1, 2 «).
Для механической системы
для электрической
Уравнения (90) выражают второй закон Кирхгофа для электрической цепи: алгебраиче-
алгебраическая сумма 9. д. с. в любом контуре цепи равна алгебраической сумме падений напря-
напряжений на элементах этого контура.
Кинетической энергии механической системы соответствует энергия магнитного
поля, потенциальной энергии — энергия электрического поля, диссипативной функ-
функции — функция Fe и об«~б ценным силам Q/ — э. д. с. ?у.
Уравнения (89) и (90) для системы с одной степенью свободы (п = 1) имеют вид
Q(() (91)
^^eit). (92)
Уравнение (91) описывает вынужденные колебания механической системы с одной
степенью свободы, уравнение (92) — вынужденные колебания в одноконтурной
электрической цепи (рис. 12).
Аналогия «сила — ток» . Для электрической системы с п парами узлов, в которой
за обобщенные координаты выбраны электрические напряжения и/, выражения (84),
АНАЛОГИИ В ДИНАМИКЕ
(85) и (86) имеют соответственно вид
(=1* = 1
п п
2 т^
53
(93)
(94)
2 ^
(95)
Здесь кинетической энергии механической системы соответствует энергия электриче-
электрического поля, потенциальной энергии — энергия магнитного поля, обобщенным силам —
скорость изменения тока.
Уравнения Лагранжа второго рода для электрической системы по аналогии «сила—
ток» выражают первый закон Кирхгофа: алгебраическая сумма токов в узле равна нулю
)e(t)
Рис. 12. Одноконтурная
электрическая цепь
Рис. 13. Электрическая
цепь с одной парой узлов
\L
=±=С
Запишем дифференциальное уравнение электрической цепи с одной парой узлов
(я= 1) (рис. 13):
+ § (96)
В табл. 2 приведены выражения для потенциальной и кинетической энергии, дис-
сипативной функции и обобщенных сил для систем с одной степенью свободы для
различных типов аналогий.
2. Выражения для аналогий «сила — напряжение» и «сила — ток»
Системы и аналогии
Неханическая
Электри ческа я:
«сила — напряжение*
«сила — ток»
Обобщен-
Обобщенная коор-
координата
Q (О
1 it)
и it)
Обобщен-
Обобщенная сила
<? V)
dt
dt
Кинети-
Кинетическая
энергия
\ т'ч'
Потенциаль-
Потенциальная энергия
1А«
Диссипатив-
ная функция
Электромеханические системы. Объединение механической и электрической систем
в общий рабочий блок, в котором преобразование механической и электромагнитной
энергии взаимно обратимо, называется электромеханической системой. Примерами
таких систем могут служить электрические генераторы, громкоговорители, микро-
Фоны, вибраторы и т. п.
54
СВОБОДНЫЕ КОЛЕБАНИЯ КОНСЕРВАТИВНЫХ СИСТЕМ
Пример. Рассмотрим электромеханическую систему (рис. 14)—вибровозбудитель, состоящий из
массы т, установленной на пружинах жесткостью с, демпфера с коэффициентом демпфирования b
и подвижной кагушки, помещенной в однородное магнитное поле с магнитной индукцией В
Катушка имеет индуктивность /„ и активное сопротивление R. На обмотку катушки подается
переменное напряжение е (t) Электрическая цепь системы приведена на рис. 15
Рис. 14. Пример электро-
электромеханической системы
(вибровозбудитель)
Рис. 15. Электрическая
цепь электромеханиче-
электромеханической системы
\e(t)
Введем обобщенные координаты: х (t) — линейное смещение массы пг; q (t) — заряд, соответ-
соответствующий току в цепи. Выражение для кинетической, потенциальной энергии и диссипативной
функции (табл. 2) имеют вид
G =
F =
схК
+ ~ Rq>.
(97)
Обобщенная сила находится по формуле Q = е (О — и 4- Hi. Здесь д! = ВЦ — обобщенная
сила, Действующая на подвижную катушку; / — эффективная длина катушки. Коэффициент
]Л = В1 называют коэффициентом связи; и = цх — индуцированное напряжение а подвижной
катушке. Уравнения Лагранжа (89), (90) можно записать так:
> ~ + ex = iu (/);
(98)
Второе уравнение (98) может быть получено непосредственно из второго закона Кирхгофа,
составленного для цепи (см. рис. 15):
L—
RI
¦-е (О
(99)
С учетом принятых в соотношении (83) обозначений выражение ('99) приводится ко второму
уравнению (98).
Глава III
СВОБОДНЫЕ КОЛЕБАНИЯ КОНСЕРВАТИВНЫХ СИСТЕМ
1. УРАВНЕНИЯ МАЛЫХ СВОБОДНЫХ КОЛЕБАНИЙ
Постановка задачи о малых свободных колебаниях. Рассмотрим механическую си-
систему с голономными стационарными идеальными связями. Все силы, действующие
на систему, являются консервативными, причем энергия всех этих сил входит в потен-
потенциальную энергию системы U (<?!, q2, ..., 7л)- При t <; 0 система находится в положении
устойчивого равновесия. При этом первая и вторая вариации потенциальной энергии
системы удовлетворяют условиям
6(/ = 0, 64/ > 0 A)
т. е. потенциальная энергия системы в положении равновесия обладает изолирован-
изолированным минимумом. Без ограничения общности можно принять, что в положении равно-
УРАВНЕНИЯ МАЛЫХ СВОБОДНЫХ КОЛЕБАНИИ 55
весия i?i = аг = ••• = 9л = О- ЭТ0 всегда может быть достигнуто соответствующим
выбором обобщенных координат.
Пусть при / = О системе дается отклонение от положения устойчивого равновесия и
(или) ее точкам сообщаются начальные скорости. Совокупность этих воздействий будем
называть начальными возмущениями, которые сообщают системе некоторое количе-
количество механической энергии, дополнительное к потенциальной энергии в положении
равновесия. Колебания, происходящие в системе при / > О, представляют собой
свободные колебания, определение которых дано в гл. 1.
Ограничимся рассмотрением таких свободных колебаний, которые описываются
линейными дифференциальными уравнениями. Для того чтобы уравнения движения
были линейными, необходимо, чтобы отклонения системы от положения равновесия
были достаточно малы (что обеспечивается малостью начальных возмущений). Кроме
того, система должна быть такова, чтобы уравнения движения допускали линеариза-
линеаризацию в окрестности положения равновесия. Последнее условие накладывает ограниче-
ограничения на структуру системы, тип связей и свойства действующих сил.
Уравнения Лагранжа для консервативных систем имеют вид
dt \ dq,-
где T — кинетическая, U — потенциальная энергия системы. Для того чтобы урав-
уравнения B) были однородно линейны относительно обобщенных координат и обобщен-
обобщенных скоростей, необходимо, чтобы кинетическая и потенциальная энергии системы
были однородными функциями второй степени (квадратичными формами) соответст-
соответственно обобщенных скоростей и координат. Это условие будет выполнено, если кине-
кинетическая и потенциальная энергии допускают разложения в сходящиеся степенные
ряды по соответствующим переменным, причем эти ряды начинаются с членов вто-
второго порядка.
Кинетическая энергия системы. Инерционные коэффициенты. При малых колеба-
колебаниях относительно положения равновесия qx = q% = ... = qn = 0 кинетическая
энергия
п п
г=4 у у a.kq.qk. C)
2 Li Li '*4'4* v '
/ = 1 к = I
Здесь cijk — постоянные, называемые инерционными коэффициентами. Они удовле-
удовлетворяют условию симметрии а,/, = а^ и образуют симметричную квадратную мат-
матрицу размерностью п. X п:
Эта матрица называется матрицей инерционных коэффициентов или просто инерцион-
инерционной матрицей.
При помощи матрицы А можно представить квадратичную форму кинетической
энергии C) в более компактном виде. Введем обычную операцию умножения матрицы
на вектор (матрицу-столбец) и скалярное произведение двух векторов х и у в п-мерном
пространстве:
п
(х, у) =2 */<//• E)
/= I
С учетом этих обозначений формулу C) можно переписать так:
r = l(Aiq). F)
56 СВОБОДНЫЕ КОЛЕБАНИЯ КОНСЕРВАТИВНЫХ СИСТЕМ
Здесь q — матрица-столбец обобщенных скоростей, т. е.
q= Ь . G)
W
Если ввести соответствующую матрицу-строку (транспонированную матрицу)
qT=(<7i, 4, 4„), (8)
то квадратичная форма кинетической энергии может быть представлена в виде произ-
произведения трех матриц:
T=iqTAq. (9)
Поскольку Т )> О, если хотя бы одна из обобщенных скоростей отлична от нуля,
то квадратичная форма C) и соответствующая ей инерционная матрица А будут поло-
положительно определенными. Исключение составляют некоторые вырожденные случаи,
например, системы с полуцелым числом степеней свободы, для которых квадратичная
форма кинетической энергии может оказаться неотрицательной. Из положительной
определенно:™ квадратичной формы C) вытекает положительность определителя
инерционной матрицы А и ее главных миноров, а также существование обратной мат-
матрицы А.
Потенциальная энергия системы. Квазиупругие коэффициенты. Пусть потенци-
потенциальная энергия системы U допускает разложение в степенной ряд в окрестности поло-
положения равновесия. Так как потенциальная энергия определяется с точностью до
аддитивчой постоянной, то значение этой энергии в положении равновесия можно
принять равным нулю. Линейные члены разложения обращаются в нуль вследствие
первого условия A). Таким образом, разложение потенциальной энергии в степенной
ряд начинается с квадратичных членов. Отбрасывая члены более высокого порядка,
получим
п п
Здесь Суд, — постоянные коэффициенты, равные значениям вторых производных от
потенциальной энергии по обобщенным координатам при q1 = q2 = ... = qn = 0.
Эти коэффициенты называют квазиупругими, а образованную из них матрицу
С1п \
называют матрицей квазиупругих коэффициентов или просто квазиупругой матрицей.
Квазиупругая матрица является симметричной с^/, = с^; и положительно определен-
определенной. Последнее свойство следует из положительности второй вариации от потенци-
потенциальной энергии системы в окрестности устойчивого положения равновесия, т. е. из
второго условия A). Отсюда, в свою очередь, вытекает положительность определи-
определителя матрицы С и всех ее главных миноров, а также существование обратной мат-
матрицы С .
Если по формуле C1) гл. II ввести обобщенные силы, соответствующие потенци-
потенциальной энергии в виде A0), то эти силы окажутся линейными функциями обобщенных
координат:
п
Q/ = - 2 clkqk (/=1, 2 п). A2)
4-1
УРАВНЕНИЯ МАЛЫХ СВОБОДНЫХ КОЛЕБАНИЙ 57
Положительная определенность квадратичной формы A0) в данном случае означает
что при любом малом отклонении от положения равновесия действующие силы будут
стремиться вернуть систему к этому положению. Силы такого типа называют восста-
восстанавливающими. Важный пример восстанавливающих сил — линейно упругие силы.
Термин квазиупругие коэффициенты связан с понятием о линейно упругих силах и соот-
соответствующих упругих коэффициентах.
Квадратичная форма потенциальной энергии может быть записана в более ком
пактном виде, если использовать обозначения G) и A1);
y(Cq, q). A3)
мат-
матЗдесь q — матрица-столбец обобщенных координат. Вводя соответствующую
рицу-строку qT, можно записать
A4)
Уравнения свободных колебаний. Подставляя C) и A0) в уравнение B), получаем
уравнения свободных колебаний линейных консервативных систем
п
2 (a/ft9*+ f/*<?*)—° (/ = '. 2 п), A5)
4 = I
или, в матричных обозначениях D), G) и A1),
A'q + Cq=0 A6)
Если исходная система нелинейна то уравнения A5) описывают малые колеба-
колебания системы относительно положения равновесия. Для получения этих уравнений
следует либо непосредственно использовать малость отклонений от положения равно-
равновесия при составлении уравнений (если последние выводятся из законов динамики),
либо линеаризировать соответствующие нелинейные уравнения, либо аппроксимиро-
аппроксимировать кинетическую и потенциальную энергию системы при помощи квадратичных
форм, коэффициенты котсрых совпадают с коэффициентами уравнений малых коле-
колебаний A5).
Пример. Рассмотрим колебания двойного маятника (см. рис. 5, гл. П). Точные выражения
для кинетической и потенциальн.й энергии даются формулами C9) и D0). Так как
COS ф! = 1 — -д- ф3 + . . . I COS ф2 = i — -^ ф2 -f . . ,
2 l 2 *
COS (фз — <pi) — I — -g- <ф2 — <PiJ2 H- . . . i
аппроксимируем эти точные выражения квадратичными формами
т ,2*2 | 1 /1 • _ • \ 2
i == 7Г "Цмф| "т* ~п~ т$ 1мф( *Т" *^Ф'/ >
1 1 •)
U — "Я* /yj о/ ф2 ' "n" maS \^1фГ "Т" ^-фй/*
Отсюда получаем уравнения свободных колебаний в форме (J5) или A6) о матрицами ннер
Ционных и квазиупругих коэффициентов:
Матрица единичных перемещений (единичных податливостей). Пусть линейная
система поочередно загружается квазистатическими силами Qj, Q2, ..., Qn, вызываю-
вызывающими обобщенные перемещения qt, qa, ..., qn. Обозначим через f,k величину обобщен-
обобщенного перемещения ц} от действия квазистатической обобщенной силы Q^ = 1. Матрицу
/hi fu ••• fm^
111, ••¦ fin
Vni 'л2 ••• Inn'
58
СВОБОДНЫЕ КОЛЕБАНИЯ КОНСЕРВАТИВНЫХ СИСТЕМ
называют матрицей единичных перемещений (единичных податливостей). Перемеще-
Перемещения от произвольного квазистатического загружения
a-
2,
п).
A8)
Матрица единичных перемещений симметрична (fjk = /jy), а соответствующая
ей квадратичная форма — положительно определенная. Из сопоставления A2) и A8)
следует, что матрицы единичных перемещений и квазиупругих коэффициентов явля-
являются взаимно обратными, т. е. F = С.
Составление уравнений свободных колебаний с использованием матрицы единич-
единичных перемещений. Вводя обобщенные даламберовы силы инерции —a^q^ и используя
соотношения A8), получим уравнения свободных колебаний линейной системы
= 0 (j=l, 2 п)
A9)
k=\l=\
или в матричной записи
FAq + q = 0. B0)
Уравнение B0) непосредственно следует из уравнения A6), если последнее умно-
умножить слева на матрицу С" = F, Вместе с тем оно имеет самостоятельное значение
в практике вибрационных расчетов, особенно
там, где упругие свойства системы рассчиты-
рассчитывают методами строительной механики.
Пример Балка с постоянной по длине изгибной
жесткостью EJ (рис. I) несет две сосредоточенные
массы mt и тг. В случае плоских изгибных колебаний
число степеней свободы равно двум. Единичные пере-
перемещения определяют путем «перемножения» соответ-
соответствующих единичных эпюр (рис. 1):
0
тт
MjM2 I Р
EJ 18 ёТ
Рис. 1. Плоские изгибные колебания
балки с двумя сосредоточенными
массами
Ы
0
3' _„
, г*|; 4 Р
122 = ]ТП~ ~ъ TJ
о
Матричные коэффициенты уравнения B0) прини
мают вид
'1 1\
BJ\1 4I \0 т,)'
18 9/
F =
2. СОБСТВЕННЫЕ ЧАСТОТЫ И СОБСТВЕННЫЕ ФОРМЫ КОЛЕБАНИЙ
Собственные частоты. Решение уравнения A6), соответствующее гармоническим
колебаниям с частотой со и начальной фазой %, имеет вид
B1)
Здесь v — постоянный вектор (матрица-столбец), характеризующий соотношение
между различными обобщенными координатами в решении данного вида. Частота
ш и вектор v удовлетворяют матричному уравнению
(С — a>2A)v = 0, B2)
СОБСТВЕННЫЕ ЧАСТОТЫ И СОБСТВЕННЫЕ ФОРМЫ КОЛЕБАНИИ
59
эквивалентному системе п линейных однородных алгебраических уравнений относи-
относительно компонентов вектора v. Условие существования ненулевого решения однород-
однороден системы B2) приводит к характеристическому уравнению
или в развернутой форме
det (С — со2А)=О
— со2а22
= 0.
B3)
B4)
Число положительных корней этого уравнения равно числу степеней свободы
п. Согласно уравнению B1) эти корни представляют собой угловые частоты свобод-
свободных колебаний линейной системы, называемые собственными частотами системы.
Упорядоченную совокупность собственных частот
Wi ^ ш2 sS ... s= ш„ B5)
называют спектром собственных частот (данной системы).
Характеристическое уравнение B3) или B4) называют уравнением собственных
частот. Его можно представить в одной из следующих эквивалентных форм:
det (E-w2C-1A) = 0, det (А-1С-и2Е) =0, det(E — cc2FA)=O. B6)
В развернутом виде последняя форма уравнения имеет вид
П (I
-co2 ? /lftoftl -co2 2]
*= 1 A —
2
1— w2 2]
2
*= i
2
k= 1
*= 1
*=!
= 0. B7)
Собственные формы колебаний. Как уже указывалось, вектор v характеризует
соотношение между обобщенными координатами при колебаниях с частотой со. Каж-
Каждой собственной частоте со; соответствует вектор vj, характеризующий форму колеба-
колебаний системы с этой собственной частотой. Векторы vb v2, ..., \п называются собствен-
собственными формами колебаний или просто собственными формами.
Собственные формы определяются из однородной системы B2) после подстановки
в нее соответствующих собственных частот. Если собственная частота <О; — простой
корень уравнения B3), то ранг системы B2) равен п — 1. Пусть отбрасывание послед-
последнего уравнения системы дает систему п — 1 линейно независимых уравнений. Тогда
для определения компонентов вектора
'vlt\
B8)
получаем систему п — 1 уравнений
(c/ft- M/a/ft) vk
(/=1,2,..., n- 1).
B9)
Форма колебаний определяется при этом с точностью до произвольного постоян-
постоянного множителя.
60 СВОБОДНЫЕ КОЛЕБАНИЯ КОНСЕРВАТИВНЫХ СИСТЕМ
Если собственная частота со/ имеет кратность г, то ранг системы B2) равен п — г.
П>сть переменные занумерованы так, что независимыми оказываются первые а — г
уравнений
2 (с/*-<а/а,*H« = ° 0'=1> 2. - ¦ «"О- C0)
Решение этой системы содержит г произвольных постоянных, которые могут быть
выбраны так, чтобы получить г независимых собственных форм, соответствующих
л-кратной собственной частоте Ш/. Итак, каждой собственной частоте соответствует
собственная форма колебаний. Дополняя спектр собственных частот B5) совокуп-
совокупностью собственных форм
vi, v,,...v,, C1)
образуем спектр собственных колебаний системы.
Свойства собственных частот и собственных форм колебаний. Как следует из урав
нения B2), квадраты собственных частот со2 равны собственным значениям матрицы
А^С, а собственные формы v равны собственным векторам этой матрицы. Поскольку
матрица А~ХС— симметризуемая и положительно определенная, то из известных тео-
теорем линейной алгебры следует.
1) все собственные частоты действительны;
2) собственные формы, соответствующие различным собственным частотам, по-
попарно ортогональны с весом матрицы А, т. е.
v?Avp = 0 (а^р) C2)
В развернутой форме это соотношение имеет вид
п п
2] 2 a;At»,aoftp = 0 (a^P); C3)
/=ik=\
3) собственные формы, соответствующие различным собственным частотам, по
парно ортогональны с весом матрицы С:
v?Cvp = 0 (o^tp) C4)
Запишем это условие ортогональности в развернутом виде:
2 S 0 (a^P); C5)
4) собственные формы vu v2, ..., \п являются линейно независимыми и образуют
базис в n-мерном векторном пространстве Wn.
В случае кратных собственных частот всегда можно провести соответствующую
ортогонализацию линейно независимых векторов; поэтому перечисленные свойства
в полной мере распространяются на кратные частоты.
Обобщенные соотношения ортогональности C2) и C4) имеют энергетический смысл.
Входящие в эти условия билинейные формы аналогичны квадратичным формам кине-
кинетической и потенциальной энергии соответственно. Условие C2) называют условием
ортогональности по кинетической энергии, условие C4) — ортогональности по по-
потенциальной энергии.
3. НОРМАЛЬНЫЕ КООРДИНАТЫ
Нормальные (главные) координаты. Сформируем по столбцам из собственных форм
квадратную матрицу V'
/vu у12 ... vln^
.. vn
НОРМАЛЬНЫЕ КООРДИНАТЫ 61
Преобразование подобия при помощи матрицы V приводит матрицу А-1С к диаго-
диагональному виду, т. е.
V-iA-iCV = diag («?), C7)
а подстановка
q = Vq', C8)
связывающая первоначальные обобщенные координаты с новыми обобщенными коор-
координатами q\, q'v ..., q'n, приводит уравнение A6) к виду
q' + dia?(u)^)q' = O. C9)
Матричное уравнение C9) описывает независимые колебания с собственными ча
стотами a>i, ш2, ..., а>„ относительно вновь введенных обобщенных координат
?и; с-
D0)
Обобщенные координаты системы, которые описывают несвязанные свободные
колебания, называют нормальными (главными) координатами. Нормальными коор-
координатами широко пользуются как при качественном описании колебательных про-
процессов, так и в прикладных вибрационных расчетах. Формула C8), связывающая про-
произвольно выбранные и нормальные обобщенные координаты, в развернутом виде запи-
записывается так:
Матрица преобразования C8) является ортогональной. Формула обратного пре-
преобразования имеет вид
а= 1
В нормальных координатах квадратичные формы кинетической и потенциальной
энергий приводятся к сумме квадратов:
п
-\ 2 ми<?;J- D3)
Свободные колебания, удовлетворяющие начальным условиям. Пусть при t =0
заданы значения всех обобщенных координат и обобщенных скоростей:
q(O) = qo; q(O) = qo D4)
Здесь q0 и q0 — числовые векторы. Общее решение уравнения свободных колебаний
A6) равно сумме п. частных решений, каждое из которых описывает колебания с соб-
собственной частотой ыа и собственной формой va. Представим это решение в виде
Ч @ = 2] va (Са cos u)ae+ Da sin ыа(). D5)
a = l
Постоянные в правой части находят из условий D4) с учетом соотношений ортого-
ортогональности C2) или C4). Например,
Г Чо Ava л ' ЧоАуа ....
Сиа=~ ~Г1 • D6)
ш vAv
v«Ava
62 СВОБОДНЫЕ КОЛЕБАНИЯ КОНСЕРВАТИВНЫХ СИСТЕМ
Эти формулы (как и некоторые последующие, в которых используются разложе-
разложения по собственным формам) можно упростить, если ввести нормированные собствен-
собственные формы, т. е. если выбрать произвольный множитель, с точностью до которого опре-
определяются собственные формы, из условий нормировки
v?Ava = 1 D7)
4. СОБСТВЕННЫЕ ЧАСТОТЫ И СОБСТВЕННЫЕ ФОРМЫ СИСТЕМ
С ОДНОЙ И НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ
Системы с одной степенью свободы. Кинетическая и потенциальная энергии си-
системы равны соответственно
T^jaqt; U = ~cq\ D8)
а дифференциальное уравнение свободных колебаний имеет вид
0 D9)
Собственная частота
(?)''•' E0)
(af)h
где / = с'1 — единичная податливость, соответствующая квазиупругому коэффици-
коэффициенту с.
Пример. Для математического маятника массой т и длиной / имеем
I • 1
Т = -г ml'if1, U = -к- mg/ф2, E1)
где ф — угол наклона маятника относительно положения равновесия. Отсюда a=ml2, c=mgl.
Применение формулы E0) дает
E2)
В виде другого примера возьмем опертую по концам балку длиной I с постоянной изгибной
сткостью EJ Единичная податливость будет (г/D8Я J). Отсюда по формуле E0)
E3)
(af) '> \ ml
Формулы для вычисления собственных частот системы с одной степенью свободы
приведены в табл. 1.
Свободные колебания системы с одной степенью свободы, удовлетворяющие на-
начальным условиям q @) = q0, q@) = q0, описываются выражением
о (Л = о0 cos шН <70 sin oat, E4)
со
которое можно трактовать как частный случай формул D5) и D6).
Системы с двумя степенями свободы. Кинетическая и потенциальная энергии си-
системы равны соответственно
T^—ianql + a^ql + iar^q^ U = i
а дифференциальные уравнения свободных колебаний имеют вид
СОБСТВЕННЫЕ ЧАСТОТЫ И СОБСТВЕННЫЕ ФОРМЫ КОЛЕБАНИЙ
63
1. Собственные частоты систем с одной степенью свободы
(масса упругой системы мала по сравнению с величиной сосредоточенной массы)
Схема системы
Квадрат собственной
частоты
Примечания
EF
Ml
nEd,d2
AMI
Продольные колебания;
F — площадь постоянного попе-
поперечного сечения;
d — диаметр кругового попереч-
поперечного сечения
О Т Ь УХТ/
- ^*'* .1
М
77лр77 Ь
3EJ
Ml'
ЗЕЛ
\2ЕЛ'
•¦ о; + ь)
ЗЕЛ'
Ма'Ь'
3EJ
МЬЧ
3EJ
Изгнбные колебания;
J — момент инерции поперечного
сечения G = const)
МЬЧЦ-~
^ Т ^
16лО A 4
MR2 C +
\bnD
v)
V)
Круговая пластина постоянной
толщины Л;
О,
12A— V») '
V — коэффициент Пуассона
;^амл*-| ' |"
/////////////////У/////
М '
Gd*
G — модуль сдвига; п — число
витков пружины; d — диаметр
сечения витка;
D — средний диаметр пружины
Но
Крутильные колебания;
С?Ур — жесткость поперечного се-
сечения вала; /0 — момент инерции
диска относительно оси системы
(диск абсолютно жесткий)
64
СВОБОДНЫЕ КОЛЕБАНИЯ КОНСЕРВАТИВНЫХ СИСТЕМ
Продолжение табл. I
Схема системы
Квадрат собственной
частоты
Примечания
М
Вертикальные колебания поплав
ка;
р — плотность жидкости; S —
площадь сечения тела А по го
ричоитлли
Колебания столба жидкости в
У-образной постоянного сечения
трубке
Ft
.
~ ~
i
2
—г
1
8A
Ad +Ft/Fa)
F,, Рг — площади поперечного се-
сечения первого и второго сосудов;
Fo — площадь поперечного сече-
сечения соединительной трубки
У////////.
Математический маятник
Движение шара радиуса г по ци
линдрической поверхности радиу-
радиуса R
3 (Я — г)
Движение цилиндра радиуса г
по цилиндрической поверхности
радиуса R
ga
г2
Абсолютно жесткое тело;
г — радиус инерции; С — центр
масс
СОБСТВЕННЫЕ ЧАСТОТЫ И СОБСТВЕННЫЕ ФОРМЫ КОЛЕБАНИИ 65
Составим характеристическое уравнение (уравнение собственных частот)
си — со2аи с13 — со2а1;
с21 — со
или в развернутом виде
(апа22 — а?2)со4 — (аис22
= 0,
— 2а12с12) со2 + с„с22 - с?2 = 0.
E7)
Положительные корни сох и со2 биквадратного уравнения E7) представляют собой
собственные частоты системы. Собственные формы задаются парой векторов
которые можно определить с точностью до постоянных множителей. Для отношения
составляющих t^i/fa и Vvjv-^ этих векторов имеем формулу
2а __.
У1а
2
ша2
= 1, 2).
E8)
Парциальные частоты и диаграмма Вина. Введем параметры
i- ; со = _22_ , E9)
имеющие размерность частоты и совпадающие с собственными частотами системы при
"i2 = a2i ~ 0; Cj2 = с21 = 0. Эти частоты называются парциальными; их введение
соответствует разделению системы на
две подсистемы, называемые парциальны-
парциальными системами. В большинстве случаев
такое разделение допускает механическое
истолкование. Связанность между пар-
парциальными системами может быть инер-
инерционной (через инерционные коэффи-
коэффициенты о12), квазиупругой (через квази-
квазиупругие коэффициенты с12) или ком-
комбинированной. Различают слабую связан-
связанность, при которой побочные элементы
матриц удовлетворяют неравенствам
занность.
Понятие о парциальных системах поз-
позволяет сформулировать некоторые общие
качественные выводы о влиянии парамет-
о
1,0
Рис. 2. Диаграмма Вина
ров системы на ее собственные частоты. Один из выводов можно выразить в виде
неравенств
(OjiSminJWj, cujjJ; ю23=тах jcci], и>ц}, (СО)
где равенство достигается в случае отсутствия связанности между парциальными си-
системами. Неравенства F0) удобны для предварительной оценки собственных частот
На основании данных, относящихся к парциальным системам.
Более подробную информацию дает график (рис. 2), называемый диаграммой
Вина. Штриховые линии на рисунке соответствуют слабой связанности, сплошные
линии •— более сильной связанности. В связанной системе одна из собственных частот
системы всегда меньше, вторая — больше, чем любая из парциальных частот, причем
влияние связанности на частоты будет тем больше, чем связанность сильнее и чем
ближе друг к другу парциальные частоты.
3 п/р. Болотина В, В, т. 1
66
СВОБОДНЫЕ КОЛЕБАНИЯ КОНСЕРВАТИВНЫХ СИСТЕМ
2. Инерционные и квазиупругие коэффициенты (или единичные податливости)
для систем с двумя степенями свободы (собственная масса упругой системы мала
по сравнению с величинами сосредоточенных масс)
Схема системы
Инерционные коэффициенты
Квазиупругге коэффициенты
или единичные податливости
о22 = ml",
ot, = о2! — О
си = mgl -t cti',
<г22 = mgl ! cd'.
/11 =
ЗЯЛ '
On = a2, = 0,
a22 = тг
/12=/..=
есл
g'b'
flu =»i,i
a12 =a2! = 0;
o»2 = m,
a,, = in,
a22 = "i,
o12 = аг, = О
а»Ь'
12EJP
X C/1 — 3/га — 31 b' + ab*)
c, + e;
'12 = t.i =-
'//////////////У,
a,, = m,,
o22 = тг,
я„ = а2, = 0
022
Й21
(•/1. ^2 — моменты инерции
дисков при крутильных коле-
колебаниях)
СОБСТВЕННЫЕ ЧАСТОТЫ И СОБСТВЕННЫЕ ФОРМЫ КОЛЕБАНИЙ 67
Продолжение табл 2
Инерционные коэффициенты
Схема системы
Квазиупругие коэффициенты
или единичные податливости
а22 = - ml'.
«и = °2i — 2 ml1
(масса стержней т равномер-
равномерно распределена по длине I)
С12 = ^i - 0.
а
»m< (
с
Ь
ь
1
ау2 = а2, = О,
а'6»
х
P - 3; (а + Ь) \- 2а1)];
а3
~з~е7;
а' Bа + с)
6EJ
3! J
Сведения об инерционных и квазиупругих коэффициентах. Формулы для собствен-
собственных частот систем с двумя степенями свободы, как правило, слишком громоздки.
Поэтому ограничимся тем, что приведем в табл. 2 выражения для инерционных и ква-
квазиупругих коэффициентов. Там, где это целесообразно, вместо квазиупругих коэф-
коэффициентов даны соответствующие единичные податливости В табл. 3 содержатся
также некоторые данные для систем с тремя и большим числом степеней свободы.
Свободные колебания систем с циклическими координатами. Понятие о цикличе-
циклических координатах было дано в гл. II. Приведенная выше теория свободных колебаний
в линейных консервативных системах неприменима к системам, содержащим цикличе-
циклические координаты. В таких системах квадратичная форма потенциальной энергии A3)
не будет содержать членов с циклическими координатами. Поэтому в положении
q = 0 потенциальная энергия не будет обладать изолированным минимумом, т. е.
не будут выполнены условия A) Между гем системы с циклическими координатами
часто встречаются в технике. Примером могут служить свободно вращающиеся в опо-
опорах роторы (циклическая координата — >гол поворота ротора как твердого тела),
неуправляемые летательные аппараты (если не учитывать влияния внешних сил, то
все шесть обобщенных координат, описывающих движение аппарата как твердого
тела, будут циклическими).
Вообще, циклические координаты описывают монотонные, происходящие вследствие
инерции процессы. Если по отношению к остальным обобщенным координатам потен-
потенциальная энергия системы является положительно определенной формой, то измене-
изменение этих координат во времени является колебательным процессом. Для вибрацион-
вибрационных расчетов наибольший интерес представляют нециклические координаты. Из
Уравнений движения можно исключить все циклические координаты. Но можно также
пользоваться уравнениями B2) и B3). При этом циклическим координатам соогвег-
3*
68
СВОБОДНЫЕ КОЛЕБАНИЯ КОНСЕРВАТИВНЫХ СИСТЕМ
8. Матрицы инерционных и квазиупругих коэффициентов (или единичных гтодатливостей)
для систем с тремя, и ббльшим числом степеней свободы
Схема системы
Инерционные коэффициенты
Квазиупругие коэффициенты
(или единичные податливости)
¦¦ diag (m,, m2, m,)
3 _1
С =с | —1 2
О -] 3,
V/////////////////////
= тЕ
А =
/4 1 1
\ 1 1 О
\1 0 1
2сЕ
= mg; diag D, 1, 1)
A = diag (mi, m2, m5)
F —
/77f FT?2 IV3
A = diag (mi, m2, m3)
(т, +¦ т2 + т3) Мг (т2 -f ma)
А = | /,/2 (яг2 + т3) /| (т2 + т3)
nil + тг + т3) ^1 О О
С = g ( 0 (т2 + т3) /, О
О 0 т3/.
ВАРИАЦИОННЫЕ ПРИНЦИПЫ
69
ствуют нулевые собственные частоты, остальным обобщенным координатам — собст-
собственные частоты, отличные от нуля.
Пример. Упругий вал с двумя дисками (рис. 3) свободно вращается в подшипниках и может
совершать крутильные колебания. Квазиупругий коэффициент вала с жесткостью на кру-
кручение GJ к и расстоянием между дисками I ра-
рачени к
вен c—OJbft- Моменты инерции дисков обозна-
обозначим через J\ и У,, их углы поворота — через qh
и т Кинетическая и потенциальная энергия
и т К
системы соответственно равны
Г = j
С (ф2
Обобщенные координаты ф, и ф2 не являют-
являются циклическими; однако потенциальная энергия
системы не удовлетворяет условию A). Вводя
новые координаты д, = <р, и q2 = <р2 — Ф1 (угол
поворота одного из дисков и угол закручивания
вала), получим
Т = ^ [Ji'q! + J'2 (qi + Ч2J], U^^cq-y
Рис. З. Крутильные колебания вала с дву
мя дисками
Отсюда видно, что координата gi циклическая Уравнение собственных частот при первом выборе
обобщенных координат
'J ~c
а во втором случае
— С С — (O2J2
>2 (Л -J- Л) — <1>2Л
— и2 У j с — и'У2
= О,
= 0.
Корни этих уравнений, разумеется, совпадают. Одна из собственных частот нулевая; она
соответствует вращению вала как твердого тела с постоянной угловой скоростью, задаваемой
начальными условиями. Ненулевая собственная частота
J2 \V«
JiJ,
F1)
5. ВАРИАЦИОННЫЕ ПРИНЦИПЫ ДЛЯ СОБСТВЕННЫХ ЧАСТОТ
И СОБСТВЕННЫХ ФОРМ КОЛЕБАНИЙ
Формула Релея. Квадраты собственных частот и собственные формы связаны между
собой тождественным соотношением
которое называют формулой Релея. Выражение, стоящее в правой части, называют
дробью Релея. Формула F2) непосредственно следует из матричного уравнения B2).
Развернутая запись этой формулы имеет вид
0J =
п
/=1*=1
F3)
2j
/= 1
Числитель формулы F3) с точностью до 1!2 равен максимальному во времени значе-
значению потенциальной энергии системы A0) при свободных колебаниях по соответствую-
соответствующей форме. Знаменатель с точностью до ш2/2 равен максимальному во времени значе-
значению кинетической энергии C). Формула F3) может быть также непосредственно полу-
получена из теоремы о сохранении полной механической энергии.
Вариационные принципы для собственных частот и форм колебаний. Точное
(хотя и тривиальное) соотношение F3) служит исходным пунктом для следующих
вариационных принципов:
70 СВОБОДНЫЕ КОЛЕБАНИЯ КОНСЕРВАТИВНЫХ СИСТЕМ
1) среди всех возможных значений вектора v истинными формами колебаний будут
те, которые сообщают дроби Релея стационарное значение;
2) вариационный принцип Релея—форма колебаний, соответствующая низшей
(основной) собственной частоте, сообщает дроби Релея минимальное значение. Иначе
говоря, низшая (основная) собственная частота удовлетворяет соотношению
vTCv
сох =min ¦ т> , F4)
1 vTAv ' ч '
в котором к сравнению допускаются любые значения вектора \ф 0;
3) расширенный вариационный принцип Релея — собственная частота ьук удовле-
удовлетворяет соотношению
со? = min -~т—, F5)
где v т^ 0; vb v2 vn_k — первые k — 1 собственных форм; ЧРп_кл — подпро-
подпространство, элементы которого v удовлетворяют условиям ортогональности
v'Ava = 0 (a=l, 2 /с—I); F6)
4) минимаксный вариационный принцип Куранта — собственная частота соА
удовлетворяет соотношению
vTCv
(й|= max min —^—, F7)
".."« "*^"V*-i vAv
где v Ф 0; Wj, w2, ..., ч/!{ i — произвольные линейно независимые векторы; Wn-k-\ —
подпространство, элементы которого удовлетворяют условиям ортогональности
v1Awtt = 0 (a=l, 2 k — l). F8)
Вариационные принципы широко используют для построения приближенных алго-
алгоритмов вычисления собственных частот и форм колебаний при больших п. Кроме того,
они позволяют оценить влияние некоторых изменений условий задачи на поведение
собственных частот.
Влияние изменений инерционных и квазиупругих параметров на собственные ча-
частоты. Пусть параметры системы изменяются при неизменном числе степеней свободы.
Тогда увеличение инерционности уменьшает или хотя бы оставляет неизменными соб-
собственные частоты исходной системы. Возрастание жесткости увеличивает или хотя бы
оставляет неизменными собственные частоты. Для системы с одной степенью свободы
это непосредственно следует из формулы E0). Для систем с произвольным конечным
числом степеней свободы точная формулировка основана на теоремах о сравнении.
Пусть спектр собственных частот упорядочен с учетом кратности: а>1 sg ш2 ^
==: ... sg <в„. Тогда прибавление к матрице А положительной матрицы не может уве-
увеличить ни одну частоту в этой последовательности, а прибавление к матрице С поло-
положительной матрицы не может уменьшить ни одну частоту в последовательности.
Влияние наложения связей на собственные частоты. Пусть на систему с п степенями
свободы наложено г идеальных голономных связей. При рассмотрении частот и форм
колебаний это означает, что в я-мерном пространстве собственных форм v выделено
(п — г)-мерное подпространство Wn_r. Рассмотрим спектр собственных частот си-
системы со связями со', sc (Og =б ••• °>л_/-' Выполняются следующие неравенства:
ша^<^юа+г (а=1> 2 "-'¦)• F9)
Эти соотношения обобщают неравенства F0), связывающие частоты системы с дву-
двумя степенями свободы с ее парциальными частотами. Согласно неравенствам F9)
парциальные частоты всегда лежат в интервале, ограниченном частотами связанной
системы, что согласуется g неравенствами F0).
СВОБОДНЫЕ КОЛЕБАНИЯ ТВЕРДОГО ТЕЛА
71
Поимер На рис. 4 показаны собственные формы и обозначены частоты как тройного
ятника, так и систем, получаемых из него наложением связей. Из неравенств F9) выте-
вытекает, что,' например,
О ^ (О' ^S (On. @ :? 0)' ^ &)¦.¦ СО, ^ СО' ? @„.
1 ~ ( "¦ 2 2 ~ 2 3 1 1 " 3
Рис. 4. К влиянию наложения связей на собственные частоты
6. СВОБОДНЫЕ КОЛЕБАНИЯ УПРУГО ПОДВЕШЕННОГО
ТВЕРДОГО ТЕЛА
Определение положения твердого тела. Наряду с неподвижной системой осей
O511S введем систему подвижных осей Охуг, жестко связанную с телом. В начальный
момент времени полюса обеих систем совместим с центром масс тела (рис. 5). В ка-
качестве обобщенных координат выберем перемещения центра масс тела q1 = |, q2 = т),
q3 = ? и три угла поворота тела относительно осей инерциальной системы qi = a,
Чъ ~ Р> <?е= !¦ Положительные направления обобщенных координат показаны
Рис. 5. Упруго подвешенное
твердое тело
Рис. 6. Положительные направ-
направления обобщенных координат
на рис. 6. Будем предполагать, что линейные и угловые перемещения твердого тела
при колебаниях достаточно малы, чтобы величинами второго и более высоких поряд-
порядков малости можно было пренебречь. Тогда кинематические соотношения [см. фор-
формулу G3) гл. II] примут вид
da, d& dy ,__
озл-^т-; ш,-^; «o,~-Jk G0)
72
СВОБОДНЫЕ КОЛЕБАНИЯ КОНСЕРВАТИВНЫХ СИСТЕМ
4. Косинусы углов между осями
Матрица инерционных коэффициентов. Если система подвижных осей Охуг
совпадает с главными центральными осями инерции твердого тела, то матрица инер-
инерционных коэффициентов
A = diag(M, М, М, Jx, Jy, Jz), G1
где М — масса твердого тела; Jx, Jy, Jг — главные центральные моменты инерции
твердого тела.
Матрица жесткостей упругого подвеса. Предположим, что упругий подвес состоит
из Л'о произвольно ориентированных амортизаторов. Каждый s-й (s = 1, 2, .... No)
амортизатор не обладает вращательной жесткостью
и может быть представлен в виде системы трех уп-
упругих взаимно перпендикулярных элементов, нап-
направленных по главным осям жесткости амортиза-
амортизатора. Главные оси жесткости образуют систему
координатных осей Osxsyszs, называемую в дальней-
дальнейшем s-й системой осей (см. рис. 5). Внешняя сила,
приложенная к s-му амортизатору в направлении
одной из его главных осей жесткости, деформирует
его по направлению силы.
Координаты точки крепления s-ro амортизатора
к телу обозначим через ls, r\s, E,s; ориентацию осей
s-й системы будем задавать направляющими коси-
косинусами (табл. 4). Обозначим через CjcS> cys, czs коэффициенты жесткости s-ro аморти-
амортизатора в направлении соответствующих осей s-й системы координат.
Матрица квазиупругих коэффициентов упругого подвеса имеет вид
Оси
s
11
I
xs
als
$ls
«2S
hs
Zs
a3s
$3s
/Си
С41
C13 Cj4 Cj5 Cig ^
^23 ^24 ^25 C[
C43 C44 C45 С
^53 C&i C55 ^5g
G2)
Элементы этой матрицы выражаются через коэффициенты жесткости всех амор-
амортизаторов, образующих упругий подвес [5]:
Л'о
2j си
s=l s=l
Л'о /V»
s=l
Л'о
s=l
Л'о N,
N,
s = l
No
C13 —
2 2
s=l s=l
Л'о Л'о
5= 1 S= 1
G3)
СВОБОДНЫЕ КОЛЕБАНИЯ ТВЕРДОГО ТЕЛА
73
=«4i=s2
Wo
— C5i= Zj
Wo
-(Г1
s = l
Wo
s = l
W»
COO
C14
C15
C16
00
s = l
Wo
s=l
= 2
s=l
s = l
/•<s>T
s=l s=l
s=l
y-
s=l
Wo
Wo
4f
w
C34
(s)
As)
С36
= 2]
s=l
Wo
S= ]
Wo
s=l
Wo
ci3r
Zj 36 Zj
s=l s=l
G4)
w0
s = l
Wo
Zj c88
s=l
Wo
s = l
Wo
s=l
W
s = l
Wo
Wo
s = l
Wo
s=l
W.
Wo Wo
6 — Ce6— Zj Cb6 — Zj 1С1бЬ
s=l s=l
С
G5)
Главные оси жесткости и центр жесткости упругого подвеса. Выражение сп ?2 +
+ С2Щ2 + с33?2 = 1 определяет эллипсоид жесткостей упругого подвеса. Если
система неподвижных осей О^лЕ параллельна главным осям жесткости подвеса, то
74 СВОБОДНЫЕ КОЛЕБАНИЯ КОНСЕРВАТИВНЫХ СИСТЕМ
матрица С принимает вид
'сп О О си сп си\
О г23 О с21 с25 с.
л<
-41 Г42 С43 С44 ^45
^51 CB! С53 С54 С'>Ь
G6)
В этом случае можно найти три непересекающиеся друг с другом прямые ?,.,
Л*. ?*> которые параллельны соответствующим осям О|, От], О? и для которых выпол-
выполняются условия с14 = С25 = сзв = 0. Эти прямые являются осями поступательной
жесткости упругого подвеса [27]. На плоскости Orjg ось жесткости |# проектируется
в точку, координаты которой
т, = -^»; ? = —• G7)
Аналогичным образом можно определить положение оси жесткости т]^, парал-
параллельной оси От]:
E = ^t; | = ^-, G8)
и положение оси жесткости ?„, параллельной оси ОС:
?_ С35. „_ С34
s —> л —•
G9)
Если в число координатных осей, параллельных главным осям эллипсоида, вклю-
включить одну из осей поступательной жесткости ?„, ц^, или ?„, то обращаются в нуль
коэффициенты жесткости, являющиеся числителями в выражениях G7), G8), G9),
а в матрице G6) по каждую сторону от главной диагонали появятся еще два нулевых
элемента. При некотором упорядоченном расположении амортизаторов три оси
жесткости 1^, т].,, ?„ могут пересекаться в одной точке D — главном центре жестко-
жесткости упругого подвеса. В этом случае эти оси являются главными центральными осями
жесткости подвеса. Если неподвижную систему осей совместить с осями О^т],.^,
то матрица жесткости С примет вид
Здесь элементы матрицы
C=diag(cE, cn, c?, ca, cp, cY).
(80)
cys'
(81)
характеризуют поступательные жесткости подвеса, а элементы
= 1]
s=l
(82)
s=l
— его вращательные жесткости.
Уравнение собственных частот. Матричную форму уравнений свободных коле-
колебаний упруго подвешенного тела можно записать так:
Aq+Cq = 0,
(83)
где q = (|, г], ?, а, р", у) — вектор, характеризующий перемещение тела при колеба-
колебаниях; А — матрица инерционных коэффициентов G1); С — матрица упругих коэф-
СВОБОДНЫЕ КОЛЕБАНИЯ ТВЕРДОГО ТЕЛА
75
(Ышиентов G2). Характеристическое уравнение для определения собственных ча-
частот таест вид
j —}.-М С18 Cl3 С14 С15 С1в
С23
С35 «38
?2
4 Л t/ ,v
С55 Л ^ V С56
= 0. (84)
Разделение форм колебаний. Возможные разделения обобщенных координат
Е "Л, ?> ai Р> У на ГРУППЫ по формам колебаний определяют наличием у упругого под-
подвеса центра жесткости D, а также взаимным расположением осей Oxyz и осей жест-
жесткости |*, Л*, Е*.
5. Варианты разделения обобщенных координат при свободных колебаниях
№ варианта
1
2
3
4
5
6
7
8
9
10
1 ругпы обобщенных
координат
I, л, Е; «, Р, v
?, П, V, ?, а, р
л, ь. «; S. Р, 7
|, :, Р; л, а, у
|, л, С ?, Р> V
1, л, Р; ?, «. v
g, г, а; л, Р, V
1, 1, у; ц, а, р
|, а, Р; л. S> V
|, а, у. Л. ?, Р
Коэффициенты жесткости, равные нулю
^14, ^1Б» ^1в, ^24i С2Б, С2в> ^34, С35, ^Зв
^13, С14, ^15, ^23t С24) ^25, ^зв, С40| Сб6
<*12, Cl3l ^14, C2S, Cj», ^35, C3S, С45, С4»
С13, С15, С1в, С23, С25, С2в, С34, ^45, ^48
С12> Clui С1в, С23, С24, ^35» С3с, ^45» Cie
«12, Cl3, Cl6, C24, ^25, «34, С35, С1в, <Г6в
«12> «13, «IS, «24, «2в, «34, «3«, «45, «5в
Пример. Центр жесткости упругого подвеса D совпадает с центром масс тела О; главные
цен!ральные оси инерции и жесткости не совпадают. Возможные варианты разделения обобщен-
обобщенных координат на две группы по три координаты в каждой сведены в табл 5; здесь же указаны
коэффициенты жесткости, которые должны быть равны нулю, чтобы такое разделение коор-
координат было возможным. Например, для варианта № I (табл. 5) система уравнений (83) распа-
распадается на две независимые с тремя уравнениями в каждой. Уравнение частот (84) примет вид
1
122
2
— Х'М
"3
= о,
-Я'У.
6
-ДА/,
= 0
31 32 53 4 65 6 '" "г
Пример. Центр жесткости упругого подвеса D совпадает с центром масс тела О; одна
из главных осей жесткости подвеса (например, ось О|„) совпадает с одной из главных цент-
центральных осей инерции тела (например, с осью О|). Матрицу С G2) можно записать в виде
11
0
0
0
0
0
0
«22
«32
0
0
0
0
«23
«33
0
0
0
0
0
0
«44
«5*
«64
0
0
0
«45
«В 5
«65
0
0
0
«4
«5
«а
76
СВОБОДНЫЕ КОЛЕБАНИЯ КОНСЕРВАТИВНЫХ СИСТЕМ
Пример. Центр жесткости упр\гого подвеса D совпадает с центром масс тела О, главные
центральные оси инерции и жесткости совпадают Матрица С G2) принимает вид С = diag (с,.,
\ cz; V
(83) pacnaj
с ). элементы которой определяются формулами (81)—(82) Система уравнений
дается на шесть независимых уравнений.
7. СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ УПРУГО ПОДВЕШЕННЫХ
ТВЕРДЫХ ТЕЛ
Построение матрицы преобразования усилий. Уравнения (83) можно распростра-
распространить на механические системы, состоящие из N абсолютно твердых тел, соединенных
друг с другом и основанием No упругими элементами, амортизаторами и опорами.
Число твердых тел, их взаимное расположение, число, расположение и динамические
характеристики упругих элемен-
тов могут быть произвольными.
Наряду с неподвижной сис-
системой координат О|т]? введем
систему координат OjX^y^j
(/= 1, 2 N), жестко свя-
связанную с /-ым телом (рис. 7).
Введем вектор обобщенных ко-
координат q системы как прямую
сумму векторов q, при у = 1,
2, ..., N. Обозначим множества
целых чисел, определяющие но-
номера упругих опор, располо-
расположенных между /-м и k-м телами
системы, через N^ (/, k — 1,2,
..., N), и множества целых чи-
чисел, определяющие номера уп-
упругих опор, присоединенных к
/-му телу, через /V, (/ = 1, 2,
N
..., N), причем Nj~ U Nlk.
Предположим далее, что s-ая (s=
= 1, 2, ..., yvo) упругая опора произвольно ориентирована в пространстве; характе-
характеристики такой опоры будем описывать матрицей в главных осях жесткости s-й опоры
С'*'; элементы этой матрицы заданы.
Введем матрицу Fx6) 8'Дпреобразования усилия, заданного в fc-й системе от-
отсчета в точке Р при приведении его в точку Q, в /-й системе отсчета.
Матрица преобразования Sj^, строится следующим образом. Положение произ-
произвольных /-й и k-й систем координат задается в системе осей О?т]? координатами
полюса и косинусами углов наклона соответствующих осей. Тогда косинусы углов
между произвольными системами осей определяются следующим образом: cty/, =
= «o]aofe- Здесь a,k — матрица (ЗуЗ) косинусов углов между осями /-й и k-й систем
координат; aOj, aoj, —заданные матрицы Cx3) косинусов углов между осями /-й
или k-h систем координат и осями системы координат О|г|?. Вследствие того, что все
системы координат ортогональные, выполняется соотношение
Рис. 7. Система упруго подвешенных твердых тел
«О*-
(85)
Главный вектор F и главный момент G сил, определяемые в k-й системе коорди-
координат, при проведении к различным точкам той же системы преобразуются следую-
следующим образом:
-FP FQ~~C,P r
QP v
СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ ТВЕРДЫХ ТЕЛ 77
где г 1Р = fAx*> ^Ук> ^гк\ — вектоР в &-й системе координат с началом в точке Р
и концом в точке Q. Проекции этого вектора на оси k-й системы координат
_,,Q „Р. Л? — ,0
(86)
Здесь х% У ft, •••> Ц — координаты точек Р и Q в k-й системе осей.
Выразим составляющие вектора г0^ через величины, задаваемые в неподвижной
ОР ПР ПР
системе координат г^ = a/jg r q , где г^ —вектор, заданный в неподвижной си-
системе. Тогда соотношения (86) примут вид
- Cp) .
(87)
где \р, 'Цр, ¦••> Zq — координаты точек Р, Q в неподвижной системе координат.
Матрица преобразования S^ включает как преобразование переноса в k-й си-
стеме осей, так и преобразование поворота до совпадения ее с осями /-й системы
координат:
Подставляя выражения (85) и (87) в выражение (88), получим матрицу преобра-
преобразования в виде
+ «пг^
-f
О
О
О
О
О
О
о\
о
о
• (89)
^Xk v-lyk ^zkl
I
Косинусы углов a/k определяются по формуле (85), приращения Дл^, Д(//г, ДгА —
по формулам (87).
Матричная форма уравнений свободных колебаний. Уравнения свободных коле-
колебаний системы упруго подвешенных тел имеют вид (83), где А и С — матрицы размер-
размерностью QN X 67V. Матрица А имеет блочно-диагональную структуру:
(90)
где А^ — матрица инерционных коэффициентов размерностью 6x6 отдельно взя-
взятого у'-го тела. Если главные оси инерции /-го тела совпадают с осями неподвижной
78 МГТОДЫ ВЫЧИСЛЕНИЯ СОБСТВЕННЫХ ЧАСТОТ И ФОРМ
системы координат Olrfe, то матрица А/ будет диагональной. Матрица С имеет блоч-
блочную структуру:
/11IN \
С= : I . (91)
\4^
Построение блоков матрицы (91) аналогично построению матрицы G2), а именно:
V s° °/c(s)/V1 °/
Глава IV
МЕТОДЫ ВЫЧИСЛЕНИЯ СОБСТВЕННЫХ ЧАСТОТ
И СОБСТВЕННЫХ ФОРМ ДЛЯ СИСТЕМ
С БОЛЬШИМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
1. ОБЗОР ЧИСЛЕННЫХ МЕТОДОВ РЕШЕНИЯ
АЛГЕБРАИЧЕСКОЙ ЗАДАЧИ О СОБСТВЕННЫХ ЗНАЧЕНИЯХ
Предварительные замечания. В вибрационных расчетах наиболее распростра-
распространенными являются следующие задачи о собственных колебаниях, в которых необ-
необходимо вычислить: все собственные частоты и соответствующие им формы; только
собственные частоты; наименьшую (наибольшую) собственную частоту или несколько
низших (высших) собственных частот и соответствующие им формы; несколько соб-
собственных частот, ближайших к заданному числу, и соответствующие им формы.
Отыскание собственных форм v и соответствующих им частот со эквивалентно ре-
решению обобщенной алгебраической проблемы о собственных значениях
(С — coSA)v=0. A)
Для систем с несколькими степенями свободы решение задачи A) не представляет
серьезных затруднений. Если число степеней свободы п велико, то необходимо при-
применять специальные численные методы линейной алгебры [22, 106, 108].
Если используется симметричная матрица единичных податливостей F = С, то
вместо A) имеем
(Е —co3H)v=0, B)
где матрица Н = FA, вообще говоря, несимметричная. Аналогично, вводя матрицу
G = А"ХС = Н, которая тоже является несимметричной, получим
(G —co2E)v=O. C)
Задача о собственных значениях симметричной матрицы. Задачи в форме уравне-
уравнений B) и C) можно привести к аналогичным задачам с симметричной матрицей [22].
Рассмотрим задачу в форме B).
Первый прием заключается в предварительном представлении матрицы инерцион-
инерционных коэффициентов А в виде произведения двух треугольных матриц
(Sll S12 S13 ... \
0 *>2? S24 •••
о о о ...
ОБЗОР ЧИСЛЕННЫХ МЕТОДОВ РЕШЕНИИ 79
Элементы матрицы S вычисляются по следующим формулам (метод квадратного
/-1
/
Полагая v = S^w получим
(E —co2Hi)w = 0, D)
где Hj = SFST—симметричная матрица. В случае диагональной матрицы А =
= diag (a,), aj > 0 имеем Hj = diag (Vaj) F diag (Vaj), v= diag (l/(^o,) w.
Второй прием состоит в предварительном приведении матрицы А посредством
ортогонального преобразования подобия к диагональному виду U^AU = diag (d-j.) =
= D2. Отыскание U ad2 эквивалентно отысканию собственных векторов и собственных
значений матрицы А. После подстановки v = UD^w задача B) сводится к уравнению
(Е —(o2H2)w = 0 E)
с симметричной матрицей Н2 = DU^FUD.
Итак, для отыскания собственных частот и собственных форм систем с конечным
числом степеней свободы применимы численные методы решения алгебраической
проблемы собственных значений (G — %Е) х = 0 или (|хЕ — Н) х = 0, где ц, = 1 /X =
= 1/а>2, G и Н — или симметричные матрицы, или каждая из них есть произведение
двух симметричных матриц.
Другие типы задач. Задачи колебаний и устойчивости неконсервативных ли-
линейных систем (см. гл. V) приводят к квадратичной проблеме о собственных значе-
значениях
= 0 F)
с вещественными матрицами. При этом матрица С, вообще говоря, несимметричная.
Задачу в форме F) легко привести к задаче (G — ХЕ) х = 0 с несимметричной
матрицей
порядка Ъг и вектором х размерности In. Характеристические показатели X в этих
задачах комплексные.
Краткая характеристика численных методов решения стандартной алгебраи-
алгебраической проблемы. Отыскание собственных значений эквивалентно отысканию кор-
корней алгебраического полинома. Все методы решения алгебраической проблемы
являются в сущности итерационными. Численные методы решения алгебраической
проблемы получили свое дальнейшее развитие в связи с широким применением ЭВМ.
При выборе метода следует руководствоваться общими требованиями к устойчивости
счета, точности результатов, простоте реализации алгоритма на ЭВМ и экономич-
экономичности по затратам машинного времени. Основные методы решения алгебраической
проблемы, машинно-ориентированные версии методов и особенности реализации
можно найти в [22, 106, 107, 108].
Краткие характеристики некоторых из наиболее распространенных методов при-
приведены в табл. 1. Мотивировки алгоритмов и дополнительные сведения для случая
вещественных матриц приведены ниже.
Отдельную группу образуют методы, основанные на предварительном вычисле-
вычислении коэффициентов характеристического полинома и численных методах решения
алгебраического уравнения. Вычисление коэффициентов полинома осуществляется
за конечное число шагов. В этом смысле их можно было бы назвать прямыми мето-
методами. В случае вещественных собственных значений коэффициенты полинома сильно
80
МЕТОДЫ ВЫЧИСЛЕНИЯ СОБСТВЕННЫХ ЧАСТОТ И ФОРМ
чувствительны к малым изменениям элементов матрицы и промежуточным ошибкам
округления. По этой причине эти методы следует применять с осторожностью. При-
Применительно к задачам устойчивости линейных систем (см. гл. V) некоторые из этих
методов описаны в п. 4 на с. 85. По возможности описание методов иллюстрируется
ссылками на ФОРТРАН — подпрограммы транслятора для ЕС ЭВМ [60—65].
1. Основные методы решения
Метод
Вращений
Обобщенных вращений
Ортогональный степенной
QR-алгоритм
Треугольный степенной
1Я-алгоритм
Предварительного приве-
приведения к трехдиагональ-
ной форме
Предварительного приве-
приведения к почти треуголь-
треугольной форме
Назначение
Полная проблема соб-
собственных зпаченчй
Полная или частичная
проблема собственных
значений
Частичная проблема
собственных значений
алгебраической проблемы
Тип матрицы
Симметричная эрми-
эрмитова
Произвольная
С вещественными соб-
собственными значениями
Симметричная эрми-
эрмитова
Произвольная
Характеристика
сходимости
Квадратичная
Асимптотически
квадратичная
Используются прие
мы ускорения
Высокая
2. РЕШЕНИЕ ПОЛНОЙ ЗАДАЧИ О СОБСТВЕННЫХ ЗНАЧЕНИЯХ
Метод вращений или метод Якоби. Вещественная симметричная матрица G
всегда имеет линейные элементарные делители. Отыскание собственных значений
и собственных векторов такой матрицы равносильно построению такой ортогональ-
ортогональной матрицы U, для которой
UTGU = diag (X/). G)
В этом случае столбцы матрицы U будут собственными векторами, а X/ — собствен-
собственными значениями матрицы G.
Для квадрата евклидовой (или сферической) нормы матрицы ||G||? =
п п п
= 22 I йГ/ft C справедливо неравенство 2 §J/ *S ||G ||g, причем равенство
возможно лишь тогда, когда G — диагональная матрица. Эта норма инвариантна
относительно ортогональных преобразований. Поэтому среди всех ортогональных
преобразований матрицы G преобразование типа G) делает сумму квадратов
диагональных элементов наибольшей, а внедиагональных элементов наименьшей.
В методе вращений матрица U получается как предел произведения (теоретически
бесконечного числа) элементарных матриц вращения
/1
R (Р, я; 6) =
cos 8... —sin б р-я строка
sin 0 ... cos 6 I q-я строка,
V
(8)
РЕШЕНИЕ ПОЛНОЙ ЗАДАЧИ О СОБСТВЕННЫХ ЗНАЧЕНИЯХ 81
каждая из которых отличается от единичной матрицы только строками и столбцами
с номерами р и q.
На каждом шаге желательно вращение выбирать таким, чтобы максимально
уменьшить сумму квадратов внедиагональных элементов. В классической схеме
метода матрица вращения Rk на k-ou шаге выбирается такой, чтобы в позиции наи-
наибольшего по модулю внедиагонального элементаg'*"^" (p < q) матрицы G (fe ~ '\ по-
чученной на предыдущем шаге, в матрице G'*' был нуль. Элементарный шаг состоит
"в преобразовании О1*1-^*^. При этом tgM^-1)/^-"-^")'
|8|^п/4, cos 6 = cosf-2-arctg26j, sin 6= sin fyarctg 28
Тогда последовательность G=G10', GA) Glftl, ... стремится к диагональной мат-
матрице, а матрица собственных векторов получается как результат накопления произ-
произведений U = R0RiR2--- •
Метод имеет квадратичную сходимость. Если внедиагональные элементы мат-
матрицы Olkl уже имеют порядок не выше е, то их порядок станет не выше е2 после
выполнения одного цикла, состоящего из п (п — 1)/2 вращений.
Метод вращений имеет несколько вычислительно-ориентированных модификаций,
сокращающих непроизводительные затраты машинного времени на поиск наиболь-
наибольшего по модулю внедиагонального элемента (циклический метод вращений, метод
вращений с барьерами [22]) или уменьшающих влияние ошибок округления [106].
Метод гарантирует точность, сравнительную с точностью вычислительной машины,
на которой реализован алгоритм. Для этого требуется от 6 до 10 циклов или от Зя2
до 5я2 вращений. Метод прост и компактен. Этот метод неэффективен при использо-
использовании двухступенчатой памяти. По затратам машинного времени он уступает мето-
методам, основанным на предварительном приведении к трехдиагональной форме, по-
поскольку не использует преимуществ симметричных ленточных матриц.
Применение стандартных подпрограмм. Оператор обращения к подпрограмме
метода вращений имеет вид CALL EIGEN (G, U, N, MV). Здесь G — симметричная
матрица порядка N; U — матрица вычисленных собственных векторов порядка N;
MV — входной признак (если MV = 0, то вычисляются собственные значения и соб-
собственные векторы, если MV = 1 — только собственные значения; массив U в этом
случае не используется, но его имя должно быть обязательно в обращении). Собст-
Собственные значения располагаются на главной диагонали массива G в порядке убы-
убывания.
Задача B) может быть решена двукратным обращением в подпрограмме EIGEN.
Вначале решаем задачу для матрицы А посредством обращения CALL EIGEN (A, U,
N, О) и формируем симметричную матрицу Н = Н2 = DIT^FUD. При этом элементы
диагональной матрицы D равны корню квадратному из диагональных элементов
преобразованной матрицы А, а матрица U ортогональная, и поэтому U'1 = UT.
После второго обращения CALL EIGEN (H, W, N, О) можно найти собственные
частоты и собственные формы: соа = 1/|^ц,а, va — суть столбцы матрицы U-1W.
Этот алгоритм реализован в подпрограмме NROOT. Оператор обращения к под-
подпрограмме в случае задачи C) с матрицей G = AZ имеет вид CALL NROOT (N,
С, А, X, V). Здесь N — число степеней свободы; А и С — матрицы инерционних
и квазиупругих коэффициентов соответственно; X — вектор, содержащий вычислен-
вычисленные частоты со^; V — матрица, столбцы которой являются собственными формами \а.
Обобщение метода вращений. В основе обобщений лежит следующее соотношение:
inf || U-iGU \\% = 23 I Я,/ |», det U Ф О,
и /=1
справедливое для произвольной матрицы G. Это значит, что можно построить такую
невырожденную матрицу U, что матрица IT'GU будет сколь угодно близка к нор-
нормальной; тогда необходимо решить задачу для почти нормальной матрицы. Однако
более удобно объединить процессы нормализации матрицы и диагонализации нор-
нормальной матрицы [22].
82
МЕТОДЫ ВЫЧИСЛЕНИЯ СОБСТВЕННЫХ ЧАСТОТ И ФОРМ
В случае вещественных несимметричных матриц строится последовательность
матриц G'01, G'1', ..., G'*', ..., каждая из которых получается из предыдущей при
помощи элементарного шага G<mi — U^G"n~14Jm. Матрица Um выбирается в виде
произведения двух матриц Rm (р, q; 6) и Sm (p, q; а), где Rm (p, q; 6) — матрица
вращения в плоскости (р, q), a Sm (p, q; a) — невырожденная матрица, зависящая
от параметра а. Параметр а при фиксированных р и q выбирается так, чтобы умень-
уменьшилась норма ||G'm) \\-E. Пара индексов (р, q) на каждом шаге выбирается путем цик-
циклического перебора.
В качестве матрицы S (р, q; а) можно взять
/1
\
\
р-я строка
(/-я строка
или
ch a,
sh a
— sh a
ch а
\
\
Если представить матрицу G(ml в виде суммы G<ml = А11 -\- B(ml, где A<ml
и в<т>—соответственно симметричная и кососимметричная матрицы, то справед-
справедливо соотношение
Эти равенства означают, что с точностью до перестановки строк и столбцов все мат-
матрицы G'mi при достаточно больших значениях т будут близки к квазидиагональной
матрице. Блоки размера 1 X 1 содержат действительные собственные значения,
а блоки размера 2X2
/. /+1
,jnf!i
G.
соответствуют комплексным собственным значениям g(j."'± igA'Vi матрицы
Может оказаться, что один из блоков имеет BimgE -+- S, где S — кососимметричная
матрица. Тогда действительные части собственных значений этого блока равны g,
а мнимые части равны собственным значениям матрицы S.
Если матрица G имеет лишь вещественные собственные значения, то предельная
матрица будет диагональной.
Методы, основанные на приведении симметричной матрицы к трехдиагональной
форме. Эти методы позволяют использовать свойства симметричных трехдиагональ-
ных матриц
'<*! р2 0 ... О 0\
р2 а2 р3 ¦¦• О О
О В, а, ... О О
0 0 0
\0 0 0
ап-1
Характеристический полином рп (к) такой матрицы вычисляют по рекуррентной
формуле р0 (к) = 1, рг (Я) = аг - I, р, {%) = (а} — Щ.^К) — р/^_2 (К) (/ = 2, 3,
..., п). Здесь рь (к) —главный диагональный минор порядка k характеристической
матрицы. Нули этого полинома являются собственными значениями подматрицы
главного диагонального минора порядка k трехдиагональной матрицы и, следова-
следовательно, вещественные.
Последовательность полиномов р0 (к), pi (к) рп (к) является последователь-
последовательностью Штурма. Пусть величины р0 if со), рг (к>) рп (со) вычислены для некоторого
РЕШЕНИЕ ПОЛНОЙ ЗАДАЧИ О СОБСТВЕННЫХ ЗНАЧЕНИЯХ 83
значения А = со. Тогда число совпадений знаков в последовательных членах этой
последовательности равно числу тех собственных значений матрицы, которые строго
больше, чем со. Это свойство позволяет отделить собственные значения для последую-
последующего уточнения, например, по методу половинного деления.
Для симметричной трехдиагональной матрицы существует явное выражение для
компонент собственного вектора х, соответствующего собственному значению X,
Xl = I, Xf = (—l)-^1/?/ (^)/(РаРз-"Р/) (/ = 2, 3, ..., п). Однако оно непригодно в прак-
практических расчетах из-за неустойчивости процесса вычислений: при достаточно хо-
хорошем приближении X к точному значению X можно получить вектор, не являющийся
собственным и даже почти ортогональный к нему.
В методе Гивеиса исходная симметричная матрица приводится к симметричной
трехдиагональной форме путем элементарных преобразований подобия с матрицами
вращения (8). С учетом симметрии для этого требуется выполнить около 4п3/3 умно-
умножений и л2/2 извлечений квадратных корней. В классической схеме метода Якоби
на одном цикле выполняется около 2я3 умножений и «2/2 извлечений квадратных
корней.
В методе Хаусхолдера приведение к трехдиагональной форме осуществляется
при помощи матриц отражения Р = Е — 2wwT, wTw = 1. Процесс приведения тре-
требует приблизительно 2«3/3 умножений и около п извлечений квадратных корней.
Свойство последовательности полиномов р0 (X), р1 (к), ..., рп (X) позволяет вы-
вычислять собственные частоты из заданного диапазона или найти несколько собствен-
собственных частот, ближайших к некоторому числу, или построить гистограмму распре-
распределения собственных частот без вычисления самих частот.
Для вычисления отдельных собственных векторов трехдиагональной матрицы
эффективен метод обратной итерации [106]. Если требуется вычислить все собствен-
собственные векторы, то наиболее эффективным окажется применение методов LR- и (^^-алго-
(^^-алгоритмов к трехдиагональной матрице.
Задачи о собственных колебаниях в форме B) или C) необходимо предварительно
привести к задачам с симметричной матрицей по методу квадратного корня. В про-
противном случае несимметричные матрицы Н и G преобразуют к верхней или нижней
почти треугольной форме (форме Хессенберга). Этот процесс может быть осуществлен
теми же устойчивыми преобразованиями и требует того же числа действий, что и
для симметричных матриц.
LR- и QR-алгоритмы. Они относятся к универсальным алгоритмам. Алгоритм
Рутисхаузера [22, 106] основан на разложении матрицы G на произведение двух
треугольных G = LR, где L — нижняя треугольная матрица с единичными эле-
элементами на главной диагонали, R — верхняя треугольная матрица. Такая факто-
факторизация всегда существует, если главные диагональные миноры матрицы G не обра-
обращаются в нуль. Из соотношения Ir'GL = L (LR) L = RL следует, что произве-
произведение сомножителей в обратном порядке является матрицей, подобной G. В LR-
алгоритме этот процесс повторяется многократно: G'*'= \.k.t Rk-ъ G(ftl = Rfe_iL^._i-
В пределе L^ стремится к Е, a G'*' — к верхней треугольной матрице с собствен-
собственными значениями Ха = ш^ на главной диагонали в порядке убывания. Объем вычис-
вычислений на одном шаге составляет около 2п3/3 умножений, причем половина из них
необходима для разложения на сомножители; поддиагональные элементы стремятся
к нулю, как (Xf+i/Xj)k. Поэтому для сокращения объема вычислений исходную матри-
матрицу следует сначала привести к верхней почти треугольной форме. Эта форма является
инвариантной относительно Lft-алгоритма (этим же свойством обладает и ленточная
форма). Если вместо G использовать матрицу G — уЕ, то элемент gn ^^ стремится
к нулю, как [(Хп — Y)/(^7*j — Y)l*> и если У — достаточно хорошее приближение
к ^л> то ёп п\ будет быстро убывать. Один из способов ускорения сходимости состоит
в том, что сдвиг осуществляется на каждом шаге: G'*'—ykE = L^R^., Ri^-k = G'*+1),
причем в качестве у/пг принимают последний диагональный элемент матрицы RftLj.
В <2/?-алгоритме Френсиса—В. Н. Кублановской осуществляется факторизация
G = QR, где Q—ортогональная матрица; R — верхняя треугольная матрица.
Алгоритм метода определяется соотношениями G(*' = QftRA, G(*+1* = QjG(*)Qft =
==Q^Q<;RAQft= RftQft,которые напоминают предыдущий алгоритм.
84 МЕТОДЫ ВЫЧИСЛЕНИЯ СОБСТВЕННЫХ ЧАСТОТ И ФОРМ
3. ОПРЕДЕЛЕНИЕ НИЗШИХ (ВЫСШИХ) СОБСТВЕННЫХ ЧАСТОТ
Формула Релея дает тем лучшее приближение сверху к низшей собственной
частоте, чем ближе v к первой форме колебаний Vj.. Однако в сложных системах
удачно выбрать аппроксимацию v трудно. Поэтому кажется естественным использо-
использовать методы итерации.
Для определения низших собственных частот и форм следует воспользоваться
уравнениями B) в форме (xv = Hv, |л = 1/со2. Собственные значения нумеруют в по-
порядке убывания: ць ц2. •••. V-n-
Прямые итерации одного вектора. Начиная с произвольного вектора v@) строится
последовательность векторов v'*' и ulft) по формулам и*1' = Hv(A), v('ir1' =
_ u<k+i>/ || и(*+1) || /1| и || = max I uj \\. Очевидно, что после выполнения т итераций
v<m> _jjmv@)/ || Hmvl01||. Если предположить, что v@) = ^ aava> т0 С точностью
до нормирующего множителя
?1 ? MV
a=2
Из этого соотношения следует, что при ai ф О и цг > ц2 с увеличением числа
итераций v(mi -*¦ vx/ II \х II и ||u'mi || ->- (хх = [imax = l/wmin- Скорость сходимости
будет медленной, если (fVfJi) близко к единице. Если fxx имеет кратность /, то \(т> =
г I п ~\
==1ЛЛ -S ааУа~^~ 2 аа (Pa/Pif* va и у'™' близка к некоторой линейной ком-
бинации форм v , v2, ..., V/.
Более быструю сходимость к минимальной собственной частоте дает процесс
одновременной итерации двух векторов, соответствующих Н и Нг. Строят две после-
последовательности векторов v'*' = Hv'*' и w'^'^H^'*"', где v""= w'0) — произвольный
вектор. При этом (w(ft), v(/j))/(wl*), v1*') = цх + О (Цг/^гJ* и Для получения той же
точности потребуется вдвое меньше итераций. В задаче A) о собственных колебаниях
эта схема эквивалентна итеративному применению формулы Релея [F2) гл. III].
Степенной метод. Для матрицы Н имеем
H = Vdiag((xa)V-1=Vdiag(tia)WT= 2] I^X-
a=l
Здесь V = (Vj, v2, ..., \n), va — формы собственных колебаний; строки w^ мат-
матрицы wT удовлетворяют условию нормировки w?va = 1.
В k-й степени матрицы
() |>
a=l
главным членом в сумме справа является матрица \ik v^ №т, где Ц] = Итах- Поэтому
вместо итерирования вектора можно построить последовательность степеней мат-
матрицы Н, Н2, Н4, ..., Н2т, причем при различных (г, в Н2"* доминирующей является
матрица ji-^'v^wT, у которой все строки параллельны wT, а все столбцы параллельны v^.
Скорость сходимости теперь определяется величиной (m/dJ"* и поэтому потребуется
небольшое число шагов даже тогда, когда значения цх и (х2 близкие. Во избежание
переполнения или получения машинного нуля можно умножать каждую степень матри-
матрицы на подходящую степень двойки, чтобы наибольший по абсолютной величине эле-
п Bт) 2т
мент имел нулевой порядок. Так как след матрицы tr Н2 = 2^ hkk =щ wTivi =
А1
РАЗВЕРТЫВАНИЕ ХАРАКТЕРИСТИЧЕСКОГО ОПРЕДЕЛИТЕЛЯ ^5
= а-т, то легко вычислить (х1( а векторы vi и Wj можно найти, используя свойство
матрицы VjWy и условие нормировки.
Двусторонние оценки низших частот дают формулы следов [22], которые можно
получить из алгебраического соотношения trHm= |х™ + ••• + р™- В частности
„ля низшей частоты
2mA — г trHm--
Для получения оценок высшей частоты следует рассматривать следы степеней
матрицы Н = G.
Пример. Для безынерционной балки, несущей три одинаковые сосредоточенные массы т,
уравнение B) принимает вид
mhi — 1 шгт/12 @!mf13
| агт[г1 а>'т[гг - I a'mf23 j г„ = О,
'" ~ 'аз ~ 3888 EJ' '12 ~ '21 "" '" ~ 23 ~~ 3888 EJ' '" ~ '" ~ 3888 EJ' 22 ~ 48 EJ'
«Точное» значение безразмерной низшей частоты
И, =<о1/шо = 5,693 [ (Во = 1/ — )•
Формула Релея при vT = A, 2, 1) дает Sit — 5,82. Вычислив следы
Н = ~ 4- -- 4- ?L = Ш- на 4- 14473
3888 + 48 + 3888 "~ 3888' + C888J '
получим двустороннюю оценку для низшей частоты: 5,45 < Qt <5,93.
Вычисление следующих собственных частот и форм. Для отыскания последующих
собственных частот ш2 = 1/\х и форм (кроме уже вычисленных Шц и Vj) можно при-
применить методы исчерпывания. Например, при использовании преобразования по-
подобия вычисления осуществляют по такой схеме. Выбираем неособенную матрицу U
такую, что Uv! = aei, a Ф 0. В качестве U можно взять матрицу отражения или
матрицу, равную произведению вращений в плоскостях A, 2), A,3), ..., A,п). Тогда
LHU (Uvj) = fij (Uvj) или UHU^ej = j-ijej. Отсюда следует, что первый столбец
матрицы UGLT1 равен ji^j и
Матрица В порядка (п — 1) имеет собственные значения (х2, ..., \in. Собственное
значение ц2 находят одним из методов вычисления наибольшего собственного зна-
значения. Далее из равенства
\ и и / \х2/ \х2
определяют число у и затем форму v2 = U (у, xl)T.
4. РАЗВЕРТЫВАНИЕ ХАРАКТЕРИСТИЧЕСКОГО ОПРЕДЕЛИТЕЛЯ
Характеристический полином матрицы G запишем в виде
det(G-XE) = (-l)»(V + /»1V»-i + ... + pn_iA,+pII). A0)
Рассмотрим некоторые методы вычисления коэффициентов этого полинома.
Метод А. Н. Крылова. Алгебраическая сущность алгоритма метода состоит в сле-
следующем [22, 106, 108]. Если вектор v есть собственный вектор матрицы G, то
векторы v и Gv линейно зависимы. Для произвольного вектора b существует наи-
86 МЕТОДЫ ВЫЧИСЛЕНИЯ СОБСТВЕННЫХ ЧАСТОТ И ФОРМ
меньшее значение т ^ п степени k, при котором векторы b, Gb, G2b, ..., G*b явтя-
ются линейно зависимыми, и тогда
(G<"+CiG»'-i + ... + cmE)b = O. (И)
Полином Хт + с1Хт+ ... + ст, соответствующий левой части выражения A1),
является минимальным полиномом вектора b относительно G,a его степень назы-
называют высотой вектора b относительно G. Если матрица G имеет различные собствен-
собственные значения или различным собственным значениям соответствует лишь одна жор
данова клетка в канонической форме, то почти все векторы имеют высоту п.
Пусть Ьо — вектор высоты п. Тогда векторы b/, = G''b0 (k = 0,1, ..., п) в сил\
теоремы Гамильтона—Кэли удовлетворяют уравнению
Ьл + Р1Ь„-1 + --- + Р«Ьо = 0, A2)
где Хп + Pi к"'1 + ... + рп — характеристический полином матрицы G.
Уравнение A2) удобно записать в матричной форме
Вр = -ЬЛ1 A3)
где В = (bQ, bi, ..., Ь„_!) — матрица, столбцами которой являются указанные век-
векторы; р = (р„, рп_г, ..., РхУ — вектор коэффициентов характеристического полинома.
Таким образом, развертывание характеристического определителя сводится
к решению системы линейных алгебраических уравнений A3). Эту систему удобно
решать по методу Гаусса с исключением по столбцам. Для этого требуется Зя2 (п-\-
-+- 1)/2 умножений и делений. За начальный вектор Ьо можно принять любой вектор,
не совпадающий с собственным вектором.
Пример. Методом А. Н Крылова вычислим коэффициенты характеристического полинома
матрицы
/1 2
0=1 7 4 . A4)
\5 1 2/
Для этого положим Ьо = A, 0, 0)т. Последовательное умножение на матрицу G дает: t), =
= Gb0 = A, 1, 5)т, Ь2 = G2bo = A8, 28, 16)т, b3 = G3bo = A22, 278, 150)т. Система A3) прини-
принимает вид
Рз + р2+ 18р, = - 122;
pa + 28Pl = -278;
5р2 + 1бр, = - 150.
Ее решение, как легко видеть р3 = 56, р2 = 2, pt = — 10. Непосредственное развертывание
характеристического определителя приводит к тому же результату
Метод А. М. Данилевского [108]. Сопровождающей матрицей характеристиче-
характеристического полинома называется матрица
где pj — коэффициенты характеристического полинома. Эта матрица является част-
частным случаем канонической формы Фробениуса. Ее характеристический определи-
определитель легко раскрывается и совпадает с полиномом A0). В этом методе матрицу G
приводят к форме A5) путем выполнения (я — 1) неортогональных преобразований
подобия.
Геометрическая интерпретация алгоритма такова. Исходной матрице G в базисе
е^ (/= 1, 2, ..., я) евклидова пространства соответствует оператор. При этом /-й
столбец матрицы — коэффициенты разложения вектора Ge, по базису е,. Пред-
Предположим, что ех = A, 0 0)т — вектор высоты п. Тогда соотношение A2) можно
записать в таком виде.
A6)
РАЗВЕРТЫВАНИЕ ХАРАКТЕРИСТИЧЕСКОГО ОПРЕДЕЛИТЕЛЯ 87
Так как векторы ei, Gex, .... G" e, линейно независимы, то они принимаются в ка-
качестве нового базиса е^:
р' = р р' = Пе e? = fi'J~1e р'— fi^-ip
Исходный оператор в новом базисе ву, очевидно, имеет матрицу в форме Фробениуса
A5).
Переход от базиса е к базису е' осуществляют за (п — 1) шагов, при этом на каж-
каждом шаге изменяется только один вектор. Получается последовательность базисов,
при этом в k-м базисе первые k векторов уже совпадают с первыми k векторами но-
нового базиса, т. е. он имеет вид ej, е?, ..., е?, е , ...,еп. Пусть G'*' матрица опера-
оператора в k-м базисе. В первых столбцах она уже совпадаете матрицей A5), а k-й столбец
суть компоненты вектора G е? = G*ej в k-м базисе. Очевидно, что G1 ' = G, так как
е[ = ег
Переход от ?-го к (k f- 1)-му базису осуществляют путем преобразования с мат-
матрицей 11д.+1. Столбцами ее, как известно, служат коэффициенты разложения (k + 1)-го
базиса по векторам k-то базиса. Очевидно, что она будет отличаться от единичной
матрицы только (k + 1)-м столбцом. Последний будет совпадать с координатами век-
вектора е'к ] в k-м базисе, т. е. с k-м столбцом матрицы G(*).
Итак, элементарное преобразование подобия на k-м шаге имеет вид
где
На всех п — 1 шагах потребуется выполнить п2 (п — 1) умножений и делений.
Пример Вычислим по методу А М Данилевского коэффициенты характеристического
полинома матрицы A4) из предыдущего примера Необходимо выполнить два шага. Так как
ej = ej, то Uj = Е и G'H = G Строим матрицы
110 ,1-1
и2 = |о 1 о], ufi = [o i о).
,0 S 1/ \0 -5 1/
Матрица Ua отличается от единичной лишь вторым столбцом, который равен первому столбцу
матрицы G'n Вычисляем
,\ - 1 0ч /1 2 Зч ,1 1 0\ уО — 10 —
/
10I740 10=1 28 4
0 — 5 1/ \5 1 2/ \0 ^ 1/ \0 —124 —18/
В матрице U3 последний столбец должен быть равен второму столбцу матрицы G<2>
/10— 10 v /10— 5/62 ч
U3 = /o 1 28 j, UJ> = (о 1 7/31 j.
\0 0 — 124/ \0 0 — 1/124/
Последний шаг
/1 0 — 5/62 > ,0 —10 — 1 ч ,1 0 — 10 ч ,0 0 —56ч
G'3'= Uj1O(slU!1 = j0 I 7/31 jfl 28 4)(° ' 28j = jl 0 — 2]
\О 0 — 1/124/ \0 — 124 — 18/ \0 0 — 124/ \0 I 10/
приводит к ~o\fy же результату pd = Г6, /?s = ?, р% =* — 10.
88 МЕТОДЫ ВЫЧИСЛЕНИЯ СОБСТВЕННЫХ ЧАСТОТ И ФОРМ
Подпрограмма вычисления коэффициентов характеристического полинома по
методу А. М. Данилевского. Оператор обращения имеет вид
CALL EVCPD (G, P, R, RN, В, N, О, IER).
Здесь G — матрица, N — порядок матрицы, Р — массив коэффициентов полиномз
размерности N + 1; R, RN, В — массивы размерности N -f- 1. Матрица G не со-
сохраняется. Если фактическое значение предпоследнего параметра равно 1, то под-
подпрограмма вычисляет дополнительно и корни характеристического уравнения по
методу Берстоу [62]. Для этого используется соответствующая подпрограмма PRBM.
Метод Д. К. Фаддеева [108]. Алгоритм метода сводится к вычислению после-
последовательности матриц GA), G'2) Gln> по нижеприведенной схеме:
G=GB, -JtrG = <?n-j. B = G9,,_1E,
Tt — 1
G"I1 = GB(n-1>, —trG'n) = 7n> B"!> = Gm) —9„Е.
При этом В(Л) = 0; р1 = —Gi, Pi = — Чь •••. Рп = — Чп> гДе Pj — коэффициенты
характеристического полинома матрицы G. Кроме того, если detG ф 0, то —В~1|/рл=
= G. Для нахождения коэффициентов характеристического полинома требуется
п3 (п — 1) умножений. Этот алгоритм представляет собой видоизмененный метод
Пример. Для матрицы A4) эта схема выглядит так:
;1 2 3, /—9 2 3'
G(I)=G = M 7 Д tr G'"= 10, В'П = | 1 —3
\5 1 2/ \ 5 1—8,
/ 8 — 1 — 13\ , 10 — 1 — IS-
ISC'2' = j 18 - 15 - 1 j, ~ tr G'S) = — 2, B'S) = I 18-13—1
\— 34 9 3 / \— 34 9 S ,
)— 56 0 0 \ /0 0 0ч
G'3) = ( 0 -56 0 ), j tr G'S) = - 56, B'3i=r(o 0 Oj.
) j ( j
0 0 — 56/ \0 0 0/
Следовательно, имеем р3 = 56, p2 = 2, p, = — 10.
Подпрограмма метода Д. К- Фаддеева. Оператор обращения имеет вид [162]
CALL FADD (G, N, GINV, DET, GDJUG, Р).
Здесь G, GINV, GDJUG — матрицы порядка N; Р — массив коэффициентов характе-
характеристического полинома размерности N; DET — значение определителя матрицы G;
GINV—вычисленная матрица G, если detG ф 0; GDJUG—вычисленная присо-
присоединенная матрица.
О методе косвенного вычисления коэффициентов характеристического уравнения.
Вычислив значения определителя р (к) = det (G — ХЕ) при некоторых заранее
выбранных Xv %„, ..., hn+1, можно получить систему уравнений р Я? + Р-^п71 +
+ ... + Pn-S-j + Рп= Р; И = U 2 п + 1) относительно коэффициентов харак-
характеристического полинома. Здесь Pj — вычисленные значения определителя. Воз-
Возможны другие варианты с использованием интерполяционных полиномов. Подроб-
Подробный анализ [108] показал, что этот метод приводит к большим относительным по-
погрешностям коэффициентов полинома и собственных значений.
Вычисление корней характеристического полинома. Рассмотрим характеристи-
характеристический полином, заданный в явном или неявном виде [р (к) = det (G — ЯЕ)]. Метод
Мюллера основан на применении квадратичной интерполяции (отсюда происходит
КЛАССИФИКАЦИЯ ЛИНЕЙНЫХ НЕКОНСЕРВАТИВНЫХ СИСТЕМ 89
другое название — метод парабол). Для произвольных начальных значений \<и>,
jjii), Х|2) независимой переменной вычисляют значения полинома р (V01), р (^A))
и р'(^'2')- По найденным значениям строят интерполяционный полином Лагранжа
второй степени и вычисляют его корни. Тот из его корней, который ближе
к V2', принимают в качестве следующего приближения А,13' и т. д. После вы-
вычисления приближенного корня X = а удаляют этот корень путем деления на мно-
множитель (^ —«) и метод применяют к полиному меньшей степени.
Если полином р (к) задан в неявном виде, а Яь Х2, ..., Aft — вычисленные значения
его корней, то для нахождения следующего корня рассматривают функцию
Оператор обращения к подпрограмме вычисления корней характеристического
полинома явного вида записывают в форме
CALL POLRT (P, COF, N, ROOTR, ROOTI, IFR).
Здесь Р = (р„, Рп-Ь ¦••< Ри 1)—массив коэффициентов характеристического поли-
полинома; COF — рабочий массив размерности N + 1; N — порядок полинома (N =g 36);
ROOTR и POOTI — массивы размерности N, содержащие вычисленные значения
действительных и мнимых частей корней полинома соответственно.
Глава V
НЕКОНСЕРВАТИВНЫЕ АВТОНОМНЫЕ СИСТЕМЫ
С ПОСТОЯННЫМИ ПАРАМЕТРАМИ.
УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ
1. КЛАССИФИКАЦИЯ ЛИНЕЙНЫХ НЕКОНСЕРВАТИВНЫХ СИСТЕМ
Предварительные замечания. Понятие о консервативных и неконсервативных
системах было введено в гл. II. В настоящей главе будут рассмотрены линейные
автономные системы, колебания которых описываются уравнениями
Здесь q (t) — матрица-столбец обобщенных координат; А, В и С — квадратные мат-
матрицы с постоянными действительными элементами ajk, bjk и Cjk соответственно.
Матрица А является матрицей инерционных коэффициентов; в дальнейшем будем
ее считать симметричной и положительно определенной. На свойства матриц В и С
не накладывается ограничений. Тогда уравнения A) будут соответствовать некото-
некоторой неконсервативной системе.
Классификация сил. Слагаемые, входящие в левую часть уравнения A), можно
истолковать как взятые с противоположным знаком обобщенные силы, действую-
действующие на систему. В левой части последовательно стоят даламберовы силы инерции,
силы, пропорциональные обобщенным скоростям
Q/'— S Ь,кцк, B)
А1
90 НЕКОНСЕРВАТИВНЫЕ АВТОНОМНЫЕ СИСТЕМЫ. УСТОЙЧИВОСТЬ
и силы, пропорциональные обобщенным координатам (позиционные),
п
~ C)
Представим матрицы В и С в виде сумм симметричных и антисимметричных мат-
матриц: В = Bj -)- В2; С = Cj + C2. Вновь введенные матрицы удовлетворяют соотно-
соотношениям Вг = В ; Вт = —В ; Ст = С ; Ст = —С , а их элементы
1 l' ¦• 2' 1 Г 2 2'
1 1
TATt'v''-*?''-^ D>
Обобщенные силы, соответствующие матрицам Bj и В2, называют соответственно
диссипативными и гироскопическими. Если матрица Bi — положительно определен-
определенная, то мощность диссипации при любых движениях будет величиной положитель-
положительной. В этом случае диссипативные силы обладают полной диссипацией. Если мат-
матрица Bj положительно полуопределенная, то говорят о неполной диссипации; если
матрица В1 отрицательно определенная, то любое движение будет сопровождаться
отрицательной диссипацией, т. е. амплитуды будут возрастать. Соответствующие
силы будем называть силами с отрицательной диссипацией или ускоряющими силами.
Этоттермин будем применять и для сил B) со знакопеременной матрицей коэффициен-
коэффициентов, т. е. со знакопеременной квадратичной формой мощности диссипации. Мощ-
Мощность гироскопических сил на любых действительных перемещениях равна нулю;
в этом смысле гироскопические силы являются консервативными.
Рассмотрим силы, зависящие от положения. Если коэффициенты в соотношениях
C) образуют симметричную матрицу, то эти силы являются консервативными. Они
совпадают с квазиупругими силами, введенными в гл.II при рассмотрении малых
свободных колебаний консервативных систем. Позиционные силы с антисимметрич-
антисимметричной матрицей коэффициентов неконсервативны. Для этих сил общепринятого тер-
термина нет. Их называют псевдогироскопическими, циркуляционными,следящими; мы
будем пользоваться термином неконсервативные позиционные силы.
Приведенная классификация основана на формальных свойствах коэффициентов
дифференциальных уравнений движения A). Одни и те же силы могут вносить вклад
в различные группы членов уравнений движения. Например, силы, зависящие от
положения, могут иметь несимметричную (не обязательно антисимметричную) мат-
матрицу коэффициентов, а разложение матрицы коэффициентов на симметричную и
антисимметричную составляющие может не допускать физической интерпретации.
В этом случае термин неконсервативные позиционные силы можно применять к си-
силам с несимметричной (не обязательно антисимметричной) матрицей коэффициентов.
Классификация линейных систем. Введенная классификация сил позволяет
классифицировать линейные системы с постоянными параметрами. Системы, нахо-
находящиеся под действием одних только консервативных позиционных сил, называют
консервативными системами. Системы, находящиеся под действием одних только
гироскопических сил или гироскопических и позиционных консервативных сил,
называют гироскопическими. Для этих систем выполняется теорема о сохранении
полной механической энергии, т. е. эти системы также являются консервативными.
Все остальные системы можно отнести к неконсервативным. Будем считать, что
во всех колебательных системах имеются позиционные консервативные (квазиупру-
(квазиупругие) силы. Системы, находящиеся под действием диссипативных сил, будем называть
диссипативными системами. В зависимости от характера сил диссипации будем
различать системы с полной диссипацией, с неполной диссипацией и с отрицательной
диссипацией. Первые два типа систем называют также пассивными системами. Си-
Системы с отрицательной диссипацией и (или) с позиционными неконсервативными
силами относят к активным системам. В пассивных системах возможны либо стацио-
стационарные, либо затухающие колебания. В активных системах возможно самовозбуж-
самовозбуждение колебаний. Активные линейные системы являются линейными моделями авто-
автоколебательных или потенциально автоколебательных систем.
СВОБОДНЫЕ КОЛЕБАНИЯ ДИССИПЛТИВНЫК СИСТЕМ 91
2. СВОБОДНЫЕ КОЛЕБАНИЯ ДИССИПАТИВНЫХ СИСТЕМ
Общее решение задачи о свободных колебаниях. Рассмотрим линейную диссипа-
тивную систему, движение которой описывается матричным уравнением A) с сим-
симметричными матрицами А, В и С. Уравнение будет удовлетворено, если положить
q (t) = veM, E)
где % комплексное число; v — комплексная числовая матрица-столбец. Числа X
называют характеристическими показателями, а числа iX или —iX — комплексными
частотами. Характеристические показатели X равны корням характеристического
уравнения
det (А?.2 + ВХ + С)=0, F)
или в развернутом виде,
... alnXz+blnX + cln
21 ^ 2л 2,1 =0, G)
••• апгр + ЬппХ^спП
Система с п степенями свободы имеет 2п характеристических показателя Хь Хг,
¦ •¦, Х2п- Поскольку коэффициенты уравнения G) являются действительными величи-
величинами, то все характеристические показатели либо действительные, либо попарно
комплексно сопряженные величины. Каждому характеристическому показателю
соответствует одно из частных решений уравнения A). Если все характеристические
показатели — простые корни уравнения G), то общее решение уравнения A) будет
равно сумме 2я частных решений типа E):
*= 1
Здесь Cji — произвольные комплексные постоянные, w^ — числовые матрицы-столбцы.
Так как по условию решение q (t) является действительной величиной, а характе-
характеристические показатели связаны соотношением X*k = Xk (звездочка означает пере-
переход к комплексно-сопряженной величине), то должно выполняться условие
{Cn+kv/n+k) * = Ckv/k.
Представим характеристические показатели в виде
где 8j>0 и й)?е !> О — действительные числа, называемые коэффициентами демп-
демпфирования и собственными частотами демпфированной системы соответственно.
Взяв действительную часть от выражения (8), получаем
" -8 t
где Fk и G/, — действительные постоянные величины; и^ и v^ —• действительные
матрицы-столбцы. При заданных начальных значениях всех обобщенных координат
и скоростей постоянные F/, и Gk однозначно определяются из начальных условий.
Если среди корней уравнения G) имеются кратные, вид общего решения зависит
от структуры элементарных делителей некоторой матрицы, формируемой из матриц
А, В и С. Поскольку для рассматриваемого класса систем все эти матрицы симмет-
симметричные, то все элементарные делители простые. Общее решение по-прежнему имеет
вид (8) или A0), где каждому характеристическому показателю соответствует такое
количество решений, какова кратность показателя.
Зависимость характера колебаний системы от свойств ее коэффициентов. Дей-
Действительные характеристические показатели, представленные в виде (9), соответ-
соответствуют монотонным (неколебательным) движениям системы, комплексные показа-
показатели — колебательным движениям. При этом частное решение будет затухающей,
92
НЕКОНСЕРВАТИВНЫЕ АВТОНОМНЫЕ СИСТЕМЫ. УСТОЙЧИВОСТЬ
периодической или неограниченно возрастающей функцией времени в зависимости
от того, будет ли действительная часть соответствующего характеристического
показателя отрицательна, равна нулю или положительна.
Для консервативной системы все характеристические показатели —¦ чисто мнимые
(рис. 1, а) и равны с точностью до ±i собственным частотам системы. Все частные
решения являются периодическими функциями времени, а движение в общем слу-
случае — стационарным (почти периодическим).
Если система диссипативная и обладает полной диссипацией, то все характеристи-
характеристические показатели лежат в левой полуплоскости комплексного переменного (рис. I, б).
ImK
I 9
Яе А
a)
T*
ReA
imX
ReA
8)
ImK
°6
Рис. 1. Расположение характеристических показателей на комплексной
плоскости для различных систем:
a — консервативной; б — с полной диссипацией; в —с неполной дисси-
диссипацией; г—с отрицательной диссипацией
Все частные решения — затухающие функции, и, следовательно, общее решение —
затухающая функция времени. Если система обладает неполной диссипацией, то
часть ее показателей лежитвлевой полуплоскости, ачасть —намнимойоси (рис. 1, в).
Среди частных решений содержатся периодические, отвечающие незадемпфирован-
ным степеням свободы.
Если система обладает отрицательной диссипацией, то среди характеристических
показателей могут найтись такие, действительные части которых положительны
(рис. 1, г). Соответствующие частные и общее решения будут неограниченно воз-
возрастающими во времени функциями.
Свободные колебания диссипативной системы с одной степенью свободы.
При п = 1 уравнение A) принимает вид
где а > 0; b J== 0; с > 0. Это уравнение можно также представить в виде
dt
A2)
СВОБОДНЫЕ КОЛЕБАНИЯ ДИССИПДТИВНЫХ СИСТЕМ 93
g коэффициент демпфирования; <в0 — собственная частота соответствующей
консервативной системы ^ ^^
Характеристические показатели
Ki = -u±iVK=r^, ('4)
т е. собственная частота демпфированной системы равна соЕ = j/"wj> — е2. Общее
решение A0) имеет вид
q (t) =<r e' (Fcos ^^IT^ /+Q sin V^l^ t)- A5)
При e = 0 движения системы будут иметь периодический характер, при е ]> 0
они будут неограниченно затухать во времени, при е < 0 будут неограниченно
возрастающими. Если 0 <^ е < со0, то затухание будет сопровождаться колебаниями.
При е > Шо затухание будет монотонным (кроме, может быть, небольшого началь-
начального отрезка времени). Значение коэффициента демпфирования е = ш0, соответ-
соответствующее переходу от колебательного процесса затухания колебаний к монотон-
монотонному, называют критическим.
Характеристики демпфирования. Коэффициент демпфирования е, задаваемый
первой из формулA3), имеет размерность с. За безразмерную характеристику демп-
демпфирования может быть принята одна из следующих величин;
^ = 4яе bJto е ,
(О0 Шо Сй0
При в2 <^ а>1 первая величина может быть истолкована как относительное рассеяние
энергии за один цикл колебаний, т. е. как отношение величины рассеянной энергии
к среднему значению энергии колебательного процесса. Параметр 0 равен натураль-
натуральному логарифму отношения двух последовательных максимальных значений обоб-
обобщенной координаты (логарифмический декремент колебаний):
A7)
Параметр E, равный отношению коэффициента демпфирования к его критиче-
критическому значению, называют относительным демпфированием. Критическому демпфи-
демпфированию соответствуют значения \|) = 4я, & = 2я, Р= 1. Демпфирование можно
считать малым, если выполнено хотя бы одно из условий: \|>2 <^ 1, д2 < 1, Р2 <; 1.
Нормальные координаты для диссипативных систем. По аналогии с консер-
консервативными системами (гл. III) будем называть нормальными координатами для
диссипативных систем такие обобщенные координаты, при переходе к которым си-
система уравнений A) распадается на независимые уравнения. Запишем эти уравне-
уравнения в виде
^ + 2е/;^ + со|^ = 0 D=1,2 «). A8)
Нормальные координаты диссипативных систем существуют только при некоторых
ограничениях, накладываемых на матрицы А, В и С. Это является отражением ал-
алгебраического факта — невозможности одновременного приведения трех произ-
произвольных квадратичных форм к сумме квадратов посредством линейного преобразо-
преобразования переменных.
Укажем два простейших частных случая, когда такое приведение возможно.
Пусть диссипативная матрица В с точностью до числового множителя пропорцио-
пропорциональна матрице инерционных коэффициентов, т. е. В = 2еА, где е — некоторая
постоянная. Тогда нормальные координаты диссипативной системы совпадают с нор-
нормальными координатами соответствующей консервативной системы, а коэффициенты
демпфирования для всех нормальных координат равны гх = е2 = ... = гп = е.
94
НЕКОНСЕРВАТИВНЫЕ АВТОНОМНЫЕ СИСТЕМЫ. УСТОЙЧИВОСТЬ
Примером может служшь система, изображенная на рис. 2. Уравнения диссипатив-
ной системы можно привести к виду A8), если все диссипативные силы, прило-
приложенные к сосредоточенным массам, пропорциональны этим массам: Q " = —2гт.д
Демпфирование такого типа называют внешним.
Во втором случае диссипативная матрица пропорциональна квазиупругой мат-
матрице. Пусть В = г|С, где г\ — некоторая постоянная. Вновь нормальные координаты
м совпадают с таковыми для консер-
консервативной системы. Коэффициенты
демпфирования пропорциональны
квадратам собственных частот
е/; = г\<л-к (k = 1, 2, ..., re). Этот
тип демпфирования иногда назы-
называют внутренним (по аналогии с
трением Фойхта в распределенных
системах).
Случай малой диссипации. На-
Назовем диссипацию маной, если эле-
элементы матрицы (А"'ВK достаточно
малы по сравнению с элементами матрицы А^С, собственные значения которой
равны квадратам собственных частот консервативной системы. Сравнивая матрицы
по некоторой норме, представим условие малости диссипации в виде
|| (A-W || . ,
Рис. 2. Система с внешним трением
АС|
A9)
В случае, если п = 1, это условие равносильно соотношению е2 -^ ш2.
При малой диссипации можно в первом приближении пренебречь недиагональ-
недиагональными элементами матрицы А^В. Тогда уравнение A) приближенно приведется к виду
A8) с коэффициентами демпфирования 8А = -?г {А^В}/^. Этот прием оправдан в тех
случаях, когда отсутствует достаточно достоверная информация о диссипативных
связях в системе. Заметим, что при малой диссипации собственные частоты будут
мало отличаться от собственных частот соответствующей консервативной системы.
3. УСТОЙЧИВОСТЬ АВТОНОМНЫХ СИСТЕМ
Предварительные замечания. Свойства общего решения (8) уравнения A) характе-
характеризуют поведение фазовых траекторий колебательной системы в окрестности ее по-
положения равновесия и определяют свойство этого решения — устойчивость по отно-
отношению к малым возмущениям начальных условий, малым возмущениям коэффициен-
коэффициентов и к добавлению малых внешних сил. Строгое определение устойчивости соответ-
соответствует определению устойчивости по Ляпунову. Чтобы ввести это определение, за-
запишем уравнение A) относительно 2я-мерной матрицы-столбца фазовых перемен-
переменных х
% = Ох, B0)
где G — матрица размерностью 2п X 2п:
G = / °
B1)
Равновесию системы соответствует тривиальное решение х = 0 уравнения B0).
Близость решения к положению равновесия будем оценивать одной из норм типа
х =
х == max
\xk\
B2)
УСТОЙЧИВОСТЬ АВТОНОМНЫХ СИСТЕМ
95
о Определения устойчивости будем формулировать применительно к частному
учаю равновесия.
Определение устойчивости по Ляпунову. Равновесие х = 0 называют устой-
ивым по Ляпунову, если для любого е >¦ 0 можно найти такое б > О, что из условия
Их (to) II < ^ ПРИ Л1°б°м ' > ^о следует неравенство II х (t) II <; е. В противном слу-
случае равновесие х = 0 называют неустойчивым.
Практически устойчивость по Ляпунову означает, что при достаточно малых
начальных возмущениях фазовые траектории системы будут достаточно мало откло-
отклоняться от положения равновесия. Неустойчивость равновесия означает, что система
может удалиться от положения равнове-
равновесия даже в том случае, если начальные
возмущения сколь угодно малы.
Равновесие х = 0 называют асимпто-
асимптотически устойчивым, если оно устойчиво
по Ляпунову и, кроме того, выполняется
условие
lim || х @ ||=0. B3)
Рис. 3. К понятию
устойчивости по Ля-
Ляпунову
Графическая иллюстрация определе-
определения устойчивости по Ляпунову на при-
примере двухмерного фазового пространства
дана на рис. 3.
Теоремы об устойчивости линейных
автономных систем. Устойчивость равно-
равновесия q = 0 линейной автономной систе-
системы, движение которой описывается урав-
уравнением A), полностью определяется свойствами характеристических показателей
\ъ Хг Х2л — корней характеристического уравнения F) или, что то же, корней
уравнения
p(X) = det(G-XE) = O. B4)
Здесь G — матрица B1).
Равновесие системы устойчиво по Ляпунову, если действительные части всех
характеристических показателей неположительны, причем чисто мнимые характе-
характеристические показатели с нулевой действительной частью — либо простые, либо
имеют простые элементарные делители.
Равновесие системы асимптотически устойчиво, если все характеристические по-
показатели имеют отрицательные действительные части.
Равновесие системы неустойчиво, если среди характеристических показателей
имеется хотя бы один с положительной действительной частью.
Четыре наиболее типичных случая расположения характеристических корней
на комплексной плоскости представлены на рис. 1. Равновесие диссипативной си-
системы A2) с одной степенью свободы будет асимптотически устойчиво при е > 0,
устойчиво по Ляпунову при е = 0 и неустойчиво при е <^ 0.
Наиболее труден для исследования случай устойчивости по Ляпунову при крат-
кратных показателях с нулевыми действительными частями. Техника установле-
установления структуры элементарных делителей связана с приведением матриц к нормальной
форме Ж.ордана и излагается в руководствах по линейной алгебре. Здесь ограни-
ограничимся указанием на то, что неустойчивость при кратных чисто мнимых показателях
—4(Ofc с непростыми элементарными делителями связана с наличием у уравнения A)
частных решений вида Р (t) sma>itt, Q(t)cosa>kt, где P(t) и Q(t) — полиномы,
степень которых не больше, чем степень кратности показателя минус единица. Если
матрицы А, В и С симметричные, то все кратные чисто мнимые характеристические
показатели имеют простые элементарные делители.
Теорема Ляпунова об устойчивости по первому приближению. Линейные урав-
уравнения типа A) обычно получают путем линеаризации более полных и точных нели-
нелинейных уравнений. Ответ на вопрос, при каких условиях выводы об устойчивости
равновесия линеаризованной системы могут быть отнесены к соответствующей не-
нелинейной системе, дае! юорема Ляпунова об устойчивости по первому приближению.
96 НЕКОНСЕРВАТИВНЫЕ АВТОНОМНЫЕ СИСТЕМЫ УСТОЙЧИВОСТЬ
Пусть уравнения нелинейной системы отличаются от линеаризованных уравнений
нелинейными членами, которые являются непрерывными и дифференцируемыми функ-
функциями фазовых переменных и времени. Если положение равновесия линейной системы
асимптотически устойчиво, то равновесие нелинейной системы будет устойчиво по
Ляпунову независимо от нелинейных членов.
Если при тех же условиях среди характеристических показателей линейной си-
системы найдется хотя бы один, имеющий положительную действительную часть, то
равновесие нелинейной системы будет неустойчиво независимо от нелинейных членов.
Теорема Лагранжа об устойчивости консервативных систем. Пусть система с голо-
номными стационарными связями находится в равновесии под действием одних кон-
консервативных сил. Если потенциальная энергия системы имеет в положении равнове-
равновесия изолированный минимум, то это положение равновесия устойчиво по Ляпунову.
Эту теорему использовали ранее при рассмотрении малых свободных колебаний
консервативных систем.
Влияние диссипативных и гироскопических сил на устойчивость равновесия
(движения) линейных систем. Приведенные ниже теоремы, связанные с именами
Кельвина и Тета, относятся к изменению характера устойчивости систем, находя-
находящихся под действием консервативных позиционных сил, при добавлении диссипа-
диссипативных и (или) гироскопических сил [114].
Равновесие, устойчивое при одних консервативных силах, становится асимптоти-
асимптотически устойчивым при добавлении диссипативных сил с полной диссипацией, а также
диссипативных сил с полной диссипацией и гироскопических сил.
Равновесие, устойчивое при одних консервативных силах, остается устойчивым
при добавлении диссипативных сил (не обязательно обладающих полной диссипацией)
и (или) гироскопических сил.
Равновесие, неустойчивое при одних консервативных силах, может быть стабили-
стабилизировано путем добавления гироскопических сил только в том случае, если степень
неустойчивости (число отрицательных коэффициентов у квадратичной формы по-
потенциальной энергии) четная.
Равновесие, неустойчивое при одних консервативных силах, не может быть стаби-
стабилизировано добавлением гироскопических сил и диссипативных сил, если последние
обладают, полной диссипацией.
4. КРИТЕРИИ АСИМПТОТИЧЕСКОЙ УСТОЙЧИВОСТИ
Для того чтобы доказать асимптотическую устойчивость линейной автономной
системы, достаточно убедиться, что все корни характеристического уравнения имеют
отрицательные действительные части. Ниже сформулированы необходимые и доста-
достаточные условия, при которых корни характеристического уравнения B4) лежат
в открытой левой полуплоскости.
Критерий Рауса—Гурвица и родственные алгебраические критерии. Рассмотрим
алгебраический полином с вещественными коэффициентами. Пусть левая часть урав-
уравнения B4) задана в виде полинома
р(?.) = ро^-Ьр1^-1 + ...+рл_Д+рл. B5)
Коэффициенты этого полинома можно получить одним из методов, описанных в гл. V.
Необходимым условием того, чтобы действительные части корней полинома B5)
были отрицательными, является положительность всех его коэффициентов: р^^> О
(k — О, 1, 2 л). Поэтому можно считать, что р0 > 0.
Составим из коэффициентов полинома квадратную матрицу порядка п
jPi Рз Ръ ¦•¦ Р2П-А
Ра рг рх ... Ргп
л = | 0 Pl Рз ... р2п_3 ) B6J
,0 0 0 ... ра
КРИТЕРИИ АСИМПТОТИЧЕСКОЙ УСТОЙЧИВОСТИ
97
по следующим правилам: в верхний левый угол ставим коэффициент pt; далее мат-
матрицу заполняем гак, чтобы индексы коэффициентов в строках увеличивались на двой-
двойку а в столбцах — уменьшались на единицу. При этом вместо коэффициентов с ин-
индексами к < 0 или k > n ставим нули.
Для того чтобы все корни полинома B5) имели отрицательные действительные
части, необходимо и достаточно, чтобы были положительными все главные диаго-
диагональные миноры его матрицы Нл {критерий Рауса—Гурвица):
= р1>0;
Pi Рз
Ро Р-2
0;
B7)
В табл. 1 приведены условия устойчивости для полиномов до четвертой степени
включительно. В случае полиномов более высокой степени проверка условий B7)
требует вычисления определителей и проводится на ЭВМ по стандартной подпро-
подпрограмме.
1. Условия устойчивости для полиномов
Полином
РОХ -f" Pi
F(A2 + Pi*- 4~ Pa
+ р,
Условия устойчи-
устойчивости
Ро > 0, Pi > 0
Ро > 0, р, > 0,
Рг >0
Ро > 0, pt > 0. р2 >0,
Рз >0,
PlP2 — РоРЗ > 0
Полином
РоХ* + Pi*.3 + РЛ2 +
+ РъК + Pi
Условия устойчи-
устойчивости
Ро > 0, pi > 0,
Рг > 0, Рз > 0,
Pi >0, Pi (ргр3 —
- "л) - PoPi > °
Критерий В. И. Зубова. Рассмотрим алгебраический полином с вещественными
коэффициентами, заданный в неявном виде. Чаще всего в теории устойчивости
систем с конечным числом степеней свободы характеристический полином встре-
встречается в виде B4), где G — вещественная матрица порядка п. При помощи дроб-
дробно-линейного преобразования
Х= (р-\- 1)/(р—1) B8)
левая полуплоскость ReX<0 отображается на единичный круг I р I <; 1. При этом
вместо B4) получаем
det(r — pE) = O, B9)
где Г = (G — Е) (G + Е). Корни полинома B9) являются собственными значе-
значениями матрицы Г, и все они по модулю меньше единицы.
Для того чтобы корни полинома B4) лежали в левой полуплоскости, необходимо
и достаточно, чтобы
Г*-*-0 при k-yco, C0)
где Г = (G — Е)*1 (G + Е) = Е + 2 (G — Е). Условие C0) будет выполнено,
6^
=; а/п для всех / и т, где
элемент
fccjiH для какого-либо s окажется, что
матрицы Vs; 0 <^ а <; 1.
Алгебраический полином с комплексными коэффициентами. Пусть коэффициенты
полинома B5) — комплексные числа. Если корни полинома р (К) лежат в левой полу-
4 п/р. Болотина В. В., т. 1
98
НЕКОНСЕРВАТИВНЫЕ АВТОНОМНЫЕ СИСТЕМЫ. УСТОЙЧИВОСТЬ
плоскости, то корни полинома Р (со) = р (iw) находятся в верхней полуплоскости
т. е. имеют положительные мнимые части. Положим X = ко. Отделяя действительную
и мнимую части, получим
Р (со) =з р (i(o) = а0соя + ajco"~г -|-... -\- ап _ jco -f а„ + i (boa>n + &iw" +...
... + 6n-iw + 6n). C1)
где аА, ЬА (А =¦- 0, 1,2 и) —вещественные числа. Составим из коэффициентов
полинома C1) вещественную матрицу порядка In:
а, а,
h h
а»
bo
ь,
.«о
а,
Z
Ьп\
ап
C2)
Элементы вне блоков равны нулю.
Число корней полинома р (к) с комплексными коэффициентами, имеющих отри-
отрицательные действительные части, равно числу перемен знака в ряду 1, А2, Д4> ...,
^2п-2. Дат гДе &гк — главные диагональные миноры четного порядка матрицы Н2л.
Поменяем местами строки в каждом блоке матрицы Н2Я. В результате получим
матрицу
l
а0
\
ь,
bo
"о
а,
¦ь0
'" ««
а, ...
Для того чтобы все корни полинома р (X) с комплексными коэффициентами лежали
в левой полуплоскости [или все корни полинома Р (со) находились в верхней полу-
полуплоскости], необходимо и достаточно, чтобы главные диагональные миноры Д^
(k = 1, 2, ..., п) матрицы И'т были положительные (критерий Рауса—Гурвица).
Пример. Исследование устойчивости цилиндрической оболочки в потоке газа [11] приводит
к решению проблемы Рауса — Гурвица для полинома р (к) = № — Q? — *' {Е -f- у) К -\- iykU.
Здесь е, у, /г, U, Qt — вещественные параметры. По физическому смыслу задачи невозмущенное
движение оболочки будет устойчивым, если этот полином не имеет корней в нижней полуплос-
полуплоскости. Составим матрицу Н^п полинома
\
^0 — (Е + V) fkU О
1 о — af о
О 0 _ (е 4- v) v№
\0 1 0 -Of/
Условия Payca — Гурвица дают Дг = (? + V) > 0, 4^ = Я? (е + v)a —
> 0.
Критерий Крши—Михайлова—Найквиста. Рассмотрим полином р (к) B5) с ве-
вещественными коэффициентами, Кривую г = р (гсо) [где со -^ вещественный параметр
КРИТЕРИИ АСИМПТОТИЧЕСКОЙ УСТОЙЧИВОСТИ
99
in
ш <. °°)\ называют годографом Михайлова полинома р (А). Каждой точке годо-
оафа соответствует вектор г, выходящий из начала координат. В силу необходимых
условий р @) = а„ > 0.
Для того чтобы все корни полинома B5) лежали в левой полуплоскости, необхо-
необходимо и достаточно, чтобы угол поворота против хода часовой стрелки вектора р (ко)
lm l
1тг
ы=0 Rez
Ret
lm i
п=3
1т 1
ы=0 Rez
Рис. 4. Примеры устойчивых годографов для полиномов степени п
при изменении параметра ш от 0 до оо был равен «я/2, где я — степень полинома
(критерий Коши—Михайлова—Найквиста).
Таким образом, график годографа полинома, имеющего все корни в левой полу-
полуплоскости, выходит из точки р @) = ап > 0 положительной полуоси Re г > 0,
при ш -*• оо будет последовательно пересекать полуоси \тг > 0, Re г <^ 0, lm г < 0,
..., а вектор г асимптотически стремиться к n-й по счету полуоси. Примеры годографов
для полиномов, имеющих все корни в ле-
левой полуплоскости, показаны на рис. 4.
Представим выражение р (/со) в виде
суммы действительной и мнимой частей:
р ((со) = и (х) -J- Ituf (JC).
Здесь х = (о2; « (х) — полином степени
п/2 при четном л или (« — 1)/2 при не-
нечетном п; и (х) — полином степени я/2 — 1
при четном я или (я — 1)/2 при нечет-
нечетном п.
Для того чтобы все корни полинома B5)
с положительными коэффициентами имели
отрицательные действительные части, необходимо и достаточно, чтобы корни поли-
полиномов и (х) и v (х) были вещественными, положительными и перемежались между
собой, причем наименьшим должен быть корень полинома и (х).
Например, для полинома восьмой степени с положительными коэффициентами условия вы-
выглядят так: все корни полиномов и (к) — р0*4 — р^х" -\- ptx2 — рвх + pg,v (*) = — pjX3 + Р„хг —
~ Рьх + р7 должны быть вещественными положительными и располагаться, как на рис. 5.
Устойчивость линейных систем с постоянными параметрами и запаздыванием.
Уравнения возмущенного движения таких систем являются дифференциально-
4*
Рис. 5. Графики полиномов и (х) и v (x)
100 НЕКОНСЕРВАТИВНЫЕ АВТОНОМНЫЕ СИСТЕМЫ. УСТОЙЧИВОСТЬ
разностными запаздывающего типа:
2/2 ^
dx,- (t) v
k ~ 1 / -= 0
Здесь %i — постоянные запаздывания, удовлетворяющие условию 0 = т0 <^ тх <-
< Т2 < ... < тот (сосредоточенные запаздывания). Отрезок [/„— хт, /0] (t0 — началь^
ный момент времени) называют начальным множеством. В случае распределенного
запаздывания система C3) будет интегро-дифференциальной.
Решение х (i) э 0 называют устойчивым по отношению к возмущениям на началь-
начальном множестве [t0 —%т, /0], если для любого е > 0 найдется такое б (е) > 0, что
для любой непрерывной начальной функции xQ (t), удовлетворяющей неравенству
II хэ (О II < б, t <= [t0 — хт, t0], решение х (t) с этой начальной функцией будет удовле-
удовлетворять неравенству II х (t) II < е при всех t > /0. Если, кроме того, выполняется
неравенство
Jim || х @11 = 0,
то тривиальное решение называют асимптотически устойчивым по отношению к воз-
возмущениям на начальном множестве.
Решение системы C3) можно искать в виде
X/@ = V-' (/==1, 2, .... 2п), C4)
где X,- и Я — постоянные. После подстановки C4) в выражение C3) получаем характе-
I т \
ристическое уравнение системы det I ^ ajkie l—°/
V=o /
где 6^ — символ Кронекера. Раскрывая определитель, получим характеристическое
уравнение в виде квазиполинома раA)е ° + Pi W е г +¦••+ Рт (Я.) е т ,
где Pj (К) — алгебраические полиномы. Квазиполином является целой трансцендент-
трансцендентной функцией, а множество его корней — бесконечным счетным множеством, не
имеющим конечных точек сгущения. Имеются общие методы, решающие проблему
Рауса—Гурвица для квазиполиномов, однако они очень громоздки и малопригодны
для приложений. Чаще всего на практике прибегают к методу Л-разбиений.
Выделение областей устойчивости в пространстве параметров системы. Харак-
Характеристическое уравнение зависит от параметров рь E2, ..., рг системы. Каждой точке
r-мерного пространства параметров соответствует некоторое расположение корней
характеристического уравнения в комплексной плоскости. При перемещении точки
в пространстве параметров непрерывным образом изменяется расположение корней
характеристического уравнения. Различным областям пространства параметров
будет соответствовать различное число корней характеристического уравнения
в правой полуплоскости. Таким образом, пространство параметров можно разделить
на области D (/г), где k — число корней характеристического уравнения в правой
полуплоскости (Ь-разбиение). Поскольку при переходе в правую полуплоскость
корень характеристического уравнения пересекает мнимую ось, то уравнение гра-
границ разбиения имеет вид Р («со) = 0. Оно эквивалентно паре вещественных уравнений
PR(co) = 0; P,(co)=O, C5)
где со — параметр (—°° <^ ш <^ оо). Области D @) соответствуют асимптотической
устойчивости системы. Если в выражении C5) -исключить со, то получим уравнение
границ областей D-разбиения в пространстве параметров. Остается решить проблему
идентификации областей. Если левая часть характеристического уравнения —
полином, то граница областей D @) в пространстве параметров определяется либо
уравнением Ап^ = 0, либо рп = 0.
НЕДИССИПАТИВНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ Ю1
Глава VI
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
1, НЕДИССИПАТИВНЫЕ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ
СВОБОДЫ
Действие гармонической силы. Дифференциальное уравнение вынужденных ко-
колебаний системы имеет вид
а-\-чАа=—Fit), A)
а
где F (t) — Fo cos <at — обобщенная вынуждающая сила; Fq и со — ее амплитуда и
частота; остальные обозначения совпадают с принятыми в гл. III, Установившиеся
вынужденные колебания происходят с частотой (о, совпадающей с частотой вынуж-
вынуждающей силы. Таким колебаниям соответствует частное решение уравнения (I):
<?ст
•l-Ti»
-cos
где </ст = FJc — статическое смещение под действием амплитудного значения вы-
вынуждающей силы: т) = ш/ш0 — частотное отношение; ф — фазовый угол. Отношение
X
4,0
3,0
2,0
1,0
Рис. 1. Амплитудно-частот-
Амплитудно-частотная характеристика в случае
гармонической внешней
силы ф = 0)
У
\
\
Pq COSUt
Г
\»
Ж
—,
X
4,0
3,0
Zfi
1,0
\
J
1
\
\
\
1—-х
„то
ил
1,0
Zfi
Рис. 2. Амплитудно-частотная ха-
характеристика в случае амплитуды
внешней силы, пропорциональной
квадрату частоты (О — 0)
амплитуды динамического смещения q к статическому смещению <7СТ называют коэф-
коэффициентом динамического усиления (коэффициентом динамичности):
При низких частотах {х\ •< 1) амплитуда колебаний близка к статическому сме-
смещению, колебания происходят в фазе с колебаниями внешней силы (ц> = 0). С уве-
увеличением частоты оз амплитуда колебаний возрастает, а при со -»- щ амплитуда q ->-oo.
Это явление называют резонансом, а частоту, при которой осуществляется резонанс, —
резонансной частотой. Колебания, частота которых выше резонансной (т) > 1),
происходят в противофазе (ср = я); при со —• оо амплитуда q -*¦ 0. График зависимо-
зависимости B), которую называют амплитудно-частотной характеристикой, представлен
на рис. 1. В реальных системах амплитуда колебаний при резонансе ограничена.
На практике распространен случай, когда амплитуда вынуждающей силы про-
пропорциональна квадрату частоты F0 = 7«2 (коэффициент у определяется параметрами
102
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
системы). Для этого случая коэффициент динамического усиления
C)
График амплитудно-частотной характеристики C) представлен на рис. 2.
Случай кинематического возбуждения колебаний. При этом справедливо уравые
ние A), если в качестве внешней обобщенной силы принять переносную силу инерции.
Пусть точка подвеса массы т совершает колебания f — f ih
(рис. 3). Если q — относительное перемещение массы, то
УРавнение (!) примет вид q + wjfr = — /, где — mf — пере-
носная сила инерции. Предположим, что / = A cos Ш
(Л — амплитуда перемещения точки подвеса, w — ее часто
та). Тогда коэффициент динамического усиления
, 1
с-^. f=Acosut
т
Рис. 3. Кинематиче-
Кинематическое возбуждение ко-
колебаний
ч,
График зависимости D) показан на рис. 2.
D)
2. СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ ПРИ УЧЕТЕ СИЛ
ВЯЗКОГО СОПРОТИВЛЕНИЯ
Действие гармонической силы. Дифференциальное уравнение вынужденных коле-
колебаний имеет вид
1
q + 2eq -f- colq=— /^ cos at, E)
где е — коэффициент трения. Частное решение уравнения E), соответствующее уста
новившимся вынужденным колебаниям,
имеет вид
9 = q" , тт^г— eosH-q).
где ¦& = 2яе/со„ — декремент колебаний,
Ф — фазовый угол, который находят из
формулы
arctg
F)
Коэффициент динамического усиления
2,0 -
1.0
HI
ill
5^
0,5
Рис. 4 Зависимость х от отношения час-
частот Г)
Графики амплитудно-частотных характе-
характеристик G) ДЛЯ различных значений §
представлены на рис. 4. Во всем частотном
диапазоне амплитуды установившихся
колебаний остаются конечными. Силы вязкого сопротивления оказывают заметное
действие лишь в околорезонансной области. Максимальное значение к при фикси-
СИСТЕМЫ С ОпНОИ СТЕПЕНЬЮ СВОБОДЫ
103
рованном 0 и частоте возбуждения
«*=»o(l+-
¦2 \- V,
-V,
При малых силах вязкого трения можно считать (с погрешностью ~ Ф2), что х^ -"
= max х яа л/Ф.
График изменения фазового угла <р представлен на рис. 5. При резонансе незави-
независимо от величины Ф сдвиг фаз всегда равен я/2 и энергия, поступающая в систему
Гис. 5. Фазочастотные характерис
тики
Рис. 6. Изменение коэффициента
передачи силы на фундамент в за-
зависимости от г)
от внешней силы, максимальна. При переходе через резонанс угол ф изменяется
тем быстрее, чем меньше трение.
Вязкое трение существенно влияет на силу F,j,, передающуюся от колеблющегося
объекта основанию. Амплитудное значение этой силы Рф = xnF0, где хП = коэффи1
циент передачи при виброизоляции, равный отношению виброперемещения (вибро*
скорости, виброускорения) колеблющегося объекта или воздействующей на него
силы к значению этой же величины источника возбуждения:
V'
я
На рис. 6 показана зависимость изменения коэффициента кп от т| при различных
значения d/л. Все кривые проходят черед одну точку, абсцисса которой равна j/2,
а ордината равна единице. Для значений т| »^2 с ростом сил трения коэффициент
кп увеличивается.
Случай произвольной периодической возмущающей силы. Пусть F (t) = F (t -f-
+ Т), где Т — период колебаний. Представим функцию Г @ в виде ряда Фурье
(a/ cos/co/ + b; sin /ш<),
гДе й0) а,, 6; — постоянные, определяемые по следующим формулам гармонического
анализа:
1 т т
dt, o;== if (t) cos jut dt; b,= — \ / {t) sm/w/d/.
о о
104 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
Частное решение уравнения E) можно представить в виде разложения
оо
-\~ V (A/ cos }(at -)- Вi sin /Чо/),
где
Л — с° • 4 — 1 ' Г| "' ' Л ^ ' •
о —' ъ— I / ~~
аш:.
Дифференциальное уравнение E) можно записать также в виде
где ho = ao/a; h,=z—
Тогда его частное решение будет
где
л
. ¦&
1'
tg e; = tg (<p, - ?/) =-j_/2t)a
Метод комплексных амплитуд. При рассмотрении установившихся вынужденных
колебаний этот метод является более экономичным, чем непосредственное аналити-
аналитическое решение. Вместо уравнения E) рассматривают уравнение для комплексной
обобщенной координаты q:
Если q = u-\-iv — частное решение уравнения (8), то и — частное решение этого же
уравнения для правой части, равной (?>lqCTcosAt, а у—для a>lqc! sin со/. Пусть
частное решение уравнения (8) имеет вид q = Aelb>t,
где
Л= 2«__
— комплексная амплитуда гармонического колебания. Обозначим комплексную ве»
личину Л = Aoe"f, где модуль
Л,= -
У (i-n2J+(|-)V
НЕДИССИПАТИВНЫЕ СИСТЕМЫ MB
и аргумент
ш = arctg —-
1—if
Частное решение уравнения E) имеет вид
q = Re q = Re (Aeiai) = A cos (tttf — tp). (9)
Динамические жесткость и податливость, механический импеданс. Динамиче-
Динамической жесткостью механической системы называют отношение амплитуды внешней
гармонической силы к комплексной амплитуде колебаний. Для системы с одной сте-
степенью свободы динамическая жесткость
А \ л
Это понятие вводится по аналогии со статической жесткостью, как отношение силы
к смещению в системе, вызванному данной силой. Для системы без демпфирования
с (rfi — действительная величина. При резонансе система обладает минимальной
динамической жесткостью. В частности, для системы без демпфирования при резо=
нансе динамическая жесткость равна нулю.
Динамической податливостью системы / (г|) называют величину, обратную дина-
динамической жесткости:
1 _г [ . d \-i
11 ~ с (Л) ~~а \ ^
В окрестности резонанса динамическая податливость системы оказывается наи-
наибольшей (для системы без демпфирования она при резонансе принимает бесконечно
большое значение). При значениях т], малых по сравнению с единицей, функция
/ (ц) мало отличается от статической податливости.
Механическим импедансом системы Z (ц) или просто импедансом называют от-
отношение амплитуды гармонической вынуждающей силы к комплексной амплитуде
скорости при установившихся вынужденных колебаниях:
3. НЕДИССИПАТИВНЫЕ СИСТЕМЫ С КОНЕЧНЫМ ЧИСЛОМ
СТЕПЕНЕЙ СВОБОДЫ
Уравнение вынужденных колебаний имеет вид
Aq + Cq = F0coscof, A0)
где q — вектор обобщенных координат; А и С — матрицы инерционных и квази-
упругих коэффициентов; Fo — вектор амплитуд внешних вынуждающих сил.
Непосредственное решение. Оно основано на представлении вектора обобщенных
координат в виде q = q0 cos <W. После выделения временного множителя задача об
установившихся вынужденных колебаниях сводится к решению неоднородной си-
системы линейных алгебраических уравнений:
(C-w2A)qo=Fo. A1)
Решение этой системы существует, если det (С — и2А) Ф 0. Тогда
q = (C-ftM)-iF0. A2)
Определитель системы A1) равен нулю при совпадении частоты внешнего воз-
возбуждения с одной из собственных частот рассматриваемой механической системы со/.
106
ВЫНУЖДЕННЫЕ КОЛЕБАНИИ
При со = W/ амплитудные коэффициенты обобщенных координат становятся неоп-
неопределенными. В этих случаях говорят о резонансах на определенных частотах. Напри-
Например, «резонанс на первой собственной частоте» и т. д. Условием существования резо-
резонанса является совпадение частоты внешнего возбуждения с одной из собственных
частот to = со,-. Однако возможен случай, когда при совпадении частот со = ш; ре-
резонанса не будет; он реализуется при выполнении дополнительного условия
(Fo.V;) = 0, означающего, что внешние силы не совершают работы на перемещениях,
FgCOSCjt
m,
]
J
А
////////////,
Рис. 8. Двухмас-
совая система
Рис. 9. Амплитудно-частотная
характеристика Для массы т,
двухмассовой системы
Рис. 7. Пример отсутствия резонанса на первой частоте системы
соответствующих /'-й форме собственных колебаний. При этом существует решение си-
системы алгебраических уравнений A1) с определителем, равным нулю, когда ранги
матрицы системы и расширенной матрицы равны (рис. 7).
Пример. Рассмотрим уравнения вынужденных колебаний двухмассовой системы (рис. 8):
miQt ~h ct9i + C2 (Qs -~ Qi) — ^o cos at;
Частное решение системы A3), описывающее стационарную часть процесса, имеет вид <?,
= Ai cos to/, <7a = А2 cos at Амплитуды колебаний масс т, и тп2 соответственно равны
, Fo (с2 — т,и2)
A3)
A4)
Из выражений A4) видно, что масса mt остается неподвижной, если га» = (сг/тг)'/г. В этом
случае At = 0, А2 — — F0/c2 (рис. 9). Режим вынужденных колебаний системы при а = со»
FoCOSCJt
т1
т.
WV\i
/7777777777777777777777777777777777777777777777А
Гис. 10, Система с четырьмя степенями свободы
соответствует антирезонансу на первой обобщенной координате qt. Возможность возникнове-
возникновения антирезонанса используют при устройстве динамического гасителя колебаний.
Пример. Система с четырьмя степенями свободы, совершающая установившиеся вынужден-
вынужденные колебания, показана на рис. 10. Периодическая внешняя сила приложена к массе т^.
НЕДИССИПАТИВНЫЕ СИСТЕМЫ
107
Амплитуды установившихся вынужденных колебаний А,, А2, А3 и Л, масс mt, шг, тъ и т,
^подставлены на рис. 11 как функции от возбуждающей частоты (о. Резонансы установившихся
колебаний возникают при частоте <о, совпадающей с одной из собственных частот ю,, <й2, оз3 и
CJ
Рис. 11. Амплитуды установившихся вынужденных колебаний как функ-
функции от возбуждающей частоты
«4. Масса ш, имеет три частоты антирезонанса, находящиеся в интервалах между соседними
собственными частотами. Масса тг обладает двумя антирезонансами, масса т3 — одним анти-
резонансом. Для массы т4 антирезонансное состояние невозможно.
Использование главных нормальных координат. Основной идеей введения главных
нормальных координат является представление движения в виде разложения по фор-
формам собственных колебаний. С математической точки зрения введение главных нор-
нормальных координат заключается в преобразовании переменных, приводящем одно-
одновременно к главным осям матрицы инерционных и квазиупругих коэффициентов.
Следствием этого является расчленение исходной системы на отдельные, независи-
независимые уравнения.
Введем преобразование
q = Vq*, A5)
где V — матрица, составленная по столбцам из форм собственных колебаний. С уче-
учетом соотношений
/ ! * A6)
и преобразования вектора статического перемещения к главным осям Г„о — V'xf0,
fo = C^Fq исходная система представляется в виде
' */0
cosco< (/=1, 2,
A7)
Каждое уравнение A7) описывает поведение системы с одной степенью свободы.
Решение каждого уравнения A7) имеет вид
/
<?*/ = /*/о ( 1 —
cos <ot (со Ф со;).
108 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
Для получения решения в исходных обобщенных координатах необходимо учесть
преобразование A5)
п
VI / ш2 А
k=\ ^ ~k '
При этом /tto должно быть выражено через статические перемещения.
4. ДИССИПАТИВНЫЕ СИСТЕМЫ С КОНЕЧНЫМ ЧИСЛОМ
СТЕПЕНЕЙ СВОБОДЫ
Уравнения движения диссипативной системы с конечным числом степеней свободы
под действием гармонических сил можно записать в форме
=F0cosco/. A9)
Матрица коэффициентов демпфирования В без ограничения общности может рас-
рассматриваться как симметричная. Среди диссипативных систем с конечным числом сте-
степеней свободы различают системы с полной и неполной диссипацией. К первым
относят системы, для которых диссипативная функция Релея R = 1/2 (Bq, q) яв-
является положительной (R > 0); матрица В при этом является положительно опреде-
определенной. Для систем с неполной диссипацией функция Релея является неотрицатель-
неотрицательной, а матрица В — неотрицательно определенней.
Диссипация существенно влияет на установившиеся вынужденные коелбания.
Для систем с полной диссипацией амплитуды при резонансах становятся конечными,
исчезают антирезонансы, сдвиги по фазам колебаний для обобщенных координат
не равны 0 и я.
Непосредственное решение. Получается путем представления вектора q в виде
q = ft cos wt -f- f2 sin a>t. B0)
Компоненты векторов fx и f2 находят из системы уравнений
[ '
Уравнения B1) для систем с полной диссипацией обладают отличным от нуля оп-
определителем и, следовательно, всегда имеют единственное решение. В системе с непол-
неполной диссипацией возможны случаи отсутствия единсгвенного решения (наличие бес-
бесконечных значений амплитуд при определенных собственных частотах).
Применение метода комплексных амплитуд. Вместо уравнения A9) следует рас-
рассмотреть
B2)
Записывая решение уравнения B2) в виде q = fe't0'1 для комплексной амплитуды
получим уравнение (С — со2А -f-io)B) f = Fo, откуда
B)-1/1,, =(C — w2A + «oB)-iCfo, B3)
где f0 — вектор статических смещений под действием амплитудных значений внеш-
внешней нагрузки.
Решение исходного уравнения A9) можно записать следующим образом: q =
= Req, fj = Ref, f = — Im f.
Метод комплексных амплитуд является предпочтительным при аналитическом
решении задачи об установившихся вынужденных колебаниях систем с конечным
числом степеней свободы.
Использование главных нормальных координат. Решение задачи об установив-
установившихся вынужденных колебаниях в диссипативных системах с конечным числом сте-
степеней свободы может быть получено при введении главных нормальных координат
НЕУСТАНОВИВШИЕСЯ ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ '09
яля соответствующей системы без диссипации. Использование преобразования A5)
с учетом A6) приводит к уравнениям
q*+2 [eyftlq^ + diag (w/)q* = diag (cof)f *0 cos at. B4)
В общем случае матрица [е;/,] не является диагональной и разделения на незави-
независимые уравнения не происходит (между вновь введенными парциальными системами
имеются диссипативные связи). В двух случаях имеет место полное разделение:
в случае внешнего трения, когда матрица коэффициентов демпфирования пропорцио-
пропорциональна матрице инерционных коэффициентов В = 2сА. Тогда [е^] = diag (e);
в случае внутреннего трения, когда матрица коэффициентов демпфирования про-
пропорциональна матрице квазиупругих коэффициентов В = т|С; 2 [е/А] = tjV^A^CV =
= т| diag (юр.
Приближенное решение получают, если в преобразованной системе пренебрегают
диссипативными связями (пренебрежение недиагональными элементами матрицы
[s.^,] в предположении, что б/А ^е,у, е^). Это приводит к разделяющейся системе
уравнений
2 / (/=1, 2 п).
Решение каждого из этих уравнений, соответствующее установившимся колебаниям,
имеет вид
г/ ю2
¦МЫ
со*
Решение в исходных обобщенных координатах получается как сумма
п
9'= 2
5. НЕУСТАНОВИВШИЕСЯ ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
В СИСТЕМАХ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
Неустановившиеся колебания в системе описывают уравнением
q+^q + <*lq = ~F{t) B5)
с начальными условиями q @) = q0, q @) = q0.
Импульсная переходная функция. Рассмотрим вспомогательную задачу о дей-
действии на систему единичного мгновенного импульса Ь (t — т), приложенного в момент
времени t = т, при нулевых начальных условиях. Соответствующее решение диффе-
дифференциального уравнения B5) называют импульсной переходной функцией h (t, x) (ино-
(иногда эту функцию называют весовой функцией или функцией Грина). Решение имеет вид
( 0, t *й т
Частное решение. Пусть начальные условия — нулевые. Представим внешнюю
вынуждающую силу F (I) в виде совокупности бесконечно малых импульсов F (x) dx
(рис. 12). Суммируя реакцию системы от каждого такого импульса на отрезке времени
[О, t,\ (рис. 12), получим
. (t, x) F (х) dx. B7)
но
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
Представление решения в форме B7) называют интегралом Дюамеля.
Если вынуждающую силу F (t) представить в виде последовательности бесконечно
малых приращений F (т) di (рис. 13), то частное решение уравнения B5) примет вид
(f) = TF(f)--F{
I e"Et i cos co6
~ sin wE/) -
B8)
Здесь сохранены обозначения, принятые в гл. V.
Воспользуемся частными решениями в форме B7) или B8) для вычисления безраз-
безразмерной функции q (i) aa>l/F0, представляющей собой реакцию системы на действие
F
F
Рис. 12. Бесконечно малые импуль-
импульсы силы F
at
Рис, 13. Бесконечно малые
приращения силы F
о
ft
6) О
J*
Рис. 14 Частные случаи внеш
ней силы
произвольной вынуждающей силы F (i) = Fof (I). Результаты вычислений для раз-
различных законов изменения вынуждающих сил, распространенных в расчетной прак-
практике, представлены в табл. 1.
Пример. Пусть вынуждающаяся сила сначала возрастает по закону F = $t, а затем,
достигнув в момент tt значения F* = [itt, остается постоянной (рис. 14, о). Такую силу можно
представить в виде двух сил (рис. 14, б, в). Тогда реакцию системы на действие Ft при нуле-
нулевых начальных условиях можно определить по 1абл 1, строка 9 (для случая е =0):
9i = ~ ¦— sin ftW.
С ССОо
Реакцию, вызываемую силой F2, можно определить по той же строке таблицы, если заме-
заменить / на t — t* и изменить знак результата:
При t >U
«Йц
sin «о (/ — /«
ей ¦
F,
— 2
sin —
¦ COS Шо [С —
НЕУСТАНОВИВШИЕСЯ ВЫНУЖДЕННЫЕ КОЛЕБАНИИ
111
1. Неустановившиеся вынужденные колебания в системе
с одной степенью свободы
f @ = F U)/Fo
q (I) aa>yF0
Примечания
e-«t
lite
-at
_L_[(.-a/_,-e/(C
-2 ¦
2u, cos @g
f>2 t -at
• — 2
1 -
A
.— Rt
X
A — Зи,2) COS (Dg/ + |X C — |X2) Sin (Og
A + Д2J
e—at
cos |j^_ jlj sjn
cos p* + ц2 sin
e ci cos (
sin
~at Г и, cos fit + sin P
2 I (l+v)(l+n;)
ц2 cos p/ — sin fit
e — a
e
e — a
e~E' Г nt cos Og/ — sin me
H, cos о)„/ — sin
s о)е/ — sin <Bg< "j
-v)(l+Mj) J
112
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
Продолжение табл. 1
№.
строки
ИЛ = F @/Fo
ц (i) offlo/Fo
Примечания
>v>
Lcosljit
e~xtsin2j3t
cat
2 cos 2fi< — и, sin 2|
+ cos 2P< + ц, sin 2ft< 1 _
e~zi г cos o)?/ + p. sin
cos we/ -f- (x2 sin
(I - v) (I + ».*)
i v-^ +
_Л _2-?M sin 'я„М f
Общее решение уравнения B5). Его представляют в виде суммы общего решения
соответствующего однородного уравнения, удовлетворяющего начальным условиям,
и частного решения, записанного в форме B7) или B8). Например, используя вы-
выражение B7), получим
Я @ =
(cos °W -\ sin
°
B9)
Применение преобразования Лапласа. Интегрирование уравнения движения
с заданными начальными условиями можно осуществить также путем применения
преобразования Лапласа. Переход от оригинала функции и if) к ее изображению
оо
«* (Р) производят по формуле прямого преобразования Лапласа ut(p) = \ и [t) e~P' dt
о
при условии, что и (t) кусочно-непрерывна в любом конечном промежутке; сущест-
существуют такие числа М > 0, с > 0, что I и (f) I < Мес и и (t) = 0 для / < 0.
Для уравнения B5) с начальными условиями q0 и <jo решение относительно изобра-
изображений q^ (p) и F^. (p) имеет вид
C0)
Искомое решение (? @ находят путем обратного преобразования Лапласа.
НЕУСТАНОВИВШИЕСЯ ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
113
Пример. Пуоь механическая системе (рис. 15, а) находится под действием ступенчатого
внешнего возбуждения (рис. 15, б) Решение относительно изображения ?, (р) запишем
в форме C0):
(р + 2е) !?„ -f io Л -2- г / л л i л
ар _ Fp /Л, Л2р + А3
Используя правило преобразования простых дробей, получим А, = 1/йо", Аг — —
л = — 2е/<»о; At = 2е<7о + <!«'¦ As — qa.
Подставим эти значения в решение C1):
Р +8
(р + ЕJ + 0K
• <7о-
Р +
(р
(р
Обратное преобразование Лапласа дает
реакцию системы
9 О = ^
+ 75
f(t)
Рис. 15. Ступенчатое внешнее возбуждение
C2)
Установление вынужденных колебаний. Пусть на систему в момент ( = 0 начи-
начинает действовать гармоническая сила F (t) = Fo s'n ш^ При нулевых начальных ус-
условиях, используя решение B7), получим
q (t) =—V 1— 2ew cos co/ + (tog — w2)
flcoj I
2еш cos wst -\- в2 + и
Sin С081\ ) .
C3)
Процесс установления вынужденных колебаний в случае гармонической возбуж-
возбуждающей силы для различных соотношений между частотами сое и со показан на рис. 16.
2Л/ш
Рис. 16 Процесс установления вынужденных колебаний
Прохождение системы через резонанс. Пусть F (t) = Fo sin,-~
й
, где b
угловое ускорение; ф — начальный фазовый угол возбуждающей силы; со = Ы —
мгновенная частота силы (в момент резонанса tt мгновенная частота равна частоте соб-
собственных колебаний системы шо> т- е- t* = щ/b). Реакцию системы определим, ис-
используя решение B7):
-t) sin(~
C4)
Н4
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
Результат вычисления интеграла C4) для случая, когда е = 0, представлен на рис. 17.
Для каждого параметра (й|/2яЬ, изменяя фазовый угол ф, можно получить семейство
подобных кривых; показанные на рисунке огибающие позволяют определить наиболь-
наибольшую амплитуду. Чем больше ускорение
Ь, тем меньше максимальная амплитуда
колебаний и тем больше ее смещение от
резонанса («0 = btt). Аналогичные ре-
результаты были получены при учете сил
вязкого трения [114]
Рис. 17. Прохож-
Прохождение системы че-
через резонанс
получ
[114].
6. РАСЧЕТ СИСТЕМ С ОДНОЙ
СТЕПЕНЬЮ СВОБОДЫ
НА ИМПУЛЬСНЫЕ ВОЗДЕЙСТВИЯ
Действие постоянной силы. Пусть пос-
постоянная вынуждающая сила Fa, внезапно
приложенная к системе в момент времени
t - О, действует в течение некоторого
промежутка времени т. Колебания систе-
системы при нулевых начальных условиях
(при t <^ т) описываются по формуле,
приведенной в табл. 1 (строка 1). После
прекращения действия силы движение
системы становится свободным и осуществляется за счет начальных условий цх и
q%, сообщаемых системе в момент времени t = т:
Icoscug (/-x) + -f- sin соЕ (t
~x)\
J
sin щ (f-
C5)
максимальное значение q
1
График колебаний изображен на рис. 18. При t > я/сое
достигается при ^ = я/»е = Tg/2 и равно qm^ = Fo [I + ехр( eTg
При этом коэффициент динамического усиления у. = 1 -f- exp (—&TJ2) всегда больше
м.
г/т
Рис. 18. Реакция системы на импульс длитель
ности т
О 0,5 t
Рис. 19. Ударный спектр для
импульса прямоугольной формы
единицы, а при отсутствии сил вязкого трения равен двум. В случае, когда т <; Те/2,
максимальное значение qmax достигается вне отрезка |0, т] в момент времени
'* = 7Г агс4§
cos иЕт —
и равно
р
С
cos ш8 (^ — т) — cos o)E/,).
НЕУСТАНОВИВШИЕСЯ ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ 45
Для системы без диссипативных сил t^ = я/2со0 + т/2 и коэффициент динамиче-
динамического усиления -л = 2 sin (wc/2). Зависимость qmax от параметра импульса т/Г8
называют ударным спектром. График к (т/Г) при 8 = 0 изображен на рис. 19.
Действие ударных импульсов. Импульсом силы S называют величину Fox. Если
•j уменьшается, а величина Foz остается постоянной, то предел F = hm /^т называют
цдарным импульсом. После перехода в выражении C5) к пределу получим
п = F (aWg) e"e'sin co<g. Максимальное значение </max = F (аш^) e~e'*, где t^ =
= ш-1 arctg <ое/е. Если е < <в0, т.е. «е я; aQ, то 4max = /"m^expf—ея/2шH.
Пусть на систему действуют через равные промежутки времени т. одинаковые
ударные импульсы. При совпадении т с периодом колебаний ТЁ = 2я/<вЕ имеет место
ударный резонанс. В этом случае
^ <
4 аше11— ехр(— еТ8I
где <х = / — (п — 1) Tg; « — число импульсов. Максимальное значение по сравне-
сравнению с действием одиночного импульса увеличивается в [1 — ехр (— п&Те)] X
X [1 —ехр (—eTg)] раз. При е = 0 это увеличение будет происходить в п раз.
Действие других форм импульса. Для формы импульса, отличного от прямоуголь-
прямоугольного, решение при t < т находят по формуле B7). Движение системы при t > т вы-
вычисляется по формуле C5). Например, для импульса в виде полуволны синусоиды
решение при t <^т вычисляется по формуле B7) или определяется по табл. 1 (строка 6)
при ф = 0.
Реакцию системы на действие любой кратковременной (т. ^ Т) силы приближенно
можно оценить ее импульсом
$ F (т) dx
sin щ1. C7)
q
ащ
t
Движение системы определяется величиной импульса I F (т) dt, форма им-
о
пульса за промежуток времени |0, т.) не играет роли.
7. НЕУСТАНОВИВШИЕСЯ ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
В СИСТЕМАХ С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
Для системы с п степенями свободы уравнения вынужденных колебаний имеют
вид
Aq + Bq + Cq=F(O C8)
Здесь F (f) — матрица-столбец обобщенных внешних сил.
Операторный метод решения. Применение преобразования Лапласа к дифферен-
дифференциальным уравнениям C8) приводит к системе линейных алгебраических уравнений
(Ар»+ В/7 + С) си (р) = F. (р) + (Ар + В) «7с + \q0. C9)
Здесь q^p) и F» (р) — матрицы-столбцы изображений, соответствующие матри-
матрицам q (t) и ?(t)\ векторы q0 и q0 определяют начальные условия. Решая полученную
систему, например по правилу Крамера, находим вектор изображений q,. (p). Приме-
Применение обратного преобразования Лапласа дает искомое решение.
Метод функций Грина. Частное решение системы уравнений C8) можно предста-
представить в виде
п t
9/@=2 j й,* С t)FA(T)dT, D0)
k=l 0
116 ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ
где hjk (t, x) — решения системы C8) с правой частью F} = 6yfe 6 (i — т). Матрицу,
составленную из функций h^ (t, т), называют матрицей Грина.
Метод разложения по собственным формам. Введем нормальные координаты
4 = Vq*. D1)
Предположим, что преобразование подобия при помощи матрицы V приводит
матрицу А-1В к диагональному виду, т. е. V^A^BV = 2diag (е-а). После перехода
к нормальным координатам уравнение C8) приводится к виду
g(pa)q:(, + diag(wa)q* = F' (/), D2)
где F' (f) — вектор-функция внешних сил в главных координатах, связанная с век-
вектором F (t) следующим соотношением:
F' ({) =V~1\~1F (t).
Система уравнений D1) описывает независимые вынужденные колебания обоб-
обобщенных координат q% (l). Каждое из решения q^- (/) находится по формулам B8)
с начальными условиями
я п
Q*fo~ ^j va;Qaa\ 9*/о = 2^ vaj4ats-
a=l a=l
Переход к искомому решению осуществляется преобразованием D1).
Глава VII
ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ
1. ОБЩИЕ СВЕДЕНИЯ
Предварительные замечания. Понятие о параметрически возбуждаемых колеба-
колебаниях было введено в гл. I. В отличие от вынужденных колебаний параметрически
возбуждаемые (параметрические) колебания поддерживаются за счет изменения пара-
параметров системы. Наиболее часто встречаются колебания с периодическим параметри-
параметрическим возбуждением, которые описываются дифференциальными уравнениями с пе-
периодическими коэффициентами. В этой главе рассматриваются колебания, возбуждае-
возбуждаемые периодическими параметрическими воздействиями.
Примеры параметрически возбуждаемых колебаний в машиностроении. Параме-
Параметрические колебания часто встречаются в задачах динамики механизмов и машин.
Вал, сечение которого имеет неодинаковые главные жесткости при изгибе, может
испытывать незатухающие поперечные колебания даже в том случае, когда он пол-
полностью уравновешен. Причиной поперечных колебаний является периодическое (при
постоянной угловой скорости) изменение изгибных жесткостей относительно непод-
неподвижных осей. В неподвижной системе координат поперечные колебания вала описы-
описываются дифференциальными уравнениями с периодическими коэффициентами. Если
использовать координатную систему, которая вращается вместе с валом, то придем
к дифференциальным уравнениям с постоянными коэффициентами. Поэтому в данном
примере изгибные колебания можно трактовать и как параметрически возбуждаемые
колебания, и как автоколебания. Для вала, который может совершать поперечные
колебания только в одной плоскости, причиной поперечных колебаний является
периодическое изменение изгибной жесткости вала в этой плоскости. Примером
системы с периодически изменяющейся приведенной массой служит шатунно-криво-
шипный механизм. Параметрическое возбуждение колебаний возможно во многих
системах, где движение передается через упруго деформируемые звенья, например,
в спарниковой передаче в локомотивах.
Исследование устойчивости периодических движений в нелинейных системах,
как правило, также приводит к линейным дифференциальным уравнениям с перио-
ПАРАМЕТРИЧЕСКИЕ РЕЗОНАНСЫ 117
яическими коэффициентами. Применительно к конкретным физическим и техниче-
техническим объектам неустойчивость невозмущенных движений обычно может быть истол-
истолкована как параметрическое возбуждение колебаний (и наоборот). Некоторые из рас-
рассмотренных выше примеров также можно интерпретировать как неустойчивость
установившихся периодических движений.
дифференциальные уравнения параметрических колебаний. Уравнения параметри-
параметрических колебаний линейных систем с конечным числом степеней свободы в общем
случае могут быть представлены в виде
где q @ — матрица-столбец обобщенных координат; А (О, В (t) и С@ — квадратные
матрицы, элементы которых — действительные функции времени. Матрица A (t)
при всех t является положительно определенной. На матрицы В (t) и С (t) это огра-
ограничение не накладывают. Если не оговорено, то все коэффициенты уравнения A) —
непрерывные периодические функции времени с периодом Т:
А(* + Г) = А@, В(< + 7-) = В@, С(< + Т)=С@. B)
Соответствующую этому периоду частоту ш = 2п/Т называют частотой парамет-
параметрического возбуждения или частотой возбуждения.
Вводя, как и в гл. V, матрицу-столбец фазовых переменных, запишем уравнение
A) в нормальной форме:
-J- = G(Qx. C)
Здесь G @ — матрица размерностью 2л X 'In:
/О Е \
0@ = 1 Д-1Г A-lR ¦ D)
\—А С —А В/
При периодическом параметрическом возбуждении
G(t+T) = O(t). E)
Понятие о параметрических резонансах. Уравнение A) имеет тривиальное ре-
решение q = 0, которое отвечает невозмущенному равновесию или невозмущенному
периодическому движению системы. Пусть коэффициенты уравнений зависят от не-
некоторых параметров, характеризующих свойства параметрического воздействия и
(или) системы. При некоторых значениях параметров решение q = 0 может оказаться
неустойчивым. Это означает, что имеет место параметрическое возбуждение колебаний
механической системы. Множества точек, соответствующих неустойчивости, как
правило, образуют области в пространстве параметров, которые называют областями
неустойчивости (областями динамической неустойчивости) механической системы.
Если параметрическое воздействие — периодическое и если среди варьируемых па-
параметров содержатся частоты параметрического воздействия, то особый интерес пред-
представляет нахождение частотных соотношений, при которых наблюдается наиболее ин-
интенсивное параметрическое возбуждение. Эти частотные соотношения, как и возбуж-
возбуждаемые при этих соотношениях колебания, называют параметрическими резонансами.
2. ПАРАМЕТРИЧЕСКИЕ РЕЗОНАНСЫ
Фундаментальная матрица Коши и матрица перехода. Рассмотрим систему линей-
линейных дифференциальных уравнений C) с периодической матрицей коэффициентов
G (/). Совокупность N = 2п независимых решений системы C) образует фундамен-
фундаментальною матрицу
й W (t)
называют фундаментальной матрицей Коми или матрицантом.
Значения матрицанта в конце первого периода, т. е.
118 ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ
где первый индекс обозначает номер функции, второй — номер решения. Фундамен
тальную матрицу, удовлетворяющую начальному условию
X @) = Е, G)
Я = Х(Г). (8)
называют матрицей перехода (матрицей монодролши).
Мультипликаторы. Если известно решение системы C) при { = tlt то решение
чри t = t1 + Т [Т — период матрицы G (/)] выражается как
x(tl + T) = Vx(t1). (9)
Собственные значения матрицы перехода — корни уравнения
det(R —рЕ)=0 A0)
называют мультипликаторами. Свойства решений уравнения C), в частности устой-
устойчивость или неустойчивоегь его нулевого решения, полностью определяются свой-
свойствами мультипликаторов, точнее, свойствами характеристического уравнения A0).
Для всякого мультипликатора р найдется хотя бы одно решение, обладающее свой-
свойством
A1)
В частности, мультипликатору р = 1 отвечает периодическое решение с периодом Т,
мультипликатору р = — 1 — решение с периодом 27". Далее эти решения называют
соответственно Т- и 2Т-периодическими.
Мультипликаторы системы уравнений с действительными коэффициентами —
действительные или попарно комплексно-сопряженные числа. Если в уравнении A)
матрица В = 0, а матрицы А (/) и С (t) — четные функции времени, т. е. А (—0 =
= А (/), С (—0 = С @, то мультипликаторы попарно связаны соотношением
PkPk,n=l (*=1, 2, ..., л). A2)
Соотношение A2) справедливо также для канонических систем (см. ниже).
Канонические системы. Уравнение C) можно представить в виде
-^ = JH(/)x. A3)
Здесь Н (t) — симметричная матрица-функция; J — матрица вида
ЧЛ о)
(Еп — единичная матрица размерности га). Уравнения A3) в компонентах имеют
ту же структуру, что и канонические уравнения Гамильтона в аналитической меха-
механике. Системы уравнений, приводимые к виду A3), а также соответствующие меха-
механические системы называют каноническими. Наиболее важный пример механических
систем канонического типа — системы с идеальными голономными стационарными
связями, нагруженные силами, которые выражаются через силовую функцию.
Сели силовая функция — периодическая функция времени, то уравнения движения
можно привести к виду A3) с периодической матрицей Н (f).
Аналитическая форма решений. Пусть все мультипликаторы рх, р2, ... , р2я —
простые корни уравнения A0). Тогда независимые решения уравнения C) имеют вид
**(Q = eA*W) (*=1. 2, .... 2п), A4)
ПАРАМЕТРИЧЕСКИЕ РЕЗОНАНСЫ
119
где X* О — ^-периодические непрерывные функции;
Л1ир
A5)
характеристические показатели.
Если среди мультипликаторов имеются кратные, то структура решений зависит
от свойств элементарных делителей матрицы R — рЕ. При простых элементарных де-
делителях решения, соответствующие кратному корню, по-прежнему имеют вид A4),
причем каждому мультипликатору кратности г отвечает г решений типа A4) с незави-
независимыми периодическими функциями ik (t). Если же кратному корню соответствует
блок нормальной формы Жордана размерностью г, то решение имеет вид
xftlS(/) = eh*'p?s) @ (s = 0, 1 /-—I), A6)
где Vk's' {f) — матрицы-столбцы, компоненты которых — полиномы от t степени s
с Т-периодическими коэффициентами.
Условия устойчивости систем с периодическими параметрами. Решение q eh О
уравнения A) устойчиво по Ляпунову, если все мультипликаторы рь р2, ... , р,„
Рис. 1. Типичные случаи расположения мультипликаторов р = о + «т. на комп-
комплексной плоскости:
а — устойчивость по Ляпунову; б — асимптотическая устойчивость; в — неустой-
неустойчивость
лежат в единичном круге lp| =g 1, причем мультипликаторы, лежащие на граничной
окружности |Р = 1, — либо простые корни уравнения (9), либо имеют простые
элементарные делители.
Решение q = 0 уравнения A) асимптотически устойчиво, если все мультипли-
мультипликаторы лежат внутри единичного круга |р'< 1. Решение q ее 0 уравнения A)
неустойчиво, если среди мультипликаторов имеется хотя бы один, по модулю боль-
u и1 единицы, или найдутся кратные |р = I с непростыми элементарными делителями.
Случаи расположения мультипликаторов на комплексной плоскости представлены
на рис. 1. Этим случаям соответствует рис. 1 гл. V для систем с постоянными пара-
параметрами, если характеристические показатели определять согласно A5).
Классификация параметрических резонансов. Рассмотрим механическую систему,
движение которой описывается уравнением A). При отсутствии параметрического
возбуждения уравнение системы имеет вид
57-+СоЧ = О, A7)
где Ао, Во и Со — симметричные положительно определенные матрицы. Пусть коэф-
коэффициенты параметрически возбуждаемой системы заданы с точностью до двух пара-
параметров: частоты возбуждения ш и коэффициента возбуждения [г, который характери-
характеризует интенсивность параметрического возбуждения (глубину модуляции параметров).
Например, пусть уравнение A) получается из A7) заменой Ао на Ао + [Mt (t),
Во на Во Н- (J,Bx @, Со на Со + [xCj (t), где Ах (t), Bx (J) и Сх Щ — периодические с пе-
периодом Т = 2я/ш матрицы достаточно произвольной структуры. Диссипацию будем
считать достаточно малой, например, удовлетворяющей условию A9) гл V. Для этого
120
ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ
класса параметрических систем область динамической неустойчивости на плоскости ц,
со имеет ряд клиньев, заостряющихся в сторону малых (х. Клинья примыкают к оси
частот вблизи значений со, находящихся в некоторых соотношениях с собственными
частотами соответствующей консервативной системы, т. е. с положительными корнямн
о>1( ш2, ... , (оя уравнения del (Ао — <й2В(|) = 0. Именно эти частотные соотношения
соответствуют параметрическим резонансам [9].
Параметрические резонансы, возникающие вблизи частот
2@»,
-=1, 2, .... п\
>=1, 2, ... )
A8)
называют простыми. В механических системах, для которых уравнение A) распа-
распадается на независимые уравнения, описывающие изменение каждой обобщенной коор-
координаты в отдельности, возможны только простые резонансы.
Рис. 2. Движение мультипликаторов р = о + (т при пересечении границы об-
области устойчивости:
а, б, в — канонические системы, г, д, е — системы с диссипацией
Параметрические резонансы, возникающие вблизи частот
± «ft
//, k=\, 2, ..., п; /:
=1, 2, ...
A9)
называют комбинационными. Эти резонансы, обусловленные попарным взаимодей-
взаимодействием форм колебаний, возможны только в системах, совершающих связанные коле-
колебания. В зависимости от знака в правой части формулы A9) различают комбинацион-
комбинационные резонансы суммарного типа (суммарные резонансы) и комбинационные резонансы
разностного типа (разностные резонансы). В канонических системах и (в силу не-
непрерывности) в системах, достаточно близких к каноническим, возможны только ре-
резонансы суммарного типа.
В зависимости от значения целых чисел р в соотношениях A8) и A9) различают
главные (при р = 1) и побочные резонансы (при р :> 2). Число р называют порядком
резонанса. Согласно этой терминологии резонанс при «> = —- | coj—ы>2 | будем пазы-
пать комбинационным резонансом разностного типа третьего порядка.
СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ 121
Характер решений на границах областей неустойчивости. Для канонической си-
системы [116] все мультипликаторы в области устойчивости находятся на единичной
окружности. При переходе в область неустойчивости, соответствующую простому
резонансу, мультипликаторы становятся кратными, принимая значения либо р = 1,
либо р = — 1 (рис. 2, а и б). В первом случае одно из решений на границе будет
^-периодическим, во втором оно будет 2Т-периодическим. При комбинационных ре-
зонансах мультипликаторы покидают единичную окружность через точки, отличные
от р -= гЬ 1 (рис. 2, в). Этим значениям мультипликаторов отвечает почти периодиче-
периодическое решение уравнения A). Такой же характер поведения будет в системах более
общего типа, мультипликаторы которых удовлешоряют соотношению A2).
Для систем, где условие A2) не выполняется (например, для систем с диссипацией),
типичны случаи, показанные на рис. 2, г—е: в области устойчивости все мультипли-
мультипликаторы лежат внутри единичного круга, а на границе области один или пара комплекс-
комплексно-сопряженных мультипликаторов попадает на единичную окружность. Уравнение
A) имеет при этом соответственно хогя бы одно периодическое или почти периодиче-
периодическое решение.
3. СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ.
ОБЛАСТИ НЕУСТОЙЧИВОСТИ УРАВНЕНИЯ МАТЬЕ — ХИЛЛА
Уравнение Матье — Хилла. Уравнение колебаний диссипативной системы с од-
одной сгепенью свободы приводится к виду
^ ^ 1д = 0, B0)
где использованы обозначения, приведенные в гл. III. Кроме того, введены обозначе-
обозначения для Г-периодической функции возбуждения Ф (t) и коэффициента возбуждения р..
При е = 0 из уравнения B0) получаем уравнение Матье — Хилла
Jg ]? = 0. B1)
Если е Ф 0, то уравнение B0) приводится к виду B1) подстановкой
q(t)=<r«u{f). B2)
Функция и (/) удовлетворяет уравнению
B3)
Области неустойчивости уравнения Магье — Хилла на плоскости ц, со примыкают
к частотным соотношениям
со = -^ (р=1, 2, ...). B4)
Гармоническое параметрическое возбуждение. Области неустойчивости уравнения
Матье. При гармоническом возбуждении уравнение B1) называют уравнением Матье.
Запишем его в виде
g = 0 B5)
или в другой употребительной форме
-0-+ (а + 2ft cos 2*) «7-0. B6)
Переход or одной записи к другой осуществляется при помощи формул
2^w/; e==i^L; /J = i^tt. B7)
(о2 (и2
122
ПАРАМЕТРИЧЕСКИЬ КОЛЕБАНИЯ
о
: cos о:
см
«о
3
+
о-
О
ti
Сз-
о
а
та
Is
3
к
з"
грами
щ
s
а
с
>>
си
Е
Л
п
тс
и
О
_^
К
а
я
метрам:
03
о.
с
?•»
межд
(ЯЗЬ
8
а:
ичес
нне
иод:
еше
на
0J
С
Я
Г
Э Ь
Ь У
и О
>>«
Q
К
О
+
-
со
-t-
+1
1 1
3
II
3
?
о
-с
_
.
536
1
1+
is
1!
а
2
й
2
1 1
э
о
*
4
+
"да
Ц
3
о
+
л
3 824 "
5
1
II
II
а
№
V
*
о
ГО
3
3
О
*
763
13 824 "
¦в
+
а
2
—1
—¦
о
+
a
+1
—1
1
3°
3
г-
о
-
1
¦si
S
1+
•с
+
и
в
?
2
8
"С
(
—1
5
о
1
4112
Й
+
g
э
1
3
S
о
+
317 ь.
о
аз
-С
-|?
II
о
2
¦ч
О
+
ОС
ОС
со
t~-
-ч
a
1
ода
и
3
о
433
1
+
-
II
0
g
s
a.
CO
о
1>.
+1
QC
381
i
=t -4-
ю
CO
00
1
II
3
о
t
1
-
**¦
f
74 14
r
CO
II
2
ft
5
a?
у
СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
123
Распределение областей неустойчивости на плоскости h, а показано на рис. 3. На
границе областей уравнение B6) имеет периодические решения, обозначаемые се„ (х)
и sen М (Функции Матье целого порядка). Диаграмму, приведенную на рис. 3, назы-
называют диаграммой Айнса —
Стретта.
На рис. 4 изображены
первые три области неустой-
неустойчивости на плоскости [х, ц =
= й)/2<в0. Клинья областей
примыкают к частотам B4).
Относительная ширина обла-
области главного параметрическо-
параметрического резонанса имеет порядок ц.
4
Рис.
Диаграмма Айнса—
Стретта
Рис. 4. Первые три области не-
неустойчивости для уравнения
Матье
10 -
0,1 0,2 0,3 Ofi Ofi/L
40 u
При достаточно малых ц =^ 1 границы этой области могут быть рассчитаны по формуле
© = 2шо1/"ПГ^- B8)
Относительная ширина второго, третьего и т. д. побочных резонансов имеет поря-
порядок ц2, ц3 Формулы для расчета границ первых пяти областей неустойчивости
даны в табл. 1.
Кусочно-постоянное параметрическое возбуждение. Области неустойчивости урав-
уравнения Мейсснера. Если функция Ф (f) ¦— кусочно-постоянная, то фундаментальная
система решений и, следовательно, матрица перехода могут быть построены в замкну-
замкнутом виде в элементарных функциях.
Границы областей неустойчивости вычисляют из условия
\h(T)+fi(T)\='2, B9)
гДе /i @ и /2 (/) — решения уравнения B1), удовлетворяющие начальным условиям
'1 (°) = 1, f[ @) = 0, /г @) = 0, f2 @) = 1. Пусть, например,
C0)
-1 -k
124
ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ
Уравнение BJ) с функцией Ф (t) в виде C0) называют уравнением Мейсснера.
Условие B9) для этого уравнения
cos
s2T
4
- COS —7;
s,T
__
__ 1
Si,2 = aoV 1 -t 2ц. C1)
Области неустойчивости для уравнения Мейсснера показаны на рис. 5. В отличие
от рис. 4 по оси ординат отложено обратное частотное отношение 2шо/ш. Характерным
для этой системы является «перекручивание» областей неустойчивости.
Рис. 5. Области неустойчивости для урав-
уравнения Мейсснера
Рис. 6. Области неустойчивости для урав-
уравнения Матье с демпфированием при
Е/Шо = 0,01
1,0
0,8
0,6
0А
0,2
0 0,1 0,2 0,3 0,4 0,5/и.
Определение областей неустойчивости уравнения Матье — Хилла в общем случае.
Пусть функция Ф (t) представлена в виде сходящегося ряда Фурье
ф (/) = ^ (На cos Ш + v/, sin Ш).
C2)
На границах первой, третьей и т. д. областей неустойчивости одно из решений будет
2Т-периодическим. Используя этот факт, ищем границы этих областей из условия
существования решения с этим периодом. Уравнение для нахождения границ имеет
вид условия равенства нулю некоторого бесконечного определителя (ц = 1):
СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
125
Границы второй, четвертой и т. д. областей неустойчивости ищем из условия су-
существования Г-периодического решения. В результате приходим к уравнению
+ Ио-36п'
Mi + Hs '
Н2 + И4
Из
v» —v2
v6 — v,
Ve
И1 + И5
+ И4— IGn
Hi + Из
H2
vs— vt
V4
V1+V5
Н2 + И4
2 Hl + Из
1 + H2 — 4ri2
Hi
v2
v» +v3
Va+V4
Нз
И2
Hi
1
v, 1
Vi
v3
V4 — Va
V3 — Vj
Vj
Vi
-H2-4T12
И, - Hj
Н2-И4
v6
Vi
Hi
Hi
— V,
v4
+ v3
Vj
— Из
4-16T12
-И,
V»
Vi +VS
v«+v4 :
V3
Из — Н4 !
Mi - Ms
1—H» — 36т)г '
=0.
C4)
Приближенные аналитические и численные результаты можно получить, рас-
рассматривая конечные определители, соответствующие усеченным рядам Фурье. В пер-
первом приближении (с точностью до членов порядка (х) границы областей неустойчивости
находят по формуле
¦)'/2]'\ C5)
из которой видно, что ширина k-& области зависит в первую очередь от соответствую-
соответствующих коэффициентов Фурье в разложении C2).
Влияние диссипации на устойчивость параметрически возбуждаемых систем. Па-
Параметрические колебания системы с одной степенью свободы описываются уравнением
B0). Согласно B2) области неустойчивости при s =^0 лежат внутри соответствующих
областей уравнения B3), но могут быть смещены относительно областей неустойчи-
неустойчивости уравнения B1). Наличие демпфирования делает невозможным параметрическое
возбуждение при достаточно малых \i. При этом влияние демпфирования тем силь-
сильнее, чем выше порядок р побочного параметрического резонанса. Типичные области
неустойчивости для уравнения Матье с демпфированием
C6)
приведены на рис. 6.
Расчет границ областей неустойчивости при наличии диссипации. На границах
уравнение B0) имеет решение с периодом Т или 2Т. Условие существования этих
решений для случая C6) приводит к уравнению для нахождения границ первой,
третьей и т. п. областей неустойчивости:
1—V
— и-
0
— ц 0
1 + IX — Т12 Т)
я
я
0 -ц
К
0
= 0,
C7)
126
ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ
где т) = <о/2а>о — частотное отношение; ¦& — 2яе/<»0 — декремент свободных колеба-
колебаний. Аналогичный вид имеет уравнение для границ областей четного порядка:
; l — i6if
'. — )i
0
; о
Я
— ц
1—41J
0
0
0
0
1
-2м
0
0
я
—
1—'
—
2т)
4т)
0
0
— и
1-16тJ
= 0.
C8)
Приближенный расчет производят с использованием усеченных определителей
[9]. Для главного параметрического резонанса
C9)
Границы следующей области неустойчивости могут быть найдены по формуле
:i-n2) D0)
и т. д. Более точные формулы получаются путем систематического разложения по сте-
степеням малого параметра и,.
Критические значения коэффициентов возбуждения. Наименьшее значение коэф-
коэффициента возбуждения, при котором возможно возникновение неустойчивости, на-
называют критическим. Приближенное критическое значение ji^. для главного парамет-
параметрического резонанса в системе, описываемой уравнением B0), легко найти из соот-
соотношения C9):
>«= —• D1)
Для второго резонанса аналогично получаем
Вообще для р-й области неустойчивости
D2)
D3)
4. ОБЛАСТИ НЕУСТОЙЧИВОСТИ ДЛЯ СИСТЕМ
С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
Общая схема метода малого параметра. Метод малого параметра позволяет
получить достаточно простые приближенные соотношения для границ областей неус-
неустойчивости, если глубина модуляции параметров, а также диссипация в системе
достаточно малы. В этом случае уравнение A) может быть записано в виде
(t, ц)] -^L
{t, |»I -^ +IC0+hCi A. l»)l 4-0.
D4)
ОБЛАСТИ НЕУСТОЙЧИВОСТИ 127
где Ао, Во и Со — симметричные положительно определенные постоянные матрицы;
Ai(^ [>-)< Bi(f, Ц) и Ci(t, ц) — периодические матрицы-функции; |j, —малый параметр.
Матрицы Ах, Вх и Съ кроме того, являются аналитическими функциями в окрестности
и == 0.
По предположению диссипация в системе и глубина модуляции параметров имеют
одинаковый порядок малости. В реальных задачах эти факторы, как правило, изме-
изменяются независимо. Можно также построить схему вычислений, где используется
разложение по степеням двух независимых малых параметров.
Пусть ш1; со2, ... , соя — собственные частоты соответствующей консервативной
системы, т.е. корки уравнения det (Со — <м2А0) = 0. В обычной схеме вычислений,
помимо разложения в ряд по степеням малого параметра искомого решения, исполь-
используют разложение частоты возбуждения или соответствующего периода. Допустим,
что нужно построить решение в окрестности одной из критических частот, задаваемых
соотношениями A8) или A9). Обозначим эту частоту через со,.. Введя безразмерное
время т = со/ и разлагая частоту со в ряд со = со,. + ju.6г + jx262 + ¦•¦ , ищем решение
уравнения D4) в виде
Ч @ = Чо @ + № @ + №* @ + • ¦ • D5)
Последовательно решая уравнения метода малого параметра, найдем приближен-
приближенные значения характеристических показателей A5) также в виде рядов по степеням ц.
В области асимптотической устойчивости действительные части всех характеристиче-
характеристических показателей должны быть отрицательны. Отрезки границ областей неустойчи-
неустойчивости, примыкающие к частоте со.,., найдем, приравняв нулю действительные части
соответствующих характеристических показателей.
Формулы первого приближения. Приведем формулы первого приближения (рас-
(рассчитанные с точностью до fi) для случая, когда уравнение параметрических колебаний
имеет вид
^^ = 0. D6)
Здесь матрицы А, В и С — симметричные, положительно определенные постоянные
матрицы; F — постоянная матрица произвольной структуры. Параметр малости
в диссипативный член не введен, хотя предполагается, что диссипация имеет порядок
малости (х (или менее). Используя нормальные координаты [см. формулу C8) гл. III],
преобразуем уравнения D6) к главным осям матрицы А-1С:
^ ^ = 0. D7)
При этом
В' =V"lA"lBV;
D8)
где V — матрица, составленная по столбцам из собственных форм консервативной
системы. Введем обозначения для безразмерных диагональных элементов матрицы дис-
диссипации: yk = yb^k/u>k. При малой диссипации именно эти величины в основном
определяют демпфирование свободных колебаний. Элементы матрицы F' обозначим
Рг//* х - .
Границы областей неустойчивости при простых главных резонансах со = 2coft оп-
определяют по приближенной формуле [9J
1
со **, 2coft A ± 1 VV/?ft-4Yl) . D9)
128 ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ
Таким образом, в первом приближении взаимодействие главных обобщенных коор-
координат не влияет на условия возбуждения основных резонансов. Формула D9) экви-
эквивалентна по точности формуле C9) для системы с одной степенью свободы. Одна фор-
формула переходит в другую, если разложить внешний радикал в C9) в] степенной ряд,
удержать два члена и заменить обозначения. Расхождение в формулах C9) и D9)
объясняется тем, что они получены различными приближенными методами.
Формула для случая отсутствия диссипации вытекает из D9) при у* -*¦ 0:
n/i E0)
Результат с точностью до членов порядка ц совпадает с приближенной формулой
C5).
Для главных комбинационных резонансов суммарного типа со = ы/ -\- сод. анало-
аналогично получаем [137, 142]
V V/Vft
VV
Эта формула включает в себя только парное взаимодействие форм колебаний v,
и \к, входящих в условие комбинационного резонанса (независимо от числа степеней
свободы и характера взаимодействия остальных форм). Если fjhfkj <С 0, то резонанс
на сумме частот не обнаруживается даже при сколь угодно малой диссипации. Вместо
него появляется резонанс разностного типа с граничными частотами
со «, | со,— щ \ ± ' ' Vv? I f,kfkj 1 - 4Y;Yft • E2)
2 V №
Если диссипация отсутствует, то граничные частоты главных комбинационных
областей неустойчивости даются приближенными формулами
Метод обобщенных определителей Хилла. Метод малого параметра приводит
к простым формулам первого приближения типа D9)—E3) для границ главных обла-
областей неустойчивости. Уточнение этих формул, а также расчет побочных резонансов
требует построения высших приближений. Эти приближения громоздки и плохо ал-
алгоритмизируются для численной реализации. К тому же метод становится ненадеж-
ненадежным, если глубина модуляции параметров и (или) коэффициенты диссипации у/г не
малы. Наконец, применение метода встречает затруднения при переходе к сущест-
существенно неканоническим системам.
В основе метода обобщенных определителей Хилла [9] лежит представление од-
одного из решений общего уравнения C) в форме A4). Пусть матрица-функция G (О
в уравнении C) разложена в ряд Фурье по времени:
00
G @ = Go + 2 (Gft cos Ш -f Hk sin kat) E4)
4=1
с постоянными коэффициентами — матрицами G^ и Нк. Разлагая периодическую
вектор-функцию в решении A4) в аналогичный ряд, ищем это решение в виде
x (t) = ehl | 7j- a0 -f- ^ (ад cos k(at + b/; sin /not)
E5)
ОБЛАСТИ НЕУСТОЙЧИВОСТИ
129
Здесь h — неизвестный характеристический показатель; &к и Ьд. — неизвестные чис-
числовые векторы. Подстановка рядов E4) и E5) в уравнение C) после приравнивания
коэффициентов при одинаковых функциях времени приводит к бесконечной системе
линейных однородных алгебраических уравнений относительно компонентов векто-
векторов — коэффициентов ряда E5). Условие существования ненулевого решения этой
системы состоит в равенстве нулю ее определителя. Таким образом, характеристиче-
характеристические показатели h являются корнями алгебраического уравнения
det(K—АЕ) = 0,
E6)
где К и Е — матрицы бесконечного порядка, причем матрица К имеет следующую
блочную структуру:
К =
G
1
1
1
2
1
(Gi +
G2
(Ha-
H4 +
G4
G3)
HO
2wE
1
G
1
2
1
2
(Gt+Оз)
0+2 G2
Gi
H2 + coE
(Hx + Ha)
1
2"
1
2~
1
1
2
G2
G,
Hj
H2
" — [CM
1
2
(H.-HO
H2 —coE
Hi
Go— 9- G2
1
2"
(G1-G3)
1
Y
1
1
'2
0
Н4-2шЕ
(Hi + Нз)
н2
(G1-G3)
0 9
E7)
При достаточно широких предположениях о свойствах матриц G* и Hft бесконеч-
бесконечный определитель оказывается сходящимся и, следовательно, допускает редукцию
к определителям конечного порядка.
Приближенные уравнения для основных параметрических резонансов. На границах
областей неустойчивости, отвечающих простым резонансам A8), уравнение C) имеет
хотя бы одно либо Т-, либо 2Г-периодическое решение. Отсюда можно вывести, что
коэффициенты уравнения на границах этих областей удовлетворяют следующим со-
соотношениям:
при Г-периодическом решении <МК = 0 или
'. G
: 1
• 1
\ 1
(Gi
G
(Hs
1
+ G3)
2
-но
+ 2coE
1
Go+ 2 G2
Gi
1
2
у (Hi+Hg)
1
2
1
1
"
1
2~
G2
Gi
Go
Hi
2 ( —Hi)
2-Н2-иЕ
Hi
Go—2
(Gx — G3)
2 H4 —
Y(Hl +
H2
[(Gi-
*-}
h3) :
Ga) :
G4
= 0, E8)
б п/р. Ьолотина В. В., т. 1
130 ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ
при 2Г-периодическом решении
Go+
(H2-Hi)
I (Gjl + Gj) Go+~ i
1 1 1
I @,-G,) Go-Jo,
= 0. E9)
Пусть параметрические колебания описываются уравнением D6). Границы глав-
главных областей неустойчивости вблизи простых резонансов со — 2й)д (k = 1, 2, ... , п)
могут быть найдены из приближенного уравнения
C + nF — - ш2А —
ушВ
С —[iF —--ю2А
= 0.
F0)
Левая часть обобщает центральный определитель в уравнении C7). Если у = 0,
то вместо F0) получаем уравнение, обобщающее формулу C5):
det (c± fiF — -4 w2AJ=0.
F1)
Тогда приближенные значения характеристических показателей могут быть найдены
как корни алгебраического уравнения достаточно высокой степени, а исследование
устойчивости решения ssO уравнения C) сводится к чисто алгебраической задаче.
Все вычисления в методе Хилла производят над матрицами блочной структуры,
что упрощает алгоритмы и программы для вычислений на ЭВМ. Точность вычислений
может быть оценена сопоставлением результатов, относящихся к двум или несколь-
нескольким приближениям последовательно возрастающего порядка. В этом методе не ис-
используется ни малость глубины модуляции, ни малость демпфирования, ни близость
системы к канонической. Необходимое для удержания число членов в рядах E4)
и E5) зависит от области частот, в которой ищется решение. Для расчета области
неустойчивости вблизи побочного резонанса порядка р нужно сохранить в разложе-
разложениях E4) и E5) по крайней мере гармоники до порядка р включительно.
Алгоритм метода обобщенных определителей Хилла. Для системы с п степенями
свободы при сохранении в рядах Фурье E4) и E5) первых р0 и р гармоник соответ-
соответственно размерность матрицы К равна In Bр0 + 1) Bр + 1)- В связи с высокой
размерностью могут встретиться затруднения при проверке условий устойчивости.
Если система обладает полной и достаточно сильной диссипацией, то следует отдать
предпочтение критерию Зубова. Если диссипация отсутствует или она не является
полной, то в области устойчивости все или часть характеристических показателей —
чисто мнимые. Критерии Рауса — Гурвица и Зубова в этих случаях непригодны.
Устойчивость проверяют непосредственным вычислением комплексных корней урав-
уравнения E6).
Метод матриц перехода. Весьма эффективный численный метод, приспособлен-
приспособленный для ЭВМ [14], основан непосредственно на общей теории. Этот метод состоит
в вычислении матрицы перехода (монодромии) R и исследовании мультипликаторов
как собственных значений этой матрицы. Первая часть алгоритма — построение
матрицанта X (t) непосредственным численным интегрированием уравнения C),
например, по методу Рунге — Кутта; для этого нужно решить 2п задач Коши с на-
начальными условиями, следующими из G). Матрица перехода R находится как зна-
значение матрицанта в конце первого периода, Другая существенная часть алгоритма —
СВОЙСТВА ПАРАМЕТРИЧЕСКИ ВОЗБУЖДАЕМЫХ СИСТЕМ 131
проверка условий | р j <^ 1 (ищутся условия асимптотической устойчивости) или
|р I sS 1 (условия устойчивости по Ляпунову). В первом случае наиболее эффектив-
эффективным Методом, особенно при высоких размерностях матрицы R и при немалом демпфи-
демпфировании, является исследование норм матриц в последовательности R, R2, R4 R2P.
Этот метод входит как составная часть в критерий Зубова для систем с постоян-
постоянными параметрами. Во втором случае приходится непосредственно вычислять корни
уравнения A0) и проверять условие | р | s? 1.
Расчет на ЭВМ устойчивости систем с кусочно-постоянными коэффициентами.
Эти системы рассматривают не только как самостоятельные модели, но и используют
для аппроксимации весьма общего класса систем с кусочно-непрерывными коэффи-
коэффициентами. Матрица перехода выражается при этом через элементарные функции.
Пусть в уравнении C)
G@ = Gft, ts(tk_b tk); ?=1,2 N; <0 = 0, tN = T0. F2)
Здесь Gfc — постоянные матрицы. Матрицант X (t) вычисляется как произведение
экспоненциальных матричных функций
X@ = exp|(/-^)Gftll]exp|(/fc-^_1)Gft] ... ехр 1(^-4) Oil (tetk,tk+1). F3)
Матрица перехода имеет вид
R = exp[(T-/jV 1)GN]exp[(lN ,-/„_,) G^_J... exp [(f,-g OJ. F4)
При реализации на ЭВМ целесообразно вычислять матричные экспоненты при
помощи разложения в ряд Тейлора
со
ехр (АО = 2 Ж А*'*- F5)
Для нормы остаточного члена можно дать оценку
N
sup
ехр
(-АО- У ^
.|| A ||W+irw+iexp(| а |, n.
Ряд F5) обрывается, как только величина, стоящая в правой части соотноше
ния F6), станет меньше, чем установленная малая часть (например, 10~9) от частичной
суммы.
5. СВОЙСТВА ПАРАМЕТРИЧЕСКИ ВОЗБУЖДАЕМЫХ СИСТЕМ
Относительная ширина областей неустойиивости. Пусть система с несколькими
степенями свободы находится под действием гармонического параметрического воз-
возбуждения. Если все элементы матрицы F в уравнении D6) имеют одинаковый порядок,
то относительная ширина всех главных областей неустойчивости, измеряемая по от-
отношениям частот, имеет одинаковый порядок ц. При слабой связи между обобщенными
координатами области комбинационных резонансов могут оказаться уже областей
простых резонансов. Напротив, если диагональные элементы матрицы F в главных
осях матрицы A~JC равны нулю или малы по модулю по сравнению с недиагональными
элементами, то области простых резонансов будут уже областей комбинационных
резонансов того же порядка. Например, при fkk = 0 формула E0) указывает на слия-
слияние границ основного резонанса (в действительности ширина этой области может
иметь порядок ц2 или менее).
Влияние диссипации на области неустойчивости. Как и в системах с одной степенью
свободы, диссипация приводит к невозможности возникновения неустойчивости при
малых глубинах модуляции, причем это проявляется в большей степени на побочных
резонансах, чем на главных,
Б*
132
ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ
В системах с несколькими степенями свободы возможен дестабилизирующий
эффект диссипации. Он состоит в расширении малых комбинационных областей
при введении в систему без диссипации диссипативных сил с существенно различными
парциальными коэффициентами. Этот эффект виден непосредственно из формулы E1).
В самом деле, коэффициент перед радикалом может быть сколь угодно большим. Для
этого достаточно принять, например, что y& ^ Y/- На рис. 7 показаны результаты
вычислений по этой формуле при coft = —u)y; y; = 0,01 и различных значениях yk.
Еще один эффект диссипации — образование конечных (ограниченных) областей
неустойчивости в системах с полигармоническим и кусочно-постоянным возбужде-
возбуждением. На рис. 8 видно, как изменяются области неустойчивости при введении в сис-
систему Мейсснера диссипации с коэффициентом у = е/со
0,2
0,3
Рис. 7. Дестабилизирующий эффект диссипации при
B« = f аГ у1 = 0'01
Рис. 8. Влияние диссипации на устойчивость системы
Мейсснера
Влияние структуры коэффициентов возбуждения. Все приводимые ниже резуль-
результаты, полученные численным методом матриц перехода, относятся к системе с двумя
степенями свободы типа D6). При этом
А = Е, В = Е, C0 = diag (cof, соз). F = (
где J — одна из матриц вида
1 1
1 I)'
:)•
1 1
-1 ii-
О 1
—1 О
F7)
F8)
На рис. 9 показаны области неустойчивости для случая и>2 = ~ ш2; у1 = у2 = 0,01.
Первые два графика относятся к системам, которые при у = 0 становятся канониче-
каноническими. На рис. 9, a (J = Jj) видны как простые, так и комбинационные резонансы
нескольких порядков. Например, клин у и>/и>1 = 2,5 соответствует главному ком-
комбинационному резонансу ш = ш1 + Щ- Рис. 9, б (J == J2) построен для системы,
СВОЙСТВА ПАРАМЕТРИЧЕСКИ ВОЗБУЖДАЕМЫХ СИСТЕМ
133
обобщенные координаты которой связаны лишь через недиагональные элементы
матрицы F. Простые резонансы вблизи ш = 2ч>1 и со = 2со2 на диаграмме не обнару-
обнаруживаются, а доминируют области неустойчивости, отвечающие комбинационным ре-
зонансам на сумме частот.
Рис. 9, в и г (J = J3, J = J4) соответствуют существенно неканоническим систе-
системам. При малых значениях коэффициента возбуждения граница области устойчивости
оказывается весьма изрезанной На рис. 9, в выделяются клинья области неустойчи-
неустойчивости, соответствующие главным простым резонансам ю = 2»! и со = 2со2, а также
главному комбинационному резонансу разностного типа со = | coi — со2 |. На рис. 9, г,
0,5 1,0 1,5 р О
В)
0,5 10 1,5 JU
в)
Рис 9 Области неустойчивости для систем
с двумя степенями свободы при со2 = ^-<Bi.
Yi = Чг = 0,01
который построен для системы с антисимметричной матрицей коэффициентов воз-
возбуждения, ясно видны клинья, отвечающие простым резонансам второго порядка со =
= сох и со = со2, а также главному комбинационному резонансу при со = \ и>1 — со2 j.
Увеличение диссипации во всех случаях приводит к смещению областей неустойчи-
неустойчивости в сторону больших (я, а также к сглаживанию границ этих областей. При
очень малых т} = со/2% ^ 1 численные методы становятся неэффективными.
Параметрические резонансы в системах, находящихся под действием позиционных
неконсервативных сил. Если система нагружена постоянными позиционными не-
неконсервативными силами, то матрица С в уравнении D6) не будет симметрич-
симметричной. Влияние этих сил учтем, полагая, например, что C = C0 + PcoiJ. гДе J —одна
из несимметричных матриц типа F8), р" — коэффициент, характеризующий величину
неконсервативных позиционных сил. Устойчивость системы
-+ [Со + fto
Fj q = 0
F9)
134
ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ
при [1 = 0 исследуется методами гл. V. При п = 2, В = а^Е, J = J4 решение q = 0
уравнения F9) устойчиво, пока Р < Р*, где Р„ — критическое значение параметра р1:
¦К (<oi-a>f)s
I + «Ю2
G0)
Из рис. 10 видно, как последовательное возрастание параметра р влияет на устойчивость
системы в присутствии параметрических сил Вычисления проделаны для случая, когда функ
ция Ф @ имеет вид C0) При р = 0 области неустойчивости весьма похожи на изображенные
на рис. 9, г. С ростом р* появляются аналоги главных простых резонансов <о = 2<Oj и со = 2шг,
однако соответствующая область неустойчивости имеет необычную серповидную форму
(рис. Ю, а) При дальнейшем увеличении р области неустойчивости приближаются к оси частот,
а при р > р* все точки на этой оси принадлежат области неустойчивости (рис 10, в) Но при
этом обнаруживаются изолированные области устойчивости, которые соответствуют некоторым
достаточно большим значениям коэффициента возбуждения
2,0
1,5
1,0
0,5
О 0,2 ОА 0,6 ju О 0,1 0,4
а) 6)
0,2 Ofi ju.
1}
Рис. 10. Области неустойчивости для систем с двумя степенями свободы:
а) р = 0,1 Р.; б) Р = 0,9 Р.», в) р = 1.1 р,
Параметрическая стабилизация динамически неустойчивых систем. Описанный
только что факт означает возможность параметрической стабилизации динамически
неустойчивых систем: система, динамически неустойчивая при ц = 0, становится
устойчивой при добавлении параметрических сил с надлежаще выбранными частотами
и коэффициентами возбуждения. Аналогичное явление известно для систем, находя-
находящихся под действием консервативных сил. Например, известна возможность стаби-
стабилизации обращенного маятника путем сообщения его опоре определенного колеба-
колебательного движения (стабилизация связана с попаданием в область устойчивости на
диаграмме Айнса — Стретта при а < 0). Возможность стабилизации существенно не-
непотенциальных систем является не столь очевидной.
Параметрическая стабилизация возможна также в системах, равновесие которых
q = 0 неустойчиво из-за наличия ускоряющих сил. Так, можно стабилизировать
систему с двумя степенями свободы, диссипативная функция Релея которой — зна-
знакопеременная функция. Если же эта функция является отрицательно определенной
(т. е. любое движение сопровождается притоком энергии в систему), то параметри-
параметрическая стабилизация невозможна. Параметрическая стабилизация обнаруживается
также в системах, неустойчивых при наличии гироскопических и диссипативных сил.
Области устойчивости для этих систем по структуре напоминают области, показанные
на рис. 10, в [109].
Часть вторая
КОЛЕБАНИЯ ЛИНЕЙНЫХ
РАСПРЕДЕЛЕННЫХ СИСТЕМ
Глава VIII
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ РАСПРЕДЕЛЕННЫХ
КОЛЕБАТЕЛЬНЫХ СИСТЕМ
1. ПРИНЦИП ГАМИЛЬТОНА — ОСТРОГРАДСКОГО ДЛЯ УПРУГИХ
РАСПРЕДЕЛЕННЫХ СИСТЕМ
Предварительные замечания. Под упругими распределенными системами пони-
понимают упругие механические системы с непрерывно распределенными массой и жест-
жесткостью. Они имеют бесконечное число степеней свободы. В отличие от систем с сосре-
сосредоточенными параметрами (с конечным числом степеней свободы п), динамическое
поведение которых можно описать системой обыкновенных дифференциальных урав-
уравнений относительно обобщенных координату (t) (/ = 1, 2 я) (см. часть первую),
поведение распределенных систем описывают дифференциальными уравнениями
в частных производных относительно некоторых функций координат и времени.
Распределенные упругие системы называют линейными, если они описываются ли-
линейными уравнениями в частных производных. При решении задач динамики для
распределенных упругих систем, кроме начальных условий, требуется формули-
формулировка краевых условий.
Вариационный принцип. Сформулированный в гл. II принцип Гамильтона
для систем с конечным числом степеней свободы может быть распространен на
распределенные системы. Если внешние силы обладают потенциалом П, то после
введения интеграла действия
tx
J='\(T~U — U)dt A)
to
(где Т — кинетическая энергия; U — потенциальная энергия деформации упругой
системы) вариационный принцип Гамильтона — Остроградского принимает форму
6J = 0. B)
Для упругого тела, занимающего объем V, ограниченный поверхностью S, интег-
интеграл действия может быть представлен в следующем виде:
где L — объемная плотность лагранжиана; R — поверхностная плотность; So —
часть поверхности S, где заданы усилия. При этом L и R зависят от перемещений
точек тела в направлениях координатных осей и, v, w и их первых производных по
координатам и времени.
В общем случае поведение упругой системы при введении соответствующих гипо-
гипотез описывает вектор-функция u (t) с компонентами и; (t) (/ может быть как меньше,
так и больше 3). Объемная и поверхностная плотности лагранжиана зависят от Uj
136
РАСПРЕДЕЛЕННЫЕ КО ЧЕБАТЕ ПЬНЫЕ СИСТЕМЫ
и их производных по координатам и времени t (порядок производных может быть
любым, но в большинстве практически используемых случаев порядок производных
по координатам < 2, а по времени sg: 1)
Уравнения движения и краевые условия. Уравнения Остроградского — Эйлера
вариационной задачи B) дают уравнения движения и естественные краевые условия
Например, для двухмерной упругой системы, когда лагранжиан L не содержит тре-
третьих и более высокого порядка производных от и,, уравнения и естественные крае
вые условия имеют вид
D)
на Г, E)
\ дха дх$
где па — компоненты вектора внешней нормали к границе Г, vna и\>/а — соответ
ственно направляющие косинусы нормали и касательной к контуру
Здесь использовано правило суммирования по немым (повторяющимся) индек
сам аи Р Это правило будет использоваться в дальнейшем (по греческим индексам
суммирование от 1 до 2, по латинским — от 1 до 3)
Выражения в E) являются коэффициентами в подынтегральном выражении
/ди,\
поверхностною интеграла при вариациях 6uj, б(^—) и т д Следовательно, естест
венные краевые условия соответствуют незакрепленному по граничной поверхности
телу В противоположном случае, когда соответствующие смещения (повороты и г д )
отсутствуют, то вариации равны н>лю Таким образом, в зависимости от характера
закрепления граничной поверхности должны выполняться условия
j = 0 либо
дп
F)
Краевые условия, записанные в виде F), называют альтернативными
УРАВНЕНИЯ ДИНАМИКИ УПРУГИХ ТЕЛ
137
2. УРАВНЕНИЯ ДИНАМИКИ УПРУГИХ ТЕЛ
Основные соотношения классической теории упругости Линейная классическая
теория базируется на ряде гипотез, основными из которых являются предположе-
предположения о сведении системы сил, действующих на элементарную площадку, только к рав
недействующей (отсутствие моментов), о малости градиентов перемещений (линей
пая связь между деформациями и перемещениями), об идеальной упругости мате-
материала (линейная связь между напряжениями и деформациями)
Каждая точка упругого тела, отнесенного к прямоугольной декартовой системе
координат, характеризуется вектором перемещения и с компонентами иъ и2, щ
в направлении осей координат В каждой точке определены компоненты тензоров
напряжений и деформаций
/ап а12 о13
0=1 а21 а22 о23
W азг стзз
еи е12 е13
е21 е22 е23
G)
В классической теории упругости эти тензоры симметричны (а]/г = akl, г^ = г]1г)
Компоненты тензора напряжении представляют собой нормальные и касательные
напряжения на трех взаимно перпендикулярных площадках в данной точке тела
Знание тензора о позволяет подсчитать компоненты вектора напряжения р, на любой
произвольно ориентированной площадке в данной точке (п — нормачь к площадкеI
Pi =сГд cos ^п, XiJ-f~o"y2 cos \п> хг)~t~°уз cos \п хз)' (8)
Компоненты тензора деформаций связаны с перемещениями форму гами Коши
1 (ди, _ duk
Компоненты Zjj характеризуют относительные удлинения в направлении соответст-
соответствующих осей, a s;fc (] ф k) — относительные сдвиги (изменение углов между осями
Ох, и 0xk).
Помимо прямоугольных декартовых координат упругое тело может быть отне-
отнесено к различным криволинейным системам координат В качестве примера приве-
приведем формулы выражения компонент тензора деформаций через перемещения в цилинд-
цилиндрических координатах
_диг _ иг \ дич _диг _д«Ф «ф
е,— дг , еф_ г + г -^-, гг—^-, е,ф—^- r
диг
диг
дпг диг
в сферических координатах
диг
иг
див
иг
див щ
диг
див
диг <3иф
g i Z. L.
rff> r sin 6 dq> дг г '
Связь между напряжениями и деформациями Закон Гука. Для упругого тела
в случае малых деформаций между компонентами тензоров напряжений и деформа
138 РАСПРЕДЕЛЕННЫЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
ций существует линейная зависимость
A2)
где %/kim — тензор упругих постоянных. Этот тензор обладает свойствами симмет-
симметрии:
^!klm = ^lmjk = ^ikml—^kilm A3)
В частных случаях число независимых постоянных в законе Гука A2) умень-
уменьшается. Для изотропного тела (все направления эквивалентны) число независимых
упругих постоянных равно двум. В этом случае упругие постоянные выражают
через постоянные Ламе X и ц:
+ S7m6/;/), A4)
С 0, если / Ф k;
где о,ь = < —символ Кронеккера. Закон Гука принимает следующею
{ I, если j=k
форму:
Ojj — ХЭ + 2|j.e,7 (по / не суммировать); ~i
Здесь 0 = ^ относительное изменение объема. Между средним напряжением
о— Tj- (an-f-ff22 + азз) и объемной деформацией имеется линейная связь
о
Щ A6)
где К — объемный модуль. В технических обозначениях соотношения закона Гука
содержат модуль упругости Е, коэффициент Пуассона v и модуль сдвига G —тгп г.
2A -f-v)
Выраженные относительно компонент тензора деформаций соотношения закона Гука
имеют вид
[
«аг = ?-[Са2—v(O3s + On)]; 8I3 = 2g a13; !¦ A7)
Потенциальная энергия деформации. Потенциальную энергию деформации можно
подсчитать по формуле Клапейрона:
причем справедливы следующие зависимости:
дФ дФ
а ^
Использование связи между напряжениями и деформациями позволяет выра-
выразить потенциальную энергию деформации либо только через напряжения, либо
только через деформации. Для изотропного тела
Ф = ? [Oii+o|s+o|,—2v (а11о22+о22озз+о33о11) +
B0)
B1)
УРАВНЕНИЯ ДИНАМИКИ УПРУГИХ ТЕЛ 139
Более подробные сведения по теории упругости можно найти в справочных руко-
руководствах [87, 101].
Выражения для плотностей лагранжианов. Для упругой консервативной системы
существует потенциал внешних сил
п=—5 5 5 xj uJdv—И Р) uidS+const- B2>
Соотношения Коши (9) и закон Гука A2) позволяют записать выражение для
потенциальной энергии деформации A8) через перемещения:
ди, dui
-—- dV. B3)
Кинетическая энергия
р(аг) dV- B4)
v
-ИИ
Объемная и поверхностная плотности лагранжиана имеют вид
B5)
ди, dui
Уравнения движения и естественные краевые условия. С использованием B5)
уравнения D) переходят в динамические уравнения Ламе
д I duts
' ' ¦ "' B6)
Естественные краевые условия на поверхностях, ограничивающих тело, где
заданы нагрузки, имеют вид
jklm ;5— rik==~Pj на *ЪG, B7)
где nh — компоненты вектора внешней нормали к поверхности.
Уравнения движения для изотропного упругого тела. Уравнения Ламе B6) при-
принимают форму
_^__^ 5^ ^\ [ B8)
[ дх* ~
дх* ~dx'i+dxl+dxlj- J
Естественные краевые условия запишутся так:
[да/ (ди, дик \~|
Гк + 1ь})\п»=* ™ s°' B9)
Кроме того, на остальной поверхности задаются перемещения
и/ = и0; на Su. C0)
При решении динамических задач должны быть заданы еще начальные условия
ди,-
"/=«';. -^=«/ при <=°- <3i)
Операторная запись уравнений движения. При использовании различных моде-
моделей для двухмерных и одномерных систем в рассмотрение вводят обобщенный вектор
перемещений u (x, t), размерность которого может быть как меньше, так и больше 3
140 РАСПРЕДЕЛЕННЫЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
Общую запись уравнений движения для всех случаев (включая рассмотренный выше
случай упругого тела) можно получить, если использовать операторную запись
A-g-+Cu = f, C2)
где А и С — линейные положительно определенные матричные операторы, соответ-
соответственно инерционный и упругий; f — вектор внешних нагрузок. Конкретный вид
этих операторов для упругого тела нетрудно получить, сопоставляя C2) с B6) или
B8). Для других случаев выражения для А и С будут даны ниже.
Замечание. Уравнение C2) нключает фактически и краевые условия через области опре-
определения операторов А и С
3. УЧЕТ ДИССИПАЦИИ В УРАВНЕНИЯХ ДВИЖЕНИЯ.
ВЯЗКОУПРУГОЕ ПОВЕДЕНИЕ ДЕФОРМИРУЕМЫХ МАТЕРИАЛОВ
Классификация моделей диссипации. Причины, приводящие к рассеянию энергии
в упругих системах, условно могут быть разбиты на три группы. Первую группу
составляют потери энергии в окружающую среду («внешнее» трение). Ко второй
группе относят потери, вызванные внутренними процессами в материале системы
(«внутреннее» трение). Наконец, третью группу образуют потери, связанные с тре-
трением в опорах, шарнирах и т. п. («конструкционное» трение). Границы между ука-
указанными группами не всегда можно провести достаточно четко.
С учетом диссипативных сил уравнения движения можно записать следующим
образом:
+ В+Си = (> C3)
где В — диссипативный оператор. Вид диссипативного оператора существенно за-
зависит от вида модели трения.
Учет конструкционного трения приводит, как правило, к нелинейным соотно-
соотношениям. В связи с этим эту группу причин диссипации энергии в упругих системах
при динамических процессах в данной книге не рассматривают.
Относительно простой линейной моделью является модель внешнего трения.
Считается, что диссипативные силы вязкие и пропорциональны скоростям движения.
В случае внешнего трения и полной диссипации диссипативный оператор В пропор-
пропорционален инерционному оператору:
В = 2еА, C4)
так что уравнения движения можно записать так:
<* = '• <35>
Внутреннее трение связано с диссипативными процессами, происходящими во
время колебаний в материале системы. Разнообразие свойств конструкционных
материалов, в частности их диссипативных свойств, обусловило многообразие мо-
моделей учета диссипации энергии при динамических процессах. Условно эти модели
можно разделить на два класса: к первому относят нелинейные модели, описываю-
описывающие гистерезисные явления при циклическом деформировании (использование этих
моделей приводит к нелинейным уравнениям движения, поэтому эти модели в дан-
данной книге не рассматривают [82, 84]); ко второму — модели, связанные с вязкоупру-
гим поведением материалов при деформировании.
Поведение материала, коюрое объединяет в себе свойства упругости и вязкости,
называют вязкоупругим. Предельными противоположными случаями большого числа
вязкоупругих сред являются упругое тело и вязкая жидкость.
Простейшие модели вязкоупругого поведения. Дифференциальная форма связи
между напряжениями и деформациями. Для описания одномерного процесса дефор-
деформирования вязкоупругих сред могут быть использованы механические модели,
УЧЕТ ДИССИПАЦИИ В УРАВНЕНИЯХ ДВИЖЕНИЯ
141
состоящие из линейных пружин и демпферов, соединенных определенным образом.
Различные соединения'позволяют моделировать различные уравнения, связывающие
напряжение сх, деформацию е и их производные по времени. Некоторые наиболее
употребительные модсл i описаны в табл. 1.
1. Модели вязкоупругого поведения материалов
Модель
Максвелла
Фойхта —
Кельвина
Стандартное
линейное
тело
Обобщенная
модель
Кельвина
Обобщенная
модель
Максвелла
Трехэлемент-
Трехэлементная модель
вязкоупру
гости
Схема
-Ту
HVWS
L-^—[м
Уравнение
1 до о де
до , г. ,
Т° дГ °= °°е
я
1 = 1
х~д7
?" 7" +1Га =
Й28 ЙЕ
~ %° dt2 + ~дТ
Диссипативный
оператор
Е ^Ж
h°°[l+ ?OT д{)Х
Г ч I"
V '
1 | ?", -4- у\, -— 1
п
1=1 V ' ^
д
dt
д^ д
То -ТТ-, + -Г,
С/ ог
15 1
В общем случае связь между напряжением и деформацией может быть записана
в следующей дифференциальной форме:
m n
2dko ^ V ^е_
4 = 0 /=0
или в операторной форме
= Q(|)e. C7)
142 РАСПРЕДЕЛЕННЫЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
При переходе к трехмерной теории линейной вязкоупругости эффекты формо-
формоизменения и изменения объема изучают независимо. Математически это соответствует
разложению тензоров напряжений и деформаций на шаровую часть и девиатор:
oy* = S/ft + e/*-^L; ejk = eJk + bjk f-. C8)
Основные соотношения линейной вячкоупругосги в дифференциальной форме
имеют вид
(?)(!)
Замечание. Довольно часто считают, что изменение объема происходит чисго упруго и
последнее соотношение заменяют на A6)
Интегральная форма связи между напряжениями и деформациями. Если в мо-
момент t = О мгновенно приложено напряжение а0, которое в дальнейшем остается
постоянным, то происходит изменение деформации со временем, которое называют
ползучестью:
<L(f) = J(t)o0, D0)
где J (t) — функция ползучести. Если в момент t = 0 мгновенно фиксируется дефор-
деформация е0, которая затем остается со временем неизменной, то происходит изменение
напряжения со временем, которое называют релаксацией:
a(t) = H(t)eB, D1)
где Н (t) — функция релаксации.
В линейной теории вязкоупругости применим принцип суперпозиции. Поэтому
представление процесса нагружения во времени как последовательного ступенча-
ступенчатого нагружения позволяет получить зависимость между деформацией и напряже-
напряжением в виде интеграла наследственности
е(/)= \ J(t-T)^Jp-dr. D2)
Предположение, что до t= 0 в теле отсутствовали напряжения и деформации
и что в момент t = 0 имело место ступенчатое нагружение, позволяет записать
выражение
t
f (/-т)^Ф<*т. D3)
При t < 0 J (t) = 0, а при t = 0 /@) =-?-, где Ео — мгновенный модуль упру-
упруго
гости. После интегрирования по частям выражение D3) принимает вид
D4)
О „ /Л ' dJ @ Д
Здесь К @ = т~т —-j, — Я"Р° ползучести
УЧЕТ ДИССИПАЦИИ В УРАВНЕНИЯХ ДВИЖЕНИЯ 143
Соотношения, подобные D3) и D4), но разрешенные относительно а, получаются
в результате аналогичных рассуждений при использовании функции релаксации
(t-x)^^dv, D5)
о
Г ' 1
a(t) = E0\e(t)~\R (t-x) г (т) dx .
I о J
D6)
При полу 'ении последнего соотношения путем интегрирования по частям D5) исполь-
использовано, что Еа= Н @). Входящая в D6) функция R (t) = ——^ называется
л (и) at
ядром релаксации.
Если D6) рассматривать как интегральное уравнение Вольтерра относительно
е (t), то ядро ползучести будет резольвентой этого уравнения.
Для стандартного тела (см. табл. 1) для определения Н (t) имеем уравнение
Я + Т°1Г = ?» D7)
которое необходимо проинтегрировать при условии Н @) = Еа.
Искомый интеграл имеет вид
Я@ = (?0-Соо)ехр(-//т0) + ?оо. D8)
Отсюда
R(t)=~<f-1exp -f). D91
Итак, для стандартного тела ядро релаксации является экспоненциальной функ-
функцией. Следовательно, и ядро ползучести будет экспоненциальной функцией. Вообще
при связи между напряжением и деформацией, заданной дифференциальным соот-
соотношением с постоянными коэффициентами, ядра релаксации и ползучести будут
представлять собой суммы экспоненциальных функций. Дифференциальные соот-
соотношения описывают поведение определенных линейных вязкоупругих сред, так
называемых сред с дискретным спектром времен релаксации. Большинство же поли-
полимерных материалов, как показывают эксперименты, обладают сплошным спектром.
Для сред со сплошным спектром ядра ползучести и релаксации были предложены
многими авторами (см. [46, 55, 90]). Некоторые из предложений сведены в табл. 2,
где представлены ядра релаксации и их резольвенты.
Зависимости типа D4), D6) обобщаются на случай трехмерного состояния. Напри-
Например, вместо D6) получим
S,„ @ = 2G0 eJk (I) -^R(t-x)eJk (т) dx
L о
t
, @ = Я/С„ | ел (t) - \ Rx (t- т) ЕЛ (т) dx
0
E0)
где Go — мгновенный модуль сдвига;/Со — мгновенный объемный модуль; R(t) —
ядро релаксации для девиатора; Rx (t) — ядро 'релаксации для объемной дефор-
деформации.
Комплексные модули и податливости. Если задано напряжение, изменяющееся
по гармоническому закону
a = a0 cos со/, E1)
то в результате устанавливается деформированное состояние, меняющееся по гар-
гармоническому закону с той же частотой, но со сдвигом по фазе:
е = е0 cos (at — у). E2)
144
РАСПРЕДЕЛЕННЫЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
2. Ядра релаксации и их резольвенты
Ядро
^e-P(/-s)*«
tf-sI ft.
"""""
„„-„-,„
(t - s)'-«i
Л.-^-s)
«-*>' «
Ла
« - sI a
д ц s\Oi
Г A + a)
n-
X
X
i
CO 1
n = l
CO |
si
\
ад,,
-s)
CO
Резольвента
^-PW-s)*'
U - s)k'
+ *2- 1 \1
ft. У 1 ('
r\n(k'+k
[ \ ft
-5I-
rK9-
-PW-S)«. v
5)]*<
г[«(а-
CO
[ЛГ (a)]" U -
Г (an)
CO
V лря «
^™^ T* f (rt -[-
X
s)fl (ft, +k, - I)
I
i)J
- s)"(l +a)
D(l+«)]
Обобщение описания вязкоупругого поведения достигается представлением на-
напряжения и деформации в комплексной форме
а = 0„е'и/; e = e0e'(M/-Y>. E3)
При таком представлении связь между напряжением и деформацией записывают
с введением комплексного модуля
а = Е (со) е = [ЕГ (со) + (?,• (со)] е. E4)
Для модели C7) комплексный модуль
?(co)=Q(ue)/P(«o). E5)
КОЛЕБАНИЯ СТРУНЫ И СТЕРЖНЕЙ 145
Отношение мнимой части комплексного модуля к его действительной части назы-
называют тангенсом потерь:
Эта характеристика может служить мерой рассеяния энергии в единице объема
вязкоупругого материала при колебаниях.
При введении комплексной податливости можно записать
e = J (ш)а = уг(<о) — и{((й)}а. E7)
При распространении основных понятий на трехмерный случай вводят комплекс-
комплексный модуль сдвига и комплексный объемный модуль на классе гармонических дви-
движений следующим образом:
G((o)e/* = 2[0((o) + «G,(a))]e*; 1
Уравнения динамики линейных вязкоупругих систем. Уравнения движения вяз-
вязкоупругого тела по форме аналогичны уравнениям движения упругого тела при
условии, что вместо упругих констант в эти уравнения должны быть внесены опера-
операторы. Динамические уравнения Ламе примут вид
2
,1 = 0, X = K-g-G. F0)
Операторы G и К устанавливают связь между напряжениями и деформациями
(компонентами девиаторов и средними значениями):
S,k = 2Ge/k, a//=3Kty/. F1)
Эти операторы берут либо в виде интегралов наследственности E0), либо диф-
дифференциальных операторов C9), либо комплексных модулей E8).
При использовании уравнений движения в форме C3) необходимо получить явное
выражение для диссипативного оператора В. Так, если для описания вязкоупругого
поведения материала используется модель Фойхта (см. табл. 1), то
В = т)С, F2)
где т) — положительная постоянная (коэффициент внутреннего трения). Для систем
из линейного вязкоупругого материала с наследственным трением вводится наслед-
наследственный оператор с ядром R (t, т), так что
t
В"Ж= I R{t' т>|г(т)Л- F3)
Ядро R (t, т.) выбирают по табл. 2.
Более подробные сведения по вопросам вязкоупругости можно найти в моногра-
монографиях [49, 55, 90].
4. КОЛЕБАНИЯ СТРУНЫ. ПРОДОЛЬНЫЕ И КРУТИЛЬНЫЕ
КОЛЕБАНИЯ СТЕРЖНЕЙ
Поперечные колебания струны. Под струной понимают тонкое упругое одномер-
одномерное тело с пренебрежимо малой жесткостью на изгиб. Колебания струны длины /,
растянутой усилием N и закрепленной по концам, происходящие в плоскости Охг,
описываются уравнением
146 РАСПРЕДЕЛЕННЫЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
Здесь w — отклонение струны в направлении Ог; р — плотность материала струны;
F — площадь поперечного сечения; q — интенсивность нагрузки, действующей в пло-
плоскости Охг. На концах струны
ш @, t) = w(l, 0 = 0. F5)
При t = 0 должны выполняться начальные условия
ш(х, 0)=f(x);^-(x, 0)=g (x). F6)
Замечание. В силу линейности задачи и одномерности упругого объекта произвольные
малые пространственные колебания могут быть представлены как суперпозиция колебании
в двух взаимно перпендикулярных плоскостях.
Техническая теория продольных колебаний стержней. Под стержнем понимают
одномерное упругое тело (два размера малы по сравнению с третьим), обладающее
конечной жесткостью на растяжение, кручение и изгиб. Пусть стержень, отнесен-
отнесенный к прямоугольной декартовой системе координат Охуг, совершает продольные
колебания. Параметры стержня являются функциями только одной продольной
координаты х. По гипотезе плоских сечений любые точки, лежащие в плоскости,
перпендикулярной к оси стержня, имеют одинаковые перемещения и1 — и (х),
«2 = «з = 0. Все компоненты тензоров напряжений и деформаций, кроме 0"п и еи,
считают пренебрежимо малыми. Выражения для потенциальной энергии деформа-
деформации, кинетической энергии и потенциала внешних сил имеют вид
;
ди \2
-=- dx;
F7)
П = — \qu dx — Nu 'g+const.
о ' )
Продольные колебания описывают уравнением
w = q{x,t). F8)
Возможные типы краевых условий сведены в табл. 3. Решение уравнения F8),
удовлетворяющее на каждом конце одному из условий, приведенных в этой таб-
таблице, должно также удовлетворять начальным условиям, аналогичным F6).
Уточненная теория продольных колебаний стержней. Эта теория учитывает влия-
влияние поперечных деформаций (е22 = е3з = — ven)- Поправка вводится только в выра-
выражение для кинетической энергии
о
где полярный момент инерции сечения
Уравнение продольных колебаний принимает вид
дх ! ' *" Л'2 " '"' я*~я> \'°я^Ш1 — ч v*t ч- G0)
Краевые и начальные условия .остаются без изменения.
КОЛЕБАНИЯ СТРУМЫ И СТЕРЖНЕЙ 147
3. Основные типы краевых условий для продольных колебаний стержней
Схема
Тип закрепления
Условия при х — О
Заделка
Свободный конец
дх
конце действует
Упругое закрепление
EF — + га = 0 (при * => I)
На конце закреплена
масса
dx dt*
Техническая теория крутильных колебаний стержней. Для стержня с прямоли-
прямолинейной осью, центр тяжести поперечного сечения которого совпадает с центром изгиба
(выполнение этого условия гарантирует существование чисто крутильных колебаний),
используют гипотезы статической задачи о чистом кручении призматических стерж-
стержней, основной из которых является гипотеза плоских сечений.
Существенными считаются только напряжения с12 = 0а1, а13 = а31. Введенные
гипотезы позволяют описать процесс деформирования при помощи одной перемен-
переменной 9 (х, t) —• угла закручивания. Потенциальную энергию деформации, кинетиче-
кинетическую энергию и потенциал внешних сил определяют по формулам
1 I
1 {' ^, I дВ \3 ,„ If / дв \2
и = ^т \ g/k hjr dx< r=w \ РЛ>Hrr dx-
\
П — — \ liO dx — Ш ;'q-f const.
0 '
G1)
148
РАСПРЕДЕЛЕННЫЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
4. Геометрические характеристики поперечных сечений стержней
при изгибе и кручении
Вид сечения
~w
яР'
64
ЯР'
~32~
яР*
*
~64~
яР4
64
D'
яР< /
~аГ V
яр* / а* \
32 Г Р4 )
-ч
J
к
a
i
,У
nab3
na'b
nab
(a2 +
>
rff-
У
-Si) *^
MI-<
n A -
a2 + i
A - С) — X
X (a2 + 62)
12
12
-^ №¦ +
i
t« - F - :
12
b' -(b- 2d)*
12
;P= - 1.2704P2-
+ 0,661 p -
- 0,1043] d-
при
b* — (b —
Вид сечения
КОЛЕБАНИЯ СТРУНЫ И СТЕРЖНЕЙ 149
Продолжение табл. 4
П(Г
У
U Ж
- d')
К 2 -0,46 4W'
3 V b I
При -j- > 3;
-=¦ B -f- 0,44660 -
О
- 2.683P2 -f.
+ 0,1845p»Vbd>
/
при
+ bd' - d»)
~W
b'h
48
6ft»
¦4-)
36
6"
при b > h
В эти формулы кроме полярного момента инерции /„ входит момент инерции
при кручении
где ф — функция кручения. Для некоторых видов сечений моменты инерции приве-
приведены в табл. 4. Уравнение крутильных колебаний имеет вид
р/0-р + |л (х, 0 = 0- G2)
Характерные типы краевых условий представлены в табл. 5. Начальные усло-
условия аналогичны F6).
Уточненная теория крутильных колебаний стержней. Эта теория учитывает
депланационные эффекты при кручении (учет сти). Использование выражений для
энергий
I
у _
дЧ \2
G3)
РАСПРЕДЕЛЕННЫЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
5. Основные типы краевых условий для крутильных колебаний стержней
•
|
vvf-
о-
0
С
Схема
3
i
X
1 ¦»-
_l
1 *
1 i
1
X
Z
i{ i4*-
Вид закрепления
Заделка
Свободный коней
Упругое закрепление
На конец действует момент Л(
Инерционный элемент на
конце
Условия при х = 0
к Лг
с/ бе е 0
(при х — 1)
G/K -у- = Л4
С/к у — / -т—
К dt dt*
(при х = 1)
ным уравнениям крутильных колебаний стержней
[GI [р/) + р1
в которые введен депланационный момент инерции 1щ = \ «р2 d/7, приводит к уточнен-
G4)
G5)
На каждом конце стержня должно быть поставлено по два условия
з-=0 либо
ф дх2
д
6 = 0 либо G/K---3- ?/ф ^
КОЛЕБАНИЯ СТРУНЫ 11 СТЬРЖНСП П1
Техническая теория крутильных колебаний тонкостенных стержней открыюго
профиля. Предположим, что выполнено условие существования чисто крутильных
колебаний стержня с тонкостенным поперечным сечением, т. е. центры кручения
всех сечений совпадают с центрами тяжести и лежат на прямолинейной оси. Выра-
Выражение для кинетической энергии совпадает с G1). Потенциальная энергия
о
где векториальный момент инерции 1&=\ <й2 dF (ш — секториальная площадь).
F
Уравнение крутильных колебании тонкостенных стержней открытого профиля
имеет вид
[GI ) + /( ° G7)
Начальные условия аналогичны F6), а альтернативные краевые условия можно
записать в форме
дЧ 3d .
-д-^-=0 либо -д^ —О,
G8)
Во втором условии левая часть представляет собой сумму момента касательных
усилий чистого кручения и момента от касательных сил сдвига срединной поверх-
поверхности.
Уточненная теория крутильных колебаний тонкостенных стержней открытого
профиля. Если при кручении тонкостенного стержня открытого профиля учитывать
наряду с чистым кручением и депланационными эффектами также напряжения сдвига
срединной поверхности, то потенциальная энергия деформации
где
ь и
При этом кинетическая энергия
^ = ~2~ \ М3'0 (~Ъ7) "^" Р''ш (д д/) ^ • (SO)
о
Уравнение крутильных колебаний тонкостенных стержней открытого профиля
по уточненной теории имеет вид
дх
=М(*. О- (8')
152 РАСПРЕДЕЛЕННЫЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
5. ИЗГИБНЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ
Техническая теория. Рассмотрим стержень длины / с прямолинейной осью пере-
переменного, но незакрученного сечения, совершающий изгибные колебания в плоско-
плоскости Oxz (ось Ох направлена вдоль оси стержня и проходит через центры тяжести
сечений, оси Оу и Ог являются главными, так что ^ yz dF = \ у dF — \ г dF = 0)
F F F
Предположим, что поперечные сечения при деформировании остаются плоскими и
перпендикулярными к деформированной оси стержня, а нормальные напряжения на
площадках, параллельных оси, пренебрежимо малы. Существенными из компонент
тензоров напряжений и деформаций являются только ап и еХ1. Растяжением оси
пренебрегают. Потенциальная энергия деформации и кинетическая энергия связаны
с прогибом стержня w следующим образом:
где J= [ z2 dF—момент инерции сечения относительно Оу (см. табл. 4). Изгибные
F
колебания стержня описывают уравнением
Основные типы граничных условий сведены в табл. 6. Начальные условия анало-
аналогичны F6).
Учет продольных сил. Если в сечениях стержня действует продольная сила N (х),
то вместо (83) следует пользоваться уравнением
EJ -3-5- — з- [N ir) + PF ~л7$- — Я(х, f)- (84)
дх2 J дх\ дх) v dt2 ¦» v • / \ /
5— [EJ -3-5- — з- [N ir) + PF ~л7$
дх2 \ дх2 J дх\ дх) v dt2
Геометрические граничные условия и условия, содержащие изгибающий мо-
момент | М = EJ-p-j-\, не изменяются. В условия, содержащие поперечную силу
Q==-^— lEJ -3-2")' Д°лжно быть внесено ее новое выражение Q=^-l EJ -3-^-) +
дх
Уточненная теория Тимошенко изгибных колебаний стержней. Техническую тео-
теорию изгиба стержней применяют, когда масштаб изменения напряженно-деформиро-
напряженно-деформированного состояния вдоль оси стержня велик по сравнению с характерным размером
поперечного сечения в направлении оси Ог. Если указанные величины сопоставимы,
то применяют уточненные теории, в которых учтены поперечные сдвиги и инерция
поворота сечений. В уточненной теории Тимошенко введены предположения: попе-
поперечные сечения остаются плоскими, но не перпендикулярными деформированной
оси стержня; нормальные напряжения на площадках, параллельных оси, равны
нулю; учитываются инерционные составляющие, связанные с поворотом сечений.
Потенциальная энергия деформации
ИЗГИБНЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ 153
в. Основные типы краевых условий для изгибных колебаний стержней
Вид
закрепления
Схема
Условия при х = О
Заделка
0. 4^
дх
Свободное
опирание
ш = 0,
дх2
Свободный
конец
д ( djw
дх \ дх'
Плавающая
заделка
дх
Упругое закреп-
закрепление
'.с,
г—
Ji
* X.
Т/ ?
L %С,
а.
(при л; = /)
дх3 дх
w = 0, „ , d*w , „ аш _
(при л; = I)
(при
154
РАСПРЕДЕЛЕННЫЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
Продолжение табл
Вид
закрепления
Схема
Условия при х = О
Упругое
закрепление
, с ¦,
EJ
f 17 I ' A
~dx \ dx'J ~ '
I 7777
¦ = 0.
<3ш
{при х — /)
-7/////
'///////. г.
(при jc = I)
77777/.
(при х — I)
Сосредоточенный
инерционный эле-
элемент на конце
1 га, Г
дгш> __
'дх'~
dx \ dv2] ~ m dt-
(при x — I)
EJ -P^r = — '
dxdi'
(при х = !)
Здесь Р — средний угол сдвига; х —¦ коэффициент, зависящий от характера распре-
распределения сдвигов по сечению и способа определения среднего значения для угла
сдвига. Если под Р понимают среднеквадратическое значение
(86)
а касательные напряжения при изгибе определяют по формуле Д. И. Журавского
(87)
QS
' Jb
(Q — поперечная сила; S — статический момент части сечения, отсеченного плоско-
плоскостью г = const; Ь — ширина поперечного сечения при г = const), то
(88)
Для прямоугольного сечения к = 5/6.
ИЗГИБНЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ 155
Кинетическая энергия
о
2
О" О
Изгибные колебания стержней по уточненной теории описывают системой урав-
уравнений
д2
дх2
„. ,' d*w д&\ г, , dw „ „ 1
\ дх2 дх ] дх м I
Альтернативные краевые условия имеют вид
д&\ г, , dw
5==^ либ° "^
\ дх ] дх (g
— xGfp^Q либо tiu = O. j
Между функциями Р и ш существует связь
^x(yGF^) = 9F^—q, (92)
которая позволяет из уравнений (90) исключить р\ Так свободные колебания стержня
постоянного поперечного сечения будут описываться уравнением
которое известно как уравнение Тимошенко.
В дополнение к краевым условиям (91) (два условия на каждом конце стержня)
необходимо задать четыре начальных условия
w (х, 0) = /[ (х); р (х, 0) =/3 (х);
~ (х, 0) = /2 (х); -J (х, 0) = /4 (х). (94)
Уравнения изгибных колебаний криволинейных стержней. Считаем, что ось
стержня лежит в плоскости, которая совпадает с главной плоскостью инерции сече-
сечения стержня и с плоскостью действия сил. Стержень отнесен к криволинейной си-
системе координат Osyz (Os по оси стержня). Кроме того, предполагаем, что r/min R <^ 1,
где г — характерный размер сечения, R (s) — начальный радиус кривизны.
Для потенциальной энергии деформации и кинетической энергии имеем выра-
выражения
i I
(95)
u'[EF(^- + ^Jds + ±-[Ej\^-d(±)}
2 J \ds ^ Rl T2 J Yds2 ds\Rj\
Уравнения колебаний криволинейного стержня будут следующими:
д Г /аи . w\] , a \EJ\d*w д
EF (ди w\ д*
(96)
156
РАСПРЕДЕЛЕННЫЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
При R -*¦ оо (96) распадаются на два независимых уравнения, описывающих про-
продольные и изгибные колебания стержня. В общем случае на концах стержня должно
быть поставлено по три условия. Альтернативные условия имеют вид
i = 0 или
ЬЛ—-a (ttW\-Q-
*l = 0 или Ej\^--^h)] = a;
ds L*a ds\Rj\
\
u = 0 или
Начальные условия
RJ R Ids*
dw , „,
(97)
w(s, 0)=/x(S); 5r
u(s, 0) = /8(s); -^-(s, 0)=/4(s).
(98)
Если деформацией оси стержня можно пренебречь, то из уравнений (96)
следует
Замена w = —R -^— приводит к уравнению шестого порядка для и
A00)
Соответствующее уравнение для стержня с круговой осью и постоянными пара-
параметрами EJ — const, EF = const, R = const, s = Ra можно записать в виде
FI d2 I <92 \i d2 l д2 \ c)a
?¦•/ <j i и , i \ .. , г- « /_u j>u__0 _i__^5. /101)
R* da2 \ da* '
Это уравнение является уравнением изгибных колебаний кольца. Если, кроме того,
кольцо загружено радиальной постоянной нагрузкой q0, то
Уравнения изгибно-крутильных колебаний стержней. Считаем, что стержень
имеет прямолинейную ось и незакрученное поперечное сечение. На основе допуще-
допущений элементарной теории изгиба и теории кручения и учета эффектов депланации
получают следующие выражения для кинетической энергии и потенциальной энер-
энергии деформации:
I I !
dt
dx;
G/K
дх
A03)
ИЗГИБЫЫЕ КОЛЕБАНИЯ ПЛАСТИН
157
где «2 и Дз — координаты центра изгиба. Перемещения v и w центра изгиба сечения
в направлении осей Оу и Ог и угол закручивания 6 удовлетворяют уравнениям
A04)
дв
где / = /0 + (а| + а|) f — полярный момент инерции относительно центра изгиба.
Если а2= а3= 0, то A04) разделяются на уравнения изгибных колебаний в двух
в аимно перпендикулярных плоскостях и уравнение крутильных колебаний. Альтер-
Альтернативные концевые условия для общего случая имеют вид
д
ИЛИ з-
дх
-5— = 0 или EJ,
дх
8 = 0 или
-1r)
х2 J
w = 0 или ъ- I
дх '
д2а>Л
— з- [ ?/ш -3-5-) +G/* з- = Ж;
дх[ ш дх2 j " дх
A05)
6. ИЗГИБНЫЕ КОЛЕБАНИЯ ПЛАСТИН
Под пластиной понимают тонкое двухмерное тело, один размер которого (тол-
(толщина) много меньше двух других размеров и срединная поверхность которого есть
плоскость. Срединной поверхностью называют поверхность, равноотстоящую от
внешних (лицевых) поверхностей двухмерного тела.
Классическая теория. В основе теории лежит совокупность допущений, назы-
называемая гипотезами Кирхгофа — Лява: прямолинейный элемент, нормальный к сре-
срединной поверхности до деформации, остается прямым и нормальным к срединной
поверхности, не меняя своей длины. Деформации предполагаются малыми. В пла-
пластине реализуется обобщенное плоское напряженное состояние, в силу предположе-
предположения о том, что ст3з пренебрежимо малы. Существенные компоненты тензоров дефор-
деформаций и напряжений вар и аар (а, |3 = 1,2) линейно изменяются по толщине. Дефор-
Деформацию срединной поверхности при изгибе пластин не учитывают.
Пусть пластина отнесена к прямоугольной декартовой системе координат OxiX2z.
Потенциальная энергия деформации
где D =
а
Eh3
.....
A06)
¦ цилиндрическая жесткость пластины. При подсчете кинети-
12A—v2)
ческой энергии учитывают только нормальные силы инерции
A07)
158
РАСПРЕДЕЛЕННЫЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
Предполагаем, что на пластину действует нормальная нагрузка ?, а на контуре
приложены поперечные силы Q, изгибающие и крутящие моменты Ma, Mi (я и / -_
нормаль и касательная к контуру), тогда потенциал внешних сил
wdQ-[ (- Qw+ Mn |J + М, ^ dr + const. A08)
а г
На элемент пластины действуют изгибающие и крутящие моменты и поперечные
силы
A09)
где А = т.—: + -г оператор Лапласа.
дх\ dx'i
Уравнение изгибных колебаний имеет следующий вид:
— 2-
D
¦Pl'-gp- = q(X. 0- (ПО)
Если толщина h однородной пластины постоянна (цилиндрическая жесткость
D = const), то уравнение колебаний принимает форму
, t).
Альтернативные граничные условия имеют вид (хг •¦
I v) ^ 1,
= 0 или
dw
const)
, дМ21
+
дх2
= 0 или
d2w , C2а) \
r-r- + v-3-r =
д d
дх\
dxl
(Ill)
A12)
Другие виды краевых условий аналогичны подобным условиям для стержня (см.
табл. 6).
Криволинейные координаты. Пусть пластина отнесена к криволинейной системе
координат Ох^х^г. Уравнение A11) для пластин постоянной жесткости остаётся
справедливым, только для оператора Лапласа следует взять выражение
Н1Н2
Я,
дхг\ Н
A13)
Пример. Круглые пластины, отнесенные к полярной системе координат Xi = r, *2=9 (пара
метры Ламе равны Hi = 1, И2 = г), при колебаниях подчиняются уравнению (D — const)
0/ii + ±J> +±.
I dw
1 d'w
d*w
= Q
A14)
Приведем также выражения для моментов и поперечных сил в криволинейных
координатах:
_ (J_ d_(J_dw_
11 ~ \ Я, дхл \ Ht Ш[
НХИ\ дх2 дх2
п 1 д ,
Я2
Я2 i?x2 \Я; 5xj у Я] dxj \Я| dx2/J'
A15)
ИЗГПБНЫЕ КОЛЕБАНИЯ ПЛАСТИН 159
Ортотропные пластины. Колебания ортотропных пластин постоянной толщины
описывают уравнением
где Di я D2 — цилиндрические жесткости соответственно в направлении осей 0хх
и 0хг; D12 — смешанная жесткость. Введенные жесткости определяют по формулам
п ?Уг3 Еф?
Ы' "~~ 12(l~v12v21) :
A17)
12A—vJ2v2l) ' " 12(l~v12v21)'
G/z3
Z? + 2Z>Df2?> D
где Z)K — жесткость при кручении.
Учет тангенциальных усилий в срединной поверхности. При действии постоянных
усилий в срединной поверхности вместо уравнения A11) с учетом A13) следует взять
При формулировке краевых условий необходимо учесть вклад тангенциальных
усилий в поперечные силы. Так, для незакрепленного загруженного края xt = const
должно быть
п , дМ12 .. 1 dw ., 1 dw « , дМ, гг ,.п
Учет поперечных сдвигов и инерции вращения в теории колебаний пластин.
Классическая теория пластин применима, когда толщина пластины мала по сравне-
сравнению с характерным масштабом изменения напряженно-деформированного состоя-
состояния (Л2 < X2). В этом случае оправдано пренебрежение влиянием деформаций попе-
поперечных сдвигов и инерцией вращения нормальных элементов. Если указанное выше
условие нарушается (Л — X), то при рассмотрении задач колебаний пластин необходим
учет деформаций поперечных сдвигов и инерции вращения нормальных элементов.
Распространение теории Тимошенко для стержней на пластины приводит к уравне-
уравнениям
\U1 dxj 12" df-
dw \ ph3 <Э62 „.
2 dx\ + 2 дх2дх1~хОП\в*~дх^)~ 12
'
12 dt*)\dX
A20)
где 6X и 6 2 —осредненные углы сдвига. Параметр х, также зависящий от распреде-
распределения сдвигов по толщине пластины, может быть принят равным х = в/е (распреде-
(распределение сдвигов, как в классической теории), или х = 2/з (отношение среднего каса-
касательного напряжения к максимальному), или х = х„., где х„ — корень уравнения
расположенный на отрезке [0, 1] (наилучшее совпадение скоростей распространения
малых возмущений с результатами трехмерной теории).
160 РАСПРЕДЕЛЕННЫЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
Естественные краевые условия на краю хх = const следующие:
дв2
-v —— 1 =
dx2j
дха дх,
A22)
При решении задач динамики пластин в уточненной постановке удобно бывает
ввести потенциальные функции
дФ dW дФ дУ
Тогда уравнения движения принимают следующую форму [69, 87]:
"—v)
ДФ —-
.(Ф_,)=?(!^^;
2p(l+v) д*У
h-
д (ф_ш)=-
A24)
q-ph
При использовании этих уравнений краевые условия также должны быть выражены
через потенциальные функции Фи t.
Дополнительные сведения о различных типах уравнений колебаний пластин
можно найти в [1, 2, 7, 9, 19, 20, 25, 33, 35, 77, 87, 100, 101, 109, 128, 139].
7. КОЛЕБАНИЯ ТОНКИХ УПРУГИХ ОБОЛОЧЕК
Перемещения и деформации в тонких оболочках. Оболочкой называют тело, огра-
ограниченное двумя поверхностями, расстояние между которыми мало по сравнению
с основными размерами тела. В классической теории оболочек справедливы гипотезы
Кирхгофа — Лява, состоящие в следующем: нормальный элемент к недеформирован-
ной срединной поверхности оболочки остается прямолинейным и нормальным к де-
деформированной срединной поверхности и не изменяет своей длины; нормальные
напряжения ст3з пренебрежимо малы. Энергетическая погрешность гипотез Кирх-
Кирхгофа — Лява в случае оболочек равна rf = max {Л2/Х2, h/R}, где R — минимальный
радиус кривизны оболочки.
Пусть оболочка отнесена к ортогональной криволинейной системе координат
Охххгг, так что ось Oz направлена по нормали к срединной поверхности, а линии
Xi = const и х2 = const совпадают с линиями кривизны. Перемещения в любой
точке оболочки
ua = va~z(fa; u3 = w (a =1, 2), A25)
где vu i>2> w — перемещения точек срединной поверхности, а углы поворота
где ka — главные кривизны; На — параметры Ламе.
Существенные компоненты деформации связаны с деформациями срединной по-
поверхности еар и изменениями кривизн хар соотношениями
(а, р=1, 2),
A27)
КОЛЕБАНИЯ ТОНКИХ УПРУГИХ ОБОЛОЧЕК
161
где
е12— ~2
«12 =
tfi
Я,
Я2 дх2
дх2 \ Н2 дх2
7. to 1 дН
A28)
dv1
дНЛ kt /dv2
~дх~2] ~ 77!
A29)
Здесь и далее в тексте запись A -»¦ 2, 2->- 1) означает, что не выписанные вторые
соотношения получаются круговой перестановкой индексов 1 и 2. Выражение для и12
приведено в форме, данной В. В. Новожиловым [78].
Уравнения движения. Потенциальная энергия деформации тонких упругих обо-
оболочек
+0
Кинетическая энергия
-2 A -v)
A30)
Использование выражения для виртуальной работы внешних сил
б'Л = \l\j (<7i 6vi + qa 8v2 + q3 5w) НхНг dxx dx2 +
A32)
и применение принципа Гамильтона — Остроградского приводит к уравнениям
движения
-ktQi-ph^ + q^O, A-2,
2, 2-> 1);
A33)
6 п/р. Болотина В В , т. I
162
РАСПРЕДЕЛЕННЫЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
Уравнения движения в перемещениях. Для их получения необходимо исполь-
использовать связь между усилиями Na$ и моментами Ма$ с деформациями
Eh
A-2,2-1),
1);
A34)
A-2, 2
v) x12 = M21.
В свою очередь, деформации связаны с перемещениями формулами A28), A29)
Усилия Nu и ^21 выбраны так, чтобы удовлетворялось шестое уравнение A33) (соот-
(соотношения Балабуха — Новожилова).
Краевые и начальные условия. На каждом краю оболочки должны быть заданы
краевые условия, соответствующие характеру закрепления края. Альтернатив-
Альтернативные краевые условия имеют вид (х1 = const)
vx = 0 или
у2 = 0 или iV1
= 0 или
дх2 '
ф1=0 ИЛИ Мп—Ма.
Различные виды условий приведены также в табл. 7.
A35)
7. Основные типы краевых
Вид закрепления
Опертый край, свободный в направлении х,
(условия Навье)
Опертый неподвижный край
Опертый край, свободный в тангенциальных
направлениях
Полностью защемленный край
Защемленный край, свободный в направле-
направлении *j
Защемленный край, свободный в направле
нии х2
Защемленный край, свободный в танген-
тангенциальных направлениях
Свободный край
условии для оболочек
Условия при *j
и>= Ми — Nu —
w = M u = vt =
w = М и = N и = N12 -
„ = „, = „, = „
— Ф. = "»-*.*.
и, = ф1 = ЛГ,1 = ЛГ1._
-о
f 2 = 0
Us = 0
- кгМ1г = 0
2 = 0
,2 = 0
, = о, = 0
~ N12 — k2M 12 =¦ С
КОЛЕБАНИЯ ТОНКИХ УПРУГИХ ОБОЛОЧЕК
163
При решении динамических задач должны быть поставлены начальные условия
dt
dt
, = 0.
dw
~di
, = w0.
A36)
Уравнения безмоментной теории. Безмоментное состояние имеет место, если
энергией изгиба и кручения можно пренебречь по сравнению с энергией растяжения-
сжатия срединной поверхности. В уравнениях A33) в этом случае следует пренебречь
изгибающими и крутящими моментами и поперечными силами:
dX,
dfi
+ ^22 + РЛ "^ <?3 = 0.
A37)
Число граничных условий на одном краю должно быть уменьшено вдвое. Из A35)
следует сохранить только первые два условия. Энергетическая погрешность безмо-
ментной теории т]2 s? Л2/?2Д4. Таким образом, безмоментная теория пригодна для до-
достаточно тонких оболочек при колебательных процессах с большим масштабом изме-
изменения напряженно-деформированного состояния срединной поверхности I.
Уравнения технической теории. Если характерные тангенциальные перемеше-
нияиО??:-= ш0 (ю0 — характерное нормальное перемещение), то вместо A26) и A29)
Н
справедливы соотношения
dw , .
фа = з—¦ (а= 1. 2);
1 3 / 1 dw
I dH1 I 1 dw
^ ^^ A-2,2-1);
dN1 dw
dx1
I dH2 dw
H2 dxx dx2
A38)
и уравнения движения для оболочек постоянной толщины (h = const) принимают
вид
A39)
где оператор Д определяется согласно A13).
Пологие оболочки. Уравнения Доннелла — Муштари — Власова. Считают, что
для пологих оболочек интенсивности тангенциальных усилий qt и q2, как и танген-
тангенциальных перемещений, составляют величины порядка X/R (и менее) от интенсив-
интенсивности <73 и нормального перемещения соответственно. Кроме того, предполагают, что
тангенциальными силами инерции можно пренебречь. Тогда первым двум уравне-
уравнениям в A33) можно удовлетворить, если ввести функцию напряжений % по формулам
A-2,2-1);
дЧ
~НХ dx2 dxx H2 дх! дх2,
A40)
164
РАСПРЕДЕЛЕННЫЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
Недостающее уравнение, связывающее w и %, получают, используя уравнения
совместности деформаций срединной поверхности. В результате получают систему
уравнений
A41)
где оператор Д определяется согласно A13), а
(
dXl\ Ht
М
Н2
Если метрика срединной поверхности меняется достаточно медленно по сравнению
с w и х» то Нх и #2 можно считать постоянными и пренебречь производными от этих
величин по координатам
1 Э2 1 &
Щ дх\ + Щ дх\
k2 d2 ki <Э2 _
1
:77?
A43)
дх2
Если оболочка достаточно Пологая, так что криволинейные координаты мало
отличаются от координат на плоскости, то можно положить Н1 = Н2 = 1. Уравне-
Уравнения движения тогда принимают вид
ЖДАХ"
дх\
дх\
Л д V |^ V
A44)
Уравнения полубезмоментной теории. Эту теорию можно применять в том случае,
когда при колебаниях характер напряженно-деформированного состояния таков,
что масштаб изменяемости в одном направлении много меньше, чем в перпендику-
перпендикулярном направлении (>ч < к2). В этом случае оболочку в одном направлении рас-
рассматривают как моментную, а в другом — как безмоментную. Уравнения движения
в данном случае принимают вид
D
Н\ дх\ "¦" Я|
1 дЧ
EhH\ дх\
Н\ дх\
~~ "
A45)
Уравнения краевого эффекта. Для изучения напряженно-деформированного со-
состояния у края оболочки (например, хх = const), быстро убывающего при удалении
во внутреннюю область, можно использовать уравнения, которые получаются из
A41), если пренебречь зависимостью от координаты х2. Уравнения движения будут
в данном случае следующими:
D
k2 дЧ
Jh ~dxf
EhH\ ~дх\
cP-w _
+ Р "Л2" ~"
2 d*w _
дх\ ~ '
(Н6)
КОЛЕБАНИЯ ТОНКИХ УПРУГИХ ОБОЛОЧЕК
165
При исключении из этих уравнений х получим
D д4
A47)
где flo определяется тангенциальными краевыми условиями.
Учет влияния предварительного безмоментного состояния. Параметрические
члены. Члены, входящие в уравнения колебаний и содержащие компоненты пред-
предварительного безмоментного состояния, называют параметрическими. Наиболее
общие выражения для этих членов имеют вид
i
\ Я.2 дх2
а=1 6=1
A48)
где jV^o соответствуют предварительному безмоментному напряженному состоянию.
Величины фа и еар определяют согласно A26) и A28) и, кроме того,
A49)
Если удлинения и сдвиги малы по сравнению с углами поворота q>t и ф2 и с углом
вращения элемента срединной поверхности относительно нормали б12, то в A48)
следует опустить члены, содержащие еар. Далее, если деформации срединной по-
поверхности еар и вращение элемента вокруг нормали 612 пренебрежимо малы по срав-
сравнению с углами наклона (еар <; фа, S12 ¦< фа), то вместо A48) можно использовать
выражения
4
2, 2 -+ 1);
A50)
При изучении преимущественно изгибных форм колебаний с применением соот-
соответствующих гипотез параметрические члены следует взять в виде
Н\ дх\
1
2N\,
дх2
дх\ ¦
A51)
Пример. Цилиндрическая оболочка радиуса /? находится под внутренним давлением р„ и
продольным растягивающим усилием УУо- Параметрические члены имеют вид
A52)
P°R
!d'w 2 dv' w
166
ОБЩИЕ СВОЙСТВА СОБСТВЕННЫХ ЧАСТОТ И ФОРМ
В случае колебаний с большим числом волн в окружном направлении в A52) следует сохра
нить только подчеркнутые члены
Более подробные сведения, касающиеся различных вариантов уравнений дви-
движения тонких упругих оболочек, можно найти в [1, 9, 25, 26, 27, 33, 35, 78, 79, 87,
100, 101, 102, 109, 132].
Глава IX
ОБЩИЕ СВОЙСТВА СОБСТВЕННЫХ ЧАСТОТ
И СОБСТВЕННЫХ ФОРМ УПРУГИХ СИСТЕМ
1. ОСНОВНЫЕ СООТНОШЕНИЯ
Общие замечания. Распространение теории свободных колебаний систем с конеч-
конечным числом степеней свободы (см. гл. III) на распределенные системы осуществляется
в рамках функционального анализа. Теория свободных колебаний упругих систем
может рассматриваться как физическая интерпретация спектральной теории линей-
линейных самосопряженных операторов в гильбертовом пространстве. Операторные обо-
обозначения весьма удобны при изложении общих вопросов теории колебаний упругих
систем, поскольку они придают предельную краткость и общность. Чтобы облегчить
интерпретацию операторных обозначений, в табл. 1 и 2 дана их развернутая запись
для некоторых классов упругих систем.
1. Операторы теории колебаний
Система
Струна
Стержень, продольные
колебания
Стержень, крутильные
колебания
Тонкостенный стержень
открытого профиля, кру-
крутильные колебания
Стержень, изгибные
колебания
Тонкостенный стержень
открытого профиля, из-
гибно-крутильные коле-
колебания
Инерционный
оператор Аф
pFcp
pF<p
р/оф
р/оф
pFq,
Р{-Раг IA )[VJ
Упругий оператор
С<р
дх \ дх )
-A-{EF d(M
дх [Ь^ дх)
-Л (ai %\
дх \UJKdx)
д* (ei а2фЧ1 д (г, д<?\
дх' \ а> дх' } дх \ к дх j
ОСНОВНЫЕ СООТНОШЕНИЯ
167
Уравнение свободных колебаний. Общая запись уравнений свободных колеба-
колебаний упругих систем имеет вид
d2
где и (х, 0 — поле перемещений, заданное при х eS s R" и на некотором отрезке
времени, например, при 0 =g: t < 00; А — инерционный оператор; С — упругий
оператор.
Операторное уравнение A) включает в себя не только дифференциальные уравне-
уравнения, но и граничные условия (через область определения операторов). В дальней-
дальнейшем множество функций, дифференцируемых по всем переменным должное число
раз, интегрируемых с квадратом в области S и удовлетворяющих всем граничным
условиям (как кинематическим, так и динамическим), обозначим через D (С). Это
множество обычно совпадает с областью определения упругого оператора С, что
учтено в обозначениях. В дальнейшем полагаем, что D (A) s D (С).
Реализации уравнения A) для различных типов упругих систем получаются из
дифференциальных уравнений гл. VIII, если в этих уравнениях приравнять нулю
члены, учитывающие внешние силы.
Собственные частоты и собственные формы упругих систем. Подстановкой типа
u(x, /)=q>(x)sin(orf + X) B)
уравнение A) приводится к уравнению относительно функции координат <р (х), опи-
описывающей формы колеблющейся системы:
(С — ш2А)ф =
C)
упругих одномерных систем
Скалярное произ-
произведение (ф, t|>)
Энергетическое про-
произведение [ф, i|)]^j
Энергетическое произведение
[ф. 4>]с
Примечание
J pFqn|) dx
О
dx
-dx
См F4) гл. VIII
J pFcnb dx
0
J фф dx
0
J р/0ф1|) dx
0
> dx
dx
dx
\EJT$-l&rdx
Cm F7), F8) гл.
Vlll
Cm. G1), G2) ГЛ.
VIII
Cm G1), G6), G7)
гл VIII
Cm. (82), (83) гл
VIII
J (Ф„*„
) \hJz dx' dx'
El,,
dx
01
к дх dx
¦ +
dx
Cm. A03), A04)
гл. VIII
Oz — ось симмет-
симметрии
a — расстояние
от центра
инерции до
центра изги-
изгиба
168
ОБЩИЕ СВОЙСТВА СОБСТВЕННЫХ ЧАСТОТ И ФОРМ
2. Операторы теории колебаний
Система
Инерцион-
Инерционный опера-
оператор Аф
Упругий оператор Сф
ОД Дф
Упругая пластина
(классическая тео-
теория)
р/ир
+
д'
— 2
д'
дх, дх2
дх,дх2
Упругая круговая
цил индрическая
оболочка (техниче-
(техническая теори.1)
дх, дхг
— v дг , д2 \ я, и
2 дх\ дх%) R ~
й „. . , А,
Значения параметра со2, при которых операторное уравнение C) имеет решения,
отличные от <р = 0, называют собственными значениями уравнения, а соответствую-
соответствующие ненулевые решения «р (х) — собственными элементами уравнения. Совокуп-
Совокупность собственных значений называют спектром уравнения. Положительные значе-
значения квадратных корней из собственных значений уравнения C) имеют смысл собст-
собственных частот, а собственные элементы совпадают с собственными формами колеба-
колебаний упругой системы.
Уравнение C) есть уравнение Остроградского — Эйлера для вариационной
задачи о стационарных значениях квадратичного функционала
Здесь Uo (<р) — максимальное во времени значение потенциальной энергии упру-
упругой деформации системы, колеблющейся по закону B); То (<р) — максимальное во
времени значение кинетической энергии, взятое с точностью до множителя со2.
2. СВОЙСТВА СОБСТВЕННЫХ ЧАСТОТ И СОБСТВЕННЫХ ФОРМ
Скалярное и энергетические произведения. Скалярным произведением элементов (jp
называется величина
(ф. ¦*) = ^ (фА + Ф
• • ¦)
СВОЙСТВА СОБСТВЕННЫХ ЧАСТОТ И СОБСТВЕННЫХ ФОРМ
упругих двухмерных систем
169
Скалярное
произведение
( Ч>
Энергетическое
произведение
Гф. Ч>]л
Энергетическое произведение [ф,
Примечания
J | ф-ф dxx dx2
Q
—2A — v)X
52ф б2* 1 ,
oxt дх2 охх дхг\)
ft=const [см. A06),
A07), A11) гл.
VIII];
ft ф const [cm. A06),
A07), A10) гл
VIIIJ
II (%%
xt dxt
X dx, dx.
+ '
Eft
1— V1
' а^ a«i
2 V ад;, дх,
i a* a^/])
где под знаком интеграла стоит сумма произведений одноименных компонент вектор
функций ip (х) и i| (х)
Энергетические произведения вводят при помощи квадратичных функционалов
Uu (ф) и Го (ф) из формулы D). А именно, произведением элементов ф и \р по кинети-
кинетической энергии называют билинейный функционал [ф, if]^ в соотношении
\> (г(з) + [ф,
F)
а произведением элементов ф и ty по потенциальной энергии— билинейный функцио-
функционал в соотношении
Энергетические произведения симметричны по отношению к сомножителям и
связаны с энергетическими функционалами формулами
= 2Г0
При ip, \feD (С)
); [ф,
= 2С/0 (ф).
[ф, г|)]д = (А<р, ф); [ф, г|5]с =
(8)
(9)
Для конкретных упругих систем эти равенства доказываются интегрированием
по частям (если система одномерна) или применением формулы Гаусса — Остроград-
Остроградского. Примеры скалярных и энергетических произведений для некоторых систем
приведены в табл. 1 и 2.
170 ОБЩИЕ СВОЙСТВА СОБСТВЕННЫХ ЧАСТОТ И ФОРМ
Свойства операторов уравнений свободных колебаний. Операторы А и С являются
самосопряженными, т. е. для них на любых ф и ijj из области определения этих опе-
операторов выполняются равенства
(Аф, ф) = (ф, Аг|5);|
(Сф, 1|>) = (ф, Щ. /
Операторы А и С являются положительно определенными, т. е. для них на любом
Ф <= D (С) при ф ф 0 справедливы неравенства
(Аф, ф)>0; (Сф ф)>0. A1)
Исключения могут встретиться в некоторых переупрощенных схемах. Напри-
Например, если массу некоторых элементов системы принять равной нулю при отличной
от нуля упругой податливости, то
(Аф, ф) ss 0. A2)
Для ограниченных упругих систем обратный оператор С является вполне не-
непрерывным (исключения могут составить системы с сильно «заостренными» элемен-
элементами, однако эти системы следует рассматривать как искусственно сконструирован-
сконструированные примеры). Определение вполне непрерывного оператора требует использования
понятия сходимости и компактности в гильбертовых пространствах. Вполне непре-
непрерывный оператор улучшает сходимость последовательностей в соответствующем
пространстве, преобразуя ограниченную последовательность в компактное множе-
множество, слабо сходящуюся последовательность в последовательность, сходящуюся
по норме, и т. п.
Интегральные уравнения собственных колебаний. Для большинства задач теории
упругих колебаний оператор С реализуется в форме интегрального оператора с сим-
симметричным регулярным или слабо полярным ядром
С-^ф = J G (х, х') ф (х') dx'. A3)
J
Уравнению A3) соответствует интегральное уравнение Фредгольма или родственное
ему интегро-дифференциальное уравнение (если оператор А — дифференциальный):
Ф(х) —ш2 f О (х, х') Аф (х') dx' = 0. A4)
Свойства собственных частот и собственных форм. В дальнейшем будем считать,
что операторы А и С — самосопряженные и положительно определенные, а опера-
оператор С — вполне непрерывный.
Спектр собственных частот — дискретный (точечный) и не имеет точек сгуще-
сгущения, кроме, может быть, бесконечно удаленной точки. Все собственные частоты —
действительные. Спектр собственных частот упорядочивается в порядке возрастания
Ш! «с ш2 sg ш3 ;? ... , A5)
а собственным формам придается номер соответствующей частоты.
Свойства собственных форм. Собственные формы колебаний попарно ортогональны
по кинетической энергии, т. е.
(Аф/, (Ы = 0 ЦФк). A6)
Собственные формы колебаний попарно ортогональны по потенциальной энергии,
т. е.
(Cq>/, ф*) = 0 Цфк) A7)
Собственные формы образуют в D (С) полный базис, т. е. любой элемент u e Д (С)
может быть представлен в форме ряда
со
и(х)=2 и/ф/М A8)
/=1
который, во всяком случае, сходится по энергетической норме.
ВАРИАЦИОННЫЕ ПРИНЦИПЫ 1?!
Перечисленные факты являются аналогами свойств собственных частот и собст
венных форм линейных консервативных систем с конечным числом степеней свободы
(см. гл. III). При этом разложение A8) соответствует введению нормальных коорди-
координат, а его коэффициенты аналогичны нормальным обобщенным координатам.
3. ВАРИАЦИОННЫЕ ПРИНЦИПЫ В ТЕОРИИ
СОБСТВЕННЫХ КОЛЕБАНИЙ УПРУГИХ СИСТЕМ
Формула Релея. Собственные частоты и соответствующие им собственные формы
связаны между собой тождественным соотношением
у '
(Аф, ф)
которое непосредственно следует из уравнения C). Выражение, стоящее в правой
части формулы A9), будем называть дробью Релея. Формула Релея может быть также
записана в одном из следующих вариантов:
[ф, ф]с Uо (ф)
[ф ф]д ^о (ф) *¦ '
Последний вариант поясняет энергетический смысл формулы Релея.
Основной вариационный принцип. Среди форм движения истинными формами
собственных колебаний будут те, которые сообщают дроби Релея стационарные
значения. Этот принцип является отправной точкой для получения ряда других
вариационных принципов. В дальнейшем будем выражать дробь Релея через энер-
энергетические функционалы. Это позволит расширить область допустимых функций за
счет функций, которые удовлетворяют кинематическим граничным условиям, но
не обязательно динамическим. Кроме того, снижаются требования к дифференци-
дифференцируемое™ функций (требуется существование производных, входящих в энергетиче-
энергетические произведения, что уменьшает вдвое требуемый порядок производных). Допол-
Дополненное таким образом энергетическое пространство будем обозначать через ?„.
Среди всех |ре?с истинными собственными формами колебаний будут те,
которые удовлетворяют одному из следующих эквивалентных условий стационар-
стационарности:
[^М1 = 0; B1)
о(ф)J v ;
-^Го(ф)] = 0; B2)
бг/0(ф) = 0; Г0 (ф) = const; B3)
6Г0(ф) = 0; ?/0(ф) = const. B4)
Вариационный принцип Релея. Низшая (основная) собственная частота упругой
системы удовлетворяет соотношению
«oj- min Ш, B5)
фЕ?С ' О iff)
где к сравнению допускаются любые ненулевые элементы энергетического прост-
пространства Ес.
Для определения высших собственных частот и собственных форм служит рас-
расширенный вариационный принцип Релея' собственная частота со^ удовлетворяет соот-
соотношению
«1= т,п -^М B6)
172 ОБЩИЕ СВОЙСТВА СОБСТВЕННЫХ ЧАСТОТ И ФОРМ
где Vk — подпространство энергетического пространства Ес, элементы которого
удовлетворяют условиям ортогональности
Гф. ф], = 0 (/'=1, 2, .... k—l). B7)
Иначе говоря, при определении k-й собственной частоты и соответствующей формы
к сравнению допускаются только те элементы, которые ортогональны ко всем низ-
низшим формам колебаний.
Вариационный принцип Куранта. Собственная частота о>? удовлетворяет соот-
соотношению
w|= max min r° \ ¦, B8)
где ijjj,^1 ••• • tyk-i— произвольные линейно независимые элементы пространства ?С)
Wk — подпространство Ес, элементы которого, удовлетворяют условиям ортогональ-
ортогональности
[Ф, ^]А = 0 0" = 1. 2 ?-1). B9)
4. СТРУКТУРА СПЕКТРА СОБСТВЕННЫХ ЧАСТОТ
Дискретный (точечный) спектр. Если С — вполне непрерывный, а А — поло-
положительно определенный оператор, то спектр частот — точечный. Это характерно
для большинства прикладных задач теории упругих колебаний.
Сплошной спектр. Этот случай типичен для неограниченных упругих тел. Напри-
Например, уравнение для изгибных колебаний бесконечной балки постоянного сечения
имеет вид
EJ —2—рАо2ф = 0, C0)
а дополнительные условия сводятся к требованию ограниченности функции ф (х)
и ее первых трех производных всюду при х е (— °о, о°). Эти условия будут
удовлетворены, если положить
. . пх_ „.
где К — любое положительное число (длина полуволны у собственной формы), со —
собственные частоты:
я2 / EJ V/.
Ш = Т? -пг . I32)
т. е. любое число из интервала @, сю) будет собственной частотой (рис. 1, а).
Спектр может начинаться с частоты щ > 0 (рис. 1, б). Для примера достаточно
дополнить рассмотренную балку упругим безынерционным основанием Винклера
с коэффициентом упругости с. Тогда
(^Г C3)
Смешанный спектр. Можно сконструировать примеры упругих систем, где наряду
с участками сплошного спектра имеются точечные частоты. Так, добавляя к беско-
бесконечной балке на основании Винклера сосредоточенную массу М, получим спектр,
изображенный на рис. 1, в. При этом точечная частота а>м является действительным
корнем уравнения
Ш /с—
8EJ ~\ 4? )
а сплошной спектр начинается с частоты <в0 C3).
ПЛОТНОСТЬ СОБСТВЕННЫХ ЧАСТОТ
173
Полосовой спектр. Спектр частот, состоящий из счетного множества отрезков при
О <^ш < оо, показан на рис. 1, г. Такой спектр имеет, например, бесконечная
неразрезная балка с равными пролетами. Нижняя частота для каждой полосы ча-
частот равна собственной частоте однопролетной балки с опертыми концами, верхняя
частота — собственной частоте однопролетной балки с защемленными концами.
CJM CJ0
О cj1H
г)
Рис. 1. Примеры спектров собственных частот:
а — сплошной; 6 — сплошной, начинающийся с некоторой частоты щ\ в — смешан-
смешанный; г — полосовой
Общие замечания о структуре спектра. Если рассматривать неограниченные
системы как предел систем конечных размеров, то в результате предельного перехода
получим системы с точечным, хотя и сколь угодно плотным спектром. С теоретиче-
теоретической точки зрения вопрос о структуре спектра является весьма существенным.
Например, если спектр сплошной, то вместо разложения A8) в ряд по собственным
элементам необходимо использовать аналогичное интегральное преобразование.
С практической точки зрения, начиная с некоторого достаточно плотного спектра,
различие между этим спектром и сплошным спектром становится несущественным.
Из-за наличия демпфирования и конечной разрешающей способности виброизме-
виброизмерительных приборов, из-за случайного дрейфа частот и т. п. при эксперименте не
всегда удается разделить вклад близких собственных частот в вибрационное поле.
5. ПЛОТНОСТЬ СОБСТВЕННЫХ ЧАСТОТ
Понятие о функции распределения и плотности собственных частот. Пусть спектр
собственных частот — точечный, но достаточно плотный, так что в диапазоне частот,
представляющем интерес для приложений, находится достаточно много собственных
частот. Это типично для тонких пластин и оболочек, а также для трехмерных тел,
находящихся под действием широкополосного возбуждения. Функция распределе-
распределения собственных частот вводится следующим образом:
(Ok), C4)
где т) (со) —единичная функция Хевисайда. Производная от функции распределения
dN (со)
V ((О) = -
C5)
называется плотностью собственных частот. Так как т)' (со) = 6 (<в), где б (со) — дельта-
функция, то точное выражение для плотности собственных частот можно записать
через сумму дельта-функций.
174
ОБЩИЕ СВОЙСТВА СОБСТВЕННЫХ ЧАСТОТ И ФОРМ
Асимптотические распределения и плотность собственных частот. Задание
точного распределения частот полностью определяет весь спектр. Для качествен-
качественных и некоторых количественных выводов о динамическом поведении упругих
систем достаточно иметь приближенные сведения о распределении собственных частот.
Пусть рь Р2>... — некоторые безразмерные параметры системы, малые по сравне-
сравнению с единицей (например, относительная толщина пластины или оболочки). Функ-
Функцию частоты Л/(со) называют асимптотической функцией распределения собственных
Рис. 2. Распределение частот:
а — точное; б — асимптотическое; в — эмпирическое
частот по отношению к параметрам Рь р2,
распределения соотношением
N (со) "~
если она связана с точной функцией
2, ...).
C6)
В отличие от N (со) асимптотическая функция распределения — дифференцируемая
или кусочно-дифференцируемая функция со. Производную
v (со) =
dN(a)
dco
C7)
называют асимптотической плотностью собственных частот. Асимптотические рас-
распределения особенно удобны в том случае, когда они позволяют выделить наиболее
существенные факторы и получить приближенные оценки для целого класса упру-
упругих систем.
Эмпирическое распределение собственных частот. Группируя собственные частоты
по некоторым достаточно широким отрезкам, вычислим среднюю плотность спектра
на каждом отрезке, т. е. число частот, приходящихся на единицу частотной оси.
Эту плотность будем называть эмпирической и обозначать через v (со). Связь с точ-
точной функцией распределения видна из формулы
-^ (fibi ^ со ^ Оь), C8)
ПЛОТНОСТЬ СОБСТВЕННЫХ ЧАСТОТ
175
где Qi, Q2> ¦•• — точки разбиения спектра. Как и асимптотическая плотность частот,
эмпирическая плотность не определяется единственным образом, так как ее значения
зависят от способа разбиения частотной оси. Введенные понятия проиллюстрированы
на рис. 2.
Общие формулы для вычисления асимптотических плотностей собственных частот.
Для получения асимптотических распределений необходимо иметь точные или при-
приближенные аналитические выражения для собственных частот во всем интересую-
интересующем нас частотном диапазоне. Пусть собственные частоты упорядочены при помощи п
параметров ku k2, ¦¦¦ , kn, принимающих дискретные положительные значения.
Чаще всего этими параметрами являются волновые числа, характеризующие собствен-
собственные формы (например, числа, обратные длинам
волн вдоль координатных осей). Назовем со-
соответствующий вектор к = (?ь k2, ... , kn)
волновым вектором. Зависимость со = Q (к),
а также объем ячейки Дк, приходящийся на
одну частоту спектра, будем считать задан-
заданными. Асимптотическая функция распределе-
распределения собственных частот (рис. 3)
ям-ш 1 *• C9)
Q (k)<co
Эта формула будет тем точнее, чем медленнее
меняется функция Q (к) в рассматриваемой
области. Асимптотическую плотность частот
вычисляют согласно C7) дифференцирова-
дифференцированием функции jV (со):
Г(и)
v (со) = ¦
1
Дк J | grad Q (k)
Г (<o)
D0)
Рис. З. К обоснованию формулы для
асимптотического распределения частот
где Г (со) = { k: Q (к) = со}, т. е. интегрирование в D0) производится по поверх-
поверхности Г (со) равных значений собственных частот в пространстве волновых чисел.
Если функция Q (к) неоднозначная, то следует выделить однозначные ветви Qy (к)
и применить к каждой ветви формулы C9) и D0). В результате получаем
Д,к'
v(co)
-2 J
dk
Гу <
| grad Q/ (к) | Д,к
D1)
где Гу (со) = {к : Qy (к) = со}, причем предусмотрена возможность изменения объема
ячейки Дук в пространстве волновых чисел. Если упругая система такова, что может
быть разбита на части, в каждой из которых плотность частот подсчитывается неза-
независимо, то плотность частот для системы в целом получают суммированием по ча-
частям системы. Если число таких частей достаточно велико, афункция v (со) достаточно
медленно меняется при переходе от одной части к другой, то для приближенной оценки
плотности частот можно провести интегрирование «локальной» плотности по всей
области, занятой системой.
Асимптотические точки сгущения собственных частот. Если в какой-либо точке
поверхности Г (со,,) градиент функции Q (к) обращается в нуль, то интеграл D0)
при частоте cos может расходиться. В этом случае говорят, что частота соответствует
асимптотическому сгущению собственных частот. В этой точке оси со касательная
к кривой N = N (со) становится вертикальной. Необходимо подчеркнуть, что асим-
асимптотические точки сгущения характеризуют лишь асимптотические (приближенные)
распределения. Вблизи точек сг>щения наблюдается некоторое увеличение средней
176
ОБЩИЕ СВОЙСТВА СОБСТВЕННЫХ ЧАСТОТ И ФОРМ
sfi
3 3
т
з
\ X
3 3
V/
я
V/
о а
V/V/
V/V/
v/v/v/
V/V/V/
оо°
Стру
a) s
¦Л №
я aj а
QJ В си
&^
5g
eg
a3
ерны
пара
ипед
X X щ
ТОЧНЫЕ МЕТОДЫ 177
плотности частот, тем более резкое, чем ближе асимптотическая оценка к точному
распределению.
Асимптотическое распределение собственных частот для некоторых классов упругих
систем. Данные об асимптотических распределениях даны в табл. 3. Для стержней,
совершающих продольные или крутильные колебания, а также для колеблющихся
струн собственные частоты распределены приблизительно равномерно. Асимпто-
Асимптотически равномерное распределение наблюдается также для тонких пластин и для
трехмерных упругих тел, все измерения которых сопоставимы. Плотность частот
для стержней, совершающих изгибные колебания, с увеличением частоты умень-
уменьшается. Более сложный характер носит распределение собственных частот для тон-
тонких упругих оболочек (см. гл. XIII).
Глава X
ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ЧАСТОТ
И СОБСТВЕННЫХ ФОРМ УПРУГИХ СИСТЕМ
1. ТОЧНЫЕ МЕТОДЫ
Собственные частоты и собственные формы колебаний являются собственными
значениями и собственными элементами краевой задачи для уравнения C) гл. IX
при краевых условиях
Nav(<Tl°) = 0:
Мау(ф'аа) = 0 (а=1, ..., т; у=\, 2, .... п).
Одномерные системы (т = 1). Функция ф, входящая в C) гл. IX, зависит только
от одной координаты xt = x. Точное решение можно построить, если удается найти
фундаментальную систему для C) гл. IX: <pj (х), <р2 (х), ... , фя (х). Функции ф7 (х)
зависят от частоты со, как от параметра. Общее решение
содержит столько констант, сколько необходимо для удовлетворения краевым усло-
условиям A). Подстановка B) в краевые условия приводит к системе линейных алгебраи-
алгебраических уравнений типа
2 ft/A(o)*)C* = O (/=1, 2 л), C)
к— 1
условие существования ненулевого решения которой [равенство нулю определителя
системы B)] дает уравнение частот
Л (соа) = det blk (со2) = 0. D)
Корни уравнения D) есть собственные частоты системы, а ненулевое решение
системы C), отвечающее какому-либо корню уравнения D), определяет форму коле-
колебаний, происходящих с соответствующей частотой.
Двухмерные системы (т = 2). Метод разделения переменных. Пусть упругое тело
занимает прямоугольную в обобщенном смысле область с границами, совпадающими
с координатными линиями ха = const.
Краевой задачей с разделяющимися переменными называют задачу, собственные
функции которой могут быть представлены в виде произведения функций каждого
аргумента в отдельности:
т
ФР=П ЬаЫ Ф = !. 2 ")• E)
«= 1
178
ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ЧАСТОТ И СОБСТВЕННЫХ ФОРМ
Краевой задачей с квазиразделяющимися переменными называют задачу, которая
соответствующим выбором краевых условий A) превращается в задачу с разделяю-
разделяющимися переменными, т. е. допускает решение вида E); кроме того, она допускает
решение в виде
П
F)
причем подстановка F) в C) гл. IX приводит к уравнению относительно Ф„а , а вид
решения F) переводит A) в условия, содержащие только Ф^а.
Пример. Для двухмерных систем, движение которых описывается одним уравнением
с постоянными коэффициентами, переменные разделяются, если все края свободно оперты или
на них реализуется «плавающая» заделка. К разделению переменных приводит решение в виде
sin
- &i> sin
Значения волновых чисел km и фазовых постоянных |а для различных сочетаний условий
даны в табл. 1.
Случай с квазиразделяющимися переменными в двухмерных системах реализуется, когда
два противоположных края свободно оперты, либо на них имеет место «плавающая» заделка
В этом случае решение имеет вид
sin km, (x> ~ ?i>.
Фт, = фт1 ( m, (> ?i.
а для Фт (х ) получается одномерная краевая задача на собственные значения
1. Значения волновых чисел и фазовых постоянных для различных типов
краевых условий
(8)
Опирание
«Плавающая»
Опирание
«Плавающая»
Условия
| ха = аа
заделка
заделка
Опирание
«Плавающая» заделка
«Плавающая» заделка
Опирание
та
аа
тал
аа
(»« + т)-^-
/ 1 \ л
(»«+t)v
«.
0
Л
2
0
Я
2
Метод факторизации. Если операторы исходного уравнения таковы, что результат
их действия можно представить как последовательное действие двух операторов при
условии коммутативности
(С — (D2A)(p = La)LB)(p = L<21L(i)q) = 0 (9)
и у уравнений
L'i'(pl = O и L'21<p2 = 0 A0)
известны фундаментальные системы решений (jpn, ф12> •••> 4>in и фгъ фгг. ••• . фгт> то
в качестве фундаментальной системы C) гл. IX можно взять совокупность фунда-
фундаментальных систем уравнений A0). Общее решение имеет вид
2
1=1
(И)
А=1
После удовлетворения A) из условия существования ненулевого решения полу-
получается уравнение частот.
МЕТОД МАЛОГО ПАРАМЕТРА (МЕТОД ВОЗМУЩЕНИЯ) 179
2. МЕТОД МАЛОГО ПАРАМЕТРА (МЕТОД ВОЗМУЩЕНИЙ)
Метод применяется в том случае, когда для рассматриваемой задачи можно ука-
указать «близкую» систему, решение которой получается достаточно просто. Пусть
краевая задача для уравнения
(С0-ш2Ао)(р = 0 A2)
при краевых условиях A) имеет собственные значения (собственные частоты) со0у и
собственные функции (собственные формы колебаний) ф0/ и коэффициенты операто-
операторов Со и Ао мало отличаются от коэффициентов операторов С и А исходного урав-
уравнения C) гл. IX. Система, описываемая уравнением A2), называется порождающей
или невозмущенной, а исходная система — возмущенной. Если для порождающей
системы требуется выполнение условия самосопряженности, то для возмущенной
системы этого не требуется. Считается, что операторы возмущений пропорциональны
некоторому малому параметру ц:
цС, = С-С0, цА1 = А-А0 A3)
Решение исходной (возмущенной) системы представляется в виде разложения по
степеням малого параметра ц:
<р/=Фо/+та+v?
v+¦ ¦ ¦ -1 A4)
Поправку к форме собственных колебаний находят из решения неоднородных
краевых задач
(Со —cog/Ao) XA7=fft («о, hj в*/. фо/, Xi/> •••• Xft-i./). A5)
которые получаются после подстановки A4) и A3) в C) гл. IX и приравнивания коэф-
коэффициентов при одинаковых степенях малого параметра \i. Поправку к частоте в ка-
каждом следующем приближении определяют из условия существования решения
рассматриваемого приближения, состоящего в требовании выполнения условий орто-
ортогональности правых частей неоднородных систем A5) к собственной функции поро-
порождающего решения <р0;-:
(f*. Фо/) = О. A6)
Поправка к частоте в первом приближении
A7)
, Фо/)
Поправка к собственной функции должна удовлетворять при этом уравнению A5)
при k = 1 с учетом A7) и исходным краевым условиям A). Решение задачи для %у
неоднозначно. Оно определяется с точностью до (pOj с постоянным множителем. Этот
член обычно отбрасывают, считая, что он учитывается в разложении A4). При полу-
получении окончательного решения следует принять ц = 1.
Замечание. Если ад имеет кратность а, так что этому значению соответствуют а собствен-
собственных форм колебаний <рАу C= 1* ... , ct), то необходимо поставить условия ортогональности
ко всем фЖ , что приведет к расщеплению частот В первом приближении поправка к каждой
из «расщепленных» частот
1УР=~ AfA? '
180 ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ЧАСТОТ И СОБСТВЕННЫХ ФОРМ
3. МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ
Метод заключается в построении последовательности функций, сходящихся
к одной из собственных форм колебаний, и нахождении по приближенным значениям
для форм соответствующих собственных частот колебаний. Для построения итера-
итерационного процесса производят замену (Ар —>¦ tyii-i> ф ~*"*|>Ь так что Для определения
\|5А по известному if&_i служит уравнение
Ctfu = Ai|)ft_1> A9)
которое на каждом приближении решают при краевых условиях A) исходной задачи
Начальную функцию \?>0 выбирают достаточно произвольно, но так, чтобы выполня-
выполнялись следующие условия: функция tf0 должна быть непрерывной вместе с необходи-
необходимым числом ее производных; она может не удовлетворять всем краевым условиям;
достаточно, чтобы для любой функции сравнения и (функции, удовлетворяющей
всем краевых условиям и нужное число раз дифференцируемой) выполнялось усло-
условие
(г|з0, Аи)-(и, А-фо) = О; (,f0, Аг|з0) > 0. B0)
Построенный итерационный процесс без наложения дополнительных ограниче-
ограничений сходится к первой собственной форме колебаний. При использовании формулы
Релея [A9) гл. IX] оценка для основной частоты
Рекуррентные формулы A9) пригодны для определения высших собственных
форм и собственных частот колебаний, однако при получении каждого следующего
приближения необходимо выполнить требования ортогональности к ifj/', являю-
являющимся достаточно хорошим приближением для предыдущих форм колебаний. Так,
при определении второй частоты и формы на от-м шаге приближения должны выпол-
выполняться условия
ш' и/ '"' *п о ^
На каждом шаге из фД' вычитают, кроме того, компоненту, соответствующую
первой собственной функции:
B3)
где г|)^' — решение рекуррентной системы A9). Оценка для второй частоты
ССгЬ12'*, \b'2)*\
a>i=). , ' ,.,/.. B4)
При определении третьей собственной функции на каждом шаге итерационного
процесса вычитают компоненты первой и второй собственных функций. Аналогично
поступают и при определении других высших собственных функций [50].
4. МЕТОДЫ ТЕОРИИ ЛИНЕЙНЫХ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ
Задачу о колебаниях упругих систем можно свести к интегральному уравне-
уравнению A4) гл. IX. Поэтому при определении собственных частот и собственных форм
используют специфику интегральных уравнений. В частности, рекуррентные соот-
соотношения метода последовательных приближений имеют в данном случае вид tf>? =
а частота определяется по формуле
М__. B5)
АСИМПТОТИЧЕСКИЙ МЕТОД 181
Если уравнение A4) гл. IX (для одномерного случая) является уравнением Фред-
гольма
ср (х) -tf\m (I) G (х, I) Ф A) d% = О, B6)
о
где G {х, 5) = G (?, х) — функция Грина, то собственные частоты могут быть опре-
определены из уравнения Д (со2) = 0. Здесь А (со2) — определитель Фредгольма, первые
члены разложения которого в ряд по степеням со2 имеют вид
Д (ш2)= 1 — со2 $ т (х) G (х, х) dx +
о
l l
т (х) G (х, х) т (|) G (х,
т (х) G (|, х) т (I) G (|,
dxdt — .... B7)
о о
Использование первых двух членов в B7) приводит к оценке
m(x)G(x, x)dx. B8)
Эта формула дает для основной частоты оценку снизу. Для получения оценки сверху,
а также оценки для второй частоты необходимо в разложении B7) сохранить три
члена ряда и т. д.
5. АСИМПТОТИЧЕСКИЙ МЕТОД
Предварительные замечания. Асимптотические методы, использующие свойства
спектра упругих колебаний при высоких частотах, предназначены для эффективного
определения высших частот и форм. В некоторых случаях асимптотические методы
оказываются пригодными и при определении основных частот и форм. Асимптотиче-
Асимптотический метод [10, 87) применим для упругих тел, занимающих прямоугольную в
обобщенном смысле область в пространстве 0 sc ха ^ аа (а = 1 я). Он пригоден
для краевых задач с квазиразделяющимися переменными. Исходными будут урав-
уравнения C) гл. IX с краевыми условиями A).
Идея метода заключается в использовании при высоких частотах свойств малой
зависимости спектров упругих колебаний от краевых условий и концепции динами-
динамического краевого эффекта. Полагают, что для внутренней области справедливо
порождающее решение типа E), вообще говоря, не удовлетворяющее краевым усло-
условиям. На это порождающее решение накладывают у каждого края корректирующие
решения, которые убывают при удалении от края во внутреннюю область и позво-
позволяют удовлетворить всем краевым условиям. Полученные решения для двух про-
противоположных краев стыкуются. Процедура стыковки позволяет получить систему
трансцендентных уравнений для параметров, определяющих порождающее (внутрен-
(внутреннее) решение и динамические краевые эффекты, а затем получить асимптотические
выражения для частот.
Схема метода. Порождающее решение характеризуется волновыми числами ka и
фазовыми характеристиками |а. Подстановка порождающего решения в уравнение C)
гл. IX дает связь между параметром со2 и волновыми числами ka. Затем в уравне-
уравнениях со2 заменяют ее выражением через ka. Далее строят решение у каждого края.
С использованием условия квазиразделяемости находят уравнение для Ф„а (ха ),
одним из решений которого является "ФраСо (*„0) [см. E) и F)]. Кроме того, для воз-
возможности построения решения необходимо, чтобы полученная система допускала
р — 1 Bр — порядок системы) линейно независимых решений, обладающих свой-
свойством краевого эффекта, т. е. затухающих при удалении во внутреннюю область.
182 ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ЧАСТОТ И СОБСТВЕННЫХ ФОРМ
Сумма порождающего и корректирующего решений содержит р + 1 постоянных
при помощи которых удовлетворяются р условий на границе и условие нормировки'
Волновые числа на этом этапе предполагаются известными. Требуется, чтобы ре-
решения, построенные у двух противоположных сторон области, занимаемой упругим
телом, совпадали во внутренней области с точностью до малой невязки. Условия
стыковки дают уравнения для определения волновых чисел. По известной связи
между со2 и ka находят частоты собственных колебаний.
Примеры приложения асимптотического метода для определения частот и форм
собственных колебаний пластин и оболочек приведены в гл. XII и XIII.
6. МЕТОД РЕЛЕЯ И РОДСТВЕННЫЕ МЕТОДЫ
Метод Релея. Для приближенного нахождения первой собственной частоты можно
использовать формулу Релея A9) гл. IX или B0) гл. IX, если в качестве ф выбрать
некоторую допустимую вектор-функцию (функцию, удовлетворяющую по крайней
мере кинематическим граничным условиям) ф е Ес, близкую к предполагаемой пер-
первой форме собственных колебаний:
«>! ~ !!' IiC • B9)
Эта формула дает оценку сверху.
Для определения k-й собственной частоты необходимо знать первые k — 1 соб-
собственных форм колебаний. При применении формулы Релея требуется удовлетво-
удовлетворить дополнительным условиям
[ф. <Ыл = ° или [Ф- Ф/]С = ° (/='¦ 2 *-!) C°)
Особенностью применения формулы B9) является необходимость задания вектор-
векторной функции ф. Если зависимость каждой компоненты от координат нетрудно по-
подобрать исходя из физического представления о характере деформирования упругой
системы и необходимости удовлетворения по крайней мере кинематическим гранич-
граничным условиям, то соотношения между компонентами ф задать достаточно сложно.
В этом случае может быть использован следующий прием. Вводят параметры а;,
характеризующие амплитудные отношения между компонентами вектора:
фг = М(*); ф/ = /а,Ф/*(Дс) (/ = 2 л). C1
Отношение Релея B0) гл. IX будет зависеть ото,. Использование экстремальных
свойств собственных частот колебаний приводит к уравнениям
д? = 0 (/ = 2, ...,„), C2)
служащим для нахождения at. Для каждой совокупности решений (всего их п) из
B0) гл. IX находят значение для частоты, соответствующей форме с преимуществен-
преимущественным движением по одной из компонент ф.
Методы Данкерли и Саутвелла. Если уравнение C) гл. IX можно представить
в виде
s
Сф-ш2 2 АаФ = 0, C3)
а= 1
где Аа — симметричные, положительно определенные операторы, то уравнения
Сфа-62Аафа = О (а=1, 2, .... s) C4)
МЕТОПЫ РИТЦА, БУБНОВД-ГАЛЕРКИНА, КОЛЛОКАЦИЙ 183
можно рассматривать как уравнения собственных колебаний парциальных по кине-
кинетической энергии систем. В этом случае получается формула Данкерли
C5)
Здесь е1се — собственная частота колебаний парциальной системы C4).
Если уравнение C) гл. IX можно представить в виде
2 СаФ-со2Аф = 0, C6)
а= 1
(т. е. исходная система состоит из парциальных по потенциальной энергии систем),
то получается формула Саутвелла
<°!** ? Ча U^ 2 ejA C7)
а—1 \ а= 1 /
Формулы Данкерли и Саутвелла дают для основной частоты оценки снизу.
Использование теорем сравнения. Если имеются две системы I и II с уравнениями
(Ct — со2А) ф = 0 и (Си — со2А) ф = 0 и совпадающим классом допустимых функций
и для любых допустимых функций [ф, ф]с 3; [ф, ф]с , то со 3=03 . Аналогично,
если есть две системы I и II с уравнениями (С — w2Aj) ф = 0 и (С — <о2Аи) ф = О
и для любых допустимых функций выполняется неравенство [ф, ц>]А 5э [q>, ф]^ >
то cOj sg (Bjj. В первом случае система I более жесткая, чем система II, во втором слу-
случае система I более инерционная, чем система II.
7. МЕТОДЫ РИТЦА, БУБНОВА — ГАЛЕРКИНА, КОЛЛОКАЦИЙ
И РОДСТВЕННЫЕ МЕТОДЫ
Метод Ритца. Этот метод основан на замене задачи нахождения минимума функцио-
функционала нахождением минимума функции нескольких переменных. Исходным является
вариационный принцип B1) гл. IX. Согласно методу Ритца решение представляется
в виде ряда
N
4>W= Ц ЛиЫх). C8)
k— 1
Последовательность (система) координатных элементов г|)д, должна подчиняться
трем требованиям: координатные функции должны удовлетворять по крайней мере
кинематическим граничным условиям: if>A e Ес; при любом N линейно независимы;
система {\|з^} полна по энергии. На практике при ограниченном числе членов ряда
C8) обычно требуется, чтобы система {г|з^} была представительной, т. е. чтобы любую
допустимую функцию можно было аппроксимировать данной системой функций с за-
заданной степенью точности.
Подстановка C8) в B0) гл. IX дает
2 cibfifk
C9)
где
c/ft=[4> **]c; «/*=[*/• %Ь- <40)
184 ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ЧАСТОТ И СОБСТВЕННЫХ ФОРМ
Очевидно, что Cjk = ckf и ауд, = akJ. Условия экстремума B1) гл. IX приводят
к уравнениям для обобщенных координат
N
Л (c/*-fiAl/*)/ft = 0 O'=U 2, ...,„). D1)
ft — 1
Условие существования ненулевого решения системы D1) дает уравнение частот
\c,k-aPajk\ = 0. D2)
Формы собственных колебаний находят в результате определения ненулевого ре-
решения D1) при со = coy и использования разложения C8). Формы собственных коле-
колебаний при простых частотах определяют с точностью до постоянного множителя. При
кратных частотах всегда удается выбрать столько линейно независимых форм, какова
кратность частоты. Метод Ритца легко поддается алгоритмизации и поэтому удобен
для решения на ЭВМ.
Метод Стодолы. Идея сведения вариационной задачи к задаче отыскания минимума
функции нескольких переменных, являющаяся основной в методе Ритца, используется
и в методе Стодолы. Отличие заключается лишь в том, что вместо процесса мини-
минимизации по обобщенным координатам (коэффициентам при координатных функциях) в
методе Стодолы рассматривают минимизацию по некоторым параметрам, входящим
в выражения для форм собственных колебаний (в аппроксимирующие функции).
Метод Бубнова—Галеркина. Уравнения колебаний упругой распределенной сис-
системы C) гл. IX решают с использованием C8). Однако (в отличие от метода Ритца)
координатные функции должны удовлетворять всем краевым условиям A), т. е.
я|Э? е D (С). Согласно методу Бубнова—Галеркина результат подстановки ряда C8)
в C) гл. IX должен быть ортогонален ко всем координатным функциям
N \ / N \
2 /*t*. +/)-«>• А Ц М>*. */1 = ° (/ = '. ••¦• N). D3)
*=1 / \ к= 1 /
После введения обозначений
%) = <*/* D4)
(очевидно, что $]к = $jk и а/к = aft;) из условия существования ненулевого решения
системы D3) получается уравнение частот
|P/ft-co*a,ft| = O. D5)
Собственные формы колебаний определяются после нахождения ненулевого реше-
решения системы D3) рядом C8).
Связь между методами Бубнова—Галеркина и Ритца. Если координатные функции
принадлежат области определения симметричных и положительно определенных опе-
операторов А и С, то скалярные и энергетические произведения совпадают (см. гл. IX):
(А*,. **) = [*,. %]а\ (с%> %) = [%' %]с
и, следовательно, а^к = ujk\ $fk = C]k. В этом случае уравнения частот D5) и D2),
получаемые по методу Бубнова—Галеркина и методу Ритца, совпадают.
Замечание 1. Процедура вычислений по методу Бубнова — Галеркина часто оказывается
несколько проще.
Замечание 2. Метод Ритца допускает большую свободу выбора координатных функции
(удовлетворяются по крайней мере кинематические граничные условия).
Замечание 3. Для приближенного определения частот можно применять процедуру метода
Бубнова — Галеркина с выбором координатных функций, удовлетворяющих «смягченным» усло-
условиям (как в методе Ритца).
Замечание 4. Метод Бубнова — Галеркина можно трактовать как дискретизацию нахожде
ния экстремума в вариационном принципе B2) гл IX.
Замечание 5. Для сходимости метода Бубнова — Гйлеркина достаточно потребовать полной
непрерывности оператора С, положительной определенности оператора А и полноты системы
базисных функций {Ч5^! принадлежащих области определения операторов А и С [68]
Применение метода Бубнова—Галеркина к интегральным уравнениям. Метод
Граммеля. Рассмотрим интегральное уравнение в форме A4) гл. IX. Представление
МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ 185
решения в виде C8) и выполнение формальной процедуры метода Бубнова—Галер-
Бубнова—Галеркина приводит к уравнению вида D5), где
Р/* = (ф*. ifr); «yA = (C-1A^, %). D6)
Описанная процедура нахождения частот называется методом Граммеля.
Обобщение метода Бубнова—Галеркина. Обобщение состоит в ортогонализации
результата подстановки ряда C8) в уравнение C) гл. IX по отношению к новой сис-
системе функций{%&}> от которой требуется по крайней мере представительности. Резуль-
Результат разложения по введенному базису можно представить в форме
I N \
2 * v <А 2 /***• х/)=° (/ = •> •••• N)- D7)
к=\ I \ 4=1 /
Введение обозначений
(С%, Х/) = Р/й! (Иь X/) = «yfe D8>
приводит к уравнению частот вида D5).
Метод Власова—Канторовича. Данный метод состоит в частичном применении
метода Бубнова—Галеркина (по одной или двум координатам), в результате чего
задача сводится к решению ряда одномерных краевых задач на собственные значения.
Метод внутренней коллокации. Решение уравнения собственных колебаний C)
гл. IX при краевых условиях A) аппроксимируется функцией
ф = <Р(х, h, ft, .... /») D9)
или рядом C8), где координатные функции г|^ удовлетворяют всем краевым условиям
tjijefl (С). Коэффициенты fk выбирают так, чтобы удовлетворить уравнению C)
гл. IX в N точках коллокации 3Cfc внутри области определения этого уравнения.
Это приводит к системе алгебраических уравнений относительно /*,. В случае аппро-
аппроксимации C8) эта система имеет вид D1), где
C/* = C**I« = V a/* = A^|x = x/ E°)
Условие существования нетривиального решения /^ системы дает частотное уравнение.
Собственные формы находят по C8) после определения /,, для каждого ч>к.
При назначении точек коллокации должна быть учтена геометрическая и упругая
симметрия системы. Вообще задача выбора этих точек связана с теорией интерполя-
интерполяции и аппроксимации [50].
Связь мегода внутренней коллокации с методом Бубнова—Галеркина. Формулы
E0) получаются из D8) выбором в качестве %к дельта-функций /д. = б (х — хд,).
Метод граничной коллокации. Для границ сложной формы может оказаться полез-
полезным представление решения в виде ряда C8) по координатным функциям if^,, удовлет-
удовлетворяющим уравнению C) гл. IX, но не удовлетворяющим краевым условиям A).
Уравнения для определения коэффициентов fk получают из удовлетворения краевых
условий в N 1у точках границы G — число граничных условий).
Метод комбинированной коллокации. Если координа Нглефункциив C8) удовлетво-
удовлетворяют только части граничных условий, например, толы о кинематическим условиям,
то точки коллокации выбирают и внутри области, и на ее границе.
Метод минимума среднеквадратичной ошибки [50]. Решение задачи C) гл. IX
и A) аппроксимируется D9) или C8). Квадраты собственных частот со2 и коэффициенты
Ik определяют из требования минимума среднеквадратичной ошибки 6 (<р) = ( (Аф —
s
— co2C(pJdS = min. Для нахождения со2 и fk служат уравнения дЫд (со2) = 0,
dS/dfk = 0 (k = 1, 2, ...,). При использовании ряда C8) и k = 1 получаем формулу
Релея A9) гл. IX.
8. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
Применение метода к одномерным системам. Обласгь определения 0 гс х =? I
уравнения C) гл. IX делится на п интервалов точками хк (k = 0, 1, ..., п; х0 = 0;
хп = /). Ограничимся случаем равных интервалов хк = khx {k = 0, 1, ..., п), Д* =
186
ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ЧАСТОТ И СОБСТВЕННЫХ ФОРМ
= IIп. Неизвестную функцию представляют дискретным множеством значений в узлах
Ф* — Ф ixk) (математическая дискретизация). Аналогичную операцию выполняют
с коэффициентами операторов С и А из C) гл. IX. Дифференциальные операторы ап-
аппроксимируются конечными (центральными) разностями в точке хк
Ф
1
(ф
'*+!¦
IV .
ф
и т. д. Уравнение C) гл. IX заменяют системой алгебраических уравнений относи-
относительно фа, составленных для внутренних точек области (к = 1, 2, ..., я — 1). Контур-
Контурные и законтурные значения функции ф0, ц>,1 и т. д. определяют из разностной аппрок-
аппроксимации граничных условий. Например, из ф @) == ф" @) = 0 следует ф0 = 0,
-
дхду
Рис. 1. Схемы разностной аппроксимации смешанных производных
ф_! = —фх. Условие существования нетривиального решения однородной системы
алгебраических уравнений относительно фд. дает уравнение собственных частот.
Применение метода конечных разностей к двухмерным системам. Выбирают
сетку значений координат xk = х0 + kAx, у; = у0 + jAy (/, к = 0, 1,...). Неизвестные
функции аппроксимируют дискретным множеством значений ф;у = ф (xk, y;). Диффе-
Дифференциальные операторы заменяют разностными. Некоторые схемы составления цент-
центрально-разностных операторов показаны на рис. 1 (в кружках даны весовые коэффи-
коэффициенты), остальные аналогичны одномерному случаю. После составления системы раз-
разностных уравнений для внутренних точек области удобно перенумеровать подряд
все узлы сетки (xk, t/j) = р (р = 1,2, ...) и соответствующие значения функций фй;- =
= фР-
Законтурные значения, как и в одномерных системах, исключают из граничных
условий. Для границы, не совпадающей с координатной линией, область определения
сеточной функции q>k} должна включать в себя область определения ф (х, у). Далее,
функция ф (х, у) должна быть разложена в ряд Тейлора в точках пересечения границы
с линиями сетки. Значения сеточной функции в законтурных точках получаются выра
женными через граничные условия и значения во внутренних точках. Для обеспече-
обеспечения такого же порядка точности, как в уравнениях для внутренних точек, в разложе-
разложениях необходимо удержать члены до порядка, совпадающего с порядком уравнения.
Порядок точности. Сходимость разностной аппроксимации. Все приведенные выше
конечно-разностные соотношения имеют второй порядок аппроксимации [30, 95],
что соответствует удержанию в разложении ф (х, у) в ряд Тейлора слагаемых до вто-
второго порядка включительно. В этом случае конечно-разностная аппроксимация схо-
сходится к точному решению при Ах, Ау -*¦ 0 со скоростью О (\ h |2), где h — максималь
ный шаг. Если требуется повысить скорость сходимости, необходимо повысить поря-
МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
187
док аппроксимации. На рис. 2 показаны некоторые разностные операторы четвертого
порядка аппроксимации [30, 95].
Устойчивость разностных схем. Устойчивыми называют такие разностные схемы,
решения которых непрерывно зависят от параметров системы и равномерно от h.
Для сложных систем априорные оценки устойчивости затруднены, поэтому о них
судят, непосредственно сопоставляя результаты вычислений для различных значений
h и входных параметров.
d(AxJ
Рис. 2. Разностная аппроксимация производных четвертого порядка
точности
Для двухмерных систем отношение шагов зависит от отношения порядков старших
производных по х и у и коэффициентов при дифференциальных операторах. Напри-
Например, для Сф = д2ц)/дх2 + а2д2Ц)/ду2 необходимо выполнение условия Ду/Лх < а;
для Сф == д2ф/дх2 + а?д(р/ду необходимо Д(//Д* < a Y2.
Методы решения разностных уравнений. При вычислении собственных частот
разностными методами используют стандартные процедуры отыскания собственных
значений матриц. Для построения форм собственных колебаний системы разностных
уравнений наиболее часто решают методом прогонки в различных модификациях,
в частности, методом матричной прогонки [30, 95]. В случае периодических решений
(полярные координаты) применяют метод циклической прогонки [30, 95].
9. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
Общая схема метода конечных элементов (МКЭ). Континуальная система объема
V, ограниченная поверхностью S, для которой ищется минимум функционала
6/ = 0, 1 = UO —
E1)
аппроксимируется совокупностью М элементов конечных размеров (физическая диск-
/ М \
Vk = V • Элементы мо-
ретизация) — конечными элементами (КЭ) объемов V
.*=¦
. /
гут быть произвольной формы, но должны быть достаточно малыми, чтобы перемеще-
перемещения и (х) любой точки элемента можно было выразить через перемещения некоторых
точек на его поверхности (узлов).
Чаще всего для трехмерных областей используют КЭ в форме тетраэдров или па-
параллелепипедов (в осесимметричных — тело вращения треугольного или прямоуголь-
прямоугольного сечения), для двухмерных областей — КЭ треугольной и прямоугольной формы.
Пусть для определенности пространство трехмерно, конечные элементы — произ-
произвольные тетраэдры. Занумеруем все узлы в 7+ S:;'= 1, 2, ..., N. Аппроксимируем
поле перемещений в КЭ с номером k (рис. 3):
E2)
188
ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ЧАСТОТ И СОБСТВЕННЫХ ФОРМ
WJ
vj
где и* = (и, v, w)r; fk = (fy, ft, fm fn)T — вектор узловых перемещений КЭ составлен
из векторов перемещений узлов fy = («у, vj, wf)T. Здесь и далее верхний индекс обозна-
обозначает номер КЭ, нижний — номер узла. Элементы матрицы функции формы КЭ N*
C X 12) представляют в виде N* = (N*, N*. N^, N*), где N* C X 3)— подматрица
влияния вектора fy. Элементы Nft выбирают так, чтобы совокупность перемещений E2)
удовлетворяла условиям непрерывности
внутри V.
Подстановка E2) в E1) приводит к за-
задаче отыскания минимума функции мно-
многих переменных (узловых перемещений).
Условие минимума имеет вид матричного
уравнения
(С —co2A)f = 0. E3)
Здесь f = (fu f2, ..., /Л,)т — полный век-
вектор узловых перемещений системы. Мат-
Матрицу жесткости системы С и матрицу масс
А составляют из соответствующих под-
М м
матриц КЭ С= ^ с*. А= 2 А*' ко"
А=1 4=1
торые вычисляют по формулам
С*= \ DrADdV, A*= \ NTpNdV,
V V
Щ
Рис. 3. Объемный конечный элемент
где D — матрица, определяемая соотношениями, по которым вычисляют деформации
через перемещения; А — матрица упругих постоянных; р — плотность; т — верхний
индекс, означающий транспонирование матрицы.
Из E3) следует уравнение det (С — со2А) = 0, определяющее собственные частоты.
По найденным частотам из E3) определяют собственные формы колебаний системы.
МКЭ дает оценки сверху для собственных частот.
Для повышения порядка точности вместо дробления области на более мелкие КЭ
часто используют элементы с большим числом степеней свободы, что достигается введе-
введением внутренних узлов в КЭ. В целях лучшего приближения для областей сложной
формы применяют криволинейные — изопараметрические КЭ [43, 86].
Применение МКЭ к задачам колебаний пластин [86]. Разобьем срединную плос-
плоскость пластины на конечные элементы прямоугольной формы. В качестве обобщенных
перемещений узла / принимают нормальный прогиб пластины w/ и углы поворота
нормали f- = (w,, dwJdy, dwJdx).
Аппроксимируем функцию нормальных перемещений срединной плоскости плас-
пластины внутри конечного элемента с номером k полиномом
wk = аг + агх + а3у+а4*2 -f сс^ху + аву2 -f- а-,х3 + авх^у +
E4)
Коэффициенты ау определяют из условий совпадения w, dw/dy, dw/dx с обобщен-
обобщенными перемещениями четырех узлов КЭ /', /, т, п:
dw
dwp
dw
дх
СР>УР
dwp
или в компактной форме C*o* = f* [f*T = (f-, fJ, ^, fTn)]-
О E4)
Отсюда с учетом E4)
где
QT = (
х, у,
w= Nf*
N .= QTC !;
ху, уг, Xя, х2у, ху*, у»,
у, ху3).
метопы динамических жесткостея и податливостеи 189
Матрицы D C X 12) и Л C X 3) для конечного элемента имеют вид
d4
12
Eh3
A—V2)
Iх
V
V°
V
1
0
1
0
0
9
V
/
где Е, v —• упругие постоянные материала.
Интегрирование при вычислении С и А ведется по площади КЭ на срединной
плоскости пластины, a dV = h (x, y)dxdy (ft — толщина пластины).
Применение МКЭ к задачам колебаний оболочек. Каждый из конечных элементов
на которые разбита срединная поверхность оболочки, можно рассматривать как плас-
пластину с двумя системами напряжений и деформаций — мембранной и изгибной. Вектор
узловых перемещений, отнесенный к локальной системе координат элемента с номе-
номером k, имеет шесть составляющих:
'/ = («;. ",¦ *,. V V V-
где первые три компонента — перемещения узла, а последние — углы поворота
относительно соответствующих осей. Перемещения в плоскости КЭ и из плоскости
аппроксимируют независимо. Подматрицы жесткости и масс КЭ вычисляют в локаль-
локальной системе координат, затем находят их компоненты в общей для всей оболочки сис-
системе координат (глобальной). Матрицы жесткости и масс формируют в глобальной
системе координат.
Для определения собственных форм колебаний после вычисления собственных час-
частот и соответствующих векторов узловых перемещений в глобальной системе коорди-
координат к этой системе надо перейти и в выражениях, аппроксимирующих перемещения
в каждом КЭ.
Связь МКЭ с методом Ритца. МКЭ можно рассматривать как один из вариантов
метода Ритца. В классической форме метода Ритца функции, аппроксимирующие соб-
собственные формы, определены на всей области, занятой системой. В МКЭ функции
подбираются для отдельных участков этой области (КЭ), достаточно малых, чтобы
можно было применять функции наиболее простого вида.
10. МЕТОДЫ ДИНАМИЧЕСКИХ ЖЕСТКОСТЕЙ
И ПОДАТЛИВОСТЕИ
Метод динамических жесткостей. Его применяют для систем, которые могут быть
легко разбиты на такие подсистемы, поведение которых известно при задании гармо-
гармонических перемещений. Суть метода состоит в том, что систему условно расчленяют
на достаточно простые части. В местах расчленения системы снимают условия сопря-
сопряжения обобщенных динамических сил. Определяют в каждой /п-й подсистеме реак-
реакции /¦("' (to) по направлениям /-го обобщенного перемещения от &-го единичного
гармонического перемещения l-cosco^. Действительные обобщенные перемещения
Zk cos Ы должны быть определены из условий сопряжения динамических обобщен-
обобщенных сил
I] Zkrik (со) = 0 (/ = 1, 2, ... , л; Пк =2 rft\ E5)
ft = 1 \ m /
Здесь п — число условий сопряжения, rjk (со) — динамические жесткости, которые
определяют суммированием по всем подсистемам, реагирующим на k-e обобщенное
перемещение.
Условие det R (со) = 0, где R (со) — матрица системы, дает уравнение для первых
п собственных частот системы; далее из E51 определяют п векторов Z^7' (co?), по кото-
которым строят собственные формы. Остальные собственные частоты и собственные формы
находят независимо для всех подсистем при однородных краевых условиях Z^ = О
190 СОБСТВЕННЫЕ ЧАСТОТЫ И ФОРМЫ УПРУГИХ СТЕРЖНЕЙ
(k = 1, 2, ..., п). В применении к статике стержневых систем этот метод совпадает
с методом перемещений.
Связь метода динамических жесткостей с методом конечных элементов. Этот метод
можно рассматривать как частный случай МКЭ. Для стержневых систем конечные
элементы — это элементарные балки, на которые разделяется система, линейные и
угловые перемещения узла составляют вектор f/.
Метод динамических податливостей. Этот метод альтернативен методу динамичес-
динамических жесткостей. Ограничимся рассмотрением неразветвленной системы. Как и в ме-
методе динамических жесткостей, систему условно расчленяют на простые части. В мес-
местах расчленения снимают условия сопряжения обобщенных перемещений и вместо
них вводят неизвестные гармонические обобщенные силы Xk cos (sit. Вычисляют мат-
матрицу F(co), элементы которой fJk (со) есть относительные перемещения двух сосед-
соседних подсистем по направлению j-тл обобщенной силы от k-й единичной гармонической
силы 1-cos со/ (динамические податливости). Действительные силы Xk cos со^ опре-
п
деляют из условий сопряжения по перемещениям ^ X^fjk (со) = 0 (/ = 1,2 я).
*= 1
Условие det F (со) = 0 дает первые п собственных частот системы. По соответствую-
соответствующим значениям Х^ (со ) и решениям для парциальных подсистем можно построить п
собственных форм. Остальную часть спектра колебаний вычисляют с использованием
условий X/i = 0. В применении к статике стержневых систем этот метод совпадает
с методом сил.
Глава XI
СОБСТВЕННЫЕ ЧАСТОТЫ И СОБСТВЕННЫЕ ФОРМЫ
УПРУГИХ СТЕРЖНЕЙ И СТЕРЖНЕВЫХ СИСТЕМ
1. ПРОДОЛЬНЫЕ И КРУТИЛЬНЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ
Дифференциальное уравнение и краевые условия продольных колебаний стержней.
В качестве исходного может быть использовано уравнение технической теории
(см. гл. VIII) при q = 0. Если стержень имеет постоянные по длине характеристики
EF = const, pF = const, то уравнение для исследования собственных колебаний бу-
будет следующим:
^"-1^"-0 A)
дх* eg дР~ ' A)
где с0 = (El p)'/2 имеет смысл скорости распространения продольных волн в стержне
(см. гл. XVI).
Функция и (х, t) на концах стержня должна удовлетворять краевым условиям,
соответствующим характеру закрепления концов стержня. Некоторые основные виды
граничных условий приведены в табл. 3 гл. VIII.
Общее решение. Для стержня, совершающего собственные продольные колебания,
переменные разделяют введением временного множителя, гармонически изменяю-
изменяющегося со временем:
и(х, t) = U(x) cos (at-х), B)
где со и х — соответственно частота и фаза колебаний. При рассмотрении собственных
колебаний фаза несущественна и может быть положена равной нулю х = 0. Подста-
Подстановка B) в A) приводит к уравнению
0, C)
где
ПРОДОЛЬНЫЕ И КРУТИЛЬНЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ
191
Общее решение C) можно представить в виде
U (х) = d cos p*+C2 sin fix.
E)
Определение собственных частот и форм продольных колебаний. Подстановка E)
в краевые условия дает систему линейных однородных уравнений для определения
Сг Из условия существования ненулевого решения этой системы (равенство нулю ее
определителя) следует уравнение частот. Формы собственных колебаний определяются
ненулевым решением Cj при со = wh, где (од, — одна из собственных частот. Для раз-
различных случаев закрепления концов стержня собственные частоты или уравнения для
их определения и выражения для форм собственных продольных колебаний стержней
представлены в табл. 1.
1. Собственные частоты и формы продольных и крутильных колебаний
для некоторых граничных условий
Схема закрепления
стержня
Собственные частоты
Собственные формы
JN
_ я Bft - 1)с„
к 21
Ik = 1, 2 )
Ub (х) = sin
я Bk -l) х
21
Частотное уравнение
usl и/ _ pFl
Uk (х) = sin -S-
(k = 1, 2, . .)
Частотное уравнение
со/ сГ
U ь (х) = sin
Пример. Рассмотрим процесс решения задачи определения частот и форм собственных
колебании консольного стержня с сосредоточенной массой М на свободном конце (х = I) Из
краевого условия при х = 0 следует, что Ct = 0. Из условия при х = I (см табл 3 гл VIII)
приходим к уравнению
где и = |У = —. В правой части F) стоит отношение массы стержня и сосредоточенной массы
Для различных отношений масс значения первого корня уравнения F) приведены ниже:
/7
Л<
0,01 0,1 0,3 0,5 0,7 1,0
у. 0,10 0,32 0,52 0,65 0,75 0,86
Высшие частоты находят по приближенной формуле
2,0
1,08
5,0
1,32
10,0 со
1,42 1,57
G)
192
СОБСТВЕННЫЕ ЧАСТОТЫ И ФОРМЫ УПРУГИХ СТЕРЖНЕЙ
Из рассмотрения данной задачи следуют некоторые частные случаи. При М ^ pFl собст-
собственные частоты близки к частотам собственных колебаний консольного стержня [уравнение F)
при М -* 0 переходит в уравнение cos к — 0, что совпадает с уравнением для консольного
стержня]. При очень большой массе (М —> со) собственные частоты будут близки к частотам
для закрепленного на обоих концах стержня [уравнение F) переходит при М -» со в частотное
уравнение для закрепленного на обоих концах стержня sin к = 0]. Еще один частный случай
получается, когда отношение массы стержня к сосредоточенной массе мало, так что инерцион-
инерционностью стержня можно пренебречь и учитывать только его упругость (переход к системе с одной
степенью свободы). В этом случае tg и =
EF
~Ш
М '
W
откуда
(8)
где с?Т — жесткость стержня на растяжение-сжатие.
Форма собственных колебаний с учетом E) и того, что С2 ¦
0 описывается функцией
Фк (х) — sin
sin -
(9)
Колебания составных стержней. При получении частотного уравнения системы,
состоящей из нескольких стержней и совершающей продольные колебания, может
быть использован метод начальных параметров Коши. Решение E) для каждого из
участков составного стержня можно переписать так:
U (х) = U) @) cos р*; -\
U,
sin
A0)
(для каждого участка введена своя система координат).
При применении этого метода последовательно выражают постоянные решения
для каждого участка через постоянные решения для предыдущего участка. Уравне-
Уравнение частот получают при удовлетворении краевым условиям на последнем участке.
Характерные условия сопряжения решений на отдельных участках для различных
типов составных стержней приведены в табл. 2. Описанная выше процедура получения
уравнения частот может быть проведена в матричной форме с использованием матриц
перехода.
2. Условия сопряжения при продольных колебаниях составных стержней
Схема
Условия сопряжения
<*">.¦&=
с ,«, -
= {BFh ^1 = {EF),
Дифференциальное уравнение и краевые условия крутильных колебаний стержней.
Исходным может являться уравнение технической теории (см. гл. VIII) при ц = 0.
ИЗГИБНЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ
193
Для стержня постоянного сечения (G/K = const, p/0 = const) уравнение будет сле-
следующим:
дЧ 1 д2в п
0 <и>
/G/K\l/2
где ск= ~) имеет смысл скорости распространения крутильных волн в стержне
\Р'о /
(см. гл. XVI).
На концах стержня функция 6, характеризующая угол закручивания, должна
удовлетворять условиям, соответствующим характеру закрепления. Некоторые основ-
основные виды условий приведены в табл. 5 гл. VIII.
Аналогия между продольными и крутильными колебаниями. Между продольными
и крутильными колебаниями стержней постоянного поперечного сечения, движение
которых описывается по технической теории, имеется аналогия (табл. 3). Используя
эту аналогию, все результаты предыдущего параграфа, относящиеся к продольным
колебаниям, нетрудно перенести на крутильные.
3. Аналогичные параметры
Продольные колебания
Перемещение и
EF
Жесткость на растяжение-сжатие —-.—
ди
Продольная сила EF -^-~
Инерционная сила рг -^—-
Уравнение — - — — = 0
Краевые условия (см табл. 3, гл. VIII)
Скорость продольных волн с0 = ( — J 2
продольных и крутильных колебаний
Крутильные колебания
Угол поворота 6
GI
Жесткость на кручение —j-
дЪ
Крутящий момент 67., —^—¦
к ох
Инерционная сила р/0 -^|-
д'О I дЩ
Уравнение ¦ = 0
дх' ей д('
Граничные условия (см. табл. 5 гл. VI11)
Скорость крутильных волн
2. ИЗГИБНЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ
Дифференциальные уравнения и краевые условия. Исходными служат уравнения
технической теории стержней (см. гл. VIII) при q = 0. На каждом краю должно быть
поставлено по два условия. Основные виды краевых условий представлены в табл. 6
гл. VIII. Решение может быть получено методом разделения переменных. Выделение
временного множителя путем подстановки
w = W (x) cos at A2)
приводит для стержня с постоянными по длине параметрами к уравнению
WiV-^\V=0, A3)
7 п/р. Болотина В, В., т, 1
194 СОБСТВЕННЫЕ ЧАСТОТЫ И ФОРМЫ УПРУГИХ СТЕРЖНЕЙ
.
Граничные условия для W (х) получают после подстановки в исходные условия
выражения A2) и сокращения на временной множитель cos со^.
Общее решение. Применение метода начальных параметров. Функции Крылова.
Решением уравнения A3) является функция
W (x) = C14m$x + Cacas$x + C3sh$x + Cich$x A5)
Представление общего решения в виде A5) не явпяется единственным В качестве фун-
фундаментальной системы могут быть использованы другие функции, являющиеся линей-
линейными комбинациями ф>нкций, входящих в A5). В частности, вместо A5) можно взять
выражение
W (х) = С; sin рдг + С, cos Р* + C'j?* + CJe-P*. A6)
При решении большого класса задач удобно использовать фундаментальную
систему Коши т])у. Линейно-независимые функции г|);, составляющие эту систему,
являются линейными комбинациями функций, входящих в A5), и обладают тем свой-
свойством, что матрица Коши для этих функций при х — 0 является единичной
' ]
У" @) ф»' @) w @) %" @)/
х колебаний стержней с
A8}
Фундаментальной системой Коши в случае изгибных колебаний стержней с по-
постоянными по длине параметрами являются функции
где Sj фх) — функции Крылова:
A9)
3 ф-V — 7Г V4-^ P1* — COS u-VJ
/
54 (pjc) = ¦— (sh Рл: — sin px)
Общее решение, соответствующее методу начальных параметров, имеет вид
W @) W" @) W" @)
Функции Крылова Sj (x) и их производные по х, как это следует из A8) и A7), при
х = 0 составляют единичную матрицу. Таблицы численных значений функций Кры-
Крылова можно найти в [87, 100]. Функции Крылова и их производные связаны соотно-
соотношениями (штрих означает дифференцирование по х)
( ;
И31 ИБНЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ
195
Используя эти выражения, нетрудно получить выражения для производных от W (х)
W (х) = W @)
х) + W @) Sx (рде)
(И
" @)
.(И;
= № @) 0»S, фх) + W'@)
W" @)
@)
'" (д) = «7 @) p3S2 (px) + W' @) p»
+ W" @) pS4 (fix) + W" @) Sx
B2)
Собственные частоты и собственные формы колебаний. Для получения частотного
уравнения необходимо привлечь краевые условия (см. табл. 6 гл. VIII). Подстановка
в краевые условия одного из видов общих решений A5), A6) или B0) с учетом B2)
приводит к однородной системе уравнений относительно постоянных, входящих в эти
решения. Условия существования ненулевого решения для постоянных дает уравнение
частот. Ненулевое решение определяет форму собственных колебаний. Для некоторых
основных видов краевых условий частотные уравнения и их корни, а также формы
собственных колебаний представлены в табл. 4.
4. Уравнения собственных частот и собственных изгибных колебаний стержней
для некоторых граничных условий
Схема закрепления
стержня
Уравнение
частот
Корни уравнения
частот
Номер Значение
Формы собственных колебаний
sin p; = о
3 142
6 2SS
W (р1*) = sin f,x
4,730
7,859
cos p/ch p; = 1
W фх) = (sin p/ - sh PO X
X (ch P* — cos p*) — (ch p/ -
- cos p/) (sh P* - sin P?)
tgP'-
¦ th ft/ = 0
3,927
7,069
W фх) = (sh |W -(- sin p/) x
X (ch fix — cos fix) — (ch p/ —
— cos p/) (sh p* — sin fix)
cos p/ X
X ch p/ = - 1
1 875
4,694
W фх) = (sh p/ + sin P0 x
X (ch p* - cos p*) _ (ch p/ +
+ cos p/) (sh ft* — sin pj;)
Пример. Рассмотрим процедуру получения собственных частот и собственных форм колеба
ний Если стержень, защемленный на одном конце, на другом оперт на линейно упругую опору
с коэффициентом с (рис 1), то краевые условия для W
W iO) = 0, W ,,0j ¦= 0, W" {I) = 0, W" (/) = - ~ W (О. B3)
196
СОБСТВЕННЫЕ ЧАСТОТЫ И ФОРМЫ УПРУГИХ СТЕРЖНЕЙ
Первые два условия B3) позволяют переписать решение B0) в виде
W (х) = C,S3 (рлг) + C.S, фх).
Подстановка B4) в последние два условия B3) с учетом B1) и B2) дает
С,[р«1(р/) + ^5,<|
Уравнение частот имеет вид
S,
JL St
= 0.
где
2
Si (К) - S, (х) S. (и) + Л.
= 0,
- S, (у.) Ss (*)] = 0,
B4)
B5)
B6)
B7)
B8)
Используя выражения для функций Крылова A9), получим следующее уравнение частот
I + ch и cos и -J- ф (sh и cos и - ch x sin к) = о. B9)
ch к cos и = — 1, ^30)
ИеМ ДЛЯ консольного стеРжня 'см «бл 4) При и„ _ оо (е - оо) уравне-
tgx=thx, C1)
*"* СТСрЖНЯ' один коне« КОТОР°™ заделан, а второй свободно
«о
3,926
Рис. 1. К примеру определения частот
и форм собственных колебаний
Рис. 2. Зависимость корней уравнения
B9) от х„
0 200 400 600 800 Хо
Если и = и. — корень уравнения B9), то собственная частота
с
. ^-
^Второй
^Первый
тон
тон
Форма колебаний определяется функцией
C2)
C3)
Балочные функции. Собственные формы изгибгых колебаний стержней с постоян-
постоянными по длине характеристиками для различных краевых условий называют балоч-
балочными функциями. Так, формула C3) определяет балочную функцию для стержня
с одним заделанным и другим опертым на линейную пружину концом. Для других
ИЗГИБНЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ
197
видов краевых условий балочные функции представлены в табл. 4. Функции, соответ-
соответствующие /г-ой собственной частоте, обозначают обычно через X/, (х). Балочные
функции широко используют в качестве системы базисных функций для приближен-
приближенного решения различных задач теории колебаний упругих распределенных систем.
Это обусловлено тем, что будучи собственными формами колебаний, они обладают
свойствами ортогональности и полноты, что вытекает из общей теории собственных
колебаний распределенных систем (см. гл. IX).
Замечание 1. В табл 4 балочные функции не нормированы. Обычно производят норми.
ровку
Х%(х) dx=>\.
C4)
о
Замечание 2. В приложениях, в частности при применении вариационных методов (Ритца,
Бубнова — Галеркина и др ), приходится вычислять интегралы, содержащие балочные функ-
функции и их производные. Вычисление этих интегралов or балочных функций можно найти
в руководствах [3, 87, 100, 109]
5. Условия сопряжения участков для стержней с кусочно-постоянными
характеристиками
Условия на границе
участков
-ж
м
М,1
Аналитические условия сопряжения
W_=1S7+; W'_=W^. (ЯJW")_ = {EJW")+\
(EJW'")_ = (EJW'")+
W_ = W+ = 0; W' = W+; (EJW")_ = (EJW")^;
(EJW'")_ = (EJW'")+- R
W - W+; W - W'+; (EJW") —[EJW);
(EJW'")_ = (EJW'")+ + cW+
W -W+-0; W - W'+; (EJW") - [EJW )+ - cW'+;
(EJW")_ = (EJW')+ - R
«7_=«7+, W'_=W+; {EJW")_ = {EJW")+;
(EJW'")_ = (EJW'")+ - Ma*W+
W = W+, W> = W'+; (EJW") =(EJW")+ + ta>'W"+;
iEJW'")_ = (?УЦ7'")+ _ Ma>'W+
198
СОБСТВЕННЫЕ ЧАСТОТЫ И ФОРМЫ УПРУГИХ СТЕРЖНЕЙ
Колебания стержней с кусочно-постоянными характеристиками. Уравнение
собственных частот колебаний стержней в этом случае может быть получено путем
применения метода начальных параметров. Решение для каждого участка записы-
записывается в виде B0). Две константы, входящие в выражение B0), для первого участка
выражают при помощи краевых условий для этого участка при хх = 0. Условия со-
сопряжения при переходе от одного участка к другому позволяют последовательно вы-
выразить все константы на любом участке через две константы первого участка, остав-
оставшиеся неопределенными. Удовлетворение условий на последнем участке при кп = /„
для неопределенных постоянных дает линейную однородную систему алгебраических
уравнений, из условия существования ненулевого решения которой следует уравнение
частот. Условия сопряжения при переходе от одного участка к другому приведены
в табл. 5.
6. Зависимости для частотных коэффициентов для стержней,
имеющих промежуточные опоры и сосредоточенные массы
Схема закрепления
стержня
Зависимости для ча-
частотных коэффи-
коэффициентов
Схема закрепления
стержня
Зависимости для ча-
частотных коэффк-
ииснтов
Основной тон симмет-
симметричных колебаний
^te
5,52
V>
2,0
f
A
••-
100 200 300
5,0
4,0
3,926
3,0
г
i
\
\
\
0 0,25 0,5 0,75 Ц
Основной тон симмет-
симметричных колебаний
. I _
to 20
X
3,0
0,3
— —
n-v
—-—
0,2! 0,5 0,15
2,0
Колебания неразрезных балок. Описанный выше метод применим для неразрезных
балок. Однако более предпочтительно в этом случае использовать уравнения трех
моментов (т — номер пролета, совпадающий с номером правой опоры):
-f
1
4, m
($EJ)m+i
+ мт+1
2, m -f J — огм, m -
S4, m+i
5-2,
, m-Si,
J
i — Sfn, m + i
= 0.
¦ +
C5)
ИЗГИБНЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ
199
Если все пролеты одинаковы, то C5) принимает вид
E2, mS3l m — Sb mS4
i=0.
C6)
Некоторые данные, определяющие частотные параметры, для различных стержней
с промежуточными опорами и сосредоточенными массами приведены в табл. 6. Дан-
Данные для многопролетных неразрезных стержней приведены в табл. 7 [100].
7. Корни уравнения
частот и Для
Схема закрепления стержня
'Л
'''
7, 7?,
ni
tJLJL ... ф^
* nL
Г
"* *'* *' ni
7?
Число
тов
1
2
3
4
5
10
1
2
3
4
5
10
1
2
3
4
5
10
многопролетных стержней
Номер формы
1
3,142
3,142
3,142
3,142
3,142
3,142
4,730
3,927
3,550
3,393
3,299
3,205
3,927
3,393
3.267
3,205
3,205
3,142
2
6,283
3,927
3,550
3,393
3,299
3,205
7,853
4,744
4,304
3,927
3.707
3,299
7,069
4,461
3,927
3,644
3,487
3,236
3
9,425
6,283
4,304
3,927
3,707
3,299
10,995
7,069
4,744
4,461
4,147
3,487
10,210
6,535
4,587
4,210
3,927
3,456
4
12,566
7,069
6 283
4,461
4,147
3,487
14,137
7,855
6,692
4,744
4,555
3,707
13.352
7,603
6,409
4,650
4,367
3,582
5
15,708
9,425
6,692
6.283
4,555
3,707
17,279
10,210
7,446
6,535
4,744
3,927
16,494
9,677
7,069
6,347
4,681
3,801
Замечание. Частоты неразрезных стержней с равными пролетами образуют «зоны cry
щения». В каждой такой зоне находится чигло частот, равное числу пролетов стержней, а значе
ния частот близки между собой.
Влияние начальных осевых усилий на собственные колебания. Исходным является
уравнение (84) гл. VIII при q = 0 и jV = const. Общее решение этого уравнения может
быть записано в следующей форме:
W (х) = Сх sin 7 ix + С2 cos 7i* + С3 sh у2х + ^4 сп Уъх>
где
N
N
^ 2EJ г У \ 2EJ
Для опертой по концам балки форма определяется функцией
а частоты при N = —Р
„ . кпх
W (x)=sm-r,
C7)
C8)
C9)
D0)
200
СОБСТВЕННЫЕ ЧАСТОТЫ И ФОРМЫ УПРУГИХ СТЕРЖНГЯ
1Де Од — собственные частоты [см. C2), где xfc = feri] стержня без учета продольной
силы; Pk = —; значение А-й эйлеровой критической силы. Таким образом,
наличие растягивающей продольной силы приводит к увеличению собственных час-
частот, а при действии сжимающей продоль-
продольной силы — к уменьшению. При Р = Pk
k-я собственная частота обращается в
нуль (рис. 3).
Замечание 1. Формулы, аналогичные D0),
могут быть получены для других краевых
условий стержня
Замечание 2. При больших растягивающих
значениях силы вместо D0) может быть исполь-
использована приближенная формула
*л / N у/,
~—r{w)
D1)
(на рис. 3 эта зависимость дана штриховыми
линиями).
Влияние сдвигов и инерции вращения.
Для стержней небольшой длины уравне-
уравнения технической теории (см. гл. VIII)
становятся неприменимыми. В этом слу-
случае необходимо использовать уравнения
Тимошенко (см. формулу (93) гл. VIII), учитывающие влияние поперечных сдви-
сдвигов и инерции вращения поперечных сечений.
Общее решение для прогиба W (х) имеет форму C7), где параметры Yi и у2'-
Рис. 3. Влияние начальных осевых усилий
на собственные частоты изгибных коле-
колебаний стержней
Здесь
a =P4-f
Е
Для опертой по концам балки частоты определяют по формуле
Ы A1
/
'/.
D2)
D3)
D4)
Замечание. Для стержней переменного сечения задачу о собственных колебаниях решают
приближенными методами (см. гл. X). Точное решение в бесселевых функциях возможно для
балок в форме клина или конуса. Примеры применения приближенных методов для
Определения собственных частот и собственных форм изгибных колебаний стержней можно
найти в [2, 35, 87, 100, 109].
3. ИЗГИБНО-КРУТИЛЬНЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ
Рассмотрим колебания шарнирно-опертого стержня, имеющего плоскость симмет-
симметрии [109]. Система уравнений [см. формулу A04) гл. VIII] (q2 = 0, q3 = 0, (х = 0,
а2 = 0) распадается на две независимые системы, из которых уравнение
?/гр + pF тр = 0 D5)
описывает чисто изгибные колебания в плоскости симметрии, а два других уравнения
у дх*
д*в
к яЛ ~ Ela з^ - р/. ш - pFa3 ш = 0
D6)
РАСЧЕТ СОБСТВЕННЫХ ЧАСТОТ И ФОРМ КОЛЕБАНИЯ 201
— изгибно-крутильные колебания. Граничные условия при х = 0 и х = / имеют вид
, = 0; е = 0; 0 = 0; g- = 0. D7)
Граничные условия и уравнения удовлетворяются, когда
, „ . knx
w (х, t) = we sin —-— cos at;
Ь(х, 0 = в0 sin-^-cos м/ {k=\, 2, ...). D8)
Собственные частоты колебаний определяют из характеристического уравнения
[а>\ — со2)(ш|>р — со2) —(o4a|s = O, D9)
где
я20/к
— частоты чисто изгибных и крутильных колебаний соответственно; s = у. Собст-
'0
венные частоты колебаний, найденные из D9), равны
«1,9- 2 A -я|) ¦ (°^
Если а3 = 0, т. е. центр тяжести сечения и центр изгиба совпадают, то щ = сокр
4. РАСЧЕТ СОБСТВЕННЫХ ЧАСТОТ И СОБСТВЕННЫХ ФОРМ
КОЛЕБАНИЙ ПО МЕТОДАМ ДИНАМИЧЕСКИХ ЖЕСТКОСТЕЙ
И ДИНАМИЧЕСКИХ ПОДАТЛИВОСТЕЙ
Общая характеристика методов динамических жесткостей и динамических подат-
ливостей дана в гл. X. Преимущество этих точных методов для систем, составленных
из прямолинейных стержней, заключается в том, что заранее могут быть построены
и затабулированы вспомогательные решения для элементов расчлененной системы.
Применение метода динамических жесткостей. По этому методу основная система
образуется наложением п дополнительных кинематических связей таким образом,
чтобы исходная система была расчленена на однопролетные стержни с неподвижными
опорами.
Обобщенные перемещения по направлению этих связей
г, @ = 2; cos М-Х), E3)
где Zj — амплитудные значения перемещений. Налагаемые связи могут быть как угло-
угловыми, так и линейными. Полагая поочередно Zk = 1 при всех остальных Zj = 0
(/, k = 1,2, ..., п), находим обобщенные силы, возникающие во всех введенных свя-
связях. Амплитудные значения этих сил называют динамическими реакциями (динами-
(динамическими жесткостями), элементы которых г/А (ш) образуют квадратную матрицу
R («>) порядка п. При этом /",¦? (со) = г^ (ш).
Амплитуды перемещений Zu Z2, ..., Zn выбирают так, чтобы формы колебаний
основной и заданной систем совпадали. Условие равенства нулю обобщенных сил
имеет вид
2 rlk(fs,)Zk = 0 (/ = 1, 2 я). E4)
*= 1
202 собственные частоты и формы упругих стержней
8. Формулы для определения единичных реакций
Реакции
Схема стержня
Расчетные формулы
Единич
ный
поворот
to, U
ПК
kk
aEJ (
S
a'EJ
S
' mk <
StSi — 52S,)
2 — S2S4
(sis3 - s!)
-' — S2S
aEJS,
J2 — S S '
— a'EJS,
nk s, _ s^
O.EJ (S2 _ S2)
'fk
a'Ej
st
s.
\s4 - s
st -s2
a'EJS,
,S, - S,
st
s3
S1S4 —
Единич-
Единичное
смещение
o-
1
rmi
rnj
a*EJ (SI
a'E
S4
-V3)
S2S4 '
-S.S.
a'EJ (S| - S«)
O S,S4 - S2S3 '
_ a'EJ (S^; — S,S4)
**/ OJO4 *~" 02*^8
' fij S S — S S J
Ф= с с _3g о
Примечание. В таблице принято a = р, где р определяют по формуле A4)*
ПЛАСТИНЫ, ПРЯМОУГОЛЬНЫЕ В ПЛАНЕ 203
Условие существования нетривиального решения системы линейных алгебраичес-
алгебраических уравнений E4) приводит к уравнению частот
detR(<o) = O. E5)
Выражения для динамических реакций г^, вычисленные для некоторых частных
случаев, приведены в табл. 8 [87].
Применение метода динамических податливостей. При динамическом расчете
стержневых систем по методу динамических податливостей основная система обра-
образуется (так же как и при статическом расчете) путем отбрасывания п. «лишних» свя-
связей. За «лишние» неизвестные принимают реакции в отброшенных связях X/ =
= X, cos (bit — у), удовлетворяющие каноническим уравнениям
21 //*(ш)Х* = 0 (/ = 1, 2 п). E6)
*= 1
Здесь fjfi = fjk (со) — амплитуда перемещения по направлению неизвестной реакции
отброшенной связи от единичной силы Хь = 1. При этом реакции в остальных отбро-
отброшенных связях равны нулю. Перемещения
MfMk
-?j-dz, E7)
(О "._
где М} — изгибающие моменты от статической силы X/ = 1. Величины М^ являются
амплитудными значениями изгибающих моментов от динамической силы Xk (Xk =
= 1). Для существования нетривиальных решений необходимо, чтобы определитель
матрицы F (w), составленной из коэффициентов канонических уравнений E6), был
равен нулю:
detF(co) = O. E8)
Раскрывая определитель, приходим к трансцендентному уравнению для определения
собственных частот колебаний стержневой системы.
Глава XII
СОБСТВЕННЫЕ ЧАСТОТЫ И СОБСТВЕННЫЕ ФОРМЫ
УПРУГИХ ПЛАСТИН
1. ПЛАСТИНЫ, ПРЯМОУГОЛЬНЫЕ В ПЛАНЕ
Уравнения. В случае свободных колебаний в уравнении A11) гл. VIII следует
положить q = 0. Подстановка w = ф {хъ x2)-cos (Ш —%) приводит при D = const
к уравнению
D ДДф — рЛю2ф = 0. A)
Краевые условия имеют тот же вид, что и A12) гл. VIII при замене w на ф.
Краевые условия Навье. Для шарнирно опертых по контуру пластин
= J=0 при ж1 = 0, aj
= й-^ = 0 при лг2 = 0, а2
B)
204
СОБСТВЕННЫЕ ЧАСТОТЫ И ФОРМЫ УПРУГИХ ПЛАСТИН
переменные разделяются. Формы собственных колебаний описываются функциями
(П1Ъ Щ" ' • ¦¦•)" ()
Колебания по форме cpm m происходят с собственной частотой
DV/2
D)
Краевые условия Леви. Если на двух противоположных сторонах пластины реали-
реализуются условия свободного опирания типа B), то формы колебаний описываются сле-
следующими функциями:
где Фт удовлетворяет уравнению
(m = 1, 2, ...),
E)
F)
и краевым условиям, соответствующим характеру закрепления на других сторонах.
Эти условия служат для определения произвольных постоянных, входящих в общее
решение
sin
+ Сзт ch
sh y2mx2,
G)
где
Уравнение частот получается в виде равенства нулю определителя системы для
С/т. Например, если остальные кромки защемлены, так что выполняются условия
@) = Фт (а2) = Ф'т @) = Ф'т
0,
то уравнение частот имеет вид
0
sin vlmea
ch yima2 sh у
ch Y2
=0
(9)
Формы колебаний определяются функциями E) с учетом G), если для Cjm взять
ненулевое решение соответствующей однородной системы при со = со^т, где со^т —
k-й корень уравнения (9). Если на двух противоположных сторонах при хг = const
реализуются одинаковые условия, то уравнение частот распадается на два уравне-
уравнения, соответствующие симметричным и антисимметричным формам. Уравнения час-
частот для различных сочетаний краевых условий приведены в табл. 1.
Замечание. Разделение переменных возможно также при реализации на двух противопо
ложных сторонах условий скольэящей заделки или комбинации опирания и скользящей за-
заделки. Вместо E) следует принять в первом случае
<f(x
во втором
ПЛАСТИНЫ, ПРЯМОУГОЛЬНЫЕ В ПЛАНЕ
1 Уравнения частот для прямоугольных пластин
205
Краевые условия
Опирание — опирание
Опирание — заделка
Опирание — свободный край
Заделка — заделка
Заделка — свободный край
Свободный край — свободный
край
a th
(th
2A + ab)
Уравнения частот
sin y a = 0
т vlm m 2
vlm
V2ma2 v2m t Vlma2 \
+(a + 6) ch V2ma2 cos Vlma2
V2ma2 v2m vlfflcs2 \
+
- 0
Примечание В таблице приняты обозначения:
Защемленные или свободные по контуру пластины. Точного решения для данного
случая в замкнутом виде получить не удается. Здесь можно применять различные при-
приближенные подходы: вариационные методы (Релея, Ритца, Бубнова—Галеркина.
и др.), численные методы (конечных разностей, конечных элементов), комбинирован-
комбинированные методы и т. д. Так, по формуле Релея основная частота
о о
A0)
р/ир2 dx2 rfx2
о о
В качестве аппроксимирующих функций для форм собственных колебаний могут
быть использованы произведения балочных функций (см. гл. XI):
Выражение для частоты записывается в виде
=*_._5?/.?Y\ (i2)
206
СОБСТВЕННЫЕ ЧАСТОТЫ И ФОРМЫ УПРУГИХ ПЛАСТИН
Значения безразмерного коэффициента kmn для различных случаев закрепления
пластин можно найти в руководствах [2, 20, 35, 77, 87, 93, 100, 101, 109, 139]. Там же
можно найти значения этого коэффициента для анизотропных пластин, пластин пере-
переменной толщины, пластин с сосредоточенными элементами и для других случаев.
2. КРУГОВЫЕ И КОЛЬЦЕВЫЕ В ПЛАНЕ ПЛАСТИНЫ
Общий случай (пластины постоянной толщины). Подстановка w—<p(r, 9) х
X cos(w^ — %) в уравнение A14) гл. VIII (q = 0) дает уравнение A) с заменой опера-
оператора Лапласа на его выражение в полярных координатах:
З2 1 д 1 д2
~~ дг2 г дг г1 <Эв2'
Краевые условия для края г = const приведены в табл. 2.
A3)
Вид закрепления
Заделка
Опирание
Свободный край
Упругое закрепление
2. Краевые
Схема
условия для круговых пластин
Условия при г = const
\ дг^ г of J
\ д (д^ц> 1 dtp 1 д^ф "\
/ I д2(р 1 ^ф \ Т
\ т dfdB f^ дВ 1\
Q -f- с,ф = 0; М +с2 -^- — 0
Для замкнутых в окружном направлении пластин
Ф(л, 6) = 0n(/-)cos[/i(e-eo)] (n = 0, 1, 2, ...),
где п — число узловых диаметров. Функция Фп удовлетворяет уравнению
л21
I d
r dr
dr*
r dr
где
IF
A4)
A5)
A6)
КРУГОВЫЕ И КОЛЬЦЕВЫЕ В ПЛАНЕ ПЛАСТИНЫ
207
и краевым условиям, получающимся из условий, приведенных в табл. 2 после подста-
подстановки A4) и сокращения на cos \п (б — 90)].
Общее решение уравнения A5) может быть найдено по методу факторизации
(см. гл. X) и записано в форме
где использованы стандартные обозначения для цилиндрических функций.
Круговые в плане пластины. Для круговых пластин из условия ограниченности
решения в центре (г = 0) постоянные С2п = С4п = 0. Для определения оставшихся
констант используют краевые условия (см. табл. 2). Уравнение частот получают из
условия существования ненулевого решения для Cjn (равенство нулю определителя
соответствующей системы). Для некоторых случаев закрепления уравнения частот
приведены в табл. 3.
3. Уравнения частот для круговых пластин
Вид закрепления
Схема
Уравнения частот
Заделка
1
- = 0
Опирание
• + •
(РЛ)
1 — v
V)
Свободный край
«2/„ (PR) - A -v) [fLRl'n (PR) - n2ln (PR)] ~
3R34 (PK) + С - v)V [PRJn (PR) - ¦/„ (PR)]
3R3/^ (PR) - ( 1 - v2) «2
- In (PR)]
4. Значения коэффициентов v.mn Для круговых пластин
/n
0
1
2
3
0
1
2
0
1
п
2
3
Заделанная пластина
3,196
6 306
9.439
12 5S
4,611
7.799
10,96
14,11
5,906
9 197
12,40
15,58
7,144
10.54
13,79
17,00
Опертая пластина
2,231
5,455
8,614
3,733
6,965
10,139
5,065
8,375
11,59
-
0
1
2
3
0
1
1
2
3
Свободная пластина
3.014
6,209
9,370
4,630
7.737
10,91
2.292
5,937
9,160
12.41
3,497
7,274
10,55
13.86
208 СОБСТВЕННЫЕ ЧАСТОТЫ И ФОРМЫ УПРУГИХ ПЛАСТИН
Ч астота
Значения коэффициентов ктп приведены в табл. 4.
При больших п для заделанной по контуру пластины
а для свободной пластины
л,
п
-тг I п.
A8)
A9)
B0)
Кольцевые в плане пластины. В этом случае все константы в A7) отличны от нуля.
Частотные уравнения имеют достаточно громоздкий вид. Например, для пластины,
заделанной по внутреннему контуру радиу-
радиуса Rx и внешнему контуру радиуса R2, это
уравнение имеет вид
= 0.
/h=0, S = 1
/
/-п=0
K'n(f>Ri
B1)
Зависимости
n
0
0,2
0,4
от а = -^ для данного
случая показаны на рис. 1. Аналогичные
уравнения и зависимости для различных
сочетаний краевых условий на внутреннем
и внешнем контурах можно найти, напри-
например, в [35, 87].
Применение приближенных подходов.
Для пластин переменной толщины (хотя
в ряде случаев и может быть получено точное
решение) применение различных прибли-
приближенных методов, например метода Ритца, более эффективно. Для оценки основных
частот удобной оказывается формула Релея
Рис. 1. Зависимость частотного пара-
параметра для кольцевой заделанной плас-
пластины от а = R,IR,
Пгя«,
\ \
о к,
B2)
Широкое применение для определения собственных частот колебаний кольцевых
и круговых пластин переменной толщины находит метод Стодолы. Его отличие от
метода Ритца заключается в том, что минимизация проводится по параметру s, вхо-
входящему в выражение для аппроксимирующих функций. 1 ак, для кольцевой круговой
пластины с защемленным внутренним контуром радиуса а решение ищется в классе
функций
Ф = (г — a)scosnF — 6„) (п = 0, 1, 2, ...)
Для каждого п находят частоту по схеме метода Ритца с дальнейшей минимиза-
минимизацией по параметру s.
ПРИМЕНЕНИЕ АСИМПТОТИЧЕСКОГО МЕТОДА
209
3. ПРИМЕНЕНИЕ АСИМПТОТИЧЕСКОГО МЕТОДА К УПРУГИМ
ПЛАСТИНАМ
Динамический краевой эффект. Асимптотический метод [10] применяют для пластин,
занимающих прямоугольную (в обобщенном смысле) область. Он дает хорошие резуль-
результаты для высших частот. Однако в ряде случаев и для основной частоты этот метод
дает приемлемые результаты. Для пластины постоянной толщины, когда уравнение
колебаний имеет вид A), порождающее решение будет следующим:
(xi — %i) sin k2 (x2 —12) • B3)
ф (*i. Ч) = sin
Собственную частоту выражают через волновые числа
и k2
B4)
Вблизи края *i = 0 решение можно записать в следующем виде
qp (х1, х2) = Ф (*]} sin k2 (x2~l2) B5)
Используя исходное уравнение A), нетрудно получить уравнение для Ф. Реше-
Решение этого уравнения, удовлетворяющее условию ограниченности при удалении во
внутреннюю область, будет следующим:
/•]. B6)
Это решение описывает динамический
краевой эффект, вблизи края Xi = 0.
Первое слагаемое соответствует порож-
порождающему решению, второе — корректи-
корректирующему или собственно краевому эф-
эффекту. Таким образом, в пластинах имеет
место невырожденный неосциллирующий
динамический краевой эффект. Протяжен-
Протяженность краевого эффекта, определяемая
экспоненциальным множителем во втором
слагаемом B6), не превышает длины по-
полуволны порождающего решения.
Постоянные С и |] в B6) выражают
через волновые числа &, и ka при удов-
удовлетворении краевым условиям на этом
краю.
Условия стыковки. Решения, анало-
аналогичные B6), строят вблизи всех краев
пластины Требование, чтобы с точностью до динамических краевых эффектов ре
шения противоположных кромок совпадали, приводит к условиям стыковки
-
\
\
•*>
4
J
г
\
Рис. 2. Графическое решение уравнений
стыковки асимптотического метода
kxax = arctg un
arctg u12 (ku
k2) + arctg игг (klt
+ т2я,
B7)
где mt и m2 — целые числа или нули, a ujk равны тангенсам фазовых постоянных
%г Для различных краевых условий выражения для «^ и С даны в табл. 5.
Полученная система B7) может быть решена относительно волновых чисел ?j
и k2 методом последовательных приближений или графически. В качестве примера
на плоскости волновых чисел (рис. 2) показаны зависимости, построенные согласно
B7) для заделанной пластины. Точки пересечения кривых отвечают волновым числам,
соответствующим определенным формам колебаний Частоты при этом находятся
по формуле B4).
Пластины при различных краевых условиях. Точное решение уравнений стыковки
получается для следующих случаев:
210
СОБСТВЕННЫЕ ЧАСТОТЫ И ФОРМЫ УПРУГИХ ПЛАСТИН
о
3
вне
о
3,
а
CQ
рае
я
О)
и
к
к
Вид
закреплен
о
о
о
[1
Э-
+
М-.
е-
|
||
¦я
X
33
та
к
О
¦ад*
™
+
•ад"
ГМ
_+
^^
о
||
и
11
Заделке
-
>
+
а
+
•ад
1
i
т
(N
_|_
1
-f
'•ад
11
*-ад"
о
II
I I"
-
*
^ +
©¦
^»
-о
п
1
Свободны
край
¦ад
•ад*
-ад
(М
+
1
Q
|
'•ад
^.
+
•ад
•ад
"г
'-ад
Q
*^
о э-
я—
& и
>г
Q
|
Si
?3.
с я
+
1
•ад
+
¦ад
-ад*
+
1
-[-
j«
-lei
9-
о*
II <.
н
II ?¦
е-
«2
^ Гч I.
1*0 ||
е-
«1
Опора н
пружин
ПРИМЕНЕНИЕ АСИМПТОТИЧЕСКОГО МЕТОДА
211
бесконечная в одном направлении, заделанная по кромкам пластина при цилиндри-
цилиндрическом изгибе:
' 1 \2
TJ л3 (DVU
квадратная заделанная пластина при я^ = т2 = /п:
квадратная пластина, два противоположных края которой защемлены, а два опер-
оперты:
а2
oh
Асимптотический метод оказывается достаточно эффективным, так как он быстрее
приводит к результатам, чем другие методы О точности можно судить по табл. 6 и 7,
где дано сравнение значений частот, полученных асимптотическим и вариационным
методами ю == — ш ?_ .
L я2 \D / J
Влияние тангенциальных усилий. Основное уравнение записывается в виде
D ДДФ -
Частота
N2 J|- р/г«2ф= 0.
B8)
B9)
1
1
2
1
3
1»!
]
2
2
3
3
6. Результаты для оценки точности асимптотического
(заделанная пластина)
Я
4/3
1,2027
7/3
1,1420
10/3
кгаг
я
4/3
2.4372
7/3
3,4688
10/3
<о по методу
асимптоти-
асимптотическому
3,556
7,386
10,889
13,337
22,222
вариацион-
вариационному
3,646
7,437
10,865
13,393
метода
Рас-
Расхождение,
%
2,53
0 69
0,70
0,42
Невязка,
%
2.66
0,93
0,18
0,24
0,01
7. Результаты для оценки точности асимптотического метода (квадратная пластина)
Закрепление
*, = 0
Заделка
*i = а,
Опирание
Заделка
Опирание
дг2=0
Заделка
Опиранне
Заделка
Опирание
х2 = а2
Заделка
Опирание
Лг@ ПО
асимпто-
асимптотическому
31,37
28,96
26,87
23,68
методу
вариаци-
вариационному
31,96
28,99
27,10
23,70
Расхож-
Расхождение, %
1,88
0,24
0,86
0,25
212 СОБСТВЕННЫЕ ЧАСТОТЫ И ФОРМЫ УПРУГИХ ПЛАСТИН
Решение вблизи края хх = 0 будет следующим:
Если край хх = О заделан, то
Краевой эффект может вырождаться при отрицательных N (при I N |
„ — эйлерова критическая нагрузка).
Ортотропная пластина. Уравнение для форм колебаний имеет вид
<Э4ф
д4а>
д4ф р/гсо2
C0)
C1)
, где
C2)
где
Частота связана с волновыми числами соотношением
ю = (*• + 2aI2Af
Вблизи края л:! = 0 решение выглядит следующим образом:
Ф2 (*х) = sin ftx (^ - |i) + Cx exp [— хх {k\
а вблизи х2 = 0
Ф2 (х2) = sin *2 (дс-Ь) + C2 exp [-
Для заделанных сторон пластины ual и Ca равны:
«21 = -
C3)
C4)
C5)
C6)
4. МНОГОПРОЛЕТНЫЕ ПЛАСТИНЫ
Основные уравнения и граничные условия. Пусть прямоугольная пластина,
отнесенная к системе координат Оху, разделена на п пролетов длиной aj (j = 1, 2,
..., п) жесткими линейными опорами. Для каждого пролета будет справедливо урав-
уравнение колебаний
D, ДДФ/ - Р/Л;0*ру = 0
= JJ + |1).
C7)
Удобно для каждого пролета ввести свою систему координат Oxji/j. На краях
х\ =0; хп = ап; yt- = 0; уп= b условия ставят, как обычно. На промежуточной
опоре
d<fj
ф/ \х/ = а/ = ф/И U/+1 = о = °: 577
C8)
^/+1
МНОГОПРОЛЕТНЫЕ ПЛАСТИНЫ 213
Если опора не является жесткой в нормальном направлении, то первые два усло-
условия C8) заменяют на
Р3Ф/
+ B-v/.
ds(ff+1 I
Xuidysl + .\
C9)
где С/ — жесткость /-и опоры в нормальном направлении.
Точное решение. Точное решение возможно, если на краях у/ = 0, у/ =6 имеют
место условия свободного опирания. Тогда подстановка
D0)
сводит задачу к одномерной. Пусть Dj = D; Vy = v; р;- = р; fy = ft. После подста-
подстановки D0) в C7) получают уравнения, аналогичные F), решения которых имеют вид
Ф/т = С/mi cos ylmx, + C/m2 sin vim*/ + C/m3 ch у2тх,- + Cimi sh у2т-«/. D')
где Уют и 72m определяют согласно (8) с заменой а3 на 6. Входящие в D1) постоянные
определяют из четырех условий на краях *j = 0 и хп = ап и 4 (п — 1) условий C8)
или C9) на опорах. Равенство нулю определителя получающейся системы для C/mj
дает уравнение частот. Например, для заделанных краев хх = 0; хп = ап и условий
C8) это уравнение будет иметь вид формулы D2) на стр 214,
Замечание. Уравнение частот может быть получено при использовании метода начальных
параметров (см. гл. XI). В этом случае решение для Ф-т следует записать в форме
ф/т(*/)-ф/« ^^/яцЛЗ + Ф/тв»^/ямСЛ + Ф/т^/таС/)-*-*/™ «^mity). D3)
где функции 4f;mbi образующие фундаментальную систему Коши, имеют вид
V|m
(Ch
Применение асимптотического метода. Уравнение частот при точном решении
достаточно громоздко. Для других, пусть даже одинаковых на всех пролетах,условий
при у, = 0, у/ = b точное решение вообще найти не удается (кроме условий скользя-
скользящей заделки). Для нахождения собственных частот и собственных форм можно реко-
рекомендовать асимптотический метод. Будем считать, что при у/ = 0 и t/j = b условия
закрепления по всем пролетам одинаковы. Порождающие решения для каждого
пролета имеют вид
ф/ (*/. Уд = A, sin kx (x, — If) sin ky (у,- — г)) D4)
всех
D5)
Здесь А, — произвольные постоянные. Заметим, что kx, ky и х\ одинаковы для всех
п р олетов. Ч астота
214
СОБСТВЕННЫЕ ЧАСТОТЫ И ФОРМЫ УПРУГИХ ПЛАСТИН
<з
S
с*
р-
1
I
5
C
В
Е
S
р-
с
I
s
S
р-
е
6
РАСЧЕТ ПО УТОЧНЕННЫМ ТЕОРИЯМ 215
Решение типа динамического краевого эффекта у края х/ = о,- обозначим
Ф (х,\а/). Тогда
Фу (xj ; 0) = A, sin kx (х, -1/) + В, exp [-Xj {k% + 2ky)v'];
Фу (Xj | aj) = Af sin kx (x/-1/) + Cj exp [*y (^ + 2ky)v'];
Ф, ((// | 0) = Лу sin *„ (y, - n) + F, exp [- ,/y D + 2*J) '/•];
Ф/ fey | 6) = Л/ sin ky (у, ~ц) + Gj exp
Постоянные Лу в последних двух выражениях несущественны. Удовлетворяя
условиям C8), получим после исключения В/, С/ и А/
kx sin kx (a,- ^ + |/+I) = 2 (^ + 2/$ V. X
X sin kx (aj — Jy) sin *A|y+i (/ = 1, 2, ... , n — 1). D6)
Эти уравнения следует дополнить условиями при хх = 0 и хп = ап
**li=arcte «SI' (kx- ky)' К K-U = arcte "S^1 (*,- *й) D7)
и, кроме того, условиями стыковки решения по направлению Оу
kyb = arctg на1 (fe^., ^) + arctg «22 (йЛ, fey) + /пая. D8)
Вместо D6) можно использовать соотношение
ctgAx(a/-E/)+ctgft^/+1 = -i—г ^ . D9)
кх
Возможные потерянные корни при переходе к D9) содержатся среди корней урав-
уравнений
sin kx {ai — I,) = 0; sin kx\hl = 0. E0)
Уравнения D6) или D9) и E0) вместе с D7) и D8) образуют замкнутую систему для
определения фазовых постоянных h и волновых чисел kx и ky. Частоты определяют
затем по формуле D5) [см. [71, 87J).
5. РАСЧЕТ СОБСТВЕННЫХ ЧАСТОТ И СОБСТВЕННЫХ ФОРМ НА ОСНОВЕ
УТОЧНЕННЫХ ТЕОРИЙ
Уравнения и краевые условия. Условие применимости классической теории
в терминах волновых чисел имеет вид
(*? + *•) А«<1. E1)
При невыполнении этого условия применяют уточненные теории. Для варианта
A24) гл. VIII выделение гармонического множителя
© = <pcos(o>/ — x); 4 = tycos (wt—%); w = wcos(at—x) E2)
дает уравнения
. 6хA— V), -ч , рШ2A—V2)
12х 2pw(l + v) , „ , ._о.
^+ ^^^ 0; } E3)
., -л 2pco2(l+v)- .
Д (ф — w) —V. w — 0.
Y.E
На каждой стороне пластины должно выполняться по три условия. Для условий
опирания типа условий Навье
w- п-2- при *!_ , х,~аъ I ^
216
СОБСТВЕННЫЕ ЧАСТОТЫ И ФОРМЫ УПРУГИХ ПЛАСТИН
где б 1>2 связаны сФи? формулами A23) гл. VIII. Если пластина заделана по кром-
кромкам, то
ш = е1 = б2 = 0 при лгх == 0, ах, дг2 = 0, аг. E5)
Пластина с краевыми условиями Навье. Для краевых условий E4) переменные
разделяются при подстановке
ф = фо81П
tp = г|?0 cos
w = w0 sin
О,
sin
cos
«2
E6)
«i
sm
Уравнение частот получают после подстановки E6) в E3) и приравнивания
нулю определителя системы для ф0, i)j0, ш0:
О
—v)
-f-v)
где
Одна из частот
Две другие определяют из уравнения
1 со \* /со \ Г/. , 1— v \
- - — Н—к- у-)
где характерная частота
12х
+
A-v)]
= 0,
= 0, E7)
E8)
E9)
F0)
F1)
имеет смысл собственной частоты продольных колебаний пластины в направлении,
нормальном к срединной плоскости. При условии 0<х<^1и/Уг>0 частота, опре-
определяемая E9) (обозначим ее сог), расположена между частотами, являющимися кор-
корнями уравнения F0), так что ш1 <^ со2 <^ со3. Таким образом, у пластин при учете
сдвигов и инерции вращения нормальных элементов существуют три серии частот.
Наименьшая частота при этом
F2)
где g = ?—— — + т-у ¦ Эта частота соответствует преимущественно изгибным коле-
колебаниям и при малых kh близка к значению частоты, определяемому по классической
теории. Вообще при выполнении условия k2h? <; 1 имеют место следующие оценки:
СО "-' TV Ш(Ь С02 -^ <й3 ~^ С00.
Приближенное выражение для со3 имеет вид
ш3 «»со0 [6ч A -v)
F3)
РАСЧЕТ ПО УТОЧНЕННЫМ ТЕОРИЯМ
217
Результаты определения частот изгибных колебаний по уточненным теориям,
по классической теории и по трехмерной теории для квадратной опертой пластины
(h/a = 0,025, v = 0,3) представлены в табл. 8.
8. Результаты применения различных методов определения изгибных частот
прямоугольных пластин
Теории
Гипотезы
Кирхгофа —
Лява
Уточненные
теории:
и=з
_ 5
* 6
Трехмерная
теория
mt = 1;
0,0642
0,0639
0,0640
0,0640
"т — 2
0,160
0,159
0,159
0,159
"т — У
0,321
0,316
0,317
0,317
@0
т, = 2;
0,257
0,254
0,254
0,254
т, = 2;
0,417
0,409
0,411
0,411
0,577
0,564
0,566
0,566
т, = 7;
3,14
2,80
2,84
2,86
т1 = 10;
6,40
5,21
5,36
5,39
Применение асимптотического метода. Метод применяют при условии, что дина
мические краевые эффекты не вырождаются. Порождающее решение имеет вид
ф = Фо sin kx (xt — ?j) sin k2 (x.2 — ?2);
г|> = -ф0 cos k, (хг — %{) cos fe2 (x2 —12); F4)
w = w0 sin kx fa — li) sin ?2 (x2 — ^2
Подстановка F4) в E3) приводит к уравнению частот, совпадающему с E7). Решение,
соответствующее динамическому краевому эффекту для края Xi = 0, можно записать
следующим образом:
K<i — \%)\ {?} == w \Х\) Sin «2 (*^2 — S2)" ( )
Функции Ф, У и # находят из системы уравнений
=0;
F6)
Характеристическое уравнение
о 6И {I — V) р@г A — У»<
6и A - v)
> _ k»
имеет корни
=o
F7)
F8)
218 СОБСТВЕННЫЕ ЧАСТОТЫ И ФОРМЫ УПРУГИХ ОБОЛОЧЕК
При этом для первой серии частот щ
F9)
для второй серии частот со2
1
2м, \ 2,
и для третьей серии
Из формул G0) и G1) видно, что динамический краевой эффект для второй и третьей
серий частот оказывается вырожденным. Для первой серии краевой эффект вырож-
вырождается при kx > k0, где k0 ~ — . Таким образом, при учете деформаций сдвига и инер-
инерции вращения нормальных элементов динамический краевой эффект для преимуще-
преимущественно изгибных колебаний вырождается при больших волновых числах (сильное
влияние условий на контуре на поведение во внутренней области). Область приме-
применения асимптотического метода фактически совпадает с областью, где уточненная тео-
теория дает достоверные результаты.
Глава XIII
СОБСТВЕННЫЕ ЧАСТОТЫ И СОБСТВЕННЫЕ ФОРМЫ
УПРУГИХ ОБОЛОЧЕК
1. КЛАССИФИКАЦИЯ СОБСТВЕННЫХ ФОРМ КОЛЕБАНИЙ
Дифференциальные уравнения и граничные условия. Различные варианты урав-
уравнений динамики оболочек приведены в гл. VIII. Для свободных колебаний (<jy = 0)
уравнения движения оболочек в перемещениях после выделения гармонического
временного множителя могут быть записаны в форме
A)
(индекс * означает амплитудное значение величины). На краях оболочки, которые для
простоты будем считать совпадающими с координатными линиями, должно выпол-
выполняться по четыре условия (см. табл. 7 гл. VIII). Вид операторов L^ в A) зависит от
введенных предположений, его можно легко определить на основе общих уравнений
(см. гл. VIII).
КРУГОВЫЕ ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ 219
Классификация собственных форм. Уравнения A) есть реализация операторного
уравнения (С — <о2А) <р = 0 для оболочек. Собственные формы колебаний опреде-
определяет вектор-функция
Ф=( »?(*!. *2>|. B)
Каждой собственной форме колебаний ц>, соответствует определенная частота со,.
Собственные формы колебаний обладают свойством ортогональности по потенциаль-
потенциальной и по кинетической энергии. Например, условие ортогональности по кинетической
энергии
$ \ Ch (y*iy!i + v%vk2 + wfwl) dQ==0 (/ Ф k)- C)
Q
В некоторых случаях собственные формы колебаний, соответствующие различным
собственным частотам, отличаются друг от друга только числовыми коэффициентами,
характеризующими отношения между максимальными значениями перемещений
vlt v-2 и w при колебаниях.
Среди различных собственных форм колебаний можно выделить серии преимуще-
преимущественно нормальных и преимущественно тангенциальных форм колебаний. Частоты
для указанных серий имеют порядок
h IE VI, 1 IE \Ч,
Здесь и далее введены характерные величины для толщины k, радиуса кривизны R,
размера области L, масштаба изменения напряженно-деформированного состояния К.
Поскольку отношение шп/(о( ~ h/k <; 1, то низшим частотам соответствуют преимуще-
преимущественно нормальные формы колебаний. Данные соотношения выполняются при усло-
условиях
'1 < I < R.
Замечание 1. При использовании уточненных теорий, когда дополнительно вводятся функ-
функции, характеризующие поперечные сдвиги, размерность вектор-функции формы колебаний уве-
увеличивается; кроме преимущественно нормальных и тангенциальных форм колебаний появляются
преимущественно сдвиговые формы колебаний. Частоты таких форм колебаний обычно выше,
чем частоты форм колебаний первых двух типов.
Замечание 2. Для оболочек характерным является то, что не всегда низшей собственной
частоте соответствует самая простая собственная форма колебаний.
2. КРУГОВЫЕ ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ
Дифференциальные уравнения. Пусть одна из координат, к которым отнесена
оболочка, отсчитывается вдоль образующей, а вторая —¦ в окружном направлении,
тогда параметры Ламе равны Н1 = Н2 = 1, a kt = 0; кг = MR. Входящие в A)
дифференциальные операторы имеют вид
__ д / w I ' " _^_ \. д __ _ Eh 1
дх\ ' 2 дх\ }' 1—
п
L3, = DAA + 4; L19=L21 = ,4-^ . д\ ¦ LJ3 = L31=^ ~
33 ~ /?2 ' '" 21 2 дх1 дх2 ' J3 31 R dXi
__ __ = _ E№
R "" "¦""¦""
D)
220
СОБСТВЕННЫЕ ЧАСТОТЫ И ФОРМЫ УПРУГИХ ОБОЛОЧЕК
Уравнения технической теории получаются, если в операторах, кроме Lss. опус-
опустить члены, содержащие цилиндрическую жесткость D:
E)
3 = LSx — -^- — • L 23 = ?32 = "ft
А д
Если пренебречь тангенциальными силами инерции и использовать техническую
теорию, то после введения функции усилий % уравнения принимают вид
1
D ДДш* + о-
р/гсо2а>* = 0;
F)
При применении этой системы тангенциальные краевые условия должны быть вы-
выражены через функцию усилий %• Например, условия свободного опирания, анало-
аналогичные условиям Навье (условия Власова), можно записать следующим образом
(xi = const):
d* ? *
дх\
—
дх\
Краевые условия Навье. Условиям свободного опирания при хх = 0 и Х\ = I
удовлетворяют функции
v* = Vi cos
cos
А
(8)
Параметр т1 равен числу полуволн формы колебаний в продольном направлении,
а т2 — числу волн в окружном направлении. Число узловых линий формы колебаний,
параллельных образующей, равно 2т2, а в окружном направлении т1 — 1 (не счи-
считая опорных линий). Случай т2 = 0 соответствует осесимметричным формам коле-
колебаний цилиндрической оболочки, а т2 = 1 — балочной форме колебаний.
Подстановка (8) в A) при учете D) приводит к системе линейных однородных урав-
уравнений для Vi, V2 и W, из условия существования ненулевого решения которой следует
где
1—v
det (С — р/гсо2Е) = О,
1 —v
(9)
D
vA
Dkl
Уравнение (9) является кубическим относительно квадрата частоты со2. Паре чисел
т1 и т2 соответствуют три значения частоты, каждому из которых отвечает своя фор-
форма колебаний, характеризующаяся отношением V1:V2: W. Это отношение получает-
получается как ненулевое решение системы для Vi, V2, W при равенстве со одной из найденных
КРУГОВЫЕ ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ
221
частот. Итак, имеются три серии частот, отвечаюдих преимущественно нормальным
формам колебаний, преимущественно крутильным и преимущественно продольным
формам колебаний. При осесимметричных колебаниях крутильные колебания не свя-
связаны с продольно-поперечными колебаниями. Полное разделение форм колебаний
возможно в осесимметричном случае при v = 0.
Для случая преимущественно нормальных форм колебаний могуг быть использо-
использованы уравнения F). Решение в форме
w* = W sm ¦ cos -—
* v . т<пх<
у* = X sin l. x cos
I
приводит к следующей формуле для частоты:
A0)
где
Eh \V.
DRi '
(И)
A2)
0,2
Формула A1) позволяет исследовать влияние волновых чисел ki и k2 на величины
собственных частот преимущественно нормальных форм колебаний. Минимум по 6,
достигается при ki = —г- (щ = 1). так что наи-
наименьшей частоте соответствует форма с одной
полуволной в продольном направлении (без-
(безузловая форма в продольном направлении); ми-
минимум по k2 имеет место вблизи А2 ?~ 'Ь-ЪлЧ*
или с учетом обозначений A2) вблизи
ТD
Следовательно, чем меньше отношение дли-
длины оболочки к радиусу и отношение h/R, тем
больше т2. На рис. 1 приведены зависимости
Lp (i -"vJJ
нормальной формы колебаний опертой по тор-
торцам круговой цилиндрической оболочки от вол-
волнового числа для разных чисел волн в окруж-
окружном направлении п при R/h = 100. Минималь-
Минимальной частоте оболочки может соответствовать
число т2 от 2 до 6 (и более).
Произвольные краевые условия. Задача о собственных колебаниях круговой ци-
цилиндрической оболочки постоянной толщины допускает точное решение при любых
краевых условиях (однородных в окружном направлении). Подстановка
A3)
безразмерной частоты ffi
0
Рис. I. Зависимость безразмерной
частоты нормальной формы .колеба-
.колебаний опертой цилиндрической обо
лочки от волнового числа Для раз-
разных чисел волн в окружном направ
лен и и
222 СОБСТВЕННЫЕ ЧАСТОТЫ И ФОРМЫ УПРУГИХ ОБОЛОЧЕК
приводит задачу к одномерной для системы с постоянными коэффициентами
А {v" ~
A
VI -
(W]V-2klW"
+4
tt w) -phuW = 0
A4)
(уравнения выписаны для технической теории при k2 = tnJR). Разделение происхо-
происходит и в краевых условиях. Так, в случае заделки условия имеют вид
Общее решение A4) можно записать следующим образом:
2
1= 1
A6)
где Г/ — корни характеристического уравнения, соответствующего системе A4):
0, A7)
a akJ — постоянные являющиеся ненулевым решением системы, получаемой из A4)
при г = Г]. Удовлетворение краевых условий приводит к однородной системе алгеб-
алгебраических уравнений относительно Cj, равенство нулю определителя которой дает
уравнение частот. Процесс нахождения собственной частоты состоит в последователь-
последовательном подборе значения со, удовлетворяющего уравнению частот с предварительным
нахождением для каждого фиксированного со корней уравнения A7), определением
коэффициентов ak/ и вычислением левой части уравнения частот, являющейся опре-
0,10
щ
o,os
0,0i
0,02
А
X
--J
Ж
//
J
f
10
Рис. 2. Зависимость низшей часто-
частоты цилиндрической оболочки от
числа волн в окружном направле-
направлении для различных сочетаний крае-
краевых условий:
/ — свободный край — свободный
край; 2 — заделка — заделка: 3 —
опирание — заделка; 4 — опирание —
опирание; 5 — заделка — свободный
край; 6 — опирание—свободный край
СФЕРИЧЕСКИЕ ОБОЛОЧКИ
223
Рис. 3. Зависимость низших частот Q
для защемленной цилиндрической обо- gt
лочки от 1/R '
делителем восьмого порядка. При
этом часть корней и коэффициентов
akj оказываются комплексными; это
необходимо учитывать при проведе-
проведении вычислений. В [87] можно найти
обширные числовые данные определе- o,i -
ния частот при различных соотноше-
соотношениях Ri'h и R/1. В качестве примера
приведем зависимость низшей час-
частоты для различных видов краевых
условий от числа волн в окружном
направлении (рис. 2) и зависимости
безразмерных значений низшей
о Г Е "-'/г
частоты со = сок — ^- от
IIR при различных R/h (рис. 3).
Полуэмпирические формулы. Раз-
Различными авторами были предло-
предложены полуэмпирические прибли-
приближенные формулы для вычисления
собственных частот преимущест-
преимущественно изгибных колебаний круго- "'""'0,2 I
вых цилиндрических оболочек с заделанными торцами,
ведем формулу
VN
500
ч
ч
13
N
и
N
V
\
\
=500
ч
N
ч
\
\
в
\
\
*/*
ч
в
ч
=100
\J°
\
\
ч
где
¦г
В качестве
phj •
20 100
примера при-
A8)
щ = k0R\
100 ^ R/h:
200-с R/h:
100 si R/h:
; 200);
I 500);
:800)
3. СФЕРИЧЕСКИЕ ОБОЛОЧКИ
Дифференциальные уравнения. Пусть оболочка отнесена к географической системе
координат хх = а, х2 = {5 (а — угол широты, Р — угол долготы). Параметры Ламе
#! = R; #2 = R sin a, a параметры кривизны ki — k2 = l/R. Наиболее удачным
вариантом являются уравнения Власова
A9)
где функции 8и? связаны с перемещениями формулами
1 Г д
' 2 sin a
B0)
224 СОБСТВЕННЫЕ ЧАСТОТЫ И ФОРМЫ УПРУГИХ ОБОЛОЧЕК
и, кроме того, использованы обозначения
да
№ /?2 A — v2)
• а2 — к '
а -
Eh • (Z/i>
Замечание. Хотя из уравнения A9) выделилось уравнение для V, такого разделения
в граничных условиях в общем случае не происходит.
Первые два уравнения A9) при пренебрежении тангенциальными силами инерции
могут быть после исключения 0 сведены к уравнению
=Г^ (Д + 1 )^ + 1J (Л + 2) ^ + рЛ (А + 1 — V) ^ =
ич которого после упрощения можно получить уравнение
D
О,
д2
^ ^^Aw^O B3)
для колебаний с большой изменяемосгью напряженно-деформированного состоя-
состояния по поверхности оболочки. Эго уравнение получается так же как результат
исключения функции усилий % из уравнений {хг = Ra; x2 = Rf>)
=ДХ
АДХ
B4)
Собственные колебания замкнутой сферической оболочки. Краевые условия в дан-
данном случае не ставят. Выделение временного множителя в A9) приводит к сле-
следующей системе уравнений:
(Д + 1 — v) в* — (у2Д + 1 — v) (Д + 2) w* + а2р/гсо2 (в* -2w*) = 0; ^
— 1— vN*— Т2(Д + 1 — v) (Д + 2)ш*+ауш2^* 0 / ( '
и уравнению
ДЧ'* + ХЧГ* = О, B6)
где
Собственными функциями уравнения B6) являются поверхностные сферические
функции
V* (а, р) = К<-У > (а, р) = pW (cos а)™8 ^, B7)
где Р(",' (х) — присоединенные полиномы Лежандра. Собственные значения \т =
= т (т + 1), а собственные частоты
[ ~ 2]'/2(|-I\ B8)
где т принимает целые значения, начиная с m = 2. Каждой частоте соответствует
2/п + 1 форм собственных колебаний. Например, для т = 2 виды узловых линий
форм собственных колебаний показаны на рис. 4.
Для системы B5) решение имеет вид
w*=CiYm '"(«. Р), О* =?./<„' п) («, Р) (/»!=><>. 1, 2, ...; ;,=.0, 1, 2, ... , т).
B9)
СФЕРИЧЕСКИЕ ОБОЛОЧКИ 225
Входящие в B9) функции с учетом выражения для кт удовлетворяют уравнениям
Из требования равенства нулю определителя системы для Сх и С2 получаем урав-
уравнение частот
аи — (о26ц а12 — со2
= 0.
C0)
Здесь использованы обозначения
а12 =
[m (m +l)-2];
В результате решения уравнения C0) получают значения частоты, каждому из
которых соответствует семейство собственных форм колебаний. Среди возможных
т=2,п = 0 т=2, п=1 т=2,п=2
Рис. 4. Формы колебаний сферической оболочки
собственных форм можно выделить чисто радиальные при т = 0, у2
дящие с частотой
2?
p(l-v)
¦ 0, происхо-
C1)
При больших т можно выделить две серии собственных форм колебаний: преиму-
преимущественно нормальных и преимущественно тангенциальных. Для преимущественно
изгибных (нормальных) форм колебаний, происходящих с более низкими частотами,
можно получить приближенное выражение, если воспользоваться уравнением B3)
C2)
Замечание. Для форм колебаний B9) справедливы те же выводы, что и для B7), т. е.
каждой собственной частоте соответствует 2т -f- 1 форм собственных колебаний.
Колебания пологих сферических сегментов. Исходными являются уравнения для
пологих оболочек. При граничных условиях, не зависящих от полярного угла, реше-
решение можно представить в виде
к> = ф (г) cos \п (9 — 60)] cos (со^ — г|);
3!;=i|) (г) cos [п F — 90)] cos (otf — т)).
Уравнения B4) после исключения ф приводятся к виду
где
C3)
D
Ek
8 ч/Р- Болотина В. В., г. 1
226 СОБСТВЕННЫЕ ЧАСТОТЫ И ФОРМЫ УПРУГИХ ОБОЛОЧЕК
Применение метода факторизации (см. гл. IX) приводит к общему решению C3)
вида
Тогда
г-т-2)
**[*
4(л—1
C5)
Если сферический сегмент полный, то из условия ограниченности решения при
г = О следует, что С2 — Сь = Св = С8 — 0. Остальные четыре постоянные находят
из условий на краю г = г0. Условие существования ненулевого решения для по-
постоянных дает уравнение частот.
Пример. Пусть на краю реализуется скользящая заделка (осесимметричные колебания)
dw n dw dib
w — -^— = jV,, —и или ф = ~~ — — = 0 при г = Гц.
Уравнение частот имеет вид
где
Тогда частоты
. = 7fl' + (*?-)] Ы <"='.2,...).
C7)
Здесь кт —корень уравнения C6).
4. КОНИЧЕСКИЕ ОБОЛОЧКИ
Дифференциальные уравнения. Пусть коническая оболочка отнесена к ортого-
ортогональной системе координат х и ф, где х отсчитывают от вершины конуса вдоль обра-
образующей, а ф — в окружном направлении. Тогда параметры Ламе Ях = 1; Н2 —
= xsina (о —угол полураствора конуса), кроме того, kx = 0, k%= (xtgaf1.
Уравнения колебаний имеют вид
1 д ... . , 1 dNri 1 ,, , .&V!
х дхv ' х sin а дф л: 21 л: tg a
sin а дф * х tg а
х sin а
а усилия и моменты связаны с деформациями и изменениями кривизн выражениями
A34) гл. VIII. В свою очередь, деформации и изменения кривизн выражаются через
перемещения:
d 1 d
12 2 L x sin a дф ' дх \
d2a> 1 3 /dai \ 1 to _n
xu = ^-v; x22 =¦ . 5-3 u2 cos a M -т—: C8)
дх2 ' л:3 sni2a^ \Cф / ' л: дл: ' v '
л:3
1 / d-
х sin а \с<л" Уф х dip дх j
КОНИЧЕСКИЕ ОБОЛОЧКИ
Для изучения форм колебаний с большим показателем изменяемости в окружном
направлении могут быть использованы следующие уравнения:
D Alw*
x tg a dx2
x tg a
=0;
\ dx2 x dx ^ x- sin2 a дф2
(индекс * означазт ампитуднээ знаиниз взтлчиня).
Функция усилий в C9) введена по формулам
C9)
—_ -А д. __ .Л. Л' = ¦
1 sin2 а Лр2 дг дх' с
л: sin a \дх д(р х Эф/ '
Исследование собственных колебаний конических оболочек на основе уравнений
с большим показателем изменяемости. Применение общих уравнений затруднительно
из-за их громоздкости и переменности коэффициентов. Известны решения для кони-
конических оболочек на основе общих уравнений, полученные методом Бубнова—Галер-
кина [87]. Для исследования преимущественно изгибных форм колебаний могут быть
использованы уравнения C9) с применением метода Бубнова—Галеркина. Функции
прогиба w и усилий % в случае опертой по контуру оболочки можно аппроксимировать
при помощи рядов
О)* = COS Пф
1
Пт= I
I sin ут ¦
— Ч)
X* = cosmp 2^ smsinvm(—т-1). Vm~
D0)
Здесь xt — расстояние до торца меньшего радиуса от вершины конуса; / — длина
образующей.
Замечание 1. Функции D0) удовлетворяют только кинематическим граничным условиям
Замечание 2. Учет тангенциальных сил инерции приводит к появлению двух серий частот
преимущественно тангенциальных колебаний и дает снижение частоты, соответствующей пре-
преимущественно изгибным колебаниям (до 15 — 20%) Большее влияние оказывает учет инерцион
ных членов в окружном направлении
Применение энергетического метода. Выражения для потенциальной энергии
деформации и кинетической энергии в случае конических оболочек имеют вид
2л Xi+l 1
D1)
-f- D 1(кп -f x22J — 2 A — v) (xux2? — xf2)]} x sin a dx;
2л *t -b '
-47 ) \x sin a dx,
где е,-? и К/// определяют по формулам C8).
8*
228
СОБСТВЕННЫЕ ЧАСТОТЫ И ФОРМЫ УПРУГИХ ОБОЛОЧЕК
Для опертой по торцам оболочки с краевыми условиями w = v2 = Nn = Мп ¦¦
= 0 перемещения могут быть аппроксимированы выражениями
/4j (t) (x sin aJ cos
гпя (х
—
cos rup;
z= Az (t) (x sin aJ sin -- - sin ncp;
¦¦ A3 (t) (x sin aJ sin
I
тя (х —;
/
cos rup.
D2)
Рассматривая A/ (t) как обобщенные координаты и составляя уравнения Лагранжа
второго рода, получим по стандартной схеме feo(°6 + *1ш4 + Ь2<а2 + Ь3 = 0.
Коэффициенты bk имеют довольно сложный вид и здесь не приводятся (см. [87]).
Некоторые результаты для наименьшей бе,размерной частоты шф = а
для различных а и hlRa (Ro= I sin а) даны в табл. 1.
1. Наименьшая частота колебаний конической оболочки
и-
Ь
10
15
30
45
h/Ro
0,001
0,0448 F)
0,0656 G)
0,0814 (8)
0,119 (9)
0.147 A0)
0,005
0,0967 C)
0,138 D)
0,169 E)
0,244 F)
0,299 F>
0,010
0.141 B)
0,193 C)
0,236 D)
0.337 E)
0,408 E)
0,030
0,419 B)
0,562 C)
0,693 C)
60
75
80
85
h/Ro
0,001
0,172 (9)
0,207 G)
0,229 F)
0,283 C)
0,005
0,350 F)
0,400 D)
0,432 D)
0,488 C)
0,010
0,479 E)
0,548 D)
0,553 C)
0,643 B)
0,030
0.776 C)
0,877 C)
0,891 B)
0,963 B)
Примечание. В скобках указано число волн в окружном направлении
5. ПОЛОГИЕ КРИВОЛИНЕЙНЫЕ ПАНЕЛИ
Дифференциальные уравнения. Для пологих оболочек, т. е. оболочек, у которых
стрела подъема не превышает V5 характерного размера, можно принять допущение,
что метрика срединной поверхности совпадает с евклидовой. Использование гипотез
для пологих оболочек (см. гл. VIII) приводит к уравнениям для форм колебаний
х2
дх-
+ х,
= 0;
D3)
д2 , &
где Д = -г-^- + ^~j- • Xj и и2—кривизны срединном поверхности, которые для пологих
оболочек можно приближенно считать постоянными. На каждом контуре должны
быть сформулированы четыре условия.
Краевые условия Навье. Эти условия будут удовлетворены, если
-W,
--Х„
. тпх, .
sin sin
ППХц
D4)
Требование существования ненулевого решения для Wmn и Хтп приводит к уравне-
уравнению частот, решение которого можно записать в виде)
D5)
ПРИМЕНЕНИЕ АСИМПТОТИЧЕСКОГО МЕТОДА 229
где ki = тл/ai, k2 = nnla2. Если щ = х2 = 0, то приходим к формуле частот для
пластины D) гл. XII. Если щ— 0 (или х2 = 0), получаем формулу для определе-
определения частот цилиндрической панели. При хх= х2= V/? получаем формулу для сфе-
сферической панели.
Другие виды краевых условий. В том случае, если на двух противоположных кром-
кромках заданы условия типа свободного опирания (пусть это кромки х2 = const), то под-
подстановка
D6)
в D3) сводит задачу к одномерной:
D «v -2фГ +k\
Эта задача может быть решена по схеме, описанной в п. 2 данной главы. Для других
случаев краевых условий необходимо использовать приближенные или численные
методы. При решении задачи методом Релея, Ритца, Бубнова—Галеркина и др.
в качестве аппроксимирующих могут быть использованы балочные функции (см.
гл. X).
6. ПРИМЕНЕНИЕ АСИМПТОТИЧЕСКОГО МЕТОДА К РАСЧЕТУ
СОБСТВЕННЫХ ЧАСТОТ И СОБСТВЕННЫХ ФОРМ КОЛЕБАНИЙ
Построение решений типа краевого эффекта. Пусть оболочка является пологой
и занимает прямоугольную (в обобщенном смысле) область, ограниченную линиями
Xi = const и х2 = const. Исходными являются уравнения D3). Порождающее решение,
справедливое во внутренней области, будет следующим [10]:
w = т=гг ,, —=V- sin k, (x, — S.) sm л, (*2 — ?2); I
Eh ХъЩ + щЩ > D8)
X* = sin kt (x-i — \\) sin k2 (x2 —12), I
где ^ и k2 — волновые числа; %х и ?2 — фазовые постоянные. Частота со связана с вол-
волновыми числами соотношением D5).
Решение вблизи края Х\ = 0 имеет вид
X (i) sin ftj (*.-&«). I
Функции WbX удовлетворяют уравнениям D7). Характеристическое уравнение имеет
корни г = ± iki, соответствующие порождающему решению. Остальные корни на-
находят из уравнения
XI z-t+2zt-^-^—"' ' ~a2A—^-1 = 0, E0)
где безразмерные параметры
__L. —h. —Ь.. ь —(—h ^V*
(xi и щ предполагаются конечными и хх Ф 0).
230
СОБСТВЕННЫЕ ЧАСТОТЫ И ФОРМЫ УПРУГИХ ОБОЛОЧЕК
Замечание. Если исследуется краевой эффект вблизи неасимптотического края у оболочки
нулевой гауссовой кривизны (xt = 0) (под гауссовой кривизной понимают произведение глав-
главных кривизн и,х2), то уравнение E0) непригодно, так как и -» со. В этом случае вместо E1)
вводят обозначения
, _ I Eh W4
E2)
и уравнение E0) примет вид
E3)
Динамический краевой эффект будет невырожденным, если уравнение E0) отно-
относительно s2 имеет только действительные положительные или комплексные корни
(не имеет отрицательных дейст-
действительных или нулевых корней).
Достаточное условие невырож-
невырождения динамического краевого
эффекта можно записать в виде
г! A-
E4)
Если х 5- 1, то это условие вы-
выполняется при всех гх и z2. Сле-
Следовательно, у края х1 = const
при х2 ~--j: X] динамический крае-
краевой эффект всегда существует.
В оболочках нулевой гауссовой
кривизны (XjX2 = 0) динамичес-
динамический краевой эффект всегда не-
невырожден вблизи неасимптоти-
неасимптотического (кругового) края. При
х <^ 1 краевой эффект вырож-
вырождается при малых волновых чис-
числах гх и г2. Границы областей
Рис. 5. Области вырождения динамического краевого
эффекта в оболочках
вырождения определяются не-
неравенством E4). На рис. 5 гус-
густой штриховкой показаны обла
сти вырождения динамического краевого эффекта в зависимости от изменения
параметра х [87].
Типы динамических краевых эффектов. Если динамический краевой эффект не вы-
вырождается, то возможны следующие случаи:
все корни уравнения E0) действительные положительные; тогда решение вблизи
края хх = 0 имеет вид
X
E5)
ПРИМЕНЕНИЕ АСИМПТОТИЧЕСКОГО МЕТОДА
231
один корень действительный положительный и два комплексных, тогда решение
будет иметь вид
W (*,) = -
V DEh
X cos SihXi + (C,ar —
ач) = [sin
где
sin
xi sin
sin
r+C2a;)(? ''*»*!
E6)
Замечание. Два кратных действительных положительных корня появляются только для
сферической оболочки В этом случае кратный корень s| = г| и решение у края ^ = 0 может
быть записано в виде
г
YDEh
2г2
С Г"!
(Z| + 2-2J + I 3
ХА sir
(х2
X (х,) = [sin г,А„ (дс, - Ii) +
где
E7)
] sin z2klt (xt — \,\.
Первый случай и случай, приведенный в замечании, соответствуют неосциллирую-
щему краевому эффекту, а второй случай соответствует осциллирующему динамичес-
динамическому краевому эффекту. Второй случай реализуется при выполнении условия р3 +
+ ф > 0, где
1
sin2 9 [2кA— x) + (l-xJsin2e]};
2 sin2 6 fx A — x>— A — xJ sin2 в]}.
E8)
Здесь введены полярные координаты
Замечание. Если Ki = 0 и краевой эффект не вырождается, то условие, при котором он
будет осциллирующим, можно записать в виде
г<—ту- [A + 4 sin» 9)*/»- 1 + 10sin2 9+2sin«ei
2 I*
E9|
Пример применения асимптотического метода. Дальнейшая процедура приме-
применения асимптотического метода [после построения решений типа E5), E6), E7)] будет
такой же, как описано выше, т. е. составляют уравнения стыковки типа B7) гл. XII,
из которых находят волновые числа kx и кг (или zx и z2). Частоты определяют затем
по формуле D5). В качестве примера приведем уравнения стыковки для сферической
панели. Частота в этом случае связана с волновыми числами соотношением
[I/г ¦ F0)
Решение вблизи края хг = 0 определяют согласно E7). Пусть на краю оболочки
t = 0 выполняются условия (скользящая в тангенциальном направлении заделка)
@) = W ¦ @) = А'@) = К' @) = 0.
F1)
232 СОБСТВЕННЫЕ ЧАСТОТЫ И ФОРМЫ УПРУГИХ ОБОЛОЧЕК
Удовлетворение условиям F1) приводит к выражению для тангенса фазовой по-
постоянной
«и («i, «a) = 'g «xSi = ; 1 . УЬЧ
1 2-bgl(klt ftg)
ri
где
^__. F3)
Если на всех краях оболочки выполняются условия, аналогичные F1), то уравне-
уравнения стыковки можно записать следующим образом:
"'-?,-
F4)
Здесь т.у и m2 — целые положительные числа; гг и g2 находя г по формулам F3), если
в них произвести круговую замену индексов. Система F4) может быть решена методом
последовательных приближений. Более подробные сведения о применении асимпто-
ческого метода можно найти в работах [10, 87).
7. ПЛОТНОСТЬ СОБСТВЕННЫХ ЧАСТОТ
Основные формулы. Для пологой оболочки, прямоугольной в плане, из формулы
C9) гл. IX следует [13]
Л'(ш)
= v0w3 — f f 1 - -^| (x cos2 8 + sin2 6J1 '''2 clb F5)
Здесь введены полярные координаты ki = k cos 8; k2 ~ k sin 0 и использовано обо-
обозначение x = x2/xj = Wj/coj, где характерные частоты
— J 2; ">*=*¦*{—J '. F6)
Интервал бх ^ 9 sc 82 определяется неотрицательностью подкоренного выражения
под интегралом F5). Параметр v0 совпадает с плотностью частот для пластин
Замечание. Координаты Xi и х2 можно занумеровать так, чтобы х ^ 1
Оценка для плотности частот получается дифференцированием F5) по со:
е2
2
v (со) = ve -| f [l -^ (хcos26 + sin^бK!"" '/2d8. F7)
в,
Интегралы, входящие в F7), могут быть выражены через эллиптические интегралы
или вычислены в конечном виде [13]. Для некоторых типов оболочек выражения для
асимптотической плотности распределения v (со) = v (co)/vo приведены в табл. 2.
ПЛОТНОСТЬ СОБСТВЕННЫХ ЧАСТОТ
233
а; к
з з
v л
з з
а- о;
3 3
V Л
3 3
а а
V/V/
н н
V/V/
о о
Я СЗ -j q
ЦП
234 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ УПPi Г ИХ СИСТЕМ
Точки сгущения частот собственных колебаний оболочек. Анализ результатов инте-
интегрирования F7) позволяет выявить интересные свойства плотности частот собственных
колебаний тонких упругих оболочек [13]. У зависимостей плотности частотсуществуют
полюса, где v (со) обращается в бесконечность. Эти точки соответствуют точкам сгу-
сгущения (см. гл. IX).
У оболочек положительной гауссовой кривизны (х1к2 !> 0) имеется одна точка
сгущения при со — со2. В интервале 0 < со <[ сох плотность частот равна нулю и при
(о > ша стремится к v0 — плотности частот для пластин. Для оболочек нулевой гаус-
гауссовой кривизны (хцХг = 0) характер зависимостей v (со) будет аналогичным, но сох -> 0.
Частоты собственных колебаний оболочек отрицательной гауссовой кривизны (XjX^ <^
< 0) имеют две точки сгущения при со = ш1 и со = со2; при увеличении частоты плот-
плотность собственных частот для оболочек отрицательной гауссовой кривизны стремится
к плотности частот для пластин.
Рассмотренные точки сгущения принадлежат асимптотическим оценкам распре-
распределения собственных частот. Эмпирические плотности частотбудут иметь соответствую-
соответствующие максимумы, если плотность v0 достаточно высока.
Глава XIV
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ УПРУГИХ СИСТЕМ
1. УСТАНОВИВШИЕСЯ ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
НЕДИССИПАТИВНЫХ СИСТЕМ ПОД ДЕЙСТВИЕМ
ПЕРИОДИЧЕСКИХ ВНЕШНИХ СИЛ
Вынужденные колебания упругой недиссипативной системы описываются урав
не ни ем
Cu + A^=f(/). A)
Если внешние силы изменяются со временем по гармоническому закону с часто-
частотой о) и амплитудой f0 (x), т.е. i(t) = f0 (х) cos at, то при установившихся вынужден-
вынужденных колебаниях в системе устанавливается периодический режим с той же частотой
и (х, t) = u0 (х) cos cut. B)
После подстановки B) в A) исследование сводится к неоднородной краевой задаче
для уравнения
(С —co2A)uo = f0 C)
при краевых условиях, получающихся из формулы A) в гл. X подстановкой в них B)
и сокращением на временной множитель cos со/.
Предполагается, что система имеет дискретный спектр собственных колебаний.
Если частота внешних сил со не равна ни одной из собственных частот системы coj,
то неоднородное уравнение C) имеет единственное решение
При совпадении частоты внешних сил с одной из собственных частот со = ак
уравнение C) решения не имеет. Исключение составляет случай, когда правая часть
уравнения C) ортогональна ко всем собственным элементам однородного -уравнения,
отвечающим частоте со/,:
Со, ф*а) = ° («=1. 2 т). E)
Здесь <$ка — нетривиальные решения однородного уравнения
(С-со|А)Фл = 0 F)
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ 235
(учитывается, что собственные частоты могут быть кратными). При выполнении E)
уравнение C) имеет бесчисленное множество решений, которые представляют собой
произвольную линейную комбинацию собственных элементов, соответствующих
частоте ю^.
Теория установившихся вынужденных колебаний упругих систем с вполне не-
непрерывными операторами аналогична теории вынужденных колебаний линейных
систем с конечным числом степеней свободы. Если С^А не является вполне непре-
непрерывным оператором (это имеет место, например, для неограниченных упругих си-
систем), то указанная аналогия может частично или полностью утрачиваться.
2. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ
Продольные колебания. Пусть на стержень, заделанный на одном конце и сво-
свободный на другом, действует периодически изменяющаяся во времени продольная
сила Р cos Ш на свободном конце. Использование технической теории приводит
задачу к решению уравнения
дх* Е
при краевых условиях
Ц(О) = О; EP*L
*-/
= Р cos at. (8)
Представление решения в виде B) сводит исследование к неоднородной краевой
задаче
при
{/0@) = 0; i/J(/) = -^. A0)
Замечание. Данная задача служит примером неоднородной краевой задачи, обусловленной
неоднородностью краевых условии.
Решение краевой задачи (9) при краевых условиях A0) можно записать в виде
(и)
?3
COS
Со
а общее решение исходной задачи будет следующим:
. (ОХ
sm
и(х, 0 = -
Решение A1) является реализацией D) для рассматриваемого случая, оно су-
существует для всех со, кроме
где Шд — собственные частоты колебаний, являющиеся корнями уравнения
cos—= 0. A4)
Замечание. Аналогичное решение имеет задача об установившихся вынужденных колеба
ниях консольного стержня при действии на свободном конце крутящего момента М cos (ot.
236 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ УПРУГИХ СИСТЕМ
Изгибные установившиеся колебания стержня. Пусть стержень постоянного
поперечного сечения, опертый по концам, находится под действием равномерно
распределенной нагрузки интенсивностью q0 cos со/. Уравнение колебаний и крае-
краевые условия имеют вид
+P lF = (?oCOS ' ( )
= -^- = 0 при «=±у^ ('6)
(начало координат выбрано в середине пролета). Подстановка в A5) решения типа
B) w — w0 (х) cos в t приводит к уравнению
^-*Ч = ^, A7)
где введено обозначение
Решение уравнения A7) можно представить в виде суммы общего решения соот-
соответствующего однородного уравнения, содержащего четыре постоянные, и частного
решения (q0 = const)
= C1 sin >a + C2 cos
T
Выполнение краевых условий A6) приводит к выражению
~2 ~2 I
которое является реализацией соотношения D) для рассматриваемой задачи. Как
известно, для стержня с опертыми концами собственные частоты
так что нетрудно заметить, что при ю = сод. выражение B0) не определено.
Решения, аналогичные B0), можно получить также для некоторых других видов
нагрузок и других типов граничных условий.
3. МЕТОД РАЗЛОЖЕНИЯ ПО СОБСТВЕННЫМ ФОРМАМ
Условия применения метода. Метод применим, если оператор С вполне непре
рывный, а оператор А положительно определенный. В этом случае элементы, при-
принадлежащие области определения оператора С, могут быть представлены в виде
разложения по собственным элементам оператора С~ХА, т. е. по нетривиальным
решениям уравнения F).
Применительно к амплитудам установившихся вынужденных колебаний и0 (х),
удовлетворяющих уравнению C), разложение имеет вид
со
ио(х)=2] "*<Р*(х). B2)
k=\
Здесь <pfc (x) — собственные формы колебаний; uk — коэффициенты, подлежащие
определению. Для определения коэффициентов и^ может быть использован метод
ПРИМЕНЕНИЕ ВАРИАЦИОННЫХ МЕТОДОВ 237
Бубнова—Галеркина. Подстановка B2) в уравнение C) и умножение последнего
скалярно на элементы <р7 (х) (/= 1, 2, ...) приводит к выражениям
оо оо
2 (СфА, Ф,')«а-о>2 ? (А(Р*- »/>«*=№>¦ 4V> (Z^1- 2> ••¦)• B3>
4=1 *=1
Использование условий ортогональности форм собственных колебаний
(dp*, Ф,) = 0; (Aq>ft, <р,) = 0 (/^/г) B4)
и формулы Релея (см. гл. IX) дает
Здесь через
P*=) B6)
обозначены амплитудные значения обобщенных сил. Из соотношений B5) при ш Ф
=f= шк находят коэффициенты uk. Окончательно для амплитуд установившихся вы-
вынужденных колебаний имеем
2^S- <27)
4. ПРИМЕНЕНИЕ ВАРИАЦИОННЫХ МЕТОДОВ К РАСЧЕТУ
ВЫНУЖДЕННЫХ КОЛЕБАНИЙ
Многие из приближенных методов (см. гл. X) могут быть распространены на
задачи о вынужденных колебаниях. Так, при применении вариационного метода
Бубнова—Галеркина приближенное решение уравнения C) ищется в виде ряда
п
«oW=2«*(x), B8)
4=1
где uk — некоторые коэффициенты; ^ (х), ijJ (x), ... — совокупность элементов из
области определения оператора С (например, функции, удовлетворяющие как кине-
кинематическим, так и динамическим граничным условиям). Подстановка ряда B8)
в уравнение C) и требование ортогональности результата подстановки к каждому
элементу -ф] (х), if2 (x) ,... приводят к системе п линейных алгебраических уравнений
2 (Ч*. t/)"*-«2 S (А**, *,)«* = (to. 47) (/=!. 2' •••• я). B9)
Использование ранее введенных обозначений позволяет записать уравнения B9)
в виде
п
2 (с/к - ш2а, й) и* = (fо, if/) (J = 1, 2, ... , п). C0)
*=1
Система уравнений C0) разрешима, когда частота со не совпадает ни с одним из
корней уравнения det [сд. — сЛг,/,] = 0, которое служит для определения собст-
собственных частот колебаний по методу Бубнова—Галеркина. Если базисные элементы
в B8) совпадают с формами собственных колебаний системы, т. е. ifft =<Pa. мат-
матрицы С и А становятся диагональными. Для случая, когда система ipi, i|j2, ...—пол-
...—полная, решение системы C0) переходит в точное решение B7).
238 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ УПРУГИХ СИСТЕМ
5. НЕУСТАНОВИВШИЕСЯ ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
Неустановившиеся вынужденные колебания систем без демпфирования мог^т
быть исследованы методом собственных функций, непосредственно примененным
к уравнению A). При этом кроме краевых условий должны быть сформулированы
начальные условия
u|/-o = vi(x), -дт- =v2(x). C1)
При применении метода собственных функций непосредственно к уравнению A)
решение можно записать в виде
оэ
и (х, 0=2 "*¦ @ф* (х), C2)
где, в отличие от B2), ик (/) — функции времени (обобщенные координаты). Метод
Бубнова—Галеркина приводит к уравнениям
iS 2Сф*' ^uk=(i' »/> (/='•2> ¦•¦)• (зз)
которые при использовании условия ортогональности и формулы Релея имеют вид
^Г+аа*«* = <г* (А = 1, 2. ...). C4)
где
— обобщенные силы.
Решение уравнения C4) должно удовлетворять начальным условиям при t = О
C6)
Постоянные gk и h/t определяют из соотношений
, _ (АфЬ у8)
"* (А )
Общее решение, удовлетворяющее заданным начальным условиям, записывают
с использованием интеграла Дюамеля в виде
°° ( • )
и(х, 0= У \gk cos akt + -±- sin to^ + -— \ sin wft (<—x) Qk (т) Л/фй (х). C8)
*=1 I 0 I
6. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ДИССИПАТИВНЫХ СИСТЕМАХ
Установившиеся колебания в системах с «внешним» трением. Уравнение вынуж-
вынужденных колебаний системы при наличии «внешнего» трейия (В = 2еА) имеет вид
g. + 2pA-g-=f(Q. C9)
При установившихся вынужденных колебаниях под действием нагрузки f =
= fo (x) cos u>t наличие трения в системе приводит к сдвигу фаз между нагрузкой
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ДИССИПАТИВНЫХ СИСТЕМАХ 239
f (x, t) и перемещением u (x, t). В этом случае решение для u (x, t) следует предста-
представить в виде
u = \r (x) cos Ы — v{ (x) sin со/, D0)
где \г (х) и v,- (х) •— некоторые вектор-функции координат. Если u (x, t) представ-
представляет собой скалярное поле u (x, t), то
и = у(х) cos [w/+ у(*I- D1)
Здесь v (х) — амплитуда и у (х) — начальная фаза колебаний, которые соответ-
соответственно равны
а =(?>* +г,*I/» и Y = arctg^-. D2)
Функции vr(x) и v, (х) определяют из системы уравнений^
(С - Ш2А) v,. - 28u)Av, = f0;
, = f0; \
(С — со2A) Vi + 2swAvr = 0. J ^ '
Подстановка D0) в краевые условия после приравнивания коэффициентов при
cos wt и sin (at дает условия для определения vr и v,-.
Используя метод комплексных амплитуд (см. гл. VI) при рассмотрении внеш-
внешней нагрузки в виде f = f*e!C0\ где f* — комплексная амплитуда нагрузки, и раз-
разложение типа B2) для комплексной амплитуды перемещения v (u = vemt)
v(x)= ? У*Ф*(х), D4)
получим для V), уравнения
Здесь со| — собственное значение уравнения F); Г k — амплитуды обобщенных
сил, определяемые согласно B6) с заменой f0 на f^.
После решения уравнения D5) выражение для искомого перемещения u (x, t)
записывается в виде
со
u(x, /) = Re У -/**?? У eto'. D6)
Установившиеся вынужденные колебания в вязкоупругих системах. При приме-
применении метода комплексных амплитуд (см. гл. VI) исходным является уравнение
^=f,e"»', D7)
где С — линейный вязкоупругий оператор. Подстановка u = Ve'w' приводит к урав-
уравнению
(Cr + iCi — toaA)V = f,, D8)
связывающему комплексные амплитуды V (я) и f# (x) перемещения и нагрузки. При
этом Cr + i'C,- — образ оператора С в пространстве Фурье преобразований. Если С
содержит в качестве множителя единственный вязкоупругий оператор (например,
аналог модуля упругости), то имеет место соотношение С; = Сг% (со), где % — тан-
тангенс потерь, зависящий только от частоты. Уравнение D8) преобразуется в этом
случае к виду
[<V(l)«2A]V = f*. D9)
Далее стандартными методами решают краевую задачу для уравнения D9) при
соответствующих краевых условиях. Для определения установившихся вынужден
ных колебаний используют действительную часть найденного решения.
240 ДИНАМИЧЕСКАЯ УСТОЙЧИВОСТЬ РАСПРЕДЕЛЕННЫХ СИСТЕМ
Применение метода разложения по собственным формам дает
со
F*k(fk (X)
k = 1
В E0) через со| г обозначена собственная частота системы с оператором Сг.
Неустановившиеся вынужденные колебания в диссипативных системах. Коле-
Колебания системы описываются уравнением
Cu + A^ + B J=f(O, E1)
где В — линейный диссипативный оператор. П>сть оператор В такой, что е^ =
= Е/,6^. Тогда относительно обобщенных координат имеем следующую систему урав-
уравнений:
^¦ + 2e*^- + M|«ft = QA@ (fe=l,2, ..). E2)
Здесь обобщенные силы Q/, определяют по формуле C5). Уравнения E2) рассматри-
рассматривают при начальных условиях C6), где g^ и Ад, связаны с vx (x) и v2 (x) соотношениями
C7). Общее решение задачи может быть записано в форме
со ,
u(x, 0=2]
\gk cos ч>к&{ + ^—^^- sin
1 I
< 1
. 1 (' —ek(t — x) . . ,,_ ... ,. , . . .„
0 J
где cofte = yco|-
Глава XV
ДИНАМИЧЕСКАЯ УСТОЙЧИВОСТЬ
РАСПРЕДЕЛЕННЫХ СИСТЕМ
1. СВОБОДНЫЕ КОЛЕБАНИЯ РАСПРЕДЕЛЕННЫХ
НЕКОНСЕРВАТИВНЫХ СИСТЕМ
Понятие о распределенных неконсервативных системах. В этой главе рассматри-
рассматриваются свободные колебания линейных распределенных систем, которые описы-
описываются уравнениями
ii Cu=0, A)
где А, В и С — линейные операторы, действующие на функции координат х. Точ-
Точками обозначено частное дифференцирование по t. В отличие от операторов консер-
консервативных систем операторы в уравнениях A), вообще говоря, не будут симметрич-
симметричными.
Распределенные диссипативные системы. Если неконсервативный характер си-
системы определяется только ее диссипативными свойствами, то систему называют
диссипативной. Операторы А и С при этом обладают свойствами инерционного и
квазиупругого операторов. Оператор В описывает рассеяние энергии в системе.
Некоторые конкретные реализации диссипативных операторов были рассмотрены
в гл. VIII.
УСТОЙЧИВОСТЬ РАСПРЕДЕЛЕННЫХ СИСТЕМ 241
Метод нормальных координат для распределенных неконсервативных систем.
Решение уравнения A) с заданными начальными условиями естественно искать
в виде
где ф/, (х) — собственные формы соответствующей консервативной системы. Относи-
Относительно обобщенных координат qk (t) получаем систему обыкновенных дифференциаль-
дифференциальных (в случае наследственного трения — интегро-дифференциальных) уравнений.
В общем случае эта система будет бесконечной. Для прикладных расчетов беско-
бесконечную систему заменяют конечной, что соответствует ^чету конечного числа членов
в разложении B).
Разделение обобщенных координат для диссипативных систем. Пусть диссипатив-
н ли оператор В и собственные формы <р^ (х) удовлетворяют условию (Вф,, ф^) =
= 0 (/ ф к).
Тогда обобщенные координаты в уравнениях разделяются:
Для модели внешнего трения парциальные коэффициенты диссипации е^ =
= р (k = 1, 2, ...); для модели внутреннего трения е^ = -= Т|(о|(й =1,2, ...), т. е.
парциальные коэффициенты демпфирования растут пропорционально квадратам
собственных частот. Если В — наследственный оператор, то вместо уравнений C)
получаем
Г { ~1
= 0 (k = \, 2, ...). D)
2. УСТОЙЧИВОСТЬ РАСПРЕДЕЛЕННЫХ СИСТЕМ
Постановка задачи об устойчивости равновесия распределенных систем. Дисси-
пативные системы образуют частный класс неконсервативных систем. Для этих
систем каждое (или почти каждое) движение сопровождается уменьшением полной
механической энергии. Ниже рассмотрим такие системы с не зависящими от вре-
времени параметрами, в которых возможно возрастание полной механической энергии
за счет ее притока извне. Равновесие таких систем u (x, t) = 0 при определенных
значениях параметров может стать неустойчивым. В связи с этим возникает задача
об отыскании условий устойчивости распределенных неконсервативных систем.
Строгое определение устойчивости распределенных систем строится путем соот-
соответствующего обобщения определения устойчивости по Ляпунову. При этом сущест-
существенное значение имеет выбор метрики, при помощи которой оценивается близость
двух движений распределенной системы. Так, близость скалярной функции и (к,1)
(где х е S) к решению и (х, I) = 0 может оцениваться по нормам типа
\ и |) = sup J и (х, t)'
xeS
S
i и2 (х, 0 dx
и т. д. В теории устойчивости упругих систем широко применяют нормы (метрики)
энергетического типа: так, за меру близости двух состояний системы принимается
близость их полной механической энергии.
Области устойчивости и критические параметры. Пусть операторы А, В и С в урав-
уравнении A) зависят от числовых параметров а, р, у Выделим в пространстве этих
параметров область значений, при которых решение u (x, t) = 0 уравнения A) устой-
устойчиво. Эта область называется областью устойчивости. Остальная часть пространства
принадлежит обгасти неустойчивости. Поверхность, отделяющую область устой-
устойчивости, называют критической, а соответствующие значения параметров а, р\ у,
... — критическими параметрами.
242
ДИНАМИЧЕСКАЯ УСТОЙЧИВОСТЬ РАСПРЕДЕЛЕННЫХ СИСТЕМ
Типы неустойчивости распределенных систем. В зависимости от поведения си-
системы непосредственно после выхода ее параметров из области устойчивости разли-
различают два типа неустойчивости. Если все решения u (x, i) имеют вблизи критической
поверхности монотонный характер, то говорят о потере устойчивости по типу ди-
дивергенции или о монотонной неустойчивости. Если среди решений имеются колеба-
колебательные, то говорят о потере устойчивости типа флаттера или о колебательной
неустойчивости. Поэтому критическую поверхность разбивают на части, одни из
которых соответствуют переходу от устойчивого равновесия к дивергенции, другие—
переходу от устойчивого равновесия к флаттеру.
1тХ
1т*
ReX
Рис. 1. Типы неустойчивости распределен-
распределенных систем:
а — дивергенция; б — флаттер; в — переход
от квазиустойчивости к неустойчивости
Рис. 2. Упругие системы, нагруженные не-
неконсервативными позиционными силами:
а — задача
Николаи; б — задача Реута;
в — задача Бека
Связь с поведением характеристических показателей на комплексной плоскости.
Представим решение уравнения A) в виде
и (х, /) = i|) (х) е>-<, E)
где \|) (х) — функция координат; К — характеристический показатель. Для опре-
определения г|э (х) и А, имеем обобщенную задачу о собственных значениях
(Я2А+ХВ + С)г|з = 0. F)
Все дальнейшие выводы относятся также к более общему классу задач
D (X) Ч> = 0, G)
где оператор D является достаточно произвольной функцией показателя К.
Распределенные системы, как правило, имеют бесконечное множество харак-
характеристических показателей X. При изменении параметров а, р1, у, ... показатели пере-
перемещаются по комплексной плоскости. В области устойчивости все ReX <; 0. На
той части критической поверхности, которая соответствует переходу к дивергенции,
хотя бы один из показателей X обращается в нуль (рис. 1, а). На части критической
поверхности, которая соответствует переходу к флаттеру, хотя бы пара комплексно-
сопряженных характеристических показателей попадает на мнимую ось и при
дальнейшем изменении параметров переходит на правую полуплоскость (рис. 1, б).
Примеры распределенных неконсервативных систем. Большую группу хорошо
изученных неконсервативных систем образуют упругие системы, нагруженные
неконсервативными позиционными (следящими) силами. На рис. 2, а показан кон-
консольный упругий вал, который скручивается следящим моментом М, т. е. момен-
моментом, вектор которого остается направленным по касательной к деформированной оси
вала. На рис. 2, б показан консольный стержень с жесткой траверсой, который на-
нагружен силой Р, сохраняющей фиксированную в пространстве линию действия.
Эта сила не связана с материальными точками траверсы, а скользит по ней. На
рис. 2,в изображен консольный упругий стержень, нагруженный силой, которая на-
метопы исследования устойчивости
243
правлена по касательной к деформированной оси стержня. Во всех трех случаях
внешние силы не обладают потенциалом. Чтобы реализовать эти силы, нужны элек-
электромеханические следящие устройства, струйные устройства и тому подобные си-
системы с внешним источником энергии. По именам авторов, впервые рассмотревших
эти задачи, они названы соответст-
соответственно задачами Николаи (рис. 2, а),
Реута (рис. 2,6) и Бека (рис. 2, в).
Вторую группу неконсерватив-
ных систем образуют упругие си-
системы, взаимодействующие с пото-
потоком газа или жидкости. Таковы
задачи об устойчивости крыла
(рис. 3, й) И ПЛОСКИХ ИЛИ криВОЛИ- рис- 3- Упругие системы в потоке жидкости или
нейных панелей (рис. 3, б) в потоке газа:
газа, об УСТОЙЧИВОСТИ труб И обо- а — крыло; б — упругая панель; в — оболочка, со
ЛОЧек, содержащих движущуюся держащая движущуюся жидкость
жидкость (рис. 3, в).
Теория колебаний и устойчивости упругих систем, нагруженных неконсерва-
неконсервативными силами или взаимодействующих с потоком жидкости или газа, изложена
в работе [11]. Обзор некоторых более поздних работ можно найти в [25, 129]. Обзор
задач устойчивости применительно к аэроупругим системам, а также сводка числен-
численных результатов, относящихся к различным частным случаям, имеется в [87].
3. МЕТОДЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ
Основной метод. Метод состоит в исследовании обобщенной задачи о собственных
значениях G). К сожалению, даже в простейших случаях, когда эта задача допу-
допускает решение в замкнутом виде, исследование ее характеристических показателей
и выделение областей устойчивости представляет трудную вычислительную задачу.
Действительно, результат решения записывается в виде неявной зависимости харак-
характеристических показателей X от параметров а, р, у, ...
F(k, а, р, у, ...)=0. (8)
В отличие от систем с конечным числом степеней свободы, где левая часть урав-
уравнения (8) — полином от X, уравнение (8) для распределенных систем трансцендент-
трансцендентное. Для нахождения критической поверхности обычно применяют метод, аналогич-
аналогичный методу D-разбиения (см. гл. V). Полагая % = ('со (где со пробегает значения
О ¦<; и < сю), ищут отображение мнимой оси при помощи функции F (к, а, C, у, ...)
на пространство параметров а, C, у, ... Исследование устойчивости несколько упро-
упрощается, если из предварительного анализа известны некоторые точки в пространстве
параметров, заведомо принадлежащие области устойчивости.
Для численной реализации метода целесообразно применить алгоритм, основан-
основанный на минимизации модуля от левой части уравнения (8), которая рассматривается
как функция параметров а, р\ у, ... Таким образом, алгоритм включает в себя цикл
по частоте со, формирование модуля комплексной функции F («со, а, C, у, ...) и мини-
минимизацию модуля этой функции по а, р\ у, ...
Метод нормальных координат. Решение ищу г в виде ряда B), где ф/, (х) — соб-
собственные формы соответствующей консервативной системы или, в более общем слу-
случае, некоторые функции, удовлетворяющие граничным условиям для и (х, /) и об-
обладающие в некотором смысле полнотой. Уравнения относительно обобщенных
координат ць (/) могут быть получены, например, методом Бубнова—Галеркина.
Если функция и (х, /) аппроксимируется конечным числом членов ряда, то прихо-
приходим к задаче об устойчивости некоторой неконсервативной системы с конечным чис-
числом степеней свободы. Дальнейший анализ проводят,пользуясь методами из гл. V.
Метод функционалов Ляпунова. Строгий метод для получения достаточных усло-
условий устойчивости (неустойчивости) распределенных систем дает метод функций
Ляпунова, распространенный на распределенные системы. Вместо функций Ляпунова
в классическом методе используют функционалы Ляпунова, по поведению которых
244
ДИНАМИЧЕСКАЯ УСТОЙЧИВОСТЬ РАСПРЕДЕЛЕННЫХ СИСТЕМ
вдоль фазовых траекторий системы можно судить об устойчивости (неустойчивости).
Выбор функционалов Ляпунова обусловлен выбором метрики, по отношению к ко-
которой исследуется устойчивость и которая входит в строгое определение устой-
устойчивости распределенных систем.
Упрощенный метод исследования устойчивости. Большое число опубликованных
численных результатов относится к задачам, которые приводят к уравнениям F)
при В = 0, т. е. к таким задачам об устойчивости упругих систем при действии
следящих нагрузок, где с самого начала не учитываются диссипативные силы. Урав-
Уравнение F) при подстановке X = i'w принимает вид
(С — ю2А)г|) = 0. (9)
Если все частоты со действительные, то это квалифицируется как устойчивость ре-
решения u (x, t) = 0. Критические соотношения параметров ищут из условия, что при
этих параметрах впервые появляется хотя бы одна пара кратных частот, которые
затем становятся комплексными (рис 1, в).
К полученным таким упрощенным способом результатам следует относиться
с осторожностью. Случай чисто мнимых характеристических показателей является
сомнительным по Ляпунову, если рассматривать линейные уравнения как результат
линеаризации соответствующих нелинейных задач. Даже
введение сколь угодно малого демпфирования может
существенно изменить выводы об устойчивости, полу-
полученные упрощенным методом [II, 100]. Исключение состав-
составляет случай внешнего трения. Если ввести в систему внешнее
трение, а затем устремить его к нулю, то получатся условия
устойчивости, совпадающие с теми, которые дает упрощен-
упрощенный метод. Чтобы избежать недоразумений, случай на-
нахождения всех характеристических показателей на мнимой
оси следует называть квазиустойчивостью, а значения пара-
параметров, при которых первая пара показателей покидает
мнимую ось, — квазикритическими параметрами.
Пример. Консольный стержень. Пусть консольный стержень
из вязкоупругого материала нагружен следящей силой Р и силой
веса О (рис. 4). Материал стержня — стандартный вязкоупругий,
описываемый уравнением механического состояния
Рис. 4. Консольный
стержень с неконсер-
неконсервативной нагрузкой
е + те —
о
о
')'
(Ю)
Здесь Еп— мгновенный модуль; Е,х — длительный модуль; т —время релаксации. Уравнение
малых колебаний стержня имеет вид
д
-со" у-г ' ~м J ~дхТ + V +~ЁТ~ Ж,
Оно решается при граничных условиях
-PF-хТГ- = °-
d'w
ю=„г = 0 „ = 0);
д \ д'ю I
д \ dw
Et, dt i дх
Введем безразмерные параметры
¦ = -г-; а = ¦
где
PI'
1 / ?a
OT Z» \ pF j
Производя подстановку w (x, t) = W(x) e " °° , получим обобщенную задачу о собственных
значениях
¦ W = 0;
W"=
«7=W7' = 0 E = 0);
ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ РАСПРЕДЕЛЕННЫХ СИСТЕМ
245
Уравнение (8), связывающее характеристические показатели с параметрами задачи, имеет вид
F(K, се, Р, V, Л) =
(а
sh r, sh r, - а (а + В)
A - chr, ch/-,) = О,
A2)
где
A3)
и г3 — корни уравнения
Задача сводится к отысканию условий, накладываемых на а, р, у, Л, при которых все корни
уравнения A2) находятся в левой полуплоскости. Вид
уравнений A2) и A3) дает представление о характере
трудностей при вычислениях даже в этой относительно
простой задаче.
Диаграмма устойчивости на плоскости параметров
а, р* при различных значениях Т| и при у = 0,2 пока-
показана на рис. 5. Область устойчивости оставлена не-
заштрихованной. Штриховой линией показана граница
области квазиустойчивости, которая получается, если
вместо вязкоупругого стержня взять чисто упругий
стержень. Существенно, что при учете демпфирования
значительная часть области квазиустойчивости в дей-
действительности оказывается областью колебательной
неустойчивости, причем с уменьшением л область не-
неустойчивости расширяется
4. ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ
РАСПРЕДЕЛЕННЫХ СИСТЕМ
Введение. Определение параметрических ко-
колебаний, данное в гл. VII применительно к си-
системам с конечным числом степеней свободы,
справедливо для систем с распределенными па-
параметрами. Параметрически*, колебания рас-
распределенных систем описываются дифференци-
дифференциальными и интегро-дифференциальными уравне-
уравнениями в частных производных с переменными
коэффициентами. Наиболее важный случай —
системы с параметрами, периодически меняю-
меняющимися во времени. Далее будут рассмотрены
системы, описываемые уравнениями в частных
производных с коэффициентами — периодичес-
периодическими функциями времени.
Задачи динамической устойчивости упругих
систем. -Большая часть задач параметрических
колебаний упругих систем связана с теорией
упругой устойчивости. Примером служат колебания упругого прямолинейного
стержня, нагруженного периодической во времени продольной силой (рис. 6, я).
0,5-
о
Рис. 5. Области флаттера и дивер-
дивергенции при у — 0,2 и различных
значениях п
\
\
а, 6) Ь) г) --' д)
Рис. в. Примеры упругих систем, нагруженных параметрическими силами
При такой нагрузке имеют место продольные колебания. Однако при определен-
определенных соотношениях между частотой внешней силы и собственными частотами
стержня прямолинейная форма последнего может оказаться динамически неустой-
246
ДИНАМИЧЕСКАЯ УСТОЙЧИВОСТЬ РАСПРЕДЕЛЕННЫХ СИСТЕМ
чивой: малые поперечные возмущения влекут за собой возбуждение интенсивных
поперечных колебаний.
На рис. 6 приведены и другие примеры упругих систем, нагруженных параме-
параметрическими силами: круговое кольцо, нагруженное равномерно распределенной ра-
радиальной периодической во времени нагрузкой (рис. 6, б), изгибно-крутильные
колебания упругой балки, нагруженной периодическими силами в одной из главных
плоскостей инерции (рис. 6, в), изгибные колебания пластин и оболочек, нагружен-
нагруженных периодическими силами, действующими в срединной поверхности, и т. п.
(рис. 6, г, д).
Перечисленные примеры относятся к широкому классу задач теории динамической
у;тойчивости упругих систем. Во всех этих задачах причиной параметрического воз-
возбуждения колебаний служит периодическое изменение во времени нагрузок, кото-
которые, будучи приложены статически, могут вызвать потерю устойчивости путем раз-
разветвления форм равновесия. Параметрические колебания этих систем можно интер-
интерпретировать и как результат изменения во времени их эффективной жесткости под
eft)
k"(Q
u(t)
а)
Uuft>
В)
в)
Рис. 7. Примеры распределенных систем с переменными параметрами
влиянием приложенных периодических сил. Эти силы обычно называют параме-
параметрическими (по отношению к возбуждаемым ими параметрическим колебаниям).
Другие примеры параметрических колебаний распределенных систем. Примеры
систем, в которых изменение параметров можно увидеть непосредственно из расчет-
расчетной схемы, показаны на рис. 7, а и б. В первом случае изгибные колебания стержня
возбуждаются за счет периодического изменения во времени коэффициента упру-
упругости опоры, во втором случае — за счет периодического изменения длины стержня.
В обоих случаях изменение параметров системы в процессе изгибных колебаний
требует поступления энергии от внешнего источника.
Примером параметрически возбуждаемой гидродинамической системы служит
тяжелая жидкость, находящаяся в сосуде, который совершает периодическое дви-
движение в направлении силы тяжести (рис. 7, в). При некоторых соотношениях между
частотой движения сосуда и собственными частотами колебаний жидкости относи-
относительное равновесие жидкости становится неустойчивым и возникают ее интенсив-
интенсивные колебания. Если стенки сосуда к тому же деформируются упруго, то возникает
задача о параметрических колебаниях гидроупругой системы.
Примером параметрически возбуждаемой электрической системы может слу-
служить пассивная линейная цепь с распределенными емкостью, индуктивностью и
омическим сопротивлением, один из параметров которой (например, сосредоточен-
сосредоточенная емкость) периодически изменяется во времени.
5. УРАВНЕНИЯ ДИНАМИЧЕСКОЙ УСТОЙЧИВОСТИ
Динамическая устойчивость сжатого стержня. Пренебрегая продольными коле-
колебаниями от действия силы N (t), запишем уравнение, которое в линейном прибли-
приближении описывает изгибные колебания стержня
EJ
= 0.
A4)
УРАВНЕНИЯ ДИНАМИЧЕСКОЙ УСТОЙЧИВОСТИ
247
Здесь и в дальнейшем при обсуждении частных задач используются обозначения,
принятые в предыдущих главах. Сила N (/) считается положительной при сжатии.
Уравнение A4) отличается от аналогичного уравнения (84) гл. VIII тем, что сила
N (t) является функцией времени. Граничные условия для функции поперечного
прогиба w (х, t) берутся в соответствии с данными таблиц гл. VIII. В простейшем
случае (при шарнирном опирании концов стержня) имеем условия
=o x=i)-
A5)
Задача состоит в нахождении условий, связывающих параметры стержня и внешней
силы, при которых решение w = 0 поставленной задачи устойчиво.
Параметрические колебания упругого стержня как неустойчивость режима уста-
установившихся вынужденных продольных колебаний. Пусть и (х, t) — продольное
перемещение точек оси стержня, EF — жесткость сечения при растяжении (сжатии).
С учетом наиболее существенных нелинейных членов уравнения совместных продоль-
продольных и поперечных колебаний имеют вид
r,,,dev , „ д2и „
JLU)
дх , дх ]
A6)
где гх = 5—гс(а~] —продольная деформация оси стержня. Решение уравнений
A6) должно удовлетворять граничным условиям
J=^=°: -efb^n® (x = i
A7)
В случае установившихся продольных колебаний под действием силы N {() =
No + N( cos (at получаем
Nax Nt sin vx
U^U°-~~E~F~ vEF cos vl
cos at;
A8)
где
A9)
Для исследования устойчивости решения A8) положим в уравнениях A7) и =
= и0 + п, w = w0 + w и линеаризируем уравнения относительно малых возмуще-
возмущений п и w'.
дх*
дР
р . д*&) Рр д (ди0 дю\
дх1 дх \ дх дх j
B0)
Второе уравнение обобщает уравнение A4) на случай, когда при исследовании
устойчивости учитывают перемещения невозмущенного движения. Это уравнение
можно также представить в виде
д
B1)
где N (х, t) — продольная сила в стержне, найденная с учетом невозмущенного
движения. Если частота возбуждения w <; соо (где ш0 — наименьшая собственная
248 ДИНАМИЧЕСКАЯ УСТОЙЧИВОСТЬ РАСПРЕДЕЛЕННЫХ СИСТЕМ
частота продольных колебаний), то силу N (х, t) можно заменить ее квазистатиче-
квазистатическим приближением. В результате возвращаемся к уравнению A4).
Общие уравнения динамической устойчивости упругих систем. Пусть соотноше-
соотношение между частотами возбуждения и наименьшей собственной частотой в невозму-
невозмущенном движении таково, что при нахождении невозмущенного напряженно-деформи-
напряженно-деформированного состояния допустимо использовать квазистатическое приближение и
пренебречь перемещениями в этом состоянии. Тогда уравнения динамической устой-
устойчивости каждой конкретной упругой системы могут быть получены из уравнений
нейтрального равновесия для задачи статической устойчивости добавлением далам-
беровых сил инерции и заменой усилий (напряжений) невозмущенного состояния
соответствующими функциями времени. Если необходимо учитывать диссипацию,
то в уравнения добавляют также диссипативные силы.
Иначе уравнения динамической устойчивости получают из уравнений свободных
колебаний упругой системы при отсутствии внешних сил путем добавления параме-
параметрических членов, учитывающих параметрические силы, зависящие от времени. Эти
члены могут быть взяты из уравнений нейтрального равновесия для соответствую-
соответствующей задачи статической устойчивости.
Пусть операторное уравнение свободных колебаний имеет вид
Aii + Си = 0, B2)
а уравнение нейтрального равновесия при действии статически приложенных пара-
параметрических сил
Cu + Gu = 0. B3)
Здесь А и С — инерционный и квазиупругий операторы, введенные в гл. IX; G —
линейный оператор, учитывающий параметрические силы в уравнениях нейтраль-
нейтрального равновесия. Операторное уравнение динамической устойчивости получают пу-
путем объединения уравнений B2) и B3) и замены параметров нагрузки в операторе G
заданными функциями времени:
Aii + Cu + G@u —0. B4)
Область определения решений u (x, f) уравнения B4) обычно совпадает с областью
определения оператора С, общего для уравнений B2) — B4).
Если параметрические силы заданы с точностью до двух множителей, один из
которых а характеризует постоянную составляющую нагрузки, а второй E — со-
составляющую, изменяющуюся во времени по закону Ф (/), то уравнение B4) можно
записать так:
Aii + [C-f «F + p<D@G]u = 0. B5)
Здесь учтено то, что операторы для постоянной и переменной составляющих нагруз-
нагрузки различны.
6. МЕТОДЫ СВЕДЕНИЯ К СИСТЕМАМ ОБЫКНОВЕННЫХ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Общая схема сведения. Поскольку непосредственный анализ устойчивости по
уравнениям в частных производных затруднителен, то в прикладных расчетах их
обычно сводят к системам обыкновенных дифференциальных уравнений. Для этого
функции u (x, t) разлагают по некоторому базису с коэффициентами — функциями
времени.
Полагая в уравнении B5)
и (х, 0 = S ?* @ ** (х), B6)
4 = 1
где ij!i (х), л|?-2 (х), ...,ij)n (х)—достаточно представительная система вектор-функ-
вектор-функций, удовлетворяющих всем граничным условиям для u (x, t), и применяя вариа-
вариационный метод Бубнова—Галеркина, придем к системе обыкновенных дифферен-
дифференциальных уравнений относительно коэффициентов ряда B6). Представим эту систему
МЕТОДЫ СВЕДЕНИЯ К СИСТЕМАМ ОБЫКНОВЕННЫХ УРАВНЕНИИ 249
в матричной форме, используя (поскольку это не приведет к недоразумениям) для
матриц те же обозначения, что и для соответствующих им операторов:
Aq + [C + aF + pO@G]q=0. B7)
Здесь q (t) — вектор-столбец из функций qk (t). Элементы матриц А, С, F и G вы-
вычисляют по формулам
/у* = (Fife, $,У, g/k = (Gfk, %)¦ B8)
Вместо метода Бубнова—Галеркина можно использовать вариационный прин-
принцип Гамильтона—Остроградского для соответствующего квадратичного функцио-
функционала. Это позволяет расширить класс допустимых базисных функций, введя в рас-
рассмотрение функции, которые удовлетворяют всем кинематическим, но не обязательно
всем динамическим граничным условиям. Уравнения относительно функций qk (I)
сохраняют вид B7), а элементы матриц А, С, F и G определяют по формулам B8)
с заменой скалярного произведения на соответствующие энергетические произве-
произведения.
Разложение по собственным формам колебаний. Собственные формы колеба-
колебаний — ненулевые решения уравнения
(С-со2А)(р = 0 B9)
образуют полную систему функций данной задачи, так что разложение
со
и (х, 0 = Ц Qk (О ф* (х) C0)
k=i
позволяет получить систему обыкновенных дифференциальных уравнений относи-
относительно обобщенных координат qk (t), эквивалентную исходным уравнениям в част-
частных производных. Система типа B7) приводится при этом к бесконечной системе
уравнений [113]
сю со
+РФ @ 2 g)kqk = 0, (/=1, 2, ...), C1)
где шу — собственные частоты незагруженной системы. В отличие от B8) в уравне-
уравнениях C1) использованы обозначения
Ф/) (Оф*. 9/)
Г^): ^=(Аф7^Г- C2)
Особый случай. Пусть собственные элементы задачи B9) и задач
= 0 C3)
совпадают. Это значит, что собственные формы колебаний совпадают с формами
потери устойчивости при действии статических нагрузок, заданных с точностью до
параметров а и р\ В этом случае, называемом особым, уравнения бесконечной систе-
системы C1) распадаются на независимые уравнения, каждое из которых описывает пове-
поведение одной из обобщенных координат qx (t), q2 (t), ...:
Ф*=0- C4)
(k=l, 2, ...).
Здесь ак и Pft — критические значения параметров а и E в задачах статической устой-
устойчивости, равные собственным значениям операторных уравнений C3) при \|з = х =
= ф*-
Стержень постоянного сечения, опертый по концам и сжатый постоянной по дтине
продольной силой, — пример особого случая. Уравнение A4) и граничные условия
250 ДИНАМИЧЬСКАЯ УСТОЙЧИВОСТЬ РАСПРЕДЕЛЕННЫХ СИСТЕМ
A5) удовлетворяются при помощи подстановки
со
w(x,t)=\kqk(t)smR-~. C5)
4 = 1
Здесь функции qk (f) — решения уравнений типа C4):
*ф^гЬ C6)
При этом
Неизвестные в уравнениях типа C1) разделяются также в более общем случае,
когда совпадают собственные элементы уравнений
(С — Q2A + aF)<p=0; (C + aP+PG)if = O. C8)
Первое из них отвечает задаче о собственных колебаниях системы, загруженной
статическими силами с параметром ос. Его собственные значения Q2 (се) равны ква-
квадратам собственных частот загруженной системы. Уравнения типа C1) принимают
вид
[|^] = 0 (* = 1,2,...), C9)
где Р/; (а) —собственные значения второго из уравнений C8), имеющие смысл кри-
критических значений параметра Р при совместном статическом действии обеих групп
нагрузок.
Уравнения C4) могут быть приведены к виду C9), если положить
Тогда вместо C4) имеем
qk + Qh[<x)[\+2y.k<b(t)\qk = Q (ft=l, 2, ...). D1)
Наиболее часто встречающиеся задачи динамической устойчивости, приводя-
приводящие к уравнениям типа C4) и C9), приведены в табл. 1.
Обобщенный особый случай. Представляют интерес такие задачи, для которых
бесконечная система C1) распадается на группы, состоящие из конечного числа
независимых уравнений. Пусть в операторном уравнении B5) u (x, f) есть вектор-
функция размерности г:
/«1 (х, <)\
и(х, ,)= «2(х, 0 , D2)
причём собственные элементы уравнений B9) и C3) распадаются на группы по г эле-
элементов в каждой и допускают представление
Здесь q/'\x) — вектор-функции координат; Р(р, Q^ и R? — числовые матрицы раз-
размерностью г X г. Верхний индекс указывает номер группы, нижний — номер эле-
элемента в группе. Представление D3) означает, что вектор-функции, описывающие
формы колебаний и формы статической потери устойчивости, составляются для одно-
одноименных координат из одинаковых функций. При Р^1 = Q^ = R^' приходим к осо-
особому случаю.
МЕТОДЫ СВЕДЕНИЯ К СИСТЕМАМ ОБЫКНОВЕННЫХ УРАВНЕНИИ 251
1. Параметрические колебания упругих систем (особый случай)
Упругая система и нагрузка
Собственная частота
системы
Критический параметр
Шарнирно опертый стержень
Pit)
(
\~PF
Замкнутое круговое кольцо, нагру-
нагруженное радиальной силой
k{k2— I)
E.I
ч
2— \)EJ
Шарнирно опертая пластина, нагру-
нагруженная вдоль краев равномерно рас-
распределенными силами
N,(t)
w/*=^i
Шарнирно опертая панель, нагру-
нагруженная вдоль краев равномерно рас-
распределенными силами
N,(t)
[(»/
Dm%{n) ± mkf
*i(t)
' a.
Ал
Сферическая оболочка под действием
равномерно распределенной по по-
поверхности радиальной нагрузки
Eh i\
2Eh
«(X-l+v)
252
ДИНАМИЧЕСКАЯ УСТОЙЧИВОСТЬ РАСПРЕДЕЛЕННЫХ СИСТЕМ
Решение операторного уравнения B5) для каждой группы ищут в виде ряда по
собственным формам, входящим в эту группу:
и(х, 0=
(х)
(/=1. 2, ...).
D4)
В результате приходим к последовательности систем обыкновенных дифферен-
дифференциальных уравнений, каждая из которых содержит г уравнений:
D5)
Здесь (Hjif — собственные частоты, упорядоченные при помощи двух индексов /
и &; /^ и g$ — коэффициенты, определяемые по формулам типа C2):
D6)
Такой случай частичного разделения обобщенных координат в уравнениях тео-
теории динамической устойчивости упругих систем называют обобщенным особым слу-
случаем.
Уравнения типа D5) для частных задач проще получить, если представить иско-
искомое решение в форме
и(х, /) =
D7)
Здесь <pji/' (x) — компоненты вектор-функции ф(/) (х). Полученные уравнения пере-
переходят в D5) при помощи линейного преобразования
С матРицей р(к]-
Пример. Рассмотрим задачу о динамической устойчиво-
устойчивости плоской формы изгиба балки. Пусть упругая балка оперта
по концам и нагружена в плоскости наибольшей жесткости
моментами М (t) (рис. 8). Рассмотрим изгибно-крутильные
колебания, происходящие из этой плоскости. Поперечный про-
прогиб v (х, t) и угол поворота v (*¦ О удовлетворяют уравнениям
С
Рис. 8. Упругая балка, опер-
опертая по концам и нагружен-
нагруженная в плоскости наибольшей
жесткости моментами М (/)
d2v
d2v
d2v
¦PF
= 0;
D8)
где G/K —жесткость при кручении; г — радиус инерции сечения. Граничные условия имеют вид
Решение ищем в виде
»<*, 0= V
v = у = 4j^j- = 0 (х = 0, х = I).
^l; -fix, t) =rft(/)sin^yl D=1,2,...),
D9)
E0)
где V^(O и FfcU) — искомые функции времени. Представление E0) соответствует формуле D7).
Подстановка формул E0) в уравнения D8) позволяет записать
= 0 (?= 1, 2, ...).
E1)
МЕТОДЫ СВЕДЕНИЯ К СИСТЕМАМ ОБЫКНОВЕННЫХ УРАВНЕНИЯ
253
н +
s
a
с: о —
254
ДИНАМИЧЕСКАЯ УСТОЙЧИВОСТЬ РАСПРЕДЕЛЕННЫХ СИСТЕМ
Здесь a>kv и
ственно, т. е.
. — собственные частоты изгибных и крутильных колебаний балки соответ-
E2)
I2
Другие примеры задач, относящихся к обобщенному особому случаю, приведены в табл 2
Приближенное сведение к конечным системам обыкновенных дифференциальных
уравнений. В общем случае для приближенного расчета приходится проводить редук-
редукцию бесконечных систем уравнений к конечным системам. Количество членов, удер-
удерживаемых в разложениях C0), устанавливается из физических соображений. Если
для данной упругой системы и для рассматриваемого диапазона частот собственные
формы колебаний достаточно близки к формам потери устойчивости, то в первом
приближении можно пренебречь связью обобщенных координат, заменив бесконеч-
бесконечную систему C1) последовательностью независимых уравнений [ИЗ]:
Элементы filk и gb,k выражают через приближенные значения критических пара-
параметров аир:
(Fqjfc, (fit) 1 (бф^, фд.) 1
(АфА, ф/,) <хк 5 (АфЛ) щ) pft
В результате приходим к уравнениям особого случая C4).
Пример. Рассмотрим задачу о динамической устойчивости круговой пластины, защемленной
по контуру Пусть пластина нагружена в срединной плоскости равномгрнычи усилиями интен-
интенсивностью р (t) (рис 9) Поперечные колебания пластины описы-
описываются уравнением
ОДДю + р (О Дда + pft
- = О
с граничными условиями
= о (г = R)
E5)
E6)
Собственные формы фу- (г, 0) и собственные частоты @t на-
находят из выражений A4), A7) и A8) гл. XII Первый индекс
у ц>1гп {г, 6) равен числу узловых окружностей минус единица,
второй — числу узловых диаметров у собственных форм Урав-
Уравнения типа E3) принимают вид
I ис. 9, Круговая пласти-
пластина, защемленная по кон-
контуру и нагруженная в
срединной плоскости рав-
равномерными усилиями ин-
интенсивностью р (t)
где Рь„ — приближенные значения критических параметров статической нагрузки, определяе
мые по формуле
R 2л
I J 4>kn {Г' 6) ' dr ^в
, , о о
Ркп = ~ Р'Ш*«7Г2Й ¦ "¦
J I b<Pkn(
0 0
7. ПОСТРОЕНИЕ ОБЛАСТЕЙ НЕУСТОЙЧИВОСТИ
Предварительные замечания. Если задача о параметрических колебаниях распре-
распределенной системы сведена к системе обыкновенных дифференциальных уравнений,
то дальнейший анализ может быть проведен методами, описанными в гл. VII. Для
обобщенного особого случая, а также для общего случая используют численные
методы из гл. VII. Области параметрического резонанса для распределенных систем
строят либо путем совмещения областей неустойчивости, полученных для отдельных
ПОСТРОЕНИЕ ОБЛАСТЕЙ НЕУСТОЙЧИВОСТИ
255
обобщенных координат, либо по результатам численного анализа усеченных систем,
соответствующих бесконечным системам типа C1), В качестве примера на рис. 10
построены главные области неустойчивости для опертого на одном конце и защемлен-
защемленного на другом конце стержня, сжатого периодической силой Pt cos со/ [131].
o,t -
200/,.
12 3 4 5 6 7 в 9 10 11
Рис. 10. Области неустойчивости для стержня, сжатого
периодической силой Рi cos to/
Случай плотного спектра собственных частот. Если спектр собственных частот
достаточно птотен, то области неустойчивости, соответствующие различным обоб-
обобщенным координатам, могут накладываться друг на друга, заполняя обширные об-
области в пространстве параметров. Примером может служить задача о параметриче-
параметрических колебаниях тонкостенной сферической оболочки под действием пульсирую-
пульсирующего давления q0 + qt cos ю^ (см. табл. 1). Спектр собственных частот, рассчитан-
рассчитанный согласно теории пологих оболочек,
начинается с частоты
и тем плот-
плотнее, чем меньше относительная толщи-
толщина оболочки h/R. Допустим, что нас
интересует область неустойчивости,
получившаяся в результате наложения
главных областей для каждой из обоб-
обобщенных координат. По приближенной
формуле B8) из гл. VII нижняя гра-
граница главной области неустойчивости
для обобщенной координаты с собст-
собственной частотой Q (к) и критическим
параметром q.t (к) определяется из вы-
выражения
»v
1
1 —
E8)
OS ¦
о
0,5
Рис. 11. Область неустойчивости для сфери-
сферической оболочки, находящейся под действием
пульсирующего давления q0 -f q^ cos bit
Здесь к = n (n + I) — безразмерный
параметр, характеризующий собствен-
собственные формы замкнутой оболочки. Явное
выражение для Q (к) и q%(k) содер-
содержится, например, в табл. 1. При достаточно плотном спектре собственных частот
параметр А. можно считать непрерывным (рис. 11). Строя обычным способом оги-
огибающую семейства кривых E8), приходим к формуле
"R
1/-
1 ~2
Qo + ~o qt\
E9)
Здесь @^ —¦ минимальная собственная частота, упоминавшаяся ранее; q — ми-
минимальное критическое давленге в классической теории упругой устойчивости'
2Elfl 1
I 3(l-v";
((,0)
256 РАСПРОСТРАНЕНИЕ ВОЛН И УДАРНЫЕ ПРОЦЕССЫ
Учет диссипации энергии. Уравнение параметрических колебаний в линейной
системе с учетом диссипативных сил имеет вид
Aii+ Bii + [C + aF + pO> @ G] u = 0. F1)
Оно отличается от уравнения B5) наличием члена с диссипативным оператором В.
Используя разложение B6), придем к системе уравнений относительно обобщенных
координат. Обычно это обыкновенные дифференциальные уравнения того типа,
который был подробно рассмотрен в гл. VII. Исключение составляет случай наслед-
наследственного оператора В. При этом получается система интегро-дифференциальных
уравнений относительно обобщенных координат с интегральными операторами нас-
наследственного типа. Эти уравнения могут быть исследованы, например, методом
обобщенных определителей Хилла.
Достаточные условия устойчивости систем с диссипацией. Структура областей
неустойчивости для распределенных систем может быть весьма сложной, особенно
по частотным параметрам. Если система обладает диссипацией, то практический
интерес представляют достаточные условия устойчивости со слабой зависимостью
от возбуждающей частоты. Примером может служить нестрогий критерий устойчи-
устойчивости для особого случая, основанный на использовании критических значений
коэффициентов возбуждения (см. гл. VII). Этот критерий отделяет область заведомой
устойчивости, проходя через «носики» главных областей неустойчивости. Аналити-
Аналитическая запись этого критерия следует из формулы D1) гл. VII:
Здесь соА, е^, а^, C^ — значения собственной частоты, коэффициентов демпфирова-
демпфирования и критических параметров нагрузки для k-й формы колебаний. Другой способ
получения достаточных условий устойчивости основан на методе функционалов Ля-
Ляпунова [54, 114]. Применительно к особому случаю этот метод приводит к строгим
результатам, близким к тому, который содержится в критерии F2).
Глава XVI
РАСПРОСТРАНЕНИЕ ВОЛН И УДАРНЫЕ ПРОЦЕССЫ
В УПРУГИХ СИСТЕМАХ
1. ВОЛНЫ В НЕОГРАНИЧЕННОЙ УПРУГОЙ СРЕДЕ
Под упругими волновыми процессами понимают динамическое распространение
возмущений напряженно-деформированного состояния в упругой среде или упругих
телах.
Исходные уравнения. Процесс распространения волн в упругой среде описывается
динамическими уравнениями Ламе B6) гл. VIII, которые после введения вектора
перемещений и = (ии и2, «3)т могут быть записаны в форме
<Э2и
|х Au + (X+n)graddiv u — р-^ = 0. A)
Вектор перемещений раскладывается на эквиволюмиальную и безвихревую
составляющие:
u = rot ip + gradtp. B)
Здесь ф и if — скалярный и векторный потенциалы, удовлетворяющие системе не-
независимых друг от друга волновых уравнений
ВОЛНЫ В НЕОГРАНИЧЕННОЕ УПРУГОЙ СРЕДЕ 257
Эти уравнения описывают два типа волн, которые могут существовать в неограни-
неограниченной упругой среде. Эти волны распространяются с постоянными скоростями
l~\V~) ~LpA+v)A-2v)J ' E)
-
Со скоростью С[ распространяются безвихревые возмущения, описываемые по-
потенциалом ср. Волны этого типа называют дилатационными, или волнами расшире-
расширения-сжатия. Со скоростью cf распространяются вихревые возмущения при неизмен-
неизменном объеме, описываемые векторным потенциалом л|э. Волны этого типа называют
эквивомомиальными (волнами искажения, волнами сдвига).
Отношение скоростей распространения волн искажения и волн расширения-
сжатия зависит только от коэффициента Пуассона v:
\ G)
Поскольку O^v^ 0,5, то отношение Р меняется в пределах
°^w (8)
Замечание 1. Если возмущения распространяются только в одном направлении, например
в направлении оси Oxlt и перемещения зависят только от одной координаты xt и,=и- (хЛ, то
из уравнения A) следует
дХ2 с) dt' ( О>
д'и, 1_ д'и3
dx* с? д<> " ' )
Первое уравнение описывает распространение продольных возмущений, поэтому с^ назы-
называют скоростью продольных волн. Второе и третье уравнения описывают распространение по-
поперечных возмущений, и поэтому с, называют скоростью поперечных волн.
Замечание 2. Решение уравнения A) может быть записано для прямоугольной системы
координат в форме (решение Даламбера)
либо для сферически симметричного случая (когда и зависит только от радиуса г) в форме
", = 7 [/('-<*) +g С"+ <*)]¦ A1)
Здесь Пу — направляющие косинусы; с — соответствующая скорость распространения. Два сла-
слагаемых, входящие в A0) и A1), описывают волны, распространяющиеся в двух противополож-
противоположных направлениях. Функции fug определяют из начальных условий.
Понятия о дисперсионном уравнении. Фазовая и групповая скорости. Анализ
одномерных волновых явлений в неограниченной среде или среде с граничными по-
поверхностями может быть осуществлен на основе уравнения
где ф — обобщенная вектор-функция перемещений; L — матричный оператор, коэф-
коэффициенты которого являются полиномами от операторов з~ и зт • Исследование вол-
волновых явлений приводит к изучению поведения бесконечной гармонической (моно-
(монохроматической) волны
<p
9 п/р. Болотина В, В, т, 1
258 РАСПРОСТРАНЕНИЕ ВОЛН И УДАРНЫЕ ПРОЦЕССЫ
характеризуемой волновым числом k, частотой со и длиной волны "Х = —г- Величи-
Величина Ф, входящая в A3), — комплексная амплитуда (физический смысл имеет Req>).
Из уравнения A2) для вида решения A3) нетрудно получить связь между волновым
числом k и частотой со:
detL(i?, — !ш)=0. A4)
Уравнение тина A4) называют дисперсионным. В результате решения этого урав-
уравнения находят зависимость частоты от волнового числа со = со (k).
Фазовой скоростью называют скорость распространения монохроматической
волны A3)
с = со/й. A5)
Групповой скоростью называют скорость распространения пакета волн, волно-
волновые числа которых лежат вблизи заданных значений k и со (совокупность волн с близ-
близкими длинами). Со скоростью, равной групповой скорости, переносится энергия
волновых движений с заданными значениями k и со. Групповую скорость определяют
по формуле
д д д
Если с, определенная согласно A5), не зависит от волнового числа k или от дли-
длины волны X, то форма волны при распространении не изменяется (волна распростра-
распространяется без дисперсии). В противном случае форма волны меняется за счет разной
скорости распространения отдельных компонент. Если dc/dk <^ 0 (или дс/дХ > 0),
то cg <; с и энергия в этом случае переносится медленнее, чем распространяется мо-
монохроматическая волна. Это явление называют нормальной дисперсией. Если dc/dk >
> 0 (или дс/дХ < 0), то с» > с. Скорость переноса энергии больше, чем скорость
монохроматической волны." Это явление называют аномальной дисперсией.
2. ПОВЕРХНОСТНЫЕ ВОЛНЫ РЕЛЕЯ
Краевые условия. Поверхностными волнами (волнами Релея) называют волны,
распространяющиеся вдоль поверхности упругого полупространства при условии,
что возмущения, соответствующие этим волнам, характеризуются затуханием при
удалении от граничной поверхности полупространства. Исходными уравнениями
для изучения таких волн являются динамические уравнения Ламе B6) гл. VIII или
A). На свободной поверхности (х3 = 0) должны обращаться в нуль напряжения
<?13> 02з и стзз- Это приводит к условиям
дх3 "* дхх ' дх3 ^ дх2 ' .
\ при *8 = 0. 17)
Вид решения. Определение скорости распространения. Уравнения A) с учетом
E), F) можно записать следующим образом:
<Э2«,- д2ик
Для волн, распространяющихся в направлении оси Охъ для которых и2 = 0,
решение имеет вид
и, = С) ехр [-?*, + «•*(*!-«:/)] (/=1,3), A9)
где q — некоторая положительная постоянная; k — волновое число; с — скорость
распространения поверхностной волны.
УПРУГИЕ ВОЛНЫ В СТЕРЖНЯХ
259
Из условия существования нетривиального решения системы A8) в виде A9)
следует уравнение для определения скорости поверхностных волн Релея
где а = c/cf, Р = ctlC[. Параметр а должен удовлетворять неравенству 0 < а <[ 1
0,6
0,1
0,1
0,2 0,3
0,8
0,6
0,4
0,2
О
0,2
1
\
\
\
\
«о
ч
к—
\
—-
\
*-*
\
*•—
ч
0,2 0/t 0,6 0,8 1,0 1,2
Рис. 1. Зависимость скоростей распро-
распространения волн от коэффициента Пу-
Пуассона v
Скорость поверхностных волн Релея
Рис. 2. Распределение перемещений,
связанных с поверхностными волна-
волнами Релея (V = 0,29)
B1)
Поскольку Р зависит только от коэффициента Пуассона v, cR также зависит от
этого коэффициента. Эта зависимость показана на рис. 1. На рис. 2 показано распре-
распределение перемещений, характеризующее форму поверхностной волны (ы0 = «зл:3-о)-
3. УПРУГИЕ ВОЛНЫ В СТЕРЖНЯХ
Продольные волны (техническая теория). Исходным при исследовании продоль-
продольных волн в стержнях постоянного сечения, когда процесс деформирования описы-
описывается в рамках гипотез сопротивления материалов, является уравнение продольных
колебаний стержня F8) гл. VIII, которое можно представить в виде
B2)
Последнее равенство определяет скорость распространения продольных волн
в стержнях. Эта скорость оказывается меньше скорости волн расширения-сжатия
с{ E) и больше скорости волн искажения с{ F)' с„ < с( < с ^ c[t
Продольные волны, описываемые элементарной теорией, распространяются без
дисперсии (cg0 = со).
Крутильные волны (техническая теория). Уравнение крутильных колебаний G2)
гл. VIII, описывающее крутильные волны в стержнях постоянного сечения, когда
используются гипотезы сопротивления материалов, можно переписать в виде
B3)
Для стержня кругового или кольцевого поперечного сечения /к = /0 и ск = ct.
Параметр ск определяет скорость распространения крутильных волн по техниче-
технической теории. Так как /к =~; /0, то ск sg ct. Крутильные волны, описываемые техни-
технической теорией, распространяются без дисперсии (с^к = с&).
9*
260
РАСПРОСТРАНЕНИЕ ВОЛН И УДАРНЫЕ ПРОЦЕССЫ
Изгибные волны (техническая теория). Решение исходного уравнения, которым
является уравнение изгибных колебаний стержня постоянного сечения (83) гл. VIII
(<7 = О, EJ = const), можно представить в виде монохроматической волны
w = W exp[i{kx — at)].
Дисперсионное уравнение имеет решение
Фазовую и групповую скорости определяют по формулам
_м_ /?Л'/2
c-k-n[pT) >
\'/г
Ct
= *°=2^-
dk \ pF
= 2с.
B4)
B5)
B6)
B7)
Таким образом, при распространении изгибных волн, описываемых техниче-
технической теорией, имеет место аномальная дисперсия. Поскольку скорость волн расши-
расширения-сжатия с, является верхней гранью для скоростей распространения возмеще-
возмещений в упругих телах, то cg <^ с;. При достаточно больших волновых числах k или
при достаточно малых длинах волн к = 2л/& это условие нарушается и техническая
теория оказывается непригодной. Необходимо применять уточненную теорию.
Изгибные волны (уточненная теория). За исходное в данном случае принимают
уравнение Тимошенко (93) гл. VIII. Нахождение решения в виде B4) приводит к ча-
частотному уравнению
1,0
0,8
0,6
0,4
0,2
0,2 Ofi 0,6 0,8 1,0 1,1 Я/Л
Рис. 3. Зависимость фазовых скоростей изгиб
ных волн в стержне от волнового числа по
различным теориям
\
1
1
1
'//
/'
\
V
>\
1
1
1
1
1
1
N
¦¦—
\v
ч
ж
т
—
(О4 —
где использованы F), B2) и, кроме
того, обозначение для радиуса инер-
инерции сечения г ¦= (J/F)^'-
Для каждого фиксированного вол-
волнового числа существует два значения
фазовой скорости
B9)
которые соответствуют преимущест-
преимущественно изгибным и преимущественно
сдвиговым формам распространяющих-
ся волн. При k2r2 <; I cx
krc0
^, так что
совпадает со скоростью
изгибных волн, вычисленной по элементарной теории B6). Скорость с2 при
kr ->- 0 бесконечно возрастает (групповая скорость стремится к нулю). При
&V2 > 1 характер явления меняется. Из оценок сг к. -л1гси с2 « с0 следует,
что сх близка к скорости сдвиговых волн. При kr ~ 1 колебания при распростране-
распространении волн носят связанный характер. На рис. 3 штриховой линией изображена зави-
зависимость, полученная по элементарной теории, штрихпунктиром — по уточненной
теории Тимошенко. Сплошными линиями показаны зависимости, являющиеся ре-
результатом точного решения динамических уравнений Ламе для стержня кругового
СОУДАРЕНИЕ ДВУХ УПРУГИХ ШАРОВ 261
поперечного сечения. Цифрами /, //, /// отмечены кривые, соответствующие первым
трем формам колебаний. Сравнение приведенных кривых показывает, что уточнен-
уточненная теория Тимошенко дает удовлетворительное совпадение с низшей серией. Для
второй серии имеет место лишь качественное совпадение. При малых длинах волн
(больших k) расхождение существенно. При k -*¦ со точное значение дает в пределе
скорость релеевских волн с„, в то время как по теории Тимошенко предельным зна-
значением является скорость продольных волн с0.
4. СОУДАРЕНИЕ ДВУХ УПРУГИХ ШАРОВ
Основные положения. При соударении тел обычно разделяют деформации на
местные и общие. В случае соударения массивных тел (в частности, шаров) об-
общей деформацией можно пренебречь по сравнению с местной. В этом состоит основ-
основное предположение теории Герца. Другим предположением является гипотеза, что
контактные сила и деформация связаны при ударе той же зависимостью, что и при
статическом сжатии тел (силами инерции в области контакта пренебрегают).
Пусть два шара массы т1 и т2 радиусов R1 и R2 к моменту соударения имели
скорости Vi и у2. Удар предполагается прямым и центральным (скорости v1 и v2 на-
направлены вдоль линии удара, проходящей через центры шаров). Пусть qx nq2 — обоб-
обобщенные координаты, отсчитываемые от начала соударения; а = q1 — q2 — сближе-
сближение тел. Предполагается, что зависимость контактной силы от сближения имеет
вид Р = koa'^2, где k0 зависит от свойств материала и кривизны в точке контакта.
Для шаров
, 2? (Л&\1'(.ы
Замечание. В ряде случаев может быть использована зависимость Р = &оап(' ==="^3/2).
Определение максимального сближения, максимальной контактной силы и вре-
времени соударения. Уравнения движения шаров будут следующими:
= /"(а). C0)
Отсюда нетрудно получить уравнение для а
dt2 m1mt w т ' у '
Интеграл этого уравнения при начальных условиях а @) = 0; у ' = у0 =
= I Vi — v2 | имеет вид
- — j P (a) da
C2)
Максимальное сближение определяют из условия обращения в нуль подкорен-
подкоренного выражения в C2). Для шаров
amax ~ [ 4 k0 } ' {6>
Соответствующая контактная сила
;/D'Я1'?)</1. C4)
262 РАСПРОСТРАНЕНИЕ ВОЛН И У ПАРНЫЕ ПРОЦЕССЫ
Время соударения
атах
т = 2 Г da = 2,9432 (~ )V bv~v\ C5)
v\--\P (ос) da
о
Приведенные результаты справедливы при отсутствии у шаров пластических
деформаций при ударе.
5. ПРОДОЛЬНЫЙ УДАР В УПРУГИХ СТЕРЖНЯХ
Применение элементарной теории. Приведенная масса. В элементарной теории
соударения твердых деформируемых тел используют ряд упрощающих гипотез,
основными из которых являются предположения о возможности пренебрежения ло-
локальными инерционными силами и о возможности аппроксимации динамических
смещений статическими. Так, в задаче об ударе твердого тела массы М по свобод-
свободному концу стержня, заделанного на другом конце принимается равномерное распре-
распределение напряжений. Напряжение а определяют из теоремы об изменении кинетиче-
кинетической энергии
-y-Mvl^ — , C6)
где и0 — скорость ударяющего тела; F, I, E — соответственно площадь сечения,
длина, модуль упругости материала стержня.
В случае соударения свободных стержней, движущихся в одном направлении
со скоростями v-i и v2 (v1 > t'2), принимают линейное по длине каждого стержня рас-
распределение напряжений. Применение теоремы Карно и теоремы об изменении кине-
кинетической энергии позволяет записать
После присоединения к C7) условия o1F1 = o2F2, выражающего закон равенства
действия противодействию, можно найти выражения для напряжений
- („ г, Ч ( 3/Wl/
1 = \Pl — V2)
Частично инерционные свойства стержней учитывают приведенной массой, кото-
которая вводится так, чтобы кинетическая энергия или количество движения материаль-
материальной точки, условно заменяющей стержень, равнялись соответствующим величинам
для стержня после аппроксимации динамических смещений статическими:
C9)
&L
где я1>2 — коэффициенты приведенной массы соответственно по кинетической энер-
энергии и по количеству движения; и (х) — статическое смещение; х0 — координата при-
приведенной массы.
В качестве примера приведем формулу для динамического удлинения при ударе
массы М по стержню массы m с вертикальной осью и заделанным вторым концом.
ПРОДОЛЬНЫЙ УДАР В УПРУГИХ СТЕРЖНЯХ
Это смещение (положительное при сжатии)
где
263
D0)
ДЛ.Т =
Mgt
EF
V+^M
Используя формулу D0), можно оценить максимальное динамическое напряжение
) D1)
Здесь eg = ?/р; у = M/m; aCT = Mg/F.
Волновая теория соударения стержней. Пусть стержень, имеющий закрепленный
конец х = 0, испытывает удар, наносимый твердым телом массы М по свободному
концу. Исходным является уравнение B2). Оно должно быть решено при следующих
начальных и краевых условиях:
D2)
ди
dt
=„ = 0;
t-o
dt
— щ
t-
С -
= 0
=');
@<x
ff(9u)
\dx 1
<0;
<Э2«
x=*i dt
x-l '
Решение B2) выбирается в форме A0), данной Даламбером:
« = /i (cot—х)+Ъ (cot + x).
При удовлетворении условию D2) при х = 0 получим
D3)
D4)
Определяют функцию / (г) последовательно для участков Bп — 1)/ <^ г <^
<; Bм + 1)/, п = 0, 1, 2 при использовании условий D2) и условий непрерыв-
непрерывности. Результаты определения / (г) сведены в табл. 1.
1. Функция / для задачи о продольном ударе твердого тела
по свободному концу консольного стержня
Интервал
-/<г< 1
Кг<31
31<г<Ы
Ы<г<11
1 (г)
0
A \'@ J
2-ЗМ
X B - 3/)] е~ У1 )
X B - 6Z)«J e У1 |
0
f — °° „ У1
f — V \- Р° Г| 2 v
8 ~ ! Со L V'
г —зг
X B - 3/I е У
f -1' 4- v° \l 4 v
'j~'2 + 77 L v'
X (г - 6() + -L (z — 50» 1 X
xe Y'
264
РАСПРОСТРАНЕНИЕ ВОЛН И УДАРНЫЕ ПРОЦЕССЫ
Используя данные табл. 1, определяют напряжения
o^EdJ = -E[f'(c0t-
¦x)+f (cot + x)]. D5)
Интерпретацию полученного решения можно дать на основе D4). Если 0 <; t <С —•,
го / (cot — х) = О и и = —/ (с0^ + х). Смещения представляют волну, пере-
перемещающуюся в отрицательном направлении оси Ох со скоростью с0. В момент / =
= 1/с0 волна доходит до заделанного конца, и на следующем интервале времени ре-
решение представляет собой суперпозицию двух волн, распространяющихся в проти-
противоположных направлениях. Форма этих волн определяется / (г) для / <^ г <; 3/
подстановкой вместо г соответственно cot — х и cot + x в D4). Таким же образом мож-
можно найти решение для последующих интервалов времени. Полученные соотношения
имеют смысл лишь при условии контакта между ударяющим телом и стержнем.
ди
Окончание удара определяется моментом времени т, в который производная ^~
обращается в нуль. Продолжительность удара т зависит от отношения массы ударя-
М „
ющего тела к массе стержня у = ——. Продолжительность удара увеличивается с уве-
увеличением у (табл. 2).
2. Продолжительность
продольного удара
твердого тела
по свободному концу
консольного стержня
3. Максимальные напряжения при продольном ударе
твердого тела по свободному концу консольного
стержня
Отношение
масс
V < 1,7283
1,7283 < у<
< 4,1511
4,1511 < у<
< 7,35
Продолжи-
Продолжительность
Удара
21 < сах < U
4/ < сох < 6/
6/ < с„т < 8/
Отношение
масс
Y < 5,686
5,686 < у <
< 13,816
13,816 < у<
< 25,16
max
^fi(i+. v)
4 6 "I
Анализ решения показывает, что максимальные напряжения возникают при
х = 0. Зависимость максимальных напряжений от отношения масс у представлена
в табл. 3.
В случае продольного удара твердого тела по свободному стержню последнее
условие D2) необходимо заменить следующим:
ди_
дх
= 0.
D6)
Решение, удовлетворяющее этому условию, имеет вид и = / (cot — х) + / (cot + х),
где функция / (г) определяется выражениями, сведенными в табл. 4.
Удар заканчивается при t = — , т. е. когда волна сжатия пройдет длину стержня
в одном направлении и, отразившись от ненагруженного конца в виде волны расши-
расширения, возвратится к концу стержня, подвергнутому удару.
ПОПЕРЕЧНЫЙ УДАР ПО УПРУГИМ БАЛКАМ 265
4. Функция / для задачи о продольном ударе твердого тела по ссободному стержню
Интервал
-К г < 1
1 < 2 < 3/
3/ < г < Ы
Иг)
0
Voyl ( , — yl )
Со ' '
-
z
Со
X (z
0
v°
са
1
V/ +
-3/)j
)
z-l
yi
z-U
e V/
Замечание. В приведенных выше задачах о соударениях стержней не учитывались местные
деформации. При их учете результаты будут существенно зависеть от геометрии ударяющего
тела и стержня. Например, получено решение для удара сферического тела по стержню со сфе-
сферическими концами, а также для других случаев [34, 48].
6. ПОПЕРЕЧНЫЙ УДАР ПО УПРУГИМ БАЛКАМ
Элементарная теория. Пусть с высоты h на балку постоянного сечения падает
тело массы М. В элементарном подходе массой балки пренебрегают и используют
теорему об изменении кинетической энергии. Предположения, что балка свободно
оперта по концам и что удар приходится посредине между опорами, приводят к вы-
выражению для динамического смещения при ударе
D7)
где /ст — статический прогиб, определяемый элементарными методами сопротивле-
сопротивления материалов. Следующий шаг уточнения состоит в учете приведенной массы балки
(для опертой балки приведенная к середине балки масса равна 17 т/35). Вместо
D7) применяют формулу
'лин 'ст"'"
/е
в
17
D8)
Замечание. Формула D7) пригодна для любой упругой системы, если ее масса пренебре-
пренебрежимо мала по сравнению с массой груза, а форма динамического прогиба совпадает с формой
жимо мала по сравнению с массой груза, а форма динамического прогиба совпадает с форм
статического прогиба. Формула D8) также допускает обобщение, если надлежащим образ
вычислить приведенную массу.
Сен-Венан решил задачу в предположении, что тело после удара движется вместе
с балкой (абсолютно неупругий удар). При таком предположении задача сводится
к интегрированию (83) гл. VIII (</2 = О, EJ = const) при условиях:
dw
dw
—
= 0
I dw
-^-' ~dJ = Va при
, - /I
D9)
266 РАСПРОСТРАНЕНИЕ ВОЛН И УДАРНЫЕ ПРОЦЕССЫ
Решение получено в виде разложения по собственным формам малых колебаний.
Недостатком подхода Сен-Венана является предположение об абсолютно неупругом
ударе, не позволяющее учесть возможность отскока массы и повторного удара.
Обобщение элементарной теории. Рассматривается прямой центральный удар
двух тел с массами, равными массе ударяющего тела и приведенной массе балки.
Для характеристики взаимодействия тел вводят коэффициент восстановления 8
(приведенная масса вычисляется по кинетической энергии). Скорости тел после
удара
М-етпр М(\+г)
vi = тп vo'< Щ = -гг-; vo- E0)
М + т 2 М + т ^
Отсюда следует, что v2 > vlt так что дальнейшее движение балки будет происходить
отдельно от ударяющего тела. Далее снова применяется теорема об изменении кине-
кинетической энергии, и в результате для динамического прогиба получается формула
Приведенное решение не учитывает возможности повторного удара, когда тело
догоняет балку, скорость которой уменьшается за счет действия упругих восстанав-
восстанавливающих сил.
Теория поперечного удара Тимошенко. Эта теория объединяет существенные
положения теории Сен-Венана и Герца. Она учитывает местные деформации ударя-
ударяющего по балке тела. Пусть тело в момент соприкосновения с балкой имеет скорость
v0. Если прогиб балки в точке удара х — \ обозначить через у, смещение тела — через 5,
а местное сжатие через а, то s = а + У- Это соотношение служит уравнением сов-
совместности при использовании метода расчленения, состоящего в раздельном рас-
рассмотрении движения тела и балки под действием сил контактного давления Р (t).
Исходными являются уравнения движения тела и балки
E2)
Эти уравнения должны быть проинтегрированы при начальных условиях
E3)
w(x, 0) = 0; ^(х, 0) = 0
и краевых условиях для балки, соответствующих характеру закрепления концов.
Дополнительным условием является зависимость между сближением а и силой кон-
контактного давления Р (а = кРг^3). На параметр k влияют геометрия соударяемых
тел и упругие характеристики их материалов.
Решением E2), удовлетворяющим E3), является
U
Р (У dt2 dtx. E4)
ПОПЕРЕЧНЫЙ УДАР ПО УПРУГИМ БАЛКАМ
267
Задачу о движении балки можно решить методом собственных функций, представ-
представляя решение в виде разложения по балочным функциям Хп (х) (для опертой балки
w(x, 0=2ji
п
Обобщенную координату /„ находят из уравнения
E5)
E6)
решение которого при нулевых начальных условиях можно представить в виде ин-
интеграла Дюамеля (см. гл. VI)
pF Xl (x) dx
/„ =
unpF ( Xl (x) dx
о
sin сол (t-x) dx.
E7)
Прогиб балки в месге уцара
b, 0=2"
An I
n (x) dx
i
\ P (t) sin U)n (t—%) dx.
E8)
Контактное давление определяется из функционального уравнения
J !
'—¦" 2
о о
E9)
Это основное уравнение теории удара - °
Тимошенко. Решалось оно различ-
различными авторами [34, 48] Поскольку
уравнение E9) справедливо только
при наличии контакта между уда-
ударяющим телом и балкой, при отсут-
отсутствии контакта должны использо
ваться уравнения E2) при Р = 0.
На рис. 4 представлены харак-
характерные результаты, относящиеся к
случаю свободно опертой стальной
балки, ударяемой посредине проле-
пролета стальным шаром при уо= 13 см/с,
/=39 см, F= 1,6 см2.
При рассмотрении поперечного удара по пластинам
I
/J
г t
/ У/л *
—i
A
f
-i
у
0
IDT0
20TB 30T0
of
Рис. 4. Зависимость силы взаимодейст-
взаимодействия (/), перемещения тела B) и прогиба
балки C) при поперечном ударе
р рр р удр и оболочкам также может
быть использовано как обобщение элементарной теории Кокса, так и обобщение
подхода Тимошенко [34, 48].
Часть третья
КОЛЕБАНИЯ ЛИНЕЙНЫХ СИСТЕМ
ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
Глава XVII
СВЕДЕНИЯ ИЗ ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ
И ПОЛЕЙ
1. МЕТОДЫ ОПИСАНИЯ СЛУЧАЙНЫХ ФУНКЦИЙ
Стохастические модели. Математическая формулировка и исследование стоха-
стохастических моделей основаны на методах теории вероятностей, теории случайных
функций и математической статистики. Многие задачи прикладной теории колеба-
колебаний могут быть удовлетворительно сформулированы и решены лишь с использова-
использованием стохастических моделей. К ним относятся прежде всего задачи о колебаниях си-
систем, возбуждаемых случайными нагрузками. Примером служат нагрузки от атмо-
атмосферной турбулентности, пульсаций в пограничном слое, акустического излучения
работающих двигателей, морского волнения, транспортировки по неровной дороге
и т. п. Многие технологические процессы также сопровождаются случайным изме-
изменением динамических нагрузок (например, нагрузки, действующие на элементы
горнодобывающих и горнообрабатывающих машин). Случайные факторы помимо
нагрузок могут войти в вибрационные расчеты также через параметры системы.
Так, случайный разброс собственных частот или коэффициентов демпфирования
может оказать сильное влияние на выводы о виброустойчивости.
Статистическая динамика и родственные вопросы. Предметом статистической
динамики является математическое описание и методы анализа стохастических
моделей систем самой общей природы. Это могут быть модели механических, элек-
электрических, биологических и тому подобных систем. Теорию случайных колебаний
можно рассматривать как приложение статистической динамики к системам опреде-
определенного класса. Для расчета случайных колебаний необходимо иметь статистические
данные о нагрузках и о свойствах системы. Поэтому к теории случайных колебаний
примыкает теория статистической обработки опытных данных, а также теория
идентификации динамических систем. Интерпретация вероятностных выводов о ко-
колебаниях требует применения методов теории надежности.
Случайные функции. Предполагается, что читатель знаком с элементами теории
вероятностей, включая распределения многомерных (векторных) случайных вели-
величин. Необходимые сведения можно найти в [88]. Ниже на инженерном уровне изла-
излагаются элементы теории случайных функций. Рассматриваются только непрерывно
распределенные функции непрерывных аргументов.
Случайные функции U (t) времени t называют случайными процессами. Область
изменения аргумента t, как правило, совпадает с действительной прямой Т —
— (—оо, оо). При рассмотрении задач с начальными данными будем в качестве этой
области брать полупрямую Т = [0, оо). Случайные функции 0 (х) координат х =
= (хх хт) евклидова пространства Rm называют случайными полями. Случай-
Случайные функции времени t и координат х называют либо пространственно-временными
случайными процессами, либо пространственно-временными случайными полями.
Далее будем называть эти функции случайными полями. Совокупность случайных
функций t/j (t), ..., Un (t) называют п-мерным случайным процессом или векторным
случайным процессом в пространстве R™. Если в контексте встречаются векторные или
тензорные величины, то во избежание недоразумений рекомендуется применять пер-
первый термин. Реализации (выборочные значения) случайных функций будем обозна-
МЕТОДЫ ОПИСАНИЯ СЛУЧАЙНЫХ ФУНКЦИИ
269
чать, в отличие от самих случайных функций, соответствующими строчными бук-
буквами. Например, реализации случайного процесса U (t) будут обозначаться щ (t),
щ (t), ... (рис. 1). Случайный процесс U (t) может быть истолкован либо как сово-
совокупность всех его реализаций, об-
образующих некоторое пространство
выборочных функций, либо как
случайная величина U, зависящая
от параметра t.
Плотности вероятности и функ-
функции распределения одномерного слу-
случайного процесса. Плотность веро-
вероятности р (и, 0. зависящая от /
как от параметра, характеризует не-
непрерывное распределение значений
функции U (t) при любом I. e T
так что
р(и, t)du =
A)
Рис. 1. 1 еализации случайного процесса
Здесь и в дальнейшем Р { А } — вероятность наступления события А. Функцию
распределения F (и, t) вводят через плотность вероятности р (и, t):
F(u, 0
p(u, t)du.
B)
Для исчерпывающего описания случайного процесса необходимо задать совмест-
совместные m-мерные распределения для любого m и любой комбинации значений t1 =< ... =<:
=S tm e Т. Соответствующие плотности вероятности вводят при помощи соотношений
. k
; k=\, ..., m). C)
Они должны удовлетворять условиям нормировки
оо
J Р(«ь .... «т. к, •••> tm)du1...dum~-l,
согласованности
D)
E)
и симметрии относительно любых попарных перестановок аргументов и^, tk. Од-
Одномерную плотность вероятности р (и, t) называют также одновременной или одно-
одноточечной, многомерные плотности р {их ит, tt tm) — многовременными или
многоточечными.
Моментные функции случайного процесса. Составляя произведения значений
функции U (t) при различных / и производя осреднение по множеству реализаций,
получим последовательность моментных функций
(U @), (U
U
(U (h) U (У U
F)
Угловые скобки обозначают операцию вероятностного осреднения (математиче-
(математического ожидания). Число сомножителей в F) называют порядком моментной функции.
Моментная функция первого порядка есть математическое ожидание случайной
функции. Для задания случайного процесса необходимо знать полную систему
моментных функций, включающую функции сколь угодно высокого порядка при
любых комбинациях значений tu ..., tm s Т. Моментные функции связаны с плот-
270 СВЕДЕНИЯ ИЗ ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ И ПОЛЕЙ
ностями вероятности следующими соотношениями:
(U @> = J up (и, 0 du;
— СО
со
(U (к) U (t2)) = J Ulu2p (И1, и,, fb /2) dHj rf«2;
G)
(f/ (к) U (t2) U (t3)\ = J «1«2«зР («1. «2. «3. *Ъ 4. 4) ^«1 ^«2 ^«
—оо
И Т. Д.
Корреляционная функция случайного процесса. Вспомогательный процесс
U (f) = t/ @—{U (t)) называют центрированным, а его моментные функции —
центральными (в отличие от моментных функций F), называемых начальными).
Центральную функцию второго порядка
К (к, U=°(D(QU(tJ) (8)
называют корреляционной функцией процесса U (I). В переводной литературе ис-
используют также термин ковариационная функция, а термин корреляционная функция
сохраняется за аналогом коэффициента корреляции
, h)
Корреляционная функция связана с двухмерной плотностью вероятности соот-
соотношением
со со
К (k, t2) = J J [и (к) - а (к)] [и D) - а (к)] р (uv иг, к, (г) dux du2. (9)
— со —со
Здесь и в дальнейшем a (f) = {U (()). Корреляционная функция обладает свой-
свойствами
К (t, t) > 0, К (к, t2) = К (/» к), К2 (к, к) === К (к, к) К (к, у. A0)
Дисперсия случайного процесса
ol(t) = D[U(t)] = K(t, t).
Рассмотрим т несовпадающих моментов времени к tm. Квадратную матрицу
К (к к) К {к, t2) ...К (к, tm)
. к) к (t2 tt) ...K(tz, tm)
K{tm \)...к(tm tm)
называют корреляционной (ковариационной) матрицей. Она является симметрич-
симметричной и неотрицательной; если значения функции при различных t/ и tk линейно неза-
независимы, то корреляционная матрица — положительно определенная.
Спектральные представления случайных процессов. Пусть случайная функция
U (/) допускает разложение в конечный или бесконечный ряд
где i|)j (t), i|J (t), ... — некоторая система детерминистических (неслучайных) функ-
функций; 11Ъ U2, ... — случайные величины. Система базисных функций предполагается
полной. Случайный процесс U (/) задается совместной плотностью вероятности для
СТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ 271
случайных коэффициентов Фурье Ult U2, ... или полной системой моментов для этих
коэффициентов. Разложение
l/@=a@ + 2]t/a*aW. A3)
а
где базисные функции выбраны таким образом, что все
. A4)
называют стохастически ортогональным или каноническим.
Рассмотрим спектральное разложение в виде обобщенного интеграла Фурье
оо
U @ = а @ + j У (со) i|> (/, и) dco. A5)
— 00
Здесь г|э (t, со) — детерминистическая функция времени t и действительного пара-
параметра со; U (со) — случайная функция параметра со. Без ограничения общности
принято, что со е (— оо, оо). Функцию U (со) называют спектром процесса U (t).
Если выполняется условие
<t7*(co)i7 (co'))=S(coN(co —со'), A6)
где S (со) — детерминистическая функция параметра со, б (со)—дельта-функция,
то разложение называют каноническим (звездочка обозначает комплексно-сопряженную
величину). Функцию S (со) называют спектральной плотностью процесса U (f).
Корреляционная функция процесса связана со спектральной плотностью соотноше-
соотношением
K(tu У= J S (со) i|>* ft, соЖ'2. «)rfco. A7)
— со
Обычно U (со) — обобщенная функция со, так что интеграл A5) в обычном смысле
не существует и соотношение A6) не имеет точного смысла. Более строгая трактовка
спектрального разложения A5) имеет вид
со
U(t) = a(t)+ \ г|) (t, co)dZ(co). A8)
— оэ
Здесь Z (со) — случайная функция, значения которой равны сумме комплексных
амплитуд процесса с частотами, меньшими чем со. Условие стохастической орто-
ортогональности A6) записывается в виде
I 0 (А
где Z(Aco)= \ dZ(co).
Дш
2. СТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
Понятие стационарного случайного процесса. Процесс U (t) называют стацио-
стационарным, если все его вероятностные характеристики инвариантны относительно вы-
выбора начала отсчета времени. В частности, математическое ожидание и одномерная
плотность вероятности этого процесса не зависят от времени, а двухмерная плотность
вероятности и моментная функция второго порядка зависят от разности аргумен-
аргументов t2 — ti, но не от каждого аргумента в отдельности. Если накладываются только
ограничения на одномерные и двухмерные распределения, то процесс называют
стационарным в широком смысле. Стационарные случайные процессы служат удоб-
удобной моделью для реальных процессов, свойства которых достаточно медленно из-
изменяются во времени.
272 СВЕДЕНИЯ ИЗ ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ И ПОЛЕЙ
Корреляционная функция стационарного случайного процесса. Корреляционная
функция К (h, B) зависит лишь от разности t2 — tlt так что К (h, t2) = Ki (t% — tx).
Обычно применяют обозначения Ki (т); т = 1г — tlt а индекс при К\ опускают. Кор-
Корреляционная функция стационарного случайного процесса удовлетворяет условиям
/С(О)згО; К(т) = К(-х); К (т) === К @).
Эргодические случайные процессы. Стационарный случайный процесс называют
эргоджеским, если одна его реализация содержит всю информацию о вероятност-
вероятностных свойствах процесса. Эргодические процессы выявляют свои свойства не только
на множестве реализаций, но и во времени. Важной их особенностью является воз-
возможность замены осреднения по множеству реализаций осреднением по времени.
В частности,
Г/2
<{/@> = а= lim ' С u{t)dt;
Г-оо I .'
-Г/2
Г/2
/f(T)=hm i С [u{t)-a\[u(t + x)—a\dt.
-Г/2
Вопрос о принадлежности стационарного случайного процесса к эргодическим
процессам обычно решается на основе физических соображений или предваритель-
предварительной обработки ансамбля реализаций.
Спектральное разложение стационарных случайных процессов. Стационарный
процесс U (t) может быть представлен в виде обобщенного интеграла Фурье
U(i)=a+ \ U (to) еш Ло, A9)
где и — действительный параметр, спектр (/(со)—комплексно-значная функция,
удовлетворяющая условию U* (—со) = U (со). Разложение A9) является канони-
каноническим в том смысле, что спектр U (со) удовлетворяет соотношению типа A6):
(U* (со) U (ш')> =S (со) б (со —со'), B0)
где S (со) — спектральная плотность процесса.
Интеграл Фурье A9) в обычном смысле не существует, поэтому соотношения A9)
и B0) не имеют точного смысла. Общепринятая запись стохастического интеграла
Фурье — Стильтьеса имеет вид
оо
U(t) = a+ $ e'w dZ (со).
Спектральная плотность S (и) пропорциональна мощности случайного процесса,
отнесенной к единице частотного диапазона. Для действительного стационарного
процесса она является действительной неотрицательной четной функцией частоты со.
Для процессов с ограниченной дисперсией S (со) — интегрируемая на отрезке
(— сю, оо) функция.
В табл. 1 приведены выражения для корреляционных функций и спектральных
плотностей наиболее распространенных типов стационарных случайных процессов.
Стационарные случайные процессы
273
з
V/
о э
3
л
л
8
*ц
274
СВЕДЕНИЯ ИЗ ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ И ПОЛЕЙ
э,
со
-
%
I
V/ л
Л
8
+ л
и 8
8 5
0 +
МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ 275
3. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
Плотности вероятности многомерного случайного процесса. Плотность вероят-
вероятности «-мерного случайного процесса р (и, t), характеризующая распределение зна-
значений непрерывной векторной случайной функции U (f) для любых значений пара-
параметра (еГ, вводится как
р (u, f)du = P {и sell @ <u + du} B1)
Здесь и ниже неравенства в правой части означают п неравенств для соответствую-
соответствующих компонентов векторного процесса, du — элемент объема в R".
Совместные плотности вероятности многомерного случайного процесса вводятся
при помощи соотношении
Р(Щ, ¦¦•> ит> к, ¦•¦, tm)dul ..dum =
A=l, ..,m} B2)
Здесь Uji — реализация векторного процесса в момент времени t^. Совместные плот
ности вероятности, как и в случае одномерного процесса, должны удовлетворять
условиям нормировки, согласованности и симметрии.
Моментные функции многомерного процесса. Последовательность моментных
функций векторного случайного процесса U (t) получается перемножением значений
компонентов вектора U (t) при различных t и осреднением по множеству реализаций-
(U,(t)), <?/,&) t/ft&)>, (и,(Цик(Ци,т> - (I, Ь 1 = 1, ...п) B3)
Для исчерпывающего описания многомерного случайного процесса необходимо
задать либо полную систему совместных плотностей вероятности B2), либо полную
систему моментных функций B3). Связь между двумя способами описания дается
формулами типа G), обобщенными на многомерный случай.
Взаимная корреляционная функция. Центральные моментные функции от компо
центов многомерного процесса
К,к {к, к) = ф, ft) Uk (t2)) A, k = 1, ... , п) B4)
называют взаимными корреляционными функциями. Свойства взаимных корреля-
корреляционных функций аналогичны свойствам элементов корреляционной матрицы A1),
но эти свойства не тождественны. Например, условие симметрии A0) принимает вид
Kjkik, k) = Kk,(t2,k) B5)
Спектральное разложение многомерного случайного процесса. Рассмотрим слу-
случай канонического интегрального разложения типа A5)
U, @ = а, @ + ^ U, (со) t; (t, w) A», B6)
— СО
в котором спектры Uj (со) удовлетворяют условию стохастической ортогональности
<?/,» (со) Uk (со') } = Slk (со) 6 (со - со'). B7)
Функции S/4 (со) называют взаимными спектральными плотностями векторного
процесса V(t).
Стационарные и стационарно связанные многомерные процессы. Многомерный
случайный процесс называют стационарным, если все его компоненты стационарны,
или стационарно связанным, если все его взаимные вероятностные характеристики
инвариантны относительно выбора начала отсчета времени. Взаимная корреляцион-
корреляционная функция Kjk (к, к) стационарного и стационарно связанного процесса зависит
лишь от разности t2 — /, = т. При этом свойство симметрии B5) принимает вид
K,h W = Кк, (-т.).
Спектральное разложение стационарных и стационарно связанных процессов.
Для стационарных и стационарно связанных процессов функция г|>, (t, со) в разло
276 СВЕДЕНИЯ ИЗ ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ И ПОЛЕЙ
жении B6) определяется как "фу (t, со) = ехр (—icofj, а спектры (У,- (со) являются
комплексно-значными функциями частоты. Взаимные спектральные плотности
Sjk (со) стационарного и стационарно связанного процесса — действительные функ-
функции частоты при / = k и комплексно-значные при / =? k. Свойства взаимной спек-
спектральной плотности действительного многомерного процесса следуют из свойств
взаимной корреляционной функции:
S,7(co)=sO; S//(co) = S//(-co); Sfk (<o) = S*/ (со). B8)
Нормальные (гауссовские) процессы. Действительный случайный процесс
U (t) называют нормальным (гауссовским), если его m-мерные плотности вероят-
вероятности при любом т являются гауссовскими. Например, в случае т = 2 плотность
вероятности нормального процесса U (t)
Р("ь «2, к, к) =
r(Hi
р») L
о0 ( - Д (/i)) (»-»~ a (t2)) (и, - д
Здесь а? = D [(/ (<.)J — дисперсия процесса в момент времени t = Л-; р (tv t^) —
коэффициент корреляции. Плотность вероятности р («i, ..., ит, tt tm) пол-
полностью задается математическим ожиданием a (f) = (U (/)) и корреляционной функ-
функцией К (к, к)-
Совместные плотности вероятности B2) для многомерного случайного про-
процесса подчиняются нормальному закону распределения. Например, для я-мерного
случайного процесса одноточечная плотность вероятности
- ? 2 2 L'" (t) liU'-a' {t)) {U«-a>
" (' ^p^/'ldet К (,)]¦'¦ Р { ? 2 2 L'" () li'a' {t)) {U«a>
Здесь К (t) — матрица, элементами которой являются взаимные корреляционные
функции B4), взятые в совпадающие моменты времени tx = t2 = t; LJk (t) — эле-
элементы обратной матрицы. Многомерный нормальный процесс полностью задается
математическим ожиданием a/ (t) s {U/ (t)) и взаимными корреляционными функ-
функциями Kjk (к> к) (/. k= \, ..., п).
4. МАРКОВСКИЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
Определение марковского процесса. Случайный процесс называют марков-
марковским или процессом без последействия, если для любых моментов времени t0 <ik<C
< ... <С}т выполняется условие
Р(«ш. <ml И/п-1. (т-Ь ¦•• ; «0. to) = p(un, tm\um_b tm_j). B9)
Условная плотность вероятности
Р(ит, 1т\ит-Ъ *т-Ъ •¦• '< «о, 'о) =
k sS U (tk) <ull + duk \
= 0, 1, ... , m-1 /• W
Марковский процесс полностью определяется начальным распределением
Р (мо> А;) и переходной вероятностью р («m, tm I Mm_i, 'm-i). равной условной плот-
плотности вероятности перехода из состояния um_t, tm_^ в состояние ит, tm.
Интегральное и дифференциальные уравнения для переходной вероятности.
Переходная вероятность р (и, t \ и0, t0) удовлетворяет интегральному уравнению
Смолуховского
оо
Р («2, k\u0, to)= ^ р(и2 t2\ult к)р{и1г к\и0, /0)rf"i C1)
277
C2)
где К/, (и, /) — интенсивности марковского процесса, вводимые при помощи соот-
соотношений
МАРКОВСКИЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
и дифференциальному уравнению параболического типа
со
(«, t)~ lim т-r \ (u —
(, t~Af)du.
C3)
Решение уравнения C2) должно удовлетворять начальному условию
р (и, t\ «о, t0) \t-t0 = б (« ~ fo)-
Для непрерывного марковского процесса все Хд = 0 при А > 2. Уравнение C2)
принимает вид
др д I д2
dt ди 2 дм2
его называют уравнением Фоккера — Планка — Колмогорова. Интенсивности щ (и, /)
и х2 (и, t) — соответственно коэффициенты сноса и диффузии. Переходная вероят-
вероятность как функция переменных иа, t0 удовлетворяет также уравнению
др_
др_
^ = -Xla4~T'
C5)
которое является сопряженным по отношению к C4).
Многомерный марковский процесс. Векторный случайный процесс U (t) =
= {6\ (t), ..., Un (I)} называют п-мерным марковским процессом, если его исчерпыва-
исчерпывающей характеристикой является переходная вероятность р (u, t | и0, t0), удовлетво-
удовлетворяющая уравнению Колмогорова
с начальным условием р (u, t\ и0, tB) I t-t0 = б (и — и0). Интенсивности равны
со
х, (и, /)= lim — \ (и/ — u/i) p (и, /1 иь t — At) du;
— со
со
1 с
v.jk (и, 0= !im гт \ ("/ —u/i) («* —«Ai)P (и> '! Uj, t — At) du,
Дг —*¦ 0 «/
\ C7)
где их — значение случайного векторного процесса U (f) в момент времени t — At.
Обратное уравнение Колмогорова имеет вид
dt0
rt n
V
C8)
/=¦1
где Uq/ — компоненты вектора ufl.
278
СВЕДЕНИЯ ИЗ ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ И ПОЛЕЙ
5. ВЕРОЯТНОСТНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПОЛЕЙ
Моментные функции случайного поля. Рассмотрим «-мерное векторное про-
пространственно-временное случайное поле U (x, f) (рис. 2). Система моментных функ-
функций порядка г (г = 1, 2, ...) поля U (x, t) образуется путем перемножения реали-
реализаций его компонентов при различных значениях координат х и времени t и осред-
осреднения по множеству реализаций
?/;(х, 0>, WMx, t, х',О
t, x', t>; x", t")) (;, *. '.
..= 1, .... я).
C9)
u(r;t)
Моментные функции порядка г = 1 представляют собой математические ожи-
ожидания компонентов функции U (x, t) в произвольной точке х и в произвольный
момент времени t. Моментные функции порядков г > 1 характеризуют стохастиче-
стохастическую связь компонентов в г различных точках
поля в г различные моменты времени.
Взаимные корреляционные функции прост-
пространственно-временного случайного поля. Мо-
Моментные функции порядка г центрированного
поля U (x, t) = U (х, 0 — (U (х, 0) назы-
называют центральными моментными функциями,
а моментные функции второго порядка — кор-
корреляционными функциями. Совокупность корре-
корреляционных функций Kjk (x, t; х, t') образует
тензорное поле удвоенного числа переменных
х, (, х', ?.
Спектральные разложения пространственно-
временных случайных полей. Простейший тип
спектрального разложения имеет вид
u(r't)
xz
Рис. 2. К определению понятия
пространственно-временного слу-
случайного поля
U(X, 0=
Фа
D0)
здесь сра (х) — некоторая полная система детерминистических вектор-функций;
коэффициенты Ua (t) — случайные функции времени t. Случайное поле V (х, t)
задается полной системой совместных плотностей вероятности или полной системой
моментных функций для процессов Ua (/). Система моментных функций поля U (x, t)
с использованием разложения D0) находится по формулам
<?/, (х, 0> =
a @> Ф,« (х);
(U, (х, f) Uk (%', t')) =
a @ ^Р (П) Ф/а W
а= 1
и т. д.
Стационарные пространственно-временные случайные поля. Здесь и ниже огра-
ограничимся рассмотрением скалярного поля Поле U (x, t), t e (—¦ оо, со) называется
стационарным, если его вероятностные характеристики не меняются во времени.
Моментные функции порядка т> 1 зависят от разностей V—Л t" — t и не зависят
от выбора начального момента наблюдения. Стационарное пространственно-вре-
пространственно-временное поле U (x, t) называют эргодическим, если одна его достаточно продолжи-
продолжительная реализация содержит всю информацию о вероятностных свойствах поля.
В этом случае моментные функции определяют путем осреднения соответствующих
произведений сначала по времени, а затем по множеству реализаций.
Спектральное разложение стационарных пространственно-временных случай-
случайных полей. Рассмотрим случай канонического интегрального разложения типа A9),
ВЕРОЯТНОСТНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПОЛЕЙ 279
Стационарное случайное поле U (x, t) допускает спектральное разложение
со
U(x, 0 = я(х)+ $ U (х, ы)еш'ёа. D1)
— от
Случайная функция U (х, ш) в пространстве х, со обладает свойством стохасти-
стохастической ортогональности по со, т. е.
(U* (х, ш)(/(х', co')>=S(x, х'; со) б (со —со')- D2)
Здесь 5 (х, х'; &>) — детерминистическая функция, связанная с соответствующей
корреляционной функцией соотношением
S(x, x'; «) = 2^- f ^(x, *, х', <+т)е~"«Л D3)
— со
и обладающая свойствами корреляционной функции по пространственным коор-
координатам и свойствами спектральной плотности по времени.
Однородные пространственно-временные случайные поля. Поле U (x, t),
заданное во всем пространстве Rm, называют однородным, если его вероятностные
характеристики инвариантны относительно сдвигов системы координат. Моментные
функции порядка г > 1 зависят от разностей координат р' = х' — х, р" = х" — х
и т. д Если однородное поле является эргодическим, то осреднение по множеству
реализаций может быть заменено осреднением по всему пространству.
Спектральное представление однородных пространственно-временных случай-
случайных полей. Ограничимся случаем канонического интегрального представления
однородного по х и стационарного по t поля U (x, t) В этом случае поле допускает
представление
со со
U(x, t) = a+ j j U (k, со) el (k " + at) dk dco, D4)
— CO — CO
где k — вектор с компонентами klt ..., km; kx = k^x^ + ... + kmxm. Спектр
U (k, со) обладает свойством стохастической ортогональности
(U* (к, со) (У (к', со')} =5 (к, со) б (к—к') б (со — со')- D5)
Здесь S (к, со) —¦ спектральная плотность. Корреляционная функция К (р, т)
и спектральная плотность S (к, со) связаны соотношениями
со
(р, т) = j j 5 (к, со) е1 (кх + Ш) dk Ло,
— СО — СО
СО СО
D6)
Разложение D4), как и разложения A9), D1), носит формальный характер.
Строгая интерпретация этих разложений требует применения понятия стохастиче-
стохастического интеграла Фурье—Стильтьеса.
Однородные и изотропные случайные поля. Однородное случайное поле назы-
называют изотропным, если его вероятностные характеристики инвариантны относи-
относительно сдвигов, вращений и отражений системы координат во всем пространстве Rm.
Корреляционная функция однородного и изотропного поля зависит только от модуля
вектора р = |х' —х I, а спектральная плотность —-только от модуля волнового
вектора k = I k |. Корреляционная функция и спектральная плотность однородного
280 СВЕДЕНИЯ ИЗ ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ И ПОЛЕЙ
и изотропного поля связаны соотношениями
К (р) = Bл)т'2р- <т - 2>/2 J S (k) Jm_ 2 (k p) km/2 dk;
О —2~
СО
S (k) = Bл)- т'2 к~ "" ~ 2)/2 \ K(p)Jm_2 (k р) pm/2 dp;
D7)
здесь Jv (г) — функции Бесселя.
в. СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ
ПРОЦЕССОВ И ПОЛЕЙ
Методы моделирования случайных процессов и полей. Метод статистического
моделирования (метод Монте-Карло) [18, 41, 53, 138] применительно к моделиро-
моделированию на ЭВМ случайных процессов и полей заключается в решении задачи вос-
воспроизведения дискретных последовательностей, имитирующих непрерывные слу-
случайные функции с заданными вероятностными характеристиками.
Ограничимся рассмотрением наиболее употребительных алгоритмов моделиро-
моделирования стационарных гауссовских скалярных процессов и полей. Будем считать
все рассматриваемые процессы и поля центрированными.
Существуют два типа алгоритмов, при помощи которых на ЭВМ могут выра-
вырабатываться дискретные реализации случайного процесса U (t). Алгоритмы первого
типа предусматривают вычисление дискретной последовательности значений ит —
= и (tm), т. е. значений реализаций процесса U (t) в совокупности заранее выбран-
выбранных моментов времени tm (m = 0,1, 2...). Шаг дискретизации обычно принимается
постоянным: At = const, тогда из стационарности процесса U (t) следует стацио-
стационарность последовательности {ит}.
В основе алгоритмов этого типа положено линейное преобразование стацио-
стационарной последовательности независимых гауссовских чисел ? с параметрами (?) =
= 0, (?2) = 1 в последовательность \ит), коррелированную по заданному
закону
< >*/AQ D8)
где К (т) — корреляционная функция моделируемого процесса. При этом опера-
оператор соответствующего линейного преобразования записывается или в виде сколь-
скользящего суммирования с весом а^
N
«т= 2 а*Ст-*. D9)
4=1
или в виде рекуррентного уравнения типа
4=0 4=1
Вид корреляционной функции воспроизводимого при помощи соотношений D9),
E0) случайного процесса определяет набор значений коэффициентов а^, Ь^, с^ [18].
Ко второму типу относятся алгоритмы, основанные на представлении модели-
моделируемых процессов в виде разложений
U(t) = ^%(V, 0. E1)
а
где i|Ja — некоторая система детерминистических функций; U — случайный вектор.
При этом моделирование случайного процесса сводится к воспроизведению реа-
реализаций векторов U и последующему вычислению значений ит = и (tm) по фор-
СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
28!
муле E1). Алгоритмы моделирования случайных векторов в рамках корреляцион
ной теории можно найти, например, в [18, 31].
Целью статистического моделирования случайных полей является воспроиз-
воспроизведение совокупности реализаций значений поля U (х) в дискретных точках х„ [х =
= (*i хт), n=l N].
В дальнейшем не будем делать формального различия между пространственными
координатами и временем и ограничимся случаем однородных случайных полей.
Алгоритмы моделирования случайных полей, как правило, являются обобщением
соответствующих алгоритмов моделирования случайных процессов на случай т
переменных.
Моделирование гауссовского белого шума. При статистическом моделирова-
моделировании случайных процессов и полей возникает необходимость в моделировании ста-
стационарного дельта-коррелированного гауссовского процесса Ъ, (t) (белого шума интен-
интенсивности s) или его многомерного аналога | (х). На ЭВМ можно воспроизводить
только усеченный белый шум Ъ, (t) с конечной дисперсией, спектральная плотность
и корреляционная функция которого приведены в табл. 1 Параметр шс при мо-
моделировании подбирается таким образом, чтобы последовательность %т = % (m\t)
была некоррелированной. Это условие будет выполняться, если выбрать сос = n/At,
где Д^ — шаг дискретизации. Моделирующий алгоритм при этом имеет вид [18]
4m. E2)
Метод скользящего суммирования для моделирования случайных процессов.
Алгоритм D9) позволяет воспроизводить на ЭВМ последовательности {ит} сколь
угодно большой длины, которые с самого начала обладают свойством стационарности.
Весовые коэффициенты ak могут быть вычислены различными способами. Эффектив-
Эффективным является способ, основанный на разложении в ряд Фурье спектральной плот-
плотности моделируемого процесса. Преобразование D9) при этом берется в виде
а коэффициенты
я/д/
C0S (Шс0)
E3)
E4)
Шаг дискретизации At и число членов ряда Р выбираются из условия
* = -Р
где 8 — допустимая погрешность; а2и = К @).
Моделирование стационарных случайных процессов с дробно-рациональной
спектральной плотностью. Для моделирования случайных процессов с дробно-
рациональной спектральной плотностью (см. табл. 1, процессы № 3, 4, 7, 8) вида
В (ко)
С (ia,)
E5)
где В (им) и С (to) — полиномы относительно (((о) порядка г и р соответственно
(л < р), эффективным является алгоритм типа E0). Спектральная плотность после-
последовательности
со
E6)
282 СВЕДЕНИЯ ИЗ ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ И ПОЛЕЙ
может быть приведена к виду
В (г) р E7)
"*"*-2я С {г)
где В (г) = 2 6лг*; С (г) = 1 + 2 ckz"> г =
Коэффициенты й^,, с^. используются в рекуррентных уравнениях E0).
Соотношения E0) позволяют получать дискретные реализации случайных про-
процессов сколь угодно большой длины. Начальные условия в E0) при вычислении
первых значений последовательности {ит\ можно выбрать произвольными (напри-
(например, нулевыми). Вследствие этого возникает переходный процесс, в пределах кото-
которого начальный участок вырабатываемой реализации будет искажен. Величина
этого участка реализации зависит от корреляционных свойств моделируемого про-
процесса.
Моделирование случайных процессов с использованием канонического разложе-
разложения. Для стационарных гауссовских случайных процессов справедливо разложение,
аналогичное A9):
со
U(t) = \ [U (со) cos со* + V (со) sin со*] da.
где U (и), V (со)—взаимно-независимые и стохастически ортогональные случай-
случайные функции. Принимая, что S (и) = 0 при jcol > <йс, и заменяя интеграл конеч-
конечной суммой, получим [18]
TV
U @ = Ц Vk cos (okt + Vk sin ukt). E8)
Здесь coft = kAa (Дсо = aJN); U^, Vk — гауссовские случайные величины со сле-
следующими вероятностными характеристиками:
^=a;V (/, ft = 0, 1, ... , N);
al = S @) Дщ; a| = 25 (ak) Аи (А Э= 1).
Число членов ряда E8) выбирается из условия
Наряду с E8) можно использовать разложение
N
U (t) = ^ ЛА cos (
Здесь Аи, &и — случайные величины с совместной плотностью вероятности
N
Р(А1 AN. «¦! <*ЛГ)= П р1 (Ak) рг (аА);
Ak ( А%\
"к > ZOA'
Реализации, получаемые при помощи выражений E8), E9), являются перио-
периодическими (Т = 2я/Дй>), следовательно, свойством эргодичности не обладают.
Общее достоинство разложений E8) и E9) — простота алгоритма моделирования,
а недостаток =• необходимость учитывать большое число членов ряда.
СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ 283
Разложения E8) и E9) удобно использовать для получения дискретных реа-
реализаций случайных процессов в неравноотстоящих точках.
Другие методы моделирования случайных процессов. Во многих случаях эффек-
эффективным оказывается метод моделирования, основанный на использовании разло-
разложения [138]
N
*)• F0)
Здесь ak, ak — случайные величины с совместной плотностью вероятности
N
p(wv ... , mN, av ... , aN)= Д рх (шЛ) р2 (ak),
)=cf~u!S (со) (—oo<w<co), ра(аЛ) = Bя)-1 @ s=:aft =S 2л).
Согласно центральной предельной теореме распределение реализаций F0)
при N ->- оо стремится к гауссовскому. Кроме того, при N -> оо реализации будут
асимптотически эргодическими по отношению к математическому ожиданию и кор-
корреляционной функции.
Наряду с F0) можно использовать разложение
N
U(t)= 21 (Akcos(okt + Bksm(okt). F1)
k=\
Здесь Ak, В/г, Wk — случайные величины с совместной плотностью вероятности
N
p(Av ...,AN,BV..., BN, ttl, ... , вЛГ)= П МЛМ^РаК).
А1
Кроме того, (Ak) = (Bfe) = 0; (А'гк) = (В|) = o^/N. Закон распределения величин
Лй и Вд, можно принять равномерным на интервале @,1), при этом их реализа-
реализации моделируются при помощи соотношений
«.«.(?Г(т;-9.
Здесь 7^i Tft ~" случайные числа, равномерно распределенные на интервале @,1),
которые вырабатываются на ЭВМ с помощью программных датчиков. Моделиро-
Моделирование реализаций со^. выполняют одним из методов моделирования случайных вели-
величин с заданным законом распределения. Соответствующие алгоритмы можно найти,
например, в [18, 31].
В табл. 2 приведены наиболее распространенные типы корреляционных функ-
функций стационарных случайных процессов и соответствующие им моделирующие алго-
алгоритмы.
Методы скользящего суммирования для моделирования случайных полей. Алго-
Алгоритмы этого типа связаны с преобразованием однородного дельта-коррелированного
поля X (х) в поле с заданной корреляционной функцией К. (р). Это преобразование
имеет вид
со
U (х) = j h (х) \ (х — х') dx'.
— со
Функция Грина находится из уравнения
284 СВЕДЕНИЯ ИЗ ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ И ПОЛЕЙ
2. Алгоритмы моделирования случайных процессов
Корреляционная
функция
Моделирующий
алгоритм
Параметры алгоритма
"я, = Ъ ak ^m-k
fe=-P
т* < 'Л; v* =
= р;
Р =
е—a i t I A + а | т |
а > О
Р; с,=2р; с2 = -р2
Ро= P3(l +V*)-PA +V*);
, = 1 -4p2v* - р4; р =e-V*
V» = аА'
i/J
а*«—«I 11 (cos aot+
-J sin (oo | т
a > 0
6t = ар„/Р; ct = 2p cos Vol
c,—— p2;
P, = p (pz- 1) cos Vo +
P, = 1 - 4p» -?p sin Vo cos Vo - P4;
p = e~V*; уд. = аД(; ?0 = ю,,ДГ
a > 0
64 = o-Po/fl; c, = 2p cos Vo;
c,=- P2;
Po = P (P2 — 1) cos Vo; Pi = 1 — p4;
p = e~-4*'< V* = О.Ы; Vo = «0Д/
iV-1
I X | > T0
— целая часть числа
L v* J v*
V* = aAt
СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ 285
Дискретные реализации поля U (х) воспроизводятся при помощи формулы
скользящего суммирования
\ пт = ДхЦ---1! \, ... , *m4-<V - ¦ nm-km. F3)
Здесь Ax = Ax± ... Axm — константа, определяемая выбором шага дискретизации;
?д,..., j —дискретные значения поля ? (х), реализации которого воспроизво-
воспроизводятся по формуле типа E2):
F4)
Практически суммирование в F3) производят по всем значениям kf, ..., km,
при которых слагаемые не являются пренебрежимо малыми.
Другие методы моделирования случайных полей. Эффективные алгоритмы
моделирования случайных полей основаны на разложениях типа E8), E9) и F0),
F1), обобщенных па случай т переменных [138]. В качестве примера рассмотрим
разложение однородного гауссовского случайного поля U (х) в виде
N
U (х) = 2j И/ cos (k/x) + Вi sin (к;-х)]. F5)
Здесь A/, Bj — случайные величины; ку — гауссовские случайные волновые век-
векторы. Величины А/, В/ удовлетворяют условиям
-^б F6)
Совместную плотность вероятности величин А/, В;- и волновых векторов к,- можно
представить в виде
N
р (Аг ... , AN, В ... , BN, kr ... , кд,)= Yl.Pi (Aj) Pi (S/)^°2 (ty'
/=i
где
p2(k/) = a~u S (к). F7)
Для моделирования поля U (х) согласно F5) необходимо для каждой реали-
реализации получить 2N значений случайных величин A/, Bj и N-т значений компонент
волновых векторов ку. При получении реализаций Aj, Bj могут быть использованы
соотношения, аналогичные F2). Для получения реализаций компонент волнового
вектора необходимо воспользоваться алгоритмами моделирования гауссовских
случайных векторов. Соответствующие алгоритмы можно найти в [18].
Применение стандартных программ. В математическом обеспечении ЭВМ серии ЕС для
образования случайных чисел предназначены подпрограммы RANDU и GAUSS f60].
Подпрограмма RANDU вычисляет равномерно распределенные случайные действительные
числа на интервале @, 1) и случайные целые числа на интервале @,231). Каждое обращение
CALL RANDU (IX, IY, YFL) использует для ввода целое случайное число. В результате вы-
выдаются новые целое и действительное случайные числа. При первом обращении к подпрограмме
параметр IX должен содержать некоторое целое нечетное число с девятью или меньшим числом
цифр. При последующих обращениях IX должен быть равен предшествующему значению IY,
вычисленному этой подпрограммой. Параметр YFL — образованное равномерно распределенное
случайное число.
Подпрограмма GAUSS вычисляет гауссовские случайные числа с заданным средним (AM) и
средним квадратическим отклонением [S]. При первом обращении CALL GAUSS (IX, S, AM,
V) параметр IX должен содержать некоторое целое нечетное число с девятью или меньшим
числом цифр. После этого IX будет содержать равномерно распределенное целое число, полу-
полученное в ходе выполнения подпрограммы и необходимое для следующего обращения. Пара-
Параметр V — образованное гауссовское число В ходе выполнения подпрограммы GAUSS исполь-
используется подпрограмма RANDU,
286 СИСТЕМЫ С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
Глава XVIII
СЛУЧАЙНЫЕ КОЛЕБАНИЯ СИСТЕМ
С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
1. ЗАДАЧИ ТЕОРИИ СЛУЧАЙНЫХ КОЛЕБАНИЙ
Основные понятия. Пусть некоторая система находится во взаимодействии
с окружающей средой. Состояние системы характеризуется элементами и из про-
пространства U, а внешнее воздействие — элементами f из пространства F. Система
задается оператором Н, посредством которого каждой реализации процесса f (t)
приводится в соответствие реализация процесса u (t):
и = Ш. A)
Уравнение A) разрешается относительно f, если существует оператор L = Н:
Lu = f. B)
Далее случайные функции обозначены строчными, а их коэффициенты (образы)
Фурье — соответствующими прописными буквами.
Большая часть задач теории колебаний формулируется при помощи дифферен-
дифференциальных уравнений относительно вектора состояний, т. е. в форме B). Переход
к соотношению A) обычно требует построения функции Грина для данной системы
дифференциальных уравнений.
Классификация систем. Будем считать в дальнейшем, что внешнее воздейст-
воздействие f (t) и, следовательно, состояние системы u (t) являются случайными процес-
процессами, а операторы L и Н (если не оговорено) — детерминистическими; соответствую-
соответствующие системы также будем называть детерминистическими системами в отличие
от стохастических, свойства которых также случайны.
Систему, описываемую уравнением A), называют линейной, если для любых
fj, fjeFn произвольных чисел аь а2 выполняется условие
Н (a.
В противном случае систему называют нелинейной. Линейность дифференциаль-
дифференциальных уравнений и дополнительных условий относительно и (I) еще не означает линей-
ности оператора Н. Так, параметрические системы нелинейны по отношению к пара-
параметрическим возмущениям, что находит отражение, например, в методах их анали-
аналитического исследования (см. гл. XIX). Как и в теории детерминистических колеба-
колебании, вводятся понятия о стационарных и нестационарных системах, о системах
с конечным, бесконечным счетным и континуальным числом степеней свободы. Опера-
Операторное уравнение B) для распределенных систем обычно реализуется в виде диф-
дифференциальных уравнений в частных производных с соответствующими граничными
и начальными условиями. Поэтому применительно к задачам случайных колеба-
колебаний распределенных систем применяют также термин стохастическая краевая
задача.
Классификация задач теории случайных колебаний. Основная (первая) задача
заключается в отыскании вероятностных характеристик состояния системы по за-
заданным вероятностным характеристикам внешнего воздействия и (или) системы.
Если внешнее воздействие задано вероятностными распределениями, то ставится
задача о нахождении вероятностных характеристик вектора состояния. Если внеш-
внешнее воздействие задано его моментами, например, математическими ожиданиями и кор-
корреляционными функциями, то ставится задача об отыскании аналогичных харак-
характеристик вектора состояния и т. п.
Вторая задача теории случайных колебаний — обратная по отношению к пер-
первой — состоит в отыскании характеристик внешних воздействий по известным веро-
вероятностным характеристикам вибрационного поля. Решение этой задачи может суще-
существенно осложниться при задании неполной информации относительно вибрацион-
вибрационного поля или при наличии случайных помех.
МЕТОД ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 287
Третья задача заключается в определении оператора системы или ее пара-
параметров по известным характеристикам на входе и выходе системы. Эту задачу назы-
называют задачей идентификации. Если структура системы и часть ее параметров из-
известны, то цель задачи состоит в отыскании остальных параметров. Такие задачи
возникают в технической диагностике и, в частности, в вибрационной диагностике,
где на основании измерений и надлежащей статистической обработки вибрационного
поля делают заключения о техническом состоянии системы и о ее надежности.
Четвертая задача предусматривает синтез систем, обладающих заданными
свойствами по отношению к некоторому классу внешних воздействий. Пример такой
задачи — подбор оптимальной структуры и оптимальных параметров виброзащиг-
ных систем при случайных воздействиях (см. гл. XXI).
2. МЕТОД ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ОТНОСИТЕЛЬНО
МОМЕНТНЫХ ФУНКЦИЙ
Стационарные линейные системы с конечным числом степеней свободы. Ниже
будут рассмотрены методы решения основной задачи применительно к системе урав-
уравнений
i f. C)
Здесь u (t) — вектор обобщенных координат (матрица-столбец размерностью и);
f (/) — вектор обобщенных сил той же размерности; А, В и С — постоянные матрицы
(соответственно инерционная, диссипативная и квазиупругая). Случай переменных
коэффициентов представляет особые трудности и будет рассмотрен отдельно в гл. XIX.
Векторы u (t) и f (t) являются случайными процессами. Уравнения C) рассматри-
рассматривают либо совместно с начальными условиями, либо (для стационарных процес-
процессов) совместно с условиями стационарности, требующими инвариантности вероят-
вероятностных характеристик процессов u (t) и f (/) относительно выбора начального мо-
момента времени.
Матрицы А, В и С будем считать детерминистическими. Если же они случайны,
то решение задачи можно разбить на два этапа: на первом рассмотреть условные
процессы в системе с заданными матрицами А, В и С; на втором этапе перейти к без-
безусловным процессам, применяя формулу полной вероятности или производя осред-
осреднение по всему ансамблю систем со случайными параметрами.
Дифференциальные уравнения относительно моментных функций. Оператор L
для системы C) — линейный, стационарный и детерминистический. Он переставим
с оператором осреднения по ансамблю реализаций процесса u (t). Для получения
дифференциальных уравнений относительно моментных функций перемножаем
уравнения B) при различных tlt t2,..., затем осредняем почленно результат:
D)
L L L (u ft) u (t2) u (ts)) = (f ft) f (t2) f (t3))
ti t% tz
Здесь L — оператор, действующий на функции переменной tk, т. е. переводящий
процесс и D) в процесс f (tk). Первое уравнение D) связывает математические ожи-
ожидания входного и выходного процессов. Остальные уравнения связывают моментные
функции второго, третьего и т. д. порядков. Если u (t) и f (t) — векторные процессы,
то произведения в уравнениях D) должны трактоваться как прямые (тензорные)
произведения. Например, произведение u (t{) и (t2) есть квадратная матрица раз-
размерностью п X п, составленная из упорядоченных попарных произведений компо-
компонентов иь @, так что второе уравнение D) имеет вид
п п
2 Ц LjaLw (ua (h) up (h)) = <J} ft) /* (t2)) (/, *= 1, ... , n).
a=l 8=1 *i '•
288 СИСТЕМЫ С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
Решения уравнений D) должны удовлетворять начальным условиям, которые
получаются из аналогичных условий для u (t), или (для стационарных процессов)
условиям стационарности.
Дифференциальное уравнение для корреляционной функции одномерного процесса.
Для корреляционной функцииК„ (tlf t2) одномерного процесса u (t) имеем уравнение
LLKU (tu tJ^Kfih, t2). E)
Здесь Kj (tu t2) — корреляционная функция для одномерного процесса / (f). Урав-
Уравнение E) — дифференциальное уравнение в частных производных. Если начальные
условия для и {t) — нулевые, то дополнительные условия для функции Ки (t\, 4)
При отыскании стационарной реакции системы на стационарное внешнее воз-
воздействие введением новой переменной т = t2 — tt уравнение E) приводится к обык-
обыкновенному дифференциальному уравнению относительно функции Ки ($)•
Пример. Пусть уравнение C) имеет вид
а + 2гй + alu = / (<), F)
где Шо — собственная частота; е — коэффициент демпфирования. Уравнение E) для этого слу-
случая будет
\- 2е (- и2 I | Ь 2е —
6t\ dtt V \ 5<j a;.
Для стационарных процессов корреляционные функции процессов и (/) и / {t) связаны
уравнением
Функция Ки (т) и ее производная должны быть ограничены на бесконечности; кроме того,
функция Ка (т) должна быть четной. В качестве простейшего примера возьмем процесс/(<)
в виде белого шума с интенсивностью s. Тогда
Kf (х) = s6 (т). G)
Ищем решение однородного уравнения на отрезке @, со) с начальными условиями
dK,. d'K,, 1
? W +
и с условием ограниченности на бесконечности. В результате находим
*« (Х) = 4Ш ^ Х ' (C0S V + ^ sit)
где сор = ((о2 — е2) /з — собственная частота системы, вычисленная с поправкой на демпфиро-
демпфирование (е < о>о).
3. МЕТОД ФУНКЦИЙ ГРИНА (ИМПУЛЬСНЫХ ПЕРЕХОДНЫХ ФУНКЦИЙ)
Интегральная связь моментных функций входного и выходного процессов.
Если оператор L в уравнении B) — линейный дифференциальный оператор, то опе-
оператор Н в уравнении A) является линейным интегральным оператором типа Воль-
терра с матрицей Грина Н (t, т) (см. гл. VI). Запишем уравнение A) в форме
u(Q = Hf(T). (9)
т
Здесь нижний индекс равен аргументу у f (т), верхний индекс — аргументу у u (Q.
В компонентах получаем
п t
«, @=21 $*/*('. т)/*(т)Л 0 = 1 л). (Ю)
I
X
U (ti) U (/2)) =
u(^...u(/m
(ТГ
Ti
)>=
'2
H (f
T2
'1
= H..
Ti
%)
tm
. H
Tm
f(T2)>;
(f (Tj) ...f (Xm)).
МЕТОД СПЕКТРАЛЬНЫХ РАЗЛОЖЕНИЙ 289
Для вывода операторных соотношений между моменгными функциями входного
и выходного процессов нужно перемножить уравнения (9) или A0), записанные
для различных аргументов tlt t2, ..., и осреднить результат:
(И)
Здесь, как и в дифференциальных уравнениях D), произведения трактуют как пря-
прямые (тензорные) произведения. Например, второе соотношение A1) записывают
в виде
п п ti t2
(и, ft) uk (t2)) =2 2j S \ hia(h,i\)y>
a=l E=1 _co —00
X /ЗД (t2, т2) </„ (Ti) /p (t2)> dTj dx2 (/, *= 1 n).
Аналогичные соотношения можно записать для взаимных корреляционных
функций входного и выходного процессов:
п п /i t2
J a=l|5=l— 00 — 00
Применение метода к стационарным процессам. Для стационарных систем
элементы матрицы Грина зависят только от разности аргументов: hjk (t, x) = hlti (t—т).
Если внешнее воздействие является стационарным и стационарно связанным, то вы-
выходной процесс будет обладать такими же свойствами. Переходя в формуле A2)
к новым переменным t2 — tx = т, tx—ti= $ъ t2—т2 = 92, получим
п п оо со
S«*(T)=2 2 ИА'«(81)Л/
a=lp=l0 о
j (т + e1 62)de1dd2 (/, k=l, ... , п). A3)
Пример. Рассмотрим одномерные процессы и (/) и f (t), связанные дифференциальным урав-
уравнением F). Переход от дифференциального уравнения к интегральному осуществляется с по-
помощью функции Грина h (t — т) в форме и (t) = J h (t — т) f (t) dx. Для корреляционной
— со
функции выходного процесса при заданной корреляционной функции процесса f {t) в виде G)
после вычисления интегралов в A3) приходим к формуле (8), полученной методом дифферен-
дифференциальных уравнений относительно моментных функций.
4. МЕТОД СПЕКТРАЛЬНЫХ РАЗЛОЖЕНИЙ
Сущность метода. Пусть входной процесс f (t) допускает каноническое интег-
интегральное разложение типа B6) [см. гл. XVII]
оо
// « = if, @) + \ F,- (со) Ф/ (t, со) dco (/ = 1 п),
— со
причем спектры F/ (со) удовлетворяют условию стохастической ортогональности
(Ff (со) Fk (to')) = i/;/fc (со) б (со-со').
Ю п/р, Болотина В, В, т. 1
290 СИСТЕМЫ С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
Взаимные спектральные плотности S/,/fc(w) процесса f (t) связаны с взаимными
корреляционными функциями соотношениями
со
Kf,fh Сь к) = J S!jfk (to) ФГ (h, со) ФА (*2, со) Ло. A4)
— со
Решение уравнения B) ищут в форме
п со
и, @ = <иу @) + 2 $ ^ N V С ш) rfM- A5)
k= 1 _ со
Детерминистические функции i|?/fc (^, со) находят из решения системы уравне-
уравнений
п
? 4°№a.k = &j№ {j, k=\, ... ,п) A6)
а=1 <
с соответствующими начальными условиями, взятыми в той же форме, что и для
процесса u (t). Взаимные корреляционные функции выходного процесса
К„/Вк (h, к) = |] J] J Sfaf (со) ^« ft, со) %р D, со) dco (/. k = 1, ... , я).
A7)
Пример. Рассмотрим применение этого метода к нестационарным процессам. Пусть движе-
движение колебательной системы описывается уравнением F). При t < 0 система находится в покое,
а в момент времени i — 0 начинает действовать случайная нагрузка, заданная в следующем виде:
I" 0 (* < 0),
(. -со
Уравнение A6) при этом принимает вид
а начальные условия будут нулевыми. Решение г|) (/, со) легко получается методом вариации
произвольных постоянных
i]> (<, га) = 5 ^
cos + 2ieo) — и2
Для корреляционной функции выходного процесса после вычисления интеграла в A7) по
теореме вычетов при S, (со) = s/2n получим
«а Сг У -^r{e~e'h~h] [cos ие С. - h) + ^ -"
_ г-«С + '•> [cos соЕ (/2 - tl} + ± sin «e (/, +
Для моментов времени, удовлетворяющих условию /t + t2 > , ^, — t2 |, это выражение совпа-
совпадает с полученным ранее (8), что соответствует установившейся реакции системы на стационар-
стационарное воздействие.
5. СТАЦИОНАРНЫЕ КОЛЕБАНИЯ ЛИНЕЙНЫХ СИСТЕМ
Применение метода спектральных представлений. Стационарный и стацио-
стационарно связанный векторный процесс f (t) допускает каноническое спектральное раз-
разложение в форме
со
h W = (fj W> + J F, И e'w! *o (/= 1 я). A8)
СТАЦИОНАРНЫЕ КОЛЕБАНИЯ ЛИНЕЙНЫХ СИСТЕМ 291
Базисные функции \|)а/, (t, со), определяемые как частное решение системы
уравнений A6), имеют вид
Фа* С. «) = Я а* (/«) ехР ('«0.
где Яай (г'со) удовлетворяют уравнениям
^ L;-a (ia) Hak (ia) = 6yft.
Функции Lyj (ico) есть результат действия оператора L на функцию е'га . Их
можно трактовать так же, как образы Фурье операторов Ljk. Например, для опе-
оператора L, заданного в форме C), функции L^ (ia) определяются как Ljk (ia) =
= Cj/г + tobjk ¦— (ifiajii, где ajk, bj^ и Cj^ — соответственно элементы матриц А, В
и С. В задачах теории колебаний функции Lj^ (ia) имеют смысл динамических
жесткостей. Функции Н^ (ia) (элементы матрицы Грина Н в пространстве Фурье),
называемые передаточными функциями системы или динамическими податливостями,
вычисляются как элементы матрицы, обратной матрице динамических жесткостей.
Таким образом, приходим к следующей форме записи разложения A5) для
стационарных и стационарно связанных выходных процессов:
uj (f) = (uj @> + 2 j Ft (со) Hlk (to) e^' fa (j = 1 п). A9)
4= 1 — оо
Разложение A9) обычно записывается в виде
со
и/@ = <«/@)+ I Ui((y>)eia'd&. B0)
— со
Спектры выходного процесса Uj (а) связаны со спектрами входного процесса
Fj (а) алгебраическими уравнениями
(/,(«)= J] W/fc(to)Fs(«)
или в обратной форме
В силу стохастической ортогональности спектров F;- (со) спектры U/ (со) явля-
являются также стохастически ортогональными:
(U* (ш) Uk (w')) = Sajak (со) б (со-со'), B1)
а взаимные спектральные плотности SUJIIIl (со) и S^ft (со) связаны соотношениями
UJIIIl
•V* N =¦ 2] 2] ^^ ('») Я*3 (М S/a/« И B2)
или
V* 2]
a=l
2 2 ^)i*p(to)SeeB ((o) = S/>/ft((B). B3)
10*
292 СИСТЕМЫ С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
Взаимную корреляционную функцию К,у„А (т) находят путем преобразования
Фурье взаимной спектральной плотности выходного векторного процесса:
со
К«у«*(т)= $ SUjUk (со) е'°« Ло. B4)
— со
Метод спектральных разложений для процессов, удовлетворяющих условиям
стационарности, позволяет довольно просто находить вероятностные характери-
характеристики производных случайного процесса. Например, по известным взаимным спек-
спектральным плотностям S,, -i,k (а) находят взаимные корреляционные функции обоб-
обобщенных скоростей и ускорений:
со
К... (т)= [ co2S (со)е'атЛо;
U;Uu J "/«ft
"/«ft
— СО J
CO
К.... (т)= С co4S (и) e/fi>t doi.
B5)
Пример. Предположим, что система уравнений C) допускает полное разделение обобщенных
координат, что соответствует приведению исходной системы к главным координатам при неко-
некоторых ограничениях на свойства матрицы В (см, гл. VI). Запишем эти уравнения в виде
-щ- + 2ej чг + *)и1 -'/(t) у =' ">•
где йь и е- — парциальные собственные частоты и коэффициенты демпфирования. Функции
Wy? (ta) и L^ (ico) образуют при этом диагональные матрицы L.,, (ico) = /iT^ (ico) = L• (ш) б.-ь
где L, (ш) = coy + 2<есо — со2. Тогда B2) и B3) можно привести к виду
s (ш) V*(ю)
По известным взаимным спектральным плотностям вычисляют взаимные корреляционные
функции выходного процесса и его производных по формулам B4), B5), а также дисперсии и
корреляционные моменты Последние находят по формуле
со S,, (со) day
>= I .» • <26>
Вычисление корреляционных моментов. Интеграл в правой части B6) берется
по теореме вычетов. В табл. 1 приведены выражения К„,а)) @) для различных типов
спектральных плотностей S<.fk (со). При этом принято, что $f-fk (со) = Sf (со) — дей-
действительная функция частоты со. Это будет иметь место, например, если процессы
Ь (О и /* @ отличаются постоянным множителем. Как частный случай в таблице
содержатся значения дисперсий KUj @) компонентов выходного процесса. В этом
случае нужно положить со,- = wk = coo, ej = 8^ = 8.
Вычисление интегралов типа B6) по теореме вычетов при числе полюсов в верх-
верхней полуплоскости, большем двух, довольно сложно. Для случая / = k и дробно-
рациональных спектральных плотностей S^ (со) интеграл B6) сводится к сле-
следующему:
1 r> gjn (/со) dco
К''/@)=27Г 3 1,п(-шI,-п(Ш)' B?)
- со
где
1/п (х) = а/охп + оцх" ~ 1 +... + aJn;
СТАЦИОНАРНЫЕ КОЛЕБАНИЯ ЛИНЕЙНЫХ СИСТЕМ
1. Корреляционные моменты обобщенных координат
293
2а
' (со2 -
а2
2
Sf (со)
s/2n
о2 а
я а2 + со2
я х
а2 + ю|
0J - а»J + 4а2ша
б (' о) | — соо)
2s
Ak(a)
-+
K*j uk @)
е/ + е6
-Г ¦¦¦ Cm8 гл1\' I
¦с • °/ft Vм/ ak) 1
/ft
С.. + 4cc -fe-0) ,* + ef to]
_/« I J j l К "
X [<x! + 2a (e;. + e
су* (и/ + 2е/а + а2)(°
'— ~ Гf)
,_ (E,/ + ?/j) Mfte
o'fte == l^ ^A — ^й co^
о" Г 8a CoJ + а2} В ..
V о ' / j/г
= ('col — el — со2J + (e. + a
X (»ft-eft + coj;
= fy(-«)/A(«) + 4»S(e/ +
fy (a) = ®l - co| + 2E/a
'/ 2 2\2 1.2 21 Г/ 2
(o)ft-oH) + ^co0j [(co;-
4(.y
)
fteeft
' AJ
)' + 2
h4 (a
2E* +
a) fft
-a2
.«.J.y.
+ eJx
+ e,)x
Efta + a^)
—Va .
ft
4.
(a)J'
(eft + aJ x
-«) +
-*
-4e;4]
причем все корни полинома /у„ (д:) лежат в левой полуплоскости. Очевидно, что
интеграл B7) рационально выражается через коэффициенты а^ и Ъ^ полиномов
ljn М и ё)л W:
/г rm (~ 1)д+1 Dab
К@) 7
2a
/0
B8)
где ?>а — определитель n-го порядка (Da = det {dap})- Элементы dap выражаются
через коэффициенты aj^:
Bа-р<0, 2а-Р>п).
Определитель Doi, получается из Da заменой элементов первого столбца коэф-
коэффициентами b/i, bj%, ..., bjn.
294 СИСТЕМЫ С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
Интеграл B7) можно вычислить также рекурентно:
если представить полином gin (х) виде
gjn М = //я (*) fjn(—x); fjn (x) = спх"-! + .•• + cjn.
Коэффициенты в B9) связаны с а^ и су; рекуррентными соотношениями [80]
ujQ, k ~ 1 ^ fylk == ®j'2> k +1 ^y. йч 1^/3. ,
Вычисления по формуле B9) могут быть проведены при помощи подпрограммы COLOSS
(А, В, N, IERR, V, IN) [80]. Здесь А, В — векторы коэффициентов полиномов I- и f. со-
соответственно; N —порядок полинома /. ; IERR = 1, если a-0>0, IERR = 0, если a,Q < 0;
IN —длина вектора А; V — выходное значение интеграла
Учет взаимных корреляций обобщенных координат. Корреляционные момен-
моменты Kn-uk @) в общем случае зависят от параметров затухания в^, е,/,, парциаль-
парциальных частот coy, (Од, и характера спектральных плотностей S /.-/ft(w)> действительную
часть которых можно охарактеризовать параметром остроты максимума а и некото-
некоторой преобладающей частотой воздействия ш0 (см. табл. 1).
Анализ формул для К,,.-,,^ @) и К,,.- @) позволяет сделать некоторые выводы
относительно условий, когда взаимной корреляцией обобщенных координат можно
пренебречь, т. е. когда
K,,j,,k @) < Ка, @) (/ Ф k). C0)
Предположим, что выполняются условия е,- ~ е^ ~ в, |@у — «J
ф C0)
(co
y
е
+
р у , ^ , у J ^ (y
Если а велико, то при малом демпфировании условие C0) выполняется, если е^ -^
<^ (со,- — wfeJ, т. е. частоты должны быть не слишком близки друг к другу.
Если |шу — со/,1 ~ (шу + шА) /2, то условие C0) будет удовлетворено при малом
демпфировании.
Если а ~ е, то условие C0) выполняется при близости частоты со0 к одной
из собственных частот и (или) при значительном удалении собственных частот
друг от друга.
В остальных случаях взаимной корреляцией пренебрегать нельзя. Исследо-
Исследования показывают, что при малом демпфировании вкладом мнимой части взаимной
спектральной плотности обобщенных сил можно пренебречь при выполнении усло-
условия 8 <^ |«у — (D^l.
6. МЕТОДЫ ТЕОРИИ МАРКОВСКИХ ПРОЦЕССОВ
Вводные замечания. Методы, основанные на теории марковских процессов,
позволяют в некоторых случаях найти распределения выходных процессов. При
использовании теории непрерывных марковских процессов (см. гл. XVII) необ-
необходимо наложить некоторые ограничения на вид оператора L и внешнее воздейст-
воздействие f (t) в уравнении B).
Одномерные процессы. Для того чтобы уравнение B) описывало одномерный
марковский процесс, дифференциальный оператор L должен иметь первый порядок,
а внешнее воздействие должно быть белым шумом. Запишем уравнение B) в виде
u + h(u,t)^[(t), C1)
МЕТОДЫ ТЕОРИИ МАРКОВСКИХ ПРОЦЕССОВ 295
где / (t) — нормальный белый шум с интенсивностью s: (/ @) = 0, (/ (t{) f (t2)) =
= s6 \t.t — tj); h (u, t) — детерминистическая функция. При этом интенсивности
марковского процесса
Kj = — A (u, t); K2 = s.
Функция h (и, t) в C1) имеет смысл коэффициента сноса, взятого с обратным
знаком, а интенсивность белого шума s равна коэффициенту диффузии. Уравнение
Фоккера — Планка — Колмогорова принимает вид
Если оператор L задан в форме
й + 2гй+к (и, 0=/@> C2)
то даже в том случае, когда / (f) — белый шум, выходной процесс и (t) не будет мар-
марковским процессом; но он может рассматриваться как компонента двухмерного
марковского процесса в фазовом пространстве. Полагая at = и (t); u2 = и (t),
вместо C2) получим
и2 =— 2eu2 —Л {и,
Система уравнений C3) описывает двухмерный марковский процесс u (t) =
= {%(/); u2{t)}.
Многомерный выходной процесс. Уравнение B), записанное в виде
uj + 2sjuj + hj(u, t)=fj (/=1, ... , ft), C4)
описывает выходной процесс u (f), который совместно с процессом й (() можно рас-
рассматривать как 2л-мерный марковский процесс, если входные воздействия являются
стационарными белыми шумами:
<fj @) = 0; (/у @ h if+т)) = sjk8 (т).
Вводя обозначения х;- = uj (t); xn+j = uj (t), уравнения C4) перепишем в виде
xn+j = ~~2exn+j — hJ(x1, ...xn, f)+fj (/' = 1, ... , ft)
или
у и' /у. у А _1 Г (Ь^^Х 2fl\ C5^
где
(k ~fi),
¦' _ ( *ПА
/0 (k^n),
^ ] /; (и <Z k < 2/2)
Входной белый шум |/г (t) будет иметь интенсивности
Sj_n, k~n (ra < /. k =? 2n).
Уравнение C5) описывает 2п-мерный марковский процесс, интенсивности кото-
которого
Уравнение Колмогорова принимает вид
2п 2л 2/1
рр (х> 0 V1 д /<,' ' V V д*Р /чк\
—д7 """ — / д— \lkp) ~\~ ~с)~ / / Cjk ~^—д~— \ ty
296 СИСТЕМЫ С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
или, после перехода к первоначальным обозначениям,
п
др (и, и, t)
Ft
¦ = У [— и
/= i
i=\4=1
, , , .. ар] . 1 v v д*р
7. МЕТОД СТАТИСТИЧЕСКОГО МОДЕЛИРОВАНИЯ В ЗАДАЧАХ
СЛУЧАЙНЫХ КОЛЕБАНИЙ
Общая схема метода. Предположим, что поведение системы описывается one
раторным уравнением B). Требуется найти вероятностные характеристики вектора
состояний системы при условии, что вероятностные характеристики внешнего воз-
воздействия известны. Ограничимся рассмотрением установившихся стационарных
колебаний системы.
Вычислительный алгоритм метода Монте-Карло для данной задачи можно про-
проиллюстрировать при помощи следующей схемы (рис. 1), которая содержит четыре
основных блока: датчик случайных чисел (ДСЧ); блок моделирования внешнего
воздействия (вход); блок численного решения уравнений, описывающих поведение
Дсч
/
К
вход
Г~ ~\
Параметры
с и стемы
1_ J
\
s
Модель
системы
А СП
Рис. 1. Схема реализации метода Монте-Карло
системы (модель системы), блок анализа случайных процессов (АСП) для опреде-
определения статистических оценок вероятностных характеристик вектора состояний
системы.
В случае, когда параметры системы — скалярные или векторные случайные
величины с известными вероятностными характеристиками, схема должна быть
дополнена блоком моделирования их реализаций (параметры системы).
Воспроизведение реализаций вектора состояний системы. Эта задача может
быть решена различными методами. Если система задается оператором Н и матрица
Грина для него известна, то воспроизведение реализаций u (t) может быть осущест-
осуществлено при помощи численной реализации соотношений A0) для фиксированных
реализаций f (t) и параметров системы. Если система задается оператором L, то вос-
воспроизведение реализаций u (f) производится путем интегрирования уравнения C)
методом Рунге — Кутта или другими численными методами.
При воспроизведении стационарных реализаций последовательностей и (tn) =
= и (п АО шаг дискретизации At, длительность начального интервала Та = jV0A^
и интервала наблюдения Г* = NAt выбирают из условий At <J Т, То ;> t0, Т„ ^> т#.
Здесь Т — характерный период колебаний (например, период, соответствующий
высшей парциальной частоте системы); t0 — интервал затухания переходных про-
процессов; т, — интервал корреляции выходных процессов. Начальные участки реа-
реализаций при определении статистических оценок вероятностных характеристик,
соответствующих стационарному решению, не используют.
Статистический анализ выходных последовательностей. Вопросы определения
статистических оценок вероятностных характеристик случайных последователь-
последовательностей достаточно полно освещены, например, в [6, 51, 99]. Поэтому ограничимся
МЕТОД СТАТИСТИЧЕСКОГО МОДЕЛИРОВАНИЯ 297
рассмотрением простейших оценок вероятностных характеристик последователь-
последовательностей {«„} = и (tn) (п= 1 N).
Оценки для функции распределения и плотности вероятности. Используя
N значений реализации последовательности {ип}, оценки для одномерной функции
распределения F (и) и одномерной плотности вероятности р (и) могут быть полу-
получены по формулам
F (u)^F (u)=l/V(«); C7)
t-. i C8)
где N (и) — число элементов, меньших и. Рационально принимать Ахи = А2и = -~- Аи .
Тогда C8) можно записать в виде
p(u)J(u\/{u-]; C9)
здесь
Средние квадратические погрешности оценок C7), C9) в случае статистически
зависимой последовательности
и и
L *} J J
п >т — со — оэ
И
п > т u_ u_
где AF = F (u+)-F (и_).
Близость эмпирического распределения к теоретическому оценивают при по-
помощи статистических критериев согласия [51, 99].
Оценки математического ожидания, корреляционной и взаимной корреляцион-
корреляционной последовательностей. Несмещенной оценкой математического ожидания после
довательности {«„} является статистическое среднее
N
1
Дисперсия этой оценки равна
N
= лг 2 В|- D2)
N
D[<")|=4 2 О-тгКю. D3)
/ = _ ЛГ
Оценки корреляционной и взаимной корреляционной последовательностей
(соответствующих аналогов корреляционных функций) двух стационарных и ста-
стационарно связанных последовательностей {«„}, {vn\ находят по формулам
N — \ И
Kv^^N-lll 2 Umum+\l\i D4)
здесь a = max A,1 — /); b = min (N, N — I); um= um — («т>.
298 СИСТЕМЫ С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
Математические ожидания оценок D4), D5)
(Ka(l))=Ku(t)-2zulll + zuo-
D6)
где
N — n N
1 у \
J V
2 Кп{р->пУ,
1
Ь N
Zw\l\~N (N-\l\)
m = a p = )
Для гауссовских последовательностей дисперсии оценок D6)
/v - \
« WJ =
1
N-[H
I / I - N
i_
N - |
m= | i I _ N
D7)
Из формул D6), D7) следует, что оценки D4), D5) являются асимптотически
несмещенными и состоятельными.
Оценки спектральных плотностей стационарных случайных последовательно-
последовательностей. Оценки спектральных и взаимных спектральных плотностей стационарных
случайных последовательностей {и„} (п = 1, 2, ,.., N) получают обработкой перио-
периодограмм — функций безразмерной частоты
D8)
N N
где Uc = ^ и„ cos na; fs= ^ un sin па.
п=1 л=1
Математическое ожидание и дисперсия оценки D8) соответственно равны
N
л. 1
<SH(co)) = 2T
п = — N
N -
DP« (u))J= <Л„
N — \т
т = I — N
N - 1
X
I X
m = 1 — N
Л/ - \т\
X
I ml -|2
sinBn+|ffl|)(o .
=1 J
D9)
Периодограмма Su (со) является асимптотически несмещенной, но несостоятель-
несостоятельной оценкой спектральной плотности. Периодограмма представляет собой сумму
ОПРЕДЕЛЕНИЕ СТОХАСТИЧЕСКОЙ УСТОЙЧИВОСТИ ?99
математического ожидания и быстроколеблющейся около нуля функции. Поэтому
состоятельною оценку спектральной плотности можно получить только путем отфиль-
тровывания быстроменяющейся составляющей.
Оценки для взаимной спектральной плотности последовательностей {и„\ и {vnj
(п — 1 iV) могут быть получены при помощи периодограмм
$»v(a) = 2^l(UcVc + UsVs) + l(UsVe-UeVs)]. E0)
Здесь
N N
Uc= 2 «„cosruo; Ус= ^ uncos паз;
N N
Us= 2 ип sin псо; Vs— ^ vn sin nco.
rt= 1 л = 1
Применение стандартных программ. При решении задач о случайных колеба-
колебаниях методом статистического моделирования с использованием ЭВМ серии ЕС
могут быть использованы подпрограммы RANDU, GAUSS, RKGS, AUTO и CROSS.
Описание подпрограмм RANDU и GAUSS приведено в гл. XVII. Эти под-
подпрограммы могут быть использованы для воспроизведения реализаций внешних
воздействий на систему f (t).
Для воспроизведения реализаций вектора состояний системы u (t) путем инте-
интегрирования уравнения C) может быть применена подпрограмма RKGS [61]. При
этом уравнение C) предварительно должно быть преобразовано к системе обык-
обыкновенных дифференциальных уравнений первого порядка.
Вычисления статистических оценок вероятностных характеристик реализаций
состояний системы могут быть проведены с использованием подпрограмм AUTO
и CROSS.
Подпрограмма AUTO вычисляет оценку D4). Обращение к подпрограмме AUTO
осуществляется следующим образом: CALL AUTO (A, N, L, R, S). Здесь А —вход-
—входной вектор, содержащий последовательность {«„} (я = 1, . , N); L —запаздывание
0, 1, ..., L — 1; R — выходной вектор длины L.
Подпрограмма CROSS вычисляет оценку D5). Обращение к подпрограмме
CROSS осуществляется следующим образом: CALL CROSS (А, В, N, L, R, S).
Здесь А, В — входные векторы, содержащие последовательности {ип}, {vn\ соот-
соответственно; L — запаздывание; R, S — выходные векторы длины L (R соответствует
запаздыванию по {vn}, S —запаздыванию по {«„})•
Глава XIX
ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ
ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
1. ОПРЕДЕЛЕНИЯ СТОХАСТИЧЕСКОЙ УСТОЙЧИВОСТИ
Понятие о параметрически возбуждаемых случайных колебаниях. В гл. VII были
рассмотрены параметрические колебания в линейных системах, возбуждаемые детер-
детерминистическими воздействиями В технических приложениях часто встречаются
также случайные параметрические воздействия. Любой пример из первой части
(гл. VII) можно сформулировать в терминах теории случайных колебаний, если
параметрическое воздействие является случайной функцией времени.
К случайным параметрическим воздействиям, которые могут поддерживать
незатухающие колебания системы типа параметрических резойансов в соответствую-
соответствующих детерминистических системах, относят, например, стационарные и периоди-
периодически нестационарные воздействия. Распространение теории параметрических
300 СЛУЧАЙНЫЕ ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ
колебаний на стохастические системы требует введения определений стохастиче-
стохастической устойчивости, которые могут быть введены по-разному [56, 122]. Наиболее упо-
употребительные из них приведены ниже.
Устойчивость по вероятности. Пусть состояние системы в каждый момент вре-
времени t описывается случайным вектором х (t) в некотором фазовом пространстве U.
Эволюция системы описывается дифференциальным уравнением
^ = Н(х,0х, A)
где Н ¦— матрица соответствующей размерности с элементами — случайными функ-
функциями времени. Эта матрица может также зависеть от х (f). Пусть уравнение A)
имеет тривиальное решение х (t) s 0. Начальное условие
х(д=х0 B)
будем считать детерминистическим. В пространстве U введем норму ||х||. По анало-
аналогии с классическим определением устойчивости по Ляпунову (см. гл. V) введем
определение устойчивости по вероятности. Решение х (t) = 0 стохастического урав-
уравнения A) называют устойчивым по вероятности, если для любых 8 > 0, р > 0
можно найти такое б (8, р) > 0, что
||хо||<б=>Р{ sup ||х@11<е}>1-р- C)
to<t<cc
Смысл соотношения C) состеит в том, что при устойчивом решении х (f) s 0
начальные возмущения всегда можно выбрать такими, что вероятность больших
отклонений системы при t^>t0 от начала координат будет меньше любого наперед
заданного значения р > 0.
Решение х (t) = 0 называют асимптотически устойчивым по вероятности,
если оно устойчиво по вероятности и, кроме того, при любом е > 0 выполняется
условие
lim Р{||х@||<е} = 1. D)
/->00
Аналогично вводят понятия неустойчивости по вероятности, устойчивости
по вероятности на ограниченном интервале времени и т. п.
Устойчивость по математическому ожиданию нормы и родственные определе-
определения. Некоторые определения могут быть введены на основе числовых характеристик,
связанных с вероятностью, которая входит в определение C).
Решение х (t) = 0 называют устойчивым по математическому ожиданию нормы
||х|| в пространстве U, если для любых е > 0 можно найти б (е) > 0 такое, что
||хо||<6=Э sup <||x(<)||><e. E)
/0 < t < со
Решение х (t) = 0 называют асимптотически устойчивым по математическому
ожиданию нормы ||х||, если оно устойчиво по математическому ожиданию нормы и,
кроме того, выполняется условие
lim <|| х @11)= 0. F)
/->00
Решение х (t) = 0 называют экспоненциально устойчивым по математическому
ожиданию нормы ||х||, если существуют такие постоянные С > 0 иа>0, что при
любом t > t0
<1|х(О1|>=?=С||хо||е-а<'-'»>. G)
Обычно норму в U вводят соотношением
1/р
2 • P=sl- (8)
.*=! /
В этом случае говорят о р-устойчивости. При р = 2 имеем устойчивость в среднем
квадратическом.
МЕТОД СТОХАСТИЧЕСКИХ ФУНКЦИЙ ЛЯПУНОВА 301
Устойчивость по совокупности моментных функций. Рассмотрим моментные
функции случайного векторного процесса х (t): моменты первого порядка (мате-
(математические ожидания компонентов), моменты второго порядка (математические
ожидания квадратов и попарных произведений компонентов) и т. д., используя
для этого обозначение
тт ... (t) = (xf(t)xk(t)xi(t)...), (9)
р раз
где число индексов означает порядок момента. Сформируем вектор моментных
функций до порядка г включительно [122]:
mr(i) = {m1(t), m2(t), ... ; ти (t), mn{t), ... ; ...}. A0)
Его размерность существенно уменьшается, если использовать свойства сим-
симметрии моментных функций (9). Соответствующее евклидово пространство обозначим
через Мг. Норму вектора тг обозначим через ||mr||, причем
. (И)
г раз
Решение х (t) = 0 называют устойчивым по совокупности моментных функций
до порядка г включительно, если для каждого е > 0 можно найти такое S (е) > 0,
что
|| т, (*„) ||< 6 =Э sup ||тг@||<е. A2)
to < t < СО
Решение х (t) = 0 называют асимптотически устойчивым по совокупности
моментных функций до порядка г включительно, если оно устойчиво по этой сово-
совокупности и, кроме того,
lim || nv @11=0. A3)
t-+ оо
В дальнейшем будем использовать термины устойчивость и асимптотическая
устойчивость в пространстве Мг.
Связь между определениями стохастической устойчивости. Между некоторыми
из введенных определений существует связь. Например, если решение устойчиво
в среднем квадратическом, то оно устойчиво по вероятности (обратное утвержде-
утверждение, вообще говоря, неверно). Устойчивость в пространстве Мх по существу эквива-
эквивалентна устойчивости в среднем, а устойчивость в пространстве М2, грубо говоря,
отвечает совокупности требований устойчивости в среднем и среднем квадратиче-
квадратическом. В формулировку условий устойчивости по совокупности моментных функций
входит математическое ожидание от нормы моментов в начальный момент времени,
что включает в рассмотрение случайные начальные условия.
2. МЕТОД СТОХАСТИЧЕСКИХ ФУНКЦИЙ ЛЯПУНОВА
Общая характеристика метода. Классический метод функций Ляпунова исполь-
используют для получения строгих достаточных (иногда необходимых и достаточных)
условий устойчивости и неустойчивости. В основе метода лежит идея построения
таких функций, по знаку производных которых вдоль фазовых траекторий можно
судить об устойчивости невозмущенного движения. Если система является сто-
стохастической, то необходимо исследовать поведение всего множества реализаций,
смежных с невозмущенным движением [56, 142].
Метод стохастических функций Ляпунова разработан применительно к систе-
системам, эволюция которых представляет собой диффузионный марковский процесс,
рассмотренный в гл. XVII. Существенную роль в этом методе играет производящий
302 СЛУЧАЙНЫЕ ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ
дифференциальный оператор марковского процесса, заданный на множестве функций
v (x, f) от процесса х {I) и времени t:
dv , V dv
+ 2
X X
2 2
где xy — коэффициенты сноса; v.j^ — коэффициенты диффузии [см. C7) в гл. XVII].
Оператор Lv совпадает с оператором обратного уравнения Колмогорова [см. C8)
в гл. XVII], если оно представлено в виде Lp[(x0, t0)] = 0. В литературе по теории
д
случайных процессов производящим оператором называют также оператор L —-^
Выражение Li> имеет смысл производной по времени от математического ожидания
функции v (х, /) при условии, что в момент времени t процесс имеет значение х.
Таким образом, величина Lv характеризует скорость изменения функции v (x, t)
на множестве всех траекторий системы, проходящих в момент времени t через точку
фазового пространства х.
Задача состоит в построении таких функций v (к, t), чтобы по знаку Lv в неко-
некоторой области фазового пространства можно было судить о стохастической устой-
устойчивости. Для этого используют функции, аналогичные классическим функциям
Ляпунова.
Функцию v (x, t), заданную в некоторой окрестности полупрямой х = 0, t 5= t0,
называют положительно определенной (по Ляпунову), если в этой окрестности
выполняются условия v (x, t) = w (х) — 0 при х = 0, v (х, 0 > w (х) ]> 0 при
х =jL 0. Функцией, имеющей бесконечно малый верхний предел (равномерно малой
по х), называют функцию v (x, t), если для любого А > 0 существует такое б {К) > 0,
что при любом t > t0 имеет место || х (t)\\ < б :=> || v (x, t) || < h.
Ниже сформулированы три теоремы об устойчивости решения х (t) = 0 стоха-
стохастической системы дифференциальных уравнений, описывающих непрерывный
марковский процесс х (t) с производящим оператором L [56, 112].
Теоремы об устойчивости по вероятности. Пусть в окрестности х = 0, t ^ t0
существует непрерывная положительно определенная функция v (x, t), принадле-
принадлежащая области определения оператора L и удовлетворяющая при х ф 0 условию
Lv ^ 0. Тогда решение х (t) = 0 устойчиво по вероятности.
Пусть в окрестности х = 0, t >: t0 существует непрерывная имеющая беско-
бесконечно малый предел положительно определенная функция, принадлежащая области
определения оператора L и удовлетворяющая при х^0 условию Lv <; 0. Тогда
решение х (t) = 0 асимптотически устойчиво по вероятности.
Теорема об асимптотической устойчивости линейных систем. Пусть для ка-
какой-нибудь положительно определенной квадратичной формы « (х, t) с коэффи-
коэффициентами — непрерывными ограниченными функциями времени — нашлась ква-
квадратичная положительно определенная форма w (x, t), удовлетворяющая условию
Lv = —w. A5)
Тогда решение х (t) s 0 будет асимптотически устойчивым в среднем квадра-
тическом.
Пример. Рассмотрим простейшую линейную колебательную систему, коэффициент демпфи
рования которой «зашумлен» белым шумом ц? (/) интенсивностью jj.2s:
<г+[27+й1 @1 9 + 9 = 0. A6)
Система, возбуждаемая белыми шумами, может быть представлена также в виде
п
dXj = / (х, t)dt+ ^ eJa (x, t) dta (t) A=1, 2, ..., n), A7)
a= 1
где f (/) — независимые нормальные белые шумы единичной интенсивности; х = (<?, я). Коэф-
Коэффициенты сноса к в зависимости от определения стохастического интеграла можно записать
по-разному. При использовании стохастического интеграла Ито [28]
«, = //(* t). A8)
МЕТОД МОМЕНТНЫХ ФУНКЦИИ 303
Если использовать симметризованный стохастический интеграл Стратоновича [103], то
п п
2 E ё
В первом случае процессы ?а (О называются шумами Ито, во втором — шумами Стратоновича.
Коэффициенты диффузии в обоих случаях
п
jk — ^-j /ct Аи* \ЛУ})
Трактуя белый шум ? @ по Стратоновичу, найдем коэффициенты диффузии и сноса (xt s q,
х2 == q):
х, = *„ х, — дг, - 2у*. + ~ д-«,: \ B1)
И,, = к1г = K2i = 0; У.гг = |A*:j. J
Отсюда производящий оператор A4)
^ д / \ \ д I д2
Применим теорему об асимптотической устойчивости. Квадратичные формы О и w ищем
в виде
где с ? — неопределенные коэффициенты, которые находят из условия A5), т. е.
_ 1 1 / 1 \ _ 1 _ 1
Форма У будет положительно определена тогда и только тогда, если
H!s < 2v. B3)
Это дает достаточное условие для асимптотической устойчивости системы A6) в среднем
квадратическом [112].
3. МЕТОД МОМЕНТНЫХ ФУНКЦИЙ
Основы метода. Метод состоит в исследовании детерминистических дифферен-
дифференциальных уравнений относительно моментных функций процесса. Метод позволяет
исследовать устойчивость стохастических систем в среднем, в среднем квадрати-
квадратическом и т. п., а также устойчивость по отношению к совокупности моментных функ-
функций до некоторого порядка включительно. Применительно к системам, поведение
которых является диффузионным марковским процессом, можно указать два основ-
основных способа получения этих уравнений.
Применение формулы Ито. Пусть процесс х (/) описывается дифференциальными
уравнениями Ито A7). Рассмотрим функцию V (х, t), имеющую непрерывные част-
частные производные до второго порядка включительно по х и первого порядка по t.
Тогда стохастический дифференциал Ито от процесса V (х, t)
п Inn
dV . ц.№ 1 у
а=1/=1А=1
2••?
/1
а=1/=1
Эта формула Ито отличается от формулы дифференцирования сложных функций
в математическом анализе последним членом в скобках перед dt. Для получения урав-
уравнения, содержащего производную от моментной функции rtij^i.... (t) по времени,
достаточно положить V ^Х/х^х;... и провести осреднение левой и правой частей в фор-
формуле B4).
304 случайные параметрические колебания
Применение уравнения Колмогорова. Запишем уравнение Колмогорова
[см. C6) в гл. XVII]:
*". = _
/=1 ' /=1*=1
y°(KlP) + L у у "Ъг , B5)
dt ш~ дх, ' 2 А^ Li dxjdxk v '
Здесь p (x, t) — плотность вероятности вектора х (t), удовлетворяющая некоторым
начальным условиям. Моментные функции myW .. (t) связаны с плотностью веро-
вероятности р (х, t) соотношением
tn,ki... (t) = ] XjXkxt ...p(x, t) dx, B6)
где интегрирование производится по всему фазовому пространству. Чтобы полу-
получить уравнение, содержащее производную от m]kl... (^.необходимо умножить урав-
уравнение B5) на XjX/gX/... и произвести почленное интегрирование. Интегралы в правой
части преобразуются далее при помощи формулы Гаусса — Остроградского с тем,
чтобы правая часть содержала в качестве неизвестных только моментные функции
от процесса х (t). В результате приходим к искомым уравнениям относительно
моментных функций.
Дальнейшее исследование сводится к определению условий устойчивости нуле-
нулевого решения уравнений моментных функций.
Пример. Применим метод моментных функций для линейной колебательней системы A6).
Коэффициенты уравнений A7) для случая белого шума Стратоновича имеют в«д ^ьщ
/2 = — Xi — 2ух2; glt = g12 = gM = 0; g22 = — nYsx2
Применяя один из указанных выше способов, получим уравнения относительно математи-
математических ожиданий т, = A7) и тг s (<?)'
«, B7)
Нулевое решение системы B7) асимптотически устойчиво, если
(A2s < 4v B8)
Это условие накладывает ограничение на интенсивность белого шума в 2 раза менее жесткое,
чем достаточное условие устойчивости в среднем квадратическом B3)
Модифицированный метод моментных функций. Применение метода моментных
функций усложняется, если параметрические воздействия не являются белыми
шумами, например, в случае, когда параметрические воздействия получаются путем
пропускания нормальных белых шумов через некоторые линейные фильтры.
Пусть совокупность процессов, происходящих в фильтрах, описывается вектором
г (/) размерностью пь совпадающей с суммарным порядком стохастических дифферен-
дифференциальных уравнений для фильтров. Введем расширенное (п + п^-мерное фазовое
пространство U' с элементами у (t) = x (t) + z (t).
Эволюция вектора у (t) в пространстве U' будет представлять собой диффузи-
диффузионный марковский процесс. Однако стохастические уравнения B4) для линейных
параметрических систем оказываются нелинейными по отношению к части из ком-
компонентов вектора у (t). Поэтому уравнения относительно моментных функций обра-
образуют бесконечную систему. В уравнения, содержащие производные от моментных
функций низших порядков, войдут моментные функции более высокого порядка.
В связи с этим возникает проблема замыкания, т. е. приближенного сведения беско-
бесконечной системы дифференциальных уравнений к конечной системе. Кроме того, после
замыкания уравнения будут содержать смешанные моменты процессов х (t) и z (f),
которые не входят в определение устойчивости по совокупности моментных функций.
Поэтому вводят модифицированное определение устойчивости.
Гипотеза квазигауссовости. Для замыкания системы уравнений относительно
моментных функций применяют гипотезу квазигауссовости, которая аналогична
гипотезе М. Д. Миллионщикова в теории турбулентности. При замыкании системы
на уровне г все моменты порядка выше г связываются с моментами низших порядков
метоп моментных функции
305
соотношениями, справедливыми для многомерного нормального процесса. Условия
замыкания на уровне г центральных моментов
записываются в виде
... = {(У) — т,) (уи — mk) (yi — т,)...)
(p = 2s+l>r).
B9)
C0)
Сумма, стоящая в правой части, содержит все возможные разбиения 2п индек-
индексов а1; а2 ais (включая повторяющиеся) на s пар {а^Ь {a3ai}---{a2s-ia2s}-
Общее число слагаемых равно Bп — 1)!!.
Гипотеза квазигауссовости может быть сформулирована также в терминах
кумулянтов (семиинвариантов):
C1)
Кумулянты
функцию
следующим образом:
случайного вектора у вводят через характеристическую
\ /= I /
до In ф F)
1 = 0
Замыкание на уровне г = 2 эквивалентно предположению, что действительное
распределение компонентов вектора y(t) близко к нормальному. Весьма правдопо-
правдоподобно утверждение, что повышение уровня замыкания уменьшает ограничения,
накладываемые на распределение; следовательно, повышение уровня должно при-
приводить к повышению точности. Однако модельные примеры и численный анализ
фактического поведения кумулянтов показывают, что это не всегда так. Во всяком
случае, до сих пор не предложено более эффективного способа замыкания [122].
Выражения для начальных моментов процесса через моменты низших поряд-
порядков при различных уровнях замыкания имеют вид
mjklm = 2 ma1a2a3ma 4
+ 2 '
C2)
m;klmn =
Хтазта
В этих формулах суммирование производится по всем перестановкам индек-
индексов /, к, I, т и п, кроме перестановок внутри maia2, maia2a3 и таха2аза^.
Модифицированное определение устойчивости. Рассмотрим вектор m'r (t), ана-
аналогичный вектору моментных функций тг (/), задаваемому формулой A0). Век-
Вектор m'r (t) содержит все моментные функции процесса х (/) и все смешанные моменты
процессов х @ и z (t) до порядка г включительно. Соответствующее евклидово про-
пространство обозначим через М'г, а норму в нем — через [ т'г
306 СЛУЧАЙНЫЕ ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ
Введем следующее модифицированное определение устойчивости по совокуп-
совокупности моментных функций [122]: решение х (f) = 0 называют устойчивым в про-
пространстве М'г для заданного входного процесса г (t), если для каждого е > 0 суще-
существует б (е) > 0 такое, что || m'r (t0) || < б => sup || m'r (t) \\ < ?.
Со < I < со
Решение х (/) =0 называют асимптотически устойчивым в пространстве М'г
для заданного входного процесса z (/), если оно устойчиво в М'г и, кроме того, вы-
выполняется условие lim || m'r (t) || = 0.
t -» со
Устойчивость в М'г влечет за собой устойчивость в Мг (для того же порядка г).
Противоположное утверждение неверно. Если z (t) имеет ограниченные моменты до
порядка г включительно, то устойчивость в Milr_v влечет за собой устойчивость
в пространстве М'г. Для частного случая г — 2 устойчивость в М'г есть необходимое
и достаточное условие устойчивости в Мг. Целесообразность модификации опре-
определения устойчивости видна из того, что после замыкания и линеаризации система
дифференциальных уравнений относительно моментных функций имеет вид
— = Anv, C3)
т. е. содержит смешанные моменты входного и выходного процессов. При необхо-
необходимости может быть исследована устойчивость по отношению к части составляющих
вектора т'г
4. СИСТЕМЫ, ВОЗБУЖДАЕМЫЕ БЕЛЫМИ ШУМАМИ
Предварительные замечания. Используя метод моментных функций и определе-
определение устойчивости по совокупности моментных функций, рассмотрим систему с двумя
степенями свободы
+ |хФ (t) (bnqi + buq2)] = 0; j
2)] = 0, /
<?2 + 2y2co2?2 + coH</2 + ^Ф @ (Mi + b22q2)]
где Ф (f) = % (t) — белый шум интенсивностью s.
Типичные матрицы В, составленные из коэффициентов 6/<(, имеют вид
¦¦-(_ !!)•
При Yi — Y2 = 0 матрицы C5) соответствуют гамильтоновским системам, мат-
матрицы C6) — негамильтоновским.
Систему уравнений относительно моментных функций т;^/... (t) порядка г век-
векторного процесса х (/) запишем в матричной форме
^-Ап,,. C7)
Уравнения C7) могут быть исследованы численно, а в некоторых случаях ана-
аналитически.
Условия устойчивости имеют вид [72] (п = Wa/coj)
Yi + «Y2>0 (при /-=1); C8)
чФ'\д-[(пъЬъ-ъь*п)г+
(ПРИ г = 2). C9)
СИСТЕМЫ, ВОЗБУЖДАЕМЫЕ БЕЛЫМИ ШУМАМИ
307
Устойчивость по моментам высоких порядков. Области асимптотической устой-
устойчивости могут быть получены относительно моментных функций различного
порядка. Однако при повышении уровня замыкания г изменяется определение сто-
стохастической устойчивости. Вопрос о том, насколько результат зависит от определе-
определения устойчивости, может быть исследован на примере стохастического аналога
1,0
0,5
0 0,5 1,0 1,5/, 0
V а)
3,0
2,0
1,0
г. 2
У з~/
—^
\
\
V \
\\
\ \
\ \
\
\
0,5
г)
1.0
_^~-—¦
бф,.фг- 1,0
г
1,0
в)
2.0
0,5
1.0
Рис. 1. Границы областей устойчивости уравнения Матье-Хилла с коэффициентами,
возбуждаемыми случайными процессами:
а — в — частота, возбуждаемая белым шумом, s = 1 (а), экспоненциально-корре-
экспоненциально-коррелированным процессом, 0"i? = р = (д0 = 1,0 (б), процессом со скрытой периодичностью,
О =@о=1,0, у = 0,025, р = 0,02 (в); г — д — частота и демпфирование, возбуж-
возбуждаемые: белыми шумами Ито (штриховая линия — г = 2) и Стратоновича (сплошная
линия— г = 2) (г), экспоненциально-коррелированными процессами, г = 2, v = Pi =
= р2 = 0,5 (д)
уравнения Матье — Хилла C4) F12 = 62i = Ьгг — 0, Ьп = 1). Результаты числен-
численного анализа [73] приведены на рис. 1, а. Увеличение порядка г моментов ведет к мо-
монотонному уменьшению критических значений параметра [г. Анализ показывает,
что из устойчивости по отношению к моментам нечетного порядка г = 2я + 1 не сле-
следует устойчивость при г = 2я. Для малых значений параметра демпфирования Yi
границы области устойчивости практически не зависят от г.
Системы с двумя случайными параметрическими воздействиями. Пусть воз-
возмущенное движение системы описывается дифференциальным уравнением
@] <7 =
D0)
308 случайные параметрические колебания
коэффициенту которою возмущены гауссовскими белыми шумами Ф/ (f) = т]у (t)
с корреляционной матрицей
<П/(9П*('-1)>=«/*6(т) (/, k=\, 2). D1)
Вместо зависимых шумов r\j (t) можно рассматривать линейные комбинации неза-
независимых белых шумов \j (f):
tyW=2 fjklk(t)- D2)
Для двухмерного вектора x = (q,q) коэффициенты сноса зависят от определения
стохастического интеграла (по Ито или Стратоновичу).
Уравнения C7) для моментов можно получить разными способами. Отличные
от нуля элементы матрицы А для системы стохастических уравнений в форме Стра-
тоновича имеют вид
-/ (/ = 1, 2, ..., г);
si2-l]/ (/=1, 2, ... , /¦);
(/=2, 3, ...,
4
Трактуя белые шумы I, (/) по Ито, получим
/[(/— 1)^1^12 — Ч (/ = 1, 2, ...,/•);
[4 ] (/ = 2. 3
D3)
Коэффициенты Я;,;41 и о/,/_2 определяют по формулам D3). На рис. 1,г при-
приведены границы областей устойчивости, полученных для двух форм записи сто-
стохастического интеграла при г = 2.
5. СИСТЕМЫ, ВОЗБУЖДАЕМЫЕ ПРОЦЕССАМИ
С КОНЕЧНОЙ ДИСПЕРСИЕЙ
Предварительные замечания. Для параметрических воздействий в виде белых
шумов относительно моментных функций удается получить замкнутую систему диффе-
дифференциальных уравнений с постоянными коэффициентами. Если случайное воздействие
не является белым шумом, то уравнения относительно моментов имеют бесконечный
порядок. Применение модифицированного метода моментных функций позволяет
замыкать бесконечную систему уравнений относительно моментов на любом уров-
уровне г и рассматривать устойчивость в М'г.
Параметрическое возбуждение экспоненциально-коррелированными процессами.
В качестве примера рассмотрим стохастический аналог уравнения Матье — Хилла
?+27а>0? + ш§[1+1иФ@]<7 = 0, D5)
где Ф (t) — экспоненциально-коррелированный процесс (гл. XVII, табл. 1), кото-
который получается, если белый шум \ (t) (Ито или Стратоновича) интенсивности s =
= 2ао"ф поступает на вход линейного фильтра
D6)
Замыкая систему уравнений относительно моментов от/*/... (t) при помощи
C3) Р
у ур /*/ () р
гипотезы квазигауссовости, после линеаризации приходим к системе C3). Раз-
Размерность матрицы А равна 7 при г = 2; 16 при г = 3 и 30 при г = 4. Результаты
СИСТЕМЫ, ВОЗБУЖДАЕМЫЕ ПРОЦЕССАМИ С КОНЕЧНОЙ ДИСПЕРСИЕЙ 309
численного исследования устойчивости системы D5), D6) при различных г пред-
представлены на рис. 1, б сплошными линиями. Штриховой линией нанесены резуль-
результаты [118], полученные при условии узкополосности выходного процесса:
№ф B%) < ^ (Vя < 1). D7)
где Бф (со) — спектральная плотность процесса Ф (t).
Система с двумя случайными параметрическими воздействиями. Применим
модифицированный метод моментных функций к задаче об устойчивости уравне-
уравнения D0), в котором процессы Ф} (t) соответствуют зависимым экспоненциально-
коррелированным процессам. Эти процессы получаются, если зависимые белые
шумы г)у (<?) D2) пропустить через линейные фильтры:
Ф/+ «/!>; = rvW (/=1,2). D8)
Выбор модели белого шума (по Ито или Стратоновичу) при <Zj^= 0 не влияет
на вид уравнения Колмогорова и, следовательно, на выводы об устойчивости си-
системы.
Некоторые численные результаты приведены на рис. 1, д, отражающем влияние
коэффициента корреляции аф ф на устойчивость системы при г = 2.
Параметрическое возбуждение процессом со скрытой периодичностью. Пара-
Параметрические резонансы возникают при выполнении определенных соотношений
между частотами системы. Если параметрическое воздействие представляет собой
случайный процесс со скрытой периодичностью, то можно ожидать, что аналогичные
резонансные явления будут наблюдаться и в стохастической системе. Подробное
обсуждение этого вопроса с использованием модифицированного метода моментных
функций приведено в [15].
Системы с одной степенью свободы. Рассмотрим уравнение D5), в котором
Ф (t) — процесс со скрытой периодичностью (см. гл. XVII, табл. 1). Уравнение филь-
фильтра имеет вид
Ф + 2аФ + 62Ф = ?@. D9)
Интенсивность s белого шума ? (t) равна 4а62аф. После применения гипотезы
квазигауссовости и линеаризации приходим к системе C3). Размерность матрицы А
равна 9 при г = 2; 25 при г = 3 и 55 при г = 4. Результаты численного анализа
при различных уровнях замыкания представлены на рис. 1, в сплошными линиями.
Анализ результатов позволяет сделать следующие выводы. Во-первых, границы
области устойчивости обладают относительной стабильностью по отношению к уров-
уровню г замыкания системы для моментов mjki... (t) (особенно в области аналога глав-
главного параметрического резонанса при v= 6/шо= 2). Во-вторых, при увеличе-
увеличении г обнаруживается более тонкая структура границы области устойчивости:
в дополнение к аналогам главного параметрического резонанса (v = 2) и первого
дробного резонанса (v = 1) наблюдаются аналоги дробных параметрических резо-
нансов (v ш 0,66; 0,5; 0,4; ...). Заметим, что критерий устойчивости D7) (штрихо-
(штриховая линия) (см. рис. 1, в) дает лишь область, аналогичную главному параметриче-
параметрическому резонансу.
Параметрическое возбуждение периодически модулированными процессами.
Модифицированный метод моментных функций может быть применен также к систе-
системам, параметрически возбуждаемым периодически нестационарными воздействиями.
Примером такого воздействия может служить стационарный процесс, модулиро-
модулированный периодической функцией. Используя метод моментов, приходим к системе
уравнений типа C3); однако матрица А будет содержать члены, зависящие от вре-
времени. Дальнейшее исследование устойчивости может проводиться различными мето-
методами, например, методом матриц перехода (см. гл. VII).
310 СЛУЧАЙНЫЕ КОЛЕБАНИЯ РАСПРЕДЕЛЕННЫХ СИСТЕМ
Глава XX
СЛУЧАЙНЫЕ КОЛЕБАНИЯ РАСПРЕДЕЛЕННЫХ СИСТЕМ
1. МЕТОДЫ МОМЕНТНЫХ ФУНКЦИЙ
Стохастические краевые задачи в теории колебаний. Рассмотрим методы решения
стохастических краевых задач для случайных полей u (x, t) — функций времени t
и координат х, заданных в области х е V пространства R". Операторная форма
записи уравнений имеет вид
Lu = f, A)
где f (x, t) — случайное поле с заданными вероятностными характеристиками; L —
линейный детерминистический оператор. Рассмотрим также в терминах теории
колебаний линейных систем системы более частного вида
А*-+В*+С«-.. B)
Здесь А, В, С — соответственно инерционный, диссипативный и квазиупругий опера-
операторы, свойства которых и конкретные реализации были подробно рассмотрены в гл.
VIII, IX и далее.
Пример. Пусть упругий стержень постоянного сечения совершает случайные изгибные ко-
колебания под действием случайной поперечной нагрузки f (x> t). Запишем уравнение относи-
относительно функции прогиба w (х, t) в виде
*'& + *>% + »»%-'¦
Концы стержня к = 0 и х = I будем считать опертыми. Рассмотрим случайные колебания,
которые начинаются из состояния покоя, а также установившиеся колебания под действием
стационарной случайной нагрузки, когда на решение накладывается требование стационарности
во времени. Примем, что нагрузка f (x, t) дельта-коррелнрована как по координате, так и по
времени, причем
</<*.'» = 0; 1
</ (х, 0 / (*', t')) = sd (х - х') 6 (< - П, )
где интенсивность s = const.
Метод дифференциальных уравнений относительно моментных функций. Метод
отличается от описанного ранее (см. гл. XVIII) тем, что оператор L действует на
функции координат х и времени t. Например, уравнения относительно моментных
функций второго порядка принимают вид
L L <u(x, 0 и(х', /')> = <! (х, Q f (*'.<')>. E)
X, t X', /'
где выражения u (x, f) и (х\ t') и f (x, t) f (x', t') понимаются в смысле прямого (тен-
(тензорного) произведения. Уравнение E) включает в себя также осредаенные граничные
условия.
Для рассмотренного выше примера уравнение, связывающее корреляционные функции на-
нагрузки f (x, t) и прогиба w (х, t), т. е. функции
Kf (х, t; x', t') = </ (х, t)J(x', Г)); \
Kw (х, i; x', t') = <ш (х, О w (*'. *')>. J
F)
Кт (х, t< х', I') = <ш (х, О w (*', <')>. )
пудет следующим-
дх* dt* д( } \ дк' dt
(x, t; x', t') = Kf {x, t; x', t'). G)
МЕТОДЫ МОМСНТНЫХ ФУНКЦИЙ
311
Для колебаний, начинающихся из состояния покоя, граничные и начальные условия вво-
вводятся так:
<52К
Л»=-в^=° <* = "¦* = ');
*™ = т" = ° (*' = 0, *' = /);
. = 0 (< = 0);
Стационарные случайные колебания. Если f (*, t) и w (x, /(—стационарные случайные
процессы, то корреляционные функции зависят от разности t' — t (а не от каждого аргумента
порознь) Вводя новую переменную т = /' — /, вместо уравнения G) получим
-^+pF— 2PFb--)(ej ^T
dx* dx2 dx/\ dx'4
dx
— )kw(x, x> x) = K, (x, x', x) (9)
dx I w >
Граничные условия из (8) остаются без изменения, а вместо прежних начальных условий
нужно взять следующие:
дх
дх3
= 0 (т =
|<оо (т-±со)
A0)
Ес^ти входящке в (@) производные не существуют, то следует взять соответствующие усло-
условия скачка при т= 0. Уравнение (9) с условиями A0) легко решается по методу разделения
переменных. Если нагрузка f (x, t) задана соотношениями D), то получаем
со
т. , S е I т I Х~1 1
*»<*¦*¦ т) = 2^ire ' L ^
где и^е = (ffl| — е2I^ _ собственные частоты стержня, вычисленные с поправкой на дисси
пацию.
Метод функций Грина. Метод является естественным обобщением метода импульс-
импульсных переходных функций (см. гл. XVIII). За исходное в этом методе принято уравне-
уравнение A), разрешенное относительно u (x, t):
и = Ш.
A2)
Для раскрытия конкретного содержания оператора Н необходимо построить
функцию Грина (тензор Грина) для соответствующей краевой задачи. Если и (х, t)
и / (х, f) — скалярные поля, то функцию Грина G (x, t; |, т) определяют как решение
уравнения
LG(x, /; |, т) = б(х —§N(/ —т), A3)
х, /
удовлетворяющее граничным условиям для и (х, t) и нулевым начальным условиям
при t = х. По переменным х и § функция G (x, t\ |, т) является функцией Грина
в обычном смысле, по переменным t и т — импульсной переходной функцией. Реше-
Решение уравнения A2) запишем в виде
в(х,
С(х, /;
A4)
Реализацию операторного соотношения A3) в случае, когда u (x, f) и f (х, <) —
векторные поля, записывают при помощи тензора Грина о. компонентами Gjk (x, <;|, т):
иу(х, 0=
ft = l —оо V
A5)
312 СЛУЧАЙНЫЕ КОЛЕБАНИЯ РАСПРЕДЕЛЕННЫХ СИСТЕМ
Выражения типа A4) и A5) можно представить в виде
u(x, O = XH/{f(|, т)}, A6)
где первая пара аргументов у функции (тензора) Грина выписана над знаком опера-
оператора, вторая — под этим знаком. Осредняя соотношение A6), а также соотношения,
получаемые почленным перемножением при различных х и t, получим формулы для
моментных функций вибрационного поля. Так, для моментных функций второго по-
порядка
<u(x, Ou(x\ 0>="н *Н {</(!', x)f(l', т')>} A7)
1.x 1',т'
и т. д.
Для рассмотренного выше примера функция Грина имеет вид
О (/ < Т),
G(x, t\l, T) = J 2 ^i 1 о»_т> . , %1 . Ых . *л| . A8)
4 = 1 "е
Подстановка формул D) и A8) в соотношение типа A7) для корреляционной функции при-
приводит к формуле A1)
2. МЕТОДЫ СПЕКТРАЛЬНЫХ ПРЕДСТАВЛЕНИЙ
Метод канонических разложений. Одним из эффективных методов решения сто-
стохастических краевых задач является метод канонических разложений. Рассмотрим
случай, когда L в B) является линейным скалярным оператором. Скалярное поле
/ (х, t) можно представить в виде разложения
со
f(x, 0=1] Fa9a(x. 0, A9)
08 = 1
которое является обобщением разложений A2) (см. гл. XVII) для пространственно-
временных случайных полей. Решение уравнения A) можно искать в виде разло-
разложения, аналогичного A9),
со
и(х, 0= 2 РаЦа(х, 0, B0)
се = 1
где t|;a (x, t) — неслучайные функции, которые могут быть найдены из решения
вспомогательной детерминистической задачи
М>а = Фа B1)
методами, изложенными в гл. XIV. Моментныефункции поля и (х, t) определяют при
этом следующим образом:
оэ \
(и* (х, /) и (Х\ П) = 2 2
ц = 1 8=1
B2)
и т. д. Если исходное разложение A9) выбрано каноническим (см. гл. XVII), то,
например, для моментной функции второго порядка имеем
оэ
(и* (х, 0 и (х\ ('))= 2 (! ^а I2) Фй (х, 0 Фа (х'. <')• B3)
МЕТОДЫ СПЕКТРАЛЬНЫХ ПРЕДСТАВЛЕНИЙ
313
Метод временных преобразований Фурье. В случаях, когда внешняя нагрузка
и вибрационное поле являются стационарными случайными процессами, эффективен
метод временных преобразований Фурье.
Пример. Если ввести по формулам типа D3) (см. гл. XVII) спектральные плотности для
полей I (х, t) и w (х, 1}
*-х'-т = ы
К, (х, х', х) е~ 'шт dx;
Sw (х, к', со) =~ $ Kw (х, х', х) е-ш dx,
B4)
то они будут связаны между собой уравнением, которое получается после применения к урав-
уравнению (9) преобразования Фурье по
времени:
EJ pFco* — 2pFeis> ] X
дх* j 0,8
0,6
Ofi
0,1
X Sw (х, х', со) = Sj (к, х', со). B5)
Граничные условия для функции
Sw (х, х', со) остаются такими же,
как и для Kw (х, х', и>) (8). Решение
уравнения B5) можно представить
в виде
Здесь
(со)
Sw(x,
со
¦*—' La
Р — 1
апх
Xsin -у-
X', СО) =
(—to) La
sin —-—.
/ /
(ico) x
B6)
X', СО) X
0
(*М
3,0
2,5
1
\
\
\ u -
\
-0,2
0,9
ч
,ч
1,0
/
^—
¦——,
1,05
/
1
—¦—
н
¦
10,0
=^=
— —
00
2,0
B7)
1,5
1,0
1
/
/
/
А,
о,г\
0J
\
Л
\
4,0
1,0
\
\
/0,0
. алх . вях' ,
х sin _— sin !—7—dx dx'.
Корреляционная функция
Kw (x, x', x) =
со
— I sw (x> *¦'< ю) e'mT d(s>- *28>
— CO
Если нагрузка / (х, I) задана со-
соотношениями D), то выражение для
Kw(x, x', x) имеет вид A1).
Передача случайных вибра-
вибраций через конструкции. Пусть
на элемент конструкции дейст-
действуют стохастически заданные
стационарные возмущения. Рас-
Рассмотрим вопрос об определении вероятностных характеристик реакции системы
в различных точках конструкции. Исследование передачи случайных вибраций
сводится к решению стохастических краевых задач.
На рис. 1, а показаны характерные графики безразмерной спектральной плотности нормального
прогиба Sw (х, <u)iSw (со) для полубесконечной цилиндрической оболочки со стохастически
заданным на торце нормальным прогибом w (О, I), а на рис. 1,6 — графики Sw (x, со)/[ДМ>^ (со)]
для стохастически заданного угла поворота v @, t), построенные при значениях параметров
2е/со = 0,05, hjR — 0,004 [92].
Рис. 1. Зависимость спектральной плотности прогиба
цилиндрической оболочки от осевой координаты при
заданном на торце перемещении (а) и угле поворота (б)
314 СЛУЧАЙНЫЕ КОЛЕБАНИЯ РАСПРЕДЕЛЕННЫХ СИСТЕМ
Метод пространственных преобразований Фурье. Рассмотрим применение этого
метода с использованием канонических разложений. Предположим, что нагрузка
/ (х, t) образует центрированное однородное случайное поле, т. е. допускает разло-
разложение
оо со
f(x, 0= U J F (k, &)e"kx+at>dkd& B9)
— со — со
со спектром F (k, ш), обладающим свойством стохастической ортогональности
(F*(k, u>)F (?', a>'))=Sf(k, (f>)&(k~k')8((u-oir). C0)
Здесь Sf (k, w) — пространственно-временная спектральная плотность внешней
нагрузки.
Пример. Решение уравнения C), если справедливо представление B9), можно искать в виде
со со
w(x,t)=\ I F (к, со) \р (х, 11 к, <s>)dk da C1)
— со — со
Функции i|> (х, t | k, и) при этом будем определять из решения детерминистической задачи
EJ ?-* + PF "-^ + 2pFe, "* = е'<*-« + <¦">. C2)
<?л:4 ot2 at
Если случайные колебания стержня начинаются из состояния покоя, то функция ф (л:, t \ k, со)
должна удовлетворять условиям
г|) — ^—J- = 0 (х ~ 0, 1), ф = ^- =^=0 (^ = 0), C3)
если же рассматривать установившиеся колебания под действием стационарной нагрузки, то
условиям
ф = ~^~^ = 0 (л: = 0, /), | "ф [ < со (/ —f + со). C4)
После решения вспомогательной детерминистической задачи C2) — C4) корреляционную
функцию прогиба w {x, /) определяют по формуле
со со
Kw (х, t\ х', П = \ J Sj (k, @) ф* (х, t\k, @) ф (х\ V \ k, (a)dh4&. C5)
— со — со
Метод пространственных преобразований Фурье наиболее эффективен в случае
бесконечных и полубесконечных областей.
Случай однородных и стационарных пространственно-временных полей. В случае,
когда нагрузка f (x, t) и вибрационное поле и (л;, t) являются центрированными
однородными и стационарными случайными функциями, их можно представить
в виде интегральных канонических разложений
со со
f (х, *)= ([ j F(k, &)ei{]
— со — оо
со со
и (х, t) = j j
— со — со
C6)
со стохастически ортогональными спектрами
(F'j(k, ffl)Fft(k', w')) = Sfjfk(k, coN(k-k'N(co-co'); C7)
<Gf (k, a>)tffc(k', co'))=--5H;Hfc(k, coN(k-k'N((o-(o').
Взаимные спектральные плотности S^,/fe(k, со) и S,, nft(k, to) связаны соотношением
S«ye/t (k, со) = 2 Ц ^*« (k. ») ^ft3 (k. to) S/A (k, со). C8)
a p
Здесь Я;а (k, to) ^ передаточные функции системы.
МЕТОД РАЗЛОЖЕНИЯ ПО СОБСТВЕННЫМ ФОРМАМ 315
Корреляционная функция поля u (x, t)
— со — оо
Случайные колебания бесконечной пластины с сосредоточенной массой. При действии на
пластину, выполненную из линейного вязкоупругого материала и несущую в точке х0 сосредо-
сосредоточенную массу М, случайных внешних сил можно записать уравнение колебаний
d2w d2w
D ДЛю + Ph -^ + /Мб (х - хо) щ^ — I (х, .), C9)
где D —линейный вязкоупругий оператор.
Для бесконечной пластины решение при однородной пространственной функции нагрузки
ищется в форме пространственно-временного канонического разложения C6). Спектральная плот-
плотность прогиба w
°? S|(k, to)
Sw (х, х', «) = J I t (k' to) I' ** (X> k> M> * <X'' k> й) dk'
— 00
где
CO ,
2 /|<y /> ?K ^X X )
1
(х, к,
"•" 4л2 [1 —А (со)] J L (kb со)
— oo
oo
L (k, a) = D i k ,« — рЛсог; А (со) = ^^ f rfk
J L (к, со)'
— со
Здесь D = Dft A + t'x) — образ Фурье оператора D; % — тангенс потерь
3. МЕТОД РАЗЛОЖЕНИЯ ПО СОБСТВЕННЫМ ФОРМАМ
Применение метода обобщенных координат. При решении стохастических краевых
задач в теории колебаний часто применяют метод, основанный на представлении
вибрационных полей и внешней нагрузки в виде разложения в ряд по собственным
формам колебаний <ра(х) системы без учета диссипации:
оо
и(х, .)= _ УоЮфаОО- D0)
а = 1
Применение разложений типа D0) по существу эквивалентно замене рассматри-
рассматриваемой системы системой со счетным числом степеней свободы. При практических
расчетах ряд D0) усекают, т. е. распределенную систему заменяют дискретной с ко-
конечным числом степеней свободы. Количество учитываемых членов ряда определяется
требуемой точностью вычислений, частотным диапазоном внешнего воздействия и
т. д. Случайные функции времени Ua(t) при этом можно интерпретировать как обоб-
обобщенные координаты для соответствующей системы с конечным числом степеней
свободы. Поэтому метод решения задач случайных колебаний распределенных систем,
основанный на использовании выражений, аналогичных D0), называют методом
обобщенных координат.
Путем подстановки ряда D0) в уравнения A) с использованием, например, вариа-
вариационного метода Бубнова — Галеркина можно получить уравнения относительно обоб-
обобщенных координат. Как правило, при определенных ограничениях, накладываемых
на свойства операторов А, В и С, эти уравнения имеют стандартный вид
dt* ' u dt
=l, 2, ...)• D1)
Здесь соа — собственные частоты рассматриваемой системы без учета диссипации,
еа — коэффициенты диссипации; Fa (f) — случайные функции времени, имеющие
316
СЛУЧАЙНЫЕ КОЛЕБАНИЯ РАСПРЕДЕЛЕННЫХ СИСТЕМ
смысл обобщенных сил:
= 4-(Чх. 0.
D2)
где va — нормы собственных форм; скобки означают скалярное произведение в функ-
функциональном пространстве вектор-функций:
(U, V) = j (U1O1 + U2Vi +¦¦¦ + UmVm) dx.
Разделение системы уравнений относительно обобщенных координат происходит
вследствие ортогональности форм собственных колебаний системы, вычисленных
без учета диссипации.
Вследствие разделения системы D1) оказывается возможным исследование по-
поведения каждой из обобщенных координат Ua (t) методами, изложенными в гл. XVIII.
Однако для исчерпывающего описания поведения рассматриваемой системы необ-
необходимо учитывать взаимную корреляцию обобщенных координат [12].
Рассмотрим скалярное поле и (х, t). Моментные функции для поля и (х, t) нахо-
находятся осреднением соответствующих рядов:
<и(х,0>=2] <*/„(')> Фа №;
1
а (Q
Фа
= ! 13 = 1
V
D3)
Моментные функции обобщенных координат находятся из уравнений D1) при
помощи методов, изложенных в гл. XVIII. Эти функции выражают через моментные
функции обобщенных сил Fa (t), которые можно вычислить, если известны простран-
пространственно-временная корреляционная функция нагрузки и формы собственных коле-
колебаний системы.
В случае неустановившихся колебаний моментные функции поля и (х, f)
со /
<и(х,0>= 2 Фо(х) j ha(t-x)(Fa(x))dx;
а = 1 —со
со со
(и (х, t) и (х, Г)) = 2 2 Фа (х) фр (х') X
а=16=1
X
t'~x') {Fa (т) /=р (т')> d% dx1
D4)
и т. д. Здесь ha (t — т) — импульсная переходная функция для системы D1).
Пример. Решение уравнения C) будем искать в виде ряда
со
w (х, /) = V W (О sin ^. D5)
Разлагая нагрузку / (х, t) в ряд
a= 1
D6)
и подставляя ряды D5) и D6) в уравнение C), получим систему уравнения типа D1)
d'Wa dW
D7)
МЕТОД РАЗЛОЖЕНИЯ ПО СОБСТВЕННЫМ ФОРМАМ 317
С учетом D2) моментные функции обобщенных сил определяют по формуле
(Fa «) Fp 0'» = (~^-) $ \ Kf <*. Л *'. /') sin «Н sin ^ dx d*. D8)
О О
Если ограничиться случаем, когда пространственно-временная корреляционная функция
имеет вид D), то
26
D9)
В случае установившихся стационарных колебании взаимные корреляционные функции
обобщенных координат
sin °« т '•) • <50)
При этом корреляционная функция прогиба Кщ (х, х', t) имеет вид (II).
Вычисление спектральных плотностей обобщенных сил. Ограничимся рассмотре-
рассмотрением установившихся стационарных колебаний. Предположим, что / (х, t) и и (х, t)
являются стационарными пространственно-временными скалярными полями. Тогда
из D3) получаем
со со
SB(x. х', со)= 2 И Sv УоИф (х)Ф.(х'). E1)
<! = I Р = 1 ° Р ° Р
Здесь Sy ц (со) — элементы матрицы взаимных спектральных плотностей обобщен-
обобщенных координат. Они могут быть найдены с использованием уравнений D1). Оконча-
Окончательно получаем
S ()
иаи$ ^ = (и^—и2 — 2eaico) (со| — ш2
Здесь
со
E3)
— элементы матрицы взаимных спектральных плотностей обобщенных сил, которые
могут быть найдены по формулам
) = ^?ГГ \ \ S/ (х> х''
ОС $ v J
E4)
Случайные колебания пластины с сосредоточенной массой. Для прямоугольной пластины
конечных размеров, колебания которой описываются уравнением C9), внешнюю нагрузку f (x, t)
и нормальный прогиб w (x, t) представим в виде разложения D0) по собственным формам ф (х)
и преобразования Фурье по времени. Спектральная плотность прогиба пластины
ОС ОО
S (х, х', со) = V] ^ SF F (го ф^ (х, со; ф» (х'. со)
р
SF F (го ф^ (х, со; ф» (х'.
а р
Взаимные пектральные плотности обобщенных сил Sp- p (&)) определяются через спект-
ральную плотность S, (х, со) по формуле E4) Функции
Г М(°гф« (хо) v фз(х) фз<Хо)
где Vr — квадраты норм базисных функций фо (х);
<Pa) '
318
СЛУЧАЙНЫЕ КОЛЕБАНИЯ РАСПРЕДЕЛЕННЫХ СИСТЕМ
4. ШИРОКОПОЛОСНЫЕ СЛУЧАЙНЫЕ КОЛЕБАНИЯ
Предварительные замечания. Обычный метод расчета вынужденных колебаний
упругих систем основан на разложении искомого решения по собственным элементам
соответствующей задачи собственных колебаний (см. гл. ХШ). Ответ на вопрос о том,
при каких условиях допустимо аппроксимировать систему с дискретным спектром
системой со сплошным спектром, дает теория распределения собственных частот
(см. гл. IX). Эта теория применима и к задачам случайных колебаний [13].
Интегральные оценки для вероятностных характеристик. Рассмотрим некоторый
параметр напряженно-деформируемого состояния системы v (х, t), который можно
представить в виде ряда
в(х, t) = ^Ua(t)ca(x). E5)
а
Функции са(х) здесь таковы, что почти все обобщенные координаты Ua(t) достаточно
равномерно представлены в E5).
Пусть уравнение B) после подстановки ряда D0) приводится к виду
Предположим, что выполняются следующие условия: плотность собственных
частот достаточно высока; для частот <ва и форм колебаний <ра (х) могут быть взяты
асимптотические выражения (см. гл. IX); <ва, фа (х), са(х) и спектральные плотности
обобщенных сил могут быть представлены в виде функций волнового вектора к;
перечисленные функции мало изменяются на расстояниях, сопоставимых с размером
одной ячейки в пространстве волновых чисел. Тогда, пренебрегая взаимной корреля-
корреляцией обобщенных координат, для дисперсии
функции v (x, t) E5) при
демпфировании получаем
<02>
f
[
f
\
/
<0г>
достаточно малом
neb. (x) Sf (coa)
E6)
Заменяя функции индекса а соответствующи-
соответствующими функциями от волнового вектора к, а сумми-
суммирование в формуле E6) — интегрированием в
пространстве волновых чисел, получим интег-
интегральную оценку
10
(х j k) Sf (k) dk
t (k) to» (k)
E7)
Ы'с
Рис. 2. Интегральные оценки для
дисперсий перемещений и напряже-
напряжений в тонкой упругой пластине
где Akj — объем ячейки в К, соответствующий
одному слагаемому в E6).
На рис. 2 приведены оценки типа E6) и E7)
для дисперсии перемещений и напряжений
в тонкой упругой пластине под действием нагрузки, которая представляет
собой усеченный временной белый шум [13]. При этом а'с и со" — нижняя и верхняя
частоты спектра.
Для временной спектральной плотности функции v (x, 0 получаем аналогичную
оценку:
п д с с2 (х к) 5* (к) dk
Sv (х, со) ~ —- з- \ , „ t '' . E8)
&kida J г|> (к) со3 (к) у '
а (к><ш
При некоторых условиях асимптотическая плотность частот v (со) явно входит
в окончательные аналитические результаты. Если функции с (х | k), Sf(k) и г|)(к)
ОСНОВНЫЕ ПОНЯТИЯ
319
медленно меняются по сравнению с асимптотической функцией распределения соб-
собственных частот N ((о), то, применяя теорему о среднем, выражение E8) можно пред-
представить в виде
яДк с2 (х , к) S, (к) v (со)
5«<*-»>~Ж VHCO3 • (^)
Таким образом, если функция v (со) при некоторой частоте имеет особенность,
то эта особенность сохраняется в спектральной плотности.
Пример. Рассмотрим изгибные колебания упругой защемленной по контуру пластины под
действием случайных сил с широким спектром. Пусть центрированная нормальная нагрузка на
пластину f (х, t) задана при помощи функции S. (х, х', (о) = ЧЧю) 6 (х — х'), где V (а) — вре-
временная спектральная плотность.
Дисперсии перемещений и максимальных нормальных напряжений во внутренней области
пластины определяются согласно E7) по формулам [13]
2D2 \ph ) J
p/i ) i г|) (ft) fts '
CO
J Ф (ft) ft ¦
0
При тех же условиях дисперсия максимальных нормальных напряжений в заделке
j
Применение метода статистического моделирования. Этот метод для исследования случай-
случайных колебаний в распределенных системах особенно эффективен в сочетании с методом обоб-
обобщенных координат. Статистическое моделирование в этом случае осуществляют по сле-
следующей схеме На основании заданных вероятностных характеристик внешнего воздей.ст-
вия f (x, t) моделируют реализации компонент вектора обобщенных сил Fa (t) D2). Для
каждой полученной реализации компонент вектора Fa (t) воспроизводят реализации компо-
компонент вектора обобщенных координат Ua (t). Эту задачу можно решить методами, изложенными
в гл. XVIII. Реализации вектора состояний системы u (x, t) вычисляют при помощи разложе-
разложений D0). Статистические оценки вероятностных характеристик находят путем обработки ан-
ансамбля полученных реализаций.
ГЛАВА XXI
ОСНОВЫ ТЕОРИИ ВИБРАЦИОННОЙ НАДЕЖНОСТИ
1. ОСНОВНЫЕ ПОНЯТИЯ
Случайные колебания и теория надежности. Многие приложения теории случай-
случайных колебаний требуют применения понятий и методов теории надежности, особенно
того ее направления, в котором отказ рассматривается как результат изменения во
времени параметров системы (общая, физическая или параметрическая теория на-
надежности). Оценка надежности систем, испытывающих вибрации, в значительной
степени основана на анализе случайных выбросов колебательных процессов и свя-
связанных с ними процессов накопления повреждений.
Отказ как случайное событие. Полную или частичную утрату системой способ-
способности выполнять возложенные на нее функции называют отказом. Последний может
быть как результатом развития дефектов, содержащихся в системе к началу эксплуата-
эксплуатации, так и результатом накопления повреждений и необратимых изменений в про-
процессе эксплуатации. Начальное распределение дефектов, условия эксплуатации
и взаимодействия системы с окружающей средой носят случайный характер. Поэтому
отказы следует рассматривать как случайные события.
320
ОСНОВЫ ТЕОРИИ ВИБРАЦИОННОЙ НАДЕЖНОСТИ
В теории надежности принято различать внезапные и постепенные отказы. Понятие
внезапного отказа используют, если описание процессов, ведущих к отказу, затруд-
затруднительно или нецелесообразно. Тогда для анализа надежности применяют эмпири-
ко-статистический подход. Поведение механических систем может быть описано и
исследовано с высокой степенью подробности и точности. Это позволяет отказаться
от понятия внезапного отказа и трактовать все отказы как результат взаимодействия
системы с окружающей средой [12].
Пространства теории надежности. Рассмотрим поведение некоторой системы при
внешних воздействиях. Запишем уравнение системы в виде
Lu = f, A)
где f — элемент из пространства входных параметров F; и — элемент из простран-
пространства выходных параметров [/; L — оператор системы. Пространство U выбирают
таким образом, чтобы при помощи его элементов и можно было полностью охаракте-
охарактеризовать любое состояние системы; его называют пространством состояний. Эволю-
Эволюция состояния во времени описывается функциями u (t); их геометрическим образом
служат траектории в пространстве состояний U.
Введем пространство для описания качества системы. Пусть каждому качеству
системы соответствует элемент v e V; при этом время t играет роль параметра.
,W(t)
\J
Рис. 1. Пространства теории надежности
Каждой траектории и (() в пространстве U соответствует некоторая траектория v (t)
в пространстве качества V. Элементы этих простраьств и траектории в них связаны
операторным соотношением
v = Mu. B)
Оператор М может быть, в частности, тождественным оператором. В некоторых
случаях пространство V оказывается подпространством от U.
Множество состояний системы, допустимых с точки зрения качества, образует
в пространстве качества V область допустимых состояний Q. Граница области Q
соответствует предельным состояниям. Эту границу будем называть предельной
поверхностью и обозначать через Г. Если v e Q, то это означает, что параметры
качества системы сохраняются в установленных допусках. Первое пересечение
траекторией v (/) предельной поверхности Г в направлении внешней нормали соот-
соответствует отказу системы.
Еще одним пространством теории надежности является диагностическое (прост-
(пространство признаков) W. В результате наблюдений и измерений фиксируют значения
w (t) некоторых параметров, косвенно характеризующих качество системы. Вектор
признаков w (t) связан с вектором качества v (/) операторным соотношением
w=Nv, C)
где N — оператор, отражающий неполноту информации, наличие шумов в системе
измерения и т. п.
Введенные понятия приобретают особую наглядность, если система является
конечномерной. Тогда пространства F, U, V и W — евклидовы пространства. На
рис. 1 схематически показаны траектории f (t), u (t), v (t) и w {f) для случая, когда
ОСНОВНЫЕ ПОНЯТИЯ 321
F, U, V и W являются трехмерными евклидовыми пространствами. Здесь п' и Г' —
образы допустимой области Й и предельной поверхности Г в пространстве W.
Функция надежности. Эта функция служит основной характеристикой надеж-
надежности, определяющей способность системы к безотказной работе на заданном отрезке
времени. Пусть внешнее воздействие f (t) и (или) оператор системы L являются сто-
стохастическими. Тогда траектории v (/) в пространстве качества V будут также стоха-
стохастическими, а отказ — случайным событием. Функция надежности определяется [12]
как вероятность пребывания элемента v (т) в допустимой области Q на отрезке вре-
времени [0, t]\
P(t) = P \v(r)e=Q; те[0, (]}. D)
Определение функции надежности в форме D) легко обобщается на случай, когда
допускаются повторные отказы, предусматриваются ремонт, восстановление и т. п.
Роль параметра t может играть не только физическое время, но и наработка, число
циклов или другие подходящие для данного типа систем параметры. Область до-
допустимых состояний может быть стохастической, например, может случайно меняться
при переходе от одного элемента ансамбля систем к другому. Если стохастические
свойства системы и внешнего воздействия характеризуются конечным числом слу-
случайных параметров, то задачу определения функции надежности целесообразно
решать в два этапа. На первом этапе рассматривают систему с фиксированными пара-
параметрами, для которой строится функция надежности. Эта функция представляет
собой вероятность пребывания системы в допустимой области при условии, что пара-
параметры системы г и воздействия s фиксированы:
P(t\r, s) = P{v(T|r, s)efi(r); те[0, t]}.
По аналогии с условной вероятностью будем называть функцию Р (t \ s, г) условной
функцией надежности. На втором этапе при помощи формулы полной вероятности
вычисляется функция надежности для выбранных наугад системы, принадлежащей
данному ансамблю, и воздействия:
P(Q = J$P(f|r, s)p(r, s)drds.
Здесь р (г, s) — совместная плотность вероятности для параметров г и s.
К характеристикам надежности относятся также вероятное пь отказа системы
на отрезке [0, t], вычисляемая как Q (f) = 1 — Р (t); плотность распределения (час-
(частота) отказов f (t) = —Р' (t); интенсивность отказов — плотность вероятности от-
отказов на множестве систем, не отказавших до момента времени t: X (t) —— Р' (t)IP (t).
Функция надежности и интенсивность отказов связаны формулой
Р(/) = Р @)exp \~\%{x)d% . E)
Характеристики долговечности. Время до первого отказа (срок службы)
Т является случайной величиной с функцией распределения
Средний срок службы
оо оо
(Т) = \ TF' (T)dT=[ P @ dt. F)
о 6
Таким образом, характеристики долговечности содержатся в функции надежности
Р (t). Учет ремонта, восстановления, промежуточного контроля и т. п. требует вве-
введения специальных показателей долговечности [29, 85].
Нормативная надежность. Условие надежности системы имеет вид
где Р„ @ — нормативная надежность (вообще говоря, функция времени); Т, —
нормативный срок службы. Обычно условие G) ставится при^=Т^. Обозначая
Р* (Т*) = Р*. перепишем G) в виде Р G"J =s Pt.
11 и/р. Бологина В. В , т. 1
322 ОСНОВЫ ТЕОРИИ ВИБРАЦИОННОЙ НАДЕЖНОСТИ
Для массовых систем функция надежности допускает статистическое истолкование.
Ее нормативные значения устанавливают путем статистического анализа опыта
эксплуатации. Другой путь получения нормативных значений основан на вероят-
вероятностно-оптимизационном подходе, при котором нормативные значения определяют
из условия минимума математического ожидания некоторой функции потерь, свя-
связанных с отказом. Если система не является массовой, то статистическое истолкование
утрачивает смысл. Но характеристики надежности все же остаются при этом важными
показателями качества системы и могут быть использованы для сопоставления ва-
вариантов технических решений или для оптимизации параметров. Так, из некоторого
набора технических решений виброзащитной системы наилучшим (при прочих рав-
равных или сопоставимых условиях) будет то, которое обеспечивает максимальную на-
надежность.
2. КРИТЕРИИ ВИБРАЦИОННОЙ НАДЕЖНОСТИ
Предварительные замечания. Цель расчета на вибрацию и проектирования вибро-
виброзащитных систем состоит в том, чтобы свести до минимума или до допустимого пре-
предела уровни вибраций и вибронапряженности в машинах, конструкциях и приборах.
При расчетах на случайные вибрации требования к этим уровням целесообразно
формулировать в терминах общей теории надежности путем задания пространства
качества, т. е. совокупности параметров вибрационного поля и связанных с ним
физических полей, и области допустимых состояний в этом пространстве качества —
ограничений на параметры этих полей.
Основные критерии вибрационной надежности. Простейшей и наиболее употреби-
употребительной мерой вибронапряженности служит максимальная величина виброускорения
a (t), либо измеряемая в абсолютных величинах, либо относимая к ускорению силы
тяжести на земной поверхности g. Условие качества требует, чтобы максимальное
виброускорение в точках системы не превышало предельно допустимых значений а^..
Другая мера вибронапряженности — виброперемещения. В зависимости от назначе-
назначения элементов системы ограничения могут накладываться как на абсолютные, так
и на относительные перемещения.
Прочность системы, как правило, оценивают величиной вибронапряжений, возни-
возникающих в ее элементах. Условие качества требует, чтобы максимальные напряжения
(в случае сложного напряженного состояния — некоторые максимальные эквива-
эквивалентные напряжения) не превышали допускаемых значений. Включение в число
параметров качества усилий и моментов, возникающих в элементах системы, позво-
позволяет вести расчет по несущей способности элементов. Поскольку вибрационное на-
гружение, которое в конечном счете приводит к отказу элемента системы, обычно
сопровождается накоплением повреждений, то более правильный подход к оценке
вибрационной надежности основан на рассмотрении процесса накопления поврежде-
повреждений. В число параметров качества системы при этом включаются меры повреждения
и остаточных деформаций, размеры трещин и других дефектов и т. п. Условие ка-
качества сводится к требованию, чтобы характеристики повреждаемости не превышали
предельно допустимых значений. Одно из преимуществ подхода к вибрационным
расчетам на основе методов теории надежности состоит в возможности комплексного
учета всего разнообразия факторов, влияющих на надежность и долговечность [12].
Пример. Рассмотрим абсолютно твердое тело, помещенное в контейнер, совершающий слу-
случайные колебания (рис. 2, а). Пусть u (x, t) — поле перемещений тела относительно контейнера,
а (х, t) — поле абсолютных ускорений. Если по условиям эксплуатации виброперегрузки огра-
ограничены по модулю величиной а*, а относительные перемещения тела —- величиной и„, то допу-
допустимая область дается условиями
|]а(х, t)H < а», || и (х, 011 < и,. (8)
Здесь х принимает все значения для объема, занятого телом. Если поверхность тела — много-
многогранник, то вместо (8) имеем
li a ("у 0 [| < a*' II u ("/• 0 il < ". (/=1.2,...), (9)
ты вершин многогранника. Функция надежности D) вводится как
Р 10 = р\ т '' ~" т '' '""""* |. A0)
V= 1, 2, .. .; те[0, /] }
КРИТЕРИИ ВИБРАЦИОННОЙ НАДЕЖНОСТИ
323
Пример. Рассмотрим приборы, установленные на упругой пластине. Пусть пластина совер-
совершает случайные колебания в направлении, ортогональном ее плоскости (рис. 2, б) Вибрацион-
Вибрационное поле характеризуется функцией прогиба пластины w (x, /) и абсолютными перемещениями
приборов а. (t) 0 = 1,2,.. .). Аналогично условиям (9) наложим ограничения на вибропере-
6)
Рис. 2. Абсолютно твердое тело в контейнере, совершающем случайные
колебания (а), и приборы, установленные на упругой пластине (б)
грузки каждого прибора и на перемещения приборов относительно пластины. Допустимая об-
область Q дается системой неравенств
| а- (/) ! < а-^, I и • (/) — w (х., /J | < ы. (/ = 1,2, .. .). A1)
Другие примеры выбора параметров качества и допустимой области. Если два прибора соеди-
соединены связью, которая может быгь повреждена или нарушена из-за взаимных смещений (рис. 3, а),
то к (9) и A1) добавляются еще условия и}- (t) — и. {t) I ^ и .. . Аналогичные условия ста-
ставятся, если амортизируемые элементы смонтированы с зазором, причем требуется, чтобы при
ю
Рис. 3. Примеры выбора параметров качества и допустимой
области
вибрациях зазор не перекрывался (рис. 3, б). Системе сообщаются вибрации в горизонтальном
направлении. Зазор между элементами т1 и т2 в начальном состоянии равен и,. Допустимая
область Я дается неравенствами | at (t) | <| alt, | а2 @ | ^ a2t, ut (t) — иг (t) ^ ut, а функция
надежности
С sup | а, (т) | sg ait, sup [ a2 (т) | < aj»"\
x T,
Р @ = Р <
sup [и, (т) — u2 (т)]
x
¦:[0,П
К условиям вибронадежности часто добавляются ограничения, накладываемые на усилия и
деформации в амортизирующих элементах (амортизаторах) Условия нормальной работы аморти-
амортизаторов записываются в виде
(/= 1, 2, ...),
A2)
где и, — относительные перемещения опорных плоскостей амортизаторов вдоль основной оси;
F- — усилия, действующие на амортизаторы; F. —их предельно допустимые значения Напри-
Например, для линейных амортизаторов с коэффициентами жесткости с. и коэффициентами демпфиро-
демпфирования Ь, условия A2) можно записать в виде
\ciui
U =1.2, . .).
11'
324 ОСНОВЫ ТЕОРИИ ВИБРАЦИОННОЙ НАДЕЖНОСТИ
3. МЕТОДЫ АНАЛИТИЧЕСКОЙ ОЦЕНКИ ФУНКЦИИ НАДЕЖНОСТИ
Связь теории надежности с теорией выбросов случайных процессов. Чтобы вычис-
вычислить функцию надежности по известным вероятностным характеристикам процесса
v (f), нужно уметь находить вероятность пребывания случайных процессов в заданной
области на заданном отрезке времени, что является задачей теории выбросов случай-
случайных процессов 112, 105].
Выбросом процесса v (f) из области Q называют пересечение процессом v (t) пре-
предельной поверхности Г в направлении внешней нормали к ней. Выброс является
случайным событием, а число выбросов jV (t) на отрезке {0, t]—случайной величиной.
К сожалению, даже для одномерного случайного процесса v (t) и одностороннего
ограничения типа v (/) =g v^ задача теории выбросов допускает полное решение
только в некоторых частных случаях. Для многомерных случайных процессов и для
допустимых областей сложной конфигурации и тем более для функциональных про-
пространств качества приходится применять приближенные методы. Эффективное прибли-
приближенное решение задачи теории выбросов удается найти для высоконадежных систем,
у которых выброс вектора качества из допустимой области является редким событием.
Кумулятивные модели отказов. Для выпуклых областей Q функцию надежно-
надежности Р (t) можно записать при помощи надлежаще выбранной нормы в пространстве V:
P(O = P{|]V(T)||S=^, IE[0, t]}.
Здесь и, — предельно допустимое значение этой нормы. Например, для допустимой
области в виде A1) норму можно представить как
. 01
«2* «1*
\
причем 1^=1.
Процесс v (t) называют кумулятивным (квазимонотонным) на отрезке Т по норме
II v ||, если при любых t-i, t2 e T
I|vft)ll2s|lvft)||, h>tt.
Важным примером кумулятивного процесса служит процесс, компоненты которого
равны мерам «незалечивающихся» повреждений. Так, мера усталостного поврежде-
повреждения вводится как
f(k, sk), A3)
где / — некоторая неотрицательная функция от меры повреждения иь и некоторого
характерного (например, максимального) напряжения fe-ro цикла нагружения s^.
При этом принимается, что v0 = 0, v^ = 1.
Функция надежности кумулятивного процесса непосредственно выражается
через одномерную плотность вероятности вектора v в момент времени t:
P(t)= ( р (v, 0 dv,
!lv|j<i
или
Р®=* I Р(Ъ, -. t>n, 0*1 •¦• dva. A4)
Формула A4) совпадает по виду с формулой для вероятности ненарушения усло-
условия уейв элементарных расчетах на надежность, когда качество системы описы-
описывается при помощи числового вектора v.
Марковские модели отказов. Если эволюция вектора v (t) в пространстве V есть
диффузионный марковский процесс, то его переходная плотность вероятности
р (v, t | v0, ^o) удовлетворяет уравнениям Колмогорова [см. C6) и C8) в гл. XVII] с со-
соответствующими начальными условиями. Условная по отношению к вектору на-
начальных данных v0 функция надежности Р (t | v0) связана с переходной вероятностью
соотношением (t0 = 0)
vo)dv.
МЕТОДЫ АНАЛИТИЧЕСКОЙ ОЦЕНКИ ФУНКЦИИ НАДЕЖНОСТИ 325
Пусть интенсивности ху и ^д. процесса v (t) не зависят от времени. Тогда функция
надежности Р (/ I v0) удовлетворяет обратному уравнению Колмогорова
с начальным условием Р (< I v0) == 1 (t = 0, v0 e Q) и граничным условием
P(/|vo)=O (у,еГ). A6)
Точное решение уравнения A5) удается получить лишь в немногих частных слу-
случаях, не представляющих большого интереса для вибрационных расчетов. Вид гра-
граничного условия A6) подсказывает простой и эффективный путь нахождения прибли-
приближенных решений- функцию надежности представляют в форме ряда по координатным
функциям, обращающимся в нуль на Г, а коэффициенты ряда — функции времени —
определяют из обыкновенных дифференциальных уравнений метода Бубнова —
Галеркина.
Приближенные и двусторонние оценки функции надежности. Рассмотрим вероят
ностные модели, в которых отказы образуют ординарный поток, т. е. вероятность
повторения отказа на малом отрезке времени А^ имеет порядок о (At). Для таких
моделей известны эффективные оценки функции надежности, выраженные через
моменты числа выбросов [12].
Пусть Р@)= 1, т. е. в начальный момент времени система с вероятностью, равной
единице, находится в допустимой области. Тогда для функции надежности имеет
место строгая оценка снизу [12]:
P(t)=?\-{N(t)). A7)
Если привлечь моменты второго, третьего и т. д. порядков от числа выбросов, то
можно получить двусторонние оценки, например,
1 - (N @> s? Р @ «с 1 —i (N @> +y (N* @>.
К сожалению, нахождение моментов высших порядков связано с возрастающими
аналитическими и вычислительными трудностями.
Функция надежности высоконадежных систем. Пусть выполняется условие
1 — Р (t) <; 1, ^е [О, Г*]. Системы, удовлетворяющие этому условию, называют
высоконадежными. Для таких систем может быть использована приближенная
оценка, основанная на соотношении A7), взятом со знаком равенства
Р (Q я» 1-<#(/)>. A8)
Эта оценка близка к той, которая получается при условии, что отказы образуют
пуассоновский поток:
Р (9 я* ехр [-<#(/)>]. A9)
В самом деле, переход от A9) к A8) соответствует разложению экспоненты в степенной
ряд с удержанием первых двух членов. Введя математическое ожидание числа вы
бросов в единицу времени
М0 = ^<л/@>> B0)
представим формулы A8) и A9) в виде
t
P{t)^\-\\ {%)&%; B1)
B2,
326
ОСНОВЫ ТЕОРИИ ВИБРАЦИОННОЙ НАДЕЖНОСТИ
Сравнение формул B2) и E) показывает, что функция к (t) имеет смысл интенсив-
интенсивности отказов. При X = const из B1) и B2) получаем соответственно линейную и эк-
экспоненциальную зависимость функции надежности от времени (рис. 4). В связи
с этим говорят о линейной и об экспоненциальной оценках функции надежности. Фор-
Формулы A8) и B1) сравнительно простые; они особенно предпочтительны, если требуется
дальнейшая аналитическая обработка.
Учет вероятности отказа в начальный момент времени. Оценки A7)—A9) полу
чены при условии Р @) = 1. Если Р @) < 1, то обобщением оценки A9) будет зави-
зависимость
При этом в правую часть формулы должно входить число выбросов, определенное на
множестве реализаций, выходящих при t = 0 из области Q. Таким образом, приходим
Рис 4. Функция надежности и ее
оценки
Рис. 5. Функция надежности с учетом
вероятности отказа в начальный момент
времени
к необходимости рассматривать условные процессы. Однако неравенство Р (t) >z
5= Р @) [1 — {N (I))] справедливо и в том случае, если под N (t) понимается число
выбросов безусловного процесса (рис. 5).
Применение теории надежности к распределенным упругим системам. Общие прин-
принципы теории надежности могут быть распространены на распределенные системы
[12], в которых векторами качества будут некоторые функции координат и времени
(пространственно-временные случайные поля), а пространство V будет функциональ-
функциональным. Приближенные оценки A8) и A9) функции надежности справедливы и в этом
случае, если число выбросов JV (t) трактовать определенным образом. Например,
пусть v (х, f) — скалярное поле, и условие качества задается в виде v (x, t) < vt,
хей, Тогда N (t) равно числу выбросов поля v (x, t) за уровень vt в пространственно-
временном цилиндре Й(=ЙХ [0, t]. В свою очередь, математическое ожидание
числа выбросов может быть выражено через математические ожидания числа крити-
критических точек поля v (x, t) в Q^. Существует подход к оценке надежности распределен-
распределенных систем, основанный на представлении вектора качества в виде ряда по некоторым
координатным функциям с коэффициентами — случайными функциями времени.
В результате оценка функции надежности сводится к вычислению среднего числа
выбросов из области в конечномерном пространстве.
4. ТЕОРИЯ ВЫБРОСОВ СЛУЧАЙНЫХ ПРОЦЕССОВ
Среднее число выбросов одномерного процесса за уровень. Для отыскания оценок
функции надежности необходимо определить числовые характеристики выбросов
случайных процессов из области допустимых состояний, в частности, математическое
ожидание положительных пересечений {N (/)) векторным процессом v (t) предель-
предельной поверхности Г в пространстве качества V и среднее число выбросов в единицу
времени B0).
ТЕОРИЯ ВЫБРОСОВ СЛУЧАЙНЫХ ПРОЦЕССОВ
327
Рассмотрим непрерывный дифференцируемый одномерный случайный процесс
v @ с заданной совместной плотностью вероятности р (у, z>, f) процесса и его произ-
производной в совпадающие моменты времени. Среднее число положительных пересечении
в единицу времени процессом у (t) детерминистического уровня у# (t) (рис. 6)
Я (у*, 0= j (» — *•) Р(у*. ». 0 ^- B3)
о.
Если ввести вспомогательный процесс ух (^) = у (t) — у„ (/), то задачу о выбросах
Рис. в. Реализация случайного процесса v (() и Детерминистическая
функция о, (/)
процесса v (t) за переменный уровень vt (t) можно свести к вычислению характеристик
выбросов процесса ух (t) за нулевой уровень [105]:
B4)
Если ограничения являются двусторонними, то среднее число выбросов
в единицу времени из области [vtt, v^] находят как сумму положительных пересе-
пересечений уровня и, и отрицательных пересечений уровня vtt:
B5)
Для нахождения характеристик выбросов B3)—B5) необходимо вычислить сов-
совместную плотность вероятности р (v, v, f). Для этого нужно знать двухмерную плот-
плотность вероятности рх (их, v2) процесса v (t) в несовпадающие моменты времени, т. е
i>i = t> (/х), иа= у (У.
Если обозначить v± = у (/), у2 = у @ + v (t) At (где &t = /2 — /х), то искомую
плотность вероятности можно найти после перехода от переменных vlt y2 к v, v no
формуле
р (у, о, /)= lim [рх (у, Д]
Пересечения нормального процесса с детерминистической кривой. Для нормаль-
нормального процесса совместная плотность вероятности
р (у, ii, 0 = X
2яа а. /1—р2
где а, а, а2, а2, и р — соответственно математические ожидания, дисперсии и коэффи-
коэффициент корреляции процесса и его производной. В общем случае ли параметры явля-
328 ОСНОВЫ ТЕОРИИ ВИБРАЦИОННОЙ НАДЕЖНОСТИ
ются функциями времени. Формулы B3) или B4) принимают вид
B6)
где
У 1—Р2
a~~v* ], ф(ц) =—i_- f
Формулу B6) можно обобщить на случай, когда v^ есть также нормальный слу-
случайный процесс. При этом среднее число положительных пересечений в единицу
времени находят по формуле B6), если в последней сделать замену
p о о . + p a a ¦
V V У V, V, Vt
где р„ — коэффициент корреляции процесса v (f) и его производной. Предпола-
Предполагается, что процессы v (t) и t;, (t) не коррелируют.
Некоторые примеры применения формулы B6) для стационарного процесса v {t)
приведены в табл. 1.
1. Среднее число выбросов в единицу времени [к (с*, /)] для различных уровней v*(t)
Dt = ao _ Ol<>
a0, at — const
o« = a0 — A cos и?,
a0, A, to — const
f <, = const
"•* = const
a-
V
2ла7
a.
D
Г
I exp
a-
Г (а
L
(a-
Г (-
Г
— a0 + a
За"
0
ao+ A
2О2
0
¦ I/O . /4
a. = Л<о
V
,-aJ'
ч
, 0
(o. -aJ
2^
/ я/
1
J
:os coO2 "I Г
I
"I
> (n) ;
sin at
+ exp
]
\
2a? +
о /
l "Л+
[ 2J'
.-а,.-П
ТЕОРИЯ ВЫБРОСОВ СЛУЧАЙНЫХ ПРОЦЕССОВ
329
Среднее число максимумов (минимумов) и их распределение. При исследовании
процесса накопления повреждений важную роль играет изучение максимальных
(минимальных) значений случайного процесса. Среднее число максимумов в единицу
времени, превышающих уровень v%.
Ятах(г>„ /)= \ dv J р@. О, v, t)\v\db.
При этом предполагают, что процесс v (t) является непрерывным и дважды диф-
дифференцируемым с заданной совместной плотностью вероятности р (v, v, v, t) npo-
процесса и его первых двух производных.
Аналогично определяют среднее число ми-
минимумов в единицу времени, превышающих
уровень vt:
\nin
со
о, 0, v, t)"vdv-
о
При расчете вибрационной надежности
важно знать не только числовые характерис-
характеристики экстремумов случайного процесса, но и
их распределения. Плотность вероятности
максимумов
Р
B7)
J
/
/
0,5
о,*
(
V
/К
up
Лии
Л
\
\\
\\
У
\
\
-3-2
-1
о
цесса
Z
н-а.
Штрихом обозначена операция дифференци- ^¦яо
рования по vt. Аналогичный вид имеет
плотность вероятности минимумов.
Для стационарного нормального процесса v (t) выражение для плотности вероят-
вероятности максимумов B7) имеет вид [12]
B8)
где
а.-а X (— со)
о v max
МО)
— коэффициент широкополосное™ процесса, который изменяется от х\ (для узко-
узкополосного процесса) до значений *> 1 (для широкополосного процесса). Если
C «= 1, то распределение максимумов приближенно следует распределению Ре-
лея. При Р j> 1 распределение B8) приближается к нормальному с математиче-
математическим ожиданием и, — аи дисперсией а*. Для промежуточных значений параметра
Р вид распределения B8) показан на рис. 7.
Выбросы многомерного процесса из области допустимых состояний. Для много-
многомерного пространства качества V среднее число выбросов в единицу времени ста-
стационарного гауссовского процесса v (t) за пределы поверхности Г вычисляют по
формулам, приведенным в табл. 2.
330
ОСНОВЫ ТЕОРИИ ВИБРАЦИОННОЙ НАДЕЖНОСТИ
ание
Э"
S
а
сх
С
с
a
a
и
Э4
s
а
О
а
о
1
о.
С
к
го
ИЗВОДИ
про
к
к
.а
норм*
|
"О
• a
о
"—'Л
с
¦а
•—>и
а
Ш
«г
>
Ш
-—
X
„ о"
—л
It. О.
X
си
-
1!
1
a
К
«-*!
a
!
ь.
*-*
a
a
—
f
a"
-—
i
ь 1
I
а *-
! а
1
е
X
+
*
*
a
*
*
о
1
ft.
1
i
D
. 1
*-*
^^
" +
г г
v v
s s
i? о"
V V
1 1
"at
Ш
О
II
II
а
^-—
i
•ад
а
i
¦—'
—1 1
—^^
С?-
X [^ [
^ ш _ N
•О*
&** j_
К ^~
а
R
i
+
i——
+
—i
—^
е
1
ТЕОРИЯ ВЫБРОСОВ СЛУЧАЙНЫХ ПРОЦЕССОВ
331
о;
V
ос,
ш
о;
Ш
¦а |о
332
ОСНОВЫ ТЕОРИИ ВИБРАЦИОННОЙ НАДЕЖНОСТИ
5. РАСЧЕТ ВИБРАЦИОННОЙ НАДЕЖНОСТИ
Пример, Для расчета оптимальной виброзащиты рассмотрим систему! поведение которой опи-
описывается уравнением
и + 2е« + оз^« = — а0 (О.
Условия качества запишем в виде
| a(t) |
B9)
где а = Оо ~f" # — абсолютное виброускорение. В качестве критерия оптимальности системы
по надежности выберем такое условие, чтобы функция надежности A0) в момент времени t = T%
принимала максимальное значение. Для стационарных колебаний высоконадежных систем это
условие согласно B1) эквивалентно условию к (Г) = tnin, где среднее число выбросов в еди-
Е, @0
ницу времени подсчитывают для прямоугольной области допустимых состояний B9)
Пусть процесс а0 @ на входе системы — узкополосный с несущей частотой 9. На рис. 8 при-
приведены результаты вычислений К (Г) при и, = 10~3 м, at = 20 М'С~2. На рис 9 показан при-
ю"
1
/
-Г
VI
'Л
Л/а
20
1.5
1,0
0,5
О 0,05
0,10
к
\
L
\
/
\
\\
.
—
50
100
150
гоо
250 ыо/а
Рис. 8. Оптимизация по надежности
при узкополосном входном воздействии
Рис. 9. Оптимизация по надежности при
экспоненциально-коррелированном входном
воздействии
мер вычисления X (Г) для случая экспоненциально-коррепированного процесса на входе с корре-
корреляционной функцией К (т) = of ехр (— а | т |) Вычисления проводили для значений парамет-
"о
ров е/(|H — 0,5, а+ = 2(J0, и* = (со/а2)-1О~4. Кривые
полосы | а | < а,, кривые 2 — выбросам из полосы
марпого числа выбросов [12, 91].
/ на рис. 8 и 9 соответствуют выбросам из
| и | < иг, кривые 3 построены для сум
Учет усталостных повреждений. Как правило, вибрационное нагружение сопро-
сопровождается процессом накопления усталостных повреждений. Рассмотрим простой
одномерный случай, когда повреждения характеризуются одномерным процессом
v (t). Если этот процесс является достаточно медленным, то можно от A3) перейти
к непрерывному аналогу — кинетическому уравнению
^ = 8(v's)- C0)
Мера повреждения v (t) есть неубывающая функция, 0 ^ v =g: 1. В уравнении C0)
s (f) — некоторое характерное значение для процесса нагружения / (t), например,
амплитудное. Условие качества выбирают в виде v < в# = 1, s < s^ (и),где s#(a) —
предельное значение несущей способности с учетом накопленных повреждений. При
этом функция надежности
Р@ = РМт)<1, s(t)<s*(u), те[0, /]}.
Гипотеза линейного суммирования повреждений. Обычно в качестве меры уста-
усталостного повреждения принимают
-2
РАСЧЕТ ВИБРАЦИОННОЙ НАДЕЖНОСТИ 333
где N (Sj) — число циклов, приводящих к разрушению с характеристикой S/. Тогда
условие усталостного разрушения принимает вид
V 1
Li N (sj)
i
__. j
Для оценки долговечности используют величину 71,, равную времени нагружения,
которое необходимо для достижения условия v = vt = 1. При малом разбросе
долговечности величина Tt близка к математическому ожиданию (Т). Назовем
величину Tt ожидаемой долговечностью. Если не учитывать вероятность мгновенного
разрушения вследствие выброса процесса / (t) за уровень st (v), то формула для
ожидаемой долговечности имеет вид
где Те — некоторый эффективный период цикла; р (s) — распределение параметра s
процесса нагружения / (t).
Вычисление ожидаемой долговечности для различных процессов иагружения.
Для стационарных нормальных узкополосных процессов нагружения в качестве
характерного значения s (t) принимают максимальное значение s (f) = /max@- При
этом распределение максимумов нормального процесса находят по формуле B8).
Вычисления по формуле C1) при степенной аппроксимации кривой усталости
/V ->- оо (s < st)
дают
* 2"'/2ГA+т/2)Р(х2>
где %= Sx/a^Ni, slt nt — эмпирические константы; Р (%г, т) — функция ^-распре-
^-распределения Пирсона. Эта же формула, выраженная через неполную гамма-функцию
Г (а, х), имеет вид
* 2"!/2ГA+т/2, х2/2)'
Для широкополосных процессов нагружения существуют различные способы
выбора параметра нагружения s, приводящие к различным оценкам долговечности.
В качестве параметра цикла можно рассматривать следующие друг за другом макси-
максимумы, максимальные значения огибающей, полуразность следующих друг за другом
максимумов и минимумов, максимальные значения процесса на некотором характер-
характерном интервале времени и т. д. Для схематизации заданного процесса нагружения
некоторым эквивалентным узкополосным процессом существуют различные методы:
выбросов (число циклов совпадает со средним числом нулей процесса), максимумов
(число циклов берется как среднее число максимумов процесса), размахов (цикл
характеризуется амплитудой, равной половине приращений процесса между сосед-
соседними экстремумами), полных циклов (метод, состоящий в последовательном исключе-
исключении из процесса промежуточных циклов со все более возрастающими амплитудами)
и т. д.
Приведем выражения для плотности вероятности р (s) параметра нагружения s (/) в случае
стационарного нормального процесса / (О Распределение максимумов р± (s) дается формулой B8),
По методу выбросов
s
Pa (S) = — е:
по методу размахом
?34
ОСНОВЫ ТЕОРИИ ВИБРАЦИОННОЙ НАДЕЖНОСТИ
¦а по методу полных циклов [37]
5 * уи-ъ- \
— txp / г~ 1 is
-пЛ^[-~) (s>.ft).
где 0 — коэффициент широкополосности процесса а, с, s^ — некоторые константы Характер за-
зависимости ожидаемой долговечности C1) от параметра широкополосности E изображен на рис 10
10 '
10 2
I
Z
0 3
\ \
ь
I
1
¦
1,0 1,5
2,0
3,0
Рис. 10. Сравнение оценок ожидаемой долго
вечности при схематизации различными ме
тодами:
0 — выбросов; / — максимумов; 2 — размахов,
3 — полных циклов
Через Т обозначена ожидаемая долговечность, соответствующая плотности вероятности р, (s)
При вычислениях принято, что Si = 0, m ~ 5. Метод максимумов дает оценку снизу для ожи-
ожидаемой долговечности, методы размахов и полных циклов — завышенные значения этой оценки
Для узкополосных процессов все методы приводят к практически одинаковым результатам.
СПИСОК ЛИТЕРАТУРЫ
1. Амбарцумян С. А. Общая теория анизотропных оболочек. М., «Наука», 1974.
446 с.
2. Ананьев И. В., Тимофеев П. Г. Колебания упругих систем в авиационных кон-
конструкциях и их демпфирование М., «Машиностроение». 1965. 526 с.
3. Бабаков И. М. Теория колебаний. М., «Наука», 1968. 560 с.
4. Бахвалов Н. С. Численные методы. В 2-х т. т. 1. М., «Наука», 1973. 631 с.
5. Беляковский Н. Г. Конструктивная амортизация механизмов, приборов и аппа-
аппаратуры на судах. Л., «Судостроение», 1965. 523 с.
6. Бендаг Д. С, Пирсол А. Дж. Измерение и анализ случайных процессов. Пер.
с англ. М., «Мир», 1971. 390 с.
7. Бидерман В. Л. Прикладная теория механических колебаний. М., «Высшая
школа», 1972. 416 с
8. Бишоп Р. Э. Д. Колебания. Пер. с англ. М., «Наука», 1968. 143 с.
9. Болотин В. В. Динамическая устойчивость упругих систем. М., Гостехиздат,
1956. 600 с.
10. Болотин В. В. Краевой эффект при колебаниях упругих оболочек. — «ПММ»,
т. 24. 1960, № 5, с. 831—842.
11. Болотин В. В. Неконсервативные задачи теории упругой устойчивости. М.,
Физматгиз, 1961. 339 с.
12. Болотин В. В. Применение методов теории вероятностей и теории надежности
в расчетах сооружений. М., Стройиздат. 1971. 256 с.
13. Болотин В. В. Теория распределения собственных частот упругих тел и ее при-
применение к задачам случайных колебаний. — «Прикладная механика», т. 8,
1972, вып. 4, с. 3—29.
14. Болотин В. В. Численный анализ устойчивости линейных дифференциальных
уравнений с периодическими коэффициентами. — В кн.: Избранные проблемы
прикладной механики. М., изд. ВИНИТИ, 1974, с. 155—166.
15. Болотин В. В., Москвин В. Г. О параметрических резонансах в стохастических
системах. —«Изв. АН СССР. МТТ». 1972, № 4, с. 88—94.
16. Бреховских Л. М. Волны в слоистых средах. М., Изд-во АН СССР, 1957. 502 с.
17. Бусленко Н. П. Моделирование сложных систем. М., «Наука», 1968. 355 с.
18. Быков В. В. Цифровое моделирование в статистической радиотехнике. М., «Со-
«Советское радио», 1971. 328 с.
19. Вайнберг Д. В., Писаренко Г. С. Механические колебания и их роль в технике.
М., «Наука», 1965. 276 с.
20. Вайнберг Д. В. Справочник по прочности, устойчивости и колебаниям пластин.
Киев. «Будтелышк», 1973. 488 с.
21. Валишвили Н. В. Методы расчета оболочек вращения на ЭЦВМ. М., «Машино-
«Машиностроение», 1976. 278 с.
22. Воеводин В. В. Численные методы алгебры. Теория и алгоритмы. М., «Наука»,
1966. 248 с
23. Волоховский В. Ю. Некоторые задачи теории надежности для оболочек. Теория
оболочек и пластин,
336 СПИСОК ЛИТЕРАТУРЫ
[Труды IX Всесоюзной конференции по теории оболочек и пластин.]. Л., «Судо-
«Судостроение», 1975, с. 170—173.
24. Вольмир А. С. Нелинейная динамика пластин и оболочек. М., «Наука», 1972
314 с.
25. Вольмир А. С. Устойчивость деформируемых систем. М., «Наука», 1967. 984 с.
26. Вольмир А. С. Оболочки в потоке жидкости и газа. Задачи аэроупругости. М.,
«Наука», 1976. 416 с.
27. Ганиев Р. Ф., Кононенко В. О. Колебания твердых тел. М., «Наука», 1976.
431 с.
28. Гихман И. И., Скороход А. В. Стохастические дифференциальные уравнения.
Киев, «Наукова думка», 1968. 354 с.
29. Гнеденко Б. В., Беляев Ю. Км Соловьев А. Д. Математические методы в теории
надежности. М., «Наука», 1965. 524 с.
30. Годунов С. К-, Рябенький В. С. Разностные схемы. М., «Наука», 1973. 400 с.
31. Голенко Д. И. Моделирование и статистический анализ псевдослучайных чисел
на электронных вычислительных машинах. М., «Наука», 1965. 227 с.
32. Голоскоков Е. Г., Филиппов А. П. Нестационарные колебания механических
систем. Киев, «Наукова думка», 1966. 336 с.
33. Гольденблат И. И., Сизов А. М. Справочник по расчету строительных конструк-
конструкций на устойчивость и колебания. М., Стройиздат, 1952. 252 с.
34. Гольдсмит В. Удар. Теория и физические свойства соударяемых тел. Пер. с англ.
М., Стройиздат, 1965. 448 с.
35. Гонткевич В. С. Собственные колебания пластинок и оболочек. Киев, «Наукова
думка», 1964. 288 с.
36. Григолюк Э. И., Селезов И. Т. Неклассические теории колебаний стержней,
пластин и оболочек. М., Изд. ВИНИТИ, 1973. 271 с.
37. Гусев А. С. О распределении амплитуд в широкополосных случайных процес-
процессах при схематизации их по методу полных циклов. — «Машиноведение», 1974,
№ 1, с. 65—71.
38. Ден-Гартог Дж. Механические колебания. Пер, с англ. М., Физматгиз, 1960.
580 с.
39. Джанелидзе Г. Ю. Устойчивость упругих систем при динамических нагрузках —
В кн.: Проблемы устойчивости в строительной механике. М., Стройиздат, 1965,
с. 68—84.
40. Дженкинс Г., Ватте Д. Спектральный анализ и его приложения. Пер. с англ. М.,
«Мир», вып. 1, 1971. 316 с; вып. 2, 1972. 287 с.
41. Ермаков С. М., Михайлов Г. А. Курс статистического моделирования. М.,
«Наука», 1976. 320 с.
42. Жинжер Н. И. О дестабилизирующем влиянии трения на устойчивость не-
неконсервативных упругих систем. — «Изв. АН СССР. МТТ», 1968, № 3, с.
44—47.
43. Зенкевич О. К- Метод конечных элементов в технике. Пер. с англ. М., «Мир»,
1975. 541 с.
44. Зубов В. И. Математические методы исследования системы автоматического
регулирования. Л., «Машиностроение», 1974. 336 с.
45. Ивович В. А. Переходные матрицы в динамике упругих систем. М., «Машино-
«Машиностроение», 1969. 199 с.
46. Ильюшин А. А., Победря Б. Е. Основы математической теории термовязко-
упругости. М., «Наука», 1970. 280 с.
47. Иориш Ю. И. Виброметрия. М., Машгиз, 1963. 771 с.
48. Кильчевский Н. А. Динамическое контактное сжатие твердых тел. Удар., Киев,
«Наукова думка», 1976. 319 с.
49. Кожешник Я. Динамика машин. Пер. с чеш. М., Машгиз, 1961. 421 с.
50. Коллатц Л. Задачи на собственные значения с техническими приложениями.
Пер. с англ. М., «Наука», 1968. 503 с.
51. Кокс Д., Льюис П. Статистический анализ последовательностей событий. Пер
с англ. М., «Мир», 1969. 312 с.
52. Кольский Г. Волны напряжения в твердых телах. Пер. с агл. М., Изд-во иностр.
лит. 1955. 192 с.
СПИСОК ЛИТЕРАТУРЫ 337
53. Корн Г. Моделирование случайных процессов на аналоговых и аналого-цифро-
аналого-цифровых машинах. Пер. с англ. М., «Мир», 1968. 315 с.
54. Красовский Н. Н. Некоторые задачи теории устойчивости движения. М., Физ-
матгиз, 1959. 211 с.
55. Кристенсен Р. Введение в теорию вязкоупругости. Пер. с англ. М., «Мир»,
1974. 338 с.
56. Кушнер Г. Дж. Стохастическая устойчивость и управление. Пер. с англ. М.,
«Мир», 1969. 198 с.
57. Ломакин В. А. Статистические задачи механики твердых деформируемых тел.
М., «Наука», 1970. 138 с.
58. Лурье А. И. Аналитическая механика. М., Физматгиз, 1961. 824 с.
59. Мак-Лахлан Н. В. Теория и приложения функций Матье. Пер. с англ. М., Изд-во
иностр. лит. 1953 475 с.
60. Математическое обеспечение ЕС ЭВМ. [Пакет научных подпрограмм]. Пер.
с англ. Под ред Т. И. Пыльцевой, Н. Д. Соколовой. Вып. 1, ч. 1, Минск, 1973
228 с.
61. Математическое обеспечение ЕС ЭВМ. [Пакет научных подпрограмм]. Пер
с англ. Под ред. Н. С. Жаврид, М. Л. Петрович. Вып. 2, ч. 2. Минск, 1973.
272 с.
62. Математическое обеспечение ЕС ЭВМ. [Пакет научных подпрограмм]. Пер
с англ. Под ред. С. П. Ерашевской, Н. Д. Соколовой. Вып. 3, ч. 3, Минск, 1973
240 с
63. Математическое обеспечение ЕС ЭВМ. [Пакет научных подпрограмм]. Пер.
с англ. Под ред. Н. С. Жаврид, В. Н. Кузнецовой, Л. В. Ходыко. Вып. 4, ч. 4.
Минск, 1974. 284 с.
64. Математическое обеспечение ЕС ЭВМ. [Пакет научных подпрограмм]. Вып. 6,
ч. 5, Минск, 1975. 216 с.
65. Математическое обеспечение ЕС ЭВМ. [Пакет научных подпрограмм]. Вып. 10,
ч. 6. Минск, 1976. 240 с.
66. Митропольский Ю. А. Проблемы асимптотической теории нестационарных коле-
колебаний. М., «Наука», 1964. 431 с.
67. Михлин С. Г. Численная реализация вариационных методов. М., «Наука»,
1966. 432 с.
68. Михлин С. Г. Вариационные методы в математической физике. М., «Наука»,
1970. 512 с.
69. Москаленко В. Н. К применению уточненных теорий изгиба пластинок в задаче
о собственных колебаниях. — «Инженерный журнал», 1961, т. 1, вып. 3,
с. 93—101.
70. Москаленко В. Н. Случайные колебания многопролетных пластин. — «Инже-
«Инженерный журнал. МТТ», 1968, № 4, с. 79—84.
71. Москаленко В. Н., Чен-де-Лин. О собственных колебаниях многопролетных не-
неразрезных пластинок. — «Прикладная механика», 1965, т. 1, вып. 3, с. 59—66.
72. Москвин В. Г., Окопный Ю. А. Исследование устойчивости систем с двумя сте-
степенями свободы при случайном параметрическом воздействии. — «Изв. вузов.
Сер. Машиностроение», 1972, № 3, с. 31—35.
73. Москвин В. Г., Смирнов А. И. К устойчивости линейных стохастических си-
систем. — «Изв. АН ССР. МТТ», 1975, № 4, с. 62—65.
74. Мышкис А. Д. Линейные дифференциальные уравнения с запаздывающим аргу-
аргументом. М., «Наука», 1972. 325 с.
75. Мэнли Р. Анализ и обработка записей колебаний. Пер. с англ. М., «Машинострое-
«Машиностроение», 1972. 368 с.
76. Николаенко Н. А. Вероятностные методы динамического расчета машинострои-
машиностроительных конструкций. М.( «Машиностроение», 1967. 368 с.
77. Новацкий В. Динамика сооружений. Пер. с польск. М., Стройиздат, 1963. 376 с.
78. Новожилов В. В. Теория тонких оболочек. Л., Судпромгиз, 1962. 431 с.
79. Огибалов П. М. Вопросы динамики и устойчивости оболочек. М., Изд-во МГУ,
1963. 419 с.
80. Острей К. Ю. Введение в стохастическую теорию управления. Пер. с англ.
М., «Мир», 1973. 322 с.
338 СПИСОК ЛИТЕРАТОРЫ
81. Пальмов В. А. Тонкие оболочки под действием широкополосной случайной на-
нагрузки — «ПММ», 1965, т. 29, № 4, с. 763—770.
82. Пановко Я- Г. Внутреннее трение при колебаниях упругих систем. М., Физмат-
гиз, 1960. 193 с.
83. Пановко Я. Г. Основы прикладной теории упругих колебаний. М., «Машиност-
«Машиностроение», 1967. 316 с.
84. Писаренко Г. С. Колебания механических систем с учетом несовершенной упру-
упругости материала. Киев, «Наукова думка», 1970. 380 с.
85. Половко А. М. Основы теории надежности. М., «Наука», 1964. 446 с.
86. Постнов В. А., Хархурим И. Я. Метод конечных элементов в расчетах судовых
конструкций. Л., Судпромгиз, 1974. 341 с.
87. Прочность, устойчивость, колебания. Справочник в 3-х т. Под ред.
И. А. Биргера и Я- Г. Пановко. М., «Машиностроение», 1968. т. 1—831 с; т. 2 —
463 с; т. 3 — 567 с.
88. Прохоров Ю. В., Розанов Ю. А. Теория вероятностей. Основные понятия, пре-
предельные теоремы, случайные процессы. М., «Наука», 1967. 495 с.
89. Пугачев В. С. Теория случайных функций и ее применение к задачам автомати-
автоматического управления. М., Физматгиз, 1962. 884 с.
90. Работнов К). Н. Ползучесть элементов конструкций. М., «Наука», 1966.
752 с.
91. Радин В. П. Об оптимизации линейных виброзащитных систем по надеж-
надежности. — «Прикладная механика», 1972, т. 8, вып. 9, с. 134—137.
92. Радин В. П., Чирков В. П. О передаче случайных вибраций через тонкостенные
конструкции. — В кн.: Проблемы надежности в строительной механике. Виль-
Вильнюс, РИНТИП, 1971, с. 128—135.
93. Расчеты на прочность в машиностроении. Т. 3. М., Машгиз, 1959, 1118 с.
Авт.: С. Д. Пономарев, В. Л. Бидерман, К- К- Лихарев, В. М. Макушкин,
Н. Н. Малинин, В. И. Феодосьев.
94. Расчет сооружений с применением вычислительных машин. М., Стройиздат,
1964, 380, с. Авт.: А. Ф. Смирнов, А. В. Александров, Н. Н. Шапошников,
Б. Я- Лащеников.
95. Самарский А. А. Введение в теорию разностных схем. М., «Наука», 1971. 552 с.
96. Светлицкий В. А. Случайные колебания механических систем. М., «Машино-
«Машиностроение», 1976. 216 с.
97. Свешников А. А. Прикладные методы теории случайных функций. М., «Наука»,
1968. 463 с.
98. Случайные колебания. Под ред. С. Кренделла. Пер. с англ. М., «Мир», 1967.
356 с.
99. Смирнов Н. В., Дунин-Барковский Л. В. Курс теории вероятностей и матема-
математической статистики для технических приложений. Изд. 3. М., «Наука», 1969.
511 с.
100. Справочник по динамике сооружений. Под ред. Б. Г. Коренева и И. М. Раби-
Рабиновича. М., Стройиздат, 1972. 511 с.
101. Справочник по теории упругости. Под ред. П. В. Варвака и А. Ф. Рябова.
Киев, «Буд1вельник», 1971. 418 с.
102. Статика и динамика тонкостенных оболочечных конструкций. М., «Машино-
«Машиностроение», 1975, 375 с. Авт.: А. В. Кармишин, В. А. Лясковец, В. И. Мяченков,
А. Н. Фролов.
103. Стратонович Р. Л. Условные марковские процессы и их применение в теории
оптимального управления. М., Изд-во МГУ, 1966. 319 с.
104. Тимошенко С. П. Колебания в инженерном деле. Пер. с англ. М., «Наука»,
1967. 444 с.
105. Тихонов В. И. Выбросы случайных процессов. М., «Наука», 1970. 392 с.
106. Уилкинсон Дж. X. Алгебраическая проблема собственных значений. Пер.
с англ. М., «Наука», 1970. 564 с.
107. Уилкинсон Дж. X., Рейнш К- Сборник алгоритмов на АЛГОЛе. Линейная ал-
алгебра. Пер. с англ. М., «Машиностроение», 1976. 390 с.
108. Фаддеев Д. К., Фаддеева В. Н. Вычислительные методы линейной алгебры. М.,
физматгиз, 1960. 655 с.
СПИСОК ЛИТЕРАТУРЫ
339
109. Федоров Ю. А. О параметрической стабилизации неконсервативных систем с
двумя степенями свободы.—В кн.: Механика деформируемого твердого тела и
теория надежности. М., изд. МЭИ, вып. 280, 1976, с. 29—33.
ПО. Филиппов А. П. Колебания деформируемых систем. М., «Машиностроение»,
1970. 736 с.
111. Фролов К- В. Некоторые проблемы параметрических колебаний элементов ма-
машин — В кн.: Колебания и устойчивость приборов, машин и элементов систем
управления. М., «Наука», 1968, с. 5—20.
112. Хасьминский Р. 3. Устойчивость дифференциальных уравнений при случай-
случайных возмущениях их параметров. М., «Наука», 1969. 368 с.
113. Челомей В. Н. Динамическая устойчивость элементов авиационных конструк-
конструкций. М., «Аэрофлот», 1939. 77 с.
114. Четаев Н. Г. Устойчивость движения М., Гостехиздат, 1955. 207 с.
115. Чирков В. П. Случайные колебания тонкостенных конструкций, несущих
сосредоточенные массы. — «Изв. АН СССР. МТТ», 1975, № 3, с. 159—164.
116. Якубович В. А., Старжинский В. М. Линейные дифференциальные уравнения
с периодическими коэффициентами и их приложения. М., «Наука», 1972.
718 с.
117. Anderson R. Fundamentals of vibrations. New York, The Macmillan Company
London, Collier—Macmillan Limited, 1967. 412 p.
118. Ariaratnam S. T. Dynamic stability of a column under random loading. Dynamic
stability of structures. Oxford a. o., Pergamon Press, 1967, p. 61—80.
119. Bishop R. E. D., Gladnell G. M.L., Michaelson S. The matrix analysis of vibration.
Cambridge, Univ. Press, 1965. 404 p.
120. Bishop R. E. D., Johnson D. С The mechanics of vibration. Cambridge, Univ.
Press, 1966. 592 p.
121. Bolotin V. V. Broadband random vibration of elastic systems. — «Intern. Journ.
of Solids and Struct.», 1966, vol. 2, N 1, p. 105—124.
122. Bolotin V. V. Reliability theory and stochastic stability. In: Study on Stability,
Univ. of Waterloo, 1971, N 6, p. 385—422.
123. Burton R. Vibration and impact. New York, Dover, 1968, 310 p.
124. Crandall S. H., Mark W. D. Random vibration in mechanical systems. New
York, Academic Press, 1963. 166 p.
125. Drgania i fale. Warszawa, Bemovo, 1964, 467 p. Auth.: Z. Dzygadlo, S. Kaliski,
L. Solarz, S. Wlodarczyk.
126. Duggan T. V. Stress analysis and vibrations of elastic bodies. London, Tempi.
Press, 1964. 588 p.
127. Evan-Ivanowski R. M. On the parametric response of structures. — «Appl. Mech.
Rev.», 1965, vol. 18, N 9, p. 699—702.
128. Handbook of engineering mechanics. Edited by \V. Flugee. New York, Me Graw—
Hill. 1962. 1632 p.
129. Herrmann G. Stability of equilibrium of elastic systems subjected to nonconser-
vative forces. — «Appl. Mech. Rev.», 1967, vol. 20, N. 2, p. 103—108.
130. Hsu C. S., Lee Т. Н. A stability study of continuous systems under parametric
excitation via Liapunov's direct method. In: Instability of continuous systems.
Berlin — Heidelberg — New York, Springer — Verlag, 1969, p. 112—118.
131. Iwatsubo Т., Sugiyama Y., Ogino S. Simple and combination resonances of co-
columns under periodic axial loads. — «Journ. Sound and Vibr.», 1974, vol. 33B),
p. 211—221.
132. Koiter W. T. A consistent first approximation in the general theory of thin elastic
shells. Proc. IUTAM Symposium on the theory of thin shells (Delft, 1959), Amster-
Amsterdam, North Holland Publ., 1960, p. 12—33.
133. Krajcinovic D., Herrmann G. Numerical solution of the dynamic stability prob-
problems. — «Intern. Journ. Numer. Methods in Engng.», 1970, vol 2, p. 551—561.
134. Lin Y. К- М-, Probabilistic theory of structural dynamics. New York a. o.,
Me Qraw—Hill, 1967. 336 p.
135. Mettler E. Stability and vibration problems of mechanical systems under periodic
excitation. Proc. Int. Conf. on Dynamic Stability of Structures(Evanston, 1965).
Oxford, Pergamon Press, 1967, p. 169—189.
340 СПИСОК ЛИТЕРАТУРЫ
136. Thomson W. Т. Vibration theory and applications. London, Allen and Unwin,
1971. 384 p.
137. Schmidt G. Parametererregte Schwingungen. Berlin, Deutscher Verl. der Wiss.
1975. 313 s.
138. Shinozuka M. Simulation of multivariate and multidimensional random proces-
processes. — «Journ. Acoust. Soc. Am.», 1971, vol. 49, N 1, p. 556—583.
139. Shock and vibration handbook. Edited by С. М. Harris, С. Е. Crede. New York,
Me draw—Hill, 1976. 1211 p.
140. Vernon J. B. Linear vibration theory. Generalized properties and numerical
methods. New York a. o., John Wiley and Sons, 1967. 365 p.
141. Volterra E. G., Zachmanoglou E. C. Dynamic of vibrations. Columbus, Merril,
1965. 622 p.
142. Weidenhammer F. Zufallschwingungen. — «Zeitschr. angew. Math, und Mech.»,
Sonderheft (QAMM — Tagung), Bd. 47, 1967, s. 25—28.
143. Weigand A. Einfuhrung in die Berechnung mechanischer Schwingungen. Leipzig,
Fachbuchverl., 1967. 176 s.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автоколебания — Определение 18
Алгоритм моделирования —Типы 280—
281
— - Рутисхаузера 83
— — Френсиса — Кублановской 83
Амплитуда действительная 20
— — комплексная 20, 104, 108
— — установившихся вынужденных
колебаний 106
Аналогии динамические — Виды 51—53
Антирезонанс 106
Балка упругая 265—268 — Динами-
Динамическая устойчивость 252
Белый шум 281
Ито 303, 307—309
Стратоновича 303, 307, 309
Биения ~- Определение 28
В
Вариационный принцип 69—71
172
— — Гамильтона 36, 37, 135
— — Куранта 172
Релея 70, 171
— — Релея расширенный 70
Вектор волновой 175
— — признаков 320
— — состояний системы 296
Вероятность отказа системы 321
Вибрации 16
171,
— — случайные — Передача 313
Вибродиагностика 16
Виброзащита 16
Виброиспытание 36
Виброметрия 16
Вибронадежность 16
Вибронапряжение 322
Виброобработка 16
Виброперемещение 322
Вибропрочность 16
Вибротранспортировка 16
Виброускорение 322
— — опорное 30
Виброустойчивость 16
Возбуждение кусочно-постоянное 123,
124
— — начальное 55
— — параметрическое 117
— — ступенчатое внешнее 113
Воздействие импульсное 114
— — параметрическое 299
случайное 286
Волновое число 181, 209, 213, 217, 229,
258
Волновой упругий процесс — Понятие
256
Волны — Амплитуда 257, 258 — Длина
258 — Частота 258
— — дилатационные (расширения-сжа-
(расширения-сжатия) 257
— — изгибные 260, 261 — Фазовая
скорость 260 — Волновое число
260
— — крутильные 259 — Скорость рас-
распространения 259
— — поверхностные 258, 259 — Поня-
342
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
тие 258 — Скорость распростра
нения 258, 259
— — продольные 259 — Скорость рас
пространения 259
упругие 259, 260, 261
эквиволюмиальные (искажения
или сдвига) 257
Выброс процесса 324
Вынужденные колебания
— — в системе распределенной 101—
105, 109 115, 116, 234—238
— — в системе с конечным числом сте
пеней свободы 101—116
Вынужденные колебания неустановив
шиеся 109, 115, 232
— — в распределенных системах 238
— — в системе с конечным числом
степеней свободы 102—109
в системе с одной степенью сво
боды 109
Вынужденные колебания установив-
установившиеся 101, 234
в вязко-упругих системах 239
— — в диссипативных системах 102
238—240
изгибные 236
— — продольные 235
Гамильтона принцип 36—38
Гамильтона—Остроградского принцип
135, 136
Гармонические колебания — Закон из-
изменения 19
— Комплексное представление 20
— Круговая диаграмма 19, 20
— Начальная фаза 19
— Угловая скорость 19
Гауссовский (нормальный) процесс 276
— — стационарный дельта-коррелиро
ванный 281
Гипотеза квазигауссовости 304, 305
Кирхгофа—Лява 157, 160 217
— — линейного суммирования повре-
повреждений 332, 333
— — Миллионщикова 304
Гука закон 137, 138
Д
Даламбера принцип 34, 35
Движение абсолютное 35
— — истинное 36, 37
колебательное 19
— — относительное 35
— — относительно неподвижной оси
51
— — относительно неподвижной точки
51
— — переносное 35
— — плоскопараллельное 50, 51
— — равномерное вращательное 40
— — равномерное поступательное 40
— — смежное 36
Декремент колебаний 102
— — логарифмический 93
Демпфирование внешнее 94
— — внутреннее 94
— — относительное 93
Деформации местные 261
общие 261
Диагностика вибрационная 287
техническая 287
Диаграмма Айнса — Стретта 123
— — Вина 65
Диапазоны стандартные октавные 30
Динамика статистическая 268
Динамические аналогии — см. Анало-
Аналогии динамические
Динамический гаситель колебаний 106
Дисперсия аномальная 258, 260
— — нормальная 258
случайного процесса 270
Диссипация малая 94
неполная 90, 92
— — отрицательная 92
•— — полная 92
Долговечность ожидаемая — Вычисле-
Вычисление 333
— Сравнение оценок 334
Ж
Жесткость динамическая 291
деление 105
¦ Опре-
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
343
Задача алгебраическая о собственных
значениях 78, 79
Бека 242, 243
краевая стахостическая 286, 310
— Операторная форма записи
310 — Пример 310
Николаи 242
— — обобщенная алгебраическая о
собственных значениях 78, 79
— — полная о собственных значениях
80—83
Реута 242
Затухающие колебания — Декремент
93, 102 — Определение 27
И
Изгибно-крутильные колебания стерж-
стержней 156, 157, 200, 201
Изгибные колебания 193—200 — Влия
ние начальных усилий 199, 200 — Кра-
Краевые условия 153, 154, 193, 194 — При-
Примеры 195—196— Собственные формы
195 — Собственные частоты 195 —
— Уравнения 155, 193
— — оболочек — Уравнения 160—
166 — Частоты и формы 218—
234
— — пластин — Уравнения 157 — Ча-
Частоты и формы 203—218
— — стержней — Уравнения 152—
156 — Частоты и формы 193—
200
Импеданс механический 105
Импульс 114
— —• прямоугольный 114, 115
— — силы 115
• ударный — Определение 115
Инерция вращения — Учет 159 160
Интеграл действия 38
Дюамеля 109, НО, 238
— — Фурье—Стильтьеса 272
Интенсивность белого шума 281
марковского процесса 277
отказов 321
Итерации прямые 84
Квазиустойчивость 244
Кирхгофа закон второй 53
первый 53
Колебания — Виды см под их назва-
названиями, например Вынужденные колеба-
колебания — Определение 18
стержней 145, 146, 147, 148, 149,
150, 151
— — струны 145, 146
— — тонких упругих оболочек 160—
166 — Уравнения 163
Колебательный процесс — Амплитуд-
Амплитудный спектр 21
— Классификация 18
— Несущая частота 27
— Определение 15
— Пиковые значения 28
— Пример 21, 22
— Размах 29
— Реализация 18
— Уровень 30
Колебательный процесс многомерный
31
— — модулированный 28
непериодический 26—28
— — неустановившийся 18
— — периодический 18 — Амплитуда
21 — Амплитудный спектр 192 —
Анализ спектральный 21 — Ко-
Коэффициенты Фурье 21, 22, 23 —
Спектр частот 21
установившийся 26, 27
Количество движения 33
Координаты декартовы 47, 49
— — нормальные (главные) 93, 108,
109 — Использование 107
— — обобщенные 40 — Вариации
36
— — сферические 137
— — циклические 40, 67
— — цилиндрические 137
Коэффициент возбуждения 119
критический 126
344
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Коэффициент демпфирования 91, 93
— — динамического усиления (дина-
(динамичности) 102 — Определение
101
— — диффузии 277
инерционный 55, 66, 67, 68
квазиупругий 56, 66, 67, 68
— — корреляции 270
— — Пуассона 138
— — сноса 277
Фурье 21, 25
Краевая задача с квазиразделяющими-
ся переменными 178
— — с разделяющимися переменными
177
стахостическая 286
Краевые условия 178
альтернативные 136
¦ естественные 139
Кривизны главные 160
Критерий Зубова 97
Коши—Михайлова—Найквиста
98, 99
— — оптимальности системы по на-
надежности 332
Рауса—Гурвица 98, 99
Кронекера символ 44
Кумулятивный (квазимонотонный) про-
процесс 324
Л
Лагранжиан 139
Ламе параметры 160
Ламе постоянные 138
Лапласа преобразования — Примене-
Применение 112 — Примеры 113
Лиссажу фигуры — Определение 1Ь —
Примеры 26
М
Марковский процесс
276
— — диффузионный 324
— — многомерный (я-мерный) 277,
295, 296
— — непрерывный 277
— — одномерный 294
Математическое ожидание 278
— — числа выбросов в единицу вре-
времени 325, 326
Матрица Грина 116
— — единичных перемещений (еди-
(единичных податливостей) 57, 58
— — жесткостей упругого подвеса 72,
73
— — инерционных коэффициентов
(инерционная) 55, 72
квазиупругих коэффициентов
(квазиупругая) 56
— — корреляционная (ковариацион-
(ковариационная) 270
Коши 117
коэффициентов диссипации 39
— — моментов инерции 45
перехода (монодромии) 117, 118
— — преобразования усилий 76, 77
Матрицант (фундаментальная матрица
Коши) 118
Мера усталостного повреждения 324
Метод асимптотический — Применение
209—212, 229 — Примеры 231, 232
— Схема 181
Бубнова—Галеркина 227, 238 —
Обобщение 185 — Применение
184, 185
— — Власова—Канторовича 185
— — внутренней коллокации 185
вращения (Якоби) 80 — Обоб-
Обобщение 81
— — временных преобразований Фу-
Фурье 313
— — выбросов 333
— — Гаусса 86
— — Гивенса 83
— — Граммеля 184—185
— — граничной коллокации 185
— — Данилевского 86—87
— — Данкерли 182
— — динамических жесткостей 189,
201, 202
— — динамических податливостей 203
— — дифференциальных уравнений
относительно моментных функций
310
предметный указатель
345
— — исчерпывания 85
Метод канонических разложений 312
— — комбинированной коллокации
189
— — комплексных амплитуд 104 —
Применение 108
— — конечных разностей — Примене-
Применение 185—186
— — конечных элементов 190 — При-
Применение 187 —Схема 187, 188
— — Крылова 85, 86 — Пример 86
Кули и Тьюки 25
Леверье 88
малого параметра (возмущений)
126, 127, 179
— — минимума среднеквадратичной
ошибки 185
Метод моментных функций 303—306,
310—312
— — модифицированный 304
Метод Монте-Карло 280
Мюллера (метод парабол) 88, 89
начальных параметров Коши 192
— — нормальных координат 243
— — обобщенных определителей Хил-
ла 128, 129
— — обратной итерации 83
— — операторный 115
— — полных циклов 333, 334
— — последовательных приближений
180
— — пространственных преобразова-
преобразований Фурье 314 — Применение
314
— — разделения переменных 177, 178
— — разложения по собственным фор-
формам (собственных функций) 116,
238, 249, 315—317
— — размахов 333
Релея 182
Ритца 183
— — Саутвелла 182
— — скользящего суммирования 281,
283, 284
— — спектральных
289, 312—315
— — степенной 84, 85
представлении
— — Стодолы 184
— — стохастических функций Ляпу-
Ляпунова 301—303
— — Фаддеева 88
— — факторизации 178, 207
— — функций Грина 115, 116, 311,
312
— — функционалов Ляпунова 243,
244
Хилла 265
Михайлова годограф 99
Модели отказов кумулятивные 324
марковские 324, 325
Модель вязкоупругого поведения ма-
материала 141
диссипации 140 — Классифика-
Классификация 140
— — Кельвина обобщенная 141
Максвелла 141
— — Максвелла обобщенная 141
стандартного линейного тела 141
•— — стохастическая 268
трехэлементная вязкоупругости
141
— — Фойхта—Кельвина 141, 145
Модуль упругости 138
¦ комплексный 143, 144
— — сдвига 138
Модуляция амплитудная 27
— — фазовая 27
— — частотная 27
Момент главный инерции 46
— — количества движения (момент
импульса) 133
Момент инерции — Вычисление 48 —
Тензорные свойства 45, 46 — Техниче-
Технические обозначения 45
дилатационный 150
— — осевой 45, 48
— — полярный 44
— — при кручении 149
— — секториальный 151
— — сечения полярный 146
тела относительно координатных
осей 45
— — тонких тел 47
— — тонкостенных тел 42
346
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
— — центробежный 45, 48
Момент масс статический 41
Момент распределения масс 41
Мощность диссипации 39
Мультипликатор 118, 119
Н
Надежность вибрационная — Расчет
332—334
нормативная 321
Непериодические колебания нестацио-
нестационарные — Определение 26
— — стационарные (установившие-
(установившиеся) — Определение 26
Неустойчивость колебательная 242
монотонная 242
Нормальная форма системы дифферен-
дифференциальных уравнений 117
— — Жордана 95
О
Области неустойчивости 120, 133, 134,
254 — Влияние диссипации 131 — От-
Относительная ширина 131 — Построение
254—256 — Расчет 125, 126
Область дивергенции 245
— — допустимых состояний 320 323
— — устойчивости 307
— — флаттера 245
Оболочка безмоментная 163
коническая — Собственные ко-
колебания 227 — Уравнения колебаний
226,227
— — круговая цилиндрическая —
Уравнения колебаний 219, 220
— — пологая 163
— — сферическая 223 — Собствен-
Собственные колебания 224, 225 — Уравнения
колебаний 223
— — тонкая упругая — Деформация
161 — Перемещения 160 = Ура-
Уравнения 161, 162
Оператор Лапласа 158
положительно определенный 170
— — производящий дифференциаль-
дифференциальный марковского процесса 302
— — самосопряженный 170
Определитель характеристический -т
Развертывание 85—89
Оси жесткости главные 73, 74
— — инерции главные 74
поступательной жесткости упру-
упругого подвеса 74
— — центральные главные жесткости
подвеса 74
Отказ 319
— — внезапный 320
— — постепенный 320
Отношение частотное 101
Оценка функции надежности двусто-
двусторонняя 325
— — линейная 326
— — строгая снизу 325
— — экспоненциальная 326
П
Панель пологая криволинейная — Ура-
Уравнения 164, 228
Параметр инерционный 70
качества — Выбор 323
— — квазикритический 244
— — квазиупругий 70
— — критический 241
Параметрические колебания распреде-
распределенных систем 245, 256 — Области не-
неустойчивости 254—256 — Примеры
245 — Уравнения 246—248
— — систем с конечным числом степе-
степеней свободы — Области неустой
чивости 121, 128—131 —Приме-
—Примеры — 116 — Уравнения 121
систем с одной степенью свободы
121—128
Перемещения виртуальные (возмож-
(возможные) 32
Периодограмма 298
Пластина бесконечная =- Колебания
315
защемленная по контуру 205,
206
— — кольцевая в плане 158, 208
— — круговая в плане 158, 207 —
Устойчивость 254
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
347
— — многопролетная — Граничные
условия 212 — Точное решение
213 — Уравнения 212, 213
— — ортотропная 159, 212
— — переменной толщины 158
— — прямоугольная в плане — Крае-
Краевые условия 202, 204, 205 —
Уравнения 203, 205
с сосредоточенной массой 317
Плотность распределения отказов 321
Плотность собственных частот асимп-
асимптотическая 174—177, 234, 318
— — эмпирическая 234
Плотность спектральная — Вычисле-
Вычисление 281, 282, 317
спектральная взаимная 275
Поведение вязкоупругое материалов —
Понятие 140
Поверхность критическая 241
Повреждение усталостное — Учет 332
Податливость динамическая — Опре-
Определение 105
— — комплексная 145
Подпрограмма 25, 81, 88, 89
Показатель характеристический 91
Поле случайное 268 — Вероятностные
характеристики 278—280 — Статисти-
Статистическое моделирование 280—285
изотропное 279, 280
— — однородное 280
пространственно-временное одно-
однородное 279
пространственно-временное ста-
стационарное 278
— — стационарное 278
Полигармонические колебания — Опре-
Определение 20 — Пример 20
Полином алгебраический с веществен-
вещественными коэффициентами 96
с вещественными коэффициента-
коэффициентами, заданный в неявном виде 97
— — с комплексными коэффициентами
97, 98
Полином характеристический — Корни
88—89
Полоса частот декадная 30
октавная 30
— — полуоктавная 30
третьоктавная 30
Порядок моментной функции 269
резонанса 120
Поток ординарный 325
— — пуассоновский 325
Почти гармонические колебания — Оп-
Определение 27
Почти периодические (квазипериодиче-
(квазипериодические) колебания — Квазипериоды 27 —
Определение 27 — Пример 27 —
Спектральное представление 27
Принцип суперпозиции 17, 142
Проблема замыкания 304
квадратичная 79
Программа стандартная — Применение
285
Произведение энергетическое 169
Пространство диагностическое (призна-
(признаков) 320
качества 320
— — конфигураций (конфигурацион-
(конфигурационное) 36
состояний 36, 320
Процесс — Виды см. под их названия-
названиями, например Гауссовский процесс —
Понятие 256
Процесс с конечной дисперсией перио-
периодически модулированный 309
со скрытой периодичностью 307,
309
. экспоненциально коррелирован-
коррелированный 308
Равновесие асимптотически устойчивое
95
неустойчивое 95
— — устойчивое по Ляпунову 95
Распределение масс 40, 47, 48
скоростей 49
ускорений 49
Расходящиеся колебания — Определе-
Определение 27
Реакции единичные — Формулы 202
связей 32
348
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Резонанс параметрический 101, 117
главный 120, 123
— — главный комбинационный раз
ностного гипа 128
— — главный комбинационный сум-
суммарного типа 128
— — побочный 120
— — простой 120
Резонанс ударный 115
Релаксация 142
Релея дробь 62, 170
Решение асимптотически устойчивое
в среднем квадратическом 302
— — асимптотически устойчивое по
вероятюсти 300
— — асимптотически устойчивое по
отношению к возмущениям на
начальном множестве 100
— — Даламбера 257
— — 2Г-периодическое 118
— — порождающее 209
— — Г-периодическое 118
— — устойчивое по вероятности 300
— — устойчивое по математическому
ожиданию нормы 300
— — устойчивое по отношению к воз-
возмущениям на начальном множе-
множестве 100
— — устойчивое по совокупности мо-
ментных функций 301
— — экспоненциально устойчивое по
математическому ожиданию 300
Свободные колебания — Определение
116—134
— — диссипативных систем 91—94
— — консервативных систем 54—78
— — неконсервативных систем 89^.
100
Связанность сильная 65
— — слабая 65
Связь
— — геометрическая 32
— — голономная 32
— — идеальная 32, 36
— — кинематическая (дифференци»
альная) 32
— - неголономная 32
— — нестационарная (реономная) 32
— — неудерживающая 32
— — стационарная (склерономная) 32
— — удерживающая 32
Сдвиг поперечный — Учет 159, 160
Сегмент пологий сферический — Коле
бания 225, 226
Сила внешняя 32, 310 — Действие 234
235
— — внутренняя 32, 37
— — возмущающая 103
— — восстанавливающая 57
— — вязкого сопротивления 102 —
Учет 102
— — гармоническая 102—Действие
101
— — гироскопическая 90
— — диссипативная 39, 90
— — консервативная 38
— — неконсервативная 37
-- — неконсервативная позиционная
90, 243
— — обобщенная 37
— — параметрическая 246
— — постоянная 114
— — с отрицательной диссипацией (ус-
(ускоряющая) 90
Система — Вид 15 — Классификация
16, 17 — Колебания 15 — Параметры
15, 16 — Понятие 17 — Состояние
15
— — автономная — Устойчивость 94
— Теоремы 95
— — возбуждаемая белыми шумами
306
— — высоконадежная 325
— — гироскопическая 90
— — детерминистическая 286
— — каноническая 118—120
— — консервативная 17
— — материальных точек 31, 32
— — Мейсснера 132
— — неконсервативнся 17
— - нестационарная 286
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
349
— — параметрически возбуждаемая
131—134
— — парциальная 65
Система распределенная 17, 135, 166—
169, 171—173, 177, 245, 246, 251, 310,
319 — Динамическая устойчивость 241,
242 — Устойчивость 241 — Учет дис-
диссипации 256
— — вязкоупругая 239
с внешним трением 238, 239
Система с двумя случайными парамет-
параметрическими воздействиями 307—309
Система с конечным числом степеней
свободы 15, 17, 31, 35, 78, 126 — Выну-
Вынужденные колебания 105—109 — Сво-
Свободные колебания 63, 64
— — диссипативная 91—94
— — недиссипативная 105
Система с кусочно-постоянными коэф-
коэффициентами 130
Система с одной степенью свободы 62,
92, 102, 111, 121, 307, 309 —Вынуж-
—Вынужденные колебания 101—105 — Свобод-
Свободные колебания 63, 64
диссипативная 39, 91—92
— — недиссипативная 101
Система с отрицательной диссипацией
90
— — с периодическими параметрами
119
— — с постоянными параметрами 17
_ — стохастическая 286
— — стационарная 286, 288, 289
— — упругоподвешенных твердых тел
76
— — уравнений динамики замкнутая
33
Скорость групповая 257, 258
поперечных волн 257
— — продольных волн 257
фазовая 257, 258
Случайные колебания 310—319
— — распределенных систем с конеч-
конечным числом степеней свободы
292
— — распределенных систем с одной
степенью свободы 288
Случайные параметрические колеба-
колебания 299—309
— — систем, возбуждаемых белыми
шумами 306
— — систем, возбуждаемых процесса-
процессами с конечной дисперсией 308
Случайный процесс 268 — Реализации
267, 327 — Спектральные представле-
представления 270, 271 — Статистическое модели-
моделирование 280—285
— — векторный 268
— — пространственно-временной 268
— — стационарный — Понятие 271 —
Спектральная плотность 273, 274
Случайный процесс многомерный 275,
276
— — стационарно связанный 275, 276
стационарный 275, 276
Собственные значения уравнений 168
Собственные формы 59, 60, 170, 171,
215—218 — Дифференциальные урав-
уравнения 218
— Классификация 219
— Методы вычисления 78
— Определение 177
— Расчет 201—203, 229—232
— Свойства 60, 168, 169, 170, 171
Собственные частоты 62—64, 69, 70,
71 — Асимптотическое распределение
176, 177
— Методы вычисления 78
— Определение 84, 174
— Плотность 173—177, 232—234
— Расчет 201—203,215—218,229—232
— Свойства 60, 168—171
— Точки сгущения 234
— Уравнение 74
— Формулы 232
Собственные частоты высшие 84
демпфированной системы 91
низшие 84
— — нулевые 69
Составляющая безвихревая 257
— — эквиволюмиальная 257
Спектр—Структура 173
— — дискретный 172
— — полосовой 173
350
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
— — смешанный 172
сплошной 172
Среда упругая 256
Срок службы нормативный 321
Стационарные колебания 290—294
Стержень — Геометрические характе-
характеристики 148, 149 — Колебания 146,
147, 152—157, 235, 236, 247, 248 —
Устойчивость 246 — Понятие 146
— — консольный 244—245
— — криволинейный 155, 156
— — опертый 255 — Области неустой-
неустойчивости 255
— — с кусочно-постоянными характе-
характеристиками 197, 198 — Колеба-
Колебания 198
— — тонкостенный открытого профи-
профиля 151
— упругий 265 — Собственные формы
190—Собственные частоты 190
Струна — Понятие 145
Схема разностная — Определение 187—
Устойчивость 187
Сходимость — Скорость 84
— — разностной аппроксимации 186
Тангенс потерь — Определение 145
Тело абсолютно твердое 40, 48—51, 323
деформируемое 40
— — упругое — Уравнения динамики
137—140
Тензор упругих постоянных 138
Теорема Даламбера — Эйлера 48
— — Кельвина—Тета — Определение
96
— — Лагранжа 95, 96
— — Ляпунова 95, 96
— — об асимптотической устойчиво
сти 302, 303
— — об изменении главного' момента
количества движения системы 33,
35
— — об изменении кинетической энер-
энергии системы 33, 35
— — об изменении количества движе-
движения системы 33
— — об устойчивости по вероятности
302
— — о сохранении полной механиче-
механической энергии 34
— — о сравнении 70, 183
Шаля 48
Теория вероятностей 268
выбросов 324, 336—337 — Пере-
Пересечения 327, 328 —Среднее чис-
число выбросов 327—328 — Среднее
число максимумов 329
Герца 261, 266
— — динамической устойчивости —
Задача 246
— — идентификации динамических
систем 268
Кокса 267
колебаний 268, 267
— — марковских процессов—Методы
294, 295, 296
— — надежности 268 — Критерий
322, 323 — Понятия 319—322 —
Применение 326
— — поперечного удара 266, 267
— — Сен-Венана 266
— — случайных процессов и полей
268—286
— — случайных функций 268
— — соударения волновая 263
— — статистической обработки опыт-
опытных данных 268
техническая 259, 260
— — Тимошенко 260
упругости классическая — Ос-
Основные соотношения 137
уточненная 215, 217,218,260,261
— — элементарная — Обобщения 266
Трение внешнее 109
внутреннее 109
Фойхта 94
У
Удар поперечный 267 — Силы взаимо-
взаимодействия 267 — Смещение тела 267 —
Элементарная теория 265, 266
•= — продольный 263 — Задача о со
ударении 263—265 — Макси
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
351
малыше напряжения 264 — Про-
Продолжительность 264 — Элемен-
Элементарная теория 262
Уравнение Даламбера—Эйлера 34
— — движения 139 — Операторная
запись 139, 140
— — динамики 148—51
— — дисперсионное 258 — Понятие
257
— — кинетическое 332
— — Колмогорова 277, 304
Лагранжа 36, 38, 40, 52, 55 —
Определение 38
Ламе 139, 256
— — Матье—Хилла 121 — Области
неустойчивости 121—125
— — Мейсснера — Области неустой-
неустойчивости 123, 124
— — Остроградского—Эйлера 136
— — относительного движения 34, 35
— — разностное — Методы решения
187
— — свободных колебаний линейных
консервативных систем — При-
Пример 57
— — свободных колебаний с использо-
использованием матрицы единичных пере-
перемещений — Пример 58
Смолуховского интегральное 276
— — собственных частот 59
— — Тимошенко 155
— —- Фоккера—Планка — Колмогоро-
Колмогорова 277
Фредгольма 170, 181
— — Эйлера 49, 50
Усилие тангенциальное — Учет 159
Ускорение мгновенное угловое 44
— — осестремительное 49
поступательного движения 49
— — тангенциальное 49
— — центра масс 49
Условие нормировки 269
— — симметрии 269
— — согласованности 269
Условие ортогональности по кинетиче-
кинетической энергии 60
— ^ по потенциальной энергии Ь0
Условная плотность вероятности 276
Устойчивость — Исследование 243,
245 — Определение 305, 306 — Усло-
Условия 99
асимптотическая 119, 301 — Кри-
Критерии 96—100
— — в среднем квадратическом 300
— — динамическая 246, 247, 248
— — линейных систем 89
— — по Ляпунову 119 — Определение
94—95
¦— — по моментам высоких порядков—
Исследования 307 — Результаты
анализа 307
по совокупности моментных фун-
функций 301
— — стохастическая — Определение
299—301
Ф
Флуктуации амплитуды 27
фазы 27
частоты 27
Формула Ито 303
Клайперона 138
Коши 137
Релея 62, 84, 85, 171
— — Штейнера 48
— — Эйлера 49
Формы собственных колебаний — см
Собственные формы
Фурье анализ численный — Стандарт-
Стандартные программы 25
Фурье преобразование 24
быстрое — Понятие 24, 25
Фурье ряд — Коэффициенты 22, 23
— — в действительной форме 22
— — в комплексной форме 22
Функции моментные начальные 269,
270
центральные 270, 278
Функция балочная 196, 197, 205
Грина (тензор Грина) 181, 311
— — имеющая бесконечно малый верх-
верхний предел 302
— — импульсная переходная 109
— — ковариационная 270
352
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
— корреляционная 270, 278
— Лагранжа 40
— надежности — Определение 321
— Оценки 325, 326
— надежности условная 321
— передаточная системы (динами-
(динамическая податливость) 291
— положительно определенная (по
Ляпунову) 302
— распределения 269
— Релея диссипативная 39, 40,108
— Хевисайда 173
Характеристика амплитудно-частотная
101, 106
— — демпфирования 93
— — фазочастотная 103
Центрированный процесс 270
Центр масс 40, 42—44
Частота возбуждения 117, 119
— — комплексная 91
— — отказов 321
— — парциальная 65
— — резонансная 101
Частоты собственных колебаний <~ см.
Собственные частоты
Члены параметрические 165
Ш
Шары упругие — Время соударения
261, 262
— Контактная сила 261
Штурма последовательность 83
Э
Эйлера углы 48
нутации 48
— — прецессии 48
— — собственного вращения 48
Экспоненциально-коррелированный
процесс 307
Энергия кинетическая 33
потенциальная 34
Эргодический процесс 272
Эффект динамический краевой 209 —
Области вырождения 230
— — динамический краевой невырож
денный неосциллирующий 209
— — диссипации дестабилизирующий
131, 132
Ядро ползучести 142
— — релаксации 143, 144 — Резоль-
Резольвенты 144
ИБ № 713
Иван Иванович Артоболевский, Алексей Николаевич Боголюбов,
Владимир Васильевич Болотин и др.
ВИБРАЦИИ В ТЕХНИКЕ. В 6-ги томах
Том 1
КОЛЕБАНИЯ ЛИНЕЙНЫХ СИСТЕМ
Редактор Т Д Онегина
Художественный редактор Я Я Рогачеа. Технический редактор Л А Макарова
Корректоры О Е Мишина и А А Снастина Переплет художника А Я Михайлова
Сдано в набор 1910 77 Подписано в печать 04 05 78. Г-09612. Формат 6OX9O'/i«. Бумага
типографская № 1. Гарнитура литературная Печать высокая. Усл. печ. л. 22,0. Уч.-изд.
л 29,65. Тираж 30 000 экз. Заказ 1565. Цена 1 р. 80 к.
Издательство «Машиностроение», 107885, Москва, Б-78, 1-й Басманный пер., 3
Ордена Октябрьской Революции, ордена Трудового Красного Знамени Ленинградское
производственно техническое объединение «Печатный Двор» имени А. М Горького
Союзполиграфпрома при Государственном комитете Совета Министров СССР по делам
издательств, полиграфии и книжной торговли 197136, Ленинград, П-136, Гатчинская
ул., 26,